---
title: "Análise descritiva"
subtitle: "Aula 4"
author: "Bruno Montezano"
institute: "Grupo Alliance
Programa de Pós-Graduação em Psiquiatria e Ciências do Comportamento
Universidade Federal do Rio Grande do Sul"
date: last-modified
date-format: long
lang: pt-br
execute:
echo: true
format:
revealjs:
incremental: true
smaller: true
theme: [default, ../assets/custom.scss]
logo: "../assets/logo_ufrgs.png"
---
## Conteúdo de hoje
- Medidas de tendência central
- Medidas de dispersão
- Medidas de assimetria e curtose
- Distribuição normal
- Transformação de dados
- Tabelas de frequência
## Dados dos `pinguins`
::: columns
::: {.column width="70%"}
Hoje nós usaremos os dados dos `pinguins` do pacote `dados`.
Este conjunto de dados contém 14 variáveis de 344 observações de pinguins adultos
perto da Estação Palmer na Antártida.
Os dados incluem a espécies de pinguins e ilhas do Arquipélago Palmer,
medidas de cada espécie, sexo do pinguim e ano de documentação.
:::
::: {.column width="30%"}

:::
:::
## `pinguins`
```{r glimpse-pinguins}
library(dados)
library(tidyverse)
glimpse(pinguins)
```
```{r printar-pinguins}
pinguins
```
## Revisão de conceitos matemáticos
{fig-align="center" width=45%}
## Variáveis
**Variáveis** são símbolos que representam conjuntos de um ou mais **elementos**
que podem assumir qualquer quantidade de valores.
::: {.nonincremental}
- Letras como $x$, $y$ e $z$ são comumente usadas para indicar variáveis
- Por exemplo: $x = 3$
:::
. . .
::: {.nonincremental}
- Letras maiúsculas ($X$) ou letras com um índice ($x_i$) referem-se a variáveis
com múltiplos valores — ou seja, com dimensões
- Por exemplo: $X = x_i = (15, 16, 32)$
- Variáveis com uma dimensão (comprimento) são chamadas de **vetor**
:::
. . .
::: {.nonincremental}
- Variáveis como $x_i$ são usadas para **indexar** elementos de vetores
- $i$ é uma variável que indica a posição indexada
- Por exemplo: $x_1 = 15, x_2 = 16, x_3 = 32$
:::
## Somatório
$$\sum_{i=1}^{n}x_i$$
"Soma de todos os valores de $x$ do primeiro ($i = 1$) até o último ($n$)"
. . .
Dado $x = [9, 12, 12, 14, 27]$:
$$\sum_{i=1}^{n}x_i = x_1 + x_2 + x_3 + x_4 + x_5 = 9 + 12 + 12 + 14 + 27 = 74$$
. . .
```{r soma-x}
x <- c(9, 12, 12, 14, 27)
sum(x)
```
É comum ao somar todos os elementos de um vetor, omitirmos os sobrescritos e subscritos,
por exemplo: $\sum{x_i} = \sum_{i=1}^{n}x_i$
## Medidas de tendência central
{fig-align="center" width=85%}
## Média
A média (aritmética) é o *valor esperado* de uma variável.
$$\bar{x} = \frac{1}{n}\sum_{i=1}^{n}x_{i}$$
. . .
Se você extrair elementos aleatoriamente dessa variável, a média seria o chute menos errado
que você poderia fazer sobre esse valor^[Tecnicamente, a média
minimiza o *erro quadrático*.].
Dito de outra forma, as diferenças positivas e negativas entre todos os valores e a média
equivalem entre si.
. . .
```{r calcular-media-massa-corporal}
pinguins |>
summarise(media_massa = mean(massa_corporal, na.rm = TRUE),
media_comprimento_bico = mean(comprimento_bico, na.rm = TRUE))
```
## Mediana
O valor para o qual não mais da metade dos
valores é superior ou inferior^[Tecnicamente, a mediana minimiza o erro absoluto].
. . .
A **mediana** tem essa fórmula esquisita:
$$m(x_i) = \begin{cases} x_{\frac{n+1}{2}},& \text{se } n \text{ ímpar}\\ \frac{1}{2}(x_{\frac{n}{2}} + x_{\frac{n}{2} + 1}), &\text{se } n \text{ par}\end{cases}$$
"Se $x$ tem um número ímpar de elementos, ao colocá-los em ordem, a mediana é o valor do meio. Se $x$ tem um número par de elementos, a mediana é a média dos dois valores do meio".
. . .
```{r calcular-mediana-massa-corporal}
pinguins |>
summarise(mediana_massa = median(massa_corporal, na.rm = TRUE),
mediana_comprimento_bico = median(comprimento_bico, na.rm = TRUE))
```
## Moda
A **moda** é o valor mais **frequente** na variável.
. . .
Existem fórmulas para a moda, mas elas não são nada intuitivas, apesar da moda
ser a medida de tendência central mais intuitiva.
. . .
Vocês podem usar `count()` para ver a frequência de valores:
```{r funcao-count-especie}
pinguins |>
count(especie)
```
. . .
E vocês podem achar a moda diretamente com um `filter()`:
```{r achar-moda-especie}
pinguins |>
count(especie) |>
filter(n == max(n))
```
## Valores extremos
A média é sensível a valores extremos:
```{r outliers}
z <- c(2, 5, 3, 5, 105)
mean(z)
```
. . .
A mediana não é:
```{r mediana-outlier}
median(z)
```
. . .
Isso significa que a mediana pode ser uma "média" mais útil quando os dados
têm valores extremos.
Isto é comum com variáveis como renda e números de episódios auto-relatados.
## Medidas de dispersão
{fig-align="center" width=65%}
## Variância
A variância mede como os dados estão dispersos em torno da média.
Normalmente usamos a variância *amostral*:
$$
s^2 = \frac{\sum (x_i - \bar{x})^2}{n - 1}
$$
. . .
```{r variancia-massa-corporal}
pinguins |>
filter(!is.na(massa_corporal)) |>
summarise(variancia_na_mao_massa = sum(
(massa_corporal - mean(massa_corporal))^2 /
(length(massa_corporal) - 1)),
variancia_massa = var(massa_corporal)
)
```
. . .
Se todos os valores são iguais, a variância é *zero*.
## Desvio padrão
O desvio padrão ($s$ ou $sd$, ou $dp$ em português) é simplesmente a raíz quadrada
da variância:
$$s = \sqrt{s^2}$$
. . .
Você pode interpretar como a distância "típica" dos valores em relação à média.
. . .
```{r desvio-padrao-massa-corporal}
pinguins |>
filter(!is.na(massa_corporal)) |>
summarise(desvio_padrao_na_mao_massa = sqrt(var(massa_corporal)),
desvio_padrao_massa = sd(massa_corporal)
)
```
. . .
O desvio padrão se apresenta na mesma unidade de medida da variável.
## Amplitude
A amplitude ($R$) é a medida de dispersão mais fácil de calcular. Nós subtraímos
o menor valor ($L$) do maior valor ($H$) da variável.
$$R = H - L$$
. . .
```{r amplitude-massa}
pinguins |>
filter(!is.na(massa_corporal)) |>
summarise(
massa_max = max(massa_corporal),
massa_min = min(massa_corporal),
massa_amplitude = max(massa_corporal) - min(massa_corporal)
)
```
## Intervalo interquartil
O intervalo interquartil representa a diferença entre o primeiro quartil (o 25º
percentil) e o terceiro quartil (o 75º percentil) de um conjunto de dados.
$$IQR = Q_3 - Q_1$$
. . .
Em termos simples, o quão distantes estão os 50% valores do meio da variável.
. . .
```{r intervalo-interquartil-massa}
pinguins |>
filter(!is.na(massa_corporal)) |>
summarise(
intervalo_interquartil_massa = IQR(massa_corporal),
primeiro_quartil = quantile(massa_corporal)["25%"],
terceiro_quartil = quantile(massa_corporal)["75%"]
)
```
## Distribuição normal
A distribuição normal é uma das distribuições mais importantes em
estatística.
* Também conhecida como distribuição de Gauss, é frequentemente
usada para modelar fenômenos naturais
* Muitos testes estatísticos assumem
que os dados seguem uma distribuição normal
* 68% dos dados estão dentro de um desvio padrão da média,
95% estão dentro de dois desvios padrão e 99,7% estão dentro de três
desvios padrão
. . .
```{r plot-distribuicao-normal}
#| fig-align: "center"
#| out.width: "60%"
#| echo: false
# Gerando uma amostra aleatória de uma distribuição normal padrão
set.seed(123)
amostra <- rnorm(1000)
# Calculando a média e o desvio padrão da amostra
media <- mean(amostra)
desvio_padrao <- sd(amostra)
# Criando um data frame com os limites das proporções 68-95-99
proporcoes <- data.frame(
limite_inf = c(
media - desvio_padrao,
media - 2 * desvio_padrao,
media - 3 * desvio_padrao,
media - 4 * desvio_padrao
),
limite_sup = c(
media + desvio_padrao,
media + 2 * desvio_padrao,
media + 3 * desvio_padrao,
media + 4 * desvio_padrao
),
proporcao = c(0.6826, 0.9544, 0.9972, 0.9998)
)
# Criando o histograma
ggplot(data.frame(x = amostra), aes(x)) +
geom_rect(xmin = -1,
xmax = 1,
ymin = 0,
ymax = 250,
fill = "tan1",
alpha = 0.2) +
geom_rect(xmin = -1,
xmax = -2,
ymin = 0,
ymax = 250,
fill = "gold",
alpha = 0.2) +
geom_rect(xmin = 1,
xmax = 2,
ymin = 0,
ymax = 250,
fill = "gold",
alpha = 0.2) +
geom_rect(xmin = 2,
xmax = 3,
ymin = 0,
ymax = 250,
fill = "pink",
alpha = 0.2) +
geom_rect(xmin = -2,
xmax = -3,
ymin = 0,
ymax = 250,
fill = "pink",
alpha = 0.2) +
geom_rect(xmin = 3,
xmax = 4,
ymin = 0,
ymax = 250,
fill = "palegreen",
alpha = 0.2) +
geom_rect(xmin = -3,
xmax = -4,
ymin = 0,
ymax = 250,
fill = "palegreen",
alpha = 0.2) +
geom_vline(
xintercept = c(proporcoes$limite_inf, proporcoes$limite_sup),
color = rep("grey30", 8),
linetype = rep("dashed", 8),
size = rep(1, 8),
alpha = rep(1, 8)
) +
geom_histogram(bins = 20,
color = "black",
fill = "lightblue") +
geom_vline(
xintercept = media,
color = "grey20",
linetype = "solid",
size = 1
) +
annotate("text", label = "34,13%",
x = -0.5, y = 240,
size = 4.5, family = "Charter") +
annotate("text", label = "34,13%",
x = 0.5, y = 240,
size = 4.5, family = "Charter") +
annotate("text", label = "13,59%",
x = 1.5, y = 240,
size = 4.5, family = "Charter") +
annotate("text", label = "13,59%",
x = -1.5, y = 240,
size = 4.5, family = "Charter") +
annotate("text", label = "2,14%",
x = 2.5, y = 240,
size = 4.5, family = "Charter") +
annotate("text", label = "2,14%",
x = -2.5, y = 240,
size = 4.5, family = "Charter") +
annotate("text", label = "0,13%",
x = 3.5, y = 240,
size = 4.5, family = "Charter") +
annotate("text", label = "0,13%",
x = -3.5, y = 240,
size = 4.5, family = "Charter") +
scale_x_continuous(
breaks = -4:4,
limits = c(-4.5, 4.5),
labels = c(
latex2exp::TeX("$\\mu - 4\\sigma$"),
latex2exp::TeX("$\\mu - 3\\sigma$"),
latex2exp::TeX("$\\mu - 2\\sigma$"),
latex2exp::TeX("$\\mu - \\sigma$"),
latex2exp::TeX("$\\mu$"),
latex2exp::TeX("$\\mu + \\sigma$"),
latex2exp::TeX("$\\mu + 2\\sigma$"),
latex2exp::TeX("$\\mu + 3\\sigma$"),
latex2exp::TeX("$\\mu + 4\\sigma$")
)
) +
scale_y_continuous(limits = c(0, 250)) +
theme_classic(base_size = 16, base_family = "Charter") +
labs(x = "Valores da amostra", y = "Frequência")
```
## Como testar normalidade?
Em muitos casos, é necessário verificar se uma amostra segue uma distribuição
normal antes de aplicar determinados testes estatísticos.
* O teste de Shapiro-Wilk é um teste de normalidade que verifica se uma amostra segue uma distribuição normal
* Se o $p$-valor do teste for menor do que o nível de significância (geralmente 0,05), rejeita-se a hipótese nula e conclui-se que a amostra não segue uma distribuição normal
. . .
::: columns
::: {.column width="50%"}
```{r shapiro-amostra-simulada}
# Exemplo de distribuição normal
# Amostra de 500 sujeitos
# com média de 175cm e 10cm de desvio padrão
alturas_adultos <- rnorm(n = 500,
mean = 175,
sd = 10)
shapiro.test(alturas_adultos)
```
:::
::: {.column width="50%"}
```{r shapiro-massa-pinguins}
# Exemplo de variável que não segue uma
# distribuição normal
pinguins |>
pull(massa_corporal) |>
shapiro.test()
```
:::
:::
## Assimetria
A assimetria mede o quão assimétrica é uma distribuição. Pode assumir valores
positivos ou negativos. A média, mediana e moda em geral *não* são iguais em
distribuições assimétricas
* Uma assimetria negativa indica que a cauda está no lado esquerdo da
distribuição
* Uma assimetria
positiva indica que a cauda está no lado direito da distribuição
* Um valor de zero indica que não há assimetria na
distribuição
## Exemplo de distribuição assimétrica
```{r histograma-distribuicao-assimetrica}
#| fig-align: "center"
#| out.width: "65%"
#| echo: false
set.seed(1)
tibble(x = rchisq(1000, 10)) |>
ggplot() +
aes(x = x) +
geom_histogram() +
labs(x = "Valores", y = "Frequência",
title = "De que lado a cauda se encontra?",
subtitle = "Um exemplo de assimetria positiva.") +
geom_segment(x = 32, xend = 25, y = 75, yend = 40,
arrow = arrow(length = unit(0.5, "cm")),
color = "steelblue4",
size = 2) +
ggthemes::theme_clean(base_size = 16, base_family = "Charter")
```
## Curtose
Curtose é a medida da forma da distribuição em relação à sua média.
* A curtose de uma distribuição normal é 3
* Se uma dada distribuição tem uma curtose menor que 3, ela é chamada de platicúrtica
* Se uma dada distribuição tem uma curtose maior que 3, diz-se que é leptocúrtica
. . .
*Quanto maior a curtose, maior a propensão a outliers.*
## Visualizando a curtose
```{r exemplo-curtose}
#| fig-align: "center"
#| out.width: "100%"
#| echo: false
set.seed(1)
alta_curtose <- tibble(valores = rnorm(1000, mean = 0, sd = 1) * 5,
curtose = "Alta")
baixa_curtose <- tibble(valores = rnorm(1000, mean = 0, sd = 2),
curtose = "Baixa")
dados_curtose <- bind_rows(alta_curtose, baixa_curtose)
dados_curtose |>
ggplot() +
geom_histogram(aes(x = valores, fill = curtose), alpha = 0.5) +
labs(title = "Comparação de alta e baixa curtose", x = "Valores",
y = "Frequência", fill = "Curtose") +
ggsci::scale_fill_lancet() +
theme_bw(base_size = 16, base_family = "Charter")
```
## Medidas de assimetria e curtose
Tanto a assimetria quanto a curtose podem ser calculados com funções do
pacote `moments`.
::: columns
::: {.column width="50%"}
```{r calcular-assimetria-massa}
library(moments)
pinguins |>
pull(massa_corporal) |>
skewness(na.rm = TRUE)
```
:::
::: {.column width="50%"}
```{r calcular-curtose-massa}
pinguins |>
pull(massa_corporal) |>
kurtosis(na.rm = TRUE)
```
:::
:::
. . .
```{r histograma-massa-corporal}
#| echo: false
#| fig-align: "center"
#| out.width: "75%"
pinguins |>
filter(!is.na(massa_corporal)) |>
ggplot(aes(x = massa_corporal)) + geom_histogram(fill = "brown") +
labs(x = "Massa corporal (em gramas)", y = "Frequência") +
ggthemes::theme_clean(base_size = 16, base_family = "Charter")
```
## Transformação de dados
Em alguns casos, os dados podem apresentar distribuições muito distorcidas, o
que pode afetar a validade dos testes estatísticos aplicados.
. . .
Para resolver esse problema, uma solução comum é aplicar uma transformação aos dados para deixá-los mais próximos de uma distribuição normal.
. . .
```{r plot-transformacao-de-dados}
#| fig-align: "center"
#| out.width: "70%"
#| echo: false
library(patchwork)
set.seed(123)
amostra <- rexp(10000)
original <- ggplot(data.frame(x = amostra), aes(x)) +
geom_histogram(bins = 20, color = "black", fill = "lightblue") +
labs(title = "Distribuição Original", y = "", x = "") +
theme_minimal(base_size = 14, base_family = "Charter")
amostra_log <- log10(amostra)
logaritmo <- ggplot(data.frame(x = amostra_log), aes(x)) +
geom_histogram(bins = 20, color = "black", fill = "lightgreen") +
labs(title = "Transformação logarítmica", x = "", y = "") +
theme_minimal(base_size = 14, base_family = "Charter")
amostra_sqrt <- sqrt(amostra)
raiz_quadrada <- ggplot(data.frame(x = amostra_sqrt), aes(x)) +
geom_histogram(aes(y = ..density..), bins = 20, color = "black", fill = "darksalmon") +
labs(title = "Transformação raíz quadrada", x = "", y = "") +
theme_minimal(base_size = 14, base_family = "Charter")
amostra_raiz_cubica <- amostra^(1/3)
raiz_cubica <- ggplot(data.frame(x = amostra_raiz_cubica), aes(x)) +
geom_histogram(aes(y = ..density..), bins = 20, color = "black", fill = "aquamarine") +
labs(title = "Transformação raíz cúbica", x = "", y = "") +
theme_minimal(base_size = 14, base_family = "Charter")
((original + logaritmo) / (raiz_quadrada + raiz_cubica)) +
plot_annotation(title = "Dados simulados de 10.000 observações",
theme = theme(text = element_text(family = "Charter", size = 16)))
```
## Transformando a `massa_corporal`
::: columns
::: {.column width="50%"}
```{r histograma-massa-corporal-dois}
#| fig-align: "center"
#| out.width: "100%"
pinguins |>
ggplot(aes(x = massa_corporal)) +
geom_histogram(fill = "coral2") +
labs(x = "Massa corporal (em gramas)",
y = "Frequência") +
theme_bw(base_size = 16,
base_family = "Charter")
```
:::
::: {.column width="50%"}
```{r log-massa-corporal}
pinguins |>
mutate(massa_log = log10(massa_corporal)) |>
ggplot(aes(x = massa_log)) +
geom_histogram(fill = "deepskyblue4") +
labs(x = "Log da massa corporal",
y = "Frequência") +
theme_bw(base_size = 16,
base_family = "Charter")
```
:::
:::
## Tabelas de frequência
A função `count()` do pacote `dplyr` pode ser usada para
contar valores (frequência) a partir de uma ou mais
variáveis.
. . .
```{r exemplo-basico-count}
pinguins |>
count(especie)
```
. . .
```{r tabulacao-cruzada-count}
pinguins |>
count(especie, ilha)
```
## Tabelas de frequência com `janitor()`
O pacote `janitor` oferece uma função `tabyl()` para produzir tabulações e
tabulações cruzadas, que podem ser modificadas para exibir porcentagens,
proporções, etc.
. . .
```{r exemplo-basico-tabyl}
library(janitor)
pinguins |>
tabyl(especie)
```
. . .
```{r tabulacao-cruzada-tabyl}
pinguins |>
tabyl(especie, ilha)
```
## Funções de enfeite do `janitor`
Função|Desfecho
-----|-----:
`adorn_totals()`|Adicionar totais.
`adorn_percentages()`|Converter contagens para proporções.
`adorn_pct_formatting()`|Converte proporções para porcentagens.
`adorn_rounding()`|Arredondar proporções com `digits =`.
`adorn_ns()`|Adicionar contagens a uma tabela de proporções ou porcentagens.
`adorn_title()`|Adicionar título da linha e coluna.
## Exemplo de tabela cruzada
::: {.panel-tabset}
## Básica
```{r tabyl-simples}
pinguins |>
tabyl(especie, ilha)
```
## Totais e porcentagens
```{r totais-porcentagens}
pinguins |>
tabyl(especie, ilha) |>
adorn_totals(where = "row") |>
adorn_percentages(denominator = "col") |>
adorn_pct_formatting(digits = 1)
```
## Completa
```{r tabyl-completa}
pinguins |>
tabyl(especie, ilha) |>
adorn_totals(where = "row") |>
adorn_percentages(denominator = "col") |>
adorn_pct_formatting() |>
adorn_ns(position = "front") |>
adorn_title(
row_name = "Espécie",
col_name = "Ilha")
```
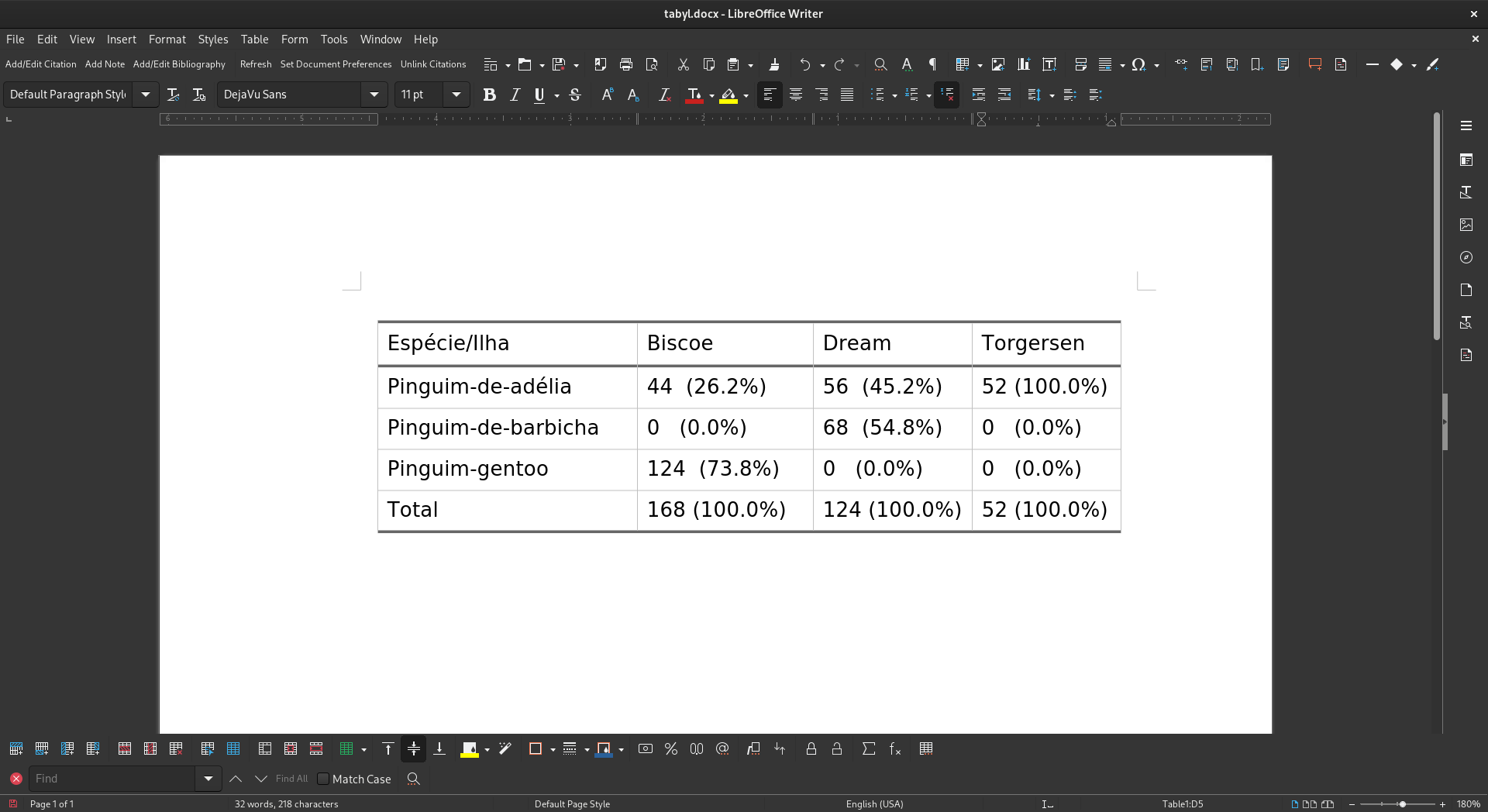
## Salvando em Word
```{r tabyl-em-word}
#| eval: false
pinguins |>
tabyl(especie, ilha) |>
adorn_totals(where = "row") |>
adorn_percentages(denominator = "col") |>
adorn_pct_formatting() |>
adorn_ns(position = "front") |>
adorn_title(
row_name = "Espécie",
col_name = "Ilha",
placement = "combined") |>
flextable::flextable() |>
flextable::save_as_docx(path = "tabela_especie_ilha.docx")
```
{fig-align="center" width=50%}
:::
## Tarefa de casa
* Para a tarefa de casa, vamos seguir usando a base `pinguins` do pacote `dados`.
1. Filtre a base para manter apenas as observações do ano de 2009.
2. Verifique se a variável `comprimento_bico` da base de
dados segue uma distribuição normal através de um histograma
e um teste de normalidade de Shapiro-Wilk.
3. Com a função `count()`, verifique a frequência da
variável `sexo` na base de dados.
4. Com a função `summarise()`, calcule a média, mediana e
desvio padrão da variável `comprimento_nadadeira`.
* Dica de leitura: Capítulos 4 e 5 do livro
[Introduction to Modern Statistics](https://openintro-ims.netlify.app/).