---
title: "Modelos de regressão"
subtitle: "Aula 6"
author: "Bruno Montezano"
institute: "Grupo Alliance<br>Programa de Pós-Graduação em Psiquiatria e Ciências do Comportamento<br>Universidade Federal do Rio Grande do Sul"
date: last-modified
date-format: long
lang: pt-br
execute:
  echo: true
format:
  revealjs:
    incremental: true
    smaller: true
    theme: [default, ../assets/custom.scss]
    logo: "../assets/logo_ufrgs.png"
---

## Conteúdo de hoje

- Conceito
- Regressão linear simples
- Regressão linear múltipla
- Coeficiente de determinação
- Preditores categóricos
- Desafios

## Ciclo da ciência de dados

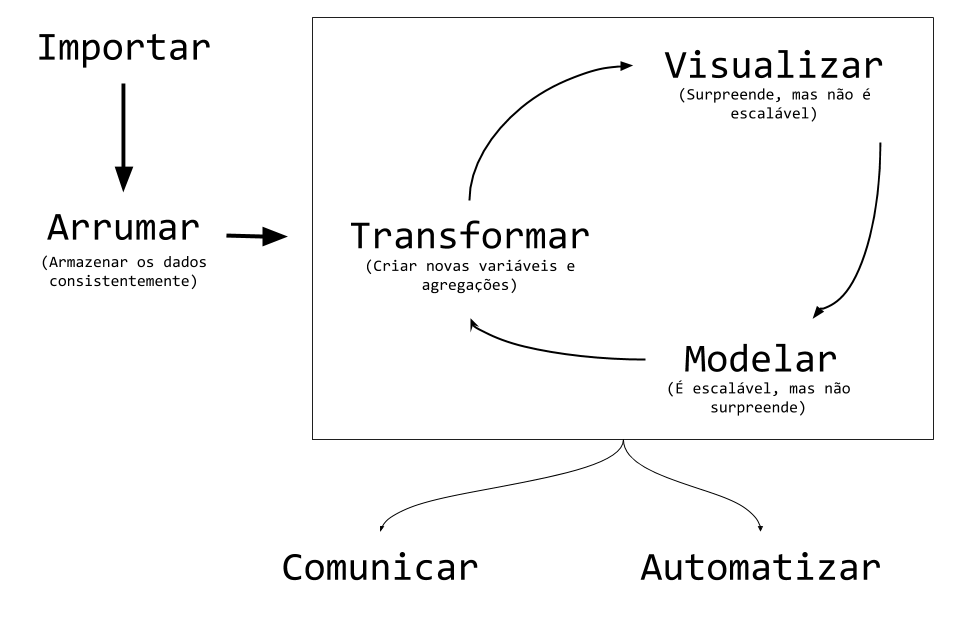![](../assets/ciclo_data_science.png){fig-align="center" width=85%}

## Regressão linear

* Método estatístico para sumarizar e estudar relações entre duas variáveis
contínuas

* $X$: preditor ou variável explicativa ou variável independente

* $Y$: desfecho ou variável resposta ou variável dependente

* Exemplo: salário ($Y$) e anos de estudo ($X$)

. . .

```{r altura-peso-scatter}
#| echo: false
#| fig-align: "center"
#| out.width: "70%"
set.seed(1)

library(ggplot2)

altura <- round(runif(10, 150, 195), 1)

peso <- 0.5 * altura + rnorm(10, mean = 0, sd = 3)

medidas <- data.frame(altura, peso)

modelo <- lm(peso ~ altura,
                  data = medidas)

medidas$predito <- predict(modelo)
medidas$residuos <- medidas$peso - medidas$predito

ggplot(medidas,
       aes(x = altura, y = peso)) +
  geom_point(size = 4, color = "slateblue4") +
  scale_x_continuous(labels = \(x) paste0(as.character(x), " cm")) +
  scale_y_continuous(labels = \(x) paste0(as.character(x), " kg")) +
  geom_smooth(method = "lm",
              color = "grey20",
              se = FALSE,
              fullrange = TRUE) +
  labs(x = "Altura",
       y = "Peso") +
  theme_minimal(base_size = 16,
                base_family = "Charter")
```

## Qual a utilidade das retas?

```{r exemplos-retas}
#| echo: false
#| fig-align: "center"
#| out.width: "100%"
library(patchwork)
library(dplyr)

neg <- openintro::simulated_scatter |> filter(group == 1)
pos <- openintro::simulated_scatter |> filter(group == 2)
ran <- openintro::simulated_scatter |> filter(group == 3)
bad <- openintro::simulated_scatter |> filter(group == 5)

bad_reg <- bad |> 
  mutate(y = max(y) + min(y) - y) |> 
  ggplot(aes(x = x, y = y)) +
  geom_point(size = 2,
             alpha = 0.8,
             color = "slateblue4") +
  geom_smooth(method = "lm",
              se = FALSE,
              color = "gray20") +
  labs(x = NULL,
       y = NULL) +
  theme_minimal(base_size = 16, base_family = "Charter")

p_neg <- ggplot(neg, aes(x = x, y = y)) +
  geom_point(size = 2, alpha = 0.8, color = "slateblue4") +
  geom_smooth(method = "lm", se = FALSE, color = "gray20") +
  labs(x = NULL, y = NULL) +
  theme_minimal(base_size = 16, base_family = "Charter")

p_pos <- ggplot(pos, aes(x = x, y = y)) +
  geom_point(size = 2, alpha = 0.8, color = "slateblue4") +
  geom_smooth(method = "lm", se = FALSE, color = "gray20") +
  labs(x = NULL, y = NULL) +
  theme_minimal(base_size = 16, base_family = "Charter")

p_ran <- ggplot(ran, aes(x = x, y = y)) +
  geom_point(size = 2, alpha = 0.8, color = "slateblue4") +
  geom_smooth(method = "lm", se = FALSE, color = "gray20") +
  labs(x = NULL, y = NULL) +
  theme_minimal(base_size = 16, base_family = "Charter")

p_neg + p_pos + p_ran + bad_reg +
  plot_annotation(title = "Um modelo linear pode ser útil mesmo quando os pontos não passam diretamente pela reta.",
                  subtitle = "Em alguns casos, não será o método mais adequado.",
                  caption = "Adaptado do livro Introduction to Modern Statistics (Çetinkaya-Rundel e Hardin, 2023).",
                  theme = theme(text = element_text(family = "Charter")))
```

## Como a reta é construída?

Construída a partir da fórmula:

<center>
$Y = \beta_0 + \beta_1x_1 + e$ $\color{red}\longrightarrow$ $peso = -4.47 + 0.527 \times altura$
</center>

* $\beta_0$: intercepto, ou valor de $Y$ quando $X = 0$

* $\beta_1$: coeficiente angular (*slope*)
  - Entendido como a mudança no $Y$ a partir do aumento de 1 unidade
  no $x_1$
  
. . .
  
```{r altura-peso-ilustracao-equacao}
#| echo: false
#| fig-align: "center"
#| out.width: "70%"
ggplot(medidas,
       aes(x = altura, y = peso)) +
  geom_point(size = 2.5, color = "slateblue4",
             alpha = 0.9) +
  scale_x_continuous(labels = \(x) paste0(as.character(x), " cm"),
                     limits = c(0, 195)) +
  scale_y_continuous(labels = \(x) paste0(as.character(x), " kg")) +
  geom_smooth(method = "lm",
              color = "grey20",
              se = FALSE,
              fullrange = TRUE) +
  geom_point(aes(x = x, y = y),
             data.frame(x = 0, y = -4.47),
             size = 5,
             color = "indianred1") +
  labs(x = "Altura",
       y = "Peso") +
  geom_segment(x = 150, xend = 150, y = 75, yend = 0,
               color = "tan1",
               linewidth = 1.5) +
  geom_segment(x = 150, xend = 0, y = 75, yend = 75,
               color = "tan1",
               linewidth = 1.5) +
  geom_point(x = 150, y = 74.58,
             size = 5,
             color = "maroon1") +
  theme_minimal(base_size = 16,
                base_family = "Charter")
```

## Definições e nomenclaturas

* $x_1, x_2, \cdots, x_p$: variáveis explicativas (variáveis independentes ou
*features* ou preditores)

* $X = x_1, x_2, \cdots, x_p$: conjunto de todos os preditores

* $Y$: variável resposta (ou variável dependente ou *target*)

* $\hat{Y}$: valor esperado (ou predição ou valor estimado ou *fitted*)

* $f(X)$ pode ser entendida como "modelo" ou "hipótese"

. . .

No primeiro exemplo:

* $x_1$: `altura` --- Altura em centímetros

* $Y$: `peso` --- Peso em quilogramas

## Observado *vs.* Esperado

* $Y$ é um valor observado (ou verdade) a partir dos dados

* $\hat{Y}$ é um valor esperado (predição, ou valor estimado, ou *fitted*)

* $Y - \hat{Y}$ é o resíduo (ou erro)

. . .

Por definição, $\hat{Y} = f(X)$ que é o valor que a função $f$ retorna.
Em suma, nosso modelo.

```{r altura-peso-erro}
#| echo: false
#| fig-align: "center"
#| out.width: "60%"

ggplot(medidas,
       aes(x = altura, y = peso)) +
  geom_segment(
    aes(
      x = altura,
      y = peso,
      xend = altura,
      yend = predito
    ),
    color = "chocolate1",
    linewidth = 1.5,
    alpha = 0.8,
    data = medidas
  ) +
  geom_point(size = 3.5, color = "slateblue4") +
  scale_x_continuous(labels = \(x) paste0(as.character(x), " cm")) +
  scale_y_continuous(labels = \(x) paste0(as.character(x), " kg")) +
  geom_smooth(method = "lm",
              color = "grey20",
              se = FALSE,
              fullrange = TRUE) +
  labs(x = "Altura",
       y = "Peso") +
  theme_minimal(base_size = 16,
                base_family = "Charter")
```

## Por que ajustar uma $f$?

::: columns
::: {.column width="50%"}
### Predição

* Em muitas situações, $X$ está disponível facilmente mas $Y$ não é fácil de
descobrir (ou mesmo não é possível descobrí-lo).

* Queremos que $\hat{Y}=f(X)$ seja uma
boa estimativa (preveja bem o futuro).

* Exemplo: Com quantos gramas irá nascer um bebê na maternidade do HCPA?
:::

::: {.column width="50%"}
### Inferência

* Em inferência estamos mais interessados em entender a relação entre as variáveis explicativas $X$ e a variável resposta $Y$.

* Exemplos:
  - Qual o efeito da idade na função cognitiva dos pacientes bipolares?
  - Os níveis de estresse podem explicar a severidade de sintomas depressivos?
  
* Nessa aula, nosso foco é **inferência**.
:::
:::

## Vamos trabalhar com `gambás`


::: columns
::: {.column width="65%"}
Os dados apresentam informações de gambás da Austrália e Nova Guiné.

```{r ler-e-mostrar-gambas}
library(readr)

gambas <- read_csv("../dados/gambas.csv")

glimpse(gambas)
```
:::

::: {.column width="35%"}
![O gambá brushtail da Austrália. Foto de Greg Schecter. Licença CC BY 2.0.](../assets/gamba.jpg){fig-align="center" width=85%}
:::
:::

## Exemplo com `gambás`

::: columns
::: {.column width="50%"}
#### Regressão linear simples

<center>
$y = \beta_0 + \beta_1x$
</center>

<br>

#### Exemplo

<center>
$cabeça = \beta_0 + \beta_1total$
</center>

<br>

```{r lm-cabeca-comprimento-total}
#| eval: false
# No R
lm(comprimento_cabeca ~ comprimento_total,
   data = gambas)
```

:::

::: {.column width="50%"}
::: {.panel-tabset}
## Gráfico

```{r scatterplot-gambas}
#| echo: false
ggplot(gambas) + 
  geom_point(aes(x = comprimento_total, y = comprimento_cabeca),
             size = 4,
             alpha = 0.7)  +
  labs(x = "Comprimento total (em cm)",
       y = "Comprimento da cabeça (em mm)") +
  theme_minimal(18, "Charter")
```

## Reta na mão

```{r reta-na-mao-gambas}
#| echo: false
ggplot(gambas, aes(x = comprimento_total, y = comprimento_cabeca)) +
  geom_point(size = 4,
             alpha = 0.7)  +
  #geom_smooth(method = "lm",
  #            se = FALSE,
  #            color = "firebrick1",
  #            size = 2) +
  geom_abline(intercept = 36,
              slope = 0.7,
              color = "dodgerblue4",
              size = 2) +
  labs(x = "Comprimento total (em cm)",
       y = "Comprimento da cabeça (em mm)") +
  theme_minimal(18, "Charter")
```

## Melhor reta

```{r melhor-reta-gambas}
#| echo: false
ggplot(gambas, aes(x = comprimento_total, y = comprimento_cabeca)) +
  geom_point(size = 4,
             alpha = 0.7)  +
  geom_smooth(method = "lm",
              se = FALSE,
              color = "firebrick1",
              size = 2) +
  geom_abline(intercept = 36,
              slope = 0.7,
              color = "dodgerblue4",
              alpha = 0.6,
              size = 2) +
  labs(x = "Comprimento total (em cm)",
       y = "Comprimento da cabeça (em mm)") +
  theme_minimal(18, "Charter")
```
:::
:::
:::

## Melhor reta no R

<center>
$comprimento \,da \,cabeça = \beta_0 + \beta_1comprimento \,total$
</center>

<br>

. . .

```{r regressao-linear-gamba}
melhor_reta <- lm(comprimento_cabeca ~ comprimento_total, data = gambas)

melhor_reta
```

<br>

. . .

<center>
$comprimento \,da \,cabeça = 42.7 + 0.57 \times comprimento \,total$
</center>

<br>

. . .

<center>
Como a melhor reta é escolhida?
</center>

## "Melhor reta" baseado em que?

A gente quer a reta que *erre menos*.

. . .

Exemplo de medida de erro: **E**rro **Q**uadrático **M**édio.

<center>
$$
EQM = \sqrt{\frac{1}{N}\sum(y_i - \hat{y_i})^2}
$$

```{r comparar erro-reta-na-mao-e-melhor}
#| echo: false
#| fign-align: "center"
#| out.width: "70%"
set.seed(1)

melhor_reta <- lm(comprimento_cabeca ~ comprimento_total, data = gambas)

gambas_com_preds <- melhor_reta |> 
  broom::augment() |> 
  rename(pred_melhor_reta = .fitted) |> 
  mutate(
    pred_reta_a_mao = 36 + 0.7 * comprimento_total
  )

grafico_residuos_melhor_reta <- gambas_com_preds |> 
  ggplot(aes(x = comprimento_total, y = comprimento_cabeca)) +
  geom_point(size = 2) +
  geom_abline(
    intercept = melhor_reta$coefficients[1], 
    slope = melhor_reta$coefficients[2], 
    size = 1,
    colour = "salmon"
  ) +
  geom_segment(aes(xend = comprimento_total, yend = pred_melhor_reta), colour = "purple", size = 0.8) +
  labs(
    subtitle = "Resíduos da Melhor Reta",
    y = "Comprimento da cabeça (em mm)",
    x = "Comprimento total (em cm)"
  ) +
  theme_minimal(15, "Charter")

grafico_residuos_reta_a_mao <- gambas_com_preds |> 
  ggplot(aes(x = comprimento_total, y = comprimento_cabeca)) +
  geom_point(size = 2) +
  geom_abline(
    intercept = 36, 
    slope = 0.7, 
    size = 1,
    colour = "orange"
  ) +
  geom_segment(aes(xend = comprimento_total, yend = pred_reta_a_mao), colour = "purple", size = 0.8) +
  labs(
    subtitle = "Resíduos da Reta Escolhida a Mão",
    y = "Comprimento da cabeça (em mm)",
    x = "Comprimento total (em cm)"
  ) +
  theme_minimal(15, "Charter")

grafico_residuos_melhor_reta + grafico_residuos_reta_a_mao +
  plot_annotation(title = "Os segmentos roxos são os resíduos (ou o quanto o modelo errou naqueles pontos).",
                  theme = theme_minimal(15, "Charter"))
```

## E se quisermos usar mais preditores?

::: columns
::: {.column width="50%"}
#### Regressão linear múltipla

<center>
$y = \beta_0 + \beta_1x_1 + \cdots + \beta_px_p$
</center>

<br>

#### Exemplo

<center>
$cabeça = \beta_0 + \beta_1total + \beta_2cauda$
</center>

<br>

```{r linear-multipla-no-r-gambas}
#| eval: false
# No R
lm(comprimento_cabeca ~ comprimento_total + comprimento_cauda,
   data = gambas)
```

:::

::: {.column width="50%"}
```{r multipla-plotly}
#| echo: false
#| fig-align: "center"
#| out.width: "100%"
set.seed(1)

library(plotly)

x <- gambas$comprimento_total
y <- gambas$comprimento_cauda
z <- gambas$comprimento_cabeca

fit <- lm(z ~ x + y)

grid.lines <- 26

x.pred <- seq(min(x), max(x), length.out = grid.lines)
y.pred <- seq(min(y), max(y), length.out = grid.lines)

xy <- expand.grid(x = x.pred, y = y.pred)

z.pred <- matrix(predict(fit, newdata = xy), 
                 nrow = grid.lines, ncol = grid.lines)

fig <- plot_ly(data = gambas) |>
  add_trace(
    x = ~ comprimento_total,
    y = ~ comprimento_cauda,
    z = ~ comprimento_cabeca,
    type = "scatter3d",
    mode = "markers",
    opacity = .8
  ) |>
  add_trace(
    z = z.pred,
    x = x.pred,
    y = y.pred,
    type = "surface",
    opacity = .9
  ) |>
  layout(scene = list(xaxis = list(title = "Total (cm)"),
                      yaxis = list(title = "Cauda (cm)"),
                      zaxis = list(title = "Cabeça (mm)"))) |> 
  hide_legend() |> 
  hide_colorbar()

fig
```
:::
:::

## O que o R nos diz?

```{r modelo-cabeca-pelo-total-e-cauda}
modelo_linear_multiplo <-
  lm(comprimento_cabeca ~ comprimento_total + comprimento_cauda,
     data = gambas)

summary(modelo_linear_multiplo)
```

. . .

<center>
$$
cabeça = 46.8 + 0.64total - 0.28cauda
$$
</center>

## Coeficiente de determinação

* O $R^2$ (coeficiente de determinação) é a proporção da variância na variável
resposta que pode ser explicada pelos preditores

* Varia de 0 a 1

. . .

```{r r-quadrado-modelo-cabeca}
# Extrair o R^2
summary(modelo_linear_multiplo)$r.squared

# Extrair o R^2 ajustado
summary(modelo_linear_multiplo)$adj.r.squared
```

. . .

<br>

<center>
"O modelo demonstra que `r paste0(format(round(summary(modelo_linear_multiplo)$adj.r.squared * 100, 1), decimal.mark = ","), "%")` da variação no comprimento da cabeça dos gambás pode ser explicado pelo
comprimento total e comprimento da cauda dos gambás."
</center>

## Preditores categóricos

#### Preditores com apenas duas categorias

Pergunta de pesquisa: O tamanho das nadadeiras dos pinguins variam conforme
o sexo?

::: columns
::: {.column width="50%"}
```{r boxplot-nadadeira-sexo}
#| echo: false
#| out.width: "100%"
#| fig-align: "center"
dados::pinguins |> 
  filter(!is.na(sexo)) |> 
  mutate(
    sexo = if_else(sexo == "macho", "Macho", "Fêmea")
  ) |> 
  ggplot(aes(y = comprimento_nadadeira, x = sexo, fill = sexo)) +
  geom_boxplot(show.legend = FALSE) +
  ghibli::scale_fill_ghibli_d("MarnieLight1") +
  labs(y = "Comprimento da nadadeira (mm)",
       x = "Sexo") +
  theme_minimal(20, "Charter")
```
:::

::: {.column width="50%"}
```{r scatterplot-nadadeira-sexo}
#| echo: false
#| out.width: "100%"
#| fig-align: "center"
set.seed(1)

dados::pinguins |> 
  filter(!is.na(sexo)) |> 
  mutate(
    sexo_macho = if_else(sexo == "macho", 1, 0)
  ) |> 
  ggplot(aes(y = comprimento_nadadeira, x = sexo_macho)) +
  geom_jitter(width = 0.05, height = 0,
              alpha = 0.7, size = 2) +
  geom_smooth(method = "lm", se = FALSE,
              color = "#0E84B4FF", linewidth = 1.5) +
  labs(y = "Comprimento da nadadeira (mm)",
       x = "Sexo (macho)") +
  scale_x_continuous(breaks = 0:1) +
  theme_minimal(20, "Charter")
```
:::
:::

```{r regressao-nadadeira-sexo}
lm(comprimento_nadadeira ~ sexo, data = dados::pinguins)
```

## Preditores categóricos

#### Preditores com 3 ou mais categorias

::: columns
::: {.column width="50%"}
```{r boxplot-nadadeira-especie}
#| echo: false
#| out.width: "100%"
#| fig-align: "center"
dados::pinguins |> 
  ggplot(aes(y = comprimento_nadadeira, x = especie, fill = especie)) +
  geom_boxplot(show.legend = FALSE) +
  ghibli::scale_fill_ghibli_d("MononokeMedium", direction = -1) +
  labs(y = "Comprimento da nadadeira (mm)",
       x = "Espécie") +
  theme_minimal(20, "Charter")
```

```{r linear-nadadeira-especie}
lm(comprimento_nadadeira ~ especie, data = dados::pinguins)
```
:::

::: {.column width="50%"}
Modelo:

$$
y_i = \beta_0 + \beta_1x_{1i} + \beta_2x_{2i}
$$

Em que:

$$
x_{1i} = \Bigg \{ \begin{array}{ll} 1 & \text{se for }\texttt{Pinguim-de-barbicha}\\0&\text{caso contrário}\end{array}
$$

$$
x_{2i} = \Bigg \{ \begin{array}{ll} 1 & \text{se for }\texttt{Pinguim-gentoo}\\0&\text{caso contrário}\end{array}
$$
:::
:::

## Heteroscedasticidade

* Inconstância da variabilidade dos erros

. . .
  
```{r plot-heteroscedasticidade}
#| out.width: "100%"
#| echo: false
#| fig-align: "center"
set.seed(1)

hetero_df <- tibble(
  x = runif(50),
  y = rnorm(50, mean = x, sd = x * 0.5)
)

cru <- ggplot(hetero_df, aes(x = x, y = y)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE) +
  theme_minimal(20, "Charter") +
  labs(x = unname(latex2exp::TeX("$x_1$")), y = "Y",
       title = unname(latex2exp::TeX("$Y = \\beta_0 + \\beta_1x_1$")))

cru
```

## Lidando com a heteroscedasticidade

* Como diagnosticar?
  - Visualização dos resíduos (`gglm::gglm()`)
  - Testes (Breuch-Pagan através da função `lmtest::bptest()`)
  
* Como tratar?
  - Transformações na variável resposta ($log(Y)$, $\sqrt{Y}$, $\frac{1}{Y}$)
  - Regressão com pesos
  
. . .

```{r plot-heteroscedasticidade-contornada}
#| out.width: "50%"
#| echo: false
#| fig-align: "center"
raiz <- ggplot(hetero_df, aes(x = x, y = sqrt(y))) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE) +
  theme_minimal(20, "Charter") +
  labs(x = unname(latex2exp::TeX("$x_1$")),
       y = unname(latex2exp::TeX("$\\sqrt{Y}")),
       title = unname(latex2exp::TeX("$\\sqrt{Y} = \\beta_0 + \\beta_1x_1$")))

cru + raiz
```

## Multicolinearidade

* Ocorre quando duas ou mais variáveis preditoras são altamente correlacionadas umas com as outras

* Não fornecem informações exclusivas

* Exemplo: preço de um imóvel ($Y$) explicado pela área ($x_1$) e número de cômodos ($x_2$)

. . .

```{r exemplo-multicolinearidade-preco-area-quartos}
#| echo: false
#| out.width: "80%"
#| fig-align: "center"
set.seed(1)

area <- rnorm(100, mean = 1500, sd = 500)
comodos <- round(rnorm(100, mean = 3 + 0.5 * area/100, sd = 1), 0)
preco <- rnorm(100, mean = 200000 + 100 * area + 50000 * comodos, sd = 50000)
area <- area / 10

dados <- data.frame(area, comodos, preco)

ggplot(dados, aes(x = area, y = preco, color = comodos)) +
  geom_point() +
  scale_color_viridis_c(name = "Cômodos") +
  scale_y_continuous(labels = scales::dollar_format(prefix = "R$ ",
                                                    big.mark = ".")) +
  scale_x_continuous(labels = \(x) unname(latex2exp::TeX(paste0(as.character(x), "$m^2$")))) +
  theme_minimal(20, "Charter") +
  labs(x = "Área",
       y = "Preço do imóvel")
```

## Lidando com a multicolinearidade

::: columns
::: {.column width="50%"}
* Problemas
  - Instabilidade numérica
  - Desvios padrão inflados
  - Interpretação comprometida
  
* Soluções
  - Eliminar uma das variáveis muito correlacionadas
  - Consultar o *variance inflation factor* (VIF)
:::

::: {.column width="50%"}

```{r calcular-vif-preco-imovel}
library(car)

regressao_linear <- lm(preco ~ area + comodos,
                       data = dados)

vif(regressao_linear)
```

* Regra geral
  - Valor 1: sem correlação entre o preditor e os demais preditores
  - Valor entre 1 e 5: Correlação moderada entre o preditor e demais preditores
  - Valor maior que 5: Correlação severa que pode afetar $p$-valores e coeficientes
  da regressão, sendo potencialmente não confiáveis
:::
:::

## Outliers

* As observações distantes das outras do conjunto de dados são consideradas **outliers**

. . .

```{r ilustracao-influencia-outlier}
#| echo: false
#| fig-align: "center"
#| out.width: "90%"
set.seed(1)

x <- 1:10
y <- 2*x + rnorm(10, mean = 0, sd = 1)
df <- data.frame(x, y)

# Criando o gráfico sem outlier
p_sem_outlier <- ggplot(df, aes(x = x, y = y)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE) +
  scale_x_continuous(limits = c(0, 12.5)) +
  scale_y_continuous(limits = c(0, 50)) +
  theme_minimal(18, "Charter") +
  labs(x = unname(latex2exp::TeX("$x_1$")),
       y = unname(latex2exp::TeX("$Y$")))

# Adicionando um outlier aos dados
df[11, ] <- c(12, 50)

# Criando o gráfico com outlier
p_com_outlier <- ggplot(df, aes(x = x, y = y)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE) +
  theme_minimal(18, "Charter") +
  scale_x_continuous(limits = c(0, 12.5)) +
  scale_y_continuous(limits = c(0, 50)) +
  labs(x = unname(latex2exp::TeX("$x_1$ com \\textit{outlier}")),
       y = NULL)

p_sem_outlier + p_com_outlier
```

## Lidando com outliers

::: columns
::: {.column width="40%"}
* Como diagnosticar?
  - Visualização univariada (histograma, boxplot)
  - Comparação do valor com o desvio padrão
  - Distância de Cook
  
* Como tratar?
  - Transformações $log()$, etc
  - Categorização
  - Remover valores extremos (não recomendado)
:::

::: {.column width="60%"}

```{r distancia-cook-codigo}
modelo_com_outlier <- lm(y ~ x, data = df)

cooks.distance(modelo_com_outlier)

4 / nrow(df)
```

```{r distancia-cook-com-outlier-plot}
#| echo: false
#| fig-align: "center"
#| out.width: "100%"
modelo_com_outlier <- lm(y ~ x, data = df)

distancia_cook <- cooks.distance(modelo_com_outlier)

df_cook <- data.frame(distancia_cook, row.names = NULL)

ggplot(df_cook, aes(x = as.numeric(row.names(df_cook)), y = distancia_cook)) +
  geom_point(size = 3) +
  scale_x_continuous(breaks = 1:11) +
  geom_hline(yintercept = 4/nrow(df_cook),
             color = "darkred", size = 2) +
  labs(x = "Observação", y = "Distância de Cook") +
  theme_minimal(20, "Charter")
```

:::
:::

## Correlação *vs.* Regressão linear

::: columns
::: {.column width="50%"}
#### Similaridades

* Coeficiente de regressão padronizado é o mesmo que o coeficiente de
correlação de Pearson

* O quadrado do coeficiente de correlação de Pearson é o mesmo que o
$R^2$ na regressão linear simples

* O sinal do coeficiente não-padronizado da regressão será o mesmo do
coeficiente de correlação

* Nenhum dos métodos respondem perguntas de causalidade
:::

::: {.column width="50%"}
#### Diferenças

* A equação da regressão ($\beta_0 + \beta_1x_1$) pode ser usada para
fazer predições de $Y$ baseado em $X$

* Apesar da correlação se referir comumente a relações lineares, o
conceito pode estar associado a outros tipos de associação

* Correlação entre $X$ e $Y$ é a mesma correlação de $Y$ e $X$.
Já na regressão linear, o coeficiente muda
quando comparamos um modelo que prediz $Y$ a partir de $X$ e um modelo
que prediz $X$ a partir de $Y$
:::
:::

## Tarefa de casa

* Ler Capítulo 8 do
[livro OpenIntro Statistics](https://www.openintro.org/book/os/) sobre
*Introduction to linear regression*
  - Caso queira se aprofundar, ler Capítulo 9 sobre
*Multiple and logistic regression*

* A partir dos dados `dados_iris` do pacote `dados`,
crie um modelo de
regressão linear simples e um modelo de regressão
linear múltipla
com as variáveis da sua escolha
  - Lembre-se que o desfecho deve ser contínuo (numérico)
  
* Crie um gráfico de dispersão/pontos (*scatterplot*) para acompanhar
sua análise de regressão linear simples