{
 "cells": [
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "# Lecture 1: Probability and Counting\n",
    "\n",
    "## Stat 110, Prof. Joe Blitzstein, Harvard University\n",
    "\n",
    "\n",
    "----"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Definitions\n",
    "\n",
    "We start with some basic definitions:\n",
    "\n",
    "#### Definition: sample space\n",
    "\n",
    "> A __sample space__ is the set of all possible outcomes of an experiment.\n",
    "\n",
    "\n",
    "\n",
    "#### Definition: event\n",
    "\n",
    "> An __event__ is a subset of the sample space.\n",
    "\n",
    "\n",
    "#### Definition: naïve definition of probability\n",
    "> Under the __naïve definition of probability__, the probability of a given event $A$ occurring is expressed as\n",
    ">\n",
    "> \\begin\\{align\\}\n",
    ">   P(A) &= \\frac{ \\text{# favorable outcomes}}{\\text{# possible outcomes}}\n",
    "> \\end\\{align\\}\n",
    ">\n",
    "> assuming all outcomes are equally likely in a finite sample space.\n",
    "\n",
    "----"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Counting\n",
    "\n",
    "With the __multiplication rule__, if we have an experiment with $n_1$ possible outcomes; and we have a 2<sup>nd</sup> experiment with $n_2$ possible outcomes; ..., and for the r<sup>th</sup> experiment there are $n_r$ possible outcomes; then overall there are $n_1 n_2 ... n_r$ possible outcomes (product).\n",
    "\n",
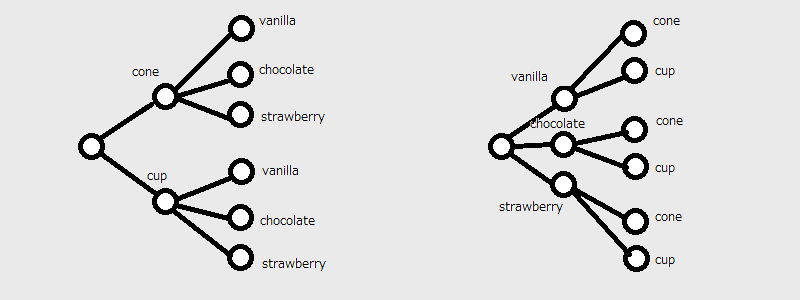
    "Let's say you are ordering ice cream. You can either get a cone or a cup, and the ice cream comes in three flavors. The order of choice here does not matter, and the total number of choices is $2 \\times 3 = 3 \\times 2 = 6$. This can be represented with a very simple [probability tree][1].\n",
    "\n",
    "[1]: https://en.wikipedia.org/wiki/Tree_diagram_(probability_theory)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "![title](images/L0101.png)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "The __binomial coefficient__  is defined as \n",
    "\n",
    "\\begin{align}\n",
    "  \\binom{n}{k} =\n",
    "    \\begin{cases}\n",
    "      \\frac{n!}{(n-k)!k!} & \\quad \\text{if } 0 \\le k \\le n \\\\\n",
    "      0 & \\quad \\text{if } k \\gt n\n",
    "    \\end{cases}\n",
    "\\end{align}\n",
    "\n",
    "This expresses the number of ways you could choose a subset of size $k$ from $n$ items, where order doesn't matter.\n",
    "\n",
    "----"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Sampling\n",
    "\n",
    "Choose $k$ objects out of $n$\n",
    "\n",
    "|           | ordered | unordered |\n",
    "|-----------|:---------:|:-----------:|\n",
    "| __w/ replacement__   | $n^k$     |   ???     |\n",
    "| __w/o replacement__  | $n(n-1)(n-2) \\ldots (n-k+1)$ | $\\binom{n}{k}$  |\n",
    "\n",
    "\n",
    "* __ordered, w/ replacement__: there are $n$ choices for each $k$, so this follows from the multiplication rule.\n",
    "* __ordered, w/out replacement__: there are $n$ choices for the 1<sup>st</sup> position; $n-1$ for the 2<sup>nd</sup>; $n-2$ for the 3<sup>rd</sup>; and $n-k+1$ for the $k$<sup>th</sup>.\n",
    "* __unordered, w/ replacement__: ???\n",
    "* __unordered, w/out replacement__: the binomial coefficient; think of choosing a hand from a deck of cards.\n",
    "\n",
    "Out of the 4 ways of choosing $k$ objects out of $n$, the case of __unordered, with replacement__ is perhaps not as clear-cut and easy to grasp as the other three. Move on to Lecture 2.\n",
    "\n",
    "-----"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "View [Lecture 1: Probability and Counting | Statistics 110](http://bit.ly/2vSEEeI) on YouTube."
   ]
  }
 ],
 "metadata": {
  "kernelspec": {
   "display_name": "Python 3",
   "language": "python",
   "name": "python3"
  },
  "language_info": {
   "codemirror_mode": {
    "name": "ipython",
    "version": 3
   },
   "file_extension": ".py",
   "mimetype": "text/x-python",
   "name": "python",
   "nbconvert_exporter": "python",
   "pygments_lexer": "ipython3",
   "version": "3.6.3"
  }
 },
 "nbformat": 4,
 "nbformat_minor": 1
}