{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Lecture 2: Story Proofs, Axioms of Probability\n",
"\n",
"\n",
"## Stat 110, Prof. Joe Blitzstein, Harvard University\n",
"\n",
"----"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Sampling, continued\n",
"\n",
"Choose $k$ objects out of $n$\n",
"\n",
"| | ordered | unordered |\n",
"|-----------|:---------:|:-----------:|\n",
"| __w/ replacement__ | $n^k$ | ??? |\n",
"| __w/o replacement__ | $n(n-1)(n-2) \\ldots (n-k+1)$ | $\\binom{n}{k}$ |\n",
"\n",
"\n",
"* __ordered, w/ replacement__: there are $n$ choices for each $k$, so this follows from the multiplication rule.\n",
"* __ordered, w/out replacement__: there are $n$ choices for the 1st position; $n-1$ for the 2nd; $n-2$ for the 3rd; and $n-k+1$ for the $k$th.\n",
"* __unordered, w/ replacement__: _we will get to this shortly..._\n",
"* __unordered, w/out replacement__: the binomial coefficient; think of choosing a hand from a deck of cards.\n",
"\n",
"To complete our discussion of sampling, recall that of the four ways of sampling as shown above, all except the case of __unordered, with replacement__ follow immediately from the multiplication rule. \n",
"\n",
"Now the solution is $\\binom{n+k-1}{k}$, but let's see if we can prove this."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### A simple proof\n",
"\n",
"We start off with some simple edge cases.\n",
"\n",
"If we let $k=0$, then we are not choosing anything, and so there is only one solution to this case: the empty set.\n",
"\\begin\\{align\\}\n",
" \\text{let }k = 0 \\Rightarrow \\binom{n+0-1}{0} &= \\binom{n-1}{0} \\\\\\\\\n",
" &= 1\n",
"\\end\\{align\\}\n",
"\n",
"If we let $k=1$, then there are $n$ ways we could select a single item out of a total of $n$. \n",
"\\begin\\{align\\}\n",
" \\text{let }k = 1 \\Rightarrow \\binom{n+1-1}{1} &= \\binom{n}{1} \\\\\\\\\n",
" &= n\n",
"\\end\\{align\\}\n",
"\n",
"Now let's consider a simple but non-trivial case. If we let $n=2$, then\n",
"\\begin\\{align\\}\n",
" \\text{let }n = 2 \\Rightarrow \\binom{2+k-1}{k} &= \\binom{k+1}{k} \\\\\\\\\n",
" &= \\binom{k+1}{1} \\\\\\\\\n",
" &= k+1\n",
"\\end\\{align\\}\n",
"\n",
"Here's an example of $n=2, k=7$:\n",
"\n",
"\n",
"\n",
"But notice that we are really doing here is placing $n-1$ dividers between $k$ elements. Or in other words, we are choosing $k$ slots for the elements out of $n+k-1$ slots in total.\n",
"\n",
"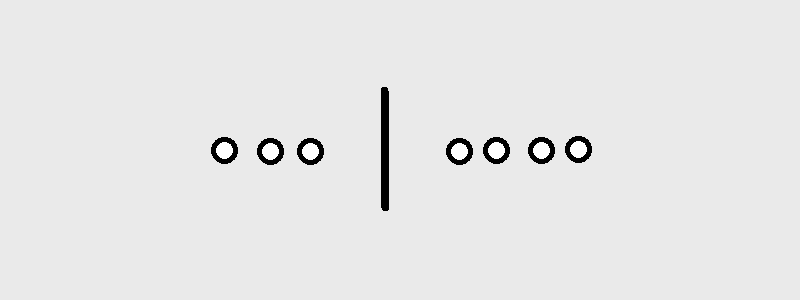\n",
"\n",
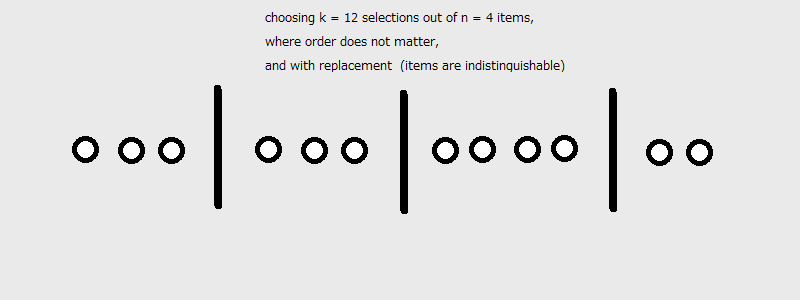
"And we can easily build on this understanding to other values of $n$ and $k$.\n",
"\n",
"\n",
"\n",
"And the number of ways to select $k$ items out of $n$, unordered and with replacement, is:\n",
"\n",
"\\begin\\{align\\}\n",
" \\text{choose k out n items, unordered, with replacement} &= \\binom{n+k-1}{k} \\\\\\\\\n",
" &= \\binom{n+k-1}{n-1}\n",
"\\end\\{align\\}"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Story Proof\n",
"A story proof is a proof by _interpretation_. No algebra needed, just intuition.\n",
"\n",
"Here are some examples that we have already come across.\n",
"\n",
"### Ex. 1 \n",
"$$ \\binom{n}{k} = \\binom{n}{n-k} $$\n",
"\n",
"Choosing $k$ elements out of $n$ is the same as choosing $n-k$ elements out of $n$. We've just seen this above!\n",
"\n",
"### Ex. 2\n",
"$$ n \\binom{n-1}{k-1} = k \\binom{n}{k} $$\n",
"\n",
"Imagine picking $k$ people out of $n$, and then designating of the $k$ as president. You can either select all $k$ people, and then choose 1 from among those $k$. Or, you can select a president, and then choose the remaining $k-1$ out of the $n-1$ people.\n",
"\n",
"### Ex. 3\n",
"$$ \\binom{m+n}{k} = \\sum_{j=0}^{k} \\binom{m}{j} \\binom{n}{k-j} $$\n",
"\n",
"Suppose you had $m$ boys and $n$ girls, and you needed to select $k$ children out of them all. You could do this by first choosing $j$ out of the $m$ boys, and then choosing $k-j$ of the girls. You would have to apply the multiplication rule to get the total number of combinations, and then sum them all up. This is known as [Vandermonde's identity](https://en.wikipedia.org/wiki/Vandermonde%27s_identity).\n",
"\n",
"----"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Non-naïve Definition of Probability\n",
"\n",
"Now we move from the naïve definition of probability into the more abstract and general.\n",
"\n",
"#### Definition: non-naïve definition of probability\n",
"> Let $S$ be a sample space, the set of all possible outcomes of some experiment. $S$ might not be _finite_ anymore, and all outcomes might not be _equally probable_, either.\n",
"> \n",
"> Let $A$ be an event in, or a subset of, $S$.\n",
">\n",
"> Let $P$ be a function that maps an event $A$ to some value from $0$ to $1$.\n",
"\n",
"And we have the following axioms:\n",
"\n",
"### Axiom 1\n",
"\n",
"> \\begin\\{align\\}\n",
"> P(\\emptyset) = 0 \\\\\\\\\n",
"> P(\\Omega) = 1\n",
"> \\end\\{align\\}\n",
"\n",
"The probability of the empty set, or a null event, is by definition $0$.\n",
"\n",
"The probability of the entire space is by definition $1$.\n",
"\n",
"These are the 2 extremes, and this is why Prof. Blitzstein lumps them together in one rule.\n",
"\n",
"### Axiom 2\n",
"\n",
"> $$ P(\\bigcup_{n=1}^{\\infty} A_{n}) = \\sum_{n=1}^{\\infty} P(A_{n}) \\iff A_1, A_2, ... A_n \\text{ are disjoint (non-overlapping)} $$\n",
"\n",
"Every theorem about probability follows from these 2 rules. You might want to have a look at [Kolmogorov's axioms](http://mathworld.wolfram.com/KolmogorovsAxioms.html).\n",
"\n",
"----"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"View [Lecture 2: Story Proofs, Axioms of Probability | Statistics 110](http://bit.ly/2nOw0JV) on YouTube."
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.3"
}
},
"nbformat": 4,
"nbformat_minor": 1
}