{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 第7章 支持向量机\n",
"求解目的: \n",
"支持向量机的本质并不复杂,其实质仍然是在求解一个线性分割面,这个分割面由参数$w$确定,但是对于这个分割面,我们增加了一些限制和约束,约束围绕“最大间隔距离”这个概念展开,为什么需要加这个约束呢?因为,当我们拿到一组二分类问题的数据时,能够区分开不同类数据的分割面不止一个,如何确定一个最好的分割面就成了需要进一步确定的问题,SVM以及最大间隔距离概念的出现,使求解最佳分割面的问题成为可能。 \n",
"\n",
"---"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 7.1 线性可分支持向量机\n",
"### 7.1.1 对线性分割面的理解\n",
">给定数据$T=\\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\\}$,我们期望得到参数$w^*$和$b^*$,$w^*$和$b^*$可以对$x$进行函数映射,此时得到一个分割超平面,即$$w^* x + b^* = 0$$\n",
"然后,决策函数被定义为:\n",
"$$f(x) = sign(w^*x + b^*)$$\n",
"但是这里,我们考虑以下一种情况:当给定以下数据及其类别标签"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"import numpy as np\n",
"x = np.array([[3,4],[1,1],[4,3],[1,0],[2,1],[4,2],[4,0]])\n",
"y = np.array([1,-1,1,-1,-1,1,1]).T"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
">并将之绘制在二维空间时,会得到以下图像:"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"import matplotlib.pyplot as plt\n",
"posindex = x[y[:] == 1]\n",
"negindex = x[y[:] == -1]\n",
"plt.scatter(posindex[:,0], posindex[:,1], c='red', alpha=1, marker='+', label='pickup') \n",
"plt.scatter(negindex[:,0], negindex[:,1], c='green', alpha=1, marker='o', label='pickup') \n",
"plt.axis([0,5,-1,5])\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
">给定以下三组参数方程,绘制分割曲线来区分数据\n",
"* f1 = -5.00 + 1.81 * x_ + 0.55 * y_\n",
"* f2 = -5.30 + 1.61 * x_ + 0.95 * y_\n",
"* f3 = -6.00 + 1.91 * x_ + 0.55 * y_"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAlUAAADCCAYAAABg+jdgAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAIABJREFUeJzt3Xl8VOW9P/DPM5ONhBC2sAYSdgiELJOZCROVTREygaFa64JLQaAqoLb2Wi21vbali3ZBFm0RFKvUrYpscQMFhZCVAAHCvq8JOyQEsjz3j8DvhxY0JGfmOcvn/XrN65qUe85n7vVDv2eeM88RUkoQERERUePYVAcgIiIiMgMOVUREREQa4FBFREREpAEOVUREREQa4FBFREREpAEOVUREREQa4FBFREREpAEOVUREREQa4FBFREREpIEgFSdt3bq1jIuLU3Fqpc4eP4ej+8oQ17cTQsKCVcehywoLC49LKaNVZtBrJ0oPHMfZ4+cQ27cTgkOU/HVBCrATxrK/5CBsdhtienZQHcW06tsJJX9LxsXFoaCgQMWplSo9cBxjYh/FuDH34d5nf6A6Dl0mhNinOoNeO1F64Dge7vMkUrr1x/MLn1YdhwKEnTCWV3/xFj74+1J88MVriGgWrjqOKdW3E1z+C6A2nVqjZ2o3ZC/OVx2FqF7adGqNMc/9ENmL8pG7rFB1HCK6hrRMB2qqa1D42QbVUSyPQ1WAeXxObM3dgRNHTqmOQlQvd/7Ui859OmLW46/h4oWLquMQ0bfED+iJyBYRyM1apzqK5XGoCrD00S4AQPYiflpFxhAcEowps8bj6J5SvPOnj1THIaJvsQfZkTo8CXnL1qG2tlZ1HEvjUBVgsfEx6NC9HdZyCZAMJGlwPwy+Nx3vvrAIh3YeUR2HiL4lzevA6bKz2F6wS3UUS+NQFWBCCKT7nChaUYzysxWq4xDV20/+8hCCQ4Iw+/HXIKVUHYeIrpI6PAk2m0DOUt77qBKHKgU8o12orqpBXlaR6ihE9daqfQs89PzdyP9kPVYvzFMdh4iu0qxlJOI9vZC7jPdVqcShSoE+aT3QvE0UvwVIhuObPBxd+8filSdfx4XyStVxiOgqbq8DO4v24PihE6qjWBaHKgXsdjvSMh3Iy1qHqktVquMQ1Zs9yI4ps8ej7OAJLPjdf1THIaKruL0pAMBVEIU4VCmSPtqFirMXsP7LzaqjEN2Qfum9MezHg/Cfvy3FvpKDquMQ0WVxfTuhbWw0crinnDIcqhRJuTUBYRGhyP6I96aQ8Uz48/0IjwzDrMlzedM6kU4IIeD2pqBoeTEuVV5SHceSOFQpEhIWgtTbk7B2SQH3FSHDaR4dhbHT7sP6Lzfjy3fWqI5DRJe5vQ5UVlzEhpVcBVGBQ5VCHp8TJw6fwrZ87itCxpMxYSh6pnbDP596A+VnylXHISIASYP7Iiw8lFsrKMKhSiG3NwU2u427q5Mh2e12PD57PE4dO4M3fvOe6jhEhLpVkORbE5CXtY5L8wpwqFKoWctI9B8Yj+xFvK+KjKmXszu8E2/FolkfY9eGvarjEBHqdlc/urcMezcfUB3FcjhUKZbuc2F/ySEc3H5YdRSiBhk77V5EtmyKGZPm8v5AIh1wZSQD4NYKKnCoUszjSwUArPmIS4BkTM1aRmL8nx/Aluxt+OyNVarjEFle646t0D25C3K5tULAcahSrE3naPRI6cIlQDK0YQ8NRLynF+b+4k2cPXlOdRwiy3N7U7B5zVb2McA4VOmAx+dCSc4OnDx6SnUUogax2Wx44uUJOHeqHK9PfVt1HCLLc3sdqK2VKPhkveoolsKhSgfSRzshpUTOEn5US8bVtX8sfJOGY9mc5diWv1N1HCJL6+XshubRzZCbxQcsB5JmQ5UQwi6EKBJCLNXqmFYR168z2ndtizV6XwIcNKjuRfVixU489Nu70aJdc7z02KuoqalRHcf/2IkbYsVOqGKz2eDMSEb+x0WoqQ5gFy3eCS0/qXoCQImGx7MMIQQ8PieKVmxCxbkLquOQdizXiYhm4fjJXx7EjsLdyHp1heo4pD+W64RKaV4Hzp0qx5a121VHsQxNhiohRAwAL4C5WhzPijw+J6ouVqHgUx2uf1+58li1qu5l8SuR+rByJwbfk46kwX3x2i//jVOlZ1TH8Q924oZZuROqOIYlwh5kD8zu6uwEAO0+qZoO4GkA192kRggxUQhRIIQoKCsr0+i05tHX0wtRrSO5u7p5WLYTQghMnvkwLpyvxLxnFqiOQ/ph2U6oEtEsHP0HxnNrhQAKauwBhBCZAEqllIVCiEHX+3NSyjkA5gBAamoq987/FnuQHWmZqVi9MBfVVdUICm70/2u0s3Jl3f+8ctVx5We6JnYCiI3vhDt/mon3XlyE4Q8PQb/03qojaYuduCHshDrujBT846k3cHRvKdrFtfHfidgJANp8UpUOYJQQYi+AdwAMEUK8pcFxLcfjc6L8TAWfLm587ASA+5+7E9ExrTBz0tzA3ihLesROKOLOdAAAH7AcII0eqqSUz0opY6SUcQDuAfCFlPL+RiezoJTb+iO0SYh+lwBXrrTs1ceNYCfqNGnaBI9OH4vdG/dh0exPVMfxD3aiXtgJdWJ6tEdMz/bIC9TWChbvBPep0pGw8FCk3p6I7EX5fLo4mcJNP3DBOTwJb/z6XZw4ws1tiVRwZ6Rg/ZebcaG8UnUU09N0qJJSrpRSZmp5TKvx+Fw4fugkthfsUh2FNGD1TgghMGnGOFRdqsY/f/6G6jikA1bvhAruTAeqLlahaHmx6iimx0+qdCYt0wGb3abfJUCiG9Sxe3vc/bQPX769BkVf8C91okDrd1NvhEc24bcAA4BDlc40axWJhJv7cKgiU7nnmdFo16UNZk6eh6pLVarjEFlKcEgwHLcnIjdrHW8t8TMOVTrk8Tmxd/MBHNp5RHUUIk2ENgnF5BnjcGDrIXw4PUt1HCLLSfM6cOLwKews2qM6iqlxqNIhj88JAMheVKA4CZF23F4HPD4n3vrt+yg9cFx1HCJLcY5IhhACucv4gGV/4lClQ+3i2qBrYiyy9f6AZaIb9Nj0sZBS4pWfzlcdhchSWrSJQi9Xd95X5WccqnQq3efCluxt5n12GllS29ho3Df1Tqz+MBf5enzOJZGJpXkd2Ja/C6eOnVYdxbQ4VOmUZ7QTtbUSOUu4BEjm8sOnRiKmZ3vMmjwXlyovqY5DZBlubwqklMj7uEh1FNPiUKVT3RLj0DY2mt8CJNMJCQ3GlFnjcXjXMbz7wiLVcYgso1tSHFp1aMFH1vgRhyqdEkLA43Oi8PONuHD+guo4RJpKubU/Bv5oAN7500Ic2X1MdRwiSxBCIM3rwLrPN3JrEz/hUKVjHp8TVRerUPDpBtVRiDT3yF8fgj3IjtlPvMa9c4gCxOVNQcW5Cyj+eqvqKKbEoUrHEm7ug8gWEchezCVAMp/WHVvhwf/9EXKXreMyN1GAJA9NQHBoMO/X9RMOVTpmD7IjbWQqcpcWorqqWnUcIs2NnjICcf064eUnX0dlxUXVcYhMr0lEGJKG9EPuskJ+QuwHHKp0zuNz4typchR/XaI6CpHmgoKD8PjsCSjdfxz/nvaB6jhEluDOSMHhXcdwcPth1VFMh0OVzjmGJSIkLBjZH3F5hMwp4eY+uO3BgXj/L4txYNsh1XGITM/tTQEA5Czl7upa41Clc00iwuAYlojsxfn8qJZMa8Kf70doeChmTZnHf8+J/KxdXBvE9euEvCxuraA1DlUG4PG5ULr/OB+ESabVom1zjP39vVi3vBhfvb9WdRwi00vzOlD89VaUnylXHcVUOFQZQFpmCmw2gTUf8VmAZF6Zj9yGHild8MrP5qPiHPdmI/IntzcFNdU1KPx8o+oopsKhygCaR0ehb3pvrF3Mr8CSedntdkyZPQEnj5zGm8+/rzoOkan1SeuJyJZNkcMHLGuq0UOVECJMCJEnhNgghNgshHhei2D0TR6fE7s37rPW7tODBtW9DIadaLg+7h4Y8fAQfPjSMuzZtF91HP1hJ0gj9iA7XCOSkZ9VhJqaGtVxGk5nndDik6qLAIZIKRMBJAEYLoRI0+C4dJX00S4A4CaJxsBONMLDfxyDps0jMHPSXN60bh7shA65MlJwuuwstuXvUh3FNBo9VMk65y//GHz5xb8JNda+a1t0SeiMNYsscF/VlSuPVavqXjq7Evk+7ETjNGsViYf/OAbFX5dg+ZtfqY6jD+wE+UHq7Ymw2W3INeIDlnXaCU3uqRJC2IUQ6wGUAvhcSpl7jT8zUQhRIIQoKCsr0+K0luPxObF59VacOX5WdRT6HuxE4wwfNxh90npgztNv4vxpfjvJDNgJ/WnWMhJ9Pb14X5WGNBmqpJQ1UsokADEAXEKIftf4M3OklKlSytTo6GgtTms56aNdqK2VyDHiVcWNWLmy7jVwYN3rys8Gwk40js1mw+OzJ+Ds8bN4/Vdvq46jHjtBfuL2OrB7wz6UHTyhOsqN0WknNP32n5TyNICVAIZreVyq0z25C6I7teLWCgbCTjRc9+QuGPno7Vj6j8+wY91u1XFII+yEvlzZXT13GXdX14IW3/6LFkI0v/zPTQDcCmBrY49L/00IAc8oJ9Z9vtEaD5/VyZXHjWIntPPj392DZq2bYcZjr6K2tlZ1HPXYCdJYbHwM2nVpg1yj7q6us05o8UlVewBfCiE2AshH3Vr5Ug2OS9fgGe3CxQuXUPjZBtVR6PrYCY00bR6BiS8+gK15O/HJvC9Ux6GGYyd0SggBd0YKipYX4+IFC1ys+5kW3/7bKKVMllL2l1L2k1L+VotgdG39b+mDyBYR1vgWoEGxE9q69f5bkHBLH8x9dgG/pGFQ7IS+uTMduHjhEtZ/uVl1FMPjjuoGExQcBJc3BblL16Gm2sAbthHVkxACU2aNR/mZCsx79t+q4xCZTuLAeISFh/K+Kg1wqDKgdJ8LZ0+cw6Y1vCWBrKFLv8644wkvPp63AltytquOQ2QqIWEhSLmtP3KXFXLD3UbiUGVAqbcnIjg0GGsWcgmQrOOB39yF1h1bYsZjr/JTWiKNub0OlO4/jr18PFSjcKgyoCZNmyDl1gSsXZzPqwqyjPDIJnjkrw9h1/q9WPLKZ6rjEJmKKyMZALdWaCwOVQbl8blwdG8Zdm/cpzoKUcDcctcApNyagNefexsnj55SHYfINFp3aIkeKV24u3ojcagyqAEjHRBCcAmQLOXKTetVlVV49RdvqY5DZCqujBSUrN3Ob9k2Aocqg2rRtjniPT2RvThfdRSigIrp2QE/fGoklr/5FTZ+tUV1HCLTSMt0oLZWouBT7oPYUByqDCzd58Ku9XtxbB8fPErWct/UO9E2NhozJ81FdVW16jhEptAztRuat4niEmAjcKgysAE+JwAgexE/rSJrCQsPxWPTx2Lv5gNY+FKW6jhEpmCz2eDKSEbBJ+v5DdsG4lBlYDE92iOubydkc3d1sqABo1Lh9qbgX8+/h7KDJ1THITKFNK8D50+XY3P2NtVRDIlDlcF5fE5s/KoEZ0+cUx2FKKCEEJj00jjU1tTiH0+9oToOkSmk3NYfQcF25CwpUB3FkDhUGZzH50RtTS33FiFLat+1Le599g589f5aFH7Om2uJGiuiWTj6D4xHbhb/O6UhOFQZXA9HV7Tu2JIPWCbL+tHTPnTo3g4zJ8/DpYtVquMQGZ47w4H9JYdwZPcx1VEMh0OVwdlsNgwY5UThpxtw8cJF1XGIAi4kNBiTZz6MQzuO4P2/LFYdh8jw3JkpALi7ekNwqDKB9NFOVFZcxLrlxaqjECnhvD0JN9/pxtt/+BBH95aqjkNkaB27t0enXh24tUIDcKgygf4D4xERFc7d1cnSHvnbjyFsAi8/+brqKESG5/Y6sHHlZlw4f0F1FEPhUGUCwSHBcHtTkLO0ADU13FuErKlNp9a4/7m7sHZxAXKW8gqbqDHSMh2oulTNFZAbxKHKJDyjnDhz/By2ZG9XHYVImTuezEDnPh0x+4nXeI8hUSP0Te+FiKhwXqDcoEYPVUKITkKIL4UQJUKIzUKIJ7QIRjcmdXgSgkOCsGZhruoolsdOqBMcEozHZ0/A0T2lePuPC1XHocvYCeMJCg5C6u2JyMtah9raWtVxDEOLT6qqATwlpewDIA3AJCFEvAbHpRsQ0SwcSUMTkL24AFJK1XG0MWhQ3ct42AmFEgf1xZD7bsJ7LyzCwR1HVMfRFjtBAeTOcODk0dPYWbRHdZTr01knGj1USSmPSCnXXf7ncwBKAHRs7HHpxqX7nDiy+xj2bj6gOoqlsRPqTXzxQQSHBWP24/PMc5FhYOyEMTlHJEEIgdyl3FqhvjS9p0oIEQcgGQDXoBQYMCoVQgjjfwvwypXHqlV1L51didwIdkKNVu1b4Me/vQcFn27A6g9N8H96doIUaB4dhd7u7vrcWkGnndBsqBJCNAXwAYAnpZRnr/GfTxRCFAghCsrKyrQ6LV2lZbsW6JPWA9mL81VHIbATqo167HZ0TYzFKz+dz6+F6wQ7YTxurwPbC3bh5NFTqqMYgiZDlRAiGHVFWSCl/PBaf0ZKOUdKmSqlTI2OjtbitHQNHp8LOwp3o3S/gf9CWrmy7jVwYN3rys8Gwk6oZw+y4/HZE1B28ATe+u1/VMdpHHaCFEnLdAAA8rKKFCf5Fp12Qotv/wkA8wCUSCn/1vhI1BgeXyoAIHsxnzCuCjuhH309vXD7jwfjg+nLeK+hQuyEcXXtH4vomFb6XALUIS0+qUoH8ACAIUKI9ZdfGRoclxqgU6+O6NS7I9Z8ZPD7qgDdXHk0ADuhI+P/PAbhkWGYOXmu8W9aZycowIQQcHtTsO7zjfp8YLnOOqHFt/9WSymFlLK/lDLp8itLi3DUMOk+Jzau2oJzp86rjmJJ7IS+NI+Owrg/jMHGVVvwxb9Xq45jSeyEsbm9Dlw4X4nir7aojqJ73FHdhDyjXaitqdXfGjiRIhkThqKXsxv++fM3UH6mXHUcIkNJGtIPIWHByF3GrRW+D4cqE+rl7IaW7VtgzSITLAESacBms2HK7Ak4XXoW83/9ruo4RIYSFh6KpCH9kLus0PhL6H7GocqEbDYbPKNSkf9xES5VXlIdh0gXeqV2Q+ZPbsPi2Z9g53od7xBNpEPuDAcO7zqGA9sOq46iaxyqTMoz2oXK8osoWsEnjBNdMXbavWjWKhIzJ83l88yIbkBaZgoAcAnwe3CoMqnEQX0RHtkEaz7iRqBEV0S2aIrxf74fW9Zux2fzV6qOQ2QYbTpHo0tCZ+Rya4XvxKHKpEJCg+HKSMbaJQWoqalRHYdIN257cCD6pvfC3GfewtmT51THITIMt9eBTau34vxpftnjejhUmZjH58Lp0jMoydmhOgqRbthsNjw+ewLOnSrHa798W3UcIsNIy3SgproGBZ+uVx1FtzhUmZhrRBKCgu3INsNGoEQa6to/FqMnj0DWq8uxNY8XHUT10dvdHc1aRXJ39e/AocrEIqIikDSkH9YsyufXYIm+5cHnf4QW7ZpjxqS5XCInqge73Q7niCTkf7yenbkODlUm5/G5cHjnUewvOag6CpGuRDQLx0/+8iB2FO5G1pzlquMQGUKa14GzJ85ha+5O1VF0iUOVyQ0YVfeA5dULuQRI9G2D70lH0uC+eG3q2zhVekZ1HCLdS709CTa7DTlLuQR4LRyqTK51h5bo7eqOtYu5tQLRtwkhMHnWeFSWV2LuM2+pjkOke02bR6DfTb2Rl8X9qq6FQ5UFeHwubMvfhbKDJ1RHIdKd2D4x+OHPRuKz+SuxaXWJ6jhEupfmdWD3xn0oPXBcdRTd4VBlAZ7RTgDA2sUFipMQ6dN9v7oT0Z1a1d20Xs0bcIm+i8t7eXd1LgH+Fw5VFtC5d0fE9GyPbC4BEl1Tk4gwPPr3sdhTvB8fzfxYdRwiXevcuyPad22LXC4B/hcOVRYghIDH58L6LzZxJ1yi67jpBy44RyTjjd+8i+OHT6qOQ6RbQgi4vSkoWlGMyoqLquPoCocqi/D4nKipruHNhUTXIYTA5BnjUF1Vg3/+/F+q4xDpWlqmA5cqq7D+i02qo+gKhyqL6O3ujhZto7gESPQdOnRrh3t+MRor31mDoi+KVcch0q2EW+IRFhHKByx/iyZDlRDiNSFEqRCCI6tO2e12DBiZirysIly6WKU6jumxE8Z19y98aN+1LWZOnoeqS+yKVtgJcwkJDYZjWCJys9bxiR1X0eqTqvkAhmt0LMNaULwAcdPjYHvehrjpcVhQvEBX5/KMduHC+Up+XBsY88FO6L4T1xLaJBSTZozDga2H8MHfl2mc0tLmw+KdCGQfAnE+d0YKyg6cwJ7i/Zoe18g0GaqklF8BsPSdnQuKF2DikonYd2YfJCT2ndmHiUsm+qU0DT1X8pB+aNI0jA9YDgB2whiduB53RgrSRzux4Hf/Qen+Mo3TWpPVOxHIPgTqfK6My1srLOO9ulfwniqNTF0xFRVVFd/4XUVVBaaumKqbc4WEhcA5IhlrlxSgtrZW81xEVzNCJ77Lo38fCwB4+afzGxONCEBg+xCo87Vq3wI9HF2Rs5R7IF4RsKFKCDFRCFEghCgoKzPfld/+M9f++PN6v1d1rnSfEyePnsbWPD4MUzV2Qt/nahsbjfum3ok1C/OQ93FRg49D9WfmTgSyD4E8X5rXgZKcHThz/KymxzWqgA1VUso5UspUKWVqdHR0oE4bMJ2jOt/Q71Wdy5WRAnuQnUuAOsBO6P9cP3wqE516dcDsx+fhUuWlRh2Lvp+ZOxHIPgTyfO5MB6SUyMvihQfA5T/NTBs6DeHB4d/4XXhwOKYNnaarczVtHoHEwX2RvYhbK5B/GaUT3yU4JBiTZ43H4V3H8O6fFzXqWGRtgexDIM/XI6ULWrZrjtwsbq0AaLelwtsA1gLoJYQ4KIR4WIvjGsmYhDGYM3IOYqNiISAQGxWLOSPnYEzCGN2dK93nwoFth7F/6yHNs1EddsJYnfguKUMTMOhuD97+00Ic3nVUg7TWZPVOBLIPgTyfzWaDa0QyCj7dgOqqak2PbURCxf4SqampsqCAN7apUnbwBO7r/Age/sN9uOeZH6iOo5wQolBKmaoyAzuhb8cPn8S43k+g3819MG3psxBCqI7kV+wE3YjVC3Px/J1/wYsrfoOkwf1Ux/GL+naCy38WFB3TCj1Tu3F3daJ6at2hJR56/m7kf1zEpXOib0m5tT+CQ4K4tQI4VFmWx+dESc4OnDhySnUUIkMYPWUEuiR0xuwnXsOF8krVcYh0IzyyCRIGxiOXz5blUGVV6aNdAMCrbqJ6sgfZMWXWeJQdOIF/T/tQdRwiXUnzOnBg6yEc2nlEdRSlOFRZVGx8DDp0b4e1XAIkqreEm/vgtgcH4j9/XcwvehBdxe3l7uoAhyrLEkIg3edE0YpilJ+t+P7/BSICAEx44QGERYRh1pR5fJAs0WUdurVDp94dLb8EyKHKwjw+J6qralDwyXrVUYgMo0WbKIz9/b0oWlGMVe9lq45DpBvujBRsXLkZFecuqI6iDIcqC+szoCeaRzfDau6uTnRDvD+5FT0cXfGPp96w9H+BEF0tLdOB6qoarFu+UXUUZThUWZjdbkfayFTkZa1D1aUq1XGIDMNut+Px2eNx8shp/Os376qOQ6QLfdN7ISIqHLlLrbu7Oocqi0sf7ULF2QvYsHKL6ihEhtLb1QMZ44di4cyPsad4n+o4RMoFBQfBOTwJuVnrUFtbqzqOEhyqLC55aD+ERYTyActEDTDuD/ehafMIzJg0lzetEwFwex04dewMdqzbozqKEhyqLC60SSicw5OQvTjfslcWRA3VrFUkxv9pDDat3orP/7VKdRwi5ZzDk2CzCeQsseYjhjhUEQaMcuLE4VPYXrBLdRQiw7l97GDED+iJV59+E+dOnVcdh0ipqNbN0GdAT8turcChiuD2psBmt2HNR9wIlOhG2Ww2TJk9HmdPnMPrv3pHdRwi5dwZDuwo3G3Jx6BxqCI0axmJ/gPjsYb3VRE1SPekLhj12HAs/cdn2F7IT3zJ2tIyrbu7OocqAgCk+1w4sPUQDm4/rDoKkSH9+Hd3o3mbZpg5aS7vTyRLi+vXGdGdWiEvy3pbK3CoIgCAx5cKAFwCJGqgiKgITHzxQWzN24mP565QHYdIGSEE0rwOFH6+EZcuWmsPRA5VBABo0zka3ZO7IHsRlwCJGmromJvRf2A85j27AKfLzqiOQ6SMO9OByvKL2LBys+ooAcWhiv4fj8+JkpwdOHnUejcXEmlBCIEps8aj4lwl5j2zQHUcImWSBvdFaJMQy+2urslQJYQYLoTYJoTYKYR4RotjUuClj3ZBSomcJdYqgT+wE9YV17cT7nzSi09e/xJb1m5THUc32AlrCW0SiuShCchdVmipjXEbPVQJIewAZgMYASAewL1CiPjGHteIFhQvQNz0ONietyFuehwWFBvrSrVLQme069IGa/SyBDhoUN3LYNiJ/8/onWio+3/9Q0THtMKMSXNRU12j3YHZCUOzWh/cXgeO7i3D/pKD/juJzjqhxSdVLgA7pZS7pZSXALwDwKfBcQ1lQfECTFwyEfvO7IOExL4z+zBxyURDlUYIgXSfE0XLi1Fx7oLqOEbGTsAcnWioJk2b4JG/PYRd6/diySufqY6jB5bvhBX74MpIBmCtrRW0GKo6Ajhw1c8HL//OUqaumIqKqopv/K6iqgJTV0xVlKhhPKNdqLpUjfxP1qsLceXKY9WqupfOrkTqgZ2AeTrRUDffmQbHsES8/tzbjb9PkZ0wPCv2oU2n1uiaGIucZX64pUSnndBiqBLX+N1/LaAKISYKIQqEEAVlZWUanFZf9p/Zf0O/16u+6b0Q1ToSaxdza4VGYCdgnk40lBACk2eMQ1VlFeb8z5uq46hm+U5YtQ9pXgc2r9lmmUc4aTFUHQTQ6aqfYwD81w6SUso5UspUKWVqdHS0BqfVl85RnW/o93plt9uRlpmKnKWFqK6qVhNi5cq618CBda8rPxsHOwHzdKIxYnp2wF0/H4UVC75u3FfL2QnDs2of3N4U1NbUouDTDdoeWKed0GKoygfQQwjRRQicUGw7AAAIcklEQVQRAuAeAIs1OK6hTBs6DeHB4d/4XXhwOKYNnaYoUcN5fE6Un6nAxlVbVEcxKnYC5upEY9z7yzvQLi4aMyfPVXehop7lO2HVPvRydUdU60jk+mMJUIcaPVRJKasBTAbwKYASAO9JKa212xeAMQljMGfkHMRGxUJAIDYqFnNGzsGYhDGqo92wlNv6Iyw8FNmLFC8B6uTK40axE3XM1InGCAsPxaPTx2LfloP4cPqyxh2MnTAsq/bBbrfDOSIZeR8XoaZGw2/CXqGzTggV+0ekpqbKgoKCgJ+X6u9/73gB2wt2Y8G+VyDEtW6HMA8hRKGUMlVlBnbC/J4b9Ses/3ITXit5CdExrVTH+U7sBGlp1XvZ+P09f8ffv/ot+t3UR3WcBqlvJ7ijOl2Tx+dC2cET2LFut+ooRKbw2EtjUVtTi1d+Nl91FKKAcgxLhD3IbomtFThU0TWlZTpgswmsWaiTjUCJDK59l7a475d34uv/5KDgM41v2iXSsabNI5Bwc2/kZnGoIotq1ioSCbfEI5tbKxBp5q7/GYWOPdpj1pR5uHSxSnUcooBxZTiwp3g/ju0z11YZ38ahiq7L43Ni76YDOLzrqOooRKYQEhqMyTMfxqEdR/D+i5b68htZXFpmCgAgz+SfVnGoouvy+JwAgDUf8dMqIq2kDkvELXcNwL//8AGO7DmmOg5RQMT07IAO3dr6Z3d1HeFQRdfVLq4NuiXFcXd1Io098teHYLPb8PKTr6uOQhQQQgi4vQ6s/2ITKisuqo7jNxyq6Dt5RjmxafVWnCo9ozoKkWlEx7TCA7++CzlLCrF2CbcNIGtIy3TgUmUV1n+xSXUUv+FQRd/J43NCSokc/sVPpKk7nvQiNj4GLz/xmqmv3ImuSLilD5o0DUPOUvMuAXKoou/ULSkObWOj+S1AIo0FBQdhyuzxOLq3DO/8caHqOER+FxwSDMewROQuK4SKjccDgUMVfSchBDw+Jwo/24gL5y+ojkNkKokD+2Lo/TfjvRcX4eCOI6rjEPmdOyMFxw+dxK4Ne1VH8QsOVfS90ke7UHWxSvunjBMRJr7wAILDgjFryjzTXr0TXeHKSAYA5C4159YKHKroe/W7qTciWzblEiCRH7Rs1wJjf3cvCj/bgK8/yFEdh8ivWrZrgV7ObsjNMud9VRyq6HvZg+xIy3Qgd2khqquqVcchMp2Rjw5Dt6Q4vPLT+VxmJ9Nzex3YmrsTp8vM961yDlVULx6fE+dOlWPT6q2qoxCZjj3Ijsdnj8fxQyfx5vPvq45D5FdubwqklMjLKlIdRXMcqqheHMMSERIWjDUf8QHLRP4QP6AXho8bgg9fysLezQdUxyHym+7JXdCyfQtTPmCZQxXVS5OIMDiGJSJ7UT5vpiXyk/F/GoPwyDDMmPQqe0amZbPZ4M5IQcGn6013SwmHKqo3j8+F0v3HsbNoj+ooRKYU1boZxv1hDIq/KsGKBV+rjkPkN2mZDlScvYDir0tUR9EUhyqqt7TMFNhsAtmL+C1AIn8ZMX4Ieru6Y87//AvlZ8pVxyHyi+Sh/RAcEoTcZeZaAuRQRfXWPDoKfdN7c6gi8iO73Y4ps8fjdOlZzH/uXdVxiPyiSdMmSBzcF7nLzLW1QqOGKiHEXUKIzUKIWiFEqlahSL88Pid2b9yHI3uOqY6iS+wEaaGnoxsyHxmGxS9/YvjldnaCrsed4cDB7UdM9TSBxn5StQnAHQC+0iALGYDH5wQArF3EByxfBztBmhj7+3vQrFUkZkx6FbW1tarjNAY7Qdfk9qYAAPJMtATYqKFKSlkipdymVRjSvw7d2iHe0wvlZytUR9EldoK0EtmiKSa88ABOHjmNsgMnVMdpMHaCrqd917aIH9ATF8orVUfRTFCgTiSEmAhg4uUfzwshAlmy1gCOB/B8gaTmva0BHvxNQM4UiPcX6+fjXxM74Teme28L4l65+kd2wj9M9+/NVfT93rKB+3/VqCPophPfO1QJIZYDaHeN/2iqlHJRfdNIKecAmFPfP68lIUSBlNKUa/lmfm+APt8fO6FvZn5vgD7fHzuhb2Z+b4C+3t/3DlVSylsDEYTIKNgJom9iJ4jqcEsFIiIiIg00dkuFHwghDgIYAGCZEOJTbWJpTsnHyQFi5vcGGOz9sRO6YOb3Bhjs/bETumDm9wbo6P0JPl+KiIiIqPG4/EdERESkAQ5VRERERBow9VAlhBguhNgmhNgphHhGdR4tCSE6CSG+FEKUXH4ExBOqM2lNCGEXQhQJIZaqzmIW7ISxsRPaYyeMTW+dMO1QJYSwA5gNYASAeAD3CiHi1abSVDWAp6SUfQCkAZhksvcHAE8AKFEdwizYCVNgJzTETpiCrjph2qEKgAvATinlbinlJQDvAPApzqQZKeURKeW6y/98DnX/UnVUm0o7QogYAF4Ac1VnMRF2wsDYCb9gJwxMj50w81DVEcCBq34+CBP9y3Q1IUQcgGQAuWqTaGo6gKcBGPpJsjrDThgbO6E9dsLYdNcJMw9V4hq/M93+EUKIpgA+APCklPKs6jxaEEJkAiiVUhaqzmIy7IRBsRN+w04YlF47Yeah6iCATlf9HAPgsKIsfiGECEZdURZIKT9UnUdD6QBGCSH2ou7j+CFCiLfURjIFdsK42An/YCeMS5edMO3mn0KIIADbAQwFcAhAPoD7pJSblQbTiBBCAHgDwEkp5ZOq8/iLEGIQgJ9LKTNVZzE6dsIc2AntsBPmoKdOmPaTKillNYDJAD5F3c1575mlKJelA3gAddP5+suvDNWhSL/YCaJvYidIa6b9pIqIiIgokEz7SRURERFRIHGoIiIiItIAhyoiIiIiDXCoIiIiItIAhyoiIiIiDXCoIiIiItIAhyoiIiIiDfwfdb7+PTiE/HMAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"import matplotlib.pyplot as plt\n",
"x_ = np.arange(-1,5,0.1)\n",
"y_ = np.arange(-1,5,0.1)\n",
"x_, y_ = np.meshgrid(x_, y_)\n",
"plt.figure(figsize=(10, 10)) \n",
"plt.subplot(3,3,1)\n",
"plt.scatter(posindex[:,0], posindex[:,1], c='red', alpha=1, marker='+', label='pickup') \n",
"plt.scatter(negindex[:,0], negindex[:,1], c='green', alpha=1, marker='o', label='pickup') \n",
"f = -5.00 + 1.81 * x_ + 0.55 * y_\n",
"plt.contour(x_, y_, f,0)\n",
"plt.subplot(3,3,2)\n",
"plt.scatter(posindex[:,0], posindex[:,1], c='red', alpha=1, marker='+', label='pickup') \n",
"plt.scatter(negindex[:,0], negindex[:,1], c='green', alpha=1, marker='o', label='pickup') \n",
"f = -5.30 + 1.61 * x_ + 0.95 * y_\n",
"plt.contour(x_, y_, f,0)\n",
"plt.subplot(3,3,3)\n",
"plt.scatter(posindex[:,0], posindex[:,1], c='red', alpha=1, marker='+', label='pickup') \n",
"plt.scatter(negindex[:,0], negindex[:,1], c='green', alpha=1, marker='o', label='pickup') \n",
"f = -6.00 + 1.91 * x_ + 0.55 * y_\n",
"plt.contour(x_, y_, f,0)\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"可以发现不同的参数方程都可以确定一个分割方程来区分数据,但是无法确定最好的分割函数为哪一个。"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"---\n",
"\n",
">### 7.1.2 于是,SVM出现了!关于SVM的推导\n",
"两个基本概念 \n",
"\n",
">函数间隔\n",
">>首先,当给出参数方程$(w,b)$的时候,任意样本点$x_i$到分割面的函数间隔被定义为$$\\hat \\gamma_i = y_i(wx_i+b)$$\n",
"其中,$y_i \\in \\{1,-1\\}$ \n",
"对整个训练数据集$T$而言,我们的目的是找到最小的$\\hat \\gamma $,即$$\\hat \\gamma = \\mathop \\min_{i=1,...,N} \\hat \\gamma_i$$\n",
"所以这里可以一定程度上知晓,$T$数据中一定存在起决定性作用的样本$x_i$,其可以使$\\hat \\gamma $的值尽可能得小。 \n",
"\n",
">几何间隔 \n",
">>某个点到分割面的距离为\n",
"$$\\gamma_i = \\frac{w}{||w||}x_i + \\frac{b}{||w||}$$\n",
"因为$y_i \\in \\{1,-1\\}$,所以,若点$x_i$被正确分类,则有点到分割面的距离为$$\\gamma_i = y_i (\\frac{w}{||w||}x_i + \\frac{b}{||w||})$$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"为了更直观了解何为“几何间隔”,这里定性地绘制两幅图,左边的图中,几何间隔较大,右边的图,集合间隔较小。"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"fig1. 点(2,1)到分割面几何间隔 γ1 = 0.8703913642249845\n",
"\n",
"fig2. 点(2,1)到分割面几何间隔 γ2 = 0.6044768974731611\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAeYAAADxCAYAAAAeNxRYAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAIABJREFUeJzs3XdU1EfXB/Dv7LJ0BAREBARRQPou7GLv4i622I0dTGJ98lhioompGhMTjSVvokajYMFuNBqNWLErRUCKYgVFUVER6fX3/oH4pBFFZofdZT7n7DlR8d7xfc8897e/mblDBEEAx3Ecx3GaQVTfA+A4juM47n94YeY4juM4DcILM8dxHMdpEF6YOY7jOE6D8MLMcRzHcRqEF2aO4ziO0yC8MHMcx3GcBuGFmeM4juM0CC/MHMdxHKdB9OojqbW1teDs7FwfqTVK9p1HqCivRNMWTZjlvHstC0amRmhsZ8EkX3lpOe7dfIDGTS1gamHCJKcuiYuLeyQIgk19j6Mm6p7LRXlFyLr5EA7uzaBvKKEe/96NBxCJCZo605+DhXlFuK/GsXPapTZzuV4Ks7OzM2JjY+sjtUb5furPOLwhCrvOhEHfgM3EndZhLirKK/DDhYVM8pWXlWOw9Xh069EB03+ayCSnLiGEZNT3GP6NuudyzsNchLr/F57N3bBg/0cghFCNv/bDCGz9Zg+W/7YAnm3dqMbOeZiLELd34e3cGgt++4hqbE771GYu81fZ9SgwWIbighIkn77CLKdCJcPV2Jt4mp3LJJ+eRA+ynj6IiUwA78vO1ZZlE3OM+XQoYg4mIPrARerxR3w0CI3tLLFyehgqKyupxq4ee/SBeFxQw9g53cULcz3y6+oJib4eYn6PZ5ZToZJCEATEHbrELqdSioe3H+H25UxmOTnd0X+qEo7uzbBy5nqUlZZRjW1sZoS3vx6FK9HXcWTjSaqxAeCN/6jg6N4Mq2aGUx87p7t4Ya5HRqZG8O7kgdjIBGY5XQNcYG5thphIhg8DwTIAQMxBdv9OTndI9CWYtCQEd69lYc/3v1OP32N0J7Ru44q1H0agMK+IauzqsWdezcKvPxykGpvTXbww1zOFSob0lDt4eOcRk3wikQhypRRxkYnUX93VpImjNZw8HRBzkN3DAKdbAoNlaNPHH5vm78ST+zlUY4tEIkxZFoon959i84JdVGMDVWMP7C3Dxnk7kPPgKfX4nO7hhbmeKVRSAEAsw2+TcqUUT7Of4VrcTWY5FSoZkk5eRlFBMbOcnG6Z9N04lBaXYt1HW6jH9mjjiqBxXfDLsv24ez2LevxJ341DSWEp1s2lP3ZO9/DCXM+cPB1g42iFaIbfJuVKPxBCEBuZyCynQiVFWWk5Eo+nMMvJ6RYHt2YY+N/eOLQ+CmmxN6jHf+urUdDT18Pq9zdSj+3obo8B7wYjMuw4rsbRHzunW3hhrmeEECiUUsQfTUJ5WTmTnBY25nANcGH6MODdyQOGxgb8dTZXJ6M+Hgxzm0ZYMT2M+i5/KztLjJw7GGd/jUHcYfoPraM/GQJzazO1jJ3TLbwwawBFsAyFz4qQeu4qu5wqKa6cv4q8nHwm+fQNJJB29+YbwLg6MTE3wfgFI5B6Ng3Ht5ymHn/Q9D5o1tIWK2eEU39QNrUwQeiCkUg5k4aobWepxuZ0Cy/MGkDWwwdiPTHjY1MyVFYKuHiY3bEpuVKKrJsPkHmN/hoe13AoQ7vBNcAFa2Zvor5nQd9AgomLxyEjNRP7Vh6iGhsAlKFd0UrWAms+2Mj3W3A14oVZA5g0MoZXB3fEMDw21TqwFcwsTZh+gw18fmyK5UY3TveIRCJMXT4ej+4+wbaFe6jHb9dfDv8gX2z4fDtyHz2jGlssFmPq8lBkZz7G9m9/pRqb0x28MGsIhVKKGwnpeJxF9yhITcR6YvgH+TLtyGXnYgt7VzumZ6g53eTV3h3dR3bE9sV7cT/9IdXYhBBMXhKCwrwirP90G9XYAODd0QNd3+yA7Yt+pT52Tjfwwqwh5NXHphh+a5YrZXiSlYObl9i1Y1aopEg8noKSohJmOTnd9PbC0RCLRVj9/gbqsZ29HNF/shL7Vx9Wy/x455vRIIRgzexN1GNz2o8XZg3R0s8ZjZtaMC3M1WeoWa9tlxSVIukUu/7gnG6ycbDCm3MG4tSuC0g4nkw9/pjPh8LU0lQtu6ibOFpj+AcDcHLHOSSe4EcIuT/jhVlDEEIgV0kRdygRFRUVTHJa2VnCxc+J6dq2X1dP6BtKmD4McLpryHt9Yetkg5UzwlFRTnfeNGpshpB5w5EYlYJTu85TjQ0AQ9/vjybNrbFiehizOc9pB16YNYhCKUVeTgHSoq8zzZlyJg0FzwqZ5DMwMoBvF0+mDwOc7jIwMsCERWNw81IGDqw5Qj1+7wk94eLrhNXvb6S+/GJobIAJ347BzcQM/P7zMaqxOe3GC7MG8Q/yhUhEEM3y1XKwDBXlFYg/msQup0qGO1fuIuvWA2Y5Od3VaXBb+HX1Qvin26ifyxeLxZiyLBQPMrKxY/E+qrEBoPPQdvDp7IGwj7cw6ynAaT5emDVIo8ZmaN3Glek6s1d7dxibGTE9wvSiPzjDlqCc7iKEYPLSEOTn5GPD59upx/fr6oVOg9tg2zd7kJ35mGpsQgimLAtF3hP1jJ3TTrwwaxi5UoqrsTfxNDuXST49iR5kPX0QfTCe2bEpB7dmaOpsw/QBhNNtLf2c0fudnti7IhIZqXeox3/n2zGoqKjEz3Po76JuJW2B3m/3UNvYOe3DC7OGCQyWQRDYduRSKKXIvvMYGamZTPIRQqBQyRB/NIlfHs9REzL/TRibGWHFjHDqD5l2LWwxbFZ/HNt8Gsln6J8oCPnyTRiZGmLlzPW8jzbHC7OmcQ1wgbm1GdMLJhT1cYZaJUVRfjGST/NjUxwd5taNMPbzYbh4+BLO7YulHn/4nAGwtm+MFdPDqN9lbmFjjrGfD0PcoUSc/y2OamxO+/DCrGFEIhHkSiniIhOpT/6aNGluAydPB6Y3P8m6e0NPIubtOTmq+k3uBSdPB6yauR6lJXTfxhiZGOKdb0bjWtxNHAqPohobAPpPUcKxtT1WvUd/7Jx24YVZA8mVUjzNfoZrF28xzZl08jKzxvpGpkbw7uTBj01xVOlJ9DB5aQiybj7AL8v2U4/fbURHeLZ3x9qPNlM/Ylg99nvX72P38gNUY3PahRdmDRTQyw8A245cgcEylJWWI/E4uy5ECqUUt5Ju49FdujtduYYtIMgP7frLsXnBLuq95wkhmLo8FLnZzxAxfyfV2EDVnGjbLwARX+5k1jef0zy8MGsgyybmcA1wYfpt0ruTBwyNDZi+zlY8v22K39HM0Tbpu3EoLy3H2o8iqMd2C2iJXuO6Yvf3B5B59R71+BMXj0NZSRnC5m6hHpvTDrwwa6hAlQxXzl9l1nRA30ACaXdvphvAnL0cYW3fmL/O5qhr1rIpBk3vg8PrT+BK9DXq8cd/NQL6hvpY9d566rEdXO0waHpfRIYfR1oMuy6AnObghVlDKYJlqKxke2xKrpTi3o0HyLyWxSQfIQRypRQXD1+i3ueY40bOHYzGTS3w4zT6u6gbN7XEqI8H48L+i2rp1Ddy7iBY2pqr5QINTvNRK8yEEDEhJJ4Q8hutmA1Z68BWMLM0qZdjU2xvm5KiILcQqeeuMsvJvZwuzGdjMyO89fUoXLlwDUcjTlGPP3Bab9i72mHVzHCUl5VTjW3SyBhvfT0Kqeeu4tjm01Rjc5qP5jfmaQAuU4zXoIn1xPAP8kVsZCKzJ+ZmLZvC3tUOsYfYvVr27+kLkVj097Xtrl2rPlx90Yn53HNMZ7grWuLnOREoyi+iGluiL8HkJeNwJ+0efv3hINXYABA0tgvc5C2xZvZG6mNnis/lWqNSmAkhDgD6APiZRjyuilwpw5OsHNxITGeWU6GUIvF4CkqLS5nkM7UwgWc7N96eU4Po0nwWiUSYsnw8nmTlYPNXu6nHD+ztD4VKio3zdiDnId02uiKRCFOXh+LxvRxs+Zr+2DnNResb8zIAHwBg0xGjgZArq45NsbzsQREsQ0lRKRJPpLLLqZLh2sVbyHnw9H9P1ydOVH3403Z90Kn57NnWDT3HdMauJfuQdZPujWaEEExaEoLighKEf0x/F7VnO3f0GNUJO5f8pn23sfG5/NrqXJgJIX0BPBQE4V/7yBFCJhBCYgkhsdnZ2XVN2yBYN2sMFz8npkeYfLt4QmIg4bdNNVCvMp+1cS6/9fUoiCVi/DSL/i7q5q3tMeA/Kvy+9hiux9NvCvT2wlEQi0VY/f5G6rE5zUTjG3MHAP0JIekAtgLoTgj52xUsgiCsFgRBLgiC3MbGhkLahkGhlCLlTBr1LkM1MTQ2gF9XT6ZHmFpKnWFpa1610S0qqurTpUvVp/rXHCsvnc/aOJetmzXGyI8G48yeGFw8Qv+kw+hPh8Lc2kwtu6it7a3w5ocDcfqXC4g/xu7e9Drjc/m11bkwC4LwoSAIDoIgOAN4E8AxQRBG13lkHICqV8sV5RWIP8puQiqUMty5chf30x8yyScSiSBXSRF3KBEVFfzYVH3S5fk8eEYfNG3RBCumh1E/nmdqYYLQL0cg6dRlnNh+lmpsABgysy+aOtuoZeyc5uHnmDWcV3t3GJsZMT3CJK8+NsXydbZShrwn+UiLuVH1G/zpmqNM31AfExePRUZqJvatOkQ9vnJ8N7SUOmP1BxtRXFhCNbaBkQEmLBqL9OQ72L/6CNXYasfncq1RLcyCIEQJgtCXZsyGTk+iB1kPb8QeYndsytG9GWydbJiubQcE+UIkIojj68waQxfnc4cBgZD18MGGz7bh2eM8qrHFYjGmLAtF9p3H2LFoL9XYANBxUBtIu3kh/NOtePaE7tg5zcK/MWsBhUqGh7cf4fblTCb5CCFQqKSIP5qEslI21881sjKDe2Arpg1VuIaHEILJS0NQkFuI8E+3UY/v29kTXYa1w7Zv9+Dhbbob4wghmLIsFAVPC7Dhs+1UY3OahRdmLVB92UP07yx3SstQXFCC5NNX2OVUypAWfZ36NxmO+6MW3s3Rd1Iv7P/pEG4lZVCPP+HbMRAEAWtm/20PbJ218HFCn4m9sG/VIdxKvk09PqcZeGHWAk0creHk6cC0I5eshzf0JGKmR5jkKikEQUDsIf46m1OvcfOGw8TCRC27qJs0t8HwDwYgattZJJ2i3zwtZN5wmDQywsoZ4byPto7ihVlLKFQyJJ1IRVFBMZN8RqZG8O7kwXSd2U3ugkZWZrwLGKd2jRqbYdwXw5FwPAWnd0dTjz/sgzdg42iFH6eto37SoJGVGcZ+MRzxR5NwZg/9sXP1jxdmLaFQSVFWWo7E4ynsciqluJV0G9mZj5nkE4vFCOjli5iDCdRvA+K4v+o7MQjO3o5Y/f4G6i1oDY0NMOHbMbiRkI6Da49RjQ0A/Sb1grOXI36aRX/sXP3jhVlLeHfygKGxAdNvk//ryMV2bfvpw1zcSEhnlpNrmMR6Vbuo7996iJ1L6F+i1WVYe/h08kD4J1uR/7SAamyxnhiTl4aobexc/eKFWUvoG0gg7e7N9NWys3dzWNs3ZtoFTN6rqj+4Ou645bi/knX3QcdBbbDl61/w6C7dN0PVu6hzH+Vh07wdVGMDVTezdRigqBr7vSfU43P1hxdmLSJXSnHvxgPcvZ7FJB8hBHKlFBcPX2LWbcjS1gKuAS58nZljZsK3Y1BRXomfP4ygHruVrAWC3+qOPT8cRIYajjtOXDwOFWUVWKuGsXP1hxdmLRL4/NhUDNNjU1IU5BYi9dxVdjmVUqSeu0r99R/H/RM7F1sMmdkXRzedQuq5NOrxQxeMgKGJAVbNpL+L2s7FFoNn9sORjSeRep7dHOXUixdmLWLnYgt7VzvERLJ7zevf0xcisYj52nZlRaVaLhvguH8y4sOBsGpmiR+nhVHfeGhhY44xnw5FbGQiog9cpBobAEZ+NBCN7Syxcjr9sXP1gxdmLaNQSpF4PIXZTkxTCxN4tnNjurbt0dYNJubGTHt1cw2bkakR3l44Gldjb+DwhhPU4/efqoSjezOsnLmeejc9I1MjvP31KFyJvo4jG09Sjc3VD16YtYwiWIaSolJcOkm/cUGNOVUyXLt4CzkPnjLJJ9YTwz/IFzEH43kDBY6Z7iM7wqOtK9Z+GEH9mlWJvgSTl4bg7rUs7Pn+d6qxAaDH6E5o3aZq7IV5RdTjc2zxwqxlfLt4QmIgYXrb1ItjUww7cgWqZHh8LwfpvO0gx4hIJMLU5eOR8yAXmxf8Qj2+QiVDmz7+2DR/J/WH3Kqxh+LJ/afY8hX9sXNs8cKsZQyNDeDbxZPpEaaWUmdY2pozfZ0tV1Ydm+KvszmW3BWt0CukK35Z9hsyr9E//TDpu3EoLS7Fuo82U4/dOtAVQWO7YNfS35id3ODUgxdmLRSokuHOlbu4n/6QST6RSAS5Uoq4Q5eotxesibW9FVr4NGf6MMBxAPDWVyMhMZDgp1nrqcd2cGuGgf/tjcjwKKTF3qAef/xXIyGWiLH6/Y3UY3Ps8MKsheTPXy2z/DapUMnw7HEersbeZJoz+fQVvmbGMdW4qSVGfTwE5/fFqeXN1KiPB8PcppFaLtCwbtYYo+YOxtlfYxB3mF8Go614YdZCju7N0NTZhukRpoAgXxBCEMv0YUCK8rIKJBxPZpaT4wBg4LTeaNaqKVbNDEd5WTnV2CbmJhi/YARSz6bh+JbTVGMDwKDpfWDnYosV08Ooj51jgxdmLVTdkSv+aBL1oxc1aWRlBvfAVohm+GrZq4M7jEwNmW504zigqgXupO/G4fblu9i7IpJ6fGVoN7gGuGDN7E3Ub4zTN9RX69g59eOFWUspgmUoyi9Gyhn6nYpqzKmUIi36Op49zmOST6IvgayHD2IjE/ixKY65tn0DENDLDxs+346n2blUY1fvAH909wm2LdxDNTYAtOsvh39PH2z8YgdyHz2jHp9TL16YtZS0mzf0JGK2x6aCZRAEgemxKYVKhvvp2biTdo9ZTo4Dqt5MTV4agqL8Yqz/dBv1+F7t3dF9ZEdsX7yX+kbOqrGHojCvSC1j59SLF2YtZWxmBO+OrZkem3KTu6CRlRnTte0Xx6b462yuHjh5OOCNqSocWHMENxLTqcd/e+FoiMUirP6A/i5qZy9H9J+sxP7Vh9Uydk59eGHWYgqVDLeSblO/rq4mYrEYAb18ERuZwKwnb1PnJnBsbc/0AYTj/mjMZ0Nh1tgUP05bR31JxcbBCm/OGYhTO88jMSqFamwAGPvFMJhammLlDPoXaHDqwwuzFlPUx7EppQw5D3JxIyGdYU4pLp1IRXFhCbOcHFfNzNIU4+a9iaSTl3Fyxznq8Ye81xe2Tjb4cdo66termlmaImTecCRGpeDUrvNUY3PqwwuzFnP2bg5r+8ZMv03WR0cuRbAMZSVluHQilVlOjvuj3u/0gIuvE1Z/sBElRXQfEA2MDDBh0RjcSrqNAz8fpRobAHpP6Fk19vfpj51TD16YtVj1samLhy9Rf9KuiaWtBVz9WzDtyOXb2QMGRvp8nZmrN2KxGFOWheLh7UfYsXgf9fidBreFX1cvhH+yFXk5+VRjV4/9QUY2dn73G9XYnHrwwqzlFCopCnILcZnhJelypRSp564i/2kBk3z6hvrw6+bF15m5euXX1QudhrTF1oW78fDOI6qxCSGYsiwU+Tn52PDZdqqxgedjH9xGLWPn6KtzYSaEGBJCogkhiYSQFELIFzQGxr0a/56+EIlFiGb4bTIwWIbKikpcPHKJWU6FUoa717Jw78Z9ZjkbIj6f/93ERWMhCALWzN5EPbaLrxP6TAjC3pWRSE+5Qz3+O9+OQUVFJdZ+GEE9NkcXjW/MJQC6C4LgB0AKQEUIaUshLvcKTC1M4NnOjekRJo+2bjAxN2a8zsx+oxsAoGvXqk/Dwefzv7B1ssHQWf0RtfUMkk/TvxN93LzhMDYzwsoZ9Pto27WwxbBZ/XFs82kkn7lCNbZW0KK5XOfCLFSpXhSRPP/wffkMyZVSXLt4i/odrzUR64nhH+TLtCOXfSs7NGtpy2+bUjM+n19u+OwBsHGwwo/TwqjftmZu3QhjPx+Gi0eScG5fLNXYADB8zgBY2zfGiulhzI48crVHZY2ZECImhCQAeAjgsCAIF2jE5V5NYLAMABAbybAjl1KKR3ef4FbSbWY55UopEo+noLS4VP3Jqp+uT5yo+mjR03Zd8fn874xMDPH2N6NxPf4WIsOiqMfvN7kXnDwd8NN761FaQrcXvpGJId5eOBrX4m4iMuw41dgaSwvnMpXCLAhChSAIUgAOAAIJId5//RlCyARCSCwhJDY7O5tGWu65llJnWNqaIyaSYXvO52eoWb5CDwyWobiwBMmnG+BrOIZeNp/5XAa6vdkBXh3cETZ3Mwpy6W6C1JPoYfLSENy78QC/LNtPNTYAdB/ZEZ7t3bFu7hYUPCukHp+rO6q7sgVBeAogCoDqH/5stSAIckEQ5DY2NjTTNngikQhypRRxhy5Rf7VWE2t7K7Twac722FRXL0j09dhsdIuKqvp06VL1qf51A1LTfOZz+X+7qHMf5WHT/F3U4wcE+aH9GwpsXrALj7NyqMauHvvTh7mImL+TamyNpIVzmcaubBtCiMXz/zYC0BMA/0rDmFwpxbPHebgae5NZToVKhuTTV1CYV8Qkn5GJIXy6eDL9lt7Q8Pn86twCWkIZ2g27vz+AO2l3qcefsGgMykvLsfYj+ruo3eUtoQypGnvmVX5BjKah8Y3ZDsBxQsglADGoWpPip9gZCwjyBSGE7W1TKinKyyqQcCyZXU6lFBmpmXh4m9ErVC14uqaMz+daGP/VSBgY62PVe+upx7ZvZYdB0/vg8PoTuHzhGvX4478aAX1D9YxdI2nRXKaxK/uSIAgyQRB8BUHwFgRhHo2BcbVjbt0I7oGtEHuI3bdJrw7uMDI1ZPo6uz76gzckfD7XjmUTc4z+ZCiiD8TjwoGL1OOPnDsYjZtaqGUXdeOmlhj18WBc2H+RaR8E7uV45y8dolBKceXCdTx7nMckn0RfAlkPH8QcZHdsqrmHA2wcrfixKU5jDHhXBQc3O6yaGY6yUrq7qI3NjPDW16Nw5cI1HI04RTU2AAyc1hv2rlVjLy8rpx6fez28MOsQRbAMgiAg9hC7Y1NypRQPMrJx+wr9NbZ/QghBoEqGi0eSqP+PIMe9Dom+BJOWhCDzahb2/N9B6vF7jumM1oGt8POcCOr7OST6EkxeMg530u7h1x/oj517Pbww6xA3uQvMGpsy3Rz14tgUw1fLcpUURfnFSD3Hrj84x/2bNr39oQiWYdP8Hch5mEs1tkgkwuRloXiSlYMtX++mGhsAAnv7Q6GSYuM8+mPnXg8vzDpELBYjoJcfYiMTmHX1aercBI6t7Zmubct6+ECsJ+a3TXEaZdJ341BSWIqwuVuox/Zs64aeYzpj15J9yLr5gGpsQggmLQlBcUEJwj+mP3au9nhh1jGBKhlyHuTiRkI6s5wKpRSJUakoLmRz16tJI2N4dXDnG8A4jdK8tT0GvBuMg+uO4dpF+scW3/p6FMQSMX6aRX8XdfPW9hjwHxV+X3sM1+NvUY/P1Q4vzDpGrvQDwHbXsiJYhrKSMiRGpbDLqZLh5qUMPLr3hFlOjnuZMZ8Ogbm1GX6cto76hkjrZo0x8qPBOLMnRi03u43+dCgaWZlixXT6F2hwtcMLs46xtLWAq38LpuvMvp09YGCkz3Sd+X8tQdltdOO4lzExN0HogpFIOZOGqG1nqccfPKMP7FxssXJGOCrK6Xb5M7UwQeiXI5B06jJObKc/du7V8cKsg+RKKVLOpiH/Kd0evjXRN9SHXzcvxDB8GHDxdUJjO0vEMuwPznGvQhnaFa1kLbDmg40oKiimGlvfUB8TF49Fesod7Ft1iGpsAFC91R0tpc5Y/cFGZktT3N/xwqyDAoNlqKyoRPzRJGY5FUoZ7l7Lwr0b95nkI4RAUd0fnPI3B46rC7FYjCnLQpGd+RjbvtlDPX77NxSQ9fDBhs+2Ue9ZIBaLMXX5eGTfeYzt3/5KNTb36nhh1kEebd1gYm7MdJ1ZXg8duRTBMuQ/LcCV6OvMcnLcq/Dp5IGub3bAjsV78SCDbvvY6ksoCp4VYf1n26jGBp6PfXh7bF/0K7vWt9yf8MKsg8R6YvgH+SLmYDyzTRwOrnZo1tKW6dq2f08fiERs+4Nz3Kt655vRIIRgzeyN1GM7ezmi36Re+G3VIdxKyqAe/51vRkMQBKyZvYl6bO7leGHWUQqlFI/uPkF68m1mOeVKKRKOJaO0uJRJPjNLU3i0c2O6ts1xr6qJozWGzx6AE9vPIfEE/RMLY78YBhMLE7Xsom7S3AbDPxiAqG1ncelkKtXY3Mvxwqyj5MqqV8vRv7MrWoHBMhQXliD5NLtbAhVKGa7G3uAdiziNNHRWfzRpbo0V08Oo35XeqLEZxn0xHAnHU3B6dzTV2AAw7IM3YONopZaxc/+OF2YdZeNgBWdvR6YduXy7ekGir8f0pprqte04hv3BOe5VGRobYMK3Y3AzMQO//3yMevy+E4Pg7O2I1bPWU39TVT32GwnpiFx3nGps7t/xwqzDAlUyJJ+6jKJ8uo3va2JkYgifLp5M15ld/VvAwqYR05wcVxudh7aDT2cPhH28BXk5+VRji/WqdoDfT8/Gju/2UY0NAF2GtYdPJw+sm7uZ2fFLjhdmnSZXSVFeVoH4Y8nMciqUUmSkZjLbzSkSiRCgZNsfnONqo3oXdd6TfGz8Ygf1+LLuPug4qA22fr0bj+4+phq7euzPHqtn7Nw/44VZh3l3bA0jU0Od78ilUMqQ+ygP1+Lo9yfmOBpaSVug9zs9sXdFJDIuZ1KPP2HRGFRUVOLnORHUY7eStUDwW93x648HmV3v2tDxwqzDJPoSyHr4MD021dzDATaOVog+yG6dOaCXLwgh/FILTqOFzB8OQxMDrJoZTn0+2rWwxZCZfXE04hRSz6VRjQ0AoQtGqG3s3N/xwqzj5Eop7qdnI/PqPSb5CCEIVMkQfyQJ5WXlTHJa2JjDTe7Cj01xGs2kz1XHAAAgAElEQVTCxhxjPx+G2MhEnP8tjnr8ER8OhFUzS6yYHkZ9WcfCxhxjPh2KmIMJuLD/ItXY3N/xwqzjql8txzA8NiVXSVGYV4SUs/Sf3GvMqZTiyvmrePaEbotCjqOp/xQlmnvYY9V761FaUkY1tpGpEd5eOBppMTdweMMJqrEBoP9UJRzdm2HVe+tRVkp37Nyf8cKs45o6N4Fja3umr5ZlPXwg1hMzXdsODJahslJA/BF2/cE5rrb0JHqYtCQE967fx57vD1CP331kR3i0dcXaDyNQ8KyQamyJvgSTloTg7rUs7Pn+d6qxuT/jhbkBUCilSDqZipIiNrfFmDQyhlcHd6YPA+6KVjCzNGGak+Neh0IpRdt+AYj4chee3M+hGlskEmHq8vHIeZCLzQt+oRobqHoAbtPHH5vm70TOg6fU43NVeGFuAOQqKUqLy5AYxa61nkIpxc3EDDy694RJvur+4LEHE/jmFE7jTVw8DqXFpVj70Wbqsd0VrdArpCt+WfYbMq9lUY8/6buqsa9Tw9i5KrwwNwC+nT1gYKSPGIbfJhXBMgCMj02pZHhy/yluJKYzy8lxr8PB1Q6DpvXBofAopMXQvx1t/IKRkBhI8NOs9dRjO7g1w8D/9kZkeBTSYm9Qj8/xwtwgGBgZwLerF9PjRC6+TmhsZ4nYSIbtOZ/3B2e5ts1xr2vkx4NhaWuulksorOwsMXLuYJzfF6eW0wqjPh4Mc5tGahk7xwtzg6FQSnH3Whbu3bjPJB8hBAqlFBcPX0JFOZsG+FZ2lmgpdebHpjitYNLIGOO/GoXUc1dxNOIU9fiDpvdBs5a2WDkjnPrRRRNzE4xfMAKpZ9NwbPNpqrE5CoWZEOJICDlOCLlMCEkhhEyjMTCOrupXyyy/NStUUuTlFOBKNP1XdTXnlCHlTBoKcnlf39fB5zNbvcZ1gZu8JX6es4l6T3t9AwkmfjcOd67cxd4VkVRjA4AytBtcA1yqxl5QTD1+Q0bjG3M5gPcEQfAA0BbAVEKIJ4W4HEX2rZrCzsWW6WUP/kG+EIkI27VtlRQV5RT7g3ftWvVpOPh8ZqhqF3UoHt/LwdaFe6jHb9dPDv8gX2z4fDueZtO9GrV6B/iju0+w7Rv6Y6dOi+ZynQuzIAhZgiBcfP7feQAuA7Cva1yOLkIIFCopEo4lU78eriZmlqbwaOfG9Fu6Zzs3GJsZIYbh1ZO6hM9n9jzbuaPHqE7Y8d0+ZN16QDU2IQRTloagKL8Y6z/dRjU2AHi1d0f3kR2xY/Fe3E9/SD1+Q0V1jZkQ4gxABuACzbgcHQqVDMWFJUg6dZldTqUMV2NvIOch3af1muhJ9CDr6YOYuh6bqn66PnGi6qNFT9u08PnMztsLR0EsFmH1+xupx3bydMQbU1U4sOYIrifcoh7/7YWjIRKJsPr9DdRjU6GFc5laYSaEmALYBWC6IAjP/uHPJxBCYgkhsdnZbK4E5P7Mr5sXJPp6TL/Byp+3BL14+BKznIEqGbIzHyMjlf4tPg3Fv81nPpfps7a3wpsfDsTpXy4g/hj97nVjPhsKU0tTrJxB/xIKGwcrvDlnIE7tuoDEqBSqsRsqKoWZECJB1SSOEAThH9vNCIKwWhAEuSAIchsbGxppuVoyMjGET2cPpuvMrv4tYGHTiOk6s/xFf/A65IyKqvp06VL1qf51A/Cy+cznsnoMmdkXTZ1tsHJGOPWTDGaWpgiZ/yYunUjFqV3nqcYGgCHv9YWtkw1WTA9jdgrjlWnhXKaxK5sAWAvgsiAIS+o+JE6dFCoZMlIz8fA2m286IpEIAUo/xEYmUL/xpiZNHK3h7OWI2EP82FRt8flcfwyMDDBh0VjcSrqN/auPUI/f+50ecPF1wur3N1Jvz1s19jG4eSkDB9bQH3tDQ+MbcwcAYwB0J4QkPP/0phCXU4MXt02xPDallCH3UR6uxd1kllOulCLp5OW6H0HRgqdryvh8rkcdB7WBtJsXwj/dSv2mNLFYjCnLQvEgIxs7Fu+jGhsAOg1uC7+uXgj/dBvycvKpx68zLZrLNHZlnxYEgQiC4CsIgvT5h/61KRwVzT0c0KS5NdMmHAG9fEEIYfswECxDWWk5Eo7zNa/a4PO5fhFCMGVZKAqeFmDDZ9upx/fr6oVOQ9pi68LdeHjnEdXY1WPPz8nHhs/pj70h4Z2/GpjqjlzxR5KY3alqYWMON7kL03Vm746tYWhiwPRhgONoaOHjhD4Te2HfqkO4lXybevyJi8ZCEAT8PGcT9dguvk7o/U5P7F0RifSUO9TjNxS8MDdAcpUUhXlFSD17lV1OpRRXLlyj/nquJvoGEki7eyPmYDzv5ctpnZB5w2HSyEgtu6htnWwwdFZ/HN9yBsmn6R+dDJn/JozNjLByJv2xNxS8MDdAsh4+EOuJme7OVqhkqKwUEH+E/lGQGnMqZbh/6yHuquHqO45Tp0ZWZhj7+XDEH03C2V9jqMcfPnsAbBys8OO0MFRU0N1FbW7dCGM/H4aLhy/h3L5YqrEbCl6YGyCTRsbw6uCOaIavllsHtoKZpQnzXt0A241uHEdL30lBcPJ0wE+zNlDv1mdkYoi3vxmN6/G3EBkWRTU2APSb3Ktq7O+tR2kJmyUzXcILcwOlUMlwMzEDj+49YZJPrCeGf5AvYiLr2JGrFuxcbOHgZsd0bZvjaNGT6GHKslBk3XyAXUv3U4/f7c0O8OrgjrC5m6lf+qIn0cPkpSG4d+MBfln6G9XYDQEvzA1U9bfJ2MhEhjlleJKVgxuJ6cxyypVSJEalUD+3yXEs+Pf0Rfs3FNj81S7qD9GEEExdPh65j/Kwcd5OqrEBICDID+36y7H5q1/wOCuHenxdxgtzA+Xi64TGdpaIY9iEQ658/jDA8NVyYLAMpcVluHSSXX9wjqNp4uKxqCirwNoPI6jHdvV3gTK0G/b83++4k3aXevyJi8eivLQcaz+iP3ZdxgtzA1V9bCruUCKzFnpWdpZoKXVmeobat4sn9A0l/LYpTms1a9kUg2f0xZGNJ5F6nv5JivELRsDAWB8rZ66nHtu+lR0GTe+Dw+tP4PKFa9Tj6ypemBswhUqKvJwCXIm+zi6nUoqUM2nU17RqYmBkAL+uXnydmdNqIz4ahMZ2llg5PYx6a1tLWwuM/mQoYn6Px4UDF6nGBoCRcwejcVMLrFDD2HUVL8wNmH+QL0QiwvyCiYryCsQfS2aXUylF5tUs6nfdchwrxmZGePvrUbgSfR1HN52iHn/Auyo4uNlh1cxw6o2HjM2M8NbXo3DlwjUcjaA/dl3EC3MDZmZpitZt3ZieZ/Zq7w5jMyPm68wA27VtjqOtx+hOaN3GFT/P2YTCvDr2gP8Lib4Ek5aEIPNqFn794SDV2ADQc0xntA5shZ/nRNS9f30DwAtzAxeokuFq7E08zc5lkk9PogdZTx9EM+zIZe9qh6YtmjBd2+Y42kQiEaYsC8WT+0+x5at/vF23Ttr09ociWIaN83Yg5yHd/z0QiUSYvCwUT7JysPmr3VRj6yJemBs4uUoKQRCYHpsKVMmQfecxMlIzmeQjhEChkiH+aBJvdsBpNY82rgga2wW7lv6Gu9fpd7SbvGQcSgpLETZ3C/XYnm3d0HNMZ+xasg9ZN/my0r/hhbmBc/VvAQubRkxfZ8vr4+pJlRTFBSVIOXOFWU6OU4e3vh4FPX09rH5/I/XYju72GPjf3ji47hiuXaR/TetbX42EWCLGT+9voB5bl/DC3MCJRCIEKP0QG5nAbMdkE0drOHs5IjaS3aYzaTcvSPT1+LEpTutZ2Vli5EeDcPbXGMQdpv+ma/Qng2FubYYfp62jvtxkbW+FER8Owpnd0bh4lF3ffG3DCzMHhVKG3Ed5uBZH/wm5JnKlFEknL6OooJhJPiNTI3h38uDrzJxOGDS9D+xcbLFyRjjKy8qpxjYxN0HogpFIOZOG41vPUI0NAENm9kXTFk2wcnoYsx4K2oYXZg4BvXxBCGH+armstByJx1PY5VRKkZ58B9mZj5nl5Dh10DfUx6TvxiEjNRP7Vh6iHl8Z2hWu/i3w8+xN1B+e9Q31MXHxWKSn3MG+VfTHrgt4YeZgYWMON7kL02+T3p08YGhswPQMteL5sSl+2xSnC9r1l8M/yBcbPt+O3EfPqMYWi8WYvDQU2ZmPse2bPVRjA0CHAYGQ9fDBhs+24dljNne0axNemDkAVa+Wr5y/irycfCb59A0kkHb3ZrrpzMnTATYOVkzXtjlOXQghmLwkBIV5RVj/6Tbq8X06eaDdoC7YsXgvHmRkU41NCMHkpSEoyC1EuBrGru14YeYAVDXhqKwUcPHwJWY5FSoZ7t14gMxr9I99/BNCCORKKeIOX6K+Lsdx9cHZyxH9Jyuxf/Vh3LyUQS1uVhYwahSwI3kSBOhhzWz6O8BbeDdH30m9sP+nQ7iVRG/suoAXZg4A4K5oBTNLE0SzbM/5/LYpljulFSopCp8V4fJ53lCf0w1jvxgGU0tTrJgeVudd1OXlwNKlgLs7sGsXMHSYHobMegMntp9D4gn6+0HGzRsOEwsTKmPXJbwwcwAAsZ4Y/kG+iD2YoLYJIgjAlSvAd98B3bsD362whYObHdO1bf+ePhCJRYjmx6Y4HWFmaYqQecORGJWC079cqFMsQoBNm4COHYHkZGDePGDknL5o0twaK6aHoaKC7i7qRo3NMO6L4Ug4noIze6KpxtZmvDBzLyhUMjy5/xQ3EtOpx370CHB1BTw8gFmzgOxswMGh6ltz4vFklBSVUM/5T0zMTeDV3p3p2jbHqVvvd3qihU9z/DRrQ63nUlYWMGkS8OQJIBYDR48C+/cDrVpV/bmhsQEmfDsGNxMz8PvPx6iPve/EIDh7O+Kn99ajtLiUenxtxAsz90L1q+W6XvZw9y6wZg0wYAAweXLV71lZAZ07Az/+CKSnA0lJwIwZVQ8DpcVluHTych1H/+oUKhmux9/Ck/s5zHJynDqJ9cSYsiwUDzKysfO7317p75SXA8uWVb22DgsDTp+u+n0Li6pvzn/UeWg7+HT2QNjHW6hvEK0e+/30bOxc8mpj13W8MHMvWNlZwsXP6bVfLf/wAyCTVX0TnjABSEioKshA1URftw6YMgVwcvrf3/Ht4gmJgYTpzU+K5y1BWfYH5zh1k3bzRqfBbbB14e6XntU/ebJqrs6Y8b/X1v371/zzhBBMWRaK/Jx8bJq3k/LIAVl3H3QYGIgtX/2CR3d5nwFemLk/CVTJkHImDQXPCv/153JygK1bgXfeAaqXndLTATMzYOHCqol+6xbw5Zf/ns/Q2AB+XT2ZrjO3lDqjcVMLpmeoOY6Fd74dg4qKSvw8Z9O//tyyZUBeHrB7d9Vra1fXl8duJW2B4Ld74tcfDyLjMv0LaCYuHvt87BHUY2sbKoWZELKOEPKQEJJMIx5XfxTBMlSUVyD+H/rYZmYC33xT9UraxgYYMaJqYt983slz0aKqJ/HZswEvr7+/Dqsxp0qGO1fuIusWmxtnCCEIUPoh7vAl6ptZtB2fy9rNroUths3qj2ObTyP5Dxe2lJcDy5cDV69W/fqnn4DU1KrlpledpwAQMn84DE0MsHJGOPVNonYtbDFkZl8cjTiFlLNpVGNrG1rfmMMBqCjFalAikiLgvMwZoi9EcF7mjIik+nlarB6H7IgPKgwqsGXzThQVVT1Npz2fI2lpwJw5VU/ac+YAZ88CDx7872m7NhP8j+rj1XKgSoa8J/lIi7nBLKeWCAefy69FU+by8DkDYNzEEJNHzITocxGavjsULp45mD4diHg+JBsbwNi49rEtbMwx9rNhiDuUiAv7L9IdOIARHw6EVTNLrJgexuxSHU1EpTALgnASwBMasRqSiKQITNg3ARm5GRAgICM3AxP2TWA+of84jso8e1y1aIete4bConE5+vYF1q+v+rnOnYE7d4D4+KpX1O3aVe3irCsHt2Zo2qIJ01fL/j19IRIRpmvb2oDP5dejKXMZAH65uQsJnc+D3LGH4dqdePDDDmRm52Ha0hP4/PO6x+8/VQnH1vZYOTOc+v3mRqZGeHvhaFyNvYHDG05Qja1N+BpzPZp7dC4Ky/68lltYVoi5R+fWzzgqxMDKS7h7/30UlTeHsddmREYCn31W9XMSSdXGLtoIIVAopYg/moSyUroTvSaNrMzgHtiKrzNzVGjKXK4ey23P67hm1h3Fmf1A2n8FYUpr7MG4136r9Ud6Ej1MXhqCe9fvY/fyA3UP+BfdR3aER1tXrP0w4qV7XXQVs8JMCJlACIklhMRmZ9Ptu6qtbufertXvq30c4gpg4FhIxvmhPd6FudUC9OoFGBiofwxylRTFBSVIPn3l5T9MiUIlQ1rMDeoXAOg6Ppf/TlPm8oucBMgfPAdt8R5akq2AfhHVsSiUUrTtF4DNC3ZRP3YoEokwdfl45DzIxeYFv1CNrS2YFWZBEFYLgiAXBEFuY2PDKq1Ga27evFa/z2QcrfehrMUlFDTJhX2GU81/iTJZd2/oScTM23MKgoC4Q/zYVG3wufx3mjKX/5gz3/k2cmVn0fy8K4wfm1Ify8TF41BaXIp1H22hGheoahHcK6Qrfln2G7Ne+pqEv8quRwt6LICx5M87MIwlxljQY0G9jyPX7TFMb1miKL+IyRiMTI3g3cmD6bEp1wAXNLIyY5qT002aMpf/OpbrPZJRqVeB1of9qY/FwdUOg6b1QWT4caTFXKcaGwDGLxgJiYEEP81aTz22pqN1XGoLgHMA3AkhmYSQt2jE1XWjfEZhdb/VcDJ3AgGBk7kTVvdbjVE+o+p9HKFjR6OyrBIJx+k3rq9JoEqG9OQ7L22OQItYLIZc6YfYgwkNegfoH/G5/Ho0ZS7/dSxlpqXI6XUfjdOawO2uJ/VcIz8eDEtbc7VcQmFlZ4lRHw/B+X1xDe/hWRAE5p+AgACB02wlxaVCX5NRwvdT1zDLeTMpQ+hJhgj71xxhlvPQhiihJxkipMVeZ5azNgDECvUwR1/1w+ey5istKRXGub0rhHpME8pKy6jH/33dMaEnGSIc2XSSeuyS4lJhbKupwnhP9YydpdrMZf4qm/tH+gYSSLt7M73swdnLETYOVoiNrIerJ/mxKU5HSfQlmPTdONy5che//nCQevxe47rAXdESa2ZvpL70pW8gwcTvxuH25bvYuyKSamxNxgszVyO5Uop7Nx7UuPlCpVLBwsICffv2pZKPEAK5Uoq4w5dQXlZOJebLWDYxh2uACz82xem0Nn38IVf6YcMX25HzMPdvf56QkIB27drBy8sLvr6+2LZt2yvHFolEmLIsFI/v5WDL17tpDhsA0K6fHAG9/LDh8+14mv33sesiXpi5GgUGywDUfNvU+++/j40bN1LNqQiWofBZES6fv0Y17r8JVMlw+fw15D8tYJaT41gihGDSkhCUFJZi/Sdb//bnxsbG2LBhA1JSUnDw4EFMnz4dT58+feX4nu3c0WNUJ+xc8hv11rqEEExeMg5F+cUI/+TVHxi0GS/MWmL+/Plo3bo1goKCMGLECCxevBhr1qyBQqGAn58fBg8ejMLCqsP4ISEhmDx5Mrp16wYXFxecOHEC48ePh4eHB0JCQl7ENDU1xezZsxEQEICePXsiOjoaXbt2hYuLC/bu3Qs7F1uYO5vg3c8mw9/fH/7+/jh79uyLv9+jRw+YmZlR/Xf69/CGSCxi+g1WrpKisqISF49cYpaTa9jqYz47eTig42g5vlj9Mbw8vP80n93c3OD6vLdus2bN0KRJE9T2jPrbC0dBLBZhzQd0H9YBwMnTEW9MVeHAmiO4nnCLenyN86qL0TQ/fMNI7cTExAh+fn5CYWGh8OzZM6FVq1bCokWLhEePHr34mblz5wrff/+9IAiCMG7cOGH48OFCZWWlsGfPHsHMzEy4dOmSUFFRIfj7+wvx8fGCIAgCAOHAgQOCIAjCgAEDhKCgIKG0tFRISEgQ/Pz8BEEQhCWTVwgqo+FCSVGJcPXqVeGv/787fvy40KdPH6r/3hmdPxEm+b9PNea/KS8rF96wGCssHv8js5yvCnzzl86pz/n84O5DYYD1GGFG50+EtLS0v81nQRCECxcuCK1btxYqKipq/W/b9OVOoScZIsQfS6r1332ZZ0/yhEHWocKMLp8IlZWV1OOrW23mMv/GrAVOnz6NN954A0ZGRjAzM0O/fv0AAMnJyejUqRN8fHwQERGBlJT/HW3q168fCCHw8fGBra0tfHx8IBKJ4OXlhfT0dACAvr4+VKqq+wp8fHzQpUsXSCQS+Pj4vPgZv+5eSCg6B08PLwwdOhSpqalq//cqVDJcj79FvaNQTcR6YvgH+SImMgFV84fj1Kc+57OBiT5yW97D6pPL0btXn7/N56ysLIwZMwZhYWEQiWpfHobM7IumzjZYMT0MFeV0b24zszRFyPw3kXTyMk7uPE81tqbhhVkL1FQsQkJC8MMPPyApKQmfffYZiouLX/yZwfM+miKR6MV/V/+6vLxqY5VEIgF53jz3jz/3x585Fn8IRnrGmPHGh4iNjUVpaSn9f+BfVN82FXeI3avlQJUMj+/lID2ZfQtFrmGpz/m8dOlSSNv7YpT0HSiE7n+az8+ePUOfPn3w5Zdfom3btq/1bzMwMsCERWNxK+k29q8+8lox/k3vd3rAxdcJq9/fgJKiEurxNQUvzFqgY8eO2LdvH4qLi5Gfn4/9+/cDAPLy8mBnZ4eysjJERKjnFpuCwgI4t3RGXGQiNm7cyOT+Yhc/J1jamiOa5Tqz0g8AEP07PzbFqVd9zufc3FzY29tj6vLxuHT74ov5XFpaioEDB2Ls2LEYOnRonXJ0HNQG0m5eCP90K549yaMx7BfEYjGmLA/Fw9uPsH3RXqqxNQkvzFpAoVCgf//+8PPzw6BBgyCXy2Fubo758+ejTZs2CAoKQuvWrdWSe8qUKbjx7Ap2XdmEi9HxMDExefFnnTp1wtChQ3H06FE4ODggMpLOOUORSAS5Soq4Q4lMHgQAwNreCi6+TvzYFKd29T2f169fjwkfjIeVRyOIoYeHt7Oxfft2nDx5EuHh4ZBKpZBKpUhIeL2HVEIIpiwLRcHTAmz4bDvlfwHg18ULnYa0xbZv9uDhnUfU42uEV12MpvnhG0ZqLy8vTxAEQSgoKBACAgKEuLg4ZrlvX8kUepIhwt6VkcxyHt96WuhJhggp59KY5Vwze6Og0h8uFDwrZJbzZcA3f+mk+pzP1R5kPBR6G40QvnxziVriL5+yRuilN0y4mZRBPfb99KqxLxi5lHpsdanNXObfmLXEhAkTIJVK4e/vj8GDB8Pf359Zbge3ZmjqbMP026R/T1+IRKTGM9TqoFDJUF5WgYRjycxycg1Tfc7nak2a22D4BwMQte0skk5dph4/ZN5wmDQywsoZ4dQ3Vdo62WDorP44vuUMkk/TH3t944VZS2zevBkJCQm4cuUKPvzwQ6a5CSFQqGRIOJaMstIyJjkbWZnBPbAV04cBz/ZuMDI1RDTDqye5hqk+5/MfDfvgDdg4WOHHaeuoLxs1sjLD2C+GI/5oEs7+GkM1NgAMnz3g+djDmC15scILM/dK5CopivKLkXz6CrOcCqUMaTE3kPvoGZN8En0JZD18EHMwnh+b4hoEQ2MDTFg0BjcS0hG57jj1+P0m9YKzlyN+mrUBpcV0T3QYmRji7W9G43r8LUSGRVGNXd94YeZeibSbN/QkYravloOlEAQBcYfZHZtSqGR4ePsRbl+5yywnx9WnLsPaw7tja6ybu5l6W1qxnhiTl4Ui6+YD7Fq6n2psAOj2Zgd4dXBH2NzNKMjVnZa6vDBzr8TYzAjenTyYHmFyDXBBIyszpq+zq89Qs3wA4bj6RAjB1OXj8exxPjbN20E9vn8PH3QYoMDmr3bh0b0nVGNX7wDPfZSHTfN3UY1dn3hh5l6ZQilFevIdZGc+ZpJPLBZDrvRDbGQiKisrmeS0dbJBcw97pg8gHFffWslaIPit7tjzw0G1vC2asGgsKsoqsPZD+uez3QJaQhnaDbu/P4A7abrxposXZu6Vvfg2yfCOZrlSiqcPc3EjIZ1ZToVSiqSTl1FcqLudhTjur0K+HAEDY32sem899djNWjbF4Jn9cGTjSaSev0o9/vivRqpt7PWBF2bulTl7N4e1fWPEMC7MAJjulFYEy1BWUobEqJSX/zDH6QjLJuYY8+lQxPwejwv746jHH/HhQDS2s8TK6WHU34BZNjHH6E+GIvpAPC4cuEg1dn3ghZl7ZYQQyJVSXDx8iXqD+ppYNjGHa4AL03Vmn04eMDDSRww/NsU1MG/8RwVH92ZY9d566kcjjc2M8PbXo3Al+jqObDxJNTYADHhXBQc3O6yaGc7sWKe68MLM1UpgsAwFuYVIPUf/dVRNFEopLp+7irycfCb59A314dfNi7fn5Bocib4Ek5aEIPNqFvb830Hq8XuM7oTWbVyx9qPNKMwrohr7j2P/9Qf6Y2eJF2auVvx7+kAkFrHdKR0sQ2WlgPijSexyqmS4d+MB7l7PYpaT4zRBYLAMbfr4Y9P8Hch58JRqbJFIhCnLQvEkKwdbvvqFamwAaNPbH4pgGTbO24Gch7nU47PCCzNXKybmJvBq7850A5hHG1eYWpgghml7zuqNbonMcnKcppj03TiUFJZi3Uebqcf2aOOKoLFdsGvpb2p58K0ee9jcLdRjs8ILM1drcqUU1y7ewpP7OUzyifXE8A/yZdqRy76VHZq1aspfZ3MNkoNbMwz8b29EhkchLfYG9fhvfT0Kevp6+GnWBuqxm7e2x4B3g3Fw3TFcu3iTenwWeGHmai0wWAYAiDvEsCOXUorH93KQnnybac7E4ynUWwlynDYY/clgmNs0worpYdQfiK3sLDHyo0E4tzcWcYfpv5Ua8+kQmFub4cdp67SyvS4vzFytufg5wdLWHDGR7L5NypV+AIDo39m+zi4uLBRxVqEAABMFSURBVFHLzTscp+lMzE0wfsEIpJ5Nw/Etp6nHHzS9D+xcbLFyRjjKy8qpxjYxN0HolyOQciYNx7eeoRqbBV6YuVoTiUSQK6WIjUxkdquLtb0VXHydmL5a9uvmDYmBhB+b4hqsXiFd4erfAmtmb0JRQTHV2PqG+pi4eCwyUjOxb+UhqrEBQDm+G1rJWuBnNYxd3agUZkKIihCSRgi5TgiZQyMmp9kUKhnynuQjLYb++lNN5Eopkk9foX7MoiaGxgbw7eLJtKGKJuDzmasmFosxZfl4PLr7BNu+2UM9fvs3FPDv6YMNn2+nfoucWCzGlGWhyM58jO3f/ko1trrVuTATQsQAfgQQDMATwAhCiGdd4zYUEUkRcF7mDNEXIjgvc0ZEEv1esuoQEOQLQgjb26ZUUlSUVyDhWDK7nNfP4Pblu3iQkc0sZ33i8/n1aetcfhnvDq3RbUQH7Fi8F/fTH1KNTQjB5KWhKMwrwvpPt1GNDVQ1C+o6vD22L/oVD9p2B7p2pZ5DHWh8Yw4EcF0QhJuCIJQC2ArgDQpxdV5EUgQm7JuAjNwMCBCQkZuBCfsmaMWEbmRlBvfAVky/TXp1cIeRqSHT19nyxlUbv1geD6tnfD6/Bm2ey6/inW/GQCQSYfX79HdRO3s5ov9kJfavPoyblzKox3/n2zEghGDNLRPqsdWFRmG2B3DnD7/OfP573EvMPToXhWWFf/q9wrJCzD06t55GVDuBKhnSoq9TfwVVE4m+BLIePog5mKD+nZZduwJdu6J5zDHYCgWImft/WvO0XUd8Pr8GbZ/LL2PjYIXhswfg1K4LaukhP+bzoTC1NFXLDvAmY4ZgeJMcnMg2ROKJlBdzW5PRKMzkH37vb/+XJYRMIITEEkJis7MbxmvBl7md+89Hf2r6fU0jV0khCALiDjM8NqWS4UFGtlqupvsnBIAc9xH/VIIyNjdP1reXzmc+l/9O2+fyqxg6qx9snWywYnoY9V75jRqbIWTecCRGpeD0LxeoxgaAYQ6FaCIUYAWkqNCC01M0CnMmAMc//NoBwL2//pAgCKsFQZALgiC3sbGhkFb7NTdvXqvf1zRuchc0sjJj256zuiOXute2o6KqPl26QOFljcIKEVLn/ajenJrhpfOZz+W/0/a5/CoMjAwwYdEY3LyUgQM/H6Uev/c7PdHCpzlWv78BJUUUr1yNioLBqShM8KzATWKB30fOrZrbGoxGYY4B4EoIaUEI0QfwJoC9FOLqvAU9FsBYYvyn3zOWGGNBjwX1NKLaEYvFCOjli9jIROrXuNXE1skGzT3sma5tyyzKINYTN5QuYHw+vwZtn8uvqtPgtvDt4onwT7ZSv1RGrFe1i/p+ejZ2fvcb1dgA0Nm6BD7mpQj7eAuzC3FeV50LsyAI5QD+AyASwGUA2wVB4BfZvoJRPqOwut9qOJk7gYDAydwJq/utxiifUfU9tFemUMnw9GEursffYpdTKcWlE6koLqT4VF2TqCgYnz4O746tmfbqri98Pr8eXZjLr4IQgqnLxyM/Jx8bPt9OPb60mzc6DW6DrQt3IzvzMdXY5EQUphxfhrwn+dj4xQ6qsakTBIH5JyAgQOB0w5P7OUJPMkTYNH8ns5yxhxKEnmSIcH5/HLOcWxbuFnqSIUL23cfMcgqCIACIFephjr7qh8/lhmnZpJ+EXnrDhPSU29Rj37t5Xwg2HCF8PXo59diCIAhLJ6xS29j/TW3mMu/8xdWJpa0FXP1bMG3P6dPJAwZG+kzPUFf3B2eZk+M0Vcj8N2FsZoQVM8Kp76K2a2GLYbP642jEKaScTaMaGwBCvnwTRqaGWDlzvcb20eaFmaszhUqGy+evIf9pAZN8+ob68OvmhWiGa74tfJrDqpllg+sCxnH/xNy6EcZ8NhQXD1/Cub2x1OMPnzMA1vaN8eO0ddT3r1jYmGPsZ8MQdygR53+LoxqbFl6YuTpTBMtQWVGJi0fYHpu6d/2+Wu5z/SeEECiUUlw8fIn6URGO00b9pyjR3MMeP81aj9KSMqqxjUwM8fbC0bgWdxOHwqOoxgaA/lOVcGxtj1Xv0R87Dbwwc3Xm0cYVJubGTC97qD42xXJDllwlQ/7TAly+cI1ZTo7TVHoSPUxeGop7Nx7gl2X7qcfvPrIjPNu7Y+1Hm1HwrPDlf6EWqsYegnvX72P38gNUY9PACzNXZ2I9MfyDfBETyaAj13P2rezQrKUt01aZAUG+EIlF/LYpjntO3ssP7frLsXnBLjzOyqEamxCCKctC8fRhLiLm76QaG6g63dG2bwAivtxJfex1xQszR0WgSobH93JwK4ldpyOFSoaEY8koLS5lks/UwgQebV35OjPH/cHExWNRXlqOtR/R7wvuLm8JZUg37P7+ADKv/q1vVZ1N/G4cykrKEDZ3C/XYdcELM0eFXOkHgO2rZYVKipKiUiT9f3v3HVxllcZx/PvcS0JCCb2HJiAEAuRigiAiCkqCoAjY6CIu2GZALCvqLOuuA66sbXalOIjAggVWQZFdAQERFektEFgi0hGQIlUg4ewfSViGDSXJued9A89nJjMJ5Tm/Cffh3Lznfc9ZlOZuzOQQm1ds4dC+X52NqZSfVatbha6DOzJ34kI2LrW/zPPw8O5ERkUy5umJ1mvH1qtC10EdmT1hAZuWpVuvn186MSsrylcrx3VNarLc4WNTTW5tRETRCLdr2x2ytwTVn5qVOqfHi90oW7k07wx63/pd1GUrl6HnS91YMmtlWHbf6/FSN8pUKsU7g8b75vEpnZiVNYnJCaR+u5ETR086GS+6eBSNb4lzemm5bqg2pSuWula251TqihQrGc3Dw3uwcclm5k1eZL1+l0F3Uq1eFUY/NYGMMxlWaxePKcbDw3uS9sNm5k2xnz0/dGJW1jTvECLjTCar56e6GzMlxPa0Xezb7uaUo0AgQGJyU1bMWUtmpj42pVSOO/q0oX5SHcYNncLJY3bfnEdERvDYG33ZsWk3n78z22ptgPZ923B9Yh3GPT/Zevb80IlZWdPwpuuJLhHl9KfJRA8em0pKTuDIgaNsXrHF2ZhK+V0gEODxt/pxcM8hPhwx3Xr95nc2IyklgUkvT+Xwfrv3eAQCAZ54ux8Hdh/io1dnWK2drzxeB1BXj4jICELtGrPsS3ePTdVoUI2KNco7fTNwQ/umiMg1caiFUnnRsGV92vVqzT9fn8meLXut1hYRBr7el9+On2LCSx9ZrQ3Z2Xu2ZloYsueVTszKqsTkBPZu28/2jbucjHduR66v1nHmtJsdfEqVj6F+Uh1dZ1YqF4+82otgRJCxz06yXrtmXCydn0jhX+PmheVEu/4jehIMBnj3uX9Yr50XOjErq7w47CGpQ4iTx35jw/f/cTdmSohNS9M5cuCoszGVKgzKVy1L96Fd+W76UlbOW2e9fu9h9xFTrgSjBr9v/cpchdhyPPh8F779dAmr5tvPfqV0YlZWVapZgRpx1ZzeKZ3QNp5gkaDzte2zZw0r5rrbH1ypwuLeIZ2oXLsiowe/b31v+RKli9Pvle6sW5TGN9MWW60NcO/TnahcqwKjwpD9SunErKxLSk5g7cIN/HbilJPxiscUI/7mBk7XfOsn1aFk2RJ6OVupXERGRTLwr33Yun4HM8fMsV4/pX9b6iTUYuyzk6z/P1M0uigDRvZha+oOvhg712rtK6UTs7IuqUOIM6fOsObr9e7GTAmxZe02ftl90Ml4wWCQG9o3Zfns1dY3VFDqatDqnuYktI1n0rCPrS/5BINBHn+rH/t3HGDayM+t1ga4ueuNJNzWiInDPubIQffLVToxK+sat46jaHSk23XmlJwduda4GzM5gUN7f2XL2m3OxlSqsMg5hOL4kZNM+MPH1us3uaUhbe5vycevzbC+j4GI8Nib/Th++DiThk21WvtK6MSsrIuMiqTpbY1Y6vAyb+3GNShXtYzbdeac/cH/rY9NKZWb2vE1uOvR9swaO4ef1tl/A/u7v/TGGBOWu6iva1KTjgPuYOaYOfyU6u5wHtCJWYVJUnKI3ek/syt9j5Pxzj02NXetsxs2ylYuQ91QbV1nVuoS+rx8P8VLF2fUUxOs30VdqWYF7n+2MwunLg7LYTYP/flBisdEMzoM2S9FJ2YVFjmHPbi8ISsxJcSxw8dJW2L/hJuLSUpJYP33mzj+63FnYypVmMSULUnflx9g9fxUvpux1Hr9B35/DxWql8u6i9ryNrkx5UrS548PsGreOr7/bJnV2peiE7MKi2p1q1C1TiWnpzA1u70xgYA4XtsOcTbzLCvnudsfXKnCptPAO6gVX52xz0yyfn56VLGiDHitN+mrfmL2+AVWawPc9Vh7ajUKT/aL0YlZhU1SSojV81OdvZhLlilBXMvrna5tx7WoR7GYaKdHTypV2ASLBHnszX78/NM+pr0+03r9NvffROPWcYx/8QOOHbZ79Sor+0Ps2bKXT96cZbX2xejErMImKSWBUydPh2Xt56JjJofYvGILh/bZ3eT+YopEFOGGO5qwfLa7/cGVKoyatWtMqy7N+WjEdH7ZdcBq7Zw7wI8cOMbkP02zWhug2e1NaHVPEh8M/8TJI5k6MauwaXJrIyKKRrg9+Sl7bXvFHHePTSUmh9i/8wDbNux0NqZShdHAkX3IzDzLuKFTrNeuG6pNh/5tmfH3L8OyV/+AkX3IPJPJ+Bc+sF77Qjoxq7CJLh5F41vinN61XDdUm9IVSzkdM+cZar2crdSlVbmuEvcO6cS8yYvYsHiT9foPvdKdosUiGTNkgvXaVetUptuQu5g7aSEbfgjvvvwFmphF5D4RWS8iZ0Uk0VYodfVISk5ge9ou9m6zuwHAxQQCARKTm7J89hrrd2heTIXYctSKr+50bTsctJ+VC92HdqFc1TKMGvy+9V3zylQsRe8/3MeyL1ezZNYKq7UBerzQhbJVyjA6DNnPV9CfmFOBrsA3FrKoq9D/duRyeDk7OYEjB46SvtL+sXCXGjN1URonj510NmYYaD+rsIsuEc0jr/Zi07IfmTtpofX6nZ9MoXr9qoweMtH6UbDRJaJ5ZERPNi5NZ97kRVZrn69AE7MxJs0YY/96hLpq1IiLpWKN8k5Pm7qhfVNExPHadoiMM5msXuBuf3DbtJ+VK2173Exci3q8N3QKx4+csFo7IjKCR994iF2b9zDjb19arQ3QrldrGjSvy7ihUzhxNDxvxHWNWYWViHDT3UlOxyxVPoZQu3hnj2kBNGrVgKp1KnH04DFnYypVWAUCAR5/qx+ZGWfZmrrDev3mHULc2LEZm1f+aL12IBDg8bcfJuN0BlvDtFWnXO4RDxH5Cqicy2+9aIz5LPvPfA08Y4xZfok6A4AB2V/Gk3XZzGvlgV+8DpHNL1n8kgP8k8XLHDWNMRVsFbPRzz7tZdDXS278kkVz5KGXLzsxX1GRK5iYL/jzy40xnt9c4pcc4J8sfskB/snilxyu5KWf/fS98UsWv+QA/2TRHHmjl7KVUkopHyno41JdRGQn0BKYJSKz7cRSSrmm/ayUPxQpyF82xkwHpufjr75bkHEt8ksO8E8Wv+QA/2TxS46wymc/++l745csfskB/smiOfLAyhqzUkoppezQNWallFLKRzybmL3e/k9EUkRkk4iki8jzrsc/L8d4EdknIp4+ciIi1UVkgYikZf+7DPIoR5SILBWRNdk5XvYix3l5giKySkS+8DKHn2kvn8uhvfz/WbSf88HLn5g92/5PRILAO0AHoCHQXUQaus6RbQKQ4tHY58sAnjbGxAEtgCc8+p6cAtoaY5oCCUCKiLTwIEeOQYC7cysLJ+3lLBPQXr6Q9nM+eDYxe7z9X3Mg3RizxRhzGvgI6OxFEGPMN0D4D/i8fI49xpiV2Z8fJevFW82DHMYYk7N9VkT2hyc3QohILNARGOfF+IWF9nIW7eVcs2g/58O1usZcDTh/H7idePTC9SMRqQWEgCUejR8UkdXAPmCuMcaTHMBbwHNA+I6RUQWlvXwJXvdydgbt5zwK68QsIl+JSGouH568oz0/Wi6/prenAyJSAvgEGGyMOeJFBmNMpjEmAYgFmotIvOsMItIJ2GeMsX92XCGkvVz4+KGXQfs5Pwr0HPPlGGNuD2f9AtgJVD/v61hgt0dZfENEIshq5CnGmE+9zmOMOZy9PWQK7vdjbgXcLSJ3AlFAjIhMNsb0cpzDF7SXCxe/9TJoP+fFtXopexlQT0Rqi0gk8CDwuceZPCUiArwHpBlj3vAwRwURKZ39eTRwO7DRdQ5jzFBjTKwxphZZr4/5fm3ia5z28gX80svZWbSf88HLx6U82/7PGJMBPAnMJuvGiKnGGE8O0hWRD4HFQH0R2Ski/b3IQdY7yt5AWxFZnf1xpwc5qgALRGQtWf/pzjXG+PrRhmud9nIW7eVcaT/ng+78pZRSSvnItXopWymllPIlnZiVUkopH9GJWSmllPIRnZiVUkopH9GJWSmllPIRnZiVUkopH9GJWSmllPIRnZiVUkopH/kv3FEGAtbhfJsAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"## 注:以下示意图仅为定性示意使用,非定量分析\n",
"x_ = np.arange(-1,5,0.1)\n",
"y_ = np.arange(-1,5,0.1)\n",
"x_, y_ = np.meshgrid(x_, y_)\n",
"plt.figure(figsize=(8, 3.8)) \n",
"\n",
"plt.subplot(1,2,1)\n",
"plt.scatter(posindex[:,0], posindex[:,1], c='red', alpha=1, marker='+', label='pickup') \n",
"plt.scatter(negindex[:,0], negindex[:,1], c='green', alpha=1, marker='o', label='pickup') \n",
"f = -4.50 + 1.91 * x_ + 0.55 * y_\n",
"f_1 = -6.10 + 1.91 * x_ + 0.55 * y_\n",
"f_2 = -7.70 + 1.91 * x_ + 0.55 * y_\n",
"plt.contour(x_, y_, f,0)\n",
"plt.contour(x_, y_, f_1,0)\n",
"plt.contour(x_, y_, f_2,0)\n",
"plt.plot([2,2.8],[1,1+0.8*0.55/1.91],'b--')\n",
"plt.text(1.2, 0.6,'gamma1')\n",
"print 'fig1. 点(2,1)到分割面几何间隔 γ1 = ', -1*(1.91*2+0.55*1 - 6.10)/np.sqrt(1.91**2 + 0.55**2)\n",
"\n",
"plt.subplot(1,2,2)\n",
"plt.scatter(posindex[:,0], posindex[:,1], c='red', alpha=1, marker='+', label='pickup') \n",
"plt.scatter(negindex[:,0], negindex[:,1], c='green', alpha=1, marker='o', label='pickup') \n",
"f = -4.20 + 1.61 * x_ + 0.95 * y_\n",
"f_1 = -5.30 + 1.61 * x_ + 0.95 * y_\n",
"f_2 = -6.40 + 1.61 * x_ + 0.95 * y_\n",
"plt.contour(x_, y_, f,0)\n",
"plt.contour(x_, y_, f_1,0)\n",
"plt.contour(x_, y_, f_2,0)\n",
"plt.text(1.2, 0.6,'gamma2')\n",
"plt.plot([2,2.5],[1,1+0.95/1.61 * 0.5],'b--') #在点到x轴画出垂直线\n",
"print '\\nfig2. 点(2,1)到分割面几何间隔 γ2 = ', -1*(1.61*2+0.95*1 - 5.30)/np.sqrt(1.61**2 + 0.95**2)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
">间隔最大化 \n",
"虽然对数据进行线性分割的时候,可以得到无穷多个分割面方程,但是,几何间隔gamma最大的时候的分割面只有一个(这里暂时不讨论“软间隔”问题),实际上,通过上述的图像可以发现,几何间隔越大,分割面越好,因为数据点离分割面越远,就愈加确定其属于某一类,因此其属于某一特定类别地置信度越高。所以这里我们定义如下式子来描述我们接下来的目的,即\n",
"$$\\mathop \\max_{w,b} \\gamma$$\n",
"但是这个写法是有条件的,因为我们打算最大化的是最靠近分割面的点到分割面之间的距离,所以附加条件约束为对任意$(x_i,y_i)$\n",
"$$s.t. y_i (\\frac{w}{||w||}x_i + \\frac{b}{||w||}) \\geq \\gamma$$\n",
"这个条件,隐性地要求超平面$(w,b)$关于每个训练样本点$(x_i,y_i)$的几何间隔至少为$\\gamma$ \n",
"又因为 \n",
"$$几何间隔\\gamma = \\frac{由T中某个样本x_i确定的函数间隔最小值\\hat \\gamma}{||w||}$$\n",
"所以有\n",
"$$\\mathop \\max_{w,b} \\gamma = \\mathop \\max_{w,b} \\frac{\\hat \\gamma}{||w||}$$\n",
"$$s.t. y_i (wx_i + b) \\geq \\hat \\gamma$$\n",
"由于${\\hat \\gamma}$ 对求解 $\\mathop \\max_{w,b} \\gamma$ 无用,因此\n",
"$$\\mathop \\max_{w,b} \\frac{\\hat \\gamma}{||w||} 等价于 \\mathop \\max_{w,b} \\frac{1}{||w||}$$\n",
"该式子进一步的推导可知\n",
"$$\\mathop \\max_{w,b} \\frac{1}{||w||} 等价于 \\mathop \\min_{w,b} \\frac{||w||^2}{2} $$\n",
"因此得到最终优化问题: \n",
"$$\\mathop \\min_{w,b} \\frac{||w||^2}{2} $$\n",
"此时条件$y_i (wx_i + b) - \\hat\\gamma\\geq 0 $等价于\n",
"$$s.t. y_i (wx_i + b) - 1 \\geq 0 $$\n",
"当解出相应的$w$和$b$之后,可以直接构造预测函数,即:\n",
"$$f(x) = sign(wx+b)$$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"---\n",
"## 7.2 编写代码测试示例数据"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"w includs 2 parameters\n"
]
}
],
"source": [
"# 确定w的维度dim\n",
"n,dim = x.shape\n",
"print 'w includs',dim,'parameters'"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
">$w$包含了两个参数,这里定义两个参数$w1$和$w2$ \n",
"此时我们要最小化目标函数为\n",
"$$\\mathop \\min_{w,b} \\frac{||w||^2}{2} = \\mathop \\min_{w,b} \\frac{w_1^2+w_2^2}{2}$$\n",
"$$s.t. y_i (w x_i + b) - 1 \\geq 0, 其中(x_i,y_i) \\in T$$\n",
"约束条件为"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"约束条件:\n",
" + 1 *( 3 * w1 + 4 * w2 + b )≥ 1\n",
" -1 *( 1 * w1 + 1 * w2 + b )≥ 1\n",
" + 1 *( 4 * w1 + 3 * w2 + b )≥ 1\n",
" -1 *( 1 * w1 + 0 * w2 + b )≥ 1\n",
" -1 *( 2 * w1 + 1 * w2 + b )≥ 1\n",
" + 1 *( 4 * w1 + 2 * w2 + b )≥ 1\n",
" + 1 *( 4 * w1 + 0 * w2 + b )≥ 1\n"
]
}
],
"source": [
"print '约束条件:'\n",
"for i in range(len(x)):\n",
" if y[i] == 1:\n",
" print ' +',y[i],'*(',x[i,0],'* w1 +',x[i,1],'* w2 + b )≥ 1'\n",
" if y[i] == -1:\n",
" print ' ',y[i],'*(',x[i,0],'* w1 +',x[i,1],'* w2 + b )≥ 1'"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
">此时,问题已经转化为求解一个条件极值问题。一般来说,直接使用拉格朗日乘子法,构造一个多元函数,最后解出这个线性方程组,就可以直接得到最终的参数,其中,拉格朗日函数记为\n",
"$$L(w,b,\\lambda) = \\frac{||w||^2}{2} + \\sum_{i=1}^N \\lambda_i y_i (wx_i+ b -1)$$\n",
"然后,拉格朗日函数对其参数w和b求偏导,并令其等于$0$,有:\n",
"$$\\nabla_w L(w,b,\\lambda) = w + \\sum_{i=1}^N \\lambda_i x_i y_i = 0$$\n",
"$$\\nabla_b L(w,b,\\lambda) = \\sum_{i=1}^{N} \\lambda_i y_i = 0$$\n",
"所以上式中,得到$$\\nabla_w L(w,b,\\lambda) = (w_1, w_2) + \\lambda_1*(3,4) - \\lambda_2*(1,1) + \\lambda_3*(4,3) - \\lambda_4*(1,0) - \\lambda_5*(2,1) + \\lambda_6*(4,2) + \\lambda_7*(4,0) = 0$$ \n",
"得到$$\\nabla_b L(w,b,\\lambda) = \\lambda_1 - \\lambda_2 + \\lambda_3 - \\lambda_4 - \\lambda_5 + \\lambda_6 + \\lambda_7 = 0$$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"---\n",
"## 7.3 核函数\n",
">核函数是为了SVM中的解决线性不可分的问题,一个经典的图如下所示,在没有进行核函数映射之前,数据呈现为两个包围状的数据分布,无法求解得到一个线性分割面对数据进行分割;进行核函数映射之后,数据分布可以被一个线性分割面分割。 \n",
"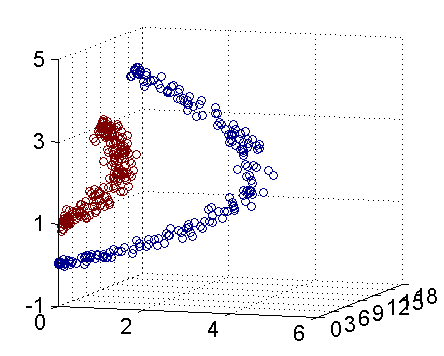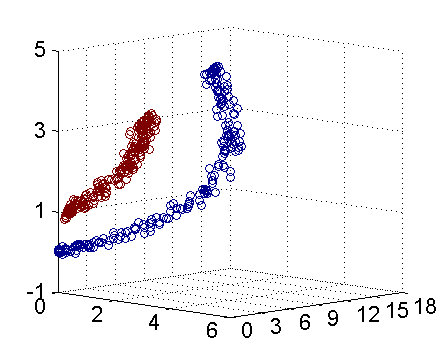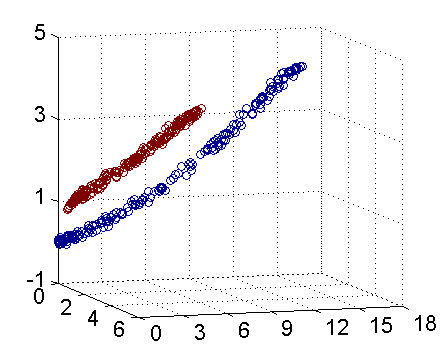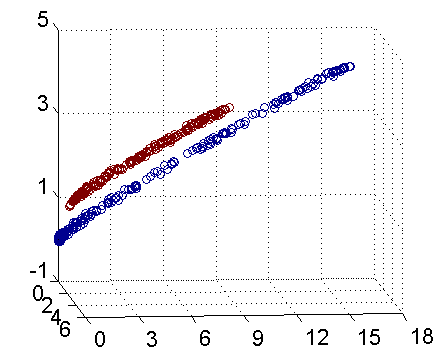"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.2"
}
},
"nbformat": 4,
"nbformat_minor": 2
}