{
"cells": [
{
"cell_type": "markdown",
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T02:19:02.272939Z",
"start_time": "2019-04-07T02:19:02.268259Z"
},
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"***\n",
"***\n",
"\n",
"# Introduction to Neural Network\n",
"\n",
"\n",
"***\n",
"***"
]
},
{
"cell_type": "markdown",
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T05:41:09.971531Z",
"start_time": "2019-04-07T05:41:09.967172Z"
},
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
"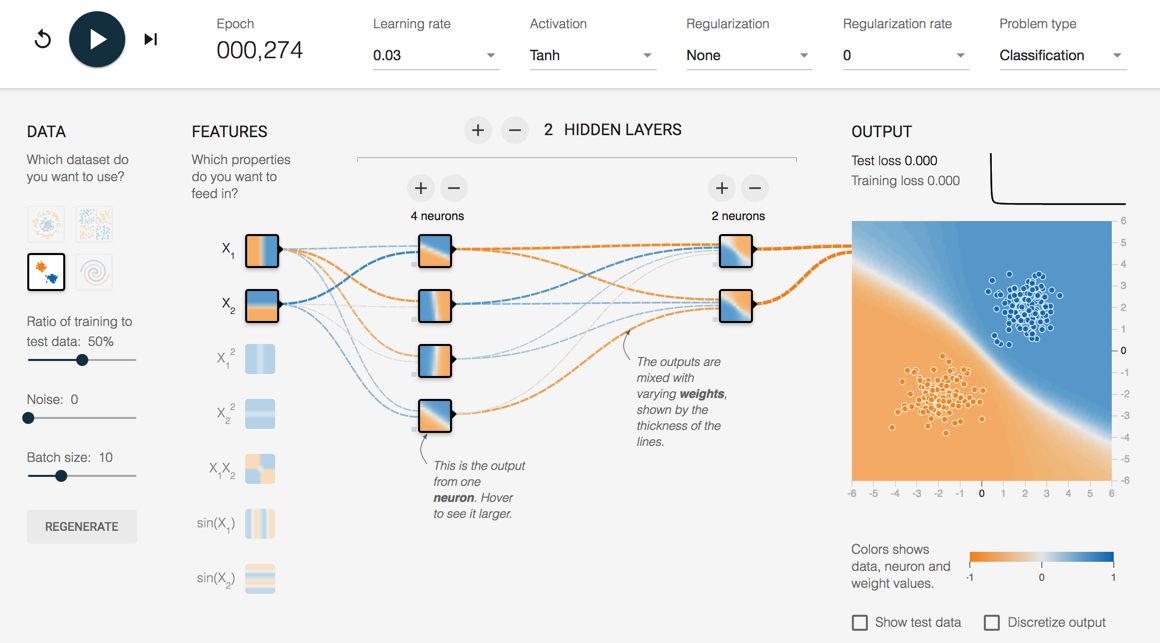 \n",
"\n",
"http://playground.tensorflow.org/"
]
},
{
"cell_type": "markdown",
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T09:37:45.438709Z",
"start_time": "2019-04-07T09:37:45.434406Z"
},
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"- Deep Learning http://www.deeplearningbook.org\n",
" - An MIT Press book by Ian Goodfellow, Yoshua Bengio and Aaron Courville\n",
"\n",
"- Neural Networks and Deep Learning http://neuralnetworksanddeeplearning.com/index.html\n",
"\n",
" - A free online book explaining the core ideas behind artificial neural networks and deep learning. [Code](https://github.com/mnielsen/neural-networks-and-deep-learning). By [Michael Nielsen](http://michaelnielsen.org/) / Dec 2017"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## House Price\n",
"\n",
"Let’s start with a simple example. \n",
"- Say you’re helping a friend who wants to buy a house.\n",
"\n",
"- She was quoted $400,000 for a 2000 sq ft house (185 meters). \n",
"\n",
"Is this a good price or not?"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"So you ask your friends who have bought houses in that same neighborhoods, and you end up with three data points:\n",
"\n",
"\n",
"\n",
"| Area (sq ft) (x) | Price (y) | \n",
"| -------------|:-------------:|\n",
"|2,104|399,900|\n",
"|1,600|329,900|\n",
"|2,400|369,000|"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
"$$y = f(X) = W X$$\n",
"\n",
"- Calculating the prediction is simple multiplication.\n",
"- But before that, we need to think about the weight we’ll be multiplying by. \n",
"- “training” a neural network just means finding the weights we use to calculate the prediction.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"A simple predictive model (“regression model”)\n",
"- takes an input, \n",
"- does a calculation, \n",
"- and gives an output \n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"
\n",
"\n",
"http://playground.tensorflow.org/"
]
},
{
"cell_type": "markdown",
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T09:37:45.438709Z",
"start_time": "2019-04-07T09:37:45.434406Z"
},
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"- Deep Learning http://www.deeplearningbook.org\n",
" - An MIT Press book by Ian Goodfellow, Yoshua Bengio and Aaron Courville\n",
"\n",
"- Neural Networks and Deep Learning http://neuralnetworksanddeeplearning.com/index.html\n",
"\n",
" - A free online book explaining the core ideas behind artificial neural networks and deep learning. [Code](https://github.com/mnielsen/neural-networks-and-deep-learning). By [Michael Nielsen](http://michaelnielsen.org/) / Dec 2017"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## House Price\n",
"\n",
"Let’s start with a simple example. \n",
"- Say you’re helping a friend who wants to buy a house.\n",
"\n",
"- She was quoted $400,000 for a 2000 sq ft house (185 meters). \n",
"\n",
"Is this a good price or not?"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"So you ask your friends who have bought houses in that same neighborhoods, and you end up with three data points:\n",
"\n",
"\n",
"\n",
"| Area (sq ft) (x) | Price (y) | \n",
"| -------------|:-------------:|\n",
"|2,104|399,900|\n",
"|1,600|329,900|\n",
"|2,400|369,000|"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
"$$y = f(X) = W X$$\n",
"\n",
"- Calculating the prediction is simple multiplication.\n",
"- But before that, we need to think about the weight we’ll be multiplying by. \n",
"- “training” a neural network just means finding the weights we use to calculate the prediction.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"A simple predictive model (“regression model”)\n",
"- takes an input, \n",
"- does a calculation, \n",
"- and gives an output \n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T03:15:14.317623Z",
"start_time": "2019-04-07T03:15:14.313438Z"
},
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
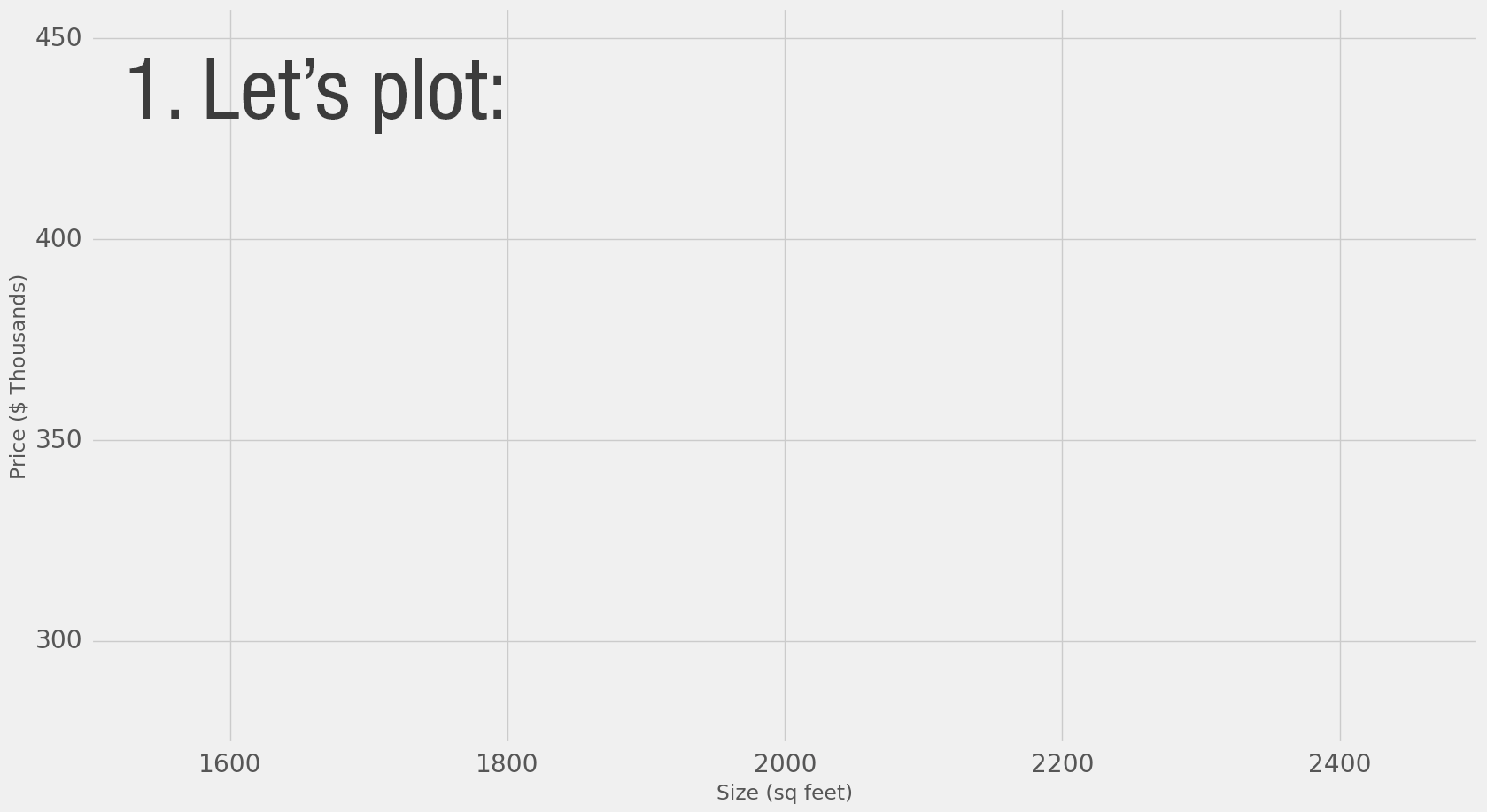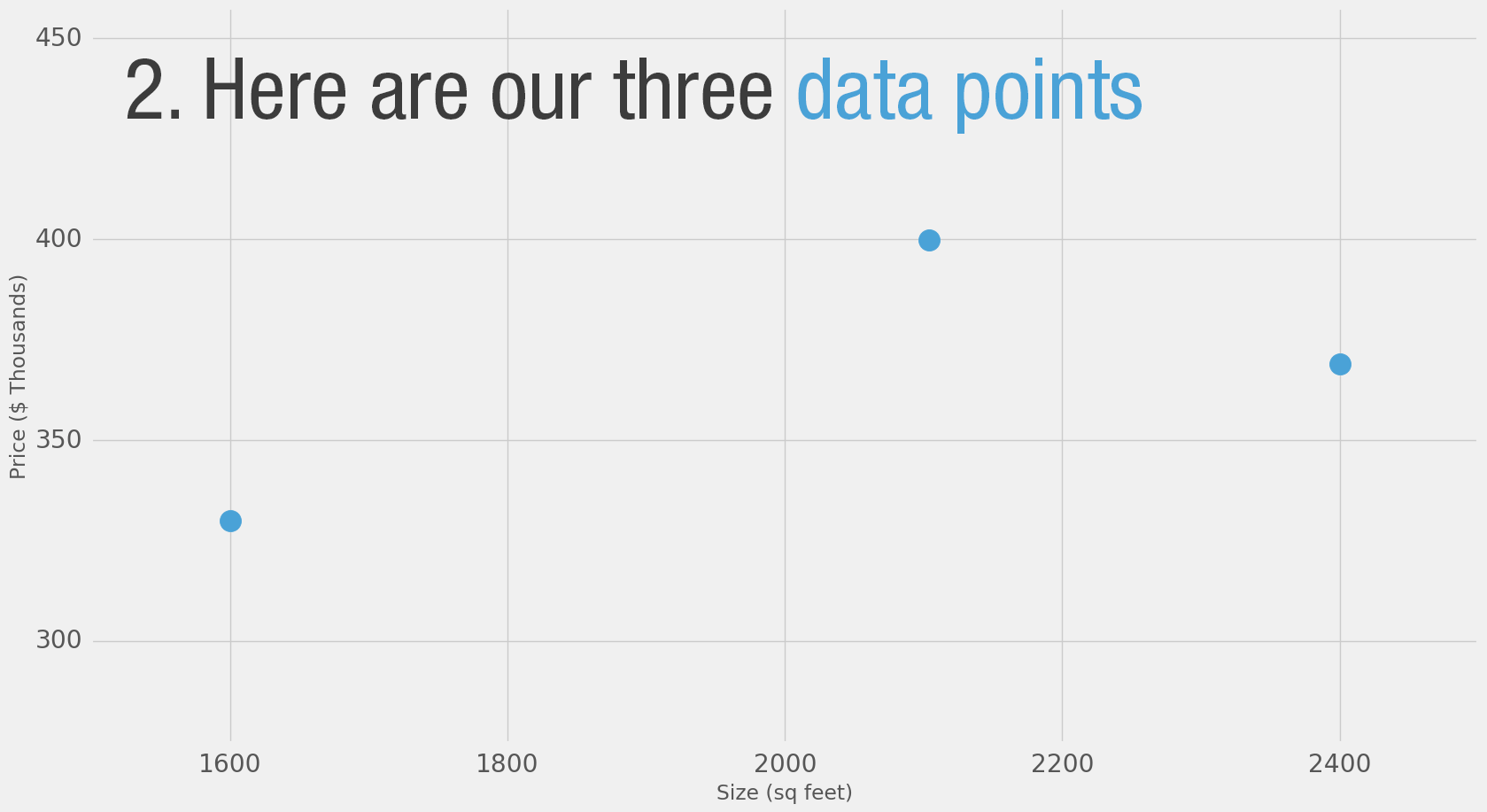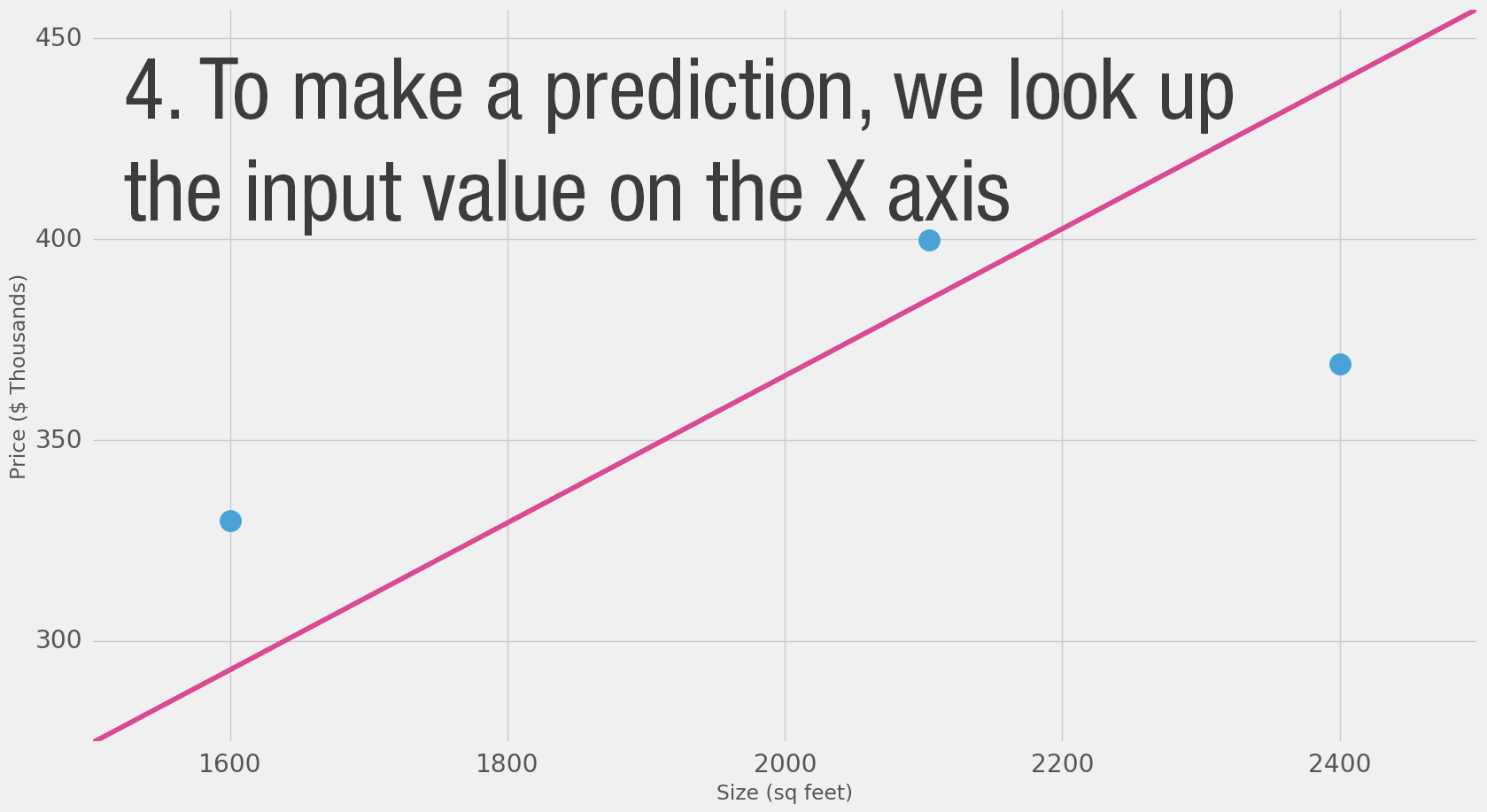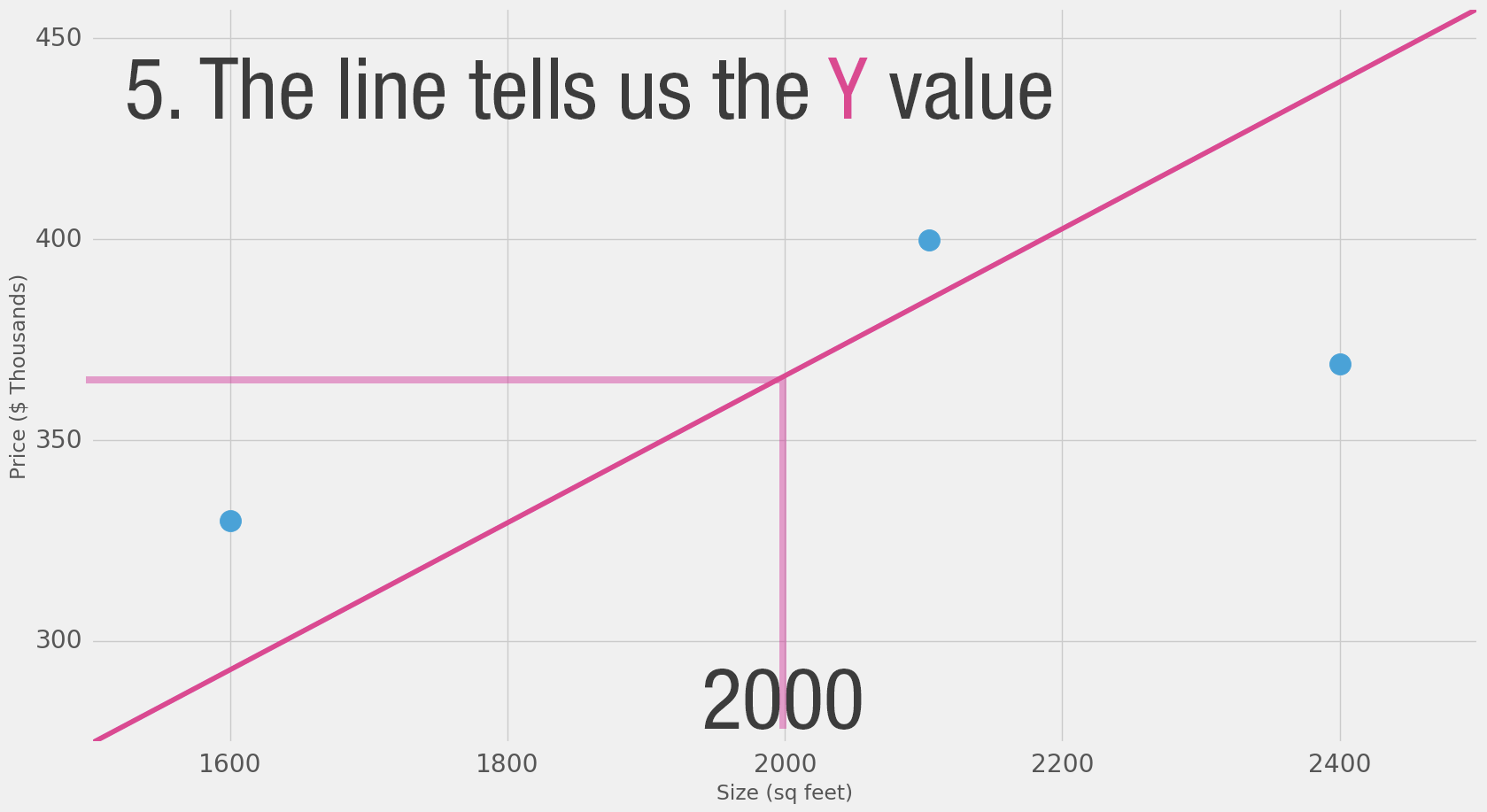
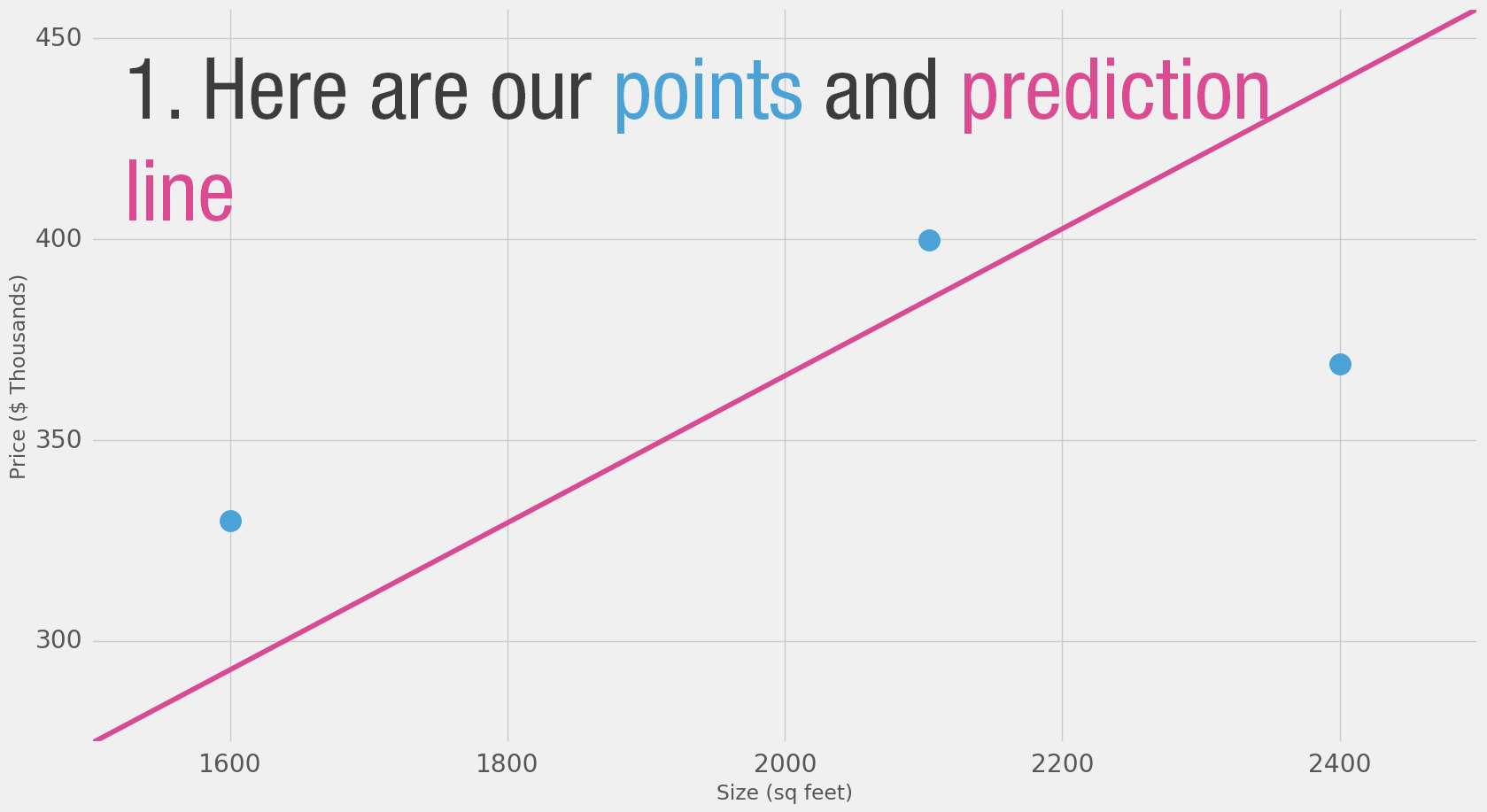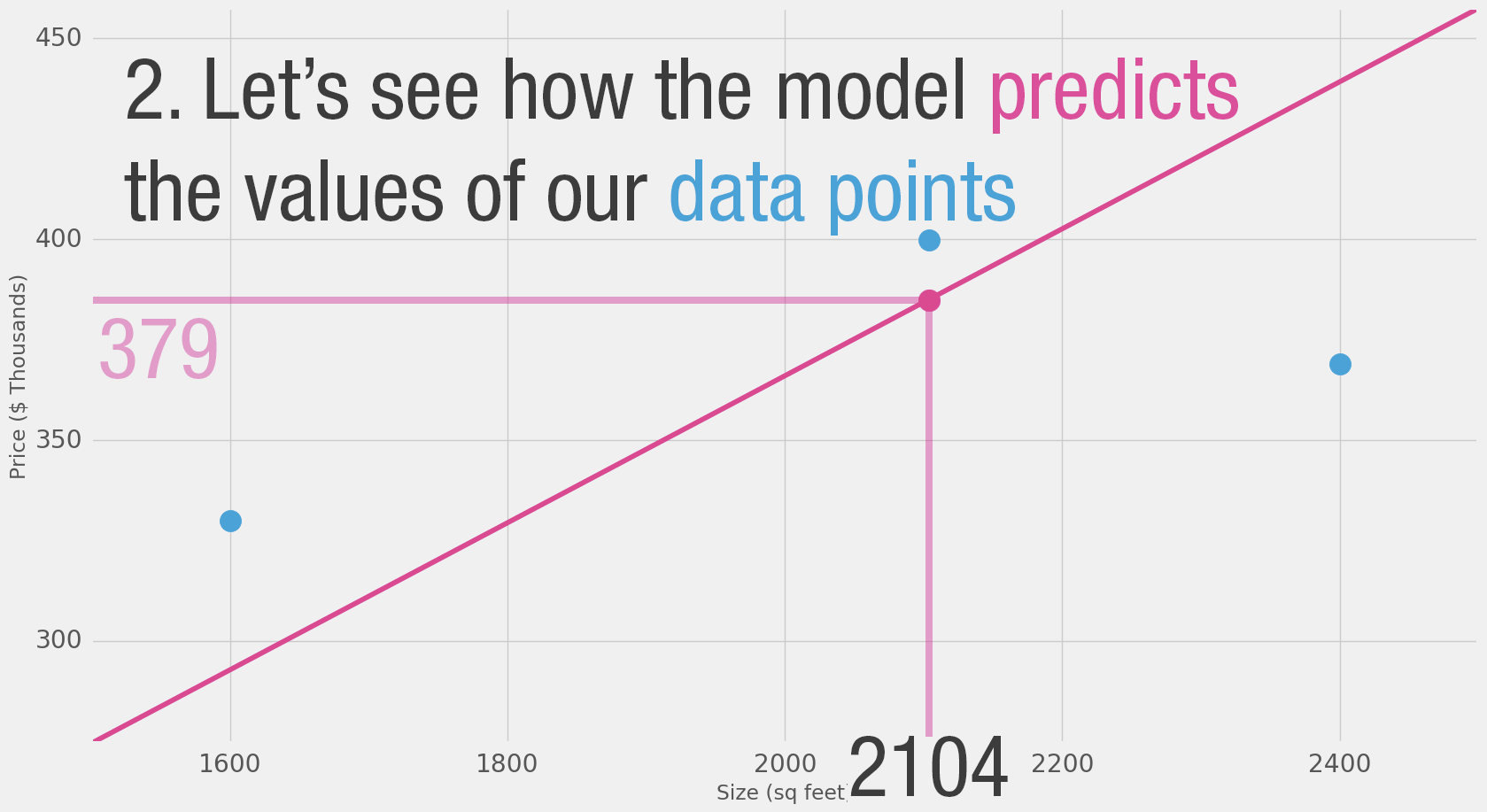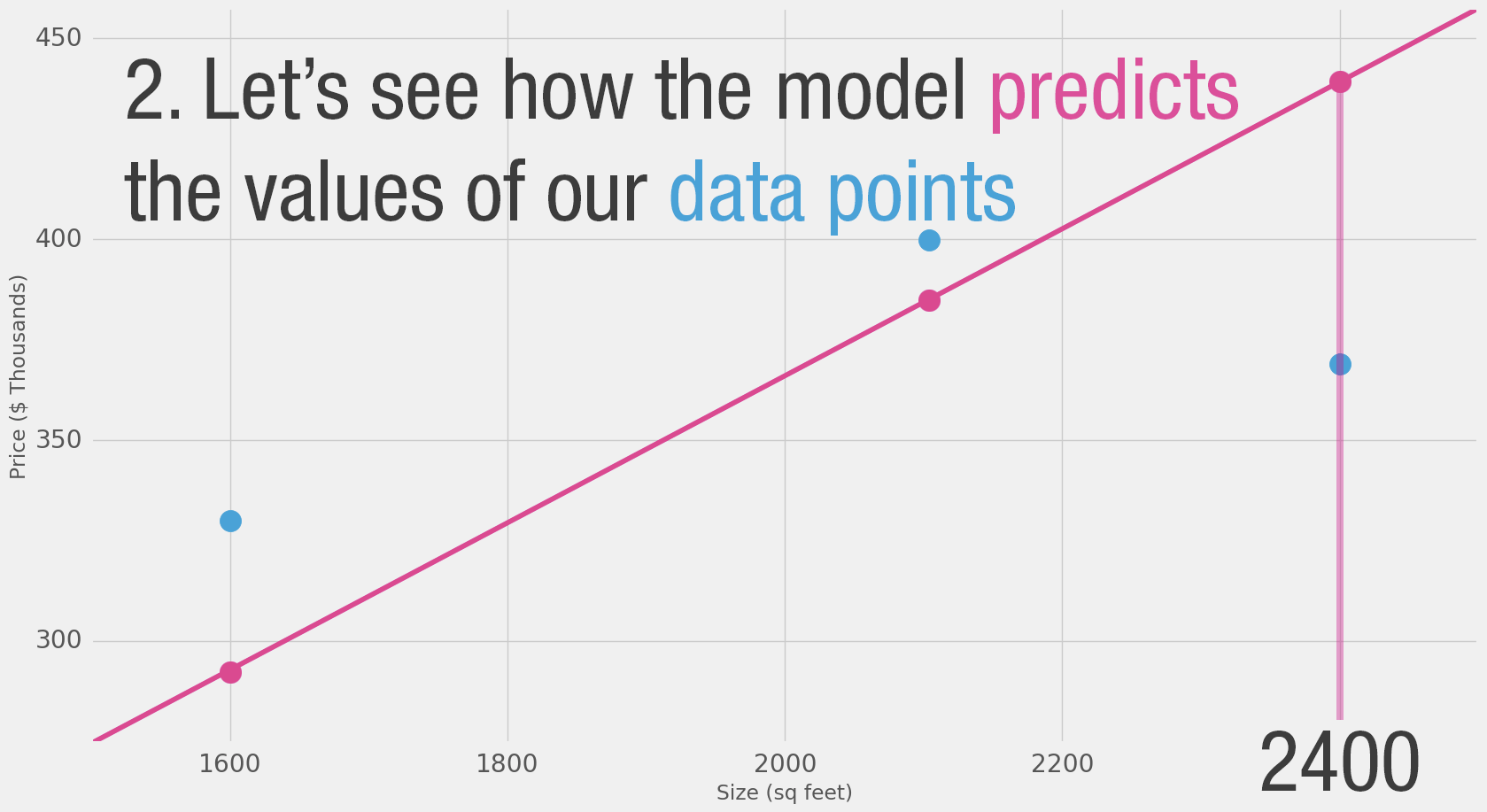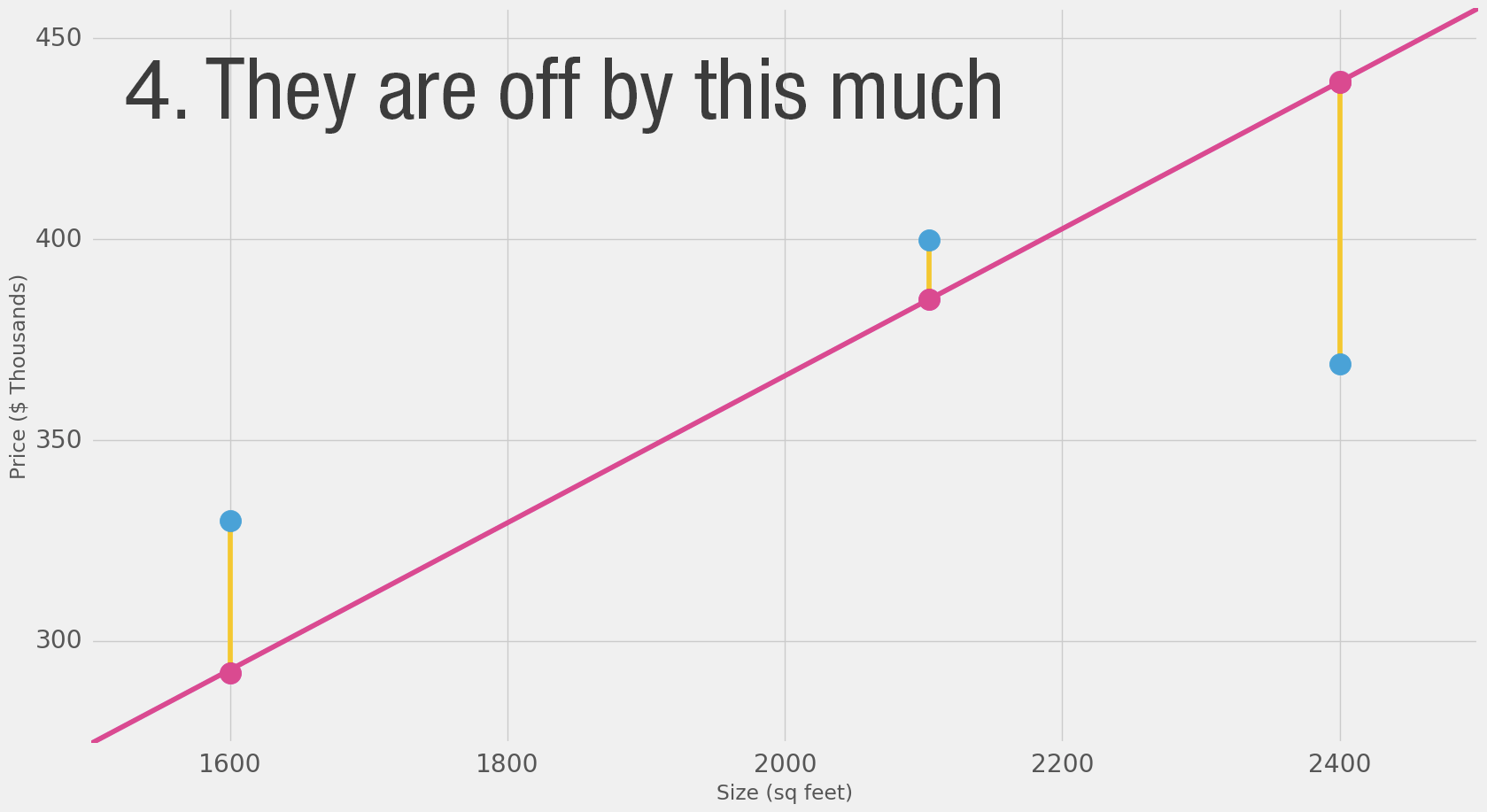
"Model Evaluation\n",
"- If we apply our model to the three data points we have, how good of a job would it do?"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T03:15:14.317623Z",
"start_time": "2019-04-07T03:15:14.313438Z"
},
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"Model Evaluation\n",
"- If we apply our model to the three data points we have, how good of a job would it do?"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"**Loss Function (also, cost function)**\n",
"\n",
"- For each point, the error is measured by the difference between the **actual value** and the **predicted value**, raised to the power of 2. \n",
"- This is called **Mean Square Error**. "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"**Loss Function (also, cost function)**\n",
"\n",
"- For each point, the error is measured by the difference between the **actual value** and the **predicted value**, raised to the power of 2. \n",
"- This is called **Mean Square Error**. "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
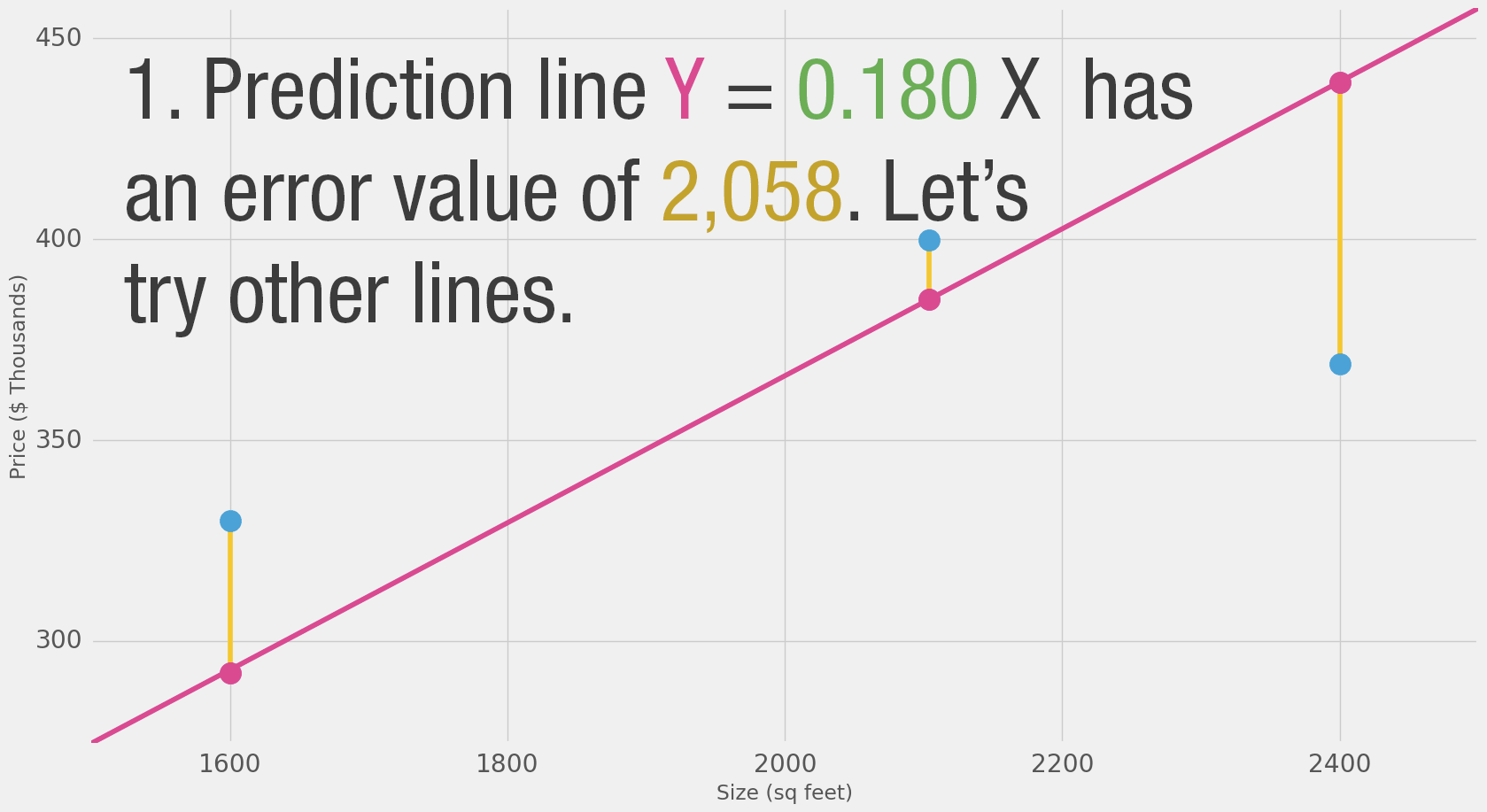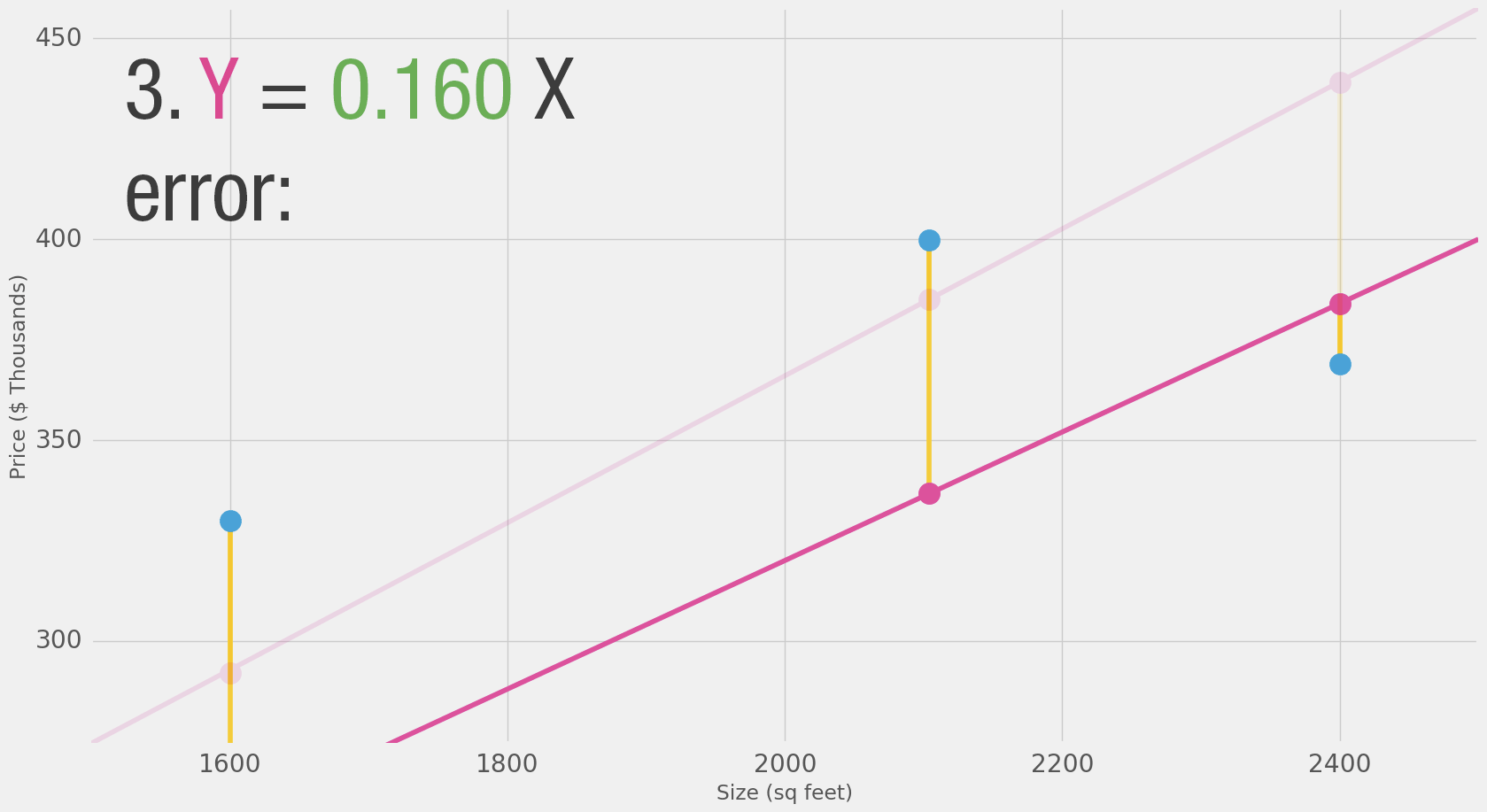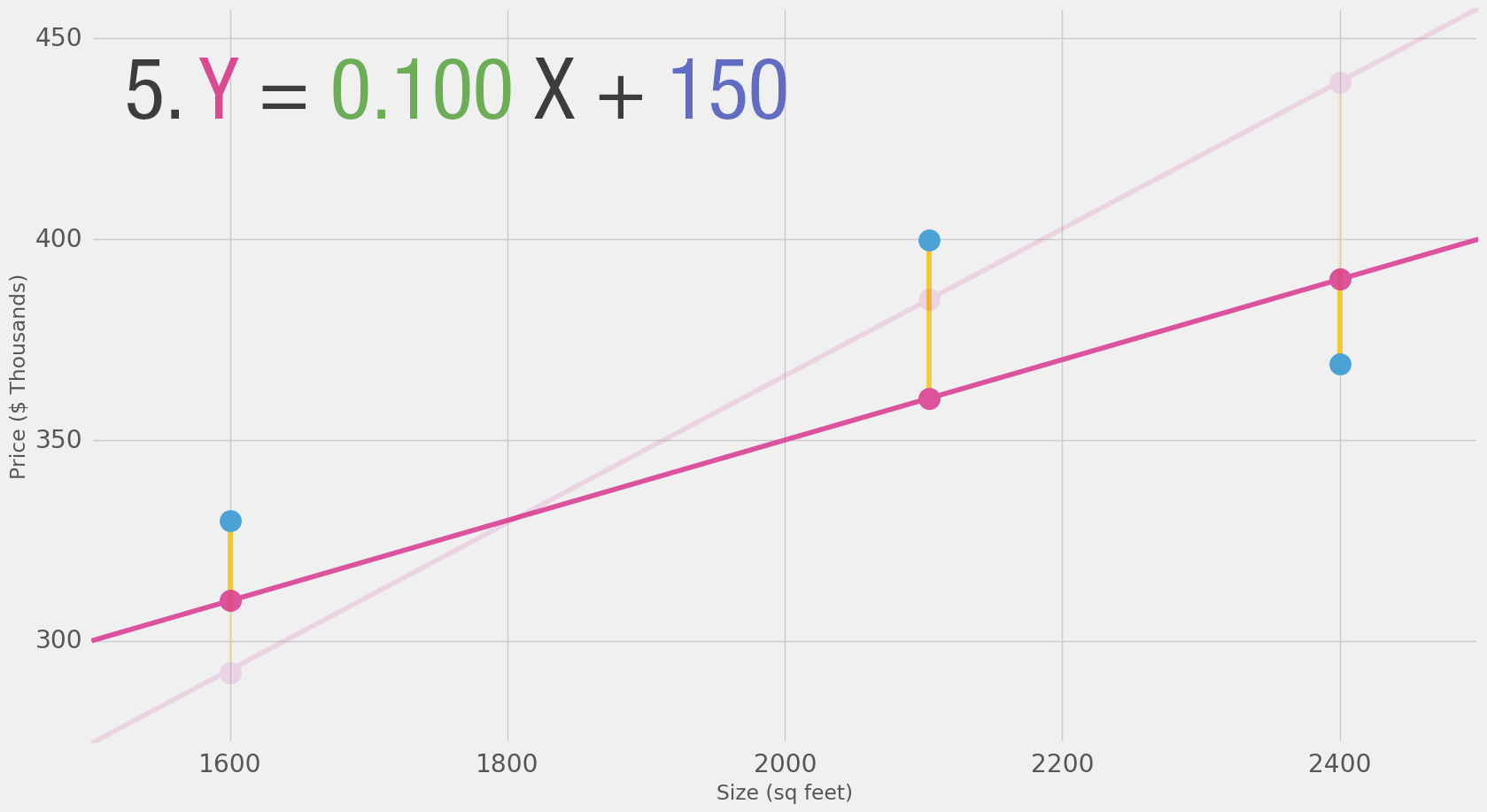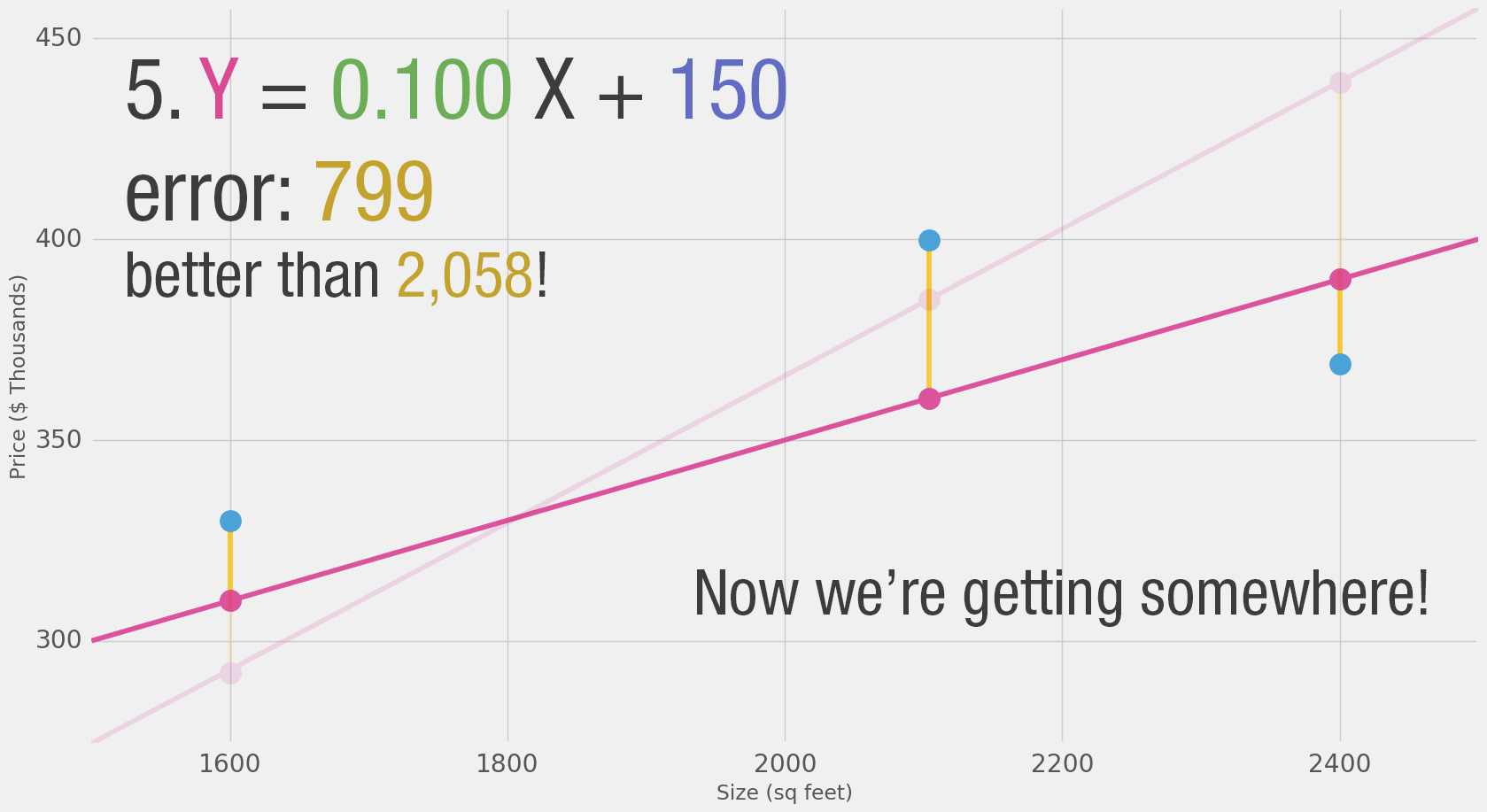
"- We can't improve much on the model by varying the weight any more. \n",
"- But if we add a bias (intercept) we can find values that improve the model.\n",
"\n",
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"- We can't improve much on the model by varying the weight any more. \n",
"- But if we add a bias (intercept) we can find values that improve the model.\n",
"\n",
" \n",
"\n",
"$$y = 0.1 X + 150$$"
]
},
{
"attachments": {},
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"**Gradient Descent**\n",
"\n",
"- Automatically get the correct weight and bias values \n",
"- minimize the loss function.\n",
"\n",
"
\n",
"\n",
"$$y = 0.1 X + 150$$"
]
},
{
"attachments": {},
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"**Gradient Descent**\n",
"\n",
"- Automatically get the correct weight and bias values \n",
"- minimize the loss function.\n",
"\n",
"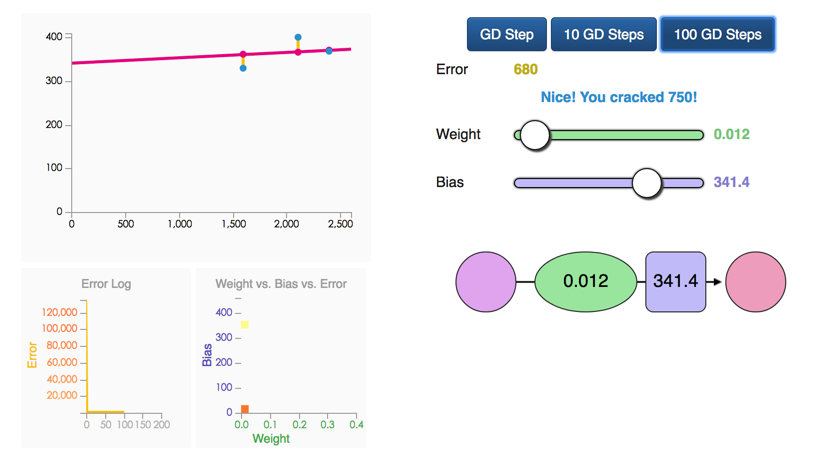 \n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
"
\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
" \n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
"
\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
" \n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## softmax\n",
"\n",
"The softmax function, also known as softargmax or normalized exponential function, is a function that takes as input a vector of K real numbers, and normalizes it into a probability distribution consisting of K probabilities. \n",
"\n",
"$$softmax = \\frac{e^x}{\\sum e^x}$$\n"
]
},
{
"cell_type": "code",
"execution_count": 128,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T13:57:33.466056Z",
"start_time": "2019-04-07T13:57:33.459580Z"
},
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"text/plain": [
"array([0.02364054, 0.06426166, 0.1746813 , 0.474833 , 0.02364054,\n",
" 0.06426166, 0.1746813 ])"
]
},
"execution_count": 128,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"def softmax(s):\n",
" return np.exp(s) / np.sum(np.exp(s), axis=0)\n",
"\n",
"softmax([1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0])"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
"That is, prior to applying softmax, some vector components could be negative, or greater than one; and might not sum to 1; but after applying softmax, each component will be in the interval (0,1), and the components will add up to 1, so that they can be interpreted as probabilities. \n",
"\n",
"Furthermore, the larger input components will correspond to larger probabilities. \n",
"\n",
"Softmax is often used in neural networks, to map the non-normalized output of a network to a probability distribution over predicted output classes."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## Activation Function\n"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T03:59:39.599371Z",
"start_time": "2019-04-07T03:59:39.593104Z"
},
"code_folding": [],
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"text/plain": [
"0.6224593312018546"
]
},
"execution_count": 12,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"import numpy as np\n",
"def sigmoid(x):\n",
" return 1/(1 + np.exp(-x))\n",
"\n",
"sigmoid(0.5)"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T04:01:24.575040Z",
"start_time": "2019-04-07T04:01:24.567328Z"
},
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"text/plain": [
"0.5"
]
},
"execution_count": 13,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Naive scalar relu implementation. \n",
"# In the real world, most calculations are done on vectors\n",
"def relu(x):\n",
" if x < 0:\n",
" return 0\n",
" else:\n",
" return x\n",
"\n",
"relu(0.5)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# WHAT IS PYTORCH?\n",
"\n",
"It’s a Python-based scientific computing package targeted at two sets of audiences:\n",
"\n",
"- A replacement for NumPy to use the power of GPUs\n",
"- a deep learning research platform that provides maximum flexibility and speed"
]
},
{
"cell_type": "code",
"execution_count": 44,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T04:43:15.243401Z",
"start_time": "2019-04-07T04:43:14.333403Z"
}
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"import matplotlib.pyplot as plt\n",
"import torch\n",
"from torch import nn, optim\n",
"from torch.autograd import Variable\n",
"import numpy as np"
]
},
{
"cell_type": "code",
"execution_count": 104,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T05:26:28.414285Z",
"start_time": "2019-04-07T05:26:28.201996Z"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXoAAAD8CAYAAAB5Pm/hAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvDW2N/gAAFRdJREFUeJzt3X+QXWd93/H3B0n+0RIswEuiWKKisWkSPLHsbISVhERI40Q2TEQbu3HKDC526oFAQphM+FE6mXFdxjFu69QdxoxTh8iUBrvmRxwHJri2FcKMLGVFZAWDgQVMbeHiBWwTD7Uci2//uI/weitp77XuatcP79fMmfuc5zzn3u89u/vZs+ecuydVhSSpX89Z7AIkSQvLoJekzhn0ktQ5g16SOmfQS1LnDHpJ6pxBL0mdM+glqXMGvSR1bvliFwBw8skn19q1axe7DEl6Vtm9e/c3q2pivnFLIujXrl3L1NTUYpchSc8qSb42zDgP3UhS5wx6SeqcQS9JnTPoJalzQwd9kmVJ/jbJrW3+JUl2JplOcmOS41r/8W1+ui1fuzClS5KGMcoe/VuAz8+avxK4uqpOBR4GLmn9lwAPt/6r2zhJ0iIZKuiTrAZeBfy3Nh9gE3BzG7INeE1rb23ztOWb23hJ47RjB1xxxeBROoJhr6P/Q+BtwA+1+RcCj1TVk23+AeCU1j4FuB+gqp5M8mgb/82xVCxpEO6bN8MTT8Bxx8Htt8OGDYtdlZaoeffok7waeKiqdo/zhZNcmmQqydTMzMw4n1rq3/btg5A/cGDwuH37YlekJWyYQzc/B/xKkvuADzE4ZPNfgJVJDv5FsBrY19r7gDUAbflJwLfmPmlVXVdVk1U1OTEx7yd4Jc22ceNgT37ZssHjxo2LXZGWsHmDvqreWVWrq2otcCFwR1W9FrgTOL8Nuwj4s9a+pc3Tlt9RVTXWqqUfdBs2DA7XXH65h200r6P5XzdvBz6U5D8Afwtc3/qvBz6QZBr4NoNfDpLGbcMGA15DGSnoq2o7sL21vwKsP8SYx4ELxlCbJGkM/GSsJHXOoJekzhn0ktQ5g16SOmfQS1LnDHpJ6pxBL0mdM+glqXMGvSR1zqCXpM4Z9JLUOYNekjpn0EtS5wx6SeqcQS9JnTPoJalzBr0kdc6gl6TOGfSS1DmDXpI6N2/QJzkhya4kdye5J8llrX9Tks8k+WySbUmWt/4kuSbJdJK9Sc5a6DchSTq8Yfbo9wObquoMYB2wJcnPAtuAC6vqdOBrwEVt/LnAaW26FLh27FVLkoY2b9DXwGNtdkWbDgBPVNUXW/9twK+29lbghrbeXcDKJKvGXLckaUhDHaNPsizJHuAhBqG+C1ieZLINOR9Y09qnAPfPWv2B1jf3OS9NMpVkamZm5pnWL0max1BBX1UHqmodsBpYD7wMuBC4Osku4O8Z7OUPraquq6rJqpqcmJgYsWxJ0rBGuuqmqh4B7gS2VNWOqnpFVa0HPgUcPIyzj6f27mHwy2HfOIqVJI1umKtuJpKsbO0TgXOAe5O8qPUdD7wdeF9b5Rbgde3qm7OBR6vqwQWpXpI0r+VDjFkFbEuyjMEvhpuq6tYkVyV5deu7tqruaOM/DpwHTAPfBV6/AHVLkoaUqlrsGpicnKypqanFLkOSnlWS7K6qyfnG+clYSeqcQS9JnTPoJalzBr0kdc6gl6TOGfSS1DmDXpI6Z9BLUucMeknqnEEvSZ0z6CWpcwa9JHXOoJekzhn0ktQ5g16SOmfQS1LnDHpJ6pxBL0mdM+glqXPzBn2SE5LsSnJ3knuSXNb6Nyf5TJI9ST6d5NTWf3ySG5NMJ9mZZO3CvgVJ0pEMs0e/H9hUVWcA64AtSc4GrgVeW1XrgP8B/Ls2/hLg4ao6FbgauHL8ZUuShjVv0NfAY212RZuqTc9r/ScBX2/trcC21r4Z2JwkY6tYkjSS5cMMSrIM2A2cCry3qnYm+Q3g40n+L/Ad4Ow2/BTgfoCqejLJo8ALgW/Oec5LgUsBXvziF4/hrUiSDmWok7FVdaAdolkNrE9yOvBW4LyqWg28H/jPo7xwVV1XVZNVNTkxMTFq3ZKkIY101U1VPQLcCZwLnFFVO9uiG4Gfbe19wBqAJMsZHNb51liqlSSNbJirbiaSrGztE4FzgM8DJyV5aRt2sA/gFuCi1j4fuKOqaqxVS5KGNswx+lXAtnac/jnATVV1a5J/A3w4yfeAh4GL2/jrgQ8kmQa+DVy4AHVLkoY0b9BX1V7gzEP0fxT46CH6HwcuGEt1kqSj5idjJalzBr0kdc6gl6TOGfSS1DmDXpI6Z9BLUucMeknqnEEvSZ0z6CWpcwa9JHXOoJekzhn0ktQ5g16SOmfQS1LnDHpJ6pxBL0mdM+glqXMGvSR1zqCXpM7NG/RJTkiyK8ndSe5Jclnr/+ske9r09SQfa/1Jck2S6SR7k5y10G9CknR4894cHNgPbKqqx5KsAD6d5BNV9YqDA5J8GPizNnsucFqbXg5c2x4lSYtg3j36Gnisza5oUx1cnuR5wCbgY61rK3BDW+8uYGWSVeMtW5I0rKGO0SdZlmQP8BBwW1XtnLX4NcDtVfWdNn8KcP+s5Q+0PknSIhgq6KvqQFWtA1YD65OcPmvxrwN/OuoLJ7k0yVSSqZmZmVFXlyQNaaSrbqrqEeBOYAtAkpOB9cBfzBq2D1gza35165v7XNdV1WRVTU5MTIxatyQ9++3YAVdcMXhcQPOejE0yAfxDVT2S5ETgHODKtvh84NaqenzWKrcAb07yIQYnYR+tqgfHXLckPbvt2AGbN8MTT8Bxx8Htt8OGDQvyUsPs0a8C7kyyF/gbBsfob23LLuT/P2zzceArwDTwR8BvjqlWSerH9u2DkD9wYPC4ffuCvdS8e/RVtRc48zDLNh6ir4A3HXVlktSzjRsHe/IH9+g3blywlxrmOnpJ0rht2DA4XLN9+yDkF+iwDRj0krR4NmxY0IA/yP91I0mdM+glqXMGvSR1zqCXpM4Z9JLUOYNekjpn0EtS5wx6SeqcQS9JnTPoJalzBr0kdc6gl6TOGfSS1DmDXpI6Z9BLUucMeknqnEEvSZ2bN+iTnJBkV5K7k9yT5LLWnyTvTvLFJJ9P8tuz+q9JMp1kb5KzFvpNSJIOb5hbCe4HNlXVY0lWAJ9O8gngJ4A1wI9X1feSvKiNPxc4rU0vB65tj5KkRTBv0FdVAY+12RVtKuCNwL+qqu+1cQ+1MVuBG9p6dyVZmWRVVT049uolSfMa6hh9kmVJ9gAPAbdV1U7gx4BfSzKV5BNJTmvDTwHun7X6A61PkrQIhgr6qjpQVeuA1cD6JKcDxwOPV9Uk8EfAH4/ywkkubb8kpmZmZkatW5I0pJGuuqmqR4A7gS0M9tQ/0hZ9FPip1t7H4Nj9Qatb39znuq6qJqtqcmJiYtS6JUlDGuaqm4kkK1v7ROAc4F7gY8Ar27BfBL7Y2rcAr2tX35wNPOrxeUlaPMNcdbMK2JZkGYNfDDdV1a1JPg18MMlbGZys/Y02/uPAecA08F3g9eMvW5I0rGGuutkLnHmI/keAVx2iv4A3jaU6SdJR85OxktQ5g16SOmfQS1LnDHpJ6pxBL0mdM+glqXMGvSR1zqCXpM4Z9JLUOYNekjpn0EtS5wx6SeqcQS9JnTPoJalzBr0kdc6gl6TOGfSS1DmDXpI6Z9BLUufmDfokJyTZleTuJPckuaz1/0mSrybZ06Z1rT9JrkkynWRvkrMW+k1Ikg5v3puDA/uBTVX1WJIVwKeTfKIt+72qunnO+HOB09r0cuDa9ihJWgTz7tHXwGNtdkWb6girbAVuaOvdBaxMsuroS5UkPRNDHaNPsizJHuAh4Laq2tkWvbsdnrk6yfGt7xTg/lmrP9D6JEmLYKigr6oDVbUOWA2sT3I68E7gx4GfAV4AvH2UF05yaZKpJFMzMzMjli1JGtZIV91U1SPAncCWqnqwHZ7ZD7wfWN+G7QPWzFptdeub+1zXVdVkVU1OTEw8s+olSfMa5qqbiSQrW/tE4Bzg3oPH3ZMEeA3w2bbKLcDr2tU3ZwOPVtWDC1K9JGlew1x1swrYlmQZg18MN1XVrUnuSDIBBNgDvKGN/zhwHjANfBd4/fjLliQNa96gr6q9wJmH6N90mPEFvOnoS5MkjYOfjJWkzhn0ktQ5g16SOmfQS1LnDHpJ6pxBL0mdM+glqXMGvSR1zqCXpM4Z9JLUOYNekjpn0EtS5wx6SeqcQS9JnTPoJalzBr0kdc6gl6TOGfSS1DmDXpI6Z9BLUufmDfokJyTZleTuJPckuWzO8muSPDZr/vgkNyaZTrIzydrxly1JGtYwe/T7gU1VdQawDtiS5GyAJJPA8+eMvwR4uKpOBa4GrhxjvZKkEc0b9DVwcI99RZsqyTLgKuBtc1bZCmxr7ZuBzUkypnolSSMa6hh9kmVJ9gAPAbdV1U7gzcAtVfXgnOGnAPcDVNWTwKPACw/xnJcmmUoyNTMzczTvQZJ0BEMFfVUdqKp1wGpgfZJfAC4A/uszfeGquq6qJqtqcmJi4pk+jSRpHiNddVNVjwB3Aq8ETgWmk9wH/KMk023YPmANQJLlwEnAt8ZVsCRpNMNcdTORZGVrnwicA+yuqh+pqrVVtRb4bjv5CnALcFFrnw/cUVU1/tIlScNYPsSYVcC2dvL1OcBNVXXrEcZfD3yg7eF/G7jw6MuUJD1T8wZ9Ve0FzpxnzHNntR9ncPxekrQE+MlYSeqcQS9JnTPoJalzBr0kdc6gl6TOGfSS1DmDXpI6Z9BLUucMeknqnEEvSZ0z6CWpcwa9JHXOoJekzhn0ktQ5g16SOmfQS1LnDHpJ6pxBL0mdM+glqXPzBn2SE5LsSnJ3knuSXNb6r299e5PcnOS5rf/4JDcmmU6yM8nahX0LkqQjGWaPfj+wqarOANYBW5KcDby1qs6oqp8C/jfw5jb+EuDhqjoVuBq4cgHqliQNad6gr4HH2uyKNlVVfQcgSYATgWpjtgLbWvtmYHMbM347dsAVVwweJUmHtHyYQUmWAbuBU4H3VtXO1v9+4Dzgc8DvtuGnAPcDVNWTSR4FXgh8c6yV79gBmzfDE0/AccfB7bfDhg1jfQlJ6sFQJ2Or6kBVrQNWA+uTnN76Xw/8KPB54NdGeeEklyaZSjI1MzMzYtnA9u2DkD9wYPC4ffvozyFJPwBGuuqmqh4B7gS2zOo7AHwI+NXWtQ9YA5BkOXAS8K1DPNd1VTVZVZMTExOjV75x42BPftmywePGjaM/hyT9ABjmqpuJJCtb+0TgHOALSU5tfQF+Bbi3rXILcFFrnw/cUVXFuG3YMDhcc/nlHraRpCMY5hj9KmBbO07/HOAm4C+Av07yPCDA3cAb2/jrgQ8kmQa+DVw49qoP2rDBgJekecwb9FW1FzjzEIt+7jDjHwcuOMq6JElj4idjJalzBr0kdc6gl6TOGfSS1DmDXpI6l4W4xH3kIpIZ4GvPcPWTGfe/VxgP6xqNdY1uqdZmXaM5mrr+SVXN+4nTJRH0RyPJVFVNLnYdc1nXaKxrdEu1NusazbGoy0M3ktQ5g16SOtdD0F+32AUchnWNxrpGt1Rrs67RLHhdz/pj9JKkI+thj16SdARLMuiT/HGSh5J8dk7/byW5t92k/D2z+t/Zbkb+hSS/PKt/S+ubTvKOhair3Qh9T5vuS7JnidS1Lsldra6pJOtbf5Jc0157b5KzZq1zUZIvtemiQ73WGOo6I8mOJH+X5M/bf0A9uOxYba81Se5M8rn2vfSW1v+CJLe1939bkue3/mOyzY5Q1wVt/ntJJuess+Db7Ah1XdV+Hvcm+WjavzNfAnVd3mrak+STSX609S/q13HW8t9NUklOPmZ1VdWSm4BfAM4CPjur75XA/wKOb/Mvao8/yeDfJB8PvAT4MrCsTV8G/ilwXBvzk+Oua87y/wT8/lKoC/gkcG5rnwdsn9X+BIN/L302sLP1vwD4Snt8fms/fwHq+hvgF1v7YuDyRdheq4CzWvuHgC+2138P8I7W/w7gymO5zY5Q108A/wzYDkzOGn9MttkR6volYHnrv3LW9lrsup43a8xvA+9bCl/HNr8G+EsGnxs6+VjVtST36KvqUwz+l/1sbwT+oKr2tzEPtf6twIeqan9VfRWYBta3abqqvlJVTzC4C9bWBagL+P4NWP4l8KdLpK4CDu4tnwR8fVZdN9TAXcDKJKuAXwZuq6pvV9XDwG3MupPYGOt6KfCp1r6Np+5Mdiy314NV9ZnW/nsGt8I8haff2H4b8JpZtS34NjtcXVX1+ar6wiFWOSbb7Ah1fbKqnmzD7mJwq9GlUNd3Zg37xwx+Fg7WtWhfx7b4auBts2o6JnUtyaA/jJcCr0iyM8lfJfmZ1v/9m5E3D7S+w/UvlFcA36iqLy2Run4HuCrJ/cB/BN65ROq6h6d+uC+g3XZysepKspbB/RZ2Aj9cVQ+2Rf8H+OHFqm1OXYezlOq6mMFe6ZKoK8m72/f+a4HfXwp1JdkK7Kuqu+cMW/C6nk1Bv5zBnzBnA78H3NT2opeKX+epvfml4I3AW6tqDfBWBnf+WgouBn4zyW4Gf9Y+sViFJHku8GHgd+bsBVKDv50X5ZK0I9W1mA5XV5J3AU8CH1wqdVXVu9r3/geBNy92XQy2z7/lqV86x9SzKegfAD7S/rzZBXyPwf+I+P7NyJvVre9w/WOXwU3Q/wVw46zuxa7rIuAjrf0/GfzZvOh1VdW9VfVLVfXTDH4xfnkx6kqygsEP4Qer6uB2+kb7k5n2ePDw4DGr7TB1Hc6i15XkXwOvBl7bfjkuibpm+SBPHR5czLp+jMH5iruT3Nde4zNJfuSY1PVMDuwfiwlYy9NP4r0B+Pet/VIGf9IEeBlPP/HzFQYnfZa39kt46sTPy8ZdV+vbAvzVnL5FrYvBccGNrb0Z2N3ar+LpJ3521VMnfr7K4KTP81v7BQtQ18GT6M8BbgAuPtbbq733G4A/nNN/FU8/GfueY7nNDlfXrOXbefrJ2GOyzY6wvbYAnwMmFuN7/wh1nTar/VvAzUvp69jG3MdTJ2MXvK6j+iFeqInBnt6DwD8w2JO/pH1j/Hfgs8BngE2zxr+LwZ7hF2hXmrT+8xic8f4y8K6FqKv1/wnwhkOMX7S6gJ8Hdrcfpp3AT8/6Jnxve+2/4+nBcTGDE2fTwOsXqK63tPf+ReAPaB/aO8bb6+cZHJbZC+xp03nAC4HbgS8xuMLrBcdymx2hrn/ett9+4BvAXx7LbXaEuqYZ7HAd7HvfEqnrwwxyYi/w5wxO0C7613HOmPt4KugXvC4/GStJnXs2HaOXJD0DBr0kdc6gl6TOGfSS1DmDXpI6Z9BLUucMeknqnEEvSZ37fx1iIYZvFmeYAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"x_train = np.array([[2104],[1600],[2400]], dtype=np.float32)\n",
"y_train = np.array([[399.900], [329.900], [369.000]], dtype=np.float32)\n",
"\n",
"# x_train = np.array([[3.3], [4.4], [5.5], [6.71], [6.93], [4.168],\n",
"# [9.779], [6.182], [7.59], [2.167], [7.042],\n",
"# [10.791], [5.313], [7.997], [3.1]], dtype=np.float32)\n",
"\n",
"# y_train = np.array([[1.7], [2.76], [2.09], [3.19], [1.694], [1.573],\n",
"# [3.366], [2.596], [2.53], [1.221], [2.827],\n",
"# [3.465], [1.65], [2.904], [1.3]], dtype=np.float32)\n",
"\n",
"plt.plot(x_train, y_train, 'r.')\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 105,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T05:26:28.745318Z",
"start_time": "2019-04-07T05:26:28.741971Z"
}
},
"outputs": [],
"source": [
"x_train = torch.from_numpy(x_train)\n",
"y_train = torch.from_numpy(y_train)"
]
},
{
"cell_type": "markdown",
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T04:47:17.479477Z",
"start_time": "2019-04-07T04:47:17.468259Z"
}
},
"source": [
"`nn.Linear`\n",
"\n",
"Applies a linear transformation to the incoming data: $y = xA^T + b$"
]
},
{
"cell_type": "code",
"execution_count": 106,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T05:26:30.527459Z",
"start_time": "2019-04-07T05:26:30.516864Z"
}
},
"outputs": [],
"source": [
"# Linear Regression Model\n",
"class LinearRegression(nn.Module):\n",
" def __init__(self):\n",
" super(LinearRegression, self).__init__()\n",
" self.linear = nn.Linear(1, 1) # input and output is 1 dimension\n",
"\n",
" def forward(self, x):\n",
" out = self.linear(x)\n",
" return out\n",
"\n",
"model = LinearRegression()"
]
},
{
"cell_type": "code",
"execution_count": 107,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T05:26:31.378932Z",
"start_time": "2019-04-07T05:26:31.375266Z"
}
},
"outputs": [],
"source": [
"# Define Loss and Optimizatioin function\n",
"criterion = nn.MSELoss()\n",
"optimizer = optim.SGD(model.parameters(), lr=1e-9)#1e-4)"
]
},
{
"cell_type": "code",
"execution_count": 108,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T05:26:32.848256Z",
"start_time": "2019-04-07T05:26:32.681980Z"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Epoch[50/1000], loss: 3798.923096\n",
"Epoch[100/1000], loss: 2773.092773\n",
"Epoch[150/1000], loss: 2336.129639\n",
"Epoch[200/1000], loss: 2150.003906\n",
"Epoch[250/1000], loss: 2070.720459\n",
"Epoch[300/1000], loss: 2036.951782\n",
"Epoch[350/1000], loss: 2022.566162\n",
"Epoch[400/1000], loss: 2016.437866\n",
"Epoch[450/1000], loss: 2013.828125\n",
"Epoch[500/1000], loss: 2012.717407\n",
"Epoch[550/1000], loss: 2012.243286\n",
"Epoch[600/1000], loss: 2012.041260\n",
"Epoch[650/1000], loss: 2011.954956\n",
"Epoch[700/1000], loss: 2011.918335\n",
"Epoch[750/1000], loss: 2011.904053\n",
"Epoch[800/1000], loss: 2011.897217\n",
"Epoch[850/1000], loss: 2011.894409\n",
"Epoch[900/1000], loss: 2011.893311\n",
"Epoch[950/1000], loss: 2011.892456\n",
"Epoch[1000/1000], loss: 2011.890991\n"
]
}
],
"source": [
"num_epochs = 1000\n",
"for epoch in range(num_epochs):\n",
" inputs = Variable(x_train)\n",
" target = Variable(y_train)\n",
"\n",
" # forward\n",
" out = model(inputs)\n",
" loss = criterion(out, target)\n",
" # backward\n",
" optimizer.zero_grad()\n",
" loss.backward()\n",
" optimizer.step()\n",
"\n",
" if (epoch+1) % 50 == 0:\n",
" print('Epoch[{}/{}], loss: {:.6f}'\n",
" .format(epoch+1, num_epochs, loss.data.item()))\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"$$\n",
"\\ell(x, y) = L = \\{l_1,\\dots,l_N\\}^\\top, \\quad\n",
" l_n = \\left( x_n - y_n \\right)^2,\n",
"$$\n",
" where :`N` is the batch size. "
]
},
{
"cell_type": "code",
"execution_count": 109,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T05:26:38.112863Z",
"start_time": "2019-04-07T05:26:38.108523Z"
}
},
"outputs": [
{
"data": {
"text/plain": [
"LinearRegression(\n",
" (linear): Linear(in_features=1, out_features=1, bias=True)\n",
")"
]
},
"execution_count": 109,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"model.eval()"
]
},
{
"cell_type": "code",
"execution_count": 118,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T05:54:13.026497Z",
"start_time": "2019-04-07T05:54:12.777585Z"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZEAAAETCAYAAAD3WTuEAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvDW2N/gAAIABJREFUeJzt3Xl8VNX5x/HPY1gCAoKIgGyhij9ZjRpXfloFF2oRrNL+sLjghlWpuGFVrFTRFoWKtIKKQgWbVlREqKKCAu6y7yASNEBQISCgNIIs5/fHuUMWCJAhM3cy832/XvPKPWfuzDyZLM8899x7jjnnEBERicZhYQcgIiIVl5KIiIhETUlERESipiQiIiJRUxIREZGoKYmIiEjUlERERCRqSiIiIhI1JREREYlapbADiLWjjjrKZWRkhB2GiEiFMmfOnA3OuXoH2i/pk0hGRgazZ88OOwwRkQrFzFYdzH46nCUiIlFTEhERkagpiYiISNSSfkxkX3bs2EFeXh7btm0LOxQB0tPTady4MZUrVw47FBEpo5RMInl5edSsWZOMjAzMLOxwUppzjo0bN5KXl0fz5s3DDkdEyiglD2dt27aNunXrKoEkADOjbt26qgpFykmDBmC2961Bg9i8XkomEUAJJIHoZyFSftatK1v/oUrZJCIiIodOSSQkeXl5dO3alRYtWnDsscfSp08ffvrpp33u+/XXX9OtW7cDPufFF1/M5s2bo4rnT3/6E4MHDz7gfjVq1Njv/Zs3b2b48OFRxSAiFY+SyMHIzoaMDDjsMP81O/uQns45x2WXXcall17KihUr+OKLL9i6dSv9+vXba9+dO3dyzDHH8Oqrrx7weSdNmkTt2rUPKbZDpSQiEo4tW6BXr/i/rpLIgWRn+5/MqlXgnP/aq9chJZKpU6eSnp7OtddeC0BaWhpDhgxh1KhRFBQU8MILL9ClSxc6dOhAx44dyc3NpU2bNgAUFBTwm9/8hlatWvGrX/2K008/fc+0LhkZGWzYsIHc3FxatmzJjTfeSOvWrbnwwgv58ccfAXjuuec49dRTOfHEE7n88sspKCjYb6xfffUVZ555Jm3btuWBBx7Y079161Y6duzIySefTNu2bZkwYQIA9957LytXriQzM5O+ffuWup+IlJ+JE6FVKxg5Mv6vnRBJxMzSzGyemb0RtLPNbLmZLTazUWZWOeg3M/ubmeWY2UIzOznmwfXrByX/0RYU+P4oLVmyhFNOOaVYX61atWjatCk5OTkAzJ07l1dffZX333+/2H7Dhw+nTp06LF26lAEDBjBnzpx9vsaKFSu49dZbWbJkCbVr12bcuHEAXHbZZcyaNYsFCxbQsmVLRh7gt65Pnz7cfPPNLFq0iIYNG+7pT09PZ/z48cydO5dp06Zx11134Zxj4MCBHHvsscyfP59BgwaVup+IHLr166F7d+jaFerWhRkzoH79fe9bWv+hSogkAvQBlhVpZwMnAG2BasANQf8vgBbBrRfwdMwjW726bP3l5IILLuDII4/cq/+jjz6ie/fuALRp04Z27drt8/HNmzcnMzMTgFNOOYXc3FwAFi9ezNlnn03btm3Jzs5myZIl+43j448/5oorrgDgqquu2tPvnOP++++nXbt2nH/++axdu5Z1+zj942D3E5GD55w/GNKqFYwfDwMGwOzZkJUF337r7y95+/bb2MQSehIxs8bAL4HnI33OuUkuAMwEGgd3dQXGBHd9BtQ2s4Z7PWl5atq0bP0HoVWrVntVEN9//z2rV6/muOOOA+Dwww+P+vkBqlatumc7LS2NnTt3AtCzZ0+eeuopFi1aRP/+/Q/q+ox9nYKbnZ1Nfn4+c+bMYf78+dSvX3+fz3Ww+4nIwVmzBi65BK68Elq0gHnz4IEHoEqVcOIJPYkATwL3ALtL3hEcxroKeDvoagSsKbJLXtBX8nG9zGy2mc3Oz88/tOgefRSqVy/eV726749Sx44dKSgoYMyYMQDs2rWLu+66i549e1K95GuV0L59e15++WUAli5dyqJFi8r02j/88AMNGzZkx44dZB/EuE779u156aWXAIrtv2XLFo4++mgqV67MtGnTWLXKzxpds2ZNfvjhhwPuJyJls3s3PPMMtG4N06bBk0/CRx/5aiRMoSYRM+sMrHfO7fvAPgwHPnDOfViW53XOjXDOZTnnsurVO+CaKvvXoweMGAHNmvnLPps18+0ePaJ+SjNj/PjxvPLKK7Ro0YLjjz+e9PR0/vznPx/wsbfccgv5+fm0atWKBx54gNatW3PEEUcc9GsPGDCA008/nfbt23PCCScccP+hQ4cybNgw2rZty9q1a/f09+jRg9mzZ9O2bVvGjBmz57nq1q1L+/btadOmDX379i11PxE5eCtWQIcOcPPNcPrpsHgx9OkDaWlhRwYW5iCnmf0FX2nsBNKBWsBrzrkrzaw/cBJwmXNud7D/s8B059y/g/Zy4Fzn3DelvUZWVpYruSjVsmXLaNmyZSy+pZjbtWsXO3bsID09nZUrV3L++eezfPlyqoRVy5aTivwzEYmVnTthyBB48EGoWhWeeAKuvdZ/no01M5vjnMs60H6hTsDonLsPuA/AzM4F7g4SyA3ARUDHSAIJTAR6m9lLwOnAlv0lkGRUUFDAeeedx44dO3DOMXz48AqfQERkbwsWwPXXw5w5cOmlMGwYHHNM2FHtLVFn8X0GWAV8GgzqvuacexiYBFwM5AAFwLWhRRiSmjVrarlfkSS2fTs88ggMHAhHHgkvvwzdusWn+ohGwiQR59x0YHqwvc+4grO1bo1fVCIi8fPpp776WLYMrr7aH76qWzfsqPYvEc7OEhFJaf/9L9x+O7RvD1u3wqRJMHp04icQSKBKREQkFb37Ltx4I+Tmwq23wl/+AjVrhh3VwVMlIiISgk2b/KGrCy7wFwp+8AE89VTFSiCgJBKatLQ0MjMz99xyc3OZPXs2t912GwDTp0/nk08+2bP/66+/ztKlS/e0H3zwQd59991yiSUycWNREydOZODAgeXy/CJS3Pjx/iLB0aPh3nv9mVhnnx12VNHR4awDaNBg3yuC1a9/aHPRVKtWjfnz5xfry8jIICvLn5Y9ffp0atSowVlnnQX4JNK5c2daBZenPvzww9G/+EHo0qULXbp0ielriKSadevg97+HV16BzEx48004OfbTyMaUKpEDiOdSk9OnT6dz587k5ubyzDPPMGTIEDIzM3n//feZOHEiffv2JTMzk5UrV9KzZ889a4xkZGTQv3//PdOtf/755wDk5+dzwQUX0Lp1a2644QaaNWu2V8VRmhdeeIHevXsDfr6t2267jbPOOouf/exnxdY2GTRoEKeeeirt2rWjf//+5fyOiCQH52DMGGjZEiZM8LMmzZxZ8RMIqBLh9tuhREFw0M49d9/9mZl+Xpv9+fHHH/fMstu8eXPGjx+/576MjAx+97vfUaNGDe6++27AVwadO3cudYXDo446irlz5zJ8+HAGDx7M888/z0MPPUSHDh247777ePvttw847fv+fPPNN3z00Ud8/vnndOnShW7dujF58mRWrFjBzJkzcc7RpUsXPvjgA84555yoX0ck2axeDTfdBG+/DWed5df8SKbZf1I+iYRlX4ezDsVll10G+GnfX3vtNcBPGx9JTp06daJOnTpRP/+ll17KYYcdRqtWrfZM5T558mQmT57MSSedBPiFqlasWKEkIoKfMPHpp/2Yh3Pw97/DLbf4BVKTSconkQNVDPu7SnT69HIN5ZBEpn4vOu17LJ4f2LOolHOO++67j5tuuqncX0+kIlu+HG64wc+ye+GF8OyzfmXtZJRkOTF5lJxSvWT7YBSdNn7y5Mls2rSpXGO86KKLGDVqFFu3bgVg7dq1rF+/vlxfQ6Qi2bHDT1dy4omwZAm88II/jJWsCQSURA4o3ktNRlxyySWMHz+ezMxMPvzwQ7p3786gQYM46aSTWLly5UE9R//+/Zk8eTJt2rThlVdeoUGDBtQs5ST0du3a0bhxYxo3bsydd955UM9/4YUX8tvf/nbPGuzdunUrc6ITSRbz5vlp2u+7Dzp3hqVL4ZprEnfOq/IS6lTw8ZBsU8GXxfbt20lLS6NSpUp8+umn3HzzzeU6DlOeUuVnIsln2za/PO1jj8FRR/nZdi+/POyoDl2FmApeYmv16tX85je/Yffu3VSpUoXnnnsu7JBEksrHH/urzpcv9+t8DB7sZ95NJUoiSaxFixbMmzcv7DBEks7WrXD//X6akqZN4Z13/AB6KkrZMZFkP4xXkehnIRXJO+/4dc6fespffb54ceomEEjRJJKens7GjRv1zysBOOfYuHEj6enpYYcisl/ffQc9e0KnTlC9Onz4IQwdCjVqhB1ZuFLycFbjxo3Jy8sjPz8/7FAEn9QbN24cdhgipRo3zk/TvmED9OsHDzwA+tzjpWQSqVy5Ms2bNw87DBFJcN98A717w2uvwUkn+Ws+gtmKJJCSh7NERPbHOX+hYKtWfqbdgQP9hIlKIHtLiCRiZmlmNs/M3gjazc1shpnlmNlYM6sS9FcN2jnB/Rlhxi0iySc3Fy66yJ+y27YtLFwIf/gDVErJ4zYHlhBJBOgDLCvSfgwY4pw7DtgEXB/0Xw9sCvqHBPuJSHnKzvbzdBx2mP+anR12RHGxaxf87W/Qpg18+qm/aHD6dDj++LAjS2yhJxEzawz8Eng+aBvQAYgsWjEauDTY7hq0Ce7vGOwvIuUhOxt69YJVq/wxnVWrfDvJE8myZXDOOdCnj19hcMmS5JxxNxYS4S16ErgH2B206wKbnXORqWjzgEbBdiNgDUBw/5Zg/2LMrJeZzTaz2ToDS6QM+vWDgoLifQUFvj8J7djhF4jKzITPP/cLR02a5C8glIMTahIxs87AeufcnPJ8XufcCOdclnMuq169euX51CLJbfXqsvVXYHPnwqmn+tN1L73UT5h41VXJP2FieQu7EmkPdDGzXOAl/GGsoUBtM4sMYzUG1gbba4EmAMH9RwAb4xmwSFIr7SN4En00//FHv1DUaafB+vUwfjyMHRv7mbmTVahJxDl3n3OusXMuA+gOTHXO9QCmAZF1YK8BJgTbE4M2wf1TnS47Fyk/jz7qL8cuqnp1358EPvjAr/Xx2GP+6vOlS30VItELuxIpzR+AO80sBz/mEVkcfCRQN+i/E7g3pPhEklOPHjBiBDRr5o/rNGvm2z16hB3ZIfn+e3/F+c9/Djt3wrvvwvPPQ+3aYUdW8aXkeiIikjreegtuugny8vzZV488AocfHnZUiU/riYhIStu4Ee64A1580V95/skncMYZYUeVfBL1cJaISFScg5dfhpYt4d//hj/+0Z+JpQQSG6pERCRpfP21v0hwwgTIyvJjH+3ahR1VclMlIiIVnnMwcqQ/bPXOOzBokJ+6RAkk9lSJiEiF9uWXcOONMHWqP/vq+efhuOPCjip1qBIRkQpp1y548kk/0+6sWfDMMz6RKIHElyoREalwliyB66+HGTPgl7/0CUSLY4ZDlYiIVBg//QQDBvhVBnNy/OTC//mPEkiYVImISIUwa5avPhYtgiuugKFDQfOrhk+ViIgktIIC6NvXX+fx3XcwcSL8619KIIlClYiIJKzp0/2ZVzk5fm2sxx+HI44IOyopSpWIiCScLVvgd7+D887z14BMnQrPPqsEkoiUREQkobz5JrRuDc89B3fdBQsX+mQiiUlJREQSQn6+n3G+c2eoU8dfcT548N7Lm0hiURIRkVA55ydKbNUKXnkF/vQnmDPHrzwoiU8D6yISmrw8uPlmeOMNnzRGjoQ2bcKOSspClYiIxN3u3X7BxNat4b334Ikn/HofSiAVjyoREYmrnBx/2u706X7A/Lnn4Nhjw45KoqVKRETiYtcu+Otf/fTsc+f65PHee0ogFV2oScTM0s1sppktMLMlZvZQ0N/RzOaa2Xwz+8jMjgv6q5rZWDPLMbMZZpYRZvwicnAWLYIzz4S774bzz4elS+GGG8As7MjkUIVdiWwHOjjnTgQygU5mdgbwNNDDOZcJ/At4INj/emCTc+44YAjwWAgxi8hB2r4d+veHk0+G3Fx46SW/6mCjRmFHJuUl1CTivK1Bs3Jwc8GtVtB/BPB1sN0VGB1svwp0NNNnGZFENGMGnHIKPPwwdO/uq4//+z9VH8km7EoEM0szs/nAemCKc24GcAMwyczygKuAgcHujYA1AM65ncAWoO4+nrOXmc02s9n5+fnx+DZEJPDf/8Kdd/rDV1u2+NN3X3wRjjoq7MgkFkJPIs65XcFhq8bAaWbWBrgDuNg51xj4B/BEGZ9zhHMuyzmXVU9TfYrEzdSpfuB8yBA/99WSJX7RKEleoSeRCOfcZmAa8AvgxKAiARgLnBVsrwWaAJhZJfyhro1xDlVESti82Z+227EjHHaYP313+HCoVeuAD5UKLuyzs+qZWe1guxpwAbAMOMLMjg92i/QBTASuCba7AVOdcy6OIYtICRMn+osGR42Ce+7xEyb+/OdhRyXxEvbFhg2B0WaWhk9oLzvn3jCzG4FxZrYb2ARcF+w/EnjRzHKA74DuYQQtIrB+Pdx2G4wd6w9hTZgAWVlhRyXxFmoScc4tBE7aR/94YPw++rcBv45DaCJSCuf82uZ9+sDWrX7N8z/8ASpXDjsyCUPYlYiIVCBr1vgB80mT/HK1I0f62XcldSXMwLqIJK7du+Hpp/3Yx/Tp8OST8NFHSiCiSkREimjQANat27u/cmXYscNPWTJiBDRvHv/YJDEpiYjIHvtKIOATyKhR0LOnrjiX4pREROSgXHtt2BFIItKYiIiIRE1JREQAv9aHSFkpiYikuHXr/DjH3XeHHYmUm+xsyMjwc9BkZPh2jCiJiKSwe+7xZ2RFlDZfaf368YlHykF2NvTqBatW+StDV63y7RglEiURkRT05Ze++hg0yLf/8hf//2b9ev+15O3bb8ONV8qgXz8oKCjeV1Dg+2NAZ2eJpJirroJ//rOwvWkT1K4dXjxSzlavLlv/IVIlIpIiFizw1UckgYwc6asMJZAk07Rp2foPkZKISJJzzq/zkZnp27Vq+aMb1123/8dJBfXoo1C9evG+6tV9fwwoiYgksQ8+8CfoTJ3q26+/7pesrVYt3Lgkhnr08HPTNGvmS89mzXy7R4+YvJzGRESS0M6d0KYNLF/u2yecAIsWQSX9xaeGHj1iljRKUiUikmQmTPATJkYSyPvvw7JlSiASG/q1EkkSP/4IRx/tF4oC6NAB3n1XEyZKbKkSEUkCo0b5sdNIApk/H957TwlEYk+ViEgFtnkz1KlT2L7ySnjxxfDikdQTaiViZulmNtPMFpjZEjN7KOg3M3vUzL4ws2VmdluR/r+ZWY6ZLTSzk8OMXyRMjz1WPIGsXKkEIvEXdiWyHejgnNtqZpWBj8zsLaAl0AQ4wTm328yODvb/BdAiuJ0OPB18FUkZ33wDxxxT2O7bFx5/PLx4JLWFmkSccw4IjuJSObg54Gbgt8653cF+64N9ugJjgsd9Zma1zayhc+6bOIcuEoo77vDrm0d8+60mR5RwhT6wbmZpZjYfWA9Mcc7NAI4F/s/MZpvZW2bWIti9EbCmyMPzgr6Sz9kreOzs/Pz8WH8LIjGXk+MHySMJZPBgfyW6EoiELfQk4pzb5ZzLBBoDp5lZG6AqsM05lwU8B4wq43OOcM5lOeey6pU2t7VIBeAcdO8OLVoU9m3ZAnfdFV5MIkWFnkQinHObgWlAJ3yF8Vpw13igXbC9Fj9WEtE46BNJOvPm+SlLxo717dGjfVKpVSvcuESKCvvsrHpmVjvYrgZcAHwOvA6cF+z2c+CLYHsicHVwltYZwBaNh0iy2b0bzj4bTg7OPaxb119IePXV4cYlsi9lGlg3s/rOuXXl+PoNgdFmloZPaC87594ws4+AbDO7Az/wfkOw/yTgYiAHKACuLcdYREI3bZq/0jzijTfgl78MLx6RAynr2Vmrzex14Fnn3NRDfXHn3ELgpH30bwb2+tMJzsq69VBfVyTR7NjhJ0n88kvfbtcO5s6FtLRw4xI5kLIezvoC+DUwJbgQ8C4zqxuDuERSxrhxUKVKYQL5+GO/gJQSiFQEZUoizrm2wP8CL+JPrR0E5JlZtpmdE4P4RJJWQYFf16NbN9/u1MmPh5x1VrhxiZRFmQfWnXOfOOd6AscAffDjE1cA08xsqZn1MbM6+3sOkVQ3YgQcfjhs2+bbixbBW29pwkSpeKI+O8s5t8U59/ci1ckYoBnwBL46ecHMssopTpGk8N13PlHcdJNvX3utP223TZtw4xKJVnmd4rsB2ARsAwx/seDVwAwze93Mjiyn1xGpsB55xJ+uG/HVV34Kd5GKLOokYmaVzay7mU0DlgG3A/nAncBRQAfgHaALMKwcYhWpkNau9dXHH//o2/ff76uPjIxQwxIpF2WegNHMjgN6AT2BusBu/MWBw51z7xXZdTow3cxexV+FLpJyeveGYUU+Qq1fD5qJR5JJWS82fA84F3/I6htgADDCOff1fh42B/hVtAGKVETLl/vrPiKGDoXbbgsvHpFYKWslch5+fqvhwOvOuV0H8Zj/APtLMiJJwzl/yu5rrxX2ff891KwZXkwisVTWJNLSObe8LA9wzi0GFpfxdUQqnFmz4LTTCtvZ2fDb34YXj0g8lCmJlDWBiKSC3bvhzDNh5kzfbtAAcnOhatVQwxKJi4SZCl6kIpoyxU9PEkkgb73ll69VApFUEfYa6yIV0k8/wbHHQl6eb59yCsyYofmuJPWoEhEpo5df9pVGJIF8+inMnq0EIqlJlYjIQdq6FY44wo+BAFxyCUyYoPmuJLWpEhE5CMOG+dN0IwlkyRKYOFEJRESViMh+bNhQ/Arzm26CZ54JLx6RRKNKRKQU/fsXTyCrVyuBiJSkJCJSwpo1/jDVww/7dv/+/kr0Jk3CjUskEYWaRMws3cxmmtkCM1tiZg+VuP9vZra1SLuqmY01sxwzm2FmGfGOWZLbTTdB06aF7Q0b4E9/Ci0ckYQXdiWyHejgnDsRyAQ6mdkZAMGCViVXSLwe2OScOw4YAjwWz2AleS1d6quPESN8e9gwX30UXf9DRPYWahJxXqTSqBzcnJml4ddvv6fEQ7oCo4PtV4GOZjo/RqLnHHTuDK1b+3ZaGvzwA9xyS7hxiVQUYVcimFmamc0H1gNTnHMzgN7AROfcNyV2bwSsAXDO7QS24Nc0KfmcvcxstpnNzs/Pj+03IBXWZ5/BYYfBm2/69tixsHMn1KgRblwiFUnop/gG08lnmlltYLyZnQP8Gr9uSbTPOQIYAZCVleXKI05JHrt2wamnwrx5vt20KaxYAVWqhBuXSEUUeiUS4ZzbjF+r5DzgOCDHzHKB6maWE+y2FmgCYGaVgCOAjfGPViqqt9+GSpUKE8iUKbBqlRKISLRCrUTMrB6wwzm32cyqARcAjznnGhTZZ2swkA4wEbgG+BToBkx1zqnSkAPavh2aNYN163z7jDPg44/94SwRiV7Yf0INgWlmthCYhR8TeWM/+48E6gaVyZ3AvXGIUSq4f/0L0tMLE8isWX7SRCUQkUMXaiXinFsInHSAfWoU2d6GHy8ROaAffoBatQrbl10Gr76q+a5EypM+i0lSGjq0eAL5/HMYN04JRKS8hX52lkh5Wr8e6tcvbPfuDX//e3jxiCQ7VSKSNPr1K55A8vKUQERiTUlEKrzcXH+Y6s9/9u1HHvFXojdqFGpYIilBh7OkQrvuOvjHPwrbGzfCkUeGF49IqlElsi/Z2ZCR4c8BzcjwbUkoixb56iOSQJ591lcfSiAi8aVKpKTsbOjVCwoKfHvVKt8G6NEjvLgE8ImiUyeYPNm3q1Xz07VXrx5uXCKpSpVISf36FSaQiIIC3y+hilxhHkkg48b5H40SiEh4VImUtHp12fol5nbtgsxMWLzYt487zq//UblyuHGJiCqRvRVd1u5g+iWm3njDT5gYSSBTp/oZd5VARBKDkkhJjz669/GR6tV9v8TNtm1+kPySS3z7nHN8RXLeeeHGJSLFKYmU1KOHXyO1WTN/+k+zZr6tQfW4GT3aD5hv2uTbc+bA++9rwkSRRKQxkX3p0UNJIwRbtkDt2oXt7t39DLya70okcemznSSEv/61eAJZsQL+/W8lEJFEp0pEQrVuHTRoUNi+4w544onw4hGRslElIqHp27d4Avn6ayUQkYpGSUTi7ssv/WGqwYN9e+BAfyV6w4bhxiUiZafDWRJXV15ZfCqyTZuKj4WISMWiSkTiYsECX31EEsjIkb76UAIRqdhCTSJmlm5mM81sgZktMbOHgv5sM1tuZovNbJSZVQ76zcz+ZmY5ZrbQzE4OM345MOf8BYKZmb5dq5af7+q668KNS0TKR9iVyHagg3PuRCAT6GRmZwDZwAlAW6AacEOw/y+AFsGtF/B03COWg/bBB/4CwenTffv11/21INWqhRqWiJSjUMdEnHMO2Bo0Kwc355ybFNnHzGYCjYNmV2BM8LjPzKy2mTV0zn0Tz7hl/3buhNat4YsvfPuEE/z6H5U0AieSdMKuRDCzNDObD6wHpjjnZhS5rzJwFfB20NUIWFPk4XlBX8nn7GVms81sdn5+fuyCl728/rqfHDGSQN5/H5YtUwIRSVahJxHn3C7nXCa+2jjNzNoUuXs48IFz7sMyPucI51yWcy6rXr165RmulOLHH6FGDfjVr3y7QwfYvdtPnCgiySv0JBLhnNsMTAM6AZhZf6AecGeR3dYCTYq0Gwd9EqKRI/1Ex//9r2/Pnw/vvacpS0RSQdhnZ9Uzs9rBdjXgAuBzM7sBuAi4wjm3u8hDJgJXB2dpnQFs0XhIeDZv9onihuC0hyuv9GdjnXhiuHGJSPyEfaS6ITDazNLwCe1l59wbZrYTWAV8av7j7GvOuYeBScDFQA5QAFwbTtgycCDcd19he+VK+NnPwotHRMIR9tlZC4GT9tG/z7iCs7JujXVcUrqvv4ZGRU5luOceeOyx8OIRkXCFXYlIBXLHHfDkk4Xtb7+F+vXDi0dEwpcwA+uSuFas8GMfkQQyeLAf+1ACERFVIlIq5/zqgi+/XNi3ZYufukREBFSJSCm8CQyyAAANOElEQVTmzvVTlkQSyJgxPqkogYhIUapEpJjIBYIff+zbRx0Fa9ZAenq4cYlIYlIlIntMmwZpaYUJ5I03ID9fCURESqdKRNixA/7nf+Crr3y7XTt/OCstLdy4RCTxqRJJcePGQZUqhQnk44/9AlJKICJyMFSJpKj//hfq1oXt2327UyeYNEnzXYlI2agSSUHPPutn3I0kkEWL4K23lEBEpOxUiaSQ777z1UfEddf5GXhFRKKlSiRFDBhQPIF89ZUSiIgcOlUiSW7tWmjcuLB9//3w6KPhxSMiyUVJJIn17g3DhhW2168HLfQoIuVJh7OS0PLlfpA8kkCGDvVTliiBiEh5UyWSRJyDyy6D118v7Pv+e6hZM7yYRCS5qRJJErNm+QkTIwkkO9snFSUQEYklVSIV3O7dcOaZMHOmbzds6M+8qlo13LhEJDWoEqnApkzx05NEEsjbb/vla5VARCReQk0iZpZuZjPNbIGZLTGzh4L+5mY2w8xyzGysmVUJ+qsG7Zzg/oww4w/LTz9BkyZw4YW+fcopsHMnXHRRuHGJSOoJuxLZDnRwzp0IZAKdzOwM4DFgiHPuOGATcH2w//XApqB/SLBfShk71lcaeXm+/dlnMHu2JkwUkXCEmkSctzVoVg5uDugAvBr0jwYuDba7Bm2C+zuapcaMT1u3+oHz7t19u0sXPx5y+unhxiUiqS3sSgQzSzOz+cB6YAqwEtjsnNsZ7JIHNAq2GwFrAIL7twB1KcHMepnZbDObnZ+fH+tvIeaeesqfZeWcby9dChMmaMJEEQlf6EnEObfLOZcJNAZOA04oh+cc4ZzLcs5l1avAV9ht2OATxe9/79s33eQTScuW4cYlIhIRehKJcM5tBqYBZwK1zSxy+nFjYG2wvRZoAhDcfwSwMc6hxsWDDxa/wnz1anjmmfDiERHZl7DPzqpnZrWD7WrABcAyfDLpFux2DTAh2J4YtAnun+pc5CBPcli92lcfAwb4dv/+vvpo0iTcuERE9iXsiw0bAqPNLA2f0F52zr1hZkuBl8zsEWAeEJm0fCTwopnlAN8B3cMIOlZ69YLnnitsb9hQfPp2EZFEE2oScc4tBE7aR/+X+PGRkv3bgF/HIbS4WroUWrcubA8bBrfcEl48IiIHK+xKJKU5B5dcAm++6duVKsHmzXD44eHGJSJysBJmYD3VfPqpv+4jkkDGjoUdO5RARKRiUSUSZ7t2wamnwrx5vt20KaxYAVWqhBuXiEg0VInE0Vtv+UNWkQQyZQqsWqUEIiIVlyqRONi+3Vcc69f79plnwkcf+cNZIiIVmf6NxVh2NqSnFyaQWbPgk0+UQEQkOagSiZHvv4cjjihsX345vPKK5rsSkeSiz8Mx8OSTxRPI8uXw6qtKICKSfFSJlKP166F+/cJ2797w97+HF4+ISKypEikn999fPIHk5SmBiEjyUxI5RLm5/jDVX/7i24884q9Eb9Rovw8TEUkKOpx1CHr2hNGjC9vffQd16oQWjohI3KkSicKiRb76iCSQESN89aEEIiKpRpVIGTgHF13krzQHqFbNT9devXq4cYmIhEWVyEH6+GN/gWAkgYwbBwUFSiAiktpUiZTQoAGsW1f6/cceC8uWQeXK8YtJRCRRqRIpYX8JZNo0yMlRAhERiVASKYNzzw07AhGRxKIkIiIiUQs1iZhZEzObZmZLzWyJmfUJ+jPN7DMzm29ms83stKDfzOxvZpZjZgvN7OQw4xcRSXVhD6zvBO5yzs01s5rAHDObAjwOPOSce8vMLg7a5wK/AFoEt9OBp4OvIiISglArEefcN865ucH2D8AyoBHggFrBbkcAXwfbXYExzvsMqG1mDcszpqLzXx1Mv4hIKgu7EtnDzDKAk4AZwO3AO2Y2GJ/ozgp2awSsKfKwvKDvmxLP1QvoBdC0adMyxfHtt2UOXUQkZSXEwLqZ1QDGAbc7574HbgbucM41Ae4ARpbl+ZxzI5xzWc65rHr16pV/wCIiAiRAEjGzyvgEku2cey3ovgaIbL8CnBZsrwWaFHl446BPRERCEPbZWYavMpY5554octfXwM+D7Q7AimB7InB1cJbWGcAW51yxQ1kiIhI/YY+JtAeuAhaZ2fyg737gRmComVUCthGMbwCTgIuBHKAAuDa+4YqISFGhJhHn3EdAaSuPn7KP/R1wa0yDEhGRg2b+/3LyMrN8YFWUDz8K2FCO4ZQXxVU2iqvsEjU2xVU2hxJXM+fcAc9MSvokcijMbLZzLivsOEpSXGWjuMouUWNTXGUTj7hCPztLREQqLiURERGJmpLI/o0IO4BSKK6yUVxll6ixKa6yiXlcGhMREZGoqRIREZGopVwSMbNRZrbezBaX6P+9mX0erGvyeJH++4L1S5ab2UVF+jsFfTlmdm8s4jKzscGaKvPNLLfIBZlhx1Xm9V7M7BozWxHcrolRXCea2admtsjM/mNmtYrcF6/3q7Q1co40synB9z/FzOoE/XF5z/YT16+D9m4zyyrxmJi/Z/uJa1Dw97jQzMabWe0EiWtAENN8M5tsZscE/aH+HIvcf5eZOTM7Km5xOedS6gacA5wMLC7Sdx7wLlA1aB8dfG0FLACqAs2BlUBacFsJ/AyoEuzTqrzjKnH/X4EHEyEuYDLwi2D7YmB6ke238BeQngHMCPqPBL4MvtYJtuvEIK5ZwM+D7euAASG8Xw2Bk4PtmsAXwes/Dtwb9N8LPBbP92w/cbUE/geYDmQV2T8u79l+4roQqBT0P1bk/Qo7rlpF9rkNeCYRfo5BuwnwDv66uKPiFVfKVSLOuQ+A70p03wwMdM5tD/ZZH/R3BV5yzm13zn2Fn27ltOCW45z70jn3E/BSsG95xwXsmWPsN8C/EySusq73chEwxTn3nXNuEzAF6BSDuI4HPgi2pwCXF4krXu9XaWvkdAVGB7uNBi4tElvM37PS4nLOLXPOLd/HQ+Lynu0nrsnOuZ3Bbp/hJ1tNhLi+L7Lb4fi/hUhcof0cg7uHAPcUiSkucaVcEinF8cDZZjbDzN43s1OD/tLWLymtP1bOBtY55yITUYYd1+3AIDNbAwwG7kuQuJZQ+I/j1xTO+BxKXFZ8jZz6rnCy0G+ByDJncY+tRFylSaS4rsN/mk6IuMzs0eB3vwfwYCLEZWZdgbXOuQUldot5XEoiXiV8WXcG0Bd4Ofj0nyiuoLAKSQSHtN5LDF0H3GJmc/Cl/k9hBWJ7r5Gzh/PHE0I5LXJ/cYWptLjMrB9+Ge3sRInLOdcv+N3PBnqHHRf+/bmfwoQWV0oiXh7wWlDyzQR24+ecKW39krita2J+JuPLgLFFusOOq6zrvcQlLufc5865C51zp+CT7sow4rJ9r5GzLjiMQPA1csg0brGVEldpQo/LzHoCnYEeQeJNiLiKyKbwkGmYcR2LHx9aYGa5wWvMNbMGcYkrmoGUin4DMig+IPs74OFg+3h8mWdAa4oP4n2JH8CrFGw3p3AQr3V5xxX0dQLeL9EXalz447DnBtsdgTnB9i8pPog30xUO4n2FH8CrE2wfGYO4IidEHAaMAa6L9/sVfO9jgCdL9A+i+MD64/F8z0qLq8j90yk+sB6X92w/71cnYClQL4zf/f3E1aLI9u+BVxPp5xjsk0vhwHrM4zqkP+KKeMN/Qv0G2IGvQK4Pfun+CSwG5gIdiuzfD/+JdjnBGUlB/8X4MyNWAv1iEVfQ/wLwu33sH1pcwP8Cc4I/1BnAKUV+wYcFr72I4v+UrsMPguYA18Yorj7B9/4FMJDgYto4v1//iz9UtRCYH9wuBuoC7+EXWHs38gcbr/dsP3H9Knj/tgPrgHfi+Z7tJ64c/Ie5SN8zCRLXOPz/iYXAf/CD7aH/HEvsk0thEol5XLpiXUREoqYxERERiZqSiIiIRE1JREREoqYkIiIiUVMSERGRqCmJiIhI1JREROLAzK4Ppuh+az/7vBnsc0s8YxM5FEoiInHgnBsJTAQ6mdmtJe83s5sJpu12zg2Pd3wi0dLFhiJxYmZH4692Phy/JsTyoP94YB7wI9DGOfdteFGKlI0qEZE4cX6dmhuB6sA/zaxSMMHmP4O+XkogUtFUCjsAkVTinJtgZqPw8xZFpu4+FXjBHXhmXZGEo8NZInFmZjXxk1c2DbrWAO2cX6lOpELR4SyROAuSxcMUrg1+sxKIVFRKIiJxZmbVgD8U6fp1WLGIHColEZH4exw4ARiKXw/iOjO7JNyQRKKjMRGRODKzC4G38af6ngq0AGYDm/Gn924IMTyRMlMlIhInZnYk8A/8aoxXOue2O+cWA38E6gNPhxmfSDSURETi5xngGOAB59zCIv1/BT4EupnZlaFEJhIlHc4SiQMzuwoYA3wAnOec213i/ub4dbN3Am2dc3nxj1Kk7JRERGLMzJriE4ThrwdZVcp+NwDPAVOAi5z+OKUCUBIREZGoaUxERESipiQiIiJRUxIREZGoKYmIiEjUlERERCRqSiIiIhI1JREREYmakoiIiERNSURERKKmJCIiIlH7f1gLS3bZv0mkAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"predict = model(Variable(x_train))\n",
"predict = predict.data.numpy()\n",
"plt.plot(x_train.numpy(), y_train.numpy(), 'ro', label='Original data')\n",
"plt.plot(x_train.numpy(), predict, 'b-s', label='Fitting Line')\n",
"plt.xlabel('X', fontsize= 20)\n",
"plt.ylabel('y', fontsize= 20)\n",
"plt.legend()\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"使用pytorch建立卷积神经网络并处理MNIST数据。\n",
"https://computational-communication.com/pytorch-mnist/"
]
}
],
"metadata": {
"celltoolbar": "Slideshow",
"kernelspec": {
"display_name": "Python [default]",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.4"
},
"latex_envs": {
"LaTeX_envs_menu_present": true,
"autoclose": false,
"autocomplete": true,
"bibliofile": "biblio.bib",
"cite_by": "apalike",
"current_citInitial": 1,
"eqLabelWithNumbers": true,
"eqNumInitial": 1,
"hotkeys": {
"equation": "Ctrl-E",
"itemize": "Ctrl-I"
},
"labels_anchors": false,
"latex_user_defs": false,
"report_style_numbering": false,
"user_envs_cfg": false
},
"toc": {
"base_numbering": 1,
"nav_menu": {},
"number_sections": false,
"sideBar": true,
"skip_h1_title": false,
"title_cell": "Table of Contents",
"title_sidebar": "Contents",
"toc_cell": false,
"toc_position": {},
"toc_section_display": true,
"toc_window_display": false
}
},
"nbformat": 4,
"nbformat_minor": 2
}
\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## softmax\n",
"\n",
"The softmax function, also known as softargmax or normalized exponential function, is a function that takes as input a vector of K real numbers, and normalizes it into a probability distribution consisting of K probabilities. \n",
"\n",
"$$softmax = \\frac{e^x}{\\sum e^x}$$\n"
]
},
{
"cell_type": "code",
"execution_count": 128,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T13:57:33.466056Z",
"start_time": "2019-04-07T13:57:33.459580Z"
},
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"text/plain": [
"array([0.02364054, 0.06426166, 0.1746813 , 0.474833 , 0.02364054,\n",
" 0.06426166, 0.1746813 ])"
]
},
"execution_count": 128,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"def softmax(s):\n",
" return np.exp(s) / np.sum(np.exp(s), axis=0)\n",
"\n",
"softmax([1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0])"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
"That is, prior to applying softmax, some vector components could be negative, or greater than one; and might not sum to 1; but after applying softmax, each component will be in the interval (0,1), and the components will add up to 1, so that they can be interpreted as probabilities. \n",
"\n",
"Furthermore, the larger input components will correspond to larger probabilities. \n",
"\n",
"Softmax is often used in neural networks, to map the non-normalized output of a network to a probability distribution over predicted output classes."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## Activation Function\n"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T03:59:39.599371Z",
"start_time": "2019-04-07T03:59:39.593104Z"
},
"code_folding": [],
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"text/plain": [
"0.6224593312018546"
]
},
"execution_count": 12,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"import numpy as np\n",
"def sigmoid(x):\n",
" return 1/(1 + np.exp(-x))\n",
"\n",
"sigmoid(0.5)"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T04:01:24.575040Z",
"start_time": "2019-04-07T04:01:24.567328Z"
},
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"text/plain": [
"0.5"
]
},
"execution_count": 13,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Naive scalar relu implementation. \n",
"# In the real world, most calculations are done on vectors\n",
"def relu(x):\n",
" if x < 0:\n",
" return 0\n",
" else:\n",
" return x\n",
"\n",
"relu(0.5)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# WHAT IS PYTORCH?\n",
"\n",
"It’s a Python-based scientific computing package targeted at two sets of audiences:\n",
"\n",
"- A replacement for NumPy to use the power of GPUs\n",
"- a deep learning research platform that provides maximum flexibility and speed"
]
},
{
"cell_type": "code",
"execution_count": 44,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T04:43:15.243401Z",
"start_time": "2019-04-07T04:43:14.333403Z"
}
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"import matplotlib.pyplot as plt\n",
"import torch\n",
"from torch import nn, optim\n",
"from torch.autograd import Variable\n",
"import numpy as np"
]
},
{
"cell_type": "code",
"execution_count": 104,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T05:26:28.414285Z",
"start_time": "2019-04-07T05:26:28.201996Z"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXoAAAD8CAYAAAB5Pm/hAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvDW2N/gAAFRdJREFUeJzt3X+QXWd93/H3B0n+0RIswEuiWKKisWkSPLHsbISVhERI40Q2TEQbu3HKDC526oFAQphM+FE6mXFdxjFu69QdxoxTh8iUBrvmRxwHJri2FcKMLGVFZAWDgQVMbeHiBWwTD7Uci2//uI/weitp77XuatcP79fMmfuc5zzn3u89u/vZs+ecuydVhSSpX89Z7AIkSQvLoJekzhn0ktQ5g16SOmfQS1LnDHpJ6pxBL0mdM+glqXMGvSR1bvliFwBw8skn19q1axe7DEl6Vtm9e/c3q2pivnFLIujXrl3L1NTUYpchSc8qSb42zDgP3UhS5wx6SeqcQS9JnTPoJalzQwd9kmVJ/jbJrW3+JUl2JplOcmOS41r/8W1+ui1fuzClS5KGMcoe/VuAz8+avxK4uqpOBR4GLmn9lwAPt/6r2zhJ0iIZKuiTrAZeBfy3Nh9gE3BzG7INeE1rb23ztOWb23hJ47RjB1xxxeBROoJhr6P/Q+BtwA+1+RcCj1TVk23+AeCU1j4FuB+gqp5M8mgb/82xVCxpEO6bN8MTT8Bxx8Htt8OGDYtdlZaoeffok7waeKiqdo/zhZNcmmQqydTMzMw4n1rq3/btg5A/cGDwuH37YlekJWyYQzc/B/xKkvuADzE4ZPNfgJVJDv5FsBrY19r7gDUAbflJwLfmPmlVXVdVk1U1OTEx7yd4Jc22ceNgT37ZssHjxo2LXZGWsHmDvqreWVWrq2otcCFwR1W9FrgTOL8Nuwj4s9a+pc3Tlt9RVTXWqqUfdBs2DA7XXH65h200r6P5XzdvBz6U5D8Afwtc3/qvBz6QZBr4NoNfDpLGbcMGA15DGSnoq2o7sL21vwKsP8SYx4ELxlCbJGkM/GSsJHXOoJekzhn0ktQ5g16SOmfQS1LnDHpJ6pxBL0mdM+glqXMGvSR1zqCXpM4Z9JLUOYNekjpn0EtS5wx6SeqcQS9JnTPoJalzBr0kdc6gl6TOGfSS1DmDXpI6N2/QJzkhya4kdye5J8llrX9Tks8k+WySbUmWt/4kuSbJdJK9Sc5a6DchSTq8Yfbo9wObquoMYB2wJcnPAtuAC6vqdOBrwEVt/LnAaW26FLh27FVLkoY2b9DXwGNtdkWbDgBPVNUXW/9twK+29lbghrbeXcDKJKvGXLckaUhDHaNPsizJHuAhBqG+C1ieZLINOR9Y09qnAPfPWv2B1jf3OS9NMpVkamZm5pnWL0max1BBX1UHqmodsBpYD7wMuBC4Osku4O8Z7OUPraquq6rJqpqcmJgYsWxJ0rBGuuqmqh4B7gS2VNWOqnpFVa0HPgUcPIyzj6f27mHwy2HfOIqVJI1umKtuJpKsbO0TgXOAe5O8qPUdD7wdeF9b5Rbgde3qm7OBR6vqwQWpXpI0r+VDjFkFbEuyjMEvhpuq6tYkVyV5deu7tqruaOM/DpwHTAPfBV6/AHVLkoaUqlrsGpicnKypqanFLkOSnlWS7K6qyfnG+clYSeqcQS9JnTPoJalzBr0kdc6gl6TOGfSS1DmDXpI6Z9BLUucMeknqnEEvSZ0z6CWpcwa9JHXOoJekzhn0ktQ5g16SOmfQS1LnDHpJ6pxBL0mdM+glqXPzBn2SE5LsSnJ3knuSXNb6Nyf5TJI9ST6d5NTWf3ySG5NMJ9mZZO3CvgVJ0pEMs0e/H9hUVWcA64AtSc4GrgVeW1XrgP8B/Ls2/hLg4ao6FbgauHL8ZUuShjVv0NfAY212RZuqTc9r/ScBX2/trcC21r4Z2JwkY6tYkjSS5cMMSrIM2A2cCry3qnYm+Q3g40n+L/Ad4Ow2/BTgfoCqejLJo8ALgW/Oec5LgUsBXvziF4/hrUiSDmWok7FVdaAdolkNrE9yOvBW4LyqWg28H/jPo7xwVV1XVZNVNTkxMTFq3ZKkIY101U1VPQLcCZwLnFFVO9uiG4Gfbe19wBqAJMsZHNb51liqlSSNbJirbiaSrGztE4FzgM8DJyV5aRt2sA/gFuCi1j4fuKOqaqxVS5KGNswx+lXAtnac/jnATVV1a5J/A3w4yfeAh4GL2/jrgQ8kmQa+DVy4AHVLkoY0b9BX1V7gzEP0fxT46CH6HwcuGEt1kqSj5idjJalzBr0kdc6gl6TOGfSS1DmDXpI6Z9BLUucMeknqnEEvSZ0z6CWpcwa9JHXOoJekzhn0ktQ5g16SOmfQS1LnDHpJ6pxBL0mdM+glqXMGvSR1zqCXpM7NG/RJTkiyK8ndSe5Jclnr/+ske9r09SQfa/1Jck2S6SR7k5y10G9CknR4894cHNgPbKqqx5KsAD6d5BNV9YqDA5J8GPizNnsucFqbXg5c2x4lSYtg3j36Gnisza5oUx1cnuR5wCbgY61rK3BDW+8uYGWSVeMtW5I0rKGO0SdZlmQP8BBwW1XtnLX4NcDtVfWdNn8KcP+s5Q+0PknSIhgq6KvqQFWtA1YD65OcPmvxrwN/OuoLJ7k0yVSSqZmZmVFXlyQNaaSrbqrqEeBOYAtAkpOB9cBfzBq2D1gza35165v7XNdV1WRVTU5MTIxatyQ9++3YAVdcMXhcQPOejE0yAfxDVT2S5ETgHODKtvh84NaqenzWKrcAb07yIQYnYR+tqgfHXLckPbvt2AGbN8MTT8Bxx8Htt8OGDQvyUsPs0a8C7kyyF/gbBsfob23LLuT/P2zzceArwDTwR8BvjqlWSerH9u2DkD9wYPC4ffuCvdS8e/RVtRc48zDLNh6ir4A3HXVlktSzjRsHe/IH9+g3blywlxrmOnpJ0rht2DA4XLN9+yDkF+iwDRj0krR4NmxY0IA/yP91I0mdM+glqXMGvSR1zqCXpM4Z9JLUOYNekjpn0EtS5wx6SeqcQS9JnTPoJalzBr0kdc6gl6TOGfSS1DmDXpI6Z9BLUucMeknqnEEvSZ2bN+iTnJBkV5K7k9yT5LLWnyTvTvLFJJ9P8tuz+q9JMp1kb5KzFvpNSJIOb5hbCe4HNlXVY0lWAJ9O8gngJ4A1wI9X1feSvKiNPxc4rU0vB65tj5KkRTBv0FdVAY+12RVtKuCNwL+qqu+1cQ+1MVuBG9p6dyVZmWRVVT049uolSfMa6hh9kmVJ9gAPAbdV1U7gx4BfSzKV5BNJTmvDTwHun7X6A61PkrQIhgr6qjpQVeuA1cD6JKcDxwOPV9Uk8EfAH4/ywkkubb8kpmZmZkatW5I0pJGuuqmqR4A7gS0M9tQ/0hZ9FPip1t7H4Nj9Qatb39znuq6qJqtqcmJiYtS6JUlDGuaqm4kkK1v7ROAc4F7gY8Ar27BfBL7Y2rcAr2tX35wNPOrxeUlaPMNcdbMK2JZkGYNfDDdV1a1JPg18MMlbGZys/Y02/uPAecA08F3g9eMvW5I0rGGuutkLnHmI/keAVx2iv4A3jaU6SdJR85OxktQ5g16SOmfQS1LnDHpJ6pxBL0mdM+glqXMGvSR1zqCXpM4Z9JLUOYNekjpn0EtS5wx6SeqcQS9JnTPoJalzBr0kdc6gl6TOGfSS1DmDXpI6Z9BLUufmDfokJyTZleTuJPckuaz1/0mSrybZ06Z1rT9JrkkynWRvkrMW+k1Ikg5v3puDA/uBTVX1WJIVwKeTfKIt+72qunnO+HOB09r0cuDa9ihJWgTz7tHXwGNtdkWb6girbAVuaOvdBaxMsuroS5UkPRNDHaNPsizJHuAh4Laq2tkWvbsdnrk6yfGt7xTg/lmrP9D6JEmLYKigr6oDVbUOWA2sT3I68E7gx4GfAV4AvH2UF05yaZKpJFMzMzMjli1JGtZIV91U1SPAncCWqnqwHZ7ZD7wfWN+G7QPWzFptdeub+1zXVdVkVU1OTEw8s+olSfMa5qqbiSQrW/tE4Bzg3oPH3ZMEeA3w2bbKLcDr2tU3ZwOPVtWDC1K9JGlew1x1swrYlmQZg18MN1XVrUnuSDIBBNgDvKGN/zhwHjANfBd4/fjLliQNa96gr6q9wJmH6N90mPEFvOnoS5MkjYOfjJWkzhn0ktQ5g16SOmfQS1LnDHpJ6pxBL0mdM+glqXMGvSR1zqCXpM4Z9JLUOYNekjpn0EtS5wx6SeqcQS9JnTPoJalzBr0kdc6gl6TOGfSS1DmDXpI6Z9BLUufmDfokJyTZleTuJPckuWzO8muSPDZr/vgkNyaZTrIzydrxly1JGtYwe/T7gU1VdQawDtiS5GyAJJPA8+eMvwR4uKpOBa4GrhxjvZKkEc0b9DVwcI99RZsqyTLgKuBtc1bZCmxr7ZuBzUkypnolSSMa6hh9kmVJ9gAPAbdV1U7gzcAtVfXgnOGnAPcDVNWTwKPACw/xnJcmmUoyNTMzczTvQZJ0BEMFfVUdqKp1wGpgfZJfAC4A/uszfeGquq6qJqtqcmJi4pk+jSRpHiNddVNVjwB3Aq8ETgWmk9wH/KMk023YPmANQJLlwEnAt8ZVsCRpNMNcdTORZGVrnwicA+yuqh+pqrVVtRb4bjv5CnALcFFrnw/cUVU1/tIlScNYPsSYVcC2dvL1OcBNVXXrEcZfD3yg7eF/G7jw6MuUJD1T8wZ9Ve0FzpxnzHNntR9ncPxekrQE+MlYSeqcQS9JnTPoJalzBr0kdc6gl6TOGfSS1DmDXpI6Z9BLUucMeknqnEEvSZ0z6CWpcwa9JHXOoJekzhn0ktQ5g16SOmfQS1LnDHpJ6pxBL0mdM+glqXPzBn2SE5LsSnJ3knuSXNb6r299e5PcnOS5rf/4JDcmmU6yM8nahX0LkqQjGWaPfj+wqarOANYBW5KcDby1qs6oqp8C/jfw5jb+EuDhqjoVuBq4cgHqliQNad6gr4HH2uyKNlVVfQcgSYATgWpjtgLbWvtmYHMbM347dsAVVwweJUmHtHyYQUmWAbuBU4H3VtXO1v9+4Dzgc8DvtuGnAPcDVNWTSR4FXgh8c6yV79gBmzfDE0/AccfB7bfDhg1jfQlJ6sFQJ2Or6kBVrQNWA+uTnN76Xw/8KPB54NdGeeEklyaZSjI1MzMzYtnA9u2DkD9wYPC4ffvozyFJPwBGuuqmqh4B7gS2zOo7AHwI+NXWtQ9YA5BkOXAS8K1DPNd1VTVZVZMTExOjV75x42BPftmywePGjaM/hyT9ABjmqpuJJCtb+0TgHOALSU5tfQF+Bbi3rXILcFFrnw/cUVXFuG3YMDhcc/nlHraRpCMY5hj9KmBbO07/HOAm4C+Av07yPCDA3cAb2/jrgQ8kmQa+DVw49qoP2rDBgJekecwb9FW1FzjzEIt+7jDjHwcuOMq6JElj4idjJalzBr0kdc6gl6TOGfSS1DmDXpI6l4W4xH3kIpIZ4GvPcPWTGfe/VxgP6xqNdY1uqdZmXaM5mrr+SVXN+4nTJRH0RyPJVFVNLnYdc1nXaKxrdEu1NusazbGoy0M3ktQ5g16SOtdD0F+32AUchnWNxrpGt1Rrs67RLHhdz/pj9JKkI+thj16SdARLMuiT/HGSh5J8dk7/byW5t92k/D2z+t/Zbkb+hSS/PKt/S+ubTvKOhair3Qh9T5vuS7JnidS1Lsldra6pJOtbf5Jc0157b5KzZq1zUZIvtemiQ73WGOo6I8mOJH+X5M/bf0A9uOxYba81Se5M8rn2vfSW1v+CJLe1939bkue3/mOyzY5Q1wVt/ntJJuess+Db7Ah1XdV+Hvcm+WjavzNfAnVd3mrak+STSX609S/q13HW8t9NUklOPmZ1VdWSm4BfAM4CPjur75XA/wKOb/Mvao8/yeDfJB8PvAT4MrCsTV8G/ilwXBvzk+Oua87y/wT8/lKoC/gkcG5rnwdsn9X+BIN/L302sLP1vwD4Snt8fms/fwHq+hvgF1v7YuDyRdheq4CzWvuHgC+2138P8I7W/w7gymO5zY5Q108A/wzYDkzOGn9MttkR6volYHnrv3LW9lrsup43a8xvA+9bCl/HNr8G+EsGnxs6+VjVtST36KvqUwz+l/1sbwT+oKr2tzEPtf6twIeqan9VfRWYBta3abqqvlJVTzC4C9bWBagL+P4NWP4l8KdLpK4CDu4tnwR8fVZdN9TAXcDKJKuAXwZuq6pvV9XDwG3MupPYGOt6KfCp1r6Np+5Mdiy314NV9ZnW/nsGt8I8haff2H4b8JpZtS34NjtcXVX1+ar6wiFWOSbb7Ah1fbKqnmzD7mJwq9GlUNd3Zg37xwx+Fg7WtWhfx7b4auBts2o6JnUtyaA/jJcCr0iyM8lfJfmZ1v/9m5E3D7S+w/UvlFcA36iqLy2Run4HuCrJ/cB/BN65ROq6h6d+uC+g3XZysepKspbB/RZ2Aj9cVQ+2Rf8H+OHFqm1OXYezlOq6mMFe6ZKoK8m72/f+a4HfXwp1JdkK7Kuqu+cMW/C6nk1Bv5zBnzBnA78H3NT2opeKX+epvfml4I3AW6tqDfBWBnf+WgouBn4zyW4Gf9Y+sViFJHku8GHgd+bsBVKDv50X5ZK0I9W1mA5XV5J3AU8CH1wqdVXVu9r3/geBNy92XQy2z7/lqV86x9SzKegfAD7S/rzZBXyPwf+I+P7NyJvVre9w/WOXwU3Q/wVw46zuxa7rIuAjrf0/GfzZvOh1VdW9VfVLVfXTDH4xfnkx6kqygsEP4Qer6uB2+kb7k5n2ePDw4DGr7TB1Hc6i15XkXwOvBl7bfjkuibpm+SBPHR5czLp+jMH5iruT3Nde4zNJfuSY1PVMDuwfiwlYy9NP4r0B+Pet/VIGf9IEeBlPP/HzFQYnfZa39kt46sTPy8ZdV+vbAvzVnL5FrYvBccGNrb0Z2N3ar+LpJ3521VMnfr7K4KTP81v7BQtQ18GT6M8BbgAuPtbbq733G4A/nNN/FU8/GfueY7nNDlfXrOXbefrJ2GOyzY6wvbYAnwMmFuN7/wh1nTar/VvAzUvp69jG3MdTJ2MXvK6j+iFeqInBnt6DwD8w2JO/pH1j/Hfgs8BngE2zxr+LwZ7hF2hXmrT+8xic8f4y8K6FqKv1/wnwhkOMX7S6gJ8Hdrcfpp3AT8/6Jnxve+2/4+nBcTGDE2fTwOsXqK63tPf+ReAPaB/aO8bb6+cZHJbZC+xp03nAC4HbgS8xuMLrBcdymx2hrn/ett9+4BvAXx7LbXaEuqYZ7HAd7HvfEqnrwwxyYi/w5wxO0C7613HOmPt4KugXvC4/GStJnXs2HaOXJD0DBr0kdc6gl6TOGfSS1DmDXpI6Z9BLUucMeknqnEEvSZ37fx1iIYZvFmeYAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"x_train = np.array([[2104],[1600],[2400]], dtype=np.float32)\n",
"y_train = np.array([[399.900], [329.900], [369.000]], dtype=np.float32)\n",
"\n",
"# x_train = np.array([[3.3], [4.4], [5.5], [6.71], [6.93], [4.168],\n",
"# [9.779], [6.182], [7.59], [2.167], [7.042],\n",
"# [10.791], [5.313], [7.997], [3.1]], dtype=np.float32)\n",
"\n",
"# y_train = np.array([[1.7], [2.76], [2.09], [3.19], [1.694], [1.573],\n",
"# [3.366], [2.596], [2.53], [1.221], [2.827],\n",
"# [3.465], [1.65], [2.904], [1.3]], dtype=np.float32)\n",
"\n",
"plt.plot(x_train, y_train, 'r.')\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 105,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T05:26:28.745318Z",
"start_time": "2019-04-07T05:26:28.741971Z"
}
},
"outputs": [],
"source": [
"x_train = torch.from_numpy(x_train)\n",
"y_train = torch.from_numpy(y_train)"
]
},
{
"cell_type": "markdown",
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T04:47:17.479477Z",
"start_time": "2019-04-07T04:47:17.468259Z"
}
},
"source": [
"`nn.Linear`\n",
"\n",
"Applies a linear transformation to the incoming data: $y = xA^T + b$"
]
},
{
"cell_type": "code",
"execution_count": 106,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T05:26:30.527459Z",
"start_time": "2019-04-07T05:26:30.516864Z"
}
},
"outputs": [],
"source": [
"# Linear Regression Model\n",
"class LinearRegression(nn.Module):\n",
" def __init__(self):\n",
" super(LinearRegression, self).__init__()\n",
" self.linear = nn.Linear(1, 1) # input and output is 1 dimension\n",
"\n",
" def forward(self, x):\n",
" out = self.linear(x)\n",
" return out\n",
"\n",
"model = LinearRegression()"
]
},
{
"cell_type": "code",
"execution_count": 107,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T05:26:31.378932Z",
"start_time": "2019-04-07T05:26:31.375266Z"
}
},
"outputs": [],
"source": [
"# Define Loss and Optimizatioin function\n",
"criterion = nn.MSELoss()\n",
"optimizer = optim.SGD(model.parameters(), lr=1e-9)#1e-4)"
]
},
{
"cell_type": "code",
"execution_count": 108,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T05:26:32.848256Z",
"start_time": "2019-04-07T05:26:32.681980Z"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Epoch[50/1000], loss: 3798.923096\n",
"Epoch[100/1000], loss: 2773.092773\n",
"Epoch[150/1000], loss: 2336.129639\n",
"Epoch[200/1000], loss: 2150.003906\n",
"Epoch[250/1000], loss: 2070.720459\n",
"Epoch[300/1000], loss: 2036.951782\n",
"Epoch[350/1000], loss: 2022.566162\n",
"Epoch[400/1000], loss: 2016.437866\n",
"Epoch[450/1000], loss: 2013.828125\n",
"Epoch[500/1000], loss: 2012.717407\n",
"Epoch[550/1000], loss: 2012.243286\n",
"Epoch[600/1000], loss: 2012.041260\n",
"Epoch[650/1000], loss: 2011.954956\n",
"Epoch[700/1000], loss: 2011.918335\n",
"Epoch[750/1000], loss: 2011.904053\n",
"Epoch[800/1000], loss: 2011.897217\n",
"Epoch[850/1000], loss: 2011.894409\n",
"Epoch[900/1000], loss: 2011.893311\n",
"Epoch[950/1000], loss: 2011.892456\n",
"Epoch[1000/1000], loss: 2011.890991\n"
]
}
],
"source": [
"num_epochs = 1000\n",
"for epoch in range(num_epochs):\n",
" inputs = Variable(x_train)\n",
" target = Variable(y_train)\n",
"\n",
" # forward\n",
" out = model(inputs)\n",
" loss = criterion(out, target)\n",
" # backward\n",
" optimizer.zero_grad()\n",
" loss.backward()\n",
" optimizer.step()\n",
"\n",
" if (epoch+1) % 50 == 0:\n",
" print('Epoch[{}/{}], loss: {:.6f}'\n",
" .format(epoch+1, num_epochs, loss.data.item()))\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"$$\n",
"\\ell(x, y) = L = \\{l_1,\\dots,l_N\\}^\\top, \\quad\n",
" l_n = \\left( x_n - y_n \\right)^2,\n",
"$$\n",
" where :`N` is the batch size. "
]
},
{
"cell_type": "code",
"execution_count": 109,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T05:26:38.112863Z",
"start_time": "2019-04-07T05:26:38.108523Z"
}
},
"outputs": [
{
"data": {
"text/plain": [
"LinearRegression(\n",
" (linear): Linear(in_features=1, out_features=1, bias=True)\n",
")"
]
},
"execution_count": 109,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"model.eval()"
]
},
{
"cell_type": "code",
"execution_count": 118,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T05:54:13.026497Z",
"start_time": "2019-04-07T05:54:12.777585Z"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZEAAAETCAYAAAD3WTuEAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvDW2N/gAAIABJREFUeJzt3Xl8VNX5x/HPY1gCAoKIgGyhij9ZjRpXfloFF2oRrNL+sLjghlWpuGFVrFTRFoWKtIKKQgWbVlREqKKCAu6y7yASNEBQISCgNIIs5/fHuUMWCJAhM3cy832/XvPKPWfuzDyZLM8899x7jjnnEBERicZhYQcgIiIVl5KIiIhETUlERESipiQiIiJRUxIREZGoKYmIiEjUlERERCRqSiIiIhI1JREREYlapbADiLWjjjrKZWRkhB2GiEiFMmfOnA3OuXoH2i/pk0hGRgazZ88OOwwRkQrFzFYdzH46nCUiIlFTEhERkagpiYiISNSSfkxkX3bs2EFeXh7btm0LOxQB0tPTady4MZUrVw47FBEpo5RMInl5edSsWZOMjAzMLOxwUppzjo0bN5KXl0fz5s3DDkdEyiglD2dt27aNunXrKoEkADOjbt26qgpFykmDBmC2961Bg9i8XkomEUAJJIHoZyFSftatK1v/oUrZJCIiIodOSSQkeXl5dO3alRYtWnDsscfSp08ffvrpp33u+/XXX9OtW7cDPufFF1/M5s2bo4rnT3/6E4MHDz7gfjVq1Njv/Zs3b2b48OFRxSAiFY+SyMHIzoaMDDjsMP81O/uQns45x2WXXcall17KihUr+OKLL9i6dSv9+vXba9+dO3dyzDHH8Oqrrx7weSdNmkTt2rUPKbZDpSQiEo4tW6BXr/i/rpLIgWRn+5/MqlXgnP/aq9chJZKpU6eSnp7OtddeC0BaWhpDhgxh1KhRFBQU8MILL9ClSxc6dOhAx44dyc3NpU2bNgAUFBTwm9/8hlatWvGrX/2K008/fc+0LhkZGWzYsIHc3FxatmzJjTfeSOvWrbnwwgv58ccfAXjuuec49dRTOfHEE7n88sspKCjYb6xfffUVZ555Jm3btuWBBx7Y079161Y6duzIySefTNu2bZkwYQIA9957LytXriQzM5O+ffuWup+IlJ+JE6FVKxg5Mv6vnRBJxMzSzGyemb0RtLPNbLmZLTazUWZWOeg3M/ubmeWY2UIzOznmwfXrByX/0RYU+P4oLVmyhFNOOaVYX61atWjatCk5OTkAzJ07l1dffZX333+/2H7Dhw+nTp06LF26lAEDBjBnzpx9vsaKFSu49dZbWbJkCbVr12bcuHEAXHbZZcyaNYsFCxbQsmVLRh7gt65Pnz7cfPPNLFq0iIYNG+7pT09PZ/z48cydO5dp06Zx11134Zxj4MCBHHvsscyfP59BgwaVup+IHLr166F7d+jaFerWhRkzoH79fe9bWv+hSogkAvQBlhVpZwMnAG2BasANQf8vgBbBrRfwdMwjW726bP3l5IILLuDII4/cq/+jjz6ie/fuALRp04Z27drt8/HNmzcnMzMTgFNOOYXc3FwAFi9ezNlnn03btm3Jzs5myZIl+43j448/5oorrgDgqquu2tPvnOP++++nXbt2nH/++axdu5Z1+zj942D3E5GD55w/GNKqFYwfDwMGwOzZkJUF337r7y95+/bb2MQSehIxs8bAL4HnI33OuUkuAMwEGgd3dQXGBHd9BtQ2s4Z7PWl5atq0bP0HoVWrVntVEN9//z2rV6/muOOOA+Dwww+P+vkBqlatumc7LS2NnTt3AtCzZ0+eeuopFi1aRP/+/Q/q+ox9nYKbnZ1Nfn4+c+bMYf78+dSvX3+fz3Ww+4nIwVmzBi65BK68Elq0gHnz4IEHoEqVcOIJPYkATwL3ALtL3hEcxroKeDvoagSsKbJLXtBX8nG9zGy2mc3Oz88/tOgefRSqVy/eV726749Sx44dKSgoYMyYMQDs2rWLu+66i549e1K95GuV0L59e15++WUAli5dyqJFi8r02j/88AMNGzZkx44dZB/EuE779u156aWXAIrtv2XLFo4++mgqV67MtGnTWLXKzxpds2ZNfvjhhwPuJyJls3s3PPMMtG4N06bBk0/CRx/5aiRMoSYRM+sMrHfO7fvAPgwHPnDOfViW53XOjXDOZTnnsurVO+CaKvvXoweMGAHNmvnLPps18+0ePaJ+SjNj/PjxvPLKK7Ro0YLjjz+e9PR0/vznPx/wsbfccgv5+fm0atWKBx54gNatW3PEEUcc9GsPGDCA008/nfbt23PCCScccP+hQ4cybNgw2rZty9q1a/f09+jRg9mzZ9O2bVvGjBmz57nq1q1L+/btadOmDX379i11PxE5eCtWQIcOcPPNcPrpsHgx9OkDaWlhRwYW5iCnmf0FX2nsBNKBWsBrzrkrzaw/cBJwmXNud7D/s8B059y/g/Zy4Fzn3DelvUZWVpYruSjVsmXLaNmyZSy+pZjbtWsXO3bsID09nZUrV3L++eezfPlyqoRVy5aTivwzEYmVnTthyBB48EGoWhWeeAKuvdZ/no01M5vjnMs60H6hTsDonLsPuA/AzM4F7g4SyA3ARUDHSAIJTAR6m9lLwOnAlv0lkGRUUFDAeeedx44dO3DOMXz48AqfQERkbwsWwPXXw5w5cOmlMGwYHHNM2FHtLVFn8X0GWAV8GgzqvuacexiYBFwM5AAFwLWhRRiSmjVrarlfkSS2fTs88ggMHAhHHgkvvwzdusWn+ohGwiQR59x0YHqwvc+4grO1bo1fVCIi8fPpp776WLYMrr7aH76qWzfsqPYvEc7OEhFJaf/9L9x+O7RvD1u3wqRJMHp04icQSKBKREQkFb37Ltx4I+Tmwq23wl/+AjVrhh3VwVMlIiISgk2b/KGrCy7wFwp+8AE89VTFSiCgJBKatLQ0MjMz99xyc3OZPXs2t912GwDTp0/nk08+2bP/66+/ztKlS/e0H3zwQd59991yiSUycWNREydOZODAgeXy/CJS3Pjx/iLB0aPh3nv9mVhnnx12VNHR4awDaNBg3yuC1a9/aHPRVKtWjfnz5xfry8jIICvLn5Y9ffp0atSowVlnnQX4JNK5c2daBZenPvzww9G/+EHo0qULXbp0ielriKSadevg97+HV16BzEx48004OfbTyMaUKpEDiOdSk9OnT6dz587k5ubyzDPPMGTIEDIzM3n//feZOHEiffv2JTMzk5UrV9KzZ889a4xkZGTQv3//PdOtf/755wDk5+dzwQUX0Lp1a2644QaaNWu2V8VRmhdeeIHevXsDfr6t2267jbPOOouf/exnxdY2GTRoEKeeeirt2rWjf//+5fyOiCQH52DMGGjZEiZM8LMmzZxZ8RMIqBLh9tuhREFw0M49d9/9mZl+Xpv9+fHHH/fMstu8eXPGjx+/576MjAx+97vfUaNGDe6++27AVwadO3cudYXDo446irlz5zJ8+HAGDx7M888/z0MPPUSHDh247777ePvttw847fv+fPPNN3z00Ud8/vnndOnShW7dujF58mRWrFjBzJkzcc7RpUsXPvjgA84555yoX0ck2axeDTfdBG+/DWed5df8SKbZf1I+iYRlX4ezDsVll10G+GnfX3vtNcBPGx9JTp06daJOnTpRP/+ll17KYYcdRqtWrfZM5T558mQmT57MSSedBPiFqlasWKEkIoKfMPHpp/2Yh3Pw97/DLbf4BVKTSconkQNVDPu7SnT69HIN5ZBEpn4vOu17LJ4f2LOolHOO++67j5tuuqncX0+kIlu+HG64wc+ye+GF8OyzfmXtZJRkOTF5lJxSvWT7YBSdNn7y5Mls2rSpXGO86KKLGDVqFFu3bgVg7dq1rF+/vlxfQ6Qi2bHDT1dy4omwZAm88II/jJWsCQSURA4o3ktNRlxyySWMHz+ezMxMPvzwQ7p3786gQYM46aSTWLly5UE9R//+/Zk8eTJt2rThlVdeoUGDBtQs5ST0du3a0bhxYxo3bsydd955UM9/4YUX8tvf/nbPGuzdunUrc6ITSRbz5vlp2u+7Dzp3hqVL4ZprEnfOq/IS6lTw8ZBsU8GXxfbt20lLS6NSpUp8+umn3HzzzeU6DlOeUuVnIsln2za/PO1jj8FRR/nZdi+/POyoDl2FmApeYmv16tX85je/Yffu3VSpUoXnnnsu7JBEksrHH/urzpcv9+t8DB7sZ95NJUoiSaxFixbMmzcv7DBEks7WrXD//X6akqZN4Z13/AB6KkrZMZFkP4xXkehnIRXJO+/4dc6fespffb54ceomEEjRJJKens7GjRv1zysBOOfYuHEj6enpYYcisl/ffQc9e0KnTlC9Onz4IQwdCjVqhB1ZuFLycFbjxo3Jy8sjPz8/7FAEn9QbN24cdhgipRo3zk/TvmED9OsHDzwA+tzjpWQSqVy5Ms2bNw87DBFJcN98A717w2uvwUkn+Ws+gtmKJJCSh7NERPbHOX+hYKtWfqbdgQP9hIlKIHtLiCRiZmlmNs/M3gjazc1shpnlmNlYM6sS9FcN2jnB/Rlhxi0iySc3Fy66yJ+y27YtLFwIf/gDVErJ4zYHlhBJBOgDLCvSfgwY4pw7DtgEXB/0Xw9sCvqHBPuJSHnKzvbzdBx2mP+anR12RHGxaxf87W/Qpg18+qm/aHD6dDj++LAjS2yhJxEzawz8Eng+aBvQAYgsWjEauDTY7hq0Ce7vGOwvIuUhOxt69YJVq/wxnVWrfDvJE8myZXDOOdCnj19hcMmS5JxxNxYS4S16ErgH2B206wKbnXORqWjzgEbBdiNgDUBw/5Zg/2LMrJeZzTaz2ToDS6QM+vWDgoLifQUFvj8J7djhF4jKzITPP/cLR02a5C8glIMTahIxs87AeufcnPJ8XufcCOdclnMuq169euX51CLJbfXqsvVXYHPnwqmn+tN1L73UT5h41VXJP2FieQu7EmkPdDGzXOAl/GGsoUBtM4sMYzUG1gbba4EmAMH9RwAb4xmwSFIr7SN4En00//FHv1DUaafB+vUwfjyMHRv7mbmTVahJxDl3n3OusXMuA+gOTHXO9QCmAZF1YK8BJgTbE4M2wf1TnS47Fyk/jz7qL8cuqnp1358EPvjAr/Xx2GP+6vOlS30VItELuxIpzR+AO80sBz/mEVkcfCRQN+i/E7g3pPhEklOPHjBiBDRr5o/rNGvm2z16hB3ZIfn+e3/F+c9/Djt3wrvvwvPPQ+3aYUdW8aXkeiIikjreegtuugny8vzZV488AocfHnZUiU/riYhIStu4Ee64A1580V95/skncMYZYUeVfBL1cJaISFScg5dfhpYt4d//hj/+0Z+JpQQSG6pERCRpfP21v0hwwgTIyvJjH+3ahR1VclMlIiIVnnMwcqQ/bPXOOzBokJ+6RAkk9lSJiEiF9uWXcOONMHWqP/vq+efhuOPCjip1qBIRkQpp1y548kk/0+6sWfDMMz6RKIHElyoREalwliyB66+HGTPgl7/0CUSLY4ZDlYiIVBg//QQDBvhVBnNy/OTC//mPEkiYVImISIUwa5avPhYtgiuugKFDQfOrhk+ViIgktIIC6NvXX+fx3XcwcSL8619KIIlClYiIJKzp0/2ZVzk5fm2sxx+HI44IOyopSpWIiCScLVvgd7+D887z14BMnQrPPqsEkoiUREQkobz5JrRuDc89B3fdBQsX+mQiiUlJREQSQn6+n3G+c2eoU8dfcT548N7Lm0hiURIRkVA55ydKbNUKXnkF/vQnmDPHrzwoiU8D6yISmrw8uPlmeOMNnzRGjoQ2bcKOSspClYiIxN3u3X7BxNat4b334Ikn/HofSiAVjyoREYmrnBx/2u706X7A/Lnn4Nhjw45KoqVKRETiYtcu+Otf/fTsc+f65PHee0ogFV2oScTM0s1sppktMLMlZvZQ0N/RzOaa2Xwz+8jMjgv6q5rZWDPLMbMZZpYRZvwicnAWLYIzz4S774bzz4elS+GGG8As7MjkUIVdiWwHOjjnTgQygU5mdgbwNNDDOZcJ/At4INj/emCTc+44YAjwWAgxi8hB2r4d+veHk0+G3Fx46SW/6mCjRmFHJuUl1CTivK1Bs3Jwc8GtVtB/BPB1sN0VGB1svwp0NNNnGZFENGMGnHIKPPwwdO/uq4//+z9VH8km7EoEM0szs/nAemCKc24GcAMwyczygKuAgcHujYA1AM65ncAWoO4+nrOXmc02s9n5+fnx+DZEJPDf/8Kdd/rDV1u2+NN3X3wRjjoq7MgkFkJPIs65XcFhq8bAaWbWBrgDuNg51xj4B/BEGZ9zhHMuyzmXVU9TfYrEzdSpfuB8yBA/99WSJX7RKEleoSeRCOfcZmAa8AvgxKAiARgLnBVsrwWaAJhZJfyhro1xDlVESti82Z+227EjHHaYP313+HCoVeuAD5UKLuyzs+qZWe1guxpwAbAMOMLMjg92i/QBTASuCba7AVOdcy6OIYtICRMn+osGR42Ce+7xEyb+/OdhRyXxEvbFhg2B0WaWhk9oLzvn3jCzG4FxZrYb2ARcF+w/EnjRzHKA74DuYQQtIrB+Pdx2G4wd6w9hTZgAWVlhRyXxFmoScc4tBE7aR/94YPw++rcBv45DaCJSCuf82uZ9+sDWrX7N8z/8ASpXDjsyCUPYlYiIVCBr1vgB80mT/HK1I0f62XcldSXMwLqIJK7du+Hpp/3Yx/Tp8OST8NFHSiCiSkREimjQANat27u/cmXYscNPWTJiBDRvHv/YJDEpiYjIHvtKIOATyKhR0LOnrjiX4pREROSgXHtt2BFIItKYiIiIRE1JREQAv9aHSFkpiYikuHXr/DjH3XeHHYmUm+xsyMjwc9BkZPh2jCiJiKSwe+7xZ2RFlDZfaf368YlHykF2NvTqBatW+StDV63y7RglEiURkRT05Ze++hg0yLf/8hf//2b9ev+15O3bb8ONV8qgXz8oKCjeV1Dg+2NAZ2eJpJirroJ//rOwvWkT1K4dXjxSzlavLlv/IVIlIpIiFizw1UckgYwc6asMJZAk07Rp2foPkZKISJJzzq/zkZnp27Vq+aMb1123/8dJBfXoo1C9evG+6tV9fwwoiYgksQ8+8CfoTJ3q26+/7pesrVYt3Lgkhnr08HPTNGvmS89mzXy7R4+YvJzGRESS0M6d0KYNLF/u2yecAIsWQSX9xaeGHj1iljRKUiUikmQmTPATJkYSyPvvw7JlSiASG/q1EkkSP/4IRx/tF4oC6NAB3n1XEyZKbKkSEUkCo0b5sdNIApk/H957TwlEYk+ViEgFtnkz1KlT2L7ySnjxxfDikdQTaiViZulmNtPMFpjZEjN7KOg3M3vUzL4ws2VmdluR/r+ZWY6ZLTSzk8OMXyRMjz1WPIGsXKkEIvEXdiWyHejgnNtqZpWBj8zsLaAl0AQ4wTm328yODvb/BdAiuJ0OPB18FUkZ33wDxxxT2O7bFx5/PLx4JLWFmkSccw4IjuJSObg54Gbgt8653cF+64N9ugJjgsd9Zma1zayhc+6bOIcuEoo77vDrm0d8+60mR5RwhT6wbmZpZjYfWA9Mcc7NAI4F/s/MZpvZW2bWIti9EbCmyMPzgr6Sz9kreOzs/Pz8WH8LIjGXk+MHySMJZPBgfyW6EoiELfQk4pzb5ZzLBBoDp5lZG6AqsM05lwU8B4wq43OOcM5lOeey6pU2t7VIBeAcdO8OLVoU9m3ZAnfdFV5MIkWFnkQinHObgWlAJ3yF8Vpw13igXbC9Fj9WEtE46BNJOvPm+SlLxo717dGjfVKpVSvcuESKCvvsrHpmVjvYrgZcAHwOvA6cF+z2c+CLYHsicHVwltYZwBaNh0iy2b0bzj4bTg7OPaxb119IePXV4cYlsi9lGlg3s/rOuXXl+PoNgdFmloZPaC87594ws4+AbDO7Az/wfkOw/yTgYiAHKACuLcdYREI3bZq/0jzijTfgl78MLx6RAynr2Vmrzex14Fnn3NRDfXHn3ELgpH30bwb2+tMJzsq69VBfVyTR7NjhJ0n88kvfbtcO5s6FtLRw4xI5kLIezvoC+DUwJbgQ8C4zqxuDuERSxrhxUKVKYQL5+GO/gJQSiFQEZUoizrm2wP8CL+JPrR0E5JlZtpmdE4P4RJJWQYFf16NbN9/u1MmPh5x1VrhxiZRFmQfWnXOfOOd6AscAffDjE1cA08xsqZn1MbM6+3sOkVQ3YgQcfjhs2+bbixbBW29pwkSpeKI+O8s5t8U59/ci1ckYoBnwBL46ecHMssopTpGk8N13PlHcdJNvX3utP223TZtw4xKJVnmd4rsB2ARsAwx/seDVwAwze93Mjiyn1xGpsB55xJ+uG/HVV34Kd5GKLOokYmaVzay7mU0DlgG3A/nAncBRQAfgHaALMKwcYhWpkNau9dXHH//o2/ff76uPjIxQwxIpF2WegNHMjgN6AT2BusBu/MWBw51z7xXZdTow3cxexV+FLpJyeveGYUU+Qq1fD5qJR5JJWS82fA84F3/I6htgADDCOff1fh42B/hVtAGKVETLl/vrPiKGDoXbbgsvHpFYKWslch5+fqvhwOvOuV0H8Zj/APtLMiJJwzl/yu5rrxX2ff891KwZXkwisVTWJNLSObe8LA9wzi0GFpfxdUQqnFmz4LTTCtvZ2fDb34YXj0g8lCmJlDWBiKSC3bvhzDNh5kzfbtAAcnOhatVQwxKJi4SZCl6kIpoyxU9PEkkgb73ll69VApFUEfYa6yIV0k8/wbHHQl6eb59yCsyYofmuJPWoEhEpo5df9pVGJIF8+inMnq0EIqlJlYjIQdq6FY44wo+BAFxyCUyYoPmuJLWpEhE5CMOG+dN0IwlkyRKYOFEJRESViMh+bNhQ/Arzm26CZ54JLx6RRKNKRKQU/fsXTyCrVyuBiJSkJCJSwpo1/jDVww/7dv/+/kr0Jk3CjUskEYWaRMws3cxmmtkCM1tiZg+VuP9vZra1SLuqmY01sxwzm2FmGfGOWZLbTTdB06aF7Q0b4E9/Ci0ckYQXdiWyHejgnDsRyAQ6mdkZAMGCViVXSLwe2OScOw4YAjwWz2AleS1d6quPESN8e9gwX30UXf9DRPYWahJxXqTSqBzcnJml4ddvv6fEQ7oCo4PtV4GOZjo/RqLnHHTuDK1b+3ZaGvzwA9xyS7hxiVQUYVcimFmamc0H1gNTnHMzgN7AROfcNyV2bwSsAXDO7QS24Nc0KfmcvcxstpnNzs/Pj+03IBXWZ5/BYYfBm2/69tixsHMn1KgRblwiFUnop/gG08lnmlltYLyZnQP8Gr9uSbTPOQIYAZCVleXKI05JHrt2wamnwrx5vt20KaxYAVWqhBuXSEUUeiUS4ZzbjF+r5DzgOCDHzHKB6maWE+y2FmgCYGaVgCOAjfGPViqqt9+GSpUKE8iUKbBqlRKISLRCrUTMrB6wwzm32cyqARcAjznnGhTZZ2swkA4wEbgG+BToBkx1zqnSkAPavh2aNYN163z7jDPg44/94SwRiV7Yf0INgWlmthCYhR8TeWM/+48E6gaVyZ3AvXGIUSq4f/0L0tMLE8isWX7SRCUQkUMXaiXinFsInHSAfWoU2d6GHy8ROaAffoBatQrbl10Gr76q+a5EypM+i0lSGjq0eAL5/HMYN04JRKS8hX52lkh5Wr8e6tcvbPfuDX//e3jxiCQ7VSKSNPr1K55A8vKUQERiTUlEKrzcXH+Y6s9/9u1HHvFXojdqFGpYIilBh7OkQrvuOvjHPwrbGzfCkUeGF49IqlElsi/Z2ZCR4c8BzcjwbUkoixb56iOSQJ591lcfSiAi8aVKpKTsbOjVCwoKfHvVKt8G6NEjvLgE8ImiUyeYPNm3q1Xz07VXrx5uXCKpSpVISf36FSaQiIIC3y+hilxhHkkg48b5H40SiEh4VImUtHp12fol5nbtgsxMWLzYt487zq//UblyuHGJiCqRvRVd1u5g+iWm3njDT5gYSSBTp/oZd5VARBKDkkhJjz669/GR6tV9v8TNtm1+kPySS3z7nHN8RXLeeeHGJSLFKYmU1KOHXyO1WTN/+k+zZr6tQfW4GT3aD5hv2uTbc+bA++9rwkSRRKQxkX3p0UNJIwRbtkDt2oXt7t39DLya70okcemznSSEv/61eAJZsQL+/W8lEJFEp0pEQrVuHTRoUNi+4w544onw4hGRslElIqHp27d4Avn6ayUQkYpGSUTi7ssv/WGqwYN9e+BAfyV6w4bhxiUiZafDWRJXV15ZfCqyTZuKj4WISMWiSkTiYsECX31EEsjIkb76UAIRqdhCTSJmlm5mM81sgZktMbOHgv5sM1tuZovNbJSZVQ76zcz+ZmY5ZrbQzE4OM345MOf8BYKZmb5dq5af7+q668KNS0TKR9iVyHagg3PuRCAT6GRmZwDZwAlAW6AacEOw/y+AFsGtF/B03COWg/bBB/4CwenTffv11/21INWqhRqWiJSjUMdEnHMO2Bo0Kwc355ybFNnHzGYCjYNmV2BM8LjPzKy2mTV0zn0Tz7hl/3buhNat4YsvfPuEE/z6H5U0AieSdMKuRDCzNDObD6wHpjjnZhS5rzJwFfB20NUIWFPk4XlBX8nn7GVms81sdn5+fuyCl728/rqfHDGSQN5/H5YtUwIRSVahJxHn3C7nXCa+2jjNzNoUuXs48IFz7sMyPucI51yWcy6rXr165RmulOLHH6FGDfjVr3y7QwfYvdtPnCgiySv0JBLhnNsMTAM6AZhZf6AecGeR3dYCTYq0Gwd9EqKRI/1Ex//9r2/Pnw/vvacpS0RSQdhnZ9Uzs9rBdjXgAuBzM7sBuAi4wjm3u8hDJgJXB2dpnQFs0XhIeDZv9onihuC0hyuv9GdjnXhiuHGJSPyEfaS6ITDazNLwCe1l59wbZrYTWAV8av7j7GvOuYeBScDFQA5QAFwbTtgycCDcd19he+VK+NnPwotHRMIR9tlZC4GT9tG/z7iCs7JujXVcUrqvv4ZGRU5luOceeOyx8OIRkXCFXYlIBXLHHfDkk4Xtb7+F+vXDi0dEwpcwA+uSuFas8GMfkQQyeLAf+1ACERFVIlIq5/zqgi+/XNi3ZYufukREBFSJSCm8CQyyAAANOElEQVTmzvVTlkQSyJgxPqkogYhIUapEpJjIBYIff+zbRx0Fa9ZAenq4cYlIYlIlIntMmwZpaYUJ5I03ID9fCURESqdKRNixA/7nf+Crr3y7XTt/OCstLdy4RCTxqRJJcePGQZUqhQnk44/9AlJKICJyMFSJpKj//hfq1oXt2327UyeYNEnzXYlI2agSSUHPPutn3I0kkEWL4K23lEBEpOxUiaSQ777z1UfEddf5GXhFRKKlSiRFDBhQPIF89ZUSiIgcOlUiSW7tWmjcuLB9//3w6KPhxSMiyUVJJIn17g3DhhW2168HLfQoIuVJh7OS0PLlfpA8kkCGDvVTliiBiEh5UyWSRJyDyy6D118v7Pv+e6hZM7yYRCS5qRJJErNm+QkTIwkkO9snFSUQEYklVSIV3O7dcOaZMHOmbzds6M+8qlo13LhEJDWoEqnApkzx05NEEsjbb/vla5VARCReQk0iZpZuZjPNbIGZLTGzh4L+5mY2w8xyzGysmVUJ+qsG7Zzg/oww4w/LTz9BkyZw4YW+fcopsHMnXHRRuHGJSOoJuxLZDnRwzp0IZAKdzOwM4DFgiHPuOGATcH2w//XApqB/SLBfShk71lcaeXm+/dlnMHu2JkwUkXCEmkSctzVoVg5uDugAvBr0jwYuDba7Bm2C+zuapcaMT1u3+oHz7t19u0sXPx5y+unhxiUiqS3sSgQzSzOz+cB6YAqwEtjsnNsZ7JIHNAq2GwFrAIL7twB1KcHMepnZbDObnZ+fH+tvIeaeesqfZeWcby9dChMmaMJEEQlf6EnEObfLOZcJNAZOA04oh+cc4ZzLcs5l1avAV9ht2OATxe9/79s33eQTScuW4cYlIhIRehKJcM5tBqYBZwK1zSxy+nFjYG2wvRZoAhDcfwSwMc6hxsWDDxa/wnz1anjmmfDiERHZl7DPzqpnZrWD7WrABcAyfDLpFux2DTAh2J4YtAnun+pc5CBPcli92lcfAwb4dv/+vvpo0iTcuERE9iXsiw0bAqPNLA2f0F52zr1hZkuBl8zsEWAeEJm0fCTwopnlAN8B3cMIOlZ69YLnnitsb9hQfPp2EZFEE2oScc4tBE7aR/+X+PGRkv3bgF/HIbS4WroUWrcubA8bBrfcEl48IiIHK+xKJKU5B5dcAm++6duVKsHmzXD44eHGJSJysBJmYD3VfPqpv+4jkkDGjoUdO5RARKRiUSUSZ7t2wamnwrx5vt20KaxYAVWqhBuXiEg0VInE0Vtv+UNWkQQyZQqsWqUEIiIVlyqRONi+3Vcc69f79plnwkcf+cNZIiIVmf6NxVh2NqSnFyaQWbPgk0+UQEQkOagSiZHvv4cjjihsX345vPKK5rsSkeSiz8Mx8OSTxRPI8uXw6qtKICKSfFSJlKP166F+/cJ2797w97+HF4+ISKypEikn999fPIHk5SmBiEjyUxI5RLm5/jDVX/7i24884q9Eb9Rovw8TEUkKOpx1CHr2hNGjC9vffQd16oQWjohI3KkSicKiRb76iCSQESN89aEEIiKpRpVIGTgHF13krzQHqFbNT9devXq4cYmIhEWVyEH6+GN/gWAkgYwbBwUFSiAiktpUiZTQoAGsW1f6/cceC8uWQeXK8YtJRCRRqRIpYX8JZNo0yMlRAhERiVASKYNzzw07AhGRxKIkIiIiUQs1iZhZEzObZmZLzWyJmfUJ+jPN7DMzm29ms83stKDfzOxvZpZjZgvN7OQw4xcRSXVhD6zvBO5yzs01s5rAHDObAjwOPOSce8vMLg7a5wK/AFoEt9OBp4OvIiISglArEefcN865ucH2D8AyoBHggFrBbkcAXwfbXYExzvsMqG1mDcszpqLzXx1Mv4hIKgu7EtnDzDKAk4AZwO3AO2Y2GJ/ozgp2awSsKfKwvKDvmxLP1QvoBdC0adMyxfHtt2UOXUQkZSXEwLqZ1QDGAbc7574HbgbucM41Ae4ARpbl+ZxzI5xzWc65rHr16pV/wCIiAiRAEjGzyvgEku2cey3ovgaIbL8CnBZsrwWaFHl446BPRERCEPbZWYavMpY5554octfXwM+D7Q7AimB7InB1cJbWGcAW51yxQ1kiIhI/YY+JtAeuAhaZ2fyg737gRmComVUCthGMbwCTgIuBHKAAuDa+4YqISFGhJhHn3EdAaSuPn7KP/R1wa0yDEhGRg2b+/3LyMrN8YFWUDz8K2FCO4ZQXxVU2iqvsEjU2xVU2hxJXM+fcAc9MSvokcijMbLZzLivsOEpSXGWjuMouUWNTXGUTj7hCPztLREQqLiURERGJmpLI/o0IO4BSKK6yUVxll6ixKa6yiXlcGhMREZGoqRIREZGopVwSMbNRZrbezBaX6P+9mX0erGvyeJH++4L1S5ab2UVF+jsFfTlmdm8s4jKzscGaKvPNLLfIBZlhx1Xm9V7M7BozWxHcrolRXCea2admtsjM/mNmtYrcF6/3q7Q1co40synB9z/FzOoE/XF5z/YT16+D9m4zyyrxmJi/Z/uJa1Dw97jQzMabWe0EiWtAENN8M5tsZscE/aH+HIvcf5eZOTM7Km5xOedS6gacA5wMLC7Sdx7wLlA1aB8dfG0FLACqAs2BlUBacFsJ/AyoEuzTqrzjKnH/X4EHEyEuYDLwi2D7YmB6ke238BeQngHMCPqPBL4MvtYJtuvEIK5ZwM+D7euAASG8Xw2Bk4PtmsAXwes/Dtwb9N8LPBbP92w/cbUE/geYDmQV2T8u79l+4roQqBT0P1bk/Qo7rlpF9rkNeCYRfo5BuwnwDv66uKPiFVfKVSLOuQ+A70p03wwMdM5tD/ZZH/R3BV5yzm13zn2Fn27ltOCW45z70jn3E/BSsG95xwXsmWPsN8C/EySusq73chEwxTn3nXNuEzAF6BSDuI4HPgi2pwCXF4krXu9XaWvkdAVGB7uNBi4tElvM37PS4nLOLXPOLd/HQ+Lynu0nrsnOuZ3Bbp/hJ1tNhLi+L7Lb4fi/hUhcof0cg7uHAPcUiSkucaVcEinF8cDZZjbDzN43s1OD/tLWLymtP1bOBtY55yITUYYd1+3AIDNbAwwG7kuQuJZQ+I/j1xTO+BxKXFZ8jZz6rnCy0G+ByDJncY+tRFylSaS4rsN/mk6IuMzs0eB3vwfwYCLEZWZdgbXOuQUldot5XEoiXiV8WXcG0Bd4Ofj0nyiuoLAKSQSHtN5LDF0H3GJmc/Cl/k9hBWJ7r5Gzh/PHE0I5LXJ/cYWptLjMrB9+Ge3sRInLOdcv+N3PBnqHHRf+/bmfwoQWV0oiXh7wWlDyzQR24+ecKW39krita2J+JuPLgLFFusOOq6zrvcQlLufc5865C51zp+CT7sow4rJ9r5GzLjiMQPA1csg0brGVEldpQo/LzHoCnYEeQeJNiLiKyKbwkGmYcR2LHx9aYGa5wWvMNbMGcYkrmoGUin4DMig+IPs74OFg+3h8mWdAa4oP4n2JH8CrFGw3p3AQr3V5xxX0dQLeL9EXalz447DnBtsdgTnB9i8pPog30xUO4n2FH8CrE2wfGYO4IidEHAaMAa6L9/sVfO9jgCdL9A+i+MD64/F8z0qLq8j90yk+sB6X92w/71cnYClQL4zf/f3E1aLI9u+BVxPp5xjsk0vhwHrM4zqkP+KKeMN/Qv0G2IGvQK4Pfun+CSwG5gIdiuzfD/+JdjnBGUlB/8X4MyNWAv1iEVfQ/wLwu33sH1pcwP8Cc4I/1BnAKUV+wYcFr72I4v+UrsMPguYA18Yorj7B9/4FMJDgYto4v1//iz9UtRCYH9wuBuoC7+EXWHs38gcbr/dsP3H9Knj/tgPrgHfi+Z7tJ64c/Ie5SN8zCRLXOPz/iYXAf/CD7aH/HEvsk0thEol5XLpiXUREoqYxERERiZqSiIiIRE1JREREoqYkIiIiUVMSERGRqCmJiIhI1JREROLAzK4Ppuh+az/7vBnsc0s8YxM5FEoiInHgnBsJTAQ6mdmtJe83s5sJpu12zg2Pd3wi0dLFhiJxYmZH4692Phy/JsTyoP94YB7wI9DGOfdteFGKlI0qEZE4cX6dmhuB6sA/zaxSMMHmP4O+XkogUtFUCjsAkVTinJtgZqPw8xZFpu4+FXjBHXhmXZGEo8NZInFmZjXxk1c2DbrWAO2cX6lOpELR4SyROAuSxcMUrg1+sxKIVFRKIiJxZmbVgD8U6fp1WLGIHColEZH4exw4ARiKXw/iOjO7JNyQRKKjMRGRODKzC4G38af6ngq0AGYDm/Gn924IMTyRMlMlIhInZnYk8A/8aoxXOue2O+cWA38E6gNPhxmfSDSURETi5xngGOAB59zCIv1/BT4EupnZlaFEJhIlHc4SiQMzuwoYA3wAnOec213i/ub4dbN3Am2dc3nxj1Kk7JRERGLMzJriE4ThrwdZVcp+NwDPAVOAi5z+OKUCUBIREZGoaUxERESipiQiIiJRUxIREZGoKYmIiEjUlERERCRqSiIiIhI1JREREYmakoiIiERNSURERKKmJCIiIlH7f1gLS3bZv0mkAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"predict = model(Variable(x_train))\n",
"predict = predict.data.numpy()\n",
"plt.plot(x_train.numpy(), y_train.numpy(), 'ro', label='Original data')\n",
"plt.plot(x_train.numpy(), predict, 'b-s', label='Fitting Line')\n",
"plt.xlabel('X', fontsize= 20)\n",
"plt.ylabel('y', fontsize= 20)\n",
"plt.legend()\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"使用pytorch建立卷积神经网络并处理MNIST数据。\n",
"https://computational-communication.com/pytorch-mnist/"
]
}
],
"metadata": {
"celltoolbar": "Slideshow",
"kernelspec": {
"display_name": "Python [default]",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.4"
},
"latex_envs": {
"LaTeX_envs_menu_present": true,
"autoclose": false,
"autocomplete": true,
"bibliofile": "biblio.bib",
"cite_by": "apalike",
"current_citInitial": 1,
"eqLabelWithNumbers": true,
"eqNumInitial": 1,
"hotkeys": {
"equation": "Ctrl-E",
"itemize": "Ctrl-I"
},
"labels_anchors": false,
"latex_user_defs": false,
"report_style_numbering": false,
"user_envs_cfg": false
},
"toc": {
"base_numbering": 1,
"nav_menu": {},
"number_sections": false,
"sideBar": true,
"skip_h1_title": false,
"title_cell": "Table of Contents",
"title_sidebar": "Contents",
"toc_cell": false,
"toc_position": {},
"toc_section_display": true,
"toc_window_display": false
}
},
"nbformat": 4,
"nbformat_minor": 2
}
 \n",
"\n",
"http://playground.tensorflow.org/"
]
},
{
"cell_type": "markdown",
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T09:37:45.438709Z",
"start_time": "2019-04-07T09:37:45.434406Z"
},
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"- Deep Learning http://www.deeplearningbook.org\n",
" - An MIT Press book by Ian Goodfellow, Yoshua Bengio and Aaron Courville\n",
"\n",
"- Neural Networks and Deep Learning http://neuralnetworksanddeeplearning.com/index.html\n",
"\n",
" - A free online book explaining the core ideas behind artificial neural networks and deep learning. [Code](https://github.com/mnielsen/neural-networks-and-deep-learning). By [Michael Nielsen](http://michaelnielsen.org/) / Dec 2017"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## House Price\n",
"\n",
"Let’s start with a simple example. \n",
"- Say you’re helping a friend who wants to buy a house.\n",
"\n",
"- She was quoted $400,000 for a 2000 sq ft house (185 meters). \n",
"\n",
"Is this a good price or not?"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"So you ask your friends who have bought houses in that same neighborhoods, and you end up with three data points:\n",
"\n",
"\n",
"\n",
"| Area (sq ft) (x) | Price (y) | \n",
"| -------------|:-------------:|\n",
"|2,104|399,900|\n",
"|1,600|329,900|\n",
"|2,400|369,000|"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
"$$y = f(X) = W X$$\n",
"\n",
"- Calculating the prediction is simple multiplication.\n",
"- But before that, we need to think about the weight we’ll be multiplying by. \n",
"- “training” a neural network just means finding the weights we use to calculate the prediction.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"A simple predictive model (“regression model”)\n",
"- takes an input, \n",
"- does a calculation, \n",
"- and gives an output \n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"
\n",
"\n",
"http://playground.tensorflow.org/"
]
},
{
"cell_type": "markdown",
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T09:37:45.438709Z",
"start_time": "2019-04-07T09:37:45.434406Z"
},
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"- Deep Learning http://www.deeplearningbook.org\n",
" - An MIT Press book by Ian Goodfellow, Yoshua Bengio and Aaron Courville\n",
"\n",
"- Neural Networks and Deep Learning http://neuralnetworksanddeeplearning.com/index.html\n",
"\n",
" - A free online book explaining the core ideas behind artificial neural networks and deep learning. [Code](https://github.com/mnielsen/neural-networks-and-deep-learning). By [Michael Nielsen](http://michaelnielsen.org/) / Dec 2017"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## House Price\n",
"\n",
"Let’s start with a simple example. \n",
"- Say you’re helping a friend who wants to buy a house.\n",
"\n",
"- She was quoted $400,000 for a 2000 sq ft house (185 meters). \n",
"\n",
"Is this a good price or not?"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"So you ask your friends who have bought houses in that same neighborhoods, and you end up with three data points:\n",
"\n",
"\n",
"\n",
"| Area (sq ft) (x) | Price (y) | \n",
"| -------------|:-------------:|\n",
"|2,104|399,900|\n",
"|1,600|329,900|\n",
"|2,400|369,000|"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
"$$y = f(X) = W X$$\n",
"\n",
"- Calculating the prediction is simple multiplication.\n",
"- But before that, we need to think about the weight we’ll be multiplying by. \n",
"- “training” a neural network just means finding the weights we use to calculate the prediction.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"A simple predictive model (“regression model”)\n",
"- takes an input, \n",
"- does a calculation, \n",
"- and gives an output \n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T03:15:14.317623Z",
"start_time": "2019-04-07T03:15:14.313438Z"
},
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"Model Evaluation\n",
"- If we apply our model to the three data points we have, how good of a job would it do?"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T03:15:14.317623Z",
"start_time": "2019-04-07T03:15:14.313438Z"
},
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"Model Evaluation\n",
"- If we apply our model to the three data points we have, how good of a job would it do?"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"**Loss Function (also, cost function)**\n",
"\n",
"- For each point, the error is measured by the difference between the **actual value** and the **predicted value**, raised to the power of 2. \n",
"- This is called **Mean Square Error**. "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"**Loss Function (also, cost function)**\n",
"\n",
"- For each point, the error is measured by the difference between the **actual value** and the **predicted value**, raised to the power of 2. \n",
"- This is called **Mean Square Error**. "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"- We can't improve much on the model by varying the weight any more. \n",
"- But if we add a bias (intercept) we can find values that improve the model.\n",
"\n",
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"- We can't improve much on the model by varying the weight any more. \n",
"- But if we add a bias (intercept) we can find values that improve the model.\n",
"\n",
" \n",
"\n",
"$$y = 0.1 X + 150$$"
]
},
{
"attachments": {},
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"**Gradient Descent**\n",
"\n",
"- Automatically get the correct weight and bias values \n",
"- minimize the loss function.\n",
"\n",
"
\n",
"\n",
"$$y = 0.1 X + 150$$"
]
},
{
"attachments": {},
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"**Gradient Descent**\n",
"\n",
"- Automatically get the correct weight and bias values \n",
"- minimize the loss function.\n",
"\n",
" \n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
"
\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
" \n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
"
\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
" \n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## softmax\n",
"\n",
"The softmax function, also known as softargmax or normalized exponential function, is a function that takes as input a vector of K real numbers, and normalizes it into a probability distribution consisting of K probabilities. \n",
"\n",
"$$softmax = \\frac{e^x}{\\sum e^x}$$\n"
]
},
{
"cell_type": "code",
"execution_count": 128,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T13:57:33.466056Z",
"start_time": "2019-04-07T13:57:33.459580Z"
},
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"text/plain": [
"array([0.02364054, 0.06426166, 0.1746813 , 0.474833 , 0.02364054,\n",
" 0.06426166, 0.1746813 ])"
]
},
"execution_count": 128,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"def softmax(s):\n",
" return np.exp(s) / np.sum(np.exp(s), axis=0)\n",
"\n",
"softmax([1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0])"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
"That is, prior to applying softmax, some vector components could be negative, or greater than one; and might not sum to 1; but after applying softmax, each component will be in the interval (0,1), and the components will add up to 1, so that they can be interpreted as probabilities. \n",
"\n",
"Furthermore, the larger input components will correspond to larger probabilities. \n",
"\n",
"Softmax is often used in neural networks, to map the non-normalized output of a network to a probability distribution over predicted output classes."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## Activation Function\n"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T03:59:39.599371Z",
"start_time": "2019-04-07T03:59:39.593104Z"
},
"code_folding": [],
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"text/plain": [
"0.6224593312018546"
]
},
"execution_count": 12,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"import numpy as np\n",
"def sigmoid(x):\n",
" return 1/(1 + np.exp(-x))\n",
"\n",
"sigmoid(0.5)"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T04:01:24.575040Z",
"start_time": "2019-04-07T04:01:24.567328Z"
},
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"text/plain": [
"0.5"
]
},
"execution_count": 13,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Naive scalar relu implementation. \n",
"# In the real world, most calculations are done on vectors\n",
"def relu(x):\n",
" if x < 0:\n",
" return 0\n",
" else:\n",
" return x\n",
"\n",
"relu(0.5)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# WHAT IS PYTORCH?\n",
"\n",
"It’s a Python-based scientific computing package targeted at two sets of audiences:\n",
"\n",
"- A replacement for NumPy to use the power of GPUs\n",
"- a deep learning research platform that provides maximum flexibility and speed"
]
},
{
"cell_type": "code",
"execution_count": 44,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T04:43:15.243401Z",
"start_time": "2019-04-07T04:43:14.333403Z"
}
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"import matplotlib.pyplot as plt\n",
"import torch\n",
"from torch import nn, optim\n",
"from torch.autograd import Variable\n",
"import numpy as np"
]
},
{
"cell_type": "code",
"execution_count": 104,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T05:26:28.414285Z",
"start_time": "2019-04-07T05:26:28.201996Z"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXoAAAD8CAYAAAB5Pm/hAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvDW2N/gAAFRdJREFUeJzt3X+QXWd93/H3B0n+0RIswEuiWKKisWkSPLHsbISVhERI40Q2TEQbu3HKDC526oFAQphM+FE6mXFdxjFu69QdxoxTh8iUBrvmRxwHJri2FcKMLGVFZAWDgQVMbeHiBWwTD7Uci2//uI/weitp77XuatcP79fMmfuc5zzn3u89u/vZs+ecuydVhSSpX89Z7AIkSQvLoJekzhn0ktQ5g16SOmfQS1LnDHpJ6pxBL0mdM+glqXMGvSR1bvliFwBw8skn19q1axe7DEl6Vtm9e/c3q2pivnFLIujXrl3L1NTUYpchSc8qSb42zDgP3UhS5wx6SeqcQS9JnTPoJalzQwd9kmVJ/jbJrW3+JUl2JplOcmOS41r/8W1+ui1fuzClS5KGMcoe/VuAz8+avxK4uqpOBR4GLmn9lwAPt/6r2zhJ0iIZKuiTrAZeBfy3Nh9gE3BzG7INeE1rb23ztOWb23hJ47RjB1xxxeBROoJhr6P/Q+BtwA+1+RcCj1TVk23+AeCU1j4FuB+gqp5M8mgb/82xVCxpEO6bN8MTT8Bxx8Htt8OGDYtdlZaoeffok7waeKiqdo/zhZNcmmQqydTMzMw4n1rq3/btg5A/cGDwuH37YlekJWyYQzc/B/xKkvuADzE4ZPNfgJVJDv5FsBrY19r7gDUAbflJwLfmPmlVXVdVk1U1OTEx7yd4Jc22ceNgT37ZssHjxo2LXZGWsHmDvqreWVWrq2otcCFwR1W9FrgTOL8Nuwj4s9a+pc3Tlt9RVTXWqqUfdBs2DA7XXH65h200r6P5XzdvBz6U5D8Afwtc3/qvBz6QZBr4NoNfDpLGbcMGA15DGSnoq2o7sL21vwKsP8SYx4ELxlCbJGkM/GSsJHXOoJekzhn0ktQ5g16SOmfQS1LnDHpJ6pxBL0mdM+glqXMGvSR1zqCXpM4Z9JLUOYNekjpn0EtS5wx6SeqcQS9JnTPoJalzBr0kdc6gl6TOGfSS1DmDXpI6N2/QJzkhya4kdye5J8llrX9Tks8k+WySbUmWt/4kuSbJdJK9Sc5a6DchSTq8Yfbo9wObquoMYB2wJcnPAtuAC6vqdOBrwEVt/LnAaW26FLh27FVLkoY2b9DXwGNtdkWbDgBPVNUXW/9twK+29lbghrbeXcDKJKvGXLckaUhDHaNPsizJHuAhBqG+C1ieZLINOR9Y09qnAPfPWv2B1jf3OS9NMpVkamZm5pnWL0max1BBX1UHqmodsBpYD7wMuBC4Osku4O8Z7OUPraquq6rJqpqcmJgYsWxJ0rBGuuqmqh4B7gS2VNWOqnpFVa0HPgUcPIyzj6f27mHwy2HfOIqVJI1umKtuJpKsbO0TgXOAe5O8qPUdD7wdeF9b5Rbgde3qm7OBR6vqwQWpXpI0r+VDjFkFbEuyjMEvhpuq6tYkVyV5deu7tqruaOM/DpwHTAPfBV6/AHVLkoaUqlrsGpicnKypqanFLkOSnlWS7K6qyfnG+clYSeqcQS9JnTPoJalzBr0kdc6gl6TOGfSS1DmDXpI6Z9BLUucMeknqnEEvSZ0z6CWpcwa9JHXOoJekzhn0ktQ5g16SOmfQS1LnDHpJ6pxBL0mdM+glqXPzBn2SE5LsSnJ3knuSXNb6Nyf5TJI9ST6d5NTWf3ySG5NMJ9mZZO3CvgVJ0pEMs0e/H9hUVWcA64AtSc4GrgVeW1XrgP8B/Ls2/hLg4ao6FbgauHL8ZUuShjVv0NfAY212RZuqTc9r/ScBX2/trcC21r4Z2JwkY6tYkjSS5cMMSrIM2A2cCry3qnYm+Q3g40n+L/Ad4Ow2/BTgfoCqejLJo8ALgW/Oec5LgUsBXvziF4/hrUiSDmWok7FVdaAdolkNrE9yOvBW4LyqWg28H/jPo7xwVV1XVZNVNTkxMTFq3ZKkIY101U1VPQLcCZwLnFFVO9uiG4Gfbe19wBqAJMsZHNb51liqlSSNbJirbiaSrGztE4FzgM8DJyV5aRt2sA/gFuCi1j4fuKOqaqxVS5KGNswx+lXAtnac/jnATVV1a5J/A3w4yfeAh4GL2/jrgQ8kmQa+DVy4AHVLkoY0b9BX1V7gzEP0fxT46CH6HwcuGEt1kqSj5idjJalzBr0kdc6gl6TOGfSS1DmDXpI6Z9BLUucMeknqnEEvSZ0z6CWpcwa9JHXOoJekzhn0ktQ5g16SOmfQS1LnDHpJ6pxBL0mdM+glqXMGvSR1zqCXpM7NG/RJTkiyK8ndSe5Jclnr/+ske9r09SQfa/1Jck2S6SR7k5y10G9CknR4894cHNgPbKqqx5KsAD6d5BNV9YqDA5J8GPizNnsucFqbXg5c2x4lSYtg3j36Gnisza5oUx1cnuR5wCbgY61rK3BDW+8uYGWSVeMtW5I0rKGO0SdZlmQP8BBwW1XtnLX4NcDtVfWdNn8KcP+s5Q+0PknSIhgq6KvqQFWtA1YD65OcPmvxrwN/OuoLJ7k0yVSSqZmZmVFXlyQNaaSrbqrqEeBOYAtAkpOB9cBfzBq2D1gza35165v7XNdV1WRVTU5MTIxatyQ9++3YAVdcMXhcQPOejE0yAfxDVT2S5ETgHODKtvh84NaqenzWKrcAb07yIQYnYR+tqgfHXLckPbvt2AGbN8MTT8Bxx8Htt8OGDQvyUsPs0a8C7kyyF/gbBsfob23LLuT/P2zzceArwDTwR8BvjqlWSerH9u2DkD9wYPC4ffuCvdS8e/RVtRc48zDLNh6ir4A3HXVlktSzjRsHe/IH9+g3blywlxrmOnpJ0rht2DA4XLN9+yDkF+iwDRj0krR4NmxY0IA/yP91I0mdM+glqXMGvSR1zqCXpM4Z9JLUOYNekjpn0EtS5wx6SeqcQS9JnTPoJalzBr0kdc6gl6TOGfSS1DmDXpI6Z9BLUucMeknqnEEvSZ2bN+iTnJBkV5K7k9yT5LLWnyTvTvLFJJ9P8tuz+q9JMp1kb5KzFvpNSJIOb5hbCe4HNlXVY0lWAJ9O8gngJ4A1wI9X1feSvKiNPxc4rU0vB65tj5KkRTBv0FdVAY+12RVtKuCNwL+qqu+1cQ+1MVuBG9p6dyVZmWRVVT049uolSfMa6hh9kmVJ9gAPAbdV1U7gx4BfSzKV5BNJTmvDTwHun7X6A61PkrQIhgr6qjpQVeuA1cD6JKcDxwOPV9Uk8EfAH4/ywkkubb8kpmZmZkatW5I0pJGuuqmqR4A7gS0M9tQ/0hZ9FPip1t7H4Nj9Qatb39znuq6qJqtqcmJiYtS6JUlDGuaqm4kkK1v7ROAc4F7gY8Ar27BfBL7Y2rcAr2tX35wNPOrxeUlaPMNcdbMK2JZkGYNfDDdV1a1JPg18MMlbGZys/Y02/uPAecA08F3g9eMvW5I0rGGuutkLnHmI/keAVx2iv4A3jaU6SdJR85OxktQ5g16SOmfQS1LnDHpJ6pxBL0mdM+glqXMGvSR1zqCXpM4Z9JLUOYNekjpn0EtS5wx6SeqcQS9JnTPoJalzBr0kdc6gl6TOGfSS1DmDXpI6Z9BLUufmDfokJyTZleTuJPckuaz1/0mSrybZ06Z1rT9JrkkynWRvkrMW+k1Ikg5v3puDA/uBTVX1WJIVwKeTfKIt+72qunnO+HOB09r0cuDa9ihJWgTz7tHXwGNtdkWb6girbAVuaOvdBaxMsuroS5UkPRNDHaNPsizJHuAh4Laq2tkWvbsdnrk6yfGt7xTg/lmrP9D6JEmLYKigr6oDVbUOWA2sT3I68E7gx4GfAV4AvH2UF05yaZKpJFMzMzMjli1JGtZIV91U1SPAncCWqnqwHZ7ZD7wfWN+G7QPWzFptdeub+1zXVdVkVU1OTEw8s+olSfMa5qqbiSQrW/tE4Bzg3oPH3ZMEeA3w2bbKLcDr2tU3ZwOPVtWDC1K9JGlew1x1swrYlmQZg18MN1XVrUnuSDIBBNgDvKGN/zhwHjANfBd4/fjLliQNa96gr6q9wJmH6N90mPEFvOnoS5MkjYOfjJWkzhn0ktQ5g16SOmfQS1LnDHpJ6pxBL0mdM+glqXMGvSR1zqCXpM4Z9JLUOYNekjpn0EtS5wx6SeqcQS9JnTPoJalzBr0kdc6gl6TOGfSS1DmDXpI6Z9BLUufmDfokJyTZleTuJPckuWzO8muSPDZr/vgkNyaZTrIzydrxly1JGtYwe/T7gU1VdQawDtiS5GyAJJPA8+eMvwR4uKpOBa4GrhxjvZKkEc0b9DVwcI99RZsqyTLgKuBtc1bZCmxr7ZuBzUkypnolSSMa6hh9kmVJ9gAPAbdV1U7gzcAtVfXgnOGnAPcDVNWTwKPACw/xnJcmmUoyNTMzczTvQZJ0BEMFfVUdqKp1wGpgfZJfAC4A/uszfeGquq6qJqtqcmJi4pk+jSRpHiNddVNVjwB3Aq8ETgWmk9wH/KMk023YPmANQJLlwEnAt8ZVsCRpNMNcdTORZGVrnwicA+yuqh+pqrVVtRb4bjv5CnALcFFrnw/cUVU1/tIlScNYPsSYVcC2dvL1OcBNVXXrEcZfD3yg7eF/G7jw6MuUJD1T8wZ9Ve0FzpxnzHNntR9ncPxekrQE+MlYSeqcQS9JnTPoJalzBr0kdc6gl6TOGfSS1DmDXpI6Z9BLUucMeknqnEEvSZ0z6CWpcwa9JHXOoJekzhn0ktQ5g16SOmfQS1LnDHpJ6pxBL0mdM+glqXPzBn2SE5LsSnJ3knuSXNb6r299e5PcnOS5rf/4JDcmmU6yM8nahX0LkqQjGWaPfj+wqarOANYBW5KcDby1qs6oqp8C/jfw5jb+EuDhqjoVuBq4cgHqliQNad6gr4HH2uyKNlVVfQcgSYATgWpjtgLbWvtmYHMbM347dsAVVwweJUmHtHyYQUmWAbuBU4H3VtXO1v9+4Dzgc8DvtuGnAPcDVNWTSR4FXgh8c6yV79gBmzfDE0/AccfB7bfDhg1jfQlJ6sFQJ2Or6kBVrQNWA+uTnN76Xw/8KPB54NdGeeEklyaZSjI1MzMzYtnA9u2DkD9wYPC4ffvozyFJPwBGuuqmqh4B7gS2zOo7AHwI+NXWtQ9YA5BkOXAS8K1DPNd1VTVZVZMTExOjV75x42BPftmywePGjaM/hyT9ABjmqpuJJCtb+0TgHOALSU5tfQF+Bbi3rXILcFFrnw/cUVXFuG3YMDhcc/nlHraRpCMY5hj9KmBbO07/HOAm4C+Av07yPCDA3cAb2/jrgQ8kmQa+DVw49qoP2rDBgJekecwb9FW1FzjzEIt+7jDjHwcuOMq6JElj4idjJalzBr0kdc6gl6TOGfSS1DmDXpI6l4W4xH3kIpIZ4GvPcPWTGfe/VxgP6xqNdY1uqdZmXaM5mrr+SVXN+4nTJRH0RyPJVFVNLnYdc1nXaKxrdEu1NusazbGoy0M3ktQ5g16SOtdD0F+32AUchnWNxrpGt1Rrs67RLHhdz/pj9JKkI+thj16SdARLMuiT/HGSh5J8dk7/byW5t92k/D2z+t/Zbkb+hSS/PKt/S+ubTvKOhair3Qh9T5vuS7JnidS1Lsldra6pJOtbf5Jc0157b5KzZq1zUZIvtemiQ73WGOo6I8mOJH+X5M/bf0A9uOxYba81Se5M8rn2vfSW1v+CJLe1939bkue3/mOyzY5Q1wVt/ntJJuess+Db7Ah1XdV+Hvcm+WjavzNfAnVd3mrak+STSX609S/q13HW8t9NUklOPmZ1VdWSm4BfAM4CPjur75XA/wKOb/Mvao8/yeDfJB8PvAT4MrCsTV8G/ilwXBvzk+Oua87y/wT8/lKoC/gkcG5rnwdsn9X+BIN/L302sLP1vwD4Snt8fms/fwHq+hvgF1v7YuDyRdheq4CzWvuHgC+2138P8I7W/w7gymO5zY5Q108A/wzYDkzOGn9MttkR6volYHnrv3LW9lrsup43a8xvA+9bCl/HNr8G+EsGnxs6+VjVtST36KvqUwz+l/1sbwT+oKr2tzEPtf6twIeqan9VfRWYBta3abqqvlJVTzC4C9bWBagL+P4NWP4l8KdLpK4CDu4tnwR8fVZdN9TAXcDKJKuAXwZuq6pvV9XDwG3MupPYGOt6KfCp1r6Np+5Mdiy314NV9ZnW/nsGt8I8haff2H4b8JpZtS34NjtcXVX1+ar6wiFWOSbb7Ah1fbKqnmzD7mJwq9GlUNd3Zg37xwx+Fg7WtWhfx7b4auBts2o6JnUtyaA/jJcCr0iyM8lfJfmZ1v/9m5E3D7S+w/UvlFcA36iqLy2Run4HuCrJ/cB/BN65ROq6h6d+uC+g3XZysepKspbB/RZ2Aj9cVQ+2Rf8H+OHFqm1OXYezlOq6mMFe6ZKoK8m72/f+a4HfXwp1JdkK7Kuqu+cMW/C6nk1Bv5zBnzBnA78H3NT2opeKX+epvfml4I3AW6tqDfBWBnf+WgouBn4zyW4Gf9Y+sViFJHku8GHgd+bsBVKDv50X5ZK0I9W1mA5XV5J3AU8CH1wqdVXVu9r3/geBNy92XQy2z7/lqV86x9SzKegfAD7S/rzZBXyPwf+I+P7NyJvVre9w/WOXwU3Q/wVw46zuxa7rIuAjrf0/GfzZvOh1VdW9VfVLVfXTDH4xfnkx6kqygsEP4Qer6uB2+kb7k5n2ePDw4DGr7TB1Hc6i15XkXwOvBl7bfjkuibpm+SBPHR5czLp+jMH5iruT3Nde4zNJfuSY1PVMDuwfiwlYy9NP4r0B+Pet/VIGf9IEeBlPP/HzFQYnfZa39kt46sTPy8ZdV+vbAvzVnL5FrYvBccGNrb0Z2N3ar+LpJ3521VMnfr7K4KTP81v7BQtQ18GT6M8BbgAuPtbbq733G4A/nNN/FU8/GfueY7nNDlfXrOXbefrJ2GOyzY6wvbYAnwMmFuN7/wh1nTar/VvAzUvp69jG3MdTJ2MXvK6j+iFeqInBnt6DwD8w2JO/pH1j/Hfgs8BngE2zxr+LwZ7hF2hXmrT+8xic8f4y8K6FqKv1/wnwhkOMX7S6gJ8Hdrcfpp3AT8/6Jnxve+2/4+nBcTGDE2fTwOsXqK63tPf+ReAPaB/aO8bb6+cZHJbZC+xp03nAC4HbgS8xuMLrBcdymx2hrn/ett9+4BvAXx7LbXaEuqYZ7HAd7HvfEqnrwwxyYi/w5wxO0C7613HOmPt4KugXvC4/GStJnXs2HaOXJD0DBr0kdc6gl6TOGfSS1DmDXpI6Z9BLUucMeknqnEEvSZ37fx1iIYZvFmeYAAAAAElFTkSuQmCC\n",
"text/plain": [
"
\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## softmax\n",
"\n",
"The softmax function, also known as softargmax or normalized exponential function, is a function that takes as input a vector of K real numbers, and normalizes it into a probability distribution consisting of K probabilities. \n",
"\n",
"$$softmax = \\frac{e^x}{\\sum e^x}$$\n"
]
},
{
"cell_type": "code",
"execution_count": 128,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T13:57:33.466056Z",
"start_time": "2019-04-07T13:57:33.459580Z"
},
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"text/plain": [
"array([0.02364054, 0.06426166, 0.1746813 , 0.474833 , 0.02364054,\n",
" 0.06426166, 0.1746813 ])"
]
},
"execution_count": 128,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"def softmax(s):\n",
" return np.exp(s) / np.sum(np.exp(s), axis=0)\n",
"\n",
"softmax([1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0])"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
"That is, prior to applying softmax, some vector components could be negative, or greater than one; and might not sum to 1; but after applying softmax, each component will be in the interval (0,1), and the components will add up to 1, so that they can be interpreted as probabilities. \n",
"\n",
"Furthermore, the larger input components will correspond to larger probabilities. \n",
"\n",
"Softmax is often used in neural networks, to map the non-normalized output of a network to a probability distribution over predicted output classes."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## Activation Function\n"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T03:59:39.599371Z",
"start_time": "2019-04-07T03:59:39.593104Z"
},
"code_folding": [],
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"text/plain": [
"0.6224593312018546"
]
},
"execution_count": 12,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"import numpy as np\n",
"def sigmoid(x):\n",
" return 1/(1 + np.exp(-x))\n",
"\n",
"sigmoid(0.5)"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T04:01:24.575040Z",
"start_time": "2019-04-07T04:01:24.567328Z"
},
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"text/plain": [
"0.5"
]
},
"execution_count": 13,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Naive scalar relu implementation. \n",
"# In the real world, most calculations are done on vectors\n",
"def relu(x):\n",
" if x < 0:\n",
" return 0\n",
" else:\n",
" return x\n",
"\n",
"relu(0.5)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# WHAT IS PYTORCH?\n",
"\n",
"It’s a Python-based scientific computing package targeted at two sets of audiences:\n",
"\n",
"- A replacement for NumPy to use the power of GPUs\n",
"- a deep learning research platform that provides maximum flexibility and speed"
]
},
{
"cell_type": "code",
"execution_count": 44,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T04:43:15.243401Z",
"start_time": "2019-04-07T04:43:14.333403Z"
}
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"import matplotlib.pyplot as plt\n",
"import torch\n",
"from torch import nn, optim\n",
"from torch.autograd import Variable\n",
"import numpy as np"
]
},
{
"cell_type": "code",
"execution_count": 104,
"metadata": {
"ExecuteTime": {
"end_time": "2019-04-07T05:26:28.414285Z",
"start_time": "2019-04-07T05:26:28.201996Z"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXoAAAD8CAYAAAB5Pm/hAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvDW2N/gAAFRdJREFUeJzt3X+QXWd93/H3B0n+0RIswEuiWKKisWkSPLHsbISVhERI40Q2TEQbu3HKDC526oFAQphM+FE6mXFdxjFu69QdxoxTh8iUBrvmRxwHJri2FcKMLGVFZAWDgQVMbeHiBWwTD7Uci2//uI/weitp77XuatcP79fMmfuc5zzn3u89u/vZs+ecuydVhSSpX89Z7AIkSQvLoJekzhn0ktQ5g16SOmfQS1LnDHpJ6pxBL0mdM+glqXMGvSR1bvliFwBw8skn19q1axe7DEl6Vtm9e/c3q2pivnFLIujXrl3L1NTUYpchSc8qSb42zDgP3UhS5wx6SeqcQS9JnTPoJalzQwd9kmVJ/jbJrW3+JUl2JplOcmOS41r/8W1+ui1fuzClS5KGMcoe/VuAz8+avxK4uqpOBR4GLmn9lwAPt/6r2zhJ0iIZKuiTrAZeBfy3Nh9gE3BzG7INeE1rb23ztOWb23hJ47RjB1xxxeBROoJhr6P/Q+BtwA+1+RcCj1TVk23+AeCU1j4FuB+gqp5M8mgb/82xVCxpEO6bN8MTT8Bxx8Htt8OGDYtdlZaoeffok7waeKiqdo/zhZNcmmQqydTMzMw4n1rq3/btg5A/cGDwuH37YlekJWyYQzc/B/xKkvuADzE4ZPNfgJVJDv5FsBrY19r7gDUAbflJwLfmPmlVXVdVk1U1OTEx7yd4Jc22ceNgT37ZssHjxo2LXZGWsHmDvqreWVWrq2otcCFwR1W9FrgTOL8Nuwj4s9a+pc3Tlt9RVTXWqqUfdBs2DA7XXH65h200r6P5XzdvBz6U5D8Afwtc3/qvBz6QZBr4NoNfDpLGbcMGA15DGSnoq2o7sL21vwKsP8SYx4ELxlCbJGkM/GSsJHXOoJekzhn0ktQ5g16SOmfQS1LnDHpJ6pxBL0mdM+glqXMGvSR1zqCXpM4Z9JLUOYNekjpn0EtS5wx6SeqcQS9JnTPoJalzBr0kdc6gl6TOGfSS1DmDXpI6N2/QJzkhya4kdye5J8llrX9Tks8k+WySbUmWt/4kuSbJdJK9Sc5a6DchSTq8Yfbo9wObquoMYB2wJcnPAtuAC6vqdOBrwEVt/LnAaW26FLh27FVLkoY2b9DXwGNtdkWbDgBPVNUXW/9twK+29lbghrbeXcDKJKvGXLckaUhDHaNPsizJHuAhBqG+C1ieZLINOR9Y09qnAPfPWv2B1jf3OS9NMpVkamZm5pnWL0max1BBX1UHqmodsBpYD7wMuBC4Osku4O8Z7OUPraquq6rJqpqcmJgYsWxJ0rBGuuqmqh4B7gS2VNWOqnpFVa0HPgUcPIyzj6f27mHwy2HfOIqVJI1umKtuJpKsbO0TgXOAe5O8qPUdD7wdeF9b5Rbgde3qm7OBR6vqwQWpXpI0r+VDjFkFbEuyjMEvhpuq6tYkVyV5deu7tqruaOM/DpwHTAPfBV6/AHVLkoaUqlrsGpicnKypqanFLkOSnlWS7K6qyfnG+clYSeqcQS9JnTPoJalzBr0kdc6gl6TOGfSS1DmDXpI6Z9BLUucMeknqnEEvSZ0z6CWpcwa9JHXOoJekzhn0ktQ5g16SOmfQS1LnDHpJ6pxBL0mdM+glqXPzBn2SE5LsSnJ3knuSXNb6Nyf5TJI9ST6d5NTWf3ySG5NMJ9mZZO3CvgVJ0pEMs0e/H9hUVWcA64AtSc4GrgVeW1XrgP8B/Ls2/hLg4ao6FbgauHL8ZUuShjVv0NfAY212RZuqTc9r/ScBX2/trcC21r4Z2JwkY6tYkjSS5cMMSrIM2A2cCry3qnYm+Q3g40n+L/Ad4Ow2/BTgfoCqejLJo8ALgW/Oec5LgUsBXvziF4/hrUiSDmWok7FVdaAdolkNrE9yOvBW4LyqWg28H/jPo7xwVV1XVZNVNTkxMTFq3ZKkIY101U1VPQLcCZwLnFFVO9uiG4Gfbe19wBqAJMsZHNb51liqlSSNbJirbiaSrGztE4FzgM8DJyV5aRt2sA/gFuCi1j4fuKOqaqxVS5KGNswx+lXAtnac/jnATVV1a5J/A3w4yfeAh4GL2/jrgQ8kmQa+DVy4AHVLkoY0b9BX1V7gzEP0fxT46CH6HwcuGEt1kqSj5idjJalzBr0kdc6gl6TOGfSS1DmDXpI6Z9BLUucMeknqnEEvSZ0z6CWpcwa9JHXOoJekzhn0ktQ5g16SOmfQS1LnDHpJ6pxBL0mdM+glqXMGvSR1zqCXpM7NG/RJTkiyK8ndSe5Jclnr/+ske9r09SQfa/1Jck2S6SR7k5y10G9CknR4894cHNgPbKqqx5KsAD6d5BNV9YqDA5J8GPizNnsucFqbXg5c2x4lSYtg3j36Gnisza5oUx1cnuR5wCbgY61rK3BDW+8uYGWSVeMtW5I0rKGO0SdZlmQP8BBwW1XtnLX4NcDtVfWdNn8KcP+s5Q+0PknSIhgq6KvqQFWtA1YD65OcPmvxrwN/OuoLJ7k0yVSSqZmZmVFXlyQNaaSrbqrqEeBOYAtAkpOB9cBfzBq2D1gza35165v7XNdV1WRVTU5MTIxatyQ9++3YAVdcMXhcQPOejE0yAfxDVT2S5ETgHODKtvh84NaqenzWKrcAb07yIQYnYR+tqgfHXLckPbvt2AGbN8MTT8Bxx8Htt8OGDQvyUsPs0a8C7kyyF/gbBsfob23LLuT/P2zzceArwDTwR8BvjqlWSerH9u2DkD9wYPC4ffuCvdS8e/RVtRc48zDLNh6ir4A3HXVlktSzjRsHe/IH9+g3blywlxrmOnpJ0rht2DA4XLN9+yDkF+iwDRj0krR4NmxY0IA/yP91I0mdM+glqXMGvSR1zqCXpM4Z9JLUOYNekjpn0EtS5wx6SeqcQS9JnTPoJalzBr0kdc6gl6TOGfSS1DmDXpI6Z9BLUucMeknqnEEvSZ2bN+iTnJBkV5K7k9yT5LLWnyTvTvLFJJ9P8tuz+q9JMp1kb5KzFvpNSJIOb5hbCe4HNlXVY0lWAJ9O8gngJ4A1wI9X1feSvKiNPxc4rU0vB65tj5KkRTBv0FdVAY+12RVtKuCNwL+qqu+1cQ+1MVuBG9p6dyVZmWRVVT049uolSfMa6hh9kmVJ9gAPAbdV1U7gx4BfSzKV5BNJTmvDTwHun7X6A61PkrQIhgr6qjpQVeuA1cD6JKcDxwOPV9Uk8EfAH4/ywkkubb8kpmZmZkatW5I0pJGuuqmqR4A7gS0M9tQ/0hZ9FPip1t7H4Nj9Qatb39znuq6qJqtqcmJiYtS6JUlDGuaqm4kkK1v7ROAc4F7gY8Ar27BfBL7Y2rcAr2tX35wNPOrxeUlaPMNcdbMK2JZkGYNfDDdV1a1JPg18MMlbGZys/Y02/uPAecA08F3g9eMvW5I0rGGuutkLnHmI/keAVx2iv4A3jaU6SdJR85OxktQ5g16SOmfQS1LnDHpJ6pxBL0mdM+glqXMGvSR1zqCXpM4Z9JLUOYNekjpn0EtS5wx6SeqcQS9JnTPoJalzBr0kdc6gl6TOGfSS1DmDXpI6Z9BLUufmDfokJyTZleTuJPckuaz1/0mSrybZ06Z1rT9JrkkynWRvkrMW+k1Ikg5v3puDA/uBTVX1WJIVwKeTfKIt+72qunnO+HOB09r0cuDa9ihJWgTz7tHXwGNtdkWb6girbAVuaOvdBaxMsuroS5UkPRNDHaNPsizJHuAh4Laq2tkWvbsdnrk6yfGt7xTg/lmrP9D6JEmLYKigr6oDVbUOWA2sT3I68E7gx4GfAV4AvH2UF05yaZKpJFMzMzMjli1JGtZIV91U1SPAncCWqnqwHZ7ZD7wfWN+G7QPWzFptdeub+1zXVdVkVU1OTEw8s+olSfMa5qqbiSQrW/tE4Bzg3oPH3ZMEeA3w2bbKLcDr2tU3ZwOPVtWDC1K9JGlew1x1swrYlmQZg18MN1XVrUnuSDIBBNgDvKGN/zhwHjANfBd4/fjLliQNa96gr6q9wJmH6N90mPEFvOnoS5MkjYOfjJWkzhn0ktQ5g16SOmfQS1LnDHpJ6pxBL0mdM+glqXMGvSR1zqCXpM4Z9JLUOYNekjpn0EtS5wx6SeqcQS9JnTPoJalzBr0kdc6gl6TOGfSS1DmDXpI6Z9BLUufmDfokJyTZleTuJPckuWzO8muSPDZr/vgkNyaZTrIzydrxly1JGtYwe/T7gU1VdQawDtiS5GyAJJPA8+eMvwR4uKpOBa4GrhxjvZKkEc0b9DVwcI99RZsqyTLgKuBtc1bZCmxr7ZuBzUkypnolSSMa6hh9kmVJ9gAPAbdV1U7gzcAtVfXgnOGnAPcDVNWTwKPACw/xnJcmmUoyNTMzczTvQZJ0BEMFfVUdqKp1wGpgfZJfAC4A/uszfeGquq6qJqtqcmJi4pk+jSRpHiNddVNVjwB3Aq8ETgWmk9wH/KMk023YPmANQJLlwEnAt8ZVsCRpNMNcdTORZGVrnwicA+yuqh+pqrVVtRb4bjv5CnALcFFrnw/cUVU1/tIlScNYPsSYVcC2dvL1OcBNVXXrEcZfD3yg7eF/G7jw6MuUJD1T8wZ9Ve0FzpxnzHNntR9ncPxekrQE+MlYSeqcQS9JnTPoJalzBr0kdc6gl6TOGfSS1DmDXpI6Z9BLUucMeknqnEEvSZ0z6CWpcwa9JHXOoJekzhn0ktQ5g16SOmfQS1LnDHpJ6pxBL0mdM+glqXPzBn2SE5LsSnJ3knuSXNb6r299e5PcnOS5rf/4JDcmmU6yM8nahX0LkqQjGWaPfj+wqarOANYBW5KcDby1qs6oqp8C/jfw5jb+EuDhqjoVuBq4cgHqliQNad6gr4HH2uyKNlVVfQcgSYATgWpjtgLbWvtmYHMbM347dsAVVwweJUmHtHyYQUmWAbuBU4H3VtXO1v9+4Dzgc8DvtuGnAPcDVNWTSR4FXgh8c6yV79gBmzfDE0/AccfB7bfDhg1jfQlJ6sFQJ2Or6kBVrQNWA+uTnN76Xw/8KPB54NdGeeEklyaZSjI1MzMzYtnA9u2DkD9wYPC4ffvozyFJPwBGuuqmqh4B7gS2zOo7AHwI+NXWtQ9YA5BkOXAS8K1DPNd1VTVZVZMTExOjV75x42BPftmywePGjaM/hyT9ABjmqpuJJCtb+0TgHOALSU5tfQF+Bbi3rXILcFFrnw/cUVXFuG3YMDhcc/nlHraRpCMY5hj9KmBbO07/HOAm4C+Av07yPCDA3cAb2/jrgQ8kmQa+DVw49qoP2rDBgJekecwb9FW1FzjzEIt+7jDjHwcuOMq6JElj4idjJalzBr0kdc6gl6TOGfSS1DmDXpI6l4W4xH3kIpIZ4GvPcPWTGfe/VxgP6xqNdY1uqdZmXaM5mrr+SVXN+4nTJRH0RyPJVFVNLnYdc1nXaKxrdEu1NusazbGoy0M3ktQ5g16SOtdD0F+32AUchnWNxrpGt1Rrs67RLHhdz/pj9JKkI+thj16SdARLMuiT/HGSh5J8dk7/byW5t92k/D2z+t/Zbkb+hSS/PKt/S+ubTvKOhair3Qh9T5vuS7JnidS1Lsldra6pJOtbf5Jc0157b5KzZq1zUZIvtemiQ73WGOo6I8mOJH+X5M/bf0A9uOxYba81Se5M8rn2vfSW1v+CJLe1939bkue3/mOyzY5Q1wVt/ntJJuess+Db7Ah1XdV+Hvcm+WjavzNfAnVd3mrak+STSX609S/q13HW8t9NUklOPmZ1VdWSm4BfAM4CPjur75XA/wKOb/Mvao8/yeDfJB8PvAT4MrCsTV8G/ilwXBvzk+Oua87y/wT8/lKoC/gkcG5rnwdsn9X+BIN/L302sLP1vwD4Snt8fms/fwHq+hvgF1v7YuDyRdheq4CzWvuHgC+2138P8I7W/w7gymO5zY5Q108A/wzYDkzOGn9MttkR6volYHnrv3LW9lrsup43a8xvA+9bCl/HNr8G+EsGnxs6+VjVtST36KvqUwz+l/1sbwT+oKr2tzEPtf6twIeqan9VfRWYBta3abqqvlJVTzC4C9bWBagL+P4NWP4l8KdLpK4CDu4tnwR8fVZdN9TAXcDKJKuAXwZuq6pvV9XDwG3MupPYGOt6KfCp1r6Np+5Mdiy314NV9ZnW/nsGt8I8haff2H4b8JpZtS34NjtcXVX1+ar6wiFWOSbb7Ah1fbKqnmzD7mJwq9GlUNd3Zg37xwx+Fg7WtWhfx7b4auBts2o6JnUtyaA/jJcCr0iyM8lfJfmZ1v/9m5E3D7S+w/UvlFcA36iqLy2Run4HuCrJ/cB/BN65ROq6h6d+uC+g3XZysepKspbB/RZ2Aj9cVQ+2Rf8H+OHFqm1OXYezlOq6mMFe6ZKoK8m72/f+a4HfXwp1JdkK7Kuqu+cMW/C6nk1Bv5zBnzBnA78H3NT2opeKX+epvfml4I3AW6tqDfBWBnf+WgouBn4zyW4Gf9Y+sViFJHku8GHgd+bsBVKDv50X5ZK0I9W1mA5XV5J3AU8CH1wqdVXVu9r3/geBNy92XQy2z7/lqV86x9SzKegfAD7S/rzZBXyPwf+I+P7NyJvVre9w/WOXwU3Q/wVw46zuxa7rIuAjrf0/GfzZvOh1VdW9VfVLVfXTDH4xfnkx6kqygsEP4Qer6uB2+kb7k5n2ePDw4DGr7TB1Hc6i15XkXwOvBl7bfjkuibpm+SBPHR5czLp+jMH5iruT3Nde4zNJfuSY1PVMDuwfiwlYy9NP4r0B+Pet/VIGf9IEeBlPP/HzFQYnfZa39kt46sTPy8ZdV+vbAvzVnL5FrYvBccGNrb0Z2N3ar+LpJ3521VMnfr7K4KTP81v7BQtQ18GT6M8BbgAuPtbbq733G4A/nNN/FU8/GfueY7nNDlfXrOXbefrJ2GOyzY6wvbYAnwMmFuN7/wh1nTar/VvAzUvp69jG3MdTJ2MXvK6j+iFeqInBnt6DwD8w2JO/pH1j/Hfgs8BngE2zxr+LwZ7hF2hXmrT+8xic8f4y8K6FqKv1/wnwhkOMX7S6gJ8Hdrcfpp3AT8/6Jnxve+2/4+nBcTGDE2fTwOsXqK63tPf+ReAPaB/aO8bb6+cZHJbZC+xp03nAC4HbgS8xuMLrBcdymx2hrn/ett9+4BvAXx7LbXaEuqYZ7HAd7HvfEqnrwwxyYi/w5wxO0C7613HOmPt4KugXvC4/GStJnXs2HaOXJD0DBr0kdc6gl6TOGfSS1DmDXpI6Z9BLUucMeknqnEEvSZ37fx1iIYZvFmeYAAAAAElFTkSuQmCC\n",
"text/plain": [
"