 "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# latent Dirichlet allocation (LDA)\n",
"\n",
"潜在狄利克雷分配\n",
"\n",
"The simplest topic model (on which all others are based) is latent Dirichlet allocation (LDA). \n",
"- LDA is a generative model that **infers unobserved meanings** from a large set of observations. \n",
"\n",
"## Reference\n",
"\n",
"- Blei DM, Ng J, Jordan MI. **Latent dirichlet allocation**. J Mach Learn Res. 2003; 3: 993–1022.\n",
"- Blei DM, Lafferty JD. Correction: a correlated topic model of science. Ann Appl Stat. 2007; 1: 634. \n",
"- Blei DM. **Probabilistic topic models**. Commun ACM. 2012; 55: 55–65.\n",
"- Chandra Y, Jiang LC, Wang C-J (2016) Mining Social Entrepreneurship Strategies Using Topic Modeling. PLoS ONE 11(3): e0151342. doi:10.1371/journal.pone.0151342"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# 阅读文献\n",
"\n",
"### Blei DM. Probabilistic topic models. Commun ACM. 2012; 55: 55–65."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## LDA(Latent Dirichlet Allocation)是一种**文档主题**生成模型\n",
"- 三层贝叶斯概率模型,包含词、主题和文档三层结构。\n",
"\n",
"所谓**生成模型**,就是说,我们认为一篇文章的每个词都是通过这样一个过程得到:\n",
"\n",
"> 以一定概率选择了某个主题,并从这个主题中以一定概率选择某个词语\n",
"\n",
"- 文档到主题服从**多项式分布**,主题到词服从多项式分布。"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## 多项式分布(Multinomial Distribution)是二项式分布的推广。\n",
"- 二项分布的典型例子是扔硬币,硬币正面朝上概率为p, 重复扔n次硬币,k次为正面的概率即为一个二项分布概率。(严格定义见伯努利实验定义)。\n",
"- 把二项分布公式推广至多种状态,就得到了多项分布。\n",
" - 例如在上面例子中1出现k1次,2出现k2次,3出现k3次的概率分布情况。"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## LDA是一种**非监督机器学习技术**\n",
"\n",
"可以用来识别大规模文档集(document collection)或语料库(corpus)中潜藏的主题信息。\n",
"- 采用了词袋(bag of words)的方法,将每一篇文档视为一个词频向量,从而将文本信息转化为了易于建模的数字信息。 \n",
"- 但是词袋方法没有考虑词与词之间的顺序,这简化了问题的复杂性,同时也为模型的改进提供了契机。\n",
"- 每一篇文档代表了一些主题所构成的一个概率分布,而每一个主题又代表了很多单词所构成的一个概率分布。"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# latent Dirichlet allocation (LDA)\n",
"\n",
"潜在狄利克雷分配\n",
"\n",
"The simplest topic model (on which all others are based) is latent Dirichlet allocation (LDA). \n",
"- LDA is a generative model that **infers unobserved meanings** from a large set of observations. \n",
"\n",
"## Reference\n",
"\n",
"- Blei DM, Ng J, Jordan MI. **Latent dirichlet allocation**. J Mach Learn Res. 2003; 3: 993–1022.\n",
"- Blei DM, Lafferty JD. Correction: a correlated topic model of science. Ann Appl Stat. 2007; 1: 634. \n",
"- Blei DM. **Probabilistic topic models**. Commun ACM. 2012; 55: 55–65.\n",
"- Chandra Y, Jiang LC, Wang C-J (2016) Mining Social Entrepreneurship Strategies Using Topic Modeling. PLoS ONE 11(3): e0151342. doi:10.1371/journal.pone.0151342"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# 阅读文献\n",
"\n",
"### Blei DM. Probabilistic topic models. Commun ACM. 2012; 55: 55–65."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## LDA(Latent Dirichlet Allocation)是一种**文档主题**生成模型\n",
"- 三层贝叶斯概率模型,包含词、主题和文档三层结构。\n",
"\n",
"所谓**生成模型**,就是说,我们认为一篇文章的每个词都是通过这样一个过程得到:\n",
"\n",
"> 以一定概率选择了某个主题,并从这个主题中以一定概率选择某个词语\n",
"\n",
"- 文档到主题服从**多项式分布**,主题到词服从多项式分布。"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## 多项式分布(Multinomial Distribution)是二项式分布的推广。\n",
"- 二项分布的典型例子是扔硬币,硬币正面朝上概率为p, 重复扔n次硬币,k次为正面的概率即为一个二项分布概率。(严格定义见伯努利实验定义)。\n",
"- 把二项分布公式推广至多种状态,就得到了多项分布。\n",
" - 例如在上面例子中1出现k1次,2出现k2次,3出现k3次的概率分布情况。"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## LDA是一种**非监督机器学习技术**\n",
"\n",
"可以用来识别大规模文档集(document collection)或语料库(corpus)中潜藏的主题信息。\n",
"- 采用了词袋(bag of words)的方法,将每一篇文档视为一个词频向量,从而将文本信息转化为了易于建模的数字信息。 \n",
"- 但是词袋方法没有考虑词与词之间的顺序,这简化了问题的复杂性,同时也为模型的改进提供了契机。\n",
"- 每一篇文档代表了一些主题所构成的一个概率分布,而每一个主题又代表了很多单词所构成的一个概率分布。"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## 多项分布的参数服从Dirichlet分布\n",
"- Dirichlet分布是多项分布的参数的分布, 被认为是“分布上的分布”。"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## LDA的名字由来\n",
"\n",
"存在两个隐含的Dirichlet分布。\n",
"\n",
"- 每篇文档对应一个不同的topic分布,服从多项分布\n",
" - topic多项分布的参数服从一个Dirichlet分布。 \n",
"- 每个topic下存在一个term的多项分布\n",
" - term多项分布的参数服从一个Dirichlet分布。\n",
" \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
"### Topic models assume that each document contains a mixture of topics.\n",
"\n",
"It is impossible to directly assess the relationships between topics and documents and between topics and terms. \n",
"\n",
"- Topics are considered latent/unobserved variables that stand between the documents and terms\n",
"\n",
"- What can be directly observed is the distribution of terms over documents, which is known as the document term matrix (DTM).\n",
"\n",
"Topic models algorithmically identify the best set of latent variables (topics) that can best explain the observed distribution of terms in the documents. "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"The DTM is further decomposed into two matrices:\n",
"- a term-topic matrix (TTM) \n",
"- a topic-document matrix (TDM)\n",
"\n",
"Each document can be assigned to a primary topic that demonstrates the highest topic-document probability and can then be linked to other topics with declining probabilities."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"Assume K topics are in D documents.\n",
"\n",
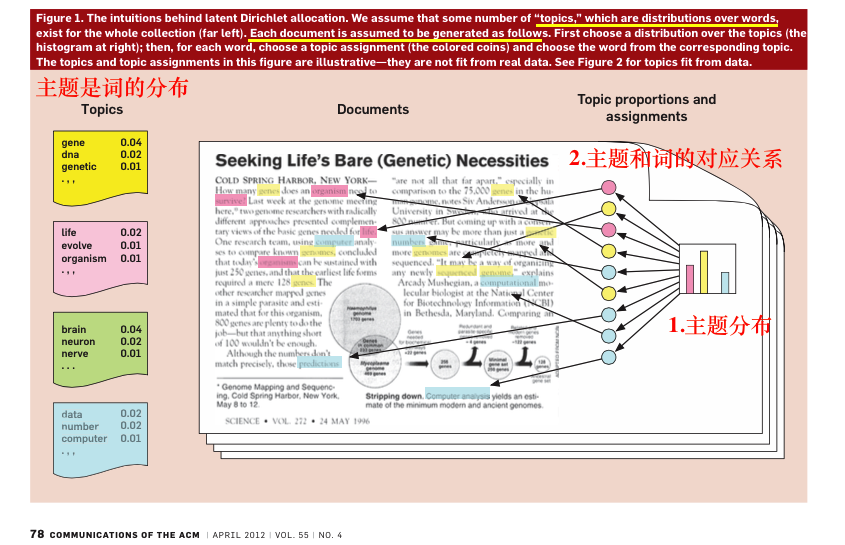
"## 主题在词语上的分布\n",
"\n",
"Each topic is denoted with $\\phi_{1:K}$, \n",
"\n",
"- 主题$\\phi_K$ 是第k个主题,这个主题表达为一系列的terms。\n",
"- Each topic is a distribution of fixed words. \n",
"\n",
"## 主题在文本上的分布\n",
"\n",
"The topics proportion in the document **d **is denoted as $\\theta_d$\n",
"\n",
"- e.g., the kth topic's proportion in document d is $\\theta_{d, k}$. "
]
},
{
"cell_type": "markdown",
"metadata": {
"ExecuteTime": {
"end_time": "2017-09-22T22:12:40.058178",
"start_time": "2017-09-22T22:12:40.051172"
},
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## 主题在文本和词上的分配\n",
"\n",
"topic models assign topics to a document and its terms. \n",
"- The topic assigned to document d is denoted as $z_d$, \n",
"- The topic assigned to the nth term in document d is denoted as $z_{d,n}$. "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## 可以观察到的是?\n",
"词在文档中的位置,也就是文档-词矩阵(document-term matrix)\n",
"\n",
"Let $w_{d,n}$ denote the nth term in document d. "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## 多项分布的参数服从Dirichlet分布\n",
"- Dirichlet分布是多项分布的参数的分布, 被认为是“分布上的分布”。"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## LDA的名字由来\n",
"\n",
"存在两个隐含的Dirichlet分布。\n",
"\n",
"- 每篇文档对应一个不同的topic分布,服从多项分布\n",
" - topic多项分布的参数服从一个Dirichlet分布。 \n",
"- 每个topic下存在一个term的多项分布\n",
" - term多项分布的参数服从一个Dirichlet分布。\n",
" \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
"### Topic models assume that each document contains a mixture of topics.\n",
"\n",
"It is impossible to directly assess the relationships between topics and documents and between topics and terms. \n",
"\n",
"- Topics are considered latent/unobserved variables that stand between the documents and terms\n",
"\n",
"- What can be directly observed is the distribution of terms over documents, which is known as the document term matrix (DTM).\n",
"\n",
"Topic models algorithmically identify the best set of latent variables (topics) that can best explain the observed distribution of terms in the documents. "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"The DTM is further decomposed into two matrices:\n",
"- a term-topic matrix (TTM) \n",
"- a topic-document matrix (TDM)\n",
"\n",
"Each document can be assigned to a primary topic that demonstrates the highest topic-document probability and can then be linked to other topics with declining probabilities."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"Assume K topics are in D documents.\n",
"\n",
"## 主题在词语上的分布\n",
"\n",
"Each topic is denoted with $\\phi_{1:K}$, \n",
"\n",
"- 主题$\\phi_K$ 是第k个主题,这个主题表达为一系列的terms。\n",
"- Each topic is a distribution of fixed words. \n",
"\n",
"## 主题在文本上的分布\n",
"\n",
"The topics proportion in the document **d **is denoted as $\\theta_d$\n",
"\n",
"- e.g., the kth topic's proportion in document d is $\\theta_{d, k}$. "
]
},
{
"cell_type": "markdown",
"metadata": {
"ExecuteTime": {
"end_time": "2017-09-22T22:12:40.058178",
"start_time": "2017-09-22T22:12:40.051172"
},
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## 主题在文本和词上的分配\n",
"\n",
"topic models assign topics to a document and its terms. \n",
"- The topic assigned to document d is denoted as $z_d$, \n",
"- The topic assigned to the nth term in document d is denoted as $z_{d,n}$. "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## 可以观察到的是?\n",
"词在文档中的位置,也就是文档-词矩阵(document-term matrix)\n",
"\n",
"Let $w_{d,n}$ denote the nth term in document d. "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## 联合概率分布\n",
"According to Blei et al. the joint distribution of $\\phi_{1:K}$,$\\theta_{1:D}$, $z_{1:D}$ and $w_{d, n}$ plus the generative process for LDA can be expressed as:\n",
"\n",
"$ p(\\phi_{1:K}, \\theta_{1:D}, z_{1:D}, w_{d, n}) $ = \n",
"\n",
"$\\prod_{i=1}^{K} p(\\phi_i) \\prod_{d =1}^D p(\\theta_d)(\\prod_{n=1}^N p(z_{d,n} \\mid \\theta_d) \\times p(w_{d, n} \\mid \\phi_{1:K}, Z_{d, n}) ) $\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
"## 后验分布\n",
"\n",
"Note that $\\phi_{1:k},\\theta_{1:D},and z_{1:D}$ are latent, unobservable variables. Thus, the computational challenge of LDA is to compute the conditional distribution of them given the observable specific words in the documents $w_{d, n}$. \n",
"\n",
"Accordingly, the posterior distribution of LDA can be expressed as:\n",
"\n",
"## $p(\\phi_{1:K}, \\theta_{1:D}, z_{1:D} \\mid w_{d, n}) = \\frac{p(\\phi_{1:K}, \\theta_{1:D}, z_{1:D}, w_{d, n})}{p(w_{1:D})}$"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"Because the number of possible topic structures is exponentially large, it is impossible to compute the posterior of LDA. \n",
"\n",
"Topic models aim to develop efficient algorithms to **approximate** the posterior of LDA. There are two categories of algorithms: \n",
"- sampling-based algorithms\n",
"- variational algorithms \n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## Gibbs sampling\n",
"\n",
"> In statistics, Gibbs sampling or a Gibbs sampler is a **Markov chain Monte Carlo (MCMC)** algorithm for obtaining a sequence of observations which are approximated from a specified **multivariate probability distribution**, when direct sampling is difficult. \n",
"\n",
"Using the Gibbs sampling method, we can build a Markov chain for the sequence of random variables (see Eq 1). \n",
"\n",
"The sampling algorithm is applied to the chain to sample from the limited distribution, and it approximates the **posterior**. "
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"\n",
"# Gensim: Topic modelling for humans\n",
"\n",
"\n",
"\n",
"Gensim is developed by Radim Řehůřek,who is a machine learning researcher and consultant in the Czech Republic. We must start by installing it. We can achieve this by running the following command:\n",
"\n",
"> # pip install gensim\n"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"ExecuteTime": {
"end_time": "2017-09-22T23:49:19.060373",
"start_time": "2017-09-22T23:49:17.621027"
},
"collapsed": false,
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"from gensim import corpora, models, similarities, matutils\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Download data\n",
"\n",
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## 联合概率分布\n",
"According to Blei et al. the joint distribution of $\\phi_{1:K}$,$\\theta_{1:D}$, $z_{1:D}$ and $w_{d, n}$ plus the generative process for LDA can be expressed as:\n",
"\n",
"$ p(\\phi_{1:K}, \\theta_{1:D}, z_{1:D}, w_{d, n}) $ = \n",
"\n",
"$\\prod_{i=1}^{K} p(\\phi_i) \\prod_{d =1}^D p(\\theta_d)(\\prod_{n=1}^N p(z_{d,n} \\mid \\theta_d) \\times p(w_{d, n} \\mid \\phi_{1:K}, Z_{d, n}) ) $\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"\n",
"## 后验分布\n",
"\n",
"Note that $\\phi_{1:k},\\theta_{1:D},and z_{1:D}$ are latent, unobservable variables. Thus, the computational challenge of LDA is to compute the conditional distribution of them given the observable specific words in the documents $w_{d, n}$. \n",
"\n",
"Accordingly, the posterior distribution of LDA can be expressed as:\n",
"\n",
"## $p(\\phi_{1:K}, \\theta_{1:D}, z_{1:D} \\mid w_{d, n}) = \\frac{p(\\phi_{1:K}, \\theta_{1:D}, z_{1:D}, w_{d, n})}{p(w_{1:D})}$"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"Because the number of possible topic structures is exponentially large, it is impossible to compute the posterior of LDA. \n",
"\n",
"Topic models aim to develop efficient algorithms to **approximate** the posterior of LDA. There are two categories of algorithms: \n",
"- sampling-based algorithms\n",
"- variational algorithms \n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## Gibbs sampling\n",
"\n",
"> In statistics, Gibbs sampling or a Gibbs sampler is a **Markov chain Monte Carlo (MCMC)** algorithm for obtaining a sequence of observations which are approximated from a specified **multivariate probability distribution**, when direct sampling is difficult. \n",
"\n",
"Using the Gibbs sampling method, we can build a Markov chain for the sequence of random variables (see Eq 1). \n",
"\n",
"The sampling algorithm is applied to the chain to sample from the limited distribution, and it approximates the **posterior**. "
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"\n",
"# Gensim: Topic modelling for humans\n",
"\n",
"\n",
"\n",
"Gensim is developed by Radim Řehůřek,who is a machine learning researcher and consultant in the Czech Republic. We must start by installing it. We can achieve this by running the following command:\n",
"\n",
"> # pip install gensim\n"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"ExecuteTime": {
"end_time": "2017-09-22T23:49:19.060373",
"start_time": "2017-09-22T23:49:17.621027"
},
"collapsed": false,
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"from gensim import corpora, models, similarities, matutils\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Download data\n",
"\n",
"| \n", " | Page | \n", "Author | \n", "Title | \n", "Title2 | \n", "Sentence | \n", "
|---|---|---|---|---|---|
| 0 | \n", "0001.1 | \n", "和岘 | \n", "导引 | \n", "导引 | \n", "气和玉烛,叡化着鸿明。缇管一阳生。郊禋盛礼燔柴毕,旋轸凤凰城。森罗仪卫振华缨。载路溢欢声。皇... | \n", "
| 1 | \n", "0001.2 | \n", "和岘 | \n", "六州 | \n", "六州 | \n", "严夜警,铜莲漏迟迟。清禁肃,森陛戟,羽卫俨皇闱。角声励,钲鼓攸宜。金管成雅奏,逐吹逶迤。荐苍... | \n", "
| 2 | \n", "0001.3 | \n", "和岘 | \n", "十二时 | \n", "忆少年 | \n", "承宝运,驯致隆平。鸿庆被寰瀛。时清俗阜,治定功成。遐迩咏由庚。严郊祀,文物声明。会天正、星拱... | \n", "