{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Introducing Keras\n",
"> In this first chapter, you will get introduced to neural networks, understand what kind of problems they can solve, and when to use them. You will also build several networks and save the earth by training a regression model that approximates the orbit of a meteor that is approaching us! This is the Summary of lecture \"Introduction to Deep Learning with Keras\", via datacamp.\n",
"\n",
"- toc: true \n",
"- badges: true\n",
"- comments: true\n",
"- author: Chanseok Kang\n",
"- categories: [Python, Datacamp, Tensorflow-Keras, Deep_Learning]\n",
"- image: images/plot_orbit.png"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"import numpy as np\n",
"import pandas as pd\n",
"import tensorflow as tf\n",
"import matplotlib.pyplot as plt\n",
"\n",
"plt.rcParams['figure.figsize'] = (8, 8)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
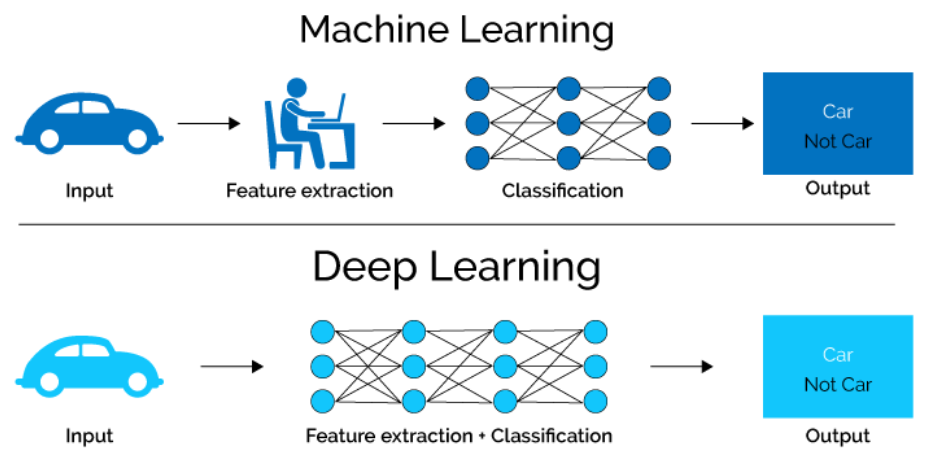
"## What is Keras?\n",
"- Keras + Tensorflow\n",
" - Tensorflow's high level framework of choice\n",
" - Keras is complementary to Tensorflow\n",
"- Feature Engineering\n",
"\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
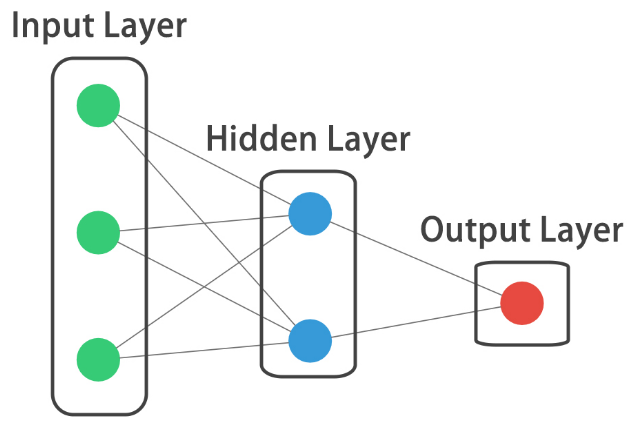
"## Your first neural network\n",
"- Neural Network\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
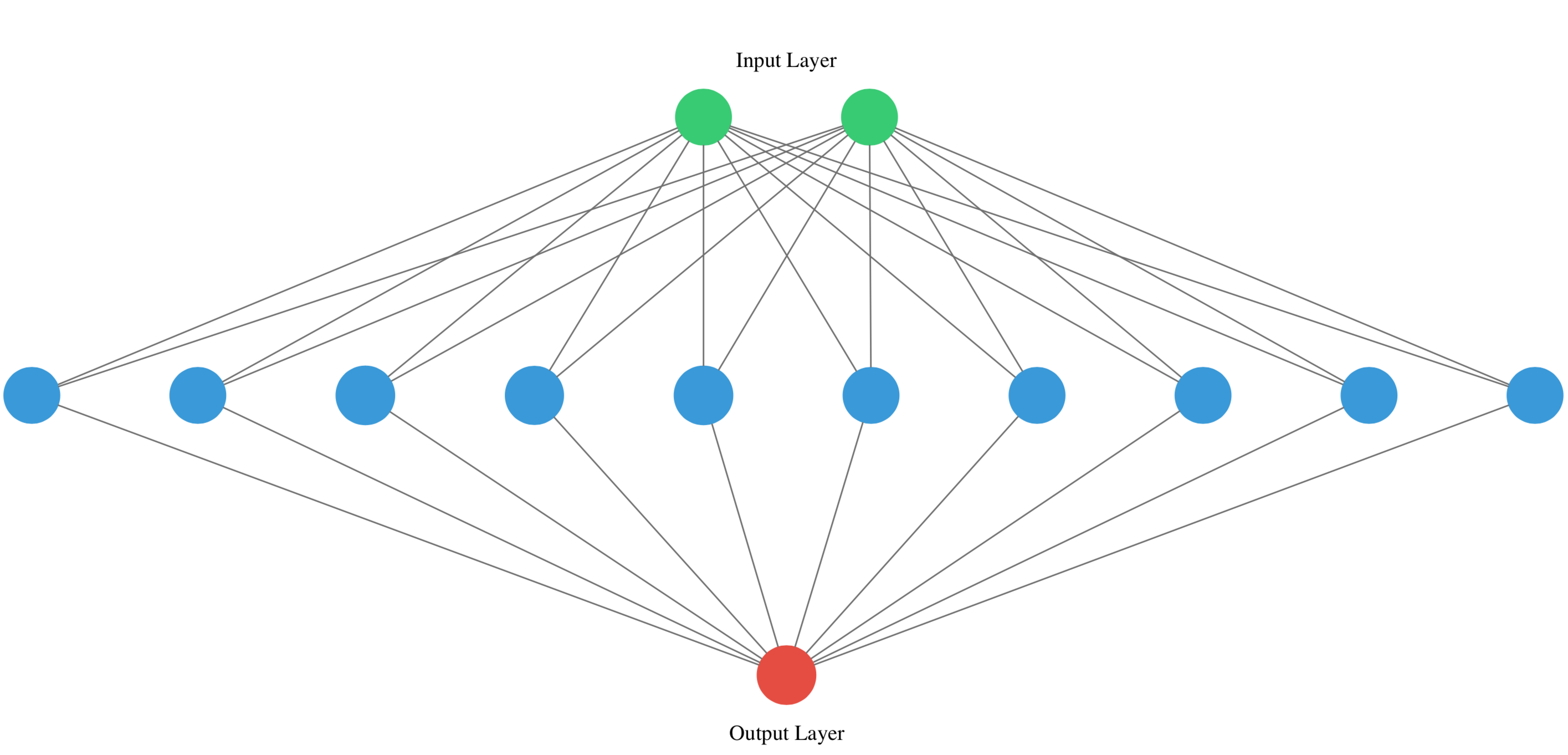
"### Hello nets!\n",
"You're going to build a simple neural network to get a feeling of how quickly it is to accomplish this in Keras.\n",
"\n",
"You will build a network that takes two numbers as an input, passes them through a hidden layer of 10 neurons, and finally outputs a single non-constrained number.\n",
"\n",
"A non-constrained output can be obtained by avoiding setting an activation function in the output layer. This is useful for problems like regression, when we want our output to be able to take any non-constrained value.\n",
""
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Model: \"sequential\"\n",
"_________________________________________________________________\n",
"Layer (type) Output Shape Param # \n",
"=================================================================\n",
"dense (Dense) (None, 10) 30 \n",
"_________________________________________________________________\n",
"dense_1 (Dense) (None, 1) 11 \n",
"=================================================================\n",
"Total params: 41\n",
"Trainable params: 41\n",
"Non-trainable params: 0\n",
"_________________________________________________________________\n"
]
}
],
"source": [
"from tensorflow.keras import Sequential\n",
"from tensorflow.keras.layers import Dense\n",
"\n",
"# Create a Sequential model\n",
"model = Sequential()\n",
"\n",
"# Add an input layer and a hidden layer with 10 neurons\n",
"model.add(Dense(10, input_shape=(2, ), activation='relu'))\n",
"\n",
"# Add a 1-neuron output layer\n",
"model.add(Dense(1))\n",
"\n",
"# Summarize your model\n",
"model.summary()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
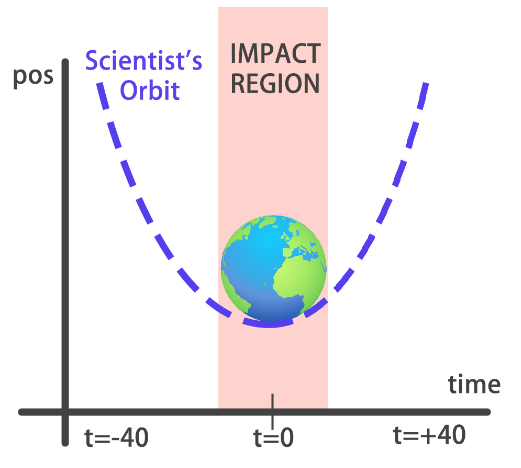
"## Surviving a meteor strike\n",
"- Scientific prediction\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Specifying a model\n",
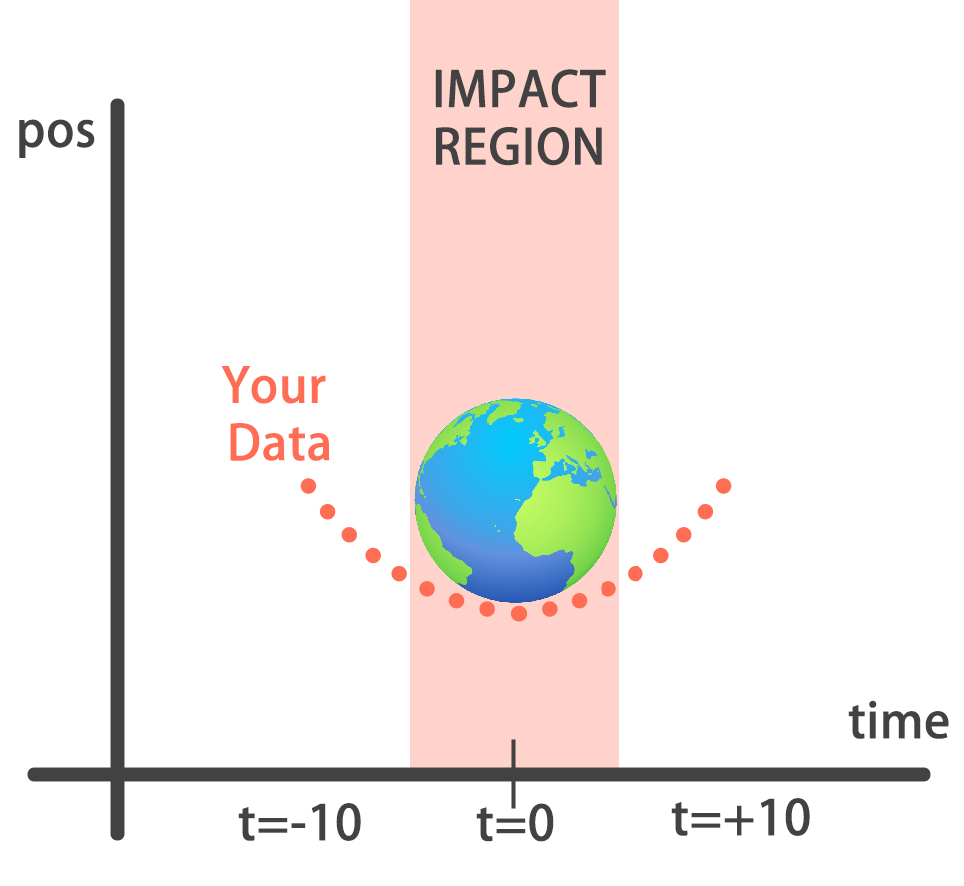
"You will build a simple regression model to predict the orbit of the meteor!\n",
"\n",
"Your training data consist of measurements taken at time steps from -10 minutes before the impact region to +10 minutes after. Each time step can be viewed as an X coordinate in our graph, which has an associated position Y for the meteor orbit at that time step.\n",
"\n",
"Note that you can view this problem as approximating a quadratic function via the use of neural networks.\n",
"\n",
"This data is stored in two numpy arrays: one called `time_steps` , what we call features, and another called `y_positions`, with the labels. Go on and build your model! It should be able to predict the y positions for the meteor orbit at future time steps."
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"
\n",
"\n",
"
\n",
" \n",
"
\n",
"
\n",
"
time_steps
\n",
"
y
\n",
"
\n",
" \n",
" \n",
"
\n",
"
0
\n",
"
-10.000000
\n",
"
100.000000
\n",
"
\n",
"
\n",
"
1
\n",
"
-9.989995
\n",
"
99.800000
\n",
"
\n",
"
\n",
"
2
\n",
"
-9.979990
\n",
"
99.600200
\n",
"
\n",
"
\n",
"
3
\n",
"
-9.969985
\n",
"
99.400601
\n",
"
\n",
"
\n",
"
4
\n",
"
-9.959980
\n",
"
99.201201
\n",
"
\n",
" \n",
"
\n",
"
"
],
"text/plain": [
" time_steps y\n",
"0 -10.000000 100.000000\n",
"1 -9.989995 99.800000\n",
"2 -9.979990 99.600200\n",
"3 -9.969985 99.400601\n",
"4 -9.959980 99.201201"
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"orbit = pd.read_csv('./dataset/orbit.csv')\n",
"orbit.head()"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [],
"source": [
"time_steps = orbit['time_steps'].to_numpy()\n",
"y_positions = orbit['y'].to_numpy()"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [],
"source": [
"# Instantiate a Sequential model\n",
"model = Sequential()\n",
"\n",
"# Add a Dense layer with 50 neurons and an input of 1 neuron\n",
"model.add(Dense(50, input_shape=(1, ), activation='relu'))\n",
"\n",
"# Add two Dense layers with 50 neurons and relu activation\n",
"model.add(Dense(50, activation='relu'))\n",
"model.add(Dense(50, activation='relu'))\n",
"\n",
"# End your model with a Dense layer and no activation\n",
"model.add(Dense(1))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Training\n",
"You're going to train your first model in this course, and for a good cause!\n",
"\n",
"Remember that before training your Keras models you need to compile them. This can be done with the `.compile()` method. The `.compile()` method takes arguments such as the `optimizer`, used for weight updating, and the `loss` function, which is what we want to minimize. Training your model is as easy as calling the `.fit()` method, passing on the features, labels and a number of epochs to train for.\n",
" Train it and evaluate it on this very same data, let's see if your model can learn the meteor's trajectory."
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Training started..., this can take a while:\n",
"Epoch 1/30\n",
"63/63 [==============================] - 0s 1ms/step - loss: 1746.0275\n",
"Epoch 2/30\n",
"63/63 [==============================] - 0s 982us/step - loss: 399.4369\n",
"Epoch 3/30\n",
"63/63 [==============================] - 0s 1ms/step - loss: 139.0688\n",
"Epoch 4/30\n",
"63/63 [==============================] - 0s 1ms/step - loss: 118.3568\n",
"Epoch 5/30\n",
"63/63 [==============================] - 0s 1ms/step - loss: 95.8330\n",
"Epoch 6/30\n",
"63/63 [==============================] - 0s 1ms/step - loss: 72.0429\n",
"Epoch 7/30\n",
"63/63 [==============================] - 0s 1ms/step - loss: 49.8471\n",
"Epoch 8/30\n",
"63/63 [==============================] - 0s 1ms/step - loss: 33.6600\n",
"Epoch 9/30\n",
"63/63 [==============================] - 0s 1ms/step - loss: 19.1619\n",
"Epoch 10/30\n",
"63/63 [==============================] - 0s 988us/step - loss: 12.1949\n",
"Epoch 11/30\n",
"63/63 [==============================] - 0s 1ms/step - loss: 7.3504\n",
"Epoch 12/30\n",
"63/63 [==============================] - 0s 1ms/step - loss: 4.9665\n",
"Epoch 13/30\n",
"63/63 [==============================] - 0s 1ms/step - loss: 3.8602\n",
"Epoch 14/30\n",
"63/63 [==============================] - 0s 1ms/step - loss: 2.3850\n",
"Epoch 15/30\n",
"63/63 [==============================] - 0s 1ms/step - loss: 1.8201\n",
"Epoch 16/30\n",
"63/63 [==============================] - 0s 1ms/step - loss: 1.3465\n",
"Epoch 17/30\n",
"63/63 [==============================] - 0s 1ms/step - loss: 1.1194\n",
"Epoch 18/30\n",
"63/63 [==============================] - 0s 1ms/step - loss: 0.9593\n",
"Epoch 19/30\n",
"63/63 [==============================] - 0s 1ms/step - loss: 0.7892\n",
"Epoch 20/30\n",
"63/63 [==============================] - 0s 1ms/step - loss: 0.6329\n",
"Epoch 21/30\n",
"63/63 [==============================] - 0s 1ms/step - loss: 0.5182\n",
"Epoch 22/30\n",
"63/63 [==============================] - 0s 1ms/step - loss: 0.5441\n",
"Epoch 23/30\n",
"63/63 [==============================] - 0s 952us/step - loss: 0.5981\n",
"Epoch 24/30\n",
"63/63 [==============================] - 0s 938us/step - loss: 0.3490\n",
"Epoch 25/30\n",
"63/63 [==============================] - 0s 1ms/step - loss: 0.3329\n",
"Epoch 26/30\n",
"63/63 [==============================] - 0s 984us/step - loss: 0.2688\n",
"Epoch 27/30\n",
"63/63 [==============================] - 0s 927us/step - loss: 0.2527\n",
"Epoch 28/30\n",
"63/63 [==============================] - 0s 964us/step - loss: 0.2108\n",
"Epoch 29/30\n",
"63/63 [==============================] - 0s 1ms/step - loss: 0.2097\n",
"Epoch 30/30\n",
"63/63 [==============================] - 0s 980us/step - loss: 0.2139\n",
"63/63 [==============================] - 0s 754us/step - loss: 0.3520\n",
"Final loss value: 0.35198938846588135\n"
]
}
],
"source": [
"# Compile your model\n",
"model.compile(optimizer='adam', loss='mse')\n",
"\n",
"print('Training started..., this can take a while:')\n",
"\n",
"# Fit your model on your data for 30 epochs\n",
"model.fit(time_steps, y_positions, epochs=30)\n",
"\n",
"# Evaluate your model\n",
"print(\"Final loss value:\", model.evaluate(time_steps, y_positions))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Predicting the orbit!\n",
"You've already trained a `model` that approximates the orbit of the meteor approaching Earth and it's loaded for you to use.\n",
"\n",
"Since you trained your model for values between -10 and 10 minutes, your model hasn't yet seen any other values for different time steps. You will now visualize how your model behaves on unseen data.\n",
"\n",
"Hurry up, the Earth is running out of time!\n",
"\n",
"Remember `np.arange(x,y)` produces a range of values from `x` to `y-1`. That is the `[x, y)` interval."
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [],
"source": [
"def plot_orbit(model_preds):\n",
" axeslim = int(len(model_preds) / 2)\n",
" plt.plot(np.arange(-axeslim, axeslim + 1),np.arange(-axeslim, axeslim + 1) ** 2,\n",
" color=\"mediumslateblue\")\n",
" plt.plot(np.arange(-axeslim, axeslim + 1),model_preds,color=\"orange\")\n",
" plt.axis([-40, 41, -5, 550])\n",
" plt.legend([\"Scientist's Orbit\", 'Your orbit'],loc=\"lower left\")\n",
" plt.title(\"Predicted orbit vs Scientist's Orbit\")"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAecAAAHiCAYAAADSwATnAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjMsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+AADFEAAAgAElEQVR4nO3deZhcVZ3/8fc3+76HEJKQBcIaIAQSGAjIJptsP5UBZTcjOiKKoA6CjogbqCOOuDLIJjCCKIK4sQiDyBICYV9MCJCEhKxk7XTSy/n9UTfYCd3pTtKdOt15v56nn6577qlb31NV3Z86t27VjZQSkiQpH+3KXYAkSVqX4SxJUmYMZ0mSMmM4S5KUGcNZkqTMGM6SJGXGcFabEBEjIiJFRIdi+U8RcdYWuN3LIuLmZtxeiogdG1h3WkTc21y31dIiYkVEjGqhbb8YEYe0xLabU2PPj9YyDm15hrO2mIh4IyJWFf+050XE9RHRoyVuK6V0TErpxibWdERL1NDcUkq3pJSOXLu8oSBvThFxYkQ8ExHLImJhRDwQESMau15KqUdKaUYz3P4NEfGN9ba9e0rpoUaut84LtqLt7Ii4YRPrODsino+Iioh4OyJ+GhF9NmVba9UdR3O/0FPrZjhrSzs+pdQDGAeMB768foco2aqem3UDJCdF+N8EXAT0BkYCPwFqy1nXlhYRFwFXAl+gdD/sDwwH7ouITg1cJ8vHVK3DVvUPUPlIKb0F/AkYAxARD0XENyPi70AFMCoiekfELyJibkS8FRHfiIj2Rf/2EfG9YiY3A/hA3e0X2/u3Ossfj4iXI2J5RLwUEeMi4pfA9sDvi9n8F4u++0fEoxGxJCKerbvbMSJGRsT/Fdu5DxiwoXEWtzs9IhZHxN0RsV2ddSkizouIacC0Olc7NiJmFGP77toXKsXM7ZHi8sNF32eL2k9Z73Y7F/WPqdM2sNhzsU1EDIiIe4o+iyPibw28IBoLvJ5SeiCVLE8p/SalNLPO43BJRLxW3CdPRcSwOuPbsU4934uImcVek59FRNdi3SERMTsiLoqI+cXjfU6x7lzgNOCLxTh/X7S/u8cjIiZExJRiZj8vIr5f1L72PlpSXPdf1ruPukTEzRGxqLgfnoyIQfU8hr2ArwHnp5T+nFKqSim9AfwrpYA+veh3WUTcUWxzGXB2sYkuEXFbcf88HRF71dn2GxFxREQcDVwCnFLU+mw9j4W2Jiklf/zZIj/AG8ARxeVhwIvA14vlh4CZwO5AB6Aj8Dvg50B3YBtgMvCJov8ngVeK7fQDHgQS0KHO9v6tuHwy8BalmXoAOwLD16+pWB4CLAKOpfTi9f3F8sBi/WPA94HOwMHAcuDmBsZ7GLCQ0l6CzsDVwMN11ifgvqL+rnXaHizatgf+UWccZwOPrHf9HTdwf18HfLPO8nnAn4vL3wZ+VtzPHYGDgKhnG6OASuAq4FCgx3rrvwA8D+xc3Ld7Af3Xrw/4AXB3Ma6ewO+BbxfrDgGqgcuLWo6l9AKtb7H+BuAbG3guPQacUVzuAexfXB5R9zlRz9g+UdTRDWgP7AP0qqff0UV979kOcCPwv8Xly4Aq4KTiudO1TtuHi7F9Hngd6FjPOC5r6Lnkz9b348xZW9rvImIJ8Ajwf8C36qy7IaX0YkqpmtI/8WOAC1JKK1NK8ykFxKlF338FfpBSmpVSWkwpbBryb8B3UkpPppLpKaU3G+h7OvDHlNIfU0q1KaX7gCmUZrPbUwr4r6SUVqeUHqb0z70hpwHXpZSeTimtBr4E/Eus+37tt1NKi1NKq+q0XVm0zaQUah/ZwG1syK3rXfejRRuUAmMwpRcpVSmlv6WU3vNF+6n0nvEhlF603A4sjNJ7wGuPFfg34MsppVeL+/bZlNKiutuIiAA+DnyuGNdySo/7qXW6VQGXF7X8EVhBKfCbogrYMSIGpJRWpJQe34jr9af0AqImpfRUSmlZPf0GAAuL5+X65rLu3pPHUkq/K547ax/Tp1JKd6SUqii9sOtCabe41CDDWVvaSSmlPiml4SmlT60XSrPqXB5OaaYxt9jluITSLHqbYv126/VvKGyhNLt+rYn1DQdOXnubxe1OpBRk2wHvpJRWNvF2t6u7PqW0gtIsfEidPrPWvxLvHdd29fRpir8CXSNiv4gYTmkX9Z3Fuu8C04F7i13oFze0kZTS4ymlf00pDaQ0wz4YuLRY3ZT7diCl2elTde7TPxftay1aL/wqKM2Cm2ISsBPwSrFr+rgmXu+XwF+AX0XEnIj4TkR0rKffQmBA1P8e8uBi/VobfDxTSrXAbDb9MdVWwnBWTurO3GYBq4EBRZj3SSn1SintXqyfSykY1tp+A9udBezQhNtc2/eXdW6zT0qpe0rpiuI2+0ZE9ybe7hxKYQ9Acb3+lHaxN3T78N5xzdnAbTSoCILbKc2ePwrcU8xaSaX3ji9KKY0CjgcujIjDm7DNJ4HfUhwrwIbv27UWAquA3evcp71T6cDAJg2lkZqmpZQ+QumF25XAHcV93dj1qlJKX0sp7QYcABwHnFlP18coPRc/WLexuI1jgAcaqfXdx7N4X38o9T+mniJQ7zKclaWU0lzgXuC/IqJXRLSLiB0i4n1Fl9uBz0TE0IjoCzQ48wOuBT4fEftEyY7FTBJgHqX3Vde6GTg+Io4qDnbqUhywNLTYFT4F+FpEdIqIiZSCrSG3AudExNiI6ExpV+4TqXQw0YZ8ISL6FgdWfRa4rYF+69feUA2nUNrFvnaXNhFxXHE/BLAMqCl+1hERE6N0UNs2xfIuwAnA2l3H1wJfj4jRxX27Z0T0r7uN4kXC/wBX1dnOkIg4qpHamzTOiDg9IgYWt7OkaK4BFlA6qrze60bEoRGxR5QOMlxGaTf3e+6DlNJSSgeEXR0RR0dEx+KtiV9TmgX/spH694mIDxYz7wsoBX19u97nASNiK/ukgurnk0A5OxPoBLwEvAPcQWk3IpT+2f8FeBZ4mtJsrl4ppV8D36QUTsspHWjWr1j9beDLxe7Wz6eUZgEnUjpydgGlmeEX+OffykeB/YDFwFcpfcyoodt9APgK8BtKs+4dWPd91obcBTwFPAP8AfhFA/0uA24sav/XBmp4AlhJaTfqn+qsGg3cT+m93ceAn6T6Pze8hFIYPx8RKyjtjr4T+E6x/vuUXijdSyngfkHpQKj1/Qel3eiPF0cy30/T31P+BbBbMc7f1bP+aODFor7/Bk5NKVWmlCooPe5/L667/vu821J6Ti0DXqZ0DES9nzNOKX2H0nPie0X/Jyg9Nw4vjifYkLsovUB6BzgD+GDx/vP6fl38XhQRTzeyTbVxUc8xIJIkqYycOUuSlBnDWZKkzBjOkiRlxnCWJCkzhrMkSZnJ4qwpAwYMSCNGjCh3GZIkbRFPPfXUwuJb9+qVRTiPGDGCKVOmlLsMSZK2iIjY0Ff/ultbkqTcGM6SJGXGcJYkKTOGsyRJmTGcJUnKjOEsSVJmDGdJkjJjOEuSlBnDWZKkzBjOkiRlxnCWJCkzhrMkSZkxnCVJyozhLElSZgxnSZIyYzhLkpQZw1mSpMwYzpIkZcZwliQpM4azJEmZMZwlScqM4SxJUmYMZ0mSMmM4S5KUGcNZkqTMGM6SJGXGcJYkKTOGsyRJmTGcJUnKjOEsSVJmDGdJkjJjOEuSlBnDWZKkzDQpnCPijYh4PiKeiYgpRVu/iLgvIqYVv/sW7RERP4yI6RHxXESMa8kBSJLU1mzMzPnQlNLYlNK+xfLFwAMppdHAA8UywDHA6OLnXOCnzVWsJElbg83ZrX0icGNx+UbgpDrtN6WSx4E+ETF4M25HkqStSlPDOQH3RsRTEXFu0TYopTQXoPi9TdE+BJhV57qzizZJktQEHZrY78CU0pyI2Aa4LyJe2UDfqKctvadTKeTPBdh+++2bWIYkSW1fk2bOKaU5xe/5wJ3ABGDe2t3Vxe/5RffZwLA6Vx8KzKlnm9eklPZNKe07cODATR+BJEltTKPhHBHdI6Ln2svAkcALwN3AWUW3s4C7ist3A2cWR23vDyxdu/tbkiQ1rim7tQcBd0bE2v63ppT+HBFPArdHxCRgJnBy0f+PwLHAdKACOKfZq5YkqQ1rNJxTSjOAveppXwQcXk97As5rluokSdoK+Q1hkiRlxnCWJCkzhrMkSZkxnCVJyozhLElSZgxnSZIyYzhLkpQZw1mSpMwYzpIkZcZwliQpM4azJEmZMZwlScqM4SxJUmYMZ0mSMmM4S5KUGcNZkqTMGM6SJGXGcJYkKTOGsyRJmTGcJUnKjOEsSVJmDGdJkjJjOEuSlBnDWZKkzBjOkiRlxnCWJCkzhrMkSZkxnCVJyozhLElSZgxnSZIyYzhLkpQZw1mSpMwYzpIkZcZwliQpM4azJEmZMZwlScqM4SxJUmYMZ0mSMmM4S5KUGcNZkqTMGM6SJGXGcJYkKTOGsyRJmTGcJUnKjOEsSVJmDGdJkjJjOEuSlBnDWZKkzBjOkiRlxnCWJCkzhrMkSZkxnCVJyozhLElSZgxnSZIyYzhLkpQZw1mSpMwYzpIkZcZwliQpM4azJEmZMZwlScqM4SxJUmYMZ0mSMmM4S5KUGcNZkqTMGM6SJGXGcJYkKTOGsyRJmTGcJUnKjOEsSVJmDGdJkjLT5HCOiPYRMTUi7imWR0bEExExLSJui4hORXvnYnl6sX5Ey5QuSVLbtDEz588CL9dZvhK4KqU0GngHmFS0TwLeSSntCFxV9JMkSU3UpHCOiKHAB4Bri+UADgPuKLrcCJxUXD6xWKZYf3jRX5IkNUFTZ84/AL4I1BbL/YElKaXqYnk2MKS4PASYBVCsX1r0X0dEnBsRUyJiyoIFCzaxfEmS2p5GwzkijgPmp5SeqttcT9fUhHX/bEjpmpTSvimlfQcOHNikYiVJ2hp0aEKfA4ETIuJYoAvQi9JMuk9EdChmx0OBOUX/2cAwYHZEdAB6A4ubvXJJktqoRmfOKaUvpZSGppRGAKcCf00pnQY8CHy46HYWcFdx+e5imWL9X1NK75k5S5Kk+m3O55z/A7gwIqZTek/5F0X7L4D+RfuFwMWbV6IkSVuXpuzWfldK6SHgoeLyDGBCPX0qgZOboTZJkrZKfkOYJEmZMZwlScqM4SxJUmYMZ0mSMmM4S5KUGcNZkqTMGM6SJGXGcJYkKTOGsyRJmTGcJUnKjOEsSVJmDGdJkjJjOEuSlBnDWZKkzBjOkiRlxnCWJCkzhrMkSZkxnCVJyozhLElSZgxnSZIyYzhLkpQZw1mSpMwYzpIkZcZwliQpM4azJEmZMZwlScqM4SxJUmYMZ0mSMmM4S5KUGcNZkqTMGM6SJGXGcJYkKTOGsyRJmTGcJUnKjOEsSVJmDGdJkjJjOEuSlBnDWZKkzBjOkiRlxnCWJCkzhrMkSZkxnCVJyozhLElSZgxnSZIyYzhLkpQZw1mSpMwYzpIkZcZwliQpM4azJEmZMZwlScqM4SxJUmYMZ0mSMmM4S5KUGcNZkqTMGM6SJGXGcJYkKTOGsyRJmTGcJUnKjOEsSVJmDGdJkjJjOEuSlBnDWZKkzBjOkiRlxnCWJCkzhrMkSZkxnCVJyozhLElSZgxnSZIyYzhLkpSZRsM5IrpExOSIeDYiXoyIrxXtIyPiiYiYFhG3RUSnor1zsTy9WD+iZYcgSVLb0pSZ82rgsJTSXsBY4OiI2B+4ErgqpTQaeAeYVPSfBLyTUtoRuKroJ0mSmqjRcE4lK4rFjsVPAg4D7ijabwROKi6fWCxTrD88IqLZKpYkqY1r0nvOEdE+Ip4B5gP3Aa8BS1JK1UWX2cCQ4vIQYBZAsX4p0L85i5YkqS1rUjinlGpSSmOBocAEYNf6uhW/65slp/UbIuLciJgSEVMWLFjQ1HolSWrzNupo7ZTSEuAhYH+gT0R0KFYNBeYUl2cDwwCK9b2BxfVs65qU0r4ppX0HDhy4adVLktQGNeVo7YER0ae43BU4AngZeBD4cNHtLOCu4vLdxTLF+r+mlN4zc5YkSfXr0HgXBgM3RkR7SmF+e0rpnoh4CfhVRHwDmAr8ouj/C+CXETGd0oz51BaoW5KkNqvRcE4pPQfsXU/7DErvP6/fXgmc3CzVSZK0FfIbwiRJyozhLElSZgxnSZIyYzhLkpQZw1mSpMwYzpIkZcZwliQpM4azJEmZMZwlScqM4SxJUmYMZ0mSMmM4S5KUGcNZkqTMGM6SJGXGcJYkKTOGsyRJmTGcJUnKjOEsSVJmDGdJkjJjOEuSlBnDWZKkzBjOkiRlxnCWJCkzhrMkSZkxnCVJyozhLElSZgxnSZIyYzhLkpQZw1mSpMwYzpIkZcZwliQpM4azJEmZMZwlScqM4SxJUmYMZ0mSMmM4S5KUGcNZkqTMGM6SJGXGcJYkKTOGsyRJmTGcJUnKjOEsSVJmDGdJkjJjOEuSlBnDWZKkzBjOkiRlxnCWJCkzhrMkSZkxnCVJyozhLElSZgxnSZIyYzhLkpQZw1mSpMwYzpIkZcZwliQpM4azJEmZMZwlScqM4SxJUmYMZ0mSMmM4S5KUGcNZkqTMGM6SJGXGcJYkKTOGsyRJmTGcJUnKjOEsSVJmDGdJkjJjOEuSlBnDWZKkzDQazhExLCIejIiXI+LFiPhs0d4vIu6LiGnF775Fe0TEDyNiekQ8FxHjWnoQkiS1JU2ZOVcDF6WUdgX2B86LiN2Ai4EHUkqjgQeKZYBjgNHFz7nAT5u9akmS2rBGwzmlNDel9HRxeTnwMjAEOBG4seh2I3BScflE4KZU8jjQJyIGN3vlkiS1URv1nnNEjAD2Bp4ABqWU5kIpwIFtim5DgFl1rja7aJMkSU3Q5HCOiB7Ab4ALUkrLNtS1nrZUz/bOjYgpETFlwYIFTS1DkqQ2r0nhHBEdKQXzLSml3xbN89buri5+zy/aZwPD6lx9KDBn/W2mlK5JKe2bUtp34MCBm1q/JEltTlOO1g7gF8DLKaXv11l1N3BWcfks4K467WcWR23vDyxdu/tbkiQ1rkMT+hwInAE8HxHPFG2XAFcAt0fEJGAmcHKx7o/AscB0oAI4p1krliSpjWs0nFNKj1D/+8gAh9fTPwHnbWZdkiRttfyGMEmSMmM4S5KUGcNZkqTMGM6SJGXGcJYkKTOGsyRJmTGcJUnKjOEsSVJmDGdJkjJjOEuSlBnDWZKkzBjOkiRlxnCWJCkzhrMkSZkxnCVJyozhLElSZgxnSZIyYzhLkpQZw1mSpMwYzpIkZcZwliQpM4azJEmZMZwlScqM4SxJUmYMZ0mSMmM4S5KUGcNZkqTMGM6SJGXGcJYkKTOGsyRJmTGcJUnKjOEsSVJmDGdJkjJjOEuSlBnDWZKkzBjOkiRlxnCWJCkzhrMkSZkxnCVJyozhLElSZgxnSZIyYzhLkpQZw1mSpMwYzpIkZcZwliQpM4azJEmZMZwlScqM4SxJUmYMZ0mSMmM4S5KUGcNZkqTMGM6SJGXGcJYkKTOGsyRJmTGcJUnKjOEsSVJmDGdJkjJjOEuSlBnDWZKkzBjOkiRlxnCWJCkzhrMkSZkxnCVJyozhLElSZgxnSZIyYzhLkpQZw1mSpMwYzpIkZcZwliQpM4azJEmZaTScI+K6iJgfES/UaesXEfdFxLTid9+iPSLihxExPSKei4hxLVm8JEltUVNmzjcAR6/XdjHwQEppNPBAsQxwDDC6+DkX+GnzlClJ0taj0XBOKT0MLF6v+UTgxuLyjcBJddpvSiWPA30iYnBzFSttCdXViWkvVZFSKncp2kjTXqqiusrHTa3fpr7nPCilNBeg+L1N0T4EmFWn3+yiTWo1nnl8DTdevYI5M2vKXYo2wvzZK+HBo3j1/r+UuxRpszX3AWFRT1u9L2Mj4tyImBIRUxYsWNDMZUibbsyol/ngTp/huceXl7sUbYS3H/sVo/s+yKidPM5Vrd+mPovnrd1dXfyeX7TPBobV6TcUmFPfBlJK16SU9k0p7Ttw4MBNLENqfl2Yx7hBN7P6tTuornYXaWtQW5vot+QaltbsSNdRR5S7HGmzbWo43w2cVVw+C7irTvuZxVHb+wNL1+7+llqNwe9nTacd2bvvtUx7sarc1agJZk19iqHdJ1Mx+FwIZ85q/ZryUar/BR4Ddo6I2RExCbgCeH9ETAPeXywD/BGYAUwH/gf4VItULbWkaEeH3T7F8N6TeWPy5HJXoyaofvGnVNV2ZeC/TCp3KVKz6NBYh5TSRxpYdXg9fRNw3uYWJZVbux3PofqZLzNoxc+oWHEA3Xo4G8tV5bIlDIvbmNvuw2zfvV+5y5Gahf9xpPp06sPqwaexx4Df8NJk35nJ2fxHb6BT+5V0GuOOOrUdhrPUgO57n0/H9pWsefn6cpeihqREz3k/5+1VezNoj/3KXY3UbAxnqSF99mBpx4ns0uVa5s9ZU+5qVI9l0x6kb8dXWNL/E0TU90lOqXUynKUN6LTHp+nX9U1mP/b7cpeieqx69qdUVPVh2wNPK3cpUrMynKUN6LrTB6moHUyfhT+lttbPPOckVcxlwJrfMaPqNPoM7FHucqRmZThLG9KuI8sHfpxRPR9g1rMvl7sa1bFkyrW0j2ra7fTJcpciNTvDWWpEvwM+SU1tR1Y//5Nyl6K1amvoPOsaZix9HztM2L3c1UjNznCWGtGx52DmtjuJ7fklq1f4fds5qJ55D91iNvO6f4LOXTwQTG2P4Sw1QcfdP02XDst4++83Nt5ZLa7imZ+wdPVgBk04qfHOUitkOEtNsM0eE5lfuQc93v4ZeJ7n8loxg54r7+OFpWcxYqcu5a5GahGGs9QE0a4dS7f5FP07vsiiFx8qdzlbtYpnf04iaDf6Y7Rr5y5ttU2Gs9REQw46nVXVfah87upyl7L1qllD+zev59XFR7PHQTuUuxqpxRjOUhN1692DWe3OYnC6m8rFs8tdzlap+o076cwC5vf4N3r08t+X2i6f3dJG6DX+U0AtCx/5ablL2SpVPPtT3qncnuEHHlvuUqQWZThLG2HbnXdiZuWR9F1yLal6dbnL2aqkpa/Qq/L/eHnl2Qwf3anc5UgtynCWNlL1iPPo3mE+C568vdylbFVWPP1zamo70Hn3SZ7kQm2e4SxtpOETj2Vx5Shi+o/LXcrWo3oVnebcxCvvHMeYA4aVuxqpxRnO0kbq2Lk987p/goHtn2DlzKfKXc5WYfW02+kci1na/+N+I5i2CoaztAkGTZzEmppuLJ3sx6q2hNXP/4wFFTuyw8FHlrsUaYswnKVN0G9If16vOoWBlbdRU7Go3OW0abWLn6NX9eO8Vv0xBg3tUO5ypC3CcJY2Ucfdz6Nju0oWPvo/5S6lTVv25M+oqu1Mr73PLncp0hZjOEubaMT4ccxaeQDd5v4camvKXU7bVLWCbgtv4dUlJ7LTPtuWuxppizGcpU3Url2wbJtP0bP9Gyx54e5yl9MmrXzu53SKZVQM+RQdOnggmLYehrO0GUYccjJLVg+j+vnvlbuUtqdmDe1e/T6vLz2QXQ49qNzVSFuU4Sxthu69O/FWl08zIB5l+YzHyl1Om1L58k10ZQ5zen6BXn38V6Wti894aTNtd9i5rKruxYrJzp6bTW0NNc9/hzkr9mTnIz5Q7mqkLc5wljZT30F9mBmTGFTzO1bNe63c5bQJa2bcSfc0jRkdLmLAtn58Slsfw1lqBv0OvICU2rHwb98vdymtX0qsfvrbLKzYgZGHnVLuaqSyMJylZjBw1Pa8WX0yg1bdyJrli8tdTqtW/dZ99Kx+mldqLmDIiM7lLkcqC8NZaiZdx11Ep/YrmfugJ8TYHBVPfJtlqwcz+KCzy12KVDaGs9RMBu+5D7NXH0r/d35CzRrP9bwpahc8Qa/VD/FCxXmM2rV7ucuRysZwlppR2uUienR8m1kP/bLcpbRKyx/7FhVVfeg74ZOes1lbNcNZakZD9zuGRWt2o8dbV1FbU1vuclqVtOQleq+4m+eWfZyd9+lX7nKksjKcpWYU7dqxctjnGND5JWY//qdyl9OqLH/sm6yp6UaXsZ+lXTtnzdq6Gc5SMxty0OmsqNqW9q9e4ey5idLiZ+m5+H+ZumgSY/bfrtzlSGVnOEvNrH2nLrwz+D8Y0uUR3vibs+emWPnIxVRW96Lj3pfQoaOzZslwllrAkEP/nWVV29P9tUuprvJ0khtSM/cheqz4M1OWXMheEweVuxwpC4az1ALadezMylGXMajrs8y473/LXU6+UmLV3/+DpasHM+Cgz9K+vbNmCQxnqcVse8AZLK7ajf5vX0blyjXlLidLVW/cSY81k5m68hJ22btXucuRspHtN8pXVVUxe/ZsKisry12KNkOXLl0YOnQoHTt2LHcpW1y070DtHt9kwCv/j5f/fA27fujT5S4pL7XVVD3xJd6pGM2IIyf5uWapjmzDefbs2fTs2ZMRI0b4R9tKpZRYtGgRs2fPZuTIkeUupywG7H0iC17cjyHLv8XyxefQs5/ferXW6pevo1vtP5icbuWQnbqWuxwpK9nu1q6srKR///4GcysWEfTv33/r3vsRQacJV9Cr01xm/vkH5a4mH9UVpGcvY+ay8ex67MnlrkbKTrbhDBjMbYCPIfTe+RDmcRQjq77HotmLyl1OFiqm/jddmMvr3b/OoCHZ7sCTyibrcC63b37zm+y+++7sueeejB07lieeeKLBvlOmTOEzn/nMJt/Wt771rXWWDzjggI3qP2LEiCbf1po1a7jgggvYYYcdGD16NCeeeCKzZ89usH+PHj3qbf/P//xP7r//fgB+8IMfUFFR0eQatjY9D/423Tou4e37ryh3KeVXuZAO/7iSf7xzJGOPe3+5q5HylFIq+88+++yT1vfSSy+9p21LevTRR9P++++fKisrU0opLViwIL311lstdnvdu3ffrP7Dhw9v8nUvuuii9LGPfSxVV1enlFK67rrr0vjx41Ntbe06/Wpra1NNTU2Tahs+fHhasGBBvevK/VjmYu5tp6TVN3VLM194vdyllNWKe89I1b/skB65Y3K5S5HKBpiSNpCLzpwbMHfuXAYMGEDnzqWTvQ8YMIDttit9reCTTz7JAQccwF577cWECRNYvnw5Dz30EMcddxwAK7FAajgAABMTSURBVFeu5GMf+xjjx49n77335q677gLghhtu4IMf/CBHH300o0eP5otf/CIAF198MatWrWLs2LGcdtppwD9nq3PnzuXggw9m7NixjBkzhr/97W/19h84cGCD/euqqKjg+uuv56qrrqJ9+/YAnHPOOXTu3Jm//vWvvPHGG+y666586lOfYty4ccyaNQuAiy66iHHjxnH44YezYMECAM4++2zuuOMOfvjDHzJnzhwOPfRQDj300BZ4NNqGfkd8i4hE1d//nao1W+fXeta8dR/dF/ySJxZ8hn2O3bfc5UjZilKAl9e+++6bpkyZsk7byy+/zK677grAH26vYO7s5v2WpcFD2/OBf+3W4PoVK1YwceJEKioqOOKIIzjllFN43/vex5o1a9hll1247bbbGD9+PMuWLaNbt2488sgjfO973+Oee+7hkksuYbfdduP0009nyZIlTJgwgalTp/LrX/+ayy+/nKlTp9K5c2d23nlnHnnkEYYNG0aPHj1YsWLFu7e/dvm//uu/qKys5NJLL6WmpoaKigp69uz5nv5rNdR/reeee46zzjqLqVOnrnO9z33uc4wcOZITTjiBUaNG8eijj7L//vsDpfeNb775Zk477TQuv/xy5s+fz49+9CPOPvtsjjvuOD784Q8zYsQIpkyZwoABA95TU93Hcmu34KHvMnDOF3m+y43s8cEzy13OllVdwao7xrByRTsW7vO0n2vWVi0inkopNfgK1ZlzA3r06MFTTz3FNddcw8CBAznllFO44YYbePXVVxk8eDDjx48HoFevXnTosO4BLffeey9XXHEFY8eO5ZBDDqGyspKZM2cCcPjhh9O7d2+6dOnCbrvtxptvvrnBOsaPH8/111/PZZddxvPPP79O0G5K/5RSvQdp1W0fPnz4u8EM0K5dO0455RQATj/9dB555JEN1qCGDTz4QhbX7suo5Rcy7/W3y13OFlXxxGV0rX2dZ+OHBrPUiFZxmOSGZrgtqX379hxyyCEccsgh7LHHHtx4442MGzeu0SOQU0r85je/Yeedd16n/Yknnnh3N/na7VdXV29wWwcffDAPP/wwf/jDHzjjjDP4whe+wJlnNjzjaqz/jjvuyJtvvsny5cvXCe6nn36a448/HoDu3Tf8WVyPwN4M7drT5bDr6PzXfZhz//kMnHT7VnF6xNpFz9Dlje/zzMLTmXD20eUuR8qeM+cGvPrqq0ybNu3d5WeeeYbhw4ezyy67MGfOHJ588kkAli9f/p6APeqoo7j66qtZ+5bB+ruQ69OxY0eqqqre0/7mm2+yzTbb8PGPf5xJkybx9NNPb1L/tbp3785ZZ53FhRdeSE1N6a2Cm266iYqKCg477LB6a6utreWOO+4A4NZbb2XixInv6dOzZ0+WL1/e6DgF3bbbg/kDLmZ09zv4x19+W+5yWl5tDase/DgVVf1IY79Dz97+25Ea0ypmzuWwYsUKzj//fJYsWUKHDh3Ycccdueaaa+jUqRO33XYb559/PqtWraJr167vfpxora985StccMEF7LnnnqSUGDFiBPfcc88Gb+/cc89lzz33ZNy4cdxyyy3vtj/00EN897vfpWPHjvTo0YObbrppk/rX9e1vf5vPf/7z7LTTTrRr145ddtmFO++8s8EZcffu3XnxxRfZZ5996N27N7fddlu99R9zzDEMHjyYBx98cINjFWx7xKUsvvW3bDfvfJbOO5Teg/qVu6QWU/nc1XRfM4UHK67jkIO3LXc5UqvQKg4IU+vmY1m/ZTOeoMdjB/DamjPY8ezr2+bbBSvfpOp3u/P6kgPo9+E/MmCQ8wEJPCBMylavUfsxt8cFjO58IzP+7y/lLqf51daw4v5zqK2FxSOvNpiljWA4S2U0+Jivs6RqRwa+8TEWzZpT7nKa1arJX6XHygf5++IrGX/UTuUuR2pVDGepjNp16ka7g2+ja4clVN57MmtWtY3zPlfPvIeuM77JMwtOZ6+PfJL27dvgLnupBRnOUpn1GjmORSN+ypCuj/LGrz9HDseBbJYVb1D7tzOZs2IPuhz8I/pv077cFUmtjuEsZWDbiWcxq9N57NThJ0z/0w3lLmfT1VSy8s8foqamhhkDf8Uue/cud0VSq2Q4S5kYctL3mVd9IMMXncfc56Y0foUMrXzofLqveZq/r7yGA070CH1pUxnODUgpMXHiRP70pz+923b77bdz9NHl+Xaja6+9lgsuuOA97TU1NRx00EEAzJgxg1/96ldbujQ1k3YdOtHruF+zurYvXZ/6MMsXLCx3SRtl9UvX033etTy+4HP8yxknbxXffCa1FMO5ARHBz372My688EIqKytZuXIll156KT/+8Y83a7uNfV3nxl6nffv27555ynBu/br2G8zq8bfTo+NcltxzKjVVG/98KYeaeY/Rfup5zFh6EENP+Bbde/ivRdoc/gVtwJgxYzj++OO58sor+drXvsaZZ57JDjvswHe+8x3GjBnDmDFjuPrqqwGYPn06Y8eOffe6V1xxBd/4xjcAmDhxIpdeeikHH3wwP/rRj9a5jYULF3LCCSew5557csABB/DCCy8A8OUvf5lPfOITvP/97+ecc84BSl/NedRRR7Hzzju/u+3q6mr69OkDlE49+eCDDzJ27Fh++MMftuydoxYzYLcDmTvo+wzr/ABv3npm9gFds3AqNfcfw9LKbVm6280MHdml3CVJrV7r+FaApy6Ad55p3m32HQv7/KDRbl/96lcZN24cnTp1YsqUKUyePJlbbrmFyZMnU1NTw4QJE3jf+95Ht24bPjnHsmXLePjhh9/T/pWvfIX99tuPu+++m3vvvZezzz6btd+WNnXqVB5++GG6dOnCtddey+TJk3nhhRfo1KkT48eP57jjjmPMmDHvbuuKK67gRz/6Eb/73e828s5Qboa9/zxm3j2fUSsu57Vb2zP8ozfQoWN+Rz3XvPMSVX85ksrVPZg++E/s977ty12S1CY4c25E9+7dOeWUUzjjjDPo3Lkzf/vb3/jQhz5Et27d6NmzJyeddFKTTqF46qmn1tv+yCOPcMYZZwBw5JFHMmfOHFauXAnAiSeeSJcu/5yFHHXUUfTt25fu3bs3+XbVem1/wteY1f1Sduh4M2/cMonqquY9p/nmqln6Gqv/cARVVe2YNvjP7Hfszo1fSVKTtI6ZcxNmuC2pXbt2tGtXeh3T0GdQO3ToQG1t7bvLlZWV65znuaHTMK6/vbrL619n/e9ebpPfxax1DDvh68z+fTU7rriSabe0Z+Rp/0OHjuV/TV2zfBarfn8E7Woq+cc29zL+mDGNX0lSk5X/r7yVOfjgg7nzzjtZtWoVK1as4K677uKggw5i2223Zc6cObzzzjtUVlbyhz/8ocnbW3tWqfvvv5+hQ4c2GOT33nsvS5YsoaKigrvuuosDDzxwnfWetrENimDo8d/mrR6fZ3Sn63jt5k9SXVXb+PVaUM3Keay863A61C7kHwPvZp9jG/zufkmbqHXMnDMyYcIEPvKRjzB+/HgA/v3f/5099tgDgEsuuYTx48czatQodttttyZt7/LLL+ecc85hzz33pEePHlx//fUN9p04cSIf/ehHee211zjjjDMYO3bsOkdy77333tTU1LDXXnsxadIkPvOZz2zGSJWNCIYc/x3m3F3DzlzFP26qZPD/+wk9+/XY4qVUvPkYNQ9/lC7M45UBdzP22Pee21vS5vOUkWpxPpbNJCXm/vFLDF56JQsrd2L5bjcxcv/9tsxt19aw8MFv0u/ty1m2ejvmDLuJ3d5/yJa5bakN8pSRUlsRweAPXMGSsX+hS4cVbD99Ii/dejlrKlv2o1ZVS2ay6FeHMGDeV5m+4iRWHz7VYJZamOEstTJ9djuSLh96jgUdjmc3vsr8mw9m3j+mN/8NpcQ7z9xOze/3pEf1MzzT7hpGnnM7g4b3b/7bkrSOFgnniDg6Il6NiOkRcXFL3Ia0NevQvT/bnvIb5g3/BQM7v0Dvx/fm5ZsuYs4rr2/+xmtrWPTU7Sy6ZT/6vnQKi1fvwJwxkxl76sfp2MnX89KW0Ox/aRHRHvgxcAywG/CRiGja0VHryeH9cG0eH8MWFMGgAz9G7VFTeafjEezc/gcMemo00/7nQ7z6fw9TXbVx9311ZQWz77uapTfvRP9XTyHWLOB5vk/vkx9l5DiPGZC2pJY4WnsCMD2lNAMgIn4FnAi8tDEb6dKlC4sWLaJ///5+nreVSimxaNGidb5IRc2v6zY70PUjd7J60esseuS/2b72ejq/9Vvm3LAPi7t9kPa9h9Ol//b0HDyc3tttR8dOHaiuXMXS2dNZ9farVC2eRqz4B9tU/56hHRbxdtU43h5wM8MPOYU9uvmBDqkcWuIvbwgwq87ybGCjDykdOnQos2fPZsGCBc1WmLa8Ll26MHTo0HKXsVXo3H8k2534A9Kar7Pg8evp8ebVbBeXwjJKP69DTW0HVtb0pWuHhfSPf86sK6r7sah2fxaNupAh4w9l2/buvpbKqSXCub5p7nv2r0XEucC5ANtv/97v4+3YsSMjR45s9uKkti469WTgwZ+BdD5ULWHVwjdZ+fZMKhfNpHrZTKhcQG3n7WjfdzRdBu5Ez2E7061vfzb87fCStqSWCOfZwLA6y0OBOet3SildA1wDpc85t0Ad0tYtAjr1pet2fem63djG+0vKRkvsu3oSGB0RIyOiE3AqcHcL3I4kSW1Ss8+cU0rVEfFp4C9Ae+C6lNKLzX07kiS1VVl8fWdELAdeLXcdLWQAsLDcRbQQx9Z6teXxObbWaWsb2/CU0sCGrpDL5yRe3dB3jLZmETHFsbU+bXls0LbH59haJ8e2Lj8vIUlSZgxnSZIyk0s4X1PuAlqQY2ud2vLYoG2Pz7G1To6tjiwOCJMkSf+Uy8xZkiQVsgjniPh8RKSIGFAsR0T8sDjl5HMRMa7cNW6siPh6UfszEXFvRGxXtLeFsX03Il4p6r8zIvrUWfelYmyvRsRR5axzU0TEyRHxYkTURsS+661r1WODtnU614i4LiLmR8QLddr6RcR9ETGt+N23nDVuqogYFhEPRsTLxfPxs0V7qx9fRHSJiMkR8Wwxtq8V7SMj4olibLcVX2LVKkVE+4iYGhH3FMsbPbayh3NEDAPeD8ys03wMMLr4ORf4aRlK21zfTSntmVIaC9wD/GfR3hbGdh8wJqW0J/AP4EsAxalBTwV2B44GflKcQrQ1eQH4IPBw3ca2MLbmPJ1rJm6g9FjUdTHwQEppNPBAsdwaVQMXpZR2BfYHziseq7YwvtXAYSmlvYCxwNERsT9wJXBVMbZ3gEllrHFzfRZ4uc7yRo+t7OEMXAV8kXVPjnEicFMqeRzoExGDy1LdJkopLauz2J1/jq8tjO3elFJ1sfg4pe9Ph9LYfpVSWp1Seh2YTukUoq1GSunllFJ9X4jT6sdGndO5ppTWAGtP59oqpZQeBhav13wicGNx+UbgpC1aVDNJKc1NKT1dXF5O6R/9ENrA+Ir/fSuKxY7FTwIOA+4o2lvl2AAiYijwAeDaYjnYhLGVNZwj4gTgrZTSs+utqu+0k0O2WGHNJCK+GRGzgNP458y5TYytjo8Bfyout7Wx1dUWxtYWxtCYQSmluVAKOGCbMtez2SJiBLA38ARtZHzFbt9ngPmU9sS9Biyp86K/NT83f0BpwllbLPdnE8bW4t8QFhH3A9vWs+pS4BLgyPquVk9bdoeVb2hsKaW7UkqXApdGxJeATwNfpY2MrehzKaXdb7esvVo9/Vvl2Oq7Wj1t2Y2tEW1hDFuViOgB/Aa4IKW0rDQJa/1SSjXA2OJ4lTuBXevrtmWr2nwRcRwwP6X0VEQcsra5nq6Njq3FwzmldER97RGxBzASeLZ4wg0Fno6ICTTxtJPl1tDY6nEr8AdK4dwmxhYRZwHHAYenf34er02MrQGtYmyNaAtjaMy8iBicUppbvF00v9wFbaqI6EgpmG9JKf22aG4z4wNIKS2JiIcova/eJyI6FDPM1vrcPBA4ISKOBboAvSjNpDd6bGXbrZ1Sej6ltE1KaURKaQSlfxzjUkpvUzrF5JnFkc37A0vX7sppLSJidJ3FE4BXisttYWxHA/8BnJBSqqiz6m7g1IjoHBEjKR30NrkcNbaAtjC2reF0rncDZxWXzwIa2hOSteJ9yl8AL6eUvl9nVasfX0QMXPsJj4joChxB6T31B4EPF91a5dhSSl9KKQ0tMu1U4K8ppdPYlLGllLL4Ad4ABhSXg9JRpa8BzwP7lru+TRjPbygd+fsc8HtgSBsa23RK710+U/z8rM66S4uxvQocU+5aN2Fs/4/SC8XVwDzgL21lbMUYjqV0hP1rlHbjl72mzRjL/wJzgariMZtE6f29B4Bpxe9+5a5zE8c2kdKuz+fq/J0d2xbGB+wJTC3G9gLwn0X7KEoveKcDvwY6l7vWzRznIcA9mzo2vyFMkqTM5PBRKkmSVIfhLElSZgxnSZIyYzhLkpQZw1mSpMwYzpIkZcZwliQpM4azJEmZ+f8hhRjVtqRtrAAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# Predict the twenty minutes orbit\n",
"twenty_min_orbit = model.predict(np.arange(-10, 11))\n",
"\n",
"# Plot the twenty minute orbit\n",
"plot_orbit(twenty_min_orbit)"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAecAAAHiCAYAAADSwATnAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjMsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+AADFEAAAgAElEQVR4nOzdeXycV3n3/881M7JlS5ZlWftmeZGT2FkcLylbn1+B0rL1gVLoRilQaICEhCULWVhCEgrZl5KNlpYUSoHSp5C2tJBStj6/QrwncezEu6xdsuVdljQz5/nj3OM4jmxrmZl7lu/79fLL0iz3fUkzuq8551znHHPOISIiIrkjEnYAIiIi8lJKziIiIjlGyVlERCTHKDmLiIjkGCVnERGRHKPkLCIikmOUnKUgmFmbmTkziwXf/7uZvTcL573FzL6RxuM5M1tyhvvebWY/Ste5Ms3MjprZogwde4uZ/UYmjp1O53p/5MvPIdmn5CxZY2Z7zGw4uGj3mdnfmll5Js7lnHuTc+7xCcb0m5mIId2cc3/vnPut1PdnS+TpZGZvM7NNZnbYzAbN7Mdm1nau5znnyp1zu9Jw/q+Z2e2nHXu5c+6n53jeSz6wBbe9z8y+NsU43mdmz5jZcTPrNbNHzKxyKsdKOfXnSPcHPclvSs6Sbb/jnCsHVgJrgE+f/gDziuq9eWoCySVB8v874BpgLrAQeBhIhhlXtpnZNcAdwHX438MrgAXAk2Y24wzPycnXVPJDUV0AJXc457qAfwcuBDCzn5rZF8zs/wLHgUVmNtfMvmpmPWbWZWa3m1k0eHzUzO4OWnK7gLecevzgeB885fs/N7OtZnbEzJ4zs5Vm9nWgFfiXoDV/ffDYV5jZ/29mB81s86ndjma20Mx+FhznSaD6bD9ncN4dZnbAzJ4ws8ZT7nNmdqWZbQe2n/K0N5vZruBnuyv1QSVouf138PXPg8duDmL/g9POOzOI/8JTbqsJei5qzazazP41eMwBM/vFGT4QrQB2O+d+7Lwjzrl/cs51nPI63GRmO4PfyXozaznl51tySjx3m1lH0GvyqJnNCu77DTPrNLNrzKw/eL3fH9x3OfBu4Prg5/yX4PaTPR5mdpmZrQta9n1mdm8Qe+p3dDB47itP+x2Vmtk3zGx/8HtYa2Z147yGFcDngaucc//hnBtzzu0Bfh+foP8keNwtZvbd4JiHgfcFhyg1s28Hv58NZnbJKcfeY2a/aWZvBG4C/iCIdfM4r4UUE+ec/ulfVv4Be4DfDL5uAbYAtwXf/xToAJYDMaAE+B7wGFAG1AJPAR8KHv9hYFtwnCrgJ4ADYqcc74PB1+8CuvAtdQOWAAtOjyn4vgnYD7wZ/+H1DcH3NcH9/wPcC8wE/hdwBPjGGX7e1wGD+F6CmcBfAj8/5X4HPBnEP+uU234S3NYKvHDKz/E+4L9Pe/6Ss/y+/wb4winfXwn8R/D1F4FHg99zCfDrgI1zjEXACeA+4LVA+Wn3Xwc8A5wX/G4vAeafHh9wP/BE8HPNAf4F+GJw328AceDWIJY34z+gzQvu/xpw+1neS/8DvCf4uhx4RfB126nviXF+tg8FccwGosAqoGKcx70xiO9lxwEeB/4h+PoWYAx4e/DemXXKbe8MfrZrgd1AyTg/xy1nei/pX/H9U8tZsu17ZnYQ+G/gZ8BfnHLf15xzW5xzcfxF/E3Ax51zx5xz/fgE8YfBY38fuN85t885dwCfbM7kg8Cdzrm1ztvhnNt7hsf+CfAD59wPnHNJ59yTwDp8a7YVn+A/45wbcc79HH9xP5N3A3/jnNvgnBsBbgReaS8dr/2ic+6Ac274lNvuCG7rwCe1PzrLOc7mm6c994+D28AnjAb8h5Qx59wvnHMvW2jf+THj38B/aPkOMGh+DDhVK/BB4NPOueeD3+1m59z+U49hZgb8OfCJ4Oc6gn/d//CUh40Btwax/AA4ik/4EzEGLDGzaufcUefcLyfxvPn4DxAJ59x659zhcR5XDQwG78vT9fDS3pP/cc59L3jvpF7T9c657zrnxvAf7Erx3eIiZ6TkLNn2dudcpXNugXPuitOS0r5Tvl6Ab2n0BF2OB/Gt6Nrg/sbTHn+mZAu+db1zgvEtAN6VOmdw3tfgE1kjMOScOzbB8zaeer9z7ii+Fd50ymP2nf4kXv5zNY7zmIn4L2CWmf2amS3Ad1H/c3DfXcAO4EdBF/oNZzqIc+6Xzrnfd87V4FvY/wu4Obh7Ir/bGnzrdP0pv9P/CG5P2X9a8juObwVPxAeApcC2oGv6rRN83teBHwLfMrNuM7vTzErGedwgUG3jjyE3BPennPX1dM4lgU6m/ppKkVByllxyasttHzACVAfJvNI5V+GcWx7c34NPDCmtZznuPmDxBM6ZeuzXTzlnpXOuzDn3peCc88ysbILn7cYnewCC583Hd7Gf6fzw8p+r+yznOKMgEXwH33r+Y+Bfg1Yrzo8dX+OcWwT8DvBJM3v9BI65Fvg/BLUCnP13mzIIDAPLT/mdznW+MHBCP8o5YtrunPsj/Ae3O4DvBr/rcz1vzDn3eefcMuBVwFuBPx3nof+Dfy++49Qbg3O8CfjxOWI9+XoG4/rNjP+aaotAOUnJWXKSc64H+BFwj5lVmFnEzBab2f8XPOQ7wNVm1mxm84AztvyAvwauNbNV5i0JWpIAffhx1ZRvAL9jZr8dFDuVBgVLzUFX+Drg82Y2w8xeg09sZ/JN4P1mtsLMZuK7cn/lfDHR2VxnZvOCwqqPAd8+w+NOj/1MMfwBvos91aWNmb01+D0YcBhIBP9ewsxeY76orTb4/nzgfwOpruO/Bm4zs/bgd3uxmc0/9RjBh4S/Au475ThNZvbb54h9Qj+nmf2JmdUE5zkY3JwABvBV5eM+18xea2YXmS8yPIzv5n7Z78A5dwhfEPaXZvZGMysJhib+Ed8K/vo54l9lZu8IWt4fxyf68bre+4A2K7KZCjI+vQkkl/0pMAN4DhgCvovvRgR/sf8hsBnYgG/Njcs594/AF/DJ6Qi+0KwquPuLwKeD7tZrnXP7gLfhK2cH8C3D63jxb+WPgV8DDgCfw08zOtN5fwx8BvgnfKt7MS8dZz2T7wPrgU3AvwFfPcPjbgEeD2L//TPE8CvgGL4b9d9Puasd+E/82O7/AA+78ecNH8Qn42fM7Ci+O/qfgTuD++/Ff1D6ET7BfRVfCHW6T+G70X8ZVDL/JxMfU/4qsCz4Ob83zv1vBLYE8T0A/KFz7oRz7jj+df+/wXNPH+etx7+nDgNb8TUQ484zds7diX9P3B08/lf498brg3qCs/k+/gPSEPAe4B3B+PPp/jH4f7+ZbTjHMaXA2Tg1ICIiIhIitZxFRERyjJKziIhIjlFyFhERyTFKziIiIjlGyVlERCTH5MSuKdXV1a6trS3sMAre8WOOof1J6hqjxHLilReRbEskoLcrQeW8CGVzLOxwitb69esHg1X3xpUTl+i2tjbWrVsXdhgFr2NXnK/cdYT3XFHOeReNt0qhiBS6ndvG+NsHjvL+j5Wz+HxdB8JiZmdb+lfd2sWkuta/3IP9L1sESUSKxP5+vxV3dV005EjkbJSci8js8gizyozBPiVnkWI12JegZAbMmasu7Vym5FxkqusiDPYlww5DREIy2J+gujZKJKLknMuUnItMdW2U/erWFila+/uSzK/TpT/X6RUqMvNrIxw+6Bg5oTXVRYpNPO5nbFTXarw51yk5F5maoAhk/4BazyLFZmgwSTLph7ckt+kVKjLzU8lZ484iRSdVDKpK7dyn5Fxk5tdEMIMBVWyLFJ1UMej8Wl36c51eoSJTMsOYOy9ycq6jiBSPwf4EZXOMWbN16c91eoWK0Py6iOY6ixSh/f0qBssXSs5FqLo2ymBfAudUsS1STAb7EppGlSf0KhWh6roIIyfg2BElZ5FicWLYcfSwOzljQ3KbknMRSlVqqmtbpHikFh9SMVh+0KtUhOaf3ABDRWEixSJVqa1pVPlBybkIVVZFiMVgsFctZ5FiMdiXwAyqqnXZzwd6lYpQJGLMr4tqAwyRIjLQl6CqOkKsRBte5AMl5yJVUxfRQiQiRWSwN0l1vbq084WSc5Gqro8yNJgkPqaKbZFCl0w6BvsT1GgaVd7QK1WkauqiJJNwYFBd2yKF7uCBJPEx1HLOI0rORaqm3r/0AyoKEyl4g73+Q3iNknPeUHIuUvODJfyUnEUKX6q+RN3a+UOvVJGaWWrMnWeq2BYpAgO9CWaXG7PLdcnPF3qlilh1fVQtZ5EiMNiX1LKdeUbJuYjV1GkDDJFiMNCboLpel/t8oleriNXU+w0wjhxSchYpVMePJTl2xKkYLM8oORex1Bq76toWKVypuhJ1a+cXJecilvokrd2pRApX6sO3urXzi16tIjZnrjGzFAZ6VbEtUqgG+xJEYzBvvi73+USvVhEzM6rrolpjW6SADfQmqa6NEIlow4t8ouRc5Grqo9o6UqSADfYmtGxnHlJyLnLVdREODTlGTqhiW6TQxOOOA4Oa45yPlJyLXKoobH+/Ws8ihebAQJJkUsVg+UivWJFLJWcVhYkUnsGTa2qr5ZxvJpSczWyPmT1jZpvMbF1wW5WZPWlm24P/5wW3m5k9aGY7zOxpM1uZyR9ApqeqOkIkornOIoWovyeYRqXknHcm03J+rXNuhXNudfD9DcCPnXPtwI+D7wHeBLQH/y4HHklXsJJ+sRJjXnVEFdsiBWiwL0nFPGNmqSq18810urXfBjwefP048PZTbv875/0SqDSzhmmcRzKspk4V2yKFaKA3oS7tPDXR5OyAH5nZejO7PLitzjnXAxD8Xxvc3gTsO+W5ncFtkqOq6yMM9idJJlWxLVIonHMM9iW0pnaeik3wca92znWbWS3wpJltO8tjx+s/edlVP0jylwO0trZOMAzJhJr6KIk4DO1PMr9Gf8giheDIIcfICT9dUvLPhF4151x38H8/8M/AZUBfqrs6+L8/eHgn0HLK05uB7nGO+RXn3Grn3Oqampqp/wQybalur0FVbIsUjFSRp1rO+emcydnMysxsTupr4LeAZ4EngPcGD3sv8P3g6yeAPw2qtl8BHEp1f0tuSn2yVlGYSOE4OY1KyTkvTaRbuw74ZzNLPf6bzrn/MLO1wHfM7ANAB/Cu4PE/AN4M7ACOA+9Pe9SSVrPLI5SVm6ZTiRSQgd4kM2b6DW4k/5wzOTvndgGXjHP7fuD149zugCvTEp1kTXV9VN3aIgVkICgGCxpWkmdUKSAA1NRrrrNIIRnsTWjxkTym5CyALwo7ftRx7KhazyL5buSE49CQo0ZrauctvXICcHJLucE+JWeRfJfayEYLkOQvJWcBoCZVsa2iMJG8l9rIRvs45y8lZwGgcn6EWAwt4ylSAAb6EpjB/Bpd4vOVXjkBIBIx5tdFGVC3tkjeG+xNUFUdIVaiSu18peQsJ9XURdRyFikAA31JdWnnOSVnOam6PsqBwSTxMW2AIZKvkknH/r7EyToSyU969eSk2voozsFgv7q2RfLV0GCSeBxqGtRyzmdKznJSbUNQsd2jrm2RfNUf/P3WKjnnNSVnOWl+XRSzF/+4RST/9AfTqLThRX5TcpaTSkqMquqI5jqL5LGBngQVlUbpLFVq5zMlZ3mJmoaoWs4ieWygN6Hx5gKg5CwvUdsQZX9/kkRCFdsi+SaZdAz0JqhVl3beU3KWl6hpiJBIwIEBVWyL5JtDQ0lGR1QMVgiUnOUlUp+41bUtkn8GeoJiMCXnvKfkLC9Ro+Qskrf6g2LOWm0Vmff0CspLzJhpVM6PaK6zSB7q70lQXmHMLtelPd/pFZSXqa2PnJwrKSL5Y6AnofnNBULJWV6mpiHKYG+CZFIV2yL5wjlHf48qtQuFkrO8TG1DlHgchvar9SySL44ccoyc8DMuJP/pVZSXSX3y1rizSP7QmtqFRclZXiY1DaO/Ry1nkXwxoORcUJSc5WVKZxkVlabpVCJ5pL83wawyo2yO1tQuBErOMq6ahqg2wBDJI/09SWrro5gpORcCJWcZV229T86q2BbJfalKbRWDFQ69kjKumoYooyN+rV4RyW3HjjiGjzlNoyogSs4yrtTyfwMqChPJeallO7WmduFQcpZxpSo+Ne4skvtSH6JVqV04lJxlXLPLI5TNUcW2SD4Y6E0wsxQqKlUMViiUnOWMahuiJ7vLRCR39QdraqtSu3AoOcsZ1dZHGehJ4pwqtkVyWX9PQl3aBUbJWc6opiHCiWHHkUNKziK56vixJEcPOyXnAqPkLGeU2npO484iuWsg2N5VW0XmqA3XwDO3TfppSs5yRicrtpWcRXJW6sOzFiDJQfvXwbb7YGRg0k/VqylnVF5hzJptKgoTyWEDPQlKSqCySpfznJJMwNoPQ2kdXDz5lnMsAyFJgTAzahoi2p1KJIelKrUjEVVq55Qdj8GB9fCqb8KMuZN+uj5qyVnVagMMkZw20JvQymC5ZrgXNt8Eda+HBX84pUMoOctZ1dZHOX7UceyIWs8iuebEsOPQkKNW4825ZeN1kDgOax6CKc491ysqZ5X6RK6KbZHcM9jn/y41jSqH9P0U9nwDLrgeKs6b8mFyIzmf6As7AjmD2pPJWS1nkVzzYqW2knNOSIzC2iugbCEsv3lah8qN5Hy8Cw49F3YUMo6KSmNmqVrOIrmovztBNAbz5ufGpbzobbsXDm+F1X8JsVnTOlRuvKIWgac+DE6ts1xjZn6NbSVnkZyTqtSORlWpHbpje+HZW6H5d6HpLdM+XG4k59nNMPAL2PW1sCORcdQ2RunrSmiNbZEc09edoK5RXdo5Yd3VgMGq+9NyuNxIzjOroeY1vsLtxORXUpHMqmuMcvyY49gRJWeRXHGyUlvJOXydT0DXE3DRLVDWmpZD5kZyBljzKIwd9glackrqk3lft7q2RXJFf/D3WNeYO5fxohQ/BuuvhrnL4fyPp+2wufOqVi6HC66D3Y/7UnTJGUrOIrmn72RyVss5VM/e7seb1zwCkZK0HTZ3kjPAhZ/2JehrPwKJkbCjkUDZHGN2uSk5i+SQvu4EM2bC3Hm5dRkvKoeeg613w8L3Qu2vp/XQufWqxmbDmofh8DbYelfY0UjAzKhrjJ7sRhOR8PV1J6ht0JraoXEO1l4JJXPg0vTnq9xKzgCNb4TWd/mugiM7wo5GAnWNUfq6VbEtkiv6Vakdrj1/D/0/hUu+CKU1aT987iVngJX3Q3SmX2lFySAn1DZGGR2Bgwc0F10kbEcPJzl21Ck5h2V0CDZeA/MvgyV/npFT5GZynt0IF38Bep+Evd8KOxrhxaKT/m4lZ5Gwpeo/NI0qJJs/DSODfpaRZSaN5mZyBmj/CFSthg2fgNGDYUdT9FK73milMJHwpf4O1XIOwf61sP0RaL8Sqi7N2GlyNzlHonDZYzAyAJtuDDuaojdrdoSKSlVsi+SCvu4Es8qM8goVg2VVMuFnE5XWwcW3ZfRUuZucAapWwtKrYcdjMPjLsKMpeqmiMBEJV6oYzKa4V7BM0Y5H4cB6WHkfzJib0VPldnIGuPhWmN0ET30IkmNhR1PUahujDPQkSCZVpCcSFuecX1Nb20Rm13AvbL4Z6l4PC/4g46fL/eRcMgdWPQgHn4bnHwg7mqJW1xglHocDAyoKEwnLoSHHyAkVg2XdxmshMezX4shCj0XuJ2eA5rdD0+/A05+DYx1hR1O0tIynSPi0pnYI+n7i5zVfcD1ULM3KKfPj1TXzm1cDrLsq3FiKWE19FDMlZ5EwaRpVliVG/ZobZQth+U1ZO21+JGeAsgV+O66uJ2Df98KOpijNmGnMq45oGU+REPV1J5gz15hdlj+X77y27R6/pPTqL0NsVtZOm1+v7vkfh8qLYP1VMHYk7GiKkiq2RcKlZTuz6OgeePY2aP5daHpzVk+dX8k5UgJrHoPjXX78WbKutiHK/v4k8TFVbItkWzLp6O9Vcs6a9VcDBqvuz/qp8ys5A9S8EpZcDi88AAc2hh1N0alrjJJMwmC/KrZFsm1oMEl8TOPNWdH5BHT9ix9OLWvN+unzLzkDrPgizKwO5j6rizWbVLEtEp6+bi3bmRXxY774eO5yP5wagvxMzjPm+RVaDqz1q4dJ1syvixCJoKIwkRCkknNNvZJzRj17OxzvgDWP+OHUEORncgZY8EdQ/5uw+UYY7gk7mqIRixnVdRG1nEVC0N+dYN78CDNLtWxnxhx6DrbeDYveB7W/HloY+ZuczfynmsQIrP9E2NEUlVpVbIuEok+V2pnlHKy90q9MueLOUEPJ3+QMMGcJLL8ZOr4N3f8RdjRFo64xytBgktERVWyLZEs87hjsS6oYLJP2/D30/xRWfAlKa0INJb+TM8Cy66HiPFh3JcSHw46mKKQ+uWtvZ5Hs2d+XJJlUMVjGjB6EjdfA/F+DxR8MO5oCSM7Rmb57++gu2HJ72NEUhVpVbItkXZ/W1M6szTfDyKDPJxb+73jCEZhZ1Mw2mtm/Bt8vNLNfmdl2M/u2mc0Ibp8ZfL8juL8tM6Gfou61sPBPYetdfjBfMqqqOkKsRBXbItnU150gEoHqOrWc027/Otj+CLR/FKouDTsaYHIt548BW0/5/g7gPudcOzAEfCC4/QPAkHNuCXBf8LjMu/RuiM2Bpz4MTgtkZFIkYtTWR9WtLZJF/T0J5tdGiJWoUjutkglY+2GYVQ+X3BZ2NCdNKDmbWTPwFuCvg+8NeB3w3eAhjwNvD75+W/A9wf2vDx6fWaU1cOmdMPAL2PW1jJ+u2KliWyS7tKZ2hux4DA6sh0vvhZKKsKM5aaIt5/uB64FUk3Q+cNA5Fw++7wSagq+bgH0Awf2Hgse/hJldbmbrzGzdwMDAFMM/zaL3Q81rYON1cCJNx5Rx1TVGOXzQcfyYeilEMm10xHFgMEltg5JzWg33wuab/JoZC/4g7Ghe4pzJ2czeCvQ759afevM4D3UTuO/FG5z7inNutXNudU1NmkrWLQJrHoWxw7Dp+vQcU8ZV3xwUhXWp9SySaf09CZx78e9O0mTjdZAYhtUP+bUzcshEWs6vBv63me0BvoXvzr4fqDSzWPCYZqA7+LoTaAEI7p8LHEhjzGdXuRwuuNZ3bff9LGunLTb1Tf4i0avkLJJxvZ3+7yz1dydp0PcT2PMNWPYpqFgadjQvc87k7Jy70TnX7JxrA/4Q+C/n3LuBnwDvDB72XuD7wddPBN8T3P9fzrnsrlZx4WegbKEf5E+MZPXUxaK8wphdbkrOIlnQ25VgxkyonB/+FJ+CkBiFtVdA+SJYdmPY0YxrOq/0p4BPmtkO/JjyV4PbvwrMD27/JHDD9EKcgthsWPMQHN7mp1dJ2pkZ9U1RdWuLZEFvV4K6piiRSG51veatbff4/LD6yxCbFXY044qd+yEvcs79FPhp8PUu4LJxHnMCeFcaYpuexjdB67v87iIL/tAv9SlpVd8UZe0vRkgmnS4aIhninKO3M8FFq8PZHangHN0Dz94GLe/weSJHFXYfycr7ITLDd19kuWe9GNQ1RRkbgwMDqtgWyZRDQ44Tw07jzemy/mpfPLzy/rAjOavCTs6zG+GSL0Dvk7D3W2FHU3AamlUUJpJpqaGj+uZJdXTKeDqfgK5/gYtugbKWsKM5q8JOzgDtV0DVatjwCb+wuaRNTUMUMyVnkUzq7fLLSWgBkmmKH4N1V8HcC+G8j4UdzTkVfnKOROGyx2BkADblZlVeviopMarrIioKE8mg3q4ElfMjlM5SXce0PHs7HO/wG1tEcn/8vvCTM0DVSlh6lV+mbfCXYUdTUOqbovR0KjmLZEpvZ0LjzdN16DnYejcseh/UvibsaCakOJIzwMW3waxGeOpDkBwLO5qCUdcU5eD+JCeGVXAnkm5jY47BvqSS83Q454uCS+bAijvDjmbCiic5l8yB1Q/Cwafh+QfCjqZgnFzGU5tgiKTdQGrZTiXnqdvzDej/Gaz4kt8gKU8UT3IGaP5daHwrPP05ONYRdjQFob7JV5D2qmtbJO16T1ZqKzlPyegQbLwW5v8aLP5g2NFMSnElZzNY/ZeA81V7Mm1z5xmls4y+rvi5Hywik9LblaCkBKpqiutSnTabb4aRQV8EZvn1O8yvaNOhvM3Pcet6AvZ9L+xo8p6ZUd8c1XQqkQzo7UxQ26hlO6dk/1rY/ii0XwlVl4YdzaQVX3IGOP8TUHkRrL8Kxo6EHU3eq2/yyTmZVFGYSLo45+jtUqX2lCQTsPYjUFrni4HzUHEm50iJ3/f5eCc8c0vY0eS9uqYooyNwcL+W8RRJl6OHHcePatnOKdnxKBxYDyvvgxlzw45mSoozOQPUvAqWXO4rt4c2hR1NXtPeziLpl/p7qlMx2OQM98Lmm6Du9bDgD8KOZsqKNzmDL62fOT+Y+6zEMlV1jVrGUyTdUjMg1HKepI3XQuIErHnYFwHnqeJOzjPmwaX3wv6n/OphMiUzZhpVNVrGUySdersSVMwzZpcV92V6Uvp+Anv+Hi64HiqWhh3NtOhVb/tjqP9N2HwjDPeEHU3eShWFiUh69KkYbHISo34lsLKFsPymsKOZNiVnM1j9MCRGYP0nwo4mb9U1RTkwkGR0RBXbItMVjzsGehMnF/mRCdh2DxzeBqu/DLFZYUczbUrOABXt/pNWx7eh+4dhR5OX6puiOKdlPEXSYbA3QSLhP/TKBBzdA8/eBi3vgKY3hx1NWig5pyz7FMxZCuuugPhw2NHkHVVsi6TPyWU7lZwnZv3VfgWwlfeHHUnaKDmnRGfCZY/C0V2w5QthR5N3KudHmDETFYWJpEFvV4JoDKrrdIk+p87vQ9e/+JUfy1rCjiZt9Mqfqu610PYe2HonHNoadjR5JRIxFYWJpElfV4LahijRaP5OBcqK+DFYdzXMvRDO+1jY0aSVkvPpVt4NsXJY+2G/D6hMWH1TlN7OBE6/N5Fp6elUpfaEPHsbHO/wG1tESsKOJq2UnE9XWus35O7/Oez6WtjR5JW6phgnhh2HhpScRabq6OEkRw9r2c5zOvQcbL0HFr0Pal8TdjRpp+Q8nsV/BjWvhk3XwYnBsKPJG6k9Z3u1faTIlKVmPKhS+yyc83OaS+b4xlQBUnIej5E4FhQAACAASURBVEVgzWMwegg2XR92NHmjrjFIzp0adxaZKlVqT8Ceb0D/z2DFHVBaE3Y0GaHkfCaVy+GCa2HX3/oubjmn0lnGvPkRJWeRaejZl6C8wiiv0OV5XKNDsOEamP8KWPyBsKPJGL36Z3PhZ/xScE992C8NJ+fU0BKlZ5+Ss8hU9XQmaGxRq/mMNt8Mo/vhskd8L2eBKtyfLB1is2HNQ3B4K2y9K+xo8kJDS5T9A0lGTqgoTGSyxsYcAz0J6pu1bOe4Bp+C7Y9C+0dh3oqwo8koJedzaXwTtL4LttwOR3aGHU3Oawg+8feoa1tk0vq7EySTqOU8nmQC1n4EZtXDJbeFHU3GKTlPxMr7ITLDVwdqDu9ZNbb4T/w9+1SxLTJZqSGhBiXnl9v+CAxtgJX3QUlF2NFknJLzRMxuhIu/AL0/gr3fDjuanDZnrjG73NRyFpmCns4EM0thXrUuzS8x3AtP3+y39239/bCjyQq9Ayaq/SNQtRo2fBxGD4YdTc4yMxWFiUxRz7449U0xIhEt2/kSG66BxAlY/ZDf5rcIKDlPVCQKlz0GIwOwOf838s6kxpYo/d0J4nENAYhMVDLp6O1KqEv7dL3/BXu/6XcOrFgadjRZo+Q8GVUrYelVvlpw8FdhR5Oz6ptjJBIw0KvWs8hEHRhIMjqi8eaXSIz4bXzLF8GyG8OOJquUnCfr4ttgViM89SFIquhpPKlKU3Vti0ycisHGse0eOPw8rP4yxGaFHU1WKTlPVskcWP0gHNwMzz8YdjQ5aX5thJIZSs4ik9G9L040CrUNSs4AHN3td51q+T0/pbXIKDlPRfPvQuNb4ZnPwrGOsKPJOam9nVWxLTJxvZ0JahqixGLFUfB0Vs7BuqvAon7qVBFScp4KM1jzZf8GWn912NHkpIaWGD374iSTKgoTORfnHN37VAx2Uuf3ofvf4KJboKwl7GhCoeQ8VWUL/Bun8/v+n7xEQ0uUkRNwcH8y7FBEct7Rw45jRxyNzUrOxI/5Rs/cC+G8j4UdTWiUnKfj/I9D5UW++2XsaNjR5JSGZhWFiUxUd/B3Uq+WMzxzKxzfB2segUhJ2NGERsl5OiIlft/n453wzOfCjian1DVFiURevOiIyJmllrttKPYNLw5ugW33wqL3Q+1rwo4mVErO01XzSlhyOTz/AAxtCjuanFFSYtTUa29nkYno6UxQVROhdFYRF4M55+c0l8yBFXeEHU3olJzTYcUXYeb8YO6zklFKfXOMbm2AIXJOPfsSJ4eCitbur0P/z31iLq0JO5rQKTmnw4x5cOm9sP8p2PFY2NHkjMaWKEcOOY4eVlGYyJmcGHYcGEgWd6X26BBsvBbmvwIWfyDsaHKCknO6tP2x3zFl840w3BN2NDlBezuLnFtvZzDe3FLE482bboLR/XDZI2BKS6DknD5msPphvxbs+k+EHU1OqFfFtsg5nVy2s1i7tQeDHselV8G8FWFHkzOUnNOpoh2W3wQd34buH4YdTehml0WorIqcrEQVkZfr7kxQNseYM7cIi8GSCVj7EZjVABffGnY0OUXJOd2WfQoqzvNVh/HhsKMJXUOLlvEUOZvefQkaW6JYkexT/BLbH4GhDX6JzpKKsKPJKUrO6Rad6SfPH90FW74QdjSha2iOsr8/ycgJLeMpcrp43NHfkzg5BFRUhnvh6Zuh/g3Q+q6wo8k5Ss6ZUPdaWPinsPVOOLQ17GhC1dASxTno61LrWeR0/T0JEgloLMZisA3XQOIErH7I1+zISyg5Z8qld0GsHNZ+2E+uL1KpCtSeTo07i5yuaPdw7v0v2PtNWHaDr9WRl1FyzpTSWlhxp59Uv+trYUcTmrnzjFllpmU8RcbRsy/BjJlQVVNEl+LEiK/JKV/sk7OMq4jeESFY/GdQ82rYdB2cGAw7mlCYGQ3NUU2nEhlHz74E9U1RIpEi6tbddg8cfh5Wfxlis8KOJmcpOWeSRfzGGKOHfIIuUo0tUfq7EyQSxdu9L3K6ZNLR2xUvrsVHju6BZ2+HlndC4xvDjianKTlnWuVyuOBa37Xd97OwowlFQ0uMeNwXv4iId2AgyciJIhpvds5vr2sRWHVf2NHkPCXnbLjwM1DW5ovDEiNhR5N1TQv8xae7Q8lZJKUr+HtI/X0UvK4noPtf4aJbYXZz2NHkPCXnbIjN9tMFDm+DrXeFHU3WVdVEmFkK3XuVnEVSujvixGJQ21AEyTl+DNZdDZUXwXlXhR1NXlByzpamN/txlmdvhyM7wo4mqyIRo7E1RleHplOJpHTt9YuPRKNFUAz27G1wvMMv0BQpCTuavKDknE2rHoDIDFh7RdHNfW5sjdLbqaIwEfDFYD374jS1FkEx2MEtsPUeWBTMXpEJUXLOptmNcMkXoPdJ2PutsKPJqqbWoCisW13bIn5JW2gs9PFm5/yc5pIKWHFH2NHkFSXnbGu/AqpWwYZPwOjBsKPJmtRFqEtFYSIniyObWgs8Oe/+ul+IacUdUFoddjR5Rck52yJRuOwxGBmAzTeFHU3WVFVHKJ1ldO/VuLNIV0ecWAnUFHIx2OgQbLwWql/pF2SSSVFyDkPVKmj/KGx/FAZ/FXY0WRGJGA0tUbWcRfAt54ZCLwbbdBOM7vdFYKZUM1n6jYXlktv8BuNPfQiSxdGabFoQpbcrQTyuojApXsmko7sjTtOCAi4GG3wKdjwGS6+CeZeEHU1eUnIOS0kFrHoQDm6G5x8MO5qsaGqNkdBKYVLk9vcnGR3xMxgKUjIBaz/iGx8X3xp2NHlLyTlMLe+AxrfAM5+FYx1hR5NxqYtRlxYjkSLWFdRdNBbqNKrtj8DQBlh5n2+EyJQoOYfJzO/M4pKw/mNhR5NxVTVBUZgWI5Ei1t2RoKQEauoL8PI73ANP3wz1b4DWd4UdTV4rwHdHnilvg4tugc7vQecTYUeTUWZGY2tULWcpal17E9S3FGgx2IZrIXHCL1dsBfjzZZGScy44/xN+zdl1H4Wxo2FHk1FNC6L0dSWIj6koTIpPMuno6SzQlcF6fwx7vwnLboCK9rCjyXvnTM5mVmpmT5nZZjPbYmafD25faGa/MrPtZvZtM5sR3D4z+H5HcH9bZn+EAhApgTWPwvF98MwtYUeTUY2tMRIJ6NNKYVKEBvsKtBgsMQLrroTyRT45y7RNpOU8ArzOOXcJsAJ4o5m9ArgDuM851w4MAR8IHv8BYMg5twS4L3icnEvNq2DJ5fD8/TC0OexoMia1IpK2j5RilNr8peCmUW27Bw4/72toYrPCjqYgnDM5Oy/V11oS/HPA64DvBrc/Drw9+PptwfcE97/eTIMPE7LiSzCjKpj7XJjJa151hFmzTTtUSVHq3pugZEaBFYMd3e13nWr5PWh8U9jRFIwJvUPMLGpmm4B+4ElgJ3DQOZe6wnYCTcHXTcA+gOD+Q8D8dAZdsGbMg5X3wv5fwc6vhB1NRqSKwrS3sxSjro44DS1RIpECaa84B+uuAovCqvvDjqagTCg5O+cSzrkVQDNwGXDBeA8L/h/vXfey6h8zu9zM1pnZuoGBgYnGW/ja3g11r4dNN8Jwb9jRZERja5S+bhWFSXHx20QmCqsYrPP70P1vcNHnYXZz2NEUlEn1rTjnDgI/BV4BVJpZ6l3WDHQHX3cCLQDB/XOBA+Mc6yvOudXOudU1NTVTi74QmcGahyEx7HeuKkBNC1QUJsVnoDfJ2GgBbRMZPwbrr/YzTc67OuxoCs5EqrVrzKwy+HoW8JvAVuAnwDuDh70X+H7w9RPB9wT3/5dzTk2kyahYCstv8ns+9/wo7GjS7uRKYSoKkyKSWnynYFrOz9zqZ5isecTPOJG0mkjLuQH4iZk9DawFnnTO/SvwKeCTZrYDP6b81eDxXwXmB7d/ElBd/VQsuwHmLIW1V0B8OOxo0mre/AizyuzkMoYixaBrb4IZM6G6rgCKwQ5ugW33wqI/g5pXhx1NQTrnRzjn3NPApePcvgs//nz67ScArds2XdGZcNmj8OPXwZa/8LtYFYiTRWFqOUsR6e6I09Acy/9iMOdg3RV+3ewVmimbKQXwEa6A1b0W2t4DW++AQ1vDjiatmlpj9HUlGFNRmBSBRCIoBiuE8ebdX4f+n/vEXFoddjQFS8k51628G2Llfgu2Ahq6b2qNkkxCX5daz1L4BnuTjI0VwMpgIwdg47VQ/UpY/GdhR1PQlJxzXWktrLgT+n8Gux8/9+PzRKpiVZtgSDEomJXBNt8Mo/t9EZgpfWSSfrv5YHFQdLHxWjgxGHY0aVFZFWF2uYrCpDikisHm1+bxJXfwKdjxGCy9GuZdEnY0BS+P3ylFxCJ+Y4zRQ7Dp+rCjSQszo3lBVMlZikLnnjhNC/K4GCyZgLUfhlkNcPHnw46mKCg554vKC+GCa2DX3/pijALQ3BajvyfJyInCGUsXOd3YmKO3M0FzWx6PN29/GIY2wsr7fJW2ZJyScz658LNQ1gZPfRgSo2FHM23NbTGcQ61nKWi9+xIkEv79npeGe+DpT0P9G6BVs2SzRck5n8Rmw+qH4PBW2HpX2NFMW6ol0blHRWFSuDr3+A+fLQvzNDlvuAYSJ/y1RxsMZo2Sc75pejO0vBO23A5HdoYdzbTMLo9QVRM5efESKUT79iSYM9eoqMzDy23vj2HvP/gVCyvaw46mqOThu0VYdT9YiV/aM8/nPje3xZScpaB17YnnZ6s5MeKvMeWLfXKWrFJyzkezm+CS26H3R9DxnbCjmZaWtiiHDzoOH0yGHYpI2h0/mmT/QDI/x5u33g1HXoDVX4bYrLCjKTpKzvmq/UqoWgXrPw6jB8OOZspSFy21nqUQdQaL7ORdpfbR3X7orOWd0PjGsKMpSkrO+SoShcseg5F+v2pPnqpviRKNwr7dSs5SeDp3xzHLs5XBnIN1HwWLwqr7wo6maCk557OqVdD+Udj+iF+9Jw+VlBj1zVFVbEtB6twbp6Y+wszSPKpy7vwedP8ALroVZjeHHU3RUnLOd5fc5lftWfshSOZn67O5LUbX3jjJZH4Xt4mcyjlH5+4EzflUDDZ2FNZ/DCovgvOuCjuaoqbknO9KKmDVgzC0CZ5/MOxopqS5LcroCAz0qihMCsfQYJLjx1x+FYM9eysc3+c3toiUhB1NUVNyLgQt74DGt8Azn4VjHWFHM2kqCpNCtC8YqmnJl2Kwg8/CtvtgUbDRjoRKybkQmPnpDs7B+qvDjmbS5tdGKJ1lKgqTgtK5O05JCdQ25kFyds7PaS6pgBV3hB2NoORcOMrb4KLPQef3/b88EokYTW1RulQUJgWkc2+cxtYY0WgeFIPt/jsY+IVPzKXVYUcjKDkXlvM/4Qs51l3lCzvySEtbjL7uBKOjKgqT/BePO3o6EjQvzINW88gB2HgdVL/S7x0vOUHJuZBESvy+z8f3wTOfCzuaSWlui5JMQneHWs+S//q6EsTjebIT1eabYPSALwIzpYRcoVei0NS8CpZcDs8/4Cu484SKwqSQpN7HOb8y2OCvYMdXYOlVMO+SsKORUyg5F6JLvggzqvy+z8n8aImWV0SorNIOVVIYOvckKJtjVFbl8CU2GYe1H/HrJFx8a9jRyGly+J0jUzazClbeC/t/BTu/EnY0E9a8MErn7vz4MCFyNp174rS0xbBc3v94+yMwtNHvclcyJ+xo5DRKzoWq7d1Q93rYdCMM94YdzYQ0t8U4eCDJ0cNajETy14lhx0BvkqZc7tIe7oGnPw31v+U3t5Cco+RcqMxgzcOQGIYNnwg7mgnRuLMUgtT7N6f3cN5wjd+vec1D/lohOUfJuZBVLIXlN8Heb0HPj8KO5pwaW6NEImgTDMlrqeTctCBHW869P4a9/wDLboA5S8KORs5AybnQLbsB5iz1hR/x4bCjOasZM4y6xij71HKWPNa5J0F1XYRZs3Pw8poY8SuBlS+G5TeEHY2cRQ6+eyStojPhskfh6C7Y8oWwozmn1Eph2qFK8pFzjs498dyd37z1bjjyAqx+CKKlYUcjZ6HkXAzqXgtt74Gtd8KhrWFHc1YtC2OcGHYM9qkoTPKPL2h0uTm/+ehu2HI7tL4LGn877GjkHJSci8XKuyFW7ru3Xe62SlsX+RaHNsGQfNSxy9dLtC7OsZazc35ZX4vByvvCjkYmQMm5WJTW+kXt+38Gux8PO5ozqq6LMKvM6Nip5Cz5Z9+uODNmQl2u7UTV+X3o/je/2MjsprCjkQlQci4miz/g92ndeC2cGAw7mnGZGa2LYnTsUnKW/NOx048359ROVGNH/VaylRf7ZTolLyg5FxOL+I0xRg/BpuvDjuaMWhdFGehNcvyYxp0lf4yccPR2JXKvS/vZ2/xmOGsegUiOxSZnpORcbCovhAuugV1/C/0/Dzuacb047qz5zpI/uvbGSSZffP/mhIPPwrZ7g16zV4UdjUyCknMxuvAzUNbmN8ZIjIYdzcs0tcWIRNC4s+SVvTtTK4PlyHizc35Oc0kFXPKlsKORSVJyLkaxMlj9ZTi8FbbeFXY0LzNjhtHQEtW4s+SVfbvi1Dbk0OIju/8OBn4Bl94JpdVhRyOTlCPvIsm6prdAy+/5eY9HdoYdzcu0LorRuSdOIpG7075EUpJJR8euHBpvHjkAG6+D6lfCoveHHY1MgZJzMVv1AFgJrLsy5+Y+ty6KMTYKvZ0ad5bcN9iX5MSwy53x5s03wegBXwBqusznI71qxWx2E1xyO/T8EDq+E3Y0L9ESXOTUtS35IFUfkRPJefBXsOMrsPRqmHdx2NHIFCk5F7v2K6FqFaz/OIweDDuakyqrIlTMMyVnyQsdu+LMLjPm14Z8SU3G/SqAsxrg4s+HG4tMi5JzsYtE4bLHYKQfNt8cdjQv4RcjUbe25L6OXXFaF8WwsPdG3v4IDG2EVfdDyZxwY5FpUXIW33Ju/6j/wx58KuxoTmpdFOPQgSSHhrQYieSuY0eTDPYlaQm7GGy4B57+NNT/FrS8M9xYZNqUnMW75DbfFfbU5b5rLAecXIxEXduSw1KbtLQuCnl+84Zr/H7Nax6CsFvwMm1KzuKVVMCqB+HgZnj+wbCjAaChJUpJiYrCJLd17EwQiUDTghBbzr3/CXv/AZbdAHOWhBeHpI2Ss7yo5R3Q+GZ45rNwrCPsaIhGjaY2bYIhua1jV5yGligzZoTUWk2MwNoroXwxLL8hnBgk7ZSc5UVmsPohcElY/7GwowF813Z3R4Kx0dyahy0CkEg4uvbEWRDmePPWu+DIC37Vv2hpeHFIWik5y0uVt8FFn4PO70HnE2FHQ+viKMkkdO5V61lyT8++BGNjIc5vProLtnzBF4A1vjGcGCQjlJzl5c7/JMy9ENZ91O8FG6KWhanFSDSlSnJPasilJYzk7BysuwosBqvuy/75JaOUnOXlIiV+7vPxffDMLaGGUlYeobouwj7tUCU5qGNXnLlVEebOC+FS2vk96P4BXPR5mN2c/fNLRik5y/hqXgWL/xyevx+GNocail+MJI7LsfW/RfziIyFMoRo76utCKi+G867O/vkl45Sc5cxWfAlmVMFTH/JFYiFpXRTj+DHH/n4tRiK54+CBJIeHQtrs4tlbfc/WmochkgPreUvaKTnLmc2sgpX3wP5gIf2QpLbh05QqySWpxXGynpwPPgvb7oPFH4CaV2f33JI1Ss5ydm1/AnWvg003wHBvKCFU10UonWXs1biz5JC9O+OUzID65ix2azsHa6/wiwZd8qXsnVeyTslZzs7Md50lhmHDJ0MJIRIxFiyJsXeHkrPkjr074rQsjBGNZnHxkd1/BwO/gEvvhNLq7J1Xsk7JWc6t4jxYdqNfHrDnR6GE0LYkxmBfkiOHNO4s4Rs+lqS3K0Fbexa7tEcOwMZrofqVsOj92TuvhELJWSZm+Q0wp913qcWHs3761EVQrWfJBXt3xXGO7CbnzTfB6BCseRRMl+5Cp1dYJiZa6i8KR3fClr/I+ukbW6OUzIA9Ss6SA/ZsjxONQktblpLzYFCUufRqmHdxds4poVJylomrf50vENt6BxzamtVTR6NG66IYe7YrOUv49myP09QWpSQbm10k47D2I35L14s/n/nzSU5QcpbJWXkPxMr9xSLLi4K0tcfo605w/JjGnSU8Iycc3R0JFraXZOeE2x+GoY2w6n4omZOdc0rolJxlckprYcUd0P8z2P14Vk/d1h7DOejQlCoJ0b7dcZLJLI03D/fA5k9Dw2/7zS2kaCg5y+Qt/gBUv8pXjo7sz9ppm9tiRGOoa1tCtWdHHLMsLT6y4ZOQHPXbQVpI+0VLKJScZfIsApc9CqOHYOP1WTttSYnR3BZTUZiEas/2OI2tUWaWZjhZ9v4n7P0WLLsB5izJ7Lkk5yg5y9RUXuS3ltz1N9D/i6ydtm1JjO6OBCMntAmGZF98zNG5O07bkgy3mhMjsPZKKF/spzFK0VFylqm76LNQtsBvjJEYzcop29pjJJN+3E8k2zr3JojHszDevPUuOPICrH7IT2OUoqPkLFMXK/MXj8NbYdvdWTll66IYkYjGnSUce7aPAbBgcQaT89FdsOUL0PouaPztzJ1HcpqSs0xP01ug5ffg2dvgyM6Mn25mqdHQEtW4s4Ri7444dY0RZpdn6NLpHKy7CiwGK+/LzDkkLyg5y/StegCsBNZdmZW5z23tMTp3xxkb07izZE8i4di7M07bkgzOb+78HnT/AC6+FWY3Ze48kvOUnGX6ZjfBJbdDzw+h4x8zfrqF7THicejao9azZE9vZ4LREWhbmqEu7bGjsP5qqLwYll6VmXNI3jhncjazFjP7iZltNbMtZvax4PYqM3vSzLYH/88Lbjcze9DMdpjZ02a2MtM/hOSA9iuhahWs/5ifYpVBCxbHMIPdGneWLEq93zJWqf3srXC8E9Y8ApEsbqghOWkiLec4cI1z7gLgFcCVZrYMuAH4sXOuHfhx8D3Am4D24N/lwCNpj1pyTyQKlz0GI/2w+eaMnmpWWYS6Ro07S3bt2R5nfm2EOXMz0OF48FnYdp9f4KfmVek/vuSdc77LnHM9zrkNwddHgK1AE/A2ILV+4+PA24Ov3wb8nfN+CVSaWUPaI5fcU7UK2j/q1wIefCqjp2prj7FvV5xEQuPOknnJpGPvjgzNb3bOr1U/Y65fGleESY45m1kbcCnwK6DOOdcDPoEDtcHDmoB9pzytM7hNisElt/ndc9Z+yO+mkyFtS2KMjkDPvkTGziGS0t+TZPi4y8z85t2Pw8B/+8Q8c376jy95acLJ2czKgX8CPu6cO3y2h45z28uaN2Z2uZmtM7N1AwMDEw1Dcl1JBax6EIY2wQt/mbHTLAhaMJrvLNmQmt+c9uQ8cgA2XufXql/0/vQeW/LahJKzmZXgE/PfO+f+T3BzX6q7Ovi/P7i9E2g55enNQPfpx3TOfcU5t9o5t7qmpmaq8UsuankHNL4Znv4MHNt37sdPwZy5EaprI0rOkhV7dsSZO8+orErzePPmG2F0yBeBmSbPyIsmUq1twFeBrc65e0+56wngvcHX7wW+f8rtfxpUbb8COJTq/pYiYeZXDnNJPzUkQxa0+00wkkmNO0vmOOfYsz1OW3sJls6doQZ/CTv+CpZeDfMuTt9xpSBM5KPaq4H3AK8zs03BvzcDXwLeYGbbgTcE3wP8ANgF7AD+Crgi/WFLzitvg4s+5xdV6HwiI6dY2B7jxLCjt0vjzpI5g31Jjh526S0GSyZg7RW+PuPiz6fvuFIwzvluc879N+OPIwO8fpzHO+DKacYlheD8T8Lub8C6j0Ld66CkPK2HX3SeX6lp1/NxGls0L1QyY9fzfrx50flpfI9tfwSGNsKrvw0lc9J3XCkYGuSQzImU+LnPx/fBs+lvHVRURqipj7Br21jajy2SsnNbnMqqCFXVabpcDvfC0zdD/Rv85hYi41BylsyqeRUs/nO/wMLQ5rQfftHSEvbs0HxnyYxk0rH7hTiLzoulb7x543WQOAGrv+zrM0TGoeQsmbfiSzCjCp76sC8SS6NF5/v5zp17NO4s6dfbmWD4uEtfl3bfT2HPN+CC66FiaXqOKQVJyVkyb2YVrLwX9v8SdnwlrYdeuNSvs71TXduSATu3+al6i89Lw05UiVG/c1vZQlh+0/SPJwVNyVmyo+3dvihs0w1+zC1NZpdFaGiOsut5zXeW9Nv1/Bg19WlaT/v5++HQc7D6QYjNmv7xpKApOUt2mMGahyExDBs+mdZDLzo/xr7dcUZHNe4s6ROPO/bsiLP4/DS0mo91wDOfh+a3QdNbp388KXhKzpI9FefBshth7z9Az4/SdtjF55eQiMNe7VIladS5O87YKCw6Lw3jzRs+CThYef/0jyVFQclZsmv5DTCn3S/AEB9OyyEXLI4Rjb44H1UkHXY9H8fML3YzLT1Pwr5/guU3+8V5RCZAyVmyK1oKax6Fozthy1+k5ZAzZhrNC2Mad5a02vl8nMbWKLPKpnGZTIz6JWzLF8MF16QvOCl4Ss6SffWvg7Y/ga13wKGtaTnk4vNidHckGD6W3qlaUpxGRxydu+PT79J+/gE4vM3v1BYtTU9wUhSUnCUcK++BaJnfZN5Nv5Br0fklOAe7tUuVpMHenXESCaZXDHa8C569FZp+B5renL7gpCgoOUs4Smvh0jug/2d+s/lpam6LUjIDdW1LWuzcNkY0Bq2Lp9Fy3ng9JMdglYrAZPKUnCU8iz/oN5nfeC2M7J/WoWIxo21JTIuRSFrs2hanZWGMGTOmuLxm389g7zdh2aegfFF6g5OioOQs4bEIXPYojB7yrYxpWnx+CQO9SQ4f1LizTN3xY0l6OhMsnuqSncm434mtbIFPziJToOQs4aq8yG8tuetvoP8X0zpUqnhn1wtqPcvU7X4hjnMvbkk6adsfhkPP+jnNsdnpDU6KhpKzhO+iz/pWxlMf8lNPpqi+OcqsMmPXNo07y9Tt2hZnxkxfxzBpL3V+IgAAIABJREFUJ/rh6c9Cw2/71cBEpkjJWcIXK/Pb5x3eCtvunvJhIhFj0dIYO5+P49JQAS7FaefzY7S1x4hGpzDevPnTED8Gqx7QdpAyLUrOkhua3got74Bnb4MjO6d8mEXnxTh0IMmBQY07y+QdPphksC85tS7tAxth51/D0qv8UrUi06DkLLlj1QNgMb+t3hRbvqmLqrq2ZSp2BkvALp7s4iPOwYaPw8z5fphGZJqUnCV3zG6Gi2+Hnh9Cx3emdIjquggVlcYOTamSKdi5Nc7sMqOuaZLjzfu+C/0/9+/fGZWZCU6KipKz5JalH4V5K2H9x2H04KSfbmYsWVbCzq1xEgmNO8vEJZOOHVvHWHJBjEhkEuPF8WHYcC1UXuzn7oukgZKz5JZIFC57DEb6fXHNFCxdVsKJYUfXnkSag5NC1tuV4OhhR/vySY43b7sHjnf4YZnIFCq8Rcah5Cy5Z/5qaL/SzxcdfGrST198fgwzeOE5dW3LxG3f4t8vSy6YRHI+3glbvggtvwd1v5GZwKQoKTlLbrrkdphVD2s/5FdcmoRZZRFaFkZPXmxFJmL7c3EaWqLMmTuJy+KmG8Al4NK7MheYFCUlZ8lNJRW+m3BoE7zwl5N+evvyEro7Ehw7oilVcm4nhh0dO+O0L5tEq3ngf2DP38MF10L5wswFJ0VJyVlyV8s7oeFN8PRn4Ni+ST21fZnfQnLHVk2pknPb9fwYySS0L5/gFCqXhPUfg1kNsOyGzAYnRUnJWXKXGax56MUL4SQ0tkaZXW5s17izTMALW8aYWQqtiyaYnHd/Aw6shUu+BCXlmQ1OipKSs+S28oVw4Weh85+h84kJPy0SMdqXlbD9uTGSSU2pkjNzzrH9uTiLzy+Z2JKdY0dh8w0w/zJY+CeZD1CKkpKz5L4LroG5y2HdVX7d4glqXxbj2BFHb6emVMmZDfQmOXQgOfEpVM99CYZ7/K5TpkuoZIbeWZL7IiV+7vPxDnjmlgk/LTUl5gVVbctZpIY+JlQMdnQPbL0bFvwx1Lwys4FJUVNylvxQ82q/+tK2+2Bo84SeUl4RobE1yvbnVBQmZ7Z9yxi1DREqqyZwOdx0vW8tr/hS5gOToqbkLPljxR0wYx489WFfJDYB7ctK2LcrzolhjTvLy42OOvZsn+AUqv6fQ8c/wrJPQVlL5oOToqbkLPljZhVceg/s/yXs+MqEntK+vIRkEnZqIwwZx54X4sTjnHu8OZnw673PboYLrstOcFLUlJwlvyx8D9S91q/MNNx3zoe3LIxSOktTqmR8258bo6QEFiw5xxSq3V+DoY2+9yY2OyuxSXFTcpb8YgZrHoHEMGz45DkfHo0ai8+PsX3LGG6Ke0RL4dq+ZYyF58UoKTnLFKqxw7D5Zqh+JSz4o+wFJ0VNyVnyT8V5flWmvd+EnifP+fD2ZSUcGnIM9GopT3nRgYEEg/3Jc483b/kinOgLpk5NYitJkWlQcpb8tPxGKF8Ca6+AxImzPnRJcPHVRhhyqlQV/1nHm4/u/n/t3Xl8VNXdx/HPmclkDwGSAIFAEiCEJYQQDFIEREUBi2C1PmgVAXnUVqtFaa2KdcENd+te6iNKxYq1RajWFhcoIgoCgRD2HUJCNsieSWY5zx8zYICEhGx3lt/79cqLzJ07M9/DJPPLPffcc2Dni5AwDaKHt1MyIaQ4C29lDobhb0LFXtj+zDl37djZRJdYkywhKU6zZ7uNTtEmomLO8TG4+fegzJD2VPsFEwIpzsKbdRsHvaa6uh3L951z16RBFg7usVNbI+edBdjtmv27bPQbaEE11FVd8M2Pl06FxrVvQOH3pDgL75b+gmsGsY13wzkGfPUbZMFhl0uqhMuB3XZqayAppYFR2toJm+6RS6eEYaQ4C+8W2gMGPwa5/4KcTxrcLSEpgOAQxY4sKc4CdmbZsARCn+QGzjcf+Asc3whDnpZLp4QhpDgL75d8F3Qc7FpWsoGFMcxmRb9BAezKklWq/J3Wmp1ZtfQdYMESWE+Xtr0StjzoWnUq4RftH1AIpDgLX2CywAVvQNURyH6iwd36pwZSWaHJOSCrVPmzvBwHpSc0/VMbOGre/ixU50L6S7LqlDCM/OQJ39BlFCROh50vQOnOendJGhSAyQQ7smrbOZzwJDu32FAKklPqKc6VR2DHcxB/PcSMbP9wQrhJcRa+Y+izYA6DDXfWOzgsJNREYr8Adsp5Z7+2M8tGz95mwjvU8/G35QHXYDBZdUoYTIqz8B3BXVzXo+Z/DYc+rHeX/qkWCo85KSqQrm1/VHLcSe4RBwNSA8++s2g9HFwMA+ZAWHz7hxOiDinOwrf0uQ06D4PM39U7OOzkeUY5evZPu7a6Tmmcdb5Za8ic4/oDb+D9BiQT4nRSnIVvMZlh2CtQfdQ1OckZOkWZ6dbDLMXZT+3MshHVxUR01zM++o78AwrXQOrjYIkwJpwQdUhxFr4nZiQk3Ag7noeK/Wfd3X+IhUN77VRWyEIY/sRardm/y86A1DNmBXPUwOb7IDIFet9iXEAh6pDiLHxT2jNgCnB1b59hQKoFrWF3thw9+5O92204HPV0ae9+3fVHXPoLrp8ZITyAFGfhm0J7wKAHXd2Vx74+7a7YnmYiIpV0bfuZHVk2QsMUPXvXKcDWIsieB7ETIPYK48IJcQYpzsJ39b8XwhJdM4c57ac2m0yK/qkW9my3YbPJbGH+wOHQ7M620S/Fgtlcp0s7ex7Yy2Ho88aFE6IeUpyF7zIHu7oqS7Nhz1un3TUgNZDaGjiwy97Ag4UvObTPTnWVZsCQOl3aZbtgz5uuEf4dBxkXToh6SHEWvi3uauh6GWx9GGqKT21OTA4gMAh2ymxhfmFnlg1zAPQdUKc4Z94H5hBIfcy4YEI0QIqz8G1KwbA/gq0Msh4+tdliUfQdYGFHlg19jqUmhfdzLXRho09yAEHB7i7t/JVwdDkMesB1bbMQHkaKs/B9HQdB0h2w9y04kXVqc/9UC+WlmtzDMluYLyvIc3K80En/k7OCOR2w6V7XLGD97zE2nBANkOIs/MPgR8HSETbdc2re7eTBFpSCHVtk1LYvO3nq4tQlVAf/Aic2u9ZqNgcbmEyIhklxFv4hqDOkznPNu52zDICwcBPxfQPYvlnOO/uybZk2esSb6dDRVGet5gtdK08J4aGkOAv/0fd2iBzkmkPZUQNASrqFgjwn+bnSte2Ligsd5B52MHiYu0t7+3NQnQfpL7rGIwjhoaQ4C/9hCoBhL7tmg9r1MgCDhgaiFGRvlKNnX5S9yXXKYlC6BaqOutZq7vU/slaz8HhSnIV/6TYOekyG7CegOo+ISBMJSQFkb6qVUds+aNvGWuISzHSKMkPWQ6Dtslaz8ApSnIX/SX8BnDWwZS7g6touPOakIFcWwvAlxQUOco84SBkWCMc3wf73IPk3EJ5odDQhGiXFWfifiL6QPBv2L4TiDQxMc3Vtb90kXdu+JNv9fg5KC4BNcyAoyjXfuhBeQIqz8E8pD7kmn9g0m4gOytW1vVG6tn1J9kYbPRPNdLL+CwpWuS6nC+xodCwhmkSKs/BPlg4w5Cko/BYOfUhKeiBF+U7ypWvbJxQVOMjLcTB4qHItG9qhP/S9zehYQjSZFGfhvxJnQKehsPl+BqU6ZNS2Dzn5PqZFL4Ty3TD0OTBZGnmUEJ5DirPwXyaza6nAqsOE571OYj/p2vYV2Zts9OlTRui+x1wLn3T/qdGRhDgvUpyFf+t2qeuDe9uTpKWVUVTgJP+oTEjizYryHRzLcXBF35eg9oRrdL5MOCK8jBRnIYY+C/ZyUgKfcY3a3ihzbXuz7E21dA4+QPfqN6D3DOg0xOhIQpw3Kc5CRA6EPv9L4KE3GTLgoExI4uWyN9q4OmUeymSB1CeMjiNEszRanJVS7yilCpRS2XW2dVZKfaGU2uP+t5N7u1JKvaKU2quUylJKpbdleCFazeDHwBzEpXGPU1zg5FiOdG17o8JjDgLLv6V3yDIYeB+Edjc6khDN0pQj53eBCWdsux/4SmudBHzlvg0wEUhyf90GvNk6MYVoYyHdYMB9dK5eSnzkulNzMgvvkr3RysTEh3AGdYcBvzU6jhDN1mhx1lqvBo6fsXkK8J77+/eAq+tsX6Rdvgc6KqViWyusEG1qwBwIiWXKgEfI3lgjXdteqGb3Enp22IRp6JMQEGZ0HCGarbnnnLtqrfMA3P92cW/vARyps1+Oe5sQni8gDFIfp4tlPd30J+Qelq5tb1JwtIoRkY9QETAEEm82Oo4QLdLaA8Lqu16h3sMPpdRtSqkNSqkNhYWFrRxDiGZKnIEzIoXxiY+x+bsKo9OI83Bs7Yd0DM7BnP4kKBnrKrxbc3+C8092V7v/LXBvzwF61tkvDsit7wm01gu01hdorS+IiYlpZgwhWpnJjCn9aToHH8S2/2Psduna9gZOp6ZzyZ8oc/QhpM9Eo+MI0WLNLc7Lgenu76cDy+psv9k9ansEUHqy+1sIr9H9SmoD+zK005/Zs00GhnmDI5kbiQtbT2XsbXLULHxCUy6l+ivwHZCslMpRSs0C5gOXK6X2AJe7bwP8C9gP7AX+DNzRJqmFaEvKRMDAO4iPXM/B9T8YnUY0gX3bm9icwUT/ZJbRUYRoFQGN7aC1vqGBuy6rZ18N3NnSUEIYzdR3JvbND9Gl4i2qKn5CaLgcjXkqa1kpPdUS8kzX0Sssyug4QrQK+cQRoj6BHamJvZHU6I/Ztv6Y0WnEORSsfZdAcyVBKb8yOooQrUaKsxANCBt6FxazFduOd4yOIhqiNRH5b3GseihdBo8wOo0QrUaKsxAN6TiYUsso+ge/TUGurPPsicr2rKKTZSclUbejZOUp4UOkOAtxDoGDf03nkEPkrP2n0VFEPao3v0G1PZJuF91odBQhWpUUZyHOIaTfNVQ5Y+lY/CZOp1zz7El0VR7Rtk/YV3sTHWPCjY4jRKuS4izEuZgslMfcSu+IrziyZYfRaUQdJRvexqzsmPr90ugoQrQ6Kc5CNKLzyF/icFqo2fqG0VHESU4HQUcWsL/0YvoMH2R0GiFanRRnIRphiYglz3Q1vfgLNRXlRscRgP3wp4SqHPLDbicoWAaCCd8jxVmIJrAM+jXBAWUc+/a9xncWba5q8xuU1sTSdfjVje8shBeS4ixEE3QZPIoC62DCj70Fss6zsSr2E1H5Bdml00noF2x0GiHahBRnIZpAmUyUdrmDKMs2iretMjqOX6va8ic0ClPSLZhM0qUtfJMUZyGaqMfom6i2d8Sa9arRUfyXoxbzoYXsOj6BwaP7GJ1GiDYjxVmIJgqNDOeIaTqxejnW4zlGx/FL9oNLCaKQgvD/JbyDfHwJ3yU/3UKchw4ZdwBOita8aXQUv1S15U1OWHsRf9GVRkcRok1JcRbiPHRL7sdh6xV0Knkbba8xOo5f0aU76WD9LzsqZxCfFGh0HCHalBRnIc6TPeFOwgIKKPzhI6Oj+JWKTX/C4QwgaNAsWeRC+DwpzkKcp/hRV3Lc2hu193Wjo/gPezWBuYvYeWISKSN7Gp1GiDYnxVmI82QJMpMfdjsx5nVUHt5odBy/ULPnI4LUcUqjbpUZwYRfkOIsRDN0HTWLWkcopevlsqr2ULP1LQqr+tJnzBVGRxGiXUhxFqIZOveI4oBtKjHWJTiqio2O49Ocx7PoYP+effZb6BoXYHQcIdqFFGchmsky6E4sJitFa/9sdBSfVvbDW9icQXQYOsPoKEK0GynOQjRTQkY6RypHEpr3J3A6jI7jm2wVhBYtZlfJFPoN62Z0GiHajRRnIZrJZFKUdbmDCPNBSrKXGx3HJ1Vm/YlAVUZVjzsICJCBYMJ/SHEWogUSxl5HSU1P7FufNzqK73HUYtr1IgdKL6L/JaONTiNEu5LiLEQLhEUGcjT410SrtZTv/87oOD7FumMRIeSSG/E7OnSUjyrhX+QnXogW6n7pbVTbO1CxXo6eW43TgWPrs+RWpJI87qdGpxGi3UlxFqKFOnXtyGE1i66OT6jO32d0HJ9Qu38pYXoP+wPmEN1NLp8S/keKsxCtoPNFs9HaRNE3LxodxftpTc2mpymq6kPipVONTiOEIaQ4C9EKYnr34pD9OrpWv0dt+XGj43g1+9EviLBvYqdjNj0SgoyOI4QhpDgL0UpC0ucQaK4kb6UsiNESVeuepqwmltjRM4yOIoRhpDgL0UpiU4eRU3MJUSfewFEraz03h7NwHR1qVpFddSe9B4QZHUcIw0hxFqIV6f5zCLcc48iqvxgdxSuVf/cUVbaOdBr+S1mzWfg1Kc5CtKK4CydSXDuQ8KMv4XQ4jY7jVXTJdiIrlpNVdivJwzobHUcIQ0lxFqIVKZOJyp73EB20nZzvPzc6jlcp/+5Jah2hBKf9BpNJjpqFf5PiLEQr6zH6Jips3TDvmi9Hz02kj28h4vhfySyeRcqI7kbHEcJwUpyFaGXmwGBOxP6eHsFrOPiNHD03ReWa+7HaO2AZ+iABFjlqFkKKsxBtoMclv6LM1ouwfXOx22Q5yXNx5K0ivOLfbCi5lyGjuhodRwiPIMVZiDZgsgRR2ftRuoZsYf8XfzU6jufSmupvf09pTSzRo3+D2SxHzUKAFGch2ky3kdM4bhtI1LFHsVbWGh3HI9kOLiW8dj2ZlQ/Sf2gHo+MI4TE8dkZ5m81GTk4OVqvV6CiiBYKDg4mLi8NisRgdpd0pcwDOwU8SvfNn7Pj3AgZc+2ujI3kWpx3bugc4UZVEwhWz5LpmIerw2OKck5NDREQECQkJ8kvrpbTWFBcXk5OTQ2JiotFxDBE9dAqF2y6kR/lTlB+fSURnmfXqpJod7xDq3M16/QFj+4UYHUcIj+Kx3dpWq5WoqCgpzF5MKUVUVJR/934oReDw+XQIzOPwv182Oo3nsFehtzzK4bIMBlx5ndFphPA4HlucASnMPkDeQ4hMHks+40m0PU9xTrHRcTxCVeYfCSaPA2GP07WHx3bgCWEYjy7ORnvyyScZNGgQqamppKWlsW7dugb33bBhA3fffXezX+upp5467fbIkSPPa/+EhIQmv1ZtbS2zZ8+mT58+JCUlMWXKFHJychrcPzw8vN7tDz/8MF9++SUAL7/8MlVVVU3O4G8ixjxNqKWEY1/ONzqK8axFBOx+ht0nriBt0uVGpxHCM2mtDf8aNmyYPtP27dvP2tae1q5dq0eMGKGtVqvWWuvCwkJ99OjRNnu9sLCwFu0fHx/f5MfOmTNH33LLLdput2uttX7nnXd0RkaGdjqdp+3ndDq1w+FoUrb4+HhdWFhY731Gv5eeIm/JVF2zKFQfzj5gdBRDVayYpu1/CdBrPl5vdBQhDANs0Oeoi3Lk3IC8vDyio6MJCnIt9h4dHU337q5pBX/44QdGjhzJkCFDGD58OOXl5axatYpJkyYBUFlZyS233EJGRgZDhw5l2bJlALz77rtcc801TJgwgaSkJO677z4A7r//fqqrq0lLS+PGG28EfjxazcvLY8yYMaSlpZGSksI333xT7/4xMTEN7l9XVVUVCxcu5KWXXsJsNgMwc+ZMgoKC+Prrrzl48CADBgzgjjvuID09nSNHjgAwZ84c0tPTueyyyygsLARgxowZfPzxx7zyyivk5uZyySWXcMkll7TBu+EbOo97CqU0tm9/ha3WP6f1dBz9grDCv7Cu8G6GXXmB0XGE8FjKVcCNdcEFF+gNGzactm3Hjh0MGDAAgM8+qiIvp3VnWYqNM/PT/wlt8P6KigpGjRpFVVUV48aNY+rUqVx88cXU1tbSv39/lixZQkZGBmVlZYSGhrJmzRqef/55Pv30Ux588EEGDhzITTfdRElJCcOHDyczM5O//e1vzJs3j8zMTIKCgkhOTmbNmjX07NmT8PBwKioqTr3+ydsvvPACVquVuXPn4nA4qKqqIiIi4qz9T2po/5OysrKYPn06mZmZpz3unnvuITExkcmTJ9O7d2/Wrl3LiBEjANd54/fff58bb7yRefPmUVBQwGuvvcaMGTOYNGkSP//5z0lISGDDhg1ER0eflanue+nvClc9R0zufWwNfo/B19xsdJz2Za+i+uMUKitMFA3bJNc1C7+mlNqotW7wL1Q5cm5AeHg4GzduZMGCBcTExDB16lTeffdddu3aRWxsLBkZGQB06NCBgIDTB7SsWLGC+fPnk5aWxtixY7FarRw+fBiAyy67jMjISIKDgxk4cCCHDh06Z46MjAwWLlzIo48+ytatW08rtM3ZX2td7yCtutvj4+NPFWYAk8nE1KlTAbjppptYs2bNOTOIhsWMuZfjzgvoXX4v+QeOGR2nXVWte5QQ5wG2qFekMAvRCK8YJnmuI9y2ZDabGTt2LGPHjmXw4MG89957pKenNzoCWWvN3//+d5KTk0/bvm7dulPd5Cef3263n/O5xowZw+rVq/nss8+YNm0av/vd77j55oaPuBrbv2/fvhw6dIjy8vLTCvemTZu46qqrAAgLO/e1uDICuwVMZoIvfYegr4eR++VdxMz6yC+WR3QWbyb44ItsLrqJ4TMmGB1HCI8nR84N2LVrF3v27Dl1e/PmzcTHx9O/f39yc3P54YcfACgvLz+rwI4fP55XX32Vk6cMzuxCro/FYsFms521/dChQ3Tp0oVbb72VWbNmsWnTpmbtf1JYWBjTp0/n3nvvxeFwnSpYtGgRVVVVXHrppfVmczqdfPzxxwB88MEHjBo16qx9IiIiKC8vb7SdAkK7D6Yg+n6Swj5m93/+YXSctud0UL3yVqpsndFpzxIRKR87QjTGK46cjVBRUcFdd91FSUkJAQEB9O3blwULFhAYGMiSJUu46667qK6uJiQk5NTlRCf94Q9/YPbs2aSmpqK1JiEhgU8//fScr3fbbbeRmppKeno6ixcvPrV91apVPPfcc1gsFsLDw1m0aFGz9q/r6aef5re//S39+vXDZDLRv39/li5d2uARcVhYGNu2bWPYsGFERkayZMmSevNPnDiR2NhYVq5cec62Cug2bi7HP/gH3fPvojT/EiK7djY6UpuxZr1KWO0GVla9w9gx3YyOI4RX8IoBYcK7yXtZv7L96wj/biT7aqfRd8ZC3zxdUHkI2yeDOFAyks4//xfRXeV4QAiQAWFCeKwOvS8kL3w2SUHvsf+//zE6TutzOqj4ciZOJxxPfFUKsxDnQYqzEAaKnfg4Jba+xBy8heIjuUbHaVXV6x8hvHIl3x5/hozx/YyOI4RXkeIshIFMgaGYxiwhJKAE64rrqK32jXWf7Yc/JWT/k2wuvIkhN/wSs9kHu+yFaENSnIUwWIfEdIoT3qRHyFoO/u0ePGEcSItUHMT5zc3kVgwmeMxrRHUxG51ICK8jxVkID9Bt1HSOBN5Jv4A32Pv5u0bHaT6Hlcp/X4vD4WB/zIf0HxppdCIhvJIUZyE8RI+rXyTffhHxxXeSl7Wh8Qd4oMpVdxFWu4lvKxcwcoqM0BeiuaQ4N0BrzahRo/j8889Pbfvoo4+YMMGY2Y3efvttZs+efdZ2h8PB6NGjAdi/fz8ffvhhe0cTrcQUEEiHSX+jxtmJkI0/p7ywyOhI56Vm+0LC8t/m+8J7+Mm06/xi5jMh2ooU5wYopXjrrbe49957sVqtVFZWMnfuXF5//fUWPW9j03We72PMZvOplaekOHu/kM6x1GR8RLglj5JPr8dhO/+fFyM48r/DnHkn+0tHEzf5KcLC5aNFiJaQ36BzSElJ4aqrruKZZ57hscce4+abb6ZPnz48++yzpKSkkJKSwquvvgrA3r17SUtLO/XY+fPn88QTTwAwatQo5s6dy5gxY3jttddOe42ioiImT55MamoqI0eOJDs7G4CHHnqI22+/ncsvv5yZM2cCrqk5x48fT3Jy8qnnttvtdOzYEXAtPbly5UrS0tJ45ZVX2vY/R7SZ6IEXkdf1RXoGfcWhD272+ALtKMrE8eVESq3dKB34PnGJwUZHEsLrecesABtnw4nNrfucndJg2MuN7vbII4+Qnp5OYGAgGzZsYP369SxevJj169fjcDgYPnw4F198MaGh516co6ysjNWrV5+1/Q9/+AMXXnghy5cvZ8WKFcyYMYOTs6VlZmayevVqgoODefvtt1m/fj3Z2dkEBgaSkZHBpEmTSElJOfVc8+fP57XXXuOTTz45z/8M4Wl6Xn4nh5cX0LtiHvs+MBP/i3cJsHjeqGfHie3Y/nMF1ppw9sZ+zoUX9zI6khA+QY6cGxEWFsbUqVOZNm0aQUFBfPPNN1x77bWEhoYSERHB1Vdf3aQlFK+//vp6t69Zs4Zp06YBcMUVV5Cbm0tlZSUAU6ZMITj4x6OQ8ePH06lTJ8LCwpr8usJ79Zr8GEfC5tLH8j4HF8/CbmvdNc1bylG6j5rPxmGzmdgT+28uvDK58QcJIZrEO46cm3CE25ZMJhMmk+vvmIauQQ0ICMDpdJ66bbVaT1vnuaFlGM98vrq3z3zMmXMv++RczOI0PSc/Ts4/7fSteIY9i80k3vhnAizG/03tKD9C9T/HYXJY2d1lBRkTUxp/kBCiyYz/LfcyY8aMYenSpVRXV1NRUcGyZcsYPXo03bp1Izc3lxMnTmC1Wvnss8+a/HwnV5X68ssviYuLa7CQr1ixgpKSEqqqqli2bBkXXXTRaffLso0+SCnirnqao+G/JSnwHfa9/0vsNmfjj2tDjsp8KpddRoCziN0xyxl2ZYNz9wshmsk7jpw9yPDhw7nhhhvIyMgA4Fe/+hWDBw8G4MEHHyQjI4PevXszcODAJj3fvHnzmDlzJqmpqYSHh7Nw4cIG9x01ahS/+MUv2LdvH9OmTSMtLe20kdxDhw7F4XAwZMgQZs2axd13392ClgqPoRQ9rnqW3OUOknmJ3YusxP7sDSI6h7d7lKpD3+FY/QuCyWdn9HLSrjx7bW8hRMvJkpGizcl72Uq0Ju9fDxBb+gxF1n6vaWg2AAAIHklEQVSUD1xE4ogL2+e1nQ6KVj5J52PzKKvpTm7PRQy8fGz7vLYQPkiWjBTCVyhF7E/nU5L2H4IDKui1dxTbP5hHrbVtL7WylRym+MOxROc/wt6Kq6m5LFMKsxBtTIqzEF6m48ArCL42i8KAqxjIIxS8P4b83Xtb/4W05sTmj3D8M5Vw+2Y2mxaQOPMjusZHtf5rCSFO0ybFWSk1QSm1Sym1Vyl1f1u8hhD+LCAsim5T/05+/P8RE5RN5PdD2bFoDrk7D7T8yZ0Oijd+RPHiC+m0fSrHa/qQm7KetOtvxRIof88L0R5a/TdNKWUGXgcmAgOBG5RSTRsddQZPOB8uWkbewzakFF0vugXn+ExOWMaRbH6ZrhuT2PPna9n139XYbef3f2+3VpHzxauUvt+PqF1TUbWFbOVFIq9bS2K6jBkQoj21xWjt4cBerfV+AKXUh8AUYPv5PElwcDDFxcVERUXJ9bxeSmtNcXHxaROpiNYX0qUPITcspab4AMVr/kgv50KCjv6D3HeHcTz0GsyR8QRH9SIiNp7I7t2xBAZgt1ZTmrOX6mO7sB3fg6rYTRf7P4kLKOaYLZ1j0e8TP3Yqg0Plgg4hjNAWv3k9gCN1bucA5z2kNC4ujpycHAoLC1stmGh/wcHBxMXFGR3DLwRFJdJ9ysvo2scp/H4h4YdepbuaC2W4vg6AwxlApaMTIQFFRKkfj6yr7J0pdo6guPe99Mi4hG5m6b4WwkhtUZzrO8w9q39NKXUbcBtAr15nz8drsVhITExs9XBC+DoVGEHMmLtB3wW2EqqLDlF57DDW4sPYyw6DtRBnUHfMnZIIjulHRM9kQjtFce7Z4YUQ7aktinMO0LPO7Tgg98ydtNYLgAXgus65DXII4d+UgsBOhHTvREj3tMb3F0J4jLbou/oBSFJKJSqlAoHrgeVt8DpCCCGET2r1I2ettV0p9WvgP4AZeEdrva21X0cIIYTwVR4xfadSqhzYZXSONhINFBkdoo1I27yXL7dP2uad/K1t8VrrmIYe4CnXSew61xyj3kwptUHa5n18uW3g2+2Ttnknadvp5HoJIYQQwsNIcRZCCCE8jKcU5wVGB2hD0jbv5MttA99un7TNO0nb6vCIAWFCCCGE+JGnHDkLIYQQws0jirNS6rdKKa2UinbfVkqpV9xLTmYppdKNzni+lFKPu7NvVkqtUEp1d2/3hbY9p5Ta6c6/VCnVsc59D7jbtkspNd7InM2hlLpOKbVNKeVUSl1wxn1e3TbwreVclVLvKKUKlFLZdbZ1Vkp9oZTa4/63k5EZm0sp1VMptVIptcP98/gb93avb59SKlgptV4ptcXdtsfc2xOVUuvcbVvinsTKKymlzEqpTKXUp+7b5902w4uzUqoncDlwuM7miUCS++s24E0DorXUc1rrVK11GvAp8LB7uy+07QsgRWudCuwGHgBwLw16PTAImAC84V5C1JtkA9cAq+tu9IW2teZyrh7iXVzvRV33A19prZOAr9y3vZEdmKO1HgCMAO50v1e+0L4a4FKt9RAgDZiglBoBPAO85G7bCWCWgRlb6jfAjjq3z7tthhdn4CXgPk5fHGMKsEi7fA90VErFGpKumbTWZXVuhvFj+3yhbSu01nb3ze9xzZ8OrrZ9qLWu0VofAPbiWkLUa2itd2it65sQx+vbRp3lXLXWtcDJ5Vy9ktZ6NXD8jM1TgPfc378HXN2uoVqJ1jpPa73J/X05rg/6HvhA+9yffRXumxb3lwYuBT52b/fKtgEopeKAnwJvu28rmtE2Q4uzUmoycFRrveWMu+pbdrJHuwVrJUqpJ5VSR4Ab+fHI2SfaVsctwOfu732tbXX5Qtt8oQ2N6aq1zgNXgQO6GJynxZRSCcBQYB0+0j53t+9moABXT9w+oKTOH/3e/LP5Mq4DTqf7dhTNaFubzxCmlPoS6FbPXXOBB4Er6ntYPds8blj5udqmtV6mtZ4LzFVKPQD8GngEH2mbe5+5uLrfFp98WD37e2Xb6ntYPds8rm2N8IU2+BWlVDjwd2C21rrMdRDm/bTWDiDNPV5lKTCgvt3aN1XLKaUmAQVa641KqbEnN9eza6Nta/PirLUeV992pdRgIBHY4v6BiwM2KaWG08RlJ43WUNvq8QHwGa7i7BNtU0pNByYBl+kfr8fzibY1wCva1ghfaENj8pVSsVrrPPfpogKjAzWXUsqCqzAv1lr/w73ZZ9oHoLUuUUqtwnVevaNSKsB9hOmtP5sXAZOVUlcCwUAHXEfS5902w7q1tdZbtdZdtNYJWusEXB8c6VrrY7iWmLzZPbJ5BFB6sivHWyilkurcnAzsdH/vC22bAPwemKy1rqpz13LgeqVUkFIqEdegt/VGZGwDvtA2f1jOdTkw3f39dKChnhCP5j5P+X/ADq31i3Xu8vr2KaViTl7hoZQKAcbhOqe+Evi5ezevbJvW+gGtdZy7pl0PfK21vpHmtE1r7RFfwEEg2v29wjWqdB+wFbjA6HzNaM/fcY38zQL+CfTwobbtxXXucrP766069811t20XMNHorM1o289w/aFYA+QD//GVtrnbcCWuEfb7cHXjG56pBW35K5AH2Nzv2Sxc5/e+Ava4/+1sdM5mtm0Urq7PrDq/Z1f6QvuAVCDT3bZs4GH39t64/uDdC/wNCDI6awvbORb4tLltkxnChBBCCA/jCZdSCSGEEKIOKc5CCCGEh5HiLIQQQngYKc5CCCGEh5HiLIQQQngYKc5CCCGEh5HiLIQQQngYKc5CCCGEh/l/ycZFA6JBq08AAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# Predict the eighty minute orbit\n",
"eighty_min_orbit = model.predict(np.arange(-40, 41))\n",
"\n",
"# Plot the eighty minute orbit\n",
"plot_orbit(eighty_min_orbit)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Your model fits perfectly to the scientists trajectory for time values between -10 to +10, the region where the meteor crosses the impact region, so we won't be hit! However, it starts to diverge when predicting for new values we haven't trained for. This shows neural networks learn according to the data they are fed with. Data quality and diversity are very important."
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.6"
}
},
"nbformat": 4,
"nbformat_minor": 4
}