{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 前言\n",
"EM算法是机器学习十大算法之一,它很简单,但是也同样很有深度,简单是因为它就分两步求解问题,\n",
"- E步:求期望(expectation)\n",
"- M步:求极大(maximization)\n",
"\n",
"深度在于它的数学推理涉及到比较繁杂的概率公式等,所以本文会介绍很多概率方面的知识,不懂的同学可以先去了解一些知识,当然本文也会尽可能的讲解清楚这些知识,讲的不好的地方麻烦大家评论指出,后续不断改进完善。\n",
"\n",
"### EM算法引入\n",
"概率模型有时候既含有观测变量,又含有隐变量或潜在变量,如果概率模型的变量都是观测变量,那么给定数据,可以直接用极大似然估计法,或贝叶斯估计方法估计模型参数,但是当模型含有隐变量时,就不能简单的使用这些方法,EM算法就是含有隐变量的概率模型参数的极大似然估计法,或极大后验概率估计法,我们讨论极大似然估计,极大后验概率估计与其类似。\n",
"参考统计学习方法书中的一个例子来引入EM算法, 假设有3枚硬币,分别记做A、B、C,这些硬币正面出现的概率分别是$\\pi$、$p$、$q$,进行如下实验:\n",
"\n",
"- 先掷硬币A,根据结果选出硬币B和硬币C,正面选硬币B,反面选硬币C\n",
"- 通过选择出的硬币,掷硬币的结果出现正面为1,反面为0\n",
"如此独立地重复n次实验,我们当前规定n=10,则10次的结果如下所示:\n",
"$$\n",
"1,1,0,1,0,0,1,0,1,1\n",
"$$\n",
"假设只通过观测到掷硬币的结果,不能观测掷硬币的过程,问如何估计三个硬币出现正面的概率?\n",
"我们来构建这样一个三硬币模型:\n",
"$$\n",
"\\begin{aligned}\n",
"P(y|\\theta) &=\\sum_{z}P(y,z|\\theta)=\\sum_{z}P(z|\\theta)P(y|z,\\theta) \\\\\n",
" &=\\pi p^{y}(1-p)^{1-y}+(1-\\pi)q^{y}(1-q)^{1-y}\n",
"\\end{aligned}\n",
"$$\n",
"\n",
"- 若$y=1$,表示这此看到的是正面,这个正面有可能是B的正面,也可能是C的正面,则$P(1|\\theta)=\\pi p+(1-\\pi)q$\n",
"- 若$y=0$,则$P(0|\\theta)=\\pi (1-p)+(1-\\pi)(1-q)$\n",
"\n",
"y是观测变量,表示一次观测结果是1或0,z是隐藏变量,表示掷硬币A的结果,这个是观测不到结果的,$\\theta=(\\pi,p,q)$表示模型参数,将观测数据表示为$Y=(Y_1,Y_2,...,Y_n)^{T}$,未观测的数据表示为$Z=(Z_1,Z_2,...,Z_n)^{T}$,则观测函数的似然函数是:\n",
"$$\n",
"\\begin{aligned}\n",
"P(Y|\\theta)&=\\sum_{Z}P(Z|\\theta)P(Y|Z,\\theta)\\\\\n",
"&=\\prod_{i=0} ( \\pi p^{y_i}(1-p)^{1-y_{i}}+(1-\\pi)q^{y_{i}}(1-q)^{1-y_{i}})\n",
"\\end{aligned}\n",
"$$\n",
"考虑求模型参数$\\theta=(\\pi,p,q)$的极大似然估计,即:\n",
"$$\n",
"\\hat{\\theta}=arg\\max_{\\theta}logP(Y|\\theta)\n",
"$$\n",
"这个问题没有解析解,只有通过迭代方法来求解,EM算法就是可以用于求解这个问题的一种迭代算法,下面给出EM算法的迭代过程:\n",
"- 首先选取初始值,记做$\\theta^{0}=(\\pi^{0},p^{0},q^{0})$,第i次的迭代参数的估计值为$\\theta^{i}=(\\pi^{i},p^{i},q^{i})$\n",
"- E步:计算在模型参数$\\pi^{i},p^{i},q^{i}$下观测变量$y_i$来源于硬币B的概率:\n",
"$$\n",
"\\mu^{i+1}=\\frac{\\pi^{i}(p^{i})^{y_i}(1-p^i)^{1-y_i}}{\\pi^{i}(p^{i})^{y_i}(1-p^i)^{1-y_i}+(1-\\pi^{i})(q^{i})^{y_i}(1-p^i)^{1-y_i}}\n",
"$$\n",
"备注一下:这个公式的分母是$P(Y|\\theta)$,分子表示是来源与B硬币的概率。\n",
"\n",
"- M步:计算模型参数的新估计值:\n",
"$$\n",
"\\pi^{i+1}=\\frac{1}{n}\\sum_{j=1}^{n}\\mu_{j}^{i+1} \n",
"$$\n",
"因为B硬币A硬币出现正面的结果,所以A硬币概率就是$\\mu_{j}$的平均值。\n",
"$$\n",
"p^{i+1}=\\frac{\\sum_{j=1}^{n}\\mu_{j}^{i+1}y_j}{\\sum_{j=1}^{n}\\mu_{j}^{i+1}}\n",
"$$\n",
"分子乘以$y_{i}$,所以其实是计算B硬币出现正面的概率。\n",
"$$\n",
"q^{i+1}=\\frac{\\sum_{j=1}^{n}(1-\\mu_{j}^{i+1})y_j}{\\sum_{j=1}^{n}(1-\\mu_{j}^{i+1})}\n",
"$$\n",
"$(1-\\mu_{j}^{i+1})$表示出现C硬币的概率。\n",
"\n",
"闭环形成,从$P(Y|\\theta)$ 到 $\\pi、p、q$一个闭环流程,接下来可以通过迭代法来做完成。针对上述例子,我们假设初始值为$\\pi^{0}=0.5,p^{0}=0.5,q^{0}=0.5$,因为对$y_i=1$和$y_i=0$均有$\\mu_j^{1}=0.5$,利用迭代公式计算得到$\\pi^{1}=0.5,p^{1}=0.6,q^{1}=0.6$,继续迭代得到最终的参数:\n",
"$$\\widehat{\\pi^{0}}=0.5,\\widehat{p^{0}}=0.6,\\widehat{q^{0}}=0.6$$\n",
"如果一开始初始值选择为:$\\pi^{0}=0.4,p^{0}=0.6,q^{0}=0.7$,那么得到的模型参数的极大似然估计是$\\widehat{\\pi}=0.4064,\\widehat{p}=0.5368,\\widehat{q}=0.6432$,这说明EM算法与初值的选择有关,选择不同的初值可能得到不同的参数估计值。\n",
"\n",
"这个例子中你只观察到了硬币抛完的结果,并不了解A硬币抛完之后,是选择了B硬币抛还是C硬币抛,这时候概率模型就存在着隐含变量!\n",
"### EM算法 \n",
"输入:观测变量数据Y,隐变量数据Z,联合分布$P(Y,Z|\\theta)$,条件分布$P(Z|Y,\\theta)$;\n",
"输出:模型参数$\\theta$\n",
"- (1)选择参数的初值$\\theta^0$,开始迭代\n",
"- (2) E步:记$\\theta^i$为第i次迭代参数$\\theta$的估计值,在第i+1次迭代的E步,计算\n",
"$$\n",
"\\begin{aligned}\n",
"Q(\\theta,\\theta^i)&=E_{Z}[logP(Y,Z|\\theta)|Y,\\theta^i]\\\\\n",
"&=\\sum_{Z}logP(Y,Z|\\theta)P(Z|Y,\\theta^i)\n",
"\\end{aligned}\n",
"$$\n",
"这里,$P(Z|Y,\\theta^i)$是在给定观测数据Y和当前的参数估计$\\theta^i$下隐变量数据Z的条件概率分布;\n",
"\n",
"- (3) M步:求使$Q(\\theta,\\theta^i)$极大化的$\\theta$,确定第i+1次迭代的参数的估计值$\\theta^{i+1}$,\n",
"$$\n",
"\\theta^{i+1}=arg \\max \\limits_{\\theta}Q(\\theta,\\theta^{i})\n",
"$$\n",
"$Q(\\theta,\\theta^{i})$是EM算法的核心,称为Q函数(Q function),这个是需要自己构造的。\n",
"- (4) 重复第(2)步和第(3)步,直到收敛,收敛条件:\n",
"$$\n",
"|| \\theta^{i+1}-\\theta^{i} || < \\varepsilon_1\n",
"$$\n",
"或者:\n",
"$$\n",
"||Q(\\theta^{i+1},\\theta^{i})-Q(\\theta^{i},\\theta^{i})|| <\\varepsilon_2\n",
"$$\n",
"收敛迭代就结束了。我们来拆解一下这个M步骤,\n",
"\n",
"### 推导逼近\n",
"主要讲解Jensen不等式,这个公式在推导和收敛都用到,主要是如下的结论:\n",
"- $f(x)$是凸函数\n",
"$$\n",
"f(E(X)) \\le E(f(x))\n",
"$$\n",
"- $f(x)$是凹函数\n",
"$$\n",
"f(E(X)) \\ge E(f(x))\n",
"$$\n",
"\n",
"推导出Em算法可以近似实现对观测数据的极大似然估计的办法是找到E步骤的下界,让下届最大,通过逼近的方式实现对观测数据的最大似然估计。统计学习基础中采用的是相减方式,我们来看下具体的步骤。\n",
"- 增加隐藏变量\n",
"$$\n",
"L(\\theta)=\\sum_{Z}logP(Y|Z,\\theta)P(Z,\\theta)\n",
"$$\n",
"则$L(\\theta)-L(\\theta^{i})$为:\n",
"$$\n",
"\\begin{aligned}\n",
"L(\\theta)-L(\\theta^{i})=log(\\sum_{Z} P(Y|Z,\\theta^i)\\frac{P(Y|Z,\\theta)P(Z,\\theta)}{P(Y|Z,\\theta^i)})-L(\\theta^{i})\\\\\n",
"\\ge \\sum_{Z} P(Y|Z,\\theta^i)log(\\frac{P(Y|Z,\\theta)P(Z,\\theta)}{P(Y|Z,\\theta^i)})-L(\\theta^{i})\n",
"\\end{aligned}\n",
"$$\n",
"$\\ge$这一个步骤就是采用了凹函数的Jensen不等式做转换。因为$Z$是隐藏变量,所以有$\\sum_{Z} P(Y|Z,\\theta^i)==1,P(Y|Z,\\theta^i)>0$,于是继续变:\n",
"\n",
"$$\n",
"\\begin{aligned}\n",
"L(\\theta)-L(\\theta^{i})&=log(\\sum_{Z} P(Y|Z,\\theta^i)\\frac{P(Y|Z,\\theta)P(Z,\\theta)}{P(Y|Z,\\theta^i)})-L(\\theta^{i})\\\\\n",
"&\\ge \\sum_{Z} P(Z|Y,\\theta^i)log(\\frac{P(Y|Z,\\theta)P(Z,\\theta)}{P(Z|Y,\\theta^i)})-L(\\theta^{i})\\\\\n",
"&=\\sum_{Z} P(Z|Y,\\theta^i)log(\\frac{P(Y|Z,\\theta)P(Z,\\theta)}{P(Z|Y,\\theta^i)})-\\sum_{Z} P(Z|Y,\\theta^i)L(\\theta^{i})\\\\\n",
"&= \\sum_{Z} P(Z|Y,\\theta^i)log(\\frac{P(Y|Z,\\theta)P(Z,\\theta)}{P(Z|Y,\\theta^i) (P(Y|\\theta^{i})}) \\\\\n",
"& \\ge0\n",
"\\end{aligned}\n",
"$$\n",
"也就是:$L(\\theta)\\ge L(\\theta^{i})+ \\sum_{Z} P(Z|Y,\\theta^i)log(\\frac{P(Y|Z,\\theta)P(Z,\\theta)}{P(Y|Z,\\theta^i) L(\\theta^{i})})$,有下界,最大化下界,来得到近似值。这里有一个细节:$P(Y|Z,\\theta^i)$ 变为$P(Z|Y,\\theta^i)$?如果要满足Jensen不等式的等号,则有:\n",
"$$\n",
"\\frac{P(Y|Z,\\theta)P(Z,\\theta)}{P(Y|Z,\\theta^i)} = c\n",
"$$\n",
"c为一个常数,而$\\sum_{Z}P(Y|Z,\\theta^i)=1$则:\n",
"$$\n",
"\\begin{aligned}\n",
"\\sum_{Z}P(Y|Z,\\theta)P(Z,\\theta)= c\\sum_{Z}P(Y|Z,\\theta^i)&=c\\\\\n",
"&=\\frac{P(Y|Z,\\theta)P(Z,\\theta)}{P(Y|Z,\\theta^i)}\\\\\n",
"P(Y|Z,\\theta)=\\frac{P(Y|Z,\\theta)P(Z,\\theta)}{\\sum_{Z}P(Y|Z,\\theta)P(Z,\\theta)}=\\frac{P(Y,Z,\\theta)}{P(Y,\\theta)}=P(Z|Y,\\theta)\n",
"\\end{aligned}\n",
"$$\n",
"\n",
"大家是不是很奇怪$P(Y|Z,\\theta)P(Z,\\theta)$加上$\\sum$之后等于什么,其实有的博客这里使用$P(Z,\\theta) = P(Y^i,Z^i,\\theta^i)$来替代$P(Y|Z,\\theta)$参与计算,这样$\\sum_{Z}P(Y^i,Z^i,\\theta^i)$,这样就方便理解来了。\n",
"\n",
"于是最大化如下:\n",
"\n",
"$$\n",
"\\begin{aligned}\n",
"\\theta^{i+1}&=arg \\max_{\\theta}\\sum_{Z} P(Z|Y,\\theta^i)log(\\frac{P(Y|Z,\\theta)P(Z,\\theta)}{P(Z|Y,\\theta^i)})\\\\\n",
"&=arg \\max_{\\theta}\\sum_{Z} P(Z|Y,\\theta^i)log(P(Y|Z,\\theta)P(Z,\\theta))\\\\\n",
"& =arg \\max_{\\theta}\\sum_{Z} P(Z|Y,\\theta^i)log(P(Y,Z|\\theta))\\\\ \n",
"&=arg \\max_{\\theta}Q(\\theta,\\theta^i)\n",
"\\end{aligned} \n",
"$$\n",
"其中$log$分母提出来是关于$Z$的$\\sum_{Z} P(Z|Y,\\theta^i)logP(Z|Y,\\theta^i)$,可以去掉。当然也有博客写的形式是:\n",
"$$\n",
"arg \\max_{\\theta}\\sum_{i=1}^{M}\\sum_{Z^{i}} P(Z^{i}|Y^{i},\\theta^i)log(P(Y^{i},Z^{i};\\theta))\\\\ \n",
"$$\n",
"形式其实一样,表示的不一样而已。\n",
"### 证明收敛\n",
"我们知道已知观测数据的似然函数是$P(Y,\\theta)$,对数似然函数为:\n",
"$$\n",
"\\begin{aligned}\n",
"L()=\\sum_{i=1}^{M}logP(y^{i},\\theta) &=\\sum_{i=1}^{M}log(\\frac{P(y^i,Z|\\theta)}{P(Z|y^i,\\theta)})\\\\\n",
"&=\\sum_{i=1}^{M}logP(y^i,Z|\\theta) - \\sum_{i=1}^{M}logP(Z|y^i,\\theta)\n",
"\\end{aligned} \n",
"$$\n",
"要证明收敛,就证明单调递增,$\\sum_{i=1}^{M}logP(y^{i},\\theta^{j+1})>\\sum_{i=1}^{M}logP(y^{i},\\theta^{j})$\n",
"由上文知道:\n",
"$$\n",
"\\begin{aligned}\n",
"Q(\\theta,\\theta^i)&=\\sum_{Z}logP(Y,Z|\\theta)P(Z|Y,\\theta^i)\\\\\n",
"&=\\sum_{i=1}^{M}\\sum_{Z^j}logP(y^i,Z^j|\\theta)P(Z^j|y^i,\\theta^i)\n",
"\\end{aligned}\n",
"$$\n",
"我们构造一个函数$H$,让他等于:\n",
"$$\n",
"H(\\theta,\\theta^{i})=\\sum_{i=1}^{M}\\sum_{Z^j}log(P(Z|y^i,\\theta)P(Z|y^i,\\theta^i))\n",
"$$\n",
"让$Q(\\theta,\\theta^i)-H(\\theta,\\theta^{i})$:\n",
"$$\n",
"\\begin{aligned}\n",
"Q(\\theta,\\theta^i)-H(\\theta,\\theta^{i})&=\\sum_{i=1}^{M}\\sum_{Z^j}logP(y^i,Z^j|\\theta)P(Z^j|y^i,\\theta^i) - \\sum_{i=1}^{M}\\sum_{Z^j}log(P(Z^j|y^i,\\theta)P(Z^j|y^i,\\theta^i)) \\\\\n",
"&=\\sum_{i=1}^{M}\\sum_{Z^j}log\\bigg(P(y^i,Z^j|\\theta)-P(Z^j|y^i,\\theta)\\bigg) \\\\\n",
"&=\\sum_{i=1}^{M}logP(y^{i},\\theta) \n",
"\\end{aligned}\n",
"$$所以:\n",
"$$\n",
"\\sum_{i=1}^{M}logP(y^{i},\\theta^{j+1})-\\sum_{i=1}^{M}logP(y^{i},\\theta^{j}) \\\\\n",
"= Q(\\theta^{i+1},\\theta^i)-H(\\theta^{i+1},\\theta^{i}) - (Q(\\theta^{i},\\theta^{i})-H(\\theta^{i},\\theta^{i}))\\\\\n",
"= Q(\\theta^{i+1},\\theta^i)- Q(\\theta^{i},\\theta^{i}) -( H(\\theta^{i+1},\\theta^{i}) - H(\\theta^{i},\\theta^{i}))\n",
"$$\n",
"该公式左边已经被证明是大于0,证明右边:$H(\\theta^{i+1},\\theta^{i}) - H(\\theta^{i},\\theta^{i})<0$:\n",
"$$\n",
"\\begin{aligned}\n",
"H(\\theta^{i+1},\\theta^{i}) - H(\\theta^{i},\\theta^{i}) &=\\sum_{Z^j}\\bigg(log(\\frac{P(Z^j|Y,\\theta^{i+1})}{P(Z^j|Y,\\theta^i)}) \\bigg)P(Z^j|Y,\\theta^i) \\\\\n",
"&=log\\bigg(\\sum_{Z^j}\\frac{P(Z^j|Y,\\theta^{i+1})}{P(Z^j|Y,\\theta^i)}P(Z^j|Y,\\theta^i) \\bigg)\\\\\n",
"&=logP(Z|Y,\\theta^{i+1})=log1=0\n",
"\\end{aligned}\n",
"$$\n",
"其中不等式是由于Jensen不等式,由此证明了$\\sum_{i=1}^{M}logP(y^{i},\\theta^{j+1})>\\sum_{i=1}^{M}logP(y^{i},\\theta^{j})$,证明了EM算法的收敛性。但不能保证是全局最优,只能保证局部最优。\n",
"### 高斯混合分布\n",
"EM算法的一个重要应用场景就是高斯混合模型的参数估计。高斯混合模型就是由多个高斯模型组合在一起的混合模型(可以理解为多个高斯分布函数的线性组合,理论上高斯混合模型是可以拟合任意类型的分布),例如对于下图中的数据集如果用一个高斯模型来描述的话显然是不合理的:\n",
"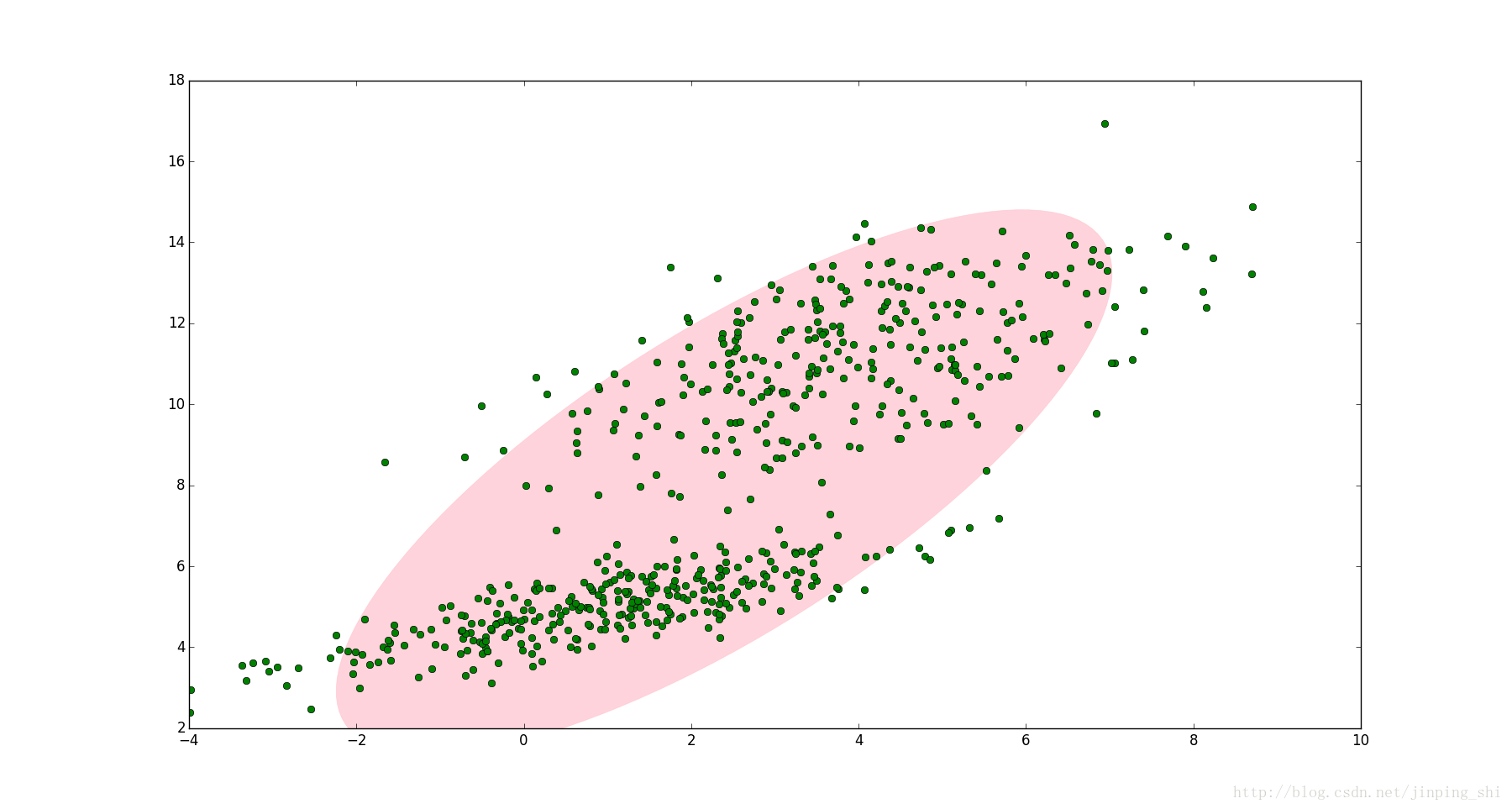\n",
"\n",
"两个高斯模型可以拟合数据集,如图所示:\n",
"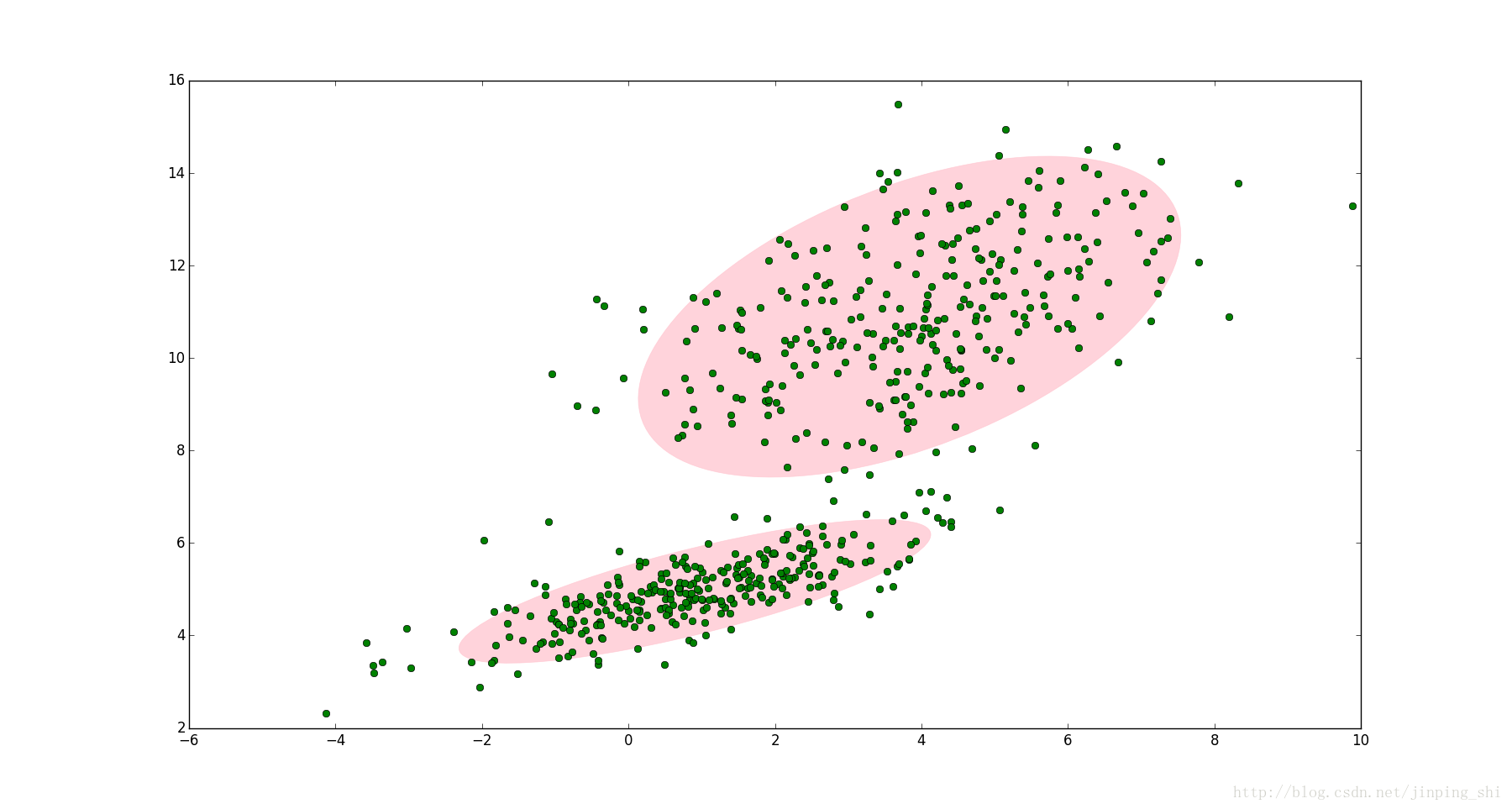\n",
"\n",
"如果有多个高斯模型,公式表示为:\n",
"$$\n",
"P(y|\\theta)=\\sum_{k=1}^{K}a_k\\phi(y|\\theta_{k}) \\\\\n",
"\\phi(y|\\theta_{k})=\\frac{1}{\\sqrt{2\\pi}\\delta_{k}}exp(-\\frac{(y-\\mu_{k})^2}{2 \\delta_{k}^{2}}) \\\\\n",
"a_k>0,\\sum a_k =1\n",
"$$\n",
"$\\phi(y|\\theta_{k})$表示为第k个高斯分布密度模型,定义如上,其中$a_k$表示被选中的概率。在本次模型$P(y|\\theta)$中,观测数据是已知的,而观测数据具体来自哪个模型是未知的,有点像之前提过的三硬币模型,我们来对比一下,A硬币就像是概率$a_k$,用来表明具体的模型,而B、C硬币就是具体的模型,只不过这里有很多个模型,不仅仅是B、C这两个模型。我们用$\\gamma_{jk}$来表示,则:\n",
"$$\n",
"\\gamma_{jk} =\n",
"\\begin{cases}\n",
"1& \\text{第j个观测数据来源于第k个模型}\\\\\n",
"0& \\text{否则}\n",
"\\end{cases}\n",
"$$\n",
"所以一个观测数据$y_j$的隐藏数据$(\\gamma_{j1},\\gamma_{j2},...,\\gamma_{jk})$,那么完全似然函数就是:\n",
"\n",
"$$\n",
"P(y,\\gamma|\\theta)= \\prod_{k=1}^{K}\\prod_{j=1}^{N}[a_{k}\\phi(y|\\theta_{k})]^{\\gamma_{jk}}\n",
"$$\n",
"\n",
"取对数之后等于:\n",
"\n",
"$$\n",
"\\begin{aligned}\n",
"log(P(y,\\gamma|\\theta))&=log( \\prod_{k=1}^{K}\\prod_{j=1}^{N}[a_{k}\\phi(y|\\theta_{k})]^{\\gamma_{jk}})\\\\\n",
"&=\\sum_{K}^{k=1}\\bigg(\\sum_{j=1}^{N}(\\gamma_{jk}) log(a_k)+\\sum_{j=1}^{N}( \\gamma_{jk})\\bigg[log(\\frac{1}{\\sqrt{2\\pi}})-log(\\delta_{k})-\\frac{(y_i-\\mu_{k})^2}{2 \\delta_{k}^{2}}\\bigg]\\bigg)\n",
"\\end{aligned}\n",
"$$\n",
"\n",
"- E 步 :\n",
"$$\n",
"\\begin{aligned}\n",
"Q(\\theta.\\theta^i) &= E[log(P(y,\\gamma|\\theta))]\\\\\n",
"&=\\sum_{K}^{k=1}\\bigg(\\sum_{j=1}^{N}(E\\gamma_{jk}) log(a_k)+\\sum_{j=1}^{N}(E\\gamma_{jk})\\bigg[log(\\frac{1}{\\sqrt{2\\pi}})-log(\\delta_{k})-\\frac{(y_i-\\mu_{k})^2}{2 \\delta_{k}^{2}}\\bigg]\\bigg)\n",
"\\end{aligned}\n",
"$$\n",
"其中我们定义$\\hat{\\gamma_{jk}}$:\n",
"$$\n",
"\\hat{\\gamma_{jk}} = E(\\gamma_{jk}|y,\\theta)=\\frac{a_k\\phi(y_i|\\theta_{k})}{\\sum_{k=1}^{K}a_k\\phi(y_i|\\theta_{k}) }\\\\\n",
"j=1,2,..,N;k=1,2,...,K\\\\\n",
"n_k=\\sum_{j=i}^{N}E\\gamma_{jk}\n",
"$$\n",
"于是化简得到:\n",
"$$\n",
"\\begin{aligned}\n",
"Q(\\theta.\\theta^i) &= \\sum_{K}^{k=1}\\bigg(n_k log(a_k)+\\sum_{j=1}^{N}(E\\gamma_{jk})\\bigg[log(\\frac{1}{\\sqrt{2\\pi}})-log(\\delta_{k})-\\frac{(y_i-\\mu_{k})^2}{2 \\delta_{k}^{2}}\\bigg]\\bigg)\n",
"\\end{aligned}\n",
"$$\n",
"\n",
"E 步 在代码设计上只有$\\hat{\\gamma_{jk}}$有用,用于M步的计算。\n",
"\n",
"\n",
"- M步,\n",
"$$\n",
"\\theta^{i+1}=arg \\max_{\\theta}Q(\\theta,\\theta^i)\n",
"$$\n",
"对$Q(\\theta,\\theta^i)$求导,得到每个未知量的偏导,使其偏导等于0,求解得到:\n",
"$$\n",
"\\hat{\\mu_k}=\\frac{\\sum_{j=1}^{N}\\hat{\\gamma_{jk}}y_i}{\\sum_{j=1}^{N}\\hat{\\gamma_{jk}}}\n",
"\\\\\n",
"\\\\\n",
"\\hat{\\delta_k}=\\frac{\\sum_{j=1}^{N}\\hat{\\gamma_{jk}}(y_i-\\mu_k)^2}{\\sum_{j=1}^{N}\\hat{\\gamma_{jk}}}\n",
"\\\\\n",
"\\\\\n",
"\\\\\n",
"\\hat{a_k}=\\frac{\\sum_{j=1}^{N}\\hat{\\gamma_{jk}} }{N}\n",
"$$\n",
"给一个初始值,来回迭代就可以求得值内容。这一块主要用到了$Q(\\theta.\\theta^i)$的导数,并且用到了E步的$\\hat{\\gamma_{jk}}$。\n",
"\n",
"### 总结\n",
"这里其实还有很多问题没讲,大家想了解的可以去学习统计学习方法这本书,讲解的还是挺全的。\n",
"\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 混合高斯分布模型\n",
"EM算法更多是一种思想,用概率来解决问题的一种方法,具体的代码看自己选用模型,所以并没有通用的模型,本此代码主要是讲解混合高斯分布模型的\n",
"\n",
"这其中的M步 完全按照了 公式来计算。"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"import numpy as np\n",
"import random\n",
"import math\n",
"import time"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [],
"source": [
"'''\n",
"数据集:伪造数据集(两个高斯分布混合)\n",
"数据集长度:1000\n",
"------------------------------\n",
"运行结果:\n",
"----------------------------\n",
"the Parameters set is:\n",
"alpha0:0.3, mu0:0.7, sigmod0:-2.0, alpha1:0.5, mu1:0.5, sigmod1:1.0\n",
"----------------------------\n",
"the Parameters predict is:\n",
"alpha0:0.4, mu0:0.6, sigmod0:-1.7, alpha1:0.7, mu1:0.7, sigmod1:0.9\n",
"----------------------------\n",
"'''\n",
"\n",
"def loadData(mu0, sigma0, mu1, sigma1, alpha0, alpha1):\n",
" '''\n",
" 初始化数据集\n",
" 这里通过服从高斯分布的随机函数来伪造数据集\n",
" :param mu0: 高斯0的均值\n",
" :param sigma0: 高斯0的方差\n",
" :param mu1: 高斯1的均值\n",
" :param sigma1: 高斯1的方差\n",
" :param alpha0: 高斯0的系数\n",
" :param alpha1: 高斯1的系数\n",
" :return: 混合了两个高斯分布的数据\n",
" '''\n",
" # 定义数据集长度为1000\n",
" length = 1000\n",
"\n",
" # 初始化第一个高斯分布,生成数据,数据长度为length * alpha系数,以此来\n",
" # 满足alpha的作用\n",
" data0 = np.random.normal(mu0, sigma0, int(length * alpha0))\n",
" # 第二个高斯分布的数据\n",
" data1 = np.random.normal(mu1, sigma1, int(length * alpha1))\n",
"\n",
" # 初始化总数据集\n",
" # 两个高斯分布的数据混合后会放在该数据集中返回\n",
" dataSet = []\n",
" # 将第一个数据集的内容添加进去\n",
" dataSet.extend(data0)\n",
" # 添加第二个数据集的数据\n",
" dataSet.extend(data1)\n",
" # 对总的数据集进行打乱(其实不打乱也没事,只不过打乱一下直观上让人感觉已经混合了\n",
" # 读者可以将下面这句话屏蔽以后看看效果是否有差别)\n",
" random.shuffle(dataSet)\n",
"\n",
" #返回伪造好的数据集\n",
" return dataSet\n"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [],
"source": [
"\n",
"# 高斯分布公式,没有什么特殊的\n",
"def calcGauss(dataSetArr, mu, sigmod):\n",
" '''\n",
" 根据高斯密度函数计算值\n",
" 依据:“9.3.1 高斯混合模型” 式9.25\n",
" 注:在公式中y是一个实数,但是在EM算法中(见算法9.2的E步),需要对每个j\n",
" 都求一次yjk,在本实例中有1000个可观测数据,因此需要计算1000次。考虑到\n",
" 在E步时进行1000次高斯计算,程序上比较不简洁,因此这里的y是向量,在numpy\n",
" 的exp中如果exp内部值为向量,则对向量中每个值进行exp,输出仍是向量的形式。\n",
" 所以使用向量的形式1次计算即可将所有计算结果得出,程序上较为简洁\n",
" \n",
" :param dataSetArr: 可观测数据集\n",
" :param mu: 均值\n",
" :param sigmod: 方差\n",
" :return: 整个可观测数据集的高斯分布密度(向量形式)\n",
" '''\n",
" # 计算过程就是依据式9.25写的,没有别的花样\n",
" result = (1 / (math.sqrt(2*math.pi)*sigmod**2)) * np.exp(-1 * (dataSetArr-mu) * (dataSetArr-mu) / (2*sigmod**2))\n",
" # 返回结果\n",
" return result\n",
"\n",
"\n",
"def E_step(dataSetArr, alpha0, mu0, sigmod0, alpha1, mu1, sigmod1):\n",
" '''\n",
" EM算法中的E步\n",
" 依据当前模型参数,计算分模型k对观数据y的响应度\n",
" :param dataSetArr: 可观测数据y\n",
" :param alpha0: 高斯模型0的系数\n",
" :param mu0: 高斯模型0的均值\n",
" :param sigmod0: 高斯模型0的方差\n",
" :param alpha1: 高斯模型1的系数\n",
" :param mu1: 高斯模型1的均值\n",
" :param sigmod1: 高斯模型1的方差\n",
" :return: 两个模型各自的响应度\n",
" '''\n",
" # 计算y0的响应度\n",
" # 先计算模型0的响应度的分子\n",
" gamma0 = alpha0 * calcGauss(dataSetArr, mu0, sigmod0)\n",
" #print(\"gamma0=\",gamma0.shape) # 1000, 维向量\n",
" # 模型1响应度的分子\n",
" gamma1 = alpha1 * calcGauss(dataSetArr, mu1, sigmod1)\n",
"\n",
" # 两者相加为E步中的分布\n",
" sum = gamma0 + gamma1\n",
" # 各自相除,得到两个模型的响应度\n",
" gamma0 = gamma0 / sum\n",
" gamma1 = gamma1 / sum\n",
"\n",
" # 返回两个模型响应度\n",
" return gamma0, gamma1\n",
"\n",
"def M_step(muo, mu1, gamma0, gamma1, dataSetArr):\n",
" # 依据算法9.2计算各个值\n",
" # 这里没什么花样,对照书本公式看看这里就好了\n",
" \n",
" # np.dot 点积:[1,2] [2,3] = [2,6]\n",
" mu0_new = np.dot(gamma0, dataSetArr) / np.sum(gamma0)\n",
" mu1_new = np.dot(gamma1, dataSetArr) / np.sum(gamma1)\n",
"\n",
" # math.sqrt 平方根 \n",
" sigmod0_new = math.sqrt(np.dot(gamma0, (dataSetArr - muo)**2) / np.sum(gamma0))\n",
" sigmod1_new = math.sqrt(np.dot(gamma1, (dataSetArr - mu1)**2) / np.sum(gamma1))\n",
"\n",
" alpha0_new = np.sum(gamma0) / len(gamma0)\n",
" alpha1_new = np.sum(gamma1) / len(gamma1)\n",
"\n",
" # 将更新的值返回\n",
" return mu0_new, mu1_new, sigmod0_new, sigmod1_new, alpha0_new, alpha1_new\n",
"\n",
"\n",
"## 训练主函数\n",
"def EM_Train(dataSetList, iter=500):\n",
" '''\n",
" 根据EM算法进行参数估计\n",
" 算法依据“9.3.2 高斯混合模型参数估计的EM算法” 算法9.2\n",
" :param dataSetList:数据集(可观测数据)\n",
" :param iter: 迭代次数\n",
" :return: 估计的参数\n",
" '''\n",
" # 将可观测数据y转换为数组形式,主要是为了方便后续运算\n",
" dataSetArr = np.array(dataSetList)\n",
"\n",
" # 步骤1:对参数取初值,开始迭代\n",
" alpha0 = 0.5\n",
" mu0 = 0\n",
" sigmod0 = 1\n",
" alpha1 = 0.5\n",
" mu1 = 1\n",
" sigmod1 = 1\n",
"\n",
" # 开始迭代\n",
" step = 0\n",
" while (step < iter):\n",
" # 每次进入一次迭代后迭代次数加1\n",
" step += 1\n",
" # 步骤2:E步:依据当前模型参数,计算分模型k对观测数据y的响应度\n",
" gamma0, gamma1 = E_step(dataSetArr, alpha0, mu0, sigmod0, alpha1, mu1, sigmod1)\n",
" # 步骤3:M步\n",
" mu0, mu1, sigmod0, sigmod1, alpha0, alpha1 = M_step(mu0, mu1, gamma0, gamma1, dataSetArr)\n",
"\n",
" # 迭代结束后将更新后的各参数返回\n",
" return alpha0, mu0, sigmod0, alpha1, mu1, sigmod1\n"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"---------------------------\n",
"the Parameters set is:\n",
"alpha0:0.3, mu0:0.7, sigmod0:-2.0, alpha1:0.5, mu1:0.5, sigmod1:1.0\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"gamma0= (1000,)\n",
"----------------------------\n",
"the Parameters predict is:\n",
"alpha0:0.4, mu0:0.6, sigmod0:-1.9, alpha1:0.7, mu1:0.6, sigmod1:0.8\n",
"----------------------------\n",
"time span: 0.19019794464111328\n"
]
}
],
"source": [
"\n",
"\n",
"if __name__ == '__main__':\n",
" start = time.time()\n",
"\n",
" # 设置两个高斯模型进行混合,这里是初始化两个模型各自的参数\n",
" # 见“9.3 EM算法在高斯混合模型学习中的应用”\n",
" # alpha是“9.3.1 高斯混合模型” 定义9.2中的系数α\n",
" # mu0是均值μ\n",
" # sigmod是方差σ\n",
" # 在设置上两个alpha的和必须为1,其他没有什么具体要求,符合高斯定义就可以\n",
" \n",
" alpha0 = 0.3 # 系数α\n",
" mu0 = -2 # 均值μ\n",
" sigmod0 = 0.5 # 方差σ\n",
"\n",
" alpha1 = 0.7 # 系数α\n",
" mu1 = 0.5 # 均值μ\n",
" sigmod1 = 1 # 方差σ\n",
"\n",
" # 初始化数据集\n",
" dataSetList = loadData(mu0, sigmod0, mu1, sigmod1, alpha0, alpha1)\n",
"\n",
" #打印设置的参数\n",
" print('---------------------------')\n",
" print('the Parameters set is:')\n",
" print('alpha0:%.1f, mu0:%.1f, sigmod0:%.1f, alpha1:%.1f, mu1:%.1f, sigmod1:%.1f' % (\n",
" alpha0, alpha1, mu0, mu1, sigmod0, sigmod1\n",
" ))\n",
"\n",
" # 开始EM算法,进行参数估计\n",
" alpha0, mu0, sigmod0, alpha1, mu1, sigmod1 = EM_Train(dataSetList)\n",
"\n",
" # 打印参数预测结果\n",
" print('----------------------------')\n",
" print('the Parameters predict is:')\n",
" print('alpha0:%.1f, mu0:%.1f, sigmod0:%.1f, alpha1:%.1f, mu1:%.1f, sigmod1:%.1f' % (\n",
" alpha0, alpha1, mu0, mu1, sigmod0, sigmod1\n",
" ))\n",
"\n",
" # 打印时间\n",
" print('----------------------------')\n",
" print('time span:', time.time() - start)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### E步主要计算内容\n",
"其中我们定义$\\hat{\\gamma_{jk}}$:\n",
"$$\n",
"\\hat{\\gamma_{jk}} = E(\\gamma_{jk}|y,\\theta)=\\frac{a_k\\phi(y_i|\\theta_{k})}{\\sum_{k=1}^{K}a_k\\phi(y_i|\\theta_{k}) }\\\\\n",
"j=1,2,..,N;k=1,2,...,K\\\\\n",
"n_k=\\sum_{j=i}^{N}E\\gamma_{jk}\n",
"$$\n",
"\n",
"### M步 主要计算内容\n",
"这一步骤主要是对Q函数求导后的数据进行计算,利用了 E 步 的$\\hat{\\gamma_{jk}}$"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [],
"source": [
"import math\n",
"import copy\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"from mpl_toolkits.mplot3d import Axes3D\n",
" \n",
"#生成随机数据,4个高斯模型\n",
"def generate_data(sigma,N,mu1,mu2,mu3,mu4,alpha):\n",
" global X #可观测数据集\n",
" X = np.zeros((N, 2)) # 初始化X,2行N列。2维数据,N个样本\n",
" X=np.matrix(X)\n",
" global mu #随机初始化mu1,mu2,mu3,mu4\n",
" mu = np.random.random((4,2))\n",
" mu=np.matrix(mu)\n",
" global excep #期望第i个样本属于第j个模型的概率的期望\n",
" excep=np.zeros((N,4))\n",
" global alpha_ #初始化混合项系数\n",
" alpha_=[0.25,0.25,0.25,0.25]\n",
" for i in range(N):\n",
" if np.random.random(1) < 0.1: # 生成0-1之间随机数\n",
" X[i,:] = np.random.multivariate_normal(mu1, sigma, 1) #用第一个高斯模型生成2维数据\n",
" elif 0.1 <= np.random.random(1) < 0.3:\n",
" X[i,:] = np.random.multivariate_normal(mu2, sigma, 1) #用第二个高斯模型生成2维数据\n",
" elif 0.3 <= np.random.random(1) < 0.6:\n",
" X[i,:] = np.random.multivariate_normal(mu3, sigma, 1) #用第三个高斯模型生成2维数据\n",
" else:\n",
" X[i,:] = np.random.multivariate_normal(mu4, sigma, 1) #用第四个高斯模型生成2维数据\n",
" \n",
" print(\"可观测数据:\\n\",X) #输出可观测样本\n",
" print(\"初始化的mu1,mu2,mu3,mu4:\",mu) #输出初始化的mu\n",
"\n",
"\n",
"# E 期望\n",
"# \\hat{\\gamma_{jk}}\n",
"def e_step(sigma,k,N):\n",
" global X\n",
" global mu\n",
" global excep\n",
" global alpha_\n",
" for i in range(N):\n",
" denom=0\n",
" for j in range(0,k):\n",
" # sigma.I 表示矩阵的逆矩阵\n",
" # np.transpose :矩阵转置 np.linalg.det():矩阵求行列式\n",
" denom += alpha_[j]* math.exp(-(X[i,:]-mu[j,:])*sigma.I*np.transpose(X[i,:]-mu[j,:])) /np.sqrt(np.linalg.det(sigma)) #分母\n",
" for j in range(0,k):\n",
" numer = math.exp(-(X[i,:]-mu[j,:])*sigma.I*np.transpose(X[i,:]-mu[j,:]))/np.sqrt(np.linalg.det(sigma)) #分子\n",
" excep[i,j]=alpha_[j]*numer/denom #求期望\n",
" print(\"隐藏变量:\\n\",excep)\n",
"\n",
" \n",
"def m_step(k,N):\n",
" global excep\n",
" global X\n",
" global alpha_\n",
" for j in range(0,k):\n",
" denom=0 #分母\n",
" numer=0 #分子\n",
" for i in range(N):\n",
" numer += excep[i,j]*X[i,:]\n",
" denom += excep[i,j]\n",
" mu[j,:] = numer/denom #求均值\n",
" alpha_[j]=denom/N #求混合项系数\n",
"\n",
" # #可视化结果\n",
"def plotShow():\n",
" # 画生成的原始数据\n",
" plt.subplot(221)\n",
" plt.scatter(X[:,0].tolist(), X[:,1].tolist(),c='b',s=25,alpha=0.4,marker='o') #T散点颜色,s散点大小,alpha透明度,marker散点形状\n",
" plt.title('random generated data')\n",
" #画分类好的数据\n",
" plt.subplot(222)\n",
" plt.title('classified data through EM')\n",
" order=np.zeros(N)\n",
" color=['b','r','k','y']\n",
" for i in range(N):\n",
" for j in range(k):\n",
" if excep[i,j]==max(excep[i,:]):\n",
" order[i]=j #选出X[i,:]属于第几个高斯模型\n",
" probility[i] += alpha_[int(order[i])]*math.exp(-(X[i,:]-mu[j,:])*sigma.I*np.transpose(X[i,:]-mu[j,:]))/(np.sqrt(np.linalg.det(sigma))*2*np.pi) #计算混合高斯分布\n",
" plt.scatter(X[i, 0], X[i, 1], c=color[int(order[i])], s=25, alpha=0.4, marker='o') #绘制分类后的散点图\n",
" #绘制三维图像\n",
" ax = plt.subplot(223, projection='3d')\n",
" plt.title('3d view')\n",
" for i in range(N):\n",
" ax.scatter(X[i, 0], X[i, 1], probility[i], c=color[int(order[i])])\n",
" plt.show()\n",
" \n",
" \n",
" \n",
" \n",
" \n",
" "
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"可观测数据:\n",
" [[34.10078398 41.99939702]\n",
" [17.97196632 19.52471006]\n",
" [32.34127531 41.41768696]\n",
" [43.55623437 15.6460001 ]\n",
" [26.75126564 35.50622855]\n",
" [13.2335205 32.86586681]\n",
" [12.70538568 11.48725734]\n",
" [45.06316267 8.41118073]\n",
" [47.57630029 18.86976153]\n",
" [46.24701093 8.09261051]\n",
" [31.6856349 38.3816145 ]\n",
" [41.64126306 3.1628792 ]\n",
" [46.14857455 7.21170413]\n",
" [21.93536542 27.07271141]\n",
" [14.02413964 29.70759751]\n",
" [28.00761242 41.35510063]\n",
" [-1.48775397 40.97093856]\n",
" [48.65773485 16.15378227]\n",
" [22.48474941 27.32601426]\n",
" [50.67364683 13.88159845]\n",
" [37.79824479 11.1916526 ]\n",
" [37.72662908 36.09471673]\n",
" [27.49916272 40.96482288]\n",
" [28.19440799 16.28953534]\n",
" [39.80916916 8.45412261]\n",
" [48.62197899 26.63845404]\n",
" [41.0543496 7.4001902 ]\n",
" [28.9050116 44.98388131]\n",
" [24.17507743 16.95299992]\n",
" [16.94171114 34.58447536]\n",
" [34.608337 16.77946838]\n",
" [41.51172038 16.48020012]\n",
" [42.77898465 12.35588339]\n",
" [45.12250132 17.42877677]\n",
" [42.67598701 6.58295637]\n",
" [19.34219222 23.05409255]\n",
" [30.31108537 25.63345344]\n",
" [30.4130082 40.52392205]\n",
" [41.46644655 16.94538105]\n",
" [43.8056078 10.78415563]\n",
" [ 6.84141737 15.4165794 ]\n",
" [49.18263591 10.5222882 ]\n",
" [44.26373762 21.7874918 ]\n",
" [34.97029744 10.60403938]\n",
" [41.59429269 24.13482791]\n",
" [ 4.63391475 31.2073789 ]\n",
" [33.40104196 42.23381551]\n",
" [22.64400842 18.27278289]\n",
" [41.13874878 19.34870817]\n",
" [48.9296952 17.82749922]\n",
" [ 1.35837365 37.43428297]\n",
" [22.85980648 35.7114185 ]\n",
" [43.23194757 1.80047766]\n",
" [43.97224829 16.33780178]\n",
" [19.81974073 9.21257053]\n",
" [52.87644002 17.03347397]\n",
" [38.11937795 17.52775566]\n",
" [48.70514656 22.21187488]\n",
" [28.42904897 40.05690694]\n",
" [37.78525025 16.60381937]\n",
" [54.44856232 16.97833772]\n",
" [20.00792055 12.55996805]\n",
" [29.24710253 20.00953972]\n",
" [ 4.36216746 29.47967659]\n",
" [ 5.64290401 36.84855284]\n",
" [49.44880872 17.70366146]\n",
" [38.97919295 14.17682754]\n",
" [44.35047857 16.96203349]\n",
" [20.16578155 28.27155509]\n",
" [17.84314586 26.07604556]\n",
" [48.5369958 14.78976177]\n",
" [37.56664902 9.64744929]\n",
" [41.90612082 27.98063948]\n",
" [19.39379041 23.38263542]\n",
" [40.78311853 22.7069765 ]\n",
" [31.31100649 4.74654749]\n",
" [27.81850002 23.88740218]\n",
" [24.40281112 19.21007619]\n",
" [52.79444648 11.10367651]\n",
" [48.69136118 18.48706472]\n",
" [27.36179794 38.96839341]\n",
" [14.3955137 23.73250706]\n",
" [12.83638793 22.67206662]\n",
" [41.21627903 15.91466713]\n",
" [21.99014159 17.60699749]\n",
" [22.43105158 18.31396831]\n",
" [39.65773965 9.57539553]\n",
" [44.87559084 19.75504824]\n",
" [24.05663756 24.77172765]\n",
" [ 3.87301084 29.96607249]\n",
" [25.53648145 5.98228589]\n",
" [38.85213406 23.97987467]\n",
" [47.4766735 16.58538884]\n",
" [37.75225065 13.17503997]\n",
" [14.76537384 23.60775947]\n",
" [46.88185733 18.04404044]\n",
" [ 1.34308284 38.55982558]\n",
" [51.5799769 7.27271334]\n",
" [48.76146614 12.94900173]\n",
" [50.67032735 14.53052206]\n",
" [43.33943081 20.38314748]\n",
" [50.29498112 20.16756997]\n",
" [18.97445258 20.88689473]\n",
" [45.72879937 15.14860253]\n",
" [44.00399859 15.5586213 ]\n",
" [-4.55563736 27.92724986]\n",
" [38.93040102 15.69105206]\n",
" [49.34375964 12.73842381]\n",
" [44.71506179 16.2445931 ]\n",
" [41.99812117 16.20963758]\n",
" [45.80468869 6.82945586]\n",
" [21.62171107 13.85136938]\n",
" [37.90647348 16.27884234]\n",
" [18.30524585 24.91855222]\n",
" [46.37665861 7.71412768]\n",
" [48.60522007 21.0196075 ]\n",
" [19.74846478 27.93769448]\n",
" [29.4137209 37.82860776]\n",
" [14.74758561 24.42050311]\n",
" [11.17655821 17.80424563]\n",
" [38.65076781 3.01710606]\n",
" [43.72088098 18.15703023]\n",
" [19.7418687 19.31755897]\n",
" [53.27530711 17.87916791]\n",
" [25.43497442 28.87639188]\n",
" [48.88182112 16.57530126]\n",
" [ 9.11179244 34.60472006]\n",
" [26.9252331 17.07561473]\n",
" [36.18748449 17.53461272]\n",
" [44.43474823 14.12185961]\n",
" [19.06719824 19.67077106]\n",
" [45.44463698 18.19513106]\n",
" [44.24167965 14.24678861]\n",
" [37.04531475 15.51170619]\n",
" [46.56082908 16.95933005]\n",
" [47.62363791 14.43358361]\n",
" [ 6.77763595 28.0281931 ]\n",
" [14.31363065 33.04536861]\n",
" [30.91101949 44.57098876]\n",
" [21.51916492 26.69631943]\n",
" [20.82663718 26.60433864]\n",
" [40.26843255 10.57322165]\n",
" [50.5349425 9.64935112]\n",
" [50.3974125 30.13343422]\n",
" [18.90279678 18.37681572]\n",
" [20.31276064 26.8056216 ]\n",
" [43.58181405 15.3611326 ]\n",
" [49.37506208 8.14037624]\n",
" [ 2.79605425 30.40621777]\n",
" [40.00938791 8.38742237]\n",
" [47.06648275 19.08476278]\n",
" [ 3.39154166 36.30283386]\n",
" [26.56273594 20.95872678]\n",
" [37.85733711 44.63804562]\n",
" [50.46537897 30.58691539]\n",
" [25.88870663 45.27153535]\n",
" [38.35374961 11.15656457]\n",
" [42.79144313 16.74488319]\n",
" [11.35150002 35.95308486]\n",
" [ 8.01775495 20.17951082]\n",
" [40.05358933 14.59760428]\n",
" [42.28819614 29.31538571]\n",
" [ 5.71898699 48.49639906]\n",
" [55.43513184 0.98679793]\n",
" [24.36822266 32.23987359]\n",
" [30.83996661 34.40822302]\n",
" [26.75868065 21.9874932 ]\n",
" [49.76002442 15.45076927]\n",
" [44.74063527 27.85118268]\n",
" [ 8.38057535 36.68918615]\n",
" [12.82896812 18.08989977]\n",
" [39.98610321 24.20054852]\n",
" [42.86457138 5.27643928]\n",
" [46.09962776 17.91291264]\n",
" [47.19816647 6.52083557]\n",
" [17.33488067 29.76100635]\n",
" [38.45174576 12.54518776]\n",
" [48.70756491 12.71376596]\n",
" [46.36148576 18.05755857]\n",
" [37.47166178 18.92720756]\n",
" [48.87596147 22.12670257]\n",
" [49.57591528 15.8568224 ]\n",
" [41.6613632 43.66814863]\n",
" [16.84380237 19.89880443]\n",
" [13.69768659 21.43724681]\n",
" [48.8103184 19.02706345]\n",
" [25.19055568 19.21318208]\n",
" [52.45524162 21.14514719]\n",
" [48.92908397 12.14609127]\n",
" [41.45363577 20.60158731]\n",
" [46.54136475 12.15508256]\n",
" [16.32041319 26.76891283]\n",
" [19.17556278 39.88809292]\n",
" [27.7398478 35.26056078]\n",
" [39.53534295 24.1502645 ]\n",
" [23.6101855 24.64636073]\n",
" [41.07545864 14.45243467]\n",
" [45.5412231 12.03696757]\n",
" [15.74960785 9.18036224]\n",
" [42.66313033 18.15568087]\n",
" [51.82521638 10.03603077]\n",
" [-0.35168172 32.66732811]\n",
" [47.56228723 16.19234061]\n",
" [25.01004746 36.024799 ]\n",
" [39.01422316 11.64893375]\n",
" [49.57822452 6.50447041]\n",
" [50.22347651 8.6984849 ]\n",
" [49.40633658 10.5228405 ]\n",
" [52.98362025 14.95409286]\n",
" [29.55097051 45.21370681]\n",
" [38.70075406 25.64772518]\n",
" [27.04561708 37.20857784]\n",
" [12.33882511 23.57754988]\n",
" [26.66212044 48.28846805]\n",
" [52.90164768 7.1837463 ]\n",
" [46.74388686 3.66289806]\n",
" [25.06656585 16.56052017]\n",
" [25.43402908 46.22534413]\n",
" [45.96332029 11.3173738 ]\n",
" [29.85637153 51.65605238]\n",
" [27.07764357 37.39973973]\n",
" [46.47346365 12.4928957 ]\n",
" [13.96086543 18.11571644]\n",
" [ 2.00023769 34.75667918]\n",
" [29.46834876 29.7450956 ]\n",
" [50.40919421 12.3811701 ]\n",
" [16.3574766 29.32949119]\n",
" [42.57880543 17.92591292]\n",
" [29.29295357 21.90832228]\n",
" [ 9.12679085 34.57291242]\n",
" [47.98138458 19.63154583]\n",
" [14.15676853 33.0779678 ]\n",
" [44.31645946 9.1684328 ]\n",
" [13.05676502 21.49522895]\n",
" [14.93788973 29.12945902]\n",
" [15.70135648 12.07938282]\n",
" [ 3.91738347 39.61418558]\n",
" [46.15150294 9.26044012]\n",
" [18.62293325 25.83742768]\n",
" [22.28719741 19.12155356]\n",
" [35.46021241 15.66913954]\n",
" [22.91646716 16.309418 ]\n",
" [40.9333429 26.38609539]\n",
" [20.61107052 18.47615901]\n",
" [41.99606722 7.94909265]\n",
" [24.55782096 31.00108147]\n",
" [40.59990055 15.8564243 ]\n",
" [39.44811928 19.05314726]\n",
" [30.52537538 35.1964212 ]\n",
" [43.84205217 14.66079242]\n",
" [52.76015224 22.27392048]\n",
" [ 0.53635851 33.2155064 ]\n",
" [44.88162761 18.73865156]\n",
" [44.44014864 21.48709943]\n",
" [47.82606872 10.38403453]\n",
" [36.26157604 37.82367763]\n",
" [43.62612613 14.47178666]\n",
" [31.02987893 37.47201458]\n",
" [ 8.6870975 28.72764772]\n",
" [47.03787343 10.6021404 ]\n",
" [-2.2273671 31.534357 ]\n",
" [-5.5527884 35.78317105]\n",
" [33.97410704 18.27894531]\n",
" [35.08805903 36.54684565]\n",
" [47.11719623 12.60702487]\n",
" [18.59791274 14.80784179]\n",
" [16.88512604 36.87556821]\n",
" [-2.46728743 31.69879922]\n",
" [10.2195111 28.01834712]\n",
" [17.14716289 26.71018422]\n",
" [15.87912908 15.55351361]\n",
" [28.07369566 32.33877451]\n",
" [37.92413287 15.7082284 ]\n",
" [47.21946769 11.55866576]\n",
" [22.04470036 29.11036652]\n",
" [47.56019889 7.58746674]\n",
" [46.80805009 15.61906449]\n",
" [20.87034473 16.54594974]\n",
" [10.83385054 23.77147518]\n",
" [47.22374574 15.79694751]\n",
" [ 7.10622286 38.56567066]\n",
" [39.1541188 23.47717576]\n",
" [18.90596043 14.20053477]\n",
" [47.18290947 14.80314809]\n",
" [16.27962629 21.10193262]\n",
" [19.48056864 29.96877045]\n",
" [41.07311764 14.65460825]\n",
" [51.49046834 12.43188518]\n",
" [36.13700081 7.18562116]\n",
" [26.31326858 39.45031334]\n",
" [46.29175628 9.84302885]\n",
" [ 8.18468255 32.50658552]\n",
" [47.6801346 15.10827806]\n",
" [38.3127991 22.32224051]\n",
" [19.87856263 16.29540339]\n",
" [35.93030051 46.78499113]\n",
" [50.54193438 16.49593679]\n",
" [26.98983193 39.50752382]\n",
" [41.10864415 8.75050624]\n",
" [-0.59134994 36.04513784]\n",
" [32.76561906 39.77393837]\n",
" [17.47044798 16.49877386]\n",
" [22.50429257 41.66412521]\n",
" [37.70944163 49.69855197]\n",
" [43.86133668 12.2038014 ]\n",
" [22.17456317 14.30107001]\n",
" [16.30903718 17.13935 ]\n",
" [24.6073783 16.97211229]\n",
" [40.30644112 4.22253284]\n",
" [-2.84953878 43.48700219]\n",
" [32.91453906 44.90119634]\n",
" [46.44308873 18.02404918]\n",
" [37.3836467 14.75452789]\n",
" [47.33363318 20.36012798]\n",
" [41.74642063 27.03559179]\n",
" [29.31598311 41.93510181]\n",
" [48.22347798 21.62569022]\n",
" [ 3.17735918 29.25572957]\n",
" [31.6461558 20.78888781]\n",
" [33.50294755 14.46878239]\n",
" [18.9812725 22.14299312]\n",
" [43.8738558 12.67516662]\n",
" [57.97405644 23.14127176]\n",
" [33.65001616 44.37996747]\n",
" [40.08608404 34.53885576]\n",
" [48.11079596 7.78926236]\n",
" [33.82549885 42.27612509]\n",
" [20.86273026 30.79132298]\n",
" [18.70056825 20.62206572]\n",
" [33.15880447 44.88629903]\n",
" [37.4362346 37.41992638]\n",
" [ 3.81016154 39.48962836]\n",
" [47.79564803 21.70275157]\n",
" [39.0008174 21.08286979]\n",
" [39.67007978 15.6638161 ]\n",
" [50.3540132 6.97142327]\n",
" [51.22993184 20.86038852]\n",
" [25.34780084 36.04993353]\n",
" [25.8099056 16.31838414]\n",
" [17.87456001 17.24086795]\n",
" [42.18432075 19.49102872]\n",
" [ 0.77389513 35.73945298]\n",
" [28.84158093 25.9747731 ]\n",
" [44.56458945 16.8096007 ]\n",
" [16.48325211 12.82712674]\n",
" [55.54813167 10.13983485]\n",
" [44.84227321 20.04591581]\n",
" [39.9303047 14.88429312]\n",
" [46.73229805 18.87442115]\n",
" [44.06042308 17.75104303]\n",
" [48.43173896 15.30141463]\n",
" [ 9.28491339 40.59064676]\n",
" [23.91953267 21.67275322]\n",
" [59.15488587 15.28271498]\n",
" [28.2029577 28.71580638]\n",
" [39.84986713 34.12515617]\n",
" [31.4900022 35.49798299]\n",
" [52.43744267 7.0471627 ]\n",
" [18.09728084 58.96694133]\n",
" [53.03410082 9.34412334]\n",
" [21.76734261 3.69027898]\n",
" [ 1.8458268 36.28669624]\n",
" [22.7322565 12.94515186]\n",
" [12.95886653 21.36141223]\n",
" [55.62274463 18.8514422 ]\n",
" [33.72616719 26.7407725 ]\n",
" [52.61860902 14.89879178]\n",
" [48.22746409 15.64536993]\n",
" [17.88394301 12.51091537]\n",
" [50.26283254 22.46648565]\n",
" [44.72663488 19.76503597]\n",
" [24.40311185 14.73062202]\n",
" [27.19901717 43.47928673]\n",
" [43.05060849 13.06655809]\n",
" [44.77230721 18.24725475]\n",
" [47.75525156 15.90833203]\n",
" [31.79166009 48.4449465 ]\n",
" [37.22065533 37.27995287]\n",
" [ 5.8327125 42.18174967]\n",
" [40.84405302 37.99263624]\n",
" [50.31672717 5.0201574 ]\n",
" [19.56157411 9.62681703]\n",
" [17.65180009 26.36157925]\n",
" [50.47905327 12.56459176]\n",
" [43.72288064 17.30236971]\n",
" [32.58711875 41.67314512]\n",
" [28.0813277 43.36109863]\n",
" [49.24188116 15.69614044]\n",
" [44.53679433 23.40222034]\n",
" [24.55634024 44.41905486]\n",
" [24.19807813 32.17738141]\n",
" [51.44755427 19.31466872]\n",
" [48.37459525 15.61966358]\n",
" [37.19591127 18.58052694]\n",
" [35.03470148 37.96630752]\n",
" [55.94714181 17.28201297]\n",
" [13.11359375 10.95151261]\n",
" [20.62450402 16.97277941]\n",
" [29.51375629 26.29389605]\n",
" [ 5.81029283 40.88280446]\n",
" [43.18504329 15.81468197]\n",
" [12.85033004 39.56089251]\n",
" [40.95846471 9.10179159]\n",
" [24.629248 20.91898324]\n",
" [36.43034188 43.2707104 ]\n",
" [24.58811257 48.16267479]\n",
" [27.1293558 45.31207983]\n",
" [37.14752856 16.18811707]\n",
" [15.2655828 23.78727062]\n",
" [17.96962961 23.15933344]\n",
" [41.67960922 18.31257833]\n",
" [23.25010001 21.61212361]\n",
" [21.06446702 47.65133533]\n",
" [46.58973596 10.44750494]\n",
" [ 3.07615683 36.82828907]\n",
" [50.9135076 3.37674452]\n",
" [40.34920095 15.44876942]\n",
" [35.89000167 13.66760966]\n",
" [42.04094777 24.76482129]\n",
" [17.52525829 17.42764559]\n",
" [12.31690045 9.24433637]\n",
" [26.58200859 8.23591132]\n",
" [41.63966598 8.21667593]\n",
" [20.17877755 11.99634565]\n",
" [61.67708583 19.70748798]\n",
" [39.39037903 11.41986853]\n",
" [22.41528605 19.21555276]\n",
" [42.81675312 15.6921447 ]\n",
" [40.99616294 19.58223833]\n",
" [ 4.84589475 42.2913667 ]\n",
" [47.36320583 22.13312622]\n",
" [52.32460463 17.48055118]\n",
" [ 0.26061262 31.53116015]\n",
" [37.73788355 33.97179794]\n",
" [58.36581659 16.59819707]\n",
" [37.90636038 38.94282108]\n",
" [-2.08168895 26.54818442]\n",
" [26.74718411 22.59862955]\n",
" [ 9.43625799 34.59995523]\n",
" [50.25594578 21.10792157]\n",
" [43.74002138 0.81621241]\n",
" [49.24369694 9.0857212 ]\n",
" [38.46565583 12.40154322]\n",
" [42.66611695 14.7283639 ]\n",
" [32.86484795 41.9641505 ]\n",
" [10.03732253 27.4766204 ]\n",
" [44.17206352 18.83111666]\n",
" [50.19790216 28.45569455]\n",
" [10.62002631 46.26260766]\n",
" [31.48815931 33.47984284]\n",
" [46.75121958 17.81070944]\n",
" [34.39886357 4.23348705]\n",
" [28.85252696 35.99002672]\n",
" [18.61944798 18.18903209]\n",
" [22.88495677 26.06605579]\n",
" [40.56233268 15.8406341 ]\n",
" [39.45243605 15.0994373 ]\n",
" [42.29944358 25.88846118]\n",
" [42.47641326 11.39220724]\n",
" [ 6.6793156 35.23439658]\n",
" [46.50270477 16.2841948 ]\n",
" [41.46867499 17.08656174]\n",
" [11.15994409 27.95130881]\n",
" [18.2132395 14.15072105]\n",
" [15.5741201 38.92002488]\n",
" [ 2.80455719 36.14087444]\n",
" [26.16868621 24.99967331]\n",
" [43.25652286 18.74812046]\n",
" [32.49424606 42.57789034]\n",
" [46.69719091 17.97622407]\n",
" [42.59649352 6.88890803]\n",
" [29.69650488 50.13363846]\n",
" [38.32543452 19.95682787]\n",
" [37.84187112 16.8230419 ]\n",
" [33.55352019 3.02575625]\n",
" [43.71207664 10.60423708]\n",
" [18.90667597 24.6764515 ]\n",
" [41.53240143 13.88091882]\n",
" [-0.61351581 39.39421656]\n",
" [40.45059704 7.36019341]\n",
" [31.43807884 18.12233643]\n",
" [23.86321692 18.36065462]\n",
" [13.82747253 25.04157229]\n",
" [42.23238901 18.73489884]\n",
" [42.14302727 18.98447353]\n",
" [34.92707606 35.73705217]\n",
" [59.57320284 22.57352783]\n",
" [28.0682902 42.716359 ]\n",
" [48.18341538 10.49951822]\n",
" [35.93596481 13.21017045]\n",
" [37.44002969 45.99082288]\n",
" [34.38998009 38.6183042 ]\n",
" [47.86510206 13.87264923]\n",
" [26.725038 31.32641901]\n",
" [49.08552279 22.01980689]\n",
" [42.26343175 17.49672525]\n",
" [19.17560368 16.79761814]\n",
" [10.10778035 41.93231823]\n",
" [19.84391871 16.86139614]\n",
" [39.46129257 9.06815109]]\n",
"初始化的mu1,mu2,mu3,mu4: [[0.28947187 0.22554279]\n",
" [0.01447452 0.5124134 ]\n",
" [0.10294728 0.15686306]\n",
" [0.69678914 0.89667212]]\n",
"隐藏变量:\n",
" [[0.05365836 0.06384243 0.02906718 0.85343203]\n",
" [0.15315695 0.15935179 0.11238167 0.5751096 ]\n",
" [0.05700052 0.06926734 0.03164486 0.84208727]\n",
" ...\n",
" [0.08445446 0.15580072 0.06167289 0.69807193]\n",
" [0.16159985 0.15439595 0.11726983 0.56673436]\n",
" [0.15675736 0.09005354 0.09236928 0.66081983]]\n",
"迭代次数: 1\n",
"估计的均值: [[31.65316945 19.89603321]\n",
" [25.63672599 23.62681403]\n",
" [29.12939399 20.41782732]\n",
" [33.98478206 22.99299238]]\n",
"估计的混合项系数: [0.11594808400275008, 0.10335377348283055, 0.0726856257795488, 0.7080125167348705]\n",
"隐藏变量:\n",
" [[1.86457199e-03 2.85967847e-02 1.33872895e-03 9.68199914e-01]\n",
" [2.30863410e-02 8.53065626e-01 1.14413670e-01 9.43436345e-03]\n",
" [2.63762082e-03 7.08943099e-02 2.49520575e-03 9.23972863e-01]\n",
" ...\n",
" [4.38501025e-06 9.99763774e-01 1.77933738e-04 5.39068213e-05]\n",
" [7.35055781e-02 6.60969408e-01 2.42338324e-01 2.31866902e-02]\n",
" [4.12377547e-01 2.04232730e-04 3.82123353e-02 5.49205885e-01]]\n",
"迭代次数: 2\n",
"估计的均值: [[37.93594076 11.89499695]\n",
" [14.94926956 29.41774966]\n",
" [23.87998539 15.98752609]\n",
" [42.25358839 20.87200857]]\n",
"估计的混合项系数: [0.08962512910647233, 0.3122664181489847, 0.0458092402134442, 0.5522992125310985]\n",
"隐藏变量:\n",
" [[1.45579396e-07 2.73216520e-01 7.88678857e-06 7.26775448e-01]\n",
" [1.19872635e-06 4.83243646e-01 5.16755073e-01 8.30533287e-08]\n",
" [6.16268676e-08 8.69089952e-01 1.48147901e-05 1.30895172e-01]\n",
" ...\n",
" [6.20162624e-23 1.00000000e+00 1.91685195e-11 2.97877121e-19]\n",
" [2.69593702e-05 2.74863433e-02 9.72486047e-01 6.50327626e-07]\n",
" [9.39414030e-01 9.36434253e-15 4.19840895e-05 6.05439856e-02]]\n",
"迭代次数: 3\n",
"估计的均值: [[42.37627335 9.36451582]\n",
" [16.89398296 33.74959707]\n",
" [21.50625389 16.41879915]\n",
" [44.36491724 20.05770285]]\n",
"估计的混合项系数: [0.13721527301326916, 0.3192554988084501, 0.12350162509023202, 0.4200276030880484]\n",
"隐藏变量:\n",
" [[3.12549924e-12 9.99213728e-01 1.22839180e-07 7.86149425e-04]\n",
" [1.76764670e-10 6.08404926e-03 9.93915950e-01 5.77003877e-10]\n",
" [4.05315118e-13 9.99946530e-01 1.40146325e-07 5.33302850e-05]\n",
" ...\n",
" [6.93222853e-30 1.00000000e+00 8.30495647e-11 6.90625379e-23]\n",
" [8.41518850e-09 1.58636581e-04 9.99841350e-01 5.27312644e-09]\n",
" [9.68388979e-01 1.93080615e-16 4.12504064e-06 3.16068958e-02]]\n",
"迭代次数: 4\n",
"估计的均值: [[43.96279316 9.55068753]\n",
" [18.58478664 36.00242554]\n",
" [20.55945572 17.68515427]\n",
" [44.81944502 19.37490103]]\n",
"估计的混合项系数: [0.17185168724460861, 0.3074291907473439, 0.16934105280452583, 0.351378069203522]\n",
"隐藏变量:\n",
" [[1.26665428e-13 9.99990181e-01 3.42010021e-08 9.78512085e-06]\n",
" [8.56718548e-12 2.94268706e-04 9.99705731e-01 1.06661317e-10]\n",
" [1.80026578e-14 9.99999086e-01 5.52014979e-08 8.59295700e-07]\n",
" ...\n",
" [3.34757769e-31 9.99999998e-01 1.57716450e-09 6.28738008e-24]\n",
" [6.73977093e-10 8.89987050e-06 9.99991098e-01 1.63188631e-09]\n",
" [9.56871950e-01 5.23428791e-17 1.05708319e-06 4.31269930e-02]]\n",
"迭代次数: 5\n",
"估计的均值: [[44.3557747 9.86047413]\n",
" [19.31929982 37.09815726]\n",
" [20.11945741 18.66625064]\n",
" [44.88231194 19.04166866]]\n",
"估计的混合项系数: [0.1844119832193132, 0.2900644571819827, 0.19672913292266966, 0.32879442667603415]\n",
"隐藏变量:\n",
" [[6.89800882e-14 9.99998169e-01 4.27354628e-08 1.78847723e-06]\n",
" [4.16967660e-12 5.61096046e-05 9.99943890e-01 6.51173638e-11]\n",
" [1.05204618e-14 9.99999741e-01 7.95172047e-08 1.79613630e-07]\n",
" ...\n",
" [3.15915229e-31 9.99999987e-01 1.29045243e-08 3.38633772e-24]\n",
" [4.09940187e-10 1.92483548e-06 9.99998073e-01 1.33931556e-09]\n",
" [9.47725564e-01 1.91542764e-17 4.08579022e-07 5.22740273e-02]]\n",
"迭代次数: 6\n",
"估计的均值: [[44.46539955 10.04135093]\n",
" [19.69535999 37.70332355]\n",
" [19.82497396 19.28491523]\n",
" [44.88414162 18.91438842]]\n",
"估计的混合项系数: [0.18995262821351014, 0.27699894857210305, 0.21264147641363979, 0.3204069468007472]\n",
"隐藏变量:\n",
" [[5.85113374e-14 9.99999082e-01 5.45832562e-08 8.63774619e-07]\n",
" [3.45561681e-12 2.17989925e-05 9.99978201e-01 5.47493727e-11]\n",
" [9.35986763e-15 9.99999797e-01 1.09815570e-07 9.32516225e-08]\n",
" ...\n",
" [4.11144706e-31 9.99999952e-01 4.81717031e-08 2.98562705e-24]\n",
" [3.86179802e-10 8.15007830e-07 9.99999183e-01 1.33392377e-09]\n",
" [9.43893505e-01 9.74540406e-18 2.02833939e-07 5.61062925e-02]]\n",
"迭代次数: 7\n",
"估计的均值: [[44.50082855 10.14475691]\n",
" [20.04384496 38.12278518]\n",
" [19.46089664 19.72459962]\n",
" [44.87762301 18.89435699]]\n",
"估计的混合项系数: [0.19320256483830528, 0.26639964137438127, 0.22388405490169302, 0.3165137388856205]\n",
"隐藏变量:\n",
" [[4.82182890e-14 9.99999394e-01 5.21341944e-08 5.53937350e-07]\n",
" [3.21142567e-12 1.09341973e-05 9.99989066e-01 4.98368138e-11]\n",
" [8.10051153e-15 9.99999823e-01 1.13942694e-07 6.34166756e-08]\n",
" ...\n",
" [5.59822405e-31 9.99999856e-01 1.43817067e-07 3.38500246e-24]\n",
" [4.00442972e-10 4.48422050e-07 9.99999550e-01 1.37760851e-09]\n",
" [9.43616112e-01 6.60605412e-18 9.73807060e-08 5.63837906e-02]]\n",
"迭代次数: 8\n",
"估计的均值: [[44.51294892 10.21402556]\n",
" [20.42147939 38.46538952]\n",
" [19.08715875 20.08667662]\n",
" [44.8699599 18.89649596]]\n",
"估计的混合项系数: [0.19580352468051282, 0.2574765384508134, 0.232962652015997, 0.3137572848526768]\n",
"隐藏变量:\n",
" [[3.76353825e-14 9.99999586e-01 4.28522928e-08 3.71445831e-07]\n",
" [3.12305135e-12 6.10569437e-06 9.99993894e-01 4.70329401e-11]\n",
" [6.66992385e-15 9.99999853e-01 1.02208497e-07 4.50817376e-08]\n",
" ...\n",
" [7.85012587e-31 9.99999607e-01 3.93168371e-07 4.21026049e-24]\n",
" [4.30438953e-10 2.75967508e-07 9.99999722e-01 1.45067960e-09]\n",
" [9.44227384e-01 5.29607071e-18 4.70061383e-08 5.57725691e-02]]\n",
"迭代次数: 9\n",
"估计的均值: [[44.51659086 10.26681568]\n",
" [20.86320703 38.77253123]\n",
" [18.69400516 20.42946739]\n",
" [44.86354283 18.89699992]]\n",
"估计的混合项系数: [0.1979459404889354, 0.24924043990967576, 0.24128415618953222, 0.3115294634118566]\n",
"隐藏变量:\n",
" [[2.75232341e-14 9.99999728e-01 3.17535046e-08 2.40476083e-07]\n",
" [3.10654268e-12 3.54197403e-06 9.99996458e-01 4.52787040e-11]\n",
" [5.18591272e-15 9.99999885e-01 8.34133368e-08 3.11294393e-08]\n",
" ...\n",
" [1.15823784e-30 9.99998893e-01 1.10736899e-06 5.58975265e-24]\n",
" [4.73670829e-10 1.78799168e-07 9.99999819e-01 1.55745993e-09]\n",
" [9.44786821e-01 4.84826810e-18 2.18795988e-08 5.52131572e-02]]\n",
"迭代次数: 10\n",
"估计的均值: [[44.51565341 10.30842795]\n",
" [21.43276391 39.07327891]\n",
" [18.23994635 20.78992309]\n",
" [44.85816428 18.88697641]]\n",
"估计的混合项系数: [0.19965596054308057, 0.24089341257986294, 0.24975523521632426, 0.30969539166073223]\n",
"隐藏变量:\n",
" [[1.80439987e-14 9.99999839e-01 2.03651273e-08 1.40567770e-07]\n",
" [3.14552243e-12 2.00908389e-06 9.99997991e-01 4.43775932e-11]\n",
" [3.67185567e-15 9.99999920e-01 6.01826568e-08 1.97019015e-08]\n",
" ...\n",
" [1.89337958e-30 9.99996350e-01 3.65043303e-06 8.20726494e-24]\n",
" [5.37076656e-10 1.16466278e-07 9.99999881e-01 1.72413708e-09]\n",
" [9.44939924e-01 5.13442016e-18 9.04154556e-09 5.50600669e-02]]\n",
"迭代次数: 11\n",
"估计的均值: [[44.51044378 10.33983496]\n",
" [22.06860091 39.34021697]\n",
" [17.79698777 21.15088757]\n",
" [44.85355819 18.85827476]]\n",
"估计的混合项系数: [0.20090931105285778, 0.2331030840659099, 0.25778076668923877, 0.3082068381919933]\n",
"隐藏变量:\n",
" [[1.13438434e-14 9.99999909e-01 1.26321625e-08 7.82249456e-08]\n",
" [3.26255045e-12 1.16901176e-06 9.99998831e-01 4.45545091e-11]\n",
" [2.51152046e-15 9.99999946e-01 4.22119458e-08 1.19556436e-08]\n",
" ...\n",
" [3.32225956e-30 9.99987290e-01 1.27102415e-05 1.27386639e-23]\n",
" [6.23789697e-10 7.88388525e-08 9.99999919e-01 1.95931797e-09]\n",
" [9.44405981e-01 6.11986530e-18 3.69829549e-09 5.55940152e-02]]\n",
"迭代次数: 12\n",
"估计的均值: [[44.50038062 10.35961563]\n",
" [22.76929317 39.55082345]\n",
" [17.3679637 21.54275188]\n",
" [44.85193968 18.81389727]]\n",
"估计的混合项系数: [0.2016000793485042, 0.2255791330762731, 0.2656444273257188, 0.3071763602495035]\n",
"隐藏变量:\n",
" [[6.90389153e-15 9.99999950e-01 8.04169460e-09 4.21035382e-08]\n",
" [3.47131685e-12 7.15061911e-07 9.99999285e-01 4.57375716e-11]\n",
" [1.67375693e-15 9.99999962e-01 3.04651682e-08 7.05697508e-09]\n",
" ...\n",
" [6.30756141e-30 9.99950747e-01 4.92531749e-05 2.11081306e-23]\n",
" [7.47091497e-10 5.73417347e-08 9.99999940e-01 2.29239744e-09]\n",
" [9.43292809e-01 8.51653238e-18 1.46972428e-09 5.67071894e-02]]\n",
"迭代次数: 13\n",
"估计的均值: [[44.48151997 10.36648065]\n",
" [23.73843833 39.77616388]\n",
" [16.85545872 22.07914985]\n",
" [44.85412021 18.75909663]]\n",
"估计的混合项系数: [0.20173564954496506, 0.2155247715339381, 0.27605908657628914, 0.3066804923448076]\n",
"隐藏变量:\n",
" [[3.56081176e-15 9.99999976e-01 4.82714071e-09 1.93334246e-08]\n",
" [3.87845045e-12 3.85933627e-07 9.99999614e-01 4.87834910e-11]\n",
" [9.77595119e-16 9.99999975e-01 2.14974401e-08 3.66933233e-09]\n",
" ...\n",
" [1.58110864e-29 9.99684272e-01 3.15727615e-04 4.55604755e-23]\n",
" [9.75270740e-10 3.93485647e-08 9.99999957e-01 2.89582686e-09]\n",
" [9.41847479e-01 1.45270003e-17 4.47667275e-10 5.81525204e-02]]\n",
"迭代次数: 14\n",
"估计的均值: [[44.43908486 10.35888692]\n",
" [25.3551494 40.08155987]\n",
" [16.17698522 22.89592521]\n",
" [44.861286 18.68629281]]\n",
"估计的混合项系数: [0.2015024059465105, 0.19976276060095488, 0.292177097022309, 0.30655773643022516]\n",
"隐藏变量:\n",
" [[1.33132745e-15 9.99999991e-01 2.46484690e-09 6.34314391e-09]\n",
" [4.92836796e-12 1.37839339e-07 9.99999862e-01 5.68653803e-11]\n",
" [4.49457067e-16 9.99999984e-01 1.40863196e-08 1.47552851e-09]\n",
" ...\n",
" [8.36106857e-29 9.93716355e-01 6.28364485e-03 1.95352368e-22]\n",
" [1.55313832e-09 2.04935868e-08 9.99999974e-01 4.30630145e-09]\n",
" [9.40168904e-01 3.52977402e-17 7.95846430e-11 5.98310963e-02]]\n",
"迭代次数: 15\n",
"估计的均值: [[44.32409353 10.32999173]\n",
" [27.66608038 40.27920082]\n",
" [15.44236836 23.9050458 ]\n",
" [44.88203118 18.57037908]]\n",
"估计的混合项系数: [0.20129542511928245, 0.18166595193465496, 0.3105827951405498, 0.3064558278055118]\n",
"隐藏变量:\n",
" [[4.51409792e-16 9.99999997e-01 1.24644519e-09 1.73877405e-09]\n",
" [8.03898336e-12 3.47797028e-08 9.99999965e-01 7.38305901e-11]\n",
" [2.04349425e-16 9.99999990e-01 9.86649662e-09 5.35594454e-10]\n",
" ...\n",
" [9.77080058e-28 7.06305656e-01 2.93694344e-01 1.48599261e-21]\n",
" [3.29104016e-09 8.73391250e-09 9.99999980e-01 7.50213128e-09]\n",
" [9.38637029e-01 1.50407536e-16 9.72404747e-12 6.13629712e-02]]\n",
"迭代次数: 16\n",
"估计的均值: [[44.11021577 10.27957514]\n",
" [29.29752543 40.26127808]\n",
" [15.06648473 24.65560201]\n",
" [44.91815172 18.45347115]]\n",
"估计的混合项系数: [0.2007998901723772, 0.1698846742772788, 0.32170723450813465, 0.3076082010422088]\n",
"隐藏变量:\n",
" [[2.71946365e-16 9.99999998e-01 1.13633387e-09 8.23533469e-10]\n",
" [1.48193003e-11 1.39371068e-08 9.99999986e-01 9.03465887e-11]\n",
" [1.53052080e-16 9.99999989e-01 1.10487251e-08 3.07051987e-10]\n",
" ...\n",
" [1.53845053e-27 9.64456987e-02 9.03554301e-01 1.23355645e-21]\n",
" [7.13680630e-09 5.15356777e-09 9.99999976e-01 1.12740769e-08]\n",
" [9.38938337e-01 4.49690948e-16 2.39370099e-12 6.10616634e-02]]\n",
"迭代次数: 17\n",
"估计的均值: [[43.90799179 10.23217418]\n",
" [29.99645232 40.24409958]\n",
" [14.97380216 25.02371628]\n",
" [44.97768692 18.38637751]]\n",
"估计的混合项系数: [0.198899008582842, 0.16362705463830654, 0.3271201171767318, 0.3103538196021196]\n",
"隐藏变量:\n",
" [[2.35419007e-16 9.99999998e-01 1.32275683e-09 6.05451409e-10]\n",
" [2.31070585e-11 9.10434020e-09 9.99999991e-01 9.29923341e-11]\n",
" [1.47439497e-16 9.99999986e-01 1.39034953e-08 2.43794082e-10]\n",
" ...\n",
" [1.47337407e-27 2.52402799e-02 9.74759720e-01 6.60131784e-22]\n",
" [1.18174727e-08 3.97922215e-09 9.99999971e-01 1.27769033e-08]\n",
" [9.40446503e-01 6.71889803e-16 1.34650460e-12 5.95534967e-02]]\n",
"迭代次数: 18\n",
"估计的均值: [[43.73712019 10.18955783]\n",
" [30.29694755 40.23075774]\n",
" [14.95075648 25.18962827]\n",
" [45.04836594 18.33624019]]\n",
"估计的混合项系数: [0.19669177551084918, 0.16074450952333744, 0.32961186348714566, 0.31295185147866755]\n",
"隐藏变量:\n",
" [[2.23803200e-16 9.99999998e-01 1.46943505e-09 5.04723829e-10]\n",
" [3.16826574e-11 7.57066367e-09 9.99999992e-01 8.72105829e-11]\n",
" [1.48301141e-16 9.99999984e-01 1.59315299e-08 2.09085982e-10]\n",
" ...\n",
" [1.61758933e-27 1.37127341e-02 9.86287266e-01 4.31869585e-22]\n",
" [1.65070469e-08 3.55665326e-09 9.99999967e-01 1.25975803e-08]\n",
" [9.42024396e-01 7.85681846e-16 1.05123940e-12 5.79756036e-02]]\n",
"迭代次数: 19\n",
"估计的均值: [[43.58723142 10.15440641]\n",
" [30.40662594 40.23023582]\n",
" [14.94813378 25.25689745]\n",
" [45.11717428 18.29185387]]\n",
"估计的混合项系数: [0.1946357821395416, 0.15962401271301882, 0.3305547576731, 0.3151854474743397]\n",
"隐藏变量:\n",
" [[2.21597201e-16 9.99999998e-01 1.55156613e-09 4.41555515e-10]\n",
" [4.05803293e-11 7.03370734e-09 9.99999993e-01 7.91005250e-11]\n",
" [1.51582420e-16 9.99999983e-01 1.70002997e-08 1.84109941e-10]\n",
" ...\n",
" [1.92614657e-27 1.08859597e-02 9.89114040e-01 3.20260312e-22]\n",
" [2.11387584e-08 3.39160958e-09 9.99999964e-01 1.17592228e-08]\n",
" [9.43394647e-01 8.08067697e-16 9.45055278e-13 5.66053532e-02]]\n",
"迭代次数: 20\n",
"估计的均值: [[43.45473785 10.12788427]\n",
" [30.44574987 40.23124592]\n",
" [14.94909103 25.28562747]\n",
" [45.18028862 18.25146157]]\n",
"估计的混合项系数: [0.19279393655512383, 0.15921316638064156, 0.33088217127266967, 0.3171107257915648]\n",
"隐藏变量:\n",
" [[2.23878788e-16 9.99999998e-01 1.59422986e-09 3.95000563e-10]\n",
" [5.00328374e-11 6.84885976e-09 9.99999993e-01 7.14436569e-11]\n",
" [1.56424195e-16 9.99999982e-01 1.75272865e-08 1.64499584e-10]\n",
" ...\n",
" [2.34729364e-27 9.97758354e-03 9.90022416e-01 2.52748855e-22]\n",
" [2.58849145e-08 3.33461667e-09 9.99999960e-01 1.08358212e-08]\n",
" [9.44521690e-01 8.01497696e-16 8.94003186e-13 5.54783101e-02]]\n",
"迭代次数: 21\n",
"估计的均值: [[43.33632476 10.10904766]\n",
" [30.46084276 40.23034995]\n",
" [14.94947544 25.30041093]\n",
" [45.23672955 18.21455063]]\n",
"估计的混合项系数: [0.1911895249313257, 0.15907476157654166, 0.33097108537334624, 0.3187646281187865]\n",
"隐藏变量:\n",
" [[2.28924606e-16 9.99999998e-01 1.61756303e-09 3.58208928e-10]\n",
" [6.02527648e-11 6.80208761e-09 9.99999993e-01 6.49610430e-11]\n",
" [1.62587372e-16 9.99999982e-01 1.78036963e-08 1.48663268e-10]\n",
" ...\n",
" [2.86212379e-27 9.60925187e-03 9.90390748e-01 2.06651639e-22]\n",
" [3.08974329e-08 3.32717846e-09 9.99999956e-01 1.00132607e-08]\n",
" [9.45451762e-01 7.91161298e-16 8.60556983e-13 5.45482383e-02]]\n",
"迭代次数: 22\n",
"估计的均值: [[43.22921326 10.0965657 ]\n",
" [30.46768182 40.22780556]\n",
" [14.9488227 25.31008279]\n",
" [45.28707373 18.18090294]]\n",
"估计的混合项系数: [0.18981460809415082, 0.1590409262643288, 0.33096357124902875, 0.32018089439249126]\n",
"隐藏变量:\n",
" [[2.36052592e-16 9.99999998e-01 1.63180021e-09 3.28177067e-10]\n",
" [7.13866486e-11 6.81219654e-09 9.99999993e-01 5.95927004e-11]\n",
" [1.69971247e-16 9.99999982e-01 1.79676738e-08 1.35669763e-10]\n",
" ...\n",
" [3.46961268e-27 9.41431420e-03 9.90585686e-01 1.73040816e-22]\n",
" [3.62660951e-08 3.34248211e-09 9.99999951e-01 9.31579594e-09]\n",
" [9.46245027e-01 7.82570267e-16 8.33745116e-13 5.37549731e-02]]\n",
"迭代次数: 23\n",
"估计的均值: [[43.13125256 10.08930782]\n",
" [30.4715465 40.2243953 ]\n",
" [14.94741595 25.3176842 ]\n",
" [45.33240999 18.15026971]]\n",
"估计的混合项系数: [0.18864671832823302, 0.15904731429667726, 0.3309157275910514, 0.32139023978403847]\n",
"隐藏变量:\n",
" [[2.44977733e-16 9.99999998e-01 1.64152560e-09 3.03141221e-10]\n",
" [8.35433159e-11 6.84557991e-09 9.99999993e-01 5.51062492e-11]\n",
" [1.78544054e-16 9.99999982e-01 1.80782177e-08 1.24843415e-10]\n",
" ...\n",
" [4.17809360e-27 9.28165996e-03 9.90718340e-01 1.47491213e-22]\n",
" [4.20444073e-08 3.36765030e-09 9.99999946e-01 8.72387553e-09]\n",
" [9.46949643e-01 7.76003719e-16 8.10283776e-13 5.30503565e-02]]\n",
"迭代次数: 24\n",
"估计的均值: [[43.0407747 10.08642401]\n",
" [30.47423868 40.22065945]\n",
" [14.94556125 25.32426646]\n",
" [45.3738127 18.12234054]]\n",
"估计的混合项系数: [0.1876606110527325, 0.15906894376118258, 0.3308510136613136, 0.32241943152477065]\n",
"隐藏变量:\n",
" [[2.55607808e-16 9.99999998e-01 1.64878118e-09 2.81902476e-10]\n",
" [9.68252217e-11 6.88788193e-09 9.99999993e-01 5.12856739e-11]\n",
" [1.88332342e-16 9.99999982e-01 1.81605428e-08 1.15679120e-10]\n",
" ...\n",
" [5.00194671e-27 9.17526049e-03 9.90824740e-01 1.27458495e-22]\n",
" [4.82738251e-08 3.39660080e-09 9.99999940e-01 8.21316159e-09]\n",
" [9.47598918e-01 7.70879668e-16 7.89099404e-13 5.24010823e-02]]\n",
"迭代次数: 25\n",
"估计的均值: [[42.95645749 10.08728947]\n",
" [30.47639717 40.2168795 ]\n",
" [14.94346252 25.33021277]\n",
" [45.41218244 18.09678529]]\n",
"估计的混合项系数: [0.186833065987643, 0.15909603348929255, 0.33077961998129995, 0.3232912805417645]\n",
"隐藏变量:\n",
" [[2.67960279e-16 9.99999998e-01 1.65451211e-09 2.63599880e-10]\n",
" [1.11346910e-10 6.93297597e-09 9.99999993e-01 4.79662699e-11]\n",
" [1.99410629e-16 9.99999982e-01 1.82258931e-08 1.07801134e-10]\n",
" ...\n",
" [5.96064808e-27 9.08267100e-03 9.90917329e-01 1.11351933e-22]\n",
" [5.49967520e-08 3.42656710e-09 9.99999934e-01 7.76377051e-09]\n",
" [9.48214897e-01 7.66695588e-16 7.69734088e-13 5.17851032e-02]]\n",
"迭代次数: 26\n",
"估计的均值: [[42.8772295 10.09143987]\n",
" [30.47826297 40.21317812]\n",
" [14.94123556 25.33568316]\n",
" [45.44823624 18.07328666]]\n",
"估计的混合项系数: [0.18614414235881865, 0.15912478341423905, 0.33070601461798116, 0.32402505960896094]\n",
"隐藏变量:\n",
" [[2.82124371e-16 9.99999998e-01 1.65918467e-09 2.47599742e-10]\n",
" [1.27244852e-10 6.97833547e-09 9.99999993e-01 4.50287927e-11]\n",
" [2.11893388e-16 9.99999982e-01 1.82796391e-08 1.00929959e-10]\n",
" ...\n",
" [7.07894055e-27 8.99912163e-03 9.91000878e-01 9.81247128e-23]\n",
" [6.22626402e-08 3.45637179e-09 9.99999927e-01 7.36097988e-09]\n",
" [9.48812104e-01 7.63130002e-16 7.51901518e-13 5.11878964e-02]]\n",
"迭代次数: 27\n",
"估计的均值: [[42.80220589 10.09852384]\n",
" [30.47993676 40.20959588]\n",
" [14.93893976 25.34076246]\n",
" [45.48253979 18.05155433]]\n",
"估计的混合项系数: [0.18557709053751037, 0.15915378197659005, 0.3306320856964241, 0.3246370417894752]\n",
"隐藏变量:\n",
" [[2.98244451e-16 9.99999998e-01 1.66304888e-09 2.33427348e-10]\n",
" [1.44683654e-10 7.02302127e-09 9.99999993e-01 4.23874282e-11]\n",
" [2.25931469e-16 9.99999982e-01 1.83245893e-08 9.48560592e-11]\n",
" ...\n",
" [8.38766722e-27 8.92242111e-03 9.91077579e-01 8.70624570e-23]\n",
" [7.01310676e-08 3.48558464e-09 9.99999919e-01 6.99412663e-09]\n",
" [9.49400163e-01 7.59992405e-16 7.35372662e-13 5.05998372e-02]]\n",
"迭代次数: 28\n",
"估计的均值: [[42.73064355 10.10827167]\n",
" [30.48146758 40.20613493]\n",
" [14.93660178 25.34550892]\n",
" [45.51554323 18.03132768]]\n",
"估计的混合项系数: [0.18511787588441114, 0.15918257769742047, 0.3305585181503539, 0.32514102826781466]\n",
"隐藏变量:\n",
" [[3.16514448e-16 9.99999998e-01 1.66625196e-09 2.20721210e-10]\n",
" [1.63861425e-10 7.06679220e-09 9.99999993e-01 3.99797742e-11]\n",
" [2.41712445e-16 9.99999982e-01 1.83623713e-08 8.94203722e-11]\n",
" ...\n",
" [9.92512848e-27 8.85129127e-03 9.91148709e-01 7.76634519e-23]\n",
" [7.86738105e-08 3.51411954e-09 9.99999911e-01 6.65545744e-09]\n",
" [9.49985467e-01 7.57171053e-16 7.19949484e-13 5.00145330e-02]]\n",
"迭代次数: 29\n",
"估计的均值: [[42.66190873 10.12047473]\n",
" [30.48288418 40.20278101]\n",
" [14.93422995 25.34996998]\n",
" [45.54761048 18.01237338]]\n",
"估计的混合项系数: [0.1847546615022768, 0.15921110234578367, 0.33048541999163134, 0.32554881616030806]\n",
"隐藏变量:\n",
" [[3.37178434e-16 9.99999998e-01 1.66888849e-09 2.09201684e-10]\n",
" [1.85015683e-10 7.10970922e-09 9.99999993e-01 3.77597505e-11]\n",
" [2.59463917e-16 9.99999982e-01 1.83940255e-08 8.45004244e-11]\n",
" ...\n",
" [1.17389734e-26 8.78481429e-03 9.91215186e-01 6.95667961e-23]\n",
" [8.79768132e-08 3.54204433e-09 9.99999902e-01 6.33926363e-09]\n",
" [9.50572211e-01 7.54599478e-16 7.05459271e-13 4.94277887e-02]]\n",
"迭代次数: 30\n",
"估计的均值: [[42.59545288 10.13497148]\n",
" [30.48420648 40.19951388]\n",
" [14.93182232 25.35418727]\n",
" [45.57904126 17.99448121]]\n",
"估计的混合项系数: [0.18447735258954256, 0.15923943610555813, 0.33041261550303164, 0.3258705958018675]\n",
"隐藏变量:\n",
" [[3.60535105e-16 9.99999998e-01 1.67102334e-09 1.98649204e-10]\n",
" [2.08430483e-10 7.15195932e-09 9.99999993e-01 3.56928011e-11]\n",
" [2.79459179e-16 9.99999981e-01 1.84202678e-08 8.00005632e-11]\n",
" ...\n",
" [1.38887268e-26 8.72224492e-03 9.91277755e-01 6.25075300e-23]\n",
" [9.81424583e-08 3.56949248e-09 9.99999892e-01 6.04128322e-09]\n",
" [9.51163040e-01 7.52237603e-16 6.91752452e-13 4.88369604e-02]]\n",
"迭代次数: 31\n",
"估计的均值: [[42.5307944 10.15163761]\n",
" [30.4854499 40.19631189]\n",
" [14.92937107 25.35819824]\n",
" [45.61008692 17.97745956]]\n",
"估计的混合项系数: [0.18427721837847763, 0.15926771224672237, 0.33033978548351434, 0.32611528389128575]\n",
"隐藏变量:\n",
" [[3.86945214e-16 9.99999998e-01 1.67270263e-09 1.88889021e-10]\n",
" [2.34445263e-10 7.19377784e-09 9.99999993e-01 3.37526688e-11]\n",
" [3.02025016e-16 9.99999981e-01 1.84416128e-08 7.58450896e-11]\n",
" ...\n",
" [1.64491304e-26 8.66294323e-03 9.91337057e-01 5.62877094e-23]\n",
" [1.09292349e-07 3.59662282e-09 9.99999881e-01 5.75829626e-09]\n",
" [9.51759454e-01 7.50061545e-16 6.78700421e-13 4.82405462e-02]]\n",
"迭代次数: 32\n",
"估计的均值: [[42.46750452 10.17037868]\n",
" [30.48662716 40.19315394]\n",
" [14.92686478 25.36203684]\n",
" [45.6409619 17.96113119]]\n",
"估计的混合项系数: [0.18414658119284794, 0.15929607920851013, 0.3302665351304893, 0.3262908044681525]\n",
"隐藏变量:\n",
" [[4.16841710e-16 9.99999998e-01 1.67395928e-09 1.79780375e-10]\n",
" [2.63465875e-10 7.23541506e-09 9.99999992e-01 3.19192050e-11]\n",
" [3.27551752e-16 9.99999981e-01 1.84584344e-08 7.19733908e-11]\n",
" ...\n",
" [1.95145610e-26 8.60634704e-03 9.91393653e-01 5.07572440e-23]\n",
" [1.21570762e-07 3.62360183e-09 9.99999869e-01 5.48785031e-09]\n",
" [9.52362076e-01 7.48058133e-16 6.66193082e-13 4.76379241e-02]]\n",
"迭代次数: 33\n",
"估计的均值: [[42.40519623 10.19112446]\n",
" [30.48774908 40.1900201 ]\n",
" [14.9242897 25.36573383]\n",
" [45.67185185 17.94532943]]\n",
"估计的混合项系数: [0.18407855680900317, 0.15932468629465307, 0.33019242667662335, 0.3264043302197197]\n",
"隐藏变量:\n",
" [[4.50742747e-16 9.99999998e-01 1.67481604e-09 1.71208718e-10]\n",
" [2.95978369e-10 7.27712271e-09 9.99999992e-01 3.01768599e-11]\n",
" [3.56505836e-16 9.99999981e-01 1.84709985e-08 6.83364541e-11]\n",
" ...\n",
" [2.32048967e-26 8.55195754e-03 9.91448042e-01 4.58008976e-23]\n",
" [1.35148937e-07 3.65059636e-09 9.99999856e-01 5.22807193e-09]\n",
" [9.52970812e-01 7.46221926e-16 6.54136384e-13 4.70291880e-02]]\n",
"迭代次数: 34\n",
"估计的均值: [[42.34351542 10.2138244 ]\n",
" [30.488825 40.18689177]\n",
" [14.92163035 25.36931723]\n",
" [45.70291943 17.92989474]]\n",
"估计的混合项系数: [0.1840668314634411, 0.15935367892495772, 0.3301169943319753, 0.32646249527962556]\n",
"隐藏变量:\n",
" [[4.89267935e-16 9.99999998e-01 1.67528730e-09 1.63080060e-10]\n",
" [3.32566243e-10 7.31914939e-09 9.99999992e-01 2.85136222e-11]\n",
" [3.89445473e-16 9.99999981e-01 1.84794825e-08 6.48943416e-11]\n",
" ...\n",
" [2.76733505e-26 8.49932951e-03 9.91500670e-01 4.13292711e-23]\n",
" [1.50230409e-07 3.67777128e-09 9.99999841e-01 4.97753524e-09]\n",
" [9.53584954e-01 7.44553567e-16 6.42450043e-13 4.64150460e-02]]\n",
"迭代次数: 35\n",
"估计的均值: [[42.28213364 10.23844383]\n",
" [30.48986304 40.18375158]\n",
" [14.91886981 25.37281257]\n",
" [45.73430827 17.91467157]]\n",
"估计的混合项系数: [0.1841054634718351, 0.15938319757839967, 0.3300397500414968, 0.3264715889082682]\n",
"隐藏变量:\n",
" [[5.33158468e-16 9.99999998e-01 1.67538022e-09 1.55316822e-10]\n",
" [3.73932124e-10 7.36173985e-09 9.99999992e-01 2.69202599e-11]\n",
" [4.27039980e-16 9.99999981e-01 1.84839867e-08 6.16143410e-11]\n",
" ...\n",
" [3.31169992e-26 8.44806335e-03 9.91551937e-01 3.72724202e-23]\n",
" [1.67057651e-07 3.70528922e-09 9.99999825e-01 4.73516854e-09]\n",
" [9.54203234e-01 7.43058858e-16 6.31065556e-13 4.57967659e-02]]\n",
"迭代次数: 36\n",
"估计的均值: [[42.220742 10.26496075]\n",
" [30.4908703 40.18058328]\n",
" [14.91598978 25.37624327]\n",
" [45.76614573 17.8995055 ]]\n",
"估计的混合项系数: [0.184188699952516, 0.1594133779937191, 0.3299601842810219, 0.3264377377727428]\n",
"隐藏变量:\n",
" [[5.83301945e-16 9.99999998e-01 1.67509549e-09 1.47854762e-10]\n",
" [4.20925154e-10 7.40513591e-09 9.99999992e-01 2.53897659e-11]\n",
" [4.70093743e-16 9.99999981e-01 1.84845431e-08 5.84695989e-11]\n",
" ...\n",
" [3.97910376e-26 8.39779813e-03 9.91602202e-01 3.35752469e-23]\n",
" [1.85920390e-07 3.73331137e-09 9.99999806e-01 4.50018671e-09]\n",
" [9.54823847e-01 7.41748261e-16 6.19924503e-13 4.51761525e-02]]\n",
"迭代次数: 37\n",
"估计的均值: [[42.15904587 10.29336303]\n",
" [30.49185298 40.17737161]\n",
" [14.91297061 25.37963101]\n",
" [45.79854449 17.88424044]]\n",
"估计的混合项系数: [0.18431080122740917, 0.15944435163709425, 0.32987776401960217, 0.32636708311589374]\n",
"隐藏变量:\n",
" [[6.40762976e-16 9.99999998e-01 1.67442789e-09 1.40640685e-10]\n",
" [4.74575811e-10 7.44957806e-09 9.99999992e-01 2.39169418e-11]\n",
" [5.19575964e-16 9.99999981e-01 1.84811213e-08 5.54381011e-11]\n",
" ...\n",
" [4.80282259e-26 8.34820537e-03 9.91651795e-01 3.01941080e-23]\n",
" [2.07166072e-07 3.76199857e-09 9.99999785e-01 4.27204096e-09]\n",
" [9.55444450e-01 7.40636651e-16 6.08977138e-13 4.45555497e-02]]\n",
"迭代次数: 38\n",
"估计的均值: [[42.09675996 10.32364591]\n",
" [30.4928165 40.17410219]\n",
" [14.90979114 25.38299606]\n",
" [45.83160348 17.86871599]]\n",
"估计的混合项系数: [0.18446586712714413, 0.15947624605474087, 0.32979192890764314, 0.326265957910472]\n",
"隐藏变量:\n",
" [[7.06821017e-16 9.99999998e-01 1.67336668e-09 1.33630729e-10]\n",
" [5.36140559e-10 7.49530723e-09 9.99999992e-01 2.24980763e-11]\n",
" [5.76657729e-16 9.99999981e-01 1.84736326e-08 5.25019066e-11]\n",
" ...\n",
" [5.82656497e-26 8.29898334e-03 9.91701017e-01 2.70942684e-23]\n",
" [2.31213157e-07 3.79151269e-09 9.99999761e-01 4.05038022e-09]\n",
" [9.56062138e-01 7.39743234e-16 5.98181209e-13 4.39378617e-02]]\n",
"迭代次数: 39\n",
"估计的均值: [[42.03360349 10.35580987]\n",
" [30.49376561 40.1707614 ]\n",
" [14.90642861 25.3863576 ]\n",
" [45.86540802 17.85276465]]\n",
"估计的混合项系数: [0.18464766076531805, 0.15950918498654104, 0.32970208616473073, 0.3261410680834102]\n",
"隐藏变量:\n",
" [[7.83017351e-16 9.99999998e-01 1.67189587e-09 1.26789068e-10]\n",
" [6.07159643e-10 7.54256660e-09 9.99999992e-01 2.11306878e-11]\n",
" [6.42758457e-16 9.99999981e-01 1.84619332e-08 4.96465625e-11]\n",
" ...\n",
" [7.10818906e-26 8.24985201e-03 9.91750148e-01 2.42479497e-23]\n",
" [2.58568158e-07 3.82201796e-09 9.99999734e-01 3.83502027e-09]\n",
" [9.56673409e-01 7.39091593e-16 5.87500961e-13 4.33265909e-02]]\n",
"迭代次数: 40\n",
"估计的均值: [[41.96929513 10.38985885]\n",
" [30.49470445 40.16733639]\n",
" [14.90285842 25.38973405]\n",
" [45.90002961 17.83620911]]\n",
"估计的混合项系数: [0.1848494264738752, 0.15954328823184044, 0.32960760427381663, 0.3259996810204678]\n",
"隐藏变量:\n",
" [[8.71213844e-16 9.99999998e-01 1.66999443e-09 1.20086922e-10]\n",
" [6.89532805e-10 7.59160351e-09 9.99999992e-01 1.98133076e-11]\n",
" [7.19604588e-16 9.99999982e-01 1.84458267e-08 4.68606526e-11]\n",
" ...\n",
" [8.72492041e-26 8.20054814e-03 9.91799452e-01 2.16328029e-23]\n",
" [2.89847766e-07 3.85368243e-09 9.99999703e-01 3.62591747e-09]\n",
" [9.57274112e-01 7.38709820e-16 5.76906285e-13 4.27258877e-02]]\n",
"迭代次数: 41\n",
"估计的均值: [[41.90354726 10.42579905]\n",
" [30.4956366 40.16381501]\n",
" [14.89905387 25.39314349]\n",
" [45.93552533 17.81885915]]\n",
"估计的混合项系数: [0.18506369957026028, 0.15957867131938236, 0.3295078053004223, 0.3258498238099352]\n",
"隐藏变量:\n",
" [[9.73667200e-16 9.99999998e-01 1.66763640e-09 1.13501777e-10]\n",
" [7.85619805e-10 7.64267145e-09 9.99999992e-01 1.85452883e-11]\n",
" [8.09304499e-16 9.99999982e-01 1.84250654e-08 4.41354354e-11]\n",
" ...\n",
" [1.07807651e-25 8.15082064e-03 9.91849179e-01 1.92306887e-23]\n",
" [3.25807981e-07 3.88667962e-09 9.99999667e-01 3.42314502e-09]\n",
" [9.57859385e-01 7.38630759e-16 5.66371956e-13 4.21406150e-02]]\n",
"迭代次数: 42\n",
"估计的均值: [[41.83605909 10.4636384 ]\n",
" [30.49656521 40.16018577]\n",
" [14.89498588 25.39660396]\n",
" [45.97193706 17.80050844]]\n",
"估计的混合项系数: [0.18528210646135795, 0.15961544507854117, 0.3294019553617604, 0.3257004930983405]\n",
"隐藏变量:\n",
" [[1.09312412e-15 9.99999998e-01 1.66479097e-09 1.07016760e-10]\n",
" [8.98376002e-10 7.69603239e-09 9.99999991e-01 1.73266259e-11]\n",
" [9.14445491e-16 9.99999982e-01 1.83993517e-08 4.14645423e-11]\n",
" ...\n",
" [1.34171869e-25 8.10042572e-03 9.91899574e-01 1.70266832e-23]\n",
" [3.67383082e-07 3.92119035e-09 9.99999625e-01 3.22687029e-09]\n",
" [9.58423575e-01 7.38892350e-16 5.55876919e-13 4.15764249e-02]]\n",
"迭代次数: 43\n",
"估计的均值: [[41.76650813 10.50338719]\n",
" [30.49749298 40.15643784]\n",
" [14.8906225 25.40013399]\n",
" [46.00929088 17.78093079]]\n",
"估计的混合项系数: [0.18549515420559307, 0.15965371525500055, 0.3292892524056833, 0.32556187813372317]\n",
"隐藏变量:\n",
" [[1.23294552e-15 9.99999998e-01 1.66142241e-09 1.00620080e-10]\n",
" [1.03153849e-09 7.75195985e-09 9.99999991e-01 1.61577880e-11]\n",
" [1.03822157e-15 9.99999982e-01 1.83683372e-08 3.88437092e-11]\n",
" ...\n",
" [1.68287328e-25 8.04912170e-03 9.91950878e-01 1.50082578e-23]\n",
" [4.15738738e-07 3.95740514e-09 9.99999577e-01 3.03733197e-09]\n",
" [9.58960147e-01 7.39538137e-16 5.45403582e-13 4.10398532e-02]]\n",
"迭代次数: 44\n",
"估计的均值: [[41.6945391 10.54506023]\n",
" [30.49842229 40.15256101]\n",
" [14.88592839 25.40375306]\n",
" [46.04759663 17.7598757 ]]\n",
"估计的混合项系数: [0.18569200888347653, 0.1596935823665739, 0.3291688099593771, 0.32544559879057294]\n",
"隐藏变量:\n",
" [[1.39727242e-15 9.99999998e-01 1.65748986e-09 9.43045193e-11]\n",
" [1.18988671e-09 7.81074288e-09 9.99999991e-01 1.50395442e-11]\n",
" [1.18460551e-15 9.99999982e-01 1.83316216e-08 3.62705209e-11]\n",
" ...\n",
" [2.12863224e-25 7.99666282e-03 9.92003337e-01 1.31645961e-23]\n",
" [4.72345811e-07 3.99552740e-09 9.99999521e-01 2.85481640e-09]\n",
" [9.59461564e-01 7.40618014e-16 5.34937076e-13 4.05384361e-02]]\n",
"迭代次数: 45\n",
"估计的均值: [[41.61974956 10.58868123]\n",
" [30.49935526 40.14854553]\n",
" [14.88086395 25.40748236]\n",
" [46.08684824 17.73706315]]\n",
"估计的混合项系数: [0.18586026168975883, 0.15973514205326683, 0.3290396348000742, 0.32536496145689997]\n",
"隐藏变量:\n",
" [[1.59125352e-15 9.99999998e-01 1.65294690e-09 8.80669072e-11]\n",
" [1.37961537e-09 7.87269189e-09 9.99999991e-01 1.39727963e-11]\n",
" [1.35858640e-15 9.99999982e-01 1.82887488e-08 3.37441545e-11]\n",
" ...\n",
" [2.71727035e-25 7.94279174e-03 9.92057208e-01 1.14860294e-23]\n",
" [5.39085148e-07 4.03577787e-09 9.99999454e-01 2.67963312e-09]\n",
" [9.59919139e-01 7.42189347e-16 5.24464441e-13 4.00808606e-02]]\n",
"迭代次数: 46\n",
"估计的均值: [[41.54167092 10.63429018]\n",
" [30.50029385 40.14438201]\n",
" [14.8753842 25.41134559]\n",
" [46.12702483 17.71217691]]\n",
"估计的混合项系数: [0.1859856801836716, 0.1597784862332621, 0.3289005954955445, 0.3253352380875214]\n",
"隐藏变量:\n",
" [[1.82136671e-15 9.99999998e-01 1.64774074e-09 8.19075803e-11]\n",
" [1.60888043e-09 7.93814712e-09 9.99999990e-01 1.29584117e-11]\n",
" [1.56650713e-15 9.99999982e-01 1.82391986e-08 3.12651141e-11]\n",
" ...\n",
" [3.50377573e-25 7.88722977e-03 9.92112770e-01 9.96358033e-24]\n",
" [6.18399707e-07 4.07840099e-09 9.99999375e-01 2.51208976e-09]\n",
" [9.60322833e-01 7.44318669e-16 5.13973714e-13 3.96771668e-02]]\n",
"迭代次数: 47\n",
"估计的均值: [[41.45974338 10.68195499]\n",
" [30.50123998 40.14006105]\n",
" [14.86943705 25.41537022]\n",
" [46.16809319 17.68485613]]\n",
"估计的混合项系数: [0.18605193922833357, 0.1598237054191537, 0.3287503773465937, 0.3253739780059189]\n",
"隐藏变量:\n",
" [[2.09588769e-15 9.99999998e-01 1.64181080e-09 7.58298135e-11]\n",
" [1.88861835e-09 8.00749092e-09 9.99999990e-01 1.19970647e-11]\n",
" [1.81655799e-15 9.99999982e-01 1.81823740e-08 2.88349586e-11]\n",
" ...\n",
" [4.56871770e-25 7.82966393e-03 9.92170336e-01 8.58861170e-24]\n",
" [7.13520587e-07 4.12367410e-09 9.99999280e-01 2.35246724e-09]\n",
" [9.60660969e-01 7.47084305e-16 5.03452871e-13 3.93390311e-02]]\n",
"迭代次数: 48\n",
"估计的均值: [[41.37328278 10.73178848]\n",
" [30.50219576 40.13557282]\n",
" [14.86296085 25.419589 ]\n",
" [46.21001159 17.65468443]]\n",
"估计的混合项系数: [0.1860403216280052, 0.15987089255161996, 0.32858741728655927, 0.3255013685338153]\n",
"隐藏变量:\n",
" [[2.42559398e-15 9.99999998e-01 1.63508647e-09 6.98392601e-11]\n",
" [2.23380717e-09 8.08116572e-09 9.99999990e-01 1.10890936e-11]\n",
" [2.11952097e-15 9.99999982e-01 1.81175790e-08 2.64560365e-11]\n",
" ...\n",
" [6.03291361e-25 7.76972942e-03 9.92230271e-01 7.35258082e-24]\n",
" [8.28811000e-07 4.17192076e-09 9.99999165e-01 2.20099664e-09]\n",
" [9.60919825e-01 7.50580384e-16 4.92888636e-13 3.90801749e-02]]\n",
"迭代次数: 49\n",
"估计的均值: [[41.28143709 10.78397272]\n",
" [30.5031636 40.13090643]\n",
" [14.85588077 25.4240423 ]\n",
" [46.25273514 17.62117575]]\n",
"估计的混合项系数: [0.18592937283626168, 0.15992014862910228, 0.3284098095488631, 0.3257406689857727]\n",
"隐藏变量:\n",
" [[2.82485357e-15 9.99999998e-01 1.62748356e-09 6.39434687e-11]\n",
" [2.66546068e-09 8.15969992e-09 9.99999989e-01 1.02343854e-11]\n",
" [2.48992496e-15 9.99999982e-01 1.80439843e-08 2.41312573e-11]\n",
" ...\n",
" [8.08253927e-25 7.70698553e-03 9.92293014e-01 6.24690145e-24]\n",
" [9.70302828e-07 4.22352993e-09 9.99999023e-01 2.05783998e-09]\n",
" [9.61083030e-01 7.54923025e-16 4.82265139e-13 3.89169695e-02]]\n",
"迭代次数: 50\n",
"估计的均值: [[41.18312957 10.83879254]\n",
" [30.50414658 40.12604912]\n",
" [14.84810357 25.42878115]\n",
" [46.29622212 17.58375627]]\n",
"估计的混合项系数: [0.18569448958535423, 0.15997159018086787, 0.3282151691288174, 0.3261187511049607]\n",
"隐藏变量:\n",
" [[3.31335414e-15 9.99999998e-01 1.61889906e-09 5.81515994e-11]\n",
" [3.21387144e-09 8.24374476e-09 9.99999989e-01 9.43230166e-12]\n",
" [2.94788974e-15 9.99999982e-01 1.79605755e-08 2.18639468e-11]\n",
" ...\n",
" [1.10137906e-24 7.64088260e-03 9.92359117e-01 5.26291260e-24]\n",
" [1.14655539e-06 4.27898346e-09 9.99998847e-01 1.92307734e-09]\n",
" [9.61130658e-01 7.60259782e-16 4.71562468e-13 3.88693424e-02]]\n",
"迭代次数: 51\n",
"估计的均值: [[41.07698556 10.8966806 ]\n",
" [30.50514873 40.12098516]\n",
" [14.83951008 25.43387177]\n",
" [46.34044026 17.54174206]]\n",
"估计的混合项系数: [0.18530742494927321, 0.160025358120896, 0.328000434919629, 0.3266667820102022]\n",
"隐藏变量:\n",
" [[3.91891900e-15 9.99999998e-01 1.60920346e-09 5.24745268e-11]\n",
" [3.92404373e-09 8.33412619e-09 9.99999988e-01 8.68166581e-12]\n",
" [3.52214929e-15 9.99999982e-01 1.78660786e-08 1.96578584e-11]\n",
" ...\n",
" [1.53157233e-24 7.57071641e-03 9.92429284e-01 4.39195061e-24]\n",
" [1.37006739e-06 4.33889502e-09 9.99998624e-01 1.79670445e-09]\n",
" [9.61037857e-01 7.66784043e-16 4.60755211e-13 3.89621427e-02]]\n",
"迭代次数: 52\n",
"估计的均值: [[40.96124084 10.95827601]\n",
" [30.50617541 40.11569488]\n",
" [14.82994447 25.43940187]\n",
" [46.38537026 17.49431361]]\n",
"估计的混合项系数: [0.184735716419081, 0.1600816264967176, 0.3277615877129701, 0.327421069371231]\n",
"隐藏变量:\n",
" [[4.68220052e-15 9.99999998e-01 1.59823003e-09 4.69255983e-11]\n",
" [4.86508296e-09 8.43191674e-09 9.99999987e-01 7.98083648e-12]\n",
" [4.25513812e-15 9.99999982e-01 1.77588539e-08 1.75174394e-11]\n",
" ...\n",
" [2.18311289e-24 7.49556571e-03 9.92504434e-01 3.62551537e-24]\n",
" [1.65966416e-06 4.40406491e-09 9.99998334e-01 1.67864603e-09]\n",
" [9.60772799e-01 7.74756856e-16 4.49811146e-13 3.92272010e-02]]\n",
"迭代次数: 53\n",
"估计的均值: [[40.8336336 11.02449641]\n",
" [30.50723375 40.11015359]\n",
" [14.81919921 25.44548984]\n",
" [46.43100144 17.44049186]]\n",
"估计的混合项系数: [0.18394211959930148, 0.1601406076683685, 0.32749325065983137, 0.32842402207249816]\n",
"隐藏变量:\n",
" [[5.66467222e-15 9.99999998e-01 1.58576041e-09 4.15223995e-11]\n",
" [6.14695322e-09 8.53853319e-09 9.99999985e-01 7.32790844e-12]\n",
" [5.21176015e-15 9.99999982e-01 1.76367544e-08 1.54484789e-11]\n",
" ...\n",
" [3.20849856e-24 7.41420725e-03 9.92585793e-01 2.95551455e-24]\n",
" [2.04465055e-06 4.47555591e-09 9.99997949e-01 1.56879355e-09]\n",
" [9.60293591e-01 7.84539685e-16 4.38690306e-13 3.97064094e-02]]\n",
"迭代次数: 54\n",
"估计的均值: [[40.69129382 11.09661731]\n",
" [30.50833313 40.10433146]\n",
" [14.80699457 25.45229772]\n",
" [46.47730953 17.37912843]]\n",
"估计的混合项系数: [0.1828843178614694, 0.16020254671699616, 0.3271881347376156, 0.32972500068391886]\n",
"隐藏变量:\n",
" [[6.96248675e-15 9.99999998e-01 1.57150638e-09 3.62899205e-11]\n",
" [7.95135785e-09 8.65586519e-09 9.99999983e-01 6.72110377e-12]\n",
" [6.49484069e-15 9.99999982e-01 1.74969468e-08 1.34592751e-11]\n",
" ...\n",
" [4.89920772e-24 7.32500325e-03 9.92674997e-01 2.37455683e-24]\n",
" [2.57223578e-06 4.55479611e-09 9.99997422e-01 1.46708132e-09]\n",
" [9.59543753e-01 7.96642659e-16 4.27344639e-13 4.04562474e-02]]\n",
"迭代次数: 55\n",
"估计的均值: [[40.53067202 11.17633652]\n",
" [30.50948549 40.09819498]\n",
" [14.79295201 25.46004941]\n",
" [46.52419917 17.30893878]]\n",
"估计的混合项系数: [0.1815155746104749, 0.160267691122327, 0.32683630047037193, 0.3313804337968262]\n",
"隐藏变量:\n",
" [[8.73078129e-15 9.99999998e-01 1.55508948e-09 3.12653373e-11]\n",
" [1.05903432e-08 8.78643527e-09 9.99999981e-01 6.15944578e-12]\n",
" [8.27279932e-15 9.99999983e-01 1.73357117e-08 1.15623890e-11]\n",
" ...\n",
" [7.84698791e-24 7.22576013e-03 9.92774240e-01 1.87623630e-24]\n",
" [3.32112579e-06 4.64371243e-09 9.99996673e-01 1.37362269e-09]\n",
" [9.58445817e-01 8.11792629e-16 4.15718151e-13 4.15541833e-02]]\n",
"迭代次数: 56\n",
"估计的均值: [[40.34760412 11.26576874]\n",
" [30.51070545 40.09171229]\n",
" [14.77656328 25.46905472]\n",
" [46.57138437 17.22863236]]\n",
"估计的混合项系数: [0.17978768556597496, 0.16033621063248138, 0.32642425845205764, 0.3334518453494864]\n",
"隐藏变量:\n",
" [[1.12262556e-14 9.99999998e-01 1.53602454e-09 2.65038221e-11]\n",
" [1.46200862e-08 8.93357464e-09 9.99999976e-01 5.64381307e-12]\n",
" [1.08294665e-14 9.99999983e-01 1.71482826e-08 9.77675464e-12]\n",
" ...\n",
" [1.33328100e-23 7.11357183e-03 9.92886428e-01 1.45529111e-24]\n",
" [4.42679271e-06 4.74488897e-09 9.99995567e-01 1.28893341e-09]\n",
" [9.56892928e-01 8.31020608e-16 4.03746137e-13 4.31070715e-02]]\n",
"迭代次数: 57\n",
"估计的均值: [[40.13768544 11.36726759]\n",
" [30.5120098 40.08486537]\n",
" [14.75716361 25.47973794]\n",
" [46.61818128 17.13721784]]\n",
"估计的混合项系数: [0.17765839298491456, 0.16040802773653048, 0.32593408289085357, 0.3359994963877011]\n",
"隐藏变量:\n",
" [[1.48801015e-14 9.99999998e-01 1.51372243e-09 2.20827065e-11]\n",
" [2.10642639e-08 9.10156104e-09 9.99999970e-01 5.17835632e-12]\n",
" [1.46525623e-14 9.99999983e-01 1.69288791e-08 8.12915285e-12]\n",
" ...\n",
" [2.43148803e-23 6.98469760e-03 9.93015302e-01 1.10742811e-24]\n",
" [6.12852660e-06 4.86171869e-09 9.99993865e-01 1.21425432e-09]\n",
" [9.54739388e-01 8.55751661e-16 3.91349583e-13 4.52606122e-02]]\n",
"迭代次数: 58\n",
"估计的均值: [[39.89715097 11.48294739]\n",
" [30.51341605 40.07767315]\n",
" [14.73393004 25.4926633 ]\n",
" [46.66323003 17.03453417]]\n",
"估计的混合项系数: [0.17510526517615915, 0.16048251125708687, 0.32534303080515775, 0.3390691927615959]\n",
"隐藏变量:\n",
" [[2.04163116e-14 9.99999998e-01 1.48754288e-09 1.80979821e-11]\n",
" [3.18497291e-08 9.29559280e-09 9.99999959e-01 4.77186409e-12]\n",
" [2.05845185e-14 9.99999983e-01 1.66712380e-08 6.65285646e-12]\n",
" ...\n",
" [4.80439240e-23 6.83459155e-03 9.93165408e-01 8.28565284e-25]\n",
" [8.85550786e-06 4.99846410e-09 9.99991138e-01 1.15191418e-09]\n",
" [9.51793217e-01 8.87845054e-16 3.78418302e-13 4.82067826e-02]]\n",
"迭代次数: 59\n",
"估计的均值: [[39.62424089 11.61388578]\n",
" [30.51494023 40.07022749]\n",
" [14.70594105 25.50854127]\n",
" [46.70428496 16.92189458]]\n",
"估计的混合项系数: [0.17214460805033135, 0.16055801287460342, 0.324624565887793, 0.3426728131872722]\n",
"隐藏变量:\n",
" [[2.90260185e-14 9.99999999e-01 1.45693804e-09 1.46459234e-11]\n",
" [5.06344440e-08 9.52139123e-09 9.99999940e-01 4.43801392e-12]\n",
" [3.00608117e-14 9.99999984e-01 1.63700539e-08 5.38087178e-12]\n",
" ...\n",
" [1.03150109e-22 6.65827151e-03 9.93341728e-01 6.13487613e-25]\n",
" [1.33784266e-05 5.16007503e-09 9.99986615e-01 1.10553105e-09]\n",
" [9.47816227e-01 9.29489959e-16 3.64781366e-13 5.21837729e-02]]\n",
"迭代次数: 60\n",
"估计的均值: [[39.320443 11.75930774]\n",
" [30.51659579 40.06273657]\n",
" [14.67232629 25.52819558]\n",
" [46.73835341 16.80244355]]\n",
"估计的混合项系数: [0.16884637410757108, 0.16063132610391867, 0.3237516024972363, 0.34677069729127347]\n",
"隐藏变量:\n",
" [[4.25903537e-14 9.99999999e-01 1.42169670e-09 1.17908145e-11]\n",
" [8.43208838e-08 9.78425446e-09 9.99999906e-01 4.19334302e-12]\n",
" [4.54474794e-14 9.99999984e-01 1.60234331e-08 4.33425182e-12]\n",
" ...\n",
" [2.38870006e-22 6.45115836e-03 9.93548842e-01 4.54579950e-25]\n",
" [2.10644068e-05 5.35161442e-09 9.99978929e-01 1.07977735e-09]\n",
" [9.42536061e-01 9.82873984e-16 3.50183582e-13 5.74639391e-02]]\n",
"迭代次数: 61\n",
"估计的均值: [[38.99048155 11.91637126]\n",
" [30.51839728 40.0555578 ]\n",
" [14.63246332 25.55249296]\n",
" [46.76236677 16.6807344 ]]\n",
"估计的混合项系数: [0.1653307785575671, 0.1606973011126511, 0.32270115186046233, 0.3512707684693197]\n",
"隐藏变量:\n",
" [[6.39232340e-14 9.99999999e-01 1.38218391e-09 9.53635143e-12]\n",
" [1.45747457e-07 1.00877495e-08 9.99999844e-01 4.05339454e-12]\n",
" [7.04680225e-14 9.99999984e-01 1.56353221e-08 3.51196345e-12]\n",
" ...\n",
" [5.86300176e-22 6.21015299e-03 9.93789847e-01 3.41747899e-25]\n",
" [3.42964143e-05 5.57738922e-09 9.99965697e-01 1.07971136e-09]\n",
" [9.35665405e-01 1.04969085e-15 3.34303283e-13 6.43345945e-02]]\n",
"迭代次数: 62\n",
"估计的均值: [[38.64033301 12.08104155]\n",
" [30.52037102 40.04919636]\n",
" [14.586055 25.58229189]\n",
" [46.77410884 16.56148606]]\n",
"估计的混合项系数: [0.16174075772368837, 0.16074892097158994, 0.3214564938537436, 0.3560538274509778]\n",
"隐藏变量:\n",
" [[9.70441021e-14 9.99999999e-01 1.33933442e-09 7.82245257e-12]\n",
" [2.58622251e-07 1.04329615e-08 9.99999731e-01 4.02983993e-12]\n",
" [1.10754173e-13 9.99999985e-01 1.52154827e-08 2.89010964e-12]\n",
" ...\n",
" [1.49267302e-21 5.93417594e-03 9.94065824e-01 2.63850642e-25]\n",
" [5.72059747e-05 5.84043189e-09 9.99942787e-01 1.11022631e-09]\n",
" [9.26906174e-01 1.13080561e-15 3.16813723e-13 7.30938256e-02]]\n",
"迭代次数: 63\n",
"估计的均值: [[38.27388054 12.24988444]\n",
" [30.52256858 40.04425748]\n",
" [14.53288421 25.61851847]\n",
" [46.77276322 16.44816031]]\n",
"估计的混合项系数: [0.15820441527017362, 0.1607779586472253, 0.3200016136861318, 0.3610160123964695]\n",
"隐藏变量:\n",
" [[1.47708218e-13 9.99999999e-01 1.29422409e-09 6.54892227e-12]\n",
" [4.67715347e-07 1.08197703e-08 9.99999521e-01 4.13150241e-12]\n",
" [1.74843251e-13 9.99999985e-01 1.47752043e-08 2.43078861e-12]\n",
" ...\n",
" [3.87958184e-21 5.62332329e-03 9.94376677e-01 2.10615108e-25]\n",
" [9.71704650e-05 6.14346404e-09 9.99902822e-01 1.17640109e-09]\n",
" [9.15901837e-01 1.22651971e-15 2.97418650e-13 8.40981628e-02]]\n",
"迭代次数: 64\n",
"估计的均值: [[37.88961141 12.42206154]\n",
" [30.52507419 40.04137937]\n",
" [14.47219721 25.66247917]\n",
" [46.7586846 16.34210162]]\n",
"估计的混合项系数: [0.15481075556720164, 0.16077582816619168, 0.3183055613571243, 0.36610785490948294]\n",
"隐藏变量:\n",
" [[2.24936997e-13 9.99999999e-01 1.24737452e-09 5.60661606e-12]\n",
" [8.63622989e-07 1.12512144e-08 9.99999125e-01 4.37024034e-12]\n",
" [2.76732555e-13 9.99999986e-01 1.43202709e-08 2.09344143e-12]\n",
" ...\n",
" [1.02834424e-20 5.27655085e-03 9.94723449e-01 1.73819507e-25]\n",
" [1.68430800e-04 6.49233062e-09 9.99831561e-01 1.28533454e-09]\n",
" [9.02094962e-01 1.33769692e-15 2.75786068e-13 9.79050376e-02]]\n",
"迭代次数: 65\n",
"估计的均值: [[37.47779006 12.60109607]\n",
" [30.52800608 40.04122323]\n",
" [14.40180527 25.71650602]\n",
" [46.73257528 16.24235448]]\n",
"估计的混合项系数: [0.15160844115035227, 0.16073362130535315, 0.31629734144872823, 0.3713605960955666]\n",
"隐藏变量:\n",
" [[3.45442547e-13 9.99999999e-01 1.19813110e-09 4.89806067e-12]\n",
" [1.65282712e-06 1.17410893e-08 9.99998335e-01 4.77203893e-12]\n",
" [4.43083918e-13 9.99999986e-01 1.38446341e-08 1.84221766e-12]\n",
" ...\n",
" [2.83826446e-20 4.88856600e-03 9.95111434e-01 1.47441809e-25]\n",
" [3.02080435e-04 6.90246235e-09 9.99697911e-01 1.45015631e-09]\n",
" [8.84418358e-01 1.46780960e-15 2.51391490e-13 1.15581642e-01]]\n",
"迭代次数: 66\n",
"估计的均值: [[37.01661203 12.79689641]\n",
" [30.53152763 40.04463006]\n",
" [14.3167694 25.78514983]\n",
" [46.69445466 16.14571705]]\n",
"估计的混合项系数: [0.14862287255789436, 0.16063996067563394, 0.3138265696414943, 0.3769105971249776]\n",
"隐藏变量:\n",
" [[5.46450185e-13 9.99999999e-01 1.14415085e-09 4.34391803e-12]\n",
" [3.39102020e-06 1.23260713e-08 9.99996597e-01 5.39788157e-12]\n",
" [7.34672173e-13 9.99999987e-01 1.33251796e-08 1.64818041e-12]\n",
" ...\n",
" [8.58003002e-20 4.44635493e-03 9.95553645e-01 1.27181096e-25]\n",
" [5.77982795e-04 7.41022467e-09 9.99422008e-01 1.69864562e-09]\n",
" [8.60616875e-01 1.62632990e-15 2.23317848e-13 1.39383125e-01]]\n",
"迭代次数: 67\n",
"估计的均值: [[36.46411752 13.02947946]\n",
" [30.53589305 40.053079 ]\n",
" [14.20688552 25.87756984]\n",
" [46.64245783 16.04652179]]\n",
"估计的混合项系数: [0.14588932149846032, 0.1604750936159448, 0.3105888822684617, 0.38304670261713264]\n",
"隐藏变量:\n",
" [[9.27034073e-13 9.99999999e-01 1.08054656e-09 3.88095836e-12]\n",
" [7.94688656e-06 1.30903547e-08 9.99992040e-01 6.39399603e-12]\n",
" [1.31896084e-12 9.99999987e-01 1.27127414e-08 1.48849143e-12]\n",
" ...\n",
" [3.12821415e-19 3.92526397e-03 9.96074736e-01 1.09826416e-25]\n",
" [1.24938049e-03 8.09721124e-09 9.98750609e-01 2.09543856e-09]\n",
" [8.25550007e-01 1.83537779e-15 1.90022855e-13 1.74449993e-01]]\n",
"迭代次数: 68\n",
"估计的均值: [[35.74115028 13.33655987]\n",
" [30.54155883 40.06967601]\n",
" [14.05125878 26.01253574]\n",
" [46.57091622 15.9358256 ]]\n",
"估计的混合项系数: [0.1435070573122507, 0.16019873833298473, 0.30597399553547105, 0.3903202088192929]\n",
"隐藏变量:\n",
" [[1.80835795e-12 9.99999999e-01 9.97976591e-10 3.45851225e-12]\n",
" [2.38693462e-05 1.42289023e-08 9.99976116e-01 8.14380885e-12]\n",
" [2.77106660e-12 9.99999988e-01 1.19107527e-08 1.34515940e-12]\n",
" ...\n",
" [1.63706412e-18 3.28741896e-03 9.96712581e-01 9.27948972e-26]\n",
" [3.38372548e-03 9.15171800e-09 9.96616263e-01 2.81130828e-09]\n",
" [7.66355914e-01 2.14423874e-15 1.49258022e-13 2.33644086e-01]]\n",
"迭代次数: 69\n",
"估计的均值: [[34.70650727 13.78371025]\n",
" [30.54938584 40.10092568]\n",
" [13.80905977 26.22661878]\n",
" [46.46660268 15.80097576]]\n",
"估计的混合项系数: [0.14166678166935626, 0.1597299383180467, 0.29884108996230074, 0.39976219005029595]\n",
"隐藏变量:\n",
" [[4.48993861e-12 9.99999999e-01 8.80229337e-10 3.04429363e-12]\n",
" [1.11090618e-04 1.62133550e-08 9.99888893e-01 1.18188651e-11]\n",
" [7.65076418e-12 9.99999989e-01 1.07416858e-08 1.20748358e-12]\n",
" ...\n",
" [1.63652020e-17 2.50259899e-03 9.97497401e-01 7.44527312e-26]\n",
" [1.35486556e-02 1.10011779e-08 9.86451329e-01 4.37141415e-09]\n",
" [6.48997394e-01 2.64525287e-15 9.94211395e-14 3.51002606e-01]]\n",
"迭代次数: 70\n",
"估计的均值: [[33.17333966 14.44706145]\n",
" [30.56052809 40.15633747]\n",
" [13.42380137 26.57063798]\n",
" [46.30308443 15.63304666]]\n",
"估计的混合项系数: [0.14021097938818317, 0.15895839334785702, 0.2877502696370239, 0.41308035762693557]\n",
"隐藏变量:\n",
" [[1.49317722e-11 9.99999999e-01 7.12899490e-10 2.66715189e-12]\n",
" [9.70504583e-04 2.01259483e-08 9.99029475e-01 2.16726883e-11]\n",
" [2.97857460e-11 9.99999991e-01 9.01234800e-09 1.08918520e-12]\n",
" ...\n",
" [4.21240813e-16 1.64257991e-03 9.98357420e-01 5.66685380e-26]\n",
" [8.95247896e-02 1.39517167e-08 9.10475188e-01 8.33718843e-09]\n",
" [4.09525046e-01 3.31099796e-15 4.64200583e-14 5.90474954e-01]]\n",
"迭代次数: 71\n",
"估计的均值: [[30.95950165 15.31216757]\n",
" [30.57336207 40.22633276]\n",
" [12.86126436 27.09834686]\n",
" [46.045063 15.45544285]]\n",
"估计的混合项系数: [0.13843343486474635, 0.15801810386239543, 0.271614234084118, 0.43193422718874025]\n",
"隐藏变量:\n",
" [[5.18862674e-11 9.99999999e-01 5.19894929e-10 2.49566882e-12]\n",
" [1.62160544e-02 2.90632175e-08 9.83783916e-01 5.67855098e-11]\n",
" [1.30314113e-10 9.99999993e-01 6.90760404e-09 1.06220721e-12]\n",
" ...\n",
" [2.81422560e-14 8.99826923e-04 9.99100173e-01 4.48486434e-26]\n",
" [5.61163242e-01 1.14923117e-08 4.38836734e-01 1.25877865e-08]\n",
" [1.14859259e-01 3.39307042e-15 1.03399276e-14 8.85140741e-01]]\n",
"迭代次数: 72\n",
"估计的均值: [[27.75447595 16.1102132 ]\n",
" [30.58169421 40.26751703]\n",
" [12.00835501 28.1180865 ]\n",
" [45.68847699 15.33629634]]\n",
"估计的混合项系数: [0.14126305514391388, 0.15743584783201778, 0.24578295866804803, 0.45551813835601956]\n",
"隐藏变量:\n",
" [[7.75734118e-11 1.00000000e+00 3.63953207e-10 2.80957452e-12]\n",
" [3.80991492e-01 4.48316955e-08 6.19008463e-01 1.85639194e-10]\n",
" [2.75805390e-10 9.99999995e-01 5.15051396e-09 1.25589462e-12]\n",
" ...\n",
" [2.59125894e-12 3.25762837e-04 9.99674237e-01 3.27909525e-26]\n",
" [9.73706107e-01 2.23634644e-09 2.62938860e-02 5.10336845e-09]\n",
" [8.24472702e-03 2.70582169e-15 4.95080864e-16 9.91755273e-01]]\n",
"迭代次数: 73\n",
"估计的均值: [[24.18481322 16.72521839]\n",
" [30.58800887 40.26191858]\n",
" [10.83601077 29.94099522]\n",
" [45.31122055 15.29381746]]\n",
"估计的混合项系数: [0.15512103977319425, 0.1573885153765887, 0.20937043945270897, 0.4781200053975075]\n",
"隐藏变量:\n",
" [[3.50965942e-11 1.00000000e+00 2.54643702e-10 3.64024354e-12]\n",
" [9.69711820e-01 1.36676300e-08 3.02881660e-02 1.17053648e-10]\n",
" [1.85299170e-10 9.99999996e-01 3.85466136e-09 1.70452938e-12]\n",
" ...\n",
" [7.79783158e-11 7.12686544e-05 9.99928731e-01 1.71698841e-26]\n",
" [9.99435295e-01 4.79639174e-10 5.64702009e-04 2.17217390e-09]\n",
" [2.18970741e-04 2.22677834e-15 3.37759077e-18 9.99781029e-01]]\n",
"迭代次数: 74\n",
"估计的均值: [[22.16143103 17.85451889]\n",
" [30.59146778 40.1796643 ]\n",
" [ 9.43204805 31.51845207]\n",
" [45.04951426 15.23633496]]\n",
"估计的混合项系数: [0.17385816539748147, 0.1583035583442353, 0.17639541875459394, 0.4914428575036888]\n",
"隐藏变量:\n",
" [[5.80629509e-11 1.00000000e+00 7.47065506e-11 4.11046873e-12]\n",
" [9.98548160e-01 5.91107447e-09 1.45183381e-03 7.32530873e-11]\n",
" [3.70984422e-10 9.99999998e-01 1.25071111e-09 1.98361096e-12]\n",
" ...\n",
" [1.18676203e-09 2.57646553e-05 9.99974234e-01 1.07104540e-26]\n",
" [9.99973756e-01 3.21863221e-10 2.62412667e-05 2.03159583e-09]\n",
" [1.26294778e-05 2.28970153e-15 1.61151948e-20 9.99987371e-01]]\n",
"迭代次数: 75\n",
"估计的均值: [[21.07057908 18.92872365]\n",
" [30.58327787 40.15870099]\n",
" [ 7.86752405 33.07317914]\n",
" [44.94592973 15.20710569]]\n",
"估计的混合项系数: [0.19961752116565756, 0.15867330470271623, 0.1456995211977265, 0.4960096529338994]\n",
"隐藏变量:\n",
" [[1.46135887e-10 1.00000000e+00 1.18901554e-11 4.25460003e-12]\n",
" [9.99925523e-01 3.78847527e-09 7.44732837e-05 5.45151474e-11]\n",
" [1.01606717e-09 9.99999999e-01 2.24766732e-10 2.07693447e-12]\n",
" ...\n",
" [8.81629296e-09 1.35246042e-05 9.99986467e-01 6.77889956e-27]\n",
" [9.99998834e-01 2.86424191e-10 1.16346901e-06 2.07747606e-09]\n",
" [1.91415360e-06 2.24771057e-15 4.54072715e-23 9.99998086e-01]]\n",
"迭代次数: 76\n",
"估计的均值: [[20.46290344 19.65548765]\n",
" [30.58961798 40.2088799 ]\n",
" [ 6.46178113 34.44884838]\n",
" [44.90233988 15.19254951]]\n",
"估计的混合项系数: [0.22052491225632445, 0.15811820425237072, 0.12359386916714006, 0.49776301432416503]\n",
"隐藏变量:\n",
" [[2.81489306e-10 1.00000000e+00 1.71311214e-12 4.27558449e-12]\n",
" [9.99995027e-01 2.80103294e-09 4.96998067e-06 4.70920450e-11]\n",
" [2.04885885e-09 9.99999998e-01 3.63029413e-11 2.10471557e-12]\n",
" ...\n",
" [3.29808867e-08 9.86671092e-06 9.99990100e-01 5.38461057e-27]\n",
" [9.99999935e-01 2.57800980e-10 6.26307446e-08 2.19620635e-09]\n",
" [5.89089063e-07 1.97529213e-15 1.89085096e-25 9.99999411e-01]]\n",
"迭代次数: 77\n",
"估计的均值: [[20.21669697 19.99330773]\n",
" [30.60039866 40.26974669]\n",
" [ 5.78603385 35.07081951]\n",
" [44.88470835 15.18924617]]\n",
"估计的混合项系数: [0.22991920130746002, 0.15739033846211842, 0.11422715905115136, 0.49846330117927035]\n",
"隐藏变量:\n",
" [[3.83870443e-10 1.00000000e+00 6.03074509e-13 4.28903286e-12]\n",
" [9.99998667e-01 2.35942330e-09 1.33016284e-06 4.51671827e-11]\n",
" [2.84880023e-09 9.99999997e-01 1.35534711e-11 2.12366234e-12]\n",
" ...\n",
" [6.43522095e-08 9.37060736e-06 9.99990565e-01 5.37001150e-27]\n",
" [9.99999982e-01 2.35534803e-10 1.51058269e-08 2.30271283e-09]\n",
" [3.48993981e-07 1.72780104e-15 1.32912232e-26 9.99999651e-01]]\n",
"迭代次数: 78\n",
"估计的均值: [[20.14397814 20.12084303]\n",
" [30.6032376 40.30506238]\n",
" [ 5.56441975 35.23952042]\n",
" [44.87833768 15.18934672]]\n",
"估计的混合项系数: [0.2330242314210044, 0.1569689088904177, 0.11128805974430009, 0.4987187999442781]\n",
"隐藏变量:\n",
" [[4.37371971e-10 1.00000000e+00 4.16118529e-13 4.30303432e-12]\n",
" [9.99999109e-01 2.19211908e-09 8.88850375e-07 4.48241633e-11]\n",
" [3.26305373e-09 9.99999997e-01 9.55178241e-12 2.13581271e-12]\n",
" ...\n",
" [8.37588449e-08 9.48986813e-06 9.99990426e-01 5.53795086e-27]\n",
" [9.99999988e-01 2.24553295e-10 9.83612267e-09 2.35695536e-09]\n",
" [2.92595615e-07 1.59930591e-15 5.84569358e-27 9.99999707e-01]]\n",
"迭代次数: 79\n",
"估计的均值: [[20.12348176 20.16513877]\n",
" [30.60459524 40.32169934]\n",
" [ 5.49645354 35.28652594]\n",
" [44.87631581 15.18958496]]\n",
"估计的混合项系数: [0.23405467200711402, 0.15676215519392384, 0.11038173829883739, 0.4988014345001249]\n",
"隐藏变量:\n",
" [[4.59337829e-10 1.00000000e+00 3.70028349e-13 4.30809591e-12]\n",
" [9.99999209e-01 2.12508062e-09 7.88804602e-07 4.47489620e-11]\n",
" [3.43204492e-09 9.99999997e-01 8.55307845e-12 2.14053372e-12]\n",
" ...\n",
" [9.16903067e-08 9.55309450e-06 9.99990355e-01 5.61206951e-27]\n",
" [9.99999989e-01 2.19355185e-10 8.67327104e-09 2.37695353e-09]\n",
" [2.76798855e-07 1.54280140e-15 4.57633811e-27 9.99999723e-01]]\n",
"迭代次数: 80\n",
"估计的均值: [[20.11782904 20.1801906 ]\n",
" [30.60553293 40.32873992]\n",
" [ 5.47532397 35.30076728]\n",
" [44.87569365 15.18969428]]\n",
"估计的混合项系数: [0.2344031276976603, 0.15667033457081828, 0.11009911592178995, 0.4988274218097313]\n",
"隐藏变量:\n",
" [[4.67541888e-10 1.00000000e+00 3.56614745e-13 4.30928498e-12]\n",
" [9.99999238e-01 2.09808236e-09 7.60326552e-07 4.47289373e-11]\n",
" [3.49495899e-09 9.99999996e-01 8.26208479e-12 2.14209204e-12]\n",
" ...\n",
" [9.44701434e-08 9.56895076e-06 9.99990337e-01 5.63715758e-27]\n",
" [9.99999989e-01 2.17055082e-10 8.34521061e-09 2.38369767e-09]\n",
" [2.72085222e-07 1.51993007e-15 4.24331689e-27 9.99999728e-01]]\n",
"迭代次数: 81\n",
"估计的均值: [[20.11630152 20.18530195]\n",
" [30.60603973 40.33155351]\n",
" [ 5.46868505 35.30523074]\n",
" [44.87550475 15.189735 ]]\n",
"估计的混合项系数: [0.23452201334750492, 0.1566323361541897, 0.11001016890393013, 0.4988354815943756]\n",
"隐藏变量:\n",
" [[4.70510140e-10 1.00000000e+00 3.52475420e-13 4.30944017e-12]\n",
" [9.99999246e-01 2.08746526e-09 7.51605120e-07 4.47229202e-11]\n",
" [3.51767313e-09 9.99999996e-01 8.17250935e-12 2.14257439e-12]\n",
" ...\n",
" [9.54028861e-08 9.57136931e-06 9.99990333e-01 5.64513376e-27]\n",
" [9.99999989e-01 2.16099678e-10 8.24517351e-09 2.38592228e-09]\n",
" [2.70642125e-07 1.51102667e-15 4.14382513e-27 9.99999729e-01]]\n",
"迭代次数: 82\n",
"估计的均值: [[20.1159003 20.18704225]\n",
" [30.60627381 40.33264022]\n",
" [ 5.4665835 35.3066504 ]\n",
" [44.87544751 15.18974936]]\n",
"估计的混合项系数: [0.2345627479815288, 0.15661730139851904, 0.10998197185946357, 0.4988379787604886]\n",
"隐藏变量:\n",
" [[4.71570479e-10 1.00000000e+00 3.51168828e-13 4.30940765e-12]\n",
" [9.99999249e-01 2.08338854e-09 7.48862179e-07 4.47210211e-11]\n",
" [3.52577391e-09 9.99999996e-01 8.14434053e-12 2.14272054e-12]\n",
" ...\n",
" [9.57128445e-08 9.57117177e-06 9.99990333e-01 5.64763275e-27]\n",
" [9.99999989e-01 2.15719777e-10 8.21380780e-09 2.38665466e-09]\n",
" [2.70194991e-07 1.50764186e-15 4.11277215e-27 9.99999730e-01]]\n",
"迭代次数: 83\n",
"估计的均值: [[20.11579942 20.18763644]\n",
" [30.6063728 40.33305044]\n",
" [ 5.46591388 35.30710594]\n",
" [44.87543014 15.18975436]]\n",
"估计的混合项系数: [0.23457674172793627, 0.1566115282588881, 0.10997297462917778, 0.49883875538399763]\n",
"隐藏变量:\n",
" [[4.71946878e-10 1.00000000e+00 3.50751668e-13 4.30936968e-12]\n",
" [9.99999250e-01 2.08185336e-09 7.47988609e-07 4.47204104e-11]\n",
" [3.52864567e-09 9.99999996e-01 8.13538485e-12 2.14276459e-12]\n",
" ...\n",
" [9.58159010e-08 9.57078320e-06 9.99990333e-01 5.64841524e-27]\n",
" [9.99999989e-01 2.15573240e-10 8.20384580e-09 2.38689662e-09]\n",
" [2.70055418e-07 1.50637710e-15 4.10290490e-27 9.99999730e-01]]\n",
"迭代次数: 84\n",
"估计的均值: [[20.11577584 20.18783983]\n",
" [30.6064125 40.33320276]\n",
" [ 5.46569916 35.30725315]\n",
" [44.87542484 15.18975609]]\n",
"估计的混合项系数: [0.23458155854284657, 0.1566093577686685, 0.10997008553797614, 0.4988389981505082]\n",
"0.0007879452125143516 1.011916284210379e-05\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXQAAAD3CAYAAAANMK+RAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8QZhcZAAAgAElEQVR4nOy9eZxcV3km/Ly3lq5eqrfqllpSL+q2JYy1WFK3bNlGYCyTgEGAADtDIIEEG0gyM+GDGXCS75vAfJlgki+EzCTBGPyxBCaAiTcZDMECG9nY2q2WLAlb6l3qraqXqu7a657547mn7+1SdXe11JJa6np/v/pV1V3Pufc9z3n3I0opFKhABSpQga5+Mq50AwpUoAIVqEALQwVAL1CBClSga4QKgF6gAhWoQNcIFQC9QAUqUIGuESoAeoEKVKACXSNUAPQCFahABbpG6JoHdBH5vIh890q341oiEfmoiLwwj+O7ROSuS9mmxULzfTYXcP1nROQjjv9/JSJBERkQkUYRmRAR1wVcd7WIKBFx53n8t0Tkr+Z7n4WixcRTIvKciNx3pdsBLAFAL9D5tJgYMJssULn+SrdjsZJS6h1KqW8DgIg0APgMgBuVUnVKqR6lVJlSKnNlWzmdLpbfrvTksZAkIneIiGlNvM7Prdb+56wxcFPWeU9Y2++Y7fqLCtDzlQ4KNDMVnuGSoiYAIaXU0JVuyGKmRTgmzlkTr/PzkmP/awB+X/8RkQCAbQCG57rwFQd0S3X6nIi0A5gUEbeIPCAiZ0QkIiInRGSX4/iPisgLIvL/icioiHSKyDsc+5tF5Hnr3J8DqMm637tF5FURGbNmwzdmteW/iki7iEyKyCMistxScyMi8qyIVM3Sl8+KSL+InBOR+5zSpogUWW3uEZFBEXlIRIqtfXeISJ+IfEZEhqxr/IHjuvmc+zkRGQDwTRGpEpGnRWTYekZPi0i9dfz/ALAdwD9aksE/WttvEJGfi8iIiPxGRO513D8gIk+JSFhE9gO4bo53+nsi0i0iIRH5i6x9N4vIS9bz7xeRfxQRr7XvV9ZhR622/c5sfbmSJCINIvKY1a6Qfo45jvsHEem1nt0hEdnu2HeziBy09g2KyJet7T4R+a513TEROSAiy619z1m8dReAnwNYaT2rb0mW2UREKiwe7heRs0LzjMva57J4KigiHQDeOUd/N4vIYWsc/ACAz7HvQvhtxueSdd+PA/gQgM9a5+927N4kHKvjIvIDEfFZ55w3Jqzt94vIaYvHnxKRldb288xN4tAqrGf1d9az6hSR/5h9PIAmEXnRej7/LiLTcGee9D0AvyO26eyDAB4HkJzzTKXUFf0A6ALwCoAGAMXWtnsArAQnnN8BMAlghbXvowBSAO4H4ALwRwDOARBr/0sAvgygCMCbAUQAfNfat9a61tsAeAB8FsBpAF5HW14GsBzAKgBDAA4D2Gxd7xcA/nKGfrwdwACAdQBKAPwLAAXgemv/VwA8BaAagB/AbgBftPbdASAN4L9b7bobQBRA1TzO/ZLVxmIAAQDvt9rhB/AogCccbX0OwH2O/6UAegH8AQA3gC0AggDWWfu/D+CH1nHrAZwF8MIMz+FGABPWsy+y3kUawF3W/lZQ2nADWA3gJIBPOc6fembW/1n7coV41gXgKIC/t56JD8CbHPz5guPYD1t9cIPmkQEAPgev/p71uwzANuv3J6x3XGLdqxVAefa7s959n+Neq63n57b+PwHga1YblwHYD+AT1r5PAjgFjrtqAL90npvVXy+AbgD/F8ifHwDH4F/l846y+W2u55Lj/t/S98rCjf0gTlRbfPTJWcbEnSBPb7G2/S8Av8r13HI8508COAGgHkAVgGeznvNzAM6A+FJs/X9whr5Me2c59j8H4D4A/w7gHda2/QBuBdAH4I5ZefNKDgzHi/nDOY55BcB7HAPmtGNfifVw6wA0Wi+y1LH/f8MG9P8HwA8d+wwQnO5wtOVDjv3/BuCrjv//CTOACYD/HxbIWv+vt9p1PQABJ5LrHPtvBdDpeMmxLIYaAoEvn3OTmGEwWMdsAjA60wADJ829Wed8DcBfgoCSAnCDY99fY2ZA/28Avu/4X2q1764Zjv8UgMcd/6cB+lx9uUI8eyuo/uYCv4/O9Gys/aMAbrJ+/wrAFwDUZB3zhwB+DWBjjvOn3h1mAXRQKEnAEpKs/R8E8Evr9y9gAaD1/7cwM6C/GQ6hydr2a2SBbL78NtdzybHvW9n3Asfqhx3//wbAQzONCQCPAPgbx/8yi69XY25A/wWsidD6fxfOB/T/27H/jwH8dIa+3AHABDCW9Sl13hec8P4VwBsAvGbtmxPQF4ttqdf5R0R+H8CnwQcN8OE7VZgB/UMpFRUR5zGjSqlJx7HdoBQCcDbvdpxrikgvKI1rGnT8juX4XzZDH1YCODhDn2rBieeQ1VaAQO2MRggppdKO/1HrXvmcO6yUik/tFCkBpce3gxIFAPhFxKVyO8yaANwiImOObW5Qy6i1fjv7042ZaaXzWKXUpIiEHG1bC0rtbVa/3AAOzXSxC+jL5aAGAN1Z7ysnichnwAG6EgSBcti8/DFQKzslIp0AvqCUehp87g0Avi8ilQC+C+AvlFKpebSxCZSm+x18Y8B+N9PeE+Z+p2eVhSrZx1/IO5rjueRLA47fUetamqaNCWvfYf1HKTVh8eUqUKibjbKfVW+OY7LbMhNOALShz2U2fAzA3wEIgfyQF11xG7pFU4wiIk0Avg7gPwIIKKUqARwHQWwu6gdQJSKljm2Njt/nQEbX9xJw4Mz1QvOhflAl09Tg+B0EJ4N1SqlK61OhlJrtpc/nXJV1zmfAmf0WpVQ5KGEB9jPMPr4XwPOO61cqOmr+CJRE01n9acTM1O881hrsAcf+r4Kq/hqrbX+O2d/tXH25EtQLoFHmcLZZduHPAbgXNJ9VAhiH1Xal1OtKqQ+C5pAvAfiRiJQqpVJKqS8opW4EcBuAd8HhJJtHGxOg9K/fablSap21f9p7wtzvdJU4Zoas4+fFb3M9lxyUza/5UPY52WO/FOTLs6AGDFDA0FTn+D3b2L4kpJSKAngGNClfdYDupFLwZQwDgNA5uD6fE5VS3aCU/AUR8YrImwDsdBzyQwDvFJEdIuIBGTEBqo8XSz8E8Aci8kYLxP6bo10mOEn9vYgss/q1SkR+O48+Xci5fnASGBORatB04qRBAC2O/08DWCt0Znqsz1YReaMlYT0G4PMiUiIiNwL4yCz3/hGAd4nIm4TOzv+O6XzmBxAGMCEiN4AMO1vb5urLlaD94CB/UERKhU7M23Mc5wcnw2EAbhH5b6AkCgAQkQ+LSK31jrV2lBGRt4rIBsspFgZNA/PSRpRS/aAd9u9EpFxEDBG5TkTeYh3yQwD/WUTqhY7+B2a53EtWP/6zMGjhfQBuzurnfPht1ueSg7LPvxD63+D43CQiRaDZcJ9SqkspNQwC+4ctB+gfYrrj/4cA/tQad5XgZHQ56M8BvEUp1ZXvCYsO0JVSJ0BV4yXwRW4A8OI8LvG7AG4BMAIy1ncc1/4NaJv6X6DkuxPATqXU3N7judv9DID/CTqXTlvtBzhhAGSC0wBeFpEw6Fh5Q56Xn++5XwGdM0HQyfvTrP3/AOADwoiE/6mUioA21P8ASjIDsB1KALWlMmv7t2BFDeQipdSrAP4EHED9oG20z3HIfwHfUQScqH6QdYnPA/i2MLrj3jz6ctnJmuR2gv6RHrB/v5Pj0J+BUtZroIkijunq+tsBvCoiE+A7+Q+WmaAOnBjDoLPvedDsMl/6fdCheQJ8Dz8CsMLa93WrfUdBU8RjM13EGh/vA/0Do2BfncfPi98w93PJpkcA3GjxxBOz9njmPuwBfWj/BvLldSC/a7ofwH8FTRzrMF3I+zo4ObYDOALgJ+CEdKEmPx2Z5Py8P0ebzyml5pWkpiNDCrTAJAyHPA6gKB9ba4EKVKCrg4Rh0g8ppZrmPPgy06KT0K9mEpFdlqmnCpRwdxfAvEAFurpJRIpF5G7L3LQK1Pwfv9LtykUFQF9Y+gRoFzwDqmPZ9uECFahAVx8JGF46CppcTsLhI1tMVDC5FKhABSrQNUIFCb1ABSpQga4RyrdUZiWAb4DhgwrMZPsNGKGwGszaulcpNTrbdWpqatTq1asvvLUFKtAsdOjQoaBSqvZy37fA1wW61JQvb+ebKfoPYCrrB6zY4hIwRnKPUupBEXkAjGOdNT5z9erVOHjw4GyHFKhAF0wiMlu24yWjAl8X6FJTvrw9p8lFRHTm1yMAY1KVUmMA3gPg29Zh3wbw3gtr6tVNSgE9PcDhw/wuuCSuLhKRShH5kYicEpGTInKriFQLK0++bn3PWGGzQAVaTJSPhN4CRm58U1h0/RCAPwWw3MpGg1KqX2cxZpOw/OXHAaCxcbbs4quPlAIefxw4cAAwDMA0ga1bgV27ALmSiekFmg8tiPZZoAItBsrHKarLqX5VKbUZrHswW5rwNFJKPayUalNKtdXWXnbz5iWl3l6CeVOT/TlwgNsLtPipoH3mQQUV9KqifCT0PrBE5z7r/49AQB8UkRWWdL4CLPe6pCgYpGRuWNOi/h0MAteYMnKt0kVpn9c8FVTQq47mlNCVUgMAekVE1w7ZAdaGeAp2kaaPAHjykrRwEVNNDXncNPlf/665mLVKCnQ56YK1TxH5uHC1oYPDw3OuDHZ1UkEFveoo3yiX/wTge5aNsQNc2cYA8EMR+RhYoOieS9PExUsNDRRYsgWYhkteXLNAC0QXrH0qpR4G8DAAtLW1XZt2iIIKetVRXoCulHoFXJAgm3YsbHOuLhKh9tnWRh6vqSGYF7TRq4OUUgPCdS3fYFXi1NrnCVDrfBBLVPsEMF0F1RJLQQVd1LRYViy6akmEwkpBYLlqqaB9zkQFFfSqowKgF2hJU0H7nIUKKuhVRwVAL1CBCjQzFVTQq4oKxbkKVKACFegaoYKEfhWQUowUK2i9BSpQgWajAqAvcirkdhSoQAXKlwqAvsjJmduhAf3AAfqpCmbNAl3VVFA9F5wKgL7IaXgYiESAvj6grAyoqpp/bkdh3BRo0VFB9bwkVAD0RUxKAYcO8VNRwW1NTQT1fHM7CuOmQIuSenuB/fuB8nIgGgX8fv4vqJ4XRdc0oF9Nkmmutvb2Ap2dwMaNLHQHAO3twEc+wuMPH567XwWTTYEWJQ0PA6dPAxMTNmOWlXF7QfW8YLpmAX0xSKaz8ZtzXyAAHDzIj7OtGoS3bAGam8n7Y2P8fuih/PpVKMdx7ZJSCr29vQgGg6ipqUFDQwPkagG0ZBI4e5aMrRm5s5OSi8jcAL0YBvgipGsW0K+0ZDobvwHT942NAf39wNveBrhcdltXrOBvpYDqaqCyEhgdBTo6KLXn069COY5rk5RSePzxx3HgwAEYhgHTNLF161bs2rXryoN6tiRTX08nkFOy8XqBlSvJ0CI2oz/1FLfPBdBXeoAvUrpmAf1KS6az8RswfR8AHDkCjI8TuHVbvd7zS2k0NwMjI7P3K1v6L5TjuPaot7cXBw4cQFNT0xSgHzhwAG1tbZdnZbCZ1M9ckkwmw99aWtm6FWhtBdaupe08GqXEvncvsGaNLYXMBtBXeoAvUrpmAX0+kumlMMXNxm/O/0oB6TTNKL29dHgqxbbW1tLc4iyloRTNLTP1K3s8ZTLA6tXAm97E/evXk9+vtBBXoIujYDAIwzBgWAymfweDwUsP6LOpn9mSTDAI7N4N7Nw5HahbW6dLGsEgsGoVJRB2aHZJJZEoqJ456JoF9HwLxV0qU9xcE4oWXI4eBU6eBMJh4PnnaU5Zvhy49Vbyd08PcPw4zwkE5u6XczyJ0HH6/PMcP34/x8ESFmCuGaqpqYFpmjBNc0pCN00TNTkAbcFt7bOpn1qSEaEqeeYMkEoBk5Nkfg3UodD0wl+JBPDkkxyQ2gQzm6SSTlOlHRgASkvpUL355iWvel6zgJ5vobhLZYqbC3i3bgWeeIJgq23kySRw4gQl885O4IEHGAgwOMhz6uqA3/5tgvOKFYDbzfb39ADf+hbw1rdynOgxMzICdHcz5FGE2/bs4flNTRfetwJdeWpoaMDWrVvPs6E3ZAHaJbG1z6Z+aklGr0E6OmpLJaWltme/uvp8O3t///wklfZ2mm2iUTqV3vveJa96XrOADuRXKO5SmeJmm1CU4icUIi9WVdFenkrRzFhRwfDcH/2IUnVzM6/56qvAww9Tei8tBU6d4mdigvvr64E/+ANK/qZpbx8cBOJxoKSEY+nRR4HPfGbJ8/5VTSKCXbt2oa2tbVbJ+5LY2mdTP+vrybw//jEZMRol4/3qV8CxY5RK6uqABx+kVK6l65YW2hdXrAA8Hko3IyPAt79NCUdL7tmSSnk5P0ePEvSXuKSyKAH9coaXXsookJkmlN5ehig2NxOQKyvZV7ebY2BwkCaYSMSeaGIx/q+r4/HJJLBvHwG/vp7PbHgYePFF2ss7OynwdHezHStX2ppsRwfbkMs0WQjnvXpIRNDY2DgrMF8SW/tM6md9PdXO117jcWNjtBuuWEGvf1kZsH07mW33bjpAfT6e//zzlLjLyjgITp+mujoxwW3NzUBxMe+dj6SyRJl60QH65Q4vvRKLsmitYNUqCheTkzQJjo0R1F99lZpqJELeLS6mIKMUhZeyMo6ZVIpAn0hQwhehWbG1lb8HByn9d3fTTr98OR2kegJpbCyE814pulwx5POxtedNM6mf2iyyZg0ZNJMhc4+Pk7FLSgjSp09TFS0uBoqKCOSNjWTMkhKqph4Pj1m1iteIxXjv9nZK/bNJKg0NS5apFx2gL4RNW0/Ow8OUZL1eam0zTdKtreQr4PJEgWitoLISuOUWgm0mw3b7/RwjOtIrHqc2uXw5x8TatTxvZIT70mnyu35WqRQBvrOT1167FvjpT7l90yY+154eWwMphPNefrpYu/Z8JoN8be3zplzqp5ZUAgFK1L/+NbeHw2SsM2cIuhMTtkpZW8tjkklKKpGIrY6KcHs8TiZvbqbtPR6fXVIBlixTLzpAv1ibtlPifO014Nw5TvLXX08nuHOSziWdXoookFx5FlorqK7mJLJ5M3l3chJ49lmOiVCIQkoiQZ5dv55mw+PHaU5xgj/Afh05Anzta+yzYfD6b3wjBZvhYR7j1EAK4byXny7Gru2cDEQE4+PjaG5uxj333IPGxsacwN7a2ooiS2JZv379jMddEOUKJVSKdj+laDdfvZoqZzJpx+oClNQ1WGtA1oxqmpTEdcRMLEY1taRkbkllCTP1ogP0bJt2JmNnUvb0zG0K0xKn308+WbaMoN7SMr32j1LAyy8DTz9NsA8EuG2hJ/KZTBrvfW/u+HKA46K/nzxcXk7JfONG7rvhBmqwv/wl+V0/C8PgsX4/AwAAW0C56SZODHffDWzYMP0ZFjJJLz9l27VFBJFIBHv37sX27dtnlbj1ZNDY2IijR4+iq6sLR44cQUdHB+66665pUn4uTSCRSCxcnHqupAfTpORsGBxEb3kLQTiZJGO63VSZIxEyeiRCs0ksRjA/eJDXjUSofmrSgKwdo3NJKkuUqfMGdBFxATgI4KxS6l0i0gzg+wCqARwG8HtKqeTFNshp0xah0xCgs++FF+Y2henJeXISGBoiz8TjPHflSr57bWLbvZtSfH8/wW/z5oubyGcqsDWb9ud0TG7dCnzlK7ZGaprk86IiTkq6P2NjvK7HQ543TbsNmoerq+1xZZrAjh0E9OznVljY/fKT064tIjh8+DDa29sBAMePH5/V/KIng/HxcXR1dcHn8yESiUBEsH///ikpXymFl19+GU8//TSuv/56BAIBKKUWNps0F3N3dQHvfjeZVg+Cnh7gn/+ZjOu0DZaWAnfcQZv70aME+njcZmLd/5ISSlwiHAR6/0ySyhJm6vlI6H8K4CSAcuv/lwD8vVLq+yLyEICPAfjqxTbI6W85dow8sGGDnYuwezed5tu2nQ9OWjg4doyS6tiYnXhWW8taQMnkdN9Nf79tjmtstCfy+TrJZ5LENa/nk6rv8VCAWbaMAorOiHa76Utqbrb9TSIzg7nbDdx7L007c7V/qS/sfrkEFSc57dqRSATt7e3YuHEjNmzYMCvoKqWQSCTQ39+PsbExDA0NIR6PIx6Pw+12o7a2FsPDw2hoaMDjjz+O3bt347XXXkN/fz+ampqwefNmGIaB4eFhAJifQzbXgMhl2nC5COZbtkw/3+Oxo0+0WUZ78V98kXb2gQEOWu0Q1RK6223fZ+3auSWVJczUeQG6iNQDeCeA/wHg08K3fyeA37UO+TaAz2MBAJ33I9gFg/aCDkeOcPKPRICvf51A3NpKkK+poc34z/6M4a6jo3QaattyZSUl26oq+mRGRniPQICmO33d06eBd72LQDiTmSS7xpDmkZkkcV1ga65U/f37+Tl2jCCuFH1Epkl+Doc5KVVVEfBLSsjzqRSvo+3/8Thw5500M7pctnlptslpiS/sflkEFSc5Y8j37t0LgLbt0dFRTExMIBKJYHh4eBqgK6Xw2GOP4dlnn0V3dzf6+voQDAZRV1eHhoYGrFy5El1dXUgmk1NmmTVr1qC/vx9VVVXo7u5GY2MjTNPEwYMH0dXVdZ5DFkBuZ+tM0kpr69ymDW1Hd7nskC6l7ONPnuR1lCJjt7dTLdWDQCkydSpFFfv++22JSEtrR46cz9hLlKnzldC/AuCzAPzW/wCAMaWUNnL1AViV60QR+TiAjwOYt5qn7buhEEG3uprv6brrgO9+l87DqioeU17O2j4tLbZm9sorTMJpauKk3tEBvPQSjx8Y4PvfvJnv/PXXySvbtuUG5/37yUOdnbkjoWbyw+QqsJUrAc7vZ5ihaVIw0dK330+7eThsn1NWxv7qySyR4LU9HmDdOv5/5BHgvvvYttmqPi7BUN0putyCSta90djYiO3bt+PYsWM4cuQIuru7AQDj4+PYsGEDampqEAqFpkw03/ve9xCNRuH1elFaWoqRkRH4/X6UlJRgbGwMVVVV6OjowMjICEQEgUAAq1evRldXFyKRCE6fPo1t27aho6MDq1evnuaQbW1txaFDh3JH3swkrWTXY8lmbqWAxx6jBHb4MMEcoARfUsLBMT5Oe+INN/C8sjJu0/bEdJrXrq0F3vMeDlbDWNKhibPRnIAuIu8CMKSUOiQid+jNOQ5Vuc5XSj0M4GEAaGtry3nMTKRNYbt321FMmqcGBij9ihD0XnqJk7gG1GXLOAFEIgRDXXJ2wwYb0I8fp/RumqwdpM04ucB5YoJO1Jtvzm0Ln8m5mKvAlhM49b0GBiiYlJRQIHFbb+YNb6BW+YtfEHyPHCH/V1eT55cvpxba0cFJLBzmed/8JjWRdeuA732P0TG1tXx+eiweOrTkx8MVEVSc1NDQgObmZjz//POorKwEAGzcuBE/+9nPcPToUVRVVU3FkA8MDKC5uRkigqKiIgwODmLt2rVoaGhAV1cXOjo68NJLL8E0TQwMDKChoQGbN29GY2MjXn/9ddx///3wer3o7u4+L9Ho+PHjM0fezCStZNdjyaW27tlDxtYJQ9EoQdrrJXMPDHAA3XQTJTCXi8lGLhePKS/n8StXUqoyDNa/ePVVXnv9+uk1p9vabOfVEpRU8pHQbwfwbhG5G4APVE2/AqBSRNwW89cDOLfQjdOmsBUrOMnraJTubvLSq68SAJUin0xM8B0WF5MnqqpoQhkaIuht3szrjo8T4NraCPLZMeq5wHlykj4czdMinCz27mXymzMUMVtYmU370/fKZAjAyST/a2d+PM4s6hUr7BWMWlrsJCO3m59Egv1qauLYGRggkKdSNBOVlvKzZg0nmOPHl2yoLoArK6hktQNtbW04duwYKisrUVZWBqUUjh07hhUrVkBE4Pf7cfjwYUQiEYyMjMDn86G4uBhlZWUYGRlBPB7HmTNn0Nraig0bNkwB+vHjx1FZWQnTNLFz505s27YNvb29ORONABvclVIYGxvD4OAgjh07hob16yEzmVZmY24dyphKEZwrKnheWRmZUUvfx47RcRoKcZCOjXFgj47yvHCYgzudBr78ZUrmdXWMiDl1ikyrF8oYHub2JSqpzAnoSqk/A/BnAGAx/n9RSn1IRB4F8AHQgfQRAE9eigaKUHLu7+eEfPo0gcs0+U4TCYLtmTN8fwcOEOAqKhjVdOYM97/2GkFehOabcJjAX1FBgHNmCw8Pkz+c5pVt23ieBltdGwggOOYKRZxLMDBNgm0sxmvEYmy7TqCbmOD5W7ZwDPT3c391NfsSDvNeFRWcDHQRrr4+jo1AgJOZ388Jw+228zCAJRuqq+mKCSrZVFtbC7/fj/r6ehiGga6uLoRCIRw/fhyGYSAWiyEUCk05Qr1eLwKBAMrLy1FVVYWwpZaJCJRSGB8fR0VFBdra2rBx40bU1tZO2cNnSjRav349XnjhBWQymalwyHA4jB//+MdIJBLY1dYGyV5Sa66okZoaMrIGa8MguOswroYGRrlEIpS+i4spwfh83B+LcbD7fFSlx8e5bWyMDN/XxwF7+jSl/S1bKBEtYUnlYuLQPwfg+yLyVwCOAHjkQi6SbzSJ9o+I8FNaSlCNxSidRyLcVlxMybW6mlJtczOPT6XsUMjaWtv84tTSskNqm5u5r7bWLlNx4ADv1d5uXyM7fj0X32T3Uztx9+5lm86dsyciwA7XHR7mxDI2xvsqRV4uKSFQL1sG/P7vU8j55jdpRtGRX0rxGuk0z00mbU1g3TqGci7BUF0Al1dQmSuzU4Psnj17EIvFMDY2hkQigfHxcUxOTk45SX0+H1wuF1KWJ/zGG2/EbbfdhvHxcTz33HPo6urC5OQkgsEgwuEwiouLUVFRgS1WxElPTw+CwSBaW1vR2to6ZZ/XWaO6De3t7SgvL5+KvDlw4ADaPvlJNG7dOvd6ijpzrreXUsrkpF2UKJPh4AQoVWzYwEHb1cUBoSWYaJRefb34xdmzDPNyXiuZ5MAMhcjg7e0sN+r1LmlJZV6ArpR6DsBz1u8OADdfzM3zrSOii1lt3Mjtv/oVpVWXi/tTKW73eglwqRQn89FROzFt9WoCo2ky10E7WPW7BkS449AAACAASURBVHKH1L7jHTYfaHOhFZiADRvsCWY2nsnVT+3E1Zri5CT5Nh63zSmJBK+tqzH29pKPtbaRSAA33siorXXrgB/8gNdxu/mtx46+X0UFr19ZaedhLMFQ3bloQQQVTfmm+SuloKwMyv7+fkSjUYyNjQEA4vH4lN28rq4O8XgchmGgoqICLpcLlZWVCAQCOHz4MHp6etDY2DgNjGd1eDrasGvXLhQVFSEej2PNmjWoqqqCiMAwDARDITRu2XI+g+dKLspkqBoPDFAiSaUogWiG1Kn9p09TzRwbs0MUdUapywX8yZ+Q2f/2b207uS5TWlZmS3luN88fGFjymXJXNFM03zoiTp/MyAjfZ0UFvzMZu25PMjk9uUzbpo8eJTjrRLOuLoJaRwedjFVVdLJrYAZyT+zaXLh9O4UPXf62pGR2nsnVz5/8xHbiaj+R1jhLStin6moKMH19tnPXNLlNhBNTZSX3nzjB826+mUAfDHK7x8N2+nwE+euuozB0/DgnibVrOQku5ZWMFlpQcVI+af69vb04ePAgNm7ciLGxMZw5cwZutxulpaWIRqOYtKJD4vE4JiYm4Pf7YZomlFJTJpKglkpAE86GDRtw7NgxHD9+fEqqb25unrENAE02GzZswAsvvADTNNHb24uSkhLMWswr1wpFzrrPbjdNLoZB88vkJBm+spJhXckknWJeLwdiebldVXHrVtsZpqUcLaXr0MaaGu4PBsnohw5x369/TUYHlpSkckUBPd+SC85JV1fOrK62K2vqcD9tTxchUO3YQU2svZ18cvPN5Iv2dpae1QuMnzxJUFu9mu9dCwMzgXR9PSeK3bttgNaO0Xz7WVVl2+TjcW4vK2O/KirIkz4f2718OQWVQIDbvV57XOioHE0lJQT8qiq28e67gX//d7sUhs8HPPccAwoiEZ5TVwd86ENLQiO97JRP+VrnMRMTEygpKUF1dTWCwSCSySRcLheUUjAMAxHrpd14443YsWMH2tvbp0wkra2tCAaDGBoawj/90z/h3LlzSKfTePXVV1FdXY1Pf/rTM7ZBU319PTKZDHbv3j0F/tu3b0d9vswdjZLx0mnbNlpcbFdMdLnIpDfcQMlchIw/OUnpfHiYzq+VKwnQIhwAy5fblfa6uwnu3d0c9GfPMlLgtdeAz3+e14vHee4XvmAvirEE6IoCer7akZ6s9+zh++7rs5NslCJIaR5yuRgNc999wPveBzzzDN/t2rU8HiAPHjpEgNTbhofJT8eO2bHtzc10Kvb1cR9ASRZge3futCX0cJjHzRbJ4uxnXR1w223UHlIp8vb117MvNTXURAIBahHl5eRln4/fqRT7euAA+fmTn+SxdXW278k0ycdvfzujgXSdo8lJ9tXnw9TCGaEQn+3WrQVQX2jKp3yt85iysjKYponq6mr4fD709vbCZdkWRQQigvr6etx333143/veh2eeeQbxeBxr165FZWUlXnnlFfzyl79Eb28vysvL4ff7UVxcjM7OThw9ehRbtmyZulcikcDBgwfR29uLaDSKlpYWrFixAoZhYOfOnYhGoygpKUE4HEZfX1/u8Mxs5tYZb243B2dREaXxoiLur6nhQCkutmORvV47g1SEAH30KPBHf0TGXrHCZuB4nIz76U8Df/EXHJilpRwYp0+zKFh5Oa+l63qsXn2Z3vaVpysK6PMpuaDNZcGgXQ5ZV9G8/XZO0N3dlEjvvNM2H2zYQOefthtnMrSvA7b9G+D9KyqAd77Tjog6cwb42c+mr+lZV8dkJc2bmiYnZ7ahZ/cznWZ71q+nY7642J40Ojr4qaqiEPLud7MP3/kOTYQTE3YGrK7ECPC+H/6wHfZbXEwNxeejMFReznPHx22TpbPv2kxTAPSFpXzK1zqPCYfDOHfuHCYnJ6fi0q+77jq8+c1vRjQaxfDwMD71qU/h1ltvnWYiqayshGEY2LhxI/bt2wePx4NAIICysjIAgNfrxYkTJxAIBGCaJjKZDB5//HHs3bsXPT09KCsrQ3V1NdauXYuVK1dOm3C0ozUnoGczdypFCfs3v6EqXFpK6VpHqWiJe2TEjmjwW2kA6bS9bNdcjF1fzwFZXMz79vXxeO1Y01pDRwcH7BKhKwros5VcUMpeinBoiFFN9fUE2fXr+f7Ky8kjetWqD37wfIdqrmJfqZQdt66UnVxUUUHwBGgO0XZ6l8vmw2iUUrxOy8/H7+Ls59AQ8I1v0LHrNNd88YsUTIaGgJ//nMJFaSkl/2SSPPxP/0TBx+ezs0VvvJFtbGqaec0B3cfqantlJC1AAWyDrqVUoIWl2ZaKM00T+/btm8rcbGxsxJ49e6CUQmVlJZYvX44bbrgBHR0diMViKC8vx44dO6bAHJg+GYgITp06haKiImQyGYyMjCCVSqG8vBw+nw8f/vCH0dbWhkQigSeffBKmaWJwcBArV65ELBbDsmXLcPz4cZimOc3mP6sNPRdzd3SQuVIpDtq/+Rse9/nP286bSIQD+YYbgH/9Vw7g4uL8GfvIkemSSlMT8NRTtm1RD8qWlsv3shcBXfHyubnyErTj/LvftaXSRIKRHMPDds0Sn8+WmN/85umTgTOKSseH62JfO3ZwgfFXXuH1w2FqZe95j80r2lnpzD7VKfZut60RzKRZ5ArHbGy0tcnmZvYhGmUJA33vwUGed/PN0xPgPvEJCjX/+q92HHpTE4UbPdZyPctcWtCOHSx10NnJY+rquG2J+I0uO+VaKs40TTzwwAPYu3cvDMNAPB6Hy+XCqlWrEI1GoZTCb37zG9x6661obW3FrbfeOlVaF7BDEGtqavDe9753KjlpbGwMd955J77xjW+gs7MTExMTCIfD2LZtGz72sY/B5XLh8OHDcLlcGB4enopiAYBUKoWioiIEAoGpbNJcGsX5vC0QJ3PrUDOPh9sGBuyIgx07uL20lKD+u7/LffNlbF1BT0sqK1cyjnloiNfVktItt1z6F7yI6IoDei7SGcPRKIEvGiWf6MJay5fb8eRDQ/YkfOQItbCDB/nJDoXUxb48HtrXN23iObffDnz0o7bvRJsF/X4eq017RUW2s/Kee2yHZK6w3JnCMTs6pif/iLBPX/witYPBQWoRpmmX89XRPZ/7HPv38st2HPpcDvxcWpAzTBhYuAgX06SzuaOD7+SWW+zJsEDTad++fdi7d+9U5EkoFMLhw4eRTqfh8/mmTCWdnZ3YtGkTWlpaEAwGoZTCwYMHcfDgwfNCEIPBIKqqquD1evGJT3wC7e3tOHHiBN797nfjU5/61JQtXtvsdUldnSnq8XiglMK9996L+vr6nHHzs4Yad3TQbhgO25JVOg388Ifc5rRpNzbSTnmhjJ1LUvnsZ6mu63TqBWBA0zQRiexDPN4Bn68Ffv8tUxPgYqRFCejBIIHTMGxHeUUFJXVdQkIvlLxyJatv6gqKfX30jWzaxHdeWWmHQmb7b1paKAX/4R/mlmr37+fk39NDu3VPD0F/x47zwyoBAmVfHzWBmcpMtLRQMo/HybdKkde7uugkrahgklFXF/m+osJe4KOmhs7et799fmUqcgk4TU0Lu0C6aQIPPMDYeqcp6cEHC6Ceizo6OqZFvxQXF8M0TaTT6amiXPF4HEVFRZicnMSTTz4JwzDQ19eH06dPY9OmTWhoaEBlZeVUCKLTuepyuXDTTTehsrIS99xzzxSYA7aZZt++fVi2bNlUXfXe3l7s2HEXVq7chuFhA8lkI6xKu3nxdmNJib1ghWaCnh5KD62tdq3qri4y7sUw9mz22ttumzqMJYd7kUoF4fHUoKgo/7VbTdNER8cDGB/fC8AAYKKiYjtaWh5ctKC+KAG9pobmNJ1HAFCLa2khnzQ321pbXx8n5PXr7UUwgkHyUE0NTReBALdt3pyfE1bzSmsrhYvSUts8csMNdGR2dzPctqPDtsGbJpl8aMheJ3Tz5ul1X26/nW3ds4cmHKXYznSavL1uHYG8vZ0CjZVbct4CH5d6mbz51jPat296opRp8v++fUvKJ5U3tbS0TIt+8fl8U/HlJSUlMAwDgUAApaWlKC0tRWNjI1588UW88MILCAaD6O3tRU1NDW6++WYEAgEEg0Fs3rx5Wp31aDSKbdu2nRdyqO36ra2tCAQCePnlfQiHK+D1rsT4+Hvw1a8KTp+2l2+87jryRzZvb9pE/hwcJNA31DdAGhqAoSEoCNJphaR/GUxXOcqqA5CmJqiuboSHEzj3xCmUBorR8MKLkAtl7NnqyIBgHgw+jnD4ADQgl5dvRU1Nfmu3RiL7MD6+Fz5fM0QMKGVifHwvIpF9qKhYnEy9KAG9oYFScH//dDvvBz9o12sBCJItLZTYf/1rAsjEBMEEIGCeOkWQ1HWENFA7zQ25SEfAjIzY4YWRCJd+O3yY+8bGKEHr+PWnn2YoY3k5tYT2dlvCdtZ9ue02O09idJQg2tHBY1IpZsRGo+TTVIqA6HZfurIU+WbszkZnztjhl7o66hIMMsibbrnlFmzfvn3Khm6aJt7//vfjuuuuw/79+1FSUgK/349AIIBQKIRf//rX2Lt3LyYmJqZMJIlEAqdOncKNN96IRCKBI0eOYMuWLRgeHsbLL7+M0tJSnDlzBl//+tfR2tqKVCoFr9c7rbbLyMgoamvvRzS6HNGoGz/+sR9bt04gHvejuZn8rxTH1rveZed77N9PII/FqGH++MdAYlMTdr3lDsA00XU4hK6JAHypCajTAl+VwqbNm/FK5DqMd53BAfetGFXrsXU0iF03dUIuAWPH4z0YHd0Dl6sSbrcfLlcFwuED8Pvb4PPNfZ9Y7AxMM4V0egyGUQTDKAFgIB7vKAD6XJTLkZkNvPpdZ6/F+aUvETh0BIhOQNIOzOZmHnf4MKV1Z9lYLVW2ttpF4XT1RZ0zMT5OLTEQIDPrErU+H7d1dRGcDYP37e6mH0iXH9DlBnTdl+5uhsu2t3PC8fvtiUVntZaU8LgzZ6ghOO3pCx1e2NNDjaGykm2pqLBL7M7kJ8j17vQ6qABNVZnMkgsymJWya7p88YtfxP79+9HR0YGWlhbccsstEBHcfffdU8copfClL30JHR0dcLvd8Pl8ME0TExMTMAwDLpcL0WgUTz31FAzDwOjoKAYGBvC2t70NhmHg0KFDeOihh1BSUoJYLIbVq1fjDW94A7Zu3YqmpiZMTFShu3s5AoEIRkfLUFSUQGcn35/mN+3rOXKEgsrAAIWbM2f4fm+8kbyz55UatN70FlS2/wqdsTpUVpkYbtoBpQSJ9gM4Fzcw3mEisX4zKifLUV49iQNdy9C2OojGBWZspRSGhx9FJHIEbnclAAWfrwludzWSSdqRZjPD2KaafphmDCKAy1UNpTLw+RYvUy8KQJ9NQsxl581ei7Olhap9JmPX7BEh4N50EyXmhx7itUdHyZBvexv/HzrEWHOdbr96NQu3ORdkCYenR7pYC6hPhco6QxdPniQoFxXZ2czhME02x4/TvCjCSam+ntvXrOGAGBvjoFGKdYbGxwmS2p6uTTsLGV6oFM1KL7/M5+XxsP/V1cCjj05PVJpJau/tZVvXreOABzjB7ty55IIMZqTZarrcmqXCOCNilFJoaWnBvn37kMlkkEwmUVtbCxGBz+fDmjVrUFpaOhVmqJTCK6+8gvHx8anl7EKhEIaHh1FeXo7Ozk60trbiwIEDWLFiBSYniwGYVn5PEkAJDMMzFd46OcmxFo/zPadSHF+ZDPn/3Dlu4/KOgkeb347funsdTsaDqFxTg8kq2jPHvG2I1QVx3F+DylUlwK9+BQMKhqEQDBehUeVg7IuwAyYSvYhGz0CEjl6XqwjRaCdKSgxEIocQj3cilxlGA/nk5DHE470oLl6HePy05d/tQHX1Tvj9i5epFwWgz7YgylwSoggjTjo67AgRvRZnSwtt1l1d9rWVYrji+LhdJTEUYjhkeTlNPK2t0xdkefZZgq0Oax0ethdvPnHCrsPS0mKbVjIZhtR2dvJeQ0N2iG1LC/tTW2snPRkGv3XqvsvFyaCpiRE7L71Ee2au8MIL5XuleN3HH2efdH7H+Dg1hnDYXs81l7lH31ebut73PvY3GOQzue++gkNUU66aLvv378eKFStQVFQ049qeIoJ77rkHHR0dGBwcxKlTpxCNRpFMJtHS0oJt27ZhdHR0yklXXs6V9CKRCMLhMMbHx+F2u+HxeOD3+xEMBjEwMIDy8nJ4vV5s23Y9vvWtMETGYZom/P7VGBwsQibDd+nzcVxVVNjJczqcN5GwawwFg+Tto+2C225vRN+yRrgqAUPIO6P+RlTtaMToU4C/QmGsei3OnhzHUMyNeGAI6r1baX/XdBF2QKUUJibaEY3+BqnUMDKZCQAZiBTB79+CeLwTPl/TlF1cm2GKihqmbO7J5BCi0ZMoLd0Av38z0ukgTDONFSvuW7QOUWCRAHquWici+UuIjY3AXXfZa3gODjLV//77eX5vr31ti9+nGHF8nJKIx0NACwYpwesl3rTN/dFHyeDl5XRW9vayHZOTBF+/n4Ds9doZmRMTBH7t2HW57GqHSrHd2U5aZ9113c7JSU4QExOcuHp67DDD+fC9E/i16en736dpB6C9tLiY+zdt4iCeqc6O876RCK+VStFh3NzMay5btqBsclVTdk0XEcHp06fx9a9/HStWrJgmsWeDemNjI+66664pqVqvVHT//fdDRPDQQw9NOVcrKipQV1eHsbExBINBJBIJrFq1CpOTk1PVHHWoYm1tLe6/fwtEgnj55QwymRKEw37cfLNgYIDjIBSyy5LrVeGcobw6MlFnH584QQd+W9v5ocO33EKN81/+RXDixDpMjKdR5k3j/+25DneeKcG9PWKHz+ZbuQ/TI1nc7gAikUMIBp9ALHYKgAEREyI+ZDJRZDIRuFzlENHvwQBgIJViqFo4fMAyzVQgkTiLeLwbVVXNKC5uRjzejaKixc3UiwLQc9U6GRsjE80mIWqaLYLJaQ7R6f11dby+XlBl1Sp77VrALivhzGt461sp7YdCdikKEYJ7PE7NwDDsyp+69jhtb/xMThL4R0YYIfOZz5zvpF23juB48CA1ifZ2AuPZs3ZIZmcnJ7Bdu/Ln+2zg16anFSs4CbndfB56cXZnsl2ubFjnfUUI5u3t9sS4hArc5UXZNV1CoRDOnj2LLVu2TO3LVQERmD3bVCl1XmmBD33oQ2hra8Px48enTC/pdBrBYBAej2dq8qivb0Bfn6C1tRYbNtAmrn0og4PkV12lVkvjmhcAe5lEXcJF1xz62c+AP/5jJsOFQnZNrb4+TviPPw4EAoI3vtGDUMiDUz3A0A+Azi6bryXPyn3ZkSzp9ChSqQH4fGvhclUimewHoODx+OD11iGVGgRgQilzSkIHTHg8NRaoGxAx4HZXobh4NSYm2hGLvQaPZznKy7eiqGhxM/WiAPRcOQItLQS+Od7nFM0UwZTr2h/6EAHv+HHb9JJO24CmJYr6ehsERWwpJZEgAycS9pJx0agd3qgZ3eOxF5hIp3lOUREng+eeo5T81rfSWavbpyO4du5kUa01a2h6ee01XlPXOtKgnW/Fymzg16anNWvYrsFB9tE0aT83TUraXV25Qzyz77tlC/t7662MP19CyzjmRdk1Xc6dO4eVK1ciYK1cP1sFRCB3tqnePhPYNzY2IpFIYM+ePVi5ciUymQw2btyIe+65Bw0NjXjiCZnG29pHU1JCMNd87dQyddmI4mJui8c5mStFs104zHH7+c9z6c9t26ZL6oZhR0KJULAoKbEXJZoSRvKs3JdI9CIcPgCXqwzJ5ADi8R7E42fgctVCqRhoahEoxW+PZ9mUtO20odtAbYN9aelNAAzU1LwTpaUb5hXDfqVoUQB6LglbKToy862XMp9rO9f5TCRoIy8vJ/Nu2kRTTVOTDYINDQyLfPVVMqBSlFxqaqbXY9dLJOqa+7rI3LlztsM2lbIrOPb0cFGKkhI6aV0uHrdnj10dMpm0K4FqSam8nNKS7k8efD9VC35sjIOup4cDsL+f9zp3jtf2eNjmwUFqDu94R27bfPZ9laJ0t317ocBXLsoG3kQigaeeegpKqam6LrPWTJnj2rOBfWtrG44fDwKowbp1DQAEzzxDPlu3zubtcJg8q0uMnz5NfjRNCiYAv/XCQ7oarmFwPOiggliMwsCePeSj224j32jBJZXihDE2Zhfd83im83Xj5vwq9yWTw4hGf4NotAPJZB9MMwalMojHhwEkoNf7FklaJieF8vLbkMmwfGpJyXr4fI3gAiINKC/fOi1uvbr6LlRX373ogVzTogB04HwJW6mFW1FnJuldhOGRw8OM8li+nMyq48xfeIEM9uKLBH1dU9/tpioZDpM5dXs1YxqGXc0wFrOB//rr7bDHkhJqIUND/IyPcxAdPUrTRTBIO7RWY6NR3mfzZqrE4+M2yObznAIBmoUiERbCC4XY3p/9jG1OJjkoKyr4fe4ct81E86mUmQ9dbGLT1UBO4FVKob+/f9YqjAt0Vxw61IgDBxohAjxirb/kdpMfDh6kCS8e5/seGaHQcu+95NMTJ/hutClRT+C3387ETqVoqtm/nxFemt/LyuzKpiL0/Rw7Rn6uruY9+/t5/sqVTNhz8vWskpiDlEoiFutEKjUIpWIQcUGpJJQaB+CGy1UKERcMwwMRF0xzEsHgUxBxATBhmompmHQRQU3NLvj9bReUWZpN2bZ9AEinQxd93dlo0QB6NuX5Pi+a+vpoVtBlHzIZFgV79llKEfv28TuZtOu5FBWRuRsbCcpHj9rp/AD3FRURwD/8YUaznDvHSePwYR7X0EATjV7EJRzmQDp6lFLQTTdRWjp6lGGEhsHtDQ2UrjV45vuclOJ9Tp2i1OTx2M7cgQEOMu0wPnuW99QlFXI5W2erEXMh0TbZjt22Nn5CoWsT4GczlSwkOU1tY2MUDAYHyXdjY3aYqdbMtInw2DFGOinF8aHLNsdi5JnxcUZcNTXxmCeeAP7yLymZa7u7y0WQPnyYE8fAALetWgV84AOMsDIM8l1V1XS+th7SrJmgVssh4kImMw6lAMMQAC4AaYtPi+HzrQDghtdbBZESFBevzhnhosHXMKoQi3UhFPoJSkpuRGnpZpjm6BQQA5iznIDTtq+UIBY7BRGguPgGUEvIP2N1PrRoAR3I831eJGXbgsfH7eJw2lEaDNpmFF2/X4cVavX0xRcJyNrUUlXFAfPGN9KurBQzQL/8ZTKuXsTF46GT9vBhSuShECeA7m6af3Sc+ic+QUlmZOR8gJvrOSlFJ6wOOdMx+uk0B3cmw/vU1fHe2h9w7Bjv40w20gtq69LGg4Nss1bBx8dtSW7rVmpAfX2zg3y2fT+TAb73PeAXv7DtuvPNXL0aaCZTyUKSk7911dKxMb4Hj4fPWtvAy8rsCTWZ5H4dmaLXonC5yCPj43z/2in+7ncDP/0p8PzzNn/t2MGyAV/5CnlDO1lffdVeGrS1lb8DAYYfz6dIHMMTDyOTiVjRKhkAYn1cMIxSuN3FloRcibKyTTDNDOLxzikwBgwkk8OIRA4iHD6AVGocodATyGTCECmFUkm43RWorLwDLlcJKiruRDodQiSyDy5XCVwuf05w1rZ9n68J6fQYJiaoYrvd5XC7K+eVsTofWtSAfjko2xYciZDp9ao+Xi8/WuU0DA4AvcqVUnT+nDxpL5yhbd5FRXbqu4hdV2b/fko9LhcH1kc+wlLOxcV2DZv9+9mWzk4C6u7dFw5qvb28jq5/E42yjdoBptXeUIj7dcKUDs9MJKiJNDTwuRw8SC3myBEOdtNkX91uRiW96U1s8759vMZrr00vopfdh5km1Te+kYBxqUoeLAVy8rfm2WiUkvn4uA3mqZTt4K+utiV1nTOhAV2X0NCmRoDnP/kkeUNP7BUVjM7yerktELDzQwYG2I7s7GlgfhpeItGLeLwTZWVbMDoagmlOQqlJAAYMwweXqwqG4YdpRlFd/XYsW/YxnDr1QSSTQ1MSute7DNXV77LAfASjo/9uRcIAIly4O5nsx+TkUbhc5Rgd3QPAjaKiBhiGoKioMSc4OyNmMpkJK+kLyGQm4PFUQ4dKFgB9gSnbFjw2RuDp6iLApVL2CkFFRfytgd3jIVil02Rgr5cMqKVKDYQAmfaRR+xa6JGIXfI5GuXg0mA1MWGn0TuZfj7p+E7SSR9FRXbZgnjcnpxWrLCjFsrKGJnw2mt2rL4INZA3vIHRN88+S+m9v9+2s+vCZK+8Yi+X19/Pfc3NthaRC5izJ1XdRp3odKlKHohIA4DvAKgDYAJ4WCn1DyJSDeAHAFYD6AJwr1JqdOHufOko2xdRXz99gRev156wAU7gurJpIsFJWYR83ttL4A8GyScitrlm82a7XIWz3PXGjdTezp6lwx+guVEpnl9WRv64/no6UHt7uQ3IP+9EUyoVtOLhDbjd5RARZDIJGEYRfL61MAw3gDQMAygqasTk5BEkkwMAPFAqCdOMIx7vweTkSWQyEUxOHrXKAigABpRKWL/dSCYHIDKGVGoQLpcfXm8N3O5VSCR6YBie88CZ0j8jZlyusqn6Oy5X2bRQyYWmOQH9WmP6XM43py04EAD++Z85AJSy0+HjcUqMd95JsLvpJjKetg+OjZHpTZNA5vHwujr1vbeXNvTKSt6ju5uMPzHBc7u7Ceo6YsQwFobpAfZTRxSsWkWgnpjgRNTcbK+/G41yYhoYYHuGhmygFuEzGBnhpKRTvrWtFLCTTgYG+H9oiP2NxXjfnh7uzwbmXJNqXR3bAlx4hFMelAbwGaXUYRHxAzgkIj8H8FEAe5RSD4rIAwAeAPC5Bb/7AtNMSWZ6gZdgkBEnf/3XBGrt69EmNe0UX76cPOb18rhIhGYWHaYbj3Nyb2jgPfbsofklmbQjpADbZKnzM7xetqGhgbzz/PPT49pbWjghzJV3osntDmBy8ghipUPA3AAAIABJREFUsddgGMUQcVvm0Eqk08NwuXwwjGIUFb0Bw8M/hFIppFJxKBUEkARt7Rn09X0FbrcfsdhrDhA3p/YDKWQykxCJW2BMM43HU21J3dHzwNkZMaOUwOUqgQiQToeRTo/D798KpRQikcML6iTNR0K/Zph+tqxKpw16wwbawCcnyYRaIq+tZSEipWgX7u7mb11xrr7elsyjUUYC6NjuPXsIzJEIQU0zvQ5D1ItNazNPJsNjL5bpAbYrGmU0gq5Ds3Ytf+tonWiU4Nvezna73eyXDk0D2N/BQX50XDJgay2679qEom2uw8NU4wHeJxuYsx2s2QXU9HvSBdYWykmqlOoH0G/9jojISQCrALwHwB3WYd8G8BwWOW8DcyeZNTby2W3axHcWDBLE02luX7aMPDg0xHfQ20vw1pmgWlNViqGOf/u3NOXt388JPhajiTGVsoUbveRnJsPJwufjpHLqlB3uCxDw88mn0MSFJw4hkehFJhOHYRQDUJaJI4h0egyZjA+mGUU8fgaZTAZudwWUCoNgbkDEDaUE8XgHDKMYphkB4Q4gqOvfbiu7Ng4gA6VMpNMhJBIDEAHKy3fB661HPN4zzVHqjJhxRrkwm/Ugzp17CLnqyVwMzQno1xLT55tVed11ZO5IxLYNj4+TIVtayMy6+mJPDxkznaaa6WTIRx8lWHZ02OVGUymGDWYy/BQX28xsmgR3j4eMnx02OF+mB3jNJ59k25Yto/Slq1GWlhJs9cB9/XUblBMJTmiGQVD2ejnQH33UtoXqSQaws2IDAW7XxZuSSU4aWmrftYtgnEtTck6qjY3TAf7gQbvA2qVwkorIagCbAewDsNzieyil+kXkvHxvEfk4gI+zrYvDsD9bkpleX3Z4mAJBRwffyblzBPH6emqf+/fz3FiM762szLa1myZ5U9/rkUdsQaamxl6Fy+0mzwQC5KGKCv7evJnvXQs6ejnQsjKOo6Ehjqvycp5jmgplZecQiQxOk2L1whMjIz9FKhWCaUaRSqXhdlcik4kglRqFYVTAMDwwzShMMwVAkEpNwAZp04pRpxRumjHMRKyyOAGXyw+lMjCMYigVt5yk21BZ+TYEg08gEjm/7rrP15hlJ29CPN6DSORgznoyF2tTn5cNfb5Mb52zaBg/H4YPBmlT3rED+Ld/I5MpRSC87TY6Nl98kQ7BRIJAqU0aOp5b2yVDIeA73+E16+sp9etIk6IiHtfQwEFRVkYNoLWV93/9dQ60hgab6Xt7pxdIKikhcOqJJduubppcReinP2Vb9KRTVmbHw/f30yHa2Wn7C86csZ+ZBnid7frLX9qTUTYVFfHawSDbxjAtThYlJbTN/9Zv2WFus9WfcUbu9PQQ0PMo63FBJCJlAP4NwKeUUuF8pCSl1MMAHgaAtrY2Ncfhl4VmSjILBKZnPJ88ye2rVlHIWL6cgsqyZTQRPvww3/XICHmUZgXbeapT/XWm6MmTBHAN+toOryPDtK+mt5c11fViNHo50EzG9hk99xz7UlensHPnyzCMpzA0ZINkIPBehEJPYmTkp/B4lsM040ilBJnMCAyjFEql4XKVAlBIpQYAaO+tU+J2Ug5Gzj4iMwG3uwwuVzlMMwmPpwrp9ChMM4FkchR9fX+LVGoAFRV3wTTDSKfDGBl5FmVlrSgubjrvek6HKTC9nsxlA/QLYXpgcTF+Pgyv1UOlCODt7QTRVatocnjySeD976cdeXyc0sT4OK+jbYY6k275cjJqNtOn05TAEwlOGG43rw8QqCMRRsbo1ZB0Kv7oKK+9e7fd/u3b2e5Dh863mz75JMFcJ0xpR9eqVZSAdHx8X9909dcpeQN2aQQgd7IRnU72M6iuZp+SSU5iWtMxTeBrX6NfQBc6i0Zpw92/f2aAzre8wYWQiHhAvv6eUuoxa/OgiKywBJUVAIYu7i6Xh2ZK9gKmx6LHYuQ9r5cAPjrKcw8c4LupraXTOxTiM9aFuABbc9TVRycmbF+Tdnzq39EoJ4k1ayh5V1WRpw8fnl68a3TUDn0Mh3W26ASuu+55+HyNyGTGkU5HMDLyLJLJYYRCP0YqFUIyGbIqKaagVBqmGUNZ2WZMTv7GMp/MkhmXF3lBiOS1PZ46eDzVSKdDSKeDAExkMpPweJYjmTwLpRQymRgMw0AqNYbh4UdRX/9pJJN900wxTodpdj2Zi6W8AP1aYfp8GF4Dxe7dBMtgkAA1OkoA2r+fauvEBJn+7Fk7PdrjIWDr1YX6+wmY2UwP2BEx8Tivf9ttHAA338xB4CzS5axv09nJSBMtoff1MV57wwZOLJEIo1CGh7mKzMgI2xQKsR3JJM9ZtgxTS/k5ox4uhPQkaBi8n17FSTt4IxFKgj09dCw//TS3+Xx238rKOLkB52sa+ZY3mC8JpZJHAJxUSn3ZsespAB8B8KD1/eTF3eny0ExJZkeOTI9F15nMgO3riEa5b/9+8n1np+3odxat0+GuOuFMZ0hr7c7lspdN1BVCh4dZ2kLnY+zZA9x9NwHc66Xp58UXOW6qq/lJJCYwOlqGycmjiMe7rWzVXkQiB1BaugVKiQWqNKcAJtLpGFyuBhhGJ1KpkQV4oilQqjcg4oVpRmCaYZhmHG53FTyeOqRS/UilBsGVjUZQXNwCj6cRpmkiFutAf/83zqu9Hgi897wSAwtV+CufKJdrhunzYXiAzG0YdjRJNtPv20fTyKuv2mDmjM1NJsm4r77K/9lMr23yWpqfmOAiEzfcQGn19deBn/yEoLhzJ6Xb2loOjJ6e6UCmM/2OHqUGIcIBcuoU29jeTjAdG7Mdlx4P7+1cK/ViKJ22JzGtao+NTbdvx2KcaF55hc9scJCREjrOvKMD+PnP7cVEnGaYhS4z4KDbAfwegGMi8oq17c9Bnv6hiHwMQA+Aey76TpeQZvJHaMqORXeaRUyT52vhQCkKKrquSzJJrSuRsMcBwG/9X79/wJ7YKyvJW5kM+auzkxO9vn48TqFCLyTzwgvTJ2yRElRUDCAW64LHE0Ai0WOZOYYB+CzJPFsSCSMU+hZoXlmQJwsd8cJaRbciEtkHr7cOppmAUilwNSM/XC4PAIVE4hxEXCgpuQGAIBx+GX7/1iktY3R0D8rKWhe0xICT8pHQr3qmnw/Da/ugNsWcPTs701dU8FsDNjDdbKND/rKZXqda68kgmeQ1a2sJ6t3dnGh0qdwtW3hutqRaXExp99w5thcgWJ47Z58zagWT6uJhwSAds3qd1IUgp8RXWsqwzuPHKYW73XbkTjRK1bu2ls9WLxuoK0recgufRyhESX7FCtreL0UZCKXUC6B4l4t2XNzVLw/lUw/fOSGKkI919ElnJ30o4TDfw9GjdgirYdhVEIeHeS9nLkYqZZcB0JO5ltq1rb2oyJ4MTp3ivvJye5Uu50Iy09cF8KOhQSEUOodMZhyJxAC83nokk0NIp0esBCInCQi+c9vEL+w5h5FI9MDl8sM0FQBBInEOSiXgchWjrKwV6fQYTDOJsrINKC6+EZHIfrhcpVNaBiBIp2mKaWj4TA6H6cVTPlEuVzXTz5fhNRhv387fetWhmZheZ4Q6oz50rRfN9OXltsSqpRptl3a57Fh3pQi0fj/t3FrScabcZzP+jh10Yj7+uC2dJ5Ns62OPcSBq0hKZaXJiyraVLwSZph3aqKVAEbvYVzrNGHPTpJTW0sKootdf50Qgwomsu5t9ePhhmq6yQ0sLRMoncitXWCjA3zo+PJmkz2XjRgKvz2cv3qKFEx3xpPkWsH0qPh/HivYB6UgnncykfUBK0exWVWWPB72QjN0+heLiJzA6OgoRNzKZSbjdpfB6m5FKjVrOzmwp/NK651hm4Bg8ngqYZgzMSs1AKaC4uAmVlb+FaPQoJifbwaJcPSgv34aJiaOIxbrg9QYsTZ2mmESid8HBHFgCmaIXwvA6w66vj4A4F9NrgNbgpdPrtUTuchGwa2vpoBwYsJ1NupKdTvl3mm50GONUSdHG3O18+WXaPnV9mFWr7IqNTiemM3b8UoC58z4nT3Ji0ynjGhRKSxm21tPDNmoNQ6/UFAoRzKuqePyaNYW0/9koX4dxrno/zvV6Dx8mn27ZQlNfIGCH1/b12UKLro2uM0d1MpFOTNJLM2qBRSlK4L/92xSE9Dq/TuFClxPQ7YvHe3H27AGUlm4AYGJy8iRisddhmkdBm7ZO/AFsyfxCKd/zFZRKIJMZh8+3Bm53CQAgkRgCEEUsdgJudxXq6j4Kv78NXm8tvN569PV9GRMTryCdpvOzuHg1XK7KS5L2DywBQL8Yhs/+n4vpjx2j5OFkcG2v1ioqwO/ly8nQWu3NZOzImNJSu55KPM7v1auzSopmtdOpfZgm7dOJBEGysZHX1w4qZ3LSpSadbJVO006q/Qajo3w+584RsD/6UQJ1bS0npieeoJlFm7D0M9ahmgVAP58WymHsvI4I/Rs6ga6sjO9xbMz2KzU18b36/ZyQh4fpKDVNnrt+PTXHcJgZz5OTwAc/yGtmL02X7QvRYX2G4UJZ2Wb4fE0YHk4hkeiGLo/LCJQUbGC/UBJop+rs5IVhFCGTSUOpOIqK1gIADKMYLlc5KitvRUXF9vNs4bW19yAW64DbXQm3uxwuVwUSiZ5LkvYPLAFAX8gIiVxMr+2HhkHwHR4m+FRWMvLEGZrY329Httx+OyXpEycosa9fz6iT5mYOgs5OXuO8kqIOcmofq1fTdPHMM/bCvqEQ76dXYXLShQC8toPnikHXpCMV3G67lIBeNT4ateP5c61qtGsXbeYPP0zJPBAgAFyitP9rghbKYdzQwMn1G9+wfRvJJCfheNyuOKp5wO2238/kJCfk0VHyu9//f9p78/i46nr///mZfbI2TZM2bZqmTWlaoHsKBS+CIl8REbxeWUSx91JAK35tBQX8il5QlMULwk+5LMriVaDK1SuLCNcFrsilKy1blyTNvi/NMksyyzmf3x+fOZNJMplMksnWnufjkUcyM2fOfGZy5nXe5/15f15vtaL6rLPUPMpFF6nvgjGmTZsSz4UMLeuz2XJwuRah6x6czkKCwRb6+qrRdQ3DKncgyhZD/rYzuBZ90CuhhDyZCL0PXQ8Ckv7+Zmy2OTidi5FSYrfnkp19TtyI2+UqYu7cj9Hbu5dw2EM43DOprexOeEFPZYVEYaESzl//Wgm5cWnZ3z8wWZSfr6L1/HyVK6yvHygNNOxljRPAmjVKyOMd9Mm4zg29+igpUSeJgwcHrhCMPCUMCLGRIorFsDjoG2HBXEaGuqro7Bz9c+rrU192r1d9NrEukrm5I3c1EkKlXpqb1f/LaINm9icdmZEqtxJNGEs5YH8M6hg0nDRbWwcqYQIBdUy43epqq7d34LbLpeY9FiwYKKG1WFSQEwqpCe7589Ucz0UXDR7PaHMh8ToHud0rCAQasdvnRjxUQvj9lRhGWgpDnI2o2x2t81bL/PtjPzkGIvORPqyhJwcHEMZmS6evr5xQqB2Xq5g5c84fUaBT3TRjNE54QR/vAT9UUEGlBIwFRQ6HiqaNfHFvr/oxJoOamtSinkBAHfygIm6jc3ptrUrXZGaO76CHkdvAZWWpk4/TqfLSR48OztEbpWXG68Uu044n6EZe31jYlAijDNPwwfH51CV2bq768p9/fmJxHs//62QnXrpwJKRUk+VPPz1gx7Bggcpx79qlApF589SJu7VVHUuh0EDnIbtdldcuWTLgWZSRoX7Wr1dR+QcfwCc/ORCgjPV/N1QEbbZc+vsb6O19i/7+BqzWNGy2XCyWOpS/SmxO3QK4SUtbgc2WQyjURn9/FULYI0v9dQZE3IjcbZG/LQw+KahFRcZ+bTYXUtpwOBYSDh/H4SjE6Swe9f0JISaloiUeJ7ygw9gP+P/6LzXJaAjT5s3qgN+7V4ny/PkqB9zYqLZfulQd8D6f+klLUymDefMGuhnFtqQ76yy1n4k2VI539bFihRrX3LlqnwUFKhpTs/EDgq3r6ot8xhlKqI02eIYPtlE7b+BwDDTANkoUDQyvF8OS14jiHA61oKSxUY3z//wf9VmO/gUwK1omi1ir26VL1X2dnWqNQJqa54sughNCBQgf/rAS/9dfV8d9VpY6zg1voLlzlehnZ6uc+8c+NjxAGSuGCDqdi+no+C96evZgteYQCFQjhA2ns4i+vlp0vQEiDS2MaN1icaBpftzuYnS9D4djCZrWG1k9GhvRw+CUTWy0IhkQfACBxZKDlH40rReHYz45OR/Fbs/B49lHZmYZQogpicITcVII+lior1di3tU1YLr/1FNKFA1DISP3bFSjzJ+vxKqmRi06ys1VqRlQXwBj5j8rS0UxZ5+tXmeiDZXjlaM1NKjWXg0N6gvq96vx9vUNVNVYLEpsDSOw7dtVxcmvfqW27+hQ+zfK04xWYqBE21igZAi+UbEASshhwKb34EG1n7o6tfq2pSW5LkYmk0N7uxJwj0f9r4xUiVGhlZs70AzFZlP/d6tVBQalpeo4aW9Xj5WWqon8bdvUcyfj/2l0/nG7i3G7lxIKdeL3l2OzZSBEOkI4kTL2sjKMrofQtF4CgXqk1MjKWo/Hc5BwuBlj1aeUGkrINZLLoWsEg/VYLI5IHbqMCrmuQ3v7c4RCnaTaPXGsmII+hI4OFZnX1qqD2zjQy8tVNcbixUqsa2oGeoiefrqqp87KGlgdakTqRqni4sWqSiA7W4l5qvLCRjS7ePHAlUVOjvpS2mzqsdpa9Z5gIJ8eCqkv5vvvK6FdtGig2YZhSBbrdZ6WprY3ovdYDOMuGGhfZ/i8h0JKHJqbVY5/9271GVdXT55zokl8pFR2EhUV6n/T3a2Ocbd7IH135Ij6X3q98JGPKHM3Y2L0yBEVjRtVSLW1ytfIaBuXqAXieBuADzWycjjmEQg0EQq14nLNQwiNUKgLXVfeKooA4XAIn8+PxSKw2/PJyDiNUKgJXQ9E8umxaZpYjIFZYh63R6pZ5mCxZCOEP1KXfiDSg9SNri8jI2MNqXZPHCumoA9h3jx1MPf1qQPZ4RhwWywuVpGm1arEe+NGdXDW1qqfI0eU8HV0DDSlWLdORaSTHZUaFS/FxepSurNTnYQyMgaaURs+HKDek9Ffsrp6oBNNf/9AVYwQ6uQQCqmSNKOW3MASc+VqnPiM/qRNTQOd3202lcfv61Pi0dY20JQ71c6JJiNjtCLctEmd+Ht6VGnh6tWqNryqSvmrGJOcxiTohg3KF6itTR3PfX3qf9zWpgKB0eajRlvYl4h4Rla6rgyxrNa5aJoHTfOi64YAD+TGVd24nd7eN3G7lyOEA6vVicViJxz2oetGMwtL5Ccc87exLwuGva7VmobFoiGlBSEEUgp0PYgQVkAwGe6JY8UU9CEUFqr8YWXlQA358uVKnD77WXj11YHJI01TEfgnPqEi3e5uJdZHjw7k38vKlJhbLKM3ch5vFAPDK17mzVOi2tqq/tY09QVtaxuY2AwE1N/79w8sDnG7B5oFg/rbMPgy8uPG8w3hN8yedH1glazRyb2rS+Xq+/rU52r4sk+Gc6JJYoxjxFhHYRwfW7ao/9FQn6B49f/Gwrm0tIGJ0kQk24NgJIZWvEip4XavoK+vHJdrOU7nEny+d+jp+TvhcBdSCiDWnEj5p/f3N+N0ziMQaEfTPJH3komUHgYmSmEgBaMz0LHIGUkrhggEWnA652OzZRIO62RmrgWs6Lp/UtwTx4op6ENoaFATluedp9IqdrvKNxp9MWtqBkeX+/apiKOgQN1XX69OCkZOsaJC7TPRwTvRKAbi19v7fAOTVh6Pum2L+Y8by+/tdvUcv18Js1ERYyxqCocHV78Yq2aNtIzhNml41qSlqdcx5g2MptT9/QOWBql2TjQZHeMYkVKlWnJy1Al79Wr1eKL1GqefrkQ/tv3hggUDfUVHYqLWx7EVL8FgOx7Pfvr7q9C0Xo4ffwmHYxF2ez5OZwGaFgL8Q1KCasJTCI1w2IvdngM4sduz8XgOMDx/bsVmm084fBwhnEAQKXWk1NA01ey2r88T2S6Tnp5duN1LmTv3Qvr7a0i1e+JYMQV9CB0dKsL88IfVgW7kgsvKBrsvwuCD08g/w+A67/T00Q/eiUYxEN+PZsUKlXZZvlzt+513lKtdT48SXGOVaig0UKViLBxyOlVE7fGoiLqmZmDy04jQh3qjx5ozGR4dRsnmggVqfBaLmm+oqUm5c6LJKIy2JiPRY0VF8PnPqwqZQEAdH+efP/oVZ3Oz+v4UFg5Mpo/1BG5UvAD091fjchXjcqkJ0r6+ShYs+ALd3YtpaHgQXReRKN0QalW9ImUI1UbOixAhdN2N8ks30ipGuaKqelFpk0Bk8lSlUOz2RYTDrQjhQAiwWrPRtF40rY+cnI+jfNDNKpcZRWwUM3euitaN1AqMHMUsXqxK8p58ckDMlyxREdBoB28qGjjEVry0t6s0SlWVSrO89JKKjPPz1ZVEKKS+lLGVKn19A17ubvdAV6WlSwfSNEMnQzMzVXRv+HsYqRe/f6B3qNEpqbtbvZ9LLoFrr1WpF7PKZWoZrcY/0WNCwGc+M/oqTxh8xSmEEvXmZlW/LmX8E7gytKpPKIjxJkg1zYfV6mLx4pvxePbR1fVXjAVAsXlwIdxYLDZstoLI8zWEyIi4NtpRVrwqUrFaswiHe1F9SnUgHKlh70cIJzbbHCwWGw5HHkI4cDgWomnHSUvbMOU586GYgj6E8UYxQiihklLl2NPTlZifcUbi6NOYnGxuVs+ZyHL32EqD6urBE6SVlfCFL6ixPPjggDVq7ESpIdpGHtwwyTK8aWK3MV4vLW1gH8YJQdPU6xqNpy0WdULRdXXF09ho1plPF4lq/Eer/092fcDQK87Fi9Uiug99KP5iIyklHR3/Nazhw7x5/wgQFXrlQa7FzVVbrVZKSu7j2LEb8fkOYbG4CYe7CQabI6/Rj5Q2wuE23O6V5OScj6b9AtXCrj06QWr0IbVa3aSnryYQaEFKP+Fwd+QzUNG6EHZstvzIZKlrWvLl8TAFfQgTiWIsFrj+ejVJmkz0GbuIqbdXlQ8uXKhSJRNJQ8SbIPX5lIDffLPK+//tb0q4jdV/Rp26zaZuZ2Wpx0tKlFAHgwOlj8YVitEM2PB2NxoIBwJKyD2eAf8Poz49GDQnQE8URprIH3r8Wa0qMCgoiP9/N2rNhzZNzsjYiNe7f5DQg05fX02ksmRwrtrlKsLtXo7P9wGhUBuqp2lOpCdoHhaLHZttLuFwF1lZZxEKtdHd/TektBAKNWO3zyc7+ywAfL73yMjYhKb9hXDYgsXSh5ThyOuq5tKhUCsOxwJyckZe+j/VmIIeh6mIYiB+qWFFhUpLjLSicqQvUez9RvVKvNSQ1Qr33Qff/a6qXqmtVa//zjuq4kHTBmxSLRa49FI1OVperrZvbR2oaDEmUrOzVTnbkSPquYGAqqAwnB+NqN9YYGVOgM5+Ek3kj9UQL17TZCkF3d1/pbv7b7jdp2C356KMsWqZN+8SLBZnNDUD0N9fh8/3HprmZf78qwmFWgiHPfT316PrfoSwYLE4IymTdKxWF8uW3U1v7y7a2n6Dz3cQXQ/Q31+J3T6fnJyPEQ53IIQLqzWIELnY7Tlomp/s7A8zd+6FWCyCtLTTcbmKpiVfHg9T0CeZROWII0XSRuQcb1/xvkSf/rTymYm9X9fVxKMxETV0gmvBAnXyCAaVLXB2tioxTEtTfxtL/EtLVbT9q18NNBbOzlb3G81/c3PVbaNG31idajjzhcPqRJCMl4vJ7CDRRP5YDfGG1prrukZf3xECgQr6+5sIBptxuYrJyFiPWtrvJDNTteOKTdcEg234/YfJyFA5xFCoLbLk3+giVIzFko6meXA48rBYLLhchVitbvLyroi2idO0bhYtuoFQqJn6+h8TDLbidBai7LE7EUKSmblm2vPl8TAFfRIZrRxxrJFMvC/Rnj1qXy++ONhytrZWRfpGRGx8merqVD7T64WLL1bia4i62z1QwuhwqElhl0uNd8MGZWv7+usqZ+7zqWX811yjtn/xRfX8rKyBzvF+v0o/zZ+vXvv00wdWFZrMbkabyB+LwdrQWvNwuCtS776OcNiLzZZDf38NTmcRQ+u7Y9M1Nls2gUAjPt9hhBA4HAuj9rZ9fVUIYUMIK1lZm3E4CoHB3usWi3Jy7OsDTTtOVtZmsrLOoL39d4TDXYCMNKjInpZFQ8lgCvokMlo54lgjmaFfIiHUZOehQypd09ysxHT9erWN0znQVzT25NLWphwidV2lSg4eVNF5OKwmcvPy1D68XvV3bDni1VerskePR02Wbtqk3ovhYx4MDjj1GTXsEzVqMpl5jBaMjCX1ONRdMRhsprv7Tez2ebhcS+jvryUc9tDXV8G8eZ8alK+OTdfYbDm43cX09PwvykzLhdtdTFra2kjruuPY7XMjj0sKCq6LuxLVOGkIIcjLu4z+/mqs1jnYbJkjNqhIpkpnKjAFfRIZLYoZq1Xs0C9RZ6eqGDnnHBV15+SoFEhR0fBIP/bkkp2tnldTo/6uqVHCPW+eGkdVlRrDBReo+uHY92K1qsh97lx1f2en2ufmzcq46amnVIoGlN97dbV67dk2CSqEuBB4EFWY/HMp5d3TPKQZRSr7DMBgi9n+/jq6u/8OSDIy1kecFStZuPA6srI2DxLKoYKcnr4WTfOj631kZKzHbs8lFOokHD6O211CKNQKQEvLU4CgoODaYd7rQydac3LOT9igIlGVjmnOdQKRTEplLJHM0C9RU5Oqilm2TFXJ1NaqyLmiAj71qcFfrtiTS06OiuTffVdNZPb2KvFdu1YtPDI6K1VVqdx8MhNdQqgT03vvKUHPyFCvU1c3vKplojYHk41QpQwPARcADcBeIcQLUspD0zuymcNk+tbHa3Axb97Fw8R85G0/jeGGqGk+gsEm7PYcQqFO7PbcqA9Lb+8ucnORcXp9AAAgAElEQVQvTNiAIpkGFSNV6ZjmXCcYqY9iBn+JAgF44QX12Pr1SjQrK+G664ZXyQwV5LVr1e8zzlB5+NWrVYqks1OlT5YtU4//+c/KhKyoaPT3kpenFhsVFo58AkuFzcEUcAZQKaWsAhBC7AQuBUxBj2GyfOvH0uVnpG0BsrI2RevXm5oeIxhsjuxDRlZ6pkVz4YkaUIzWoCJelc6sNOcyL0sTMxlRTOyXSMqBdm2GOF58cfySx3gnl499TFXIZGUN5NZ7etTtgwfVdt3d8NxzcNNNo7+XZE5gqbA5mAIWAfUxtxuAM2M3EEJcD1wPUDSDBn6iMJYuPyNta9ynrG7fpaXlKaQUCAFOZxFWa2ZKFgQlysNPNeMWdPOyNDkmK4ox9p3sCSPRtsb9772nFhG1tqpqGVCCG5sHH60Gf7TxpMLmYAqId8odZHwgpXwMeAygrKwsmQ4JJtOEEIKCgusAlWaxWtOwWjNTZqAVL+0zG825zMvSGcDYqgnibxvbJOPwYdVz0mgyXVysJk6Td8dLPJ6xlmpOEw1A7LexEGiaprGYpACLxcLChdeRm3thyitRproRdCImIuijXpaCeWk6mxACLrtMReRz5qh8eHb2cJ/siZDqeYVJYi9wihBiKdAIXAlcNb1DMpkok9mseSobQSdiIoI+6mUpmJems42iIrWac+9eVTHT05NawZ3M6ohUIaUMCyG+CryKmh96Qkr5wTQPy8RkVCYi6OZl6QnIVAjuZM4rpAop5cvAy9M9DhOTsSDkUJPrZJ8ohA0oB85HXZbuBa5KFMkIIdqB2nG94GDmAR0p2M9kYo4xdSQ7ziVSyrzJHsxQUnhcxzKT/zczeWxwYo4vqWN73BH6eC5LU/VlE0Lsk1KWpWJfk4U5xtQx08c5GSeRmfyeZ/LY4OQe34Tq0M3LUhMTE5OZg2W6B2BiYmJikhpmq6A/Nt0DSAJzjKljtowzlczk9zyTxwYn8fjGPSlqYmJiYjKzmK0RuomJiYnJEExBNzExMTlBmHWCLoS4UAhxVAhRKYS4dbrHAyCEWCyEeE0IcVgI8YEQYnvk/rlCiD8JISoiv3NmwFitQogDQoiXIreXCiF2R8b4ayGEY5rHN0cI8Z9CiCORz/Osmfg5ThYz7fieDcf2TD6mp/p4nlWCHuPw+AngVOBzQohTp3dUAISBm6SUq4DNwA2Rcd0K/EVKeQrwl8jt6WY7cDjm9j3AjyNj7AK2TsuoBngQeEVKuRJYixrrTPwcU84MPb5nw7E9k4/pqT2epZSz5gc4C3g15va3gG9N97jijPN5lK3wUaAgcl8BcHSax1UYOYA+CryE8uPpAGzxPt9pGF8WUE1ksj7m/hn1OU7i+5/xx/dMO7Zn8jE9HcfzrIrQie/wuGiaxhIXIUQxsB7YDcyXUjYDRH7nT9/IAHgAuBnQI7dzgW4pZThye7o/z2VAO/Bk5BL650KIdGbe5zhZzOjje4Ye2zP5mJ7y43m2CXpSDo/ThRAiA/gtsENK2Tvd44lFCHEx0Cal3B97d5xNp/PztAEbgIellOsBHydoemUEZtr/I8pMPLZnwTE95cfzbBP0GevwKISwow74p6WUv4vc3SqEKIg8XgC0CSGkEGL5OPb/iBDiOxMY4oeAS4QQNcBO1CXqA8CciNEaTP/n2QA0SCl3R27/J+oLMexznKbxTTYz8vhO9tiehqHN9GN6yo/n2Sbo0cYDkZnrK4EXpnNAQohfCSGaUWffM4DY6OUFYEvk7y2o/OO4kFJ+WUr5/Qk8/1tSykIpZTHqc/urlPLzwGvAZ1MxxokipWwB6oUQpZG7zkd1wErZ5zjDmYnHtwAeBw5LKe+PeWja/ycz/ZieluN5OiYLJjjRcBHKtvcY8O0ZMJ7TgI+gLuuOAqHI74tQ+by/ABWR33Mj2y2f5jGfB7wU+XsZsAeoBJ4DnNM8tnXAPuBd4PdATrzPcbr/75P4/mfa8f0PkWP2XeBg5CfusT3N45yRx/RUH8/m0v8UEjkTvw5sl1L+JnLfN4EbUV+K21DRzilSysohz70S+IaMsdUUQnwd+IiU8hIhxFOoy7fbIo9dDNwJFKPO+l+WUr4rhPgX4DNSyk9FtqsE3pZSXh65XQ98Skp5cHI+BRMTk+litqVcZiRCiH8XQviBI0AzEUthIcSFwDdQZV6nAB9LsJsXgFIhxCkx910FPBPn9TYATwBfQp3tHwVeEEI4gf8BzhFCWCL5OTsq14gQYhmQgYoWTExMTjBMQU8BUsqvAJnAOcDvgEDkocuBJ6WU70spfcDtCfbhR+XSPgcQEfaVxM+hXgc8KqXcLaXUpJS/iLzmZillFeBBXeqdi2pA0iiEWBm5/YaUUo+zTxMTk1mOKegpIiKsf0fNqm+L3L2QwXXFo7Upe4aIoKOi899HhH4oS4CbhBDdxg+qOmJh5PH/QeUUPxz5+3WUmJ8buW1iYnICMqGORePghE/Yb926lfT0dIAH//mf/5n58+d/HPgpQHl5OStWrKCioqIi3nNDoRAFBQUcPHhQlpaW8uMf/xjgCwBbtmyhsLAQ4NvXX389RUVFfPvb33YP2cUzwDOPPfYYL7744uerq6v54x//uO2dd97h6aef5q233uK5554D+LdJefPTTwpbWZuYzD7MCH0CtLW1sXPnTrxeL5qm8eqrr/Lss8/y0Y9+FIDLL7+cp556ikOHDuH3+7njjjsS7s9ms/HZz36Wb37zmxw/fpwLLrgg7nbXXXcdjzzyCLt370ZKic/n4w9/+AMejweAc889l9dee42+vj4KCws555xzeOWVV+js7GT9+vWp/RBMTExmDKagTwAhBA8//DCFhYXk5OTwjW98gwceeIBLL70UgE984hPs2LGDj370oyxfvjwq9Im46qqr+POf/8xll12GzRb/AqqsrIyf/exnfPWrXyUnJ4fly5fz1FNPRR9fsWIFGRkZnHPOOQBkZWWxbNkyPvShD2G1Wif+xk1MTGYkU122eMKnXEymFTPlYnJSY0boJiYmJicIpqBPAbquYy7gMjExmWymusrlpEJKSTgcJhgMEgwGsdlsWK1WrFYrFosFq9WKEAJll2FiYmIyMUxBnwQMIa+trSU3NxeHw4EQAl3X0TRNeS7EiLjFYsFms0VF3mKxYLFYTKE3MTEZE6agpxBDyMNh5a3f3d1NVlZWVNAtluEZLsNUJxgMsn//fjZu3Bh9zBD42KjeFHoTE5ORMAU9BRiRtyHkRhrFYrGMmjuPTbkIIaJlhYbQh0IhgsHgsIjeFHoTE5OhmII+TgzBDYfDaJoGMCwfLoQYll5JlpFy68YJIhwOEwqFBj1mCr2JycmNKehjJDZy1nXlcTWS+Bp581QSG80PHRcooQ8EAnzwwQesXr06uq3Vao3m6WN/TExMThxMQU8SKSW6rhMOh0cVcoNkUi6pIlbopZRomobVao2+fmxKKPY5I0X0ZlRvYjL7MAV9FAxxbG5uJjc3d0yCZ4jrVBOb5hktoh9J6I30TWxUbwq9icnMxhT0ETCEPBwOI6WkurqauXPnjknQplPQR2MkoTeeb0z0BoNBqqqqKCoqGlRHHxvVm0JvYjIzMAV9CLETnUaka0SrY82HWyyWlOfQk2UiAjtUoD0eT1S8DaEfylCRNxdNmZhMPaagRxhaQz60btxiscQVskRMZ4SeyglPXdcTRuKxEb25aMrEZPo46QU9npDHE5vxRNsTKVucCKk+iei6nvA9JBJ6Y9FU7OfQ1NREYWGhWWJpYpJiTlpBNypWRqohH8p4BV3XdY4fP05vby+ZmZmkp6eP6HOeKlJ9Ehlv6iTe86SUNDc3s2jRomGLpv77v/+bnp4errvuupSM28TkZOOkEvRkFgONxFhz6FJK/H4/HR0dZGdnk56eTktLS7S7kdPpJD09nfT0dDIyMkhLSxv3+4r32jM10tU0LZqCGUpjYyN2u30aRmVicmJwUgh67GKgY8eOkZOTQ05OzphEL9kcupSSzs5Ojh07hq7rFBQUUFJSQjAYjIqYkYbwer34fD4aGhrw+Xz4fD7ee++9qNCnp6eTlpY25nz4TBb0cDg84hVKb28vy5cvn+IRmZicOJzQgh5vMZBxe6yCN1rKRUpJR0cHVVVVpKWlcfrpp9PV1RX3JCCEwOl04nQ6yc3Njd6/Z88eli9fjs/nw+v10tHRgd/vB8DtdpORkREVerfbPeJ7mMmCbix4ikdPTw9z5syZ4hGZmJw4nJCCPrSG3EirCCGw2WzDFtIkw0iCLqWkvb2dqqoq0tPTWb16dTR90tPTM8xvJRFCCFwuF263m3nz5kXv13Wdvr4+fD4fHo+HlpYW+vr6sFgspKWlDRJ6p9OZUkFP9QTraBG6KegmJuPnhBL0eEI+NF1htVrHXH4Y73mxQp6RkcGaNWuG5cFTVbZosViigp2fnx+9X9M0/H4/Pp+Prq4uGhoaCAQCgDoJ1NfXR8Xe4XCM67VTHe0nEvSenh6ys7NT9lomJicbJ4Sgj7QYKB42m41gMDjm1zAidCklbW1tVFVVkZmZGVfIDWIFPVlRHIuAWq1WMjMzyczMHHR/V1cX9fX1WK1WOjo6qKmpIRQKYbfbB03EJlNxY9Sgp4rRUi45OTkpey0Tk5ONWS3ooy0GiofVah1XykUIQXd3N3V1dWRlZbFu3TrcbnfC54zVnCtVkbDFYsHpdLJw4cJB94dCoehE7EgVN8aPIbqpFvTRInRT0E1Mxs+sFPSx1pDHMtaUi5SS1tZWampqcDqdSQm5wWTY5ybDSFG+3W6PVvjEbhsMBqMTsY2Njfh8PnRdx+Vy4XQ6oyeC8VTcDMUoW4xHIBBI+rM1MTEZzqwSdKP0MBwOs2vXLs4+++wxR7XJCroh5NXV1WRnZ7N06VLC4fCYBCc25ZJsKiUVOfexpG1iK27mzp07aB/9/f10dnbS09NDbW3toIqb2LRNooqboYTDYVwuV9wxm5iYTIxZJ+iapk3I4W+0KhcpJS0tLVRXV5OTk8P69etxuVy0traOOfceu/Q/WbvdVJAKcRRC4Ha7yc7OxuPxsGrVKmDkihshxLD8vNPpHPaeEqVcTDMvE5OJMasEPZkc+WiMFKEbS9JramrIyclhw4YNgyLJ8Sz9n61ui7EMzaEnU3HT3d0drbixWq2DcvPGfUMJhUKTbolgYnKiM2u/QeM1vhoaoeu6TktLCzU1NcydO5eNGzfidDqHPW885Y5jLVtMVZljKksNE1WlxDJSxU04HMbv9+P1euns7KSrqwuv14vD4RhUP9/b20tWVlZKxmxicrIyq5pKxorUeBcIGcKs6zqNjY3s2rULj8fDxo0bWblyZVwxh4m5LU41qRT0iVa52Gw2srKyWLhwIaeccgqZmZls2LCB1atXk5eXF52ruPXWWzl48CBXXXXViPt65ZVXKC0tZfny5dx9993DHhdCOIUQvxZCVAohdgshimMe+1bk/qNCiI9H7lsshHhNCHFYCPGBEGL7uN+oickMYNZF6IZI2my2aG31WOnv72fXrl3k5uZSVlaW1KKb8aZcJkvQQ6EOgsFadD1EIHCM9PQy3O5SYGYJ+lCMiN9qtQ6quLnpppuYN28e991334jPu+GGG/jTn/5EYWEhmzZt4pJLLuHUU0+N3Wwr0CWlXC6EuBK4B7hCCHEqcCVwGrAQ+LMQYgUQBm6SUr4thMgE9gsh/iSlPJSyN2xiMoXMOkE3sNvtY4rQdV2nqamJ2tpadF1PWsgNxtvgYiwngWQj+s7O56ip+RJKjwaYN+96liz5t5SnXFIt6PH2193dTU5OzqBKm1gMn5tly5YBcOWVV/L8888PFfRLgdsjf/8n8FOhPohLgZ1SygBQLYSoBM6QUr4FNANIKT1CiMPAIsAUdJNZyaxKucBA2sWI0EfDWAL/1ltv0dfXx6ZNm3C5XGNeCj+eFnSGoDc2NvL+++9TVVVFW1sbfr9/3JF7KNRBTc1Whoo5QEfHY/T1HU15hJ5MDn0sxBtbb29vwkVFjY2NLF68OHq7sLCQxsbGoZstAuoBpJRhoAfIjb0/QkPkvtgxFQPrgd3Jvg8Tk5nGCRuhG0JaV1dHfn4+Z5xxxoS8tseacjHcFzs7O3G73SxdupS+vj68Xi+tra1Rc62MjIzo5GAy+6+t3ZHwcZ9vH1Ken1JBn4rqk56enoSTovFOgHHeY7w3LRPcb+wnA/gtsENK2ZvEcE1MZiSzVtBHitB1XaehoYH6+vqEQj7WKDZZQTeE/NixY6SlpZGdnU1paSnBYJCMjAzy8vKi22qaFq3nbm9vx+fzsX///qhVrvGTlpaGEIJQqIOenhcTvr7TWUIoNDNz6ImuSnp6eigqKhrx8cLCQurrB4LshoaGYdYGqMh7MdAghLAB2cDxmPujuwOaAIQQdpSYPy2l/N0Y3o6JyYxj1gn6SCkXTdNoaGigoaGB+fPnJ4zIjUqXsUSeyZQtdnV1UVFRgcvlYs2aNVitVt57772E+8zKyopGpn6/n1WrViGlxOv14vV6aW9vx+/3Y7FYcLlqUVmykcfR0vIA6en3z8gceqL0TXd3N2vWrBnxuZs2baKiooLq6moWLVrEzp07eeaZZ4Zu9gKwBXgL+CzwVymlFEK8ADwjhLgfNSl6CrAnkl9/HDgspbx/ou/PxGS6mXWCbmC32/H7/YOEfMGCBZx55pmjCvV4BD3RhGVvby8VFRVYLBZWrVoVrcU2miOP5TUAXC4XLpdrkCe6pmkcPy6oq0t8UuntfRmH4yvYbCVJv24iUplDn4gXus1m46c//Skf//jH0TSNa665htNOO43vfve7lJWVcckll4AS519GJj2PoypbkFJ+IIT4DWqyMwzcIKXUhBD/AFwNvCeEOBh5qf8npXw5JW/YxGSKmXWCboiexWLh+PHjtLa2UlBQkJSQG9hstnFVrAzF5/NRUVFBOBzmlFNOGeblncqyRavVSij051G3kxKam/+A3X45mqZF0zbj9UNPZcplNKfF0ZpbXHTRRVx00UWD7vve974X/VtK2Q9cFu+5UsofAD8Yct/fiZ9fNzGZlcw6Qdc0jZqaGurq6rBarWzevHnMk3bjtdA16Ovr49ixY/h8PpYvXz6ojVwsqXRbDIU6aGmJX6M9+DXB5XqHrKwvYbfb6ezspLa2lmAwiNPpHJabH02sUynoiVadjlblYmJiMjqzTtB7enqQUrJhwwbKy8vHVYEx3q5Fuq5z+PBhuru7KSkpIS8vL2GuOpVL/4PBWoRwoILQxGja/2KzNVFQ8A/R+2IbUxvL8A33RMNQK140n8oc+kQjdBMTk8TMOkHPzc0lKyuLcDg8pn6dsYw1Qg+FQtTU1OD3+ykpKWHlypVJuyemKuXicCxB1/uS3j4UehcYEPSRGlPruh71QjeieWMFbkZGBn6/n/7+/pR5oY8Uofv9/hE7P5mYmCTHrBN0g/FG2ZB8Dl3TNGpra2lubqaoqIj09HQKCgqSfp2xVpqMfgJIPn2jad1JbWexWOKaahnRfGdnJ83NzVRXVwNEm1LHRvNj8UKPF6Eb7zmVK1JNTE5GZp2gG+IxkbK80U4GsbXsixYtYvPmzVitVurr68e9CnOiZYR+/zskKlccisdzD6HQ9djt80bfOA4Oh4O5c+fidDpZuXIldrsdXdejzolG39JgMBiN5mNz8/Ei8UQpF0id5a+JycnKrBP0VDBShC6lpKmpiZqaGubPnz+scsZYXJTqpfCTg8Tvf4fs7PMntJfYHHrsytZYYnPz9fX1+Hw+QEXzRn4+MzOTUCgU180yHA7Pks/UxGRmM+sEfWgUN56I2Wq1Duo+ZFi4VlVVkZuby6ZNm+KW+U22oCdKuTgchWPen6b1THRISClHTYUY0XyssVZsNN/T00NjYyO9vb04nU66u7sHWR6YXugmJqlhViYtY1eLTsQT3Vimv3v3bjo7O9mwYQOlpaUj1mxPpAPRRCdHOzqeHfNzNC01tiTjSYUY0fyCBQsoKSlh7dq15OXlsXz5cvLy8tA0jcbGRg4cOMANN9xAbW0tDz74YNx9jeaDHggEuOKKK0jWBz1y/xNCiDYhxPtjfnMmJjOUWRehx2IYdI3VdMtms+H1etm7d290mX4yFRYTmYidCKFQB21tD4z5eeFwxySMZvxomobT6SQ9PX1QzfmNN97IT3/6U0477bS4zxnNB/3xxx8nJyeHZH3QpZQa8BTwU+A/JvEtm5hMKbMyQjdI1kI3FmOZfk9PD6tWrUpazGH8EfqLL4a55powO3f20tfXN2K0PlLKRU2Ijv11bbbxTYhOFiNNivr9foqKivjYxz427LFYH3SHwxH1QY/l+eefZ8uWLcbN/wTOH+qDLqWsBiqBMwCklH9D2QOYmJwwzMoIPbZrUbIpF5/PR2VlJcFgkKKiItra2oaV6o3GWAVd13X+5V82UFubDqTz29/mcOedPp54Yne0MiQzMzNaGTISwWDDmMZp4HAsHn2jKWSkyc9Ei4ri+aDv3r17xG2klGEhRKwP+q6YTYf5oJuYnEjMSkE3SKZrUbxl+v39/TQ1NY359ZIV9La2Nt5++23+8AdJbe2lxNqF1NWl8+KLZ/Od7/jxeDx4vV46Ojrw+/0EAgGklOTk5EQnDVVjjeQXFA0eb/q4njdZjLSwKJGgJ+ODPsIVz6g+6CYmJxqzUtCT6VoUDAY5duxY3GX6482FJ/O8Bx98kNtuu41wOIyUH8QbPQ8+6OKqq8KsWpU7aNXm+++/T25uLpqm0dTUhM/nQ9d1XK7s4bsZSa5iHm8+uJ3Mc8bfgGcy+qHGm2Dt7u5m0aL4gXMyPujGNoWFhSTrg25iciIyq3Podrt9mKCHQiEqKirYt28f2dnZbN68mfz8/EFCMl5BTxShe71ebrrpJm655RZCoRBS7gBWMpLqbt6cwc6dglAoRDgcRtM0hBBkZmZSWFjIqlWrKCsro6ysjPz8OCV9oxWeCPC4D9PftGuUDUcm1Q2iR8Lj8YxYthjrgx4MBtm5c6dhlRvlkksu4Re/+IVxM+qDjvJHv1II4RRCLCXigz5pb8TEZJqZlYIer2xR0zSqq6vZs2cPLpeLzZs3s3DhwrgR4XhtbeMJeiAQ4NChQ9x222089NBDkXvnAXcxsuoKpBR89atptLWpOvquri56e3uRUhIKhQiFQtGTjs02uiHXSHhfumPcz03kvTJWEq0X6OnpGdFpMdYHfdWqVVx++eVRH/QXXngBgK1bt9LZ2UnEB/1G4NbIa34AGD7orxDxQQcQQjyLaoRRKoRoEEJsTckbNTGZRmZlysXAZrMRDAapq6ujvr6ehQsXRpfpTwaxkb1h49vS0sKf//xnHnnkkZgti0lmmb6uS/793/+XzZs95OTkkJ+fTyAQwGazYbfbkVKi6zqdnTvHPWb7n9+kcvVbuBYvjk7AJvv5pDJCT7Sv0ZwWR/NBd7lcPPfccwDLhz43ng965P7PJTl0E5NZw6wVdCklXV1dNDc3s2TJkjE1uBgvFosl2iGptraWRYsW8cEHH3DXXXcN2dIDuEfdXzhs4Sc/OZ+HH/4S99yznkAggMfjwWazEQgEcDqduFxteL2vDn/yaDn0CP2LYPGxY7QvXkxzczNerxdd1wctyR+pAcZUeaEnitBNTEySZ1YKutfr5e233yYrK4s5c+awfPmwwGxS8Pv9tLa24nA4sFqtNDU1sWPHjjhbDl/NGB8BpBEOP8pNNy0hMzNAOBzm4Ycf5rLLLiMQCFBf/5fxD1hAwxWw6JYf4fzCF6J3G8vyPR4PnZ2d1NTUEAqFcLlcUefFjIyMKfVCNwXdxGTizEpBd7vdbNiwAavVyoEDB8a1D6ObUDKC5fF4OHr0KKFQiIMHD3LHHXcgpaS/P15uuxS1nmUsy+XdwHV4PCrS37ZtG+eddx55eXlkZs7j+ESWv9jAb6nG9ve/o515JhaLBSHEMJMt4/14vV48Hg/Nzc34fD40TaOioiIazY/XFz1RhO7z+YYZfpmYmIydWSnoRn5ZSjnuVnJGPjyROPX391NRUUFfXx+lpaU0NDRw++23jyDkBmeOYzQCuA34GdCB3W6nrq6OvLw8+vurRn5KkvTnQd7NN+N/441oXt6YC5BSYrVaow0w3G43eXl5AHR1ddHa2kpubi5er5fa2lr8fj9CCNLT0wdF86Pl5RN5oSdjAGZiYjI6s1LQDSbin21Y6MbzgQmHw1RVVdHR0RFN55SXl0dTE4kZvnx9gNES38VAB6FQiOL0dLR9f6FNfyjB9skRmgP2V97H+/nP03vBBdiWLSNDShwrVmArKIiKPBA1LbNYLFERHuqkqGla1C43Ni+flpYWFfjMzMxBeXnTC93EZPKZ1YI+EeK1oTMaW9TV1VFUVMTmzZv5zW9+w7Zt27BarQQCgVHq10uBLzC+RvJu4DPAPn5y9tkU/sM/0LvKAj8MQKyFeJKTobHYu9VTFr38MoteflntxulEAoduuoneiy6KCnF6ejpOp5NAIEBTUxM5OTnRk5gQIvqTnZ1NdvbAgqdYu9zjx49TV1dHMBiM5uWNZf9Dyxd1XTfF3MQkRcxKQU+VJ3ps2qGtrY1jx46Rl5fH5s2bsdlstLW1sW3bNvr6kl16P550i4FAlU/nYvvLlxBAdwnI+E6+Y8LVPvAK0VcLBAA4/cc/pnvLFnocjmju3OPxEA6Hox2LDGEG4kbyhsgbefkFCxYA6nM1KncaGxsJBoN0dnZis9miJ5DRPHVeeeUVtm/fjqZpXHvttdx6662DHg8EAnzxi19k//79HDt2bDdwhZSyBpR1LrAVVUP6NSnlq5H7LwQeBKzAz6WUyc5im5jMaGaloMOAQZchzGMtWTQWJXV3d1NeXk5aWhobNmzA5XIhpUTTNKqqqsZY075+tFEn8fh1fIn7uTj7KDXXjvCUMUbprrYED9rtuFtbcW7cSJGUm/oAABWiSURBVFpaGl1dXSxYsIDCwkL6+vrweDzRBtlG/1EjpeJ2u6OTy8CgqxdD6F0uFy6XC5/PR1paGvn5+YRCoaiPzRNPPMGhQ4f49Kc/ze9///tBQxuLdW5lZSVCiB8zinVu5GkPARegrAH2CiFekFIeSv4TNTGZmcxaQTcwDLrGKui6rlNRUYHdbmfVqlVkZmZGhdwQqCVLloyaMzcEX9OeZPzplsFk8XWsC76MJQTa0Ah9jLsXQdASuQP39REuLORYRQXd3d2sXLkyGjGnpaUN8poJh8N4PJ5oxO31egHi9hMdOvkaCARIT0+Pdnwy8vLXXHMN4XCYJ554YtjQYq1zgah1bqygP//889x+++3Gzf8EfjrUOheojqwiPSOyXaWUsgpACLEzsq0p6Caznlkr6LEWukYNdTIYpl1tbW0sXLiQFStWDBNyI4WQn5/Pj370I772ta8N2ofT6eTOO+9k4cK11Ndb+d//zeaFFzaQCjEHaOdaHmk5zGbbkA4+48ifSwd4lkPW0ZG3OXDgAPmnnUZZWVnC1JXNZiMnJ2dQzbiu63i9Xnp7e2lra8Pj8QyaIE1LS6OzsxOv10tRUdGglbZSSjo7O3E4HHFPyJNonVs/5P6J5MpMTGYMs1bQDZKx0AUlIHV1dTQ1NVFcXBytp9Z1HV3Xo3n4oYK2dauy+PjmN7+Jw+EgHA5z77330tx8Ht/5zqlYrQLVEzlVE3sCsNL0xbDKn8vInsU4X0JAxddh3t/B0TPwCgaaw8Ha7Gxsi8fnnW6xWMjKyhpkriWlxOfz0dLSwuHDh7Hb7VgsFiorK6MpGyEEjY2N3HbbbZx99tlx9z1J1rnx6iNNS12TE4JZL+ijdS2SUtLc3Ex1dTUFBQVRr5eGhga6u7vJycnB5XIlrIPeunUrl1xyCbt2HaOx0UZe3hxuvvk0+vsnpzpj8eLD/OM/PkTKij8s0HkWLHxluHJZdR1bilfaGvYIfr+fM888E7fbHV241NvbS09PD3fccQevvfYaZWVlPProo3H3M4nWuaalrskJyawV9GQaRR8/fpzy8nKysrLYtGkTDocjml7JycnB4/Fw6NAhgsEgaWlp0UgzKytrUH16MBjkV7/S+P73z8XhEASD41VaQ07FkPsG7+/88381zv2PTOtHlKDrTidC1xFuN4RCBB9+GCILiVJBZ2cnFRUVLF68mNLS0uj/SQiB2+2msrKS7du3c+GFF/LrX/8an7q8iUusde6iRYvYuXMnzzzzzKBtDOvcs846C2Ksc4UQLwDPCCHuR02KGta5AjglYqfbiJo4vSplH4CJyTQyawXdIJ4nutfrpby8HCEEq1evJj09fVie3Ol0smKFKnqQUtLX10dvby+dnZ1UV1cTCoVIS0tD13UaG4Pceee5BAIWItV+xL9KHy3JHe8x474BsS8qSvH8nICeTdD4SSj4i6B/1y4sPh96UVHKxDwUClFeXk4oFGLdunXD5jSCwSD33Xcff/rTn3jkkUdYt24dQFxTMINY61xN07jmmmui1rllZWVccsklbN26lauvvtpYAHYjSqCRUn4ghDCsc8MMts79KvAqqmzxCRm/E4mJyaxDTEZXmgSk7MU0TSMcDtPS0oLP56OkpIRAIEBlZSVer5cVK1YYneCjeXIgbp582CAjdemVlZVkZGRQUTGHr3zlFHy+2PNfvGh7IgycDB54YDNr1uxOXcrFQIPst79I18bTcLnCpKXlk5NzBjk5xRNyqjRq+JcuXcr8+fOHfb7vvvsuX/va17j44ou59dZbE4r4BDFXKJmc1Mx6Qe/s7Iw6ILa2tlJSUsL8+fPVi0XEfKQJz3h4PB7Ky8txuVwsX74cp9NJezusWuWmry+VejE0mle3L774UW688cupF/MRsQLfQtc/Qnp6OllZWWRmZpKVlTWqyAeDQY4cOYIQgtLS0mFCHQwG+dGPfsRrr73GI488wpo1aybxfQCmoJuc5MxaQdd1nWAwSEVFBfX19ZSUlFBUVBTtRmSUxSUr5MFgkMrKSvx+PytWrBjWEu3xx6187WsOJqYZkrQ0nXAYQiGBlJZBjy1efIQnnzyVSerPMSJCuFiz5hDBYBoej4fe3l48Hg+apg2aW8jMzIwao7W0tFBTU0NJSQn5+fnD9nnw4EF27NjBpZdeys033xzXM2cy3spUvIiJyUxl1ubQh3qiFxcXj1hPnghd16mrq6OlpYWlS5eyatWquM9Zt06SmQkez1hHKnG7NXRdcN11h9i40YLbvZDrr59Db+/AVh//+LN8/ev/TELTwXHUoSeDEFZCoQYyMzeSmZkZrSQxyg+NGvNjx45F2+O5XC5KSkqG+ZgHAgHuuece3njjDR5//HFWr16d+gGbmJjEZdYKusvlYt26dVitVt55550xC7mRJ6+urmbBggVs2rQp4TL/oiIVWSfYI0NTKFYr3Habl8zMGux2O2efnYXb7aW2tpJAYAMq3QHZ2e3s2LEVp3MUJ8dJij91PUw43EUo1I7dPjBJGuvPUlBQQGNjY/RqyGq10tXVRW1tbXSl7i9/+Uv+9re/ceWVV/L6669PVVRuYmISYdYKut1ux+VyEQ6H8fl8HDlyhOzsbObMmTPqqtHe3t6of8v69etxOp0JtwdVDPLww0G2bXMgJShL9MQKa7fr/OAH6cBppKUJQiG1j8su03j00TDbtlmw2ST/+I8P43SOvxH0YKyATvLZLQtCSCorP4+UIYqKfsT8+YP7Jff19XHo0CHS09PZtGlTNLdeUFAQffy+++7j6NGjnHXWWZSWlppibmIyDczaHPqBAwc4cOAAZWVlFBYWRlMDPT099PX14XK5yMrKIjs7m6ysLBwOR7QKpr+/nxUrViR0+RuJ9naoq7PwxhuC731PTQIOlDImFvjs7HaWLKnmv/5rPgsW5NHeDrW1nej6KUAg4XPHhpVkmlTn5v4zx4/vRMrBJ5MlS/4/5s/fipSS+vp6mpqaWLlyZdxGzvv27ePrX/86V1xxBTfeeOOk93UdBTOHbnJSM2sFvby8nJ07d7J3797owpOysjI2btzIxo0bycjIoLe3l97eXrq7u/H7/ei6Tn5+PgsXLiQrK2uMTorDOXIEzj7bTSAwtFoFhmrLRz/6LN/85lY0zUZ6eoD58/8vCxf+X9raHqex8fsTGsf4sSGEEymHLu6xUlr6HuXlbcyZM4dly5YN+6z6+/u566672L17N48++iirVq2aumGPjCnoJic1s1bQYzEmNnft2sWePXvYu3cvPT09lJaWkpaWxpIlS/inf/on5s+fH63i6I3MSGZmZkabNaSnp4/JV33/fgsXX+ykt3fgOW63jqYNXk2and3Ozp1LcLmG+qpbURo0vjZ6oyGEGylD49z/vaxcefWwah+AvXv3cuONN/K5z32OHTt2THdUHosp6CYnNTPmmzgRLBYLxcXFFBcXc+WVVwJq5eJdd93FX//6V4QQXHPNNVgsFtavX8+GDRvYtGkTJSUl+P1+enp6qK6uxuv1Yrfbo6ma7OxsnE7niCK/eLFGMDh0MlTwb/8W5JZbHNjtKtdeWFiNpsX7qEdPi0wEXe9D2Zskl4KJ5ZRTThkm5n19ffzgBz9g//79PP3006xcuTJ1g41Dd3c31157Le+//z5CCJ544glKS0u54oorqKmpobi4mN/85jfDKm1MTE5WTogIPakXlhKv18v+/fvZtWsXe/fupby8nHnz5kVTNWeccUbU46Wnp4fe3l76+/txu92D8vF2u52enh7Ky8t5660lfO97S7DbGTTpaeTai4p0NK2durpSxpsnl5IJLjRyYrVeQTj8S4SI9y+woCZSFUI4WLeufFDFy65du/jGN77BF77wBbZv3z7hdFUybNmyhXPOOYdrr72WYDCI3+/nhz/8IXPnzuXWW2/l7rvvpquri3vuuSc69EkflInJDOakEfR4GE6Me/bsiYp8W1sby5cvZ+PGjZSVlbFu3TpsNlt0wrWnpwe/X3W+X7hwIfn5+fT3Z9LQYKOoSB/RGqW19XFqa78W/8FJxmrNorT0JXQ9yJEjg5tYSwmBwL/gcj2NEFZAsnTpw8ybdzkAfr+fO++8kwMHDvCzn/0s6n8z2fT29rJ27VqqqqoGXSGVlpby+uuvU1BQQHNzM+eddx5Hj0bN3k1BNzmpOakFPR6apnH06FF2797N7t27OXDgAKFQiNNPPx1N0zjzzDP5xCc+QWZmZjQX7/F4EEJEV1RmZ2eTlpY2LFXT2vo4dXU3IqWR07YhhAUpg5P6niwWN2vXHsZuz6O6+iba2x+JefQzrFz5EIFAK93dR/D7s+jrU2WcDz30EG+//TZf/OIX+e53vzslUbnBwYMHuf766zn11FN555132LhxIw8++CCLFi2iu7s7ul1OTg5dXV3GTVPQTU5qTEFPAr/fz/bt26mrqyMnJ4dDhw6RlZUVjeI3bdrEggUL8Pl80VSNz+fD4XAMy8eHQu34fO8AgvT0NfT0vE5NzTZ0faTJS9sI949MQcH/o7X1xwhhR8oQxcUPM2/eZdHHW1p2U1PzCvPnn0dx8YeHnXh8Ph/f//73+eCDD1i7di3r16/n6quvHvPnNhH27dvH5s2befPNNznzzDPZvn07WVlZ/OQnPzEF3cRkBExBTxLDF8b4u7Ozc1Cqpr6+nqKiIjZt2hQtnXS73YPy8YFAIOqNYuTjbTYbfn8T5eW/IRj89rDXLSz8AU1NdyKEHV0PAnrCiD43dwslJf9OKNROIFCH01kUzYWHQiEqKioIBAKsWrVq2AIsKSVvvvkmt9xyC9dccw1f+cpXpjQqj6WlpYXNmzdTU1MDwBtvvMHdd99NZWWlmXIxMRkBU9BThK7rVFVVRVM1+/btw+fzceqpp1JWVkZZWRmrV69G07RoPt4Q+XA4zPz587Fa/52eniej+8zL+zJLl943SJyNiF5KgZT+QWOwWNJZufKPZGRsHDa+9vZ2KisrKS4uZsGCBXGj8ttvv50jR47w2GOPUVJSMjkf1Bg455xz+PnPf05paSm33357tBlGbm5udFL0+PHj3HvvvcZTTEE3OakxBX0SCQaDvPvuu1GRf++993A4HKxfv57FixcTCoW4+OKLKSgowOv10tPTg9f7ARZLOenpm5g7dy3Z2dm43e5BAqzSNu9SUXH5oFWesbny2DEcPXoUKSWlpaXDbA6klPz973/nlltu4brrrmPbtm0J2/FNJQcPHoxWuCxbtownn3wSXde5/PLLqauro6ioiOeee465c+caTzEF3eSkxhT0KURKSU9PDzt37uSHP/wha9eujfY6NfLxZWVlw0on/X4/TqdzUD7e4XDQ0fEcNTXb4ubKDfOxqqoqli1bFvWIj8Xr9fKv//qvVFRU8LOf/YylS5dOyeegaRplZWUsWrSIl156ierqaq688kqOHz/Ohg0b+OUvfzneJhimoJuc1JiCPg0YHZRsNhtSShoaGti1axe7d+9m7969HD9+nBUrVkQFft26dVgslkEiHwwGSU9PJyMjjNvdQ07OqbhcSrQDgQBHjhzBarXGNcqSUvLGG29w66238uUvf5nrr79+SqPy+++/n3379tHb28tLL73E5Zdfzmc+8xmuvPJKvvzlL7N27Vq2bds2nl2bgm5yUmMK+gwkHA5z6NAhdu/ezZ49ezhw4AAAa9eujYr8ihUrCAQC0Xy8x+NBSonVasXv97N06VIWLVo0TKg9Hg/f+c53qKmp4bHHHqO4uHhK31tDQwNbtmzh29/+Nvfffz8vvvgieXl5tLS0YLPZeOutt7j99tt59dVXx7N7U9BNTmpOiKX/Jxo2m401a9awZs0arrvuumijif3797Nnzx7uvfdejh49Sk5OTjRVk5+fj9frJT8/n6KiIrq7u2lsbMRqtZKdnU1nZye1tbU88MADfPWrX+WRRx6Zllz5jh07uPfee/FEOoV0dnYyZ86cqB9MYWEhjY2NUz4uE5MTAVPQZwFGo4lzzz2Xc889F1Bpk9bWVvbs2cOvfvUr/vKXv3DqqadGRX7Tpk1s2LABl8tFS0sLTz75JG+88Qbp6elcccUV0yLmL730Evn5+WzcuJHXX389+j6GMhaDNBMTkwFMQZ+lCCFYsGABl1xyCWeccQZZWVm4XC7Ky8vZvXs3f/jDH/j+978ftQ++4447+I//+I+ke6xOBm+++SYvvPACL7/8Mv39/fT29rJjxw66u7ujXY8aGhqiLfBMTEzGiJRyKn9Syh//+Ee5YsUKWVJSIu+6665U7/6EwO/3y3feeWe6hzGM1157TX7yk5+UUkr52c9+Vj777LNSSim/9KUvyYceemi8u53q49n8MX9m1M/MKDgeB5qmccMNN/DHP/6RQ4cO8eyzz3Lo0KHpHtaMw+12s2bNmukeRkLuuece7r//fpYvX05nZydbt24d/UkmJibDmLVVLkOrIe666y4AvvWtb6XqJUySoL6+ni9+8Yu0tLRgsVi4/vrr2b59O8ePH58O33Iz+W5yUjNrI/TGxkYWL14cvW1WR0wPNpuN++67j8OHD7Nr1y4eeughDh06xN133835559PRUUF559/Pnffffd0D9XE5IRn1gp6vCuLsUz21dfX85GPfIRVq1Zx2mmn8eCDDwJw/PhxLrjgAk455RQuuOCCWCc/kzgUFBSwYcMGQLXzW7VqFY2NjTz//PNs2bIFUI0qfv/730/nME1MTgpmraAXFhZSX18fvT3W6ggzskw9NTU1HDhwgDPPPJPW1lYKCgoAJfptbW3TPDoTkxOfqc6hpwyhmmWWA+cDjcBe4Cop5Qfj3N/zwE8jP+dJKZuFEAXA61LK0hQN+4RFCJEB/A/wAynl74QQ3VLKOTGPd0kpzeafJiaTyKyN0KVq+/NV4FXgMPCbCYh5MbAe2A3Ml1I2R16jGchPxXhPZIQQduC3wNNSyt9F7m6NnBCJ/DZDdBOTSWbWCjqAlPJlKeUKKWWJlPIH49lHJLL8LbBDStk7kfEIIaxCiANCiJcit5cKIXYLISqEEL8WQozLQnAmI9TExePAYSnl/TEPvQBsify9BXh+qsdmYnKyMasFfaJMQmS5HXW1YHAP8GMp5SlAF3AiFlh/CLga+KgQ4mDk5yLgbuACIUQFcEHktomJySQya3PoEyUSWf4COC6l3BFz/4+ATinl3UKIW4G5Usqbk9hfYWR/PwBuBD4FtAMLpJRhIcRZwO1Syo9PwtuZFIQQFwIPAlbg51JKU5RNTGYwJ3OEnurI8gHgZkCP3M4FuiO5foAGYFHKRj/JCCGswEPAJ4BTgc8JIU6d3lGZmJgk4qQ155JS/p2RVxaeP5Z9CSEuBtqklPuFEOcZd8d72bHsd5o5A6iUUlYBCCF2ApcCpr+CickM5f8HYKoZcwmJqDcAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
" \n",
"if __name__ == '__main__':\n",
" iter_num=1000 #迭代次数\n",
" N=500 #样本数目\n",
" k=4 #高斯模型数\n",
" probility = np.zeros(N) #混合高斯分布\n",
" u1=[5,35]\n",
" u2=[30,40]\n",
" u3=[20,20]\n",
" u4=[45,15]\n",
" sigma=np.matrix([[30, 0], [0, 30]]) #协方差矩阵\n",
" alpha=[0.1,0.2,0.3,0.4] #混合项系数\n",
" generate_data(sigma,N,u1,u2,u3,u4,alpha) #生成数据\n",
" #迭代计算\n",
" for i in range(iter_num):\n",
" err=0 #均值误差\n",
" err_alpha=0 #混合项系数误差\n",
" Old_mu = copy.deepcopy(mu)\n",
" Old_alpha = copy.deepcopy(alpha_)\n",
" \n",
" e_step(sigma,k,N) # E步\n",
" m_step(k,N) # M步\n",
" \n",
" print(\"迭代次数:\",i+1)\n",
" print(\"估计的均值:\",mu)\n",
" print(\"估计的混合项系数:\",alpha_)\n",
" for z in range(k):\n",
" err += (abs(Old_mu[z,0]-mu[z,0])+abs(Old_mu[z,1]-mu[z,1])) #计算误差\n",
" err_alpha += abs(Old_alpha[z]-alpha_[z])\n",
" if (err<=0.001) and (err_alpha<0.001): #达到精度退出迭代\n",
" print(err,err_alpha)\n",
" break\n",
"\n",
" "
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXQAAAD3CAYAAAANMK+RAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8QZhcZAAAgAElEQVR4nOy9eZxcV3km/Ly3lq5eqrfqllpSL+q2JYy1WFK3bNlGYCyTgEGAADtDIIEEG0gyM+GDGXCS75vAfJlgki+EzCTBGPyxBCaAiTcZDMECG9nY2q2WLAlb6l3qraqXqu7a657547mn7+1SdXe11JJa6np/v/pV1V3Pufc9z3n3I0opFKhABSpQga5+Mq50AwpUoAIVqEALQwVAL1CBClSga4QKgF6gAhWoQNcIFQC9QAUqUIGuESoAeoEKVKACXSNUAPQCFahABbpG6JoHdBH5vIh890q341oiEfmoiLwwj+O7ROSuS9mmxULzfTYXcP1nROQjjv9/JSJBERkQkUYRmRAR1wVcd7WIKBFx53n8t0Tkr+Z7n4WixcRTIvKciNx3pdsBLAFAL9D5tJgYMJssULn+SrdjsZJS6h1KqW8DgIg0APgMgBuVUnVKqR6lVJlSKnNlWzmdLpbfrvTksZAkIneIiGlNvM7Prdb+56wxcFPWeU9Y2++Y7fqLCtDzlQ4KNDMVnuGSoiYAIaXU0JVuyGKmRTgmzlkTr/PzkmP/awB+X/8RkQCAbQCG57rwFQd0S3X6nIi0A5gUEbeIPCAiZ0QkIiInRGSX4/iPisgLIvL/icioiHSKyDsc+5tF5Hnr3J8DqMm637tF5FURGbNmwzdmteW/iki7iEyKyCMistxScyMi8qyIVM3Sl8+KSL+InBOR+5zSpogUWW3uEZFBEXlIRIqtfXeISJ+IfEZEhqxr/IHjuvmc+zkRGQDwTRGpEpGnRWTYekZPi0i9dfz/ALAdwD9aksE/WttvEJGfi8iIiPxGRO513D8gIk+JSFhE9gO4bo53+nsi0i0iIRH5i6x9N4vIS9bz7xeRfxQRr7XvV9ZhR622/c5sfbmSJCINIvKY1a6Qfo45jvsHEem1nt0hEdnu2HeziBy09g2KyJet7T4R+a513TEROSAiy619z1m8dReAnwNYaT2rb0mW2UREKiwe7heRs0LzjMva57J4KigiHQDeOUd/N4vIYWsc/ACAz7HvQvhtxueSdd+PA/gQgM9a5+927N4kHKvjIvIDEfFZ55w3Jqzt94vIaYvHnxKRldb288xN4tAqrGf1d9az6hSR/5h9PIAmEXnRej7/LiLTcGee9D0AvyO26eyDAB4HkJzzTKXUFf0A6ALwCoAGAMXWtnsArAQnnN8BMAlghbXvowBSAO4H4ALwRwDOARBr/0sAvgygCMCbAUQAfNfat9a61tsAeAB8FsBpAF5HW14GsBzAKgBDAA4D2Gxd7xcA/nKGfrwdwACAdQBKAPwLAAXgemv/VwA8BaAagB/AbgBftPbdASAN4L9b7bobQBRA1TzO/ZLVxmIAAQDvt9rhB/AogCccbX0OwH2O/6UAegH8AQA3gC0AggDWWfu/D+CH1nHrAZwF8MIMz+FGABPWsy+y3kUawF3W/lZQ2nADWA3gJIBPOc6fembW/1n7coV41gXgKIC/t56JD8CbHPz5guPYD1t9cIPmkQEAPgev/p71uwzANuv3J6x3XGLdqxVAefa7s959n+Neq63n57b+PwHga1YblwHYD+AT1r5PAjgFjrtqAL90npvVXy+AbgD/F8ifHwDH4F/l846y+W2u55Lj/t/S98rCjf0gTlRbfPTJWcbEnSBPb7G2/S8Av8r13HI8508COAGgHkAVgGeznvNzAM6A+FJs/X9whr5Me2c59j8H4D4A/w7gHda2/QBuBdAH4I5ZefNKDgzHi/nDOY55BcB7HAPmtGNfifVw6wA0Wi+y1LH/f8MG9P8HwA8d+wwQnO5wtOVDjv3/BuCrjv//CTOACYD/HxbIWv+vt9p1PQABJ5LrHPtvBdDpeMmxLIYaAoEvn3OTmGEwWMdsAjA60wADJ829Wed8DcBfgoCSAnCDY99fY2ZA/28Avu/4X2q1764Zjv8UgMcd/6cB+lx9uUI8eyuo/uYCv4/O9Gys/aMAbrJ+/wrAFwDUZB3zhwB+DWBjjvOn3h1mAXRQKEnAEpKs/R8E8Evr9y9gAaD1/7cwM6C/GQ6hydr2a2SBbL78NtdzybHvW9n3Asfqhx3//wbAQzONCQCPAPgbx/8yi69XY25A/wWsidD6fxfOB/T/27H/jwH8dIa+3AHABDCW9Sl13hec8P4VwBsAvGbtmxPQF4ttqdf5R0R+H8CnwQcN8OE7VZgB/UMpFRUR5zGjSqlJx7HdoBQCcDbvdpxrikgvKI1rGnT8juX4XzZDH1YCODhDn2rBieeQ1VaAQO2MRggppdKO/1HrXvmcO6yUik/tFCkBpce3gxIFAPhFxKVyO8yaANwiImOObW5Qy6i1fjv7042ZaaXzWKXUpIiEHG1bC0rtbVa/3AAOzXSxC+jL5aAGAN1Z7ysnichnwAG6EgSBcti8/DFQKzslIp0AvqCUehp87g0Avi8ilQC+C+AvlFKpebSxCZSm+x18Y8B+N9PeE+Z+p2eVhSrZx1/IO5rjueRLA47fUetamqaNCWvfYf1HKTVh8eUqUKibjbKfVW+OY7LbMhNOALShz2U2fAzA3wEIgfyQF11xG7pFU4wiIk0Avg7gPwIIKKUqARwHQWwu6gdQJSKljm2Njt/nQEbX9xJw4Mz1QvOhflAl09Tg+B0EJ4N1SqlK61OhlJrtpc/nXJV1zmfAmf0WpVQ5KGEB9jPMPr4XwPOO61cqOmr+CJRE01n9acTM1O881hrsAcf+r4Kq/hqrbX+O2d/tXH25EtQLoFHmcLZZduHPAbgXNJ9VAhiH1Xal1OtKqQ+C5pAvAfiRiJQqpVJKqS8opW4EcBuAd8HhJJtHGxOg9K/fablSap21f9p7wtzvdJU4Zoas4+fFb3M9lxyUza/5UPY52WO/FOTLs6AGDFDA0FTn+D3b2L4kpJSKAngGNClfdYDupFLwZQwDgNA5uD6fE5VS3aCU/AUR8YrImwDsdBzyQwDvFJEdIuIBGTEBqo8XSz8E8Aci8kYLxP6bo10mOEn9vYgss/q1SkR+O48+Xci5fnASGBORatB04qRBAC2O/08DWCt0Znqsz1YReaMlYT0G4PMiUiIiNwL4yCz3/hGAd4nIm4TOzv+O6XzmBxAGMCEiN4AMO1vb5urLlaD94CB/UERKhU7M23Mc5wcnw2EAbhH5b6AkCgAQkQ+LSK31jrV2lBGRt4rIBsspFgZNA/PSRpRS/aAd9u9EpFxEDBG5TkTeYh3yQwD/WUTqhY7+B2a53EtWP/6zMGjhfQBuzurnfPht1ueSg7LPvxD63+D43CQiRaDZcJ9SqkspNQwC+4ctB+gfYrrj/4cA/tQad5XgZHQ56M8BvEUp1ZXvCYsO0JVSJ0BV4yXwRW4A8OI8LvG7AG4BMAIy1ncc1/4NaJv6X6DkuxPATqXU3N7judv9DID/CTqXTlvtBzhhAGSC0wBeFpEw6Fh5Q56Xn++5XwGdM0HQyfvTrP3/AOADwoiE/6mUioA21P8ASjIDsB1KALWlMmv7t2BFDeQipdSrAP4EHED9oG20z3HIfwHfUQScqH6QdYnPA/i2MLrj3jz6ctnJmuR2gv6RHrB/v5Pj0J+BUtZroIkijunq+tsBvCoiE+A7+Q+WmaAOnBjDoLPvedDsMl/6fdCheQJ8Dz8CsMLa93WrfUdBU8RjM13EGh/vA/0Do2BfncfPi98w93PJpkcA3GjxxBOz9njmPuwBfWj/BvLldSC/a7ofwH8FTRzrMF3I+zo4ObYDOALgJ+CEdKEmPx2Z5Py8P0ebzyml5pWkpiNDCrTAJAyHPA6gKB9ba4EKVKCrg4Rh0g8ppZrmPPgy06KT0K9mEpFdlqmnCpRwdxfAvEAFurpJRIpF5G7L3LQK1Pwfv9LtykUFQF9Y+gRoFzwDqmPZ9uECFahAVx8JGF46CppcTsLhI1tMVDC5FKhABSrQNUIFCb1ABSpQga4RyrdUZiWAb4DhgwrMZPsNGKGwGszaulcpNTrbdWpqatTq1asvvLUFKtAsdOjQoaBSqvZy37fA1wW61JQvb+ebKfoPYCrrB6zY4hIwRnKPUupBEXkAjGOdNT5z9erVOHjw4GyHFKhAF0wiMlu24yWjAl8X6FJTvrw9p8lFRHTm1yMAY1KVUmMA3gPg29Zh3wbw3gtr6tVNSgE9PcDhw/wuuCSuLhKRShH5kYicEpGTInKriFQLK0++bn3PWGGzQAVaTJSPhN4CRm58U1h0/RCAPwWw3MpGg1KqX2cxZpOw/OXHAaCxcbbs4quPlAIefxw4cAAwDMA0ga1bgV27ALmSiekFmg8tiPZZoAItBsrHKarLqX5VKbUZrHswW5rwNFJKPayUalNKtdXWXnbz5iWl3l6CeVOT/TlwgNsLtPipoH3mQQUV9KqifCT0PrBE5z7r/49AQB8UkRWWdL4CLPe6pCgYpGRuWNOi/h0MAteYMnKt0kVpn9c8FVTQq47mlNCVUgMAekVE1w7ZAdaGeAp2kaaPAHjykrRwEVNNDXncNPlf/665mLVKCnQ56YK1TxH5uHC1oYPDw3OuDHZ1UkEFveoo3yiX/wTge5aNsQNc2cYA8EMR+RhYoOieS9PExUsNDRRYsgWYhkteXLNAC0QXrH0qpR4G8DAAtLW1XZt2iIIKetVRXoCulHoFXJAgm3YsbHOuLhKh9tnWRh6vqSGYF7TRq4OUUgPCdS3fYFXi1NrnCVDrfBBLVPsEMF0F1RJLQQVd1LRYViy6akmEwkpBYLlqqaB9zkQFFfSqowKgF2hJU0H7nIUKKuhVRwVAL1CBCjQzFVTQq4oKxbkKVKACFegaoYKEfhWQUowUK2i9BSpQgWajAqAvcirkdhSoQAXKlwqAvsjJmduhAf3AAfqpCmbNAl3VVFA9F5wKgL7IaXgYiESAvj6grAyoqpp/bkdh3BRo0VFB9bwkVAD0RUxKAYcO8VNRwW1NTQT1fHM7CuOmQIuSenuB/fuB8nIgGgX8fv4vqJ4XRdc0oF9Nkmmutvb2Ap2dwMaNLHQHAO3twEc+wuMPH567XwWTTYEWJQ0PA6dPAxMTNmOWlXF7QfW8YLpmAX0xSKaz8ZtzXyAAHDzIj7OtGoS3bAGam8n7Y2P8fuih/PpVKMdx7ZJSCr29vQgGg6ipqUFDQwPkagG0ZBI4e5aMrRm5s5OSi8jcAL0YBvgipGsW0K+0ZDobvwHT942NAf39wNveBrhcdltXrOBvpYDqaqCyEhgdBTo6KLXn069COY5rk5RSePzxx3HgwAEYhgHTNLF161bs2rXryoN6tiRTX08nkFOy8XqBlSvJ0CI2oz/1FLfPBdBXeoAvUrpmAf1KS6az8RswfR8AHDkCjI8TuHVbvd7zS2k0NwMjI7P3K1v6L5TjuPaot7cXBw4cQFNT0xSgHzhwAG1tbZdnZbCZ1M9ckkwmw99aWtm6FWhtBdaupe08GqXEvncvsGaNLYXMBtBXeoAvUrpmAX0+kumlMMXNxm/O/0oB6TTNKL29dHgqxbbW1tLc4iyloRTNLTP1K3s8ZTLA6tXAm97E/evXk9+vtBBXoIujYDAIwzBgWAymfweDwUsP6LOpn9mSTDAI7N4N7Nw5HahbW6dLGsEgsGoVJRB2aHZJJZEoqJ456JoF9HwLxV0qU9xcE4oWXI4eBU6eBMJh4PnnaU5Zvhy49Vbyd08PcPw4zwkE5u6XczyJ0HH6/PMcP34/x8ESFmCuGaqpqYFpmjBNc0pCN00TNTkAbcFt7bOpn1qSEaEqeeYMkEoBk5Nkfg3UodD0wl+JBPDkkxyQ2gQzm6SSTlOlHRgASkvpUL355iWvel6zgJ5vobhLZYqbC3i3bgWeeIJgq23kySRw4gQl885O4IEHGAgwOMhz6uqA3/5tgvOKFYDbzfb39ADf+hbw1rdynOgxMzICdHcz5FGE2/bs4flNTRfetwJdeWpoaMDWrVvPs6E3ZAHaJbG1z6Z+aklGr0E6OmpLJaWltme/uvp8O3t///wklfZ2mm2iUTqV3vveJa96XrOADuRXKO5SmeJmm1CU4icUIi9WVdFenkrRzFhRwfDcH/2IUnVzM6/56qvAww9Tei8tBU6d4mdigvvr64E/+ANK/qZpbx8cBOJxoKSEY+nRR4HPfGbJ8/5VTSKCXbt2oa2tbVbJ+5LY2mdTP+vrybw//jEZMRol4/3qV8CxY5RK6uqABx+kVK6l65YW2hdXrAA8Hko3IyPAt79NCUdL7tmSSnk5P0ePEvSXuKSyKAH9coaXXsookJkmlN5ehig2NxOQKyvZV7ebY2BwkCaYSMSeaGIx/q+r4/HJJLBvHwG/vp7PbHgYePFF2ss7OynwdHezHStX2ppsRwfbkMs0WQjnvXpIRNDY2DgrMF8SW/tM6md9PdXO117jcWNjtBuuWEGvf1kZsH07mW33bjpAfT6e//zzlLjLyjgITp+mujoxwW3NzUBxMe+dj6SyRJl60QH65Q4vvRKLsmitYNUqCheTkzQJjo0R1F99lZpqJELeLS6mIKMUhZeyMo6ZVIpAn0hQwhehWbG1lb8HByn9d3fTTr98OR2kegJpbCyE814pulwx5POxtedNM6mf2iyyZg0ZNJMhc4+Pk7FLSgjSp09TFS0uBoqKCOSNjWTMkhKqph4Pj1m1iteIxXjv9nZK/bNJKg0NS5apFx2gL4RNW0/Ow8OUZL1eam0zTdKtreQr4PJEgWitoLISuOUWgm0mw3b7/RwjOtIrHqc2uXw5x8TatTxvZIT70mnyu35WqRQBvrOT1167FvjpT7l90yY+154eWwMphPNefrpYu/Z8JoN8be3zplzqp5ZUAgFK1L/+NbeHw2SsM2cIuhMTtkpZW8tjkklKKpGIrY6KcHs8TiZvbqbtPR6fXVIBlixTLzpAv1ibtlPifO014Nw5TvLXX08nuHOSziWdXoookFx5FlorqK7mJLJ5M3l3chJ49lmOiVCIQkoiQZ5dv55mw+PHaU5xgj/Afh05Anzta+yzYfD6b3wjBZvhYR7j1EAK4byXny7Gru2cDEQE4+PjaG5uxj333IPGxsacwN7a2ooiS2JZv379jMddEOUKJVSKdj+laDdfvZoqZzJpx+oClNQ1WGtA1oxqmpTEdcRMLEY1taRkbkllCTP1ogP0bJt2JmNnUvb0zG0K0xKn308+WbaMoN7SMr32j1LAyy8DTz9NsA8EuG2hJ/KZTBrvfW/u+HKA46K/nzxcXk7JfONG7rvhBmqwv/wl+V0/C8PgsX4/AwAAW0C56SZODHffDWzYMP0ZFjJJLz9l27VFBJFIBHv37sX27dtnlbj1ZNDY2IijR4+iq6sLR44cQUdHB+66665pUn4uTSCRSCxcnHqupAfTpORsGBxEb3kLQTiZJGO63VSZIxEyeiRCs0ksRjA/eJDXjUSofmrSgKwdo3NJKkuUqfMGdBFxATgI4KxS6l0i0gzg+wCqARwG8HtKqeTFNshp0xah0xCgs++FF+Y2henJeXISGBoiz8TjPHflSr57bWLbvZtSfH8/wW/z5oubyGcqsDWb9ud0TG7dCnzlK7ZGaprk86IiTkq6P2NjvK7HQ543TbsNmoerq+1xZZrAjh0E9OznVljY/fKT064tIjh8+DDa29sBAMePH5/V/KIng/HxcXR1dcHn8yESiUBEsH///ikpXymFl19+GU8//TSuv/56BAIBKKUWNps0F3N3dQHvfjeZVg+Cnh7gn/+ZjOu0DZaWAnfcQZv70aME+njcZmLd/5ISSlwiHAR6/0ySyhJm6vlI6H8K4CSAcuv/lwD8vVLq+yLyEICPAfjqxTbI6W85dow8sGGDnYuwezed5tu2nQ9OWjg4doyS6tiYnXhWW8taQMnkdN9Nf79tjmtstCfy+TrJZ5LENa/nk6rv8VCAWbaMAorOiHa76Utqbrb9TSIzg7nbDdx7L007c7V/qS/sfrkEFSc57dqRSATt7e3YuHEjNmzYMCvoKqWQSCTQ39+PsbExDA0NIR6PIx6Pw+12o7a2FsPDw2hoaMDjjz+O3bt347XXXkN/fz+ampqwefNmGIaB4eFhAJifQzbXgMhl2nC5COZbtkw/3+Oxo0+0WUZ78V98kXb2gQEOWu0Q1RK6223fZ+3auSWVJczUeQG6iNQDeCeA/wHg08K3fyeA37UO+TaAz2MBAJ33I9gFg/aCDkeOcPKPRICvf51A3NpKkK+poc34z/6M4a6jo3QaattyZSUl26oq+mRGRniPQICmO33d06eBd72LQDiTmSS7xpDmkZkkcV1ga65U/f37+Tl2jCCuFH1Epkl+Doc5KVVVEfBLSsjzqRSvo+3/8Thw5500M7pctnlptslpiS/sflkEFSc5Y8j37t0LgLbt0dFRTExMIBKJYHh4eBqgK6Xw2GOP4dlnn0V3dzf6+voQDAZRV1eHhoYGrFy5El1dXUgmk1NmmTVr1qC/vx9VVVXo7u5GY2MjTNPEwYMH0dXVdZ5DFkBuZ+tM0kpr69ymDW1Hd7nskC6l7ONPnuR1lCJjt7dTLdWDQCkydSpFFfv++22JSEtrR46cz9hLlKnzldC/AuCzAPzW/wCAMaWUNnL1AViV60QR+TiAjwOYt5qn7buhEEG3uprv6brrgO9+l87DqioeU17O2j4tLbZm9sorTMJpauKk3tEBvPQSjx8Y4PvfvJnv/PXXySvbtuUG5/37yUOdnbkjoWbyw+QqsJUrAc7vZ5ihaVIw0dK330+7eThsn1NWxv7qySyR4LU9HmDdOv5/5BHgvvvYttmqPi7BUN0putyCSta90djYiO3bt+PYsWM4cuQIuru7AQDj4+PYsGEDampqEAqFpkw03/ve9xCNRuH1elFaWoqRkRH4/X6UlJRgbGwMVVVV6OjowMjICEQEgUAAq1evRldXFyKRCE6fPo1t27aho6MDq1evnuaQbW1txaFDh3JH3swkrWTXY8lmbqWAxx6jBHb4MMEcoARfUsLBMT5Oe+INN/C8sjJu0/bEdJrXrq0F3vMeDlbDWNKhibPRnIAuIu8CMKSUOiQid+jNOQ5Vuc5XSj0M4GEAaGtry3nMTKRNYbt321FMmqcGBij9ihD0XnqJk7gG1GXLOAFEIgRDXXJ2wwYb0I8fp/RumqwdpM04ucB5YoJO1Jtvzm0Ln8m5mKvAlhM49b0GBiiYlJRQIHFbb+YNb6BW+YtfEHyPHCH/V1eT55cvpxba0cFJLBzmed/8JjWRdeuA732P0TG1tXx+eiweOrTkx8MVEVSc1NDQgObmZjz//POorKwEAGzcuBE/+9nPcPToUVRVVU3FkA8MDKC5uRkigqKiIgwODmLt2rVoaGhAV1cXOjo68NJLL8E0TQwMDKChoQGbN29GY2MjXn/9ddx///3wer3o7u4+L9Ho+PHjM0fezCStZNdjyaW27tlDxtYJQ9EoQdrrJXMPDHAA3XQTJTCXi8lGLhePKS/n8StXUqoyDNa/ePVVXnv9+uk1p9vabOfVEpRU8pHQbwfwbhG5G4APVE2/AqBSRNwW89cDOLfQjdOmsBUrOMnraJTubvLSq68SAJUin0xM8B0WF5MnqqpoQhkaIuht3szrjo8T4NraCPLZMeq5wHlykj4czdMinCz27mXymzMUMVtYmU370/fKZAjAyST/a2d+PM4s6hUr7BWMWlrsJCO3m59Egv1qauLYGRggkKdSNBOVlvKzZg0nmOPHl2yoLoArK6hktQNtbW04duwYKisrUVZWBqUUjh07hhUrVkBE4Pf7cfjwYUQiEYyMjMDn86G4uBhlZWUYGRlBPB7HmTNn0Nraig0bNkwB+vHjx1FZWQnTNLFz505s27YNvb29ORONABvclVIYGxvD4OAgjh07hob16yEzmVZmY24dyphKEZwrKnheWRmZUUvfx47RcRoKcZCOjXFgj47yvHCYgzudBr78ZUrmdXWMiDl1ikyrF8oYHub2JSqpzAnoSqk/A/BnAGAx/n9RSn1IRB4F8AHQgfQRAE9eigaKUHLu7+eEfPo0gcs0+U4TCYLtmTN8fwcOEOAqKhjVdOYM97/2GkFehOabcJjAX1FBgHNmCw8Pkz+c5pVt23ieBltdGwggOOYKRZxLMDBNgm0sxmvEYmy7TqCbmOD5W7ZwDPT3c391NfsSDvNeFRWcDHQRrr4+jo1AgJOZ388Jw+228zCAJRuqq+mKCSrZVFtbC7/fj/r6ehiGga6uLoRCIRw/fhyGYSAWiyEUCk05Qr1eLwKBAMrLy1FVVYWwpZaJCJRSGB8fR0VFBdra2rBx40bU1tZO2cNnSjRav349XnjhBWQymalwyHA4jB//+MdIJBLY1dYGyV5Sa66okZoaMrIGa8MguOswroYGRrlEIpS+i4spwfh83B+LcbD7fFSlx8e5bWyMDN/XxwF7+jSl/S1bKBEtYUnlYuLQPwfg+yLyVwCOAHjkQi6SbzSJ9o+I8FNaSlCNxSidRyLcVlxMybW6mlJtczOPT6XsUMjaWtv84tTSskNqm5u5r7bWLlNx4ADv1d5uXyM7fj0X32T3Uztx9+5lm86dsyciwA7XHR7mxDI2xvsqRV4uKSFQL1sG/P7vU8j55jdpRtGRX0rxGuk0z00mbU1g3TqGci7BUF0Al1dQmSuzU4Psnj17EIvFMDY2hkQigfHxcUxOTk45SX0+H1wuF1KWJ/zGG2/EbbfdhvHxcTz33HPo6urC5OQkgsEgwuEwiouLUVFRgS1WxElPTw+CwSBaW1vR2to6ZZ/XWaO6De3t7SgvL5+KvDlw4ADaPvlJNG7dOvd6ijpzrreXUsrkpF2UKJPh4AQoVWzYwEHb1cUBoSWYaJRefb34xdmzDPNyXiuZ5MAMhcjg7e0sN+r1LmlJZV6ArpR6DsBz1u8OADdfzM3zrSOii1lt3Mjtv/oVpVWXi/tTKW73eglwqRQn89FROzFt9WoCo2ky10E7WPW7BkS449AAACAASURBVHKH1L7jHTYfaHOhFZiADRvsCWY2nsnVT+3E1Zri5CT5Nh63zSmJBK+tqzH29pKPtbaRSAA33siorXXrgB/8gNdxu/mtx46+X0UFr19ZaedhLMFQ3bloQQQVTfmm+SuloKwMyv7+fkSjUYyNjQEA4vH4lN28rq4O8XgchmGgoqICLpcLlZWVCAQCOHz4MHp6etDY2DgNjGd1eDrasGvXLhQVFSEej2PNmjWoqqqCiMAwDARDITRu2XI+g+dKLspkqBoPDFAiSaUogWiG1Kn9p09TzRwbs0MUdUapywX8yZ+Q2f/2b207uS5TWlZmS3luN88fGFjymXJXNFM03zoiTp/MyAjfZ0UFvzMZu25PMjk9uUzbpo8eJTjrRLOuLoJaRwedjFVVdLJrYAZyT+zaXLh9O4UPXf62pGR2nsnVz5/8xHbiaj+R1jhLStin6moKMH19tnPXNLlNhBNTZSX3nzjB826+mUAfDHK7x8N2+nwE+euuozB0/DgnibVrOQku5ZWMFlpQcVI+af69vb04ePAgNm7ciLGxMZw5cwZutxulpaWIRqOYtKJD4vE4JiYm4Pf7YZomlFJTJpKglkpAE86GDRtw7NgxHD9+fEqqb25unrENAE02GzZswAsvvADTNNHb24uSkhLMWswr1wpFzrrPbjdNLoZB88vkJBm+spJhXckknWJeLwdiebldVXHrVtsZpqUcLaXr0MaaGu4PBsnohw5x369/TUYHlpSkckUBPd+SC85JV1fOrK62K2vqcD9tTxchUO3YQU2svZ18cvPN5Iv2dpae1QuMnzxJUFu9mu9dCwMzgXR9PSeK3bttgNaO0Xz7WVVl2+TjcW4vK2O/KirIkz4f2718OQWVQIDbvV57XOioHE0lJQT8qiq28e67gX//d7sUhs8HPPccAwoiEZ5TVwd86ENLQiO97JRP+VrnMRMTEygpKUF1dTWCwSCSySRcLheUUjAMAxHrpd14443YsWMH2tvbp0wkra2tCAaDGBoawj/90z/h3LlzSKfTePXVV1FdXY1Pf/rTM7ZBU319PTKZDHbv3j0F/tu3b0d9vswdjZLx0mnbNlpcbFdMdLnIpDfcQMlchIw/OUnpfHiYzq+VKwnQIhwAy5fblfa6uwnu3d0c9GfPMlLgtdeAz3+e14vHee4XvmAvirEE6IoCer7akZ6s9+zh++7rs5NslCJIaR5yuRgNc999wPveBzzzDN/t2rU8HiAPHjpEgNTbhofJT8eO2bHtzc10Kvb1cR9ASRZge3futCX0cJjHzRbJ4uxnXR1w223UHlIp8vb117MvNTXURAIBahHl5eRln4/fqRT7euAA+fmTn+SxdXW278k0ycdvfzujgXSdo8lJ9tXnw9TCGaEQn+3WrQVQX2jKp3yt85iysjKYponq6mr4fD709vbCZdkWRQQigvr6etx333143/veh2eeeQbxeBxr165FZWUlXnnlFfzyl79Eb28vysvL4ff7UVxcjM7OThw9ehRbtmyZulcikcDBgwfR29uLaDSKlpYWrFixAoZhYOfOnYhGoygpKUE4HEZfX1/u8Mxs5tYZb243B2dREaXxoiLur6nhQCkutmORvV47g1SEAH30KPBHf0TGXrHCZuB4nIz76U8Df/EXHJilpRwYp0+zKFh5Oa+l63qsXn2Z3vaVpysK6PMpuaDNZcGgXQ5ZV9G8/XZO0N3dlEjvvNM2H2zYQOefthtnMrSvA7b9G+D9KyqAd77Tjog6cwb42c+mr+lZV8dkJc2bmiYnZ7ahZ/cznWZ71q+nY7642J40Ojr4qaqiEPLud7MP3/kOTYQTE3YGrK7ECPC+H/6wHfZbXEwNxeejMFReznPHx22TpbPv2kxTAPSFpXzK1zqPCYfDOHfuHCYnJ6fi0q+77jq8+c1vRjQaxfDwMD71qU/h1ltvnWYiqayshGEY2LhxI/bt2wePx4NAIICysjIAgNfrxYkTJxAIBGCaJjKZDB5//HHs3bsXPT09KCsrQ3V1NdauXYuVK1dOm3C0ozUnoGczdypFCfs3v6EqXFpK6VpHqWiJe2TEjmjwW2kA6bS9bNdcjF1fzwFZXMz79vXxeO1Y01pDRwcH7BKhKwros5VcUMpeinBoiFFN9fUE2fXr+f7Ky8kjetWqD37wfIdqrmJfqZQdt66UnVxUUUHwBGgO0XZ6l8vmw2iUUrxOy8/H7+Ls59AQ8I1v0LHrNNd88YsUTIaGgJ//nMJFaSkl/2SSPPxP/0TBx+ezs0VvvJFtbGqaec0B3cfqantlJC1AAWyDrqVUoIWl2ZaKM00T+/btm8rcbGxsxJ49e6CUQmVlJZYvX44bbrgBHR0diMViKC8vx44dO6bAHJg+GYgITp06haKiImQyGYyMjCCVSqG8vBw+nw8f/vCH0dbWhkQigSeffBKmaWJwcBArV65ELBbDsmXLcPz4cZimOc3mP6sNPRdzd3SQuVIpDtq/+Rse9/nP286bSIQD+YYbgH/9Vw7g4uL8GfvIkemSSlMT8NRTtm1RD8qWlsv3shcBXfHyubnyErTj/LvftaXSRIKRHMPDds0Sn8+WmN/85umTgTOKSseH62JfO3ZwgfFXXuH1w2FqZe95j80r2lnpzD7VKfZut60RzKRZ5ArHbGy0tcnmZvYhGmUJA33vwUGed/PN0xPgPvEJCjX/+q92HHpTE4UbPdZyPctcWtCOHSx10NnJY+rquG2J+I0uO+VaKs40TTzwwAPYu3cvDMNAPB6Hy+XCqlWrEI1GoZTCb37zG9x6661obW3FrbfeOlVaF7BDEGtqavDe9753KjlpbGwMd955J77xjW+gs7MTExMTCIfD2LZtGz72sY/B5XLh8OHDcLlcGB4enopiAYBUKoWioiIEAoGpbNJcGsX5vC0QJ3PrUDOPh9sGBuyIgx07uL20lKD+u7/LffNlbF1BT0sqK1cyjnloiNfVktItt1z6F7yI6IoDei7SGcPRKIEvGiWf6MJay5fb8eRDQ/YkfOQItbCDB/nJDoXUxb48HtrXN23iObffDnz0o7bvRJsF/X4eq017RUW2s/Kee2yHZK6w3JnCMTs6pif/iLBPX/witYPBQWoRpmmX89XRPZ/7HPv38st2HPpcDvxcWpAzTBhYuAgX06SzuaOD7+SWW+zJsEDTad++fdi7d+9U5EkoFMLhw4eRTqfh8/mmTCWdnZ3YtGkTWlpaEAwGoZTCwYMHcfDgwfNCEIPBIKqqquD1evGJT3wC7e3tOHHiBN797nfjU5/61JQtXtvsdUldnSnq8XiglMK9996L+vr6nHHzs4Yad3TQbhgO25JVOg388Ifc5rRpNzbSTnmhjJ1LUvnsZ6mu63TqBWBA0zQRiexDPN4Bn68Ffv8tUxPgYqRFCejBIIHTMGxHeUUFJXVdQkIvlLxyJatv6gqKfX30jWzaxHdeWWmHQmb7b1paKAX/4R/mlmr37+fk39NDu3VPD0F/x47zwyoBAmVfHzWBmcpMtLRQMo/HybdKkde7uugkrahgklFXF/m+osJe4KOmhs7et799fmUqcgk4TU0Lu0C6aQIPPMDYeqcp6cEHC6Ceizo6OqZFvxQXF8M0TaTT6amiXPF4HEVFRZicnMSTTz4JwzDQ19eH06dPY9OmTWhoaEBlZeVUCKLTuepyuXDTTTehsrIS99xzzxSYA7aZZt++fVi2bNlUXfXe3l7s2HEXVq7chuFhA8lkI6xKu3nxdmNJib1ghWaCnh5KD62tdq3qri4y7sUw9mz22ttumzqMJYd7kUoF4fHUoKgo/7VbTdNER8cDGB/fC8AAYKKiYjtaWh5ctKC+KAG9pobmNJ1HAFCLa2khnzQ321pbXx8n5PXr7UUwgkHyUE0NTReBALdt3pyfE1bzSmsrhYvSUts8csMNdGR2dzPctqPDtsGbJpl8aMheJ3Tz5ul1X26/nW3ds4cmHKXYznSavL1uHYG8vZ0CjZVbct4CH5d6mbz51jPat296opRp8v++fUvKJ5U3tbS0TIt+8fl8U/HlJSUlMAwDgUAApaWlKC0tRWNjI1588UW88MILCAaD6O3tRU1NDW6++WYEAgEEg0Fs3rx5Wp31aDSKbdu2nRdyqO36ra2tCAQCePnlfQiHK+D1rsT4+Hvw1a8KTp+2l2+87jryRzZvb9pE/hwcJNA31DdAGhqAoSEoCNJphaR/GUxXOcqqA5CmJqiuboSHEzj3xCmUBorR8MKLkAtl7NnqyIBgHgw+jnD4ADQgl5dvRU1Nfmu3RiL7MD6+Fz5fM0QMKGVifHwvIpF9qKhYnEy9KAG9oYFScH//dDvvBz9o12sBCJItLZTYf/1rAsjEBMEEIGCeOkWQ1HWENFA7zQ25SEfAjIzY4YWRCJd+O3yY+8bGKEHr+PWnn2YoY3k5tYT2dlvCdtZ9ue02O09idJQg2tHBY1IpZsRGo+TTVIqA6HZfurIU+WbszkZnztjhl7o66hIMMsibbrnlFmzfvn3Khm6aJt7//vfjuuuuw/79+1FSUgK/349AIIBQKIRf//rX2Lt3LyYmJqZMJIlEAqdOncKNN96IRCKBI0eOYMuWLRgeHsbLL7+M0tJSnDlzBl//+tfR2tqKVCoFr9c7rbbLyMgoamvvRzS6HNGoGz/+sR9bt04gHvejuZn8rxTH1rveZed77N9PII/FqGH++MdAYlMTdr3lDsA00XU4hK6JAHypCajTAl+VwqbNm/FK5DqMd53BAfetGFXrsXU0iF03dUIuAWPH4z0YHd0Dl6sSbrcfLlcFwuED8Pvb4PPNfZ9Y7AxMM4V0egyGUQTDKAFgIB7vKAD6XJTLkZkNvPpdZ6/F+aUvETh0BIhOQNIOzOZmHnf4MKV1Z9lYLVW2ttpF4XT1RZ0zMT5OLTEQIDPrErU+H7d1dRGcDYP37e6mH0iXH9DlBnTdl+5uhsu2t3PC8fvtiUVntZaU8LgzZ6ghOO3pCx1e2NNDjaGykm2pqLBL7M7kJ8j17vQ6qABNVZnMkgsymJWya7p88YtfxP79+9HR0YGWlhbccsstEBHcfffdU8copfClL30JHR0dcLvd8Pl8ME0TExMTMAwDLpcL0WgUTz31FAzDwOjoKAYGBvC2t70NhmHg0KFDeOihh1BSUoJYLIbVq1fjDW94A7Zu3YqmpiZMTFShu3s5AoEIRkfLUFSUQGcn35/mN+3rOXKEgsrAAIWbM2f4fm+8kbyz55UatN70FlS2/wqdsTpUVpkYbtoBpQSJ9gM4Fzcw3mEisX4zKifLUV49iQNdy9C2OojGBWZspRSGhx9FJHIEbnclAAWfrwludzWSSdqRZjPD2KaafphmDCKAy1UNpTLw+RYvUy8KQJ9NQsxl581ei7Olhap9JmPX7BEh4N50EyXmhx7itUdHyZBvexv/HzrEWHOdbr96NQu3ORdkCYenR7pYC6hPhco6QxdPniQoFxXZ2czhME02x4/TvCjCSam+ntvXrOGAGBvjoFGKdYbGxwmS2p6uTTsLGV6oFM1KL7/M5+XxsP/V1cCjj05PVJpJau/tZVvXreOABzjB7ty55IIMZqTZarrcmqXCOCNilFJoaWnBvn37kMlkkEwmUVtbCxGBz+fDmjVrUFpaOhVmqJTCK6+8gvHx8anl7EKhEIaHh1FeXo7Ozk60trbiwIEDWLFiBSYniwGYVn5PEkAJDMMzFd46OcmxFo/zPadSHF+ZDPn/3Dlu4/KOgkeb347funsdTsaDqFxTg8kq2jPHvG2I1QVx3F+DylUlwK9+BQMKhqEQDBehUeVg7IuwAyYSvYhGz0CEjl6XqwjRaCdKSgxEIocQj3cilxlGA/nk5DHE470oLl6HePy05d/tQHX1Tvj9i5epFwWgz7YgylwSoggjTjo67AgRvRZnSwtt1l1d9rWVYrji+LhdJTEUYjhkeTlNPK2t0xdkefZZgq0Oax0ethdvPnHCrsPS0mKbVjIZhtR2dvJeQ0N2iG1LC/tTW2snPRkGv3XqvsvFyaCpiRE7L71Ee2au8MIL5XuleN3HH2efdH7H+Dg1hnDYXs81l7lH31ebut73PvY3GOQzue++gkNUU66aLvv378eKFStQVFQ049qeIoJ77rkHHR0dGBwcxKlTpxCNRpFMJtHS0oJt27ZhdHR0yklXXs6V9CKRCMLhMMbHx+F2u+HxeOD3+xEMBjEwMIDy8nJ4vV5s23Y9vvWtMETGYZom/P7VGBwsQibDd+nzcVxVVNjJczqcN5GwawwFg+Tto+2C225vRN+yRrgqAUPIO6P+RlTtaMToU4C/QmGsei3OnhzHUMyNeGAI6r1baX/XdBF2QKUUJibaEY3+BqnUMDKZCQAZiBTB79+CeLwTPl/TlF1cm2GKihqmbO7J5BCi0ZMoLd0Av38z0ukgTDONFSvuW7QOUWCRAHquWici+UuIjY3AXXfZa3gODjLV//77eX5vr31ti9+nGHF8nJKIx0NACwYpwesl3rTN/dFHyeDl5XRW9vayHZOTBF+/n4Ds9doZmRMTBH7t2HW57GqHSrHd2U5aZ9113c7JSU4QExOcuHp67DDD+fC9E/i16en736dpB6C9tLiY+zdt4iCeqc6O876RCK+VStFh3NzMay5btqBsclVTdk0XEcHp06fx9a9/HStWrJgmsWeDemNjI+66664pqVqvVHT//fdDRPDQQw9NOVcrKipQV1eHsbExBINBJBIJrFq1CpOTk1PVHHWoYm1tLe6/fwtEgnj55QwymRKEw37cfLNgYIDjIBSyy5LrVeGcobw6MlFnH584QQd+W9v5ocO33EKN81/+RXDixDpMjKdR5k3j/+25DneeKcG9PWKHz+ZbuQ/TI1nc7gAikUMIBp9ALHYKgAEREyI+ZDJRZDIRuFzlENHvwQBgIJViqFo4fMAyzVQgkTiLeLwbVVXNKC5uRjzejaKixc3UiwLQc9U6GRsjE80mIWqaLYLJaQ7R6f11dby+XlBl1Sp77VrALivhzGt461sp7YdCdikKEYJ7PE7NwDDsyp+69jhtb/xMThL4R0YYIfOZz5zvpF23juB48CA1ifZ2AuPZs3ZIZmcnJ7Bdu/Ln+2zg16anFSs4CbndfB56cXZnsl2ubFjnfUUI5u3t9sS4hArc5UXZNV1CoRDOnj2LLVu2TO3LVQERmD3bVCl1XmmBD33oQ2hra8Px48enTC/pdBrBYBAej2dq8qivb0Bfn6C1tRYbNtAmrn0og4PkV12lVkvjmhcAe5lEXcJF1xz62c+AP/5jJsOFQnZNrb4+TviPPw4EAoI3vtGDUMiDUz3A0A+Azi6bryXPyn3ZkSzp9ChSqQH4fGvhclUimewHoODx+OD11iGVGgRgQilzSkIHTHg8NRaoGxAx4HZXobh4NSYm2hGLvQaPZznKy7eiqGhxM/WiAPRcOQItLQS+Od7nFM0UwZTr2h/6EAHv+HHb9JJO24CmJYr6ehsERWwpJZEgAycS9pJx0agd3qgZ3eOxF5hIp3lOUREng+eeo5T81rfSWavbpyO4du5kUa01a2h6ee01XlPXOtKgnW/Fymzg16anNWvYrsFB9tE0aT83TUraXV25Qzyz77tlC/t7662MP19CyzjmRdk1Xc6dO4eVK1ciYK1cP1sFRCB3tqnePhPYNzY2IpFIYM+ePVi5ciUymQw2btyIe+65Bw0NjXjiCZnG29pHU1JCMNd87dQyddmI4mJui8c5mStFs104zHH7+c9z6c9t26ZL6oZhR0KJULAoKbEXJZoSRvKs3JdI9CIcPgCXqwzJ5ADi8R7E42fgctVCqRhoahEoxW+PZ9mUtO20odtAbYN9aelNAAzU1LwTpaUb5hXDfqVoUQB6LglbKToy862XMp9rO9f5TCRoIy8vJ/Nu2kRTTVOTDYINDQyLfPVVMqBSlFxqaqbXY9dLJOqa+7rI3LlztsM2lbIrOPb0cFGKkhI6aV0uHrdnj10dMpm0K4FqSam8nNKS7k8efD9VC35sjIOup4cDsL+f9zp3jtf2eNjmwUFqDu94R27bfPZ9laJ0t317ocBXLsoG3kQigaeeegpKqam6LrPWTJnj2rOBfWtrG44fDwKowbp1DQAEzzxDPlu3zubtcJg8q0uMnz5NfjRNCiYAv/XCQ7oarmFwPOiggliMwsCePeSj224j32jBJZXihDE2Zhfd83im83Xj5vwq9yWTw4hGf4NotAPJZB9MMwalMojHhwEkoNf7FklaJieF8vLbkMmwfGpJyXr4fI3gAiINKC/fOi1uvbr6LlRX373ogVzTogB04HwJW6mFW1FnJuldhOGRw8OM8li+nMyq48xfeIEM9uKLBH1dU9/tpioZDpM5dXs1YxqGXc0wFrOB//rr7bDHkhJqIUND/IyPcxAdPUrTRTBIO7RWY6NR3mfzZqrE4+M2yObznAIBmoUiERbCC4XY3p/9jG1OJjkoKyr4fe4ct81E86mUmQ9dbGLT1UBO4FVKob+/f9YqjAt0Vxw61IgDBxohAjxirb/kdpMfDh6kCS8e5/seGaHQcu+95NMTJ/hutClRT+C3387ETqVoqtm/nxFemt/LyuzKpiL0/Rw7Rn6uruY9+/t5/sqVTNhz8vWskpiDlEoiFutEKjUIpWIQcUGpJJQaB+CGy1UKERcMwwMRF0xzEsHgUxBxATBhmompmHQRQU3NLvj9bReUWZpN2bZ9AEinQxd93dlo0QB6NuX5Pi+a+vpoVtBlHzIZFgV79llKEfv28TuZtOu5FBWRuRsbCcpHj9rp/AD3FRURwD/8YUaznDvHSePwYR7X0EATjV7EJRzmQDp6lFLQTTdRWjp6lGGEhsHtDQ2UrjV45vuclOJ9Tp2i1OTx2M7cgQEOMu0wPnuW99QlFXI5W2erEXMh0TbZjt22Nn5CoWsT4GczlSwkOU1tY2MUDAYHyXdjY3aYqdbMtInw2DFGOinF8aHLNsdi5JnxcUZcNTXxmCeeAP7yLymZa7u7y0WQPnyYE8fAALetWgV84AOMsDIM8l1V1XS+th7SrJmgVssh4kImMw6lAMMQAC4AaYtPi+HzrQDghtdbBZESFBevzhnhosHXMKoQi3UhFPoJSkpuRGnpZpjm6BQQA5iznIDTtq+UIBY7BRGguPgGUEvIP2N1PrRoAR3I831eJGXbgsfH7eJw2lEaDNpmFF2/X4cVavX0xRcJyNrUUlXFAfPGN9KurBQzQL/8ZTKuXsTF46GT9vBhSuShECeA7m6af3Sc+ic+QUlmZOR8gJvrOSlFJ6wOOdMx+uk0B3cmw/vU1fHe2h9w7Bjv40w20gtq69LGg4Nss1bBx8dtSW7rVmpAfX2zg3y2fT+TAb73PeAXv7DtuvPNXL0aaCZTyUKSk7911dKxMb4Hj4fPWtvAy8rsCTWZ5H4dmaLXonC5yCPj43z/2in+7ncDP/0p8PzzNn/t2MGyAV/5CnlDO1lffdVeGrS1lb8DAYYfz6dIHMMTDyOTiVjRKhkAYn1cMIxSuN3FloRcibKyTTDNDOLxzikwBgwkk8OIRA4iHD6AVGocodATyGTCECmFUkm43RWorLwDLlcJKiruRDodQiSyDy5XCVwuf05w1rZ9n68J6fQYJiaoYrvd5XC7K+eVsTofWtSAfjko2xYciZDp9ao+Xi8/WuU0DA4AvcqVUnT+nDxpL5yhbd5FRXbqu4hdV2b/fko9LhcH1kc+wlLOxcV2DZv9+9mWzk4C6u7dFw5qvb28jq5/E42yjdoBptXeUIj7dcKUDs9MJKiJNDTwuRw8SC3myBEOdtNkX91uRiW96U1s8759vMZrr00vopfdh5km1Te+kYBxqUoeLAVy8rfm2WiUkvn4uA3mqZTt4K+utiV1nTOhAV2X0NCmRoDnP/kkeUNP7BUVjM7yerktELDzQwYG2I7s7GlgfhpeItGLeLwTZWVbMDoagmlOQqlJAAYMwweXqwqG4YdpRlFd/XYsW/YxnDr1QSSTQ1MSute7DNXV77LAfASjo/9uRcIAIly4O5nsx+TkUbhc5Rgd3QPAjaKiBhiGoKioMSc4OyNmMpkJK+kLyGQm4PFUQ4dKFgB9gSnbFjw2RuDp6iLApVL2CkFFRfytgd3jIVil02Rgr5cMqKVKDYQAmfaRR+xa6JGIXfI5GuXg0mA1MWGn0TuZfj7p+E7SSR9FRXbZgnjcnpxWrLCjFsrKGJnw2mt2rL4INZA3vIHRN88+S+m9v9+2s+vCZK+8Yi+X19/Pfc3NthaRC5izJ1XdRp3odKlKHohIA4DvAKgDYAJ4WCn1DyJSDeAHAFYD6AJwr1JqdOHufOko2xdRXz99gRev156wAU7gurJpIsFJWYR83ttL4A8GyScitrlm82a7XIWz3PXGjdTezp6lwx+guVEpnl9WRv64/no6UHt7uQ3IP+9EUyoVtOLhDbjd5RARZDIJGEYRfL61MAw3gDQMAygqasTk5BEkkwMAPFAqCdOMIx7vweTkSWQyEUxOHrXKAigABpRKWL/dSCYHIDKGVGoQLpcfXm8N3O5VSCR6YBie88CZ0j8jZlyusqn6Oy5X2bRQyYWmOQH9WmP6XM43py04EAD++Z85AJSy0+HjcUqMd95JsLvpJjKetg+OjZHpTZNA5vHwujr1vbeXNvTKSt6ju5uMPzHBc7u7Ceo6YsQwFobpAfZTRxSsWkWgnpjgRNTcbK+/G41yYhoYYHuGhmygFuEzGBnhpKRTvrWtFLCTTgYG+H9oiP2NxXjfnh7uzwbmXJNqXR3bAlx4hFMelAbwGaXUYRHxAzgkIj8H8FEAe5RSD4rIAwAeAPC5Bb/7AtNMSWZ6gZdgkBEnf/3XBGrt69EmNe0UX76cPOb18rhIhGYWHaYbj3Nyb2jgPfbsofklmbQjpADbZKnzM7xetqGhgbzz/PPT49pbWjghzJV3osntDmBy8ghipUPA3AAAIABJREFUsddgGMUQcVvm0Eqk08NwuXwwjGIUFb0Bw8M/hFIppFJxKBUEkARt7Rn09X0FbrcfsdhrDhA3p/YDKWQykxCJW2BMM43HU21J3dHzwNkZMaOUwOUqgQiQToeRTo/D798KpRQikcML6iTNR0K/Zph+tqxKpw16wwbawCcnyYRaIq+tZSEipWgX7u7mb11xrr7elsyjUUYC6NjuPXsIzJEIQU0zvQ5D1ItNazNPJsNjL5bpAbYrGmU0gq5Ds3Ytf+tonWiU4Nvezna73eyXDk0D2N/BQX50XDJgay2679qEom2uw8NU4wHeJxuYsx2s2QXU9HvSBdYWykmqlOoH0G/9jojISQCrALwHwB3WYd8G8BwWOW8DcyeZNTby2W3axHcWDBLE02luX7aMPDg0xHfQ20vw1pmgWlNViqGOf/u3NOXt388JPhajiTGVsoUbveRnJsPJwufjpHLqlB3uCxDw88mn0MSFJw4hkehFJhOHYRQDUJaJI4h0egyZjA+mGUU8fgaZTAZudwWUCoNgbkDEDaUE8XgHDKMYphkB4Q4gqOvfbiu7Ng4gA6VMpNMhJBIDEAHKy3fB661HPN4zzVHqjJhxRrkwm/Ugzp17CLnqyVwMzQno1xLT55tVed11ZO5IxLYNj4+TIVtayMy6+mJPDxkznaaa6WTIRx8lWHZ02OVGUymGDWYy/BQX28xsmgR3j4eMnx02OF+mB3jNJ59k25Yto/Slq1GWlhJs9cB9/XUblBMJTmiGQVD2ejnQH33UtoXqSQaws2IDAW7XxZuSSU4aWmrftYtgnEtTck6qjY3TAf7gQbvA2qVwkorIagCbAewDsNzieyil+kXkvHxvEfk4gI+zrYvDsD9bkpleX3Z4mAJBRwffyblzBPH6emqf+/fz3FiM762szLa1myZ5U9/rkUdsQaamxl6Fy+0mzwQC5KGKCv7evJnvXQs6ejnQsjKOo6Ehjqvycp5jmgplZecQiQxOk2L1whMjIz9FKhWCaUaRSqXhdlcik4kglRqFYVTAMDwwzShMMwVAkEpNwAZp04pRpxRumjHMRKyyOAGXyw+lMjCMYigVt5yk21BZ+TYEg08gEjm/7rrP15hlJ29CPN6DSORgznoyF2tTn5cNfb5Mb52zaBg/H4YPBmlT3rED+Ld/I5MpRSC87TY6Nl98kQ7BRIJAqU0aOp5b2yVDIeA73+E16+sp9etIk6IiHtfQwEFRVkYNoLWV93/9dQ60hgab6Xt7pxdIKikhcOqJJduubppcReinP2Vb9KRTVmbHw/f30yHa2Wn7C86csZ+ZBnid7frLX9qTUTYVFfHawSDbxjAtThYlJbTN/9Zv2WFus9WfcUbu9PQQ0PMo63FBJCJlAP4NwKeUUuF8pCSl1MMAHgaAtrY2Ncfhl4VmSjILBKZnPJ88ye2rVlHIWL6cgsqyZTQRPvww3/XICHmUZgXbeapT/XWm6MmTBHAN+toOryPDtK+mt5c11fViNHo50EzG9hk99xz7UlensHPnyzCMpzA0ZINkIPBehEJPYmTkp/B4lsM040ilBJnMCAyjFEql4XKVAlBIpQYAaO+tU+J2Ug5Gzj4iMwG3uwwuVzlMMwmPpwrp9ChMM4FkchR9fX+LVGoAFRV3wTTDSKfDGBl5FmVlrSgubjrvek6HKTC9nsxlA/QLYXpgcTF+Pgyv1UOlCODt7QTRVatocnjySeD976cdeXyc0sT4OK+jbYY6k275cjJqNtOn05TAEwlOGG43rw8QqCMRRsbo1ZB0Kv7oKK+9e7fd/u3b2e5Dh863mz75JMFcJ0xpR9eqVZSAdHx8X9909dcpeQN2aQQgd7IRnU72M6iuZp+SSU5iWtMxTeBrX6NfQBc6i0Zpw92/f2aAzre8wYWQiHhAvv6eUuoxa/OgiKywBJUVAIYu7i6Xh2ZK9gKmx6LHYuQ9r5cAPjrKcw8c4LupraXTOxTiM9aFuABbc9TVRycmbF+Tdnzq39EoJ4k1ayh5V1WRpw8fnl68a3TUDn0Mh3W26ASuu+55+HyNyGTGkU5HMDLyLJLJYYRCP0YqFUIyGbIqKaagVBqmGUNZ2WZMTv7GMp/MkhmXF3lBiOS1PZ46eDzVSKdDSKeDAExkMpPweJYjmTwLpRQymRgMw0AqNYbh4UdRX/9pJJN900wxTodpdj2Zi6W8AP1aYfp8GF4Dxe7dBMtgkAA1OkoA2r+fauvEBJn+7Fk7PdrjIWDr1YX6+wmY2UwP2BEx8Tivf9ttHAA338xB4CzS5axv09nJSBMtoff1MV57wwZOLJEIo1CGh7mKzMgI2xQKsR3JJM9ZtgxTS/k5ox4uhPQkaBi8n17FSTt4IxFKgj09dCw//TS3+Xx238rKOLkB52sa+ZY3mC8JpZJHAJxUSn3ZsespAB8B8KD1/eTF3eny0ExJZkeOTI9F15nMgO3riEa5b/9+8n1np+3odxat0+GuOuFMZ0hr7c7lspdN1BVCh4dZ2kLnY+zZA9x9NwHc66Xp58UXOW6qq/lJJCYwOlqGycmjiMe7rWzVXkQiB1BaugVKiQWqNKcAJtLpGFyuBhhGJ1KpkQV4oilQqjcg4oVpRmCaYZhmHG53FTyeOqRS/UilBsGVjUZQXNwCj6cRpmkiFutAf/83zqu9Hgi897wSAwtV+CufKJdrhunzYXiAzG0YdjRJNtPv20fTyKuv2mDmjM1NJsm4r77K/9lMr23yWpqfmOAiEzfcQGn19deBn/yEoLhzJ6Xb2loOjJ6e6UCmM/2OHqUGIcIBcuoU29jeTjAdG7Mdlx4P7+1cK/ViKJ22JzGtao+NTbdvx2KcaF55hc9scJCREjrOvKMD+PnP7cVEnGaYhS4z4KDbAfwegGMi8oq17c9Bnv6hiHwMQA+Aey76TpeQZvJHaMqORXeaRUyT52vhQCkKKrquSzJJrSuRsMcBwG/9X79/wJ7YKyvJW5kM+auzkxO9vn48TqFCLyTzwgvTJ2yRElRUDCAW64LHE0Ai0WOZOYYB+CzJPFsSCSMU+hZoXlmQJwsd8cJaRbciEtkHr7cOppmAUilwNSM/XC4PAIVE4hxEXCgpuQGAIBx+GX7/1iktY3R0D8rKWhe0xICT8pHQr3qmnw/Da/ugNsWcPTs701dU8FsDNjDdbKND/rKZXqda68kgmeQ1a2sJ6t3dnGh0qdwtW3hutqRaXExp99w5thcgWJ47Z58zagWT6uJhwSAds3qd1IUgp8RXWsqwzuPHKYW73XbkTjRK1bu2ls9WLxuoK0recgufRyhESX7FCtreL0UZCKXUC6B4l4t2XNzVLw/lUw/fOSGKkI919ElnJ30o4TDfw9GjdgirYdhVEIeHeS9nLkYqZZcB0JO5ltq1rb2oyJ4MTp3ivvJye5Uu50Iy09cF8KOhQSEUOodMZhyJxAC83nokk0NIp0esBCInCQi+c9vEL+w5h5FI9MDl8sM0FQBBInEOSiXgchWjrKwV6fQYTDOJsrINKC6+EZHIfrhcpVNaBiBIp2mKaWj4TA6H6cVTPlEuVzXTz5fhNRhv387fetWhmZheZ4Q6oz50rRfN9OXltsSqpRptl3a57Fh3pQi0fj/t3FrScabcZzP+jh10Yj7+uC2dJ5Ns62OPcSBq0hKZaXJiyraVLwSZph3aqKVAEbvYVzrNGHPTpJTW0sKootdf50Qgwomsu5t9ePhhmq6yQ0sLRMoncitXWCjA3zo+PJmkz2XjRgKvz2cv3qKFEx3xpPkWsH0qPh/HivYB6UgnncykfUBK0exWVWWPB72QjN0+heLiJzA6OgoRNzKZSbjdpfB6m5FKjVrOzmwp/NK651hm4Bg8ngqYZgzMSs1AKaC4uAmVlb+FaPQoJifbwaJcPSgv34aJiaOIxbrg9QYsTZ2mmESid8HBHFgCmaIXwvA6w66vj4A4F9NrgNbgpdPrtUTuchGwa2vpoBwYsJ1NupKdTvl3mm50GONUSdHG3O18+WXaPnV9mFWr7IqNTiemM3b8UoC58z4nT3Ji0ynjGhRKSxm21tPDNmoNQ6/UFAoRzKuqePyaNYW0/9koX4dxrno/zvV6Dx8mn27ZQlNfIGCH1/b12UKLro2uM0d1MpFOTNJLM2qBRSlK4L/92xSE9Dq/TuFClxPQ7YvHe3H27AGUlm4AYGJy8iRisddhmkdBm7ZO/AFsyfxCKd/zFZRKIJMZh8+3Bm53CQAgkRgCEEUsdgJudxXq6j4Kv78NXm8tvN569PV9GRMTryCdpvOzuHg1XK7KS5L2DywBQL8Yhs/+n4vpjx2j5OFkcG2v1ioqwO/ly8nQWu3NZOzImNJSu55KPM7v1auzSopmtdOpfZgm7dOJBEGysZHX1w4qZ3LSpSadbJVO006q/Qajo3w+584RsD/6UQJ1bS0npieeoJlFm7D0M9ahmgVAP58WymHsvI4I/Rs6ga6sjO9xbMz2KzU18b36/ZyQh4fpKDVNnrt+PTXHcJgZz5OTwAc/yGtmL02X7QvRYX2G4UJZ2Wb4fE0YHk4hkeiGLo/LCJQUbGC/UBJop+rs5IVhFCGTSUOpOIqK1gIADKMYLlc5KitvRUXF9vNs4bW19yAW64DbXQm3uxwuVwUSiZ5LkvYPLAFAX8gIiVxMr+2HhkHwHR4m+FRWMvLEGZrY329Httx+OyXpEycosa9fz6iT5mYOgs5OXuO8kqIOcmofq1fTdPHMM/bCvqEQ76dXYXLShQC8toPnikHXpCMV3G67lIBeNT4ateP5c61qtGsXbeYPP0zJPBAgAFyitP9rghbKYdzQwMn1G9+wfRvJJCfheNyuOKp5wO2238/kJCfk0VHyu9//f9p78/C2yjPv//Nolxc5jmM7ThzHiZM4AbI7EOhQKJS3lNLQ6ZRlaGlmCNCm9G1SaCn9lXagpWXpQOHXMiwtS6csaZkuLG1husCUMmQlYctiO953x/GixdZ2nvePR0eWbVmWbTm2kvO5Ll+2pKOjR/LR99znfu7ne6sV1WefreZRLrlEfRf0MW3YkHguZHhZn8WSi8MxH01zY7cXEwi00d9fi6aF0a1yB6NsMexvK0Nr0Ye8EkrIk4nQ+9G0ACAZGGjFYpmF3b4AKSVWax45OefGjbgdjhJmz/4ofX17CIXchEK9U9rK7qQX9FRWSBQXK+H85S+VkOuXlgMDg5NFBQUqWi8oULnCxsbB0kDdXlY/AaxapYQ83kGfjOvc8KuPsjJ1kjhwYPAKQc9TwqAQ6ymiWHSLg/5RFsxlZamriq6usT+n/n71Zfd41GcT6yKZlzd6VyMhVOqltVX9v/Q2aEZ/0tEZrXIr0YSxlIP2x6COQd1Js719sBLG71fHhNOprrb6+gZvOxxq3mPu3MESWpNJBTnBoJrgLixUczyXXDJ0PGPNhcTrHOR0LsPvb8ZqnR3xUAni81WjG2kpdHHWo25ntM5bLfMfiP3kGIzMR/uwhp8cbEAIiyWT/v5KgsFOHI5SZs26cFSBTnXTjLE46QV9ogf8cEEFlRLQFxTZbCqa1vPFfX3qR58MamlRi3r8fnXwg4q49c7p9fUqXZOdPbGDHkZvA+dyqZOP3a7y0keODM3R66Vl+uvFLtOOJ+h6Xl9f2JQIvQxT98HxetUldl6e+vJfeGFicZ7I/+tUJ166cDSkVJPlzzwzaMcwd67Kce/cqQKROXPUibu9XR1LweBg5yGrVZXXLlw46FmUlaV+1q5VUfkHH8AnPjEYoIz3fzdcBC2WPAYGmujre4uBgSbM5gwsljxMpgaUv0psTt0EOMnIWIbFkksw2MHAQA1CWCNL/TUGRVyP3C2Rv00MPSmoRUX6fi0WB1JasNnmEQodx2Yrxm4vHfP9CSGmpKIlHie9oMP4D/jf/lZNMurCtHGjOuD37FGiXFiocsDNzWr7RYvUAe/1qp+MDJUymDNnsJtRbEu6s89W+5lsQ+V4Vx/LlqlxzZ6t9llUpKIxNRs/KNiapr7IZ56phFpvg6f7YOu18zo222ADbL1EUUf3etEtefUozmZTC0qam9U4/8//UZ/l2F8Ao6Jlqoi1ul20SN3X1aXWCGSoeb7oIjghVIDw4Q8r8X/9dXXcu1zqONe9gWbPVqKfk6Ny7h/96MgAZbzoImi3L+DYsd/S27sbszkXv78WISzY7SX099ejaU0QaWihR+smk41w2IfTWYqm9WOzLSQc7ousHo2N6GFoyiY2WpEMCj6AwGTKRUof4XAfNlshubkXYLXm4nbvJTu7AiHECYnCE3FKCPp4aGxUYt7dPWi6/9RTShR1QyE996xXoxQWKrGqq1OLjvLyVGoG1BdAn/l3uVQUc8456nUm21A5XjlaU5Nq7dXUpL6gPp8ab3//YFWNyaTEVjcC27ZNVZw8/bTa/tgxtX+9PE1vJQZKtPUFSrrg6xULoIQcBm16DxxQ+2loUKtv29qS62JkMDV0dioBd7vV/0pPlegVWnl5g81QLBb1fzebVWBQXq6Ok85O9Vh5uZrI37pVPXcq/p965x+nsxSncxHBYBc+XyUWSxZCZCKEHSljLytDaFqQcLgPv78RKcO4XGtxuw8QCrWir/qUMowS8jDJ5dDDBAKNmEy2SB26jAq5pkFn5/MEg12k2j1xvBiCPoxjx1RkXl+vDm79QK+sVNUYCxYosa6rG+whesYZqp7a5RpcHapH6nqp4oIFqkogJ0eJearywno0u2DB4JVFbq76Ulos6rH6evWeYDCfHgyqL+b77yuhnT9/sNmGbkgW63WekaG216P3WHTjLhhsX6f7vAeDShxaW1WOf9cu9RnX1k6dc6JBfKRUdhJVVep/09OjjnGnczB9d/iw+l96PPCRjyhzN31i9PBhFY3rVUj19crXSG8bl6gF4kQbgA83srLZ5uD3txAMtuNwzEGIMMFgN5qmvFUUfkKhIF6vD5NJYLUWkJV1OsFgC5rmj+TTY9M0segDM8U8bo1Us8zCZMpBCF+kLn1/pAepE01bTFbWKlLtnjheDEEfxpw56mDu71cHss026LZYWqoiTbNZiff69ergrK9XP4cPK+E7dmywKcWaNSoineqoVK94KS1Vl9JdXeoklJU12Ixa9+EA9Z70/pK1tYOdaAYGBqtihFAnh2BQlaTpteQ6ppgrV/3Ep/cnbWkZ7Pxusag8fn+/Eo+OjsGm3Kl2TjQYHb0V4YYN6sTf26tKC1euVLXhNTXKX0Wf5NQnQdetU75AHR3qeO7vV//jjg4VCIw1HzXWwr5ExDOy0jRliGU2zyYcdhMOe9A0XYAHc+OqbtxKX9+bOJ1LEMKG2WzHZLISCnnRNL2ZhSnyE4r5W9+XCd1e12zOwGQKI6UJIQRSCjQtgBBmQDAV7onjxRD0YRQXq/xhdfVgDfmSJUqcPvMZePXVwcmjcFhF4B//uIp0e3qUWB85Mph/r6hQYm4yjd3IeaJRDIyseJkzR4lqe7v6OxxWX9COjsGJTb9f/b1v3+DiEKdzsFkwqL91gy89P64/Xxd+3exJ0wZXyeqd3Lu7Va6+v199rrov+1Q4JxokRj9G9HUU+vGxebP6Hw33CYpX/68vnMvIGJwoTUSyPQhGY3jFi5RhnM5l9PdX4nAswW5fiNf7Dr29fycU6kZKAcSaEyn/9IGBVuz2Ofj9nYTD7sh7yUZKN4MTpTCYgtEY7Fhkj6QVg/j9bdjthVgs2YRCGtnZqwEzmuabEvfE8WII+jCamtSE5fnnq7SK1aryjXpfzLq6odHl3r0q4igqUvc1NqqTgp5TrKpS+0x08E42ioH49fZe7+Ckldutblti/uP68nurVT3H51PCrFfE6IuaQqGh1S/6qlk9LaO7TeqeNRkZ6nX0eQO9KfXAwKClQaqdEw3GRj9GpFSpltxcdcJeuVI9nmi9xhlnKNGPbX84d+5gX9HRmKz1cWzFSyDQidu9j4GBGsLhPo4ffxmbbT5WawF2exHhcBDwDUsJqglPIcKEQh6s1lzAjtWag9u9n5H5czMWSyGh0HGEsAMBpNSQMkw4rJrd9ve7I9tl09u7E6dzEbNnX8zAQB2pdk8cL4agD+PYMRVhfvjD6kDXc8EVFUPdF2Howannn2FonXdm5tgH72SjGIjvR7NsmUq7LFmi9v3OO8rVrrdXCa6+SjUYHKxS0RcO2e0qona7VURdVzc4+alH6MO90WPNmXSPDr1kc+5cNT6TSc031NWl3DnRYAzGWpOR6LGSEvjsZ1WFjN+vjo8LLxz7irO1VX1/iosHJ9PHewLXK14ABgZqcThKcTjUBGl/fzVz536Onp4FNDU9iKaJSJSuC7WqXpEyiGoj50GIIJrmRPml62kVvVxRVb2otIk/MnmqUihW63xCoXaEsCEEmM05hMN9hMP95OZ+DOWDblS5zChio5jZs1W0rqdWYPQoZsECVZL35JODYr5woYqAxjp4U9HAIbbipbNTpVFqalSa5eWXVWRcUKCuJIJB9aWMrVTp7x/0cnc6B7sqLVo0mKYZPhmana2ie93fQ0+9+HyDvUP1Tkk9Per9bNoE112nUi9GlcuJZawa/0SPCQGf/vTYqzxh6BWnEErUW1tV/bqU8U/gytCqMaEgxpsgDYe9mM0OFiy4Bbd7L93df0VfABSbBxfCiclkwWIpijw/jBBZEddGK8qKV0UqZrOLUKgP1adUA0KRGvYBhLBjsczCZLJgs+UjhA2bbR7h8HEyMtad8Jz5cAxBH8ZEoxghlFBJqXLsmZlKzM88M3H0qU9Otraq50xmuXtspUFt7dAJ0upq+Nzn1FgefHDQGjV2olQXbT0Prptk6d40sdvor5eRMbgP/YQQDqvX1RtPm0zqhKJp6oqnudmoM58uEtX4j1X/n+z6gOFXnAsWqEV0H/pQ/MVGUkqOHfvtiIYPc+b8I0BU6JUHeThurtpsNlNWdh9Hj96E13sQk8lJKNRDINAaeY0BpLQQCnXgdC4nN/dCwuGfo1rYdUYnSPU+pGazk8zMlfj9bUjpIxTqiXwGKloXworFUhCZLHVMS748HoagD2MyUYzJBDfcoCZJk4k+Yxcx9fWp8sF581SqZDJpiHgTpF6vEvBbblF5/7/9TQm3vvpPr1O3WNRtl0s9XlamhDoQGCx91K9Q9GbAure73kDY71dC7nYP+n/o9emBgDEBerIw2kT+8OPPbFaBQVFR/P+7Xms+vGlyVtZ6PJ59Q4QeNPr76yKVJUNz1Q5HCU7nErzeDwgGO1A9TXMjPUHzMZmsWCyzCYW6cbnOJhjsoKfnb0hpIhhsxWotJCfnbAC83vfIytpAOPwXQiETJlM/UoYir6uaSweD7dhsc8nNHX3p/4nGEPQ4nIgoBuKXGlZVqbTEaCsqR/sSxd6vV6/ESw2ZzXDfffCd76jqlfp69frvvKMqHsLhQZtUkwkuu0xNjlZWqu3b2wcrWvSJ1JwcVc52+LB6rt+vKih050c96tcXWBkToOlPoon88RrixWuaLKWgp+ev9PT8DadzKVZrHsoYq545czZhMtmjqRmAgYEGvN73CIc9FBZeQzDYRijkZmCgEU3zIYQJk8keSZlkYjY7WLz4bvr6dtLR8Su83gNomp+BgWqs1kJycz9KKHQMIRyYzQGEyMNqzSUc9pGT82Fmz74Yk0mQkXEGDkfJtOTL42EI+hSTqBxxtEhaj5zj7Svel+hTn1I+M7H3a5qaeNQnooZPcM2dq04egYCyBc7JUSWGGRnqb32Jf3m5iraffnqwsXBOjrpfb/6bl6du6zX6+upU3ZkvFFIngmS8XAzSg0QT+eM1xBtea65pYfr7D+P3VzEw0EIg0IrDUUpW1lrU0n472dmqHVdsuiYQ6MDnO0RWlsohBoMdkSX/ehehUkymTMJhNzZbPiaTCYejGLPZSX7+ldE2ceFwD/Pn30gw2Epj448IBNqx24tR9thdCCHJzl417fnyeBiCPoWMVY443kgm3pdo9261r5deGmo5W1+vIn09Ita/TA0NKp/p8cCllyrx1UXd6RwsYbTZ1KSww6HGu26dsrV9/XWVM/d61TL+a69V27/0knq+yzXYOd7nU+mnwkL12mecMbiq0CC9GWsifzwGa8NrzUOh7ki9+xpCIQ8WSy4DA3XY7SUMr++OTddYLDn4/c14vYcQQmCzzYva2/b31yCEBSHMuFwbsdmKgaHe6yaTcnLs74dw+Dgu10ZcrjPp7PwNoVA3ICMNKnKmZdFQMhiCPoWMVY443khm+JdICDXZefCgSte0tioxXbtWbWO3D/YVjT25dHQoh0hNU6mSAwdUdB4KqYnc/Hy1D49H/R1bjnjNNars0e1Wk6UbNqj3ovuYBwKDTn16DftkjZoMZh5jBSPjST0Od1cMBFrp6XkTq3UODsdCBgbqCYXc9PdXMWfOJ4fkq2PTNRZLLk5nKb29/4sy03LgdJaSkbE60rruOFbr7MjjkqKi6+OuRNVPGkII8vMvZ2CgFrN5FhZL9qgNKpKp0jkRGII+hYwVxYzXKnb4l6irS1WMnHuuirpzc1UKpKRkZKQfe3LJyVHPq6tTf9fVKeGeM0eNo6ZGjeGii1T9cOx7MZtV5D57trq/q0vtc+NGZdz01FMqRQPK7722Vr12uk2CCiEuBh5EFSb/TEp59zQPaUaRyj4DMNRidmCggZ6evwOSrKy1EWfFaubNux6Xa+MQoRwuyJmZqwmHfWhaP1lZa7Fa8wgGuwiFjuN0lhEMtgPQ1vYUICgqum6E9/rwidbc3AsTNqhIVKVjmHOdRCSTUhlPJDP8S9TSoqpiFi9WVTL19SpyrqqCT35y6Jcr9uSSm6si+XffVROZfX1KfFevVguP9M5KNTUqN5/MRJcQ6sT03ntK0LOy1Os0NIysapmszcFUI1Qpw0PARUATsEcI8aKU8uD0jmzmMJW+9fEaXMyZc+kIMR9920+huyGGw14CgRas1lyCwS6s1ryoD0uiMvZDAAAgAElEQVRf307y8i5O2IAimQYVo1XpGOZcJxmpj2KGfon8fnjxRfXY2rVKNKur4frrR1bJDBfk1avV7zPPVHn4lStViqSrS6VPFi9Wj//5z8qErKRk7PeSn68WGxUXj34CS4XNwQngTKBaSlkDIITYAVwGGIIew1T51o+ny89o2wK4XBui9estLY8RCLRG9iEjKz0zornwRA0oxmpQEa9KJy3NuYzL0sRMRRQT+yWScrBdmy6Ol14av+Qx3snlox9VFTIu12BuvbdX3T5wQG3X0wPPPw833zz2e0nmBJYKm4MTwHygMeZ2E3BW7AZCiBuAGwBKZtDATxbG0+VntG31+5TV7bu0tT2FlAIhwG4vwWzOTsmCoER5+BPNhAXduCxNjqmKYvR9J3vCSLStfv9776lFRO3tqloGlODG5sHHqsEfazypsDk4AcQ75Q4xPpBSPgY8BlBRUZFMhwSDaUIIQVHR9YBKs5jNGZjN2Skz0IqX9klHcy7jsnQGML5qgvjbxjbJOHRI9ZzUm0yXlqqJ0+Td8RKPZ7ylmtNEExD7bSwGWqZpLAYpwGQyMW/e9eTlXZzySpQT3Qg6EZMR9DEvS8G4NE0nhIDLL1cR+axZKh+ekzPSJ3sypHpeYYrYAywVQiwCmoGrgKund0gGk2UqmzWfyEbQiZiMoI95WQrGpWm6UVKiVnPu2aMqZnp7Uyu4U1kdkSqklCEhxJeBV1HzQ09IKT+Y5mEZGIzJZATduCw9CTkRgjuV8wqpQkr5B+AP0z0OA4PxIORwk+tknyiEBagELkRdlu4Brk4UyQghOoH6Cb3gUOYAx1Kwn6nEGGPqSHacC6WU+VM9mOGk8LiOZSb/b2by2ODkHF9Sx/aEI/SJXJam6ssmhNgrpaxIxb6mCmOMqWOmj3MqTiIz+T3P5LHBqT2+SdWhG5elBgYGBjMH03QPwMDAwMAgNaSroD823QNIAmOMqSNdxplKZvJ7nsljg1N4fBOeFDUwMDAwmFmka4RuYGBgYDAMQ9ANDAwMThLSTtCFEBcLIY4IIaqFELdO93gAhBALhBCvCSEOCSE+EEJsi9w/WwjxJyFEVeR37gwYq1kIsV8I8XLk9iIhxK7IGH8phLBN8/hmCSH+SwhxOPJ5nj0TP8epYqYd3+lwbM/kY/pEH89pJegxDo8fB04D/lkIcdr0jgqAEHCzlHIFsBG4MTKuW4G/SCmXAn+J3J5utgGHYm7fA/woMsZuYMu0jGqQB4FXpJTLgdWosc7EzzHlzNDjOx2O7Zl8TJ/Y41lKmTY/wNnAqzG3vwl8c7rHFWecL6BshY8ARZH7ioAj0zyu4sgBdAHwMsqP5xhgiff5TsP4XEAtkcn6mPtn1Oc4he9/xh/fM+3YnsnH9HQcz2kVoRPf4XH+NI0lLkKIUmAtsAsolFK2AkR+F0zfyAB4ALgF0CK384AeKWUocnu6P8/FQCfwZOQS+mdCiExm3uc4Vczo43uGHtsz+Zg+4cdzugl6Ug6P04UQIgv4NbBdStk33eOJRQhxKdAhpdwXe3ecTafz87QA64CHpZRrAS8naXplFGba/yPKTDy20+CYPuHHc7oJ+ox1eBRCWFEH/DNSyt9E7m4XQhRFHi8COoQQUgixZAL7f0QI8e1JDPFDwCYhRB2wA3WJ+gAwK2K0BtP/eTYBTVLKXZHb/4X6Qoz4HKdpfFPNjDy+kz22p2FoM/2YPuHHc7oJerTxQGTm+irgxekckBDiaSFEK+rseyYQG728CGyO/L0ZlX+cEFLKL0opvzeJ539TSlkspSxFfW5/lVJ+FngN+EwqxjhZpJRtQKMQojxy14WoDlgp+xxnODPx+BbA48AhKeX9MQ9N+/9kph/T03I8T8dkwSQnGi5B2fYeBb41A8ZzOvAR1GXdESAY+X0JKp/3F6Aq8nt2ZLsl0zzm84GXI38vBnYD1cDzgH2ax7YG2Au8C/wOyI33OU73/30K3/9MO77/IXLMvgsciPzEPbaneZwz8pg+0cezsfQ/hUTOxK8D26SUv4rc93XgJtSX4jZUtLNUSlk97LlXAV+TMbaaQoivAh+RUm4SQjyFuny7LfLYpcCdQCnqrP9FKeW7Qoh/BT4tpfxkZLtq4G0p5RWR243AJ6WUB6bmUzAwMJgu0i3lMiMRQvyHEMIHHAZaiVgKCyEuBr6GKvNaCnw0wW5eBMqFEEtj7rsaeDbO660DngC+gDrbPwq8KISwA/8DnCuEMEXyc1ZUrhEhxGIgCxUtGBgYnGQYgp4CpJRfArKBc4HfAP7IQ1cAT0op35dSeoHbE+zDh8ql/TNARNiXEz+Hej3wqJRyl5QyLKX8eeQ1N0opawA36lLvPFQDkmYhxPLI7TeklFqcfRoYGKQ5hqCniIiw/h01q741cvc8htYVj9Wm7Fkigo6Kzn8XEfrhLARuFkL06D+o6oh5kcf/B5VT/HDk79dRYn5e5LaBgcFJyKQ6Fk2Akz5hv2XLFjIzMwEe/Jd/+RcKCws/BvwEoLKykmXLllFVVVUV77nBYJCioiIOHDggy8vL+dGPfgTwOYDNmzdTXFwM8K0bbriBkpISvvWtbzmH7eJZ4NnHHnuMl1566bO1tbX88Y9/3PrOO+/wzDPP8NZbb/H8888D/PuUvPnpJ4WtrA0M0g8jQp8EHR0d7NixA4/HQzgc5tVXX+W5557jggsuAOCKK67gqaee4uDBg/h8Pu64446E+7NYLHzmM5/h61//OsePH+eiiy6Ku93111/PI488wq5du5BS4vV6+f3vf4/b7QbgvPPO47XXXqO/v5/i4mLOPfdcXnnlFbq6uli7dm1qPwQDA4MZgyHok0AIwcMPP0xxcTG5ubl87Wtf44EHHuCyyy4D4OMf/zjbt2/nggsuYMmSJVGhT8TVV1/Nn//8Zy6//HIslvgXUBUVFfz0pz/ly1/+Mrm5uSxZsoSnnnoq+viyZcvIysri3HPPBcDlcrF48WI+9KEPYTabJ//GDQwMZiQnumzxpE+5GEwrRsrF4JTGiNANDAwMThIMQT8BaJqGsYDLwMBgqjnRVS6nFFJKQqEQgUCAQCCAxWLBbDZjNpsxmUyYzWaEECi7DAMDA4PJYQj6FKALeX19PXl5edhsNoQQaJpGOBxWngsxIm4ymbBYLFGRN5lMmEwmQ+gNDAzGhSHoKUQX8lBIeev39PTgcrmigm4yjcxw6aY6gUCAffv2sX79+uhjusDHRvWG0BsYGIyGIegpQI+8dSHX0ygmk2nM3HlsykUIES0r1IU+GAwSCARGRPSG0BsYGAzHEPQJogtuKBQiHA4DjMiHCyFGpFeSZbTcun6CCIVCBIPBIY8ZQm9gcGpjCPo4iY2cNU15XI0mvnrePJXERvPDxwVK6P1+Px988AErV66Mbms2m6N5+tgfAwODkwdD0JNESommaYRCoTGFXCeZlEuqiBV6KSXhcBiz2Rx9/diUUOxzRovojajewCD9MAR9DHRxbG1tJS8vb1yCp4vriSY2zTNWRD+a0Ovpm9io3hB6A4OZjSHoo6ALeSgUQkpJbW0ts2fPHpegTaegj8VoQq8/X5/oDQQC1NTUUFJSMqSOPjaqN4TewGBmYAj6MGInOvVIV49Wx5sPN5lMKc+hJ8tkBHa4QLvd7qh460I/nOEibyyaMjA48RiCHmF4DfnwunGTyRRXyBIxnRF6Kic8NU1LGInHRvTGoikDg+njlBf0eEIeT2wmEm1PpmxxMqT6JKJpWsL3kEjo9UVTsZ9DS0sLxcXFRomlgUGKOWUFXa9YGa2GfDgTFXRN0zh+/Dh9fX1kZ2eTmZk5qs95qkj1SWSiqZN4z5NS0trayvz580csmvrv//5vent7uf7661MybgODU41TStCTWQw0GuPNoUsp8fl8HDt2jJycHDIzM2lra4t2N7Lb7WRmZpKZmUlWVhYZGRkTfl/xXnumRrrhcDiaghlOc3MzVqt1GkZlYHBycEoIeuxioKNHj5Kbm0tubu64RC/ZHLqUkq6uLo4ePYqmaRQVFVFWVkYgEIiKmJ6G8Hg8eL1empqa8Hq9eL1e3nvvvajQZ2ZmkpGRMe58+EwW9FAoNOoVSl9fH0uWLDnBIzIwOHk4qQU93mIg/fZ4BW+slIuUkmPHjlFTU0NGRgZnnHEG3d3dcU8CQgjsdjt2u528vLzo/bt372bJkiV4vV48Hg/Hjh3D5/MB4HQ6ycrKigq90+kc9T3MZEHXFzzFo7e3l1mzZp3gERkYnDyclII+vIZcT6sIIbBYLCMW0iTDaIIupaSzs5OamhoyMzNZuXJlNH3S29s7wm8lEUIIHA4HTqeTOXPmRO/XNI3+/n68Xi9ut5u2tjb6+/sxmUxkZGQMEXq73Z5SQU/1BOtYEboh6AYGE+ekEvR4Qj48XWE2m8ddfhjvebFCnpWVxapVq0bkwVNVtmgymaKCXVBQEL0/HA7j8/nwer10d3fT1NSE3+8H1EmgsbExKvY2m21Cr53qaD+RoPf29pKTk5Oy1zIwONU4KQR9tMVA8bBYLAQCgXG/hh6hSynp6OigpqaG7OzsuEKuEyvoyYrieATUbDaTnZ1Ndnb2kPu7u7tpbGzEbDZz7Ngx6urqCAaDWK3WIROxyVTc6DXoqWKslEtubm7KXsvA4FQjrQV9rMVA8TCbzRNKuQgh6OnpoaGhAZfLxZo1a3A6nQmfM15zrlRFwiaTCbvdzrx584bcHwwGoxOxo1Xc6D+66KZa0MeK0A1BNzCYOGkp6OOtIY9lvCkXKSXt7e3U1dVht9uTEnKdqbDPTYbRonyr1Rqt8IndNhAIRCdim5ub8Xq9aJqGw+HAbrdHTwQTqbgZjl62GA+/35/0Z2tgYDCStBJ0vfQwFAqxc+dOzjnnnHFHtckKui7ktbW15OTksGjRIkKh0LgEJzblkmwqJRU59/GkbWIrbmbPnj1kHwMDA3R1ddHb20t9ff2QipvYtE2iipvhhEIhHA5H3DEbGBhMjrQT9HA4PCmHv7GqXKSUtLW1UVtbS25uLmvXrsXhcNDe3j7u3Hvs0v9k7XZTQSrEUQiB0+kkJycHt9vNihUrgNErboQQI/Lzdrt9xHtKlHIxzLwMDCZHWgl6MjnysRgtQteXpNfV1ZGbm8u6deuGRJITWfqfrm6LsQzPoSdTcdPT0xOtuDGbzUNy8/p9wwkGg1NuiWBgcLKTtt+giRpfDY/QNU2jra2Nuro6Zs+ezfr167Hb7SOeN5Fyx/GWLaaqzDGVpYaJqlJiGa3iJhQK4fP58Hg8dHV10d3djcfjwWazDamf7+vrw+VypWTMBganKmnVVDJWpCa6QEgXZk3TaG5uZufOnbjdbtavX8/y5cvjijlMzm3xRJNKQZ9slYvFYsHlcjFv3jyWLl1KdnY269atY+XKleTn50fnKm699VYOHDjA1VdfPeq+XnnlFcrLy1myZAl33333iMeFEHYhxC+FENVCiF1CiNKYx74Zuf+IEOJjw55nFkLsF0K8POE3amAwA0i7CF0XSYvFEq2tHi8DAwPs3LmTvLw8Kioqklp0M9GUy1QJejB4jECgHk0L4vcfJTOzAqezHJhZgj4cPeI3m81DKm5uvvlm5syZw3333Tfq82688Ub+9Kc/UVxczIYNG9i0aROnnXZa7GZbgG4p5RIhxFXAPcCVQojTgKuA04F5wJ+FEMuklPol1zbgEGBcIhikNWkn6DpWq3VcEbqmabS0tFBfX4+maUkLuc5EG1yM5ySQbETf1fU8dXVfAIa+/zlzbmDhwn9Pecol1YIeb389PT3k5uYOqbSJRfe5Wbx4MQBXXXUVL7zwwnBBvwy4PfL3fwE/EeqDuAzYIaX0A7VCiGrgTOAtIUQx8Ang+8BNKXiLBgbTRlqlXGAw7aJH6GOhL4F/66236O/vZ8OGDTgcjnEvhZ9ICzpd0Jubm3n//fepqamho6MDn8834cg9GDxGXd0Whos5wLFjj9HffyTlEXoyOfTxEG9sfX19CRcVNTc3s2DBgujt4uJimpubh282H2gEkFKGgF4gL/b+CE2R+wAeAG4Bpmf22sAghZy0EboupA0NDRQUFHDmmWdOymt7vCkX3X2xq6sLp9PJokWL6O/vx+Px0N7eHjXXysrKik4OJrP/+vrtCR/3evci5YUpFfQTUX3S29ubcFI03gkwznuM96blaPcLIS4FOqSU+4QQ5yc9WAODGUraCvpoEbqmaTQ1NdHY2JhQyMcbxSYr6LqQHz16lIyMDHJycigvLycQCJCVlUV+fn5023A4HK3n7uzsxOv1sm/fvqhVrv6TkZGBEIJg8Bi9vS8lfH27vYxgcGbm0BNdlfT29lJSUjLq48XFxTQ2DgbZTU1NI6wNUJH3AqBJCGEBcoDjMfdHdwe0AJuATUKISwAH4BJCPC2l/Nw43paBwYwh7QR9tJRLOBymqamJpqYmCgsLE0bkeqXLeCLPZMoWu7u7qaqqwuFwsGrVKsxmM++9917Cfbpcrmhk6vP5WLFiBVJKPB4PHo+Hzs5OfD4fJpMJh6MelSUbfRxtbQ+QmXn/jMyhJ0rf9PT0sGrVqlGfu2HDBqqqqqitrWX+/Pns2LGDZ599dvhmLwKbgbeAzwB/lVJKIcSLwLNCiPtRk6JLgd1SyreAbwJEIvSvGWJukM6knaDrWK1WfD7fECGfO3cuZ5111phCPRFBTzRh2dfXR1VVFSaTiRUrVkRrsfXmyON5DQCHw4HD4RjiiR4Ohzl+XNDQkPik0tf3B2y2L2GxlCX9uolIZQ59Ml7oFouFn/zkJ3zsYx8jHA5z7bXXcvrpp/Od73yHiooKNm3aBPA48IvIpOdxVGULUsoPhBC/Ag6iJh9ujKlwMTA4aUg7QddFz2Qycfz4cdrb2ykqKkpKyHUsFsuEKlaG4/V6qaqqIhQKsXTp0hFe3qksWzSbzQSDfx5zOymhtfX3WK1XEA6Ho2mbifqhpzLlMpbT4ljNLS655BIuueSSIfd997vfjf4tpRwALo/3XCnl91GVLHGRUr4OvJ5wAAYGM5y0E/RwOExdXR0NDQ2YzWY2btw47km7iVro6vT393P06FG8Xi9LliwZ0kYullS6LQaDx2hri1+jPfQ1weF4B5frC1itVrq6uqivrycQCGC320fk5scS61QKeqJVp2NVuRgYGIxN2gl6b28vUkrWrVtHZWXlhCowJtq1SNM0Dh06RE9PD2VlZeTn5yfMVady6X8gUI8QNlQQmphw+H+xWFooKvqH6H2xjan1Zfi6e6JuqBUvmk9lDn2yEbqBgUFi0k7Q8/LycLlchEKhcfXrjGW8EXowGKSurg6fz0dZWRnLly9P2j0xVSkXm20hmtaf9PbB4LvAoKCP1pha07SoF7oezesrcLOysvD5fAwMDKTMC320CN3n843a+cnAwCA50k7QdSYaZUPyOfRwOEx9fT2tra2UlJSQmZlJUVFR0q8z3kqTsU8AyadvwuGepLYzmUxxTbX0aL6rq4vW1lZqa2sBok2pY6P58Xihx4vQ9fecyhWpBganImkn6Lp4TKYsb6yTQWwt+/z589m4cSNms5nGxsYJr8KcbBmhz/cOicoVh+N230MweANW65yxN46DzWZj9uzZ2O12li9fjtVqRdO0qHOi3rc0EAhEo/nY3Hy8SDxRygVSZ/lrYHCqknaCngpGi9CllLS0tFBXV0dhYeGIyhl9cVGql8JPDRKf7x1yci6c1F5ic+ixK1tjic3NNzY24vV6ARXN6/n57OxsgsFgXDfLUCiUJp+pgcHMJu0EfXgUN5GI2Ww2D+k+pFu41tTUkJeXx4YNG+KW+U21oCdKudhsxePeXzjcO9khIaUcMxWiR/Oxxlqx0Xxvby/Nzc309fVht9vp6ekZYnlgeKEbGKSGtExaxq4WnYwnur5Mf9euXXR1dbFu3TrKy8tHrdmeTAeiyU6OHjv23LifEw73Teo1dSaSCtGj+blz51JWVsbq1avJz89nyZIl5OfnEw6HaW5uZv/+/dx4443U19fz4IMPxt3XWD7ofr+fK6+8kmR90IUQC4QQrwkhDgkhPhBCbBv3GzQwmIGkXYQei27QNV7TLYvFgsfjYc+ePdFl+slUWExmInYyBIPH6Oh4YNzPC4WOTcFoJk44HMZut5OZmTmk5vymm27iJz/5Caeffnrc54zlg/7444+Tm5tLsj7oqNWiN0sp3xZCZAP7hBB/klIenMr3b2Aw1aRlhK6TrIVuLPoy/d7eXlasWJG0mMPEI/SXXgpx7bUhduzoo7+/f9RofbSUi5oQHf/rWiwTmxCdKkabFPX5fJSUlPDRj350xGOxPug2my3qgx7LCy+8wObNm/Wb/wVcONwHXUpZC1QDZ0opW6WUbwNIKd2o5hbzMTBIc9IyQo/tWpRsysXr9VJdXU0gEKCkpISOjo4RpXpjMV5B1zSNf/3XddTXZwKZ/PrXudx5p5cnntgVrQzJzs6OVoaMRiDQNK5x6thsC8be6AQy2uRnokVF8XzQd+3aNeo2UsqQECLWB31nzKaxPugARNIza4GhOzUwSEPSUtB1kulaFG+Z/sDAAC0tLeN+vWQFvaOjg7fffpvf/15SX38ZsXbcDQ2ZvPTSOXz72z7cbjcej4djx47h8/nw+/1IKcnNzY1OGqrGGskvKBo63swJPW+qGG1hUSJBT8YHfZQrnlF90GP2kwX8GtgupUzNhIOBwTSSloKeTNeiQCDA0aNH4y7Tn2guPJnnPfjgg9x2222EQiGk/CDe6HnwQQdXXx1ixYq8Ias233//ffLy8giHw7S0tOD1etE0DYcjZ+RuRpOrmMdbD2wj+9yJB55T0Q813gRrT08P8+fHz3gk44Oub1NcXEySPugIIawoMX9GSvmbybwnA4OZQlrn0K1W6whBDwaDVFVVsXfvXnJycti4cSMFBQVDhGSigp4oQvd4PNx888184xvfIBgMIuV2YDmjqe7GjVns2CEIBoOEQiHC4TBCCLKzsykuLmbFihVUVFRQUVFBQUGckr6xCk8EuJ2HGGjZOcaGo5PqBtGj4Xa7Ry1bjPVBDwQC7NixQ7fKjbJp0yZ+/vOf6zejPugof/SrhBB2IcQiIj7okfz648AhKeX9U/S2DAxOOGkp6PHKFsPhMLW1tezevRuHw8HGjRuZN29e3Ihwora28QTd7/dz8OBBbrvtNh566KHIvXOAuxhddQVSCr785Qw6OlQdfXd3N319fUgpCQaDBIPB6EnHYhnbkGs0PC/fMeHnJvJeGS+J1gv09vaO6rQY64O+YsUKrrjiiqgP+osvvgjAli1b6OrqIuKDfhNwa+Q1PwB0H/RXGPRB/xBwDXCBEOJA5OeSeK9vYJBOpGXKRcdisRAIBGhoaKCxsZF58+ZFl+lPBbGRvW7j29bWxp///GceeeSRmC1LSWaZvqZJ/uM//peNG93k5uZSUFCA3+/HYrFgtVqRUqJpGl1dOyY8Zuuf36R65Vs4FiyITsAm+/mkMkJPtK+xnBbH8kF3OBw8//zzAEuGPzeeD7qU8u+MfY1jYJB2pK2gSynp7u6mtbWVhQsXjqvBxUQxmUzRDkn19fXMnz+fDz74gLvuumvYlm7AOeb+QiETP/7xhTz88Be45561+P1+3G43FosFv9+P3W7H4ejA43l15JPHyqFHGJgPC44epXPBAlpbW/F4PGiaNmRJ/mgNME6UF3qiCN3AwCB50lLQPR4Pb7/9Ni6Xi1mzZrFkyYjAbErw+Xy0t7djs9kwm820tLSwffv2OFuOXM0YHwFkEAo9ys03LyQ7208oFOLhhx/m8ssvx+/309j4l4kPWEDTlTD/Gz/E/rnBVpn6sny3201XVxd1dXUEg0EcDkfUeTErK+uEeqEbgm5gMHnSUtCdTifr1q3DbDazf//+Ce1D7yaUjGC53W6OHDlCMBjkwIED3HHHHUgpGRiIl9suR61nGc8VvRO4HrdbRfpbt27l/PPPJz8/n+zsORw/Po5dDccCPlMtlr//nfBZZ2EymRBCjDDZ0t+Px+PB7XbT2tqK1+slHA5TVVUVjeYn6oueKEL3er0jDL8MDAzGT1oKup5fllJOuJWcng9PJE4DAwNUVVXR399PeXk5TU1N3H777aMIuc5ZExiNAG4Dfgocw2q10tDQQH5+PgMDNaM/JUkG8iH/llvwvfFGNC+vzwVIKTGbzdEGGE6nk/z8fAC6u7tpb28nLy8Pj8dDfX09Pp8PIQSZmZlDovmx8vKJvNCTMQAzMDAYm7QUdJ3J+GfrFrrxfGBCoRA1NTUcO3Ysms6prKyMpiYSM3L5+iBjJb5LgWMEg0FKMzMJ7/0LHdpDCbZPjuAssL7yPp7Pfpa+iy7CsngxWVJiW7YMS1FRVOSBqGmZyWSKivBwJ8VwOBy1y43Ny2dkZEQFPjs7e0he3vBCNzCYetJa0CdDvDZ0emOLhoYGSkpK2LhxI7/61a/YunUrZrMZv98/Rv16OfA5JlZA4QQ+Dezlx+ecQ/E//AN9K0zwAz/EWognORkai7VHPWX+H/7A/D/8Qe3GbkcCB2++mb5LLokKcWZmJna7Hb/fT0tLC7m5udGTmBAi+pOTk0NOzuCCp1i73OPHj9PQ0EAgEIjm5fVl/8PLFzVNM8TcwCBFpKWgp8oTPTbt0NHRwdGjR8nPz2fjxo1YLBY6OjrYunUr/f3JLr2fSLpFR6DKp/Ow/OULCKCnDGR8J99x4egcfIXoq/n9AJzxox/Rs3kzvTZbNHfudrsJhULRjkW6MANxI3ld5PW8/Ny5cwH1ueqVO83NzQQCAbq6urBYLNETyFieOq+88grbtm0jHA5z3XXXceuttw553O/38/nPf559+/Zx9OjRXcCVUso6UNa5wBZUDelXpJSvRu6/GHgQMAM/k1ImO4ttYDCjSUtBh0GDLl2Yx1uyqC9K6unpobKykoyMDNatW4fD4UBKSTgcpqFOPLYAABXGSURBVKamZpw17WvHGnUSj1/PF7ifS3OOUHfdKE8ZZ5Tu6EjwoNWKs70d+/r1ZGRk0N3dzdy5cykuLqa/vx+32x1tkK33H9VTKk6nMzq5DAy5etGF3uFw4HA48Hq9ZGRkUFBQQDAYjPrYPPHEExw8eJBPfepT/O53vxsytPFY51ZXVyOE+BFjW+cCPARchLIG2COEeNGwzjU4GUhbQdfRDbrGK+iaplFVVYXVamXFihVkZ2dHhVwXqIULF46ZM9cFPxx+komnW4bi4quY534RUxDCwyP0ce5eBCCcyB24v59QcTFHq6ro6elh+fLl0Yg5IyNjiNdMKBTC7XZHI26PxwMQt5/o8MlXv99PZmZmtOOTnpe/9tprCYVCPPHEEyOGFmudC0Stc2MF/YUXXuD222/Xb/4X8JPh1rlAbWQV6ZmR7aqllDUAQogdkW0NQTdIe9JW0GMtdPUa6mTQTbs6OjqYN28ey5YtGyHkegqhoKCAH/7wh3zlK18Zsg+73c6dd97JvHmraWw087//m8OLL64jVYsPO7mOR9oOsdEyrIPPBPLn0gbuJeA6Mvo2+/fvp+D006moqEiYurJYLOTm5g6pGdc0DY/HQ19fHx0dHbjd7iETpBkZGXR1deHxeCgpKRmy0lZKSVdXFzabLe4JeQqtcxuH3T+ZXJmBwYwhbQVdJxkLXVAC0tDQQEtLC6WlpdF6ak3T0DQtmocfLmhbtmwB4Otf/zo2m41QKMS9995La+v5fPvbp2E2C1RP5FRN7AnATMvnQyp/LiN7FhN8CQFVX4U5fwdb7+Ar6IRtNlbn5GBZMDHvdJPJhMvlGmKuJaXE6/XS1tbGoUOHsFqtmEwmqquroykbIQTNzc3cdtttnHPOOXH3PUXWufHqI1NvK2lgMA2kvaCP1bVISklrayu1tbUUFRVFvV6ampro6ekhNzcXh8ORsA56y5YtbNq0iZ07j9LcbCE/fxa33HI6AwNTU52xYMEh/vEfHyJlxR8m6Dob5r0yUrnMmoYlxSttdXsEn8/HWWedhdPpjC5c6uvro7e3lzvuuIPXXnuNiooKHn300bj7mSrr3AT3GxikNWkr6Mk0ij5+/DiVlZW4XC42bNiAzWaLpldyc3Nxu90cPHiQQCBARkZGNNJ0uVxD6tMDgQBPPx3me987D5tNEAhMVGl1ORXD7hu6vwsvfHqC+x+d9o8oQdfsdoSmIZxOCAYJPPwwRBYSpYKuri6qqqpYsGAB5eXl0f+TEAKn00l1dTXbtm3j4osv5pe//CVedXkTl1jr3Pnz57Njxw6effbZIdvo1rlnn302xFjnCiFeBJ4VQtyPmhRdCuxGfdhLI3a6zaiJ06tT9gEYGEwjaSvoOvE80T0eD5WVlQghWLlyJZmZmSPy5Ha7nWXLVNGDlJL+/n76+vro6uqitraWYDBIRkYGmqbR3BzgzjvPw+83Ean2I/5V+lhJ7niP6fcNin1JSYrn5wT0boDmT0DRXwQDO3di8nrRSkpSJubBYJDKykqCwSBr1qwZMacRCAS47777+NOf/sQjjzzCmjVrAOKagunEWueGw2GuvfbaqHVuRUUFmzZtYsuWLVxzzTX6ArCbUAKNlPIDIYRunRti0DoXIcSXgVdRZYtPyPidSAwM0g4xFV1pEpCyFwuHw4RCIdra2vB6vZSVleH3+6mursbj8bBs2TK9E3w0Tw7EzZOPGGSkLr26upqsrCyqqmbxpS8txeuNPf/Fi7Ynw+DJ4IEHNrJq1a7UpVx0wpDz9ufpXn86DkeIjIwCcnPPJDe3dFJOlXoN/6JFiygsLBzx+b777rt85Stf4dJLL+XWW29NKOKTxFihZHBKk/aC3tXVFXVAbG9vp6ysjMLCQvViETEfbcIzHm63m8rKShwOB0uWLMFut9PZCStWOOnvT6VeDI/m1e1LL32Um276YurFfFTMwDfRtI+QmZmJy+UiOzsbl8s1psgHAgEOHz6MEILy8vIRQh0IBPjhD3/Ia6+9xiOPPMKqVaum8H0AhqAbnOKkraBrmkYgEKCqqorGxkbKysooKSmJdiPSy+KSFfJAIEB1dTU+n49ly5aNaIn2+ONmvvIVG5PTDElGhkYoBMGgQErTkMcWLDjMk0+exhT15xgVIRysWnWQQCADt9tNX18fbrebcDg8ZG4hOzs7aozW1tZGXV0dZWVlFBQUjNjngQMH2L59O5dddhm33HJLXM+cqXgrJ+JFDAxmKmmbQx/uiV5aWjpqPXkiNE2joaGBtrY2Fi1axIoVK+I+Z80aSXY2uN3jHanE6QyjaYLrrz/I+vUmnM553HDDLPpi+sx/7GPP8dWv/gsJTQcnUIeeDEKYCQabyM5eT3Z2drSSRC8/1GvMjx49Gm2P53A4KCsrG+Fj7vf7ueeee3jjjTd4/PHHWblyZeoHbGBgEJe0FXSHw8GaNWswm82888474xZyPU9eW1vL3Llz2bBhQ8Jl/iUlKrJOsEeGp1DMZrjtNg/Z2XVYrVbOOceF0+mhvr4av38dKt0BOTmdbN++Bbt9DCfHKYo/NS1EKNRNMNiJ1To4SRrrz1JUVERzc3P0ashsNtPd3U19fX10pe4vfvEL/va3v3HVVVfx+uuvn6io3MDAIELaCrrVasXhcBAKhfB6vRw+fJicnBxmzZo15qrRvr6+qH/L2rVrsdvtCbcHVQzy8MMBtm61ISUoS/TECmu1anz/+5nA6WRkCIJBtY/LLw/z6KMhtm41YbFI/vEfH8Zun3gj6KGYAY3ks1smhJBUV38WKYOUlPyQwsItQ7bo7+/n4MGDZGZmsmHDhmhuvaioKPr4fffdx5EjRzj77LMpLy83xNzAYBpI2xz6/v372b9/PxUVFRQXF0dTA729vfT39+NwOHC5XOTk5OByubDZbNEqmIGBAZYtW5bQ5W80OjuhocHEG28IvvtdNQk4WMqYWOBzcjpZuLCW3/62kLlz8+nshPr6LjRtKeBP+NzxYSaZJtV5ef/C8eM7kHLoyWThwv+fwsItSClpbGykpaWF5cuXx23kvHfvXr761a9y5ZVXctNNN015X9cxMHLoBqc0aSvolZWV7Nixgz179kQXnlRUVLB+/XrWr19PVlYWfX199PX10dPTg8/nQ9M0CgoKmDdvHi6Xa5xOiiM5fBjOOceJ3z+8WgWGa8sFFzzH17++hXDYQmamn8LC/8u8ef+Xjo7HaW7+3qTGMXEsCGFHyuGLe8yUl79HZWUHs2bNYvHixSM+q4GBAe666y527drFo48+yooVK07csEfHEHSDU5q0FfRY9InNnTt3snv3bvbs2UNvby/l5eVkZGSwcOFC/umf/onCwsJoFUdfZEYyOzs72qwhMzNzXL7q+/aZuPRSO319g89xOjXC4aGrSXNyOtmxYyEOx3BfdTNKgybWRm8shHAiZXCC+7+X5cuvGVHtA7Bnzx5uuukm/vmf/5nt27dPd1QeiyHoBqc0M+abOBlMJhOlpaWUlpZy1VVXAWrl4l133cVf//pXhBBce+21mEwm1q5dy7p169iwYQNlZWX4fD56e3upra3F4/FgtVqjqZqcnBzsdvuoIr9gQZhAYPhkqODf/z3AN75hw2pVufbi4lrC4Xgf9dhpkcmgaf0oe5PkUjCxLF26dISY9/f38/3vf599+/bxzDPPsHz58tQNNg49PT1cd911vP/++wgheOKJJygvL+fKK6+krq6O0tJSfvWrX42otDEwOFU5KSL0pF5YSjweD/v27WPnzp3s2bOHyspK5syZE03VnHnmmVGPl97eXvr6+hgYGMDpdA7Jx1utVnp7e6msrOSttxby3e8uxGplyKSnnmsvKdEIhztpaChnonlyKZnkQiM7ZvOVhEK/QIh4/wITaiJVIYSNNWsqh1S87Ny5k6997Wt87nOfY9u2bZNOVyXD5s2bOffcc7nuuusIBAL4fD5+8IMfMHv2bG699Vbuvvtuuru7ueeee6JDn/JBGRjMYE4ZQY+H7sS4e/fuqMh3dHSwZMkS1q9fT0VFBWvWrMFisUQnXHt7e/H5VOf7efPmUVBQwMBANk1NFkpKtFGtUdrbH6e+/ivxH5xizGYX5eUvo2kBDh8e2sRaSvD7/xWH4xmEMAOSRYseZs6cKwDw+Xzceeed7N+/n5/+9KdR/5uppq+vj9WrV1NTUzPkCqm8vJzXX3+doqIiWltbOf/88zlyJGr2bgi6wSnNKS3o8QiHwxw5coRdu3axa9cu9u/fTzAY5IwzziAcDnPWWWfx8Y9/nOzs7Ggu3u12I4SIrqjMyckhIyNjRKqmvf1xGhpuQko9p21BCBNSBqb0PZlMTlavPoTVmk9t7c10dj4S8+inWb78Ifz+dnp6DuPzuejvV2WcDz30EG+//Taf//zn+c53vnNConKdAwcOcMMNN3DaaafxzjvvsH79eh588EHmz59PT09PdLvc3Fy6u7v1m4agG5zSGIKeBD6fj23bttHQ0EBubi4HDx7E5XJFo/gNGzYwd+5cvF5vNFXj9Xqx2Wwj8vHBYCde7zuAIDNzFb29r1NXtxVNG23y0jLK/aNTVPT/0d7+I4SwImWQ0tKHmTPn8ujjbW27qKt7hcLC8ykt/fCIE4/X6+V73/seH3zwAatXr2bt2rVcc8014/7cJsPevXvZuHEjb775JmeddRbbtm3D5XLx4x//2BB0A4NRMAQ9SXRfGP3vrq6uIamaxsZGSkpK2LBhQ7R00ul0DsnH+/3+qDeKno+3WCz4fC1UVv6KQOBbI163uPj7tLTciRBWNC0AaAkj+ry8zZSV/QfBYCd+fwN2e0k0Fx4MBqmqqsLv97NixYoRC7CklLz55pt84xvf4Nprr+VLX/rSCY3KY2lra2Pjxo3U1dUB8MYbb3D33XdTXV1tpFwMDEbBEPQUoWkaNTU10VTN3r178Xq9nHbaaVRUVFBRUcHKlSsJh8PRfLwu8qFQiMLCQszm/6C398noPvPzv8iiRfcNEWc9opdSIKVvyBhMpkyWL/8jWVnrR4yvs7OT6upqSktLmTt3btyo/Pbbb+fw4cM89thjlJWVTc0HNQ7OPfdcfvazn1FeXs7tt98ebYaRl5cXnRQ9fvw49957r/4UQ9ANTmkMQZ9CAoEA7777blTk33vvPWw2G2vXrmXBggUEg0EuvfRSioqK8Hg89Pb24vF8gMlUSWbmBmbPXk1OTg5Op3OIAKu0zbtUVV0xZJVnbK48dgxHjhxBSkl5efkImwMpJX//+9/5xje+wfXXX8/WrVsTtuM7kRw4cCBa4bJ48WKefPJJNE3jiiuuoKGhgZKSEp5//nlmz56tP8UQdINTGkPQTyBSSnp7e9mxYwc/+MEPWL16dbTXqZ6Pr6ioGFE66fP5sNvtQ/LxNpuNY8eep65ua9xcuW4+VlNTw+LFi6Me8bF4PB7+7d/+jaqqKn7605+yaNGiE/I5hMNhKioqmD9/Pi+//DK1tbVcddVVHD9+nHXr1vGLX/xiok0wDEE3OKUxBH0a0DsoWSwWpJQ0NTWxc+dOdu3axZ49ezh+/DjLli2LCvyaNWswmUxDRD4QCJCZmUlWVgins5fc3NNwOJRo+/1+Dh8+jNlsjmuUJaXkjTfe4NZbb+WLX/wiN9xwwwmNyu+//3727t1LX18fL7/8MldccQWf/vSnueqqq/jiF7/I6tWr2bp160R2bQi6wSmNIegzkFAoxMGDB9m1axe7d+9m//79AKxevToq8suWLcPv90fz8W63GyklZrMZn8/HokWLmD9//gihdrvdfPvb36auro7HHnuM0tLSE/rempqa2Lx5M9/61re4//77eemll8jPz6etrQ2LxcJbb73F7bffzquvvjqR3RuCbnBKc1Is/T/ZsFgsrFq1ilWrVnH99ddHG03s27eP3bt3c++993LkyBFyc3OjqZqCggI8Hg8FBQWUlJTQ09NDc3MzZrOZnJwcurq6qK+v54EHHuDLX/4yjzzyyLTkyrdv3869996LO9IppKuri1mzZkX9YIqLi2lubj7h4zIwOBkwBD0N0BtNnHfeeZx33nmASpu0t7eze/dunn76af7yl79w2mmnRUV+w4YNrFu3DofDQVtbG08++SRvvPEGmZmZXHnlldMi5i+//DIFBQWsX7+e119/Pfo+hjMegzQDA4NBDEFPU4QQzJ07l02bNnHmmWficrlwOBxUVlaya9cufv/73/O9730vah98xx138J//+Z9J91idCt58801efPFF/vCHPzAwMEBfXx/bt2+np6cn2vWoqakp2gLPwMBgnEgpT+RPSvnjH/8oly1bJsvKyuRdd92V6t2fFPh8PvnOO+9M9zBG8Nprr8lPfOITUkopP/OZz8jnnntOSinlF77wBfnQQw9NdLcn+ng2foyfGfUzMwqOJ0A4HObGG2/kj3/8IwcPHuS5557j4MGD0z2sGYfT6WTVqlXTPYyE3HPPPdx///0sWbKErq4utmzZMvaTDAwMRpC2VS7DqyHuuusuAL75zW+m6iUMkqCxsZHPf/7ztLW1YTKZuOGGG9i2bRvHjx+fDt9yI/lucEqTthF6c3MzCxYsiN42qiOmB4vFwn333cehQ4fYuXMnDz30EAcPHuTuu+/mwgsvpKqqigsvvJC77757uodqYHDSk7aCHu/KYjyTfY2NjXzkIx9hxYoVnH766Tz44IMAHD9+nIsuuoilS5dy0UUXxTr5GcShqKiIdevWAaqd34oVK2hubuaFF15g8+bNgGpU8bvf/W46h2lgcEqQtoJeXFxMY2Nj9PZ4qyOMyDL11NXVsX//fs466yza29spKioClOh3dHRM8+gMDE5+TnQOPWUI1SyzErgQaAb2AFdLKT+Y4P5eAH4S+TlfStkqhCgCXpdSlqdo2CctQogs4H+A70spfyOE6JFSzop5vFtKaTT/NDCYQtI2Qpeq7c+XgVeBQ8CvJiHmpcBaYBdQKKVsjbxGK1CQivGezAghrMCvgWeklL+J3N0eOSES+W2E6AYGU0zaCjqAlPIPUsplUsoyKeX3J7KPSGT5a2C7lLJvMuMRQpiFEPuFEC9Hbi8SQuwSQlQJIX4phJiQheBMRqiJi8eBQ1LK+2MeehHYHPl7M/DCiR6bgcGpRloL+mSZgshyG+pqQece4EdSyqVAN3AyFlh/CLgGuEAIcSDycwlwN3CREKIKuChy28DAYApJ2xz6ZIlElj8Hjkspt8fc/0OgS0p5txDiVmC2lPKWJPZXHNnf94GbgE8CncBcKWVICHE2cLuU8mNT8HamBCHExcCDgBn4mZTSEGUDgxnMqRyhpzqyfAC4BdAit/OAnkiuH6AJmJ+y0U8xQggz8BDwceA04J+FEKdN76gMDAwSccqac0kp/87oKwsvHM++hBCXAh1Syn1CiPP1u+O97Hj2O82cCVRLKWsAhBA7gMsAw1/BwGCG8v8Au3Am9xZ5Ns4AAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# 画图\n",
"plotShow()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 参考博客\n",
"主要参考统计学习方法这本书,书籍地址:http://www.dgt-factory.com/uploads/2018/07/0725/%E7%BB%9F%E8%AE%A1%E5%AD%A6%E4%B9%A0%E6%96%B9%E6%B3%95.pdf。\n",
"\n",
"\n",
"[统计学习方法-代码解读](https://github.com/fengdu78/lihang-code)\n",
"\n",
"[EM算法 - 期望极大算法](https://blog.csdn.net/randompeople/article/details/93711747)\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "py3",
"language": "python",
"name": "py3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.4"
}
},
"nbformat": 4,
"nbformat_minor": 2
}