{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Funktionen"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"- Funktionen\n",
" - Notation und Terminologie\n",
" - total und partiell\n",
" - injektiv, surjektiv, bijektiv\n",
" - Komposition\n",
" - Identitätsfunktion\n",
" - mehrstellige Funktionen\n",
" - charakteristische Funktion einer Teilmenge\n",
" - Mengen von Funktionen\n",
" - charakteristische Funktion und Potenzmenge"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Nützlicher Link\n",
"\n",
"Vorab der [Wikipedia-Artikel zu Funktionen](https://de.wikipedia.org/wiki/Funktion_(Mathematik%29), der durchaus lesenswert ist, wenn man einen Überblick gewinnen und sich daran gewöhnen möchte, verschiedene Schreibweisen zu lesen. Besonders den Abschnitt [Notation](https://de.wikipedia.org/wiki/Funktion_(Mathematik%29%23Notation) sollte man einmal gelesen haben, da einem der Inhalt häufig begegnen wird."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
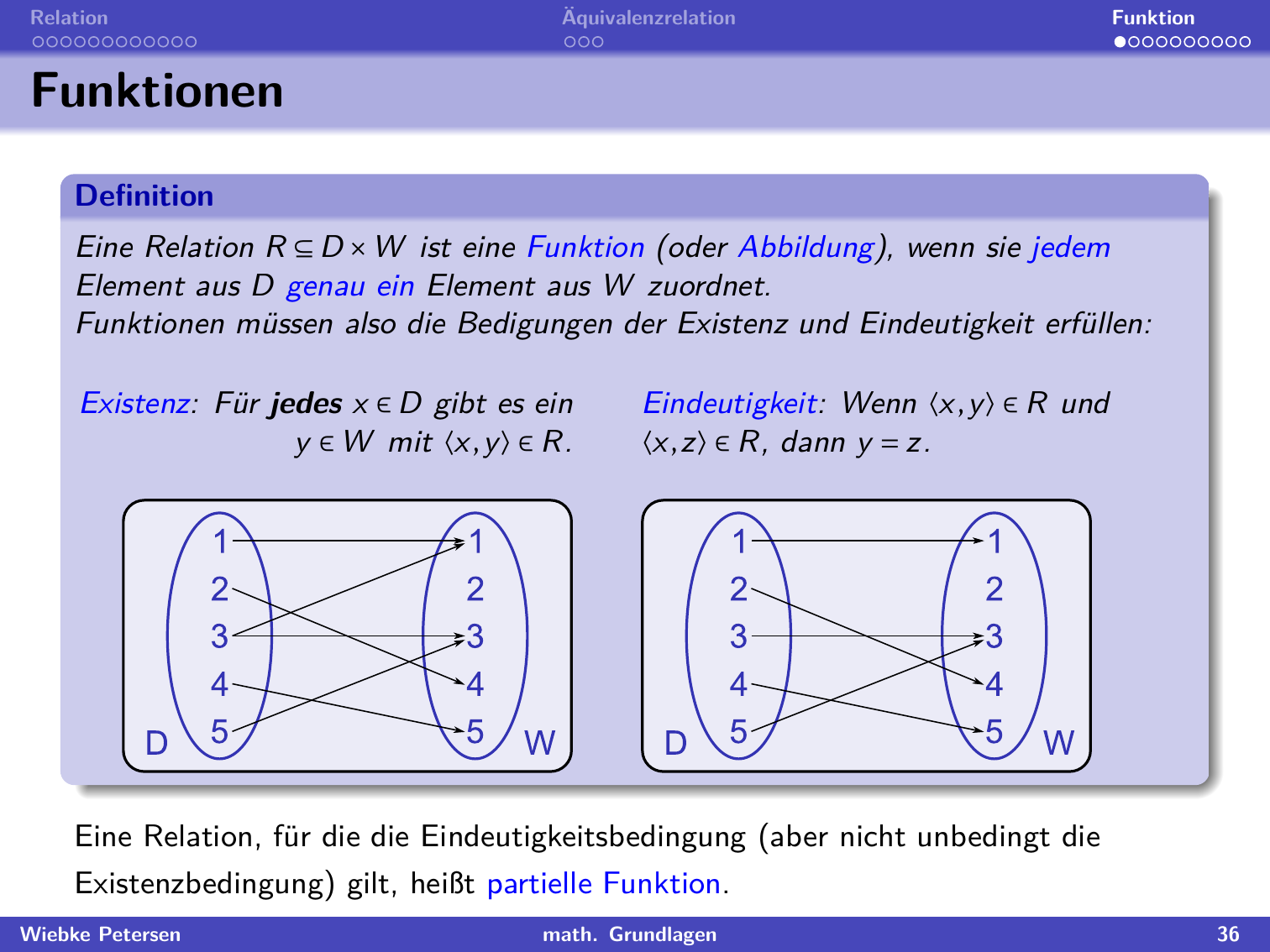
"## Funktionsbegriff, Existenz und Eindeutigkeit"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Erklärung Stichpunkt 5: Einschränkung\n",
"\n",
"Zur Erinnerung: $\\mathbb{N}$ bezeichnet die Menge der natürlichen Zahlen (alle ganzen Zahlen > 0, also $1,2,3,4,5$ usw. $\\mathbb{Q}$ bezeichnet die Menge der rationalen Zahlen (alle Zahlen, die sich als Bruch zweier ganzer Zahlen darstellen lassen). Es gilt also: $\\mathbb{N}\\subset \\mathbb{Q}$.\n",
"\n",
"Wir betrachten eine Funktion $f:A\\to B$, z.B. die Funktion $f:\\mathbb{Q}\\to\\mathbb{Q}$ mit $f(x)=2x$\n",
"\n",
"In diesem Fall gilt für die Mengen $A,B$, dass $A=B=\\mathbb{Q}$.\n",
"Außerdem gibt es eine dritte Menge $C$, sodass gilt $C\\subset A$. Nehmen wir also an, dass $C=\\mathbb{N}$. (Es gilt ja $\\mathbb{N}\\subset\\mathbb{Q}$, siehe oben).\n",
"\n",
"Die Funktion $f_{|C}:C\\to B$ ist jetzt die Einschränkung von $f$ auf $C$. $f_{|C}$ nimmt nur natürliche Zahlen als Argumente, aber keine nicht-natürlichen Zahlen. $f_{|C}$ ist also auf die natürlichen Zahlen *eingeschränkt*.\n",
"\n",
"Beispiele:\n",
"- $f(2)=4$ und $f_{|C}(2)=4$\n",
"- $f(2.3)=4.6$, aber $ f_{|C}(2.3)$ ist nicht definiert (da $2.3\\notin \\mathbb{N}$).\n",
"- $f(-\\frac{1}{3})=-\\frac{2}{3}$, aber $ f_{|C}(-\\frac{1}{3})$ ist nicht definiert (da $-\\frac{1}{3}\\notin \\mathbb{N}$)."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Video zum Funktionsbegriff und zu partiellen und totalen Funktionen"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## partielle und totale Funktionen"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Video zum Definitions- und Wertebereich sowie zur Domain und Range"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Injektivität, Surjektivität, Bijektivität"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Video zu Funktionseigenschaften"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Das Video deckt die Themen partielle und totale Funktion, Injektivität, Surjektivität und Bijektivität am Beispiel $f(x)=x+2$ ab. Folgende Abschnitte sind für die jeweiligen Themen interessant:\n",
"\n",
"$f : \\mathbb{N} \\to \\mathbb{N}$\n",
"- 0:00-1:02 partiell/total\n",
"- 1:03-2:18 injektiv\n",
"- 2:19-4:20 surjektiv (Es gilt natürlich in dem Beispiel $x \\notin D, x \\notin \\mathbb{N}$).\n",
"\n",
"$f : \\mathbb{Z} \\to \\mathbb{Z}$\n",
"- 4:21-5:27 Einführung, partiell/total\n",
"- 5:28-5:41 injektiv\n",
"- 5:42-6:53 surjektiv\n",
"- 6:54-Ende bijektiv"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
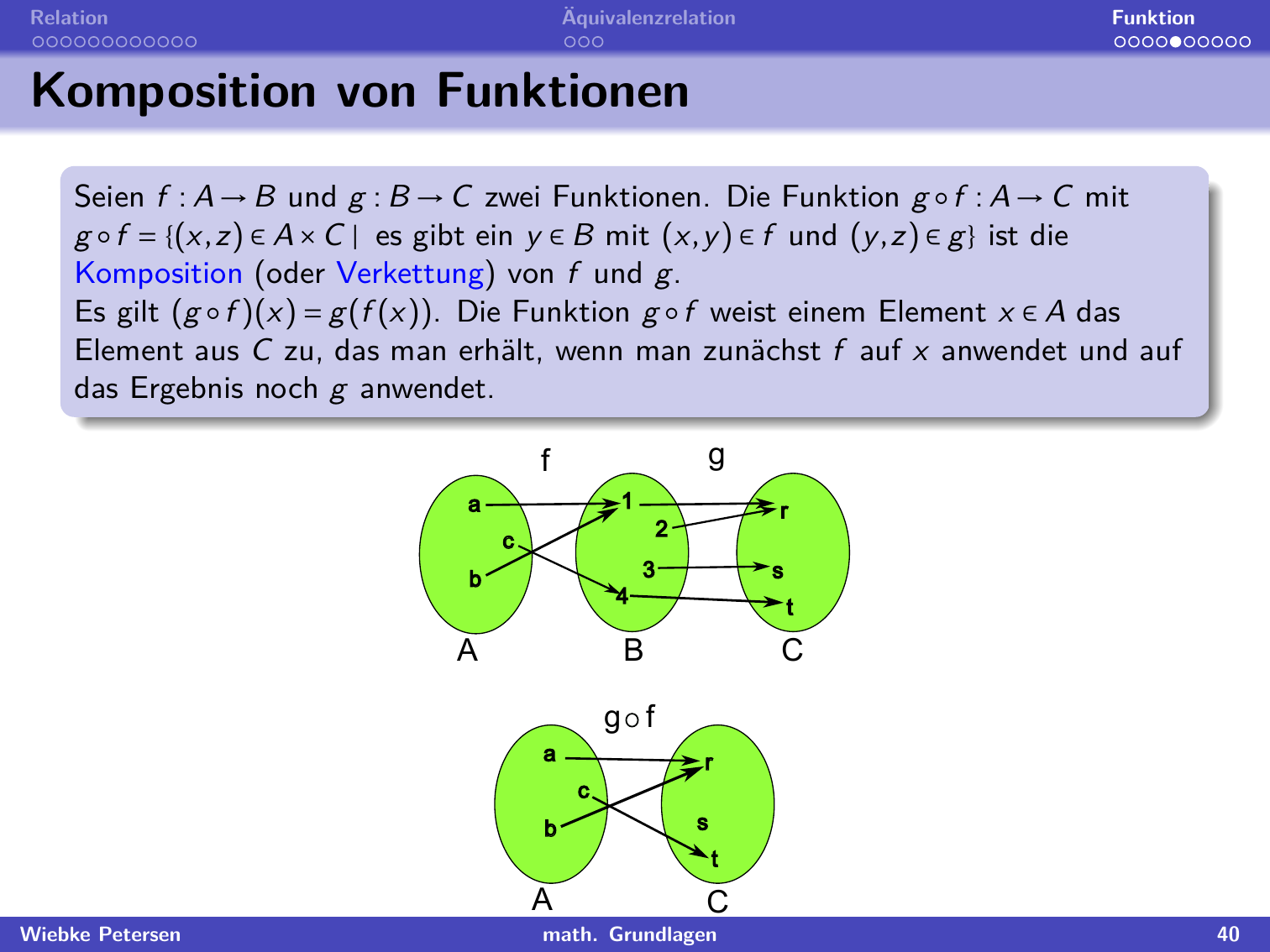
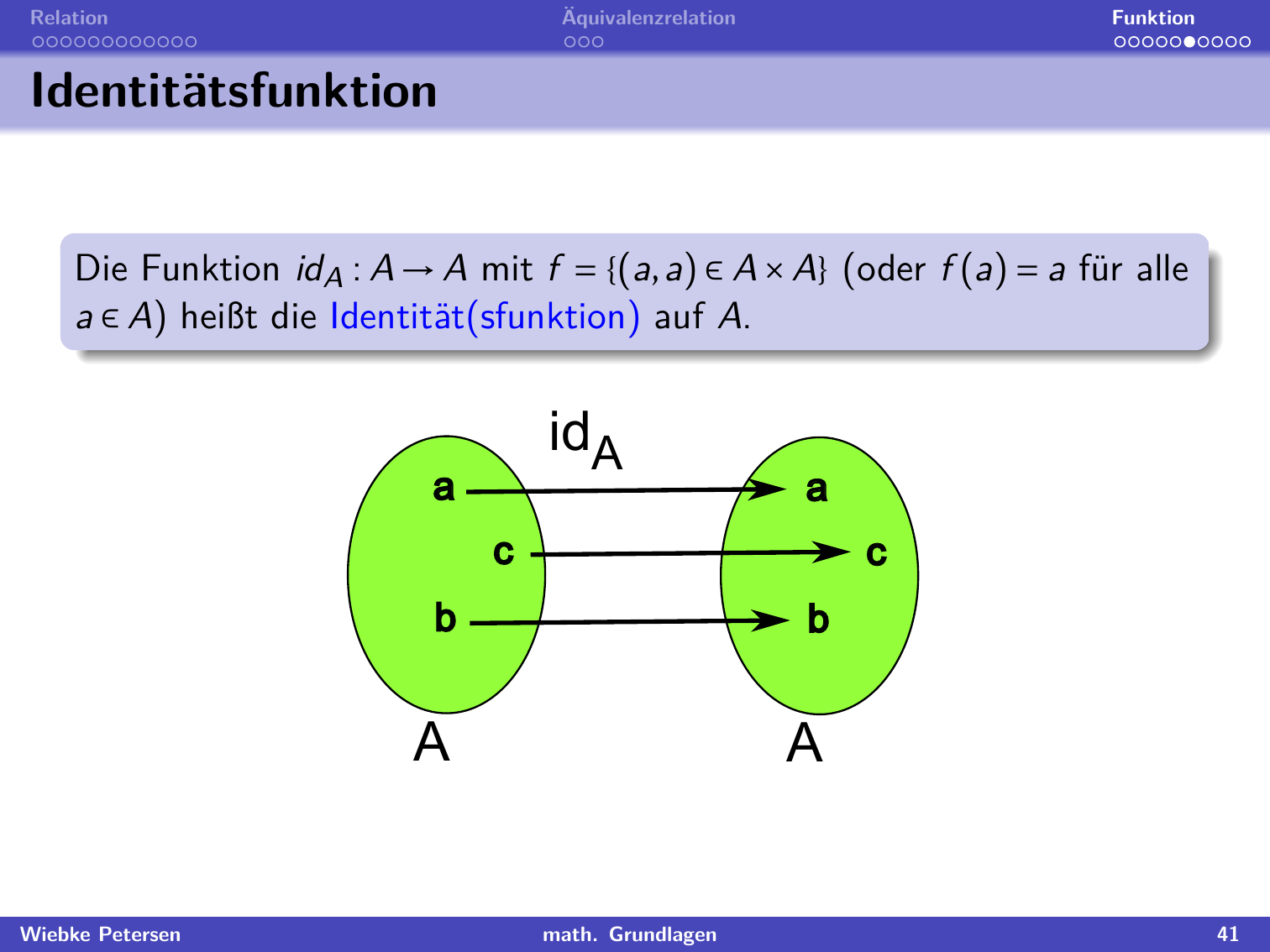
"## Komposition von Funktionen"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Komposition bedeutet also, dass mehrere Funktionen 'nacheinander ausgeführt' werden. \n",
"\n",
"Nehmen wir als Beispiel die Funktionen $f:\\mathbb{N}\\to\\mathbb{N}$ mit $f(x)=5x$ und $g:\\mathbb{N}\\to\\mathbb{N}$ mit $g(x)=x-1$. Für die Komposition $(g\\circ f)(x)=g(f(x))$ wendet man erst die Funktion $f$ und dann die Funktion $g$ an ($f$ steht in $g(f(x))$ ja weiter innen. \n",
"\n",
"Zum Beispiel gilt $(g\\circ f)(3)=g(f(3))=g(15)=14$. \n",
"\n",
"**Merke**: $(g\\circ f)(x)=g(f(x))$ ist nicht das selbe wie $(f\\circ g)(x)=f(g(x))$. Zum Beispiel gilt $(f\\circ g)(3)=f(g(3))=f(2)=10$."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Diese \"wenn...,sonst\"-Beschreibung einer Funktion mit geschweifter Klammer wird einem häufiger begegnen."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.4"
}
},
"nbformat": 4,
"nbformat_minor": 2
}