{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Endliche Automaten"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Formale (und zu einem gewissen Grad auch natürliche Sprachen) modellieren wir auf verschiedene Weisen. Die folgenden 3 sind in dieser Veranstaltung besonders relevant:\n",
"\n",
"- Durch implizite Beschreibung der formalen Sprache als Menge\n",
"- Durch die Angabe von Regeln, wie Elemente der Sprache gebildet werden (formale Grammatik)\n",
"- Durch die Angabe eines Automaten, der die Sprache akzeptiert"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
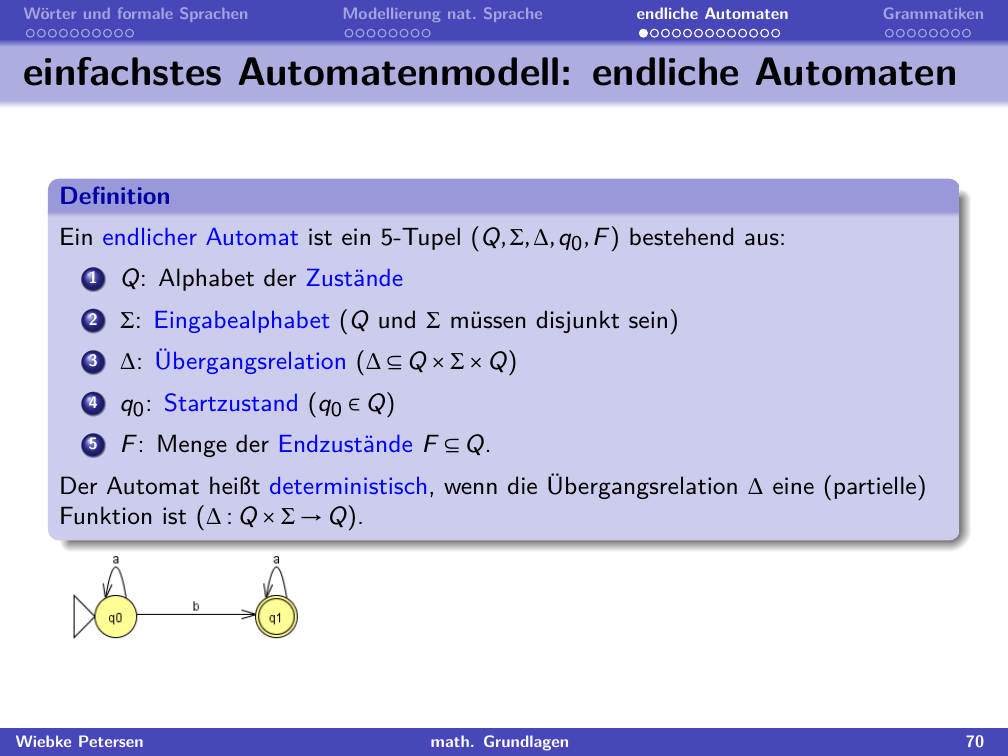
"Was ist überhaupt ein endlicher Automat? Ein Automat ist ein Objekt, mit dem man für bestimmte formale Sprachen Aussagen darüber treffen kann, ob ein Wort Teil der Sprache des Automaten ist oder nicht. \n",
"\n",
"Hier hilft es, zwei Dinge zu unterscheiden: Ein Automat kann graphisch dargestellt werden als ein Übergangsnetz, das sinnvoll ist, um die Arbeitsweise des Automaten zu zeigen und ihn anschaulich darzustellen.\n",
"Um dieses Übergangsnetz zeichnen zu können, brauchen wir aber eine formale Definition dieses Übergangsnetzes. Für diese formale Definition benötigt man lediglich Mengenoperationen und Tupel, wie wir sie schon kennengelernt haben. Hier die Definition eines endlichen Automaten:"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Unter dem Block mit der Definition sieht man das Übergangsnetz eines Automaten $A$. Dieser ist durch das folgende Tupel definiert: \n",
"\n",
"$A=(Q,\\Sigma, \\Delta, q0, F )$ mit\n",
"\n",
"- $Q=\\{q0,q1\\}$\n",
"- $\\Sigma=\\{a,b\\}$\n",
"- $\\Delta=\\{(q0,a,q0), (q0,b,q1), (q1,a,q1)\\}$\n",
"- $F=\\{q1\\}$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Diese Definition bedeutet (umgangssprachlich) folgendes: Wenn der Automat ein Wort zu erkennen versucht, kann er sich in zwei Zuständen befinden: $q0$ oder $q1$. Er startet in $q0$, denn $q0$ ist im Tupel als Startzustand genannt. Es kann immer nur einen Startzustand geben! Der Startzustand ist im Übergangsnetz durch einen Pfeil markiert. \n",
"Die Übergangsrelation $\\Delta$ gibt das Verhalten des Automaten an. Ist der Automat in $q0$ und liest ein $a$, bleibt er in Zustand $q0$. Das zugehörige Tupel ist $(q0,a,q0)$. Wenn der Automat in $q0$ hingegen ein $b$ liest, geht es in Zustand $q1$ (Tupel $(q0,b,q1)$). \n",
"In $q1$ kann man beliebig viele $a$'s einlesen und bleibt in $q1$ (Tupel $(q1,a,q1)$).\n",
"Aus $q1$ kommt man nicht mehr raus, denn es gibt ein Tupel in $\\Delta$, das die Form $(q1,x,q0)$ hat für ein $x \\in \\Sigma$. \n",
"In $q1$ kann man auch kein b mehr einlesen, denn es gibt kein Tupel $(q1,b,r)$ für ein $r \\in Q$. \n",
"\n",
"Wenn der Automat ein Wort \"fertig\" eingelesen hat und sich in $q1$ befindet, hat er das Wort akzeptiert. $q1$ ist nämlich der einzige Endzustand. \n",
"\n",
"Der Automat akzeptiert also alle Wörter, die genau ein $b$ enthalten und davor und danach beliebig viele (oder 0) $a$'s. Beim Lesen der $a$'s verändert der Automat seinen Zustand nicht, also kommt es auf die Anzahl nicht an. Beispielwörter, die der Automat erkennt, sind: $\\{b, ab, ba, aba, aaba, aabaa, aaabaaaaaaa, \\dots\\}$\n",
"Beispielwörter, die der Automat nicht erkennt, sind: $\\{bb, a, bba, abba, \\dots\\}$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Arbeiten mit endlichen Automaten und formalen Sprachen\n",
"\n",
"In den Hausaufgaben (und später im Studium/der Arbeit mit formalen Sprachen) wird man häufig mit dem folgenden Aufgabentyp konfrontiert sein. Man hat ein Objekt wie zum Beispiel einen Automaten, einen regulären Ausdruck, eine Grammatik, etc. gegeben und soll eine Grammatik, einen regulären Ausdruck, einen Automaten, etc. finden, der die selbe Sprache akzeptiert. Bei diesen Aufgaben sollte man unbedingt in mehreren Schritten vorgehen, um keine Randfälle zu übersehen, die nicht intuitiv klar sind. Als Beispiel zeige ich im Video ausführlich und Schritt für Schritt, wie man zu einem gegebenen Automaten die passende formale Sprache finden kann. Dazu vollziehe ich erst nach, wie der Automat aufgebaut ist. Dann durchdringe ich die Definition der gegebenen formalen Sprachen und versuche, Wörter zu finden, die meine Auswahl eingrenzen. Dabei darf man nicht vergessen, dass es für die selbe formale Sprache häufig verschiedene Bezeichnungen gibt."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Teil 1: Die Sprache eines Automaten verstehen"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Teil 2: Definitionen formaler Sprachen verstehen"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"- 0:00-3:40 Sprache $L1$ \n",
"- 3:50-6:25 Sprache $L2$\n",
"- 6:25-8:05 Sprache $L3$\n",
"- 8:05-Ende $L1-L3$ und der Automat $A$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Nichtdeterministische Automaten und Äquivalenz zweier Automaten"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Ein Automat entscheidet eine Sprache: Der Automat kann für jedes endlich große Wort entscheiden, ob das Wort zur Sprache gehört oder nicht. Zwei Automaten sind also **äquivalent** (gleichwertig), wenn sie die selbe Sprache erkennen. \n",
"\n",
"Eine weitere, wichtige Eigenschaft ist die Frage, ob ein Automat deterministisch ist. Wenn ein Automat deterministisch ist, gibt es in jedem Zustand für jedes Zeichen höchstens eine Möglichkeit, in den nächsten Zustand zu gelangen. Die Übergangsrelation eines deterministischen Automaten ist also eine Funktion $\\Delta: Q \\times \\Sigma \\to Q$\n",
"\n",
"Nicht deterministische Automaten können zum Beispiel die folgenden beiden Tupel in $\\Delta$ haben: $(q0,a,q0),(q0,a,q1)$\n",
"\n",
"Es gibt zu jedem nicht deterministischen Automaten einen deterministischen Automaten, der die selbe Sprache erkennt. Der Beweis dafür wird in diesem Kurs nicht behandelt. Es ist aber auch nicht unmöglich schwer zu verstehen, wie man zu jedem nichtdeterministischen Automaten einen deterministischen findet. Für Interessierte: Der Algorithmus findet sich [hier](https://www.youtube.com/watch?v=w2m6yLB-LeU)."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Reguläre Sprachen und endliche Automaten: Der Satz von Kleene"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
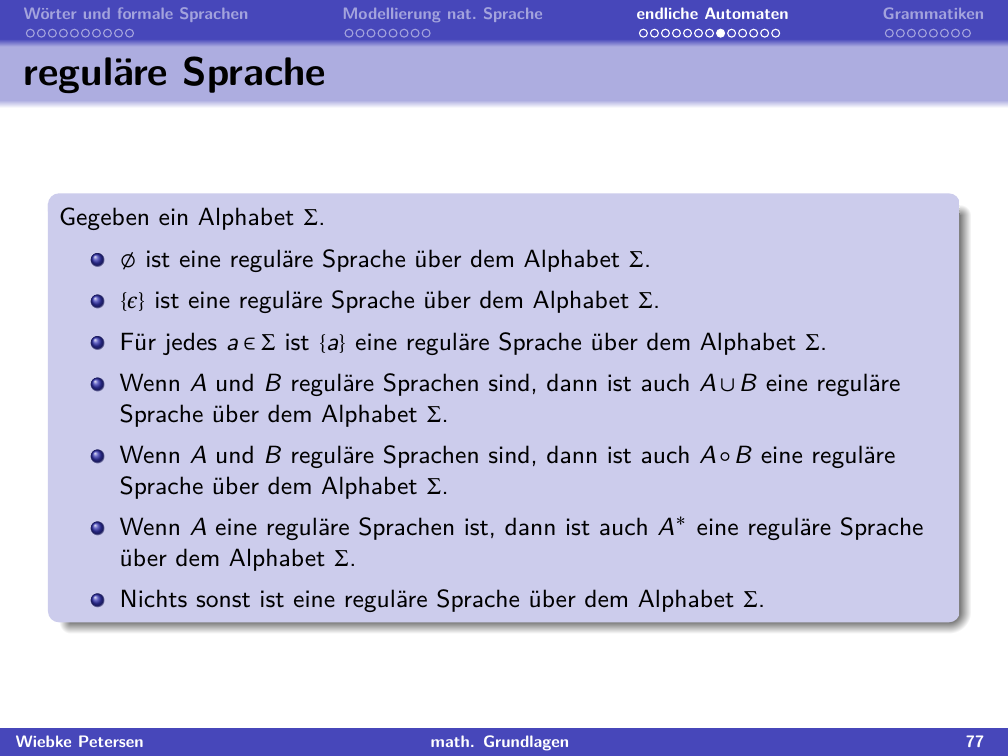
"Reguläre Sprachen sind formale Sprachen mit gewissen Beschränkungen, mit denen wir uns im Laufe des Studiums detaillierter befassen werden. Hier sehen wir die [rekursive Definition](01_Mengen.ipynb#implizite-Mengenbeschreibung-durch-rekursive-Definition) einer regulären Sprache über dem Alphabet $\\Sigma$. Erst werden die Startelemente festgelegt: $\\emptyset, \\{\\epsilon\\}$ und $\\{a\\}$ für alle $a \\in \\Sigma$.\n",
"\n",
"Als nächstes können diese Startelemente durch verschiedene Operationen verknüpft werden: Durch Vereinigung, Verkettung oder Kleene-Stern. Schließlich folgt die Ausschlussklausel: Nichts sonst ist eine reguläre Sprache über $\\Sigma$. \n",
"\n",
"Beispiel: Die Sprache $L=\\{w \\in \\{a,b,c\\}^\\ast | w = ab $ oder $w=(abc)^n $ mit $n\\in \\mathbb{N} \\}$\n",
"\n",
"Im Video wird gezeigt, wie diese Sprache aus der Definition für reguläre Sprachen abgeleitet werden kann."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Video Beispiel Definition für reguläre Sprachen"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Übrigens: Die Menge der regulären Sprachen ist gleich der Menge von Sprachen, die mit regulären Ausdrücken dargestellt werden können (reguläre Ausdrücke haben wir informell kurz eingeführt, sie werden häufig in der Programmierung verwendet.) \n",
"Außerdem sind sie äquivalent zu der Menge der Sprachen, die mit regulären Grammatiken erkannt werden können (Kein Wunder, sie heißen fast gleich). Reguläre Grammatiken behandeln wir kurz am Ende dieses Foliensatzes. \n",
"Schließlich ist die Menge der regulären Sprachen gleich zur Menge der Sprachen, die mit endlichen Automaten erkannt werden können. Warum das so ist, sehen wir im nächsten Abschnitt."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Um die Aussage von Kleene zu beweisen, müssen wir zwei Dinge tun: \n",
"1. Zeigen, dass man für jede reguläre Sprache einen Automaten konstruieren kann, der genau diese Sprache akzeptiert.\n",
"2. Zeigen, dass die Sprache jedes endlichen Automaten regulär ist und deshalb aus der obigen Definition der regulären Sprachen hergeleitet werden kann.\n",
"\n",
"Der erste Teil des Beweises findet sich auf den Folien 79-81 im Foliensatz 3. Ich illustriere ihn an einem Beispiel im folgenden Video. Um den zweiten Teil des Beweises kümmern wir uns später. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.4"
}
},
"nbformat": 4,
"nbformat_minor": 2
}