{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Ordnungserhaltende Abbildungen"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Ordnungserhaltende Abbildungen (Ordnungshomomorphismus)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Hier eine Schritt-für-Schritt-Erklärung der Definition: \n",
"\n",
"Wir haben zwei geordnete Mengen $(M,\\unlhd), (M',\\unlhd')$ gegeben und eine totale Funktion (Abbildung) $f : M \\to M'$, die die erste (geordnete) Menge $M$ als Definitionsbereich hat und die zweite (geordnete) Menge $M'$ als Wertebereich. \n",
"Diese Abbildung $f$ ist ordnungserhaltend, wenn \n",
"\n",
"- ich zwei beliebige Elemente $x,y \\in M$ nehme\n",
"- es in der ersten geordneten Menge gilt, dass $x \\unlhd y$\n",
"- und daraus folgt, dass $f(x)\\unlhd' f(y)$. \n",
"\n",
"Anders gesagt, $f(x)=x'$ und $f(y)=y'$. Und wenn $x\\unlhd y$, dann auch $x'\\unlhd' y'$."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Erläuterungen zu den Beispielen\n",
"\n",
"$f:\\mathbb{N}_0\\to\\mathbb{N}_0$ mit $f(x)=2x$ als Abbildung von $(\\mathbb{N}_0,\\leq)$ nach $(\\mathbb{N}_0,\\leq)$. Sei $x,y \\in \\mathbb{N}_0$ mit $x=3,y=4$. Es gilt: $x \\leq y$ und $f(x)\\leq f(y) \\leftrightarrow 6\\leq 8$. $f$ ist hier also eine ordnungserhaltende Abbildung. Es gibt nämlich keine $x,y$, für die $x\\leq y$ gilt, aber $f(x)\\leq f(y)$ nicht.\n",
"\n",
"$f:\\mathbb{Z} \\to \\mathbb{Z}$ mit $f(x)=x^2$ als Abbildung von $(\\mathbb{Z},\\leq)$ nach $(\\mathbb{Z},\\leq)$ ist nicht ordnungserhaltend. Hier ist ein Beispiel, das die Ordnung durcheinanderbringt: Für $x,y\\in \\mathbb{Z}$ mit $x=-6,y=2$ gilt natürlich $x \\leq y$. Es gilt aber nicht $f(x) \\leq f(y)$, denn $f(x)=36$ und $f(y)=4$."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Video zu ordnungserhaltenden Abbildungen"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Ordnungsreflektierende Abbildungen\n",
"\n",
"Hinweis: Die Begriffe *injektiv* und *bijektiv* hatten wir [hier](02_Funktionen.ipynb#Injektivität,-Surjektivität,-Bijektivität) eingeführt."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
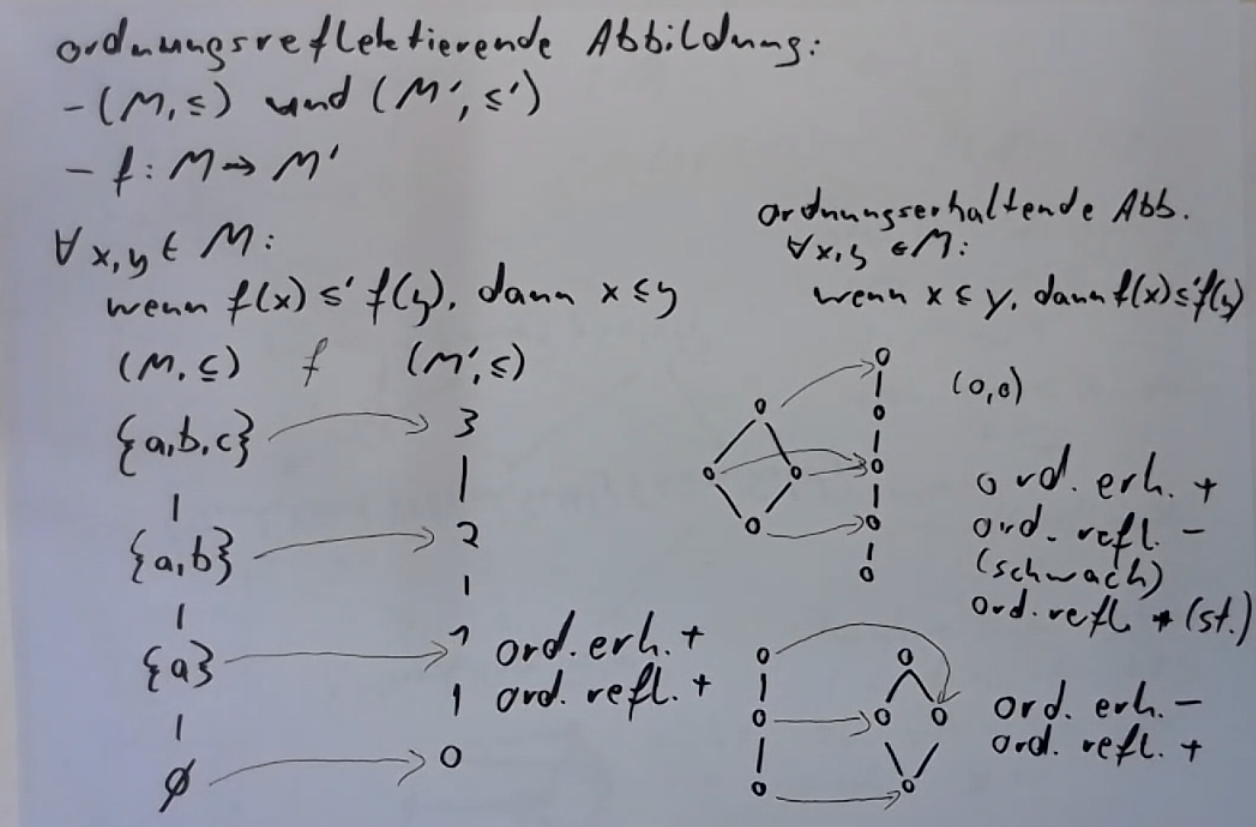
"Bei ordnungserhaltenden Abbildungen ging es um eine Implikation vom Definitions- in den Wertebereich der Abbildung $f:M \\to M'$: Wenn in der Menge $M$ etwas der Fall ist, muss es ebenso in $M'$ der Fall sein. \n",
"Bei ordnungsreflektierenden Abbildungen ist es genau anders: Eine Abbildung $f: M \\to M'$ heißt ordnungsreflektierend, wenn aus $f(x) \\unlhd' f(y)$ folgt, dass $x \\unlhd y$. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Video zu ordnungsreflektierenden Abbildungen\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Unterschied zwischen Ordnungseinbettung Isomorphismus** \n",
"\n",
"Bei ordnungserhaltenden und -reflektierenden Abbildungen wählen wir zwei Elemente $x,y$ aus $M$ und treffen Aussagen auf Grundlage dieser beiden Elemente. Uns interessiert dabei nicht, ob in $M'$ nicht vielleicht Elemente sind, die gar keinem Element aus $M$ als Wert zugeordnet wurden. Im linken Beispiel könnte die Menge $M'$ z.B. ein fünftes Element $4$ haben, das $\\le$ alle anderen Elemente aus $M'$ ist und das keinem Element aus $M$ als Wert zugeordnet wurde. \n",
"Dann ist die gezeigt Abbildung immer noch eine Ordnungseinbettung. Sie ist aber kein Ordnungsisomorphismus mehr. Für diesen muss nämlich gelten, dass die Abbildung $f$ bijektiv ist. $f^{-1}$ muss also auch eine Abbildung $f: M' \\to M$ sein oder, anders gesagt, $f$ muss jedes Element aus $M'$ erreichen. \n",
"Die linke Abbildung aus dem Video zu ordnungserhaltenden und -reflektierenden Abbildungen ist also ein Ordnungsisomorphismus:"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Zusammenfassung\n",
"\n",
"**Gegeben:**\n",
"- zwei geordnete Mengen $(M,\\unlhd),(M',\\unlhd')$\n",
"- eine Abbildung (totale Funktion) $f: M \\to M'$\n",
"\n",
"Bei zwei beliebigen Elementen $x,y\\in M$ ist $f$ eine \n",
"\n",
"- **ordnungserhaltende Abbildung** bei $(x\\unlhd y) \\to (f(x) \\unlhd' f(y))$\n",
"- **ordnungsreflektierende Abbildung** bei $(x\\unlhd y) \\leftarrow (f(x) \\unlhd' f(y))$\n",
"- **Ordnungseinbettung** bei $(x\\unlhd y) \\leftrightarrow (f(x) \\unlhd' f(y))$ (erhaltend und reflektierend)\n",
"- **Ordnungsisomorphismus** bei $(x\\unlhd y) \\leftrightarrow (f(x) \\unlhd' f(y))$ (Einbettung) und $f$ ist bijektiv ($f^{-1} : M' \\to M$ ist eine Funktion)\n",
"- **Ordnungsautomorphismus** bei Ordungsisomorphismus und nur einer geordneten Menge $(M,R)$, sodass $f: M \\to M$"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.4"
}
},
"nbformat": 4,
"nbformat_minor": 2
}