{
"cells": [
{
"cell_type": "code",
"execution_count": 60,
"metadata": {},
"outputs": [],
"source": [
"using Plots, ComplexPhasePortrait, ApproxFun, SingularIntegralEquations\n",
"gr();"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# M3M6: Methods of Mathematical Physics\n",
"\n",
"$$\n",
"\\def\\dashint{{\\int\\!\\!\\!\\!\\!\\!-\\,}}\n",
"\\def\\infdashint{\\dashint_{\\!\\!\\!-\\infty}^{\\,\\infty}}\n",
"\\def\\D{\\,{\\rm d}}\n",
"\\def\\dx{\\D x}\n",
"\\def\\dt{\\D t}\n",
"\\def\\C{{\\mathbb C}}\n",
"\\def\\CC{{\\cal C}}\n",
"\\def\\HH{{\\cal H}}\n",
"\\def\\I{{\\rm i}}\n",
"\\def\\qqfor{\\qquad\\hbox{for}\\qquad}\n",
"$$\n",
"\n",
"Dr. Sheehan Olver\n",
"<br>\n",
"s.olver@imperial.ac.uk\n",
"\n",
"Office Hours: 3-4pm Mondays, Huxley 6M40\n",
"<br>\n",
"Website: https://github.com/dlfivefifty/M3M6LectureNotes\n",
"\n",
"# Lecture 19: Logarithmic singular integrals\n",
"\n",
"1. Evaluating logarithmic singular integrals\n",
"2. Logarithmic singular integrals and orthogonal polynomials\n",
"2. Solving a logarithmic singular integral equation\n",
"2. Application: electrostatic potentials in 2D\n",
" - Potential arising from a point charge and a single plate\n",
" \n",
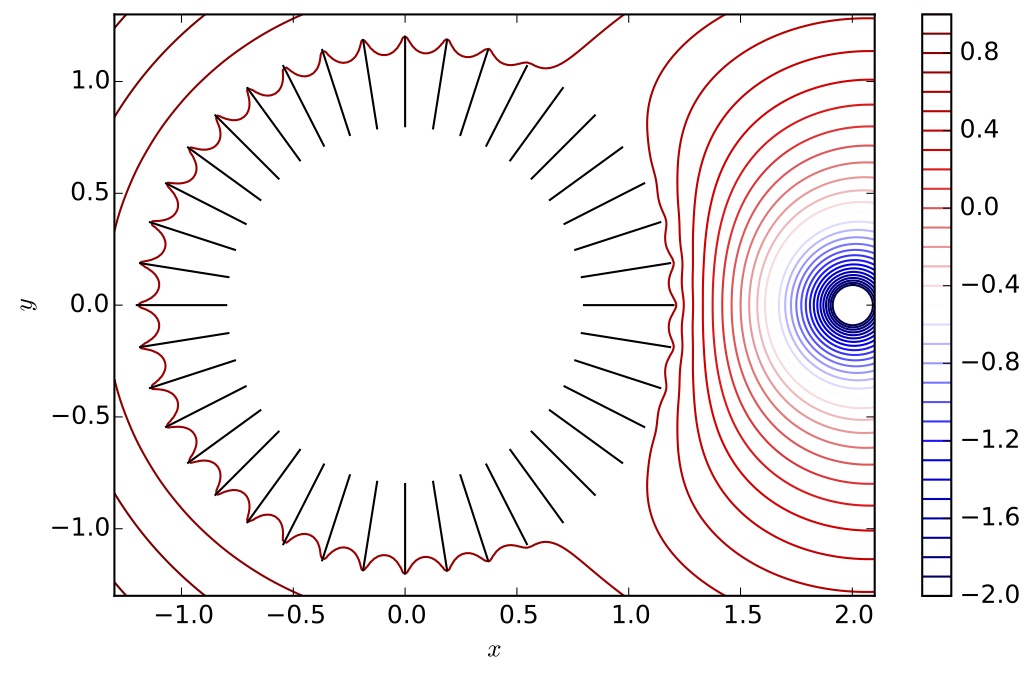
"The motivation behind this lecture is to calculate electrostatic potentials. An example is the Faraday cage: imagine a series of metal plates connected together so that they have the same charge. If configured to surround a region, this configuration will shield the interior from an external charge:\n",
"\n",
"\n",
"\n",
"Here, the coloured lines are equipotential lines, and there is a point source at $x = 2$, which corresponds to a forcing of \n",
"$$\\log\\| (x,y) - (2,0) \\| = \\log|z - 2|$$\n",
"where $z = x + \\I y$. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Logarithmic singular integrals\n",
"\n",
"From the Green's function of the Laplacian, it is natural to consider logarithmic singular integrals, and we focus yet again on $[-1,1]$:\n",
"\n",
"$$v(z) = {1 \\over \\pi }\\int_{-1}^1 f(t) \\log | z - t| \\dt$$\n",
"\n",
"Note that off $[-1,1]$, $v(z)$ solves Laplace's equation, and is continuous on $[-1,1]$:"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"data": {
"image/svg+xml": [
"<?xml version=\"1.0\" encoding=\"utf-8\"?>\n",
"<svg xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\" width=\"600\" height=\"400\" viewBox=\"0 0 2400 1600\">\n",
"<defs>\n",
" <clipPath id=\"clip5200\">\n",
" <rect x=\"0\" y=\"0\" width=\"2000\" height=\"2000\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<defs>\n",
" <clipPath id=\"clip5201\">\n",
" <rect x=\"0\" y=\"0\" width=\"2400\" height=\"1600\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<polygon clip-path=\"url(#clip5201)\" points=\"\n",
"0,1600 2400,1600 2400,0 0,0 \n",
" \" fill=\"#ffffff\" fill-opacity=\"1\"/>\n",
"<defs>\n",
" <clipPath id=\"clip5202\">\n",
" <rect x=\"480\" y=\"0\" width=\"1681\" height=\"1600\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<polygon clip-path=\"url(#clip5201)\" points=\"\n",
"149.361,1503.47 2081.26,1503.47 2081.26,47.2441 149.361,47.2441 \n",
" \" fill=\"#ffffff\" fill-opacity=\"1\"/>\n",
"<defs>\n",
" <clipPath id=\"clip5203\">\n",
" <rect x=\"149\" y=\"47\" width=\"1933\" height=\"1457\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 204.037,1503.47 204.037,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 659.674,1503.47 659.674,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1115.31,1503.47 1115.31,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1570.95,1503.47 1570.95,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 2026.58,1503.47 2026.58,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 149.361,1462.26 2081.26,1462.26 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 149.361,1118.81 2081.26,1118.81 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 149.361,775.359 2081.26,775.359 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 149.361,431.909 2081.26,431.909 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 149.361,88.4582 2081.26,88.4582 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5201)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,1503.47 2081.26,1503.47 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5201)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,1503.47 149.361,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5201)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 204.037,1503.47 204.037,1481.63 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5201)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 659.674,1503.47 659.674,1481.63 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5201)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1115.31,1503.47 1115.31,1481.63 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5201)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1570.95,1503.47 1570.95,1481.63 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5201)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 2026.58,1503.47 2026.58,1481.63 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5201)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,1462.26 178.339,1462.26 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5201)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,1118.81 178.339,1118.81 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5201)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,775.359 178.339,775.359 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5201)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,431.909 178.339,431.909 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5201)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,88.4582 178.339,88.4582 \n",
" \"/>\n",
"<g clip-path=\"url(#clip5201)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:middle;\" transform=\"rotate(0, 204.037, 1557.47)\" x=\"204.037\" y=\"1557.47\">-2</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5201)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:middle;\" transform=\"rotate(0, 659.674, 1557.47)\" x=\"659.674\" y=\"1557.47\">-1</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5201)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:middle;\" transform=\"rotate(0, 1115.31, 1557.47)\" x=\"1115.31\" y=\"1557.47\">0</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5201)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:middle;\" transform=\"rotate(0, 1570.95, 1557.47)\" x=\"1570.95\" y=\"1557.47\">1</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5201)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:middle;\" transform=\"rotate(0, 2026.58, 1557.47)\" x=\"2026.58\" y=\"1557.47\">2</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5201)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:end;\" transform=\"rotate(0, 125.361, 1479.76)\" x=\"125.361\" y=\"1479.76\">-2</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5201)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:end;\" transform=\"rotate(0, 125.361, 1136.31)\" x=\"125.361\" y=\"1136.31\">-1</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5201)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:end;\" transform=\"rotate(0, 125.361, 792.859)\" x=\"125.361\" y=\"792.859\">0</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5201)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:end;\" transform=\"rotate(0, 125.361, 449.409)\" x=\"125.361\" y=\"449.409\">1</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5201)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:end;\" transform=\"rotate(0, 125.361, 105.958)\" x=\"125.361\" y=\"105.958\">2</text>\n",
"</g>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#f3e258; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 535.901,1462.26 532.095,1460.23 529.483,1458.83 527.539,1457.78 523.154,1455.39 522.983,1455.3 518.426,1452.8 516.913,1451.96 513.87,1450.27 510.756,1448.52 \n",
" 509.314,1447.71 504.757,1445.13 504.681,1445.09 500.201,1442.53 498.688,1441.65 495.644,1439.89 492.773,1438.22 491.088,1437.23 486.934,1434.78 486.532,1434.55 \n",
" 481.975,1431.83 481.171,1431.35 477.419,1429.09 475.481,1427.92 472.863,1426.32 469.862,1424.48 468.306,1423.52 464.313,1421.05 463.75,1420.7 459.194,1417.84 \n",
" 458.833,1417.61 454.637,1414.95 453.42,1414.18 450.081,1412.04 448.073,1410.74 445.524,1409.09 442.789,1407.31 440.968,1406.12 437.569,1403.87 436.412,1403.11 \n",
" 432.411,1400.44 431.855,1400.07 427.313,1397.01 427.299,1397 422.743,1393.89 422.275,1393.57 418.186,1390.75 417.296,1390.14 413.63,1387.58 412.373,1386.7 \n",
" 409.073,1384.38 407.507,1383.27 404.517,1381.14 402.697,1379.83 399.961,1377.86 397.94,1376.4 395.404,1374.55 393.238,1372.96 390.848,1371.2 388.587,1369.53 \n",
" 386.292,1367.82 383.989,1366.09 381.735,1364.4 379.441,1362.66 377.179,1360.94 374.943,1359.23 372.623,1357.44 370.495,1355.79 368.066,1353.9 366.095,1352.36 \n",
" 363.51,1350.32 361.743,1348.92 358.953,1346.7 357.438,1345.49 354.397,1343.04 353.18,1342.05 349.841,1339.33 348.967,1338.62 345.284,1335.59 344.799,1335.18 \n",
" 340.728,1331.79 340.676,1331.75 336.597,1328.31 336.172,1327.95 332.56,1324.88 331.615,1324.07 328.567,1321.45 327.059,1320.14 324.615,1318.01 322.503,1316.16 \n",
" 320.706,1314.58 317.946,1312.13 316.837,1311.14 313.39,1308.05 313.009,1307.71 309.221,1304.27 308.833,1303.92 305.472,1300.84 304.277,1299.74 301.762,1297.4 \n",
" 299.721,1295.5 298.091,1293.97 295.164,1291.2 294.459,1290.54 290.864,1287.1 290.608,1286.85 287.306,1283.67 286.052,1282.45 283.785,1280.23 281.495,1277.98 \n",
" 280.301,1276.8 276.939,1273.45 276.853,1273.36 273.44,1269.93 272.382,1268.86 270.063,1266.49 267.826,1264.2 266.721,1263.06 263.413,1259.62 263.27,1259.47 \n",
" 260.139,1256.19 258.713,1254.68 256.9,1252.76 254.157,1249.82 253.694,1249.32 250.521,1245.89 249.601,1244.88 247.381,1242.45 245.044,1239.87 244.275,1239.02 \n",
" 241.2,1235.58 240.488,1234.78 238.157,1232.15 235.932,1229.61 235.146,1228.71 232.166,1225.28 231.375,1224.36 229.218,1221.85 226.819,1219.02 226.301,1218.41 \n",
" 223.414,1214.98 222.262,1213.59 220.557,1211.54 217.732,1208.11 217.706,1208.08 214.934,1204.67 213.15,1202.46 212.168,1201.24 209.431,1197.8 208.593,1196.74 \n",
" 206.722,1194.37 204.044,1190.93 204.037,1190.93 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#fabf26; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 974.348,1462.26 974.063,1462.21 969.507,1461.32 964.95,1460.43 960.394,1459.51 957.067,1458.83 955.837,1458.57 951.281,1457.63 946.725,1456.66 942.168,1455.67 \n",
" 940.887,1455.39 937.612,1454.67 933.056,1453.66 928.499,1452.62 925.637,1451.96 923.943,1451.57 919.386,1450.5 914.83,1449.41 911.181,1448.52 910.274,1448.3 \n",
" 905.717,1447.18 901.161,1446.04 897.419,1445.09 896.605,1444.88 892.048,1443.71 887.492,1442.51 884.268,1441.65 882.936,1441.3 878.379,1440.07 873.823,1438.82 \n",
" 871.66,1438.22 869.266,1437.55 864.71,1436.27 860.154,1434.96 859.535,1434.78 855.597,1433.64 851.041,1432.3 847.856,1431.35 846.485,1430.94 841.928,1429.56 \n",
" 837.372,1428.16 836.575,1427.92 832.816,1426.75 828.259,1425.31 825.666,1424.48 823.703,1423.85 819.146,1422.38 815.092,1421.05 814.59,1420.88 810.034,1419.37 \n",
" 805.477,1417.83 804.835,1417.61 800.921,1416.28 796.365,1414.7 794.871,1414.18 791.808,1413.11 787.252,1411.49 785.177,1410.74 782.696,1409.85 778.139,1408.19 \n",
" 775.739,1407.31 773.583,1406.51 769.026,1404.81 766.539,1403.87 764.47,1403.09 759.914,1401.35 757.565,1400.44 755.357,1399.58 750.801,1397.8 748.804,1397.01 \n",
" 746.245,1395.99 741.688,1394.16 740.244,1393.57 737.132,1392.3 732.575,1390.43 731.874,1390.14 728.019,1388.53 723.686,1386.7 723.463,1386.61 718.906,1384.66 \n",
" 715.673,1383.27 714.35,1382.69 709.794,1380.7 707.825,1379.83 705.237,1378.69 700.681,1376.65 700.132,1376.4 696.125,1374.58 692.593,1372.96 691.568,1372.49 \n",
" 687.012,1370.38 685.198,1369.53 682.455,1368.24 677.939,1366.09 677.899,1366.08 673.343,1363.89 670.818,1362.66 668.786,1361.67 664.23,1359.43 663.823,1359.23 \n",
" 659.674,1357.16 656.954,1355.79 655.117,1354.86 650.561,1352.54 650.202,1352.36 646.005,1350.19 643.567,1348.92 641.448,1347.81 637.042,1345.49 636.892,1345.41 \n",
" 632.335,1342.97 630.628,1342.05 627.779,1340.51 624.316,1338.62 623.223,1338.02 618.666,1335.5 618.105,1335.18 614.11,1332.95 611.995,1331.75 609.554,1330.36 \n",
" 605.978,1328.31 604.997,1327.75 600.441,1325.11 600.054,1324.88 595.884,1322.43 594.221,1321.45 591.328,1319.72 588.476,1318.01 586.772,1316.98 582.815,1314.58 \n",
" 582.215,1314.21 577.659,1311.4 577.238,1311.14 573.103,1308.56 571.742,1307.71 568.546,1305.69 566.326,1304.27 563.99,1302.78 560.986,1300.84 559.434,1299.83 \n",
" 555.721,1297.4 554.877,1296.85 550.531,1293.97 550.321,1293.83 545.764,1290.77 545.412,1290.54 541.208,1287.68 540.364,1287.1 536.652,1284.54 535.385,1283.67 \n",
" 532.095,1281.37 530.474,1280.23 527.539,1278.16 525.628,1276.8 522.983,1274.9 520.847,1273.36 518.426,1271.61 516.129,1269.93 513.87,1268.27 511.474,1266.49 \n",
" 509.314,1264.88 506.88,1263.06 504.757,1261.46 502.345,1259.62 500.201,1257.98 497.87,1256.19 495.644,1254.47 493.452,1252.76 491.088,1250.9 489.091,1249.32 \n",
" 486.532,1247.29 484.785,1245.89 481.975,1243.62 480.535,1242.45 477.419,1239.91 476.338,1239.02 472.863,1236.14 472.194,1235.58 468.306,1232.32 468.103,1232.15 \n",
" 464.063,1228.71 463.75,1228.45 460.073,1225.28 459.194,1224.52 456.133,1221.85 454.637,1220.53 452.242,1218.41 450.081,1216.48 448.4,1214.98 445.524,1212.38 \n",
" 444.605,1211.54 440.968,1208.21 440.857,1208.11 437.156,1204.67 436.412,1203.98 433.499,1201.24 431.855,1199.68 429.889,1197.8 427.299,1195.31 426.322,1194.37 \n",
" 422.8,1190.93 422.743,1190.88 419.321,1187.5 418.186,1186.37 415.884,1184.07 413.63,1181.79 412.49,1180.63 409.139,1177.2 409.073,1177.13 405.827,1173.76 \n",
" 404.517,1172.39 402.557,1170.33 399.961,1167.57 399.327,1166.89 396.137,1163.46 395.404,1162.66 392.986,1160.02 390.848,1157.67 389.875,1156.59 386.802,1153.16 \n",
" 386.292,1152.58 383.767,1149.72 381.735,1147.39 380.77,1146.29 377.811,1142.85 377.179,1142.11 374.887,1139.42 372.623,1136.72 372.002,1135.98 369.152,1132.55 \n",
" 368.066,1131.22 366.338,1129.11 363.561,1125.68 363.51,1125.61 360.817,1122.24 358.953,1119.88 358.11,1118.81 355.437,1115.38 354.397,1114.02 352.798,1111.94 \n",
" 350.194,1108.51 349.841,1108.04 347.622,1105.07 345.284,1101.91 345.086,1101.64 342.58,1098.2 340.728,1095.63 340.11,1094.77 337.671,1091.33 336.172,1089.2 \n",
" 335.265,1087.9 332.891,1084.46 331.615,1082.6 330.549,1081.03 328.238,1077.6 327.059,1075.82 325.959,1074.16 323.712,1070.73 322.503,1068.85 321.495,1067.29 \n",
" 319.309,1063.86 317.946,1061.69 317.155,1060.42 315.029,1056.99 313.39,1054.3 312.936,1053.55 310.87,1050.12 308.838,1046.69 308.833,1046.68 306.831,1043.25 \n",
" 304.856,1039.82 304.277,1038.8 302.909,1036.38 300.992,1032.95 299.721,1030.63 299.104,1029.51 297.244,1026.08 295.415,1022.64 295.164,1022.17 293.611,1019.21 \n",
" 291.837,1015.77 290.608,1013.36 290.092,1012.34 288.373,1008.91 286.684,1005.47 286.052,1004.17 285.021,1002.04 283.386,998.602 281.78,995.168 281.495,994.549 \n",
" 280.199,991.733 278.646,988.299 277.122,984.864 276.939,984.445 275.622,981.43 274.15,977.995 272.706,974.561 272.382,973.777 271.287,971.126 269.894,967.692 \n",
" 268.53,964.257 267.826,962.452 267.19,960.823 265.876,957.388 264.59,953.954 263.331,950.519 263.27,950.35 262.094,947.085 260.884,943.65 259.701,940.216 \n",
" 258.713,937.28 258.545,936.781 257.411,933.347 256.304,929.912 255.223,926.478 254.169,923.043 254.157,923.002 253.137,919.609 252.13,916.174 251.15,912.74 \n",
" 250.196,909.305 249.601,907.103 249.266,905.871 248.36,902.436 247.478,899.002 246.623,895.567 245.793,892.133 245.044,888.938 244.988,888.698 244.205,885.264 \n",
" 243.447,881.829 242.714,878.395 242.006,874.96 241.323,871.526 240.665,868.091 240.488,867.131 240.03,864.657 239.418,861.222 238.831,857.788 238.268,854.353 \n",
" 237.731,850.919 237.217,847.484 236.728,844.05 236.263,840.615 235.932,838.028 235.822,837.181 235.404,833.746 235.01,830.312 234.64,826.877 234.294,823.442 \n",
" 233.972,820.008 233.674,816.573 233.4,813.139 233.15,809.704 232.924,806.27 232.722,802.835 232.544,799.401 232.389,795.966 232.259,792.532 232.152,789.097 \n",
" 232.069,785.663 232.01,782.228 231.974,778.794 231.962,775.359 231.974,771.925 232.01,768.49 232.069,765.056 232.152,761.621 232.259,758.187 232.389,754.752 \n",
" 232.544,751.318 232.722,747.883 232.924,744.449 233.15,741.014 233.4,737.58 233.674,734.145 233.972,730.711 234.294,727.276 234.64,723.842 235.01,720.407 \n",
" 235.404,716.973 235.822,713.538 235.932,712.691 236.263,710.104 236.728,706.669 237.217,703.235 237.731,699.8 238.268,696.366 238.831,692.931 239.418,689.497 \n",
" 240.03,686.062 240.488,683.588 240.665,682.628 241.323,679.193 242.006,675.759 242.714,672.324 243.447,668.89 244.205,665.455 244.988,662.021 245.044,661.781 \n",
" 245.793,658.586 246.623,655.152 247.478,651.717 248.36,648.283 249.266,644.848 249.601,643.615 250.196,641.414 251.15,637.979 252.13,634.545 253.137,631.11 \n",
" 254.157,627.716 254.169,627.676 255.223,624.241 256.304,620.807 257.411,617.372 258.545,613.938 258.713,613.438 259.701,610.503 260.884,607.069 262.094,603.634 \n",
" 263.27,600.369 263.331,600.2 264.59,596.765 265.876,593.331 267.19,589.896 267.826,588.267 268.53,586.462 269.894,583.027 271.287,579.593 272.382,576.942 \n",
" 272.706,576.158 274.15,572.724 275.622,569.289 276.939,566.274 277.122,565.855 278.646,562.42 280.199,558.986 281.495,556.17 281.78,555.551 283.386,552.117 \n",
" 285.021,548.682 286.052,546.553 286.684,545.247 288.373,541.813 290.092,538.378 290.608,537.363 291.837,534.944 293.611,531.509 295.164,528.552 295.415,528.075 \n",
" 297.244,524.64 299.104,521.206 299.721,520.084 300.992,517.771 302.909,514.337 304.277,511.923 304.856,510.902 306.831,507.468 308.833,504.041 308.838,504.033 \n",
" 310.87,500.599 312.936,497.164 313.39,496.419 315.029,493.73 317.155,490.295 317.946,489.033 319.309,486.861 321.495,483.426 322.503,481.865 323.712,479.992 \n",
" 325.959,476.557 327.059,474.899 328.238,473.123 330.549,469.688 331.615,468.123 332.891,466.254 335.265,462.819 336.172,461.523 337.671,459.385 340.11,455.95 \n",
" 340.728,455.09 342.58,452.516 345.086,449.081 345.284,448.812 347.622,445.647 349.841,442.683 350.194,442.212 352.798,438.778 354.397,436.694 355.437,435.343 \n",
" 358.11,431.909 358.953,430.837 360.817,428.474 363.51,425.104 363.561,425.04 366.338,421.605 368.066,419.494 369.152,418.171 372.002,414.736 372.623,413.996 \n",
" 374.887,411.302 377.179,408.608 377.811,407.867 380.77,404.433 381.735,403.324 383.767,400.998 386.292,398.14 386.802,397.564 389.875,394.129 390.848,393.052 \n",
" 392.986,390.695 395.404,388.057 396.137,387.26 399.327,383.826 399.961,383.15 402.557,380.391 404.517,378.329 405.827,376.957 409.073,373.589 409.139,373.522 \n",
" 412.49,370.088 413.63,368.931 415.884,366.653 418.186,364.349 419.321,363.219 422.743,359.841 422.8,359.784 426.322,356.35 427.299,355.406 429.889,352.915 \n",
" 431.855,351.04 433.499,349.481 436.412,346.742 437.156,346.046 440.857,342.612 440.968,342.51 444.605,339.177 445.524,338.342 448.4,335.743 450.081,334.235 \n",
" 452.242,332.308 454.637,330.19 456.133,328.874 459.194,326.202 460.073,325.439 463.75,322.272 464.063,322.005 468.103,318.57 468.306,318.398 472.194,315.136 \n",
" 472.863,314.579 476.338,311.701 477.419,310.812 480.535,308.267 481.975,307.098 484.785,304.832 486.532,303.434 489.091,301.398 491.088,299.819 493.452,297.963 \n",
" 495.644,296.253 497.87,294.529 500.201,292.734 502.345,291.094 504.757,289.261 506.88,287.66 509.314,285.834 511.474,284.225 513.87,282.451 516.129,280.791 \n",
" 518.426,279.112 520.847,277.356 522.983,275.816 525.628,273.922 527.539,272.561 530.474,270.487 532.095,269.347 535.385,267.052 536.652,266.174 540.364,263.618 \n",
" 541.208,263.04 545.412,260.183 545.764,259.945 550.321,256.889 550.531,256.749 554.877,253.869 555.721,253.314 559.434,250.887 560.986,249.88 563.99,247.941 \n",
" 566.326,246.445 568.546,245.03 571.742,243.011 573.103,242.155 577.238,239.576 577.659,239.315 582.215,236.508 582.815,236.142 586.772,233.735 588.476,232.707 \n",
" 591.328,230.995 594.221,229.273 595.884,228.287 600.054,225.838 600.441,225.612 604.997,222.968 605.978,222.404 609.554,220.355 611.995,218.969 614.11,217.773 \n",
" 618.105,215.535 618.666,215.222 623.223,212.7 624.316,212.1 627.779,210.207 630.628,208.666 632.335,207.745 636.892,205.311 637.042,205.231 641.448,202.905 \n",
" 643.567,201.797 646.005,200.527 650.202,198.362 650.561,198.178 655.117,195.855 656.954,194.928 659.674,193.559 663.823,191.493 664.23,191.291 668.786,189.048 \n",
" 670.818,188.059 673.343,186.832 677.899,184.643 677.939,184.624 682.455,182.478 685.198,181.19 687.012,180.339 691.568,178.226 692.593,177.755 696.125,176.136 \n",
" 700.132,174.321 700.681,174.073 705.237,172.032 707.825,170.886 709.794,170.016 714.35,168.024 715.673,167.452 718.906,166.055 723.463,164.112 723.686,164.017 \n",
" 728.019,162.189 731.874,160.583 732.575,160.291 737.132,158.414 740.244,157.148 741.688,156.561 746.245,154.73 748.804,153.714 750.801,152.922 755.357,151.135 \n",
" 757.565,150.279 759.914,149.37 764.47,147.627 766.539,146.845 769.026,145.905 773.583,144.205 775.739,143.41 778.139,142.526 782.696,140.868 785.177,139.976 \n",
" 787.252,139.231 791.808,137.614 794.871,136.541 796.365,136.018 800.921,134.442 804.835,133.107 805.477,132.888 810.034,131.351 814.59,129.837 815.092,129.672 \n",
" 819.146,128.341 823.703,126.865 825.666,126.238 828.259,125.409 832.816,123.972 836.575,122.803 837.372,122.556 841.928,121.156 846.485,119.778 847.856,119.369 \n",
" 851.041,118.417 855.597,117.076 859.535,115.934 860.154,115.755 864.71,114.45 869.266,113.165 871.66,112.5 873.823,111.898 878.379,110.649 882.936,109.42 \n",
" 884.268,109.065 887.492,108.207 892.048,107.013 896.605,105.838 897.419,105.631 901.161,104.678 905.717,103.538 910.274,102.416 911.181,102.196 914.83,101.31 \n",
" 919.386,100.222 923.943,99.1529 925.637,98.7617 928.499,98.0998 933.056,97.0637 937.612,96.046 940.887,95.3272 942.168,95.0455 946.725,94.0604 951.281,93.0933 \n",
" 955.837,92.1443 957.067,91.8927 960.394,91.2105 964.95,90.2935 969.507,89.3941 974.063,88.5124 974.348,88.4582 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#f3e258; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 535.901,88.4582 532.095,90.4877 529.483,91.8927 527.539,92.9415 523.154,95.3272 522.983,95.4205 518.426,97.9235 516.913,98.7617 513.87,100.452 510.756,102.196 \n",
" 509.314,103.007 504.757,105.587 504.681,105.631 500.201,108.193 498.688,109.065 495.644,110.826 492.773,112.5 491.088,113.485 486.934,115.934 486.532,116.172 \n",
" 481.975,118.886 481.171,119.369 477.419,121.627 475.481,122.803 472.863,124.397 469.862,126.238 468.306,127.196 464.313,129.672 463.75,130.023 459.194,132.879 \n",
" 458.833,133.107 454.637,135.765 453.42,136.541 450.081,138.68 448.073,139.976 445.524,141.626 442.789,143.41 440.968,144.603 437.569,146.845 436.412,147.611 \n",
" 432.411,150.279 431.855,150.651 427.313,153.714 427.299,153.723 422.743,156.828 422.275,157.148 418.186,159.965 417.296,160.583 413.63,163.136 412.373,164.017 \n",
" 409.073,166.342 407.507,167.452 404.517,169.582 402.697,170.886 399.961,172.857 397.94,174.321 395.404,176.168 393.238,177.755 390.848,179.515 388.587,181.19 \n",
" 386.292,182.899 383.989,184.624 381.735,186.321 379.441,188.059 377.179,189.781 374.943,191.493 372.623,193.28 370.495,194.928 368.066,196.819 366.095,198.362 \n",
" 363.51,200.398 361.743,201.797 358.953,204.018 357.438,205.231 354.397,207.68 353.18,208.666 349.841,211.385 348.967,212.1 345.284,215.133 344.799,215.535 \n",
" 340.728,218.926 340.676,218.969 336.597,222.404 336.172,222.764 332.56,225.838 331.615,226.648 328.567,229.273 327.059,230.58 324.615,232.707 322.503,234.56 \n",
" 320.706,236.142 317.946,238.589 316.837,239.576 313.39,242.668 313.009,243.011 309.221,246.445 308.833,246.799 305.472,249.88 304.277,250.983 301.762,253.314 \n",
" 299.721,255.221 298.091,256.749 295.164,259.514 294.459,260.183 290.864,263.618 290.608,263.864 287.306,267.052 286.052,268.273 283.785,270.487 281.495,272.741 \n",
" 280.301,273.922 276.939,277.27 276.853,277.356 273.44,280.791 272.382,281.863 270.063,284.225 267.826,286.521 266.721,287.66 263.413,291.094 263.27,291.244 \n",
" 260.139,294.529 258.713,296.037 256.9,297.963 254.157,300.9 253.694,301.398 250.521,304.832 249.601,305.837 247.381,308.267 245.044,310.848 244.275,311.701 \n",
" 241.2,315.136 240.488,315.937 238.157,318.57 235.932,321.107 235.146,322.005 232.166,325.439 231.375,326.359 229.218,328.874 226.819,331.697 226.301,332.308 \n",
" 223.414,335.743 222.262,337.125 220.557,339.177 217.732,342.612 217.706,342.643 214.934,346.046 213.15,348.26 212.168,349.481 209.431,352.915 208.593,353.975 \n",
" 206.722,356.35 204.044,359.784 204.037,359.793 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#fabf26; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1484.05,88.4582 1484.38,88.5204 1488.93,89.4072 1493.49,90.312 1498.04,91.2348 1501.23,91.8927 1502.6,92.1746 1507.16,93.13 1511.71,94.1037 1516.27,95.0958 \n",
" 1517.32,95.3272 1520.83,96.1034 1525.38,97.1288 1529.94,98.173 1532.47,98.7617 1534.5,99.2343 1539.05,100.312 1543.61,101.409 1546.82,102.196 1548.17,102.524 \n",
" 1552.72,103.656 1557.28,104.807 1560.49,105.631 1561.83,105.976 1566.39,107.162 1570.95,108.368 1573.54,109.065 1575.5,109.593 1580.06,110.834 1584.62,112.096 \n",
" 1586.05,112.5 1589.17,113.376 1593.73,114.675 1598.08,115.934 1598.29,115.994 1602.84,117.329 1607.4,118.686 1609.66,119.369 1611.95,120.062 1616.51,121.456 \n",
" 1620.84,122.803 1621.07,122.873 1625.62,124.306 1630.18,125.761 1631.65,126.238 1634.74,127.235 1639.29,128.729 1642.13,129.672 1643.85,130.244 1648.41,131.779 \n",
" 1652.29,133.107 1652.96,133.336 1657.52,134.912 1662.07,136.51 1662.16,136.541 1666.63,138.128 1671.19,139.768 1671.76,139.976 1675.74,141.428 1680.3,143.112 \n",
" 1681.1,143.41 1684.86,144.815 1689.41,146.543 1690.2,146.845 1693.97,148.29 1698.53,150.062 1699.08,150.279 1703.08,151.854 1707.64,153.67 1707.75,153.714 \n",
" 1712.19,155.508 1716.21,157.148 1716.75,157.37 1721.31,159.254 1724.48,160.583 1725.86,161.163 1730.42,163.095 1732.57,164.017 1734.98,165.051 1739.53,167.031 \n",
" 1740.49,167.452 1744.09,169.035 1748.25,170.886 1748.65,171.065 1753.2,173.118 1755.84,174.321 1757.76,175.197 1762.31,177.302 1763.29,177.755 1766.87,179.432 \n",
" 1770.59,181.19 1771.43,181.588 1775.98,183.77 1777.75,184.624 1780.54,185.979 1784.78,188.059 1785.1,188.215 1789.65,190.477 1791.68,191.493 1794.21,192.768 \n",
" 1798.45,194.928 1798.77,195.086 1803.32,197.432 1805.11,198.362 1807.88,199.806 1811.65,201.797 1812.43,202.21 1816.99,204.642 1818.08,205.231 1821.55,207.104 \n",
" 1824.41,208.666 1826.1,209.596 1830.63,212.1 1830.66,212.119 1835.22,214.672 1836.74,215.535 1839.77,217.256 1842.76,218.969 1844.33,219.872 1848.69,222.404 \n",
" 1848.89,222.52 1853.44,225.2 1854.52,225.838 1858,227.913 1860.26,229.273 1862.55,230.66 1865.91,232.707 1867.11,233.441 1871.48,236.142 1871.67,236.256 \n",
" 1876.22,239.106 1876.97,239.576 1880.78,241.992 1882.37,243.011 1885.34,244.914 1887.7,246.445 1889.89,247.873 1892.95,249.88 1894.45,250.87 1898.12,253.314 \n",
" 1899.01,253.904 1903.22,256.749 1903.56,256.977 1908.12,260.09 1908.25,260.183 1912.67,263.242 1913.21,263.618 1917.23,266.436 1918.1,267.052 1921.79,269.671 \n",
" 1922.93,270.487 1926.34,272.949 1927.68,273.922 1930.9,276.27 1932.38,277.356 1935.46,279.635 1937.01,280.791 1940.01,283.045 1941.57,284.225 1944.57,286.502 \n",
" 1946.08,287.66 1949.13,290.005 1950.53,291.094 1953.68,293.556 1954.92,294.529 1958.24,297.157 1959.25,297.963 1962.79,300.807 1963.52,301.398 1967.35,304.51 \n",
" 1967.74,304.832 1971.91,308.264 1971.91,308.267 1976.02,311.701 1976.46,312.073 1980.08,315.136 1981.02,315.937 1984.09,318.57 1985.58,319.857 1988.04,322.005 \n",
" 1990.13,323.836 1991.95,325.439 1994.69,327.874 1995.81,328.874 1999.25,331.973 1999.62,332.308 2003.37,335.743 2003.8,336.135 2007.09,339.177 2008.36,340.363 \n",
" 2010.75,342.612 2012.91,344.657 2014.37,346.046 2017.47,349.019 2017.95,349.481 2021.48,352.915 2022.03,353.453 2024.97,356.35 2026.58,357.96 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#f3e258; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 2026.58,154.71 2025.13,153.714 2022.03,151.595 2020.09,150.279 2017.47,148.513 2014.98,146.845 2012.91,145.463 2009.82,143.41 2008.36,142.446 2004.59,139.976 \n",
" 2003.8,139.461 1999.3,136.541 1999.25,136.507 1994.69,133.583 1993.94,133.107 1990.13,130.691 1988.52,129.672 1985.58,127.828 1983.02,126.238 1981.02,124.995 \n",
" 1977.46,122.803 1976.46,122.192 1971.91,119.418 1971.83,119.369 1967.35,116.671 1966.12,115.934 1962.79,113.953 1960.34,112.5 1958.24,111.263 1954.48,109.065 \n",
" 1953.68,108.601 1949.13,105.966 1948.54,105.631 1944.57,103.358 1942.52,102.196 1940.01,100.776 1936.42,98.7617 1935.46,98.2206 1930.9,95.6912 1930.24,95.3272 \n",
" 1926.34,93.187 1923.97,91.8927 1921.79,90.7086 1917.61,88.4582 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#fb9c07; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 2026.58,600.012 2025.16,596.765 2023.61,593.331 2022.03,589.896 2022.03,589.884 2020.43,586.462 2018.78,583.027 2017.47,580.341 2017.11,579.593 2015.4,576.158 \n",
" 2013.65,572.724 2012.91,571.292 2011.88,569.289 2010.07,565.855 2008.36,562.672 2008.22,562.42 2006.35,558.986 2004.43,555.551 2003.8,554.441 2002.48,552.117 \n",
" 2000.5,548.682 1999.25,546.55 1998.48,545.247 1996.42,541.813 1994.69,538.964 1994.33,538.378 1992.21,534.944 1990.13,531.657 1990.04,531.509 1987.84,528.075 \n",
" 1985.6,524.64 1985.58,524.606 1983.32,521.206 1981.02,517.789 1981.01,517.771 1978.66,514.337 1976.46,511.188 1976.26,510.902 1973.83,507.468 1971.91,504.788 \n",
" 1971.36,504.033 1968.85,500.599 1967.35,498.572 1966.3,497.164 1963.71,493.73 1962.79,492.53 1961.08,490.295 1958.41,486.861 1958.24,486.648 1955.69,483.426 \n",
" 1953.68,480.923 1952.93,479.992 1950.13,476.557 1949.13,475.341 1947.29,473.123 1944.57,469.893 1944.4,469.688 1941.46,466.254 1940.01,464.578 1938.48,462.819 \n",
" 1935.46,459.385 1935.46,459.382 1932.39,455.95 1930.9,454.306 1929.27,452.516 1926.34,449.338 1926.11,449.081 1922.89,445.647 1921.79,444.479 1919.63,442.212 \n",
" 1917.23,439.721 1916.32,438.778 1912.96,435.343 1912.67,435.059 1909.54,431.909 1908.12,430.492 1906.08,428.474 1903.56,426.014 1902.56,425.04 1899.01,421.622 \n",
" 1898.99,421.605 1895.36,418.171 1894.45,417.314 1891.68,414.736 1889.89,413.086 1887.94,411.302 1885.34,408.936 1884.15,407.867 1880.78,404.86 1880.3,404.433 \n",
" 1876.39,400.998 1876.22,400.856 1872.41,397.564 1871.67,396.923 1868.38,394.129 1867.11,393.058 1864.29,390.695 1862.55,389.259 1860.13,387.26 1858,385.524 \n",
" 1855.9,383.826 1853.44,381.85 1851.61,380.391 1848.89,378.238 1847.25,376.957 1844.33,374.684 1842.82,373.522 1839.77,371.187 1838.32,370.088 1835.22,367.747 \n",
" 1833.75,366.653 1830.66,364.36 1829.11,363.219 1826.1,361.027 1824.39,359.784 1821.55,357.745 1819.59,356.35 1816.99,354.514 1814.71,352.915 1812.43,351.333 \n",
" 1809.75,349.481 1807.88,348.2 1804.7,346.046 1803.32,345.114 1799.57,342.612 1798.77,342.074 1794.36,339.177 1794.21,339.08 1789.65,336.13 1789.05,335.743 \n",
" 1785.1,333.223 1783.65,332.308 1780.54,330.359 1778.15,328.874 1775.98,327.537 1772.55,325.439 1771.43,324.757 1766.87,322.017 1766.85,322.005 1762.31,319.315 \n",
" 1761.04,318.57 1757.76,316.652 1755.13,315.136 1753.2,314.028 1749.1,311.701 1748.65,311.442 1744.09,308.892 1742.96,308.267 1739.53,306.379 1736.69,304.832 \n",
" 1734.98,303.901 1730.42,301.46 1730.3,301.398 1725.86,299.051 1723.78,297.963 1721.31,296.677 1717.12,294.529 1716.75,294.338 1712.19,292.03 1710.32,291.094 \n",
" 1707.64,289.756 1703.38,287.66 1703.08,287.515 1698.53,285.303 1696.27,284.225 1693.97,283.124 1689.41,280.977 1689.01,280.791 1684.86,278.858 1681.58,277.356 \n",
" 1680.3,276.771 1675.74,274.713 1673.97,273.922 1671.19,272.685 1666.63,270.686 1666.17,270.487 1662.07,268.714 1658.17,267.052 1657.52,266.773 1652.96,264.858 \n",
" 1649.97,263.618 1648.41,262.972 1643.85,261.112 1641.54,260.183 1639.29,259.28 1634.74,257.475 1632.88,256.749 1630.18,255.696 1625.62,253.943 1623.96,253.314 \n",
" 1621.07,252.216 1616.51,250.516 1614.78,249.88 1611.95,248.84 1607.4,247.19 1605.31,246.445 1602.84,245.565 1598.29,243.965 1595.53,243.011 1593.73,242.389 \n",
" 1589.17,240.837 1585.41,239.576 1584.62,239.311 1580.06,237.807 1575.5,236.328 1574.92,236.142 1570.95,234.871 1566.39,233.438 1564.03,232.707 1561.83,232.029 \n",
" 1557.28,230.642 1552.72,229.279 1552.7,229.273 1548.17,227.936 1543.61,226.618 1540.87,225.838 1539.05,225.322 1534.5,224.046 1529.94,222.795 1528.49,222.404 \n",
" 1525.38,221.563 1520.83,220.354 1516.27,219.168 1515.49,218.969 1511.71,218.001 1507.16,216.856 1502.6,215.733 1501.78,215.535 1498.04,214.63 1493.49,213.547 \n",
" 1488.93,212.487 1487.24,212.1 1484.38,211.446 1479.82,210.426 1475.26,209.427 1471.72,208.666 1470.71,208.448 1466.15,207.488 1461.59,206.549 1457.04,205.631 \n",
" 1455.01,205.231 1452.48,204.732 1447.92,203.851 1443.37,202.992 1438.81,202.153 1436.83,201.797 1434.26,201.332 1429.7,200.53 1425.14,199.748 1420.59,198.986 \n",
" 1416.76,198.362 1416.03,198.244 1411.47,197.518 1406.92,196.812 1402.36,196.126 1397.8,195.459 1394.06,194.928 1393.25,194.812 1388.69,194.181 1384.14,193.569 \n",
" 1379.58,192.976 1375.02,192.403 1370.47,191.848 1367.45,191.493 1365.91,191.311 1361.35,190.792 1356.8,190.291 1352.24,189.809 1347.68,189.345 1343.13,188.9 \n",
" 1338.57,188.474 1334.02,188.065 1333.94,188.059 1329.46,187.673 1324.9,187.3 1320.35,186.944 1315.79,186.607 1311.23,186.287 1306.68,185.986 1302.12,185.703 \n",
" 1297.56,185.437 1293.01,185.19 1288.45,184.96 1283.9,184.749 1280.98,184.624 1279.34,184.554 1274.78,184.377 1270.23,184.217 1265.67,184.076 1261.11,183.951 \n",
" 1256.56,183.845 1252,183.756 1247.44,183.685 1242.89,183.632 1238.33,183.596 1233.78,183.578 1229.22,183.577 1224.66,183.594 1220.11,183.629 1215.55,183.681 \n",
" 1210.99,183.751 1206.44,183.838 1201.88,183.943 1197.32,184.066 1192.77,184.206 1188.21,184.364 1183.66,184.54 1181.67,184.624 1179.1,184.733 1174.54,184.943 \n",
" 1169.99,185.17 1165.43,185.416 1160.87,185.679 1156.32,185.96 1151.76,186.259 1147.2,186.575 1142.65,186.91 1138.09,187.262 1133.54,187.633 1128.98,188.021 \n",
" 1128.56,188.059 1124.42,188.426 1119.87,188.849 1115.31,189.29 1110.75,189.749 1106.2,190.227 1101.64,190.723 1097.08,191.237 1094.89,191.493 1092.53,191.768 \n",
" 1087.97,192.317 1083.42,192.885 1078.86,193.471 1074.3,194.076 1069.75,194.7 1068.13,194.928 1065.19,195.341 1060.63,196 1056.08,196.677 1051.52,197.375 \n",
" 1046.96,198.091 1045.28,198.362 1042.41,198.825 1037.85,199.577 1033.3,200.348 1028.74,201.139 1025.04,201.797 1024.18,201.95 1019.63,202.777 1015.07,203.624 \n",
" 1010.51,204.492 1006.72,205.231 1005.96,205.379 1001.4,206.283 996.845,207.207 992.288,208.153 989.865,208.666 987.732,209.117 983.176,210.099 978.619,211.103 \n",
" 974.185,212.1 974.063,212.128 969.507,213.169 964.95,214.233 960.394,215.317 959.496,215.535 955.837,216.42 951.281,217.544 946.725,218.69 945.632,218.969 \n",
" 942.168,219.854 937.612,221.04 933.056,222.248 932.478,222.404 928.499,223.475 923.943,224.724 919.95,225.838 919.386,225.996 914.83,227.286 910.274,228.6 \n",
" 907.977,229.273 905.717,229.935 901.161,231.291 896.605,232.671 896.487,232.707 892.048,234.07 887.492,235.494 885.45,236.142 882.936,236.94 878.379,238.407 \n",
" 874.809,239.576 873.823,239.899 869.266,241.412 864.71,242.951 864.535,243.011 860.154,244.51 855.597,246.095 854.603,246.445 851.041,247.702 846.485,249.334 \n",
" 844.981,249.88 841.928,250.989 837.372,252.67 835.648,253.314 832.816,254.374 828.259,256.104 826.583,256.749 823.703,257.858 819.146,259.639 817.77,260.183 \n",
" 814.59,261.443 810.034,263.275 809.192,263.618 805.477,265.132 800.921,267.016 800.835,267.052 796.365,268.925 792.691,270.487 791.808,270.863 787.252,272.826 \n",
" 784.744,273.922 782.696,274.818 778.139,276.837 776.982,277.356 773.583,278.884 769.399,280.791 769.026,280.961 764.47,283.064 761.988,284.225 759.914,285.198 \n",
" 755.357,287.361 754.736,287.66 750.801,289.553 747.641,291.094 746.245,291.777 741.688,294.03 740.692,294.529 737.132,296.314 733.886,297.963 732.575,298.631 \n",
" 728.019,300.979 727.215,301.398 723.463,303.358 720.676,304.832 718.906,305.771 714.35,308.218 714.261,308.267 709.794,310.697 707.97,311.701 705.237,313.211 \n",
" 701.795,315.136 700.681,315.761 696.125,318.345 695.732,318.57 691.568,320.965 689.78,322.005 687.012,323.621 683.933,325.439 682.455,326.316 678.188,328.874 \n",
" 677.899,329.048 673.343,331.817 672.544,332.308 668.786,334.626 666.996,335.743 664.23,337.475 661.541,339.177 659.674,340.365 656.177,342.612 655.117,343.296 \n",
" 650.901,346.046 650.561,346.269 646.005,349.286 645.712,349.481 641.448,352.345 640.608,352.915 636.892,355.45 635.585,356.35 632.335,358.601 630.642,359.784 \n",
" 627.779,361.798 625.777,363.219 623.223,365.043 620.988,366.653 618.666,368.337 616.274,370.088 614.11,371.681 611.632,373.522 609.554,375.077 607.061,376.957 \n",
" 604.997,378.525 602.561,380.391 600.441,382.027 598.128,383.826 595.884,385.584 593.762,387.26 591.328,389.198 589.462,390.695 586.772,392.87 585.226,394.129 \n",
" 582.215,396.602 581.052,397.564 577.659,400.395 576.941,400.998 573.103,404.252 572.891,404.433 568.9,407.867 568.546,408.174 564.968,411.302 563.99,412.164 \n",
" 561.093,414.736 559.434,416.224 557.275,418.171 554.877,420.355 553.513,421.605 550.321,424.561 549.806,425.04 546.153,428.474 545.764,428.843 542.553,431.909 \n",
" 541.208,433.206 539.005,435.343 536.652,437.651 535.509,438.778 532.095,442.182 532.065,442.212 528.669,445.647 527.539,446.803 525.324,449.081 522.983,451.517 \n",
" 522.028,452.516 518.78,455.95 518.426,456.328 515.578,459.385 513.87,461.241 512.425,462.819 509.318,466.254 509.314,466.259 506.256,469.688 504.757,471.391 \n",
" 503.24,473.123 500.269,476.557 500.201,476.637 497.341,479.992 495.644,482.009 494.458,483.426 491.618,486.861 491.088,487.51 488.82,490.295 486.532,493.148 \n",
" 486.066,493.73 483.353,497.164 481.975,498.932 480.681,500.599 478.052,504.033 477.419,504.87 475.461,507.468 472.914,510.902 472.863,510.972 470.403,514.337 \n",
" 468.306,517.254 467.935,517.771 465.504,521.206 463.75,523.724 463.113,524.64 460.76,528.075 459.194,530.399 458.446,531.509 456.169,534.944 454.637,537.294 \n",
" 453.932,538.378 451.73,541.813 450.081,544.43 449.567,545.247 447.438,548.682 445.524,551.829 445.35,552.117 443.294,555.551 441.277,558.986 440.968,559.52 \n",
" 439.294,562.42 437.348,565.855 436.412,567.536 435.436,569.289 433.56,572.724 431.855,575.907 431.721,576.158 429.912,579.593 428.142,583.027 427.299,584.693 \n",
" 426.404,586.462 424.7,589.896 423.033,593.331 422.743,593.94 421.396,596.765 419.794,600.2 418.228,603.634 418.186,603.728 416.691,607.069 415.189,610.503 \n",
" 413.723,613.938 413.63,614.16 412.285,617.372 410.882,620.807 409.513,624.241 409.073,625.37 408.174,627.676 406.867,631.11 405.595,634.545 404.517,637.532 \n",
" 404.355,637.979 403.144,641.414 401.966,644.848 400.822,648.283 399.961,650.941 399.709,651.717 398.625,655.152 397.573,658.586 396.554,662.021 395.568,665.455 \n",
" 395.404,666.044 394.61,668.89 393.683,672.324 392.788,675.759 391.925,679.193 391.094,682.628 390.848,683.682 390.291,686.062 389.518,689.497 388.777,692.931 \n",
" 388.068,696.366 387.389,699.8 386.742,703.235 386.292,705.741 386.124,706.669 385.535,710.104 384.977,713.538 384.449,716.973 383.952,720.407 383.486,723.842 \n",
" 383.051,727.276 382.645,730.711 382.27,734.145 381.926,737.58 381.735,739.66 381.611,741.014 381.324,744.449 381.069,747.883 380.843,751.318 380.647,754.752 \n",
" 380.482,758.187 380.347,761.621 380.242,765.056 380.167,768.49 380.122,771.925 380.107,775.359 380.122,778.794 380.167,782.228 380.242,785.663 380.347,789.097 \n",
" 380.482,792.532 380.647,795.966 380.843,799.401 381.069,802.835 381.324,806.27 381.611,809.704 381.735,811.059 381.926,813.139 382.27,816.573 382.645,820.008 \n",
" 383.051,823.442 383.486,826.877 383.952,830.312 384.449,833.746 384.977,837.181 385.535,840.615 386.124,844.05 386.292,844.978 386.742,847.484 387.389,850.919 \n",
" 388.068,854.353 388.777,857.788 389.518,861.222 390.291,864.657 390.848,867.037 391.094,868.091 391.925,871.526 392.788,874.96 393.683,878.395 394.61,881.829 \n",
" 395.404,884.675 395.568,885.264 396.554,888.698 397.573,892.133 398.625,895.567 399.709,899.002 399.961,899.777 400.822,902.436 401.966,905.871 403.144,909.305 \n",
" 404.355,912.74 404.517,913.187 405.595,916.174 406.867,919.609 408.174,923.043 409.073,925.349 409.513,926.478 410.882,929.912 412.285,933.347 413.63,936.558 \n",
" 413.723,936.781 415.189,940.216 416.691,943.65 418.186,946.991 418.228,947.085 419.794,950.519 421.396,953.954 422.743,956.779 423.033,957.388 424.7,960.823 \n",
" 426.404,964.257 427.299,966.026 428.142,967.692 429.912,971.126 431.721,974.561 431.855,974.812 433.56,977.995 435.436,981.43 436.412,983.183 437.348,984.864 \n",
" 439.294,988.299 440.968,991.198 441.277,991.733 443.294,995.168 445.35,998.602 445.524,998.89 447.438,1002.04 449.567,1005.47 450.081,1006.29 451.73,1008.91 \n",
" 453.932,1012.34 454.637,1013.42 456.169,1015.77 458.446,1019.21 459.194,1020.32 460.76,1022.64 463.113,1026.08 463.75,1026.99 465.504,1029.51 467.935,1032.95 \n",
" 468.306,1033.47 470.403,1036.38 472.863,1039.75 472.914,1039.82 475.461,1043.25 477.419,1045.85 478.052,1046.69 480.681,1050.12 481.975,1051.79 483.353,1053.55 \n",
" 486.066,1056.99 486.532,1057.57 488.82,1060.42 491.088,1063.21 491.618,1063.86 494.458,1067.29 495.644,1068.71 497.341,1070.73 500.201,1074.08 500.269,1074.16 \n",
" 503.24,1077.6 504.757,1079.33 506.256,1081.03 509.314,1084.46 509.318,1084.46 512.425,1087.9 513.87,1089.48 515.578,1091.33 518.426,1094.39 518.78,1094.77 \n",
" 522.028,1098.2 522.983,1099.2 525.324,1101.64 527.539,1103.92 528.669,1105.07 532.065,1108.51 532.095,1108.54 535.509,1111.94 536.652,1113.07 539.005,1115.38 \n",
" 541.208,1117.51 542.553,1118.81 545.764,1121.88 546.153,1122.24 549.806,1125.68 550.321,1126.16 553.513,1129.11 554.877,1130.36 557.275,1132.55 559.434,1134.5 \n",
" 561.093,1135.98 563.99,1138.55 564.968,1139.42 568.546,1142.54 568.9,1142.85 572.891,1146.29 573.103,1146.47 576.941,1149.72 577.659,1150.32 581.052,1153.16 \n",
" 582.215,1154.12 585.226,1156.59 586.772,1157.85 589.462,1160.02 591.328,1161.52 593.762,1163.46 595.884,1165.14 598.128,1166.89 600.441,1168.69 602.561,1170.33 \n",
" 604.997,1172.19 607.061,1173.76 609.554,1175.64 611.632,1177.2 614.11,1179.04 616.274,1180.63 618.666,1182.38 620.988,1184.07 623.223,1185.68 625.777,1187.5 \n",
" 627.779,1188.92 630.642,1190.93 632.335,1192.12 635.585,1194.37 636.892,1195.27 640.608,1197.8 641.448,1198.37 645.712,1201.24 646.005,1201.43 650.561,1204.45 \n",
" 650.901,1204.67 655.117,1207.42 656.177,1208.11 659.674,1210.35 661.541,1211.54 664.23,1213.24 666.996,1214.98 668.786,1216.09 672.544,1218.41 673.343,1218.9 \n",
" 677.899,1221.67 678.188,1221.85 682.455,1224.4 683.933,1225.28 687.012,1227.1 689.78,1228.71 691.568,1229.75 695.732,1232.15 696.125,1232.37 700.681,1234.96 \n",
" 701.795,1235.58 705.237,1237.51 707.97,1239.02 709.794,1240.02 714.261,1242.45 714.35,1242.5 718.906,1244.95 720.676,1245.89 723.463,1247.36 727.215,1249.32 \n",
" 728.019,1249.74 732.575,1252.09 733.886,1252.76 737.132,1254.4 740.692,1256.19 741.688,1256.69 746.245,1258.94 747.641,1259.62 750.801,1261.17 754.736,1263.06 \n",
" 755.357,1263.36 759.914,1265.52 761.988,1266.49 764.47,1267.65 769.026,1269.76 769.399,1269.93 773.583,1271.83 776.982,1273.36 778.139,1273.88 782.696,1275.9 \n",
" 784.744,1276.8 787.252,1277.89 791.808,1279.86 792.691,1280.23 796.365,1281.79 800.835,1283.67 800.921,1283.7 805.477,1285.59 809.192,1287.1 810.034,1287.44 \n",
" 814.59,1289.28 817.77,1290.54 819.146,1291.08 823.703,1292.86 826.583,1293.97 828.259,1294.61 832.816,1296.34 835.648,1297.4 837.372,1298.05 841.928,1299.73 \n",
" 844.981,1300.84 846.485,1301.38 851.041,1303.02 854.603,1304.27 855.597,1304.62 860.154,1306.21 864.535,1307.71 864.71,1307.77 869.266,1309.31 873.823,1310.82 \n",
" 874.809,1311.14 878.379,1312.31 882.936,1313.78 885.45,1314.58 887.492,1315.22 892.048,1316.65 896.487,1318.01 896.605,1318.05 901.161,1319.43 905.717,1320.78 \n",
" 907.977,1321.45 910.274,1322.12 914.83,1323.43 919.386,1324.72 919.95,1324.88 923.943,1325.99 928.499,1327.24 932.478,1328.31 933.056,1328.47 937.612,1329.68 \n",
" 942.168,1330.86 945.632,1331.75 946.725,1332.03 951.281,1333.17 955.837,1334.3 959.496,1335.18 960.394,1335.4 964.95,1336.49 969.507,1337.55 974.063,1338.59 \n",
" 974.185,1338.62 978.619,1339.62 983.176,1340.62 987.732,1341.6 989.865,1342.05 992.288,1342.57 996.845,1343.51 1001.4,1344.44 1005.96,1345.34 1006.72,1345.49 \n",
" 1010.51,1346.23 1015.07,1347.09 1019.63,1347.94 1024.18,1348.77 1025.04,1348.92 1028.74,1349.58 1033.3,1350.37 1037.85,1351.14 1042.41,1351.89 1045.28,1352.36 \n",
" 1046.96,1352.63 1051.52,1353.34 1056.08,1354.04 1060.63,1354.72 1065.19,1355.38 1068.13,1355.79 1069.75,1356.02 1074.3,1356.64 1078.86,1357.25 1083.42,1357.83 \n",
" 1087.97,1358.4 1092.53,1358.95 1094.89,1359.23 1097.08,1359.48 1101.64,1360 1106.2,1360.49 1110.75,1360.97 1115.31,1361.43 1119.87,1361.87 1124.42,1362.29 \n",
" 1128.56,1362.66 1128.98,1362.7 1133.54,1363.09 1138.09,1363.46 1142.65,1363.81 1147.2,1364.14 1151.76,1364.46 1156.32,1364.76 1160.87,1365.04 1165.43,1365.3 \n",
" \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#fb9c07; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1165.43,1365.3 1169.99,1365.55 1174.54,1365.78 1179.1,1365.99 1181.67,1366.09 1183.66,1366.18 1188.21,1366.35 1192.77,1366.51 1197.32,1366.65 1201.88,1366.78 \n",
" 1206.44,1366.88 1210.99,1366.97 1215.55,1367.04 1220.11,1367.09 1224.66,1367.12 1229.22,1367.14 1233.78,1367.14 1238.33,1367.12 1242.89,1367.09 1247.44,1367.03 \n",
" 1252,1366.96 1256.56,1366.87 1261.11,1366.77 1265.67,1366.64 1270.23,1366.5 1274.78,1366.34 1279.34,1366.16 1280.98,1366.09 1283.9,1365.97 1288.45,1365.76 \n",
" 1293.01,1365.53 1297.56,1365.28 1302.12,1365.02 1306.68,1364.73 1311.23,1364.43 1315.79,1364.11 1320.35,1363.77 1324.9,1363.42 1329.46,1363.05 1333.94,1362.66 \n",
" 1334.02,1362.65 1338.57,1362.25 1343.13,1361.82 1347.68,1361.37 1352.24,1360.91 1356.8,1360.43 1361.35,1359.93 1365.91,1359.41 1367.45,1359.23 1370.47,1358.87 \n",
" 1375.02,1358.32 1379.58,1357.74 1384.14,1357.15 1388.69,1356.54 1393.25,1355.91 1394.06,1355.79 1397.8,1355.26 1402.36,1354.59 1406.92,1353.91 1411.47,1353.2 \n",
" 1416.03,1352.48 1416.76,1352.36 1420.59,1351.73 1425.14,1350.97 1429.7,1350.19 1434.26,1349.39 1436.83,1348.92 1438.81,1348.57 1443.37,1347.73 1447.92,1346.87 \n",
" 1452.48,1345.99 1455.01,1345.49 1457.04,1345.09 1461.59,1344.17 1466.15,1343.23 1470.71,1342.27 1471.72,1342.05 1475.26,1341.29 1479.82,1340.29 1484.38,1339.27 \n",
" 1487.24,1338.62 1488.93,1338.23 1493.49,1337.17 1498.04,1336.09 1501.78,1335.18 1502.6,1334.99 1507.16,1333.86 1511.71,1332.72 1515.49,1331.75 1516.27,1331.55 \n",
" 1520.83,1330.36 1525.38,1329.16 1528.49,1328.31 1529.94,1327.92 1534.5,1326.67 1539.05,1325.4 1540.87,1324.88 1543.61,1324.1 1548.17,1322.78 1552.7,1321.45 \n",
" 1552.72,1321.44 1557.28,1320.08 1561.83,1318.69 1564.03,1318.01 1566.39,1317.28 1570.95,1315.85 1574.92,1314.58 1575.5,1314.39 1580.06,1312.91 1584.62,1311.41 \n",
" 1585.41,1311.14 1589.17,1309.88 1593.73,1308.33 1595.53,1307.71 1598.29,1306.75 1602.84,1305.15 1605.31,1304.27 1607.4,1303.53 1611.95,1301.88 1614.78,1300.84 \n",
" 1616.51,1300.2 1621.07,1298.5 1623.96,1297.4 1625.62,1296.78 1630.18,1295.02 1632.88,1293.97 1634.74,1293.24 1639.29,1291.44 1641.54,1290.54 1643.85,1289.61 \n",
" 1648.41,1287.75 1649.97,1287.1 1652.96,1285.86 1657.52,1283.95 1658.17,1283.67 1662.07,1282 1666.17,1280.23 1666.63,1280.03 1671.19,1278.03 1673.97,1276.8 \n",
" 1675.74,1276.01 1680.3,1273.95 1681.58,1273.36 1684.86,1271.86 1689.01,1269.93 1689.41,1269.74 1693.97,1267.59 1696.27,1266.49 1698.53,1265.42 1703.08,1263.2 \n",
" 1703.38,1263.06 1707.64,1260.96 1710.32,1259.62 1712.19,1258.69 1716.75,1256.38 1717.12,1256.19 1721.31,1254.04 1723.78,1252.76 1725.86,1251.67 1730.3,1249.32 \n",
" 1730.42,1249.26 1734.98,1246.82 1736.69,1245.89 1739.53,1244.34 1742.96,1242.45 1744.09,1241.83 1748.65,1239.28 1749.1,1239.02 1753.2,1236.69 1755.13,1235.58 \n",
" 1757.76,1234.07 1761.04,1232.15 1762.31,1231.4 1766.85,1228.71 1766.87,1228.7 1771.43,1225.96 1772.55,1225.28 1775.98,1223.18 1778.15,1221.85 1780.54,1220.36 \n",
" 1783.65,1218.41 1785.1,1217.5 1789.05,1214.98 1789.65,1214.59 1794.21,1211.64 1794.36,1211.54 1798.77,1208.64 1799.57,1208.11 1803.32,1205.61 1804.7,1204.67 \n",
" 1807.88,1202.52 1809.75,1201.24 1812.43,1199.39 1814.71,1197.8 1816.99,1196.2 1819.59,1194.37 1821.55,1192.97 1824.39,1190.93 1826.1,1189.69 1829.11,1187.5 \n",
" 1830.66,1186.36 1833.75,1184.07 1835.22,1182.97 1838.32,1180.63 1839.77,1179.53 1842.82,1177.2 1844.33,1176.03 1847.25,1173.76 1848.89,1172.48 1851.61,1170.33 \n",
" 1853.44,1168.87 1855.9,1166.89 1858,1165.2 1860.13,1163.46 1862.55,1161.46 1864.29,1160.02 1867.11,1157.66 1868.38,1156.59 1871.67,1153.8 1872.41,1153.16 \n",
" 1876.22,1149.86 1876.39,1149.72 1880.3,1146.29 1880.78,1145.86 1884.15,1142.85 1885.34,1141.78 1887.94,1139.42 1889.89,1137.63 1891.68,1135.98 1894.45,1133.4 \n",
" 1895.36,1132.55 1898.99,1129.11 1899.01,1129.1 1902.56,1125.68 1903.56,1124.7 1906.08,1122.24 1908.12,1120.23 1909.54,1118.81 1912.67,1115.66 1912.96,1115.38 \n",
" 1916.32,1111.94 1917.23,1111 1919.63,1108.51 1921.79,1106.24 1922.89,1105.07 1926.11,1101.64 1926.34,1101.38 1929.27,1098.2 1930.9,1096.41 1932.39,1094.77 \n",
" 1935.46,1091.34 1935.46,1091.33 1938.48,1087.9 1940.01,1086.14 1941.46,1084.46 1944.4,1081.03 1944.57,1080.83 1947.29,1077.6 1949.13,1075.38 1950.13,1074.16 \n",
" 1952.93,1070.73 1953.68,1069.8 1955.69,1067.29 1958.24,1064.07 1958.41,1063.86 1961.08,1060.42 1962.79,1058.19 1963.71,1056.99 1966.3,1053.55 1967.35,1052.15 \n",
" 1968.85,1050.12 1971.36,1046.69 1971.91,1045.93 1973.83,1043.25 1976.26,1039.82 1976.46,1039.53 1978.66,1036.38 1981.01,1032.95 1981.02,1032.93 1983.32,1029.51 \n",
" 1985.58,1026.11 1985.6,1026.08 1987.84,1022.64 1990.04,1019.21 1990.13,1019.06 1992.21,1015.77 1994.33,1012.34 1994.69,1011.75 1996.42,1008.91 1998.48,1005.47 \n",
" 1999.25,1004.17 2000.5,1002.04 2002.48,998.602 2003.8,996.278 2004.43,995.168 2006.35,991.733 2008.22,988.299 2008.36,988.047 2010.07,984.864 2011.88,981.43 \n",
" 2012.91,979.427 2013.65,977.995 2015.4,974.561 2017.11,971.126 2017.47,970.378 2018.78,967.692 2020.43,964.257 2022.03,960.834 2022.03,960.823 2023.61,957.388 \n",
" 2025.16,953.954 2026.58,950.707 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#fabf26; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 2026.58,1192.76 2024.97,1194.37 2022.03,1197.27 2021.48,1197.8 2017.95,1201.24 2017.47,1201.7 2014.37,1204.67 2012.91,1206.06 2010.75,1208.11 2008.36,1210.36 \n",
" 2007.09,1211.54 2003.8,1214.58 2003.37,1214.98 1999.62,1218.41 1999.25,1218.75 1995.81,1221.85 1994.69,1222.85 1991.95,1225.28 1990.13,1226.88 1988.04,1228.71 \n",
" 1985.58,1230.86 1984.09,1232.15 1981.02,1234.78 1980.08,1235.58 1976.46,1238.65 1976.02,1239.02 1971.91,1242.45 1971.91,1242.45 1967.74,1245.89 1967.35,1246.21 \n",
" 1963.52,1249.32 1962.79,1249.91 1959.25,1252.76 1958.24,1253.56 1954.92,1256.19 1953.68,1257.16 1950.53,1259.62 1949.13,1260.71 1946.08,1263.06 1944.57,1264.22 \n",
" 1941.57,1266.49 1940.01,1267.67 1937.01,1269.93 1935.46,1271.08 1932.38,1273.36 1930.9,1274.45 1927.68,1276.8 1926.34,1277.77 1922.93,1280.23 1921.79,1281.05 \n",
" 1918.1,1283.67 1917.23,1284.28 1913.21,1287.1 1912.67,1287.48 1908.25,1290.54 1908.12,1290.63 1903.56,1293.74 1903.22,1293.97 1899.01,1296.81 1898.12,1297.4 \n",
" 1894.45,1299.85 1892.95,1300.84 1889.89,1302.85 1887.7,1304.27 1885.34,1305.8 1882.37,1307.71 1880.78,1308.73 1876.97,1311.14 1876.22,1311.61 1871.67,1314.46 \n",
" 1871.48,1314.58 1867.11,1317.28 1865.91,1318.01 1862.55,1320.06 1860.26,1321.45 1858,1322.81 1854.52,1324.88 1853.44,1325.52 1848.89,1328.2 1848.69,1328.31 \n",
" 1844.33,1330.85 1842.76,1331.75 1839.77,1333.46 1836.74,1335.18 1835.22,1336.05 1830.66,1338.6 1830.63,1338.62 1826.1,1341.12 1824.41,1342.05 1821.55,1343.61 \n",
" 1818.08,1345.49 1816.99,1346.08 1812.43,1348.51 1811.65,1348.92 1807.88,1350.91 1805.11,1352.36 1803.32,1353.29 1798.77,1355.63 1798.45,1355.79 1794.21,1357.95 \n",
" 1791.68,1359.23 1789.65,1360.24 1785.1,1362.5 1784.78,1362.66 1780.54,1364.74 1777.75,1366.09 1775.98,1366.95 1771.43,1369.13 1770.59,1369.53 1766.87,1371.29 \n",
" 1763.29,1372.96 1762.31,1373.42 1757.76,1375.52 1755.84,1376.4 1753.2,1377.6 1748.65,1379.65 1748.25,1379.83 1744.09,1381.68 1740.49,1383.27 1739.53,1383.69 \n",
" 1734.98,1385.67 1732.57,1386.7 1730.42,1387.62 1725.86,1389.56 1724.48,1390.14 1721.31,1391.46 1716.75,1393.35 1716.21,1393.57 1712.19,1395.21 1707.75,1397.01 \n",
" 1707.64,1397.05 1703.08,1398.87 1699.08,1400.44 1698.53,1400.66 1693.97,1402.43 1690.2,1403.87 1689.41,1404.18 1684.86,1405.9 1681.1,1407.31 1680.3,1407.61 \n",
" 1675.74,1409.29 1671.76,1410.74 1671.19,1410.95 1666.63,1412.59 1662.16,1414.18 1662.07,1414.21 1657.52,1415.81 1652.96,1417.38 1652.29,1417.61 1648.41,1418.94 \n",
" 1643.85,1420.47 1642.13,1421.05 1639.29,1421.99 1634.74,1423.48 1631.65,1424.48 1630.18,1424.96 1625.62,1426.41 1621.07,1427.85 1620.84,1427.92 1616.51,1429.26 \n",
" 1611.95,1430.66 1609.66,1431.35 1607.4,1432.03 1602.84,1433.39 1598.29,1434.73 1598.08,1434.78 1593.73,1436.04 1589.17,1437.34 1586.05,1438.22 1584.62,1438.62 \n",
" 1580.06,1439.88 1575.5,1441.13 1573.54,1441.65 1570.95,1442.35 1566.39,1443.56 1561.83,1444.74 1560.49,1445.09 1557.28,1445.91 1552.72,1447.06 1548.17,1448.19 \n",
" 1546.82,1448.52 1543.61,1449.31 1539.05,1450.41 1534.5,1451.48 1532.47,1451.96 1529.94,1452.55 1525.38,1453.59 1520.83,1454.62 1517.32,1455.39 1516.27,1455.62 \n",
" 1511.71,1456.62 1507.16,1457.59 1502.6,1458.54 1501.23,1458.83 1498.04,1459.48 1493.49,1460.41 1488.93,1461.31 1484.38,1462.2 1484.05,1462.26 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#f3e258; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1917.61,1462.26 1921.79,1460.01 1923.97,1458.83 1926.34,1457.53 1930.24,1455.39 1930.9,1455.03 1935.46,1452.5 1936.42,1451.96 1940.01,1449.94 1942.52,1448.52 \n",
" 1944.57,1447.36 1948.54,1445.09 1949.13,1444.75 1953.68,1442.12 1954.48,1441.65 1958.24,1439.46 1960.34,1438.22 1962.79,1436.77 1966.12,1434.78 1967.35,1434.05 \n",
" 1971.83,1431.35 1971.91,1431.3 1976.46,1428.53 1977.46,1427.92 1981.02,1425.72 1983.02,1424.48 1985.58,1422.89 1988.52,1421.05 1990.13,1420.03 1993.94,1417.61 \n",
" 1994.69,1417.14 1999.25,1414.21 1999.3,1414.18 2003.8,1411.26 2004.59,1410.74 2008.36,1408.27 2009.82,1407.31 2012.91,1405.26 2014.98,1403.87 2017.47,1402.21 \n",
" 2020.09,1400.44 2022.03,1399.12 2025.13,1397.01 2026.58,1396.01 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#f57d15; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1698.53,1144.53 1695.63,1146.29 1693.97,1147.29 1689.87,1149.72 1689.41,1149.99 1684.86,1152.65 1683.98,1153.16 1680.3,1155.27 1677.96,1156.59 1675.74,1157.84 \n",
" 1671.8,1160.02 1671.19,1160.36 1666.63,1162.85 1665.5,1163.46 1662.07,1165.29 1659.04,1166.89 1657.52,1167.69 1652.96,1170.05 1652.43,1170.33 1648.41,1172.38 \n",
" 1645.65,1173.76 1643.85,1174.66 1639.29,1176.91 1638.7,1177.2 1634.74,1179.12 1631.56,1180.63 1630.18,1181.29 1625.62,1183.42 1624.23,1184.07 1621.07,1185.52 \n",
" 1616.7,1187.5 1616.51,1187.58 1611.95,1189.62 1608.94,1190.93 1607.4,1191.61 1602.84,1193.57 1600.96,1194.37 1598.29,1195.5 1593.73,1197.4 1592.73,1197.8 \n",
" 1589.17,1199.26 1584.62,1201.09 1584.25,1201.24 1580.06,1202.89 1575.5,1204.66 1575.47,1204.67 1570.95,1206.4 1566.39,1208.11 1566.39,1208.11 1561.83,1209.79 \n",
" 1557.28,1211.44 1556.98,1211.54 1552.72,1213.06 1548.17,1214.65 1547.2,1214.98 1543.61,1216.21 1539.05,1217.74 1537.03,1218.41 1534.5,1219.25 1529.94,1220.73 \n",
" 1526.42,1221.85 1525.38,1222.18 1520.83,1223.6 1516.27,1225 1515.33,1225.28 1511.71,1226.37 1507.16,1227.71 1503.68,1228.71 1502.6,1229.03 1498.04,1230.32 \n",
" 1493.49,1231.58 1491.41,1232.15 1488.93,1232.82 1484.38,1234.04 1479.82,1235.23 1478.43,1235.58 1475.26,1236.39 1470.71,1237.53 1466.15,1238.65 1464.6,1239.02 \n",
" 1461.59,1239.74 1457.04,1240.81 1452.48,1241.85 1449.77,1242.45 1447.92,1242.87 1443.37,1243.86 1438.81,1244.83 1434.26,1245.78 1433.73,1245.89 1429.7,1246.71 \n",
" 1425.14,1247.61 1420.59,1248.49 1416.13,1249.32 1416.03,1249.34 1411.47,1250.18 1406.92,1250.99 1402.36,1251.77 1397.8,1252.54 1396.47,1252.76 1393.25,1253.28 \n",
" 1388.69,1254.01 1384.14,1254.7 1379.58,1255.38 1375.02,1256.04 1373.91,1256.19 1370.47,1256.67 1365.91,1257.28 1361.35,1257.87 1356.8,1258.44 1352.24,1258.99 \n",
" 1347.68,1259.51 1346.69,1259.62 1343.13,1260.02 1338.57,1260.51 1334.02,1260.97 1329.46,1261.41 1324.9,1261.83 1320.35,1262.23 1315.79,1262.61 1311.23,1262.97 \n",
" 1309.97,1263.06 1306.68,1263.3 1302.12,1263.62 1297.56,1263.92 1293.01,1264.19 1288.45,1264.45 1283.9,1264.68 1279.34,1264.9 1274.78,1265.09 1270.23,1265.26 \n",
" 1265.67,1265.42 1261.11,1265.55 1256.56,1265.66 1252,1265.75 1247.44,1265.82 1242.89,1265.87 1238.33,1265.9 1233.78,1265.91 1229.22,1265.9 1224.66,1265.87 \n",
" 1220.11,1265.82 1215.55,1265.75 1210.99,1265.66 1206.44,1265.55 1201.88,1265.42 1197.32,1265.27 1192.77,1265.1 1188.21,1264.9 1183.66,1264.69 1179.1,1264.46 \n",
" 1174.54,1264.21 1169.99,1263.93 1165.43,1263.64 1160.87,1263.32 1157.3,1263.06 1156.32,1262.99 1151.76,1262.63 1147.2,1262.26 1142.65,1261.86 1138.09,1261.45 \n",
" 1133.54,1261.01 1128.98,1260.55 1124.42,1260.07 1120.35,1259.62 1119.87,1259.57 1115.31,1259.05 1110.75,1258.51 1106.2,1257.95 1101.64,1257.37 1097.08,1256.76 \n",
" 1092.91,1256.19 1092.53,1256.14 1087.97,1255.49 1083.42,1254.83 1078.86,1254.14 1074.3,1253.43 1070.12,1252.76 1069.75,1252.7 1065.19,1251.95 1060.63,1251.17 \n",
" 1056.08,1250.38 1051.52,1249.56 1050.25,1249.32 1046.96,1248.72 1042.41,1247.86 1037.85,1246.97 1033.3,1246.07 1032.42,1245.89 1028.74,1245.14 1024.18,1244.19 \n",
" 1019.63,1243.21 1016.14,1242.45 1015.07,1242.22 1010.51,1241.2 1005.96,1240.16 1001.4,1239.09 1001.08,1239.02 996.845,1238.01 992.288,1236.9 987.732,1235.76 \n",
" 987.034,1235.58 983.176,1234.6 978.619,1233.42 974.063,1232.22 973.817,1232.15 969.507,1230.99 964.95,1229.73 961.324,1228.71 960.394,1228.45 955.837,1227.15 \n",
" 951.281,1225.82 949.452,1225.28 946.725,1224.47 942.168,1223.09 938.123,1221.85 937.612,1221.69 933.056,1220.26 928.499,1218.8 927.288,1218.41 923.943,1217.32 \n",
" 919.386,1215.82 916.89,1214.98 914.83,1214.28 910.274,1212.72 906.886,1211.54 905.717,1211.13 901.161,1209.52 897.244,1208.11 896.605,1207.88 892.048,1206.21 \n",
" 887.934,1204.67 887.492,1204.51 882.936,1202.78 878.93,1201.24 878.379,1201.03 873.823,1199.24 870.21,1197.8 869.266,1197.43 864.71,1195.58 861.754,1194.37 \n",
" 860.154,1193.71 855.597,1191.81 853.543,1190.93 851.041,1189.87 846.485,1187.9 845.56,1187.5 841.928,1185.91 837.795,1184.07 837.372,1183.88 832.816,1181.82 \n",
" 830.237,1180.63 828.259,1179.72 823.703,1177.59 822.869,1177.2 819.146,1175.43 815.685,1173.76 814.59,1173.23 810.034,1171 808.675,1170.33 805.477,1168.74 \n",
" 801.831,1166.89 800.921,1166.43 796.365,1164.09 795.145,1163.46 791.808,1161.72 788.609,1160.02 787.252,1159.3 782.696,1156.85 782.217,1156.59 778.139,1154.36 \n",
" 775.966,1153.16 773.583,1151.83 769.846,1149.72 769.026,1149.26 764.47,1146.64 763.854,1146.29 759.914,1143.99 757.986,1142.85 755.357,1141.29 752.237,1139.42 \n",
" 750.801,1138.55 746.601,1135.98 746.245,1135.76 741.688,1132.93 741.077,1132.55 737.132,1130.05 735.661,1129.11 732.575,1127.13 730.348,1125.68 728.019,1124.15 \n",
" 725.135,1122.24 723.463,1121.13 720.02,1118.81 718.906,1118.05 715,1115.38 714.35,1114.93 710.073,1111.94 709.794,1111.74 705.237,1108.51 705.235,1108.51 \n",
" 700.681,1105.22 700.485,1105.07 696.125,1101.86 695.82,1101.64 691.568,1098.45 691.237,1098.2 687.012,1094.98 686.736,1094.77 682.455,1091.44 682.314,1091.33 \n",
" 677.97,1087.9 677.899,1087.84 673.701,1084.46 673.343,1084.17 669.506,1081.03 668.786,1080.44 665.383,1077.6 664.23,1076.62 661.332,1074.16 659.674,1072.74 \n",
" 657.35,1070.73 655.117,1068.78 653.436,1067.29 650.561,1064.73 649.589,1063.86 646.005,1060.6 645.807,1060.42 642.09,1056.99 641.448,1056.39 638.437,1053.55 \n",
" 636.892,1052.08 634.845,1050.12 632.335,1047.68 631.315,1046.69 627.846,1043.25 627.779,1043.18 624.435,1039.82 623.223,1038.58 621.083,1036.38 618.666,1033.87 \n",
" 617.788,1032.95 614.551,1029.51 614.11,1029.04 611.368,1026.08 609.554,1024.09 608.241,1022.64 605.17,1019.21 604.997,1019.01 602.15,1015.77 600.441,1013.8 \n",
" 599.184,1012.34 596.272,1008.91 595.884,1008.44 593.409,1005.47 591.328,1002.93 590.599,1002.04 587.839,998.602 586.772,997.254 585.129,995.168 582.47,991.733 \n",
" 582.215,991.401 579.857,988.299 577.659,985.354 577.295,984.864 574.779,981.43 573.103,979.099 572.312,977.995 569.891,974.561 568.546,972.618 567.518,971.126 \n",
" 565.19,967.692 563.99,965.888 562.909,964.257 560.673,960.823 559.434,958.882 558.482,957.388 556.336,953.954 554.877,951.57 554.236,950.519 552.178,947.085 \n",
" 550.321,943.914 550.167,943.65 548.195,940.216 546.271,936.781 545.764,935.859 544.387,933.347 542.547,929.912 541.208,927.353 540.751,926.478 538.994,923.043 \n",
" 537.283,919.609 536.652,918.311 535.612,916.174 533.983,912.74 532.398,909.305 532.095,908.633 530.851,905.871 529.347,902.436 527.886,899.002 527.539,898.164 \n",
" 526.463,895.567 525.081,892.133 523.743,888.698 522.983,886.686 522.444,885.264 521.184,881.829 519.966,878.395 518.791,874.96 518.426,873.858 517.653,871.526 \n",
" 516.554,868.091 515.498,864.657 514.483,861.222 513.87,859.061 513.507,857.788 512.569,854.353 511.672,850.919 510.816,847.484 510.001,844.05 509.314,841 \n",
" 509.227,840.615 508.488,837.181 507.789,833.746 507.132,830.312 506.515,826.877 505.939,823.442 505.403,820.008 504.907,816.573 504.757,815.447 504.449,813.139 \n",
" 504.029,809.704 503.65,806.27 503.311,802.835 503.012,799.401 502.753,795.966 502.534,792.532 502.355,789.097 502.216,785.663 502.116,782.228 502.056,778.794 \n",
" 502.037,775.359 502.056,771.925 502.116,768.49 502.216,765.056 502.355,761.621 502.534,758.187 502.753,754.752 503.012,751.318 503.311,747.883 503.65,744.449 \n",
" 504.029,741.014 504.449,737.58 504.757,735.272 504.907,734.145 505.403,730.711 505.939,727.276 506.515,723.842 507.132,720.407 507.789,716.973 508.488,713.538 \n",
" 509.227,710.104 509.314,709.719 510.001,706.669 510.816,703.235 511.672,699.8 512.569,696.366 513.507,692.931 513.87,691.658 514.483,689.497 515.498,686.062 \n",
" 516.554,682.628 517.653,679.193 518.426,676.861 518.791,675.759 519.966,672.324 521.184,668.89 522.444,665.455 522.983,664.033 523.743,662.021 525.081,658.586 \n",
" 526.463,655.152 527.539,652.555 527.886,651.717 529.347,648.283 530.851,644.848 532.095,642.086 532.398,641.414 533.983,637.979 535.612,634.545 536.652,632.408 \n",
" 537.283,631.11 538.994,627.676 540.751,624.241 541.208,623.366 542.547,620.807 544.387,617.372 545.764,614.859 546.271,613.938 548.195,610.503 550.167,607.069 \n",
" 550.321,606.805 552.178,603.634 554.236,600.2 554.877,599.149 556.336,596.765 558.482,593.331 559.434,591.837 560.673,589.896 562.909,586.462 563.99,584.831 \n",
" 565.19,583.027 567.518,579.593 568.546,578.101 569.891,576.158 572.312,572.724 573.103,571.62 574.779,569.289 577.295,565.855 577.659,565.365 579.857,562.42 \n",
" 582.215,559.318 582.47,558.986 585.129,555.551 586.772,553.465 587.839,552.117 590.599,548.682 591.328,547.788 593.409,545.247 595.884,542.276 596.272,541.813 \n",
" 599.184,538.378 600.441,536.919 602.15,534.944 604.997,531.705 605.17,531.509 608.241,528.075 609.554,526.629 611.368,524.64 614.11,521.679 614.551,521.206 \n",
" 617.788,517.771 618.666,516.852 621.083,514.337 623.223,512.139 624.435,510.902 627.779,507.535 627.846,507.468 631.315,504.033 632.335,503.036 634.845,500.599 \n",
" 636.892,498.635 638.437,497.164 641.448,494.33 642.09,493.73 645.807,490.295 646.005,490.115 649.589,486.861 650.561,485.988 653.436,483.426 655.117,481.944 \n",
" 657.35,479.992 659.674,477.98 661.332,476.557 664.23,474.095 665.383,473.123 668.786,470.284 669.506,469.688 673.343,466.545 673.701,466.254 677.899,462.876 \n",
" 677.97,462.819 682.314,459.385 682.455,459.274 686.736,455.95 687.012,455.738 691.237,452.516 691.568,452.266 695.82,449.081 696.125,448.855 700.485,445.647 \n",
" 700.681,445.503 705.235,442.212 705.237,442.21 709.794,438.974 710.073,438.778 714.35,435.792 715,435.343 718.906,432.664 720.02,431.909 723.463,429.589 \n",
" 725.135,428.474 728.019,426.564 730.348,425.04 732.575,423.59 735.661,421.605 737.132,420.664 741.077,418.171 741.688,417.786 746.245,414.955 746.601,414.736 \n",
" 750.801,412.169 752.237,411.302 755.357,409.427 757.986,407.867 759.914,406.729 763.854,404.433 764.47,404.075 769.026,401.462 769.846,400.998 773.583,398.89 \n",
" 775.966,397.564 778.139,396.359 782.217,394.129 782.696,393.869 787.252,391.416 788.609,390.695 791.808,389.001 795.145,387.26 796.365,386.626 800.921,384.287 \n",
" 801.831,383.826 805.477,381.983 808.675,380.391 810.034,379.717 814.59,377.486 815.685,376.957 819.146,375.289 822.869,373.522 823.703,373.127 828.259,370.998 \n",
" 830.237,370.088 832.816,368.903 837.372,366.842 837.795,366.653 841.928,364.811 845.56,363.219 846.485,362.814 851.041,360.847 853.543,359.784 855.597,358.912 \n",
" 860.154,357.009 861.754,356.35 864.71,355.134 869.266,353.292 870.21,352.915 873.823,351.477 878.379,349.693 878.93,349.481 882.936,347.936 887.492,346.211 \n",
" 887.934,346.046 892.048,344.511 896.605,342.842 897.244,342.612 901.161,341.199 905.717,339.585 906.886,339.177 910.274,337.996 914.83,336.436 916.89,335.743 \n",
" 919.386,334.902 923.943,333.395 927.288,332.308 928.499,331.915 933.056,330.459 937.612,329.031 938.123,328.874 942.168,327.626 946.725,326.249 949.452,325.439 \n",
" 951.281,324.896 955.837,323.567 960.394,322.266 961.324,322.005 964.95,320.986 969.507,319.732 973.817,318.57 974.063,318.504 978.619,317.296 983.176,316.115 \n",
" 987.034,315.136 987.732,314.958 992.288,313.822 996.845,312.711 1001.08,311.701 1001.4,311.626 1005.96,310.559 1010.51,309.518 1015.07,308.501 1016.14,308.267 \n",
" 1019.63,307.504 1024.18,306.53 1028.74,305.58 1032.42,304.832 1033.3,304.653 1037.85,303.746 1042.41,302.862 1046.96,302.001 1050.25,301.398 1051.52,301.163 \n",
" 1056.08,300.343 1060.63,299.547 1065.19,298.774 1069.75,298.022 1070.12,297.963 1074.3,297.29 1078.86,296.579 1083.42,295.891 1087.97,295.225 1092.53,294.58 \n",
" 1092.91,294.529 1097.08,293.955 1101.64,293.35 1106.2,292.767 1110.75,292.206 1115.31,291.666 1119.87,291.147 1120.35,291.094 1124.42,290.647 1128.98,290.168 \n",
" 1133.54,289.709 1138.09,289.272 1142.65,288.856 1147.2,288.46 1151.76,288.086 1156.32,287.731 1157.3,287.66 1160.87,287.396 1165.43,287.082 1169.99,286.787 \n",
" 1174.54,286.514 1179.1,286.26 1183.66,286.027 1188.21,285.815 1192.77,285.623 1197.32,285.451 1201.88,285.3 1206.44,285.168 1210.99,285.057 1215.55,284.967 \n",
" 1220.11,284.896 1224.66,284.846 1229.22,284.816 1233.78,284.806 1238.33,284.816 1242.89,284.847 1247.44,284.897 1252,284.968 1256.56,285.06 1261.11,285.171 \n",
" 1265.67,285.303 1270.23,285.456 1274.78,285.629 1279.34,285.822 1283.9,286.036 1288.45,286.27 1293.01,286.525 1297.56,286.801 1302.12,287.097 1306.68,287.415 \n",
" 1309.97,287.66 1311.23,287.753 1315.79,288.11 1320.35,288.488 1324.9,288.888 1329.46,289.308 1334.02,289.75 1338.57,290.213 1343.13,290.698 1346.69,291.094 \n",
" 1347.68,291.204 1352.24,291.729 1356.8,292.276 1361.35,292.845 1365.91,293.436 1370.47,294.049 1373.91,294.529 1375.02,294.683 1379.58,295.337 1384.14,296.014 \n",
" 1388.69,296.714 1393.25,297.436 1396.47,297.963 1397.8,298.18 1402.36,298.944 1406.92,299.732 1411.47,300.543 1416.03,301.378 1416.13,301.398 1420.59,302.232 \n",
" 1425.14,303.11 1429.7,304.013 1433.73,304.832 1434.26,304.939 1438.81,305.886 1443.37,306.857 1447.92,307.853 1449.77,308.267 1452.48,308.872 1457.04,309.913 \n",
" 1461.59,310.981 1464.6,311.701 1466.15,312.072 1470.71,313.186 1475.26,314.326 1478.43,315.136 1479.82,315.492 1484.38,316.68 1488.93,317.895 1491.41,318.57 \n",
" 1493.49,319.135 1498.04,320.4 1502.6,321.692 1503.68,322.005 1507.16,323.008 1511.71,324.351 1515.33,325.439 1516.27,325.722 1520.83,327.117 1525.38,328.542 \n",
" 1526.42,328.874 1529.94,329.992 1534.5,331.47 1537.03,332.308 1539.05,332.976 1543.61,334.509 1547.2,335.743 1548.17,336.072 1552.72,337.662 1556.98,339.177 \n",
" 1557.28,339.283 1561.83,340.93 1566.39,342.611 1566.39,342.612 1570.95,344.317 1575.47,346.046 1575.5,346.058 1580.06,347.825 1584.25,349.481 1584.62,349.627 \n",
" 1589.17,351.458 1592.73,352.915 1593.73,353.322 1598.29,355.217 1600.96,356.35 1602.84,357.146 1607.4,359.108 1608.94,359.784 1611.95,361.103 1616.51,363.134 \n",
" 1616.7,363.219 1621.07,365.197 1624.23,366.653 1625.62,367.297 1630.18,369.432 1631.56,370.088 1634.74,371.603 1638.7,373.522 1639.29,373.812 1643.85,376.057 \n",
" 1645.65,376.957 1648.41,378.341 1652.43,380.391 1652.96,380.664 1657.52,383.025 1659.04,383.826 1662.07,385.427 1665.5,387.26 1666.63,387.87 1671.19,390.355 \n",
" 1671.8,390.695 1675.74,392.881 1677.96,394.129 1680.3,395.452 1683.98,397.564 1684.86,398.067 1689.41,400.727 1689.87,400.998 1693.97,403.432 1695.63,404.433 \n",
" 1698.53,406.184 1701.27,407.867 1703.08,408.985 1706.79,411.302 1707.64,411.836 1712.19,414.736 1712.19,414.737 1716.75,417.689 1717.49,418.171 1721.31,420.694 \n",
" 1722.67,421.605 1725.86,423.753 1727.75,425.04 1730.42,426.868 1732.74,428.474 1734.98,430.04 1737.62,431.909 1739.53,433.272 1742.41,435.343 1744.09,436.563 \n",
" 1747.11,438.778 1748.65,439.917 1751.71,442.212 1753.2,443.335 1756.23,445.647 1757.76,446.819 1760.67,449.081 1762.31,450.371 1765.02,452.516 1766.87,453.993 \n",
" 1769.29,455.95 1771.43,457.689 1773.49,459.385 1775.98,461.46 1777.6,462.819 1780.54,465.309 1781.64,466.254 1785.1,469.239 1785.61,469.688 1789.51,473.123 \n",
" 1789.65,473.253 1793.33,476.557 1794.21,477.355 1797.09,479.992 1798.77,481.549 1800.77,483.426 1803.32,485.837 1804.39,486.861 1807.88,490.225 1807.95,490.295 \n",
" 1811.44,493.73 1812.43,494.718 1814.87,497.164 1816.99,499.32 1818.24,500.599 1821.55,504.033 1821.55,504.035 1824.79,507.468 1826.1,508.874 1827.98,510.902 \n",
" 1830.66,513.838 1831.11,514.337 1834.19,517.771 1835.22,518.939 1837.21,521.206 1839.77,524.181 1840.17,524.64 1843.08,528.075 1844.33,529.577 1845.93,531.509 \n",
" 1848.73,534.944 1848.89,535.134 1851.48,538.378 1853.44,540.867 1854.18,541.813 1856.83,545.247 1858,546.787 1859.43,548.682 1861.98,552.117 1862.55,552.908 \n",
" 1864.48,555.551 1866.93,558.986 1867.11,559.247 1869.33,562.42 1871.67,565.826 1871.69,565.855 1874,569.289 1876.22,572.668 1876.26,572.724 1878.48,576.158 \n",
" 1880.65,579.593 1880.78,579.801 1882.78,583.027 1884.86,586.462 1885.34,587.258 1886.9,589.896 1888.9,593.331 1889.89,595.078 1890.85,596.765 1892.76,600.2 \n",
" 1894.45,603.305 1894.63,603.634 1896.46,607.069 1898.24,610.503 1899.01,612.013 1899.98,613.938 1901.68,617.372 1903.34,620.807 1903.56,621.27 1904.97,624.241 \n",
" 1906.55,627.676 1908.08,631.11 1908.12,631.188 1909.59,634.545 1911.05,637.979 1912.47,641.414 1912.67,641.922 1913.86,644.848 1915.2,648.283 1916.51,651.717 \n",
" \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#f57d15; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1916.51,651.717 1917.23,653.681 1917.77,655.152 1919.01,658.586 1920.2,662.021 1921.35,665.455 1921.79,666.79 1922.47,668.89 1923.55,672.324 1924.6,675.759 \n",
" 1925.6,679.193 1926.34,681.819 1926.57,682.628 1927.51,686.062 1928.41,689.497 1929.27,692.931 1930.09,696.366 1930.88,699.8 1930.9,699.903 1931.63,703.235 \n",
" 1932.35,706.669 1933.03,710.104 1933.68,713.538 1934.29,716.973 1934.86,720.407 1935.4,723.842 1935.46,724.218 1935.91,727.276 1936.38,730.711 1936.81,734.145 \n",
" 1937.21,737.58 1937.58,741.014 1937.91,744.449 1938.2,747.883 1938.46,751.318 1938.69,754.752 1938.88,758.187 1939.03,761.621 1939.15,765.056 1939.24,768.49 \n",
" 1939.29,771.925 1939.31,775.359 1939.29,778.794 1939.24,782.228 1939.15,785.663 1939.03,789.097 1938.88,792.532 1938.69,795.966 1938.46,799.401 1938.2,802.835 \n",
" 1937.91,806.27 1937.58,809.704 1937.21,813.139 1936.81,816.573 1936.38,820.008 1935.91,823.442 1935.46,826.501 1935.4,826.877 1934.86,830.312 1934.29,833.746 \n",
" 1933.68,837.181 1933.03,840.615 1932.35,844.05 1931.63,847.484 1930.9,850.816 1930.88,850.919 1930.09,854.353 1929.27,857.788 1928.41,861.222 1927.51,864.657 \n",
" 1926.57,868.091 1926.34,868.9 1925.6,871.526 1924.6,874.96 1923.55,878.395 1922.47,881.829 1921.79,883.929 1921.35,885.264 1920.2,888.698 1919.01,892.133 \n",
" 1917.77,895.567 1917.23,897.038 1916.51,899.002 1915.2,902.436 1913.86,905.871 1912.67,908.796 1912.47,909.305 1911.05,912.74 1909.59,916.174 1908.12,919.53 \n",
" 1908.08,919.609 1906.55,923.043 1904.97,926.478 1903.56,929.449 1903.34,929.912 1901.68,933.347 1899.98,936.781 1899.01,938.705 1898.24,940.216 1896.46,943.65 \n",
" 1894.63,947.085 1894.45,947.414 1892.76,950.519 1890.85,953.954 1889.89,955.641 1888.9,957.388 1886.9,960.823 1885.34,963.46 1884.86,964.257 1882.78,967.692 \n",
" 1880.78,970.918 1880.65,971.126 1878.48,974.561 1876.26,977.995 1876.22,978.05 1874,981.43 1871.69,984.864 1871.67,984.893 1869.33,988.299 1867.11,991.471 \n",
" 1866.93,991.733 1864.48,995.168 1862.55,997.811 1861.98,998.602 1859.43,1002.04 1858,1003.93 1856.83,1005.47 1854.18,1008.91 1853.44,1009.85 1851.48,1012.34 \n",
" 1848.89,1015.59 1848.73,1015.77 1845.93,1019.21 1844.33,1021.14 1843.08,1022.64 1840.17,1026.08 1839.77,1026.54 1837.21,1029.51 1835.22,1031.78 1834.19,1032.95 \n",
" 1831.11,1036.38 1830.66,1036.88 1827.98,1039.82 1826.1,1041.85 1824.79,1043.25 1821.55,1046.68 1821.55,1046.69 1818.24,1050.12 1816.99,1051.4 1814.87,1053.55 \n",
" 1812.43,1056 1811.44,1056.99 1807.95,1060.42 1807.88,1060.49 1804.39,1063.86 1803.32,1064.88 1800.77,1067.29 1798.77,1069.17 1797.09,1070.73 1794.21,1073.36 \n",
" 1793.33,1074.16 1789.65,1077.47 1789.51,1077.6 1785.61,1081.03 1785.1,1081.48 1781.64,1084.46 1780.54,1085.41 1777.6,1087.9 1775.98,1089.26 1773.49,1091.33 \n",
" 1771.43,1093.03 1769.29,1094.77 1766.87,1096.73 1765.02,1098.2 1762.31,1100.35 1760.67,1101.64 1757.76,1103.9 1756.23,1105.07 1753.2,1107.38 1751.71,1108.51 \n",
" 1748.65,1110.8 1747.11,1111.94 1744.09,1114.16 1742.41,1115.38 1739.53,1117.45 1737.62,1118.81 1734.98,1120.68 1732.74,1122.24 1730.42,1123.85 1727.75,1125.68 \n",
" 1725.86,1126.97 1722.67,1129.11 1721.31,1130.03 1717.49,1132.55 1716.75,1133.03 1712.19,1135.98 1712.19,1135.98 1707.64,1138.88 1706.79,1139.42 1703.08,1141.73 \n",
" 1701.27,1142.85 1698.53,1144.53 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#e65e2d; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1621.07,1085.52 1616.81,1087.9 1616.51,1088.07 1611.95,1090.57 1610.53,1091.33 1607.4,1093.02 1604.08,1094.77 1602.84,1095.42 1598.29,1097.77 1597.44,1098.2 \n",
" 1593.73,1100.08 1590.6,1101.64 1589.17,1102.35 1584.62,1104.57 1583.56,1105.07 1580.06,1106.74 1576.29,1108.51 1575.5,1108.87 1570.95,1110.97 1568.78,1111.94 \n",
" 1566.39,1113.02 1561.83,1115.03 1561.03,1115.38 1557.28,1117 1553,1118.81 1552.72,1118.93 1548.17,1120.82 1544.67,1122.24 1543.61,1122.68 1539.05,1124.5 \n",
" 1536.03,1125.68 1534.5,1126.28 1529.94,1128.02 1527.04,1129.11 1525.38,1129.73 1520.83,1131.41 1517.66,1132.55 1516.27,1133.05 1511.71,1134.66 1507.87,1135.98 \n",
" 1507.16,1136.23 1502.6,1137.77 1498.04,1139.28 1497.62,1139.42 1493.49,1140.76 1488.93,1142.2 1486.82,1142.85 1484.38,1143.61 1479.82,1144.99 1475.45,1146.29 \n",
" 1475.26,1146.34 1470.71,1147.66 1466.15,1148.95 1463.37,1149.72 1461.59,1150.21 1457.04,1151.44 1452.48,1152.64 1450.49,1153.16 1447.92,1153.81 1443.37,1154.96 \n",
" 1438.81,1156.07 1436.64,1156.59 1434.26,1157.16 1429.7,1158.22 1425.14,1159.25 1421.62,1160.02 1420.59,1160.25 1416.03,1161.23 1411.47,1162.18 1406.92,1163.1 \n",
" 1405.1,1163.46 1402.36,1164 1397.8,1164.87 1393.25,1165.71 1388.69,1166.53 1386.58,1166.89 1384.14,1167.32 1379.58,1168.09 1375.02,1168.83 1370.47,1169.54 \n",
" 1365.91,1170.23 1365.21,1170.33 1361.35,1170.89 1356.8,1171.53 1352.24,1172.14 1347.68,1172.73 1343.13,1173.3 1339.19,1173.76 1338.57,1173.84 1334.02,1174.35 \n",
" 1329.46,1174.84 1324.9,1175.31 1320.35,1175.75 1315.79,1176.17 1311.23,1176.57 1306.68,1176.94 1303.23,1177.2 1302.12,1177.28 1297.56,1177.61 1293.01,1177.91 \n",
" 1288.45,1178.18 1283.9,1178.43 1279.34,1178.66 1274.78,1178.87 1270.23,1179.05 1265.67,1179.21 1261.11,1179.34 1256.56,1179.46 1252,1179.54 1247.44,1179.61 \n",
" 1242.89,1179.65 1238.33,1179.67 1233.78,1179.67 1229.22,1179.64 1224.66,1179.59 1220.11,1179.52 1215.55,1179.42 1210.99,1179.3 1206.44,1179.16 1201.88,1178.99 \n",
" 1197.32,1178.8 1192.77,1178.59 1188.21,1178.36 1183.66,1178.1 1179.1,1177.82 1174.54,1177.51 1170.19,1177.2 1169.99,1177.18 1165.43,1176.83 1160.87,1176.46 \n",
" 1156.32,1176.06 1151.76,1175.64 1147.2,1175.2 1142.65,1174.73 1138.09,1174.23 1133.93,1173.76 1133.54,1173.72 1128.98,1173.18 1124.42,1172.62 1119.87,1172.03 \n",
" 1115.31,1171.42 1110.75,1170.79 1107.59,1170.33 1106.2,1170.13 1101.64,1169.44 1097.08,1168.74 1092.53,1168.01 1087.97,1167.25 1085.89,1166.89 1083.42,1166.47 \n",
" 1078.86,1165.67 1074.3,1164.84 1069.75,1163.98 1067.05,1163.46 1065.19,1163.1 1060.63,1162.2 1056.08,1161.27 1051.52,1160.31 1050.2,1160.02 1046.96,1159.33 \n",
" 1042.41,1158.32 1037.85,1157.29 1034.85,1156.59 1033.3,1156.23 1028.74,1155.15 1024.18,1154.03 1020.67,1153.16 1019.63,1152.89 1015.07,1151.73 1010.51,1150.54 \n",
" 1007.46,1149.72 1005.96,1149.32 1001.4,1148.07 996.845,1146.8 995.058,1146.29 992.288,1145.5 987.732,1144.17 983.334,1142.85 983.176,1142.8 978.619,1141.42 \n",
" 974.063,1140 972.22,1139.42 969.507,1138.56 964.95,1137.08 961.624,1135.98 960.394,1135.58 955.837,1134.04 951.492,1132.55 951.281,1132.48 946.725,1130.88 \n",
" 942.168,1129.25 941.785,1129.11 937.612,1127.6 933.056,1125.9 932.458,1125.68 928.499,1124.18 923.943,1122.43 923.475,1122.24 919.386,1120.64 914.83,1118.82 \n",
" 914.809,1118.81 910.274,1116.97 906.439,1115.38 905.717,1115.08 901.161,1113.15 898.341,1111.94 896.605,1111.19 892.048,1109.2 890.492,1108.51 887.492,1107.17 \n",
" 882.936,1105.1 882.877,1105.07 878.379,1103 875.49,1101.64 873.823,1100.85 869.266,1098.67 868.307,1098.2 864.71,1096.45 861.321,1094.77 860.154,1094.19 \n",
" 855.597,1091.89 854.521,1091.33 851.041,1089.54 847.898,1087.9 846.485,1087.16 841.928,1084.73 841.441,1084.46 837.372,1082.26 835.147,1081.03 832.816,1079.74 \n",
" 829.002,1077.6 828.259,1077.18 823.703,1074.57 823.004,1074.16 819.146,1071.91 817.147,1070.73 814.59,1069.2 811.423,1067.29 810.034,1066.45 805.828,1063.86 \n",
" 805.477,1063.64 800.921,1060.78 800.358,1060.42 796.365,1057.87 795.008,1056.99 791.808,1054.9 789.773,1053.55 787.252,1051.88 784.649,1050.12 782.696,1048.79 \n",
" 779.634,1046.69 778.139,1045.65 774.723,1043.25 773.583,1042.44 769.914,1039.82 769.026,1039.18 765.204,1036.38 764.47,1035.84 760.589,1032.95 759.914,1032.44 \n",
" 756.068,1029.51 755.357,1028.97 751.637,1026.08 750.801,1025.42 747.295,1022.64 746.245,1021.8 743.039,1019.21 741.688,1018.11 738.867,1015.77 737.132,1014.33 \n",
" 734.778,1012.34 732.575,1010.46 730.769,1008.91 728.019,1006.51 726.838,1005.47 723.463,1002.47 722.984,1002.04 719.206,998.602 718.906,998.327 715.502,995.168 \n",
" 714.35,994.086 711.87,991.733 709.794,989.738 708.309,988.299 705.237,985.28 704.818,984.864 701.396,981.43 700.681,980.703 698.041,977.995 696.125,976 \n",
" 694.753,974.561 691.568,971.166 691.531,971.126 688.372,967.692 687.012,966.189 685.277,964.257 682.455,961.063 682.245,960.823 679.274,957.388 677.899,955.772 \n",
" 676.364,953.954 673.515,950.519 673.343,950.308 670.724,947.085 668.786,944.652 667.993,943.65 665.32,940.216 664.23,938.79 662.704,936.781 660.146,933.347 \n",
" 659.674,932.701 657.643,929.912 655.199,926.478 655.117,926.362 652.806,923.043 650.561,919.74 650.472,919.609 648.189,916.174 646.005,912.803 645.964,912.74 \n",
" 643.788,909.305 641.671,905.871 641.448,905.503 639.602,902.436 637.59,899.002 636.892,897.782 635.628,895.567 633.72,892.133 632.335,889.571 631.865,888.698 \n",
" 630.06,885.264 628.31,881.829 627.779,880.759 626.609,878.395 624.961,874.96 623.368,871.526 623.223,871.204 621.821,868.091 620.328,864.657 618.891,861.222 \n",
" 618.666,860.667 617.501,857.788 616.164,854.353 614.882,850.919 614.11,848.763 613.652,847.484 612.471,844.05 611.345,840.615 610.275,837.181 609.554,834.742 \n",
" 609.258,833.746 608.291,830.312 607.38,826.877 606.525,823.442 605.728,820.008 604.997,816.619 604.987,816.573 604.297,813.139 603.664,809.704 603.091,806.27 \n",
" 602.576,802.835 602.121,799.401 601.725,795.966 601.389,792.532 601.115,789.097 600.9,785.663 600.747,782.228 600.655,778.794 600.625,775.359 600.655,771.925 \n",
" 600.747,768.49 600.9,765.056 601.115,761.621 601.389,758.187 601.725,754.752 602.121,751.318 602.576,747.883 603.091,744.449 603.664,741.014 604.297,737.58 \n",
" 604.987,734.145 604.997,734.099 605.728,730.711 606.525,727.276 607.38,723.842 608.291,720.407 609.258,716.973 609.554,715.977 610.275,713.538 611.345,710.104 \n",
" 612.471,706.669 613.652,703.235 614.11,701.956 614.882,699.8 616.164,696.366 617.501,692.931 618.666,690.052 618.891,689.497 620.328,686.062 621.821,682.628 \n",
" 623.223,679.515 623.368,679.193 624.961,675.759 626.609,672.324 627.779,669.96 628.31,668.89 630.06,665.455 631.865,662.021 632.335,661.148 633.72,658.586 \n",
" 635.628,655.152 636.892,652.936 637.59,651.717 639.602,648.283 641.448,645.216 641.671,644.848 643.788,641.414 645.964,637.979 646.005,637.916 648.189,634.545 \n",
" 650.472,631.11 650.561,630.979 652.806,627.676 655.117,624.357 655.199,624.241 657.643,620.807 659.674,618.018 660.146,617.372 662.704,613.938 664.23,611.929 \n",
" 665.32,610.503 667.993,607.069 668.786,606.067 670.724,603.634 673.343,600.411 673.515,600.2 676.364,596.765 677.899,594.947 679.274,593.331 682.245,589.896 \n",
" 682.455,589.656 685.277,586.462 687.012,584.529 688.372,583.027 691.531,579.593 691.568,579.552 694.753,576.158 696.125,574.718 698.041,572.724 700.681,570.016 \n",
" 701.396,569.289 704.818,565.855 705.237,565.439 708.309,562.42 709.794,560.98 711.87,558.986 714.35,556.633 715.502,555.551 718.906,552.392 719.206,552.117 \n",
" 722.984,548.682 723.463,548.252 726.838,545.247 728.019,544.208 730.769,541.813 732.575,540.256 734.778,538.378 737.132,536.393 738.867,534.944 741.688,532.614 \n",
" 743.039,531.509 746.245,528.916 747.295,528.075 750.801,525.296 751.637,524.64 755.357,521.751 756.068,521.206 759.914,518.279 760.589,517.771 764.47,514.877 \n",
" 765.204,514.337 769.026,511.543 769.914,510.902 773.583,508.275 774.723,507.468 778.139,505.07 779.634,504.033 782.696,501.926 784.649,500.599 787.252,498.843 \n",
" 789.773,497.164 791.808,495.818 795.008,493.73 796.365,492.85 800.358,490.295 800.921,489.937 805.477,487.078 805.828,486.861 810.034,484.27 811.423,483.426 \n",
" 814.59,481.514 817.147,479.992 819.146,478.808 823.004,476.557 823.703,476.152 828.259,473.542 829.002,473.123 832.816,470.979 835.147,469.688 837.372,468.462 \n",
" 841.441,466.254 841.928,465.991 846.485,463.561 847.898,462.819 851.041,461.176 854.521,459.385 855.597,458.833 860.154,456.531 861.321,455.95 864.71,454.27 \n",
" 868.307,452.516 869.266,452.049 873.823,449.867 875.49,449.081 878.379,447.723 882.877,445.647 882.936,445.62 887.492,443.55 890.492,442.212 892.048,441.52 \n",
" 896.605,439.525 898.341,438.778 901.161,437.566 905.717,435.643 906.439,435.343 910.274,433.753 914.809,431.909 914.83,431.9 919.386,430.077 923.475,428.474 \n",
" 923.943,428.291 928.499,426.535 932.458,425.04 933.056,424.814 937.612,423.123 941.785,421.605 942.168,421.466 946.725,419.837 951.281,418.243 951.492,418.171 \n",
" 955.837,416.676 960.394,415.143 961.624,414.736 964.95,413.637 969.507,412.162 972.22,411.302 974.063,410.717 978.619,409.3 983.176,407.915 983.334,407.867 \n",
" 987.732,406.554 992.288,405.224 995.058,404.433 996.845,403.922 1001.4,402.646 1005.96,401.401 1007.46,400.998 1010.51,400.181 1015.07,398.988 1019.63,397.825 \n",
" 1020.67,397.564 1024.18,396.685 1028.74,395.573 1033.3,394.489 1034.85,394.129 1037.85,393.429 1042.41,392.396 1046.96,391.389 1050.2,390.695 1051.52,390.409 \n",
" 1056.08,389.452 1060.63,388.522 1065.19,387.618 1067.05,387.26 1069.75,386.738 1074.3,385.882 1078.86,385.053 1083.42,384.249 1085.89,383.826 1087.97,383.469 \n",
" 1092.53,382.712 1097.08,381.98 1101.64,381.274 1106.2,380.593 1107.59,380.391 1110.75,379.933 1115.31,379.298 1119.87,378.687 1124.42,378.101 1128.98,377.539 \n",
" 1133.54,377.001 1133.93,376.957 1138.09,376.485 1142.65,375.992 1147.2,375.524 1151.76,375.079 1156.32,374.658 1160.87,374.261 1165.43,373.887 1169.99,373.537 \n",
" 1170.19,373.522 1174.54,373.208 1179.1,372.903 1183.66,372.621 1188.21,372.362 1192.77,372.127 1197.32,371.915 1201.88,371.726 1206.44,371.56 1210.99,371.418 \n",
" 1215.55,371.299 1220.11,371.202 1224.66,371.129 1229.22,371.079 1233.78,371.052 1238.33,371.048 1242.89,371.067 1247.44,371.109 1252,371.175 1256.56,371.263 \n",
" 1261.11,371.375 1265.67,371.51 1270.23,371.668 1274.78,371.85 1279.34,372.056 1283.9,372.285 1288.45,372.537 1293.01,372.813 1297.56,373.113 1302.12,373.437 \n",
" 1303.23,373.522 1306.68,373.784 1311.23,374.153 1315.79,374.547 1320.35,374.965 1324.9,375.408 1329.46,375.875 1334.02,376.367 1338.57,376.883 1339.19,376.957 \n",
" 1343.13,377.422 1347.68,377.985 1352.24,378.574 1356.8,379.188 1361.35,379.828 1365.21,380.391 1365.91,380.493 1370.47,381.18 1375.02,381.894 1379.58,382.634 \n",
" 1384.14,383.4 1386.58,383.826 1388.69,384.192 1393.25,385.007 1397.8,385.85 1402.36,386.721 1405.1,387.26 1406.92,387.617 1411.47,388.538 1416.03,389.488 \n",
" 1420.59,390.466 1421.62,390.695 1425.14,391.468 1429.7,392.499 1434.26,393.559 1436.64,394.129 1438.81,394.646 1443.37,395.759 1447.92,396.904 1450.49,397.564 \n",
" 1452.48,398.076 1457.04,399.276 1461.59,400.508 1463.37,400.998 1466.15,401.767 1470.71,403.056 1475.26,404.378 1475.45,404.433 1479.82,405.726 1484.38,407.108 \n",
" 1486.82,407.867 1488.93,408.52 1493.49,409.963 1497.62,411.302 1498.04,411.441 1502.6,412.947 1507.16,414.489 1507.87,414.736 1511.71,416.061 1516.27,417.669 \n",
" 1517.66,418.171 1520.83,419.309 1525.38,420.986 1527.04,421.605 1529.94,422.695 1534.5,424.442 1536.03,425.04 1539.05,426.223 1543.61,428.042 1544.67,428.474 \n",
" 1548.17,429.897 1552.72,431.792 1553,431.909 1557.28,433.721 1561.03,435.343 1561.83,435.693 1566.39,437.702 1568.78,438.778 1570.95,439.752 1575.5,441.844 \n",
" 1576.29,442.212 1580.06,443.976 1583.56,445.647 1584.62,446.153 1589.17,448.372 1590.6,449.081 1593.73,450.635 1597.44,452.516 1598.29,452.944 1602.84,455.299 \n",
" 1604.08,455.95 1607.4,457.701 1610.53,459.385 1611.95,460.152 1616.51,462.653 1616.81,462.819 1621.07,465.202 1622.91,466.254 1625.62,467.804 1628.86,469.688 \n",
" 1630.18,470.46 1634.65,473.123 1634.74,473.171 1639.29,475.937 1640.3,476.557 1643.85,478.76 1645.8,479.992 1648.41,481.643 1651.17,483.426 1652.96,484.587 \n",
" 1656.41,486.861 1657.52,487.594 1661.53,490.295 1662.07,490.666 1666.52,493.73 1666.63,493.804 1671.19,497.011 1671.4,497.164 1675.74,500.29 1676.17,500.599 \n",
" 1680.3,503.643 1680.82,504.033 1684.86,507.072 1685.37,507.468 1689.41,510.581 1689.82,510.902 1693.97,514.174 1694.17,514.337 1698.43,517.771 1698.53,517.852 \n",
" 1702.59,521.206 1703.08,521.621 1706.65,524.64 1707.64,525.483 1710.63,528.075 1712.19,529.445 1714.52,531.509 1716.75,533.509 1718.33,534.944 1721.31,537.682 \n",
" 1722.06,538.378 1725.7,541.813 1725.86,541.969 1729.26,545.247 1730.42,546.378 1732.75,548.682 1734.98,550.914 1736.16,552.117 1739.5,555.551 1739.53,555.584 \n",
" 1742.77,558.986 1744.09,560.402 1745.96,562.42 1748.65,565.371 1749.08,565.855 1752.14,569.289 1753.2,570.507 1755.12,572.724 1757.76,575.82 1758.04,576.158 \n",
" 1760.9,579.593 1762.31,581.328 1763.69,583.027 1766.42,586.462 1766.87,587.043 1769.08,589.896 1771.43,592.988 1771.69,593.331 1774.23,596.765 1775.98,599.187 \n",
" 1776.71,600.2 1779.14,603.634 1780.54,605.665 1781.5,607.069 1783.81,610.503 1785.1,612.455 1786.07,613.938 1788.26,617.372 1789.65,619.599 1790.4,620.807 \n",
" 1792.49,624.241 1794.21,627.147 1794.52,627.676 1796.5,631.11 1798.43,634.545 1798.77,635.167 1800.3,637.979 1802.12,641.414 1803.32,643.744 1803.89,644.848 \n",
" 1805.61,648.283 1807.28,651.717 1807.88,652.994 1808.9,655.152 1810.46,658.586 1811.98,662.021 1812.43,663.08 1813.45,665.455 1814.87,668.89 1816.25,672.324 \n",
" 1816.99,674.258 1817.57,675.759 1818.85,679.193 1820.08,682.628 1821.26,686.062 1821.55,686.933 1822.4,689.497 1823.49,692.931 1824.53,696.366 1825.53,699.8 \n",
" 1826.1,701.888 1826.48,703.235 1827.39,706.669 1828.25,710.104 1829.06,713.538 1829.83,716.973 1830.55,720.407 1830.66,720.945 1831.24,723.842 1831.87,727.276 \n",
" 1832.47,730.711 1833.01,734.145 1833.52,737.58 1833.97,741.014 1834.39,744.449 1834.76,747.883 1835.08,751.318 1835.22,752.922 1835.37,754.752 1835.61,758.187 \n",
" 1835.81,761.621 1835.96,765.056 1836.07,768.49 1836.13,771.925 1836.15,775.359 1836.13,778.794 1836.07,782.228 1835.96,785.663 1835.81,789.097 1835.61,792.532 \n",
" 1835.37,795.966 1835.22,797.797 1835.08,799.401 1834.76,802.835 1834.39,806.27 1833.97,809.704 1833.52,813.139 1833.01,816.573 1832.47,820.008 1831.87,823.442 \n",
" 1831.24,826.877 1830.66,829.773 1830.55,830.312 1829.83,833.746 1829.06,837.181 1828.25,840.615 1827.39,844.05 1826.48,847.484 1826.1,848.831 1825.53,850.919 \n",
" 1824.53,854.353 1823.49,857.788 1822.4,861.222 1821.55,863.786 1821.26,864.657 1820.08,868.091 1818.85,871.526 1817.57,874.96 1816.99,876.461 1816.25,878.395 \n",
" 1814.87,881.829 1813.45,885.264 1812.43,887.639 1811.98,888.698 1810.46,892.133 1808.9,895.567 1807.88,897.725 1807.28,899.002 1805.61,902.436 1803.89,905.871 \n",
" 1803.32,906.974 1802.12,909.305 1800.3,912.74 1798.77,915.552 1798.43,916.174 1796.5,919.609 1794.52,923.043 1794.21,923.572 1792.49,926.478 1790.4,929.912 \n",
" 1789.65,931.119 1788.26,933.347 1786.07,936.781 1785.1,938.264 1783.81,940.216 1781.5,943.65 1780.54,945.054 1779.14,947.085 1776.71,950.519 1775.98,951.532 \n",
" 1774.23,953.954 1771.69,957.388 1771.43,957.731 1769.08,960.823 1766.87,963.676 1766.42,964.257 1763.69,967.692 1762.31,969.391 1760.9,971.126 1758.04,974.561 \n",
" 1757.76,974.899 1755.12,977.995 1753.2,980.211 1752.14,981.43 1749.08,984.864 1748.65,985.348 1745.96,988.299 1744.09,990.317 1742.77,991.733 1739.53,995.134 \n",
" 1739.5,995.168 1736.16,998.602 1734.98,999.805 1732.75,1002.04 1730.42,1004.34 1729.26,1005.47 1725.86,1008.75 1725.7,1008.91 1722.06,1012.34 1721.31,1013.04 \n",
" 1718.33,1015.77 1716.75,1017.21 1714.52,1019.21 1712.19,1021.27 1710.63,1022.64 1707.64,1025.24 1706.65,1026.08 1703.08,1029.1 1702.59,1029.51 1698.53,1032.87 \n",
" 1698.43,1032.95 1694.17,1036.38 1693.97,1036.55 1689.82,1039.82 1689.41,1040.14 1685.37,1043.25 1684.86,1043.65 1680.82,1046.69 1680.3,1047.08 1676.17,1050.12 \n",
" 1675.74,1050.43 1671.4,1053.55 1671.19,1053.71 1666.63,1056.91 1666.52,1056.99 1662.07,1060.05 1661.53,1060.42 1657.52,1063.12 1656.41,1063.86 1652.96,1066.13 \n",
" \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#e65e2d; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1652.96,1066.13 1651.17,1067.29 1648.41,1069.08 1645.8,1070.73 1643.85,1071.96 1640.3,1074.16 1639.29,1074.78 1634.74,1077.55 1634.65,1077.6 1630.18,1080.26 \n",
" 1628.86,1081.03 1625.62,1082.91 1622.91,1084.46 1621.07,1085.52 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#d24742; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1557.28,1034.23 1553.06,1036.38 1552.72,1036.55 1548.17,1038.83 1546.13,1039.82 1543.61,1041.04 1539.05,1043.21 1538.96,1043.25 1534.5,1045.33 1531.51,1046.69 \n",
" 1529.94,1047.4 1525.38,1049.42 1523.77,1050.12 1520.83,1051.39 1516.27,1053.32 1515.71,1053.55 1511.71,1055.21 1507.31,1056.99 1507.16,1057.05 1502.6,1058.85 \n",
" 1498.52,1060.42 1498.04,1060.6 1493.49,1062.32 1489.31,1063.86 1488.93,1064 1484.38,1065.63 1479.82,1067.23 1479.63,1067.29 1475.26,1068.79 1470.71,1070.3 \n",
" 1469.41,1070.73 1466.15,1071.79 1461.59,1073.23 1458.58,1074.16 1457.04,1074.64 1452.48,1076.01 1447.92,1077.35 1447.06,1077.6 1443.37,1078.65 1438.81,1079.92 \n",
" 1434.71,1081.03 1434.26,1081.15 1429.7,1082.36 1425.14,1083.52 1421.35,1084.46 1420.59,1084.66 1416.03,1085.76 1411.47,1086.83 1406.92,1087.86 1406.75,1087.9 \n",
" 1402.36,1088.87 1397.8,1089.85 1393.25,1090.79 1390.53,1091.33 1388.69,1091.7 1384.14,1092.59 1379.58,1093.44 1375.02,1094.26 1372.1,1094.77 1370.47,1095.05 \n",
" 1365.91,1095.82 1361.35,1096.55 1356.8,1097.26 1352.24,1097.93 1350.34,1098.2 1347.68,1098.58 1343.13,1099.2 1338.57,1099.79 1334.02,1100.36 1329.46,1100.89 \n",
" 1324.9,1101.4 1322.61,1101.64 1320.35,1101.88 1315.79,1102.33 1311.23,1102.76 1306.68,1103.15 1302.12,1103.52 1297.56,1103.87 1293.01,1104.18 1288.45,1104.47 \n",
" 1283.9,1104.73 1279.34,1104.97 1277.08,1105.07 1274.78,1105.18 1270.23,1105.36 1265.67,1105.52 1261.11,1105.65 1256.56,1105.75 1252,1105.83 1247.44,1105.88 \n",
" 1242.89,1105.91 1238.33,1105.91 1233.78,1105.88 1229.22,1105.83 1224.66,1105.75 1220.11,1105.64 1215.55,1105.51 1210.99,1105.35 1206.44,1105.17 1204.41,1105.07 \n",
" 1201.88,1104.96 1197.32,1104.72 1192.77,1104.46 1188.21,1104.17 1183.66,1103.86 1179.1,1103.52 1174.54,1103.15 1169.99,1102.76 1165.43,1102.34 1160.87,1101.89 \n",
" 1158.44,1101.64 1156.32,1101.42 1151.76,1100.92 1147.2,1100.4 1142.65,1099.84 1138.09,1099.27 1133.54,1098.66 1130.26,1098.2 1128.98,1098.03 1124.42,1097.37 \n",
" 1119.87,1096.68 1115.31,1095.97 1110.75,1095.23 1108.05,1094.77 1106.2,1094.46 1101.64,1093.66 1097.08,1092.84 1092.53,1091.98 1089.17,1091.33 1087.97,1091.1 \n",
" 1083.42,1090.2 1078.86,1089.26 1074.3,1088.29 1072.5,1087.9 1069.75,1087.3 1065.19,1086.28 1060.63,1085.22 1057.44,1084.46 1056.08,1084.14 1051.52,1083.03 \n",
" 1046.96,1081.89 1043.62,1081.03 1042.41,1080.72 1037.85,1079.52 1033.3,1078.29 1030.81,1077.6 1028.74,1077.02 1024.18,1075.73 1019.63,1074.4 1018.81,1074.16 \n",
" 1015.07,1073.05 1010.51,1071.66 1007.53,1070.73 1005.96,1070.24 1001.4,1068.79 996.845,1067.3 996.835,1067.29 992.288,1065.78 987.732,1064.22 986.685,1063.86 \n",
" 983.176,1062.64 978.619,1061.01 977,1060.42 974.063,1059.36 969.507,1057.66 967.733,1056.99 964.95,1055.93 960.394,1054.17 958.845,1053.55 955.837,1052.36 \n",
" 951.281,1050.52 950.3,1050.12 946.725,1048.65 942.168,1046.73 942.068,1046.69 937.612,1044.77 934.133,1043.25 933.056,1042.78 928.499,1040.74 926.465,1039.82 \n",
" 923.943,1038.67 919.386,1036.54 919.042,1036.38 914.83,1034.38 911.858,1032.95 910.274,1032.18 905.717,1029.93 904.888,1029.51 901.161,1027.64 898.127,1026.08 \n",
" 896.605,1025.29 892.048,1022.91 891.556,1022.64 887.492,1020.47 885.173,1019.21 882.936,1017.99 878.959,1015.77 878.379,1015.45 873.823,1012.86 872.914,1012.34 \n",
" 869.266,1010.23 867.026,1008.91 864.71,1007.53 861.287,1005.47 860.154,1004.78 855.691,1002.04 855.597,1001.98 851.041,999.116 850.235,998.602 846.485,996.193 \n",
" 844.912,995.168 841.928,993.208 839.716,991.733 837.372,990.16 834.641,988.299 832.816,987.045 829.686,984.864 828.259,983.863 824.844,981.43 823.703,980.61 \n",
" 820.113,977.995 819.146,977.285 815.49,974.561 814.59,973.885 810.97,971.126 810.034,970.406 806.551,967.692 805.477,966.847 802.23,964.257 800.921,963.203 \n",
" 798.004,960.823 796.365,959.471 793.871,957.388 791.808,955.647 789.828,953.954 787.252,951.726 785.873,950.519 782.696,947.704 782.004,947.085 778.22,943.65 \n",
" 778.139,943.576 774.518,940.216 773.583,939.336 770.896,936.781 769.026,934.978 767.353,933.347 764.47,930.494 763.888,929.912 760.499,926.478 759.914,925.877 \n",
" 757.184,923.043 755.357,921.117 753.942,919.609 750.801,916.205 750.773,916.174 747.673,912.74 746.245,911.128 744.644,909.305 741.688,905.875 741.685,905.871 \n",
" 738.791,902.436 737.132,900.427 735.965,899.002 733.206,895.567 732.575,894.769 730.511,892.133 728.019,888.879 727.882,888.698 725.314,885.264 723.463,882.729 \n",
" 722.811,881.829 720.37,878.395 718.906,876.288 717.991,874.96 715.673,871.526 714.35,869.517 713.417,868.091 711.221,864.657 709.794,862.367 709.086,861.222 \n",
" 707.009,857.788 705.237,854.771 704.994,854.353 703.035,850.919 701.138,847.484 700.681,846.636 699.297,844.05 697.517,840.615 696.125,837.838 695.797,837.181 \n",
" 694.132,833.746 692.529,830.312 691.568,828.18 690.985,826.877 689.497,823.442 688.071,820.008 687.012,817.348 686.705,816.573 685.396,813.139 684.149,809.704 \n",
" 682.964,806.27 682.455,804.723 681.839,802.835 680.773,799.401 679.772,795.966 678.834,792.532 677.96,789.097 677.899,788.845 677.143,785.663 676.387,782.228 \n",
" 675.687,778.794 675.036,775.359 675.687,771.925 676.387,768.49 677.143,765.056 677.899,761.874 677.96,761.621 678.834,758.187 679.772,754.752 680.773,751.318 \n",
" 681.839,747.883 682.455,745.996 682.964,744.449 684.149,741.014 685.396,737.58 686.705,734.145 687.012,733.371 688.071,730.711 689.497,727.276 690.985,723.842 \n",
" 691.568,722.539 692.529,720.407 694.132,716.973 695.797,713.538 696.125,712.881 697.517,710.104 699.297,706.669 700.681,704.083 701.138,703.235 703.035,699.8 \n",
" 704.994,696.366 705.237,695.948 707.009,692.931 709.086,689.497 709.794,688.352 711.221,686.062 713.417,682.628 714.35,681.201 715.673,679.193 717.991,675.759 \n",
" 718.906,674.431 720.37,672.324 722.811,668.89 723.463,667.99 725.314,665.455 727.882,662.021 728.019,661.84 730.511,658.586 732.575,655.95 733.206,655.152 \n",
" 735.965,651.717 737.132,650.292 738.791,648.283 741.685,644.848 741.688,644.844 744.644,641.414 746.245,639.591 747.673,637.979 750.773,634.545 750.801,634.514 \n",
" 753.942,631.11 755.357,629.602 757.184,627.676 759.914,624.842 760.499,624.241 763.888,620.807 764.47,620.225 767.353,617.372 769.026,615.741 770.896,613.938 \n",
" 773.583,611.382 774.518,610.503 778.139,607.143 778.22,607.069 782.004,603.634 782.696,603.014 785.873,600.2 787.252,598.993 789.828,596.765 791.808,595.072 \n",
" 793.871,593.331 796.365,591.248 798.004,589.896 800.921,587.516 802.23,586.462 805.477,583.872 806.551,583.027 810.034,580.312 810.97,579.593 814.59,576.834 \n",
" 815.49,576.158 819.146,573.434 820.113,572.724 823.703,570.109 824.844,569.289 828.259,566.856 829.686,565.855 832.816,563.674 834.641,562.42 837.372,560.559 \n",
" 839.716,558.986 841.928,557.51 844.912,555.551 846.485,554.525 850.235,552.117 851.041,551.603 855.597,548.74 855.691,548.682 860.154,545.934 861.287,545.247 \n",
" 864.71,543.185 867.026,541.813 869.266,540.492 872.914,538.378 873.823,537.854 878.379,535.268 878.959,534.944 882.936,532.732 885.173,531.509 887.492,530.247 \n",
" 891.556,528.075 892.048,527.813 896.605,525.425 898.127,524.64 901.161,523.083 904.888,521.206 905.717,520.79 910.274,518.54 911.858,517.771 914.83,516.334 \n",
" 919.042,514.337 919.386,514.174 923.943,512.053 926.465,510.902 928.499,509.976 933.056,507.941 934.133,507.468 937.612,505.944 942.068,504.033 942.168,503.991 \n",
" 946.725,502.072 950.3,500.599 951.281,500.195 955.837,498.354 958.845,497.164 960.394,496.552 964.95,494.786 967.733,493.73 969.507,493.058 974.063,491.364 \n",
" 977,490.295 978.619,489.707 983.176,488.083 986.685,486.861 987.732,486.496 992.288,484.941 996.835,483.426 996.845,483.423 1001.4,481.934 1005.96,480.481 \n",
" 1007.53,479.992 1010.51,479.059 1015.07,477.67 1018.81,476.557 1019.63,476.315 1024.18,474.988 1028.74,473.695 1030.81,473.123 1033.3,472.432 1037.85,471.2 \n",
" 1042.41,470 1043.62,469.688 1046.96,468.828 1051.52,467.686 1056.08,466.577 1057.44,466.254 1060.63,465.494 1065.19,464.441 1069.75,463.419 1072.5,462.819 \n",
" 1074.3,462.426 1078.86,461.459 1083.42,460.522 1087.97,459.616 1089.17,459.385 1092.53,458.735 1097.08,457.881 1101.64,457.058 1106.2,456.263 1108.05,455.95 \n",
" 1110.75,455.494 1115.31,454.751 1119.87,454.037 1124.42,453.351 1128.98,452.693 1130.26,452.516 1133.54,452.06 1138.09,451.453 1142.65,450.874 1147.2,450.322 \n",
" 1151.76,449.798 1156.32,449.3 1158.44,449.081 1160.87,448.828 1165.43,448.381 1169.99,447.961 1174.54,447.568 1179.1,447.201 1183.66,446.861 1188.21,446.547 \n",
" 1192.77,446.259 1197.32,445.998 1201.88,445.763 1204.41,445.647 1206.44,445.553 1210.99,445.369 1215.55,445.211 1220.11,445.079 1224.66,444.973 1229.22,444.893 \n",
" 1233.78,444.84 1238.33,444.813 1242.89,444.811 1247.44,444.837 1252,444.888 1256.56,444.966 1261.11,445.07 1265.67,445.2 1270.23,445.357 1274.78,445.541 \n",
" 1277.08,445.647 1279.34,445.75 1283.9,445.986 1288.45,446.248 1293.01,446.536 1297.56,446.852 1302.12,447.195 1306.68,447.566 1311.23,447.963 1315.79,448.389 \n",
" 1320.35,448.842 1322.61,449.081 1324.9,449.322 1329.46,449.828 1334.02,450.362 1338.57,450.925 1343.13,451.517 1347.68,452.138 1350.34,452.516 1352.24,452.786 \n",
" 1356.8,453.461 1361.35,454.166 1365.91,454.9 1370.47,455.666 1372.1,455.95 1375.02,456.458 1379.58,457.279 1384.14,458.132 1388.69,459.017 1390.53,459.385 \n",
" 1393.25,459.929 1397.8,460.872 1402.36,461.847 1406.75,462.819 1406.92,462.856 1411.47,463.89 1416.03,464.96 1420.59,466.064 1421.35,466.254 1425.14,467.196 \n",
" 1429.7,468.363 1434.26,469.565 1434.71,469.688 1438.81,470.797 1443.37,472.065 1447.06,473.123 1447.92,473.37 1452.48,474.705 1457.04,476.079 1458.58,476.557 \n",
" 1461.59,477.487 1466.15,478.932 1469.41,479.992 1470.71,480.415 1475.26,481.933 1479.63,483.426 1479.82,483.493 1484.38,485.086 1488.93,486.724 1489.31,486.861 \n",
" 1493.49,488.396 1498.04,490.114 1498.52,490.295 1502.6,491.869 1507.16,493.67 1507.31,493.73 1511.71,495.51 1515.71,497.164 1516.27,497.397 1520.83,499.325 \n",
" 1523.77,500.599 1525.38,501.301 1529.94,503.323 1531.51,504.033 1534.5,505.391 1538.96,507.468 1539.05,507.51 1543.61,509.675 1546.13,510.902 1548.17,511.893 \n",
" 1552.72,514.165 1553.06,514.337 1557.28,516.486 1559.75,517.771 1561.83,518.864 1566.22,521.206 1566.39,521.3 1570.95,523.79 1572.47,524.64 1575.5,526.341 \n",
" 1578.53,528.075 1580.06,528.954 1584.41,531.509 1584.62,531.631 1589.17,534.372 1590.11,534.944 1593.73,537.18 1595.64,538.378 1598.29,540.058 1601,541.813 \n",
" 1602.84,543.009 1606.22,545.247 1607.4,546.035 1611.29,548.682 1611.95,549.138 1616.22,552.117 1616.51,552.323 1621.01,555.551 1621.07,555.593 1625.62,558.95 \n",
" 1625.67,558.986 1630.18,562.4 1630.21,562.42 1634.62,565.855 1634.74,565.947 1638.91,569.289 1639.29,569.595 1643.1,572.724 1643.85,573.35 1647.17,576.158 \n",
" 1648.41,577.219 1651.13,579.593 1652.96,581.207 1654.99,583.027 1657.52,585.323 1658.75,586.462 1662.07,589.573 1662.41,589.896 1665.98,593.331 1666.63,593.969 \n",
" 1669.45,596.765 1671.19,598.52 1672.83,600.2 1675.74,603.237 1676.12,603.634 1679.32,607.069 1680.3,608.138 1682.44,610.503 1684.86,613.234 1685.47,613.938 \n",
" 1688.42,617.372 1689.41,618.549 1691.29,620.807 1693.97,624.1 1694.08,624.241 1696.8,627.676 1698.53,629.922 1699.43,631.11 1701.99,634.545 1703.08,636.041 \n",
" 1704.48,637.979 1706.89,641.414 1707.64,642.5 1709.24,644.848 1711.51,648.283 1712.19,649.351 1713.71,651.717 1715.84,655.152 1716.75,656.664 1717.9,658.586 \n",
" 1719.9,662.021 1721.31,664.524 1721.83,665.455 1723.7,668.89 1725.49,672.324 1725.86,673.061 1727.23,675.759 1728.9,679.193 1730.42,682.455 1730.5,682.628 \n",
" 1732.05,686.062 1733.53,689.497 1734.95,692.931 1734.98,693.009 1736.31,696.366 1737.61,699.8 1738.84,703.235 1739.53,705.252 1740.02,706.669 1741.14,710.104 \n",
" 1742.2,713.538 1743.2,716.973 1744.09,720.245 1744.13,720.407 1745.02,723.842 1745.85,727.276 1746.61,730.711 1747.32,734.145 1747.97,737.58 1748.56,741.014 \n",
" 1748.65,741.553 1749.1,744.449 1749.58,747.883 1750.01,751.318 1750.37,754.752 1750.68,758.187 1750.94,761.621 1751.14,765.056 1751.28,768.49 1751.36,771.925 \n",
" 1751.39,775.359 1751.36,778.794 1751.28,782.228 1751.14,785.663 1750.94,789.097 1750.68,792.532 1750.37,795.966 1750.01,799.401 1749.58,802.835 1749.1,806.27 \n",
" 1748.65,809.166 1748.56,809.704 1747.97,813.139 1747.32,816.573 1746.61,820.008 1745.85,823.442 1745.02,826.877 1744.13,830.312 1744.09,830.474 1743.2,833.746 \n",
" 1742.2,837.181 1741.14,840.615 1740.02,844.05 1739.53,845.466 1738.84,847.484 1737.61,850.919 1736.31,854.353 1734.98,857.71 1734.95,857.788 1733.53,861.222 \n",
" 1732.05,864.657 1730.5,868.091 1730.42,868.263 1728.9,871.526 1727.23,874.96 1725.86,877.658 1725.49,878.395 1723.7,881.829 1721.83,885.264 1721.31,886.195 \n",
" 1719.9,888.698 1717.9,892.133 1716.75,894.055 1715.84,895.567 1713.71,899.002 1712.19,901.367 1711.51,902.436 1709.24,905.871 1707.64,908.219 1706.89,909.305 \n",
" 1704.48,912.74 1703.08,914.678 1701.99,916.174 1699.43,919.609 1698.53,920.797 1696.8,923.043 1694.08,926.478 1693.97,926.619 1691.29,929.912 1689.41,932.17 \n",
" 1688.42,933.347 1685.47,936.781 1684.86,937.484 1682.44,940.216 1680.3,942.581 1679.32,943.65 1676.12,947.085 1675.74,947.482 1672.83,950.519 1671.19,952.199 \n",
" 1669.45,953.954 1666.63,956.75 1665.98,957.388 1662.41,960.823 1662.07,961.146 1658.75,964.257 1657.52,965.396 1654.99,967.692 1652.96,969.512 1651.13,971.126 \n",
" 1648.41,973.5 1647.17,974.561 1643.85,977.369 1643.1,977.995 1639.29,981.124 1638.91,981.43 1634.74,984.772 1634.62,984.864 1630.21,988.299 1630.18,988.319 \n",
" 1625.67,991.733 1625.62,991.769 1621.07,995.126 1621.01,995.168 1616.51,998.395 1616.22,998.602 1611.95,1001.58 1611.29,1002.04 1607.4,1004.68 1606.22,1005.47 \n",
" 1602.84,1007.71 1601,1008.91 1598.29,1010.66 1595.64,1012.34 1593.73,1013.54 1590.11,1015.77 1589.17,1016.35 1584.62,1019.09 1584.41,1019.21 1580.06,1021.76 \n",
" 1578.53,1022.64 1575.5,1024.38 1572.47,1026.08 1570.95,1026.93 1566.39,1029.42 1566.22,1029.51 1561.83,1031.85 1559.75,1032.95 1557.28,1034.23 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#ba3655; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1502.6,990.358 1499.53,991.733 1498.04,992.4 1493.49,994.389 1491.66,995.168 1488.93,996.325 1484.38,998.208 1483.4,998.602 1479.82,1000.04 1475.26,1001.83 \n",
" 1474.71,1002.04 1470.71,1003.57 1466.15,1005.25 1465.54,1005.47 1461.59,1006.9 1457.04,1008.5 1455.83,1008.91 1452.48,1010.05 1447.92,1011.56 1445.5,1012.34 \n",
" 1443.37,1013.03 1438.81,1014.46 1434.46,1015.77 1434.26,1015.84 1429.7,1017.19 1425.14,1018.49 1422.54,1019.21 1420.59,1019.75 1416.03,1020.98 1411.47,1022.17 \n",
" 1409.58,1022.64 1406.92,1023.32 1402.36,1024.43 1397.8,1025.51 1395.29,1026.08 1393.25,1026.55 1388.69,1027.55 1384.14,1028.52 1379.58,1029.45 1379.26,1029.51 \n",
" 1375.02,1030.35 1370.47,1031.22 1365.91,1032.05 1361.35,1032.84 1360.72,1032.95 1356.8,1033.61 1352.24,1034.34 1347.68,1035.04 1343.13,1035.7 1338.57,1036.33 \n",
" 1338.19,1036.38 1334.02,1036.94 1329.46,1037.51 1324.9,1038.04 1320.35,1038.55 1315.79,1039.03 1311.23,1039.47 1307.39,1039.82 1306.68,1039.88 1302.12,1040.27 \n",
" 1297.56,1040.62 1293.01,1040.94 1288.45,1041.24 1283.9,1041.5 1279.34,1041.73 1274.78,1041.93 1270.23,1042.11 1265.67,1042.25 1261.11,1042.36 1256.56,1042.45 \n",
" 1252,1042.5 1247.44,1042.53 1242.89,1042.52 1238.33,1042.49 1233.78,1042.43 1229.22,1042.34 1224.66,1042.22 1220.11,1042.07 1215.55,1041.89 1210.99,1041.68 \n",
" 1206.44,1041.45 1201.88,1041.18 1197.32,1040.89 1192.77,1040.56 1188.21,1040.21 1183.66,1039.82 1183.57,1039.82 1179.1,1039.41 1174.54,1038.97 1169.99,1038.5 \n",
" 1165.43,1038 1160.87,1037.48 1156.32,1036.92 1152.2,1036.38 1151.76,1036.32 1147.2,1035.71 1142.65,1035.06 1138.09,1034.38 1133.54,1033.67 1129.07,1032.95 \n",
" 1128.98,1032.93 1124.42,1032.16 1119.87,1031.37 1115.31,1030.53 1110.75,1029.67 1109.95,1029.51 1106.2,1028.78 1101.64,1027.86 1097.08,1026.9 1093.3,1026.08 \n",
" 1092.53,1025.91 1087.97,1024.89 1083.42,1023.84 1078.86,1022.76 1078.4,1022.64 1074.3,1021.64 1069.75,1020.49 1065.19,1019.31 1064.83,1019.21 1060.63,1018.09 \n",
" 1056.08,1016.84 1052.3,1015.77 1051.52,1015.55 1046.96,1014.24 1042.41,1012.88 1040.63,1012.34 1037.85,1011.49 1033.3,1010.07 1029.67,1008.91 1028.74,1008.61 \n",
" 1024.18,1007.11 1019.63,1005.58 1019.32,1005.47 1015.07,1004.01 1010.51,1002.4 1009.52,1002.04 1005.96,1000.75 1001.4,999.062 1000.18,998.602 996.845,997.338 \n",
" 992.288,995.571 991.27,995.168 987.732,993.766 983.176,991.917 982.732,991.733 978.619,990.03 974.54,988.299 974.063,988.096 969.507,986.123 966.665,984.864 \n",
" 964.95,984.103 960.394,982.039 959.075,981.43 955.837,979.931 951.749,977.995 951.281,977.773 946.725,975.571 944.676,974.561 942.168,973.32 937.828,971.126 \n",
" 937.612,971.017 933.056,968.667 931.202,967.692 928.499,966.264 924.775,964.257 923.943,963.807 919.386,961.297 918.541,960.823 914.83,958.732 912.489,957.388 \n",
" 910.274,956.11 906.606,953.954 905.717,953.428 901.161,950.687 900.886,950.519 896.605,947.886 895.324,947.085 892.048,945.021 889.909,943.65 887.492,942.09 \n",
" 884.635,940.216 882.936,939.092 879.497,936.781 878.379,936.024 874.49,933.347 873.823,932.884 869.608,929.912 869.266,929.67 864.846,926.478 864.71,926.378 \n",
" 860.202,923.043 860.154,923.007 855.67,919.609 855.597,919.553 851.248,916.174 851.041,916.012 846.931,912.74 846.485,912.381 842.716,909.305 841.928,908.655 \n",
" 838.6,905.871 837.372,904.831 834.581,902.436 832.816,900.903 830.655,899.002 828.259,896.866 826.821,895.567 823.703,892.715 823.075,892.133 819.416,888.698 \n",
" 819.146,888.442 815.843,885.264 814.59,884.041 812.352,881.829 810.034,879.504 808.941,878.395 805.61,874.96 805.477,874.822 802.357,871.526 800.921,869.984 \n",
" 799.179,868.091 796.365,864.979 796.076,864.657 793.046,861.222 791.808,859.795 790.087,857.788 787.252,854.416 787.2,854.353 784.38,850.919 782.696,848.824 \n",
" 781.63,847.484 778.946,844.05 778.139,843 776.327,840.615 773.774,837.181 773.583,836.92 771.283,833.746 769.026,830.555 768.856,830.312 766.49,826.877 \n",
" 764.47,823.871 764.185,823.442 761.939,820.008 759.914,816.829 759.752,816.573 757.622,813.139 755.551,809.704 755.357,809.379 753.533,806.27 751.571,802.835 \n",
" 750.801,801.458 749.662,799.401 747.806,795.966 746.245,792.999 746.002,792.532 744.246,789.097 742.54,785.663 741.688,783.909 740.881,782.228 739.267,778.794 \n",
" 737.699,775.359 739.267,771.925 740.881,768.49 741.688,766.81 742.54,765.056 744.246,761.621 746.002,758.187 746.245,757.72 747.806,754.752 749.662,751.318 \n",
" 750.801,749.26 751.571,747.883 753.533,744.449 755.357,741.34 755.551,741.014 757.622,737.58 759.752,734.145 759.914,733.89 761.939,730.711 764.185,727.276 \n",
" 764.47,726.847 766.49,723.842 768.856,720.407 769.026,720.164 771.283,716.973 773.583,713.799 773.774,713.538 776.327,710.104 778.139,707.719 778.946,706.669 \n",
" 781.63,703.235 782.696,701.895 784.38,699.8 787.2,696.366 787.252,696.303 790.087,692.931 791.808,690.924 793.046,689.497 796.076,686.062 796.365,685.739 \n",
" 799.179,682.628 800.921,680.735 802.357,679.193 805.477,675.897 805.61,675.759 808.941,672.324 810.034,671.215 812.352,668.89 814.59,666.677 815.843,665.455 \n",
" 819.146,662.277 819.416,662.021 823.075,658.586 823.703,658.004 826.821,655.152 828.259,653.852 830.655,651.717 832.816,649.816 834.581,648.283 837.372,645.888 \n",
" 838.6,644.848 841.928,642.063 842.716,641.414 846.485,638.338 846.931,637.979 851.041,634.707 851.248,634.545 855.597,631.166 855.67,631.11 860.154,627.712 \n",
" 860.202,627.676 864.71,624.34 864.846,624.241 869.266,621.049 869.608,620.807 873.823,617.835 874.49,617.372 878.379,614.695 879.497,613.938 882.936,611.627 \n",
" 884.635,610.503 887.492,608.628 889.909,607.069 892.048,605.698 895.324,603.634 896.605,602.833 900.886,600.2 901.161,600.031 905.717,597.29 906.606,596.765 \n",
" 910.274,594.609 912.489,593.331 914.83,591.987 918.541,589.896 919.386,589.422 923.943,586.912 924.775,586.462 928.499,584.455 931.202,583.027 933.056,582.052 \n",
" 937.612,579.702 937.828,579.593 942.168,577.399 944.676,576.158 946.725,575.148 951.281,572.946 951.749,572.724 955.837,570.788 959.075,569.289 960.394,568.68 \n",
" 964.95,566.616 966.665,565.855 969.507,564.596 974.063,562.623 974.54,562.42 978.619,560.689 982.732,558.986 983.176,558.802 987.732,556.953 991.27,555.551 \n",
" 992.288,555.148 996.845,553.381 1000.18,552.117 1001.4,551.656 1005.96,549.969 1009.52,548.682 1010.51,548.323 1015.07,546.712 1019.32,545.247 1019.63,545.143 \n",
" 1024.18,543.606 1028.74,542.111 1029.67,541.813 1033.3,540.649 1037.85,539.225 1040.63,538.378 1042.41,537.836 1046.96,536.481 1051.52,535.164 1052.3,534.944 \n",
" 1056.08,533.878 1060.63,532.627 1064.83,531.509 1065.19,531.413 1069.75,530.228 1074.3,529.078 1078.4,528.075 1078.86,527.964 1083.42,526.877 1087.97,525.826 \n",
" 1092.53,524.808 1093.3,524.64 1097.08,523.819 1101.64,522.863 1106.2,521.939 1109.95,521.206 1110.75,521.048 1115.31,520.184 1119.87,519.353 1124.42,518.554 \n",
" 1128.98,517.787 1129.07,517.771 1133.54,517.046 1138.09,516.336 1142.65,515.658 1147.2,515.01 1151.76,514.394 1152.2,514.337 1156.32,513.804 1160.87,513.244 \n",
" 1165.43,512.714 1169.99,512.214 1174.54,511.745 1179.1,511.305 1183.57,510.902 1183.66,510.895 1188.21,510.511 1192.77,510.157 1197.32,509.833 1201.88,509.538 \n",
" 1206.44,509.272 1210.99,509.035 1215.55,508.828 1220.11,508.65 1224.66,508.501 1229.22,508.381 1233.78,508.29 1238.33,508.228 1242.89,508.195 1247.44,508.192 \n",
" 1252,508.217 1256.56,508.272 1261.11,508.356 1265.67,508.47 1270.23,508.613 1274.78,508.786 1279.34,508.988 1283.9,509.221 1288.45,509.483 1293.01,509.776 \n",
" 1297.56,510.099 1302.12,510.453 1306.68,510.837 1307.39,510.902 1311.23,511.25 1315.79,511.693 1320.35,512.168 1324.9,512.674 1329.46,513.213 1334.02,513.784 \n",
" 1338.19,514.337 1338.57,514.387 1343.13,515.018 1347.68,515.682 1352.24,516.38 1356.8,517.112 1360.72,517.771 1361.35,517.878 1365.91,518.672 1370.47,519.502 \n",
" 1375.02,520.368 1379.26,521.206 1379.58,521.269 1384.14,522.2 1388.69,523.168 1393.25,524.174 1395.29,524.64 1397.8,525.213 1402.36,526.288 1406.92,527.402 \n",
" 1409.58,528.075 1411.47,528.553 1416.03,529.739 1420.59,530.966 1422.54,531.509 1425.14,532.231 1429.7,533.534 1434.26,534.881 1434.46,534.944 1438.81,536.263 \n",
" 1443.37,537.69 1445.5,538.378 1447.92,539.158 1452.48,540.668 1455.83,541.813 1457.04,542.223 1461.59,543.82 1465.54,545.247 1466.15,545.466 1470.71,547.153 \n",
" 1474.71,548.682 1475.26,548.893 1479.82,550.675 1483.4,552.117 1484.38,552.511 1488.93,554.394 1491.66,555.551 1493.49,556.33 1498.04,558.319 1499.53,558.986 \n",
" 1502.6,560.361 1507.07,562.42 1507.16,562.462 1511.71,564.615 1514.27,565.855 1516.27,566.83 1520.83,569.107 1521.18,569.289 1525.38,571.442 1527.82,572.724 \n",
" 1529.94,573.845 1534.21,576.158 1534.5,576.315 1539.05,578.852 1540.35,579.593 1543.61,581.46 1546.28,583.027 1548.17,584.145 1551.99,586.462 1552.72,586.907 \n",
" 1557.28,589.749 1557.51,589.896 1561.83,592.674 1562.83,593.331 1566.39,595.687 1567.98,596.765 1570.95,598.793 1572.96,600.2 1575.5,601.996 1577.77,603.634 \n",
" 1580.06,605.301 1582.43,607.069 1584.62,608.714 1586.94,610.503 1589.17,612.241 1591.31,613.938 1593.73,615.89 1595.53,617.372 1598.29,619.668 1599.63,620.807 \n",
" 1602.84,623.585 1603.59,624.241 1607.4,627.651 1607.42,627.676 1611.14,631.11 1611.95,631.879 1614.74,634.545 1616.51,636.282 1618.22,637.979 1621.07,640.877 \n",
" 1621.59,641.414 1624.85,644.848 1625.62,645.685 1628,648.283 1630.18,650.728 1631.05,651.717 1634,655.152 1634.74,656.035 1636.85,658.586 1639.29,661.641 \n",
" 1639.59,662.021 1642.25,665.455 1643.85,667.597 1644.81,668.89 1647.27,672.324 1648.41,673.957 1649.65,675.759 1651.93,679.193 1652.96,680.802 1654.12,682.628 \n",
" 1656.23,686.062 1657.52,688.245 1658.25,689.497 1660.19,692.931 1662.03,696.366 1662.07,696.444 1663.8,699.8 1665.49,703.235 1666.63,705.692 1667.09,706.669 \n",
" 1668.61,710.104 1670.04,713.538 1671.19,716.437 1671.4,716.973 1672.68,720.407 1673.88,723.842 1675,727.276 1675.74,729.754 1676.03,730.711 1677,734.145 \n",
" 1677.89,737.58 1678.69,741.014 1679.42,744.449 1680.07,747.883 1680.3,749.291 1680.64,751.318 1681.14,754.752 1681.56,758.187 1681.91,761.621 1682.18,765.056 \n",
" 1682.37,768.49 1682.48,771.925 1682.52,775.359 1682.48,778.794 1682.37,782.228 1682.18,785.663 1681.91,789.097 1681.56,792.532 1681.14,795.966 1680.64,799.401 \n",
" 1680.3,801.428 1680.07,802.835 1679.42,806.27 1678.69,809.704 1677.89,813.139 1677,816.573 1676.03,820.008 1675.74,820.965 1675,823.442 1673.88,826.877 \n",
" 1672.68,830.312 1671.4,833.746 1671.19,834.282 1670.04,837.181 1668.61,840.615 1667.09,844.05 1666.63,845.027 1665.49,847.484 1663.8,850.919 1662.07,854.274 \n",
" 1662.03,854.353 1660.19,857.788 1658.25,861.222 1657.52,862.474 1656.23,864.657 1654.12,868.091 1652.96,869.917 1651.93,871.526 1649.65,874.96 1648.41,876.762 \n",
" 1647.27,878.395 1644.81,881.829 1643.85,883.122 1642.25,885.264 1639.59,888.698 1639.29,889.078 1636.85,892.133 1634.74,894.684 1634,895.567 1631.05,899.002 \n",
" 1630.18,899.991 1628,902.436 1625.62,905.034 1624.85,905.871 1621.59,909.305 1621.07,909.841 1618.22,912.74 1616.51,914.436 1614.74,916.174 1611.95,918.84 \n",
" 1611.14,919.609 1607.42,923.043 1607.4,923.067 1603.59,926.478 1602.84,927.134 1599.63,929.912 1598.29,931.051 1595.53,933.347 1593.73,934.829 1591.31,936.781 \n",
" 1589.17,938.478 1586.94,940.216 1584.62,942.005 1582.43,943.65 1580.06,945.418 1577.77,947.085 1575.5,948.723 1572.96,950.519 1570.95,951.926 1567.98,953.954 \n",
" 1566.39,955.032 1562.83,957.388 1561.83,958.045 1557.51,960.823 1557.28,960.97 1552.72,963.812 1551.99,964.257 1548.17,966.574 1546.28,967.692 1543.61,969.258 \n",
" 1540.35,971.126 1539.05,971.867 1534.5,974.404 1534.21,974.561 1529.94,976.874 1527.82,977.995 1525.38,979.277 1521.18,981.43 1520.83,981.612 1516.27,983.889 \n",
" 1514.27,984.864 1511.71,986.104 1507.16,988.257 1507.07,988.299 1502.6,990.358 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#9e2a62; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1457.04,951.503 1452.48,953.24 1450.55,953.954 1447.92,954.925 1443.37,956.556 1440.97,957.388 1438.81,958.136 1434.26,959.668 1430.7,960.823 1429.7,961.148 \n",
" 1425.14,962.585 1420.59,963.969 1419.61,964.257 1416.03,965.313 1411.47,966.609 1407.52,967.692 1406.92,967.858 1402.36,969.07 1397.8,970.235 1394.18,971.126 \n",
" 1393.25,971.357 1388.69,972.442 1384.14,973.483 1379.58,974.481 1379.2,974.561 1375.02,975.445 1370.47,976.369 1365.91,977.251 1361.88,977.995 1361.35,978.094 \n",
" 1356.8,978.904 1352.24,979.676 1347.68,980.408 1343.13,981.103 1340.86,981.43 1338.57,981.763 1334.02,982.39 1329.46,982.98 1324.9,983.533 1320.35,984.051 \n",
" 1315.79,984.534 1312.42,984.864 1311.23,984.982 1306.68,985.399 1302.12,985.782 1297.56,986.13 1293.01,986.444 1288.45,986.725 1283.9,986.972 1279.34,987.186 \n",
" 1274.78,987.367 1270.23,987.515 1265.67,987.63 1261.11,987.713 1256.56,987.764 1252,987.782 1247.44,987.768 1242.89,987.722 1238.33,987.644 1233.78,987.534 \n",
" 1229.22,987.392 1224.66,987.218 1220.11,987.012 1215.55,986.773 1210.99,986.502 1206.44,986.2 1201.88,985.864 1197.32,985.497 1192.77,985.096 1190.32,984.864 \n",
" 1188.21,984.665 1183.66,984.203 1179.1,983.708 1174.54,983.181 1169.99,982.62 1165.43,982.025 1161.11,981.43 1160.87,981.397 1156.32,980.741 1151.76,980.05 \n",
" 1147.2,979.325 1142.65,978.566 1139.37,977.995 1138.09,977.773 1133.54,976.95 1128.98,976.092 1124.42,975.197 1121.3,974.561 1119.87,974.269 1115.31,973.31 \n",
" 1110.75,972.314 1106.2,971.28 1105.54,971.126 1101.64,970.216 1097.08,969.115 1092.53,967.975 1091.43,967.692 1087.97,966.803 1083.42,965.593 1078.86,964.344 \n",
" 1078.55,964.257 1074.3,963.062 1069.75,961.74 1066.67,960.823 1065.19,960.38 1060.63,958.984 1056.08,957.545 1055.59,957.388 1051.52,956.072 1046.96,954.555 \n",
" 1045.2,953.954 1042.41,953 1037.85,951.404 1035.39,950.519 1033.3,949.766 1028.74,948.087 1026.09,947.085 1024.18,946.365 1019.63,944.6 1017.23,943.65 \n",
" 1015.07,942.791 1010.51,940.937 1008.78,940.216 1005.96,939.039 1001.4,937.093 1000.69,936.781 996.845,935.103 992.922,933.347 992.288,933.062 987.732,930.976 \n",
" 985.461,929.912 983.176,928.839 978.619,926.649 978.27,926.478 974.063,924.411 971.34,923.043 969.507,922.118 964.95,919.771 964.642,919.609 960.394,917.371 \n",
" 958.171,916.174 955.837,914.913 951.901,912.74 951.281,912.396 946.725,909.821 945.829,909.305 942.168,907.185 939.942,905.871 937.612,904.487 934.226,902.436 \n",
" 933.056,901.723 928.674,899.002 928.499,898.893 923.943,895.996 923.281,895.567 919.386,893.028 918.037,892.133 914.83,889.988 912.935,888.698 910.274,886.872 \n",
" 907.969,885.264 905.717,883.679 903.134,881.829 901.161,880.405 898.424,878.395 896.605,877.047 893.834,874.96 892.048,873.602 889.361,871.526 887.492,870.068 \n",
" 884.999,868.091 882.936,866.438 880.745,864.657 878.379,862.711 876.596,861.222 873.823,858.881 872.548,857.788 869.266,854.942 868.597,854.353 864.741,850.919 \n",
" 864.71,850.891 860.979,847.484 860.154,846.721 857.305,844.05 855.597,842.426 853.718,840.615 851.041,837.998 850.216,837.181 846.796,833.746 846.485,833.43 \n",
" 843.457,830.312 841.928,828.713 840.195,826.877 837.372,823.837 837.01,823.442 833.899,820.008 832.816,818.793 830.861,816.573 828.259,813.567 827.893,813.139 \n",
" 824.995,809.704 823.703,808.147 822.165,806.27 819.4,802.835 819.146,802.517 816.699,799.401 814.59,796.661 814.062,795.966 811.486,792.532 810.034,790.56 \n",
" 808.97,789.097 806.512,785.663 805.477,784.192 804.112,782.228 801.767,778.794 800.921,777.535 799.477,775.359 800.921,773.184 801.767,771.925 804.112,768.49 \n",
" 805.477,766.527 806.512,765.056 808.97,761.621 810.034,760.159 811.486,758.187 814.062,754.752 814.59,754.058 816.699,751.318 819.146,748.202 819.4,747.883 \n",
" 822.165,744.449 823.703,742.572 824.995,741.014 827.893,737.58 828.259,737.152 830.861,734.145 832.816,731.926 833.899,730.711 837.01,727.276 837.372,726.881 \n",
" 840.195,723.842 841.928,722.006 843.457,720.407 846.485,717.289 846.796,716.973 850.216,713.538 851.041,712.721 853.718,710.104 855.597,708.293 857.305,706.669 \n",
" 860.154,703.997 860.979,703.235 864.71,699.828 864.741,699.8 868.597,696.366 869.266,695.777 872.548,692.931 873.823,691.838 876.596,689.497 878.379,688.008 \n",
" 880.745,686.062 882.936,684.28 884.999,682.628 887.492,680.651 889.361,679.193 892.048,677.116 893.834,675.759 896.605,673.672 898.424,672.324 901.161,670.314 \n",
" 903.134,668.89 905.717,667.04 907.969,665.455 910.274,663.847 912.935,662.021 914.83,660.731 918.037,658.586 919.386,657.691 923.281,655.152 923.943,654.723 \n",
" 928.499,651.826 928.674,651.717 933.056,648.996 934.226,648.283 937.612,646.232 939.942,644.848 942.168,643.533 945.829,641.414 946.725,640.898 951.281,638.323 \n",
" 951.901,637.979 955.837,635.806 958.171,634.545 960.394,633.348 964.642,631.11 964.95,630.948 969.507,628.601 971.34,627.676 974.063,626.308 978.27,624.241 \n",
" 978.619,624.07 983.176,621.88 985.461,620.807 987.732,619.743 992.288,617.656 992.922,617.372 996.845,615.615 1000.69,613.938 1001.4,613.626 1005.96,611.679 \n",
" 1008.78,610.503 1010.51,609.781 1015.07,607.928 1017.23,607.069 1019.63,606.119 1024.18,604.354 1026.09,603.634 1028.74,602.632 1033.3,600.953 1035.39,600.2 \n",
" 1037.85,599.315 1042.41,597.718 1045.2,596.765 1046.96,596.163 1051.52,594.647 1055.59,593.331 1056.08,593.174 1060.63,591.735 1065.19,590.339 1066.67,589.896 \n",
" 1069.75,588.978 1074.3,587.657 1078.55,586.462 1078.86,586.375 1083.42,585.126 1087.97,583.916 1091.43,583.027 1092.53,582.744 1097.08,581.604 1101.64,580.503 \n",
" 1105.54,579.593 1106.2,579.439 1110.75,578.405 1115.31,577.409 1119.87,576.45 1121.3,576.158 1124.42,575.521 1128.98,574.627 1133.54,573.769 1138.09,572.946 \n",
" 1139.37,572.724 1142.65,572.153 1147.2,571.394 1151.76,570.669 1156.32,569.978 1160.87,569.322 1161.11,569.289 1165.43,568.694 1169.99,568.099 1174.54,567.538 \n",
" 1179.1,567.01 1183.66,566.516 1188.21,566.054 1190.32,565.855 1192.77,565.623 1197.32,565.222 1201.88,564.854 1206.44,564.519 1210.99,564.216 1215.55,563.946 \n",
" 1220.11,563.707 1224.66,563.501 1229.22,563.327 1233.78,563.185 1238.33,563.074 1242.89,562.996 1247.44,562.95 1252,562.937 1256.56,562.955 1261.11,563.006 \n",
" 1265.67,563.089 1270.23,563.204 1274.78,563.352 1279.34,563.533 1283.9,563.747 1288.45,563.994 1293.01,564.275 1297.56,564.589 1302.12,564.937 1306.68,565.32 \n",
" 1311.23,565.737 1312.42,565.855 1315.79,566.185 1320.35,566.668 1324.9,567.186 1329.46,567.739 1334.02,568.329 1338.57,568.955 1340.86,569.289 1343.13,569.616 \n",
" 1347.68,570.311 1352.24,571.043 1356.8,571.814 1361.35,572.625 1361.88,572.724 1365.91,573.468 1370.47,574.35 1375.02,575.273 1379.2,576.158 1379.58,576.238 \n",
" 1384.14,577.236 1388.69,578.277 1393.25,579.362 1394.18,579.593 1397.8,580.484 1402.36,581.649 1406.92,582.861 1407.52,583.027 1411.47,584.11 1416.03,585.406 \n",
" 1419.61,586.462 1420.59,586.75 1425.14,588.134 1429.7,589.571 1430.7,589.896 1434.26,591.051 1438.81,592.582 1440.97,593.331 1443.37,594.163 1447.92,595.794 \n",
" 1450.55,596.765 1452.48,597.479 1457.04,599.215 1459.54,600.2 1461.59,601.008 1466.15,602.857 1468.01,603.634 1470.71,604.763 1475.26,606.732 1476.02,607.069 \n",
" 1479.82,608.757 1483.62,610.503 1484.38,610.852 1488.93,613.007 1490.84,613.938 1493.49,615.232 1497.73,617.372 1498.04,617.531 1502.6,619.898 1504.3,620.807 \n",
" 1507.16,622.343 1510.59,624.241 1511.71,624.869 1516.27,627.478 1516.61,627.676 1520.83,630.17 1522.37,631.11 1525.38,632.956 1527.9,634.545 1529.94,635.838 \n",
" 1533.22,637.979 1534.5,638.821 1538.32,641.414 1539.05,641.912 1543.23,644.848 1543.61,645.117 1547.95,648.283 1548.17,648.444 1552.48,651.717 1552.72,651.9 \n",
" 1556.85,655.152 1557.28,655.496 1561.05,658.586 1561.83,659.245 1565.08,662.021 1566.39,663.159 1568.97,665.455 1570.95,667.255 1572.7,668.89 1575.5,671.553 \n",
" 1576.3,672.324 1579.75,675.759 1580.06,676.076 1583.06,679.193 1584.62,680.853 1586.25,682.628 1589.17,685.92 1589.3,686.062 1592.22,689.497 1593.73,691.33 \n",
" 1595.02,692.931 1597.7,696.366 1598.29,697.143 1600.26,699.8 1602.69,703.235 1602.84,703.452 1605.02,706.669 1607.22,710.104 1607.4,710.396 1609.31,713.538 \n",
" 1611.28,716.973 1611.95,718.199 1613.15,720.407 1614.9,723.842 1616.51,727.231 1616.53,727.276 1618.07,730.711 1619.48,734.145 1620.78,737.58 1621.07,738.414 \n",
" 1621.97,741.014 1623.06,744.449 1624.02,747.883 1624.87,751.318 1625.61,754.752 1625.62,754.837 1626.24,758.187 1626.76,761.621 1627.16,765.056 1627.45,768.49 \n",
" 1627.62,771.925 1627.68,775.359 1627.62,778.794 1627.45,782.228 1627.16,785.663 1626.76,789.097 1626.24,792.532 1625.62,795.881 1625.61,795.966 1624.87,799.401 \n",
" 1624.02,802.835 1623.06,806.27 1621.97,809.704 1621.07,812.304 1620.78,813.139 1619.48,816.573 1618.07,820.008 1616.53,823.442 1616.51,823.488 1614.9,826.877 \n",
" 1613.15,830.312 1611.95,832.519 1611.28,833.746 1609.31,837.181 1607.4,840.322 1607.22,840.615 1605.02,844.05 1602.84,847.267 1602.69,847.484 1600.26,850.919 \n",
" 1598.29,853.575 1597.7,854.353 1595.02,857.788 1593.73,859.389 1592.22,861.222 1589.3,864.657 1589.17,864.799 1586.25,868.091 1584.62,869.866 1583.06,871.526 \n",
" 1580.06,874.643 1579.75,874.96 1576.3,878.395 1575.5,879.166 1572.7,881.829 1570.95,883.464 1568.97,885.264 1566.39,887.56 1565.08,888.698 1561.83,891.474 \n",
" 1561.05,892.133 1557.28,895.222 1556.85,895.567 1552.72,898.819 1552.48,899.002 1548.17,902.275 1547.95,902.436 1543.61,905.601 1543.23,905.871 1539.05,908.806 \n",
" 1538.32,909.305 1534.5,911.897 1533.22,912.74 1529.94,914.881 1527.9,916.174 1525.38,917.763 1522.37,919.609 1520.83,920.548 1516.61,923.043 1516.27,923.241 \n",
" 1511.71,925.85 1510.59,926.478 1507.16,928.376 1504.3,929.912 1502.6,930.821 1498.04,933.188 1497.73,933.347 1493.49,935.487 1490.84,936.781 1488.93,937.711 \n",
" 1484.38,939.867 1483.62,940.216 1479.82,941.961 1476.02,943.65 1475.26,943.987 1470.71,945.956 1468.01,947.085 1466.15,947.862 1461.59,949.711 1459.54,950.519 \n",
" 1457.04,951.503 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#821f6b; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1416.03,917.473 1411.47,918.855 1408.89,919.609 1406.92,920.188 1402.36,921.473 1397.8,922.703 1396.49,923.043 1393.25,923.891 1388.69,925.031 1384.14,926.121 \n",
" 1382.58,926.478 1379.58,927.169 1375.02,928.174 1370.47,929.131 1366.56,929.912 1365.91,930.043 1361.35,930.919 1356.8,931.75 1352.24,932.538 1347.68,933.283 \n",
" 1347.27,933.347 1343.13,933.993 1338.57,934.662 1334.02,935.29 1329.46,935.878 1324.9,936.426 1321.72,936.781 1320.35,936.936 1315.79,937.411 1311.23,937.848 \n",
" 1306.68,938.247 1302.12,938.608 1297.56,938.932 1293.01,939.219 1288.45,939.469 1283.9,939.683 1279.34,939.861 1274.78,940.004 1270.23,940.11 1265.67,940.182 \n",
" 1261.36,940.216 1261.11,940.218 1256.56,940.219 1256.17,940.216 1252,940.185 1247.44,940.116 1242.89,940.012 1238.33,939.873 1233.78,939.699 1229.22,939.491 \n",
" 1224.66,939.248 1220.11,938.969 1215.55,938.656 1210.99,938.307 1206.44,937.924 1201.88,937.505 1197.32,937.05 1194.83,936.781 1192.77,936.561 1188.21,936.04 \n",
" 1183.66,935.482 1179.1,934.889 1174.54,934.259 1169.99,933.592 1168.39,933.347 1165.43,932.893 1160.87,932.158 1156.32,931.386 1151.76,930.576 1148.19,929.912 \n",
" 1147.2,929.73 1142.65,928.851 1138.09,927.933 1133.54,926.976 1131.25,926.478 1128.98,925.984 1124.42,924.956 1119.87,923.887 1116.4,923.043 1115.31,922.779 \n",
" 1110.75,921.637 1106.2,920.452 1103.06,919.609 1101.64,919.228 1097.08,917.968 1092.53,916.664 1090.87,916.174 1087.97,915.322 1083.42,913.939 1079.59,912.74 \n",
" 1078.86,912.512 1074.3,911.047 1069.75,909.536 1069.07,909.305 1065.19,907.986 1060.63,906.389 1059.19,905.871 1056.08,904.75 1051.52,903.065 1049.86,902.436 \n",
" 1046.96,901.336 1042.41,899.559 1041.01,899.002 1037.85,897.737 1033.3,895.865 1032.59,895.567 1028.74,893.948 1024.54,892.133 1024.18,891.978 1019.63,889.962 \n",
" 1016.84,888.698 1015.07,887.892 1010.51,885.769 1009.45,885.264 1005.96,883.596 1002.35,881.829 1001.4,881.365 996.845,879.081 995.505,878.395 992.288,876.74 \n",
" 988.906,874.96 987.732,874.339 983.176,871.88 982.532,871.526 978.619,869.361 976.373,868.091 974.063,866.778 970.408,864.657 969.507,864.131 964.95,861.417 \n",
" 964.628,861.222 960.394,858.638 959.028,857.788 955.837,855.788 953.592,854.353 951.281,852.866 948.313,850.919 946.725,849.869 943.183,847.484 942.168,846.795 \n",
" 938.196,844.05 937.612,843.643 933.345,840.615 933.056,840.408 928.624,837.181 928.499,837.089 924.028,833.746 923.943,833.682 919.552,830.312 919.386,830.184 \n",
" 915.19,826.877 914.83,826.59 910.94,823.442 910.274,822.898 906.796,820.008 905.717,819.102 902.754,816.573 901.161,815.198 898.812,813.139 896.605,811.181 \n",
" 894.965,809.704 892.048,807.045 891.21,806.27 887.545,802.835 887.492,802.785 883.969,799.401 882.936,798.395 880.476,795.966 878.379,793.867 877.064,792.532 \n",
" 873.823,789.192 873.732,789.097 870.478,785.663 869.266,784.366 867.298,782.228 864.71,779.375 864.19,778.794 861.154,775.359 864.19,771.925 864.71,771.344 \n",
" 867.298,768.49 869.266,766.353 870.478,765.056 873.732,761.621 873.823,761.526 877.064,758.187 878.379,756.852 880.476,754.752 882.936,752.324 883.969,751.318 \n",
" 887.492,747.934 887.545,747.883 891.21,744.449 892.048,743.673 894.965,741.014 896.605,739.538 898.812,737.58 901.161,735.521 902.754,734.145 905.717,731.617 \n",
" 906.796,730.711 910.274,727.821 910.94,727.276 914.83,724.129 915.19,723.842 919.386,720.535 919.552,720.407 923.943,717.037 924.028,716.973 928.499,713.63 \n",
" 928.624,713.538 933.056,710.311 933.345,710.104 937.612,707.076 938.196,706.669 942.168,703.923 943.183,703.235 946.725,700.85 948.313,699.8 951.281,697.853 \n",
" 953.592,696.366 955.837,694.931 959.028,692.931 960.394,692.081 964.628,689.497 964.95,689.302 969.507,686.588 970.408,686.062 974.063,683.94 976.373,682.628 \n",
" 978.619,681.358 982.532,679.193 983.176,678.839 987.732,676.379 988.906,675.759 992.288,673.979 995.505,672.324 996.845,671.638 1001.4,669.354 1002.35,668.89 \n",
" 1005.96,667.123 1009.45,665.455 1010.51,664.95 1015.07,662.827 1016.84,662.021 1019.63,660.757 1024.18,658.741 1024.54,658.586 1028.74,656.77 1032.59,655.152 \n",
" 1033.3,654.854 1037.85,652.981 1041.01,651.717 1042.41,651.16 1046.96,649.383 1049.86,648.283 1051.52,647.654 1056.08,645.968 1059.19,644.848 1060.63,644.33 \n",
" 1065.19,642.733 1069.07,641.414 1069.75,641.183 1074.3,639.671 1078.86,638.207 1079.59,637.979 1083.42,636.78 1087.97,635.397 1090.87,634.545 1092.53,634.055 \n",
" 1097.08,632.751 1101.64,631.49 1103.06,631.11 1106.2,630.267 1110.75,629.082 1115.31,627.94 1116.4,627.676 1119.87,626.832 1124.42,625.763 1128.98,624.735 \n",
" 1131.25,624.241 1133.54,623.742 1138.09,622.785 1142.65,621.868 1147.2,620.989 1148.19,620.807 1151.76,620.143 1156.32,619.333 1160.87,618.561 1165.43,617.826 \n",
" 1168.39,617.372 1169.99,617.127 1174.54,616.46 1179.1,615.83 1183.66,615.236 1188.21,614.679 1192.77,614.157 1194.83,613.938 1197.32,613.669 1201.88,613.214 \n",
" 1206.44,612.795 1210.99,612.411 1215.55,612.063 1220.11,611.75 1224.66,611.471 1229.22,611.228 1233.78,611.019 1238.33,610.846 1242.89,610.707 1247.44,610.603 \n",
" 1252,610.534 1256.17,610.503 1256.56,610.5 1261.11,610.501 1261.36,610.503 1265.67,610.537 1270.23,610.609 1274.78,610.715 1279.34,610.858 1283.9,611.036 \n",
" 1288.45,611.25 1293.01,611.5 1297.56,611.787 1302.12,612.111 1306.68,612.472 1311.23,612.871 1315.79,613.307 1320.35,613.783 1321.72,613.938 1324.9,614.293 \n",
" 1329.46,614.841 1334.02,615.429 1338.57,616.057 1343.13,616.726 1347.27,617.372 1347.68,617.436 1352.24,618.181 1356.8,618.969 1361.35,619.8 1365.91,620.676 \n",
" 1366.56,620.807 1370.47,621.588 1375.02,622.545 1379.58,623.55 1382.58,624.241 1384.14,624.598 1388.69,625.688 1393.25,626.828 1396.49,627.676 1397.8,628.016 \n",
" 1402.36,629.246 1406.92,630.531 1408.89,631.11 1411.47,631.863 1416.03,633.246 1420.14,634.545 1420.59,634.686 1425.14,636.172 1429.7,637.72 1430.44,637.979 \n",
" 1434.26,639.317 1438.81,640.978 1439.97,641.414 1443.37,642.694 1447.92,644.476 1448.84,644.848 1452.48,646.316 1457.04,648.228 1457.16,648.283 1461.59,650.199 \n",
" 1464.97,651.717 1466.15,652.247 1470.71,654.364 1472.34,655.152 1475.26,656.557 1479.32,658.586 1479.82,658.834 1484.38,661.187 1485.93,662.021 1488.93,663.628 \n",
" 1492.22,665.455 1493.49,666.163 1498.04,668.794 1498.21,668.89 1502.6,671.521 1503.9,672.324 1507.16,674.358 1509.33,675.759 1511.71,677.31 1514.51,679.193 \n",
" 1516.27,680.386 1519.47,682.628 1520.83,683.594 1524.19,686.062 1525.38,686.944 1528.71,689.497 1529.94,690.451 1533.03,692.931 1534.5,694.128 1537.15,696.366 \n",
" 1539.05,697.996 1541.09,699.8 1543.61,702.078 1544.85,703.235 1548.17,706.404 1548.43,706.669 1551.85,710.104 1552.72,711.007 1555.1,713.538 1557.28,715.943 \n",
" 1558.19,716.973 1561.12,720.407 1561.83,721.28 1563.89,723.842 1566.39,727.121 1566.51,727.276 1568.97,730.711 1570.95,733.638 1571.28,734.145 1573.44,737.58 \n",
" 1575.44,741.014 1575.5,741.131 1577.29,744.449 1578.98,747.883 1580.06,750.323 1580.5,751.318 1581.86,754.752 1583.03,758.187 1584.02,761.621 1584.62,764.22 \n",
" 1584.81,765.056 1585.4,768.49 1585.77,771.925 1585.89,775.359 1585.77,778.794 1585.4,782.228 1584.81,785.663 1584.62,786.498 1584.02,789.097 1583.03,792.532 \n",
" 1581.86,795.966 1580.5,799.401 1580.06,800.395 1578.98,802.835 1577.29,806.27 1575.5,809.587 1575.44,809.704 1573.44,813.139 1571.28,816.573 1570.95,817.081 \n",
" 1568.97,820.008 1566.51,823.442 1566.39,823.598 1563.89,826.877 1561.83,829.439 1561.12,830.312 1558.19,833.746 1557.28,834.776 1555.1,837.181 1552.72,839.712 \n",
" 1551.85,840.615 1548.43,844.05 1548.17,844.315 1544.85,847.484 1543.61,848.64 1541.09,850.919 1539.05,852.722 1537.15,854.353 1534.5,856.591 1533.03,857.788 \n",
" 1529.94,860.268 1528.71,861.222 1525.38,863.775 1524.19,864.657 1520.83,867.125 1519.47,868.091 1516.27,870.333 1514.51,871.526 1511.71,873.409 1509.33,874.96 \n",
" 1507.16,876.361 1503.9,878.395 1502.6,879.198 1498.21,881.829 1498.04,881.925 1493.49,884.556 1492.22,885.264 1488.93,887.091 1485.93,888.698 1484.38,889.532 \n",
" 1479.82,891.885 1479.32,892.133 1475.26,894.162 1472.34,895.567 1470.71,896.354 1466.15,898.472 1464.97,899.002 1461.59,900.52 1457.16,902.436 1457.04,902.491 \n",
" 1452.48,904.403 1448.84,905.871 1447.92,906.243 1443.37,908.025 1439.97,909.305 1438.81,909.74 1434.26,911.402 1430.44,912.74 1429.7,912.999 1425.14,914.547 \n",
" 1420.59,916.033 1420.14,916.174 1416.03,917.473 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#63146e; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1384.14,885.289 1379.58,886.357 1375.02,887.372 1370.47,888.335 1368.66,888.698 1365.91,889.254 1361.35,890.129 1356.8,890.955 1352.24,891.734 1349.76,892.133 \n",
" 1347.68,892.471 1343.13,893.166 1338.57,893.817 1334.02,894.423 1329.46,894.986 1324.9,895.507 1324.33,895.567 1320.35,895.99 1315.79,896.432 1311.23,896.833 \n",
" 1306.68,897.193 1302.12,897.513 1297.56,897.793 1293.01,898.033 1288.45,898.235 1283.9,898.397 1279.34,898.521 1274.78,898.606 1270.23,898.654 1265.67,898.663 \n",
" 1261.11,898.635 1256.56,898.569 1252,898.466 1247.44,898.325 1242.89,898.146 1238.33,897.93 1233.78,897.677 1229.22,897.386 1224.66,897.057 1220.11,896.69 \n",
" 1215.55,896.285 1210.99,895.843 1208.38,895.567 1206.44,895.364 1201.88,894.849 1197.32,894.297 1192.77,893.705 1188.21,893.075 1183.66,892.405 1181.9,892.133 \n",
" 1179.1,891.7 1174.54,890.958 1169.99,890.176 1165.43,889.354 1161.97,888.698 1160.87,888.492 1156.32,887.595 1151.76,886.657 1147.2,885.677 1145.36,885.264 \n",
" 1142.65,884.66 1138.09,883.603 1133.54,882.503 1130.85,881.829 1128.98,881.362 1124.42,880.183 1119.87,878.959 1117.83,878.395 1115.31,877.695 1110.75,876.389 \n",
" 1106.2,875.036 1105.95,874.96 1101.64,873.646 1097.08,872.207 1094.99,871.526 1092.53,870.726 1087.97,869.199 1084.76,868.091 1083.42,867.626 1078.86,866.009 \n",
" 1075.16,864.657 1074.3,864.341 1069.75,862.63 1066.11,861.222 1065.19,860.867 1060.63,859.058 1057.52,857.788 1056.08,857.196 1051.52,855.286 1049.35,854.353 \n",
" 1046.96,853.323 1042.41,851.306 1041.55,850.919 1037.85,849.238 1034.09,847.484 1033.3,847.113 1028.74,844.934 1026.93,844.05 1024.18,842.698 1020.05,840.615 \n",
" 1019.63,840.402 1015.07,838.049 1013.43,837.181 1010.51,835.634 1007.04,833.746 1005.96,833.155 1001.4,830.613 1000.87,830.312 996.845,828.008 994.912,826.877 \n",
" 992.288,825.333 989.142,823.442 987.732,822.589 983.553,820.008 983.176,819.774 978.619,816.886 978.136,816.573 974.063,813.923 972.881,813.139 969.507,810.883 \n",
" 967.778,809.704 964.95,807.761 962.82,806.27 960.394,804.557 958,802.835 955.837,801.266 953.312,799.401 951.281,797.887 948.75,795.966 946.725,794.415 \n",
" 944.308,792.532 942.168,790.847 939.982,789.097 937.612,787.18 935.767,785.663 933.056,783.409 931.658,782.228 928.499,779.529 927.652,778.794 923.943,775.536 \n",
" 923.744,775.359 923.943,775.182 927.652,771.925 928.499,771.19 931.658,768.49 933.056,767.31 935.767,765.056 937.612,763.539 939.982,761.621 942.168,759.871 \n",
" 944.308,758.187 946.725,756.304 948.75,754.752 951.281,752.832 953.312,751.318 955.837,749.453 958,747.883 960.394,746.162 962.82,744.449 964.95,742.958 \n",
" 967.778,741.014 969.507,739.836 972.881,737.58 974.063,736.795 978.136,734.145 978.619,733.833 983.176,730.945 983.553,730.711 987.732,728.129 989.142,727.276 \n",
" 992.288,725.385 994.912,723.842 996.845,722.711 1000.87,720.407 1001.4,720.105 1005.96,717.563 1007.04,716.973 1010.51,715.085 1013.43,713.538 1015.07,712.67 \n",
" 1019.63,710.317 1020.05,710.104 1024.18,708.021 1026.93,706.669 1028.74,705.784 1033.3,703.606 1034.09,703.235 1037.85,701.48 1041.55,699.8 1042.41,699.413 \n",
" 1046.96,697.396 1049.35,696.366 1051.52,695.433 1056.08,693.523 1057.52,692.931 1060.63,691.661 1065.19,689.852 1066.11,689.497 1069.75,688.089 1074.3,686.378 \n",
" 1075.16,686.062 1078.86,684.71 1083.42,683.093 1084.76,682.628 1087.97,681.519 1092.53,679.993 1094.99,679.193 1097.08,678.512 1101.64,677.073 1105.95,675.759 \n",
" 1106.2,675.683 1110.75,674.33 1115.31,673.024 1117.83,672.324 1119.87,671.76 1124.42,670.535 1128.98,669.356 1130.85,668.89 1133.54,668.216 1138.09,667.116 \n",
" 1142.65,666.059 1145.36,665.455 1147.2,665.042 1151.76,664.062 1156.32,663.123 1160.87,662.227 1161.97,662.021 1165.43,661.365 1169.99,660.543 1174.54,659.761 \n",
" 1179.1,659.018 1181.9,658.586 1183.66,658.313 1188.21,657.644 1192.77,657.013 1197.32,656.422 1201.88,655.869 1206.44,655.355 1208.38,655.152 1210.99,654.876 \n",
" 1215.55,654.433 1220.11,654.029 1224.66,653.662 1229.22,653.333 1233.78,653.042 1238.33,652.788 1242.89,652.572 1247.44,652.394 1252,652.253 1256.56,652.149 \n",
" 1261.11,652.084 1265.67,652.055 1270.23,652.065 1274.78,652.112 1279.34,652.198 1283.9,652.322 1288.45,652.484 1293.01,652.685 1297.56,652.926 1302.12,653.206 \n",
" 1306.68,653.525 1311.23,653.885 1315.79,654.286 1320.35,654.729 1324.33,655.152 1324.9,655.212 1329.46,655.732 1334.02,656.295 1338.57,656.902 1343.13,657.553 \n",
" 1347.68,658.248 1349.76,658.586 1352.24,658.985 1356.8,659.764 1361.35,660.59 1365.91,661.464 1368.66,662.021 1370.47,662.384 1375.02,663.347 1379.58,664.362 \n",
" 1384.14,665.43 1384.24,665.455 1388.69,666.538 1393.25,667.702 1397.68,668.89 1397.8,668.923 1402.36,670.187 1406.92,671.512 1409.59,672.324 1411.47,672.893 \n",
" 1416.03,674.327 1420.37,675.759 1420.59,675.828 1425.14,677.379 1429.7,679.002 1430.22,679.193 1434.26,680.68 1438.81,682.434 1439.3,682.628 1443.37,684.247 \n",
" 1447.73,686.062 1447.92,686.142 1452.48,688.099 1455.6,689.497 1457.04,690.142 1461.59,692.262 1462.98,692.931 1466.15,694.465 1469.92,696.366 1470.71,696.761 \n",
" 1475.26,699.146 1476.46,699.8 1479.82,701.628 1482.65,703.235 1484.38,704.217 1488.51,706.669 1488.93,706.919 1493.49,709.736 1494.06,710.104 1498.04,712.677 \n",
" 1499.32,713.538 1502.6,715.758 1504.32,716.973 1507.16,718.989 1509.07,720.407 1511.71,722.385 1513.58,723.842 1516.27,725.962 1517.87,727.276 1520.83,729.744 \n",
" 1521.94,730.711 1525.38,733.759 1525.8,734.145 1529.46,737.58 1529.94,738.038 1532.92,741.014 1534.5,742.628 1536.2,744.449 1539.05,747.606 1539.29,747.883 \n",
" 1542.2,751.318 1543.61,753.052 1544.93,754.752 1547.48,758.187 1548.17,759.133 1549.86,761.621 1552.08,765.056 1552.72,766.097 1554.12,768.49 1556,771.925 \n",
" 1557.28,774.363 1557.76,775.359 1557.28,776.356 1556,778.794 1554.12,782.228 1552.72,784.622 1552.08,785.663 1549.86,789.097 1548.17,791.586 1547.48,792.532 \n",
" 1544.93,795.966 1543.61,797.667 1542.2,799.401 1539.29,802.835 1539.05,803.113 1536.2,806.27 1534.5,808.091 1532.92,809.704 1529.94,812.681 1529.46,813.139 \n",
" 1525.8,816.573 1525.38,816.959 1521.94,820.008 1520.83,820.974 1517.87,823.442 1516.27,824.756 1513.58,826.877 1511.71,828.334 1509.07,830.312 1507.16,831.73 \n",
" 1504.32,833.746 1502.6,834.961 1499.32,837.181 1498.04,838.041 1494.06,840.615 1493.49,840.983 1488.93,843.8 1488.51,844.05 1484.38,846.502 1482.65,847.484 \n",
" 1479.82,849.091 1476.46,850.919 1475.26,851.573 1470.71,853.957 1469.92,854.353 1466.15,856.254 1462.98,857.788 1461.59,858.456 1457.04,860.577 1455.6,861.222 \n",
" 1452.48,862.619 1447.92,864.577 1447.73,864.657 1443.37,866.472 1439.3,868.091 1438.81,868.285 1434.26,870.038 1430.22,871.526 1429.7,871.716 1425.14,873.34 \n",
" 1420.59,874.89 1420.37,874.96 1416.03,876.391 1411.47,877.826 1409.59,878.395 1406.92,879.206 1402.36,880.532 1397.8,881.796 1397.68,881.829 1393.25,883.017 \n",
" 1388.69,884.181 1384.24,885.264 1384.14,885.289 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#470b69; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1361.35,854.7 1356.8,855.496 1352.24,856.241 1347.68,856.937 1343.13,857.585 1341.6,857.788 1338.57,858.192 1334.02,858.754 1329.46,859.271 1324.9,859.742 \n",
" 1320.35,860.17 1315.79,860.553 1311.23,860.893 1306.68,861.191 1306.12,861.222 1302.12,861.45 1297.56,861.666 1293.01,861.841 1288.45,861.974 1283.9,862.066 \n",
" 1279.34,862.117 1274.78,862.128 1270.23,862.098 1265.67,862.028 1261.11,861.917 1256.56,861.766 1252,861.575 1247.44,861.344 1245.39,861.222 1242.89,861.075 \n",
" 1238.33,860.767 1233.78,860.419 1229.22,860.031 1224.66,859.603 1220.11,859.134 1215.55,858.625 1210.99,858.075 1208.77,857.788 1206.44,857.487 1201.88,856.861 \n",
" 1197.32,856.193 1192.77,855.484 1188.21,854.733 1186.03,854.353 1183.66,853.943 1179.1,853.114 1174.54,852.242 1169.99,851.327 1168.04,850.919 1165.43,850.372 \n",
" 1160.87,849.377 1156.32,848.337 1152.73,847.484 1151.76,847.253 1147.2,846.132 1142.65,844.963 1139.22,844.05 1138.09,843.75 1133.54,842.497 1128.98,841.195 \n",
" 1127.02,840.615 1124.42,839.85 1119.87,838.46 1115.82,837.181 1115.31,837.021 1110.75,835.54 1106.2,834.007 1105.44,833.746 1101.64,832.431 1097.08,830.803 \n",
" 1095.75,830.312 1092.53,829.128 1087.97,827.4 1086.63,826.877 1083.42,825.625 1078.86,823.795 1078,823.442 1074.3,821.916 1069.81,820.008 1069.75,819.979 \n",
" 1065.19,817.994 1062.02,816.573 1060.63,815.949 1056.08,813.85 1054.57,813.139 1051.52,811.693 1047.43,809.704 1046.96,809.475 1042.41,807.201 1040.59,806.27 \n",
" 1037.85,804.864 1034,802.835 1033.3,802.463 1028.74,800 1027.66,799.401 1024.18,797.471 1021.54,795.966 1019.63,794.874 1015.62,792.532 1015.07,792.206 \n",
" 1010.51,789.469 1009.91,789.097 1005.96,786.66 1004.38,785.663 1001.4,783.775 999.014,782.228 996.845,780.812 993.814,778.794 992.288,777.77 988.768,775.359 \n",
" 992.288,772.949 993.814,771.925 996.845,769.906 999.014,768.49 1001.4,766.944 1004.38,765.056 1005.96,764.059 1009.91,761.621 1010.51,761.249 1015.07,758.512 \n",
" 1015.62,758.187 1019.63,755.845 1021.54,754.752 1024.18,753.248 1027.66,751.318 1028.74,750.719 1033.3,748.256 1034,747.883 1037.85,745.854 1040.59,744.449 \n",
" 1042.41,743.518 1046.96,741.243 1047.43,741.014 1051.52,739.025 1054.57,737.58 1056.08,736.869 1060.63,734.769 1062.02,734.145 1065.19,732.725 1069.75,730.739 \n",
" 1069.81,730.711 1074.3,728.803 1078,727.276 1078.86,726.924 1083.42,725.094 1086.63,723.842 1087.97,723.318 1092.53,721.591 1095.75,720.407 1097.08,719.916 \n",
" 1101.64,718.288 1105.44,716.973 1106.2,716.712 1110.75,715.179 1115.31,713.698 1115.82,713.538 1119.87,712.259 1124.42,710.869 1127.02,710.104 1128.98,709.524 \n",
" 1133.54,708.222 1138.09,706.969 1139.22,706.669 1142.65,705.756 1147.2,704.587 1151.76,703.465 1152.73,703.235 1156.32,702.382 1160.87,701.342 1165.43,700.347 \n",
" 1168.04,699.8 1169.99,699.392 1174.54,698.477 1179.1,697.605 1183.66,696.776 1186.03,696.366 1188.21,695.986 1192.77,695.235 1197.32,694.525 1201.88,693.858 \n",
" 1206.44,693.232 1208.77,692.931 1210.99,692.644 1215.55,692.094 1220.11,691.585 1224.66,691.116 1229.22,690.688 1233.78,690.3 1238.33,689.952 1242.89,689.644 \n",
" 1245.39,689.497 1247.44,689.375 1252,689.144 1256.56,688.953 1261.11,688.802 1265.67,688.691 1270.23,688.621 1274.78,688.591 1279.34,688.601 1283.9,688.653 \n",
" 1288.45,688.745 1293.01,688.878 1297.56,689.053 1302.12,689.269 1306.12,689.497 1306.68,689.528 1311.23,689.825 1315.79,690.166 1320.35,690.549 1324.9,690.976 \n",
" 1329.46,691.448 1334.02,691.965 1338.57,692.527 1341.6,692.931 1343.13,693.134 1347.68,693.782 1352.24,694.478 1356.8,695.223 1361.35,696.018 1363.23,696.366 \n",
" 1365.91,696.858 1370.47,697.745 1375.02,698.686 1379.58,699.682 1380.09,699.8 1384.14,700.721 1388.69,701.817 1393.25,702.972 1394.24,703.235 1397.8,704.175 \n",
" 1402.36,705.437 1406.59,706.669 1406.92,706.764 1411.47,708.139 1416.03,709.585 1417.59,710.104 1420.59,711.089 1425.14,712.661 1427.57,713.538 1429.7,714.3 \n",
" 1434.26,716.007 1436.72,716.973 1438.81,717.788 1443.37,719.643 1445.16,720.407 1447.92,721.575 1452.48,723.594 1453.02,723.842 1457.04,725.687 1460.34,727.276 \n",
" 1461.59,727.879 1466.15,730.16 1467.2,730.711 1470.71,732.536 1473.65,734.145 1475.26,735.022 1479.74,737.58 1479.82,737.623 1484.38,740.329 1485.48,741.014 \n",
" 1488.93,743.164 1490.9,744.449 1493.49,746.136 1496.04,747.883 1498.04,749.254 1500.92,751.318 1502.6,752.53 1505.54,754.752 1507.16,755.977 1509.93,758.187 \n",
" 1511.71,759.612 1514.1,761.621 1516.27,763.454 1518.07,765.056 1520.83,767.524 1521.85,768.49 1525.38,771.849 1525.46,771.925 1528.89,775.359 1525.46,778.794 \n",
" 1525.38,778.869 1521.85,782.228 1520.83,783.195 1518.07,785.663 1516.27,787.265 1514.1,789.097 1511.71,791.106 1509.93,792.532 1507.16,794.741 1505.54,795.966 \n",
" 1502.6,798.189 1500.92,799.401 1498.04,801.465 1496.04,802.835 1493.49,804.583 1490.9,806.27 1488.93,807.555 1485.48,809.704 1484.38,810.39 1479.82,813.096 \n",
" 1479.74,813.139 1475.26,815.697 1473.65,816.573 1470.71,818.182 1467.2,820.008 1466.15,820.558 1461.59,822.84 1460.34,823.442 1457.04,825.031 1453.02,826.877 \n",
" 1452.48,827.125 1447.92,829.144 1445.16,830.312 1443.37,831.075 1438.81,832.931 1436.72,833.746 1434.26,834.712 1429.7,836.419 1427.57,837.181 1425.14,838.058 \n",
" 1420.59,839.63 1417.59,840.615 1416.03,841.134 1411.47,842.58 1406.92,843.955 1406.59,844.05 1402.36,845.282 1397.8,846.544 1394.24,847.484 1393.25,847.747 \n",
" 1388.69,848.902 1384.14,849.998 1380.09,850.919 1379.58,851.037 1375.02,852.033 1370.47,852.973 1365.91,853.861 1363.23,854.353 1361.35,854.7 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#270b52; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1338.57,826.896 1334.02,827.388 1329.46,827.832 1324.9,828.23 1320.35,828.582 1315.79,828.888 1311.23,829.151 1306.68,829.368 1302.12,829.543 1297.56,829.674 \n",
" 1293.01,829.762 1288.45,829.807 1283.9,829.81 1279.34,829.77 1274.78,829.689 1270.23,829.565 1265.67,829.399 1261.11,829.192 1256.56,828.943 1252,828.651 \n",
" 1247.44,828.318 1242.89,827.942 1238.33,827.524 1233.78,827.064 1232.08,826.877 1229.22,826.564 1224.66,826.024 1220.11,825.441 1215.55,824.815 1210.99,824.146 \n",
" 1206.5,823.442 1206.44,823.433 1201.88,822.683 1197.32,821.888 1192.77,821.049 1188.21,820.165 1187.44,820.008 1183.66,819.242 1179.1,818.275 1174.54,817.261 \n",
" 1171.58,816.573 1169.99,816.204 1165.43,815.105 1160.87,813.957 1157.75,813.139 1156.32,812.764 1151.76,811.529 1147.2,810.244 1145.36,809.704 1142.65,808.914 \n",
" 1138.09,807.537 1134.05,806.27 1133.54,806.109 1128.98,804.638 1124.42,803.113 1123.62,802.835 1119.87,801.542 1115.31,799.918 1113.9,799.401 1110.75,798.245 \n",
" 1106.2,796.519 1104.78,795.966 1101.64,794.742 1097.08,792.908 1096.17,792.532 1092.53,791.024 1088.01,789.097 1087.97,789.08 1083.42,787.085 1080.26,785.663 \n",
" 1078.86,785.029 1074.3,782.915 1072.86,782.228 1069.75,780.743 1065.77,778.794 1065.19,778.507 1060.63,776.212 1058.98,775.359 1060.63,774.507 1065.19,772.212 \n",
" 1065.77,771.925 1069.75,769.976 1072.86,768.49 1074.3,767.804 1078.86,765.69 1080.26,765.056 1083.42,763.634 1087.97,761.639 1088.01,761.621 1092.53,759.695 \n",
" 1096.17,758.187 1097.08,757.811 1101.64,755.977 1104.78,754.752 1106.2,754.2 1110.75,752.473 1113.9,751.318 1115.31,750.801 1119.87,749.176 1123.62,747.883 \n",
" 1124.42,747.606 1128.98,746.081 1133.54,744.61 1134.05,744.449 1138.09,743.182 1142.65,741.805 1145.36,741.014 1147.2,740.475 1151.76,739.19 1156.32,737.954 \n",
" 1157.75,737.58 1160.87,736.762 1165.43,735.614 1169.99,734.515 1171.58,734.145 1174.54,733.458 1179.1,732.444 1183.66,731.476 1187.44,730.711 1188.21,730.554 \n",
" 1192.77,729.669 1197.32,728.83 1201.88,728.036 1206.44,727.286 1206.5,727.276 1210.99,726.573 1215.55,725.903 1220.11,725.277 1224.66,724.694 1229.22,724.154 \n",
" 1232.08,723.842 1233.78,723.655 1238.33,723.194 1242.89,722.777 1247.44,722.401 1252,722.068 1256.56,721.776 1261.11,721.527 1265.67,721.319 1270.23,721.154 \n",
" 1274.78,721.03 1279.34,720.949 1283.9,720.909 1288.45,720.912 1293.01,720.957 1297.56,721.045 1302.12,721.176 1306.68,721.35 1311.23,721.568 1315.79,721.83 \n",
" 1320.35,722.137 1324.9,722.489 1329.46,722.887 1334.02,723.331 1338.57,723.823 1338.73,723.842 1343.13,724.355 1347.68,724.935 1352.24,725.565 1356.8,726.245 \n",
" 1361.35,726.976 1363.1,727.276 1365.91,727.753 1370.47,728.579 1375.02,729.459 1379.58,730.396 1381.02,730.711 1384.14,731.38 1388.69,732.419 1393.25,733.518 \n",
" 1395.71,734.145 1397.8,734.672 1402.36,735.881 1406.92,737.156 1408.36,737.58 1411.47,738.486 1416.03,739.881 1419.55,741.014 1420.59,741.345 1425.14,742.867 \n",
" 1429.64,744.449 1429.7,744.47 1434.26,746.127 1438.81,747.874 1438.84,747.883 1443.37,749.68 1447.29,751.318 1447.92,751.579 1452.48,753.547 1455.13,754.752 \n",
" 1457.04,755.607 1461.59,757.756 1462.46,758.187 1466.15,759.989 1469.32,761.621 1470.71,762.327 1475.26,764.765 1475.78,765.056 1479.82,767.298 1481.86,768.49 \n",
" 1484.38,769.947 1487.62,771.925 1488.93,772.714 1493.1,775.359 1488.93,778.005 1487.62,778.794 1484.38,780.772 1481.86,782.228 1479.82,783.42 1475.78,785.663 \n",
" 1475.26,785.953 1470.71,788.392 1469.32,789.097 1466.15,790.729 1462.46,792.532 1461.59,792.962 1457.04,795.112 1455.13,795.966 1452.48,797.172 1447.92,799.14 \n",
" 1447.29,799.401 1443.37,801.039 1438.84,802.835 1438.81,802.845 1434.26,804.592 1429.7,806.249 1429.64,806.27 1425.14,807.852 1420.59,809.373 1419.55,809.704 \n",
" 1416.03,810.838 1411.47,812.232 1408.36,813.139 1406.92,813.562 1402.36,814.838 1397.8,816.047 1395.71,816.573 1393.25,817.201 1388.69,818.3 1384.14,819.339 \n",
" 1381.02,820.008 1379.58,820.323 1375.02,821.26 1370.47,822.14 1365.91,822.966 1363.1,823.442 1361.35,823.743 1356.8,824.474 1352.24,825.154 1347.68,825.784 \n",
" 1343.13,826.364 1338.73,826.877 1338.57,826.896 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#0d0829; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1334.02,799.559 1329.46,799.909 1324.9,800.213 1320.35,800.47 1315.79,800.681 1311.23,800.846 1306.68,800.966 1302.12,801.042 1297.56,801.073 1293.01,801.059 \n",
" 1288.45,801.002 1283.9,800.9 1279.34,800.755 1274.78,800.566 1270.23,800.333 1265.67,800.056 1261.11,799.735 1256.93,799.401 1256.56,799.371 1252,798.967 \n",
" 1247.44,798.519 1242.89,798.027 1238.33,797.491 1233.78,796.91 1229.22,796.284 1227.05,795.966 1224.66,795.617 1220.11,794.908 1215.55,794.153 1210.99,793.352 \n",
" 1206.58,792.532 1206.44,792.505 1201.88,791.619 1197.32,790.685 1192.77,789.704 1190.08,789.097 1188.21,788.678 1183.66,787.609 1179.1,786.491 1175.87,785.663 \n",
" 1174.54,785.325 1169.99,784.116 1165.43,782.855 1163.25,782.228 1160.87,781.547 1156.32,780.193 1151.79,778.794 1151.76,778.784 1147.2,777.332 1142.65,775.825 \n",
" 1141.28,775.359 1142.65,774.894 1147.2,773.387 1151.76,771.935 1151.79,771.925 1156.32,770.526 1160.87,769.171 1163.25,768.49 1165.43,767.864 1169.99,766.603 \n",
" 1174.54,765.394 1175.87,765.056 1179.1,764.228 1183.66,763.11 1188.21,762.041 1190.08,761.621 1192.77,761.015 1197.32,760.033 1201.88,759.1 1206.44,758.214 \n",
" 1206.58,758.187 1210.99,757.367 1215.55,756.566 1220.11,755.811 1224.66,755.102 1227.05,754.752 1229.22,754.434 1233.78,753.809 1238.33,753.228 1242.89,752.692 \n",
" 1247.44,752.2 1252,751.752 1256.56,751.348 1256.93,751.318 1261.11,750.984 1265.67,750.663 1270.23,750.386 1274.78,750.153 1279.34,749.964 1283.9,749.819 \n",
" 1288.45,749.717 1293.01,749.66 1297.56,749.646 1302.12,749.677 1306.68,749.752 1311.23,749.873 1315.79,750.038 1320.35,750.249 1324.9,750.506 1329.46,750.809 \n",
" 1334.02,751.16 1335.82,751.318 1338.57,751.555 1343.13,751.996 1347.68,752.485 1352.24,753.023 1356.8,753.612 1361.35,754.252 1364.64,754.752 1365.91,754.942 \n",
" 1370.47,755.678 1375.02,756.467 1379.58,757.312 1384,758.187 1384.14,758.214 1388.69,759.159 1393.25,760.165 1397.8,761.232 1399.37,761.621 1402.36,762.35 \n",
" 1406.92,763.527 1411.47,764.772 1412.46,765.056 1416.03,766.068 1420.59,767.431 1423.94,768.49 1425.14,768.863 1429.7,770.351 1434.26,771.921 1434.27,771.925 \n",
" 1438.81,773.542 1443.37,775.252 1443.64,775.359 1443.37,775.467 1438.81,777.177 1434.27,778.794 1434.26,778.798 1429.7,780.368 1425.14,781.856 1423.94,782.228 \n",
" 1420.59,783.288 1416.03,784.651 1412.46,785.663 1411.47,785.947 1406.92,787.192 1402.36,788.368 1399.37,789.097 1397.8,789.487 1393.25,790.554 1388.69,791.559 \n",
" 1384.14,792.505 1384,792.532 1379.58,793.407 1375.02,794.252 1370.47,795.041 1365.91,795.776 1364.64,795.966 1361.35,796.466 1356.8,797.107 1352.24,797.696 \n",
" 1347.68,798.234 1343.13,798.723 1338.57,799.164 1335.82,799.401 1334.02,799.559 \n",
" \"/>\n",
"<defs>\n",
" <clipPath id=\"clip5204\">\n",
" <rect x=\"2129\" y=\"47\" width=\"73\" height=\"1457\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<g clip-path=\"url(#clip5204)\">\n",
"<image width=\"72\" height=\"1456\" xlink:href=\"data:image/png;base64,\n",
"iVBORw0KGgoAAAANSUhEUgAAAEgAAAWwCAYAAAD+FAeUAAALO0lEQVR4nO3dQWoTUBSG0cS8QRyY\n",
"iYhr6L67B1fRFRQsjREqFASLGZRgXEH7Dd8bnLOCy8c/v9vLv9vrhjd9mH3A6gQKAgWBgkBBoCBQ\n",
"ECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBB\n",
"oCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWB\n",
"gkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFMb5\n",
"57fZNyzNgoJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAg\n",
"UBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJA\n",
"QaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIF\n",
"gYJAQaAgUBAoCBQECgKFsf9+N/uGpVlQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgI\n",
"FAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQ\n",
"ECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBB\n",
"oCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoDC29w+zb1iaBQWBgkBBoCBQECgIFAQKAgWB\n",
"gkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQK\n",
"AgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgI\n",
"FAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQK4/XxMPuGpVlQ\n",
"ECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBB\n",
"oCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWB\n",
"gkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQK\n",
"AgWBgkBBoDD+HL/OvmFpFhQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAg\n",
"UBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJA\n",
"QaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIF\n",
"gYJAQaAgUBAoCBQECgIFgYJAQaAgUBAojOdfX2bfsDQLCgIFgYJAQaAgUBAoCBQECgIFgYJAQaAg\n",
"UBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJA\n",
"QaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIF\n",
"gYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBTG0+/Ps29YmgUFgYJAQaAg\n",
"UBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJA\n",
"QaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIF\n",
"gYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQE\n",
"CuPHy2H2DUuzoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQ\n",
"ECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBB\n",
"oCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWB\n",
"gkBBoCBQECgIFAQKAgWBgkBhnP5+nH3D0iwoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAo\n",
"CBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAg\n",
"UBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJA\n",
"QaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBjH8272DUuzoCBQECgIFAQKAgWBgkBB\n",
"oCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWB\n",
"gkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQK\n",
"AgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBhnM6X2Tcs\n",
"zYKCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgU\n",
"BAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQ\n",
"KAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGg\n",
"IFAQKAgUBAoChfGweZp9w9IsKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGC\n",
"QEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoC\n",
"BYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgU\n",
"BAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFDYftrfXGcfsTILCgIFgYJAQaAgUBAoCBQECgIFgYJA\n",
"QaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIF\n",
"gYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQE\n",
"CgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBS2m83OA7Z3WFAQKAgU\n",
"BAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQ\n",
"KAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGg\n",
"IFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGC\n",
"QEGg8B++FCk4XRJKMAAAAABJRU5ErkJggg==\n",
"\" transform=\"translate(2129, 47)\"/>\n",
"</g>\n",
"<g clip-path=\"url(#clip5201)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 1515.55)\" x=\"2237.26\" y=\"1515.55\">-</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5201)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2265.37, 1515.55)\" x=\"2265.37\" y=\"1515.55\">0.75</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5201)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 1250.32)\" x=\"2237.26\" y=\"1250.32\">-</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5201)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2265.37, 1250.32)\" x=\"2265.37\" y=\"1250.32\">0.50</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5201)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 985.085)\" x=\"2237.26\" y=\"985.085\">-</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5201)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2265.37, 985.085)\" x=\"2265.37\" y=\"985.085\">0.25</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5201)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 719.853)\" x=\"2237.26\" y=\"719.853\">0</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5201)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 454.621)\" x=\"2237.26\" y=\"454.621\">0.25</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5201)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 189.39)\" x=\"2237.26\" y=\"189.39\">0.50</text>\n",
"</g>\n",
"<polyline clip-path=\"url(#clip5201)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 2201.26,1503.47 2201.26,1501.9 2225.26,1501.9 2201.26,1501.9 2201.26,1236.67 2225.26,1236.67 2201.26,1236.67 2201.26,971.433 2225.26,971.433 2201.26,971.433 \n",
" 2201.26,706.202 2225.26,706.202 2201.26,706.202 2201.26,440.97 2225.26,440.97 2201.26,440.97 2201.26,175.738 2225.26,175.738 2201.26,175.738 2201.26,47.2441 \n",
" \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5203)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1570.77,775.359 1569.33,775.359 1566.47,775.359 1562.19,775.359 1556.5,775.359 1549.43,775.359 1540.99,775.359 1531.21,775.359 1520.12,775.359 1507.76,775.359 \n",
" 1494.16,775.359 1479.37,775.359 1463.43,775.359 1446.4,775.359 1428.33,775.359 1409.27,775.359 1389.29,775.359 1368.45,775.359 1346.81,775.359 1324.44,775.359 \n",
" 1301.41,775.359 1277.8,775.359 1253.68,775.359 1229.12,775.359 1204.2,775.359 1179,775.359 1153.61,775.359 1128.09,775.359 1102.53,775.359 1077.01,775.359 \n",
" 1051.62,775.359 1026.42,775.359 1001.5,775.359 976.944,775.359 952.82,775.359 929.208,775.359 906.181,775.359 883.812,775.359 862.172,775.359 841.328,775.359 \n",
" 821.346,775.359 802.289,775.359 784.217,775.359 767.187,775.359 751.252,775.359 736.462,775.359 722.865,775.359 710.502,775.359 699.413,775.359 689.632,775.359 \n",
" 681.191,775.359 674.116,775.359 668.429,775.359 664.147,775.359 661.286,775.359 659.853,775.359 \n",
" \"/>\n",
"<g clip-path=\"url(#clip5204)\">\n",
"<image width=\"72\" height=\"1456\" xlink:href=\"data:image/png;base64,\n",
"iVBORw0KGgoAAAANSUhEUgAAAEgAAAWwCAYAAAD+FAeUAAAMbklEQVR4nO3dwY3sRhAFQY5Q/lsh\n",
"L6XfLQtUeSQPERYMEg9LNMmZ/f17/r4P/+uvtz/A1wkUBAoCBYHCnPvv25/h0ywoCBQECgIFgcJc\n",
"V7GVBQWBgkBBoCBQmHtcxTYWFAQKAgWBgqNGsKAgUBAoCBQECq5iwYKCQEGgIFAQKLiKBQsKAgWB\n",
"gkDBU41gQUGgIFAQKAgUHDWCBQWBgkBBoCBQcBULFhQECgIFgcI8bpitLCgIFAQKAgWBgqtYsKAg\n",
"UBAoCBQECvO4YbayoCBQECgIFBw1ggUFgYJAQaAgUHAVCxYUBAoCBYGCQGGe88/bn+HTLCgIFAQK\n",
"AgVPNYIFBYGCQEGgIFBwwyxYUBAoCBQECgIFV7FgQUGgIFAQKAgU5nf/vP0ZPs2CgkBBoCBQmOf4\n",
"I72xoCBQECgIFAQK83MVW1lQECgIFAQKAgVnsWBBQaAgUBAozOOpxsqCgkBBoCBQECi4YRYsKAgU\n",
"BAoCBYGCG2bBgoJAQaAgUHDUCBYUBAoCBYGCQMFRI1hQECgIFAQKAoX5nfP2Z/g0CwoCBYGCQMFR\n",
"I1hQECgIFAQKAgVXsWBBQaAgUBAoCBS8vBAsKAgUBAoChXk81VhZUBAoCBQECgIFR41gQUGgIFAQ\n",
"KAgUPPYJFhQECgIFgYJAwVUsWFAQKAgUBAq+zBIsKAgUBAoCBYGClxeCBQWBgkBBoCBQcMMsWFAQ\n",
"KAgUBAqOGsGCgkBBoCBQECi4igULCgIFgYJAQaDg5YVgQUGgIFAQKHiqESwoCBQECgIFgYIbZsGC\n",
"gkBBoCBQECi4igULCgIFgYJAwR/pYEFBoCBQECgIFOY59+3P8GkWFAQKAgWBgkBhnusstrGgIFAQ\n",
"KAgU3DALFhQECgIFgYJAwQ2zYEFBoCBQECgIFJzFggUFgYJAQaAgUHAVCxYUBAoCBYGCG2bBgoJA\n",
"QaAgUBAoOGoECwoCBYGCQEGgMI+L2MqCgkBBoCBQ8Ec6WFAQKAgUBAoChfGNzJ0FBYGCQEGgIFBw\n",
"FgsWFAQKAgWBgj/SwYKCQEGgIFAQKLiKBQsKAgWBgkBBoDCPL/usLCgIFAQKAoW55/f2Z/g0CwoC\n",
"BYGCQEGg4IZZsKAgUBAoCBQECvM4i60sKAgUBAoChbnXH+mNBQWBgkBBoCBQcNQIFhQECgIFgYJA\n",
"wVUsWFAQKAgUBAoCBXcUgwUFgYJAQaDgqBEsKAgUBAoCBYHCPEejjTpBoCBQECgIFNwwCxYUBAoC\n",
"BYGCG2bBgoJAQaAgUBAo+HmcYEFBoCBQECgIFOa5Gm3UCQIFgYJAwVEjWFAQKAgUBAoCBVexYEFB\n",
"oCBQECgIFLwnHdQJAgWBgkDBa8DBgoJAQaAgUBAoeE86WFAQKAgUBAoChblumK3UCQIFgYJAwQ2z\n",
"YEFBoCBQECgIFNwwCxYUBAoCBYGCQMENs6BOECgIFAQKAgV3FIMFBYGCQEGg4CuZwYKCQEGgIFAQ\n",
"KMz1G2YrdYJAQaAgUBAoeHkhWFAQKAgUBApumAULCgIFgYJAQaDg2XywoCBQECgIFAQK3pMO6gSB\n",
"gkBBoOCoESwoCBQECgIFgYLHPsGCgkBBoCBQECg4iwULCgIFgYJAwVONoE4QKAgUBAoCBUeNYEFB\n",
"oCBQECgIFDz2CRYUBAoCBYGCo0awoCBQECgIFAQKHvsEdYJAQaAgUBAoOIsFCwoCBYGCQEGg4CoW\n",
"LCgIFAQKAgV/pIMFBYGCQEGgIFDwhlmwoCBQECgIFAQKc/wDtpU6QaAgUBAouGEWLCgIFAQKAgWB\n",
"ghtmwYKCQEGgIFAQKDiLBQsKAgWBgkDBH+lgQUGgIFAQKAgUXMWCBQWBgkBBoCBQcBULFhQECgIF\n",
"gcIcf6RXFhQECgIFgYJAwVEjWFAQKAgUBAoCBVexYEFBoCBQECj4Ix0sKAgUBAoCBYGCq1iwoCBQ\n",
"ECgIFAQKrmLBgoJAQaAgUBAoeAUvWFAQKAgUBAqOGsGCgkBBoCBQECi4igULCgIFgYJAQaDgX9cE\n",
"dYJAQaAgUHDUCBYUBAoCBYGCQMGz+WBBQaAgUBAoCBScxYIFBYGCQEGg4KgRLCgIFAQKAgWBgqNG\n",
"sKAgUBAoCBQECq5iwYKCQEGgIFBwwyxYUBAoCBQECgKFuY+r2MaCgkBBoCBQECg4iwULCgIFgYJA\n",
"wVONYEFBoCBQECgIFObctz/Ct1lQECgIFAQKAgVnsWBBQaAgUBAoCBQ89gkWFAQKAgWBwhxvmK0s\n",
"KAgUBAoCBYGCG2bBgoJAQaAgUBAouGEWLCgIFAQKAgVHjWBBQaAgUBAoCBTmvP0JPs6CgkBBoCBQ\n",
"ECg4iwULCgIFgYJAwVONYEFBoCBQECgIFPwSZ7CgIFAQKAgUBArOYsGCgkBBoCBQ8BtmwYKCQEGg\n",
"IFAQKLhhFiwoCBQECgIFgYI3zIIFBYGCQEGg4MsswYKCQEGgIFAQKDhqBAsKAgWBgkBBoOAsFiwo\n",
"CBQECgIFgYKzWLCgIFAQKAgUfJklWFAQKAgUBAoChfFln50FBYGCQEGgIFBwFgsWFAQKAgWBgqNG\n",
"sKAgUBAoCBQECo4awYKCQEGgIFAQKDiLBQsKAgWBgkDBUSNYUBAoCBQECgIFvycdLCgIFAQKAgWB\n",
"gt+TDhYUBAoCBYGCo0awoCBQECgIFAQKcxw1VhYUBAoCBYGCQGGus9jKgoJAQaAgUPCGWbCgIFAQ\n",
"KAgUBAq+zBIsKAgUBAoCBYGClxeCBQWBgkBBoCBQ8PJCsKAgUBAoCBQ8mw8WFAQKAgWBgkDB/3oO\n",
"FhQECgIFgYJAwSt4wYKCQEGgIFBwwyxYUBAoCBQECgIFN8yCBQWBgkBBoCBQcBYLFhQECgIFgYLX\n",
"gIMFBYGCQEGgIFDwlcxgQUGgIFAQKAgU/DxOsKAgUBAoCBQcNYIFBYGCQEGgIFBwFQsWFAQKAgWB\n",
"gkDB/3oOFhQECgIFgYKjRrCgIFAQKAgUBAqezQcLCgIFgYJAQaDgLBYsKAgUBAoCBYGCq1iwoCBQ\n",
"ECgIFNwwCxYUBAoCBYGCQMFRI1hQECgIFAQKAgW/Jx0sKAgUBAoCBT+XHCwoCBQECgIFgYIbZsGC\n",
"gkBBoCBQECh4eSFYUBAoCBQECo4awYKCQEGgIFAQKMx9XMY2FhQECgIFgYJAwVksWFAQKAgUBAqe\n",
"agQLCgIFgYJAQaDgqBEsKAgUBAoCBYGCs1iwoCBQECgIFBw1ggUFgYJAQaAgUPDDAsGCgkBBoCBQ\n",
"ECjM8Z70yoKCQEGgIFAQKDiLBQsKAgWBgkDBUSNYUBAoCBQECgIFP/ofLCgIFAQKAgWBwlx3zFYW\n",
"FAQKAgWBgqNGsKAgUBAoCBQECr7tEywoCBQECgIFgYLfkw4WFAQKAgWBgqNGsKAgUBAoCBQECt6T\n",
"DhYUBAoCBYGCQMENs2BBQaAgUBAoOGoECwoCBYGCQEGg4CoWLCgIFAQKAgWBwhxfyVxZUBAoCBQE\n",
"Cp5qBAsKAgWBgkBBoOCGWbCgIFAQKAgUBAquYsGCgkBBoCBQECi4igULCgIFgYJAYe7jtzg3FhQE\n",
"CgIFgYJAwVEjWFAQKAgUBAoChTk/Z7GNBQWBgkBBoDDHDbOVBQWBgkBBoCBQcBULFhQECgIFgYJA\n",
"wcsLwYKCQEGgIFCY8/NsfmNBQaAgUBAoCBTcMAsWFAQKAgWBgkDBVSxYUBAoCBQECp5qBAsKAgWB\n",
"gkBBoDDn+fP2Z/g0CwoCBYGCQEGg4IZZsKAgUBAoCBTmOmqsLCgIFAQKAgWBgqNGsKAgUBAoCBQE\n",
"Cq5iwYKCQEGgIFAQKLijGCwoCBQECgIFR41gQUGgIFAQKAgUHDWCBQWBgkBBoCBQ8J3VYEFBoCBQ\n",
"ECjMuf5IbywoCBQECgIFgYKjRrCgIFAQKAgUBApzncVWFhQECgIFgYKjRrCgIFAQKAgUBAreMAsW\n",
"FAQKAgWBgkDBywvBgoJAQaAgUHDDLFhQECgIFAQKAgXP5oMFBYGCQEGgIFDw2CdYUBAoCBQECo4a\n",
"wYKCQEGgIFAQKHjsEywoCBQECgIFgYKzWLCgIFAQKAgUBAoe+wQLCgIFgYJAwVEjWFAQKAgUBAoC\n",
"BY99ggUFgYJAQaAgUJh73TDbWFAQKAgUBAqOGsGCgkBBoCBQECjMc+/bn+HTLCgIFAQKAgWBwjzO\n",
"YisLCgIFgYJAwRtmwYKCQEGgIFAQKDhqBAsKAgWBgkBBoODlhWBBQaAgUBAozOOG2cqCgkBBoCBQ\n",
"ECg4agQLCgIFgYJAQaDgsU+woCBQECgIFP4DPcHwb7pfSUoAAAAASUVORK5CYII=\n",
"\" transform=\"translate(2129, 47)\"/>\n",
"</g>\n",
"<g clip-path=\"url(#clip5201)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 1515.55)\" x=\"2237.26\" y=\"1515.55\">-</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5201)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2265.37, 1515.55)\" x=\"2265.37\" y=\"1515.55\">0.75</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5201)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 1250.32)\" x=\"2237.26\" y=\"1250.32\">-</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5201)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2265.37, 1250.32)\" x=\"2265.37\" y=\"1250.32\">0.50</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5201)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 985.085)\" x=\"2237.26\" y=\"985.085\">-</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5201)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2265.37, 985.085)\" x=\"2265.37\" y=\"985.085\">0.25</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5201)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 719.853)\" x=\"2237.26\" y=\"719.853\">0</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5201)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 454.621)\" x=\"2237.26\" y=\"454.621\">0.25</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5201)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 189.39)\" x=\"2237.26\" y=\"189.39\">0.50</text>\n",
"</g>\n",
"<polyline clip-path=\"url(#clip5201)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 2201.26,1503.47 2201.26,1501.9 2225.26,1501.9 2201.26,1501.9 2201.26,1236.67 2225.26,1236.67 2201.26,1236.67 2201.26,971.433 2225.26,971.433 2201.26,971.433 \n",
" 2201.26,706.202 2225.26,706.202 2201.26,706.202 2201.26,440.97 2225.26,440.97 2201.26,440.97 2201.26,175.738 2225.26,175.738 2201.26,175.738 2201.26,47.2441 \n",
" \n",
" \"/>\n",
"<g clip-path=\"url(#clip5201)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:66px; text-anchor:middle;\" transform=\"rotate(-90, 2378.86, 775.359)\" x=\"2378.86\" y=\"775.359\"></text>\n",
"</g>\n",
"<polygon clip-path=\"url(#clip5201)\" points=\"\n",
"1608.73,251.724 2009.26,251.724 2009.26,130.764 1608.73,130.764 \n",
" \" fill=\"#ffffff\" fill-opacity=\"1\"/>\n",
"<polyline clip-path=\"url(#clip5201)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1608.73,251.724 2009.26,251.724 2009.26,130.764 1608.73,130.764 1608.73,251.724 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5201)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1632.73,191.244 1776.73,191.244 \n",
" \"/>\n",
"<g clip-path=\"url(#clip5201)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 1800.73, 208.744)\" x=\"1800.73\" y=\"208.744\">contour</text>\n",
"</g>\n",
"</svg>\n"
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"t = Fun()\n",
"f = sqrt(1-t^2)*exp(t)\n",
"v = z -> logkernel(f, z) # logkernel(f,z) calculates 1/π * \\int f(t)*log|t-z| dt\n",
"\n",
"xx = yy = -2:0.01:2\n",
"V = v.(xx' .+ im*yy)\n",
"\n",
"contour(xx, yy, V)\n",
"plot!(domain(t); color=:black, label=\"contour\")"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"data": {
"image/svg+xml": [
"<?xml version=\"1.0\" encoding=\"utf-8\"?>\n",
"<svg xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\" width=\"600\" height=\"400\" viewBox=\"0 0 2400 1600\">\n",
"<defs>\n",
" <clipPath id=\"clip5400\">\n",
" <rect x=\"0\" y=\"0\" width=\"2000\" height=\"2000\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<defs>\n",
" <clipPath id=\"clip5401\">\n",
" <rect x=\"0\" y=\"0\" width=\"2400\" height=\"1600\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<polygon clip-path=\"url(#clip5401)\" points=\"\n",
"0,1600 2400,1600 2400,0 0,0 \n",
" \" fill=\"#ffffff\" fill-opacity=\"1\"/>\n",
"<defs>\n",
" <clipPath id=\"clip5402\">\n",
" <rect x=\"480\" y=\"0\" width=\"1681\" height=\"1600\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<polygon clip-path=\"url(#clip5401)\" points=\"\n",
"507.195,1503.47 1723.43,1503.47 1723.43,47.2441 507.195,47.2441 \n",
" \" fill=\"#ffffff\" fill-opacity=\"1\"/>\n",
"<defs>\n",
" <clipPath id=\"clip5403\">\n",
" <rect x=\"507\" y=\"47\" width=\"1217\" height=\"1457\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 507.195,1417.45 952.366,1159.38 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 952.366,1159.38 952.366,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 603.577,1428.2 1048.75,1170.13 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1048.75,1170.13 1048.75,57.9971 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 699.96,1438.96 1145.13,1180.88 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1145.13,1180.88 1145.13,68.7501 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 796.342,1449.71 1241.51,1191.64 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1241.51,1191.64 1241.51,79.5031 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 892.725,1460.46 1337.9,1202.39 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1337.9,1202.39 1337.9,90.2561 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 989.107,1471.22 1434.28,1213.14 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1434.28,1213.14 1434.28,101.009 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1085.49,1481.97 1530.66,1223.9 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1530.66,1223.9 1530.66,111.762 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1181.87,1492.72 1627.04,1234.65 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1627.04,1234.65 1627.04,122.515 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1278.25,1503.47 1723.43,1245.4 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1723.43,1245.4 1723.43,133.268 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 507.195,1417.45 1278.25,1503.47 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 507.195,1417.45 507.195,305.316 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 562.841,1385.19 1333.9,1471.22 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 562.841,1385.19 562.841,273.057 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 618.488,1352.93 1389.55,1438.96 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 618.488,1352.93 618.488,240.798 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 674.134,1320.67 1445.19,1406.7 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 674.134,1320.67 674.134,208.539 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 729.781,1288.41 1500.84,1374.44 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 729.781,1288.41 729.781,176.28 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 785.427,1256.16 1556.49,1342.18 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 785.427,1256.16 785.427,144.021 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 841.073,1223.9 1612.13,1309.92 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 841.073,1223.9 841.073,111.762 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 896.72,1191.64 1667.78,1277.66 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 896.72,1191.64 896.72,79.5031 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 952.366,1159.38 1723.43,1245.4 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 952.366,1159.38 952.366,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 507.195,1417.45 952.366,1159.38 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 952.366,1159.38 1723.43,1245.4 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 507.195,1278.43 952.366,1020.36 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 952.366,1020.36 1723.43,1106.39 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 507.195,1139.42 952.366,881.345 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 952.366,881.345 1723.43,967.369 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 507.195,1000.4 952.366,742.328 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 952.366,742.328 1723.43,828.352 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 507.195,861.383 952.366,603.312 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 952.366,603.312 1723.43,689.335 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 507.195,722.366 952.366,464.295 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 952.366,464.295 1723.43,550.319 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 507.195,583.35 952.366,325.278 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 952.366,325.278 1723.43,411.302 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 507.195,444.333 952.366,186.261 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 952.366,186.261 1723.43,272.285 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 507.195,305.316 952.366,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 952.366,47.2441 1723.43,133.268 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 414.201,1194.29 436.372,1181.44 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 452.385,1152.41 448.69,1156.2 446.226,1162.56 444.995,1171.51 444.995,1176.44 446.226,1183.96 448.69,1187.47 452.385,1186.97 454.849,1185.54 458.544,1181.75 \n",
" 461.008,1175.39 462.239,1166.45 462.239,1161.51 461.008,1153.99 458.544,1150.49 454.849,1150.98 452.385,1152.41 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 472.093,1172.25 470.862,1174.61 472.093,1175.55 473.325,1173.19 472.093,1172.25 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 496.729,1126.7 484.411,1133.84 483.179,1149.37 484.411,1147.01 488.106,1143.22 491.802,1141.08 495.497,1140.58 497.96,1142.45 499.192,1146.67 499.192,1149.96 \n",
" 497.96,1155.61 495.497,1160.33 491.802,1164.12 488.106,1166.26 484.411,1166.76 483.179,1165.83 481.947,1163.25 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 489.338,852.954 485.643,856.742 483.179,863.108 481.947,872.05 481.947,876.987 483.179,884.502 485.643,888.011 489.338,887.514 491.802,886.086 495.497,882.298 \n",
" 497.96,875.933 499.192,866.99 499.192,862.053 497.96,854.539 495.497,851.03 491.802,851.526 489.338,852.954 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 452.385,596.343 448.69,600.131 446.226,606.496 444.995,615.439 444.995,620.376 446.226,627.89 448.69,631.399 452.385,630.903 454.849,629.475 458.544,625.687 \n",
" 461.008,619.321 462.239,610.379 462.239,605.442 461.008,597.927 458.544,594.418 454.849,594.915 452.385,596.343 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 472.093,616.186 470.862,618.546 472.093,619.478 473.325,617.118 472.093,616.186 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 496.729,570.636 484.411,577.777 483.179,593.302 484.411,590.943 488.106,587.155 491.802,585.013 495.497,584.516 497.96,586.379 499.192,590.602 499.192,593.894 \n",
" 497.96,599.545 495.497,604.265 491.802,608.053 488.106,610.195 484.411,610.691 483.179,609.76 481.947,607.182 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 448.69,327.034 451.153,323.96 454.849,316.881 454.849,351.441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 472.093,338.153 470.862,340.512 472.093,341.444 473.325,339.084 472.093,338.153 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 489.338,296.887 485.643,300.675 483.179,307.04 481.947,315.983 481.947,320.92 483.179,328.434 485.643,331.943 489.338,331.447 491.802,330.019 495.497,326.231 \n",
" 497.96,319.866 499.192,310.923 499.192,305.986 497.96,298.471 495.497,294.962 491.802,295.459 489.338,296.887 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 507.195,1417.45 507.195,1417.45 499.759,1421.76 507.195,1417.45 507.195,1278.43 503.477,1280.59 507.195,1278.43 507.195,1139.42 499.759,1143.73 507.195,1139.42 \n",
" 507.195,1000.4 503.477,1002.56 507.195,1000.4 507.195,861.383 499.759,865.694 507.195,861.383 507.195,722.366 503.477,724.522 507.195,722.366 507.195,583.35 \n",
" 499.759,587.66 507.195,583.35 507.195,444.333 503.477,446.488 507.195,444.333 507.195,305.316 499.759,309.627 507.195,305.316 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 653.17,1469.76 682.429,1473.02 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 698.683,1461.67 701.934,1460.39 706.811,1455.99 706.811,1490.55 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 875.193,1474.78 870.317,1475.88 867.066,1480.45 865.44,1488.5 865.44,1493.44 867.066,1501.85 870.317,1507.15 875.193,1509.34 878.444,1509.7 883.321,1508.6 \n",
" 886.572,1504.02 888.197,1495.98 888.197,1491.04 886.572,1482.63 883.321,1477.33 878.444,1475.14 875.193,1474.78 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1063.08,1502.32 1066.33,1501.04 1071.21,1496.65 1071.21,1531.21 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1252.6,1525.11 1252.6,1523.47 1254.22,1520.36 1255.85,1518.89 1259.1,1517.61 1265.6,1518.33 1268.85,1520.34 1270.48,1522.17 1272.1,1525.64 1272.1,1528.93 \n",
" 1270.48,1532.04 1267.22,1536.62 1250.97,1551.26 1273.73,1553.8 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 507.195,1417.45 507.195,1417.45 499.759,1421.76 507.195,1417.45 603.577,1428.2 599.859,1430.36 603.577,1428.2 699.96,1438.96 692.524,1443.27 699.96,1438.96 \n",
" 796.342,1449.71 792.624,1451.87 796.342,1449.71 892.725,1460.46 885.289,1464.77 892.725,1460.46 989.107,1471.22 985.389,1473.37 989.107,1471.22 1085.49,1481.97 \n",
" 1078.05,1486.28 1085.49,1481.97 1181.87,1492.72 1178.15,1494.88 1181.87,1492.72 1278.25,1503.47 1270.82,1507.79 1278.25,1503.47 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1410.77,1477.37 1432.94,1464.52 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1445.26,1444.21 1447.72,1441.13 1451.42,1434.06 1451.42,1468.62 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1544.23,1380.25 1540.54,1384.04 1538.07,1390.4 1536.84,1399.34 1536.84,1404.28 1538.07,1411.8 1540.54,1415.31 1544.23,1414.81 1546.7,1413.38 1550.39,1409.59 \n",
" 1552.86,1403.23 1554.09,1394.28 1554.09,1389.35 1552.86,1381.83 1550.39,1378.32 1546.7,1378.82 1544.23,1380.25 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1651.83,1324.46 1654.29,1321.38 1657.99,1314.3 1657.99,1348.86 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1760.66,1263.01 1760.66,1261.37 1761.89,1257.36 1763.12,1255 1765.59,1251.93 1770.51,1249.07 1772.98,1249.29 1774.21,1250.22 1775.44,1252.8 1775.44,1256.09 \n",
" 1774.21,1260.09 1771.75,1266.46 1759.43,1290.06 1776.67,1280.06 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1278.25,1503.47 1278.25,1503.47 1293.68,1505.2 1278.25,1503.47 1333.9,1471.22 1341.61,1472.08 1333.9,1471.22 1389.55,1438.96 1404.97,1440.68 1389.55,1438.96 \n",
" 1445.19,1406.7 1452.9,1407.56 1445.19,1406.7 1500.84,1374.44 1516.26,1376.16 1500.84,1374.44 1556.49,1342.18 1564.2,1343.04 1556.49,1342.18 1612.13,1309.92 \n",
" 1627.55,1311.64 1612.13,1309.92 1667.78,1277.66 1675.49,1278.52 1667.78,1277.66 1723.43,1245.4 1738.85,1247.12 1723.43,1245.4 \n",
" \"/>\n",
"<g clip-path=\"url(#clip5403)\">\n",
"<image width=\"1216\" height=\"1456\" xlink:href=\"data:image/png;base64,\n",
"iVBORw0KGgoAAAANSUhEUgAABMAAAAWwCAYAAAC7Hz3jAAAgAElEQVR4nOzdabM0SZoW5szq6u6p\n",
"7p6lZ8D017RjSDIZwgAxQoxALJpVLY2EZhjaZsYQYhFCiN+k1SQZGCCWYZbq7qp6Ux/eE5GxPOnh\n",
"HuERGennur6c82ZEuntEZkae8vI7nuvtdrsAAAAAQKs+efYAAAAAAGBPJsAAAAAAaJoJMAAAAACa\n",
"ZgIMAAAAgKaZAAMAAACgaSbAAAAAAGiaCTAAAAAAmmYCDAAAAICmmQADAAAAoGkmwAAAAABomgkw\n",
"AAAAAJpmAgwAAACAppkAAwAAAKBpJsAAAAAAaJoJMAAAAACaZgIMAAAAgKaZAAMAAACgaSbAAAAA\n",
"AGiaCTAAAAAAmmYCDAAAAICmmQADAAAAoGkmwAAAAABomgkwAAAAAJpmAgwAAACAppkAAwAAAKBp\n",
"JsAAAAAAaJoJMAAAAACaZgIMAAAAgKaZAAMAAACgaSbAAAAAAGiaCTAAAAAAmmYCDAAAAICmmQAD\n",
"AAAAoGkmwAAAAABomgkwAAAAAJpmAgwAAACAppkAAwAAAKBpJsAAAAAAaJoJMAAAAACaZgIMAAAA\n",
"gKaZAAMAAACgaSbAAAAAAGiaCTAAAAAAmmYCDAAAAICmmQADAAAAoGkmwAAAAABomgkwAAAAAJpm\n",
"AgwAAACAppkAAwAAAKBpJsAAAAAAaJoJMAAAAACaZgIMAAAAgKaZAAMAAACgaSbAAAAAAGiaCTAA\n",
"AAAAmmYCDAAAAICmmQADAAAAoGkmwAAAAABomgkwAAAAAJpmAgwAAACAppkAAwAAAKBpJsAAAAAA\n",
"aJoJMAAAAACaZgIMAAAAgKaZAAMAAACgaSbAAAAAAGiaCTAAAAAAmmYCDAAAAICmmQADAAAAoGkm\n",
"wAAAAABomgkwAAAAAJpmAgwAAACAppkAAwAAAKBpJsAAAAAAaJoJMAAAAACaZgIMAAAAgKaZAAMA\n",
"AACgaSbAAAAAAGiaCTAAAAAAmmYCDAAAAICmmQADAAAAoGkmwAAAAABomgkwAAAAAJpmAgwAAACA\n",
"ppkAAwAAAKBpJsAAAAAAaJoJMAAAAACaZgIMAAAAgKaZAAMAAACgaSbAAAAAAGiaCTAAAAAAmmYC\n",
"DAAAAICmmQADAAAAoGkmwAAAAABomgkwAAAAAJpmAgwAAACAppkAAwAAAKBpJsAAAAAAaJoJMAAA\n",
"AACaZgIMAAAAgKaZAAMAAACgaSbAAAAAAGiaCTAAAAAAmmYCDAAAAICmmQADAAAAoGkmwAAAAABo\n",
"mgkwAAAAAJpmAgwAAACAppkAAwAAAKBpJsAAAAAAaJoJMAAAAACaZgIMAAAAgKaZAAMAAACgaSbA\n",
"AAAAAGiaCTAAAAAAmmYCDAAAAICmmQADAAAAoGkmwAAAAABomgkwAAAAAJpmAgwAAACAppkAAwAA\n",
"AKBpJsAAAAAAaJoJMAAAAACaZgIMAAAAgKaZAAMAAACgaSbAAAAAAGiaCTAAAAAAmmYCDAAAAICm\n",
"mQADAAAAoGkmwAAAAABomgkwAAAAAJpmAgwAAACAppkAAwAAAKBpJsAAAAAAaJoJMAAAAACaZgIM\n",
"AAAAgKaZAAMAAACgaSbAAAAAAGiaCTAAAAAAmmYCDAAAAICmmQADAAAAoGkmwAAAAABomgkwAAAA\n",
"AJpmAgwAAACAppkAAwAAAKBpJsAAAAAAaJoJMAAAAACaZgIMAAAAgKaZAAMAAACgaSbAAAAAAGia\n",
"CTAAAAAAmmYCDAAAAICmmQADAAAAoGkmwAAAAABomgkwAAAAAJpmAgwAAACAppkAAwAAAKBpJsAA\n",
"AAAAaJoJMAAAAACaZgIMAAAAgKaZAAMAAACgaSbAAAAAAGiaCTAAAAAAmmYCDAAAAICmmQADAAAA\n",
"oGkmwAAAAABomgkwAAAAAJpmAgwAAACAppkAAwAAAKBpJsAAAAAAaJoJMAAAAACaZgIMAAAAgKaZ\n",
"AAMAAACgaSbAAAAAAGiaCTAAAAAAmmYCDAAAAICmmQADAAAAoGkmwAAAAABomgkwAAAAAJpmAgwA\n",
"AACAppkAAwAAAKBpJsAAAAAAaJoJMAAAAACaZgIMAAAAgKaZAAMAAACgaSbAAAAAAGiaCTAAAAAA\n",
"mmYCDAAAAICmmQADAAAAoGkmwAAAAABomgkwAAAAAJpmAgwAAACAppkAAwAAAKBpJsAAAAAAaJoJ\n",
"MAAAAACaZgIMAAAAgKaZAAMAAACgaSbAAAAAAGiaCTAAAAAAmmYCDAAAAICmmQADAAAAoGkmwAAA\n",
"AABomgkwAAAAAJpmAgwAAACAppkAAwAAAKBpJsAAAAAAaJoJMAAAAACaZgIMAAAAgKaZAAMAAACg\n",
"aSbAAAAAAGiaCTAAAAAAmmYCDAAAAICmffrsAQDA3r76Bz95e7hxsOVr//rvXA8YDgAAcDArwAAA\n",
"AABomgkwAAAAAJp2vd0ep0IA4JV99b/8xPxLrvB772v/xu+KRQIAwIuzAgwAAACAppkAAwAAAKBp\n",
"IpAANOWrv//jdb/YbrNfLl/7N39PLBIAAF6IFWAAAAAANM0EGAAAAABNE4EEoAlh9LF7ZBhY/LDv\n",
"997X/i3xSAAAOBsrwAAAAABomgkwAAAAAJomAgnAy/rqf/7O/UvsbF9ng+/Xr/3bvy8WCQAAT2QF\n",
"GAAAAABNMwEGAAAAQNNEIAF4OV/9ve9s//Iq/f7b6fvya//OH4hHAgDAzqwAAwAAAKBpJsAAAAAA\n",
"aJoIJAAvo48+dt9d1yA9+OHDgSOqaPB1/LV/VywSAABqsgIMAAAAgKZZAQbAqX31d791vi+q2/SX\n",
"YMFW5e/Xr/2Rz60KAwCAlawAAwAAAKBpJsAAAAAAaJoIJACntDr6eIv+EaUHb8H+59Df4z/aFvzj\n",
"0z8qHgkAAClWgAEAAADQNBNgAAAAADRNBBKA0/jqfwxij8NwX7f12d9d0+6DMYZJzAOJRQIAwJ0V\n",
"YAAAAAA0zQQYAAAAAE0TgQTg6b76O58d/mXUf/0Ne14su3hyC2P99N8TiwQA4H2yAgwAAACAppkA\n",
"AwAAAKBpIpAAPMWq2OOkwuJiYvFVv+KeUTVSPBIAgIZZAQYAAABA00yAAQAAANA0EUgADvXV355H\n",
"H2+zX07urOOMKlrmVrkM9vv03xeLBACgDVaAAQAAANA0E2AAAAAANE0EEoBDfPm3VlR9XONVv9Zy\n",
"x32S4/v0PxCPBADgdVgBBgAAAEDTTIABAAAA0DQRSAB2Uxx7jPa+Lmx/hpxxnGWsS0qPJaou+ebT\n",
"/1AsEgCAc7ICDAAAAICmmQADAAAAoGkikABU10cfX+Er5sOzBxDozttS/DPaL6fdA4lFAgBwBlaA\n",
"AQAAANA0E2AAAAAANE0EEoAqvvybhRUf17hNfkbhumd/reX2/+xx5thynqfbgzjnp39MPBIAgGNY\n",
"AQYAAABA00yAAQAAANA0EUgANsmOPqb2OstXUTSOa7DtLOOdKo0lnpBYJAAAe7ACDAAAAICmWQEG\n",
"QLEv/4fBqq9nfo1Efb/q11pLN8+/XC63ScGC6zXYFtwYP+Xrf9zqMAAA1rECDAAAAICmmQADAAAA\n",
"oGkikABk+/JvZN7wfq0Pg9+jsNtZvrJyxnGWsQ5kf+VPI4onPJaOWCQAADmsAAMAAACgaSbAAAAA\n",
"AGiaCCQASdmxxzNXZDzz2CKJKom3aL8zio5hui31vOFzC4/z639CLBIAgDErwAAAAABomgkwAAAA\n",
"AJomAglA6Mv//i36+KyviTPHFjPifbcoyhe1caTcWGJp9PAsr0vK2xi//ifFIwEA3iMrwAAAAABo\n",
"mgkwAAAAAJomAgnAyJd/PbPq49RS5O9DYtsTv4oWvwbP9jXZUiwxUjruaP+gembK1/+UWCQAQOus\n",
"AAMAAACgaSbAAAAAAGiaCCQAcezxxFG77qsrTLqd5WstN5qX2u+Mx5KKsOaO92zHt0BEEgDg9VkB\n",
"BgAAAEDTTIABAAAA0DQRSIB37MvfXlnxcYuux0Go7PYh3PN5bg9+77xChC81tlcZd07wMHqtoqhp\n",
"KrpZWjXyT4tEAgC8GivAAAAAAGiaCTAAAAAAmiYCCfDObIo9JiJjT/86Ke3/Fcb77DHmKj2WV4iQ\n",
"biAiCQBwPlaAAQAAANA0E2AAAAAANE0EEuCd+PK33qKPQThrVIVxuv3Ir4mlvp7xlfWqUcXc6pWp\n",
"/XLbPY3ozd1tmud3b7ePv1+vH2aP5ZWgzPeNn/19sUgAgCeyAgwAAACAppkAAwAAAKBpIpAADfvi\n",
"twYVH/e+3EftPzuyGIXOXqlaZG7fL/BVfo8WXi7XMI6YenaU3TxxojBRLTXyjf9EPBIAYG9WgAEA\n",
"AADQNBNgAAAAADRNBBKgQV/85mfrL+7TZy5VCXxGtLLm/luceWyZ7pUQo22Xt22Dgb/tfztzBDFX\n",
"f1iZb+hbcMxROrOib/yZ32vgRAMAPJ8VYAAAAAA0zQQYAAAAAE0TgQRoyCz6eAt+PzK++GgsJdv2\n",
"kop2RuftxO4VFpde3JOk6aL3Ymq/3OjhznHEQyU+r9/4T8UiAQBKWQEGAAAAQNOsAAN4cV98f8MN\n",
"73MsLST6sGvvY6mVQ7fJz1N5u3F8MLbu5vPjbSdZ4BPeJH628YHuwOoN51CplWXDFWldgYDRYxvb\n",
"3+Abf/Z3T/LmAQA4FyvAAAAAAGiaCTAAAAAAmiYCCfCiiqOPqSjjh+Cxvb8ectt/+tdUFF88Wcos\n",
"94b+rxBLLI4GLsQRz3yse+tumv9zYpEAAFaAAQAAANA0E2AAAAAANE0EEuCFfPHXBrHHKNT0YbLt\n",
"yEt81NdTvmLuJ+aWVcXwJOmw4bnqInzXYIfbScY7dAuildeM8/uO/gS5vZ2j69t5uZ3odfzmz/2r\n",
"8wwGAGAnVoABAAAA0DQTYAAAAAA0TQQS4AV88RuFFR9LpVo/5GvicWbzdhv+v5onxhaTVSAHG08U\n",
"bZvJrrx54mNISMUKr9F76yzx12dIVdscnBbxSACgFVaAAQAAANA0E2AAAAAANE0EEuCkNsUen1yR\n",
"MRlFuy7vU28gfa/Rg/NtZ/lKjJKeHzLOV+own2z4ep+xEmJV0es3ey8uvEB9JdDzxmu/+ed+51wD\n",
"AgBIsAIMAAAAgKaZAAMAAACgaSKQACfzxV8Noo/RpTozSbXexw6GXxOHxhc74fFdH287IgaYKkYZ\n",
"xi5nGy/JYzhQ9Fp2FRO7KonDCoqnqZxYWhA0jBROtj2S+qzt/jl8LWKRAMBZWQEGAAAAQNNMgAEA\n",
"AADQNBFIgJPoo481L8uDaFefGBsWPdwryrgUTbxcxlUNzxIju50jlhjpXqtrEOE7TSwxZfGcJt4E\n",
"J6t+eKjhsXev/Yuej2/++X/5mgMHAJpgBRgAAAAATTMBBgAAAEDTRCABnuiLXw8qPiYMI4vpioyl\n",
"JfIKRfHFYXRt74hW6qwNu/5wjsTVoVUzS+VUNozGv3RIr/TnRVCcc7x9UkHyzK/nXqJzlHosqsa6\n",
"8JiIJACwJyvAAAAAAGiaCTAAAAAAmiYCCfAE9+jjoEpj8nK8Mhm0FO3qIoKjbQfFvJa+fp4ZMxsV\n",
"WnyBVFY/3ihjNnzolY7lcumPJ4we7hzz3dtSpHBts6OY9G31Y2fzY3/hX5x3cADAS7ACDAAAAICm\n",
"mQADAAAAoGkikAAH+dGvfWtwwd0pzXObZKn2ijSlKgdeLnG08qCvmyjGdR10/pRIY9axD8b1al/N\n",
"J47OFUtVLAx3v77tHrzHdoo5Nmt67pci3G/EIwGAHFaAAQAAANA0E2AAAAAANE0EEmBnP/q1b5dd\n",
"aKcxxtFjlaUK6T0xxjjs6+lVGHPO0RlF75mwmmL/hOGOe4woLaeoY1Sdcylm2FL0MBXPDI+z4gkZ\n",
"vmei99G02WddNyZ+7C/98xN/SAGAI1kBBgAAAEDTrAAD2MFo1Vd0md37puHhpT1YMbN3/8P7uh91\n",
"o/SlhUy3ycYzfg2Gq2hOspAlWJl37VcEpZ72wjf576RWqS2tkCppf0sbFLFCDADeDyvAAAAAAGia\n",
"CTAAAAAAmiYCCVDRj/7Kd/a5qKZuWn5gROo2jQ8e0unwH9N+DygUEJkWKjhjVLGz8I4MbyZ/Nsno\n",
"4dJzu2IOIoWbRAUIGvfZX/5n7+NAAaABX/72Zw//Kvz0j31+vVysAAMAAACgcSbAAAAAAGiaCCTA\n",
"Spvijk+s0nhYNcZZx9MHDqwKmKoMmYxYHiAz3te/btdghzPG+rqxp8YdPu+Ex1JB9+fWdZKe/fjr\n",
"xwevgwffS8zwVYlHAsAxvvjNx9HG4Z9L1+CbuYs+dqwAAwAAAKBpJsAAAAAAaJoIJEChMPo4rQoY\n",
"btvHUyKNUWzwGV8nJ47Ljb5ezzLOqIpnXx0x9cQD46obzGKGo41vP4eH8va6XK+32WPNi2LB04qZ\n",
"w8d2G0f0XgzGUaON6Fii6qAVK4Z+9vP/9J28oQAgzxffz4s0Ft8N4m3/r/9Hnz98phVgAAAAADTN\n",
"BBgAAAAATROBBMgwij1+CKraVbyU7h7BisYaRoMS+9cWRkifF+28nTnydzvx2EoFlRCbUiNWt9RG\n",
"xbgexxKPBKAlX/xGItq4ZenVdfJzwdf/uAgkAAAAAO+UCTAAAAAAmiYCCZDwo//mxzdfJHevNBel\n",
"BqOY5mXnqNTTq1G+GSYEPxw0pqXkZlR9cbbxfNHGW6q66atFFpMVMDfEEqdtrWnvFYRVI+ePRZU4\n",
"U9fA6yV47G2/0XWyu6RlthHHRS/L+w+fM3rqZExLEfjUeyuV+A7a+tYv/pMG31AAnN0Xv75TpHFt\n",
"G9G34eCxVPRxbZcAAAAA8FJMgAEAAADQNBFIgIml2OOhkcZe0H7Ny3cq4XZknGuYQsqJIR08pvtj\n",
"J0kkBenJflMydvlk4fkLTvT0PZh73l8hjrgQf+uqYo7ieonH4nbnMbwoXhhGDnkJ4pEA5PrRr337\n",
"4X89DP+7ZvV/ZBxY6bHz9T+xHHscsgIMAAAAgKaZAAMAAACgaSKQAG9+9Ksfo4+zSNEe+iqNO0W1\n",
"EtG4QyJhXfIqKpW2WxXK0v13Pg+ZlSEPeb/lSEbyhiX9gvdust2THF+u6LPTvVapin6ptob7+bMr\n",
"X3j+oiqepQ0vlnB8PJZr8uI6+DWoFtk9N7r+Tyv4TrfP2k1Ujw3aFZUEaM+P/sp3Hn8Ddt8FG67+\n",
"1+uH9U/uVK702CmNPq4dDgAAAAC8FBNgAAAAADRNBBJ49374qz9RdiGMEjDTSMshMcN9+4iqCB5a\n",
"hTF1ni/BtgO/zqbHfw06PzTaWPp6nCWWuBATvSVW7/cVEaNqrO/xT5sompp67D2eIxZ965f/8Uku\n",
"DgDvT7IS/ScVvrifGYu8Pvi94Llf/5PrYo9DVoABAAAA0DQTYAAAAAA0TQQSeJeyY49HxoV2jzS+\n",
"RcaiuN6RkcZUhbW9ug6O7xpUkHtKRcbo3J8lolhodJ4zi+WdQm61xmQlwoVqfC/6mp7H/IXpr2lh\n",
"RdJg/8v8GnhvY/jcedR73sc8fz3efz6iPtIbVHCcb1u4bgX7ROchdXy5H87ovIlKAqQt/bdG/N2V\n",
"Ibqeb7kir45F3sdffCyZlR47X/9T26OPHSvAAAAAAGiaCTAAAAAAmiYCCbwrP/yvfvLjRW/vaNJe\n",
"caeFS/buUcYoEpqKjO3skOhm39lC7K20jb31Cc+FPqPoVf/LSVJOUXw2+RqkKiEGUcWXEX3Ypo8t\n",
"RfOWH4tieMMIXXq/qFLs47Fty23wKr79K//ICw28tP6/IS6X4Ktr8L1c4Wq3Oh55uTy5WmSFWOSg\n",
"z5rRx44VYAAAAAA0zQowoFmj/1NT0y21CmNLu5N/HrH65kO3OiYYyEE35X+aF1i9NRK87Z5+Djvp\n",
"27zO90mt3ooWCZ1EfNP1stcgXj0VtWWFVBVrXqrSBWu595Sfbl8a2x59Lj33iawSA47ww+/91OO/\n",
"LrasvJqqsBJr00qwSOmYwpvV57Yx3i/7WIYrwP5jK8AAAAAAoIgJMAAAAACaJgIJNGVV7HGHGNnw\n",
"0ton155xY/wDInJPjeFFfS+NZ+0N7JPjiB4Kbra+FFd6puTN5J914/jSCgsf94/fk6k2Gkhe5cb2\n",
"opc0jGCubHhWdGD4WGGzqSjwUhusk/uRy9kvigoHD137Shz3TbdEPH/00Ns/xCfhffnBr3x3fvWZ\n",
"XlOCbZvUiCMOx1GhvSoRybWxyOK+826Q//U/XT/2OGQFGAAAAABNMwEGAAAAQNNEIIEmhNHHvas1\n",
"puIaNS6tt0S8aEfT+NhwKfltr6hY6rieELHsX8/LZfA6B5GuI2W9p54VVZz3P/vzIjqlA+kYXuRk\n",
"peyGb49LVOmxdJyJ+KnI3zGGr1ntSlyP+or6OXIc78R3vvcPT3LhgPfnB7/002UXsuF1r0qU8e1H\n",
"zevplrai5244ztXHtSWeWRyLnO/3jZ/9g0Ouy1aAAQAAANA0E2AAAAAANE0EEnhZP/zeT9ZdE92l\n",
"DG9BVutVI4236NcDY4xRdOcZx3yWyGJqHIfG2pY666oppvY/SYJooVJg93nuIwG3+bZHz33Y16tF\n",
"EKMUeOqzGVZwLHwsav/DJ/PHSsexpPQ6U3P/NePdaqnPnPHmVs4dSkU2U693af+5cZonxETFKHmP\n",
"Pv/Fn1n9AYsqvq4W3Z7idPHICmMrrdAYWHUs0/HmtlEYo/zGz/7+4ddRK8AAAAAAaJoJMAAAAACa\n",
"JgIJvJwffu+nVl+4ZtUaL5dK8cbLuN0P+6zoHUa2uqXk1SszTqMtSzGWnaI+yaqAR351dceXito9\n",
"6au0f+2jdFG36Rnxz0zjsX08iOvD7dONe41qZ6l432JkOMhg1ogNwntR+h2WivBUjlqKVFLT5z//\n",
"h+u+Qfv3e8UYY9RN7QhzcXXCjLYulcZZo42VEcni8W+pxBm8Bs+IPnasAAMAAACgaSbAAAAAAGia\n",
"CCRwamHcMUgBhXG5mtHG3WJ+O0caR+cgEbMaPWef/mfHVfvrJ1WcMDwPlfsv1lVaPEnqJbfYWul4\n",
"nxET3VJ9tGaUUBzxcrkElTgzH4vea7ltnK5a6Ymkzm8fRQ4qqUZtlOwz6yl4/Zq2dJw514ilNjLO\n",
"pajl8f7gL/5r8xcmqmI427aPa4XKgnHDiWqvmwzqmNc8N93YNrQZXr+2jLE4mri9jeLqnCsrcH7j\n",
"z/zeKa49VoABAAAA0DQTYAAAAAA0TQQSOKUf/pcfo4+jWEXNKNWwjT7yVK/98aV1p0hjP96oSmKF\n",
"PhNVD287VblclIo37f51du8rWaFy7+hV9B7oNqXe18MnHxHHi6KEOfsnjm9TtPHFlMYGgdiaz8vL\n",
"xjK3VHY7m9K0/aHH0kWFD+zzGvxtsVP/fUx60NcuVQ8rtHktjOFlNPhme7tVoqZbzlFhxHPTa5xR\n",
"bVMEEgAAAAAOYAIMAAAAgKaJQAKn0cUeL5cVsZ7oUhZFwFZe8kbVGpMVtEobHvy+d6Qx0eco0rh3\n",
"1b6w3b0qM6YOpqvCGO1/nHnVust5Yn2llRPzG377+dzjjKKsqQjAu44bhteqhcdSG6Pr3SzWmtvp\n",
"8KG37d01LarEuRQLjuK101hMaltuX0sVa6NIyYfpczP7HD00OTfD/WftD9pIfZcufTRKP/LnuERs\n",
"UudvhXlVztMavk9PFq0cXdefeC6v1w8HdPL2c/gS1Kz62F0i9nqNd3ofVY9wrn0fDb86ise0smrl\n",
"hkqVxWMctvv23LNEHztWgAEAAADQNBNgAAAAADRNBBJ4uh/8ynfzLkTdXhWjjZfLvLJa9ZjTTpHG\n",
"7vIdRSNuUYyldvXM3vHxxdvtk/m2cPedV113iaZDq1HO+8+OmEXvuxNXU5xGFJuqfhhG7gbb10aR\n",
"F6N8iQhfFDvzZyJHWfO+S1Vsi6oVV6zw9ipeqqJl7lh3i9+9/YwSYzVjhJni167yOD5JfP9scI0i\n",
"1qsbO3EssrPh/bEporv2GAr7XFNt8xt/9ndPeXW1AgwAAACAppkAAwAAAKBpIpDAocK4YxS7iaIL\n",
"FayOTR1ZrTE4H7edzkdYbW0aH9kUh3r85Oi1GMY5q0bcUuM+4jyXCs/9OcZ2L9V6jvFUN62QN3ws\n",
"3P+St//e1VVfTRi3HJ/7peq7/W9BNLZ4/+EwJm0sDnu216D/oMLufdvg/0Nfb6Nto+2Dx66TCGuY\n",
"Wlo4vmlkJjrP4x0S0elI9Bl6dUsVO9e2EWbtCts9iUOjluH7tN843++IsU2u8cdEJud93P+Oqlz1\n",
"8FLxc12zkuRSGyv72DS2ClHrTRHS4sqNpX09rk571tjjkBVgAAAAADTNBBgAAAAATROBBA7xg19+\n",
"iz5WruDYN1E1Llc52hhFGnMiVVv66h1XnTA+pr2im/Pmw8qX0/33svT+eEJcMFkl9MzxxeRrFbyf\n",
"c6OKQROniSOGscu3nwuv3zTqN6zUdAufnIh4ZleNzHis9HXh/cmpQDuMfwaPdcI4aWL/Ra8e4wy/\n",
"js97LE+pVHmWipPDh3Y7D+N2q/dTs5Lk8GulZkSy8jEXjy3avzQWWRqr3RTjLItFfvPn/tXLfNFb\n",
"AQYAAABA00yAAQAAANA0EUhgN33s8XIpjsBE8a0qsa1UvDEnjjF63uD3t6eEY6xxmY3a2DlOek0d\n",
"06YO3n5GpyqomLZbTC2qGNVvWzrmxEFUdOqo4lB3Om7B6zfd53Ip/6w9Qxjv635c5/stRQ3WXmeo\n",
"JvW9ElZ8TFRHXKqcmG53Po7ptuH2uGJuWZ9k2BLbDc75rIUzvi6FVd+2tVHPqFrq5Lv86dUod+p/\n",
"U1XALMNqs/PHVhuNd/sxzF7fLeejQjxyW7XIdedjU4XRihUiXyn2OGQFGAAAAABNswIMqOIHv/TT\n",
"qy8mu6/sqmA0xr0um9ObuFfpZ34Oxpf9ff7nTXRD+u7m3Lutakq+B2rcmTVzGGde2ROej85xBROK\n",
"vY07ehXHj729x6IVWvcHglZe13Q1UbyCaPiM1z9mXs+0WEMsWoEy2Jq5Eq5JieNc/ETvfY5qrMB5\n",
"gtZXig2/B/c41uv1Q4VGoscqrMZ65VVhK0bDqRwAACAASURBVFd37X6D/ME5/eZ/9jsv/YeEFWAA\n",
"AAAANM0EGAAAAABN+/TZAwBeWxR9jG7EWzfm2N1Eus4cfj/eGhG9cEVxENZK9ZG9KvktFrZbpLD7\n",
"seHG/sNDLl2TnjxHpcdcWoThyau7U+c3NbbsggiVY8epG4hH441uBF94c/iwLkTWce0U+w1uin7k\n",
"+yi6o8VL3OUiLCby9s/c05coSBJGUZZSsEGNi+Kb2idSxv3+wbalcST7zOj7WfI+C/d9ct+7z7lW\n",
"fxxc9vuzSpePO1s8VZPnxvGsYXY6e1SZA0g9N6Oz68LYVtakKX3vbIq15d6mY1JwZU0cLjqu/rH+\n",
"x4bXu29z/jf4+BxljD1V4OlyKT7++98dw0HNO0t+dqO/XQpjkZvi2h8mz808B8MiUllxyIW/4eb7\n",
"Zw3jJVgBBgAAAEDTTIABAAAA0DRVIIFiqdjjJqNKi9067czYYNhe8NDaceZWUdt0SR1HJcfLy1eu\n",
"8Q+Molo1KzMuxdmmr+lO0ZUoivZo+66i90xqWf6TYpfhUv1uW7/T+Qr+3P98iaKHl8Fj3f7nO4Zn\n",
"GsUlJpHNKL4eRtqj63Oq8OqW62ONNhjLLArbS+53mz00+swl9usvjx/m+9eIar2al6ts+TbeVS9P\n",
"zWNNvp+Pfx89rcpkjX53+vzNz8mGsXbj2VKtcWXFxZFP1lfDXP0eKRx3/nE+fr2/+edeu/LjkBVg\n",
"AAAAADTNBBgAAAAATROBBBZ1kcdt1RGv6X+vaXIUr9vS0NvPfvl8pXZ783X597G/QKQxrKKWWdFo\n",
"J1XjbEsV4T5cg23HxBZT8cRgNOmqUo+2H6SFCGJutb/+khLst1uV3BYtfTZr9lFacXIpIlharW5t\n",
"yv2Ic9S6jHhmq54et5xWPQxO+HVDxCx/HJN/D09LjZhcquuFyHmdTsqqGK5tv0Zl1Ot1w+vdH+eW\n",
"/le2USmGWvzal8YhC4/vm3/+XzZ3FbQCDAAAAICmmQADAAAAoGkikEDo81/8mbKLwy3K+qyfY++X\n",
"gYexwdxG3n6OhhaUCSqOHz0ucxZVpitV5djDhoNI44dP5o/tHuvrfjtgVXV4LDvHF1N9jh7pSp9V\n",
"qHi6k1v0eemdY4xDYWXILhacKk84eui5VTmzpCosRvHM3Mhm/+/U+Vt4bG3VyAdjmyk9vtL2WxPE\n",
"+2bv7dxzNHj9wkqPk/1GW3IqPZbGUEuec5RwPI/PR0ueFqecvN/Cb6sjxlYhfpfVTZUqj9G1uG4l\n",
"ySoVFrvPTnQLilJbKoF2p6j0vGw4p4dFIS+X8Hy0GH3sWAEGAAAAQNNMgAEAAADQNBFIID/uGMYH\n",
"182jV69cGFXqW315uzcSXyLXjXPxmFPr98MGM6Jzo7b2Wc28ewW7KF7bPfQh6HunyFNYdTR62z2h\n",
"Gma0VP40lQUTr8FoU854zxJnS0UQL/do4DgGON09HSm8v8fOF419P56RrTzLm/yESr8jw6+HvJja\n",
"bfY3xYkrRGaPY37innEsqWjX8G+uGhUF0wav6bSvKjHDoKstMbxiiePLFZ2HLedmmr6uEbVcUzVy\n",
"+rlec35KK19WOJfZ52tlHPKb/3m7scchK8AAAAAAaJoJMAAAAACaJgIJ71gy+jiKe22P/FVJckwj\n",
"mKvGNc9Q3Me5pXLjWwuJSlebzkF0rDvFofaPNL79HHaTijKWnrdRrDQqeXcdN3uSWNmhkcWFc3qv\n",
"UBlsTMSKDnvvPBhH+JTb+FhGscRUIwsxx5eVrMgYXFvDx7rnXdKPZUmVdVxqLOdNsPSmiS5Ia23p\n",
"K2fbYHNmtdnwXOa0EW5KxNHDWyNEca9kmcnH42lNbrXI5P4VbWj/adUfD+5//N2xc987V5SsPu5+\n",
"vOvbvVY55i6WuCWmWTaOsK/SWOReUcjMY/mxv/AvzvGH8EGsAAMAAACgaSbAAAAAAGjap88eAHCM\n",
"z3/hZ+Zr6/to0JboXyIqVdxYbmQyb7y3KIbRPzc3PzXffV4d6r5fmCpPHcvO0cZbFFmpsaZ+qTpm\n",
"zvthaZ9U9cDc81bhXE7jrdnjOVL3/gsqCwa7bTsvUao08Z4KK1XeRj8+bo+aT41z5TVn1WuV1dfC\n",
"Z6003ZfqIqzuGn2+E5/5LZ+h0utctlkpth3aLN1+VF+Z21Z/Nxa2sfh6TveL+o76LD3fS/unIptR\n",
"G7lxpZ1jdYnv0HBTNOwt0aus8WQ+tfCaei2sUFe9/5XxuKifsO+g/eI+U39bj7pcFxvMPWfZ4079\n",
"98QneVUaw/+eiE5vckzXcVuDBq/ReQsHEo3j8XmOzmX099dyrHzSV8Koqnxq/+mtYx6N452xAgwA\n",
"AACAppkAAwAAAKBpqkBCg0bVHWvGHPsHVjeVXta9aLyUdzyu7ZGuvr2FtERem9f494qiaNnqKF60\n",
"5DyKem6qwNk1MY959K/s0nLw3eKh/aOTER0giC8eWvgso6/FsW2J9W22FPmbDCq6biy+x1L5xRfI\n",
"EyxlTQtTlFEseHo9GkU0gmt2tF9qHGGl0dwKlRnbwuto6tq39D2xchzLxzzZP2zj/mCqMnEYkw6O\n",
"r99v+HpPvh9GbaU+Ei/20cmXE3l6jf/mqlONr4JE/0dWntyvr/mF7poZF8xSISoZNlvzfGw43m0R\n",
"4JXVIq+Z17noqaWfq8IKkfmVIT/++LG/+M+f/Ql/GivAAAAAAGiaCTAAAAAAmiYCCQ35/Bf+0Fte\n",
"InNVayLusqmq3eqY43wgW2KOt2C1cZVqfX1EZHCAH+r//4TqlQUT1SurCKJJt+F5ieJKW7uMqu/U\n",
"iISGnQWPRfGiybbFNiqKYk7xjvuOY1EYde22BY+lnnekwoTs8E+sPorWPbYQB+wfC8tODX7PiS/C\n",
"qwkvEdHfBann3uZNNRn6iaJgB374r7kXxqgaX32jvwGCMe0dn9yt/evK2N6SilU5q4xtFDMsa69G\n",
"fPd6LYxlFp6/64YYZW5kNPU6/Nhfer/Rx44VYAAAAAA0zQQYAAAAAE0TgYQX9fnP/+FVH95RdKBK\n",
"hcPSJ79VAAyfV7gqd1i4rUYFxyhWEcUdC2NYh1VrvFyqxAz78U7+PXJAZcawStwOxu/FhbhZ1Y67\n",
"H0FEo4v6jPZPlcQat1lPZqXMs1TU7HrOLQ7VxxKDa1rpe1z08KPsSpKPr4ulFR+HFQhv02t2WEEx\n",
"eG2XIsupa2tiW/K6v/Qei6Jlk4fiYx80EVVwvN23TtsIL4G35f1u0aZXDtpMX6qsKo+N6N93x1/I\n",
"rsM4War72ud+8lk7osrkXn1UqSTZnd8KY6xynBWO6VocVdzQZ2ZfxZHN7PMwjhuLPY5ZAQYAAABA\n",
"06wAgxeQvdqrxk3tJ/9neNxI7v9AOGiV15rLV3+D/u2rpqqvVpq+fjVW643an69m629SX3lFV9VV\n",
"b9l9dr9tee+W9jlfGXH/7fGqjcmOG8zuEj/flt3Pc/8HYXRz+PmQ5md37/fVotRCt9QN/Ye7hZ+X\n",
"7pelVVAr3+OpFVqpm+w/egxKTVaxld7cfvRQxudr+NzT3Bg/7Hv+wUoO8elrO7pVLEsXhH0vHOFq\n",
"mpoLkaNFmi9yQ/1ZO1vajVbSrjy/T1sd1l17im+yv9MN8odf6Tljyjzmz/7yP3v61eGMrAADAAAA\n",
"oGkmwAAAAABomggknEzpze1vHyqsbq0QtRtHDNbFHG9R9GnLjewr3sB+kzD+VhpPi9qdn6Tohurz\n",
"/Qu72evG9FFaL7qJdHST5wpSN3YOP1dV4ou5jQTvjyga+wyZx36LjuGJoohseGPrbv8wwrpvpPZY\n",
"NTKQc+HlrksmBTdivwZNha9KIlIfRkdDecd3Da9Ht+xt4+1BTCjYlttu99jt9sno3x/3m5/9+DyP\n",
"T9L4Gh/vM233UVvvQvj1cP6b5BfHzXYbf+K9teXG44WiG+73n6DKx158s/O17W9qJLqWrG+jxrFm\n",
"jSPaJ3f8FWKt2bHI3PdAaTyzb/e+v+hjmhVgAAAAADTNBBgAAAAATROBhCcqjjuuiSpGlcSKdVUd\n",
"t1c4nFVyHGxbbmMSafywfg6/SqwvGU/bHrtcrKB4tkjjYr9vfQbj2Nrm5fIgSvUheL/1Gzd3f294\n",
"MS3UfQAO/P9OiepX46/+1MmpGGPMTVQFz0lHe4ftBQf9lD9zUhnuvBhe6joQXxu2xxehjtIPe1D1\n",
"MIhiRrHP+f6P+n9N19wqcrt0Xrj7zhURP3YyySpG2/bu+5JXfTS/3cGvFY+h9utxXVNt8XKJz1Fx\n",
"HDc496XPLYxF7h6FHPSV3H3pGvDW3mf/xf/nyz2TFWAAAAAANM0EGAAAAABN+/TZA4D3ojTueLkM\n",
"oi2lzyysDLkciVtu7xas6A2rqD369+UyjvSlYo6Z0bncKGFWFO9DMLZkJHUhstid5+HxTdqtExFM\n",
"t1HaR1Q5sbiN3I1RRcZpV8Okaarh7M9QqiRdqmreUp8rP5NLybWc41qVgkhU+Uuej+FDGce8lNYr\n",
"VfyZ6T5rg0f6anypxxauB5dgv6xteden9GeudByB3BRl6rHR22MSXx8+lnqTL+0ftdvt9iHRZxhP\n",
"Dl7T4X5Re6lxhJVcE++VZJ/BeKf9DLeF14rc/YLHctKLo33WfQ5HzYbXmZz91/SfF8F8hiqVvjul\n",
"0a7CQ1/6WyDVb/82WozFp75zM9/Qa1/bQfu32S/zdrMrSY7+jpl85kffQ5lVBKdtBdbEI2/Tv8dz\n",
"q0am/t7PjQMG5z7/fZxoOLyev/0IKtMn38ODW1wk45Cp63+0++AaEMYhm6hKfSwrwAAAAABomgkw\n",
"AAAAAJqmCiTsZHWFx9KPZHFlyMEy4hoRu9Ll+TtVMyx/8uD3fqn5ytcgaj4RbaylbkRyIbpT3PC4\n",
"qXFf3ab1Mcq03M9EhfdPKo0RRY72rk44jFJc5nHV6baH46gRR8ySjqxMKxwOYwXz6ofD56bafVJc\n",
"YNr9UtQsPPeF2cMwjpjbFySUXiNSsbMwEhTs/7JJn7yTlBeZe86HNVmJbu9L6yhqN+mzWr+T49ur\n",
"ouQoVVcWaUy3F5yjLc1WOP57ZLOwrQ2VT4vHvbJCZG5f2ZUhh1LHH0QxP/v5f/qyV8ZnsQIMAAAA\n",
"gKaZAAMAAACgaSKQUMF5447DPsvmu0eXhrXxtNF4nxBz7BuJHtsQ3YwqZVaM8NWMNo5ihskKh6Ud\n",
"DH9NVGcrtlDFqX8f75O5iM59FFOoWpkr9RoEMbXwdYwq2R3qY7/RnxRRVcXTZJmSccCc0neD/XKr\n",
"/b2oMHQ5qlDWPdbFVfMuLrltpNpNVzKeR4Oi/aP2xv33z3g4tqG4onJZn1H76Spkeee+O5YaUalT\n",
"mh7Xmu+52blZaOSJ53JbXK3ifwcufH2XVjGsITw3Ve+4MPpjuWLDb81viAOOG3r7UTPauOa5n6yI\n",
"BF4up45F5r5G93Es7J8RgfzWL/yTVq/eh7ACDAAAAICmmQADAAAAoGkikJDh81/8mUHW4Tr++UiX\n",
"gNlUqXBdVHLcZ0b/w4TZ2mhgEBHMjf9UiTl2kbThkuW1scudKjjWiTbef+/jPDXjeJd5fLJuhcZh\n",
"R1G7tc/zbdbq7HhqVMOLEnELkb/dz2/gHpEaPdqP6L7fZfLYUsnCnaRej7ByXDvRw9wY4PzPuFQc\n",
"MP8xKLEUCV16ziO34G+Lpt6ltSJuq5X1XyNCl+7gOf3318Ag4rze8A+2euMejW3lh6F2NHTt+Vod\n",
"ibxcij87q6OQ098f7b44nlvZOIL2vvWLoo81WAEGAAAAQNNMgAEAAADQNBFImPj8F/7QPO6YqTiK\n",
"VqHSYnHcMXpu7mUgN/6Z6GtT1GYac9wQ1xlXcOx+qdHe+uqE08pctaONVWK5yfaHUZXgsbXNJlb7\n",
"38I+SzsY/J4Ybhhp3P0rNBVLHNo5orh0jvriRsHrEbXR71Ojcmhd/Yg2RQSD60BD8cwsYdnI+WPJ\n",
"CocL0eKwquPkjXYLIqHjKraRcQx82s6sn9Q4hl810+q8Qfx6dMjBWyXZxqSth9un+72Tt+RHXQzp\n",
"ycPYyxMqLfZdX4dxtvkA7m+3yl+c07sa7BXTHF7Oa/ZRo5JkcFuD68PtBc1WiOjmn6v5ezfruaP/\n",
"DNopFllaGTLzczj+zEw3fvzxrV/6x61erZ7GCjAAAAAAmmYCDAAAAICmiUDyLo2qOk59KJ8XzooS\n",
"Hhh3jON9uZ0EWZVb2TkpryT59jOqxlcj5vjsCo7B8fXxxtwKhKlzNHzoNmk3+/WPsjjRGCuch6DL\n",
"8PxW/HqKokl9pKn61+Djk38bfZYSJ6SmhWqU8RvpHCvuZ9HiRMJyvP+LWogNhlUgJ3G9aVQvp93Z\n",
"Y1E0Nbr25F6/OJec74cgUpW8Low+m4/jn9H7LhnnfGnj4zr14VWoLLip+77/pYvV2g4Gv3cvy04V\n",
"OLt2k/HubHUrSW465gqf19LzcK/OmdlGP6ay93NxFHL6+6P2NkQgv/XLoo97sQIMAAAAgKaZAAMA\n",
"AACgaSKQNCUZbRwaRQSXV5iuihSWVljsDau+7TS2fv8nRgS3jDvqs1ZFyNWNTNraEA2aVfmq1G76\n",
"HFWMNl4qjTejr1Hca6dYVioqGVWhq6o0wnrCr/TTxRLXFMycfL6jCGJ55b3zVcCsq8YHMagkN6oC\n",
"mSpj+DiGFL0nR69pF1UePHadtDeuIhj1Nd42HOe94m8Uk86NTaXiYZlR53D/E15Epqq/tYKqeeF+\n",
"z7NbZcNSyfNxXIwyqjhZs8rkKCpYs1pqaYXDRWXVCUNvz91SGXVttHLNObgWVmTsZY4xe0yfJCo4\n",
"9o3ltTt8P4s+7s8KMAAAAACaZgIMAAAAgKZ9+uwBQK4f/NJPP1w7mh2xKY38RUVpcvbPfM44vpUR\n",
"d/ywYVXshrjj6qqOw+d1S38L27qtqMo5a6NCPHIUj+krOCYiTEuv/zQyebnMEi2L1dz6xwbnaOV5\n",
"Thm970qLMiX2G0eZEn1dEuc5s8/wPdAfy5b3R9k4Ypmv885S0atDY4yJKGF0vsdpqCiOmPGZWBlT\n",
"3tRe2EZuqcV5VD6K990fG/TQx3ajQUUf8NLHSttdL/06RPHJx/vHlWgH53nS3vj8paKahX0ubp++\n",
"B3LPY05b6f3i2Ocno3+Pegz2j6RipfETHm/KFrx+YbMVr8VbKvBtuwZP+01HZJNRuOQhZN7a4pq4\n",
"luT+eZ6oTh797TSOrXddJd6T0d/bC2njrOjc8M+ZKIpd/B5J/G0/Gk/q8zSOZq8ZT3S+ciohLsXR\n",
"k88J/j5PxiKHY0wc16z69OXBZ6L775NUFDLzKy/1fqY+ZxsAAACAppkAAwAAAKBpqkDydD/4le++\n",
"raMfPFgaU0jJrRQYRdKy283YfdTuukjhurEVRg7XLrMvreo4ipYstJfTXMWY45aoabKC4ybrI6z3\n",
"gYybulwqjzdY6r0pPpnqKlmJ7ZPZY2s/cyPDJvoYbPSEIIZXQWpZ/lMqLWYeX6qK5nOKzy11mhP5\n",
"G0YQU+3mZome8PrtbUuK8hZsCqKb8fv/9nBbf52LroFhRcZ5X8ltw3jTg+ct9TnesR942bY1+72s\n",
"pehlvM/LSLxuz6wMeUjfqe/X6v2P27umYppLgnFfZ79kipKNNaptXjMqGC41sSLSW/qc0vdZcYXI\n",
"mpUhF6KYqUjot3/lHzV7hT4jK8AAAAAAaJoVYFTxw+/91OyNdMtdEdTfzDDdR/EKh8ybp98y+78/\n",
"oftZduPZ3PGPPpLJFWvpG/bm9XXQaq/hU/sVQeXnY+1ql/im0OuPIecG9vltRW1sX+XVrbrZsrKr\n",
"O/fD/5uebGPD10nfbrg4p+6qt/u2xIt2wIqq3VdtLa246sfR/RK8F8Nlg5tHtlruORu/Z/tHoxYT\n",
"23aWuwCsdNXUwvUuvAZOCwVEBT6WFrj5c7KOGuc0t41ohU3qMza6RIxXM6Rv2L9hBczTFkomTlzw\n",
"kch63klsuRl/lf73Wj0WXR+rHmt0U/QK7Sc+V6uaKz7mqM+cFU/BQ7mvbfcZWvFeKF2NVb56a2Xf\n",
"mTfjH74+Vn49hxVgAAAAADTNBBgAAAAATRtFIL/6Bz/ZrYu/7xFFJD8klv99CG6q97b/1/7I55b5\n",
"ncAPf/Unxi9gbuRu9JzH+2XfQLzwRuNZ0Zel2OMkHjZ8LN1ublwvc045itDlyIx1hl3WuHn6lojl\n",
"gTe179tYezP70SUwFc1LtVEh2hjdVz2MvpY1e8TN6qObPN8/HzvFzqLx7hwz7Lus3U/mKepjqv2/\n",
"j/yavfd1C8Z7nW4bbLzH8PL7qGYhUpUaUxzyit7rQbS+wufq1YWnI4hnrt1/+Jzs/ZM3wU+MrUK7\n",
"S9GcJwZ0nyOdolzRzu1hs2c+qdcKNyivIrwR/Nu/DrwB/259DaOCVT9sb++7CuPeFFfdElHsnzD6\n",
"j8TC/bs+c/vq9q94Y/rBmNLxxfn+m/r/5PFn+Dvf+4cnvvq8D1aAAQAAANA0E2AAAAAANC27CuRX\n",
"f//H5ztGUciuvdLo5OVyuU1XCy4NLbVCuHTbQuoz67lh/CaxbbhbKjqXinFlxhezK7eVVh0M2siO\n",
"4GTE0/LbSpy/0QrnIJYy27+82tl9nLlRyaCv5BOu45/Z41khZ2yDbWsrMoZxoexGVj4vaGNTO+Hz\n",
"1o+pPzeXoEpbdiPjYWyqdhm6ztutmR2I2j0w1rdbhDCIX8+qqK2N7G6Uvn5Fb5rnrd4PY2fRNT58\n",
"cvDYE2OJRxa3K64Cybu1FAW975iIF0bPy9j/ZWQfRBe92m0kD6XiWePq2vtc/PrrzPCx2S/79Fmn\n",
"sWDkNSKNpZHCsJHhP9a9x7ZFK9dHdPvjT413eNnIOOerKkkmIop9/1uikP1x3reJPp6HFWAAAAAA\n",
"NM0EGAAAAABNy45ARkaxyGm8MaoGOdoeLbHufgn2XxsvjIaxMLRkFLO0r9w+94pABrGbovZHbSUi\n",
"lkttFEb+8iOby9HH7IqPxVUp8+aPs2NNhTHH+zh2jjsOtm/pqzwqOe77crmUx5WqRCWjeFhZ5O/e\n",
"/zCrtS72OXo7R5XmCvUV7AaNVK3WGI5t+7jDro6Mb02vL0tJwdXHmn7fzb7Co4/L7cEOe0uMrcpn\n",
"cydhTHuyz3Vp/xMe1+GCBNFS5cR5hHvQRCqhO7oulu2fGm8qp5pdBXLYyLTfpRxs1cp0ry8d68s8\n",
"Sc+IYiY7K/tyqB+nzPtQ7F31MYxM7vUi1XwPhPG30kYen9tV572velj+1L6J0ohkYSwyKwo52F69\n",
"MmS3fyoKmXkOUn1+57/+f129T8gKMAAAAACaZgIMAAAAgKZtikBGvvp733mcbcysDLk6ChltX1qR\n",
"GWyfRSBz23tGBDIzXhcuDc+NT2XEEReXnmf0ld1G6rGoGtjS8RVXo8yLZ2b334+jbD76/nEqjVjm\n",
"7Xdk3HFtHGoUQekqJ+ZGXkcNTWOO5fXZuqhrWGGtUB+bHS6rLj03WdHGj3sUNpzYVreq3G7Rstv0\n",
"n8F7pkp8cWEY/fFF27rfdlo9vxTZzBpHlHHbNKrNst4fGz5Xu1uK4a1ttrQKZHSOllLga8dZ2sbe\n",
"+x+hxmvbH9fC+7l/+RLX0dE/5/GpMG4/bTf3T5EoEXqyj+GSveOA6c4z9xue5y0V/3I6uPd0/21D\n",
"pcCk6/zis8frUaXN0X86rG2vbgx1y3thj1hkXEGx7nhS5+0exVxoK9FX1L7o47lZAQYAAABA00yA\n",
"AQAAANC06hHIlK/+p28P11/Pd5jEIZNRxMslXn1bGkNM7B/2nxvPLIxi7hWBTFdTTERWcqs1bqlQ\n",
"2W3KjaBkRASzKy5mR0dLY4mJ+N1o2/qoX3rHsvbvsYYD447R87Kjiiv7zI2wppqI4palr8tSpKR0\n",
"HH2UafA+XRs9jKJXfRTzwX6FppHG6nHG7pQOP98VY2RR9cV7TCiKmg5lZg4Lzd5HQZRp/Mbb3GWx\n",
"WxSr6zeeLyUQRW+nVT9HcbK3n+OPyePI2P0JJ45iVrH9wjGMJ18z24heo/mYlmLg82vUNOayWNEy\n",
"bH/Sxorje1lrr8XhR+M239zAR+iZ0cqwkuloe83eHl8Yq0cP++/qKHtboast482thJg0jyxnfciC\n",
"cS++xtPk9KoKlYWxyMSYSiOZyShkqhrkcByJNn78V/+fBq5C74MVYAAAAAA0zQQYAAAAAE07NAIZ\n",
"+ervfms+gKgyZGplYm4UsjAemaxGmYpHRs9JbbtsiEAuxMiSEaPcdhOSkcMtFSqjcaRilBWjj6Wx\n",
"x8X+N8QMsyJiucfetVlYbXL03OJo5eDBjPhDGItMpmgWxlMjaro2nrkp3nQNxhNm3LLHNXpqhYjg\n",
"YlW5Giaxs9Q+q5oPqjDGx1Dx3CfGEec5gydUiqROm0gd+ZERvVGVuJxuR0nF6NqT8fqdJn2W/szP\n",
"o7er353pz3B4/Vq6oM8ynvNOs9tN2Xv/Wta+Mrlt5Maq5zGre4w/qgz8ts9CpOr+Xol6Ps0H6rHF\n",
"l+W2vNtJAk9PrUr5qP8q52b+/o+PtV5sskqlxZoxzlVtrYtFFr+O1/m1NfvYc6uEZrwuNapBjttL\n",
"jC3Rlwjk67ACDAAAAICmmQADAAAAoGlPj0BG+lhkaRTycpmv8CyNQgbbF/usELfsogBh1GevKpAb\n",
"IpBZFeyqVKhcirhltFW54mN23HI6pmCM5dUM0+2lxnH/qFeIpkb7FUfohv8oPQ/92vDM/Yf9zpdp\n",
"Zx3rvCDcgzElmliMDa48D8Nl3YWR2LDZPao1Ru1fCl+DRfNIVSriU7MK46iCW/eRqPBarB3PKSQj\n",
"rN3GE403aXwdzb5+hIe+8hr0aiokD4vjsJfLPCa68NHv9w+2R9V/k2nEpaTi9M+C3ON7VopzF0GF\n",
"t+z3/+OI1itEMEur1j3L3pHK0bWvf6xeu+PP1cpjGUaG++ra8fYy90ZWH/OG99E1N3rY7V/a17Xw\n",
"+AqjkB/bTYwpM8q6uiJkcD5EH1+PFWAAAAAANM0EGAAAAABNO2UEMuWrv/PZvShVqkpj9FhuVDGx\n",
"8jGMQ5bGHVPtRzG8VFTsWRHIvas/aGuMMQAAIABJREFUpioVBnG25H6Lcc7leeBVscdU1crSuEvp\n",
"OS2NL2ZaG3f8+Nzul9KVwnnnNO6zcLzBfuVV8KIYXmFkMzGe8fkobG6n6FX/+dhU+XI+nnQEs96K\n",
"81FcImj+fnzRk6sNY3ycfeRip5X1UeXEYTRj+sjSOFJxs6qG43hcJXGcl5iey6U4bI3qfSstFFrs\n",
"XqtRfHhSfSt6Py/GtqfnKPosh48FY0+e5sw2Ukr338vSOHLebkvjz9kv97p7zfx89y9LdGEcmESc\n",
"F/d/CaVxr+Gvx8UGO3GP8+/5ugMJvpveHqv9svfXtMUqkDmWKhZuj0p2bWyJc9aIbJZWjtwtFnkt\n",
"PB+Z40j2nxmB7HcP9suNQIo+vi4rwAAAAABomgkwAAAAAJr2chHIyFd/O4hF9g8ETzgyClkYj1yM\n",
"402jcKPIXdRexQhkbvQw0W523CoRgUzGERfORzyOxHhLo481ooeZxxDtn3N+V0XeuhXv2cfX/ZLa\n",
"P4g25kY5gvFsqVhYHu2sGHMcqlg1sEq0MVWtMTuG9DgjFX/9VDgHS9fCHeJ68XtxuEe94woLUSXi\n",
"clEbdeRlwHL/zLhGH8OzVEecxr0WY8RRjHIcHWq+CuRJLBVui6Lh022Ptm9VpajcqwkPdB6h669f\n",
"S4nlSRvh5kNO7nIsa8ngr7mNY8nuaPeKj8vRwwqmsbdNH6wgErc6ljh4T1Z4DxaPozgWORxvYYwy\n",
"OxaZ0X5mNLVvY+kODYmxhRHIvt35th//b//vd3OpbpkVYAAAAAA0zQQYAAAAAE1rIgKZ8uXf+myQ\n",
"MQh2yIktRlHFpUIVGW0k45GXB3HIwuqLh1WBHK1WXRmBXKigmI4+Lvc97j9zjKmPR2bFx7DdsP3l\n",
"GN6tsM+H/Sb3X9n+4qWkLCa6ra/uCZPnbZAbm70/YV4hqTjeOmwuarfoiZf7SzCM9VyC6GhWRPBx\n",
"tPFje9F+Zbo2htGBeUXGzNjslj4rth932v1IRen26z/8fEwfOklEL6zYOdweRhS7XwpzSCf88yhV\n",
"yTWKgW+JhvMq5jGrpdd7GvuJrwGJSGH03Mz9X0V2pGsXpVX89okUjnTfjdF5iRLfNYZR8bhG18wK\n",
"Ucz7czeMsbRK4qzv9X0uv1broqCln5vl/R/HEXPPXyoqGR/TbTY20ce2WAEGAAAAQNOaXwEW+fJv\n",
"fjY/6NwVWsGE/y36nwCFN78vviF+tBqq9ObzNVeALbSbtRokceP7j20kVv8kbx4+XJWScY4W/2dE\n",
"3kqm5DFH23JWflW5yf7w19xjLtz/Gau9ps/b9NzMcadWeWX2nV6tUX4n1+mN69fd/H28Y9xGegVY\n",
"cmypVSkVvpKis3bkCpi9jivV/v3/gEY3Vo9eq9GzVw5koanEdaN/DwRPGD+y7jqwl9QKrJFo1ee8\n",
"teETtg+O0NKN7Pe6CX7OVdE7YGz/G7I/SfbKk526v3b/kfFxIPGlu8J4lo6z4kqx1CrYTe1uWvmX\n",
"WpGU126NlYflN8svWxWW237OTeo3rQDLbS+xUix1LD/x3/1fLsuNsgIMAAAAgKaZAAMAAACgae8y\n",
"AhkZxSKnkcZUFHLw+y14LIpMlsYjn3Iz/Mo3wc+6+X3l2OW977x53nT7mW1kRg+TN7wftJFz8+3V\n",
"N7lfaHf0nGTENHpC2dx6btxxdjPr0dL6xDkaRU3Xxwt7pecjkPW6BUNc8/rNGgljcqn9FvoJdgtj\n",
"nCtjiNmRxqzYWWaf0ef10aAqiQst3IKH9l+VP3v9TnIT9Vv0j1FmMi/O9qrcBJ+U3Nc76yb4wc31\n",
"X888gvWqh/KMm/KH19FuW60vwe7PueC1qtJ8jahpF6EbPVbaSFl8MBzGhvdAVr/D9pN//q2MQj5s\n",
"b7Jf+Gdp9B/ZwW5hBDIYR2KMoo/tswIMAAAAgKaZAAMAAACgaSKQGb78G+urRt66x1LxyOHvqXjk\n",
"JYjzFVaD/NjGZHuNCORCe+mKiI8jkIvRu2kkbtRnVAEtaCInzpZboTLc2P1yDR4b7hdU56kQfcw6\n",
"vtGq58Kqa4WVE/OrbU72zzaIkJY+N/F+KrUpchQde5TczOh/GF1ZfT6W2gijaDljW4piZlhIsk6r\n",
"Ym7qK3tI0Xs8pxZc+bimUcXwJQjjoolhrJA6gtwqe/FA9n6tynoJ37v9L+8vehjGkyf/Hu0/TMIE\n",
"se7ZY9ElMNx//s4PtwVRpq69KOYX9ZWzbdzv9ijhUl/taCF2efeUqpY5EbO9ug6ui3WqSw7eF7Nf\n",
"NjRb+XyURxTn+2eNKfpKzz6WxxUR477y4ov3cSz8h2xOHHFDZcjUc1PbfvLX/s8GrjjksgIMAAAA\n",
"gKaZAAMAAACgaSKQK41ikRlxyNvSPqlY5DCelqqulxmHnEUylqrKlUYTS6tQpqpAjo69LO6ZjECm\n",
"2s09B7nRltS5qlzxMYyaZnzEl2OSidcobLD7kTmO1XHHQRO5UcxUBcnCy2F5Bc5BROpSGpGax2nS\n",
"FRxTA5nvPmqr4tdCFD/aEjHt40ph+9ETSnsIosh9WzutkI+iptFnsn8oeO/u5NDzUCisNHod/Xiw\n",
"/+uK4nrTx27B91tcNTKvjeixUjXaaMk1+CxH78+c85YbLR5Hnh7HoD4EsfG4jcei8Z4n0jivNHea\n",
"ob1JxcMOCYhH0bKanY3+/ura33KBmf6zLLa3rDA22HVdGB8cP3chSpjqq7DP7HOfqtLYt7U9Ajna\n",
"PRWHDPpKVZKM2hJ9fJ+sAAMAAACgaSbAAAAAAGiaCGRFYSwyVRlyKPVYEIsMo5A1Yom5FSFTkbWs\n",
"WGLQ/poqkMm+Hs/vJtsdne95G1Wij+E4VkYfMys49h/1NTGg1LksjA+W7p9sYzHu2P0sjSoO/7W2\n",
"bNewvdI2NkRuE88rj13mtbu+jfvvfdRn+JkIEm5peTHRe4W+T2b718hLxFVvM+Kfwe75fQbR3n7j\n",
"eVf4PzuWmFsBcPrWiuKDo8/aJ/PXO9VX1OdrxAajN230wU19mBOfkzAmM99/dO6nz4li2GF7mWPL\n",
"2nZZOIbMNl5I9JlY89xBK8GOox9P95Qqj5l2H9t1/vneq89hrK77O3dTdcn+fVQYUYyqUW5QWjVy\n",
"UywyY8A1o5Af21se79I5SEUaowhkKmI57Ev08X2zAgwAAACAppkAAwAAAKBpIpAH+fKvz+ORxVHI\n",
"4LFxfOTt97XVIC+XODIWxnneNqUik1F0M6zIWC8CGZ6P0Q7RftM20/PCuXHEZDXHRB/Z8bvcyonT\n",
"cx995JfOW6r5zEjj2gjm4mva77iu/cd95ew//MfafocRqYw2DqjgWCWWFlU2rBF/nb4Hws9LYaRx\n",
"6ZxGO063b4kvRk2cLLYYVfN8xniXr4/LcbPwz55Dk2i52d7cKOH0sfk1Ja4CGTzWRQqT0cZHj5Uq\n",
"baNGn9O2HrWX6uu4Y49fj3Eboy19vDv63hzEt/rN0XsmGMds/xcTJOtjj49vvyqWSxekrv+a5z79\n",
"/q/aV3DZGMXeanyc+u+k7eMujSWGbZSev+H7s/C59/3znpeMFCbbjzYOf099doL/IAzaSFWyjLc9\n",
"jlhGr+NP/dX/41x/WPE0VoABAAAA0DQTYAAAAAA0TQTyib787c9mJ38xFjndPvp3F+8YrPDMiENu\n",
"qQaZjChmxy4LI5C5McNUBcdUDDAaR2bMcG3sMbuvW+X9wlhk4vhzLxdR5DX53CiaVC/uGFUIy41s\n",
"TaNBH7tPnY/HEaXsmFgYGZ5XlSu1Oqa2kNCoGW2MY3WFkcao/VvmucxNp6X66n+J2k/EKCuIoorP\n",
"rgKZW2nxHs1L77eHuIpg6rzNB7QUO8tr7x0lNAoPOYpuztoqaI/aggp50ffEwnOnsitE7mxLLHC/\n",
"+GTU10HnpnJFxL6tQXQt+ZlPCi4Io/FmtLdwUDlj2vRadLHO7JM7jDgXjq1GHLITRkgTY8uMf8bR\n",
"1O6Pi/mxRG2JQNKxAgwAAACAppkAAwAAAKBpIpAn9sVvfdaV/7lLRSCD+GQfA4yqxOVGFDPikGFU\n",
"Mbf9fv8gslgYgVyqGJiMaiUrM66PQN77XKg9lIxzLpyHyWNZscelMY2K9KSiozl9Rm2VxQFzn7Ol\n",
"Gt3aSpXjfktjjnd9aOrJMcd0pcVIXtxrHmncfpz50dT1DqtwOPi9xnshu9+siGI0jqUY4ESQQt3k\n",
"ra+lpqbHVeecni9zV1zxMfHYcmz8HUY2nyAnsh9FfZaq2KZiVVH0/MgI33Gi49vnv4nS53u+32Ex\n",
"xgd91fx0j64zNdqteo7KYoO1x7G+4uN8HMvPTVRMzKwMuT4CuX0cYQQyswqk6CNTVoABAAAA0DQT\n",
"YAAAAAA0TQTyxXzxm5PKkVEEchQZe/sRVETsI4propDTWMxS1cGcPqIIYmG74XEOt6finKURxMQ4\n",
"xn2mopXDfz2OOaYikKMmkpHGvIheTkW/0bgz45ZZsaMoqpvafUuUaem9Nevr/jpmVZIMElL55y3q\n",
"f17JKC8SOhhGP46y8xyNYxyf6s5NZiwsyEEkv4pGlQ2Drgql4l417dbu4PdpD0sxtdR5vua+HvGz\n",
"Hz4vHS+KxpbKSu71Wg16yLlURVUjgxhxFDM8tSijlPtYjXa37h9tX5NWTfTVR4aHD+YewzvRR9NH\n",
"15R1J2JUsW/3c1n3v4n2jjLG7c+vPXv0WXrNfNxgd/3cMO7Z3RVus03h/kkb4pHd8xbigOFz1sYi\n",
"K0QhR+ctdTeD3DEmKjeWVnyMq1Z2xz5/rX7qN8QeecwKMAAAAACaZgIMAAAAgKaJQDbki+9/Nn8x\n",
"P0x+XoKY4CjaWBhpDCIrqytC3jaMo5eO3JVGINMRt3SMLB19zFuZG4532sbSRzgj+pjqZ9V+OZUe\n",
"V8QB82KU81/HKZqciOfwGSujiisurbOY44pKmeUVHCNdnC3KG5aej/kz78c53DHRRtD73vHC0dCS\n",
"FdW2jyMV/Vs6znusdcsIcnKl86hi+Ll6gugcXaNjiSLAeyuN5uWmiMNo8/jfHx9LRDFT/Wd+Nodm\n",
"keIVbRRHnFP7p66ja8ZWMp6HY5r8e2Gfa+o6cB3vU7Lfw/EM2sjd/9UcWWExRzKSVr2vIyOT8y+K\n",
"Gm+fGuMsjQ3eLUTzkp0mxpF6Wmb7pXHLxfddd91I9b8UNU2MKVkNMopAZlaB/O5f+98buEqxNyvA\n",
"AAAAAGiaCTAAAAAAmiYC2bg+FjlcJXob/xxFIhPxxbwo5OXSx6fWRiEvl7AiZE57S9G1qhHIhTjg\n",
"2ghkskLfUiQ0jPcdE31cqsB537H7Wb5KOataY+Yxxe3mRTb7Cm9L0ZPJU5djdalBBs8rjErexz0c\n",
"R9/YYt/D3aIqeKNzXxpl6scTtFs5sjZtr0alvvirdB4bHPebem7K45zV+HN4S+y9U4Q0iiMGVcPC\n",
"2E33dn5Gzir6fAdjCwXv9VQUrThyt1dcb2dhpcyd+jhbrO1dCqKbj7Z3kt/X/abMq9YTLhtHvu/6\n",
"OOyB4xi3u+9nrWa7WypJRhVM8/sti7P2342jx/KfV7Rf6qOWOe5UzDI5psJqkKURSLFHSlkBBgAA\n",
"AEDTrAB7h2arwlI3yL9c7iudPgxXM1zjfS6XeCVV6eqtYFVW8ubi4cqyzFVkpSvAUuOIxhvtltoW\n",
"jnH5eeP+16/6qrraayir3eG/Mv6HzuKKuOgpj1/veEyJ1zvneUVPmjx3tAIlt73pis3yG9hPb4Jc\n",
"awVW1mqz4jaj5THr20+t1PoweA/Xufl839pbY483fewrOq7pk45b2VW/k7efpYsjM8cWrUo59Ib4\n",
"B1laRZn3WPl1gzqrSUvPfW6fuatGWlhVV3pD8KM865xOV+GOVxnVuKn8ZdT+5XK5fPLJfOVvzuqm\n",
"cbuPr1WlbdRQ/Ubz4XPKVqDl34S/W3GVais93vTYEu1XXwH28ffvfv9/8+XEKlaAAQAAANA0E2AA\n",
"AAAANE0EkpEvfmN+0/w+7jaMsKXii/2N8cuikDVvhv+xvdwIZPcz2L/wJvhrb3z/cGwZ28YZqXXx\n",
"yeyb4acillF8MXF5WRMPKY0jZt3cfkX74U3t+19S0df77/fIwPD1yxjk6Mbq66KSSzdsL497Bm2s\n",
"tFckbXTMk3O/WMwgSoUlRdejaNv2yOa8n6WY5Mq+cpsIbibfRx0uwbaF2GfyFO3050vqRv6p/Zei\n",
"aHsVdXglpXGoI26kn6uFaOBRWjxHuTcUP1LVeN/we3Dw6L2v8jjfw74G4y6NRS61d1hb/bhzj+Vx\n",
"5C97PMn4Ytm44/2HxxLdDyInRvn4ecP+syOQwXi/+/3/9SSfQF6VFWAAAAAANM0EGAAAAABNE4Fk\n",
"UVYsMqoQmaq4eBnE7m7BtrVxyNG/g2hlKg4YtV9YBTKsZJloazH+lowvPo6ahn2k4ohhBHL4eswf\n",
"m44xN0KXXa0xM5Y5b7c0znnJilJtiS2VV5IM3rvd8u/F13vYQp1x16lsFkQ2N7X11tTwZQwq2KXH\n",
"+zjbOI5epdqqH2Mc9lXr3Od1Ovi9O+bCz+Gz5ZyjQ8/pAabvlRpVIKNz1Np5O6stVR3XVoEsjf0+\n",
"TRfBevIwSiXP/Wi/540j3/w77x6PDG8MUWbQxCerx7s9YrnmXM2es9h3WSwytwplsr1kBHKorEpj\n",
"su8gAhlGaoOxdX2JPVKTFWAAAAAANM0EGAAAAABNE4Fkky9+/WM8clRxMTcW+fbYlsqQ6Qhk13du\n",
"Jcl9qkAmqy8uxPCS8aPguLLavT3Yr5c492GbefG+nPZuCzHK/5+9O4+25svr+l7nPE9MIGIQm0ZQ\n",
"RGgh0ulR4kJkEBnCKHOMSxNdhCgxIC6SaGLIMmSZyWSZZC0jKgQkYtQkIAEVQabuppHRNLY9MDXi\n",
"YmECi6RDBBvw95zKH/fsqj186ru/u2qf4dbzfv1z763atfc+deqce5/z7E99R2fss7Xf4jBvTNOK\n",
"FW05H96Ah6PCp1fXaOMwNMcbVaTxdOoZvSqjGfN7Q1nzarxQpLG7LI0i3zOSTdvjp175Y06ex+mb\n",
"+001tFYgrMUMHz8Vb1Kvq/J1a/Vhn+fW9vEx3n1WtNnXr79CpDU3NZ/H+Tf6XcYnN7rKYzIuj2n8\n",
"2suwxzQuVFVx/j2/vn/r2Na4Y/M8DuXfCmbzOCrofq7qscjelSHltTXtK6OKdvv1EcjpfEX9vtuf\n",
"+eE9/RLFnWAFGAAAAAAAAHaND8AAAAAAAACwa0Qg0d0Uizw9mTeGSGMcz5mqQKoooRGjjJ0jh1aM\n",
"Mq1mKOJ9eRXKWrXGov943s5Y4tTeXtlb7E/6EMcakTh/NM/4XPzGFR+tSo9j/jw28MwzeatsHiNc\n",
"d+U2e9B4/NZIYb/4YPO8F44tqylumZvqo4w0rs2G1GJWXaJteSRiS2zW2Uere47w9bjGbxFV1HE5\n",
"bzRv6sU4tvydp8+Rr48+OavWPta2V8dseT/o0W9ru9ocQ0Tq/JNZnTaOhbVWgdT93YPHErGc3l/C\n",
"hktV26ykZqdoWcfIZL/nIL2ee1xrR2e1RKX9canXmtG/e271KORDg/z8Vdo19xE/vnQu6rHI+cp2\n",
"yxHId/sSYo+4LFaAAQAAAAAAYNf4AAwAAAAAAAC7RgQSV/VL/+0vny+4Z1kcsVYhUlZ4DMd6opA6\n",
"QldWknRWcuxRBdJ6TMMgVoKX56jWX9GvfMlXoqb5NlWhsXvcse3zeddj9/a1Iu6YR43SMa25ibG8\n",
"kTjR+7Wikna0cZ7d+mjjUh/9V8YncccwZmMlThVBycICy8d2VDvf9xP5S/fdzvKLrR4Ly9vX+r31\n",
"Y70OVdHVvgbm7/P3ktb2558W91n9qefW6tffR7mttVqdYo15XSre5Gt3z+4lZpnPo/s7yvRnh7pQ\n",
"O3S/6Tw6I3bmBMKXxqhih+ffXYXRjEUuRxDTTnzjmvsq8cw8ttgjAhn3QfQR18IKMAAAAAAAAOwa\n",
"H4ABAAAAAABg14hA4uZ+6b/75x8uwhfmz2NlLDJUkhyNbVEE0YpDqkiVbn8U7dO+Yj2qQJoRwUos\n",
"UB7rqQxZi2e5InF2m/aIojHfxret6twa+zXPm3mgf071sS/Tvt5HGaGbo0be/vpVa9T9l5En8zyI\n",
"aag4WxyhuFZ07xrjqKqAdoW5a/JEFNXz7ekz6a2yfx0d1/Mda7dfvsZVnDnedhqXr2f1etHbyrn1\n",
"fXzb219aGvFc3m/NV1Va9FZktF6bqr2KfZ1Oh8X2y/1dizPuda0xO7hGrNKKmm8a/5D/OC7ua+o2\n",
"zGlThUpnxURDa+VI31htscth8FWJVBUUW/tS80+2ifn2iEDmffyqP/dDt/4jA88hVoABAAAAAABg\n",
"1/gADAAAAAAAALtGBBJ37Zf+m3eZLtBpuf8zEXOU8UhvZcgs5hi/JDpWhHRHIGUVyDA3b3t7jPlY\n",
"4zNwd7VGo39r7MF4nGnD8hj1OKdvnPNufnyV9tMq/uUYUrWqY49Y5BQnsJ73qLmIurX/WlDX5fI+\n",
"k4wjlhHMTZmL7PGl50+3WTVMaxSzg2TaZkTqmnHO8P4cj1+2Wn3NdOCv4GiU/Uz6e/5SHZ4YZdI+\n",
"7DP6sPq/JM9Ytev5eTE/9loFuYtPZbP2a+sy12Ly/hy2XWQk/+vV11nZb490uX8+66ofpu1ax2wf\n",
"w9N+2lc5Z3MfbZFGObZ6/pJjGiOQ4jGEPog+4pZYAQYAAAAAAIBd4wMwAAAAAAAA7BoRSDxqv/hf\n",
"/4qHC/iZiDt6Y5FTO1HxcUyPK/ZnfcRWRyBlNM+IQFaifPn+NHqockhGzHBTvPCQdtuhMqM7ZuSN\n",
"UTZWd6zFT5v7cLTzRtfCW3taqWw5iuav4Ghcn426RARVZDK+/jpEGlvPfU+XG8eOvOZxpXpE0B5j\n",
"rXxuuvKeeCwioWjHLi+vjAjO+3rGw+qvq0uHquAWx4U6vtZrUazyfaW9Wt2l2fPo+8Jd/5h974He\n",
"qn1rpb+bwrYePZe/YLtEkCtRO/tQXzTQ7MOIDVrt3ZUcO0Yh4/cIPb5RAdM4tjZHHW9sjECe97/o\n",
"z7/1Tt5VgAesAAMAAAAAAMCu8QEYAAAAAAAAdo0IJHZlikQOwxyLlFUjrUqS0efCoYiNilHWopBT\n",
"3ExEMUOT+OUnIn/FMaJqo4wbGn2kP4s4oBmrM/bVopiOeKG/D2ebxrc3OcesuqO33y2Roy3V8PKY\n",
"o46MxcpYZL6vVsbJiltuig2q198FIo1qXj3ijtUqeB0iT/NjUfusIy+TSFDVRK25Xeq8bFG7Hjzt\n",
"H7tapdi1MajWPuqvoXSO7n3R99NbinjP1v12jILtyGM+H765b7/+vfPQ8ejtY3at+Gj0362PlW+t\n",
"6+ZhRAmNMXrHIu04pK8vFblVcUVrTCsCaUYfo31EH3GvWAEGAAAAAACAXeMDMAAAAAAAAOwaEUg8\n",
"V37xv3zXcRiGYXyhrOo4PnvysOHZodiXVBlTMUojDplXg1xqP/Wr4otGfNBbSdKMIFZig3a1QRGj\n",
"lMetiz6a8aJRfasei6p454wjVmKZc7+OeGb0vWptnmfRZo7uWKNuj5V2Oy6bZ49oY5dKkt6xkh8u\n",
"EV+MY5fHYpuu2OmJBUetzaikiO3K56WMzbZWE7VsiefcSxzRCj1vqdJmRYuteNO9nBcEl6rEWY9u\n",
"ets/FreIXnoj51ZMrke1Rh2ZvGw88yZ9JH8q9KwC6W2/XMVTxgeNufWIQlpxxodjxXyNa9GOQI5F\n",
"u7BPxVVf9KVvecTvJnhesAIMAAAAAAAAu8YHYAAAAAAAANg1IpB47oXKkeMvPh2GIY0sThUkoxhc\n",
"iCYl0ThVGTKLzo2VyKQryuisAqljeyG21DkCacYXlz9j71Hx0ayYmVCxVjVm+KZvbHB9zNDbh4iu\n",
"hWjvhkqSzfGpJJJaKb3mmsdwnkc5ty2sKm7r+y+fg/T6L+MHPR+L7r/fOGs8htid/1pII2v3WL3y\n",
"Xnhimqp9vL+1fW18e25Tb6v7Lft63LHCFo+1+qNVVfTcotq+zzxq+3uMm79/xRG5dfcf8L6+W/pZ\n",
"q+ij+zm9TIVIT3/eCo1pg/P44jk1KziKdlZFyfi4F30Z0Uc8HqwAAwAAAAAAwK6xAgww/MJ//isf\n",
"Vof906fTtrAqLFnRZd0YX67QEivGxGqNnivAzJvgm+1Lat7pfnXj//Cd96b5y/w3zV//GMzx1Qq+\n",
"6RvvTfPLvlpXXOnntH5z5eYxxd37vcUBrO6SWRurRrbosyqnvOn7UpsWeX/x/xafTodiW3Rk1Mdl\n",
"/9P1nlc1WTf17n9z8XX0ay1smNu1zta7asp8XcX/65+tJLyX8weP9YUyHt/qLXWn+eTLXel5fq0b\n",
"6R9rK4Kaxzqd+7dXRfr6uuHN8wfHaqnVY9VXhcX77NVgvnb+1WDLc7NWgOl98wqwfOUXq77wWLEC\n",
"DAAAAAAAALvGB2AAAAAAAADYNSKQwErv+OJ3n1NvL4RIYxSBfOHJeVvIJIi4o4hMyljkFDeL9x2y\n",
"fdEuM1q5PgJp3STeuuH90jytsdb3Yd98fTQimK3z8R7TfDNyFVGyihgY8/FGCs1YpPPXRC1a2XxT\n",
"/coYW+lzFK5jkfs051NGGE6nQ7HNii+qG9jXqEIBS/3finWO7m+OydZiy73N+xqsYhRW3FIVEfD2\n",
"4W1fHlfu73HT/KX9rj7ED/u4Qf7yjb5bXx/XjGIWUeTllkn7PoOr2LFo1iU2GA3VMypp3GB9U7cr\n",
"b0z/cKxngLaxWqOQtWPCHHWb9RHIQfa7PQIZoo/pNqKP2AdWgAEAAAAAAGDX+AAMAAAAAAAAu0YE\n",
"EujoF/+rf2F6QT37uXcahmEYTueqkbUKkaoyZIj8yShac0XI5YiljjQa26oVHEXVPG9VyWxu7mqU\n",
"VkzNWbHQHS+cvlmOifojINHzXRzTGsOzmZGjDb8K7qVa4/z4VL++cyn7nb4pI11q3roSW5trRuz0\n",
"Y9geV/WNHY+59ljvgbetcGjFVec2l48RYy/WRxAfV/VHe673Fie9RZyz/bj5+/l9qTFSmFiOi2/5\n",
"46L18TWfj8bH7O0/rpxosSIIqZ6VAAAgAElEQVSpMr5oRSwrFRzzqGT6fI9Jm4f+ng3DMAwv/vI3\n",
"39krDNiOFWAAAAAAAADYNT4AAwAAAAAAwK4RgQSu5Oe/6D2jqpFZhchhmOKQsjLkKf36IOSsyshk\n",
"bDpWtM/HTo5T8T6zna+91b+3WmOt4uTq8ad98U9tq79PZtzSijvamiNPzVFMa8wN8cEe0UZR/bQH\n",
"9fguUWUy5q3K2XPMhZbR95d9zPfGWxXQcunn8ZJ0Vcd025oopqf6ojfOuaWSZMu++v7liJS/QuQQ\n",
"tVts5orI7t114oNqjMtWZPS61Fh9q0ouR2/XzWdtjNMbR1wXi6w9Pl8lSTsKaVflXJ5HvbpjPeaY\n",
"7DuG9vN8X/wVb3qO34mwd6wAAwAAAAAAwK7xARgAAAAAAAB2jQgkcEO/8CfebXoBvvBz7zwMwzCM\n",
"z6IIZFYZckyqRqpIo2iXVfmT8cFNEUhRjdKqFjl90xaZXBrL00d73DD+abnSYxpptMa8TGxQzeNg\n",
"VCe0x2qrOLkuApaOpeNQznirjHFdL9LYsxqfqk1ovU56q0U1l9r0n0e5rayo+ThSGWb87vy19kis\n",
"19pjjmAGt63J+Zil0Sjv898aBavFTy9PvSEkX+7KtaKSvcfpG49c369u7+wjxBabRqxUVYz3GR33\n",
"qAzZoxpkrQrkHHMci/aH40O7F385sUc8H1gBBgAAAAAAgF3jAzAAAAAAAADsGhFI4M6844vffQ77\n",
"PHk2DMMw/NLbf8UwDGkkQVaGPMfHrGqQshLhNSOQql+jvVk5Ma4aafXrZLW3qzuqvrxRPme/Xas6\n",
"Xv44HdU6JtvaY5rDoOKTa106Tralmqh/DF+lu+3jzN/bleysMS9TebLGqq5nVyCMN4YD1LzvK8zn\n",
"r744RNuGdJvK4ybbHJUb42vSG7XO+kiC5Od9p/ixiGjeyfGaSCqgZfviecp+s7kmfSSDZTuH8hGr\n",
"a6wajc1+vo+rrpflqpu9+p3ZAzzWSOPl4qo9qj+Gr63xSLuaYtm+/Zy64pCVxx7ej3S7sjKjksch\n",
"10Qg1fkK+4/nuOPx/O+LYRiGd//yN+/rbQSoYAUYAAAAAAAAdo0PwAAAAAAAALBrRCCBR+Qd/+mL\n",
"5njkeRnzL/zMu07758qQx2KbihlOMb04+mFE7dwRSE+kshJfnCpaNkYm18XqlveNxTflHB+OKbe1\n",
"zikfdEv08NLHpZGqsC1uUe+vFm3U/Xr6u0zUTs23R/+tEb0e/er2dnTuWqy45TVipa1UxU4Zo5z3\n",
"nr/Eb4LprqR/d6TxPs4H6mRk0mwfxbQd133SQsWlsvGT6ykaSXe4uKmvlZX9rulaMcn+Y14mauqv\n",
"iLilD1+UsL1fR7uDs53Rphbn7BmBTCs9Pnz/q7/y793zSwq4ClaAAQAAAAAAYNf4AAwAAAAAAAC7\n",
"RgQSeOT+yR9/8Ry+e/pQ1SVeHv2On/pVwzAsVI08S2KMRnxxSxVIM3Ko+g1rzZ1RTM84S/vLt0EV\n",
"bVR9daj06DxHzf1ObeKf2qoezvt80T+zqpw4pj3a2Dfu1TMyWauS2Lci43IFvkuNuUYZCy5jN83X\n",
"fPR9az3GMJ84QjadN7O643zMY4sbqhisZ1v9tbn8XtJ6jqz3I72vdh2N7n1t/ZZz8vRhtetfqe++\n",
"OH5DVQ/oc4rurwrkpfrv2a/1+r7GPHT8T7WsxwZb9re0PxyNfdX4Yrm/NQIZxo+jlXnFx2EYhvf4\n",
"yjfu/N0G8GMFGAAAAAAAAHaND8AAAAAAAACwa0QggR36+S96zzl89OQciwzLqqMl0f/kH71oGIaF\n",
"KF8UM5wikFYlyYinCqQVY1zs16z+GL7zRSDVW58dB7T/v8AXR4xzN9Xmzf2vaa9iDTr6aPV/iVji\n",
"dY+9Rf9WHOqaETs91vYql2YccfpGZZ7K6oiq8p1VSU+FdntSsVy134rObIv2XqbSKR675Wil+9q6\n",
"s+qLXaJ0HeYh+71mFciuz8v2KpC9HntrP3lEsN5nv8hmNVrpiC+m+8uKkKsjkNHf9u/1VW+4l5cv\n",
"cJdYAQYAAAAAAIBd4wMwAAAAAAAA7BoRSOA58XN/7L3GYRiG4zkSOQzDMExLp6P3gfMy6p//ifco\n",
"+lDVIFVcbn0EUvVbO8Zo76pwWMYh0+PaooRmm0rss6Wvde2zKOtifz3GWte+3l/4rnUe8/dlhbfL\n",
"VIG0o4Xrx1Ljrq2q6B8n6lfFOsJ7gzjWiipew9rqhCqKeT/BsGW1aqzTtuSgvL14vmVk0xrLV2XP\n",
"qrSootaVUK3Y76sa2VoVsFZdsrWdan/piN3LPvN1i/ve9DUf0Xk0b0W//g7OKpC3qPzY5/nufW7X\n",
"VikV8z/Ib12858MTi0zfB9oqN7rnc1g+b3aUsZxb6COJO4Z9x3jbw9/s7/WXiD0CXqwAAwAAAAAA\n",
"wK7xARgAAAAAAAB2jQgk8Bz7x3/0vcdhmCtFDkMUkYyXWIfvz8uvfy6KR4ZYX60apCcCWa20mB1T\n",
"j/KpMerH1uZh979cqbJ27Nox0+joeYuMEFmPef3cbl390e5rXTVDf6Rxu7WxTnf/lY2hwmIyuhn3\n",
"uow8zqn23WME0Yq6WpE4VXlVV2MFLPM18/JzpLH5T3vVvrGPN39d78hk6apVFw1yHsb717bBplK4\n",
"/fqPY3Wth/aoyunsw9/u4Wu47uuRyPD+vH4eZlRSjK/7sKpAlr9DQqXHX/bP/eK07cVf8SZ+UQCN\n",
"WAEGAAAAAACAXWMFGIDEP/73f915VVj0P1Pn/3U6hm3x/2SJm3KG9j/7tl87bVq7Aiw5zrxZvbGt\n",
"Mq41vtVvuoomfNPxpvnO1V7elV2hnVpl0vPG90vHNt+EvPNcPH2unaO/j7ab4NdaT2OIG5X3/O2u\n",
"VsTpdss7e6xu8s5DH+s9YN2qwd7Uijhrm6o2YN4E37hma6vTirGT8Y3iEklhgR7n13Nj/MrrsJh3\n",
"tMu8Zms31w87l1fbeG+Q/7JPe2250eJ98W9p1/gGowrmvOUbPqytk7WcBS0utcLsGF5f8UbjdeVX\n",
"XuPXXKHVsw9/+/oN+pNVU2a/l7kx/rStcjN8awVYaPfPvvM7pn2s9gL6YAUYAAAAAAAAdo0PwAAA\n",
"AAAAALBrRCABVP1//+6vf4hFPn24QX6y5Pscd4wjkNOybnUj0PO2t7/t18wbpxiefSP9aZt5A3u7\n",
"vYoNtvanoh/NfTj2pe3a/r/CE21cmkdrDLD1Bt46xrXuJuCt0S4v/03wfXE5M4xl7NwWFz13W+ni\n",
"Fjdbr8dDg9slPtR1ZO3T14zYNnXSNx78GLQFgB0R4I37vPPo7eWf/pqHb8oE1DZj9tVN/Y7U+5fH\n",
"Xr5dgZuI7L/5Gz+0nM2Nb4ZvveZ79v8wSPq7cdu1W48PuuZ00ePKaPGWMUIf/hveL78ot9wM37oJ\n",
"frwvRCB/2Ts93Oj+Pf7CG/f9SwG4AVaAAQAAAAAAYNf4AAwAAAAAAAC7RgQSQLOf/cL3nd44jk+e\n",
"nb8RS72P81LyQxaHTJaZi6jk29/23sMw+COQepu1z/j8PykYleeW2udhsdvXopvWtrVj2u29US0V\n",
"P1obQ1RRyZ7cUc/o+6LOnVkNr3dFxuXqZZeK0PkjoffhFufIy47DOqOVsmOj0mJlWx5Brr3mD2EG\n",
"yQs87Ve1H+NqdeohuPZF8zYq+clrQMzDM59kf6h8HO07ncd65ad+u+hloUMXFWVfef2qPtan06Jt\n",
"219P7tekquAo5vSWb/mQ5Oc0Wi/6EO16unRk8igeX2v/Wx77pY/tXVHyKP7mLPsQUUijoqsaV0cg\n",
"y23v9MvnSo+nZw9/m77nX/yB+/0FCzxyrAADAAAAAADArvEBGAAAAAAAAHaNCCSALv7fP/x+USwy\n",
"VIYsY44qHhmkMcms/TDMy8/PC8P/7x9+n7m1OwJ5MNo7qzU2VoH0tpn3Lz+W1rhjy/jWWMttdMW7\n",
"1pjOPLft9dnSx+mr0lj2UU4jjXSlvdf6UHGU/DFfOupZ7/f6VRi9kaBLxxar1Qbz8ZNIoTjQiB56\n",
"o3y4vVd+ymsW93W/JkXcv1nPiKK6FcCGPtbPozUeKeZb+V351m//4KYpWVHhLS7W7+q+4jfotK+m\n",
"Y6fx60f5qzVubxfvK+dWq+BY36YikO/8Lj8/j3B+zYfY4zAMw3v9pTfwywC4MFaAAQAAAAAAYNf4\n",
"AAwAAAAAAAC7RgQSwMW8/Q+9ZI5FPj3HIkMFLSseGatGJc/bVMWec7uffuv7TptU9Ucr8qeqUM7H\n",
"rduXiiON9cihP8bYsxrl+n63HJtXpkv7WBdtjI+c+hf7mvt0V8rcHvFcGvcS1HPQOo8t1ReLKpvy\n",
"lJbVNg8iemj2H/HEW3uTFU+z+Swf21jB0bPNef5iZb/VYKmxr5/4WnjF73htOnQynQvNo0f1Rav7\n",
"NfPOf+f1mM+W89f4+00du2X81nF/8HW/2dWurP54H5HJ5KYQq+dhxQcr43eu6tijv+lv0+mxrI9A\n",
"vsuv/NmHHqK/N8PfkvFzRaVH4DZYAQYAAAAAAIBd4wMwAAAAAAAA7BoRSABX9fbPf/9xGIbh8OTZ\n",
"tO0gIpAHEX28VFTy/3rrS9INcfqnMebojxKqKOYh+7nWh6dK44rYmRGpWjuf1rHd7St9rI2z+SON\n",
"65XPb9/zZ8VCtlTslP05etJjllXGVKTxFvQ1EDbM7Q5m+30nXFoDvX0DwLNXfvJro0GMV/1Nqqtu\n",
"6Th87dz/ht8PeR/Nj31LJDSM2TrvpIrzytsDNM4xHuuHvvvVTWP2iEdu6U+dod6xxbXt7XZ5jLGh\n",
"j/MxR9l/+bfnu777//Ow5xTFHEOlXxF3DNuo8gjcHivAAAAAAAAAsGt8AAYAAAAAAIBdIwIJ4CZ+\n",
"5nM/cHrzefLPvPDwTRRPnGKRUYwxX7auKkkm+51RyXzMVLn0/R+96f0X+7BjiVYFSm8ffas79q3M\n",
"2Has+zj5w6Hc5xh7zfi36F9VBVRjrR3TG0VTkb8Q67EqKC6N5aFeE+E8xPv0ubFmovq9bFTROs9b\n",
"4oDW9aZem95tU/XHLeejuY95Hq/6pNeleyqR3q7PWy2iO7XrOeYVIpmeF6Bso15g3gmEL1silof0\n",
"6zD4r63V8czG8+as4qz6tNr/yPe9YnnE5HUbttWHXuqjVRhqTWSxdb49YpGt+8K2d3vxz0zb9O0u\n",
"Hv6eiyuF5xHI07Mn075f+1e+n+gjcCdYAQYAAAAAAIBd4wMwAAAAAAAA7BoRSAB3I45FHs9VIpNY\n",
"4jki6YlHPuwXccfQLk5VWMvsGyOToa+f/PsfMG3Ty+eX91nH6XbJDDb316O9J1rmbb+lguNa16kC\n",
"mcbODmpfa59iW9zTScUnnf0UbTbFET11I69HvYaS6E6yx46hLu1/DGTi1bstu55f9YlpnDE5MCFi\n",
"Z2vLt3rJ56dDjco44mb1seVx5cde6n2p1anv/6m7qy+q95lLxBfjIVsrQ04H+qpRuucjqoT+6A+8\n",
"dBiGPpUkW/vQFRSV+G+3fvPwxh1f9J4/Xc5oOpfnaKOIwyZVHbO448O2h2NPzx6+vvdf/b7H+YsA\n",
"2DlWgAEAAAAAAGDX+AAMAAAAAAAAu0YEEsBdi2ORIdI4RSCjqpFTjCyJTIZ20SZvVDLwVpec2qvY\n",
"ZfgyFtt+4u/9i0XzLbHI1dE5Z4yydRwVk5uiA865bRlftV8babQeS29mxEy0tOJWKrpWHd+IZ9rz\n",
"uT73PKYKcsnGdWNWepCVFleN5OjXqK66dpu6Zl79CSLSmEyuYyXJVqpY4/RN53lM/VWe0c5R7O2d\n",
"qZzyliqN4cvKOKCah7OP9Ly0VnoMX5yRSSvK3VgBud6w8TwYsdMtv9/U4/rxtzxUv3bHEadvxnKb\n",
"au/s91e/z08+fGPMVz52UYEzjTmKbXl7EXeMt1HpEXgcWAEGAAAAAACAXeMDMAAAAAAAAOwaEUgA\n",
"j87P/P6XjsMwDIcnc9xwikfGy+jDYvRD3E5FINNtcil+vIxf7Rf9Fl1U+h2sCkbn/v/hGz6wOs4w\n",
"1GKUSc/VY9dUt1sbc+xdwbFHHz0jk3EVxjwiIisLxv2tHFPvv35SQ53Tpf1N/Ubfe3pIRlZjWlEc\n",
"cV0fHDHUNXoWQoz7+E0f/x2+htMmO050UdUKgLe9jtd30hiJa+5fbOoQd+wf63T0N4pvW+exIf7Z\n",
"/J4pqgd623ueo2oblfQuIoLxT95qm464pbzulueRHKvO72n5sVoxR3WNpRUcy/nkjyFtX8Ydw34q\n",
"PQKPDyvAAAAAAAAAsGt8AAYAAAAAAIBdIwIJ4NH66X/zZdMb2DHEIaMoYqgSWasMGUcki/bWNjOy\n",
"aFSWjOahUxVijpbaWGc//oaXliO1xvpWHrdpzA7VF61ooDvWGX1fxNPiPlSVPdFHOcc1EUFVL3Id\n",
"GcFcGf9cNb6rURRBEbvlLLOqhJf6q0fGZuNphHbZz2v6fdXHvl50LK6yvDJjsi0exDmZC5urUF4m\n",
"VmoPXlaEk+etx1CnDs+BN5rX2K8ZSWuUVtlb24l4XtaMv3bc1sqUF4pWjkYcUM/DauSLoVpj1p7b\n",
"uTpoJULtqeCY7C+Ps8ZSj0FVdZz3LccdT9G29/lfv5foI/BIsQIMAAAAAAAAu8YKMAC78lOf/fJi\n",
"VViymuYYVlct3xhfrfbKV4ktt7NWb8Wr08Sh1kouc8WYaG7dyFv2u9z+x/7uy6bvvb8xVt/QPDmu\n",
"vlZmy83qrRVESR9rV3SJfpP9PVeUiG3ysZhHG+e50oM8H/m4HW98v4ZarSevmfAajo8NK5M6rIh7\n",
"9ce8fnGfXjH2SBca1G48nq3Muwa18mpabdbl5vZqY4dVUGoo46bkzX05VxfZnaxfqTUd1uNG/WvG\n",
"DyuCLrzCbM2KONdz413R5VzV5lv51bayK+0j/ik795XXkDrn+XxrbdRrJ+wfxbXw7NmTYRiG4X2/\n",
"+rse6ZsxgBgrwAAAAAAAALBrfAAGAAAAAACAXSMCCWD3fuqzXxHFIp8Nw5BFBLN44cEZd9wUlXTs\n",
"S9ptueF+4BzLM6Y+QJzTyI9+/8uHYbBjI7Ub3nsiaObN6pOxet7kuRZ4dPQleugdEVRhx7H4Zige\n",
"wqWiitXo4fSNygwbETpx8/It5QJe9dF/J91Qi/LdIN7XlbgW5OvwdIPHXM0WZ6/JS127KtqYXLwd\n",
"x40v5679tt24PTm0Z2S0d1EVR3+bCrk0Rka90cP5xSa2bejX0y49H1a8cbkv/VzE3y4/PqsogHUj\n",
"+3q78qb2qo/8Rven05Np3/t9zd95pG/kABRWgAEAAAAAAGDX+AAMAAAAAAAAu0YEEsBz5f/8va8a\n",
"h2GuEDkMc+TxMFWIFO+LUXxQRSSL6o9xMkj1p/rI26tkVxIzXOzCHltkiOwKlGpb+++O1ZFKFS07\n",
"f/2h73lVsa+1WmPs0lUJN8Vuzl/NipLqHKu4yepZaPbj2hI+rHvlR373Rfp9tGoZ4GmbCJuq62ja\n",
"tjDG1cWxpXJbF8YlK+NvrW80csx1Ub5VQzVXSbR2euN9oa/o+Su+8c1r0/uoO44YDhBjeuO+nkqd\n",
"Kt5qvNa8lSTT+YaNYr5WxcfkB6Odq2pkNJFqLFIduzxWXtUxiTYa0ceTqAx5evbw9SVf+53EHoGd\n",
"YgUYAAAAAAAAdo0PwAAAAAAAALBrRCABPPdCLDJE9OI44LxtLLYlsgqLOiYZ73dWlZx2GpHJ1kqS\n",
"zoX97sjiFP/0tk+PG4ahS0puU9VKa5vDW7771fMPjRUq1T557LlfGYGsHOvpNzZV+ZsazW1e+RHf\n",
"E1rVet4wK9j5xVlxlt2n/U4SPsbbgI5xXWoelVeWJ87WOuSlItfxOeo4Rhq/295v6+OXkVfrehC/\n",
"V6Y+qmNn+6txx/ClcW7xJrNCsrwXgWgoXijZsdXz3vhY8ghisq9SMTOfiyfiWOvXqu4Y9xe3o9Ij\n",
"8PxgBRgAAAAAAAB2jQ/AAAAAAAAAsGtEIAHg7Cd/zwedK0Q+m7apCOQU+YsyAXkMUVZrVLHHxmij\n",
"uwqk0W9tDLONO6qYVcVc4ZBVfFzXSVvs05zHTVSe71vOzVkVcI5TijiNiAXHf5YU14+oHiafH2/W\n",
"1Eq9ea8Z1V5EiA5ZldJ43tY2f1XH5XlclVVJMhb2n47lNqt959jgqCJjPeKh1nVUiYW1jSOqKi7s\n",
"Xz2Epw/1a2JV9NCah7eP7LWTvCaMY1V1QrFPtndd96qCqd6/2IeMTlb6sNqbsct+0cbasTLmKN4D\n",
"PTHRNO54KPoP217y16j0CDyPWAEGAAAAAACAXeMDMAAAAAAAAOwaEUgAMIRYZBxVDJHAOK40xQQd\n",
"8cj82Hlj+NoWlYzbF5GxSuXJmYraOatLeqtQHpcjYF5d4oitVSsdfd26oN5tY5qdWREiGXc8+Pab\n",
"++LX1yHdFx+rqtC1RvMuFOW7pvCnYxpxW35d++JhnbkjZj3GWr7GxpP4v+aLxzlbD1Tfbj9XadXI\n",
"xjnlMcalOZnjh29qcb1z7+J69s57fqxWxFLlpNdHCZsrTw4hDugcc0ulSnmsL+ZojaVijmb/p/Ix\n",
"v+RriT4CzzNWgAEAAAAAAGDX+AAMAAAAAAAAu0YEEgAcfuJ3/ebpzfL45CEuVYtF5vuScInZbrlN\n",
"wooeiiimbGb24ZxHNuaDtt8t3hjlfMD5S5fonxEh3eJgP98XZ0ZZrfKHC7vxfLtmpLCVEZVKXDF+\n",
"ujqO6O2/QyXJHpUZZ3H8rUcUsy2CKGOc7nmEmFy5rTbWvK01nulr73me077aqi9O+5Ifll/Xet7L\n",
"568ei6xHKuM21rbpZ1EF8jf876/ntxqAYRhYAQYAAAAAAICd4wMwAAAAAAAA7BoRSABYKY5F5hHI\n",
"9nhktE1VfDQif+54nREzNKtMOueRtiujRq6Y44YYpdWfO9oYHt8V44C3qeAYj1l/gIejuD7iCEpo\n",
"t6dqlI9FXoFQVK+MI0IHx7akVp1VwfGaVR3z+UTi6+7S0cN5oPjbxriedwjPY3GP2VqR0RnRs2KU\n",
"ouih7iR8WR+p9cYArfEvFWO044O1fq2IYPimsZKkePuvRS1VhcVpnxWtbJxbrbqjrAyZVXqM27z/\n",
"130H0UcACVaAAQAAAAAAYNf4AAwAAAAAAAC7RgQSADr4h7/zg8dhGIbjMVSIjCoAThHIMkamI5Dn\n",
"bUkVQTVqW7QyP2653zNnZUZ3fDK0b634mIwVzk3rkXGksePvvStGJrect0tIY2fTVrNdLv4TpGsF\n",
"zufQFF8UcUDvtijMermJeohplHOcdyexqLJZ1zmFmF78mu8Tu/RWHez43DRG85JDrVidW149cMVj\n",
"UzHAxmug9fG3VuC04oNpw7b5mO1GXzsz2thcDVIMH7XT8cawzdgnHouuDPnwWD7g61/LbxMAi1gB\n",
"BgAAAAAAgF3jAzAAAAAAAADsGhFIAOjoxz7zt47DMAxPnrwwbTuqKpCimuL8/bm9irwdyvhPsru1\n",
"0qOjqqO7sp9q566+eH7MzszK+ijk4HrM7VQE8oq/Xy/ymNbPI6GmJKKjqpJecT2LynvqMZvRyloB\n",
"TCsFaOyTYxqPXVZiW5GkzadUjQNeKiJ4AWnMyjr5vUc2nnwZGbOe6DbJn+VTtc3KUEUfbdUJvVR1\n",
"wrmC6FDsq4+ZveYbH2c5J88B645bU2VSRfj8YzS0Ef3b0cb4h3VxS/V8q4hjfK5U1DU/R7LKoxF3\n",
"jMf9jX/jNUQfAVSxAgwAAAAAAAC7xgdgAAAAAAAA2DUikABwYf/gsz5kHIY0gqhikXmUK45/5fHI\n",
"pXZLfdXa68qQrX2Idq2RPBETbZWO2Tp++LJhHlesDOlzoQqYl2LEoJLKheqAkIyNrs88dpNcH1ll\n",
"v4dWIlKZHyuqkqVjGmMZ7atRxWn8g73tUTCiXNNjv/xjCtdHMlJ4OuJIlxWlXT24ms9lHvOaCF/Z\n",
"idrYFvOT3XqrQIrXa2t80qo6aI65ospka6QxvPfIGOB0nivVFx0RyWoFR7NqZF65cxjKap7ztlq/\n",
"4TVWiz4Gp9Mx+ToMw/CBf/PbH9ubH4AbYgUYAAAAAAAAdo0PwAAAAAAAALBrRCAB4Ere9ukfOr3h\n",
"Hp88xCFrschAbpPRx1O1Ta3fYp8zXCCrTKp2zvikHsNxbJL0WTvWcjS1O3F+b1HNccvzclveCnxG\n",
"FUERVUzaiehjMZSsWCgamjFG2bFz250Qp3mKfcZVPz0VDldUBWydWzGfpcE6RhPbY47eqorGsc0V\n",
"H53juztU01hbJdFZHXQ6Lv6hrbKmijN7IoK1fufYoLMKo6ywaLR3Rgrnfa19tEUc18ztdHpSzC1E\n",
"H1/6Dd92Z298AB4LVoABAAAAAABg11gBBgA39LbPiFaFHdNVYYfo/zfD/z57V4cNU3uxS6zU6nJT\n",
"ezFfW/sqq9ZVaWYfW+SFAjb9X7R6Tpf3bdKlsMCOWDezvubKpHvjXHSW3MD7kN7AWxWBqN7w23lz\n",
"cZ/lztJ5l0d2vRG99ViucsP7Hh2GL97VTcvziM+37ybx5bFyRZdzHvl1WjtGtlerpczVbM7VWNYq\n",
"LKPYRf2xnLs4NztVVpON4/L6iN6rvMK5OYmb4Yfv4xve/0t/61tZ+QVgE1aAAQAAAAAAYNf4AAwA\n",
"AAAAAAC7RgQSAO7Ej37ah43DEMUdo1jiHIE8iW1DsU3x3kh/bm/c1H7DmFZ/rVG7tP1lx6qPfwFd\n",
"bui/YthsrHHxB/s47FUZLywjY/P/serYmbd4wUa1OOfKm8S7h5exr/K9e3VsManfcJnHYt34XLc/\n",
"t67FS1fO033jeOsG9tWo4vmanc5pZUx1k//GeGZrO++N68t9ZcywOr4Rm/TGHcN7QhpzTNurCCSx\n",
"RwA9sQIMAAAAAAAAu8YHYAAAAAAAANg1IpAAcGd++FM+YhyGuSrkMNixSKua4jGOOIY+xJhmjLFS\n",
"IdKMSjb3V1aOM7MPKoqpIk+m+PyJeax1UP32tlzt86rM6OPB0QaPkvsp9VW8u5ZLVUlMqIecx8g6\n",
"VBNNH0u/x9VaabHaX1bN7NQAACAASURBVIe+7PhiPFZaiTStXumL8hWx3dqYjY/LOh8qKuyLNg6D\n",
"dQ2YfVQrQx7Mnx+22esqrEqPKgL5sm/8llv/ZgOwQ6wAAwAAAAAAwK7xARgAAAAAAAB2jQgkADwC\n",
"P/KpH55UiIy/V5FCTzxyGLKI5NRwOSpp9ZXst2KOU/++3z9JX+FbZzBibVXJJN4hqm3aVPvL/K6d\n",
"Ht8dB0Ws5yD9E6Ss2Ib7ND9vd3jhZe8RMvZVu8RktUjH0EmErhzMXVHQNVgYSM0j/qFjLDL5wdFv\n",
"lwqVZcXA1utuS+XJ5mijUa0x/p1wao5Wros2JvtXV42MtolrOK/kuHxs+KZsdzo9rMl4+Td98x2+\n",
"qQDYE1aAAQAAAAAAYNf4AAwAAAAAAAC7RgQSAB6RH/zkj5zetJ88eTYMg46M+eKR8baykmOIa1j9\n",
"L3LEKJPmlUqTsxAvbPzdtaEiY9dIXpysDIGQroEPZ6z0CvHM4nGptG18bkXsbMx2Eo80qEic2Kbi\n",
"WPm2auzL8zR0qHDoV8ax5jhz/H+94jUnH2tj1lr1IB/z2hhg1G/a08LYG95URDHdWVuUsF6dsP5o\n",
"VEy6d4xRvybq51DNzf5nlYoI2mWLzXmI6KFs1hhz1I8l3aajnpUIpKj0GKKgryD6COBKWAEGAAAA\n",
"AACAXeMDMAAAAAAAAOwaEUgAeKTe+km/fRyGYXjyJI4vPrynH48q0iiijI6IZFKtUUXQDmU7HTOs\n",
"V1NsrtrojU7GEcgidtP+e/DS1Rd7Rv388dJb8JXjUxFdFdN5XBHJNRnBtms2RI3i8+LZpqoZpttE\n",
"tVTzddXxhVLpdnosg5qjOO5Cl0zXSpmqmmJ4Px3Evg2VFsWQ0Q/OxzLFKEVkMn6NumKGW2KorRUc\n",
"txwb1hQsX6DePr1VPO1oYzSL7DVsxR6HYRhOp3oUU0ZTRXsVizxF2175t/820UcAV8UKMAAAAAAA\n",
"AOwaH4ABAAAAAABg14hAAsAj95ZP/KjpjTxEH+cKjnN0bKoM6azqaEXnalEzHVkLc2yMORpj1aJd\n",
"Zr/N0cA44plWmEvH9MYy0/at1Sk3Uc/3xccU26oJyDTmNYpO5PMtImOy6qa32J/VbnvBwLKvhv6K\n",
"CnaqDxHt8kYgp2sl2eYb6xJUFFPuF5VoN1VHnDoJgxv7hi1xRNFtLcZZjN/4OGXlVTGY87FMzaqx\n",
"WU8fYh5xO6Oq6Xxdl/tqbwStEVb5uLJux1PldWX15R1z2re8xkFFHP39euOO56+i8iWxRwC3xAow\n",
"AAAAAAAA7BofgAEAAAAAAGDXiEACwA6FWGQcEQrfpxHEMhZZVIGsRSZlOqdeJdEbG+wZmex+7BQ1\n",
"7f27VMUir/f7+r4rR6bMGJyz3Zbnz+rjQnUQzfFrqUSZVMxig57qfFdRO4Eijjg/9yoae6nHVVYk\n",
"nfbIubXR1TZVw36PT14f3mNVzLaxL/U8+mOleSTP90psr/woqlx6269sV6vgmMc/dR/lsVa00TuP\n",
"eNtJxCJf9c3fdCdvLACeZ6wAAwAAAAAAwK7xARgAAAAAAAB2jQgkAOzYmz/ho+daVqIKpN4WvpaV\n",
"HL0VGeeNzmMdkUndh/07rDU+uTxOy8Fl9bkusqqRw9CncuT8WO/k7wFn2kudD1WtbopzjmXr0D55\n",
"vkX1suJ6WBHNm3aJqnX5vmS/OgdGAbukSuIQYpFqmyIiZjes+Fi/GERMbopzqsMuk8CyKgv2qEI5\n",
"inM/PbwLxTpVTM7bPlxvx6TSaPjaFgOsV3C05tIYaUyqNIaN1ji+Kpfe+Occ8Vxud6rMsT0+6Wun\n",
"Kj1Oc1LbTg9rLF79Ld9I7BHAXWEFGAAAAAAAAHaND8AAAAAAAACwa0QgAeA58aaP/5jFypBWFUgd\n",
"I1xuv7SteZ9VQdIZmdRjWuOX7a3ImtfaSGX/6pJqEGtnawXOTTNpVMsGnreco7y6gtwhaRNvk3HE\n",
"oYw56eqP537FHM2qkSpSlZQ4zOcTX5/LEaw+bpBk8kZNk03GPC/0clKRO291Ulf/0fdF6q3z8636\n",
"9f1TIW5fvq7mx94agRTx1sZjvdUaN1WBdM3HPlZvWze+d9/aSo9x7FFdM0QfAdwrVoABAAAAAABg\n",
"1/gADAAAAAAAALtGBBIAnjNv/LiPnd74j0YE0htttCotqkqSVl/udiJcsTZ2WR8/PAZfeUKrup+q\n",
"ttk+n/v4vX3zeTirJBaVENXlFMesRCfTflUhUsRxPTFHb+VJVY0vjlZOccvmCGQ8fsj+junP85B3\n",
"UyRUR1Pj/ddJXiWnIz9/Q98qjaoK5HTNdH+8ZQTYFVsUVSCbiWqG3SOQjuPq1DlK96X9lvtao40q\n",
"ir82vlhrP6pt2bFq32/61r9F7BHA3WMFGAAAAAAAAHaNFWAA8Bz7gY/9uHEYhuHJcV6p5VsBVq5k\n",
"qq0IuslKMaPdOP3sOmzjKrLyvPWQ35z9mjehv/kKMLfpmS72eG9UnrdL25TnvnkFmOg3v04fflhe\n",
"FWOvdhFLiJIVaMYKsDtj3hA+aXjZx1D78zlcD6fTpVdoXeZxNq8s8xYkcL5tbFsBNpyP9R5XXknW\n",
"Tftbb1ZvHaf76Leyq9bu5Owv33Y6zWsoPujbvuF+3zAAIMMKMAAAAAAAAOwaH4ABAAAAAABg157e\n",
"egIAgNt51Td/02EYhuENH/Px843xz3FIdYP8WRkBU/Gt2LNny9Gv43H5/2PSm14vRyWtaJnVLo4o\n",
"WceqG5R700feubWaz42KQF4mong43n9MLmXEiUQLT5wobbMcn5JxvdYbVyc/1KNJ8ublyQM8lJuy\n",
"bde6kfwa8cPTkbH0/SiNpvaYQS1i+mCOiNXeP9e52HMkCjLk+1Z12zjf9qifiPedlvel/Z5bRReL\n",
"FV1de+5rr2/r9eeNvJpjiPclfYP+Q/I1PiZsiyOQAPCY8O4FAAAAAACAXeMDMAAAAAAAAOwaVSAB\n",
"AFKoEBnH9o5T9C+qAhm+mlUj7W2efTFdUbJtrNYxex87TBHT9V3YevR/qTle72+PuRLc8j4VRIrb\n",
"h+tNx4XOW+Jr0qgkKf/smrJPogpk3O254VFUxptjXMsVIhe3hQnITKiY792oV+NT1TmzIxb72mKO\n",
"lYrzvKnjdfNoHqZyLbaer/Z5tEUg06h8um1LlUSrXWuFynqss34t1mKUnuioN14aV4icoo/nrx/8\n",
"mr9xvzlpADCwAgwAAAAAAAC7xgdgAAAAAAAA2DUikAAAU1wh8iAqQx5XRh91fDCKVhoBCztG2dZe\n",
"t2v73dglCrm+h0r/8bdt1Ss1Md+7DsPkz81yPHEYdMxxrj5axiPDtrRCadluHkPtW5z8oKpLptfb\n",
"Idt3MtvPUScreiVr0zVuu81FMT++688jiQ2K95AianrB8a/dl64CXEaF26OT6+e05ThPtdYeEcja\n",
"/vxSaa+OaZ/7PNq41O+zc9XH3/Lav37X7/YAUMMKMAAAAAAAAOwaH4ABAAAAAABg14hAAgDc/o+P\n",
"/oSiMqSKRQbeeKQVA+xRNdIbrQx0lcnl8XX853oxyk0RTNcAtQaNMc6rhmjaonAhuqYq9k3nWVRm\n",
"VM+BiibZ10x5bK3fvL96nHN5fHfVyI5Ru2YidWme59OhaH8QsdJruGVE0W855uul/2mh+m2ztkqj\n",
"N3rYHmmMf9oegQwxRBVO9kQyk23JD4fFvqxIZRyLJPoIYC9YAQYAAAAAAIBd4wMwAAAAAAAA7BoR\n",
"SABAs+//qE+cfnkcRQTSUwVSxSNrUcUeccjWuKCnfRKdOQdY9OOLLUfzblKNsrdLV7f0TiPEoJwV\n",
"+Ir20TEyjij6PYQIrRWVVPNQ2SchnltebdCKNsZzM9v1KAJ5RbXH7Nl3KclY03PfY3xvHHBte9+Y\n",
"3n9GlNU5/XMq+2iTHueLRPeo6ji3CyOvH7M1/qmqOqq+wvfx83gaH9ZHfMjrvv7Wb98A0B0rwAAA\n",
"AAAAALBrfAAGAAAAAACAXSMCCQDY5Pt++ycVlSFVLDJQ8T4r7nipypDePqxqfNaxtSp/874wTrmt\n",
"tXqlbn+r3/PhGrjR8AVf9MlTzdFbmdHbR2vFR8ua6pJW1bzV2+Kxb1hpsVbZr2csMj0f09Z4tHM7\n",
"q5ce8yj7a/1z3zpXS/vX9tca72u15rjmCKTxWHo8vimqKHdGkUbrWNH/Sewj+ghgz1gBBgAAAAAA\n",
"gF3jAzAAAAAAAADsGhFIAEAX3/uRnzzXGxMRyGMWfYyjca2RxoO1r3OVx7WVFbfMQ1VMa40Szs9B\n",
"23F+tXKKyZft/W3UGrdKn49pa7GvbFNr1xaprQnjqufZE3dU25KZ3TjS2KqMc8b/11u+JnR1wqCt\n",
"yl/ttZb/yd07dnkpfeYZvlvf19pKku4IojgmVFlVFRzbo432vM2YoxhTxi2nb5bbxRUiw/cf+h1f\n",
"d78vagDoiBVgAAAAAAAA2DU+AAMAAAAAAMCuEYEEAHT33b/td4zDEMcey1jkcUV8Md9fa6/GaOm/\n",
"Zayt7dWxrRUAe8/D7ldt3T5We2SzLQ6lo41Ji6LfslJn/Lycim2edmnVT6tCZe3xpddK+nwvR6/S\n",
"a+u02Ef7tvTnuF0axVKP2VepM6cqqFox4tPJrtZ46VihPw647nzoMS/zmLb02xqLbK48KY5TkUYV\n",
"YS2vnwtVd0x+KCOQnnNkVXdUfaQRyIe1EB/++q8lAgngucAKMAAAAAAAAOwaH4ABAAAAAABg14hA\n",
"AgAu5rs+4lOKypDHLAqZfx+0RiR77LMyID0ija3tk2hLOG8XHnuLa46lxy+3WX/m6PmqiOLUm+j/\n",
"YefxuFw1Uo1Vqxqp5m3HC/O5lnNU7dN+rfZt26x45NJ8L/0nqVWB8xrVFC33XBFS9dtaVVX11dqH\n",
"jgMuV2ncMqZnTt55h8ihCvvaMWxffFJVhhxFwxB3jM8V0UcAzxtWgAEAAAAAAGDX+AAMAAAAAAAA\n",
"u0YEEgBwFd/54Z86DsMwPDk+VJxT0UMVTVrTztKj0mOIZ3prtLVHA0NMNNpixLf6jt3u1tHHrbyR\n",
"OOtx1ip2rn3+alr7lRHF81dvFspTGfLWkcJAR1nj/beLRaoYbNai3LVyTqraYA9rKzPG89jyiugZ\n",
"VdTHOKtAGte9GWOsRTGzdvWqkcvjhwjkR3znX7uPFycA3AArwAAAAAAAALBrrAADAFzV6z/s05KV\n",
"YMPQfhN8a7WLOk71oZUrLnrcGN9auWYeZ6yw8Xdi3+T/Uv3ei/Km7/Zs9Uqg9NjauTJXFblmcXmt\n",
"N9Jv7zd+7L6bqF9r9diaVWHe62f9nC69Kst+Psz+pm/Ec2WOqeYWzeKQ7/P20XbN6IIP0Y3jwz51\n",
"jGjfOg9rbqcVj9k6Vq0UCyu/fhsrvwCAFWAAAAAAAADYNz4AAwAAAAAAwK4RgQQA3MR3fNinT7+A\n",
"jofT+WvlJvghAin2KWujkj1uqN+7vYplufIson3rDd7XuNcb43tjbVtueF/2vy1WeG06Mta2rVbA\n",
"wdo2XbNXuJF++03wLxtiVTdWt6LLq8bo0Mc8j/DdmhvNrz927kPEALNe1U3iD6K96teONs7fq2hl\n",
"3lftHdF6LHa/djyS6CMAzFgBBgAAAAAAgF3jAzAAAAAAAADsGhFIAMDNve4chzxGIRFV8TGPLca5\n",
"DhVh8lR8VNG0Wr9t45RjLo1rtVeBHk8fydxCsix6hIfGypc93DIeWa/gOLV0H7NnOtJY31aLh/mq\n",
"QK6vXLhFeyxy5TjVjWV0Lh99y5W5JeJZRgTjvW2VDVv78FZ1tMe2xyqv5+V4Ynqc0a5y7VhVHee+\n",
"7DahtvLpNK9x+Kjv+moikABwxgowAAAAAAAA7BofgAEAAAAAAGDXiEACAO7Gaz/0M6LKkKECmrcK\n",
"ZBlpzNvHelZ6tCpKbum3Rx+yyl7SYPkcbVEEkpwDbJmHjqzVe36eI45e16wCaVXeq17PjdQzr6ul\n",
"pu8vqrLgpTyG/ldFIKdvsuqfDXMqKofG/Rnta9dRHgSN44nTtqi9VWHXW3VTH5vFYEXUM4lAnr8n\n",
"9ggAGivAAAAAAAAAsGt8AAYAAAAAAIBdIwIJALhLr/mtn/lQGfI4B02m6OMUR7IrP7ZGH60ooxmT\n",
"q4xp9dc78neLPmatVS4vLzyn5qMUlQhls9DGOfZtahja1j6GMgxob1tTBXLItsl4ZDw5VUkym09v\n",
"doXIZHLdxzz/dB6/1m5t/85jpm/UcxXarD8HW2KZ1rHeyo1F+w1VID37HvqrxydVtcu44uNHf/f/\n",
"di9vNQBwl1gBBgAAAAAAgF3jAzAAAAAAAADsGhFIAMBdC1HIYZhjNiqqeBCBFBVTWhtz9FZ69EcK\n",
"l6NMsl8RPLufCGTbY7mF1sd5j/HFPfFUi6xGJrN9S/svoRZL9FQf3T5uw3HiB1XR0hv1c43preR4\n",
"/qoitVZFx8VjQ1ywsb05To8IZFkbtz5GFn1U1UeJPQKAHyvAAAAAAAAAsGt8AAYAAAAAAIBdIwIJ\n",
"AHg0vu1DPuuhMmSooBhXXzSqKsbxyEvHHFXVQSuf4o3mWbGwVrVKmT73UfHRew5UJK1vBUz0YlaB\n",
"rMQdrahkew3MNqqiZZp16xBfnDYux/y2sKOHy+9qMq6aNKhXWlQRyB4VKqtjWZHJxvGtypcnI+KY\n",
"blvuL25P9BEA2rECDAAAAAAAALvGB2AAAAAAAADYNSKQAIBH51t/y786DkMah1KxyEBF/lTVSNVe\n",
"8UQl5Tyi78Pe1shkbYxLHCers7mPGfMNV62q+HhjjpeN6z1WrZUhe1eNVFeT6iHE3bIAW3JE7coM\n",
"x265gldXjdwQaZyaVNrnj0u9B7orSYr4aWsVSk9MM51dScUcpz7G4l3RrPyo+o37/7jv/V94cwCA\n",
"RqwAAwAAAAAAwK7xARgAAAAAAAB2jQgkAODR+uYP/p3TL7Hj4TQMQ1qRUEUV52qRY9F+alMLHRkV\n",
"J62xZVcb4ojXikD6ba8MqQ8T83Xnw8rqgXh8dPU+tTG7glQlSbF/bVSwxTxGv3irjBmqa90RQYxn\n",
"pPrdFMU05qHmo+bRHFctzvfcc1xdMbzfqwqO6hqz5mHuE+1qEcgpKnmewL/yPcQeAWALVoABAAAA\n",
"AABg1/gADAAAAAAAALtGBBIAsAshDmnFHuPvD2KfYkUZt1SSXJpPi+b4pBhrFLGp5rlseAxr3XOk\n",
"0UpnqnMk24XHJ+JQW8ZSkb9DFslLA2NlPMyzTVUOXVNNdK35z9u2qpFL+y+h9zhWZcEu/ct+y2fX\n",
"CnhuqtaoIp6uyKGv/1PymjhvEz1Y87WqQCZzE7HSedvcR+jv47/3rxJ9BIAOWAEGAAAAAACAXeMD\n",
"MAAAAAAAAOza01tPAACAHl44PRmGYRieHE/TtqnSY9TuECrBidieypicxLYpdnZIf47Fdxiwsiut\n",
"9eB8ISRbEvVxRu2K8ePIZIcqca2sGNLl45GqXp3em29VlebmaF7Ueiz/j1JF+EZzX1npdDwdk/bD\n",
"MAynfKwkDrjc3upDnYNbh1bDda/ibKN4TWyJErojqdbceoxtxD2bqyrKjeV1OmZfF/s7rft/+PS1\n",
"sfzupyKhdsVHVX2xZMUcZVXH6Zvl6o5L/Z5OJB8BoCdWgAEAAAAAAGDX+AAMAAAAAAAAu0YVSADA\n",
"rvzNf/l3T7/YQhzymFQ4HItt0z61zdhnHaf2+2OObRUk7b6296Hap38+2FX1FvtKfhqXujJGaWeH\n",
"FzsRsdJplzgvVlVCHWeLq5qmfdT6t54/FY3zbotGS/pc3nZ9ZhVN9ViMypDJeb5QBPjS1Si3VI1s\n",
"j0+GiOe4uE3GEqPv9XNVHptfbd5rdxSD6Xa+CGR+Pag5Ju3P38dRyE/6/r9MBhIAOmIFGAAAAAAA\n",
"AHaNFWAAgN0Kq8Hi1V7h+3lVVrk67FD5P/d8RVd1tVPjCjC1Ok1261lzIlaqJDewd87JHMJYOXdp\n",
"l7/hfWVMY/WPnFtYHBadoaNc7RU6ifrLdmW7i31hRUl8PVnrswaxikzeSNyxKuwgVk+1bktvXl4+\n",
"vkvZslJs7sRYJWT0X2tn9Wse17H/tA+1siuw+xqzb9QKsOr4YlVkGNd6fNUb9BvnwboJftJHmIcx\n",
"ZjxO6JdVXwBwOawAAwAAAAAAwK7xARgAAAAAAAB2jQgkAGD3/voH/Z7pl93T843x1Y3pVSxy2ifa\n",
"Lf2ct2+NQJo33I/ndki+uHlvsm930jlGWRnD1b4nFR21mqubzyc/LN+kXrX33l6+B/sG+ucxD23b\n",
"LnYD98bnJWadP3mzddlJGWeb+nMWONgij6tu6qPDlaTPUdm/9Y4jH5NRSCI5VkQg5+jhuauDal+O\n",
"H++xYo7eqGbowxoz3kf0EQAujxVgAAAAAAAA2DU+AAMAAAAAAMCuEYEEADxXQhwyVMaLK+RZschY\n",
"HiE8OOOA3mijXYWyDF95KyF6q1zaluOctQhfMZ9bVHCs7PfMSFVVTDsxIoVGv2vOqSfW19pvLQ54\n",
"8YqMRmW/pJk4NFzjayoKtkj/fC7HUpUsLzKPDY9TxfCCg4gUevp6+GG5wqfZRy3u2HisrHgqKuHq\n",
"Y40IpDGW1e4kKj7Gx33K3/2fiUACwIWxAgwAAAAAAAC7xgdgAAAAAAAA2DUikACA59LXhyhktO0Y\n",
"KkRG22QE0qjqaFVYPFoRSG+MUVTBaz02juZ4jlURz5Poo39+51L9LnNVaVSRsRvEOR8Lqxqfisl5\n",
"K2XOG+8jOaZic61RwrS/khVXVRUqm8eRz0s5uhmvVc/3tM93Dqzrw2qfbHONpJ+XvLpk3EadD2tO\n",
"p/PP8Xtm6OJTiT0CwFWxAgwAAAAAAAC7xgdgAAAAAAAA2DUikACA59rXnaOQwzD/r9BRRP68UUhP\n",
"1UjFW0mydmw5dkw9Bqvn5aDTlsjf1Js8V721znN5Bp7ncWlkck7byIp+oQqqeF7Wv5ra5rM0QmvF\n",
"QtXX2ldYrUKleaw1jzh9PZ37Ylc0jzImreamqzWqjb6Ip6tqZWNk8qSeMxFpjPsYs/nG+4g+AsBt\n",
"sAIMAAAAAAAAu8YHYAAAAAAAANi1p7eeAAAAt/Ts9GT+4fBQr0vFm9T/GIVt9ahbWdGsaDfKbxd6\n",
"ylsa1dGS3o7FPNSdEOZYkxF9bK28p8YcK/8P16W6ZNvRVqXOcViOYNVG4YYT+nUitxlVI0dVkTQ6\n",
"+4esvYrZqmu3NjdLczurmmFjX97rzlt90ZqHFV+s9TGe1HvPckQwb/MwYlmRUTllFSRl3DHZttxv\n",
"cT0N+nmUc5+ODfNi3QEA3BrvxAAAAAAAANg1PgADAAAAAADArlEFEgCAs6959e8dh2EYnpyjkMOg\n",
"I3F5UEa1saJ0w1BWUUz6NKJ/rZUIk3GyaNCqPjpQVSB7lkTrPV9v3KyFt9pfrZ0V11Nx1THfN5QR\n",
"sfga81TUU/PoUc3QK/5TNsQmVQRSxdnUtbI2Lug9Sp4PUeHQ6m/LOc0fn7uipazq6KvMOPfVFmnU\n",
"EdlK9DCL0HorPlrPu6oCWesjj59++hu+isqPAHBjrAADAAAAAADArvEBGAAAAAAAAHaNCCQAAJkQ\n",
"hRyGYTiegyxxVCqPNx4Wvp+2yRhl6Hd5HrUo36GxSmJzfFLMcbyTGKUco0cfV5inZ2wzhidirbqP\n",
"aWuxX/Vv7fOH8+6LGY8cBhk3nqoIxo95yt/5onCKp7qkqrTYyn0Fq9ilEZtNx0jPkTcqaz/29sfr\n",
"OaYWgfRUylTt1TlSEcjPIPoIAHeDFWAAAAAAAADYNT4AAwAAAAAAwK4RgQQAwPDVr/p94zAMwzGq\n",
"DBnyLCqC6I0l5n2ofbUqiVZcT8WtQnTTH2Yr69t5Y5T5Y0gq72X76vPwuWV8MXYQ582s9Ois1jjv\n",
"LNup51ZV/TQr+qm5heYiNmhdSKrSYnVbFqdTlSSvW11yuVpkGpdrqwNpnWfZzoqkJtNoq8g496Se\n",
"A3t2+SNW111tHkUflTijvAaMsVQlUG9FyHyfPE7GROdtIUr7WT/wPxGBBIA7wQowAAAAAAAA7Bof\n",
"gAEAAAAAAGDXiEACAOAQopDDMMehjiI8oyJredXIYbDDUmsjkNXYpTMimMfTDmIeOv22nIlrrUBZ\n",
"Ix+r4/H1jlq2Vq5Tz4FVkTFpN33ji+ZZY7XuU3SkMfzs6qISi7TDunbVyu1GMXwY6VSJ9M6drK8a\n",
"KedUjKq2+KKEeqevEmK+LY0l5jOyeaOKal+4Bk7Oa8CMSgqq3ykWqaKhUXuijwBwf1gBBgAAAAAA\n",
"gF3jAzAAAAAAAADs2tNbTwAAgMfgn57m/zN6cq4IOR5ERFAUZ3tmRMtUPHKKFckqY7ND1q+uLhfH\n",
"io6L80jGz/utzEMFNctYWNSHiDzZkVAjDphsrCeOvPEzq6fa+Qji57aoJueMKlarOmbtahXyVMU9\n",
"qxqfijSaY4n4oopWqn5Pp/T6DNdrvE1FD72VJK2KpNXrIit8OYrgby05WosmtlBxWKtYpDW2usZq\n",
"8dPcKf7BiDSq2plWtcvac+WJPsqIo6qMqo4djCqTYoxnJ1KPAHDPWAEGAAAAAACAXeMm+AAANPor\n",
"r/jscRjmlWBHtcBArm4qt6nVP2Fb9ab2jrnK/p39qpVl3vUN1o3011KreRb3X4n35v75M9+7KMDz\n",
"Il7JlK/2qrHaJyslG68kvfLygVqhJG+ar1b8Gf16b0iv5CuiqqsMF46r9V/rw7P6rnY+5ErCbLVZ\n",
"vDpNrRq0xp2fv3JVZCy0+9fe+JUsAQOAO8YKMAAAAAAAAOwaH4ABAAAAAABg14hAAgCwUohCxvGp\n",
"cOPzOJJjxh0HFXcs+1DUDfQtrfFFFYfS/ZbRsjzmtSYX5IlNplEm33lrnocxH3OGlRvdW32ZN+F3\n",
"trul3nOUN9432suom7gJ/rRL3LBd7ffGAJX8WF38IGmx3NfqWcSdlLFLK86pbvqet1nqw7MvaWfe\n",
"SF/EVVVhiux9LHaqXJV5AQkr9jgMw/C7iD4CwKPACjAAAAAAAADsGh+AAQAAAAAAYNeIQAIAsNFf\n",
"Pkchh2EYjiLkiuZuxwAAIABJREFUo6KKoXKkFY1TfcVaKyteKjKp2qsKknm71jhbHIdqzxtdJh6p\n",
"qtBdk1VJb21sr/a8qDFbKzLeCxmtVOfLiNOtHTPp3mhnPX/uV7SIgqp9rf8q2NQ+ixnWrrv5nyzl\n",
"+dBVMY3zVnkeT+HpNo6NY5S/+41/4XFd+ADwnGIFGAAAAAAAAHaND8AAAAAAAACwa09vPQEAAB67\n",
"Z6f5/5PGc7wojhueRI5mPIdrjlOlxbLNqRaqOR9bi0pO/Rn75FAixujN+Zymim0lM+4oYo7Tlii2\n",
"dBK5KXtu5/l0uPNDvXrfpYkqeKqVGfMqn9XwuE6VKolqf/6s1aoqtrJict7erfbWa+Ph4HNcT50b\n",
"YywvFXf0RCVXXXbZY2iuzDiUEedk38p+dYxxFvqNo4fWWOq5suYUv0/nc0qvu4efiD0CwOPDCjAA\n",
"AAAAAADsGh+AAQAAAAAAYNeoAgkAQEdf9bLPGYchjUBOVQ+T6Ny4uE9VSbSqDFrVIA8q6tahumQy\n",
"HVEhr7VCpXusC4jPx7WqOarnRZ2x+DpSUdAiohWf99BOPReqD/E8FvsGZwywMo8esUjFjMRlbeLv\n",
"T2KbOlYyInxqbq4+V7RbfayqELmlMqS7amX6bI1JtNFXVdQTc6z9UyfsPo3L6wLi2G+4Vv6Nv/8V\n",
"RCAB4JFhBRgAAAAAAAB2jQ/AAAAAAAAAsGtEIAEAuIAQhRyGOT6m8jLHaZ8vlqjiW+Eb1b83ipj2\n",
"u+5vgy2xxzDmpSKIt84qzfHCacu0z4o+JvtE1C6/LuI/60J8rBajzCv6xQOE56NWkXC04pZCaK+i\n",
"ldN81BxFtUHZv2sWfVgVKj3H5cd6j1lu1CO+2DY7HTltizSqa13tT6+7+lxU1VI1zySgblTK/NeJ\n",
"PgLAo8UKMAAAAAAAAOwaH4ABAAAAAABg14hAAgBwYX/xHIdMqzouxyJ13LH8fW3FBvN45NJY+ZjD\n",
"oKNGi/0POt7kiVFWKwtmcbrWiFl+THGkM8jUmndqriLoHMfzvKyJ1fWQz21LvM/qo9av1ccWRb+j\n",
"uBrFa82K9XmrRvZ4DP7KjNZM1hybj79c/VRFG2vRyqmCpPn47CtQRSTH7CsVHwFgH1gBBgAAAAAA\n",
"gF3jAzAAAAAAAADs2tNbTwAAgL174fSQnnlynAM9x1DRT0UhZbW/oWwXmhs5pGPUixVXOiQV9x6+\n",
"nsLP+oDp29N4PB8Xj5UedRjKfQcRI5OVBZMWuXmrioKq4Gilw8U+DiLqJtuLSo95X0dRLXFU3zsr\n",
"MnaJyYVxKv17Ipi1OeqI4PnLtDOqZnjId87bZGVIsU9ty9vH+1XkVp/n8omxHr9+DZthXZfolRB9\n",
"J6qJiqqHrv4r1RTzecjzJ869dW5P4n0pfb8Lj0XEIo0rtVYZcurJ2Q4A8DiwAgwAAAAAAAC7xgdg\n",
"AAAAAAAA2DWqQAIAcCVf8dJ/a/qlGyJwIdaj/kcqjhTKapFGFUhFV5K0xy33PXyN/3w4NpdJXK6A\n",
"KZufv3qr5ukw2H2wzu1Vxj9/7T2LS/W7VRK5U7HIbF+6X1QMbYzEqfOhejiFWLCzj1bWY14Vv8yq\n",
"NHortG6piqkijaOawLTP97hGETkP3/++N335vb2FAAA2YAUYAAAAAAAAdo0PwAAAAAAAALBrRCAB\n",
"ALiBEIcM8UEVjavFIqdtzjEPRvRQxSM9fXnncVAZqbhAX9PodpRQVf7rkWPyVD8chrTyZgtvpcVt\n",
"ljNjViQurpLYGgO8FCt+532utDICaVU1XWrTohbLtNq5+hc/TOdKnEAVB7SqV1YrfMo5LT8W+dyG\n",
"xy7jquWxsl/R/iTahSqRn/3m//E+LnYAQBesAAMAAAAAAMCu8QEYAAAAAAAAdu3prScAAMDz6Nn4\n",
"8H9Q4zmAc0yq1T18PakqkEbkp1phUMSV5v7LankLnVTnYR0W9x8PE2JIca9WlOowxaHK9um4y4+5\n",
"lfc8nzoGGOuVL9MWKlZ2EAG1uN10nqf4W7yvfL7Dft1vOaanfTKP7OfaNlnZT2xrZ13j0fkwY4ne\n",
"OpBl69CvWRlyFNucpvN3KuunqufPfldQNVid8zCijaOKmqrzLRK6odWp8l6lYpxEHwFgn1gBBgAA\n",
"AAAAgF3jAzAAAAAAAADsGlUgAQC4oS/7wD9wrgYZh6vKyoVTpTYRi8y/pqL2RqjHm/cJ82ytWFiP\n",
"xBnHGpUcvRUf5RxVsUPXjC7EWWmxtTrgIYmWTVsX+xvH5X3xfqvfg4izqW231lpJcrR2Wu0FM9q4\n",
"uO2w3NDJG2WcRxwX9+lqjWrjcv9qXlb8OT6n4T3NW91RXf/Bs6jfz3kLEUgA2CNWgAEAAAAAAGDX\n",
"WAEGAMAd+NLzSrBhmFdZpTeEL39fH+c74z+0qaxoMleI1W4mb/Rr7j9MSz/mfavXVqhbkK9XzLHW\n",
"riN5DsQ01MyOB7G/PM1Tu6QPTzu1wkbMQ62asqhVQgf1WFp5lw6JibT+GWyvDitXI+pOypu+yz5c\n",
"8/E+C8bKq8rzrVbweYpLuE+tcRN81Z+7EILRR/yYwzn8nLd8Gau+AGDnWAEGAAAAAACAXeMDMAAA\n",
"AAAAAOza01tPAAAADMMzEdeJtxxFOOc0hqikEW8SN81PxzjHm5JIUNZGRbUWR8z2h/hUvM+Zjcpv\n",
"fh/Hvbz3IvfcwDu94XwZP+1xs4jyRvOiUSX+Fvo4qedKxNRCu1p8MW+nnqtaytCMBoqiB1N78VhU\n",
"/+5tYb7yfBjFF4y4nBqrdrP6g+wv7SVuY90c3svdh3FDeuu1aUUK5UYZNTWijWP5+lbt4nmMIi5+\n",
"yucprrH4sRN9BIDnByvAAAAAAAAAsGt8AAYAAAAAAIBdowokAAB35s/+xs8dh2EYntTii1P8p4wB\n",
"qePs6ovRWKEom9HK+z9oKj5pthdjbckn5eNfKuskY3VO+llefk51H0a8r1Et/mkVWvQUYbwGXTFQ\n",
"RTHLGavIbY+rsYgW19rUsqtZGysC2VoosyaPmKb/nCgrRFoR1pNjnIcDQnazfJwn48Go6HTc7+9/\n",
"65cSgQSA5wQrwAAAAAAAALBrfAAGAAAAAACAXSMCCQDAnQpRyGGY40JHESkM+w4yMlmrAlnuzNvV\n",
"Yowq3nTMtumMkQhEVWKfW3n7TNuNbQe3EifJH31sa3+tvm7N+1jMKoZDGb8bRVXTQVVJrVT0XKvn\n",
"X+2qUqaq1uiJuqqwaHWuY4hKWr3M21TMcY5R+uKfoULkHyD2CADPJVaAAQAAAAAAYNf4AAwAAAAA\n",
"AAC79vTWEwAAANoLpzml8/T4EOQ5RdGqOb6YxrPifQcR44pNQaPolghltToxpuoj6v9Z1l7Hocp+\n",
"9WNwmqpiijmGfp1VKWXtSCOC5WVG80b5rY+okCeja552SSRuOfKXPFdTv+FLuU+3L+cRqjRW+1Dt\n",
"sr42VTqMvj9Mcb36vmtKq0a2XY2qIqIVRlwc19NmXH4nmF+b5bZaHc4QfZTjXyiGCgB4vFgBBgAA\n",
"AAAAgF3jAzAAAAAAAADsGlUgAQB4BP70B/zb4zAMw5M40WhE/qxqkWqbVenxUAl3yX4d6aODito5\n",
"I4oqUGVWuewqGlUMYMZELzGdBlYktXXe6tx7KgbWWM+td8xbm+ZkxvDEdVSJ7bU+Vu/zV7SP5yHi\n",
"p9YIZmVI8wHEfSzPXEU2FRXx/Nwf/PO3fgkCAG6IFWAAAAAAAADYNT4AAwAAAAAAwK4RgQQA4BEJ\n",
"UchhGIbjIXxdjjvGkUIr+2PtU/3rPtr+pojHDJHJWqRxNibHlXt0H7X8k/UIvNkpV7v4nE7f+kZQ\n",
"MVEdufOdo8GIn1rR1PhPSE/k1f/cGn2ISpKjiOuFweJ5jbISocqwlhUqPftqsVJPXE/x9mH2mxyY\n",
"zz2uALv8zCTPd3Zkep69cztkP5f9n5yVHONjT1MFyXPl3GicP0gEEgCea6wAAwAAAAAAwK7xARgA\n",
"AAAAAAB27emtJwAAAPyeiYjbHFOb94R42LFSMW0uPrcclazFkOY4VBlPm9vEMauSik3ZlRMPRV+e\n",
"Snej+MkT31N9bbIi2hX+11JV49PP7fkcGee2NiermuG4+INWa5I/39WKj6O4BrJt8WOf+6+ce+O5\n",
"UefeqkYpz5ExvHxuZVw2H90eM4koZt9YscelfsMxU8zQW71SvH+p13L1XGbU+CH6SOwRABCwAgwA\n",
"AAAAAAC7xgdgAAAAAAAA2DWqQAIA8Ej99+//B8dhmKtBxjHDw7RtiLaNxbZpn7FNVQCsHWu1Cb15\n",
"q0vOfbT/zWLF0w7FN+urEyYjtHbirAJZex6yWcyRycbpyLEXxsj3q5Sfp31vch6qomWIzhkVMItj\n",
"hjyqaGUbfbUvZbVGo7tt5y2NHKbxZMcc1UZZbdNnzL7G3Xnjvkl8MovBft4P/TkikACAYRhYAQYA\n",
"AAAAAICd4wMwAAAAAAAA7BoRSAAAHrk8ChlLYpHhq6gWaWWE3JFJZ6TRqvKn2oV+rUhafUwRcTPG\n",
"tPtyD+pjTGR1mnKIH/OGBNhBZe6sqJ9zrKnf66XTvDNsjWyGfSeVghVJSW9M1GOUvTRWdaw8t+vn\n",
"1rY/iTuK68OMPkbtwvPw+T9M9BEAkGIFGAAAAAAAAHaND8AAAAAAAACwa09vPQEAALDNs6zq2TDM\n",
"8bfjoYwQHaLbHxzOkafWSKO3Yps3qmjFmw6qEpwa63yEqmSnqmJ659He5hwr3XKXCeNYd7fhQcdF\n",
"D41mssLgVDmxMoF8LHGi47tuHEMlwjg2eEjbJddYtm9xWzbF2rS959JqN1cxLEezKiKuuTxG4/xO\n",
"G0VsUFW+bB3ffa5Etc28MqPqV1XsVP3KPirXOAAAw8AKMAAAAAAAAOwcN8EHAGAn/tRv+HemX+ph\n",
"dcxRrIdQN8uPhZVU6kbeh3LTtNTJe8dp64b38WyP2c3vW2+yH7MWzqTblleReceaRjO6qPe+7gb2\n",
"9Zv9L6+cm9sfFvfVZmbvs/vNrwLVvnVbPI61rcbzbMhVkUYnehWjPWqPv9pbVznqx5Kuxuqx0k7f\n",
"BH/edJLLCsO+2Rdw83sAwAJWgAEAAAAAAGDX+AAMAAAAAAAAu8ZN8AEA2IkXogjR03M26HSI42EP\n",
"TuL2B8lNzvPQk7jBdHpTdONG+iFOGe08TftEv9G2UxYRq91kX0Ul8yPiqJSMdhlFAZST3Hruw3kj\n",
"ex3tLG9gr2YVdk9xUaPNww/iBuVDGmeTd58X/VVjctY88jGHYciv1DQSd+5DzE1vO38V1+lYu/DU\n",
"DdiN5kMW1Y3bSe4CB+tuoK+e77TbcXGfFV/0P7di/1heIaN11ZzbnyodT3Mzig0AABCwAgwAAAAA\n",
"AAC7xgdgAAAAAAAA2DWqQAIAsEN/8iWfNw5DWvExVIRUVSBVVT5dLXK54qMVQhJJOn2sEV80j4vo\n",
"WJ3P2nm4+93A+ott9eN09tv612Kt/7X9XoOnymWP/tWFKs+bFYMVEeDWeax5nGYccopEi5iteMxh\n",
"m7eSpIrGxnHpL/yRLyEPCQCQWAEGAAAAAACAXeMDMAAAAAAAAOwaEUgAAHbsT77f502/6A/n//Z6\n",
"IgJGhzJVFP1s/61wEPEtz7HuWKT4+SAq76lqilbMy4rheTNUsp1V/tE4bs1fZK1ZL+t8WP3XztFj\n",
"/WtSzjtE8qIHOF1nhzICfBKVNecDfZUW19rSlyyAOX0TvyGUrzVPH/E/MQ6HcttcCXT5qvRWgfzC\n",
"H/mzxB4BAFWsAAMAAAAAAMCu8QEYAAAAAAAAdu3prScAAAAu51kUK3p6zh+dRPbwEGWTDtnXMWo/\n",
"fxdlk8ZiS3GsjPyJeFNaOS7t65S0K/udomhqrKyvh7mVcbYwJ1FoTpLRQEc1vl4xuNWV/OK43hii\n",
"aKLZoTwhod3xUD5Xo3oOVFxVzTyLEKp4a3Xbud/ReNa80U15lxBxrlRs8BaRUBlfzPcNZaxVPZb0\n",
"NVFWcDxkncSvTeUkztvUhXq9iE3qOa1FJAEAiLECDAAAAAAAALvGB2AAAAAAAADYNapAAgDwnPgv\n",
"3u/zx2EYhmMURApRpqORQlKVHFX7OODkKcmWVnXMe7CrUY5TBLJSodKxszZXTyXJZOa+RNdq8SPO\n",
"/yez9lddc5zTaLd2n/dYK7a3RY/qlTIOqNrJH9QFoipILrcvw6dzO6uypequ/k+B8uyP2bY0mrrc\n",
"00mcNzW+ijuq6pL/3o9+CdUfAQBurAADAAAAAADArvEBGAAAAAAAAHaNKpAAADwnnk0F/ebU0HEu\n",
"HVe0nyKQogrkaSxDWIehbKdihnOlvpmOQWXzEfOwqv2lc1sewBv9U5Xu5scZHSGrW15GqGSpY2+i\n",
"at75q6rgKI8T0TyzcmL4qqo1inZWHFEWYTTG9hrV45OVCKNzlFW3rF275vhyo8gAK9kEate/NQF9\n",
"7HKIVcUcRyN2WTsvp+ycV5/vUHHSUWUVAACFFWAAAAAAAADYNT4AAwAAAAAAwK5RBRIAgOfMf/a+\n",
"n1/Ul4sTfCEueBT7FLX/mAWaaqEla4xapUerr/BnTtjmD08tV7S0o2OXizuq52p5FgsbjfOg0rBq\n",
"LB0r7feoZcxQjOLZJitJOh+f3GiUo6ymF42qh6oPPdT281yML05gbR7zY6lXiIx7GUXHVhVIFYH8\n",
"I2/7M2QgAQCrsAIMAAAAAAAAu8YHYAAAAAAAANg1IpAAADzH/sQ5Dpn8j9g5YBRijCpvlEYm7f1l\n",
"m+V+ZR9ZjLHGG5k00mzp3BzxSW8lyS1ao6B2XzOrV+scWe0OtVid6Dg/9pp/oqrYrHWW4hisel6s\n",
"GKC2XH3Rau3lPZf6Ol6u9Kj6l8+f2KbPUbpPzfuPEoEEAKzECjAAAAAAAADsGh+AAQAAAAAAYNee\n",
"3noCAADgdp6dQt4xqmJ4/vYk4liHqbmKLUXtsq9J63MnB9E+qSaXVZg7iDiUiirOx0VxLNHejHTF\n",
"3Z4fqxVzVPu8MTV3nsubATWpx1KP5unKl8vtkkic6GOqzimqB9pxvctUntSVCOORVIg3fH8oN06x\n",
"2fm4kxXlHcuY4aH4xp6vop439XzM7cshT/lO0S45H6oypKwWGb5Znkfc739A9BEAsBErwAAAAAAA\n",
"ALBrfAAGAAAAAACAXaMKJAAAGL74ff7Q9AfBMcS3DmW1xinaKMJIcZzNyipZfSTtjP0qxnUU26zK\n",
"iSpiNgW1ZJxNWa5oWY8N1nnPaTobqz+jM1GtMVwLo2iX9Ju1U1UBky7GtP94W96Xt73sY0V1Qnls\n",
"6L98KKvp62N9PVHzT3rn8y37HUJkWcQXxZmxIqEqRmnFh+PH9Md+jAgkAGAbVoABAAAAAABg17gJ\n",
"PgAAmG90PQzT8otjuCl5tOt4XhWmV8eUN5+f25SrR6o3tc/bJyt9DsU2ddP+efVK3tvc/jCW61mS\n",
"PsZ0X3rjfePm5UZfkliJlhxrbvMujlle9qP6OhkTTp7vrF1txVjYdFL7erR3bptvPq9u2F7OwF61\n",
"JW7y73xarBvCy3atS9KMc6pXTJavmOSxh8sorI4c1Sssam48H+HIk3qVElQBAHTECjAAAAAAAADs\n",
"Gh+AAQAAAAAAYNe4CT4AAEj88fMN8cP/kiU3wc9ukB9TN8vPj1tqr7JORR+ide2m6EWfzvZqLD2v\n",
"5Zvgq2O8f3V5o3MmYzB5Y3rVztl93s4bCbX6dYc61Q3sRR+em+aredQ3tjU7iIvBjrcmR9f79/Yl\n",
"T5Job1y8RhdpO2cEM9/5H/2D/4Eb3wMAumEFGAAAAAAAAHaND8AAAAAAAACwa1SBBAAAiWdjGrOK\n",
"447HEBmLqr5Nka6oXREbrFZ8LJNOZpTxPMIzVY1SReKyinPx9yfVx/LQabxPVIHU81VHL7WpVIs0\n",
"uOdRid8VBzjjeur8WTG5gxW/q0QVPZUea3E8VW1QRwhDNVFVDbKMwVrVOfVzW27UFSfr1Ln3XtDW\n",
"1KzXlRXXfNi/XCnTH/8EAGAbVoABAAAAAABg1/gADAAAAAAAALtGFUgAACB90a/7gqQa5DDMcUgV\n",
"JVTVIvPjlqg+ijbORJhVpdFbnfCw+IPuxBtW61LdsYODeBB2ZUG7/aE4ugx9evuY44Y1ZRyxtdqm\n",
"pVbZsJXnT+7uYxpj5zHG2kxGuV9FQpcnMhoPMP7xP6b6IwDgAlgBBgAAAAAAgF3jAzAAAAAAAADs\n",
"GlUgAQCA9GzOrk2Oo4iuqVhkUXWxkmg6lDGrInlYrSRZbhzP81XRQxXNU/G7QzbwmA6wOA8Vo1TV\n",
"KG9CnBAzoldtv5wFndrV+sgqalpVBx+2HUQfQ9KHvKCMOGDcX2sEsRavLSplWvP2DOJob+4XjzO8\n",
"XvTFG7ULzcT7gTmk0fA03vxVAQDYOVaAAQAAAAAAYNf4AAwAAAAAAAC7RhVIAABg+g/f+wumPxae\n",
"GFUP0yqQ9WhgHDvzhJ+8lSRb99VK77VWbizrHzrnsaKdxZtoNCsnihisbB+inUbUNBnfs6+SKfSc\n",
"o1oC0vXYo4YywmpVU4zPWxY5HGsXnurE0U61MKPF6ofKkEWcs72LrCTkMJyi7/+TH//T5CEBAN2x\n",
"AgwAAAAAAAC7xgdgAAAAAAAA2DUikAAAwC3EIZO44/nr0Yg0qvhitXJitq0WRQxjqOqBqn8V1bJi\n",
"cmYncj7L+2T75Keef5+VEzkY/VeSfOYxVrvWKonX5I9KesKbdr9h66geae0kGe2t6GPr8+KNNM5x\n",
"1fjRLR8RP+Z8LGKPAIBLYwUYAAAAAAAAdo0PwAAAAAAAALBrT289AQAA8Hg8Oz2klJ4c55CUJwx2\n",
"HEW6qVLVMafu2pCGrEI5PjWhEI8sy/KpyGTcb1ydLjosaRe3UVUMXWm2JEJ6mTRYmNKxEtdbPnIY\n",
"PNUG44iljPpZMUAZlytjddZYB6OP2ra8//z7fB5WzjC+Bsbp2joU+6xM6JYwrBVftPqVj30sz72+\n",
"BtSJKK+ZqTvuxgIAuBJWgAEAAAAAAGDX+AAMAAAAAAAAu0YVSAAA0OyP/Jo/PP0BcTxnAo8q5Ri+\n",
"igqRtYqMU/v/v717+7Vlz+oCXrU4T+6zwfvtyXi/xBtGQzQmRk00REQgEoRABAkRge6Y+B+oifqi\n",
"59DaELpJBwXlElGU8ECQByXEGDHGqNFETbxgEEXoc/abPcuHNWvOuowa9ZtrzXUb+/N56L1W1a9+\n",
"VbPmPMnssX7fGvfoIHmeY3GixTVdIrqeKFqZXs/eOS6/rLu7MIo23rfZ8CEe03Ub0dWGOWbjVz9M\n",
"5k3bE27P+aCC82eX0nq56f5TxnJnlkUccTr6Jtg2dnWcxnLT+GTyvkTHHY7X8xf/6/u6QALwoKwA\n",
"AwAAAKA0BTAAAAAAStMFEgC42DTKdEiiV6dIVRKD67o4AnbaHXSQjKJUYxQzmiM8/7A4T7dO0EXm\n",
"XQSD/VHHy+WYyb1KGgA+ipsknjaaxeSCgctNUQfMvbjjMpI3/Svt2GVz+hEbVj+sJ9t7b6Nth8Zx\n",
"2en7hnu6N0c4ruGzFU+c/Dc0OfkhfIG3G6edTpuSpjufk/Fn0UcAHosVYAAAAACUpgAGAAAAQGm6\n",
"QAIA9/IXjh0hpzmmsVPiGHNs7doYxSLT8TvXNl7H+HUn6vy4F3Vbxrz2riOMxEUDk/keU9TVcimM\n",
"pqYHrLtitrr0Pl98bXdwjgv26/OcPmPRmzvNbM67L7Zf6zD5KTj/alS+c3nf9uaKYo4t72h0P4Zg\n",
"5r8kAgnAI7ECDAAAAIDSFMAAAAAAKE0XSADgXv7fMdX0WbPU2zGqdYoeBl0Pd7JXp4hWEpBK44Zd\n",
"EMPa6Uw3Xudh2sVwf4r2CGTSnXBrvnzjHc3u83zivdMcgm3LY2b3tKUTYbD3EOzbi95FHRxb7EX+\n",
"lt1Eh+CzPoQHTAYuOkOGrz3pwrg8Jvp9S9Ioc3f8Mv55++PyRqxjmvF8531/WfQRgEdmBRgAAAAA\n",
"pVkBBgDcy9/4yff6ruu6P/8rP7pa6zOunroJVrH0wRqUPvgleoZ6tnQke9D97gPTFw8qX/+yddL1\n",
"oCF5EPydVpE9UN+iZT+k6K+ju6de3OAh2hm8wCEYlu2bXmsfvKnZCqk+mSPqCZU+9H39bPv57mCl\n",
"3yhapTasfsi1rt46b8xX37Vsm6+sXI6JbsL69HpvAfCUrAADAAAAoDQFMAAAAABKE4EEAK7iM5N4\n",
"080yvjhNA44/RNmxPsmz7Twye/mg8qkwUhhE6KL45PIlhDHKnYjZGIdMX8JOxvGx0mPRQ+4j8YPu\n",
"t8dlb23X5fG4cF8Yt7xs/tbPSrYveu3pg+6PZo0Wok9X9mGJPm/hhbRFH5f79u7pKd6b/EfR+vkA\n",
"gMdiBRgAAAAApSmAAQAAAFBaP2jHAgBc2Tf9ituOkJ8VNAAc3QSxyLy7Y/6dZdl5ck8WaYw69EWR\n",
"yW65r1E0/MIpHkzfGMObdrk8/RR2wzzu2nuBp1hdEuXbi/mN+6PxV9w2BNHC6edzCOc4jZz/Op0j\n",
"2LbbuTQY17Ive1+G6KQ7EdaWc/6V//b+c/mYA/AWsgIMAAAAgNIUwAAAAAAoTQQSAHgwHzlGIW+C\n",
"4NN0UxTDWm7qk32zcUlUcnodQYPKcP5sXHj+YNtqjobXe8k5H8qlkbvW643uaXafW/ZN91/6nl16\n",
"bdf49vwY38BbumFO/9tr/b8Fq2FBWjTa/1f/uwgkAE/HCjAAAAAASlMAAwAAAKC0d576AgCAug5J\n",
"pOomiF6l3Rd3nOJpYQbreD07wbPsnK2xvWzbaV/UzHDycxi1a4xN3lUWaYxey33mzcZl9691/mxb\n",
"63uVXdts34XdFPtoXzB/+N4uPhh3iVGm8cVofPD6htWN6yf7gk6gl10iADwIK8AAAAAAKE0BDAAA\n",
"AIDSdIEEAB7cN/7yj66+cESdIfe6Rab7+vW2ZYRvN2I27ks6Se7F5frgOpbj9qKLz61VXhhDTaJz\n",
"0fsSje+DmzTuiyKy4Ula9zVuCztI9vPraP0M3Lmr4obl23CvCGQUbQwmjmOi/fHf8U2b7D3+t9NP\n",
"tv21//GPWeRFAAAgAElEQVTec/tIA/AWsgIMAAAAgNIUwAAAAAAoTRdIAODBfWYSqRqjbbNtx38P\n",
"wbFRpDAUdMbLOkiO5wwTcZP4VhY7G6OS886Tw2rcMmsXRjGDKNrea84idq3dM1tMz5NNG3VLTDte\n",
"JtcfdRBtnTdMsEbjk0jjbHhyneGu48bpa8jejzTKOI0jLjtJNk8yHbb4LO60Go1ijud7tN0u1UNW\n",
"AHhurAADAAAAoDQFMAAAAABKE4EEAB7cx3/q3AXu63/ZbUfIWews6Zq37OQ4+3k3I7i96xAMGeOZ\n",
"s22LcbNTDv1q/Kwj3sp2xGyn0eLGHA3ZvPtEIbOY4Xb6rdk08toSrWx85eG+U9wxiJruXveQ/Bp1\n",
"kgw+R6u4ZdjlcucVXhgvPEdNo7s75imTdp4b5xrft7gRp4aPADxPVoABAAAAUJoCGAAAAACliUAC\n",
"AI/qEETRIqfdUQarn881Gx/MkcX1pruizoPLqOQsihlE3aLIZnbO02+NObz5ubZvYtZpsQ/bJF4m\n",
"6nyZjr90/nvsP0fzgu6cF1731swnh+0o4excy3s+66oYZRuD93acI43Zri4j3xd0PI0ijVGcM/zo\n",
"XiN6CwAPwAowAAAAAEpTAAMAAACgtH6I2i0BADywr/ulHz19CRm7L0bxwizaGJnGHbM4YjQ+mv+u\n",
"ia7oOqL4Z+vru2tY71rj8kkui+aNEcwhGp/MNY1uRsem8z6Q8PMRvIbl+3efIGarNAIZpC77IAMZ\n",
"df1s+b8Pf/0n3xOCBOBZsQIMAAAAgNIUwAAAAAAoTQQSAHhyYxzyJokGRvHIyKXxyL1x3SK2GHV8\n",
"bL2OLE7ZB7/sdahczXOH0Nn419DWqGfSlLP5uOU5r2WZ4Gt9r+6j9X5kEchDFwi7dyZDGi9k+dV/\n",
"7x5d3L3zeMB7/1MEEoDnxQowAAAAAEp756kvAAAgWt00uklWsew9rH61Uix4uPfUaZVXtPomWwrT\n",
"+NT85tU0wQPKm469w5Kqzyx+D+/3zrlWq5t25vhM0AxgNW5yQDgumGNY7Nt9Xy7cNiyXmE3GDcH1\n",
"Riv4opWErYGMi4MbyfholVx2O8KlYsH8siUAPFdWgAEAAABQmgIYAAAAAKV5CD4A8Gx87S/56OqL\n",
"SRTJiyJmzQ+1T8a3PLU7PG4awwuieUli7LQvi/ltXcBDPGX8OT65vOX+be2/7/hWrQ+Tv8aD5q9h\n",
"FRediO5RloCcjn/fw+8BeKasAAMAAACgNAUwAAAAAErTBRIAeDaiKFjUIfL0F7zWsFXSrS7qIjiV\n",
"neI0RzR/0BUw7F45xjmn44//HqLrybovRhd5YSBt2PzlON0TBNyyiOAVGyPey96843t/er+Dfc1a\n",
"PpSNu6Ph4bbp526RgfRAFQBeAivAAAAAAChNAQwAAACA0kQgAYBn45M/fe4g9zW/+NgRMoh7HYLW\n",
"dFG3yFG/+mHyY2N+K4pMpuOCjWFHvSBGlnU9DLsN9sm+K+fTohjnakx0HTvtD8cfb4LXMv4SxlWz\n",
"1/dALR/33qvoM5Bdbxh1bb2A7U3psfeKjso8AvACWQEGAAAAQGkKYAAAAACUJgIJADxL3/6/b+OQ\n",
"X32MQkbxt2lM7BBF8xY5sqiD4hDFIrv1uO0NDbsXXSD3OjNenDC7RyTurg0Fp8f1UWxxnCPIfUYx\n",
"0nF31PUzig9mMdEo/pnd+yiqmG2LOiJGXT+nTp/P4F5FXSCz1/XQnS9347irG3LhCQDgCVgBBgAA\n",
"AEBpCmAAAAAAlCYCCQA8a2m3v70o4SIWGcYjg1hdv5eJ27rGybBpZ79+ee07ryWKxKXdFBs1RTx3\n",
"ZJ0sm+dIxl8z3hfua4yw7nXgXG5MI4Jd/jm+9DVHXSNDLRnWxusJu1wef/j4T713j08lADwOK8AA\n",
"AAAAKE0BDAAAAIDSRCABgGftU8dukF/1iz56SmHdBPGtUyyrNaqYRL/6YOP4V8NZtDE7R2MobBkn\n",
"m82RHdAF1/uIQbQwEvd4p788+vhA46POkKuun9Ofow6Y2Q3c6Th5qeXnbbfjY7CttZspADwnVoAB\n",
"AAAAUJoCGAAAAACliUACAC9CcwSrpfPdJSc7OgSRsTGKGcXIWrvr9cEcd80UTqNxUZytZbq9MS3R\n",
"wzCGuhPxXB2zF2+NInxZhi+7IZd2sdzZduo+mnWBbOwQGZ3kHgnI1bHhf1fTbVns8j4XAgCPzAow\n",
"AAAAAEpTAAMAAACgtH64TxsZAIAn8JWTjpCj01/1JtGyZaouSuaFkb9gY/Ox2bggcjfG5KZzHbr1\n",
"tuX4aP7dr3UNF7w3pCU1eJekaXbMc2s6eIUUZRekOXfP1bSzMRbces7w9S3ekG/7X+89l7cGADZZ\n",
"AQYAAABAaQpgAAAAAJSmCyQA8OIcki57USfEU4wriEe2dnCMdqVdIPcOHjeNryUY1jrvoTEK1zfk\n",
"9PaG3CQXEl13lF+Mphhjn13w3kbXlnVavEYeb8hygDvXlm887pped/AZGH+5+GklO+Nbpotee3Qd\n",
"nxB9BOAFsQIMAAAAgNIUwAAAAAAoTRdIAODF+opfuO4G2QdRu6yb4qUZrt0uiUFkLIsN3ue847as\n",
"a+Rd5r30gLu+vKwTYmMzw3u5xjmW78F02yyOuzjZXRo4hlHJ1UnDy0zPe5cxXdd1n/xpEUgAXg4r\n",
"wAAAAAAozUPwAYAX6zt/5rwC5cvH1WDRg+aP//bBkqNo5U62rGX2fPDGJUTLh/aHK4NalwQlp2pd\n",
"uZOtvNrVcp3JezA7LLl/h8Zx4fvRsK/r5g+iP21LmhKEjROSh8RnD+1vDWFEw7IH7re+n1ETgZb5\n",
"bw9qPAkAPCNWgAEAAABQmgIYAAAAAKWJQAIAJYyNfebxtNusVvZQ8ijq1pz2CmJnN0nMMYy9RXG9\n",
"5QV10c71fP3mL/NN136YfBbnS1OirTHAxkhlGgNszBK2DBuCX1qjikP2fu8c2+Iw/dwl47L59+73\n",
"pzz8HoAXyAowAAAAAEpTAAMAAACgNBFIAKCEv/t/3++7ruu+7Bd85JzWamh1txc1O3WGTLrlTXcd\n",
"kixcGIXsZ0N2tXYPTLthZsfdJdyWXVMy37TT4/Ie7Z4mGL+MsN6n2+Ww8fPWXFHHx1DUjXL8N4i3\n",
"hrHWZP7oultjqGksMtkHAC+BFWAAAAAAlKYABgAAAEBpIpAAQCl/7xiF7LpzHHIIMmnnaOM6IBZG\n",
"5+4Y85se2kexxNao4vGXsMtfY2xxHHZI9j1U1m0Irrv5VI3dHVuiilNhNDC5uNZOj6nGnGFLl8vW\n",
"iGe2L4qhzmQdTAHgBbECDAAAAIDSFMAAAAAAKE0EEgAoa4wLpp0FJ9muKA55Ghdsi2KD4bi7dFZc\n",
"nr8xBng+6fawKM526SW2vqYs4hkfsD1mL/J3YfPF+PQNUb/7dJdMzx39Er2P0T1qfIGnaVujjcf9\n",
"3/F/3rvCpxgAno4VYAAAAACUpgAGAAAAQGkikABAWd/zs7cdIb/05992g5zG9sII3TEPFmW9wo6B\n",
"4769TpKLk01/jaJoUbxwSCJxoSTa9qgN/Rq7Z646VO5kIMM45/LeBPumm8Zjo89F+H6M0cMoA7m3\n",
"rWF8a7x1vEf9zrh0uiSamt1SAHiprAADAAAAoDQFMAAAAABKE4EEAMob42yHSbbrJsh29UFM7qIT\n",
"RJNNh4XHBvuu2PFxL8/W2h1xNX9yQHNsbqd75iXnbJ1kb46wa+Xi/eiD697bdsm+vW0t+zaPybpL\n",
"BhM/alwWAB6QFWAAAAAAlKYABgAAAEBpIpAAQHnf+3O33SC/5HM+ckp0jXHI+3S5G1OOh2hfkKXr\n",
"k5aPw14byEwWmQzGRZvSM17YeTK8jqDjYzrVPW5HPOHsn9k5ml9ecLPusy3b1y/37UleROsczecC\n",
"gBfICjAAAAAASlMAAwAAAKC0frDWGQB4C33x53zT6ktQf8yRTdNkY/wuSphdGs27NMnXT04wfmeb\n",
"blvOt9Pw8SrXdA2nl9DYCTEbH76AIO4YzTEs9802bs/XODzctrqe7jrRwyzKmt22vVN/18+89xQf\n",
"EQC4OivAAAAAAChNAQwAAACA0nSBBADeSqcOgNMoWpjJO3ZpPP6axdqW+1dTjWMaQ2Xhoyom287z\n",
"rTtJhpG4fh3xfIqHYUTdF5fXO7uu7CKv0OEw3NcYz7zztiCKGQ9o+7AMp3/Ps53v5XqO9Sfl/KMH\n",
"pABQkRVgAAAAAJSmAAYAAABAaSKQAMBb6fs//c1913XdF332uhvkvHvgfPcsTDaso2U3SRu+Mfo4\n",
"jdxdvC2avrWN4HFcNrq/tLXlXZyidsGVBOc/nI6bxPuS64w6Zi737c0RHhPNF43P5jifPJ3/HBMN\n",
"PgRbc25eh1AjAFgBBgAAAEBpCmAAAAAAlNY3L5kHACjuCz/7G4eu67p+EnRcht72UnPbR8b9/Pqg\n",
"7WEUd2wK6/Xhj1f10AHJqKNlNi7qirkaMxk3RPuDc136DfnanTVbekDufT4uvo7jAd/9s+8/Qg4W\n",
"AB6XFWAAAAAAlOYh+AAAR9lDw8dVYYfmh6hvr7+Zrdw5/dIH29bHBIuaTkdeexXS6Xqm57zGhMny\n",
"pms+0H/2wPvFqadzhMe2XUU47zXvfetc8YP3r3ghAPDCWQEGAAAAQGkKYAAAAACUJgIJAHD0A5/+\n",
"WN91XfcFx4fhT/XHkNksZjist6WPLY+euX4anj+I/Tysn+yfZwnvEnnrFz+ED1N/jCjdGOfcfi79\n",
"fhRzSPadJjn/eBhWm+L3aHn+yb7DeN+CNyt8n5N5w3NOfk7jnheOTycBgIKsAAMAAACgNAUwAAAA\n",
"AEoTgQQAWJhG0U7xtG7+b9dtxAWDqOR53qjtYbApisudriOKSgbxzOD8ffDT8oC919e2M7ATrxvv\n",
"+fjX2b2uhnfrvznfeXGMMnqvovHhxSeX1PjhyjteHv+dZjGjz1vi+37u/UvfVQB4MawAAwAAAKA0\n",
"BTAAAAAAShOBBABY+McffOwUBftjr287QkZd9rpFPHLPTTJyln4LI3T9etxyzLRLYpqBPO9cv65+\n",
"tW9nirsL4oiH8ffJC+ijPGB077OYYfwOLvbl+2/GbpvtQdHwSlbH9cG2IFq5/Qom1xTekDsHRgGg\n",
"DCvAAAAAAChNAQwAAACA0vohXB8PAMDU57/+hqHr5mGyMJo37mtMxkXDoiaQUXfEZWxx3gVy7Ay5\n",
"cyHL3cFXw2u3Blx21twdvxH6W86xHhdFPde9MuM5spjo/OqW47Nt0fsSdw5dxy2X19Z6/6KupuPB\n",
"f//T36zzIwBvBSvAAAAAAChNAQwAAACA0nSBBABocDhGxm5mnRaPG6MmhdPYWRYiDHZF0bZDsK8/\n",
"/bsdiZtH6NY/ja8hi/fdp+dhpCm6F3Uz3Dn56tEe0b2d5QGjU63PNWQZyOgzcNw2zBo9LrZNrmNI\n",
"5h2yeYMbOXu/+/X7p+kjAG8rK8AAAAAAKE0BDAAAAIDSdIEEALjAH3n3z52+PEXRxrHL3rxb5Lbd\n",
"Lo3ZscsoXBTFDH4+bOzfmCI+d+O4VuNLuAlmPr28IH6a3b+4g+L2ube39vPzD+tRcZ/KYI70nPlV\n",
"9adI6vZZhwszjv/w0x/TBRKAt4IVYAAAAACUpgAGAAAAQGkikAAAd3SOQ677KzZHCRsbRJ7jb+v9\n",
"WQwvmn/WCPGyBpWpS8dH30L7ICSYxQan0cYs/hfNe+m34LCLZreOYubXcbdzT48+n3N7354fEH0E\n",
"4C1jBRgAAAAApSmAAQAAAFDaO099AQAAL9Xh1IlwEqvr593+pqJOhNHTKG6Ow+bdGrejbVk08DBs\n",
"dyIMzz/ttLjeFF5vS6wvjGIG46IIX5bVa438RbHB+Px3O2f7dbTti88/bM5xeqzJXrDR008AeEtZ\n",
"AQYAAABAaQpgAAAAAJQmAgkAcEc//Objfdd13R9+9fWnYFkfZgSz7n1rh/Nskzlu/wk7OB63DbPh\n",
"2wG/edRucTXB9cepuX61P48Ntjm9pOCA2XX3wbbkZOO9mf71dwgufFj90K3vffRCJ+PHc/XJtiHK\n",
"Yu7Ne7qe8X3cyZX2Le8MALwdrAADAAAAoDQFMAAAAABK64dofTkAAHfyh1792aHrlqGz+W83UUvE\n",
"qbGhX2NyLeou2UeRyeByssjhuPPSAN1dAnfj6W+So+cRyGMMcPb6+s3x3Sl+GnTi3O2/uH1sdq64\n",
"52TUMzPozpn8FF/h7dbpX7cPQeT2Bz/4m/KQALyVrAADAAAAoDQPwQcAuKIfefMtfdd13R88rgS7\n",
"NV+Jcxjy1T+Lw2Y/9pNlYee1RMGD64ftlUbzeZN1RcPsn/moZB1R23qq2OE06DwqeuB9HmJYP+y/\n",
"fdz2i45WZY2rwqL3oP3R/22NB8bXPAQr88ZUxyF6oD8AYAUYAAAAALUpgAEAAABQmggkAMADCGOJ\n",
"x39vgsedR7HBIYwlToJ4y5Tj9OH247g+OFdwsj4JzE0f/j5GFPvGfN2lMbzovqVPbY/inFk8cyda\n",
"mcY+w9xlEKNM0qenOYIn3g/T+OL2sMk1tsVbf+jDv+XB9wC89awAAwAAAKA0BTAAAAAAShOBBAB4\n",
"AD/65ltPsbM/8OrrZgm5w3p4aO8vlauYXNQ1MkjtTc+/2t/nfRvHCOE0nhkeckdhV8XgNQyL8bNt\n",
"y6zgceRyy3h/hygTOj3XMCz2TftBZjHVINN4iipG8cV1n8k4Qrr9Hg2rLQBA11kBBgAAAEBxCmAA\n",
"AAAAlNYPYTcbAACubRmF3NInbQznkb/b6W6C2GA0R9accPwp6jq4ty1zaTqyT/KUuzcvany5HDKZ\n",
"JOoCmQZAG+bfPVcwR7wt6mi5OHHcznM1xw+/+bgukAC89awAAwAAAKA0BTAAAAAAStMFEgDgkRyO\n",
"Gbq9PFoWMxyCIGDUVXIIzjWOm887D0ZGXQTb83NBB8XmY8cZtls+7kUVW04eXc80SXh6zVEDx+TY\n",
"Pjgg68gYXkfw87xL5/yo+f1Y3yTRRwA4swIMAAAAgNIUwAAAAAAoTRdIAIBH9vtffe20P+Bqf7+5\n",
"Zzlu7P64Hh91fFweF50zHr/9W7zl7rLrmI+LOl9uzTa1DlLGc0S9L5N9swjk1nGxS7ttZu/RdN+P\n",
"vPkWEUgAOLICDAAAAIDSFMAAAAAAKE0EEgDgCf2+YxxyHl/cTq5lmbZojnm877JE3KXjo+u4jijg\n",
"t96WRUIz+7HP+bi2YGV718rWCOSw+Gk+/+3IfyL2CAAhK8AAAAAAKE0BDAAAAIDS3nnqCwAAeJv9\n",
"2JtP9F3Xdb930hmyD0J5WXfCMf52mI2PYnLbj75o637YFi9sjRRm9uOD0VnWr3k5On91+9fSMiYb\n",
"33odQ7Ive50AQMwKMAAAAABKUwADAAAAoDQRSACAZ2BY9fibd2E8b4vikdtRxeXI7b3rfVlcL48o\n",
"rrdc2mlxb2tLlDC/B/N7nlt31DzPkd3TvWvZ3teybfraf/TNt+r+CAAJK8AAAAAAKE0BDAAAAIDS\n",
"RCABAJ6BH3/zyVOE7fNe/Zlj2i2PNvanaN62eS4u6gw57mmLA0bdItdxxHyultBga1fFKAQZR0hv\n",
"t97MRm8HKYfZK53PO7+esRNnNG90nev55zPN58i7RUo9AkArK8AAAAAAKE0BDAAAAIDS+mFo7X4D\n",
"AMBj+rxXX7NuyTjR9/sRuL4xJtfSH3L581IUKBx/u35Yb4wIbnd1jLtodqvxrfdo+yraX9/9vnnP\n",
"z/ZP33ybDCQANLICDAAAAIDSrAADAHgBfs/P++rVl7bTArChn/8+HxX81CZfGTWsxrU/jP9uLl1l\n",
"FT1APp5j71Hzy9eXr5PrgwfdLx+k3ypqWDD6Z28+YQUYADSyAgwAAACA0hTAAAAAAChNBBIA4AX5\n",
"3a/+9DoKGQT7+mMssusnw4f1A+mX0cCWB+tf4j4PmF/PFZkGE1uaAkyPvOwh+FmMMosqZnNNx8+3\n",
"RTHKWz8m+ggAF7MCDAAAAIDSFMAAAAAAKO2dp74AAADaHbrD6eeb498yp9tGUZRx2TXy9sdj8G78\n",
"J8jmzWKDw3rbsv1kFDN8KEP4WxQq3D42ji+ut8avZX9ffG1nhyCKeX5HLw1XAgARK8AAAAAAKE0B\n",
"DAAAAIDSdIEEAHihfterr9r8ItcH0bxxWz8L+i3id5MZw46QpwhksK9fDJpsbA3vZR0Z92OGi9P3\n",
"6ajzbJNpb9a34Tx+fO2TybLOkK2ibpTRth9/80kZSAC4IyvAAAAAAChNAQwAAACA0kQgAQBeuM99\n",
"9ZVNX+iyeGG2b3dcQw4wOq6tR2LsPD7II0bnP0Ubg66KQzRusm3eKHMRgYzii/Pjum7WeHN65vn4\n",
"YNs/f/PtYo8AcAVWgAEAAABQmgIYAAAAAKW989QXAADA/fzEm7/dd13X/c5XX7FqbBhFD6POkC37\n",
"pvtnkb9+vS07Zz7//Z2usV/HEmevLzjZEPw0hhMPabfGbK7pb32wLxoPAFyTFWAAAAAAlKYABgAA\n",
"AEBpukACABT0O159+epLXh/E785xvu0+jH3yW2QvdpmNu3Te1vHZ+aN9s3HHFo5R1DN9XbMukNvn\n",
"iF7Xv3jzKd0fAeCKrAADAAAAoDQFMAAAAABKE4EEACjst7/7pyaNDffijft74/HbsywDlvcxjQrG\n",
"cchhdq5LO2DunXfoDqctlxy3PG+Lf/nmO0QgAeCKrAADAAAAoDQFMAAAAABKE4EEAHhL/LZ3v+z4\n",
"xS+JLE5iklHXw6iZ4XjI+djo++WlYct81HYA8vxTP/lbb2sXyJZtWfxy++rm1xGN+Ik3f0fsEQAe\n",
"iBVgAAAAAJSmAAYAAABAaSKQAABvmd96ikKuY31R58Iw8pck/ma/BrHI1u6LuZb+knkXyJsw7ngT\n",
"bFtGIKfzRWdq6VB59q/efKfoIwA8MCvAAAAAAChNAQwAAACA0kQgAQDeYr/l3S8duu5+scTs2D6L\n",
"Kg7r4+6TBVzFC/u8W+PYtTKMQPbTcd18XDDvvDtmvz3H8dB//eF3iT0CwCOyAgwAAACA0hTAAAAA\n",
"ACjtnae+AAAAns6//fB7+q7rut/87p9cZRTj+OJ+ci/qoBiaRgRPxz5Mh8ghiGCeRs2u47A569Bv\n",
"Pzpkdof6cdt5rqEfu2wCAE/BCjAAAAAASvMQfAAATn7Tu18y+XKYPaR+e1/07fJ+D9m/bO94rmjV\n",
"V3TkfH1b9GD8+bb4taxXyc3nuPVvPvxui8AA4AlYAQYAAABAaQpgAAAAAJQmAgkAQOg3vv7i2y+K\n",
"s1BklOBbhgnXQckoZjiXfSfdTg22Rivz+OJ6vtYIZPxw/fUcY7MBAOBpWAEGAAAAQGkKYAAAAACU\n",
"JgIJAEDqN7z+otUXxn6YJPqS9o+nOGC/7pLYX+FraB/+PXeV3Fxdz55pfPFmFWlsm+Pfffi9Yo8A\n",
"8ExYAQYAAABAaQpgAAAAAJQmAgkAwMV+/es/sY5FRh0Ux6hkGAZcd4sMJV9Xo0jjOZ0ZdGgc9lKJ\n",
"68jm+ZggAjmOm8z77z/8PtFHAHhmrAADAAAAoDQFMAAAAABKE4EEAOBeft3rL9z9QtnafbF13PSI\n",
"s/3vtfMI5LFb5KyhZRLjDE45jvsPH3y/2CMAPGNWgAEAAABQmgIYAAAAAKWJQAIAcFW/9vUfT79g\n",
"RjHD5b69bS1mMcbjHNO5xv3TcTfHvw9Hx47bpnOIPgLAy2AFGAAAAAClKYABAAAAUJoIJAAAD+bX\n",
"vP6C45fN7UjhuLWb/XbdZGE83zD53+1rG2OR//GDfyDuCAAvlBVgAAAAAJSmAAYAAABAaSKQAAA8\n",
"ql/9+vOPX0C3Oz5G8chL84fTGW5Of/cdJvujLpTrLpD/6YN/JPoIAC+cFWAAAAAAlKYABgAAAEBp\n",
"IpAAADwbYzwy6xB5F3EE8tZ//uAHRRwBoDgrwAAAAAAoTQEMAAAAgNJEIAEAeHF+1es/uvsltp9E\n",
"J//LBz8k5ggAbzErwAAAAAAoTQEMAAAAgNJEIAEAAAAozQowAAAAAEpTAAMAAACgNAUwAAAAAEpT\n",
"AAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAA\n",
"AEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUw\n",
"AAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACg\n",
"NAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMA\n",
"AACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpT\n",
"AAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAA\n",
"AEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUw\n",
"AAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACg\n",
"NAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMA\n",
"AACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpT\n",
"AAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAA\n",
"AEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUw\n",
"AAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACg\n",
"NKPGmbIAAAXESURBVAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACg\n",
"NAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMA\n",
"AACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpT\n",
"AAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAA\n",
"AEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUw\n",
"AAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACg\n",
"NAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMA\n",
"AACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpT\n",
"AAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAA\n",
"AEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUw\n",
"AAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACg\n",
"NAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMA\n",
"AACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpT\n",
"AAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAA\n",
"AEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUw\n",
"AAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACg\n",
"NAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMA\n",
"AACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpT\n",
"AAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAA\n",
"AEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUw\n",
"AAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACg\n",
"NAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMA\n",
"AACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpT\n",
"AAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAA\n",
"AEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUw\n",
"AAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACgNAUwAAAAAEpTAAMAAACg\n",
"tP8PeEhLEATAIfsAAAAASUVORK5CYII=\n",
"\" transform=\"translate(507, 47)\"/>\n",
"</g>\n",
"<defs>\n",
" <clipPath id=\"clip5404\">\n",
" <rect x=\"1891\" y=\"47\" width=\"73\" height=\"1457\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<g clip-path=\"url(#clip5404)\">\n",
"<image width=\"72\" height=\"1456\" xlink:href=\"data:image/png;base64,\n",
"iVBORw0KGgoAAAANSUhEUgAAAEgAAAWwCAYAAAD+FAeUAAAMbklEQVR4nO3dwY3sRhAFQY5Q/lsh\n",
"L6XfLQtUeSQPERYMEg9LNMmZ/f17/r4P/+uvtz/A1wkUBAoCBYHCnPvv25/h0ywoCBQECgIFgcJc\n",
"V7GVBQWBgkBBoCBQmHtcxTYWFAQKAgWBgqNGsKAgUBAoCBQECq5iwYKCQEGgIFAQKLiKBQsKAgWB\n",
"gkDBU41gQUGgIFAQKAgUHDWCBQWBgkBBoCBQcBULFhQECgIFgcI8bpitLCgIFAQKAgWBgqtYsKAg\n",
"UBAoCBQECvO4YbayoCBQECgIFBw1ggUFgYJAQaAgUHAVCxYUBAoCBYGCQGGe88/bn+HTLCgIFAQK\n",
"AgVPNYIFBYGCQEGgIFBwwyxYUBAoCBQECgIFV7FgQUGgIFAQKAgU5nf/vP0ZPs2CgkBBoCBQmOf4\n",
"I72xoCBQECgIFAQK83MVW1lQECgIFAQKAgVnsWBBQaAgUBAozOOpxsqCgkBBoCBQECi4YRYsKAgU\n",
"BAoCBYGCG2bBgoJAQaAgUHDUCBYUBAoCBYGCQMFRI1hQECgIFAQKAoX5nfP2Z/g0CwoCBYGCQMFR\n",
"I1hQECgIFAQKAgVXsWBBQaAgUBAoCBS8vBAsKAgUBAoChXk81VhZUBAoCBQECgIFR41gQUGgIFAQ\n",
"KAgUPPYJFhQECgIFgYJAwVUsWFAQKAgUBAq+zBIsKAgUBAoCBYGClxeCBQWBgkBBoCBQcMMsWFAQ\n",
"KAgUBAqOGsGCgkBBoCBQECi4igULCgIFgYJAQaDg5YVgQUGgIFAQKHiqESwoCBQECgIFgYIbZsGC\n",
"gkBBoCBQECi4igULCgIFgYJAwR/pYEFBoCBQECgIFOY59+3P8GkWFAQKAgWBgkBhnusstrGgIFAQ\n",
"KAgU3DALFhQECgIFgYJAwQ2zYEFBoCBQECgIFJzFggUFgYJAQaAgUHAVCxYUBAoCBYGCG2bBgoJA\n",
"QaAgUBAoOGoECwoCBYGCQEGgMI+L2MqCgkBBoCBQ8Ec6WFAQKAgUBAoChfGNzJ0FBYGCQEGgIFBw\n",
"FgsWFAQKAgWBgj/SwYKCQEGgIFAQKLiKBQsKAgWBgkBBoDCPL/usLCgIFAQKAoW55/f2Z/g0CwoC\n",
"BYGCQEGg4IZZsKAgUBAoCBQECvM4i60sKAgUBAoChbnXH+mNBQWBgkBBoCBQcNQIFhQECgIFgYJA\n",
"wVUsWFAQKAgUBAoCBXcUgwUFgYJAQaDgqBEsKAgUBAoCBYHCPEejjTpBoCBQECgIFNwwCxYUBAoC\n",
"BYGCG2bBgoJAQaAgUBAo+HmcYEFBoCBQECgIFOa5Gm3UCQIFgYJAwVEjWFAQKAgUBAoCBVexYEFB\n",
"oCBQECgIFLwnHdQJAgWBgkDBa8DBgoJAQaAgUBAoeE86WFAQKAgUBAoChblumK3UCQIFgYJAwQ2z\n",
"YEFBoCBQECgIFNwwCxYUBAoCBYGCQMENs6BOECgIFAQKAgV3FIMFBYGCQEGg4CuZwYKCQEGgIFAQ\n",
"KMz1G2YrdYJAQaAgUBAoeHkhWFAQKAgUBApumAULCgIFgYJAQaDg2XywoCBQECgIFAQK3pMO6gSB\n",
"gkBBoOCoESwoCBQECgIFgYLHPsGCgkBBoCBQECg4iwULCgIFgYJAwVONoE4QKAgUBAoCBUeNYEFB\n",
"oCBQECgIFDz2CRYUBAoCBYGCo0awoCBQECgIFAQKHvsEdYJAQaAgUBAoOIsFCwoCBYGCQEGg4CoW\n",
"LCgIFAQKAgV/pIMFBYGCQEGgIFDwhlmwoCBQECgIFAQKc/wDtpU6QaAgUBAouGEWLCgIFAQKAgWB\n",
"ghtmwYKCQEGgIFAQKDiLBQsKAgWBgkDBH+lgQUGgIFAQKAgUXMWCBQWBgkBBoCBQcBULFhQECgIF\n",
"gcIcf6RXFhQECgIFgYJAwVEjWFAQKAgUBAoCBVexYEFBoCBQECj4Ix0sKAgUBAoCBYGCq1iwoCBQ\n",
"ECgIFAQKrmLBgoJAQaAgUBAoeAUvWFAQKAgUBAqOGsGCgkBBoCBQECi4igULCgIFgYJAQaDgX9cE\n",
"dYJAQaAgUHDUCBYUBAoCBYGCQMGz+WBBQaAgUBAoCBScxYIFBYGCQEGg4KgRLCgIFAQKAgWBgqNG\n",
"sKAgUBAoCBQECq5iwYKCQEGgIFBwwyxYUBAoCBQECgKFuY+r2MaCgkBBoCBQECg4iwULCgIFgYJA\n",
"wVONYEFBoCBQECgIFObctz/Ct1lQECgIFAQKAgVnsWBBQaAgUBAoCBQ89gkWFAQKAgWBwhxvmK0s\n",
"KAgUBAoCBYGCG2bBgoJAQaAgUBAouGEWLCgIFAQKAgVHjWBBQaAgUBAoCBTmvP0JPs6CgkBBoCBQ\n",
"ECg4iwULCgIFgYJAwVONYEFBoCBQECgIFPwSZ7CgIFAQKAgUBArOYsGCgkBBoCBQ8BtmwYKCQEGg\n",
"IFAQKLhhFiwoCBQECgIFgYI3zIIFBYGCQEGg4MsswYKCQEGgIFAQKDhqBAsKAgWBgkBBoOAsFiwo\n",
"CBQECgIFgYKzWLCgIFAQKAgUfJklWFAQKAgUBAoChfFln50FBYGCQEGgIFBwFgsWFAQKAgWBgqNG\n",
"sKAgUBAoCBQECo4awYKCQEGgIFAQKDiLBQsKAgWBgkDBUSNYUBAoCBQECgIFvycdLCgIFAQKAgWB\n",
"gt+TDhYUBAoCBYGCo0awoCBQECgIFAQKcxw1VhYUBAoCBYGCQGGus9jKgoJAQaAgUPCGWbCgIFAQ\n",
"KAgUBAq+zBIsKAgUBAoCBYGClxeCBQWBgkBBoCBQ8PJCsKAgUBAoCBQ8mw8WFAQKAgWBgkDB/3oO\n",
"FhQECgIFgYJAwSt4wYKCQEGgIFBwwyxYUBAoCBQECgIFN8yCBQWBgkBBoCBQcBYLFhQECgIFgYLX\n",
"gIMFBYGCQEGgIFDwlcxgQUGgIFAQKAgU/DxOsKAgUBAoCBQcNYIFBYGCQEGgIFBwFQsWFAQKAgWB\n",
"gkDB/3oOFhQECgIFgYKjRrCgIFAQKAgUBAqezQcLCgIFgYJAQaDgLBYsKAgUBAoCBYGCq1iwoCBQ\n",
"ECgIFNwwCxYUBAoCBYGCQMFRI1hQECgIFAQKAgW/Jx0sKAgUBAoCBT+XHCwoCBQECgIFgYIbZsGC\n",
"gkBBoCBQECh4eSFYUBAoCBQECo4awYKCQEGgIFAQKMx9XMY2FhQECgIFgYJAwVksWFAQKAgUBAqe\n",
"agQLCgIFgYJAQaDgqBEsKAgUBAoCBYGCs1iwoCBQECgIFBw1ggUFgYJAQaAgUPDDAsGCgkBBoCBQ\n",
"ECjM8Z70yoKCQEGgIFAQKDiLBQsKAgWBgkDBUSNYUBAoCBQECgIFP/ofLCgIFAQKAgWBwlx3zFYW\n",
"FAQKAgWBgqNGsKAgUBAoCBQECr7tEywoCBQECgIFgYLfkw4WFAQKAgWBgqNGsKAgUBAoCBQECt6T\n",
"DhYUBAoCBYGCQMENs2BBQaAgUBAoOGoECwoCBYGCQEGg4CoWLCgIFAQKAgWBwhxfyVxZUBAoCBQE\n",
"Cp5qBAsKAgWBgkBBoOCGWbCgIFAQKAgUBAquYsGCgkBBoCBQECi4igULCgIFgYJAYe7jtzg3FhQE\n",
"CgIFgYJAwVEjWFAQKAgUBAoChTk/Z7GNBQWBgkBBoDDHDbOVBQWBgkBBoCBQcBULFhQECgIFgYJA\n",
"wcsLwYKCQEGgIFCY8/NsfmNBQaAgUBAoCBTcMAsWFAQKAgWBgkDBVSxYUBAoCBQECp5qBAsKAgWB\n",
"gkBBoDDn+fP2Z/g0CwoCBYGCQEGg4IZZsKAgUBAoCBTmOmqsLCgIFAQKAgWBgqNGsKAgUBAoCBQE\n",
"Cq5iwYKCQEGgIFAQKLijGCwoCBQECgIFR41gQUGgIFAQKAgUHDWCBQWBgkBBoCBQ8J3VYEFBoCBQ\n",
"ECjMuf5IbywoCBQECgIFgYKjRrCgIFAQKAgUBApzncVWFhQECgIFgYKjRrCgIFAQKAgUBAreMAsW\n",
"FAQKAgWBgkDBywvBgoJAQaAgUHDDLFhQECgIFAQKAgXP5oMFBYGCQEGgIFDw2CdYUBAoCBQECo4a\n",
"wYKCQEGgIFAQKHjsEywoCBQECgIFgYKzWLCgIFAQKAgUBAoe+wQLCgIFgYJAwVEjWFAQKAgUBAoC\n",
"BY99ggUFgYJAQaAgUJh73TDbWFAQKAgUBAqOGsGCgkBBoCBQECjMc+/bn+HTLCgIFAQKAgWBwjzO\n",
"YisLCgIFgYJAwRtmwYKCQEGgIFAQKDhqBAsKAgWBgkBBoODlhWBBQaAgUBAozOOG2cqCgkBBoCBQ\n",
"ECg4agQLCgIFgYJAQaDgsU+woCBQECgIFP4DPcHwb7pfSUoAAAAASUVORK5CYII=\n",
"\" transform=\"translate(1891, 47)\"/>\n",
"</g>\n",
"<g clip-path=\"url(#clip5401)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 1999.43, 1515.55)\" x=\"1999.43\" y=\"1515.55\">-</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5401)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2027.54, 1515.55)\" x=\"2027.54\" y=\"1515.55\">0.75</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5401)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 1999.43, 1250.32)\" x=\"1999.43\" y=\"1250.32\">-</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5401)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2027.54, 1250.32)\" x=\"2027.54\" y=\"1250.32\">0.50</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5401)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 1999.43, 985.085)\" x=\"1999.43\" y=\"985.085\">-</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5401)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2027.54, 985.085)\" x=\"2027.54\" y=\"985.085\">0.25</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5401)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 1999.43, 719.853)\" x=\"1999.43\" y=\"719.853\">0</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5401)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 1999.43, 454.621)\" x=\"1999.43\" y=\"454.621\">0.25</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5401)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 1999.43, 189.39)\" x=\"1999.43\" y=\"189.39\">0.50</text>\n",
"</g>\n",
"<polyline clip-path=\"url(#clip5401)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1963.43,1503.47 1963.43,1501.9 1987.43,1501.9 1963.43,1501.9 1963.43,1236.67 1987.43,1236.67 1963.43,1236.67 1963.43,971.433 1987.43,971.433 1963.43,971.433 \n",
" 1963.43,706.202 1987.43,706.202 1963.43,706.202 1963.43,440.97 1987.43,440.97 1963.43,440.97 1963.43,175.738 1987.43,175.738 1963.43,175.738 1963.43,47.2441 \n",
" \n",
" \"/>\n",
"<g clip-path=\"url(#clip5401)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:66px; text-anchor:middle;\" transform=\"rotate(-90, 2021.03, 775.359)\" x=\"2021.03\" y=\"775.359\"></text>\n",
"</g>\n",
"</svg>\n"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"surface(xx, yy, V)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Continuity follows since $\\log|x-t|$ is integrable for $-1 \\leq x \\leq 1$ provided $f(t)$ has weaker than pole singularities. \n",
"\n",
"For $z \\notin (-\\infty,1]$ this can also be seen since $v$ is the real part of an analytic function:\n",
"$$\n",
" v(z) = \\Re {1 \\over \\pi} \\int_{-1}^1 f(t) \\log ( z - t) \\dt\n",
"$$\n",
"Note that the integrand avoids the branch cut of $\\log z$. To extend this to $z\\in (-\\infty,-1]$ (or more generally, $z \\notin [-1,\\infty)$), we can use the alternative expression\n",
"$$\n",
" v(z) = \\Re {1 \\over \\pi} \\int_{-1}^1 f(t) \\log (t-z) \\dt\n",
"$$\n",
"which follows from $\\log|z-t| = \\log|t-z|$."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"v(z) = 0.7068168642791222\n",
"sum(f * log(abs(z - t))) / π = 0.7068168642791223\n",
"sum(f * log(z - t)) / π = 0.7068168642791222 + 0.5923597267719309im\n",
"sum(f * log(t - z)) / π = 0.7068168642791222 - 1.1831399624402499im\n"
]
}
],
"source": [
"z = 2.0 +3.0im\n",
"@show v(z)\n",
"@show sum(f*log(abs(z-t)))/π\n",
"@show sum(f*log(z-t))/π\n",
"@show sum(f*log(t-z))/π;"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Evaluating logarithmic singular integrals\n",
"\n",
"How can we actually evaluate \n",
"$$\n",
"Lu(z) = {1 \\over \\pi} \\int_{-1}^1 u(t) \\log (z-t) \\dt\n",
"$$\n",
"for $z$ in the complex plane? We relate this to the indefinite integral of the Cauchy transform, and then use that to reduce it to a Cauchy transform itself.\n",
"\n",
"#### Integrated Cauchy transform\n",
"\n",
"For $z$ away from the branch cut our integrand is \"nice\" (assuming $u$ itself is \"nice\") and we can exchange integration and differentiation to determine\n",
"$$\n",
"{\\D \\over \\D z} Lu(z) = {1 \\over \\pi} \\int_{-1}^1 u(t) {1\\over z -t} \\dt = -2 \\I \\CC u(z)\n",
"$$\n",
"thus if we can calculate $\\int^z Cu(\\zeta) \\D \\zeta$, we are in good shape. \n",
"\n",
"\n",
"_Example_ If $u(x) = {1 \\over \\sqrt{1-x^2}}$, then recall\n",
"$$\n",
"Cu(z) = {-1 \\over 2 \\I \\sqrt{z-1} \\sqrt{z+1}}\n",
"$$\n",
"We therefore have\n",
"$$\n",
"{\\D \\over \\D z} Lu(z) = {1 \\over \\sqrt{z-1} \\sqrt{z+1}} \n",
"$$\n",
"and therefore for some constant of integration $D$ we have\n",
"$$\n",
"Lu(z) + D = \\pi \\int^z {\\D z \\over \\sqrt{z-1} \\sqrt{z+1}} = 2 \\pi \\log\\left(\\sqrt{z-1} + \\sqrt{z+1}\\right)\n",
"$$\n",
"We need the right constant of integration. we can find that via the behaviour as $x \\rightarrow \\infty$:\n",
"$$\n",
"Lu(x) ={1 \\over \\pi} \\int_{-1}^1 u(t) \\log(x-t) \\dt = {\\log x \\over \\pi} \\int_{-1}^1 u(t) \\dt + {1 \\over \\pi} \\int_{-1}^1 u(t) \\log(1-t/x) \\dt = {\\log x \\over \\pi}\\int_{-1}^1 u(t) \\dt + O(x^{-1})\n",
"$$\n",
"Since we have\n",
"$$\n",
"\\int_{-1}^1 {1 \\over \\sqrt{1-x^2}} \\dx = \\pi\n",
"$$\n",
"and\n",
"$$\n",
"2 \\log(\\sqrt{x-1} + \\sqrt{x+1}) = 2 \\log \\sqrt x + 2 \\log(\\sqrt{1-1/x} + \\sqrt{1 + 1/x}) = \n",
"\\pi \\log x + 2\\pi \\log(2) + O(1/x)\n",
"$$\n",
"therefore, \n",
"$$\n",
"Lu(z) = 2 \\log\\left(\\sqrt{z-1} + \\sqrt{z+1}\\right) - 2 \\log 2\n",
"$$\n",
"\n",
"_Demonstration_ We want to calculate the log kernel of $1/\\sqrt{1-x^2}$:"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"0.3681278813450904 + 0.9045568943023814im"
]
},
"execution_count": 10,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x = Fun()\n",
"u = 1/sqrt(1-t^2)\n",
"z = 1+im\n",
"sum(u*log(z-x))/π"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We saw that its derivative is given in terms of the Cauchy transform, here we test it using finite difference approximation:"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(0.3515911336637867 - 0.5688482444998755im, 0.35157758425414287 - 0.5688644810057831im, 0.3515775842541429 - 0.568864481005783im)"
]
},
"execution_count": 17,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"h = 0.0001;\n",
"(sum(u*log(z+h-x))/π - sum(u*log(z-x))/π)/h , sum(u/(z-x))/π, -2im*cauchy(u,z)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"But we already know the Cauchy transform in closed form:"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"0.3515775842541429 - 0.568864481005783im"
]
},
"execution_count": 22,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Cu = z -> -1/(2im*sqrt(z-1)sqrt(z+1))\n",
"\n",
"-2im*Cu(z)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This we can integrate in closed form to determine:"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"0.36812788134509056 + 0.9045568943023812im"
]
},
"execution_count": 24,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Lu = z -> 2*log(sqrt(z-1) + sqrt(z+1)) - 2*log(2)\n",
"Lu(z)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Reduction to a Cauchy transform\n",
"\n",
"The representation is not ideal as it involves indefinite integration in the complex plane. However, we will see that we can actually express $L u (z)$ as a Cauchy transform of $\\int_x^1 u(t) \\dt$. \n",
"\n",
"**Lemma (Log kernel as Cauchy transform)** Suppose $u$ is \"nice\" (as in Plemelj). Then \n",
"$$\n",
"Lu(z) = {\\log(z-a) \\over \\pi} \\int_a^b u(x) \\dx +2 \\I C U(z)\n",
"$$\n",
"where \n",
"$$\n",
"U(x) = \\int_x^b u(t) \\dt\n",
"$$\n",
"\n",
"**Proof**\n",
"\n",
"We use Plemelj to prove this result (of course!) and assume $[a,b] = [-1,1]$. Note that $Lu$ satisfies the following Riemann–Hilbert problem:\n",
"\n",
"1. $Lu(z) \\sim {1 \\over \\pi} \\int_{-1}^1 u(t) \\dt \\log z + o(1)$\n",
"2. $L^+ u(x) - L^- u(x) = 2 \\I \\int_x^1 u(t) \\dt $ for $-1 < x < 1$\n",
"3. $L^+ u(x) - L^- u(x) = 2\\I \\int_{-1}^1 u(t) \\dt $ for $x < -1$\n",
"\n",
"\n",
"The first part follows immediately by noting for $z \\rightarrow + \\infty$ we have \n",
"$$\\log(z - x) = \\log(z (1 - x/z)) = \\log z + \\log(1-x/z) = \\log z + o(1)$$\n",
"\n",
"We now see where the jumps come from. Since\n",
" $Lu'(z) = -2 \\I Cu(z)$ and\n",
" This let's us think of $Lu (z)$ as (2 is arbitrary here)\n",
"$$\n",
"L u(z) = Lu(2) + \\int_2^z C u (\\zeta) \\D\\zeta\n",
"$$\n",
"where the contour is a straight line (just like in the problem sheet for $\\log z$ that I'm sure everyone has done by now), but we can think of it also as an arc that avoids $[-1,1]$.\n",
"\n",
"Consider $x < -1$. Given an ellipse $\\gamma$ surrounding $[-1,1]$ we can write the integral representations and exchange orders to get: \n",
"$$\n",
"L u^+(x) - L u^-(x) = -2 \\I \\oint_\\gamma C u(\\zeta) \\D\\zeta = -2 \\I \\int_{-1}^1 u(t) {1\\over 2 \\pi \\I} \\oint_\\gamma {1 \\over t-z} \\dt \\D \\zeta = 2 \\I \\int_{-1}^1 u(t) \\dt \n",
"$$\n",
"\n",
"For $-1 < x < 1$, note that\n",
"$\n",
"L u(1) \n",
"$\n",
"is well-defined as there is only a logarithmic singularity times an algebraic one. Thus deforming the contour onto the interval we have \n",
"$$\n",
"L^\\pm u(x) = -2 \\I \\int_1^x C^\\pm u(t) \\dt + L u(1),\n",
"$$\n",
"hence\n",
"$$\n",
"L^+ u(x) -L^- u(x) = 2 \\I \\int_x^1 (C^+ u(t) - C^- u(t)) \\dt =2 \\I \\int_x^1 u(t) \\dt\n",
"$$\n",
"⬛️\n",
"\n",
"\n",
"\n",
"_Example_\n",
"For the problem above, we have that $\\int_x^1 {1 \\over \\sqrt{1-t^2}}\\dt = {\\rm arccos}\\, x$, which gives us:"
]
},
{
"cell_type": "code",
"execution_count": 37,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(0.36812788134509017 + 0.9045568943023812im, 0.36812788134509056 + 0.9045568943023812im)"
]
},
"execution_count": 37,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x = Fun()\n",
"\n",
"u = 1/sqrt(1-x^2)\n",
"U = acos(x)\n",
"\n",
"\n",
"Lu = z -> 2*log(sqrt(z-1) + sqrt(z+1)) - 2*log(2)\n",
"\n",
"sum(u) * log(z+1)/π + sum(U/(x-z))/(π), Lu(z)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Log transforms of weighted orthogonal polynomials\n",
"\n",
"\n",
"Now consider ${1 \\over \\pi} \\int_a^b p_k(x) w(x) \\log |z-x| \\dx$, which we write in terms of the real part of\n",
"$$\n",
"L_k(z) = L[p_k w](z) = {1 \\over \\pi } \\int_a^b p_k(x) w(x) \\log (z-x) \\dx\n",
"$$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For $k > 0$ we have $\\int_a^b p_k(x) w(x) dx = 0$ due to orthogonality, and hence we actually have no branch cut:"
]
},
{
"cell_type": "code",
"execution_count": 40,
"metadata": {},
"outputs": [
{
"data": {
"image/svg+xml": [
"<?xml version=\"1.0\" encoding=\"utf-8\"?>\n",
"<svg xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\" width=\"600\" height=\"400\" viewBox=\"0 0 2400 1600\">\n",
"<defs>\n",
" <clipPath id=\"clip5800\">\n",
" <rect x=\"0\" y=\"0\" width=\"2000\" height=\"2000\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<defs>\n",
" <clipPath id=\"clip5801\">\n",
" <rect x=\"0\" y=\"0\" width=\"2400\" height=\"1600\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<polygon clip-path=\"url(#clip5801)\" points=\"\n",
"0,1600 2400,1600 2400,0 0,0 \n",
" \" fill=\"#ffffff\" fill-opacity=\"1\"/>\n",
"<defs>\n",
" <clipPath id=\"clip5802\">\n",
" <rect x=\"480\" y=\"0\" width=\"1681\" height=\"1600\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<polygon clip-path=\"url(#clip5801)\" points=\"\n",
"149.361,1503.47 2321.26,1503.47 2321.26,47.2441 149.361,47.2441 \n",
" \" fill=\"#ffffff\" fill-opacity=\"1\"/>\n",
"<defs>\n",
" <clipPath id=\"clip5803\">\n",
" <rect x=\"149\" y=\"47\" width=\"2173\" height=\"1457\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<polyline clip-path=\"url(#clip5803)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 149.361,1503.47 149.361,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5803)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 511.344,1503.47 511.344,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5803)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 873.327,1503.47 873.327,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5803)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1235.31,1503.47 1235.31,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5803)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1597.29,1503.47 1597.29,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5803)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1959.28,1503.47 1959.28,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5803)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 2321.26,1503.47 2321.26,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5803)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 149.361,1503.47 2321.26,1503.47 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5803)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 149.361,1260.77 2321.26,1260.77 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5803)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 149.361,1018.06 2321.26,1018.06 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5803)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 149.361,775.359 2321.26,775.359 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5803)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 149.361,532.654 2321.26,532.654 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5803)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 149.361,289.949 2321.26,289.949 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5803)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 149.361,47.2441 2321.26,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,1503.47 2321.26,1503.47 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,1503.47 149.361,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,1503.47 149.361,1481.63 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 511.344,1503.47 511.344,1481.63 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 873.327,1503.47 873.327,1481.63 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1235.31,1503.47 1235.31,1481.63 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1597.29,1503.47 1597.29,1481.63 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1959.28,1503.47 1959.28,1481.63 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 2321.26,1503.47 2321.26,1481.63 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,1503.47 181.939,1503.47 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,1260.77 181.939,1260.77 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,1018.06 181.939,1018.06 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,775.359 181.939,775.359 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,532.654 181.939,532.654 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,289.949 181.939,289.949 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip5801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,47.2441 181.939,47.2441 \n",
" \"/>\n",
"<g clip-path=\"url(#clip5801)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:middle;\" transform=\"rotate(0, 149.361, 1557.47)\" x=\"149.361\" y=\"1557.47\">-3</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5801)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:middle;\" transform=\"rotate(0, 511.344, 1557.47)\" x=\"511.344\" y=\"1557.47\">-2</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5801)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:middle;\" transform=\"rotate(0, 873.327, 1557.47)\" x=\"873.327\" y=\"1557.47\">-1</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5801)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:middle;\" transform=\"rotate(0, 1235.31, 1557.47)\" x=\"1235.31\" y=\"1557.47\">0</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5801)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:middle;\" transform=\"rotate(0, 1597.29, 1557.47)\" x=\"1597.29\" y=\"1557.47\">1</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5801)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:middle;\" transform=\"rotate(0, 1959.28, 1557.47)\" x=\"1959.28\" y=\"1557.47\">2</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5801)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:middle;\" transform=\"rotate(0, 2321.26, 1557.47)\" x=\"2321.26\" y=\"1557.47\">3</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5801)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:end;\" transform=\"rotate(0, 125.361, 1520.97)\" x=\"125.361\" y=\"1520.97\">-3</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5801)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:end;\" transform=\"rotate(0, 125.361, 1278.27)\" x=\"125.361\" y=\"1278.27\">-2</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5801)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:end;\" transform=\"rotate(0, 125.361, 1035.56)\" x=\"125.361\" y=\"1035.56\">-1</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5801)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:end;\" transform=\"rotate(0, 125.361, 792.859)\" x=\"125.361\" y=\"792.859\">0</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5801)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:end;\" transform=\"rotate(0, 125.361, 550.154)\" x=\"125.361\" y=\"550.154\">1</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5801)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:end;\" transform=\"rotate(0, 125.361, 307.449)\" x=\"125.361\" y=\"307.449\">2</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5801)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:end;\" transform=\"rotate(0, 125.361, 64.7441)\" x=\"125.361\" y=\"64.7441\">3</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip5803)\">\n",
"<image width=\"2172\" height=\"1456\" xlink:href=\"data:image/png;base64,\n",
"iVBORw0KGgoAAAANSUhEUgAACHwAAAWwCAYAAAAlz8STAAAgAElEQVR4nOzd3XLsyK0mUHqsef8n\n",
"nu25cEyED5s9zIKBBLK01qVaifwhq1TaTeH7x7/+9/Wv6+6ff/nKu/+18D0VdSetdWXM5P1Mvobf\n",
"fra7rs/O+2DKnrP2s2ueinObftaTz7brPj5pP5PP4KnOrjF3TzUi79lTrmHVmKw9Tx5Tca80jvk/\n",
"L0Oe/vufhDFv8+4cc/+ep/291Zk0puts3+6LrDEra6mau+qejLymMu6VSWfw6byVc1fc61XvpZEx\n",
"GWfQ+R6+672m6z1u18+TyfdX1phJP9//XP94GdX5y8bkMVM+RD+NmzRmyjnt+mV90j82rMxd9Q9E\n",
"U65HZO6qfyzpWtvK3J331+R/uK1Yy7f9z4RJa9n1OozUnXQGn9ZcrXv62U6p2/XwwHvdSAUAAAAA\n",
"AAAAABp54AMAAAAAAAAA4DA/j1+99xdc6TZy7zn49ChJRd2nXohvdZ/6I77VjXRpWZk7Yz8rVvZT\n",
"dQ3frOw5Y/2Tz3ZlbRnXZ9c8K3V2rSXr9b5rngo7r3vE5LOd/L4SUbGfrPsrUjcispaq10fV561P\n",
"VV33jDHXVXfNusbsuld2jWmy8qM6Y0yWlY9kGWMydM379PJZiTPgr2d30rl1vi4znHTWT04660k6\n",
"z61r7si8XWuNvC7Pey1UtNv+DWMi5/ZtY6rqVo3ZdW9U1Kxq3151bisq6k7eT+fadsV0VDkpPiNj\n",
"LbvmWalzWgxM13v25NfYbzjbiMlxOZEx+Z/ndfgAAAAAAAAAADiMBz4AAAAAAAAAAA7zE2qVf119\n",
"sSmTo2O69rNy1m81o3WzomI+NSkOpMvkqJKVOp3xLJNNicKJyLpXToozyZj3ae6uyLMVFe/p1zXr\n",
"M0HX6+NtHStrqbruu0yOl9k1ZvJnjweR+I+T4idOj5tgTVeMDfDfmfzzgxynXePIes/a46Soj7vJ\n",
"UTKTnH5OVffGpEidk1rwd0WeiIGpm7szrmGXjFiIk6JXstbS5fQz2LW2zjiTip/NVe+lXREuez6/\n",
"nP7uDAAAAAAAAADw63jgAwAAAAAAAADgMD+PXz2p/XxnxMNb3c79VLXc/21xE5GznXwG/NuuCKdd\n",
"90qF3/BeVDHv09wZ8562n66fuxGR+IxJkRuR19jkMcTsuo8b7/1IDExXdMzTkeyauyuapGvezrPO\n",
"IDKIb3DSa+5J52uua+6ua9Z5r0TOuu+c/hEYVdXSmjyTo1Sm3AuTomMmRdJ0RYRMjh2J6IwqmRw3\n",
"sWJKNElnXA6zIoMq4jNWnH4fd51t5/tvxXtrV8zNe90pn+gAAAAAAAAAAFjkgQ8AAAAAAAAAgMM8\n",
"R7rcVcWmTI6OibQhX1lrV6v/zgiRt7pZ99fJZzspbiYrpuOkPWfspzOeZcpZR3Wd7enxUm91J+0n\n",
"MqYqFi1iV6zNpCicyWMmR9JUfX7MGNMkElnRGXMhBub7Y2CydN0r8K1Ofw2JZ9mn66wj8572s212\n",
"7MiuqJJvG3NaNEnGmIqaVS34OyNpKs5hcgxBpO5viIHpumaToj0yzilrnkl73nV/db2v7Frb6e8R\n",
"EV2RJ50/q7v289+vAgAAAAAAAACARh74AAAAAAAAAAA4zE+oZfp15cQovNVcqTspduSt5lPdqhiF\n",
"ioiHlTpZrcsnRZNU+Paokqe5Ttpzp5PjWXbeKxEV7/OT9xMxKRKlqm7VWibHf1Soer08mRwvM+V6\n",
"rPj2/V2/L5qkMwbm9DiT09c/hXPMc17sw0ynn2PXa6jz3E6KZ+k1Kcqjwq79fduYKqfvecpaOtv4\n",
"T6pbESnwG6JKIiZFk3TJWP+3Ra/sXEvXvTHpDCo+0+y6D6rqVn3O63ovnbSf/1lXhw8AAAAAAAAA\n",
"gMN44AMAAAAAAAAA4DA/j1+NtG+uilHYFfFwd1IkQtZjOxnXsCoOoCuaZNIZsE9WTMdvi2fZGZ/T\n",
"9Tqsuh4nxaR1nUHUlLVErmHVdc8YQ1zV5+yMMQki8SadsRBiYM6K4eg6t2/kLL+Pa5jnpPfFu98Y\n",
"z9J5vSJz96038mFw1xhiqlqzd41ZsWvPK6qiSCpaxVddw0lnkFGzKwZmZe6q+/ikKIzJUTKsmXSv\n",
"dL0nZEXjdL0ndMaKTY7LmVHXp3AAAAAAAAAAgMN44AMAAAAAAAAA4DDPkS53k1rJr6ho9d8Zb7Ar\n",
"FuJuV9xE5P5acVLkxqS4mYxze5rr9D1n7KfqPe/N9HiWye8RU6I9InV3XZ+I6BlkRHdlrKXqGlZF\n",
"0J08ZmXcrhib3xCXc1B0TGc0yW+LgcnSGd3zTVY+mkOU12We08/yt8Wz9MbC/CMw6qS29lWRD3fT\n",
"o0p2zbXrvCvuwUn7PT3Gpqtu5xl07WdyDEznz4qTYmBOixCZspZd8+w6t4istVVFOu0624q6VZ8J\n",
"un6m7vmMM/mfnAEAAAAAAAAAeOCBDwAAAAAAAACAw6xFujypaB2fFTvwVjerbX9X1MpJMSpPdXfF\n",
"dFQRVRKLUfi2PVeZcn9FRK7P09xd7/NV0R5VEQkZUV0nncHquE/rVkVWNMVcPJq852+LsclwejTR\n",
"gq5oks4YmJPjTESI/FvGfXvyfQCfyHiP+I3vM3enn0HXe1znufXNfXKMR+Xcxsz6W8+T9zwpOqYz\n",
"kqbiHDrPoGs/nTE9u+JAKkyKz5h01r8x+qbCpCiciM73xa7rXhXhkrGfiEDdf/3PaMhJn/oAAAAA\n",
"AAAAAFjggQ8AAAAAAAAAgMPEI13uJsemvNVcqZv1aExXlERWPEDFuUyK6ehq3z7pDLLula7Io10y\n",
"zunb4ll2vWeszN35XhrR9bMuousMssZMWsukPZNj1zXtigwSA3Nd11kxMF3nlqXiDK7rvHMAYrLe\n",
"r09/z8g4B/EsO3X+bV5VDETGGPaZfB9U/fIx6T6u2OOkSJqsuStqdu5ncoTApGiSLlNiYHaupSKO\n",
"KcuU69H5M6nrPW1ybFVVDNygurcIl8isAAAAAAAAAAAM4oEPAAAAAAAAAIDD/JQ1ua2KTZkcHVPV\n",
"krsiuiCyn6e6XXETu9Y2+Qz4tykxNlnvEeJZcuJMVlS9drv20/UzKGstK6o+N/y361hZy64xkc8E\n",
"k8c8jauKPNk1pkvTWiO/aWTFqHTFmZweIZJxbqefAUC2rPfArmiVDKfHs0TOvvd6Tf5gelfVKvvb\n",
"x1TFdJw0pqrupOiYqrb9Fe8RVWvtii6YHgPTFblxUgxM5zXkrHvlN7xequpWfI7LeA+MzFtVNz++\n",
"5bquv/yS490MAAAAAAAAAOAwHvgAAAAAAAAAADjMz/OXixogV7S5nxwdsytqZVcsxErdydERu852\n",
"1xlMjip5qvPte94V0zP5NRa5Pk9zV0WITI7LueuKL4uoiirZFRkyKWJn15jJcSeTY2yy7HrtZrze\n",
"D4u5uU/1G2NgMs4AgO+W8bOtM54l42db58/HP9dCe+a/yPigenosR8W8O/e3a67JETQVvxhMWvuk\n",
"10vVWirOrvMMuvZT9Uvy5FiLFbsiHk6KEDkt+mbKnjvfV3adQUTX2WbteUjUStU1DES43OnwAQAA\n",
"AAAAAABwmL/p8HGX9TdnLyV2/QVz1V/zZnQWiNjVXWFl7sldG6qcdAY7u0O81Zm05yoZ1/2kbh07\n",
"X5eTOyxFdF3Dt3U8raWr08CTkzolPNnVPWFyt5FJ1+PTeVfmPq37SNPZdnXVuK6zu4JkyTiDinO8\n",
"rr4uJ1lrybg3dG2h25RuEFn3/pT9XFfOnk77mXN3+hn0zd3VRWNXN4Wu/V3XrI4Rd5O7mJzWqSJj\n",
"zJvoP+xUdGCo+ofQrus+qUvLrrknr63zbN9M6igxaS2n7bnCSZ1RqupO7jY0ad6mjh6BXzR0+AAA\n",
"AAAAAAAAOIwHPgAAAAAAAAAADvPz/MzHSlPFgubFWRECb3WrIjfeaq7U3RW1Ejnr1bnfnBRNMrmt\n",
"+qQz6IzCyHBSLE/E5LWtzF31Oqx6/63YT+fPx4hdUSUrInuctH5y7LqmXfdBZ3zZkBiY6zqrrf2k\n",
"2BG+n3vldxL/w6pJETVdet8Tu35x6PyFpaqddsYY9jn9PpgSHROte1JsyrfFA6zYFbkRMSkGZtL/\n",
"YLibFIkilmdOFE7ErjOoqlv187LrZ05BfMt1xX4huf0C5pMvAAAAAAAAAMBhPPABAAAAAAAAAHCY\n",
"n+cvR5oMF0S8PJXJiB3pjDfYFQtxt7LWyREoJ0VuVF3D3+DkGBvxLLHr8zR3VYxC1/WIOCnepCqi\n",
"ZmXcrs8E3z4mcm67xjyNq4or6ooe64pj2nkNb4p+a/h43ujcGXEscKKu1+5v5Gz5rTLu/c7XT85n\n",
"gl0xF1lzd7V437XWyWN2xZvsGjPprCft+fQYm46a11XX6n9yNMa3x8DsiniYHG8y3ZQYm8mRQTuj\n",
"Sip+LnW9t67MPSgybFOEy53/zQwAAAAAAAAAcBgPfAAAAAAAAAAAHOZnrbnx03Mhb40Ks5omv5SI\n",
"xDVEZEVJvNWNxBAktdd+nXdl7knr37W2jLicb4wqyVjLaXv+1KT7627XPRk1Oe7rrur+mhJvsiLj\n",
"3FbHvan6WX3SmF1xJxljVsZV3bcrToqOmRJZc12h13JXjErWbzQZURgZZ2A/dWsB9suI7sh6vWfU\n",
"sZ+/6nw/zpj7z7XQzrlMV7v5XVEeGXZGZZwecdI1ZkqcyaS4o9NibCqu+6QzyJo7I0YhMmZyDMyu\n",
"tU2KEPmN0TdTrmHEpDOI6Dzbive8FU0RLgXxLU91dfgAAAAAAAAAADiMBz4AAAAAAAAAAA7z8/zl\n",
"lSa9kca3Gc1/F0rsimvIiJKI2BVzEZl7UjRJhKiSnGtatZaqyI0M7v3e95WIjLicSN3OiJ27riiy\n",
"rLVURVRMXv+k69w1JkPV67DKrmuYMW8CMR2cKBKC+hv9htdlRozFt/vG685sUyJq4jI+hE2Jxqia\n",
"t/NvGr8t3mTXmEkxKZP2POWaVV2fk+JYquYVUdEX5XVdcyJEss76pNiUndE3nzrtDKrqTj7biroF\n",
"8S3XtS3C5U6HDwAAAAAAAACAw3jgAwAAAAAAAADgMH8T6XK30lh5SMTLU5mq2JG7XfEZbzVX6ma1\n",
"4F9xUjRJl0lnkBHtsVqny5Rz+sZ4ljed0SQV0RGdcTMRkTOoWEv03KZEhuyKA9k1JvJ6r3qPWLHr\n",
"Ps6490+Ljjk4BuZpqq4YmKxIGvv5q98QB1L0GzKk+cbX3V3G6y6jRtZZ209NjbiMD3Zd/5jVGcGx\n",
"a+6uf7yavL/JkTUrJu+5qu6k6JuOmtfVF5/TeR+cHgPTFYWxy2nnNDmW581pUTgRu+JlPq25+j0V\n",
"cxe9R3RFuARqTvnf3QAAAAAAAAAALPLABwAAAAAAAADAYX6en/nIiGOJ1M1qGPxSYle8wc74jLuK\n",
"yIqnOlVtu0+K3Dg93qRL1jU86V6JyLi/Jq+tau6qiIpJcTNdZ/C2jpW1RM5tZdxp0SR3XbEju0TP\n",
"+qRz6VrraRE7N6dHWGTEjER/IyPm9HvuzW+IviHm2+71O/f6PpPiWTrlnMNJESJPqtqBV6iIb8ga\n",
"0+nkPU6+pl2RItExVdExFXUnncGKrtiHyTEwu9Ym3qTXpGs4OTJoyn0crdsVHdMU4VIR35JUd8qn\n",
"MwAAAAAAAAAAFnngAwAAAAAAAADgMD/PX440gV1pjFtV90OdMR27IkQidkVHdK1/13X/jVElk9by\n",
"7fEsVfEZu9YWmbvqfWXy+/zbOlbX8qYiMmznWnaNOSlSZEXVe0TFmJVx0feetzpVe8wgBiYtAuXb\n",
"oj0y9iOiZs233TvQ7dtfQ5MiUL7trDP2k3V9/lwvLaDLdMazdM2bsdaqCIuscSdHrTzZdd6Tx1TV\n",
"rVjLaTE2XdExVa/trrMUAzMrBuY37jljLV0xSit1J7/GVup2RscURCu9xbdc1+gIl7vJnwIBAAAA\n",
"AAAAAHjggQ8AAAAAAAAAgMP8rGVJRJryRuo2RbysOD1GIWNt0bpd619xUmxKVzxLNOZi0loqTH7t\n",
"rqiKZ/l03pW5sx5NrDjLSVErVa+XKbE20bVM2fNpYyafdYbOaKWu6JiMGo0xMBVRJdfVFwMzaT+T\n",
"fXtsym+4hny/b3tdPvn2PU6Km8lYy6T9xEyKZ+mKlpgSabGqqnX5t4/ZFVmza0xnnElkzJTXWdVr\n",
"t+rvnDPiDiI6Ix4mRZNUmBSJclJsyqQYmK54k0lnUFW3K8Kl6P2gK8JlUyyMDh8AAAAAAAAAAIfx\n",
"wAcAAAAAAAAAwGF+nr+80jy3Io6lKjpmwaSW9W92xWlEnBZNEjElqmTXPJHYkaq1REw+p6xuY7si\n",
"g+4yXstVc0ciaSZHdz3pOoO3dTytJWLX+nft+dvGVMU+rfj26JiquXfFz7ytI7oWykyJqKkiNiXG\n",
"uc3i7GMmvRc9mRKBQqWsD8hd8SwZTotamRwpcNKYyVEyU6JMonWrxpwUY/ONZ1Cxp84YmNOjMP7b\n",
"eVfm3nnvfFsMTMRJZxCxM1boU43vv28RLpuiVnbV1eEDAAAAAAAAAOAwHvgAAAAAAAAAADjM30S6\n",
"3K3EplREvFTWfdHVtr+qtXxWpECktffJ0SRajs+SdQ0n3yvfHmeUMe/K3DsjaT6tuyt2ZMWuaIyu\n",
"WJvOMZF7Z/KYiniQ1bl37XHKvGJgsgIbU2JGsmItvj02JcP0CJFvP3+YZtLr/27y2rJMiZvJeq+d\n",
"sp9/y/hg1/WPVZ0RNV2xNp3xH5PXGxkzOYKmopV89J6dEkVUdY0nxbF0xYFU7SdjbjEw/ofQCU66\n",
"VyZHRXW+zxecy1t8y3WdFeESqKnDBwAAAAAAAADAYX7if0v19jdOkbqdnUReRP7aMuuv0rv+wryz\n",
"k8CuDgy7uins2s+Uc5u0lpVreHq3joqOBVWv/873xYoOJVX316SOJV3dILLWMnnPk8dkyFjryris\n",
"jhhdZ9vVFSSrc9CUM3gY1tWJY3KnikkdS6pMXluV37hnckx5b9pp8p4ndcSo8I3dOv5cC39J+Crj\n",
"w3lnR4CujiWnndtJXVmq/hr528dU1Z3UEaNiLVX3aNW5dXV26epysjL3b+hYknF9dnVtmLTnSfeX\n",
"7jZ9HT2Kft50dfSY1CXkNkaHDwAAAAAAAACAw3jgAwAAAAAAAADgMD/PX66KTamoWxUdsyDSwnpX\n",
"xEPEpJiOiCnxGadFlVSc20qdzoidiCn3V8SuyKAnVTEjn877d3N/qvP999Mxu6IxdkWeVa1l0p67\n",
"xjyp+IyTNSZD1XtEZO7GCJQ2CWeQ9Gl+tCkRNVUmr63Kb9wzv9NvvLcn73lSBMpUedfvtA9ld13x\n",
"LBk6z76qRXrGmLtdkSK79jcpsmby+quiCrpiOiKq1toZL5MRuRExKQ4kYkp8xq7olUlr2RV903l/\n",
"TYnCieo624QIl0lRK5siXO5O/00EAAAAAAAAAODX8cAHAAAAAAAAAMBhftYaIlfFppwUHbOgqv15\n",
"V4zKpJiOqhiYk+JZMu6VnbEjk+NZppxTVVxDV4xKZ0xHVZRERYzNrgiRFbsiOLqivDrHVEUgVYi8\n",
"F3Xex13RMadF7FTUyNrPIFNiUyZH1ER+E9ylam2T9wy/VdV74pT32ie/YW0Z763f9/6c9eEq45eJ\n",
"jLV0RZdc1774kq55u+JzonN/25iqmievvzP6pmK9k85g19xV0T6nx3Rk3CunndO3Rd9EnBSFExm3\n",
"M1bow7pv8S3XNStq5a1uQXzL07yH/xMtAAAAAAAAAMDv44EPAAAAAAAAAIDD/Dx/uSs25bTomBeR\n",
"1uWTIkSefFs0ScSUM8i6Vyrm+bu5Kpx0ThFdr/esqKWTolY6I3be6k4+t6wxp69/13XOmPek/UXn\n",
"7opAmRSb8mUxMJNiUzJiYKpYG1EZr7FddasikKruyaq6k+M+mP0eN3ltGff1pLiZvH8YmRLP0rmf\n",
"rjPI+sfEXXN37XHyWgtazYfrThpTFd3x6ZhJsSmTI2k674OKf+SfFIXR9TfxvzEGpvN6TDmDroiq\n",
"rLmL3lu7IlwmxcIEIlzudPgAAAAAAAAAADiMBz4AAAAAAAAAAA7zN5Eud52xKSdFxyzIaI29soyK\n",
"CJGokyI3qs6AWTE2VZFHbyav7fT3iLuq13tVjM1JETUZY3bdxytr2TUmS1XcT8aYDJ3Xo+szwKDY\n",
"lLaYobd1BNcyOUJkUkTNW93fEBtRteeKezDymyysqnq9nxaXM1nFnmdFoNTIWNufa6HV9BLxLDm6\n",
"zqDzHwp3rbdrj6fvb/L6q2I7JsWxVETHVEUvTJ57Z8zIpybFm0yOivkNdsWmTI4M2rX+iIQIl0lR\n",
"K10RLoFfYLzrAAAAAAAAAAAcxgMfAAAAAAAAAACH+Yk3he2KTZkUHZOgKx4gEnewUicruiAj1mLX\n",
"PN8WVZJ1T56058n3cVUUQ0UcSGQ/T3UnRa1UxFpE4kw6z61rTGdsSoXIdZ88ZqXOpPvprjMCZUps\n",
"StZ1n7KfIlmxKZPjZSrWJm4GOFnFe0vV+9Xk98GMtU3e379l/IIyKZ6laz+nn0FXrMius54Um9Jl\n",
"53095bp2vZafnBRjUxV30hm1sivWYvL1mBIhMmktu6Jvvu3cInUnv/4X6r7Ft0R1RbhUxLeszLtQ\n",
"9+T/dQIAAAAAAAAA8Ct54AMAAAAAAAAA4DA/z1+O9KOuik2ZHB1T0FR4cvzESp2qFvwZa/uN8Sxd\n",
"5/Y016Q9R0y5v57suic/nTdad8WUqJXO9+yIXfETu/b8bWMmX5+7qmiiKpMiUCKmxKZ0nsGCjE/m\n",
"vy16ZbqqPf/Gs4TfoCr+4ze+R0zec8baZkfFTIpn6fqgN+kMds2btdZd8Su79jgl3uQ3jKmqe1J0\n",
"TGckTcU5dMXaXNe+mI6IKfEZ3xgDM2XPnREoGTUnR7gs1IxEuGREnlTEt0TrNu1Hhw8AAAAAAAAA\n",
"gMN44AMAAAAAAAAA4DA/az34n7w1wo3Epjw5KTqmIOLlqUxGjMppMR0RGXETk85gUtzMpD1HTDqn\n",
"T1XFs0TmznotV9Stur+6Ynkia6k6t64x1zU78uTbYmzuOqOJpsTW7IpAyfpclHEGVT+HE+pGf4N5\n",
"q5Px6f03rO2t7uxW+TWcLd+qItrDffxvJ51tRt2qmJhZa6uKUZgSz9IZLdF1Blnr75pbvInImuvq\n",
"ixSJjqm4zl3RJdExXbE8k2NtOmNgJkWITFnLaXEzFffGaVE4RXUrIlyqolYy6k6KjrnV1eEDAAAA\n",
"AAAAAOAwHvgAAAAAAAAAADjMz/OXI41jV2JUKupGomMyIl5W6hY19s2I04g6KZokYlJUyUlxM1Wx\n",
"PCtOOqe3mit1s17vXZE73xa1Enkv2hXDNSm6pOpe+fYxu+6vJ13RMSJQvs+k61Mk8pvGLlVrq6hb\n",
"FYnCM1Ex32fSe8+3mxyb8mTyvTH5vefPFWhP/Re7/mHkNFMianbFnWTN3XVuk6I+MsZMjpLZOVdG\n",
"LMSuMSfF2FRd98mRDp2xNhnXo+tn9WkxMCfFzUScFoUTkbD+iviW6+qLcFmpOTjC5W7QP5UCAAAA\n",
"AAAAALDCAx8AAAAAAAAAAIf5WWueG2mw+/QsyVvkya7omJW1vdVcqZsVa/NiV4TIk2+LJqniDNwr\n",
"T3V3ra3zPSLy42Ry1MqumIuuczttzORImowYm10xKp3RMbvO9i7rfb7i/O2n7Odw5DeAJxVRGOJM\n",
"6lSdrUgUyFUROzI5yuR0VWeb8V5ad92z/mbu5DiTqjqT9rMr8iRj3qx/0JsU3dE1ZnIEzaTYmil7\n",
"7oouiY7pijzp3E/F/3DImndXfE7X39qfdk4Vvi0Kp6ruQo2uCJfOGJWu6JhPaz7U1eEDAAAAAAAA\n",
"AOAwHvgAAAAAAAAAADjMz/OXVxrUVsSxdEbHrMSx3GVExxQ1A66IxniqczcpciMjoiJrnpNkRXt8\n",
"ezzL5PtrV3zO27xPYzrfV+4y7q8nFWOqzu2kMdc1O15mcoxNxrwZUR/R9+Nvixmxn78q+iyV8Sk7\n",
"KwbmrW5W+/mT4maqzqCq7i6nr5/vd3p8UdX6T4qkqTqDirpZZ1B332b848LpcSYVNU7fT1YL+13x\n",
"GV3znh5vctKYrkiRnWMq6p52bl3xMpNjYHatbWcMTFdMSpUp99ekKJzIvEnrr4hwyYpaqajbGR1T\n",
"UPf0/zUNAAAAAAAAAPDreOADAAAAAAAAAOAwfxPpchfJa8iIeKmqu7KfioiXlbpFTZOzogsy2na/\n",
"1Xyquyui4tuiSrrO7anOpD1/Ou/T3FXXPaIiniVj3qe5s2I7psSmVI2pOreTx6yMmxxJExmTFbmx\n",
"K5roLiOyZufcb2uJrMN+nhX9PCwKSkxRsbbT4mZO51zeVd2T32bSe9NkzunZ5NiUXXUz1K1NnMlf\n",
"TdpPV9xJ1txd8TKTYjsyxkyOn4mOm3Lek2J6Totjqfi77M54kCkxHZG6p0WIZNT5tj1POreITeuv\n",
"iG+5rr7Ik5WaJ0W4BGrq8AEAAAAAAAAAcJif+N/hRP58/+2RlJW1dHUSiZxTVieRgr8JjPyF+XXV\n",
"dKp4clIXjUmdK6ac20qdqi4HKyad011XJ5Fd93Fk7kldNLo6yDzJ6J7QueeMMSd1KKka81ZjpU5n\n",
"J5GKzhWrc1esxX7+qqrLVFHdyV1CTldxtkW9Eb+Ozhu/k9fCmqpzcv51arqcBP7CcYnuFs+m7Cfr\n",
"L3O7Om/s6gSRNfek7g/fPmbS9Zmy50mdObLOratLS9dZVp3JiikdJbLWclIXjdPO7dN5V+omnUFX\n",
"R4/OrhpDOm/s6hKiwwcAAAAAAAAAwGE88AEAAAAAAAAAcJif5y+vxIzcRXrwZ8SxdEbHVJxTVazN\n",
"gknRJBFTYlO+LZ5lZ/xPxEnndLcrMuhJ12u56l6ZFJuScU/eRcbsivbYGSEixmbOvJ3RMZNiRr4t\n",
"NqXqZ3WGorVFPs1/WjOrblXcjKiVv9q1/tPPCa5r3z17egxR1fpPiqSpWmvdvTH5b+ROjzO5s5/e\n",
"uJyu858S9XHamMlnXRWBMmktFdExK+Mmx71eodQAACAASURBVMtMjrWpiqhZMSUSZeV7JsWmDIpA\n",
"CZlyBldNhMumaJJQ3cFRK7vqTv7tBQAAAAAAAACABx74AAAAAAAAAAA4zM9aI9lIf/CVupH+7SuN\n",
"l7uiY6qicCpibRacFk0SsWttJ8WOVEVjrDjpnCJ2RQa91XwaUxW1VBVJMyU2per9a9eYydElYmzW\n",
"fpTvup/udkXHZNWZFJvybfu5G7y2qviMk6JWquJmdqmI4AG4O/m9pWrtJ0XS1MUMTYoMqar5bfEs\n",
"GWvpjFq5j+mKwhBvsm9MdNzka1QRgdIZIRIZU/U31xVnuzNm5FPiQNbmPu2cdkWgRBx0BhXxLdfV\n",
"F3myUrMraiXyi1HWWb/U1eEDAAAAAAAAAOAwHvgAAAAAAAAAADjMz/OXKyJRonXfxqw0Ju7aT6Rp\n",
"clZ0TFFz6ZMiN6oiKjLWNukMquJZvu2cPp33ae5dcUZV171iPytzV0XsVMWmTI5J2XXd7zLGrIz7\n",
"thibjLiQlTpZ8RkZP0+yXu9ZMUL/7To69/O2ll0/71cUra0qaqUiVqQqaqXqDO5Oj1rZtf5d8+y6\n",
"7pxn12tz1zyn39u71n9SbMppkTRzIlCq6k6OZ9kZsZFd47r6znZSRE3VmIy4j0gL/qoxk8+6akzX\n",
"6/uuMzpmUrzMrsiNitf7afEmEZNiU04+p19wBhmxIl0xKlVzb4pa2VVXhw8AAAAAAAAAgMN44AMA\n",
"AAAAAAAA4DA/sUiU63rvSVIVtbIy5q1Zbud+Io18u2JtFkyK3OiKz/h2WTEdGdewM8Zm8v2Vsba7\n",
"XfFMK3OvXMO7XWvZFVFTNSaScFYVhfM2ZnVcxdyTxkyZtzMGJhoJ9P+bd3XuT9fybTEwT7rWtqlu\n",
"5LeGSN3TYgl2rf/0c/p2rk8eZzfbrutzWhzWXcX666Jj/lFUuSqmY0q0yqR4lreaK7LOesr1idbp\n",
"Ov+sa1Yx5m7nfRGJA8iIEOga0xVD8jR3VdRCRoRLZ7xMREaESFeszS+I9jjervtryr3y4F8Ln2Xf\n",
"PkhnRa1U1O2MjqmIcNkUC6PDBwAAAAAAAADAYTzwAQAAAAAAAABwmJ/nL6/EjmT0hc+IWlkZM3k/\n",
"FREvK3WLGlSfFs8yJW7m285t51oqYlImx5lEYjqyIh4q4k1W5o5ER1RFoFRF1OwakxGfMXnPT972\n",
"WBV5lDHmya5rmDFv5KNU1tx3VfEmFT9zOtdWEbVSdW5FdSOfzDvr7phnJTwyw655rkskDez2bZEo\n",
"u+apizPZ46z1V/09XFUr9snxLJNqdp3TpKiYkyJqImOy9rdrvZ17vDt5z5PW3hljU7Gnb4u1WXFa\n",
"tMeuazhlz7/x3G4y4luuqy/CZaVmV4TLpqiVXXV1+AAAAAAAAAAAOIwHPgAAAAAAAAAADvM3kS53\n",
"Kw12KyJRonXfxkT286QiOibSzLgz1mbBlJiR02JTTj63zrW81Vypu2ttu+7JJ7teL2/zrsydFUnz\n",
"tpass50yZlIUTsaYp3GRLpJTrs/KmCcV1/DJrlieu6z1T46BuZu0tikRNRvrVnz6LQpObJuniriT\n",
"PLsig/g+Xnd5Tj7LXWuvmqdu/VVxLJMjUCqiPE6PZ7nr3M9vjKjpOqdv219VNMmkPe9af0XcTFbd\n",
"rvifybE2nZFIGdd00jmdFANz2rnd7Ipw6YpRWfmeL4taCdUN1NThAwAAAAAAAADgMB74AAAAAAAA\n",
"AAA4zE+8x/hb49iMSJSVuhkRL09zr/RLqYiOmby2pzpFvi2eJWM/J8XaZK0lYtI5fTrv09y7Yjo6\n",
"4012RUdUnG3VmEi0x6QonIoxK+MiPx5X6uzaY0YsR2R/T6pied7WEjmDyL3yZEoMzJNvX9tbzaS6\n",
"VZ9sd8Vp7IpA+baolUhgZsTpETuw067YoW98De7a065rVDFP3dqrIl4m1528towPs5PiZrIiEXbF\n",
"WtztiibJ2N+kGJUnk6NJKuJMOiM3do3pirHpjM+puBc617Zr3pNiUybFwEw6t4C3CJesSJGuCJff\n",
"GLXSdNY6fAAAAAAAAAAAHMYDHwAAAAAAAAAAh/lZ+7aVBrUVsSMrdSPNc0/fT9faVuu8qIoQOCme\n",
"JWM/k2Ntomu5O+mcnuy6Jz+dd+V7dkaVVERHZMUkvdU9LdamIgrn9DFPuu7JFbuuYca8b+uIrqVi\n",
"P9fVFwNzN3ltVXFsVXEzRXV3RZ7siooRScOqXffKlHmvq+/+2bnH30YkSsyuc6ua58/10io7rOLv\n",
"6Kr+Nm9KjEpV3awW/ZPOqSuWZ1JETWTMlEiUJ5NiRnaNmbKWSde4M8ZmV/xP5HsiY6bEm0TG7Fzb\n",
"lHPaFX3T+Xp5qfsW33JdsyNcVmpOjlr5tOZq3a6zvtHhAwAAAAAAAADgMB74AAAAAAAAAAA4zM/z\n",
"Mx8ZESGRullxJhW9/iftp2ttT3ULIl6eyr4t47rOjmfJ2s+UWJuok87prvNsM+7j3xBVUhUn9emY\n",
"SbE2GWOqXi8r46rGTJm3MzpmSgxM1lomx8Dcda7tre6un/eD6kZ/U/pUJKRy8jy7zq1TV8zIrmvI\n",
"79T5Ov32+/j0SJS78yNrJsem7KpbFTsinuVZVzzL3a5YiyeR9XfdT7vGTI6fOS3OJDJm0nXuirHp\n",
"ivKZHGtTdR+vmBSbMiUGZlLczKc1r5wIl65IkdW6olb++5rRurcxOnwAAAAAAAAAABzGAx8AAAAA\n",
"AAAAAIf5ef5ypEHtSrRHRd2qOJPJ++la20rdpCbDFa2+T4tn2RXTURE/sTL3aed013W2u+7jJ5Pu\n",
"lbd5IvEGkbONrGVSdElkTNXr5W3MyrisMZ/WeKoT3eN/6oqsWakTeS08WTn/yGv30xordSdFrVSt\n",
"7S4jPudJRdxMUt2EsMIlu+JAds2z69zufkN0DFCr8z3j/FiU/+ns2JqqKJann1QVsRyTIlCqamZ8\n",
"gMw4t6cxGdEEXXEn0bkzony65p0Ub5I1bvKYSCxERpREZEzkdblrLSsGx1ocH2uTcU923ivfdk4V\n",
"7xErEiJcJkeVrNTNWn9F3UlRK5siXO50+AAAAAAAAAAAOMzPWkeGqi4aJ3USmbyfXWuL1k34m7+M\n",
"bgoRk7pQZHRtiHZgePNt5/Rk19o+nfdp7q5uF5H9PI3r6iARaf60cy0njZncoWRSR4xdXSfefuxW\n",
"3Qd3nWfwVuOJtfXW3TTPrs4U3zbPrs4hd12dRDrn7jpr+H92vs7+U+e93rXnsztk9M1Td69Ufai5\n",
"q/pbvMmdRDL2fF/L5LXtrNPVAeNtHbvmjc49pdvFaWMmnfWUPUfv4yldTbLmztjP5C4nGZ0qOn/+\n",
"O6eU9b9187iuvs4VWXW7Onqc1nmj4hoGzl6HDwAAAAAAAACAw3jgAwAAAAAAAADgMD/PX47EjNxF\n",
"oj0ivdg7o1Yi+9kVhVOxtqy6BREvT2Wroj0yVMTPZMk6t8nxLG8615YRz3JavMmUKI9I5NGuaI/I\n",
"dX+ya8zbuUXjpbpibO665r2ufdExGT+nst6fK2J4sn7uTjqnu66ou4iqGJu7qvUvlKxoN7/yo/qk\n",
"eZ50xZnsuoaTdV53/srZ955B1+v//EiUrnkW2muHPP10qPhHpKp/mOpsif5m8p4nRcV07edpTFf8\n",
"x2+IN4lEYewa82bS9ZkU03NSjE1GBEd0TMU9uSLjGu6Mz5n0P5Ludv3Ptci8CfdXRoTL9KiSjPVH\n",
"5p0ctVK154L9TH53AAAAAAAAAADggQc+AAAAAAAAAAAO8xOL4Liu934jVdEeXXEmkXyDlSicSTEq\n",
"VdE3b3WTGgbvisKoiIV4sms/FfOs1IlEoOyKwqg6p7td9+TK3LviTSJ1I/fXk8g9+baWqlibu8lR\n",
"OE8iHxHe5l0Zt2vMSp2qs73LiAPJ+rlVsZ/oWjLOJfK+EqlbFYlSEXE2OW7myabovoSwwiW74k26\n",
"YlREiPzbrvsJotyTvyNeZtce953lrr93mxybclfVdj2jblV8TtXaIqbs57r6omImRdRUjMm6jyeN\n",
"iUTsTFl/5HqcFMWyOndkTORs3+yKN+k6k+vKWdukc9r1np2x56Rze4twmRxVslK3M84kI2rl05qr\n",
"dSv2vGk/OnwAAAAAAAAAABzGAx8AAAAAAAAAAIf5ef5yRmxKpG5ndEyk5/tb3ZX9RHq+74pRqYq+\n",
"qbq/XoZUxbPsiirZtZ+sCJFde/503qe5q87prisyKOs+fqu7M3ak6vw/HRP50Vd1DU8akxWV0XUf\n",
"PKk4pycZr6nIOjKuWeT1smJSDMxbzWjdjJikFSfHzTxJWH/WyyNj7qq2910RIpOiSyatBVi3K95k\n",
"Rddadr1f7drffZ66/d3f+SfHm+yse//wNCkC5W7S2iIxF281onUyrmFX3EzVGVSNybjuk8fsijPp\n",
"jEC5+7Y4ls4z6NpP1TWctLYpa/my6Ju3+JbrOj+q5PT1V0StVEXWNJ2TDh8AAAAAAAAAAIfxwAcA\n",
"AAAAAAAAwGH+JtLlLhKb8mRXtMfk6Jiu/WSd9UqdT+tmne2L3xjPkrGfyDxPc3XFf+w6pye71vbp\n",
"vE9zV8WbZNRdub/uqsZU3Ae/YUxVjMqkPVbM+2RXdExGvElWPEhFnEnkPeJJxdqqIlCyopTeVETj\n",
"XFdN3MyDrhiVJxXt8yOBjVVzd0YxTFlL5/W4E2tznilxJlPWcV2z7tuutey6Hk/7+7Z4mbq/kauo\n",
"mxWF8WZSBMrd5LU91e2qkRVHEVlLxlnuiqjJiH2KXq+uPa6YEkEzab+7om9WVK13V+RGZMyueJOK\n",
"ut8YAzNlzws1MiJcsqJKquqevP6qqJWuCJeqeW90+AAAAAAAAAAAOIwHPgAAAAAAAAAADvMT76s+\n",
"JdrjyUnRMRXzrtSNnnXkbO8yomMisTwLQ749niVrP7v2/Dbv05hd5/RWc6XurqiVyfEmWXUj9+Rd\n",
"VsxQ1fq/fcxJESgrP26qzukuI+ZicgzMddVErXSu7a1u1uPYFdEqWVFLkXmyomHuNkXFdEWIdMV0\n",
"JH1STzF5LZPiJyDTlHt7yjquqzf65tvjZf5cCy25U1R9GKmKEHmbZ3LdrJoVZ1u1tojT42Yyrs9p\n",
"ETWTx0yOkolEPGTET0TGRF+XXTE2XZE0nVE4b3Umr22lzqRzGhQ38xbhkhUHUhGBkhEpsjLPap1P\n",
"63ZGrWSsrWLeoro6fAAAAAAAAAAAHMYDHwAAAAAAAAAAh/lZ+7bJ0R6RupE4k11RK5Gmw1n72RUV\n",
"81ZzpW5WLM/LkN8Qz5Kxn6w93006p0/nXfmezqiViniTaMxFxb1RFRmUMabqup80JhrX0BWBkhH5\n",
"kHW2d9Fkvk/WsVJjtc5b3UlRK1Vru8uIz3lyUtzMXdUj6ZuiYjojRLoiQ7oia55MWstkk89pcvTN\n",
"pHO6m3ROk026ht8etXK3b787/7YtEiEQUVE3K9bire6kCJSqmhn3XNb1qIhJ2RV38mRXZEjXvJPH\n",
"TI6fqYqsqVpL5HXZFWOz6wx2zZ0Va9O1tkkxMAfFzbzFt1xXXxxIVqzK6euviDypiqyZvJ8bHT4A\n",
"AAAAAAAAAA7jgQ8AAAAAAAAAgMP8xJsOT472eKsbiTOJ9EzPilqpiJeJnPVKndNjeRaGfHs8S8Z+\n",
"Vr/n0zG7zulJRfRNVoRFV7xJ5BwnrWVXzNBdVcTOpDF3kXt/UgRKRmxKV2TNdfVFrUyOgZm8tl11\n",
"q+Jm7jbFqPztXP+p6FH3rmiMyG9bWaZEbnTG56yYck7QbVKMyt2k12XXWjrPYN+9cX9Hrvowclf1\n",
"d3YZsR0rJtetio7JWNvTWiriciI6I3Yq4mYiYybHmzyN2xXtsSuaJCuiImNMRvxExpiVcZ0xNhXn\n",
"0HkfTF5bxtxZ6981T8LrMCPCpSoOJKNuVqRI1/onry0ypiK+JamuDh8AAAAAAAAAAIfxwAcAAAAA\n",
"AAAAwGF+nr+c0Xd8Jdrj7qlnSSTa463uadExGb3lV/aza/2Tz3bBlNiRyXEzT3XuJp/Tk4qzjUQK\n",
"dMabVEXSRFrw74oMuou8Pt7W8VT39DF3kbifruiV64p9XIk8Qht5rd5NioGp2M+Tb4uBucu6HndV\n",
"cTN3GfdBZJ6iubLeViIiP04qdEbH3HXF56yYdE5306NvqDHl/nsy/f6bcnad67jPveua3efZdwY7\n",
"/x5uV5xMxTxVa6+K3KmIQMm6VybFs1RE7ERkRSRURV9UjNkVFdO1v6wxGZE1nWupus5dMTZVZxCJ\n",
"EHkbMylGpWLerDqTzikhwmVyBMpKzV3r74wmmXy2n85bVTdQU4cPAAAAAAAAAIDDeOADAAAAAAAA\n",
"AOAwP/Hms2/ZBFl9+99iOSL9tbOiY97OKSveJLLnjP3sWv9pZ/sy5NviWbI6RJ50Tk+6znbyfu46\n",
"438y1rIrQiTrup885smkc7mrio7ZFZcT+ZEaWUtGnMykGJiqaJKM63HXGTdzl/G5Ydc8K3Nvejx+\n",
"UuRGwqfjNJPWcjd5bXCiKTEqTya9vqespXMdf66XNt5pqqI87iKt8SfN07X+iKprmrHnrGiSjOuR\n",
"EbFTtZ+IitiLlTHR+2JXlMqu6zEltmbS2quu8a4YmxUV0TErMuruijeJylj/Qef0Ft9yXTkxI51R\n",
"HxnRK1lRKxV1J59tZO7BsTA6fAAAAAAAAAAAHMYDHwAAAAAAAAAAh/l5/vJKFMbdSlPbijiWzuiY\n",
"SKZARdRKRsTL09yd66+4B6vOdmHI5HiWqoiEt7knndNd59lO3s9d1xk81b3bea9njJkcL9M15kkk\n",
"AqUrNqUrQiRyBlVrqYrl2BUDk9F9M+t6vNWt6hT6bfN0RsXcRD7pZoikZ+0yKdbmSdc1izhprew1\n",
"6TX1ZvJaJ72m7mvpjVrpsitS5MmuuXbNU/F3gVV/a/gb4llW6n4q65y69pNx3U+LqOnc48ljIlES\n",
"nXEsJ8XYdJ3BrvsgUqczBiYjwmXQOWVEuGyKzwjVzYpe6Ypwmby2wVEru+rq8AEAAAAAAAAAcJif\n",
"tb+livxp60rdyJ/8RrpQvNVcqTupk0jG2qLXvWv9VV1nKs52YUhXt46sv36vWv+uc/p03qe5d51t\n",
"V7eLSNeD6F+yZ3SDeauZNSby1pP1dnVXdc3extxVdZ15Evmx+zb3ri4aWR0lKs4gupa7jC4Nk7uC\n",
"PMm4Hp/WjNbtmqezq8auziE3GW9nWRJ615WZ3IViereRu8nX+c3Kb5yTnXTWT0466+lrnXwvdJ3d\n",
"/Ux6r2FXh4yqeXfNs6uLxq71R1SddVW3joy/Du/qvNHZpSXjOneOifz1/sljJl2fXV00qjpIZHR2\n",
"6OwkUnFdB3W7KOvws+u6J3T02NkR49O6KzUz1t/VMWO1bkZXkE9rrn5PV5eTT2sm1dXhAwAAAAAA\n",
"AADgMB74AAAAAAAAAAA4zM/zlzN6y69ErUT6m0diR95qrtTN2s+ueJOKLImVuXed7WnX/WVIVYRI\n",
"pIX9yphd68+Y58nJZ7srqqRqP08yYnky1hK917vGVF2ztzF3u85kdVzV3P9pV3RMNPrmbnLUyklr\n",
"e1IReTI5biYy7664lidFe8xIcMoQ+VGxy6RYmxWT42WAvzfpfeTu/j4yaa2Tolb61rIrEmVl7l3z\n",
"TI5NucuKKnmr+43xLCt1O2pcV19UTNc5Rs8t4z7dtd5dYyIRFV1xLE/zZkWEZKwlYx1V+8mI8umK\n",
"l9kVA7Na59O6m9b2Ft9yXfsiUD6tuVo3Iw7k9BibrgiXwVEru+rq8AEAAAAAAAAAcBgPfAAAAAAA\n",
"AAAAHOZnLRoj0v+8qm5G7MiTjAiRriicqniTSfEs33bdF4ZEIjcqoiRWIgV2rb8zziRyTp/O+zT3\n",
"rniTXffKk0jEzl3GWiaPqbr3q8bcVUWgZMyddQ3vMqJjMmpcV18MzOS17apbFTdzlxWBFJnnrupx\n",
"8qrom0/n3Tn3y7STYkcSPg1vddp6/1PkNz9YddJr4clp65+83ilr+3MttP4us+sH/v2n0q54mar9\n",
"7YqS2bX+rBpT4lme1tEVtZJxr2RFG+yauyui5tvG7Irt6Iouqay7K8bmrUbWGZwca5N1f3XtcaFG\n",
"RoRLV3TJSt1d0SuTz2C1zqd1J0etdJ71S10dPgAAAAAAAAAADuOBDwAAAAAAAACAw/w8f7kiGqOq\n",
"biR25ElFhMiuKJxdZ73yPbvWnxU3c7drbQsq4jOyIkSqIlAia3k72s61fTrv09y74k0ibfozzuBp\n",
"XEa0R9b12DUmksL1VqMqRiVjzJOq888424yoj6xYiIxYi6oonLvJMTBZdTPurxWRn3WT5/l03uuq\n",
"6wa+6xq+yEqxqpDxVtvp9AiUk+Nn+A4n33Mnvdav66/rnXT297X0nu2uyJC7p3l2/R3drj1nxE10\n",
"zVN1faoid6riTKoiaT5VdU6RuaviP97GRM9gUsTJ25iqCJHJcTIZMR1ZdSsiQ7JiRique9XadkXH\n",
"7Ipw2RV59OAtwmVXBEqk7krNXXEgkyNcqtb25VEru+rq8AEAAAAAAAAAcBgPfAAAAAAAAAAAHOYn\n",
"HokS6X+8K3Ij0vj22yNEMmJtnupOimfJiJt5q7lSN7K2BZMiRKoiUDLW8lZzpW40xubTMZ3xJrv2\n",
"cxeJ2HmSEe1REWsTHfO2/qwon0/nfZp715gnb/dp5GyfVMTWZJ3Brv3cZcTaPJkSUROdJ+McOtdf\n",
"Mc+Uea+rLnooweSYjshvNF0mR+FEnXT+EZPv/Szfds3uTt/frGiSz01e75zXc2f0yq5IlLtIq/+I\n",
"XWd7WmRN1XWeEq2Sdd2rYmx21Kg6g+jcn46piva4i8zTFcGxc0zGnqvWsmJX1EpF3c5zzIiB2RkV\n",
"8+GYt/iW6zo/pmNXvMmuGJiquhURLl8WtbJrrTp8AAAAAAAAAAAcxgMfAAAAAAAAAACH+Xn+ciSm\n",
"4y4rcuOtblbsyF1VhMhdV7zJk4y6k+JZMuJmnuxaW8CuCJGuqJhdcSbRGJtPx+yKN8mKEMm4PisR\n",
"O5ExGZEnGbE2nWN2xahkxDNE7oO/G/efItE+kTqd0TFvNZ5kRAZVRa10ndtK3btJMTYrqmJ43ua5\n",
"2/l4+a49v8h6K6qQ9aOhy7fFgaz85gTTfeM9e9KeJkfU3Ncy61ybPiQ8zr1rLV2xNlky4kBWTIpA\n",
"eaubFQ8yJTqmcz9dcTNPYyIRFZ3rrRhTEcMRuVd2xg51raUr8qTqepwea7MrKqboM8HJMR274k12\n",
"xcBU1c2IwonMW1V38lkH6urwAQAAAAAAAABwGA98AAAAAAAAAAAc5icWP3Fdsf7NGbEWVbEjd7ti\n",
"OibFm9xl1Z0Sz5IVNzPErniWaJzGrrW8zbszxubTMVlRJW9jst7CK87gumIxCl2RJ6eP6YqkuYtm\n",
"CkS6LlZE3WScwcpaJkeiVMXAZJzbzrpd81Sdf9c8Kyat5Xad/3mbt7Nl/dvtNfiTbehH+Wm+LZJm\n",
"xUG/XZX5Ddf57tuu8+xokncnxb78uf7Rso68iIQMu9ZSFe3RNU/VuWXEqHTWzaiRFfmQEaOwM2Lj\n",
"P3WeQVXkRteYyVEykSiMrJiOXWvpir7piqTpOseVOjsjahLO6V9dn9Ee7Iod2RUHkhEDU1W3K8Ll\n",
"y6JWytZ6+x4dPgAAAAAAAAAADuOBDwAAAAAAAACAw/w8fzkSM3KXFbnxVrcqzmRXhMhbzZW6u846\n",
"Wvetn35nPMtJcTMLKiJEonEau9by6bwr37OytrudZ/vpmEg0xq64mZW1VI3JWv9JY7rOemXM3a7Y\n",
"lMjr/Unk/eptLZMjUapiYCbHtVStPzLPt8W17LqGKyatJTDtpDb9d2+302kRCXenXx+oNDlSJMvJ\n",
"sS9Pa52z/t8YtbIi0n4+oip2pGueqnP79niWlboRGWuZFDdzWrzJrmiPt/VGrkfWmDdV13TS+qvu\n",
"wcn7qZg7K9YmY49J5/QW4TIpziQjdiRrnikxMFV1u+ZdrfNp3clnHRijwwcAAAAAAAAAwGE88AEA\n",
"AAAAAAAAcJifWDTGdb33JMmK3HiruyvOpCpC5K3mSt1dZx2t+3bNfmM8S8Z+FmREiKzENZweZxJZ\n",
"21vNpzG74k0i59h1fZ7mvqsaE+m9nrXnrjGRc8uYNyMO5LpyYp7uMmpcVyz2qWItkyJRsq77XUZ8\n",
"zkrdu6r1V80T+blVYVJEyqS1BKadHIGQ8SPoNJHfrr5dUkjl13Mmz779XJ72d9L7xuzIml1xICt2\n",
"Ra2s6Ip9+bZ4mUl1J0fSZKwtEgeyUmdXlMfbOirnrjr/ijG7rkck1iIypitCZHXuT8fsjLF5qzMo\n",
"3iQ0ZtfaEuq8xbdc11lxJqfFzWScW1VdUSs5dQviW57m1eEDAAAAAAAAAOAwHvgAAAAAAAAAADjM\n",
"z/OXM2ItInVPi46ZvJ/I2u46Y1N+WzxL1n5eZMWBdEbFfDomsv7OqJWKqJKqt7y3dayuJRKFUTGm\n",
"as8njcl4za2MeVIVmxK57p/W+Lu5/1NW1ErkUd1da8uom3U9dtXtmmdSNMmU6JjrmrWWD6ee3NZf\n",
"XMuzb9tzhFibPM7ur2ZHiNS47/G0+2L2NZsU+zJlLU/zVnxY2jXPU82Ms62KUZkcz/JWMypjz5Oi\n",
"SzKiL6piLu52jZkcJTMpsqZqLZHXR1eMza4ziNSJ/NzatbaVOgs1MiJcJsWZnBQ3s+vconUz1h+Z\n",
"96Solaq1JpyTDh8AAAAAAAAAAIfxwAcAAAAAAAAAwGF+YlES15UTERKJ3HiruVI3Y61PdSftJyMO\n",
"ZFJsym+MZ8nYz4JIHEhGPEs0KubTMZH1R442K2olI7Ki4hyfvudtHZVribTtz0jUuquK5aka81Yj\n",
"6/q8jXmyKzYlsv63GtE6FfuJ1rkTA/NXu2JUOuNaIi0HK9YS7WHfFdlyW+8/H+63WW3t/6dIQtjp\n",
"MtK+gH6nR6BEnLznp7X+uRZaim+xEtew64PGpLXsmnfXPJFYghUnxb5kRZPsWltE136y7q+uuJJd\n",
"0R6njzktjuXTMZ0xNhVnUHWOk9aWIXN9ZAAAIABJREFUEOFyWpzJlNiUSecWqXt61EpnvMyndTdF\n",
"x+jwAQAAAAAAAABwGA98AAAAAAAAAAAc5uf5yxmxFpG6Wf30K+JMImfQuZ/IWd9Njk35jfEsVa/L\n",
"lyEr0RinxZm8rT8S19AZtbJyPT4ds+sMnmSsZdeYqvu4asxdVtrX29yRx0uzruFdJOomUqMqliPj\n",
"bHetLaPmdeVcjxVV6++a59N5K+e+6zqDFVNibZKsLO2kOIAVGW/zPEv4TYNFzjbH0zl+23ve3fl7\n",
"XmnnPukHb1fUyt3TT7+uCJqqvy08PV5mcjzLSt1PZd2TFVErFTEYlXV2RZXcVUV7nDTmpCiW1bkj\n",
"Yyrqdp7BSbE2gTpv8S3XdVacyaTYlJPOrWruTdEk4Tqf1q2KhWk6Jx0+AAAAAAAAAAAO8xPrLHBd\n",
"OR0jIh0L3mqu1M1Y60rdrD9P3tUd4u60Lhq/rVtHVXebhSGRbh2RThVv8z6NiXSHiPzFfFUnkbuM\n",
"/TyJnMHbend1H4mOiXQJyNhz1Zi7qg4ydxldAjo7iVR1OYic5d2us+1a2866XfNUnf+bk7p3XFff\n",
"H79mvfc0qWroc5Joj0Le6Ywy29Nr2fXIcX5HjM/d93z+GUzpsvGkqgNDRNc57TqDXV1OquapqlvV\n",
"3aKqQ8mnstaWMSZr3pM6XkS6EUwes2JXZ4qM9UdeH51dTbo6iUS6nFRdn09rXDkdPSZ1tzipi8ak\n",
"c4uMO73zRme3kU/HVHUSudUd/E+aAAAAAAAAAAA88cAHAAAAAAAAAMBhfp6/nBFrEam7ElHxVnOl\n",
"bsZaV+qurO1t3qcxVXEgd50xIxln+xvjWSruyYUhVVErb/M+jYlEe2REolRFx2Ts50nkDN7Wuytu\n",
"Jjrmbf1Ve64ac5cRGbQyd0Y//Z3RKxlRKxlnuSsSpSrzQVxLbxxIRuxTRKSNYWcX9Yz3nia/MU5D\n",
"RE2vhOBHhvH6qHN/ffzGiJ2VM5jtpNiXXdEkT6bEvlR9aNs1z+R4lpW6ERn3zs64nE/HdO4nY0wk\n",
"OqJrrZ1jJkfJZMWm7Kr7NmZydEzn9UmIcDktzmRK7Mi3nVvV3JuiScJ1Pq1bEd+yMm9R3cH/7AkA\n",
"AAAAAAAAwBMPfAAAAAAAAAAAHOYnFo3x9D2R/uyRiIq3mit1M9a6UndlbW81n8ZUxYHcTYoZyYhN\n",
"+Y3xLBn7WVAVtXKXFc/yFn2RFRNRER0T2c+TyBlkJGxVRXBMHlMV5VMx5snbHrPicz6d97pmRa1U\n",
"RG7sOqfJcS3XVbP+yDxZj0lPiUnZeQ0/Fe2LP6U7+8PZ/vPl/vm2KIDfGFEzScaPLc739Bpz3fc5\n",
"PwLlc297/nO9tCBvtRK9MOlv5qZEr1zXvrV8e+xL1rllrP/b17ZyH0fqVMRerI7ZFYvSuceKMZPi\n",
"ZCriS55qvNXtjLHpio6ZdH1u3uJbruusOJPTYlNOOrfI3KdHrVTFpkyJjgmc/aTfVgAAAAAAAAAA\n",
"WOCBDwAAAAAAAACAw/w8f3kl4iEjIiQSUfFWc6VuxlpX6q6s7a3mU92qOJC3eaN1J8emVMyz4vRz\n",
"W1ARtfIkI5qkYt6nuasiRCriP1b2cxcZE13L3eQxVVE+b2OeZNyDU+a9rpzYmqy1VMSi7Dynu4qI\n",
"midV6++aZ1JMyq5r+CbSYnHSI+lTIngaRbYjrqWOuBYy3V+rXrt7vUWg/I7r8dYiffoP1bf1dn6o\n",
"6Yp9ucuKn3gTiS7ImuekeJms9VfcX5PWlvFeFD2TrqiYjJiOyWO6Yjt2jqmK6am4/zujYyJrq9jP\n",
"g4wIl0lxJhkZh78xBqYzzmRINEm4zqd1O/dTUHfSP6cCAAAAAAAAALDAAx8AAAAAAAAAAIf5iUdW\n",
"ZPRnj0RUvNVcqZux1pW6K2t7q7lSNysO5G3eaN1dMSMZcTMZLQgj9/GKyee2YHI0ScW8T3NnpEtF\n",
"9vOk6ww619I1pirK523Mk8iPoLcxVdErkUdSo7FCFWupivaoOqe7ih9bT6rWnzHPXWdcy+RYkSnR\n",
"MStOj5cJ2JWIRExFGhhke4sZcU/uFbke3/c+/tZyf/oP7ynrXWlZv+uD3K74mZV5JsWmdM0zKZ5l\n",
"pe6nsq7FlLiZ6JjOuaeMqYhWid77FXuOrKUz+mbXGdw1RexkxLdcV1+cyaS1fVpzte6uGJiKM8iq\n",
"2xW1UhWbMnk/n9Z8qDv9tyAAAAAAAAAAAG488AEAAAAAAAAAcJif5y9nxHQ8yYj2eKu5UjfSk/u0\n",
"6JjIWb/NG63bFTNSFRnUdQZ3k84tIeLlqWxVNMlbXEbGvE9zR2I6MvbzpOsMOtcyZUxnBErkR2pG\n",
"XENWFMbb2WWcwcpaqiJRdq1tV8ZDVVxLV0ZFZ1zLrke0Iy0GuyJbTlprksjyv6+N/xxVQZDwDd5i\n",
"Rp7em7we9vmdMTBvMSqTPiSstODvWu9KDMyuuXfFz1RF8Jy0/qrrPmltGdcj617JiMvoijfZFQey\n",
"MiZyPTLGrNi156q1rOiKjsnYT1EUzq4Il6o4k8lrWzFlbZPPYKXu5LVFxnRGBhXU1eEDAAAAAAAA\n",
"AOAwHvgAAAAAAAAAADjMTyzi4bpy4ksyYi2yYkfe6p4WHZOR8XB6PMuu6951Bk92nVtk/Qt2RZNE\n",
"olYyojDe5l2pG9nPk4y4mYxzexpXtZaTxuyKl7lbiVpaGfNpjdU6kY8EFWuJPC47eW2RlniT41pW\n",
"5qp65Pm0qJi7ru7gJ6016vYe8M/APSjuII84FphvpYv0SlQMOSKxPH+uhdblo620kp/ygWQl1mLX\n",
"3/ytnNuktWSoOuu39VfFy0TqTl5bVdxJV+xLxvVZqZP12u3cY8eY6L1SsefIWjqjbyoiXBpjed4i\n",
"XHZGe0TiTHZFe+yKWqmou1Lj289gtc6ndbPO9tN5q+puWqsOHwAAAAAAAAAAh/HABwAAAAAAAADA\n",
"YX6ev5wRURGp2xk7cjc5QiRjbU9Oj2fJiBnKWNukiJqumJ7VOi+qokkiUSsZURhv867UjeznSUbc\n",
"TMa5PY3LeMuePOZJV7zMXca9E5k3OvfdruiYSN3JazstRiUrHidjnruqR6knreXNSWtdkZXbMaXj\n",
"+2Gqjk0cC/wOT6/1+8eV6PcQsdJaviuGJMukOJM3KxE1u9a6Mm/Fp4Jd8zzVPSleJivOaNfauiJp\n",
"siKEMs52SrzJyphI5EZVPEjGmBW79ly1lhUZUSuRdWTsJ/Cz4S2+5br2xWdEakxeW6ROZ9THlDOo\n",
"qtu5tq6olar9ROZ5qTvltwwAAAAAAAAAABZ54AMAAAAAAAAA4DA/8WiMiviSztiRu9OjYzL2PDme\n",
"ZeW6v9VcqZu1tilnsCumZ6VOU8TL01JWIioiUQVvL6mMJKysuhWxMNdVF8sTWcuUMU8yfnyszBsZ\n",
"c1cVN/NWI1oncs1W1nIXefv9tMa0ul3z7IprmZQl0RUHctJaV3Tdb7/ApDQjgGpPP07eYmCexniP\n",
"i3qLAzjth3dXnEnESnzGrrXuip/ZFdOzct0nRaC81ciKgKjac0eN6+qLismK+iiIwnjUucf/dkz0\n",
"Pq7Yc2QtndE3FTE2RfvJiHDZGe1REeHybTEwkbqnnUFV3clnO6XuprXq8AEAAAAAAAAAcBgPfAAA\n",
"AAAAAAAAHObn+cuRmI67XVErnXEzk6NjKuJNVr6nav2TzzYSgbJrnpV7vyKmZ6XOyvoDIjEjK5Eo\n",
"GfEZK29fb+2dIrfXk4q4mci5PY1bieWJrGXKmCcZMTYr80bG3E2KN8k4/11ryYq1uZsUA9M1z6TY\n",
"kc6omLuMPvFTuodf1/ftZ5NdW074BAfw673Fwqx8z0rczO/01q59cozKk0jMSNd+Os+2K/7nqW7F\n",
"XLsiUKriTDKiPiL7zTq3STE2kXPJOMtd57ZrfxljVuzac9ZaKiJcqmJ7suJlbt4iXHZFe6zUiXwY\n",
"7FxbxVqqIlBOOoPVOp/WPf1sP615WF0dPgAAAAAAAAAADuOBDwAAAAAAAACAw/zEYyEycgdWoiPe\n",
"6kZiR57sis84Od7kqc6kaJKueJaMCJRd82REvDzNvWv9C9NEYkaqolYiUSWR+ImMt7xdZ7AybiWW\n",
"564i1qZqzJOMGJuVeU+KN6mKy7nbFR3zJGNtn9aM1u2a57pq4nJWRFrr/Ya1fCojiuW65uynSGfK\n",
"EAC/y0oMzNv3/M6fL5HYlMl/ZzcpBmZl3klrOWmeqnuyYv1Z8T8ZkTRVcSdT9hMdE4npyIrdOWVM\n",
"9LpXRLhE1lIV7TPpDF5qvMW3XNfsaI/TYlOmRKB0xnZMOYOqugdFopTV3bTWyb95AAAAAAAAAADw\n",
"4Of5y5HOCHdV3QcyulA82dSNYFtHibuMbhcrdao6PbzVXKnb2UUj0n1k1zxvr7uqeyVr/S/fUtV5\n",
"o6pzReQv/iONd97qVnUfWRmXcdZVXTUyxjzJ6GqyMu+UbhcZHUxW60Q+rkTWsqtuV1eQu4q1Z86V\n",
"MXfVY9EndeuIXrP/dHpnjowzWOExfAAO9+e6/0VspGtDV4eJnSJ7nvJBYeWvxXettevcVs4g677d\n",
"1UGmYv1Z3S3e6kZqVnXe6OwCEjmXjLPc1bFk1/4yxqyoOuuq9Vd03sjqIPNpjYc6GR09dnV6eKpz\n",
"UgeJSR0xsvb8ad3Oe2XFrrP9dN6VuhXX67C6U35jAAAAAAAAAABgkQc+AAAAAAAAAAAO8xOLVbiu\n",
"WE/xlbpv81RFrVTETzzZFSFylxFvslInK5rk03lX6nbGjmTEzeyaJ5IlMemcFv5zRtRKVVRJJH7i\n",
"LWZkZa274mZWxlWc9ZNIjErGmCcZMTYr8+6KN8mIHamKy7k7Ka7lumoiW7Ie/901T6TlXdUjzpPW\n",
"8uaktUZVxK+cdgYA8PUiMRddsSNVInvustK2f9daO89t154r7vXJ8SxPKqJWsiI4MuI/sqJjImPe\n",
"zqEqouakMSvxZSt1q+JkMmJTImN2xdgs1HiLcJkebzIlMmT6OXXNU1F3ZwxMpO5vi1qpug8i89y+\n",
"5/TfcAAAAAAAAAAAfh0PfAAAAAAAAAAAHObn+cuRKIy7SFzDk66olUj8xNs6VupOjo5ZqROJJnny\n",
"7fEsGfvpjLV5m3dl7l3rX5gmErVSFVUSiZ94ixmJpFrtipt5smtMRoxKVQRKRmxK17zXtS86pipa\n",
"JSMGJtLeLWvPdxUxME+qYmwy5lkxaS13GVElU7p6X1fsPl7hUXYAIGSlBf/pUTEn7WdSDMzKvBXx\n",
"Jk91M65H9F5/s3JOXdEqd5PWlnU/ZYzZFYkSmfekMV1RLE9zR8aszJ0R4ZIVGfRpjQeT401Oi02Z\n",
"EgMz6dw+rblatyuaZOf6P63bFbmzs+7LmMm/iQAAAAAAAAAA8MADHwAAAAAAAAAAh/mJxSo8yYhr\n",
"iNTdFbWysp+VdUzZTzQ6JiNy463m05hvj2fJ2k/XuT2ZfE4v31IVm7IypiJmJHK5dsXNPNk1JiPO\n",
"pCoCJSM2pWve69oXiVIR17JSN+ucInUzOthWrb9rnujcdxVdoTOiWK5rziPaWfuZFC9zEMd2vqyX\n",
"EJzmfu8/fRx762C9Mub+PU+vuYzviYzZtf6qtREViSaZ8sHvyeT9TIqoiUQVRGRFk3TNk3F9Jq8t\n",
"6z6IxGlUxc28ncOkiJpJYzrjWD4dE7lvq+7JhDP41z/++rXJ8SYnxaZMih056dwidXeu7duiVipi\n",
"d6qifBLOafJvEQAAAAAAAAAAPPDABwAAAAAAAADAYX6evxyIREiJa4jU7YxaifR8n7yfqsiNu8ie\n",
"f2M8S8Z+us7tyeRzWvjPGbEpK2MqYkYiERa74mYmjZkUgbIrNqVi3pW5s86tKrYj8mP3v60ZrRtp\n",
"I1e1/rusrsW79vhmyjpWRdb75jc8Kj6oh/0/b+c9aGkEVcXyuDfIUhU7wvnu1/TP9dAi/bVde1Yc\n",
"yG8MOXs7l5UYhUkf5N7ujV1rjdyTWVbmqYgmmRyBslI3I8Ii631lUiRNxpiueJNdcSBVY7KiWCJx\n",
"OW81smJTMtayIuEM7hEuk+NNdsZ0TIkM2RU7ctq5VdV9qyNqpfcaFpz/pE/7AAAAAAAAAAAs8MAH\n",
"AAAAAAAAAMBhfmKxCk8y4hoidVciN95qrtTNyFV4+p5J+5l8DXed7eTYkZPO7anO27wrc+9c/8u3\n",
"VMWOZESGrFz2SBxIRdzMaWN2RaDsik2pmHdl7l3RMU+qolW6YmAiZ9AVTRLNHKjoohw5g13dw7Oy\n",
"GU7udt6ZT3HyufFr7fpRwFlW4lnEAfEdItEYGXEzp8uK2NklEmuzYx3XtW8tuyKPdsWzZNStOoOq\n",
"uJNd0TEZZx0520kRNVVjdkXfdEW4RO7bqnuyKcKlKk7jtNiUKTEwv/HcPq25Wndy1ErnuXxaN1Jz\n",
"09nr8AEAAAAAAAAAcBgPfAAAAAAAAAAAHObn+csrkQh3GREPWZEbb3WjcSaf1n06gyn7qYrp6IxN\n",
"+W3xLJPPbbXOp2M6z+nlW7JiU94iQzIiXv5u7k/HZK3lpDG7IlB2xaZUzLsy9/S4lorIk10xKlVn\n",
"exdpX5fV2Tgjh6Cqy3JGb/zJj2PvyoCYfAbwJSp+bLHX/RqJZ4EOkQiUKdEkWSL72bXHjOvTuZYM\n",
"XfEsVREoGbEdWdc4o27WPbgrKqZr3q4xO2NVMmJTImMy9rxSNyHC5R7fcl2zYzqmrG3SWnbFjnzb\n",
"uUXrnhy1UnUmXWf9pGAt/jkVAAAAAAAAAOAwHvgAAAAAAAAAADjMz754k6e6d9HoiLd5suJM7jKi\n",
"Pbr2s+usV+pWxaZ0xbOs+PZzW6mTEfHyNHfW+j+0EoESiVp4i3j5u7l3jFl5i5i8/pUxbzWqIlC6\n",
"YlN2RaJEO6hm1K2KPKnYc+Stadc8WY8Md0bD3GXkF0x6lLqit/9pHcaBsMhHKeo4e/jt3iIDnj6k\n",
"nRQVs7LWrv10xsDsiv/ZNU9F3ZV7ZcW3rW1XxM7bvJlzfzpmeoRLxpiuPb/VjI65eYpwedMV07Er\n",
"QmSlzuQ4k654kJU6k89txaT1f1qzs27VWX+6jqS6k/5ZGgAAAAAAAACABR74AAAAAAAAAAA4zM/z\n",
"l3fFjLzVXK37Nk9XnEnWGVTsZ+Wsn3TFjGREiOxq9xg924q5q86t6x7sjOUJ9FTKiP9YiYWJRHtk\n",
"RIisjNm1/qoxdxkRKJ2xKVMiUaJ9yTPqZsXwROreVcTAdEakTIpnmbSWN1V9+id37a7y5ZkH//yy\n",
"R/W//HJ9pcjHIGIyUsbodb+GT6+Xt+95ug/eOmOvjIms7c91b6u+0rY/EoWREe0RWdtvVHU9ukT2\n",
"U6VzLd8ez7Ir6uNtHU91s6JLTop92TVvVUTNp/NmjcmKQEmITfm4ZrRuQoTLygeWlTGf1niqc1KE\n",
"SHQtGeufdE4VdXddw+gv3lPWH6k7KTal6x4M1JzyqRwAAAAAAAAAgEUe+AAAAAAAAAAAOMzPWtzB\n",
"k0jMyF1V9EJFlEQkCmMl5uKt5lPdqhiVt3mjdStiRrKeVdp1tpPPIPJ66TqnJ11nmxDx8uQt/iMr\n",
"puM+JvLWmhHx8lT39DFvNTLiWlbmXnnproz5tMZKnejbV0bdrEidSN27KTEwkXmeZPxYysoH6EpS\n",
"izjp8evp+Q0nnSWtYYvkWEnuY437dJ9dsSmcJhrBsSuS5iQrMRdVMSOfepp3VyTKylp2zV0xz65o\n",
"pZV5VlS8DietLTKmKm4mMqYq9iVytl1jVuza813gXn+Lb7mutQ9gb2OeRKIkMqIXdsVnRD6oZq1/\n",
"yjmdHgNz+vo/rblat2LPk6JjEvZ3+m8RAAAAAAAAAAC/jgc+AAAAAAAAAAAO8/P85Ui/9pWIh7tI\n",
"9MLbOlbqRva3Es/SFR2zKwpnpW5V9E3GNdt1trvOoOreXzHpnD6d92nujNduU8TLdcX6aVeMicZp\n",
"dK3/blcESsZaV+Z+uh5TIlGiPd8z6kbeBk+Pgdk1z5R5n1T1We/qPn23K0fBo+IcaNfbJrGPHr+R\n",
"6Js897OMdP6GM7xFYWTFzUxRFZ9TpWstu2JgopFHFfNk1M2KyqiKWtkV+5IRsbMr3uRuV0RN1pgV\n",
"BbEpZesPvKa6IlwiNTqjV1Zq7IozyYjC6DynT+t0RnvsOoOquhVRK1V77ozL+XSeQE3/bAsAAAAA\n",
"AAAAcJifWOeH64p1RriL/CX+2zpW6kb+BPi0TiIVnVFW5s7q1vGms4vG5G4dU7pqROvu6rxRcbar\n",
"c/+XQ1b+dDKjSdPOLhsV618Zc5fVEeNtTMZan+be1XljZf2RH90rMupGnriNflTKqHvX1TVj1/5W\n",
"TFrLm11/Wjz5DzThQJGXlE4C8N95+6NO3WJgh7e/2l75C/OKzg9ZVjoa7Fpv5Gwz7OrWsasjRtY1\n",
"rOiMMmltK9fjbd6suau6gFR0LMkaE7mGkTGD1v/W0WNS54pd3SEia5vU3WLyOVXUWKnT2WHi2zpv\n",
"dHX0qOrm0VR30qduAAAAAAAAAAAWeOADAAAAAAAAAOAwP2vflhXT8daDPxLXUBVRURXxsCva424l\n",
"/6ArcqMzniUj2uP0eJaKa/o0ruucnkyKvkkYkhHtsfIWEYnTyErQuqvY88qYu6f9RVKG3mpkrPW6\n",
"9kWiRFLFVmTUjTzqmhV1E6l7tysG5i6jo21WL/aq+JKKPIZvi1qRWTHKP5Me3XdZc1Slf50ukgD4\n",
"bUSRiGfZaaVD+kq38D/XvRX7Sjv3txb8K/EGkZiLrrWtfE/W+r9N1fWokHFNT1/LrutRFbGTcSZV\n",
"ZzAp9mVX7Mjd5IiaXWOexmVEuGxa/1t8y3XNiiqZHAcyKc5k8jlVrGXXuUXm3hkDU1G3Kt5kUnRM\n",
"RfxP4Nx0+AAAAAAAAAAAOIwHPgAAAAAAAAAADvMT79++EoFw99a3P7KWqriZSMTDW82Vup3RMV3x\n",
"MpPiWTKiPU6PZ6m6J1dMiVrJOtu7yJgF96VVxZ1E3vKyEqfu3vZcNeYuK/rmrUZWn/hdkShvdar6\n",
"3lfVzYq6idS92xUDc5fxdlX1mHFWPsDk7tlTet9PPiPCdv0FwJTbuJPYl9jH1NN8457+f57u2d92\n",
"BitWzmkl+ibSEZ1vMCUuZ7KV/XTuLyOKqGIdq2uZMk/kPo7UzbhXqtZWFUmzYlfcTEVEzeljqs4t\n",
"sJZIhMuKisiNzjiQKZEoK3VOi02ZEoGSNU9V3a6olarYlMn7idSNzPNS96RP7gAAAAAAAAAAXB74\n",
"AAAAAAAAAAA4zk88EqUiZuTJW6//lYiKt3Ws1M3a30nRMZ3xMlPiWbKiPU6OZ4mcW3Qtd7vO6W3e\n",
"pzGR/USux8J/vpdZiQOJRG5UjHkaF0nHicSZ7Bpzt2t/kbl3Rcdk7WdX3ayom0jdu4zuupF5qx4R\n",
"zuj53hkzsquPuke0+QK7UqxO9xsiTzibe/L5DFbiWOB8K7EjGXEznTL2U6VrLZG4nKp5Mupm3W+T\n",
"Y192Rcd0nUHk3p885mlcV4TLQ423CJdIJEJVLERXHMjOmIuM9Z8Um/Ibz+3Tmqt1q6JWdp3tp/NW\n",
"1a1aa2SeW13/fAwAAAAAAAAAcBgPfAAAAAAAAAAAHObn+ctdMSNP3uIZApEIabEQb3W/LTpmxeSY\n",
"kWh80UkmndtJ8UUrr7uK/UTjcl6+ZSUOJJJ8FekxvmvMlLiW66qJvsmY9+/m/k+7ziBrP5PqRlqz\n",
"ZTx22zVvVp/yqkePd+VAnP6x4U7/+Trfdq9ssista7KqH0HwZCWq5Ns87fn+tW8/g31W2vZnxIFE\n",
"xkTWtvI9u9b/bbLOOiNuIiLrulespSo25S76mvq0blasTeT++rTmU90VGWupio7ZFfuya96uMX/3\n",
"tU/rRsbc5n2Lb7muvsiTlQ9tn9ZcqfFU56RIlJXveZrnpKiVT2uu1j35DLLqVkWRnBS1clBdHT4A\n",
"AAAAAAAAAA7jgQ8AAAAAAAAAgMP85MUdVMUoRKJWdsVCvNXNihDZFdNxF6n7bfEsu9a2ch9HruGK\n",
"yNomXcOu10fVfhLipVZelm9tpVbGRN5GInEmuyJQqmJTMqJWMmpcV+y6V6wlaz+T6kZ+5GT0B++a\n",
"t+qR4awshsldrifnTUw+t9Ntuu7/vL02J99uVarSvSaLfPSYIvIxdZKT1vrk9PW/+Y0RNSvuZ/Dn\n",
"emrfLnbkLOJmYrLif6pkRBFVzLu6lk9lRaC81c26RyfFvuyKy/l0HStricSbrNb5dMzOCJc3m9aS\n",
"EeGyKw5kVwTK5HiTlTqRD8CdZ1uxlsgvxN92BlV1O892St3Ba9XhAwAAAAAAAADgMB74AAAAAAAA\n",
"AAA4zM/zlwMRAqEYhbtdUSudcTNvdSdHY6zUzYom+bZ4lsh9/HbfVr1eVkw6p7tda3ub92lMRcTL\n",
"38398p/vZVZaRlWNibwtVkSGdMW1XFcsaiXSQi1yDe92Rcd0rS1aN+N6RHTNW9UPfdejyJ15Byd1\n",
"ueZ4Vbfb6ZEIb+fybfs7fT/kOSnuZ8V9P992r6905F45g2+77pymM25ml0jUyq6omMjZZqiK/6mK\n",
"tamI8slaWyRaaWXeyPWouIZV81ZF1GSMqbqGC2PeIlwisQNVURi74id27SerxpTIkOnnVDFPZN5J\n",
"Z1BVt2Luzv1MqvvhPDp8AAAAAAAAAAAcxgMfAAAAAAAAAACH+dkbBxKZZ1fUypS4mV3xE5F4k6e6\n",
"GdEkEafHs0QikDKiibLOLWLXOUVUvRdV7Cf62n35lq6Il5VxWWPejuXpkkbG3O08y+wa11UTGbJS\n",
"s2ttlXUz5rnLeIuOtJDb2TG5og/56Y88f1vP+klOvzc2iRzTSZECVQlhwLpvi2uJxLOwKhLxkBEh\n",
"svI9WdEeFevPipuYLOMMOj8cRq57xbxV8SxvNZ/qRq5H1b2/K/Zl8toyxqzUmRT7EhkTuR4ZYxZ0\n",
"RZ7siiqZHG+SFZUxKTJkSgzMpHP7tOZq3aw6n9btmreq7klrXRjjnzQBAAAAAAAAAA7jgQ8AAAAA\n",
"AAAAgMP8PH+5KjblbZ5IvMFJ9b9KAAAgAElEQVSuqJXOuJkp0TErdbKu4W+LZ8naz5Rze6rzNu/K\n",
"3FXn9FZzpW5GxMvT3Cuv74T345W3vIroladxu8ZEfkzddcW1XNf7+rOiSzLO4NOa15Wztml1M+a5\n",
"y+hvntUJuKrXetfjyZN7x39bt+1JJl33L7vOGUlkk9zfmiZHMURS6zjfadf4tPeAu2+LoHknduR3\n",
"EDfzV9F4k11RMVPOdldczspZR2RE1lRF4UyOpKmKN3mbd2XuXWNWrvvKuIQIl3/9469fi8QbVMSB\n",
"VMVaTI432RXhMinOZNd+Tjq3SN3Ote06209rnlj303kC69DhAwAAAAAAAADgMB74AAAAAAAAAAA4\n",
"zM9aZMWTrpiRu86olV1xM1OiY57qRET2/BvjWTL203Vuq3U+teucnmRcw7d1PI2piHj5u7lf/nNG\n",
"OtOkCJTIUa7MGxlzlxE7khVdsms/kbpVcTJVdTPmuat6a43Y1WV5V4/6KV2j+b0y7vWDHu/flaZV\n",
"perHYZXIx61dJsflTFrL3aRreBfp4t3prQP35LNe8ee6t3hfaVnvgxHT7Iqb2SUr+qZiLZ3xLBUR\n",
"KFnXver6dEWtvK0jupaMqJKs2JdPx1RF1GRdj5t7hEtV7EhXhMtTja4ojIxYiJ0xHVMiQ7L2c1Lc\n",
"zORoks5IlIoIlIqa0Xmq4nPubms56J8AAQAAAAAAAAC4Lg98AAAAAAAAAAAc5+f5y1lxLHcVkQiR\n",
"yI0nGbEQb+t4GpMRozI5OmalbuQa7jrb0+06t857cNf9dTd5P3dJ75Nv3/K0vcjRZox5EukPXhEv\n",
"U7XWlXVURKvsio550hknc1e1/jeTIh929Wef/Ljy6T3ev923f+x7ENny9KiF/xRJVuskRoVMk6/R\n",
"pHv7zeRzXLHSif2k61EnEr1QFRmSETPybWubLLKfqmiSFRnXvWIdq2uZMk/VfZwRl5W154xIml37\n",
"6RqzWidjTOAaTolweapREbnRGdOREe0xOTZlUgTK5DiQSTEwkbqTz/bTmqfVrYqOuZn8T+YAAAAA\n",
"AAAAADzwwAcAAAAAAAAAwGF+4n3Wd8WMvNV9Wn9F3awzeItRmBSj8qQiPiNyDVfONqIroibrDHY9\n",
"wzXpnD6d92nujPtr0n7uss7g828J9QefPCYjQmQl+mZlzF1G3EykZdmutV1XrP1Z5G1xVwzMlDiW\n",
"rD7fXZ2ZJ/ViP6k79W/Uea8cdG/sSrWqUpUiViHykQCmmXzPPr3WJ693pbv25PW/64wdYbZJcTNd\n",
"sl4fFWvZFc8SjcupmCdyb2SdScV92xlJsytip2JM1f4C1+P/snd3y47kOJpolVN7+v2ft+Zk5blo\n",
"a7MuD0YSQgH8kda6ix0iSKe7JFeENr5nfMvr1ROjkIm16IoquT3epCtCZFVkyKoIlFOiVjJ1T4qB\n",
"yYyrWv8pdU9a66Zr8qQ7WwAAAAAAAAAAAn5yv5n/es2/fpKtO5unostB12/iZ7oenNRV4+n2ThWR\n",
"vb6pW8eurhpVvzFw8rXS9dztOJ6uMZk9eO+vh9NGxu0c826NUZ3svvxvqzpkdHXZqKqbebp3dS15\n",
"WtUV5Kni19S7fjFs1a+gfuPXl3e1J/ALs3kVz4eD9/+mrhqvV+7OaZXnaT7p6X7SOfw2J+39yWs5\n",
"ufvF/d06dv3GP/+to7tFZMw36ug687txHU45711dNHbNU7VvXdfKKR1KMsezcw92dfQIjHl29Dip\n",
"i0ZXx4KOzhWrul2cvLZInZP3KVPnG7qC7Opm0bEnt9Xt2vvMPI+67uQBAAAAAAAAAC7jCx8AAAAA\n",
"AAAAAJf5Gf94VWzKU1XswKxuJkoiU7dqDzoiRCJznxS50bW2b4tnWbVvv5vr3TGr9umpK/qm4nhG\n",
"OsZk9iAwzUhFBMqu2JSqGJJMSlpHVMmq41lZN/O2m7EqBuapojNwVz/xnV287+qR/r5de3v7vt7+\n",
"VffM/h90zCfHqDydFGeSueWBSqdcc6es43duipfJRVTcriMSJfKYzJiD3rxT8RMn7dvJe1uxT13H\n",
"s2tvM3E5FdEfXXWrYmBOOuZd0TFde9ARN5OMqOmIcKmKTemIqOiK3FgVb3JyhMtJMTA3xc2cHANz\n",
"eiRKR8TJrsia7Jiu/X9znpPudAEAAAAAAAAACPCFDwAAAAAAAACAy/zsjQN5qoo36IgdqYrPmNWN\n",
"7EFFa81sXMMpETtdcSDfGM/SsW+jx1R8v2zVPkXmzkTfzGpG6u6KeHm9SpqZd0WG7IpNyVw6kTqZ\n",
"MU+ZtmCRp3K2zn9as6vuriiW7NwdmQJdX//d2cvcV5oZ6crkOLnr/eOY/xF4buyKLsl8iljplGiV\n",
"qrfqjF17kLlNqrLr+bDr+tp1vCMnr+WkuJZIh/R/vf4Y/PRUnxaJwtlWxc2MHtNltt6d8SyZvc3o\n",
"eI2I7NvOqJWOY85cxztjbCpiXxat9RnfErEqNqUr4qErcmNVTMeq43m3xmlrOeWYb9u3zJhV63+3\n",
"5m11u6JjMvMU1PUpCAAAAAAAAADgMr7wAQAAAAAAAABwmZ/xj0+OTXk6OXYkU7dqD1bFXETsihmp\n",
"2Ntv0BE3E3nMzqiViteIrjimjtfWnWMSVkWgdI3pmHdktt0VMTeRtWT2pGptmbq75qnq/V3xtrWr\n",
"9/9OJ/Ve51cnXSsZFdfXQXvQ9RJd4aTYl50xI/CJToqxOeW2YbSOs19rZhECO2MuVqmIz6iKsemI\n",
"9rh9bSfpOuaOf+fcGa20ap7MXs90xedE6kZ0RNJEjidz7T9lxmyMqIlEuFREhuyKcMncsGTmXRVz\n",
"sep4uup0rf+mqJVM3Z3XV2aerrq79vbdmtm6O/f/3XkSNU++8wUAAAAAAAAAYMAXPgAAAAAAAAAA\n",
"LvMTiyEYWRWb8lQR7ZGp2xVRs2oPKo4nMveqeJYuq/Z2VUTNrn0czb0qaiWiI/4ncz66omMi53nX\n",
"mMBDTo5rqeglP6pRESuSaR3WdTzv1lhZd9c8VS+/J61l5qSe477ifLZV18rJSX4VkWELZT4FrbIr\n",
"amW0J+JlON1JMSqrnBLX8nrlOrGvsypGYZWK2JGqGAX22RU3M3rMKhWxPFUq9jYzT1f8T0cMTKRu\n",
"REX8T1UkzarjqZi3YEwmvuX1WhfTMbsRWhUlE5m7K0KkYw8ydbLZfavWf/I+daylK8Zj1R501d0Z\n",
"L/Nu3ZOiYzbFwtz2CQ0AAAAAAAAA4Ov5wgcAAAAAAAAAwGV+xj/eFcdSESUzqvvUFSUR2ZOOul1R\n",
"EidFk8xqRuquik3ZGc9ye+TOrhibrudu5nx0RMd8WMTL6zVvi1U15inzNhUZk3nJm807UhEd83Ty\n",
"2kYy7dEqXuKqenRXdNcVnzF2Vh/1PW47Z++q6uN/yj7tej0rmkbUSp+K1LeIzKd5xlZdG7ve6nZd\n",
"GzuvyUxX8j6zVvinvLGNZCIFTj6eLpG4hopoj6rz0bG221Qcc1U0ycxJz8OueJanrr2u2Keu58eq\n",
"tVWMidQ5OMJlVWxKVxRGV3xGR4TIzjiQUyJRInVOik25KQYmM2blee+oe1Jsys59eneeRbEwOnwA\n",
"AAAAAAAAAFzGFz4AAAAAAAAAAC7zk+9hf3JsylNXREVFfMasZqRuV3TMqniWiF3xLFWxKTfHs2T2\n",
"LbuWp1X7NJt3NCZzPBGZ+KVde1Ax5nfjJn+d6ZHeEZtSFWcyq1PVG79iDyI1q+rMrIqBqeh/vur4\n",
"IlZ1P76tt//tXaErnHzOTjo/Ffu063gGryv/eLwurroMVsWOjHx61Arstuva3pnOdsox/+sVaC2/\n",
"TCYO5KQ3/KeTY1M4P25m1znriuXpWMuqeJbIHuycJ/MaMXNyJE0memVj3MwswmV0Q3BThEtm/VVj\n",
"3q0xqrMrDmRlhEjF+m+KTfm0fcvU7YpEOTle5qTomF3xOYm6PiEAAAAAAAAAAFzGFz4AAAAAAAAA\n",
"AC7zk48DmfUkWRWbMtIRO3JyZEVGNqbj2+JZvlHVvt0c/1Mx72juzLwdES9Va1k1JvCQit7so6Vl\n",
"olYq4kwqanTFnVREx4x0xcDsil7YFQMzsqu/+ad9rXhXzgX/7eYYlZFV0VdN03Q8HTJ3OFV2Ra2M\n",
"jrnjGFfNw1lWXcffEKOS6bJeYTTPviiokyMrInZFSXyD2V5Wxdp8morIo53xPxXnPWPVHqyKgamq\n",
"m7lWZjUya6s6H5kIl4rXlceYWXzL61UTxRIZNxrTEQOxasxIJibllD3IzH1yrE2kzkn79G7NaN1T\n",
"9qCr7kmxKSfH5bxbc+U8j7rfcAcNAAAAAAAAAPBRfOEDAAAAAAAAAOAyP+Mfd0WgVMSmPHXFKHRF\n",
"Iszq7tyDikianfEsHVbtbeT50jXPSXEmFfs0qxmpW/X86DgfO/dgtpZsXEvmmCcPqepHn+nxnnnJ\n",
"fqroa9/Vk7+rblWcTKbu080xMCOrYiz29RhfY+etx81uj1EZ2fWV+cj6N8W+rLpsV0WvZAJNER0T\n",
"5VrKWXkt7bpuz4lreb3OeQP/xDiQiniZrtiUzNpWuXnfoo9ZoeuYK9ayat9Ga6+YpysqKlK3Igam\n",
"a23vriNSpykKZ1WEy0kxHbsiTzK5dSftQcW8kToVsSOjuh01InVOioHZFWfSFYlycrzMSdExO+su\n",
"mOf0T0EAAAAAAAAAADz4wgcAAAAAAAAAwGV+1kWVjGTiQJ66okm6Ym1mdSvWGqmbjfZYFU2SsSo6\n",
"pmJvM5FBq+apuParVOxTRtdztysqKrMHq+JmVkbDxP96OE3XmKeqfucV/fRXxahU9afOvO1mZN6W\n",
"Knp/d718reJrxIyszNxYpeI1u8tsv5vW0fV2MrMyQmRVjM2q2JpV87DOqnNonrp51kXHRGIsVuiK\n",
"UejSFf8BI5nnx0nX5EnxLJkon455IseXqRtRES9TtbaK89Exb0DmzTv7ht8R4bJq/SdFleyKN1kV\n",
"iRJ5zEmxKSdFoNwctZL90LDrmHdFxxwSq9JadzKPTx4AAAAAAAAAAJfxhQ8AAAAAAAAAgMv8jH9c\n",
"FSvyVBEHMltHZC1V0R6zuqvicrIxCjOrokkic39aPEvF8ayaJxub1BEVs2qfRk45nl0RL1VrKYhr\n",
"eb1esefqmw8ZLS0z5inSjqsiqiTz0hqxKjrmadU8q+JmRjr6eK/6Kq/e/99pZ4zK087nbkZVBNh/\n",
"KhNfViTzCa1jnqq5VkWirIqSgd9Zdc11zLMyRiXT2btm3j8eP1l1M7gqriHjpJiLKrMIhMz5qNon\n",
"a6t5zM4b7cwxnxLPUvXcXTVP5hqM/H1FDEzFMWeOJ1KnKcLlr8d7aEV0QbbVf0f0wqoxIx0RLqO1\n",
"7Yo3WRWJcltsyikxMCft27s1o3V3xabcFoGyKVplSc2B0z/RAAAAAAAAAADw8JP/HaiKzhuR3yif\n",
"1a3qRlKxlorf+F+1b11dGzIinV1WdevgV5lr8vXq6xzyrqrrK2PV8czWm+melDmnIxVjRjLP98RS\n",
"Kn59t6tDRmYtFb9e3dVJZNc8q34VfKTrJWEFb5/faVULg5VO6bwxMltb0zoy78IVqt7qMnN1vW3p\n",
"xtGz113XStf15jr4Vdder7ot2jnPuuup4rfFK5zcSWSkq1MF36miq0nmmqzQ1aUlM/eqebr2elXn\n",
"jUjdzDFn5p3VSYx5dvN4vXo6Soys+s31k8dE/n5Xd4iTOmSc3G3ktn16d+6T9uDdmtG6Xa9fN3XE\n",
"WNRpY9f58CkCAAAAAAAAAOAyvvABAAAAAAAAAHCZn3xsx6wnSVUcSEfsSyYSoSqyYlZ31b5VxXQ8\n",
"VUXSdJzDiFXRMRXnPXNNrorpiVi1Txld0Updx1Mxpmr9J4+Z9LzKRLxElvJUFVWSSfKZqepHXxEd\n",
"UzFP1VwVHay7+m/vfMnmbjtjVJ6qrq9TolZGOp6rVSlpCR0xHSOZYLiKebrepk6OM+naA/p0nKPb\n",
"Ym1WXaefNs++uJZMxMMqo3m7YiBWWRUHUhFr8elrGz3m5OtrttbXa180UcV5r5qn4vWrav0VUSuz\n",
"mtG1zOp0nY+HZ4TLqqiMbBxFJm7i5DGzx1TFHdwUb3JSZMjJ+7Rrnkzdk9cWqXtSVMnJ5/DdmlXz\n",
"JK4vHT4AAAAAAAAAAC7jCx8AAAAAAAAAAJf5Gf94VQTK06qolUw//Uy0R6buzhiVjFXRJBmfHs9S\n",
"dTwd80TrvGvVPo10XMddUVE3RbxExq3a24GKWJSKSJSqeJaqOt01d8/V0U+76m13V7SKrwh/nlXX\n",
"0spO1B25FlVmrytdz7FFsS9VaWXvzrMyLeum9cNuHW8xK2+BOuYaPd97jikSD9DllKiYbOTGKqui\n",
"Sfg8qyJpuq6njoidinV0zdO111Xrr4jlycT/zGqMxnxYhEsmuuDkMavqZm6mdkbHnBK9ctJaKvat\n",
"ap6TI0S61lY197t1uyJQbqtbMWayNv98DwAAAAAAAABwGV/4AAAAAAAAAAC4zM+6uIORTCzEU9f6\n",
"V8XarNq3VXW74lkya9sVz/JpMvv2eq2LWpnpijzqOp6KmKGnqjEd0SujcbvGJPpoRVp8dUS8VK0l\n",
"U+Opam0RHevPzNM590zHW86umBh6ndLZu+r6WnW7FVlvx1oqXsOzFt3adsSZdEWv3KbgjuYX9vYs\n",
"XXsvVqhvD9Y9X1a9QZ4S1/J67fs3mKr4jFNkjqcrQqQi2uPktXXV3fX8f73ujmfJ7FvVHmTmWrX+\n",
"iNnzLhMDkzieZ3zL67UuDmQ2ZvT3J8exVERHZI55VeROZO6uPXjaGS9zSsxIR0RKtO4pe5CpWxWF\n",
"8+68t9XtWmtmnk1rOfmTBwAAAAAAAAAAA77wAQAAAAAAAABwmZ/xj6viP5464kBWRa10xdpE7Nq3\n",
"k+JZKiJEVrUcXRUdc3KMSsTOiJ2To4kyOvYgMuamuJbsmD//9o/DIbP2W5m3k4iKXvmr1lZVd9c8\n",
"2blndvVV9/Xfz7Sql/yq66frNS1j11oi57Thtegfg3PcERlSdcl2RMeM6opNgf92W9xM13o76o72\n",
"4F+vQRv7/1hVq/+KeVbdWGTiQFZZFU3CZ8rEjFTEs1SIXMeZaz9i1R6ctP6nzLUSURD78oxwWRV7\n",
"kWnbn40yyEQVrBqTib6Z1dgZ07EqPmNVJE1HjUidrn3qqNFVd2cMzK592RkDk5mnq+67Yxatw90+\n",
"AAAAAAAAAMBlfOEDAAAAAAAAAOAyP/n+5x2xKbuiZKrq7oq1ieiKxlgVTdJldg4/LZ6l63iqrqeZ\n",
"rteVzNyRvZ1dx13Hc1PES2TczjETkdOeadlV0ee+K94k89aws25mnqdV/fVPip/gLqtum0Z2PS8j\n",
"ul7jMmZr6Up5a5qnIzYlk5IW0RWb0hUdU8Ha9jo5lufb1tZ1fd0WN5Nr7Z8RiUnpsCt+YiSzlp03\n",
"ck8V8RkVe9AV7bFrbVV1T76+uo6nYv2r9q0rKqrrNW5WtyoGZra2wZhnhEvETREuJ4/piqjoiipZ\n",
"FT+x6njerXHaWk455p1RK6uicN6dN1p3VwzMuzWz83TF5zxtur50+AAAAAAAAAAAuIwvfAAAAAAA\n",
"AAAAXOYnH28y6zfSFZtSETPSFVHzFOn1vytGJWtVNMnTrtiU2yJqMjr2LfKYqteImaoYm4q5M5En\n",
"Fa9fO8dUHPPOMU+BXlsVaV9Pq2JUqvpIZ94eK+pWzvW/dSVSrXLyW9DTqn26aU8iVvXo7/qqeNV5\n",
"70hBjKjYl8g5XHVblHD729RJ0TEnR56cvLZPc/LeVqzttkiUirqjGj37sCqupeumIBMLUSETP9G1\n",
"lpFV0SSfZlWMyk12xs1U2BVrk43ymel67na9fjVE30TiWyJxGh1xIJk37+wb/s0RLqv2qSum47YI\n",
"kV17e3IcyEnnMFN31R58Q9135zllHdl5HnW/4e4eAAAAAAAAAOCj+MIHAAAAAAAAAMBlfsY/roio\n",
"2BmbUhHXsCp2pGItq/ZtVPfTomNW2RVRc9IeVD13O46xa28zz/+IirWsGnNSXMumiJeRip71FX3W\n",
"M6c0o6v3/8jstN4WIXJyj/cKqzokr4pA6bKrk3TV9dd1OzI7r137FtmXVbEvmXlm6y86Xx1vdVVP\n",
"5a7omAoVa6uKm+EuVS/ZJ18rXWs7ObamJ6ogEilQYdU8kblX3UxlYiBO+nebruiYTBzIyVErXcdc\n",
"sbcVa6syO55V0USrImpWRkVVrL9ibYExFREumeiFTKzCqliVyLiqMR3RNyv3aTb3SfEZFddtZu6q\n",
"9YtaWReF8+680bq7InberdlZNzPmpMiWN+c56VMEAAAAAAAAAAABvvABAAAAAAAAAHCZn7qIhJNj\n",
"U3atvypqpSJKYlc0RqTup0XH7IxnmZ3nlTEqFXEZs5qjul1rq9jbp67n+01jXq9c5sYpY0YmvbV2\n",
"Rbxk15KpW9HDumv9mXmedsaq3B7lcZOTvxa9qr/+zgiUp4q1VGVhZCyKTVl2+1Ww3ookstHhdb0F\n",
"VazvG19K4fWqedvqev5UvaV2vDX/6xVoe5/SdZNzSizEquOLrKXLqtiUk+2KUcleBxXxLLvsjJvJ\n",
"qDjvJ81z0vpn8w7GzCJcIlElnxbhsmrMSbEjXVElszG3Hc+7Narq3BY3c3IMzKo9+PS6XXEt766j\n",
"s27DPCf/UzYAAAAAAAAAAAO+8AEAAAAAAAAAcJmf8Y93xrG8O09VbMps/V2xI5n4jF37VlX3pniW\n",
"qtiUU9owZmT27fWqiYrp6t+eWVvF3BXXelV0TMeYlTpieSJjnrIxNm8+JPN2ElERHTOSeRvO6NqX\n",
"ma6XiJPd/DaWdXL2wqqX44prtOs2L6IrzmTXPJm9jOxbYv2RO8F3jQ6vIoWn6y1n19rEzfA7J8Wm\n",
"VNTpuk369LX1xUKsii45aZ5d0Tcr1zJzcmzKN8rE8qyKmzn5+ZJ5HamK8nl3nkjdyF53PacKjjkT\n",
"jfFUFe2RiRRYFTdzcoRLV+RGRcTDScfzbo1snZNiRjpiLE6KgdkVGZL9kNBR9+S4nJFd1+S7NYvm\n",
"cbcMAAAAAAAAAHAZX/gAAAAAAAAAALjMTy7G4/X6vNiUp4poj2zdd0XOT8W+VdWNODk6pkIkuuSU\n",
"iJoumfVn9imj6/o66XVl175FxmWuwVURL09VcTnvP+QXFb3ZV0WkrIxiqTqtHW6K5WBsV9RNV/ZC\n",
"x/FUZE1kNcWZbJvn4AS67CfKd+tWXU7iS2p0xed8I3vXo2pfK14zMt3nY7puRjrqdsXNRGqu2qdV\n",
"kTSzdbxed8emrIqOicxTFW+yK/pm1weWVXEzGVXnvWKeqtfFivUXrO2vP379WSbCZTYm0/q/Yt7I\n",
"3Nk3/FUxHavGzGpUxXR01N0ZvVIx96p5Topa2RUhUrUHN9VdFWey87xn5jkkbuaUO3kAAAAAAAAA\n",
"AIJ++n7D/LYuGrN5ujqWPEXm2fnrfR3n4xs6iWSur1XzZK6vkzuH7Fpb5jUi4pROQtm17Oq8kXn9\n",
"zXYoearouPLeXw+t+nXrqrq75snO/XTyr+b6em+fXee96y214ni6mtdFrHruZo5xNk/X2jNrbbqF\n",
"62hElb1UKupE7rLfrfF67d2XHUaX6E3rv2mtIxXrP72LRsZJ+/Krihflit9cH9n1m/gV6181z0hV\n",
"B4kOu7po0OfTuo9UHU9FV43MvkWctP6HZ0eP0Ztf5rf3T+nosbKLQ6ZrQ0dnhJM6V+zqDnFbh4yT\n",
"umjc1BXk0zpknNwVpGpMxXl/t2Z2nk3dR/wXAAAAAAAAAADAZXzhAwAAAAAAAADgMj/jH3dFoDyd\n",
"HJuS0REl01U3EiGSIZ7lO62KiqmK3Hjqeh52HM/OPegYExlXdcy74mUaIl6CD5nq6gE/O8RV83TO\n",
"/dTxFdrb+8R/o13pZVU6ksgiutIJu+aZHWNXPMuqt76npuiYjliVqjpVl3FVvMQKN8fCfKubz1HV\n",
"2ivqVD1PayJpHq3x26JWMroiODoiHnbOk4m1qJCJTYmMWWVVdEwmGqNibZHHdJ3DrrV16DqeirV0\n",
"RdRUxeW8WyP6mIdZhEtFjMroMZG/XxUds2pM197Oxox0RJ6ManTEgZwUIbIr1iZS56R9erdmtO6q\n",
"Peiom/2gsSte5qTomE3RKiXzJGrq8AEAAAAAAAAAcBlf+AAAAAAAAAAAuMxPvhFuJq5hNk9mTFVs\n",
"SmaejrpdETUVax2Nuz2epcOq6Jiq85OZZ9VertqnjK7rqyN2JLMHK6NXdkWtnBLx8nq1ZKBkWoll\n",
"3lIzsuk/FVYdY4WTvpa7qm/8ScecsWqfurpt74pjyexbV6RT1/HsSo+c1RhJ7EEm3DMybcUlecpL\n",
"epRoFU53+zVZsf6qPah5feqKKum4KdsZo5KxKjriqSs6ImNVbMrtvnGfTombichELVXE2mT2YPSY\n",
"zFwF63/Gt7xePTEjO+NNMu30O8aMHrMrvmTVMe+KkonU2Rkdc3K8TEeNSJ2TI0ROjoFZWXdXdMzN\n",
"cS1N89z+z+oAAAAAAAAAAF/HFz4AAAAAAAAAAC7zM/7xydEqu9aW6c2cjTeYqYgUyNbtOB8741lW\n",
"ra3i+qo4P13z3B4VU7G2rmilrud75rm8av2nRLxE6kR6bUWu61mfr8DzMHJKV8WxVPS5XjVPdu6Z\n",
"2zIEZnamot2sqwtzxbXfdSsVseo5VpW6VVF3tt7M+Vi1B4m1Vb0F7Yo3GR1yRfLQrtSnnWlTt8d/\n",
"dNj5Vrdr7op5d15LJ8XA1LyJdsWDVEQgzGpW1V0VkZKNdKhQEZ/RJRM/0REHsirao0rFMXfFzey6\n",
"viLH0xWjsmoPKs5hoO4zwqWqrX9FK/xV0TGrxmT2aeeYWY2uqJKuOJBTIlFWzROpc1sMzM1RKzvj\n",
"TTriWqJzZ+q+O8+Hx7VE6PABAAAAAAAAAHAZX/gAAAAAAAAAALjMTy7u5PWatzpbFYEymqdibRXx\n",
"M1UxN6dE1EREzsft8Sz0OfkcdtTtin3KrHVXxEtk3KoxkTqbeuNnrv2qt8eMVT3ss7cwK3R1hf60\n",
"yJNVdr2d77z2Z6qupU239jkAACAASURBVMxaKrIxqubpiH3piHx5vWr2oOstKKDireE5bXbbVs1d\n",
"Yde88D9ujoHJ1tg597/rilqpqFF1c9VRtyquIVN31Ty7ImmqYlN22RUdE3nMzniWVdfT0664mYiu\n",
"+JynqricxDyZCJdZ5EYmUqArquTkCJeKiJqTxqyqO6qxKtojc02esraT1lIV//PuvJG6nxYDE6m7\n",
"63iydTPzfFhky2yM/80GAAAAAAAAALiML3wAAAAAAAAAAFzmZ12EyMiueU4+5q74nIq1VtWN6Nin\n",
"KqtiRypieTKRQRXzROqs+r7Zzuu4o24mjqlqTFeMSkU0TNeYjhpVkVqJ14hZq7CqvveRuk9d/cK7\n",
"ohV2Oakj8k1OOqcV57DieLre6iKqYkUq6nbEs0ReNzte9jM1snUKbut2RpWIZ5kbXRYnr/fT3bb3\n",
"XYlmp85bN3dXnEnGTTEwq2JUMnbGZ1TEgXSsI7KWrngTcj4tbmbn9VUR5TMyGfOMb3m9auIzKiJc\n",
"qmJHVsWBZCISTo5jqYrheaqI5YmMebfGqE5FRMWq6JVIndtiYE6Jm8nUPTkGJjtm1z69WzM7z8Vx\n",
"LUOPtenwAQAAAAAAAABwGV/4AAAAAAAAAAC4zM/4xyfHsVTMk4kqyLTg74q52Bk/ccr5iKg4npOj\n",
"Sk63K5KmYv8z570qUiRzPKvGnOyUiJdsnYrzkegvVhE7UNVjPJs01qErfYm7dL0sdlwbHVEmUR2x\n",
"Sdm974iXiezTSQlhT10ft56ex5OokUkVq0oie9bJvD2uetnPHLN4lu+0qotslVXddU+Z97/rDFrs\n",
"v60iUqDqpqeiTsXaVsaodOxlZv1Vx1MRa7EqRiVyTndFx2T26aTom1Vrq7DyHM5UXJOZeQZ1RxEu\n",
"M883t6rIjY7YkUwsQdWYjhiY6NyRuWY1Ks7huzVHNbpiOlZFouw6P5G5T4qO2RXLcXsMzLs1o48R\n",
"rbKmZtWYxNpu/x8+AAAAAAAAAICv4wsfAAAAAAAAAACX+clFcrxe+yJQMvNURMms6odcVbciTiNj\n",
"5/moiGfpsio6ZleMyqp9XLVPGV3RRCfFtayK5eqKN5mtt+o1oqNPf9f7yXt/PbQyimVR0k2Jrq/U\n",
"fmMP/lVvMU+r9rojxS5i0ctKS+RL51y7olW6omMqEuhGJtdP5O4x4lknsrTI3W+HzDFXRdLATpmX\n",
"7J23M6u69lbMWxeJUPGmXxGJ0hXxsCtGpWqurg8OmciNCqtiR3bJXiunxMt0xYxk7IqbyVgZtZQ4\n",
"h7MIl0h0REXkRlWEyCkRLisjRTqiYqrO4axuVZRER+xLVbTEyWs7aS0nHfO7dXfGkMzqZj+MVMTy\n",
"vFuzs+6qeQ6ObJnNo8MHAAAAAAAAAMBlfOEDAAAAAAAAAOAyP7lojJFVrf4zcROr1l9xzCfH2lTV\n",
"jchEk3T0RO+KjtkVO5KROZ7IY0465q7XlZlMtFJXHFNm77teVyrGjKw6xo4aq3r9J6eeeZ6ulf3q\n",
"V8ZJrHBKJ+OVTs436EoEe9fO6zzzEj6T3deKeJmTolVmNTJvhRvfUjPxLBVGS5vNnRnDWEUsT1eU\n",
"z6ookpPfxm6yqrNuldzcFTcWXbEjGV0xChVxMlW//5aJ3Hi35qhu1/FUxIF0rCOyllWRKN/o0+Jm\n",
"uo4n8lyoiPIJiMRPVLyxVsRc7Iw32RVnctKYk9ZSET+xag86amTrrFp/ZsxJcTM3xcDsOp6uuifF\n",
"tWTmOWktk3nctQIAAAAAAAAAXMYXPgAAAAAAAAAALvMz/vHOOJaKed6tGalbFbWSibmYrWVVjEpX\n",
"3a6Iikjv7I6InVU+LToma9c57Nrbjte8zB6sGvN65Y65Y58iOiJesnVmdS+KeBnZ2Tv/02Jg6Htr\n",
"6+gV35X6FFER7VFRc2OKVeot6GlVdEzkdWfVR4vE23Im7WtnQlhm7l1xJplL4/T9/zarusau6jT7\n",
"DXEsuVvBis8wFZEhmRf+SLxBREVcw6p4k6obyor9f6qKqMi4KTalIk4jG+2xKgLllOibpqiS6Toi\n",
"81Qdz0z22p/M9dcfv/5sFpNSFRPREeFStbZMZMWu6JjIuFXxJV2RGx1RGFXxGaccT1ednfuUmefk\n",
"qJWOtX1aXEt2nlNiUk5ZR9E8OnwAAAAAAAAAAFzGFz4AAAAAAAAAAC7zk++rnokzWRWbMot0OCmy\n",
"JqJjLdkYlVPiWU6KJonMWxE7UrEHVc+XrrVURB5F7LqOT4pjOjnKZ1XES8X1VRXP0nE+qtaW6DlW\n",
"EW9yW6zKrrecm+z8mvGqvvAdiWFZq55DFbEjTxWxKq/XvpfjqtuIjrepVelyo/M+qTNa2uzyyYwZ\n",
"LUU0CXyGk2Nt/vUatOBPqYhNWTXvU1eESEZVpEhHDMRoTEcESlUcSIWK2JSqmKEuHREoXfu064Pb\n",
"yfEsIxXnNOAZ4RKJM6mIA6mKTelYWyYuYGesyq74kq5z+O46RjVWxZusOp5MnZNiYD7tmHfGkHTM\n",
"nf0Hi5P3KVO3Yp7bom/enEeHDwAAAAAAAACAy/jCBwAAAAAAAADAZX5iD+uKM+mKTVkVx7IqaqUj\n",
"Pifi0+JZMrEpVdcXNboinDJzZ2J5KubdGdeyKzYlI/P6VfWaV7H/J8X/PP35t38cll0VQ5J5677N\n",
"SV2J33V6HE3XrVOFRWlMLfN0Rcusin2pio7JZJPMalSdr0wsT2LuyKeep0z0SmZM5m0rM2bV8UCl\n",
"Vd1pT+ri+7TqeH6VuTnZGZvSEWdSFYmSOZ6umIuOuqtiOqriMzr+XWBnHMgpkShdTo6bqbq+MnFG\n",
"mT14GtSdRbiM3mAyMQqzyJOqGJKKte2KcFkZxZKJXuiIz9gVPxOps2oPInVWxY6sihn5hqiVjrWt\n",
"PIcn1X13nts/6J2yjwGfdgcKAAAAAAAAAPDxfup+HXZXF43Mr5xlfot71TwRmd/47+qqcVO3jpM6\n",
"C1R0qqnag0zXmV1r6dJ1rVTs7VPmV3MjVnXv2HnMuzqUdHT8GKlYW6bu4PxUvE116dom9ul6ye6S\n",
"WW/m+XHKPFUdMp5WdQHZ2Ulk1d7e1MCLkFVdTthr1S89sVJVN4t3x+ya9/Xa13mjohvJSMXaMp0E\n",
"MjIdGLrmOamLRkenh8hjVu3T7WvLWNV9JLGWZzeP1yvXPeEp0o2g4kaiouvBzm4Xu7pb7OpYEhkT\n",
"WUvFb8RnusGctAcdNarqfNoxVx1Ppu6uzhXq1o25uWNJYm7/NAcAAAAAAAAAcBlf+AAAAAAAAAAA\n",
"uMxvIl26erFXxKZk+gd3RZWsmqeiblV7yo6Iip3xLB2xKZl4FsYy0TcV12REV/xMx7VS1Se+Y8xo\n",
"XGbMTfE/mYiwiF2vk4ExXclwq3RdXp/eL3/V03LVPnbdSmVE1pKZpyNapSoS5alqDzpSHUcqPlo8\n",
"db3FZm5xEmMyESIVY16vXJJPx5jR2m56axADU+fmvTu5G292X9fF5WTeUCriSyI6YlMyquat2Ouq\n",
"uImOeJauGJiKOJAqq2JHVqnY253xLLv2clfcTERgnmeES1WcySzGoitqpaJuVbxJxb7tGjMatyq+\n",
"pCtyoyKmoyNKJlLn5OiYyGNO2qd3a0brdlxfEVXrf7fuSbEqXXtwSlxLdp6KyJaC4/G/zgAAAAAA\n",
"AAAAl/GFDwAAAAAAAACAy/yMf9wVGZJphHt7HEvFPO/WjNQdnYtVURgnx7PsEtnrTLxJRURN9nl5\n",
"8vnYtbaua3/V69fJMu9JFa/HVa+THe8Nq17DRyavK9k2Z5m3tpOd8hbU5eTzUfV0r5B5WmbWsita\n",
"pSJWZWTny28mp6Ni3lmNSJ2qjw0NKW+rYlRer3VxMh1uj4HhbCddS6s6Aa/qHlwTq9I1puqzYMV6\n",
"Vx1zR43XqydGZVSnK0qmYh+6oko61hLZ64oIkdFjPt3JcTNVrzOTeZ7xLa9XzRvV6E2oIw4kMs+s\n",
"ZrTubExFjaoxFXuQnXvFWqrGzGqsikBZdTyZOlWxI1371LGWldE3747ZFddyW92TP3CZ5/r/4QMA\n",
"AAAAAAAA+Dq+8AEAAAAAAAAAcJmfXAzJ61UTGRIZM1vfqr7EJ81zSpRMdC0dcRNdkRu7YlO+rbVj\n",
"VlX0TYeu+IxdxzOSWcuqMRWqXlcq4nJ2vmZXmK1/8HypiMtYFY3BXl2JRxUqnu4nzbMr3qSrTlWs\n",
"TUOcScm8ozqZMave3gNruzl65fWKBWY+Pbel4uUq8olmlY7jO80psShd68jUPWVPXq+VXXsHrfyn\n",
"KmI6IiriDHautSvO5N0a2Tod8RJdESInz1NxTiMqIkQij1kVL/MNa8so2INnhEs2umAW7TGq2xG1\n",
"UhEL87u5Z2M64liqjqdiTNU+rRozq9EVTXJyhEhFnMbKeJNV+9RRd2X0zbt1d+1JtE6mbmaek9by\n",
"5fPo8AEAAAAAAAAAcBlf+AAAAAAAAAAAuMxPLrJipCK2oyLqY6QjUmTnPBFd6++IIjk5nmWn2V5X\n",
"xZt0RNR0raVL5LruWFvXtX9TP/fIuFVjInVOiXjJruVpV8RLwKoe72Jg1ulKJuqyKjYlM29XPMtT\n",
"V7zJU0V0TKROZN+6bvkr4mZWpaRV3EYk4lp2xZ1k654UTdKxltEp9Pa3T9fen3ROV3XO7aqbW0tF\n",
"lEfXmJNiU3bNuyv6pirGZlZ3VVzObTEwXdEwFWtZFc9y0toyFsXNPCNcIjIRKM/HdEWtVNTNxBB0\n",
"RZWcHOGyKkJkV1RJV92dx3NS7EjHPmXqrDqerg8J3xgDk6l7cbzJN85z0v9uAwAAAAAAAAAQ4Asf\n",
"AAAAAAAAAACX+Rn/+OTIk5PXtmueTKv/SARHxqjuzfEst0eVfIPZ/ndd6xEVcSBPmePZuQcnqTgf\n",
"HREvr1dNdkTX9fXU1eI2MPcpfce/8elTYef5q3i6V6mIHXnKRG5U1a2IKlkV+7IqAiUz96rb+cyY\n",
"Rclqo7/uSknKXCoVa3nW7XqZgd063vIzNc+KwtkVbxKxM1pm19xV81bsd1eMTcfaus571/HM5l0V\n",
"iULeKXEzAZEoicxjIjJRK5nYgY4Il6qYjlOOJzL3qjEju455VjM75t0akTqZ62vV2iJ1ToqOebdm\n",
"9DEVe/BuzWjdU2JgInUzYy6KN/nGedyBAgAAAAAAAABcxhc+AAAAAAAAAAAu85Pv1dzRY7hqnpPX\n",
"1jFPRFV/6kycyazubfEsHbqiYzLxJlURNRVRK7vOR+R5mImbijgl/mdlVFTmmCv2adf1NXLT8aya\n",
"J9G3TG/871CVpFRh1Voyt48zmXiTTJ1IjarYl0ycyVPkduXdeUd1MmO6ImlWJVs23OJko1cyp7lr\n",
"Le/WrXqr66ibic/5RmfFjOyp23XLtqojb8zJ0SqromJWxZ1UxGlURYhURKBEIkMiZvElVee0I84k\n",
"M09XDExVHMjsMaviZawtdV389cevP5tFY0QiKzLxBplokqoIkUyMwqq1ZcZUHE+k5smxLxURG1UR\n",
"O+/WGNVZFQdyU/TKSWvZFYkSqbszBmZV3Z37b56aeSZjdPgAAAAAAAAAALiML3wAAAAAAAAAAFzm\n",
"py5OY1Uv4FVO3oOqyI1M3YyOujvjQG6OKvkGFXEzFfOO6na95q3q377KIX3iQ7IxNit0RYTtmuf1\n",
"+mW/M3EHesufJfN0WXUOV11PVdEqTxXxJpGaFXWqYl9mdbreTj4tRmVVlEzAc7mZhJ2ql4yOuiJQ\n",
"+AQnxbNErOrQG7MrJuWkMSdHxUTmnR1zNv7j3TFdMTYdUTJd80TOT2ZMRtdaKiJQvnFtEY8xzwiX\n",
"TDxLNtpjVVRMx/p3rm22lsyYVdExo3EVkQ5d5/DdmpEaozpdezCrsSreZFVcy8q1ZMasur466t4W\n",
"1/K0M5Jm1Ty7PvxtOoen/K8UAAAAAAAAAABBvvABAAAAAAAAAHCZn/GPd0aRnDrvzrV0RBVkYwgq\n",
"4kxmNSN1T4pn6bIqOma2t5l5InUyUSs7z8euyJCT4lpW9YXfper6qrhWborYiszzVPX8mUS8dE3d\n",
"19f7XF0veav2suKWMyPzMllVN7O3s32K1KyIqIncImTmziRQZeaNnNOKMVXHMxuTeXvM3D4GruvI\n",
"FmR01e2Kl5m5bZ9mdu3j6rn+t9tiUma69vGkuv96/TF5xO2xKpkIkUi0x2wtO/dg1Xq7jrkjxiYS\n",
"0xFREQeSsSp2pEtX1MqueJaKaz8iMM8swiUSjVHVwr4jaiWz/or4mUidqr1ddTwdYyLjuqJWdh7z\n",
"0yl7MLIr1ubktaw85nfrnhwDk6mb/dCzK5Jm1Twnr7+iRmKtOnwAAAAAAAAAAFzGFz4AAAAAAAAA\n",
"AC7zk+8J3dH7NzL3yXEzs3VE1rJzr3fVbWrtv6ylYkVUCX2q4mY6jJ5ju66NiriWbHbBqh78q2LE\n",
"OmpUHU+kbsc8Twvftzp6fX/jS/jJMTZdsSkRFXEg79bM1q3Yp8xteKZO9iUvs/6OY171Fho5nq61\n",
"NNzaZk5Ptm7FS9op8Sav177YET7PzmupY+77onEqIjciMlElEV1rmY2JzHtbVMxsTEeMyugxmbod\n",
"UTKRupGokoiOeJOqut+o4Xw841ter1wcSKZV/qqomMz6K+I/MnEHXfEmJ8eZrBpTdT5mYyJrqYhn\n",
"qIp4OHltJ62lYp7MvKv24N2anXW/MfLk5riZqg+uDet15wgAAAAAAAAAcBlf+AAAAAAAAAAAuMxP\n",
"XS/gir6+J0egdLXTX7XXXbEjq+JZuiJqTon2qIodmZ3DyLUfuQ4qeoqvOuYumX3aFbXUFZ9xm0+L\n",
"Vlp1PKvisipyIAJ19b0/W+YUd/VVr4ovecq8ZP+nNV+v2D5VrG1X9Epk7lVvoauSyKpu62Zr2fhR\n",
"Yxab0hVvsjM25ZSoGG+X59uVtrbr2tgZz5I75siL585YkRPXUTWm6ngic8/iTDJzVx1zxX6vWltH\n",
"lExknqp/F+laS0e8zBeu7RnhUhUH8hSJ09gVZxKJjumaZ1Y3s7ZVxxOZ+6QxJ62lIq5h1R501IjU\n",
"OSkG5rZj7qh7W1xLZp5T4lo661bMs2ptDfN+4//4AQAAAAAAAABc7Wf841WdHVZ1lDh5noiT1tKx\n",
"lyf9SmNEx/Fwlp3n8JQuFKt+PXk0bmd3oZmublYV5/nTOn6MzL4uG7kOdPxYpurp0SFxqZTNk/nW\n",
"d+bld6ZrbZF96+okMhuXOebMmKqmXx0fAaq6nOxqdBgQ6ZDR0c0i0hUk83SpsLNjyczoUtrVuSLj\n",
"lH0c2bm2il+czOj6JbuYjs8jXd0tTuq0ken0kBmT6eywq/NGVUeMTAeGd2tG5onUyXSHiOjoQlH1\n",
"XO9ay6xrxqpuHRvXNuvokbnRiHSUyHSu6OqIUdEZYdX6qzo9dHQFWTVmNK7qnHWMearap3drjB5z\n",
"UheKUzqJRB6zstvIu3VP7gqSGaN7R75uxTwnr61gXh0+AAAAAAAAAAAu4wsfAAAAAAAAAACX+cn1\n",
"Bn69avp03x7HckrUSqY3c1dkxaq6qyJqdkYvVETH7Iq96FJ1zLtiU1bFDIkQiumIJnu9at4fT349\n",
"fup6ncwoatJ9cn/2XTJPj5372BGBMpK53ZrJRJWMVKytIvomk9eQnbfj9ndV8uBIRVph121RR8Jh\n",
"IHulI4rl9cp9AlgVOxI55l1r436Ra2XX9dTVuThiVvdfrz8mjxjJxFxEZKI9KupGohdWrGNkVWTN\n",
"63VOVEzVMWfqdkSgVMWBVMwTiTfJRJNkVKylK55l09qe8S1ZmdiRzJiuCJSOOJDM+qvWNhtTFZFS\n",
"cTwVY0bjumJgVh3zrEZVDt+u2JSTomN2xXJ8YwzMyceTqZuZ6+RIlJPXVvXBdTL37f/7CwAAAAAA\n",
"AADwdXzhAwAAAAAAAADgMj+5KImIrv7H5smpiJ+pWsuueJYukSiGk6NVOqJjInUi+3RSNElH7/KK\n",
"eVfWvWnMSddORtfxrHqdvOl8JPqw3dYrvyshaJdM3ETXPJl9mb2kVcW3VKytIvYlcjxV887GZeJy\n",
"qm7rMi+/HcmDXYmAFWmFCZHEoNE0qxKnZlErmcSj20Qu20/3aef0aWf0ykxXF+yYyAt9R/RIV5zJ\n",
"SdEqs2iPSN2uMatiRiJ/33HMVbE8mbVlalTME9mDVbEpFariWTLXSkf8z0BHJEpmTDZSIFN39ma2\n",
"av2RtVXEm6yK4FgZ9ZGJdFg1ZlZjVTTJquPJ1OmKjsk85qRjfrdmtG7H2nbFtXTWzcxzcizKyWtb\n",
"Nc9k3pP+1xkAAAAAAAAAgABf+AAAAAAAAAAAuMzP+McVvbK7ehuv6qH8afNEnLSWjrpdPawrVEWi\n",
"8Kvbz3uGayWnKpbn5Ainp10RLyMn7dOff/vH655SJ/fPr3iKZWSSojKq8hoyMR1P2TS/WY3MmFmN\n",
"bJxOR9pi5hZtpOLWIzKmo+7GlMddcSCZqJiTX2oz7MFamU7sn6ajM3OV2Ft3xw1iJkKkqm7m3nxW\n",
"NxNZ0bGOqjGvV01ky66omKqYnszaMhEiFec1E1WScXJsym0e6//rj3//c1ckSkWMykhFBEom8qFr\n",
"nkxczmwdo59VxIxUHU/FmKp96ogZ6YomOTk2pSLmYlVcS2Suk6NJdq6t4hxm5j0pUuTkqJKT13ZI\n",
"XEvESf+7AgAAAAAAAABAgC98AAAAAAAAAABc5icf37Kqzf3JMSmfNk9Ex1oy/bV3xnTs6nsdUbHX\n",
"kWsnsre71nJSu8qOa7Dr+srs46oe/KvGROrsinhZ9bqy8/Xr5CicScQLYxUJgVWea8m04xvJxIHM\n",
"RN7qIipiR54y0TEVcSeRMZFxmYidzC3OSMftY2RMxVt15varKbUu8lSOxIx0vSSsUBW1sisuhz4V\n",
"XXxvvw4ie9DV7XiuKkalKobjP625M26mI0IkMiZzDrvGzGpE6kTGVKy/KpanYp7ImNkeZPZ651oq\n",
"omM2rm0W4VIVVbIr3iT7mKfM+juOsSrqoyLe5OQIl1WxI1U3PVWxNX9XMzvm3RqROl3RMbvmidRZ\n",
"uZZ361ZF4bw7b1fdm9ZaNc/Jazt5nsTcJ/1vCgAAAAAAAAAAAb7wAQAAAAAAAABwmZ+6PsVPmRiY\n",
"rmgP89TME9HUv3lbPEuX26NKODt+4qnrecleXdFdpzj5uh2s7fYe6O+KnIpVe7JqLZFb5ojMbd27\n",
"NV6vXFRJJhLl3XlHc2eOOfMSkfl40pUiWJWgNxuzKGplWdrfRrPLtipqJfP0gJVO6mC9T+TFqSue\n",
"paJm5sW16pjfHdMRYZMd0xWbEnFKVExVTE+mbkVUSURHJMpJa6mKgWlY2zO+5fXqiSrZGW+Secyq\n",
"tcxqRupWxZt0rC27ltmYk6JjTj7mWc1IjVWxI1XxGadE1FSt5d2a0bodmZM7I1BOiYGJ1K2a69Oi\n",
"VE6eZzLvQf+EBgAAAAAAAABAhC98AAAAAAAAAABc5mf848z3QDKt5TORFV09kyvmyTj5eFbFvpwc\n",
"zxJptLwrViHSl/ym2JEqFXE5O3uKn3LOup7/VSr63Gf2tqLG6Xv7dMo1+XrV5E10+fNv/3idTMxF\n",
"l1Vr6Zgn8haUqZOpMbt9qZo3E/tSdSu7KsZmtpaqva245Tw5aiWztv/zt38clq2KWgHOsyo65l+v\n",
"QczALzruQ3dGx8zGdEWKZI65ay0d+xYZs2pvIzEdsxqjMZlrMlPjqSqqpGOek9aSiYFpio55Rrhk\n",
"olYykSiZz3VV8SaRx6yKWslECHREuFRFe1QcT2TMruiYkVVRMRXXZGTMuzUidXbtyahuR41onY66\n",
"XWtbtbfv1ryxbsU8Jx1zZp6KeU+e5+Eb/vcXAAAAAAAAAOCj+MIHAAAAAAAAAMBlfvJtJ3dFkZwU\n",
"x3LKvCO7Yl+q2pjuimfpsiv2JSLTl7yrD3nFWk7W9RpxyvUViRkaOWX9tzs5imyVSO+zTfcEO/MB\n",
"KtKLVqmKQJnJRHtEVESvVO1BJmYkk2tREfsSGVNxPJnbiE+LWsnc1mXWdvstW0DkkGdPqVUvedCp\n",
"qmPv51/7VdErmciNmVVry4zpilWpiniZ7V1mTCSmo2JMJqYjMncmnqUidiRTd9U8K9cyE7lWmiJq\n",
"ZhEuVVElFS3rK+JZMnEzI11redq1/q61zdYRGbMqOmY0bldUTNUxz2qsijNZdaO6KqLmpLXsimvJ\n",
"zv1pMTAV81Sdj0zdXfPsmnfRPCf9Lw0AAAAAAAAAAAG+8AEAAAAAAAAAcJmfXGzH61XT/7hiniq7\n",
"Imp2xaZk9/qU9XfFs1T0sM6o6q9Nn1kT7q5r8qbYpNtU7G02xmZW56YYq51xWRkV2RhF886WUvV0\n",
"z7SN65C5zaiSiQOZ1RipuLwykSgjs2OM3OJE5s1cx5kxmZfsTJrc06dFrWRk1taU3BfZ6k+LWuk6\n",
"nkwqT+blipyTOkufcp5XHs98rqp4k0wcSIWKtZ0UHVNV9ylTNzOmK4KmIg6ka96KqJ6KWJ6iqJKQ\n",
"RbEpLTEwI5N5nvEtr1dNbErGqniWqriZjrWMdKx/59pma+k6nooxo3FdkRsdN5A7I0QqYjpWxZuc\n",
"FLXSFS9RcX1l5v20GJiKeSLjPizOZFsszMq5J2NO/h8ZAAAAAAAAAAAGfOEDAAAAAAAAAOAyP7GH\n",
"nRRvMps3MnemBf+qiJrbonCeTlr/rsiKk6OJqnpy30RcTp2ufvpPmfPhHJ7l087Hpmbmp/RQz4pk\n",
"L3TMM5JprRfJN3i3xkikbsVeZmJtKuJmqsZ01T05amXVbd3JL9mTtUWiSkaHc/vL66ki5wN7slJd\n",
"d+eTXhifVkXHVERwjJwSHVOx1lGdyJhVcS2ZCJHZvNG5Z3UqonF2rq3rvHesJRKxsyoWJuH5or0z\n",
"nmX2mGwMQcdaInNn9vZp1doyb/CrYlWqznvFmK4IlI74mUidrny/k9a2K/JkXS7i+3V3xbV01n13\n",
"nuw/YHxalMrJ81TMW/APVSd/agUAAAAAAAAAYMAXPgAAAAAAAAAALvOTb8uW6f2b6WW8a95MrMWu\n",
"ta2aJzrXu3WrazaJkgAAIABJREFU1t9xzrriWTLHc9L3syr6g+/skX6KrufYzXuyU9f5yOg6h7uu\n",
"jZNfz3b682//eLRM0lKVrqiYirod0StVdTIRLl1xM5m3+666s2NcdYszMqubWVvkre6keRaJJDjN\n",
"HhO5bCvmud2nH9/rddfbeUZFN+edXa/7VMSmZGIguuaZ1YnET7xbM/qYigiUyN93xeV0xKZkxmQi\n",
"RCJzV8TlVF1fFVElFdEr0blmYyrW0hQd89cf//7nrqiVXfEsmbWNrFrLrOZoTEXMReZ8ZOvOxuya\n",
"N3uTk4nc6IjC6LpJuyl25LaImoo6OyNRdsXAvFuzs+6nxZuYp6ZGYq3+xwUAAAAAAAAA4DK+8AEA\n",
"AAAAAAAAcJmfXJzG6zVvRVfVGv+myJOT13bSPBEddUfX5Kp4lg4nxU98o11xM10xQyI36tjLOa9f\n",
"YwdHvOzswR+JinhXJKIiU2dV9MqsRqRO1ZjMS14mEuWpKmrlaVcEysisbtXabp5nsI+RU3hzrEhV\n",
"dAzfqSJq5WRVnZj/9fpj8oidsSkd81REyWTHdOzBydExK9cSieV4d0zVvBURNZnrdtXaqmJTZvNk\n",
"1pLZ28HxzCJcqqJWdsWzZNY2W0fnWiriQCoiOKrWllnLquPpGBMZtytGZVRnV5zJp0WtrDqe6GPe\n",
"nXtnBMpNMTAnx46YJzdP1b/XN6zX/64AAAAAAAAAAFzmZ92voEVkfuN3Z/eRb3RKF5Cuc5jp2hJx\n",
"SheQVV0obuc1Iubka+fTzuGq17yb9+gTDc57R9ePTEeGLpmuExEdnTiq6mSOL/Pr+xXdLiK33avW\n",
"UtV14umkjhgZmbXNHpO5fexqrLdIppnNbZ1EOponVTl5bSet5en2tVX8EuHZKrpdRB5TNU/Gqk4i\n",
"mfV3dVPJ1J0d400dPyJzZ7pdjMzGVO3bqq4mmbVEVMzzeMyzm8fr1dN5Y2e3joq1zdZRtZaqzggd\n",
"3SwynSsiY3Z159jV/eK0tXR0DqnqjLBrbSd1EsmMWbX+d2veVvekLhSf1kWj6h9PVnXwqFhvwbz+\n",
"ZwcAAAAAAAAA4DK+8AEAAAAAAAAAcJmf8Y9XxXSsige5PW6mI6Ims7aIkyJ2uqIKOmJfus5Hhcja\n",
"qnqXz/a2a56TvvvW0eP9pOsr83z/tHgWxk6OCDrJn3/7x5CKSJEqXWvpiHDJrK0qoiZzPF0RLrMx\n",
"kb+f1c0m0GViRp5OjkA5+fYlo2DfMneTo7K7IkSqomM6VKVYUWPnW/XJUSsVXZZje1sRtXKbVdEx\n",
"HfOsjI7piP/YGR2TGdMRFdMVo/JUFb0SmXdWZ9VaAvM8I1y6olZ2xbNUrW1WI3M8kcdUxYF0HGNV\n",
"9M2uOJNVY3ZFlYzqdEV7rLpJWxWbckoMTOQxq445U/e2OJNTIk+yHwZPWf/OeSpq7FprYt7b/5kQ\n",
"AAAAAAAAAODr+MIHAAAAAAAAAMBlfnKRKK9XTSzKqjiWjJPjZjKRIhVri87VYVU8S0eUzOvVE8tx\n",
"W1QJIitu1BEJdvLz8qTX/ZPWcrJAxMspES5V8SaRupta5/1yiVbUeL3mxxPJrHhaFbVSFSVTEYEy\n",
"kolNmT0ms37z1M3TZLaUzNOwSsVLz03zfqJde7crjqWrM3OdTF7ZUyYOZNc8VZE1J8+zK6Lm5OiY\n",
"qjGZqJLMvJl4k8y+zcZkonBG4yrWXxTLM4twqYod2RXPUrG2kY7jiT5m1VreHVMVb5KJz+g4nqox\n",
"u6JjRjqiYlbtwcgpUSur4loic3VFVnxaDMzOfcrUNU/NmIoPmbvmDcx98v86AQAAAAAAAAAw4Asf\n",
"AAAAAAAAAACX+emLhci0Yo/0Ic/MfXIcy6fFvnTNE7EqnqWj7qqYgkyvfxEKMTvjJzrOmTgNTuT1\n",
"6VeBPnK7eqJ39frviqjJxIE8ZW4ROmJIRjL7VhW18m7dTKxN5DGZjz2RY65I3TNP2Ut65KXnudxV\n",
"sRanzLtybvbZeY53zd3VZTnm5DiTd2t8wzxdMR2Rv++4VrriWiL79JSJKomMycTyZGJU3q0RfUxF\n",
"3a61PFTEgeyMZ6lY22wdkXkyxzN6TFfUyqoYm8y8mYiHXbEpu2JURnW6oklmY247nndrROqsimvp\n",
"qnvy2jJ1xbXcP8/Jaztp7se8OnwAAAAAAAAAAFzGFz4AAAAAAAAAAC7zM/5xpp/uqjiQ2byRuXfG\n",
"zXyjU2JfbjuHu2JfIip6fd9GlMTc6c+xT7smP+14Mr7xeTl7bxg8D1f1Va+IRImoiHDJRoY8ZWJS\n",
"VkW4ZCJ1KmJfZusY1a04vtG4SN2KeBnz9L0cZ6JjCt4OM5ftSelSJ+mIsYmcn4yuBLTbz+HTrn3q\n",
"mvdfrz8Cj+q6x8zEgTx1xY6YJxeNUVE3EtMR+fvMTdpsTGZtXcdTES9TFQOTecxs3qa1/DV4zauI\n",
"eNgVz1K1tlmNVccTnbtjLbOakbpV8SYVa8uMqYqkicxdsZaOqJjINfluzUiNSJ2q8/5ujUidnREi\n",
"q6Jv3q0ZrXtK3MdJESLiWcZO3pdD5v3G/x0CAAAAAAAAALiaL3wAAAAAAAAAAFzmJ9+aMhM3UdF+\n",
"/pR4kIiT42Yy84zm2tU+/6ToiF2RAqM9uCnOoKsPeaTX96xZ9kn7+A2xHZnn0DdGeexy015n39tO\n",
"kckDifjzb/+YUhWJkpmrInqlosbrta6dYKYD9GyezPFExmTOV6b7eeQ2IvIWmlm/eXIqomMSRiVm\n",
"S6mKjrgpzuTTomS+QUfEyclpbCO7YmDqIkM65q6IRDFPvMbzZ5kYmMz6uyJpZseTiTOpimfJxJtk\n",
"5q2IqMk+ZjZXYp5nhEtVrEWmRkU8y8mRKBVxM78bt2ItkXXsist5WjVmVdzMaNyqMe/+/Wiek2JH\n",
"uqJjds2zMvbl3bo741pOifY4OUZl5Vyn78MXzfuJ/3MIAAAAAAAAAPDRfOEDAAAAAAAAAOAyP7Hv\n",
"fFTFjBS0IU+t9+R5b5onMlfmvHfFs+y6dlbWnTk5qoS9viEqpsNN8Sb8t5PP2XNtmyLnOiJGsrqi\n",
"YjKt8yIJYTM7o1Zma4kcT0VKWmYtmQS3SJ3M+s0ztis6JrDWrmiSm+JZOtb6evVF3/CrrmiVjrq7\n",
"4lqyYuvN3C9WRIZkbrAq4mWqYke+bZ7IYyJxJpExs8dURbycEh3TdTxdcTORMZnom0SMzSzCpSs2\n",
"5alqntljTopEqYqb2bW3kXVk5pnNWzWm4ngiNTvGjMZ1RYZ0xHScFLWyK9YmU+fkuJZI3U+Pa+ms\n",
"e9M8J6+t4oPornmb5vY/fAAAAAAAAAAAl/GFDwAAAAAAAACAy/zEHrYrRiVSpyoO5OQ4Fs6Kn+g4\n",
"h5n4nCqz2JeuyB32nnf28Zza65SIrdfrnPM+WNvsbff0/u0VmQ4V3dwr4k1GMucj05W8om4kniVz\n",
"65GJM8lExXzjPE9V0TEZFdExA7On3ahEJo2pI/ZFjAqrnRIDE1lHbq1dUSsRFTEw79aMPqYjdsQ8\n",
"4zqZOJBZzdGYTFTJqoiXzB5U7Fsm1iYTvTJ6TMHePuNbXq99sSkVkRWRKIyKKImT4mZOiqSpmGck\n",
"s7bZWrqOZ9eY0biuaJJdsSknRaCcErWSvck+JfomM2ZX/Ey2bmaekyNQPj02peqD6665C/b6lP9p\n",
"AAAAAAAAAAAgyBc+AAAAAAAAAAAu85NvZV7Rt7ciRqUqOma2/p3RCyfHzdwea3NTPMtJ+/Z0clTB\n",
"ThWvV8Cdbn/+P9bflSFQEb0yknkLeo7JrKVi3shjumJfMp3lKyI3qlp0zvaya57I8czORyaepWqe\n",
"2byZtY3M1tJ0Cz0qUfGStirBKSLzlDolKqYrCmeVkyJ2Mms5KaGtYy1911Im1iKiKjLk3bpdUSUV\n",
"86yK3MjM87u5ZmPerRFZS2ZtO6NjMvEmmb2ezRM5nopYm0idxPnoivboikB5ioxZNc8p+zZ6zFPV\n",
"+eiYZ2TXtTKrcdKY0biuaJKT40wqokpWRa3sjPZYdQ4zYzqiML4hBqZinpPXVvVB79MjaQrm9T+y\n",
"AAAAAAAAAACX8YUPAAAAAAAAAIDL/OT6775eNVEqq75vsqutembfVsXNZCM4To596TjPt8Wz3BT7\n",
"kukLv0rkvO96PYvoWtsp5wcqVb3vPt3+/Pjzb/9YpuLlKfJ2EpEZc1PUSmTM7O2jIlYlUicbIZKJ\n",
"l8m8vT/nyZzDTPRN5G2441a96+NJ5tY9c34C12RFotNIJjalay0r3B7Pssrte7Kqw3BE7u3+j8Cj\n",
"MvdxmSiMinV05clVRJVkYkcy8SazeTM1oo+ZxXKsjAx5d55I3ZOjYyJ7XbG3meiVqvP+eMxfj9ev\n",
"rmiPVREoER3xHyfv2+gxs3kjdVfNM5I5H7O1dB3PrjG/G9exllmNVXEmVbEjFdfT084IkVWRNB3z\n",
"nlT35KiSlR+mPm0fviyeZWiylpP+hxIAAAAAAAAAgABf+AAAAAAAAAAAuMxPvmfyzM4YmIrYga4e\n",
"w08iEtaJ9PH+dF0RNatURa143gF/Z9Zn7Ru+Lzvp65lpRVcVvfJU1SE9c0yZuSuiVt6tOapblUyU\n",
"iR2piBCpuiXIxNhUpLytiqiZzTuaO3ObVHHeR5pS6jKxKZl4lg6Zl4hI+k/FGPqs6jx70jk+a/0d\n",
"ES/RxzxVxJlkxlRFoLw7d1f0yq55InUicSAdcS3ZugVRJanomMxzrGIPMrE2kTqDGs8Il0ysRcWY\n",
"qgiUzNpmdq6tY99+N9e7Y1bNk4moyESIrDqeXWNWrmVW46TYkVXznBRRU1Xn3TFd8+6s++48J8ez\n",
"ZD/k3BRfsmr/T5k3O/fTYy3f8D8WAAAAAAAAAAAf5Wf841WdOJ4y3Qciv6aWmTvT0WNVl4CKtWa6\n",
"j0TmypyPnee9QtOvHrbVndH9AuC7jN6HZ+85g/fhjm/Lj2R+NX9WIzsm82v1FfsU6fSQqTvb26ou\n",
"FLMaI8+6mQ4SkVvOik4Vkd++2tWxpKrxWea8J15WKj5GZJ6GqzpiZF5W4DSrfrGt7xfFqlqFVYzp\n",
"6PgxesyujhhVe1Cxtsw8kc4OFV0oRjKdXRIdJaZ1R2MqznPFmMjaVu1BonPIs5vH61Xzm/e7unV0\n",
"daH49LX9bq7ZmIq1RObJdOeo6Oyy6ni6xnR1qujobrGqC8Wndd44uXtHZO7bunec3EHi5LWdPM8p\n",
"8+6cu+Afg3T4AAAAAAAAAAC4jC98AAAAAAAAAABc5if/nY+K2IeKmJGKeaNzV8jEwOyK9rjdruur\n",
"ai3v1qyqGyH2ZZ9MBBLwe6Pnz6xt7z+b1rJLUxRZ1+1LRZu8TI3MmEyH7kgLv8hjOqJVqjqkd0SV\n",
"jGRibDLRJJkYmFURNU9V0TGZMbO1VETJJM2SfUYy6VKZMZmncuZ4+A6rutOe3DE5pita5d0xkViI\n",
"FeuIzDt6TEVUSWZtmeiVSExHZO5IjUwMTEWcyaxmpG7mOqiKWunYt6prJbH+Z4RLVzTJqgiUyDyZ\n",
"Mf8vMeapa20d+/a7uVasZVYzWnc2pqJG1/FUjMlEr3StpSvOpOLfLD4tauXkuJbs3J8WA5OZ56S1\n",
"7Jpn17w741medu11ooZvDgAAAAAAAAAAXMYXPgAAAAAAAAAALvOTixR5vXLfFcn04K3oB74rBmZn\n",
"9MKqvsonz9PlpjiTnft20z4B3yPTHP/pvwY/uznmpavZ/2Nvq6ap6LJ+Uo5CV+xLpsP47LahK94k\n",
"E1VSFU0ya08bGZOJgYnMk9nbp4rzMXJyhMtJHxsusiqihrGz4kw+XeZF4ZSIl5FMxEZEJmolEyHy\n",
"bo3RYyqiV6rWVnE+uubJRJM8VUWtzGpURcdkxlTEwAweM4twuS2eZfaYzJhnfEtkzEmRKBX79ruf\n",
"rVhLZB0V0R5dsTwVxxMZ0xG9kl3LrjiTb4xa6Yg3OTmuJVL3pGiPVR+mTjrmm+Y5ae6Kf5ve+eF9\n",
"sn7//AUAAAAAAAAAcBlf+AAAAAAAAAAAuMxPrk9xxM4IlF0xMB3zRuYe7XVmzO3f/1nVW7pD5hze\n",
"bmfkEewU6ad/kkjWwskqIlwinjEvN0W8dL3///m3f0xb1fZvVcf3itiX0cvKrG7mNik6d8c8kQ7c\n",
"FVExzxqRzuUVMTAjFdExmTGzdYzqVoxZ+JGmIn2pK/Iks7bMmF1WvSvvdPL+P63q/LvqrTt3PXXF\n",
"qFSM6YqFea6lKs6kYi2Rv6+IRKnap1mcSeRGYtc8I7MxkQiUrjGZ6JiKMRUxMANdsSm7YmAyY54R\n",
"LlVRJZG1VMzTsW/RuTvWMqs5GtOx19kxHVErq6JjImupOuZ3a4we82lRK7siQ1btwUl1T/5QsDM+\n",
"p2KenXPviknZNW9VnYb13/4//AAAAAAAAAAAX8cXPgAAAAAAAAAALvMz/nFF7+WTI1C61pJxWwzJ\n",
"qvXuOh8VuuJyIj3GM06JtRk5eW1dvvGYb/INjchvdlJczk0RL13N5wO9aDP5BqviWbp61meOpyKe\n",
"pSLeZDRPR4xKJBIls2+ZGJjIbd1J0TFPXbfus/V33e5XHE9gXORSfzrpHSgiEzfD2W46h6tiYf71\n",
"+iMx6vXaF/OyM1rl6ZSolYpYmFGdTIRIZu6qc9oxT+QcZiJQZjVHYyLnfVd0zKzmYMxfg9eeigiU\n",
"yJiKaI+K2JTRmFmES1WsTWYPnnbtW/QxFWvJRGFk5pnNuyo2JXI8kZodY343blajIs7k5LWdFB2T\n",
"GbNqDz697skxKifPk52rYu5D4k221tl0PDf9LzoAAAAAAAAAAC9f+AAAAAAAAAAAuM5Prt/u61XT\n",
"G3tX9MrOGJhdcQ0VsSrRcafKnPeueJabVD1fuohA4VtFMgQ+zayl8Ml78Ix4eb3OiXnpagKfyGfo\n",
"etvNXBqZztgVLVMzuRCZKJmR2TF3zVMRiRJ5TKRzeeS24vmYk6JjZmvJjMk8L6uOZ9HHrUy8SWRr\n",
"360RqZMZU2VXDEzFXmfturPYNW9XR+uIVTEvNZEoXdEkT1UxHbMxJ0etRMZE5s2MebfG6DFdMSO7\n",
"5hmZ1Y2sLfL3s7pd0TGBMc8Il0i8QVdsSkW0R0VsyjO+JTKmKtamYw9GOvatay2Zva2aZzbvqtiU\n",
"ndExXdEkFVEYu9ZWFbVSEZvSMW+kTldMR1eMzc54nKeOmJGboktWzn1TLExXnZPiZiZr+bb/uQYA\n",
"AAAAAAAAuJ4vfAAAAAAAAAAAXOY3kS7P/iIVcSevlxiYrIo4llXf7cnEwGSuldNjRma6YkjEm/zq\n",
"pGtl1/MSojJZEl1OWkuXZ8zLroiXrtfEop59FTkJXfkMmZfxTAfrp0zkRuQtqCLaIzNPZq9HdWdz\n",
"V8WZrIqOear4SND1MWJX0mXyNm/VS0RHjYzI04XPs/McV8y9rkNy1WeyiqiYiI6bj5GO41kVtZKJ\n",
"XonMHVl/VyRN5jEd80RiYDL7VhED0xUd83jMM77l9aqJz8hEe0TubVfFpjwjXKqiVjriWarW9m6N\n",
"lWup2NuRVWvLxHSsih3pGPO7cbMaN8WmVFwr2bnfHXPSvq2quzOu5eQolU+bZ9e84lnGGtbifxsB\n",
"AAAAAAAAAC7jCx8AAAAAAAAAAJf5Gf+4IjZFDEyux3DVHmTs6sV8EnuQs/O6rRA5h5k+8d94LUBW\n",
"psH+p/m014yi94E/E9fCqm7ns/Z7kTiTp0yH8ZGT58lEomRiYCLdwWdznxQdk4nYmUXuRMaMnBJJ\n",
"k6nxek2PcVR2V4RL5BR2qApW2xVjc5KKY965b7viWWpqZO9FMi+MFXNXxKhURZVUjNkZtfLumMgN\n",
"y0gmNmU2d2QtkSiZU+YZqYiBWRUd83hMJkIk8phMtMczRiUypis2pWIPdsazVKxtto6qtWSiF7Jr\n",
"eXdMRSxMZC1d52PXmN+N61jLuzUidU6KQNkVUZOt01G3K3Lj5PiPneejYp5d81Z9yOyK+5n58HiW\n",
"jJv+RxYAAAAAAAAAgJcvfAAAAAAAAAAAXOcn/52PjtgUMTA5t8VpdPRzjow5eU9GOtZ/27UCnyDS\n",
"6//dGtk6s7qrGoZXNYqnT8e1MOo5HPHn3/5xKLP8qqfmuzUzeQ2Zuk+ZeTKRKJlbj0hKWqRu5FZq\n",
"9jIYWUvFrW3kdmxV8mBmD2Y1ImOqblMT+9QRvTJaSqbOrhp8pkM6zZZdk7k6FRF6OyNeKmJfusZ0\n",
"7EtmDzJjMhE1o3EVETuRx2QiaSJjMvPMalTtW0VETSIG5q8//v3PmQiR1+v1+ufkMasiUKoiRJ4f\n",
"7TIxHbviWVatbaTrmDMRD5l5ZnWrYkcqjuemMSvX8m6NSJ1VESifFlFzUt1vjFExT93c4ll+tWlP\n",
"/E8vAAAAAAAAAMBlfOEDAAAAAAAAAOAyP7mew6/XvtiUCicdz20xMKecw9vcHi9ToSLCCf5HpLf/\n",
"Uya+ZFfkyaexj/fpeJ/KnvdJn9iq27qqTuvv1oxsy+wlL5L6FHnZzMwzm3dk1oG76zZ1tLbMPs06\n",
"ikfGRF4WZ/tfdTyZ7vOzte2MtclcK4nnf0f0SlWdTI2KWBvWqjhHp9R4vaq63v4xf9AvdsamROIl\n",
"OmpkXvgrokoyYzLHU7UHXeufzb0ykqZinorjyexbU3TMM8KlIhIl8phM5MaqaJJRMmdF7Miufdu5\n",
"ttm8kbpVsSkd68/EjmSfU6eMecpE1GTrnhK1UhXtcUrUyulxLR2RGyfFjnxabMrOuBPxLPvO2dOi\n",
"D83f+L/OAAAAAAAAAABX84UPAAAAAAAAAIDL/OR6QEdU9dd+2hUpcnsMzM4olszcq44xEzNySjzL\n",
"qA9QxXkV2wP7dUWgZKJwMkS4fJ5RH993Zd8vZ+MG13Hmkuto85dJjvq0eSKZFVW3eZmYkdmYyEel\n",
"TMRO5ng6oleyYxJPy1SX/orb0qJb5o4Il6534V1G2+oO4FffsCfnRMVUfZatiHipiHyprPPuGFEx\n",
"uTiTyFoi8ySiScwzf8wzvuX16olRidSNxDU8P5LtnKcidqQrnuWmtY10xPJE5qlYfybOZNXxdI2J\n",
"/H1XbMpNESgnRa2s2rdVdXdF0HxajMqnzVNVRzxL3wf4hrXp8AEAAAAAAAAAcJmf8Y93da4Yqeim\n",
"oCtITubX4bo6u3y6rm4dUOn2rhOrnNLdIvLr4hUiv8rO/Xb+rm5i3J+Ja73il18zNSu6c3TNE3l5\n",
"nr3kReaN/FJnputE5LfUMuuf7cto/bMxO7toVHRcyXxcyex1RMFHp0hjmoiOO5yqd/dnnZPeuU9e\n",
"28l3qed01eipW7e2in+fiHQfyNSp6CQSkemQMavxu5/9p2Mib6oVY7LdVGZvvFXrf3feUZ3M2k6e\n",
"p6ArSFV3iEiXgIoOEl2dKmYdPTJrW9Wt49PWNtK1lqfM+iN/H1n/TWM6uoJk13JKR4zbOm+s2rdM\n",
"3ZM6h+gK0jNP1dy6dayb96nrHwUK1uZ/4gEAAAAAAAAALuMLHwAAAAAAAAAAl/nJx0ZURK08VfXx\n",
"FQOzb/0ZmWM+OQJldDynrO10Ha8rcIObYm1OiaxhrOt8/N+CGtnrOjP3n3/7x6HZ1mXSizIduUc6\n",
"5okcT9e+PX9WEdcy+lnkpXXWDTwTm1IVtTI7HxXRK6/X/Po5KGolFZ8TUPEuPJq24hX55HiTk9d2\n",
"m5Pv/DrOa1XNmjqZmJFs3XdVRbxU1FlVI/OGmRmTWVtXVExFnMnIbEzk2o/M2zHPSMG+/fXHv/85\n",
"ElkxizsZ1cnEvozGVEStdK1tVwTKp6/td+M61jKrm13/zWN2Ra+M6pwUgfJpUSu7Ykd2RsWcHHFy\n",
"SgzMzrnFs6yb92nnHswk1uZ/UwEAAAAAAAAALuMLHwAAAAAAAAAAl/nJ95GuiKjoiF55vcTAvF7r\n",
"1n9TBEfmWqna211uivaBSpnshaq8hl1NubtiYU6OcIm0Ap69T42OZ/aYzLWySkX0SkTmvfC/Bj/7\n",
"56K5H/2Qq9LkZqpaa87WFjmeSLTHu/OOHlMRvZIZ83rNn+6j48mMme1l5HarK2ql4nY+0zU+8pGg\n",
"4rY78/RvqtsVZ9JRtytuhrN13ZGeXTcTE7GqblV0TMULYyRy490av/vZu3UqokpGboqKGY2ZrSUy\n",
"Zjbv6GeZeSJjKuYJ7NszwqUiniUTA1NVtyKaJLO2VfsUGbNq32Y1I3Wz8T8dcSyZ6Jida5utZVVc\n",
"S9daInOvikD5tKiVVcfTMW92bjEwZ82zK6pEPMtZ8SybPjTf9D/XAAAAAAAAAAC8fOEDAAAAAAAA\n",
"AOA6P7l+yBGRvienRK+ctJbbYmAq5va9o/s4hzmRPvezWI6ToyS64k1Oik2pUHUOOyJcTtrrSBvf\n",
"U679kWe0ys7XyY6Yl67wgq65A/1RM2VnW5vpFj4yu10cPU1nW1sx7+gxmaiYqq7qmRibWX5GVSLg\n",
"rOt4JnakKmqlIjKoImrl4LiW1yt3qVfMU1H35LgZxs6OTemvOapbN08mciNTN+Om6JiuSJSnrqiS\n",
"zJiuqJWKqJhMbEpm3khmW2TMbJ9GN9mTus/4ltdrXxzIqniWk2NTRtExmT3YtW+ZeI2KearWUrG3\n",
"I6vWVjFmV3TMSEdcS6TOyWvL1D1p3zrm/Za6N80jnmXdvE/iWWIex+d/aQEAAAAAAAAALuMLHwAA\n",
"AAAAAAAAl/kZ/3hXvMlIReSJGJg6u6I8MvPu3KeZTzsezorCuCn2YqeOSJTb7NqDSKyN8/F6/bNp\n",
"noqIl6qYmMzrU0Vb8oE/E9fcrGxVwmGmA/fscKpSxZ4ia521vc7macz2O9NRPBMZMppntpeZW8Gq\n",
"OJNZ3aqPTid/DHrWLfqIM7u8RK30xdqscvvdyn1xLP/uX69BhEOJiheXVdExmbqZOJCquk8V+WWZ\n",
"3LdM7MhI5pgrIlAifz875kjcTFesTSaiZlI3E7USibnIRHBkYkaqIlBmES5VsSmZeWaP2RnP0rG2\n",
"kVWRNJG/71j/qtiUyPHMaoysijepitPIfObPjHm3RqTOzhiSij3IzHtb3VXz7IodOWkPOubdPff/\n",
"9mnxLH2dY94wAAAgAElEQVQfbv9jOnwAAAAAAAAAAFzGFz4AAAAAAAAAAC7zk//OR0c/3Uhf4ohT\n",
"YmCqnNz/OOKkvZzJ7NNNxwf/Y1fsS6S3f0XdruPJzFOxtqp9WxXhMmtLfFOz9p3+a/CzjpiXqniW\n",
"TJ2KuUf9j58SvT8rWk9WRK+M5sm89ET+PhNRM8uSqIqOqYhaGcnEmcyOMZMEGYmoidyW7lpbxUeN\n",
"qj1YVfchkuRT4dPmIWbV3t8/TyQa4+S6FfNE4jMq6lZEvmTrroq1eeqKWnmqikCZnffIDVdmTOR6\n",
"K5jnr0ekUyZqpSqqZDZmNO45pioGpiOaJDNP5nysimc5aW0jmbod0SpdETWzdUTmrooq6Yg3WRU7\n",
"MpprVdRKxTF2RWPcHjdzUt2b5jl5bafMm537adVeR5wUz9JwjP/nr8SY+mUAAAAAAAAAANDJFz4A\n",
"AAAAAAAAAC7zE+lYMm5sWPFdkY7oldfrnO+xnLy2iEzP5ypiUtbZGffDubqiVzJzf2P8x6rolQo7\n",
"r5Vv9Ix56Yh4eb1q3nczNSpi66rqPnoXZ27rMksbvQ1nbotmc4/myUTUrIqOWRW18pwn0iH9KXKt\n",
"ZDrJZ6JvImZ1uz6iVXTkH81TUXdg1my+653aPPe5PxZlzzyZ9LKcTP5XRd1V81TUzNbt2IOuSJTI\n",
"WjKxKSdFrWTeeCuibiI3Eom1PSNcKiJRIrFvFWNGP6uIDOmKJslE1FTEjnTFs9y0tpGKWJ6RivXP\n",
"akbGVMXAnDwm85iOuJZInaoIkY7YlJP24N2anXUz85wcgXLy2k6Zd+fcVR/STopjeSo4xkwcS6ju\n",
"f/j3AAAAAAAAAAAcxhc+AAAAAAAAAAAuM4x06Wok/2tDvoq23VXxExURIidF1OyK6RADw6e6KWJj\n",
"lduiVzLncNWYDl1RKyed98haZo+J7FOkLXFXtMrMM+Kl63p79vVdWWM2LnPMkbUEeqhmIlAS07w9\n",
"72juSI5CJmpldsuZGZOJA4nUiXQ7z+xTpmN9xdoydau69mfmydg0zz8GdTteXSOnQ7QKUZ8XvRKZ\n",
"p+szf0W21a55InEgmXkyb8QVdSsiRSJ1qt6IM2Mix9yxT5F5Mue9INbmGd/yeuWiSp4f0SqiPUYf\n",
"IyKRG7OYlEh0RCTGpmL9FXEmmTGjtVXEjqyKKqnYt5VrmdWtijOpiLFZNeapKqKmou5JUSsVa9kZ\n",
"gdIRN3NbjIp4lnPm3Tn3p8WzNH0wrYhn6frUmgmtBAAAAAAAAADgIL7wAQAAAAAAAABwmZ/RDyu6\n",
"p4wa9mXq1sTAPFXFjoiBqXFbDMyufYoQa8NpuuI/TolNqVKxTxV7Emnr29W4O5PpcFKM0CxaZfR6\n",
"XBGTsktm7dnzNRv33PvXax6xk8lEGfhz8jyriF6JjInMHVnLrAN3Jt5kJBOJEmkxPKsTiZeJ3ObN\n",
"xmRibEYy82RuS2d1uz5qZGJtMqqu24RZwtGqu5fR4e2a+/Y7toxdx7zzLmlX7EtNdElmnq65b5+n\n",
"INojVTey1szaqtaSiU15t0ZkLVVjZutPjIlESVTEZ2QiRLKRFZloklmES1UMTEdsSlc8S0UsT9ce\n",
"zGqOxlStZTbPyvXP6tw+piMG5nfjqmtE6lRFk6yap6Pu7TEqXfOsWsuuecWz/LcPi2epiGP5pWZR\n",
"nY5Pqv43GAAAAAAAAADgMr7wAQAAAAAAAABwmZ+qTi8VrVqrYmDmdSt6EI8rf5+T401Oktkn8Sx8\n",
"i46Yjsw7SmZMJHegYsxIR4RLV9PxyDn+xibvTydF1GR0RdRk3v9m77OZTJSRP//2j6lpIttY1en7\n",
"qWL9XZEoT5Eu5JG1zI45Ms+sZqRuppN8ZJ7ZnkTmGVkVN/PuvK/XslvoyNbuelUXo8LvnHKnEenA\n",
"36cqyuM/nXf0s4oXrEyESGbeSEzHrnkidSI1Im/WmbV0RK1E1lYRN/N/B2Nm6w9c+3/98e9/zkRJ\n",
"ZKI9qiJEIvfzs7qRMRUxMFXHvGqeTMTOquiYzNpmNarWMqsZrTurc3L0SkdcS9VaMnNXRaBURMec\n",
"FFHTUXdXlEy2bsU8J6/t5Hmq5n7aGUlzUBzLU0U8S9f/sFZ8eqxYm/9BBgAAAAAAAAC4jC98AAAA\n",
"AAAAAABc5ifSoSXSjiTTpaWr1WxHg/p/lH03piICpaJP8e0RNZEe1hC1KtYCsqpCz1bF53TM841G\n",
"LZOfe9sVo5Kxqudg5Jhna8lmhszq/Pn3f900TWhMZi0V0TEVXdZHP8tEeWTqVs3zFDmnHZ3xq+ap\n",
"+NjwXEsk/mfVx5XBef/H/5k+ZInINu26kx1dKu6qf3XSnmTeKlb5tWv8H8PHrZF5Q+mYN7KWqhfK\n",
"TBxIZu5MVMlsnsiYyDwVdTNRMVWxPLO1VEXHJPbgGeHSFdNREQfyz8A8FevPRNJkomO6jrkiAiWz\n",
"t5+2tpFVdbvWdsqYruiVk6JWKtbyaRE1mbq7omSydSvGnBybcls8S8XcHxbPUhHF8nr1fNrq+iem\n",
"XdEx/occAAAAAAAAAOAyvvABAAAAAAAAAHCZn1FHllVRKxXdbbraxlYEPIzbq1TEr+yKgTltLf/p\n",
"vCvnhqxID/vZK9boOp89lyPPl1VNn6viTJ4yx5MZk3lHqXgXipz3jJMikCItrGfPh8id0PMxXXtb\n",
"Yec6RhE0M//1+POzf/BI5Bgza5kZ9UyezPNn4PmReempikmZrSXzdhLJB5h9KIi05I483SMfPjK3\n",
"tqvmmdXItC7vuvWNzFMRSZMR2add0TEDmafHLl3/bvCNTjqvT5mO6OtkIitWWZWPFdERm1Ix7+tV\n",
"c84yMSqReTJ1ZzWidWdjKqJWMuejaMzzheR5mz16UZzFjETiTSLzZOJAMnWfYyIxI5kxs3lHj1kV\n",
"gVJxPF2RLrOaVfNUrSUTGfRujdFjnnaO6YgQWRk70jH3qniWTN3b1/ZuzWzdT4tNEc+yr8br9XHx\n",
"LDfFsaxaq//tBgAAAAAAAAC4zM/ohzd13qj6glfFbyd1/c7zP3wv56UrCJ/p5C4BGZlOIq/XOX2Z\n",
"Rk7uAlIx72wdVXUjKjpvnOTZ+WHn872j20XXvM+OH6/Xr7/Ol6kbee+u+JWgwDzPrh+ZzhuZl5WK\n",
"TiKRr6RHvl4+O+bsL+bO6kZu606aJ/KLuO/KdLuI/Obkrs4hkfOzsVvHU2RpJ7+zndTj69OdfB08\n",
"ZX7Jdq9dL8ARFV0bul6QMy/AFS/ImRf6qnky56Pi+qra246bj8SY/++PX4fM7jWqOhhk5pl1nRh1\n",
"yKioO3rhz4zZ1UUj0+VkVbeOzDyZMbN1ZOtGjrlinqfs+jvGVHSDqOokMquxsnNFR1eTTJ2dHTE6\n",
"ukx0da74tC4aunX0jXkq2reK7hxdnzQqPm2dvLaRjvX6n2sAAAAAAAAAgMv4wgcAAAAAAAAAwGV+\n",
"6mJH/t1JUStPJ7fOrQo7+LVO5rs9o13JNLDZFceyixgY/ofG1zl9AVk9dXfpiHBZtdefFmdUJRID\n",
"0zHPKtl5Z/cemX0a9WKumCfRl7QiaiUwTUl0TKalaiRCJPJBIlM389LTNU9GRZzJqniTzL5Frq+D\n",
"bqEz72wdn2W7ZJ6GrHP7+Yh0c8+kl+2TiVqJRG50OSVXbCSzb5kYm4rzUzFPpG5VlE/FMSfG/PWI\n",
"cMnEZ0SyoiIvGrM4k6p5IrEvs7qZMVXRMavWtiue5eS1jVTEF0Xmrfis1zVmV3TMU1UUzrs1oo/p\n",
"iKTJ1Kk65lPqdsV2nByb8g3xLBUfxsWzDH1bHMvJaz3on9AAAAAAAAAAAIjwhQ8AAAAAAAAAgMv8\n",
"ZDvI3BS10tVKtyLG5uQ2v/+4/vtAs37hfIeqoCTO0hFFkrlWTh4TqbNr36pEYm1mj4m0Pz45kua5\n",
"1n8mauyKeHm9+r57POo7/L9Vna/nPInclD8Dz5dMn/tMlEdFx/dMzkVkrV11Z/sSiRmJzJOJjqm4\n",
"dc3EpmSiY06+ze465otkLknuE+n4freqyIqTVbwAZ97sMqpiRzIvyDOrbhK66lad94obu8SYTPxE\n",
"JBJlFjMSienomicT/1FRtysGpiLOZNUeZCKDqmI6OmJgRipibDJ1Pz2uZVRnVYzKbVErq6JjOup2\n",
"xbO8u47OujfNc9Lcm2JsKqJYXq+af57o+qT06WsbWfVpa+bif7YCAAAAAAAAAPhOvvABAAAAAAAA\n",
"AHCZn0jnmm+MWnkafTPmlBapVWuraPQ/bjOT+V7Rt8WxdPXxpk8kSqJDpM995Nk8W3+mn37kOs6s\n",
"JaMrZiTzSrlqzKxGts7s/HS9e6+6Vro8Y1JWxcD81+BnmXM0W/8sMiU7b6RuZN9mj0lEr6QeMzqe\n",
"ydyjiJfZckepPBXtaSOZD5k2srO62ad/Rd2KTvIjs7fQ/5+9u+mSJEnWhGzZFbequffOmWGALfxU\n",
"/icbdqzhwAzTTWcni8scutS1SiSkRNXUPJ5nF5GmH6Zmbm4W6S5vpXp7Zg1Oup2srEG0z09bgwZd\n",
"pwpfU1Tl/pS/cay1Kgpj1RvICrvWYNUFuBLlU4mbifqo9tsRy1N5E82MM95UJtr87duvf868V48p\n",
"lJV7zo6Yi65xov2p9htFnpwUm7JrnMz9/YqolVUxMF2xL5X5jzr2ObM/q9pEfayKUfmK8Syf7TPb\n",
"74poj5PiTcSz9I3dMV/xLFMnzWW04ulq19NKl2gNTn4CBQAAAAAAAABgwgc+AAAAAAAAAAAe5iOz\n",
"0VeMWllVBrcjxuYrlOj96bbPIkW1plmrI8bi6azBq1VRGKvW+q4Il464k1VrnZmbc/2+GJguYx3f\n",
"MV5mrHVc7XeWX9KhMk5Hnkmiz0pCTaWyfEf19sy/V8bJVCEfZW7rOiJDKtExHboiajrWILPWbqtT\n",
"z3HRUnq3ZLdK2tfJdyv3qcSBdEV7RNvsyr7qWoMVNywzHTE2d8azVI57MLcfQ3zLdcX3BJXIilmb\n",
"8VZ97GP2qFGJN+kYp9LvLAlyRQzM0+JZVpxfd84t6qM6l6jfrtiUVVExmbGjPlZEouyKa8n087To\n",
"mF39duxPZR7vFs/SdfP+oHiWjjiWrj9xdNyJr/pzy7vPbVe/u/4c5s9uAAAAAAAAAAAP4wMfAAAA\n",
"AAAAAAAP87Gq1OZXjFoZzUq/nFLatGtuKyJq+vrxeSaqus5K9slEhtwVtRL1We23EuESlfHtuop3\n",
"xMtUxs7kG4xzycSmZPYnWttqnEkkEwMzqw8cGfup9BFFvFxXbl2i86cjeiUzzmxto9iaWZtovpN5\n",
"fA/mX4kdmemI9oj6zPRbybmY/S5zKxj1uyqSZlVsCtuifH760+/+c7pb+AoyFdJfK76P0RF3Rnt8\n",
"RSfHzVRy3ip97NrnVTE2Ub+FuWVevJk4kKhN5b4oc/8Yjds1TqbfVesUzbcrOqYSOxLNvxIhsirS\n",
"Jepz1qZj3WZ29dsRFbMq3mRVm13xJidFreyKjqn0e1c8S2Wcd4tn6fpvj5viZMSzzJ00l9GK2JRV\n",
"ES9PWgNPugAAAAAAAAAAD+MDHwAAAAAAAAAAD/NRrdYTlRv5ilErK+Z6XetibHj106M+A5WJrPgK\n",
"VkRurLIr5mKUiRDpiESpjDMb665jWola2RX/k1m3jjYz0fHoiKO5rlrUysmv99EszqTyOuxQiWfp\n",
"6GPWJopEua5cZMtoXMuOcToyUWYKOSRjxEulYv1sd1fEm2SSljqqn19XLSpmxa1TJZKmq8r9iric\n",
"p88N4HdVojwqbVZlhD19bivsipuZ9VvZ544Ym1mb8WavcK78bYhW6opaie4BuqJjogiRSjxLZZxM\n",
"P10RKB3RMZUYmI6olVXxLHfNbaZjLpV+T4pROSWuZdZvpo9dkSi74lk+22e23xVji2dZN05XP4X5\n",
"nhLH0nWX+m5zGa26m39SHMuuJ5rK3P05DAAAAAAAAADgYXzgAwAAAAAAAADgYVKRLrsK1otamX8C\n",
"Z0WMTXWuq9byyV7PW5+j+pq64jMqnhRr0yXa51XHo7LWlTaVaI9VbSrnU1QyeWc4WVQiOZM3kYmb\n",
"6YhJyRhLM49zqcyj63h0xLzMom/G+JVKxEtlnHFtM+NW1jLTJqjFnCmVParEplRKcs9E/VbKhV/X\n",
"mqiYyj5/xYQ9ACg5OW4ms82Kuaza50SbH0GESyXaI9MmilGptqnEm0TbVMaZ9VPpt6PNquiYStRK\n",
"x/5UIl1mormtio7JzKUSeZQZ98ltdkXHVMbeFdeycy6VNnfFs1TGebd4lq7/FnhQPEvHn2C6/kdv\n",
"xZ+DTp7bqn5X/Q/rk6JjZqL5+59pAAAAAAAAAICH8YEPAAAAAAAAAICH+ZhV5tkV27EqhOBJUSur\n",
"nBy90jG3rvifU9bpJ5+92uzOeInPuiuuJROJ0hGNkelnVbBYx9xm3i32ZZQpObwiPmc2ViZq5a7X\n",
"d2Vuq94LKmtQiU0ZZSJeMnMb41cqES+VnJHRbH8qsS+ZCKpRkCHyPXHNGKdWiU3pqjAe9VsZ57rW\n",
"RMV07fOK6JiTY21Ontt11c7Bjssi8AdUIjcybXZd6Lvmb27nzC079mf7XbXP4xvZpE0Ua5GJklgV\n",
"IRK16YoQibapjNPVb0ebrniWqN9VMTAdcTNdcxt1xc1U4kw64ktOatOx/tE8do3b1c+qOJC7Ik/E\n",
"s6xr0/Rn0Eo8S8dfNd8tnuWUNVnZ7ylxJhVPi44ZZZ5oAAAAAAAAAAA4mA98AAAAAAAAAAA8zMfs\n",
"l6siUEYdBflXFfrf5ZRIkZmnxdh8NWJgdlsRA3PnFexJsTYZXfEyf3Tc3xr7jjaVeJNMm8o5mimH\n",
"nKmzSk/M01jOeXbcxxq9mTaRWc3kSkZCpVR2RxZD5pox7mMmdyTqY9ZP4g5yRWxKJlMvU157dGdM\n",
"x659rkTHiBA5y3DMfvrT7/7zdV21AIGOZKInJeyseimPc8tU7c9U4F91PDpSFN5tbr6fdLpdETtd\n",
"b953xf8cvM8/vr02qVwkKlEr4+/GxMZMm0xUSUfsSGUNKuuUeaOK1m22TUc8SyXGZlc8y9PmFo1b\n",
"ncvo5Da7YlM64j92xbV0zWVV/Id4lp5xNs2tEsUy7afQ5t0iUE6ay4p+nxZn8uTomJkV++MJGgAA\n",
"AAAAAADgYXzgAwAAAAAAAADgYT66CqZnyrl22BWB0lEwPdPvqvickwrhnxxbg2iYte6KELkrrqUy\n",
"t+t6nd+qK3Bk1dxWtYnK+GbG6ThXZsd91TkYlT+ejRNtkznulUiajrl1GceZ1QuOVNpU+l2VYVEZ\n",
"p3I8KnkmmXEr/Q77fHIuRMZXjECp5Fp05IFk1rojqwTgrT0pmqQyt3ez6o0r02/lGBbiZsYIl0rW\n",
"VVfUStRvZW6ZNlGsymybjnFmY2XWqRJ9U9nnSoRIRwxMR2zKqhiYSsxFJSetY5zfGuuzbTqiPTLH\n",
"Y1Wbz/aR6adrrT/bR7WNeBbxLFffHVvlLuiUCJQ712BXn0+KY3nSXGeeFCXz7k9sAAAAAAAAAABv\n",
"56P6XdK7Km08qXJI5vu/Hf12rcnJlThOnttXVKsKUvkm+10VC76izLrdVXljJprLnZVEVlT0yOzP\n",
"KPNtso7XVGXdKlU1Ztu8u1m5ghXXuEofuyp+XNeasg2zcca1zYwbvVYrlURmr6nKGgz9fh/6XVW1\n",
"YVdFiZmxn8xN811VTTJf4o7mlvnG2clVT+6qPnJdZ68L0KhSXSGzTabNyTZVlCjdSNw1t4yuc6Xj\n",
"RqKwTpnKCOMtcqVaR6UiRmVulSoUlUoimTXoqBwyaxNV9MjM/0nVOjLjPGluMx1zqfRbqfywqqLE\n",
"0ytvdFQf2VWto9LvqsoVJ1XrOLg6x0sfhTZ3VpA4pULBqrvyU/ZvZtU+P2m+T6rEkdHxP7AAAAAA\n",
"AAAAABzOBz4AAAAAAAAAAB7mY1bBKFOSZEVR9dmnT1YEBmQqJleIHTnbrvOLnFoszCq74mYyVvS7\n",
"KmCqMnamNn4UvTLrZ1WUTzT/ytqu2p+ONpX9qcSzVI9PVK65a22jbSr7XJlbJTYlEwNT7SeyKnJn\n",
"XIeOLIbMXMdxZ+v48yf7mPUz/jzrc6znXCn9PZxvlXiTTOncu+JNZr/riP9YFWOzK6GqYw2qx+Nk\n",
"K+J/Trq1hQf6+/Vt+M2umI473RWbssqD4k1a5pbZZlVkUGJuP4bXVOW+LhPPUonHi6JjMu/DUdzJ\n",
"7HeVeJbKGnRFxVTmX2nTEQPTEVWyKmplVYzKrnEq/Y4yxz3T54rYlDujVk6KZ1nR79PiWSr9HhzP\n",
"clc0Sdfd8F1jv3sci+iVOfOvyTw9AgAAAAAAAABwMB/4AAAAAAAAAAB4mI/ZL+8q9L+qEvDTo1ZW\n",
"zH9VwMOquBzOclcF67NiYCreLQZm1f6scld0TEeszcyuNqOO454pmVypH9qlEulSiV+piOZSmcfs\n",
"eIw1kscYlcwadESvzFTGqZzrldiXjrvb2TFckCHyffJ6WlFVvRKNkblM7oomyVyKOk71yj5Xjscu\n",
"q+J/Vl1WGnSdXrveTaBLJRXi9KeGV5XYlExMxy67YlM6LIo3WRK9ktlmVSxPYm6VF2LHG1claqUS\n",
"iVJpk4lnibbJrMGqqJiONrviWVZFBnVEoFTmVomOman0O6rMP9PPrjajVVErHREiu8bJ9HNSjIp4\n",
"lpSnR6Ls2ucVfcyctLajJ8WZPGmuM/v+H/MeT//fUwAAAAAAAACAL8cHPgAAAAAAAAAAHuZjV4zK\n",
"zKoynk+OihGJ8m92HcOKjrk9PWboWV6vRnFJpdkV7K6z8EkxMJVxZ2Nnoj2i+WeO4ao16IiOifqc\n",
"9burTWadorWtrnUlaiXaZlXI2aq5jTWSK3PJ+Llh3LsiXlaONep4b6jEs2SueYUsjP+ncO5XLscd\n",
"lcx3RcVkTqVd+9xh1brteslF6XLXddaDQ0HlJQVdKpeI56nEf+zSESGyq9j0qtiUjMoarIhemf2u\n",
"Yy7jffh1vb7RDj//7dtrk0pMRyUGphK1EsWbZGJHKjEqlTaV6JiuqJgVbSrxLF3RMR1RKx1xM5U2\n",
"Mx37U+n35LiWXREolbW9c24ZHf2+eTzLriiWmV3xLB13cXfu84o+Ttqf0clzu65nx5c8ee53ju3v\n",
"RQAAAAAAAAAAD+MDHwAAAAAAAAAAD/OxKhzg3aJinl4teNXxEU3CTrPzdl95p2ikSnzGqiiJu2Jg\n",
"TorC6XJXdEymTVSGOBOFk2kzyrSJ9rES7fNbY31WZv5RaeZMvkEm0mVWGzcylnjOrFsUrZJpE42b\n",
"sTN6ZRyrI6ejMtfM6yNTLrxjnaI1ua6XuWXq+EenceYmOjPOqtiUaGkzL/dK3EzFqvSfjtNrUcpQ\n",
"i5PWaZHMqQ7X1Reyd4+T4k0y7oqO6VqnFYW8u968I7uiV2a/q9x8ZO7Nh9/9GCJcMu91Y0JjJmql\n",
"EiFSiYGJxs30W4kdybSpxMCsioqJjulsm451qhz3VeNUoomieVTHWRWBsmL+Mx1tRpU/D3VFiuwa\n",
"J+pnV3TMzn4XxNjsimfZFcVy0thdd7+nxLF07c+uu+4Oq57nnzbf0V1PdrvG7VhHfwsCAAAAAAAA\n",
"AHgYH/gAAAAAAAAAAHiYj0rx9plVpUB3RcWMdkWViFqhKhPwcLI741l2iWNgar2+enIMzHXFURiZ\n",
"fd41TiU2pSPCZVdk0KzNitiXyprM2lXiWU6OGcrEwKzIhVjV5s5+I7Maw+N6jzE2s5rJlTLkY78Z\n",
"URxLV27K8Lvvw2uuUok9czmuVL2v7PJMwzKV0n86Ymy6YkfuShmqrPWdl/DKOh0i83KphIxxlmfH\n",
"tVxX7kK/SyUCZcVFoPLG2zXOrhiYjrXOrEEleiWzTcf8C2tbiU3peN+d3Q5XYmCie6lKJMpsnCjG\n",
"JhNXmIkqyUS6rIiKqcw/c89Z2Z9V8SyVc2XX3D47blc/u+JaVkWgiGfJEc/yYldEytNiYDr6ODlC\n",
"5KS1HZ28bhlPn/9dT4t3/ukn2ueD/ywFAAAAAAAAAMCMD3wAAAAAAAAAADzMRyYW4q4YlevaV4Z0\n",
"1z4/PWplxfwzJYYrnr7Wu0TBGO+oss+ZoIWOccaee45HJdojEyUhBqYvNqUSVTKqtOmIn6nEjmTa\n",
"VM6nSiRNZi6V6JiO8ytjzFXIlJoeaxvPshnGfsa6vpk2mX/P9Nuhsrbj3LreIaN+K/W1u/JAgrun\n",
"ytQqDxuV0t/X9Tr98XRatUzjOF0xNiviWbpO48opuULlPFhkVejeLuP8Rbyc70nn10npTLn4jB3j\n",
"zn63Kp5lVwxMJarks31k+s2MU4moqcTLZO7NE21+fPv1z5VbwUoMTCbiIZrL7A2lErUS9TuLm6nM\n",
"LYo3qbTJjJ05Hpl16mizKzqmEoHSEQPTFW9SyVKrzD8a9/Q20TbiWXL9rhp3kIlnOTkm5a4Ika67\n",
"ybviWFbdDb/73GZEx9w3zslRK6s8KGkYAAAAAAAAAIAZH/gAAAAAAAAAAHiYj9kv3y1GZbQrOmZV\n",
"VMnozigcuK5ctfZdY3+FSJpXlRiYjiiJqM9Zv08veF6xKjpmV5uoTmlXJMpoVb8ZUZnlTKRLx1wy\n",
"sSmZiJqx3u7Pw8+baoOmzOofb8pjaFHJJulYy1W5KcPP3yfjRPUDZ4e0UMm8FIGSuVx1RJ5kbkYq\n",
"hznqt+tluCueJSph3RVrMzoo9uVJ5TYzp7HYl3XOikD5fZWK7+usyrEaVeM/njROxxWr8gbf0W8m\n",
"RiUzj454mdkbTCGSphLPUnl/j+JLMnEmHXObjRNFuFT2Zza3jjaVCJTM2lYiacY2meibVfEsK2Jg\n",
"ZlbEwKyKa+nq9642T4paOSk6ZtGfYDJxLC9tPt/k6HiWu+JY7opiqY49Ojky5OS5zayY787/73q3\n",
"+JVTolbefVwAAAAAAAAAAIp84AMAAAAAAAAA4GE+VhXSz5RKuWvsVeVFx0/P7Nq/XftzXe8fvMC9\n",
"7opnqYybCVF40jg/pXpeFZ/RETOSmVsUrVKJpMnEKKwa57PjzsbO1OyMShln5rYqEqXSb2b+K97t\n",
"MkQrQQsAACAASURBVPEsHccwo9Imk9OxKhNhHGtXxMtJBfWj60jXmkTjTM7JSrnwSlRJR1pOpk3m\n",
"36N+Zy/d8RB1zG2mY24Zp5ySq8a5MSMwemcQo8Jular2a3TFgVTG2lVM+uQYmEwfUb+VuWXWPjO3\n",
"6Jhm5lbJnCvM5ce31yYdESir4lkq41RiUyrxJpUYlUqbStRKR1RMV2zKiqiVyjGsRKCsmls0j+o4\n",
"Hf3OdLTJ/Lt4lto2nx33WhfPcnJMyleLY+l65DxpLqN3n9vMrj8liF7pcWdFjBX7rMIHAAAAAAAA\n",
"AMDD+MAHAAAAAAAAAMDDfKwqyL+rzGem0P+use8s9P0kd50rJzmoavTbsbY1tXX79at53kYMTE8M\n",
"zEzH3EZdbZ4U+1KZf2adOvan8rncTHRMZd0qIVRRnzOZce6KeMmoxCRlysZHd5035o58H/rJ7E40\n",
"lUrF9Ew/mX475jI7JStzG/upzC3z8lgRm5I59Tteupm31C6HpDzNdu+umBdxM31O+VvCvc/mlSiP\n",
"il1xLavGqdyjVfqI+s3cr2TmFs2lErXSFR1TmUtDm0zcxF+Df5/9LhPP0hGPlxkn2mZVRM2qNuMa\n",
"jMdnts1JkS6VuJzoGHZFoHREulSiPSrjRH1m+13RZlXUiniWtniWd4tN2TXOk+NYuu4M320uI9Er\n",
"c6JW1nnyPqvwAQAAAAAAAADwMD7wAQAAAAAAAADwMB+VovEzu0qQio5Zt9aiVuj05GiVSnXwTFjD\n",
"u4+T89rL61wq8ROZCJF3i4HpmNtdbTJrPdumEoHSEWNTmX8l0qVSDL9y7mciUaI2P0/ajLWLK3kN\n",
"szWYjRW1qYx9SkH9ikp0zOw8HtcgyhSZ/C5T+jt6uWSmNhNdRjr6yPTTFTPSEbWSeQuK+lkVz7Lr\n",
"ZjFTfn7ROD8N67Qq8uSUaBXfJsk56d1m1zP/awX4b4tGuisWpmusjhiYrrmtmEumj0oeW+bfd82l\n",
"0ObH8HqYXSSiaI+udL9KbMr4CJBpUxkniiqp7E+lzWytxzXIHMNMjE0UFZO5z87MvxK1smucSmTQ\n",
"Z/vIbNMVd9I138rYn51LV4zNZ/vI9NMVz1K4KYviWap3A5UgtT/a553j3BXFUh17tGudMk6JqLmu\n",
"NXfeq9Zt1/9VvVv0iqiVe614rwAAAAAAAAAA4EYfme+b3lnpYVd1i9FXrCTydHedK+/mpMocHXPp\n",
"+pJtRWX+mXoFd43z2T6z/cbzz1QFqXhSVZCZqE3lHaVrfyrjdFR2qVTrOPndIvOq6ng1V9ag66s7\n",
"mflW5pepYvJZlSoas/2L7lgqX9HM7F9H6Y3ZOEM/34c+ZkswHp6Oy/Hsd2M/iemnvlE39pNZ2s+O\n",
"m+mnq3JFZf4r+tjZbzTOIrsqcZxS8YPz7Lrr2fc3jF3f+esYJ3P/W+lnVx+ZNYn6mbWJ1jbTJnN8\n",
"ojbVccbfjZXpEm0ylR6iqgaZCgxRJY7qONF7deWerVJRolIVpFJ9JFMVpKvCR1S1YVWbSqWKVVU0\n",
"7ppb1Ge230qbFVU0VlXeUK3jqCoa716d4ytWBZlZcfd78tyeXrni6fPP+GqVN05KMuioyQgAAAAA\n",
"AAAAwI184AMAAAAAAAAA4GE+Zr+8KzZl5q4oFdEx68Y6uXj+050Ux/JunrS2q2JhToqbWRMDk4kD\n",
"OSkGZkV0TDVH4bNtquPsWttKbEq0za65ZVQihDrOg+o2HfEsKyJe7lS5amf2Oar9OzvuY79DH5Uy\n",
"3pkknErCTqXNbNkqyTeVNqNdcTPRuF39dDwUrHqwyKxtg9krd0X8yq5xZnzD5L6IVvEtu/vtiIFZ\n",
"0Uemn0qbTD8dUSsz0X12Jm4mc6+eKZJciPf78e3XP2ciQ6L30Ew0SSVqpRKbkmkTxct0jXNXDMzJ\n",
"kS6ZSJq7Il1WxcCsil6pRJXsik1ZFbVySDxLFMUybZPY5qTYlFVxMndFkzwpBmbGXO7rd9fz5DtG\n",
"r4hauc9da+DvLwAAAAAAAAAAD+MDHwAAAAAAAAAAD/Oxs7zoKdEemXiAVb5adAz8V5U4kNHsvK2U\n",
"auqYS8WqeJO7dOzPdfXsU08MzKufwtndGQOzIt4k02bcprIGlTazdpW6pR3HoxLpkjn7O+Y2U9mf\n",
"qI9Z/eBdMSkrIl6uq5axURHV084c90o8S6YseRDPkiplPpzH3yf7E52SldLMmX4q0SSVm4/KIVx1\n",
"2DtOlVXjRn109ZM51Tv6bbpkjKfXquiVk+4p6bHrbwvrxumIM4n6XNnvrn5Wxb5EMs8NUZvKPWdX\n",
"m2jdKm0y20zaVOImoviPzL1TJZokE7kRbTPGt8zG6YhayUSVrIqBqUStZKJ8ouOcGSdzD70r0mVF\n",
"DExmblGfmX4rUSWZN8yu2JSOqJWOfc70O3i3eJbqPfZd7+YnjfPkcWdWPW+ddCc7WrHP7xa1cmfs\n",
"yFeMWjnl7x7vdh4DAAAAAAAAANDEBz4AAAAAAAAAAB7mo6scZ+aTI3fFiJwSo3Jd7x+l8m77PCu1\n",
"c1cU0V1WRXA83V0RNZU2lWO4a5zZWJlrdsf8V8XAjD29ttkVA3NSdEymvn7H/Cv9Zso3V+ZfiXTJ\n",
"7M84t7FG8ixToBIDE407E/XbVXj1s+NWjbWNC3Em07l15D5kskp+/mQfs9+NfWTaJIIEKy/LTD5h\n",
"R2xKZmlHu9pUoko64k0qUSu7komqL6eOCJqoz+tquWl+t4iXr/Acsev599kRLicXub6uWnzJjj6q\n",
"bSoxlSvaZJ41Mm0KMSqf7uO6alExwzY/vr02qURUrIgzqUTHZKJWMnEzlRi+FXNbFekyi7GJ4lgq\n",
"kS6ZNpUIlI7IoK7YlMrr5bPjzrZZFYFyV5uZjn0eZOJZVkWKVN5N/mif1X7fLYrlpAiUjrl03aV+\n",
"teiV63p2bMVXiB25cx9HXzFeJnLS9QsAAAAAAAAAgE184AMAAAAAAAAA4GE+MtW6Oop4r3JSlMxd\n",
"0TEzmarXT/Zu0TFfUVdUTC1y4/fnsiuepWsulTWotNk1t1VRK4XQgdJ1Pep3PtcVMTAnRcdkxumY\n",
"f1fUyihTkjvKHeiKdInmWzmGM5U20Ttx5qpRuXua1VXuyGe4S+b1UcnCyPQRnceZ8u1jv5Nj+v37\n",
"729SKf09+92qCJRKzEg0t0ybSlRMRiXepCNqpSNWpRI3s2ouEyviWHxjg5VW/Q1j3d9GOl4RXa+q\n",
"jviVrgiXjjarYlI+2yYTozLK3K9U4loysS/DNpXIjUysRRQPUm0TRXlk4mY6olZmkSgrxqlE4VRi\n",
"YK6rJ9KlI/6nEunSFbXSEekS9Znpd9U4HW1m7ToexQtz6YpnqVyx/2ifK/s9OSbl5HE6xp05ZS6i\n",
"V/7Nu0WTvNv+jE7628JJUSsnzWVUCd0EAAAAAAAAAOBgPvABAAAAAAAAAPAwH5mNTorKEJvyalZi\n",
"Zte6nLIGzHXEncx0RKCs8vR4lg5PioW5rnh+laiVrn1e0W9mDfbFwFTaZMosR31UC39GtVi7Il2i\n",
"bQrlnEtRK7P9GevrjrkDmXLUmXfrjhiYz/57dpyMO+8QIyuyMDJZJZmaydEV6+dJm6jWdyITpSN6\n",
"ZdauKypmFMV/ZOaWaROdCpWIl1Vtoj4yTopn6ZrL4KR75siT5voVPO05e8278J3RKx19dBVaj/qZ\n",
"tYme1CpPu5WC+l1F+KM4lswadMTPTH7349uvf67EWmQiQzIRFZWYjqhNZW6ZqJUxwqUSzyLSpd6m\n",
"cgx3Rbp8dtyd4+yKdGno96R4llURIiveyXZFpOwc664IlFOiVzr7+Uddd6miVnLebX9Gdz6LnxJn\n",
"cso8rutZfxt50lwBAAAAAAAAALh84AMAAAAAAAAA4HE+Tip4XSmVv8udsSkjMSq8q68WFVOJQNkV\n",
"UbMqeiXTrmNdMtfFjqiVSr+JcIPDY2AqMSqZGJhVsSnR2JVIl654lmj+XXE5lSvJikiXavBTxV13\n",
"R5ksjFksymf7HfvIZJVUMkQy52SlrPowt79//91/Tk+lMv1om0oMTEcszGybTPpPJc5kV2RLR5td\n",
"467sZ4GT7pl5loNP6+u+6JXrqkUYRn08rc2KOJbMfUQmaiXaJnPfHc1j9rvENpWolUwURhQH0hXt\n",
"EbUZo1dmbVZFx7xbpMu4lruOYSYO5K5Il5nK66VjnFUxMNG4iX6fFs/S8VeCFeNW+333cU4a++R4\n",
"k5PnNiNqpeau5+yT4kxOmsvJf/c4ZZ1OXiMAAAAAAAAAACZ84AMAAAAAAAAA4GE+7owDyZSsv4vY\n",
"lDnrskY1CuMUq+ZfifoYVaJJdtkZmxKNXYnUWhVJUxln1dx2xc08KwamEjNSiYHpik2JomK6xonG\n",
"rUStdJ3JlXEy9Y5H0bpUaulW7brSR7EpGZmaw1FWSWbcSobIuE0moiazJsM434efM6dxJWplJtrl\n",
"SvLNbJejuWT2Z9SVytNxet0VtVLt486x/8GqK9WT+j3lvrxq1fPwk/rt+zvOXREuXU/ep8SxdMWZ\n",
"RNt0FfuPtukq3F+JoCvEy0TRK5ltZi/UMf6jErmRiSapRMdUxon6fcdIl2ibSjxLZpzMY/ZdkS4d\n",
"MSmZcaI+s/1GbcSztFz1K+Ou7Pfdx+kY9+R4kztjbSI7/+/n6fMfvVt0TOQrrHXFKcdn5q51O/l4\n",
"AQAAAAAAAAAw4QMfAAAAAAAAAAAP87EqRqVStv9O4mXOZg16PD06psuKqJg7Pz3XMZe74lpmKtfj\n",
"SmzKqBK1UpnLbB4rYmBmosLF+2JgZiONPa2KTRllyl5XImky+xPNP3NExvq6XeNE486O/Fhretxm\n",
"Vgs4Gidj1iYzVoeOO5JMHysiXDKvw8xrLCqRnnmNDeP8fbImmZdhtE0lBiZT8jlz0Y7mkoln6Yio\n",
"qbTJzC3qM9PmzgewQyJerss3Mjhfz7P4nTEqd427qk3XvdNnx65EoMzaVO4jovvSytwy9yuTbf72\n",
"7dc/ZyIeouiIyv1KVwxMJUJkRdTKqjbjmnRF4axa20rUSkekSyb6Juo302ZUGWdVpEslbmYwi2u5\n",
"K55lVaTIrhiYz/ZZHefOYLi7xu7oo+v55aS5jFbccT5prjN3Prc+6Qmgw0l/Izj5/xJPWqeMJ11X\n",
"AAAAAAAAAABYxAc+AAAAAAAAAAAe5qNajjMqN3JyJMrMKREhmVL/u2QqZcNv6YhNGWXCDSo65toV\n",
"l1MJn4jm0jWPaOxKXEtm7K59rqxtZS2jNpXYlJmO/akEeWTmEcfAxEd1vk1HbMqoEoEyOxOio7Yq\n",
"0iUTm1LJuYjGrWRLZPqtRLHs+vxyJaMi008lc2M0Ox4/B9vM1i3K8pjNNXpdZs7j4efvk/2tRK1E\n",
"6UzX1bPLn/337DiVVJ7KXD47bnabu9ocFM9yCt/y+Jre79n9zhiYXW0yr9YVES67Cvd3hBlktqlE\n",
"x2TaTLapRMNFERVj7Mhsm/GWOTNOJqYjijzZFQMzm1sl0qWyP9G6zY5P5nhU1il6gO+KdInmX4km\n",
"OjnSpTC3SjxL9aq5ItKlss3TYlN2RaI8OXrluu6NrflHJ8XAjESt5NwZ7SFa5axolZPWJXLSukVW\n",
"BXcCAAAAAAAAAHAQH/gAAAAAAAAAAHiYj2rDk8uDZgpJn6JSxp99umI6TrYiemWnk6NjVsytck52\n",
"xHbMxr4zKqayzx3jVNYys27RtT8TUZN5P4n2pxJrU1nraqxNFAWTi4GJ4k1mbTJxJlEuRObIVyJd\n",
"MkdxrNGbybmIolYyc8vEs3QUFK3EwNxpRTxLJnNjXOtMVkk0bqbfytVockwrL93Mv0f9ZmJgOqJV\n",
"ToqbqbQ5OeKlK42popJT98ebbHPy3J7m5L8DdMzt79e3hl4qqk9gu4q8d0SgjLriWTqK/XcED1Ti\n",
"WSrjzsYZfvdjch6PL5Do5+uKb6srcSCZGJhMHMhdMTBjH39JtKlEreyKqMkcw3G+mfvUzDgdMTCV\n",
"2JRKpEslyzbzGgv62BXP0hVDsuuKfVdsyrtFsTw9euXkOJOT55bx9PnfNe5Jz5wn/b/ZSesyOmmd\n",
"IievY8W77Q8AAAAAAAAAwNvzgQ8AAAAAAAAAgIf5OLl06EymHMzJ+3Ry3Ix4mbM8PWpltGt/Gipn\n",
"T62KMxndFR1T6ePOqJho7Ew0ySgTm1IZZ0UszKzfzDpW9uezfcz66YiBmbWrxMBEsTC5kSqrkNnr\n",
"StRK5qoXRaBk2mRiVCqFcDNxLCdHuFTuliqRLlEfldyRSjRR5lwZ+62UYp+0+fswl0xpaTEwPTEw\n",
"Mx1zu6vNrN2qNoOOq1n1SrpiLpyl4/m9628APf3sKqS+Ioql2mbVPj8pnmXcZlE8SyoGZvhdJaKi\n",
"cr+SGacSIZKJZ+mIQMm0WRED0zW3Fes2a1c5hpXzKzP/jvN4VaRLMM4snmXUEbWyKp5lZ+zLZ/u9\n",
"K+JlZb8dbUZ3Ra9Uxx59xaiVXd+A3/V/Oe8erXLS/4mdXD3hpHUanbxuGSev7ejpaw0AAAAAAAAA\n",
"8OV8nFxhYubkqhNPqj5S+eb3TqqN3OeuShzXteYTaJnKCBVPqiTSUTWkOpe7KodU5l85JzPjdFT0\n",
"qFyzM9fNTD2JaH8yVU66qsFUzu3Kl4jiqiCrKnxUqnVUShhk5hZVAZmdlePX7CpVQWbzP/l755U7\n",
"lKjSxqxsQFRaIPMVunFtM+NkvoMWzSXzLdvEuf996DdTqSJTkaFywapcgKO5dIybGaer+sioa/6j\n",
"XZU4bqr4wdzJ1Uc8l66kokdOpYrGqKOiR6WyyKpKIqu+rz9ss6rKQabSQ1QFZHahjOaSqW4RzTWz\n",
"zfiIMNtmV1WQXRVLKtU6uo7hisobXed+4b57rOBxV7WOjlpKs34r/XS9u6yoTHFyZQ6VOP7NSXMZ\n",
"rfh/gXersnFdX6/SxskVC06v/HDy2o1OX8vIKWt9yjwAAAAAAAAAAEjygQ8AAAAAAAAAgIf52FmS\n",
"tFJO/2RiR9hpV9TKaFf0ynXdFyfTsT8nR8dUoj0ycxl1xXJV4rFWzT+abyVqJTPOiliYar+VNRid\n",
"FOnSEwPz2strYelVkS7RNrMjEsW+ZOaWqTUdtanGtURlu2f9RlExmbicVSpBQ1H9458L48yO4bgG\n",
"mTyQ6ApWOT6zYzGcK7OpRKd25aLXFYHSETdTGbdjnMwaVDzt4W+BxJkOx/N3kP9qxX3EyfEsmW06\n",
"ggdm/x71m7nPS8TC/Pj2658zt0GVKIyOqJXZ3CrRJGM/UYxKdZzxd38Jxs202RUDU1nr64qjbzJR\n",
"K5nomLsiXRJtnhzPsjNG5a7YlFX9Pil+RezL3JOiVnb9VWfXt+jvjLk4pVLAyVEfp6zRbzl57SKn\n",
"r+1nvdu1CQAAAAAAAACAJj7wAQAAAAAAAADwMB/VSrqrYgVO0VWi/hTiZ3iiFdErM6uiZHZFx4wq\n",
"818VHbNrLh3rUpn/nVErlev6XXEzleOTict5UgzMa8TL/He/3+us50qN3kz94Kjw7axOcaXN6OkB\n",
"Bx3ZHjOV4z4ej0weSFSbeXZ8ooLHszZjBE3mVTf08/fEumXiWaJDlinfXolayYwTRavMYlWisXfF\n",
"wKx6UFq1tne1aVK52u7oo9rPu+t6Fu/o576/C+wq8F59ArureHlH0f2u4IG7QgUqQQqZe4/CumVi\n",
"LSq32ZXbuij2JRNnktmfjniWSptMdEwU4ZKJgVm1P7tieSpRK5lkzoZ4lpd/n/yu8tQQ9XtSPMud\n",
"sSkdwV0dbbrWtmOcFeNWxx6941zuGufdo1Xu/Lb+KXEgJ1csOGWNsk5ey4qnrf9n7XpiBgAAAAAA\n",
"AADgRj7wAQAAAAAAAADwMB/VEvxPijPJeLfIk0rJ/btkIgR41RWfUbEramW0a59nr5eT41hGq+JZ\n",
"Rl3vFdH8ds2lci3KjJsJRNg1t8o4n+1j1k9lDe487h1txm1mVX3jkraZGJjMKz7aplILODNOpk1m\n",
"pcZtop9nv8uEBnU4KdJl3KYQm5IqgFxpEx3DRCn275N97ohn6TiEmQiUjmiVGyNESlbEwJz8kFPU\n",
"Ea0CK73fs/qqQvdPKjLcFURwV9jCohiYStRKdPuV6XdVm1VxJlEcS2WcMb5lts04bqZNRwxMJQrn\n",
"uuLHq65kzuhcSbQZ41rujGephEt1BFLtilHZFcJVHfvdx+kYd9T1N/JVdxEr+n23WJWvGKNyclWA\n",
"J91RX9fZazl62tpG3m1/MjJ/IQcAAAAAAAAA4GA+8AEAAAAAAAAA8DAfs1++W4nOd4+oEYnC3b5C\n",
"vExHtEfGiv1ZFSXTEddyXT1re1d0TEe8SWack+bWsdZd504lEWHUFX2zIgYmE7QyRrzMYmBqI0UF\n",
"dmcrG0W4ZIJtZkfk5ECDyh1Xpq7yKKoPvqie87Y2leiYyXmxIp6lK6UnilqpjJPR0W9mfzKxNhWr\n",
"HtIq/Vb2cWyz6esWYmH4Lff9naBy8u9qk7Hq6Taa78nF/rv6rIyzIAbmx7fXJh23QZXIkHdrM3sT\n",
"+i+FNlGESyY6Joqfycwl0ybzqBTFtcz6aYgZGuNarit+8uuKdNkVz/KkSJeu2JdKv+8+Tse4Mx1z\n",
"ueuuosvT5z8So3J2FMZJ65Rx8lpmPH3+kaedT5/17vsHAAAAAAAAAPB2fOADAAAAAAAAAOBhPp4W\n",
"ZVL5hMq7xZtUyvbzNeyKN8l4jR24Z9yZFXPJBCJU7NqfroiNUcf8nx4dc1Icy11RMaOdkS6VuVTO\n",
"lbECb6YMbiUGplI6909B7Mv83I9qDFciNzIrlyn1XSkYnImOWaFyhmX6GetRz4/872/zbm2u6/r7\n",
"sLaVeJZRplR2Jdoj08eK2JFMPIsYGOCtrboH6AgR6AgauDMgoBK1sqOPRL+ZuJbMbd27tcnEmUTR\n",
"KpkIlLGPWXRMNM4YE5OZSyXSZTa3SjxLFPGSaPP0eJaOK96dkS67xqn0++7jdI29oo+nhcuNnh4L\n",
"Mzrp2+4nRWWctC6Rk9Yt42nzjTzpXFnlScfU8QIAAAAAAAAAeBgf+AAAAAAAAAAAeJiPk+JOusrp\n",
"P1lHLMHpnh5Jc1JsSuSuWJWZk9Zt17p0RIhkVGIhKlbtT8f8nx4dU1mDjlCIjMr+RG1Oj3SJ+si0\n",
"yVxnOmJgKnMb28xSFF5jX35JjDTudWZ2417PaiRX4llWlQPfYfYKGs+Wn4efK3W8M+NEcTrXFa/1\n",
"rjbXdX0f9imzyytiX7outlHESeVi1BWbcpeTYmAKbaLgq642HTLvW+xz598ANr08rtp79dMLp+8S\n",
"rdOu+6RKMMRMJbQiaJO5lcrEvtzVJhNNMt5mZ9pUxhmjVWZRK1GEy/jvs34y8SyVNtE2mVvoWb9R\n",
"QuPkHBwjWzJRK+OtUSVWpCMGJjPOrjaf/feucarvUCv67XpXu2vsk6JWVt0hiFLpcdId3En/Z3TS\n",
"ukSeNNeMk86DVd7tmFWccpxPmQcAAAAAAAAAAEk+8AEAAAAAAAAA8DAfq+I0Kp8keXpUScXT402g\n",
"qiOCo0tXvMRn7VqDXeOsWseu+e+KjhlVrvPjXDrGzYxdiY5ZERNzXX0xbysiXWYVeqNSs5k2lXXp\n",
"KLc7W4O4UPbrSD+HrWZ7mInyiIJsMmW7M6/wFVf62epGNblnbcYzqJJVEoUIXddrEehMHe/ouM/G\n",
"Ofgz55nDUYkVGfvpuHh2xZlE/Wbm2hEvU4m1yfCABV/YnYXXdwUPrNrHFVErXX0cXDi6ch9RuRXM\n",
"xIyM/XTEmczaRFExmTZjhMssBiaKjpmNM/YbxdzMtoluw7P9Du3GuJbZLU8lvGjF82IlAmVVm444\n",
"lqdHunSNdVfUyslhbCfPLePdYmFGJ/0V4eA7kaknzfek49zhSWvf5d2O4Sorzg1rDwAAAAAAAADw\n",
"MD7wAQAAAAAAAADwMB+rSv2rnLsuHuBpxNacY3a+nVxWKiriv1P0Wl21jrviZp4eL9OxTl2xKaO7\n",
"Ilx2jbtqnEo6QMa4TpmolVEmdGRXm3H+d5b1fb1m/7rVT5ORfkrFf4xHulLq+86S6KNKHe8/B9vM\n",
"Xg3j2ZHJ6RjrT2fWsaMIdCUGZrbNsM+r4llGmcMR9bsqOibqM9vvqcTApCReLdvG3jXuSe565n+z\n",
"0/g6K7rkZB1BBJl+uwIEOp5mC/eGP779+udMOl7mvTrz71HMW2YumdS98bYuepCY/S6KRJn9Lope\n",
"mfWbiWcZt8nMLeq3sj+J2+6PH6+bRHfMs9uXXc9xlQiUSpvKc3ZHbMqq2JGT+u3oo+Nq3PWOuuLv\n",
"v3eGvHV4t1iYmZPvyE6e2+jp3/B/0lpXPP34dHn347xKdP44vwAAAAAAAAAAHsYHPgAAAAAAAAAA\n",
"HuYjs9FXiB2piMrOvF8JVWbG18fTyhFVIgXusit2pGJX9MrMrriZyjWtss+rolVW9Nu1JrsiXDJz\n",
"WTFuZZxV+9MRFZMpjZ85JyvBF1GbXTEws5LD0fvhbJx/eol9+WUyl3EPOmJGZlYEV83OpjGepSN3\n",
"JJNrkTnyPwdtZkc+ioHpKjZd6Pfvw7p0lVXvuMnviJJZFWeSmVu0TWaNKhfkk+NnNj383RnPwvvb\n",
"9zeMk54yMzLzrQQcVLY5udD9iiCCSsxbok3m9qtyTxD9POsnE88SbZOZ/9hmvIWbbVOJQMnEs9wV\n",
"A9MQ6ZKJa5ndrlTO2rGfXfEslXDMjmfbmV2RLl0hVSva7Jpbx7gzK/5Ou+ouQmzK+42b8bS70pPX\n",
"suJp6/9HvdvxW+WrnRddrBsAAAAAAAAAwMP4wAcAAAAAAAAAwMN8iGv5N5VSOtbu1WwdRds82+w8\n",
"P7n01J3RKpG7Iml2RX3MrIpnGa3axxXz7+qzY58rc9l1Pt0Z6RL1O6v8Ox6jSmxKJhYmmkulRO9s\n",
"blG/mfeGTFnf8XhkYl9+fol9mbUaf5eZzax29ArjXo8RL5VIl9lZOW6TaVM5WypHvjLOgz6nXjmE\n",
"mX46+qhu824OiYp50FkNv+msS8jJT6qrrIqtqwQ0RH087KpXSd3LpPtF/WbiWTJxM1F8yWyc4Ca2\n",
"wgAAIABJREFUKPZldvs4Rq2M24z/fl2vt93jz11tojWYxNr8aVjL6I76ul7P7DEkcbZNLv7y99vM\n",
"NAQevbizzWf7qPZ7ctRKx5Wz693x5FCx0a53nDvvPE656zn53f2UNao6eW27PP0YdfgKx3kH55Jz\n",
"CQAAAAAAAADgcT7O+jZGj8qnWFTrqMl84/ereVpFjIqTq2hkROfpncfrzmoc/2hXZY6ZXWuwah9X\n",
"zL9rrh39PL3CR6YiRqXfaL6VKhqV+guZ6iOV+gtjv10VPsZ+Z9+YG9f2tc1rq5/DahazrwCOMt+7\n",
"q4i++jlW/Jhtk/muYbS6lTaZM6zyHbqu78cN/Xwf1q3yzdxKm0q1iNmLqqOfjsoVXXPb5ZDqHcCp\n",
"Tn5SHa2aa8eTW9fTX3RPUKkulmiTqZCRkblvGEVjZ6p1jNvMbtE62ow/zwrijVUyokocs9+Nt+b/\n",
"OdEmM7fhd1H1jtnvMtU7ojbXVXtWim5huuroRf121RHqqPBxZxWQu8bpGHdmxd8+T37XOmmcmVPu\n",
"Tp72fxinrFvF09a6w5OP105f8dy4y7udk++2PwAAAAAAAAAAb88HPgAAAAAAAAAAHubj9AiOSvma\n",
"d4ypOcX4CaHTz59TjOv0FcoynRybEjklViXrzviVf1S99nasXce1aFVcy2i2vyvm3/VeuGttR13z\n",
"j86vTEBFps+OqJhVcTOV8sHR2Jl1q5Q2HitCX9dr2eSx39m5Mv5ujH35KVUAORP7UhHV/p7tURTH\n",
"kilIPR612RGpFIGOyqhnjnzm31dF7NykI3akcqFc9aCU2Z9o7Mzc7oxr8ZCZihGjh9Ptus4urN4V\n",
"PLBiH3cFE6zs5wazh55K7EslGi4zTkebKK7lul5vxjNtxlvm8edZ1EoU4VKJgZm0+fjx658zd9DR\n",
"s8esTSUycxyncsfcFR2T6Tca57P/3jXOXbEqd479tNiUXe/mp7wDnfT37lPWJOuktevwtPVf4d2O\n",
"6V2cS2c5+bx2rgAAAAAAAAAAPIwPfAAAAAAAAAAAPMzHrpLpVSJD7jMrTaO0bI9xHb/iJ68yr+2T\n",
"yyONTolVyToptuauyJDRrvfDrve1FREuq+JmKnObVQveVTK14/VRiWeJ+pzJhFxEc+kaJyr1P2sz\n",
"lkSerdPYz9hmLIc82+b159fZ/Pn652A2mZXKnD3jNtEeXtfrXmbaRNEqs9WOYmAyUSvRz5m5VN9x\n",
"grMwU649Iyqj3jXOij5OGucrsJbw/3nSk93pdq1lxzgd9wRN4/z49uufKw85mRzBTNRKtE1mnDF6\n",
"JdMminiZ/S4T6TL+LopemW0z/jxGvEy2+dOwBr9MmkTPDZlQxEpM5azfStRKRxxLJVyqI2plpiMs\n",
"67N93jlO19h39bvrb9Un3SGc/Pf5k9Yp4+S17PC047HLux/3kzgH38/JsW8AAAAAAAAAACziAx8A\n",
"AAAAAAAAAA/z0dWRarXPkvmkjzidfWZrrSzTWbEjK6yK9lhl1TXhpDiWUeV82hVRsyLCZdUxvjM+\n",
"rhKtkokiiUTxJpk2Mx3RMatKA1dCOjLzj0JGZmtbKd88nv9/HgpD/9T2DjPO+M/BTGZtMmE4cbBN\n",
"PE7mKEbrklm3SuHoRe9+mXiW2dKtMI5dGbejj6/goHW6q3x25n3qLnfO9UnPxF8z9clTc07HleWu\n",
"tc7cdTaYndiZC0C0TaaPTAxMFPsyuzCOsS/jNplbziiuZfa7TJsxsmX8+T+9NvkY5jveQY8/X1ft\n",
"bji6y84EKXY9K1Xufjue9aJ5VPqo9nvXOCv6uK73i0m562+wJ7/7P+nv0jMnr+0qTz9md/mK58rT\n",
"OEZfj+sZAAAAAAAAAMDD+MAHAAAAAAAAAMDDjBXxeBNRuZ6zyrAyMx4jn87KqVzTnl7eakW0x04r\n",
"3oe6juldc9sVUbPrHuCkyJ1KBEpGFLUyE5WoX1Wu9q7Yl0yZ4tk2lbLK4za/DD9nIl3G8/aXSauf\n",
"r3+e9PR7vV5XXE87E1JTWYVMUejxCGTOhEqx6Wib6iszmu/BTz5dF8pdN/kHRaCE7ozl2cRzAlXv\n",
"/3eBp706ds23Y5yHrW10o1fpo2ubzNyi2JfZuGObTAxMtM2szRjZEv18XWGEyy+T/Rnv5yuRLuM2\n",
"Xc8elTvmVTGbUZuZFdEqlT5Pik1Z9XfCrxiBcvK7xdP/Hjw6ea13ebdjehJr+35cM96PYwoAAAAA\n",
"AAAA8DA+8AEAAAAAAAAA8DAf71/C8/kqn8o5uGA1RZljqrRWzUlxE3fZdc3YdY7uem87+fo8W+u7\n",
"3htOfo3NqhJ3nKeZuUWxL5USvZUomUy/mT4y8SyVNlEZ5Uwp5nFdZqWYo4rV89fPr3t6jXjJ1OT+\n",
"6+/2Of9dZRWiuJbr6inoXCk23VWQOjA7HLsujB2l5FdZEc/yBWJUAD5n1dPhSX8FqMS8rRi3aa0z\n",
"79XRNpV4lowormXWb+bmNrohnj1sjL8b41rGn68rjHCZhSaOv6tEukQ/X9fr2fNz8O/Xte85aLQq\n",
"rmXTnfm25+6Kd4t0mTnp3WN00jp1OHmt72JNzvJurznW8do9m9cyAAAAAAAAAMDD+MAHAAAAAAAA\n",
"AMDDfIj+WKervM1JFZ85W+Vc8amvdVZcX59eNuvO69mKc/3O99DoXDhprU9ep5mOqJWM6Jzsimf5\n",
"7LiZfrvKFGfGjfqZlWKOYmC6Il3G19m/vkS8/DJpNUa4jAWo/zJpUylIHZVVr0St7Dr7M2fLojuY\n",
"Son0TJsVnh6bkomSqZTK32VFFA58aXc96XSFIjz5SW3X3DOhFR1BFwWZB5bMNh3vS7NxorEzN6pR\n",
"xMt1vd6mZiJdxlvX/xL8+/Ua4fLvhn+vRLrM7rrHt+ZMPMvYpuuMXBF6uCrS5ZS4lutac8d/0tX6\n",
"5L/JnrROHd5tf3Y6+TzllXOdJ3BdWcO6AgAAAAAAAAA8jA98AAAAAAAAAAA8zMc7xoWc8ikWcTk8\n",
"Qcd5qlTYPidfs0+59v6Wk6/JldeQcyFnrDrccb3KRK2MutZknH9lLk+KgZm1q5RVjkozX9dr9emx\n",
"TPRsraPX4X+cFqQee/rPw8+zXIhoDzIrV4lJyfRRKcUe9VHljmSJk99wAN6a97Vluh4OK1ErlWi4\n",
"sU0lgiYad/a7TKTL+LshwuVP//drkzHC5V+Df7+uONJl/Pm64ijIyrNHps2MeJb7/k5w8pX05LlV\n",
"nPS3oKd5t3OBGq8h2Ovdrr2uIQAAAAAAAAAAD+MDHwAAAAAAAAAAD/Nx9wRWUHUY9rrzNedTa+c4\n",
"OTKlaldZr3d73zr5dbkrAmWVFWu7qzRwZpzMNlGZ5cw2s/mPJZ7HstBj5Mt1xefTL5Pf/UtYgHqM\n",
"eLmueA9mq1CJWjnpbB91nKkPf6capz9L//lsH9V+ADhU193iyXf0BZUHrpNvG8b9mc01iorJxM2M\n",
"P89ufseb5OHnWcDhGOHyH4efK5Eus9uZyh10ZpuozcxJz1wn9Fn1Zlemo9b2Sd7tPOAsXpfAU3l/\n",
"BAAAAAAAAAB4GB/4AAAAAAAAAAB4mI+TKxQCRL7aNUxZub3eLWpll3f7NGklBibj5NfzKdEx19VT\n",
"yrgSgDKWhZ6Vo/5L0Meszb+89LyquHSHVeOcfPYDABSt+gPFrgfTKPYlEwMzPDzN7of/w/Dz/zD8\n",
"PEa+XNd1/cvwc3RHfV21Z4LIzmeayMl31O/2N4FVTj6G8F95PQM8g+s1AAAAAAAAAMDD+MAHAAAA\n",
"AAAAAMDDiHQBeBDXbJ5AWdKcVVExp7rzvMh8wjma31g2+rpeS1T/Mvz8307afB9m81NYbPrftvp9\n",
"HcE3AAA8UiXyJdNm3GbWZvjdx49f//znSZN/P/z8Pw4/j/Et1zW/F/9HHff7K/nGJTOeyACALu43\n",
"AQAAAAAAAAAe5tv/fP34EW8GAJCjEg0zlS8edsmck9H8ZhVZ/tPw8/8y/Py/Ttr8b8PPf/vvhl/8\n",
"x0mj8WuQ4zb/LtFm3GYsT5LZZjbOuE3083W9ftWzo81sm/Hnn/82afSX4ef/Evx8Z5u/Bv+e6Xd2\n",
"Jkdzm7UZt4nmOttm7He2BtE2mbll9rkyl8+3+dOwLrNvK4+/G0/jTJux2tDPhTazccZ+Mm069ifq\n",
"Y1WbWbtMm4593tVm17kSvuSuK37pVtpkXsqzS2l0uV01l+jSmmlT2edZm2h/Km9Bd7b5Hr1ixjP7\n",
"ul7rTGS2ieq/ZdqsukkbtxlvFmfbjDedsza/3ub79d//6ufx3ve6Xu+Rx3vo/zxpE1VH7LjfX8kz\n",
"MjPOCwCgiwofAAAAAAAAAAAP4wMfAAAAAAAAAAAP86F0GMBz3FmCFLLcW+Sc/HpecQyr+1uZy9hm\n",
"HHvW57jNWDZ6jG+5ruv6v4af/4/h51mF9L99G34xfvx69nHs6CPalY9w+9g3AMCbqNwxZ+7Oo7vq\n",
"121+Grb58+Sm8z8MP/9Pw8//52SUMeZlvFefrUDlmSCy85km8tWeJ9/RT3dPABK8ngGewZ96AQAA\n",
"AAAAAAAexgc+AAAAAAAAAAAe5uPk8m8AEWXlWMl7ZM27vS5POg9WrO2uUsaZcdYUls6Vbx7LQo9x\n",
"LGMZ6et6LTf9vyfaXP80/DzW8Z3V9R1/t+sj26vGUbsYAHhLq56Edj1h9Qcj/vP1y0uLfx/0+tri\n",
"9b56vFcf7+VnM+t4jpjJHJ2Tnrk+qzKP8ZGni781cF3vdx6c7qt9Y9zrEniqr3a9BgAAAAAAAAB4\n",
"PB/4AAAAAAAAAAB4mI+7J7CCsl6wl1JnXJdr7x/xbq+hk8+Fu+bWdYw75n9XHEu1j7FdpRTzWOJ5\n",
"1mYsC12JdPm/Em2uPwc/z+ofR7Evs4iU8WPd48+ZNiepxMCcvD8lHVeSd3vHAeBXZu+Xs6yLz/ZT\n",
"6eMop4RjdKncEUc/z/qJ7qqvK7qL/pdJQMtfJr38o9nt8HjLPI466zOafWUFMis9s+pZKdJxFne9\n",
"EjruQitRMSe/kt/tznzXWr/dY971fufCk92ZQHvy9Qre0btde9/x/REAAAAAAAAA4K35wAcAAAAA\n",
"AAAAwMN8KBO0zruVg+E9uQY8i+tK3bud6yfvz0nn6Yp1Es+S6yNT/jjTb6Ww9Njmr4k2YxnoTKTL\n",
"+Lsx4uXv/82k0VjVeqxLPKtTPP4uimu5rlzsy2fbzMaJomIq41bdWXv1rZ38jgPwxnxFa6Gu97ao\n",
"n67AwvF3mTvrqM1s7tGd9uwuevzdeBf9enP7r9c/T/r5/81O/bGXKOJlNrNMpEsUBZlZtZlMP1Gb\n",
"jnEzxn4rMSonPTOP8z/pzvakv52MKut08tvWyWt9XWc/yp70mnl3Ha+h0891uK5zrisnv29VvNv+\n",
"AAAAAAAAAAC8PR/4AAAAAAAAAAB4mA8lfs53Snkbzuf1fBav3VfvtiYnv+ZOWutV67RqHzvmuyuu\n",
"pTLOqvLBHWWKM/2O8SyzuUblm2fFqMcy0JVIl7+MdVjH+Jbreq0/HUW8zH73c6JNFMfSEfFSFX3k\n",
"fGcMzItMWfVKKfYVTrrSV1TCoUZ3vhM/ff3hMON1ffZmvULma1CZbe6af4fZe+qK+Vei4TJtWlQi\n",
"UqrbRCqhIZk2mWDEjrvo8WZ3vHG9rp+Hm9d/HX7OpBVmUhHH2WZiHscjmImBWfUc1HEXVLlbWdVv\n",
"ZZwoTqYyj0xEza6/YdwZ4xGt3Z3fEl6x/iev9elWnAsn/z316Srn+tPPUfbpeu2eHGP1ZCp8AAAA\n",
"AAAAAAA8jA98AAAAAAAAAAA8zIdyPe9JWaz347W6jrV9v2vGycf0KxafPznSpWtuK6JVKnPriGuZ\n",
"9dPRJlOmOBPPkilGPfYzFpquRLr8ZdLmJcLlX4af/3nSaPxdph51tM2sFmK0TVeJ9KjfrlL5LR9T\n",
"z8SzrBKVVb/Tirm8250FwB+0KjblpCiZKJ5l1dwy9zilt7qOYItMAEjHXf+sjyicpCsYcfzdGHoY\n",
"33T+HN4g90S6jPfzs6PT8exRiX3Z9YxW3WZUiQD9o33OzI77SX8nGN31zdvZ/uwqp185HifPrWLX\n",
"cX/SE9iqY3zSU/aTZM7RJ51f5FReLypInM3xAQAAAAAAAAB4GB/4AAAAAAAAAAB4mA+leL4m5a3O\n",
"5xjVfMVr2tPPlZOP2btFoIx27d+dsSkdfayKVqmM0xED01EKuKtM8apIl0ox6ijS5W+zmqNRhMuf\n",
"J23G340/ZyJdxo9sz9pE0Sqz/anEs4xtMrVZo22q9V0z+3isrivlrneQk9+9R0+aa41vcVD19q+O\n",
"VTEqq+yKQOm4aDzuwlO5A4766NqmcqddCU/M3EVH2/x10mYMSonCV2bb/NprxMt1/TT0k7ntG2c/\n",
"ziTzHBEF41zXvc9KK9qMKn3Mjvpnx63OZRz7pIiXu6I97ozPWLHPXcdjxbrc+Tfajv15+t+YK+fb\n",
"298PNxnPr6efK19BdG4/6k9mpDzuEQ0AAAAAAAAA4KvzgQ8AAAAAAAAAgIf56OpICZ/345juo3TY\n",
"3Lufg0877icfj5PW8mkxKf9o1dy7+j0pWuWz46yae6aYc9RvV2ngaJvZ3KK4llk/mXiWqPj0rM1Y\n",
"jPrvPw+/mMWzjNWmM5EuY43hKOJl1mb8eVaHcdxm3J9MDEwmriX6+HhHxMtsm2UfW6+8qlY5qQD1\n",
"uzvnLmfXNzKe9M2PO0vNVkrU32XXXI+6quyKQHm6jnW6a60zEXQtMpEoM9ErIvOKieJaZnPpCDnM\n",
"3J2PP493zNcVR7iMQYk1Pw03yf9y/fK7s7iuWqRL9Nwwu7ZmjkZ0h1mJgZm5q00lwmVss+qZuSPi\n",
"5fRIlxURLrviWipre2dETWTXMV6la23PebqKVfb5Sfu3yuxcP+o54c3dFanFOh2vH8ccAAAAAAAA\n",
"AOBhfOADAAAAAAAAAOBhPk4vP3T6/L4aZZl6OK/f71x62jE9af1PWbtda3J6bMqoY13uLJm6YuyO\n",
"4s6ZflaNkynZW1mDsc1YDrkSA3NdcWHpcZxMm799mzQao1R+Cf599ruoj9k2UVxLZptZmygCZfax\n",
"7zH2JdMmGicTA5MZJ2Mc69uP4RfVcu1Rm8yrquMqvesd85R35ndgLeG6Ll816vSk3KfMPUFHZFtm\n",
"nJeMja6nhI57gkq4RyZoJIqKqQQjzsYZ24wRLpmDmtnm99f2z5Ob9X8a+s1EQ0axL7Nnj0y8SbT6\n",
"Xc9klTPys+Nm+pn1UYlWieZSuWTcGVmxKgJlRYRL19tNdAxPihC5K6Im42mxI5W1POlv1ZHM8fiK\n",
"T4LjunzFNVhh1XWfmlXn9YrHLwAAAAAAAAAADucDHwAAAAAAAAAAD3N8pEvFk8o/Pd07nj8rfMVz\n",
"8snnxtOO1ylrfee6Pb3I/Yq165rrkyJdVo2T6bdS0rYyTkdJ3kyMStTvrPxxR3TMrN8oGiZTjPrv\n",
"Y63DTDzLWHN41uafh58zMTDjNuPPmUiXMXol02Zcg0zUSkebTAxM5t8z5dofpePquutK2dXvriCr\n",
"VU6547qPb4vsM55ts8v827vzhBvfY8Ybi66Eimicio5IlKoV+7NN5o648l436zeKWqlEx2TaZAJN\n",
"om1mbaIIl1U3bfFa/zTcaP80XE1np/74u0ySYiaeJbquz9pEL6GukKHP9nFdPfEsK/rI9hP1m3FX\n",
"nEzXHemKCJddcTMzp8SxVPd3xZPG02JVnhZbE4nW/2n//1Ah4qVmVcQWryqvw5P/HOlcAQAAAAAA\n",
"AAB4GB/4AAAAAAAAAAB4mI+vUDooQzmhHs6nr3EuPf04n3yMTlnbO9do19ir1nrF/Lvm2jG3k6JW\n",
"KuPcFftSiU1Z1SZTojfqY1ZeuBIdE8W1zMYK41quK448mdX+jeJYMvEsmTbj78a5ztpE85/tz7gu\n",
"HW1ma52JcBl1VPrOxL6Uyqp3tKlYVZy5wyl3J1lPmy+w1ZNiR2bvdR3z7ViDrrlF8XGZaLhKm+9d\n",
"7+UdgRmZ6JhxccebtEw8S6XN+PMY33Jdrwv+l+HnrsLX41qPN+Izvx+k8vPkhnj83fi8Mju9Mitb\n",
"iVqplMLviPMc96fSJhPnOco8RmTu8jqiYjJ2xWV0lPbvilqJ1nJVJMeutb4zUuSU+JWnxao8OTYl\n",
"s9Yn/x9Gxex4nXyMdhmP88mRIServF7erSLGu+0PAAAAAAAAAMDb+3i3T4nt5NNnOV/tHHu38+Jp\n",
"x+/k9b9rLe88hruOx6p9XDH/rrl2zO2kyhsdbToqcWT66fqGUEeljco3tkaZNuM2mW+tZeY29jOb\n",
"69++Db/IVKqItslU0Ri3mX2JMKroMWszjjNuM9ufqGJJ5quGmWodYz/Rz7PfRd+6zWyT+Wbu0TJV\n",
"QTIqV4moj5mT755WOeMO17cveAdHXUGeVL2jS6WyVkalgteKPm41nt2Vu+ZMnYPKHX1mnKhax+ym\n",
"M2ozuyEbq36M28yqgqwwW7fxRjtzTH/9u7Hix0+TEzlTgaFy1KMKH5mzq1J5IzO3qN/KN9dnZ2Tl\n",
"WXbUVTmk0u8p43RVbVixz6sqSuyqVHFnZY5TqnGseo11eHoVDRUx3k9XxaV3V3ldWscHPm4BAAAA\n",
"AAAAAHx1PvABAAAAAAAAAPAwH5mNlAmqObkc1E7vfv48/Tg/6ficvNZiU/qs2p8V8++aa8fcdkWt\n",
"VPo4KYRgVaRLpU1H1EqlTUeh6UzR6Mw4YVzLdb3W5NsV6TJWgM60ycxt7Kdjf8bIl9k2mXiWKPYl\n",
"c3wy5dujuVTiZqbtMmdh5RWy6+q5o4+ZjoCsrqv4k+5U98zVNzZYafbKnV36/7CnnciZqJhonzL7\n",
"nBlnRWzN7H230m/H3DruCTJtvldiVHbFs8wWbnwl/jX499k4UVzLdcUHMbO4Y4RL5qatowh35d4j\n",
"c5/3659/msz1p0LsS+aoj710PMdl4gEqMTCr2kRnRuaor4rcWNVv5ph1jLNr3BWxI6vWZFdEyp1R\n",
"LNHarXqiOTla5eRImpmO6+JJovc63tOKuK+vYMX7IwAAAAAAAAAAN/KBDwAAAAAAAACAh/l4Uun8\n",
"d/QVSxS927nxpGP4tLU/ab53Heenx6iM7iw+HzlpbncV+t81146wgK5+uuaSKd68o01XPEulOPVL\n",
"pMsY1zL7mPEYRTKrRj22y0SgRP2OcS2zbaLoldk2q2Jgxn4zbcZ1y6x1VF27q6x6NG618ve3H8Mv\n",
"Kmd7ReaV+Nk+fut3kY6r3pOsevc+6S70j7vzWx5Ksb6eTUsiUhLj7hx7iVUnclecySky+1NZy8x7\n",
"9Wf7qPYT9Zu5j3g5xpU74t/63R/ttxJBlwkEGa8AmUiXMZ4lcxDHbf4yabNC5amtstazE2yMfXm9\n",
"2r5Gwfzpd36aj9wRGNQVAxP1satNJsxo3KbrbwCVaIzMfVFHXEklPuOucWdWRLasihTZFQeyKxLl\n",
"zuiVu+JmMsZ1OflpMfN+wj6V6+TTrbrOv5vK6zI6f6wrAAAAAAAAAMDD+MAHAAAAAAAAAMDDfJxU\n",
"fkhpobPLQXV5t+P8pGN20lxPOg/uWpenx6iMTo8IOyX2ZVfUyq6xnx7pUhnnzjaVAtBRH7NizlEp\n",
"4Je4luuKI0RmHzPORJOM9eoybaJtKlErszZj1EomNmX8XaVNZQ0yUStRv5WolUybo6yKgamEOEV9\n",
"dOm4UnZctU+/kwAe584YmDBC5Irnl5l/ZpyKSr9RzFtl3FI8y50qMTCZNtEJNrsZjO76ZydydAD+\n",
"OmkT3WTODuKKF2fmPuLlqaawTaZY/qzf34/Y+TkRl5O5S32J2fzdUef9dDyXVsaptJnpiIWoXH5H\n",
"1TvQFVExs7k8OTpmpuN4rIpn2RWT8m7xMqeMO7NrreEJvmJszWhVJNgJfQIAAAAAAAAAsJAPfAAA\n",
"AAAAAAAAPMzH00oLKcj7fuWgnnZMnzTfk86Vk9ZNlErNqv15ctTKzK4i/U8epyvSpSNAoBLWsCqe\n",
"JTPOinK700LGY2TLWF83rjica5OJDIkiT7oiUMbIlnGbMb7lul7nNm4zi4GJxumKtamsW1SBu1L5\n",
"e1eb67oSYUSFNhmVcKWoj4xK6fKnO+lu5PNtKt+2uOsbGl+xDOvJZmf+7DK+Y+zMuGOb1Pl00gvk\n",
"6MiQgmh/OqJXZv2OuuJZovuGzH3quM336j1C6U57QZvZwlVuuKIb+sw4u3TcO2WeuDJXwUy/4zpl\n",
"omJ+Gn76p+Hn1zYvp3Yw6mzkSojNuCqZFeiI2MjsT6bNZ/vI9FPtY0VUTFeMyoromI64lt8a+zPz\n",
"6JrLziifilXzH+3an1HlOrPKSXOJrvMnOWndKt4t3qQrDuvJut6ndnj3YwEAAAAAAAAA8HZ84AMA\n",
"AAAAAAAA4GE+nlYSp+LkEkUdnn4Mnzb/k8+nk9byrnW6aw1W7e/TY2GeHrUyOiUS5fRxon47oli6\n",
"+umKWnlUPMuqyI0onqUSVTL7XSXSJYo3mf1ujGcZ+5htU5lb1Mfsd5l4k+iYvVub67riV0jXVW9V\n",
"CfEV41T67Li6dl3FK066IwaOc1cMTCYCJTO3aJvMOB0xKpmxK+Nk4lk6omPGbb5X7rxnv3t6m3Gb\n",
"Vfk/u75/GN0LVtZtdo+TCTSJtqlExbyu7Rjz8lPiRjtalUrg0aoYmGgevzX2781j5s5Il9G4j5V+\n",
"K5EolTa75jbzbtExo651iqya/2i2Pyue4nbtT8ZJUSUnzYWzvFskzWhXLNpdnjRXAAAAAAAAAAAu\n",
"H/gAAAAAAAAAAHicj9kvT46sWOXdyhY9aX+edr6dvLZfLUbluvbt85OjVU4vmH5X1MropEiUk8dZ\n",
"FaPy2T5WzmVFPEumn0qR5TCu5bri0tiZNlFcS6ZNJgZmVsk4ioaZtYkiXGZtogiXTNTKnwttoviZ\n",
"d2xTiQwaf/ftx2SjSoRLRwxMptR3pOvKWOk32iYz7snhcDOV+e5q88e9W9lV+mQCBJboiPboih2p\n",
"ePcYmEqbXckelXiWTD+p86sSbDH+POu44+Z8V5txm45sn4yT38kyT4OZeJZKoMnYZnZKJd/aAAAg\n",
"AElEQVROjscoDlsZY1/GWJhMbEom0mVUiYGJ5nFdtRiYTL+jXZEuu2JS3i0qZvRu0TEzd8WxdD2x\n",
"daxtxV3xJpVrHnSqxKKdrOv6+ySV90sAAAAAAAAAAA7iAx8AAAAAAAAAAA/zUS0TdHKsRYd327+n\n",
"lYM6ef1PWcuvEKMyenKsynXtm/9d8SYzT5/LrriZXTEvHUX7V61jRyRKZuxKuMGueJaXfx/jWq4r\n",
"LkedKZWdiVqJxplVKY4qQGfiTSqxL5XYlEoMzBj5Uh0nijzp2p8ohqerinelTcd5XHtVTX63IgZm\n",
"pnJl6QjIOkk03xXvbM/zbiVGeT+3xcKssiLu5LpqkTR3yUTHZPanEpuyIp6lEoUza/O9FLgY/Dzr\n",
"pyM6JtPmr8PPlRu7zLtUx0HtUlm36BjOrnqZfqMIl8yDUKZNJZvz98NVxsiXf/vd7x+zSgxqVwxM\n",
"R5tK5EamrHolEqUjpqNStn/WZyUuJ4r/mamMc0qUz67omMxcZlbEl9wVJXNda54G74xaES/zLE+L\n",
"RKm8B53s3eNMKu+X77YGAAAAAAAAAABvzwc+AAAAAAAAAAAe5mNnEdx3K7j75LJGpx+Lk9f2lLW7\n",
"c42eHq0yWrU/K/o9OW7mK0SvdIxbKfyfcVccS1dkzUkhCivaLItnydRuq1RmHrcZY0cy42SqB2ei\n",
"SaJ+KxEo4/7MthkjXCoxMKviWTJrO65bJTqm45zMVKeuRMeUIlFWxcB89t+z41T67Qjv6pjLqrur\n",
"yjvvrjb3PSV0lGI9pY+vYHamVGJROqJVbotnyURu3NXmutZ8NaorBibapis9IxqnsraVcbviWSrr\n",
"9n1VbEp0f5K5X8kckGhhZvtTWdzRSZEuK1Sv4tEVN3N+VdpkYmD6HzIzMTCVUux3xcBkyvZ3RXlE\n",
"61KJWqnsc2V/umJsonWqxE90HZ+OyI2u+IxVcxmtiGPpenKqRAZV3BW1An/EkyNPOuK/TrLq+tzR\n",
"BgAAAAAAAACAG/nABwAAAAAAAADAw2yNdImcHOORcdJaRk5f65PX8q61u2tNdu7vrn0UtVLz9Lns\n",
"Ks5+V2zKZ/vM9ntSpMvR8SyjSmnpStTKqkiXKNojE88SRbHM+slErdwVmzKbWxT70jW3cezM2kb9\n",
"Zs6vSuRO5ZzMlG//9mP4xeyqEZWw7oqBicbd1W/XFXjFu1DGyXf8ezypBCn8lq6Imsdb8XWqTJzJ\n",
"rhiYyjgdSR5d8Swd6SapqJXo51k/UVzLdcWLO5tbdLJkFioTHTOqnAgduo5PdM+WucLN+h3bjf3O\n",
"HjaisILMA1bmHjR6QWQCKDLBCr8f+zI/u54bAzNTudyOOmJhrmtNhEslbiYTlzPqGicatytSoBIV\n",
"U+ljVTzLijiTrlib0a7olbuiZK5r31P0rn2E63p2/Mx19cSKdXjaugEAAAAAAAAAfHk+8AEAAAAA\n",
"AAAA8DAfTyvF8/TCvyev98lre9K6vXu0ypNjVWZOjlqZ6ZjvV4xe6Rj3ztiUFf2uirCpzG1Vv6va\n",
"vES2ZCJQRquiVjoiXSrRHpV4lsw4lciQXZEuY1XlrhiYcZto3TLbZNYtM04lniXan67zeFvwU8cV\n",
"K1O+/bP/nhk3s01XRE2lTeWdaVebXXcOZJwcdVMp7E9SJjLkSW064kwqbbpiYKJxKrkEmblV1m1V\n",
"3MxLXfjM+3smaiWKcJlNriMGZuwj06Zysvw1+PeMJ70TXFcuaiV6B8nEwFTiWaKb9Uy/s+PxxyNd\n",
"KiEorzEw8fl1VwzMTCUCZVc8S+bfo/l3xMLM+h1VYi66xvnsuLOxO2JVsmNH/VT6WBX18aTomNHO\n",
"6BVRK/c5OXakEnW1S0es1Z26IrV2OGUeAAAAAAAAAAAkfbzj95Ke9Km2k9f/pHU8aZ3erdLGrnGf\n",
"vm6nVN6YuWtud1YB2TXfFePcWUlk1/e+K+OsqmoSVuuYqVQ5iPrYVeEjU0WjMk6lKkimQkam6kQ0\n",
"dleFj2i+u6qCVNpUqqd0VeuovF4q5/7LK3z6ih9+zlTvqFxZom/Z7rqadr07rHgnPrmax3XdVdGj\n",
"41srXd98OfkbNNR0VB+ZneUd/ZTOt7uqd2TarWqzouLHbOyo4sdsm46KJZn7iMrX6jP3EdHX0Gfj\n",
"vBTryDzFZO4Jou+HZu5xMgcoqrRRKQczUznwkZPepSpX18rVNHPPmXkIiM7B2Twq1TqiK/2aCh+V\n",
"i0SmKki0N5UKH5UKGTMd1UW6qnVU3t8rV7yo38z+jLrGicbNHNOTK4d0VA2ZefdKIjPvVonj3fbn\n",
"6Z5UbeSku7rR06uPjE46DwAAAAAAAAAASPCBDwAAAAAAAACAh/moNnxSyZ6T4kAiJ63rSet217rc\n",
"uQa7xha18qprrqfM7c7olY4+TolieVq/J8ezVMd9iWcZZaIjMv8eVTuujNMVaxG1mVXorYxTifao\n",
"RK9k5h/FpGSiSaLolUybXyZtVsTAVI5HZm3HfmdrEB2zTLnzTKXpKAbm249Jo1XxLJVS7J8d97fG\n",
"/sy/d81l1TvZrjiWe6JYqv50zc7lzzm5fOjJc3uak/4OMGqZ211fNapEr8za3dVmVcSLGJhaDMz0\n",
"mFbCCqLFnL1vRfEss8lFCzVrM/Ybjftb/fzePE7XEZBVuXfK3NBn2lSiVqKb/ko8y+w8rlxYKpEu\n",
"n79IjLEvr/++JwZm1m8lAiVT6j8qub8qNmVFLMxvjR2NEz0l7BonM/auqJjKPmesio7peNJ7elTJ\n",
"0+cfWXVO0ufkeJnRu8XNjE5eewAAAAAAAAAAJnzgAwAAAAAAAADgYT5Wlb85KQ4k4+QyQCet5VeL\n",
"Vrlz7UWtvDp5rifFwDwpemXn2KfEyewq2p8Ze1WkS9RHGM1yXbVS05kKsFEfsza7Il0q42QiNzoi\n",
"XTJzq0S6ZOI/opiUzFyi6JXMOJW5ZSJ27oqBqRzDTAxMZpxwm0xYVGabVfEsHVf6jneDjqt4tc3J\n",
"cSx33Qmd6+Qypaxz8t84Srq+rlTp55SIl2q/0T53RLxktrkzbqZyf5+5Z/5eufcYOx63qSxuptD9\n",
"rniWykmaGafST0XHvVMmBiZzr1Ep1F+JWolibCqRLpUi/JkYmI5xMm2i1+maGJjZyKOOs+C3xv7M\n",
"PGb9Zq5EHVElmTMlmsfKuUTjzDw5KqYrdqBy9e2Iion67Or33aNXWKcSsbVK5f1kl67r8S6V637k\n",
"pP0DAAAAAAAAACDBBz4AAAAAAAAAAB7m4ytEVlScXMT3znU7ZV12zePd1nrn/pw8/465nRSHddf+\n",
"nBKRsnOcVf3uioFZEc8y3WaMbOmKZxllyizvinSJ+u0apxK1siLSZValeOy3EolyUmzKSW0q+xPF\n",
"sWTOyUo8S+bcH3/38WP4xexKM16hMttEP2f6nY1TKd9emVvUx8yKCJcnRbFUnRMDc0o5VPgtLc9B\n",
"d8az3DVuJaEi02ZVdEzlHjrKKsjUgM6kNVTuV6JxZvuTmcv3SlhBdB+RuceJ4yb2nSxRm4pd74az\n",
"tc7EsWT6GVViUzLbjDqiVsa5znIdO8bJnMfR3DIv3lFlbjMdMTCv40QRFatiU6I+Zv1k4jSiuWRe\n",
"7ZW5jSpvW9W5jHZFxZwSiVLVMRexKX1xOdRe7+/m5DWovJ/scle8zEnHBwAAAAAAAACABB/4AAAA\n",
"AAAAAAB4mI+TyvmcEhcyY53m7prLruPxbtExq/bnpHiT0clz2xVVcufYTx9nRUH6LxnPkvn3Sr+Z\n",
"aJJonErUyq5xVkW6VOJZKm3Gyr+V/Zltc1KkSxRjkxknU4Y8alMZpysGpjLOyz5WolcyJZ9TV7ng\n",
"37uiVirvDtHcKu8od737dbXp6qPjjuqP97Hq2xerSpmu6PeksqsVq541ntRvW58dL4hKH3fGy3RE\n",
"w0SpHdf1epAybcZtMvcro8r9fWVulYiajti665qkTUSLPev4r4nJVHZ6RYRLZqEy40R9jGuyys6/\n",
"sEQviMo92mzcKAamK86kkse0IjYlE4GUCYqIxqnkPlWzosZezomBicbpioEZdcyt2m/HOCfPLRo3\n",
"M3bm/LpL19xWRMWcvG4ZomPWOTlG5U4nr8sp8TInrQkAAAAAAAAAAAk+8AEAAAAAAAAA8DAfTyoT\n",
"dF1nlQU6Ze3unMddx0PUSs3J8SbXtWZ+XXO7K17mSeNWj9+KsVYVll+1lrfFs4wycSCf/fdZv5U2\n",
"s3arYmB2jbMi0qUyTlekS7TNO0a6VI5H1O8YozLrJ7O2HccjU+482ufMaywVxVKJa8nEmUSlsTPx\n",
"MiuiZDLjZNpknNzmpVZ+Qx9VJz2J/ppvcVB17ll93RfxMmu3K67llFiY2TaZpJKONJDKvUemhnIl\n",
"1iaTvDD+7nsl4KByH5RZ3EouTxQv0xHX0tVvh66/GHXknmauyJVQgV1RK5kQkRURKLM1iLaZ7V80\n",
"/8w4mXv3qE1m7PjC+LqSz4qBGWUu8yv63RW9khmr0qYrcmPXunSMu8vJc4M/4pTYlMz7yS4dwX27\n",
"nDIPAAAAAAAAAACSfOADAAAAAAAAAOBhPjIbnVzm86RySSfNRdRKj6fvz6r5nzzfuyJQZt49juWk\n",
"cVbN5a64mbePZ+mKdKm0ycSmdIyzKtIliukQ6ZKbS1ekyxi/UplbZm07omMqUSsd58rsuH/7Mfwi\n",
"E6MyykStZPpdEceSGSfTJlJZp8q70K53/JOiV9bc7T7p2xZ3lUtl7uS/ycwsme/spKykQGTiTFbM\n",
"pSuuJeqnq00kswaZRISozWxdKzEw0f1KZW6zdi/zzcTJjZMbY1Vm22SK5Y/jtOzQRCX/5xRd78yV\n",
"8IjP/vtsnMpfNTLHfbzpnx3DStTKXbEpn49Eyd0PV2J6KudKJgYmOheeFQPz2XFX9VuJRKlEr8zG\n",
"6lqXjjYdOsa9M6Jml1Vz64jYYZ27YlROjk25828nmRixu1SivAAAAAAAAAAAOJgPfAAAAAAAAAAA\n",
"PMzHSdEFq9w1t5NKIz09miRjxT4+PTrm3aNXrqtnH58eA/P0OJZKmxVzuSvi5bqK8SyjTFxDR78n\n",
"t6nEmcx0RK10RLpk2qyKdIn2pyvSZYxEycS+rIqBibYZ57pqnEwZ8sw4UeXvSptMDEzm+ISlmDNx\n",
"LbOraxTPUrnSZ8pRr4pW6Yhjyehoc1eEy0kxMK9WfLvCNzZYadfzY1tZ3LviWbrm0pGEURk3cyHJ\n",
"xKREc6nUls/UUI7WKdOmEgNTiYr5PluESvZN9L6byb7pOFm6XjCnmN0QV/anI9JlVehDJWol6mPW\n",
"T2acaJtMbErmHSS6n6/sTyZGJdMmsz9Rv5U2a+a/KgZmVIlaqbwlZc7iVf0+aZx3i2fpiDupRvlw\n",
"jkxU1NOJTaldS3epXLNH73bOAgAAAAAAAAC8PR/4AAAAAAAAAAB4mI+dpYVOKWP0brEjGV9hn58c\n",
"v/IVoldGJ8VJ7YoquWvck6JYZjoKm362z2y/pQL1K+JZMtt09JuJKrmrzWybSmxKZtxdkS4rYmAy\n",
"MR2ZKrJRzEgl0qUyzmybXZEumeMelfqu7E9lbpU1qMSzVM79bz8mjaLyzZlS5pnYl8y/R7EplXeL\n",
"SptUANimNlEfGZmy0ZV+TrqDHD0nFubOcXaVar3TrufSu55/Z29Tn7YqFaIj4mXWT0fUyuyARf1U\n",
"1mlVBMrYJnNflPn3jjaVtc60qSStZBIRwvuG2U7/Ndhm1iY6WTKL2/HC7DqIlRdiReUdMfPuFl21\n",
"u/5QEPU7m8d4ZR/Pt0qESCXSJRPykAkEic6nSqTLquiVTOxL5n44uvjcGR3z+RiY3++htmqVCJFM\n",
"TEdHjMqs39Gq+d81TqafU/4v8U6iYnK3aE/yFaJjRnfu813RMaNdUTLvfi4BAAAAAAAAALwdH/gA\n",
"AAAAAAAAAHiYrZEuoztjRkZfLWpl5/4+OWplZsX+rJr7XbEjM+ayL46lY9xVcSfiWYrbdMWmRH3s\n",
"apNZk0p0RGbsjtiUzNxWxcBUIl0q40RRHpk2lbiZSpxJpk1HnEllnJ8T42ReH5W5Vc7JSnRMeG50\n",
"xahkShlH/WTKg2f+fUWbVREolTY7g926+5j1c3q/v/ZuES7s8+iIl+vqiVGJ+lzZb0c/HVExlT5W\n",
"RdRU2mTuOaM2XTF8mdrylWSS79H9SSXOJHOyr8omigIOVkWvjFefSm5Spt9V84/GnY1difOrBE5k\n",
"2kSRIasiXTrmNtMRUdMRvZKZSybQpHI87oqOyezP+K97YmAqqhEclVfqLpV1umt/Oo5pJdZm1Vzg\n",
"j8hEW61wV4zKSXE5d62Bv/MAAAAAAAAAADyMD3wAAAAAAAAAADzMx+yXJ5WMErWyz9OjV548/64+\n",
"T46buSuaZGZXgfS7xr0zNqXSb2WcsJh+FMUyc2c8S9RH19wyJZKjNplxV0XFdETfdMSmrIqBWTW3\n",
"jniWOyNdOqJWOmJgMm3GCJdV41RKl2fGifrNHPdvP4ZfZMqSV0qZZ8ofZ9pkShdHbTLvXCtiU+4a\n",
"t6ufk2JgdvX7a1+hrOeufTzZSX9baItfuWGcthiVUdcLJPPefEcfmX6q9eejfjIJIivazF50lTaZ\n",
"+6AoqWC29i9rG2XUZDrOvBgqOTa74kxW6YhnqfRRiV6ZqYQiVOJMKuNG22QCNFZFunTMrRJvUolR\n",
"yRyfSmxKpk1HLE9HdMyuGJiZP/3uNl0xMJVXciVVrKvfU5wcc/N01nafXdEen78qrhv7K0bHjO5a\n",
"AxU+AAAAAAAAAAAexgc+AAAAAAAAAAAe5mNVGf9VTiqHusuTo0pmnr4/K/rtWpO7YkcydsWBdIw7\n",
"8/Q4lh3jVNf6y8WzVPrJRHt0jFtZk11xLbN2HbEpM1FMyqp4liiGZOc4Y5sxqmS2Bh2RLuM4s20y\n",
"0SQrYmAqx6NSkTszTmZtx7Ws7E9mnJd+MrEdfy206drms21WxaZU4maiPrJjV+ayo4+ZFTEwmXHW\n",
"+AoRLpxtPNOXRK9sHGfZyd4RrRL1We33ruiYyj1O5t874mYq9/eZPjJJBdHJnkqpGzup5Nhkiv1n\n",
"okh23dxW4v063qs7Il4yJ1zXX9u7cp0iHbEpJ4niWCrRMV3jROPO2lViUyrjVOKAMvvcER3TEQPz\n",
"eV0xMJl+O65wJ8XNdIzTIfNqzzgpCkccS4+74kCeTnTMvedKtAYn350BAAAAAAAAADDxcee33zt8\n",
"hcobo6dX4tg1/1XjrFiXk16H7zYXlTnOGidVraPyUcSnV+uI+ugYd9bPrrl0VNlY1W/XOB2VNzJz\n",
"G7+U1jFOpmpDVGUj0+9s3SqVQzIVSiptOqqCVNqMa1AZJ3PcK1/QzBzDbz+GX2S+oVn5VmfqXabQ\n",
"72f7yPRTnX9lLnf0Ue0n6mPV08eqbwn/2p+u8bWw75sfp3wbybdJck76Ft5dFT9+elJljsw41/X6\n",
"QqwUDsh86TnqN/Ol50qhh0ofmfvUsZ/MMYzWOnOPkzlelblkvmAefXE9deA7Jlc5wU5WecHPrnrR\n",
"GsxKElbWbRx7rIA3G2scZ3YMoyommfuiyp1FZpzoe+mZ7w1nXmTR/GfjdFQ56apCUakc0tGmUtYo\n",
"U/egcgxPrgry+/1mqoJUVKqCVKpbvNs4JzmpSgjPt6vaxV3VLVQSmev47y0AAAAAAAAAAA7iAx8A\n",
"AAAAAAAAAA/z8fTYjhlRK/8ve3e340hurAtUMy74/Z/XGxtzLowD7MliD0PREfxRrXXnGjHIZKak\n",
"VFuKr4bolbFdMSMRJ63tpjiWihonxaZk5kk1eBfP0he1EqkxG7MrrmX0mKdM7Ei2bkfUSlWkS8fa\n",
"Rl2JT4l0yUTUROpEIlAyYyLxLLMYnsx5j7T+zlxfkbU9u0aHYqCe7zKz/101JtJiOFJ31ko6u5bZ\n",
"mI4a0Tqzuh1xLVV1d80zqrvnE+8p8S2vl1+PVFoVrTIzuqqXrWVXHEskZiSjIp4lU7ciriVSN9IZ\n",
"P7K2TOrIrLd0Jk0uczyjv2USBL7VGD0Tnxdu5ITMGlJX3XRmIvV2NcuOmEWijETenWf3J5l/OIjc\n",
"80SiSTKv9BURKJE4jYonWeYfPiL3xxV1Ix/kZjWqxmTiTSriWW6LgcmY1/3+l/n+iwjJibxakWNv\n",
"z77DOZnomJprxfUGAAAAAAAAAHAZX/gAAAAAAAAAALjMl+iVPp8WvdI118nxJiMV6/0JaxPHctc8\n",
"4lmKakTqVB1PJGbk1DGZuJbRuK6olaeuqJVVcTPPmI7IPLOolciYTNxMJiqmaszsGCPHHJln9phM\n",
"PEtVRM2si/cffw0GTfuSJ8Zk4lqya5m901ZFx7xbI1rn3bpVd3pddZ8i18ZN88yFkpRgoa7m5m+L\n",
"3OdVRLGM6mZiU3bNk0n2iMikgTxVpY7M5s0klWTGjP4WuTef1R2+pWbycjJmF+XOf0Velfv0lIl4\n",
"qZhnNFfm/qTiCR+5H47EZ3SEhFWtrSP2JZPNO6obuTvMxNh0RLisimcRAzPyr6YYmMyYTLTHqnkq\n",
"iC5hpUjYX5VV0Sqrom9mz81Vx7dqbh0+AAAAAAAAAAAu4wsfAAAAAAAAAACX+Rr98dOjVkY+LX7l\n",
"5MiQp5vW+nrVrPfT1tbVHDxiV4zNSfEsoTiWp454lqpIlK66u6JjumJtbhpTEdcyqlNxPqpiYDri\n",
"WapiR2axKVVjZusf7XWkbiYCZTYmEn1TEYGyKp4l0y48s7ZQ7Mjzf4/aXmdiRzKRG7M2y9m6mRod\n",
"dVfFs9w2z2ze12vXJ97M29gumbQG6kRa3HY0xs+oesUrEenEXpHGEOmMX/GSlo0Z6ZgnE58TWWtF\n",
"3ch5nyWgRM5p5jZi9ERNJdtlsm8yN4MVT5CqvJxTRaJXqmT25XmtPD/kjNY6i77oimeJzDN7TNW1\n",
"0xHPErkHjdSNvMHMwjAy0SRVcSZd5+xUmX17vWo+GWRiYJ4+/fx8d0oszMq54fVaFxUzuq47/i1k\n",
"ZfTN06oonKdV0TgAAAAAAAAAADTxhQ8AAAAAAAAAgMt8ZZohr/Tp8TK3xZk83bT+qrXuihCJ2BXH\n",
"snNvb49j+TamI54l00NKPEusTiauZWd0zKpIlKdM7EikTkVsSqSDalcMTMXaMvEsFdExozGZSJdM\n",
"nElm/c///exsPKoT6TT9HDOLhYnUzVyTmXiWSHftP/56/CHSy7wiRiUTHfOrv/1u3UwcSGSeiiiZ\n",
"kUyf+Ip5VsWzPGWugx63R6CcHC/D2PNKPyXiZSTTjL7NqtiXp53xLLNjzhxvJgIlsteZeJZMnE5k\n",
"nkiP5ExqSuZe8NsxVeTNRBpfZ+JZMjk9ERV1u96Zn6/AkdiUyH+f1Y2M+c/jf0eevJl3lEgowixu\n",
"oirSJRNRk7k2ZvNE3tmysS8VY96P/6g5h0+romMyUTgrI2oq1j+rOar7vkwMzGynq8bsimfZ6Sce\n",
"c0ZH9EVXVMntMR2r1n9KjMrrdU50zG3XCgAAAAAAAADAj+cLHwAAAAAAAAAAl/k6KeYiYle8zKp5\n",
"u/bxpAiRiI71Vq21Ym0nxcLsOp6fEAMjniVY9+Z4lqp5KtbWFfGSWVtF7EtXbMqsZtU8keOZRZWs\n",
"mmc05hlNEtmDWSRKJgYm8phM1EqkG3UkLme2l5G1zdYaqZvprh05nlSMSkU8S6YteXTud+tm42Vm\n",
"Mnsb2aeMVTEws3m79rpK1/73Cz3duV6kde7JsS8tsSNZFe+7FTKxKaviWap6Gc/6tVdF4VRE6mVu\n",
"TyK9vlO3OBUbtSr/Z3Rzm9m4ZzTJs+6qfKaIrt9XZup2ZUV1xVp0iNzDzUIRuuI0MjEqXbEps3lf\n",
"r/lrRFX8TEV0jBiYmppVdf/uX0e/ZrxvdNZ3fnJ9V+RVnvt1Ra2silbZFXWz6/hGZsf8Wa+sAAAA\n",
"AAAAAAA/gC98AAAAAAAAAABc5uumSI7T5u7Yu5vX/nrtjemYOWltFWu5/Xhui4GZxrN0RaJkxuyK\n",
"Z8n2s+qIM8nUWRW1Eqlz8phdcS1VdVdFx3StLRPPMotEiRxP15jMYzJRMZkxkbiZTCxPxXmf/e/X\n",
"ax5jM5rnj78ef4i01362yn7+70z0SjbaY9buOHUHEPhbZJ6Ou7/MPq0Keozs2yon7VOPyEsPvF7r\n",
"AptaRDqk7+rzO5KJA6lIn6jap44UiEwEXSalIxNRk02Ky6SmzLKVIvN8e8yqC2y0+FX5P8+5I+/V\n",
"zzGrsqJG+5SZ63mMzxv8Uc3nMT7XEhkzmzciMs8sRmW0lky0R8Wd0eh6m+1bZN5VsS+R2JSKqJWR\n",
"itiUmyKEInYe8ykxMO/HJK2Kgbk9noX73B610iGSilihIkYlq+P83P7uCAAAAAAAAADw4/jCBwAA\n",
"AAAAAADAZb5Er9RZ1SC5wk1rfb1q1nvy2lZFolTN/bQqnqUlimVEPEuubkWsSlWdVfNE4jMq5t0V\n",
"1xKpk4k3GamITamKWnmqiFrpioGpiCqpio6ZjYmsbfSYiqiYrjGz9UeOpyIGJhOx8/WMb3m95vEs\n",
"/xmMyURjZKJXMrEpVVExM5EaFb3kK1TFm+z6FHlydEyNTDoAVMmkWszSKY4TeVI931e7Uh9m80be\n",
"6la9SETu1Sve6iJ7Pdunqn1bdcwVT6r/qYg3Gf0tk//TkQfUpSp6JTNXZp7nvXgmaiWzt6PPAJn4\n",
"iY4oiapojNljMv/ol4moidTJ/EPU+/EZfWMyexCxKjqmImaoy00xMBmZGJgRn6i6VESTnBxDcvLa\n",
"VumKWlmVzLnqHO6KivHqBgAAAAAAAABwGV/4AAAAAAAAAAC4zNfoj6c06O1yW5zJ023rPyWOpWvf\n",
"bopEOWlu8SyH162KZ+mqe0rUSqROxTmsilqp2LeKCJSqGJiKCJSuqJVV8SyR45nFjkTWVjEmEqPS\n",
"FRWTiY7JjIl0tH52Xo7swaxuJgYmFe2RiVpZGb3S0Vd9VZzJyuibFbqur3NlnoZ+fcEnGD3bM2+P\n",
"R7dEjnRrn7387sxTnt03VL29VyRhzDr/v141F1hXmlxFVEzZ7VbF4iI3nZkTP87Ab1kAACAASURB\n",
"VKsbqZl5F42MqYheiYjM8zyxzzGRqJWI59y74hsie1ARtZIRiemo2reKyJNMja4xmX2piE3pio7p\n",
"UhFJ0zHvaXX3+Nei9Udug7jbqkiUrrq3PZM/LSrm6fbzAwAAAAAAAADw4/nCBwAAAAAAAADAZb6y\n",
"bYFujy956jienxi9MiKOZS6zjqrrYNfcR8WzdEWTZObZFc/ybs1o3a54lsw8q2JTZjW69rZiLRVx\n",
"LVV1u6JWKiJdTl5bVQzMLGbkGUsSqRuJRImsvyIqJhK1EhnznCeytlndTERNpCP3H389/tAVb7Ir\n",
"eiW7lo7YlGwkTYddsTyn+/1j/vP1fE4BvyUT01GRCrHTrmiSrn2pOIeR+9SO24jM2l6vnqiYqhib\n",
"b3UqFjeKEHneRFfk/4w+bGQu5IrfOa6KeMmsdfTBYWZ0PjJ1ZjEwkebykciH2WMyUStVa5uJfA7K\n",
"hJxF1r8rwiVyPp52xrOsio7ZFW/yE2Jgzo3uWRUDw3eRWyn26ogi6YrLeVp1fUX+P1ixwQAAAAAA\n",
"AAAAl/OFDwAAAAAAAACAy3ztjIXIuD1K5idGx3Ssr6rmKXEzmXXs3IOj4lgqxqxaW1U0ybt1V8az\n",
"dMy9KmolUyfTfTMzpio6pmKvK9ayap7IYyLn4/Z4lllkSGTMLO5kVGcWqxJdy+wxmaiYqn2aXSuZ\n",
"eJbIHmTWdlW8SVXoZEU0SWb9q2JTIms7WVdkUOR8AD9CJg5k9LdM/MfJnvtSFSHSEW8SeXtcFf8T\n",
"uZ4qomLaYmwqmmePbm4zdZ91IveP79Z4vXriV0Z70BXzkqlb8WIUiU3JxMDcLBPPkm0kX1E3EnNR\n",
"ER2TieDoigOZHfOqKJ8qkbWcG2dytsy+7YmbEQuzV0fsSJWutT2v9IpXla5wqVXnp2NPRiqO56Rr\n",
"FAAAAAAAAACAgK/Tu0PM3N5Z5OT971rbro4YI6esJbOOqj3QraNxnpO7dWTqZjpXZObp6rwxq9G1\n",
"/szerlp/xZjMD0UyHTKya+noNnLy2iLdLiLHM+voEelCMeuYMaqTeUymc0im80ZmbzP7lOk6M1rb\n",
"H389/nBSt4uMn9i1oeTnvJP/HXlM5BeNmbUBfLBlXRsm847+VrG2roYGu2S7wXTU7epq8u3tPHIS\n",
"MxNFROq+W2PkeZPcdeGumidT9zmm634s0hVk9piqDgyzx2TW1tWFIrKWTN2KLiCRF7Cujh6zMV2/\n",
"F4+oWFvVec+YnfeutelGsoquIGe5qUvI61Wzvq6OGKteRW7uHHLS9QUAAAAAAAAAQIAvfAAAAAAA\n",
"AAAAXOZr9Mfb41g61n9bdMynx7FUHd8pa8msIxXFMiKe5ex4lndrRuueHDfTFZvSsf5Pj2sZPSby\n",
"3ysiUUYq6u6KZ6mK6aiYZxZ3MqrTNSZTNxMrlFlLpNP0LPom0vW6Yg++xbe8XvtiOrrmOTmapGtt\n",
"nOXv5z3zdI80yp49JvMSYW355tqzV4RIG9yKY86srSsVoiup5FuL3mfhT4sQuV3kxFfEzUTubTNv\n",
"3RVP5tHfMp9pTjrm1LN39uSMXCyZeJmM54135F/jMv94Mvogl3kRe64vEh0zGxMheiFm9qTK5N9G\n",
"5sn8g0omAiUzJhMHsjNCpCu6Z5ddz10xMJ9INMw5uqJXqpwcWzPTFRAW+Re+jvicm/YeAAAAAAAA\n",
"AICXL3wAAAAAAAAAAFznK9K87rY4kyfRMWdFoDydtLbMWirmTcWzVH1dSzxLXd135+la6654k9vW\n",
"UrH+SO/y28dk4k1m82YiUSKPWbWW0T7OYjm6YmBm8SCRtWSOp2oPKupWHfOqGJtMJsL0MaM7mGeL\n",
"50gf70zsyPNvmU8XFdErkcesOmZrW7e2lfE/wFaZ7JiumI6TMnZ+4to6omMy11fkMZk8qa5jjiR7\n",
"/G/mxD+FsmMeIlErmeiYp8j6n2v5z+N/PzMds/NU5FRl4lq6fvsZaSp+SuPxyGeN59pWRVZE1pKp\n",
"G3l+rBqTOb7ImI74j8h5j8xbES/TFTwQccpzN0IMzE67YmAqIkVGz/bM1XNyvMnJa3vqirF5nueq\n",
"V4hVrzwVd+oAAAAAAAAAABzEFz4AAAAAAAAAAC7zlW1W2xW/8tTRTPe26JiT96BibZ+2lmXxLFV9\n",
"gU6JN1k5z654lndrRh9zctxMRZ1IrEXHvKPHrIqOWTWma95VdSvW0hW10rW2Z9feyJhZBMqq6JjR\n",
"mEzdSGzK7Bir1l9xzJkxf/z1+EOm9/eq+IxVESJda8lGhgAAU7M+xCfH2oz+VhF/2XXMs5qv1+CW\n",
"5lkkEkOS+QeKTNTKc23P6JXX63v8SiZGZRbxUjVPRcTL65Xb/1kUZCY6JmO0B5molVlj9VURD11x\n",
"LZGYkZMiXFbFvry7jtFaboouqbLrmHdG1HCWv19zroK66JWO+JLbo1Y61vp69Vy3mVfJn/CuBQAA\n",
"AAAAAADwUXzhAwAAAAAAAADgMl+3xZvctN6T96BqbZ+2llQcy5N4lrXznLL+qniWd+eN1F0Vz7Iq\n",
"4qVqLbtiVEYyESKzeSrmjT7m3TGZSJRfjXt3TFfUSkUESsX5qIqBma2/KjomE88SOYeZ9c8eE9mn\n",
"SEvu2fpHY76eES6ZeJNni+RMJEqkLfGsZqRuphf76G+7oldOjpv5tLWJ0wF+0+j9PZM8VnFPkHmr\n",
"u31tHS/jmeiVzB6M/pZ5O6yYZ7SPsxSO0K1U5ARFDvqp4kPm0+iAn/Erz+iVzL8kZuZ5vfbFvFRF\n",
"xTzNolVG185oX04VibmYPSb7j72zvczUzTSGXxW5kZknEmvTZXbeM9ExkTqjPcm8oeyKbDk5qOOm\n",
"tXaJ3BCf61/6GrQRtdKz1tdr/gxb9X/BAgAAAAAAAACwkS98AAAAAAAAAABc5mtlE9yOJkBd6/8J\n",
"cSxPJ61tWzxLxVegMr12qnohnRJvsnKeXfEsmTG7Ym1WRa2simsZ1enap469rRqTOR8dMTZV+9YV\n",
"tdIRL3PS2iJRJbN5Rl2JO6JjMrE2kcdE6lbMk4mkqYqOmUZsZOIzunqxd0WvZB4TURFjs/OY+a4n\n",
"d+DP19+jlSJP3Z/YDBhGIm1wv916RN6HZ4/JxLXwX8+9y5zEivNRdbvylIlR6YrLmdWM1M18xozM\n",
"8zSMeMlErTw3NxKJMnuyRj7cRi6OWRZOZJ7n8bxe34+pIuIl8wI2mvdZZ7YHWc99ycRPVEStZLKW\n",
"qkQ+k2X+8XC2/sjxVOxBV4RIZm2Ra0WUx112RtTwef5+7awKy4rUyVzVXXEmFW6PWulY6+vV8+rl\n",
"FREAAAAAAAAA4DK+8AEAAAAAAAAAcJmvyIO6OlzeFMdy8h5Ure2ktaTiWJ5uimep+uqVeJaY2Tw7\n",
"j6/jeFat7eS4llGdrhibjjGZmI7I3B0RL6PHVO19RQRKJi7npniWzDyZcxiJgckcz6h7c6bu7Bir\n",
"5um4vv746/VdJg6kIp4lEwOTiSrJ9G+P6OoLn4mB6XBy3Iz4mZGKhApYLfMq6ToeiMSZnBybUmG0\n",
"ttkx74zy2bW3mduVyPFUrG349p6JWplmx0z+++v1/WY9E5ESUTXPLLama/0VIrEpXTEwN4lEiHQ1\n",
"hq8IEaiIcIm842fGRHTEs1Tt9afpOoc3sQd7Pfd7z78//OsDz3tFnImolZ61vl7zK/3zrkgAAAAA\n",
"AAAAgA/nCx8AAAAAAAAAAJf5ynZp7GiS09V45yfEsTydtLZt8SwVfXLEs6ydZ9X6V0WgdNS9PZ4l\n",
"85hdcS2jOl1jOqJVqtbacTzZeTLX7azuybEpmYiaUSfdzPmYxZlUHc+zk3FV3YpzmJkncjzPv309\n",
"I1wi8RnPls+3xbNUxIFU1V0VRVIRY5OJmzlJRd/72/fg90WSojSa5ldmzc5Hz8KPu552RYZ0/eNP\n",
"RmYPIhfLqj2YrSVyixDZg0g6QEUkzaxmpG7k82Okv/YslWO4t7P33dGgWXxJ5IAy0RFd82TiWCL3\n",
"K8+6FTEqo3lHeZe/6/YYmMhnp44IkdFcmX+UmdUc1c3U6Ypw6YjL6IpniVwHkePJ3KXNYi0ya9kZ\n",
"Y9P1nKJH5Pr6NJHn5cz35/+uUK6uOJMKt0etdKz19ar5v9EAAAAAAAAAADiIL3wAAAAAAAAAAFzm\n",
"q6rh7U1xLCevtWptFWspiWJ5vWq+VnRTPEtVH6Db41ky8+yKZ8msY1fdVVErq+JaInNVRXvMatwU\n",
"15IdkznvmZiLWY1MVEnkMZE+9xXxMjvXNouKyRxPVwxMVZTPrG5k/ZG8g4p5Mue9JGqlKwoj04s9\n",
"EpGyq27mDrmqZ31FjE1GVyzPTa1aqyKP7hV6KeJ6kTayV//ipypG5eTUp67YlI63nEwUTuQeuuIt\n",
"qGueSF/lirpdkUGZLuSp6JhMU+vnYjIRKSOzuavmedp5H5GJSfnP43/vukuIxMBURFZEojFW7UFV\n",
"1MqsbqZmJtojczyrxkSIFPk8XdcK96mIYznHvw66jiviTD49aiWiYq3nXBUAAAAAAAAAAIT4wgcA\n",
"AAAAAAAAwGXKIl2euhrinLzek9d2fTxLRU8c8Sznz9Oxlp3xMx37tGptq+JaRnW6Imk69nZndExF\n",
"FE5FJE1VJMps3kjdnfEsFWt7dt/tOp6KeUadgjuiYyJ1I1kFs7iWqnkix/PHX48/VEStVEVWZGJH\n",
"KqJjZjWzdSN357O6VfNkZM5hRYxNRsX5OTlnoSap4GSZrv2sM3p23HTOMikXRzdVHy1m1oM3cu/R\n",
"9TLYETtStdbn2jLZRJF97JgnUidbt2Kep8w5rEjhS2XHRBbzNHpiZiJbMvNEZKJWKnTN+9ynXcd3\n",
"ksznrap3t44Il6PeeRMq9mTk0/ZpFfvG6xW7mfo0FTf8kfiy99eSeRZmwr5WOTlqZaQjxubkfxMA\n",
"AAAAAAAAAGDAFz4AAAAAAAAAAC7zNfrjTXEsJ6+1am0lcSxVX+2p6CsjnuVnznNyBMq7NaN1b17b\n",
"qqiSk+aOxDVEau4aUxFJs2pt2biZU9ayKjal6nhma8kcT9ceRGJfMnUz11fmWnn+769nfMvr1RO1\n",
"UtWLfTama22ZGJXMnXambtU8mb3t+KRTFeWzqu1qxfV1jkwy3En8WmSdrraxHSJtfY+61mfxJqO/\n",
"rUrLmsWOvF65fKmKl+zIfVHHW93J80TqVqWvZWJ5nio+Q6eiYzLZMZHFPFXN8/T88PGfwWP+XVB3\n",
"lVXzjs7XTTEwkXvOzJNq1VoydTPrz8SmZOY9OQrnKZMrNnrMTT7teDjLzhiYVfmL9/hX0SfTilf1\n",
"m6JWIh/rMrrCywAAAAAAAAAAWOQr8t3mru8tndyd4+njunVUfclSt46fOU/X2jrq7lxrxdp2devI\n",
"1Dm5e8eozqq17BpTNW/H2iLdIXZ2xMjs7a61PX9M1tUVpKuTSFcnlFnd0Y/JMns7XX+m00PVmIqu\n",
"DZlfSlbUiHShyNTJ1n13nq6OGF3nsMLJnTcyXWb2ObozwoNfj9Tp+BVRldkvp7ZeB7u6XURUdBLp\n",
"Wkvk53AVP2iMnI/ZfV6m8UPVPJm6mb2N7HXmHD5lrreKTiIj064fo5v1/wkUflekw0TkgJ5dP27q\n",
"+PF6nfOOHukK8nxM5Mkbue876Q5sV9eJiMzabu4CUtVNJSNyPLO9jZz3yPnp6rACXW7vCpK5IT55\n",
"Ld/PR0VHj5s6b1S9ah792RwAAAAAAAAAgPf5wgcAAAAAAAAAwGW+qhrZVHSePDk6piSKZeT2eJaT\n",
"1v9psSm3x7Nk5umouytKJlK3am27olY6aozqdO3TqrVUjKk6vsy1UhE7ElnHrniWTLzMqrWNuvqu\n",
"micTa5NZW2RvZ9EqmbpV5/D5tz/+evwhEiFSEdORiazI9JaPrC0To5KJIamKsXm3RrZuxTxdn7gy\n",
"UTgVIvPsiYH58/V8Lp/TuDiSDrDLKXt0utFVvWvvMukTq3xr2XtSZ+bIfUTFy1eke3vXS+nseDJv\n",
"75l5In2WM13vM7c4mbojFW+7XdE3TxXRMZG6bRPN6kTmyUTJVGQg7fQ85tFe74yguVnk/r4jwqUi\n",
"vuX1Ous6hderJwKJn2nnh40KkRvViFNiYEZVf//53RVQlbmTfcp8BHjyCggAAAAAAAAAcBlf+AAA\n",
"AAAAAAAAuMxXV5Pck6JivtWsimc5Jc5kZyTK065YmJVzV+x317wn78GuaJVdUTKRulXndFfUSlWN\n",
"jn26Ka4lMqZq3zJRMasiUWY1qtZSEQdStbZnF9zMec/swXPezDnMxMBkxkQeE+k/n4mkiczzLcIl\n",
"0st81kN81Da6I2qlKjom0789czyZnvWr+qrPap40T9entIqYm4hMFE6PyMvKLn7Vwa88n7mnRMm8\n",
"Xrm0iZTnQWciQzIi9ysV82buizIxMJlYm8w8VbE2s73OdsHOnMPZmEyaScXt10jkReJ561qy/oq4\n",
"lkidqpiLCpnomJO4+4hFS3S981bEWlTUGL0YzY551ZiT43PgBpkb1Z5oj89jn77riaipeIXOvANF\n",
"6lS8I7kbAwAAAAAAAAC4jC98AAAAAAAAAABc5mv0x64muBWNaMriWJ7Es3z3E+JZds2bmeemGJXs\n",
"PB11d+7BrO7pUSvv1snEjkTm7oqB6Yg3yY7JnMOOeJmqve6IRMmuJRPt0RHPUhV9k9nbWYRL5Bxm\n",
"YmAi7akzUSvPOqOomIprMPR8n0WeRCJQMmMqolYyfdUzUSuZ6JjI3Jkoj6q1ZOJMMp+wZnWrPrV9\n",
"2jyzeTvn+rtlERUTO3/loan1vhiV0Sv6qrln7WmXxbVk3uoy84zqVrzEjeaZbW5XDExmnsiJXxWJ\n",
"Muu4n02ty8TYPGWibyo+l1YkooweU5HG8r+Z+7HMRP8Z/O3fv1mzctzNMS+RmMrneZ7t/UqZz1td\n",
"77KRtVTEr1Q0pL/9zq8i1mbk0/aJ+3XkF1bJxJvsOp6q2JGKuX8/7uS/Kj60VKyl6sNTxfn4/ViY\n",
"qhiYWV0dPgAAAAAAAAAALuMLHwAAAAAAAAAAl/mqapKXURLP0vWVFfEs4lk65zlpbauOeVe0yqrY\n",
"lMyYnVErFWupWn9FnMlNY1ZFlVSd00jkxlNmbV1xJh3xMietbRYlE6lbFQOTWdssOiYyd2Qtz+7A\n",
"mWv9j78GgyqiPSJjMrEpmXiWWbvgTDRGpp9+ZEzkE0pXjE2k7kzmvFfUrfpk11V31zx/r7vqVxGR\n",
"dIMuGkl/nlXRMZFX4465h21wK7oHj1TEdOyaJ9LJOPL2PqsbeUutqJtJUcjcRkTuDTNRK5FO2Zno\n",
"m9k6RvNUdEgfyfSSztx+pSbKRKLMLtxszEpFPEtXxMsp0SqjiJ3ZhTu6DmaPiUSi7LxT6oj/6Gom\n",
"n5GJTVk1ZiexL9/ddg65ixgYMTC/Ur+2qlf02TuFV0kAAAAAAAAAgMv4wgcAAAAAAAAAwGW+ss1i\n",
"SuJYnnZGiHTUGFkVn1Ex74h4lpoxJ8WoZOa5qe6q2JHM3KviZk6OaxnN1RVjs2pMRQxMxTmr2vtV\n",
"81Q8Zmc8y6q1zWJSMlElkbbRFfNE9iBzPqrO4XNvv0W4VEWgVESTZKJjIvPO1p8ZUxVrkwmijNSd\n",
"1ch8WqqKpOmosapu1x5k5qkReenpsKqZ86fNs9OuaJVPm6dt3sg9QUVH4UwcSMQpMTAjHXuQiVqJ\n",
"3NtGOkA/5xk9JhO1UpFsF1lHxb8TZDKcKqJiIhE1qXiTqhybTN2KMR01Rp7RKrsiXn6Ck6JWIsSO\n",
"7NuD264V1unKOOS7nxgDU6EqBqbDSRE1T9/XVnF7DwAAAAAAAADAQXzhAwAAAAAAAADgMl9l0Sxd\n",
"Xx05JZ7lpLiZXREpO+feFYXTtdaT92Dn+nfFptweN7MqqiTzmI64llGdruibSCTFrE7FmKo9ma1l\n",
"VSRKZO6qaJKOeJZVa3tGjETGZGJ5qubJxM3MxozGRcZkzsc0wqUqAmUWM3Jb1Mps3kgbw4qYm1/9\n",
"7d06kRoV+zSrma1TEWszq1lVNzPPSXX/7tMiUTSIPkskRcE8r1j2Uubpv6tuZp6qOJN3a0TqrIpa\n",
"iRxPJm4mE30TOebneiNjZuv41d/e+e+jeSOf6zK3i7N5Q/NUxbVkomKeRh+wOsZ01vm/nhEvr5eY\n",
"l4hIvGfX/6FSMU9VhEgmAmVVbErHPDujV0TucKPMjelNMTa7YmBer5p92rn+p4q1dOxJdi1Pv782\n",
"HT4AAAAAAAAAAC7jCx8AAAAAAAAAAJf5Gv51Z2TIirriWfbuwa5jvj1GJTOPun0RIpka79aM1u2I\n",
"Nzl5baM6XWO6okneHVN1fKvWVhGJctJaKvY2EoFScTxVkSizeVbFzYwekznm0HNqFpNSFYEy6/0d\n",
"madiTFXUSkckStVaImNm+5A5h5E6XfEzq2Jt3q3ZWff3/fl6RjrVyCTDVcxzk5vX/nrtbdpdoavx\n",
"96xu2R51dRju6BZc9bK4Ks6ko27kCZN5687EszxloldGj8lE0lTckmViYLqS+ir+LSHTXft/K7Jk\n",
"qsZU/aNrRTxLR8TL6/U95uWmd78qsyfiyj1ZFRVzMnsQc0rsy+130T9B5oblpPiPp5uORwxMLEtx\n",
"11qqIoTq1+adDwAAAAAAAADgMr7wAQAAAAAAAABwma+y9voZp0SivF7nrEU8S9+Y2+NZMvOctP6u\n",
"9VZErVSs/6TomEw0RsU8J8W1RObeFR1TtbeZWJ5da+uK9niqWsspsSmZeJPRmNlaVu1bpNX0qn36\n",
"YxTfMOs7/j+DMZkIkVmP9MiYp0jv8kwcSEWv765Ym1XRMZmWiple8pExFW3IUz3SA3Uzzo2OibxN\n",
"VTj5Y/bKuny3Kmql4uN8JOWiom42EXA6KPO2m61bUWNWN9L9OBPLkYlaidzndUStZMZU7VtmTEV0\n",
"TGQtT5Fj7pg38phMCsnweVvxqrfqH/mq5p7piniJeJ74nWuZiXxG2/U72q4ojIpIlE+L6eg67yfv\n",
"UyaLbLQnp0TH3ObkSBRiTomBWTm3GJjYWp7q16bDBwAAAAAAAADAZXzhAwAAAAAAAADgMl/pbkod\n",
"XZjEs9y/ByfHs6ya+6QYlcw8O+vuOh8nRa1UHM+uiJquvb4prmXlmI44lkicxqxmpG5mTOQxq+Jl\n",
"Tl7bqCvuKceTWVvkMaP1P+f6FuESiYHIRJNEIkQqIlC6okoqolYi/70ioiYyLjJmVVRMR42qHIKf\n",
"GB3z+3Vvik3RQPln2hm1sq1uRSRKV92qyJDZfVCmRqYDdCY2JbOWTGf5zJhI1/7IPmXGZM5hRVTM\n",
"6JrM3KLN5h3J3K7M6oZui0YRjTOZF43/DP7270VzZ5wSrTI6ybPoiMiTN/MicdLdU1c0RkWES4VM\n",
"bEomEuXkGBXoVhG5sUvmRrUq2mOVzE10R4xKdO4KYmDm3l+bDh8AAAAAAAAAAJfxhQ8AAAAAAAAA\n",
"gMvkI12eur46Ip7l8+NZRk6KOFkxz0lr76q7KyrmpKiVirWcHFHTtdeZ62vV+qvGZM57R1RMJk5j\n",
"ZNYNNTtPRzTJzniWjrV1Hc+zy+/KKJ/Z3KP1TyNcIr3YM9Eekf7gsyiPTNxMZp6R2ZjMvq2KVYmM\n",
"y/Tgz4zJrC1S55QaWRUtVCuiY76r+NjW9XH45F9oaIJdpysmpULH2qriZkqa3Efug3Z19d0ZtfLc\n",
"g8zbSWQfM/EmsxSCSPfjiuiVUd3MmKdMJEomxmak4t8JKubJJC+komQyT+5s/EnF/VRX9MpJ7zr0\n",
"Rbh0OCUWBlbriG/4CTJ5cqtU3bSdcjwjYmDOioF5+v21eRcGAAAAAAAAALiML3wAAAAAAAAAAFzm\n",
"a/jXXREoEeJZ1sWQVNU5JTbl0+bZFZGSHbMrgubkCJSd82T2rWuvO2Jsdo7J7FPmvGciRGZ1q2I6\n",
"OuaJPCayT7viWbrW9uzqW3U8HfuW2YNI3eE1OIsViURuVMSZjObJRKDsmuepIhZmNE8m9mVVVExk\n",
"TOZ4KqJJInubrfPumEyNTIxSpu77qj76dfy64uS1VTm5cfmnR69URa3M6mZqjp7ZJREuVVErmbqz\n",
"e6WK6JXImMwtQaSTcaTT/2wtmb2OdAvPRK+M9qTiM1hmLZmO1hVxLCfNUzHmf6teADrHVdfgLJn8\n",
"oozIC9gqN0XWRHTF2nzaPvF5umItPl0mEmXnXouB6Ytwql+bO0UAAAAAAAAAgMt8tf3if6Tj6yU/\n",
"sVvHU1dHhpGbOqycNM8p69/ZvWNXR5KdHTF2zdO1b1173VF355hMx5KO7hxV57Ci00Nmnq5OFau6\n",
"dXStbdbRo6pLy6p5Ins7q/vHX4NBme4WFV1BIj8F/WnzjGS6qXR12vi0ziGzGhGZPZnV+NXfMnV2\n",
"1PC73IhPP74qXV00TjJrRrCqRtmPySo6b2Te2rJdJzJreZrdf0V+LB7Zt1mHksiYyJ5kxkS61T1F\n",
"brc6unNkbitun+fdmuF5ZpNnf1Fb8Uvc/ymowV6rujboOgGfq6IrwKxmVd2Mk1rePXV9KOiy6hgr\n",
"5p2tI7uWjI5zVnU8/7y2T/t3BQAAAAAAAACAj+cLHwAAAAAAAAAAl/m6LtrjSTzL3sidk2JTPm2e\n",
"jrq7YlU6654SgbIzaqVjLZG4hsy8VXVPHtMVZ/LumK7jqYj2GOmKDFkVz9KxtmesSmRMVSzPKfs2\n",
"+tu3CJdMNMloTCYGZjYmsraKSJHMY6qiSzLHM5s7c35+9bfZvJkxFeuPjJmtrWoPKqJiqmJf3h2T\n",
"a+n552sUBfWeUz4+VtXxS5D7PK/+zDnsiF6pqlMS4ZLpsjxaTFe35kzMyFPkXmrW2T/SYTjSKXs2\n",
"JvIWlBmTOZ6KuJbIWqr+nWB2bWTOeyZuput4ZuuIqEq++7YvFa+2vzPun+xqt09M5ElGTCZKZtUY\n",
"+JVMzMinqYgH+Ymq8v9W7bcYmO/2HI9/1wEAAAAAAAAAuIwvfAAAAAAAAAAAXObr4yJRXq9z1iKe\n",
"5ax5d8WorJynYy079+2kCJSTo1Y61hKJa3j3v2frnjxmVZxJRcTL6DFdLG6RoQAAIABJREFUa8tE\n",
"e8zmHY3bFTPStbZnhEvV8awa83zMvyf/PTLP6xWIcOmKWslEiGSiY2Y1R2MqImoy84xURJVkeudX\n",
"RdJUjKnqIT5TEYGSGZOpsWpPRt5fb8VHsKqPcad8lOUzdUS47IyBSTVer+iuG4nPeMp0GI7E7kVe\n",
"8iqibioiakZma8vsQSamJxOJ8qu//VONyNyjMZkImop0v8w8Ff9mUdX1umLMt33M3q/8T3LcP/GO\n",
"f5bIi0aXjiiSqkgaMSmwVlesxe3xLBU3xF030buIganbg4oIp98/HneGAAAAAAAAAACX8YUPAAAA\n",
"AAAAAIDLfA3/elIf2VPWsrNH76qYkV3z/sR5uuJ+Oo4x+/y5KQKlY95RnZMiajL71rW2zFpWjamI\n",
"gam4ViqiVyLzjOyKRDlpLasiUCqOJzPmGSUTGbMqPuf1etVErVTEwGTGjMzqRnp/V0TU7JxnViPy\n",
"mK5Imor1RvZpto7IWjJjMmuL1pmpiHlZExVzUjzLrqbXVR/n/cIkllDxbo1snYyKCJeKZu6pPchE\n",
"r4wKd0SVVI2JrC0TITJLJshEoEQ6Jke6Ic/WH4lEyXy+yqylKmr0KROxs2ueTCpE5gVuWcJeVavz\n",
"k1u8Z/zEmI6dES5wu8yNROaN+GQ74zROsupG+2Q37UHmus1+KJvNLQbmWcOdCAAAAAAAAADAZXzh\n",
"AwAAAAAAAADgMl9tMREj4ln2rX9XLMzKuTuiPVatfVdcS6Ru9jqoqLsrHmdnbMop+7ZybRWxKRVj\n",
"uqJjKuJYMue0Kt5kNs+qSJSVa+mITRmt7Rmlkjmeij3oOoeZtf3x1+BBmaiVd2tkx3REx0SiSt79\n",
"77+qe8o8mX3LzF0VtTKrUbVPFWOW9TdfNOYp17J310ejXc3Of2KTdcbPjlXXQkeMTaRGKjqmqiNv\n",
"RRxLVYRLxZiOSJpIN+dIhtAp0TEjme7zmX3aNc9Ixe1jZkzmRaIigWP4XKh40aiy613/P4///e8t\n",
"q+gTyYpa5aS1wK+cErlRFSXxabqicG6O2MlcK1XxJrviWLo+fFQQAxNby99ruBsAAAAAAAAAALiM\n",
"L3wAAAAAAAAAAFzmK/2VD/Es350SXdI1b3buk6NUOubpWsen1d0V1xKZe1VsSlVUybs1svN0rW1V\n",
"9M2u6JiKaJKu4+mIn4k8JhuFsyoupyM25RnfEhmTib5ZdT4iYyJr+xbhEonc6IpayYx5yqwt07M6\n",
"EwNTsW9d87z730fzROqsiqSJjInMuyqipiLWJlKz43iidf5Z5iPBro9kO+NZdv1aZOevVCqiSTIi\n",
"qRYdIqkQkTGrIlxS+9QVvTKLy8iklXXFmVREoETeTiJjZmuJXGC7omMic2cid0ZmT4id88zGZG6T\n",
"KqJkRipexEO3UlX3shm7YhOenhEvr9fZMS+zzw0/4TezqWA0+AAnx5CIpKmLTbl537IxMKfEsXTl\n",
"Sc7mjc69Yi1rYmB+wt0KAAAAAAAAAMBH8YUPAAAAAAAAAIDLfA3/elO8SVedXes/Ocpk59xVERuZ\n",
"uhVjKiJE3q25u27HMe+MWulYS1V8RkXdSI2uKJyOqJWu6Jiuc1YRn/GUOZ6K+JnRYyoiUSKPqTo/\n",
"FbEpzwiXVVErmX3rOofP//0tvuX16ok3GdWJRHB0RKBUxY7MHtMV01ERgdI1T+QcnhS1Mpu3ap8y\n",
"a8mMyax/ViMiE9cyeu2ZjXnfbb+k0KT78+yKgcnIxMCMXjGmx5jpAD0qnInLyHQuzkSgVEXSzMZE\n",
"0g0yY06JjhmJ3Hp0HPOqeUZm121X1tKqN96K25XMtTP8Y9edw8l3JM+Yl10RL5lsItb6iZE6Nzk5\n",
"AqXLycfctbbMDeRM9ub8FBU34qviTbJuWu/tMTCzm+T39967JQAAAAAAAADAZXzhAwAAAAAAAADg\n",
"Ml9trfVGVsVnPFWsX2zKz5jnpOiYrviMmVWxKZkxJ0etZOpkauxcW9f5yZyPVevviDzJxPKsOp6u\n",
"85OZpyvOJPLfM/PMIlxWRd9URcd0XCvpCI7ZYyK9vivG7IyOqYgqiRxPZt92zTNyctRKR7RKZp+6\n",
"Il7eXUfVmFyr0FNSHavGnBzd8fQTfnGyqml/hcxaM2MyCQ+ZMZkEi1QX38yYTAfrzJjI2iKdmmfd\n",
"9CMvv5ExJ0fHVHS0HslcXx3zVGUrvVsjW7diTOa2oepF/NvcXXEAJ8UMzKyKeLk9HiT17raJuBx+\n",
"qqpYiJuMjnlXPMtNMSRdqj44VHzYiFgVj1Mx72wdkbVUxRn98x54xwUAAAAAAAAAuIwvfAAAAAAA\n",
"AAAAXOYr/ZWPiu5hu2JSqjqfnRLtcdK8J81z0lo66n5aXEtk7pOjVjJ1qqI9MnUza+s6PxWRG6vG\n",
"ZI6xIpZn1fHsjETpijPpiOV5xrdExqyKvlkVAxOZ54+/Hn+IxKhkHhOJQJnVjIyJrC0zJhKBMqsb\n",
"iU2piCbJrO3keUZzRebOnPcV82bXsqon+snRMOxKX+W/VkWe8FrX8bmiS3FVZ+OO9Uc6GWfGZGJg\n",
"Im+pFTEwVVExmb2tmOcpc4tQESXzetVkQ3XlSc1qZH27Lrtax9/8285nxMvrlYt5uT3CBfhMFXEU\n",
"WTfFl+zcp6dVsSMnz1Ph3AiUmFPiZ+Zzu+MBAAAAAAAAALiML3wAAAAAAAAAAFzmq6zvZ0WdVREi\n",
"J819e2zKrnlOWttNdU+Oa4nUOSlqpWItXfN07XXX+Vm1looxmWPsiBQZPeapKxKla56Kx5wcgXLy\n",
"2qrm+RbhEumvnYkmqYiBqYpama2/KzomE9cSWduqfXvqWn9knyriZTLHuCr6JjMms9aTI17mTv44\n",
"svMjMp8nk6JQkbzQFVGTWVvIrgiXyCbMXqIz3Y+7okq64k1m+5TpaD0SuU3NRMXM5hmp+CyeWVvm\n",
"tqHqmJ9WvYl21Hi9AtdTVVv1T4u2e8a8VOQZAb+WiV6gzq44k6r4jFndqve6m+JMbrcqp7LCzhiY\n",
"iuvr95//7oAAAAAAAAAAAC7jCx8AAAAAAAAAAJf5Gv51V1TJyKpeubvmvSkWZuVcHft/0jndVffk\n",
"uJZInduiY3ZF1HTtdcX5qaq7a0zmGCvOz6rjWTVPNj4nE5ezKwLlprWNzOb5Ft/yevXEgfxq3Ltj\n",
"KuJMInNXRJOs2oOqmI5VETWrIlC65pnNvTL6JjP3u2tZFfEyH3PyxxfRK3yC0avB7NqOJGNExsye\n",
"36F5Mp1/R4vNjJlFYVRFycy6A1dFlcziWCJvjxUxMKsiakYqolUi5yMSffPUlcc0q5tJ3Mi8SETn\n",
"nsnsbUTmmFtejAC42ymxL1XvN6dErVR9KJidj1XzjOaqyJzskomBqVjryvMxm/v3Y2B0+AAAAAAA\n",
"AAAAuMxXWzeCkdu6WeyY9+R5snPdvA9daz+p7q4uFNk679bt6pBxcseSri4nszHZ4+lYS9eYiuup\n",
"6px2HE/XPBWdK7rqVr3f7OrW0bVv044emY4SI5HODhWdQzJdGzJdJyqOZ6RiDyL/fVa3qltERXeI\n",
"ro4YXfNk6s4ek5m3qrNLpm7XPr0v89J/yi8lVq1d95GzrOqIkenW0SXStOEp05wgJPPjsYpOFSOz\n",
"MZkfnFV1H+nYp6pOIh3zRB6TOe9V/x7R0QUk82K06k0o00mkau6nqg4l3+pkXhlvl3m3A36urjfi\n",
"VV0OKty+/go6YK2V+RBQ0X3k9zti9K11Nm907vfW8hPuDAEAAAAAAAAAPoovfAAAAAAAAAAAXOZr\n",
"abTH06fHs+yce9U8J6/t5AiRd2tm654UO9JVd1UkzaoIkXdrROpEoiQy81ZFyaxaf2ZMRxxLVcxQ\n",
"x/F07XUmqmRVBMpIR+zLquibqn2bRrhkokqyMTCZWJHZmFGNzPrfnXekIjomW3c2ZraOyDyZvR5Z\n",
"FYGSmSdzDt/976N5snXeHZNpV7kvCufP1/P1a67rVxCrPl6d4ua1r3RSbEpGJjalK4QgFeFycjTJ\n",
"rOZoTFdX4opu5xWfgzLnZ2VETcVn/swtQCbGZlYzMqYrSiYz5inzwlIVvfLU1Tn/23pvb9EfOWmz\n",
"F8rMiyvcIPMGH1ERTdDlpqiVruy+Vbqur466Xec9Ew+yK7okM09krszerpqnSkUMTMaeGBgdPgAA\n",
"AAAAAAAALuMLHwAAAAAAAAAAl/naGlXytKpl3865b4qkOWlPxMDkxqyKROmquyqSZlf0zc5zWNGq\n",
"tep4VsXlZI65I46lKlKk43i69jqyj7siUEYqYlOeVkXfVO3bNxXRK9mIh4rIkIoIkcjaIsf8rPNp\n",
"0TGzmpEametg9LfM+aiIZ6nYt5XzvDtvtm7FtfK+rqiMnSmhT5m1nPLLj1PWkXVSPEsmNiUVidK0\n",
"lo7Yl660hlAn467uzR2dpKuiY1bNM5t3pOItKDNPV7zMu/99VLdrTEe63EhFDEzVrUckwqnCt2vj\n",
"pHiAiOfG3B5JA8TtilU42emRVDfHs+x8f7kp9qVrngqr4mYic6/ap9+Pgbn931cAAAAAAAAAAH4c\n",
"X/gAAAAAAAAAALjMV+hRO/vVfnpsyk+MZ1k1z0nr7zhnu+JnonU7IlAydU6KvtkV+xKJz3i35qhG\n",
"dg8qojAiYzqiSSJzV4xZdTyrokqy0Su7ImkqYlNGOqJvMvv2x1+DQZm+15kYla7IjXdrjB6TGRP5\n",
"7xV7G/nvq6JjKuo+rYpEidT5ifN0zJuVeY7NVdw+PnX9kmJXPAj8fxWpCU+ZKJzImFQsTFXkRsas\n",
"82+mK3FkTEV0jHnGdTLRN7OaI11RKxWxL5k8qVX/ftcVvdJ1GzQ7H8N5T4kD6Grbn5lbdMw6p0dU\n",
"0GPn8/3TZW5QVj3nfkI8S9eHgE93U9xM5n0rklMZUZ9lqcMHAAAAAAAAAMBlfOEDAAAAAAAAAOAy\n",
"X+mvfOzqc/vp854c17Jyroq4iXdrZufpOmcVkSjv1ozWPSkCZVfUSkeNUZ1dsTYr42cqIjci/31V\n",
"dEzHXq5a2+mRKJk4k6ddsSmZ53LXOfwW4ZKJ6RiNmUWtZCJRsnUr4mWespE0szoVY3ZGx8zqVkWV\n",
"VMSKmCc3T6Zu17zzMTdFq9y01s66fJeKJgmYpU9kjJ6VFevtWOvrFUysqOgonIkDycwbGVMRZ2Ke\n",
"WDxLV7zJrqiVWc3IWjKxNpG5d/37cCaTqnKumW/naFdr/5Pa3p8UD0CMc5YjfoJfOSX2peq5vCoy\n",
"5N2akbqZOJBsfM6qmJST5zl13kid98+7Dh8AAAAAAAAAAJfxhQ8AAAAAAAAAgMt8lbWdWxWxsWve\n",
"qq/GnBzZclLkyc0xMKsiUTJ1V66tY793xs2cHB3TsbZd8TOjOplon1XRMdloktmYVcdzUyRK9DHv\n",
"jumKTckcT0RmnmmESyTaIxMd0TVPJEYl0486E0VSETdTEVEz0hEdM9IRhVMVA9O1fvPkZJ6Xv6/r\n",
"trtq7nfdtFZ6dcS+3B7P8lxrW/JCpLvuqg7WXdEx5olFrczGRB6TWf/TqqiVkoiR5JjMk7ciBiZz\n",
"HWRURd88lUS8RBZyU3REtjX+LuJN1sns9U84PydHxey6kcjksZ0sEzfRNfeu59BJ5zATwZN5b6uK\n",
"pOmYp8qquJmOed/fI/+uAwAAAAAAAABwGV/4AAAAAAAAAAC4zNfwrxVfA7ktNuWkuI+nk+JZTp5n\n",
"V4RIZh276p68tshjdsamzGqsipvJxEKcdDwV8SaRtVSNyextRyRN1/F0nZ+OSJRfzfXumFXxLJl5\n",
"Ks7Ht/iW1ysXITJ7TFU8SMVjuqJiOiJeqsbsimsZra1iLZH/XlG3IhLFPPnHZPxz3T9fo9e83/dp\n",
"MTA7dexT1x7dFmeyS0eUzKhupKFtydyRDsNdnaZnnX6romPMUzPPSKYrfEVsSiaqJPPkrYi1yayt\n",
"InolW+dpVYTLqhuA4a1VJiDr05wSKbDTybEdGScfz0nRESf7tOdlRXTMTr8fN7FO13NsVzzIT3Rb\n",
"3EzmPFe8T/193k/79yQAAAAAAAAAgI/nCx8AAAAAAAAAAJf5WtqvdlVkyK55T4o3+bR5uup2HOPO\n",
"SJSOfVoV1xKZa1VsStf52BVrs/N4OuJNVo7piBCJ1Fl1PF3npyMSZSQyZlc8y6q1hVREomTGzNZR\n",
"VbcqBmZWNzJPJqJmNu+v/jar2TFmVXRMtm5FPM6sZqbGJ87Tca3U6LplrrAryuP2CBFyutINMnOf\n",
"NG9FcsTQrCNvVXSMeWrmmdUcqYqXmdXNHPNI11oqxsxqZMasypeqqrvrZiTULVy7eS34OU8mqiBT\n",
"d9W13nU8P8HsnO2MDOqIfTkpnqWr7qo4kMz52bW2k+aZzRuZu+o175+PWYcPAAAAAAAAAIDL+MIH\n",
"AAAAAAAAAMBlvtKt6Sq+KnJSZEhHjdtjVDJznbT+ndEq79Y9OQZmVVxLpM5Jx1yxlkxcw6rolcjc\n",
"mTEnRcesihCZ1RiN6VpbR4RLVyTKyKzuzniWXWv746/HH1ZFY2RiVLrWMtKx/pUxNrM6q6JVKqI9\n",
"VkXHROrcFmdyyjwVUTIr5+nRcTtfZdfcfj1SZ1en/1PmHc29Nf2golN2pGOyedbN8xTJ/1kVtRLp\n",
"Rj2rWzVmtneZuJzI3JkaFS8KmX3bWTcjco1+W++q1v83OSl+4qS1RFTEJojYuY9zdrbMzUdHhNCv\n",
"5n7XSfEsHbKv+2Jfaqw6vtm887n9Gw0AAAAAAAAAwGV84QMAAAAAAAAA4DJfw7/uik1ZNW9VG71P\n",
"i2zZFWeSmee249sVA9O1tptiU1ZFlWQes3NtqyJQdq1lZ0RN5tpfdTwdETurImpG43bFs+xc2zTC\n",
"pSo+oyLepCJSJLuWWd1V+zQyG9MV19IV8XJKdEykTlUsz7s1Vs5zk9/ft1W3bF2qboc7+GXIWUav\n",
"EKuu21nyxclry0THjOps63q90+x4MhEomX3LRq28O6bsYikYk7klyETJRMZk9no2b3TuWZ1Mjcj1\n",
"lVGxtioVaxHxEvRpL/x8F8nyqhjTpSv+5+Rrv+Lm4+Ssu1GdXVZdXyfHs2Se76v2LVK3av0dx1z1\n",
"WnpT3Mzvz+vfcQAAAAAAAAAALuMLHwAAAAAAAAAAl/k6Ksajau5TYkfMk59nVwTKuzV31t2597ui\n",
"VjJ1uo5n19q6jqfifGTiTarWUjEm8/yIxHQ8ZaI9MmsZraNjbasialaupWJvK9b2Lb7l9crFpmQi\n",
"NzI1KmJgRiqOOTJvR1RMVbxJJg6kIqLm3ZqjGjsjXjLXeld0TGaejJsias61MzlxFWvL6UoDqHDy\n",
"2p6vGKPnz8nRMSVOjkBZ1Sm7am2Z9WfWtio2JfIEOWktHfPOamTrVETSPFWtLSNye9WxluFzTMzL\n",
"WU6JKjjZ6cdzckzKKU4/h7tErp2um7+Zruu6I/al6/raFQ/yE62K2Dk3bkaHDwAAAAAAAACAy3yl\n",
"v/m7qoNERY3bu1182jw3ddrYudaO/V/5c8VdnTc6anTN07XXXeenojtEZNyuMTvXuup4Mue9o0NG\n",
"ZO6d3Toq9jaztm8dPbq6aKzqKBHp9NDRVSNbN7O3mXkrOm/c1mnjKdNJpGItXV1NKrqCZMZUnZ9T\n",
"9mBe48/XqPPR8zFzV3UFeIgcn1918CuzH+/f3kWjopPIcOCuThW3zfNU8YPTVZ03shd/pu5snkwH\n",
"iVVjInUqOnFU1Hi9ejp6rHxRrOi40uXb9eNX9vt+QX8b+1SnYy8zv3bP1D2pCwV7u6d0dLOI3EBm\n",
"7GqTN1LfHeKseU5eW+YaXdN95KRbRQAAAAAAAAAAAnzhAwAAAAAAAADgMl9lX/nItLSraIN3e7zJ\n",
"TfNE5jrpmHfV3RkDsyrepKtuRwxMVczQroiarlibzHO5Ig4kMm7VmIrrqWqtFedw1doykSizmivX\n",
"kpmna23TCJdVsSlVESKzebPzVMR/RNbybo3RY55WxdisimvJjKmKO6mI6amqm4mOeao4h5G6HTVW\n",
"zrPGqhTBT4+bifj043u99nb/XyGTuJGJjqmYZ6mOaJJVEShV8zzNYmEidTNRK5GoksjaVtXNxJl0\n",
"xNpEVMXAZPapo0akbteLeCbu52QiXgY+LSKhs+67du7t7TrO4e3no+vGKJOPl4m1WCWz/q54lo7s\n",
"warj6Yh9yT7HTo48+bTYlzPm1eEDAAAAAAAAAOAyvvABAAAAAAAAAHCZr9CjVsW17IyXOTlKpWOe\n",
"bFvAU455ZwzMrvOxK2plVVzLyrV0RKB07VNX3EzH8WT3oCMqJhsZ8u6YqnPacTxda+uK01kVzxKZ\n",
"55jWuVVRJbMxVdExs/Z0mXmij5nJzPO0c22ZMZnYkYr4nMh/z+x1pEZF3cyYihiYzJiuuJyT/PP6\n",
"u1IeybHXMaNnnL3rkYmOGT3mmA72I5kIlK6olaeKzt+ZDtaZzt8jkWiPirqZOJlVES4VcTMjmRe9\n",
"igynrrVFdEXQ7LLtdfDk+9aIjlb/5GXOx6q4g5NvPk5SEbVym0wQYkUESoWd56PjmDPHc1IE0qr1\n",
"75ynY20ju6Jw3vmvAAAAAAAAAAAcxxc+AAAAAAAAAAAu83V9tEfVPLvm3RXTUTVmZ7TKu3Vvi4E5\n",
"JWpl5R6sir7ZdcxdsTazMauiZLL7tuqYK6JjKvZlZQTKu2MykSgjs/Vn58nEs1TcE1TEzfzx12BQ\n",
"RRxIREU8SyZCpCrComItFfNEZCJ2ZjUiYyJ1qqJiZmMyMSNV0SRPXWv5tOiYipoVa5vPszPdb5dV\n",
"x9OVMElOJEVh1rw5Eh2TmWfX82Pl8UwbY1dFoHTEmUTcFLUSytyZ1IzWzYyZPSEia4mMmR1zZp+q\n",
"4k06omNGMnUr1paZZ+SUm4uqW8XZ8Qzn6XgBizg5NmVVa/+dbygzmRb8kTq3x3ZkdMV0dOxt5mbq\n",
"5OfyJ9oVlxO53jqu9a7Xya5cxNk80bnerbtq/V3zVDg3CueU200AAAAAAAAAAIJ84QMAAAAAAAAA\n",
"4DL5SJenk+JMds2TmXfV8Zy01zfV3Rmfsyp2pKvurt7SJ62tIkIkM2/FnnTtQdWYjhiYrjiTzB5k\n",
"4k2eVkWiRM5PRSRK9DEzFXE5kb39FuGyKjalqm1pJgamIjpm1Vqq5pnVjZzDrrWtmHekIq4lG6uS\n",
"icvJzHNK3a7omF1ru8unRcdA1qdFx7SJdPH9tKiVitiUro7JkRfxzJjI+agYs+p4njJxM5E6FU/4\n",
"TKxNRtUeVMjcbu3MZ/t2jla1Xs88EXda1aJ+Vyv8T5OJIaiKsanQFYVz8/XVdWOUuWmrWssuu6KW\n",
"To6xGjk5NqXLruu2Yt/Ojaj5uM/QAAAAAAAAAACfzhc+AAAAAAAAAAAu8zX866o4k4p5zbM2sqaj\n",
"L/Hp0STv1l0ViZKpu3JtHdEkXfPsijzJ1FgVoxJZy6oxO6NjKmJ5KiJcVq2t6vxURKJkXp8jdSvW\n",
"MjrmaYRLJtqjKzalIgamK6Jm51pmMhE7kToVUStV8SaZMV1xJpkxu2JrZjWzYzKPyYzJRBNVmK/t\n",
"z9fztfX53+eqbjmB88yiYjJxM6M6JV27M26PWqmIGRnt4+zFPxPtUXVOM52YM2kTuyJcMp/RMudw\n",
"JBNNlDGbZ+VPJ09aS4dtES8jmReJVU6Oa3jK5HCNVBxzxQvySXtdtbcVToliGM0duek5KdZilcyN\n",
"3arz2pFXGNF1HXfUzT7/V8W+nBxFtisuZ1XEzp//8L8AAAAAAAAAADieL3wAAAAAAAAAAFzmqy1a\n",
"YuTTolQ+LbJlVwTKTWuNPGbn8XREiHTV+bRjrorcmD2m63hOGrMrOiYS7fGUiRCJ1Fl1PF3npyOi\n",
"Jlu3Yi3Px3yLb3m9eqJWVsWmZOaJqJrnpLU8Zfb23Zqjupk6XfEmu+atiuWZqYhEyY7pqNvVWvPk\n",
"6Jgap6QVwm6RZImOqJWjopd2Rq3MZE5I5OU3E7VS0ck408U70/U6c05HMjEqFbEvVTE27877es33\n",
"tiq+peJFIHOtdzlpLacYXpOnRGp0RQqc5CfGXHy6267bkyN1ODsu56Z4lq7nZeYGeNWNtnnqYpP+\n",
"+Tnm35MAAAAAAAAAAC7jCx8AAAAAAAAAAJf5SreHq/iqyElRJbvmOWltJ+1tR92qPsvvzhupu2tP\n",
"InWr1tYVmzKrcXJ0TNfauo6nY8zoMbsiXKqur4p96jqejgiXzDzZa3RWt2ot0wiXrqiVXfEsXWuL\n",
"2LWWqr2dycwzktmDinlnNSJ1qsZkIkO6xlRF9XTXfL32xdj0tN+tunW6+VcPomP4leezbnSOK6JW\n",
"TlaxB6M6JakKVVErmc7SszGZrsSRMZnImkwUzmwdo7pPkb2OjMtEuFTEvnTN+5Tdp0id/6sqyiRy\n",
"rXeI3H7d9OK607dr/6SIh13xE5n28zvnqdinipiIrryvijGjcZkxu2IhIk6Oa6mIKsncGGVv9Fat\n",
"pUNVLmLGrG5XtEdmr7v2YNVazNPz3jev4/YSAAAAAAAAAOAyvvABAAAAAAAAAHCZr+FfxbXUzHPS\n",
"2k7a25Pqrooz6dj/VWtb2Tf65GPetU8nHU9mzKpj3jWmat6OtWUidroiUSIydTNjInsdinC5SSaq\n",
"ZFV0TEbFWiJmMSrZeTr2KRObMlIRb1Ixb0RXBMpTV1zOqrVEdMTNVMy779cJIlH60jAZ+/SolYjM\n",
"Hqy6BkNJGB2dl7u6RFd0Lo/U7Yo7yXTTr4ioiYzLdIWOzJsZ826NSJ3MC0/XC1jmmuya5+nkF+hV\n",
"XfurTF+vTvqsHjnxXevdFc+Q0dXm/uRjPknHtZJ9E63QEdPBf1VEx3TZdd67XmvFvphn5P15T74F\n",
"BQAAAAAAAABgwBc+AAAAAAAAAAAu89UWlTFyUqxIxTynrG3V8UbmuimuJTL3zuOpWFvXtbFr/bdF\n",
"x0TiJt6tm4nPyMybGZM9P6uOueMYq/a243iqrtGKeapibTJryax3atSW7dNiU54i83Qcz6/+NlOx\n",
"lq553q0ZmSdS56S4lkyEyKpolUwsT0RHbE3XOrrq1rd3PT12pOM6gxfrAAAgAElEQVSjxm38wuT7\n",
"lf9pexJJn9i1B6NXpmVxOZGuvh3dgjPdtSNdrzNr7eqGPDtBkRP/lM0MCuX9PGQiaSrmndXI1qk4\n",
"nqfM9ZWxap4qXVFRJ0t9vD0p5uUp8i7UMU9X7MDJex2ROZ5Vb4irxkR01O26+VilIh8vk90XqXPS\n",
"PkXWtut15aR4lndrRuvueu7O1hFZi3lic//vP/5XAAAAAAAAAAAO5wsfAAAAAAAAAACX+WqL9og4\n",
"JRKlakzX2k6Kwumouyuupavu7TEwt8Wm7IqO6VrbKVE4KyNrVu1TZkxHhMvKCJSnVZEoszGR6JhV\n",
"8Sx//DX4Y0c0SVU8y661ZWSOZ1WMTWYtXfNkIjZ2Ra1E6mQiUSrm7RpTFcsze0xXJEpmLRV139/r\n",
"P1+j1+PnY3qsTDl9V2RtfsVBViRq5flsXvVciKytKypmesyZLr6Zrt1V3dsznaVndatiRyr2rWJM\n",
"tstyJiomE0nz7ry/mvvdGk+ZiJ2RjrXtnCcjc1v6E7Lg3lXW+X9XBELmhbFqno6Ygcza17S551e6\n",
"4jS64jIq5s3c5Kxaf5eKY+666ZyJvE7+hHiWjrqZm+bMWrriZz5tntm887n92xAAAAAAAAAAwGV8\n",
"4QMAAAAAAAAA4DJfw7+uihDZNa+4lrV1M/Psio45OQam4hyumidS57bomKr4kt+tsWrMSWupGpN5\n",
"flREx6yKQIn89455ImMie5I575m1fItw6Ypa2RXPctLaMlbtU2YtVfNkInZmqtaW2euKeWc1Oueu\n",
"iFbpimPpiK1ZtY59dbs+alTU3PVri5M7wJ+8tohMWsMqo2fYKXEsXWuLxM90xcAc0/G5qiP3rG4m\n",
"diRz4iPdwivGZKNKMudjVqMqIiXzpMrE5WRqdjzhR1a96FWkT1Dn2zWXycd6Whnn0BWxMZtnVfRC\n",
"ps6q/d/1BhkZd1LMyClxLSvnpkbXjWpm7sgNWEUm4KrXlYhd0SQ713LyPPXzur0EAAAAAAAAALjM\n",
"11GdH6rmPqVTxUndOzLz3NS9o6vuyo4Y79at2uuT9qBjLSfvU9feZsasWv9JY3Z1t8ispet4uvZ6\n",
"9pjsL60y65929KjqKLGrW8enrS1j51oqOmI8ZY4nU3dl543ZmFWdQ07psjHSdTwnreX9uh0ftyJ2\n",
"/ipiV8cLvwS5T6SbRYe2DhkTq7qCjOo+jzk0b+QHWqt+cDYbk/lBduZHkF0/nKwYk+3mUdEUYFUn\n",
"kcyPEyMq1vZU0ZAhK3Mb5E30bKmOH09VT7KMmzt+7PRpx5Ox6s06s5aqG6MKkXkzN1OZTg+R53tF\n",
"p4pVx9yl4+a2Yt6VdSvOYbZuxTzvriOyllUfNqpeJ+v32i0pAAAAAAAAAMBlfOEDAAAAAAAAAOAy\n",
"X+kemKviSipq3BZ5smKe7Fd9ZnVvimuJ1N157VTs9ao9uG0tFTEdkTHv1hjV2RVj0xVvEhm3K8Kl\n",
"K85kto7sWjLHk3lNm9WNnPdVUTHf4lter544k5+oYt+ye90R5VEVYzMTiUDpiJLJ1u3Y61WRItm5\n",
"Py0q5qS1vOe2eJZd0Su75uVn6IpNieiIihm9InbVLdmnVV2XI2O66s7GVER5ZKJXsvNmOuNXzf1/\n",
"ZfY6oitaJdNdu0LXPq3yEz+WdpyP4T6e3Or/KbIpFffqVXENFftSUWNVRlg2SqIjs22VrviMiJNj\n",
"R+iLHanQFZfVcTyropYidXdGoMzW0hU/UxE3tWavdfgAAAAAAAAAALiML3wAAAAAAAAAAFzma/jX\n",
"VVElFW3ZxLWsrZsZsyuS5uQYmF17vSp6Zedadq1tZ6xNJv7npD2IRITMxuyKjsmstescrlpbZh+f\n",
"stfBNMIlEtNRoSoOpCNupmttXVbtU8aquJmu48lcKzNVa8tEr+yKiskc82jMbO7M83DnHvz+mD9f\n",
"oxiuf9bVZf22ujO3xePM7Oyu/3yW3Rxv0ll3pmsfI027K+qG9qmjo3imQ3pV7EhmE57HkxkTOYkd\n",
"e5CddzYu0yU6U6cjVuX1yj2pVsWmVHXT7rAzyePTVHysS0UrdbXKf+qKlqhoP99VtyPiJVtnlYr8\n",
"sqrjW5XZVmFX1Efk+qqIKoncHGbWErlhqZhn13Xweq1b22xvu+JNKqJKRnUzVkWgnPSa1xEjtiZu\n",
"RocPAAAAAAAAAIDL+MIHAAAAAAAAAMBlvrbGTzzdHqNy8jw3xbV01T05BmZnHMjta+mYZ2esTUXU\n",
"Sle0R8eYyLjRmIrom137cvLxZKJjVs4TinCZyUSI7Ipn+Qlry1i1TxVryUR7VM0zk7lWRirWVnWt\n",
"dO1Lx5hzolW+W7UHc6s+TkV0/FLCry/4BKNnf0daQ9VzO1O3LdpnVYfkijFd3ed37cFTV/RK5mLJ\n",
"RMeMZCKDZjLnNCPbubxD5hbnJ0avnCzz/G6JeIlM/Hr13FevmidjZzzLqjeuVU6Ka8nEmVTsZUXU\n",
"CnknR8dUrK1j3pV1I9f+niiSvbEvFc7YA//GBAAAAAAAAABwGV/4AAAAAAAAAAC4zFe6zdztESef\n",
"NM+qyJ3Xq2ctK2NG3q27KnYkM/dt0Std0Tcn71PH3maOp2sPVo2pOuaKiJ2KtZx8PJnruGueb/Et\n",
"EVVxJrsiUKwt9piMrn3qWEtVnMYs1iaiYm1V53RVjE3FmGidU8acHBXzz7o+0pxS8/Xq6wrfUVcH\n",
"+5iuCJSKJIlI3YprffQK0lE3UrNrLcu6qt8Uo1IRvTKqEzlhFfEmVeuf7XdFjdcrdyFXrO0p8/bf\n",
"9aZ60lo4S+o2dVXMS1f0SsU8J7XX33U8FWMi406K5ek677NspZ17sCqqpCJyI7OWrnm67Fpb5vxU\n",
"3Ghnj6fj/STzPFz1mlc1z8lr++d53LYCAAAAAAAAAFzGFz4AAAAAAAAAAC7zNfzrzfEm5ok/5qkq\n",
"uuPdup8WA/NpUSurjifymK5j3rVPVc/ljtiRnWN2RcdUxfJ0RLh0HU/Fa2BmnnSP8Y7IkGzMCO/L\n",
"RMdEHhOJl8nour5muq7JrvicVWuL6Nr/W+aNODcm5qTokpPWAjfqiJfJRK+sis8J1c108V3V/XhV\n",
"V+KK6JVRnYp4k8y82TqziyXToTuiKpLmqeK8Z2Rug3b+7HFX8sLtTvmpauh6WxXx0jV3RyTK65Vb\n",
"W8VaVkXjnGzVzUfErvNRFbVCzqqImoyKtWVkIkQiuj44rMqCvGmec9d2ym0TAAAAAAAAAABBvvAB\n",
"AAAAAAAAAHCZr22xF+bJz3PSWn5iDMyq2JGOuiujcDqib06Oy+m6vrqO55Qxo8fsinCpuiYr9qnr\n",
"eDKvrR3zjPzx1+MPmViLSBxIR9RHZC2r4mZOXluVVfuUUXE+Ik6KtXm3RrZOxb51xdhk5j43WmXV\n",
"mMxbRdevFVZ9POzSsZaTjo++aJJn3Z3nPbOWrvVn6qZibDKdfjMdhSsiUCpiRnbNG6kTeSOoiI55\n",
"vXIRO+/WGMm82XXFy2Tm6Zg3oqqzv59c5pwc3ZP6uNUVFZF58ZzJ5H2NVKytI+IlUmfVmNG4k24K\n",
"3l3H61VzrWciN1ZFMq+KKqmK3OhYy0nx1yfFs3TUrTqejud/tq7Yl461ud0EAAAAAAAAALiML3wA\n",
"AAAAAAAAAFzmK/2Vj5NiRT59nor4icw6Pq1ux95H5o3UWRW1sjKm5+Rj3rVPJx1Pxx5kr4uK9a+K\n",
"CKo4p6v2oOoa7ZjnW3zL67UuCuNpVQRKJm7G2n491++6PQbmpHkqYpOqntur4nLerZEdsyqOZU28\n",
"zJ+v0Wv/P1v1Ea3LKbE1t+/JbU6JSRm9GlTsf0Xcyc7rILOW1Pp3xais6ho/sqoz/rs1InVWRce8\n",
"XvMLKNPNOWJVbMpJ8SwVt9A/4Y3r0+yKgfk276pIgZGutv0V6++IeMmuJWPXG++q4xvpWEskQqRL\n",
"RbwJY7NYi1URNRlVa5vVHa31pNfs2Voyr7+Z59RPmKd+bW5bAQAAAAAAAAAu4wsfAAAAAAAAAACX\n",
"+Rr+dVfv3J1xILvmue2YPy1e5pTYkUzdk2JguiJQTo7L6bq+Oo5n1ZjsdbBqnyrGVFwrVeej45xl\n",
"9i0yz7cIl2y0x8xozK4IlIrjuV1VTE9HvExG1/VVsZaqeTLX/syqPVhZpyPGJqPqfHSMyUS+vC/b\n",
"Ab7rY9sKfrFBp64YmIyK6JVsGshsXGZMWZxJR4fhqs7lFTE2TxWdpyOq0gEqYl8yT7qqWJ5M3Yp5\n",
"Ik5aS4VP/3h48t6PZLqqp2pm3qm6sokq6nZEvLxeNS/kmRfG25+Yq7LhutYy0xW5UWFlVElF5EbF\n",
"Wk6Ovtl5rXTUjez1msiQmI4omdPnmd3AZ+Z5f4x/LwIAAAAAAAAAuIwvfAAAAAAAAAAAXOarLY5i\n",
"pCNm5Pa4lqeq+IlPr1sVM/LuvJG6J0WtVKxl1TyROidHx4z+e8fxnLQHq9ZfNSZzPipiYCrOR9fx\n",
"dO31NMIl2x5uFjfRFc/S5eS4mV1RJRmr9qnKqr1dFTNUsW+79iCi6jro2pcV80a8v7aTPl5VjLk5\n",
"JibLr0fqZOJLTpGJgVkVo5KNqFkVJ1MSgdLV7TizuRXzPmW6hVclJOyKVqmI04no2oPMPBGrXhh3\n",
"dv//JF0fpXbtW6ZL/Mi366vrhT9iV+RGxCmxHF3nZ1X+WlfkRtf56YiXyURhZKNW+C4THdMVUZNR\n",
"EZ8zqxmpW3W9/X5kSC5mKFv31HmqzvvT78e+3PTvCAAAAAAAAAAAvHzhAwAAAAAAAADgOl9Hx7Vk\n",
"5zm5B+9NETU763acj1WxI5m6J0WirDqHu6JXInWqoj3erTGqsyv2pSveJDKuYszOiJrM3mb2YFY3\n",
"s7aR2dq+xbe8XrnWeZnIjVXxLBVRKzvjWW5eW3TuCqv2KSNz7VfM0xUpUvG8rIp96TjGitfA7Jid\n",
"c3OKnxgv8xNlYkeer1bO+2EqoleqYjpmc48unkxn+Xfn/dXc1TVer75olczezmTWmpknc6u16oWm\n",
"K1GAs1RFQ3X4/U7swUJVL6ar6nbke62Kwql6s1sVDdMVy1NxzF0RFafE/2RiLjJRJZE6q9aSib7p\n",
"ihmK6IjpiNgZiVJRtyMGKlK3Ky4nM8+uKJmRf55bhw8AAAAAAAAAgMt8hR51UteJzDyndO/IzrOr\n",
"o8Squiu7Trxb96TOGxVrWdmB5ZRjznSd6FrbruNZtQfZfavYp10dParWWnEOV63tW0ePyLdaT+r0\n",
"ULGWru4jFV0CTpbZt9G4k/e26/rqWMuqeSpqZut2dd7o6mI0U3HOds1b02Qq4uSPfquOBypluoJk\n",
"xmQ6lqzqclJxPKnn8qofw0XmzvyQ7WlV95FVnURer54uIKu6aJzUKaHjB7Snufmj3el7O1Px+lUl\n",
"8obybb0VnSmqPvtV1O3o+PF69XXeqHBK947Xa107sXdrjtayaw92XivkOonc3q1jpuuarPqwUdHR\n",
"Z1cXjUynmmzdjnne+a8AAAAAAAAAABzHFz4AAAAAAAAAAC7zlW5ZdlJky7vznLKOzrqZeXbV3Xk8\n",
"FbEj79aM1q1Y203RK9m17Nqnk48ns9ZdsSqRcVVjKmJTKval6hyuWtu3CJeIigiOjNvjQCJOjps5\n",
"aZ+eVu1ThUycUdU6ZnWrIlEq1t91PnbFpox0vS72z/vn6/33jlUf0X5nHHC2iuiV12v+GpEZU9aJ\n",
"eVWH4Yp5ZzWydSqOZ2Xsy1MmdeB3a1bNM1Jx27PqjbnqFi3j5liUVfu2c49WRSlVzFvyIp6efFL3\n",
"tjeHk6JWKlTEtZwU//MUuZnqOp7Zea+KuaiIm6jap8wxZ2J5us7ZzMnxLFVRH7uiViJOiU1ZlaG5\n",
"Zh7/1gUAAAAAAAAAcBlf+AAAAAAAAAAAuMzX8K8nxYxk5jlpLe/O82lxLdkxJ+/TSREo745ZGdNR\n",
"MXdHjdFjdq1t5/nYtZZVY3ZGx3REuKxaWyi+pSIOJOK2eJaOCJSq47l5bdm6q1pAduxTxToi86y6\n",
"9itq/upv76qKganYy1WvkxF7YmxWffyq0vWxp2JMZi9v2/+fJhNNUhFnErkuKsZ0HU+VVftf0sG6\n",
"orPxSEXsSKYz/lNVrErF3lbVna23Kq0ho2uf3tV1K+9nj2fbFauSlenenhF6TdiV1TWrma27K+Jh\n",
"VcRLZp9WjYnoiFXI1n133tHcJ8f0RKyKZ9mlKzrm5HiWiJPqVkQezdYRWUtVhuasbtVrXv08bnUB\n",
"AAAAAAAAAC7jCx8AAAAAAAAAAJf52hoHUjFPVZREpu6qeTrqZr/qM6u783x8egzMbXEzHWs5eZ+6\n",
"9rYqzuTdtayKRBmNqzjmnXEzmdffzDmc1cisbagjTmNltEfGrO5tcTO3OyVeput8VFxfGZF9q4gd\n",
"WRVrM6pTEbXS9bqSUbGWriifuV0dt1fFqjB2ckTNyXEmfDd61Zntf6SZc5fUea/oKJ7pmByps6sj\n",
"f1WsSkV0TKZuZq6qizRz3it+FtiRFnCSUzrcr3TyG9fJMTCZN65s3dyDHiryviJ1V72hdL0JZTLP\n",
"utr/d0Q6rDzmd9cSubNb9SLdFaNyctTKquiYXec9cz5Wxah0va5k6nbFJGUid7piU/bEsVTMc/It\n",
"NAAAAAAAAAAAA77wAQAAAAAAAABwma90G7OTIluedkV7ZOY5KW6mKi7j3blvj1rpOocVsTw792DV\n",
"+jvm6drbrvNRESHy7jpGNbL7VnHMuyJcqq6DinOYWdsffz3+0BUlsSuyIlK3KtZiVfzKyXEzHWvb\n",
"adU+Vdi5tx3z7HyNqKhR8To5qptREcPz/vFU/apg1ce2CqtiSOA0o1eZ2XO3q8t9xKoon1mN1yvw\n",
"GlfVXf+UaJWqeJZZ3ZVRJh1zdXUHj+jowN9l18eGn/jm3ZUesGsvu14DIzKv2SV1q54wHdljVbk8\n",
"mbysVW86q1r9R6xa/0xVBt2sblfsSJdIrEVFTMdJ8SwduqJjdsWoRFSd91ndne8np5yPzGvEmnl+\n",
"4m0qAAAAAAAAAMDVfOEDAAAAAAAAAOAyX8O/3hzXkp3nlGiVnfEmmTG7zsftMTAnxc2cEh0TqbMr\n",
"RiVSZ1Vsyqo9WLnXmfOeeX5UjKnYl6q9zbz+TiNcKlr/j+pWzDMa1xW5UaEiAqUrbuamtUUe0xUv\n",
"06Vrn353HZF5VkUtZXWsvyvCqSuupSpO5j1/vp7vL5ka78umk54094p5d62VvTIRIpl4lirPuSPz\n",
"ZsbMakTqlO3Trs74t0erZLr2z2TfCjP5RTNVP82rSkn4XV232N7c7teVCtGhK4plpCIeK7W3u174\n",
"q+IzMm+IXbEpu6yKa8lEYWTOx6qolYrj6YrT+AlWRcd07H8kmqgrRqXreupY784IlF2xNnvm0eED\n",
"AAAAAAAAAOAyvvABAAAAAAAAAHCZr61xIE+nxKp01s3M01E322ZuVcxIR92dazslNmVVvEl2LSfv\n",
"U8fedsX/3D7m+ZjMea8aUxHlU7FPmeP5Ft/yeuViITIRCRWRAjvjWXZFoKyKm/mJToq+qbArBiaz\n",
"llXPy6q6XXEtFXVPiZKpqbOzE/tNcSy7+GXIWUbP/pPP0XO9q9a6a96yuSs6M2e6H0fqVHXpf6o6\n",
"xt+tGVlr1x5UzDNS8QSoWMtJL1Y+XuWcfANzSnTR61UXqTWTuSkYXvsdcRNVb0IVa1kV8VIxJjIu\n",
"ElXwlDkfVefwaVf8RNfxRHRElUTq7IykWRXP0mHn2rqu4466Xfu0Kvrm3DiWinlOuu0GAAAAAAAA\n",
"ACDAFz4AAAAAAAAAAC7zlW5jdlLkyYp5Tlp7V8TOrqib22NgbopaWRWJEqmz85g79qlqbzvqdkWV\n",
"VIwZPWZXhEtVRE3FPpVEuFTEqrxe83iGyDwV0Rijx0Rk1l8Rz9Ll5LiZjrVFHrPzfMx07VOFnRE1\n",
"s+dh1zxdcSafHgNT83yq+KVBpkbVLxx2/VLCLzTY7eZ4ltEraya5o2Lu1D+9dXXG74omqYiOeeqI\n",
"fHm91sWz7Iyb6OjAX6UraXDm5GiSk3Wdr13nY1X0ykjXm2qmA/+3MZnohYiOjLCqF9dMjErHmNG4\n",
"zJjI3nZEUlRdK09d8Rk3x47wXyefw8zaujL0KqK7MrEpuyJQqiJqKmJtnrric+azAAAAAAAAAABw\n",
"MF/4AAAAAAAAAAC4zNfwr6fEqJw+z654k8yYXZEoXXV3ru2U2JTbYmCq4jJmYyrmjdTpirXJHE/H\n",
"HnSN2XnMq46xo8ZoTCrCZVU0xqp5MnW7Ih6eKqJKdsaz7OqzfHK8TGZtXariclaspWtPuq7brn3r\n",
"qNu1B7+/tqoO3bs6fVfN+9NiYPyaJGb0DLspJiWjIt4kG89SoWL9kebHIV1d7Z86Ik86Il9er7P2\n",
"4Kkqiyij4gnSdRv3aW8Yqzr5f9q+VVxfXW8Emc7yJ88TeROdRrxEFpOJFBnpik2Z1VkVvXJSxEtE\n",
"x/oz8QaZyIqdL9CZOI2K+IyqfeqYJ3PMt8WzVKyt4vxkddTtikDZFSVTET8z8vtr+7RbRQAAAAAA\n",
"AACAj+cLHwAAAAAAAAAAl/lKtwXriCY5Ka4lM8+uCJGRjvNTVffkGJhd6789Bua2eJlV0TEdx3PS\n",
"HmSeU6uOeTQmcz4qYnkq9vZbfEtEV/zEqpiLrmiPiF1xIKtaTWasipu53e37lLn2K6yKGap6jcjM\n",
"U6FrD36/bsWvCG6Pgaly+/r5fBXxJjtFGjG/W+P1yr0OVqxlWeRJVzfnVbEpXbEvFfM8VVxMVXbl\n",
"Pt1m1QvhSR+dTvkJaaZD+qq5q66LrmNMPe8qIjciVkWg7Jo3E29QNaYiEqErSqIjlqNqD7oiQ2Z2\n",
"xqbsimfp8mnRMRWxIpnX7FUxNlXPw5tjXyJv7n+f55TbMwAAAAAAAAAAgnzhAwAAAAAAAADgMl/D\n",
"v54UrXJKZMuqPTk5EiVa5926J8fl3B610lEj+phdx7xrn046nq49qIg3iYyrGLMzoqZib0MRLhWx\n",
"I7Oa2XlmMjEXo8dkdMWzdKiKtemIm1m1tshjuo551TWZ0XUOK3RFLUWsOsaOebr2qeN18/X685WJ\n",
"GnvW+H1Vv16o6Lh9W6zF0+3r/4lujlYZvbpVRKtUJWFUdMY/Kp6lovv0rtiUrk7Zu+bpmrvrBWBn\n",
"x3rO1nFtdF0HXa95FfNWHXPFG+KsZvpBFW9Cp0S8ROpkIytOiVbpOubMdRAZs2sPKtZWFYH0aVZF\n",
"x5wUz7IqO7Er3mRVbMq7NSN1M+cjE7U0Un9+3FIDAAAAAAAAAFzm66ouG511M/N0dfB4OrlDxq66\n",
"VV0o3p03UvfTuoKc1LkiM/eqTg9VdTPHs2rM7DHZc1qx/l0dParmnXb0yHZGmMl0Soio6K4Q0dXp\n",
"ISPTHWJVtw767OqE0mXVc/fddUTXUjHXrteIjK7z0fOropO6aJzSXaTqeG7q7PB089pfr/Gz8KZj\n",
"quhKUdUho+LHyVVdTzr2pezXVh0/lB6p6CRSUTOz+avmyc5VNff/1XWruOsFzUeaPif/9LPr9Swj\n",
"spaKubvm2VZ3V8eP16uv88aszk3dO16v3P53rKWru0VFd4guVWur6BzS1UVj1Tw3devoes51HXNH\n",
"Z5pVXTS6Oot0nY9n3d9fy8m3eQAAAAAAAAAADPjCBwAAAAAAAADAZb7S7cdOiVY5KW7mpOiYjn2r\n",
"qrtr/0+KEHm3ZrTuSTEdT7vicqrWn1nbKceTGXNSlE/V3mbiizoiXKbxLa9XTYxCZExFjEpX9EJm\n",
"/TvjWWaPWdUicuTkuJnMY1bFppwcl9N1Djt0RVJl5l41T9e1smr978u83UecFJvCd/a2TlUUCX93\n",
"ctzMSOq8n9Tx/d2aI6vm6dqniI63866f8+36COPniX1WndNV53BnDEymG33HPNm5unLd3n5QVbTH\n",
"rtiUinmzcz9l3rxPijeoiM/IyMSorFpbxEmxKZmIilU+PTqmqm7HzfhJsSld+1YRUfP0/vlxCw0A\n",
"AAAAAAAAcBlf+AAAAAAAAAAAuMzX8K+nxLVk51m1/oq4hsw6Pq3uyXE5J0WtVKxl1TyROhXRGJl5\n",
"I3Ui0R7v1hzVOCk2ZdX6TxpT0X8+Ex0z1BGBEol4mNUYjamIYshGPHRE0OyMm+iIQKmKmzkpvmSX\n",
"k6NvVrnp+TJ6TIXb5+mJm+n41UBVd+2uXzRUrK9ibVXHJzLk81TEjlRFoFR0ie+KuelYW7bOU6RZ\n",
"8FRXnElkMRW3AKvm6crliai4WHZ1iT/JSV3iVzn5fDxVnZ+OY+6KSHnKdJqvmqvrNW5WtyTiJTJR\n",
"V1xLV05ahUwcwKoxEV1RGLNz1nU8keiSirXtjIrpEImoOCmiJmPX2lbVzVzrIyfHpnTsW8WezOfR\n",
"4QMAAAAAAAAA4DK+8AEAAAAAAAAAcJmvsviGp5NiYTriWkZ27eXOtXad51VRKx11T4pEOTlu5uR9\n",
"6lpb1/FkxmSu444xo3EnRbjMxkTm/eOvxx8ybfu7YhS6IhJWRVbsipuIrL8rnmWXXXEzXXVPik3J\n",
"yMTynLQHu679zHXbNffKY/w9f76e72M1KjpYd3U2F5sCtU6Km4nUzTx3K47xm9u7qj/tjHioeHus\n",
"unArrPr53sld43/im+yu87Fzr7siqGZWxbFkUkYiutafebObriXzQplp9b9zTCbG5qYxmWPOxJlU\n",
"xfJ0RElEVKwtUqdqb1dFk8wiQ35iPEtExbWSqZt5vt8Wm7InjqViHh0+AAAAAAAAAAAu4wsfAAAA\n",
"AAAAAACX+Rr+dWeUx4p5TlnHJ9atihl5d95I3ZMiRN6tGa27Kqbj3RpVdTI1dq7tlPNxUqzKqn2q\n",
"ir5piXCJtOeqiF7oijepiPbIzDOqUzFPVTTJKbEQO+NmTo4Qicw7W3/XMXdFK3Wour66RM5Zh11x\n",
"LVXzrDlnFb806Pq1wsld4SvW5lceP9PomVyRhHHS86VrbRXxLG371hGbEllcRyfzkV0RKF23K10X\n",
"5Sq3v4Gs2reTXhg7VD0/Vu1TJnGjY56q508mcSOi4o2qJRC7vhkAACAASURBVOIl/KCHrviPjjE3\n",
"xbVkdRxzV9TKqhiVnf4fe3e0HDmuHFqUHuv/f/ncB8eN8LDpISonM5EorfV22iIIglSpNC5h78qz\n",
"TPlvWdd1dp4lMrence66UiuTsylV63bXc39Of+sOAAAAAAAAAPDr+MAHAAAAAAAAAMBhfkbnQaLj\n",
"Ro6ZkqjZmQOpWoOMREXkvN+Wgek6z6RrjuQ0qua263q+LeHSdd8j6xZJx/yRb7muukxKxhhvc8vK\n",
"T7zpTKJMyWfszIGcpGudvk1XlqfKpHu6K0XUdZ6aexr50b2iaufvinGz/pJi8l9kTJ7bt8lIilSp\n",
"yJ1cV873ZdW6Vex6/yTltalrt/MnXdmXu4wfbZ3phYgpKYzTWLc/7czPdL0WvalKX0XOM7lF9uRt\n",
"3Kyd/kMDv51ocuLlut6vMZIDqDqmK2uzYldqZWUNIpmOSZmRClXpmEmJmpPTMdfVd827silTUjJP\n",
"4959fn8m/XcDAAAAAAAAAAAW+MAHAAAAAAAAAMBhfsIf+ZiSM9mZQImMGznP5AxM5JhJqZWKcbPm\n",
"dlJuJiufETl3ZJ12rW3V/ehag4pjno7bmXB580fCZWULr4yESFUCpSpv8jZudCu6XXmWlflnZEeq\n",
"VKQ9shIiVeNmzP+kue00JZv0ZNJcuu5hT/pmchKla9ydO6K/Mbe9TsqxTLofFXPrSsdcV01lIO3+\n",
"vE0u60dF13nuIgs1aS53O9/mTXrBosbkZ39F5Psj47nOyJ10jluVk6lIx0R2+l8a+C6SB+g65um4\n",
"lUWIZAYqjslap4z0woqK68k479O5I8mNrKxFV5qk4nq63kxNTsdEx31TlaSJ3MOM5zg67qfnqUrU\n",
"vB8BAAAAAAAAAMBgPvABAAAAAAAAAHCYn8d/nZQzmTKXXbmWaeNOXqcpCZTIuJPXoHPdKtZpcpIm\n",
"kkDpWoPOtY5ccyR9EzmmLOHyJpIQeRvj6ZiMuWWlSjJSGCuq0h4ZMtagat04T1eWp0skEVQlsrYZ\n",
"es7z1/Wf2/+uUbXzd9W4FeswKacBUV3ZlKzvwapxV3ao/9TjxsyRXYnfrCxC13kqzvtk0lzuun44\n",
"dFXt6LXrTzurdonPUJU36TpP1bgZP7gy5rbyRuKP82SlC046ZlLiZcVJKYmu7EiVb8uzVHn7ntqZ\n",
"Z3kTmdt1va9t1ffUiorsS082pS9r83lKxg4fAAAAAAAAAACH8YEPAAAAAAAAAIDD/GzNg2Qck5Wb\n",
"mDLupLlOyox8OubquF0ZmCm5ma51y5rLrrxMVg7kbYysrNVJCZeu+x455o98y4pIziSSEFmRsdV/\n",
"JPGwIiMlsWJnoiJynl1ZiLd5XFfN9URzM11pkq572DW3Kb4xHVMhku7K0nOeil26/fXC/5Cb+X6n\n",
"ZVNOcvzaVuwavXKeJxU/MlfO2/XjMuuFcUpK5Td+w/8GFd+HXc9K5Huj6/uy8/s/st4Z8++aW9nr\n",
"+tvW/pNzLSvHPR3z9g0fSRWsHFO1ThUJhKqEyK6MytM436YrHbOSTZqSZ8ma265xq1IrkfRV5Hv3\n",
"bR6r476d59/P39t7AAAAAAAAAIDD+MAHAAAAAAAAAMBhfh7/dWci5K4i97EzITJl3OnXM/kedq3t\n",
"t2dgJq9T1dpW5X9OPubpa0YlXDKyA5Fcw9sYT8esbBVWkVGI5CeiTs6zZHnLpFTlWfg+nVmeLhmJ\n",
"nSq7kk0ZybB3kR/LGeepUnUemRR+i4qcSVV65cnKJsSfqtopPzTIruxL1Y/cqgesStef3n37ju+/\n",
"0a4/28x6lipetLsyMJE1iF7v27my5p8xTlfi5W0eS1+UlVGpOObpuMgxKwsTSQhU5BqyshZv41al\n",
"ViKychqR+UeyPBVJmq48S1Yy6M3OPMuKiuTR5O/dlXG7cjNv88g6z9/HtcMHAAAAAAAAAMBhfOAD\n",
"AAAAAAAAAOAwP1vzLVVZjsh5KsadNNeufEZk3Elpj0/HXP2ak9agKm+ya512rm1F/uf0Y56+JnLf\n",
"I8e8JlyyshYZeYOq1EpFkqZzbhX3oytnkpVa2bU3cySNkZGbWfmarjTJt81tkoznq1NXXurTeVxX\n",
"133u+quB089TMW5VwsJfgpznpGxKxu7tTyrWYOd5qtbpD7uyL5EL6nr7knVTJ2VUdMS+T9fz1fUi\n",
"F3FSY6vqPFk/rN+ep5W5RXbTv8tap9e5ZGUUTjpmV+LlaS4Z1xzJKKzoyo5UicxfnuV9zKdxV77H\n",
"pmRUnsaNfF9Wfb9XpJWy7uFd17rdff7s++86AAAAAAAAAACH8YEPAAAAAAAAAIDD/IS3QjspgRI5\n",
"z0nj7kzHfHsGZnJqJTJO5z2dnJfpSoi8fU3V9exM39xlJKgi6/Sab7muWO4gkh1Y+b9XpFYy8ier\n",
"c3kbJ2PdnnRlIKrSHhkyEiKn50DoU5W12anitTTLnrlE3iJk6Nx5vuJcds5/dlLW5rScycmefjJU\n",
"7J5/2rNyl7FTftjbDZmcltj5o7vzoeP77fozzYzv753fCxnr1vUCnHWeyC73b7J+WGf8cI601Zae\n",
"44zcwcoFraQKIse8ze/pmEjLp+JFIesHWyQL0XU9GcmKnamYk3WlY6qer6yMSiR9MyVJk5VayRh3\n",
"8rq9nwUAAAAAAAAAgMF+Hv/1N+y08el5du6iETmm4nqyxt31rGTsSpF1nm/bFaTqmnetU9UuJ1XX\n",
"03XM2xjR5yDjdXDrjh4dY3TtiLEyZtVuHXddu07s3K3jbdys3WAqPJ03Y6eHqh1KqnZp+W1zm2TS\n",
"Tjsrpuwk8ud5/rpWfob+e5G3RRFdO5R0/eWEv9Bgt8gf1UZU7M7RuUNG5O+zUqzckIofMZEL6vpR\n",
"l/WQTtpVww+D32nyTjpvIt8/XS/IT7p2E5qyQ8aTyKYTkTEydmmJ7D6SsuNHdODIX5hn/YX/2zEZ\n",
"c8nafSTjL/4j6zbpenbtHFK1ThnXvHO3jopdKKrWICJrbd/GzXr9qngtytp5o2vd/nkufmUAAAAA\n",
"AAAAADiMD3wAAAAAAAAAABzm56isSvQ8J427Mx0zObVSNbeTsimTMjBVCZSKdepa26f/+5TrqVqD\n",
"SfP/w0reoOqYinTMyhZekcTDil1zy0jWPP3brjxLVfrmbR4rc4ncj8mpD2bJeiYnPXOTvz/2zKUr\n",
"o3LXdZ7Oc33beehTkUTZeZ7IpuoZ57mumr+M6szL/OHtgianVnb+SO3qF8F17f2TzIzvs4wXsK5E\n",
"ypOuLldGJy0jibIybla6KyNBs3I9Gcd8/gUPJ4ocs3JcVXqhIvGSNZeurEVGcqPK5GzKb8yzrIjM\n",
"rSIHEh03I1uT8b3bldhZWYO7SAIpOpe7f75mO3wAAAAAAAAAABzGBz4AAAAAAAAAAA7z8/ivWXmG\n",
"yLgd59mZTYkcU7FuO+9xV9rj9LXdlYE5LS9TkS+ZlLWZtAaRe1o1///6z+0fMvIfkfRKVnYkshVg\n",
"RQKla27RrQ+7Mgq78iyR81QlaiIy1q0q/9GVFcoQmZt1W3Pa99Rd1mvpv7crB9L11wr+KiJGJmbN\n",
"ygaw/KkrvXJdfdmau4yd/kNWTrTrR07W4k/KqHzbD5mut0rftm53XevY1ftakTGXyLpNyqhU9b4y\n",
"xo0UOCLjbMu1XLEd+FPSKyvHZRyzkkS4W8lNvM1jZS4ZiZenc3etwa65rdiZTTlpnVZ0pWOqciAV\n",
"a1v1/V6Vitq1BneR19bPn69vf7sMAAAAAAAAAPB1fOADAAAAAAAAAOAwP+PTHpFxI+epGHdyEqVq\n",
"3J3X/O2plYoxOs8TGWfXOu28h13HvI3RmZJ5O+6PfMt1vW95FU1HvB2zsqVaRs4kIyGyckxXCidr\n",
"3Mh8d+VZMvIZWTLWoGvdJuvKpvDs2/MyWUmtfy/ydixDtAyX4dsTNXIhv1NXAqUztXLXlV6JbKqe\n",
"IWs3/RRVCYQuGTdo0vVMsqt5dLpdf4KZ9Rxn3PfJGZiqjErkPFU5mYwfois74386xnW9X0/Wm4+3\n",
"NUhJvFxXTa4lekxGWmVXbmZF1Rq8qUp7RDIdv1FX3mTS89X1PVX1TL6Nm5VNidzDt3GrEjV3nz9f\n",
"dvgAAAAAAAAAADiMD3wAAAAAAAAAABzmJ7wVWkUypCpDEjlPZNxdqZXpWZ6KDMxp2ZQpGZiu86yM\n",
"8zTGrnU66XomrUHVMX8kXDIyKitW0gtv5806d2TLtYw1qErhVGUWJuVZKq4xcp5JqZWsdXv7mqx1\n",
"Iuf5qrqnk5ybPPrr+jOTtusvAHZmRn7jNUOnrtTK3f2VtvN7fco1/3dk9+Mq35ZRmfwnc5PWaZfT\n",
"fsh2fV9WrcuuHEvkvF1JqqycSUVOpisdk9VAi/xAr1iDlYrC519wxVIFVcd0JV5WVCQestZgV7Ki\n",
"KzPStU6RNMlvyLNkzC0rTVKRY6p6Laq6h5MTNf98zORfVwAAAAAAAAAAeOADHwAAAAAAAAAAh/l5\n",
"/NdJaZXIeSrGnZSO6UqVVI27cs0V6/IbMzA7czOT16liblXXM2kNKo65rsaES0XyZGduJrKNXEVq\n",
"JWtuK3PZlWfJMCk7ElnrXevWqStNIpuyz6TvwwyR790ekdJdlZ07vO86d9da++uRPF0pkinZka5n\n",
"5+kVcNc1P2l7jYicaMqPv6yH5dvf9nhBnvPMrup6AajafT4iYy6RZz3y/V+VgclIk0ye28qzUpFr\n",
"WTl35E3ByjFLz1ck87LrmEiuISvT8TZuVmqlKwcScXqepSJNMilr8zbmyrhdc3sat+tZn5xJehtz\n",
"ddy38+xJyfiVAAAAAAAAAADgMD7wAQAAAAAAAABwmJ+taY9Px4yeJzLurnTMzszNrvWflFr5dMzV\n",
"caekcCanV6Jz2fV87bqeyHm7UjKhfMt1vW9PtZI3yDimM03y6TEr84ikJFZUZF8i9+dJRtZiRWT+\n",
"VftGn5RayUiVPH1N1fPEPlXPykl7e591PZG3AF2+PaPyZNL6c5aVTX0rTEqt7PzezdgZv0xXNqHL\n",
"pJYP+0z6s8eut3UZ11xVKojo6mVVnSdj3K65ZaVjuq4n0q2rOObrEi/XlZNjqUrHdKVWKjIqnW8a\n",
"duVZqtYp8kxmmJTcudu5thWpqK516lqDJ5Fn5e7v55n0VhcAAAAAAAAAgAU+8AEAAAAAAAAAcJif\n",
"x3+dlFapyHCcdn0V4+7MwGSc+7TUSsb1nLRuVXPZuU67rucrEy5vKpIoTzKyKV25mZW5VKVK3lRl\n",
"CKryLG9jPo2bsTVg5DxdWZjIWp+WUcnI/1TlZsztfF15qR4n5VpkVOB77EqtRDdI7tBVLkiTMZk5\n",
"9bKYUTeEP0x6+9X1wpJxzVnPdWQuWVmRHeeJ3uNI1eLTMa7rfX47UysZY+w6JuxtwVfyBl3HVCRe\n",
"ssbtymesHBPJXFSlVn6byYmarBeNrmfw7bxP567Im1SNG3mdnJuoscMHAAAAAAAAAMBhfOADAAAA\n",
"AAAAAOAwP2lJgbtJeZNd11i1bpPzMjvv+5ScSdb1nJSbicxl8jpVrW3V/YisQcXr11K+ZWWb+xUZ\n",
"iZCshMubrkTN2xhP42SsQUZKZuU8K7ryLJH5Z22pWJH2qJKVudiVvuH7ZGVsznnm/rr+c/vff5qy\n",
"+3ykqNdpylx+Y8Zm5zVPyYx0rf3Tq9uu9d+1Bk8iG3t3WdrI+KSdvqseuMnXzD6TfsBkqbimrkTK\n",
"k64MTGT39n87Zua4FfPbmUB5G+dpjMgxd/dnJ6v7lvL9npU3qDgmkjeI5Ex2plYy/ltiJCGyMzOS\n",
"sU67simT1+1JxdyexomoyjFVfB/2ZFNiP4h7npUp/90KAAAAAAAAAIBFPvABAAAAAAAAAHCYn8d/\n",
"3ZkM+fQ8k9Ixu8bdmeXpSoZ8OubquFMyMKflZnZlUibPrSqbch9jV0rmaZxQwqUqo5KRrIjkZqoS\n",
"NSvz70qtVFxPdD/LXddclUTJyLNUzGNlLlnPSpWMta3KzUy57xGT1231a0628lo06fvw7yJvv3aZ\n",
"krm5rllz4XeaklbJ2sG+SkUNoExkMnN/vKwZdQMCdq3/6ev2Zudbxaq1zbimjLl1pVgi5656DYzM\n",
"vysZkjW3imzKk5Wd/T89d+S8XccsfVFWPuOu6piMHEtVOmZXduQumun4bXmWrOvpyrO8mZyOWRl3\n",
"ZW3fzvt07l3XExk38v3ek6iZ/N/ZAAAAAAAAAAB44AMfAAAAAAAAAACH+Tkub7IrX1KVRNk1bnR7\n",
"vinJkNMzMCflZiKpkpVzV63TrrWtuh+T1uA14RLdWr4r4VKR/6i6vrcxouN0rUFk3KoUQySfMfk8\n",
"n563cy6R80YSFd+W6YjYmU0h5vRM0j87KddyXbPnO2UuU+bB/3h6hdh1jyI7l1c5KaMS2Tx4lIwb\n",
"7W1F3K5vtHPeiuTpWuuq74eMF5KM+x6ZR1cGJnJ9WZmOqnV5GzdrblOyKZFzR95MdR3zfx33+gW7\n",
"MiORYyoSL9Fx3+xMbqzISN+cnmfJuJ6T8iyRHEjWuBlJlKzv3Yp1qnr9ijyTd58/K/47DgAAAAAA\n",
"AADAYX7Cn/yt2Jli0k4iu8bdOddd556088anY66Ou2sNTtpJZOVrIruNnLa2FbsNRdbgdTeP68rZ\n",
"7WLluJW/XF8Zs+KYJ107lmSc925lDTJ2KIl+4r5rF423+1F1nl1/8R/Z6WHSn/tFntvINZ+9AwPX\n",
"VXffJ39/fG5l94vJf4U+efeOu8nrCKueXvGmPNun7arR9cft2+xc7LN/NH+/078RM2StQdUft38q\n",
"so6TdwXp2iHjump2LemaW9aOGHcr88/YOWTyMUtfFNlJ4C5rp4qKv8R/OqZr541du1B0vYGZtFPF\n",
"rnXqer66dtWIjtu180Zkr8aKdcp6jajYcenz18mjfjcEAAAAAAAAAMAHPgAAAAAAAAAAjvPz+K8V\n",
"uZboMV1zmZwD2ZXPqVr7b8vAnJRN6XwmK57BnetUsbZV1zM+4VJxzEquYdcxd1WJmsj92HU9K+N0\n",
"JXay9uztOs/beSP5iaq5rJy36r7vErmertzMt89t9Wt+l5W3Uif/BcCkHeBXTF7r09aSP1/hJt3D\n",
"yM7lu0R2n58k8pNu0rPS5qSb+htNfsvW9exk/cqzK8dyF3mh6XpBq+p9ZeVaIju8R8bMGKfreiJv\n",
"eqoyKvdzZx2Tkb4py6ZkZBSqUhJvizv5eiIZlZVxVuZy0n9ni+hat8kZlZVxqzIjkbmtzCNyPW/j\n",
"Rl4nsxJIb+N+/gPGrzwAAAAAAAAAAIfxgQ8AAAAAAAAAgMP8hD/ykZFruNuZEJkyblZyI3JMVzLk\n",
"0zFXx+1a2ynZlNPXbfI6Va1t1fVEjnlNuFSlWCK5hpUcwIqMY7qyL1Wpla41iIxRNbfIuF15loys\n",
"RcU8Vuayc/vHjMzI6ekYfoe3PM6fz/Ff10qibaaVot7kv1Z4ers1OZtw2lpOIaMSk7XLfZevz6Rk\n",
"LPbkBAe/Q9c3XdevCFnXsyvHchd5jYi8NlX9gImUJFZk5GS60jFVCZS7p+vJWIOM9MrKubOOiVQU\n",
"Xq+pKpuSkYWoSiKs3PiK61mxcj27UjFd54lcc1c2pWvdIiJrcF19mZGudMyu67mLfu++neffJ2om\n",
"/U4NAAAAAAAAAMACH/gAAAAAAAAAADjMz+O/ViVD7qryJRmJh0/H3DnuzuuZfA+71nZSNmXKuj19\n",
"zeR1qlrbiuuJHPOab7muulRJ5JiV9MKuY+4mJWoysi8Z+ZOncXYmad7G3ZlnyRBJlVTN5W0Nqp6V\n",
"KhlrKzdznkn3/btE3n5NdtJfTpy+1sREdkjfaXIuZ0XGzvhHmXRB3ibVmfyNuOutU9Wzn3U9u3Is\n",
"d5F1inwvZ2VHKsaNPitv69+VWpmUQLmLrMHOXMvbMSvHrRyz9KxXZFOy8gYZaY+7rCxE19wmZVN+\n",
"W56lat3uutZgdZxPx52Ujum6nrcxV8d9O8+/X7dJv6IBAAAAAAAAALDABz4AAAAAAAAAAA7zE0oz\n",
"rIh8lCQrNzFl3Kq5Tl6n0zMwJ63BzgzM5HXatbaTr+fR29ZUkaRANEMwOeFSkTyZnJtZmcvkuWWN\n",
"25VeiGQhKvasnp5ayUigfFsuY1J2JPIaUTG3la+Ry8ny9nZl8g7wK57efp1+TXCarJ3kp4i8Eznp\n",
"+rayUHVOfwtd8WeOnW8dI8/2rhzLXWSdItdb9cNiUhKlatxIbeJtjIzzXtf7M/i0BpFjMjIqGcc8\n",
"HZdxTEri5elEd1mJirusrMWnOpMbEbuyKb8xz1LxPHWtwdM4d11r+6QrtbIrN5M17mfnscMHAAAA\n",
"AAAAAMBhfOADAAAAAAAAAOAwP4//WpVw2ZXp+HTMaeN2pT2qxp2SQIkc821rENmfuvP+RNZp19pO\n",
"vp7/+s/tH1a2g4rkGyLHZGQ7ose8baWVdUxVmuTTY7LuYdf13FVlOqoSDxn3IyKSuag479O5J+c0\n",
"Vp71qoQI9FkpxX17nuXJt1/jt10Pee4/pU7/C6C3dxHffn1RXiNotfOB6/pVo+rFpqpM8CZj3arO\n",
"G1nrjIRIZNyuvMnKuFn3I5IzuVu5nsgbloxj7p7GiBQSKnIt0WNev8+yUgUVuYbT8xNVc1tRMX95\n",
"lry5TXmOV8bdmY55GzeSJnrSlZtZGfftPH8f9/TffwEAAAAAAAAAfh0f+AAAAAAAAAAAOMxPWu7g\n",
"7tvGrZrrrtRK9KM+JyVQJj8rk3MgO/Myb2PsXNvJ17Mt4bJiUk7mLuOYnXPNyKRE5jLpelbGzdj+\n",
"sCrP8jZu1zpV5XMiInPZlYWJilyP3Mz58u/7X9f9579P81/X9+danpx830+e+3U9f+eedE0ZO75P\n",
"VrVT/un+2Ai4axG89agz+Zt38lv1rHWrusaM783I913GulSdN7LWGWmPyLhZiZrI7vN3VamVjDGq\n",
"1iBj3SJv9FaOidyPp2Mi9z2yTinphapERUZ+YnIaoyqFsWJKmuS0PEvk+Xr7xoyuwcnfH5Fxs1Ir\n",
"u3Iz/37c3/i7LQAAAAAAAADA0XzgAwAAAAAAAADgMD+P/5qVGYiM++l5TsrCrHzNzus5PYEyObVS\n",
"MZdvW7encXat0+Tr+SPfcl3vW1NlpD+eZORNVo6bfMzKOLuyL1kJnl3pmEiiYkUkhZExbtUe1pE8\n",
"S8V5V+bSuZ9zRi7nNyZQJudmMr5GLuc0b3mWyTvYZ/mNiRr2ydp9/iS7age/0rc9PJNMzqZEdH2T\n",
"Vb1ly3rWM+5rZC4Z61J13sizkZH2iIyblahZGedt7brSMVkJlE/Pe12xTl3kmIwkTdYxkfv+ds0p\n",
"iZenE91VpSQyMgpZWYiMtMfOzMhJJq1bxfO1ovMZvKvKF91lJIPexnwad+V67va8rvh1CwAAAAAA\n",
"AADgMD7wAQAAAAAAAABwmJ/RqY/oeSrGjYzZmVr5dNzJc1sZ97RsypT7MSn/8zTGrnWafD1/JFyi\n",
"2ZS7yPbzGQmX04/J2LZ/Z24mcg/fxuhagxVZeZa3cbP2/n27H1V7DFdlbSIy8hk7VeRAJl0f5Hkr\n",
"3Ukk/A/rwHSR3c+/TeQn9W9cJ75Q158N7qzjZXyzVr2dj6x/1S7xFefNyo7cZSRRIuNmJWoiu+nf\n",
"7cymZKRvunItuxIvK8dVHbNyza/PT1YWoiKFsXJMRg7kScb1TMqMVGVTus4zed3uInP7xnzRXcZ9\n",
"fxtzZdyM7/+VuXy+bnb4AAAAAAAAAAA4jA98AAAAAAAAAAAc5ie8VV1FwqUqC1M17uTUStW4u+7h\n",
"SdmUSRmYnes2eZ265hY55o+Ey4q3LaEiuYbIPpnRfVezkiAVx2Skb3ZdX9Y9nJx9qZpbxbhZ+/p2\n",
"neftvJPSK5FnZec+0RFva7uyBqfnc6jyllZZqda95Vr4H9bpd2QtflvyJGuX+G/X9RPVWn+pKTd2\n",
"8lvDrDWq+jUh44d+xvpH5lGRO3lS9QMlI4kSGTcrUZMxTlU6JiNb8zRGRi4nMteM64s+x5F7mJGT\n",
"iVzzkpXUwqfHZKVWunIgEZMyI7uyKafnWSblf3blZSalY97GrbqHkdfAf79uv/G/MQEAAAAAAAAA\n",
"HM0HPgAAAAAAAAAADvOz9FVVeYNd41alGHalVnau/a70xaRsyqQMzK51m7xOO+f2dsxSvqUrKbKy\n",
"NdWuuXQdk5HxiB5TkeVZGWdXOqYqJZGVZ3kb97Q8S0YOpGIeO+fyRALlXWQNOnMzb18zef7vx/x1\n",
"/ef2v//0lgyZsiP8N1pJ3/xGnrnYbtvfRvalT9Y7kf/+jQ/qZKfVCN9UfMNXrVHWXDO+OTPmEpnH\n",
"pAxMZNyuJMqnY66OmzFOVtYmIyGyct6KXE7XMdHnOCN9s+ual0xOrezKgUSbTiflWarWaUqeZWXd\n",
"3sZcGTeaHcloTlWt7V3G8xUZt+seVuVmPvm/AgAAAAAAAAAwjg98AAAAAAAAAAAc5if8kY+M9MKn\n",
"Y0bPsyvhMj21UjFuRnZk5TyRcb8tAzM5VbJy7qr575rbyjFtCZcVb8d0Zkd2pVRWxojkGiqSJzsT\n",
"NbuyL0+6kjQV4+7Ms2SYlF5ZuYdT0ior65SREAEyreRZ5CcgV1dlAPgHXT/cdr2V7UqTrNg1l6o0\n",
"yV3V9UXG7UqifDrm6rgZ4+xMe7zN/2mMt3NnHXOXsQP/SoXgyf0eZhyTNf+MtQ0d1JUQeTvv0zFV\n",
"OZBJ6ZvJ2ZQpeZYVu5I7T+Pcda3tyrkznq8nGc/+25ir476d598/k34/BgAAAAAAAAA4zM/jv1bt\n",
"TBE5T8W437bzRtUuJ1njnjz/SbuCVJ1nyo4l0bnsuocpO3pk7aLxNsbKMVN2Fnk6d9euGhm7Oqyc\n",
"O2tnhK4dS97OW7VuO3coeRs368+8unbreBu3ajeMqt1UIiJzOWlXjazrqdqZBvZZ2azOX0HksI5r\n",
"nl597RgTE/nJ7DnlSF0P7pS3u1UvilVvbbt2zdh13km7glTNP2OHjE/HXB038gf/K2NU7IjxJLJz\n",
"RcYfpa8cc1exy8Z1xe5h1Vwix1Tt/vLxQV07SqycXtiBEAAAIABJREFUu2tXjawfXJN366hYp6zz\n",
"vJ130hpEfuhUre3beVfGnbSTyNuYq+O+neffb9Pkd10AAAAAAAAAgMP4wAcAAAAAAAAAwGF+wtvk\n",
"ZWQgPh0zOu7k1MqnY66OWzG3lXEnzf/0DEzkPFMSNVVz2Tm3t2Ne8y3XVZdNyUi4rKhKlXQlXDLW\n",
"Pytf8ukxkxM1T3YlUFZ0ZVN25Vmy7MrARNIkO7MjkXU6OZOy8hpRlc85KbHDipWsyttbwchbNvJY\n",
"6zwrG+WSo+unh7+uOsz0G3bS28eMtey63qz7njHfqmTIircfOpHznJaBycibfDrm6rgnJVCevKVK\n",
"IueO9PEmH3Nd79mUrLXOmP+YxMvTybvSHhnJjUjmYuVrsn44TEmTRNYp643ESWvwpGttIy8sGWv7\n",
"NubKuFUpnIxxP//hMf1XGgAAAAAAAAAAbnzgAwAAAAAAAADgMD+P/7ozRRIZ99NjJudAIuN2ZS6q\n",
"zj05IRId521c67Y2zq51WjkmlHBZEcmmZMyjK6vSlUTJWvu3c3cdszLOrkRN1lpX5XMqsi9ZWwNW\n",
"JCoi+YwskUxHlUlzeVOVQPmNImmlXUma92P+uv5z+99/9/R25e1rqrIpkblxHvewT2SnbGb5tp/M\n",
"//3tD+FJyZQsVe2oXWvZlRBZsXMuXec+KQNTlUT5t2OujjspgXIXSXlEjslYp6fz7jomI/ESPaZi\n",
"/pFnfVvi5WkyGfmMrJREZP5dGZsM0TRJhq51q8ioRF+QK57BrEZYxjNZdT13Ga8RPWvw7b+yAQAA\n",
"AAAAAAB8HR/4AAAAAAAAAAA4zM/WvEnkPL8xtVIx7vS1/racyZRsSmf+JzKXKev05DXhsjOB8rZN\n",
"fOdcIsdkpEmqrvntvJFjqq7vbYyVc2flZiYnUCbP7W3Mp3Ez5r8zAxNJYVTJSHtMErkeqRjgf1Tt\n",
"9E9MZCd24ItUfMNPythk/Dli1dvWnXmWyLp0pVQqzlM196okyr8dc3XcSQmUt/NGjnkSyX+8nftp\n",
"jF3HRJ7JyfOPPG+RKsSSqnxGJLUQSUlkzH9nZiQjFbMrm3LaulXlTCpSK1lre7frelbW+i6yBk/+\n",
"ef52+AAAAAAAAAAAOIwPfAAAAAAAAAAAHObn8V8nZVMyEg+ReUxOrXw65uq4u9bl23Imp+Vmdq3b\n",
"5HV6zbdc175sysoW/J+OGT0mI1WyclzWNU855knkmJMSNSvn7UqgrHhb26rETsb+lV1JlJXzVO2r\n",
"HMnAdKVJVp6VrlxOhcj1TLo/wP93f/vrL0HO8/bTQ/IFGnS9eE5+q5SxBlVvhzNeCLPWflcaJisr\n",
"cleRm6lK2GRlRu4yMjCnJVAyzpuV/7jLyMtMPiaSQFk5JmP+kfbgyjFL35cV+YyqLERGqmRlnJUb\n",
"P2mdpmRTJq3b25jRcbOewbuutf30vFXjdt7Dt/P89Q//CwAAAAAAAACA8XzgAwAAAAAAAADgMD9b\n",
"8yaT0jGTUysV69+V06gad1LOZHI2pWKM6DiT1ykl4ZKVA3kbIyML8zRONMcy5ZiqbE3FMSvXl5E7\n",
"mJSoqUqgRFSlJE7Ks0SSGxkm5U0mzeUukkA5KQuzInp/Ius0eY90WPP2tttfefxOkZ8MnhWOtLNf\n",
"dPJbsKx161qDyHwr3uZF1y1jnaqSJ3eRfMaKjITIp2NGx81I4VTlWlbmknEPq84b2U1/5ZiMvMxp\n",
"x1RkU7ISNRnPRkni5elEXdmRu52ZjsnrNDk305X/yViDlXEiz23X2q6ce9L1vI0bvYefjev3eQAA\n",
"AAAAAACAw/jABwAAAAAAAADAYX4e//WkhMu3pVZ2rn1XMuTTMVfH7cqZTMmmTF+3yev0mnDJyqZE\n",
"jqnImUS2sI+sQXTd3o7Lmv+UY1bH+fSYyYmalfNWrcGuJM1dVTYlkrmoOk9VGmNKzmTlHk7a1/tt\n",
"nSZnbXaKvK78+9zMX9ef7018Mv/73O/p09vUt6/xXFCp6ie55/Z8f2xgPemm/oa3KxXrvbNq15Um\n",
"ebNzHpH/nt3V6opcY1VaJSMDU7XWXXPrSqB0nTcrGfJ2TFeSZucxFdeclZvJeDYia7D0BVOyI092\n",
"ZVMmr9Pk3EzkPE8q1mBlnJX78TbmyrhZqZXJ1/M2bvQefjbupF/RAAAAAAAAAABY4AMfAAAAAAAA\n",
"AACH+UnLKkSO2Zn/+HTcyamSyDGdWZtdKZ+MuU3Ppnw6TtX1TF6n13zLdeUkXKqyKZFsR0bC4klW\n",
"wiVjLicfU7XWb+d9GjfjmJVxsnIzXWmST8eIjvM2btX+1F3nyXgOot6usWsuWTmQKb7tes6ykvZ4\n",
"+5qVCl9VdmTK3Fa+ZmX+kWPgt9pZjiCH17OgrIWb8nYq688GK66nK5Gyoipvsus8K2tblZuJ7Ph+\n",
"F/khlHHNVbmWlblkrO2u815XXWbkriI7Ej0mktipuOaq3EzG85S1BqOzI2/nXTl31vwnr9Pk3Ezk\n",
"h0PFGqyMszKXtzFXxq1KrUy6nrdxe/I/dvgAAAAAAAAAADiMD3wAAAAAAAAAABzm5/FfV7Zuqsh0\n",
"RM6zKylSNe7OtZ+UDKkYN2ttp+Rmdt7Tk9bp0dvWWpFsSlZqpWLcSH4iK8Gxct6u+U85ZnWcT4+Z\n",
"nKhZOe+uNXhSkaTpuuasNehKoqzMv2sj+Mlpksj9mLL395OM65l8fQDAUar+HG5SzygjL9P19mtS\n",
"nqVrLl3niTzrK89x1fwjmYt/O+bquBlzm5RAmXLe66rLjNxVZEeix0SqAxXX3JWbqVq3ksTL04m6\n",
"siNPdmVTJq/TpNzM3cpDWbEGK+NE5j85HbPzeu4yvt8/v6d2+AAAAAAAAAAAOIwPfAAAAAAAAAAA\n",
"HOZnfEJkyrg7UyUZaY/IeSdlYD4dc3XcydmUirlExjjtWfmv/9z+YWUrp6wcy6fHVCU4unIskWN2\n",
"zn/XMRnrtvP6MhI135Z9qcqOVGVTutIkVfOPnKdrv+nJGZi7SetWJSMVM2nvdQDgDxV/unbaW6Cq\n",
"LEeFSXPdOZe3c2c9gxXnycqO3GWlVT4dtyu1UpVreZKRA8k4b9Y9XcmMZByTUQPISJWsHLdyTMY1\n",
"d+VmskoYb2vw9Ey+nntyduTJrmzK5HXqys08icyt6lnpmv/kdMzd5Ou5+/ye2uEDAAAAAAAAAOAw\n",
"PvABAAAAAAAAAHCYn8d/3ZUv2ZkmmTLu9OuZkkCJjPtta1B1PaetU0nCJTLGyjFV40auJ2MNMo65\n",
"rr75dx3TtXa7UjFVuZmuNVg57+Q8SyST9KYrc7Hy/VK1f/PKa2vXPteR7MgukXU7bU/0N5Frfj/m\n",
"r+v+/gUADtf1J2Wnv9WIZI3vdq1BZO5Vc408bxlzid6/quRJxnkqMjC7ci0r43alVrpyLdeVkwNZ\n",
"OeZtjKpcTtcxGRmb6H1/O27lmIxr7srNZCWD3tbg6ZmM3LMx2ZGncd7Ou3LurPlPWaeq3MzbmCvj\n",
"rsyt6lmJfONVre3drtTKpBTO25jv49rhAwAAAAAAAADgMD/jd5SYMm7WbgSRYzJ2evh0zNVxJ+30\n",
"EDlm1y4aFWOsjPM0xpS5rYzzx24e1/X+yb3Irgcr42Ts6JG1M8LbeSetQdZcTjomY9eWnde3a+eN\n",
"ql1Adl1P17hZ6/amc4eMXTtgfL5rQ523NZj8p66RHWQmX0+Np7dJ97dF9695etvk0/wAvKl695Kx\n",
"ccVoWRc4ZTO3Sbt1nDSXrPuXtcvErvNM3hUkY24Zc+m6nuvK2R1i5Zi3Map2T5l0TMXOFSvHRXaq\n",
"yPqj+ordR3auQcYuLdt2oVgd59NjJu9UUbVbR8UuDivjRubW+ax829reZexU8yTjOX4b831c/00Q\n",
"AAAAAAAAAOAwPvABAAAAAAAAAHCYn8d/rUpsTE6TVIw7PbVSMW5X2mPy2k7OwHTNbWWclTEeEy5v\n",
"MpIhkT06I5mOlXF2JVAiWYjofqMVc+k6JivxkHFMVyqmKjfTtQYr552SfclK7Nx15TMycjqR81zX\n",
"vkTIrvzMk0g2Zcoe409W1nbS+s+w8lbwLRWzkpsB4N/rerfyK1/DMy560tuKk64nK2tRde67jLl8\n",
"e64lOm5GLqcqb1Ixl0hlITpORgpj5Zi3MapyOZOOiaRK7iKZkScZaZJIOeJtHivjrqzBXVaeJXLP\n",
"XnWlPVbGyUi8PJ17V5okKyEyOW8SSe5EnpW3866Me9ra3mWkiZ5kXM/bmO/j2uEDAAAAAAAAAOAw\n",
"PvABAAAAAAAAAHCYn/EJkch5MlIYn465+jV3u9IeKyalPXY9g5PWYFfCpTMD85pwiWw/X5VayRi3\n",
"63qy1mDyXLqO6Up9ZGQJsq6v69x3WZtaT0mgVOUzqtIlb+Nm7bu8KzOSlfKJiKRWdolkVCablP/5\n",
"Lm9ZmJWv+ZWJAeBIVfUJf5G1KPIDY/KP913ZkYhJc+1KxXQ9b5EXgEm5loxxu+YWeS5WdtOPjFOV\n",
"QLnLymfcrRQFPj3v07knHRNJldxlZUbejsnK2mTc50hq5W0eT8dErqcsw1WVxqhIR0xOk2SdZ0re\n",
"JCvTU5EdWTl3ZP5PTk7HPNmVm/n7uH6fBAAAAAAAAAA4jA98AAAAAAAAAAAc5ufxXyfnMz4ds3Lc\n",
"yddzel7m5IzNzgzMlLmtjPOab7munBTGk4xsyqdjRsfdlUB5Ou/bXKL7pXalb7quueo+Vxyz67xZ\n",
"z0rG92pXAmVFxv150pWsqJr/23mq9omelDN5u4eT9inflempsnLfu57J3+ctA/P0lnTla4DfYWdJ\n",
"ggdZCzf5x2zkh86u65k0111z6crCXFcsVTDlPFm5g7f1njy3yE7s0blkpD0i582oA0Su70lGcqPr\n",
"mKxMT8X8s7I2Gfc5klp5m8fTMRnXsy3xcl05uYmsFMaUNEnWed7OOynPsis7snLuyPyffHs6JqOF\n",
"9fl999+/AAAAAAAAAAAO4wMfAAAAAAAAAACH+Tk+IRIZNzLmznRMxvVMzst0nWfyGkTGmDy3J6GE\n",
"y4qMzMjKeSvyMpE8QOS8VbmZSXPpOqYin7NyTCTts/P6dmVfstIRFQmUrHXaNbeMvYw7kyi7EhuT\n",
"ciZvc5m0H/pKombSfD/31/Wf2//+u6e3Uj6ZX+ct+xIpJwK5umoNrIncj/+ObC0/SeQB2lXZmzTX\n",
"SXOZklGJnivyZrDiPBlJlOuKvQZMmVtXOmZlnKwUxt1KcuPtmJVzT8rLVBwTXbeKuWRlbSLPRkZq\n",
"5W0eT8dkXE/Vs/OHaBqjKzPy6Xmfzp2RJpmcEOlag67syMq5s/IyJ6Vj3sZcGbcnM+S/IwIAAAAA\n",
"AAAAHMYHPgAAAAAAAAAADvPz+K8npVaq5tqVWvl0zNVxK+aWNe6kjM2u53hXwqVz3V4TLlWJioxk\n",
"SGQr+ay5RY6pyJlUrUHkuKz0Tdc1VxzzJCN5UpXlucvKkKxkHz4dY2fG5m2MSXNbGXNS+ubNyvy7\n",
"9h2flFp5m8uufcqfrLyWTprvv/eWIXn6GupEsjzuD7+FHMtskZ+Ox9+PyAXseks2ea5V6ZIVu1Ix\n",
"O3MtU+ZflWupypvcRXZ8/3QemXPJyFpEzhvJcEWer668zK5jImWMnXNZOSbybFSkVp5E1uDterKe\n",
"nZTMy6TMyF1XmiSrY3VyniWSHYmOuysvMzkd8zbmyriRNz2fP8d2+AAAAAAAAAAAOIwPfAAAAAAA\n",
"AAAAHOanLSEyadzJqZXIuLvSJavjds1/Us7kbdxvW7fXfMt17UuerJy3IolyXX05kLcxJq3BzvTN\n",
"XdU1Tzlm51y77mHFGNdVkybJ2tt48ty6zrMybsW+1l3nWTn3pAzMSRmVlWTQzrXMF8nA+IuAPu4H\n",
"J6japZ+YrsLDaJELmPTjPSO9kGFXIuVJVTLkLvLsTM61ZCRRnkTyDXdV97Rqbl3rlPFsrKQwKs57\n",
"XXXJkLuMtd11TPT7ctdcImmSjJTPzjV4u56sZyfy7P9hcmYkIpom+XTcyetWlZt5kjFuRl5m5zNZ\n",
"kTPKuodv437+HB//ex4AAAAAAAAAwG/jAx8AAAAAAAAAAIf5efzXyWmST8dc/Zq7jFzGzsxNxdxW\n",
"xp00/5MyMKetW0rCZWW7rsg26xn5kpUt31eO+XSM6DEVOZPOJEdX+qbrvk85ZnWcT4/ZmYrJGGfX\n",
"GjyZPLfTsy93GcmjyHl27h8+ZS4rr1+TMzArr0WT9onP9/TWMFIrJMfTWlt/olZevTxfdSI//b7u\n",
"fkzKikRMzsuclI7pyrV0NZGyntGKe1iV9rirysB0zS1jnaLpmLf5d6VXnlQlQ+4yEiK7jom+ucp4\n",
"nialSSJViK778Ta3rGfn7dkP/6w4KTOS8cMg63pOXrdIdiRr3Ehm5K5rbZ9k3Pe3MVfGzZjr+9fY\n",
"4QMAAAAAAAAA4DA+8AEAAAAAAAAAcJiftpRE57gnp1Yi4+5K8GSd+7ScScb1nLRuKfmW69qXcKlK\n",
"omTMrSsdM/n+7DymK1vTdcyU3En0mIx7mPXsTEmr/Ia5rfj2vEzXed/mcV1z0iQrrxFT5vqnv64/\n",
"3zv9tgTK01vQb7/mSX7b88YzuZa9Vn6af9tfYL3uRr+y3fku0W+GXXmZrkxK5Lx3WWsU2V07IiOn\n",
"kXGe66rJolSlPVZkpFYy5jYpaxN5Xcy6P1X5j4xjKhIi04+JPE9T0iRPIjmTirXNSq1Efga9PfvR\n",
"7NPrQZMyI5OzKd+2bk+67kekSdWVDMp4vt7GXBk3Y65P4/79a77t90sAAAAAAAAAgK/nAx8AAAAA\n",
"AAAAAIf5efzXyWmSyDG7Ei47MzcVc1s5btL8J2VgTlq3toRLVbajam4Z17MrHRMZt+r+ZGVsMlI+\n",
"px9TsW6r5/70mKxETVdy5m7S9ayM+6msZ+VtjK7ky9O5TzrPk105k5Xz7trL/Mk52Ze735hAuV/f\n",
"b1yDnfzlx/dZ2ZyWmMhPk2/7Hjs+UdOVA4nYmUm5y0hURGQlNt50pXB2JVGi40aSG3eTUit3GZmI\n",
"J7vSMVkvyBn5j7usnf7fjomkcLpSJdFjMq65KjdTkfJZWYOqdExFamXlmJV1jNzD1xM/DfxteZaM\n",
"6zl93Z7suh93XWv7pOJ6su7h27ifr8Ho38cAAAAAAAAAAPiTD3wAAAAAAAAAABzmpy0lER13Sjpm\n",
"8jpVJXhOy6ZMycCctm6vCZesVElknIyES1USZXI6JrKlfdX96UpwdM1/0jFvY3Qd05WoWR3n02Oy\n",
"9iWekkA5Lc/SleDYlZfZlXy5rn05k11rsGLSOn3u/tbv6W3etyccVtaAmJXEDvscn9MYLGtn/5N8\n",
"XaKmKwcS0ZUQWbFrLivnlWvZO24kVXCXMbeMXMuTjPzEyjF3XemYp3GqUjGRXe4rjlnJdESO6XpW\n",
"qq65KzeTkQzKyplk5Fky7k/keqKZoZTMy7fnWbKu56R1e7LrfryN+XRMxtqunLvqeiJr/Tbu52sw\n",
"+nc2AAAAAAAAAAD+9PP4r7t2qti580bFuFW7nnTtQhE592m7W2Rcz0m7j7zu5nFdfTt6dO3iEBmn\n",
"aqeEqh0MKsbtXIOMXU0icznpmKx7XLHrzJOMP53aubtFxm4Qk3cSqdqBwS4ga6bsArJzZ4tJc7m7\n",
"z+37dwX5Nr/xmrtYyz4rfwfGu9+4M0rkD8FHiUxu52Zikb/4rbBzJ5GuNeg6T8auDU8q5l913yM7\n",
"GNxV7bxxl/VCn/HHySsqdhJ5mkvG+q/sPrDrmMj9qDomY7eL68q55q7dRzJ2kNm5BhVzi+zWEd11\n",
"JmN3pF+5W0fG9Uxetye77sfbmE/jZqztyrm7rqdiru/jftvvtgAAAAAAAAAAX88HPgAAAAAAAAAA\n",
"DvPTlpKIHlORRZmcWomMm5Ud+fS8q+NOyZlkXc9JuZmUhEtWqqQqeZKRA4nM7fSsTeSYijWIHpMx\n",
"l8nHRO5z1VpXHBPdBzcjA5Gx1++kBMpJeZaqNMbTuBV7e3elPXYmRN7u+678zHXtm8u7v67/3P73\n",
"WX5jAuU3XjN8o7efBKe9Hq+I7D4/xePmxxnpiAzRhauY76SsTVcqpus8GWmPJ1Xz35WBiewSf5c1\n",
"t4z70XU9Wc9XRT7jSWTH+snHRO5hxjFZ96eiiBCZy6ScyV1kDbLm9ul5n879dt6ncarm/3rip4G/\n",
"Lc+ScT2T1u3JrvvxNubKuJG1XTn3ruvJmOv7uN/4+y8AAAAAAAAAwFfzgQ8AAAAAAAAAgMP8PP7r\n",
"roTLztRKxbg7MyoVa5017kkZmNNyM68Jl870SkZqpSohkjG3ivM+jVN1PZPXIDLutx/TlS55OiaS\n",
"Jsq4xp33I+M5nZSOqUhhdOZZMsbtyoFUPAc7z7NiUmpl0lz+7v427qRP3T/NdXIyIMPT9Z10z7pY\n",
"kzwrG/3+Nhm70Z/m9Gt+ezey9WdHRX4iaspcTs+odJ1HBiaWeHgyJZuSlaz49LzXFbvvGc9KJJfz\n",
"bcdUpUoix1Rdc8bzVZXl2bUGWXO7y8izRJNBFWv76LflWbKuZ0pGJWvcyP14G3Nl3KoXvUnX8zbu\n",
"58/x5N8VAQAAAAAAAAB44AMfAAAAAAAAAACH+dmWb7mu35laqbjmyWu9Ms6kDMxJuZnXfMt19eVN\n",
"slIrFQmHqgzMrnRM1vVEjqnKimRkbHbOP+OYXfmSydeXde6KVMzOdMzpeZYMVePuyr6cnpd5U/V8\n",
"RWQlqPKdnhC5z/Xbky/X9Tuu8VPWZE1k09jf4NuzNt+ea7mujc9xV5pkxUlzyZpHZKv/yedZ2U4/\n",
"YmUr/ze7MjBVqZK7rmxKZIysHFBkB/6M1E3kh1DXXKuO6UqVRI7JuubIc7ortRK5nrvIGmTN7S7j\n",
"/mTlf6qeldcT/4Y8S8b17MqoZI0buR9vY66MG1nblXNnPF9PZqRjJv8+CQAAAAAAAADAAx/4AAAA\n",
"AAAAAAA4zM/jv2alL+4mp1Yqxq3KqOzK2mSNOykDc1JuJiXhUpU3iYwzKSEy5byrX/PpMV3XU5Wb\n",
"mTz/ycmaXZmYFVlZhV2JmqpxMvYLrkpWnDa3ir2yu3IgXeeZlFqZkp+5rllz+bv728XTEhD3+X7b\n",
"Xx48Xc9p9wiqjM6BJHn7ST35NW/0/TkpkXJdfXPJSl9MOc/K2nadpyq1kpEEmZSBqZhbVzYla00y\n",
"MipV+YyVY97GiHz/Tz5m51pXXXPkWT8pZ/J23qdjVl5XMqoQGXmWaP6nay6vfmOeJeN6ujIqWeNG\n",
"7sfbmCvjZqVWKp6vJzNSOJN/5wQAAAAAAAAA4IEPfAAAAAAAAAAAHOZnW75l57hVqZVdCZfJa70y\n",
"TlcGpuoeVnlNuHSlVzpTJW/nimw/37VOkWO60h4r5961BtPmsuuYrhRJ1zGTUisZ93BSbubb8yxd\n",
"11y133ZGWmnSeSblTebM5a/rP7f/Pcd9LiclEp7mOmltM3zb9aw46RmssrKZ67eJbLY72cpP2cn3\n",
"NaNuUOWPZyUjExHRlS5Z8RtzLRn3eWeuJSOJ8mRyBiYjIbIrmxJZ16qMSlY+I+OYiszFacdEchp3\n",
"kQTHk0j+4y6SM6nKzXStwdt5n8aJfK92za0rFRN5jdtqSp4lKzdTkVHJGjcjl/NkV2pl8vW8jfk+\n",
"7uTfSQEAAAAAAAAAeOADHwAAAAAAAAAAh/l5/Ndd+ZLTUisZqZKK80bP3ZXL6Vrbyc9x2Z6pk/Im\n",
"XamYyDEV69SVtYkcs2sdo+NGjqlK32QcMzklk5HT6Zrr03EZ97ArwfOkIoGSdT1T5vbk9HxJ176Y\n",
"XXugZ7wmZJmx5+jkNMnTPE5KLZw01xXfdj38TisbzZ7mpCRNZCPjLpGCQJuMxENURqIiouuaq7I8\n",
"kYxCxJQkypOMDExXoiZr3bquJ+P5ykivPMlIbjypSp5MPSbyfbmS03ibx8oxT8dlJDci5YidqZW7\n",
"jARKVmKnIs8SnVvXXEK6EiJ3k/IsGbmZXdmRlXEjuZwnU9Ixk67nbcz3caf8t0cAAAAAAAAAABb5\n",
"wAcAAAAAAAAAwGF+RidRJo1blenoypvsXOuutZ2cDHob57/+szDI5LxJVyqmKsGxK18yOWsTOebp\n",
"vJPSKpH5V1xz1twj5+nKr+xKrexMhkzJzTypyLNkyRi3KknTMeZ11d33u65kzV3X/Vk594zky3XN\n",
"zgOc9BcBpydqnpy0/hHffn3XdVYOJCKyke4kkV27J5m8/mOe/apkxYqs1MLU83adJ5IuWFE1/66M\n",
"za65ZSVqdmVTVubxNv+dGZWMY55kJE9WzpuRpMk4JpL2qcqbPMmY/+k5k0/P+3TujCxPV55lZW47\n",
"MzYpKbiuhMjbmCvjduVNIrmZruzIyriR+T/pWtu7lbnuup63Md/HnfS7IQAAAAAAAAAAC3zgAwAA\n",
"AAAAAADgMD+P/yq1kjPurvOujlMxblcC5fQ1SEm47MybdKViIvPtSsdUZS4qMh271jFrLismH1O1\n",
"/pHzZByzK3cSPS4j6ZCxJ2/W3s0VCZSs74WqdapI0lTdD9mXmJ3plV3X/HeT0yRP8zjprwZOmuuT\n",
"Kc8Bv9eYTEfAyia4k0R2m+8yKoWTkYWoOO911b2FeVvcrPN2nafiHnblWrLGzUgPTU7URDIKTypy\n",
"Jl1pj+i5q9IXGcdE1nZXxqbqmIy8SWQuWSmcjJTProRI5HoiiZ2V8kLX3LoyNlnzf/UbEiJvc8vK\n",
"zVSswcq4kfk/6Vrbu8h937XWn487+XddAAAAAAAAAAAe+MAHAAAAAAAAAMBhfkYnUSaNuzLmruvZ\n",
"meDpSqCcngx6TbhU5U1WvB3TObeMDEzFeVfGieQNsuYWOWbXsxI5ripjk3HM5JTMzmTNrvnuvIe7\n",
"cjP3YyalY6pSGVX7dFeMW5W+6RjzSVVyZ8Wu1MpKhq/H5IzC5Lk9OW2+/9vJc2e+0xIod6flZybP\n",
"d2UT4hZZWYiMc1edtyrL8SaaHYiMe5exlilbyxeN25WB2Tm3t/vclUDJShfcZaQ9qs4d+d7tOqYq\n",
"JdF1TFXeJGMuWYmajJRPVTqmIoFS9ex3zW1OHpA+AAAgAElEQVTys5L2PqIrgXI3Kc+SkZtZ+Zq3\n",
"866cOzL/Jyff94xkzdO5//24J/3uDgAAAAAAAADA5QMfAAAAAAAAAADH+Xn8129LrXw65uq4u65n\n",
"ci6na20nZ2xe8y3X1Zc3qcobZCRDujIwkWNWzrsrL7Mza5Mx7qSMTVX6pisnsytbM3muTzLuYVei\n",
"5m0eO8epyrNkrFNVNqXqmt/OUzVu1/7nO/MyPee+v13ctQX/09vWKTmAp3lM/kuDKesGfGZMduRB\n",
"pAbQJbJ7e5XIruopdmVUrqsuRXL3do1Z561I33QlUZ5E5p9xTyfPLSutVJFAyUoXfDrGyjjR3EFk\n",
"B/67jLXOSH10HhN5VrryJlVzOTln8qQigZL17L9dc9bcTl/blPc4XQmUtzFXxq2aW0Z25P8619sx\n",
"XfO/O/2+3+1J4Uz6fRgAAAAAAAAAgAU+8AEAAAAAAAAAcJiftMzF3beNuzMdMzlrkzHO5GdlZYyU\n",
"hEtX3qQqT3FaBiZyTMbcIsfsyqY8jVGxBtG5vOl6DrpSMl3HTFrrleOqUkRvsr7fM9YuY4zfmGfJ\n",
"knE/7rKelTddSZR96ZW6+/7PJqVWJn+6f3JGZfK6PTltvv/b5OdgxcoGsJNFNqfdJbJBb6eT8jJT\n",
"ci3X1bhOXRmVqizHXVeSpuo8J+VmJqdWsuZWkU2JjBNNoNztSsdknfftuMj3ZdcxkWcy65iK5ysr\n",
"bxIZN+OerSQ37qpyJivz6EqIRLI8b8/gyhvVjPP8X+f69JiMtc1ap1edCZS7KXmWSHbkaZy3866c\n",
"u2r+b2OujLsyt7cxV8bNapGtrNPdP89l0u+gAAAAAAAAAAAs+Hn815N23qia6+Trmbyjx29Y29cd\n",
"PU7b7aLqr/Mzdm3oWqdPx1wdt2Jtd+4k0jXurl1NonP59mOqnrm3Y3ZeX+euJf9bxp/7TdqtI+Oe\n",
"PjlpF42qnSy+bYeMnefpWsu/2/Wp+6e3ulP+AmDKPP4vk3YSeHPSXOk1eReKu8lznbTbyMpPsa65\n",
"bbtnXbtqrJy7a+eQk86TtWvDyrgZ55m8K0jV3HatU8VOHNfVt9PDp2M8jfMbj8m471nHVOx2kTWX\n",
"rp0q7qp2bejaUeLtvE/HrFzP2/yzdoPpetarduvIWKclFTtiZOz4sTJu1tyqdjXZNf+3MVfG3bmT\n",
"yNu4kReJJ/88l0m/MwMAAAAAAAAAsMAHPgAAAAAAAAAADvMT/sjHrtTKroTLzuupSLh0zu3ktX3N\n",
"t1zXWXmTquzFipPWKTJu1druyqbsSv10HnNS3qTqmF0pmejrTNc1Zpy3KlGza/1/Y56l6+dhxnm6\n",
"UiVd5+lK7vzpr2vlvV++SQkOc1njLycgV2RD2y6T5jZlLluzNhkpiRVdqZiu82SkMJ5EkggRFQmR\n",
"J5MzMJHEw93ObMqnYzyN03V/IsdkfS9PSp5kHDMlL1OVA3mbR+dcqta64r5Pvp7IPczK9Kw4Kc/S\n",
"tk4ZCZTIu9uuPEskOxKdy923r+2TXemYf5948d+pAAAAAAAAAAAO4wMfAAAAAAAAAACH+Xn814qE\n",
"SNW4kTF3pmO6UitV476NM3n+K2OkJFyyUhIZCZFJGZXIMbvWaefcdt2PSfd5UsYm436cdEzWPT7p\n",
"GrvO+yRjf+OqHEhE1fVMybNkJXYi55k87q7zVO3f/ndPby+7tqy/n2fXJ/Un/YXApLncTcpP3E1e\n",
"N+psTW68iGyC2ymy8W+Fnev09tO8ah4ZxYqQyPb6WefqStJkvEWrWqeu3ExGDuTJrgxM1v3YlU15\n",
"G2NlnKz705UdqcrlnHxMJD/xZFcO5C6ya3/WXDKyPNEkzdsxVQmRu13ZkZ35n5PyLFUpnz9EEihP\n",
"k/v3iY2cPEt0bpG53K3ckJPX9klGOuZtzJVxP78/k36nBgAAAAAAAABggQ98AAAAAAAAAAAc5ie8\n",
"F2JFaqUqC9OVA/l0zNVxKxIoWXM7ff6vCZeszEVXBmZKbmZ1nE+P6VqnyDG71mTl3FVpj0nZjqqM\n",
"TeSYSDKk65iMfE5V2ifjmEiWJ+vcU1Ixk/Is97lMnlvWuFV7cleMW5XPWTlPlapn7p/t+gT9zjTD\n",
"lCzElHn8X/x1BfyPyIa9XSalb3at0850TFs+J7IFf4ZI3iA67l3GW7CKLEzWuL8xA1M1t64MzNtz\n",
"25VeeRLZiT0j17B63Nt5Tz6mK1USOaYra7NzLhmZjpVzr7zJicztbnJ2JFLG+A15lopn/9HbQ7jy\n",
"jrgiQ7IybmRuK+Nk9JlWviY6/7uT0jFvY66MuzLXvx/jv0EBAAAAAAAAABzGBz4AAAAAAAAAAA7z\n",
"s/RVVamVXQmXyddTkT9ZHTcj4TJ5/q/5luvqy2dk5DJOy81UZRW61ilyTMbaVpz36WuqrmfX+ldl\n",
"bE46ZlJyJ+OYf3Pcvx0j47yTEjUZa5CV6ajKs2Soet4qrrkqm9K1tl3Zl57z7EwV/Ma8zJ2/aFgz\n",
"6Z7dTb6Hk9MkbWmMw01ap11z2fUct+VzqjIqT7pSMZFt7T8d80lGduRJV0Lkzc68ycpc7iJZiMgY\n",
"uxIoK+NUpT3uqnINd5F1+rZjurIpkxIiTzKSG3dVmY67rLRHxfddV3bkSUaq5DfmWaoyQ68nfprc\n",
"5LRHVyrmbcyncbPm/3buk7I8kXE/f778NwAAAAAAAAAAgMP4wAcAAAAAAAAAwGF+wh/5qEieZCRF\n",
"IuetGjcrVVIxbtZaT55/SsKlK2cSSXBUnWfSNUeOmTy3rLX99Jid1xM5puvZ2DmXXcdMTtBkJE92\n",
"znVXKmZXbubJlOu5rpyMzd3kdEzXuFnP/puqNfnTX9fK+8WM8+yxKzcx6a8KJiU3Js0FKk1J37Ql\n",
"RBbsnMuu+9GWrKnInTypSsVUpVXuKpIo19WXm8nIctxlpVd2ZWCynskpCZQnXWmPu6p0TFcq5tuO\n",
"2ZU3eVKRRKkaNyvTcdeV9ngbc2Xcrrl1pkp+W56l6jn+w8piT057dKZi7t7GzVrbT8+7Mm7kRW9S\n",
"Oub9CAAAAAAAAAAABvOBDwAAAAAAAACAw/wsfdXOtMeu1MqnY66OW7FOWXM7ff6vCZeu5EZWJuKk\n",
"3EzXXCLj7pxb19p2jVuRwlk5rmoNIseclDf5xmMmz/fupETNk0kJlIo8S9Y6TZ7b27hV2ZSu+dfo\n",
"+jT8/a1t1/b6Oz/tPylnMmUuk/76YtJcWDMlm7KyoW2XtoTIgl1z6bofkd3ps7Q9+1WpmIq0Slai\n",
"InKerCxKxZiRa66Y29O4J2VgdiZQMsbIOOZJRW7m6dxd1zjpmF15k8gxWTmjSBHhbdxIpuNJV9rj\n",
"blJ25NPzPp07I1XyNM6kdTopN7PkbbEnpT2yciZdqZWMtX0bc2Xc09Mxn/xfAQAAAAAAAAAYxwc+\n",
"AAAAAAAAAAAO85x02ZX2kFpZkzHuzkxPxvxf8y3XdVbO5LTczKS5VIxbNbeuZ/LTMaPj7kygVK3D\n",
"p8c8zaPiHk653spjTrrGXZmYrHPvWoOs+74ybkRF4qRqblV5k4o1qErHZGWf/tnTW9KuT8zvyst0\n",
"mfSXB5PmAqybkrW5rn1z6Tpv13naUjEZuYYVaVuK31TlZipyJlVrsCtv8qQq/3GX8Q3SlV6pSsdk\n",
"ZS0qjrmL3q+KVMykYzJ2z9/5HOzKf0TG7bqHWdfzdszkuXWlSlbG+Y15lqr7/nriqozK25jRcTNS\n",
"MZEXvZW5Rdb27bwr435XOsZ/2wIAAAAAAAAAOIwPfAAAAAAAAAAAHOZna9pjV85kcqokMm7WWu9a\n",
"l5UxUhIuXTmTrO3Ep+RmJmVgdmZHMtap4ryrX/PpMZNSLJE12DmXyDGRXMak+b8dE3meJl/fk65r\n",
"zDjv3c7czN2kPEtVRuWkbEpVOqZq3D3n6dq2v+s8u/4iYGeKYRLrwHSTMiq7RDZizhLZHHjyedqe\n",
"p5RtvBdUpVYq5j85N5OVN3kbd1IGpiubsjJO1/VkrMFKUmDSMXcZ2Y7OYyLVga4cSyQLcbcrifJ0\n",
"7oxxu3IzVd9TK8/B5LlVpEqic+nKs7w5LTfzqiuj8qQqz/KWY+maW1f6JpLleTIjHWOHDwAAAAAA\n",
"AACAw/jABwAAAAAAAADAYX4e/7UqTTI5tVIx7q5kzcrXRD/qkzFuSsKlK9NRZdd5V0xK32Td50/t\n",
"fL4ysjan5Vim5D6q1i3jmKosTNcxd9HXwF33qOsad67tXcZr66QESlXaY/Lcdv18zBi3Zk3+ulYS\n",
"gRnn6dF1np25BnmZfazBLDsTIlNENsGtOnfXebvue9d52u5hZPv26Lh3FUmU66qZ/6TcTNXcKpIh\n",
"0blNWaedaZKMtMeu8+66vqdxIvcj65gpuZydeZPIMVXPU8W4VSmMrgRKxK48S/RZqfqZmWHX3EY9\n",
"X1MyKtFx337z2ZlaqcjLRLI8TzLW+m3M93Ht8AEAAAAAAAAAcBgf+AAAAAAAAAAAOMzPtnzLdZ2V\n",
"cKlap4xxp6/12ziv+Zbr2pf2yMpcZKQkujIqEd+2TpFjdqZLKu77aemYSXPZlf84/ZjJa33XdX1Z\n",
"556SipmUm3may5Q8y9M8qsbN0LVHZ838vy2L8m3nmXLe65KX4feakjPp/F7Yde6ute66vuPPk5Hg\n",
"2HmeioTIk8i4v3FukbfMJyVQ7rrSHivj7Ex5ZBxzUpJm5zFT5hJ9jityE1l5lopnvSrLc1KepSrh\n",
"Filh/MZ1qsox/WFXRiVr3JXfUHalVirOWzVuTwrHDh8AAAAAAAAAAIf5efzXk3b0mLxzRWTclTEn\n",
"7+ixMkbajh6fytqx4G2crvNM3xXk29YpckzF2p6+y0nkuMhfu3fd0507u3z7MTt3I9l1jafvWDJp\n",
"95GMj/tP3lWjaseVimuu2gGkZm2/bYeMrk/37/orAn+9APxbK383VaVrB4yunUOO3qGk669Hn2Ts\n",
"QvGka0eJNzt3u1iZy13kL+Y/HeO6cu7hpB0x7rp2V4icO7JTQtcxT8etHDN5h5LILgF3u3a7iMwl\n",
"+hyftLvF23mfjqnaTSHyB/+7dqHY+ax82zpVPMcrSnb8eBp41y4UK+N+vutE39x6dtGYvJOI/0YG\n",
"AAAAAAAAAHAYH/gAAAAAAAAAADjMT3jvQ6mVfz/m6rinr/VrwmVy1mJljK7zTMqbVG3PftI6VZx3\n",
"9Ws+PWZy1iY6buSYnYmQ/+20vEnFMVX5n8xz/W+d1/hvz5v1+lyVDImYklapup5dz8qKyUmaJ/nr\n",
"8G1JlG9L1uy06xr9xQaVIpvgZunKgezSlY7puodd5ylbt4p0SeW4ka39Px0zOu7bjc9Kr+zKwGTd\n",
"04x7WHE9K+NkbY3flRDZdd6sNM7bcZOTNFWpkl15k6y5nJ4zuetKe7yd9+mYSOGhK8+yYlI25aQ8\n",
"y65nMi0dU5FReRrnLitn8vab3M65RX5wTb6efx73236HBgAAAAAAAAD4ej7wAQAAAAAAAABwmJ+l\n",
"r8rKf1SMuzO1UjHu5LVeGec133Jd+xIuXcmNSbmZk9YtesyUdYocszNDMjlrExk3ckxXHmTn98dJ\n",
"x+xK0Ey+vqxzT8mZyM30jlmRTdmVdIv561p5X/q5b8uiyNawatdfi+y8p7syI9+eN9kpslHu5PN0\n",
"PStd5ylbt4okStW4aduDv4y7M7VyN2luu7IpT3ZlYCrOu3LurGM+HeNpnNOP+fZUSeSYyVmb65qT\n",
"M3myK4HSlQPZlf/JelZOWqdJeZaq+56S+8nIqKyO8+m4Ky8sk+f2No+nY865Hv/dAAAAAAAAAADg\n",
"MD7wAQAAAAAAAABwmJ/w/oi/LbUSGXdlzF0Jl6w1WUq4REzJdJyWTZmybitfU7Ut/KR1qhh3Vxqn\n",
"8txTMiNdSZHI/diZ/8k4Zuc9/rZrvNuVtZmUHcmaS8Y4FRmVrHEnz61jzLpPukuizPZtaRz4BpHN\n",
"diOefrKf/r0qSfOu7PmanFp5sisHsmLK3LIyMJMSKHdd289PSojcZaxTVYJj5biqexhJItx1pUoi\n",
"x0xK4UzOmbyNuTLu5ARK1v140zm3Kev0bXmWrOspEcmOXNd7IiQjO7Iy7uS5Pam4nicZ6Zj3IwAA\n",
"AAAAAAAAGMwHPgAAAAAAAAAADvOz9FW/MbVSkVFZ+Zqq825NuJyUM5mUA/lt67YyTlWaYVdqpWtu\n",
"kWMmZ206j+nKdOy6h7uOie55tyu5seue7srE7Dz3pFRM1fVMWaeqvSd3Jts+V7FFfVdC5PT0yunz\n",
"n8RaElWR0/ituhIoFboSO1XnKVv7qm27K8bNys1UpUnupswtMo+da70rHRNJe6yce9Ixu86blfLp\n",
"ynS8zWXnMZNTOJNyJne70jGTciBvY66M25UqmTSXlTd2p+dZuq4nZOUd8Ntve5F351l5lsjc7rrS\n",
"MRnXExn380Cp3+cBAAAAAAAAAA7jAx8AAAAAAAAAAId5TrpMTq18OubquBUplZ3pmIy1Lsm3XNes\n",
"nMlJ2ZST1m3lXF3XHNG5Tp8eszNDUpEQqRp31xpEx+06piuXs+uav+36nnRdY8V5o2swOc+SYVeq\n",
"qHKc6jGvq+p+VH0avmtr/4r5nzz33ec6KekAlbpyJ13n+Xxz3Vnn6Ur5VJ2nZNysTEfXuLvSHlVz\n",
"uZs0t8hW7DsTKG9zqcpcvJ135dxdx6z8cKhK7HQdU5VAmXLMt6Vwno7LyE2snHvlzVNGOmZXnmXF\n",
"SamSSXNZeVZ+Y56l4vVrycqDu/IuOvIbVUY6piKJsjJuJGsz93rs8AEAAAAAAAAAcBgf+AAAAAAA\n",
"AAAAOMzPtnzLznGrMiq7Ei5Za70t4dKV9qjKHXy7zvTKlGclcszO5ysjAxM5ZlfW5rpiqYiKdYhc\n",
"X1eSI3IPq75/dmVIrqsvv7LrGnflZSYlarru15OMrNDbmDvHycryvI2b468r8l72n1XlAE7/1L0k\n",
"Ctfl/mTqSpEQ821JmioV849ssrykIkOSNe7KBU7Jm0Tn8naNXXPLSnvsSqBkzSVj/l3nnXJ9K+NE\n",
"v18i2YG383TNv+qYroTI2zw655KRM6lK0qzoymd8et6nc5+UKnka5zc6Kc9SlWda8vbgrgQkKxIv\n",
"K+NG4pY7szYzruf0/9YIAAAAAAAAAPDr+MAHAAAAAAAAAMBhfh7/9aSEy66MysrXVJ23aq2XZKQj\n",
"utIeaXsffTjupDWoyjOs+LZ1qhh3V4Zk9dyfHrPzeiKqUhhdiY0pxzz93yPPflWCJnKet/NOOuau\n",
"6/qyzn23M2cyOc+SMZeq19JJ6/R3VZ9srxi36q17Vw7gtOzAXdf8u/7awl918H/pSoasbJR70nmq\n",
"dM2/4r5HNiWOjJu1JmXPfkXKI+st25S5TcrATL6ergxMVh6gKmux65jI81VxzNNxXRmbSfdnV7rn\n",
"bcyVcbMyHbtyJpFxu/IZT6YkN6rSRCtOSpPsXKcpa7AztbR0Q97ejUeCi1npmMhvCruyNnuu57Tf\n",
"hwEAAAAAAAAAfj0f+AAAAAAAAAAAOMzP1iTKSeNOvp7IXpT/9Z+FL+pKhuzMjkzJpkzKm1RlOVac\n",
"tE4Ru+a2857uystMSn10zWXSNX/7MTvvz65r3JWoua45OZNJ15Mxl50/6zrG+NNp2ZSKT+af/mn/\n",
"0+cPnOHkVExVaqUqiVIxbmSj6SVZKYyKbbonzS1jK/Zvu57oOG/fvFWZi8hO5StjnHxMZz5nV8am\n",
"63mK5A3uqo6pSuFU5RkyEhV3K8dU5Vne/Ibkxkl5lqx1Ovl+dOWMsnJyS4O8JU+eLjryjj4jHVOR\n",
"eFkZN+sH5kpe5u6f53LS760AAAAAAAAAAFw+8AEAAAAAAAAAcJyfx389KbVSNdfJ1zM64SIHcl4G\n",
"Zsq6RZ20TpFjdiVDsvI/kWN2rmXGMbuyPLuO6cqbdJ5r8nrfdV1fxnmzfg5MSoZ8W56l6md1hpq5\n",
"VXz6/bR0TMW4p/9VQdf8q+4pdCrLZ2w6T5Wq+Z+UWqnKzZQleKq2B89QkSq5rn3ZlG+/npVxsrZr\n",
"78qB7Drvt+dOVo47PWMzJSVzXTXPRlXKJyvT8el5n8698iYh45mclB2JqJjbyjg71ynjOZ6UtYmY\n",
"ktwJe7shK+/oKxIvK+NGftvYmY7JX6fT/1scAAAAAAAAAMCv4wMfAAAAAAAAAACH+Ql/5GNXamVX\n",
"wmXn9ZQkXLqyI6vjfDruadmUKRmYSfd9cgamc50+PWZnuqQia7Ny3KR0zKS5yJt8X7ZmVx5kZ2rl\n",
"23Imu3I5VeNMup6/++tayRV+7qQ8wGkq1tb9WmOdfqeqfMa3OS21QtHaZuVAqsaVTakZY+f1ZGwl\n",
"vzMdMynLseuYyUmaSRmbKddc9f1SlfKpSjrsSqBMyo5ETEmVrIwzKc/SlQyatG53u+b2NE7Iyg15\n",
"S55EfuPKSsdU5Fiq0jH/PvHi930AAAAAAAAAgMP8LH3Vzp03KsadfD0lu3lc194dCzLGnLSjxEm7\n",
"gpy0bp1zqRh38o4lVefdudtIxe4Jk3Z+sNuFHUyix0w6965dTrLGmbS7xZSdUCZdz58mf5K9Ym5V\n",
"1+uv0J9Zl3fWaI2dN9ZE/hbrN6hYl6pncvIuJ2Vzm7TrRMUOEq4nfj0V567aKeEu8lfDkXWafEzn\n",
"bion72rStU5Zf/F/V7WrRtW4n5736dxVO2JM2YXiyck7Vzyd66TdOrKuZ8rzVbWrRtduMCErN2Tl\n",
"N5Z/v5tFbCeRih0/qsb9fGcUvzMDAAAAAAAAABzGBz4AAAAAAAAAAA7znHTZlTypyqhMvp5tCZeq\n",
"pEDWuCdlU6pyGbv8xvRNxOTnK2NtT0qxrJ47csyUdIe8Se+5JidoMn7m7Dpv532vGGNSzsT1rMjY\n",
"nv20bErFuFVrcNradjl9/ny/01MrVfOvGPfzTXxj42a97kzOzZQlXKZkRrK2FHc973OJpDJWj6s4\n",
"d9e6Tc6QTMmdrByzctykjE1XZqgqXZCRhXgbM2vc0xMoVXN7822pkqdznf7/mpryfE16Vt7GjI5b\n",
"lXB6vSEr7+grEi8r40Z+29iZjvnnrzntd3MAAAAAAAAAgF/PBz4AAAAAAAAAAA7zsy13UjnurnTM\n",
"toRLV4KjatxJCZEqXXmTyWswKQOza512JWqy0iUn5ViqciaTsh3yJt+XrenM40w473X13cOM8z6Z\n",
"MhfXsyLrk+4nZVM4L0kDv1VFcqMqicLs3ExWBuYPp2dG3saIjuN6ctagK9Px5KTkyaRjJudlqo6Z\n",
"MpedSZS7neuWkah4O+/TMVWJnTeTkhuT0yunrVOF09ag6mdQxWvEkpV39G/Jk8hvG1npmIocS1U6\n",
"5u9f479TAQAAAAAAAAAcxgc+AAAAAAAAAAAO8/P4ryclXCYnaUryLddVlx1YkZGb2JW1WNE1t29L\n",
"4XTtxxU596R1qjhv9Ny77vtp6ZhdiZ3IMfImkjXXtTe1kvHeo+seZp37bmc6baqcZ/Kva+U98h6T\n",
"8wBVn+6vuObJ6/iN/OXH96lIovCsKmcS2Tx457gZJs+tJFVyXXv/88kUFQmUrvuTdU+70hh3XemY\n",
"rrWdfEw0uTMlY9N1zTtTK1PWLWvcqmenIrFzWnKjwsoanLZOXc9xxT07bQ0idq3t0m9PK78VRH7j\n",
"zUjHVCReasYd9bsUAAAAAAAAAADvfOADAAAAAAAAAOAwP+GPfLztlrIybmTPy10Jl6rrSUm4VG35\n",
"npVIqJj/ikk5k5NSOJOueXKaaFfqZmdip+p7eVc2ZVJapeKYb8ubRI+bnJOZnK3JOG/Wa9Guc//G\n",
"dbur+jn87+eW9an1iuTB5LlVJR78FYG15XtVpGKqkiinOWltM+b6K+a2cwvujjFOS6DcdaUynkTm\n",
"X3HPqtIxXdc3+ZiMdVs5ruqYXdc8ObXStW5Z466oyLNknHfla3bmWSalSn5bniXreiqejclr8DTO\n",
"3dbk0ds7+KeFesuxZCReVsaN/FDqScf470cAAAAAAAAAAIfxgQ8AAAAAAAAAgMP8PP5rZN/CXQmX\n",
"inzL6rglCZeqXEBXomJXSuK65mQ6JqVwTlq3rLlUPYOT1unTY3ZmSHbdj64xd93TqMnZkcl5k8nH\n",
"nJQ7qcqDdJ276vuy69ynr8G7jG3hJ38afvLcqlRd829MR8BvENkEd+e4k02+5oy5VeR00pyeQMkw\n",
"aQ0iIkmErGv+9uTJ6cdMvj8rKq55Zyrqbue6VTyDVbmGrhzIt+dZsjIdvzHP0vV8VbwmdK3B6jif\n",
"jlv1+rv07vztt4BIpPG70jGTfmcDAAAAAAAAAGCBD3wAAAAAAAAAABzmJ7xv4dtHRSryLSvn7Rz3\n",
"zWu+5br2JVy6siNV556UEOlK4Zy0bp1z6TpP5Jiu56ti3F1rUnnuKWmVSemYyamSnfmPCt+WrHky\n",
"+Rozzvtk13qfvgYVY9TI2uJ91FbxNxVzq7reyesIfI+K3Edkg+EVvy29cl3DfhZMyaZMSqDsyk9E\n",
"MipPJudA3sZYGWfyMZN1ZnqmPIM700R3Va8rUzIqK+fuzEB8ekxXDuTJlLlNynR82zV3Xc+3Pccr\n",
"42SlyHYl9FKyKZFx56ZjJv0uCAAAAAAAAADAAh/4AAAAAAAAAAA4zM/SV618LOSkhEtVFiYt4fKp\n",
"nRmFFVOyKTvXgO9L30TsSq2sqMrLZJx7V9YmekxX1iLj++WkY6rGnTT/qnOfdI0757orK5Ix/0lr\n",
"8O/n8te18p56ZZy5MuZWtaX95HWrUnXNFeOOShnwdVY2ms0YN+t7oyK9Mt3k3Mzk+5HyDO5MhrzN\n",
"5bQESoaKdbyu9zXIWreIrlxOxvMV0XU/qu5hxlb5K3OpOqYrJTM5tXJXtW4rqvIsn5736dy7Eg/f\n",
"liohrusedp0noiuXE5FyzXOzKZPTMb/xv+cBAAAAAAAAABzNBz4AAAAAAAAAAA7znHTZlXCpSq1s\n",
"S7hE9qrJygVUZSG6sildGZiIjLlNWoPTUzgnrVNExvO0M10yKZtS8bq4cw3uJs3lpPt+2jG7zrvr\n",
"+naee1de5rvyLFnXMymBMmmL+rvJnwDljewAABVUSURBVOafPDfOSgRVPUtZWYu3cbPWenI+g7qM\n",
"TYZvn9uoRM2kbMquBErWXHatQdZW7JGt/bvmuyszNPn6qnINp8+/4ponpVZ2rtvbuSPphcl5lt+Q\n",
"3HgTuT/XNXudMhIiVSmcjLlNXoNJyaO3MZ/GXTIjmzI5HTPp9zoAAAAAAAAAABb4wAcAAAAAAAAA\n",
"wGF+tuVbruushMtrvuW69iVcqrbBn5TCqNpLq2tu35bC6ZpL1X2fsk47sx0Va7vzteikHMuuTETW\n",
"uOY/65gMp13frnOflrW527UGs2V8+n1SbqbCb5zb5GuG32pl49xJ42aYPLdJ2ZTJiZoQGZi8NehK\n",
"VtxVpRfustYpoitN0nUPKxIC0S3sT55/VhLhbdyu1EpXRuXp3BG7cg2TciBVeZauTMekdZpyzTuz\n",
"PBmppV3fl1njTkqc/WFPNiU2bk865vjfgwAAAAAAAAAAfhsf+AAAAAAAAAAAOMzP47+elHCpysJs\n",
"S7hUJQZWTEqGREzJdEzKgUy6p5PSNxGT1ulTO+e26zVh5+tkREXepys/UXVMVSbtpGN2ZlMmX2OG\n",
"nWmSjGvetW5Z/v36/4bkhlTM9/mN18zvlJHpOM3ka5ZNeZeVqCnbUrxLRc6kaw2i+YwMXQmOkxI7\n",
"kWO6UjhdmY7IPc2aS+SYKSmZqnGrXiOyMh2RY6oyEG8m5UAiTk6VVM1l8jWf9nxNWYOoXWtbknh5\n",
"Gvju82zK5HTMt/2OBgAAAAAAAADw9XzgAwAAAAAAAADgMD/hfSZ3pVa2JVyqtpavyh1MyY5EnZQz\n",
"OSmb0vlMTnkGT8/AVL1G7MozdeV/IsdMSpPs/Jmz65iqcb/tmK7USobTrm/Xs54xxmnr9nd/XSsp\n",
"xZVx/r2MLfgnbeN/lzW3yX81MHluVX7jNZNjcoakyuRrrkivXNec14isuY1K1ExJoHTlM1bO3bUG\n",
"GevWldN4Om5X6qZqrl3HdGVHdm31nzWXnZmRT485LVFTlVHJyChU3dOT8xnflirpnMuUaz7tHkZU\n",
"rMHKOFk/gypeF9MyXBU5lrnpmCm/9wEAAAAAAAAAsOhn6at27rxRMe7rbh7Xte+vqyt281j9mqq/\n",
"Dv+23S3Y5zc8K5PnlvG9HDF9t5FPj6l6nY/o2hVg18+X046ZvLPIzp0sds13164Zu3Zkua4pO5Zk\n",
"fSJ90m4dU3YfmWz6XyJMnx98m8k7cUzeRSNLxvpP2rGk4nqi44zZFSRi564gGeu2a3eI1ePuJu0G\n",
"seuYKbtQRI6JPge7dry5i8x/8l+YP6m6h5+ed+XcWf+Z4OTdOibtXMFeJ+0+svM1L2P+b2OujBvd\n",
"zeYu5WddxY4fVeN+/tvHt/1OCgAAAAAAAADw9XzgAwAAAAAAAADgMM9Jl12plaoszLaEy868QUVS\n",
"YEXWtv1dGZiIruTGt6Vwdt2z09YpYtfcTk9FRY45KWdyUuoja9xvO2ZyfmbnfpYnzXdnKm5X1qZi\n",
"DCp9e25m8twm85chs/yGhEiF6es2JZtCoZ0JlLe5nJaByTj3rjTGikhCILK233ZMVXYk45gVk665\n",
"6vulYtv+b1yDinP/hjxLRbJiRdfcJq3Trms+LWeU8X0Z0TX/iKr7XpJ4eRr4buW3zD3pmEm/6wIA\n",
"AAAAAAAAsMAHPgAAAAAAAAAADvOzLd9SOe5SwuVTu7bkXxm3KkMghXHeGkzJwKx8Tdc1V5n8vbti\n",
"V/YpK/8TsSsZ1DXuziTNp8dE123K/LOOmZyTmZytybAzX7Tr3BlrvS9Rk7FFfdYn3ackUH7DJ/e/\n",
"PU3w7dfH7zA9m5Lh27MpWfdwSqJm0vWETMrARMaoyM9cV00OJEtXOiZyTNc97Dpm8lrvypt0zqUi\n",
"tbAzuRGxKyFSlaRZMSXPUmVSquSkuXSd5zc8+xUZq6xxT0p3panIsfSkY77t93CA/9feHS1HbsNY\n",
"AFVN+f//eGv3eZ1OxMYQBCCd85gMKRJSS26XjAsAAAAAAADweF74AAAAAAAAAAAY5ufjf50U4RKK\n",
"bzkZa/HtvJVxB50iQyJO1bZLbEqnGJg37jmi0/UVGZMVA1MV+1RVy06xF5WxFjvmfdqYU0TWfHaq\n",
"LjvMjmf5c/19/OKut9af1pZ/x37Ezax52rUD1cSmxOYZFVWSpFMMTJt29NcV+1EvqyX6napoiUi7\n",
"8GiL8c6RJ6eIsVlzas/frmNlLbsiHu7mPRVRk7Wf6TEKVfEsokp6rSUrmqRTrE3EjrVVRiBV1fbU\n",
"eQ/JiHjJmfcNv4sDAAAAAAAAAHgUL3wAAAAAAAAAAAzzE37l4667SFYsTFmES1YL/qwIly6xI1Gn\n",
"Ih66RIi8kRiYNZ3XNv0eERmTFTeRMe+peIqqCLTKMVmmr/9OdK2T6lIV2VTZq/nvjz39DXQRKPM8\n",
"vd7T4xnIsyMOpLOnRZV01imiptKWa+6NMTBVsSOn1prWUjzJpHP4W1bsyKkxkYigTlErO6IkPtkR\n",
"uXE356cxlTE9VREondf2tKiSN+oUz3LqWonIiBm6rj3rP1XbuzlX5t31DLq1cpP4beXb099HvEz7\n",
"LgUAAAAAAAAA8Hpe+AAAAAAAAAAAGOZn6V+tdA4ZFeFS2X7+bt7K6JisPlNd4mU690+cFm8yPcam\n",
"S52yatQ5Bibr2qmKl6m6b0ZlRdKcmrPL+iPn59TaO4/ZZdIep9V2x72n7vm/o3V/p3gW+8mZozt/\n",
"kUF3b4hN2REzsqNOkWbBn9jP/VqOXsc7WktXxcBEWnLvanN/KnZkUsROZMypc1h5rdzNuyuqZMeY\n",
"FZ2u44zW+JXnPeO+krWfzvEGb4jc2GFXfM6pOu2IWqnSqQado6Kyfo7IiopqfY/4+ziW+4iX+3n9\n",
"PgkAAAAAAAAAYBgvfAAAAAAAAAAADPM50qUqwiUlvuW66iJcsnoYnYr2yJq3c9xEp9iUSVE40/ac\n",
"oVMsT0Tl53Ly5z0yJiviISsKJzImK55sx5gVp2I4Op2zHWMmxZd0ut6yjr1jvTXnZ1dbdW+2c5Lr\n",
"bc0T4z9+2xE38XSfnlDqRKaMGJjrOnhPq4qBqWqN3ykOZEXnyJBTUTidx6zotP4u5znrc5hVt6q4\n",
"mR37+TROPEueHTEXVXEgK/NURpPcrcW1777yb/NmPfvKookyIl7u5/WdGgAAAAAAAABgGC98AAAA\n",
"AAAAAAAM81MW33JdxREu36pq/b9y7KyeiiIqetXg1H7euOesz/eOOas+Y7tqUhXH0ik2pSqOpVO8\n",
"Rqe1PC3epPOYzvEzu5yqyw418Sx/rsjP+5/mqbHruDtavu9Yi/189oaYEXiiTjEdGWuJrMN+9tkS\n",
"z1TZsr4qjqVTTMe3x105drT1d6fIkN86R9J0iSLqFDMUuQYro1YyznunGqyoikDZteeqeBZRJb33\n",
"3On6yroX3ekUuRNRWduq+0pVrE3oW81KEOr//Of/BQAAAAAAAACgOS98AAAAAAAAAAAM8/Pxv46K\n",
"cKlsr5/REj3ruJ3iMyJ2REd0qkFl+/nOJp3DqvMsoib32BnH7TRvl+iY6LnoEmPztHiTzpE1J49V\n",
"E3lSt9ZT5/2fqt4439UCXvwHb+XaP2dHFAZM1CmmJ2LLZ7cyOuJUHMgOk+JOVsadGnMqxqbzmMp4\n",
"k7sxn8Z1ibWJruVOVlRB57iZ6REoEW+MKnmjHedw0rUScXJtGT/3VD63nhb3Ffrm8N/flnT4AAAA\n",
"AAAAAAAYxgsfAAAAAAAAAADD/IRf+bjrLpIS33JddREulREDGa3jK2NHduz5VG0ro1dOxZt0iVGp\n",
"9PQ6dY6BWZk369qpeuZkRW50irDotJbOESec8/TroPIZW3Ps6fEGO966n14DzvFXHu9UGWvBLLuu\n",
"lR1xLFVKPy9VbeGzIgUix94Ro7BrDOecOqed4k2yrsmqtv136/g0JqtunaMXdhxbPMu5875LRnTM\n",
"yjxPi7GZVoOMe8KuayUr2m5Hbe/mXJl31z2i6t66IeJl0vcvAAAAAAAAAAAuL3wAAAAAAAAAAIzz\n",
"s/SvVjqHjIpwmRYPsGPO6XE5nSNDTtVgUhTOyjxieebHwFR+LifFpqzImLdTDSqfu1VjsubtPOZU\n",
"bErn5/1vk/Z3XVX9TysjBnYce/ob9F1qsOs66LKf69qzFhEcVNsR0xFpTns3R3SejP1UrmVyjMp1\n",
"7bk2KmuwY/0hnduqV43ZJVLbp42ZHlVyas/frmN1LVWt8SOqzntlPEBE53iWHZEIlbW9cyqmY1ec\n",
"xqRokumxPNNrcOqzGzEp+uZUrUO+/9Y57bsgAAAAAAAAAMDrfe7wUdbRo6rDRHTezvup+mvkXWvL\n",
"WH+njhKTOqO8sStI544ynbuCVK6t6r44bT9VNYiMmd4tovP6s34+efqYXSbt8fs5/lyR7wh77HiT\n",
"vept+E7dLQB4tk5dTiKmdwUp654wuVPCilOdRCKdBT6N6zSmc7eRO6e6XWR1MIheT3c6/QVzRreO\n",
"FStrrdpP524dWedjxds6V0SO8+lYk/a8az9V13GnGkRU1bZzJ5SsnwXTOtf8941Ehw8AAAAAAAAA\n",
"gGG88AEAAAAAAAAAMMxPXXzLdc2KcOm8n0g/mJPRCxlt058WIULcG6NvvtU5aum6cu5xO44bPXbn\n",
"/UTGZD1jIrpEd3SO5Dg15mR8ztOibqrURJFF3i7f9UZ6VbzJ9FiVHfWfXgOA3XZFoOyIM6nytBiY\n",
"67p/ZlbuuSxaJeLpcScr4zqPibRvPzVmRadooqwonFPX9p2sNvdZNbhT2ba/czzLqViITlElxJw6\n",
"h6eOE1F1HX+a57dTtV059qnom0nRMUv+/yQ6fAAAAAAAAAAADOOFDwAAAAAAAACAYX4+/tdRES5Z\n",
"7bezWnRn7GfFyQiXb52KwugcvXIqcqNTlE/n87Hi6TEwnde2cuyqe3hUxn6eVoNdY1Z0jjjRW7K3\n",
"p18HddffG+NZdryZP/3t/h31n14DIG5XnMbvp9+0+0pGnMmpGkRiVHYpi89Ja/m8oCrypPOvft7o\n",
"1DntdO10WktGvERWlM/TaiCepXfkRqVT8ROdYmyqrskVd2ubXoNdsSNV99Ksz3JGbMq06JgvDwsA\n",
"AAAAAAAAQHNe+AAAAAAAAAAAGOYnFt9yXb0jBCLzZrRvr9xP57iDzutf0SWmY1r0Sqe1VEUrrehy\n",
"fUVUrq3qvtJ5P5Ex02oQkfXc3TEmS+c9P23MDk/fn3iWaSrr1smOOqglb7Ej/qMsTqORXZE0VcTA\n",
"NI+BOTVml86RIZHW5Z3HZJm850jb/kib+Ova8znMimfKOB+VNcj4vEfW9mmeiE5xIBk6xXRUReF8\n",
"+jdP23PV9dWpBhGV98VT19dvne/zERsiXib/7hEAAAAAAAAA4JW88AEAAAAAAAAAMMzP2j/r1OJ9\n",
"xY4ojN9Oxlp8O29WrafHZ3SKENkRo3DqOJ32/Mbomwynrq+oqntEVtzXncr9dJk3WoOMSJqs52NE\n",
"5yiPjAihaWNmxabEfL/eP1c0HvLvVL61XnXsSW38P/GXBnuoI5mmR4h0UhVnsktVNEnVcStjYNpE\n",
"VmTJisKoGhNt4905kuZUjM2361hZS9aYU3VckfV5z1hvVpv7rLb9dyrjJzpHR6y4W7+okvh1/LY9\n",
"79pP53vEjhp8UhW1UnX/ytrPioxzGKjBtO+cAAAAAAAAAACv54UPAAAAAAAAAIBh/iXSpVOEy6ko\n",
"jG+PG513x5ydI1AqIwW6RIh07qXJmk7XStU9ofPaVo7d+T4ZGZMVWdHp+Zj1/DgV3XHnaVElxHW+\n",
"Fv5e5G1y8SzPP+4u/lphn+nXAv9UFYXxRJNrWRlN8rYYmOuKRfeUrfdUdExWq2z+qXOMTWW0x44x\n",
"lWvJaJ+fdd471eDb4346dlWr/+uqi2eZFLkRjbWgj05xMzuOE3GqBlGT70WRebOedVnn8GZevzMD\n",
"AAAAAAAAABjGCx8AAAAAAAAAAMP8xPut7IjP+HbO6Lw7jl25n4z27LvWVlWX7nETd3bU9lQNTsWb\n",
"7FpL5/O+ovNn9073z2VGJFXn/XSZ87p61aAyeqxqTIaTa+9c287Pk9+evr/3xaRURgxM/6uBSfEM\n",
"nanjPpFYCP5peh2r1i8GZsD9LCPioZNT+zs15lTUSpaMlum7xqzo8nk51fb+uvbUrirOJOvz0nk/\n",
"nSMRKmu7w6k4kKpaf5pn0p6z7FhbZQ0yzs/KPLue7ztqe3fcT8fufJ+/m3Nl3kDEy7TvvwAAAAAA\n",
"AAAAr+eFDwAAAAAAAACAYX7W/llW1ErWvKciEU7Nu2PO6XE5T6/tqeOcjNzoEk3SKW6mc1TJG+4R\n",
"p+atOm7n+2RkTFYNIk6tpVP0Tec9nxrTOUqmU8/U/xZpkV7ZVr3q2JVv4Vcdu337/Bv+cgL2mh7H\n",
"8rZoksoYmKpr5dNPX3f1jowpVRV5khX/cWpM53iZqnbnlWPudGrFXhnPknGtT9vPjhiFrM/Y9HiW\n",
"U7XtElWyq9aToklO7TkrAmllbZ0/Y0+v7SenPu+/DXqmTvsODQAAAAAAAADwel74AAAAAAAAAAAY\n",
"5l8iXaoiTzq1hV+RsZ+TkRsRXeIzIjpFe1SeQ/pcx52vgzfEwER0joHJmnd6NEnGnJ3iNJ4WVULM\n",
"mevgz/W/gePsEXlLXTzLOVW1bt0Wf4G/vuAJxkVW/FIZTSIGpncMTFnMUCQS4dQY4jpH0kTGZOh0\n",
"HU+Lwsk4h5Wt/qv2k/VZOBWfkaVLbErlOeR5ETsRnWoQUVXbynisqv0URcf4HRMAAAAAAAAAwDBe\n",
"+AAAAAAAAAAAGOanLr4lOm9W+/lTEQ8Z82a18e4c6XBqbZ37fnWqwam1dI5A2WVyZFDne8bKvJUx\n",
"JBmxKZUxMBFZ0TFZz+ZviVFZ07lOp+KNZj3HIm+PT3rjfNJaiXOeYaaqaBLOmRYZFImBGXUdZ7W9\n",
"fvqYTk7tuVPUSlaESFb7+UlxJm+MZ8mIHbkucRMn7Yh4qKp1dC2dI4PudDofEadiVLKe1VXP0GnP\n",
"rSbRMX63BQAAAAAAAAAwjBc+AAAAAAAAAACG+fn8nydFuGTFmWT1LOrcgr+qLqciQzrXtlMNOq1l\n",
"0p4ro0runIzliehc284xMBnzdopV6RRJUxXLs2tMxpwn137qWJ3jZDrH1tSItDuvfNM9st6qlu5v\n",
"O+4TTK7d9L9AmRY38VskfoLPT8tTtauK/4gct8taV4497rOcFWtRNSbSOrvzmOnxMqfiTbLaqldF\n",
"iNyt49Nass57VZzJjjk/zVu1n11xBxGdIypWnKrt5HiWSLTHrrVM2/O3Tq0t6zO26/nYubY7jl0U\n",
"m9I5Osb3eQAAAAAAAACAYf4PM7L2RAC3ISAAAAAASUVORK5CYII=\n",
"\" transform=\"translate(149, 47)\"/>\n",
"</g>\n",
"</svg>\n"
]
},
"execution_count": 40,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"T₅ = Fun(Chebyshev(), [zeros(2);1])\n",
"w = 1/sqrt(1-x^2)\n",
"L₅ = z->cauchyintegral(w*T₅, z)\n",
"\n",
"phaseplot(-3..3, -3..3, L₅)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"\n",
"#### Example: Weighted Chebyshev log transform\n",
"\n",
"For classical orthogonal polynomials we can go a step further and relate the indefinite integrals to other orthogonal polynomials.\n",
"\n",
" For example, recall that\n",
"$$\n",
"{\\D\\over \\dx}[\\sqrt{1-x^2} U_n(x)] = -{n+1 \\over \\sqrt{1-x^2}} T_{n+1}(x)\n",
"$$\n",
"in other words, \n",
"$$\n",
"\\int_x^1 {T_k(t) \\over \\sqrt{1-t^2}} \\dt = -{\\sqrt{1-x^2} U_{k-1}(x) \\over k}\n",
"$$\n",
"Thus for $k=1,2,\\ldots$,\n",
"$$\n",
"L_k(z) = -{1 \\over n+1} \\CC[\\sqrt{1-\\diamond^2} U_{k-1}](z)\n",
"$$\n",
"and\n",
"$$\n",
"{1 \\over \\pi} \\int_{-1}^1 {T_k(x) \\over \\sqrt{1-x^2}}\\log(z-x) \\dx = {2 \\I \\over k} \\CC[\\sqrt{1-\\diamond^2} U_{k-1}](z)\n",
"$$\n"
]
},
{
"cell_type": "code",
"execution_count": 42,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(0.00018695792399762436 - 0.0009741971129007227im, 0.0001869579239976236 - 0.000974197112900722im)"
]
},
"execution_count": 42,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"T₅ = Fun(Chebyshev(), [zeros(5);1])\n",
"U₄ = Fun(Ultraspherical(1), [zeros(4);1])\n",
"x = Fun()\n",
"L₅ = z->sum(T₅/sqrt(1-x^2) * log(z-x))/π\n",
"\n",
"L₅(z), 2im*cauchy(sqrt(1-x^2)*U₄,z)/5"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"As we saw last lecture, Cauchy transforms of OPs satisfy simple recurrences, and this relationship renders log transforms equally calculable. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"\n",
"### Solving logarithmic singular integral equations\n",
"\n",
"Oddly enough, it is easier to solve a singular integral equation involving the logarithmic kernel than to actually calculate the logarithmic singular integral, so we begin here. Consider the problem of calculating $u(x)$ such that\n",
"$$\n",
"{1 \\over \\pi} \\int_{-1}^1 u(t) \\log | x-t| \\dt = f(x) \\qqfor -1 < x < 1\n",
"$$\n",
"\n",
"\n",
"To tackle this problem we first need to understand the additive jump $Re L^\\pm(x) = {L^+(x) + L^-(x) \\over 2}$. Thinking in terms of integrals of Cauchy transforms we see that\n",
"$$\n",
"L^+u(x) + L^-u(x) = -2\\I (2\\int_2^1 \\CC u(x) \\dx + \\int_1^x [C^+ u(t) + C^-u(t)] \\dt) =\n",
" D -2 \\I \\int_1^x (-\\I H u(t)) \\dt = D + 2\\int_x^1 H u(t) dt\n",
"$$\n",
"That is, it is expressed as an indefinite integral of the Hilbert transform. We therefore have:\n",
"$$\n",
"{\\D \\over \\dx} {1 \\over \\pi} \\int_{-1}^1 u(t) \\log | x-t| \\dt = {\\D \\over \\dx} \\int_x^1 H u(t) dt = - Hu(x)\n",
"$$\n",
"where the minus sign comes from the fact that $x$ is the lower limit. In other words, our original SIE becomes equivalent to inverting the Hilbert transform:\n",
"$$\n",
"\\HH u(x) = -f'(x)\n",
"$$\n",
"recall, we can express the solution as\n",
"$$\n",
" u = {1 \\over \\sqrt{1-x^2}} \\HH[\\sqrt{1-\\diamond^2} f'] + {C\\over \\sqrt{1-x^2}}\n",
"$$\n",
"\n",
"Let's do a numerical example:"
]
},
{
"cell_type": "code",
"execution_count": 43,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"hilbert(u, 0.1) + f(0.1) = -4.440892098500626e-16\n",
"logkernel(u, 0.1) - f(0.1) = -0.18115023187927326\n",
"logkernel(u, 0.2) - f(0.2) = -0.18115023187927304\n"
]
}
],
"source": [
"x = Fun()\n",
"f = exp(x)\n",
"\n",
"C = randn()\n",
"\n",
"u₁ = hilbert(sqrt(1-x^2)*f')/sqrt(1-x^2) \n",
"\n",
"u = u₁ + C/sqrt(1-x^2)\n",
"\n",
"@show hilbert(u, 0.1) + f(0.1)\n",
"@show logkernel(u,0.1) - f(0.1) # didn't work 😩\n",
"@show logkernel(u,0.2) - f(0.2); # but we are only off by a constant"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Remember: for inverting the Hilbert transform we had a degree of freedom: every solution plus $C/\\sqrt{1-x^2}$ was also a solution. But here, since we differentiated, we use that degree of freedom to ensure that we have arrived at the right solution. \n",
"\n",
"To choose $C$, we use the fact that\n",
"$$\n",
"f(0) = {1 \\over \\pi} \\int_{-1}^1 u(t) \\log |t| \\dt\n",
"$$\n",
"If we can calculate the right integral, we can use this to choose $C$:"
]
},
{
"cell_type": "code",
"execution_count": 44,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"hilbert(u, 0.1) + f(0.1) = -4.440892098500626e-16\n",
"logkernel(u, 0.1) - f(0.1) = 0.0\n",
"logkernel(u, 0.2) - f(0.2) = 2.220446049250313e-16\n"
]
}
],
"source": [
"# choose C so that\n",
"# logkernel(u₁, 0) + C*logkernel(1/sqrt(1-x^2), 0) == f(0)\n",
"C = (f(0) - logkernel(u₁, 0))/logkernel(1/sqrt(1-x^2), 0)\n",
"u = u₁ + C/sqrt(1-x^2)\n",
"\n",
"@show hilbert(u, 0.1) + f(0.1)\n",
"@show logkernel(u,0.1) - f(0.1) # Works!\n",
"@show logkernel(u,0.2) - f(0.2); # And at all x!"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"*Example* We now do an example which can be solved by hand. Find $u(x)$ so that: \n",
"$$\n",
"\\int_{-1}^1 u(t) \\log | x-t| \\dt = 1.\n",
"$$\n",
"Differentiating, we know that \n",
"$$\n",
"\\int_{-1}^1 {u(t) \\over x-t} \\dt = 0\n",
"$$\n",
"hence $u(x)$ must be of the form ${C \\over \\sqrt{1-x^2}}$. Which $C$? Make it work for $x = 0$:\n",
"$$\n",
"1 = \\int_{-1}^1 u(t) \\log | 0 - t| \\dt = C \\int_{-1}^1 {\\log | t| \\over \\sqrt{1-t^2}} \\dt\n",
"$$\n",
"To evaluate the integral, we can use trigonmetric variables:\n",
"$$\n",
"\\int_0^1 {\\log t \\over \\sqrt{1-t^2}} \\dt = \\int_0^{\\pi \\over 2} {\\cos \\theta \\log \\sin \\theta \\over \\sqrt{1-\\sin^2 \\theta}} \\D\\theta = \\int_0^{\\pi \\over 2} \\log \\sin \\theta \\D\\theta = - {\\pi \\log 2\\over 2}\n",
"$$\n",
"(The last identity takes some work: I'll leave it as an excercise.)\n",
"\n",
"Thus we have $ C = -{1 \\over \\pi \\log 2}$"
]
},
{
"cell_type": "code",
"execution_count": 49,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"1.0"
]
},
"execution_count": 49,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x = Fun()\n",
"C = -1/(log(2))\n",
"u = C/sqrt(1-x^2)\n",
"\n",
"logkernel(u, 0.2) "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Physically, this solution gives us the potential field \n",
"$$\n",
"\\int_{-1}^1 u(t) \\log|z-t| \\dt\n",
"$$\n",
"corresponding to holding a metal plate at constant potential:"
]
},
{
"cell_type": "code",
"execution_count": 52,
"metadata": {},
"outputs": [
{
"data": {
"image/svg+xml": [
"<?xml version=\"1.0\" encoding=\"utf-8\"?>\n",
"<svg xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\" width=\"600\" height=\"400\" viewBox=\"0 0 2400 1600\">\n",
"<defs>\n",
" <clipPath id=\"clip6600\">\n",
" <rect x=\"0\" y=\"0\" width=\"2000\" height=\"2000\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<defs>\n",
" <clipPath id=\"clip6601\">\n",
" <rect x=\"0\" y=\"0\" width=\"2400\" height=\"1600\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<polygon clip-path=\"url(#clip6601)\" points=\"\n",
"0,1600 2400,1600 2400,0 0,0 \n",
" \" fill=\"#ffffff\" fill-opacity=\"1\"/>\n",
"<defs>\n",
" <clipPath id=\"clip6602\">\n",
" <rect x=\"480\" y=\"0\" width=\"1681\" height=\"1600\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<polygon clip-path=\"url(#clip6601)\" points=\"\n",
"149.361,1503.47 2081.26,1503.47 2081.26,47.2441 149.361,47.2441 \n",
" \" fill=\"#ffffff\" fill-opacity=\"1\"/>\n",
"<defs>\n",
" <clipPath id=\"clip6603\">\n",
" <rect x=\"149\" y=\"47\" width=\"1933\" height=\"1457\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 204.037,1503.47 204.037,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 659.674,1503.47 659.674,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1115.31,1503.47 1115.31,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1570.95,1503.47 1570.95,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 2026.58,1503.47 2026.58,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 149.361,1462.26 2081.26,1462.26 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 149.361,1118.81 2081.26,1118.81 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 149.361,775.359 2081.26,775.359 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 149.361,431.909 2081.26,431.909 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 149.361,88.4582 2081.26,88.4582 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6601)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,1503.47 2081.26,1503.47 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6601)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,1503.47 149.361,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6601)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 204.037,1503.47 204.037,1481.63 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6601)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 659.674,1503.47 659.674,1481.63 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6601)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1115.31,1503.47 1115.31,1481.63 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6601)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1570.95,1503.47 1570.95,1481.63 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6601)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 2026.58,1503.47 2026.58,1481.63 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6601)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,1462.26 178.339,1462.26 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6601)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,1118.81 178.339,1118.81 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6601)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,775.359 178.339,775.359 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6601)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,431.909 178.339,431.909 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6601)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,88.4582 178.339,88.4582 \n",
" \"/>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:middle;\" transform=\"rotate(0, 204.037, 1557.47)\" x=\"204.037\" y=\"1557.47\">-2</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:middle;\" transform=\"rotate(0, 659.674, 1557.47)\" x=\"659.674\" y=\"1557.47\">-1</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:middle;\" transform=\"rotate(0, 1115.31, 1557.47)\" x=\"1115.31\" y=\"1557.47\">0</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:middle;\" transform=\"rotate(0, 1570.95, 1557.47)\" x=\"1570.95\" y=\"1557.47\">1</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:middle;\" transform=\"rotate(0, 2026.58, 1557.47)\" x=\"2026.58\" y=\"1557.47\">2</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:end;\" transform=\"rotate(0, 125.361, 1479.76)\" x=\"125.361\" y=\"1479.76\">-2</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:end;\" transform=\"rotate(0, 125.361, 1136.31)\" x=\"125.361\" y=\"1136.31\">-1</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:end;\" transform=\"rotate(0, 125.361, 792.859)\" x=\"125.361\" y=\"792.859\">0</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:end;\" transform=\"rotate(0, 125.361, 449.409)\" x=\"125.361\" y=\"449.409\">1</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:end;\" transform=\"rotate(0, 125.361, 105.958)\" x=\"125.361\" y=\"105.958\">2</text>\n",
"</g>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#0d0829; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 204.037,1303.33 205.162,1304.27 208.593,1307.12 209.306,1307.71 213.15,1310.86 213.496,1311.14 217.706,1314.56 217.733,1314.58 222.017,1318.01 222.262,1318.21 \n",
" 226.349,1321.45 226.819,1321.82 230.73,1324.88 231.375,1325.38 235.161,1328.31 235.932,1328.91 239.641,1331.75 240.488,1332.39 244.173,1335.18 245.044,1335.84 \n",
" 248.757,1338.62 249.601,1339.25 253.393,1342.05 254.157,1342.62 258.082,1345.49 258.713,1345.95 262.826,1348.92 263.27,1349.24 267.626,1352.36 267.826,1352.5 \n",
" 272.382,1355.72 272.481,1355.79 276.939,1358.91 277.394,1359.23 281.495,1362.06 282.365,1362.66 286.052,1365.18 287.395,1366.09 290.608,1368.27 292.486,1369.53 \n",
" 295.164,1371.32 297.638,1372.96 299.721,1374.34 302.853,1376.4 304.277,1377.33 308.131,1379.83 308.833,1380.29 313.39,1383.21 313.474,1383.27 317.946,1386.11 \n",
" 318.885,1386.7 322.503,1388.98 324.363,1390.14 327.059,1391.81 329.91,1393.57 331.615,1394.62 335.527,1397.01 336.172,1397.4 340.728,1400.15 341.217,1400.44 \n",
" 345.284,1402.87 346.982,1403.87 349.841,1405.56 352.821,1407.31 354.397,1408.23 358.737,1410.74 358.953,1410.87 363.51,1413.48 364.733,1414.18 368.066,1416.07 \n",
" 370.81,1417.61 372.623,1418.63 376.969,1421.05 377.179,1421.16 381.735,1423.67 383.215,1424.48 386.292,1426.16 389.547,1427.92 390.848,1428.62 395.404,1431.05 \n",
" 395.968,1431.35 399.961,1433.46 402.482,1434.78 404.517,1435.85 409.073,1438.21 409.089,1438.22 413.63,1440.55 415.796,1441.65 418.186,1442.87 422.6,1445.09 \n",
" 422.743,1445.16 427.299,1447.43 429.51,1448.52 431.855,1449.68 436.412,1451.9 436.523,1451.96 440.968,1454.11 443.649,1455.39 445.524,1456.29 450.081,1458.45 \n",
" 450.886,1458.83 454.637,1460.59 458.24,1462.26 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#270b52; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 795.668,1462.26 791.808,1461.43 787.252,1460.42 782.696,1459.4 780.147,1458.83 778.139,1458.37 773.583,1457.32 769.026,1456.26 765.381,1455.39 764.47,1455.18 \n",
" 759.914,1454.08 755.357,1452.97 751.283,1451.96 750.801,1451.84 746.245,1450.69 741.688,1449.53 737.782,1448.52 737.132,1448.35 732.575,1447.16 728.019,1445.95 \n",
" 724.813,1445.09 723.463,1444.72 718.906,1443.48 714.35,1442.22 712.324,1441.65 709.794,1440.95 705.237,1439.65 700.681,1438.34 700.267,1438.22 696.125,1437.01 \n",
" 691.568,1435.67 688.617,1434.78 687.012,1434.3 682.455,1432.93 677.899,1431.53 677.329,1431.35 673.343,1430.11 668.786,1428.68 666.387,1427.92 664.23,1427.23 \n",
" 659.674,1425.76 655.756,1424.48 655.117,1424.27 650.561,1422.77 646.005,1421.24 645.421,1421.05 641.448,1419.7 636.892,1418.14 635.364,1417.61 632.335,1416.56 \n",
" 627.779,1414.96 625.565,1414.18 623.223,1413.35 618.666,1411.71 616.008,1410.74 614.11,1410.05 609.554,1408.38 606.68,1407.31 604.997,1406.68 600.441,1404.97 \n",
" 597.57,1403.87 595.884,1403.23 591.328,1401.48 588.666,1400.44 586.772,1399.7 582.215,1397.91 579.957,1397.01 577.659,1396.09 573.103,1394.25 571.435,1393.57 \n",
" 568.546,1392.39 563.99,1390.51 563.089,1390.14 559.434,1388.61 554.913,1386.7 554.877,1386.69 550.321,1384.74 546.902,1383.27 545.764,1382.78 541.208,1380.79 \n",
" 539.046,1379.83 536.652,1378.77 532.095,1376.74 531.337,1376.4 527.539,1374.68 523.773,1372.96 522.983,1372.6 518.426,1370.5 516.348,1369.53 513.87,1368.37 \n",
" 509.314,1366.22 509.053,1366.09 504.757,1364.04 501.89,1362.66 500.201,1361.84 495.644,1359.62 494.848,1359.23 491.088,1357.37 487.927,1355.79 486.532,1355.09 \n",
" 481.975,1352.79 481.121,1352.36 477.419,1350.47 474.427,1348.92 472.863,1348.11 468.306,1345.73 467.841,1345.49 463.75,1343.33 461.362,1342.05 459.194,1340.89 \n",
" 454.983,1338.62 454.637,1338.43 450.081,1335.94 448.706,1335.18 445.524,1333.42 442.523,1331.75 440.968,1330.88 436.434,1328.31 436.412,1328.3 431.855,1325.7 \n",
" 430.438,1324.88 427.299,1323.06 424.53,1321.45 422.743,1320.4 418.708,1318.01 418.186,1317.7 413.63,1314.97 412.971,1314.58 409.073,1312.22 407.318,1311.14 \n",
" 404.517,1309.42 401.744,1307.71 399.961,1306.6 396.248,1304.27 395.404,1303.74 390.848,1300.85 390.829,1300.84 386.292,1297.93 385.486,1297.4 381.735,1294.97 \n",
" 380.217,1293.97 377.179,1291.97 375.019,1290.54 372.623,1288.94 369.892,1287.1 368.066,1285.87 364.833,1283.67 363.51,1282.76 359.842,1280.23 358.953,1279.62 \n",
" 354.917,1276.8 354.397,1276.43 350.058,1273.36 349.841,1273.21 345.284,1269.94 345.262,1269.93 340.728,1266.64 340.528,1266.49 336.172,1263.29 335.857,1263.06 \n",
" 331.615,1259.9 331.245,1259.62 327.059,1256.47 326.693,1256.19 322.503,1252.99 322.199,1252.76 317.946,1249.46 317.762,1249.32 313.39,1245.89 313.382,1245.89 \n",
" 309.057,1242.45 308.833,1242.27 304.786,1239.02 304.277,1238.61 300.569,1235.58 299.721,1234.89 296.405,1232.15 295.164,1231.12 292.293,1228.71 290.608,1227.29 \n",
" 288.232,1225.28 286.052,1223.42 284.222,1221.85 281.495,1219.48 280.262,1218.41 276.939,1215.5 276.35,1214.98 272.487,1211.54 272.382,1211.45 268.672,1208.11 \n",
" 267.826,1207.34 264.903,1204.67 263.27,1203.17 261.182,1201.24 258.713,1198.94 257.506,1197.8 254.157,1194.64 253.875,1194.37 250.289,1190.93 249.601,1190.27 \n",
" 246.747,1187.5 245.044,1185.83 243.249,1184.07 240.488,1181.32 239.794,1180.63 236.381,1177.2 235.932,1176.74 233.01,1173.76 231.375,1172.08 229.681,1170.33 \n",
" 226.819,1167.34 226.394,1166.89 223.146,1163.46 222.262,1162.51 219.939,1160.02 217.706,1157.61 216.772,1156.59 213.645,1153.16 213.15,1152.61 210.555,1149.72 \n",
" 208.593,1147.51 207.505,1146.29 204.494,1142.85 204.037,1142.33 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#470b69; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 204.037,948.879 204.751,950.519 206.278,953.954 207.839,957.388 208.593,959.014 209.432,960.823 211.056,964.257 212.716,967.692 213.15,968.573 214.406,971.126 \n",
" 216.13,974.561 217.706,977.637 217.89,977.995 219.679,981.43 221.505,984.864 222.262,986.264 223.364,988.299 225.257,991.733 226.819,994.514 227.186,995.168 \n",
" 229.147,998.602 231.146,1002.04 231.375,1002.42 233.177,1005.47 235.246,1008.91 235.932,1010.03 237.348,1012.34 239.488,1015.77 240.488,1017.36 241.663,1019.21 \n",
" 243.875,1022.64 245.044,1024.43 246.124,1026.08 248.409,1029.51 249.601,1031.28 250.732,1032.95 253.092,1036.38 254.157,1037.91 255.49,1039.82 257.927,1043.25 \n",
" 258.713,1044.34 260.401,1046.69 262.916,1050.12 263.27,1050.6 265.468,1053.55 267.826,1056.68 268.061,1056.99 270.693,1060.42 272.382,1062.6 273.366,1063.86 \n",
" 276.079,1067.29 276.939,1068.37 278.833,1070.73 281.495,1074 281.63,1074.16 284.467,1077.6 286.052,1079.49 287.347,1081.03 290.271,1084.46 290.608,1084.86 \n",
" 293.236,1087.9 295.164,1090.1 296.246,1091.33 299.3,1094.77 299.721,1095.24 302.398,1098.2 304.277,1100.26 305.542,1101.64 308.732,1105.07 308.833,1105.18 \n",
" 311.968,1108.51 313.39,1110 315.25,1111.94 317.946,1114.72 318.581,1115.38 321.959,1118.81 322.503,1119.36 325.385,1122.24 327.059,1123.9 328.861,1125.68 \n",
" 331.615,1128.37 332.387,1129.11 335.963,1132.55 336.172,1132.75 339.591,1135.98 340.728,1137.05 343.27,1139.42 345.284,1141.28 347.003,1142.85 349.841,1145.43 \n",
" 350.789,1146.29 354.397,1149.51 354.629,1149.72 358.524,1153.16 358.953,1153.53 362.476,1156.59 363.51,1157.48 366.484,1160.02 368.066,1161.37 370.55,1163.46 \n",
" 372.623,1165.19 374.675,1166.89 377.179,1168.95 378.86,1170.33 381.735,1172.66 383.105,1173.76 386.292,1176.31 387.413,1177.2 390.848,1179.9 391.783,1180.63 \n",
" 395.404,1183.44 396.217,1184.07 399.961,1186.93 400.716,1187.5 404.517,1190.36 405.283,1190.93 409.073,1193.75 409.917,1194.37 413.63,1197.09 414.62,1197.8 \n",
" 418.186,1200.38 419.393,1201.24 422.743,1203.62 424.239,1204.67 427.299,1206.82 429.158,1208.11 431.855,1209.97 434.153,1211.54 436.412,1213.08 439.224,1214.98 \n",
" 440.968,1216.15 444.374,1218.41 445.524,1219.17 449.603,1221.85 450.081,1222.16 454.637,1225.1 454.916,1225.28 459.194,1228.01 460.313,1228.71 463.75,1230.87 \n",
" 465.796,1232.15 468.306,1233.7 471.368,1235.58 472.863,1236.5 477.03,1239.02 477.419,1239.25 481.975,1241.97 482.786,1242.45 486.532,1244.66 488.639,1245.89 \n",
" 491.088,1247.31 494.589,1249.32 495.644,1249.93 500.201,1252.51 500.64,1252.76 504.757,1255.06 506.798,1256.19 509.314,1257.58 513.061,1259.62 513.87,1260.06 \n",
" 518.426,1262.52 519.437,1263.06 522.983,1264.95 525.928,1266.49 527.539,1267.34 532.095,1269.7 532.535,1269.93 536.652,1272.04 539.268,1273.36 541.208,1274.34 \n",
" 545.764,1276.62 546.125,1276.8 550.321,1278.87 553.117,1280.23 554.877,1281.09 559.434,1283.28 560.243,1283.67 563.99,1285.45 567.512,1287.1 568.546,1287.59 \n",
" 573.103,1289.7 574.929,1290.54 577.659,1291.78 582.215,1293.84 582.497,1293.97 586.772,1295.88 590.23,1297.4 591.328,1297.89 595.884,1299.87 598.129,1300.84 \n",
" 600.441,1301.83 604.997,1303.77 606.202,1304.27 609.554,1305.68 614.11,1307.57 614.459,1307.71 618.666,1309.43 622.91,1311.14 623.223,1311.27 627.779,1313.09 \n",
" 631.566,1314.58 632.335,1314.88 636.892,1316.65 640.436,1318.01 641.448,1318.4 646.005,1320.13 649.532,1321.45 650.561,1321.83 655.117,1323.51 658.868,1324.88 \n",
" 659.674,1325.17 664.23,1326.81 668.458,1328.31 668.786,1328.43 673.343,1330.03 677.899,1331.6 678.323,1331.75 682.455,1333.16 687.012,1334.7 688.48,1335.18 \n",
" 691.568,1336.21 696.125,1337.71 698.948,1338.62 700.681,1339.18 705.237,1340.63 709.748,1342.05 709.794,1342.07 714.35,1343.48 718.906,1344.88 720.921,1345.49 \n",
" 723.463,1346.26 728.019,1347.61 732.481,1348.92 732.575,1348.95 737.132,1350.27 741.688,1351.57 744.484,1352.36 746.245,1352.85 750.801,1354.12 755.357,1355.36 \n",
" 756.958,1355.79 759.914,1356.59 764.47,1357.8 769.026,1358.99 769.959,1359.23 773.583,1360.16 778.139,1361.31 782.696,1362.45 783.552,1362.66 787.252,1363.57 \n",
" 791.808,1364.67 796.365,1365.76 797.813,1366.09 800.921,1366.82 805.477,1367.87 810.034,1368.91 812.834,1369.53 814.59,1369.92 819.146,1370.92 823.703,1371.9 \n",
" 828.259,1372.87 828.729,1372.96 832.816,1373.82 837.372,1374.75 841.928,1375.66 845.667,1376.4 846.485,1376.56 851.041,1377.44 855.597,1378.31 860.154,1379.16 \n",
" 863.848,1379.83 864.71,1379.99 869.266,1380.81 873.823,1381.61 878.379,1382.4 882.936,1383.16 883.564,1383.27 887.492,1383.92 892.048,1384.66 896.605,1385.38 \n",
" 901.161,1386.08 905.251,1386.7 905.717,1386.77 910.274,1387.45 914.83,1388.11 919.386,1388.75 923.943,1389.38 928.499,1389.99 929.603,1390.14 933.056,1390.59 \n",
" 937.612,1391.17 942.168,1391.74 946.725,1392.29 951.281,1392.83 955.837,1393.35 957.843,1393.57 960.394,1393.85 964.95,1394.35 969.507,1394.82 974.063,1395.28 \n",
" 978.619,1395.73 983.176,1396.16 987.732,1396.58 992.288,1396.98 992.609,1397.01 996.845,1397.37 1001.4,1397.74 1005.96,1398.09 1010.51,1398.44 1015.07,1398.76 \n",
" 1019.63,1399.08 1024.18,1399.38 1028.74,1399.66 1033.3,1399.93 1037.85,1400.18 1042.41,1400.42 1042.8,1400.44 1046.96,1400.65 1051.52,1400.86 1056.08,1401.05 \n",
" 1060.63,1401.23 1065.19,1401.4 1069.75,1401.55 1074.3,1401.69 1078.86,1401.81 1083.42,1401.92 1087.97,1402.02 1092.53,1402.1 1097.08,1402.16 1101.64,1402.21 \n",
" 1106.2,1402.25 1110.75,1402.27 1115.31,1402.28 1119.87,1402.27 1124.42,1402.25 1128.98,1402.21 1133.54,1402.16 1138.09,1402.1 1142.65,1402.02 1147.2,1401.92 \n",
" 1151.76,1401.81 1156.32,1401.69 1160.87,1401.55 1165.43,1401.4 1169.99,1401.23 1174.54,1401.05 1179.1,1400.86 1183.66,1400.65 1187.82,1400.44 1188.21,1400.42 \n",
" 1192.77,1400.18 1197.32,1399.93 1201.88,1399.66 1206.44,1399.38 1210.99,1399.08 1215.55,1398.76 1220.11,1398.44 1224.66,1398.09 1229.22,1397.74 1233.78,1397.37 \n",
" 1238.01,1397.01 1238.33,1396.98 1242.89,1396.58 1247.44,1396.16 1252,1395.73 1256.56,1395.28 1261.11,1394.82 1265.67,1394.35 1270.23,1393.85 1272.78,1393.57 \n",
" 1274.78,1393.35 1279.34,1392.83 1283.9,1392.29 1288.45,1391.74 1293.01,1391.17 1297.56,1390.59 1301.02,1390.14 1302.12,1389.99 1306.68,1389.38 1311.23,1388.75 \n",
" 1315.79,1388.11 1320.35,1387.45 1324.9,1386.77 1325.37,1386.7 1329.46,1386.08 1334.02,1385.38 1338.57,1384.66 1343.13,1383.92 1347.06,1383.27 1347.68,1383.16 \n",
" 1352.24,1382.4 1356.8,1381.61 1361.35,1380.81 1365.91,1379.99 1366.77,1379.83 1370.47,1379.16 1375.02,1378.31 1379.58,1377.44 1384.14,1376.56 1384.95,1376.4 \n",
" 1388.69,1375.66 1393.25,1374.75 1397.8,1373.82 1401.89,1372.96 1402.36,1372.87 1406.92,1371.9 1411.47,1370.92 1416.03,1369.92 1417.79,1369.53 1420.59,1368.91 \n",
" 1425.14,1367.87 1429.7,1366.82 1432.81,1366.09 1434.26,1365.76 1438.81,1364.67 1443.37,1363.57 1447.07,1362.66 1447.92,1362.45 1452.48,1361.31 1457.04,1360.16 \n",
" 1460.66,1359.23 1461.59,1358.99 1466.15,1357.8 1470.71,1356.59 1473.66,1355.79 1475.26,1355.36 1479.82,1354.12 1484.38,1352.85 1486.14,1352.36 1488.93,1351.57 \n",
" 1493.49,1350.27 1498.04,1348.95 1498.14,1348.92 1502.6,1347.61 1507.16,1346.26 1509.7,1345.49 1511.71,1344.88 1516.27,1343.48 1520.83,1342.07 1520.87,1342.05 \n",
" 1525.38,1340.63 1529.94,1339.18 1531.67,1338.62 1534.5,1337.71 1539.05,1336.21 1542.14,1335.18 1543.61,1334.7 1548.17,1333.16 1552.3,1331.75 1552.72,1331.6 \n",
" 1557.28,1330.03 1561.83,1328.43 1562.16,1328.31 1566.39,1326.81 1570.95,1325.17 1571.75,1324.88 1575.5,1323.51 1580.06,1321.83 1581.09,1321.45 1584.62,1320.13 \n",
" 1589.17,1318.4 1590.18,1318.01 1593.73,1316.65 1598.29,1314.88 1599.05,1314.58 1602.84,1313.09 1607.4,1311.27 1607.71,1311.14 1611.95,1309.43 1616.16,1307.71 \n",
" 1616.51,1307.57 1621.07,1305.68 1624.42,1304.27 1625.62,1303.77 1630.18,1301.83 1632.49,1300.84 1634.74,1299.87 1639.29,1297.89 1640.39,1297.4 1643.85,1295.88 \n",
" 1648.12,1293.97 1648.41,1293.84 1652.96,1291.78 1655.69,1290.54 1657.52,1289.7 1662.07,1287.59 1663.11,1287.1 1666.63,1285.45 1670.38,1283.67 1671.19,1283.28 \n",
" 1675.74,1281.09 1677.5,1280.23 1680.3,1278.87 1684.5,1276.8 1684.86,1276.62 1689.41,1274.34 1691.35,1273.36 1693.97,1272.04 1698.09,1269.93 1698.53,1269.7 \n",
" 1703.08,1267.34 1704.69,1266.49 1707.64,1264.95 1711.18,1263.06 1712.19,1262.52 1716.75,1260.06 1717.56,1259.62 1721.31,1257.58 1723.82,1256.19 1725.86,1255.06 \n",
" 1729.98,1252.76 1730.42,1252.51 1734.98,1249.93 1736.03,1249.32 1739.53,1247.31 1741.98,1245.89 1744.09,1244.66 1747.83,1242.45 1748.65,1241.97 1753.2,1239.25 \n",
" 1753.59,1239.02 1757.76,1236.5 1759.25,1235.58 1762.31,1233.7 1764.82,1232.15 1766.87,1230.87 1770.31,1228.71 1771.43,1228.01 1775.7,1225.28 1775.98,1225.1 \n",
" 1780.54,1222.16 1781.02,1221.85 1785.1,1219.17 1786.25,1218.41 1789.65,1216.15 1791.4,1214.98 1794.21,1213.08 1796.47,1211.54 1798.77,1209.97 1801.46,1208.11 \n",
" 1803.32,1206.82 1806.38,1204.67 1807.88,1203.62 1811.23,1201.24 1812.43,1200.38 1816,1197.8 1816.99,1197.09 1820.7,1194.37 1821.55,1193.75 1825.34,1190.93 \n",
" 1826.1,1190.36 1829.9,1187.5 1830.66,1186.93 1834.4,1184.07 1835.22,1183.44 1838.84,1180.63 1839.77,1179.9 1843.21,1177.2 1844.33,1176.31 1847.52,1173.76 \n",
" 1848.89,1172.66 1851.76,1170.33 1853.44,1168.95 1855.95,1166.89 1858,1165.19 1860.07,1163.46 1862.55,1161.37 1864.14,1160.02 1867.11,1157.48 1868.14,1156.59 \n",
" 1871.67,1153.53 1872.1,1153.16 1875.99,1149.72 1876.22,1149.51 1879.83,1146.29 1880.78,1145.43 1883.62,1142.85 1885.34,1141.28 1887.35,1139.42 1889.89,1137.05 \n",
" 1891.03,1135.98 1894.45,1132.75 1894.66,1132.55 1898.23,1129.11 1899.01,1128.37 1901.76,1125.68 1903.56,1123.9 1905.24,1122.24 1908.12,1119.36 1908.66,1118.81 \n",
" 1912.04,1115.38 1912.67,1114.72 1915.37,1111.94 1917.23,1110 1918.65,1108.51 1921.79,1105.18 1921.89,1105.07 1925.08,1101.64 1926.34,1100.26 1928.22,1098.2 \n",
" 1930.9,1095.24 1931.32,1094.77 1934.37,1091.33 1935.46,1090.1 1937.38,1087.9 1940.01,1084.86 1940.35,1084.46 1943.27,1081.03 1944.57,1079.49 1946.15,1077.6 \n",
" 1948.99,1074.16 1949.13,1074 1951.79,1070.73 1953.68,1068.37 1954.54,1067.29 1957.25,1063.86 1958.24,1062.6 1959.93,1060.42 1962.56,1056.99 1962.79,1056.68 \n",
" 1965.15,1053.55 1967.35,1050.6 1967.7,1050.12 1970.22,1046.69 1971.91,1044.34 1972.69,1043.25 1975.13,1039.82 1976.46,1037.91 1977.53,1036.38 1979.89,1032.95 \n",
" 1981.02,1031.28 1982.21,1029.51 1984.5,1026.08 1985.58,1024.43 1986.75,1022.64 1988.96,1019.21 1990.13,1017.36 1991.13,1015.77 1993.27,1012.34 1994.69,1010.03 \n",
" 1995.37,1008.91 1997.44,1005.47 1999.25,1002.42 1999.47,1002.04 2001.47,998.602 2003.43,995.168 2003.8,994.514 2005.36,991.733 2007.26,988.299 2008.36,986.264 \n",
" 2009.12,984.864 2010.94,981.43 2012.73,977.995 2012.91,977.637 2014.49,974.561 2016.21,971.126 2017.47,968.573 2017.9,967.692 2019.56,964.257 2021.19,960.823 \n",
" 2022.03,959.014 2022.78,957.388 2024.34,953.954 2025.87,950.519 2026.58,948.879 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#270b52; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 2026.58,1142.33 2026.13,1142.85 2023.11,1146.29 2022.03,1147.51 2020.07,1149.72 2017.47,1152.61 2016.98,1153.16 2013.85,1156.59 2012.91,1157.61 2010.68,1160.02 \n",
" 2008.36,1162.51 2007.47,1163.46 2004.23,1166.89 2003.8,1167.34 2000.94,1170.33 1999.25,1172.08 1997.61,1173.76 1994.69,1176.74 1994.24,1177.2 1990.83,1180.63 \n",
" 1990.13,1181.32 1987.37,1184.07 1985.58,1185.83 1983.87,1187.5 1981.02,1190.27 1980.33,1190.93 1976.75,1194.37 1976.46,1194.64 1973.11,1197.8 1971.91,1198.94 \n",
" 1969.44,1201.24 1967.35,1203.17 1965.72,1204.67 1962.79,1207.34 1961.95,1208.11 1958.24,1211.45 1958.13,1211.54 1954.27,1214.98 1953.68,1215.5 1950.36,1218.41 \n",
" 1949.13,1219.48 1946.4,1221.85 1944.57,1223.42 1942.39,1225.28 1940.01,1227.29 1938.33,1228.71 1935.46,1231.12 1934.22,1232.15 1930.9,1234.89 1930.05,1235.58 \n",
" 1926.34,1238.61 1925.83,1239.02 1921.79,1242.27 1921.56,1242.45 1917.24,1245.89 1917.23,1245.89 1912.86,1249.32 1912.67,1249.46 1908.42,1252.76 1908.12,1252.99 \n",
" 1903.93,1256.19 1903.56,1256.47 1899.38,1259.62 1899.01,1259.9 1894.76,1263.06 1894.45,1263.29 1890.09,1266.49 1889.89,1266.64 1885.36,1269.93 1885.34,1269.94 \n",
" 1880.78,1273.21 1880.56,1273.36 1876.22,1276.43 1875.7,1276.8 1871.67,1279.62 1870.78,1280.23 1867.11,1282.76 1865.79,1283.67 1862.55,1285.87 1860.73,1287.1 \n",
" 1858,1288.94 1855.6,1290.54 1853.44,1291.97 1850.4,1293.97 1848.89,1294.97 1845.13,1297.4 1844.33,1297.93 1839.79,1300.84 1839.77,1300.85 1835.22,1303.74 \n",
" 1834.37,1304.27 1830.66,1306.6 1828.88,1307.71 1826.1,1309.42 1823.3,1311.14 1821.55,1312.22 1817.65,1314.58 1816.99,1314.97 1812.43,1317.7 1811.91,1318.01 \n",
" 1807.88,1320.4 1806.09,1321.45 1803.32,1323.06 1800.18,1324.88 1798.77,1325.7 1794.21,1328.3 1794.19,1328.31 1789.65,1330.88 1788.1,1331.75 1785.1,1333.42 \n",
" 1781.91,1335.18 1780.54,1335.94 1775.98,1338.43 1775.64,1338.62 1771.43,1340.89 1769.26,1342.05 1766.87,1343.33 1762.78,1345.49 1762.31,1345.73 1757.76,1348.11 \n",
" 1756.19,1348.92 1753.2,1350.47 1749.5,1352.36 1748.65,1352.79 1744.09,1355.09 1742.69,1355.79 1739.53,1357.37 1735.77,1359.23 1734.98,1359.62 1730.42,1361.84 \n",
" 1728.73,1362.66 1725.86,1364.04 1721.57,1366.09 1721.31,1366.22 1716.75,1368.37 1714.27,1369.53 1712.19,1370.5 1707.64,1372.6 1706.85,1372.96 1703.08,1374.68 \n",
" 1699.28,1376.4 1698.53,1376.74 1693.97,1378.77 1691.57,1379.83 1689.41,1380.79 1684.86,1382.78 1683.72,1383.27 1680.3,1384.74 1675.74,1386.69 1675.71,1386.7 \n",
" 1671.19,1388.61 1667.53,1390.14 1666.63,1390.51 1662.07,1392.39 1659.19,1393.57 1657.52,1394.25 1652.96,1396.09 1650.66,1397.01 1648.41,1397.91 1643.85,1399.7 \n",
" 1641.95,1400.44 1639.29,1401.48 1634.74,1403.23 1633.05,1403.87 1630.18,1404.97 1625.62,1406.68 1623.94,1407.31 1621.07,1408.38 1616.51,1410.05 1614.61,1410.74 \n",
" 1611.95,1411.71 1607.4,1413.35 1605.06,1414.18 1602.84,1414.96 1598.29,1416.56 1595.26,1417.61 1593.73,1418.14 1589.17,1419.7 1585.2,1421.05 1584.62,1421.24 \n",
" 1580.06,1422.77 1575.5,1424.27 1574.86,1424.48 1570.95,1425.76 1566.39,1427.23 1564.23,1427.92 1561.83,1428.68 1557.28,1430.11 1553.29,1431.35 1552.72,1431.53 \n",
" 1548.17,1432.93 1543.61,1434.3 1542,1434.78 1539.05,1435.67 1534.5,1437.01 1530.35,1438.22 1529.94,1438.34 1525.38,1439.65 1520.83,1440.95 1518.3,1441.65 \n",
" 1516.27,1442.22 1511.71,1443.48 1507.16,1444.72 1505.81,1445.09 1502.6,1445.95 1498.04,1447.16 1493.49,1448.35 1492.84,1448.52 1488.93,1449.53 1484.38,1450.69 \n",
" 1479.82,1451.84 1479.34,1451.96 1475.26,1452.97 1470.71,1454.08 1466.15,1455.18 1465.24,1455.39 1461.59,1456.26 1457.04,1457.32 1452.48,1458.37 1450.47,1458.83 \n",
" 1447.92,1459.4 1443.37,1460.42 1438.81,1461.43 1434.95,1462.26 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#0d0829; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1772.38,1462.26 1775.98,1460.59 1779.73,1458.83 1780.54,1458.45 1785.1,1456.29 1786.97,1455.39 1789.65,1454.11 1794.1,1451.96 1794.21,1451.9 1798.77,1449.68 \n",
" 1801.11,1448.52 1803.32,1447.43 1807.88,1445.16 1808.02,1445.09 1812.43,1442.87 1814.82,1441.65 1816.99,1440.55 1821.53,1438.22 1821.55,1438.21 1826.1,1435.85 \n",
" 1828.14,1434.78 1830.66,1433.46 1834.65,1431.35 1835.22,1431.05 1839.77,1428.62 1841.07,1427.92 1844.33,1426.16 1847.41,1424.48 1848.89,1423.67 1853.44,1421.16 \n",
" 1853.65,1421.05 1858,1418.63 1859.81,1417.61 1862.55,1416.07 1865.89,1414.18 1867.11,1413.48 1871.67,1410.87 1871.88,1410.74 1876.22,1408.23 1877.8,1407.31 \n",
" 1880.78,1405.56 1883.64,1403.87 1885.34,1402.87 1889.4,1400.44 1889.89,1400.15 1894.45,1397.4 1895.09,1397.01 1899.01,1394.62 1900.71,1393.57 1903.56,1391.81 \n",
" 1906.26,1390.14 1908.12,1388.98 1911.74,1386.7 1912.67,1386.11 1917.15,1383.27 1917.23,1383.21 1921.79,1380.29 1922.49,1379.83 1926.34,1377.33 1927.77,1376.4 \n",
" 1930.9,1374.34 1932.98,1372.96 1935.46,1371.32 1938.13,1369.53 1940.01,1368.27 1943.23,1366.09 1944.57,1365.18 1948.26,1362.66 1949.13,1362.06 1953.23,1359.23 \n",
" 1953.68,1358.91 1958.14,1355.79 1958.24,1355.72 1962.79,1352.5 1962.99,1352.36 1967.35,1349.24 1967.79,1348.92 1971.91,1345.95 1972.54,1345.49 1976.46,1342.62 \n",
" 1977.23,1342.05 1981.02,1339.25 1981.86,1338.62 1985.58,1335.84 1986.45,1335.18 1990.13,1332.39 1990.98,1331.75 1994.69,1328.91 1995.46,1328.31 1999.25,1325.38 \n",
" 1999.89,1324.88 2003.8,1321.82 2004.27,1321.45 2008.36,1318.21 2008.6,1318.01 2012.89,1314.58 2012.91,1314.56 2017.12,1311.14 2017.47,1310.86 2021.31,1307.71 \n",
" 2022.03,1307.12 2025.46,1304.27 2026.58,1303.33 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#0d0829; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 204.037,247.384 205.162,246.445 208.593,243.599 209.306,243.011 213.15,239.859 213.496,239.576 217.706,236.163 217.733,236.142 222.017,232.707 222.262,232.512 \n",
" 226.349,229.273 226.819,228.903 230.73,225.838 231.375,225.336 235.161,222.404 235.932,221.81 239.641,218.969 240.488,218.325 244.173,215.535 245.044,214.879 \n",
" 248.757,212.1 249.601,211.472 253.393,208.666 254.157,208.103 258.082,205.231 258.713,204.772 262.826,201.797 263.27,201.478 267.626,198.362 267.826,198.22 \n",
" 272.382,194.997 272.481,194.928 276.939,191.81 277.394,191.493 281.495,188.656 282.365,188.059 286.052,185.537 287.395,184.624 290.608,182.451 292.486,181.19 \n",
" 295.164,179.398 297.638,177.755 299.721,176.378 302.853,174.321 304.277,173.389 308.131,170.886 308.833,170.432 313.39,167.506 313.474,167.452 317.946,164.609 \n",
" 318.885,164.017 322.503,161.743 324.363,160.583 327.059,158.907 329.91,157.148 331.615,156.1 335.527,153.714 336.172,153.322 340.728,150.572 341.217,150.279 \n",
" 345.284,147.85 346.982,146.845 349.841,145.156 352.821,143.41 354.397,142.49 358.737,139.976 358.953,139.851 363.51,137.237 364.733,136.541 368.066,134.65 \n",
" 370.81,133.107 372.623,132.09 376.969,129.672 377.179,129.556 381.735,127.046 383.215,126.238 386.292,124.561 389.547,122.803 390.848,122.102 395.404,119.667 \n",
" 395.968,119.369 399.961,117.256 402.482,115.934 404.517,114.87 409.073,112.508 409.089,112.5 413.63,110.168 415.796,109.065 418.186,107.851 422.6,105.631 \n",
" 422.743,105.559 427.299,103.288 429.51,102.196 431.855,101.04 436.412,98.8158 436.523,98.7617 440.968,96.6117 443.649,95.3272 445.524,94.4305 450.081,92.2711 \n",
" 450.886,91.8927 454.637,90.1323 458.24,88.4582 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#270b52; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 795.668,88.4582 791.808,89.2934 787.252,90.2955 782.696,91.3141 780.147,91.8927 778.139,92.3478 773.583,93.3962 769.026,94.4616 765.381,95.3272 764.47,95.5431 \n",
" 759.914,96.6387 755.357,97.7515 751.283,98.7617 750.801,98.8812 746.245,100.025 741.688,101.186 737.782,102.196 737.132,102.364 732.575,103.557 728.019,104.767 \n",
" 724.813,105.631 723.463,105.994 718.906,107.236 714.35,108.497 712.324,109.065 709.794,109.774 705.237,111.067 700.681,112.379 700.267,112.5 696.125,113.706 \n",
" 691.568,115.051 688.617,115.934 687.012,116.414 682.455,117.793 677.899,119.192 677.329,119.369 673.343,120.606 668.786,122.039 666.387,122.803 664.23,123.49 \n",
" 659.674,124.958 655.756,126.238 655.117,126.446 650.561,127.95 646.005,129.475 645.421,129.672 641.448,131.016 636.892,132.577 635.364,133.107 632.335,134.156 \n",
" 627.779,135.755 625.565,136.541 623.223,137.373 618.666,139.009 616.008,139.976 614.11,140.666 609.554,142.341 606.68,143.41 604.997,144.037 600.441,145.751 \n",
" 597.57,146.845 595.884,147.487 591.328,149.242 588.666,150.279 586.772,151.018 582.215,152.814 579.957,153.714 577.659,154.631 573.103,156.468 571.435,157.148 \n",
" 568.546,158.327 563.99,160.207 563.089,160.583 559.434,162.108 554.913,164.017 554.877,164.032 550.321,165.976 546.902,167.452 545.764,167.944 541.208,169.932 \n",
" 539.046,170.886 536.652,171.944 532.095,173.979 531.337,174.321 527.539,176.036 523.773,177.755 522.983,178.117 518.426,180.22 516.348,181.19 513.87,182.348 \n",
" 509.314,184.5 509.053,184.624 504.757,186.675 501.89,188.059 500.201,188.875 495.644,191.101 494.848,191.493 491.088,193.35 487.927,194.928 486.532,195.626 \n",
" 481.975,197.927 481.121,198.362 477.419,200.253 474.427,201.797 472.863,202.606 468.306,204.986 467.841,205.231 463.75,207.392 461.362,208.666 459.194,209.826 \n",
" 454.983,212.1 454.637,212.288 450.081,214.777 448.706,215.535 445.524,217.294 442.523,218.969 440.968,219.84 436.434,222.404 436.412,222.416 431.855,225.021 \n",
" 430.438,225.838 427.299,227.655 424.53,229.273 422.743,230.321 418.708,232.707 418.186,233.017 413.63,235.744 412.971,236.142 409.073,238.503 407.318,239.576 \n",
" 404.517,241.294 401.744,243.011 399.961,244.119 396.248,246.445 395.404,246.976 390.848,249.868 390.829,249.88 386.292,252.793 385.486,253.314 381.735,255.753 \n",
" 380.217,256.749 377.179,258.749 375.019,260.183 372.623,261.782 369.892,263.618 368.066,264.851 364.833,267.052 363.51,267.958 359.842,270.487 358.953,271.103 \n",
" 354.917,273.922 354.397,274.287 350.058,277.356 349.841,277.51 345.284,280.774 345.262,280.791 340.728,284.079 340.528,284.225 336.172,287.426 335.857,287.66 \n",
" 331.615,290.817 331.245,291.094 327.059,294.251 326.693,294.529 322.503,297.729 322.199,297.963 317.946,301.254 317.762,301.398 313.39,304.826 313.382,304.832 \n",
" 309.057,308.267 308.833,308.445 304.786,311.701 304.277,312.113 300.569,315.136 299.721,315.832 296.405,318.57 295.164,319.602 292.293,322.005 290.608,323.425 \n",
" 288.232,325.439 286.052,327.302 284.222,328.874 281.495,331.234 280.262,332.308 276.939,335.223 276.35,335.743 272.487,339.177 272.382,339.271 268.672,342.612 \n",
" 267.826,343.379 264.903,346.046 263.27,347.549 261.182,349.481 258.713,351.783 257.506,352.915 254.157,356.082 253.875,356.35 250.289,359.784 249.601,360.449 \n",
" 246.747,363.219 245.044,364.886 243.249,366.653 240.488,369.395 239.794,370.088 236.381,373.522 235.932,373.978 233.01,376.957 231.375,378.64 229.681,380.391 \n",
" 226.819,383.38 226.394,383.826 223.146,387.26 222.262,388.204 219.939,390.695 217.706,393.114 216.772,394.129 213.645,397.564 213.15,398.112 210.555,400.998 \n",
" 208.593,403.205 207.505,404.433 204.494,407.867 204.037,408.393 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#470b69; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 204.037,601.84 204.751,600.2 206.278,596.765 207.839,593.331 208.593,591.704 209.432,589.896 211.056,586.462 212.716,583.027 213.15,582.145 214.406,579.593 \n",
" 216.13,576.158 217.706,573.082 217.89,572.724 219.679,569.289 221.505,565.855 222.262,564.455 223.364,562.42 225.257,558.986 226.819,556.204 227.186,555.551 \n",
" 229.147,552.117 231.146,548.682 231.375,548.294 233.177,545.247 235.246,541.813 235.932,540.691 237.348,538.378 239.488,534.944 240.488,533.364 241.663,531.509 \n",
" 243.875,528.075 245.044,526.287 246.124,524.64 248.409,521.206 249.601,519.442 250.732,517.771 253.092,514.337 254.157,512.81 255.49,510.902 257.927,507.468 \n",
" 258.713,506.374 260.401,504.033 262.916,500.599 263.27,500.121 265.468,497.164 267.826,494.041 268.061,493.73 270.693,490.295 272.382,488.121 273.366,486.861 \n",
" 276.079,483.426 276.939,482.351 278.833,479.992 281.495,476.722 281.63,476.557 284.467,473.123 286.052,471.23 287.347,469.688 290.271,466.254 290.608,465.862 \n",
" 293.236,462.819 295.164,460.615 296.246,459.385 299.3,455.95 299.721,455.482 302.398,452.516 304.277,450.459 305.542,449.081 308.732,445.647 308.833,445.539 \n",
" 311.968,442.212 313.39,440.72 315.25,438.778 317.946,435.995 318.581,435.343 321.959,431.909 322.503,431.361 325.385,428.474 327.059,426.815 328.861,425.04 \n",
" 331.615,422.353 332.387,421.605 335.963,418.171 336.172,417.972 339.591,414.736 340.728,413.67 343.27,411.302 345.284,409.443 347.003,407.867 349.841,405.288 \n",
" 350.789,404.433 354.397,401.204 354.629,400.998 358.524,397.564 358.953,397.189 362.476,394.129 363.51,393.239 366.484,390.695 368.066,389.353 370.55,387.26 \n",
" 372.623,385.528 374.675,383.826 377.179,381.765 378.86,380.391 381.735,378.059 383.105,376.957 386.292,374.411 387.413,373.522 390.848,370.818 391.783,370.088 \n",
" 395.404,367.278 396.217,366.653 399.961,363.792 400.716,363.219 404.517,360.356 405.283,359.784 409.073,356.97 409.917,356.35 413.63,353.633 414.62,352.915 \n",
" 418.186,350.343 419.393,349.481 422.743,347.1 424.239,346.046 427.299,343.903 429.158,342.612 431.855,340.749 434.153,339.177 436.412,337.639 439.224,335.743 \n",
" 440.968,334.572 444.374,332.308 445.524,331.547 449.603,328.874 450.081,328.562 454.637,325.617 454.916,325.439 459.194,322.711 460.313,322.005 463.75,319.844 \n",
" 465.796,318.57 468.306,317.014 471.368,315.136 472.863,314.222 477.03,311.701 477.419,311.466 481.975,308.746 482.786,308.267 486.532,306.06 488.639,304.832 \n",
" 491.088,303.409 494.589,301.398 495.644,300.793 500.201,298.21 500.64,297.963 504.757,295.658 506.798,294.529 509.314,293.14 513.061,291.094 513.87,290.654 \n",
" 518.426,288.199 519.437,287.66 522.983,285.774 525.928,284.225 527.539,283.38 532.095,281.016 532.535,280.791 536.652,278.681 539.268,277.356 541.208,276.376 \n",
" 545.764,274.1 546.125,273.922 550.321,271.85 553.117,270.487 554.877,269.63 559.434,267.438 560.243,267.052 563.99,265.271 567.512,263.618 568.546,263.133 \n",
" 573.103,261.02 574.929,260.183 577.659,258.934 582.215,256.875 582.497,256.749 586.772,254.839 590.23,253.314 591.328,252.831 595.884,250.846 598.129,249.88 \n",
" 600.441,248.886 604.997,246.951 606.202,246.445 609.554,245.04 614.11,243.154 614.459,243.011 618.666,241.289 622.91,239.576 623.223,239.45 627.779,237.632 \n",
" 631.566,236.142 632.335,235.839 636.892,234.067 640.436,232.707 641.448,232.319 646.005,230.592 649.532,229.273 650.561,228.888 655.117,227.205 658.868,225.838 \n",
" 659.674,225.545 664.23,223.904 668.458,222.404 668.786,222.288 673.343,220.689 677.899,219.114 678.323,218.969 682.455,217.557 687.012,216.023 688.48,215.535 \n",
" 691.568,214.508 696.125,213.014 698.948,212.1 700.681,211.54 705.237,210.085 709.748,208.666 709.794,208.652 714.35,207.235 718.906,205.84 720.921,205.231 \n",
" 723.463,204.463 728.019,203.106 732.481,201.797 732.575,201.769 737.132,200.448 741.688,199.148 744.484,198.362 746.245,197.867 750.801,196.603 755.357,195.359 \n",
" 756.958,194.928 759.914,194.131 764.47,192.922 769.026,191.733 769.959,191.493 773.583,190.56 778.139,189.405 782.696,188.269 783.552,188.059 787.252,187.149 \n",
" 791.808,186.047 796.365,184.963 797.813,184.624 800.921,183.896 805.477,182.845 810.034,181.813 812.834,181.19 814.59,180.798 819.146,179.798 823.703,178.817 \n",
" 828.259,177.853 828.729,177.755 832.816,176.904 837.372,175.972 841.928,175.057 845.667,174.321 846.485,174.159 851.041,173.276 855.597,172.41 860.154,171.561 \n",
" 863.848,170.886 864.71,170.728 869.266,169.91 873.823,169.109 878.379,168.324 882.936,167.556 883.564,167.452 887.492,166.801 892.048,166.063 896.605,165.342 \n",
" 901.161,164.636 905.251,164.017 905.717,163.947 910.274,163.271 914.83,162.611 919.386,161.967 923.943,161.339 928.499,160.727 929.603,160.583 933.056,160.129 \n",
" 937.612,159.546 942.168,158.979 946.725,158.428 951.281,157.891 955.837,157.371 957.843,157.148 960.394,156.864 964.95,156.373 969.507,155.896 974.063,155.435 \n",
" 978.619,154.988 983.176,154.558 987.732,154.142 992.288,153.741 992.609,153.714 996.845,153.354 1001.4,152.981 1005.96,152.624 1010.51,152.281 1015.07,151.954 \n",
" 1019.63,151.641 1024.18,151.343 1028.74,151.06 1033.3,150.791 1037.85,150.538 1042.41,150.299 1042.8,150.279 1046.96,150.073 1051.52,149.863 1056.08,149.667 \n",
" 1060.63,149.485 1065.19,149.318 1069.75,149.166 1074.3,149.028 1078.86,148.905 1083.42,148.796 1087.97,148.702 1092.53,148.623 1097.08,148.558 1101.64,148.507 \n",
" 1106.2,148.471 1110.75,148.449 1115.31,148.442 1119.87,148.449 1124.42,148.471 1128.98,148.507 1133.54,148.558 1138.09,148.623 1142.65,148.702 1147.2,148.796 \n",
" 1151.76,148.905 1156.32,149.028 1160.87,149.166 1165.43,149.318 1169.99,149.485 1174.54,149.667 1179.1,149.863 1183.66,150.073 1187.82,150.279 1188.21,150.299 \n",
" 1192.77,150.538 1197.32,150.791 1201.88,151.06 1206.44,151.343 1210.99,151.641 1215.55,151.954 1220.11,152.281 1224.66,152.624 1229.22,152.981 1233.78,153.354 \n",
" 1238.01,153.714 1238.33,153.741 1242.89,154.142 1247.44,154.558 1252,154.988 1256.56,155.435 1261.11,155.896 1265.67,156.373 1270.23,156.864 1272.78,157.148 \n",
" 1274.78,157.371 1279.34,157.891 1283.9,158.428 1288.45,158.979 1293.01,159.546 1297.56,160.129 1301.02,160.583 1302.12,160.727 1306.68,161.339 1311.23,161.967 \n",
" 1315.79,162.611 1320.35,163.271 1324.9,163.947 1325.37,164.017 1329.46,164.636 1334.02,165.342 1338.57,166.063 1343.13,166.801 1347.06,167.452 1347.68,167.556 \n",
" 1352.24,168.324 1356.8,169.109 1361.35,169.91 1365.91,170.728 1366.77,170.886 1370.47,171.561 1375.02,172.41 1379.58,173.276 1384.14,174.159 1384.95,174.321 \n",
" 1388.69,175.057 1393.25,175.972 1397.8,176.904 1401.89,177.755 1402.36,177.853 1406.92,178.817 1411.47,179.798 1416.03,180.798 1417.79,181.19 1420.59,181.813 \n",
" 1425.14,182.845 1429.7,183.896 1432.81,184.624 1434.26,184.963 1438.81,186.047 1443.37,187.149 1447.07,188.059 1447.92,188.269 1452.48,189.405 1457.04,190.56 \n",
" 1460.66,191.493 1461.59,191.733 1466.15,192.922 1470.71,194.131 1473.66,194.928 1475.26,195.359 1479.82,196.603 1484.38,197.867 1486.14,198.362 1488.93,199.148 \n",
" 1493.49,200.448 1498.04,201.769 1498.14,201.797 1502.6,203.106 1507.16,204.463 1509.7,205.231 1511.71,205.84 1516.27,207.235 1520.83,208.652 1520.87,208.666 \n",
" 1525.38,210.085 1529.94,211.54 1531.67,212.1 1534.5,213.014 1539.05,214.508 1542.14,215.535 1543.61,216.023 1548.17,217.557 1552.3,218.969 1552.72,219.114 \n",
" 1557.28,220.689 1561.83,222.288 1562.16,222.404 1566.39,223.904 1570.95,225.545 1571.75,225.838 1575.5,227.205 1580.06,228.888 1581.09,229.273 1584.62,230.592 \n",
" 1589.17,232.319 1590.18,232.707 1593.73,234.067 1598.29,235.839 1599.05,236.142 1602.84,237.632 1607.4,239.45 1607.71,239.576 1611.95,241.289 1616.16,243.011 \n",
" 1616.51,243.154 1621.07,245.04 1624.42,246.445 1625.62,246.951 1630.18,248.886 1632.49,249.88 1634.74,250.846 1639.29,252.831 1640.39,253.314 1643.85,254.839 \n",
" 1648.12,256.749 1648.41,256.875 1652.96,258.934 1655.69,260.183 1657.52,261.02 1662.07,263.133 1663.11,263.618 1666.63,265.271 1670.38,267.052 1671.19,267.438 \n",
" 1675.74,269.63 1677.5,270.487 1680.3,271.85 1684.5,273.922 1684.86,274.1 1689.41,276.376 1691.35,277.356 1693.97,278.681 1698.09,280.791 1698.53,281.016 \n",
" 1703.08,283.38 1704.69,284.225 1707.64,285.774 1711.18,287.66 1712.19,288.199 1716.75,290.654 1717.56,291.094 1721.31,293.14 1723.82,294.529 1725.86,295.658 \n",
" 1729.98,297.963 1730.42,298.21 1734.98,300.793 1736.03,301.398 1739.53,303.409 1741.98,304.832 1744.09,306.06 1747.83,308.267 1748.65,308.746 1753.2,311.466 \n",
" 1753.59,311.701 1757.76,314.222 1759.25,315.136 1762.31,317.014 1764.82,318.57 1766.87,319.844 1770.31,322.005 1771.43,322.711 1775.7,325.439 1775.98,325.617 \n",
" 1780.54,328.562 1781.02,328.874 1785.1,331.547 1786.25,332.308 1789.65,334.572 1791.4,335.743 1794.21,337.639 1796.47,339.177 1798.77,340.749 1801.46,342.612 \n",
" 1803.32,343.903 1806.38,346.046 1807.88,347.1 1811.23,349.481 1812.43,350.343 1816,352.915 1816.99,353.633 1820.7,356.35 1821.55,356.97 1825.34,359.784 \n",
" 1826.1,360.356 1829.9,363.219 1830.66,363.792 1834.4,366.653 1835.22,367.278 1838.84,370.088 1839.77,370.818 1843.21,373.522 1844.33,374.411 1847.52,376.957 \n",
" 1848.89,378.059 1851.76,380.391 1853.44,381.765 1855.95,383.826 1858,385.528 1860.07,387.26 1862.55,389.353 1864.14,390.695 1867.11,393.239 1868.14,394.129 \n",
" 1871.67,397.189 1872.1,397.564 1875.99,400.998 1876.22,401.204 1879.83,404.433 1880.78,405.288 1883.62,407.867 1885.34,409.443 1887.35,411.302 1889.89,413.67 \n",
" 1891.03,414.736 1894.45,417.972 1894.66,418.171 1898.23,421.605 1899.01,422.353 1901.76,425.04 1903.56,426.815 1905.24,428.474 1908.12,431.361 1908.66,431.909 \n",
" 1912.04,435.343 1912.67,435.995 1915.37,438.778 1917.23,440.72 1918.65,442.212 1921.79,445.539 1921.89,445.647 1925.08,449.081 1926.34,450.459 1928.22,452.516 \n",
" 1930.9,455.482 1931.32,455.95 1934.37,459.385 1935.46,460.615 1937.38,462.819 1940.01,465.862 1940.35,466.254 1943.27,469.688 1944.57,471.23 1946.15,473.123 \n",
" 1948.99,476.557 1949.13,476.722 1951.79,479.992 1953.68,482.351 1954.54,483.426 1957.25,486.861 1958.24,488.121 1959.93,490.295 1962.56,493.73 1962.79,494.041 \n",
" 1965.15,497.164 1967.35,500.121 1967.7,500.599 1970.22,504.033 1971.91,506.374 1972.69,507.468 1975.13,510.902 1976.46,512.81 1977.53,514.337 1979.89,517.771 \n",
" 1981.02,519.442 1982.21,521.206 1984.5,524.64 1985.58,526.287 1986.75,528.075 1988.96,531.509 1990.13,533.364 1991.13,534.944 1993.27,538.378 1994.69,540.691 \n",
" 1995.37,541.813 1997.44,545.247 1999.25,548.294 1999.47,548.682 2001.47,552.117 2003.43,555.551 2003.8,556.204 2005.36,558.986 2007.26,562.42 2008.36,564.455 \n",
" 2009.12,565.855 2010.94,569.289 2012.73,572.724 2012.91,573.082 2014.49,576.158 2016.21,579.593 2017.47,582.145 2017.9,583.027 2019.56,586.462 2021.19,589.896 \n",
" 2022.03,591.704 2022.78,593.331 2024.34,596.765 2025.87,600.2 2026.58,601.84 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#270b52; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 2026.58,408.393 2026.13,407.867 2023.11,404.433 2022.03,403.205 2020.07,400.998 2017.47,398.112 2016.98,397.564 2013.85,394.129 2012.91,393.114 2010.68,390.695 \n",
" 2008.36,388.204 2007.47,387.26 2004.23,383.826 2003.8,383.38 2000.94,380.391 1999.25,378.64 1997.61,376.957 1994.69,373.978 1994.24,373.522 1990.83,370.088 \n",
" 1990.13,369.395 1987.37,366.653 1985.58,364.886 1983.87,363.219 1981.02,360.449 1980.33,359.784 1976.75,356.35 1976.46,356.082 1973.11,352.915 1971.91,351.783 \n",
" 1969.44,349.481 1967.35,347.549 1965.72,346.046 1962.79,343.379 1961.95,342.612 1958.24,339.271 1958.13,339.177 1954.27,335.743 1953.68,335.223 1950.36,332.308 \n",
" 1949.13,331.234 1946.4,328.874 1944.57,327.302 1942.39,325.439 1940.01,323.425 1938.33,322.005 1935.46,319.602 1934.22,318.57 1930.9,315.832 1930.05,315.136 \n",
" 1926.34,312.113 1925.83,311.701 1921.79,308.445 1921.56,308.267 1917.24,304.832 1917.23,304.826 1912.86,301.398 1912.67,301.254 1908.42,297.963 1908.12,297.729 \n",
" 1903.93,294.529 1903.56,294.251 1899.38,291.094 1899.01,290.817 1894.76,287.66 1894.45,287.426 1890.09,284.225 1889.89,284.079 1885.36,280.791 1885.34,280.774 \n",
" 1880.78,277.51 1880.56,277.356 1876.22,274.287 1875.7,273.922 1871.67,271.103 1870.78,270.487 1867.11,267.958 1865.79,267.052 1862.55,264.851 1860.73,263.618 \n",
" 1858,261.782 1855.6,260.183 1853.44,258.749 1850.4,256.749 1848.89,255.753 1845.13,253.314 1844.33,252.793 1839.79,249.88 1839.77,249.868 1835.22,246.976 \n",
" 1834.37,246.445 1830.66,244.119 1828.88,243.011 1826.1,241.294 1823.3,239.576 1821.55,238.503 1817.65,236.142 1816.99,235.744 1812.43,233.017 1811.91,232.707 \n",
" 1807.88,230.321 1806.09,229.273 1803.32,227.655 1800.18,225.838 1798.77,225.021 1794.21,222.416 1794.19,222.404 1789.65,219.84 1788.1,218.969 1785.1,217.294 \n",
" 1781.91,215.535 1780.54,214.777 1775.98,212.288 1775.64,212.1 1771.43,209.826 1769.26,208.666 1766.87,207.392 1762.78,205.231 1762.31,204.986 1757.76,202.606 \n",
" 1756.19,201.797 1753.2,200.253 1749.5,198.362 1748.65,197.927 1744.09,195.626 1742.69,194.928 1739.53,193.35 1735.77,191.493 1734.98,191.101 1730.42,188.875 \n",
" 1728.73,188.059 1725.86,186.675 1721.57,184.624 1721.31,184.5 1716.75,182.348 1714.27,181.19 1712.19,180.22 1707.64,178.117 1706.85,177.755 1703.08,176.036 \n",
" 1699.28,174.321 1698.53,173.979 1693.97,171.944 1691.57,170.886 1689.41,169.932 1684.86,167.944 1683.72,167.452 1680.3,165.976 1675.74,164.032 1675.71,164.017 \n",
" 1671.19,162.108 1667.53,160.583 1666.63,160.207 1662.07,158.327 1659.19,157.148 1657.52,156.468 1652.96,154.631 1650.66,153.714 1648.41,152.814 1643.85,151.018 \n",
" 1641.95,150.279 1639.29,149.242 1634.74,147.487 1633.05,146.845 1630.18,145.751 1625.62,144.037 1623.94,143.41 1621.07,142.341 1616.51,140.666 1614.61,139.976 \n",
" 1611.95,139.009 1607.4,137.373 1605.06,136.541 1602.84,135.755 1598.29,134.156 1595.26,133.107 1593.73,132.577 1589.17,131.016 1585.2,129.672 1584.62,129.475 \n",
" 1580.06,127.95 1575.5,126.446 1574.86,126.238 1570.95,124.958 1566.39,123.49 1564.23,122.803 1561.83,122.039 1557.28,120.606 1553.29,119.369 1552.72,119.192 \n",
" 1548.17,117.793 1543.61,116.414 1542,115.934 1539.05,115.051 1534.5,113.706 1530.35,112.5 1529.94,112.379 1525.38,111.067 1520.83,109.774 1518.3,109.065 \n",
" 1516.27,108.497 1511.71,107.236 1507.16,105.994 1505.81,105.631 1502.6,104.767 1498.04,103.557 1493.49,102.364 1492.84,102.196 1488.93,101.186 1484.38,100.025 \n",
" 1479.82,98.8812 1479.34,98.7617 1475.26,97.7515 1470.71,96.6387 1466.15,95.5431 1465.24,95.3272 1461.59,94.4616 1457.04,93.3962 1452.48,92.3478 1450.47,91.8927 \n",
" 1447.92,91.3141 1443.37,90.2955 1438.81,89.2934 1434.95,88.4582 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#0d0829; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1772.38,88.4582 1775.98,90.1323 1779.73,91.8927 1780.54,92.2711 1785.1,94.4305 1786.97,95.3272 1789.65,96.6117 1794.1,98.7617 1794.21,98.8158 1798.77,101.04 \n",
" 1801.11,102.196 1803.32,103.288 1807.88,105.559 1808.02,105.631 1812.43,107.851 1814.82,109.065 1816.99,110.168 1821.53,112.5 1821.55,112.508 1826.1,114.87 \n",
" 1828.14,115.934 1830.66,117.256 1834.65,119.369 1835.22,119.667 1839.77,122.102 1841.07,122.803 1844.33,124.561 1847.41,126.238 1848.89,127.046 1853.44,129.556 \n",
" 1853.65,129.672 1858,132.09 1859.81,133.107 1862.55,134.65 1865.89,136.541 1867.11,137.237 1871.67,139.851 1871.88,139.976 1876.22,142.49 1877.8,143.41 \n",
" 1880.78,145.156 1883.64,146.845 1885.34,147.85 1889.4,150.279 1889.89,150.572 1894.45,153.322 1895.09,153.714 1899.01,156.1 1900.71,157.148 1903.56,158.907 \n",
" 1906.26,160.583 1908.12,161.743 1911.74,164.017 1912.67,164.609 1917.15,167.452 1917.23,167.506 1921.79,170.432 1922.49,170.886 1926.34,173.389 1927.77,174.321 \n",
" 1930.9,176.378 1932.98,177.755 1935.46,179.398 1938.13,181.19 1940.01,182.451 1943.23,184.624 1944.57,185.537 1948.26,188.059 1949.13,188.656 1953.23,191.493 \n",
" 1953.68,191.81 1958.14,194.928 1958.24,194.997 1962.79,198.22 1962.99,198.362 1967.35,201.478 1967.79,201.797 1971.91,204.772 1972.54,205.231 1976.46,208.103 \n",
" 1977.23,208.666 1981.02,211.472 1981.86,212.1 1985.58,214.879 1986.45,215.535 1990.13,218.325 1990.98,218.969 1994.69,221.81 1995.46,222.404 1999.25,225.336 \n",
" 1999.89,225.838 2003.8,228.903 2004.27,229.273 2008.36,232.512 2008.6,232.707 2012.89,236.142 2012.91,236.163 2017.12,239.576 2017.47,239.859 2021.31,243.011 \n",
" 2022.03,243.599 2025.46,246.445 2026.58,247.384 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#63146e; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1779.8,435.343 1780.54,435.927 1784.1,438.778 1785.1,439.582 1788.32,442.212 1789.65,443.304 1792.48,445.647 1794.21,447.093 1796.57,449.081 1798.77,450.953 \n",
" 1800.59,452.516 1803.32,454.885 1804.54,455.95 1807.88,458.893 1808.43,459.385 1812.26,462.819 1812.43,462.979 1816.02,466.254 1816.99,467.147 1819.73,469.688 \n",
" 1821.55,471.4 1823.37,473.123 1826.1,475.741 1826.95,476.557 1830.47,479.992 1830.66,480.174 1833.94,483.426 1835.22,484.704 1837.35,486.861 1839.77,489.335 \n",
" 1840.71,490.295 1844,493.73 1844.33,494.072 1847.25,497.164 1848.89,498.922 1850.44,500.599 1853.44,503.887 1853.57,504.033 1856.66,507.468 1858,508.979 \n",
" 1859.69,510.902 1862.55,514.2 1862.67,514.337 1865.6,517.771 1867.11,519.563 1868.48,521.206 1871.32,524.64 1871.67,525.073 1874.1,528.075 1876.22,530.742 \n",
" 1876.83,531.509 1879.52,534.944 1880.78,536.581 1882.16,538.378 1884.75,541.813 1885.34,542.602 1887.3,545.247 1889.79,548.682 1889.89,548.819 1892.25,552.117 \n",
" 1894.45,555.251 1894.66,555.551 1897.02,558.986 1899.01,561.917 1899.34,562.42 1901.62,565.855 1903.56,568.838 1903.85,569.289 1906.05,572.724 1908.12,576.04 \n",
" 1908.19,576.158 1910.3,579.593 1912.36,583.027 1912.67,583.559 1914.38,586.462 1916.36,589.896 1917.23,591.432 1918.3,593.331 1920.2,596.765 1921.79,599.7 \n",
" 1922.06,600.2 1923.88,603.634 1925.65,607.069 1926.34,608.433 1927.39,610.503 1929.09,613.938 1930.75,617.372 1930.9,617.695 1932.37,620.807 1933.95,624.241 \n",
" 1935.46,627.596 1935.49,627.676 1937,631.11 1938.47,634.545 1939.89,637.979 1940.01,638.275 1941.29,641.414 1942.64,644.848 1943.96,648.283 1944.57,649.931 \n",
" 1945.23,651.717 1946.48,655.152 1947.68,658.586 1948.85,662.021 1949.13,662.853 1949.98,665.455 1951.08,668.89 1952.14,672.324 1953.16,675.759 1953.68,677.558 \n",
" 1954.15,679.193 1955.11,682.628 1956.02,686.062 1956.9,689.497 1957.75,692.931 1958.24,695.008 1958.56,696.366 1959.34,699.8 1960.08,703.235 1960.78,706.669 \n",
" 1961.45,710.104 1962.09,713.538 1962.68,716.973 1962.79,717.64 1963.25,720.407 1963.78,723.842 1964.28,727.276 1964.74,730.711 1965.17,734.145 1965.56,737.58 \n",
" 1965.92,741.014 1966.25,744.449 1966.54,747.883 1966.79,751.318 1967.01,754.752 1967.2,758.187 1967.35,761.553 1967.35,761.621 1967.47,765.056 1967.56,768.49 \n",
" 1967.61,771.925 1967.63,775.359 1967.61,778.794 1967.56,782.228 1967.47,785.663 1967.35,789.097 1967.35,789.165 1967.2,792.532 1967.01,795.966 1966.79,799.401 \n",
" 1966.54,802.835 1966.25,806.27 1965.92,809.704 1965.56,813.139 1965.17,816.573 1964.74,820.008 1964.28,823.442 1963.78,826.877 1963.25,830.312 1962.79,833.079 \n",
" 1962.68,833.746 1962.09,837.181 1961.45,840.615 1960.78,844.05 1960.08,847.484 1959.34,850.919 1958.56,854.353 1958.24,855.711 1957.75,857.788 1956.9,861.222 \n",
" 1956.02,864.657 1955.11,868.091 1954.15,871.526 1953.68,873.161 1953.16,874.96 1952.14,878.395 1951.08,881.829 1949.98,885.264 1949.13,887.866 1948.85,888.698 \n",
" 1947.68,892.133 1946.48,895.567 1945.23,899.002 1944.57,900.788 1943.96,902.436 1942.64,905.871 1941.29,909.305 1940.01,912.444 1939.89,912.74 1938.47,916.174 \n",
" 1937,919.609 1935.49,923.043 1935.46,923.122 1933.95,926.478 1932.37,929.912 1930.9,933.023 1930.75,933.347 1929.09,936.781 1927.39,940.216 1926.34,942.286 \n",
" 1925.65,943.65 1923.88,947.085 1922.06,950.519 1921.79,951.019 1920.2,953.954 1918.3,957.388 1917.23,959.287 1916.36,960.823 1914.38,964.257 1912.67,967.159 \n",
" 1912.36,967.692 1910.3,971.126 1908.19,974.561 1908.12,974.679 1906.05,977.995 1903.85,981.43 1903.56,981.881 1901.62,984.864 1899.34,988.299 1899.01,988.802 \n",
" 1897.02,991.733 1894.66,995.168 1894.45,995.468 1892.25,998.602 1889.89,1001.9 1889.79,1002.04 1887.3,1005.47 1885.34,1008.12 1884.75,1008.91 1882.16,1012.34 \n",
" 1880.78,1014.14 1879.52,1015.77 1876.83,1019.21 1876.22,1019.98 1874.1,1022.64 1871.67,1025.65 1871.32,1026.08 1868.48,1029.51 1867.11,1031.16 1865.6,1032.95 \n",
" 1862.67,1036.38 1862.55,1036.52 1859.69,1039.82 1858,1041.74 1856.66,1043.25 1853.57,1046.69 1853.44,1046.83 1850.44,1050.12 1848.89,1051.8 1847.25,1053.55 \n",
" 1844.33,1056.65 1844,1056.99 1840.71,1060.42 1839.77,1061.38 1837.35,1063.86 1835.22,1066.01 1833.94,1067.29 1830.66,1070.55 1830.47,1070.73 1826.95,1074.16 \n",
" 1826.1,1074.98 1823.37,1077.6 1821.55,1079.32 1819.73,1081.03 1816.99,1083.57 1816.02,1084.46 1812.43,1087.74 1812.26,1087.9 1808.43,1091.33 1807.88,1091.83 \n",
" 1804.54,1094.77 1803.32,1095.83 1800.59,1098.2 1798.77,1099.77 1796.57,1101.64 1794.21,1103.63 1792.48,1105.07 1789.65,1107.41 1788.32,1108.51 1785.1,1111.14 \n",
" 1784.1,1111.94 1780.54,1114.79 1779.8,1115.38 1775.98,1118.38 1775.44,1118.81 1771.43,1121.92 1771,1122.24 1766.87,1125.39 1766.48,1125.68 1762.31,1128.8 \n",
" 1761.89,1129.11 1757.76,1132.16 1757.22,1132.55 1753.2,1135.46 1752.47,1135.98 1748.65,1138.71 1747.64,1139.42 1744.09,1141.91 1742.72,1142.85 1739.53,1145.05 \n",
" 1737.72,1146.29 1734.98,1148.15 1732.64,1149.72 1730.42,1151.2 1727.46,1153.16 1725.86,1154.2 1722.19,1156.59 1721.31,1157.16 1716.83,1160.02 1716.75,1160.07 \n",
" 1712.19,1162.94 1711.36,1163.46 1707.64,1165.77 1705.8,1166.89 1703.08,1168.55 1700.14,1170.33 1698.53,1171.3 1694.37,1173.76 1693.97,1174 1689.41,1176.66 \n",
" 1688.49,1177.2 1684.86,1179.29 1682.5,1180.63 1680.3,1181.88 1676.4,1184.07 1675.74,1184.43 1671.19,1186.95 1670.17,1187.5 1666.63,1189.43 1663.82,1190.93 \n",
" 1662.07,1191.87 1657.52,1194.28 1657.35,1194.37 1652.96,1196.66 1650.73,1197.8 1648.41,1199 1643.99,1201.24 1643.85,1201.31 1639.29,1203.59 1637.1,1204.67 \n",
" 1634.74,1205.84 1630.18,1208.05 1630.06,1208.11 1625.62,1210.24 1622.86,1211.54 1621.07,1212.39 1616.51,1214.52 1615.51,1214.98 1611.95,1216.61 1607.99,1218.41 \n",
" 1607.4,1218.68 1602.84,1220.72 1600.28,1221.85 1598.29,1222.73 1593.73,1224.71 1592.4,1225.28 1589.17,1226.66 1584.62,1228.59 1584.32,1228.71 1580.06,1230.49 \n",
" 1576.04,1232.15 1575.5,1232.37 1570.95,1234.22 1567.53,1235.58 1566.39,1236.04 1561.83,1237.84 1558.8,1239.02 1557.28,1239.61 1552.72,1241.36 1549.83,1242.45 \n",
" 1548.17,1243.08 1543.61,1244.78 1540.6,1245.89 1539.05,1246.46 1534.5,1248.11 1531.1,1249.32 1529.94,1249.74 1525.38,1251.34 1521.3,1252.76 1520.83,1252.92 \n",
" 1516.27,1254.48 1511.71,1256.02 1511.19,1256.19 1507.16,1257.53 1502.6,1259.02 1500.73,1259.62 1498.04,1260.49 1493.49,1261.94 1489.91,1263.06 1488.93,1263.37 \n",
" 1484.38,1264.77 1479.82,1266.15 1478.68,1266.49 1475.26,1267.52 1470.71,1268.86 1467.02,1269.93 1466.15,1270.18 1461.59,1271.48 1457.04,1272.76 1454.86,1273.36 \n",
" 1452.48,1274.02 1447.92,1275.26 1443.37,1276.48 1442.17,1276.8 1438.81,1277.68 1434.26,1278.86 1429.7,1280.02 1428.87,1280.23 1425.14,1281.17 1420.59,1282.29 \n",
" 1416.03,1283.39 1414.89,1283.67 1411.47,1284.48 1406.92,1285.55 1402.36,1286.59 1400.11,1287.1 1397.8,1287.62 1393.25,1288.63 1388.69,1289.63 1384.43,1290.54 \n",
" 1384.14,1290.6 1379.58,1291.56 1375.02,1292.49 1370.47,1293.41 1367.64,1293.97 1365.91,1294.31 1361.35,1295.2 1356.8,1296.06 1352.24,1296.91 1349.54,1297.4 \n",
" 1347.68,1297.74 1343.13,1298.56 1338.57,1299.36 1334.02,1300.13 1329.79,1300.84 1329.46,1300.89 1324.9,1301.64 1320.35,1302.37 1315.79,1303.08 1311.23,1303.77 \n",
" 1307.86,1304.27 1306.68,1304.45 1302.12,1305.11 1297.56,1305.76 1293.01,1306.38 1288.45,1306.99 1283.9,1307.59 1282.92,1307.71 1279.34,1308.16 1274.78,1308.72 \n",
" 1270.23,1309.27 1265.67,1309.8 1261.11,1310.31 1256.56,1310.8 1253.35,1311.14 1252,1311.28 1247.44,1311.75 1242.89,1312.2 1238.33,1312.63 1233.78,1313.04 \n",
" 1229.22,1313.44 1224.66,1313.83 1220.11,1314.19 1215.55,1314.54 1215.1,1314.58 1210.99,1314.88 1206.44,1315.2 1201.88,1315.51 1197.32,1315.79 1192.77,1316.07 \n",
" 1188.21,1316.32 1183.66,1316.57 1179.1,1316.79 1174.54,1317 1169.99,1317.19 1165.43,1317.37 1160.87,1317.54 1156.32,1317.68 1151.76,1317.82 1147.2,1317.93 \n",
" 1143.6,1318.01 1142.65,1318.03 1138.09,1318.12 1133.54,1318.19 1128.98,1318.24 1124.42,1318.28 1119.87,1318.3 1115.31,1318.31 1110.75,1318.3 1106.2,1318.28 \n",
" 1101.64,1318.24 1097.08,1318.19 1092.53,1318.12 1087.97,1318.03 1087.02,1318.01 1083.42,1317.93 1078.86,1317.82 1074.3,1317.68 1069.75,1317.54 1065.19,1317.37 \n",
" 1060.63,1317.19 1056.08,1317 1051.52,1316.79 1046.96,1316.57 1042.41,1316.32 1037.85,1316.07 1033.3,1315.79 1028.74,1315.51 1024.18,1315.2 1019.63,1314.88 \n",
" 1015.52,1314.58 1015.07,1314.54 1010.51,1314.19 1005.96,1313.83 1001.4,1313.44 996.845,1313.04 992.288,1312.63 987.732,1312.2 983.176,1311.75 978.619,1311.28 \n",
" 977.275,1311.14 974.063,1310.8 969.507,1310.31 964.95,1309.8 960.394,1309.27 955.837,1308.72 951.281,1308.16 947.696,1307.71 946.725,1307.59 942.168,1306.99 \n",
" 937.612,1306.38 933.056,1305.76 928.499,1305.11 923.943,1304.45 922.759,1304.27 919.386,1303.77 914.83,1303.08 910.274,1302.37 905.717,1301.64 901.161,1300.89 \n",
" 900.829,1300.84 896.605,1300.13 892.048,1299.36 887.492,1298.56 882.936,1297.74 881.079,1297.4 878.379,1296.91 873.823,1296.06 869.266,1295.2 864.71,1294.31 \n",
" 862.977,1293.97 860.154,1293.41 855.597,1292.49 851.041,1291.56 846.485,1290.6 846.192,1290.54 841.928,1289.63 837.372,1288.63 832.816,1287.62 830.508,1287.1 \n",
" 828.259,1286.59 823.703,1285.55 819.146,1284.48 815.733,1283.67 814.59,1283.39 810.034,1282.29 805.477,1281.17 801.746,1280.23 800.921,1280.02 796.365,1278.86 \n",
" 791.808,1277.68 788.449,1276.8 787.252,1276.48 782.696,1275.26 778.139,1274.02 775.758,1273.36 773.583,1272.76 769.026,1271.48 764.47,1270.18 763.603,1269.93 \n",
" 759.914,1268.86 755.357,1267.52 751.937,1266.49 750.801,1266.15 746.245,1264.77 741.688,1263.37 740.711,1263.06 737.132,1261.94 732.575,1260.49 729.889,1259.62 \n",
" 728.019,1259.02 723.463,1257.53 719.432,1256.19 718.906,1256.02 714.35,1254.48 709.794,1252.92 709.318,1252.76 705.237,1251.34 700.681,1249.74 699.522,1249.32 \n",
" 696.125,1248.11 691.568,1246.46 690.019,1245.89 687.012,1244.78 682.455,1243.08 680.79,1242.45 677.899,1241.36 673.343,1239.61 671.818,1239.02 668.786,1237.84 \n",
" 664.23,1236.04 663.087,1235.58 659.674,1234.22 655.117,1232.37 654.585,1232.15 650.561,1230.49 646.299,1228.71 646.005,1228.59 641.448,1226.66 638.221,1225.28 \n",
" 636.892,1224.71 632.335,1222.73 630.336,1221.85 627.779,1220.72 623.223,1218.68 622.633,1218.41 618.666,1216.61 615.11,1214.98 614.11,1214.52 609.554,1212.39 \n",
" 607.756,1211.54 604.997,1210.24 600.56,1208.11 600.441,1208.05 595.884,1205.84 593.524,1204.67 591.328,1203.59 586.772,1201.31 586.631,1201.24 582.215,1199 \n",
" 579.886,1197.8 577.659,1196.66 573.274,1194.37 573.103,1194.28 568.546,1191.87 566.799,1190.93 563.99,1189.43 560.45,1187.5 559.434,1186.95 554.877,1184.43 \n",
" 554.224,1184.07 550.321,1181.88 548.119,1180.63 545.764,1179.29 542.128,1177.2 541.208,1176.66 536.652,1174 536.25,1173.76 532.095,1171.3 530.482,1170.33 \n",
" 527.539,1168.55 524.818,1166.89 522.983,1165.77 519.257,1163.46 518.426,1162.94 513.87,1160.07 513.795,1160.02 509.314,1157.16 508.431,1156.59 504.757,1154.2 \n",
" 503.162,1153.16 500.201,1151.2 497.984,1149.72 495.644,1148.15 492.896,1146.29 491.088,1145.05 487.896,1142.85 486.532,1141.91 482.981,1139.42 481.975,1138.71 \n",
" 478.149,1135.98 477.419,1135.46 473.4,1132.55 472.863,1132.16 468.73,1129.11 468.306,1128.8 464.138,1125.68 463.75,1125.39 459.623,1122.24 459.194,1121.92 \n",
" 455.183,1118.81 454.637,1118.38 450.816,1115.38 450.081,1114.79 446.521,1111.94 445.524,1111.14 442.297,1108.51 440.968,1107.41 438.142,1105.07 436.412,1103.63 \n",
" 434.055,1101.64 431.855,1099.77 430.034,1098.2 427.299,1095.83 426.08,1094.77 422.743,1091.83 422.189,1091.33 418.363,1087.9 418.186,1087.74 414.598,1084.46 \n",
" 413.63,1083.57 410.895,1081.03 409.073,1079.32 407.253,1077.6 404.517,1074.98 403.67,1074.16 400.146,1070.73 399.961,1070.55 396.678,1067.29 395.404,1066.01 \n",
" 393.268,1063.86 390.848,1061.38 389.915,1060.42 386.617,1056.99 386.292,1056.65 383.372,1053.55 381.735,1051.8 380.182,1050.12 377.179,1046.83 377.046,1046.69 \n",
" 373.961,1043.25 372.623,1041.74 370.929,1039.82 368.066,1036.52 367.948,1036.38 365.017,1032.95 363.51,1031.16 362.136,1029.51 359.305,1026.08 358.953,1025.65 \n",
" 356.522,1022.64 354.397,1019.98 353.788,1019.21 351.102,1015.77 349.841,1014.14 348.463,1012.34 345.871,1008.91 345.284,1008.12 343.324,1005.47 340.826,1002.04 \n",
" 340.728,1001.9 338.37,998.602 336.172,995.468 335.962,995.168 333.596,991.733 331.615,988.802 331.276,988.299 328.998,984.864 327.059,981.881 326.766,981.43 \n",
" 324.574,977.995 322.503,974.679 322.429,974.561 320.322,971.126 318.26,967.692 317.946,967.159 316.237,964.257 314.258,960.823 313.39,959.287 312.318,957.388 \n",
" 310.42,953.954 308.833,951.019 308.564,950.519 306.744,947.085 304.968,943.65 304.277,942.286 303.229,940.216 301.53,936.781 299.873,933.347 299.721,933.023 \n",
" 298.251,929.912 296.669,926.478 295.164,923.122 295.129,923.043 293.621,919.609 292.154,916.174 290.728,912.74 290.608,912.444 289.334,909.305 287.98,905.871 \n",
" 286.665,902.436 286.052,900.788 285.386,899.002 284.142,895.567 282.936,892.133 281.77,888.698 281.495,887.866 280.636,885.264 279.538,881.829 278.478,878.395 \n",
" 277.456,874.96 276.939,873.161 276.468,871.526 275.513,868.091 274.596,864.657 273.716,861.222 272.872,857.788 272.382,855.711 272.062,854.353 271.284,850.919 \n",
" 270.543,847.484 269.838,844.05 269.169,840.615 268.535,837.181 267.936,833.746 267.826,833.079 267.369,830.312 266.836,826.877 266.339,823.442 265.876,820.008 \n",
" 265.449,816.573 265.056,813.139 264.697,809.704 264.373,806.27 264.083,802.835 263.828,799.401 263.607,795.966 263.42,792.532 263.27,789.165 263.267,789.097 \n",
" 263.147,785.663 263.061,782.228 263.01,778.794 262.993,775.359 263.01,771.925 263.061,768.49 263.147,765.056 263.267,761.621 263.27,761.553 263.42,758.187 \n",
" 263.607,754.752 263.828,751.318 264.083,747.883 264.373,744.449 264.697,741.014 265.056,737.58 265.449,734.145 265.876,730.711 266.339,727.276 266.836,723.842 \n",
" 267.369,720.407 267.826,717.64 267.936,716.973 268.535,713.538 269.169,710.104 269.838,706.669 270.543,703.235 271.284,699.8 272.062,696.366 272.382,695.008 \n",
" 272.872,692.931 273.716,689.497 274.596,686.062 275.513,682.628 276.468,679.193 276.939,677.558 277.456,675.759 278.478,672.324 279.538,668.89 280.636,665.455 \n",
" 281.495,662.853 281.77,662.021 282.936,658.586 284.142,655.152 285.386,651.717 286.052,649.931 286.665,648.283 287.98,644.848 289.334,641.414 290.608,638.275 \n",
" 290.728,637.979 292.154,634.545 293.621,631.11 295.129,627.676 295.164,627.596 296.669,624.241 298.251,620.807 299.721,617.695 299.873,617.372 301.53,613.938 \n",
" 303.229,610.503 304.277,608.433 304.968,607.069 306.744,603.634 308.564,600.2 308.833,599.7 310.42,596.765 312.318,593.331 313.39,591.432 314.258,589.896 \n",
" 316.237,586.462 317.946,583.559 318.26,583.027 320.322,579.593 322.429,576.158 322.503,576.04 324.574,572.724 326.766,569.289 327.059,568.838 328.998,565.855 \n",
" 331.276,562.42 331.615,561.917 333.596,558.986 335.962,555.551 336.172,555.251 338.37,552.117 340.728,548.819 340.826,548.682 343.324,545.247 345.284,542.602 \n",
" 345.871,541.813 348.463,538.378 349.841,536.581 351.102,534.944 353.788,531.509 354.397,530.742 356.522,528.075 358.953,525.073 359.305,524.64 362.136,521.206 \n",
" 363.51,519.563 365.017,517.771 367.948,514.337 368.066,514.2 370.929,510.902 372.623,508.979 373.961,507.468 377.046,504.033 377.179,503.887 380.182,500.599 \n",
" 381.735,498.922 383.372,497.164 386.292,494.072 386.617,493.73 389.915,490.295 390.848,489.335 393.268,486.861 395.404,484.704 396.678,483.426 399.961,480.174 \n",
" 400.146,479.992 403.67,476.557 404.517,475.741 407.253,473.123 409.073,471.4 410.895,469.688 413.63,467.147 414.598,466.254 418.186,462.979 418.363,462.819 \n",
" 422.189,459.385 422.743,458.893 426.08,455.95 427.299,454.885 430.034,452.516 431.855,450.953 434.055,449.081 436.412,447.093 438.142,445.647 440.968,443.304 \n",
" 442.297,442.212 445.524,439.582 446.521,438.778 450.081,435.927 450.816,435.343 454.637,432.334 455.183,431.909 459.194,428.803 459.623,428.474 463.75,425.332 \n",
" 464.138,425.04 468.306,421.919 468.73,421.605 472.863,418.562 473.4,418.171 477.419,415.26 478.149,414.736 481.975,412.011 482.981,411.302 486.532,408.813 \n",
" 487.896,407.867 491.088,405.666 492.896,404.433 495.644,402.568 497.984,400.998 500.201,399.519 503.162,397.564 504.757,396.516 508.431,394.129 509.314,393.559 \n",
" \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#63146e; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 509.314,393.559 513.795,390.695 513.87,390.647 518.426,387.777 519.257,387.26 522.983,384.95 524.818,383.826 527.539,382.166 530.482,380.391 532.095,379.422 \n",
" 536.25,376.957 536.652,376.719 541.208,374.054 542.128,373.522 545.764,371.428 548.119,370.088 550.321,368.839 554.224,366.653 554.877,366.288 559.434,363.773 \n",
" 560.45,363.219 563.99,361.293 566.799,359.784 568.546,358.849 573.103,356.439 573.274,356.35 577.659,354.062 579.886,352.915 582.215,351.719 586.631,349.481 \n",
" 586.772,349.409 591.328,347.13 593.524,346.046 595.884,344.883 600.441,342.669 600.56,342.612 604.997,340.482 607.756,339.177 609.554,338.328 614.11,336.203 \n",
" 615.11,335.743 618.666,334.107 622.633,332.308 623.223,332.041 627.779,330.002 630.336,328.874 632.335,327.992 636.892,326.01 638.221,325.439 641.448,324.054 \n",
" 646.005,322.128 646.299,322.005 650.561,320.225 654.585,318.57 655.117,318.351 659.674,316.501 663.087,315.136 664.23,314.679 668.786,312.88 671.818,311.701 \n",
" 673.343,311.108 677.899,309.36 680.79,308.267 682.455,307.637 687.012,305.937 690.019,304.832 691.568,304.263 696.125,302.611 699.522,301.398 700.681,300.984 \n",
" 705.237,299.378 709.318,297.963 709.794,297.798 714.35,296.238 718.906,294.703 719.432,294.529 723.463,293.188 728.019,291.697 729.889,291.094 732.575,290.227 \n",
" 737.132,288.779 740.711,287.66 741.688,287.354 746.245,285.947 750.801,284.565 751.937,284.225 755.357,283.201 759.914,281.859 763.603,280.791 764.47,280.539 \n",
" 769.026,279.237 773.583,277.957 775.758,277.356 778.139,276.697 782.696,275.456 787.252,274.237 788.449,273.922 791.808,273.035 796.365,271.854 800.921,270.694 \n",
" 801.746,270.487 805.477,269.551 810.034,268.427 814.59,267.324 815.733,267.052 819.146,266.239 823.703,265.172 828.259,264.125 830.508,263.618 832.816,263.096 \n",
" 837.372,262.085 841.928,261.093 846.192,260.183 846.485,260.121 851.041,259.164 855.597,258.226 860.154,257.307 862.977,256.749 864.71,256.406 869.266,255.521 \n",
" 873.823,254.654 878.379,253.806 881.079,253.314 882.936,252.975 887.492,252.16 892.048,251.364 896.605,250.585 900.829,249.88 901.161,249.824 905.717,249.078 \n",
" 910.274,248.35 914.83,247.639 919.386,246.946 922.759,246.445 923.943,246.269 928.499,245.608 933.056,244.964 937.612,244.337 942.168,243.727 946.725,243.134 \n",
" 947.696,243.011 951.281,242.556 955.837,241.994 960.394,241.449 964.95,240.921 969.507,240.409 974.063,239.914 977.275,239.576 978.619,239.435 983.176,238.97 \n",
" 987.732,238.522 992.288,238.091 996.845,237.675 1001.4,237.276 1005.96,236.893 1010.51,236.526 1015.07,236.175 1015.52,236.142 1019.63,235.839 1024.18,235.518 \n",
" 1028.74,235.213 1033.3,234.925 1037.85,234.652 1042.41,234.395 1046.96,234.154 1051.52,233.928 1056.08,233.718 1060.63,233.524 1065.19,233.345 1069.75,233.182 \n",
" 1074.3,233.035 1078.86,232.903 1083.42,232.787 1087.02,232.707 1087.97,232.686 1092.53,232.601 1097.08,232.531 1101.64,232.476 1106.2,232.437 1110.75,232.414 \n",
" 1115.31,232.406 1119.87,232.414 1124.42,232.437 1128.98,232.476 1133.54,232.531 1138.09,232.601 1142.65,232.686 1143.6,232.707 1147.2,232.787 1151.76,232.903 \n",
" 1156.32,233.035 1160.87,233.182 1165.43,233.345 1169.99,233.524 1174.54,233.718 1179.1,233.928 1183.66,234.154 1188.21,234.395 1192.77,234.652 1197.32,234.925 \n",
" 1201.88,235.213 1206.44,235.518 1210.99,235.839 1215.1,236.142 1215.55,236.175 1220.11,236.526 1224.66,236.893 1229.22,237.276 1233.78,237.675 1238.33,238.091 \n",
" 1242.89,238.522 1247.44,238.97 1252,239.435 1253.35,239.576 1256.56,239.914 1261.11,240.409 1265.67,240.921 1270.23,241.449 1274.78,241.994 1279.34,242.556 \n",
" 1282.92,243.011 1283.9,243.134 1288.45,243.727 1293.01,244.337 1297.56,244.964 1302.12,245.608 1306.68,246.269 1307.86,246.445 1311.23,246.946 1315.79,247.639 \n",
" 1320.35,248.35 1324.9,249.078 1329.46,249.824 1329.79,249.88 1334.02,250.585 1338.57,251.364 1343.13,252.16 1347.68,252.975 1349.54,253.314 1352.24,253.806 \n",
" 1356.8,254.654 1361.35,255.521 1365.91,256.406 1367.64,256.749 1370.47,257.307 1375.02,258.226 1379.58,259.164 1384.14,260.121 1384.43,260.183 1388.69,261.093 \n",
" 1393.25,262.085 1397.8,263.096 1400.11,263.618 1402.36,264.125 1406.92,265.172 1411.47,266.239 1414.89,267.052 1416.03,267.324 1420.59,268.427 1425.14,269.551 \n",
" 1428.87,270.487 1429.7,270.694 1434.26,271.854 1438.81,273.035 1442.17,273.922 1443.37,274.237 1447.92,275.456 1452.48,276.697 1454.86,277.356 1457.04,277.957 \n",
" 1461.59,279.237 1466.15,280.539 1467.02,280.791 1470.71,281.859 1475.26,283.201 1478.68,284.225 1479.82,284.565 1484.38,285.947 1488.93,287.354 1489.91,287.66 \n",
" 1493.49,288.779 1498.04,290.227 1500.73,291.094 1502.6,291.697 1507.16,293.188 1511.19,294.529 1511.71,294.703 1516.27,296.238 1520.83,297.798 1521.3,297.963 \n",
" 1525.38,299.378 1529.94,300.984 1531.1,301.398 1534.5,302.611 1539.05,304.263 1540.6,304.832 1543.61,305.937 1548.17,307.637 1549.83,308.267 1552.72,309.36 \n",
" 1557.28,311.108 1558.8,311.701 1561.83,312.88 1566.39,314.679 1567.53,315.136 1570.95,316.501 1575.5,318.351 1576.04,318.57 1580.06,320.225 1584.32,322.005 \n",
" 1584.62,322.128 1589.17,324.054 1592.4,325.439 1593.73,326.01 1598.29,327.992 1600.28,328.874 1602.84,330.002 1607.4,332.041 1607.99,332.308 1611.95,334.107 \n",
" 1615.51,335.743 1616.51,336.203 1621.07,338.328 1622.86,339.177 1625.62,340.482 1630.06,342.612 1630.18,342.669 1634.74,344.883 1637.1,346.046 1639.29,347.13 \n",
" 1643.85,349.409 1643.99,349.481 1648.41,351.719 1650.73,352.915 1652.96,354.062 1657.35,356.35 1657.52,356.439 1662.07,358.849 1663.82,359.784 1666.63,361.293 \n",
" 1670.17,363.219 1671.19,363.773 1675.74,366.288 1676.4,366.653 1680.3,368.839 1682.5,370.088 1684.86,371.428 1688.49,373.522 1689.41,374.054 1693.97,376.719 \n",
" 1694.37,376.957 1698.53,379.422 1700.14,380.391 1703.08,382.166 1705.8,383.826 1707.64,384.95 1711.36,387.26 1712.19,387.777 1716.75,390.647 1716.83,390.695 \n",
" 1721.31,393.559 1722.19,394.129 1725.86,396.516 1727.46,397.564 1730.42,399.519 1732.64,400.998 1734.98,402.568 1737.72,404.433 1739.53,405.666 1742.72,407.867 \n",
" 1744.09,408.813 1747.64,411.302 1748.65,412.011 1752.47,414.736 1753.2,415.26 1757.22,418.171 1757.76,418.562 1761.89,421.605 1762.31,421.919 1766.48,425.04 \n",
" 1766.87,425.332 1771,428.474 1771.43,428.803 1775.44,431.909 1775.98,432.334 1779.8,435.343 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#821f6b; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1716.12,483.426 1716.75,483.903 1720.6,486.861 1721.31,487.406 1725,490.295 1725.86,490.979 1729.31,493.73 1730.42,494.624 1733.54,497.164 1734.98,498.346 \n",
" 1737.69,500.599 1739.53,502.146 1741.76,504.033 1744.09,506.028 1745.75,507.468 1748.65,509.996 1749.67,510.902 1753.2,514.054 1753.52,514.337 1757.29,517.771 \n",
" 1757.76,518.205 1760.99,521.206 1762.31,522.455 1764.62,524.64 1766.87,526.808 1768.18,528.075 1771.43,531.27 1771.67,531.509 1775.09,534.944 1775.98,535.847 \n",
" 1778.45,538.378 1780.54,540.546 1781.75,541.813 1784.98,545.247 1785.1,545.374 1788.15,548.682 1789.65,550.341 1791.25,552.117 1794.21,555.452 1794.3,555.551 \n",
" 1797.28,558.986 1798.77,560.724 1800.2,562.42 1803.07,565.855 1803.32,566.162 1805.88,569.289 1807.88,571.785 1808.63,572.724 1811.32,576.158 1812.43,577.607 \n",
" 1813.96,579.593 1816.54,583.027 1816.99,583.643 1819.06,586.462 1821.53,589.896 1821.55,589.917 1823.95,593.331 1826.1,596.456 1826.32,596.765 1828.63,600.2 \n",
" 1830.66,603.286 1830.89,603.634 1833.1,607.069 1835.22,610.444 1835.25,610.503 1837.36,613.938 1839.42,617.372 1839.77,617.98 1841.42,620.807 1843.38,624.241 \n",
" 1844.33,625.947 1845.29,627.676 1847.15,631.11 1848.89,634.409 1848.96,634.545 1850.72,637.979 1852.44,641.414 1853.44,643.482 1854.1,644.848 1855.73,648.283 \n",
" 1857.3,651.717 1858,653.285 1858.83,655.152 1860.31,658.586 1861.75,662.021 1862.55,664.015 1863.14,665.455 1864.49,668.89 1865.79,672.324 1867.04,675.759 \n",
" 1867.11,675.965 1868.25,679.193 1869.42,682.628 1870.54,686.062 1871.62,689.497 1871.67,689.661 1872.66,692.931 1873.65,696.366 1874.6,699.8 1875.5,703.235 \n",
" 1876.22,706.13 1876.36,706.669 1877.18,710.104 1877.96,713.538 1878.69,716.973 1879.38,720.407 1880.03,723.842 1880.63,727.276 1880.78,728.177 1881.2,730.711 \n",
" 1881.72,734.145 1882.2,737.58 1882.64,741.014 1883.04,744.449 1883.39,747.883 1883.7,751.318 1883.97,754.752 1884.2,758.187 1884.39,761.621 1884.53,765.056 \n",
" 1884.63,768.49 1884.7,771.925 1884.72,775.359 1884.7,778.794 1884.63,782.228 1884.53,785.663 1884.39,789.097 1884.2,792.532 1883.97,795.966 1883.7,799.401 \n",
" 1883.39,802.835 1883.04,806.27 1882.64,809.704 1882.2,813.139 1881.72,816.573 1881.2,820.008 1880.78,822.542 1880.63,823.442 1880.03,826.877 1879.38,830.312 \n",
" 1878.69,833.746 1877.96,837.181 1877.18,840.615 1876.36,844.05 1876.22,844.589 1875.5,847.484 1874.6,850.919 1873.65,854.353 1872.66,857.788 1871.67,861.058 \n",
" 1871.62,861.222 1870.54,864.657 1869.42,868.091 1868.25,871.526 1867.11,874.754 1867.04,874.96 1865.79,878.395 1864.49,881.829 1863.14,885.264 1862.55,886.704 \n",
" 1861.75,888.698 1860.31,892.133 1858.83,895.567 1858,897.434 1857.3,899.002 1855.73,902.436 1854.1,905.871 1853.44,907.236 1852.44,909.305 1850.72,912.74 \n",
" 1848.96,916.174 1848.89,916.31 1847.15,919.609 1845.29,923.043 1844.33,924.772 1843.38,926.478 1841.42,929.912 1839.77,932.739 1839.42,933.347 1837.36,936.781 \n",
" 1835.25,940.216 1835.22,940.274 1833.1,943.65 1830.89,947.085 1830.66,947.433 1828.63,950.519 1826.32,953.954 1826.1,954.263 1823.95,957.388 1821.55,960.802 \n",
" 1821.53,960.823 1819.06,964.257 1816.99,967.075 1816.54,967.692 1813.96,971.126 1812.43,973.112 1811.32,974.561 1808.63,977.995 1807.88,978.933 1805.88,981.43 \n",
" 1803.32,984.557 1803.07,984.864 1800.2,988.299 1798.77,989.995 1797.28,991.733 1794.3,995.168 1794.21,995.267 1791.25,998.602 1789.65,1000.38 1788.15,1002.04 \n",
" 1785.1,1005.34 1784.98,1005.47 1781.75,1008.91 1780.54,1010.17 1778.45,1012.34 1775.98,1014.87 1775.09,1015.77 1771.67,1019.21 1771.43,1019.45 1768.18,1022.64 \n",
" 1766.87,1023.91 1764.62,1026.08 1762.31,1028.26 1760.99,1029.51 1757.76,1032.51 1757.29,1032.95 1753.52,1036.38 1753.2,1036.66 1749.67,1039.82 1748.65,1040.72 \n",
" 1745.75,1043.25 1744.09,1044.69 1741.76,1046.69 1739.53,1048.57 1737.69,1050.12 1734.98,1052.37 1733.54,1053.55 1730.42,1056.09 1729.31,1056.99 1725.86,1059.74 \n",
" 1725,1060.42 1721.31,1063.31 1720.6,1063.86 1716.75,1066.82 1716.12,1067.29 1712.19,1070.25 1711.56,1070.73 1707.64,1073.62 1706.9,1074.16 1703.08,1076.93 \n",
" 1702.15,1077.6 1698.53,1080.18 1697.31,1081.03 1693.97,1083.36 1692.37,1084.46 1689.41,1086.49 1687.33,1087.9 1684.86,1089.57 1682.2,1091.33 1680.3,1092.59 \n",
" 1676.96,1094.77 1675.74,1095.55 1671.61,1098.2 1671.19,1098.47 1666.63,1101.34 1666.15,1101.64 1662.07,1104.16 1660.58,1105.07 1657.52,1106.93 1654.89,1108.51 \n",
" 1652.96,1109.66 1649.08,1111.94 1648.41,1112.34 1643.85,1114.97 1643.15,1115.38 1639.29,1117.57 1637.08,1118.81 1634.74,1120.12 1630.89,1122.24 1630.18,1122.64 \n",
" 1625.62,1125.11 1624.56,1125.68 1621.07,1127.54 1618.08,1129.11 1616.51,1129.94 1611.95,1132.29 1611.45,1132.55 1607.4,1134.61 1604.67,1135.98 1602.84,1136.9 \n",
" 1598.29,1139.15 1597.73,1139.42 1593.73,1141.36 1590.62,1142.85 1589.17,1143.54 1584.62,1145.69 1583.33,1146.29 1580.06,1147.8 1575.86,1149.72 1575.5,1149.88 \n",
" 1570.95,1151.94 1568.19,1153.16 1566.39,1153.95 1561.83,1155.94 1560.32,1156.59 1557.28,1157.9 1552.72,1159.82 1552.24,1160.02 1548.17,1161.72 1543.93,1163.46 \n",
" 1543.61,1163.59 1539.05,1165.43 1535.38,1166.89 1534.5,1167.24 1529.94,1169.03 1526.57,1170.33 1525.38,1170.78 1520.83,1172.52 1517.49,1173.76 1516.27,1174.22 \n",
" 1511.71,1175.9 1508.12,1177.2 1507.16,1177.54 1502.6,1179.17 1498.44,1180.63 1498.04,1180.77 1493.49,1182.34 1488.93,1183.89 1488.42,1184.07 1484.38,1185.42 \n",
" 1479.82,1186.92 1478.03,1187.5 1475.26,1188.4 1470.71,1189.85 1467.25,1190.93 1466.15,1191.28 1461.59,1192.69 1457.04,1194.07 1456.03,1194.37 1452.48,1195.43 \n",
" 1447.92,1196.77 1444.33,1197.8 1443.37,1198.08 1438.81,1199.38 1434.26,1200.65 1432.1,1201.24 1429.7,1201.9 1425.14,1203.13 1420.59,1204.33 1419.28,1204.67 \n",
" 1416.03,1205.52 1411.47,1206.68 1406.92,1207.83 1405.78,1208.11 1402.36,1208.95 1397.8,1210.05 1393.25,1211.14 1391.5,1211.54 1388.69,1212.2 1384.14,1213.24 \n",
" 1379.58,1214.26 1376.33,1214.98 1375.02,1215.26 1370.47,1216.25 1365.91,1217.21 1361.35,1218.15 1360.08,1218.41 1356.8,1219.08 1352.24,1219.98 1347.68,1220.87 \n",
" 1343.13,1221.74 1342.54,1221.85 1338.57,1222.59 1334.02,1223.42 1329.46,1224.23 1324.9,1225.02 1323.36,1225.28 1320.35,1225.79 1315.79,1226.55 1311.23,1227.29 \n",
" 1306.68,1228.01 1302.12,1228.71 1302.07,1228.71 1297.56,1229.39 1293.01,1230.06 1288.45,1230.71 1283.9,1231.34 1279.34,1231.95 1277.8,1232.15 1274.78,1232.54 \n",
" 1270.23,1233.12 1265.67,1233.68 1261.11,1234.23 1256.56,1234.75 1252,1235.26 1248.98,1235.58 1247.44,1235.75 1242.89,1236.22 1238.33,1236.68 1233.78,1237.12 \n",
" 1229.22,1237.54 1224.66,1237.95 1220.11,1238.34 1215.55,1238.71 1211.58,1239.02 1210.99,1239.06 1206.44,1239.4 1201.88,1239.73 1197.32,1240.03 1192.77,1240.32 \n",
" 1188.21,1240.59 1183.66,1240.85 1179.1,1241.08 1174.54,1241.31 1169.99,1241.51 1165.43,1241.7 1160.87,1241.87 1156.32,1242.03 1151.76,1242.17 1147.2,1242.29 \n",
" 1142.65,1242.4 1139.82,1242.45 1138.09,1242.49 1133.54,1242.56 1128.98,1242.62 1124.42,1242.66 1119.87,1242.68 1115.31,1242.69 1110.75,1242.68 1106.2,1242.66 \n",
" 1101.64,1242.62 1097.08,1242.56 1092.53,1242.49 1090.8,1242.45 1087.97,1242.4 1083.42,1242.29 1078.86,1242.17 1074.3,1242.03 1069.75,1241.87 1065.19,1241.7 \n",
" 1060.63,1241.51 1056.08,1241.31 1051.52,1241.08 1046.96,1240.85 1042.41,1240.59 1037.85,1240.32 1033.3,1240.03 1028.74,1239.73 1024.18,1239.4 1019.63,1239.06 \n",
" 1019.04,1239.02 1015.07,1238.71 1010.51,1238.34 1005.96,1237.95 1001.4,1237.54 996.845,1237.12 992.288,1236.68 987.732,1236.22 983.176,1235.75 981.644,1235.58 \n",
" 978.619,1235.26 974.063,1234.75 969.507,1234.23 964.95,1233.68 960.394,1233.12 955.837,1232.54 952.819,1232.15 951.281,1231.95 946.725,1231.34 942.168,1230.71 \n",
" 937.612,1230.06 933.056,1229.39 928.546,1228.71 928.499,1228.71 923.943,1228.01 919.386,1227.29 914.83,1226.55 910.274,1225.79 907.259,1225.28 905.717,1225.02 \n",
" 901.161,1224.23 896.605,1223.42 892.048,1222.59 888.082,1221.85 887.492,1221.74 882.936,1220.87 878.379,1219.98 873.823,1219.08 870.541,1218.41 869.266,1218.15 \n",
" 864.71,1217.21 860.154,1216.25 855.597,1215.26 854.294,1214.98 851.041,1214.26 846.485,1213.24 841.928,1212.2 839.119,1211.54 837.372,1211.14 832.816,1210.05 \n",
" 828.259,1208.95 824.842,1208.11 823.703,1207.83 819.146,1206.68 814.59,1205.52 811.341,1204.67 810.034,1204.33 805.477,1203.13 800.921,1201.9 798.518,1201.24 \n",
" 796.365,1200.65 791.808,1199.38 787.252,1198.08 786.287,1197.8 782.696,1196.77 778.139,1195.43 774.59,1194.37 773.583,1194.07 769.026,1192.69 764.47,1191.28 \n",
" 763.374,1190.93 759.914,1189.85 755.357,1188.4 752.593,1187.5 750.801,1186.92 746.245,1185.42 742.204,1184.07 741.688,1183.89 737.132,1182.34 732.575,1180.77 \n",
" 732.183,1180.63 728.019,1179.17 723.463,1177.54 722.502,1177.2 718.906,1175.9 714.35,1174.22 713.132,1173.76 709.794,1172.52 705.237,1170.78 704.052,1170.33 \n",
" 700.681,1169.03 696.125,1167.24 695.243,1166.89 691.568,1165.43 687.012,1163.59 686.69,1163.46 682.455,1161.72 678.379,1160.02 677.899,1159.82 673.343,1157.9 \n",
" 670.297,1156.59 668.786,1155.94 664.23,1153.95 662.427,1153.16 659.674,1151.94 655.117,1149.88 654.759,1149.72 650.561,1147.8 647.289,1146.29 646.005,1145.69 \n",
" 641.448,1143.54 640.002,1142.85 636.892,1141.36 632.889,1139.42 632.335,1139.15 627.779,1136.9 625.949,1135.98 623.223,1134.61 619.166,1132.55 618.666,1132.29 \n",
" 614.11,1129.94 612.542,1129.11 609.554,1127.54 606.065,1125.68 604.997,1125.11 600.441,1122.64 599.73,1122.24 595.884,1120.12 593.537,1118.81 591.328,1117.57 \n",
" 587.473,1115.38 586.772,1114.97 582.215,1112.34 581.54,1111.94 577.659,1109.66 575.732,1108.51 573.103,1106.93 570.044,1105.07 568.546,1104.16 564.471,1101.64 \n",
" 563.99,1101.34 559.434,1098.47 559.013,1098.2 554.877,1095.55 553.665,1094.77 550.321,1092.59 548.424,1091.33 545.764,1089.57 543.287,1087.9 541.208,1086.49 \n",
" 538.25,1084.46 536.652,1083.36 533.312,1081.03 532.095,1080.18 528.47,1077.6 527.539,1076.93 523.722,1074.16 522.983,1073.62 519.065,1070.73 518.426,1070.25 \n",
" 514.497,1067.29 513.87,1066.82 510.017,1063.86 509.314,1063.31 505.623,1060.42 504.757,1059.74 501.311,1056.99 500.201,1056.09 497.082,1053.55 495.644,1052.37 \n",
" 492.933,1050.12 491.088,1048.57 488.862,1046.69 486.532,1044.69 484.868,1043.25 481.975,1040.72 480.949,1039.82 477.419,1036.66 477.105,1036.38 473.334,1032.95 \n",
" 472.863,1032.51 469.634,1029.51 468.306,1028.26 466.004,1026.08 463.75,1023.91 462.444,1022.64 459.194,1019.45 458.952,1019.21 455.526,1015.77 454.637,1014.87 \n",
" 452.166,1012.34 450.081,1010.17 448.872,1008.91 445.642,1005.47 445.524,1005.34 442.474,1002.04 440.968,1000.38 439.368,998.602 436.412,995.267 436.325,995.168 \n",
" 433.34,991.733 431.855,989.995 430.416,988.299 427.552,984.864 427.299,984.557 424.744,981.43 422.743,978.933 421.995,977.995 419.302,974.561 418.186,973.112 \n",
" 416.665,971.126 414.085,967.692 413.63,967.075 411.558,964.257 409.088,960.823 409.073,960.802 406.668,957.388 404.517,954.263 404.305,953.954 401.991,950.519 \n",
" 399.961,947.433 399.733,947.085 397.522,943.65 395.404,940.274 395.368,940.216 393.258,936.781 391.204,933.347 390.848,932.739 389.196,929.912 387.24,926.478 \n",
" 386.292,924.772 385.332,923.043 383.472,919.609 381.735,916.31 381.664,916.174 379.898,912.74 378.183,909.305 377.179,907.236 376.516,905.871 374.893,902.436 \n",
" 373.32,899.002 372.623,897.434 371.792,895.567 370.308,892.133 368.873,888.698 368.066,886.704 367.483,885.264 366.135,881.829 364.835,878.395 363.583,874.96 \n",
" 363.51,874.754 362.368,871.526 361.2,868.091 360.079,864.657 359.003,861.222 358.953,861.058 357.965,857.788 356.972,854.353 356.024,850.919 355.121,847.484 \n",
" 354.397,844.589 354.261,844.05 353.44,840.615 352.663,837.181 351.929,833.746 351.239,830.312 350.592,826.877 349.988,823.442 349.841,822.542 349.423,820.008 \n",
" 348.9,816.573 348.419,813.139 347.981,809.704 347.585,806.27 347.231,802.835 346.92,799.401 346.65,795.966 346.421,792.532 346.235,789.097 346.089,785.663 \n",
" 345.986,782.228 345.924,778.794 345.903,775.359 345.924,771.925 345.986,768.49 346.089,765.056 346.235,761.621 346.421,758.187 346.65,754.752 346.92,751.318 \n",
" 347.231,747.883 347.585,744.449 347.981,741.014 348.419,737.58 348.9,734.145 349.423,730.711 349.841,728.177 349.988,727.276 350.592,723.842 351.239,720.407 \n",
" 351.929,716.973 352.663,713.538 353.44,710.104 354.261,706.669 354.397,706.13 355.121,703.235 356.024,699.8 356.972,696.366 357.965,692.931 358.953,689.661 \n",
" 359.003,689.497 360.079,686.062 361.2,682.628 362.368,679.193 363.51,675.965 363.583,675.759 364.835,672.324 366.135,668.89 367.483,665.455 368.066,664.015 \n",
" 368.873,662.021 370.308,658.586 371.792,655.152 372.623,653.285 373.32,651.717 374.893,648.283 376.516,644.848 377.179,643.482 378.183,641.414 379.898,637.979 \n",
" 381.664,634.545 381.735,634.409 383.472,631.11 385.332,627.676 386.292,625.947 387.24,624.241 389.196,620.807 390.848,617.98 391.204,617.372 393.258,613.938 \n",
" 395.368,610.503 395.404,610.444 397.522,607.069 399.733,603.634 399.961,603.286 401.991,600.2 404.305,596.765 404.517,596.456 406.668,593.331 409.073,589.917 \n",
" 409.088,589.896 411.558,586.462 413.63,583.643 414.085,583.027 416.665,579.593 418.186,577.607 419.302,576.158 421.995,572.724 422.743,571.785 424.744,569.289 \n",
" 427.299,566.162 427.552,565.855 430.416,562.42 431.855,560.724 433.34,558.986 436.325,555.551 436.412,555.452 439.368,552.117 440.968,550.341 442.474,548.682 \n",
" 445.524,545.374 445.642,545.247 448.872,541.813 450.081,540.546 452.166,538.378 454.637,535.847 455.526,534.944 458.952,531.509 459.194,531.27 462.444,528.075 \n",
" 463.75,526.808 466.004,524.64 468.306,522.455 469.634,521.206 472.863,518.205 473.334,517.771 477.105,514.337 477.419,514.054 480.949,510.902 481.975,509.996 \n",
" 484.868,507.468 486.532,506.028 488.862,504.033 491.088,502.146 492.933,500.599 495.644,498.346 497.082,497.164 500.201,494.624 501.311,493.73 504.757,490.979 \n",
" 505.623,490.295 509.314,487.406 510.017,486.861 513.87,483.903 514.497,483.426 518.426,480.467 519.065,479.992 522.983,477.097 523.722,476.557 527.539,473.79 \n",
" 528.47,473.123 532.095,470.543 533.312,469.688 536.652,467.356 538.25,466.254 541.208,464.226 543.287,462.819 545.764,461.152 548.424,459.385 550.321,458.132 \n",
" 553.665,455.95 554.877,455.164 559.013,452.516 559.434,452.248 563.99,449.38 564.471,449.081 568.546,446.561 570.044,445.647 573.103,443.788 575.732,442.212 \n",
" 577.659,441.062 581.54,438.778 582.215,438.382 586.772,435.744 587.473,435.343 591.328,433.148 593.537,431.909 595.884,430.595 599.73,428.474 600.441,428.084 \n",
" 604.997,425.611 606.065,425.04 609.554,423.177 612.542,421.605 614.11,420.782 618.666,418.426 619.166,418.171 623.223,416.104 625.949,414.736 627.779,413.82 \n",
" 632.335,411.571 632.889,411.302 636.892,409.356 640.002,407.867 641.448,407.176 646.005,405.029 647.289,404.433 650.561,402.915 654.759,400.998 655.117,400.835 \n",
" 659.674,398.784 662.427,397.564 664.23,396.766 668.786,394.778 670.297,394.129 673.343,392.821 677.899,390.895 678.379,390.695 682.455,388.995 686.69,387.26 \n",
" 687.012,387.128 691.568,385.286 695.243,383.826 696.125,383.475 700.681,381.69 704.052,380.391 705.237,379.934 709.794,378.203 713.132,376.957 714.35,376.501 \n",
" 718.906,374.824 722.502,373.522 723.463,373.174 728.019,371.548 732.183,370.088 732.575,369.95 737.132,368.374 741.688,366.826 742.204,366.653 746.245,365.299 \n",
" 750.801,363.799 752.593,363.219 755.357,362.322 759.914,360.869 763.374,359.784 764.47,359.44 769.026,358.032 773.583,356.65 774.59,356.35 778.139,355.289 \n",
" 782.696,353.951 786.287,352.915 787.252,352.636 791.808,351.341 796.365,350.071 798.518,349.481 800.921,348.821 805.477,347.592 810.034,346.386 811.341,346.046 \n",
" 814.59,345.2 819.146,344.035 823.703,342.892 824.842,342.612 828.259,341.768 832.816,340.665 837.372,339.584 839.119,339.177 841.928,338.521 846.485,337.479 \n",
" 851.041,336.457 854.294,335.743 855.597,335.456 860.154,334.472 864.71,333.509 869.266,332.566 870.541,332.308 873.823,331.641 878.379,330.735 882.936,329.849 \n",
" 887.492,328.983 888.082,328.874 892.048,328.134 896.605,327.303 901.161,326.492 905.717,325.701 907.259,325.439 910.274,324.926 914.83,324.169 919.386,323.431 \n",
" 923.943,322.712 928.499,322.012 928.546,322.005 933.056,321.327 937.612,320.66 942.168,320.012 946.725,319.382 951.281,318.771 952.819,318.57 955.837,318.175 \n",
" \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#821f6b; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 955.837,318.175 960.394,317.597 964.95,317.036 969.507,316.493 974.063,315.968 978.619,315.461 981.644,315.136 983.176,314.97 987.732,314.495 992.288,314.038 \n",
" 996.845,313.598 1001.4,313.175 1005.96,312.77 1010.51,312.381 1015.07,312.01 1019.04,311.701 1019.63,311.655 1024.18,311.316 1028.74,310.994 1033.3,310.688 \n",
" 1037.85,310.4 1042.41,310.128 1046.96,309.873 1051.52,309.634 1056.08,309.413 1060.63,309.207 1065.19,309.019 1069.75,308.846 1074.3,308.691 1078.86,308.552 \n",
" 1083.42,308.429 1087.97,308.322 1090.8,308.267 1092.53,308.232 1097.08,308.158 1101.64,308.101 1106.2,308.06 1110.75,308.035 1115.31,308.027 1119.87,308.035 \n",
" 1124.42,308.06 1128.98,308.101 1133.54,308.158 1138.09,308.232 1139.82,308.267 1142.65,308.322 1147.2,308.429 1151.76,308.552 1156.32,308.691 1160.87,308.846 \n",
" 1165.43,309.019 1169.99,309.207 1174.54,309.413 1179.1,309.634 1183.66,309.873 1188.21,310.128 1192.77,310.4 1197.32,310.688 1201.88,310.994 1206.44,311.316 \n",
" 1210.99,311.655 1211.58,311.701 1215.55,312.01 1220.11,312.381 1224.66,312.77 1229.22,313.175 1233.78,313.598 1238.33,314.038 1242.89,314.495 1247.44,314.97 \n",
" 1248.98,315.136 1252,315.461 1256.56,315.968 1261.11,316.493 1265.67,317.036 1270.23,317.597 1274.78,318.175 1277.8,318.57 1279.34,318.771 1283.9,319.382 \n",
" 1288.45,320.012 1293.01,320.66 1297.56,321.327 1302.07,322.005 1302.12,322.012 1306.68,322.712 1311.23,323.431 1315.79,324.169 1320.35,324.926 1323.36,325.439 \n",
" 1324.9,325.701 1329.46,326.492 1334.02,327.303 1338.57,328.134 1342.54,328.874 1343.13,328.983 1347.68,329.849 1352.24,330.735 1356.8,331.641 1360.08,332.308 \n",
" 1361.35,332.566 1365.91,333.509 1370.47,334.472 1375.02,335.456 1376.33,335.743 1379.58,336.457 1384.14,337.479 1388.69,338.521 1391.5,339.177 1393.25,339.584 \n",
" 1397.8,340.665 1402.36,341.768 1405.78,342.612 1406.92,342.892 1411.47,344.035 1416.03,345.2 1419.28,346.046 1420.59,346.386 1425.14,347.592 1429.7,348.821 \n",
" 1432.1,349.481 1434.26,350.071 1438.81,351.341 1443.37,352.636 1444.33,352.915 1447.92,353.951 1452.48,355.289 1456.03,356.35 1457.04,356.65 1461.59,358.032 \n",
" 1466.15,359.44 1467.25,359.784 1470.71,360.869 1475.26,362.322 1478.03,363.219 1479.82,363.799 1484.38,365.299 1488.42,366.653 1488.93,366.826 1493.49,368.374 \n",
" 1498.04,369.95 1498.44,370.088 1502.6,371.548 1507.16,373.174 1508.12,373.522 1511.71,374.824 1516.27,376.501 1517.49,376.957 1520.83,378.203 1525.38,379.934 \n",
" 1526.57,380.391 1529.94,381.69 1534.5,383.475 1535.38,383.826 1539.05,385.286 1543.61,387.128 1543.93,387.26 1548.17,388.995 1552.24,390.695 1552.72,390.895 \n",
" 1557.28,392.821 1560.32,394.129 1561.83,394.778 1566.39,396.766 1568.19,397.564 1570.95,398.784 1575.5,400.835 1575.86,400.998 1580.06,402.915 1583.33,404.433 \n",
" 1584.62,405.029 1589.17,407.176 1590.62,407.867 1593.73,409.356 1597.73,411.302 1598.29,411.571 1602.84,413.82 1604.67,414.736 1607.4,416.104 1611.45,418.171 \n",
" 1611.95,418.426 1616.51,420.782 1618.08,421.605 1621.07,423.177 1624.56,425.04 1625.62,425.611 1630.18,428.084 1630.89,428.474 1634.74,430.595 1637.08,431.909 \n",
" 1639.29,433.148 1643.15,435.343 1643.85,435.744 1648.41,438.382 1649.08,438.778 1652.96,441.062 1654.89,442.212 1657.52,443.788 1660.58,445.647 1662.07,446.561 \n",
" 1666.15,449.081 1666.63,449.38 1671.19,452.248 1671.61,452.516 1675.74,455.164 1676.96,455.95 1680.3,458.132 1682.2,459.385 1684.86,461.152 1687.33,462.819 \n",
" 1689.41,464.226 1692.37,466.254 1693.97,467.356 1697.31,469.688 1698.53,470.543 1702.15,473.123 1703.08,473.79 1706.9,476.557 1707.64,477.097 1711.56,479.992 \n",
" 1712.19,480.467 1716.12,483.426 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#9e2a62; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1658.44,524.64 1662.07,527.226 1663.25,528.075 1666.63,530.538 1667.95,531.509 1671.19,533.923 1672.54,534.944 1675.74,537.385 1677.03,538.378 1680.3,540.927 \n",
" 1681.42,541.813 1684.86,544.553 1685.72,545.247 1689.41,548.266 1689.91,548.682 1693.97,552.072 1694.02,552.117 1698.04,555.551 1698.53,555.974 1701.96,558.986 \n",
" 1703.08,559.978 1705.8,562.42 1707.64,564.09 1709.55,565.855 1712.19,568.317 1713.22,569.289 1716.75,572.665 1716.81,572.724 1720.32,576.158 1721.31,577.143 \n",
" 1723.74,579.593 1725.86,581.759 1727.09,583.027 1730.36,586.462 1730.42,586.523 1733.56,589.896 1734.98,591.449 1736.68,593.331 1739.53,596.547 1739.72,596.765 \n",
" 1742.7,600.2 1744.09,601.835 1745.6,603.634 1748.43,607.069 1748.65,607.328 1751.2,610.503 1753.2,613.05 1753.89,613.938 1756.52,617.372 1757.76,619.025 \n",
" 1759.08,620.807 1761.58,624.241 1762.31,625.281 1764,627.676 1766.37,631.11 1766.87,631.857 1768.67,634.545 1770.91,637.979 1771.43,638.8 1773.08,641.414 \n",
" 1775.19,644.848 1775.98,646.168 1777.25,648.283 1779.24,651.717 1780.54,654.037 1781.16,655.152 1783.04,658.586 1784.85,662.021 1785.1,662.51 1786.6,665.455 \n",
" 1788.3,668.89 1789.65,671.743 1789.93,672.324 1791.51,675.759 1793.03,679.193 1794.21,681.955 1794.5,682.628 1795.91,686.062 1797.26,689.497 1798.55,692.931 \n",
" 1798.77,693.513 1799.8,696.366 1800.99,699.8 1802.12,703.235 1803.19,706.669 1803.32,707.094 1804.22,710.104 1805.19,713.538 1806.11,716.973 1806.97,720.407 \n",
" 1807.78,723.842 1807.88,724.296 1808.54,727.276 1809.24,730.711 1809.89,734.145 1810.49,737.58 1811.04,741.014 1811.53,744.449 1811.97,747.883 1812.36,751.318 \n",
" 1812.43,752.109 1812.69,754.752 1812.98,758.187 1813.22,761.621 1813.4,765.056 1813.53,768.49 1813.61,771.925 1813.63,775.359 1813.61,778.794 1813.53,782.228 \n",
" 1813.4,785.663 1813.22,789.097 1812.98,792.532 1812.69,795.966 1812.43,798.61 1812.36,799.401 1811.97,802.835 1811.53,806.27 1811.04,809.704 1810.49,813.139 \n",
" 1809.89,816.573 1809.24,820.008 1808.54,823.442 1807.88,826.423 1807.78,826.877 1806.97,830.312 1806.11,833.746 1805.19,837.181 1804.22,840.615 1803.32,843.625 \n",
" 1803.19,844.05 1802.12,847.484 1800.99,850.919 1799.8,854.353 1798.77,857.206 1798.55,857.788 1797.26,861.222 1795.91,864.657 1794.5,868.091 1794.21,868.763 \n",
" 1793.03,871.526 1791.51,874.96 1789.93,878.395 1789.65,878.976 1788.3,881.829 1786.6,885.264 1785.1,888.209 1784.85,888.698 1783.04,892.133 1781.16,895.567 \n",
" 1780.54,896.682 1779.24,899.002 1777.25,902.436 1775.98,904.551 1775.19,905.871 1773.08,909.305 1771.43,911.919 1770.91,912.74 1768.67,916.174 1766.87,918.862 \n",
" 1766.37,919.609 1764,923.043 1762.31,925.437 1761.58,926.478 1759.08,929.912 1757.76,931.694 1756.52,933.347 1753.89,936.781 1753.2,937.668 1751.2,940.216 \n",
" 1748.65,943.391 1748.43,943.65 1745.6,947.085 1744.09,948.883 1742.7,950.519 1739.72,953.954 1739.53,954.172 1736.68,957.388 1734.98,959.27 1733.56,960.823 \n",
" 1730.42,964.195 1730.36,964.257 1727.09,967.692 1725.86,968.96 1723.74,971.126 1721.31,973.576 1720.32,974.561 1716.81,977.995 1716.75,978.054 1713.22,981.43 \n",
" 1712.19,982.402 1709.55,984.864 1707.64,986.629 1705.8,988.299 1703.08,990.741 1701.96,991.733 1698.53,994.745 1698.04,995.168 1694.02,998.602 1693.97,998.647 \n",
" 1689.91,1002.04 1689.41,1002.45 1685.72,1005.47 1684.86,1006.17 1681.42,1008.91 1680.3,1009.79 1677.03,1012.34 1675.74,1013.33 1672.54,1015.77 1671.19,1016.8 \n",
" 1667.95,1019.21 1666.63,1020.18 1663.25,1022.64 1662.07,1023.49 1658.44,1026.08 1657.52,1026.73 1653.53,1029.51 1652.96,1029.91 1648.5,1032.95 1648.41,1033.01 \n",
" 1643.85,1036.06 1643.36,1036.38 1639.29,1039.04 1638.09,1039.82 1634.74,1041.97 1632.71,1043.25 1630.18,1044.84 1627.19,1046.69 1625.62,1047.65 1621.55,1050.12 \n",
" 1621.07,1050.41 1616.51,1053.12 1615.77,1053.55 1611.95,1055.78 1609.84,1056.99 1607.4,1058.39 1603.78,1060.42 1602.84,1060.95 1598.29,1063.46 1597.56,1063.86 \n",
" 1593.73,1065.93 1591.18,1067.29 1589.17,1068.36 1584.64,1070.73 1584.62,1070.74 1580.06,1073.08 1577.93,1074.16 1575.5,1075.38 1571.04,1077.6 1570.95,1077.64 \n",
" 1566.39,1079.87 1563.96,1081.03 1561.83,1082.05 1557.28,1084.19 1556.69,1084.46 1552.72,1086.31 1549.22,1087.9 1548.17,1088.38 1543.61,1090.42 1541.52,1091.33 \n",
" 1539.05,1092.42 1534.5,1094.39 1533.61,1094.77 1529.94,1096.33 1525.45,1098.2 1525.38,1098.23 1520.83,1100.11 1517.03,1101.64 1516.27,1101.94 1511.71,1103.76 \n",
" 1508.34,1105.07 1507.16,1105.53 1502.6,1107.28 1499.36,1108.51 1498.04,1109 1493.49,1110.7 1490.07,1111.94 1488.93,1112.36 1484.38,1113.99 1480.45,1115.38 \n",
" 1479.82,1115.6 1475.26,1117.18 1470.71,1118.73 1470.46,1118.81 1466.15,1120.26 1461.59,1121.75 1460.08,1122.24 1457.04,1123.23 1452.48,1124.68 1449.26,1125.68 \n",
" 1447.92,1126.1 1443.37,1127.5 1438.81,1128.87 1437.98,1129.11 1434.26,1130.22 1429.7,1131.54 1426.17,1132.55 1425.14,1132.84 1420.59,1134.12 1416.03,1135.37 \n",
" 1413.76,1135.98 1411.47,1136.6 1406.92,1137.81 1402.36,1138.99 1400.7,1139.42 1397.8,1140.16 1393.25,1141.3 1388.69,1142.41 1386.87,1142.85 1384.14,1143.51 \n",
" 1379.58,1144.59 1375.02,1145.64 1372.17,1146.29 1370.47,1146.67 1365.91,1147.68 1361.35,1148.67 1356.8,1149.64 1356.42,1149.72 1352.24,1150.59 1347.68,1151.52 \n",
" 1343.13,1152.43 1339.4,1153.16 1338.57,1153.32 1334.02,1154.19 1329.46,1155.03 1324.9,1155.86 1320.8,1156.59 1320.35,1156.67 1315.79,1157.46 1311.23,1158.23 \n",
" 1306.68,1158.98 1302.12,1159.71 1300.14,1160.02 1297.56,1160.43 1293.01,1161.12 1288.45,1161.8 1283.9,1162.46 1279.34,1163.09 1276.64,1163.46 1274.78,1163.71 \n",
" 1270.23,1164.31 1265.67,1164.9 1261.11,1165.46 1256.56,1166.01 1252,1166.54 1248.81,1166.89 1247.44,1167.05 1242.89,1167.54 1238.33,1168.02 1233.78,1168.47 \n",
" 1229.22,1168.91 1224.66,1169.33 1220.11,1169.74 1215.55,1170.12 1213,1170.33 1210.99,1170.49 1206.44,1170.84 1201.88,1171.18 1197.32,1171.49 1192.77,1171.79 \n",
" 1188.21,1172.07 1183.66,1172.34 1179.1,1172.59 1174.54,1172.82 1169.99,1173.03 1165.43,1173.22 1160.87,1173.4 1156.32,1173.56 1151.76,1173.71 1149.83,1173.76 \n",
" 1147.2,1173.84 1142.65,1173.95 1138.09,1174.04 1133.54,1174.12 1128.98,1174.18 1124.42,1174.22 1119.87,1174.24 1115.31,1174.25 1110.75,1174.24 1106.2,1174.22 \n",
" 1101.64,1174.18 1097.08,1174.12 1092.53,1174.04 1087.97,1173.95 1083.42,1173.84 1080.79,1173.76 1078.86,1173.71 1074.3,1173.56 1069.75,1173.4 1065.19,1173.22 \n",
" 1060.63,1173.03 1056.08,1172.82 1051.52,1172.59 1046.96,1172.34 1042.41,1172.07 1037.85,1171.79 1033.3,1171.49 1028.74,1171.18 1024.18,1170.84 1019.63,1170.49 \n",
" 1017.62,1170.33 1015.07,1170.12 1010.51,1169.74 1005.96,1169.33 1001.4,1168.91 996.845,1168.47 992.288,1168.02 987.732,1167.54 983.176,1167.05 981.811,1166.89 \n",
" 978.619,1166.54 974.063,1166.01 969.507,1165.46 964.95,1164.9 960.394,1164.31 955.837,1163.71 953.98,1163.46 951.281,1163.09 946.725,1162.46 942.168,1161.8 \n",
" 937.612,1161.12 933.056,1160.43 930.482,1160.02 928.499,1159.71 923.943,1158.98 919.386,1158.23 914.83,1157.46 910.274,1156.67 909.82,1156.59 905.717,1155.86 \n",
" 901.161,1155.03 896.605,1154.19 892.048,1153.32 891.224,1153.16 887.492,1152.43 882.936,1151.52 878.379,1150.59 874.202,1149.72 873.823,1149.64 869.266,1148.67 \n",
" 864.71,1147.68 860.154,1146.67 858.455,1146.29 855.597,1145.64 851.041,1144.59 846.485,1143.51 843.746,1142.85 841.928,1142.41 837.372,1141.3 832.816,1140.16 \n",
" 829.92,1139.42 828.259,1138.99 823.703,1137.81 819.146,1136.6 816.856,1135.98 814.59,1135.37 810.034,1134.12 805.477,1132.84 804.453,1132.55 800.921,1131.54 \n",
" 796.365,1130.22 792.64,1129.11 791.808,1128.87 787.252,1127.5 782.696,1126.1 781.356,1125.68 778.139,1124.68 773.583,1123.23 770.544,1122.24 769.026,1121.75 \n",
" 764.47,1120.26 760.157,1118.81 759.914,1118.73 755.357,1117.18 750.801,1115.6 750.171,1115.38 746.245,1113.99 741.688,1112.36 740.548,1111.94 737.132,1110.7 \n",
" 732.575,1109 731.258,1108.51 728.019,1107.28 723.463,1105.53 722.279,1105.07 718.906,1103.76 714.35,1101.94 713.59,1101.64 709.794,1100.11 705.237,1098.23 \n",
" 705.171,1098.2 700.681,1096.33 697.014,1094.77 696.125,1094.39 691.568,1092.42 689.096,1091.33 687.012,1090.42 682.455,1088.38 681.403,1087.9 677.899,1086.31 \n",
" 673.926,1084.46 673.343,1084.19 668.786,1082.05 666.658,1081.03 664.23,1079.87 659.674,1077.64 659.579,1077.6 655.117,1075.38 652.694,1074.16 650.561,1073.08 \n",
" 646.005,1070.74 645.979,1070.73 641.448,1068.36 639.443,1067.29 636.892,1065.93 633.064,1063.86 632.335,1063.46 627.779,1060.95 626.845,1060.42 623.223,1058.39 \n",
" 620.778,1056.99 618.666,1055.78 614.854,1053.55 614.11,1053.12 609.554,1050.41 609.072,1050.12 604.997,1047.65 603.428,1046.69 600.441,1044.84 597.914,1043.25 \n",
" 595.884,1041.97 592.526,1039.82 591.328,1039.04 587.261,1036.38 586.772,1036.06 582.215,1033.01 582.117,1032.95 577.659,1029.91 577.09,1029.51 573.103,1026.73 \n",
" 572.176,1026.08 568.546,1023.49 567.372,1022.64 563.99,1020.18 562.675,1019.21 559.434,1016.8 558.082,1015.77 554.877,1013.33 553.591,1012.34 550.321,1009.79 \n",
" 549.199,1008.91 545.764,1006.17 544.905,1005.47 541.208,1002.45 540.705,1002.04 536.652,998.647 536.599,998.602 532.584,995.168 532.095,994.745 528.658,991.733 \n",
" 527.539,990.741 524.819,988.299 522.983,986.629 521.066,984.864 518.426,982.402 517.396,981.43 513.87,978.054 513.809,977.995 510.304,974.561 509.314,973.576 \n",
" 506.877,971.126 504.757,968.96 503.529,967.692 500.259,964.257 500.201,964.195 497.063,960.823 495.644,959.27 493.942,957.388 491.088,954.172 490.896,953.954 \n",
" 487.921,950.519 486.532,948.883 485.017,947.085 482.186,943.65 481.975,943.391 479.421,940.216 477.419,937.668 476.727,936.781 474.099,933.347 472.863,931.694 \n",
" 471.539,929.912 469.045,926.478 468.306,925.437 466.616,923.043 464.253,919.609 463.75,918.862 461.951,916.174 459.715,912.74 459.194,911.919 457.539,909.305 \n",
" 455.427,905.871 454.637,904.551 453.375,902.436 451.385,899.002 450.081,896.682 449.456,895.567 447.583,892.133 445.775,888.698 445.524,888.209 444.02,885.264 \n",
" 442.325,881.829 440.968,878.976 440.692,878.395 439.109,874.96 437.588,871.526 436.412,868.763 436.125,868.091 434.713,864.657 433.36,861.222 432.066,857.788 \n",
" 431.855,857.206 430.821,854.353 429.632,850.919 428.5,847.484 427.426,844.05 427.299,843.625 426.399,840.615 425.426,837.181 424.51,833.746 423.649,830.312 \n",
" 422.842,826.877 422.743,826.423 422.083,823.442 421.378,820.008 420.726,816.573 420.127,813.139 419.582,809.704 419.09,806.27 418.651,802.835 418.263,799.401 \n",
" 418.186,798.61 417.926,795.966 417.639,792.532 417.405,789.097 417.223,785.663 417.093,782.228 417.015,778.794 416.989,775.359 417.015,771.925 417.093,768.49 \n",
" 417.223,765.056 417.405,761.621 417.639,758.187 417.926,754.752 418.186,752.109 418.263,751.318 418.651,747.883 419.09,744.449 419.582,741.014 420.127,737.58 \n",
" 420.726,734.145 421.378,730.711 422.083,727.276 422.743,724.296 422.842,723.842 423.649,720.407 424.51,716.973 425.426,713.538 426.399,710.104 427.299,707.094 \n",
" 427.426,706.669 428.5,703.235 429.632,699.8 430.821,696.366 431.855,693.513 432.066,692.931 433.36,689.497 434.713,686.062 436.125,682.628 436.412,681.955 \n",
" 437.588,679.193 439.109,675.759 440.692,672.324 440.968,671.743 442.325,668.89 444.02,665.455 445.524,662.51 445.775,662.021 447.583,658.586 449.456,655.152 \n",
" 450.081,654.037 451.385,651.717 453.375,648.283 454.637,646.168 455.427,644.848 457.539,641.414 459.194,638.8 459.715,637.979 461.951,634.545 463.75,631.857 \n",
" 464.253,631.11 466.616,627.676 468.306,625.281 469.045,624.241 471.539,620.807 472.863,619.025 474.099,617.372 476.727,613.938 477.419,613.05 479.421,610.503 \n",
" 481.975,607.328 482.186,607.069 485.017,603.634 486.532,601.835 487.921,600.2 490.896,596.765 491.088,596.547 493.942,593.331 495.644,591.449 497.063,589.896 \n",
" 500.201,586.523 500.259,586.462 503.529,583.027 504.757,581.759 506.877,579.593 509.314,577.143 510.304,576.158 513.809,572.724 513.87,572.665 517.396,569.289 \n",
" 518.426,568.317 521.066,565.855 522.983,564.09 524.819,562.42 527.539,559.978 528.658,558.986 532.095,555.974 532.584,555.551 536.599,552.117 536.652,552.072 \n",
" 540.705,548.682 541.208,548.266 544.905,545.247 545.764,544.553 549.199,541.813 550.321,540.927 553.591,538.378 554.877,537.385 558.082,534.944 559.434,533.923 \n",
" 562.675,531.509 563.99,530.538 567.372,528.075 568.546,527.226 572.176,524.64 573.103,523.985 577.09,521.206 577.659,520.812 582.117,517.771 582.215,517.705 \n",
" 586.772,514.659 587.261,514.337 591.328,511.674 592.526,510.902 595.884,508.749 597.914,507.468 600.441,505.88 603.428,504.033 604.997,503.067 609.072,500.599 \n",
" 609.554,500.308 614.11,497.6 614.854,497.164 618.666,494.941 620.778,493.73 623.223,492.332 626.845,490.295 627.779,489.772 632.335,487.257 633.064,486.861 \n",
" 636.892,484.786 639.443,483.426 641.448,482.36 645.979,479.992 646.005,479.978 650.561,477.635 652.694,476.557 655.117,475.335 659.579,473.123 659.674,473.076 \n",
" 664.23,470.852 666.658,469.688 668.786,468.669 673.343,466.524 673.926,466.254 677.899,464.413 681.403,462.819 682.455,462.341 687.012,460.302 689.096,459.385 \n",
" 691.568,458.298 696.125,456.329 697.014,455.95 700.681,454.39 705.171,452.516 705.237,452.488 709.794,450.614 713.59,449.081 714.35,448.774 718.906,446.963 \n",
" 722.279,445.647 723.463,445.185 728.019,443.434 731.258,442.212 732.575,441.715 737.132,440.023 740.548,438.778 741.688,438.362 746.245,436.726 750.171,435.343 \n",
" 750.801,435.121 755.357,433.54 759.914,431.99 760.157,431.909 764.47,430.463 769.026,428.965 770.544,428.474 773.583,427.49 778.139,426.043 781.356,425.04 \n",
" 782.696,424.621 787.252,423.222 791.808,421.851 792.64,421.605 796.365,420.502 800.921,419.177 804.453,418.171 805.477,417.878 810.034,416.6 814.59,415.347 \n",
" 816.856,414.736 819.146,414.117 823.703,412.909 828.259,411.725 829.92,411.302 832.816,410.562 837.372,409.421 841.928,408.304 843.746,407.867 846.485,407.207 \n",
" 851.041,406.132 855.597,405.079 858.455,404.433 860.154,404.047 864.71,403.035 869.266,402.045 873.823,401.077 874.202,400.998 878.379,400.127 882.936,399.198 \n",
" 887.492,398.29 891.224,397.564 892.048,397.403 896.605,396.533 901.161,395.684 905.717,394.856 909.82,394.129 910.274,394.048 914.83,393.257 919.386,392.486 \n",
" 923.943,391.735 928.499,391.004 930.482,390.695 933.056,390.291 937.612,389.596 942.168,388.92 946.725,388.264 951.281,387.627 953.98,387.26 955.837,387.007 \n",
" 960.394,386.405 964.95,385.821 969.507,385.256 974.063,384.71 978.619,384.183 981.811,383.826 983.176,383.673 987.732,383.179 992.288,382.704 996.845,382.247 \n",
" 1001.4,381.807 1005.96,381.386 1010.51,380.983 1015.07,380.597 1017.62,380.391 1019.63,380.229 1024.18,379.877 1028.74,379.542 1033.3,379.226 1037.85,378.926 \n",
" 1042.41,378.644 1046.96,378.38 1051.52,378.133 1056.08,377.903 1060.63,377.69 1065.19,377.494 1069.75,377.316 1074.3,377.155 1078.86,377.011 1080.79,376.957 \n",
" 1083.42,376.883 1087.97,376.772 1092.53,376.679 1097.08,376.602 1101.64,376.542 1106.2,376.5 1110.75,376.474 1115.31,376.466 1119.87,376.474 1124.42,376.5 \n",
" 1128.98,376.542 1133.54,376.602 1138.09,376.679 1142.65,376.772 1147.2,376.883 1149.83,376.957 1151.76,377.011 1156.32,377.155 1160.87,377.316 1165.43,377.494 \n",
" 1169.99,377.69 1174.54,377.903 1179.1,378.133 1183.66,378.38 1188.21,378.644 1192.77,378.926 1197.32,379.226 1201.88,379.542 1206.44,379.877 1210.99,380.229 \n",
" 1213,380.391 1215.55,380.597 1220.11,380.983 1224.66,381.386 1229.22,381.807 1233.78,382.247 1238.33,382.704 1242.89,383.179 1247.44,383.673 1248.81,383.826 \n",
" 1252,384.183 1256.56,384.71 1261.11,385.256 1265.67,385.821 1270.23,386.405 1274.78,387.007 1276.64,387.26 1279.34,387.627 1283.9,388.264 1288.45,388.92 \n",
" 1293.01,389.596 1297.56,390.291 1300.14,390.695 1302.12,391.004 1306.68,391.735 1311.23,392.486 1315.79,393.257 1320.35,394.048 1320.8,394.129 1324.9,394.856 \n",
" 1329.46,395.684 1334.02,396.533 1338.57,397.403 1339.4,397.564 1343.13,398.29 1347.68,399.198 1352.24,400.127 1356.42,400.998 1356.8,401.077 1361.35,402.045 \n",
" 1365.91,403.035 1370.47,404.047 1372.17,404.433 1375.02,405.079 1379.58,406.132 1384.14,407.207 1386.87,407.867 1388.69,408.304 1393.25,409.421 1397.8,410.562 \n",
" 1400.7,411.302 1402.36,411.725 1406.92,412.909 1411.47,414.117 1413.76,414.736 1416.03,415.347 1420.59,416.6 1425.14,417.878 1426.17,418.171 1429.7,419.177 \n",
" \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#9e2a62; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1429.7,419.177 1434.26,420.502 1437.98,421.605 1438.81,421.851 1443.37,423.222 1447.92,424.621 1449.26,425.04 1452.48,426.043 1457.04,427.49 1460.08,428.474 \n",
" 1461.59,428.965 1466.15,430.463 1470.46,431.909 1470.71,431.99 1475.26,433.54 1479.82,435.121 1480.45,435.343 1484.38,436.726 1488.93,438.362 1490.07,438.778 \n",
" 1493.49,440.023 1498.04,441.715 1499.36,442.212 1502.6,443.434 1507.16,445.185 1508.34,445.647 1511.71,446.963 1516.27,448.774 1517.03,449.081 1520.83,450.614 \n",
" 1525.38,452.488 1525.45,452.516 1529.94,454.39 1533.61,455.95 1534.5,456.329 1539.05,458.298 1541.52,459.385 1543.61,460.302 1548.17,462.341 1549.22,462.819 \n",
" 1552.72,464.413 1556.69,466.254 1557.28,466.524 1561.83,468.669 1563.96,469.688 1566.39,470.852 1570.95,473.076 1571.04,473.123 1575.5,475.335 1577.93,476.557 \n",
" 1580.06,477.635 1584.62,479.978 1584.64,479.992 1589.17,482.36 1591.18,483.426 1593.73,484.786 1597.56,486.861 1598.29,487.257 1602.84,489.772 1603.78,490.295 \n",
" 1607.4,492.332 1609.84,493.73 1611.95,494.941 1615.77,497.164 1616.51,497.6 1621.07,500.308 1621.55,500.599 1625.62,503.067 1627.19,504.033 1630.18,505.88 \n",
" 1632.71,507.468 1634.74,508.749 1638.09,510.902 1639.29,511.674 1643.36,514.337 1643.85,514.659 1648.41,517.705 1648.5,517.771 1652.96,520.812 1653.53,521.206 \n",
" 1657.52,523.985 1658.44,524.64 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#ba3655; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1609.36,562.42 1611.95,564.099 1614.61,565.855 1616.51,567.116 1619.72,569.289 1621.07,570.206 1624.7,572.724 1625.62,573.372 1629.54,576.158 1630.18,576.617 \n",
" 1634.26,579.593 1634.74,579.945 1638.85,583.027 1639.29,583.361 1643.32,586.462 1643.85,586.869 1647.68,589.896 1648.41,590.475 1651.92,593.331 1652.96,594.185 \n",
" 1656.05,596.765 1657.52,598.005 1660.07,600.2 1662.07,601.942 1663.99,603.634 1666.63,606.006 1667.8,607.069 1671.19,610.204 1671.51,610.503 1675.11,613.938 \n",
" 1675.74,614.548 1678.62,617.372 1680.3,619.049 1682.03,620.807 1684.86,623.722 1685.35,624.241 1688.58,627.676 1689.41,628.583 1691.71,631.11 1693.97,633.651 \n",
" 1694.75,634.545 1697.71,637.979 1698.53,638.95 1700.58,641.414 1703.08,644.506 1703.36,644.848 1706.05,648.283 1707.64,650.358 1708.67,651.717 1711.2,655.152 \n",
" 1712.19,656.544 1713.65,658.586 1716.01,662.021 1716.75,663.123 1718.3,665.455 1720.51,668.89 1721.31,670.167 1722.64,672.324 1724.7,675.759 1725.86,677.777 \n",
" 1726.68,679.193 1728.58,682.628 1730.41,686.062 1730.42,686.089 1732.16,689.497 1733.84,692.931 1734.98,695.349 1735.45,696.366 1736.99,699.8 1738.45,703.235 \n",
" 1739.53,705.904 1739.84,706.669 1741.17,710.104 1742.42,713.538 1743.6,716.973 1744.09,718.491 1744.71,720.407 1745.76,723.842 1746.73,727.276 1747.63,730.711 \n",
" 1748.47,734.145 1748.65,734.939 1749.24,737.58 1749.94,741.014 1750.58,744.449 1751.15,747.883 1751.65,751.318 1752.08,754.752 1752.44,758.187 1752.74,761.621 \n",
" 1752.97,765.056 1753.13,768.49 1753.2,770.799 1753.23,771.925 1753.27,775.359 1753.23,778.794 1753.2,779.92 1753.13,782.228 1752.97,785.663 1752.74,789.097 \n",
" 1752.44,792.532 1752.08,795.966 1751.65,799.401 1751.15,802.835 1750.58,806.27 1749.94,809.704 1749.24,813.139 1748.65,815.779 1748.47,816.573 1747.63,820.008 \n",
" 1746.73,823.442 1745.76,826.877 1744.71,830.312 1744.09,832.228 1743.6,833.746 1742.42,837.181 1741.17,840.615 1739.84,844.05 1739.53,844.815 1738.45,847.484 \n",
" 1736.99,850.919 1735.45,854.353 1734.98,855.37 1733.84,857.788 1732.16,861.222 1730.42,864.63 1730.41,864.657 1728.58,868.091 1726.68,871.526 1725.86,872.942 \n",
" 1724.7,874.96 1722.64,878.395 1721.31,880.552 1720.51,881.829 1718.3,885.264 1716.75,887.596 1716.01,888.698 1713.65,892.133 1712.19,894.174 1711.2,895.567 \n",
" 1708.67,899.002 1707.64,900.361 1706.05,902.436 1703.36,905.871 1703.08,906.213 1700.58,909.305 1698.53,911.769 1697.71,912.74 1694.75,916.174 1693.97,917.068 \n",
" 1691.71,919.609 1689.41,922.136 1688.58,923.043 1685.35,926.478 1684.86,926.997 1682.03,929.912 1680.3,931.67 1678.62,933.347 1675.74,936.171 1675.11,936.781 \n",
" 1671.51,940.216 1671.19,940.515 1667.8,943.65 1666.63,944.713 1663.99,947.085 1662.07,948.777 1660.07,950.519 1657.52,952.714 1656.05,953.954 1652.96,956.534 \n",
" 1651.92,957.388 1648.41,960.244 1647.68,960.823 1643.85,963.85 1643.32,964.257 1639.29,967.358 1638.85,967.692 1634.74,970.774 1634.26,971.126 1630.18,974.102 \n",
" 1629.54,974.561 1625.62,977.347 1624.7,977.995 1621.07,980.513 1619.72,981.43 1616.51,983.603 1614.61,984.864 1611.95,986.62 1609.36,988.299 1607.4,989.567 \n",
" 1603.97,991.733 1602.84,992.447 1598.44,995.168 1598.29,995.262 1593.73,998.019 1592.75,998.602 1589.17,1000.72 1586.89,1002.04 1584.62,1003.35 1580.88,1005.47 \n",
" 1580.06,1005.94 1575.5,1008.47 1574.7,1008.91 1570.95,1010.95 1568.33,1012.34 1566.39,1013.37 1561.83,1015.75 1561.79,1015.77 1557.28,1018.09 1555.04,1019.21 \n",
" 1552.72,1020.37 1548.17,1022.61 1548.1,1022.64 1543.61,1024.81 1540.94,1026.08 1539.05,1026.97 1534.5,1029.08 1533.56,1029.51 1529.94,1031.16 1525.94,1032.95 \n",
" 1525.38,1033.2 1520.83,1035.2 1518.07,1036.38 1516.27,1037.16 1511.71,1039.08 1509.94,1039.82 1507.16,1040.97 1502.6,1042.82 1501.53,1043.25 1498.04,1044.64 \n",
" 1493.49,1046.43 1492.82,1046.69 1488.93,1048.18 1484.38,1049.9 1483.79,1050.12 1479.82,1051.59 1475.26,1053.25 1474.41,1053.55 1470.71,1054.88 1466.15,1056.48 \n",
" 1464.66,1056.99 1461.59,1058.04 1457.04,1059.58 1454.5,1060.42 1452.48,1061.09 1447.92,1062.58 1443.91,1063.86 1443.37,1064.03 1438.81,1065.46 1434.26,1066.86 \n",
" 1432.82,1067.29 1429.7,1068.24 1425.14,1069.58 1421.2,1070.73 1420.59,1070.9 1416.03,1072.2 1411.47,1073.48 1408.97,1074.16 1406.92,1074.72 1402.36,1075.95 \n",
" 1397.8,1077.15 1396.06,1077.6 1393.25,1078.32 1388.69,1079.47 1384.14,1080.6 1382.36,1081.03 1379.58,1081.71 1375.02,1082.79 1370.47,1083.85 1367.76,1084.46 \n",
" 1365.91,1084.89 1361.35,1085.9 1356.8,1086.9 1352.24,1087.87 1352.09,1087.9 1347.68,1088.82 1343.13,1089.75 1338.57,1090.66 1335.1,1091.33 1334.02,1091.55 \n",
" 1329.46,1092.41 1324.9,1093.26 1320.35,1094.09 1316.48,1094.77 1315.79,1094.89 1311.23,1095.68 1306.68,1096.44 1302.12,1097.19 1297.56,1097.92 1295.7,1098.2 \n",
" 1293.01,1098.62 1288.45,1099.31 1283.9,1099.98 1279.34,1100.63 1274.78,1101.26 1271.94,1101.64 1270.23,1101.87 1265.67,1102.46 1261.11,1103.04 1256.56,1103.59 \n",
" 1252,1104.13 1247.44,1104.64 1243.54,1105.07 1242.89,1105.14 1238.33,1105.63 1233.78,1106.09 1229.22,1106.54 1224.66,1106.96 1220.11,1107.37 1215.55,1107.76 \n",
" 1210.99,1108.14 1206.44,1108.49 1206.22,1108.51 1201.88,1108.83 1197.32,1109.15 1192.77,1109.45 1188.21,1109.74 1183.66,1110.01 1179.1,1110.26 1174.54,1110.49 \n",
" 1169.99,1110.71 1165.43,1110.9 1160.87,1111.08 1156.32,1111.25 1151.76,1111.39 1147.2,1111.52 1142.65,1111.63 1138.09,1111.73 1133.54,1111.8 1128.98,1111.86 \n",
" 1124.42,1111.91 1119.87,1111.93 1115.76,1111.94 1115.31,1111.94 1114.86,1111.94 1110.75,1111.93 1106.2,1111.91 1101.64,1111.86 1097.08,1111.8 1092.53,1111.73 \n",
" 1087.97,1111.63 1083.42,1111.52 1078.86,1111.39 1074.3,1111.25 1069.75,1111.08 1065.19,1110.9 1060.63,1110.71 1056.08,1110.49 1051.52,1110.26 1046.96,1110.01 \n",
" 1042.41,1109.74 1037.85,1109.45 1033.3,1109.15 1028.74,1108.83 1024.4,1108.51 1024.18,1108.49 1019.63,1108.14 1015.07,1107.76 1010.51,1107.37 1005.96,1106.96 \n",
" 1001.4,1106.54 996.845,1106.09 992.288,1105.63 987.732,1105.14 987.085,1105.07 983.176,1104.64 978.619,1104.13 974.063,1103.59 969.507,1103.04 964.95,1102.46 \n",
" 960.394,1101.87 958.679,1101.64 955.837,1101.26 951.281,1100.63 946.725,1099.98 942.168,1099.31 937.612,1098.62 934.916,1098.2 933.056,1097.92 928.499,1097.19 \n",
" 923.943,1096.44 919.386,1095.68 914.83,1094.89 914.141,1094.77 910.274,1094.09 905.717,1093.26 901.161,1092.41 896.605,1091.55 895.52,1091.33 892.048,1090.66 \n",
" 887.492,1089.75 882.936,1088.82 878.528,1087.9 878.379,1087.87 873.823,1086.9 869.266,1085.9 864.71,1084.89 862.859,1084.46 860.154,1083.85 855.597,1082.79 \n",
" 851.041,1081.71 848.258,1081.03 846.485,1080.6 841.928,1079.47 837.372,1078.32 834.565,1077.6 832.816,1077.15 828.259,1075.95 823.703,1074.72 821.655,1074.16 \n",
" 819.146,1073.48 814.59,1072.2 810.034,1070.9 809.422,1070.73 805.477,1069.58 800.921,1068.24 797.802,1067.29 796.365,1066.86 791.808,1065.46 787.252,1064.03 \n",
" 786.713,1063.86 782.696,1062.58 778.139,1061.09 776.12,1060.42 773.583,1059.58 769.026,1058.04 765.964,1056.99 764.47,1056.48 759.914,1054.88 756.212,1053.55 \n",
" 755.357,1053.25 750.801,1051.59 746.834,1050.12 746.245,1049.9 741.688,1048.18 737.802,1046.69 737.132,1046.43 732.575,1044.64 729.092,1043.25 728.019,1042.82 \n",
" 723.463,1040.97 720.681,1039.82 718.906,1039.08 714.35,1037.16 712.55,1036.38 709.794,1035.2 705.237,1033.2 704.68,1032.95 700.681,1031.16 697.064,1029.51 \n",
" 696.125,1029.08 691.568,1026.97 689.684,1026.08 687.012,1024.81 682.52,1022.64 682.455,1022.61 677.899,1020.37 675.58,1019.21 673.343,1018.09 668.832,1015.77 \n",
" 668.786,1015.75 664.23,1013.37 662.289,1012.34 659.674,1010.95 655.924,1008.91 655.117,1008.47 650.561,1005.94 649.739,1005.47 646.005,1003.35 643.726,1002.04 \n",
" 641.448,1000.72 637.875,998.602 636.892,998.019 632.335,995.262 632.182,995.168 627.779,992.447 626.646,991.733 623.223,989.567 621.257,988.299 618.666,986.62 \n",
" 616.009,984.864 614.11,983.603 610.9,981.43 609.554,980.513 605.925,977.995 604.997,977.347 601.081,974.561 600.441,974.102 596.363,971.126 595.884,970.774 \n",
" 591.77,967.692 591.328,967.358 587.297,964.257 586.772,963.85 582.941,960.823 582.215,960.244 578.699,957.388 577.659,956.534 574.569,953.954 573.103,952.714 \n",
" 570.548,950.519 568.546,948.777 566.634,947.085 563.99,944.713 562.823,943.65 559.434,940.515 559.115,940.216 555.508,936.781 554.877,936.171 551.999,933.347 \n",
" 550.321,931.67 548.586,929.912 545.764,926.997 545.268,926.478 542.043,923.043 541.208,922.136 538.91,919.609 536.652,917.068 535.867,916.174 532.912,912.74 \n",
" 532.095,911.769 530.044,909.305 527.539,906.213 527.265,905.871 524.567,902.436 522.983,900.361 521.955,899.002 519.425,895.567 518.426,894.174 516.975,892.133 \n",
" 514.608,888.698 513.87,887.596 512.318,885.264 510.11,881.829 509.314,880.552 507.977,878.395 505.922,874.96 504.757,872.942 503.944,871.526 502.039,868.091 \n",
" 500.215,864.657 500.201,864.63 498.456,861.222 496.776,857.788 495.644,855.37 495.17,854.353 493.63,850.919 492.168,847.484 491.088,844.815 490.778,844.05 \n",
" 489.452,840.615 488.2,837.181 487.022,833.746 486.532,832.228 485.91,830.312 484.864,826.877 483.889,823.442 482.986,820.008 482.153,816.573 481.975,815.779 \n",
" 481.381,813.139 480.677,809.704 480.041,806.27 479.474,802.835 478.975,799.401 478.544,795.966 478.179,792.532 477.882,789.097 477.65,785.663 477.485,782.228 \n",
" 477.419,779.92 477.386,778.794 477.353,775.359 477.386,771.925 477.419,770.799 477.485,768.49 477.65,765.056 477.882,761.621 478.179,758.187 478.544,754.752 \n",
" 478.975,751.318 479.474,747.883 480.041,744.449 480.677,741.014 481.381,737.58 481.975,734.939 482.153,734.145 482.986,730.711 483.889,727.276 484.864,723.842 \n",
" 485.91,720.407 486.532,718.491 487.022,716.973 488.2,713.538 489.452,710.104 490.778,706.669 491.088,705.904 492.168,703.235 493.63,699.8 495.17,696.366 \n",
" 495.644,695.349 496.776,692.931 498.456,689.497 500.201,686.089 500.215,686.062 502.039,682.628 503.944,679.193 504.757,677.777 505.922,675.759 507.977,672.324 \n",
" 509.314,670.167 510.11,668.89 512.318,665.455 513.87,663.123 514.608,662.021 516.975,658.586 518.426,656.544 519.425,655.152 521.955,651.717 522.983,650.358 \n",
" 524.567,648.283 527.265,644.848 527.539,644.506 530.044,641.414 532.095,638.95 532.912,637.979 535.867,634.545 536.652,633.651 538.91,631.11 541.208,628.583 \n",
" 542.043,627.676 545.268,624.241 545.764,623.722 548.586,620.807 550.321,619.049 551.999,617.372 554.877,614.548 555.508,613.938 559.115,610.503 559.434,610.204 \n",
" 562.823,607.069 563.99,606.006 566.634,603.634 568.546,601.942 570.548,600.2 573.103,598.005 574.569,596.765 577.659,594.185 578.699,593.331 582.215,590.475 \n",
" 582.941,589.896 586.772,586.869 587.297,586.462 591.328,583.361 591.77,583.027 595.884,579.945 596.363,579.593 600.441,576.617 601.081,576.158 604.997,573.372 \n",
" 605.925,572.724 609.554,570.206 610.9,569.289 614.11,567.116 616.009,565.855 618.666,564.099 621.257,562.42 623.223,561.152 626.646,558.986 627.779,558.272 \n",
" 632.182,555.551 632.335,555.456 636.892,552.7 637.875,552.117 641.448,550.003 643.726,548.682 646.005,547.364 649.739,545.247 650.561,544.782 655.117,542.252 \n",
" 655.924,541.813 659.674,539.773 662.289,538.378 664.23,537.345 668.786,534.968 668.832,534.944 673.343,532.633 675.58,531.509 677.899,530.346 682.455,528.106 \n",
" 682.52,528.075 687.012,525.905 689.684,524.64 691.568,523.748 696.125,521.634 697.064,521.206 700.681,519.557 704.68,517.771 705.237,517.522 709.794,515.522 \n",
" 712.55,514.337 714.35,513.562 718.906,511.638 720.681,510.902 723.463,509.749 728.019,507.896 729.092,507.468 732.575,506.075 737.132,504.291 737.802,504.033 \n",
" 741.688,502.536 746.245,500.817 746.834,500.599 750.801,499.126 755.357,497.47 756.212,497.164 759.914,495.84 764.47,494.244 765.964,493.73 769.026,492.675 \n",
" 773.583,491.136 776.12,490.295 778.139,489.625 782.696,488.142 786.713,486.861 787.252,486.689 791.808,485.259 796.365,483.859 797.802,483.426 800.921,482.484 \n",
" 805.477,481.135 809.422,479.992 810.034,479.814 814.59,478.515 819.146,477.243 821.655,476.557 823.703,475.996 828.259,474.771 832.816,473.573 834.565,473.123 \n",
" 837.372,472.398 841.928,471.245 846.485,470.118 848.258,469.688 851.041,469.012 855.597,467.928 860.154,466.869 862.859,466.254 864.71,465.831 869.266,464.814 \n",
" 873.823,463.821 878.379,462.85 878.528,462.819 882.936,461.898 887.492,460.967 892.048,460.06 895.52,459.385 896.605,459.173 901.161,458.305 905.717,457.458 \n",
" 910.274,456.633 914.141,455.95 914.83,455.828 919.386,455.041 923.943,454.275 928.499,453.529 933.056,452.804 934.916,452.516 937.612,452.097 942.168,451.408 \n",
" 946.725,450.74 951.281,450.091 955.837,449.462 958.679,449.081 960.394,448.851 964.95,448.257 969.507,447.683 974.063,447.128 978.619,446.592 983.176,446.075 \n",
" 987.085,445.647 987.732,445.576 992.288,445.093 996.845,444.629 1001.4,444.184 1005.96,443.756 1010.51,443.347 1015.07,442.956 1019.63,442.583 1024.18,442.228 \n",
" 1024.4,442.212 1028.74,441.89 1033.3,441.569 1037.85,441.265 1042.41,440.98 1046.96,440.712 1051.52,440.462 1056.08,440.229 1060.63,440.013 1065.19,439.815 \n",
" 1069.75,439.635 1074.3,439.472 1078.86,439.326 1083.42,439.197 1087.97,439.085 1092.53,438.991 1097.08,438.914 1101.64,438.854 1106.2,438.811 1110.75,438.786 \n",
" 1114.86,438.778 1115.31,438.777 1115.76,438.778 1119.87,438.786 1124.42,438.811 1128.98,438.854 1133.54,438.914 1138.09,438.991 1142.65,439.085 1147.2,439.197 \n",
" 1151.76,439.326 1156.32,439.472 1160.87,439.635 1165.43,439.815 1169.99,440.013 1174.54,440.229 1179.1,440.462 1183.66,440.712 1188.21,440.98 1192.77,441.265 \n",
" 1197.32,441.569 1201.88,441.89 1206.22,442.212 1206.44,442.228 1210.99,442.583 1215.55,442.956 1220.11,443.347 1224.66,443.756 1229.22,444.184 1233.78,444.629 \n",
" 1238.33,445.093 1242.89,445.576 1243.54,445.647 1247.44,446.075 1252,446.592 1256.56,447.128 1261.11,447.683 1265.67,448.257 1270.23,448.851 1271.94,449.081 \n",
" 1274.78,449.462 1279.34,450.091 1283.9,450.74 1288.45,451.408 1293.01,452.097 1295.7,452.516 1297.56,452.804 1302.12,453.529 1306.68,454.275 1311.23,455.041 \n",
" 1315.79,455.828 1316.48,455.95 1320.35,456.633 1324.9,457.458 1329.46,458.305 1334.02,459.173 1335.1,459.385 1338.57,460.06 1343.13,460.967 1347.68,461.898 \n",
" 1352.09,462.819 1352.24,462.85 1356.8,463.821 1361.35,464.814 1365.91,465.831 1367.76,466.254 1370.47,466.869 1375.02,467.928 1379.58,469.012 1382.36,469.688 \n",
" 1384.14,470.118 1388.69,471.245 1393.25,472.398 1396.06,473.123 1397.8,473.573 1402.36,474.771 1406.92,475.996 1408.97,476.557 1411.47,477.243 1416.03,478.515 \n",
" 1420.59,479.814 1421.2,479.992 1425.14,481.135 1429.7,482.484 1432.82,483.426 1434.26,483.859 1438.81,485.259 1443.37,486.689 1443.91,486.861 1447.92,488.142 \n",
" 1452.48,489.625 1454.5,490.295 1457.04,491.136 1461.59,492.675 1464.66,493.73 1466.15,494.244 1470.71,495.84 1474.41,497.164 1475.26,497.47 1479.82,499.126 \n",
" 1483.79,500.599 1484.38,500.817 1488.93,502.536 1492.82,504.033 1493.49,504.291 1498.04,506.075 1501.53,507.468 1502.6,507.896 1507.16,509.749 1509.94,510.902 \n",
" 1511.71,511.638 1516.27,513.562 1518.07,514.337 1520.83,515.522 1525.38,517.522 1525.94,517.771 1529.94,519.557 1533.56,521.206 1534.5,521.634 1539.05,523.748 \n",
" 1540.94,524.64 1543.61,525.905 1548.1,528.075 1548.17,528.106 1552.72,530.346 1555.04,531.509 1557.28,532.633 1561.79,534.944 1561.83,534.968 1566.39,537.345 \n",
" 1568.33,538.378 1570.95,539.773 1574.7,541.813 1575.5,542.252 1580.06,544.782 1580.88,545.247 1584.62,547.364 1586.89,548.682 1589.17,550.003 1592.75,552.117 \n",
" 1593.73,552.7 1598.29,555.456 1598.44,555.551 1602.84,558.272 1603.97,558.986 1607.4,561.152 1609.36,562.42 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#d24742; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1561.83,593.795 1560.99,593.331 1557.28,591.288 1554.69,589.896 1552.72,588.841 1548.18,586.462 1548.17,586.454 1543.61,584.115 1541.44,583.027 1539.05,581.831 \n",
" 1534.5,579.602 1534.48,579.593 1529.94,577.414 1527.26,576.158 1525.38,575.278 1520.83,573.188 1519.79,572.724 1516.27,571.14 1512.05,569.289 1511.71,569.14 \n",
" 1507.16,567.176 1504.02,565.855 1502.6,565.256 1498.04,563.374 1495.68,562.42 1493.49,561.531 1488.93,559.727 1487.02,558.986 1484.38,557.958 1479.82,556.225 \n",
" 1478.01,555.551 1475.26,554.527 1470.71,552.863 1468.62,552.117 1466.15,551.232 1461.59,549.634 1458.82,548.682 1457.04,548.069 1452.48,546.533 1448.58,545.247 \n",
" 1447.92,545.031 1443.37,543.554 1438.81,542.112 1437.85,541.813 1434.26,540.694 1429.7,539.307 1426.58,538.378 1425.14,537.948 1420.59,536.615 1416.03,535.311 \n",
" 1414.72,534.944 1411.47,534.032 1406.92,532.779 1402.36,531.554 1402.19,531.509 1397.8,530.35 1393.25,529.174 1388.89,528.075 1388.69,528.024 1384.14,526.894 \n",
" 1379.58,525.79 1375.02,524.713 1374.71,524.64 1370.47,523.654 1365.91,522.619 1361.35,521.61 1359.49,521.206 1356.8,520.621 1352.24,519.653 1347.68,518.709 \n",
" 1343.13,517.788 1343.04,517.771 1338.57,516.885 1334.02,516.004 1329.46,515.146 1325.05,514.337 1324.9,514.309 1320.35,513.49 1315.79,512.692 1311.23,511.916 \n",
" 1306.68,511.16 1305.08,510.902 1302.12,510.422 1297.56,509.704 1293.01,509.006 1288.45,508.329 1283.9,507.671 1282.45,507.468 1279.34,507.03 1274.78,506.409 \n",
" 1270.23,505.806 1265.67,505.223 1261.11,504.659 1256.56,504.114 1255.86,504.033 1252,503.586 1247.44,503.075 1242.89,502.583 1238.33,502.11 1233.78,501.655 \n",
" 1229.22,501.218 1224.66,500.8 1222.38,500.599 1220.11,500.398 1215.55,500.013 1210.99,499.646 1206.44,499.296 1201.88,498.964 1197.32,498.65 1192.77,498.353 \n",
" 1188.21,498.074 1183.66,497.812 1179.1,497.567 1174.54,497.339 1170.76,497.164 1169.99,497.128 1165.43,496.934 1160.87,496.756 1156.32,496.596 1151.76,496.452 \n",
" 1147.2,496.326 1142.65,496.216 1138.09,496.124 1133.54,496.048 1128.98,495.989 1124.42,495.947 1119.87,495.922 1115.31,495.913 1110.75,495.922 1106.2,495.947 \n",
" 1101.64,495.989 1097.08,496.048 1092.53,496.124 1087.97,496.216 1083.42,496.326 1078.86,496.452 1074.3,496.596 1069.75,496.756 1065.19,496.934 1060.63,497.128 \n",
" 1059.86,497.164 1056.08,497.339 1051.52,497.567 1046.96,497.812 1042.41,498.074 1037.85,498.353 1033.3,498.65 1028.74,498.964 1024.18,499.296 1019.63,499.646 \n",
" 1015.07,500.013 1010.51,500.398 1008.24,500.599 1005.96,500.8 1001.4,501.218 996.845,501.655 992.288,502.11 987.732,502.583 983.176,503.075 978.619,503.586 \n",
" 974.762,504.033 974.063,504.114 969.507,504.659 964.95,505.223 960.394,505.806 955.837,506.409 951.281,507.03 948.173,507.468 946.725,507.671 942.168,508.329 \n",
" 937.612,509.006 933.056,509.704 928.499,510.422 925.539,510.902 923.943,511.16 919.386,511.916 914.83,512.692 910.274,513.49 905.717,514.309 905.568,514.337 \n",
" 901.161,515.146 896.605,516.004 892.048,516.885 887.577,517.771 887.492,517.788 882.936,518.709 878.379,519.653 873.823,520.621 871.132,521.206 869.266,521.61 \n",
" 864.71,522.619 860.154,523.654 855.909,524.64 855.597,524.713 851.041,525.79 846.485,526.894 841.928,528.024 841.728,528.075 837.372,529.174 832.816,530.35 \n",
" 828.43,531.509 828.259,531.554 823.703,532.779 819.146,534.032 815.902,534.944 814.59,535.311 810.034,536.615 805.477,537.948 804.04,538.378 800.921,539.307 \n",
" 796.365,540.694 792.772,541.813 791.808,542.112 787.252,543.554 782.696,545.031 782.041,545.247 778.139,546.533 773.583,548.069 771.803,548.682 769.026,549.634 \n",
" 764.47,551.232 762.004,552.117 759.914,552.863 755.357,554.527 752.614,555.551 750.801,556.225 746.245,557.958 743.601,558.986 741.688,559.727 737.132,561.531 \n",
" 734.938,562.42 732.575,563.374 728.019,565.256 726.601,565.855 723.463,567.176 718.906,569.14 718.567,569.289 714.35,571.14 710.83,572.724 709.794,573.188 \n",
" 705.237,575.278 703.362,576.158 700.681,577.414 696.143,579.593 696.125,579.602 691.568,581.831 689.183,583.027 687.012,584.115 682.455,586.454 682.441,586.462 \n",
" 677.899,588.841 675.934,589.896 673.343,591.288 669.631,593.331 668.786,593.795 664.23,596.363 663.532,596.765 659.674,598.992 657.632,600.2 655.117,601.69 \n",
" 651.916,603.634 650.561,604.459 646.378,607.069 646.005,607.302 641.448,610.221 641.018,610.503 636.892,613.22 635.828,613.938 632.335,616.306 630.801,617.372 \n",
" 627.779,619.484 625.931,620.807 623.223,622.759 621.214,624.241 618.666,626.137 616.646,627.676 614.11,629.626 612.223,631.11 609.554,633.234 607.942,634.545 \n",
" 604.997,636.969 603.797,637.979 600.441,640.844 599.787,641.414 595.908,644.848 595.884,644.87 592.16,648.283 591.328,649.059 588.536,651.717 586.772,653.431 \n",
" 585.035,655.152 582.215,658.007 581.654,658.586 578.392,662.021 577.659,662.81 575.246,665.455 573.103,667.871 572.214,668.89 569.295,672.324 568.546,673.229 \n",
" 566.485,675.759 563.99,678.931 563.787,679.193 561.192,682.628 559.434,685.048 558.706,686.062 556.321,689.497 554.877,691.665 554.042,692.931 551.863,696.366 \n",
" 550.321,698.912 549.787,699.8 547.806,703.235 545.931,706.669 545.764,706.987 544.143,710.104 542.458,713.538 541.208,716.243 540.872,716.973 539.371,720.407 \n",
" 537.971,723.842 536.67,727.276 536.652,727.327 535.448,730.711 534.324,734.145 533.295,737.58 532.36,741.014 532.095,742.089 531.509,744.449 530.747,747.883 \n",
" 530.077,751.318 529.498,754.752 529.01,758.187 528.611,761.621 528.302,765.056 528.082,768.49 527.95,771.925 527.906,775.359 527.95,778.794 528.082,782.228 \n",
" 528.302,785.663 528.611,789.097 529.01,792.532 529.498,795.966 530.077,799.401 530.747,802.835 531.509,806.27 532.095,808.63 532.36,809.704 533.295,813.139 \n",
" 534.324,816.573 535.448,820.008 536.652,823.392 536.67,823.442 537.971,826.877 539.371,830.312 540.872,833.746 541.208,834.476 542.458,837.181 544.143,840.615 \n",
" 545.764,843.732 545.931,844.05 547.806,847.484 549.787,850.919 550.321,851.807 551.863,854.353 554.042,857.788 554.877,859.054 556.321,861.222 558.706,864.657 \n",
" 559.434,865.671 561.192,868.091 563.787,871.526 563.99,871.788 566.485,874.96 568.546,877.49 569.295,878.395 572.214,881.829 573.103,882.848 575.246,885.264 \n",
" 577.659,887.909 578.392,888.698 581.654,892.133 582.215,892.712 585.035,895.567 586.772,897.288 588.536,899.002 591.328,901.66 592.16,902.436 595.884,905.849 \n",
" 595.908,905.871 599.787,909.305 600.441,909.875 603.797,912.74 604.997,913.75 607.942,916.174 609.554,917.485 612.223,919.609 614.11,921.093 616.646,923.043 \n",
" 618.666,924.582 621.214,926.478 623.223,927.96 625.931,929.912 627.779,931.235 630.801,933.347 632.335,934.412 635.828,936.781 636.892,937.498 641.018,940.216 \n",
" 641.448,940.498 646.005,943.416 646.378,943.65 650.561,946.26 651.916,947.085 655.117,949.029 657.632,950.519 659.674,951.727 663.532,953.954 664.23,954.356 \n",
" 668.786,956.923 669.631,957.388 673.343,959.431 675.934,960.823 677.899,961.878 682.441,964.257 682.455,964.265 687.012,966.604 689.183,967.692 691.568,968.888 \n",
" 696.125,971.117 696.143,971.126 700.681,973.305 703.362,974.561 705.237,975.441 709.794,977.53 710.83,977.995 714.35,979.579 718.567,981.43 718.906,981.579 \n",
" 723.463,983.543 726.601,984.864 728.019,985.463 732.575,987.345 734.938,988.299 737.132,989.187 741.688,990.992 743.601,991.733 746.245,992.761 750.801,994.493 \n",
" 752.614,995.168 755.357,996.192 759.914,997.856 762.004,998.602 764.47,999.486 769.026,1001.08 771.803,1002.04 773.583,1002.65 778.139,1004.19 782.041,1005.47 \n",
" 782.696,1005.69 787.252,1007.16 791.808,1008.61 792.772,1008.91 796.365,1010.02 800.921,1011.41 804.04,1012.34 805.477,1012.77 810.034,1014.1 814.59,1015.41 \n",
" 815.902,1015.77 819.146,1016.69 823.703,1017.94 828.259,1019.16 828.43,1019.21 832.816,1020.37 837.372,1021.54 841.728,1022.64 841.928,1022.69 846.485,1023.82 \n",
" 851.041,1024.93 855.597,1026.01 855.909,1026.08 860.154,1027.07 864.71,1028.1 869.266,1029.11 871.132,1029.51 873.823,1030.1 878.379,1031.07 882.936,1032.01 \n",
" 887.492,1032.93 887.577,1032.95 892.048,1033.83 896.605,1034.71 901.161,1035.57 905.568,1036.38 905.717,1036.41 910.274,1037.23 914.83,1038.03 919.386,1038.8 \n",
" 923.943,1039.56 925.539,1039.82 928.499,1040.3 933.056,1041.01 937.612,1041.71 942.168,1042.39 946.725,1043.05 948.173,1043.25 951.281,1043.69 955.837,1044.31 \n",
" 960.394,1044.91 964.95,1045.5 969.507,1046.06 974.063,1046.6 974.762,1046.69 978.619,1047.13 983.176,1047.64 987.732,1048.14 992.288,1048.61 996.845,1049.06 \n",
" 1001.4,1049.5 1005.96,1049.92 1008.24,1050.12 1010.51,1050.32 1015.07,1050.71 1019.63,1051.07 1024.18,1051.42 1028.74,1051.75 1033.3,1052.07 1037.85,1052.37 \n",
" 1042.41,1052.64 1046.96,1052.91 1051.52,1053.15 1056.08,1053.38 1059.86,1053.55 1060.63,1053.59 1065.19,1053.79 1069.75,1053.96 1074.3,1054.12 1078.86,1054.27 \n",
" 1083.42,1054.39 1087.97,1054.5 1092.53,1054.6 1097.08,1054.67 1101.64,1054.73 1106.2,1054.77 1110.75,1054.8 1115.31,1054.81 1119.87,1054.8 1124.42,1054.77 \n",
" 1128.98,1054.73 1133.54,1054.67 1138.09,1054.6 1142.65,1054.5 1147.2,1054.39 1151.76,1054.27 1156.32,1054.12 1160.87,1053.96 1165.43,1053.79 1169.99,1053.59 \n",
" 1170.76,1053.55 1174.54,1053.38 1179.1,1053.15 1183.66,1052.91 1188.21,1052.64 1192.77,1052.37 1197.32,1052.07 1201.88,1051.75 1206.44,1051.42 1210.99,1051.07 \n",
" 1215.55,1050.71 1220.11,1050.32 1222.38,1050.12 1224.66,1049.92 1229.22,1049.5 1233.78,1049.06 1238.33,1048.61 1242.89,1048.14 1247.44,1047.64 1252,1047.13 \n",
" 1255.86,1046.69 1256.56,1046.6 1261.11,1046.06 1265.67,1045.5 1270.23,1044.91 1274.78,1044.31 1279.34,1043.69 1282.45,1043.25 1283.9,1043.05 1288.45,1042.39 \n",
" 1293.01,1041.71 1297.56,1041.01 1302.12,1040.3 1305.08,1039.82 1306.68,1039.56 1311.23,1038.8 1315.79,1038.03 1320.35,1037.23 1324.9,1036.41 1325.05,1036.38 \n",
" 1329.46,1035.57 1334.02,1034.71 1338.57,1033.83 1343.04,1032.95 1343.13,1032.93 1347.68,1032.01 1352.24,1031.07 1356.8,1030.1 1359.49,1029.51 1361.35,1029.11 \n",
" 1365.91,1028.1 1370.47,1027.07 1374.71,1026.08 1375.02,1026.01 1379.58,1024.93 1384.14,1023.82 1388.69,1022.69 1388.89,1022.64 1393.25,1021.54 1397.8,1020.37 \n",
" 1402.19,1019.21 1402.36,1019.16 1406.92,1017.94 1411.47,1016.69 1414.72,1015.77 1416.03,1015.41 1420.59,1014.1 1425.14,1012.77 1426.58,1012.34 1429.7,1011.41 \n",
" 1434.26,1010.02 1437.85,1008.91 1438.81,1008.61 1443.37,1007.16 1447.92,1005.69 1448.58,1005.47 1452.48,1004.19 1457.04,1002.65 1458.82,1002.04 1461.59,1001.08 \n",
" 1466.15,999.486 1468.62,998.602 1470.71,997.856 1475.26,996.192 1478.01,995.168 1479.82,994.493 1484.38,992.761 1487.02,991.733 1488.93,990.992 1493.49,989.187 \n",
" 1495.68,988.299 1498.04,987.345 1502.6,985.463 1504.02,984.864 1507.16,983.543 1511.71,981.579 1512.05,981.43 1516.27,979.579 1519.79,977.995 1520.83,977.53 \n",
" 1525.38,975.441 1527.26,974.561 1529.94,973.305 1534.48,971.126 1534.5,971.117 1539.05,968.888 1541.44,967.692 1543.61,966.604 1548.17,964.265 1548.18,964.257 \n",
" 1552.72,961.878 1554.69,960.823 1557.28,959.431 1560.99,957.388 1561.83,956.923 1566.39,954.356 1567.09,953.954 1570.95,951.727 1572.99,950.519 1575.5,949.029 \n",
" 1578.7,947.085 1580.06,946.26 1584.24,943.65 1584.62,943.416 1589.17,940.498 1589.6,940.216 1593.73,937.498 1594.79,936.781 1598.29,934.412 1599.82,933.347 \n",
" 1602.84,931.235 1604.69,929.912 1607.4,927.96 1609.41,926.478 1611.95,924.582 1613.97,923.043 1616.51,921.093 1618.4,919.609 1621.07,917.485 1622.68,916.174 \n",
" 1625.62,913.75 1626.82,912.74 1630.18,909.875 1630.83,909.305 1634.71,905.871 1634.74,905.849 1638.46,902.436 1639.29,901.66 1642.08,899.002 1643.85,897.288 \n",
" 1645.59,895.567 1648.41,892.712 1648.97,892.133 1652.23,888.698 1652.96,887.909 1655.37,885.264 1657.52,882.848 1658.41,881.829 1661.33,878.395 1662.07,877.49 \n",
" 1664.14,874.96 1666.63,871.788 1666.83,871.526 1669.43,868.091 1671.19,865.671 1671.91,864.657 1674.3,861.222 1675.74,859.054 1676.58,857.788 1678.76,854.353 \n",
" 1680.3,851.807 1680.83,850.919 1682.81,847.484 1684.69,844.05 1684.86,843.732 1686.48,840.615 1688.16,837.181 1689.41,834.476 1689.75,833.746 1691.25,830.312 \n",
" 1692.65,826.877 1693.95,823.442 1693.97,823.392 1695.17,820.008 1696.3,816.573 1697.33,813.139 1698.26,809.704 1698.53,808.63 1699.11,806.27 1699.87,802.835 \n",
" 1700.54,799.401 1701.12,795.966 1701.61,792.532 1702.01,789.097 1702.32,785.663 1702.54,782.228 1702.67,778.794 1702.71,775.359 1702.67,771.925 1702.54,768.49 \n",
" 1702.32,765.056 1702.01,761.621 1701.61,758.187 1701.12,754.752 1700.54,751.318 1699.87,747.883 1699.11,744.449 1698.53,742.089 1698.26,741.014 1697.33,737.58 \n",
" 1696.3,734.145 1695.17,730.711 1693.97,727.327 1693.95,727.276 1692.65,723.842 1691.25,720.407 1689.75,716.973 1689.41,716.243 1688.16,713.538 1686.48,710.104 \n",
" 1684.86,706.987 1684.69,706.669 1682.81,703.235 1680.83,699.8 1680.3,698.912 1678.76,696.366 1676.58,692.931 1675.74,691.665 1674.3,689.497 1671.91,686.062 \n",
" 1671.19,685.048 1669.43,682.628 1666.83,679.193 1666.63,678.931 1664.14,675.759 1662.07,673.229 1661.33,672.324 1658.41,668.89 1657.52,667.871 1655.37,665.455 \n",
" 1652.96,662.81 1652.23,662.021 1648.97,658.586 1648.41,658.007 1645.59,655.152 1643.85,653.431 1642.08,651.717 1639.29,649.059 1638.46,648.283 1634.74,644.87 \n",
" 1634.71,644.848 1630.83,641.414 1630.18,640.844 1626.82,637.979 1625.62,636.969 1622.68,634.545 1621.07,633.234 1618.4,631.11 1616.51,629.626 1613.97,627.676 \n",
" 1611.95,626.137 1609.41,624.241 1607.4,622.759 1604.69,620.807 1602.84,619.484 1599.82,617.372 1598.29,616.306 1594.79,613.938 1593.73,613.22 1589.6,610.503 \n",
" 1589.17,610.221 1584.62,607.302 1584.24,607.069 1580.06,604.459 1578.7,603.634 1575.5,601.69 1572.99,600.2 1570.95,598.992 1567.09,596.765 1566.39,596.363 \n",
" 1561.83,593.795 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#e65e2d; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1522.06,624.241 1525.38,625.788 1529.32,627.676 1529.94,627.972 1534.5,630.208 1536.28,631.11 1539.05,632.505 1542.98,634.545 1543.61,634.869 1548.17,637.295 \n",
" 1549.41,637.979 1552.72,639.79 1555.6,641.414 1557.28,642.362 1561.55,644.848 1561.83,645.015 1566.39,647.745 1567.26,648.283 1570.95,650.564 1572.75,651.717 \n",
" 1575.5,653.478 1578.03,655.152 1580.06,656.495 1583.11,658.586 1584.62,659.622 1587.99,662.021 1589.17,662.867 1592.67,665.455 1593.73,666.242 1597.17,668.89 \n",
" 1598.29,669.757 1601.48,672.324 1602.84,673.429 1605.62,675.759 1607.4,677.275 1609.58,679.193 1611.95,681.316 1613.38,682.628 1616.51,685.58 1617.01,686.062 \n",
" 1620.48,689.497 1621.07,690.097 1623.78,692.931 1625.62,694.912 1626.94,696.366 1629.94,699.8 1630.18,700.081 1632.79,703.235 1634.74,705.686 1635.5,706.669 \n",
" 1638.06,710.104 1639.29,711.839 1640.48,713.538 1642.75,716.973 1643.85,718.72 1644.89,720.407 1646.89,723.842 1648.41,726.629 1648.75,727.276 1650.49,730.711 \n",
" 1652.08,734.145 1652.96,736.206 1653.55,737.58 1654.89,741.014 1656.09,744.449 1657.16,747.883 1657.52,749.194 1658.11,751.318 1658.93,754.752 1659.63,758.187 \n",
" 1660.19,761.621 1660.63,765.056 1660.94,768.49 1661.13,771.925 1661.19,775.359 1661.13,778.794 1660.94,782.228 1660.63,785.663 1660.19,789.097 1659.63,792.532 \n",
" 1658.93,795.966 1658.11,799.401 1657.52,801.525 1657.16,802.835 1656.09,806.27 1654.89,809.704 1653.55,813.139 1652.96,814.513 1652.08,816.573 1650.49,820.008 \n",
" 1648.75,823.442 1648.41,824.09 1646.89,826.877 1644.89,830.312 1643.85,831.999 1642.75,833.746 1640.48,837.181 1639.29,838.879 1638.06,840.615 1635.5,844.05 \n",
" 1634.74,845.033 1632.79,847.484 1630.18,850.637 1629.94,850.919 1626.94,854.353 1625.62,855.807 1623.78,857.788 1621.07,860.622 1620.48,861.222 1617.01,864.657 \n",
" 1616.51,865.139 1613.38,868.091 1611.95,869.403 1609.58,871.526 1607.4,873.444 1605.62,874.96 1602.84,877.29 1601.48,878.395 1598.29,880.961 1597.17,881.829 \n",
" 1593.73,884.477 1592.67,885.264 1589.17,887.851 1587.99,888.698 1584.62,891.097 1583.11,892.133 1580.06,894.224 1578.03,895.567 1575.5,897.241 1572.75,899.002 \n",
" 1570.95,900.155 1567.26,902.436 1566.39,902.974 1561.83,905.704 1561.55,905.871 1557.28,908.357 1555.6,909.305 1552.72,910.929 1549.41,912.74 1548.17,913.424 \n",
" 1543.61,915.85 1542.98,916.174 1539.05,918.214 1536.28,919.609 1534.5,920.511 1529.94,922.747 1529.32,923.043 1525.38,924.93 1522.06,926.478 1520.83,927.054 \n",
" 1516.27,929.128 1514.5,929.912 1511.71,931.151 1507.16,933.122 1506.62,933.347 1502.6,935.052 1498.4,936.781 1498.04,936.93 1493.49,938.772 1489.82,940.216 \n",
" 1488.93,940.566 1484.38,942.324 1480.84,943.65 1479.82,944.038 1475.26,945.718 1471.46,947.085 1470.71,947.355 1466.15,948.963 1461.62,950.519 1461.59,950.528 \n",
" 1457.04,952.067 1452.48,953.567 1451.28,953.954 1447.92,955.038 1443.37,956.475 1440.4,957.388 1438.81,957.881 1434.26,959.26 1429.7,960.604 1428.94,960.823 \n",
" 1425.14,961.924 1420.59,963.214 1416.81,964.257 1416.03,964.474 1411.47,965.712 1406.92,966.919 1403.93,967.692 1402.36,968.1 1397.8,969.259 1393.25,970.389 \n",
" 1390.2,971.126 1388.69,971.495 1384.14,972.579 1379.58,973.637 1375.5,974.561 1375.02,974.67 1370.47,975.683 1365.91,976.672 1361.35,977.637 1359.62,977.995 \n",
" 1356.8,978.581 1352.24,979.505 1347.68,980.405 1343.13,981.282 1342.34,981.43 1338.57,982.141 1334.02,982.98 1329.46,983.796 1324.9,984.591 1323.3,984.864 \n",
" 1320.35,985.368 1315.79,986.126 1311.23,986.863 1306.68,987.58 1302.12,988.277 1301.97,988.299 1297.56,988.958 1293.01,989.619 1288.45,990.261 1283.9,990.884 \n",
" 1279.34,991.488 1277.43,991.733 1274.78,992.075 1270.23,992.644 1265.67,993.196 1261.11,993.729 1256.56,994.244 1252,994.741 1247.94,995.168 1247.44,995.221 \n",
" 1242.89,995.685 1238.33,996.132 1233.78,996.561 1229.22,996.973 1224.66,997.368 1220.11,997.746 1215.55,998.107 1210.99,998.451 1208.9,998.602 1206.44,998.78 \n",
" 1201.88,999.093 1197.32,999.389 1192.77,999.668 1188.21,999.932 1183.66,1000.18 1179.1,1000.41 1174.54,1000.62 1169.99,1000.82 1165.43,1001 1160.87,1001.17 \n",
" 1156.32,1001.32 1151.76,1001.45 1147.2,1001.57 1142.65,1001.68 1138.09,1001.76 1133.54,1001.83 1128.98,1001.89 1124.42,1001.93 1119.87,1001.95 1115.31,1001.96 \n",
" 1110.75,1001.95 1106.2,1001.93 1101.64,1001.89 1097.08,1001.83 1092.53,1001.76 1087.97,1001.68 1083.42,1001.57 1078.86,1001.45 1074.3,1001.32 1069.75,1001.17 \n",
" 1065.19,1001 1060.63,1000.82 1056.08,1000.62 1051.52,1000.41 1046.96,1000.18 1042.41,999.932 1037.85,999.668 1033.3,999.389 1028.74,999.093 1024.18,998.78 \n",
" 1021.72,998.602 1019.63,998.451 1015.07,998.107 1010.51,997.746 1005.96,997.368 1001.4,996.973 996.845,996.561 992.288,996.132 987.732,995.685 983.176,995.221 \n",
" 982.675,995.168 978.619,994.741 974.063,994.244 969.507,993.729 964.95,993.196 960.394,992.644 955.837,992.075 953.193,991.733 951.281,991.488 946.725,990.884 \n",
" 942.168,990.261 937.612,989.619 933.056,988.958 928.646,988.299 928.499,988.277 923.943,987.58 919.386,986.863 914.83,986.126 910.274,985.368 907.324,984.864 \n",
" 905.717,984.591 901.161,983.796 896.605,982.98 892.048,982.141 888.28,981.43 887.492,981.282 882.936,980.405 878.379,979.505 873.823,978.581 871.003,977.995 \n",
" 869.266,977.637 864.71,976.672 860.154,975.683 855.597,974.67 855.12,974.561 851.041,973.637 846.485,972.579 841.928,971.495 840.415,971.126 837.372,970.389 \n",
" 832.816,969.259 828.259,968.1 826.689,967.692 823.703,966.919 819.146,965.712 814.59,964.474 813.81,964.257 810.034,963.214 805.477,961.924 801.68,960.823 \n",
" 800.921,960.604 796.365,959.26 791.808,957.881 790.217,957.388 787.252,956.475 782.696,955.038 779.343,953.954 778.139,953.567 773.583,952.067 769.026,950.528 \n",
" 769,950.519 764.47,948.963 759.914,947.355 759.164,947.085 755.357,945.718 750.801,944.038 749.776,943.65 746.245,942.324 741.688,940.566 740.803,940.216 \n",
" 737.132,938.772 732.575,936.93 732.215,936.781 728.019,935.052 723.996,933.347 723.463,933.122 718.906,931.151 716.122,929.912 714.35,929.128 709.794,927.054 \n",
" 708.561,926.478 705.237,924.93 701.302,923.043 700.681,922.747 696.125,920.511 694.338,919.609 691.568,918.214 687.639,916.174 687.012,915.85 682.455,913.424 \n",
" 681.208,912.74 677.899,910.929 675.024,909.305 673.343,908.357 669.072,905.871 668.786,905.704 664.23,902.974 663.36,902.436 659.674,900.155 657.867,899.002 \n",
" 655.117,897.241 652.585,895.567 650.561,894.224 647.509,892.133 646.005,891.097 642.631,888.698 641.448,887.851 637.947,885.264 636.892,884.477 633.451,881.829 \n",
" 632.335,880.961 629.137,878.395 627.779,877.29 625.001,874.96 623.223,873.444 621.038,871.526 618.666,869.403 617.243,868.091 614.11,865.139 613.612,864.657 \n",
" 610.145,861.222 609.554,860.622 606.836,857.788 604.997,855.807 603.681,854.353 600.68,850.919 600.441,850.637 597.826,847.484 595.884,845.033 595.122,844.05 \n",
" 592.561,840.615 591.328,838.879 590.143,837.181 587.867,833.746 586.772,831.999 585.729,830.312 583.727,826.877 582.215,824.09 581.867,823.442 580.131,820.008 \n",
" 578.537,816.573 577.659,814.513 577.074,813.139 575.734,809.704 574.531,806.27 573.463,802.835 573.103,801.525 572.514,799.401 571.689,795.966 570.994,792.532 \n",
" 570.428,789.097 569.99,785.663 569.678,782.228 569.491,778.794 569.429,775.359 569.491,771.925 569.678,768.49 569.99,765.056 570.428,761.621 570.994,758.187 \n",
" 571.689,754.752 572.514,751.318 573.103,749.194 573.463,747.883 574.531,744.449 575.734,741.014 577.074,737.58 577.659,736.206 578.537,734.145 580.131,730.711 \n",
" 581.867,727.276 582.215,726.629 583.727,723.842 585.729,720.407 586.772,718.72 587.867,716.973 590.143,713.538 591.328,711.839 592.561,710.104 595.122,706.669 \n",
" 595.884,705.686 597.826,703.235 600.441,700.081 600.68,699.8 603.681,696.366 604.997,694.912 606.836,692.931 609.554,690.097 610.145,689.497 613.612,686.062 \n",
" 614.11,685.58 617.243,682.628 618.666,681.316 621.038,679.193 623.223,677.275 625.001,675.759 627.779,673.429 629.137,672.324 632.335,669.757 633.451,668.89 \n",
" 636.892,666.242 637.947,665.455 641.448,662.867 642.631,662.021 646.005,659.622 647.509,658.586 650.561,656.495 652.585,655.152 655.117,653.478 657.867,651.717 \n",
" 659.674,650.564 663.36,648.283 664.23,647.745 668.786,645.015 669.072,644.848 673.343,642.362 675.024,641.414 677.899,639.79 681.208,637.979 682.455,637.295 \n",
" 687.012,634.869 687.639,634.545 691.568,632.505 694.338,631.11 696.125,630.208 700.681,627.972 701.302,627.676 705.237,625.788 708.561,624.241 709.794,623.665 \n",
" 714.35,621.591 716.122,620.807 718.906,619.568 723.463,617.597 723.996,617.372 728.019,615.667 732.215,613.938 732.575,613.788 737.132,611.946 740.803,610.503 \n",
" 741.688,610.153 746.245,608.395 749.776,607.069 750.801,606.681 755.357,605.001 759.164,603.634 759.914,603.363 764.47,601.756 769,600.2 769.026,600.191 \n",
" 773.583,598.652 778.139,597.152 779.343,596.765 782.696,595.681 787.252,594.243 790.217,593.331 791.808,592.838 796.365,591.459 800.921,590.115 801.68,589.896 \n",
" 805.477,588.794 810.034,587.505 813.81,586.462 814.59,586.245 819.146,585.007 823.703,583.8 826.689,583.027 828.259,582.618 832.816,581.46 837.372,580.33 \n",
" 840.415,579.593 841.928,579.224 846.485,578.14 851.041,577.082 855.12,576.158 855.597,576.049 860.154,575.035 864.71,574.047 869.266,573.082 871.003,572.724 \n",
" 873.823,572.138 878.379,571.214 882.936,570.314 887.492,569.437 888.28,569.289 892.048,568.577 896.605,567.739 901.161,566.923 905.717,566.128 907.324,565.855 \n",
" 910.274,565.35 914.83,564.593 919.386,563.856 923.943,563.139 928.499,562.442 928.646,562.42 933.056,561.761 937.612,561.1 942.168,560.458 946.725,559.835 \n",
" 951.281,559.231 953.193,558.986 955.837,558.644 960.394,558.074 964.95,557.523 969.507,556.99 974.063,556.475 978.619,555.978 982.675,555.551 983.176,555.498 \n",
" 987.732,555.034 992.288,554.587 996.845,554.158 1001.4,553.746 1005.96,553.351 1010.51,552.973 1015.07,552.612 1019.63,552.267 1021.72,552.117 1024.18,551.939 \n",
" 1028.74,551.626 1033.3,551.33 1037.85,551.051 1042.41,550.787 1046.96,550.54 1051.52,550.31 1056.08,550.095 1060.63,549.897 1065.19,549.715 1069.75,549.549 \n",
" 1074.3,549.398 1078.86,549.264 1083.42,549.146 1087.97,549.043 1092.53,548.956 1097.08,548.885 1101.64,548.83 1106.2,548.791 1110.75,548.767 1115.31,548.759 \n",
" 1119.87,548.767 1124.42,548.791 1128.98,548.83 1133.54,548.885 1138.09,548.956 1142.65,549.043 1147.2,549.146 1151.76,549.264 1156.32,549.398 1160.87,549.549 \n",
" 1165.43,549.715 1169.99,549.897 1174.54,550.095 1179.1,550.31 1183.66,550.54 1188.21,550.787 1192.77,551.051 1197.32,551.33 1201.88,551.626 1206.44,551.939 \n",
" 1208.9,552.117 1210.99,552.267 1215.55,552.612 1220.11,552.973 1224.66,553.351 1229.22,553.746 1233.78,554.158 1238.33,554.587 1242.89,555.034 1247.44,555.498 \n",
" 1247.94,555.551 1252,555.978 1256.56,556.475 1261.11,556.99 1265.67,557.523 1270.23,558.074 1274.78,558.644 1277.43,558.986 1279.34,559.231 1283.9,559.835 \n",
" 1288.45,560.458 1293.01,561.1 1297.56,561.761 1301.97,562.42 1302.12,562.442 1306.68,563.139 1311.23,563.856 1315.79,564.593 1320.35,565.35 1323.3,565.855 \n",
" 1324.9,566.128 1329.46,566.923 1334.02,567.739 1338.57,568.577 1342.34,569.289 1343.13,569.437 1347.68,570.314 1352.24,571.214 1356.8,572.138 1359.62,572.724 \n",
" 1361.35,573.082 1365.91,574.047 1370.47,575.035 1375.02,576.049 1375.5,576.158 1379.58,577.082 1384.14,578.14 1388.69,579.224 1390.2,579.593 1393.25,580.33 \n",
" 1397.8,581.46 1402.36,582.618 1403.93,583.027 1406.92,583.8 1411.47,585.007 1416.03,586.245 1416.81,586.462 1420.59,587.505 1425.14,588.794 1428.94,589.896 \n",
" 1429.7,590.115 1434.26,591.459 1438.81,592.838 1440.4,593.331 1443.37,594.243 1447.92,595.681 1451.28,596.765 1452.48,597.152 1457.04,598.652 1461.59,600.191 \n",
" 1461.62,600.2 1466.15,601.756 1470.71,603.363 1471.46,603.634 1475.26,605.001 1479.82,606.681 1480.84,607.069 1484.38,608.395 1488.93,610.153 1489.82,610.503 \n",
" 1493.49,611.946 1498.04,613.788 1498.4,613.938 1502.6,615.667 1506.62,617.372 1507.16,617.597 1511.71,619.568 1514.5,620.807 1516.27,621.591 1520.83,623.665 \n",
" 1522.06,624.241 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#f57d15; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1482.66,651.717 1484.38,652.322 1488.93,653.975 1492.08,655.152 1493.49,655.675 1498.04,657.416 1501.01,658.586 1502.6,659.208 1507.16,661.048 1509.49,662.021 \n",
" 1511.71,662.941 1516.27,664.89 1517.55,665.455 1520.83,666.892 1525.22,668.89 1525.38,668.965 1529.94,671.091 1532.48,672.324 1534.5,673.292 1539.05,675.57 \n",
" 1539.42,675.759 1543.61,677.916 1545.99,679.193 1548.17,680.353 1552.26,682.628 1552.72,682.885 1557.28,685.509 1558.2,686.062 1561.83,688.239 1563.84,689.497 \n",
" 1566.39,691.09 1569.2,692.931 1570.95,694.073 1574.29,696.366 1575.5,697.202 1579.1,699.8 1580.06,700.494 1583.66,703.235 1584.62,703.971 1587.96,706.669 \n",
" 1589.17,707.663 1592.02,710.104 1593.73,711.607 1595.83,713.538 1598.29,715.856 1599.42,716.973 1602.77,720.407 1602.84,720.48 1605.9,723.842 1607.4,725.576 \n",
" 1608.81,727.276 1611.5,730.711 1611.95,731.316 1613.99,734.145 1616.26,737.58 1616.51,737.991 1618.33,741.014 1620.19,744.449 1621.07,746.256 1621.85,747.883 \n",
" 1623.32,751.318 1624.58,754.752 1625.62,758.173 1625.63,758.187 1626.51,761.621 1627.19,765.056 1627.68,768.49 1627.97,771.925 1628.06,775.359 1627.97,778.794 \n",
" 1627.68,782.228 1627.19,785.663 1626.51,789.097 1625.63,792.532 1625.62,792.545 1624.58,795.966 1623.32,799.401 1621.85,802.835 1621.07,804.463 1620.19,806.27 \n",
" 1618.33,809.704 1616.51,812.728 1616.26,813.139 1613.99,816.573 1611.95,819.403 1611.5,820.008 1608.81,823.442 1607.4,825.143 1605.9,826.877 1602.84,830.239 \n",
" 1602.77,830.312 1599.42,833.746 1598.29,834.863 1595.83,837.181 1593.73,839.112 1592.02,840.615 1589.17,843.056 1587.96,844.05 1584.62,846.748 1583.66,847.484 \n",
" 1580.06,850.225 1579.1,850.919 1575.5,853.517 1574.29,854.353 1570.95,856.646 1569.2,857.788 1566.39,859.629 1563.84,861.222 1561.83,862.48 1558.2,864.657 \n",
" 1557.28,865.21 1552.72,867.834 1552.26,868.091 1548.17,870.366 1545.99,871.526 1543.61,872.803 1539.42,874.96 1539.05,875.149 1534.5,877.427 1532.48,878.395 \n",
" 1529.94,879.628 1525.38,881.754 1525.22,881.829 1520.83,883.826 1517.55,885.264 1516.27,885.829 1511.71,887.778 1509.49,888.698 1507.16,889.671 1502.6,891.51 \n",
" 1501.01,892.133 1498.04,893.303 1493.49,895.044 1492.08,895.567 1488.93,896.744 1484.38,898.397 1482.66,899.002 1479.82,900.01 1475.26,901.582 1472.71,902.436 \n",
" 1470.71,903.115 1466.15,904.613 1462.21,905.871 1461.59,906.069 1457.04,907.498 1452.48,908.886 1451.07,909.305 1447.92,910.247 1443.37,911.574 1439.26,912.74 \n",
" 1438.81,912.867 1434.26,914.136 1429.7,915.372 1426.66,916.174 1425.14,916.579 1420.59,917.762 1416.03,918.914 1413.21,919.609 1411.47,920.041 1406.92,921.145 \n",
" 1402.36,922.22 1398.78,923.043 1397.8,923.271 1393.25,924.301 1388.69,925.305 1384.14,926.284 1383.21,926.478 1379.58,927.244 1375.02,928.181 1370.47,929.094 \n",
" 1366.28,929.912 1365.91,929.985 1361.35,930.859 1356.8,931.711 1352.24,932.541 1347.7,933.347 1347.68,933.35 1343.13,934.143 1338.57,934.915 1334.02,935.667 \n",
" 1329.46,936.399 1327.01,936.781 1324.9,937.113 1320.35,937.811 1315.79,938.489 1311.23,939.149 1306.68,939.791 1303.57,940.216 1302.12,940.415 1297.56,941.024 \n",
" 1293.01,941.615 1288.45,942.188 1283.9,942.744 1279.34,943.284 1276.14,943.65 1274.78,943.807 1270.23,944.315 1265.67,944.807 1261.11,945.282 1256.56,945.741 \n",
" 1252,946.184 1247.44,946.612 1242.89,947.023 1242.18,947.085 1238.33,947.421 1233.78,947.803 1229.22,948.17 1224.66,948.521 1220.11,948.858 1215.55,949.179 \n",
" 1210.99,949.485 1206.44,949.777 1201.88,950.053 1197.32,950.315 1193.57,950.519 1192.77,950.563 1188.21,950.797 1183.66,951.016 1179.1,951.221 1174.54,951.412 \n",
" 1169.99,951.588 1165.43,951.75 1160.87,951.898 1156.32,952.031 1151.76,952.15 1147.2,952.256 1142.65,952.347 1138.09,952.424 1133.54,952.487 1128.98,952.536 \n",
" 1124.42,952.571 1119.87,952.592 1115.31,952.599 1110.75,952.592 1106.2,952.571 1101.64,952.536 1097.08,952.487 1092.53,952.424 1087.97,952.347 1083.42,952.256 \n",
" 1078.86,952.15 1074.3,952.031 1069.75,951.898 1065.19,951.75 1060.63,951.588 1056.08,951.412 1051.52,951.221 1046.96,951.016 1042.41,950.797 1037.85,950.563 \n",
" 1037.05,950.519 1033.3,950.315 1028.74,950.053 1024.18,949.777 1019.63,949.485 1015.07,949.179 1010.51,948.858 1005.96,948.521 1001.4,948.17 996.845,947.803 \n",
" 992.288,947.421 988.442,947.085 987.732,947.023 983.176,946.612 978.619,946.184 974.063,945.741 969.507,945.282 964.95,944.807 960.394,944.315 955.837,943.807 \n",
" 954.48,943.65 951.281,943.284 946.725,942.744 942.168,942.188 937.612,941.615 933.056,941.024 928.499,940.415 927.051,940.216 923.943,939.791 919.386,939.149 \n",
" 914.83,938.489 910.274,937.811 905.717,937.113 903.607,936.781 901.161,936.399 896.605,935.667 892.048,934.915 887.492,934.143 882.936,933.35 882.919,933.347 \n",
" 878.379,932.541 873.823,931.711 869.266,930.859 864.71,929.985 864.338,929.912 860.154,929.094 855.597,928.181 851.041,927.244 847.411,926.478 846.485,926.284 \n",
" 841.928,925.305 837.372,924.301 832.816,923.271 831.836,923.043 828.259,922.22 823.703,921.145 819.146,920.041 817.408,919.609 814.59,918.914 810.034,917.762 \n",
" 805.477,916.579 803.959,916.174 800.921,915.372 796.365,914.136 791.808,912.867 791.365,912.74 787.252,911.574 782.696,910.247 779.552,909.305 778.139,908.886 \n",
" 773.583,907.498 769.026,906.069 768.411,905.871 764.47,904.613 759.914,903.115 757.907,902.436 755.357,901.582 750.801,900.01 747.964,899.002 746.245,898.397 \n",
" 741.688,896.744 738.544,895.567 737.132,895.044 732.575,893.303 729.611,892.133 728.019,891.51 723.463,889.671 721.132,888.698 718.906,887.778 714.35,885.829 \n",
" 713.073,885.264 709.794,883.826 705.405,881.829 705.237,881.754 700.681,879.628 698.137,878.395 696.125,877.427 691.568,875.149 691.203,874.96 687.012,872.803 \n",
" 684.631,871.526 682.455,870.366 678.364,868.091 677.899,867.834 673.343,865.21 672.421,864.657 668.786,862.48 666.778,861.222 664.23,859.629 661.416,857.788 \n",
" 659.674,856.646 656.331,854.353 655.117,853.517 651.516,850.919 650.561,850.225 646.961,847.484 646.005,846.748 642.66,844.05 641.448,843.056 638.605,840.615 \n",
" 636.892,839.112 634.788,837.181 632.335,834.863 631.204,833.746 627.848,830.312 627.779,830.239 624.72,826.877 623.223,825.143 621.809,823.442 619.115,820.008 \n",
" 618.666,819.403 616.631,816.573 614.363,813.139 614.11,812.728 612.29,809.704 610.431,806.27 609.554,804.463 608.771,802.835 607.304,799.401 606.045,795.966 \n",
" 604.997,792.545 604.993,792.532 604.11,789.097 603.428,785.663 602.943,782.228 602.653,778.794 602.557,775.359 602.653,771.925 602.943,768.49 603.428,765.056 \n",
" 604.11,761.621 604.993,758.187 604.997,758.173 606.045,754.752 607.304,751.318 608.771,747.883 609.554,746.256 610.431,744.449 612.29,741.014 614.11,737.991 \n",
" 614.363,737.58 616.631,734.145 618.666,731.316 619.115,730.711 621.809,727.276 623.223,725.576 624.72,723.842 627.779,720.48 627.848,720.407 631.204,716.973 \n",
" 632.335,715.856 634.788,713.538 636.892,711.607 638.605,710.104 641.448,707.663 642.66,706.669 646.005,703.971 646.961,703.235 650.561,700.494 651.516,699.8 \n",
" 655.117,697.202 656.331,696.366 659.674,694.073 661.416,692.931 664.23,691.09 666.778,689.497 668.786,688.239 672.421,686.062 673.343,685.509 677.899,682.885 \n",
" 678.364,682.628 682.455,680.353 684.631,679.193 687.012,677.916 691.203,675.759 691.568,675.57 696.125,673.292 698.137,672.324 700.681,671.091 705.237,668.965 \n",
" 705.405,668.89 709.794,666.892 713.073,665.455 714.35,664.89 718.906,662.941 721.132,662.021 723.463,661.048 728.019,659.208 729.611,658.586 732.575,657.416 \n",
" 737.132,655.675 738.544,655.152 741.688,653.975 746.245,652.322 747.964,651.717 750.801,650.708 755.357,649.137 757.907,648.283 759.914,647.604 764.47,646.106 \n",
" 768.411,644.848 769.026,644.65 773.583,643.221 778.139,641.832 779.552,641.414 782.696,640.472 787.252,639.145 791.365,637.979 791.808,637.852 796.365,636.583 \n",
" 800.921,635.347 803.959,634.545 805.477,634.14 810.034,632.957 814.59,631.804 817.408,631.11 819.146,630.678 823.703,629.574 828.259,628.499 831.836,627.676 \n",
" 832.816,627.448 837.372,626.418 841.928,625.414 846.485,624.435 847.411,624.241 851.041,623.475 855.597,622.538 860.154,621.624 864.338,620.807 864.71,620.733 \n",
" 869.266,619.859 873.823,619.008 878.379,618.178 882.919,617.372 882.936,617.369 887.492,616.576 892.048,615.804 896.605,615.052 901.161,614.32 903.607,613.938 \n",
" 905.717,613.605 910.274,612.908 914.83,612.229 919.386,611.57 923.943,610.928 927.051,610.503 928.499,610.304 933.056,609.695 937.612,609.104 942.168,608.531 \n",
" 946.725,607.974 951.281,607.435 954.48,607.069 955.837,606.912 960.394,606.404 964.95,605.912 969.507,605.437 974.063,604.978 978.619,604.535 983.176,604.107 \n",
" 987.732,603.696 988.442,603.634 992.288,603.298 996.845,602.916 1001.4,602.549 1005.96,602.198 1010.51,601.861 1015.07,601.54 1019.63,601.234 1024.18,600.942 \n",
" 1028.74,600.665 1033.3,600.403 1037.05,600.2 1037.85,600.156 1042.41,599.922 1046.96,599.702 1051.52,599.497 1056.08,599.307 1060.63,599.131 1065.19,598.969 \n",
" 1069.75,598.821 1074.3,598.688 1078.86,598.568 1083.42,598.463 1087.97,598.372 1092.53,598.295 1097.08,598.232 1101.64,598.183 1106.2,598.148 1110.75,598.127 \n",
" 1115.31,598.12 1119.87,598.127 1124.42,598.148 1128.98,598.183 1133.54,598.232 1138.09,598.295 1142.65,598.372 1147.2,598.463 1151.76,598.568 1156.32,598.688 \n",
" 1160.87,598.821 1165.43,598.969 1169.99,599.131 1174.54,599.307 1179.1,599.497 1183.66,599.702 1188.21,599.922 1192.77,600.156 1193.57,600.2 1197.32,600.403 \n",
" 1201.88,600.665 1206.44,600.942 1210.99,601.234 1215.55,601.54 1220.11,601.861 1224.66,602.198 1229.22,602.549 1233.78,602.916 1238.33,603.298 1242.18,603.634 \n",
" 1242.89,603.696 1247.44,604.107 1252,604.535 1256.56,604.978 1261.11,605.437 1265.67,605.912 1270.23,606.404 1274.78,606.912 1276.14,607.069 1279.34,607.435 \n",
" 1283.9,607.974 1288.45,608.531 1293.01,609.104 1297.56,609.695 1302.12,610.304 1303.57,610.503 1306.68,610.928 1311.23,611.57 1315.79,612.229 1320.35,612.908 \n",
" 1324.9,613.605 1327.01,613.938 1329.46,614.32 1334.02,615.052 1338.57,615.804 1343.13,616.576 1347.68,617.369 1347.7,617.372 1352.24,618.178 1356.8,619.008 \n",
" 1361.35,619.859 1365.91,620.733 1366.28,620.807 1370.47,621.624 1375.02,622.538 1379.58,623.475 1383.21,624.241 1384.14,624.435 1388.69,625.414 1393.25,626.418 \n",
" 1397.8,627.448 1398.78,627.676 1402.36,628.499 1406.92,629.574 1411.47,630.678 1413.21,631.11 1416.03,631.804 1420.59,632.957 1425.14,634.14 1426.66,634.545 \n",
" 1429.7,635.347 1434.26,636.583 1438.81,637.852 1439.26,637.979 1443.37,639.145 1447.92,640.472 1451.07,641.414 1452.48,641.832 1457.04,643.221 1461.59,644.65 \n",
" 1462.21,644.848 1466.15,646.106 1470.71,647.604 1472.71,648.283 1475.26,649.137 1479.82,650.708 1482.66,651.717 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#fb9c07; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1445.11,679.193 1447.92,679.883 1452.48,681.035 1457.04,682.223 1458.54,682.628 1461.59,683.437 1466.15,684.684 1470.71,685.972 1471.02,686.062 1475.26,687.285 \n",
" 1479.82,688.641 1482.59,689.497 1484.38,690.037 1488.93,691.469 1493.42,692.931 1493.49,692.955 1498.04,694.471 1502.6,696.048 1503.48,696.366 1507.16,697.666 \n",
" 1511.71,699.348 1512.89,699.8 1516.27,701.078 1520.83,702.881 1521.68,703.235 1525.38,704.738 1529.9,706.669 1529.94,706.685 1534.5,708.689 1537.54,710.104 \n",
" 1539.05,710.793 1543.61,712.99 1544.68,713.538 1548.17,715.284 1551.33,716.973 1552.72,717.705 1557.28,720.263 1557.52,720.407 1561.83,722.958 1563.23,723.842 \n",
" 1566.39,725.835 1568.51,727.276 1570.95,728.926 1573.38,730.711 1575.5,732.274 1577.85,734.145 1580.06,735.942 1581.92,737.58 1584.62,740.035 1585.61,741.014 \n",
" 1588.92,744.449 1589.17,744.72 1591.87,747.883 1593.73,750.319 1594.45,751.318 1596.68,754.752 1598.29,757.69 1598.55,758.187 1600.1,761.621 1601.29,765.056 \n",
" 1602.12,768.49 1602.62,771.925 1602.78,775.359 1602.62,778.794 1602.12,782.228 1601.29,785.663 1600.1,789.097 1598.55,792.532 1598.29,793.029 1596.68,795.966 \n",
" 1594.45,799.401 1593.73,800.4 1591.87,802.835 1589.17,805.999 1588.92,806.27 1585.61,809.704 1584.62,810.683 1581.92,813.139 1580.06,814.776 1577.85,816.573 \n",
" 1575.5,818.445 1573.38,820.008 1570.95,821.793 1568.51,823.442 1566.39,824.883 1563.23,826.877 1561.83,827.761 1557.52,830.312 1557.28,830.455 1552.72,833.013 \n",
" 1551.33,833.746 1548.17,835.435 1544.68,837.181 1543.61,837.729 1539.05,839.926 1537.54,840.615 1534.5,842.03 1529.94,844.034 1529.9,844.05 1525.38,845.981 \n",
" 1521.68,847.484 1520.83,847.838 1516.27,849.641 1512.89,850.919 1511.71,851.371 1507.16,853.053 1503.48,854.353 1502.6,854.67 1498.04,856.247 1493.49,857.764 \n",
" 1493.42,857.788 1488.93,859.249 1484.38,860.682 1482.59,861.222 1479.82,862.077 1475.26,863.434 1471.02,864.657 1470.71,864.747 1466.15,866.035 1461.59,867.282 \n",
" 1458.54,868.091 1457.04,868.496 1452.48,869.684 1447.92,870.836 1445.11,871.526 1443.37,871.96 1438.81,873.059 1434.26,874.127 1430.6,874.96 1429.7,875.168 \n",
" 1425.14,876.188 1420.59,877.181 1416.03,878.147 1414.83,878.395 1411.47,879.093 1406.92,880.017 1402.36,880.917 1397.8,881.792 1397.61,881.829 1393.25,882.652 \n",
" 1388.69,883.49 1384.14,884.306 1379.58,885.102 1378.62,885.264 1375.02,885.881 1370.47,886.641 1365.91,887.382 1361.35,888.103 1357.5,888.698 1356.8,888.807 \n",
" 1352.24,889.496 1347.68,890.167 1343.13,890.821 1338.57,891.457 1334.02,892.076 1333.59,892.133 1329.46,892.682 1324.9,893.272 1320.35,893.846 1315.79,894.404 \n",
" 1311.23,894.947 1306.68,895.474 1305.85,895.567 1302.12,895.988 1297.56,896.488 1293.01,896.974 1288.45,897.445 1283.9,897.901 1279.34,898.344 1274.78,898.772 \n",
" 1272.26,899.002 1270.23,899.188 1265.67,899.591 1261.11,899.981 1256.56,900.357 1252,900.72 1247.44,901.071 1242.89,901.408 1238.33,901.732 1233.78,902.044 \n",
" 1229.22,902.343 1227.73,902.436 1224.66,902.63 1220.11,902.905 1215.55,903.168 1210.99,903.419 1206.44,903.657 1201.88,903.884 1197.32,904.098 1192.77,904.301 \n",
" 1188.21,904.491 1183.66,904.67 1179.1,904.837 1174.54,904.992 1169.99,905.135 1165.43,905.267 1160.87,905.387 1156.32,905.496 1151.76,905.593 1147.2,905.679 \n",
" 1142.65,905.753 1138.09,905.816 1133.54,905.867 1133.12,905.871 1128.98,905.907 1124.42,905.936 1119.87,905.953 1115.31,905.958 1110.75,905.953 1106.2,905.936 \n",
" 1101.64,905.907 1097.5,905.871 1097.08,905.867 1092.53,905.816 1087.97,905.753 1083.42,905.679 1078.86,905.593 1074.3,905.496 1069.75,905.387 1065.19,905.267 \n",
" 1060.63,905.135 1056.08,904.992 1051.52,904.837 1046.96,904.67 1042.41,904.491 1037.85,904.301 1033.3,904.098 1028.74,903.884 1024.18,903.657 1019.63,903.419 \n",
" 1015.07,903.168 1010.51,902.905 1005.96,902.63 1002.89,902.436 1001.4,902.343 996.845,902.044 992.288,901.732 987.732,901.408 983.176,901.071 978.619,900.72 \n",
" 974.063,900.357 969.507,899.981 964.95,899.591 960.394,899.188 958.357,899.002 955.837,898.772 951.281,898.344 946.725,897.901 942.168,897.445 937.612,896.974 \n",
" 933.056,896.488 928.499,895.988 924.773,895.567 923.943,895.474 919.386,894.947 914.83,894.404 910.274,893.846 905.717,893.272 901.161,892.682 897.032,892.133 \n",
" 896.605,892.076 892.048,891.457 887.492,890.821 882.936,890.167 878.379,889.496 873.823,888.807 873.124,888.698 869.266,888.103 864.71,887.382 860.154,886.641 \n",
" 855.597,885.881 851.996,885.264 851.041,885.102 846.485,884.306 841.928,883.49 837.372,882.652 833.012,881.829 832.816,881.792 828.259,880.917 823.703,880.017 \n",
" 819.146,879.093 815.794,878.395 814.59,878.147 810.034,877.181 805.477,876.188 800.921,875.168 800.022,874.96 796.365,874.127 791.808,873.059 787.252,871.96 \n",
" 785.508,871.526 782.696,870.836 778.139,869.684 773.583,868.496 772.078,868.091 769.026,867.282 764.47,866.035 759.914,864.747 759.604,864.657 755.357,863.434 \n",
" 750.801,862.077 748.028,861.222 746.245,860.682 741.688,859.249 737.205,857.788 737.132,857.764 732.575,856.247 728.019,854.67 727.139,854.353 723.463,853.053 \n",
" 718.906,851.371 717.731,850.919 714.35,849.641 709.794,847.838 708.939,847.484 705.237,845.981 700.717,844.05 700.681,844.034 696.125,842.03 693.08,840.615 \n",
" 691.568,839.926 687.012,837.729 685.936,837.181 682.455,835.435 679.293,833.746 677.899,833.013 673.343,830.455 673.102,830.312 668.786,827.761 667.394,826.877 \n",
" 664.23,824.883 662.107,823.442 659.674,821.793 657.236,820.008 655.117,818.445 652.771,816.573 650.561,814.776 648.699,813.139 646.005,810.683 645.009,809.704 \n",
" 641.696,806.27 641.448,805.999 638.754,802.835 636.892,800.4 636.171,799.401 633.939,795.966 632.335,793.029 632.072,792.532 630.523,789.097 629.333,785.663 \n",
" 628.498,782.228 628.005,778.794 627.842,775.359 628.005,771.925 628.498,768.49 629.333,765.056 630.523,761.621 632.072,758.187 632.335,757.69 633.939,754.752 \n",
" 636.171,751.318 636.892,750.319 638.754,747.883 641.448,744.72 641.696,744.449 645.009,741.014 646.005,740.035 648.699,737.58 650.561,735.942 652.771,734.145 \n",
" 655.117,732.274 657.236,730.711 659.674,728.926 662.107,727.276 664.23,725.835 667.394,723.842 668.786,722.958 673.102,720.407 673.343,720.263 677.899,717.705 \n",
" 679.293,716.973 682.455,715.284 685.936,713.538 687.012,712.99 691.568,710.793 693.08,710.104 696.125,708.689 700.681,706.685 700.717,706.669 705.237,704.738 \n",
" 708.939,703.235 709.794,702.881 714.35,701.078 717.731,699.8 718.906,699.348 723.463,697.666 727.139,696.366 728.019,696.048 732.575,694.471 737.132,692.955 \n",
" 737.205,692.931 741.688,691.469 746.245,690.037 748.028,689.497 750.801,688.641 755.357,687.285 759.604,686.062 759.914,685.972 764.47,684.684 769.026,683.437 \n",
" 772.078,682.628 773.583,682.223 778.139,681.035 782.696,679.883 785.508,679.193 787.252,678.759 791.808,677.66 796.365,676.592 800.022,675.759 800.921,675.551 \n",
" 805.477,674.531 810.034,673.538 814.59,672.572 815.794,672.324 819.146,671.625 823.703,670.702 828.259,669.802 832.816,668.926 833.012,668.89 837.372,668.066 \n",
" 841.928,667.229 846.485,666.412 851.041,665.617 851.996,665.455 855.597,664.838 860.154,664.078 864.71,663.337 869.266,662.616 873.124,662.021 873.823,661.912 \n",
" 878.379,661.223 882.936,660.552 887.492,659.898 892.048,659.262 896.605,658.643 897.032,658.586 901.161,658.037 905.717,657.447 910.274,656.873 914.83,656.315 \n",
" 919.386,655.772 923.943,655.245 924.773,655.152 928.499,654.73 933.056,654.23 937.612,653.745 942.168,653.274 946.725,652.818 951.281,652.375 955.837,651.946 \n",
" 958.357,651.717 960.394,651.531 964.95,651.127 969.507,650.738 974.063,650.362 978.619,649.998 983.176,649.648 987.732,649.311 992.288,648.987 996.845,648.675 \n",
" 1001.4,648.376 1002.89,648.283 1005.96,648.089 1010.51,647.813 1015.07,647.55 1019.63,647.3 1024.18,647.061 1028.74,646.835 1033.3,646.621 1037.85,646.418 \n",
" 1042.41,646.228 1046.96,646.049 1051.52,645.882 1056.08,645.727 1060.63,645.584 1065.19,645.452 1069.75,645.332 1074.3,645.223 1078.86,645.126 1083.42,645.04 \n",
" 1087.97,644.966 1092.53,644.903 1097.08,644.852 1097.5,644.848 1101.64,644.812 1106.2,644.783 1110.75,644.766 1115.31,644.76 1119.87,644.766 1124.42,644.783 \n",
" 1128.98,644.812 1133.12,644.848 1133.54,644.852 1138.09,644.903 1142.65,644.966 1147.2,645.04 1151.76,645.126 1156.32,645.223 1160.87,645.332 1165.43,645.452 \n",
" 1169.99,645.584 1174.54,645.727 1179.1,645.882 1183.66,646.049 1188.21,646.228 1192.77,646.418 1197.32,646.621 1201.88,646.835 1206.44,647.061 1210.99,647.3 \n",
" 1215.55,647.55 1220.11,647.813 1224.66,648.089 1227.73,648.283 1229.22,648.376 1233.78,648.675 1238.33,648.987 1242.89,649.311 1247.44,649.648 1252,649.998 \n",
" 1256.56,650.362 1261.11,650.738 1265.67,651.127 1270.23,651.531 1272.26,651.717 1274.78,651.946 1279.34,652.375 1283.9,652.818 1288.45,653.274 1293.01,653.745 \n",
" 1297.56,654.23 1302.12,654.73 1305.85,655.152 1306.68,655.245 1311.23,655.772 1315.79,656.315 1320.35,656.873 1324.9,657.447 1329.46,658.037 1333.59,658.586 \n",
" 1334.02,658.643 1338.57,659.262 1343.13,659.898 1347.68,660.552 1352.24,661.223 1356.8,661.912 1357.5,662.021 1361.35,662.616 1365.91,663.337 1370.47,664.078 \n",
" 1375.02,664.838 1378.62,665.455 1379.58,665.617 1384.14,666.412 1388.69,667.229 1393.25,668.066 1397.61,668.89 1397.8,668.926 1402.36,669.802 1406.92,670.702 \n",
" 1411.47,671.625 1414.83,672.324 1416.03,672.572 1420.59,673.538 1425.14,674.531 1429.7,675.551 1430.6,675.759 1434.26,676.592 1438.81,677.66 1443.37,678.759 \n",
" 1445.11,679.193 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#fabf26; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1402.36,707.313 1397.8,706.679 1397.73,706.669 1393.25,706.058 1388.69,705.452 1384.14,704.863 1379.58,704.288 1375.02,703.729 1370.89,703.235 1370.47,703.184 \n",
" 1365.91,702.649 1361.35,702.129 1356.8,701.623 1352.24,701.129 1347.68,700.649 1343.13,700.181 1339.32,699.8 1338.57,699.725 1334.02,699.28 1329.46,698.846 \n",
" 1324.9,698.425 1320.35,698.014 1315.79,697.615 1311.23,697.228 1306.68,696.851 1302.12,696.484 1300.6,696.366 1297.56,696.128 1293.01,695.782 1288.45,695.445 \n",
" 1283.9,695.12 1279.34,694.804 1274.78,694.498 1270.23,694.202 1265.67,693.915 1261.11,693.639 1256.56,693.371 1252,693.113 1248.66,692.931 1247.44,692.864 \n",
" 1242.89,692.624 1238.33,692.393 1233.78,692.171 1229.22,691.958 1224.66,691.754 1220.11,691.559 1215.55,691.372 1210.99,691.194 1206.44,691.025 1201.88,690.864 \n",
" 1197.32,690.712 1192.77,690.569 1188.21,690.434 1183.66,690.307 1179.1,690.188 1174.54,690.078 1169.99,689.977 1165.43,689.883 1160.87,689.798 1156.32,689.721 \n",
" 1151.76,689.652 1147.2,689.591 1142.65,689.538 1138.4,689.497 1138.09,689.494 1133.54,689.457 1128.98,689.429 1124.42,689.409 1119.87,689.397 1115.31,689.392 \n",
" 1110.75,689.397 1106.2,689.409 1101.64,689.429 1097.08,689.457 1092.53,689.494 1092.22,689.497 1087.97,689.538 1083.42,689.591 1078.86,689.652 1074.3,689.721 \n",
" 1069.75,689.798 1065.19,689.883 1060.63,689.977 1056.08,690.078 1051.52,690.188 1046.96,690.307 1042.41,690.434 1037.85,690.569 1033.3,690.712 1028.74,690.864 \n",
" 1024.18,691.025 1019.63,691.194 1015.07,691.372 1010.51,691.559 1005.96,691.754 1001.4,691.958 996.845,692.171 992.288,692.393 987.732,692.624 983.176,692.864 \n",
" 981.956,692.931 978.619,693.113 974.063,693.371 969.507,693.639 964.95,693.915 960.394,694.202 955.837,694.498 951.281,694.804 946.725,695.12 942.168,695.445 \n",
" 937.612,695.782 933.056,696.128 930.023,696.366 928.499,696.484 923.943,696.851 919.386,697.228 914.83,697.615 910.274,698.014 905.717,698.425 901.161,698.846 \n",
" 896.605,699.28 892.048,699.725 891.304,699.8 887.492,700.181 882.936,700.649 878.379,701.129 873.823,701.623 869.266,702.129 864.71,702.649 860.154,703.184 \n",
" 859.73,703.235 855.597,703.729 851.041,704.288 846.485,704.863 841.928,705.452 837.372,706.058 832.89,706.669 832.816,706.679 828.259,707.313 823.703,707.964 \n",
" 819.146,708.633 814.59,709.32 810.034,710.026 809.55,710.104 805.477,710.747 800.921,711.487 796.365,712.248 791.808,713.032 788.955,713.538 787.252,713.835 \n",
" 782.696,714.658 778.139,715.505 773.583,716.379 770.592,716.973 769.026,717.277 764.47,718.197 759.914,719.148 755.357,720.131 754.131,720.407 750.801,721.139 \n",
" 746.245,722.179 741.688,723.259 739.333,723.842 737.132,724.372 732.575,725.519 728.019,726.717 725.994,727.276 723.463,727.954 718.906,729.236 714.35,730.584 \n",
" 713.947,730.711 709.794,731.97 705.237,733.433 703.157,734.145 700.681,734.96 696.125,736.565 693.449,737.58 691.568,738.263 687.012,740.056 684.78,741.014 \n",
" 682.455,741.968 677.899,744.029 677.062,744.449 673.343,746.234 670.301,747.883 668.786,748.671 664.365,751.318 664.23,751.396 659.674,754.476 659.323,754.752 \n",
" 655.117,758.156 655.085,758.187 651.666,761.621 650.561,762.919 648.985,765.056 647.081,768.49 646.005,771.884 645.991,771.925 645.59,775.359 645.991,778.794 \n",
" 646.005,778.835 647.081,782.228 648.985,785.663 650.561,787.799 651.666,789.097 655.085,792.532 655.117,792.563 659.323,795.966 659.674,796.243 664.23,799.323 \n",
" 664.365,799.401 668.786,802.048 670.301,802.835 673.343,804.485 677.062,806.27 677.899,806.69 682.455,808.751 684.78,809.704 687.012,810.663 691.568,812.456 \n",
" 693.449,813.139 696.125,814.154 700.681,815.759 703.157,816.573 705.237,817.286 709.794,818.748 713.947,820.008 714.35,820.135 718.906,821.483 723.463,822.765 \n",
" 725.994,823.442 728.019,824.002 732.575,825.199 737.132,826.347 739.333,826.877 741.688,827.46 746.245,828.54 750.801,829.58 754.131,830.312 755.357,830.588 \n",
" 759.914,831.571 764.47,832.522 769.026,833.442 770.592,833.746 773.583,834.34 778.139,835.214 782.696,836.061 787.252,836.884 788.955,837.181 791.808,837.687 \n",
" 796.365,838.471 800.921,839.232 805.477,839.972 809.55,840.615 810.034,840.693 814.59,841.399 819.146,842.086 823.703,842.755 828.259,843.406 832.816,844.04 \n",
" 832.89,844.05 837.372,844.661 841.928,845.267 846.485,845.856 851.041,846.43 855.597,846.99 859.73,847.484 860.154,847.535 864.71,848.069 869.266,848.589 \n",
" 873.823,849.096 878.379,849.589 882.936,850.07 887.492,850.538 891.304,850.919 892.048,850.994 896.605,851.439 901.161,851.873 905.717,852.294 910.274,852.705 \n",
" 914.83,853.103 919.386,853.491 923.943,853.868 928.499,854.234 930.023,854.353 933.056,854.591 937.612,854.937 942.168,855.273 946.725,855.599 951.281,855.915 \n",
" 955.837,856.221 960.394,856.517 964.95,856.803 969.507,857.08 974.063,857.348 978.619,857.606 981.956,857.788 983.176,857.854 987.732,858.095 992.288,858.326 \n",
" 996.845,858.548 1001.4,858.761 1005.96,858.965 1010.51,859.16 1015.07,859.347 1019.63,859.525 1024.18,859.694 1028.74,859.854 1033.3,860.007 1037.85,860.15 \n",
" 1042.41,860.285 1046.96,860.412 1051.52,860.53 1056.08,860.64 1060.63,860.742 1065.19,860.836 1069.75,860.921 1074.3,860.998 1078.86,861.067 1083.42,861.128 \n",
" 1087.97,861.181 1092.22,861.222 1092.53,861.225 1097.08,861.262 1101.64,861.29 1106.2,861.31 1110.75,861.322 1115.31,861.326 1119.87,861.322 1124.42,861.31 \n",
" 1128.98,861.29 1133.54,861.262 1138.09,861.225 1138.4,861.222 1142.65,861.181 1147.2,861.128 1151.76,861.067 1156.32,860.998 1160.87,860.921 1165.43,860.836 \n",
" 1169.99,860.742 1174.54,860.64 1179.1,860.53 1183.66,860.412 1188.21,860.285 1192.77,860.15 1197.32,860.007 1201.88,859.854 1206.44,859.694 1210.99,859.525 \n",
" 1215.55,859.347 1220.11,859.16 1224.66,858.965 1229.22,858.761 1233.78,858.548 1238.33,858.326 1242.89,858.095 1247.44,857.854 1248.66,857.788 1252,857.606 \n",
" 1256.56,857.348 1261.11,857.08 1265.67,856.803 1270.23,856.517 1274.78,856.221 1279.34,855.915 1283.9,855.599 1288.45,855.273 1293.01,854.937 1297.56,854.591 \n",
" 1300.6,854.353 1302.12,854.234 1306.68,853.868 1311.23,853.491 1315.79,853.103 1320.35,852.705 1324.9,852.294 1329.46,851.873 1334.02,851.439 1338.57,850.994 \n",
" 1339.32,850.919 1343.13,850.538 1347.68,850.07 1352.24,849.589 1356.8,849.096 1361.35,848.589 1365.91,848.069 1370.47,847.535 1370.89,847.484 1375.02,846.99 \n",
" 1379.58,846.43 1384.14,845.856 1388.69,845.267 1393.25,844.661 1397.73,844.05 1397.8,844.04 1402.36,843.406 1406.92,842.755 1411.47,842.086 1416.03,841.399 \n",
" 1420.59,840.693 1421.07,840.615 1425.14,839.972 1429.7,839.232 1434.26,838.471 1438.81,837.687 1441.67,837.181 1443.37,836.884 1447.92,836.061 1452.48,835.214 \n",
" 1457.04,834.34 1460.03,833.746 1461.59,833.442 1466.15,832.522 1470.71,831.571 1475.26,830.588 1476.49,830.312 1479.82,829.58 1484.38,828.54 1488.93,827.46 \n",
" 1491.29,826.877 1493.49,826.347 1498.04,825.199 1502.6,824.002 1504.63,823.442 1507.16,822.765 1511.71,821.483 1516.27,820.135 1516.67,820.008 1520.83,818.748 \n",
" 1525.38,817.286 1527.46,816.573 1529.94,815.759 1534.5,814.154 1537.17,813.139 1539.05,812.456 1543.61,810.663 1545.84,809.704 1548.17,808.751 1552.72,806.69 \n",
" 1553.56,806.27 1557.28,804.485 1560.32,802.835 1561.83,802.048 1566.26,799.401 1566.39,799.323 1570.95,796.243 1571.3,795.966 1575.5,792.563 1575.54,792.532 \n",
" 1578.95,789.097 1580.06,787.799 1581.64,785.663 1583.54,782.228 1584.62,778.835 1584.63,778.794 1585.03,775.359 1584.63,771.925 1584.62,771.884 1583.54,768.49 \n",
" 1581.64,765.056 1580.06,762.919 1578.95,761.621 1575.54,758.187 1575.5,758.156 1571.3,754.752 1570.95,754.476 1566.39,751.396 1566.26,751.318 1561.83,748.671 \n",
" 1560.32,747.883 1557.28,746.234 1553.56,744.449 1552.72,744.029 1548.17,741.968 1545.84,741.014 1543.61,740.056 1539.05,738.263 1537.17,737.58 1534.5,736.565 \n",
" 1529.94,734.96 1527.46,734.145 1525.38,733.433 1520.83,731.97 1516.67,730.711 1516.27,730.584 1511.71,729.236 1507.16,727.954 1504.63,727.276 1502.6,726.717 \n",
" 1498.04,725.519 1493.49,724.372 1491.29,723.842 1488.93,723.259 1484.38,722.179 1479.82,721.139 1476.49,720.407 1475.26,720.131 1470.71,719.148 1466.15,718.197 \n",
" 1461.59,717.277 1460.03,716.973 1457.04,716.379 1452.48,715.505 1447.92,714.658 1443.37,713.835 1441.67,713.538 1438.81,713.032 1434.26,712.248 1429.7,711.487 \n",
" 1425.14,710.747 1421.07,710.104 1420.59,710.026 1416.03,709.32 1411.47,708.633 1406.92,707.964 1402.36,707.313 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#f3e258; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1361.35,739.344 1356.8,739.079 1352.24,738.821 1347.68,738.569 1343.13,738.324 1338.57,738.086 1334.02,737.854 1329.46,737.628 1328.47,737.58 1324.9,737.407 \n",
" 1320.35,737.193 1315.79,736.984 1311.23,736.782 1306.68,736.585 1302.12,736.393 1297.56,736.207 1293.01,736.027 1288.45,735.852 1283.9,735.682 1279.34,735.518 \n",
" 1274.78,735.359 1270.23,735.204 1265.67,735.055 1261.11,734.911 1256.56,734.772 1252,734.638 1247.44,734.508 1242.89,734.383 1238.33,734.263 1233.78,734.148 \n",
" 1233.66,734.145 1229.22,734.037 1224.66,733.931 1220.11,733.829 1215.55,733.732 1210.99,733.64 1206.44,733.552 1201.88,733.468 1197.32,733.389 1192.77,733.315 \n",
" 1188.21,733.244 1183.66,733.179 1179.1,733.117 1174.54,733.06 1169.99,733.007 1165.43,732.958 1160.87,732.914 1156.32,732.874 1151.76,732.838 1147.2,732.806 \n",
" 1142.65,732.779 1138.09,732.756 1133.54,732.737 1128.98,732.722 1124.42,732.712 1119.87,732.705 1115.31,732.703 1110.75,732.705 1106.2,732.712 1101.64,732.722 \n",
" 1097.08,732.737 1092.53,732.756 1087.97,732.779 1083.42,732.806 1078.86,732.838 1074.3,732.874 1069.75,732.914 1065.19,732.958 1060.63,733.007 1056.08,733.06 \n",
" 1051.52,733.117 1046.96,733.179 1042.41,733.244 1037.85,733.315 1033.3,733.389 1028.74,733.468 1024.18,733.552 1019.63,733.64 1015.07,733.732 1010.51,733.829 \n",
" 1005.96,733.931 1001.4,734.037 996.956,734.145 996.845,734.148 992.288,734.263 987.732,734.383 983.176,734.508 978.619,734.638 974.063,734.772 969.507,734.911 \n",
" 964.95,735.055 960.394,735.204 955.837,735.359 951.281,735.518 946.725,735.682 942.168,735.852 937.612,736.027 933.056,736.207 928.499,736.393 923.943,736.585 \n",
" 919.386,736.782 914.83,736.984 910.274,737.193 905.717,737.407 902.155,737.58 901.161,737.628 896.605,737.854 892.048,738.086 887.492,738.324 882.936,738.569 \n",
" 878.379,738.821 873.823,739.079 869.266,739.344 864.71,739.616 860.154,739.896 855.597,740.183 851.041,740.477 846.485,740.779 843.039,741.014 841.928,741.089 \n",
" 837.372,741.406 832.816,741.732 828.259,742.066 823.703,742.41 819.146,742.762 814.59,743.124 810.034,743.496 805.477,743.879 800.921,744.272 798.941,744.449 \n",
" 796.365,744.675 791.808,745.089 787.252,745.514 782.696,745.952 778.139,746.403 773.583,746.868 769.026,747.348 764.47,747.844 764.122,747.883 759.914,748.351 \n",
" 755.357,748.875 750.801,749.418 746.245,749.98 741.688,750.563 737.132,751.17 736.081,751.318 732.575,751.794 728.019,752.443 723.463,753.12 718.906,753.829 \n",
" 714.35,754.576 713.35,754.752 709.794,755.349 705.237,756.161 700.681,757.025 696.125,757.952 695.086,758.187 691.568,758.923 687.012,759.966 682.455,761.12 \n",
" 680.751,761.621 677.899,762.367 673.343,763.758 669.885,765.056 668.786,765.403 664.23,767.32 662.366,768.49 659.674,769.959 657.71,771.925 655.679,775.359 \n",
" 657.71,778.794 659.674,780.76 662.366,782.228 664.23,783.399 668.786,785.316 669.885,785.663 673.343,786.961 677.899,788.351 680.751,789.097 682.455,789.599 \n",
" 687.012,790.753 691.568,791.796 695.086,792.532 696.125,792.767 700.681,793.694 705.237,794.558 709.794,795.37 713.35,795.966 714.35,796.143 718.906,796.89 \n",
" 723.463,797.599 728.019,798.276 732.575,798.925 736.081,799.401 737.132,799.549 741.688,800.156 746.245,800.739 750.801,801.301 755.357,801.843 759.914,802.368 \n",
" 764.122,802.835 764.47,802.875 769.026,803.371 773.583,803.851 778.139,804.316 782.696,804.767 787.252,805.205 791.808,805.63 796.365,806.044 798.941,806.27 \n",
" 800.921,806.447 805.477,806.84 810.034,807.222 814.59,807.595 819.146,807.957 823.703,808.309 828.259,808.652 832.816,808.987 837.372,809.312 841.928,809.63 \n",
" 843.039,809.704 846.485,809.94 851.041,810.242 855.597,810.536 860.154,810.823 864.71,811.102 869.266,811.375 873.823,811.64 878.379,811.898 882.936,812.15 \n",
" 887.492,812.395 892.048,812.633 896.605,812.865 901.161,813.091 902.155,813.139 905.717,813.312 910.274,813.526 914.83,813.734 919.386,813.937 923.943,814.134 \n",
" 928.499,814.326 933.056,814.511 937.612,814.692 942.168,814.867 946.725,815.036 951.281,815.201 955.837,815.36 960.394,815.514 964.95,815.663 969.507,815.808 \n",
" 974.063,815.947 978.619,816.081 983.176,816.211 987.732,816.335 992.288,816.455 996.845,816.571 996.956,816.573 1001.4,816.682 1005.96,816.788 1010.51,816.889 \n",
" 1015.07,816.986 1019.63,817.079 1024.18,817.167 1028.74,817.25 1033.3,817.329 1037.85,817.404 1042.41,817.474 1046.96,817.54 1051.52,817.602 1056.08,817.659 \n",
" 1060.63,817.712 1065.19,817.761 1069.75,817.805 1074.3,817.845 1078.86,817.881 1083.42,817.913 1087.97,817.94 1092.53,817.963 1097.08,817.982 1101.64,817.997 \n",
" 1106.2,818.007 1110.75,818.014 1115.31,818.016 1119.87,818.014 1124.42,818.007 1128.98,817.997 1133.54,817.982 1138.09,817.963 1142.65,817.94 1147.2,817.913 \n",
" 1151.76,817.881 1156.32,817.845 1160.87,817.805 1165.43,817.761 1169.99,817.712 1174.54,817.659 1179.1,817.602 1183.66,817.54 1188.21,817.474 1192.77,817.404 \n",
" 1197.32,817.329 1201.88,817.25 1206.44,817.167 1210.99,817.079 1215.55,816.986 1220.11,816.889 1224.66,816.788 1229.22,816.682 1233.66,816.573 1233.78,816.571 \n",
" 1238.33,816.455 1242.89,816.335 1247.44,816.211 1252,816.081 1256.56,815.947 1261.11,815.808 1265.67,815.663 1270.23,815.514 1274.78,815.36 1279.34,815.201 \n",
" 1283.9,815.036 1288.45,814.867 1293.01,814.692 1297.56,814.511 1302.12,814.326 1306.68,814.134 1311.23,813.937 1315.79,813.734 1320.35,813.526 1324.9,813.312 \n",
" 1328.47,813.139 1329.46,813.091 1334.02,812.865 1338.57,812.633 1343.13,812.395 1347.68,812.15 1352.24,811.898 1356.8,811.64 1361.35,811.375 1365.91,811.102 \n",
" 1370.47,810.823 1375.02,810.536 1379.58,810.242 1384.14,809.94 1387.58,809.704 1388.69,809.63 1393.25,809.312 1397.8,808.987 1402.36,808.652 1406.92,808.309 \n",
" 1411.47,807.957 1416.03,807.595 1420.59,807.222 1425.14,806.84 1429.7,806.447 1431.68,806.27 1434.26,806.044 1438.81,805.63 1443.37,805.205 1447.92,804.767 \n",
" 1452.48,804.316 1457.04,803.851 1461.59,803.371 1466.15,802.875 1466.5,802.835 1470.71,802.368 1475.26,801.843 1479.82,801.301 1484.38,800.739 1488.93,800.156 \n",
" 1493.49,799.549 1494.54,799.401 1498.04,798.925 1502.6,798.276 1507.16,797.599 1511.71,796.89 1516.27,796.143 1517.27,795.966 1520.83,795.37 1525.38,794.558 \n",
" 1529.94,793.694 1534.5,792.767 1535.53,792.532 1539.05,791.796 1543.61,790.753 1548.17,789.599 1549.87,789.097 1552.72,788.351 1557.28,786.961 1560.74,785.663 \n",
" 1561.83,785.316 1566.39,783.399 1568.25,782.228 1570.95,780.76 1572.91,778.794 1574.94,775.359 1572.91,771.925 1570.95,769.959 1568.25,768.49 1566.39,767.32 \n",
" 1561.83,765.403 1560.74,765.056 1557.28,763.758 1552.72,762.367 1549.87,761.621 1548.17,761.12 1543.61,759.966 1539.05,758.923 1535.53,758.187 1534.5,757.952 \n",
" 1529.94,757.025 1525.38,756.161 1520.83,755.349 1517.27,754.752 1516.27,754.576 1511.71,753.829 1507.16,753.12 1502.6,752.443 1498.04,751.794 1494.54,751.318 \n",
" 1493.49,751.17 1488.93,750.563 1484.38,749.98 1479.82,749.418 1475.26,748.875 1470.71,748.351 1466.5,747.883 1466.15,747.844 1461.59,747.348 1457.04,746.868 \n",
" 1452.48,746.403 1447.92,745.952 1443.37,745.514 1438.81,745.089 1434.26,744.675 1431.68,744.449 1429.7,744.272 1425.14,743.879 1420.59,743.496 1416.03,743.124 \n",
" 1411.47,742.762 1406.92,742.41 1402.36,742.066 1397.8,741.732 1393.25,741.406 1388.69,741.089 1387.58,741.014 1384.14,740.779 1379.58,740.477 1375.02,740.183 \n",
" 1370.47,739.896 1365.91,739.616 1361.35,739.344 \n",
" \"/>\n",
"<defs>\n",
" <clipPath id=\"clip6604\">\n",
" <rect x=\"2129\" y=\"47\" width=\"73\" height=\"1457\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<g clip-path=\"url(#clip6604)\">\n",
"<image width=\"72\" height=\"1456\" xlink:href=\"data:image/png;base64,\n",
"iVBORw0KGgoAAAANSUhEUgAAAEgAAAWwCAYAAAD+FAeUAAALO0lEQVR4nO3dQWoTUBSG0cS8QRyY\n",
"iYhr6L67B1fRFRQsjREqFASLGZRgXEH7Dd8bnLOCy8c/v9vLv9vrhjd9mH3A6gQKAgWBgkBBoCBQ\n",
"ECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBB\n",
"oCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWB\n",
"gkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFMb5\n",
"57fZNyzNgoJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAg\n",
"UBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJA\n",
"QaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIF\n",
"gYJAQaAgUBAoCBQECgKFsf9+N/uGpVlQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgI\n",
"FAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQ\n",
"ECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBB\n",
"oCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoDC29w+zb1iaBQWBgkBBoCBQECgIFAQKAgWB\n",
"gkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQK\n",
"AgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgI\n",
"FAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQK4/XxMPuGpVlQ\n",
"ECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBB\n",
"oCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWB\n",
"gkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQK\n",
"AgWBgkBBoDD+HL/OvmFpFhQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAg\n",
"UBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJA\n",
"QaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIF\n",
"gYJAQaAgUBAoCBQECgIFgYJAQaAgUBAojOdfX2bfsDQLCgIFgYJAQaAgUBAoCBQECgIFgYJAQaAg\n",
"UBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJA\n",
"QaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIF\n",
"gYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBTG0+/Ps29YmgUFgYJAQaAg\n",
"UBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJA\n",
"QaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIF\n",
"gYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQE\n",
"CuPHy2H2DUuzoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQ\n",
"ECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBB\n",
"oCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWB\n",
"gkBBoCBQECgIFAQKAgWBgkBhnP5+nH3D0iwoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAo\n",
"CBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAg\n",
"UBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJA\n",
"QaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBjH8272DUuzoCBQECgIFAQKAgWBgkBB\n",
"oCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWB\n",
"gkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQK\n",
"AgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBhnM6X2Tcs\n",
"zYKCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgU\n",
"BAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQ\n",
"KAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGg\n",
"IFAQKAgUBAoChfGweZp9w9IsKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGC\n",
"QEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoC\n",
"BYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgU\n",
"BAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFDYftrfXGcfsTILCgIFgYJAQaAgUBAoCBQECgIFgYJA\n",
"QaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIF\n",
"gYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQE\n",
"CgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBS2m83OA7Z3WFAQKAgU\n",
"BAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQ\n",
"KAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGg\n",
"IFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGC\n",
"QEGg8B++FCk4XRJKMAAAAABJRU5ErkJggg==\n",
"\" transform=\"translate(2129, 47)\"/>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 1383.93)\" x=\"2237.26\" y=\"1383.93\">-</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2265.37, 1383.93)\" x=\"2265.37\" y=\"1383.93\">4</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 1198.67)\" x=\"2237.26\" y=\"1198.67\">-</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2265.37, 1198.67)\" x=\"2265.37\" y=\"1198.67\">3</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 1013.41)\" x=\"2237.26\" y=\"1013.41\">-</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2265.37, 1013.41)\" x=\"2265.37\" y=\"1013.41\">2</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 828.156)\" x=\"2237.26\" y=\"828.156\">-</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2265.37, 828.156)\" x=\"2265.37\" y=\"828.156\">1</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 642.898)\" x=\"2237.26\" y=\"642.898\">0</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 457.641)\" x=\"2237.26\" y=\"457.641\">1</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 272.384)\" x=\"2237.26\" y=\"272.384\">2</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 87.1264)\" x=\"2237.26\" y=\"87.1264\">3</text>\n",
"</g>\n",
"<polyline clip-path=\"url(#clip6601)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 2201.26,1503.47 2201.26,1370.28 2225.26,1370.28 2201.26,1370.28 2201.26,1185.02 2225.26,1185.02 2201.26,1185.02 2201.26,999.762 2225.26,999.762 2201.26,999.762 \n",
" 2201.26,814.504 2225.26,814.504 2201.26,814.504 2201.26,629.247 2225.26,629.247 2201.26,629.247 2201.26,443.99 2225.26,443.99 2201.26,443.99 2201.26,258.732 \n",
" 2225.26,258.732 2201.26,258.732 2201.26,73.4752 2225.26,73.4752 2201.26,73.4752 2201.26,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6603)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1570.77,775.359 1569.33,775.359 1566.47,775.359 1562.19,775.359 1556.5,775.359 1549.43,775.359 1540.99,775.359 1531.21,775.359 1520.12,775.359 1507.76,775.359 \n",
" 1494.16,775.359 1479.37,775.359 1463.43,775.359 1446.4,775.359 1428.33,775.359 1409.27,775.359 1389.29,775.359 1368.45,775.359 1346.81,775.359 1324.44,775.359 \n",
" 1301.41,775.359 1277.8,775.359 1253.68,775.359 1229.12,775.359 1204.2,775.359 1179,775.359 1153.61,775.359 1128.09,775.359 1102.53,775.359 1077.01,775.359 \n",
" 1051.62,775.359 1026.42,775.359 1001.5,775.359 976.944,775.359 952.82,775.359 929.208,775.359 906.181,775.359 883.812,775.359 862.172,775.359 841.328,775.359 \n",
" 821.346,775.359 802.289,775.359 784.217,775.359 767.187,775.359 751.252,775.359 736.462,775.359 722.865,775.359 710.502,775.359 699.413,775.359 689.632,775.359 \n",
" 681.191,775.359 674.116,775.359 668.429,775.359 664.147,775.359 661.286,775.359 659.853,775.359 \n",
" \"/>\n",
"<g clip-path=\"url(#clip6604)\">\n",
"<image width=\"72\" height=\"1456\" xlink:href=\"data:image/png;base64,\n",
"iVBORw0KGgoAAAANSUhEUgAAAEgAAAWwCAYAAAD+FAeUAAAMbklEQVR4nO3dwY3sRhAFQY5Q/lsh\n",
"L6XfLQtUeSQPERYMEg9LNMmZ/f17/r4P/+uvtz/A1wkUBAoCBYHCnPvv25/h0ywoCBQECgIFgcJc\n",
"V7GVBQWBgkBBoCBQmHtcxTYWFAQKAgWBgqNGsKAgUBAoCBQECq5iwYKCQEGgIFAQKLiKBQsKAgWB\n",
"gkDBU41gQUGgIFAQKAgUHDWCBQWBgkBBoCBQcBULFhQECgIFgcI8bpitLCgIFAQKAgWBgqtYsKAg\n",
"UBAoCBQECvO4YbayoCBQECgIFBw1ggUFgYJAQaAgUHAVCxYUBAoCBYGCQGGe88/bn+HTLCgIFAQK\n",
"AgVPNYIFBYGCQEGgIFBwwyxYUBAoCBQECgIFV7FgQUGgIFAQKAgU5nf/vP0ZPs2CgkBBoCBQmOf4\n",
"I72xoCBQECgIFAQK83MVW1lQECgIFAQKAgVnsWBBQaAgUBAozOOpxsqCgkBBoCBQECi4YRYsKAgU\n",
"BAoCBYGCG2bBgoJAQaAgUHDUCBYUBAoCBYGCQMFRI1hQECgIFAQKAoX5nfP2Z/g0CwoCBYGCQMFR\n",
"I1hQECgIFAQKAgVXsWBBQaAgUBAoCBS8vBAsKAgUBAoChXk81VhZUBAoCBQECgIFR41gQUGgIFAQ\n",
"KAgUPPYJFhQECgIFgYJAwVUsWFAQKAgUBAq+zBIsKAgUBAoCBYGClxeCBQWBgkBBoCBQcMMsWFAQ\n",
"KAgUBAqOGsGCgkBBoCBQECi4igULCgIFgYJAQaDg5YVgQUGgIFAQKHiqESwoCBQECgIFgYIbZsGC\n",
"gkBBoCBQECi4igULCgIFgYJAwR/pYEFBoCBQECgIFOY59+3P8GkWFAQKAgWBgkBhnusstrGgIFAQ\n",
"KAgU3DALFhQECgIFgYJAwQ2zYEFBoCBQECgIFJzFggUFgYJAQaAgUHAVCxYUBAoCBYGCG2bBgoJA\n",
"QaAgUBAoOGoECwoCBYGCQEGgMI+L2MqCgkBBoCBQ8Ec6WFAQKAgUBAoChfGNzJ0FBYGCQEGgIFBw\n",
"FgsWFAQKAgWBgj/SwYKCQEGgIFAQKLiKBQsKAgWBgkBBoDCPL/usLCgIFAQKAoW55/f2Z/g0CwoC\n",
"BYGCQEGg4IZZsKAgUBAoCBQECvM4i60sKAgUBAoChbnXH+mNBQWBgkBBoCBQcNQIFhQECgIFgYJA\n",
"wVUsWFAQKAgUBAoCBXcUgwUFgYJAQaDgqBEsKAgUBAoCBYHCPEejjTpBoCBQECgIFNwwCxYUBAoC\n",
"BYGCG2bBgoJAQaAgUBAo+HmcYEFBoCBQECgIFOa5Gm3UCQIFgYJAwVEjWFAQKAgUBAoCBVexYEFB\n",
"oCBQECgIFLwnHdQJAgWBgkDBa8DBgoJAQaAgUBAoeE86WFAQKAgUBAoChblumK3UCQIFgYJAwQ2z\n",
"YEFBoCBQECgIFNwwCxYUBAoCBYGCQMENs6BOECgIFAQKAgV3FIMFBYGCQEGg4CuZwYKCQEGgIFAQ\n",
"KMz1G2YrdYJAQaAgUBAoeHkhWFAQKAgUBApumAULCgIFgYJAQaDg2XywoCBQECgIFAQK3pMO6gSB\n",
"gkBBoOCoESwoCBQECgIFgYLHPsGCgkBBoCBQECg4iwULCgIFgYJAwVONoE4QKAgUBAoCBUeNYEFB\n",
"oCBQECgIFDz2CRYUBAoCBYGCo0awoCBQECgIFAQKHvsEdYJAQaAgUBAoOIsFCwoCBYGCQEGg4CoW\n",
"LCgIFAQKAgV/pIMFBYGCQEGgIFDwhlmwoCBQECgIFAQKc/wDtpU6QaAgUBAouGEWLCgIFAQKAgWB\n",
"ghtmwYKCQEGgIFAQKDiLBQsKAgWBgkDBH+lgQUGgIFAQKAgUXMWCBQWBgkBBoCBQcBULFhQECgIF\n",
"gcIcf6RXFhQECgIFgYJAwVEjWFAQKAgUBAoCBVexYEFBoCBQECj4Ix0sKAgUBAoCBYGCq1iwoCBQ\n",
"ECgIFAQKrmLBgoJAQaAgUBAoeAUvWFAQKAgUBAqOGsGCgkBBoCBQECi4igULCgIFgYJAQaDgX9cE\n",
"dYJAQaAgUHDUCBYUBAoCBYGCQMGz+WBBQaAgUBAoCBScxYIFBYGCQEGg4KgRLCgIFAQKAgWBgqNG\n",
"sKAgUBAoCBQECq5iwYKCQEGgIFBwwyxYUBAoCBQECgKFuY+r2MaCgkBBoCBQECg4iwULCgIFgYJA\n",
"wVONYEFBoCBQECgIFObctz/Ct1lQECgIFAQKAgVnsWBBQaAgUBAoCBQ89gkWFAQKAgWBwhxvmK0s\n",
"KAgUBAoCBYGCG2bBgoJAQaAgUBAouGEWLCgIFAQKAgVHjWBBQaAgUBAoCBTmvP0JPs6CgkBBoCBQ\n",
"ECg4iwULCgIFgYJAwVONYEFBoCBQECgIFPwSZ7CgIFAQKAgUBArOYsGCgkBBoCBQ8BtmwYKCQEGg\n",
"IFAQKLhhFiwoCBQECgIFgYI3zIIFBYGCQEGg4MsswYKCQEGgIFAQKDhqBAsKAgWBgkBBoOAsFiwo\n",
"CBQECgIFgYKzWLCgIFAQKAgUfJklWFAQKAgUBAoChfFln50FBYGCQEGgIFBwFgsWFAQKAgWBgqNG\n",
"sKAgUBAoCBQECo4awYKCQEGgIFAQKDiLBQsKAgWBgkDBUSNYUBAoCBQECgIFvycdLCgIFAQKAgWB\n",
"gt+TDhYUBAoCBYGCo0awoCBQECgIFAQKcxw1VhYUBAoCBYGCQGGus9jKgoJAQaAgUPCGWbCgIFAQ\n",
"KAgUBAq+zBIsKAgUBAoCBYGClxeCBQWBgkBBoCBQ8PJCsKAgUBAoCBQ8mw8WFAQKAgWBgkDB/3oO\n",
"FhQECgIFgYJAwSt4wYKCQEGgIFBwwyxYUBAoCBQECgIFN8yCBQWBgkBBoCBQcBYLFhQECgIFgYLX\n",
"gIMFBYGCQEGgIFDwlcxgQUGgIFAQKAgU/DxOsKAgUBAoCBQcNYIFBYGCQEGgIFBwFQsWFAQKAgWB\n",
"gkDB/3oOFhQECgIFgYKjRrCgIFAQKAgUBAqezQcLCgIFgYJAQaDgLBYsKAgUBAoCBYGCq1iwoCBQ\n",
"ECgIFNwwCxYUBAoCBYGCQMFRI1hQECgIFAQKAgW/Jx0sKAgUBAoCBT+XHCwoCBQECgIFgYIbZsGC\n",
"gkBBoCBQECh4eSFYUBAoCBQECo4awYKCQEGgIFAQKMx9XMY2FhQECgIFgYJAwVksWFAQKAgUBAqe\n",
"agQLCgIFgYJAQaDgqBEsKAgUBAoCBYGCs1iwoCBQECgIFBw1ggUFgYJAQaAgUPDDAsGCgkBBoCBQ\n",
"ECjM8Z70yoKCQEGgIFAQKDiLBQsKAgWBgkDBUSNYUBAoCBQECgIFP/ofLCgIFAQKAgWBwlx3zFYW\n",
"FAQKAgWBgqNGsKAgUBAoCBQECr7tEywoCBQECgIFgYLfkw4WFAQKAgWBgqNGsKAgUBAoCBQECt6T\n",
"DhYUBAoCBYGCQMENs2BBQaAgUBAoOGoECwoCBYGCQEGg4CoWLCgIFAQKAgWBwhxfyVxZUBAoCBQE\n",
"Cp5qBAsKAgWBgkBBoOCGWbCgIFAQKAgUBAquYsGCgkBBoCBQECi4igULCgIFgYJAYe7jtzg3FhQE\n",
"CgIFgYJAwVEjWFAQKAgUBAoChTk/Z7GNBQWBgkBBoDDHDbOVBQWBgkBBoCBQcBULFhQECgIFgYJA\n",
"wcsLwYKCQEGgIFCY8/NsfmNBQaAgUBAoCBTcMAsWFAQKAgWBgkDBVSxYUBAoCBQECp5qBAsKAgWB\n",
"gkBBoDDn+fP2Z/g0CwoCBYGCQEGg4IZZsKAgUBAoCBTmOmqsLCgIFAQKAgWBgqNGsKAgUBAoCBQE\n",
"Cq5iwYKCQEGgIFAQKLijGCwoCBQECgIFR41gQUGgIFAQKAgUHDWCBQWBgkBBoCBQ8J3VYEFBoCBQ\n",
"ECjMuf5IbywoCBQECgIFgYKjRrCgIFAQKAgUBApzncVWFhQECgIFgYKjRrCgIFAQKAgUBAreMAsW\n",
"FAQKAgWBgkDBywvBgoJAQaAgUHDDLFhQECgIFAQKAgXP5oMFBYGCQEGgIFDw2CdYUBAoCBQECo4a\n",
"wYKCQEGgIFAQKHjsEywoCBQECgIFgYKzWLCgIFAQKAgUBAoe+wQLCgIFgYJAwVEjWFAQKAgUBAoC\n",
"BY99ggUFgYJAQaAgUJh73TDbWFAQKAgUBAqOGsGCgkBBoCBQECjMc+/bn+HTLCgIFAQKAgWBwjzO\n",
"YisLCgIFgYJAwRtmwYKCQEGgIFAQKDhqBAsKAgWBgkBBoODlhWBBQaAgUBAozOOG2cqCgkBBoCBQ\n",
"ECg4agQLCgIFgYJAQaDgsU+woCBQECgIFP4DPcHwb7pfSUoAAAAASUVORK5CYII=\n",
"\" transform=\"translate(2129, 47)\"/>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 1383.93)\" x=\"2237.26\" y=\"1383.93\">-</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2265.37, 1383.93)\" x=\"2265.37\" y=\"1383.93\">4</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 1198.67)\" x=\"2237.26\" y=\"1198.67\">-</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2265.37, 1198.67)\" x=\"2265.37\" y=\"1198.67\">3</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 1013.41)\" x=\"2237.26\" y=\"1013.41\">-</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2265.37, 1013.41)\" x=\"2265.37\" y=\"1013.41\">2</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 828.156)\" x=\"2237.26\" y=\"828.156\">-</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2265.37, 828.156)\" x=\"2265.37\" y=\"828.156\">1</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 642.898)\" x=\"2237.26\" y=\"642.898\">0</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 457.641)\" x=\"2237.26\" y=\"457.641\">1</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 272.384)\" x=\"2237.26\" y=\"272.384\">2</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 87.1264)\" x=\"2237.26\" y=\"87.1264\">3</text>\n",
"</g>\n",
"<polyline clip-path=\"url(#clip6601)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 2201.26,1503.47 2201.26,1370.28 2225.26,1370.28 2201.26,1370.28 2201.26,1185.02 2225.26,1185.02 2201.26,1185.02 2201.26,999.762 2225.26,999.762 2201.26,999.762 \n",
" 2201.26,814.504 2225.26,814.504 2201.26,814.504 2201.26,629.247 2225.26,629.247 2201.26,629.247 2201.26,443.99 2225.26,443.99 2201.26,443.99 2201.26,258.732 \n",
" 2225.26,258.732 2201.26,258.732 2201.26,73.4752 2225.26,73.4752 2201.26,73.4752 2201.26,47.2441 \n",
" \"/>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:66px; text-anchor:middle;\" transform=\"rotate(-90, 2378.86, 775.359)\" x=\"2378.86\" y=\"775.359\"></text>\n",
"</g>\n",
"<polygon clip-path=\"url(#clip6601)\" points=\"\n",
"1718.43,251.724 2009.26,251.724 2009.26,130.764 1718.43,130.764 \n",
" \" fill=\"#ffffff\" fill-opacity=\"1\"/>\n",
"<polyline clip-path=\"url(#clip6601)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1718.43,251.724 2009.26,251.724 2009.26,130.764 1718.43,130.764 1718.43,251.724 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6601)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1742.43,191.244 1886.43,191.244 \n",
" \"/>\n",
"<g clip-path=\"url(#clip6601)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 1910.43, 208.744)\" x=\"1910.43\" y=\"208.744\">y2</text>\n",
"</g>\n",
"</svg>\n"
]
},
"execution_count": 52,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"v = z -> π*logkernel(u, z)\n",
"\n",
"xx = yy = -2:0.01:2\n",
"V = v.(xx' .+ im*yy)\n",
"\n",
"contour(xx, yy, V)\n",
"plot!(domain(x); color=:black)"
]
},
{
"cell_type": "code",
"execution_count": 53,
"metadata": {},
"outputs": [
{
"data": {
"image/svg+xml": [
"<?xml version=\"1.0\" encoding=\"utf-8\"?>\n",
"<svg xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\" width=\"600\" height=\"400\" viewBox=\"0 0 2400 1600\">\n",
"<defs>\n",
" <clipPath id=\"clip6800\">\n",
" <rect x=\"0\" y=\"0\" width=\"2000\" height=\"2000\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<defs>\n",
" <clipPath id=\"clip6801\">\n",
" <rect x=\"0\" y=\"0\" width=\"2400\" height=\"1600\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<polygon clip-path=\"url(#clip6801)\" points=\"\n",
"0,1600 2400,1600 2400,0 0,0 \n",
" \" fill=\"#ffffff\" fill-opacity=\"1\"/>\n",
"<defs>\n",
" <clipPath id=\"clip6802\">\n",
" <rect x=\"480\" y=\"0\" width=\"1681\" height=\"1600\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<polygon clip-path=\"url(#clip6801)\" points=\"\n",
"507.195,1503.47 1723.43,1503.47 1723.43,47.2441 507.195,47.2441 \n",
" \" fill=\"#ffffff\" fill-opacity=\"1\"/>\n",
"<defs>\n",
" <clipPath id=\"clip6803\">\n",
" <rect x=\"507\" y=\"47\" width=\"1217\" height=\"1457\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 507.195,1417.45 952.366,1159.38 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 952.366,1159.38 952.366,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 603.577,1428.2 1048.75,1170.13 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1048.75,1170.13 1048.75,57.9971 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 699.96,1438.96 1145.13,1180.88 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1145.13,1180.88 1145.13,68.7501 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 796.342,1449.71 1241.51,1191.64 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1241.51,1191.64 1241.51,79.5031 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 892.725,1460.46 1337.9,1202.39 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1337.9,1202.39 1337.9,90.2561 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 989.107,1471.22 1434.28,1213.14 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1434.28,1213.14 1434.28,101.009 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1085.49,1481.97 1530.66,1223.9 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1530.66,1223.9 1530.66,111.762 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1181.87,1492.72 1627.04,1234.65 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1627.04,1234.65 1627.04,122.515 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1278.25,1503.47 1723.43,1245.4 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1723.43,1245.4 1723.43,133.268 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 507.195,1417.45 1278.25,1503.47 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 507.195,1417.45 507.195,305.316 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 562.841,1385.19 1333.9,1471.22 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 562.841,1385.19 562.841,273.057 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 618.488,1352.93 1389.55,1438.96 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 618.488,1352.93 618.488,240.798 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 674.134,1320.67 1445.19,1406.7 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 674.134,1320.67 674.134,208.539 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 729.781,1288.41 1500.84,1374.44 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 729.781,1288.41 729.781,176.28 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 785.427,1256.16 1556.49,1342.18 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 785.427,1256.16 785.427,144.021 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 841.073,1223.9 1612.13,1309.92 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 841.073,1223.9 841.073,111.762 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 896.72,1191.64 1667.78,1277.66 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 896.72,1191.64 896.72,79.5031 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 952.366,1159.38 1723.43,1245.4 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 952.366,1159.38 952.366,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 507.195,1417.45 952.366,1159.38 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 952.366,1159.38 1723.43,1245.4 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 507.195,1306.24 952.366,1048.17 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 952.366,1048.17 1723.43,1134.19 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 507.195,1195.02 952.366,936.952 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 952.366,936.952 1723.43,1022.98 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 507.195,1083.81 952.366,825.739 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 952.366,825.739 1723.43,911.762 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 507.195,972.597 952.366,714.525 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 952.366,714.525 1723.43,800.549 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 507.195,861.383 952.366,603.312 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 952.366,603.312 1723.43,689.335 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 507.195,750.17 952.366,492.098 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 952.366,492.098 1723.43,578.122 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 507.195,638.956 952.366,380.885 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 952.366,380.885 1723.43,466.908 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 507.195,527.743 952.366,269.671 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 952.366,269.671 1723.43,355.695 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 507.195,416.529 952.366,158.458 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#ededed; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 952.366,158.458 1723.43,244.482 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 507.195,305.316 952.366,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#cccccc; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 952.366,47.2441 1723.43,133.268 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 451.153,1228.48 473.325,1215.63 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 494.265,1183.74 481.947,1213.92 500.424,1203.21 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 494.265,1183.74 494.265,1218.3 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 451.153,1006.05 473.325,993.199 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 483.179,975.967 483.179,974.321 484.411,970.316 485.643,967.956 488.106,964.882 493.033,962.026 495.497,962.243 496.729,963.175 497.96,965.752 497.96,969.044 \n",
" 496.729,973.049 494.265,979.415 481.947,1003.01 499.192,993.015 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 489.338,741.741 485.643,745.529 483.179,751.894 481.947,760.837 481.947,765.774 483.179,773.288 485.643,776.797 489.338,776.301 491.802,774.873 495.497,771.085 \n",
" 497.96,764.72 499.192,755.777 499.192,750.84 497.96,743.325 495.497,739.816 491.802,740.313 489.338,741.741 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 483.179,531.113 483.179,529.467 484.411,525.462 485.643,523.102 488.106,520.028 493.033,517.172 495.497,517.389 496.729,518.321 497.96,520.898 497.96,524.19 \n",
" 496.729,528.195 494.265,534.561 481.947,558.158 499.192,548.161 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 494.265,294.031 481.947,324.211 500.424,313.5 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 494.265,294.031 494.265,328.591 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 507.195,1417.45 507.195,1417.45 499.759,1421.76 507.195,1417.45 507.195,1306.24 503.477,1308.39 507.195,1306.24 507.195,1195.02 499.759,1199.33 507.195,1195.02 \n",
" 507.195,1083.81 503.477,1085.97 507.195,1083.81 507.195,972.597 499.759,976.908 507.195,972.597 507.195,861.383 503.477,863.539 507.195,861.383 507.195,750.17 \n",
" 499.759,754.481 507.195,750.17 507.195,638.956 503.477,641.112 507.195,638.956 507.195,527.743 499.759,532.054 507.195,527.743 507.195,416.529 503.477,418.685 \n",
" 507.195,416.529 507.195,305.316 499.759,309.627 507.195,305.316 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 653.17,1469.76 682.429,1473.02 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 698.683,1461.67 701.934,1460.39 706.811,1455.99 706.811,1490.55 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 875.193,1474.78 870.317,1475.88 867.066,1480.45 865.44,1488.5 865.44,1493.44 867.066,1501.85 870.317,1507.15 875.193,1509.34 878.444,1509.7 883.321,1508.6 \n",
" 886.572,1504.02 888.197,1495.98 888.197,1491.04 886.572,1482.63 883.321,1477.33 878.444,1475.14 875.193,1474.78 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1063.08,1502.32 1066.33,1501.04 1071.21,1496.65 1071.21,1531.21 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1252.6,1525.11 1252.6,1523.47 1254.22,1520.36 1255.85,1518.89 1259.1,1517.61 1265.6,1518.33 1268.85,1520.34 1270.48,1522.17 1272.1,1525.64 1272.1,1528.93 \n",
" 1270.48,1532.04 1267.22,1536.62 1250.97,1551.26 1273.73,1553.8 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 507.195,1417.45 507.195,1417.45 499.759,1421.76 507.195,1417.45 603.577,1428.2 599.859,1430.36 603.577,1428.2 699.96,1438.96 692.524,1443.27 699.96,1438.96 \n",
" 796.342,1449.71 792.624,1451.87 796.342,1449.71 892.725,1460.46 885.289,1464.77 892.725,1460.46 989.107,1471.22 985.389,1473.37 989.107,1471.22 1085.49,1481.97 \n",
" 1078.05,1486.28 1085.49,1481.97 1181.87,1492.72 1178.15,1494.88 1181.87,1492.72 1278.25,1503.47 1270.82,1507.79 1278.25,1503.47 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1410.77,1477.37 1432.94,1464.52 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1445.26,1444.21 1447.72,1441.13 1451.42,1434.06 1451.42,1468.62 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1544.23,1380.25 1540.54,1384.04 1538.07,1390.4 1536.84,1399.34 1536.84,1404.28 1538.07,1411.8 1540.54,1415.31 1544.23,1414.81 1546.7,1413.38 1550.39,1409.59 \n",
" 1552.86,1403.23 1554.09,1394.28 1554.09,1389.35 1552.86,1381.83 1550.39,1378.32 1546.7,1378.82 1544.23,1380.25 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1651.83,1324.46 1654.29,1321.38 1657.99,1314.3 1657.99,1348.86 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1760.66,1263.01 1760.66,1261.37 1761.89,1257.36 1763.12,1255 1765.59,1251.93 1770.51,1249.07 1772.98,1249.29 1774.21,1250.22 1775.44,1252.8 1775.44,1256.09 \n",
" 1774.21,1260.09 1771.75,1266.46 1759.43,1290.06 1776.67,1280.06 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1278.25,1503.47 1278.25,1503.47 1293.68,1505.2 1278.25,1503.47 1333.9,1471.22 1341.61,1472.08 1333.9,1471.22 1389.55,1438.96 1404.97,1440.68 1389.55,1438.96 \n",
" 1445.19,1406.7 1452.9,1407.56 1445.19,1406.7 1500.84,1374.44 1516.26,1376.16 1500.84,1374.44 1556.49,1342.18 1564.2,1343.04 1556.49,1342.18 1612.13,1309.92 \n",
" 1627.55,1311.64 1612.13,1309.92 1667.78,1277.66 1675.49,1278.52 1667.78,1277.66 1723.43,1245.4 1738.85,1247.12 1723.43,1245.4 \n",
" \"/>\n",
"<g clip-path=\"url(#clip6803)\">\n",
"<image width=\"1216\" height=\"1456\" xlink:href=\"data:image/png;base64,\n",
"iVBORw0KGgoAAAANSUhEUgAABMAAAAWwCAYAAAC7Hz3jAAAgAElEQVR4nOzdPag1XZsn9F3nbWW6\n",
"xxmUBgNBGFpEQcxEREREURERA1MzDURhEEGDCSaYQIMBBwwmm2zAaNDcQEzFD1QUPxhQBAOlmUGd\n",
"fvsd+zllcO+qXR//fdWq/XHu+1nP7xf0c+6qVWutXbt2nbfXqf++hnEcLwAAAADQq4/vPQEAAAAA\n",
"eCcLYAAAAAB0zQIYAAAAAF2zAAYAAABA1yyAAQAAANA1C2AAAAAAdM0CGAAAAABdswAGAAAAQNcs\n",
"gAEAAADQNQtgAAAAAHTNAhgAAAAAXbMABgAAAEDXLIABAAAA0DULYAAAAAB0zQIYAAAAAF2zAAYA\n",
"AABA1yyAAQAAANA1C2AAAAAAdM0CGAAAAABdswAGAAAAQNcsgAEAAADQNQtgAAAAAHTNAhgAAAAA\n",
"XbMABgAAAEDXLIABAAAA0DULYAAAAAB0zQIYAAAAAF2zAAYAAABA1yyAAQAAANA1C2AAAAAAdM0C\n",
"GAAAAABdswAGAAAAQNcsgAEAAADQNQtgAAAAAHTNAhgAAAAAXbMABgAAAEDXLIABAAAA0DULYAAA\n",
"AAB0zQIYAAAAAF2zAAYAAABA1yyAAQAAANA1C2AAAAAAdM0CGAAAAABdswAGAAAAQNcsgAEAAADQ\n",
"NQtgAAAAAHTNAhgAAAAAXbMABgAAAEDXLIABAAAA0DULYAAAAAB0zQIYAAAAAF2zAAYAAABA1yyA\n",
"AQAAANA1C2AAAAAAdM0CGAAAAABdswAGAAAAQNcsgAEAAADQNQtgAAAAAHTNAhgAAAAAXbMABgAA\n",
"AEDXLIABAAAA0DULYAAAAAB0zQIYAAAAAF2zAAYAAABA1yyAAQAAANA1C2AAAAAAdM0CGAAAAABd\n",
"swAGAAAAQNcsgAEAAADQNQtgAAAAAHTNAhgAAAAAXbMABgAAAEDXLIABAAAA0DULYAAAAAB0zQIY\n",
"AAAAAF2zAAYAAABA1yyAAQAAANA1C2AAAAAAdM0CGAAAAABdswAGAAAAQNcsgAEAAADQNQtgAAAA\n",
"AHTNAhgAAAAAXbMABgAAAEDXLIABAAAA0DULYAAAAAB0zQIYAAAAAF2zAAYAAABA1yyAAQAAANA1\n",
"C2AAAAAAdM0CGAAAAABdswAGAAAAQNcsgAEAAADQNQtgAAAAAHTNAhgAAAAAXbMABgAAAEDXLIAB\n",
"AAAA0DULYAAAAAB0zQIYAAAAAF2zAAYAAABA1yyAAQAAANA1C2AAAAAAdM0CGAAAAABdswAGAAAA\n",
"QNcsgAEAAADQNQtgAAAAAHTNAhgAAAAAXbMABgAAAEDXLIABAAAA0DULYAAAAAB0zQIYAAAAAF2z\n",
"AAYAAABA1yyAAQAAANA1C2AAAAAAdM0CGAAAAABdswAGAAAAQNcsgAEAAADQNQtgAAAAAHTNAhgA\n",
"AAAAXbMABgAAAEDXLIABAAAA0DULYAAAAAB0zQIYAAAAAF2zAAYAAABA1yyAAQAAANA1C2AAAAAA\n",
"dM0CGAAAAABdswAGAAAAQNcsgAEAAADQNQtgAAAAAHTNAhgAAAAAXbMABgAAAEDXLIABAAAA0DUL\n",
"YAAAAAB0zQIYAAAAAF2zAAYAAABA1yyAAQAAANA1C2AAAAAAdM0CGAAAAABdswAGAAAAQNcsgAEA\n",
"AADQNQtgAAAAAHTNAhgAAAAAXbMABgAAAEDXLIABAAAA0DULYAAAAAB0zQIYAAAAAF2zAAYAAABA\n",
"1yyAAQAAANA1C2AAAAAAdM0CGAAAAABdswAGAAAAQNcsgAEAAADQNQtgAAAAAHTNAhgAAAAAXbMA\n",
"BgAAAEDXLIABAAAA0DULYAAAAAB0zQIYAAAAAF2zAAYAAABA1yyAAQAAANA1C2AAAAAAdM0CGAAA\n",
"AABdswAGAAAAQNcsgAEAAADQNQtgAAAAAHTNAhgAAAAAXbMABgAAAEDXLIABAAAA0DULYAAAAAB0\n",
"zQIYAAAAAF2zAAYAAABA1yyAAQAAANA1C2AAAAAAdM0CGAAAAABdswAGAAAAQNcsgAEAAADQNQtg\n",
"AAAAAHTNAhgAAAAAXbMABgAAAEDXLIABAAAA0DULYAAAAAB0zQIYAAAAAF2zAAYAAABA1yyAAQAA\n",
"ANA1C2AAAAAAdM0CGAAAAABdswAGAAAAQNcsgAEAAADQNQtgAAAAAHTNAhgAAAAAXbMABgAAAEDX\n",
"LIABAAAA0DULYAAAAAB0zQIYAAAAAF2zAAYAAABA1yyAAQAAANA1C2AAAAAAdM0CGAAAAABdswAG\n",
"AAAAQNcsgAEAAADQNQtgAAAAAHTNAhgAAAAAXbMABgAAAEDXLIABAAAA0DULYAAAAAB0zQIYAAAA\n",
"AF2zAAYAAABA1yyAAQAAANA1C2AAAAAAdM0CGAAAAABdswAGAAAAQNcsgAEAAADQNQtgAAAAAHTN\n",
"AhgAAAAAXbMABgAAAEDXLIABAAAA0DULYAAAAAB0zQIYAAAAAF2zAAYAAABA1yyAAQAAANA1C2AA\n",
"AAAAdM0CGAAAAABdswAGAAAAQNcsgAEAAADQNQtgAAAAAHTNAhgAAAAAXbMABgAAAEDXLIABAAAA\n",
"0DULYAAAAAB0zQIYAAAAAF2zAAYAAABA1yyAAQAAANA1C2AAAAAAdM0CGAAAAABdswAGAAAAQNcs\n",
"gAEAAADQNQtgAAAAAHTNAhgAAAAAXbMABgAAAEDXLIABAAAA0DULYAAAAAB0zQIYAAAAAF2zAAYA\n",
"AABA1yyAAQAAANA1C2AAAAAAdM0CGAAAAABd+63vPQEAfpn+4K/+i+N+69B2cGx2/9jf+b3/qLFj\n",
"AACgR54AAwAAAKBrFsAAAAAA6NowjiGBAgBv9gf/y79w+wU07H64XC7p99PJJGPs99m+6mPFLQEA\n",
"4MfjCTAAAAAAumYBDAAAAICuiUAC8F38+n/+53e/gMYhRCCXra77n8kY3sZ4RVJxONnV2SqX+/Yi\n",
"lgAAcJ4nwAAAAADomgUwAAAAALomAgnAd/Hr/+mf2/8CWkYg0++n4Wz6b9/HOP3t53RflQf6KitU\n",
"nhyr7OKgf3FLAAB+ATwBBgAAAEDXLIABAAAA0DURSAC+i1//j/9sYwRy0Wxo+btN+L222DQO74hA\n",
"Lr0pWtnU7dkqk63HtM6j2HkwprglAADv5AkwAAAAALpmAQwAAACArolAAvBd/Pp/+KfnX0BTGnFM\n",
"Ecjl76mPk3+3GXc/zDHK8W0RyMoySvju8V/R/9DYVUv0sXU+74lbilgCAPyyeQIMAAAAgK55AgyA\n",
"7+IP//t/avcLaP1UVvEE2HXTENvX447T40EfjQ8EPfprMnW/+hL/r38g6fZSzn65/iMe7fj9X7i/\n",
"2/fUE26+0B8A4OfAE2AAAAAAdM0CGAAAAABdE4EE4Ev94X/3T377xTPsf//EL8FfBvfmCOGUgQx/\n",
"x2n8vTamL9Rv/ZX4cLrviQhkbP5z+CL9b9antjV6eNbZDt8TgXx8rLDzIM4pbgkA0MYTYAAAAAB0\n",
"zQIYAAAAAF0TgQTgS/3hf/tP7Ms1DrsfFvuX7aYqkNdtyxhj/HWWNn4bY9zGKQ+sk2gPps7K49r6\n",
"LGebIqGv9qVRzOf73VW+fMlUH+nkPRHI8oCz71X8HH4jagkA/Nx5AgwAAACArlkAAwAAAKBrIpAA\n",
"fKk//G/+8RCBLNJVY9Fu9e/p5/B7bdnHHJss2q+ODdumcR+NQr7J+PGrB45qicS9wgs6+5L45WP9\n",
"va/K5YOVLe8e+lgEMjY8G+c8GEvMEgB4J0+AAQAAANA1C2AAAAAAdE0EEoAv9Zv/+h/79otnCNHG\n",
"xaZxTiimCOSw+L9T+xdEIFt/JU7VFlsDW1O/b45Mjh/P/F2rNQr5lSm1beT1hX09degrzsHjfawu\n",
"05dcUw/GLFW0BAB+RjwBBgAAAEDXLIABAAAA0DURSAC+1G/+q380RCCvf49Z/E4aQ0LxlmraJ5jG\n",
"FAVLv+OmmGBz3LF543bwcNjy705vSGEddnlyzJPVLvMpfeHr/F5VIB8e4uz5fkEfLzj29RUtXxmx\n",
"PF9d8vGxGscVtwSAnwVPgAEAAADQNQtgAAAAAHRNBBKAL/Wb//Ifuf7iCRHI1lxiiExOMb3Uw7Aa\n",
"61eHY72+yt7U1xf+3en0tFP0r4pAvivZ9coI4vK9/BlUgXyo2+8Zs3xBJcunPl8PHns45mNxx8M+\n",
"zlbNjLvutxO3BICaJ8AAAAAA6JoFMAAAAAC6JgIJwJf6zX/xD9+PQIZI49q4ab/YFaNJR5UYt2Pu\n",
"+xiLaVRzzUmzxdaGX7+rypbfJdx0rgpk3dUTf3N7NDr2qsFODvFw7PIrqkC+Ihrb1PxNMdED3yda\n",
"+d5Kkm8bs2yioiUA/fEEGAAAAABdswAGAAAAQNdEIAH4Ur/5z/+h8XLZpAGv8bhh/LxtrKo6hshk\n",
"jj5NW5dRwmFzQIpdtuQelxN6z9+TDiOQDVHM7+86p4+jc9RaBe/Jebzk0O9bBXL9tv8gVSDfEa38\n",
"ikhoIZ7np976s+9V1f75qpHx/nh6HocTuLvrd37vP/4Rb1gAdMwTYAAAAAB0zQIYAAAAAF37re89\n",
"AQB+WVYxx0mKI477eM4w7f/Ytrm1GpcZm7mLRbtdWcdljPJjt63W2u5s0me8HnWuauSr/671mi9J\n",
"uPayfNvPRttyDvaxeRxq6feor1f0cb+v9Zaqn9ZzNG7+9dhxz4zZfuwLxmyMCMbzPOa9baOP809N\n",
"faQStC3VIpfHDfevj2FsOx+3W3EYM76Uk59lAPgingADAAAAoGsWwAAAAADomggkAF9rikCm4osh\n",
"HzOkOM1niFGWscFUGTIp4pmL+M+w7SPFOpe7Y3XJhixQa6Xmuf/X5oteW6JtcY4enOaqKubp2T0T\n",
"zTvb1yv6aO2rpcrfueN21/eTY+6DygfHxsv57Oss4oOr5lO08aCPlkqgB7Hcee90/2qMDeZIamOF\n",
"yCptOd+L0+sc9ptSJ9fztp7jcH/INF0A+CKeAAMAAACgaxbAAAAAAOiaCCQAXytGjfYRwqlC2Rhj\n",
"RfejOJdh+bedaaywLUSD9hUi7/Vxr809LRHIJwKH82tvjUx+h79/tcY5k/nULObdWMFuccDZwfaH\n",
"FlHd5r6a5/OKiOTr45GrY+PlXFWtfL6C49gcVWyMCE5bPn9a/CNdA5ttq5ThsJziukGcRogeFu9H\n",
"jIE3vr5piCGmtKeNKTJ5cA7mOOk1er7aV8VrXxusBoAzPAEGAAAAQNc8AQbAlxrCF8aP16cHVg8O\n",
"jMWTV2P6Zudp2+e+XXooLH47dPVUzLj/ufW7t+OTZdtGR3+TavnS/OMml8vlMn6XP3898OTH5kvL\n",
"07Vz1G3TF7DHXc984f5+9MZBG49t7eeVT4edfCItfdF8+aXyi43xi9uv94jlk1rpKaviSbTpBhPP\n",
"yvLJspanC8ewp+XJscXB42omje/H7tzUT4flhxbH1b48j8Zr4HM6V+HzEk+0J8AA+H48AQYAAABA\n",
"1yyAAQAAANA1EUgAvtbnNcZWfFHyut1t07CJ/Ywhlrj6kuXpi/TH/bYsxLemQVfxu7NfYP/EF8C/\n",
"w2f8Ruy9o/folFecg+IL6tuP2O+NKbLH/0bY9kobI2bL6zW+Hy+MOTZ3VUTc0uclRZarCN+cwjs4\n",
"H/HzWvQ7JxvTl7mn8cPB1TldvVepwVD8q9i46PeW4J6u3bbraFhFPNfN1l9Mv3+dc+GB5fU3zjvD\n",
"mCKQAPyYPAEGAAAAQNcsgAEAAADQNRFIAL5WiCAOKco0TpHGz1XLdcNltbOi+txnii8O6+PuzG2c\n",
"/1aU8jxVLOpk1CdVOFyVmpv6e7Tq36KrMga68PGKv5N93xjl2HK+Urerl15F/nY/vOYVT+9RiNWt\n",
"p7EZrapcuDw4VlhMVTYb42ybj+aYPoexmuH5WOtu0FgFsvpsVlUVL3cqNzb0m+axOhHb+R5VoL3u\n",
"X7wv2xh4imuvouHTa4n3lzSPff5zCDHH22me3vBFHx/X6ymmbEUgAfh+PAEGAAAAQNcsgAEAAADQ\n",
"NRFIAL5WjHYdVXvL+4bGqnirGOWc5inibyuf+3bDNj65j1SNQ4oVVVpzX6+optjYR2tq6gWxzDbn\n",
"41PD6fGn2NlPbeOGOFs9YlF5MlYr3V9beTZFvwftdqnB1ZzCxhThG+80OZpHGPS1NVMPqiS2Vnzc\n",
"VUJsrOK5jJVW1S1T1DRWoC3Gv/Y7pM9mikDGSpIhah0q995msa++O35Of19f3neHXTsA+GqeAAMA\n",
"AACgaxbAAAAAAOjaMLZWggKAF/j//rO/bx/kinGwqVn6W02IKMVoUqqcWEWZqmqOB5HN3Qxb53bZ\n",
"7Ssjbmms8hw9oeF1rtu9ON700u5e0Fms3vdgJ7GLo6qA056T4zfHVQ8Pbuii9Zo52T72sT/24av+\n",
"4FrfV05dRP7Sa5l+XEUgqzHSdVHFHYs+07YUxZzHrO57l1t8svl+cL0fxf8fY9/HH/sH/1O5SAC+\n",
"hCfAAAAAAOiaBTAAAAAAuqYKJABfa6rguIj1jGOI/8zxmVS9LMUjQ1XHYbNv3UnRPrSLu7Zxyjtd\n",
"pQpsrXGilnm8S+vXJHwcRKju+srkU+v5e2XFzqJK6VEXRUSwrmx5NP+q6mJbVdV6rMbqiI+2P0iJ\n",
"1unMqcLnPg44VpUZL5fFZ3gfSxxSHLGoqJnPaLof3X81cyRzMe/5x+VrKStJ7ic7F8ctX/vikJTS\n",
"nG7LhxFIyUcAvpYnwAAAAADomgUwAAAAALomAgnAlxo+93HA4Rq3OV2YOMV6xpBpTDHHOFaoXpYq\n",
"OKa41H5yYdNi28fHpt3jcaAhRSznnV8QM/osKhbGCpU/srMRvrN9ne3zFZHC+thFiO7hsZpilKv4\n",
"Yku/jXHO9JlPEdI5Nrj4vMxTCxUcV3McN/89iH8WVRrzq5rikWG+6TM8buezeQ2bduuq79vXsB9z\n",
"CNvW9+d1H8PypV/v8Smqu46aikAC8LV+bv+rFAAAAABOsQAGAAAAQNdEIAH4WqmiWDCnkGIcsThu\n",
"DLGsFJEq57ba2LDtqApi6OPzp03zZ/4mdTZqdzC3Vw4fK0Q+OvZ3jkw9n1YNnS09E4ts7ePBmONB\n",
"fHEfo2ybR/sVkOJ91z3Lz+1c9TAcN0etWz7Td8asprZKGe6rNO5jmeOu/RDjjstKj5tKlqtqjUVV\n",
"2hAXn9+pcT+PdR8hFjm9f/FamKLkIe6uCiQA35EnwAAAAADomgUwAAAAALomAgnAl/ij/+RPbbJU\n",
"y4qIw2rPJfwrHrmI7szRoZORybUHY1CxCl1juGtq9hGqtK26Pag6d7f/cNxh3PIFschpqG3U827D\n",
"lr/JnZ9XXZ3wfC97P1qMqzHue/eYluNaPiepCuqyefjM7yobpmu3qoi4+DlWgUy9bqtGXhYfv6p8\n",
"bB0tnqvdpujoFMVcHjpHJusKtFOEcAhR8nitj/u9t1bVe5QqWjZGNuc2oUrvQ9cnALyGJ8AAAAAA\n",
"6JoFMAAAAAC6JgIJwNf4nEu2hX3T32P28ZghRIhCMmjRJkR9lp1co0ljEd1JsaxVr2W08sFSgYdR\n",
"wUfjQq+LMz42fDH+2aTd6UhrDoidPbJ2v9/x9Hv2o8TDXhyj3MUSl81T9vB+NcPNB/HkvIoY8VE8\n",
"cze3xZ45ZrzcmKrdritDHqWax3jepqj35/rfl+V9blEJN33+NlHMIbTJH9vFWNfxx7ni4zLSnjpJ\n",
"59nf4QH4Wn7zAAAAANA1C2AAAAAAdE0EEoAvcs2+fKZ40+eu9eko4ec+LnSL9iz+3jNVL2uutLif\n",
"xbiJew1pjov4TxW3LK1iRSFq9HC/4XwPd//xPqtznyKgm3l8fOXf7R6sCLpq/Uz1yFdEKx+M47ZK\n",
"OblYfTF81vYHXPbzPYqthtdXHprORxURDPOco4fLPan91Feqpjis/73atqzluI5Mfvtx2y5EPJex\n",
"yGm+i3vFuOt3f09ZxiJvhSHTedufjylmnupSplQkAHwVT4ABAAAA0DVPgAHwNeanQNITF+GpsLRt\n",
"9+TEwZMt6Uuktw89jOEJigPDdvx42OLph+uTE+mL9MsRl3P73D+19fgDFEdPN519cqhlJkfvVTpk\n",
"szE9KLhq/z2/OP6sx58wO/9kWfiS87Jd+uL2MNLqScLqs5BGKh7Vmt73sbGz6oGu+MTkmPdv28Uv\n",
"3I+VN/a74hf4b15X+nL71O/qSartE2AHn9vwZfy3V1I9uRrGXL3A65O0cd77p9m2Y297A4Cv4Akw\n",
"AAAAALpmAQwAAACArolAAvA1QoSvyRjiSjHqluI/my9qXu5P0adHrWJWsUHYNWz+e/+4y+USv+R/\n",
"F5sK56U5FBjOx/yF283RwheHmnZxtoNraD6lRSzrpRN6Vb+vlCLGi5/n6G0RRV5p/IL3bQzw4JoZ\n",
"Ytxy0336gvfY8H5hiFVMM0QP40uO95ni2p4jk2msNFiIeG7jvvfmsZvw8v6YopX3o+fNX94fv7R/\n",
"d8Di56lgR7jvhi/GB4Cv4gkwAAAAALpmAQwAAACArolAAvAlhmukJgafpn2p4mOZu2mMccU4TxUv\n",
"Ws5j3105fnNU6/o3qBR9qixSRcPu2Ff9XWvqd4oyFZXy4nHvctB/it/F66jFK2KfZ0Ne5yuS1t2l\n",
"963ov7kiYuXs+b4ftRtiu1Qpdrlp87pWn7l9tcZ9bcTFj4tjc9XMtSFGQoftln2b7fhzf/sKjrt5\n",
"xHvb8lV95uNW4y/ab+7T98a6FepM19E07yIiu+wEAL6IJ8AAAAAA6JoFMAAAAAC6JgIJwNe4VoEc\n",
"YmRmqpK4ryQ2pgqLU/uhihftD1u1K6tAjvsfWyshlpUql+0+n+s/HTuu8pGbRucNMcp09fGrg6OL\n",
"anVfWf+tinQlLect7kqx2WfikVWUNxyboo2paubR3JsOKNrfsnFFn/f62owVq6uGCOSqWVXZ8LFp\n",
"fNu9rXK5nEbb528ft1xELKuqkcvo4eY+kW9j+8q5626Le9R8L963H6rPcJjjuNoW5isBCcAX8wQY\n",
"AAAAAF2zAAYAAABA10QgAfga26xOzMIsYzXXyOSq3ce6/TJmFeI8tyRaqJQ2/XNZ6e3VMcczfRRz\n",
"POwjzucVMcMio/QZ4nXNQ74i+9RYbfO49Z2GJ8/fKmO2+s9x+yQdHPNuReSv2abf8FrK9nECrZHX\n",
"Klb3GZqlrGLY1hwtDpHXUF1yN+Tq41pU1Eyf66n54jN06yNVpb1vfX9MFTurSo/7qpFnq3cO12PH\n",
"sG8d1x6usxi3rQDgy3gCDAAAAICuWQADAAAAoGsikAB8jRQJmpQJqRSVTBG3VDUvDHUyvhhjlPe7\n",
"X+xMg5+NSh3F5KqqealS4AurL44/7bd9hL+rnSwieGICDx7XGj0s+h/CP87GLlvfi2Wl0xiJOxv5\n",
"+x4aK2pu46erKpbTZ6I4B6t2066jiq4hRjlFE9P7nJRVFcNrGO9fMzn2uI8SpuRm3cd+/xyFTJUn\n",
"F9uGGAktJhATpCEXPIQYNQC8kSfAAAAAAOiaBTAAAAAAuiYCCcDXmGNFKUpUxWmW2z7v75uLqLVW\n",
"sNv/Dag96rOOMA1pzJSGitOp4mEHkcYqrveKSpVnpcqQ1Yn4Lmm9R6KTrVUMT/RxGAXex+TeXNcz\n",
"VyRt1RLJqyLAy2NjZdSi/3WHmwPCWKvqsZf9tjm2WFVHTJUnQ1Xa1esrzsNn2Df9vPxczf2m6pXV\n",
"Sbp/XxwOY5fFecv/DAOF63n0d3gAvpbfPAAAAAB0zQIYAAAAAF0TgQTgbX76K797Mr91MoZ0VBAu\n",
"btxUk4uV2MKYq/mPm00fu33btOblskk+DR/F+Ps41Ljdt9z/TIzypZUhGytfzu3TfF43ndep4m/v\n",
"6qPK+rVGMvftHj29x8nD+/G+OWJ3EK3cXeOpOmGS2pV9HFWGbBkztWuMI1ZzO4pRVnObh0yRydXB\n",
"+2N3/afKkKGPlDiNCcy2awAA3skTYAAAAAB0zQIYAAAAAF0TgQTgfZZRnLPhqxS7qarElZUFQ+wm\n",
"FSw8WyFwHnMZOUpdjfttH8P9fWE+w/zjyahWapeila+QOiv/1HYQP/0h45CvclCp7yXHnh3j/oco\n",
"f6zC53tO3B1F6B6LZx5VUt1VNAzRxmeu+an/MUZ72+Kn9WuoKyfu24cRjqo6Vub3avHBTXH0bXz5\n",
"KGI5hrkN8SYMAG/jCTAAAAAAumYBDAAAAICuiUAC8D4xFlNEh1orlT1VSWwbNXokOraZ73I+H8N6\n",
"3z2fn+tujyKT8zSKGFKrZWRs6mJ44m9iVXzz8/4cc4yMx5QZ4NBuaXtMiBavmqeo3fqaHZrnUVQC\n",
"TYUO05irz8S9cW4d55nd2o1hasOm3xwJXfQxhE6u+4dw/sYqfrqKeo+b2e7tYqCr/m9jxDjnfOwt\n",
"njjEMe/PIL19w3x9LF+zzz8AX8sTYAAAAAB0zQIYAAAAAF0TgQTga8QqZ7tG+x8/wu6zyZlVRPHa\n",
"4WeqTPdEv5PPlljW4tjmGGCIRZaHtlZ9u3by0fi+nN2dzlH5mpfXwLqy4A+j+T34udhcWzESt2/e\n",
"1Oeyv4NKp7uT2VrNsKqI2Go53ZaqlWN6faEaZboPhH3DbediiPuvIdVxnSOFB9HRudspkrloN5YV\n",
"J8/FKId0/qqKnQDwZp4AAwAAAKBrngAD4H0+Pxf/aHjS6OiBj5bvr4/H7r9E+vQX6acnPtK++cm1\n",
"g6dotvvOPgm2Onae2Pk+5i+rX2w6/YTdyfbXA1ZfLH77Nv59x296EszzJxvxqaWzT/A9NYFpgPtj\n",
"t6qKS5QHXC6X8XO/bXfTCU8qHj2dtnsSLhUbWBaoSOf5fsGCec/qvF3/1j0uvtR+d35vfw8fru3S\n",
"02fD6iWv76PDWHxul5Nb/k7o4ulJAH5OPAEGAAAAQNcsgAEAAADQtSF+2SUAvMBP/+Gf3OdzPk7+\n",
"7SXFgIrE0WE8q9xdjFWNkX6XLl9nijwd9fmIV0XTtv2kbl/9Px+mMVtfw9n38V0a59t0up56/4qY\n",
"6FGM8ez/Fjw7z9b2VRy4NSpcfTaf6fcVdhtDuo8AACAASURBVF+Wf/DBaplTjBHXX9C/i5gexrXT\n",
"DXfTR7qeDr4E/9btt22/9c/8b0KRALyVJ8AAAAAA6JoFMAAAAAC6pgokAO+T4jQtFREvl4P4z8kq\n",
"ccuu5gJvJ3N9If2zjfCspAqYZf8no0/vtH09Hyk69kVjXy4PnI+zk3vmfLeVJH3FO1q/qnHf6Hre\n",
"htW1uN53fpxGKRJXVkRc/KO6Bo4+89tI3qpCaxHXS5/vV9vN/YEzXb7+FDOc/tYdKr9O7T6Xce3i\n",
"WmmuaFlUgUwVc9VjBeCLeAIMAAAAgK5ZAAMAAACgayKQALzcT3/5j3/LtKwqIU5xm2vEJlahW2aP\n",
"ivjk2UjceNBvUx9hHh8pxhUPeGzMs94Vo1ylOYvo2jOqaFdrBPPh19w6/6r/oz5a5lbn8Moe5uha\n",
"ip2l9qEa3/WHR87ibojwfg6N1+czV9MtaVfFLuMJ2f94ulJmOPdntX6GWypmXi6X9Yf3XrvPsO1g\n",
"btv44uE98GRsHQDewBNgAAAAAHTNAhgAAAAAXROBBOD15mTNIlozFHmsqhrYWMRommNGJ2M3yzE/\n",
"wt+K5jhnUQHwsKpcw/l4pvjhK//EFavK3Rv4DYoU18pLXvMzMcdKQ/W+1P4wWbmNlqWY2skx076D\n",
"FPHuiBSxTDHiEOG7JTL3EcSxiG4u2w1FNLA5rLoYqy0Auf/Qr5PC69e8jISORTwzRUfH5qji/j29\n",
"vR3XD9b4sdgXzvN0Dxz3lW3jXSy8B7fLc//+DVKRAHwRT4ABAAAA0DULYAAAAAB0TQQSgDco4lvN\n",
"8b4qonV2OkVltaMqcVXVytbXEisWVu1DxLOKkKZxQlHA12jNI75QFfdavi8tUzusFHk2Ljv1ezhw\n",
"MU76vIT3u6x8+WDEMjrK7za86GVcrpp3ijjPx+0/m8MqVr3pazlWGbE8eI9DFcj9uzcu9t2PW5bJ\n",
"0XHZx7Tt9vrGOfK9736Y45zL62NfxbMMcc7nKHxwQoxy+Fz0Vrz1c2QzvX/hsn97hBoArjwBBgAA\n",
"AEDXLIABAAAA0DURSABeL1VH3Jb6Wv0JJpaJ2/extUpPNUbG5n1FXm41jWu7ZTXIKpLXqohoPZwI\n",
"StXflv03xeVSv4ufh81/v7cq3pqkNi3HHc5j1eHqP6FBrKhXdFiMW1xHVV9lNi/sjEnF6rPWGqNM\n",
"2+5HCuNnL22bzsdnuD7Gg/vM/DFJr+EaB1ztasvBDtuxUlXMxXUxpIqrm9d6dOXOVR1Dy+E61hj+\n",
"Hr6qUDnFTlex1ukabzynr7hnAsCTPAEGAAAAQNcsgAEAAADQNRFIAN5mVSltm4AZwz9ao3YxdpP6\n",
"zbO633HR32eK+IR/viIaGNNhDVG3o3jYx4N/94qR0PjGPNb/q8QoXNXmuvPsaTmMc6UIZNVHS4zx\n",
"1U5GJldR09BHeX22Vqgc1/9tTs0Vec4UM4xCJDXdo8oU8b4iY4zBpnO1eenrOTXGwNN1dP28VnHK\n",
"WBVzFdG9Hru4B27f5iFGIBf79yNUzQHgLTwBBgAAAEDXLIABAAAA0DURSABer0gSpgJyOZpUVHWc\n",
"/nzzSGWxlgRkTFSdnGNrEiz9KWqOQ52scHh0PqZqbmejdilmlYpo/iiVIc/6rN7b4DBqeTbC9zMw\n",
"pms8RP6qF50if6vPTsMJO+pjGzN85KKs5lHeI1IfRw03u+LY96tRrhXVM5cf2N15q/bdqkU2V+Cc\n",
"I56p3RMVTwHgSZ4AAwAAAKBrFsAAAAAA6JoIJAAv8Ud/6bdvOZbqzytzgidEqlZCZGY6JsXvmnKX\n",
"B/um/pfVEh+JWe47Xo+Z5nG4bYoVFbHIo7mm11e2LzamsR6tMvlyISYXk3BVVPFdsayT1Re/h9Zr\n",
"vjWZV46RKkme7GMIfdw23H58aZXNg3mnqo7be1+MCIY+hnQvuV/xMbZP/c73g9T8IO64Hf+wIm8s\n",
"cwkAX+pH+V+qAAAAAPAWFsAAAAAA6JoIJACv0RjlO58220clb5UkF/s+iijO2Upsq6qAKSZ37W8o\n",
"XmBV3XH5jynO2TjF1b7tGK3pouXra0rkNXb80yKb+vHKuNlZKXf2bs25vTeN0dpvqly6iSOOjdfH\n",
"WVWEbtXuZH9VZLOMR96Z26MVV1eX3XQul3ntKi54NnYaIoXlfaMY8yhSXsYiWwa/5Hjm5rL76a/8\n",
"7tzJr/6l3/+51pQF4AfmCTAAAAAAumYBDAAAAICuiUAC8HoxUnNVVYtrjVGmKmrXWF/OzTyTz2zt\n",
"b7MrJJ9iBDJWnmyc0MOF1Rojgs/0u70GvnegqawG+cL+nxrj6MCzb0i68KbrLkUDz8Yolxo+E7FK\n",
"4sm4Zaws2CjOo2He22POjHVUTbFlHlW7o1tb+VY1RkLLjsPNvqrOWXX7cMVdAGjjCTAAAAAAuuYJ\n",
"MABeIzxkcvZBkbgvPTVSPEV21MXcbnpIYfmnoPkhhVsv9YMf6QvFNwNcLosv6C+6+jx64iIds53d\n",
"2S/Svty+yD99OfUztk9zfLcvxX/3o1/fW8MX46cna4ZwzTb1GQ/Y74pPe4X2sfhD8blKnQzpH403\n",
"h6YveG8Un7wKX/wfL8nGJ9F27VqrZ4Rm89OnqU3z47hhGtW5LB4P9gAYAG/mCTAAAAAAumYBDAAA\n",
"AICuiUAC8BpH8ZXtdyafjUe27L8zZvk91ym62TiNoTU2FeONj1pGqj6niTzfXWuM7FGrogDfI44Y\n",
"voS7x1Tk0ResDw1x3AdSdbtYXfN7XNwIjr4UPb6WTd6yOVlcRULDtub7V2u0smg3nHwT0vudLvz0\n",
"xfTlF+QX11Z6D2IXRYRVBBKAN/MEGAAAAABdswAGAAAAQNdEIAF4jVdUTHsmAvnKGM1BGqpoXm4s\n",
"6/UtokHtCcGzFQ4bK82lCnbPWlXF/Ln9/a3l/H6v/NYUN5tibUWVvZcPnaKVT0RNt/HJGIEM+cxq\n",
"HmfHPjpm6v8o1pyioEeRzm+N9j9W98pUSfIw4rlp8FkNcKePe30tt1Xld1O3IpAAvNnP7X+BAgAA\n",
"AMApFsAAAAAA6JoIJABP+aO/+Nvj5XJLYF0udwqPnf2TS1UtMnmwQmTzcVXy6miOm5TaqXFzV5uN\n",
"37Y+VVxxFVF8op8WKT72ZRUZHxnoldmsMgjb1kVMBlbxtwfGaJpHEat75Fqfrouq6mHqdzWPzQ+t\n",
"UcymeOJRu4MXvT02Vms8GKsavrnc7Vkpanr97/ye7ZvnLHljDBsA3sATYAAAAAB0zQIYAAAAAF0T\n",
"gQTgKXPRuaM/qWyL06XITGts6mzxw3Tsx+bfj/RXVWmr2qd2JytPtnqor88XRCorKY718VUZyOWJ\n",
"vo75kqHflNWNxfhS1cNz3a5t5p6iboelTosLujp09Zl/8Nys5ltEMVOs+qlo4MZRvy1jjXf/kdul\n",
"KpCx/dkKsK3HhpNaVXV8W0wTAI55AgwAAACArlkAAwAAAKBrIpAAvFysjrhNJh3GbsK2s5Ubk208\n",
"Zwz7zqbZWuffqoqVtiaIvqyq4mL8Zw4OlSH3EcxXv6h3hU0fnOeqi2sfn9vs8CMay5Se3NXeMHxw\n",
"U3zx7nF3+o/VBhuyxa2VMlunFoaao4FDiAa2xqSnc1PGEpc7i/OctjUXJC3O/UsrVd5+/Okv//Hx\n",
"crlcfvUv/43vcCcDoFeeAAMAAACgaxbAAAAAAOiaCCQAz5liK8ukVhUPKorWxVhkiihW82itLnk2\n",
"WVbNbbkvVZc8qzmqVbR7QVz0S2uypcF2f6Z704ya04tfWOlx+jC0xvVe6Sj+VpUHjVUpp9dyMNfd\n",
"scvYXogDztvCB3za9Lnfld/GcBE89RmuooHDvk1z9cXiHKXjyuvoZGRydeim39YKjlU10dYKmADw\n",
"IE+AAQAAANA1C2AAAAAAdE0EEoDnpLjesPlvah9SS8sCbinBt9226v6ZuOCjUl9n44tVv0ex0pZ5\n",
"tI7V6hWVOBuN25hqOAdfWyLuZMwrFjEMM47xvlMTW0gn6SDOttt2lAltmFz84D6Txw0xyiFECXfj\n",
"N0Ybj+KId/u/5NdXVXBMY6Z+04U0bm8w6UZ68H7Xg96fWzqkpaLknW5vh6TX2dYfAJzhCTAAAAAA\n",
"umYBDAAAAICuiUACcNrf/Au/cwt0fbwnEzc2pGJSSueoCOQ2JVQVtFsPtvi5qvRYVZc8GxNtVc3j\n",
"6PWdraz5lU4m7R52Mnr4yOm4JdfOxR3Pj1W/gNvwrS+62lfEOVNUsTVaWVUKPJr33CzEHYfitTxV\n",
"gTBEMcsqjS377mysjp13NcYX45/Brzs/D26u81DDddfBezuG97a4uJ9JywLAPZ4AAwAAAKBrFsAA\n",
"AAAA6JoIJADnhaJkMc3SGHeJ6abWCpLFkHFbQwpqSPMeQ8NXRBVb2zUmwE77OUWNjuZaxUqf6ffR\n",
"5umaqRLDrYm4wuHncE6i3Y+4xT7idbfvI36G4k1iv22q+lm/fSkOWFRCXO0qonkrJ28+MfZZjJmi\n",
"nh9V/DNMY44xHlR8rCKVY3Exrs5LiHhuK3DG117P53ZGx/2QAPAGngADAAAAoGsWwAAAAADomggk\n",
"AOelWE9M+hSVxJrjOsX+o6hiQ4HKs6mhy+VyGT7v7rolu46qO1aV2KqI5Udol1Sx0meim7/EP51t\n",
"z9czVTFfkmm8399h91WMuDGFN1mlC6t5hOuuimqeDSWmI/Jp20ftht0Ptwa5XWPsc+7qtnF7T1j1\n",
"/7k/SbdKtfuI57xveS+e5r14McO8bTHW9MNU6THFW1dRxTE027xZKRafbowt96zFP/7oL/32vPW3\n",
"/pVff696tAB04pf4P2MBAAAA+AXxBBgA530u/hB//RLmcbXt23+G9WMEj2l+YuCF0hNPT7yU4jvD\n",
"41Mj1Zehr79c/Mzgl/haTpuefvuRn8V45BGmM/21fhn/WUdPDb5S1W/j04vx+90bx6o+E41dNLU/\n",
"KgqQ5jGEJ9am11p9XpfnIz8NtpnTwVNWqWDB9tjxM+w7qqYwv77iSbejx/Cqp1TnXYu5NbR/27UO\n",
"AFeeAAMAAACgaxbAAAAAAOiaCCQAz/kM2aD5xxBAKr+c/QV5qKPI33ZKR0N+hm0tXyRefbn9clNL\n",
"NOhoPo1dbL+8/yHV+/e9vfoL5n9U1byX73Hr62v5TBxt+0HP5dg6x4NYZLGpvd3Z/k9GR9O+McU5\n",
"Xzm3eL8rvvC+jHC/IDIPAAVPgAEAAADQNQtgAAAAAHRNBBKAZn/zz/+Jb8GU5Z9PYtzxWl2sNRc1\n",
"55Ru7YfQx62qZMj17OZz2cV0vkQ1Ztp2Mpb4FS+laYxl5bjqz2k/cizxbCXEs/1+j9fylVUjU1XA\n",
"tG/SGs+c9h21f0XVzFdUJXzFOW+9X7S0r96Xo35b22yvt4NxqnR7a6wUAJ7lCTAAAAAAumYBDAAA\n",
"AICuiUAC0Gy8lhRbFnx8OKqSqrMtoju3yMxt436oKh55uVw+Gyb3SCW76Ziq0mOKb706KtUy32UM\n",
"6V1/9npl/O4oasfjsbZXjfVoH4dlSq//nT47r4ggtsYBl+0erPzarLWv6r7xPSKv1fhHvxNOxi7n\n",
"UyQKCcALeQIMAAAAgK5ZAAMAAACgayKQAJw2fqZqjTfDGLI9H1UZsGv7GO8bwrbQReh+mLodl/Od\n",
"jwj7qvxdyOe0Rn1aqrm9K+b3irjqQb9vTym9MBbZRZqyNSb3aL9HscEzfZ3pd/u5ap3HM6/9XVUS\n",
"Hz32KytPPtP/KyKQLUV9RSABeCFPgAEAAADQNQtgAAAAAHRNBBKAdlNccFGaawxxxznZsizhNVZZ\n",
"rbQvxSK344d45CqaF+Y2bo9NbfZzG8q5HcQjX5G7S6et+jNWav/T9b/L+Zyd21dWIKw8GB1tnmrj\n",
"+/f2SGVrFO2sFC/8DPvOekWMsrWqY6rWeKavZX8tfd3rt+rj1THOV0RSJ9X7fFTFdtvf0flruW8c\n",
"tPmjv/jb4+VyufzWv/7rLpLMAHw9T4ABAAAA0DULYAAAAAB0TQQSgNJv/t2//RZCmf9skhIobWUB\n",
"xzlSGAzDsmHRbzo6RCZjHut+FDNFJqdozziEPq5ZydWu675ljDJXlzyez2Zybdta9p111NcronOP\n",
"enXU9Inhz4hTPaqC98ooZvhYzcniozFbYoOPnJizx7wysvmK9s/Eg1/Z7pm+WquKjvf/OaSNVTR2\n",
"LIZcXqcqQgLwJE+AAQAAANA1C2AAAAAAdE0EEoDaKrKSKjOO632LbasKkZsITE7fLKpLVlHJJOZj\n",
"wtG3EpWpk/1xZVW7a9yxcZY5wpOqTN5v19DhdV81kcXPZytJVu2quBwrD1WjLM5za39V9DImjMdw\n",
"XBVZq8ZZdhEOHrY/HERCh4bLf9Wmuh2kIq/LsaoX9Ojn5IEKn1UXZ7eVY4bo4RCuiyqpfnjNpGtr\n",
"62x1TgAoeAIMAAAAgK5ZAAMAAACgayKQAJTGz1tAZRhCZqWszJg6DM1TZHJuvh9/avdQZHKX2Tk4\n",
"Yo4EpQqVdzes+i2TTuH85fb7ec6xraHttcTYWdr4aLW171yRsfUt/WG9uspdSvQ+OEYsrpqkiHNL\n",
"1cjQbYwvLqN2Ydu2AuEqmZ2qRt5PcB/H+u7M+850d5G/oyT5tq846MF721SYMo35GfaH81FZtSkq\n",
"drbdH+8cDAAneAIMAAAAgK5ZAAMAAACgayKQADQro4epWuTStmTbUbRlzgQtD1nnq8ZQmu2oumQ5\n",
"x2o+Y8r/FH2s8k3DvvnudIQM1kHOaF998oGIUGv1zKa+mje+16ujmO+IVn7laXlXtPJs+5OX2urS\n",
"bBxzdzkfxfYOKk1u28XbRnV7aY0lnizoOrae07NZxVABszym9TNR9RdfQ+tEAKCdJ8AAAAAA6JoF\n",
"MAAAAAC6NoweLQYg+PWf+93xcrlcho9libXid8YywZcifNvybHeO3W2rKsEt51NFk1LCMlSeHMLr\n",
"a0r6HMWipv3L/qtfvx8NbVbjNzd84tjHDMNB6b93e2Vs8WxfVRTtmeTpK2JnJxPAh9diy5zeVSX0\n",
"bOQvHXv2I/TMx6bq45FzX/WRopKPvlfPRBXnG2lbSdIp3j581hnSv+Xf/LXSkAA08wQYAAAAAF2z\n",
"AAYAAABA11SBBCC7RgPHRYJtSH82mSJ0y6Tbx/XYVX/rMOFwFFsaq53rOd7ff7+PbUXJ1bZkERW8\n",
"JXf2VTHreQxhW5BiP7eJ1GOdNZ3Dp6KQ9+c0jh9P9x97b44BfsevenigiuFLx3xlf8/EFx+tGvnq\n",
"CoOviBeePa41SvjMGC19VPfYo/NytpJk3J8q6263tZXMnO8pAHCS3yAAAAAAdM0TYAA0Gz+np7eW\n",
"j01NTxAt26Uvul//tX/5YM7cX/h+5GEonppq/VL5+KTYeLxvManY/fxd/22PqqQnxbZPk61/ekbR\n",
"y+rlnX3c5sF5PNF9de6bx288YNj9sBzz3CM5Y/HE3/CC/jc9vqCPaR7h57NfNP/INF759Nq7nrir\n",
"nqh65RNmrce2PuFWPQH20FNq1/vifOuuP+DzZfQZtu0Gv9zuy+XTwQBwjifAAAAAAOiaBTAAAAAA\n",
"uiYCCUBtGRGc4nLhi+OHoyzO9kvQj758fj/ULSqZvlS+kiKbSdnv/TnGL3hfbSpilHEe+xxSFbN8\n",
"KrwYxnrxCN/8tPj54T+/vSAi+HjdhJbeN50Ndxu0JhVbo5JjcV2v+wgfrFvL3a750KMJb6PQzVHM\n",
"kHuu2qU2Q2O7lO+LCeDQR/V97ekjFO8luwz3fl9j9DBO/Drf5bUw3ZfTttvrDMOU529/SEpVx++9\n",
"Dxtvcfe6/atD4gD88ngCDAAAAICuWQADAAAAoGvD+IpqQQB04w/+7N85Xi65MmOM+oVtQ2y3+Xes\n",
"RBgUaZchpKeWY4+hXY48bTs+iExu59taIS++zhBDSue+6v8FiaD4nr1L9frePvZRgwezj58HHe92\n",
"N3xG7krVT1urbYbP67ynOvh23DDsNi33NrWP6bvwGb7tuv7NdtyPlIptDrsf8utLob5brDtMrvxQ\n",
"3o/3LXeniGA9j/tzW76mOe64H7LeVsxxab2pIUp+eP/aXARx0HROF6/5esjf+m//P3KRABzyBBgA\n",
"AAAAXbMABgAAAEDXVIEEYG1cV4Kr4jd3u6g2XjMrQ4rCHEZm1tmaFONPMadxldW6voZQ0XI3n/2Q\n",
"qz5u/w7V4tLra9VUqTJs+zjMLRXuV3h7lyHlsk47OdvDMRsmcpQxa9L6gtNg4fps7SOU2hs/t/tS\n",
"PHNxfYz3mz3cfjmfMiEb+g3nKO7aVqq83O4Nwzrrvdq3378dsaryun+v0rePVPNI/c19rGLg4fWl\n",
"drsJ1dfT6Uv70ftXjJCG6pXpPQWABp4AAwAAAKBrFsAAAAAA6JoIJABrm8jMmOIxy6jdVP2uNc82\n",
"RSxXlRano+oKaLt+hxTdOZjHHENKZejSfKehYsm71VzvjNgWo1wq45mh31hSb9vmqKsQ42x1NiMV\n",
"oloHubfCuyJQxXU03vn54f4rZ+OOB32kvnb9Np7T0+97+HlIDaaYXyqTuI8zr9+qTYxzFfm8/zk5\n",
"ii9WL7VMUa8+5yFyuJ1anFt6/1Ipzmrbusf1oAex8Ycj3Ecn+ux9az9fxewBOMMTYAAAAAB0zQIY\n",
"AAAAAF0TgQRgZYodzYm/ZcTkGn0cP0M06YkE3TTYGKM4i3jhpt0qMjlviwMsO/zmM2awNo1uP65e\n",
"c+k6xzDmcDbqc1ZrHOipCpXnmrd39XA5xZ2h9WIsh1rGrDaRzbLMaSy0+HjMsOzjiQPK6/lgoCpW\n",
"l87RA5VI7x+XIqH3qyUexuvim/UCZYQvtU9xzpb+D85HrMC5uZ7T/XwlvanHMcfVvbtIQ8Z0axER\n",
"XyenVYEEoJ0nwAAAAADomgUwAAAAALo2jMqnAPzi/Y0/83ct8lvrzMyq+mFKvXzsf48MMeu3bZS2\n",
"HRw3V0dMlSenbkMlyUW7udhglZwJhduqanVH5yP2UcXpppdXVJ78tmndycvSXC3v37vE85z2vdAz\n",
"L/fBObXGNI8iXnM/Jws3thZt3R532Lwp/nlwbPxMpA9AqCZaOq7CeLfdLqfX+kKLKpDVPeXuUJsY\n",
"+OoeUVTkrab2GboIUxs/9tviWUjzCBH18rJIrz29byGi/sf+zF+XiwQg8gQYAAAAAF2zAAYAAABA\n",
"11SBBOAypjTWNU+3iql8TrsOonlVxChWjdxXgawr6d1PuIwhMhOLrhX5m1U8bVz957q/yqwVkaPW\n",
"CcxJqdYkT1sFxUXOtam37yJW6ItvwskOq/esta+zYy7sChym6n11F6mvsYi4Ndd5PJk0jWm6Yf0e\n",
"pXtAikav212jvEX8LV4Cxe1oCP9a32f219YcnV5NdLMvpgyH7aZ437iNP+73Ldu33HsWr+UWb91v\n",
"S/HB4XoPOroW51tVqOxZxxj3/dYftYPqlSklOt9vpR4BOOYJMAAAAAC6ZgEMAAAAgK6JQAKwKu81\n",
"XnOOQ8qbpEOrqFMVX1lWZgxjjOO+3fR3m9a5lbGYNMcQQ1pMcvePNO8hZojiBO7PrTywiH829Nh0\n",
"8I/y57H5bQ6BsuZTU0Sk2pKjtwbNFQ4ffW+Xu1sjXffzi3UFyfuZyeYC4TGKdr9dnE/1+TsolJna\n",
"7aOmB32E6oRxarvjip3Lg5fnaBsBPXiP0xjjpt8xvMDj+9e0qfFeMobBzkYOz96cQv9j+hh+npwH\n",
"AL9oP8r/xAUAAACAt7AABgAAAEDXRCABuKR8yhyP+bxtm6KNVXTmXn+7XcuIS4hF3tqHKMxcpW0f\n",
"o0yV2+oKgOcjNPsibqHqWpDikWMxx9eEe45iomHTy6siPmkXhVxurDdN4lk4HaO833/suJxuY3w3\n",
"fiaKfprnGD5/0xt/9JnYtl9urMsChj7arvIx/HTb1BZgzFObYpcHZTS3u0P1ytXuUOlxH8dNMfAU\n",
"Myy2HcVKW2K+R6dv+vkVccMi2pimFKOYjf0CwJYnwAAAAADomgUwAAAAALo2jD9czgGAr/L//jt/\n",
"93i5rKuTzRUchxCx+dhXThw+qt8jy36rmRzEj+Ztmzkt42HTj8s/7UwvJVScjHHEaV+KnbXGt4bP\n",
"TaPlvsbfuVNluuGWPz2Ond6b9xNe3d+7vSIFVWQlq3Tk97OJW7ZGwar3Nl7Xrdfu1L6t+dsdpGbf\n",
"dmw6D81VR4s+ttuO4o5lIdBwwNnrKHU7dZXSn8uhxqLq7razpdX5mKL6+xj6b//Z3/9RrkIAfhCe\n",
"AAMAAACga74EH+AXbPqi5vzQS3jK6nO/bZy3pU7CowvV4wGxh/QF0OG4+Yua9/2uv0j5+p+Pti82\n",
"vz15dRtr2L6WleJvS61PZuzGvtPHZv+rn9f62T0+0fT00eEbHvoonlSJ7Y+fGBvHcO2mB68On45c\n",
"X8fLfstjyy8UP9n+qI/TBz1z5W36KN+0e2NVxQBOzjHefMrHshY/Vl+CfzTWZlvxpNi4ureFIbf7\n",
"NsfcHfzgC/r3BUBaCxzs+2v+snwAftE8AQYAAABA1yyAAQAAANA1EUiAX7IqPlIlG6vOjvaGeMqw\n",
"++ES4znbMYaU64nTCHGzMb34MGbI/4zbsRb7hmu/R19av9ub5p3+THX2S86LyOSR7/8V+A9++Xw5\n",
"8VfE644UkcnPtLEa8fHraEwf4vk780MRiCLyF1OXn8NuW1VcYjm5+Jmfztsczd5/Ofu433Snj7u7\n",
"NjHRfR9VNPxWKGPZfj9Wfs335zbfShYdz2OF9/R2n7kZUmx9M+a3LZt7VIhprq6FcO739mdr1b4p\n",
"urn/Ivt4TpcdT/2KPQLQwBNgAAAAAHTNAhgAAAAAXRvG+nlmADrzf/9bf+oWOJmiMkPIFQ33fz8M\n",
"xb67xx4ds+03FQZryA0OKcoUxy7mE7NJjb8vWwvHNRRRGz5iPjNsCq9zjkA+EQ36OJnX+1k4iuE9\n",
"KFSBzMMXg8VdB1Ugd7tj3rHudvtZaz0frVVNG/sdiqhdUSdwHUGe2qU+Gvq/O0aLg07K11D1kbZV\n",
"+1rf72rfMt768eC9JMavx/3uot+jlOMzagAAIABJREFUWGk6do7mXvf9zp/7P+UjAbhcLp4AAwAA\n",
"AKBzFsAAAAAA6JoqkAC/MLnS282+ituqxOHdPlbxuwdjd6EYWZzJXEUtFGtMHW5rR943VX/73G1b\n",
"V44rztF8bJpcW6Rx3jUevcBC43sQAoG3LVOU6OccINpFV/eV5trP7bUi4lHELFXE21XcW5z51nzf\n",
"1CxVQozC3pNp4DtlUI/bN98DFpG4ls/CQdS07iNtnSp2ps/m/t7XtG+1fxn522wLlRZzvC9VPaza\n",
"B2P4OTX/3LS5XOY4ZD61+4qZ+V58v7JmNe9qzNWxqeKkypAAbHgCDAAAAICuWQADAAAAoGsikADk\n",
"qEiMZd3Pao0nw1irwmONFQu3EabDNFcogjduIzspJbaax/1zc5vPMh6ZXkMRo6ziZJ9H2bz1WK+u\n",
"6zxe/062j3zuGh772aWRUs5weh/belin9aYI3z5/VvV3FC2upnL7XC3aVxX3QvtbRHCxpapAGM5R\n",
"injeumiLv6WEYHPEs8nBBRojmJt9cR4hOjqXowwnMPbVum36z+I+c30j1kNd74HzkPtrbNW84Zwe\n",
"Nvmcuq9eS3jHq2qlq7kd3LMB4OIJMAAAAAA6ZwEMAAAAgK6JQAL8Qvy1P/33jJfL5TKs/vRxjbss\n",
"IjDzTz9d42/DoiLiFFVJfz45yB5W0atU1TGqKrGliYz3q5ftq/Jd5vnGyOTyHG3HHfft72Sl9oPN\n",
"fe5bnw7yHFWmO9vjHJ96QaToXJqz2XE888FKlodl7Y4dVVwNR+zGX1cCrfpr/MyluFkaa70rz7Kx\n",
"GuX8+Q7Xf+tVeotMhqqKVcXYg/7z/nHd/+qY675xvy9W5yzvG6GPMM+4bT6n25ldLssituN8s267\n",
"L5b7ntEQc1yf7yJunCpahoqa42d1VQLwS+QJMAAAAAC6ZgEMAAAAgK4NY2spIwB+1v76n/69awSy\n",
"zi0Nu+hcnc3bt79jTga2tZ/6XUWNpm37aRx0FirpfXyu/32v/Tz2oovdD4t2H+NuX4pRtljHLsuW\n",
"4djP0K555GnU6z+/8H8rvCu1VPR7GKNsmNNR9dGmvo7OcxWBbH2PdtUoD/r6/Ljf/qBCZTm36nPX\n",
"+Jl8uI9UfbE1stw6j+2YR+1eKVXKrOa9vM9cY4Or3xMt8z66dKvrruo/RBsPI5DzrmuMchGF/Nv+\n",
"vf9DLhLgF8wTYAAAAAB0zQIYAAAAAF1TBRLgFyJXTPv2j1W8b4qLxHjk6rB9d1O7OzP49p+GCNYl\n",
"V6QbNz3HsUPVtTifqf/GWNIqgljErMYyebiPXm1f07dW9/etB7vffXsFwvvthipO9i5PFa8srqki\n",
"6XZ4nnfTuV/JrnE2d/qLk1v8eP9aqU5SunTL9svYcUP7bwdVMbbQRfrshMqGTWOmmGHaN0fhDmJ1\n",
"c4XKVAXy/jzu13i9M98XfK5WlSdDbDxdn9v7eKw0uqwkGe/Z24qWRxOtru2Ga2c7z5Zxv/K+BcDP\n",
"gifAAAAAAOiaBTAAAAAAuiYCCfBLUcRBcupsn1u6xW32kaNVjLKo9JVrrU376gqVZSnEKekTo1Up\n",
"OrbfV0f+lq/5sb8fjVVGajFmmdwpT0HKOZ3rY90svLet/Q3lP89prlj9isjT8VirKOKjb9a9/s4d\n",
"Go6tq/c1fdYPI87h3rCJTqeYaHobV5fpteLk2NhHGVAM8bpbxHI1g/v9rj6T17h4c/v9WHMkO0QP\n",
"66q3y1e62ZbeqxgVbL2/7OOcOapYRCBD5DXGW+eCudN5WcTXh/W5WqtvSLvz8Fm9YAB+STwBBgAA\n",
"AEDXLIABAAAA0LVhbI4VAPBz89f+jb/3dpOfC6AtynvFSo+b3wshg1Kl62Ifl0UEZp5HiGottrVE\n",
"gg4jk3PWKO27O/0ov6Z9Cbny3MRoaDGhj1BSssovrRJKT5Ql3PSXXvv3cX4e+/fjgdfSEBlr7jeX\n",
"B9zvbL5mY65vM7fW9qn/auxw7Nm02SoC+WAfTyjfvRRZrg4I7dcRyKKPaltl+R7H+90+KrnIbN4f\n",
"6PD620w4xQxDRd76uqvncZttilEGn/u/809R3T/x5/93uUiAXyBPgAEAAADQNQtgAAAAAHRNFUiA\n",
"jq2r1a2rmF0bfJPifXPMMPW7T1auhyoqThYJrFWlsqqC3VSpbNjvHFK0Ms9k32YXDVq2LrONt3bH\n",
"hSrbLedWvpapzeLnj6qiZev41/+87c9lIV5btk/v1cEIuyHCRRN2r7rfVT9N12nd7xzFjBfIVHlv\n",
"/9lcRTiLY6MYz6zaF90fRf52G9N9JjVv/bwWqnhf/HznQ5vGGNv6raN54bjWbVWMsniB8dq6hH3b\n",
"ce4pI43h3l1VAQ4VIotfTfG1VHOMVYkB+EXyBBgAAAAAXfMEGEDPwtMBy7+eV19WX/c7pB/vDbwa\n",
"f/ri+rF8rOHOF69vByueNPjWScMTRukxssNvCN98sfRHfEwhbGp7wqV8bq144mN1zsIXQD/sbQVz\n",
"iqf8jjR/6fr05GMavnpiJnXV+IRS6LftFJ4/bh7q+rTQ8edq3/E4P+I3rtss2o0HTzzNBSnGcJ/Z\n",
"9LXcWrWL+xbvTHxKdfdN8/unYLczX/e63HN/rPxEVWi/PM/D5h447vtYadl2/yHG6xhp6/3u45fm\n",
"l/NJn4nQx7g/z7uH9cK1Wz1NfG/83QObqza++x7gl8wTYAAAAAB0zQIYAAAAAF0bxrfFGgD4Xn7/\n",
"X/v7r1mm5ZfV7799fo7MDSGYMhTfwFxFoO7s3x+wmNuUmFlEVWIEcrOvtX05/qqP/WueA1VVJHMI\n",
"rz1mqqo5tp3nyqp5GW891/Hqtf9wXyh98rpLjq7nKSbX+tKr/sovTN/vbP5cnfx+/NUB1ReaN36Z\n",
"/H4CjTHiL+2j9fNXjBXuG2X7KvN3VCigZdtYNw+D7yKCMQofjs3Rymqsxmss3pfCeY7nY4pWHpz7\n",
"bftFRPxP/vv/q1wkwC+EJ8AAAAAA6JoFMAAAAAC6pgokQIemaGCuYrbftnTbsq4Mt927GG3fV4rW\n",
"bA8d70dyVvNd9LGL8IX2SykquZ3Oet/9vwu1VgWcE1KheXvOJuUoi6PntFBj+1ZF5OjH0Rpxq6QI\n",
"2PJ6Tp+FJ/q7XPJ5HPefl6PKoaGoY1v7FL+b26T450E8czPPdQXH+YZw2x/uUbuxDlKX+R6xieut\n",
"ikCGqpEpfh3nO+3bn49U2fbWLryGMGZVdXF1z968hlX0L1VEjJHs9f0zVw5N00nXbGqZ2hX3tHjP\n",
"vL7Ocf8e5PGX53Lz+2G56xp9PKwuCUCXPAEGAAAAQNcsgAEAAADQNRFIgC7dr5IYo0mfi5jJnPba\n",
"50eGIsUSZxEiKymydatGuWh4Lcg4DiHWs/shx5D2B1xy/GjbPFWXTPGiKY4UIlhHdqdmOebH525b\n",
"7uSFMZ4iQvfjFIzeVw5d737d+VhdMg9Wz8wdV1UEDw8O3VX9PNZ+/RlKFfWKdlX8MxVSbYzLpVhk\n",
"7CNWBVx3F15K7G8I7dJnIb2G2z1qH/Uedo0u8TXfXsu+Xbg9L/Yts6NVpPHa5HPZ/m7zfPD8z3Tg\n",
"4p6W7p/zD/fv2SkWuT5v4dBtfz/M/QuA780TYAAAAAB0zQIYAAAAAF0bxh8n1wDAk/6vf/UfGC+X\n",
"y2X41WfY++1+PxSRmMvlchk+7u+/xSjTvv1Y6wbVqFMEch//iRXePu5HPOOYIW457hrd6SNFjbbD\n",
"VJUq7/VbqdoXEbY5OnnkbPyutd9XeHNxttb34myVuLPv8eG1GwdJ12d1Yb6pfUu7ozZnPxNzBDJ9\n",
"zutKiA/3+72luVXnuYgZ5iqa++NulXMXQ6R05q63xrh26zVW3QKLCqapv1WTKe65aPL507fnAf6O\n",
"/+CvKg0J0DlPgAEAAADQNQtgAAAAAHRNFUiArmyqOg77HEuszLiM8O2ObaxquCqbN1VReyJWlCqg\n",
"XecyhkRejPN87OM8u9ezjPV83K9Wt3wt2zOTK6At+n0wlnUUjdvFLQ+jRI8lfFIFt7dprDDaXNpt\n",
"+3YfVtZMB27GSqf5oN+y9mIVa11eAyG+tT12OIrEhW3bSqep6mBrv6lqaryTnI3r/f/s3fuvPV98\n",
"1/WZ8/3+BUaNMRq10IqVUovFAi0WKZSWi6VSUC5NKwiCgDEmEqLxEhKN0XiJ2AoUkFqBooK01nIr\n",
"TQstci+VUltKC0ZDjP+CfPf4w9kzsy6vea33mpm9z/nM9/n44XvOmVmz1tqzZ+Z8vvvMa95z/2Zd\n",
"un7pS8xbHmKN+dbnvOjDtI/2ofa9Is9Jec0sRxfXqyzaWF8DJ9FOzMiOuXzr5m1OuXwEFYGsr89u\n",
"/01J5cvuiDoA4IPFHWAAAAAAAAC4ND4AAwAAAAAAwKURgQSASymCNCpTMm7HQoZhjdXpQIuINprk\n",
"i4oG6riJih6aZTIvVE9IRSXnjeTcpu0KaCo6JkI3g573fc2LyhXNP6pKbDsr2vVsEok1nRyBDPfm\n",
"DsZTykWKoFrjmGr3pTdT1UEj22bHwFR8bbVX1Esut1GHs4pOqu5dVFEsG8VgkSjklnKMSebqGvHM\n",
"jb5ay04PCptjRh5P5tiVu031sV1AuKGxn937Nq9rjDOpa7f6tTZHKt05l16KnxnxBgC8Ke4AAwAA\n",
"AAAAwKXxARgAAAAAAAAubZx89gEA8M79v7/qc6pc3Ry1a1a3UuvXsmj3PtSGajs/1lh9I9pkVStt\n",
"d8E5iVVVdcvGvOc4oup4jt+YaGM2VKPK2dJ87k92G6wYeKK3r5LmopAru9q8hml6SX/Y7Gw9hvsr\n",
"UC7RwOXwa52by5ZJJ+7kEe1NHNee+0mFPD1Pc+7IPtTcDHdqts6hZVvRSeyUXxuO7rxuhSb3xurE\n",
"+x3Pk9ZdzMdd6xpVjHn6Ge8qMtp4cNaybicmWlWylOU263hmWhny7/m6HyEXCQAXxB1gAAAAAAAA\n",
"uDQ+AAMAAAAAAMClUQUSAD5wWcXCIjrXqiyoMx55zGQy69JvW4mu7kiNSlctccQx+/l1oYgLuap5\n",
"Ki80jtUiPe98W1mpL2vdGWmU1SuNuTPxZy0///fERW6jVeIODd0ca6q+GeSurGsMDksk0M0x7ypW\n",
"Sc/VM5QVGedzRlU1nfImalZZvy6a16i+6NhKtK2UdCSqGI1ABg+o9dWl78a8700kVUUs050q4ohj\n",
"dc1Jr+e3Yt26cRrvs8JxxD7LnNQ1O3zizvujVfmyGDNtE66eCQC4Iu4AAwAAAAAAwKXxARgAAAAA\n",
"AAAujQgkAHyg/p+v+dxpGIZhfBGRmSUNuGY7VHxKKqOEaRzPVDPMYin3mMtoc2RqlYiljNsRoulF\n",
"xVh8Fbwl5bjErMK5wbpfV1UuWHTNmVoxpHIfRd/jXk9JTN6P3RPiSNlxJ6q+laLnxlhVEB18VFKM\n",
"MboIYmsCgW2yFr0V/ZbrR33wqrixLK5n5hot4KjmUa6r5rk9Ez+o1Xfg68uAimC6ZaKX2yiaibj2\n",
"fD008dZhiL2q/Dw08cUoET1cxlB9BSt2rtfxNH5aRM4bc12jku8xGg4AOBN3gAEAAAAAAODS+AAM\n",
"AAAAAAAAlzZOZ2QNAABPt0Qg01jKHD0cl1zISkWZTOJjdGUdWyUf17xStUhWcJRV4mQ5xWxV2oeu\n",
"uia6jawzlTWz2apInByj7qOawBgt/WgmrOKiLYGyhPZYaOlOFdVjucKQh4i3Zay+eYa6Aub6zzM/\n",
"EffeVLFLO/qQnFe2+Qdvx1lyah/qfZHLlm+SSo+imm9knXRGdFpd2lykUWxr87DpdVdUH9XnSf66\n",
"mnOb26Xx2nvs9O/9HT908bMBAD5duAMMAAAAAAAAl8YHYAAAAAAAALg0qkACwIdurH9YK2PVQZ08\n",
"DlJHr5ZVaiwTyxpFAsX1pyscplGfeYrJsntJSh3xyStgpoNm1TCXb+5xmpepai8jM7Z6ZT0Pte/N\n",
"RrpNdH04ytRbue2ExyTYcn9KsDpiNH1abN2Kh0XCguKUa3ZSRXTNebs5EXUYBeJrMi5njs/nPh3D\n",
"nSetoOH2QRCNA4orw8ZYkT76NlBVb3XVyPTbsWiftjOVTtU+mtdl19ip7jeyP7Jj11XiNBUqk1XL\n",
"JU30m79mMUURaXTj6ygmyUcAuCLuAAMAAAAAAMClcQcYAHxA/s5Xf956D9Z8i1T67PTlIfjijpK5\n",
"ifxJPUzeUH/Yz26gmO+UiT6Mee4keQixGGsq/m4zib/YZ3d72bs/gnfd3OY7ItRdEtt3E0ytJ4mb\n",
"O8BG89B8fWNQ71P+g3ofqh3VfVeYuPNK9SXfjuLuplt6m4maRvvJ+M07fuzdgtt3MmU3sQT3+XIs\n",
"mgePq8IQ6fG5PFxc3J02ibt5VKGAsp26I1SdQ/kTzcv5p3Osm6tzeJ2FuHNT3lUamEeyqOo/Watu\n",
"gtU3xt73dzLx6j3YeA3u/XbPg1cNl2MgvcYu+2H7ofL3yeddTmL/qX0qj+u6fzntZR+ly+rpVNtm\n",
"czN3kYk78gAA18IdYAAAAAAAALg0PgADAAAAAADApY3Tc590CgA44O/8ys9LUjSv37681Ndx9QDo\n",
"UbRb40rB3wUqUhVNOUbHKPsV0cp1IiL3Ip+Pv52PSee1RGw690dGxU7nfS+n0Tmmmobo32k3m+d0\n",
"a7RrdtHhhH+PuDoB8yiqSkJnv63jP4tZFu30Q/BFHyp6aLZREbrd6dd0u5tYJidQtGvtZvOc9DDX\n",
"xxn9P5O7fqnooXmQfnqtX/+Z7w6epHsRE9VFNtyE3RjuwPCRV/1axNyKqUUfhq9inPOyv+8bfpCn\n",
"4gPABXAHGAAAAAAAAC6ND8AAAAAAAABwaVSBBIAPlIp0qejjsLQrt9yIuxR9qU5cJbvAjKt5rFUj\n",
"G92V88xiOvkc9dj18K1qey5CNIp82BrdSWJIKhIXkL8S08eBpKLVqmTpdEfPOjNr9hAUVQ+XNzya\n",
"2U03LireNavFqciVO3fEVuK4m9SpU1StVP03K6O6apHq2mCqoI7i/FuO/+SccJHUuappudfzLYdl\n",
"h+Q9FBUWRaVKtT/U9c5VfpX7NItai2XBGGK9Lp1H0Xyq203yeqCOSbEoGjN0/YoBdEXi8n1WEUTT\n",
"fTIne07K6sKN/XF25VsAwLvAHWAAAAAAAAC4ND4AAwAAAAAAwKVRBRIAPgD/9y///GkY8qp8c6Wv\n",
"aNU3GWkU0acl4hOsALim5Bq/T+axVIVKUwHRVWlMf4XZtJ4sXmaikjL+udHf1pAqUmV2UbwKpIiM\n",
"zftjs90+unLoGUTlUjuR4/2v8bc9/ZelQ1tNTAN7vmxHdZvbRNsv0TzXLhpxjlX06+/DbdtZXrLV\n",
"XJebrZcti4Lt3TJ5DRo3m9trjzzuWvs5b6bP8gMVH6vt0m9VbL1eN4m8r3x1trqkiNJOYj+X64Y6\n",
"+pvG2P/+3/MD5CMB4APFHWAAAAAAAAC4ND4AAwAAAAAAwKVRBRIAPgQq5jFXlRvTiEgeL2zF6pZq\n",
"YS8qehVLecjqXjJCOG62X+abRO5ktTpT6W4ylcpk1be692yLckw5EdXebaYaLNUoWxs8OnUj+r8d\n",
"qMjYucH+sKWqIaeOHVVZcNuocmcmYaar3KU/lNGrurpj3l6NFcjERY8j2y76hnbmjsfGebXsIxVB\n",
"LNdtDWUyguEqhq5C4IE+7HtVXx+XvWBS7pM8PpIlYldOoWPA99u7naxCXEYwG++PTC2qfpd1Iu5r\n",
"fg+p8ed2rWrBAIAPA3eAAQAAAAAA4NL4AAwAAAAAAACXRgQSAD4kWQJyjvLVFRxlRMvFWEQeZKl6\n",
"JarF6Z7SqEo7qpVVd5zXicKT2byXqFhd9XA0VdRUfEVGZ6pMTtreBuwaTORo2Q8udtXoNhzPibbr\n",
"rPrm5hneWaYypJ1Ob0RKRSbVbDrf5Ubh0HJpflq5eKaYbxIlLM/TvCqsinvV142lnTjnl3bpmDKy\n",
"uR0tG6v4Z9KHSEquEW61zvdbRhXzarOij2UzEaE7M+4olmUvT12jqm+SqLe71qd9zX/qNudoK0Z5\n",
"Cnd+mOijuv63ClQurz943dcXjnJuRCAB4Aq4AwwAAAAAAACXxgdgAAAAAAAAuLRxapedAgC8gf/r\n",
"X/opWfBlGPIqiWs8qM78LVG+seoi6yOUdEv6aCTQ6lVpzLGqTKnikenrc3kXM48sIjVHJUXMUXUZ\n",
"ThKaipONypvLsMv7oVYG5/FiXssRS+rHxBK7nfzvDTkRlYdScdxIvyp6KEaUUeF5kSnfl/Yh4syn\n",
"pFWjL31udyt+7uHGUv25eUfWbfXfe5h1Hh7RGF5viti9rjx+PW2uU32s10DRsRvbtZcb+xc6iWZr\n",
"4txExFvzMftejaljkS5+Xkdp53P+H/jG7ycXCQAfGO4AAwAAAAAAwKXxARgAAAAAAAAujSqQAPBB\n",
"EFXU5jVZ9avt9ksU5pZmUIaqXdk+jYzolM52bkVXX6wrvM0RGPtakvVrBbl0h2xXocvGL9qnVHVJ\n",
"WTXPRIj6qwe6/VfPI4vmTb3RoSAT8dw/VDTPJraUm25nxvLjzmV0RQuRm6qr8anIVD0fX3lVLQoe\n",
"OzYJLOYhzvmseqw5jpZzYvJ9VGON9XGat1bVMOvx3bo6Vr12KKvkTvUbrl6fXDbmy1S/0WXh2GdV\n",
"iVDshqwCptrPSjsCaSOTWQt3jAdjka69ijaK1ZPYD4tmdeFAtUieGAMAl8AdYAAAAAAAALg0PgAD\n",
"AAAAAADApVEFEgDemb/9S75gGoZheMkqPtaVE5dYmIiIzJUe00u8qk7oKhau/YvcZdawbrfGUkz1\n",
"xQZbwTFcYa1uOI55qbvWPlrzXs2c0GuzlzqnI+oJdu8Ppexj2vyhHr+WzHL3n8cOvKbd9dTU+9KO\n",
"PXb1VyTXZNU41YeI2i0tppeu9mmD/Jgt+hDt5dxsOx/nlHOz1RR7M39qOzfvOgLp5xFtH+xDLZvE\n",
"dWOOKJoYan5Oi/e7+Eb/M17EOTfWi5XHzd2L6K16LSqWrqpXVlUjN5TxUxXfzWKl5nxe5pu1n7+u\n",
"5/A/+E3fR0VIAPgAcAcYAAAAAAAALo0PwAAAAAAAAHBpVIEEgHdKx5zSGEZdqa+sVOYKF6arZeGx\n",
"OpW1MVHRh+i4jPi4CmvbQ7UrcmXxrFFVBSz+9tNIeLoqkGs1yqQPUXHMUfFI13BMorHtKF6P7M06\n",
"3kevUKy1Ed8T8aa+wZNOXPW5SZ0xaRf1cTqVga+ps306rnmr8plt74dRnJuynfhueavMca/7TyPc\n",
"6tzMR1Lzl68vPQRu5Uj11vLd6z7k1T6rKwvK+YpDYLmmpPtRHheFRgSyLGYot1HHYnMM00TEBtcX\n",
"LeYmFqhr/fp+i2tg1tmYT2Oqj+LsuHPRykm033wBAID3jjvAAAAAAAAAcGl8AAYAAAAAAIBLIwIJ\n",
"AB+ASVQUG0Vco6x+la/Mvty7y6uSBWbSnuNW82XuLu5V9zeKKpTudU5phEfEEavIoYqayt2XzjGf\n",
"b1pReY121X3k20Wykmq/NHKtjkzr1RnWc6OV24OrtJWPFcViopOIXrn3tr0ft4/daGXNqr3cxyZO\n",
"2dpGHnfiRat2ZUQxGVMex7KPfEi9TvQr4nfhMdeVdb/Rc9nlwN2yRhFIVcHRHyvmuHDnxPal/t5r\n",
"X382/ewSyK1rhogqzu+Dqvg7qOPDROBtpUcRu4xGGlW7x1wfAQDPwB1gAAAAAAAAuLRx2v2gWwDA\n",
"mf7WV/207B6tl5f6For0ZhD3MPlyu3Jba77ZrOorbZPeRxWZR92/vTss6dduK17TqB6QvLE+ZHnO\n",
"dtJvMXCzTzlft832nT7x+Qff8PtTw0+/p+HhN0nU58T+OzNi54l+CP68Xex9MYeu5h5ertq1phG5\n",
"8Sy761KdZKaPvevS9fJOo/oh6n4s097dyZSszzYt7qDtvWFsa1mkvb0xsHEn7bpBfSftoTtIi02n\n",
"W+N9WRq6A1rdbSVWN0+1/E6xSb6R6V1h23eWrfPwD82fX/8/9Pv/MreHAcA7xh1gAAAAAAAAuDQ+\n",
"AAMAAAAAAMCl8RB8AHgnyoe+Nx9mreIiyzdzX2n/9ZgqthVJxqcPVlaxsPLhxhuTTJap19JOkoxi\n",
"sq3typic3gd1FNP1m/ewHafJYp3jdrs0YFo13/UQ923ze3n6AxHa6Sa5gWxmFqr9oaOQov+x+mb3\n",
"Q8Bb8cuxiF7pYeooZhYts/1uz0MWksiGLc7X9Fx2xSjUfGT/93XZovqaNhavYRRRzNa5uZxjrr2M\n",
"4fkHsG+Hy1vLxDVbxNddH6oLeZyKaN6oXp8ZLHLd3dp2Xbd9/umH1ZcLBh1hNWNHr8HLdaP5wP0h\n",
"b5ceC5O4f4AH4wPAB4E7wAAAAAAAAHBpfAAGAAAAAACAS6MKJAC8oR/9yi9cwx8v21X+1mVJXOil\n",
"joiU27Yijq7iXbjaoKm2lvdRRHFEvCmv4Kj6MGXATGm1Ma2oWcSEmq/TRXHmJmo/Zz+Mm/OIWt/v\n",
"7TbtLu/zyKKYJ/w7YMy+bDhvnO1+29Xc2v1uRyVlHHFZJIKrKr011cdwrH3yvkUqOW61U+1701u9\n",
"Y7k+npkcU2M++p/BWQy9jJqm0zBRU3VtddHs6Ptj49StHZN3qCP79WB5teB8qCy6KWOi6hroYqTi\n",
"emBivsrynqXLxHVgEpHbf/ib/yK5SAB4Z7gDDAAAAAAAAJfGB2AAAAAAAAC4NKpAAsA74aoTrtGZ\n",
"pP1N9VLGV1qhtO3Ke7ISm+xkO4KTR1qKfrOxllaij1S+H7I4p4jsLPtU7qvt/uUSkV4sX1OTq17W\n",
"qN7XqgbYY0oOpFN6baczi5H6cmdrVMpnu9b3wYwlitDl/YoqjVV1wnRdfa7ZVyeO9Vh7HXfTlQ11\n",
"m3RYWS1yidXlS8s+lm2zon15PDM9XnVEeMy3E+uic/MaEdlnxiLLCqCtKoyh66I4jmRCfPvcUcd6\n",
"95VBVQGWOdv0fC3HTLqTx/N29FDPSS2so4qDiCWX69QhEz6HAQDvBneAAQAAAAAA4NL4AAwAAAAA\n",
"AACXRhVIAHgDP/IVP2MahmGGjQowAAAgAElEQVR4eVmzeUtMSBWaE1Ug1zigyubdo42qup1I2KTN\n",
"lupbYp01qmBIJxFDymKA5WtW1b3kDqz30bofGlUmTTpGVWZ08a3eHZO/diEavRT9rQv75tRvO2Z7\n",
"bB7bkVdVwbG3r+w8sbEwt62IDQruWNRVW81rF+d8eyeU/fk8oI1H2yKCrZyhi3BH2rcmUK9TryWy\n",
"LK9mWFdkHMVrWCvb5j9nM+w+7rYj6FkrGWXvjQ+KTYt48BG7+hBx+2rXyMNDRaddBFLEL001yPT7\n",
"f+R/+PMPv8oCAGK4AwwAAAAAAACXxgdgAAAAAAAAuDSqQALAG1AxmqpNGtMpqh/eF6Zflq3SbfP+\n",
"t2MeLu2SrVuih6ZaYqO/QcQXR5dAEWPJmKGIwoxqvks7GQDNt0u2lU8MMNUls+iTjYWJdS7OGRVN\n",
"PD38SQii0pxiX7KKUdaVCFXFNtfvGk1VUab0+3J9EvdtbFv2IZrrY0tWvFPt8vbRvrxWezOWifXJ\n",
"ypNZ5K9c37p+xSoFRtrnryWyTFQzlFUBVbuq0UbEef5SX13n407NsXWyhcLqretHkcpvxRfXKp59\n",
"Y+poY319lpNT124VK3Xvn/r9E4xq8pQZAHh/uAMMAAAAAAAAl8YHYAAAAAAAALg0qkACwBv4m7/o\n",
"izYvvqpa11JtMNp+iZvkS1/b29ze0p+MamU9tfs4wlVbi3ciZjyn3l7m/rMNOseJ5Qz9Pq9je+Hx\n",
"e3eHOY6eSh6ze/tav12qsh2pSKoqLUYiT2P67XblRNtevpasl9dFplJgNvaciLuN1TLZzlUllJUF\n",
"63ksixpRT3V9KS8w8txvxQZdpVij3azcEXXFR1UF0kb41HEl432B6SSOXdNEH+7wn+cYrBqZnwfl\n",
"G2423GgwuQhkNBIqM+rFdblxDVCxyNv9vLvdPhqGYRg+4w/9WapBAsAb4w4wAAAAAAAAXBofgAEA\n",
"AAAAAODSqAIJAE/yw7/wi5c0xcvL698fVDRurRY3VctStqqWK7Q1pX/72I5UrSESMQ8RywpPQMR/\n",
"IlUx1fr2PjJ93bbXquholhh72Y7YqJjo+h5FEzAusyOqktnWfh/tnUe4Jxl163sNut8p/bLZvy+c\n",
"KKpLyip/rgpkPZA6J6vzutU+n2I2p0k1NH2pjmU0b7v5RoU+1W977GFIInYu4ab2UTjSKNqb2GCc\n",
"eq/E+zKa+crKsmPy33szWTUz39HynBavWVaLjHLHRzQCuWywvf/yysDbEXXZ37i9TO6j7HfefG7W\n",
"y5RJvn/1dvnvWgDAe8CVGQAAAAAAAJfGB2AAAAAAAAC4NCKQAPAmtiN/svqhqn415zWSFOVa2TAW\n",
"mVxSOqLklytUpquMqfWq2p+KcW1HxrJtg1HJWB/rjMp1zYheIPaTdqFienWdQpXVOqFoWJ6pOrBx\n",
"LtyTirqZhrKZiVGm89DHRdGviEo1X0v1GtKYk2jvjiN3TIpYbn6q1bHPurpkstLEfG18OK2iqaJ2\n",
"88IswT1m6/wxPyz7Rl7bxLxHcc3U14P8/VbX0VYfkWVy/6Xvy/wnZndwyahi7JhRfdTXlHWhq7op\n",
"I99BLoKZVZ5cjiM11naUvFl9UbUrY8HmurDVLjJ+uk9vt+K1ZL2ccB0HAJyCO8AAAAAAAABwaXwA\n",
"BgAAAAAAgEsbp+44BACgxw/9gp85DUMel1ijIZNYpn6uoxRl+3TZNNQxHae3nYwctfookn4ykqMi\n",
"k53pkSyaVAx9lnU/zwP59+Vw//narj4OlrzbTxRnW+2cU+ulT8VBFu5PhMfSRFUZyUvP5eWAFtO5\n",
"ZQ3b7cW0W8f/5M4nGc9UfQSuF9Fqii7Rm415X+XmHT1x3dzO6CNZJveViImqOHoVv27lpF11RFsV\n",
"s47yyffWnibNk+31v6rS4TKojxmWIzTjraN4UwOn+s2MmXUh4pm20qOKU5sIa3o9+HH/8/eSiwSA\n",
"N8AdYAAAAAAAALg0PgADAAAAAADApVEFEgAebI3M3JJlw31Ze7uedtW6NDKpoleTaGdiUHqsOiri\n",
"KllOLqY2qmhLGml8Xf9SVXJMK1qKObqKd9nwInroqr4Zqg83ZtY8WOUy5uSkTWekzMc4Y7HZNanY\n",
"2ldmciqSOdWRKhWHWs/heh6T3SHp8VxE1zLzzhLxKflTfZ7UwV/dn1RcB0ZxzhUHtOnfrVNjbq9r\n",
"5ihVM7csyvWnKoeqmJys6Jnvy+y6KxOK7ZijfpJJtHKia9XK1Jbjq18s4txUlR5NLDe7xi8VhMXv\n",
"CVV8cflZnN+iedZFcfyq6pXyPTZVMQEAb487wAAAAAAAAHBpPAQfAB7gB3/ez1r/uD3WD4lXy0qq\n",
"vXpIcGtbq3wwd7KsV38f9evL7sSZynXr+uph0o0+Xl6matm6XWSuQ36LRucdXV7v07q3nfEA/n0D\n",
"Rxol7/fuPlR/4pgJ91vvL3snodpOPQ/b3RWjzrllu3pMeYeguAPG3UmYH+PRcy0fqzXfclu9Tjyc\n",
"3d7lpdbVd6e5m390//uXqbt3o/+UXo+tcpxyrGJ9umq+lk1i3dJT7DhydybFryTuLjXRLCsMMaWr\n",
"dt356go4yLvIqvdAnyfuTuV1XX0OybszxQPy5/af+S3fc/ItugAAhzvAAAAAAAAAcGl8AAYAAAAA\n",
"AIBL4yH4APAk0Yfa6223l+koTmyA5cH08qHCc0wz7d/ETVQf0txvIz5SravXR6NHKnpSzicn4lvq\n",
"AeXyPeh7c7uPBdVHMR+9dkfP7WfKb0/KbGEffC7HnMQq9TBysWxzoPWh2uJZ9UVUq5iHKNaQjqne\n",
"h2Ub0V5GamUUUxyLItJVrpTrevtQq2QEzK1TD4bX2wxD5Lya5ybiyWP+Y/3D9pzcMr0vxWZi2bJt\n",
"eD/X8cK5lsqyKHi9kcUXTkhM+wf1tzbOX/OuB/oHfneoYycbS1w3/HW8jjTK7ew+IfkIAG+BO8AA\n",
"AAAAAABwaXwABgAAAAAAgEujCiQAPEBaBXI2ztmVQcfe5kqFLmaoq/xF29XOqBq49NGI/4T6cAXh\n",
"mupBdWWw7XVq8PV92457ZX1tFw8b1E7qjUDKXt+q+uNRaaXTE7pb4ke9/ao8ZzTKuiTukuqEJtKo\n",
"4pyufdbv8k0dX1zizGJdFvt01fjEsauqQKq9u1RmvY3lqnqdGjOZ+zKWiA82K/WV10/Vx5Asq15J\n",
"8ppH8Z7auON2FLOcZrVuq01DK0rrrg29MUrdh4hAqt9dc3s5Vn3sqmqNdW/JenHYRyOVLu6oq0Ga\n",
"9rdIX+v307Tei/BZ3/rd5CIB4MG4AwwAAAAAAACXxgdgAAAAAAAAuDSqQALAif76l3/JNAxbsbY6\n",
"tpHGU24mOrHGQVTEpW7v0u0y1hO0RJla28kqeEXMsVXhzfShY6KqSlv79en2Ku7iK/+V61rmqoD+\n",
"UQR+/uH34+HqbFloRmkkqGecoREdDfYro7emwpuMrS5duIqIWViwGlIez6JfybUTFfJcRcg1Eqe6\n",
"alXjK9ZPZp0aM/lhKipmZuuOxNpUutUtc7Hn+q0aRhFxy2dZXL/Ejj7jXG7FIk+lTqHl9dVzUlVN\n",
"12thvc5V/1TzyMdSE1bHSr2mPt7F9b9VXbKsWtyYBwDg8bgDDAAAAAAAAJfGB2AAAAAAAAC4NKpA\n",
"AsCJfuDLfvY9AplGtWJVGiOV/OZKkcOgq6K5MmNpFUpnb0VBFa101RFl++bry/topUhcRFC+zmC/\n",
"rq9o/PQMT6v+2BttPDTW/sqQuppiXXXxIVQFwDO6DUaWdcXTuRJhbG7R8yUW0/NV8yJjqR7iEcH6\n",
"AqIqZcp5LNHY58fUZJRQvbdFm3ypeC2i3zPM17tJRATV7yYX429FIF07G4tsxFur9skY67EYi0DK\n",
"7mRUso59zt//hG/7LvKRAPAg3AEGAAAAAACAS+MDMAAAAAAAAFwaVSAB4AR/7ef+nM3qjyoO6JbN\n",
"VOxFVYpMI3cv9s8arsKh7m9rjjZutbFMxY+WdvM36vVluZRiHyXr5oiKWqZeso2TiZJiKjJzpApj\n",
"7AkEasw1yvq06o+iwlrKVmR0dRhVtLK7MmQykopeqWqDxQjuvJVUTLNVAbA4Z1xcM+1XRaSi59+6\n",
"MnacTGJfyXkU67TOqpGNdVPxdWtuZWQtr9YYrRa53U6d8/3Xgfq4690f67r1+6WaYrJ+DG5b67y2\n",
"yPhi3V/0tajqu9Oat0yaBd5TlQLtPifqCGR746IK5KR+QfvrBgDgXNwBBgAAAAAAgEvjAzAAAAAA\n",
"AABcGlUgAeAEawRyjrb4a+veKpDRqn+6f9Vyu7+1vQwdVWOpSNAZsghmMQu9QfK9mMZSaTIQbcz4\n",
"5GjIOfvleb+3x+qblv1zCx2fjWqUc0TY9tXoY/1nUX0g+ahn3Ue0/RlsDC/PAc4LHzyj1gnjzuad\n",
"5VgfqHxP8+jhfVm2gYq5u/ZLb2r05Psi5pjNo2+/9UcgtzfQ8b60N1FNMaC74mO62ry+cARSxeiD\n",
"/dXL1p/14wzqmOhnf/t3vp+TAAAugDvAAAAAAAAAcGl8AAYAAAAAAIBLowokAOz0/V/6pUso4qUs\n",
"OtWoAhepAqm2PVIlysWydBU8OZPgWNsVJ3sjky7SJfezyKpk7W7V6rp9o+JXNd9W8i9QebKlN950\n",
"BhWz8hr507JVVgVPbWequcndMEeI1EYiyiRivvo9ymNn6hjLq7mpueUxyrSNqmCqjhlVH3Ms2qnI\n",
"2NiYm5pTue4mKrrqKobqOL1/n0Ux1TWy6Kt5OG1fZ9Y+6whi8DAd3HuqDrHWNbM8xt2xlo8i9qXQ\n",
"e82ORyDb1x5VwTGryDtXqJSVHrep4z+9PrvqwnLaBypCRtq791TFHgEAz8UdYAAAAAAAALg0PgAD\n",
"AAAAAADApVEFEgB2SiOQS/VH0a634uORSo+9fazt058msy42nzXieRPLYrkUF/t8VJXJ+Eb3r27T\n",
"rNqgiXiqDeYlJ77O84mZn5LwiVQm1e10JTp3PMeit7oi6s72y7ETzuFZ5fmpY4w+4hmJQLp1W+vr\n",
"DdKJBsbaFYHUfab9ynnLsVwMUFRmbOyj7b7SbX003Ebll0qL+dIu0UOx2A2t2Lgs3DhtrjoUF3fC\n",
"1R8D7dI2vv328ZH3kbcfhmG43V6vaT/xj30H+UkAOAF3gAEAAAAAAODS+AAMAAAAAAAAl0YVSADo\n",
"9Fd/zs+tggxzlbXpHll5aUTXVBXIcl3Wf2e7/qpWaR/5V1fRrhhd9Fv/nUVHfdxYdQwp+tojEcLo\n",
"vsr6mrIvuqJdWgHtiZUbH07kHfurRYpuA1UudQU5Fb3drgoYf/KDiybVVRhbVSDLV5Ufd67fdJu6\n",
"r8meE/V81n1U96sigjdRNXXtV+37/Od5lq/zTtu/3Nuny/LXMsr31r+W+hqh4p+iX9muVaXRLZv7\n",
"2lxlt8vnofqrj3V1nVHXWz9osPlUfM3G7BvLTTGvtile886oZHu77dii6uOcSpJjte59x+AB4MPD\n",
"HWAAAAAAAAC4ND4AAwAAAAAAwKVRBRIAOn3fz/6yaRiG4eWlzgapapA+mldHtXzkobd9PY+oeL+v\n",
"X1WMMtdbXVJVhszH0nPsq67XipfujaAciel8cLEX837bV34gGdpbIW8dMj1Q6/W2yp55X2Tkz0zn\n",
"vJhTJLO2HQk95ux+o/m7nj52zFFUNiyv4zoSvd2+2qZY1/3Se6OKcpXJHEb7VV3cfzW2rvHluXbk\n",
"mqn2s48ZRnuOVXBszSnSxsVV52qQn/PH/+SF8vQA8HzcAQYAAAAAAIBL4wMwAAAAAAAAXBpVIAEg\n",
"4K98yZet4QRR5ayKXGTxGFWZS1Uvq/st+z8SDdJxjO2oVjyCouImKr5YRknquMvLS6vqmxq5/EFF\n",
"juqYSbTyZO+TAvZW4kwd2fZUItIrmX1od59Mp031IrFAV8gT587c3/x+Z530zc32LyYaPXb6K7qq\n",
"Hef6qP/e6eJm8VhwXQWv9/jX89gfGV6qS87XpT1/6xWX2+k2Zsvk68tSkeP2MtVeVKNU243F9bbV\n",
"fndl1uh27tzvHFtVVVTHRysqWR5HqnqsiuxHKz7uWb/V5ox+AQBx3AEGAAAAAACAS+Mh+AAQ8Fe+\n",
"5MuTO8Cm7GvKLhN3ULT+ul1L7o7p/MNw/4O22w/yPn/MVh/5X+/zO8bUtq7n1gP05z7qYgd1u7Nf\n",
"5/ty5OHUq/3H7rqhWtQ5tzH9NvhQ++XmH3WQ3dvfGu0jd5E17sSU7copyT7EandjWfSmM/d8+VZ7\n",
"tV0xvr5LJ7g/3Bwby9ydvMsdbuqurMada1W7J57yz7yTKFpIws8pdtCogij+DrB67PV61Hctie5T\n",
"167Vx/zw++XnpP3n/ok/we1hANCJO8AAAAAAAABwaXwABgAAAAAAgEsjAgkAxl/6WT9vGoY8XvES\n",
"ij76uNcS0JCxtzp6WD64vaU3RqkfcN3nSITPPTi7t1/5QP/k+/L9a0cn2wUIWnN0v2rfOvr41uNH\n",
"ROcYjV6dyiW1etu1ooeqXSACKZObaWSsiOS1YmryfC1in2pdcx5L9FC03xmj3BOBfLT2FeXerrs4\n",
"Quc8VB8isr9f7GDUBU8eE4GMPPA+7yPmSMxxbTd/V7++aXkt67o5Hvl53/HHiEICQBB3gAEAAAAA\n",
"AODS+AAMAAAAAAAAl/bxW08AAD40Ko5YRhx0hM4tSRe6NMMZOZ06XpGNUERPstdZ9aC2y5bWozcq\n",
"3UXWqRjQumyzq/uMtiuDpa2S0Yqvfh6PsveJBW8VcYxVZEziuEf7OjCf3iqX2T6dI0qt+G7xNsjY\n",
"sapEqPqT7e7nq5ivPk9i55yqTjsvUxUZZSVEsY/sPFR7d+3bTpLvWtZ7vO29Duw5M/37tsxoR89z\n",
"J9vXOxUltF0dqJLoX4v6HeZ/r7l1Z8Yde+nXnryW5ZvjjwcAAHAHGAAAAAAAAC6OD8AAAAAAAABw\n",
"aVSBBIDCX/jnfv5yYZwrBqqoQRpI6K0COUe/XJCiNaZWxxYjVLwpGq9Q0cPe8dU81vlE+43VVivH\n",
"OFIBc23vx1S/al9envP7dxxvTxmnzZUuDPZwqBpk37lxRmXU96w39om2Vgy2jsqn65alJ8zExwHr\n",
"c0Bdd1/E+ujcVCR0u6qjqgK5rgsOKfp79Hb53Ew0dfnGxx2r9mJ9Oub8HqVtfvKf+qOczABgcAcY\n",
"AAAAAAAALo0PwAAAAAAAAHBpVIEEgEIW1BLxhJdQHKoR95qrqKVbuGje/WsaZtPz2K5w6GJcvhKV\n",
"j3P6Cl71+C5i2YqgTEt5OBU1spuGx4i2OSo2j74+VawyjzItS/s6HuW3oX7X1xmLQ+n3MVplz1Ui\n",
"ddU/VdXPZG05blbdMXasRCoFts6JyDnTijaqeUTOyd5+98zD7aNo+8g8osv6Y7t1ex0DnMfxfaxz\n",
"u8n1kT6U+vEnsfOq/7roqzXW81LL+iqYtoQrU1bfpKKvofO1LuvswxHMOgBAC3eAAQAAAAAA4NL4\n",
"AAwAAAAAAACXRhVIALj7c1/8C6dhGIaXJG4yx7HSeMwSjrFRSB8bjFSVC1dhTDMaJh0hi1E+qLrd\n",
"3n6jsan+jrcja8+s8Pfosc7qf28Vz9x25bhYZTrXZzyOW27rIpavfbxUy1zVPH2c1u3K9nmf23Hm\n",
"rXHrdnvXqfWt6N/eMRU1Vm8frl8Vb40t0/G7/Oe8XXS/9bTZmpto1hkt7v1fgGdED9+i/zPm5vpw\n",
"8c9bNJJpHlOQrpv7+/zv/HaykgAgcAcYAAAAAAAALo0PwAAAAAAAAHBpVIEEgIqq5FWvVvGYum7j\n",
"2kcqEu8LxzLEUD5E4yveuXmt8R+/jaog6eI/o9invt+6D/ValrnbeEpfFT/dR9Zys/3ZMaDdx0xD\n",
"GY1qxxO3o1zre5v2vx2LdNHAMVnp4lt5/3P00UXH6nnEq63FIp5l+1YMNP5elpFeNY+xWu+im/uq\n",
"bebr9DyifZ1xHEf73V7mKvr5yrn+uJ+rteoKka1YZPs4HsUJqyssbvfR8ohI49kVH1W/ydLgtsuM\n",
"Otv7baL7XsUcAQD7cQcYAAAAAAAALo0PwAAAAAAAAHBpVIEE8Kn3v/2z//w0DEmMMa34WEUbh2qd\n",
"XJYWZtxZBfJI+97tVJXL7Rp+pVjFsV4uQnhmNUUV8cwjY8fHWuI86cLuqN1583mTMURUty+MW3Qn\n",
"Ky1G4mHpT3VlyDVytD1WK2boKk6qeHBvu2gVTRdZdhUO1fHfjmy217VikeXri/YRj1v26jsq1TET\n",
"eZ1HqPexvc2yxanjJ0vv84m2j441VP0+uoJj73b6GLhfU3aMXa6XY6bf317X36b1Hod/5ru+jfwk\n",
"ANxxBxgAAAAAAAAujQ/AAAAAAAAAcGlUgQQAR0QXVHUqV7Fq3FkF8kj73u1asYpy2zzmIeIdMvaT\n",
"7yM9j2wLMYOyXfT1pevLdedW93pG9cdHO3O+Kha8DpRUdezpa/DHgDvu1fuoKvXFx5IzrdbVsbdW\n",
"9Kl3zO0+8nnU+2F9zar/3uqZy5Kqf99+3SbaXr2+U8iCjK5KY81XKZ2/+utX73n4qOtMqy7l1tr2\n",
"MeN+F6j9Hex3+aZz/2U/dIb/VcyxuPTt+10TaZ9eR89/TAAAXAl3gAEAAAAAAODS+AAMAAAAAAAA\n",
"l0YVSACfSt/7M75iufi9iOqP5TrFVoFMl92/qhilKIy3ERnrizUciz/k27YqOrrXN6iYaLFdex77\n",
"4p+bqv3bCPO8YZTk/cRY1LF+Qq9TfQYc6zd+dKV6Y2fR9tE47JGKp5EYWWse5fpWZUG1l3vn0VvR\n",
"9ZkxYhdp1/Ydd3W4b6Nd5++CaFz7DO5Y8FuUWxWtbBQ5tbdSZzCOWMwn3VJXdYzNLR6FLqpAmnXp\n",
"snTd7f79T/3u/+XDyuIDwANwBxgAAAAAAAAujQ/AAAAAAAAAcGlEIAF8KqURyDKOmEYuVFRRcXEU\n",
"uy75fm7VG7uMctUrj9jbR7ZdZxxKe1BkMmBP//Ov3zOihI2R6kWj/PZp81irDfaOXvchW8l+YxFL\n",
"VX3u8e8R3iNV5U9Xwr03Obmq45meGYtUY6pzqN4f0VBoa9zOCo5yoajqaMfMt4uu033V1XHnJTcZ\n",
"e0x/qiOQ8/ef3L/+9D/9rVzRAHxqcQcYAAAAAAAALu3jt54AADzT93zRL5qGIf9rdPmwXfVX/9SR\n",
"h02Xfai/Lt+Cfek/4bq/V28/MFfOLXiHkrpjRj2ouexP/pVe/uU7vY0gb5fvI/MX++CdF/7B0m5f\n",
"HblboT32MWo/y28PiNxdld6RIHoInWu+D2++M0KtUwu3x3rUQ/DdnWuv7dp9qLGiD8FXd6roudXv\n",
"d3Ud7Wwf7eOZ9ywq+sHj+9rLu6KyH9rH1tl3lcXvVspfdP7e1n3ocz7/eRzT9vuvt+6uqe3fVhsP\n",
"tV++6d/PoTvRWq+lfAh+406+qfiafs9tXwDAHWAAAAAAAAC4OD4AAwAAAAAAwKXxEHwAnyp/5ou+\n",
"8h6BvC3Lyoffq5hA9mD85Zv6+tna1q0rYzEq/CP76HxY9zkP0k+X7e6u6jfl4lvLdmn7zv7PePC+\n",
"2h/RoMmjH8x/jtiD43cThRC6u2jsR/eg7eiD9GPR2Gi/222i59XZ598jnPE487NfZyR22Vq2zud9\n",
"PNw+1fuw9UeLXhddRE8dRzcZ3z3wmqe+B94vmwULIaj2dn9kEfUyAhl7lIF6kH75MPxhGIYv+jPf\n",
"8j4OFgB4Eu4AAwAAAAAAwKXxARgAAAAAAAAujSqQAC7vu7/wX1gCBR/NsZU0MlBEKNKUwouKV6g+\n",
"5lUnVH2b4w+TaK9MotJWGetszUeJxvtUkl69vnIu0XnYdiZCumcs9Z4u8RwRg5Xvn+k+i2w+KQF5\n",
"LDrmKidGx3cl8mJxHhfF7K0It6eSpItRrvr6zdvUs3TnlWrnrimtuF6sCmUrcFzEBkUE64j1kR3H\n",
"E1t7YmTrsvm74PUr+yFSlbMO/b113PKMMdXb566j5e/l1txcHPHI/ov/nupsHxzLRyq3o5uqCuSM\n",
"zCOATzPuAAMAAAAAAMCl8QEYAAAAAAAALo0qkAAu709/4VeuoZWlwqKo4Bis1hip9Ji1MdUlo+Ov\n",
"fDzG9j9vq9ImYoRoTCISd9xjfx8+nra3/1aFsoiXE/bL+9FXfTTe3/7OeiO/j2ofqRqp+0o7yb5s\n",
"jumixXurq55BR9LUMvda6va9Y6XbHYvyRY7PM2pfxnS/FlkJd1npxxKt/Pj175pToptL5O/4flbH\n",
"XbSCo4tiu2hjK0Ss5hZZp2K2WQSyWJZViLx//0Xf80dIRgL4VOAOMAAAAAAAAFwaH4ABAAAAAADg\n",
"0ohAAris7/rpv3gahjxWoyJoczQwGglyMbZojHIQ8ZyevlqiscTtumPpgu3t+hQx0V2dtOtZnR3t\n",
"ivSnKmU+OmIWFd/NacbnjP62+4++9676Ym8f7+X9OMbF8CLr9PpIBCzqzL6eqTfCHY2apmL7xr9X\n",
"Z1T06z4T5vmeUI1y/37pH+NIvzaGKJapipZnxhyVm4lWynmIeOTcx21a74n44u/9wx/WyQsAHbgD\n",
"DAAAAAAAAJfGB2AAAAAAAAC4tI/fegIAcKY/9VN/yXJ3/0fiI35ZzWr5pg4EumpPPvZS9yGrNyVd\n",
"lNHKWxqxqacRqjTXWjaoiEjZr5hHnviLRSSnIY9rqAT+2IjYRGJv7fjIHHlV83h+8mOqvulnK+TF\n",
"ewlt5Gvhbccox2RB9OkLddwr1seR6o6ReJq7Lmy1K/vdV1FyrNqt69vr0vXqNUcrVLoKjmtfsfaO\n",
"fo/V1bszUpjF0YPXStOr7EPMrKzGp1/JdnRNbSuvxeKadkoAOKseeO/d/H4Ld2veg95zWbWT13hx\n",
"DKjwqZyHqrQYmEfvula/qo3sz1SBnF0jIg4AbdwBBgAAAAAAgEvjAzAAAAAAAABcGlUgAVzKd/60\n",
"r1ouanOkML21f7nxXy1bfk6zO3WkRMWfyn57I4uyr1a7SH/idfoaY3X/vbGl135F9Krso1VFLTDH\n",
"bMxlvvlMtvqP65vJ27y43WQAACAASURBVERJtqN575GskzaW6/IYcLluXbh9LmcjiEp2NjinknOu\n",
"/7q57te0iZ6bzhl9HBmr97x1/bbCjpFlbo7ZstZpW7wgeV2UUcUkajoEjud0jMb6Hs+Mekcjdvsr\n",
"Sab91n1Vcdx0HnMfWYeiXdGHOsbyOZ0Xm41GWO2jDlTEWW73+v0ti7e+fv8z/+wf+kB+owBAHHeA\n",
"AQAAAAAA4NL4AAwAAAAAAACXRgQSwCV8x736Y1pJsayqOAxrrGEUy5TRhFDsdsHKiL39yvYHtlXb\n",
"uepbWh1EWuIj6Rhu/GFu31edKp7PiM7k/UYJz41W+uih3bI7tnR8n5YV51qiUUXZXlVGLdu1qpWK\n",
"dvMEymqoW2O6uPbNxIdbkWVX1a6cT9Y+XX1fr+bh2qtqsy669tQI5PA8Ryoc1lHv4xerN6+EKyuT\n",
"bs+ndTUv96o6r3rf77OrXC7rOseYskuKiUCaZa3tbvevn3zy0bLsS/7c//gOfysCQD/uAAMAAAAA\n",
"AMCl8QEYAAAAAAAALu3jt54AAJzBxSCOVG6zfYg4z6jWiTFfTESwN4KoIhQuPiX7MLGJdjwyGMMo\n",
"9mbWr5mdi5hlr11su8Zg6+ps8zd5rO5eLaszH3MknnjGsdgv6WXKvjxA3z7V+zLWh4rezlxlOlkR\n",
"Lms/Hyx5m7z/arqyXdFjMabvo7f63N512ZjiwHPXi2h7vQ8Dfaj4qVnWil26yKu6Qss45057+tj9\n",
"nj6RiiyHYoDB80r21YglV2NlY/Ttt972c1RYxY5bl8Uzz281VllpN53b21Q0BoDH4g4wAAAAAAAA\n",
"XBofgAEAAAAAAODSqAIJ4IP1J7/gly4XsDnqNorIn7yN37VrVFFbt9tXITLvI5XHrKIhC1lJTPQv\n",
"K6AdqFbp5nFOXG+7umSsdYzss1EV7dHRkPcTPYlVcOyvSLevMmT6T5bHVeo8M2waqz7qY3XRmnfb\n",
"63QULbkGFtEyFXtuOzek+yGJVnWMvc/R9o/VGrP33S6j59nGIg4YrtZo4rK9FR+jjySYgvM9M1qp\n",
"YqI32bJut/ZRz9vFmdN45LyMapAAPnTcAQYAAAAAAIBL4wMwAAAAAAAAXBpVIAFc1nybfxZBmSNB\n",
"aVVAEX0sO1Fxq7Ry4dyvq2aV0tXq5hzSUK2b28vgTLTilYnnpD3MsQoVv3GRyWjVKVd5b091yXqA\n",
"NKqy3deheFH1wmJ9pJu9uDjnwyJPvdHDvgqO2Ujm3In3ux20ctv2RvjUceeqRubzcO22561iifpc\n",
"q2NIrfOkXKf3laj0WIyzPd96WbnfWtVjfWxQjbmv32fGB5uxQbs+dr3rfz3yKnx4q9g80lj89u9X\n",
"1eckrlW+culmtxsx1LRF+3eXqpYY/Z0X/R1tI5uqaqTtd3u+Z1TCBIAPFXeAAQAAAAAA4NJ4CD6A\n",
"D84f/4J/cRqG/G+2H43bj4NtPeh9WW/uslL9+b/l77i2FvNszqN4aH582/pvzkceuq7+av0i7vIq\n",
"5xS9hyUbq/jr/eMehF6P+aH0W43zsI6Th6jfv0bvTpDdBfZH9K4st224fTpGaIsj3tkD5NN9dPE7\n",
"Q7qPi3ChgM47mMydyPvu4dre1jfafsC77Td4wjzqTqPuB86LbUdz3Lf2Y2R8dX3s3c+TvHMz9hs/\n",
"ekehutttXnabXu+d+NI//wevfWEAcFncAQYAAAAAAIBL4wMwAAAAAAAAXBoRSAAfjD/6U37ZNAzD\n",
"8NFLHXec44DqweKtaMto220/NDx//nNffHFtF7sG743LyUiHiK5F++iNC6l+emNsZ+cs3FiPCqI9\n",
"K+4YFQ7rdMdrmz3u7GuO1KaFJ2JiD0NPzol7M9f+jPhb+4H6rg8339Zr2e7Xzal1DC9rZUQwn0+6\n",
"bKinNpx/BpYD7O/f9RB9oLla52LE/tzxIbpnXXn2RBun4ndS8yH7wZjosi/F7zxV+MXtIxt5Fb9f\n",
"bbRyqt+1bN5zs3R2xYEhiwk0lJHGScxDzU31MW/7ybTeQ/Flf+GbiUMC+GBwBxgAAAAAAAAujQ/A\n",
"AAAAAAAAcGkfv/UEACCuXQEwi02I2IGM+BQ/j+KnLC4usy/FwkblSTW2DWiZ2OBkXp+MkbSiKuXc\n",
"G3EJNXZ3RS7VXzlm8r2KuroYSzNaU20Q7P9QTO5ZGseuNGfntnvTXYmxTIxLH/91H+OQx28252Gi\n",
"VDcRfVrb15XVbHStGcGa56vXvy7Y34eabz1L/Vrs3ExlujPOafla5Osr5pXNI1kmDtNy2zzqJuJv\n",
"IjpaddZsr47xOrbrqEhcpL2MPWadvN21J3zMzOeoXJf+EPt9Vu3Lxrnm2i2rgr8H3e/c1pjyGIhU\n",
"o2zso3JOrv+Uqga5nFfvLNYPAFHcAQYAAAAAAIBL4wMwAAAAAAAAXBpVIAG8a//r5//y5SI1V3+c\n",
"b8pXt+CrqoppO7etal9u17NNZG6q2FNUpILkWRUc1zHVwjp2FuusrqDVrDR3X/2yndDLhzBjLT8m\n",
"36topZ1POU46drRqnvE+S2vd3+8DkzvjWIxy1fjKNq8/1NHiul0d08yiyEVfrw3yGFR6/s778tbo\n",
"Q1WwS0rHVbN0VfPSfb/GQ+vYnp9H/Rp85b1k2eCWFS/pwLI8Arm97Bki1TYlc/0Kj512FxlTjX8g\n",
"yh05/9Tx76LIW+vL/Rx9ne44Uud369ipxm1M3MVlXWSypYpAqtiliFGqqOQcU70lVSDn/r78L/6B\n",
"9/krCwAS3AEGAAAAAACAS+MDMAAAAAAAAFwaEUgA79q3JxHIOc6gYmrjEsPz17TRxPVsLDL7oR35\n",
"OxLt6o3hqXpgLpqXCVbKtF1Us/ARn/n1qbhJfNBYtKu7W7EsEt25REUsERU+x1R3Go5SbcctXaxJ\n",
"H3/L2lD/aiz3PqvqhGfbGx09e27h64vrYz4skk4iVSDj/df7qndZqjdO92gyznliPLLVbl0o3q3e\n",
"89X0L6t+7og0OioSGtlWVlM0McdJrtyutJj26+bTqvo5FX2kLW7yuljPI408lmPO69II68//S7//\n",
"fZwoAFDgDjAAAAAAAABcGh+AAQAAAAAA4NI+fusJAIDybf/0r5iGYa32l1pu41cxp6x6mam0JeJe\n",
"NvaSLiuqIb3OMx/L9dUybScjNgQqRw0bFd5UJaqqcpWv1jjvh2gU5xbcz4N5r1QspLuyWTF2Nb5Z\n",
"VkV2xJiPCkX2R2SDdlQXW9hY8JxbSoZS75Hs4/4+d04ofgy4/mOV+tbjJ9l/nfN18bpmxcBQHLie\n",
"WyvyF3HGkaj2VfQ8jPW/HQlrLst+aO+j1vsX2s+dFR9b+8rGukV80Q3p5y+yrA1VNK+xr9x5pc4J\n",
"V30027b4+vrDzkqSWTsTc1z6F/MwY50R/8zXtSOTuo96f487ryMA8EzcAQYAAAAAAIBL4wMwAAAA\n",
"AAAAXBpVIAG8G9/yk3/lckH6aL6lPolEvIhlpVHE5aKVIcvtou3zberIQ3eFwECVye31eVW7aHUv\n",
"FRFp7be6Ex/dWaMk9YSCwRo7I1VdstXfXt1V+CJ9njD2kdeWRlOrfhqvd++4vVX+ZFy1Ebsp95eL\n",
"X27No4xO2zZizGGo59uKNu49xo7MTcWIXUXNLL7VWaEyUpFRzaN32RlRz7NMxTcq/iY3EPtZXu9O\n",
"ro4Y6uuEfWrno+K+B8ZX50l/H9E45H2sMf857aP1+y0Us8823I4v2piviMCr16keYaAik7fb6z0W\n",
"v+Av/z5ykQDeFe4AAwAAAAAAwKXxARgAAAAAAAAujQgkgHfjW++VH4dhjQWkFe/GIn7UitqU7bN1\n",
"JnTxImJWZ8TTonPTG3S2V10UfQ3DYKM4br+paER3ZLJhb4xM9pX9MFfNk2vLkbJ980jdUdk9Y8iF\n",
"fVXOwv0HosU2dpn04Wamqr/59vWkWq88ch3ojXNmTCXHY8zMO6sNHhjpcJ9pv73LYjX5tmKU6bbm\n",
"muNitaa6ajTefYZo5dBTxpIL8xhxtkpF5l1fYiwZaYx2sjTbF6fcXL9Uodxur6+721cTFXmNHju3\n",
"mzpOt+eR7g9XGXJedxPH+ifJsq8gDgngHeAOMAAAAAAAAFwaH4ABAAAAAADg0ohAAnhzf+Re/TGL\n",
"O85fxbIXEaHorQyZre8Mn6jx1876oopqbBW5k9EdEWM5I0ZXhRiC1Rrj/ber0MU7i1WePCIyp+go\n",
"9tg52wmx2VkrptMbE+1MJlXbvf4Qi26W0V8Xt0rb2Spx4poi45wuLif6aMU5byL6W47fjOiZ9Uv0\n",
"r27RPL/KSplyzJ0V+4bhCRHIRr97yWilm0ejSumRfbh0V44lYvE65r5/TNvextH30/OIjeEqOLpK\n",
"i7ovd6TWY2aWTWNjuuuhquC4bCfnsx3fzdapKpBi2Sf3ypBf+X3fRBQSwJvhDjAAAAAAAABcGh+A\n",
"AQAAAAAA4NI+fusJAIBjIyIiFiIrB5oIihqlFYlcokZmvq2YwjqP7RiEiu6k/aq/YNg4WDASV4Wr\n",
"6nRMvp9FJcm6r3TfxGrp6XbFa2jEgXorG9rKk26ctI9gu0fIxu6sEKY7dFunEZijffn3Sp638+tr\n",
"RfOK9lkXciKB/dY67kS76trQmo+LKwXXyeuRuH4t15feeJ1qH13WSVafE8vKKKiKlbaq8ckkWnH8\n",
"7qmqWO6vW9q/G9vNrRGZdJFKdywq8vxTjyQw7Y9YKnHKGH3fa8gjzvXCqfj9N4n2WfVk8+8SNcc1\n",
"hqrXVxMW7HVALovGP7dfi6sG2fKMSscA0MIdYAAAAAAAALg0PgADAAAAAADApVEFEsCb+MOf99XL\n",
"xeejOZrXqNY4c1UgR7Gs5SVQmSsby9z8r+bhCjupbXup1ywjGmZsFyeNxvvS/SIriI1llqSOpqai\n",
"74ebR9lX2mNv9c/w+O8s5tHcf66CqtlMVj1M92mx8Z4Kcm9ZKkxWODTtWtX7qsp7wT5a84hs26ou\n",
"ObnYoJlHuApkMXa+/vnveGtEGZMrljXPchUjK9Zl84jGKFvjBrazMe1gNd3euOw6j/S6sf0ogHh/\n",
"c1/JsurNiu1TFwuOXg+mzR82IpCqjyOVPk1EcR6/dQyp8cvoo7p+fNKIdd+KGOUwUBESwPNxBxgA\n",
"AAAAAAAujQ/AAAAAAAAAcGlEIAE81f/0T33NNAzD8NG41r+aowUy2ph9P0clt/tvxShVlKOMIkSj\n",
"mHnkL9LezyMkODfVZp1j0kd3+KB+pS4eE32dtgKajBCVW/bv0zV+42YU6+P9qCOIZ+RLXEzsSB+t\n",
"iGB1tDWuES6GKF+DiKlF2rX2qbseRNYd2faMflX7VpS76qNZffftqLkN7rgb6t8PMioo2p/B7Uv9\n",
"fors+4OdHWNc1k1ir2aLfOxuc0y1T49UQe3sY23nz04XxVwrVEZjs6/tbq1IaGCfZtdpG7tcqQjk\n",
"7T6nX/x9/x1RSABPwR1gAAAAAAAAuLSP33oCAD5deu/SUQ8vX/4I3Hgwb/jBvUW78MOsO++LSdcs\n",
"f80VY9i/C4u7FJT5td/SG4KW3VffHeAexpw9/Fe9ZvdAYLmuvpNvvh+wfQeAIe4KU/toLXrQd+dA\n",
"/11Q0T9o990lF24l3ttuvedr4PzKN/DvVbVszwPC3cObzTxcu9bDy91ek+vE3SPqjlR1p4W/eyX2\n",
"kPH11Nnuy81bbRN9MPdbi75W++BzcSdh90Pi3a12Zh7RfXrkDq291B1SuuH9zqRmj/m/AbrGN27i\n",
"93F5h1bzAfbmwfF2jqrfSa+P9OnuZbXXpfzFyLHT8VV79buXoBGA94Y7wAAAAAAAAHBpfAAGAAAA\n",
"AACAS+Mh+ACeYn74/csS80sfxL79YGu3LqUeoK+MgYdYhx/cbtrp/v2Dtst1rQfCnxNoqeOIvdQD\n",
"ymOP9xV9ZRGi7S3dvm+NGUwaVaLHmJqH8zZP/o2dV08lzk0b94k83D5t3hmJdv3qwgxp/Gf7vOot\n",
"EBHdNrIuOm5vezX+nj6qPpPvbewsezB4seyEh50fEb0GznGzVnGVs38DbM9HLfRR4VAfrn0rMtn7\n",
"kHq5cDuumu/7zrECEdlWnNn2byKNzXj+EoevH0LvqIflu8jwJJapYyaPeo/ZWF/1V7/xzX8VAbg2\n",
"7gADAAAAAADApfEBGAAAAAAAAC6NCCSAp5gjkHME4EVFsNIIXSSqKL5X1dFcDK4ct7YvItgbl1PG\n",
"RjjCveayzT51wGJvlCnbVkQ/1P6KRGzCY4p+VdVIt90zRY7/Pc7Yp8s50WzVDkf11sncU1fz3eRp\n",
"RCTvTcfUuTrTl2r/xD0tLni9Mbz48ROJxD3vtTcK7tlZdL9VRVyuObd7++jvyDxC134H1bRvjXht\n",
"WWX5yNU8Ghd0cdU1Apn2q/poH3dZzFBFvc3cVAQxej0q45Ay7qjGTOOOYqxbEctMK1f/0u8nDgng\n",
"fNwBBgAAAAAAgEvjAzAAAAAAAABcGhFIAA/zBz/3a5YLzEdz4SURV3BxyGhUMRqVVBXeym3PqAIp\n",
"x2+09/f6iziiCXa4eGSrOltv5qC3Ip3sY95OrptMwwfFF2UFMrtBrNvw/phzRaHm4Vmoql562+3x\n",
"e48P/Z7GzPshEqdM+3Xto5Xe1Pml2q9zzJe2+2jNezsm6qoj6vb1dcON1ds+Xa/aR5fVr+LcmGE0\n",
"Srs3civ3ffS6scRV6/XuHGrtoTP+lS8r8gYiveHUpajMKOOOot+II1U/VTXDdUJpHnf7vVr78se/\n",
"fZ9NNLU3ptlqLyONJgKp2rix8vjkdgTyk+n1Po1f9r//t0QhAZyGO8AAAAAAAABwaXwABgAAAAAA\n",
"gEv7+K0nAOB6vvknfe00DMPwEq0KpSofiUjEvKy3YmBeQauOKZT9TSJyoaIZR6pDVf2nc1JRmHEU\n",
"7bfjWDfVv4oiBOIr6f6Rla5cHy5yJ/pV8czsdUayL43IRUlW7HxmpT5hec2dWZ8jcUMV4VMdyuPZ\n",
"RWltNKiOt6pjfI5BqTjsKCJEvWFj3X67Xes8rK8Wvn817/l1tQ6Bcn27/faVSO+/dnvVf6sPNw/1\n",
"s6o2GFmWRhCXMUV0LRxnM5Hv3khc3knfNccd63nscl+/zZjoPF+xwd7fkYOI0KXWOGRyhi3v8/7f\n",
"x5PodyMUXnQWPa7VPEQ7cczYSKX7XWf2ZevfRI6LPu6J25avYcy+PyPACwA57gADAAAAAADApfEB\n",
"GAAAAAAAAC6NKpAATrdGINfrSxmHHLNI4Xa1M1v5MVjBsBVIGItQRLRSn4zOdeqtWJjFA4JVHes+\n",
"0uihiJaF5lH3kXpZ4otq26h2GOeMio8yhtrpjGPhHD5SGO6litac02+v3qpvkaqRKrqpokQqbinb\n",
"icqyLrK5SPtyFfVEDNy9hnTMOR52a10jighf85piIuqy4qOscBhRx7jU+eqWPePMdPPIDoEyWRyO\n",
"PW5H81qtfWnB7eiaCgBG431236vjfl7VG5kUY2brl+M0HSM0hBiz/4onq2cu/bmx0h/yf5c0qyoG\n",
"YpFnxB2j7fI4p9i26C+tArlUhky2oyIkgKO4AwwAAAAAAACXxgdgAAAAAAAAuDQikABO8Qd+0r+c\n",
"3Oz/+q2KhS1RSFFVMVr9x8XeolG06D30Szsx31a73WOeEKd7MVGmeJimDvYcqcpkQnULVXEy0lfX\n",
"PAL7V1VRs3HcA/PZmEHXIO8yE1JEA8OV6cy55iKILeHqdsF2j+7jLcfsC9w9ro+sv6k+D92y9qzu\n",
"cytjicNgK0Pqvh5TaVGN5OaxJ6bXQ/4+6Y5xxiJ0spKkjSxv9zeJ32GT3CIYwXTHXfhYrNuofVq+\n",
"lmzWrmpko6JmZJ1rH60qne5nt+0sjUDeltc3Vst+xV/7Pe/y1x6A9487wAAAAAAAAHBpfAAGAAAA\n",
"AACASyMCCeCQ3/c5v2oahjy6FopAJny0bDsO1aoCOa9txSLLilV77qvvrQK4xD57446NKGYvVZ2t\n",
"jAQdihuagIWKpbT7m78xVfPS9g+qzviofs+k98y0udIGx1pRnmBF1o3ZhNvHRXu+xzSzKnGqvQsi\n",
"3Ze0ok/lPprqq5Wch43hDfZc6I2p6fbmSiDnFq3X+Hy9lSRTkaqS6X5TMfRD0ccHiMcXe/u9f9O6\n",
"bNy/rlVT65V7/jelNwo6Vd+k4/fGbEX/pn3z5RUxR3WcqoisrMzohhF9uG3b1SDNPMS2c/RRnS8q\n",
"AplWtv3qH/jdxCEBhHEHGAAAAAAAAC6ND8AAAAAAAABwaR+/9QQAXNdNxUHuP6tKRipW5mJyoZhR\n",
"R7t1TNF8s3UxRrBSoKqGNBYxKBniClZ2ClfGk5Wcys7qmJN+r5JNlmXBqlrVlmlfojJkNIISiHLk\n",
"Y92/Nvbfo6JDhzXfd1XybnNRKPb12iCwPxrnpkxNufNUxqbu55CqNCfO0bldesyr+FbZ3yQPdn+s\n",
"jSaaJOdRbNfqV61b4lAm4pxvXM9xNFEm/b7XA4yj6reehz3eXCTULWtcM5dljYhbeVi0zombu7aa\n",
"06V1bamq+QavRS4UvCtque64qpfJXGfcuLf0973IPnZHG93vq9bv0jKx3Kp6GIjlq4qP6vh0/1bI\n",
"pmUizr1xx+gxEI1WdkcfzXbKh/AYAgDvE3eAAQAAAAAA4NL4AAwAAAAAAACXRhVIAN3++3vlx2FY\n",
"b9VXVRDzCo51lbNl3ZxYyZa1r02uQmTev++rXH8k3DYWX7cbzlGtVaRw1ouI6WTVqaLjz+1MNMRX\n",
"50zau35NZbpsTNHvXtGKkr4Pb+8IR96XyDyO7b/kfAp0FI1qnal13Olt5sjY9nxHFd9S45rIkeo9\n",
"Gu8r+0/HUBHPPDrtxqxfu5vnGDwTe9/Z7rjjE0Wud6p9sfT+9fHR6NAsOytPBoPTHTG5+dg9I8ZY\n",
"T2TcWr8xRuu64So9ukqq8fiuntfWPNTG/Y8TEMuCccfeiP/NzK213+b3T0U81Wu+qXb3ZVSDBBDB\n",
"HWAAAAAAAAC4ND4AAwAAAAAAwKURgQQQ9k0/8VdPw5DHBKIRyMG0W9pnVdfU+u1tXw4EaSLRFzfv\n",
"Zv87tztjzCPxSNlvWYFsGAZXGdLNTbV+EfPNFBXe3ktk0lVY28NFhrNxA5EW2YU8X5+pfn0+drO9\n",
"P2QcMVgN1h2zsmJbYN1ZffgKduv3Y3lCNfZRJIIcfX1qTkuVSdFH7zIXSWst69U6hyNx42Yf1dxU\n",
"vk9l+rYrFu6JBVfdb/RXtzt+lZCxwak8iNeVrbixjjTe27lzQVUONdTvPNUi3UfVeSXm0XvsxmOo\n",
"9ViynVsnl27/zmlWo7z/cDPbqgdS5NVxtyOQn9x//lqikAAM7gADAAAAAADApXEHGIAwdwdYar2L\n",
"p26n7kxS1IPx13V9D2eP3h3m+230YeZrmofJh1mLB82Xd2g195/4q2vZ75GHme+9O6bZ79qLXFqu\n",
"zQomPOlvw2fcWfZWql0UvGPslr6ny3dTucDfZZLeRRC400/t5Wj7Rx0K7sHZR+7F9P2e51H7qPXQ\n",
"8N6HrZfbpdu6u25UMZF8HtvvkXv38uvo3P/mtHeJHD2T3SOPmU++cPsuocjddZtjLYUhYneK2b7E\n",
"nPI+8v02ba4xy4q7zaJz7N4f4s5peTdW+G6v9p3Fyq3x+m7q5sblWNk+19oP0n9dfxPtv/av/y7u\n",
"BgOQ4Q4wAAAAAAAAXBofgAEAAAAAAODSiEACaPrGe/Rx/sS8FYF0D/DufTD+S/Dm9Xh8UUQoDvav\n",
"x9y/bau/o/PojYzJmId8UHM6Vmx+EWfsv6y/4uc9vR8pULBfOw4Y78kHkfojumUPfdu9/tCOCUXb\n",
"q3bD8kXENMU1TcY53QPKRR8uznkTEeB03jcXQRb9qnVrZDJZP9btqr5U/40YUhlvV69Pxp47x2rG\n",
"zpb+7z8fOFV9FLQetRUdnYrfP2c8VF5RDx6XxLFwdmyx3nD72G1FBN37HR6zZ7utMV3E08Rru+ed\n",
"9KHOod4+9HaxuGNvxFTGHU1f6reP2s9qni4C+cn9+1/9g99AFBLAMAzcAQYAAAAAAICL4wMwAAAA\n",
"AAAAXNrHbz0BAO/T7/0n/5XlTnMXZ5P1pTpvNJ+jMipWlsZX5m/nWGQe8xABlXE7ZiJjUCZils4j\n",
"Eu9TFYpkHDFYCTGSYonOQ22b9V9GtVT7ZhyijjKt7594n0UP8bG2qX1aLlERqdZ7vH9OdfWyqHFn\n",
"Za6eEWaxMXwrF+9aI2DpBtvVwFz75oxs/Ge7L7mNOJfLdZtjuQpswXXyfO3t171tsn3sQO2tPier\n",
"L3ZGxtxLWSKkSSsfOfQBRn+097Vf4qHyMQF+Zv796IxWBi8m+r3NH3UQ/p2QLTJRQjnmvFkdM4xS\n",
"lRNv7rze+LlcZqPTro/gtUefQ1sjNfpqtA9Vi/RPQbAxUVWl1FWB7J2jDlQCwCvuAAMAAAAAAMCl\n",
"8QEYAAAAAAAALo0qkAAyv/uzf800DMPwURIPeCkica2qfOqW8zL2pqow6kpe9a3sKgbkqkVmVZnM\n",
"HF30ZOy9pb5RKdNuKvbvmbfxH+lLVW5T0cZoJbHQWKky9nBgP3eP/Q7Z13zgOKriJUf6Est6tz3j\n",
"vY1W3vPt6pi0i2wOop3rvxXX09vmc8rj3e15ROemAl/RPty8nxlSctFKHX1XGUVzbVCVL1v9ld2r\n",
"bptbHXMkZr70sadhID7pg6k+gtzq74x2PX2oRx5kVR2ned1QLVtefXr8yZjh9rnZG8GcxA+9UWRd\n",
"tXI7bh+tcqnmrapAzvvvloxJRUjg0407wAAAAAAAAHBpfAAGAAAAAACASyMCCSDzez77tfpjGmeb\n",
"b8dXn5j3xvXGIk6ZbxeLVrp4muw3eLN7NPb2sjMcMYrKVdHXoiKhcx9Z9FBEKEJzE2OpdUeo+GS1\n",
"rrfPxnrXqzsW37f63DxCBU7CVeTKPkxstRVlKquPDkN/FFNWKNsuuLfGi5KVPgq93Yd6L6boPEz/\n",
"ituXal2rim05vo5q1R27KKEasxUBK5ep652mJldntpaYZutabCrYPVwwAibfF3ME2b6C7VzHvdcM\n",
"0YU/94dheU+7Cm11lAAAIABJREFUKz+mXYhldlsZSxRxxGVl/f5FxwzHEat1Ki69va2sKCl+mLbW\n",
"D0P4OM273R63OadAu6VitYhApn19Mr3+a/bX/B+/88P79Q/gMO4AAwAAAAAAwKXxARgAAAAAAAAu\n",
"jQgkgKXy4zCs8b70dv8yKpbdM24jjdtUdcd823Y0MG1RVpnMx+qbm+6knq/uI3ZN7a1XtTfSmEU/\n",
"RATxjOih6qF3/0YjIuWxGJ197/GZ6t1D0eP+LfXOQ8VO3s1rEcvsMdmI1blIaLyPuQKg6V/F8EzV\n",
"xmHwMWIVD3PniYwBiva2D7OPWn1Elh2K5gmR6Hm0j5SKcz5Kf0RxO87ZHQfcOfbrYO19FI+8HpiT\n",
"2M5Ff2/i3IzGPasKjh1zqtdFx9y+NshjQUQE1Xwi70drjr1xR9mHq/64NKojkGkVyLmPJTI5DMOv\n",
"JQ4JfGpwBxgAAAAAAAAujQ/AAAAAAAAAcGlEIIFPsW/4J37tNAx5fNBFIJef1ffNSOM2F1/M+3Ax\n",
"x+PxvpcDN8D3jrXGKFWEqDeQsl2xrRWddHHSNU6QtD8xJNCKrp0xlDo+z9Qd9eysYNqiIh/V2jMi\n",
"wAf0xsPUPtKvs75WLWuCkc21nY8b743ORePBKvK3l4pxRbc5IxoYqe4YXdaq1iir8T0hhjgMgbi2\n",
"20ZVRhVVK1VnNkIo5hY5BvNIXL1P5/Y3dV6ZcaJc5PVIDDZarVH1716Xv+5ut89fy/a2bh6tcyjS\n",
"R14ZtW7vYrPhKKZb11lBUrWXcxPzVv+bO8ch0+N5/v7X/dDvIAoJXBx3gAEAAAAAAODS+AAMAAAA\n",
"AAAAl0YEEvgU+11LBPJWrcvjgHnUSEYggxULo/eWR2KR0ahgNmakamUwNmjbnBC5G0WIIY9MxueT\n",
"9Tvu70NWbnOv9YSKk1FPjfXNX59YCbEVGT2z3zIypNqk8REXNXXvyyRyOrZ9sN+znRlRnLUq3j2z\n",
"suAj9FZ8VMvOjsSpeN+gopXzV3X9UvFFMZ9HRwPLcbJ1rWPmwcdWd1Tx/jV7LUsn6fMYtue9p4Kk\n",
"m0Cs6mEy/rKsfkeqKrKDP8aysV3lVzOn6P/eqdjg2lcsprlWkuw/nqJRybL9ZNqlr31tX/9rVUUg\n",
"P7l//Q0//Ns/zAsvgCbuAAMAAAAAAMCl8QEYAAAAAAAALo0IJPAp8zvvscdhGIaPZFzpdZmriKhi\n",
"XyoWGY2HufvM08jfHK3UcaR6abya4qtoNcq1/+T7nTfLnxOVVMvm6IVvZ/uVVfPmdZ2difFVjDIa\n",
"83tUNuEtYpTaFGnUPV9V9TASPVRj9h65+97bfD/I6FP2Q30czdEWF9NUMaRxY33Zx6jauD7UumpG\n",
"vl9XDfMWfC3p+X0rlqkoWnrOR/p4ahXITtEYpbt+ynlnDQJh3mwi21E0P9/+q3woRnmC5msx59WR\n",
"eKb/X5tgrM9ul0cbX9fWyyLZ6dbrLM8/Fe/Lz818XTqGqpYdjT6W8drWcdIdgxX7YX44x9hYVsY4\n",
"1fufviZVzbSMRf5/t7XNb/obxCGBK+EOMAAAAAAAAFwaH4ABAAAAAADg0j5+6wkAeI7f/hP+1WkY\n",
"huGj5Ebu+VZvFf27JYvWOOT2Te1yTaNSU7mtjkglt+qXqZHRRz/Wykuxm/HLiNIWFQEr5xaNCNr4\n",
"g4hZyT7ksu2qU+l36rXI6FXZvyrfly4x77N8v+9j1fVIN2ewNbRt/jq3ULM3VuR9N7go07rQvfPr\n",
"QhtXClYOjVaGVJYYS3bcb++H6DWnaifmqKJrdtYmrjMMwzC6OE9kjlvr5Dl5n6/aR66KmopBudeu\n",
"KqtF+9i5LJv/cpz6GGy5bStG6ao6ZlMrvmbruuN6seNa/q7Z6usA/TvEj1BFi8UW3a8lPZ5M9DYV\n",
"qZaq59GKNG7MMZ2nmlt2yLav49EooY71mXXq3LfXHtU+bdc+zqK/P6fNH/R7dRPLJnGsdMcuzbqP\n",
"X97PvwYAnIs7wAAAAAAAAHBpfAAGAAAAAACAS6MKJHBxX3+PPn5sKje+ZJGj7XYqOuaqGI4b37e2\n",
"2+rDtmtUpoyNFXst0fHXda9f08vtWKcldmtGfHr7K0JuaU8vorrkkLXuGCebt+plurfr7Lhj3Gd5\n",
"VgmpI+O0Ik+RcaN7VkYrTYQp2l7GLouIW7aVqkSo+ijGzK5t93at+Ge1bbCSZD63OvrrKryVc8z6\n",
"E/to+THd1r0Ws0zNuxUxi0S9daz7MdzcWmO7GKVqsze+1TpX5bV1OVbqdeF+G+vreczHfxqn3j5m\n",
"3Jit/aZjjpH2YswD1UfL+bb+l0tWODxlHp3xRROFdsfHnnhwuU0zEiqjnfm26vW6yo+qXbruk/uy\n",
"3/jDVIMEroA7wAAAAAAAAHBpfAAGAAAAAACASyMCCVzcXP1xjh28iBu4RxHFUXFAta3qQ64vvu7p\n",
"Y6vPFlXl0vd7ID6o4j/3ZWq+KuqgIpNu358xt0P9Lt/5KmAvZr9GYzeh+bxBxPEMzdcejBvvHffI\n",
"XovGYVx7t120/94IXa8zj9PeMZ89bq8q7pWs27tMXh/FsveoNyq2rhRxRBNXdWNviZzzKhacvVfz\n",
"75NgxVo5hlm3VgAU0WIRo1TbRiON5bp86+3oXNa6TJU22CqXY93O9hW8Msgxy7GHet0RqlJsfB9t\n",
"v668QmWxLj1SAnHOtL9J/NtljkV+kiz81/8GcUjgQ8UdYAAAAAAAALg07gADLujr//Fft5zY891P\n",
"L+YupNYdUvMdUctdXI2/e0XuwBk3vt/TV9pH9G4J+bB/+7pid7hFvZi7sdydA6P4y/CL+GvuIP7S\n",
"2+vsO8bcX+XVnYeRkZ76J1hxp+R7Ju/Mq28wsOQD06v+G310tj9b5G6X+EO1nydyvqj1Z9w19cw7\n",
"r47cAdY9lrkDJruzyhQUWC+uapW/e6u8o+WUfdq6Y8xtGnyIuu0jfHbU7dydS7ZXcUNcfjdW3+ty\n",
"d3QtN7jVl9HmXUXLXWyuaITYNi8WUdxp1/hXjn4t4/a6xmuI9L+Ok/60PTd155U7s9X/qup5izHF\n",
"HWBq2/Ih+eoOsFuycH4w/r/xI//Nh/DPAQAJ7gADAAAAAADApfEBGAAAAAAAAC6NCCRwIb/ts16j\n",
"jx+/1FEt9SD23jjkkQfjR+Ir7U/k76+h84bzaPOl3clRt70P1c/eqyIeWa7v6rcVYd3Zbz6GeMDw\n",
"if0v4+zat2UM6ZRH/Vbdf2i5iGy+Iv4a2rb5YOnt9mqkWxkTEu2zEUVks+w3izKJQVuRw7KNCcmF\n",
"1/XGLlW8KXrOqfZl1LUZgXSRrvuym4p3B5ep91HFEde51bG6I/v+0eIPYj9xzOR7dzzrVtt7KfoA\n",
"drlt736IRFPVnFzOdqNZaJ2IzbaOcSfyL49W/+6c6L3OyGurXLt9bjaXmejh2kYszLbJ+yjjjFv9\n",
"qm1cPDKNQM5jpsuIQwIfBu4AAwAAAAAAwKXxARgAAAAAAAAujQgkcCFfd6/++CLiP0slx/SOfdFH\n",
"GZnM121fL1QlQtm/jVjWfbhP6Y9UJGyN78ZSsY3dcUQZ3Ym9LhkhWr5R798+MjLZiJHFOvbxJj2X\n",
"839nnRGBfGruwcb7dszEVIhVVGXIc2OtyViBdtHacy7W2TjEY32Yan/pejd+MKnlq0AGK805rUjh\n",
"B/EvR/GLyJ0fzRieid/tjbqFjzu5PnYGqIhiLALZaGBeau/xrweKxdjmVmkULbJn1Eit2O5evVdK\n",
"O+/s9/38aIQ6AnmEes3Vdcasa81D9j+fXq25mX0YjT7Oy1R01PXbikDe7sv+zR/5eqKQwDvGHWAA\n",
"AAAAAAC4ND4AAwAAAAAAwKURgQQ+cHPlx2FYY4iqkuPyabeMR3plBcl4RC/5PtB/s7/Gz7U69rln\n",
"nL5tp6oTF28K9TX0xyN1f2IeJ0QlR9GxmmVZMTQcXTuiM973TH5OsajwXr3H4p4tltadle5aUULX\n",
"r9qubJf3uX2NcH20RKrbtfZL77a984i2n/+ZmO6jyLJwrC57O/Lx83+imivpg/KZvVXzVDvVX6RS\n",
"ZWT9I8i3ZWcMMDpX9b8iR157Nd/gNUX2Jeajfh+raF65rYw4NypJbvW51W9Ef1XKAxHIxlhT8U0+\n",
"Zl/c0c2nte1UfB1EPFJFINNjd45A/t37tv/W3/y69/hPD+BTjzvAAAAAAAAAcGl8AAYAAAAAAIBL\n",
"IwIJfKD+q8/69dMwDMNLWl/IRCCX+GKjclskqqi389eSMmIUjV3aNofW1/utV3dUUI0vOumfTh2K\n",
"OBSVLKqd6ThjGv0QfewdO9qJisx8CGGDh1dODEbdmpXhJrPO9dcXqY0GK3uPsf2BzXP7+BDGfGsu\n",
"0hWPnR35t+x2v9FebcStczZZH0ssrI7J2eNfxsP6zqJoxLOMsKUro/+Lod7vdZ2ILCdL5jjbGSlY\n",
"vV1fXFBFR+WeF3FHfdzvo+LUdj5iTBltDEa4y77SH8JRVhEzVO+Hna+YiDu/l77Ea2lHIOd2r+s+\n",
"Sfr4zT9KHBJ4L7gDDAAAAAAAAJfGB2AAAAAAAAC4NCKQwAfkv/zMX7+csC8iBjFX2UujHJHooYtM\n",
"Ku0YZV980UbXxuye83b7jTHcslBfnZUqz4gytcbsj2DeYxAy/ibiDDvHGYY6RmnbnMQeF8cTUu8z\n",
"kvYGVS5V3NJV61q3U8dYNIpZR1bUPOZlt2Sti4eqWF2kDxXNiweLtuNpkxgzndvNzFfNw72+fKxp\n",
"s//ePvT+2F4Wj0BuL3sLLmLWJM7bh1Va7NxJrnnvvm+dEVV8UeyC9H9TorHS8pjV1yf/W7o83m4H\n",
"3u9HHbu6ams7vrsrAtlbPTMYd4z87nAVH/O+xJgqRqzambFu8rXUEcj52/k6mvb1d+/5yN/yY0Qh\n",
"gbfGHWAAAAAAAAC4ND4AAwAAAAAAwKV9/NYTAND2n/34f20ahmH4KLtxejsMoGIpSjQxVrbLbvtX\n",
"UY5AxC79ab6FXMYiVVUh8ZJkRaK6mYwiRO5HV1GH3jGV3kpeWXzEzeO+bRpvXeNNao7bM5kaUREZ\n",
"bYtEFkT1qxYV113HjPXVHR0Vac53k2EIxF0yJjLZG9+SsSFznrSiLsu2oz/elvaijT//XF/7+4j0\n",
"316/3a+O7vTNoxX/Kdfr/ZEsE4fA+v7NC9QJE4shuXX5747tCJiNqWXR+hOih50RLfl7rXNgF2M7\n",
"Eq+L9quqL7o+ImPm75X6t8X8Nba/b+UxmXyrr3ex30kqZuiCv5E+0/V5NHart3o+aR+tmGO1bXYO\n",
"1VtMxTfpIwfW929zivd2get577mk1jX6cPso0n+rD3UUvXwQZaqBTwfuAAMAAAAAAMCl8QEYAAAA\n",
"AAAALo0qkMAH4L/4zNcI5EsaRlnu7E9vsa63HZf29bkuAwAmIhW9gdv1sfYVu/ao1Gf3jeSNqpV2\n",
"zB3r94zZ7O7+NRYOa/QlKmtmsdni/TtjzNdtt2Ow0WjlGSLH5+lj7lzZiheVv8JlSjo6j8ZYvX1s\n",
"ByWTvkR0TTdUua/taFseIcrbucjwnj5s7LNznYrmdY/ViPep8burGL4TMjJWtHHrWu3S82v+/aqi\n",
"1vZamcVE++bmIo3u/GrGM4tzoPW+j8Vrb9Hvy/Fjy75mcQ53n3+BsdPxo7+hbLxPnK+9Y7Xah2LB\n",
"opfo7xp9fLrIZt3TkTiiqxIZ7bfcJ6q6o3pNt6zduLlufgRF2u9v/lEqQgJvgTvAAAAAAAAAcGl8\n",
"AAYAAAAAAIBLIwIJvGP/+b3641z5Li0is0QbxQ3eL6pdMAK5rDMRPnXru45MTukPzTE3t92gIp97\n",
"qH1j2xdfhyEW98rVW6zxhPnnrmllvR2Jrtn+1b4Si84peNS/V19bP/73Wm8M9nBfD6SiWjP3T4RW\n",
"PPlWbNtqX1YZ22pXzXFrDLE+0uaZMdFIv2fMN9o+EimMal0f1XWuXKYiWK59uqw1Jzu34uvWtlt9\n",
"pVuk16PIvkyjWPPvfhlnW4bxEbq92pHFvutzLL5Y/5tBtZOVh02F0SNRU8VVH3UjRKON3RHIdLct\n",
"cdXg+6IivSbyOonjulyXL0vH2hdVbLVTVTm32gzDYCOy5e+tfOwx+X7ut16v9qmKQM5j/ZYfIwoJ\n",
"PBN3gAEAAAAAAODS+AAMAAAAAAAAl0YEEnhn/tMf/xuWk/LjpRpZXwQyVcYEXzqjkK/jqmBHXx9l\n",
"u2jscFe1SNcu0LA3Ein7CC7r7jeLXMzLTug3+X5f8FD35/akOhZTbu1z8wLbM3n0PIq6VJuDunmk\n",
"FbJkbCrQh5jFrm2PUjFK9c8YF3kK92EiodFYYtrHrThfVVxUxvsa8y0jrDoOVS9zJ1grghVZ1oxA\n",
"mmVuTtH20XlHq21W8xATaZ0bZ/6LOxpFm9frsWORtGgEeV24HUlTj0Y4Un00GhXu7WQ9Z9yR5OdR\n",
"LruJHvrjjnWUT1aXzLa5NxfXg3j0sP0eqfOqFfHc20dzW7PsVsaIhzr62Kr4qMffF4G8JWP92z/2\n",
"XxOHBB6MO8AAAAAAAABwaXwABgAAAAAAgEsjAgm8E//Jj3uNPn6UxDDm+KKr9KjWqciMih7ujem1\n",
"+ujpK2sX7Hdts//6lfa/O0J4IEbm9v0ZEcQjc+seSix7dExOVUc7w/vJHszx5/16K5upbdVx5OJK\n",
"+bUnfw2tKKaar6q2VrUXkaDeY7K3D7kufX1qv7ltxbqlP7WPzFgyUiXau9ccjjuaflWkMF12C0QP\n",
"9xz/676crxHpHOdxdnTcMXYqj8TFYos9Y7W2mqpvxEbZdMwRmkUEj18tbTx5o83hMeXJdnzf90b9\n",
"lthsehrOq4LVEnWkt55c5HjXsdkxWT9/I+Zmqiq2hp7Xh6tWhlqtbqZfFWl0lSx1dFS0dxHIdNmt\n",
"HnOe07/zt4hCAo/CHWAAAAAAAAC4NO4AA96J+eH3L+nflcq7t8TfnPIH42+fz7K9udPB9ZEt67zT\n",
"KDyWeUC67//4XWFnPFQ+73jf3TzuYbpb7SLzUH/BPePB/2d46z95th7M//713UX5uoU4HgLnUfQh\n",
"2b1ad1WU7VozdTe7hPswdzhE1r02yO8AkHdIbcwzMl81j967AKN9HLm78NHKu6z0nVXhe9zEsuNU\n",
"AZPIHYKvPxQtOu/SPMtbvvf6QfBpi/brb92tdyuWhV+vmJu9e0rMKb8TdHsive+BugNxeXB70k7f\n",
"WVa382OZZcl+iPTXvLuu2K+qffQB9qoP9b/K8k6x4lDM+hAPwZ99MtXt5mX/LneCAafjDjAAAAAA\n",
"AABcGh+AAQAAAAAA4NKIQAJvaH7w/TCsUYgsAlmsa0Ug13UilljEKfP2Ypl76HRr2+WbvjhWbxTz\n",
"rNheJDrayiPuvkf9hIfVu8jMi1h2ZCwX1HkvMcrUo6J5teS1BwftnVvkYdbPyUpEH7+dt1cPA1ei\n",
"Dwj37bavPephz/Vsy7Hi/adre9cp+uHU9dx8e7+sfI/29FEuUzGreKSw3ks+0ui27KfOteoB+o0B\n",
"1CuuH/Iv9kcWm52/PObMjkSMW+3CYwWi9zbq2eq/dz7pPAL9yf5lFFNE48Q4KgZ7E8vc/6b5c021\n",
"F/NYxont72hUd2/c0Y255VbGM5txx/nrdoxxEO9B3m0dCa0jkKb/jX6Xh+XfF36S7L9/72//NuKQ\n",
"wAm4AwwAAAAAAACXxgdgAAAAAAAAuDQikMAb+I8/417xMb17XkQgX4qbnV208XX9tnnbUdz7rmOU\n",
"6RiBiGDD3thifxzQR9FiUcz+62LV786xcz60eEbk0AWTXPWrM+7Dj87/UeMf8ejxVYx4b2W36Dmh\n",
"olrLtsHrzCQOpEjQTc2n1f6tj4FaNFT1/mZeesZ+lpUQi2Xp8bQsyzpRsUGxrBpcRdeS1Se8anf9\n",
"dNS+j54nj/oXvataaaOK6n1x43TP7Jxtlz6CkcboPJb3T0zOxRF1v53zUNUoD8QcI/vXxX23+o30\n",
"P4kf3P5oV3ycJfHMYnLhyo/p98XcdCS0nmfeLo9A3oa0/eu6f58oJHAId4ABAAAAAADg0vgADAAA\n",
"AAAAAJdGBBJ4kv/oM37jcrJ9JOKIKgI5K6OQw+DjkJEoZL6s7iPvN48CtKJrsZhh+sNUL+vt40C7\n",
"/ljmvuumihNEI6nxQbZjG2dWaTxr3+8e/x1WnDzTGfvt0YE7dQ67iI1qryqEuWvDLWmvYqIqHlPG\n",
"OPNKbHVcTo5VzKMVSXP9htYl6+V1ozGWJdpPxbV9Eq8970NNpOi3ESdzMSsXzX7Gmd977rjj4WHz\n",
"7X3f0017+zDn9d5YW0t0W9tuZ2w868JEdbvn0xqrt4KjnFsdvyuPxdZ5Zd9T1b+5/h+JAA9iLN1u\n",
"eywZd1Tt7Htavy4Vs1z3r9gPon1vBHLev+nY/8H/SRwS6MUdYAAAAAAAALg0PgADAAAAAADApRGB\n",
"BB7sP/zHXqOPaYxxjjmqCOQobthW0UYXw2tFGl0fY/VNfRv8nvhi7z3aLydWOOxtP5poUFsdHtgb\n",
"mczmJnIK87fpsdUfe8vjYa+L8q2PxA17YzHjxvfvwYcQu+yt2rW1bakV+Yts817ezyP76FFstFJd\n",
"j5L1bj+fUc3tUe/bGRHIt45KnmmNjyUzXxYdeBdMLP7MiOLDIpBZJydEGqMr70NN6ldkeKzyPfXv\n",
"gYpCz+f/TfxbxEXOj5wT6t89ZfSxdY1wcUS5L13cUfy7x2lVzHRVInurS07i1ZQxxqy9eC03E5nM\n",
"IpDLurX9J/eFv5UoJBDGHWAAAAAAAAC4ND4AAwAAAAAAwKURgQQe5Lf+o79pGoZh+Phljgiu59r8\n",
"yXM0Alm2yddtt0+pSpLrdv46UEYxW+b4Ym+MRrXx2yWvvfPm7yP3ipdVMbNldswkTjCM1bLIuvgc\n",
"l87SCaRfTlRHerdbPTcKNxZfH6eOLbkKWofGMPHkqzsjvtjqIxLn2TMPG3P8/9m7t6Brtv2u6z2f\n",
"va5419qbBPAAnqosFCmwoCxKjSkqiDFUTAg5QHYOUDEkIccdldLSsrQsodTyQsj5HDCQkBBDEhMD\n",
"qQBJxZCAJ9CiQKW8UQsQJCFZ682Fe79zevHM7jl69K//4/8fPXoexvP9XKx3Pt2jxxjds7ufueYz\n",
"fj2c/fFEGltEIJW96t1b+jF3ywy7l3q8UTRxlIw4otl2qHT9eb2FPAZyptNSr4w2xDJd73xlzf/q\n",
"RH9Hy5n/Fn1cjzamy2blsrp0X2NUP05ihtYtbeXRxnSZde2k9UdnZlR1WAtV9FCxo4/r54CKO8pl\n",
"6Sf6rK30x6O4xsa+vUnW/YH/86tf2kcDIIQRYAAAAAAAAOgaX4ABAAAAAACga0QggZ38wWz2x1IE\n",
"chDLnrIx2zoCKeowBqnrKOQyJ2fOMlkRwbrEKH33nNrx27PtnDNUWnVEY3sqTlAbCdV988Uo9bbj\n",
"drbxHJGzcLWMUapzQXZu2Vp0RsZbxC5vT01f5u3deqzVintZEbNTxXl0i9hs1CP0MWXFF43ktLsO\n",
"uUBUPJ4rKqI4zbyXNKAiVSpSqO7Bcevvquf4qfJb7PVJXf0vgL7mp7WqFmPdeuniSiO+2OI4l2YK\n",
"dNUhz/H13tW06dkv2Q3jd2nh0vS1qa7b2fr1tmb1ZC9U21a8VC0MxzSHYZiOjfGxxNsPs45ZBHJ5\n",
"jPI61CyQ6Tl2FOXGqOQfJAoJSIwAAwAAAAAAQNf4AgwAAAAAAABdIwIJNPQHzrHHYVjGHPM44zDo\n",
"OKKMRU7/LmdUKs1qlcfj0uL2tvWxSNXWpdxyjHrtzFw1m6noXG1EckukUdWRRyVbjF23ZrBaW2/X\n",
"t04dj+h76z6mwQikWVWzmtq3pcofxTI7Eu1jzbDm3bZ5NNaIsdlRt+ReOUWpYvEtc5a/Qh+tvul1\n",
"xtF3Hg9v3x5JKarljXVb9T6JZbUxx9I76urUhnumFb9rfacz//fBmVFsEw8V11hl5NCOZy6jt1ti\n",
"ttGY3iXaaPfDc0242zaixbPr0JhJMj1PpscrzGKAed8KMcNwzHH9PYrGF0v15tvq2SODdczWLcur\n",
"CORY7k2y7D8hDglMGAEGAAAAAACArvEFGAAAAAAAALpGBBJo4D/+J77iNAzzyEzbCOTp/K9Nz/A4\n",
"r0Ovs9vP66iJ/ll9k3UFZ3DcMrZ7sW2DmKSrnUD5KQZRmDmxNk6q27/+7wd/RPfRnI9lml65QS+8\n",
"EVbPdukyTyzTGw/zzvBmRX2idahyVn9L9UeDaLWRu3R9bflSHd5lx2xZTXwxGmn0lN8USxTbyuNr\n",
"Rl1XOjMMOrJ4hQir63wuHKw28cV5D0qRfXe92Zs1O09Ph8Wy2iihbDut1qhDXldj+yJ+7Z3dNBrH\n",
"tfph7Ut5Fkizm6Jv63HAbdftemzQ3s6uY1on6rKij57Y47x8Wm75vqhjNJ7j85khn//9T/8vopAA\n",
"I8AAAAAAAADQNb4AAwAAAAAAQNeIQAKV/qN//Cumi2eM9z0dloO5D2IIvhrm74lDluqw6lJUHQcx\n",
"Zt8TRfPG5byzRZr1imPq1TTKKN7vJvU2qEO9G/ksk+kPW+KGOraS98guv7cuopXBWPAlKpNezLN/\n",
"ynXMN7u62hiSt46Wccu9IpDetraU90Qgo7ZEIFvIo2PPy5YteaNllw3GzNH23rqPrRU3K53YRozM\n",
"e/6rLS7nyvoWNfHFaVtxMo4vjyKqqGKDizLDtkhjLXXeqccaeM7BUn/Ma9iKWCY1j++bjDkGY4lq\n",
"1mlrpsct/1vqnvFRxQaD56on+jj/cT2+qLaRsdnT8n0ZX6rHEKTXST5b5H9GFBIvGCPAAAAAAAAA\n",
"0DW+AAMAAAAAAEDXiEACQf/hOfr4vmTZFHMUs0DmZZ7XieihKKe2zam6ZuuzuISqqhRJOyxeiHUF\n",
"0dibN8Y51S/iYbXxrS3jwlUco0W9ZltN6loPIqVrntQslKJcfJ6qmC0xyupWjQ1bvBfmbHGN2vCK\n",
"xsLU7KSLbUVkeB5LWcZz8tZndRqRUBXdUXVY/ZYzro5lktct4qRjf9O+Wv1Q+2CXT/o7RZl8daiZ\n",
"6dR7NSxz8Qu+AAAgAElEQVQit6W7sXeZx/IdidZUjLBm75GKVKldmb2n2QtnevEmtsQXL3Woherm\n",
"tryW5WyNRoQu2qfocfbHVZf3KO99tDaeOdsXI+bovgrF+Zlf3eXI9zLyZ11X8X1fj1GmlVn1WhFF\n",
"7/8eWzNKqlilvG+IRZd+LOuwZpl8Xi+2ybZ9k2zwn//fxCHxsjACDAAAAAAAAF1jBBjg8B/8Yx+a\n",
"LpT3jX+pTEd0ib9e5n9OUaO41Ogta+RT6eHd1siycc2WB+R7++QZZVb6q6A16syxan2b4IPEW7W7\n",
"rGP5d9fLe3Sa/dyuzetRI8U8Z9R+fdx/RJ7FbCt7uHBVvc7rULYRHG3mrGJRvos/MTd8AHr7K3x7\n",
"67cYu+WlR8nN256tDw71UXWo60WOXjTVj+mKj3SKvQvmqMTZD+ujtvQGhZEvG1nn7pb6rBFoNaP1\n",
"8nq9fZQjNmW55Sg5uS9ZveoaKl5XQ77MblWNpFKTLC1HlCUjUx0PzU9/sN4D1TeL5yH3y7aWo96s\n",
"+uz+jtvZx3Tqm2zzsFh/FMdqXMZIMLwUjAADAAAAAABA1/gCDAAAAAAAAF0jAgk4jA++H4bLt8Yq\n",
"Smg9BD8dwX1YLpqGes+WVcYh0yhkPjB9ttlBLFNtZcPQvfHI8IPstzzYXOyLNwxyyGJNswdAO+tY\n",
"1FnRD7M+Eb3KI5Ot5P2MRt42td14X8y2rtbStnN7e9sX0V6oiKX1sUHdX6wYmXoTZpGZ7MU8onRe\n",
"Ju6tsj4r5yXqUJMSeNattZlvKx+Ovqx25UHivr7JKF+LzJihSYzSc+4MbXchjVmp63UZZyuVd55w\n",
"Zp/Kpb2xZvW7QxXfK6qotDwVzToKkWVPWrbFJSTrEAtnE1QYbcl+GzsT7+/6FVuqy/u/l9GYr/XQ\n",
"/EucsvB+O/pWuu9abVlRRVlOrRPnrNp3VYd8cP74r6rjNK67bPeR87I/9De/ilgkusMIMAAAAAAA\n",
"AHSNL8AAAAAAAADQNSKQgGGc/VFFG/eKQCoq3pevK1EzRIquueptHVU0yzfO6UTbv/QjrWOMhOr1\n",
"tfW2iEou6k0jhadldKF1fNJyb+PoW8wIur/lHFbzd6zce+81pOIu93ZsvFGtFrHPaCyx1Ga03mjM\n",
"audk41WpuL21TLFmkPPWYfcxrc9en5dTMdhpOxnX80Ys23EnK1u0ZUWGZwXX97lFHDFaX/R6nUUb\n",
"x88RKuqm6hUV55HhtXKX8tadZr3+WT8c7eg2C+VENM83a6SvjWIc0RET1bHL9ahiqQ5P9FFFFb11\n",
"qHIqAjlk655fP9fxkWTZHyYOiU4wAgwAAAAAAABd4wswAAAAAAAAdI0IJJD598+xx2G4fEOsoo1q\n",
"5jE1g536ltkbL8yLlWY789SfsmKR8z7F6r1sF7u/ePfP22Y0Uqj201tHPlI/jRaacRdRh6edSN9q\n",
"TTOTFmar09teR+t2fHOF2QXVqqMR3ZFzs6mItdEz5Vrnx3NbdVG0tfrW6o22WapDlbn0d75VaVt/\n",
"vctcz8EoX2rLbn9ev7cOu99rNd8Hq2cnNdOvN+s3bbCMF1mz9FrR2C1RTO87sPenfFm/FeM0Yp9b\n",
"ostWn7z1Wr+P1brjqXSdlKXnnyce7f3MYPVDx+aSeg/LZRbrnlKMiYajh8t6XX0sRSCNcsfK91RH\n",
"JlX59RiljCp66xCvvRHIsb60rTfn9UQh8egYAQYAAAAAAICu8QUYAAAAAAAAukYEEjj79/7R5+jj\n",
"+5KBvU9ilrhD9u8wJDMLigikGifsjRROETS1bmzTrqIQt3yW9toTi0xnwPRHBOvuNQfxw5ax1y36\n",
"oWZemtIdzmicjDpkMRp1Pm1hzXTVPEp4UOPsrYOzfq5f063b95B9FMdPxS6tuKUVGYuX130SrYu+\n",
"rZf3xr2uea5bohHnUnkrVufdL08dOg6VxL3EDHb5snnMMLZM9lLEDAdxn5niWMYse62idrWsNr3X\n",
"S7Qtz/X1/MN4gZcyY/Maa/rouV5rLM7n2UqxfyLWGmln1pZYOD0GYWXby7JynFkdrVLMMO9b3Xu1\n",
"HpPW5edtDoMdrdQxyvm6WfkNJ4gVd8zLbGlfRRDndawfw6M8Rr66VLl8n611aX1pBHLs0xiF/Oq/\n",
"RRQSj4kRYAAAAAAAAOgaX4ABAAAAAACga0Qg8eL9u1n0Uc/aeLlO1PopEpiUy8cFl75t9swM6Y07\n",
"WuXKscuRL86pPDUYFG1FFbfsn22fGN5BZBJq+yljkSKGtLfmx2h6VRuOK1Ycste4/mi90aPRiowO\n",
"bSxfFYU0Y2wqJjTGaNbrUOtUdFRdSyq2d+lGIa630p/nLZexokNWfr4PaUzoUC4frKMUqboXqm9W\n",
"/C0aEy21tQdvDFaVmdYVZqMcxPlWq+U9wt2WjBmu3yPUfs6uebFMthXp42DvszVzolm/+ByRxuU8\n",
"13Bplle1zLqu1EzXKmqnr9f5PhdjotH3w4h9zpeVY7DumSTNOuz3OI8+1sQoVT9UpDIvr2aBnNWR\n",
"lXuTrPwa4pB4IIwAAwAAAAAAQNf4AgwAAAAAAABdIwKJF+nf+Uc+NJ34U/RxQwRySkCqtIsxM6Qc\n",
"L3yQL88/W/MApW2a1brKy3KVsUTVRs1Y6egMjtbxbTFWW81WFK33sPpD7TGa90etm8WhVCUiztBC\n",
"T+PjzX0xYqi3OAbe6GFpG2tbT/kW+14TZ3vJ1LH3LCvFllpEZKP1XjOe6WlfXldqVsxZgfwmv4ym\n",
"zlY7Z7Kc6hDLPLzXlRnt2lKHihFPiwrH6PzvUSy7bLdcOY89L5e1OKeWn9jsoySvzWzhLAIpao31\n",
"R63zxRxnMwaKWr1xy7X68zYW/RRR0KlNa7uV9q02VR2WSz98v6WsGR+Ly0QbR1ku65uoV80Cqeo9\n",
"ZnUNwzB85Lzya/82UUjcP0aAAQAAAAAAoGt8AQYAAAAAAICuEYHEi/Jv/6qvPA3DMLzvaTkQ/EkM\n",
"i39yxhcPixc6brZWV/46X2jGF72xyKk/RqG1bR3bqBmmPP1Jf4h3zbfvXqqOFjHAy7B/uy2rP+os\n",
"ejqsr4u0s7qtMZNd2qa6TvbW0xj7y/1j/X5TMsUVttRRsc21eKM+0Qhdvm7Lti2ugpoI1l4xwHsg\n",
"I4VG9KlkOlaFqKI3cjiVd7bvseU63Osc0LHFw2zd/He6ynTNy1e1LRqbIpAiGqhig/52D+cq1mN7\n",
"xTqyWF9ptsZa0b7Ja0hEGudtnMuLMrUzWubtesp47sEt4o6zckbbqpyc/ffMmo1xGHR8carWqteu\n",
"1p5dUkQaoxFINTPk1xGHxJ1iBBgAAAAAAAC6xhdgAAAAAAAA6BoRSHTv959jj8MwDG+dh+UfxPB5\n",
"FYHUkbjnOqzZIPM21upQ21oxPDVsXdYfjAY+OQcpR+OALWaNVJGgTbG+ysDBQXRkNlvRVH+9vG8t\n",
"ImneGOVau562W8xGdosYpde9jeFXcWNv3MSKW5qxr4N9T7lsu8z4XCJKy9nAVJSpFFFctFnq28Z1\n",
"an3p2oy2qWZAs9raEgO0KxZRWrFsPPYHY5mOL8aXLbpYWLa2XancFtEIZnQ7q82a+5Or3VnsbPtd\n",
"UMco5+vUoxHU/6Z431MVzcvXrfdS3Wnna0r/C2XFBlU/1OMShmwfSu9FPmuk6ki538se154D3ril\n",
"vsfnvVhp49LCavkt/7trRSCtWKKK71rxUrVe1W+VHwY7ZmkdGxWBVNFKKwJ5FO8tUUjcG0aAAQAA\n",
"AAAAoGt8AQYAAAAAAICuEYFEt/6tX7mc8fF9YhBubQQyJeOQoj5PXaX285XleFoshpjPnuRpYxji\n",
"8ch5myd3O6U2t42ztt8PDxnTad7PvK597+Pu91ZkRPYe976pfmfssu17tRR996L9aRGlLfXDE0Er\n",
"7afn2JTaVJHNPEJSrmM9amRG9FQccFbgtLrO2w9PTLQUEayNEkZt6UfLtq4RgbR4o7R2JZctfRF1\n",
"b+RvWYc5m5wVXRMHusXxLseNK6N5xXqzn5fp7vD+6bhjrP/zmNq5roNYlpQb31P7Olw/x4p9MvpR\n",
"uuZds0CKvlkzTtbN+mn/vChvRB9HKopYikBa9Xu39UQgi7N+illbx9fWfqXr1MyQ4+tv/jvEInE7\n",
"jAADAAAAAABA1/gCDAAAAAAAAF1769YdAPaiIo0jbwwpmvxSs3pNdanZvdTsV0Y7sypUxEDssx17\n",
"UDGJ/EXesO6TnKnJeQDHPqomrXife5i7O4LoG3J+KW0cv3SZM680vhzPXe856X2P85mS8lrW1tbE\n",
"CcY02Gl+Mm6XneObqnREGEptmPGjnQb4b9nnvSNg3vrj0aHgOmd8RK8ztrXqNWJq6fpoP6LH1B2x\n",
"cfajRWSyRZ9q628WCc3ev0Nhpkz5fmc3xtI93npPx3KzyOIpXzuYs4SqOqL3e/mZwSxf//uq+nwr\n",
"bGjGPo36t0Qarc89aYwsnzlR/kqdfY4Y61URwfU+eqOViu7HcjvrOpXxSONYysim+xwsL1PXfqkO\n",
"+bncs126PitQ6qs6zp62SrFLz6H0Xo9qtvEv+BXPj6n51r9LFBLXxwgwAAAAAAAAdI0vwAAAAAAA\n",
"ANA1ZoFEV37/r/rK6YQev91NYwpqZsZD/m+y0vqGeMsMjmo4sFWvVWdp7LAVQ7S29c4sqGaAqh3P\n",
"XIpMLmf3skN97naNSuL1LgOxLWdpLMV383NrS7TX7sdtfndY75VZ/o7J0IER4T6qGQinF75rYst5\n",
"sTzDcU+88b5rtFVL3ufG2TPFbJvzfpSjaKX7aO0MfcrJefB17FL1Lau/tmPrrYol60fsUkM8Um7e\n",
"o6wbTTDuVdLmk8S5LhFfHCONW54IoKNw52tCxh2D9Rc6ZMbpjP0r3SMu+7DejjqmVuRv9plItmm1\n",
"YcXcC3UUfl4TnfFRxVVlvVYd6viJCKRqy4pmp/FdNRPom2zZR5L8MXFIXAsjwAAAAAAAANA1RoCh\n",
"C//mr3we+fU+MQop/WuxGnlljQCbtiu0b43asra1RoJ564+OCvM+mH5eX/lvwaW29hoVtijvHJMQ\n",
"7c9B/Gmz5lgurf89fK9RVrLfoqk2+2f040ajyCzmLleOpkyZEyJU1BcVHaVzeY/sh+NaI9DGEWuz\n",
"fTqcFss85WZ/KRd1qL/UX0YMqAMt6hAPNM/bn41CWtZqH2c1gm+cBKW0f6L9Y7ZsNrmKGMmkfjea\n",
"dWxYttjPdF8cy9SojdIoGs/IRzlSJalsmojEObriIDrsucact2KTHvHTduyvZ9RnqcWjKBCtz3IS\n",
"76o9Os0ei5a3P78OrX4stzlmP8/7VDpysdGI6h7oKa/2L/0MoN4/s47p3+W9xz8yylkuWu/0Yv19\n",
"r/nfY2syBeu+aNVVGhEn21L1We+fdRxEu1tGgJ2ycukxe3P+gZFg2BsjwAAAAAAAANA1vgADAAAA\n",
"AABA14hA4qH9G+fo4/hNbhopVDEP6yH4eZlZHUb5+bZ1Uchh8MUhrfpn5ZzLdBvOgmdP0YfliwVq\n",
"WPymiGJ028qIp9kPEYVJ3+P6gIpvyxbxwmg8xxvpvW/L2FmtFvEm2Q8jMln8lS7ugSPrYd0tQlbe\n",
"61uVi0ZnomZRLbHMijJds28t2ohGD1tcCypS5Vl2EvdRWX4Q5VQ/xLq93je7H2Pcd9l6iwfvW/3x\n",
"FpTngDhwe/9fRJOJCJLXl2j2ctkgzi2xaiXSaFleWXs9rN7c1qjPG08+inPXehi/Ovazfhg3n2ik\n",
"Ud1TpjKFB81Hj6s8lp7tCg+at3hiqN5tS5FMFee0IpAqOqr6m0cg0yLjsjfJwm8jDokdMAIMAAAA\n",
"AAAAXeMLMAAAAAAAAHSNCCQezleeY4/DsIw+qljKQczkZc1O6J25sBSLjMYh1dBwM1I21i9m4bLU\n",
"fOtdOxNjkxiZ8/1Q5a3h8GYdyevL6PzlsfVGbKLtqshkXn9tG8s218+ZLfvS0uNGK5f3nnsUjfCF\n",
"45AizibrckyKNoshieiO66IsZDdVJCjfB2vdbL33fiQuNlm+MqazpQ6zXmPZrT5dRqOH1gyBVh0p\n",
"NdtmfR/Teo311nnsjJHt/V61ji+OovcBdW2mES/PJXlMSi1DbPF9tSLAUVZ8/bnA7B+1KruW18PQ\n",
"0VhiKQNp3TfcbS3ifIV+B+O73rjj5X1YPxe8dVlxx9K2Vh3eGR8v5Z3lRPloBHLc9o1okygkWmIE\n",
"GAAAAAAAALrGF2AAAAAAAADoGhFIPIwP/cPnGR9FJG5cJqOFIgI5iDrWfn6uQ7Rpd1e2nyvV4YnE\n",
"eduy6i8ts9usbas+HjYeh1msYcPg6C3brtZZGPffOh46OTnKbFIKpKyrnZkyvAsbIq/3Ihqpyrdb\n",
"Y8W37PKPEefE7VhRJh21Wy/pP/+vH9RW0a5p1krnxu5oajDSaDRpHqHSca69H4XjnIU4oBUtttov\n",
"R1mXlVzismslym3Vziwo6zA64o/yLSvxx4Ln/fFGN0v3AU8EUr5/hVkM8zq874U/7rg95mjFmb11\n",
"qHVqXz39VXWYccdSeRVzNMrn8cj0dRqLHF9/x98jFok6jAADAAAAAABA1/gCDAAAAAAAAF0jAom7\n",
"9uX/0GXGx/eNs4AZEch0LOz4WsUCzVkgRT9K0UPPN8myH8nrKeZo1SHrdTS+0r63jZoyz206C4p6\n",
"L0PfY9ErNSw/ff+aBGbEWP3aqOF8s3nv0nfsqUF80Kphdu3kM2gF2rBt/31zi/Husk2jI2qVmg1J\n",
"xXkc1UvXD4LVWF7LpUimFcWxYllWHfN1eY989frbXN/n0n6qtnT76+++t47lslJ47XaKkao8olVx\n",
"A5O/O4xIkFVt60/Z+Xt0kOuidV7YUcl18ndNMK6X1nEsrL/Ut36kW8xCOdXlznMuF009LOeCF/Xn\n",
"M8+q2SvV/cC6vkufC6KxUmvZlgjk4IwZWte86oclGndU1Lkryzmjo9V1GP1WfZTRSaNPpQikdc/0\n",
"zBCZvk6L57FIopCIYgQYAAAAAAAAusYXYAAAAAAAAOgaEUjcpS87Rx/Tb2ifzj+omKMVgUyNMUAr\n",
"7jUrL+tYX5f214okWXHETbHIyihVdPbIVPW36EYMtbzp8ujWzjA4q7dltFFFGHYapK1jlMu1LY6R\n",
"bL/hft3nOPblfeMWrMikOWOaWDiLGp2Wy1S5aPlFDKpwzXtinN4UUm39NbyRoMi6dH00jOitQ82i\n",
"q+5VR7HMmglORg+NuJdVTM2S6E2RbRE9V+z3NHbGeSPAVj90vaKc88B567XKq7hxXnIegVzG9Tz9\n",
"UU6rP7RjRQnz62ttO08q8pgckejsnNEZHGUdzmVqnR1zXF5FZrQyeO66I5DBuKP3eKhrznvcpmVG\n",
"pHBeLhZ9zOtfbd/4ea8IpCo/vhwjkOk64pDwYAQYAAAAAAAAusYXYAAAAAAAAOgaEUjcjS/9By8z\n",
"Po6RxnQGJhVzzNfNlolyVtRP1WGNo7VmklR1lMbkemORnjbn9cbKe/ojy6+8rqUiA56onYqPPM2W\n",
"jeW2961FVFLWO1avYm0b2lHR0aktUb525sktSjOuPq5YjNKaRbAHKs7piXHKOGCpDiN+pK4nGVnO\n",
"ohxq3Vo/827Kdep+5yiv+luqY6/YYK14xNOOgF2WLetUV1M0RhblPhdUPE1VYlwU0fPO+/vQE4FU\n",
"YUbvORY9J0uR3ijzuDmv79p25uduXf3FfXdEkAu3NN+6NHo3foYsRArz9ksxPLUu372a98cTfSzF\n",
"AvPrtRhVLHdLRgpn652RTSv6aMURo+W918tYTvVLxR3VeaFmiBxjkX+MKCQMjAADAAAAAABA1/gC\n",
"DAAAAAAAAF0jAomb+5Jz9DGNPo0vt0Qgreihivd5o4K6vvMLIxJXE2NsGYv0xjk9vPHIcOzS3f7z\n",
"v9F4ZLn9ZRigduZE2Z/G/XW3ewO3iE+O3IfAKNjiMEajXS3MI8C+1tU5voyD2bVFI5tW9ErF2Voq\n",
"vS9239bXtVBzzozHy44DliJ/LfZsEWZK1s37uGz/uuQMmM5t1d6N9aWfRdQMaFakd3ytZpO21KTf\n",
"LueMqsUXX/TE9Ur/i+GJ/XtZMcY0UhWNXx+zn5/bWr/fqfN6S6TRinDLbRuVyctdIorncyf5HGjF\n",
"8EpxVeuuYdXn3gdnf/N6Cx/hZDw571PN6azihRa1L+ZMj9N2hXqD28pZIEUd+f5Z8ch0vYxFinVW\n",
"LPK7fpZYJJ4xAgwAAAAAAABd4wswAAAAAAAAdI0IJG7mi8fo4/lnNauiikCm8kUqRqnKe6OFVpzM\n",
"G5WM1mFHFX3Xa/Sb7cPqD0Y5q77gDJJW/eHxyiLVo2bV2hbPFBHaYH1mW8bY++YRR0fu4F5ilSnf\n",
"vFIt6nJuIyopxn8cdZRiGPkJ7Y/N2W3cr1v1/JbByMeijkZ0mbVSzpJY6sC4yoi6eSN/qu3oGVAK\n",
"FPusRxXlMQ3yPmJg7/+NkPWLz3oqOpbHGLNNL20YTRyd8V3rPFIzy0aPm3m9VJRbbJdE6cbPcN4Z\n",
"Br0xWB3H9a9Ll6n+DmKd7JNz2aKMEXf01lHqj3VeWNHNYr2e+mWb6+trjkcelfTEJPNl+Wq1TsUi\n",
"0/sAcciXjRFgAAAAAAAA6BpfgAEAAAAAAKBrb926A3i58ohg67Go4+hX9S2vGkY8DfkWlajh/6Ug\n",
"zmIEr4gTeKML+ew7a8Z9sGaAOYjXMlKltnG+SbKf575ZVXhn/zGjksbsNKW21PuiYw3lGY/Ks9ct\n",
"YxVTHd4x7euLZGRYlh/PcavJnSIuW6KVdpdiFUejT8/bZGdExTGy7hFqkRnVEjMf5dut1SuvK8fs\n",
"bOr9SxeNsQN1j19E3ZICdh0iAlKoI+/6bJ3YeTVT2dgBte4gDkQ0MFkbW6qquAWjLXcUxrPMeT9X\n",
"DqI/qtvW70u1g5foTunKUlfsemxRt7nWC5s3UuXNf3piU/JoeD/kGGR8UUSe7CN/aTS/dz8vK0fL\n",
"0jIy0pity5pdrIte89HI3fwcGG+M40VR2N/T8jyV98VgP2TfouVV37Nl3s+S1uf40jVU+7HIe21e\n",
"fkfGY6iee2TxGDn6VnNfj54riue2Nft/nez0H4Zh+OBHfeg0DMPw3T/31UQhXyBGgAEAAAAAAKBr\n",
"fAEGAAAAAACArjELJK5qnPlxGC7DU8eolormzWaGNKKSapk1a6Q13lXNYKiG0pbYbcTKh2d1DOax\n",
"vMdUtxUr77XXTJItEkFWVLKFMRZZikY0bXNDZU3f++C1cc90v9fvL7OIjazDvjfldXjKr9XuOeaq\n",
"/KYIX5AVg3BHICvrrUl25dtu6cc9yvcrCwmLpcsYuH3G+o7cKavXmrFP16C1fD/MaOAsXuvc1mor\n",
"q94qs7aB3HfrwhqLlKKVRhXliGm+ZvtvCnP/WtWbLdtyzxyjf+nnJWumwPWrUEc3veeaL4aql+X7\n",
"4J150tsPs5woKPtY2Q8V1dXlyhFc77p0fTiuWupvttAdgSxElnNqVkerb9YMken6k1j25lzxmyRr\n",
"/b0/Tyyyd4wAAwAAAAAAQNcYAYar+KJ/4HnkVzoqa/z21RpB9CT+AmmNVCmNIlOsb4Gt0WAtRoLN\n",
"+uEYVbRlpNZUvmJklacf8zae/50/KNpff9mpWGeJe4RbfROXOtRfxhvUfzBqGdc8XWH8yJb3IdzW\n",
"lRpo0Y73/G8hOjpFjSyzR8qsj7SZlz8lr58dpxE5yzb16AfvmE1Vx/JItBnRNS+p1qX7fhTLliP9\n",
"7D6qkYHqvcpHjJbqGMsfxTK1L7XLWozIKdEjSs7rNjRvTfrgfgh/sPzUdlpHYX1eRo088bYVFR5Z\n",
"Ni1b30KdTzWix8GqY8vIP88ontn7lz+sfhjk6CBPm/N65wtnv5uy7VRdkXIerUd55X1Tv3tLo5vW\n",
"2gn1TYw0uqyr22d7ko756CcPa4SWNXpqGMRxLtQfHYGm9sUaAeYd6WaNADtNP58W6/7k32ckWK8Y\n",
"AQYAAAAAAICu8QUYAAAAAAAAukYEErsZY4/DYD+QXj0E39xOxSKNfsxikaItz/jW0oPxp7jZTrFI\n",
"r9qIZO0D59P6w1FM58I2EcTY/pViJ09imbVtrWtGC2ftipiXx97HQ4leI0rrftdGn1QdihXPKonG\n",
"w1pEde/FlijTWl2t69tSV7QOGSES50ftslKUL99utq2qX3S8xbUm+ySWea4BuS+qYhWLD8Yuo9E1\n",
"xX/YDka9y53yRP/mW4hyO/3vifXeHsUya7twW4UYnCe+WDo5p2vH6EdNtNFzf0ljft6H2lu7Z/XJ\n",
"iv6W+m39XrMilrKcit/t9CB/K76Y+kN/86vu9ld2OhnaMNjRxnS9dTxqIpD5uuNs2Wm2bhiG4XuJ\n",
"Q3aFEWAAAAAAAADoGl+AAQAAAAAAoGtEINHcF/wKMeOjET1UURwVq5PxRWNAqjdSOa07/1sa9mzF\n",
"6bx9s+p3lzOio5aab71bRAg969z1in3fEtXK988b0ZB1BetoE/G8vFYxIav83q4xC+XI3K1gpNDd\n",
"VsPY7pbzrjlP3sWbA1TXqzPGaUU2w5Exx7pZ/el6oz/utrLjUJqpzHoPzOhhNLd0Y1Z3ZfSoFDPM\n",
"WFGpWR0iilOqLy/vjcornliWWj+Pdh1EmVhEsQUzytegXiVt6yiWWXU0jfcZMzgWD4E4cHmksVSH\n",
"GRH09sOq34j3lW49njhiKfpXex5Fr0P3TJmVs3R6lz1axLGF8f8j1+THphSb9UQg55HJ03LZ+aby\n",
"4eQN+YFf+Jqu34eeMQIMAAAAAAAAXeMLMAAAAAAAAHSNCCSa+8Lz0NU0ohGe6dFZLlrHtC5Z6Ymn\n",
"lca4umKRzjbltmbbse1atL1l1kir/i2RxpYx0WJbYv9rI5jeiIb114prRuduNTPl1L651nde3mIX\n",
"rPNzZM30trYwj2ao2Ib33uM9j6wIUdQ1zl1PtOwW50TNvlvxJm/8urYOeXV584tGdHRWRRZHLEVN\n",
"PdR+1hwjy8l9Jy9vd0i205FGb+1Gu9kOlmKiUjBeWx09dHbDu40dq97yKWS9rSE7r9NaN72PLeoQ\n",
"EVx7SiYAACAASURBVD7vDI5WP2ojm8cNx8h7HlnRandbjmNTjHOKhePL3mOOLXz+L3/+/01vBDJ1\n",
"MtapCOT4+k0yXeSbc7nvJwr5cBgBBgAAAAAAgK7xBRgAAAAAAAC6RgQSTaQzdqg4YosIpKd+pRxf\n",
"LJc7rLxe1uWMYIlx3S1njZTbbIgDeqOgi+02RCVd8c9W9WbHpnks63wcrjFGukUE85buM2K5PI89\n",
"3ZzHm+rqUL1ocYiisSF7T5JyoqDst4gEyb7lkThVsJDJXGxrrVvpW76tmolwxsoZWsULfQtWK/vo\n",
"qbcmymQZt30Sy6zy7vPO2PYkSs73z3tlnbKftl+JW+LE5sf36Ami6l+pzipndeO4WspvjJ2VPltM\n",
"8bSxXDDK5+9QbHVN9Daf0bJlRK9YR/Laat+MQIp7pXfGVatP3lN86ps3qivOMXUsrbuGOh7EHa/r\n",
"83755f9LoxHIy7rTYll6Ho3bEoV8PIwAAwAAAAAAQNf4AgwAAAAAAABdIwKJTX7vOONjskxFCq2Y\n",
"oxVBlMsO6+tVPxSz3kK0xdvPSx2xayw9VtYQ69pxttFZI2UdDfoxq+8Ks0purVf1UL1Xm9q24ho7\n",
"xSj3itM1sSG2e0u1kbH5fi631jPGrZe/9MMOPG6JQ1rl83I1karaOqx6S/33RpNqtajLiia1iEwq\n",
"3nrV+X+ZzfDkWtamH+NMXvVH2jwXVXy30JSKQe2tNmKWit4jwm0ZMxHOygdjfWYfg/HFUhnPfb/m\n",
"PrOIUSbHoHa2xpS+Xh11iZ0pxR2jx8grj6fVzB4bndXR914t1xF3vA+/+5edZ5AcP3Yn6y7n0zIC\n",
"mUa5x9XH6d9L+Q+fX//wu1/L+32HGAEGAAAAAACArvEFGAAAAAAAALpGBBJV/vXz7BpqdkfvLI2H\n",
"/N+KaJ5n21IkwY4v+vpR+01ydNbImnG0LaKSnjq871W8H23vUZ6o5JaYlRVrUNfBllnAzH4Ej1vr\n",
"fd7LLm2Jc33Lr8boTJYnkaW49Zh5T1SlFF2zritdZhlZyyOeup3l2XsS661tS/Ve4nrz/szX2bHV\n",
"vC3vvpdiVp77V3RZNO6olt3q02Ueg5LXcotM6AbeJmuP5TV26RIZO8fz1e+3Qqws+ugAuV/G+2vd\n",
"x7ecFt4oYQv5cVZHyRvF3HQenYx13jqC5WU8MxhzlOegY3bQaCQ0LTf2h7jj4/icj77MGjnFHcWJ\n",
"pc7FKQKZfi44v/xIsuyHfoE45L1gBBgAAAAAAAC6xhdgAAAAAAAA6BoRSLiNscdhWEa5ShFIFeHL\n",
"i6ntlFkdjmigKl8qZ7bvjCPmEc9yvbFrsfVsjpHys6Hnwbqs+M2WscFqNqS9ZpdU66LHwWzTyDBE\n",
"43V17ffze+Ge45zVopHNQrQyOpudiqDIckabXlYd3n60bDNcl5gVzdP2lvZlhKg0O1u2TMWLostK\n",
"be7FimJ6j+kp+9e7bal8dPerI5Cn5W8n9XvbioC1UIosLq61QgaxRRR0bOIollnbuuOR7lkafZFG\n",
"D28EUpWfrttCuT36obatuW9EZwfN20xfy9ils5L/gshjVz74UR9avPXqXDgel+vGOOQxWfjmvIwo\n",
"5O0xAgwAAAAAAABd4wswAAAAAAAAdI0IJNw2RSDHf52xvZbllZq45WJdsG/eeudt1F2f3v3zCsfI\n",
"nDFRqx0rhtQ6Kpmv28LqW1p79cyhhXpzW86FllGwYXjcaKVn/1WZUsQmUv8wlGctw44csWT3x6lo\n",
"Nsibvbqi6CyQ0TiiVb83ZuW9F7eIfnnZkd7npeo+WTuTnbc/s2rVOk/EWkQbi/U6qPfqKMp538fa\n",
"fszqbRgdVf3YEmmcjtGGCLJ5ngb7cSrsjKdL837Hjr33XmK1aZVjpseX6zPPEcl8NshhuEQgT2JZ\n",
"ev/6yLnAn3736ziProgRYAAAAAAAAOgaX4ABAAAAAACga0QgUfR55+ijFXNMf7Tib1Yc6yBelyKN\n",
"+WrVj2JbjnLe2EZN+556dSWn0HYtZsCsLS+3dUZIw/U2qm+qY6fZJc02dy4f1TpSu5vgNXHPotET\n",
"b9zLKp8uOzrKla6CaDwtGleKzavmj/V42qyJ4UX7Zi2ztvXW4Y0vWm1HtTgee5lH/pZxRHsmOFF+\n",
"5xkWp3bUD4WT3JrhcK1MTZ9KRyBvY8s9RdYfjZV66836E+mTp7yaCXGMV7Vos8V1paKNs35X1j97\n",
"X5wxX+v+FT3O4zK1HXFHWD7jA5dZI4/iDJqiksm68bPWm+Rk/BHikLtjBBgAAAAAAAC6xhdgAAAA\n",
"AAAA6BoRSEifl8z46IkyeuOOVkSwNN7TilZ6YzpWn05GmVJbnvLeGSpT1TMFbojobenvWl015ach\n",
"7WLhlr55IqzeyKvZTiEK0zJG6Y2/qYjUvXH3zVmwel/T96c2KpPU4alBRT+8LXsjR/emFMXxxGi2\n",
"1FEbafRevVbfauKOW9u8FW8Uc1pnRArdMUN1j90pqlj9/qkI1sr6S8H5Oncc0FjXJBJXqNdTv/dR\n",
"Ay3fs2HwXdfeiLO1zay80Vi0b1ab3vLFfckimNEY6jDoR0qs9SfSVjRK6/lf37TIHyb6iEqf9oGv\n",
"mE6lS7x2GYFUM0h++Pi89sdefwPnX2OMAAMAAAAAAEDXGAGGmd/zy84PvE8HImT/DoNvBFipjtqH\n",
"sqt6PdulvA/jV21aPKOLaupVdfg3nf/ZrubPCPmosJoRUvlf8lr/OeMg/lS41yi2abSgsa7F/u39\n",
"sP0tHvmvJ+Z7Uxi5enecDwmeijv+Ap+WG3lHMXpHsVkPp56VG6vKfp71Q9af9lPXubqtsc7LHLjj\n",
"HN2Ur0vXW8vk6KYWIxpvLPpgdeu8SM+J0+LFoE+4/DwSb7J7hJtYFtXioevR0TwtzO8l7X5jeke4\n",
"WRN8WMfoKJbNthW7kp8jrUfaxUdjLTsirwnPCKnSyC7jd5O1DzX7d8z2Ycv/2o6bMuoLe/nU919G\n",
"hY2jvdL7y3j+jg/GTx+a/6PvfT3nZQOP/P8wAAAAAAAAQBFfgAEAAAAAAKBrRCAxM0YgvQ+wV9FG\n",
"q7xSassSfTC+rCOryyqT/hCt36v0EH5PW9EqWkTtrGhqVX0N6pD1GmPqW0Qmp7o2rg+1lUaephex\n",
"SFy4zaqttruXsd+LfhTyNGbQx3lPUfEVz/HwRpZros14mTwPtS9FmazolXWfdvfNiEPVRNFqo1qq\n",
"LRWj3+sh5646i78v9np4gW6l9bbuCKQz8toi1rrXw+rlymA0MDzhxHqTcpmKk1pdU/3e61wh+ohb\n",
"+O3v//JFGn+KQM4+Sz7/8P+d3kzLfvz1N3HOBjECDAAAAAAAAF3jCzAAAAAAAAB0jQgkpthjyhtL\n",
"9JazYoZNYozOCJGnPm8EcUss0tuffH1NRM/a5JpRyXyY+5aoZ7TNTXVURiZLcTLPsP/DymvVhlXu\n",
"lm4xk2Xr61DJ92q3yK7RZqm8FXtR5czIpohdpsPyVTnrIHnrmLpmxD+LsbNsW2udbHNYXuvyvYhm\n",
"SGuyqRZv9nBDvDDv0pYIZEvWodzSDyu+qMpdY5/zKFo0ptasHzeo05xZ0/kLcYrZBtr1aHk8ZGyw\n",
"crZGVe/8HjjeGNNfAMsDZ13feZlIucU68Tuhdbx0bOOr/hZxR9yvT3rnORaZzgI53geOSZB4jEr+\n",
"udffyPnsxAgwAAAAAAAAdI0vwAAAAAAAANA1IpAv2O8+Rx+3RButGJuMfRmzlx1Wynnq9dTvrUOW\n",
"q6g3GlesHbfaevbFFt+KR2Nvapj7eG61npnOiqq0VIqYTasaN97yGLVwiwhkC6VjEI4jOtarmbG8\n",
"9UXjsNH03a3G1e8RIytFnzzRysc8q9dF44ueZdecVTQ6I+Ot3j9PRHFLpLHF9RqdTdFbV+3966h+\n",
"b4oftvzvzF7nymLb1rMZVs7WqNov3RerI5AiSq7eU08fS+1P5UWb6TKij3hUn/jOlz3HIpPz+c3p\n",
"+W6cRiU/PDzPEvmTr7+Fc11gBBgAAAAAAAC6xhdgAAAAAAAA6BoRyBfocz76OfpoxRxLsbp8WWlG\n",
"P6sOOTOksa5U77ROjJOujVbKegvbeqOaEeHoplhY0/T4TXmLeEXLSNyhMGa/RbzQE6dpUf9aG1O5\n",
"De9f1F5t7N332nOrFBm55xinJw4iZ0xrXG6KKxXKWaw6rL61iDSW2rRm/VT9OIpl0UhVyzhbqb97\n",
"RCCvKb2Gx+v1suyUrKuto43oe1o7+1201y1ifrPzvxRbdLS7SwSxUE72UaxU8Uz1O3qaudHZnxaR\n",
"RrN+Y1k4Aiku/tYxVG/5vE9qHbFH9OoT3v7ScywymS3yfBW8OX8a+YnX38z5n2AEGAAAAAAAALrG\n",
"F2AAAAAAAADoGhHIF+hzzxFIM3qYLnNE/qLlZ205B2WWYpZr7czWV8bIivVm9bvrdR4rq80tavut\n",
"6pjN4Fhf3aVeEUFpEUVT0dgt8dDVdgrr955dzzrXtxzFW4yhbn297k2dp9HZ3xRVxz3HM/fgjQzv\n",
"raYft4wItlCKCObLvDEuVW6vCKJlS5zTus9umQ2zxbni+V0j/1eg8MvDjA16OlaoI1qXd1tvzDFf\n",
"1/p3qfc6aXGcrfIyAikW5sch+h7XbLvoT1KJ9b+v6aqvIfqIF+jjX33Jcywyi0IOwzB8+Pz6L7z+\n",
"1hd7bTACDAAAAAAAAF3jCzAAAAAAAAB0jQjkCzHO/DgMduxNRhWNKJVaZkUVrbGWnohjpJynzWFY\n",
"Hoe9IojRfs/a2hDRq42PzUacN4iOjvXlM0rW1DttV4gONI1MpoxZofZ26/HKW87je+HZhRaztD3a\n",
"obKvJ98V641/WhE3qx+l+q31tW2qbaPlve1vmYnQW4dvWYs7dFx0Nsp83dp6T5uqvi3xVm/8zuyP\n",
"I5qX3pNP2bpSm3v/H8Be9Xsjm6pc0yjhTrOEqmXOjyJyBlpr/6Zoo4g7WrZEG70zONbW8TV/m9gj\n",
"kPqXX33xdMkcz3eJjySxyJ96YXFIRoABAAAAAACga3wBBgAAAAAAgK4RgezcZ48zPop1KspkxRyj\n",
"Mxam5b3xydHYNzXEebZdMJrnKVcT8aqOBgYjdFtmjTT7Ed1OjK2fDZ/fWP/ati3G5+41u6RFnc/K\n",
"3uOP7218c7E/lXHqa6idzcp7XqsYS8vy0XhWKRC396ymjyAaGqwJGcoZ27JlpWiSZ9mWSKHazhus\n",
"rI1AellRxdI+5zEr9TuvNEvitEx05BafxlvEP8NtBmecbH0OZNWff/BFm/Nto/fWo1jWYpbLWQRS\n",
"zFpZG/GM1mHFEtOF3v/19EQ3U19L9BFw+7hXXzRdRW+mWOTlwvqZ19/W7fXECDAAAAAAAAB0jS/A\n",
"AAAAAAAA0DUikJ377GT2x9E4nrFFBNLabrbeiCq644uOuKM3vmjFR0rlreNQ2jbKs89ynYhWRiNK\n",
"rce95jHAJnFG57JNbThmlWvWVrT8nQ1OvrPuDMNQvj7WyhxP9npPHcpt5tZbthmN49bMvOeJVJYi\n",
"RHn0XUWIovV627RsmZ2wNg7oXfZon+rMY1k40OM9UO6zEVUszQ7oOYYtYqIpbxzRc2224L1HyPcq\n",
"L5TW27jD3plZF9slrz1RxlnMMLBdWk5GIEVHrEhjzeFrcY9Y1FGINlptFaOSxrYK0UdgmzEOmc4M\n",
"Ob766Q5niGQEGAAAAAAAALrGF2AAAAAAAADoGhHIDn1WEnv0RBprYmR51HBLBNJbh2o7H5KtIgk1\n",
"sUhXeREzjAq3KX7YO2JZrKPBdouZsZKFKubXOs6599jevWeZjGpx7rbQ3ZjqjLperVnfStf3+Ota\n",
"RndUedWQcc2XojiqukU/RDlPFLKmjtpIY+sYqjeqGC2vZhvMy6fbeOvwLFPngjKLPGXbltrce5a/\n",
"vM603ppzIDrzn9WXlvvnjvJZjYr36hY80UVXPdnPNe9Z7WGwrh1vRNCK1+59vQyDHUfcFG1U95do\n",
"387/fh2xR2BXH/vqC07DcIlCvjld4pF/6Re//aGvP0aAAQAAAAAAoGt8AQYAAAAAAICuEYHsyAc/\n",
"6kOnYZgPnT6I7ES+pBQRlBHJykijVZcq540pRGOO15jJ0dunFm1Z20b39UkMUW8x26AV06mu0zh3\n",
"WmkR23W3lUUlS3GQW0Qrw/t8hWvNU8eWIxXtU8tzfAtvPMZTzorkeMupiKecjc+IY1nr0vXedXmE\n",
"NF1vxhcLB0TGmvKIYKG8Yv1uvOdPc9FrwlveipMOjnWt1O6fN08sY5yFmSytJizq9441G/JePO9t\n",
"adtRkwhkYYO9Yq2126ootPdmYcUbvdHGcFTS7tKE6CNwGx9zjkQOwyUO+eHDh6f1/9PrP/Yw1yYj\n",
"wAAAAAAAANA1vgADAAAAAABA14hAPrjPPMceh0EP8X5qEIG06vdGCj0xsi11KO79ysp524n2Zx5N\n",
"DW5c2aZSG80cBh0hmiKTabna+pPXe0cl0w63eD88sTBvDOMmY4iTiMsjjGGWfbxCJHYP0XiOtU/R\n",
"GRq99d6z1rM6PrpSvMizrHQv9iy71afLJjNwLl4kv//GVSpKmxILox+5a4/lrPxOUcUWMcOadppt\n",
"e5IvF7zvQXSWUG9E0NUPsS/W5xNr9lbZaLJ+S7TRs63q99cTewTu0r/wSz5/upw/cngzDMMw/A+v\n",
"/8u7v14ZAQYAAAAAAICuvXXrDuD2juKvmN4RMdZfSVU58y9jzjpS5kiI03I7Nfop/6tXqbwq5zlc\n",
"aXnrAc3R0R2KVcexUInVD9VvVd+4KD1+nhFd3r+EKp5zoWa9eki22s66Zk7Zv3uq/rNLMkrA7Kd4\n",
"GPIt/tRT+iu4We7MGrVR2qfxvLfOD+8DvKsfoN24fA/jwaMjJ249Wmlv3nvqYoRIxXb5g7aLIz9q\n",
"h/kWRq/kw+LV/b3UN7mvxkkSvh+N99v0fnpelj5w/jLaLHaQWoyKLH3msq6Z2uup1O/FfTf9IXj/\n",
"97Zv/f7eMupNjSS0zlnv+SzbMq7N8YfoOVx6r6z7hTkCTYw6A3Cf/uIvfvvi8v9Nrz7vMipseH5I\n",
"/l9+/Z13NSqMEWAAAAAAAADoGl+AAQAAAAAAoGs8BP9BpQ+/zx3E64ORz9Ll7fbz1eoB76Xh0eaD\n",
"8cWQdqtP13wgvSeqWGqzepuDsc5Z15ZohDo/oikWM44k8hW1D6hXbaZaRERUG9Z+eSNxeZ01/Wjp\n",
"rsYtn+NBd9Unh2hUxopWmg88FvcIFXNX5azYTc01lEdaqurYuE6tr2nzZNyPaiOspfqth0K7WZVY\n",
"ywqxLPPB2cKjRU1PKo7oiCGq+GKLh9BH47tbfr+1jPqVHqxuxe+2xAste0WhvRFCxyq7HWdkcnYv\n",
"CTZWe+9R94hj4b5hHftv+H94+D3Qg9/46nNPwzAMHz58eFr2V9/7nptd34wAAwAAAAAAQNf4AgwA\n",
"AAAAAABdIwL5YH7XL51HH1UcQ40nfHJGIOV6I77ijr05ImDefuwWi3QeS0/b3vZbRu+GoT4u2Lof\n",
"0/D5xpHGRXzLeS5sYVXbOka5qKvFsWqgeG02bOs6zjFKFWdzxpUOYjZMs0URqXpUZtw3ee2JeEbr\n",
"KNXvqbcUv57iiMF+eKOY3niRFVsvLduDjkAekmWnWbnW9+TaWGKz9s//RqOuLdrcW6kdeY45Mvut\n",
"/xejSSzYUX95YaxtK/Y8E4wIelkJ5+o6nFFMqy7Vp28k9gi8CL/h1WefhmEY/srr77r6Nc8IMAAA\n",
"AAAAAHSNL8AAAAAAAADQtbdu3QFcxzEZl5zHIb0zeW2Z/coTiXDPKCZUz7BWqF9F+cwZ08S2T859\n",
"9ijtp4ru5LNytphZyVuHPKbWbEWFSONp8cKuV9ZVmC1ptc0CT7lwdGZL5qHhgGLvrHlRNV2s3a15\n",
"Hw9qYay+yuhVNGJZKp9HKmX5pIy+9x2K5Wb1GjFONeOXtw7Vj0WZ1TXr661tLn0S/bHKiz7q2c7W\n",
"99msPylfPG5GHeo88iwrxQz1vf1QLNNC2o4nElf8fCK280Tf97ovlurIP4PoKLexYamcKH5cL5ZU\n",
"5im0eZPV7VQkz9o42rb7M6rz86IVtzTvWaIfLT+nDMOlv+77qSjv7RvRR+BlUtHHX/f2Z56GYf8Z\n",
"IhkBBgAAAAAAgK7xBRgAAAAAAAC6xiyQD+AzPnCZ+TGP09XMRHg4byTXWXWJYd3eNpVxX7wxSk+9\n",
"0Zkc0/Ut+uGd9arp7JXB8rIfhehhuN7tVdj17tRv2aYnC7NT+4+cB7Civ3vbK+ar1nvjUM7TyN1+\n",
"vu0jnytoqxRD8ixTkULvsi2s2eqsSJXVty2RsajT6g8Z4ya15V5VG+vzxkSvScXwFp8BRPktban4\n",
"4mgWcVZ11LadvG5xfsprM1vYYpZJb79L5b6J6COAzK9/+4PTbeIjw4eHYRiGv/7e9zW7VzACDAAA\n",
"AAAAAF3jCzAAAAAAAAB0jQjkHfv0c/RRzeino41imVH/uO5QyG5ZbXmjkJ5h9jWRqWgssnbspHe7\n",
"vdraEq9r0Y/x/ctjq1vqj7S/ua5CRmTv2Gd+/G7lFs2bbTpzN97fUlY8Zsu+7xUzjEZPPLGbUvzy\n",
"6CznSW95o2hW37bUET1u5ox6wX6oe2Cpb/l5VBMp9MQRW0Qgr2Gv6JXnsQbpR9+pnPPkUuXv5aN0\n",
"9BxvUe9UxpvlFsdeFd8ys6Ervtj4/WsZCzbP8UKlnn60uPZlHWKhilt+098h9ggg5te+/TtPwzAM\n",
"f+297918/2AEGAAAAAAAALrGF2AAAAAAAADoGhHIO/bpH/iKcwRyOdLPilJFo5BPzvyXN+7YcoZD\n",
"b2TMHVG01u0cM6yZsdMqM9YXjSNGo6k19ppdctFO+yoXVOxT2bsvt45PtnRvu3JY/eGZ9WsyGrtU\n",
"ERGr/GxbR7lrxJNb2Ctyd4so371oMYNjk8ik0cAsNjj+K35PnFR5FV9X7Ze70Zw3/efZbi/mDJXi\n",
"IN3LsZJR4ELnFvFMu7i73bz+Ur357IsHY136UkU2rbauEWfOu+vtY7rsW4g+Amjo17zzaadhGIb/\n",
"9d0/Fbq3MAIMAAAAAAAAXeMLMAAAAAAAAHTtrVt3AHOfdo49pqwYjTdWZsVijslYcisOadWhhtar\n",
"qqLxnKMYT62iYJ6h6qVy1jFtEk2qmLkn70tahapPzU7liQK0jvfJvmXL5IxbRr9lO87+bIl9qnOw\n",
"hWgktGU/bh2nbHlIW+yKGQ3ybmtcj8OwEhHJtpH3RxEB8870ZkaNRL0qCmrFXdT1qiKesm/eiFt+\n",
"DyzEqo+q3rzOYX3d2sI8mlfa97H8USxTx3tRf1LAigjO2l9221wWLV9a5ilU/D2YXxPO35veMt5r\n",
"pwVX3yoeE2Ddc2r70Xrnrc8nrbvhibpu2T1vlNZadhD3bvU+euotfY6OnnfeC8BzTGviqgBQS0Uf\n",
"f/U7n3IahmH4G+/+4OpvVUaAAQAAAAAAoGt8AQYAAAAAAICuMQvknfjU959nfBSD9Z7EIOdxSXFm\n",
"wcoZGVvPDOnpj7deVS4aJ2sRm9oSI4tuqvYzGuVTbdfOJFmqt7ZvpXrzofp7zCxptn9Dted6a+7m\n",
"K+89jyYaQelp36/JSulcY5Y/zFmxsOiskdd8/1r8bjIjiM7nJXijmNb9Zcu+eO5RMrJsFGzx3tU8\n",
"jsF8tIWx3aycUVDte+2+XuP8N2PdKmrtrdeow7q+v/XvMvMjgPvCCDAAAAAAAAB0jS/AAAAAAAAA\n",
"0DVmgXwAx2RQ8SEbn91kGL+or2ZmyLyO6Oxa3npVuegMjjXJhUUdhZyCOSOksc6zn2t1jfvvbdsa\n",
"Bq/q9c7waS2zFN+r4Axh8tQNxif3iuSEz7fx3506ZM0cqvpR5Dy3LLIfB0cZ1aZx0be+j7Ys34I3\n",
"YhMtF71Pl67v2nhTaV1er7dNb7xP1eWdOW6POq4pOhueOvZHUd4bB1Rt5ttWxb3GusTBN6tzzqSn\n",
"9uUo1qnj5vm9LX9HG9ulxdX7kde//KHuvYpSx0NRM7MuV4o+OX9vhT/7GkrX0OVz+fznmrbccVVx\n",
"olrHiOgjgEfCCDAAAAAAAAB0jS/AAAAAAAAA0DVmgbyhcebHNTrOdzj/q9atb5du4BmTXCpzOKz3\n",
"I9LOc12x8tE21KxFW2ZOjDosXly3fasfTesX4/JbzFhoDfdv8r6IelNqts8WEdpae7UTrte5wa0z\n",
"ELWxlFL8Mo+lyGLeWKmIm0TjXla5W78HLfS0L17R6KgnulmqdyqTzvCmZn1zLJvNWiyiV55rsyYS\n",
"WnvNl+QRMDUrs73hMqKoPoLvFXm9RkQx2o+RPMedUTsleg7sFTc2r2FjpXeGRVXemqVx0yyQjv58\n",
"G7FHAA+AEWAAAAAAAADoGiPAbuBT3v/li4P+ZAzLUX9OkeXHdd6RGQ1GcHhGgnnrmtdbv62nvL1P\n",
"2+v3SuuoHS0V/cu+u469RnQZTzdu/adD7wOrm7QV/JNzi2N5C1cdgWbcB6wHXEfrKtnr/ImOUqgd\n",
"MVMq5xkxIEexROtIGUMuZreGfFSRaHNWhTGaTo1MUg+Wdj2BvTA6JXo/kHU4utG63r1GvURH2Liv\n",
"TWM0lpwcx/mQc2uE1jV5RwGOat9H90PlIxvV1utQuib2GDnnHaW2pR/me+o8d6PttLj2GfkF4JEw\n",
"AgwAAAAAAABd4wswAAAAAAAAdO2tW3fgpfjkJPbo/tbRekDmeeVBrFQPpZXVO2Nt9vDv06zMc33r\n",
"scgtDz+NxuSi0QGl5YNiS/2wIj7eOqxl4TpUxEfFzcT4ec95pzogYw3BKGb0obcl0SiOW4M4gzfu\n",
"/AiO539nu1T5EGRZxlmXOu+shzFbcct0nYranYzyqu2T4x54TF67yxn7J+9LwTrspzcb64blsVcR\n",
"rNL7na8vPlw7elNVxRtksFQV6jrxRN9LD8nOl6kH2HuXeQ9f9Fq2olpmPKzivbD2JRoh9cY+zf4E\n",
"y8nzWX2WdFa8dzTW+5ml9twqfs40Phh5+ljqz1h9OmmK93eNVa9aF400ustlb+Ct48EAUIsR1hhs\n",
"jgAAIABJREFUYAAAAAAAAOgaX4ABAAAAAACga0Qg70Q00ngZkn1ZaW1rRaXckUmxzIpFzsoZFW+K\n",
"RU71r6/zzkKk2vH2zRPPdO+nsdE8anpeJt6/LdHN6MxjW6KSi3VpHYsXdv1SsE2lQVNmvVtSjLtF\n",
"EBzX017pyxa7tKVvU8RsSzQoGAWzIsDeyJ8qL98rcd/wlCv1zVOHFe9ercTIMln1qtkox2t+FkMS\n",
"90w1k+SiLW9EcPCxdr0mAmaWd9xTvff1aGRrSyxLRdE80cPWt8kt74HZF3UeuTaM1d9a9HfCliif\n",
"PB7WNezthzq3s59LkfZoNND73raIYC7KiOOn7pnW76s/8v8y8yOAx8QIMAAAAAAAAHSNL8AAAAAA\n",
"AADQtYOKq6GddPbHnPr28akwiNwT20qjkKp4dOY4b1TMalN5clS8ZXy1qt5TX6sx3XnsJrpdi7aH\n",
"IYknOOKRm+pvUO+sDTEGf3y59+yHafVmPHNlm2t7lBzCop+Fjj/CfhVjzI7y1nalY9Dy+vPGnnGf\n",
"ojFKa1kpirZXvLBWi3NXReJUrNW66FV8Mfoxu8WskVHXaMdzf1OzJDaPsBodUTHHvD9b+nSNOK5n\n",
"ZU0/xm3+KNFHAA+OEWAAAAAAAADoGl+AAQAAAAAAoGtEIHfySe/Mo4+lOJ4aTzxF6NRaZ5zNrEP0\n",
"zarPG+Xzjo3Oh7d7IpG1bU3ld4oBRstX7Oou/cjjkenCln0s9aNpvYVM2l77ZdZr3Gb3Ps6yzes3\n",
"2ZzcB+f1vZh9qzIuXaiiKy3iP6U6amf0i9bbuh/3Fge8Jus4tI5iqlmtrVlKrf6q33l7vX/ReOYt\n",
"ziP3deXNd1/xmKqFjrRq+/Zb1Cs6Pr5UM0+2iGJ6719EHwH0ghFgAAAAAAAA6BpfgAEAAAAAAKBr\n",
"b926A1hnRmvUsH9ztrrLqzwOeRJjoeWwcTE+essMeXm54ynto2pruTQ625qKS1zq99XhaVttq6Ic\n",
"xbYckS5vP6xyqj/m+12YmdETC6sZuu+Kj5QqdkQzamaBvJtpoc6saOWto1qtZyzMF4b3T53/othB\n",
"/GDeU8QPapaxQ1ZmrQ7v7GWL8oWYu+d6Pa70yVOH9/0w71HBdVZ57760aH/Lue6ODWax9fQ8Ucvy\n",
"c1eVU7MfyhkRRd/Uz1OMa7mZu45RPjtfqQ5ZRvwOS0Vjrd7yrr6Jer1kVNE4yWuvudIG1r3K6oc7\n",
"vh7v0ua61Lbe/srzQ1Si3j/PNeF8u8P3OzKPAHrECDAAAAAAAAB0jS/AAAAAAAAA0DVmgWzoE9/5\n",
"sulgPjlnXZyWZf+qdc+vywOSS7PKeWaGVPW5Z3dsPFtkLjpb5JYh3NOxajAOvEU/SpHXFsPVWw55\n",
"t6I7BzHsv3X/vSmMFlznSKFDTY99sLJHizq0iNc+2j57eGcIc18nKkIXrMNTf9rGlgiP2aaK/jn7\n",
"kdcnI4Kl/npihoU6evzEZsW3amars7Sow+I+F9U6EUtUjx3IK2n9Md4d7zMK7vW/FntFJaNtqRkZ\n",
"9+5HC+44+rngd/w9Zn4E0B9GgAEAAAAAAKBrfAEGAAAAAACArhGBbCCNPuZUFDIaEVTFrYilt62D\n",
"GIRvxSJLM+PV9qPUlkc0FrmlrWm7vaJre9URjLJuaqthXenF9XSlwfjXHPO/qS3HxtfYF7ONnaK6\n",
"jzBLVU0cMRecTC08K9nWco9u7/3cMqOfVYe1zBujtJa1jh5GRSOv4TrUDJiljY2D1GImySg546NF\n",
"fGZRs9h6ZwpsqXX94fhiwxinN9KrynhmrSydz3KWV0f9KaKPAHrGCDAAAAAAAAB0jS/AAAAAAAAA\n",
"0LW3bt2Bl0jNAKVYq4/ngcylKKScuWsa7r8+GLo0BH6s1xtJ8+5z3pZ3DPZR7Ohldq/DcploSzHj\n",
"FYX4g2jeV6+xblMdRtRBxQyjMROvLXUdjQLy3DLOf0tN8qF2EshNPBXuFEF0d0Os3HSOZ/GOUl1q\n",
"lj+z/mFef1owetzcM241rLd1m7d4SELrWQ898Z/oOVnTr71mhMuXecpElh2N/hRnvjRYs2FafUvr\n",
"P4pl0ffZjLoZHSn9jlTHzYweOk+u2vPokGxovafe82Kq11GmZNPMk87fBWttejd2/66JVeu/No3K\n",
"Svti3SPGfhN7BPBSMAIMAAAAAAAAXeMLMAAAAAAAAHSNCGSl3/b2cuZHFQe0oopWPPF52/OydP1K\n",
"/Wkbxdl8jDjiGIuc13FYrUvNpmNFzKwh3Lo/NlecLmlUjZ4/GB2ujUfO6jCGo1sRr1Ibe0UlrZjh\n",
"uEqd61sik1aEYstxjpYbTwXvDHkttHgfzfo3RBAtpXO3YvUwDDpqreIu7vNCVby+SJ+LRsRGRiw9\n",
"5ZMfxmXptafq9ZSTUTBnnFPNjKcYb8uMNQNaNC5k3TNLse58W28/ZvtndMAqP/udni0rxQetiOAg\n",
"lk2PNxDvY3GZ1Q9j2WAsK70vUznjjU+jemYd61XM6pCff6K/6B0xzTXmOe79HXb+13vujqzY4xZT\n",
"vd5f4Cf5cpUsEzxWFZuGnbJ/vY1uiW5GP0+1aB8AHh0jwAAAAAAAANA1vgADAAAAAABA1w4n75hr\n",
"DMOgo4+jdEh9Pup7HmP0hXc8sweWarLii942a+tVEQNv/dH+yG1rtyvMGllrS11q2y3HxlN/6/ou\n",
"s4/u2+aWGGVtm1saucW0S/c41VOLmcS8scx8JrZSZdHoZjSeeev3w3PsvYmxaP3eGGWLqI8lun9b\n",
"jkfLOmp4Yo41kXZPjFLGbI14ZlU/RMTzlqx9uMX7PvvB8TmzVMfe+1CRrNyn3UIDLdr3Rr231pte\n",
"G3/8Z5n9EcDLwggwAAAAAAAAdI2H4AeND4lXo7jSv6jkDwufP7Ty+Sf1YHxV3+wBuEZ5/RejZX/N\n",
"vzCJBjwPy/c+5D9dph6kXtsfua2xzvwLZ+Gh+aoj0REiarvoX/7ksVFteI5zuchq/d76PH+NV0Ws\n",
"B+57R1C03j9Zb4thIA25/4q/c1ve9luM3PM+fNi1/4UHNecPn1f3f6t8uo289tWD0o2Kzfu5GM2m\n",
"+ivv9WMfCyPiPA/fLj2Yu3bb0j3TGplk9eMkKjk4y8tRSHkdhfLjMm+56TND0qT3Xll7//TW5f2d\n",
"YP2ecD/U27quRF3WqLfWIw/zbWpGjk7bOjtgFmtRRwPR+rf8DrEmV2k5iku17z6HW5QT9/jx3+9k\n",
"1BeAF4wRYAAAAAAAAOgaX4ABAAAAAACgazwE3+ET3v5S8yBZD7X3xPyGoRyHnNoyih2yf1u1qcb7\n",
"e2J16XHxtFSK/0TVPiR+U5tGR2rq9UR3ausaBn2M9hoXv0e9aqKFYrmd9JgnMPepsMO3PB6ltmvj\n",
"0aqOHt93r70eYG/Vu6VNZe/yvbKild6IbDTKfm9UvFVR++d9hIFs11luq1I7La4Fz31UPmpARMmV\n",
"aB+9kdTafS7Vb8XWxyj0luuF6CMAMAIMAAAAAAAAneMLMAAAAAAAAHSNWSANH//qSxaji59Elsqa\n",
"GXIaslyYQeu4YWbISz/m/6ZtWW2mZPuVY71PhXCLOTuOM19kDlE3jpVly4yBeha602LdQUzldZDn\n",
"1r598864pWYztdoq1efhqdc9C5aznDeyvFd0596yCVtmDwvHDBvGcVtEcq7RVs573W4pp8pHZ3W0\n",
"2kzVzuBozQxZajP6fqh+WNd3NMrXIg54zxHBFjNKnsTr8IyIyevFOePN2YpYnYrZ69/zvr5ZouW2\n",
"HKMWrDjnZMNMiy1mrzwa67ZE5c3txMl4UOtER06LF77Pgd77OQCAEWAAAAAAAADoHF+AAQAAAAAA\n",
"oGtEIIOqh54bQ6JTaSxxjFSaM8Wk1QbTi3qY9DKup2KR5qw7Zj/Uq7p20jqs6Jo3/tYiKumOA4pO\n",
"jcvSKOS4bIzetp6hyDtU/mhUaJ5jG2Jtt4gUWvvZpIEH1Xo3vREi1/2rcI6p99S7bagfDVjRv9Re\n",
"kaotdexV/7WiO62jfHvXoX4X1H4+8Up/bYkU/2JZev8fl80fBSDqOP9rRlOdsbpwhE7dg4z7Us3v\n",
"smik11uvq5yzI/IznPGBp0VU0fv+tYz3Rds8ivNUFZzV4Tk/RdxxS+w5j2sPwzD8CWZ/BIAJI8AA\n",
"AAAAAADQNb4AAwAAAAAAQNcOKor10v3WV198GgZ7RsZ0jZq971LOWFeYGXKU9sMz9N4b5VPFzHrF\n",
"T9Ex1dv6FmttS/wur0PFPKK8M4Rt4Z1d0lWXWNai33lcJ6WirFuipl73kg3wvFX30tcWetqXVHiW\n",
"RnGfkXWJ+Pw007DYQEZ3RB1WvMlbx1TXsgoZ9bGi8tF7T3gGNBXbE9upbdTvBOumpmKAsrx3mUNN\n",
"tVaM8p4/JUbPmejjAfba902PUHBUsuWjfe2+t35Eg7td8UabUVNR3nysh6rD6s+GbT316seiLG9q\n",
"xB4BQGMEGAAAAAAAALrGF2AAAAAAAADoGrNAno2xx9Q4I6MVhSwZZ1VU8T3vTI5HY5y7Hgrtqzc6\n",
"BP9k/JRuadbhjBLqGXPGY5m2ul6JNXtTyozzOGeF8kTXwrNUrfTJbMOaXXKqdFlrdGalLf22tg3P\n",
"wqjarrhca5ttnS/wxFZax0fMfTBWttj3LfuyJVri6bs3zlPa1lXO2KDFjGKzckYdqkJvHer9MO8h\n",
"eXQzKW/V623TG3uLRsVkeev985av+QXhUNtUqWnrOO8VH7Tq3fL7ytpGznLp2XCtvOMa3jTTYYOD\n",
"fiwXKYq+H+Y+F27G3nufqyPCluOxJUZ6WXiarSvfu+85tAwAt8cIMAAAAAAAAHSNL8AAAAAAAADQ\n",
"NSKQZ9YI6zSCqKOM56ikkb06leowOqXji8topT1DzHKZjluuU9+WnoxXpeioOUrbOcvYKTtyukU7\n",
"npnHeWYRSxFh8B7ffIOayJij2nhdKiaZ1itPuNP6Oqstp5YRs5rR/2r2SU9brd1iyiZvnCe0XULu\n",
"k1gY3ffxXtX6umpR3ssTFfNG+aIzT0ZjSKXjbL0fVlyueG812qyNwoVn2yts4z3OjzrTomVLHLHl\n",
"NW9GFUWH5r/zlgut6K9XbRLNe0xrzuNricYS9454tj4G9udtdTKu98DbN29E9nt+7quZ/READIwA\n",
"AwAAAAAAQNf4AgwAAAAAAABdO6hZ416S3/Lq9y0OwBgrVGOIrXUpKw6Z11Uul7x2bBKdtbJm1rx8\n",
"E28V3hkc5bYNB3Vv6ce0XbJZy/HmLfez2FbLutKOi7H619qta479b/1e3Utu4V76MdoyK9ph8WK5\n",
"Lp191FN+1o/gub4lygTUKs2e6Ylnygirkfaa/UoYlxXqtdw6OrolQjvaa4ZMs22j4+a9qtTJbGf2\n",
"2qervsfOqcr3+n+n2nOG2CMA+DECDAAAAAAAAF3jCzAAAAAAAAB07UVGIFXsUTlM/y5HFqfLrHHH\n",
"YyzMHxGMxSK9Eay9Y5GHldcR0T7KfjQYBN6iH8MQj1K56rRThk1Y8Zim7RyW19A142H3mBcYD8k9\n",
"9q2F2v3a+1y8huiMj2oDec0bk4xZ9yB1UNNixyzGJtelVeQz7612eL5OxeRS4/q8P2m1R5FamsXk\n",
"sn4UI3Se6da8GcENeb3apqJxR7Ws8a7sprZvt94X73HO1y1/mG8Q/UjfIpIZnVH2msb/x5G/Q8TN\n",
"p0Ufrd9XrY8B0UcAiGMEGAAAAAAAALrGF2AAAAAAAADo2lu37sAtnMQg5OhMgN465PBrIxaZ1mv1\n",
"yR2jOTvO6nXUb0RRSv2x+mZ946r6qLTsd6kfus1lUMEc7i/6NNXQYFYmGT8wIhGl46Hq85xv0fhi\n",
"Gr+OxgJUec/Mq6U6vPbKHIyHZK+oiNlvY2Wr/W0dL/GIRnG2zEjnKe8uY2wQLldq3DjvrHPyJMrZ\n",
"HVmv37s+/TnaX+terBsProvePJ22NKWWHc//Hoxlx2SdtezeopBeal9m9amIrqMD8896yw3zOpyX\n",
"ZoNC9qat30dvfYty4nPBPPK9zHxbnz3Ma0LcfFrHF8OfbYzPsC/wiTUAsAtGgAEAAAAAAKBrfAEG\n",
"AAAAAACArr2oWSA/7tUXuXbWithZMwSqkJxZXsyCt6Vvsi7HrHJ6lst63iSa3adgm0Nstk1Zx4aN\n",
"9axaB1mmqn7RQIsZL11ttq7XWGfFD7y++wXOivQ5H/2Vd3EjlwfeGfM143pi5r8eeWemi5YrxZNb\n",
"Rpy9EaLavtXMmhfth2fyR+++vETeeHA4RmzFEoNvyDXfvy2/1zzxvnuZ0XKW0TOfmVH/+AOrfe9n\n",
"i714HsHR4n+5/uTff3mfcQCgJUaAAQAAAAAAoGt8AQYAAAAAAICudR+B/M2vvnCxg2k0TY0j9sQM\n",
"rWjjvC5fndPaYCwyOnvlMAzDU3AT777mWkQKN8UGzVcb6m1QSe15V6zXEZVsETMsZS7GNr/nBcYR\n",
"e3cvcUvlsHhxIeMpRiXyFBcXTzR20yIC3OQaxounEmsyZhhctiUCaUVNb2HLNXwLKo44Pm7DPVui\n",
"mr3camsnNbHrXfqxUwNm7F+U+69+ns9TANACI8AAAAAAAADQtbdu3YFbOIk/t6Sjb8b11oico6hD\n",
"jZRSj/pU9XofIrp8mK+9L8ox2yRtRm2p9nVkjQ4r/dXMfEZq9u9su5XXa3WoV9YIrOJfPY39Ug/n\n",
"9f7F0novx3Wl0Xiqb56/Xs72+dzE9/KgVQjf+bNf1ey8+OzCaLLqB0Y7/2Ivi52Mdc5y1ugVeX/J\n",
"Rt+k5WbHwFNOjMiZVSE652lLrZuN3PHc8EpP63Y8GX/2K3L8N6l3/P2mfq+pPlr7p94sNfLpUpmv\n",
"v56RTyXWQ9xL9crz8mT/HFlmteMtZ2275QH2LUaW7bWtdUqlaQ1rUgfZpvEm7fUe7cXqh/l58Aqd\n",
"tUYKdx62AYCHwggwAAAAAAAAdI0vwAAAAAAAANC1bh+C/7GvvuA0DHlcbj1SaMUGo/HIYfA9OL7U\n",
"N1lv8Ans0QerqxhNi4fxR6NM0QfNW8Xv8UH6U12NH6g/Xs1/6ue/hvgiumbFJ0txL6u8UvsgbC5C\n",
"PKpSzNC77JGoB8Hbz2oQj1cQswJcM56pRB/HcG9a/G9K6dEWsq3sDSn9Hoh2U5dfLv0+Ps8BQFOM\n",
"AAMAAAAAAEDX+AIMAAAAAAAAXesuAjlGHy0qnlgTR/SU90Qs8/Zr++GNR0brvdRftdm8jgahoNax\n",
"wRZjyw8ivFB7nGf1nqsg0ghsU5px8tF541OOiRbleuekh3J9bZvebb31Rieo3FK+p5Mtus9bflmN\n",
"n0nHKOHJGTOc1WH0Q9Wx1+fg2uPxaOeONdvslkPrPX7mjKGqb8E6rDbL13wsBjviMx8A7IcRYAAA\n",
"AAAAAOgaX4ABAAAAAACga2/dugOtHc//HrJ/S07ip3FZKbZnzQx5ysqs1WcPj/bF6tQw/oPIC54c\n",
"g7FVO0djKLk3lnic7cvy1fqSC++QenPyppXXa/0oD8FXMYzxvFj6gV/4Woa3A1f0XT/7Va5r7rPO\n",
"Ucn0fnqZHXf9rjW7/57LeaM7LW4G+e++Upst1+1Zr7Vf0XpvWX6L6OyLs1hWFin0LlPRw7U+Wcus\n",
"MlaE1YoleiOLdjTO+6nrwjPza3TdvWidAvXWd8peeLuxpbvqnnKUn9cWd/nFq0d4bwEAc4wAAwAA\n",
"AAAAQNf4AgwAAAAAAABd62IWyI8RMz96o2vRWQmj5b0zAXrrzQM43t6oKKR728qAzmymxcqMjxqO\n",
"viUu1GIGyaku8foHiTYCL8oHP+pDoV+i3pkCvZE/FVlb1KGibvNKinWkv0OOoo5x/dGIjspYacIz\n",
"Q5+M7RX2Jd+HWR+tvjkjglYs0Tr20Wjj2rIetZxZ89Fm5zyt/nBdpVleF+VKGwRjjlHWo0yU6Hnh\n",
"Ph4bdvD7f4HZHwFgb4wAAwAAAAAAQNf4AgwAAAAAAABde+gI5L/46veehsGO6KmYWsnBEbXzRxbr\n",
"RzPvH888/9sgF1izn9EZJK12W4wZH/shJnMbfohoI4AgFY/0xmgAxYoGtoxWPlpssAX1u7+0zLPu\n",
"mmQcUTnM/pnPjG3M+B3dPRVL9M6n6Z0lt8Uht963vd7bsbofIPYIAFfFCDAAAAAAAAB0jS/AAAAA\n",
"AAAA0LW3bt2BFk7JAOg8iidnzXLXtx6vO4qaVQTxJMp544JjG/MY5/q2qk9WRPAyVN4e1+2JSFrv\n",
"wfo2680/OQeEj+3aM/3kc2fO/fC7xBsBtPfdP/fVrnvLZwZnkvRqMWOgVUcpJufZtqbelv2w6ttS\n",
"fu/ZGlW9LZddM8mnYobWui1RNG8dar21zbhO9lf1Y1iuG7dNP/949rXqcGQzMpbqWAYT7YiiXV+s\n",
"x/J8Ldw4Dla5oFN2rFaanKSfxZefPtWRBABcEyPAAAAAAAAA0DW+AAMAAAAAAEDXHm4WyHHmx5Lo\n",
"rITWN4GqLm/te80WGe2Td6ZMs83DcjD3FltmyBxZUckfeffriDYCeGh7xSPxspxWf3hZzNhe9JkZ\n",
"J/myKe9MiMt++MLFtzgVvDPh7vW/J/ZMp+vHTT3SpLbtYRiG/5rZxQHgJhgBBgAAAAAAgK7xBRgA\n",
"AAAAAAC69jARyH/+l3z+oqNjJK82+rfG861gaWbBfF1NP2ojgt7YpdVmtIZrxiP/zHtEGwEg9bt+\n",
"6YeW0wbvNFueZ11qLJeuq63X+5HFakuti/atVP5RWfGw6LLSrJhypszs+KbH1hsHtPqRt722vtZJ\n",
"/JR+nrFnTlyPJTqTmFe193nvn2XSc8Tazr5otXg0ekHsEQBujxFgAAAAAAAA6BpfgAEAAAAAAKBr\n",
"Dx2BHEXjd6VoYb7WPUtiMBapX8XbssvVbatL1Pf3SeViDD/63tczTBwAGpjikQHR2edaaNmmd6a5\n",
"luX3qkMuSxZ64pkysnnFGKc7AukQPc6lOk4iqmj16nL40mjj7T5Lq3NBrbfWXZM34nmc3hd725Zt\n",
"qnLeNq3z+YeIPgLA3WAEGAAAAAAAALrGF2AAAAAAAADo2l1HIH/Tq8+bOjfNTnjyxRcPzshdNA7o\n",
"HcNcOxOjN0apym9pa7kuxru/P/b6GxgGDgB35DM+8ByRNGdOTF+ffziexHoVvxNtTjGy6OyLolMn\n",
"0Q8Zeaosr9r3Rvla1HEvtsQ+VcxQLyuXV8xz7E6iiql7iyUqpfd2+V6llmdIbdTVO+unomZm3Iv1\n",
"vv3wu0QgAeBeMAIMAAAAAAAAXbvLEWDpyC/L06n8/d38r9bWiKfYH2eio8KiI7tS0dFk+q9wMfGR\n",
"aBd/9vU38pcuAOjAODrsVvZ4ML63rtYPW8/HxMwf7u0bIXV0lEtHOfmXWX2LeYTRbCn5MVjshBpB\n",
"eA9Oxk/PymdvaWRcy/fUquOeDm2L95mRXwBwfxgBBgAAAAAAgK7xBRgAAAAAAAC6dpcRyH/u1e95\n",
"fiDvLIa3PorYE4V8ruP8b8MH5Kv689e+8tG2Du52SnX4y1/8+dffxLBuAHjBPv0DX7F4nLyK1Y28\n",
"D9W24nc6+jcvsdYPHQ7bp/yjxQBv6fQAMcMSK15r78ryIfHlc9xTr48z/dmk/Vu8pXufR6r6/4bY\n",
"IwDcNUaAAQAAAAAAoGt8AQYAAAAAAICu3VUEcow+KpfIn29ksRWLVDXsHYv0brVltkjVt9o6fpyI\n",
"IwAg6NNmsciXa/xo5fxosanefFkpUthjzNBfh5pFc/lKm7esZk7cMnum2i66r942bzGzpzrfbnEu\n",
"WrHPo4g2e+sY/ci7X8fnZwC4Y4wAAwAAAAAAQNf4AgwAAAAAAABdu3kE8je++txFB56M7+W8M0NO\n",
"dQVniBwGfxwy0o/Ulm8dn6ojmMvtfuL1NzNMGwBwFZ/6/ks80oo+qXifqZA7i8asHjUiuBdrdk5r\n",
"2XymTDV75nJZPhOiihmmPLOJXvNt3BQRFMs8MzK23j9zRssbXBPeSKg6V/bubno8/vR7RB8B4BEw\n",
"AgwAAAAAAABd4wswAAAAAAAAdO0uI5AjKwo5DGuzHq6PQD6cYjNJjjGIaMSxdpthiH8jOYtuijZ/\n",
"8vW3MCQbAHCX0ljkKDoL3pZZ87yiMxC2jAgeg1HC+QyH1jKrb7dlxvCS156Z+kozM3r32dune3CL\n",
"WRVL14Y92+byXbBK6Xpj1Hl0VBFqY9s/Q+wRAB4OI8AAAAAAAADQNb4AAwAAAAAAQNduFoH8Da8+\n",
"+zQMeWxvfSRxKQ55qSEWc/TOEjnVL2aItFrSM/g4I5iOZT/1+lsZfg0A6NKnvP/LZ58V5tG/4bxs\n",
"yZ6xMBYHVG1Ey98jFQGLzvjopd4rT6TQ2+Y9Hvvx47Wa1VRNNn7LJ5Kc5E924NBzTbSmeuaJLZb6\n",
"Uxv9JQIJAI+HEWAAAAAAAADoGl+AAQAAAAAAoGtXjUCOscc1l2hguyhkaZlsIxiLfFJj2R28/flp\n",
"Yo4AAEyRyJK9Z5K04oOt64guK0XRbpG0u+XskunH3PHjmvroq6KKlmj5Gp75EtNY8NMUFS7VUloT\n",
"Vzr/T6qgYwNvxLmFk7O2H33v6/lcDgAPihFgAAAAAAAA6BpfgAEAAAAAAKBrdxWBHHmikKm9Zoic\n",
"yp/qRzpH45E/8/rbGFYNAECF336OSHqiY2vL8nXp+miUr0UdPbBmRLRcI2Y41Z+226C8jtPN3/30\n",
"86iKNN6Cu3VHRPEae3Kt40XsEQD6wAgwAAAAAAAAdI0vwAAAAAAAANC1q0Qg/9m3P2vRyBgrtMYT\n",
"z6OKwdjizuVnyxwRybTEX/zFb2cYNQAAV/DJzpkjr8WKA7ZYdsUnW+zOO7Og9aGqHHk9udpS9dn1\n",
"tmO2eVqWmz19w9HhW50yJxEFzdft1nZhetC89R97/Q18dgeADjACDAAAAAAAAF3jCzAAAAAAAAB0\n",
"bbcI5K9/+4NTxd544ZNrtsVD8qpc3jtD5NZthmEehfzvfvGPMFQaAIA780nv3Fck8h7kUbQ0fnZZ\n",
"NiTLhsWySDvltpY1e9u8xSybMpq6eDEsspUqhTeISOMtqPdlbf2u/ZAHaVbg3J8lKza3JQWeAAAQ\n",
"lElEQVTrRfQRAPrCCDAAAAAAAAB0jS/AAAAAAAAA0LXdIpC/7u3PXEQg20Yh1+pb3zbaD9WO2va/\n",
"f/1HGR4NAEAHxoikFfmbT7JnzWRXX4d32dEVX/TFDO+ZPm7rZBTSmEWzFPHM3917PHrx93SfwKg1\n",
"O+f8/cjaFRHHvf4/5VR4x//s62/ksz0AdIgRYAAAAAAAAOgaX4ABAAAAAACga80jkGn0cdGYGAy9\n",
"XyyyPkaZL/sfX38Hw6ABAHih/rV3vmwRi7RYEbpbR+esKOHu/RYT+qUfQ61+RN1kNkj3jJbldWvr\n",
"430a663brlzQNwtjfMZQteX6Xlgzh+p6bX+OCCQAdIkRYAAAAAAAAOhasxFgv/bt3zmr6Mn53Vrp\n",
"AfPL8slrx6iwg7Mff/n1H+cvPQAAoOgTzyPChmFlRJXxsHXxnG/XqKxSW5vqyJbd48i1FqKjsW6h\n",
"NN4p7+X8XIiNxjqIN/e6I+byV21Hv9ltL+v/86+/if8XAIDOMQIMAAAAAAAAXeMLMAAAAAAAAHRt\n",
"twhkqiYOqX5erd/5gPzRX3n9XQxxBgAAzfy2t7/sPjJ0G4yxMPUg9tKytbrSct6Hvl8zlmg9JN73\n",
"+PWk/EmE+mQOdtmAFVtscRTsWKt6r9TW60fpOg/BVzWXtyi9tz9O9BEAXgxGgAEAAAAAAKBrfAEG\n",
"AAAAAACArm2KQP4zb396svHh/F9nbNHx3Zuqq1T/uPZ/fu9PMJwZAADcTBqLtOJ9LZepSOG2MNr1\n",
"2YG7UlxvTu25+uzrPUKemRlb0e/pen+m/buT99g/o+Wyv9fcAyKQAPByMAIMAAAAAAAAXeMLMAAA\n",
"AAAAAHStKgI5jz5mFU6DnNtFIXX9l9f/C3FHAADwAD7h7S+9i3yaNSugitXJiGD6GfIQ+yg2fv5M\n",
"Z0nMP5PeOrgZngVy9vr5pycZSV3Wunds0dqXcr899dulWsxoeYmELmuOHr+feP3N/L8DALxAjAAD\n",
"AAAAAABA1/gCDAAAAAAAAF2rikD+mrc/7TQM/hkfW8wQ+Vff+x6GKgMAgO78q2MsUkUKncusSKEV\n",
"M3w00VkgB1l+Of+gnj1z3TXimWqWxOg+P8a7fUr+uy+ijwDwsjECDAAAAAAAAF3jCzAAAAAAAAB0\n",
"zR2B/Kff+VSz4NOp/F2ajkAul/21976X4ckAAODF+vhXX9IsEWbN+KiW6XhftBbFN7+k3Y99lGZ8\n",
"VH2y6lCxvoPjGN06sqjinyo6mn+m32sWS3VM59bfLVX6J19/C/+PAQAvGCPAAAAAAAAA0DW+AAMA\n",
"AAAAAEDXihHIf+qd3xGa8dEThRyGYfjr730fQ5ABAACc/pUpFrkePawJKvoikNdXDlhGg4nLcjry\n",
"p9rSZUrlWrCih6Xy98J6p1TMtuUeEHsEAIwYAQYAAAAAAICu8QUYAAAAAAAAulaMQP7qdz5lNQLp\n",
"jUX+b+9+P0OPAQAAGvutr764ed5NRe5Ky+rbumhZ7615Z1O8BTuOuD6Dov4wvwyM1u5deSbOWCj1\n",
"v339rfz/BwBghhFgAAAAAAAA6BpfgAEAAAAAAKBrMgI5xh6LGyfDjf/3d3+AYcYAAAA39Fte/b7p\n",
"M1ztLJCPYozEpZ9H1TJPHfdM99H7sXs90nhN1h6cpn/b9vKniEACADKMAAMAAAAAAEDX+AIMAAAA\n",
"AAAAXZtFIP/Jdz55Mfb4SXxH9jfe/UGGFAMAADyANBap5fMCxkOTlxrqZ428l1kSlbxHpQ/CVqwv\n",
"Fl5sz9oXu9+q5Hotrft/yv7NWx39BaKPAIAVjAADAAAAAABA1/gCDAAAAAAAAF0rRiD/j3d/iGHE\n",
"AAAAHfm4V190fznDID0L5PLVkh3Xu7co5mn2+vmnJ9lH9ZH9fmeB9JS3Qpepnyb2CABwYAQYAAAA\n",
"AAAAujYbAQYAAICXaRwVFn8EvhqNtfx8WRqr5Cl/60+t1sgkPVpJTRSQr7HGbrXXYjTWHu34613W\n",
"/DOvv40RYACAIkaAAQAAAAAAoGt8AQYAAAAAAICuEYEEAACA9JtffeHdflDUD7z3hCUf9yH4o2gk\n",
"9D72ZH5MD1mosuZ4E30EAEQwAgwAAAAAAABd4wswAAAAAAAAdI0IJAAAANw+9tUXnIYhj7DNZ4E8\n",
"GbMfrrFnSbxeLNHqr7d1PVPm+rp8u0hbtZYzdy7XedZfG7FHAEAtRoABAAAAAACga3wBBgAAAAAA\n",
"gK4RgQQAAMAmYyxyLyqWeMr+HYbLX3ajnbl1HNHLG1u8V7P/7zgsXqQFn/8RdfylX/x2IpAAgCqM\n",
"AAMAAAAAAEDX+AIMAAAAAAAAXSMCCQAAgKb+pSQSacUXrWX3+Ql1Gc1TccRL6eVeXHNGS4v6f4DD\n",
"YexbsszYtsWMmV5EHwEAWzECDAAAAAAAAF3jCzAAAAAAAAB0jQgkAAAAdvcxO80UmUYJrXjhvUQP\n",
"LcXZKM+f21VU8f9v785WIykDMAxXzeEkuQkXxAVxQcVrEBURFUXF5cJccMUd8SYcZUTFQUVvIt3H\n",
"5YFdSaX7T3V1p3r78jxHMb0kmaPi9f+6qp5r+n35iy/82/dtXWeP/Th9z+wRgNE4AQYAAABANAEM\n",
"AAAAgGgmkAAAbNXTR+8e5AVo710Pu9fU9eIz2sdvtPPFzvN38Y/RzhFLd7Hsm5BWVVU1dbP0eWNM\n",
"TW9N3zeBBGA0ToABAAAAEE0AAwAAACCaCSQAADvXziL7ZoYl3WvZ87sjziZ6F1aJdbXwzdL7FX7+\n",
"tq6Wl00Pe59fL35v6LxxTEOnlX3P+2n6gekjAKNzAgwAAACAaAIYAAAAANFMIAEA2DtP3Xxn4SJ1\n",
"F7PErt55X134jZrFx+tm9tq6+7TN/DWrzknPXzfs9xnz9/55+qHZIwAb5QQYAAAAANEEMAAAAACi\n",
"mUACAHAQnrz59tmFaztD7E4P23nh2V0gC4+Vpod9d1rsPm/+Z5ceu4pld4EccofFVd/j4rOv/rf0\n",
"/fzSXSBbt6cfmUACsFFOgAEAAAAQTQADAAAAIJoJJAAAB+uJo7e2djE7ZIJ4lfcd29CJ52WvG+t5\n",
"fUwfAdgWJ8AAAAAAiOYEGAAAEdrTYKUPhL8x+/++pQ9iX/ZB87v4EPx1T5kt/xD89nvDXru6Ye9x\n",
"e/qxk18AbJUTYAAAAABEE8AAAAAAiGYCCQBApMeP3lz7QnfZHLHv+at++HzfbHFTH5Dfb/FvuWw0\n",
"ua5fpp+YQAKwVU6AAQAAABBNAAMAAAAgmgkkAADXxmNHb5xd/A6542PJpu4CudzlP6spfHU+o+x7\n",
"j7rnsXGZPQKwS06AAQAAABBNAAMAAAAgmgkkAADX2qNHrxcuiLvfGrLcKz2/NEy8/LUXp5XDXrmu\n",
"ofd2bOrCHSqbuv2ifdLie3Re9+vkU9NHAHbOCTAAAAAAoglgAAAAAEQzgQQAgJlHjl7b24vjs19s\n",
"Ni+sm9JksqDe9KCynwkkAPvACTAAAAAAoglgAAAAAEQzgQQAgB7zs8hlV8/FOyvOZoh9r112R8Yx\n",
"NYV3rgfd7bL82nm/TT4zewRgrzgBBgAAAEA0AQwAAACAaCaQAACwgoePX93JBXQ7PSxNFYfMEld5\n",
"3rp+n3xu+gjAXnICDAAAAIBoAhgAAAAA0UwgAQBgTe0cctldFdvHSzPGvtduerJY0v2ZdeGr+b+l\n",
"64/JFyaQAOwlJ8AAAAAAiCaAAQAAABDNBBIAAEb00PEra15gNwtfle74WH7laneBHHNiafYIwCFw\n",
"AgwAAACAaAIYAAAAANFMIAEAYMMePH65qary9HDoDHFbd4Ys3wWy+/j/7ky+NH0E4GA4AQYAAABA\n",
"NAEMAAAAgGgmkAAAsGUPHL9UuAjvfqtvfLj42PlssTtfrOe+s/juV5lT3pl8ZQIJwMFwAgwAAACA\n",
"aAIYAAAAANFMIAEAYIfuP36xcEF+PlLctqbuzCibxd/jzuRr00cADo4TYAAAAABEcwIMAAD2TOlU\n",
"2PwH1tc9/3Xh+fXlH4M/9EPw/zz9xqkvAA6aE2AAAAAARBPAAAAAAIhmAgkAAAfgvpMXLr1wr1ec\n",
"NK7KBBKAQ+cEGAAAAADRBDAAAAAAoplAAgDAAWmnkKW5Y925G2T7+LLn9fnr9FvTRwAiOAEGAAAA\n",
"QDQBDAAAAIBoJpAAAHDg7j15frSL+r9PvzN7BCCOE2AAAAAARBPAAAAAAIhmAgkAAIHuOXmuqary\n",
"HR/77hD5z+n3JpAAxHECDAAAAIBoAhgAAAAA0UwgAQAg2N0nzw664Dd9BCCZE2AAAAAARBPAAAAA\n",
"AIhmAgkAANfMXSfPNFVVVf+e/mD2CMC14AQYAAAAANEEMAAAAACimUACAAAAEM0JMAAAAACiCWAA\n",
"AAAARBPAAAAAAIgmgAEAAAAQTQADAAAAIJoABgAAAEA0AQwAAACAaAIYAAAAANEEMAAAAACiCWAA\n",
"AAAARBPAAAAAAIgmgAEAAAAQTQADAAAAIJoABgAAAEA0AQwAAACAaAIYAAAAANEEMAAAAACiCWAA\n",
"AAAARBPAAAAAAIgmgAEAAAAQTQADAAAAIJoABgAAAEA0AQwAAACAaAIYAAAAANEEMAAAAACiCWAA\n",
"AAAARBPAAAAAAIgmgAEAAAAQTQADAAAAIJoABgAAAEA0AQwAAACAaAIYAAAAANEEMAAAAACiCWAA\n",
"AAAARBPAAAAAAIgmgAEAAAAQTQADAAAAIJoABgAAAEA0AQwAAACAaAIYAAAAANEEMAAAAACiCWAA\n",
"AAAARBPAAAAAAIgmgAEAAAAQTQADAAAAIJoABgAAAEA0AQwAAACAaAIYAAAAANEEMAAAAACiCWAA\n",
"AAAARBPAAAAAAIgmgAEAAAAQTQADAAAAIJoABgAAAEA0AQwAAACAaAIYAAAAANEEMAAAAACiCWAA\n",
"AAAARBPAAAAAAIgmgAEAAAAQTQADAAAAIJoABgAAAEA0AQwAAACAaAIYAAAAANEEMAAAAACiCWAA\n",
"AAAARBPAAAAAAIgmgAEAAAAQTQADAAAAIJoABgAAAEA0AQwAAACAaAIYAAAAANEEMAAAAACiCWAA\n",
"AAAARBPAAAAAAIgmgAEAAAAQTQADAAAAIJoABgAAAEA0AQwAAACAaAIYAAAAANEEMAAAAACiCWAA\n",
"AAAARBPAAAAAAIgmgAEAAAAQTQADAAAAIJoABgAAAEA0AQwAAACAaAIYAAAAANEEMAAAAACiCWAA\n",
"AAAARBPAAAAAAIgmgAEAAAAQTQADAAAAIJoABgAAAEA0AQwAAACAaAIYAAAAANEEMAAAAACiCWAA\n",
"AAAARBPAAAAAAIgmgAEAAAAQTQADAAAAIJoABgAAAEA0AQwAAACAaAIYAAAAANEEMAAAAACiCWAA\n",
"AAAARBPAAAAAAIgmgAEAAAAQTQADAAAAIJoABgAAAEA0AQwAAACAaAIYAAAAANEEMAAAAACiCWAA\n",
"AAAARBPAAAAAAIgmgAEAAAAQTQADAAAAIJoABgAAAEA0AQwAAACAaAIYAAAAANEEMAAAAACiCWAA\n",
"AAAARBPAAAAAAIgmgAEAAAAQTQADAAAAIJoABgAAAEA0AQwAAACAaAIYAAAAANEEMAAAAACiCWAA\n",
"AAAARBPAAAAAAIgmgAEAAAAQTQADAAAAIJoABgAAAEA0AQwAAACAaAIYAAAAANEEMAAAAACiCWAA\n",
"AAAARBPAAAAAAIgmgAEAAAAQTQADAAAAINp/1zWnxVTqv2IAAAAASUVORK5CYII=\n",
"\" transform=\"translate(507, 47)\"/>\n",
"</g>\n",
"<defs>\n",
" <clipPath id=\"clip6804\">\n",
" <rect x=\"1891\" y=\"47\" width=\"73\" height=\"1457\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<g clip-path=\"url(#clip6804)\">\n",
"<image width=\"72\" height=\"1456\" xlink:href=\"data:image/png;base64,\n",
"iVBORw0KGgoAAAANSUhEUgAAAEgAAAWwCAYAAAD+FAeUAAAMbklEQVR4nO3dwY3sRhAFQY5Q/lsh\n",
"L6XfLQtUeSQPERYMEg9LNMmZ/f17/r4P/+uvtz/A1wkUBAoCBYHCnPvv25/h0ywoCBQECgIFgcJc\n",
"V7GVBQWBgkBBoCBQmHtcxTYWFAQKAgWBgqNGsKAgUBAoCBQECq5iwYKCQEGgIFAQKLiKBQsKAgWB\n",
"gkDBU41gQUGgIFAQKAgUHDWCBQWBgkBBoCBQcBULFhQECgIFgcI8bpitLCgIFAQKAgWBgqtYsKAg\n",
"UBAoCBQECvO4YbayoCBQECgIFBw1ggUFgYJAQaAgUHAVCxYUBAoCBYGCQGGe88/bn+HTLCgIFAQK\n",
"AgVPNYIFBYGCQEGgIFBwwyxYUBAoCBQECgIFV7FgQUGgIFAQKAgU5nf/vP0ZPs2CgkBBoCBQmOf4\n",
"I72xoCBQECgIFAQK83MVW1lQECgIFAQKAgVnsWBBQaAgUBAozOOpxsqCgkBBoCBQECi4YRYsKAgU\n",
"BAoCBYGCG2bBgoJAQaAgUHDUCBYUBAoCBYGCQMFRI1hQECgIFAQKAoX5nfP2Z/g0CwoCBYGCQMFR\n",
"I1hQECgIFAQKAgVXsWBBQaAgUBAoCBS8vBAsKAgUBAoChXk81VhZUBAoCBQECgIFR41gQUGgIFAQ\n",
"KAgUPPYJFhQECgIFgYJAwVUsWFAQKAgUBAq+zBIsKAgUBAoCBYGClxeCBQWBgkBBoCBQcMMsWFAQ\n",
"KAgUBAqOGsGCgkBBoCBQECi4igULCgIFgYJAQaDg5YVgQUGgIFAQKHiqESwoCBQECgIFgYIbZsGC\n",
"gkBBoCBQECi4igULCgIFgYJAwR/pYEFBoCBQECgIFOY59+3P8GkWFAQKAgWBgkBhnusstrGgIFAQ\n",
"KAgU3DALFhQECgIFgYJAwQ2zYEFBoCBQECgIFJzFggUFgYJAQaAgUHAVCxYUBAoCBYGCG2bBgoJA\n",
"QaAgUBAoOGoECwoCBYGCQEGgMI+L2MqCgkBBoCBQ8Ec6WFAQKAgUBAoChfGNzJ0FBYGCQEGgIFBw\n",
"FgsWFAQKAgWBgj/SwYKCQEGgIFAQKLiKBQsKAgWBgkBBoDCPL/usLCgIFAQKAoW55/f2Z/g0CwoC\n",
"BYGCQEGg4IZZsKAgUBAoCBQECvM4i60sKAgUBAoChbnXH+mNBQWBgkBBoCBQcNQIFhQECgIFgYJA\n",
"wVUsWFAQKAgUBAoCBXcUgwUFgYJAQaDgqBEsKAgUBAoCBYHCPEejjTpBoCBQECgIFNwwCxYUBAoC\n",
"BYGCG2bBgoJAQaAgUBAo+HmcYEFBoCBQECgIFOa5Gm3UCQIFgYJAwVEjWFAQKAgUBAoCBVexYEFB\n",
"oCBQECgIFLwnHdQJAgWBgkDBa8DBgoJAQaAgUBAoeE86WFAQKAgUBAoChblumK3UCQIFgYJAwQ2z\n",
"YEFBoCBQECgIFNwwCxYUBAoCBYGCQMENs6BOECgIFAQKAgV3FIMFBYGCQEGg4CuZwYKCQEGgIFAQ\n",
"KMz1G2YrdYJAQaAgUBAoeHkhWFAQKAgUBApumAULCgIFgYJAQaDg2XywoCBQECgIFAQK3pMO6gSB\n",
"gkBBoOCoESwoCBQECgIFgYLHPsGCgkBBoCBQECg4iwULCgIFgYJAwVONoE4QKAgUBAoCBUeNYEFB\n",
"oCBQECgIFDz2CRYUBAoCBYGCo0awoCBQECgIFAQKHvsEdYJAQaAgUBAoOIsFCwoCBYGCQEGg4CoW\n",
"LCgIFAQKAgV/pIMFBYGCQEGgIFDwhlmwoCBQECgIFAQKc/wDtpU6QaAgUBAouGEWLCgIFAQKAgWB\n",
"ghtmwYKCQEGgIFAQKDiLBQsKAgWBgkDBH+lgQUGgIFAQKAgUXMWCBQWBgkBBoCBQcBULFhQECgIF\n",
"gcIcf6RXFhQECgIFgYJAwVEjWFAQKAgUBAoCBVexYEFBoCBQECj4Ix0sKAgUBAoCBYGCq1iwoCBQ\n",
"ECgIFAQKrmLBgoJAQaAgUBAoeAUvWFAQKAgUBAqOGsGCgkBBoCBQECi4igULCgIFgYJAQaDgX9cE\n",
"dYJAQaAgUHDUCBYUBAoCBYGCQMGz+WBBQaAgUBAoCBScxYIFBYGCQEGg4KgRLCgIFAQKAgWBgqNG\n",
"sKAgUBAoCBQECq5iwYKCQEGgIFBwwyxYUBAoCBQECgKFuY+r2MaCgkBBoCBQECg4iwULCgIFgYJA\n",
"wVONYEFBoCBQECgIFObctz/Ct1lQECgIFAQKAgVnsWBBQaAgUBAoCBQ89gkWFAQKAgWBwhxvmK0s\n",
"KAgUBAoCBYGCG2bBgoJAQaAgUBAouGEWLCgIFAQKAgVHjWBBQaAgUBAoCBTmvP0JPs6CgkBBoCBQ\n",
"ECg4iwULCgIFgYJAwVONYEFBoCBQECgIFPwSZ7CgIFAQKAgUBArOYsGCgkBBoCBQ8BtmwYKCQEGg\n",
"IFAQKLhhFiwoCBQECgIFgYI3zIIFBYGCQEGg4MsswYKCQEGgIFAQKDhqBAsKAgWBgkBBoOAsFiwo\n",
"CBQECgIFgYKzWLCgIFAQKAgUfJklWFAQKAgUBAoChfFln50FBYGCQEGgIFBwFgsWFAQKAgWBgqNG\n",
"sKAgUBAoCBQECo4awYKCQEGgIFAQKDiLBQsKAgWBgkDBUSNYUBAoCBQECgIFvycdLCgIFAQKAgWB\n",
"gt+TDhYUBAoCBYGCo0awoCBQECgIFAQKcxw1VhYUBAoCBYGCQGGus9jKgoJAQaAgUPCGWbCgIFAQ\n",
"KAgUBAq+zBIsKAgUBAoCBYGClxeCBQWBgkBBoCBQ8PJCsKAgUBAoCBQ8mw8WFAQKAgWBgkDB/3oO\n",
"FhQECgIFgYJAwSt4wYKCQEGgIFBwwyxYUBAoCBQECgIFN8yCBQWBgkBBoCBQcBYLFhQECgIFgYLX\n",
"gIMFBYGCQEGgIFDwlcxgQUGgIFAQKAgU/DxOsKAgUBAoCBQcNYIFBYGCQEGgIFBwFQsWFAQKAgWB\n",
"gkDB/3oOFhQECgIFgYKjRrCgIFAQKAgUBAqezQcLCgIFgYJAQaDgLBYsKAgUBAoCBYGCq1iwoCBQ\n",
"ECgIFNwwCxYUBAoCBYGCQMFRI1hQECgIFAQKAgW/Jx0sKAgUBAoCBT+XHCwoCBQECgIFgYIbZsGC\n",
"gkBBoCBQECh4eSFYUBAoCBQECo4awYKCQEGgIFAQKMx9XMY2FhQECgIFgYJAwVksWFAQKAgUBAqe\n",
"agQLCgIFgYJAQaDgqBEsKAgUBAoCBYGCs1iwoCBQECgIFBw1ggUFgYJAQaAgUPDDAsGCgkBBoCBQ\n",
"ECjM8Z70yoKCQEGgIFAQKDiLBQsKAgWBgkDBUSNYUBAoCBQECgIFP/ofLCgIFAQKAgWBwlx3zFYW\n",
"FAQKAgWBgqNGsKAgUBAoCBQECr7tEywoCBQECgIFgYLfkw4WFAQKAgWBgqNGsKAgUBAoCBQECt6T\n",
"DhYUBAoCBYGCQMENs2BBQaAgUBAoOGoECwoCBYGCQEGg4CoWLCgIFAQKAgWBwhxfyVxZUBAoCBQE\n",
"Cp5qBAsKAgWBgkBBoOCGWbCgIFAQKAgUBAquYsGCgkBBoCBQECi4igULCgIFgYJAYe7jtzg3FhQE\n",
"CgIFgYJAwVEjWFAQKAgUBAoChTk/Z7GNBQWBgkBBoDDHDbOVBQWBgkBBoCBQcBULFhQECgIFgYJA\n",
"wcsLwYKCQEGgIFCY8/NsfmNBQaAgUBAoCBTcMAsWFAQKAgWBgkDBVSxYUBAoCBQECp5qBAsKAgWB\n",
"gkBBoDDn+fP2Z/g0CwoCBYGCQEGg4IZZsKAgUBAoCBTmOmqsLCgIFAQKAgWBgqNGsKAgUBAoCBQE\n",
"Cq5iwYKCQEGgIFAQKLijGCwoCBQECgIFR41gQUGgIFAQKAgUHDWCBQWBgkBBoCBQ8J3VYEFBoCBQ\n",
"ECjMuf5IbywoCBQECgIFgYKjRrCgIFAQKAgUBApzncVWFhQECgIFgYKjRrCgIFAQKAgUBAreMAsW\n",
"FAQKAgWBgkDBywvBgoJAQaAgUHDDLFhQECgIFAQKAgXP5oMFBYGCQEGgIFDw2CdYUBAoCBQECo4a\n",
"wYKCQEGgIFAQKHjsEywoCBQECgIFgYKzWLCgIFAQKAgUBAoe+wQLCgIFgYJAwVEjWFAQKAgUBAoC\n",
"BY99ggUFgYJAQaAgUJh73TDbWFAQKAgUBAqOGsGCgkBBoCBQECjMc+/bn+HTLCgIFAQKAgWBwjzO\n",
"YisLCgIFgYJAwRtmwYKCQEGgIFAQKDhqBAsKAgWBgkBBoODlhWBBQaAgUBAozOOG2cqCgkBBoCBQ\n",
"ECg4agQLCgIFgYJAQaDgsU+woCBQECgIFP4DPcHwb7pfSUoAAAAASUVORK5CYII=\n",
"\" transform=\"translate(1891, 47)\"/>\n",
"</g>\n",
"<g clip-path=\"url(#clip6801)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 1999.43, 1383.93)\" x=\"1999.43\" y=\"1383.93\">-</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6801)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2027.54, 1383.93)\" x=\"2027.54\" y=\"1383.93\">4</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6801)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 1999.43, 1198.67)\" x=\"1999.43\" y=\"1198.67\">-</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6801)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2027.54, 1198.67)\" x=\"2027.54\" y=\"1198.67\">3</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6801)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 1999.43, 1013.41)\" x=\"1999.43\" y=\"1013.41\">-</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6801)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2027.54, 1013.41)\" x=\"2027.54\" y=\"1013.41\">2</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6801)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 1999.43, 828.156)\" x=\"1999.43\" y=\"828.156\">-</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6801)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2027.54, 828.156)\" x=\"2027.54\" y=\"828.156\">1</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6801)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 1999.43, 642.898)\" x=\"1999.43\" y=\"642.898\">0</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6801)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 1999.43, 457.641)\" x=\"1999.43\" y=\"457.641\">1</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6801)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 1999.43, 272.384)\" x=\"1999.43\" y=\"272.384\">2</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip6801)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 1999.43, 87.1264)\" x=\"1999.43\" y=\"87.1264\">3</text>\n",
"</g>\n",
"<polyline clip-path=\"url(#clip6801)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1963.43,1503.47 1963.43,1370.28 1987.43,1370.28 1963.43,1370.28 1963.43,1185.02 1987.43,1185.02 1963.43,1185.02 1963.43,999.762 1987.43,999.762 1963.43,999.762 \n",
" 1963.43,814.504 1987.43,814.504 1963.43,814.504 1963.43,629.247 1987.43,629.247 1963.43,629.247 1963.43,443.99 1987.43,443.99 1963.43,443.99 1963.43,258.732 \n",
" 1987.43,258.732 1963.43,258.732 1963.43,73.4752 1987.43,73.4752 1963.43,73.4752 1963.43,47.2441 \n",
" \"/>\n",
"<g clip-path=\"url(#clip6801)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:66px; text-anchor:middle;\" transform=\"rotate(-90, 2021.03, 775.359)\" x=\"2021.03\" y=\"775.359\"></text>\n",
"</g>\n",
"</svg>\n"
]
},
"execution_count": 53,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"surface(xx, yy, V)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Application: Potential arising from a point charge and a single plate\n",
"\n",
"Now imagine we put a point source at $x = 2$, and a metal plate on $[-1,1]$. We know the potential on the plate must be constant, but we don't know what constant. This is equivalent to the following problem (see e.g. [\\[Chapman, Hewett & Trefethen 2015\\]](https://people.maths.ox.ac.uk/trefethen/chapman_hewett_trefethen.pdf)):\n",
"\\begin{align*}\n",
"v_{xx} + v_{yy} = 0 &\\qqfor \\hbox{off $[-1,1]$ and $2$} \\\\\n",
"v(z) \\sim \\log |z - 2| + O(1) &\\qqfor z \\rightarrow 2 \\\\\n",
"v(z) \\sim \\log|z| + o(1) &\\qqfor z \\rightarrow \\infty \\\\\n",
"v(x) = \\kappa &\\qqfor -1 < x < 1\n",
"\\end{align*}\n",
"where $\\kappa$ is an unknown constant. We write the solution as\n",
"$$\n",
"v(z) = {1 \\over \\pi} \\int_{-1}^1 u(t) \\log|t-z| \\dt + \\log|z-2|\n",
"$$\n",
"for a to-be-determined $u$. On $-1 < x < 1$ this satisfies\n",
"$$\n",
" {1 \\over \\pi} \\int_{-1}^1 u(t) \\log|t-x| \\dt = \\kappa - \\log(2-x)\n",
"$$\n",
"\n",
"We can calculate the solution numerically as follows:"
]
},
{
"cell_type": "code",
"execution_count": 133,
"metadata": {},
"outputs": [
{
"data": {
"image/svg+xml": [
"<?xml version=\"1.0\" encoding=\"utf-8\"?>\n",
"<svg xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\" width=\"600\" height=\"400\" viewBox=\"0 0 2400 1600\">\n",
"<defs>\n",
" <clipPath id=\"clip9900\">\n",
" <rect x=\"0\" y=\"0\" width=\"2000\" height=\"2000\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<defs>\n",
" <clipPath id=\"clip9901\">\n",
" <rect x=\"0\" y=\"0\" width=\"2400\" height=\"1600\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<polygon clip-path=\"url(#clip9901)\" points=\"\n",
"0,1600 2400,1600 2400,0 0,0 \n",
" \" fill=\"#ffffff\" fill-opacity=\"1\"/>\n",
"<defs>\n",
" <clipPath id=\"clip9902\">\n",
" <rect x=\"480\" y=\"0\" width=\"1681\" height=\"1600\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<polygon clip-path=\"url(#clip9901)\" points=\"\n",
"149.361,1503.47 2081.26,1503.47 2081.26,47.2441 149.361,47.2441 \n",
" \" fill=\"#ffffff\" fill-opacity=\"1\"/>\n",
"<defs>\n",
" <clipPath id=\"clip9903\">\n",
" <rect x=\"149\" y=\"47\" width=\"1933\" height=\"1457\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<polyline clip-path=\"url(#clip9903)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 204.037,1503.47 204.037,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9903)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 659.845,1503.47 659.845,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9903)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1115.65,1503.47 1115.65,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9903)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 1571.46,1503.47 1571.46,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9903)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 2027.27,1503.47 2027.27,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9903)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 149.361,1462.26 2081.26,1462.26 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9903)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 149.361,1118.68 2081.26,1118.68 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9903)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 149.361,775.102 2081.26,775.102 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9903)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 149.361,431.522 2081.26,431.522 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9903)\" style=\"stroke:#000000; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"\n",
" 149.361,87.9428 2081.26,87.9428 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9901)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,1503.47 2081.26,1503.47 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9901)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,1503.47 149.361,47.2441 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9901)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 204.037,1503.47 204.037,1481.63 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9901)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 659.845,1503.47 659.845,1481.63 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9901)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1115.65,1503.47 1115.65,1481.63 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9901)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1571.46,1503.47 1571.46,1481.63 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9901)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 2027.27,1503.47 2027.27,1481.63 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9901)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,1462.26 178.339,1462.26 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9901)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,1118.68 178.339,1118.68 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9901)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,775.102 178.339,775.102 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9901)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,431.522 178.339,431.522 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9901)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 149.361,87.9428 178.339,87.9428 \n",
" \"/>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:middle;\" transform=\"rotate(0, 204.037, 1557.47)\" x=\"204.037\" y=\"1557.47\">-4</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:middle;\" transform=\"rotate(0, 659.845, 1557.47)\" x=\"659.845\" y=\"1557.47\">-2</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:middle;\" transform=\"rotate(0, 1115.65, 1557.47)\" x=\"1115.65\" y=\"1557.47\">0</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:middle;\" transform=\"rotate(0, 1571.46, 1557.47)\" x=\"1571.46\" y=\"1557.47\">2</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:middle;\" transform=\"rotate(0, 2027.27, 1557.47)\" x=\"2027.27\" y=\"1557.47\">4</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:end;\" transform=\"rotate(0, 125.361, 1479.76)\" x=\"125.361\" y=\"1479.76\">-4</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:end;\" transform=\"rotate(0, 125.361, 1136.18)\" x=\"125.361\" y=\"1136.18\">-2</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:end;\" transform=\"rotate(0, 125.361, 792.602)\" x=\"125.361\" y=\"792.602\">0</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:end;\" transform=\"rotate(0, 125.361, 449.022)\" x=\"125.361\" y=\"449.022\">2</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:end;\" transform=\"rotate(0, 125.361, 105.443)\" x=\"125.361\" y=\"105.443\">4</text>\n",
"</g>\n",
"<polyline clip-path=\"url(#clip9903)\" style=\"stroke:#f3e258; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1248.46,1462.26 1246.92,1461.92 1244.42,1461.37 1241.91,1460.81 1239.96,1460.37 1239.4,1460.25 1236.9,1459.68 1234.39,1459.1 1231.88,1458.52 1231.71,1458.48 \n",
" 1229.38,1457.94 1226.87,1457.35 1224.36,1456.75 1223.7,1456.59 1221.86,1456.15 1219.35,1455.54 1216.84,1454.93 1215.9,1454.7 1214.33,1454.32 1211.83,1453.7 \n",
" 1209.32,1453.07 1208.3,1452.81 1206.81,1452.44 1204.31,1451.8 1201.8,1451.16 1200.89,1450.92 1199.29,1450.51 1196.79,1449.86 1194.28,1449.2 1193.65,1449.03 \n",
" 1191.77,1448.54 1189.27,1447.87 1186.76,1447.19 1186.57,1447.14 1184.25,1446.51 1181.74,1445.83 1179.65,1445.25 1179.24,1445.14 1176.73,1444.44 1174.22,1443.74 \n",
" 1172.87,1443.36 1171.72,1443.04 1169.21,1442.33 1166.7,1441.61 1166.23,1441.47 1164.2,1440.89 1161.69,1440.16 1159.72,1439.58 1159.18,1439.43 1156.67,1438.69 \n",
" 1154.17,1437.94 1153.34,1437.69 1151.66,1437.19 1149.15,1436.44 1147.07,1435.81 1146.65,1435.68 1144.14,1434.91 1141.63,1434.14 1140.91,1433.92 1139.13,1433.36 \n",
" 1136.62,1432.58 1134.86,1432.03 1134.11,1431.79 1131.61,1431 1129.1,1430.2 1128.91,1430.14 1126.59,1429.39 1124.08,1428.58 1123.06,1428.25 1121.58,1427.76 \n",
" 1119.07,1426.94 1117.3,1426.36 1116.56,1426.11 1114.06,1425.28 1111.63,1424.47 1111.55,1424.44 1109.04,1423.6 1106.54,1422.74 1106.05,1422.58 1104.03,1421.89 \n",
" 1101.52,1421.02 1100.55,1420.69 1099.02,1420.16 1096.51,1419.28 1095.13,1418.8 1094,1418.4 1091.49,1417.52 1089.79,1416.91 1088.99,1416.62 1086.48,1415.73 \n",
" 1084.52,1415.02 1083.97,1414.82 1081.47,1413.91 1079.32,1413.13 1078.96,1413 1076.45,1412.08 1074.19,1411.24 1073.95,1411.15 1071.44,1410.22 1069.13,1409.35 \n",
" 1068.93,1409.28 1066.42,1408.33 1064.13,1407.46 1063.92,1407.38 1061.41,1406.42 1059.2,1405.57 1058.9,1405.46 1056.4,1404.49 1054.33,1403.68 1053.89,1403.51 \n",
" 1051.38,1402.53 1049.52,1401.79 1048.88,1401.54 1046.37,1400.54 1044.76,1399.9 1043.86,1399.54 1041.36,1398.54 1040.06,1398.01 1038.85,1397.52 1036.34,1396.5 \n",
" 1035.41,1396.12 1033.83,1395.47 1031.33,1394.44 1030.82,1394.23 1028.82,1393.4 1026.31,1392.36 1026.28,1392.34 1023.81,1391.31 1021.79,1390.45 1021.3,1390.25 \n",
" 1018.79,1389.18 1017.34,1388.56 1016.29,1388.11 1013.78,1387.03 1012.95,1386.67 1011.27,1385.95 1008.77,1384.86 1008.6,1384.78 1006.26,1383.76 1004.3,1382.89 \n",
" 1003.75,1382.65 1001.24,1381.54 1000.04,1381 998.737,1380.42 996.231,1379.3 995.819,1379.11 993.724,1378.17 991.645,1377.22 991.217,1377.03 988.71,1375.89 \n",
" 987.512,1375.34 986.203,1374.73 983.696,1373.57 983.418,1373.45 981.189,1372.41 979.365,1371.56 978.682,1371.24 976.175,1370.06 975.35,1369.67 973.668,1368.87 \n",
" 971.372,1367.78 971.161,1367.68 968.654,1366.48 967.432,1365.89 966.147,1365.27 963.64,1364.05 963.527,1364 961.133,1362.83 959.659,1362.11 958.626,1361.6 \n",
" 956.119,1360.36 955.825,1360.22 953.613,1359.12 952.025,1358.33 951.106,1357.87 948.599,1356.61 948.259,1356.44 946.092,1355.34 944.526,1354.55 943.585,1354.07 \n",
" 941.078,1352.79 940.824,1352.66 938.571,1351.5 937.155,1350.77 936.064,1350.2 933.557,1348.9 933.516,1348.88 931.05,1347.59 929.909,1346.99 928.543,1346.27 \n",
" 926.331,1345.1 926.036,1344.94 923.529,1343.61 922.783,1343.21 921.022,1342.27 919.264,1341.32 918.515,1340.92 916.008,1339.56 915.773,1339.43 913.501,1338.19 \n",
" 912.311,1337.54 910.994,1336.82 908.876,1335.65 908.488,1335.44 905.981,1334.05 905.468,1333.76 903.474,1332.65 902.087,1331.87 900.967,1331.24 898.733,1329.98 \n",
" 898.46,1329.83 895.953,1328.41 895.404,1328.09 893.446,1326.97 892.101,1326.2 890.939,1325.54 888.824,1324.31 888.432,1324.09 885.925,1322.63 885.571,1322.42 \n",
" 883.418,1321.17 882.342,1320.53 880.911,1319.69 879.138,1318.64 878.404,1318.21 875.957,1316.75 875.897,1316.72 873.39,1315.22 872.801,1314.87 870.883,1313.71 \n",
" 869.667,1312.98 868.376,1312.19 866.556,1311.09 865.87,1310.67 863.467,1309.2 863.363,1309.13 860.856,1307.59 860.401,1307.31 858.349,1306.03 857.357,1305.42 \n",
" 855.842,1304.47 854.334,1303.53 853.335,1302.9 851.333,1301.64 850.828,1301.32 848.353,1299.75 848.321,1299.73 845.814,1298.13 845.394,1297.86 843.307,1296.52 \n",
" 842.456,1295.97 840.8,1294.9 839.538,1294.08 838.293,1293.27 836.64,1292.19 835.786,1291.63 833.761,1290.3 833.279,1289.98 830.903,1288.41 830.772,1288.32 \n",
" 828.265,1286.65 828.064,1286.52 825.758,1284.98 825.245,1284.63 823.252,1283.29 822.444,1282.74 820.745,1281.59 819.662,1280.85 818.238,1279.88 816.899,1278.96 \n",
" 815.731,1278.16 814.154,1277.07 813.224,1276.43 811.428,1275.18 810.717,1274.69 808.719,1273.29 808.21,1272.94 806.029,1271.4 805.703,1271.17 803.356,1269.51 \n",
" 803.196,1269.4 800.7,1267.62 800.689,1267.62 798.182,1265.82 798.062,1265.73 795.675,1264.01 795.441,1263.84 793.168,1262.19 792.837,1261.95 790.661,1260.37 \n",
" 790.25,1260.06 788.154,1258.52 787.679,1258.17 785.647,1256.67 785.125,1256.28 783.14,1254.81 782.588,1254.4 780.634,1252.93 780.066,1252.51 778.127,1251.04 \n",
" 777.561,1250.62 775.62,1249.14 775.071,1248.73 773.113,1247.23 772.598,1246.84 770.606,1245.31 770.139,1244.95 768.099,1243.37 767.697,1243.06 765.592,1241.42 \n",
" 765.27,1241.17 763.085,1239.46 762.858,1239.28 760.578,1237.48 760.461,1237.39 758.079,1235.5 758.071,1235.49 755.712,1233.61 755.564,1233.49 753.36,1231.72 \n",
" 753.057,1231.47 751.023,1229.83 750.55,1229.45 748.7,1227.94 748.043,1227.4 746.391,1226.05 745.536,1225.35 744.097,1224.16 743.029,1223.28 741.817,1222.27 \n",
" 740.522,1221.19 739.551,1220.38 738.016,1219.09 737.299,1218.49 735.509,1216.98 735.061,1216.6 733.002,1214.85 732.837,1214.71 730.626,1212.82 730.495,1212.71 \n",
" 728.429,1210.93 727.988,1210.55 726.245,1209.04 725.481,1208.38 724.075,1207.15 722.974,1206.19 721.919,1205.26 720.467,1203.98 719.775,1203.37 717.96,1201.76 \n",
" 717.645,1201.48 715.527,1199.59 715.453,1199.53 713.423,1197.7 712.946,1197.27 711.331,1195.81 710.439,1195 709.253,1193.93 707.932,1192.72 707.187,1192.04 \n",
" 705.425,1190.41 705.134,1190.15 703.093,1188.26 702.918,1188.09 701.065,1186.37 700.411,1185.75 699.049,1184.48 697.904,1183.4 697.046,1182.59 695.398,1181.02 \n",
" 695.055,1180.7 693.076,1178.81 692.891,1178.63 691.109,1176.92 690.384,1176.22 689.154,1175.03 687.877,1173.79 687.212,1173.14 685.37,1171.34 685.281,1171.25 \n",
" 683.362,1169.36 682.863,1168.87 681.455,1167.47 680.356,1166.37 679.56,1165.58 677.849,1163.86 677.676,1163.69 675.804,1161.8 675.342,1161.33 673.944,1159.91 \n",
" 672.835,1158.78 672.095,1158.02 670.328,1156.2 670.258,1156.13 668.432,1154.24 667.821,1153.61 666.618,1152.35 665.314,1150.99 664.814,1150.46 663.022,1148.57 \n",
" 662.807,1148.34 661.241,1146.68 660.3,1145.68 659.472,1144.79 657.793,1142.99 657.713,1142.9 655.966,1141.01 655.286,1140.28 654.229,1139.12 652.78,1137.54 \n",
" 652.504,1137.23 650.789,1135.34 650.273,1134.77 649.085,1133.46 647.766,1131.98 647.392,1131.57 645.71,1129.68 645.259,1129.17 644.039,1127.79 642.752,1126.32 \n",
" 642.378,1125.9 640.728,1124.01 640.245,1123.45 639.088,1122.12 637.738,1120.55 637.459,1120.23 635.841,1118.34 635.231,1117.62 634.233,1116.45 632.724,1114.66 \n",
" 632.635,1114.56 631.048,1112.67 630.217,1111.67 629.471,1110.78 627.905,1108.89 627.71,1108.65 626.349,1107 625.203,1105.6 624.803,1105.11 623.267,1103.22 \n",
" 622.696,1102.51 621.742,1101.33 620.227,1099.44 620.189,1099.39 618.721,1097.55 617.682,1096.24 617.226,1095.66 615.741,1093.77 615.175,1093.05 614.266,1091.88 \n",
" 612.801,1089.99 612.668,1089.82 611.346,1088.1 610.162,1086.55 609.901,1086.21 608.466,1084.32 607.655,1083.25 607.04,1082.43 605.625,1080.54 605.148,1079.9 \n",
" 604.219,1078.65 602.823,1076.76 602.641,1076.52 601.437,1074.87 600.134,1073.09 600.061,1072.99 598.694,1071.1 597.627,1069.61 597.337,1069.21 595.989,1067.32 \n",
" 595.12,1066.09 594.652,1065.43 593.323,1063.54 592.613,1062.52 592.005,1061.65 590.696,1059.76 590.106,1058.9 589.396,1057.87 588.106,1055.98 587.599,1055.23 \n",
" 586.826,1054.09 585.555,1052.2 585.092,1051.51 584.293,1050.31 583.041,1048.42 582.585,1047.73 581.798,1046.53 580.565,1044.64 580.078,1043.89 579.341,1042.75 \n",
" 578.126,1040.86 577.571,1039.99 576.921,1038.97 575.725,1037.08 575.064,1036.03 574.538,1035.19 573.361,1033.3 572.557,1032 572.193,1031.41 571.033,1029.52 \n",
" 570.05,1027.91 569.884,1027.63 568.743,1025.74 567.612,1023.85 567.544,1023.74 566.489,1021.96 565.376,1020.07 565.037,1019.49 564.272,1018.18 563.177,1016.29 \n",
" 562.53,1015.17 562.091,1014.4 561.014,1012.52 560.023,1010.76 559.947,1010.63 558.888,1008.74 557.838,1006.85 557.516,1006.26 556.797,1004.96 555.766,1003.07 \n",
" 555.009,1001.67 554.743,1001.18 553.729,999.287 552.725,997.398 552.502,996.975 551.729,995.508 550.742,993.618 549.995,992.175 549.764,991.729 548.795,989.839 \n",
" 547.835,987.949 547.488,987.261 546.883,986.06 545.941,984.17 545.008,982.28 544.981,982.226 544.082,980.39 543.167,978.501 542.474,977.058 542.26,976.611 \n",
" 541.361,974.721 540.472,972.832 539.967,971.749 539.591,970.942 538.719,969.052 537.856,967.163 537.46,966.288 537.001,965.273 536.155,963.383 535.319,961.494 \n",
" 534.953,960.66 534.49,959.604 533.67,957.714 532.86,955.825 532.446,954.85 532.058,953.935 531.264,952.045 530.479,950.155 529.939,948.84 529.704,948.266 \n",
" 528.936,946.376 528.177,944.486 527.432,942.61 527.427,942.597 526.685,940.707 525.952,938.817 525.228,936.928 524.926,936.129 524.512,935.038 523.805,933.148 \n",
" 523.106,931.259 522.419,929.373 522.417,929.369 521.735,927.479 521.062,925.59 520.398,923.7 519.912,922.296 519.743,921.81 519.095,919.92 518.457,918.031 \n",
" 517.827,916.141 517.405,914.857 517.206,914.251 516.592,912.362 515.988,910.472 515.392,908.582 514.898,906.992 514.805,906.693 514.225,904.803 513.655,902.913 \n",
" 513.093,901.024 512.54,899.134 512.391,898.617 511.995,897.244 511.458,895.355 510.93,893.465 510.41,891.575 509.9,889.685 509.884,889.626 509.396,887.796 \n",
" 508.902,885.906 508.416,884.016 507.939,882.127 507.47,880.237 507.377,879.854 507.009,878.347 506.557,876.458 506.113,874.568 505.678,872.678 505.252,870.789 \n",
" 504.87,869.063 504.834,868.899 504.423,867.009 504.021,865.12 503.628,863.23 503.243,861.34 502.867,859.45 502.499,857.561 502.363,856.845 502.139,855.671 \n",
" 501.788,853.781 501.445,851.892 501.11,850.002 500.784,848.112 500.466,846.223 500.157,844.333 499.856,842.443 499.856,842.441 499.563,840.554 499.279,838.664 \n",
" 499.002,836.774 498.735,834.885 498.475,832.995 498.225,831.105 497.982,829.215 497.748,827.326 497.522,825.436 497.349,823.929 497.305,823.546 497.096,821.657 \n",
" 496.894,819.767 496.702,817.877 496.517,815.988 496.341,814.098 496.174,812.208 496.015,810.319 495.864,808.429 495.721,806.539 495.587,804.65 495.461,802.76 \n",
" 495.344,800.87 495.235,798.98 495.134,797.091 495.041,795.201 494.957,793.311 494.881,791.422 494.842,790.333 494.814,789.532 494.754,787.642 494.703,785.753 \n",
" 494.66,783.863 494.626,781.973 494.6,780.084 494.582,778.194 494.572,776.304 494.571,774.415 494.578,772.525 494.594,770.635 494.618,768.746 494.65,766.856 \n",
" 494.69,764.966 494.739,763.076 494.796,761.187 494.842,759.867 494.862,759.297 494.936,757.407 495.017,755.518 495.108,753.628 495.206,751.738 495.313,749.849 \n",
" 495.428,747.959 495.552,746.069 495.684,744.18 495.824,742.29 495.973,740.4 496.13,738.511 496.295,736.621 496.469,734.731 496.651,732.841 496.841,730.952 \n",
" 497.04,729.062 497.247,727.172 497.349,726.278 497.462,725.283 497.686,723.393 497.917,721.503 498.158,719.614 498.406,717.724 498.663,715.834 498.929,713.945 \n",
" 499.203,712.055 499.485,710.165 499.776,708.276 499.856,707.767 500.074,706.386 500.381,704.496 500.696,702.606 501.02,700.717 501.352,698.827 501.693,696.937 \n",
" 502.043,695.048 502.363,693.356 502.4,693.158 502.766,691.268 503.14,689.379 503.522,687.489 503.913,685.599 504.313,683.71 504.721,681.82 504.87,681.143 \n",
" 505.137,679.93 505.561,678.041 505.994,676.151 506.435,674.261 506.885,672.371 507.344,670.482 507.377,670.348 507.81,668.592 508.285,666.702 508.768,664.813 \n",
" 509.261,662.923 509.761,661.033 509.884,660.579 510.27,659.144 510.787,657.254 511.313,655.364 511.847,653.475 512.391,651.585 512.391,651.584 512.941,649.695 \n",
" 513.501,647.806 514.069,645.916 514.646,644.026 514.898,643.213 515.231,642.136 515.824,640.247 516.426,638.357 517.037,636.467 517.405,635.347 517.657,634.578 \n",
" 518.284,632.688 518.92,630.798 519.565,628.909 519.912,627.908 520.219,627.019 520.88,625.129 521.551,623.24 522.23,621.35 522.419,620.832 522.918,619.46 \n",
" 523.613,617.571 524.318,615.681 524.926,614.074 525.032,613.791 525.754,611.901 526.484,610.012 527.224,608.122 527.432,607.595 527.972,606.232 528.728,604.343 \n",
" 529.493,602.453 529.939,601.364 530.267,600.563 531.049,598.674 531.84,596.784 532.446,595.353 532.641,594.894 533.449,593.005 534.266,591.115 534.953,589.543 \n",
" 535.092,589.225 535.926,587.336 536.77,585.446 537.46,583.915 537.622,583.556 538.482,581.666 539.352,579.777 539.967,578.454 540.231,577.887 541.117,575.997 \n",
" 542.014,574.108 542.474,573.146 542.918,572.218 543.832,570.328 544.754,568.439 544.981,567.979 545.685,566.549 546.625,564.659 547.488,562.942 547.575,562.77 \n",
" 548.532,560.88 549.499,558.99 549.995,558.029 550.474,557.101 551.459,555.211 552.453,553.321 552.502,553.228 553.454,551.431 554.466,549.542 555.009,548.536 \n",
" 555.486,547.652 556.515,545.762 557.516,543.942 557.554,543.873 558.601,541.983 559.657,540.093 560.023,539.444 560.722,538.204 561.796,536.314 562.53,535.035 \n",
" 562.88,534.424 563.972,532.535 565.037,530.71 565.074,530.645 566.185,528.755 567.305,526.866 567.544,526.465 568.433,524.976 569.572,523.086 570.05,522.297 \n",
" 570.719,521.197 571.875,519.307 572.557,518.201 573.041,517.417 574.216,515.527 575.064,514.174 575.401,513.638 576.594,511.748 577.571,510.212 577.797,509.858 \n",
" 579.009,507.969 580.078,506.314 580.231,506.079 581.461,504.189 582.585,502.477 582.702,502.3 583.951,500.41 585.092,498.697 585.21,498.52 586.478,496.631 \n",
" 587.599,494.973 587.756,494.741 589.043,492.851 590.106,491.303 590.341,490.962 591.647,489.072 592.613,487.684 592.963,487.182 594.288,485.292 595.12,484.115 \n",
" 595.624,483.403 596.968,481.513 597.627,480.593 598.323,479.623 599.687,477.734 600.134,477.118 601.06,475.844 602.444,473.954 602.641,473.687 603.837,472.065 \n",
" 605.148,470.3 605.241,470.175 606.653,468.285 607.655,466.954 608.076,466.396 609.508,464.506 610.162,463.649 610.951,462.616 612.403,460.727 612.668,460.383 \n",
" 613.865,458.837 615.175,457.155 615.338,456.947 616.82,455.057 617.682,453.965 618.313,453.168 619.815,451.278 620.189,450.81 621.327,449.388 622.696,447.69 \n",
" 622.85,447.499 624.383,445.609 625.203,444.604 625.926,443.719 627.48,441.83 627.71,441.551 629.043,439.94 630.217,438.53 630.617,438.05 632.201,436.161 \n",
" 632.724,435.541 633.796,434.271 635.231,432.581 635.401,432.381 637.017,430.492 637.738,429.653 638.643,428.602 640.245,426.752 640.28,426.712 641.927,424.822 \n",
" 642.752,423.881 643.585,422.933 645.253,421.043 645.259,421.037 646.933,419.153 647.766,418.221 648.623,417.264 650.273,415.431 650.324,415.374 652.035,413.484 \n",
" 652.78,412.667 653.758,411.595 655.286,409.928 655.491,409.705 657.236,407.815 657.793,407.214 658.991,405.926 660.3,404.524 660.758,404.036 662.536,402.146 \n",
" 662.807,401.859 664.324,400.257 665.314,399.216 666.125,398.367 667.821,396.597 667.936,396.477 669.759,394.587 670.328,394 671.593,392.698 672.835,391.425 \n",
" 673.439,390.808 675.296,388.918 675.342,388.872 677.165,387.029 677.849,386.34 679.045,385.139 680.356,383.829 680.937,383.249 682.841,381.36 682.863,381.338 \n",
" 684.756,379.47 685.37,378.868 686.684,377.58 687.877,376.417 688.623,375.691 690.384,373.985 690.575,373.801 692.538,371.911 692.891,371.573 694.514,370.022 \n",
" 695.398,369.18 696.501,368.132 697.904,366.805 698.501,366.242 700.411,364.448 700.514,364.352 702.539,362.463 702.918,362.11 704.576,360.573 705.425,359.789 \n",
" 706.626,358.683 707.932,357.485 708.688,356.794 710.439,355.199 710.763,354.904 712.851,353.014 712.946,352.929 714.952,351.125 715.453,350.676 717.066,349.235 \n",
" 717.96,348.439 719.193,347.345 720.467,346.219 721.333,345.456 722.974,344.014 723.486,343.566 725.481,341.825 725.652,341.676 727.832,339.787 727.988,339.652 \n",
" 730.025,337.897 730.495,337.494 732.232,336.007 733.002,335.351 734.453,334.117 735.509,333.223 736.687,332.228 738.016,331.11 738.935,330.338 740.522,329.011 \n",
" \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9903)\" style=\"stroke:#f3e258; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 740.522,329.011 741.197,328.448 743.029,326.927 743.474,326.559 745.536,324.856 745.764,324.669 748.043,322.8 748.069,322.779 750.388,320.89 750.55,320.758 \n",
" 752.721,319 753.057,318.729 755.069,317.11 755.564,316.714 757.432,315.221 758.071,314.712 759.81,313.331 760.578,312.723 762.203,311.441 763.085,310.747 \n",
" 764.611,309.552 765.592,308.785 767.033,307.662 768.099,306.835 769.472,305.772 770.606,304.897 771.926,303.882 773.113,302.972 774.395,301.993 775.62,301.06 \n",
" 776.88,300.103 778.127,299.16 779.381,298.213 780.634,297.272 781.898,296.324 783.14,295.396 784.432,294.434 785.647,293.531 786.981,292.544 788.154,291.679 \n",
" 789.547,290.655 790.661,289.838 792.13,288.765 793.168,288.008 794.729,286.875 795.675,286.19 797.346,284.986 798.182,284.384 799.979,283.096 800.689,282.588 \n",
" 802.63,281.206 803.196,280.804 805.298,279.317 805.703,279.031 807.984,277.427 808.21,277.268 810.687,275.537 810.717,275.517 813.224,273.776 813.409,273.647 \n",
" 815.731,272.045 816.149,271.758 818.238,270.325 818.907,269.868 820.745,268.616 821.683,267.978 823.252,266.917 824.479,266.089 825.758,265.228 827.293,264.199 \n",
" 828.265,263.549 830.127,262.309 830.772,261.881 832.98,260.42 833.279,260.222 835.786,258.573 835.853,258.53 838.293,256.935 838.745,256.64 840.8,255.305 \n",
" 841.658,254.751 843.307,253.686 844.591,252.861 845.814,252.076 847.544,250.971 848.321,250.476 850.518,249.082 850.828,248.885 853.335,247.304 853.514,247.192 \n",
" 855.842,245.732 856.53,245.302 858.349,244.169 859.569,243.413 860.856,242.616 862.629,241.523 863.363,241.072 865.711,239.633 865.87,239.536 868.376,238.01 \n",
" 868.816,237.743 870.883,236.492 871.944,235.854 873.39,234.984 875.094,233.964 875.897,233.484 878.268,232.074 878.404,231.994 880.911,230.511 881.466,230.185 \n",
" 883.418,229.038 884.688,228.295 885.925,227.573 887.934,226.405 888.432,226.116 890.939,224.669 891.205,224.516 893.446,223.229 894.501,222.626 895.953,221.798 \n",
" 897.822,220.736 898.46,220.375 900.967,218.961 901.17,218.847 903.474,217.554 904.544,216.957 905.981,216.156 907.944,215.067 908.488,214.766 910.994,213.384 \n",
" 911.371,213.178 913.501,212.01 914.826,211.288 916.008,210.644 918.309,209.398 918.515,209.286 921.022,207.936 921.82,207.508 923.529,206.594 925.36,205.619 \n",
" 926.036,205.26 928.543,203.933 928.93,203.729 931.05,202.614 932.53,201.839 933.557,201.303 936.064,199.999 936.159,199.95 938.571,198.703 939.821,198.06 \n",
" 941.078,197.414 943.513,196.17 943.585,196.134 946.092,194.86 947.238,194.281 948.599,193.594 950.994,192.391 951.106,192.335 953.613,191.084 954.785,190.501 \n",
" 956.119,189.84 958.609,188.612 958.626,188.603 961.133,187.374 962.469,186.722 963.64,186.151 966.147,184.936 966.363,184.832 968.654,183.728 970.294,182.943 \n",
" 971.161,182.528 973.668,181.334 974.261,181.053 976.175,180.147 978.266,179.163 978.682,178.968 981.189,177.795 982.309,177.273 983.696,176.629 986.203,175.47 \n",
" 986.391,175.384 988.71,174.318 990.514,173.494 991.217,173.173 993.724,172.035 994.677,171.604 996.231,170.904 998.737,169.779 998.882,169.715 1001.24,168.661 \n",
" 1003.13,167.825 1003.75,167.55 1006.26,166.445 1007.42,165.935 1008.77,165.347 1011.27,164.256 1011.76,164.046 1013.78,163.171 1016.14,162.156 1016.29,162.094 \n",
" 1018.79,161.022 1020.57,160.266 1021.3,159.957 1023.81,158.898 1025.05,158.377 1026.31,157.846 1028.82,156.801 1029.58,156.487 1031.33,155.761 1033.83,154.729 \n",
" 1034.16,154.597 1036.34,153.702 1038.79,152.708 1038.85,152.682 1041.36,151.668 1043.47,150.818 1043.86,150.661 1046.37,149.66 1048.21,148.928 1048.88,148.665 \n",
" 1051.38,147.676 1053.01,147.038 1053.89,146.694 1056.4,145.717 1057.87,145.149 1058.9,144.747 1061.41,143.783 1062.78,143.259 1063.92,142.825 1066.42,141.874 \n",
" 1067.76,141.369 1068.93,140.928 1071.44,139.988 1072.8,139.48 1073.95,139.055 1076.45,138.127 1077.91,137.59 1078.96,137.206 1081.47,136.29 1083.09,135.7 \n",
" 1083.97,135.381 1086.48,134.477 1088.34,133.811 1088.99,133.579 1091.49,132.687 1093.66,131.921 1094,131.802 1096.51,130.921 1099.02,130.047 1099.06,130.031 \n",
" 1101.52,129.179 1104.03,128.316 1104.54,128.142 1106.54,127.459 1109.04,126.608 1110.1,126.252 1111.55,125.763 1114.06,124.923 1115.74,124.362 1116.56,124.09 \n",
" 1119.07,123.262 1121.48,122.473 1121.58,122.44 1124.08,121.623 1126.59,120.812 1127.3,120.583 1129.1,120.006 1131.61,119.207 1133.23,118.693 1134.11,118.413 \n",
" 1136.62,117.624 1139.13,116.841 1139.25,116.803 1141.63,116.064 1144.14,115.292 1145.38,114.914 1146.65,114.526 1149.15,113.765 1151.61,113.024 1151.66,113.01 \n",
" 1154.17,112.26 1156.67,111.516 1157.97,111.134 1159.18,110.777 1161.69,110.044 1164.2,109.317 1164.45,109.245 1166.7,108.594 1169.21,107.877 1171.05,107.355 \n",
" 1171.72,107.166 1174.22,106.459 1176.73,105.759 1177.79,105.465 1179.24,105.063 1181.74,104.373 1184.25,103.689 1184.67,103.576 1186.76,103.009 1189.27,102.335 \n",
" 1191.7,101.686 1191.77,101.667 1194.28,101.003 1196.79,100.345 1198.9,99.7963 1199.29,99.6929 1201.8,99.0451 1204.31,98.4029 1206.26,97.9066 1206.81,97.7661 \n",
" 1209.32,97.134 1211.83,96.5075 1213.81,96.0169 1214.33,95.8864 1216.84,95.27 1219.35,94.6591 1221.55,94.1272 1221.86,94.0537 1224.36,93.4528 1226.87,92.8574 \n",
" 1229.38,92.2675 1229.5,92.2375 1231.88,91.682 1234.39,91.102 1236.9,90.5274 1237.69,90.3479 1239.4,89.9576 1241.91,89.3928 1244.42,88.8335 1246.12,88.4582 \n",
" \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9903)\" style=\"stroke:#f3e258; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1821.14,88.4582 1823.52,88.999 1826.03,89.5751 1828.54,90.1571 1829.35,90.3479 1831.04,90.7442 1833.55,91.3368 1836.06,91.9355 1837.31,92.2375 1838.56,92.5394 \n",
" 1841.07,93.1488 1843.58,93.7642 1845.04,94.1272 1846.08,94.3852 1848.59,95.0115 1851.1,95.6439 1852.56,96.0169 1853.6,96.2819 1856.11,96.9252 1858.62,97.5748 \n",
" 1859.89,97.9066 1861.13,98.2299 1863.63,98.8905 1866.14,99.5575 1867.03,99.7963 1868.65,100.23 1871.15,100.908 1873.66,101.592 1874,101.686 1876.17,102.282 \n",
" 1878.67,102.978 1880.81,103.576 1881.18,103.68 1883.69,104.387 1886.19,105.101 1887.46,105.465 1888.7,105.82 1891.21,106.546 1893.72,107.278 1893.98,107.355 \n",
" 1896.22,108.015 1898.73,108.758 1900.36,109.245 1901.24,109.508 1903.74,110.263 1906.25,111.025 1906.61,111.134 1908.76,111.793 1911.26,112.567 1912.73,113.024 \n",
" 1913.77,113.347 1916.28,114.133 1918.75,114.914 1918.78,114.926 1921.29,115.725 1923.8,116.53 1924.64,116.803 1926.31,117.341 1928.81,118.158 1930.44,118.693 \n",
" 1931.32,118.983 1933.83,119.813 1936.13,120.583 1936.33,120.65 1938.84,121.492 1941.35,122.342 1941.73,122.473 1943.85,123.198 1946.36,124.06 1947.23,124.362 \n",
" 1948.87,124.929 1951.38,125.804 1952.65,126.252 1953.88,126.686 1956.39,127.575 1957.98,128.142 1958.9,128.47 1961.4,129.371 1963.22,130.031 1963.91,130.28 \n",
" 1966.42,131.195 1968.39,131.921 1968.92,132.117 1971.43,133.045 1973.48,133.811 1973.94,133.981 1976.44,134.923 1978.5,135.7 1978.95,135.872 1981.46,136.828 \n",
" 1983.44,137.59 1983.97,137.791 1986.47,138.761 1988.32,139.48 1988.98,139.738 1991.49,140.721 1993.13,141.369 1993.99,141.712 1996.5,142.71 1997.87,143.259 \n",
" 1999.01,143.715 2001.51,144.727 2002.55,145.149 2004.02,145.746 2006.53,146.773 2007.17,147.038 2009.03,147.806 2011.54,148.847 2011.74,148.928 2014.05,149.895 \n",
" 2016.24,150.818 2016.56,150.951 2019.06,152.014 2020.69,152.708 2021.57,153.085 2024.08,154.163 2025.08,154.597 2026.58,155.248 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9903)\" style=\"stroke:#fabf26; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 2026.58,525.348 2026.23,524.976 2024.4,523.086 2024.08,522.749 2022.56,521.197 2021.57,520.19 2020.7,519.307 2019.06,517.671 2018.81,517.417 2016.9,515.527 \n",
" 2016.56,515.189 2014.97,513.638 2014.05,512.745 2013.02,511.748 2011.54,510.336 2011.04,509.858 2009.04,507.969 2009.03,507.963 2007.02,506.079 2006.53,505.624 \n",
" 2004.97,504.189 2004.02,503.317 2002.9,502.3 2001.51,501.043 2000.81,500.41 1999.01,498.801 1998.69,498.52 1996.55,496.631 1996.5,496.589 1994.38,494.741 \n",
" 1993.99,494.408 1992.18,492.851 1991.49,492.255 1989.96,490.962 1988.98,490.132 1987.72,489.072 1986.47,488.036 1985.44,487.182 1983.97,485.968 1983.14,485.292 \n",
" 1981.46,483.927 1980.81,483.403 1978.95,481.912 1978.45,481.513 1976.44,479.923 1976.06,479.623 1973.94,477.959 1973.65,477.734 1971.43,476.019 1971.2,475.844 \n",
" 1968.92,474.104 1968.73,473.954 1966.42,472.213 1966.22,472.065 1963.91,470.345 1963.68,470.175 1961.4,468.5 1961.11,468.285 1958.9,466.678 1958.51,466.396 \n",
" 1956.39,464.877 1955.87,464.506 1953.88,463.098 1953.2,462.616 1951.38,461.341 1950.49,460.727 1948.87,459.605 1947.75,458.837 1946.36,457.889 1944.97,456.947 \n",
" 1943.85,456.194 1942.16,455.057 1941.35,454.518 1939.3,453.168 1938.84,452.863 1936.41,451.278 1936.33,451.226 1933.83,449.609 1933.48,449.388 1931.32,448.011 \n",
" 1930.51,447.499 1928.81,446.431 1927.5,445.609 1926.31,444.869 1924.44,443.719 1923.8,443.325 1921.34,441.83 1921.29,441.8 1918.78,440.291 1918.2,439.94 \n",
" 1916.28,438.8 1915.01,438.05 1913.77,437.326 1911.77,436.161 1911.26,435.869 1908.76,434.428 1908.48,434.271 1906.25,433.004 1905.14,432.381 1903.74,431.595 \n",
" 1901.76,430.492 1901.24,430.203 1898.73,428.827 1898.32,428.602 1896.22,427.466 1894.82,426.712 1893.72,426.121 1891.27,424.822 1891.21,424.791 1888.7,423.476 \n",
" 1887.66,422.933 1886.19,422.176 1883.99,421.043 1883.69,420.891 1881.18,419.62 1880.25,419.153 1878.67,418.363 1876.46,417.264 1876.17,417.121 1873.66,415.893 \n",
" 1872.59,415.374 1871.15,414.679 1868.66,413.484 1868.65,413.479 1866.14,412.292 1864.65,411.595 1863.63,411.119 1861.13,409.96 1860.57,409.705 1858.62,408.813 \n",
" 1856.41,407.815 1856.11,407.681 1853.6,406.56 1852.17,405.926 1851.1,405.453 1848.59,404.359 1847.84,404.036 1846.08,403.277 1843.58,402.208 1843.43,402.146 \n",
" 1841.07,401.151 1838.92,400.257 1838.56,400.107 1836.06,399.075 1834.31,398.367 1833.55,398.056 1831.04,397.048 1829.61,396.477 1828.54,396.052 1826.03,395.068 \n",
" 1824.79,394.587 1823.52,394.096 1821.01,393.135 1819.86,392.698 1818.51,392.187 1816,391.249 1814.81,390.808 1813.49,390.323 1810.99,389.409 1809.63,388.918 \n",
" 1808.48,388.505 1805.97,387.613 1804.31,387.029 1803.47,386.732 1800.96,385.862 1798.85,385.139 1798.45,385.004 1795.94,384.155 1793.44,383.318 1793.23,383.249 \n",
" 1790.93,382.491 1788.42,381.675 1787.44,381.36 1785.92,380.869 1783.41,380.074 1781.48,379.47 1780.9,379.291 1778.4,378.516 1775.89,377.753 1775.32,377.58 \n",
" 1773.38,376.999 1770.88,376.256 1768.94,375.691 1768.37,375.523 1765.86,374.8 1763.35,374.087 1762.33,373.801 1760.85,373.384 1758.34,372.691 1755.83,372.009 \n",
" 1755.47,371.911 1753.33,371.335 1750.82,370.671 1748.32,370.022 1748.31,370.018 1745.81,369.374 1743.3,368.739 1740.86,368.132 1740.79,368.115 1738.29,367.499 \n",
" 1735.78,366.893 1733.27,366.298 1733.03,366.242 1730.76,365.71 1728.26,365.133 1725.75,364.565 1724.8,364.352 1723.24,364.006 1720.74,363.456 1718.23,362.916 \n",
" 1716.09,362.463 1715.72,362.385 1713.22,361.862 1710.71,361.349 1708.2,360.845 1706.82,360.573 1705.69,360.35 1703.19,359.864 1700.68,359.387 1698.17,358.919 \n",
" 1696.89,358.683 1695.67,358.46 1693.16,358.009 1690.65,357.568 1688.15,357.135 1686.12,356.794 1685.64,356.712 1683.13,356.296 1680.63,355.889 1678.12,355.492 \n",
" 1675.61,355.103 1674.3,354.904 1673.1,354.723 1670.6,354.35 1668.09,353.987 1665.58,353.632 1663.08,353.287 1661.05,353.014 1660.57,352.949 1658.06,352.62 \n",
" 1655.56,352.299 1653.05,351.986 1650.54,351.683 1648.04,351.387 1645.74,351.125 1645.53,351.101 1643.02,350.822 1640.51,350.551 1638.01,350.289 1635.5,350.035 \n",
" 1632.99,349.79 1630.49,349.553 1627.98,349.325 1626.96,349.235 1625.47,349.104 1622.97,348.891 1620.46,348.687 1617.95,348.49 1615.45,348.303 1612.94,348.123 \n",
" 1610.43,347.952 1607.92,347.788 1605.42,347.633 1602.91,347.486 1600.4,347.348 1600.36,347.345 1597.9,347.216 1595.39,347.093 1592.88,346.978 1590.38,346.872 \n",
" 1587.87,346.773 1585.36,346.682 1582.85,346.6 1580.35,346.525 1577.84,346.458 1575.33,346.4 1572.83,346.349 1570.32,346.307 1567.81,346.272 1565.31,346.246 \n",
" 1562.8,346.227 1560.29,346.217 1557.79,346.214 1555.28,346.219 1552.77,346.233 1550.26,346.254 1547.76,346.283 1545.25,346.32 1542.74,346.365 1540.24,346.418 \n",
" 1537.73,346.479 1535.22,346.548 1532.72,346.625 1530.21,346.71 1527.7,346.803 1525.2,346.904 1522.69,347.012 1520.18,347.129 1517.67,347.254 1515.95,347.345 \n",
" 1515.17,347.386 1512.66,347.527 1510.15,347.675 1507.65,347.831 1505.14,347.995 1502.63,348.167 1500.13,348.347 1497.62,348.535 1495.11,348.732 1492.6,348.936 \n",
" 1490.1,349.148 1489.11,349.235 1487.59,349.368 1485.08,349.596 1482.58,349.832 1480.07,350.075 1477.56,350.327 1475.06,350.588 1472.55,350.856 1470.11,351.125 \n",
" 1470.04,351.132 1467.54,351.416 1465.03,351.708 1462.52,352.008 1460.01,352.316 1457.51,352.633 1455,352.958 1454.57,353.014 1452.49,353.29 1449.99,353.63 \n",
" 1447.48,353.978 1444.97,354.335 1442.47,354.701 1441.1,354.904 1439.96,355.074 1437.45,355.455 1434.95,355.844 1432.44,356.242 1429.93,356.648 1429.05,356.794 \n",
" 1427.42,357.062 1424.92,357.483 1422.41,357.914 1419.9,358.353 1418.05,358.683 1417.4,358.8 1414.89,359.255 1412.38,359.718 1409.88,360.19 1407.88,360.573 \n",
" 1407.37,360.671 1404.86,361.159 1402.36,361.655 1399.85,362.161 1398.38,362.463 1397.34,362.675 1394.83,363.196 1392.33,363.727 1389.82,364.266 1389.43,364.352 \n",
" 1387.31,364.813 1384.81,365.369 1382.3,365.933 1380.95,366.242 1379.79,366.506 1377.29,367.087 1374.78,367.678 1372.88,368.132 1372.27,368.276 1369.76,368.883 \n",
" 1367.26,369.499 1365.16,370.022 1364.75,370.124 1362.24,370.756 1359.74,371.398 1357.76,371.911 1357.23,372.049 1354.72,372.708 1352.22,373.376 1350.64,373.801 \n",
" 1349.71,374.053 1347.2,374.738 1344.7,375.433 1343.78,375.691 1342.19,376.136 1339.68,376.848 1337.17,377.57 1337.14,377.58 1334.67,378.299 1332.16,379.038 \n",
" 1330.71,379.47 1329.65,379.786 1327.15,380.543 1324.64,381.309 1324.48,381.36 1322.13,382.084 1319.63,382.868 1318.42,383.249 1317.12,383.661 1314.61,384.464 \n",
" 1312.53,385.139 1312.11,385.275 1309.6,386.096 1307.09,386.926 1306.78,387.029 1304.58,387.765 1302.08,388.614 1301.19,388.918 1299.57,389.471 1297.06,390.338 \n",
" 1295.72,390.808 1294.56,391.215 1292.05,392.101 1290.38,392.698 1289.54,392.996 1287.04,393.901 1285.15,394.587 1284.53,394.815 1282.02,395.739 1280.04,396.477 \n",
" 1279.51,396.673 1277.01,397.615 1275.03,398.367 1274.5,398.568 1271.99,399.53 1270.12,400.257 1269.49,400.502 1266.98,401.483 1265.3,402.146 1264.47,402.475 \n",
" 1261.97,403.476 1260.58,404.036 1259.46,404.487 1256.95,405.507 1255.93,405.926 1254.45,406.538 1251.94,407.578 1251.37,407.815 1249.43,408.628 1246.92,409.689 \n",
" 1246.89,409.705 1244.42,410.759 1242.48,411.595 1241.91,411.839 1239.4,412.929 1238.14,413.484 1236.9,414.03 1234.39,415.14 1233.87,415.374 1231.88,416.261 \n",
" 1229.66,417.264 1229.38,417.391 1226.87,418.532 1225.51,419.153 1224.36,419.683 1221.86,420.845 1221.43,421.043 1219.35,422.016 1217.4,422.933 1216.84,423.198 \n",
" 1214.33,424.39 1213.43,424.822 1211.83,425.593 1209.51,426.712 1209.32,426.806 1206.81,428.029 1205.65,428.602 1204.31,429.262 1201.83,430.492 1201.8,430.507 \n",
" 1199.29,431.761 1198.06,432.381 1196.79,433.026 1194.34,434.271 1194.28,434.302 1191.77,435.588 1190.66,436.161 1189.27,436.884 1187.03,438.05 1186.76,438.191 \n",
" 1184.25,439.509 1183.44,439.94 1181.74,440.837 1179.88,441.83 1179.24,442.176 1176.73,443.526 1176.37,443.719 1174.22,444.886 1172.9,445.609 1171.72,446.256 \n",
" 1169.46,447.499 1169.21,447.638 1166.7,449.03 1166.06,449.388 1164.2,450.432 1162.69,451.278 1161.69,451.846 1159.36,453.168 1159.18,453.27 1156.67,454.704 \n",
" 1156.06,455.057 1154.17,456.149 1152.79,456.947 1151.66,457.605 1149.55,458.837 1149.15,459.072 1146.65,460.549 1146.35,460.727 1144.14,462.036 1143.17,462.616 \n",
" 1141.63,463.534 1140.02,464.506 1139.13,465.043 1136.89,466.396 1136.62,466.562 1134.11,468.092 1133.8,468.285 1131.61,469.633 1130.73,470.175 1129.1,471.183 \n",
" 1127.68,472.065 1126.59,472.745 1124.66,473.954 1124.08,474.316 1121.66,475.844 1121.58,475.898 1119.07,477.49 1118.69,477.734 1116.56,479.093 1115.74,479.623 \n",
" 1114.06,480.706 1112.81,481.513 1111.55,482.328 1109.9,483.403 1109.04,483.961 1107.01,485.292 1106.54,485.604 1104.14,487.182 1104.03,487.257 1101.52,488.92 \n",
" 1101.29,489.072 1099.02,490.593 1098.46,490.962 1096.51,492.275 1095.65,492.851 1094,493.967 1092.86,494.741 1091.49,495.669 1090.08,496.631 1088.99,497.38 \n",
" 1087.32,498.52 1086.48,499.1 1084.58,500.41 1083.97,500.83 1081.85,502.3 1081.47,502.569 1079.14,504.189 1078.96,504.317 1076.45,506.074 1076.45,506.079 \n",
" 1073.95,507.84 1073.76,507.969 1071.44,509.614 1071.09,509.858 1068.93,511.397 1068.44,511.748 1066.42,513.189 1065.8,513.638 1063.92,514.989 1063.17,515.527 \n",
" 1061.41,516.797 1060.55,517.417 1058.9,518.614 1057.95,519.307 1056.4,520.438 1055.36,521.197 1053.89,522.27 1052.78,523.086 1051.38,524.11 1050.21,524.976 \n",
" 1048.88,525.957 1047.65,526.866 1046.37,527.812 1045.1,528.755 1043.86,529.673 1042.56,530.645 1041.36,531.542 1040.03,532.535 1038.85,533.418 1037.51,534.424 \n",
" 1036.34,535.3 1035,536.314 1033.83,537.189 1032.49,538.204 1031.33,539.085 1030,540.093 1028.82,540.986 1027.51,541.983 1026.31,542.894 1025.03,543.873 \n",
" 1023.81,544.808 1022.56,545.762 1021.3,546.727 1020.09,547.652 1018.79,548.653 1017.64,549.542 1016.29,550.583 1015.19,551.431 1013.78,552.519 1012.74,553.321 \n",
" 1011.27,554.46 1010.3,555.211 1008.77,556.406 1007.87,557.101 1006.26,558.358 1005.45,558.99 1003.75,560.313 1003.03,560.88 1001.24,562.274 1000.61,562.77 \n",
" 998.737,564.239 998.203,564.659 996.231,566.209 995.799,566.549 993.724,568.183 993.4,568.439 991.217,570.161 991.006,570.328 988.71,572.144 988.616,572.218 \n",
" 986.232,574.108 986.203,574.131 983.852,575.997 983.696,576.121 981.477,577.887 981.189,578.116 979.106,579.777 978.682,580.115 976.74,581.666 976.175,582.118 \n",
" 974.378,583.556 973.668,584.124 972.021,585.446 971.161,586.135 969.668,587.336 968.654,588.15 967.32,589.225 966.147,590.169 964.976,591.115 963.64,592.192 \n",
" 962.636,593.005 961.133,594.219 960.301,594.894 958.626,596.251 957.971,596.784 956.119,598.287 955.646,598.674 953.613,600.328 953.325,600.563 951.106,602.374 \n",
" 951.009,602.453 948.699,604.343 948.599,604.425 946.395,606.232 946.092,606.481 944.096,608.122 943.585,608.542 941.803,610.012 941.078,610.609 939.515,611.901 \n",
" 938.571,612.682 937.234,613.791 936.064,614.761 934.96,615.681 933.557,616.847 932.692,617.571 931.05,618.941 930.431,619.46 928.543,621.042 928.178,621.35 \n",
" 926.036,623.151 925.932,623.24 923.695,625.129 923.529,625.269 921.467,627.019 921.022,627.395 919.247,628.909 918.515,629.531 917.037,630.798 916.008,631.678 \n",
" 914.836,632.688 913.501,633.836 912.645,634.578 910.994,636.006 910.465,636.467 908.488,638.188 908.295,638.357 906.138,640.247 905.981,640.384 903.993,642.136 \n",
" 903.474,642.594 901.861,644.026 900.967,644.819 899.742,645.916 898.46,647.062 897.636,647.806 895.953,649.322 895.543,649.695 893.465,651.585 893.446,651.603 \n",
" 891.405,653.475 890.939,653.901 889.359,655.364 888.432,656.223 887.33,657.254 885.925,658.569 885.317,659.144 883.418,660.941 883.322,661.033 881.346,662.923 \n",
" 880.911,663.339 879.389,664.813 878.404,665.767 877.451,666.702 875.897,668.229 875.532,668.592 873.634,670.482 873.39,670.725 871.759,672.371 870.883,673.258 \n",
" 869.905,674.261 868.376,675.833 868.072,676.151 866.263,678.041 865.87,678.453 864.479,679.93 863.363,681.122 862.718,681.82 860.981,683.71 860.856,683.846 \n",
" 859.272,685.599 858.349,686.628 857.587,687.489 855.929,689.379 855.842,689.478 854.299,691.268 853.335,692.399 852.696,693.158 851.121,695.048 850.828,695.402 \n",
" 849.576,696.937 848.321,698.498 848.06,698.827 846.574,700.717 845.814,701.697 845.118,702.606 843.693,704.496 843.307,705.015 842.3,706.386 840.939,708.276 \n",
" 840.8,708.47 839.61,710.165 838.314,712.055 838.293,712.086 837.052,713.945 835.823,715.834 835.786,715.892 834.628,717.724 833.469,719.614 833.279,719.929 \n",
" 832.344,721.503 831.255,723.393 830.772,724.253 830.201,725.283 829.183,727.172 828.265,728.942 828.204,729.062 827.258,730.952 826.352,732.841 825.758,734.129 \n",
" 825.483,734.731 824.65,736.621 823.857,738.511 823.252,740.027 823.103,740.4 822.385,742.29 821.707,744.18 821.069,746.069 820.745,747.093 820.47,747.959 \n",
" 819.908,749.849 819.387,751.738 818.907,753.628 818.469,755.518 818.238,756.611 818.068,757.407 817.706,759.297 817.385,761.187 817.105,763.076 816.866,764.966 \n",
" 816.668,766.856 816.511,768.746 816.394,770.635 816.319,772.525 816.284,774.415 816.289,776.304 816.335,778.194 816.422,780.084 816.55,781.973 816.718,783.863 \n",
" 816.927,785.753 817.177,787.642 817.469,789.532 817.801,791.422 818.174,793.311 818.238,793.602 818.584,795.201 819.034,797.091 819.525,798.98 820.057,800.87 \n",
" 820.63,802.76 820.745,803.114 821.239,804.65 821.887,806.539 822.577,808.429 823.252,810.179 823.306,810.319 824.069,812.208 824.873,814.098 825.717,815.988 \n",
" 825.758,816.077 826.595,817.877 827.512,819.767 828.265,821.26 828.467,821.657 829.457,823.546 830.485,825.436 830.772,825.951 831.548,827.326 832.647,829.215 \n",
" 833.279,830.274 833.782,831.105 834.951,832.995 835.786,834.311 836.155,834.885 837.393,836.774 838.293,838.117 838.664,838.664 839.969,840.554 840.8,841.733 \n",
" 841.307,842.443 842.677,844.333 843.307,845.189 844.079,846.223 845.512,848.112 845.814,848.507 846.976,850.002 848.321,851.706 848.47,851.892 849.995,853.781 \n",
" 850.828,854.802 851.548,855.671 853.13,857.561 853.335,857.804 854.741,859.45 855.842,860.727 856.379,861.34 858.043,863.23 858.349,863.575 859.736,865.12 \n",
" 860.856,866.358 861.453,867.009 863.195,868.899 863.363,869.08 864.963,870.789 865.87,871.751 866.755,872.678 868.376,874.37 868.569,874.568 870.408,876.458 \n",
" 870.883,876.945 872.269,878.347 873.39,879.479 874.151,880.237 875.897,881.974 876.053,882.127 877.977,884.016 878.404,884.436 879.921,885.906 880.911,886.865 \n",
" 881.884,887.796 883.418,889.263 883.865,889.685 885.863,891.575 885.925,891.634 887.881,893.465 888.432,893.98 889.916,895.355 890.939,896.303 891.966,897.244 \n",
" 893.446,898.602 894.032,899.134 895.953,900.881 896.112,901.024 898.208,902.913 898.46,903.141 900.318,904.803 900.967,905.384 902.442,906.693 903.474,907.61 \n",
" 904.578,908.582 905.981,909.82 906.726,910.472 908.488,912.015 908.886,912.362 910.994,914.197 911.057,914.251 913.241,916.141 913.501,916.367 915.435,918.031 \n",
" 916.008,918.525 917.639,919.92 918.515,920.672 919.852,921.81 921.022,922.809 922.074,923.7 923.529,924.935 924.305,925.59 926.036,927.053 926.544,927.479 \n",
" 928.543,929.161 928.791,929.369 931.046,931.259 931.05,931.262 933.309,933.148 933.557,933.356 935.579,935.038 936.064,935.442 937.856,936.928 938.571,937.522 \n",
" 940.139,938.817 941.078,939.595 942.428,940.707 943.585,941.662 944.723,942.597 946.092,943.723 947.023,944.486 948.599,945.779 949.329,946.376 951.106,947.83 \n",
" 951.641,948.266 953.613,949.875 953.957,950.155 956.119,951.916 956.279,952.045 958.606,953.935 958.626,953.952 960.937,955.825 961.133,955.984 963.273,957.714 \n",
" 963.64,958.011 965.614,959.604 966.147,960.034 967.96,961.494 968.654,962.053 970.309,963.383 971.161,964.068 972.663,965.273 973.668,966.079 975.022,967.163 \n",
" 976.175,968.086 977.385,969.052 978.682,970.089 979.752,970.942 981.189,972.088 982.124,972.832 983.696,974.082 984.501,974.721 986.203,976.073 986.882,976.611 \n",
" 988.71,978.06 989.268,978.501 991.217,980.042 991.658,980.39 993.724,982.02 994.053,982.28 996.231,983.994 996.454,984.17 998.737,985.964 998.859,986.06 \n",
" 1001.24,987.929 1001.27,987.949 1003.69,989.839 1003.75,989.89 1006.11,991.729 1006.26,991.846 1008.54,993.618 1008.77,993.797 1010.97,995.508 1011.27,995.743 \n",
" \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9903)\" style=\"stroke:#fabf26; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1011.27,995.743 1013.41,997.398 1013.78,997.684 1015.85,999.287 1016.29,999.62 1018.31,1001.18 1018.79,1001.55 1020.77,1003.07 1021.3,1003.48 1023.23,1004.96 \n",
" 1023.81,1005.4 1025.71,1006.85 1026.31,1007.31 1028.19,1008.74 1028.82,1009.22 1030.68,1010.63 1031.33,1011.12 1033.17,1012.52 1033.83,1013.01 1035.68,1014.4 \n",
" 1036.34,1014.9 1038.19,1016.29 1038.85,1016.79 1040.72,1018.18 1041.36,1018.66 1043.25,1020.07 1043.86,1020.53 1045.79,1021.96 1046.37,1022.39 1048.34,1023.85 \n",
" 1048.88,1024.25 1050.91,1025.74 1051.38,1026.09 1053.48,1027.63 1053.89,1027.93 1056.06,1029.52 1056.4,1029.77 1058.66,1031.41 1058.9,1031.59 1061.27,1033.3 \n",
" 1061.41,1033.41 1063.89,1035.19 1063.92,1035.21 1066.42,1037.01 1066.52,1037.08 1068.93,1038.81 1069.16,1038.97 1071.44,1040.59 1071.82,1040.86 1073.95,1042.36 \n",
" 1074.49,1042.75 1076.45,1044.13 1077.18,1044.64 1078.96,1045.89 1079.88,1046.53 1081.47,1047.63 1082.6,1048.42 1083.97,1049.37 1085.33,1050.31 1086.48,1051.1 \n",
" 1088.07,1052.2 1088.99,1052.82 1090.84,1054.09 1091.49,1054.53 1093.62,1055.98 1094,1056.24 1096.42,1057.87 1096.51,1057.93 1099.02,1059.61 1099.23,1059.76 \n",
" 1101.52,1061.28 1102.07,1061.65 1104.03,1062.95 1104.92,1063.54 1106.54,1064.6 1107.8,1065.43 1109.04,1066.24 1110.69,1067.32 1111.55,1067.88 1113.6,1069.21 \n",
" 1114.06,1069.5 1116.54,1071.1 1116.56,1071.11 1119.07,1072.71 1119.5,1072.99 1121.58,1074.31 1122.48,1074.87 1124.08,1075.89 1125.48,1076.76 1126.59,1077.46 \n",
" 1128.51,1078.65 1129.1,1079.02 1131.56,1080.54 1131.61,1080.57 1134.11,1082.11 1134.64,1082.43 1136.62,1083.64 1137.74,1084.32 1139.13,1085.16 1140.87,1086.21 \n",
" 1141.63,1086.67 1144.03,1088.1 1144.14,1088.17 1146.65,1089.65 1147.22,1089.99 1149.15,1091.13 1150.43,1091.88 1151.66,1092.6 1153.68,1093.77 1154.17,1094.05 \n",
" 1156.67,1095.5 1156.96,1095.66 1159.18,1096.93 1160.27,1097.55 1161.69,1098.36 1163.61,1099.44 1164.2,1099.77 1166.7,1101.17 1166.98,1101.33 1169.21,1102.57 \n",
" 1170.39,1103.22 1171.72,1103.95 1173.84,1105.11 1174.22,1105.32 1176.73,1106.68 1177.33,1107 1179.24,1108.03 1180.85,1108.89 1181.74,1109.37 1184.25,1110.69 \n",
" 1184.41,1110.78 1186.76,1112.01 1188.01,1112.67 1189.27,1113.32 1191.66,1114.56 1191.77,1114.62 1194.28,1115.9 1195.35,1116.45 1196.79,1117.18 1199.08,1118.34 \n",
" 1199.29,1118.44 1201.8,1119.7 1202.87,1120.23 1204.31,1120.94 1206.7,1122.12 1206.81,1122.17 1209.32,1123.4 1210.58,1124.01 1211.83,1124.61 1214.33,1125.81 \n",
" 1214.51,1125.9 1216.84,1127.01 1218.5,1127.79 1219.35,1128.19 1221.86,1129.36 1222.54,1129.68 1224.36,1130.52 1226.64,1131.57 1226.87,1131.67 1229.38,1132.81 \n",
" 1230.8,1133.46 1231.88,1133.94 1234.39,1135.06 1235.02,1135.34 1236.9,1136.17 1239.31,1137.23 1239.4,1137.27 1241.91,1138.36 1243.67,1139.12 1244.42,1139.44 \n",
" 1246.92,1140.51 1248.1,1141.01 1249.43,1141.58 1251.94,1142.63 1252.61,1142.9 1254.45,1143.67 1256.95,1144.7 1257.19,1144.79 1259.46,1145.72 1261.86,1146.68 \n",
" 1261.97,1146.73 1264.47,1147.73 1266.61,1148.57 1266.98,1148.72 1269.49,1149.7 1271.45,1150.46 1271.99,1150.67 1274.5,1151.64 1276.39,1152.35 1277.01,1152.59 \n",
" 1279.51,1153.53 1281.42,1154.24 1282.02,1154.46 1284.53,1155.39 1286.57,1156.13 1287.04,1156.3 1289.54,1157.21 1291.82,1158.02 1292.05,1158.1 1294.56,1158.99 \n",
" 1297.06,1159.86 1297.2,1159.91 1299.57,1160.73 1302.08,1161.59 1302.7,1161.8 1304.58,1162.44 1307.09,1163.28 1308.34,1163.69 1309.6,1164.11 1312.11,1164.93 \n",
" 1314.12,1165.58 1314.61,1165.74 1317.12,1166.54 1319.63,1167.34 1320.05,1167.47 1322.13,1168.12 1324.64,1168.89 1326.16,1169.36 1327.15,1169.66 1329.65,1170.42 \n",
" 1332.16,1171.16 1332.44,1171.25 1334.67,1171.9 1337.17,1172.63 1338.93,1173.14 1339.68,1173.36 1342.19,1174.07 1344.7,1174.77 1345.63,1175.03 1347.2,1175.47 \n",
" 1349.71,1176.15 1352.22,1176.83 1352.56,1176.92 1354.72,1177.5 1357.23,1178.15 1359.74,1178.8 1359.75,1178.81 1362.24,1179.45 1364.75,1180.08 1367.23,1180.7 \n",
" 1367.26,1180.7 1369.76,1181.32 1372.27,1181.93 1374.78,1182.53 1375.04,1182.59 1377.29,1183.12 1379.79,1183.7 1382.3,1184.27 1383.22,1184.48 1384.81,1184.83 \n",
" 1387.31,1185.39 1389.82,1185.94 1391.82,1186.37 1392.33,1186.48 1394.83,1187.01 1397.34,1187.53 1399.85,1188.04 1400.91,1188.26 1402.36,1188.55 1404.86,1189.04 \n",
" 1407.37,1189.53 1409.88,1190.01 1410.58,1190.15 1412.38,1190.48 1414.89,1190.95 1417.4,1191.4 1419.9,1191.85 1420.96,1192.04 1422.41,1192.29 1424.92,1192.72 \n",
" 1427.42,1193.14 1429.93,1193.56 1432.22,1193.93 1432.44,1193.96 1434.95,1194.36 1437.45,1194.75 1439.96,1195.13 1442.47,1195.5 1444.61,1195.81 1444.97,1195.87 \n",
" 1447.48,1196.22 1449.99,1196.57 1452.49,1196.91 1455,1197.25 1457.51,1197.57 1458.57,1197.7 1460.01,1197.89 1462.52,1198.2 1465.03,1198.5 1467.54,1198.79 \n",
" 1470.04,1199.07 1472.55,1199.35 1474.86,1199.59 1475.06,1199.62 1477.56,1199.88 1480.07,1200.13 1482.58,1200.37 1485.08,1200.61 1487.59,1200.84 1490.1,1201.06 \n",
" 1492.6,1201.27 1495.11,1201.47 1495.27,1201.48 1497.62,1201.67 1500.13,1201.86 1502.63,1202.04 1505.14,1202.21 1507.65,1202.37 1510.15,1202.53 1512.66,1202.68 \n",
" 1515.17,1202.82 1517.67,1202.95 1520.18,1203.07 1522.69,1203.19 1525.2,1203.3 1527.05,1203.37 1527.7,1203.4 1530.21,1203.49 1532.72,1203.58 1535.22,1203.65 \n",
" 1537.73,1203.72 1540.24,1203.78 1542.74,1203.84 1545.25,1203.88 1547.76,1203.92 1550.26,1203.95 1552.77,1203.97 1555.28,1203.98 1557.79,1203.99 1560.29,1203.99 \n",
" 1562.8,1203.98 1565.31,1203.96 1567.81,1203.93 1570.32,1203.9 1572.83,1203.85 1575.33,1203.8 1577.84,1203.74 1580.35,1203.68 1582.85,1203.6 1585.36,1203.52 \n",
" 1587.87,1203.43 1589.3,1203.37 1590.38,1203.33 1592.88,1203.22 1595.39,1203.11 1597.9,1202.99 1600.4,1202.86 1602.91,1202.72 1605.42,1202.57 1607.92,1202.42 \n",
" 1610.43,1202.25 1612.94,1202.08 1615.45,1201.9 1617.95,1201.71 1620.46,1201.52 1620.85,1201.48 1622.97,1201.31 1625.47,1201.1 1627.98,1200.88 1630.49,1200.65 \n",
" 1632.99,1200.41 1635.5,1200.17 1638.01,1199.91 1640.51,1199.65 1641.05,1199.59 1643.02,1199.38 1645.53,1199.1 1648.04,1198.82 1650.54,1198.52 1653.05,1198.22 \n",
" 1655.56,1197.9 1657.12,1197.7 1658.06,1197.58 1660.57,1197.25 1663.08,1196.92 1665.58,1196.57 1668.09,1196.22 1670.6,1195.85 1670.85,1195.81 1673.1,1195.48 \n",
" 1675.61,1195.1 1678.12,1194.71 1680.63,1194.31 1683.02,1193.93 1683.13,1193.91 1685.64,1193.49 1688.15,1193.07 1690.65,1192.64 1693.16,1192.19 1694.04,1192.04 \n",
" 1695.67,1191.74 1698.17,1191.28 1700.68,1190.82 1703.19,1190.34 1704.18,1190.15 1705.69,1189.85 1708.2,1189.36 1710.71,1188.85 1713.22,1188.34 1713.62,1188.26 \n",
" 1715.72,1187.82 1718.23,1187.29 1720.74,1186.75 1722.47,1186.37 1723.24,1186.2 1725.75,1185.64 1728.26,1185.07 1730.76,1184.49 1730.83,1184.48 1733.27,1183.91 \n",
" 1735.78,1183.31 1738.29,1182.7 1738.76,1182.59 1740.79,1182.09 1743.3,1181.46 1745.81,1180.83 1746.32,1180.7 1748.31,1180.19 1750.82,1179.53 1753.33,1178.87 \n",
" 1753.55,1178.81 1755.83,1178.2 1758.34,1177.51 1760.49,1176.92 1760.85,1176.82 1763.35,1176.12 1765.86,1175.4 1767.16,1175.03 1768.37,1174.68 1770.88,1173.95 \n",
" 1773.38,1173.2 1773.6,1173.14 1775.89,1172.45 1778.4,1171.69 1779.82,1171.25 1780.9,1170.91 1783.41,1170.13 1785.84,1169.36 1785.92,1169.33 1788.42,1168.53 \n",
" 1790.93,1167.71 1791.67,1167.47 1793.44,1166.89 1795.94,1166.05 1797.33,1165.58 1798.45,1165.2 1800.96,1164.34 1802.83,1163.69 1803.47,1163.47 1805.97,1162.59 \n",
" 1808.19,1161.8 1808.48,1161.7 1810.99,1160.79 1813.41,1159.91 1813.49,1159.88 1816,1158.95 1818.49,1158.02 1818.51,1158.02 1821.01,1157.07 1823.46,1156.13 \n",
" 1823.52,1156.11 1826.03,1155.14 1828.3,1154.24 1828.54,1154.15 1831.04,1153.16 1833.04,1152.35 1833.55,1152.15 1836.06,1151.13 1837.67,1150.46 1838.56,1150.1 \n",
" 1841.07,1149.05 1842.21,1148.57 1843.58,1148 1846.08,1146.93 1846.65,1146.68 1848.59,1145.84 1851,1144.79 1851.1,1144.75 1853.6,1143.64 1855.26,1142.9 \n",
" 1856.11,1142.52 1858.62,1141.39 1859.44,1141.01 1861.13,1140.24 1863.55,1139.12 1863.63,1139.08 1866.14,1137.91 1867.57,1137.23 1868.65,1136.72 1871.15,1135.52 \n",
" 1871.52,1135.34 1873.66,1134.31 1875.41,1133.46 1876.17,1133.08 1878.67,1131.84 1879.22,1131.57 1881.18,1130.58 1882.97,1129.68 1883.69,1129.31 1886.19,1128.03 \n",
" 1886.66,1127.79 1888.7,1126.73 1890.29,1125.9 1891.21,1125.41 1893.72,1124.08 1893.86,1124.01 1896.22,1122.74 1897.37,1122.12 1898.73,1121.38 1900.82,1120.23 \n",
" 1901.24,1120 1903.74,1118.61 1904.23,1118.34 1906.25,1117.2 1907.58,1116.45 1908.76,1115.78 1910.88,1114.56 1911.26,1114.33 1913.77,1112.88 1914.13,1112.67 \n",
" 1916.28,1111.4 1917.33,1110.78 1918.78,1109.91 1920.49,1108.89 1921.29,1108.4 1923.6,1107 1923.8,1106.88 1926.31,1105.33 1926.67,1105.11 1928.81,1103.77 \n",
" 1929.69,1103.22 1931.32,1102.19 1932.68,1101.33 1933.83,1100.59 1935.62,1099.44 1936.33,1098.98 1938.52,1097.55 1938.84,1097.34 1941.35,1095.68 1941.38,1095.66 \n",
" 1943.85,1094.01 1944.21,1093.77 1946.36,1092.31 1947,1091.88 1948.87,1090.6 1949.75,1089.99 1951.38,1088.86 1952.46,1088.1 1953.88,1087.11 1955.14,1086.21 \n",
" 1956.39,1085.33 1957.79,1084.32 1958.9,1083.53 1960.4,1082.43 1961.4,1081.7 1962.98,1080.54 1963.91,1079.86 1965.53,1078.65 1966.42,1077.99 1968.05,1076.76 \n",
" 1968.92,1076.1 1970.53,1074.87 1971.43,1074.18 1972.98,1072.99 1973.94,1072.24 1975.41,1071.1 1976.44,1070.28 1977.8,1069.21 1978.95,1068.29 1980.17,1067.32 \n",
" 1981.46,1066.28 1982.51,1065.43 1983.97,1064.24 1984.82,1063.54 1986.47,1062.17 1987.1,1061.65 1988.98,1060.07 1989.35,1059.76 1991.49,1057.95 1991.58,1057.87 \n",
" 1993.78,1055.98 1993.99,1055.8 1995.96,1054.09 1996.5,1053.61 1998.11,1052.2 1999.01,1051.4 2000.23,1050.31 2001.51,1049.16 2002.34,1048.42 2004.02,1046.89 \n",
" 2004.41,1046.53 2006.46,1044.64 2006.53,1044.58 2008.49,1042.75 2009.03,1042.24 2010.5,1040.86 2011.54,1039.87 2012.48,1038.97 2014.05,1037.46 2014.44,1037.08 \n",
" 2016.38,1035.19 2016.56,1035.01 2018.29,1033.3 2019.06,1032.53 2020.18,1031.41 2021.57,1030.01 2022.05,1029.52 2023.9,1027.63 2024.08,1027.46 2025.73,1025.74 \n",
" 2026.58,1024.86 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9903)\" style=\"stroke:#f3e258; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 2026.58,1394.96 2024.08,1396.04 2023.89,1396.12 2021.57,1397.12 2019.48,1398.01 2019.06,1398.19 2016.56,1399.25 2015.02,1399.9 2014.05,1400.31 2011.54,1401.36 \n",
" 2010.5,1401.79 2009.03,1402.4 2006.53,1403.43 2005.92,1403.68 2004.02,1404.46 2001.51,1405.48 2001.28,1405.57 1999.01,1406.49 1996.58,1407.46 1996.5,1407.49 \n",
" 1993.99,1408.49 1991.82,1409.35 1991.49,1409.48 1988.98,1410.47 1987,1411.24 1986.47,1411.44 1983.97,1412.41 1982.1,1413.13 1981.46,1413.38 1978.95,1414.33 \n",
" 1977.14,1415.02 1976.44,1415.28 1973.94,1416.22 1972.1,1416.91 1971.43,1417.16 1968.92,1418.09 1966.99,1418.8 1966.42,1419.01 1963.91,1419.92 1961.8,1420.69 \n",
" 1961.4,1420.83 1958.9,1421.73 1956.53,1422.58 1956.39,1422.63 1953.88,1423.52 1951.38,1424.4 1951.18,1424.47 1948.87,1425.27 1946.36,1426.14 1945.74,1426.36 \n",
" 1943.85,1427.01 1941.35,1427.86 1940.21,1428.25 1938.84,1428.71 1936.33,1429.55 1934.59,1430.14 1933.83,1430.39 1931.32,1431.22 1928.87,1432.03 1928.81,1432.04 \n",
" 1926.31,1432.86 1923.8,1433.67 1923.05,1433.92 1921.29,1434.48 1918.78,1435.28 1917.12,1435.81 1916.28,1436.07 1913.77,1436.86 1911.26,1437.64 1911.07,1437.69 \n",
" 1908.76,1438.41 1906.25,1439.18 1904.91,1439.58 1903.74,1439.94 1901.24,1440.7 1898.73,1441.44 1898.63,1441.47 1896.22,1442.19 1893.72,1442.93 1892.22,1443.36 \n",
" 1891.21,1443.66 1888.7,1444.38 1886.19,1445.1 1885.66,1445.25 1883.69,1445.82 1881.18,1446.52 1878.97,1447.14 1878.67,1447.23 1876.17,1447.92 1873.66,1448.61 \n",
" 1872.11,1449.03 1871.15,1449.3 1868.65,1449.97 1866.14,1450.65 1865.1,1450.92 1863.63,1451.31 1861.13,1451.97 1858.62,1452.63 1857.91,1452.81 1856.11,1453.28 \n",
" 1853.6,1453.92 1851.1,1454.56 1850.53,1454.7 1848.59,1455.19 1846.08,1455.82 1843.58,1456.44 1842.96,1456.59 1841.07,1457.05 1838.56,1457.66 1836.06,1458.27 \n",
" 1835.16,1458.48 1833.55,1458.87 1831.04,1459.46 1828.54,1460.05 1827.14,1460.37 1826.03,1460.63 1823.52,1461.2 1821.01,1461.78 1818.86,1462.26 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9903)\" style=\"stroke:#fb9c07; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1607.92,1027.7 1605.42,1027.88 1602.91,1028.05 1600.4,1028.2 1597.9,1028.34 1595.39,1028.47 1592.88,1028.58 1590.38,1028.67 1587.87,1028.75 1585.36,1028.82 \n",
" 1582.85,1028.87 1580.35,1028.91 1577.84,1028.93 1575.33,1028.94 1572.83,1028.94 1570.32,1028.92 1567.81,1028.89 1565.31,1028.84 1562.8,1028.78 1560.29,1028.7 \n",
" 1557.79,1028.61 1555.28,1028.5 1552.77,1028.38 1550.26,1028.25 1547.76,1028.1 1545.25,1027.94 1542.74,1027.76 1541.13,1027.63 1540.24,1027.56 1537.73,1027.36 \n",
" 1535.22,1027.14 1532.72,1026.9 1530.21,1026.65 1527.7,1026.38 1525.2,1026.1 1522.69,1025.8 1522.22,1025.74 1520.18,1025.49 1517.67,1025.16 1515.17,1024.82 \n",
" 1512.66,1024.46 1510.15,1024.09 1508.62,1023.85 1507.65,1023.7 1505.14,1023.3 1502.63,1022.88 1500.13,1022.45 1497.62,1021.99 1497.45,1021.96 1495.11,1021.53 \n",
" 1492.6,1021.05 1490.1,1020.55 1487.8,1020.07 1487.59,1020.03 1485.08,1019.5 1482.58,1018.95 1480.07,1018.39 1479.19,1018.18 1477.56,1017.81 1475.06,1017.21 \n",
" 1472.55,1016.59 1471.36,1016.29 1470.04,1015.96 1467.54,1015.31 1465.03,1014.64 1464.15,1014.4 1462.52,1013.96 1460.01,1013.26 1457.51,1012.53 1457.44,1012.52 \n",
" 1455,1011.8 1452.49,1011.04 1451.16,1010.63 1449.99,1010.26 1447.48,1009.47 1445.23,1008.74 1444.97,1008.65 1442.47,1007.82 1439.96,1006.96 1439.62,1006.85 \n",
" 1437.45,1006.09 1434.95,1005.2 1434.29,1004.96 1432.44,1004.28 1429.93,1003.35 1429.2,1003.07 1427.42,1002.39 1424.92,1001.41 1424.33,1001.18 1422.41,1000.41 \n",
" 1419.9,999.39 1419.66,999.287 1417.4,998.347 1415.17,997.398 1414.89,997.279 1412.38,996.189 1410.85,995.508 1409.88,995.074 1407.37,993.936 1406.68,993.618 \n",
" 1404.86,992.773 1402.66,991.729 1402.36,991.584 1399.85,990.37 1398.77,989.839 1397.34,989.13 1395.01,987.949 1394.83,987.862 1392.33,986.567 1391.36,986.06 \n",
" 1389.82,985.244 1387.83,984.17 1387.31,983.892 1384.81,982.51 1384.4,982.28 1382.3,981.098 1381.06,980.39 1379.79,979.654 1377.83,978.501 1377.29,978.179 \n",
" 1374.78,976.67 1374.68,976.611 1372.27,975.127 1371.62,974.721 1369.76,973.549 1368.64,972.832 1367.26,971.934 1365.75,970.942 1364.75,970.282 1362.92,969.052 \n",
" 1362.24,968.591 1360.17,967.163 1359.74,966.859 1357.49,965.273 1357.23,965.085 1354.88,963.383 1354.72,963.267 1352.34,961.494 1352.22,961.404 1349.85,959.604 \n",
" 1349.71,959.493 1347.43,957.714 1347.2,957.531 1345.07,955.825 1344.7,955.517 1342.77,953.935 1342.19,953.448 1340.52,952.045 1339.68,951.321 1338.33,950.155 \n",
" 1337.17,949.132 1336.2,948.266 1334.67,946.878 1334.12,946.376 1332.16,944.555 1332.09,944.486 1330.11,942.597 1329.65,942.156 1328.18,940.707 1327.15,939.677 \n",
" 1326.29,938.817 1324.64,937.113 1324.46,936.928 1322.67,935.038 1322.13,934.453 1320.93,933.148 1319.63,931.692 1319.24,931.259 1317.59,929.369 1317.12,928.817 \n",
" 1315.98,927.479 1314.61,925.819 1314.42,925.59 1312.9,923.7 1312.11,922.677 1311.43,921.81 1310,919.92 1309.6,919.378 1308.61,918.031 1307.26,916.141 \n",
" 1307.09,915.897 1305.95,914.251 1304.69,912.362 1304.58,912.2 1303.46,910.472 1302.28,908.582 1302.08,908.243 1301.14,906.693 1300.04,904.803 1299.57,903.968 \n",
" 1298.98,902.913 1297.96,901.024 1297.06,899.293 1296.98,899.134 1296.04,897.244 1295.14,895.355 1294.56,894.057 1294.29,893.465 1293.47,891.575 1292.7,889.685 \n",
" 1292.05,888.009 1291.97,887.796 1291.27,885.906 1290.62,884.016 1290.02,882.127 1289.54,880.52 1289.46,880.237 1288.93,878.347 1288.46,876.458 1288.02,874.568 \n",
" 1287.64,872.678 1287.3,870.789 1287.04,869.094 1287,868.899 1286.75,867.009 1286.55,865.12 1286.4,863.23 1286.29,861.34 1286.24,859.45 1286.24,857.561 \n",
" 1286.29,855.671 1286.39,853.781 1286.55,851.892 1286.77,850.002 1287.04,848.171 1287.04,848.112 1287.37,846.223 1287.76,844.333 1288.21,842.443 1288.73,840.554 \n",
" 1289.32,838.664 1289.54,838.028 1289.97,836.774 1290.69,834.885 1291.48,832.995 1292.05,831.775 1292.35,831.105 1293.29,829.215 1294.32,827.326 1294.56,826.93 \n",
" 1295.42,825.436 1296.61,823.546 1297.06,822.89 1297.89,821.657 1299.26,819.767 1299.57,819.369 1300.71,817.877 1302.08,816.231 1302.27,815.988 1303.92,814.098 \n",
" 1304.58,813.395 1305.67,812.208 1307.09,810.778 1307.53,810.319 1309.5,808.429 1309.6,808.344 1311.56,806.539 1312.11,806.079 1313.73,804.65 1314.61,803.938 \n",
" 1316.01,802.76 1317.12,801.902 1318.4,800.87 1319.63,799.956 1320.88,798.98 1322.13,798.084 1323.45,797.091 1324.64,796.272 1326.11,795.201 1327.15,794.506 \n",
" 1328.82,793.311 1329.65,792.771 1331.58,791.422 1332.16,791.049 1334.33,789.532 1334.67,789.322 1337.05,787.642 1337.17,787.563 1339.65,785.753 1339.68,785.735 \n",
" 1342.06,783.863 1342.19,783.773 1344.18,781.973 1344.7,781.522 1345.95,780.084 1347.2,778.272 1347.25,778.194 1348.01,776.304 1348.11,774.415 1347.51,772.525 \n",
" 1347.2,771.95 1346.35,770.635 1344.73,768.746 1344.7,768.707 1342.66,766.856 1342.19,766.414 1340.31,764.966 1339.68,764.447 1337.75,763.076 1337.17,762.626 \n",
" 1335.08,761.187 1334.67,760.879 1332.34,759.297 1332.16,759.162 1329.65,757.447 1329.59,757.407 1327.15,755.707 1326.86,755.518 1324.64,753.938 1324.18,753.628 \n",
" 1322.13,752.125 1321.58,751.738 1319.63,750.252 1319.07,749.849 1317.12,748.307 1316.66,747.959 1314.61,746.273 1314.35,746.069 1312.15,744.18 1312.11,744.133 \n",
" 1310.05,742.29 1309.6,741.852 1308.05,740.4 1307.09,739.421 1306.17,738.511 1304.58,736.817 1304.4,736.621 1302.71,734.731 1302.08,733.965 1301.13,732.841 \n",
" 1299.65,730.952 1299.57,730.841 1298.25,729.062 1297.06,727.324 1296.96,727.172 1295.74,725.283 1294.62,723.393 1294.56,723.281 1293.56,721.503 1292.6,719.614 \n",
" 1292.05,718.428 1291.71,717.724 1290.9,715.834 1290.16,713.945 1289.54,712.191 1289.49,712.055 1288.89,710.165 1288.35,708.276 1287.88,706.386 1287.47,704.496 \n",
" 1287.13,702.606 1287.04,701.997 1286.84,700.717 1286.61,698.827 1286.43,696.937 1286.31,695.048 1286.25,693.158 1286.23,691.268 1286.27,689.379 1286.36,687.489 \n",
" 1286.5,685.599 1286.69,683.71 1286.93,681.82 1287.04,681.131 1287.21,679.93 1287.54,678.041 1287.92,676.151 1288.33,674.261 1288.8,672.371 1289.31,670.482 \n",
" 1289.54,669.691 1289.86,668.592 1290.45,666.702 1291.09,664.813 1291.77,662.923 1292.05,662.201 1292.49,661.033 1293.25,659.144 1294.06,657.254 1294.56,656.148 \n",
" 1294.91,655.364 1295.79,653.475 1296.72,651.585 1297.06,650.915 1297.69,649.695 1298.69,647.806 1299.57,646.233 1299.75,645.916 1300.83,644.026 1301.97,642.136 \n",
" 1302.08,641.959 1303.14,640.247 1304.35,638.357 1304.58,638.005 1305.6,636.467 1306.9,634.578 1307.09,634.307 1308.23,632.688 1309.6,630.823 1309.62,630.798 \n",
" 1311.03,628.909 1312.11,627.526 1312.5,627.019 1314,625.129 1314.61,624.386 1315.55,623.24 1317.12,621.384 1317.15,621.35 1318.78,619.46 1319.63,618.512 \n",
" 1320.47,617.571 1322.13,615.749 1322.2,615.681 1323.97,613.791 1324.64,613.092 1325.79,611.901 1327.15,610.527 1327.66,610.012 1329.58,608.122 1329.65,608.047 \n",
" 1331.54,606.232 1332.16,605.65 1333.56,604.343 1334.67,603.326 1335.63,602.453 1337.17,601.071 1337.75,600.563 1339.68,598.882 1339.92,598.674 1342.15,596.784 \n",
" 1342.19,596.754 1344.44,594.894 1344.7,594.686 1346.78,593.005 1347.2,592.672 1349.19,591.115 1349.71,590.711 1351.65,589.225 1352.22,588.8 1354.18,587.336 \n",
" 1354.72,586.936 1356.77,585.446 1357.23,585.119 1359.43,583.556 1359.74,583.345 1362.17,581.666 1362.24,581.613 1364.75,579.921 1364.97,579.777 1367.26,578.269 \n",
" 1367.85,577.887 1369.76,576.655 1370.8,575.997 1372.27,575.076 1373.84,574.108 1374.78,573.534 1376.96,572.218 1377.29,572.025 1379.79,570.549 1380.17,570.328 \n",
" 1382.3,569.106 1383.48,568.439 1384.81,567.693 1386.88,566.549 1387.31,566.312 1389.82,564.96 1390.39,564.659 1392.33,563.636 1394,562.77 1394.83,562.342 \n",
" 1397.34,561.074 1397.73,560.88 1399.85,559.833 1401.59,558.99 1402.36,558.619 1404.86,557.431 1405.57,557.101 1407.37,556.267 1409.7,555.211 1409.88,555.13 \n",
" 1412.38,554.015 1413.97,553.321 1414.89,552.924 1417.4,551.857 1418.42,551.431 1419.9,550.813 1422.41,549.791 1423.03,549.542 1424.92,548.791 1427.42,547.814 \n",
" 1427.85,547.652 1429.93,546.857 1432.44,545.923 1432.88,545.762 1434.95,545.008 1437.45,544.114 1438.14,543.873 1439.96,543.24 1442.47,542.387 1443.68,541.983 \n",
" 1444.97,541.552 1447.48,540.737 1449.51,540.093 1449.99,539.943 1452.49,539.165 1455,538.408 1455.69,538.204 1457.51,537.668 1460.01,536.947 1462.28,536.314 \n",
" 1462.52,536.245 1465.03,535.559 1467.54,534.892 1469.34,534.424 1470.04,534.242 1472.55,533.609 1475.06,532.994 1476.99,532.535 1477.56,532.397 1480.07,531.814 \n",
" 1482.58,531.25 1485.08,530.703 1485.36,530.645 1487.59,530.171 1490.1,529.656 1492.6,529.157 1494.7,528.755 1495.11,528.676 1497.62,528.208 1500.13,527.757 \n",
" 1502.63,527.322 1505.14,526.904 1505.38,526.866 1507.65,526.5 1510.15,526.111 1512.66,525.739 1515.17,525.382 1517.67,525.041 1518.17,524.976 1520.18,524.714 \n",
" 1522.69,524.401 1525.2,524.104 1527.7,523.823 1530.21,523.557 1532.72,523.305 1535.04,523.086 1535.22,523.069 1537.73,522.846 1540.24,522.638 1542.74,522.445 \n",
" 1545.25,522.267 1547.76,522.103 1550.26,521.955 1552.77,521.82 1555.28,521.7 1557.79,521.595 1560.29,521.504 1562.8,521.428 1565.31,521.366 1567.81,521.318 \n",
" 1570.32,521.285 1572.83,521.266 1575.33,521.261 1577.84,521.271 1580.35,521.294 1582.85,521.333 1585.36,521.385 1587.87,521.452 1590.38,521.533 1592.88,521.628 \n",
" 1595.39,521.738 1597.9,521.862 1600.4,522.001 1602.91,522.154 1605.42,522.322 1607.92,522.504 1610.43,522.701 1612.94,522.912 1614.86,523.086 1615.45,523.138 \n",
" 1617.95,523.378 1620.46,523.632 1622.97,523.901 1625.47,524.186 1627.98,524.485 1630.49,524.8 1631.83,524.976 1632.99,525.128 1635.5,525.471 1638.01,525.829 \n",
" 1640.51,526.203 1643.02,526.592 1644.71,526.866 1645.53,526.996 1648.04,527.415 1650.54,527.849 1653.05,528.299 1655.5,528.755 1655.56,528.765 1658.06,529.245 \n",
" 1660.57,529.741 1663.08,530.254 1664.93,530.645 1665.58,530.782 1668.09,531.325 1670.6,531.885 1673.1,532.462 1673.41,532.535 1675.61,533.054 1678.12,533.662 \n",
" 1680.63,534.289 1681.16,534.424 1683.13,534.93 1685.64,535.588 1688.15,536.265 1688.32,536.314 1690.65,536.956 1693.16,537.666 1695.01,538.204 1695.67,538.394 \n",
" 1698.17,539.138 1700.68,539.901 1701.3,540.093 1703.19,540.68 1705.69,541.479 1707.24,541.983 1708.2,542.295 1710.71,543.129 1712.89,543.873 1713.22,543.984 \n",
" 1715.72,544.855 1718.23,545.747 1718.27,545.762 1720.74,546.656 1723.24,547.587 1723.42,547.652 1725.75,548.535 1728.26,549.505 1728.35,549.542 1730.76,550.494 \n",
" 1733.09,551.431 1733.27,551.505 1735.78,552.534 1737.65,553.321 1738.29,553.587 1740.79,554.659 1742.06,555.211 1743.3,555.754 1745.81,556.871 1746.31,557.101 \n",
" 1748.31,558.009 1750.43,558.99 1750.82,559.171 1753.33,560.355 1754.42,560.88 1755.83,561.563 1758.29,562.77 1758.34,562.796 1760.85,564.051 1762.04,564.659 \n",
" 1763.35,565.331 1765.69,566.549 1765.86,566.637 1768.37,567.968 1769.24,568.439 1770.88,569.325 1772.7,570.328 1773.38,570.709 1775.89,572.121 1776.06,572.218 \n",
" 1778.4,573.559 1779.34,574.108 1780.9,575.025 1782.54,575.997 1783.41,576.521 1785.66,577.887 1785.92,578.047 1788.42,579.603 1788.7,579.777 1790.93,581.189 \n",
" 1791.67,581.666 1793.44,582.807 1794.58,583.556 1795.94,584.458 1797.42,585.446 1798.45,586.142 1800.2,587.336 1800.96,587.861 1802.91,589.225 1803.47,589.615 \n",
" 1805.57,591.115 1805.97,591.405 1808.17,593.005 1808.48,593.232 1810.71,594.894 1810.99,595.098 1813.21,596.784 1813.49,597.004 1815.65,598.674 1816,598.95 \n",
" 1818.04,600.563 1818.51,600.939 1820.38,602.453 1821.01,602.972 1822.67,604.343 1823.52,605.05 1824.92,606.232 1826.03,607.175 1827.13,608.122 1828.54,609.349 \n",
" 1829.29,610.012 1831.04,611.574 1831.41,611.901 1833.48,613.791 1833.55,613.851 1835.52,615.681 1836.06,616.185 1837.52,617.571 1838.56,618.575 1839.48,619.46 \n",
" 1841.07,621.026 1841.4,621.35 1843.28,623.24 1843.58,623.54 1845.13,625.129 1846.08,626.121 1846.94,627.019 1848.59,628.771 1848.72,628.909 1850.46,630.798 \n",
" 1851.1,631.496 1852.17,632.688 1853.6,634.299 1853.85,634.578 1855.5,636.467 1856.11,637.185 1857.11,638.357 1858.62,640.157 1858.69,640.247 1860.25,642.136 \n",
" 1861.13,643.227 1861.77,644.026 1863.26,645.916 1863.63,646.395 1864.72,647.806 1866.14,649.671 1866.16,649.695 1867.56,651.585 1868.65,653.067 1868.94,653.475 \n",
" 1870.29,655.364 1871.15,656.59 1871.62,657.254 1872.91,659.144 1873.66,660.251 1874.19,661.033 1875.43,662.923 1876.17,664.066 1876.65,664.813 1877.84,666.702 \n",
" 1878.67,668.049 1879.01,668.592 1880.15,670.482 1881.18,672.22 1881.27,672.371 1882.37,674.261 1883.44,676.151 1883.69,676.606 1884.48,678.041 1885.51,679.93 \n",
" 1886.19,681.234 1886.5,681.82 1887.48,683.71 1888.43,685.599 1888.7,686.143 1889.37,687.489 1890.27,689.379 1891.16,691.268 1891.21,691.379 1892.02,693.158 \n",
" 1892.87,695.048 1893.68,696.937 1893.72,697.013 1894.48,698.827 1895.26,700.717 1896.02,702.606 1896.22,703.14 1896.75,704.496 1897.46,706.386 1898.16,708.276 \n",
" 1898.73,709.889 1898.83,710.165 1899.48,712.055 1900.11,713.945 1900.72,715.834 1901.24,717.487 1901.31,717.724 1901.88,719.614 1902.43,721.503 1902.96,723.393 \n",
" 1903.47,725.283 1903.74,726.33 1903.96,727.172 1904.43,729.062 1904.89,730.952 1905.32,732.841 1905.73,734.731 1906.12,736.621 1906.25,737.27 1906.5,738.511 \n",
" 1906.85,740.4 1907.19,742.29 1907.5,744.18 1907.8,746.069 1908.08,747.959 1908.34,749.849 1908.58,751.738 1908.76,753.267 1908.8,753.628 1909,755.518 \n",
" 1909.19,757.407 1909.35,759.297 1909.5,761.187 1909.63,763.076 1909.74,764.966 1909.83,766.856 1909.9,768.746 1909.95,770.635 1909.99,772.525 1910,774.415 \n",
" 1910,776.304 1909.98,778.194 1909.94,780.084 1909.88,781.973 1909.81,783.863 1909.71,785.753 1909.6,787.642 1909.46,789.532 1909.31,791.422 1909.14,793.311 \n",
" 1908.95,795.201 1908.76,796.943 1908.74,797.091 1908.51,798.98 1908.27,800.87 1908.01,802.76 1907.72,804.65 1907.42,806.539 1907.1,808.429 1906.76,810.319 \n",
" 1906.4,812.208 1906.25,812.933 1906.02,814.098 1905.62,815.988 1905.2,817.877 1904.77,819.767 1904.31,821.657 1903.83,823.546 1903.74,823.877 1903.34,825.436 \n",
" 1902.82,827.326 1902.28,829.215 1901.73,831.105 1901.24,832.716 1901.15,832.995 1900.56,834.885 1899.94,836.774 1899.3,838.664 1898.73,840.315 1898.65,840.554 \n",
" 1897.97,842.443 1897.27,844.333 1896.55,846.223 1896.22,847.063 1895.81,848.112 1895.05,850.002 1894.27,851.892 1893.72,853.187 1893.46,853.781 1892.64,855.671 \n",
" 1891.79,857.561 1891.21,858.822 1890.92,859.45 1890.03,861.34 1889.11,863.23 1888.7,864.06 1888.18,865.12 1887.22,867.009 1886.23,868.899 1886.19,868.971 \n",
" 1885.23,870.789 1884.2,872.678 1883.69,873.596 1883.15,874.568 1882.07,876.458 1881.18,877.983 1880.97,878.347 1879.84,880.237 1878.69,882.127 1878.67,882.157 \n",
" 1877.52,884.016 1876.32,885.906 1876.17,886.139 1875.09,887.796 1873.84,889.685 1873.66,889.953 1872.56,891.575 1871.26,893.465 1871.15,893.615 1869.93,895.355 \n",
" 1868.65,897.137 1868.57,897.244 1867.18,899.134 1866.14,900.531 1865.77,901.024 1864.33,902.913 1863.63,903.808 1862.86,904.803 1861.36,906.693 1861.13,906.978 \n",
" 1859.83,908.582 1858.62,910.045 1858.26,910.472 1856.67,912.362 1856.11,913.019 1855.05,914.251 1853.6,915.905 1853.4,916.141 1851.71,918.031 1851.1,918.707 \n",
" 1849.99,919.92 1848.59,921.432 1848.24,921.81 1846.45,923.7 1846.08,924.083 1844.63,925.59 1843.58,926.663 1842.77,927.479 1841.07,929.178 1840.88,929.369 \n",
" 1838.95,931.259 1838.56,931.628 1836.98,933.148 1836.06,934.019 1834.97,935.038 1833.55,936.352 1832.92,936.928 1831.04,938.63 1830.83,938.817 1828.7,940.707 \n",
" 1828.54,940.854 1826.53,942.597 1826.03,943.028 1824.31,944.486 1823.52,945.153 1822.05,946.376 1821.01,947.231 1819.75,948.266 1818.51,949.264 1817.39,950.155 \n",
" 1816,951.253 1814.99,952.045 1813.49,953.2 1812.53,953.935 1810.99,955.105 1810.03,955.825 1808.48,956.971 1807.47,957.714 1805.97,958.799 1804.85,959.604 \n",
" 1803.47,960.589 1802.18,961.494 1800.96,962.343 1799.45,963.383 1798.45,964.061 1796.65,965.273 1795.94,965.745 1793.79,967.163 1793.44,967.396 1790.93,969.014 \n",
" 1790.87,969.052 1788.42,970.601 1787.88,970.942 1785.92,972.157 1784.81,972.832 1783.41,973.682 1781.67,974.721 1780.9,975.178 1778.45,976.611 1778.4,976.644 \n",
" 1775.89,978.083 1775.15,978.501 1773.38,979.494 1771.76,980.39 1770.88,980.878 1768.37,982.235 1768.28,982.28 1765.86,983.567 1764.71,984.17 1763.35,984.872 \n",
" \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9903)\" style=\"stroke:#fb9c07; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1763.35,984.872 1761.03,986.06 1760.85,986.152 1758.34,987.409 1757.24,987.949 1755.83,988.64 1753.34,989.839 1753.33,989.847 1750.82,991.033 1749.32,991.729 \n",
" 1748.31,992.194 1745.81,993.333 1745.17,993.618 1743.3,994.45 1740.87,995.508 1740.79,995.543 1738.29,996.617 1736.43,997.398 1735.78,997.669 1733.27,998.7 \n",
" 1731.81,999.287 1730.76,999.709 1728.26,1000.7 1727.02,1001.18 1725.75,1001.67 1723.24,1002.62 1722.03,1003.07 1720.74,1003.55 1718.23,1004.46 1716.83,1004.96 \n",
" 1715.72,1005.35 1713.22,1006.22 1711.38,1006.85 1710.71,1007.07 1708.2,1007.91 1705.69,1008.72 1705.66,1008.74 1703.19,1009.52 1700.68,1010.3 1699.62,1010.63 \n",
" 1698.17,1011.07 1695.67,1011.81 1693.23,1012.52 1693.16,1012.54 1690.65,1013.25 1688.15,1013.94 1686.42,1014.4 1685.64,1014.61 1683.13,1015.27 1680.63,1015.92 \n",
" 1679.1,1016.29 1678.12,1016.54 1675.61,1017.15 1673.1,1017.74 1671.18,1018.18 1670.6,1018.32 1668.09,1018.88 1665.58,1019.42 1663.08,1019.95 1662.47,1020.07 \n",
" 1660.57,1020.46 1658.06,1020.96 1655.56,1021.44 1653.05,1021.9 1652.71,1021.96 1650.54,1022.35 1648.04,1022.79 1645.53,1023.21 1643.02,1023.61 1641.46,1023.85 \n",
" 1640.51,1024 1638.01,1024.37 1635.5,1024.73 1632.99,1025.08 1630.49,1025.4 1627.98,1025.72 1627.76,1025.74 1625.47,1026.02 1622.97,1026.3 1620.46,1026.57 \n",
" 1617.95,1026.83 1615.45,1027.07 1612.94,1027.29 1610.43,1027.5 1608.76,1027.63 1607.92,1027.7 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9903)\" style=\"stroke:#f57d15; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1592.88,925.664 1590.38,925.801 1587.87,925.913 1585.36,926.001 1582.85,926.063 1580.35,926.1 1577.84,926.113 1575.33,926.101 1572.83,926.063 1570.32,926.001 \n",
" 1567.81,925.914 1565.31,925.801 1562.8,925.663 1561.68,925.59 1560.29,925.5 1557.79,925.313 1555.28,925.1 1552.77,924.862 1550.26,924.597 1547.76,924.305 \n",
" 1545.25,923.986 1543.17,923.7 1542.74,923.641 1540.24,923.272 1537.73,922.875 1535.22,922.449 1532.72,921.994 1531.76,921.81 1530.21,921.514 1527.7,921.006 \n",
" 1525.2,920.467 1522.79,919.92 1522.69,919.898 1520.18,919.303 1517.67,918.676 1515.23,918.031 1515.17,918.015 1512.66,917.329 1510.15,916.608 1508.6,916.141 \n",
" 1507.65,915.854 1505.14,915.069 1502.65,914.251 1502.63,914.246 1500.13,913.393 1497.62,912.501 1497.24,912.362 1495.11,911.576 1492.6,910.61 1492.26,910.472 \n",
" 1490.1,909.61 1487.63,908.582 1487.59,908.565 1485.08,907.485 1483.32,906.693 1482.58,906.359 1480.07,905.19 1479.27,904.803 1477.56,903.977 1475.45,902.913 \n",
" 1475.06,902.716 1472.55,901.407 1471.84,901.024 1470.04,900.047 1468.42,899.134 1467.54,898.634 1465.16,897.244 1465.03,897.164 1462.52,895.638 1462.07,895.355 \n",
" 1460.01,894.05 1459.12,893.465 1457.51,892.397 1456.3,891.575 1455,890.675 1453.61,889.685 1452.49,888.881 1451.03,887.796 1449.99,887.008 1448.56,885.906 \n",
" 1447.48,885.052 1446.2,884.016 1444.97,883.006 1443.93,882.127 1442.47,880.863 1441.76,880.237 1439.96,878.613 1439.67,878.347 1437.67,876.458 1437.45,876.248 \n",
" 1435.75,874.568 1434.95,873.754 1433.9,872.678 1432.44,871.118 1432.13,870.789 1430.44,868.899 1429.93,868.319 1428.81,867.009 1427.42,865.338 1427.25,865.12 \n",
" 1425.75,863.23 1424.92,862.142 1424.31,861.34 1422.94,859.45 1422.41,858.697 1421.62,857.561 1420.37,855.671 1419.9,854.951 1419.16,853.781 1418.01,851.892 \n",
" 1417.4,850.833 1416.92,850.002 1415.87,848.112 1414.89,846.242 1414.88,846.223 1413.93,844.333 1413.03,842.443 1412.38,841.001 1412.18,840.554 1411.37,838.664 \n",
" 1410.61,836.774 1409.89,834.885 1409.88,834.833 1409.21,832.995 1408.58,831.105 1407.98,829.215 1407.42,827.326 1407.37,827.128 1406.9,825.436 1406.42,823.546 \n",
" 1405.97,821.657 1405.55,819.767 1405.17,817.877 1404.86,816.235 1404.82,815.988 1404.49,814.098 1404.2,812.208 1403.93,810.319 1403.69,808.429 1403.48,806.539 \n",
" 1403.29,804.65 1403.12,802.76 1402.97,800.87 1402.84,798.98 1402.72,797.091 1402.62,795.201 1402.54,793.311 1402.47,791.422 1402.41,789.532 1402.36,787.642 \n",
" 1402.36,787.332 1402.32,785.753 1402.29,783.863 1402.27,781.973 1402.25,780.084 1402.24,778.194 1402.23,776.304 1402.23,774.415 1402.23,772.525 1402.24,770.635 \n",
" 1402.26,768.746 1402.28,766.856 1402.31,764.966 1402.35,763.076 1402.36,762.865 1402.4,761.187 1402.45,759.297 1402.52,757.407 1402.6,755.518 1402.69,753.628 \n",
" 1402.8,751.738 1402.93,749.849 1403.07,747.959 1403.24,746.069 1403.42,744.18 1403.63,742.29 1403.87,740.4 1404.12,738.511 1404.41,736.621 1404.73,734.731 \n",
" 1404.86,733.976 1405.07,732.841 1405.44,730.952 1405.85,729.062 1406.29,727.172 1406.77,725.283 1407.28,723.393 1407.37,723.077 1407.83,721.503 1408.41,719.614 \n",
" 1409.04,717.724 1409.71,715.834 1409.88,715.375 1410.41,713.945 1411.16,712.055 1411.96,710.165 1412.38,709.204 1412.8,708.276 1413.68,706.386 1414.62,704.496 \n",
" 1414.89,703.965 1415.6,702.606 1416.63,700.717 1417.4,699.37 1417.71,698.827 1418.84,696.937 1419.9,695.25 1420.03,695.048 1421.27,693.158 1422.41,691.505 \n",
" 1422.58,691.268 1423.93,689.379 1424.92,688.061 1425.35,687.489 1426.83,685.599 1427.42,684.867 1428.38,683.71 1429.93,681.884 1429.99,681.82 1431.66,679.93 \n",
" 1432.44,679.086 1433.41,678.041 1434.95,676.449 1435.24,676.151 1437.14,674.261 1437.45,673.955 1439.12,672.371 1439.96,671.59 1441.18,670.482 1442.47,669.341 \n",
" 1443.33,668.592 1444.97,667.198 1445.57,666.702 1447.48,665.152 1447.91,664.813 1449.99,663.196 1450.35,662.923 1452.49,661.323 1452.89,661.033 1455,659.529 \n",
" 1455.55,659.144 1457.51,657.807 1458.34,657.254 1460.01,656.153 1461.25,655.364 1462.52,654.565 1464.31,653.475 1465.03,653.038 1467.51,651.585 1467.54,651.571 \n",
" 1470.04,650.156 1470.89,649.695 1472.55,648.796 1474.44,647.806 1475.06,647.487 1477.56,646.227 1478.2,645.916 1480.07,645.012 1482.19,644.026 1482.58,643.845 \n",
" 1485.08,642.719 1486.43,642.136 1487.59,641.636 1490.1,640.595 1490.97,640.247 1492.6,639.591 1495.11,638.628 1495.84,638.357 1497.62,637.701 1500.13,636.811 \n",
" 1501.13,636.467 1502.63,635.956 1505.14,635.135 1506.92,634.578 1507.65,634.35 1510.15,633.595 1512.66,632.876 1513.34,632.688 1515.17,632.186 1517.67,631.528 \n",
" 1520.18,630.903 1520.62,630.798 1522.69,630.304 1525.2,629.736 1527.7,629.199 1529.14,628.909 1530.21,628.69 1532.72,628.207 1535.22,627.754 1537.73,627.33 \n",
" 1539.7,627.019 1540.24,626.933 1542.74,626.561 1545.25,626.216 1547.76,625.898 1550.26,625.607 1552.77,625.343 1555.03,625.129 1555.28,625.105 1557.79,624.89 \n",
" 1560.29,624.702 1562.8,624.539 1565.31,624.401 1567.81,624.289 1570.32,624.202 1572.83,624.139 1575.33,624.102 1577.84,624.09 1580.35,624.102 1582.85,624.14 \n",
" 1585.36,624.202 1587.87,624.289 1590.38,624.4 1592.88,624.537 1595.39,624.699 1597.9,624.886 1600.4,625.098 1600.73,625.129 1602.91,625.333 1605.42,625.594 \n",
" 1607.92,625.88 1610.43,626.191 1612.94,626.53 1615.45,626.894 1616.25,627.019 1617.95,627.282 1620.46,627.696 1622.97,628.137 1625.47,628.606 1627,628.909 \n",
" 1627.98,629.101 1630.49,629.621 1632.99,630.169 1635.5,630.747 1635.71,630.798 1638.01,631.349 1640.51,631.981 1643.02,632.643 1643.18,632.688 1645.53,633.33 \n",
" 1648.04,634.049 1649.8,634.578 1650.54,634.798 1653.05,635.576 1655.56,636.387 1655.8,636.467 1658.06,637.225 1660.57,638.099 1661.29,638.357 1663.08,639.002 \n",
" 1665.58,639.94 1666.38,640.247 1668.09,640.911 1670.6,641.918 1671.13,642.136 1673.1,642.958 1675.59,644.026 1675.61,644.036 1678.12,645.148 1679.79,645.916 \n",
" 1680.63,646.301 1683.13,647.491 1683.78,647.806 1685.64,648.721 1687.56,649.695 1688.15,649.993 1690.65,651.307 1691.17,651.585 1693.16,652.665 1694.61,653.475 \n",
" 1695.67,654.068 1697.91,655.364 1698.17,655.518 1700.68,657.016 1701.07,657.254 1703.19,658.564 1704.1,659.144 1705.69,660.165 1707.02,661.033 1708.2,661.821 \n",
" 1709.82,662.923 1710.71,663.534 1712.53,664.813 1713.22,665.306 1715.13,666.702 1715.72,667.141 1717.64,668.592 1718.23,669.042 1720.07,670.482 1720.74,671.012 \n",
" 1722.42,672.371 1723.24,673.056 1724.68,674.261 1725.75,675.177 1726.87,676.151 1728.26,677.382 1728.99,678.041 1730.76,679.675 1731.04,679.93 1733.02,681.82 \n",
" 1733.27,682.064 1734.94,683.71 1735.78,684.556 1736.8,685.599 1738.29,687.158 1738.6,687.489 1740.34,689.379 1740.79,689.884 1742.02,691.268 1743.3,692.743 \n",
" 1743.66,693.158 1745.24,695.048 1745.81,695.751 1746.76,696.937 1748.24,698.827 1748.31,698.922 1749.67,700.717 1750.82,702.284 1751.06,702.606 1752.39,704.496 \n",
" 1753.33,705.86 1753.69,706.386 1754.93,708.276 1755.83,709.686 1756.14,710.165 1757.3,712.055 1758.34,713.806 1758.42,713.945 1759.51,715.834 1760.55,717.724 \n",
" 1760.85,718.294 1761.55,719.614 1762.51,721.503 1763.35,723.23 1763.43,723.393 1764.32,725.283 1765.17,727.172 1765.86,728.771 1765.99,729.062 1766.77,730.952 \n",
" 1767.51,732.841 1768.22,734.731 1768.37,735.163 1768.89,736.621 1769.53,738.511 1770.13,740.4 1770.7,742.29 1770.88,742.906 1771.24,744.18 1771.74,746.069 \n",
" 1772.22,747.959 1772.65,749.849 1773.06,751.738 1773.38,753.393 1773.43,753.628 1773.77,755.518 1774.08,757.407 1774.36,759.297 1774.61,761.187 1774.82,763.076 \n",
" 1775,764.966 1775.16,766.856 1775.28,768.746 1775.36,770.635 1775.42,772.525 1775.45,774.415 1775.44,776.304 1775.41,778.194 1775.34,780.084 1775.25,781.973 \n",
" 1775.12,783.863 1774.96,785.753 1774.77,787.642 1774.54,789.532 1774.29,791.422 1774,793.311 1773.68,795.201 1773.38,796.809 1773.33,797.091 1772.95,798.98 \n",
" 1772.54,800.87 1772.09,802.76 1771.61,804.65 1771.09,806.539 1770.88,807.296 1770.55,808.429 1769.97,810.319 1769.36,812.208 1768.71,814.098 1768.37,815.038 \n",
" 1768.03,815.988 1767.31,817.877 1766.56,819.767 1765.86,821.433 1765.77,821.657 1764.95,823.546 1764.09,825.436 1763.35,826.972 1763.19,827.326 1762.25,829.215 \n",
" 1761.28,831.105 1760.85,831.909 1760.27,832.995 1759.21,834.885 1758.34,836.395 1758.12,836.774 1756.99,838.664 1755.83,840.52 1755.81,840.554 1754.6,842.443 \n",
" 1753.34,844.333 1753.33,844.346 1752.03,846.223 1750.82,847.921 1750.68,848.112 1749.29,850.002 1748.31,851.28 1747.84,851.892 1746.35,853.781 1745.81,854.453 \n",
" 1744.81,855.671 1743.3,857.462 1743.22,857.561 1741.57,859.45 1740.79,860.319 1739.87,861.34 1738.29,863.045 1738.11,863.23 1736.3,865.12 1735.78,865.648 \n",
" 1734.42,867.009 1733.27,868.139 1732.49,868.899 1730.76,870.529 1730.49,870.789 1728.42,872.678 1728.26,872.822 1726.28,874.568 1725.75,875.026 1724.07,876.458 \n",
" 1723.24,877.148 1721.78,878.347 1720.74,879.192 1719.42,880.237 1718.23,881.162 1716.97,882.127 1715.72,883.063 1714.43,884.016 1713.22,884.898 1711.8,885.906 \n",
" 1710.71,886.67 1709.07,887.796 1708.2,888.382 1706.23,889.685 1705.69,890.038 1703.29,891.575 1703.19,891.639 1700.68,893.187 1700.22,893.465 1698.17,894.686 \n",
" 1697.03,895.355 1695.67,896.136 1693.69,897.244 1693.16,897.538 1690.65,898.896 1690.2,899.134 1688.15,900.211 1686.55,901.024 1685.64,901.482 1683.13,902.712 \n",
" 1682.71,902.913 1680.63,903.903 1678.67,904.803 1678.12,905.054 1675.61,906.169 1674.4,906.693 1673.1,907.246 1670.6,908.286 1669.86,908.582 1668.09,909.292 \n",
" 1665.58,910.263 1665.03,910.472 1663.08,911.201 1660.57,912.105 1659.83,912.362 1658.06,912.978 1655.56,913.818 1654.21,914.251 1653.05,914.627 1650.54,915.406 \n",
" 1648.07,916.141 1648.04,916.152 1645.53,916.873 1643.02,917.562 1641.24,918.031 1640.51,918.221 1638.01,918.855 1635.5,919.458 1633.48,919.92 1632.99,920.032 \n",
" 1630.49,920.583 1627.98,921.104 1625.47,921.597 1624.33,921.81 1622.97,922.065 1620.46,922.507 1617.95,922.922 1615.45,923.31 1612.94,923.672 1612.73,923.7 \n",
" 1610.43,924.011 1607.92,924.324 1605.42,924.611 1602.91,924.872 1600.4,925.107 1597.9,925.318 1595.39,925.503 1594.04,925.59 1592.88,925.664 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9903)\" style=\"stroke:#e65e2d; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1590.38,865.313 1587.87,865.538 1585.36,865.721 1582.85,865.862 1580.35,865.963 1577.84,866.022 1575.33,866.041 1572.83,866.019 1570.32,865.956 1567.81,865.853 \n",
" 1565.31,865.707 1562.8,865.52 1560.29,865.291 1558.72,865.12 1557.79,865.02 1555.28,864.71 1552.77,864.356 1550.26,863.956 1547.76,863.51 1546.33,863.23 \n",
" 1545.25,863.021 1542.74,862.488 1540.24,861.906 1538,861.34 1537.73,861.273 1535.22,860.597 1532.72,859.866 1531.38,859.45 1530.21,859.084 1527.7,858.25 \n",
" 1525.77,857.561 1525.2,857.357 1522.69,856.41 1520.85,855.671 1520.18,855.4 1517.67,854.331 1516.46,853.781 1515.17,853.195 1512.66,851.989 1512.47,851.892 \n",
" 1510.15,850.715 1508.82,850.002 1507.65,849.363 1505.46,848.112 1505.14,847.93 1502.63,846.411 1502.33,846.223 1500.13,844.802 1499.43,844.333 1497.62,843.093 \n",
" 1496.71,842.443 1495.11,841.276 1494.16,840.554 1492.6,839.342 1491.76,838.664 1490.1,837.279 1489.51,836.774 1487.59,835.072 1487.39,834.885 1485.38,832.995 \n",
" 1485.08,832.705 1483.49,831.105 1482.58,830.153 1481.7,829.215 1480.07,827.392 1480.01,827.326 1478.41,825.436 1477.56,824.378 1476.91,823.546 1475.48,821.657 \n",
" 1475.06,821.064 1474.14,819.767 1472.87,817.877 1472.55,817.376 1471.67,815.988 1470.55,814.098 1470.04,813.197 1469.49,812.208 1468.5,810.319 1467.57,808.429 \n",
" 1467.54,808.348 1466.7,806.539 1465.89,804.65 1465.15,802.76 1465.03,802.443 1464.45,800.87 1463.81,798.98 1463.22,797.091 1462.69,795.201 1462.52,794.543 \n",
" 1462.21,793.311 1461.77,791.422 1461.39,789.532 1461.05,787.642 1460.77,785.753 1460.53,783.863 1460.34,781.973 1460.19,780.084 1460.1,778.194 1460.04,776.304 \n",
" 1460.04,774.415 1460.08,772.525 1460.16,770.635 1460.29,768.746 1460.47,766.856 1460.7,764.966 1460.97,763.076 1461.29,761.187 1461.66,759.297 1462.08,757.407 \n",
" 1462.52,755.647 1462.55,755.518 1463.07,753.628 1463.64,751.738 1464.27,749.849 1464.95,747.959 1465.03,747.758 1465.68,746.069 1466.47,744.18 1467.33,742.29 \n",
" 1467.54,741.86 1468.24,740.4 1469.21,738.511 1470.04,737.004 1470.25,736.621 1471.36,734.731 1472.54,732.841 1472.55,732.824 1473.78,730.952 1475.06,729.136 \n",
" 1475.11,729.062 1476.51,727.172 1477.56,725.825 1478,725.283 1479.57,723.393 1480.07,722.813 1481.23,721.503 1482.58,720.05 1482.99,719.614 1484.85,717.724 \n",
" 1485.08,717.499 1486.83,715.834 1487.59,715.131 1488.92,713.945 1490.1,712.925 1491.14,712.055 1492.6,710.862 1493.49,710.165 1495.11,708.927 1496,708.276 \n",
" 1497.62,707.111 1498.67,706.386 1500.13,705.401 1501.52,704.496 1502.63,703.791 1504.58,702.606 1505.14,702.273 1507.65,700.842 1507.88,700.717 1510.15,699.488 \n",
" 1511.45,698.827 1512.66,698.212 1515.17,697.011 1515.33,696.937 1517.67,695.872 1519.61,695.048 1520.18,694.803 1522.69,693.793 1524.37,693.158 1525.2,692.846 \n",
" 1527.7,691.954 1529.77,691.268 1530.21,691.121 1532.72,690.336 1535.22,689.608 1536.07,689.379 1537.73,688.928 1540.24,688.297 1542.74,687.717 1543.82,687.489 \n",
" 1545.25,687.182 1547.76,686.691 1550.26,686.248 1552.77,685.85 1554.56,685.599 1555.28,685.496 1557.79,685.181 1560.29,684.91 1562.8,684.682 1565.31,684.496 \n",
" 1567.81,684.351 1570.32,684.248 1572.83,684.186 1575.33,684.164 1577.84,684.183 1580.35,684.242 1582.85,684.342 1585.36,684.482 1587.87,684.664 1590.38,684.888 \n",
" 1592.88,685.153 1595.39,685.462 1596.37,685.599 1597.9,685.81 1600.4,686.198 1602.91,686.632 1605.42,687.112 1607.22,687.489 1607.92,687.636 1610.43,688.2 \n",
" 1612.94,688.814 1615.07,689.379 1615.45,689.478 1617.95,690.183 1620.46,690.943 1621.47,691.268 1622.97,691.751 1625.47,692.611 1626.97,693.158 1627.98,693.526 \n",
" 1630.49,694.496 1631.84,695.048 1632.99,695.523 1635.5,696.611 1636.22,696.937 1638.01,697.759 1640.21,698.827 1640.51,698.975 1643.02,700.257 1643.88,700.717 \n",
" 1645.53,701.61 1647.28,702.606 1648.04,703.041 1650.45,704.496 1650.54,704.552 1653.05,706.147 1653.41,706.386 1655.56,707.834 1656.19,708.276 1658.06,709.621 \n",
" 1658.8,710.165 1660.57,711.514 1661.26,712.055 1663.08,713.524 1663.58,713.945 1665.58,715.662 1665.78,715.834 1667.86,717.724 1668.09,717.944 1669.83,719.614 \n",
" 1670.6,720.388 1671.69,721.503 1673.1,723.014 1673.45,723.393 1675.13,725.283 1675.61,725.854 1676.71,727.172 1678.12,728.943 1678.21,729.062 1679.64,730.952 \n",
" 1680.63,732.345 1680.98,732.841 1682.25,734.731 1683.13,736.131 1683.44,736.621 1684.57,738.511 1685.63,740.4 1685.64,740.424 1686.63,742.29 1687.56,744.18 \n",
" 1688.15,745.468 1688.42,746.069 1689.23,747.959 1689.98,749.849 1690.65,751.699 1690.67,751.738 1691.31,753.628 1691.88,755.518 1692.4,757.407 1692.87,759.297 \n",
" 1693.16,760.651 1693.28,761.187 1693.64,763.076 1693.95,764.966 1694.2,766.856 1694.4,768.746 1694.55,770.635 1694.65,772.525 1694.69,774.415 1694.68,776.304 \n",
" 1694.62,778.194 1694.51,780.084 1694.35,781.973 1694.14,783.863 1693.87,785.753 1693.55,787.642 1693.17,789.532 1693.16,789.574 1692.75,791.422 1692.27,793.311 \n",
" 1691.73,795.201 1691.14,797.091 1690.65,798.493 1690.49,798.98 1689.78,800.87 1689.02,802.76 1688.19,804.65 1688.15,804.744 1687.31,806.539 1686.36,808.429 \n",
" 1685.64,809.772 1685.35,810.319 1684.27,812.208 1683.13,814.078 1683.12,814.098 1681.91,815.988 1680.63,817.863 1680.62,817.877 1679.26,819.767 1678.12,821.258 \n",
" 1677.81,821.657 1676.29,823.546 1675.61,824.349 1674.68,825.436 1673.1,827.19 1672.98,827.326 1671.19,829.215 1670.6,829.815 1669.3,831.105 1668.09,832.258 \n",
" 1667.3,832.995 1665.58,834.541 1665.19,834.885 1663.08,836.68 1662.96,836.774 1660.6,838.664 1660.57,838.69 1658.1,840.554 1658.06,840.583 1655.56,842.369 \n",
" 1655.45,842.443 1653.05,844.056 1652.62,844.333 1650.54,845.652 1649.61,846.223 1648.04,847.163 1646.38,848.112 1645.53,848.593 1643.02,849.946 1642.91,850.002 \n",
" 1640.51,851.23 1639.16,851.892 1638.01,852.444 1635.5,853.592 1635.07,853.781 1632.99,854.681 1630.57,855.671 1630.49,855.705 1627.98,856.678 1625.55,857.561 \n",
" 1625.47,857.589 1622.97,858.453 1620.46,859.26 1619.83,859.45 1617.95,860.02 1615.45,860.728 1613.11,861.34 1612.94,861.386 1610.43,862.003 1607.92,862.571 \n",
" 1605.42,863.09 1604.68,863.23 1602.91,863.569 1600.4,864.005 1597.9,864.396 1595.39,864.743 1592.88,865.047 1592.19,865.12 1590.38,865.313 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9903)\" style=\"stroke:#d24742; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1587.87,829.267 1585.36,829.627 1582.85,829.915 1580.35,830.135 1577.84,830.288 1575.33,830.374 1572.83,830.395 1570.32,830.35 1567.81,830.24 1565.31,830.062 \n",
" 1562.8,829.816 1560.29,829.501 1558.44,829.215 1557.79,829.116 1555.28,828.668 1552.77,828.143 1550.26,827.537 1549.49,827.326 1547.76,826.861 1545.25,826.102 \n",
" 1543.28,825.436 1542.74,825.253 1540.24,824.323 1538.35,823.546 1537.73,823.292 1535.22,822.164 1534.19,821.657 1532.72,820.926 1530.57,819.767 1530.21,819.568 \n",
" 1527.7,818.083 1527.38,817.877 1525.2,816.456 1524.52,815.988 1522.69,814.666 1521.94,814.098 1520.18,812.692 1519.6,812.208 1517.67,810.503 1517.47,810.319 \n",
" 1515.53,808.429 1515.17,808.054 1513.75,806.539 1512.66,805.282 1512.13,804.65 1510.64,802.76 1510.15,802.088 1509.28,800.87 1508.05,798.98 1507.65,798.298 \n",
" 1506.93,797.091 1505.92,795.201 1505.14,793.554 1505.02,793.311 1504.21,791.422 1503.5,789.532 1502.89,787.642 1502.63,786.7 1502.37,785.753 1501.93,783.863 \n",
" 1501.58,781.973 1501.31,780.084 1501.13,778.194 1501.04,776.304 1501.03,774.415 1501.1,772.525 1501.25,770.635 1501.5,768.746 1501.82,766.856 1502.24,764.966 \n",
" 1502.63,763.493 1502.74,763.076 1503.33,761.187 1504.01,759.297 1504.79,757.407 1505.14,756.658 1505.67,755.518 1506.65,753.628 1507.65,751.898 1507.74,751.738 \n",
" 1508.94,749.849 1510.15,748.11 1510.26,747.959 1511.71,746.069 1512.66,744.922 1513.29,744.18 1515.03,742.29 1515.17,742.148 1516.92,740.4 1517.67,739.701 \n",
" 1519,738.511 1520.18,737.511 1521.28,736.621 1522.69,735.537 1523.79,734.731 1525.2,733.747 1526.57,732.841 1527.7,732.119 1529.66,730.952 1530.21,730.635 \n",
" 1532.72,729.28 1533.15,729.062 1535.22,728.039 1537.14,727.172 1537.73,726.912 1540.24,725.881 1541.84,725.283 1542.74,724.949 1545.25,724.101 1547.61,723.393 \n",
" 1547.76,723.347 1550.26,722.662 1552.77,722.062 1555.28,721.542 1555.49,721.503 1557.79,721.084 1560.29,720.699 1562.8,720.386 1565.31,720.143 1567.81,719.967 \n",
" 1570.32,719.857 1572.83,719.813 1575.33,719.833 1577.84,719.919 1580.35,720.07 1582.85,720.288 1585.36,720.574 1587.87,720.931 1590.38,721.36 1591.1,721.503 \n",
" 1592.88,721.854 1595.39,722.421 1597.9,723.069 1599.02,723.393 1600.4,723.792 1602.91,724.597 1604.84,725.283 1605.42,725.491 1607.92,726.471 1609.56,727.172 \n",
" 1610.43,727.551 1612.94,728.732 1613.59,729.062 1615.45,730.023 1617.11,730.952 1617.95,731.437 1620.24,732.841 1620.46,732.983 1622.97,734.677 1623.04,734.731 \n",
" 1625.47,736.537 1625.58,736.621 1627.89,738.511 1627.98,738.591 1629.99,740.4 1630.49,740.875 1631.92,742.29 1632.99,743.435 1633.68,744.18 1635.28,746.069 \n",
" 1635.5,746.342 1636.76,747.959 1638.01,749.72 1638.1,749.849 1639.33,751.738 1640.43,753.628 1640.51,753.795 1641.43,755.518 1642.32,757.407 1643.02,759.085 \n",
" 1643.11,759.297 1643.81,761.187 1644.42,763.076 1644.93,764.966 1645.34,766.856 1645.53,767.93 1645.67,768.746 1645.92,770.635 1646.08,772.525 1646.16,774.415 \n",
" 1646.15,776.304 1646.05,778.194 1645.86,780.084 1645.59,781.973 1645.53,782.299 1645.24,783.863 1644.8,785.753 1644.26,787.642 1643.63,789.532 1643.02,791.115 \n",
" 1642.9,791.422 1642.09,793.311 1641.17,795.201 1640.51,796.4 1640.14,797.091 1639,798.98 1638.01,800.479 1637.75,800.87 1636.37,802.76 1635.5,803.858 \n",
" 1634.86,804.65 1633.21,806.539 1632.99,806.771 1631.41,808.429 1630.49,809.328 1629.44,810.319 1627.98,811.611 1627.28,812.208 1625.47,813.666 1624.91,814.098 \n",
" 1622.97,815.527 1622.3,815.988 1620.46,817.221 1619.42,817.877 1617.95,818.767 1616.19,819.767 1615.45,820.179 1612.94,821.47 1612.55,821.657 1610.43,822.654 \n",
" 1608.36,823.546 1607.92,823.73 1605.42,824.715 1603.38,825.436 1602.91,825.603 1600.4,826.413 1597.9,827.133 1597.15,827.326 1595.39,827.781 1592.88,828.352 \n",
" 1590.38,828.846 1588.17,829.215 1587.87,829.267 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9903)\" style=\"stroke:#ba3655; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1577.84,808.621 1575.33,808.812 1572.83,808.893 1570.32,808.866 1567.81,808.73 1565.31,808.482 1564.93,808.429 1562.8,808.135 1560.29,807.673 1557.79,807.085 \n",
" 1555.88,806.539 1555.28,806.367 1552.77,805.525 1550.58,804.65 1550.26,804.524 1547.76,803.371 1546.59,802.76 1545.25,802.03 1543.35,800.87 1542.74,800.475 \n",
" 1540.64,798.98 1540.24,798.667 1538.34,797.091 1537.73,796.539 1536.34,795.201 1535.22,793.984 1534.63,793.311 1533.15,791.422 1532.72,790.793 1531.87,789.532 \n",
" 1530.78,787.642 1530.21,786.444 1529.88,785.753 1529.12,783.863 1528.53,781.973 1528.09,780.084 1527.8,778.194 1527.7,777.039 1527.64,776.304 1527.62,774.415 \n",
" 1527.7,773.15 1527.74,772.525 1528,770.635 1528.39,768.746 1528.94,766.856 1529.65,764.966 1530.21,763.76 1530.52,763.076 1531.55,761.187 1532.72,759.399 \n",
" 1532.78,759.297 1534.2,757.407 1535.22,756.22 1535.85,755.518 1537.73,753.661 1537.77,753.628 1539.98,751.738 1540.24,751.536 1542.57,749.849 1542.74,749.729 \n",
" 1545.25,748.176 1545.64,747.959 1547.76,746.832 1549.4,746.069 1550.26,745.676 1552.77,744.68 1554.25,744.18 1555.28,743.834 1557.79,743.117 1560.29,742.536 \n",
" 1561.63,742.29 1562.8,742.07 1565.31,741.711 1567.81,741.467 1570.32,741.333 1572.83,741.306 1575.33,741.386 1577.84,741.575 1580.35,741.874 1582.85,742.29 \n",
" 1582.85,742.291 1585.36,742.807 1587.87,743.452 1590.19,744.18 1590.38,744.237 1592.88,745.146 1595.04,746.069 1595.39,746.221 1597.9,747.459 1598.8,747.959 \n",
" 1600.4,748.895 1601.88,749.849 1602.91,750.561 1604.48,751.738 1605.42,752.507 1606.7,753.628 1607.92,754.813 1608.62,755.518 1610.27,757.407 1610.43,757.616 \n",
" 1611.71,759.297 1612.92,761.187 1612.94,761.218 1613.97,763.076 1614.84,764.966 1615.45,766.607 1615.54,766.856 1616.1,768.746 1616.51,770.635 1616.78,772.525 \n",
" 1616.9,774.415 1616.88,776.304 1616.72,778.194 1616.42,780.084 1615.96,781.973 1615.45,783.594 1615.36,783.863 1614.62,785.753 1613.71,787.642 1612.94,788.968 \n",
" 1612.61,789.532 1611.34,791.422 1610.43,792.58 1609.85,793.311 1608.12,795.201 1607.92,795.394 1606.13,797.091 1605.42,797.697 1603.81,798.98 1602.91,799.643 \n",
" 1601.09,800.87 1600.4,801.308 1597.9,802.74 1597.86,802.76 1595.39,803.986 1593.85,804.65 1592.88,805.054 1590.38,805.973 1588.54,806.539 1587.87,806.745 \n",
" 1585.36,807.399 1582.85,807.922 1580.35,808.323 1579.44,808.429 1577.84,808.621 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9903)\" style=\"stroke:#9e2a62; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1577.84,795.279 1575.33,795.63 1572.83,795.796 1570.32,795.783 1567.81,795.592 1565.31,795.214 1565.25,795.201 1562.8,794.674 1560.29,793.912 1558.77,793.311 \n",
" 1557.79,792.915 1555.28,791.643 1554.91,791.422 1552.77,790.031 1552.11,789.532 1550.26,787.943 1549.95,787.642 1548.25,785.753 1547.76,785.078 1546.91,783.863 \n",
" 1545.88,781.973 1545.25,780.339 1545.15,780.084 1544.64,778.194 1544.37,776.304 1544.34,774.415 1544.54,772.525 1544.98,770.635 1545.25,769.901 1545.66,768.746 \n",
" 1546.6,766.856 1547.76,765.111 1547.86,764.966 1549.44,763.076 1550.26,762.264 1551.46,761.187 1552.77,760.173 1554.07,759.297 1555.28,758.556 1557.55,757.407 \n",
" 1557.79,757.294 1560.29,756.289 1562.8,755.543 1562.92,755.518 1565.31,754.974 1567.81,754.603 1570.32,754.417 1572.83,754.405 1575.33,754.567 1577.84,754.911 \n",
" 1580.35,755.452 1580.58,755.518 1582.85,756.17 1585.36,757.136 1585.94,757.407 1587.87,758.358 1589.44,759.297 1590.38,759.919 1592.04,761.187 1592.88,761.929 \n",
" 1594.07,763.076 1595.39,764.637 1595.66,764.966 1596.91,766.856 1597.84,768.746 1597.9,768.903 1598.54,770.635 1598.98,772.525 1599.18,774.415 1599.15,776.304 \n",
" 1598.88,778.194 1598.37,780.084 1597.9,781.263 1597.62,781.973 1596.6,783.863 1595.39,785.57 1595.26,785.753 1593.56,787.642 1592.88,788.275 1591.4,789.532 \n",
" 1590.38,790.285 1588.59,791.422 1587.87,791.843 1585.36,793.067 1584.74,793.311 1582.85,794.034 1580.35,794.762 1578.21,795.201 1577.84,795.279 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9903)\" style=\"stroke:#821f6b; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1572.83,787.757 1570.32,787.758 1569.35,787.642 1567.81,787.476 1565.31,786.9 1562.8,785.931 1562.45,785.753 1560.29,784.516 1559.41,783.863 1557.79,782.356 \n",
" 1557.42,781.973 1556.07,780.084 1555.28,778.236 1555.26,778.194 1554.8,776.304 1554.75,774.415 1555.09,772.525 1555.28,772.049 1555.8,770.635 1556.99,768.746 \n",
" 1557.79,767.857 1558.78,766.856 1560.29,765.688 1561.48,764.966 1562.8,764.261 1565.31,763.317 1566.34,763.076 1567.81,762.719 1570.32,762.422 1572.83,762.423 \n",
" 1575.33,762.721 1576.8,763.076 1577.84,763.32 1580.35,764.265 1581.66,764.966 1582.85,765.694 1584.36,766.856 1585.36,767.865 1586.15,768.746 1587.34,770.635 \n",
" 1587.87,772.065 1588.05,772.525 1588.39,774.415 1588.34,776.304 1587.88,778.194 1587.87,778.222 1587.07,780.084 1585.72,781.973 1585.36,782.348 1583.73,783.863 \n",
" 1582.85,784.511 1580.69,785.753 1580.35,785.927 1577.84,786.897 1575.33,787.475 1573.79,787.642 1572.83,787.757 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9903)\" style=\"stroke:#63146e; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1575.33,782.35 1572.83,782.87 1570.32,782.884 1567.81,782.396 1566.76,781.973 1565.31,781.338 1563.57,780.084 1562.8,779.231 1561.99,778.194 1561.24,776.304 \n",
" 1561.15,774.415 1561.71,772.525 1562.8,770.957 1563.05,770.635 1565.31,768.879 1565.58,768.746 1567.81,767.792 1570.32,767.329 1572.83,767.342 1575.33,767.837 \n",
" 1577.41,768.746 1577.84,768.961 1579.96,770.635 1580.35,771.151 1581.29,772.525 1581.85,774.415 1581.77,776.304 1581.01,778.194 1580.35,779.05 1579.44,780.084 \n",
" 1577.84,781.252 1576.25,781.973 1575.33,782.35 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9903)\" style=\"stroke:#470b69; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1575.33,778.912 1572.83,779.812 1570.32,779.84 1567.81,779.029 1566.63,778.194 1565.34,776.304 1565.31,775.691 1565.2,774.415 1565.31,774.191 1566.1,772.525 \n",
" 1567.81,771.185 1569.5,770.635 1570.32,770.376 1572.83,770.411 1573.5,770.635 1575.33,771.3 1576.86,772.525 1577.76,774.415 1577.64,776.304 1576.32,778.194 \n",
" 1575.33,778.912 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9903)\" style=\"stroke:#0d0829; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1572.83,776.632 1570.32,776.776 1569.64,776.304 1569.03,774.415 1570.32,773.393 1572.83,773.545 1573.88,774.415 1573.28,776.304 1572.83,776.632 \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9903)\" style=\"stroke:#270b52; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1572.83,777.912 1570.32,777.967 1567.91,776.304 1567.81,775.424 1567.66,774.415 1567.81,774.212 1569.76,772.525 1570.32,772.254 1572.83,772.324 1573.22,772.525 \n",
" 1575.27,774.415 1575.06,776.304 1572.83,777.912 \n",
" \"/>\n",
"<defs>\n",
" <clipPath id=\"clip9904\">\n",
" <rect x=\"2129\" y=\"47\" width=\"73\" height=\"1457\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<g clip-path=\"url(#clip9904)\">\n",
"<image width=\"72\" height=\"1456\" xlink:href=\"data:image/png;base64,\n",
"iVBORw0KGgoAAAANSUhEUgAAAEgAAAWwCAYAAAD+FAeUAAALO0lEQVR4nO3dQWoTUBSG0cS8QRyY\n",
"iYhr6L67B1fRFRQsjREqFASLGZRgXEH7Dd8bnLOCy8c/v9vLv9vrhjd9mH3A6gQKAgWBgkBBoCBQ\n",
"ECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBB\n",
"oCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWB\n",
"gkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFMb5\n",
"57fZNyzNgoJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAg\n",
"UBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJA\n",
"QaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIF\n",
"gYJAQaAgUBAoCBQECgKFsf9+N/uGpVlQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgI\n",
"FAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQ\n",
"ECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBB\n",
"oCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoDC29w+zb1iaBQWBgkBBoCBQECgIFAQKAgWB\n",
"gkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQK\n",
"AgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgI\n",
"FAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQK4/XxMPuGpVlQ\n",
"ECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBB\n",
"oCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWB\n",
"gkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQK\n",
"AgWBgkBBoDD+HL/OvmFpFhQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAg\n",
"UBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJA\n",
"QaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIF\n",
"gYJAQaAgUBAoCBQECgIFgYJAQaAgUBAojOdfX2bfsDQLCgIFgYJAQaAgUBAoCBQECgIFgYJAQaAg\n",
"UBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJA\n",
"QaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIF\n",
"gYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBTG0+/Ps29YmgUFgYJAQaAg\n",
"UBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJA\n",
"QaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIF\n",
"gYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQE\n",
"CuPHy2H2DUuzoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQ\n",
"ECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBB\n",
"oCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWB\n",
"gkBBoCBQECgIFAQKAgWBgkBhnP5+nH3D0iwoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAo\n",
"CBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAg\n",
"UBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJA\n",
"QaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBjH8272DUuzoCBQECgIFAQKAgWBgkBB\n",
"oCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWB\n",
"gkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQK\n",
"AgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBBoCBQECgIFAQKAgWBgkBhnM6X2Tcs\n",
"zYKCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgU\n",
"BAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQ\n",
"KAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGg\n",
"IFAQKAgUBAoChfGweZp9w9IsKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGC\n",
"QEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoC\n",
"BYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgU\n",
"BAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFDYftrfXGcfsTILCgIFgYJAQaAgUBAoCBQECgIFgYJA\n",
"QaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIF\n",
"gYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQE\n",
"CgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBQECgIFgYJAQaAgUBAoCBS2m83OA7Z3WFAQKAgU\n",
"BAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQ\n",
"KAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGg\n",
"IFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGCQEGgIFAQKAgUBAoCBYGC\n",
"QEGg8B++FCk4XRJKMAAAAABJRU5ErkJggg==\n",
"\" transform=\"translate(2129, 47)\"/>\n",
"</g>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 1325.3)\" x=\"2237.26\" y=\"1325.3\">-</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2265.37, 1325.3)\" x=\"2265.37\" y=\"1325.3\">4</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 1112.53)\" x=\"2237.26\" y=\"1112.53\">-</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2265.37, 1112.53)\" x=\"2265.37\" y=\"1112.53\">3</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 899.748)\" x=\"2237.26\" y=\"899.748\">-</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2265.37, 899.748)\" x=\"2265.37\" y=\"899.748\">2</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 686.971)\" x=\"2237.26\" y=\"686.971\">-</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2265.37, 686.971)\" x=\"2265.37\" y=\"686.971\">1</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 474.193)\" x=\"2237.26\" y=\"474.193\">0</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 261.415)\" x=\"2237.26\" y=\"261.415\">1</text>\n",
"</g>\n",
"<polyline clip-path=\"url(#clip9901)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 2201.26,1503.47 2201.26,1311.65 2225.26,1311.65 2201.26,1311.65 2201.26,1098.88 2225.26,1098.88 2201.26,1098.88 2201.26,886.097 2225.26,886.097 2201.26,886.097 \n",
" 2201.26,673.32 2225.26,673.32 2201.26,673.32 2201.26,460.542 2225.26,460.542 2201.26,460.542 2201.26,247.764 2225.26,247.764 2201.26,247.764 2201.26,47.2441 \n",
" \n",
" \"/>\n",
"<polyline clip-path=\"url(#clip9903)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 1343.47,775.102 1342.75,775.102 1341.32,775.102 1339.18,775.102 1336.33,775.102 1332.79,775.102 1328.57,775.102 1323.68,775.102 1318.13,775.102 1311.95,775.102 \n",
" 1305.15,775.102 1297.75,775.102 1289.78,775.102 1281.26,775.102 1272.22,775.102 1262.69,775.102 1252.69,775.102 1242.27,775.102 1231.44,775.102 1220.26,775.102 \n",
" 1208.74,775.102 1196.93,775.102 1184.86,775.102 1172.58,775.102 1160.11,775.102 1147.51,775.102 1134.81,775.102 1122.04,775.102 1109.26,775.102 1096.5,775.102 \n",
" 1083.79,775.102 1071.19,775.102 1058.73,775.102 1046.44,775.102 1034.38,775.102 1022.57,775.102 1011.05,775.102 999.86,775.102 989.036,775.102 978.61,775.102 \n",
" 968.615,775.102 959.083,775.102 950.043,775.102 941.525,775.102 933.555,775.102 926.157,775.102 919.356,775.102 913.172,775.102 907.625,775.102 902.733,775.102 \n",
" 898.511,775.102 894.972,775.102 892.127,775.102 889.986,775.102 888.555,775.102 887.838,775.102 \n",
" \"/>\n",
"<g clip-path=\"url(#clip9904)\">\n",
"<image width=\"72\" height=\"1456\" xlink:href=\"data:image/png;base64,\n",
"iVBORw0KGgoAAAANSUhEUgAAAEgAAAWwCAYAAAD+FAeUAAAMbklEQVR4nO3dwY3sRhAFQY5Q/lsh\n",
"L6XfLQtUeSQPERYMEg9LNMmZ/f17/r4P/+uvtz/A1wkUBAoCBYHCnPvv25/h0ywoCBQECgIFgcJc\n",
"V7GVBQWBgkBBoCBQmHtcxTYWFAQKAgWBgqNGsKAgUBAoCBQECq5iwYKCQEGgIFAQKLiKBQsKAgWB\n",
"gkDBU41gQUGgIFAQKAgUHDWCBQWBgkBBoCBQcBULFhQECgIFgcI8bpitLCgIFAQKAgWBgqtYsKAg\n",
"UBAoCBQECvO4YbayoCBQECgIFBw1ggUFgYJAQaAgUHAVCxYUBAoCBYGCQGGe88/bn+HTLCgIFAQK\n",
"AgVPNYIFBYGCQEGgIFBwwyxYUBAoCBQECgIFV7FgQUGgIFAQKAgU5nf/vP0ZPs2CgkBBoCBQmOf4\n",
"I72xoCBQECgIFAQK83MVW1lQECgIFAQKAgVnsWBBQaAgUBAozOOpxsqCgkBBoCBQECi4YRYsKAgU\n",
"BAoCBYGCG2bBgoJAQaAgUHDUCBYUBAoCBYGCQMFRI1hQECgIFAQKAoX5nfP2Z/g0CwoCBYGCQMFR\n",
"I1hQECgIFAQKAgVXsWBBQaAgUBAoCBS8vBAsKAgUBAoChXk81VhZUBAoCBQECgIFR41gQUGgIFAQ\n",
"KAgUPPYJFhQECgIFgYJAwVUsWFAQKAgUBAq+zBIsKAgUBAoCBYGClxeCBQWBgkBBoCBQcMMsWFAQ\n",
"KAgUBAqOGsGCgkBBoCBQECi4igULCgIFgYJAQaDg5YVgQUGgIFAQKHiqESwoCBQECgIFgYIbZsGC\n",
"gkBBoCBQECi4igULCgIFgYJAwR/pYEFBoCBQECgIFOY59+3P8GkWFAQKAgWBgkBhnusstrGgIFAQ\n",
"KAgU3DALFhQECgIFgYJAwQ2zYEFBoCBQECgIFJzFggUFgYJAQaAgUHAVCxYUBAoCBYGCG2bBgoJA\n",
"QaAgUBAoOGoECwoCBYGCQEGgMI+L2MqCgkBBoCBQ8Ec6WFAQKAgUBAoChfGNzJ0FBYGCQEGgIFBw\n",
"FgsWFAQKAgWBgj/SwYKCQEGgIFAQKLiKBQsKAgWBgkBBoDCPL/usLCgIFAQKAoW55/f2Z/g0CwoC\n",
"BYGCQEGg4IZZsKAgUBAoCBQECvM4i60sKAgUBAoChbnXH+mNBQWBgkBBoCBQcNQIFhQECgIFgYJA\n",
"wVUsWFAQKAgUBAoCBXcUgwUFgYJAQaDgqBEsKAgUBAoCBYHCPEejjTpBoCBQECgIFNwwCxYUBAoC\n",
"BYGCG2bBgoJAQaAgUBAo+HmcYEFBoCBQECgIFOa5Gm3UCQIFgYJAwVEjWFAQKAgUBAoCBVexYEFB\n",
"oCBQECgIFLwnHdQJAgWBgkDBa8DBgoJAQaAgUBAoeE86WFAQKAgUBAoChblumK3UCQIFgYJAwQ2z\n",
"YEFBoCBQECgIFNwwCxYUBAoCBYGCQMENs6BOECgIFAQKAgV3FIMFBYGCQEGg4CuZwYKCQEGgIFAQ\n",
"KMz1G2YrdYJAQaAgUBAoeHkhWFAQKAgUBApumAULCgIFgYJAQaDg2XywoCBQECgIFAQK3pMO6gSB\n",
"gkBBoOCoESwoCBQECgIFgYLHPsGCgkBBoCBQECg4iwULCgIFgYJAwVONoE4QKAgUBAoCBUeNYEFB\n",
"oCBQECgIFDz2CRYUBAoCBYGCo0awoCBQECgIFAQKHvsEdYJAQaAgUBAoOIsFCwoCBYGCQEGg4CoW\n",
"LCgIFAQKAgV/pIMFBYGCQEGgIFDwhlmwoCBQECgIFAQKc/wDtpU6QaAgUBAouGEWLCgIFAQKAgWB\n",
"ghtmwYKCQEGgIFAQKDiLBQsKAgWBgkDBH+lgQUGgIFAQKAgUXMWCBQWBgkBBoCBQcBULFhQECgIF\n",
"gcIcf6RXFhQECgIFgYJAwVEjWFAQKAgUBAoCBVexYEFBoCBQECj4Ix0sKAgUBAoCBYGCq1iwoCBQ\n",
"ECgIFAQKrmLBgoJAQaAgUBAoeAUvWFAQKAgUBAqOGsGCgkBBoCBQECi4igULCgIFgYJAQaDgX9cE\n",
"dYJAQaAgUHDUCBYUBAoCBYGCQMGz+WBBQaAgUBAoCBScxYIFBYGCQEGg4KgRLCgIFAQKAgWBgqNG\n",
"sKAgUBAoCBQECq5iwYKCQEGgIFBwwyxYUBAoCBQECgKFuY+r2MaCgkBBoCBQECg4iwULCgIFgYJA\n",
"wVONYEFBoCBQECgIFObctz/Ct1lQECgIFAQKAgVnsWBBQaAgUBAoCBQ89gkWFAQKAgWBwhxvmK0s\n",
"KAgUBAoCBYGCG2bBgoJAQaAgUBAouGEWLCgIFAQKAgVHjWBBQaAgUBAoCBTmvP0JPs6CgkBBoCBQ\n",
"ECg4iwULCgIFgYJAwVONYEFBoCBQECgIFPwSZ7CgIFAQKAgUBArOYsGCgkBBoCBQ8BtmwYKCQEGg\n",
"IFAQKLhhFiwoCBQECgIFgYI3zIIFBYGCQEGg4MsswYKCQEGgIFAQKDhqBAsKAgWBgkBBoOAsFiwo\n",
"CBQECgIFgYKzWLCgIFAQKAgUfJklWFAQKAgUBAoChfFln50FBYGCQEGgIFBwFgsWFAQKAgWBgqNG\n",
"sKAgUBAoCBQECo4awYKCQEGgIFAQKDiLBQsKAgWBgkDBUSNYUBAoCBQECgIFvycdLCgIFAQKAgWB\n",
"gt+TDhYUBAoCBYGCo0awoCBQECgIFAQKcxw1VhYUBAoCBYGCQGGus9jKgoJAQaAgUPCGWbCgIFAQ\n",
"KAgUBAq+zBIsKAgUBAoCBYGClxeCBQWBgkBBoCBQ8PJCsKAgUBAoCBQ8mw8WFAQKAgWBgkDB/3oO\n",
"FhQECgIFgYJAwSt4wYKCQEGgIFBwwyxYUBAoCBQECgIFN8yCBQWBgkBBoCBQcBYLFhQECgIFgYLX\n",
"gIMFBYGCQEGgIFDwlcxgQUGgIFAQKAgU/DxOsKAgUBAoCBQcNYIFBYGCQEGgIFBwFQsWFAQKAgWB\n",
"gkDB/3oOFhQECgIFgYKjRrCgIFAQKAgUBAqezQcLCgIFgYJAQaDgLBYsKAgUBAoCBYGCq1iwoCBQ\n",
"ECgIFNwwCxYUBAoCBYGCQMFRI1hQECgIFAQKAgW/Jx0sKAgUBAoCBT+XHCwoCBQECgIFgYIbZsGC\n",
"gkBBoCBQECh4eSFYUBAoCBQECo4awYKCQEGgIFAQKMx9XMY2FhQECgIFgYJAwVksWFAQKAgUBAqe\n",
"agQLCgIFgYJAQaDgqBEsKAgUBAoCBYGCs1iwoCBQECgIFBw1ggUFgYJAQaAgUPDDAsGCgkBBoCBQ\n",
"ECjM8Z70yoKCQEGgIFAQKDiLBQsKAgWBgkDBUSNYUBAoCBQECgIFP/ofLCgIFAQKAgWBwlx3zFYW\n",
"FAQKAgWBgqNGsKAgUBAoCBQECr7tEywoCBQECgIFgYLfkw4WFAQKAgWBgqNGsKAgUBAoCBQECt6T\n",
"DhYUBAoCBYGCQMENs2BBQaAgUBAoOGoECwoCBYGCQEGg4CoWLCgIFAQKAgWBwhxfyVxZUBAoCBQE\n",
"Cp5qBAsKAgWBgkBBoOCGWbCgIFAQKAgUBAquYsGCgkBBoCBQECi4igULCgIFgYJAYe7jtzg3FhQE\n",
"CgIFgYJAwVEjWFAQKAgUBAoChTk/Z7GNBQWBgkBBoDDHDbOVBQWBgkBBoCBQcBULFhQECgIFgYJA\n",
"wcsLwYKCQEGgIFCY8/NsfmNBQaAgUBAoCBTcMAsWFAQKAgWBgkDBVSxYUBAoCBQECp5qBAsKAgWB\n",
"gkBBoDDn+fP2Z/g0CwoCBYGCQEGg4IZZsKAgUBAoCBTmOmqsLCgIFAQKAgWBgqNGsKAgUBAoCBQE\n",
"Cq5iwYKCQEGgIFAQKLijGCwoCBQECgIFR41gQUGgIFAQKAgUHDWCBQWBgkBBoCBQ8J3VYEFBoCBQ\n",
"ECjMuf5IbywoCBQECgIFgYKjRrCgIFAQKAgUBApzncVWFhQECgIFgYKjRrCgIFAQKAgUBAreMAsW\n",
"FAQKAgWBgkDBywvBgoJAQaAgUHDDLFhQECgIFAQKAgXP5oMFBYGCQEGgIFDw2CdYUBAoCBQECo4a\n",
"wYKCQEGgIFAQKHjsEywoCBQECgIFgYKzWLCgIFAQKAgUBAoe+wQLCgIFgYJAwVEjWFAQKAgUBAoC\n",
"BY99ggUFgYJAQaAgUJh73TDbWFAQKAgUBAqOGsGCgkBBoCBQECjMc+/bn+HTLCgIFAQKAgWBwjzO\n",
"YisLCgIFgYJAwRtmwYKCQEGgIFAQKDhqBAsKAgWBgkBBoODlhWBBQaAgUBAozOOG2cqCgkBBoCBQ\n",
"ECg4agQLCgIFgYJAQaDgsU+woCBQECgIFP4DPcHwb7pfSUoAAAAASUVORK5CYII=\n",
"\" transform=\"translate(2129, 47)\"/>\n",
"</g>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 1325.3)\" x=\"2237.26\" y=\"1325.3\">-</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2265.37, 1325.3)\" x=\"2265.37\" y=\"1325.3\">4</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 1112.53)\" x=\"2237.26\" y=\"1112.53\">-</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2265.37, 1112.53)\" x=\"2265.37\" y=\"1112.53\">3</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 899.748)\" x=\"2237.26\" y=\"899.748\">-</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2265.37, 899.748)\" x=\"2265.37\" y=\"899.748\">2</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 686.971)\" x=\"2237.26\" y=\"686.971\">-</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2265.37, 686.971)\" x=\"2265.37\" y=\"686.971\">1</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 474.193)\" x=\"2237.26\" y=\"474.193\">0</text>\n",
"</g>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:48px; text-anchor:start;\" transform=\"rotate(0, 2237.26, 261.415)\" x=\"2237.26\" y=\"261.415\">1</text>\n",
"</g>\n",
"<polyline clip-path=\"url(#clip9901)\" style=\"stroke:#000000; stroke-width:4; stroke-opacity:1; fill:none\" points=\"\n",
" 2201.26,1503.47 2201.26,1311.65 2225.26,1311.65 2201.26,1311.65 2201.26,1098.88 2225.26,1098.88 2201.26,1098.88 2201.26,886.097 2225.26,886.097 2201.26,886.097 \n",
" 2201.26,673.32 2225.26,673.32 2201.26,673.32 2201.26,460.542 2225.26,460.542 2201.26,460.542 2201.26,247.764 2225.26,247.764 2201.26,247.764 2201.26,47.2441 \n",
" \n",
" \"/>\n",
"<g clip-path=\"url(#clip9901)\">\n",
"<text style=\"fill:#000000; fill-opacity:1; font-family:Arial,Helvetica Neue,Helvetica,sans-serif; font-size:66px; text-anchor:middle;\" transform=\"rotate(-90, 2378.86, 775.359)\" x=\"2378.86\" y=\"775.359\"></text>\n",
"</g>\n",
"</svg>\n"
]
},
"execution_count": 133,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x = Fun()\n",
"u₀ = SingularIntegral(0) \\ (-log(2-x)) # solution with κ = 0\n",
"u = u₀ - sum(u₀)/(π*sqrt(1-x^2)) # ensure correct asymptotics\n",
"v = z -> logkernel(u, z) + log(abs(2-z))\n",
"xx = yy = -4:0.011:4\n",
"V = v.(xx' .+ im*yy)\n",
"\n",
"contour(xx, yy, V)\n",
"plot!(domain(x); color=:black, legend=false)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can solve this equation explicitly. By differentiating we see that $u$ satisfies the following:\n",
"$$\n",
"Hu(x) = -f'(x) = {1 \\over x-2}\n",
"$$\n",
"We now use the inverse Hilbert formula to determine:\n",
"$$\n",
"u(x) = -{1\\over\\sqrt{1-x^2}} H[{1 \\over \\diamond-2} \\sqrt{1-\\diamond^2}](x) + {D \\over \\sqrt{1-x^2}}\n",
"$$\n",
"Using the usual procedure of taking an obvious ansatz and subtracting off the singularities at poles and $\\infty$ we find that:\n",
"$$\n",
"C[{\\sqrt{1-\\diamond^2} \\over x -2}](z) = \\underbrace{\\sqrt{z-1} \\sqrt{z+1} \\over 2 \\I (z-2)}_{\\hbox{ansatz}} - \\underbrace{\\sqrt 3\\over 2 \\I (z-2)}_{\\hbox{remove pole near $z=2$}} - \\underbrace{{1 \\over 2 \\I}}_{\\hbox{remove constant at $\\infty$}}\n",
"$$\n",
"This implies that\n",
"$$\n",
"H[{1 \\over\\diamond-2} \\sqrt{1-\\diamond^2}](x) = \\I(C^+ + C^-)[{1 \\over\\diamond-2} \\sqrt{1-\\diamond^2}](x) = -{\\sqrt 3 \\over x -2} - 1\n",
"$$\n",
"in other words, \n",
"$$\n",
"u = {\\sqrt{3} \\over (x - 2) \\sqrt{1-x^2}} + {D \\over \\sqrt{1-x^2}}\n",
"$$\n",
"We still need to determine $D$. This is chosen so that we tend to $\\log |z|$ near $\\infty$. In particular, we know that\n",
"$$\n",
"{1 \\over \\pi} \\int_{-1}^1 \\log|z-x| u(x) \\dx \\sim {\\int_{-1}^1 u(x) \\dx \\over \\pi} \\log |z|\n",
"$$\n",
"so we need to choose $D$ so that $\\int_{-1}^1 u(x) \\dx = 0$ and only the $\\log|z-2|$ singularity appears near $\\infty$. We first note that \n",
"\\begin{align*}\n",
"C[{1 \\over (\\diamond - 2) \\sqrt{1-\\diamond^2}}](z) &= \\underbrace{{\\I \\over 2 \\sqrt{z-1} \\sqrt{z+1} (z-2)}}_{\\hbox{ansatz}} - \\underbrace{{\\I \\over 2\\sqrt{3} (z-2)}}_{\\hbox{remove pole}} \\\\\n",
"& = -{\\I \\over 2 \\sqrt{3} z} + O(z^{-2})\n",
"\\end{align*}\n",
"near $\\infty$. Since \n",
"$$\n",
"Cw(z) ={ \\int_{-1}^1 w(x) \\dx \\over -2\\pi \\I z} + O(z^{-2}) \n",
"$$\n",
"we can infer the integral from the Cauchy transform and find that\n",
"$$\n",
"\\int_{-1}^1 {1 \\over (x - 2) \\sqrt{1-x^2}} \\dx = -{ \\pi \\over \\sqrt{3}}\n",
"$$\n",
"On the other hand,\n",
"$$\n",
"\\int_{-1}^1 {\\dx \\over \\sqrt{1-x^2}} = \\pi\n",
"$$\n",
"Thus we require $D = 1$ and have the solution:\n",
"$$\n",
"u(x) = {\\sqrt{3} \\over (x - 2) \\sqrt{1-x^2}} - {1 \\over \\sqrt{1-x^2}}\n",
"$$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"_Demonstration_ We first check that differentiation reduces to the Hilbert transform:"
]
},
{
"cell_type": "code",
"execution_count": 149,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"true"
]
},
"execution_count": 149,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"t = Fun()\n",
"f = -log(2-t)\n",
"hilbert(u, 0.1) ≈ -f'(0.1) ≈ 1/(0.1-2)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In the inverse Hilbert transform we calculated the following Cauchy transform:"
]
},
{
"cell_type": "code",
"execution_count": 150,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"true"
]
},
"execution_count": 150,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"z = 1+im\n",
"cauchy((-f')*sqrt(1-t^2), z) ≈ sqrt(z-1)sqrt(z+1)/(2im*(z-2)) - sqrt(3)/(2im*(z-2)) - 1/(2im)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Which means that:"
]
},
{
"cell_type": "code",
"execution_count": 153,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(-0.08839431180585401, -0.08839431180585411)"
]
},
"execution_count": 153,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"hilbert((-f')*sqrt(1-t^2), 0.1), -sqrt(3)/(0.1-2) - 1"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Thus we have the inverse Hilbert transform:"
]
},
{
"cell_type": "code",
"execution_count": 140,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"true"
]
},
"execution_count": 140,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"D = randn()\n",
"ũ = sqrt(3)/((x-2)*sqrt(1-x^2)) + D/sqrt(1-x^2)\n",
"hilbert(ũ,0.1) ≈ -f'(0.1)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We still need to determine the constant $D$. What goes wrong if we have the wrong choice is that we don't tend to precisely $\\log z$ near $\\infty$:"
]
},
{
"cell_type": "code",
"execution_count": 141,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(-24.76573192820616, 12.206072645530174)"
]
},
"execution_count": 141,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"z = 200000\n",
"logkernel(ũ,z), log(z)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We determined the integral"
]
},
{
"cell_type": "code",
"execution_count": 142,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"true"
]
},
"execution_count": 142,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"sum(1/((x-2)*sqrt(1-x^2))) ≈ -2π/(2*sqrt(3))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Therefore:"
]
},
{
"cell_type": "code",
"execution_count": 160,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"1.743934249004316e-16"
]
},
"execution_count": 160,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"sum(u)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We thus found $u$:"
]
},
{
"cell_type": "code",
"execution_count": 154,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(0.08883962601869715, 0.08883962601869722)"
]
},
"execution_count": 154,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x = 0.1; u(x), sqrt(3)/((x-2)*sqrt(1-x^2)) + 1/sqrt(1-x^2)"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Julia 1.0.0",
"language": "julia",
"name": "julia-1.0"
},
"language_info": {
"file_extension": ".jl",
"mimetype": "application/julia",
"name": "julia",
"version": "1.0.0"
}
},
"nbformat": 4,
"nbformat_minor": 2
}