---
comments: true
difficulty: 中等
edit_url: https://github.com/doocs/leetcode/edit/main/solution/0700-0799/0743.Network%20Delay%20Time/README.md
tags:
    - 深度优先搜索
    - 广度优先搜索
    - 图
    - 最短路
    - 堆（优先队列）
---

<!-- problem:start -->

# [743. 网络延迟时间](https://leetcode.cn/problems/network-delay-time)

[English Version](/solution/0700-0799/0743.Network%20Delay%20Time/README_EN.md)

## 题目描述

<!-- description:start -->

<p>有 <code>n</code> 个网络节点，标记为&nbsp;<code>1</code>&nbsp;到 <code>n</code>。</p>

<p>给你一个列表&nbsp;<code>times</code>，表示信号经过 <strong>有向</strong> 边的传递时间。&nbsp;<code>times[i] = (u<sub>i</sub>, v<sub>i</sub>, w<sub>i</sub>)</code>，其中&nbsp;<code>u<sub>i</sub></code>&nbsp;是源节点，<code>v<sub>i</sub></code>&nbsp;是目标节点， <code>w<sub>i</sub></code>&nbsp;是一个信号从源节点传递到目标节点的时间。</p>

<p>现在，从某个节点&nbsp;<code>K</code>&nbsp;发出一个信号。需要多久才能使所有节点都收到信号？如果不能使所有节点收到信号，返回&nbsp;<code>-1</code> 。</p>

<p>&nbsp;</p>

<p><strong>示例 1：</strong></p>

<p><img alt="" src="https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/0700-0799/0743.Network%20Delay%20Time/images/931_example_1.png" style="height: 220px; width: 200px;" /></p>

<pre>
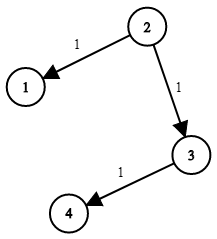
<strong>输入：</strong>times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
<strong>输出：</strong>2
</pre>

<p><strong>示例 2：</strong></p>

<pre>
<strong>输入：</strong>times = [[1,2,1]], n = 2, k = 1
<strong>输出：</strong>1
</pre>

<p><strong>示例 3：</strong></p>

<pre>
<strong>输入：</strong>times = [[1,2,1]], n = 2, k = 2
<strong>输出：</strong>-1
</pre>

<p>&nbsp;</p>

<p><strong>提示：</strong></p>

<ul>
	<li><code>1 &lt;= k &lt;= n &lt;= 100</code></li>
	<li><code>1 &lt;= times.length &lt;= 6000</code></li>
	<li><code>times[i].length == 3</code></li>
	<li><code>1 &lt;= u<sub>i</sub>, v<sub>i</sub> &lt;= n</code></li>
	<li><code>u<sub>i</sub> != v<sub>i</sub></code></li>
	<li><code>0 &lt;= w<sub>i</sub> &lt;= 100</code></li>
	<li>所有 <code>(u<sub>i</sub>, v<sub>i</sub>)</code> 对都 <strong>互不相同</strong>（即，不含重复边）</li>
</ul>

<!-- description:end -->

## 解法

<!-- solution:start -->

### 方法一：朴素 Dijkstra 算法

我们定义 $\textit{g}[u][v]$ 表示节点 $u$ 到节点 $v$ 的边权，如果节点 $u$ 到节点 $v$ 之间没有边，则 $\textit{g}[u][v] = +\infty$。

我们维护一个数组 $\textit{dist}$，其中 $\textit{dist}[i]$ 表示节点 $k$ 到节点 $i$ 的最短路径长度。初始时，我们将 $\textit{dist}[i]$ 全部初始化为 $+\infty$，但 $\textit{dist}[k - 1] = 0$。定义一个数组 $\textit{vis}$，其中 $\textit{vis}[i]$ 表示节点 $i$ 是否被访问过，初始时，我们将 $\textit{vis}[i]$ 全部初始化为 $\text{false}$。

我们每次找到未被访问的距离最小的节点 $t$，然后以节点 $t$ 为中心进行松弛操作，即对于每个节点 $j$，如果 $\textit{dist}[j] > \textit{dist}[t] + \textit{g}[t][j]$，则更新 $\textit{dist}[j] = \textit{dist}[t] + \textit{g}[t][j]$。

最后，我们返回 $\textit{dist}$ 中的最大值，即为答案。如果答案为 $+\infty$，则说明存在无法到达的节点，返回 $-1$。

时间复杂度 $O(n^2 + m)$，空间复杂度 $O(n^2)$。其中 $n$ 和 $m$ 分别为节点数和边数。

<!-- tabs:start -->

#### Python3

```python
class Solution:
    def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
        g = [[inf] * n for _ in range(n)]
        for u, v, w in times:
            g[u - 1][v - 1] = w
        dist = [inf] * n
        dist[k - 1] = 0
        vis = [False] * n
        for _ in range(n):
            t = -1
            for j in range(n):
                if not vis[j] and (t == -1 or dist[t] > dist[j]):
                    t = j
            vis[t] = True
            for j in range(n):
                dist[j] = min(dist[j], dist[t] + g[t][j])
        ans = max(dist)
        return -1 if ans == inf else ans
```

#### Java

```java
class Solution {
    public int networkDelayTime(int[][] times, int n, int k) {
        int[][] g = new int[n][n];
        int[] dist = new int[n];
        final int inf = 1 << 29;
        Arrays.fill(dist, inf);
        for (var e : g) {
            Arrays.fill(e, inf);
        }
        for (var e : times) {
            g[e[0] - 1][e[1] - 1] = e[2];
        }
        dist[k - 1] = 0;
        boolean[] vis = new boolean[n];
        for (int i = 0; i < n; ++i) {
            int t = -1;
            for (int j = 0; j < n; ++j) {
                if (!vis[j] && (t == -1 || dist[t] > dist[j])) {
                    t = j;
                }
            }
            vis[t] = true;
            for (int j = 0; j < n; ++j) {
                dist[j] = Math.min(dist[j], dist[t] + g[t][j]);
            }
        }
        int ans = 0;
        for (int x : dist) {
            ans = Math.max(ans, x);
        }
        return ans == inf ? -1 : ans;
    }
}
```

#### C++

```cpp
class Solution {
public:
    int networkDelayTime(vector<vector<int>>& times, int n, int k) {
        const int inf = 1 << 29;
        vector<vector<int>> g(n, vector<int>(n, inf));
        for (const auto& e : times) {
            g[e[0] - 1][e[1] - 1] = e[2];
        }
        vector<int> dist(n, inf);
        dist[k - 1] = 0;
        vector<bool> vis(n);
        for (int i = 0; i < n; ++i) {
            int t = -1;
            for (int j = 0; j < n; ++j) {
                if (!vis[j] && (t == -1 || dist[t] > dist[j])) {
                    t = j;
                }
            }
            vis[t] = true;
            for (int j = 0; j < n; ++j) {
                dist[j] = min(dist[j], dist[t] + g[t][j]);
            }
        }
        int ans = ranges::max(dist);
        return ans == inf ? -1 : ans;
    }
};
```

#### Go

```go
func networkDelayTime(times [][]int, n int, k int) int {
	const inf = 1 << 29
	g := make([][]int, n)
	for i := range g {
		g[i] = make([]int, n)
		for j := range g[i] {
			g[i][j] = inf
		}
	}
	for _, e := range times {
		g[e[0]-1][e[1]-1] = e[2]
	}

	dist := make([]int, n)
	for i := range dist {
		dist[i] = inf
	}
	dist[k-1] = 0

	vis := make([]bool, n)
	for i := 0; i < n; i++ {
		t := -1
		for j := 0; j < n; j++ {
			if !vis[j] && (t == -1 || dist[t] > dist[j]) {
				t = j
			}
		}
		vis[t] = true
		for j := 0; j < n; j++ {
			dist[j] = min(dist[j], dist[t]+g[t][j])
		}
	}

	if ans := slices.Max(dist); ans != inf {
		return ans
	}
	return -1
}
```

#### TypeScript

```ts
function networkDelayTime(times: number[][], n: number, k: number): number {
    const g: number[][] = Array.from({ length: n }, () => Array(n).fill(Infinity));
    for (const [u, v, w] of times) {
        g[u - 1][v - 1] = w;
    }
    const dist: number[] = Array(n).fill(Infinity);
    dist[k - 1] = 0;
    const vis: boolean[] = Array(n).fill(false);
    for (let i = 0; i < n; ++i) {
        let t = -1;
        for (let j = 0; j < n; ++j) {
            if (!vis[j] && (t === -1 || dist[j] < dist[t])) {
                t = j;
            }
        }
        vis[t] = true;
        for (let j = 0; j < n; ++j) {
            dist[j] = Math.min(dist[j], dist[t] + g[t][j]);
        }
    }
    const ans = Math.max(...dist);
    return ans === Infinity ? -1 : ans;
}
```

<!-- tabs:end -->

<!-- solution:end -->

<!-- solution:start -->

### 方法二：堆优化 Dijkstra 算法

我们可以使用优先队列（堆）来优化朴素 Dijkstra 算法。

我们定义 $\textit{g}[u]$ 表示节点 $u$ 的所有邻接边，而 $\textit{dist}[u]$ 表示节点 $k$ 到节点 $u$ 的最短路径长度。初始时，我们将 $\textit{dist}[u]$ 全部初始化为 $+\infty$，但 $\textit{dist}[k - 1] = 0$。

定义一个优先队列 $\textit{pq}$，其中每个元素为 $(\textit{d}, u)$，表示节点 $u$ 到节点 $k$ 的距离为 $\textit{d}$。我们每次从 $\textit{pq}$ 中取出距离最小的节点 $(\textit{d}, u)$。如果 $\textit{d} > \textit{dist}[u]$，则跳过该节点。否则，我们遍历节点 $u$ 的所有邻接边，对于每个邻接边 $(v, w)$，如果 $\textit{dist}[v] > \textit{dist}[u] + w$，则更新 $\textit{dist}[v] = \textit{dist}[u] + w$，并将 $(\textit{dist}[v], v)$ 加入 $\textit{pq}$。

最后，我们返回 $\textit{dist}$ 中的最大值，即为答案。如果答案为 $+\infty$，则说明存在无法到达的节点，返回 $-1$。

时间复杂度 $O(m \times \log m + n)$，空间复杂度 $O(n + m)$。其中 $n$ 和 $m$ 分别为节点数和边数。

<!-- tabs:start -->

#### Python3

```python
class Solution:
    def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
        g = [[] for _ in range(n)]
        for u, v, w in times:
            g[u - 1].append((v - 1, w))
        dist = [inf] * n
        dist[k - 1] = 0
        pq = [(0, k - 1)]
        while pq:
            d, u = heappop(pq)
            if d > dist[u]:
                continue
            for v, w in g[u]:
                if (nd := d + w) < dist[v]:
                    dist[v] = nd
                    heappush(pq, (nd, v))
        ans = max(dist)
        return -1 if ans == inf else ans
```

#### Java

```java
class Solution {
    public int networkDelayTime(int[][] times, int n, int k) {
        final int inf = 1 << 29;
        List<int[]>[] g = new List[n];
        Arrays.setAll(g, i -> new ArrayList<>());
        for (var e : times) {
            g[e[0] - 1].add(new int[] {e[1] - 1, e[2]});
        }
        int[] dist = new int[n];
        Arrays.fill(dist, inf);
        dist[k - 1] = 0;
        PriorityQueue<int[]> pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[0]));
        pq.offer(new int[] {0, k - 1});
        while (!pq.isEmpty()) {
            var p = pq.poll();
            int d = p[0], u = p[1];
            if (d > dist[u]) {
                continue;
            }
            for (var e : g[u]) {
                int v = e[0], w = e[1];
                if (dist[v] > dist[u] + w) {
                    dist[v] = dist[u] + w;
                    pq.offer(new int[] {dist[v], v});
                }
            }
        }
        int ans = Arrays.stream(dist).max().getAsInt();
        return ans == inf ? -1 : ans;
    }
}
```

#### C++

```cpp
class Solution {
public:
    int networkDelayTime(vector<vector<int>>& times, int n, int k) {
        const int inf = 1 << 29;
        using pii = pair<int, int>;
        vector<vector<pii>> g(n);
        for (auto& edge : times) {
            g[edge[0] - 1].emplace_back(edge[1] - 1, edge[2]);
        }

        vector<int> dist(n, inf);
        dist[k - 1] = 0;
        priority_queue<pii, vector<pii>, greater<>> pq;
        pq.emplace(0, k - 1);

        while (!pq.empty()) {
            auto [d, u] = pq.top();
            pq.pop();
            if (d > dist[u]) {
                continue;
            }
            for (auto& [v, w] : g[u]) {
                if (dist[v] > dist[u] + w) {
                    dist[v] = dist[u] + w;
                    pq.emplace(dist[v], v);
                }
            }
        }

        int ans = ranges::max(dist);
        return ans == inf ? -1 : ans;
    }
};
```

#### Go

```go
func networkDelayTime(times [][]int, n int, k int) int {
	g := make([][][2]int, n)
	for _, e := range times {
		u, v, w := e[0]-1, e[1]-1, e[2]
		g[u] = append(g[u], [2]int{v, w})
	}
	dist := make([]int, n)
	const inf int = 1 << 29
	for i := range dist {
		dist[i] = inf
	}
	dist[k-1] = 0
	pq := hp{{0, k - 1}}
	for len(pq) > 0 {
		p := heap.Pop(&pq).(pair)
		d, u := p.x, p.i
		if d > dist[u] {
			continue
		}
		for _, e := range g[u] {
			v, w := e[0], e[1]
			if nd := d + w; nd < dist[v] {
				dist[v] = nd
				heap.Push(&pq, pair{nd, v})
			}
		}
	}
	if ans := slices.Max(dist); ans < inf {
		return ans
	}
	return -1

}

type pair struct{ x, i int }
type hp []pair

func (h hp) Len() int           { return len(h) }
func (h hp) Less(i, j int) bool { return h[i].x < h[j].x }
func (h hp) Swap(i, j int)      { h[i], h[j] = h[j], h[i] }
func (h *hp) Push(x any)        { *h = append(*h, x.(pair)) }
func (h *hp) Pop() (x any)      { a := *h; x = a[len(a)-1]; *h = a[:len(a)-1]; return }
```

#### TypeScript

```ts
function networkDelayTime(times: number[][], n: number, k: number): number {
    const g: [number, number][][] = Array.from({ length: n }, () => []);
    for (const [u, v, w] of times) {
        g[u - 1].push([v - 1, w]);
    }
    const dist: number[] = Array(n).fill(Infinity);
    dist[k - 1] = 0;
    const pq = new PriorityQueue<number[]>((a, b) => a[0] - b[0]);
    pq.enqueue([0, k - 1]);
    while (!pq.isEmpty()) {
        const [d, u] = pq.dequeue();
        if (d > dist[u]) {
            continue;
        }
        for (const [v, w] of g[u]) {
            if (dist[v] > dist[u] + w) {
                dist[v] = dist[u] + w;
                pq.enqueue([dist[v], v]);
            }
        }
    }
    const ans = Math.max(...dist);
    return ans === Infinity ? -1 : ans;
}
```

<!-- tabs:end -->

<!-- solution:end -->

<!-- problem:end -->