---
comments: true
difficulty: 困难
edit_url: https://github.com/doocs/leetcode/edit/main/solution/0800-0899/0847.Shortest%20Path%20Visiting%20All%20Nodes/README.md
tags:
    - 位运算
    - 广度优先搜索
    - 图
    - 动态规划
    - 状态压缩
---

<!-- problem:start -->

# [847. 访问所有节点的最短路径](https://leetcode.cn/problems/shortest-path-visiting-all-nodes)

[English Version](/solution/0800-0899/0847.Shortest%20Path%20Visiting%20All%20Nodes/README_EN.md)

## 题目描述

<!-- description:start -->

<p>存在一个由 <code>n</code> 个节点组成的无向连通图，图中的节点按从 <code>0</code> 到 <code>n - 1</code> 编号。</p>

<p>给你一个数组 <code>graph</code> 表示这个图。其中，<code>graph[i]</code> 是一个列表，由所有与节点 <code>i</code> 直接相连的节点组成。</p>

<p>返回能够访问所有节点的最短路径的长度。你可以在任一节点开始和停止，也可以多次重访节点，并且可以重用边。</p>

<p>&nbsp;</p>

<ol>
</ol>

<p><strong>示例 1：</strong></p>
<img alt="" src="https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/0800-0899/0847.Shortest%20Path%20Visiting%20All%20Nodes/images/shortest1-graph.jpg" style="width: 222px; height: 183px;" />
<pre>
<strong>输入：</strong>graph = [[1,2,3],[0],[0],[0]]
<strong>输出：</strong>4
<strong>解释：</strong>一种可能的路径为 [1,0,2,0,3]</pre>

<p><strong>示例 2：</strong></p>

<p><img alt="" src="https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/0800-0899/0847.Shortest%20Path%20Visiting%20All%20Nodes/images/shortest2-graph.jpg" style="width: 382px; height: 222px;" /></p>

<pre>
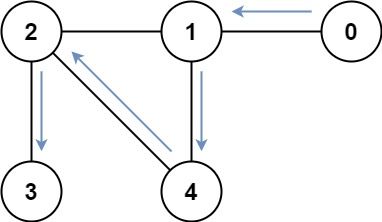
<strong>输入：</strong>graph = [[1],[0,2,4],[1,3,4],[2],[1,2]]
<strong>输出：</strong>4
<strong>解释：</strong>一种可能的路径为 [0,1,4,2,3]
</pre>

<p>&nbsp;</p>

<p><strong>提示：</strong></p>

<ul>
	<li><code>n == graph.length</code></li>
	<li><code>1 &lt;= n &lt;= 12</code></li>
	<li><code>0 &lt;= graph[i].length &lt;&nbsp;n</code></li>
	<li><code>graph[i]</code> 不包含 <code>i</code></li>
	<li>如果 <code>graph[a]</code> 包含 <code>b</code> ，那么 <code>graph[b]</code> 也包含 <code>a</code></li>
	<li>输入的图总是连通图</li>
</ul>

<!-- description:end -->

## 解法

<!-- solution:start -->

### 方法一：状态压缩 + BFS

我们注意到 $n$ 的范围不超过 $12$，因此，我们可以用一个 $12$ 位的二进制数来表示每个节点的访问情况，其中第 $i$ 位为 $1$ 表示第 $i$ 个节点已经被访问过，为 $0$ 表示该节点还没有被访问过。

我们初始化队列 $q$，其中每个元素是一个二元素 $(i, st)$，表示当前位于节点 $i$，且已经遍历过的节点的集合为 $st$。初始时，队列中只有 $n$ 个元素，即 $(i, 2^i)$，表示可以从任一节点出发开始遍历。另外，我们用一个哈希表或数组 $vis$ 记录每个状态是否已经被搜索过，防止无效的重复搜索。

在 BFS 的过程中，我们每次取出队首元素 $(i, st)$，如果当前 $st$ 包含 $n$ 个 $1$，那么我们就找到了一条从起点出发的遍历路径，返回当前的步数即可。否则我们枚举当前节点 $i$ 的所有连边 $(i, j)$，如果 $(j, st \lor 2^j)$ 没有被搜索过，那么就将 $(j, st \lor 2^j)$ 加入队列 $q$ 中，并且用 $vis$ 记录它已经被搜索过。循环此过程，直到找到一条路径。

时间复杂度 $(n^2 \times 2^n)$，空间复杂度 $O(n \times 2^n)$。其中 $n$ 是图中的节点数。

<!-- tabs:start -->

#### Python3

```python
class Solution:
    def shortestPathLength(self, graph: List[List[int]]) -> int:
        n = len(graph)
        q = deque()
        vis = set()
        for i in range(n):
            q.append((i, 1 << i))
            vis.add((i, 1 << i))
        ans = 0
        while 1:
            for _ in range(len(q)):
                i, st = q.popleft()
                if st == (1 << n) - 1:
                    return ans
                for j in graph[i]:
                    nst = st | 1 << j
                    if (j, nst) not in vis:
                        vis.add((j, nst))
                        q.append((j, nst))
            ans += 1
```

#### Java

```java
class Solution {
    public int shortestPathLength(int[][] graph) {
        int n = graph.length;
        Deque<int[]> q = new ArrayDeque<>();
        boolean[][] vis = new boolean[n][1 << n];
        for (int i = 0; i < n; ++i) {
            q.offer(new int[] {i, 1 << i});
            vis[i][1 << i] = true;
        }
        for (int ans = 0;; ++ans) {
            for (int k = q.size(); k > 0; --k) {
                var p = q.poll();
                int i = p[0], st = p[1];
                if (st == (1 << n) - 1) {
                    return ans;
                }
                for (int j : graph[i]) {
                    int nst = st | 1 << j;
                    if (!vis[j][nst]) {
                        vis[j][nst] = true;
                        q.offer(new int[] {j, nst});
                    }
                }
            }
        }
    }
}
```

#### C++

```cpp
class Solution {
public:
    int shortestPathLength(vector<vector<int>>& graph) {
        int n = graph.size();
        queue<pair<int, int>> q;
        bool vis[n][1 << n];
        memset(vis, false, sizeof(vis));
        for (int i = 0; i < n; ++i) {
            q.emplace(i, 1 << i);
            vis[i][1 << i] = true;
        }
        for (int ans = 0;; ++ans) {
            for (int k = q.size(); k; --k) {
                auto [i, st] = q.front();
                q.pop();
                if (st == (1 << n) - 1) {
                    return ans;
                }
                for (int j : graph[i]) {
                    int nst = st | 1 << j;
                    if (!vis[j][nst]) {
                        vis[j][nst] = true;
                        q.emplace(j, nst);
                    }
                }
            }
        }
    }
};
```

#### Go

```go
func shortestPathLength(graph [][]int) int {
	n := len(graph)
	q := [][2]int{}
	vis := make([][]bool, n)
	for i := range vis {
		vis[i] = make([]bool, 1<<n)
		vis[i][1<<i] = true
		q = append(q, [2]int{i, 1 << i})
	}
	for ans := 0; ; ans++ {
		for k := len(q); k > 0; k-- {
			p := q[0]
			q = q[1:]
			i, st := p[0], p[1]
			if st == (1<<n)-1 {
				return ans
			}
			for _, j := range graph[i] {
				nst := st | 1<<j
				if !vis[j][nst] {
					vis[j][nst] = true
					q = append(q, [2]int{j, nst})
				}
			}
		}
	}
}
```

#### TypeScript

```ts
function shortestPathLength(graph: number[][]): number {
    const n = graph.length;
    const q: number[][] = [];
    const vis: boolean[][] = new Array(n).fill(false).map(() => new Array(1 << n).fill(false));
    for (let i = 0; i < n; ++i) {
        q.push([i, 1 << i]);
        vis[i][1 << i] = true;
    }
    for (let ans = 0; ; ++ans) {
        for (let k = q.length; k; --k) {
            const [i, st] = q.shift()!;
            if (st === (1 << n) - 1) {
                return ans;
            }
            for (const j of graph[i]) {
                const nst = st | (1 << j);
                if (!vis[j][nst]) {
                    vis[j][nst] = true;
                    q.push([j, nst]);
                }
            }
        }
    }
}
```

#### Rust

```rust
use std::collections::VecDeque;

impl Solution {
    #[allow(dead_code)]
    pub fn shortest_path_length(graph: Vec<Vec<i32>>) -> i32 {
        let n = graph.len();
        let mut vis = vec![vec![false; 1 << n]; n];
        let mut q = VecDeque::new();

        // Initialize the queue
        for i in 0..n {
            q.push_back(((i, 1 << i), 0));
            vis[i][1 << i] = true;
        }

        // Begin BFS
        while !q.is_empty() {
            let ((i, st), count) = q.pop_front().unwrap();
            if st == (1 << n) - 1 {
                return count;
            }
            // If the path has not been visited
            for j in &graph[i] {
                let nst = st | (1 << *j);
                if !vis[*j as usize][nst] {
                    q.push_back(((*j as usize, nst), count + 1));
                    vis[*j as usize][nst] = true;
                }
            }
        }

        -1
    }
}
```

<!-- tabs:end -->

<!-- solution:end -->

<!-- solution:start -->

### 方法二：BFS(A\* 算法)

因为每条边权值一样，所以用 BFS 就能得出最短路径，过程中可以用**状态压缩**记录节点的访问情况。另外，同一个节点 u 以及对应的节点访问情况需要保证只被搜索过一次，因此可以用 `vis(u, state)` 表示是否已经被搜索过，防止无效的重复搜索。

本题也属于 BFS 最小步数模型，可以使用 A\* 算法优化搜索。

A\* 算法主要思想如下：

1. 将 BFS 队列转换为优先队列（小根堆）；
1. 队列中的每个元素为 `(dist[state] + f(state), state)`，`dist[state]` 表示从起点到当前 state 的距离，`f(state)` 表示从当前 state 到终点的估计距离，这两个距离之和作为堆排序的依据；
1. 当终点第一次出队时，说明找到了从起点到终点的最短路径，直接返回对应的 step；
1. `f(state)` 是估价函数，并且估价函数要满足 `f(state) <= g(state)`，其中 `g(state)` 表示 state 到终点的真实距离；
1. A\* 算法只能保证终点第一次出队时，即找到了一条从起点到终点的最小路径，不能保证其他点出队时也是从起点到当前点的最短路径。

<!-- tabs:start -->

#### Python3

```python
class Solution:
    def shortestPathLength(self, graph: List[List[int]]) -> int:
        n = len(graph)

        def f(state):
            return sum(((state >> i) & 1) == 0 for i in range(n))

        q = []
        dist = [[inf] * (1 << n) for _ in range(n)]
        for i in range(n):
            heappush(q, (f(1 << i), i, 1 << i))
            dist[i][1 << i] = 0
        while q:
            _, u, state = heappop(q)
            if state == (1 << n) - 1:
                return dist[u][state]
            for v in graph[u]:
                nxt = state | (1 << v)
                if dist[v][nxt] > dist[u][state] + 1:
                    dist[v][nxt] = dist[u][state] + 1
                    heappush(q, (dist[v][nxt] + f(nxt), v, nxt))
        return 0
```

#### Java

```java
class Solution {
    private int n;

    public int shortestPathLength(int[][] graph) {
        n = graph.length;
        int[][] dist = new int[n][1 << n];
        for (int i = 0; i < n; ++i) {
            Arrays.fill(dist[i], Integer.MAX_VALUE);
        }
        PriorityQueue<int[]> q = new PriorityQueue<>(Comparator.comparingInt(a -> a[0]));
        for (int i = 0; i < n; ++i) {
            q.offer(new int[] {f(1 << i), i, 1 << i});
            dist[i][1 << i] = 0;
        }
        while (!q.isEmpty()) {
            int[] p = q.poll();
            int u = p[1], state = p[2];
            if (state == (1 << n) - 1) {
                return dist[u][state];
            }
            for (int v : graph[u]) {
                int nxt = state | (1 << v);
                if (dist[v][nxt] > dist[u][state] + 1) {
                    dist[v][nxt] = dist[u][state] + 1;
                    q.offer(new int[] {dist[v][nxt] + f(nxt), v, nxt});
                }
            }
        }
        return 0;
    }

    private int f(int state) {
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            if (((state >> i) & 1) == 0) {
                ++ans;
            }
        }
        return ans;
    }
}
```

#### C++

```cpp
class Solution {
public:
    int n;

    int shortestPathLength(vector<vector<int>>& graph) {
        n = graph.size();
        priority_queue<tuple<int, int, int>, vector<tuple<int, int, int>>, greater<tuple<int, int, int>>> q;
        vector<vector<int>> dist(n, vector<int>(1 << n, INT_MAX));
        for (int i = 0; i < n; ++i) {
            q.push({f(1 << i), i, 1 << i});
            dist[i][1 << i] = 0;
        }
        while (!q.empty()) {
            auto [_, u, state] = q.top();
            q.pop();
            if (state == (1 << n) - 1) return dist[u][state];
            for (int v : graph[u]) {
                int nxt = state | (1 << v);
                if (dist[v][nxt] > dist[u][state] + 1) {
                    dist[v][nxt] = dist[u][state] + 1;
                    q.push({dist[v][nxt] + f(nxt), v, nxt});
                }
            }
        }
        return 0;
    }

    int f(int state) {
        int ans = 0;
        for (int i = 0; i < n; ++i)
            if (((state >> i) & 1) == 0)
                ++ans;
        return ans;
    }
};
```

<!-- tabs:end -->

<!-- solution:end -->

<!-- problem:end -->