---
comments: true
difficulty: 困难
edit_url: https://github.com/doocs/leetcode/edit/main/solution/2200-2299/2203.Minimum%20Weighted%20Subgraph%20With%20the%20Required%20Paths/README.md
rating: 2364
source: 第 284 场周赛 Q4
tags:
- 图
- 最短路
---
# [2203. 得到要求路径的最小带权子图](https://leetcode.cn/problems/minimum-weighted-subgraph-with-the-required-paths)
[English Version](/solution/2200-2299/2203.Minimum%20Weighted%20Subgraph%20With%20the%20Required%20Paths/README_EN.md)
## 题目描述
给你一个整数 n ,它表示一个 带权有向 图的节点数,节点编号为 0 到 n - 1 。
同时给你一个二维整数数组 edges ,其中 edges[i] = [fromi, toi, weighti] ,表示从 fromi 到 toi 有一条边权为 weighti 的 有向 边。
最后,给你三个 互不相同 的整数 src1 ,src2 和 dest ,表示图中三个不同的点。
请你从图中选出一个 边权和最小 的子图,使得从 src1 和 src2 出发,在这个子图中,都 可以 到达 dest 。如果这样的子图不存在,请返回 -1 。
子图 中的点和边都应该属于原图的一部分。子图的边权和定义为它所包含的所有边的权值之和。
示例 1:
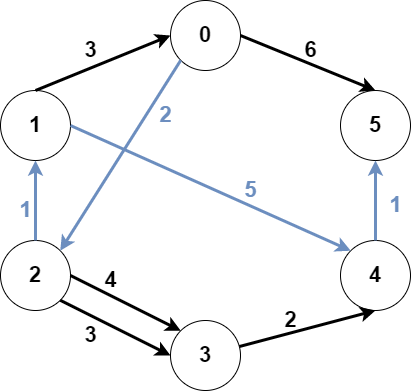
输入:n = 6, edges = [[0,2,2],[0,5,6],[1,0,3],[1,4,5],[2,1,1],[2,3,3],[2,3,4],[3,4,2],[4,5,1]], src1 = 0, src2 = 1, dest = 5
输出:9
解释:
上图为输入的图。
蓝色边为最优子图之一。
注意,子图 [[1,0,3],[0,5,6]] 也能得到最优解,但无法在满足所有限制的前提下,得到更优解。
示例 2:

输入:n = 3, edges = [[0,1,1],[2,1,1]], src1 = 0, src2 = 1, dest = 2
输出:-1
解释:
上图为输入的图。
可以看到,不存在从节点 1 到节点 2 的路径,所以不存在任何子图满足所有限制。
提示:
3 <= n <= 1050 <= edges.length <= 105edges[i].length == 30 <= fromi, toi, src1, src2, dest <= n - 1fromi != toisrc1 ,src2 和 dest 两两不同。1 <= weight[i] <= 105
## 解法
### 方法一:枚举三条最短路的交汇点
最短路问题。
我们假设从 $src1$ 出发到 $dest$ 的一条最短路径为 $A$,从 $src2$ 出发到 $dest$ 的一条最短路径为 $B$。
$A$, $B$ 两条路径一定存在着公共点 $p$,因为 $dest$ 一定是其中一个公共点。那么问题可以转换为求以下三条路径和的最小值:
1. 从 $src1$ 到 $p$ 的最短路
1. 从 $src2$ 到 $p$ 的最短路
1. 从 $p$ 到 $dest$ 的最短路(这里我们可以将原图的所有边反向,然后转换为从 $dest$ 到 $p$ 的最短路)
我们进行三次 Dijkstra 算法,就可以求出 $src1$, $src2$, $dest$ 到其他点的最短路径。
公共点可以有多个,因此我们在 $[0,n)$ 范围内枚举公共点 $p$,找出边权之和最小的值即可。
时间复杂度 $O(mlogn)$,其中 m 表示数组 $edges$ 的长度。
#### Python3
```python
class Solution:
def minimumWeight(
self, n: int, edges: List[List[int]], src1: int, src2: int, dest: int
) -> int:
def dijkstra(g, u):
dist = [inf] * n
dist[u] = 0
q = [(0, u)]
while q:
d, u = heappop(q)
if d > dist[u]:
continue
for v, w in g[u]:
if dist[v] > dist[u] + w:
dist[v] = dist[u] + w
heappush(q, (dist[v], v))
return dist
g = defaultdict(list)
rg = defaultdict(list)
for f, t, w in edges:
g[f].append((t, w))
rg[t].append((f, w))
d1 = dijkstra(g, src1)
d2 = dijkstra(g, src2)
d3 = dijkstra(rg, dest)
ans = min(sum(v) for v in zip(d1, d2, d3))
return -1 if ans >= inf else ans
```
#### Java
```java
class Solution {
private static final Long INF = Long.MAX_VALUE;
public long minimumWeight(int n, int[][] edges, int src1, int src2, int dest) {
List>[] g = new List[n];
List>[] rg = new List[n];
for (int i = 0; i < n; ++i) {
g[i] = new ArrayList<>();
rg[i] = new ArrayList<>();
}
for (int[] e : edges) {
int f = e[0], t = e[1];
long w = e[2];
g[f].add(new Pair<>(t, w));
rg[t].add(new Pair<>(f, w));
}
long[] d1 = dijkstra(g, src1);
long[] d2 = dijkstra(g, src2);
long[] d3 = dijkstra(rg, dest);
long ans = -1;
for (int i = 0; i < n; ++i) {
if (d1[i] == INF || d2[i] == INF || d3[i] == INF) {
continue;
}
long t = d1[i] + d2[i] + d3[i];
if (ans == -1 || ans > t) {
ans = t;
}
}
return ans;
}
private long[] dijkstra(List>[] g, int u) {
int n = g.length;
long[] dist = new long[n];
Arrays.fill(dist, INF);
dist[u] = 0;
PriorityQueue> q
= new PriorityQueue<>(Comparator.comparingLong(Pair::getKey));
q.offer(new Pair<>(0L, u));
while (!q.isEmpty()) {
Pair p = q.poll();
long d = p.getKey();
u = p.getValue();
if (d > dist[u]) {
continue;
}
for (Pair e : g[u]) {
int v = e.getKey();
long w = e.getValue();
if (dist[v] > dist[u] + w) {
dist[v] = dist[u] + w;
q.offer(new Pair<>(dist[v], v));
}
}
}
return dist;
}
}
```


