{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"ChEn-3170: Computational Methods in Chemical Engineering Spring 2020 UMass Lowell; Prof. V. F. de Almeida **29Apr20**\n",
"\n",
"# 21. Nuclear Chemical Reactor Point Dynamics \n",
"$ \n",
" \\newcommand{\\Amtrx}{\\boldsymbol{\\mathsf{A}}}\n",
" \\newcommand{\\Bmtrx}{\\boldsymbol{\\mathsf{B}}}\n",
" \\newcommand{\\Mmtrx}{\\boldsymbol{\\mathsf{M}}}\n",
" \\newcommand{\\Imtrx}{\\boldsymbol{\\mathsf{I}}}\n",
" \\newcommand{\\Pmtrx}{\\boldsymbol{\\mathsf{P}}}\n",
" \\newcommand{\\Lmtrx}{\\boldsymbol{\\mathsf{L}}}\n",
" \\newcommand{\\Umtrx}{\\boldsymbol{\\mathsf{U}}}\n",
" \\newcommand{\\Smtrx}{\\boldsymbol{\\mathsf{S}}}\n",
" \\newcommand{\\xvec}{\\boldsymbol{\\mathsf{x}}}\n",
" \\newcommand{\\uvar}{\\boldsymbol{u}}\n",
" \\newcommand{\\fvar}{\\boldsymbol{f}}\n",
" \\newcommand{\\avec}{\\boldsymbol{\\mathsf{a}}}\n",
" \\newcommand{\\bvec}{\\boldsymbol{\\mathsf{b}}}\n",
" \\newcommand{\\cvec}{\\boldsymbol{\\mathsf{c}}}\n",
" \\newcommand{\\rvec}{\\boldsymbol{\\mathsf{r}}}\n",
" \\newcommand{\\mvec}{\\boldsymbol{\\mathsf{m}}}\n",
" \\newcommand{\\gvec}{\\boldsymbol{\\mathsf{g}}}\n",
" \\newcommand{\\zerovec}{\\boldsymbol{\\mathsf{0}}}\n",
" \\newcommand{\\norm}[1]{\\bigl\\lVert{#1}\\bigr\\rVert}\n",
" \\newcommand{\\transpose}[1]{{#1}^\\top}\n",
" \\DeclareMathOperator{\\rank}{rank}\n",
" \\newcommand{\\Power}{\\mathcal{P}}\n",
"$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"---\n",
"## Table of Contents\n",
"* [Objectives](#obj)\n",
"* [Introduction](#intro)\n",
"* [Problem Statement](#ps)\n",
"* [Input Data](#data)\n",
"* [Degrees of Freedom](#dof)\n",
"* [One Energy Group Neutron Balance](#nbal)\n",
"* [Reactivity Step Results wihtout Feedback](#res1)\n",
"* [Reactivity Step with Negative Feedback Results](#res2)\n",
"* [Interactive Results](#ires)\n",
"---"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Objectives\n",
"+ Introduce the computational notebook approach to problem solving.\n",
"+ Combine content, problem setup, computational methods, calculations, and interactive analysis in one *live*, exchangeable, portable (web-based) document.\n",
"+ Use one-energy-group point-reactor dynamics modeling to obtain insight on neutron density behavior with a step change in reactivity."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Introduction\n",
"\n",
"Background for this topic can be found in the textbook: *Dynamics of Nuclear Reactors*, David L. Hetrick, 1993, ANS. \n",
"\n",
"**A power nuclear reactor is a heat generation device**. In most cases, nuclear heat (heat generated by nuclear fission reactions) is then converted in work through a heat-work cycle on the heated fluid passed through the reactor (figure below). A very simplified modeling of all types of nuclear reactors has been developed in the early days of nuclear engineering. The point-reactor model is an introduction to the subject of nuclear reactor dynamics. It disregards space variations of the neutron density (*i.e.* it is a pointwise approach), it considers dynamics for one-energy group of neutrons, it only applies to conditions when the reactor is near criticality and the nuclear fuel is nearly static. In this model, a pointwise neutron balance \n",
"is performed using the main components of neutron transport, namely prompt fission, delayed fission, scattering, and absorption (figure below); scattering is taking into account in the diffusion limit.\n",
"\n",
"\n",
"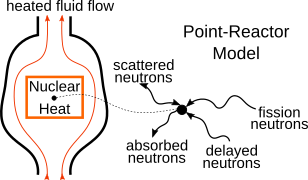"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Problem Statement\n",
"\n",
"Given the neutron generation time $\\ell$, delayed neutron fraction, $\\beta$, decay constants of a six-group delayed neutron emitters, $\\lambda_i$, and corresponding yield of delayed neutron fractions for each emitter, $\\beta_i$, calculate the pointwise neutron density variation with time for a step change in neutron reactivity, $\\rho$.\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Input Data\n",
"\n",
"Name | Parameter | Value | Unit |\n",
"--------------------------|--------------------|----------------------|------------------| \n",
"neutron generation time | $\\ell$ | $1\\times 10^{-4}$ | s | \n",
"delayed neutron fraction | $\\beta$ | $6.5\\times 10^{-3}$ | - | \n",
"reactivity feedback coef. | $\\alpha_n$ | $-3\\times 10^{-4}$ | cm$^2$ |\n",
"\n",
"\n",
"For thermal fission of $^{235}$U the following delay neutron data is typically used (*Dynamics of Nuclear Reactors*, David Hetrick, 1993, ANS textbook).\n",
"\n",
"\n",
"Delayed neutron emitter group No. | Decay cte ($\\lambda_i$,1/sec) | Relative yield ($\\beta_i/\\beta$) |\n",
"----------------------------------|-------------------------------|----------------------------------| \n",
"1 | 0.0124 | 0.033 |\n",
"2 | 0.0305 | 0.219 | \n",
"3 | 0.111 | 0.196 | \n",
"4 | 0.301 | 0.395 | \n",
"5 | 1.14 | 0.115 |\n",
"6 | 3.01 | 0.042 |"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"'''Parameters'''\n",
"\n",
"params = dict()\n",
"\n",
"params['gen_time'] = 1.0e-4 # s\n",
"params['beta'] = 6.5e-3 # \n",
"params['species_decay'] = [0.0124, 0.0305, 0.111, 0.301, 1.14, 3.01] # 1/sec\n",
"params['species_rel_yield'] = [0.033, 0.219, 0.196, 0.395, 0.115, 0.042] \n",
"params['alpha_n'] = -3e-4 # cm^2"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## One Energy Group Neutron Balance\n",
"\n",
"The space-invariant neutron balance for the point-reactor model without a startup source (or extraneous source) is \n",
"\n",
"\\begin{equation*}\n",
"\\frac{\\text{d}n}{\\text{d}t} = \\frac{\\rho(t)-\\beta}{\\ell}\\, n + \\sum\\limits_{i=1}^{6} \\lambda_i\\,c_i ,\n",
"\\end{equation*}\n",
"\n",
"where the first term on the right side of the equation represents the net production of neutrons not account for delayed neutrons, and the second term accounts for the source of delayed neutrons considering 6 groups of delayed neutron emitters resulting from the fission of $^{235}$U nuclei. Therefore a balance of neutron emitter species is also necessary\n",
"\n",
"\\begin{equation*}\n",
"\\frac{\\text{d}c_i}{\\text{d}t} = \\frac{\\beta_i}{\\ell}\\, n - \\lambda_i\\,c_i ,\n",
" \\ \\ \\ \\ \\ \\forall \\ \\ \\ \\ \\ i=1,\\ldots,6.\n",
"\\end{equation*}\n",
"\n",
"where the first term on the right side of the equation is the source of emitters as a function of the neutron density $n(t)$, and the second term is the consumption rate of the emitter by radioactive decay obtained as a function of the product of the concentration of the emmiter, $c_i(t)$, multiplied by its decay constant $\\lambda_i$. Here the concentration of of the $i$th emitter, $c_i$ is considered in terms of delayed neutron density, hence the units are the same as $n$.\n",
"\n",
"The reactivity function with feedback is postulated as\n",
"\n",
"\\begin{equation*}\n",
" \\rho(t) = \\rho_0 + \\alpha_n\\,\\bigl(n(t) - n(0)\\bigr),\n",
"\\end{equation*}\n",
"\n",
"where $\\alpha_n \\le 0$ is the feedback coefficient and the externally applied reactivity is $\\rho_0$."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Degrees of Freedom\n",
"There exists seven equations, the neutron density balance, and six neutron emitting species balance. There exists seven unknown variables, $n(t)$ and $c_i(t)$. Therefore there are as many unknowns as there are equations and the problem is potentially solvable given the initial conditions for the unknowns, and all the values of the parameters in the foregoing table."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Vector ODE System\n",
"\n",
"A vector notation for the foregoing system of equations greatly improves the generality of the derived computer code. Towards this goal let us define\n",
"\n",
"\\begin{equation*}\n",
"\\frac{d\\uvar}{dt} = \\fvar( \\uvar, t )\n",
"\\end{equation*}\n",
"\n",
"where $\\uvar(t) = (u_1,u_2,u_3,u_4,u_5,u_6,u_7)$ and we assign \n",
"\n",
"\\begin{align*}\n",
" u_1(t)&=n(t),\\\\\n",
" u_2(t)&=c_1(t),\\\\\n",
" u_3(t)&=c_2(t),\\\\\n",
" u_4(t)&=c_3(t),\\\\\n",
" u_5(t)&=c_4(t),\\\\\n",
" u_6(t)&=c_5(t),\\\\\n",
" u_7(t)&=c_6(t).\n",
"\\end{align*}\n",
"\n",
"Also for $\\fvar(\\uvar,t) = \\bigl(f_1(\\uvar,t), f_2(\\uvar,t), f_3(\\uvar,t), f_4(\\uvar,t), f_5(\\uvar,t), f_6(\\uvar,t), f_7(\\uvar,t)\\bigr)$ we assign \n",
"\n",
"\\begin{align*}\n",
" f_1 & = \\frac{\\rho(t)-\\beta}{\\ell}\\, u_1 + \\sum\\limits_{i=2}^{7} \\lambda_i\\,u_i, \\\\\n",
" f_2 & = \\frac{\\beta_1}{\\ell}\\, u_1 - \\lambda_1\\,u_2, \\\\\n",
" f_3 & = \\frac{\\beta_2}{\\ell}\\, u_1 - \\lambda_2\\,u_3, \\\\\n",
" f_4 & = \\frac{\\beta_3}{\\ell}\\, u_1 - \\lambda_3\\,u_4, \\\\\n",
" f_5 & = \\frac{\\beta_4}{\\ell}\\, u_1 - \\lambda_4\\,u_5, \\\\\n",
" f_6 & = \\frac{\\beta_5}{\\ell}\\, u_1 - \\lambda_5\\,u_6, \\\\\n",
" f_7 & = \\frac{\\beta_6}{\\ell}\\, u_1 - \\lambda_6\\,u_7 .\n",
"\\end{align*}\n",
"\n",
"Finally, the initial conditions given are as follows:\n",
"\n",
"\\begin{align*}\n",
" u_1(0)&=n_0,\\\\\n",
" u_2(0)&=c_{1_0},\\\\\n",
" u_3(0)&=c_{2_0},\\\\\n",
" u_4(0)&=c_{3_0},\\\\\n",
" u_5(0)&=c_{4_0},\\\\\n",
" u_6(0)&=c_{5_0},\\\\\n",
" u_7(0)&=c_{6_0}\n",
"\\end{align*}\n",
"\n",
"where $n_0$ is a steady-state value of the neutron density, and the corresponding steady-state values for the concentration of delayed neutron emitters is \n",
"\n",
"\\begin{equation*}\n",
"c_{i_0} = \\frac{\\beta_i\\,n_0}{\\lambda_i\\,\\ell} \\ \\ \\ \\ \\forall \\ \\ \\ \\ i=1,\\ldots,6\n",
"\\end{equation*}"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [],
"source": [
"'''ODE function'''\n",
"\n",
"def f_vec( time, u_vec, params ): \n",
" \n",
" import numpy as np\n",
" assert np.all(u_vec >= 0.0)\n",
" \n",
" n_dens = u_vec[0]\n",
" \n",
" gen_time = params['gen_time'] \n",
" beta = params['beta']\n",
" \n",
" species_decay = params['species_decay']\n",
" lambda_vec = np.array(species_decay)\n",
" \n",
" species_rel_yield = params['species_rel_yield']\n",
" beta_vec = np.array(species_rel_yield) * beta\n",
" \n",
" rho_0 = params['reactivity_0']\n",
" alpha = params['alpha_n']\n",
" n_dens_0 = params['n_0']\n",
" reactivity = rho_0 + alpha * (n_dens - n_dens_0)\n",
" \n",
" c_vec = u_vec[1:]\n",
" #print('c_vec = ',c_vec)\n",
" \n",
" f_tmp = np.zeros(7,dtype=np.float64) # vector for f_vec return\n",
" \n",
" # neutron balance\n",
" f_tmp[0] = (reactivity - beta)/gen_time * n_dens + lambda_vec @ c_vec\n",
" #print('a=',(reactivity - beta)/gen_time * n_dens)\n",
" #print('b=',lambda_vec @ c_vec)\n",
" #print('f_tmp[0]',f_tmp[0])\n",
" \n",
" # loop over 6 species balance\n",
" #for i in range(6):\n",
" #f_tmp[i+1] = species_rel_yield[i]*beta/gen_time * n_dens - lambda_vec[i] * u_vec[i+1]\n",
" f_tmp[1:] = beta_vec/gen_time * n_dens - lambda_vec * c_vec\n",
" #print('f_tmp=',f_tmp)\n",
" #print('time=',time)\n",
" #print('')\n",
" \n",
" return f_tmp"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [],
"source": [
"'''Create the point-reactor run function'''\n",
"\n",
"def run_point_reactor(f_vec, time_stamps, params):\n",
"\n",
" from scipy.integrate import odeint\n",
"\n",
" max_n_steps_per_time_step = 100 # max number of nonlinear algebraic solver iterations per time step\n",
"\n",
" n_0 = params['n_0']\n",
" c_vec_0 = params['c_vec_0']\n",
" \n",
" u_vec_0 = np.zeros(7,dtype=np.float64)\n",
" \n",
" u_vec_0[0] = n_0\n",
" u_vec_0[1:] = c_vec_0\n",
" \n",
" (u_vec_history, info_dict) = odeint( f_vec, u_vec_0, time_stamps,\n",
" args=( params, ),\n",
" rtol=1e-4, atol=1e-4, mxstep=max_n_steps_per_time_step,\n",
" full_output=True, tfirst=True )\n",
"\n",
" assert info_dict['message']=='Integration successful.',\\\n",
" 'Fatal: scipy.integrate.odeint failed %r'%info_dict['message']\n",
" \n",
" return u_vec_history"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Reactivity Step Results without Feedback "
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [],
"source": [
"'''Evolve the point-reactor from a steady state; no feedback'''\n",
"\n",
"beta = params['beta']\n",
"\n",
"# Manipulated input variable\n",
"params['reactivity_0'] = 10/100 * beta # \"10 cents\"\n",
"params['alpha_n'] = 0.0 # set no feedback\n",
"\n",
"n_0 = 5.0 # arbitrary value at steady state\n",
"params['n_0'] = n_0\n",
"\n",
"import numpy as np\n",
"c_vec_0 = np.zeros(6,dtype=np.float64)\n",
"\n",
"species_decay = params['species_decay']\n",
"lambda_vec = np.array(species_decay)\n",
"\n",
"species_rel_yield = params['species_rel_yield']\n",
"beta_vec = np.array(species_rel_yield) * beta\n",
"\n",
"gen_time = params['gen_time']\n",
"\n",
"c_vec_0 = beta_vec/lambda_vec/gen_time * n_0\n",
" \n",
"params['c_vec_0'] = c_vec_0\n",
"\n",
"time_final = 100.0 # s\n",
"n_time_steps = 100 # number of solution values in time\n",
"\n",
"import numpy as np\n",
"time_stamps = np.linspace(0.0, time_final, num=n_time_steps)\n",
"\n",
"u_vec_history = run_point_reactor( f_vec, time_stamps, params )"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [],
"source": [
"'''Plot neutron density and delayed neutron emitter concentration in the reactor'''\n",
"\n",
"def plot_results(u_vec_history):\n",
" import matplotlib.pyplot as plt\n",
" \n",
" fig, ax1 = plt.subplots(1, figsize=(12, 6))\n",
"\n",
" ax2 = ax1.twinx() \n",
" color_ids = np.linspace(0,1,u_vec_history[:,1:].shape[1])\n",
" for (j,color_id) in zip(range(u_vec_history[:,1:].shape[1]),color_ids):\n",
" color=plt.cm.nipy_spectral(color_id)\n",
" ax2.plot(time_stamps,u_vec_history[:,j+1]/params['c_vec_0'][j],'-.',color=color,label=r'$c_%i$'%(j+1) )\n",
" ax2.set_ylabel(r'$c_i/c_{i_0}$',fontsize=16,color='black')\n",
" ax2.tick_params(axis='y', labelcolor='black', labelsize=14)\n",
" ax2.legend(loc='lower right',fontsize=12)\n",
" #ax2.grid(True)\n",
"\n",
" ax1.plot(time_stamps,u_vec_history[:,0]/params['n_0'],'r-',label=r'$n/n_0$' )\n",
"\n",
" ax1.set_xlabel(r'Time [s]',fontsize=16)\n",
" ax1.set_ylabel(r'$n/n_0$',fontsize=16,color='black')\n",
" ax1.tick_params(axis='y', labelcolor='black', labelsize=14)\n",
" ax1.tick_params(axis='x', labelsize=14)\n",
" ax1.legend(loc='best',fontsize=12)\n",
" ax1.grid(True)\n",
"\n",
" plt.title(r'Point-Reactor Model: $\\rho/\\beta=$'\n",
" +str(params['reactivity_0']/params['beta'])\n",
" +r'; $\\alpha_n=$'+str(params['alpha_n']),\n",
" fontsize=18)\n",
" fig.tight_layout() # otherwise the right y-label is slightly clipped\n",
" plt.show()\n",
" print('')"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA1gAAAGoCAYAAABbkkSYAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzs3Xd8FVX6x/HPSUhPCAQIJfROQgtdEEUBGxYUse2uuC7qz46uoi4WsFAEXQuKZW2srgo2LCiC0lREXUBAegApSQhJgPR+fn/Mxb3GJNxAbm5Ivu993Zd7Z84985yZcXeenDLGWouIiIiIiIicOD9fByAiIiIiIlJbKMESERERERGpIkqwREREREREqogSLBERERERkSqiBEtERERERKSKKMESERERERGpIkqwREREREREqogSLBERERERkSqiBEtEjpsxZpgxxhpjrvF1LFLzGWN2G2OWHedva9y9Zow5zRiz2BiTYYzJM8asM8Zc7Ou4RETEt5RgidQRbg+o7p8sY8x/jTG3G2P8fRRXb2PMZGNM20r8pry2rDHG3GGMqee9iI/P8bSzCo/tfr5ml1Mm2hhT4CqzrJpDrNGMMc8ZY/YbY4zbtnOAr4EWwBRgIhABzDPGtK+muPxc9/sWV4K31xjzhDEmrBJ13GeMmW+M2em69ru9GHKNVUXn8oTrEJHaocY9hIiI170NLAQMzsPhNcBTQBxwfSXrWgGEAIUnEE9v4CFgGbC7kr91b0sz4GrgSaAblW+Lt51IO6tKHnCVMebv1tr8Uvv+gnMei6o/rJrLlVRdBCyw1lrXNj9gDrAD6GetzXVt3w0sAE4BdlZDeP8EbgM+BJ7Aue9vA+KNMSOstSUe1DEVSAfWAA28FehJoCrOZVXUISK1gBIskbpnjbX2zaNfjDFzgM3AeGPMA9baA55W5HpgyPNCjJ4q3ZbngS04bZlkrT3ou9Cqj6v3Mcham3OMoh8CV+IkDPNK7fsrTrI6vOojPKn1B2KAj9y2DQHaAjcfTa5cjv6hwX2bVxhj4oBbgQ+stWPctu8CngGuAP7jQVUdrLU7Xb/dCIR7IdwarSrOZRVeDxGpBTREUKSOs9ZmAKtwei/aAxhjGruGRe11DRvb6/reyP23Zc2LMcZc49p2pjHmLmNMgjEm3xizzRgzrtTvJwOvub4udRvG9vpxtiUb+N7Vlg6l9xtjgowx/zDG/OIawnPYGPOJMSa+VLkIY8yjxpjVxphUV/w7jDHTjTGhZdQbaIyZ6JqDk2OMOWKM+ckYc4un7azEOT96fkcYYx4wxiTgJLmXeXCK1gA/4yRT7nUOwOnBfK2sH1UmPlfZVsaYea7zkOE6x3+4Hq6yHl2TCuLqYIzp6knZUr9rYox53XV9i40xicaYh1w9Vu4uBo4AS922DXb986tSZc90/XNNZeM5Dlfi3OdPldr+MpAD/NmTSo4mV56q7Pk2xsQbYz40xhxyfd4zxkQZY1q4rveVlTm+l1TFuayS6yEitYN6sETqONcDZUfX11RjTCTwnWvbqzgPi/HAjcCZxpgB1tpMD6qeijN88EUg3/X7140xO6y137rKfAA0xxnONxWnJw0g4QSadPRBPt19ozEmAPgC5+H438BsIBK4DvjWGHOatfYnV/EYYDzwPs5fnYuA03Hm2cQDZ7vVGwgsAoYBXwJv4iQ8PYBLXMepsJ3Hec5nAQE4D3AZwFYPz89rwJPGmJbW2n2ubdcCKcCnZf2gMvEZYxrgDB1tBbwAbMI5d0tx7gf3eitzTcrzFdAG5+HWI8aY7sAS4DDOsK481zEnA2muOI66GPjMWus+DDYeyAK2u9XZEuc8/mit3V3Ocf2AKE/jBNIrGFbWHygBfnDfaK3NM8asc+33Bo/Ptyt5egNYjzNPrR3OkLk9OM8f24F3jyeIGngufXU9RKQmstbqo48+deCDkwBY4EGgMdAE6InzgG6BVa5yj7m+31Tq9ze7tj9SRp3XuG27xrVtLRDotj0GJ9F6u1S9R8sPO8G29ACec23/oYzf3OHad3ap7fVxHviWuW0LBALKqOMRVx0D3LZNdG2bWkZ5P0/aWclzfrSerUBoJc/XXUAj13X4h2tfCE6iMcv1Pcv9XBxHfFNd2/5aquxTru3u57ky1+QP95pr+27AVuLeCcZJbJe7nz+cBLgQWOu2rZvrmJeWqmMLsNL13zvjzF/bCRQAQyo4dltXfZ5+2lZQ1wbgQDn75rl+H1jRuSjjdxuB3cco49H5xukNz8VJOILdtn+L8weGXOCSysRXk8+lN66HPvroc/J+1IMlUvdMcX2OKgE+5n+LQlwMHAReKvW7F3H+wn8x8IAHx3neWltw9Iu1dr8xZhvQ6fjCLlPptoDTW3RzGWX/jPNg/F9jTONS+xYD44wxIdbaXPe4jbMiYQTgj9PrcT8wkP/9pfpPwCHg4dIHtJ5Paj+ecz7HHnvO1R9Ya9OMMR/jJGpTcXrZInF6pqoivtHAAWBuqbIzgNtLbfP4mlTQnrYVxF2WW3Eezs9yP3/W2iRjzC9AS7eyo3GS0S+ObnANEe0ELDLGtOH3PYdP4wy3LU8yMLISsSZXsC/UFVtZ8tzKFJRT5rhU4nzfjpPM3mqtdZ+nuROnx3INzpzA41XTzqVProeI1ExKsETqnpeA+Th/Uc0Gtllr3YfTtQN+stb+bjU5a22RMWYr0MfD45Q1tyMNZ3jRMRln4YYmpTbnWmuPuH0/2pYAnB6se3AekMtaeKMbTm9NRQtfNAb2uo5/E/B/OHOTSs9Xbej23zsB60o9RFbW8ZzzbSdwvNeAz4wxp+IMa/vBWrupiuJrjzNMrrhU2SRjzOFS9VbqmlSRsTi9tWUNQw3l90NLLwYWW2uz3Lb1wrkf/oszNPMCoDXOwiG349wbv5treJTrHllyog1wyQGiy9kX7FbGVy4EdlhrV5ez/wFrrT3eymvguazp10NEqpESLJG6Z7u1tqoeTCpSXM52T+fKtAJ2ldr2Bk7Py1HubfncGPMN8A3O3J8ryjjuBuDOCo55EMAYcyfOMstf4qwAlojzl+cY4HX+mHAd94PiCTiRh7VFwH6cZePPwJlLVZXKOx+lr73H16QqGGMaAv1wrmnpfVE4ieTrru8tXWWvK1W0t+ufa6y1h/jfvLXnjTGLgT8bY8bb38/ZOnqMsv5oUJGDpRNVN4lArDEmyP5xyf0YINW9J7Y6uc5lW5zXKJTWFPjFWrvwBI9R085ljb0eIlL9lGCJSGk7gS7GmHruPRauoXKdqfr3+5T3MF7WEKDECiuy9jtjzL+Bq40xz1hrv3PbvR3ngexrD4bu/QVnrsm57mWN83LZ0rYB3cp5sPpdeBXsq9Zzbq0tNsbMBe7DmQvzzjF+Upn4dgKdjTH+7g+0xpjmOEMR3VXmmlSFeJykLquMfVfh/H/i0UUXRuNcs49LleuNc84280d+QEpZyZVLWX80qEg7yn9n2o/AWcAAYOXRjcaYYFeMKypxnKrWzPXPNPeNxpjTcP6d/kNsxpiLcYabvoszXDkKmG2t/Uc5x6hp57ImXw8RqWZapl1ESvsI56F3fKnt17m2n8i8ibIcfdj93Ypg1to8a+2SUp+KhrEd9QhO71npOVFzcR78yuwtMcY0dftajPNwbdz21wPuLeOnb+EMC7u/jDrde2zKbKdLdZ9zcHr5pgD/V2rYZVkqE98CnF6Kq0uVvaeMeitzTcpUyWXDjy79Ptz92hhjugCP4qyQ97Vr88XAN/aP71KLx/n/znal4hiMsxDHvys4/tE/Gnj6qWje0Ls49+iEUtuvwxnq+JZbbAHGmK7GmNYV1FeVjg4F7eUWQzjOnD2AsDJ+E4+TrCfiDLs9B7jPtSplWWraufS4DhGp/dSDJSKlPY4zT+U5Y0wfnNUA44G/4Uzof7yKj/cjzkIbk1xDuLKBXRXM3aiQtXaHMeYd4E/GmKHW2qN/TX4a50FrpjHmTJwH6Qyc+TPDceZtneEq+x4wDWfY4Qc4q9pdxf9eJOvuaZx5OPcbY/rjDCvMw5m71QUY4UE7q/ucY63dg9Nj4InKxPc4zrl62RjTF/gFJ/E4BUgtVW9lrkl5KrNMex+c5ejbAB8bYz7HmTN2A87cq79Ya0tc1+c0nBUif+MaltYdCAJWGmOew1nQowfOXLafcRL8MlXlvCFr7QbX8W9x3aMLcea03YazQqL7S21jcHrcluNcC/c2/YX/zYtsAgQaY47+seBXa+2/S5XfDbSx1pZ7vq21icaYH4Chrh7l73ASjcY4C4acZYyZALxrrU1y/SweeMVa+7rrOL8co/016lxWsg4Rqe18vYyhPvroUz0f3Jbq9qBsE+B5YB9OUrEPZwn0xuXUeY3btmsofznyZZSxDDTOogCbcOY5WeD1E2kLzoNNMbC01PZ6OA88P+IkONk4w9TewllV7mg5f5zhcztwVgb7FSdxOLps9+RS9QYDk3CSiTycv+D/yB+XNS+3nZU45+We3yq69n9Ypr0y8bnKtsZJUjOATOATnPeT7S5ddyWuyR/uNdf23Xi4TLvr3H+B806i73GG+iXj9OZFu5W72nWsdqV+H+fa/h+cJDMfZwXJtTi9m/Wr+d9pf+DvOEluPs68uieB8FLl2lJqifxS/06Wt7R5WeVTgf0exNbGdd0zXef5O6Cr6/OLq/4ubuX3ASPcvp8O7DvJzqVHdeijjz61/2Os9cXcbBERkerjWl49A3jSWjvxGGU/xEmuepfa/iecF0kPsb+f31cnGGN64vTSXWutfa0K622C07PYyLpWNHX1cA231l5QVccREakuGiIoIiJ1QS+cHoYNHpRdhfMC7tJ64/ReeFJHbXQ2ToL1RhXXG4/Ts+2+RH4fnHdliYicdLTIhYiI1AVHF7hYf6yC1trHbdnLiMfjzEvKrNLIThLW2pnW2t626ld8jOePyVQ8ztBLEZGTjnqwRESkLogHioAtJ1BHL5zeLalC1toZZWzr4YtYRESqguZgiYiIiIiIVJE61YPl5+dnQ0JCfB0GJSUl+PlpdKb8nu4LKU33hJRF94WURfeFlKWm3Bc5OTnWWuv7QKpJnUqwQkJCyM7O9nUYLFu2jGHDhvk6DKlhdF9IabonpCy6L6Qsui+kLDXlvjDG5Po6hupUZzJJERERERERb1OCJSIiIiIiUkWUYImIiIiIiFQRJVgiIiIiIiJVpE4tclGRjIwMUlJSKCws9PqxIiMj2bx5s9ePc7zCwsJo2bJljVh1RkRERETkZKIECye5OnDgADExMYSEhGCM8erxMjMziYiI8OoxjldJSQn79+8nNTWV6OhoX4cjIiIiInJSURcFkJKSQkxMDKGhoV5Prmo6Pz8/mjZtypEjR3wdioiIiIjISUcJFlBYWEhNeAFxTREQEEBRUZGvwxAREREROekowXKp6z1X7nQuRERERESOjxIsERERERGRKqIES0REREREpIoowaolEhMTadmypa/DEBERERGp05Rg1RILFy7knHPO8XUYIiIiIiKVYoy52Riz3hiT4fqsMsaMqqB8W2OMLeNTIx6GlWCdJF544QVGjRrFzTffTOPGjWnRogWLFy/+bf/ChQs577zzPCorIiIiIrVb3vr1tHv5ZbDW16F4Yh9wD9AH6Ad8DXxkjOl5jN+dAzR3+3ztzSA95dMEq7Zlq960fv16Vq1axYUXXkhKSgo33HADM2bMAJxl5lesWMHIkSOPWVZEREREarGiInjsMY48/jgBwcGwf7+vIzoma+0Ca+3n1tod1tpt1tpJQCZwyjF+mmatTXb7FFRDuMdUz8fHP5qtbsdJ9sbhZKt9rbXrK/jdOcDPbt/TqzSqCRNg3boqrdJdSHEx9O0LTz3l8W/Wr1/Pvffey9lnnw1AbGwsK1euBGDFihX06tWLiIiIY5YFmDRpEitWrKBp06bMnTuX0NDQqmqaiIiIiPhI7vr1FDzxBJFz5xJ9+eV8d/nltDjJ5ugbY/yBsUA48N0xin9gjAnGySX+aa19z9vxecKnPVi1LVv1pg0bNnDBBRf89n3jxo3ExsYCvx8eeKyyGzduJCEhgZUrVzJixAheffXVamqBiIiIiHhFURFMm8ae1avZe/HF2HdfxFxbSL2gDF9HdlQ9Y8xPbp/rSxcwxvQwxmQB+cALwMXW2g3l1JcF3AVcBpwHfAW8a4z5s5firxRf92D9pkZlq5XoWToeuZmZv/U2eWLXrl0UFRXRpUuX37atXbuW0aNHA06C9eGHH3pUduXKlZx77rkAnHvuudxzzz3ccsstJ9wmEREREal+uRs3Uu+22whYupS248fj98gjmIhi+HAKYZG9fR3eUUXW2n7HKLMV6A00AMYAbxhjhllrN5YuaK1NBZ5w2/STMaYxMBF4s4piPm4+T7CMMT2AVUAwTjbqSbb6LVAEXIiTrY6z1pZ5Ml0Z8vUA9erVY9myZX8oExkZSWZm5gm2xHPFxcWVOt7q1auJjY0lOzv7t21r1qzhrrvuYsOGDeTl5RETE0NmZmaFZTMzM0lOTqZr165kZmbi5+dHSkpKmbHk5eWVea7Ee7KysnTO5Xd0T0hZdF9IWXRf1D2muJgmW7aQFx9PgzPOoPD0XgTFpbF78yYwfvi1eI2MnAJST5L7wjUibYfr60/GmP7AHcDfPKxiNfBXb8RWWT5PsPBytmqtfQl4CSAsLMwOGzbsD2U2b95cqR6lE5VZyR6s7du307dv399+k5aWxoEDBxg4cCAvv/wyo0aN+m1fRWWDgoJo1qwZBQUFREREkJ6eTnR0dJmxBAcHEx8fXwWtFU8tW7aMsu5Pqbt0T0hZdF9IWXRf1C2569eze/t2cgYNosGWLbQ6J4qAjbMgo4i2Z06EqO7ASX9f+AFBlSjfG0jyUiyV4vMEqzZlq97ywAMP/O57o0aNKCwsBJzhge5D/CoqC3Dqqacybdo0xo0bx6JFixgyZIgXIxcRERGRqmILCkh+7z2S2rXDv2FD2iXvoGHUm5i1X0Dz0+H0V6B+B1+HWWnGmOnAZ8BeIAK4ChgGjHLtnwYMsNYOd30fBxQCa4ES4ALgZpzF83zO5wlWGU7abNUXhg0bxhlnnOFx+R49etCmTRuGDh1KdHQ0c+fO9WJ0IiIiIlIVctetY3dCAjldutBwyxZadUon4NdJYIth8LMQdxOYk/YVt81wRqM1A44A64FzrbWLXPubA6Uzx/uBNkAxsA24trwpQ9XNpwlWbctWfWHixImV/s20adO8EImIiIiIVLmCApLmzSOpY0f8GzSg/YEdNGzwGqz7ClqcAaf9C+q393WUJ8Rae01l9ltr3wDe8GJIJ8TXPVi1KlsVEREREakyP/0E115L8Rln0MAYWg2IIWDl38AYOHUOdLv+ZO61qrV8mmDVtmxVREREROREleTkkPT++9R/5hkiUlOJOfM0zEVjoKQIUq+HHhMgvLWvw5RyKOUVEREREakpvv0WBg3iUHg4GdddB188gsm5C/JSwa8enPKkkqsaTgmWiIiIiIiPlWRmkvSvf1EyYgR+GRl0Cw8n5vrrIaY/NIp3eq8qYRe7KKHES9FKRZRguZSU6AY8ylrr6xBERERE6ozMZcvYtHw5ifHxHHlkCrz9F/wD33V2NuoJZ30Aoc08qquIIh7ncWKJ5eMWH3sxaimPEiwgLCyM/fv3U1BQUOeTC2staWlpBAcH+zoUERERkVqtOD2dX+fOZVtEBNbPj05HttOw7Vuw4VEozIKSwmNX4uZnfmYQg7iHeziXcxmaOtRLkUtFfL2KYI3QsmVLUlNT+fXXXykqqlz36/HIy8ur0QlMcHAwLVu29HUYIiIiIrXWkS++4FegsGtXordtIab1Bvw2zYKQaDjrI2h7kcd15ZPPozzKdKYTRRTzmMelXMryguXea4CUSwkW4OfnR3R0NNHR0dVyvGXLlhEfH18txxIRERGRmqMoMZG9S5aQHhdH8P79dMjbTpjfFPhlO3S5FgbNgqCGlaozl1xe5VWu4iqe5Eka0chL0YsnlGCJiIiIiHibtRS+/TabmjalqEsXmidsoVnTb/Db8gJEtIPzFkPLER5Xl0UWz/Isd3EXDWjAetYrsaohNAdLRERERMSLSnbuhHPOIeBPf6LJqlXEhofTot1m/La9BD3uhEs3VCq5AljOciYxia/4CkDJVQ2iHiwREREREW8oLiZj7lx2tW5N5337CJk9jRaXnweN46DwXmhzIUQP8Li6NNL4lm+5kAsZxSh+4Re60c2LDZDjoR4sEREREZEqZn/+GU45hZC//52Iffvw+/RTaPE+LPszWAsB4R4nVxbL27xNN7pxFVdxiEMASq5qKPVgiYiIiIhUkZKcHA68/z4Zubl03rOHgNmTaT/2MggIgZCnITASjPG4vr3s5SZu4lM+pT/9+Rf/oiGVWwRDqpd6sEREREREqkD2N9+w+csvSYyNJSAinJIPb4O8++Dn6U6BZoMhKs6juoop5lmeJZZYvuZrnuAJVrGKnvT0YgukKqgHS0RERETkBBSnpbH/k084GBdHQEgIHdK30SDoSdjwX2h9AXQdX6n6NrKR8YxnNas5m7OZwxza0c5L0UtVU4IlIiIiInI8rOXwwoXs8fOjMC6OJgnbiGm1Hv9NT0BwIxgxD9pdWqkhgf/hP4xjHA1owJu8yVVchcHz34vvKcESEREREamkwt272bt8OYe6dyd4/37a524h3E6GX3ZC5786LwwOjvK8PgoJIIAhDOEarmEa02hMY+81QLxGCZaIiIiIiKeKi+G55zi8ejWHb7mFFrsSaBr1GX5b5kJkJzj/a2hxRqWqvJM72cQmPudz2tCGl3nZS8FLddAiFyIiIiIiHshdu5Yj48fD7bfTOD2duCZNaH7pZfiV5EH8/TBmvcfJlXX9B6ATnehJT4oo8mb4Uk3UgyUiIiIiUpHsbJg8mb3t21Nw8cXUH9EH0+hLghqXOPuHv1OpeVa72c2N3MiVXMnVXM2N3OilwMUX1IMlIiIiIlKOzCVLKDz1VJg1izbbt9PllFMwF18K6evh8BankIfJVRFFPMETxBHHSlZSSKEXIxdfUQ+WiIiIiEgpRYmJ7Fu0iLSePWkydiytp40nKHQdNG4Exg+u2AF+AR7X9yM/cj3Xs451XMAFzGY2rWntxRaIr6gHS0RERETExRYXkzZ/Pr9s2kRabCxNE7bQcvBe2HML7F0E2fucgh4mVxlkcCu3MpCBpJDCe7zHAhYouarF1IMlIiIiIgLkrV/Png0byOzalbBff6VT8E5C8x+E7Qehx53QbwoEhHtUl8XyAR9wG7eRRBI3czOP8Rj1qe/lVoivKcESERERkTqtJDOTAx98QFKnTvi1bEnr/VtpHPxvzKYvoEk/OPdzaBxfuTop4VEepQlN+JAPGcAAL0UvNY0SLBERERGps0oWLmRLXh653bvTcMc2WrXcQcDBqc4QwMHPQOxN4OfvUV2FFPI8z3M1V9OQhnzKpzSlKfX0yF2naA6WiIiIiNQ5xXv2wJgx+I0aRaNvv6VjXh7te+US8MuD0Pp8uGwzdL/V4+QKYAtbuJM7+Q//ASCGGJ8lV6vS9pNvS3xy7LpO6bSIiIiI1B1FRWS/9hrbO3Sg/YED1J9+P02vGg6thkDJIIhoCzFnelzdIQ7xMR8zjnH0oAc/8zNxxHkvfg8FGD8+yT3A2b4OpA5SD5aIiIiI1Akl338P/foRcuutRO7aRcDrr0OvtbD8KigucHqrPEyuLJY3eZMudGE849nFLgC60x2D5y8dripFJSU8te1HJqxbAkC/qOZcEtKs2uMQ9WCJiIiISC1XnJZG0oIFHG7QgNgjR/B7Yyrtzh8FYc2g0UywxeAf6HF9W9jCTdzEUpYyiEG8wAu0o50XW1Cx1WmJ/N+aRaw7nMJ5zdpTWFJMgJ8/fh6+AFmqlhIsEREREamVbEkJRxYsYE9wMIW9etFoxzbsG2Ng60RYsw2GvgANu3lcXw45PMZjzGQmYYQxhzlcz/X4+WhQ2KGCPCZtXMELCWtpHhzOe6eM5pKYzhglVj6lBEtEREREap38DRvYu3YtR+LiCE7cT/vsdYQXTYEte6HreOj/WKXq+5RPuZVb2c1uruZqZjKTaKK9FH3FrLX8+9dfuGv9UtLyc7mtU18ejhtK/YAgn8Qjv6cES0RERERqjZKMDA68/z5JnTtj2rcnZt9Wmga+jdnyKUT1gOFvQ7MhlarzX/yL67iObnRjGcs4ndO9FP2x/XLkIDetWcyK1L0MjGrOoqGXEd+wqc/ikT9SgiUiIiIiJz9ryfr8c3YXFpLfsycNEnbQqsVWAlOngfGHgTOhx+3O+608UEghiSTShjaMZSyZZHIzNxOI53O1vGFOwjo2HDnIS33P5m/temmeVQ2kBEtERERETm4JCXDrrRRnZGAnTaJjXjaR5mHYtAnaXQqn/BPCW1aqytGMZg97WMtaIonkDu7wUvAVs9ayIHE7LULCGRDVgsd6nMZDcUNoEhTqk3jk2JRgiYiIiMhJyebkcHD+fEpWrqTZypVETrmXuDPPxC8oCNaNg0a9oJXnb4JKJpkGNCCYYCYwgTzyfPai4KPySoq4de0ShjZuyX8GXUik5lnVeHoPloiIiIicfBYuxPToQfaePWSNGIH99t/QcAZ+6aud/b0nepxcFVHEszxLF7rwOI8DMJKRXMAF3oq+QrnFhfxz24/kFxcR4h/AV6dfwRsDRvkkFqk89WCJiIiIyEmjcNcu9n/9NdHTpxMaGEibQb0wIy7AFOfCobEQVrmhgKtYxU3cxDrWcRZncSVXeilyzyxMSuDWtUvYmX2YtmGRXBzTmc4RUT6NSSpHCZaIiIiI1Hg2L4+D8+aR2Lo1xd27E/7QREKbLcUv9U4oPgvqhcLpr3hcXwop3Mu9vMZrxBDDfOYzhjEYfLNoxK/ZR7h93VcsSNxO14golpx2OcObtvVJLHJilGCJiIiISI2WtXgxe44cITcujojdu2gVvYuQwkdgdz70mghYj+sqppgXeIH7uZ8sspjIRB7gAcIJ914DKpBXXMSsrT8wdcsqDIbpPU7njs79CfTz90k8cuKUYImIiIhIjVS4cyf7ly4lrXdvAqzeWZKOAAAgAElEQVSlXfovNLSzMJs3QMuzYcizENnJ4/oOc5gzOZO1rGU4w3mWZ+lGNy+2oGILkxK4be0SErIPc2nLLjzR60xah9b3WTxSNZRgiYiIiEiNYnNzOTh//m/DAZvu3krzyC/w3/lvCG8NI9+HtheDh++AyiefIIKIJJJ+9ONe7mUsY302HBDgm9R9jPrmPbpERPHlaZcxsmk7n8UiVUurCIqIiIhIzfHppxQNHsz+Nm0ITUsjtmQtLTNuwH/3uxB/P1y2Gdpd4nFytYhFtKUtO9mJwfASL3EZl/kkucorLuKb1H0ADGkUw1sDL2D9WdcquapllGCJiIiIiM8VbttG0syZ2AsvJCAvj25FRXS65BJCmjeH5qfD2F+g/yPOYhYeyCcfgO50ZyADvRm6x/7+89ecvWIeqfk5GGO4qnWs5lrVQhoiKCIiIiK+k50NU6dyZPNmku6+m8g5swltt5TgBt+AGQ5tLoS2F3lcXSKJ3M3dJJLI13xNDDF8xEdebEDFtmem42cMHcIbck/XQVwS05nGQZ4liXJyUg+WiIiIiFQ/a8n45BPSr7sOpk6lUXgYcS1bEnrDTRAYAf7BTjkPhwIWUMBMZtKFLrzP+wxlKEUUebEBFcsqKuC+Dcvp/uWr3L1+GQCtQ+tr6fU6QD1YIiIiIlKt8jdsYN+PP3K4Vy9CLx1Dw6t7YY68RlBYhlNg2KuVqu8LvuB2bmcb2zif83mKp+hABy9EfmzWWubt28Lff/6a/blZjGvTnek9T/dJLOIbSrBEREREpFqUpKWR/OGHJHfrBl260GLfFpoGv4PZ8yk06AZF2ZWqL4EE7uROPuZjOtGJz/iM8zjPS9Ef2/rDKdy2bgnLD+6lT4OmzBt0EYMbt/RZPOIbSrBERERExKtsURGHP/iAfWFhFMTH03DXDlo2WUfgwSfAPwQGPQndbwG/AI/rnMY0JjOZQAKZwQxu53aCCPJiK8qXXpDLgxu/YU7CWhoGBvNCn7MZ374n/kazceoiJVgiIiIi4jW5q1axd8cOMmNjCU5KpHPmaiJyH4GtydD5GhgwDUKbeVSXxQJgMAQRxGVcxgxm0IIWXmxBxQpLiolf/Dr7cjK5qWM8U+JOJSowxGfxiO8pwRIRERGRqrdvH9xzD3tOP53cLl1olbydJkXPYrZ9B00GwNkfQbTny6enksoYxnAd1/Fn/swd3OHTFwWvPXSA3g2iCfDzZ0aP04mLbEKPyCY+i0dqDvVbioiIiEiVsbm5pL7xBoWnnALvv0+btFTievcmethpmLwUOP01GL3K4+Tq6EqAUUQRRhj+OO+N8mVytfjALvoseZ2PErcDcEXrWCVX8hslWCIiIiJy4qyFDz6gYNgw9nTpQuqECbD4IYLjvyegfn0IawGXb4Uu14AHc5MKKeQZnqEznUklFT/8WMhCruRK77elDDlFhfz3UDIAZ0a34ZneIzi7aTufxFLbGGNuNsasN8ZkuD6rjDGjjvGbHsaY5caYXGPMfmPMg8Z4uKa/lynBEhEREZETUrB+PQemTIExYwjKyaFrbi7N7rwTGjcCWwSFmU5BDxd9WMISetOb27mdjnQkm8qtLliVrLXM37uFbov+xTkr5pFTVIi/8ePWTn0Jref5ohxSoX3APUAfoB/wNfCRMaZnWYWNMfWBxcABoD9wG3A3cGe1RHsMPk2walu2KiIiIlKXlKSkkPjSS2zMzGT/WWeR//JUmB5DaNOtGGOg63Vw7kIIrO9RfTvYwUVcxEhGkksuH/ERi1hEG9p4uSVl+/lwCmcsf5vLvl9Aw4Bg3hs8WkmVF1hrF1hrP7fW7rDWbrPWTgIygVPK+cmfgFBgnLV2o7X2fWAGcGdNyAt8vcjF0Wx1O06yNw4nW+1rrV1furBbtroCJ1vtArwOZANPVFPMIiIiInWaLSjg0Pz57IuKorBvXxruTiAm6geC7NOQEgrtxzgFPXzWzSCDR3mUp3iKIIKYxjQmMIFggr3YivIdzM/h/o0r+NfO9TQMDGZOn7O4rn0vLbteDYwx/sBYIBz4rpxipwArrbW5btsWAY8AbYFd3ozxWHyaYFlrF5TaNMkYcyPOSftDgsXvs9VcYKMxphtOtvqktdZ6N2IRERGRui178WL2HjxIdteuhOzfT7vMb4jIfhTS0qDreOj/KIREe1zfZ3zGtVxLCilcwzVMZSrNae7FFpSvoKSY2Tv+y8ObviO7qJBbO/XhodhTaRjom0SvFqlnjPnJ7ftL1tqX3AsYY3oAq4BgIAu42Fq7oZz6muF01Lg74LbPpwmWqSk5iVu2OhfoW9YJNcbMBRpZa0e5besP/AC0t9b+4WQaY64HrgeoV69e38WLF3upBZ7LysoiPDzc12FIDaP7QkrTPSFl0X0hZamO+yI0MZHI9HSyBg7EPyODoKS1tCx6gYiCBA6H9GRHk1vICu7kcX3Fphh/68/W8K081/E5bkq4ia6ZXb3YgmN7JGMHX+enMTAwkpvC2tC63sn9Pqua8r8XZ5xxRo61NqyiMsaYQKA10AAYA1wHDLPWbiyj7JfAXmvt39y2tQF2A6dYa7+vwvArzecJVhnZ6p+stZ+VU/ZLYJ+19lq3ba2BX4HB1tpVFR0rLCzMZmf7bpLkUcuWLWPYsGG+DkNqGN0XUpruCSmL7gspi1fvi/R0mDKFxPx8kq+5huikvTQPmYf/nvcgoi0MnAXtLvF4OKDFcjVXE0ggr/DKb9t8tez6poxUooNCaRwUyk/pSRzMz+Hc5h18EktVqyn/e2GMOWaCVcZvlgC/uidRbvsq3elSnWrCQNKtQG9gEDAHeMMY072C8qUzQlPOdhERERE5TraggENvvUXG2LEwezZN6/kT26oVLUePwb8oHQZMg7GbnflWHiRXuTjTZQyGDnSgHe2wrsc3XyVXB/Nz6LP4dR7b7PyNvl9U81qTXNUCfkBQOftWAUONMe5jN0cCiTi9WD7l8wTLWlvgWjHkJ2vtfcA64I5yiifjjKt0d3SQ7wFERERE5MRYC599Br17kxgUxMG//AWWzsZ/6BKCowKdpdZHLYHe90K9Y89NKqaYV3mVdrTjS74EYDKTuZ/7fZJYFZQU87HrBcFNgkL594DzmdStvMXqpDoYY6YbY4YaY9q6VgyfBgwD3nLtn2aM+crtJ/8BcoDXjTHdjTGXAPcCNWJNBp8nWGU4abNVERERkZNZwcaN7Jk9m+LLLsMUFdEpJID2V18NPYZBWEsozHAKejgccDnL6U9//sbfaE97mtDEe8Efg7WWjxO3E7foFS769gN+PpwCwNhWXWkcFOqzuARwOlDexBnZ9hXOauHnWms/d+1vDvzWtWitPYKTA7QAfgKew1lR/MlqjLlcPl1F0BgzHfgM2AtEAFfhZKujXPunAQOstcNdP/kP8BBOtvoo0BknW51SE7JVERERkZNRSXIyBxYsIDk2FtuvH5FzphLZeBGBAW+C30XQsBuc/9WxK3LZwQ4mMpEP+ZBWtOJt3uZyLvfZUMD1h1O48+ev+SrlV7pFNGLhqZfSq4HnKx2Kd1lrr6nsfteCeKd5KaQT4uv3YB3NVpsBR3CWZj/XWrvItf8P2aoxZiROlvoTcIgalK2KiIiInExsbi7p8+axPzqawn79aPDrTlo2XE1Q/tNwIAT6POAMGfSwx+owh3mER3iWZwkiiMd4jDu4gxB8sxpfcl4WD2xcySu7nPdZPRs/ghva9ybAz98n8Ujd4Ov3YF1T2f01OVsVEREROSlYS9Ynn7A3J4ec7t0J3b+fdplLich4DNIyoOv10G9Kpd5n9QM/cB7nkU4613Itj/Iozf4wdb565BYX8uS2H5m+ZTX5xUXc0bk/93cbrPdZSbXwdQ+WiIiIiFSj/NWr2bdhA4fj4wlIT6dt+lqich7HJG+HlmfDoFkQVdGCzv9jsRzkINFEE0ccIxnJPdxDb3p7uRUVe2Lrjzzwy0ouienMjJ7D6Bje0KfxSN2iBEtERESkLti1C+67j4IdO8h4+mmaJybSzMzBL/FzaBgH534Orc6pVJU3cRNLWMIv/EIYYbzN214K/ti+Sd2HAYY0bsmtnfpyWpNWnNaklc/ikbpLCZaIiIhIbXb4MCnz5lG0bh0tPv6YiIk30iMujnoNGsC6X6DDaOhyLfh59liYSCLhhFOf+oxhDHHE+WzxiqOKbQl//XEh7cMiWXTa5UQGBCm5Ep+picu0i4iIiMiJKiyEZ5+Fjh3J/fVXsocPx656E1o9T72sH5wyve+Fbtd7lFxlk81kJtOJTkxnOgAjGMEt3EIAAd5sSZnSC3K5f+MKcooK8Td+LBhyCR8OvqTa4xApTT1YIiIiIrWJtWR//jn70tKIeeklwnt1p9WofphTRmNKCiD7BmjQ1ePqiinmNV7jQR4kiSTGMpbxjPdiAyqWX1zEcwlreGTTd2QUFjAoqgXnt+hIbP3GPotJxJ0SLBEREZFaIn/1avavX8+hPn2oFxxM0fT/g+zZ+O26FQacA/VCYPBTHtVlsSxiEXdzNxvZyCAG8R7vMZjBXm5FOfFYy3v7tnLvhuXszD7MWU3bMqvXmfSI9N3Li0XKogRLRERE5CQXnJzMvjlzSOndG2JjaZa4mWbmTfwTF0FkZxjyPPh7vkT5z/zM3dzNYhbTnvbMZz5jGOOzuVbfpu7jrp+X8n16It3rN+bzoWM5p1l7n8QicixKsEREREROUiVpaRx87z2CO3XiQIcONNqXQIvwxQQmvQrBjWHwsxB7A/h5PkdqBzvoQx8a0ICneIobuZFAAr3YivIlZB1i4vplfLB/G82Dw3ml37mMa9sdf6NlBKTmUoIlIiIicrLJyyPn9ddJiImhoF8/ghK20dksITTtCUj3g97/gN73QGB9j6o7whGWs5wLuZCOdOQVXuEiLqIhvn1/1I6sQyxK3sXDcadyZ+f+hNXzTaInUhlKsEREREROFiUlFL/zDv733UfgoUMEvvoqrf39sfnTCd2+ATqPg36PQHjLSlX7MA/zLM+yhz00oxnXcI134j8Gay2Pb11NQUkxD8QO4exm7dlz/o1EBYb4JB6R46EES0RERORksGQJe9auJSsmhm5NGlPv6b/Q5byREBjJf5NuoO+AIdCol0dVWSzv8z6tac0ABnAP93AVV9GMZl5uRDnxWIsxBmMMmzPSyC0u+m2bkis52WgAq4iIiEgNVrhuHSXnnw8jRxLx449ERUVhP38VUh6DLa8CkBkS63FytZKVDGYwYxnL8zwPQDTR9KWv19pQHmstC5MS6L34NdYcSgbg5X7n8O4pF2GMb19eLHK81IMlIiIiUgMV79xJ8hdfkNKzJ81at6b5P/9Ow9ObQfw5ToELVkCzIR7Xt4lN3Mu9fMIntKAFr/AK4xjnpeiP7af0JCauX8bSg3voENaAjMICAAL8/H0Wk0hVUIIlIiIiUoOUpKaS+v77JHXoQNHAgTTcm0DUxRZ2PQnroyB2PAQ1gOZDPapvH/t4iId4ndcJJ5ypTOV2bieUUC+3pGw7sg4xacMK5u3bQuPAEJ7pPYIbOvQmUImV1BJKsERERERqAJudzaF589jfuDEF/foRsX8PMX7LCEubBWlAz7sg/j4nufJAJplMZSpP8RTFFHMbtzGJSTSmsXcbUo6UvGwe2fwdLySsI9DPn/u7ncLdXQZSPyDIJ/GIeIsSLBERERFfKioi47332A/k9OxJSHIyHQ9/Rf30qZjkDNfKgFMgvHWlqi2hhFd4hTGM4REeoR3tvBO/BxYl7+TSVQvILS5kfLtePBQ7hOYh4T6LR8SblGCJiIiI+IK18NFHZL/yCtunTCEwPZ226T8QdXgaJnsvtD4fBkyFqB4eV/kxH/MiL/IxHxNJJFvZ6rN3WRWWFHMgL5uWofXp07AZF7boyIOxg+kS0cgn8YhUFyVYIiIiItUsf8UKsufNI+q55wjt2oV2qak0GDECv1UfQVgMnPkmND/No7oslmJT7NRLPgdc/2lBC5++KPiclfPJLCxg9fC/0CQolLcGXuCzWESqkxIsERERkery889w330kDhzIkTFjaNC7FX6NPiSqVxj4+8OgWeAfDB4uUb6KVdzDPXRu1ZnhDOdSLmUMY/Dz0Zt4vk75lSGNYgjyr8eETv3w01LrUgfpPVgiIiIiXlackEDic8+Rc/nlsGoVLSNDievbF79rbgVKIP+wU7BeiEfJ1S/8wmhGM5jBbGMbjQuchSsMxifJ1X8PJTNy+TsMX/4Or+7eAMAFLToyqnkHvc9K6hz1YImIiIh4SUlSEgc/+oikzp0pHjQIv3A/Qpt+TcDhlyDsdvAPhNGrPe6x+pVfeYiHmMtcIojgUR7ldm7np+SfoKuXG1OGbZnpPLBxJfP2baFRYAj/7HUm17b1fM6YSG2kBEtERESkitnDh0mbP5/EmBgKBwyg/v5facEXhBU8BfsDoMcEsEVAoEfJ1UEOMpWpPM/zGAx/5+/cy700wjcLRuzPzeThTd/yyq71BPvV48HYwfy98wAtuS6CEiwRERGRKmNzcjg8bx6J9euT16cPocmJtD3yGfVTZ8CBAug6Hvo8AGEtPK5zD3uII44ccriWa3mQB2lFKy+2onzpBblM3/I9z25fQ7Et4eYOfZjU7RSig8N8Eo9ITaQES0REROREFRaS+9Zb7A4OJqdHD4IPptD+8FIaHHwMU3AYOl4FfadAZEePqssjj9Ws5nROpzWtmchExjKWrr4YB+hm5cF9zNr6A39p050pcafSNizSp/GI1ERKsERERESOV3ExJe++i98DD1Dv0CFK5s6lTX4+jQpnYvYshdajoP9j0KhXpaq9j/uYwxz2sIdoonmAB7zUgIpZa3kuYQ2FJSXc0bk/F7boyJZzrqNzRJRP4hE5GSjBEhEREaksa+GTT9izZQs5TZrQJTKCgBljiB15GiaoPuy/H/wfhmanelRdCSXMZz5d6EJvenMnd3IRFxFNtJcbUjZrLcYYjDGsOLiXvOJiJnTqhzFGyZXIMWiZdhEREZFKyF+6lJKhQ+GiiwjbvJnImBhY+BKkz8QkvO0UijnTo+TKYvmMz+hDH67gCl7gBQBa0YphDPNiK8qJx1re37eVHl++yqaMVADeGDCKBUMu0XLrIh5SD5aIiIiIBwpWrSJpzRpS+/WjVffuRI8bQKN+zSH+LKfABcs97rECWMYy/sE/WMUqOtCBN3mTK7jCS9FXzFrLogO7uH/jSv57KJluEY04XJAHQIh/gE9iEjlZKcESERERqUDh2rUkf/stB/v0gb59aXJwBw1H7YOkz2BrB+hxK9QLhuaneVTfD/zAJCaxhCXEEMOLvMhf+SsB+CaRWXFwL5M2ruCb1H20DY3k9f7n8ec2cfgbDXQSOR5KsERERETKULRpEwe++oqU3r0pGTCARgcSaF7vI4IS50FIUxj8NHS7Afw9e/fTHvZwG7exgAU0pjFP8iQ3ciPBBHu5JWX7MT2J+zeu4MsDu2keHM7zfc7ib+16Eujn75N4RGoLJVgiIiIibop37CDl88850L07xYMH0zAxgRYBnxOc9DoENYQB0yHuFgjw7N1PhRQSQABhhLGGNTzMw0xgAhFEeLchFXgxYR3/t2YRjQJDmNXzDG7qGK+hgCJVRAmWiIiICMDevfDoo2Tu2EHi448TuW8fLYo+JDRpNgSEQ9/J0GMCBHr+7qf7uZ8lLGEVq2hEI3ayk3o+evzamplGUUkJcZFNOL9FB6bkn8qETv2oH+BZD5yIeEYJloiIiNRpNimJgx9+CN99R/S8eUTedDXdmjQhtG9f+GYR9Lobek2E4EYe1bef/UQRRQghdKMbueSSTz7BBPssuSoqKWH48nfoGRnNwqFjiQmJ4MHYIT6JRaS20+xFERERqZNsSgrcfTemQwcys7PJuPhi7HcvYbr/m9CQg06hU5+HgTM8Sq6SSWYCE+hAh9+WW/8Tf+IJnvDJPKt9ORlM2rCCwpJi6vn58fbAC3m9/3nVHodIXaMeLBEREalTbGoq6e+9R1KzZnR8/32CrziPtsO74hd/PqYwAwrWQWhzj+s7yEFmMpPZzKaAAsYxjtGM9mILKpaUm8X0Ld/z4s51lFjLqObtGdy4JUObtPJZTCJ1iRIsERERqRPsoUMcmj+fxCZNyO/fn5CUZIpfuBz2PYP/rh0Qf74zv2rwUx7Vl046T/AEz/AM2WTzJ/7EgzxIJzp5uSVlO5ifw4wt3/N8wloKSoq5pm0P7u82mLZhns8Zk9ojK6sEa30dRd2kBEtERERqNXvkCIfnzyexYUPy+vYl+OAB2h9aRIPkaZjCbOh4JfR5CIzxqL4jHOEpnuJJniSDDC7jMiYzmW5083JLypaWn8vLWXtY8NkacouL+HObOB6IHUzH8IY+iUd8KyurhNmzM5g16zB33RXMGWf4OqK6RwmWiIiI1Eo2I4PD8+aRVL8+ufHxBKem0O7QEhomTXWGAra/HPo+BA0rlxitZCWTmcxoRjOFKfSkp5dacGxzEtZyz/plZBUVcHmrbjwUO4Su9T1bjENql7w8J7GaMeMwqaklnHdeCE2aFPs6rDpJCZaIiIjULllZMHs2yYmJJI4bR1DqQdoe+pqopGmYgkPQboyTWEX18Kg6i2UmM7FY7uEeRjGKjWwkjjgvN6RsRwrzCTB+hNYLoEFAECObtuX8nCD+OkgLWNRlJSXwxBNH6NMniClTGjJoUDDLlm31dVh1klYRFBERkVrBZmVx5NVXyRk5Eu67j0YpB2hbUkLc8DNolDIb03woXLIWRr7nUXJVQAEABsMa1rCWtVgsBuOz5OpAXjZtP5vDszv+C8CVrWN5f/DFtKsX6pN4xLfmz89i6NBECgstoaF+/PxzSxYtas6gQdW/aqX8jxIsERERObllZ8OsWdhu3djdsiUHrr0WFk4mcOxWGvXpiakXBJeuh7MXQOPex66ObGYyk9a0ZiMbAZjLXN7hHQyezdOqSpmF+SxMSgCgaXAYd3buz9nN2lV7HFIz5OaWkJVVAkBIiKFePUhNdYYCRkf7+zI0cVGCJSIiIieloz1WO198EXvvvfj16ETnEEPb8eOh56kQ1gry053CgcdeSS+bbGYxi3a0YyIT6UWv3xKqQAK92ZQyZRbmM33L97Rb+CIXffsByXlZADwQO4TeDZpWezziW3l5JTzzzBE6dNjLtGmHARg1KpSlS1vQvLlm/dQkuhoiIiJyUrFZWWTMm0diUBA5vXoReCid/I/uJDjtFULqfQ5mJMQMdz4eyCabF3iBx3mcFFIYyUgmM5nBDPZyS8qWWZjPcwlrmbX1B9IKcjmvWXseihtCs+Bwn8QjvpWXV8LLL2cyffphEhOLOe20YM4+OwQA4+HKl1K9lGCJiIjIScFmZpIxf/7vEqs26cuJSpqBX14KtDoPOlzhcX3ZZDOHOcxk5m+J1UM8xBCGeLEV5SsvsRoQ1cIn8Yhv5eaW8NJLmcyYcZikpGKGDg3mzTejGTYsWIlVDacES0RERGo0m5HBkXnzSAoLK5VYTccv7yC0HgV9HoToAZWqdwpTmMlMRjCCh3iIUznVSy04tplbVzNjy2olVkJOTgkvvpjB448fITm5mNNPD+att5RYnUyUYImIiEjNlJEBs2ezKyiIQ8OGlZFYne8st96kn0fV5ZLL0zzNUIYyhCFMYAKjGe2zoYC5xYWE+AcAsPFIKgOjmv8/e/cdHlW1PXz8u2cmvZJGmiF0QgkgEJpCKBERRAT0KggIF7Er+vq7FvRey7VcEESRLiC9I4gIihQrglIFBKRISQ+pkzLJzOz3j0RFRBJKZkKyPnnyDJk5s2ft8xySWbPPWUsSK8FPPxXz9NOZdOvmztKlIXTt6uHskMRlkgRLCCGEEFWKzs4mZ9kyfF55BWNyMgFPP42v3U5gq2DU6mfOS6zaVGy8stLqAO/xHnnk0ZnOhJd9OcNX6Wfo/+1qNne9h9a1avNB21txMUgFuJrqvfdySEqy8tZbgbRv786+fRHExro5OyxxhSTBEkIIIUTVkJkJkyZRsHEjx6dNI+qhhwi+MRV//0Jo1650m3uOgW+9Cg2XTTbv8R4f8zHb2Y4HHvzETwQSWImT+HuZxYUkFppp4RdMrF8wt4bWxcNY+lZMkquaJz/fjpdXaUHvo0dLOHXKit2uMRiUJFfXOSnTLoQQQgin0mlpZE6dSvLzz8Nrr+FVL4QGQNBLL0GwN1iyQJf2/alIcnWOc7zES9ShDv/hP0QSSRZZAE5JrjIsBYz96Sui10/nvh3r0Frj7+rO4g79aOLrnGRPOE9Wlo1XXskiMvI0X35ZCMCkSYGsWxeKwSDXWFUHsoIlhBBCCKfQyclkrl5Ncng4lvbt8Yy+gdC+Rai0FfiFPA5KQdxbpbcVkE46E5nI+7yPGTMDGciLvEgrym8uXBlSi/KZcHQnU4/tocBWwl2RTRgb01EKFdRQGRk2Jk3KYfLkHHJzNXfc4UlQUOnKpckkx0R1IgmWEEIIIRzKfvo059auJaVOHYo7dMAjI5V6mR/jnzwOZS+BBoPBt37pxhVIRpJJ5m3eZjrTKaSQf/APxjKW5jSv5JlcXFJhHuOP7GTGib1YbDbuiYphbExHmvoGOSUe4VwpKVYmTMhh2rRcCgo0Awd68eKL/rRsKacB/kYp9TwwAGgMWIDvgee11gcu8Zxo4ORFHuqttd5YCWFWmFMTrOq2M4UQQgjx9+zHj5PxySekNGxISadOeKYnc0PmavzOjEdpDY2GQ+vn/0iuKqgvfdnHPoYwhOd5niY0qaQZXFp2cRFjD3zF7JP7sWo790U144WYjjTyCXBKPMK5zp61Mm5cNrNm5VFcrLn3Xm9eeMGfpk1dnR1aVRQPTAV+ABTwKvCFUqqp1jqznOfeCuw77+fytq90zl7Biqca7UwhhBBCXMThw9jGj+fgoEGU3HQTXmlnqXNuKUFJQ/gAACAASURBVL5n3kEpIzQZBS2fBZ86FRruNKcZz3je4A188GEKUwgmmPpcXmJ2rfxWbt3DaOKzlJMMq9OcZ5u0p753LafEI6qGDz/MY9q0XIYN8+G55/xp2NDF2SFVWVrrXuf/rJQaCuQAnYF15Tz9nNY6pbJiuxJOTbCq284UQgghxB9se/eS89FHBLz2GkZ3d0I6dsSrSRO8jVtRu6ZAs8eh5TPgFVGh8ezYMWAghRRmMYt+9COBBDrQoZJn8vfeOvw904/v4citD+BmNHGw1z9xMzr782vhDDk5dh5/PIP+/b0YMMCLxx/34777vImOlsTqCvhQWowvqwLbrlZKuQO/AO9orVdWamQVUNV+A1zXO1MIIYQQwPffw+uvk1a7NkkPPoiXiw232B8JbeIGdetCycPQeBh4hFRouD3s4XVeJ4AAZjKTOOJIIokAnHPq3Z6sVMI9vKnt7kW7WqGci2yCxW7DzWiS5KoGOnfORmCgEW9vxcGDxbRtW3ptlZ+fAT8/KdhdxqSU+vG8n2dqrWdeYvt3gb3A9ktsYwaeAb4FrEA/YJlSarjWeuHVBnw1lNbama//J0qp5UBDoK3W2vY32wQBw/nzzhwLXHRnKqVGA6MBTCZTm02bNlVS9BVnNpvx9vZ2dhiiipHjQlxIjglxMVX2uNAav4MH8TGbCdqwAa+9e0gcfgeJvQdT4u5Oy7P/jzSf7iT7963wkAd8D7CwzkJ2BO7Ay+rFXWfuYvip4ZU4iXLiKcljYUESO4qzudcjjNHeUU6L5UJV9rioxg4ccGXhQj9+/tmVpUuT8PDQ2O1gqEI5VVU5Lrp161agtfaqyLZKqYnAPcBNWusTl/M6SqmpZc+LvYIwr5kqk2A5Ymd6eXnp/Pz8q4jy2ti2bRvx8fHODkNUMXJciAvJMSEupsodF1pj2biRlKNHORcXhzYaCT+zizA1D3J+hsGnwM0ftK5QRUCNZjObeZ3X2cY2ggjiKZ7iUR7FDz8HTOiCeLRmc9opXv95O9vSTxPk6sFTjdrxaIMb8XOpOlXgqtxxUU1prdm0qZA33sjmyy+LCAw08NRTfowZ4/d70+CqpKocF0qpCiVYSql3KM0HummtD1/B6wwHpmutPa4gzGumSqxjX7AzLyu5KrMDGHFtoxJCCCHE37JaKVy7lpSkJDLj4lDt2xOYdZTQovm4ndsM3lEQ9yYY3Uu3Lye5smNnLWt5kzf5gR8IJ5yJTGQ0o/GiQh98X1N2rfkk+Rhv/LydHZnJhLt7807L7jxQryVeJqkCV9PY7Zo1awp4440sdu0qJiLCyDvvBPLAAz5VMrG6Himl3qU0H4i/kuSqTCsg+dpFdWWcnmBVp50phBBCVHsWC/krV5KSm0t2XByGsFBCsg5S2zwT18wd4NcIus6FhkPAUPGL+09zmkEMIppoZjKTYQzDDeesEH2dfoZHdn/OgdwM6nr5MaNNL4bXaS7XV9VAWmsWLjTz5pvZ/PxzCfXrm5g1K4ihQ31wc5PmwNeKUmoKMBToD2QppULLHjJrrc1l27wJxGmte5T9PBwoAfYAduB24FHgWQeH/xfO7oNVrXamEEIIUW2ZzTBzJtnffMPxsWMx5ucTlvEDIVnvYcr9GQJbQc/lED0ADMYKDbmIRXzLt0xlKtFE8xVf0Z72mJzw9sRis5JnLSbIzRMfF1c0sDCuL/+4IQZTVbqoRjiEzaYxGhVKKWbOzMNkUixZEsKgQV6YTJJYVYJHym43X3D/K8DLZf8Og7/0YngRqAPYgKPASGcXuADnr2BVq50phBBCVDc6I4OcFSvQGzZQa906fHv1ILKggKBOnTB+9hp4BUPniRDZq0LXWOWSixdeGDFykpPsZjeFFOKBB53p7IAZ/ZVN22nx+Rw6BIYzP64vrfxr89MtI1EVmI+ofjZsKOChhzLYsSOc0FATq1fXJijIIMdDJdJal7tztdb3X/DzPGBeZcV0NZz6kYzWWv3N98vnbXO/1jr6vJ/naa2baq29tNa+Wuu2klwJIYQQ15Y+cwaeegrq1CHFzY30YcNg4zgM9+6hdutojCYT3PIR3P4l3HBruclVGmm8yIvUoQ6rWAXAszzLdrbjgeOvR8+wFDD12G601hiVgf9rHMf90S1+f1zeTNcsKSlWTpwoAaBBAxeaNXMhL6+0EFxwsFGOB3FZnL2CJYQQQogqxH74MBkbNpAeFUWjhQtxue8W6rUIwaVtHzCfhp174LdOKi7ll38+xSne5m1mM5siihjAAJrQpPTpOL4B65mCXCYc3cmsE/spsJXQKSiCVv61eaBeK4fHIpzvxIkS3n47hzlz8ujd24OPPgqlYUMXPv00zNmhieuYJFhCCCGEwLpzJ+lff01abCzWLl3wykjEOu92XBLn4XquBFRf8KkDPRZXaLwDHGAc41jMYhSKoQzlX/zr9+TK0Q7nnmPckR0sPHUQO5ohUc14tkl7mvoGOSUe4Vx791r43/+yWb48H5MJhg3z4V//8nd2WKKakARLCCGEqKm0pviLL0jbv5/0du2wx8fjm3aS0LSleJ+Zg3Lxgdj/gxZPVnjIH/mRV3mVdazDE08e53Ge4imicE5T3p2ZSbx1eAdrEo/iZjDxYP1WPNMojjpeju+pJZxLa822bUW89VY2n39eiI+P4v/9v9IeVuHh8pZYXDtyNAkhhBA1jdVK0dq1pJw5Q2aHDuibbybg3DFqZy/HM2UteISU9rCKeai0SXA5NBobNkyY2MMevuM7XuEVHuVRAgl0wIQubvD3H7PkzM/4u7jxQkxHnmjQhhB3x/fUEs538GAxI0ems3OnhZAQI2+8UYuHH/bF379iFS+FuBySYAkhhBA1RUEBzJ0LEyaQ+PDD5Nx0E0E5idTOm4hb5nfgUw9umgqN7gdTxQpPZJFFF7owmtE8zuMMZziDGeyU5sA2bWdt4i/0C2+IyWAgPiSKNrVCGV2vJT4uzumpJZynqMhOSoqN6GgXQkKMFBTYmTYtiOHDvfHwkNL7ovJIgiWEEEJUd+fOUThvHqf9/akzfjzuUcFENvAl6sYbcSEGPp8MPZZB3YEV6mFlxswOdtCDHtSiFu1p//spgK5lX87wecpJBm5fw8qO/RkY2ZjRUriiRuvRIxmbDbZvDyc42Mj+/ZFSDVA4hCRYQgghRDWlT56kZMYMXCdPxuTmRsmSJRQvWoR7+jO42aaD62hQbnD7tgqNl0Yak5nMFKZQQAFJJBFAAB/wQeVO5G+csxQy9fhuPIwmnmncnl6h9Vh/0yBuDa3nlHiEc509a2X69FzGjvXHw8PACy/UwsPjj4RKkivhKJJgCSGEENWMbfduMrZsITUmBtfGjWkyLAGX3u40i++IcvOFpDfAxbdCjYEBjnGMiUxkLnOxYKE//fkX/yKAgEqeycWdys/hnV9++L3U+n1RzQAwKMVtYfWdEpNwnp9+Kubtt7NZvNiM1tC1qzsJCZ706ePp7NDEdUopFQLcCPgD2cAurXV6RZ9/1QmWUupG+L000Gmt9e6rHVMIIYQQl0lrSr74grR9+0hv0wZbt254Z5whNGwXuvVaVLoHKmM0RHSH8G4VGnInOxnPeFaxChdcGMpQ/o//ozGNK3kyF7cvO43xR3aw9MzPKBRDopryTOM4mvsFOyUe4Txaa7ZuLWL8+Gw2bizE01PxyCO+PPWUH9HRju+vJqoPpdQLQDvgKyAXCAMeVEr9qLV+vSJjXHGCpZRqAywCNHAaUECdsuXXwVrrXVc6thBCCCEqqKSEoo8+IiUxsbQiYNeu+J87TmjSNLySV4BbILR5GZo9Cu4V6/lUQgm96MVWtuKHH8/xHI/zOGE4vvmq1prNaacYd2QHm1J/xdvkyhMN2vBUo3bc4Onr8HiEc1mtmpUr8xk/Ppvdu4sJCTHy3/+WVgQMCJCKgOKauFVr3eWC+95RSn0FVG6CBcwEHtNaf3H+nUqpBGAWpctqQgghhKgMubkUz5/PaaORnLg41A03EJR7mJC8D3D/rSJg5/eh8QgwlX+qlAULX/EVCSTgggvNaMbt3M4oRuGDjwMmdHH7c9JJ+GoZoe5evNmiKw/Va4W/q7vT4hHOdc89aaxalU+jRi7MmBHEsGHeuLtLRUBxTe1XSk0CtlK6guUHxAP7KzrA1SRY3hcmVwBa601KqfevYlwhhBBC/A239HQsr7yC28SJmCwWij76iDCzmWDLdFxOLYXgOOi5AqLvrFBFwN9MYAIv8iJHOUoDGjCZyZU4i0ubcXwvZwtzea15F1r6h7C28wB61a6Lm1EuHa9p0tJsTJqUw9NP+xEUZOSxx3wZOtSb22/3xGCQohXi2tNaP6aUagvEAc0ovQZrodb6x4qOcTW/qdKUUiOA+VprG4BSygiMADKuYlwhhBBCXGjvXpgwgZDYWH6JjaXZnd0w9HOh2c2xKO8ISHOHFg9D6M0VKl7xK78yiUkkkEAf+jCKUcQRR32cUyQirSifYDdPlFLsz0njSF4mdq0xKEW/8IZOiUk4T0mJxsVFkZFhY9y4bFq1cuXuu72Jj69YfzYhLodSarPWuodS6kVgF7D7chKqC11NgjUcmA5MUkolld0XDuwse0wIIYQQV0NrSj7/nPS9ewl5801M1hIIDSKiXz/o/jasjEWl3QPeAyGkfYWG/IEfmMAEVrACAwZCCaUPfQghhJ70rOQJ/dWBnHQmHN3JolOH2BJ/LzcFRfJOqx64Xsbqm6getNZs2lTIhAk5+PsbWLasNk2bunL2bBShobJ6KSrVwLJbF+BRoI1SysYfydYrlzPYFR+tWusTwC1KqSD+XEVQVq+EEEKIq2GxULhyJampqWR27Iju3h33sCICPNfhZ9lJrcbvlG43NAVcyy/0YMfOOtYxgQl8zdf44svTPM2TPEkkkZU8mb/6rXDFhKM72ZhyEk+jCw/Wb0VUWdEKSa5qFotFs3ixmYkTszlwoISwMCNjxvj9/rgkV6Kyaa2zy27/89t9SqkIoE3Z92W5oiNWKeWmtbaUBZKBnBIohBBCXDWdnk7eypWkGgzktm2LqleXoNxDhOR+gHvR9+Ban0yv2wnSuvQ0wHKSqwIKmM983uEdjnKUKKKYyET+yT/xxfEV+IrtNpae/pmJR39gX04atd28eK3ZzTxcvzWBbnLqV01z7pyN6dNzef/9XFJSbLRo4cqHHwZzzz3euLnJ9VWicimlegO+WutlF3tca50IJAIfX+7Yl5VgKaXigXlApFIql9JqGruBPWW3h7TW9ssNQgghhKjJ7EeOkLV+Panh4RTGxWEy5xJ+7iuCU9/BVHgGaneGhFVQ5w6SvvqaRhVsELyABTzMw7SjHUtZykAGYrr6FphXZMbxvbx66FuSisw08w1idtveDI5qirsUrqhxkpOtvPpqFvPmmSks1PTq5cH8+X707OmBquCxLcQ18ArwLfCXBEsp1QA4+Vudict1ub/VpgAFwGNAENAa6A88WfZ4ESBts4UQQojyaA3btsHEiZxq25bMvn1xz0ynzrk1BJyegEFboO4giF1R4eurCinkMR6jM50ZyUiGMpQYYriZm1E4/o3rCXM2UZ6+mAwGUi35NPUNZHa73vSqXVfeSNcwWmuysuwEBBhRChYvNjN4sDdjxvjRvLmrs8MTNVMMpUnWxbxYdnv/lQx8uQlWXeAurfX68+9USvlT2veq1ZUEIYQQQtQYxcWUrFpFcmIitSdNwq3EQu0e7QkICsK3aR3Uyvuh2UPQ/AnwiS53OI3mCEdoQhPccec4x2lAAwA88aQLF/bLdIzvzyXSactCVnTsz8DIxrwY0wlDU0mqaqr+/VPJzrbz5ZfhhIaaSEqqg5eX9K8STmWHv/3kaQPwvysd+HITrMOUVtf4k7ILw7aUfQshhBDiAjojA9ucOZgmTUKXlHDuo4/wfvdd3Nxn4Vn8MUSNLb2uasgZMPzlT+1fFFLIIhYxiUmc4ARnOUsAAWxlq1NWq6x2O6sSj5BvLWFk3VjaBYTxRouudAqMAMAgK1Y1Slqajblz8xgzxg83N8U//uFNUZEdrTVKKUmuRFWwB+gFfHKRx1KA2lc68OUmWBOBUcCaK31BIYQQoiaxHzpE1qefkhoZidHPj8btGuA6OJLYti0xuvvAr0awFf/xhHKSq0zXTP7Nv5nGNDLIoCUtmc50vPEGcHhylV1cxAcn9zH52G5OF+TSOTCCEdEtMCoDzzXp4NBYhPMdOFDMpEk5LFxoxmLRtGrlSq9engwe7O3s0IS40BRgsVJqi9b6owseiwVSr3Tgy02wugAxSqllwL+11keu9IWFEEKIaktrSjZtIn3vXtJbtsTarRvu2WkEBhxE992OyrVjTB8ON/SC6P4VGnIf+3iHd1jcYTFWrNzO7TzFU3Slq1NWrI6bs3j3l13MObmffFsJ8cFRvN86gT5h9eX6qhrGbtds3FjIO+/k8MUXhXh4KEaM8OaJJ/yIiZHrq0TVpLVeoZRqD6xSSq0FVgJJQDPg5bKfr8jlJlidKe15VRcYpJQ6S1kDLv5oxHXF2Z4QQghxXSsoKO1flZ5e2r+qRw98M05QO2UxPonzUS6+0PzxCl9fBVBMMbdxG5vZjBde9E3qy/8i/0dDGlbuXC5Ca81XGWd45+iPfJz0CyZl4N6opoxp2JbWta74bBpxnTKb7cybl8d77+Vy9GgJERFG3nwzgAce8CEwUHqZiapPa/2MUupHShOqBec99A0w9krHvawES2vdTCnlBrSgtIJgq7LbZwEvQAPyP0oIIUTNcvYslrlzORUaSt6NN6KKLQTm/kxI4mw8sraDTz3o9C40GgGuPuUOl0ceX/IlfemLK67Upz696MUoRrHv2D4aRjo+uQLYk51K/LYlBLp6MDamI4/Uv5EwDzn1q6a6444Utmwpon17NxYvDmHQIC9cXGT1UlRdSqmOWuvt59+ntV4KLFVK1QXCgSSt9cmreZ1yE6wLAylrMPxj2fdv2yigMdDyaoIRQgghrie277+neMECPGbMwOTuTsnKlUQUFxOUNQ7T2bUQFg+3rIGovmCo+OeP4xnP67zOKU4RSSQzmFF5kyjHuMM7yLVa+G/zLrT2r82KjnfQJ6w+HsbyC3GI6uXQoWJeeSWLadOCCAgw8vLLtXj9dUWHDu7ODk2IivpGKZVGafPgj4DNWusSgLKk6qoSq99UpITLN0qpZKXUDKXUrUqpi1UR1Frrw3/XCVkIIYSoNoqLYfFiaN+eY/v2caJ7d/S/7sO4oANNu7QmtGNHTG1fgAF74PatEH3HJZMrjeZLvmQAA1hPaReUR3iE7/iOSCIdNas/OZJ37vd/HzNncSQv8/fqb4Mim0hyVYMUFtpJTbUCYLVqNm8u5MCB0qIsN9/sIcmVuN5EAK8CdSgt2pehlFqmlLpHKeV7rV6kIqcIRgB3AneUBWJRSm2kNOv7VGude62CEUIIIaoqnZqKeeVK0ktKiHrpJUxRtQn3sKFuvhnVozl80g2VcwQ8a0NIXLnjFVHEYhbzHu+xj30EEkg/+gEQWvblSDZtZ13SMd79ZRfb0k+zvft9dAiMYFqbWzAqKald05w9a2XatFxmzMjl1ls9WbgwhNhYNxIT6+DmJqcBiuuT1joFmAZMU0r5AH0pzXGmA+5KqS8pzXE+1lonXenrlJtgOSoQIYQQoiqy795N5hdfkBYVRWGHDhgLzBTNH4l3znx8QjdDyCNACAw+DYbyP7dMJJFpTGMGM8ggg+Y0ZxazGMIQPPCo/AldILu4iDm/7uf9Y7s5mZ9DlKcv42LjaewTCCDJVQ2itea77yy8914Oq1blozXccYcnDzzwx3WDklyJ6kJrnQcsAZaUnaHXk9Ic5yVgSlnxi4+01m9d7tiXW+Si0gIRQgghqgyrleKPPyb96FHS27XD1qMHHtmp1MlYScCZdzHoYoi+E1qM+eM55SRXu9nNeMazkpXYsNGPfjzJk8QT75Qy60fyzvHeL7uY9+sB8m0l3BwUyfjYbtwR3hCTQZKqmqSoyM6SJflMnpzDnj3F+PsbeOopPx591JfoaDkdVFR/ZddhbSj7fkgp1RHoDwwDKjfBqsxAhBBCCKfLyMC8YgVpxcVkdegAN9yAX9YxaidOwztlFcotEGLHQNOHwfuGcoezYEGhcMWVb/iGT/mUx3mcx3iMetRzwIQubtjOT1hw6iCuBiODo2J4ooGUWa+pNm0qYPDgNDIy7DRr5sL06UHcd583Xl6SZIuaq6zA33ZKK6VftitKsJRSbmXVBK9ZIEIIIYSz6N27Ue+/D4sXkzxuHPlt2lDbfJrg1JdxMx+CwJbQZTY0uBdMFTuN7wxnaEtb3uAN/sk/GcUoRjISbxxf1jy3xMLyM4cZUbcFRmWglX8IDb1r8WC9VoS4ezk8HuE8Wmu+/LIIT09FXJw7MTGudOnizmOP+REf7y5NokWNpJTarLXuoZR6kWvQ2/eyEiylVDwwD4hUSuUC+yltMryn7PaQ1tp+pcEIIYQQDlNSAqtXk7tpEyfvuosm27bi9kQvouJCMLXriNGSAd81g/ipENYFynnjqdFsZzu/8AvDGU4kkdzN3cQQA4Anno6Y1Z9jKqv891nKSR7YtZEG3rWID4ni6UblF+EQ1YvdrjEYFDYb3HdfGu3bu7FqVSiRkSZWrXJsQRUhqqCBZbcuwKNAG6WUjT+SrVcuZ7DLXcGaAhQAjwFBlDYZ7g88WfZ4ETjhL4gQQghRQTo5GfOqVRhWrMDrq69wj2uH9113ob/bDls74ZZtB+M9pdUAey4vd7wiiljKUiYzmd3sJpJIhjAEEyYmM9kBM/ozu9Z8lnKCycd20zkogrExnegf0ZCdPYbRLiDM4fEI5/rllxKmTs3h888L2bs3EhcXxfr1oTRqJNdWiZpNKdUb8NVaL9NaZwNorf9z3uMRQJuy78tyuQlWXeAurfX6CwL0B24EWl1uAEIIIUSl0xrb99+TuW0b6fXqUdixI/61PKn/YACuhoPU79EVTO7Qax34VuzaqDOcYRrTmMUsMsigKU2ZylSGMhTTlV/ifMVySizMPbmfKcf3cMycRai7F7eFlc7FxWCU5KoGsdk0GzYUMGVKLhs3FmIywV13eZGdbSc42EjLlm7ODlGIquAV4FvgL318lVINgJNa648pbUp8WS73L8BhSpfO/qQs69tS9i2EEEJUDYWFWFatIu3MGc516IDtllvwyE6hTvoyAgreA2xQbxAU55QmWAHNLjmcRrONbbzP+6xhDQD96MfjPE43ujmlGuDBnHTeP7abBacOkm8roVNgBK81u4kBkY1xvUSDY1H9ZGTYmDMnj2nTcvn1VythYUZefrkWo0f7EBbm+KRfiCouhtIk62JeLLu9/0oGvtz/bROBUVD2V0UIIYSogvTx4+SuXUuauzu57dpBo4bUyjlKyOkleKVvQHmEQuvnoOmD4FnxlZ1f+IXudCeQQJ7hGR7mYaKJrryJXML35xIZe+BrtqSdws1g5N6oGB5v0IYba8n1NDVNfr6dt94KYNu201gsmq5d3Rk3LoD+/b1wcZGiFUL8DTv87adiG4D/XenAl5tgdQFilFLLgH9rrY9c6QsLIYQQ15TdDp9/DlOmkOHqyukXXsBkNhOW9SVBye/iajkLtTtD9yVQdwAYXSs07Eu8RAopzGIWjWjEp3xKN7rhjnslT+iv0i0FZNqLAbDYbRwzZ/Fmi66MqhtLkJtcAl2TFBba2bevmA4d3PH0VJw968LIkT488ogvzZtX7NgWoobbA/QCPrnIYynAFfeuuNwEqzMQRem1WIOUUmcpq67BNShpKIQQQly2zExs8+ZxxmrFZ8sWAvftotYTAzH6+eHfujWG9f+B6F7Q7FEIal3ucFasfMZn9KY3BgzYy740GoWiN70dMKm/yrcWU//TGfR0qcUAoEvQDRzv/aA0Ba6hxow5x+LFZpKS6uDjY2Dy5FS6dYtxdlhCXE+mAIuVUlu01h9d8Fgs4Jgy7VrrZkopN6AFpRUEW5XdPgt4ARqQE76FEEJUOvuuXRQuX47Xe+9hKCqicNUq3Fu0AK9PMR2dRUDk62AwQN+t5ZZYB0ghhQ/4gBnM4Cxn+YIv6EEPXud1B8zmrwptJSw9/TM7MpOZ3qYXXiZX3m+dgD52BgClFCbpWVQj2Gya9esLmDo1lzffDKB1azfGjPHj3nu98fYuPQbkUBDi8mitVyil2gOrlFJrgZVAEtAMeLns5yty2Vc8ljUY/rHsGwBV2pWuMdDySgMRQgghylVUhGXNGjJOnCCjXTvsffoQa/gF4405NOkUhgrtCDn1Ifo2cPMvfc4l3nlqNN/yLVOYwipWUUIJPenJZCbTla4OmtSfHTdnMe34Huac/ImskiKa+gaSU2LBz8WNYdHN2fZrhlPiEo6XnGzlgw/ymDUrlzNnbEREGElMtNK6tRsxMa7EyIKVEFdFa/2MUupHShOqBec99A0w9krHvSYlZbTWmtIKg4evxXhCCCHE+fSxY+SuXUu6mxs5cXFQvz7+2b8QnLUCQ921UBiIyj8DdAS/hqXfl5BHHotYxFSm8hM/4Ycfj/AID/MwjWnsmEmdx6btbEw5yZRju9mYcgKDUtwZ0YhH699I1+AbULI8UWNordm6tYhp03JZsyYfqxUSEjyYNMmXfv08MZnkWBDiWtJaLwWWKqXqAuFAktb65NWMKTU7hRBCVE02G9YNG8jYu5f0Fi0ojo/HVJBHaM7XBCdPxrXoFNTuCN3mQ91BpWXWK+gmbmI/+2lFK2Yyk8EMxguvSpzMxZmtxUw9tofpJ/ZwMj+HUHcvXmraidH1WhHh4ePweIRzzZ6dy/jxORw5UkJAgIEnn/TjwQd9adhQmgILUdnKkqqrSqx+IwmWEEKIqiUlBT74gJLly/lp2jR07954Z50hImUG/klzMRhcoOEQaPpIhYpWAHzDN7zN2yxjGW64Bz8Q9AAAIABJREFU8QZvEEgg7Wnv8N5VWmsyigsJdvPEgOLNw9tp5V+bt1p0pX9EI+ldVYNorfnxRwtt2rhhMCh+/rmEWrUMzJsXzF13eeHhIQVMhLgeSYIlhBDC+bSGrVs599VXFGVkEDFlCi79OxFRkI9vbCwehz+Ck99AxwnQcNgf11ddwq/8ijvuhBJKAQXsZz8nOEEMMfShjwMmdXH//HED32YkcvjWUXiaXPil92gpsV5DffJJAf36pfL556EkJHjy5psB0rdKiGpAPhoRQgjhPJmZFM6YgY6JgR49KCguJrdfP/TORdD7O2o3LMLDxwdavwh3HYTmT1wyubJhYz3r6Utf6lGPCUwAoCc9OcYxYnB8VYCDOek8secLzlkKARgU2ZinG7XDpjWAJFc1yO7dFh58MJ333ssB4JZbPJk5M4gOHUpPb5XkSojqQVawhBBCOJbW2L//nqytW0kPCyO/bVsadmuL778aE9EyCHVjAkrbwDURQtqXPqec66tSSGEOc5jJTE5xilBCGctYHuABAAwO/jzRYrOyOvEo047v4euMs7gajPQKrUufsPrcFlbfobEI5zKb7SxZYmbmzDx+/NGCh4fi6af9AHBzUzzwgK+TIxRCXGuSYAkhhHCM3FyKVq0iIymJjA4dsPXqhVveOSIzPsaz3Xqw5mAwB5eWVVcmaPl/lxxOo9nKVqYznY/4CCtWutOdt3mbO7gDFxxfGOCEOZtZJ/cx++R+0i0F1PPyZ1xsPPdHtyBYVqpqlL17LcyYkcuiRWby8jTNm7sweXIg993njb+/XGcnRHUmCZYQQohKZd+1i5xNm0gPCCCvTRto1pRaOUcJOj0Rn/QNKI8QaPEoNBkFPtEVHncsY3mTNwkggCd5ktGMphGNKm8il7Au6RhTj+/ms5STKBR9w+vzSP3WJNSui0FKrNcomzcX8sILmezcacHdXXH33V48+KAvHTu6Sbl9IWoISbCEEEJce2YzLFkCM2dy9JFHyE9IwNWcTfi5DQQlTsalJA0iekDPZVDnDjC6ljtkEkn8i3/xBE8QRxxDGEIMMQxiEB54OGBSf5ZZXEiAa+nrzjqxj/3Z6fy7aWdG1Y0l0lNO+6pJdu+2EBxs5IYbTNhsGrPZzqRJgQwd6k1AgKxWCVHTSIIlhBDi2tmzB/NHH5Hm60v0Cy9gaFWf2m42DKGh+KoC1KZJEDMCYkaX2wwYIIssznCGWGLxwYdtbONWbiWOOJqVfTnDktOHGL5zPUd6P0BdL39mtb2VQFcPTAapHVVTaK1RSpGRYaN9+0SeesqPceMCSUjw4MCBSFmtEqIGkwRLCCHE1TGbsaxejWH+fFw2b8bWpQvmV1/Fsm0THkdup1bUXogYBToc7ksEo9slh9NotrOdGcxgOctpSEP2sQ8ffDjFKYw4fkUgpcjMnJM/0bZWKLeE1uXmoEieatQOD2Ppn9Ha7o5vUiwcT2vNjh0WZs3KIy3Nxrp1oQQFGVm7NpROnUqPa0mshBCSYAkhhLgietcusjdtIsPHh9y4OGr3uJnIAV741nWhRZcupW80g6dBcJvSJyh1yeQqiywWsICZzOQgB/HBh/u5nwd58PdmwI5MruxasyXtFNOP72Ft0jGs2s6zjdtzS2hdIj19+V9svMNiEc6VmWljwQIzH3yQy4EDJXh5Ke691xurVWMyKW67TQqYCHE1lFLPAwOAxoAF+B54Xmt9oJzntQDeB+KATGAG8JrWZX0wnMSpCVZ125lCCFHt5eZiWbWKjLNnyYiLw5qQgEt+DmFZmwkMnw2WMyhrF7AWgIsXNBxyyeE0mm/5lpnMZAUrKKKIdrRjFrO4h3vwxttBE/tDSpGZD389wKwT+ziRn02gqwdPNmzD6HqtaOQT4PB4hHPY7Zovvyxi1qxcVq8uwGLRtGvnxsyZQdxzjzc+PnI6qKjaUlNTKS4udnYYFRUPTAV+ABTwKvCFUqqp1jrzYk9QSvkCm4CvgHaU5hMfAvlQ1gTRSZy9ghVPNdqZQghRLWmNfedOcjZvJqNWLXLj4qB5c/xyfiHo7Cz8Uteg3Pyg4bDSa6tqVbyZ7wY20Ic++ODDCEbwAA/QmtaVOJm/t/1cIhOO7Px9tSo+OIr/Nr+ZOyMa4W509p9L4Uj79lkYODCV48et+PkZGDXKhwce8KFly0uf3iqEsyUmJpKbm0tMTAwWi4UdO3Zwyy23ODuscmmte53/s1JqKJADdAbW/c3ThgCewHCtdSFwQCkVAzytlJrozIUXp/7FqG47UwghqpWsLFi4EGbNIjEhgbTBg3Ex5xJ27jOCkt7HtTgZwuKh+3yIHlBuM2AAGzaGM5zmNOc5niOBBD7kQwYxCC8cfx1TSpEZH5MrXiZXdmWlsC39DE82bMMD9VrS2CfQ4fEI59Bas25dAUajok8fT+rXd6FhQxdefrkWAwd64eEhq1Wi6iouLsbV1RWtNZ06dSI2NpZ169YRFRVFq1atnB3elfIBDEDWJbbpCHxdlg/85jPgNSAaOFlp0ZWjqn0kd13vTCGEuO5pDV9/TdHy5Zxq2ZLIGTPwCjQQHOuHb3g4vkExqNUPQ5P7SvtW+ZffdyqVVL7iK+7iLowYKaEEK1YAXHBhOMMre1YXdTQvk2afzWbqjQk8UK8V/6wby6i6LWW1qgZJT7cRHGxEKcVrr2Xj72+gTx9PvL0NbNgQ5uzwhPhbZrOZjz/+mCVLlrBv3z5OnDiByWTigw8+IDo6+vftfHx8nBfkn5mUUj+e9/NMrfXMS2z/LrAX2H6JbUKBsxfcl3reY07LCVRVWvBRSi0HGgJttda2v9nmc+Cs1nrkefdFAaeATlrr7RdsPxoYDWAymdps2rSpssKvMLPZjLe3468rEFWbHBfiQo48JlwyMwneuZOAPXsI+vxzLCFBHJ7zISVmMw2K38DVmsXO6HmlhSq0Lr29BBs2dgXsYn3Yer4N/BatNCu/W0mtkloOmc/FpNssfFqUjh0Y4RWJ1pqlhcl0cQsgwlj+6ltVIb8rrk5hoeLLLz359FMvjh51ZeXKRLy9NampRoKCbBiv07ZVclxUf8XFxezcuZMtW7bw3XffYbFYCAoKonv37gwfPhxPz78WW6kqx0W3bt0KtNYVOk1BKTURuAe4SWt94hLbfQ6c0Vr/87z76gC/Ah211t9fXdRXrsp8TFe2M2+idGdeNLk6z4VZofqb+ynLjmcCeHl56fj4+KuM9Opt27aNqhCHqFrkuBAXqvRjwmbDtmkTWTt3khEVRd5dd2Hr2Jagu0y4uf9Ey+5x4BEMGY3A1Z9437rlDnma08xlLnOYw2lOE0QQT/IkoxhFTOeKX5t1rVjtdtYnH+eDk/v4NP0EdjQDIxrRtWNXlFJ0c3hEV09+V1y+38qrz56dx9KlZsxmTaNGLrzyig9dutTD1/f6PwVQjovqyWq1smXLFpYuXcrq1avJyckhKCiIkSNHcs8993DTTTdhuET/vevtuFBKvUNpctXtUslVmRRKV6rOF1J2m4oTVYkEq7rsTCGEuB7okycpWLOGjKIiMjt3xt6nD+55aUSmryAwYzpoMwT3geKc0gQr6NJFJ0ooYR3rmMUsPuMzABJI4G3eph/9cMPxhQGOm7OYfXI/H/56gOQiM2Hu3jzXpAP/rBtLPW9/h8cjnCM11cqCBWbmzMnj559L8PRU3H23FyNH+nDTTe7Ss0pUSXa7nby8PPz8/Ni7dy+9evXCx8eHO++8k3vvvZcePXrg4uLi7DCvOaXUu5TmA/Fa68MVeMp24H9KKXetdVHZfQlAEqWrWE7j9ASrOu1MIYSosoqKsH78MecOHSKjaVOKunTBUGyhVv5PBCXPwytnO8q3Ptz4LDQaDl7h5Q5ZQAGeeJJDDvdyL8EE8yIvMpKRRBNd+XO6iD1Zqfzf/q1sTjuFAUWfsPqMqhfLbaH1MV3iU15R/WRk2LjhhtOUlEDHjm7MmhXE3Xd7V4vVKlF92e12mjZtSpcuXZg5cyZt2rThk08+oUePHri7Xz+nMl8updQUYCjQH8hSSv22mGLWWpvLtnkTiNNa9yh7bDHwH+BDpdR/gUbAc8Arzi565+w+WNVqZwohRFWj9+5Fz5uHYd488m68kbP/+x+eWVlEpc0jIHEORmWDuoPg5jcgrAuoir35vJ/7+YVf+JZvCSKI7/meWGId2gj4Nz/lpGMAmvkF42kycSI/m9ea3cyIui2I8KgyF3gLBxg3LpvDh4uZMyeEoCAjkycH0bWrO02auDo7NCH+QmvN7t27WbZsGYcOHeKTTz7BYDDw0EMPUbdu6SnZSin69Onj5Egd4pGy280X3P8K8HLZv8OA+r89oLXOUUolAFOAHyktkjcBmFipkVaAs1ewqtXOFEKIKiE7G5YswbZgAYeee46gggLC7mqDX886NG3SBA8vL/j+M4j6HzQYDG6XLjyh0exgBwtYwHjG44knPehBc5pjx44Bg8N7V9m1xqAUJXYb3bctoXtIHZZ1vIPGPoEc7/2gnPpVQ2Rl2Vi5Mp8RI3wwmRQFBXby8jR2u8ZgUDz4oK+zQxTiT7TW7N+/n2XLlrF8+XKOHz+OyWQiISGB/Px8vLy8GDNmjLPDdDitdbm/tLXW91/kvp+ALpUR09Vwdh+sarUzhRDCaex27Fu3kv3ttxSlphI+dSrGTk0IsNvwfPFFSP8Qw0/v4GF6u3T7DuPLHTKNNBawgDnM4RCH8MSTIQyhE50YytBKntBfaa3Zfi6R2Sf380NWCnsTRuBiMLKyU3+a+Qb9vp0kV9WbzabZtKmQuXPzWLMmn+JiqF/fhe7dPXj55QBnhyfEX2itOXjwIMuXL2f58uUcOXIEo9FI9+7def755+nfvz+BgdJ3rzpx9gqWEEKIq3H6NAWrV5ORl0dm587Y+vTBzXyO0C4HMOR8TUSsDW64AWo/CbHPgMnjksNZsfIZnzGb2axjHVasdKADs5jFP/gHPjj+lLvUonzmnzrAnJP7OZyXiZfRhXuiYjBbi/F1caNrcJTDYxKOd/hwMfPmmZk/P4+kJBsBAQZGj/ZlxAgfWreWUwBF1VNSUoKLiwtbtmyhZ8+eGAwG4uPjGTNmDAMHDiQ4ONjZIYpKIgmWEEJcbwoLsX78MZmHDpHRqBGFN9+Mspbgn3eIoBOL8MnaivKKhNZjISSu9Dmulz5VyoaNl3iJecwjiSSCCeZJnmQkI2lKUwdM6s+sdjsbU04w++R+Pkk+jlXb6RQYwey2vbn7hiZ4m+QNdU1gtWpmz87jww/z+P57C0Yj3HqrJ+++683tt3vh5iarlaLqKS4upm3btvTv359XX32Vm2++mWnTpnHnnXdSu3ZtZ4cnHEASLCGEuB5oDbt2YVm+nMSQELI7d0Y3aIBnbiI3pC4gIHkOJm2B6Duh40YI7wGGSxecMGPmB36gG90wYuQbvuFGbmQyk+lLX1xxThJzMj+bzlsWkVxkJsTNkzEN2zKybgtizjsNUFRfVqvm8OESmjd3xWiESZNyMJng7bcDGDLEm9BQeesiqg6tNQcOHGDFihWkpqYyY8YMXF1dSUhIoFmzZgC4urry0EMPOTlS4UjyW0oIIaqytDSKVq3C9umneH3yCcbaIZiXLSdYawJT3sQzcRUEtoT2r0ODIeB+6WtQdFk/doXi3/ybKUwhmWQCCGALWzA56c/ColMHybUW83D91tTx9KN3aF36hjegb1h9XMpJFEX1MmbMORYsyCMlpQ4eHga+/jqcwECDXFsnqgytNfv27WPlypWsXLmSI0eOYDAY6NGjBzabDaPRyIQJE5wdpnAiSbCEEKKqKSlBr19P87ffRu/YwfHFizENGULjvpGYfL+gRYdWKDc/SLZC+7HlNgIGOMMZ5jOfD/mQWcwinnge4zEGMpBalFYRdGRypbVmf046Lf1L+8SvSfqF5EIzD9dvjUEpZre7zWGxCOdJS7OxZImZefPymDMnmFat3Bg1yocePTwwmUoTqqAgSbCF82mt2bVr1+9J1fHjx/90TVVFTv+z2+1kZGSQnZ2NzWZzSNx+fn78/PPPlf46RqMRf39/goKCMEjPQUmwhBCiqtD79mHesIFzQG5sLA3PHEP9uyd1oj1xbZkA2fVg12mUJRPc/Er7Vl1CEUWsYQ1zmcsmNqHRdKXr772q6pV9OVJSYR4LTh1k7q8/cSQvkyO3PkAjnwBmt+2Nj1xXVSMUFdlZt66ABQvMbNhQgNUKbdq4kpdnB6BVKzdatXJzcpRClCZEVqsVV1dXFi1axNChQzEajfTo0YNnn32W/v37X1ahirNnz6KUIjo6GhcXF4esyubl5eHjU7nFibTWlJSUkJqaytmzZ4mKksJDkmAJIYQzZWRgWbWKzLNnyWjbluKEBAzFRQTk78PwsoKSjXjrG8G1T2nBit7rLzmcRvMDP/AhH7KEJWSTTRRRvMiLDGc49f9oK+gwxXYb65KOMefkfjamnMSO5qagSJ5t3J4ID28AfF3kDXV1prXmu+8szJ+fx7Jl+eTk2ImIMPL0034MG+ZDs2aSXIuqJSMjg1atWvH888/z6KOP0rt3b+bOnUu/fv0ICLiydgD5+fk0bty42q3wKKVwdXUlIiKCI0eOODucKkESLCGEcLSSEmwbN5L9ww+ci4ggr21baNsWn5zjhCdOolbqCgwmN5I8uxAePxZC2ld46Nu4jY1sxB13BjCAEYygO90x4Pg/6HuzU5l78icWnT7EueJCwt29ea5JB+6Pbk5DH+lXVFNorenYMYkdOyx4eioGDvRi2DBvunXzwGiU66qE8xUXF7NlyxZWrVqFp6cn7777LkFBQdx55500adIEgMDAQO6///6rfq3qllydrzrP7XJJgiWEEI6ydy/Mm0fJJ59wYPZs7HfcgWt+JuEZawlInoVbcSpE9IRucyG6P0e/2UF47Q6XHPI7vmMyk5nPfFxw4W7uZgADuJu78cPPQRP7g9Vux2QwUGgrocvWxVjsNu4Ib8CI6BbcEloXo5I/wDXB+vUFzJ2bx4oVISilGDbMm0ce8WXAAC+8veUYEM5XUFDAZ599xurVq1m3bh05OTn4+PgwePDg37eZPHmyEyMU1zNJsIQQojKlpsKiRaQmJlJitRI5fSouwzpR22bFp359vI8sRyV/BC0fh4ZDwfuGSw6n0exkJxFEEEkkmWTyNV9znOM0oQkjGOGgif3VSwe+Yn3yCXb1HI6H0YU1nQfQyj+EANdLNzcW1z+LRbN+fQGdO7tRu7aJzEwbR44Uk5JiIyzMxCOPOD7ZF+JC2dnZrF+/ntWrV7NhwwYKCwsJCAhgwIABDBgwgJ49e+Lu7u7sMEU1IAmWEEJcaxYLtk8+IefHH6k1fjzKZqN43DgsrVuj/9kW9f0wwhsUg78/tHkZ4t6Cci52PstZFrKQD/mQIxxhLGP5L/+lN705xanfC1c40k856cz79SdeiOlIgKsHTX2DKLBZKbbbcDOa6B5Sx+ExCcex2zXffFPEwoVmVqzIJzvbzrvvBvLEE34MGeLNffd5S2l14XTJycn4+/vj4eHB1KlTGTt2LOHh4YwcOZIBAwbQpUsXTCZ5OyyuLTmihBDiWtAavWMHeZs2cc7FheybbsI+aBCukf+fvTuPq7LMH///us8KB5B9XwUEUVncEUFw33DJMFHLrKYpZ5xWbbF+ldVMfSeb1plppiwTFXDfQUVFMcsdU1xxQdyQfd/OOffvj2M0fTK00nMEr+d5nMdMcN8X7+twvLnf57qu91WCrdN+fEIakHoOAUMj2GjAM950nuqXR3caFA0sZjFf8zVZZCEjE0sss5jFRCYCmD2xKmmsI/XCcRacP8LBiiJUkoJBbv6M8gxisl8XJvt1MWs8gvkdO9bEokU1LF5cw4ULemxsJO67z4YHH7Rl8GDT+1mhEImVYDl6vR6VSsX+/fvp06cPy5Yt4/777+fhhx9m0KBB9OnTR6wXakVqairz5s0jPz8fFxcX5s+fT0JCgqXDalNEgiUIgvB7FBRQv3IlZeXllPbtS/OoUSib6nGqzcW58Cts1AdB1QXJ1sd0vFILQZNabXI3u/mCL0iLSaOeevzx51VeZRrTCCbYDJ36qWajgYyrZ/n6/FHWXc6nWTbSw8Gdj6IGM9mvC65andljEszv008r+fLLag4dakKhgGHDrHnnHSfGjdNhYyNuVgXLkWWZgwcPsnr1alavXs3w4cOZN28eUVFR/PWvf6VHjx4AeHt74+3tbeFo727vv/8+X375JSkpKURFRZGXl3fHy7y3RyLBEgRB+LWqqjCuXElJfj6lISHUDRgARgMdqk/jU/gVDsXrUGjsIHgKhPwXXHrcdArgOc4RQAASEl/yJctYRnxxPC95vkQccRapAijLMrO+305KQR7FjXW4aXXMDO7B9IBwIq5vECy0X5WVRrZvr2f8eBsAtm+vR6mU+PBDZ5KTbXB3F7cQguU0Nzezc+dOVq9ezZo1aygsLEShUBAXF0dUVBQAKpWKl19+2cKRtu5WRoYSExOZNWtWy/HTp09n+vTplJSUkJSU1Oq569atu+VYiouLmTt3Ljk5OURGRgIQHh5OZWUlffr04dixY3z33Xd069btltu8V4mroyAIwq3Q6zFmZdG4cSPWX3yB1NDA1YwMVBoNPnV7cDr9GmpjFfiNgaFLwXckKG9tb59VrGICE9jPfnrSk7/yVz7iI/ad3Ef8D1MJzaSooZackkKSfDojSRL5NeXEu/rysH83hnt0RK0w/1ovwXwaG2UkCTQaif/8p4oXXyzjzBlfAgPVLFnijlYrpv4JlrVp0yYWLVrE+vXrqaiowNramuHDh/PWW28xevRoXFxcLB1im5WVlUV4eHhLcvUDnU7Hhg0bmD17toUia3tEgiUIgtAKOTcXadEiWLyYgj/9iaoxY4hQlSL1OktYdw/UbpFwTQfOb0HgA2Dl3Gp7zTSTSSYLWchwhvMH/sBABvIu7+KLqYKgO+7m6FqLBoMelaRApVDwrzMHeevYbq6M8cXdyobVMRNEoYJ2zmCQ2bGjgSVLali+vJZ//9uFyZNtmT7djvh4Kzp2NN0qiORKsISioiLWrVvHI488glKpZP369WRkZDBu3Djuu+8+hg4dik7XdqcpZ2dn/+bjXVxcbnp+dXX1LbddVlaGg4PDz76uVqtxdXW95XYEkWAJgiD83KVLNK5cSdnVq5T26EHwyhVYjQrCLdwBp+7dITYK1sSgbrwCRJo2Am5lM2AZmf3sJ4UU0kijmGJccCGOOAAccOBFXjRT567HJMt8V3aZr88fJb3wOAt6j2acdyeeDOzOJN8w3K1M08JEctU+ybLMgQNNLFlSQ1paDVeuGLC1NRWr6NRJDYCbmxI3NzFiKZiXLMvk5eXh6uqKu7s727Zt4/HHHyciIoI+ffrw9ttv88EHH4jKf3dA9+7dmTNnDocPHyYiIoL8/Hz0ej1hYWGWDq3NEe9OQRAEgJoa9KtXU37sGGUdO1ITEwOAbdVZjP/PF8pzsNHagctfTMdPOnXTdVUFFLCYxaSQwglOoEXLGMYwjWmMYARq1He6Vz9zvraSRQV5LCw4yumacnRKNRO8Q/DTdQDA09oWT2tbs8clmMeJE02kptaQmlrL6dPNqNUwapSOKVNsSUzUodOJYhWC+TU3N5OTk8PatWtZu3Yt586dY968eTz//POMGTOGo0eP0qWLqUKpvb3YU+1OiYmJ4dVXXyUxMZHy8nICAgJYuHChpcNqk0SCJQjCvev6uqqq3bsp7dCBypgY5LAwtLXFeBUvx+nq12ibr4HPcOieCgHjfjz3JsnVy7zMu7wLQBxxPMdzTGQiDvx8+sWdVtXcyPKLJ1lYcJQdxYUAJLj6MSesH/d7h2Cn1po9JsF8ysoMODmZRqIefbSY775rJCHBitmz7UlKssHRUYxSCeZXUVFBRkYG69atY+PGjVRWVqLVahkyZAgvv/wyY8aMAcDW1pauXbtaONp7x+zZs8Vaq9tAJFiCINxbZBkOHoRFi5DT08n77DOaxo1D1VCLS923OJ9bgK72KJJLT+j5AgQlg87jps2e5CSv8zrv8R6++DKAAejQ8SAP0pGOZujYT8my3DK9b+jOdPaWXSHE1om3u8XxoF9X/G3Ep8D3go8/ruSFF8q4csUPR0cl//qXC25uSry8xJ9/wXLGjx/Phg0b0Ov1uLi4MGHCBMaOHcvQoUOxsbGxdHjCDYwaNYrc3FxOnjzJE088wfTp0y0d0l1NXGEFQbg3nD8PS5ZQev485aGhBP/7n0gP9cXDCtR+ftiXbkA68BF0ehA6pYNj6xvmysjsYx8aNEQRhQoVW9nKCU7giy8jrz8sYVnhCeYc3Unu0OnYqDT8tdsA7FQa+jh5ijVV7VhFhYFVq+pIS6vh5ZcdSEiwJiHBildf/XHUNCpKjFYK5vfFF1+QkZHBihUrAAgJCSEsLIwxY8bQt29flEoxinq327hxo6VDaFNEgiUIQvtVVoZ+1SrKTp/G6V//QlVdjfHlFzD26IHheA7KLdG4eiaB61hwngqh00BqfQ3KWc6ymMUsYhGnOEUSSSxjGUEEcYUrqCxwWb1UX83igmOM8OhIhIMbXta2hNu7UtbUgI1KwxD3ALPHJJhHba2RdetMSVVGRh1NTRAYqKKiwghARISWiAiRVAnmU15eTmZmJuvXr+eTTz7BycmJhoYGqqqqqK+vx9ramr///e+WDlMQ7iiRYAmC0L7U12PcsIGKgwcpc3enMjoaoqJQdTPgJK3FxeMCrgMHmo4dmQk/7DOl+OWCE6WUspSlLGIRu9kNQAIJvMALJPHjJo/mTK6qmxtZdek0KQVH2XqtABlQSBDh4EZ/Fx/6u/iYLRbBvJqaYNWqWtLSali3ro76ehkvLyV//rM9yck29O6tFSOVgtnIssyJEyfYsGED69evZ9euXRgMBlxcXDh58iQ7AxJ1AAAgAElEQVT9+vVj5syZzJw509KhCoLZiARLEIS2z2BAzs6mescOyrRaymNjMd5/P+r6StyrsnC6ugBdfT64xyD5DPvxPN/hrTabRRaf8Akb2YgePV3pyru8y2Qm44ffHe7Uz+mNRrKunSelII/Vl05TZ2gm0MaB/69LDA/6daWTnZPZYxLM43/X1P35zx7k5xfh6qpg+nQ7Jk2yITbWCqVSJFWCeTQ1NZGdnc369evZsGEDZ8+eBSA8PJwXX3yRxMRE+vTpI6b+CfcskWAJgtA2yTIcOoS8eDGXrKwoi4ujedw4FE31ONYdxvn0Imyr9iI5hEDXhyF4CnQIbLVJAwa2s51oorHFlsMcZj/7eYZneJAHiSACCcvcxP71+G4+OX2QosZaHNVWTPPvyoP+XYlx9hajFe3c559X8fe/V3DsmC9qtcS0aZVER4czcKA1KpX43QvmcenSJSoqKujatSuVlZWMGDECrVbL4MGDmTVrFqNHj8bPz/wfPAnC3UgkWIIgtC1nz9K4ahU1x4/jPH8+kkZFw9cL0el0OMuHsD86E4WVIwRPhk7/BOfurZZUl5FppBErrNjDHoYylIUs5CEe4s/8mWd4BiXm/xT2Un01S+uuECcbUUoKavTNxLh485B/V0Z5BKJVist3e6TXy+zY0UB6eg3PPmtPWJgGPz8V0dFWVFYacXFREhdXT0KCztKhCu2cXq/nzJkzhIaGAjBkyBD8/PzYtGkTrq6u7Nixg549e6LTifeiIPxf4i+0IAh3v2vXaF6xAtWiRUi7d1MyYwZX//hH7PuFolL/g6BeCqTgAVDXCTz8wWsQKFpPis5yliXXH4MYxKd8Sj/6sYpVDMc0ddAKK3P0rkV5UwMS4KCxYlfJRf5de4FHy4vo5eTJO+HxZo1FMB+DQWbnzgaWLq1hxYpaiouN2NhIDB1qTViYhuHDdQwfLm5ihTuvuLiYTZs2sXHjRjIzMzEajZSUlKBSqfjnP/+Ju7t7y7FxcXEWjFQQ7m4iwRIE4e5UXY1hzRoqjhyhzMeHqj59CDq8E4cHbHHr7olLZCSq3r1gxzEkGy/TOTpP0/MXFFNMOuksYQnf8i1g2gS4H/0AkJAYz/g73rX/1WjQs/HqWRYX5LHuyhnmdo3lpc7RjPUKZolTJL2cfrk/QttlMMjk5DSwdGktK1fWUlRkQKeTSEzUMWmSLSNHWmNt3XpFS0H4vYxGI/v372fjxo1kZGSwb98+ZFnGzc2NsWPHMnr0aIxGU0XKQYMGWThaQWg7RIIlCMLdo7ERY0YGVXv2UObgQEVsLHJYGJr6cjwqN2EdnQNNl1A32YP2eunphK9abbKGGlazmiUsYTObMWAgnHCLFqswyjK7Si6yqCCPZRdPUNHciLvWhhlBUYzyMK0Ts1aq8VSadwRNMA9ZlgkPv8jx483odBKjR+t44AEbRo3SodOJpEowj/Xr1/Poo49SXFyMJEn07duXuXPnMnLkSHr06IFCId6LgvBbiQRLEATLul4BsCY7mzKlkvK4OAxJSSibanGu24tzQQo2NblIzhHQ/WkISgZb31abbKIJ5fXHm7zJe7yHH37MYhZTmUo44Wbq3E/lVRaz6MIxllw4xoW6KmyUaib4hDDVrwuD3QJQiRuaduuf/6wkPb2WHTtMmz3/5S/2uLgoGDVKh42N+L0Ld97FixdJSkrihRdeYMKECQQGBjJs2DBGjRrFsGHDcHFxsXSIgtBuiARLEATzk2XkfftoXrMGzVdfIV25woWlS2ny9cWh8SJOZ/+KXUUOCltf6DQFglLAqestNX2IQwxhCOmkM4QhzGAGYxlLDDEoMP+N7NWGGjysbAF46/hull88yTD3jrwTHs84r2BsVBqzxyTcWT8Uqli2rIa5cx1xd1dhZ6fAw0NJba2Mra3EjBkdLB2m0I5dvXqVzZs3k5mZSWhoKK+//joeHh7Y2dmhVpv2/OvSpQuLFi2ycKSC0D6JBEsQBPM5dgxSUyE1lcvDh3Nt0iQiz32PYlgtgT1c0QT0RlmuAVVXiHsb3PvdtAJgLrmkkkoggTzJk3SmM2MZizPOAHS8/rCEpYXHSf5uLXnDHyOsgwt/6xbPx1FDcLOysUg8wp3T3CyzbVs9y5fXsmpVLaWlRnQ6iQkTbBg2TMW0aXZMm2Zn6TCFdqqpqYnc3Fw2bdpEZmYmubm5ALi5uREYaJp2rFKp2LJliyXDFNqI1NRU5s2bR35+Pi4uLsyfP5+EhARLh9WmiARLEIQ7q6CAppUrKb90ibKICPxWrcSmpxMOMV5o/P3hqyWwLBRr/XlQJoBLD9OzFfnkk0oqS1jCCU6gQsWf+BMA1ljzFa2vy7oTGgx61l/JZ3HBMSb6dmaKXxcGuPryRtdYHDWmtVSBtg5mj0u4cxobZbZsqWP58lrWrKmjosKInZ3EmDE23H+/DSNGWIs1VcIdtXTpUpYsWcK2bduorq5GpVLRv39/3nnnHYYPH05kZKRYSyX8Ku+//z5ffvklKSkpREVFkZeXh52d+HDo1xIJliAIt19REfqVKyk/c4by4GCqY2NBoUBXewnjm/5QkoGNTsLG/xXT8VMKb1pW/TKXSSedVFLZxz4kJAYwgGd5lvu5v2XEypwMspHt1y6w+EIeKy+eokrfhIeVDSM9TZ8Ye1jZ8lqX/maPS7hzZFlGkiQaG2W8vQsoLTXi4KBg7FgdSUk2DB1qjZWVuKEV7oxDhw6RkpLCe++9h1KpJCcnh8OHDzNlyhR8fHx46qmn6NBBTD9tSxISLt/0mMREHbNmObQcP326HdOn21FSYiApqajVc9etu/XkqLi4mLlz55KTk0NkZCQA4eHhfPvtt0yePBmNRoOXlxcLFy5smWoq3JhIsARBuD3KyzGsWUPl0aOmsurR0ch9+qCtK8GzbBVOV5dg1XQRvAdDwgII+J9y6DdJrv7G33iVV5GR6UEP3uM9kknGB58726cbkGWZA+VXWXLhGGmFJ7jSUIOdSsP9PiFM9evKQDc/lJK4wW6PXnqplMOHm8jI8ESrlXjlFQfCwjQMGmSNRvPLU1kF4bcwGAwcOnSIzZs3M3HiRDp16sSpU6f4z3/+wxNPPEFoaCjvvfceH3/8MZIkkZ2dLZIr4XfJysoiPDy8Jbn6gb+/P9u2bcPa2ppXXnmFNWvWkJSUZKEo2waRYAmC8NvV1CCvW4eUloacmcmxpUtpmjwZdX0VbtVZOF1dhHX9SST3GOg1GwIngrXbTZs9xSme53ne4R260Y1YYnmd15nMZEIIMUPHftnD+zaQUpCHRqFklEcgU/27MNozCGul+DSvPSktNbB2bR3r19eyaJEb1tYKvL1V1NbKGI0yCoXEs8+KKZ/C7XXx4kU2b97M5s2bycrKorS0FAAvLy86derE+PHjGT9+PNrr21RYWYmtHNq67Gyv33y8i4vypudXV1ffcttlZWU4OPz8uubl9ePPUKlUYtrpLRAJliAIv05DA2RkQFoa1zQaSkaPJuzofqQ5A/B2s0IdEoJtyTakgysh/FEImgR2/q022UgjGWTQgQ4MYhD22HOEIxRSSDe6MeD6wxJ2lVxk9uHtrI29H1etjkm+YcS7+jLBO7RlbZXQPly+rGf16lpWrKhlx44GDAbw81Nx9qyerl01/OUv9pYOUWhnmpub2bRpE5s3b2bLli2cOHECAE9PTxITExk2bBhDhgzBzc30wdQPiZUg3Andu3dnzpw5HD58mIiICPLz89Hr9YSFhQFw7tw5MjIyeOWVVywc6d1PJFiCINxcczNyVha1O3dSplLh8fnnaJTNqJ/7C7qAAIwHvkW5NAAnm1FgNxxsx0LHca02qUfPdraTSiorWUkllYxnPIMYhDvunOMcEuafdlXe1MDKSycJt3elj5MXHVQamowGLtfX4KrVMdozyOwxCXfOmTPNrFpVy8qVtXz7bSMAnTureeklByZMsKF7dw1SK5UsBeHX2rdvHxUVFQwdOhSAKVOmoNfriY+P5/HHH2fYsGF07dpVvO8Es4uJieHVV18lMTGR8vJyAgICWLhwIQBVVVU8/PDDpKSkoNGI7UVuRiRYgiDcmMGAvHMndVlZlBuNlMXG0pyUhKRvokPPEjSlC3D02oNj9Bum4x84AfadTP//F24MjBjZzW7SSGMZy7jGNeywYwITSCaZwQxuOdacyVWdvpn1V/JZcuE4GVfP0mQ08FxIb/o4eRHh4MaBodPNFotwZ8myTE2NjJ2dggsX9AQHFwLQo4eGt992ZMIEG8LCxM2DcHvIssypU6fIzc1l0qRJAMyZM4eioiK+//571Go1u3btIjQ0VIxOCXeF2bNnM3v27J98Ta/XM3nyZN544w1CQ0MtFFnbIhIsQRB+ZDTCd99Rv2kTZXV1lPfvT+OECUgGPR1qT+JY8AUOZZtRau2g8+MQPPnHcx1aXxs1n/nMZS6FFGKFFWMYQzLJjGQk1ljf4Y79XLPRQFbReZZcOM7qy6ep0TfhaWXLn4O6M8WvCz0dPcwek3DnxcZexttbxdKl7vj5qfjqK1cSEqwICBBr6ITb4+rVq2zbto2srCyysrIoLCxEoVAwfPhwHBwc+OSTT3BxcWk5PiIiwoLRCsLNpaamsmfPHt58803efPNNZsyY0fKBgXBjIsEShHudLMPBg5CWhrxsGSfefJO6sWPBaMSuNh+Pi/NwKNmASqWCgAnQdy14xoOi9cvHZS7zGZ/xJ/6EBx6oURNJJO/wDmMZix2W21fjb8e/5R+n9lHaVI+DWsuk6/tWxbv6igqA7URDg5GtWxtYvbqWgwcb2b/fG0mSmDrVFnv7H3/H06eL/V2E36e6upodO3aQlZXF1q1bOXr0KACOjo4MHjyYV155hSFDhrQUD+jcubMlwxWEX+2hhx7ioYcesnQYbYpIsAThXiTLcPQopKVRdvEilYGBdPz4Q6RJvbF3dcDZ1RXH6s2ojz4LAfdB9zTwHgLK1qdOneEMBgyEEEIFFfyVvxJFFBOYwLTrD0s4U1PO/HPf83qX/miVKlSSgiHu/kzx68Jw945oleJS2B5UVBjIyKhn1apaMjLqrk8FlBg9WkdVlYy9vcSf/iQKVQi/T1NTE7t37yYkJAQvLy/WrVvH1KlTsbKyIjY2lgcffJAhQ4YQFRWFUtn6FhSCILRP4q5CEO4lJ07QvHo15Vev4vz55ygb6mme+xoNAwZieHAgyq3xePlfBr+xoJ8CoVNB1fr0vYtcZClLSSONfexjKlNZxCK60IWrXMUVVzN17qdOVZehU6rw0XUgv6ac907uJdEziBgXH17o3NciMQm3X3GxgaVLa1i9uo7s7Hr0evDwUDJ1qi3jx9swcKA1Wq0oFiD8dgaDgQMHDqBWq+nevTtXrlxh4MCBfPjhhzz99NOMHDmSrVu3EhMTI8qmC4IAiARLENq/M2doXrmSiosXKevShZrBg0GhQBMNDvpVuPmcx33AANOolmKlaaQKQKX7xSaLKGI5y0kjjV3sAmjZAPgBHmg5ztzJ1cW6KtILT5BaeJwD5Vd5MbQv70YkMNgtgKtjZuKsNf9aL+H2kmWZo0ebsbGRCAxUc+pUMzNnlhIaqub55+0ZN86Gvn21KBQiqRJ+G6PRSF5eHtu2bWP79u3s2LGDiooKJk6cyNKlS/H39yczM5Po6GjANBVw0KBBFo5aEIS7iUiwBKE9KihAv3IlFefOUR4SQtWAAaBSYVV/Dc/S5TgVpWPVdBF8hiL5jjSdI0nQ8b5Wm13Naj7lU7azHSNGutGNt3iLSUyiE53M0LGfK26sY/nFk6RdOE5OSSEy0NvRk/cjBzLJ17R3h0qhEMlVG6bXy1y+bMDPT0V9vUyfPpd4/HE7Pv7YhehoLceP+9C5s6j8J/x2p0+fZuvWrWzbto3s7GyKi4sBCAoKIikpicGDBzNw4MCW44cPH26pUAVBaANEgiUI7cXFi7BsGfLy5ZxJSqKqXz/kAQPQ1JfiUbkBx6JUrOvPIHklQO+XoeMEsG59hKmaalazmiSSsMaaPPIooIA5zGESk+hGN/P07QaWXzzB/HPfs6XoPAZZpksHZ97sGsck3850snOyWFzC7VFdbSQzs441a+rYuLGOwEAV+/f7oNMpWLXKnchIU0KlVEoiuRJ+tQsXLnDgwAHuu8/0odKTTz7Jtm3b8PHxYeTIkQwaNIiBAwfi5+dn4UgFQWiLRIIlCG3ZlSuwfDmVR45Qp9fj+dVXSHFhKEKCcbO1xbFhC7pjzyF5xEL3pyEwCXStlx+vpZYGGnDGmb3sZRrT6EAHxjGO2cxmDnMssgFwvaGZzVfPM9YrGEmSyCoq4ERVGbND+zLZN4xwe1exMWcbV1ioZ926WtaurWP79nqamsDZWcHYsTrGj7dpOW7EiF+evioIN3L+/Hmys7OZOHEiNjY2zJ8/n7fffpuysjLs7e2ZN28etra2BAcHi+uIIAi/m0iwBKGtuXYN48qVVB49isN//oOk11P91puUxyfgPmMoikNTCOxqhIBuUO8GnSeCrU+rTTbQQAYZpJPOOtYxgxnMYx4JJLCb3URjWmugwbwjBU1GA3qjEZ1KzbLCkzy8bwPfDXqIvs5ezIscyL97DBM3Q+3AqlW1vPlmObm5TQB06qTmqafsGTNGR0yMFSqV+B0Lv05BQQHZ2dktz/PnzwPg7e3N0KFD+cMf/kBycjIdOnQAoHv37haMVhCE9kYkWILQFpSUYFy1iqrvv6fM05PKuDiMvXvTKUqmg+23eAY24d07FknWg/YyuPYynWft9otNNtHEFraQTjqrWU011bjgwkM8RBJJAChR0o9+5uhhC4NsZGdxIakXjrPi0kn+v7AYngnpzXjvTmRZT6KXk2kEzlYlpoW1VQUFzbzzTgXPPGPfMr3P1lbB3//uxNixOkJDxe9W+HUqKytZtWoVO3bs+ElC5ezsTHx8PM899xwJCQl07doVAF9fXwtGKwhCeycSLEG4W5WVYVyzhuqDByl3caEiPh5Djx4om+pwqj+A46lU7IwHQNUFpZ2vqUiFpIaI51ttNoccvuZrVrKScspxwIGJTGQSkxjEIFQWuCzIssx3ZZdJu3CcpRdPcLWhFhulmnHenejl5AlAB7WWwe4BZo9N+P2uXNGzYUMdfn4qhg3ToVJJLFlSw7BhOjp31nDffTbcd5/NzRsShOsMBgMLFiygY8eODBo0iPLych555BGcnZ0ZMGDATxIqhUJsHi4IgnmJBEsQ7iYVFbBmDYaVKymMijIlVRERKJvrcag7hGN+Gh0q9yA5hEDIJAhcAI5hrTZpwMBudtOf/ihQkE46S1nKOMaRTDJDGWr2qX8/+L7iGksuHCOt8DgFdVVoFUpGeQYx2TeM0Z5B6FRqi8Ql/D6yLHPoUBPr1tWxfn0d+/c3AjB9ui3Dhunw9lZRWhqAWi2m/gk3J8syJ06cYOfOnRiNRmbMmIFCoeC1115j1KhRDBo0iICAAPLy8ujcubNIqARBsDiRYAmCpVVVwdq1BG/aRGllJc7r1qEI9aHuLzOxt7fHsWETHY69jqJDRwicBEGfgWM304jVLzBipJlmtGhZznKSSSaHHGKJ5Q3eYB7zsMIyG2Ker60kwMYegNfydrH+Sj7D3DvyZtc4xnl3wl6ttUhcwu9TW2tk69Z61q+vY8OGOi5fNiBJEB2t5e23HRkzRkd4+I+JvEiuhF9iMBg4cuQIO3fubHn+UDa9b9++zJgxA0mS2L9/Px4ePxbt6dKli6VCFoR2JTU1lXnz5pGfn4+Liwvz588nISHhjv5MSZIGALOAnoAX8IgsywtaOT4AOHeDb42UZTnzDoT4q1g0wWpvL6Yg3LLqauR166j95hts58+HxkYa/v53yvr2xenpYUjnniMsvAOSe0+o7AChI8E5qtWkSkZmP/tbRqie4ilmMYtRjCKNNLpjWsTtgou5evljbLKMJEl8fjaXPx7YxNlRT9DRxoF5kQP5otcIXLSiKlxbdPWqHg8P05+RiROLyMiox85OYvhwHYmJOkaO1OHmprRwlEJbkZaWRkpKCrt27aKqqgoAf39/Ro4cyYABA4iPjycoKKjleE9PT0uFKgjt1vvvv8+XX35JSkoKUVFR5OXlYWdnZ44fbQscBRZef96qEcDh//nvstsZ1G9l6RGsdvViCkKramqQN2ygdvduyq2tKU9IoPnRR+nSsQZrn3PorcvoFhuLpI8Em/NIP+xRZf/LG/jKyHzP96Rff5zlLGrUDGd4yx5VdtgxiUnm6OFPXK6vZtn1DYCfDenFA75hDPcI5MOowTioTaNnwbaOZo9L+O30ehkAlUrik08qeeaZUoqK/HFxUfLSSw48/7wDcXFWaDRidEq4uaysLN59913Wrl2LTqcjLy+Ps2fPkpycTFxcHHFxcfj7+1s6TEG4oxKyl9z0mETPIGaF9m05fnpAONMDwilprCPp29Wtnruu55hbjqW4uJi5c+eSk5NDZGQkAOHh4RQVFRETE4NarUapVLJ48eLb/gGHLMsbgY0AkiQt+BWnlsqyfPW2BnMbWDTBam8vpiD8TG0t8saN1OXkUGZlRXl8PM3TpiEZmrGvO47j+U/Q2m8FvTNKY5Rp7YDGHqLntdrscY6TRhrppHOSkyhRMpjBvMIr3Md9OGKZxKWksY4VF0+RVnicHcUXkIEoBzfUCtMohp+uA0936mWR2ITfprjYQGamadrfpk31pKS4kphow5Ah1syb54Ty+gDVgAHWlg1UuGsVFxeza9cucnJyyMnJ4R//+AdxcXEYDAbKy8u5fPkywcHBzJ07l7feesvS4QrCPSsrK4vw8PCW5OoHLi4u7Nq1C4VCwYIFC5g/fz6vvvqqhaL8mZWSJFkBp4EPZFlebumAACRZli0dAwCSJNUAM29ximAhcEsvpiRJfwT+CKBSqXpu2bLl9gX9G9XU1GBra2vpMIQ7RNHQgNOePbh89x3NYWFUDBxIk5cXGJrRVeXhUrkWp/Kt6CUtxXbxFNsNpNKqKzW1da2+L4q0Rbg3ugPwetfXyXHJIaoiioRrCQwoGYBDs4O5uvgTNUY9u5rK2d5Qyv7mSoyAr9KKwVpnBmqd8VOJG+/fyhLXCqMRTp9Ws2ePNd99Z82JExpkWcLR0UDfvvWMH19NaGizWWMSfupu/hsiyzKXL1/myJEjLc/CwkIA1Go1YWFhPPLII0RFRVk40vbnbn5fCCb29vYEBweb9WcaDAaUylubqv3f//6XzZs3s3z5L+con332Gd7e3owZc+ORsfz8fCorK3/29YEDBzYBR/73x8my/N8btXGLOYEL8DDwDaAHxgKvAA/LsrzoFztgJm0twfpdL6aNjY1cW1t7ewL+HbKzs+/4YkHBzOrrITOTuu3b0X//PR127MDo7cGR1KXYaDQ4NmRinz8PldoaOt4PQZPAIw4UP170bvS+kJGRkFjAAh7hEU5zmmCCyScfW2zxwANLaDYaWkalBmxfTE7JRQJ09iT7hZHsG0aEvavYAPg2MOe1orlZ5o9/LCYjo56iIlOBij59tIwapWP0aB3du2tQKMTv9G5wN/0NaW5upqqqCmdnZ4qKioiKiuLqVdMEE0dHR/r3709sbCyxsbH06tULrVYUsblT7qb3hXBjx48fJyys9cq/t1t1dfUtr6HavXs3I0eOZOfOnURERJCfn49erycsLIzc3FyeeOIJKioq2Lx58y9O3/2lPkqSVCfL8i3tx3ErOcEvnPcvIFaW5Yhfc96dYOk1WL+KLMslwPv/86X915OuFwCLZ6vCPaahAXnTJpoyM9EuWgQ1NVz8739pHjuWrs8NRVH2HuERPijsO8I1IKg/eCWAovV/dpe5zDKWkUYaM5nJVKYyhCG8z/s4YBqlCsa8n4D9r6/PH+HZ3G2cG/0k9motb3WLw0qhoo+Tp0iq2pj//reKS5f0zJ3rhFotceaMnoEDrRg5UseIEaJAhfBzlZWVFBYW0q2baY1nSEgI8fHxLFiwADc3N8aNG0f37t2JjY0lLCxMlEwXhDYkJiaGV199lcTERMrLywkICGDhQlOJhKioKPbs2cPSpUt55513+Oyzzywc7Q3tAR6xdBDQxhKsX3DXvJjCPaCxEbZsoX7LFsplmfK4OBoeeYQI52LUXWvx6+mOKjAB6oLg4BkUktF0nlvfVpstppg1Xmt4gzfYyU5kZCKJRIvp014ffHiO5+5s326g2WhgS9F50gtP8MfASPq7+NDN3pVkvzDq9M3Yq7XEu/qZPS7h16uoMJCVVU9OTgMffOCMQiFx4EAjJ082t1R53LnTy9JhCncRWZY5d+4c33zzDd988w27d+/m6NGjBAUFcfr0aQBeeeUVfHx8AJAk6W696RIE4RbNnj2b2bNn/+RrjY2NLaPP9vb26HR3beXfKOCKpYOA9pFg3TUvptBONTXB1q00ZGZSrtdTNmAADdOmgWzEtr4Av6J/oQjIhAYlVk2jQKWCDh0h4ctWmy2nnFWsIp10trIVQ4iBMMJ4gzeYxCRCCTVTB3/KIBvZUVxI2oXjrLh0krKmBuzVWga7+dPfxYeejh70dLTM1ETh1smyTG5uE5mZdWRk1LN7dwMGA9jbK3juOXv8/dX8618uKJVi1FH40ZEjR9i8eTO7d+/mm2++oaioCIAOHTrQr18/kpKSiI2NbUnK//CHP1g4YkEQ7rSDBw/y4osvolQqsbKy4ssvW7+/+S0kSbKFluk5CsBPkqQooEyW5QuSJL0D9JFlefD14x8GmoFDgBEYA/wZePG2B/cbWHofrHb1YgrtSHMzbN+OfvVqSmSZsthY6qdNA8CmrgDfK//G8dpq1DSA/1gYshh8hoOq9c17G2lsGZWawASyySaQQF7kRYL2BfFI70eQMP8Nr1GW+bb0EmmFx1lWeJKixlpslGrGeXci2TeMYe4BaJXt4fOY9q2y0khGRh2ZmaaKf0T4VYgAACAASURBVFevGgDo3l3Diy86MHKkjuhoLSqV6T0mkivhyJEjfP3117z99ttYWVmRkpLCe++9R2BgIMOGDSMmJob+/fvTpUuXW14oLwhC+9KvXz927tx5p39ML2D7//z33OvPr4HpgCcQ9H/OeRXwBwzAKeDRu6HABVh+BKtdvZhCG6fXw44dNK1fj/6bb9Dt2wdenlxetRqdwYBPdSaO5z5GY6wG/0RI+Az8RoHq1obKU0jhL/yFs5zFCSfe5m20aOlJTyQksmuzLZJcAQzMTmVnSSFWChWjPANJ9g1jtGcQOpXaIvEIt8ZgkNm3rxEnJwUhIRqOHWti8uRrODoqGDbMmhEjdAwfbo2np6Uv9YKlNTc3k5uby7fffsu3337L888/T69evThz5gyffvop06ZNIyIigmeffZbnnnsODw8xSi0IgvnIspwNv3wTJMvy9P/z319jyhfuSpbeByubdvRiCm2QwQA5ORhWrkSZlgbFxeSnp6NMSCC0YS8q41LCuwWj1jlBQSn4fGRKrtStl8Jtooksskgjjcd4jHjiiSCCB3mQRhoB6E9/c/TwhpYVnuD9U3vJGTgVtULJYx0j+GNgJGO9grFTiypfd7NLl/QUFRno0UNLU5PMwIFXeOIJOz780IU+fbTs3u1Fnz5aMTp1j7ty5QrfffddS0K1f/9+GhoaAPD29iY5OZlevXoxatQoqqqq0Gg0ALd981BBEIR7kfhYU7j3GI2wezfNa9ZQUVpKWXQ0dfffT2TDGRRxVvj19ETl3RuqPODg96j1FYCTKbFqhQEDO9lJKqmsYAVllOGAA4MZTDzxRBLJp3xqnj7+H6eqy0gvPE6ybxid7JywUqqwU2kobqzDy9qOaQHdLBKXcHMNDUZychrYtKmeTZvqOHq0mV69tOzb5421tYKNGz0IDzfdHCuVEv36tT5NVWh/GhoaqKmpwcXFhStXrhAdHc2FCxcA0Gg09OjRgxkzZtCvXz/69evXUpTih+8LgiAIt5dIsIR7gyzDnj3oV62i4to1ynr3pnriRFAqsWoowb02E7nPDmhowLY+HqziwKovjFjXerPI7GUvqaSylKVc4Qo22DCOcUxmMsMYhgbL3MAU1FaSXniC9MLjHKwoQgK8rG3pZOfEGK9gxnhZrtS78MtkWSYvr5nNm+tIS3PlyJECGhpkNBqIi7Pm4YftGD78x2mpAweKjZzvJbIsc+nSJb777juio6ORZZnAwEBGjx7N559/jru7OwMHDiQqKoro6GiioqKwshJJtyAIgjmJBEtov2QZDh3CsGIFFRcvUtajB1UTJoBKhbaxHI/KDThdWYxVw1kkz3iIeR86TgBr11v+EcMZzha2oEHDaEaTTDKJJKLDMiVML9dXs+ziSdILj/Nt6WUA+jp58o/IQUz0CcVH18EicQmtKy424OKiQJIknn22lI8+qgLA31/FE0/YMWyYjvh4K2xsxJ5C95ry8nL27dvHnj17Wp4lJSV06dKFvLw8JEnirbfeomPHjgAoFAoWLFhg2aAFQRDucSLBEtqfo0cxLluGPjMTzd69NHfsyPlly9A0NeHeuBfH0/9CV3cCyT0GejwNgUmgu7V1B2tZyzzmkUUWGjQ8xENMYQr3cR/22N/hjrVu/DcrWXv5NDIQae/GO+HxPODTmUBbB4vGJfxcY6OMwSCj0ylYubKW++8v4vvvfQgP1/DAA7aEh2sYOlTH2bO7SEiwTLl+wXJWrlzJqlWr2Lt3L6dOnQJMe0yFhYUxZswYHBwcePjhh1uOf+yxxywVqiAIgnADIsES2odTp5DT0pDS05GPHSNv9Wp0AQEE/SEGK/djhIV2wtrGDul4Ltg/BkEPgO3NN8gtooilLGUEI+hEJ1SoMGDgKlfxw4+HeMgMnbuxzVfPseziCf7bcwSSJBFh70p3Bzcm+YbRuYOzxeISfk6WZY4ebWbLljq2bKlnxw7TZr9PPNGB6Ggtb7/tiJOTaXQqJsaKmBjTlK6zZy0ZtXAnGY2mTcgVCgWrV69m3rx5bNu2DY1GQ05ODllZWfTt25eHH36Yvn370qtXL+ztTR/iZGdnExkZacnwBUEQhFaIBEtou86fR166lOrDhykLCqIuLIwwbwekmVPxDvVC7T0ISh1hXxY6uQykDtBlxk2braKKVaxiMYvZylaMGPmAD3iGZxh1/WEJtfom1l3OZ6h7R5y11pyrrSSrqIDixjrcrGx4s1ucReISbuzSJT1ZWfVs2VJPVlY9RUWmPak6d1bz+ON29OhhWpvn5aXilVccLRmqcIf9sG5q3759P3lu2rSJvn37olAoUKlUlJSU4OXlxbvvvss//vEPJElUghQEQWiLRIIltC2XLyMvW0bt3r2U+fhQPngw+sGDUegbcWjMw5h8DKV+N05NPcCuN9iOg4DxN222kUYyyGAxi1nPehpoIJBA5jCHyUymC13M0LmfazDoybx6lrTC46y7fIY6QzNf9BrBYx0jebRjOH8MjBQ3YXcJg0FGqZQwGmV6977EwYNNALi6KhgyxJqhQ3UMHWqNj4+47LZ3tbW17Nq1qyWR2rt3L1evXgVAqVQSHh5OcnIydnZ2AIwdO5axY8e2nK/Viq0SBEEQ2jLxl164+5WWIq9YQf2OHZS5uFA2bBjNsbFIBj0OjSdxPPcP7Mu3o9C5QtijEDwZXHqazr2F5GMWs/iCL6ikEjfceJzHmcIU+tLXIhv/NhsNbL1WQNqF46y6dIoqfRMuGmum+Xcl2S+MWBdTiWW1Qmn22IQf/ZBQAcyYUcz33zfxzTfeKBQSw4bpmDzZlqFDrQkP16BQiCS4PWtoaOCTTz6hd+/eJCQkcPbsWUaMGAFAaGgoQ4YMoXfv3vTu3ZuoqCisrUXlR0EQhPZMJFjC3am6GtasQU5PR8rMpC40lBNffw1GI/ZNBTgW/g2HkkyUamtTkYqYzeAZB9LNq6yd4hQrWMFLvISEhAEDYxnLVKYymMGoLPTPQpZlZh7cQlrhcUqb6rFXa7nfJ5Rk3zAGufmjUogKcpZkNMocPtzE1q31bN1az549jRQW+mFjo6B3by1ubkpkWUaSJN55x8nS4Qp3QHV1NYcOHeLAgQPs37+fkJAQXn/9dTQaDW+//TYzZ84kISGBsLAwtm7dSs+ePVvWTQmCIAj3DpFgCXePxkbIyIDUVOR16zj18cdY9+mDX6Qbun7W+Pv54eDoiGrPQuiggx7LwGcoKNQ3bbqQQjrQAXvs2clOXuM1kkiiE534gA/M0LkbO1ReRE5JIU916oUkSVxtqGGYewDJfmEMd++IVin+iVqKLMvk5+tbEqrt2+spLTUVJggLUzN1qi11dTI2NvDoo6L8fXtTU1PDoUOHOHjwIPv37+fAgQOcOHECWZYB8PHxwdPTVH1UoVBw8eLFlil/KpWKQYMGWSx2QRCE3yM1NZV58+aRn5+Pi4sL8+fPJyEhwdJhtSni7k2wLIMBsrPRL19ORUUFdX5++G3fjvTkBGy7hqIdOxZKViLtfhoXq1mgcoX+n9xS01VUsYIVpJBCNtl8zMfMZCaTmcw4xuHKre93dbvIssz3lcV0tnNCq1Sx5vJp/n5yD9P8uwGwrN94sabKgn4Ygdq5s56pU69x8aKpMIWPj5LERB2DB1szeLA1Xl7i0tne5Obmcvz4cSZPngzA4MGD2bt3LwBeXl706tWL5ORkevXqRc+ePXF3d//J+T8kV4IgCG3Z+++/z5dffklKSgpRUVHk5eWJ69tvIO4SBPOTZdi/H2NaGpUFBZT17UvltGnIGg3apkoM0btRFi/G22EAuMWB44MQNAm0N6+0pkfPZjaTQgprWEM99QQTzBu8QSKJANhcf5jTyepS0i4cJ63wOCeqy1gdM4Fx3p14qlNPng3pjb3atKhdJFfm9cM6qpISAzExl5k9257HH++Av7+K6GgrBg+2ZtAgKzp1UovfTTtRVlbWMjKVm5vLggULUKvVfPXVV3zxxRc88MADKJVKXnvtNQB69uyJh4eHhaMWBKG9SiDhpsckksgsZrUcP/36o4QSkkhq9dx1rLvlWIqLi5k7dy45OTktW0GEh4e3fD81NZWnnnqK4uLiW27zXiUSLMF8Tp9GXrKEmtxcSsPDKR87FqOtLSp9Ha4Ne3E6+zm62jwk5+4QPQ/8x5jOU9vetOnDHOZrvmYxi7nGNZxw4hEe4SEeslixioLaStILT5BWeJxDFUVIwABXX57u1KulUIWTRix2N6fycgM7djSwfXs927bV07OnlgUL3HB2VtC3rxZvb9Ml0d9fzbJl7jdpTbjbXblypSWZ+uF/z58/3/J9f39/Ll26REBAAC+88AIvv/wySqWpeMzo0aMtFLUgCIJlZGVlER4efsN99oxGI8uXL8fX19cCkbU9IsES7qyiIkhLg8WLqSsvJ/+jj2hOTERhaMKx6ThO+V9hV7kbyc4PQqZC8DJwDLulpsspxxHTqNYc5rCFLYxhDNOYxkhGokFzJ3t2Q0ZZ5p/5B0krPM7u0ksA9HXy5IPIQUz07Yy3tRhmN6fKSiM5OfVs395AdnY9hw41IctgbS0RG2tFv36mDX0lSSIlxc3C0Qq/R0VFBVlZWcTGxuLh4cFXX33Fo48+2vL94OBgevfuzZNPPkmPHj3o0aMHzs4/bsjt7e1tibAFQbjHZZP9m493weWm51dTfcttl5WV4eDgcMPvLVmyhKSkJN5///1bbu9eJhIs4farrTVVAExJocjdHVVpKS7NTVj9OQkbPz8cvbxw+G4aiuJvTVP/4v8fuPe7pZLqP1jMYh7hEfLJxw8/PuIjHHHEGeebn3yblTc1kFtRxEA3fxSSxPxz32NE5m/dBjDJN4xA2xtfrITbr6HBiJWVqdri448X8+WX1RiNoNVK9Oun5fXXHRk0yIo+fazQasWUv7aoqamJY8eOcejQIXJzcxkxYgQjR47kwoULTJw4kcWLFzNlyhTi4uL48MMP6dGjB5GRkXToIAqRCIIgtKZ79+7MmTOHw4cPExERQX5+Pnq9npCQEJYuXcrq1atFgnWLRIIl3B4GA2zbhiE9nbqTJ7HbtQvJz4/KZ55B4+aGizIbxZ5ZBHX8C9g4Qfx/wMoVlDcfZZKR2c9+FrCARBIZyUhiiGEWs1pGqYIJvtM9/IlafRM6pWldzpwjO1hYkMe1sTOxUWnITpiMg8bKrPHcq6qqjFhbS6jVEh9/XMnLL5dRXOyPTqcgOlqLl5eShARr+vXTtiReQttRVlbG4cOHOXz4MLm5ueTm5nLs2DGam5sBsLGxwd/fn5EjRxIWFsb+/fvp1s1UMCY4OJinn37akuELgiC0KTExMbz66qskJiZSXl5OQEAACxcuZNGiRTzwwAMoxHYxt0wkWMLvc+QIckoK1UePUtqvHxXTpyNrNERc24iKHDqFNqMI6A5VDqa1VJrrnyLb3Hw6ThFFLGIRX/EVeeRhhRXBBDOSkXSkI3/jb3e4cz/VaNCTefUcqYXHWHf5DNvik+nr7MWzIb15rGMEOqWpXLxIru6cigoDu3Y1sGOH6XngQCPbt3syYIA1ffpoee45exobZXQ6eOwxMWLR1qxduxaNRsOIESNobGzE3d0dvV4PgKenJ1FRUYwaNYrIyEi6d+9OUFBQy5optVpNz549LRm+IAhCmzd79mxmz579k6+lp6dz6NAhFi1axOnTp3nqqaf4+OOPLRRh2yASLOHXKyqC1FT+//buPC7qOn/g+OszBzPc9ymHoOAF4p1H5tFtmmmZW23HWnafW7ZlZZlWm2lb65babyvTLbc8ts3KDivLTN3SPAEFFUFAQBAROWfm8/tjEMEowbiE99PH98HM95r3F97CvOf7Oco//5yCLl0ouOIKqiZPxmivxM+Wgv+BRRiPbQavLhgc5c5jvKLBa+oZT23DxhrW8CZv8gmfYMPGeZzHQhYymcn40LLN7WwOB9/kH2RZRjKrsvZyrKoCfxdXborqhW91IRXnKZPKNpeCAjvr15fz7bdlfPttOdu2OftQubjAeedZeeIJn5qBKQYPtjJ4sBS3bd3x48fZuXMn27dvZ8eOHQAsWLAAgFmzZuHj48Nll12GxWLh9ddfJzIykj59+vxiWHQhhBAt48UXX6x5PGDAACmuGkAKLNEw5eWwejX2ZcsoNJk4csUVlM6eDdqBtz0H/6yX8M79DwazK8RMhhHzIHhoo/pVLWABs5hFDjkEEcRDPMQt3EJPejbjhf2S1pqNBVksy0zmg8wU8ipK8TS5MKFTHNdF9uDCoCjMBmOLxtRRHD5so7xc07mzmf37q+jSJRMAq1UxeLCFGTN8GDHClcGDLbi6SlOFtu7gwYNs2bKFHTt21BRU+/fvr9nu7e3N+eefX/N85cqVBAWdGmxk6tQzfygjhBCi5fz000+tHcI5QQos8eu0hi1b0IsXY1uzBvP+/Th69SLj7bdxNRoJL9+AX8pMzPajEH4pjF4CUVeCqWFDj5dRxipWMZ7xeOCBHTv96Mdt3MYVXIEZczNf4Claa/IqSgm2uuNAc83G/1JYWcbY0C5cF9mTMaExuBpbLp6OQGvNwYM2cnLsDBliRWtNfPwhxo1z4+23g4iONjFnjh+DB1tkUIpzxDfffMPKlSuZP38+SilmzJjBkiVLMBgMxMbGMmDAAKZMmUJiYiK9e/cmIiKizvxikZGRrRi9EEII0TSkwBK/dPgw/OtfsHgx7N7N3n/+EzV6NHGWAswe/yO+R1dc3H1Qqbug3yMQe2OD+lSdZMOGCRNb2MIf+SP/4l/cwA3cW/2vNdz381r+k7WXjLF3YVQGPho2kThPP7yqJwAWv5/DoUlOrmL9+nLWry/nu+/KOHTITmysmb17nW+0/+//AomJcf5aUkoxbZqMwNiWlJeXk5SUxM6dO+ssX3/9Nd27dyclJYX333+fp59+msDAQKZNm8Z9991Hz549cXNza+3whRBCiBYhBZZwstng00+xL1lCUWUlR0eNIsbHB8PCOQSOGoTyDYfynfDZw1i6TwGPIRB3U4NPX045K1nJIhaRQAKv8RrDGMZ61jOUoc14Yb+UU1bC+5nJLMtM5v3B4+ns7s3E8Dh6eQdg1xqjggF+oS0aU3u1a1cln39eWlNUFRY6AAgJMXLBBVaGD7dywQWn+k1NmODeWqGKeuzbt4+lS5eya9cudu3aRWpqKg6H82dotVrp2bMnl1xySc3IUrfffjt33nlnzV2pkyP6CSGEEB2JFFgdXWoqvPkmJ77/niPDh1N4//043N2xOMqpTNiN9cB0/HIyIGY+6OHwxxwwN/xN8F72spCFvMM7FFJIF7owmckAKBTnc/4ZztA0jlaWs/LQHpZlJvNN3kE00NcnmNzyE3R292Z0UBSjg6JaJJb2LCWlkmXLSpg+3ReLRbF48XHmzTtGly4mxo93Y/hwV4YPt9Kli6lO0zDROhwOBwcPHsRsNhMeHk56ejpXXXUVs2bNYty4cWRlZTFr1iy6du1KfHw8kydPJj4+noSEBLp27YrJVPdPyMkR/YQQQoiOTAqsjqisDJYvx/7uuxR6epI/YQJlkyahHA58OUTAwdl4HPkSZQ2EhIeg+63O45RqUHFlw8bHfMzrvM6XfIkJExOYwB3cwShGYaBlBicotVWxOieN9zKSWJOznyrtINbDl6d6DuW6iJ5092r5SYnbk6wsG99/X86GDeXceqsniYkWkpOrmD27iAkT3OnTxzls+sMPexMaKr9qWpPWmszMTHbv3l1nSUpK4sSJE0ybNo05c+YQFBREaGgoVqvzruKQIUMoKSnB1bVh/SqFEEIIIQVWx7J7NyxahOP998m46y4Kn34abbHgSjkRJWvw2/cSJttxiLgULl4JkWMbNBFwbV/wBbdxG5lkEk44s5jFbdxGCCHNdFH1szkcRH+6kLyKUsKsHtwX25/rInrQ3zdE7pycBbtds3t3JRs2VLBhQznff1/OwYPO+Ync3BRDhlhJTLRw+eWuFBV1xtPTWUSHhcmvmJaWmZlJWVkZcXFx2O12hg8fzq5duzh+/HjNPiEhIfTs2ZNbb72V+Ph4hg0bBoCbmxtr1qyp2c9sNmM2y+AuQgghRGPIu5/2rqwMVqzA/vbblBYV4bl7N+rqq6m4/HL8Q0IIyFuB28+POO9Wxd8N3W93zlnVCJvZjDvuxBNPJJHEEcervMo4xmFqwRSbt+d/fJ57gC8umIzJYGB2/HBiPfwYHhiOUcmQ3o2htUYpRWGhneuuy2PTpnKKizUAoaFGhg2z8uCD3px/vpXERBfMZmfRarUasMpUVM3ObreTnp5OcnIySUlJ2O12Hn/8cQDGjh1LeHg4n3zyCUajkejoaPr370+vXr3o1asXPXv2xN9f7t4KIYQQzUUKrPYqNRUWLHCOBHj0KFkvvEDB6NH0DnHHuG8OcZFVqNAo8LkSfDtB9AQwNn7EvHLKGcMYLuMy3uVdutOdtaxt+us5jdaa7cfyWJaRzPQeQ/A2W/AwuRDg4kqF3YbFaGJqTJ9mj6M90Fpz9KgDPz9n/5nRo7Pp1s3MggWB+PgYKC3V3HCDJ0OHWhg61Ep0tPSfaklpaWls27atpphKTk5mz549lJeX1+wTHx9fU2DNmzcPb2/vmm3vvvtui8cshBBCdGRSYLUndjusWYN+/XWKKivJ+8MfCL/xRtyvHEtQYjR+1hAMFgXff4sKHQGh54N3rHNpoCMc4Q3eYG31PytWVrOaBBKa8cJOSSs5yrKMJJZlJJN8vACTMnBRcBQXB0dzR5c+3NFFiqozKStzsGVLJT/8UM7GjeX88EMFgYEGdu2KAGDIECsREc5fDQaDYv36sNYMt0MoKirCy8sLg8HAqlWrWLFiBe+99x4AM2bMYNmyZQB07tyZnj17ctFFF9GjRw969uxJjx498PE5NZz9RRdd1CrXIIQQQggnKbDag4ICeOstbEuWcKR/f/Luv5+qwEBcDArbABMk3471KzNcmwLKAH9IA0PjfvQppPAyL7OUpZRTzsVcTAEFBBLY7MOs55SV8MGhFN7LSOJ/hTkADA8IZ2HspVwT3g1/i3TA/y2ZmTbWr3cWU5s2VbBtWwU2Z/cpYmPNXH65K8OGWWuaBT73nF/rBtxOORwOMjIy2LNnDykpKXWWw4cPs2/fPmJiYsjJyWHHjh2UlJQAMH36dKZNm0ZcXBzu7jKMvRBCCNHWSYF1LktKgpdfpuyHH8ibMIGCN95Au7jg6epCZMm3eO94ElV1DEKGQ8KDp45rYHGl0WxgAy/xEh/xEVas3MRNPMAD9KRnM13UKVUOO2O/X8Ha3IM40PTxCWJO75H8IaIHEW5ezf7656q9eytZtaqUhx/2xmxWzJ1bxN//Xoy7u2LQIAuPPurD4MEWBg+2Ehgow2o3tfLycnbt2kVsbCze3t6sWbOGxx57jNTUVMrKymr28/HxoUePHlx++eV07969pni65557uOeee2r2k7mkhBBCtKRly5Yxd+5c0tLSCAgI4M0332TkyJGtHdY5RQqsc43W8M03MHcux3NyOHz77RTfdRcK8PdxJ+jIKlw3PQ+2UoiZBImPQmD/Rr2EHTsf8iEv8RKb2Yw//jzN09zDPQQS2DzXVe3zw/vZcjSX6T2GYDYYCbV68ESPIVwX2YMeXgHN+trnGrtdk5xcxebN5WzeXMF993mTkODCtm2VPP54IWPGuNK7t4X77vPmT3/yJD7eBZNJ+k41haqqKtLT09mzZw979+5lz549TJo0iYsuuoht27YxZMgQVq9ezdixY/Hy8iIiIoKLLrqI7t27061bN7p3705gYKD0ZRNCCNGmzJs3j7feeoulS5fSp08fdu/ejaenZ2uHdc6RAutcUVUFH3yAnjcPfv4ZFRRE8fz5lMbGEhbkT2DGQkzrXgFHBXT5A/R9Anwbd5dJo1EoNJppTMOAgdd5nZu5GTfcmuWybA4H6/IzGBkYiclg4Ju8DN7NSOLhuIFYjCYWD7qiWV73XJSdbWPz5oqaguqnnyooKXGO7Ofra2DMGDcSEly44go3Cgqiagat6NpVhtn+PUpKSnj33XfZu3dvzbJ//35sJ9tZAv7+/vTv7/wgIz4+npUrVzJo0CAAhg0bxscff9wqsQshhGjjVo888z6RYyHxkVP7x90C3W6B8iPw5TW/fezI1Q0OJT8/n5kzZ7J+/XoSExMBSEhIID09ncDAQHr16gXA8uXLCQxs3g/cz3VSYLV15eWwaBHMnUuFw0Ha668TXlGB95VXEmIyEWowYMABGz6EmGuchZVPt0a/zH/4D7OZzfd8jyuufMVXRBKJkaZvQqa15n+FObyXkcT7mSnkVpzgs+GTuDQkhid7DuW5hAs6/LDqx445KCtzEBJiIjPTxpAhWWRl2QEwmyEx0cLNN3ty3nkWBg2yEBdnrrkb4u5uQLrqNIzWmtzcXFJTUzGZTAwZMgStNQMGDOCqq67iqaeewuFwcOedd+Lq6kpsbCy9e/fmmmuuIS4ujtjYWLp161Zn2HMPDw8mTpzYilclhBBCNN7atWtJSEioKa5qGzFiBCtWrGiFqM5NUmC1VRUV8M9/op9/niq7HZfu3XF59FFcYmNRwcFQsAHjj0/CmC/AxRMmbgVT4yYgOsYxqqgigAD88MMLL/LJJ5JIomncXFgNkVx8hPcykngvI5n9J4qwGIxcEdqFGyJ7MiIwEgAPU+MmNm4PyssdbN9eyc8/Wxg50vmmPyoqgxtu8OC11wIICzMyerQr/ftbOO88C336uGC1duwCtLEOHz5MamoqaWlppKam1jxOS0urGUzi4osv5osvvkApRf/+/YmMdOakl5cXmZmZhIWFYTDI910IIUQTGrfu7Pe3Bpz5+FqTzJ9JYWFhnVFpa9uwYQPDhw9n+PDhPPfcc9LE/QykwGprqqrg7bdh9mwqbDYy5syhrFs3evXrh9FopGZAAmFOsAAAH/hJREFU9XIPsFdAWa6zwGpEcVVAAX/jb8xnPjdxE/OZzwhG8A3fNP3lOOy8kvoT72Uksa0oDwOKC4OjeKrnUCZ0isPb3Pi5t85lVVWa3bsr+fFHZxO/H3+sYOfOSmw2iI315aGHQCnF3//uT1ycs2mf0ahYsiSolSNv2+x2O3l5eYSGhgKwcOFCsrKymDVrFuAcunz37t0AmEwmoqOjiY2N5YILLiA2NpauXbvSo0ePmvO98cYbdc4fHh7eQlcihBBCtI6+ffsyffp0tm/fTu/evUlLS8NmsxETE0NaWhpubm5MnTqVVatWcfXVV7d2uG2aFFhthdbOSYFnzUIfPEjetGlkX3MNGI106tQJA3bYNtdZUA15GYLOg4lboBGfIBRRxMu8zCu8QgklXM3VTGFKk1/KkYpSdh7LZ1RQFCZl4M0DO/AxW3i1z4VcG9GdEKtHk79mW+RwaAwG589n3rwili8/wbZtlVRUnOo3NWCAhWnTfBg40EJV1VagOwA33SQdSk9XVlbGgQMH2Ldv3y+WAwcOYLFYKC4uRinFzz//zN69e2uOnTNnDgaDgdjYWKKiojCZ5FefEEIIUdvQoUN58sknGTt2LEePHqVz584sWbIEi8WCxeL8QHzixIls2rRJCqwzkHcZbcXbb8Ott1I2bhwH332XEy4ueHl5ERUVhcuxnbBqNBzdDZ0ngsMOBmODi6vjHOdVXmUe8yiiiGu4hmd4hl70arLwT9gqcTM6+wE9sv0bPsxOJXfcvViMJn688CY82/mdqqoqTVJSJT17umA2K15+uYgXXigiJycKk0mRl2fHalXce68X/ftbGDjQQpcupjq32Nets7fiFbQ+rTVaawwGA1u3buWTTz5h+vTpGI1GHnnkEebNm1dnf09PT7p06ULv3r2ZMGECXbp0wW63YzKZWLRoUZ19x4wZ05KXIoQQQpyTpk2bxrRp0+qsKy4uxsvLOT3O+vXr67T4EPWTAquN0IsXk/PEExyeOBGj0Uh0RAS+vr6o7K/h8/Fg8YVLP4KocQ0+5wlO8BqvMYc5FFDAlVzJTGbShz5NEnOF3caaw/tZlpHM6pw0No2+kd4+Qfyl+3k8FDcQF4NzgIz2VlxVVGh27apk69YKtm6tYMuWSnbscN6Z2rq1E337WoiPd+GPf/SgrEzj6al48UX/M5+4AyguLubAgQM1y/79++s837RpE7179+bHH39kxowZTJkyhU6dOjF69Gh8fHyIiYmhS5cuxMTEEBAQIG3AhRBCiGb27bff8swzz+Dm5kZ0dHRN83vx66TAagv27SM/LIycCRPw8/UlIiLC2YTpwH/gqz+Adxxc8QW4hTbqtAc4wGM8xqVcyrM8y0AG/u5Q7drBN3kZvJeRxKqsvRyrqiDAxZVbOifgbnL2GWqP81Xt3l3J3LlF/PxzJbt3O/tMAXh7G+jXz6XmzlRUlPO/1CWXuHHJJc0ztH1bprVGKUVubi4rVqxg7NixREVFsXr1am655RYKCwvr7O/p6UlMTAzdunXjsssuq5lr48Ybb+Tmm2/GanX2LRwzZozchRJCCCFawbhx4xg3ruEf8AspsNoEvXQpeZMm4V7d+R6Ave/At1MgcBBc9glY/Rp0ro/5mB/4ged5nnjiSSGFOOJ+X3xas6kwm2UZyXxQPay6p8mFCZ3iuC6yBxcGRWE2NP1w7i1Ja01Ojh2HA8LDTRw6ZGPUqGyefdaP665z3on65JNS+vWzMGaMD/36udC3r4WYGFOHuotSUlLCwYMHSU9PJz09vebxya8zZ87kzjvvJC8vj3vvvZfAwECioqKIiori2muvJTo6us7i5+dX7/fPza3jFadCCCGEaB+kwGptWqOWLiVm6FAcCxY41+18FTY+CJ0ugkv+A+aGDwqxiU38l//yBE/gjvtZF1daa/IrSgmyumPTDsZ+v4ITtiquCO3C9ZE9GRMag6vx3JzAtqpKk5JSxfbtFWzfXsn27ZVs21ZBfr6De+/1Yv78AIKDjfTtayEw0Dksd//+LuTmRrXrYkprTXl5Oa6urthsNubPn0/fvn0ZOXIkmZmZ9OnT5xd3oCwWS00BdeWVVxIX58y37t27k52dTXBwMAC9e/dmwcn8FkIIIYRox6TAam0//AD79+P29NPg4QG2Mkhe5BzM4sL3wPjb/ZdSSeVxHucWbmEsY3mCJ3iGZzD9zh/t1C2f8U1eBmmX347ZYOST86+hp1cAXudYf6qyMgeurga01txxxxF+/LGCpKRKKiud2y0WRa9eZsaOdaNvXwvDhzubpJnNig8+CK45T3sorMrKysjMzCQzM5OMjAwyMzM5ePAgGRkZNcukSZNYsmQJRqORp556ijvuuIORI0cSFBTEtddeS1RUFJ07d6Zz585ERUURHBxc79xQZrO5Zsh0IYQQQoiORAqsVla1fDmHZs8m9IoxWB1VYHKFcd86B7Uw/PqPp5hiZjObV3gFF1y4lEsBcMW10THsLyni/cxklh/aw8fnX02YqyeTwrsx0DcUm3ZgVkYG+3c662tsCWVlDpKTq8jOtjF2rDsAl1+eQ0WF5uuvw1BKceCAjeBgI5dc4k1iooXERBfi4syYzed+8VRZWUl2djbFxcX07t0bgBdeeAGj0cijjz4KQFRUFPn5+XWOCw0NJTIyksTERMaNG8fQoUMBZ0GZlZVVM2qQxWKRO1BCCCGEEA0gBVZrKi+ndPdujs2cSWjWCvj5a7jw3+Aa+KuHOHDwLu/yKI9ymMP8iT/xPM8TQkijXjqztJgPMlP4d2YyPx09DMAQ/zDyKkoJc/Xk0pCY33VpzaWqSrNvXxW7dlWyc2dl9dcq9u2rwuEAd3dFcXFnDAbF5Mke2Gy65tgvvzy376hs3bqVlJQUDh06VGfJzMwkNzcXrTVdunQhLS0NgC1btmA2n2rG+fzzz2OxWIiIiCAyMpJOnTrVzGtRH29v72a/JiGEEEKI9kYKrNa0ejXea9fS+y9/weBxwjm/Fb9+N+UnfuJ+7mcjGxnEIP7LfxnEoAa/XGZpMSsO7WH5oRQ2FmQD0N83hJd6j2RSeHei3NvWG+rDh21s3FjB+PFuGAyKGTMK+etfi6iqcm43GKBrVzMJCWauv96d+HgX4uNdaqYHu+WWtj1Zr9aagoICsrKyyM7O5uuvv+a7777jqaeeQinF008/zapVq9i5cycAM2fO5KOPPgKcxU94eDjh4eEkJCQQERFBREQEnTt3rjn/ihUr6rzebbfd1mLXJoQQQgjRUUmB1Yrs77+PISwMw6hRYLwIEv5c7+TBRRQxjWm8yZsEEsjbvM1N3ISBX/Z9OV2F3YbFaOKErZLYNW9Q4bCT6B3E7PjhTI7oQVcP3+a4tAarqNCkplaRnFxJUpLz67PP+hIX58JHH5Vyxx1H2L8/guhoM/37W3joIW969XIWUj16mHF1PfP3oLXk5eWxY8cORowYgdlsZuXKlfz73/8mOzubrKwscnJyqDzZGayaUoq7776bgIAAunXrxogRI2qGPp8zZw4vvvginTp1qhnOXAghhBBCtC1SYLWWvDz2jxgBt15PbOZqiBpfb3EFYMbMt3zLQzzEDGbgTcPuNE39aQ1JxQVsGP1H3E0uLB44hn6+IcR5NmzI96aWm2vj00/LSEmpJCWlipQUZ9M+u925XSmIjjaRm2snLg7Gj3ejb98wOnVypun48e6MH+/eKrED2Gw28vPzOXz4MIcPHyYnJ6feZdWqVfTt25ePPvqIqVOnkp6eTlRUFIcOHWLXrl2EhoYyfPhwOnXqRFhYWM3XjIwMJk6cWNOs7/rrr+f666+vef1u3bq11qULIYQQQogGkgKrlVSsWkXx4MGEFn4IG5ZA+KXOAS6qpZDC8zzPIhbhjjs72YmFX+8vk1ZylJWH9vBJzj7WDJ+Eu8mFYQHhRLv71NwB+UNkz2a9pspKzf79Vbi6KqKizOTk2Jg8OY9HHvHmyivdSUuzMWVKPi4uEBtrJiHBhWuucadXLxd69jQTF2fGze3UHangYBPBwc2bona7nYKCAnJzc2uWgQMHEhcXR1JSEg899BDPP/88/fv3Z/ny5XUKnpN8fHwIDQ0lNDSUYcOG1fRrGjNmDN9++y1BQUEAPPDAAzzwwAO/GktFRUWdPlNCCCGEEOLcIwVWK8kvKAA0Adn/Bxf8o05xBZBFFh/zMbvZzQAG/KK40lqz81g+H2ansvLQHnYcc44ON9A3lKyyEuI8/bilc0KTx11VpTl40EZqahWpqVWkpVXVPE5Pt2G3w5//7M28ef74+tZtvte/vwupqRF07mzCZGq+kfvsdjtGo5GKigq+/PJLunXrRmxsLBkZGUyfPr2mkMrLyyM/Px+Hw1Hn+Pnz5xMXF4fJZKKoqIjS0lIABg8ezIIFCwgJCSEkJITg4GBCQkJwda1/5MawsDDCwsKa7TqFEEIIIUTbIwVWK3BLT6dg8Hn4HNuAS2A8xEwC4Cu+Yic7eZAHuZALOchBPDnV18bmcLCh4BAfZqXyYVYq6aXHUMBQ/078LXE0E8O7Eenm9bvjs9l0TQG0cGExvr6GmhH5vLzSKS8/NTKfh4ciNtbZP+q66zzo1s3MwIHOYtBqNfDdd6cKDKvVQNeujesz5XA4qKysxGq1YrPZ+PTTT8nPz69Zjhw5Uud5fn4+d911F3PnzqWqqopx48bx4osv8uijj6K1ZuPGjQQFBRETE8PgwYMJDg4mKCioplgKDg4mPDwcgLi4ODZv3lwTS3R0NHfeeedZf1+FEEIIIdq6ZcuWMXfuXNLS0ggICODNN99k5MiRrR3WOUUKrFbgk5HB8YQEAlOXwyVvkK+O8DAPs5SldKc7d3EXFix44snxqgoKK8uJcvcmq+w4I9ctw2IwclFwZ57oMYRxYV0JtjauX1JlpSYjw0Z6ehUHDtiql1OPY2JMbNzonPfqjTeKiYkxM3myByaT4tlnfQkMNNK1q5nYWBNBQcZGTcJ7+PBhjhw5QmFhIYWFhRQUFFBQUMCRI0dqHsfHxzN79mwAOnXqxFVXXVUzB9NVV12F1s4Cz9XVlcDAwJqlR48eBAYGMmrUKADc3d3ZvHkzMTHOIeejoqLYt29fo75XQgghhBAdxbx583jrrbdYunQpffr0Yffu3TKw1llo9QJLKXUB8AjQHwgD/qS1XnyGYxKAfwCDgEJgETBLn3zn3ZbZ7dhjI7GUZ+IROYh3/LbwMA9zjGM8wRNM19MprrQTWN0isO+Xi+ntE8SqoROIcvfms+GTGBYQjofJpd7Ta605etSBn58RgE8/LSUlpZI//9kHgPHjD7N6dSm1v1MmE0RGmoiONjNunBuJiafO/f33YXX6RT3wgBtHjx6lqKiI9PQifv7Z+fjo0aM1i7u7O8888wwAN954IwBLly4FYMiQIaSnp/8ibovFgr+/P/7+/nWGGv/LX/5CbGxsdZwmtmzZgq+vL4GBgbi7/3ZhqZRi0KCGD2MvhBBCCNGS9uzZc8Z9vL29CQkJqdnf39+fgIAAbDbbGT84bkxXhfz8fGbOnMn69etJTEwEICHB2d1k3bp1zJo1C4fDwf3338+ECRMafN6GaG/1QKsXWIAHsAtYUr38JqWUF/Al8B0wEOgGLAZOAPOaLcomUvbtOkrjEgjNWsBVl6WymlcZ5BjMjUeeIjXLhd45SzlhryJr7D0YlGJO75GE1LpD1c8Yxa6fqsjOPkF2to3sbDtZWTYyM20cOmTn0CEb5eWaiopozGbFp5+Wsnz5iZoCa8QITWSkHT+/Mry9S3B3L8RkOsKJE8UcO3aM4uJi9u4tB+YD8OKLM9m0aROff/45AJdffjlff/31r16fq6sr8fHxNQXWyeLopDlz5qC1xt/fHz8/P/z8/PD398fd3b3eO2EPPvhgned9+/Zt9PdcCCGEEEL8trVr15KQkFBTXJ1UXl7OvHnzWLNmDS4u9X/A3wTaVT3Q6gWW1vpT4FMApdTiBhxyA+AG3Ky1LgN2KaV6AH9WSr3cFqrW35KbtwPleR6z41bxubGSTrtv4sekHvyPnbhgoltlKN2OhJGRVUrncHcKP/Pi0b8eZ+PGMgIDXXn00VQWLz6V3Eo58PA4gZvbMSyWo4SG5qNULrm5dxAeHkBY2DtUVDyH1gUopUhOnsE///nPX43ParXi7e3NK6+8gtFoJCAggIiIiJrtd999N1dffTU+Pj74+Pjg6+tb57HVaq1zvhkzZtR5PmnSpCb6TgohhBBCnNsaOwVL7f1NJtMZjz9+/HiDz11YWIiPj88v1v/www+4uroybtw43Nzcagb8akrtrR5o9QLrLAwB1ld/M0/6HJgFdAYOtEZQDaGLizkSEYWjbC0LgzuhPxpP1o5o2B0Eu4KoTPNjZ5WRncCXbslMnTqApKTN7Nt3mIyMSwkMjMbL6ytgBZAL5KH1UcAdg8EDi8UDDw8PPD09MRqnANCvXy/+9KebsdlsmM1mpkyZwqhRo/D09MTb2xsvLy+8vLzw9vbG09PzF59M3HfffXWeX3311S3xrRJCCCGEEC2ob9++TJ8+ne3bt9O7d2/S0tKw2Wzk5uaSlpbGpk2bWLt2Lc888wwLFy5s7XDbdD2g2tINH6VUCXDvb7W5VEp9ARzSWk+ptS4SOAgM1VpvPG3/24HbAUwmU/8vv/yyOUJvEGtODm//+wM2XuxL9sqBeOZU4WasxM2tAlfXCtzdbXh7V+HtXcXFF59PQEAAeXl5HDhwgMTERKxWK8XFxZSWluLq6orVasXFxaVRg0yItqukpAQPD4/WDkO0IZIToj6SF6I+khdtn7e3N127dm3R1zw5dU1DvfrqqyxcuJCioiIiIyNZtGgReXl5fPHFF8ydO5eKigrGjx/PZ599Vu/xaWlpHDt27BfrR40aVQnsrLXqDa31G/WdoznqgZZ2Lt7BAji9KlS/sp7qH94bAO7u7rq1h5kcfN11rFu3jpH3tm4cou1Zt26dDIMq6pCcEPWRvBD1kbxo+5KTk1t8RL7jx4836jWffPJJnnzyyTrrCgoKWLBgAR4eHiQlJREXF/er57Rarb/WX96mtR7QiNAbosH1QEs7Fwusw8DpDT+Dqr/mtnAsQgghhBBCtFv+/v5MmDCBESNGYDAYeOutt1o7JGjj9cC5WGBtBF5USlm11uXV6y4GsoH0VotKCCGEEEKIduiee+7hnnvuae0wamvT9YDhzLs0L6WUh1Kqj1KqT3U8kdXPI6u3v6CU+qrWIe8BpcBipVS8Umoi8BjQ6iOGCCGEEEIIIRqnvdUDrV5gAQOAn6sXV2Bm9eNnq7eHAl1O7qy1PoazQg0DfgJewzne/cstF7IQQgghhBCiibSreqDVmwhqrddxqlNafdtvqWfdTuCC5otKCCGEEEII0RLaWz3QFu5gCSGEEEII0e61gdZrzaY9X1tjSYElhBBCCCFEMzObzZSVlZ15x3NUWVkZZrO5tcNoE6TAEkIIIYQQopkFBQWRlZVFaWlpu7rbo7WmtLSUrKwsgoKCznxAB9DqfbCEEEIIIYRo77y8vADIzs6mqqqqRV6zvLwcq9Xa7K9jNpsJDg6uucaOTgosIYQQQgghWoCXl1eLFiHr1q2jb9++LfZ6wkmaCAohhBBCCCFEE5ECSwghhBBCCCGaiBRYQgghhBBCCNFEpMASQgghhBBCiCai2tMwkWeilHIAbWECAhNga+0gRJsjeSFOJzkh6iN5IeojeSHq01bywlVr3WFu7HSoAqutUEr9pLUe0NpxiLZF8kKcTnJC1EfyQtRH8kLUR/KidXSYSlIIIYQQQgghmpsUWEIIIYQQQgjRRKTAah1vtHYAok2SvBCnk5wQ9ZG8EPWRvBD1kbxoBdIHSwghhBBCCCGaiNzBEkIIIYQQQogmIgWWEEIIIYQQQjQRKbCEEEIIIYQQoolIgdWClFJ3K6UOKKXKlVJblFLDWzsm0XKUUo8rpX5UShUrpfKVUquVUvGn7aOUUs8opbKVUmVKqXVKqV6tFbNoWUqp6UoprZT6R611khMdlFIqVCn1TvXvi3KlVJJSakSt7ZIbHYxSyqiUmlXrvcQBpdRspZSp1j6SF+2cUuoCpdRHSqms6r8Zt5y2/Yw5oJTyVUotVUodq16WKqV8WvRC2jEpsFqIUmoy8CrwPNAX+AFYo5SKbNXAREsaCbwODAVG45xZfa1Syq/WPo8CDwP3AQOBPOBLpZRny4YqWppSajAwFdhx2ibJiQ6o+o3OBkABVwA9cOZAXq3dJDc6nr8A9wD3A92BB6qfP15rH8mL9s8D2IXz519Wz/aG5MB7QD/gcuCy6sdLmzHmDkVGEWwhSqnNwA6t9dRa61KBFVrrx3/9SNFeKaU8gGPAVVrr1UopBWQD/9BaP1e9jyvOX4yPaK0XtV60ojkppbyBrTgLrBnALq31vZITHZdS6nlghNZ62K9sl9zogJRSHwMFWuuba617B/DXWo+VvOh4lFIlwL1a68XVz8+YA0qpHkAScL7WekP1PucD64HuWus9LX8l7YvcwWoBSikXoD/wxWmbvsB5N0N0TJ44/w8erX4eDYRQK0+01mXAd0ietHdv4Pyw5evT1ktOdFxXAZuVUu8rpfKUUtuUUieLbpDc6Ki+B0YppboDKKV64mwR8Wn1dskL0ZAcGAKU4GxNddIG4ASSJ03CdOZdRBMIAIxA7mnrc4GLWj4c0Ua8CmwDNlY/D6n+Wl+edGqpoETLUkpNBboCN9azWXKi44oB7gb+BvwV6APMr972DyQ3OqoXcX44l6SUsuN8H/ec1vr16u2SF6IhORAC5Otazdi01loplVfrePE7SIHVsk5vj6nqWSc6AKXUy8D5OG/P20/bLHnSQSiluuHslzlca135G7tKTnQ8BuCnWk3If1ZKxeLsb/OPWvtJbnQsk4GbgOuB3TgL71eVUge01m/W2k/yQpwpB+rLB8mTJiJNBFvGEcDOLz8VCOKXnzCIdk4p9TfgOmC01np/rU2Hq79KnnQcQ3De4d6llLIppWzACODu6scF1ftJTnQ8OTj7SNSWDJwcGEl+X3RMLwFztdb/1lrv1FovBV7m1CAXkheiITlwGAiq1eT4ZN+tQCRPmoQUWC2g+pPpLcDFp226mLrtX0U7p5R6Fecnj6O11imnbT6A85fexbX2twLDkTxprz4EEnB+Cn1y+Qn4d/XjvUhOdFQbgG6nrYsDDlY/lt8XHZMbzg9sa7Nz6v2c5IVoSA5sxDkS4ZBaxw0B3JE8aRLSRLDlvAwsVUr9D+cfzjuBMGBhq0YlWoxS6jWc/WyuAo4qpU5+ulSitS6pbv/8CvCEUioF55vrJ3F2RH2vVYIWzUprXQQU1V6nlDoBFGqtd1U/l5zomP4G/KCUegJ4H+f0HvcD06Gmv4TkRsezGnhMKXUAZxPBvsCfgSUgedFRVI9C3LX6qQGIVEr1wfm3I+NMOaC1TlZKfQYsqu4HrIBFwMcygmDTkGHaW5BS6m6ccxOE4py/4CGt9XetG5VoKUqpX/vPNlNr/Uz1Pgp4GrgD8AU2A/ecfLMt2j+l1Dqqh2mvfi450UEppa7A2UevG5CBs+/V/JMd0yU3Op7qeYxmARNwNvnKwXnH+1mtdXn1PpIX7ZxSaiTwTT2b3tFa39KQHKieg/PvwJXVqz7COdx7EeJ3kwJLCCGEEEIIIZqI9MESQgghhBBCiCYiBZYQQgghhBBCNBEpsIQQQgghhBCiiUiBJYQQQgghhBBNRAosIYQQQgghhGgiUmAJIYQQQgghRBORAksIIcQZKaV0A5b06n0Xn3zc2qpjORnfukYea6t17G3NFKIQQoh2xtTaAQghhDgnDDnt+X+A7cAztdZVVH+dBbzaAjE11GGcE7MWN/K4YUAYsKrJIxJCCNFuSYElhBDijLTWm2o/V0pVAEdOX1+9774WC6xhKuqL80y01puVUp2bPhwhhBDtmTQRFEII0aRObyKolOpc3czuTqXUC0qpw0qp40qpfyml3JRSXZVSnyulSpRSaUqpm+s5Z6JS6iOl1FGlVJlSaoNSavjviNFDKTVfKZWhlKpQSuUqpdYqpbqf7TmFEEIIkAJLCCFEy3kcZ5O7m4EZwGRgIc7mhp/gbMa3A3hbKdXr5EFKqX7AD4AfMBW4GigA1iql+p9lLH8DrgVmAhcDdwLbAJ+zPJ8QQggBSBNBIYQQLWef1vrk3anPq+9A3QjcqLX+F4BS6ifgSuAaYHf1vi8BGcBorXVl9X6fA7uAp4CrziKWIcC7Wus3a637z1mcRwghhKhD7mAJIYRoKWtOe55S/fXzkyu01keBPCACQCnlCowAlgMOpZRJKWUCFLAWuOAsY/kRuEUpNV0pNUApZTzL8wghhBB1SIElhBCipRw97Xnlb6y3Vj/2A4w471RVnbbcC/gqpc7mb9l9wCJgCs5iK08p9TellNtZnEsIIYSoIU0EhRBCtGVFgAN4DVhS3w5aa0djT6q1LsHZJ+xxpVQUziaJf8VZ3P3lrKMVQgjR4UmBJYQQos3SWp9QSq0HEoGtZ1NMNeA1DgLzlFI3APFNfX4hhBAdixRYQggh2ro/A9/hHBjjTSAHCAD6AUat9WONPaFSaiPwEbATKMHZzysReKepghZCCNExSYElhBCiTdNab1VKDQSeBv4OeAP5wFacw7yfje9wDtP+GM6/hfuBh7TWf//9EQshhOjIlNa6tWMQQgghmoVSajEwEugKaK21vRHHGoHOQBowVWv9z2YIUQghRDsjowgKIYRo76Jwjjr4VSOPq8BZXAkhhBANJnewhBBCtFtKqc44+2sBHNda72nEsf1xzrcFkK61PtK00QkhhGiPpMASQgghhBBCiCYiTQSFEEIIIYQQoolIgSWEEEIIIYQQTUQKLCGEEEIIIYRoIlJgCSGEEEIIIUQTkQJLCCGEEEIIIZrI/wN5cDUnDj2BGAAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"\n"
]
}
],
"source": [
"plot_results(u_vec_history)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Reactivity Step with Negative Feedback Results "
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [],
"source": [
"'''Evolve the point-reactor from a steady state with negative feedback'''\n",
"\n",
"beta = params['beta']\n",
"params['alpha_n'] = -3e-4 # cm^2\n",
"\n",
"# Manipulated input variable\n",
"params['reactivity_0'] = 10/100 * beta # \"10 cents\"\n",
"\n",
"n_0 = 5.0 # arbitrary value at steady state\n",
"params['n_0'] = n_0\n",
"\n",
"import numpy as np\n",
"c_vec_0 = np.zeros(6,dtype=np.float64)\n",
"\n",
"species_decay = params['species_decay']\n",
"lambda_vec = np.array(species_decay)\n",
"\n",
"species_rel_yield = params['species_rel_yield']\n",
"beta_vec = np.array(species_rel_yield) * beta\n",
"\n",
"gen_time = params['gen_time']\n",
"\n",
"c_vec_0 = beta_vec/lambda_vec/gen_time * n_0\n",
" \n",
"params['c_vec_0'] = c_vec_0\n",
"\n",
"time_final = 300.0 # s\n",
"n_time_steps = 100 # number of solution values in time\n",
"\n",
"import numpy as np\n",
"time_stamps = np.linspace(0.0, time_final, num=n_time_steps)\n",
"\n",
"u_vec_history = run_point_reactor( f_vec, time_stamps, params )"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA1gAAAGoCAYAAABbkkSYAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzs3Xl8FdXd+PHPufuSfd8TwJCwgyyCgoLgblXUx6dWrdbaza22+qtbrXbTqq2trVZb+1i11bq0WmtrXWpBURSUHdkDIWTf97vP+f0xNyGEgAkGksD3/XrN62bmnjlz5sxNMt97llFaa4QQQgghhBBCfH6WoS6AEEIIIYQQQhwtJMASQgghhBBCiEEiAZYQQgghhBBCDBIJsIQQQgghhBBikEiAJYQQQgghhBCDRAIsIYQQQgghhBgkEmAJIYQQQgghxCCRAEsIIYQQQgghBokEWEIcQ5RS85VSWil11VCXRQx/SqlSpdTSQ9x32H3WlFInK6XeVkq1KqX8Sqm1SqnFQ10uIYQQRxcJsIQYpnrcoPZc2pVSq5RS31ZKWYeoXFOVUvcopQoGsM+BzmW1Uuo7Sinb4SvxoTmU8xzEY/esr0cOkCZNKRWMpll6hIs4rCmlHlVKVSilVI9tZwL/BbKAHwLfA2KBF5VSo49QuSzRz/uWaIC3Ryn1C6WUdwB53K6UekkptTN67UsPY5FHnEGq4wHlMZD0A0xbpJR6Vim1WSnVopTqjO73kFIqc2A1I4Q4kobdTY0QYj9/AV4HFObN4VXAr4AJwNcHmNd7gBsIfY7yTAXuBpYCpQPct+e5ZABfBh4CxjHwczncPs95DhY/8CWl1M1a60Cv967ArMfwkS/W8BUNqs4HXtVa6+g2C/AYsAOYobX2RbeXAq8Cc4CdR6B4vwRuBF4BfoH5ub8RmKaUWqS1NvqRx71AI7AaSDhcBR3BBqOOB5rHQNIPJG0OkBlNW475uz4J82/lF5VSU7XWtf04HyHEESYBlhDD32qt9Z+7VpRSjwGbgWuUUndprWv6m1H0n7f/MJSxv3qfy2+BLZjncqfWum7oinbkRFsfnVrrzs9I+gpwKWbA8GKv976CGawuHPwSjmgzgWzg7z22nQQUANd1BVdRXV809Nx2WCilJgA3AC9rrS/qsX0X8Gvgi8Bz/chqjNZ6Z3TfjUDMYSjuiDQYdTzQPAaSfqB5a63fAd7po4zvYf49uAp44GDnI4QYGtJFUIgRRmvdCnyI2XoxGkAplRLtFrUn2m1sT3Q9uee+qo9xMUqpq6LbTlVK3aKUKlFKBZRS25RSV/ba/x7gj9HVJT26sT11iOfSAXwUPZcxvd9XSjmVUncopT6NdqdpVkq9ppSa1itdrFLqJ0qpFUqp+mj5dyilfqaU8vSRr0Mp9T1ljsHpjHa/+UQpdX1/z3MAdd5Vv4uUUncppUowg9xL+lFFq4F1mMFUzzxnYbZg/rGvnQZSvmjaXKXUi9F6aI3W8X7XI5q2X9fkIOUao5Qq7k/aXvulKqWeil7fiFKqUil1d7TFqqfFQAuwpMe2E6OvvW9WT42+rh5oeQ7BpZif81/12v4E0Alc3p9MuoKr/hpofSulpimlXlFKNUWXvyqlkpRSWdHrfelAjn+EDUYdDzSPgaQflM8AsDv6mtjP9EKII0xasIQYYaI3lMdFV+uVUvHA8ui2JzFvFqcB3wJOVUrN0lq39SPrezG7D/4OCET3f0optUNr/UE0zcuYXVa+Hk2/Obq95HOcUteNfGPPjUopO/AG5s3xn4BHgHjga8AHSqmTtdafRJNnA9cAf8P8BjgMnII5zmYacEaPfB3Am8B84C3gz5gBzyTgwuhxDnqeh1jnPwfsmDdTrcDWftbPH4GHlFI5Wuvy6LargVrgn33tMJDyKaUSMLuO5gKPA5sw624J5uehZ74DuSYH8g6Qj3mj2S9KqYnAf4BmzC5W/ugx7wEaouXoshj4l9a6ZzfYaUA7sL1HnjmY9fix1rr0AMe1AEn9LSfQeJAuaDMBA1jZc6PW2q+UWht9/3Dod31Hg6engfWY49RGYXZfK8O8X9gOvHAohRjkujyQwajjgeYxkPSHVD6llAuzpdIFjAfuj771ej/ORwgxFLTWssgiyzBcMAMADfwASAFSgcmYN+ga+DCa7qfR9Wt77X9ddPuP+8jzqh7bropuWwM4emzPxgy0/tIr36708z/nuUwCHo1uX9nHPt+JvndGr+1xmDd8S3tscwD2PvL4cTSPWT22fS+67d4+0lv6c54DrPOufLYCngHW1y1AcvQ63BF9z40ZaPw8ut7esy4OoXz3Rrd9pVfaX0W396zngVyT/T5r0e2lgB7AZ8eFGdi+27P+MAPgELCmx7Zx0WNe3CuPLcCy6M9jMcev7QSCwEkHOXZBNL/+LgUHyWsDUHOA916M7u84WF30sd9GoPQz0vSrvjFbw32YN/+uHts/wPyCwQdcOJDyHa66PJx1PNA8BpL+UMsHXN+rbnYBlx3qtZBFFlkO/yItWEIMfz+MLl0M4B/snRRiMVAH/L7Xfr/D/IZ/MXBXP47zW611sGtFa12hlNoGFB5asfvU+1zAbC26ro+0l2PeGK9SSqX0eu9t4EqllFtr7etZbmXOSBgLWDFbPb4PnMDeb40vA5qAH/U+oO7/N+aHUueP6c8ec7UfrXWDUuofmIHavZitbPGYLVODUb4LgBrgmV5p7we+3Wtbv6/JQc6n4CDl7ssNmDfnp/esP611lVLqU8yJALpcgBmMvtG1IdpFtBB4UymVz74thw9jdrc9kGrgtAGUtfog73miZeuLv0ea4AHSHJIB1Pe3MYPZG7TWPcdp7sRssVyNOSbwUA1mXR7IYNTxQPMYSPpDLd/fMX/vYjBbY8/D/JJKCDFMSYAlxPD3e+AlzG8uO4BtWuue3elGAZ9orfeZTU5rHVZKbQWO7+dx+hrb0YDZvegzKXPiht7/9H1a65Ye613nYsdswboV8wa5r4k3xmG21hxs4osUYE/0+NcC38Qcm9R7fGnPsQqFwNpeN5EDdSh1vu1zHO+PwL+UUnMxu7Wt1FpvGqTyjcbsJhfplbZKKdXcK98BXZNB8j+YrbV9dUP1sG/X0sXA21rr9h7bpmB+HlZhds38ApCHOXHItzE/G/uMNewS/Yz85/OeQFQnkHaA91w90gyV84AdWusVB3j/Lq21PtTMB6suP+PvzGDU8UDzGEj6QyqfNrsGd3UP/rtS6m/Ax9EvM+47QH5CiCEkAZYQw992rfVg3eQdTOQA2/s7ViYXs+tKT09jtrx06Xku/1ZKvQ+8jzn254t9HHcD8N2DHLMOQCn1Xcwpj9/CnI2rEvNb4GzgKfYPuA75RvFz+Dw3z28CFZjTxi/AHEs1mA5UH72vfb+vyWBQSiUCMzCvae/3kjADyaei6znRtF/rlXRq9HW11rqJvePWfquUehu4XCl1jd53zFbXMfq6mT+Yut6Bag+VwHillFPvP+V+NlDfsyX2SIrWZQHmYxR6Swc+1Vp/rvE+g1iXB/s7Mxh1PNA8BpJ+UD4DWuv1Sqk1wLWABFhCDEMSYAkx8u0EipRStp4tFtGucmMZ/Of7HOhmvK8uQJUHzUjr5UqpPwFfVkr9Wmu9vMfb2zFvyP7bj657V2CONTmrZ1plPly2t23AuAPc5OxTvIO8d0TrXGsdUUo9A9yOORbm+c/YZSDl2wmMVUpZe97QKvNBpvG98h3INRkM0zCDuvY+3vsS5v+wrkkXLsC8Zv/olW4qZp1tZn8WoLav4Cqqr5v5gxnFgZ+Z9jFwOjALWNa1MTqBwVTMiUaGSkb0taHnRqXUyZi/0/uVTSm1GLO76QuY3ZWTgEe01ncc4BiDVZcH+zszGHU80DwGkn4wPwNuBjZpiBDiCJJp2oUY+f6OedN7Ta/tX4tu/zzjJvrSdbO7zz93rbVfa/2fXsvBurF1+TFm61nvMVHPYN749dlaopRK77Eawby5Vj3etwG39bHrs5jdwr7fR549W2z6PM+oI13nYLby/RD4Zq9ul30ZSPlexWyl+HKvtLf2ke9ArkmfBjhteNfU7wt7XhulVBHwE8wZ8v4b3bwYeF/v/yy1aZj/60b1KseJmBNx/Okgx++6me/vcrBxQy9gfkZv6rX9a5hdHZ/tUTa7UqpYKZV3kPwGU1dX0Ck9yhCDOWYPwNvHPtMwg/VKzG63ZwK3R2el7Mug1OVn/J3pdx1Hz7Gveh5QHgNMP9DyZdAHpdQCYCLmIy6EEMOQtGAJMfI9gDlO5VGl1PGYswFOA76KOaB/sB9E+THmRBt3RrtwdQC7DjJ246C01juUUs8Dlyml5mmtu77ZfRjzRutBpdSpmDfSrZjjZxZijttaEE37V8yuMv9WSr2MOavdl9j7INmeHsYch/N9pdRMzG6FfsyxW0XAon6c55Guc7TWZZgtBv0xkPI9gFlXTyilpgOfYgYec4D6XvkO5JocyECmaT8eczr6fOAfSql/Y44Z+wbm2KsrtNZG9PqcjDlDZLdot7SJgBNYppR6FHNCj0mYY9nWYQb4fRrMMVha6w3R418f/Yy+jjmm7UbMGRJ7PgA3G7PF7V3Ma9HznK5g77jIVMChlOr6smC31vpPvdKXAvla6wPWt9a6Uim1EpgXbVFejnnTn4I5YcjpSqmbgBe01lXR3aYB/6e1fip6nE8/4/wHczzbgY4xkDqGPup5oHkMJP0hlO+xaEvyfzGffeUCpmN2p24Dbj6EahJCHAlHcspCWWSRpf8LPabq7kfaVOC3mAOhQ9HXR4GUA+R5VY9tV3Hg6ciX0sc00JiTAmzCHOekgac+z7lg3mREgCW9ttswbz4+xgxwOjC7qT2LOatcVzorZve5HZizdO3GDBy6pu2+p1e+LuBOzGDCj/kN/sfsP635Ac9zAHV+wPodpGu/3zTtAylfNG0eZpDainnj9hrm88lKe+c9gGuy32ctur2Ufk7THq37NzCfD/QRZle/aszWvLQe6b4cPdaoXvtPiG5/DjPIDGDOILkGs3Uz7gj/Tlsxb4q3RstSATwExPRKV0CvKfJ7/U4eaGrzvtLXAxX9KFt+9Lq3Ret5OVAcXT6N5l/UI305sKjH+ilA+ZGsz89Txwer54HkcQjHHEjaS4B/YU4a449ely3Ab4C8oa5rWWSR5cCL0nooxnoLIYQQBxadXr0VeEhr/b3PSPsKZnA1tdf2yzAfJH2S3nd83zFBKTUZs5Xuaq31Hwcx31TMlsVkHZ3RNNrCtVBr/YXBOo4QQoxU0kVQCCHEcDQF89v+Df1I+yHmA7h7m4rZQtGfPI5GZ2AGWE8Pcr7TMFu2e06Rfzzms7KEEOKYJ5NcCCGEGI66JrhY/1kJtdYP6L6nEZ+GOS6pbVBLNkJorR/UWk/Vgz/j4zT2D6amYXa9FEKIY560YAkhhBiOpgFhzDEnh2oKZuuWGERa6/v72DZpKMoihBDDkYzBEkIIIYQQQohBcky1YFksFu12u4e6GBiGgcUivTNHIrl2I5tcv5FLrt3IJtdvZJPrN3INl2vX2dmptdZDX5Aj5JgKsNxuNx0dHUNdDJYuXcr8+fOHuhjiEMi1G9nk+o1ccu1GNrl+I5tcv5FruFw7pZRvqMtwJB0zkaQQQgghhBBCHG4SYAkhhBBCCCHEIJEASwghhBBCCCEGiQRYQgghhBBCCDFIjqlJLg6mtbWV2tpaQqHQYT9WfHw8mzdvPuzHOVRer5ecnJxhMeuMEEIIIYQQI4kEWJjBVU1NDdnZ2bjdbpRSh/V4bW1txMbGHtZjHCrDMKioqKC+vp60tLShLo4QQgghhBAjijRRALW1tWRnZ+PxeA57cDXcWSwW0tPTaWlpGeqiCCGEEEIIMeJIgAWEQiGGwwOIhwu73U44HB7qYgghhBBCCDHiSIAVday3XPUkdSGEEEIIIcShkQBLCCGEEEIIIQaJBFhCCCGEEEIIMUgkwDpKVFZWkpOTM9TFEEIIIYQQ4pgmAdZR4vXXX+fMM88c6mIIIYQQQghxTJPnYI0Qjz/+OK+99hoFBQW88MILOBwOnn76aU477TTADLAuv/zyfqUVQgghhBBDTGt0OIwO+NH+diyBTpRhJRwyCPmasfkqCFli8Rkapy+A9tfQolqJGCHiAk60EabO0UKQEBoD1fIB5c4cwq4C4i02YutexLuiEObNA6t1qM/2mCIB1gixfv16PvzwQ2688UZ+85vf8OMf/5j777+f0047jVAoxHvvvcfTTz/9mWmFEEIIIY4Z4TDa7yfS2YnubET72jGCneiADyPoIxTuwG90EI4EsPgrCGgbbbYkQjYPMc1v06SdtLmyGecrRtnqaHOG6LQbJPo8GMpKu9sgZFegbFDzO95wNtOcOIfTHYvJ2/ldfpcUwJZ8MV9uuRDttRCx2tEWOygbWtlB7Q18Jq0/h8Un15HlvJpvNn2T41cvZvpFEc5ruJPFajF4UrvT1vdxqsfvuZ8rLoxwRuf3+ELdfKbt/iHv7NkMoZAEWEeYBFh9uekmWLv2sGXvjkRg+nT41a/6vc/69eu57bbbOOOMMwAYP348y5YtA+C9995jypQpxMbGfmZagDvvvJP33nuP9PR0nnnmGTwez2CdmhBCCCGEyTDA50P7fIQ7OzFaqzD8behAJ0awEyPoJ2j46NQdhHUQfJWE/XXUWtMgoYj4lv/S2lnOHmcuk+3n4Ha0ELQrOtwW3CEXKBshu42I3Q7KjqfuaZbpt3klu4g7LL9hzK67eT72Xd487mR+0vKLaKEU4AWrF3o9AnV0ya38bsw7vFl4Ao9uf5Tsusf5xfHrqEw7hx+WfhG0gdJBlA7TYoRAh4EgVh0EQljcEdaMq6ciqZFpFa24Y2HTaI0/poFv7arG2tlAaayfdkeAUEccYW0QdjcRsvoIE+HveUmUteVS5e9gk36R8uNmUlyWyiqjhe81l6GMBp5zbKWCIPEd+WCx0hBXTdhqgMXBn6bfwZyaFLQ9HndBPB/nrqNjVAW4XEf2ugsJsEaKDRs28MQTT3Svb9y4kfHjxwNm98Czzz67X2k3btxISUkJy5Yt4/HHH+fJJ5/k+uuvP0JnIYQQQoihoiMRtN+P0daM0daI4WvF6GxF+zuIBDuJBJqwdpbTSgYtnlhs/m2oltVU1io21G0lHh9hR4RWDzgjTqzaSdhmI+C0gcWJs+1Dmusf4fYcJz+O/QexDX+nrfk3fG1GMs81vwnYQCWCKxH6uOdPr/4TW7wvcsnpXt5d+y4OPmJL5sfcc0IVz6+6lojuRBNEWQJ02g20EcFQASI0ENFhKmPaWZno4qNczdK6d2iMb6U0Pps1NkVT9Wom++vY4GllTWwNRlMmhmHH727G72kmiKI+M5byyKXoklTWJX9Mxylf43htp76qnaziPDJc8bzeuIWlzSWkGZk4LTbsVo3LYsdtceDMf42vWqw4I1ZOmpiDa8q1/MnfQWPQT8EliVgsFuJ9AXaVhchJd5ASb6ex0eCjjwJ0dhoU+jTXbdf4fAZlnRqf71ZyOs31rVfHMnOmixPWBrjllkYeeiiJyZOdvPpqB9/+dgM+n8bvN/D5NKEQPBit0wceSATpwHTESYDVlwG0LB0KX1tbd2tTf+zatYtwOExRUVH3tjVr1nDBBRcAZoD1yiuv9CvtsmXLOOusswA466yzuPXWWyXAEkIIIYYBHYmgOjuho4NQWxtGax3OtjIIJdMeDhMMVmOEG2mz+ECDM2LDQNHkDWNY7ahwG649D/MKiYwpuIZ0iyKj7G7uTnDw9fj/IzZhDFh63vq5wO4Cu7kW07aGlMafk3slvPTpS6S1pJLMEi67Bv674laMiAVFAAjgN4JoI0JEBzGsTYR1kHp3LWvz7bw3KZ7Xat9gsn87tZ4MSuzpLOt4nysaw1TZOng+cSv+1lTC/liCDj/t8dWELFbaEzUttmsoWpfCW9mbOG3Ktxgdup55OzbD+FFMShxNSUcjL5VvJsbqwm214bLYcFnNxW29hCstVr5ptTG6MIGECT/kDCPC3eEQcfkOrMrCQmBhH3VvGJrOTk17u0FHh6a9xXwd02FwRbumOmQjc5qD0+InsfrxXOYscDN3rovq6jA33dRAZ6emo8OIvmo6Oyujr+a2++6zcsstCdSVWzi+uJY//zmVyy5z8OmnQc49t7rPz4PFAm63wuNRLFzoZuZMc7vPZxAKmT+np1s55RQXbrfC5VK43ZYePytSUysG6dMpBkICrBFg/fr1TJo0CYtl76SPa9as4e6772bXrl0EAgGKi4s/My1AU1MTmZmZAMTHx9PY2HgEz0QIIYQ4OuhQCN3WRqS5nkhbPUZ7MxFfCzHNe9D+OBqsdlqdfmKrXqIqlEEooYgUVyaGJ0SH2wpWF1btxrA5CTvcGFYPKBuT1szlkmILp8T+gBnGdOZuu5SU/4WHtv2WCZZZ+5VDGX4sER9oHypUgZHYxo8vbOPy2gpm1zqpNxQvneQmY/smbt5Zh8XSxpvpe/AFnHS2J9BBmI6UnbRj0GgLsmv0PFyrM3jG/QnfKC4kNPUFxi77iGW5IX5QcA6+SJCr179IgkokzuLFY7XhsdlxW214raeTa72TV312xmYmUVyUjKE157Q1kjHbS4LDRaLW/BCNVfVzImsbLJg4u3t1jDeJW8eeSDAITqcCYN26AM3NBm1tBrXtmrY2g3fb/bS3+2hvN2hv14wbZ+f66+MBOPPMKhYscHPrrQkEApqkpFI6O/VBi3HttXE8+qgTpeAHP2jipz+FuXNdGAasWRPE41F4vYrYWAsZGQqPx4LXawZHHo+FWbOcAGRmWnn66VTmzDGb8KZNc7JiRRYejxkYdQVUHo8Fux2UUvuUY+pUJx98kN29Pnu2i9mzD9wFcOnSSP/qWQwqCbBGgPXr1zN16tTu9YaGBqqrq5k4cSJPPPHEPt0DD5YWIDExkZaWFgBaWlpISko6QmchhBBCDC0dDqNbW82gqLmWSFsDEV8LRrCTcMhHgCDO2g9pbVfUx+RCTjGpZfezrh3CmYsYl3IukTgnEbsXw+ruMUGBE1zp4Epn0p4bOXdhPQW2r/GNqm8wuv5GFl5qcE79LXypogCrtYOIpZOI9kGwhVAwhM/SSMDoIECAt8bGsTw/iQpjNaq9jC1TppBUk8Tj9o28wwQsthAXtr7Ajk6ItI/FYvdCUg1e5SbW6SVu1FOctzaGgtgsrpo2B3iY/yvdSFqWh+zjRwOQX7sbu8WK12rHa4suVjsemx2HZf/JEH4XSWN+wXwA3FYHf5l2eb/r3KIUxXHJ+6xXVERobw9TVOQA4J//7GD37jBtbZrWVmOfpa3NoK1NU1Bg48UX0wGYMaOCrCwbr72WAcBZZ1VTVdV3IOFyKWJiFOecs3e8eWKiGfwAOBxw3XVxeDyKmBgLXq+FmBi1z6vXq8jIMOvFblcEg6Ow2839s7JsbN2a2+/6iImx8OUv7+3FFBtrYdYsGSN1tJEAawS466679llPTk4mFG0bfv311/fp4newtABz587lvvvu48orr+TNN9/kpJNOOowlF0IIIQaHDoXQLS2EG2uINFUTaW8k4mshEvQRDvsJqDBBq4Gz5l2aGqqpcI8mdtJFZO25l0+adlObcSqzC+8CW9etjxticsylh7GB57n/lLWUZC7k/+0+jdTOAL++oAaLZzeP/6cFW6SWMm8bTY5WAi3JtBoR2uLKaXO20EqEH4zLYVXjeJZTzwlj3mVX0a/Jq6rh6fpOfrbAfF7ldRtfYX1TkCRXMrE2B7G2scTaHdGfL+enEQcpTjcXTBoLwMKOZiwo3F6zBeaf+tT9WjYO5ssFE/dZX5CWP+D6D4c1VqvZolJaGmLPnjDz5pmzRLz6agerV5utSC0t+y6trear3a6oqDCPe+ON9WzdGmLjRjMwue++ZpYvDwDmZHfx8RZiYy3Exiri4iwkJ1vIzt4b+F17bRxe794WsGeeSUUpRWysiu63NzjqCoR6+stf0rt/VkrxwAPJ+6U5mL7yFKInCbBGuPnz57NgwYJ+p580aRL5+fnMmzePtLQ0nnnmmcNYOiGEECJKa3R7O5GGesINlURaagl3NhMJtBGJBAkSJmA1sDd+gq9qIyWRdGLnXkdW9WNsq/2AdQlTWTT1d2ZetgRISICE3scIkx9ZxiszN/Ds+ADfK/OhI5pnF/rYklzCnP+uJ8uoZm1MI1viKmiqHk1TBBrjq6iPqaVOK6pGZdPQPJZgg4drpttonfomC3eX8/Tq7WRd+CU8VgfvlW7kvfo9xMU4iLc7ibc7ybE7ibM7ON3m5Pt2c3txbDIWpbjoOI0q3HtT/ujExQOqulHefU90IMHVPtWjNUopamsjbN0aZM4cFzabYulSH0uW+GhqMmhuNrpfm5sjNDcbNDTk4PPtorW1gNhYxaOPtvLoo610do4C4KWXOnj22Xbi4hTx8ZbuJSPDSlGRnfh4C8nJewOkm29OoL3d6F5/6aV0rFaIi7PgcqnPPL+vfjVun/VFi2Q2ZDG8SIA1wn3ve98b8D733XffYSiJEEKIY4JhYDQ1Ea6tJtJYQbitjrCvhUjIR8gIY2stwVKxirKmGAKnfZWE5n/gLXuVX76fyslnvRbNxAXxeebSgzICZNi38n7hdr47t5Yf7aql1ebnbzMj/DuvigkfrOSEjgY2elpYkrCFhprRVAc91HprqUwqp85w0Z6VjO74Kix3YZk6hsLid7m6upG7P/qIhIWLyYhJwFG7m7LKHSQUujguGiAl2F3dwVKCY+82C4op+VO4s0ejz5cLJu7XKnQwhxoQHUgopKmpiZCaasXpVGzbFmTJEj+NjREaGgwaGyM0NhrdPzc1GTQ2GqxYkcWUKU7++td2rruugaqqPDIybCxZ4uNHP2omPt5CYqKFhATztbDQTkKChba2JiZPzqfrNL72tVjOPdfTHbD94Q8pPPNMKhZL/87zxBP37RKXlSW3o+LoIp9oIYQQ4lgVDmM0NBCuqyJcX064vR7VWkNs5SZ0dQq7ikejjA3Yy19hfZWNjIsfR8UnYtijDxByJZtLD0kNfhpSnmDmhfDYtkvJqA2xblyY+45v5A/Ll3F6vZ9qZxtbQMjiAAAgAElEQVT/TF1HR0MBlR0JlDjr2ZOxjTo8dKTGQOgr8K6bxsJcZix4jfTmIO8seQ3PzLNJTcsnoamG6pI1JOW7yHO4SHS4SLS7SHK4zIkU7Oa2eLsTC4rzMtI5L2NcdxlPTcvn1EPoJne4dHYabN0aor4+Qn29EX01f25o2LvtgQeSOP10D//5j4+zz65m+fIs5sxxsXx5gG9+03z0rNutSE62kJRkJSnJQnGxnaQkK4mJFhITzVakc8/1MnasGTwB3HFHIj/4QSJWa98B0tKlm5g/f+/47rFjHYwdu/d9l6ufE1YIcYyQAEsIIYQ4SuhAAKO2FmvNHqhvpa2jA6N9N/F73sMoS2H3tCmEMzyEYj0E3XEY9gS0NdqaEJsJsZl4YyNk+J8h/QZ4tPQJchrjsWbXcs458PTyrSyosmBYWlmauRlrexKhjnRK7T7WZa2kVENpso3WxMXwgZd3M/zcOfentLx/KYFXdlA76UTS5s6is6OF/3z8OslxblJS3MxzuEl2ukh2uElyuEl2uEhyuMnxxBKDg7QEKD3nW93nOS0xnd/POHOIavng/H6D2lqD2toItbUR6urMpbY2wmmnuTntNA+lpSEWLKjiwQeTuPjiGD75JMApp1Ttk49S5mQMKSlWUlIs5OXZcLnMAGjKFAe/+10KBQXmbdxFF3k57TQ3SUkW3O7PDnby8mzk5e29BeyajU8IMTgkwBJCCCGGK63Rzc2ommqoqaWjpQW/r4aQ0URYQcjuIOx0E3LFEXTHYzgSsYabmbLhbL7qhfmjH2KUymBW8FU8t8KfVj7E1HYPjkgjLcY2VJuP2HY37cpgec5KGqxBqpODbE+fSUxFMk94VnBt0VxS+CexS99haVIeXz7xEoJGhK++/AuSHG5SnW5SnR5S2mczx+nhC043KU4PKQ43UxLSmEgqdaE62s+/EI/VfOBSgTee/86/dIgrt3+01rS3m13yrFYYNcqOYWh++MMmZs92cdZZHmpqwsydW0lNTYS2tr6n+3Y6FUlJVk47zUNCgoW5c12kpZktShMnOnj55XRSUiykplpJSTFbnA7UopSVZePrX987DqlrYgchxPAgAZYQQghxhOnOTiKVlYRqygg1lhPqbCYU8RO2QNDhIH3Nz9i9OULDvC/hnnk+x29YyN1+mDH6XnKOOx0wn39kCzViDzbjCDbSGtlKS6iRJmsdf51uY8mYJDYaLzPDSOH1cZcwoVbzZHoDb5/0HQDmLvkBNW1OCEVbsErmk2h3kebykO70cqrLw9yUHK5kBgAvFBWTH53FzmGxErzo/2Hp59gipRRem2OQa/HzCYfNB8vGxZmByR//2EZFRZiqqgjV1WGqqyPdS9czki691Mtzz6VjsSh+/etWQiE46ywP8fEWZs50kpZm7V5SU62kp5uvaWlWYmL2Tt6QkGDlT39K6y5LUpKVxYu9R74ShBCHhQRYUYZh7PNw3mOZ1gd/2J4QQoi+6Y4OwuXlWCtLsFTX4msN0OyCtG1PwkZF6fgZdC44i1BiEtriAFc8ZMV3768MP/ZQPQ0TglxzXRPK/QmL6vy8OQ2eGe/iQ/9/+Wfr2dhjLXy5849s8IdRu2dR5Teo0y0QdkNgPER+Ajsh4onj0WjXOmP3Umw9/s/9vugK7MpCustLmtNDmsvb5zOQupyVOWaf9f4GV0eaYWjq6w0qKsJUVkair+bP8fEWHnzQHDM2Y0YFBQU2/v5381lKd9zRSHV1hKQkc/a7jAwrc+a4SE83f05PtzJunL37OPX1+d0tTC6XheeeS9+/MEKIY5IEWIDX66WiooL09HTsdvugz/YzkmitaWhowOWSh94JIUQ3w4C6OsLl5fhqKwm1lhIMdxKyKkION0FPHEFvEmFXCtrioKjyDl5rWcemMWdyQcpPSORevnR1GS2Jbp5YMgOHbzW74qrYHLebRU2LaPDG82Lae6zyVNCikwmkL6azxk1rm4M/nngt2cc9RPmq9/lr+VZc508BIG7VF3A2VZPpiWFOcjYZrmlkumLIcHnJdHvJcMWQ7tw7ffXPJs/f55TOyyo8kjU4KMJhjc1m/o9etsxHaWmYK64wH9r69a/X8eabPqqqwvR4/CNgjmdKS7Mya5aze9t3vhO/T7e6NWuySUy09ns80oG67wkhhARYQE5ODvX19ezevZtwOHzYj+f3+4d1AONyucjJyfnshEIIcTQwDIyaGkJ7dhOsLSXYVounci3u7WX46hMo+dL/klF5H7Xr1rA5bz4FZ/8c0rIAsEQ6sQfrcAQaUMGNNFqqaLDV8uqEav6b5aUhfjer1B0UTDqZmFAiVXUREs+/mERbDA9t/De/3LIGdBCa6qB8HDCOVKeHLFcM49wxZLtjyTLy8FocfHfsTL4+eu9Mbo9NP2OIKuzwMAxznFNZWZiysjB79piv5eUR9uwx1xsbDTo6CrBaFX/+czuvvNLRHWBlZVk55RQX2dk2srOtZGXtfc3IsO73cNgrr4zdZz0jQ26JhBCDQ/6aABaLhbS0NNLS0j478SBYunQp06ZNOyLHEkKIY53u6ICyMlTZLsKVNTQoCDrqCbrcBL0JBL1phN3JYLVDZiFkFpLt+YS3xyzhe/PS+WbjXMbHGTx5JryZv5Y3Nm9jcsTC+2nVPBzzd85t+RFNHZmsMzZSGgnQ2JJBdc002rabx3/y1MuZk5zNs1Wf8t+NS2lPM0i0wXlpE8iyJ5HjjiXHE0eOO5ZMlxente9/zYWxSUew1gaf329QVhaOzoZnYckSH3/8YxtPPJGK06m4+eYGfvWr1n328XoVubk2cnNtTJzoISfHSiiksVoVP/lJEj/72d46ueeekV0/Qoijx5AGWEqpk4FbgOlAFvAVrfVT/dy3EFgNKK11zGErpBBCiGFNt7UR3rWLQEUJweZyguFOnA3bSFz9H8LvBFj/woskVfwZdjzBCzqJRWe9hSXiwx6sJmJU427fTUxDiAZPC69kLKfS00xjng2f9xTGkkVlfhMphbdwdkcsu1btJFg4B3dyAS3lW/jXW37+xXIAkh1u8jwFjPfEcUZuLHmeOHLdsRwXkwjAZfkTuCx/Qne556flMT8tr89zGomCQc3u3WF27QpRWhpm164wpaXmz9u2ZdPYWArAihVZzJrlorw8zNKlPurrI2Rn27jwQi9jxzrIzbWSl2cGVQkJlgN2209NPfB4MSEEbN68mY6OjqEuRr8cbTHBULdgxQAbgWeiS78opRzA88B7wCmHp2hCCCGGhWAQd0UFvPlv2LWbGpuNgKuVQKyHYEwKgZhMtM0FaXnmAiQ1hKjK2MPUJxVX1z5Hftx6Nh4Pzx3XyOPBFXw9cjFl9lzuDN3P5KazCLQksb2zll3NE9lTFqTc10YkOuHPKZMXcHnRLHbTwu872zAMc9zOySm5vDHvf8jzxJHniRt2s+QNNq3NLnxOpyIx0crOnSF+9KMmvvOdeKZMcfLKKx188Yu13eltNsjPt1FQYGf2bB+zZ+d2rwNccUVsd/c+gHnz3Myb5z7i5yXESNLZ2UlFRUX30tTUxPXXXw/Arbfeyrp163jjjTcAuOaaazj//PM555xzhrLI/XVUxQRDGmBprV8HXgdQSj01gF3vB9YD7zKMKlMIIcSh0c3NhEpKCOzZTqC9Ct1ZS+r6F+CfEbbedjtx6SF8my7n6a0w7aJXcHrH4AhXEtK7sLeuJt1nJ+yx8qP8Z9gd10F4QiaJjou5KpRJVlI+07Mu5AKdR8uHa7BljkeNSsPua+PZf+XzLJsAyHTFMMobz9yUNAq88YzyxjPKm8DEuBQA8r3xvH/q5d1lTnN5OSNj9JDU1+ESiWjKysKUlITYscN87fp5584QHR2aX/4ymZtuiscw4D//8XHJJTFMmQInnujiqadSGTXKxqhRdrKyrN0TQSxdupX58ycP8dkJMbx1dHRQVlbGuHHjAPjb3/7GG2+8QXl5effS3Ny8zz5KKb7xjW9gt9vJzs7ep8XqF7/4BZWVlUf0HA7V0RYTDHUL1oAppc4BzgWOBy4a4uIIIYTor6Ym2L6djj176GyvImDtxO/xEohLIxCbZbZC5RYChdhC9aTyM2bf4iXH/RYTmiKE8+Hem+B/jb/wvPEk2Dzcyu2M7ZxJWssUtrU3EG6fTKQqQEl7E2WdrUS05sLsUfzgxNNBQUdwDb6IOZlRhiuGf869mDHeBPK9cbit9oOX/yijtebxx9soLrazYIGbysowo0aVEQzuTeN0KkaPtnHccXYWLnQxZoyZFuC44+yUl+d3p83Nte03cYQQwuTz+dizZw9lZWXs2bNnn+XJJ58kKyuL3/zmN9x+++20tbURExPDihUreO2118jJyWH06NGcfPLJZGdnk5OTQ3Z2dvdit5t/u2688cZ9jjl79myWLl06BGd7ZAznmEANl2ceKaXagesP1t9SKZUJrAIu1Fp/pJS6CnjkYP0tlVJfB74OYLPZpr/99tuDWu5D0d7eTkzMsOgiKgZIrt3IJtfv8LMEArirqnC3NRC/430cJS0E8sfRMf8EilZfSe3LUHHDj2DO2SjDjzNQAcFyPC3NEOjkX2M+YWXyDjbFNOG3Z5ASyiXLl0VyczJj9Bh2Nbux+uI5z20+u+hLDWupMgLdx49RVnKsLrKsLrKtTrKsLsZYPRTaj72HuLa3K8rK7JSX29izx86ePeZrYWGQ225rBGDx4mzmzevku99twjDgD3+IJzs73L0kJ0cYjEdEyu/eyCbXr39aWlpYu3YtU6dOJT4+ng8//JCnnnqK2tra/VqeABITE0lNTeXOO+8kLy+P0tJSSkpKmDt3Lk6nE63153500HC5dgsWLAgCG3ps+r3W+vd9pT1cMcGRNNJasP4MPKa1/qi/O0Qv3u8BvF6vnj9//mEqWv8tXbqU4VAOMXBy7UY2uX6DRGt0ZSWBbVvxV+/AH2jG77Thj0/Bn5BNJGUSASA17mH+PqqObcenMs7bTKXbxTdv8+O2Pc8nHZdid8RyR9wr+CxhfsWv6AgHSetYzgmtirxa2NrWxLa2RsrDIf7gKWL+/PlctPwVSkMtPBS9jj/dlYRVWSiMTaQwJpFkh/uYepahYWiamgySk80JH+68s5Hly/1s2RKiujrSnc5qhVGjbIwb5+DUU13d3fW2bYuQnGzBYjHr7NRTD0855XdvZDvWr18kEqGqqorS0lJKS0vZvXt39+vu3bu57777uPDCC3n33Xe55557eOutt5g/fz6RSIRly5Yxf/588vLyyMvLIzc3l9zcXHJycnA6nZ998M9pGF27sNZ6xiDmN+CY4EgaaQHWqcApSqm7o+sKsCilwsC1B4qEhRBCHIJIBHbtIrx1Ky31NcRtfRn7J7tpiCmk9NZbIS4e4qYDYA/W4vKVYet8lz26hF3u3Tw4t56lmX5cnhUU08JYvsZNFJERysfuHYNCUVR6JX8p20R+22OUde6dotuCYnRMAkWxSRTHJmE0mr0t/jTrXNw9pjH/yqhjY1xPJKLZuTPM5s1BysrCXH99PACXXFLL1q1BNmzIBWDTpiCBgOass9wUFzsoKrJTVGRn9Gg7Dsf+gafMxCfEXn6/n5dffpmJEycyefJktmzZwjnnnENZWdl+z0lNS0sjPz+fyZMnk5hozhQ6Y8YM1qxZw9ixYwFYuHAhCxcuPOLncYwY1jHBSAuwJvVaPx+4E5gFVBz54gghxFEgEsHYuRPfts3463fhI4A/NpaUrS+S8PZSGtrHU/7YM4xxPcP74/bw4vEJ3F62nTS9nXXpVdyX8RzPJ31MsutM/qZeZgMWxnEe3woW8JWWBHZUdvC/ucWkOD08vP0TLl77Do3nLyLR4aLa30FD0M+8lBzGxSVTHJtMcWwSx8Uk7vM8qK5xBB7b0T1OyjDMqc4//TTIxo0hNm4M8umnQTZvDhEImEGmUvCVr8Ti9Vq48soY6uuN7v1feSVjqIouxLDW1tbGrl272LlzZ/dr18/nnXceP/vZz1BKcfnll3P33XczefJkUlNTmTVrFpdccgkFBQXk5+dTUFBAXl4eHo9nv2N4vV6mTp3ax9HFYTCsY4Khfg5WDHBcdNUC5CmlpgKNWusypdR9wCyt9UIArfXGXvvPAIze24UQQvRBa6isxFi/nubaWny6Bl+MF39SNoG4bMgwF2UEcfp302Bx8/sFbr4/azvZgYtJyN9DRbyTfLuf4IRJJHM5E6nlofB32NYSy6bq9WxsSWBjSzG/a62j2l/afejCmEROzxjF/NQ8fjFlAV1tKbcVz+a24tlDUh3Dwa5dIV57rZNrronF47Fw111N3Hvv3rEaublWJkxwsHChmwkTHIwfb6e42IHXaw6M+sIXjr2xZUIczIoVK9BaM3v2bLTWnHLKKWzZsoW6urp90sXFxTFmzBjGjRtHUVERAE6nky1btpCba7YIJycn85e//OWIn8Ox6GiLCYa6BWsGsKTH+g+jy9PAVUAmMObIF0sIIUa4jg6MjRuxrFuF3rCZ3ePG4Wn+gLSPn8N4082uZcvAKMYVKMMS2EpC7YckWb2UZYa5OvNeShKtjLKNZyIX8WMmMtE9kQnuCaSEM3mrvBRvQhrEwIaaTk577x90TZfkttqYEJfCmRmjmBiXysT4FCbEpZDtNmeXm5KQxpSEtKGrlyEQDmu2bg2xbl2QtWsDrF8f5J57Epk928XatUG+/e0GTjzRxYwZTi64wENBgY2JEx2MH+8gPn4QZpgQ4ihhGAbl5eVs376dHTt2sGPHDkpKSnC73Tz77LMA3HDDDSQmJvLmm2+ilKKgoIDi4mJGjx7NmDFjGD16NKNGjSIxMbHP8Zpd3fvEEXdUxQRD/RyspcABRyNrra/6jP2fAp4azDIJIcSIojW6ogL/xo34qnfQqTvwxSfQmTYKd+dOCluuY+1qNy3nPoJbpbJ+cgz/8yLc0fFvbtYX0+o9geMdt/IgD3IRF+Ggg+e4jMxwHlsam1jbXMva5loyk7IoKCigLtLJRR/+nZ9PXsDNRbOYEJ/CDyfMZVJ8KpPiUxnlTcByDE0y0Zvfb7BqVZA1awKsXRtk3bogGzcG8fvNENThgPHjHbS1md36Tj/dTVVVHunp5liomTNdzJzpGrLyCzHUDMOgvr6etDTzi5jf/va3vPXWW2zfvp2SkhICgb2zhjqdTkaPHs306dO7tz3xxBPEx8d3rz/zTL+fWSuG0NEWEwx1C5YQQoj+MgwoKYHVq2mqraXVG6YzPQVfymh0aiqkpqKMIC7/Tuz+D6m0f8rTiyz87GYfhuWrePEymclcylSmJMzCQjEJwKrgJtY21/CLppWsbq5hTVMNW9saMaLtUnE2BykO89lHqU4Pnyy6knGxyYD5LKm7xp80VDUy5IJBzcMPtzBtmoNFizzs3h1m7lzzwZ4pKRamTHFy3XVxTJniYOpUJ8XFduz2vfcQXq+lu7ufEMeSxsZGtm3bxtatW9m2bRt33303DoeDm2++mT/84Q+0trailGL9+vXs2LGDsWPHcvbZZ1NYWMhxxx1HYWEh2dnZWHo9R2DKlClDdEZC7CUBlhBCDEeGgbFtG+qTlahVn1Bvc9I4tZCx678Bj0DD3ffSPv1EPIEtuFr/Qauthilxc3DlTmFs8v+jzW4wjWkcz208z1SmMIUxjMGKlWV1e2gM+iHbPFTxG09QG+gEINcdy7TEdP4nt4ipCelMTUijwBO/T1ea6YnH3kQKzc0RVq8O8sknAVatCjB6tJ377kvCbof77mvmmmtiWbTIQ2GhnddeS2faNCdZWdZjasp4IfpSVVXFypUr2bp16z5LfX19dxqr1crVV1/NmDFjuOiiiygqKiISiWCz2Xj88ceHsPRCHBoJsIQQYqhpjVFSgm/9OjobdtHhVHSmZuFLGc1E323oFfVsv/irhHPtROwp3LTLSWnSU2wxbkDZTuJ6y01ADLP5BgAfs4kEEmgNBVjdVMPHTVW827GbR443xxb8fNtKtrc1cX52IQAPT11IksPNtMR0Up37z4x1rPH5DNasCbJyZYCVK/18/HGAHTv2TtE8apSNvDzz36dSit2784iNNb9Ft1gU554rE0+IY0traytWqxWv18u6deu45557eOCBBygsLOTVV1/lW9/6FgDp6ekUFRWxePFiioqKKCoqYuzYsYwaNQq73ZwhdO7cucydO3coT0eIz00CLCGEONJqawmtWkVreSkdtjY6UzLoTC9E5xdAfgHWcDPujs04mlfycrGH+/8RZl3K48DjZJPNDGZwBTMwcGPFyiM8QsiIsLqlmpWNVaxorGRFQxVb2hq6J58o8MTzYGQ+bqudh6cuIt6+9wGXX8wbPxS1MGyUlJjToZ9/vhkYnX56Ne+/7wfMWfxmzHBy9dWxTJ/uZPp0Z/dDfbt0BVdCHO3q6+vZtGkTmzZtYvPmzWzevJlNmzZRUVHBk08+yVe+8hW01t0tVIWFhZx//vlMmzaNoqIiEhIShvoUhDgiJMASQojDKRiEtWsJf/IJtZEw8Tuew7tkBT7PCZQ++iiWiA9P52bczS+Tou3EZRfzh4IP+Xbi48RZEpnFLM7jS/yYmcxgBplkAlDe2UrEBVYLPLpjNbesW4LfMFtZUhxuTkjO4ot545iVlMn0xIx9WqYKvPF9FvVY0NgYYcWKAB995Of22xNwuSw89lgrjzzSSmtrAQ6H4rbbEgiHNbNmOcnMlH+T4thTV1eHYRikp6dTUVHBTTfdRGVl5T5TnXu9XsaNG8epp57K+PHjmTlzJgBTp05l06ZN3ekyMzPJzMw84ucgxFCS/xxCCDGIdGUl/pUraa/ZSYdL461eQeqHL6He9lD9zjuQuYKSOTX8fH4i33K0MDvk5T/J6Zxju473eZ9ZzOICFnI63+U4jkOhCETCrG6uIeL2ggf+VVXCue//leWnXs6c5GwmxqfwrTFTOSE5i1lJmfuNmTpWaa3ZsiXEBx/4+eADP8uXB9i2LQSAxQIXXuhlyhQn118fxzXXxBLtocQ550g3SXFsaG5u5tNPP2Xjxo0kJiZyySWXEIlEyM3N5YYbbuDBBx8kKSmJcDjMeeedx4QJExg3bhzjx48nJydnvwkmhBAmCbCEEOJQGQbGxo10bFhHe1sl7UlxdOQUE8nNhdxcrOFmbEklbCjM4dvP57HWcTbB6U102CGbEOfRiOJUTiFIK624MKfndgeTWFPv48mG93i/vpyPG6sIGBEenDyfW4pO4ISkTB6eupB8TxwAp6TmcUpq3lDWxLCydm2Au+5qYvlyP42N5nToyckWTjzRxVVXxTBnjvnMqZgY8+awoMA+lMUV4rALBAJs3ryZDRs2dC8bN26kvLy8O82iRYu45JJLsFqtPPHEE4wfb3YddrvdPPLII8yfP3+ISi/EyCMBlhBC9FcggPHJJ1iWLYH3llNyxhk0z5kNxeOB8bh8O0lsXYZLt/FC9hKeyV3FuplgWCxMJY3LuZyTLCdxIieSS253tsqw8rc923mvfg/v15ezqbUBAJuycHxiOtcddzwnJmczLyUHgBSnhxsLZwxFDQwrWmuUUtTVRbjoohquvTaOL34xBrtdsX17iAsu8HLSSU5OOsnF2LF2adUTx4zly5ezc+dOLr/8cgBOPPFEVq9eDYDD4WDcuHHMnz+fiRMnMnHiRCZMmEBe3t4vaa644oohKbcQRwsJsIQQ4kA6Ogh99BH2996CZR+yZ/oJNJ82l0kxd6ErCyH2HDLq1+F17OG3ua9TV1TAL2P+hkbzAV/kPM7jfk7iBE4ghph9sv5L2SaCRoQrCyZhUYrr17yNoTUnpeTwpbzxzE3JYWZiJh6btK50aW6OsGyZn6VL/bz7ro8TTnDx6KMpJCdbsNvBGp17YsIEB1u25B48MyFGOL/fz6ZNm1i7di3r1q1j8+bN/Pvf/8ZqtfL000/z17/+lcsuuwylFLf9f/buPD6me//j+OvMZCb7JnuQRUJsscWW2GLX0iq1K41qVVFXtbSUql2VbigtbdFaqlo7tcXaWopQQi0RSUQIsu/JzPn9kTa3vT97xWT4PPPIo5ec+53P1yST857vOZ/vO+9gNBoJDg6mcuXKJR37hBClQwKWEEL8JSeHwgMHyDx/mkyLXDJ9Asl38SXYZzF6e0dyKjtw3T6GjXWr8e6BNLKsPyKGGAB0OFALVwAUFL7ne6B4leVidhork09wISuVGbXCAfg2LpqMwnxe9AtGq2g41jYCHxsHtIrc0/CX9HQj+/blsmtXHhs2eHLhQhyqCpaWCo0bW1KjRvFJokajsHOnt4mrFaL0pKWlcfToUY4fP17yeebMGQwGA1DccCI4OJiUlBTc3NyYNGkSM2fOLFm17d69uynLF+KJIwFLCPHkys+n6OBBMs+cJFObQ6ZPJfJc/aFBGBpDFnaZx7G8HsnWmpWY3S2ePY7vAeCGG+F/fhgxokHDKEaVDBufk0Fkchy7kuPZlRxHQm4mAF5WdrxXvQk2FjqWN3rmH63S/W2lfXFRkYqFRfEJYf/+ySxbloXRWByoqlUzMmGCM+HhVjRqZImVlQRR8fi6dOkSS5Ys4ZVXXsHb25slS5YwYsQIAMqXL0+dOnXo3LkztWvXpk6dOgQEBPyj4YSHh4epShdCIAFLCPEkMRgwHD2KuicSi12bybyZz7k5c6BBKBpDNnZZxymXdBCHci5s8InlJc+F5FqACy6EE84cwmlJS6pTHYV/3s9zLPUqi2J/Z8e1S5zPSgWK26WHu/vwjpsPLd19qGrvUvKOspPe6pFPv6wpKlLRaIpXoD79NJ3Jk1O5csUXvV4hNNQKf38LWra0pnFjSw4e3Et4+JO9X5d4vKiqSmxsLEePHuXYsWMcPXqUYcOG8eyzz5KcnMzEiRNp3Lgx3t7edOnShRo1alCnTh1cXV1NXboQ4i4kYAkhHmvqpUsURe5Et30tjSMPc2LNGovzvJ0AACAASURBVLw8z+JVJQoLbQQumTdwtYwmpryBEK+32aDbRQtaUJmjTKEqrWlNMMFo+OeKyZXcTOZcOEZ/3xpUc3DlYnYa38ZF08KtIkMC6tLK3Zeajm5opLHCP1y6VMjWrbls25bDzp157NjhRf36ltSqpSciwp6cHCN6vZbXXnMwdalCPDR/hakjR45w5MiRklCVlpYGgIWFBTVr1iQ/Px+AevXqkZmZia1t8ebXPj4+/2hCIYQo2yRgCSEeL1lZFOzZQ8bFP8iw15ARWAtb72wq191CSlpr9HkJnK1qycImVZjpu4ixuDOWsfiRzhtklXT3C/nzA4pPjs5lpbD1aiwBdk487RUAwOyzh6nh4Eo1B1ee9a5MSufK6DRak029LMrKMhIZmcu2bcWf588X70NVsaKW7t1tsbEpDqAtW1rTsqW1KUsV4qFav349tra2tG7dmszMTAICil83dDodtWrVokePHtSrV4+QkBCCg4OxtPzvJcMWFhZYWMgpmhDmSn56hRDmTVUxnjpF1qEDpOenkFEpgDzPSuDpia7gOo4Zv4ISy4qOoYwaeoJE214AVKIS/elPc5oD4IgjE5lYMmxWUQGRyXFsSbrIz1djuZSTDsAr/rV52isAb2t70p4bUdLlTy/B6h+Skw306ZPMvn25FBSAjY1Cy5bWDBvmQLt21gQFSdt08XhITU3lt99+4/DhwxQVFfH+++8D8O677+Lr60vr1q1xcHBg2bJlBAUFUbNmzX+EKSHE40cClhDC/GRlwc6dsHkzSdbWXO3eFWPdEBRjAXZZUbgkHcDR1ZWZvjuZ6bmPHE0htthS+0Ztxtq+R3vaE0DA/xv2QlYqm5Ji2JwUw+7rCRQYDdhZ6Gnl7sOooIa09/QnwM655Hhpof5Po0bdxNFRw7hxzri4aMjPVxk+3JGnnrKhSRMrLC0lUAnzVlBQwPHjxzl06BCHDh3i8OHDnD9/vuTroaGhJQFr3bp1eHl5lXytT58+j7pcIYSJSMASQpiH2FjYuJHMU6dIaNuSylHD0B3KwbLTSMplXsUx+zBRvpnMqHmWVda7Acglg8HU4WmepilNOXDqAOHh4SVDFhoNRKVdo2G54hbfw45tZ+u1WKrZu/B6YD2e9gqgqWsFWZ26hcTEIjZuzOHMmQI++cS15O9yc4v/rbRahX37pHW6MF+qqpKQkFBy79O7777L7NmzS+6T8vLyolGjRgwYMICGDRsSEhKCk9N/u4FWqlTJJHULIUxPApYQomwyGDAcOkTm0d9I0xfgHLMGx18PYGHdBq3ts+TVCmb/y3X5wv8CnzEcJ3oQwyKyuUw22dhiywxm/L9hUwvysNFaYKm1YObZQ4w/tY+rzwzD3cqWmbXC+dyiHZXspGX6/1JVlWPHCli/PpsNG3KIiioAoFIlC6ZONWJrq2H5cmkNLcxXbm4uR44cITg4GCcnJ+bNm8frr79OUlISnp6e1K5dm9dff51GjRrRqFEjKlSoIJe5CiFuSQKWEKLsyM2lMDKStLPRpLnbklm5LmpYU7RFmdi6HSa9dTe+ah/KOmbyC79gYDceeHCe87jjzst/fvyvuOx01l45z5K0M/y+/jA/hXXhWe/K9K5YnZoObjj8uR9VLSf3Rz3jMq2wUGXv3jzWrs1m3bpsEhIMaDQQGmrJjBnleOYZG6pVk3uphHm6fPkyv/76a8lnVFQURUVF/PTTT3Tp0oW2bdsyb968kvulevToQY8ePUxctRDCHEjAEkKYVmoq+du2kXY5hlRfT7L9gsHTE33+ZdxurkdjlcEvvqkMqfsHB/SngNUEE8wYxvAMz1Cf+v+vhbqqqpzOuMGaxPOsSTzHsbRrAPhqrRkd1Iiq9i4AVLJzktWq/5GdbaSoCBwdNWzYkMPzz1/D2lqhfXtrJk+2pWNHG1xd5ZJJYX7S0tL49ttvSwJVfHw8ANbW1jRs2JBRo0YRGhpKs2bNAAgKCiIoKMiUJQshzJQELCHEI6deu0bh5s3o1yyGLb8Ss2QJueHtsc45i9fV5Vg76XDy70ha4zdx03hhxEgYYcxiFl3oQiVufW9DkdHIuFN7WZN4nnNZKQCEungzs1Y4XcpX4fKRE4QHt3iEMzUPqqqiKAqpqQYqVIhn3Dgnxoxxpl07a9as8aBdO2tsbDR3H0iIMsRoNDJ16lSqVq1K9+7dKSoqYvjw4ZQvX54mTZrw5ptvEhYWRu3atdHppGGNEOLhkYAlhHgk1KQkWLMGZfUPJAVV5Vq/vtR+5hCa2hH4BASg89ZiqatKO5dvKFAK2c1MnIE1rKEhDfHg1vf3RKVeIzrjBi/41sBCo2FHchy+tg6MqFKfzt6BeFvblxx7+RHN1RykphrYsCGH1auzsbRU+OEHD5ydtUyY4EyrVsX7UdnZaXjuOVsTVyrE3aWkpLB//3727t2LRqNh5syZaDQaVqxYQatWrejevTuurq4kJibi7S3NV4QQpUsClhCi1KhJSeRu2UJqahKpNarhn/E5ts4pOAZ2QmtpJL7eSyzqW8hPNgM4xjHAipcYiAFDyRjP8Mw/x1RVjqZeJcTZE0VR+OLicVYl/EHPilXRabQcbNUPC42sttxKRoaR9euzWbkym23bcigsLN7wt08fu5JjRo+WSyZF2ZeUlMTevXvZt28fe/fu5eTJkwDo9XqeeuqpkuOOHz+OXq8v+bOEKyHEoyABSwjxcKWkkLdpEylX40mtEURe7dqg1sA+8yjGyn5c7P4CCwKusZIXSCABSyzpQAducpPylKcXvW457Kn066yIP8PKhDNczE7jUOt+NCznzXvVw5ge3ALdn63UJVz9U06OkY0bc/j++yw2bcolP1/Fx8eC//zHke7dbWnQwFKaVAizMXfuXD777LOSvadsbW1p0qQJPXv2pHnz5jRo0AArK6uS4/8eroQQ4lGRgCWE+PeysijYuJGUuAukBvmRU706VKuKXVYUPkk7MXg5sKpeDvMcz3OOTVhgQXvaM53pPMuz2GN/y2Fjs9NYEX+GFfGnOZVxA62i0Nrdl/HVw0oaVfz9EkBRrLBQxWgES0uFr77KZPjwm3h6ann1VXt69rSjcWNLNBoJVaLs+uu+wE2bNjFixAgOHDiAq6srGo2GqlWrMmjQIFq0aEHdunWxsJBTGSFE2SKvSkKIB1NUhLp9O8p3S1HXbeCP1asprPwUNtmnqHBlEU4enljWep6Ycq0JJBAFhXDCeYu3eJ7nKUe5Ww6bbyhiUezvfBcXzcGUKwA0cSnP3Lpt6V4hCHcruSfoTuLjiwgJuczMmS4MGGBPr152BAfradbMCq1WQpUom5KTk9m9ezeRkZHs2rWL2bNn06lTJ9zc3KhevTrp6em4uroyZMgQhgwZYupyhRDijiRgCSHunarC0aPw3XdcLSzkRsc21Ki7CsW5H34ODli65WJZIYgX3LeBksl31CQAWMpS2tAGL7xuOWy+oYgLWanUcHTDQqNh6pkDuFpaMyO4Bb0qVsPX1vHRztOMnDtXwHffZWFhofDee85UrKilVy87goKKu6K5uWkJD7c2cZVC/FN6ejp79uxh586dREZGcurUKQDs7e1p3rw5dnbF9wU2bNiQdevWmbJUIYS4bxKwhBB3pSYmkrNuHTdzU/E8Ogf9sZtYPfcmjlYWGGr34fCr7Vhtv5rZzAYUgtiOwn9XS/rR747jv/jbJvZdv0x8p9fQKhqOt42Qlao7SEszsGpVNosXZ3LgQD6KAt26Ff97KYrCnDmuJq5QiFvLycmhdevWHD58GKPRiLW1NU2bNqVv3760atWKevXqySV/QgizJ69iQohby8+ncONGUs5GcyM4iLxGjVCMedhX3IF+WFPSwgayhCUsZj+X+A4HHBjKUAIIYDzjbzvstbxsvo07xeJLp9jUtBu+to6MqFyfCL/gkmMkXP1/BoPKjh25LF6cydq1OeTlqVSvrmPmzHL07WuHt7e8nIuyacCAASQmJhIeHo6NjQ1+fn60bduW1q1b07hxYywtLU1dohBCPFTyG1kI8Q/q0aOk79jOTWcr0uqEgp8ftlkn8bkyH3tvX35+6jnm2K8nkikoKLSmNdOYxnM8hzW3vhSt0Ghgy9WLfB17ko1JFzCoKmEu5blZkIuvrSONXco/4lmaly1bcnj55etcuWLA2VnDwIH2RETYExKilw6AosxITExk+/btbN++nejoaKKiolAUBX9/f4xGY8lxK1asMGGVQghR+iRgCSEgPR2WL+fK1atcDw+jqE1bLApv4HFjFS42BoxV2vG2l57vlNmkk44//kxkIi/yIr743nbYC1mpLLx4giWXTnEtPxsPS1verNKQAX7BVHVweYQTNC8FBSqrV2dTpYqO+vUt8fW1oG5dSz77zI5OnWyxtJRQJUwvLy+PvXv3snXrVrZu3Up0dDQA7u7utGnThszMTBwcHHjvvffYvXu3aYsVQohHSAKWEE8qVcV48CBZW7bgsGYmnMkn/+PPsDXcwPXaKqz86nG63jNU0IdjwMB23qATnRjIQFrQAg23329KVVU6//ITG5IuoFUUOnoFMNC/Fk95VirZr0r8f6mpBpydtRiNKsOG3aBPHzvq17ekenU9Gzd6mro8IQA4cOAAkyZNYvfu3eTl5aHX62nWrBkvvvgi7dq1Izg4GI3sRyeEeIJJwBLiSZOeDt9+C198wfWaNbn81ltUD1yGtdcr+LUeioIKmr70pCe7mUQCCejRE000Fnd4ybiUnc7GpAsMCwxBURSqO7hQv5wnA/1rUV72qrqt3Fwjq1ZlM39+BjdvGjh3riJWVhoOHy5PpUryEi1M7/r160yYMIFevXrRvHlzjEYjsbGxDBo0iPbt29OiRQtsbeW+SSGE+Iv89hbiCaGeOEH6pk1c93SkXOZmXMJu4tKoLVZenmjtx7OykpG5muYsZSmVqMTbvM1whqOjuN33rcKVUVUxqioWGg3rrpxn5PFInvYMoJKdEzNqhT/iGZqXc+cKWLAgk8WLM0lNNRIUpGPoUEcKC0Gvh8BAnalLFE8gVVU5e/YsmzdvxtXVlf79+2NnZ8fq1aupW7cuzZs3JywsjD/++MPUpQohRJklAUuIx1lBAUVr1nDjj9NcbxxCQfv26AqSUZ2soc1Akhq0ZQGfs4hFJJNMZSqTSCKVqEQ96t122LSCPBZfOsm8mCjGVG3MS/61GOAXTNfyVaho4/AIJ2heiopU1q3L5vPPM4iMzMPCArp2tWXwYAfCw62kYYUwiby8PPbs2cOmTZvYtGkTFy9eBKBnz570798fa2trkpKS0GqLL++V71MhhLgzCVhCPI6SkshesYJkCkht0hw1MBC7zCNUuLIKR7/G7OsUwaf6b1iHHwCd6MRQhtKGNne8t+pU+nXmXjjGt3HR5BgKCXMpT3nr4g1BHXSWOOik3fLtXLxYSIsWV7h82YCPjwVTpzrz0kv2eHrKy7B49K5cuVISqLZv305OTg7W1ta0bt2aUaNG8dRTT+Hr+98GNn+FKyGEEHcnv9mFeJwcPUrG6tUkVQ8kq0ULNIZsXG+ux013E+tqvVjmbctM5UN+53dccGE0o3mVV/H7M2jdilFV2Xr1Ih+d+40dyXFYarT08anOsMB61HOWxgt3EhWVT2xsEV272uLnZ0GrVtY8/7wtHTvaoNXKKoB4dFRV5ffff6dWrVooisLYsWNZsmQJvr6+RERE0LFjR1q2bIm19a23WhBCCHHvJGAJYe6KijCsWwefz0F7cA+FHbpS0KENFRLn4erhTUbTXljb1wEgkoGoqHzFV/ShD1ZY3XHoDVcu8PbvuzmTeRNvKzum1WzOK5Vq42pp8yhmZpaMRhWNpjg8TZqUSlRUAc89Z4NGo7BkibuJqxNPkry8PIxGIzY2NixdupSIiAhOnjxJzZo1eeedd3jrrbeoUaOGXPInhBAPmQQsIcxVZiYsWkTh4sWcmjMHr4F+eD6fR7k+X1HO0RHFEMZ2i/10ohH72U8DGvAZn2GDDQq3P6G6lpeNldYCR50l2UUFWGkt+LZhJ3pUrIpeWqzfVkaGkUWLMpg7N4OtW72oXFnHJ5+44OioKQlcQpS21NRUNm3axLp169iyZQuzZ8/m1VdfpUOHDnzzzTdUqFABgKpVq5q4UiGEeHxJwBLC3CQlkb10KTkxv+MWuxydY1M8CwtxqNEM1bkHu52iKKKIthZtaUxjXuM13CleObHlzq2Uk3KzqLT5C8ZXD2NstVB6VKxGz4rV5B3uO4iPL+LTT9NZuDCDzEyV5s2tyM42AuDrK50ARemLj49n3bp1rF27lj179mAwGPDy8qJfv36EhIQA4OHhQUREhGkLFUKIJ4QELCHMhHrmDBmrVnHNx4PMNm2waBGCy8m1aLovwt0pkJ/4iZlM4AhHCCectrTFHns+4ZM7jhuVeo0DNxMZElgPL2s7ZtYKp72nPwAaCVa3deRIPrNmpbF6dTYAPXrYMnKkE/XrS6MP8Wh8+OGHfP/99xw9ehSA6tWrM3r0aJ577jnq168vm/0KIYSJSMASooxTDx0iZf16roXUJLdTJ3QFyZRP/Bw3VxcKekfxjd1OZtORGGKoTGW+4Av60//OY6oqe64nMOOPg2y9Fks5vRX9fGtgr7Pk9cohj2hm5ikyMpdp09LYuTMXBweFN95wZPhwRypWlJdTUbpOnTrF/v37GTx4MACRkZHodDo++OADnnvuOapUqWLiCoUQQoAELCHKJlXFuHs3Kdu2kdS8MQVdu2KVexHfhNmUq1iDnHYT+MTqB2bRgqtcpSENmclMOtMZLbe/T0pVVX6+epFJp3/lYMoV3C1tmB7cgsGV6mAvLdZv6++NK1auzOL06QJmzizHq6864OAgqwSidBiNRg4ePEjdunWxtrbmp59+YsqUKfTq1QsnJyfWr1+PTieXoQohRFkjZwZClCWqCps2YQwPJzozk7hu3bCwTSfg8gyqO13HtdMiTod0xs+qHm/xFjWoQSSRHOQgXel623Clqiobrlyg4c6lPL1/NVfysvi8XjsudRzMO1Ub46S/czfBJ9nJkwUEBSVw4EAeADNmlCM21odRo5wkXImHzmAwsHfvXoYPH07FihVp0qQJ27ZtA2DIkCEkJSXh5OQEIOFKCCHKKFnBEqIsMBoxrFlDxpbNOB/5Gk1aRdwMBqwtzuLgbiCl6Rx+0VygKTYEEURnOvMyLxNK6F2HLjIaabLrOw6nJOFv68ii+h3o51tTOgLeQU6Okbi4IqpV0+Pvb4G/vw5jcd8KypWTfzfxcBkMBvbt28eqVav46aefuHbtGlZWVjz11FN069aNli1bAuDq6mriSoUQQtwLCVhCmJKqwtq18P77JNerx5Vhw6hxahtWTT7CM7BLyWERPMNRjhJHHDp0fMVXdxlW5cDNRMJcK2Ch0fCUZyVeC6hLX5/q6CRY3VZWlpH58zOYNSsdJycNp09XwM5Ow7ZtXqYuTTyGCgsLGTlyJKtXr+bq1atYW1vTsWNHunfvztNPP42dnZ2pSxRCCPEAJGAJYQqqinHDBq7v349V8q84BlzFvV07HAIDsXKZR7pPUz5hIgMZSAUqMJ3pKCjouLdLghbFnmDQ0a0cbt2fBuW8eL9G01KekHnLyDAyd246H32Uzs2bRtq0sWb8eCe0WumiKB6uI0eOcOrUKSIiItDpdBw9epQmTZrQo0cPOnbsiK3tnbdSEEIIUfZJwBLiUVJVjFu2cGPXLpI6tKGoZ0/ckjU45hvRdu6FUcliquNJZvEiaaThhReDGERNat516F9uXCbfaKCVuy+9faqj12ip6+TxCCZlvjIzjXz2WTqzZqWTlmakY0cbxo1zonFjuSdNPByqqnLy5EmCg4NRFIWvvvqKH374gb59+6LT6di/f7+0UxdCiMeMvKoL8Yioe/dyfdQoTlmoJPTqhZU2jiqXJ+ITGEzus9uYpczGH3/GMY5mNOMYxxjEoLuOeyz1Kk/v+4Gmu5Yx6fQvANhZ6HnRLxgLOXG7pfx8lZkz0/D3j2fcuFSaN7fiyJHybNzoKeFKPBTnzp1j4sSJVK9endq1a3Po0CEAJkyYwMWLF0saVEi4EkKIx4+sYAlRytTjx0lbtozEZqHk9+6NbdYJ/OLnY1+1K4bmq/has5wJVOMyl2lPeyYxiYY0vOu4sdlpjD25l5UJZyint+KD4HCGBdZ7BDMyX6pa/F+NBr78MoMGDSyZNMmZBg0kVIl/LykpiZUrV7Js2TKOHj2Koii0aNGCESNGEBQUBICnp6eJqxRCCFHaJGAJUVouXiT/ww+5GBZKTq9eWOXGEBA/EcfK7VGa/shBbRQDCeE0p2lIQ77lW8IJv+uwKQW5TD1zgLkXjqFVFMZVC+WtoEY4yj5Wd7RuXTajRnly/LgRGxsNv/1WHmdnafgh/p3CwkKWLVvGsmXLiIyMxGg0EhISwuzZs+nZsyfly5c3dYlCCCEeMQlYQjxsyckYpk9H+8VcdDobNJ0745u2BhcnHUqn5RTo9OjR44gjAD/yI13ogsKdGyoUGA3MOX+UKWd+Jb0wnwF+wUyq2Yzy1vaPYlZmyWhUyctTsbHR4OqqxcrKSHKyAT8/jYQr8cAKCwuJiYmhatWqaDQaxo4di7W1NWPHjqVv375UrVrV1CUKIYQwIQlYQjwseXnw6ackXbrEjS4dqVH5azTtdxAU0ADU9qAovMALFFDAKlZRjWqc4tRdg9XffR4TRWMXb2bWakmwo1spTsa8qarKtm25jBmTQmioFfPmudKkiRWffZaMn191U5cnzNyAAQPYtWsX8fHxaLVaDh06RIUKFVAU6TophBBCmlwI8e+pKoZVqzDUrQOT3sFOq8XZ1Rk1qDN4eJJOOuqf5111//xQKb4Z6G7h6ve0ZHocWEtOUSF6jZbDrfuzpVkPCVd3cOhQHq1aJdGhw1XS0ow0ayb3V4kHl5CQwPTp06lRowaxsbEADB06lAULFpQcU7FiRQlXQgghSsgKlhD/gnrwICkrVpDYqQNOU7rgk7MN+xfmYK8oFNKQ+XzBBCawiEV0oQtv8uZ9jZ9emM/e65c5k3mTEGdPXCytS2km5i8mppB33klh9eps3Nw0fPaZC6++6oBeLye+4v7k5OSwZs0aFi9ezM6dO1FVlaZNm5Kamoq/vz+hoaGmLlEIIUQZJgFLiAeRkEDWp5+SUK8WOf37Y5MdTTnlKIQWB6gtbGEkI/mDP2hJSwIIuKdhC40G5l44xo38XKYGN6eZW0ViO76KtfbeNhh+EqWmGpgyJY05c9LR6RQmTHDizTedsLeXBXpx71RV5ZdffmHx4sWsWrWKzMxM/P39mTBhAv369aNSpUqmLlEIIYSZkIAlxH1QCgoo+OgjEovySendG11BMn5xUyjnWwclbC0xFkn8h2fYxCYCCWQta3mWZ+/pPqttV2P5z/Ed/JGZQievAIyqikZRJFzdQXq6kaCgBG7cMDJggD2TJzvj7S0va+L+GI1G6taty++//46trS3du3cnIiKCZs2ayT5VQggh7puciQhxj9TNm6m0aRPRfXqi6i3wurIQD9s8tO3mkGNXjhnMYCYz0aHjQz5kOMPRo7/ruEm5WbxxYiffJ/xBoJ0zG5o8T0evALmn4zZUVeXYsQJCQixxdNQwdqwzLVtaUbu2tKkX9y4yMpJ169bx6aefotFo6NOnDyNHjuT555/Hzs7O1OUJIYQwYxKwhLibixcxvvUWZ3r1Iu+ll3BM20fF6xuxbPw+eDblLGfpQDMucYne9GYWs/DG+67DGlQj82OiePfkXvKNBibVaMrooEZYauXH8k4WLMhkyJAbREWVp04dS0aMcDR1ScJMREdH4+vri52dHdHR0fz444+MGzcONzc33n77bVOXJ4QQ4jEh1z4IcTt5eRgmT4Za1dBs24qTRoP11e0EuitYPvszBZ4NAfDDj9rUZhe7WM7yewpXx1Kv0njnt7wetYNGLt6caj+Q8dWbSLi6jdRUA9HRBQD07WvHF1+4UrPm3VcHhcjOzubrr78mNDSUmjVrsnLlSgAGDRpEXFwcbm7SkVMIIcTDJQFLiFvZtYvM3r052bwZOZ9Uh12zKN+tG8m2jSH4P3ytWUpNapJNNpZYspa1hBN+z8N/ev4oCTmZrGj0DFub9SDQzrn05mLGDAaVL7/MoHLlBHr1uoaqqjg4aBg0yAELC7mEUtze0aNHGTx4MF5eXgwcOJD09HQ++ugjOnfuDIClpSVarWw2LYQQ4uGTt8uF+LubN1Hffhvl66+wrlETRwsd2oDGUKEmQMn+VdWoRl3qkkcettje09A/X71IRWt7aji68VHtVmjrKDjpZY+m29m/P4/hw28QFVVAixZWfPaZi9yXJu4oIyOD5cuX8+WXXxIVFYW1tTU9evTglVdeISwsTL5/hBBCPBISsIQAUFWMy5eTdOI4GZ3CqVp3PRa9N+FfzgdoQgYZjGUYVwKv0JKWhP75ca+yiwp48fAm2nr48V2jZ2Q/qztITjYwatRNli7NomJFLd9/70737rZycizuqmfPnvz888/Url2buXPn0rdvX5ycnExdlhBCiCeMSS8RVBSluaIo6xVFSVQURVUUJeIux1dXFGWXoijXFEXJUxTloqIo0xRFkZsxxIOLiSFjyBBOO9hytWcvrK3PY/SpDbri1ap1rKM61fmcz9Gq2pJVrHsRmRyHQTVia6FnW/OeLKr/VGnNwuwZDCoLFmQQFJTAihVZjB3rxJkzFenRw07ClbilQ4cO0aRJE65duwbAhAkTOHjwIFFRUQwdOlTClRBCmInHLROYegXLDjgFLP3z824KgCVAFJAG1AYWUjyP0aVUo3hcGY0ULVjA5ZSb3Hz5ZSzz4qkSMxL7mn2g2laSlRsMoRs/8iPBBPMjP5Ibk4tS8e4n+zfzcxl+fAfL40+zMKQDL1eqTW0n90cwKfPVrds11q7NjOSBiQAAIABJREFUoWVLKz7/3JWqVcvEa6QoY86cOQNAtWrVcHJyIj09nYSEBDw8PGjcuLGJqxNCCPGAHqtMYNKAparqZmAzgKIoi+/h+AvAhb/9VZyiKOFAs9KoTzzGYmJInzmTuK6dKWxQH8+kr/HSJ6PpuBxsy7Oa1bzGa2SQwVSmMopR6NCxm913HXpd4nkGHf2ZlII83q/ehP5+NUt/PmYqPd2ItbWCXq8wYIA93brZ0qePrFiJfyosLGTPnj1MnjyZyMhIunfvzqpVqwgKCuLkyZPy/SKEEGbuccsEpl7B+lcURQkEOgDrTV2LMBNGI4YFC0i4fp2bgwZhlXuRgNgp2NYfCZW6cZObDKM3K1lJCCEsYQk1qHFPQ2cVFfDG8Z0siv2duk4ebG/ek1qyanVbV68WUa9eIiNGODJ6tBPPPntvzULEkyMpKYmFCxfyxRdfcOXKFXx8fJg2bRoDBw4sOUbClRBCiLKWCRRVvff7SUqToihZwDBVVRffw7G/AvUAS4qXAwerqmq8zbGDgEEAFhYWIdu3b39oNT+orKws7OzsTF3GE8cqMZGqM2di9PIidvJkPK4tRZ8ZzXm31ym0KG6T/lngZ2zw3kD/uP70ju+NhfrP9yBu99ydLsxiWuYFrhjy6W3tRYRtBXSK7IJwKwUFoP/z6r9Fixxp1iyXoKCCR/LY8rNX9qmqyqlTp1izZg179+7FYDDQoEED2rdvT3h4uLRWN1Pys2fe5PkzX2XluWvZsmUBcPJvf/Wlqqpf3urY0soEj5SqqmXiE8gCIu7x2IpAdaA3cBkYcy//PxsbG7Us2LVrl6lLeLIYjWrRggVqRlioqta2VY1ff63mZGer6vVjqmo0qilqihqjxqiqqqopaop6XD1+26H+97krMhrUidH7Ve0PH6g+Gz9X9yTHl+ZMzJrBYFTnz09X3d0vqWfP5pukBvnZK/vmz5+vAqqjo6P6xhtvqOfOnVNVVZ47cyfPn3mT5898lZXnDshWy1AmKO1Ps7xEUFXVhD//52lFUbTAIkVRPlRVtciUdYkyKDkZXnqJhJAQUmd9QK3op9A+UwdrGxuwqYuKShvaoEXLIQ7h/OfHvVJQ2J0cT++K1Zlbry2OOstSnIz5+uOPAl555Qb79+fRqpUVOp1c1iWK5eTkMGXKFMLCwujUqRNdunQB4IUXXigT77oKIYQou8pqJjDLgPU/NBTPQwtIwBIl1M2bMQwbhkVKIt6dOuESVAWty3xwqUMhhWjQoEXLB3yAI44o3PtJ/6qEMzR3q4inlR2bmnXDWqsrxZmYr6IilZkz05g4MRVbWw1ff+1GRIQ0sXjSqapKUlIS3t7eWFpasnr1arRaLZ06dcLDw4PBgwebukQhhBDmp8xkApMGLEVR7IDAP/+oAXwURakDpKiqGq8oynSgoaqqrf88vh+QR/E1nAVAfWA6sFpV1fxHPgFRNuXmUvD++8RWDkD59B0qp85A3/sF9Do7KNePGGLoQx+60IV3eIc2tLmv4ZNys4j4bTOvBdRldu1WEq5u49SpAiIikjl6tIDu3W2ZM8cFD4/H4T0d8aAKCwtZvXo1n3zyCRcvXiQ+Ph5ra2tOnDiBtbVsvi2EEE+qxy0TmPpspz6w629/nvjn5xIgAvACAv729SJgDFAZUIA4YB7w8SOoVZiD48dJ+fRT4iP6o1pb4BP/AVTtCRo9Kirf8R1DGIIFFgSW/Bzfm2t52QB4WduxJ7wPdaRD4C0VFal8+GEa77+fiqOjhtWr3Xn+ebnU60l28+ZNvvzyS+bNm0diYiJVqlRh4sSJJSuZEq6EEOKJ91hlAlPvg7Ubbn9dlqqqEf/z5xXAitKtSpglVf2z/XoyN4cNwzbrFP6xn2LZ9EMo35oMMniNASxnOc1oxnd8hw8+9zz8qoQzvHzkZ4ZaVyAcaFDOq9SmYu4SE4uYMiWNzp1tmTfPFTc36fr2pDp37hwff/wxS5YsITc3l7Zt2/Lll1/SoUMHNBrpsimEEKLY45YJTL2CJcS/l5FB7ttvc7FNK/Ia1MczaRHeFkkonbeBlSsnOEE3uhFLLJOZzBjGoOXeTvrzDEW8eSKSz2OiCHXxpq7qUMqTMU9FRSpr1mTTrZstvr46Tp6sQKVKcunkkyo7O5vevXuzceNG9Ho9L7zwAiNGjKBmTdl0WwghxONP3kIU5u3ECW4OH84fL/SlqLwzlS/8h/L+NVHarwErV77hGxrTmGyy2c1uxjHunsNVfE4GTXct4/OYKN6s0oA94X1w10qXwFtZvjyLHj2S2bUrD0DC1ROosLCQI0eOAGBjYwPA+PHjiYuLY9GiRRKuhBBCPDFkBUuYJ1WFRYtI+/57Ln3wAXaZUfgnfo6+9UJwCwFgFrMYxSha0YrlLMcDj3sefv+Nyzz/6xpyDUWsDetK5/KVS2smZktVVeLji/D11fHCC3a4u2tp2dLK1GUJE3nnnXf4/PPPSUhIwNXVlfXr15u6JCGEEMIkZAVLmJ+sLNQXX4RBg3C0sMDH2ZkqboXon91REq4AetGLyUxmG9vuK1x9EXOcVrtX4Kiz5FDrfhKubuH6dQNdu14jJCSR5GQDGo1Chw420n79CXLt2jXGjRtXsmr12muvsWrVKsqVK2fiyoQQQgjTkhUsYV7Onyd9/Hgu93yeKk2PontuGm7ulYDXAFjLWlb8+VGBCoxj3H0NP+X0r4yP3kcHT39WNHoWJ72syPyvzZtzeOml66SmGpg2rRyurvI+zZPk3LlzzJ49myVLllBQUICzszP169cnMDCQwMD768wphBBCPI4kYAnz8fPP0Ls3usBALDy9UBUPMGT945BrXCOWWNJIoxz3/0561wpVyDcW8X6NpmgVCQ5/l5Nj5K23Upg/P4PgYD3btnlSq5bck/akOHLkCNOnT2fNmjXo9XoiIiIYOXIkVapUMXVpQgghRJkiAUuUfaqK4eOPSd2/D9d2dthMX0FQpUBQd4CiIZNMTnCCpjRlEIN4iZfQce9NFqJSr/HD5T+YWrM51R1cmVyzeSlOxjydPFlAr17XOH26kDffdGTKFGesrCSAPu5UVSUyMpLp06ezc+dOnJycGDNmDMOHD8fD494vuxVCCCGeJHKGJMq2nBzyX3uNs+W9iRs7htyOlmAsvucDRcNFLhJKKJ3oRBppKCj3Fa4A1l05z3dx0VzPzymFCZg3VVVZsCCDhg0TuXnTyLZtnsya5SLh6gkxd+5c2rRpQ3R0NDNnziQuLo6pU6dKuBJCCCHuQFawRNkVH0/m228T88rLYKul8oX/YF33dQjoCcAudtGNbqiorGY1Tjjd1/A38nNwtbRhQvUmvB4YgouldWnMwqydOVPIsGE3aNPGmiVL3PDwkJeMx1lRURHLly/Hx8eH8PBwevTogV6v58UXX8TKSu5HFEIIIe6FvA0tyiR13z6SJ07k3Bsj0OnTqRozBIcm70Pwf0BRmM982tEODzw4zGHa0Obex1ZVxp3aS42tX5GQk4GiKBKu/kd8fBEA1avr2b/fm82bPSVcPcZUVS357/jx41m6dCkAHh4evPrqqxKuhBBCiPsgAUuUOery5cRv3UrCkCE4Zh6g6pWJWD29Biq2p4gihvz50Z72HOAAgdx757ICo4H+hzcx9cwBnvUOxMvKrhRnYp62bs0hICCebduKL5ls3NgKjUbarz+OcnJy+PTTT2nUqBF5eXnodDr279/PV199ZerShBBCCLMlAUuUHaqK4YMPuHD9Oje6dMHj6mIC8jaj7bwbnILIJpvneI75zGcUo1jHOhxxvOfh0wry6LB3Fd/FRzOlZjO+DOmAhUZ+BP5XixZWvPWWE40ayarF4yozM5MZM2bg5+fHiBEjsLGxITk5GYCKFSvKfmZCCCHEvyBnl6JsKCyEQYOIMxrJaBKGT9w0KjgaUZ7aDJbOGDHSgQ5sYQvzmc9MZqJFe8/DX87JoOmuZey7cZmlDTvybrUwOYn8m0OH8mjbNomMDCNWVhqmTy+Ho6O8PDxu0tPTmTJlCn5+fowZM4aQkBD27dvH7t278fHxMXV5QgghxGNBzqCE6WVmwjPPwKJFeAOBPp64VWsPTeaCpvi+Hw0ahjKUNaxhMIPva/iYrFSa7lpGfE4GPzfrTj/fmqUwCfOkqipz56bTrNkVLlwo5MqVIlOXJEpBWloakyZNws/Pj/HjxxMWFsbhw4fZsmULTZs2NXV5QgghxGNF7loXppWYSOaIEaTVD6ZC13ysBo7ESmsJ7oMAOMQhEkigG93oRa/7Hv50xg3a7PmefGMRu8J7E+Ls+bBnYLYyM4288sp1vv8+m06dbFi61A1n53tfFRTmo0uXLuzevZvOnTvz3nvvUa9ePVOXJIQQQjy2ZAVLmM6pU9C4MVlubqR36ojB6jyknv7HIROZyHu8RyGFD/QQW6/GoqKyJ7yPhKu/iY4uoEGDRH74IZsZM8qxbp2HhKvHSHp6OpMnTyY1NRWAadOmERUVxdq1ayVcCSGEEKVMVrCEaRw+TGHPnuh0hXi+8grutWqhrXMcrFwBKKIICyxYxjIKKbzvzYPzDUVYai14o0oD+vnWwNXSpjRmYZZ++CGLAQOuY2enYedOL8LDpUX94yYuLo4JEyZQqVIl+vbtS2hoqKlLEkIIIZ4YsoIlHjl1926SvvmG6CVfkT/JEcUrB61WWxKuPuZj2tCGHHJwxhl33O9r/H3XE6i85Ut+TyvuiibhqpiqqowZk0KPHsnUqqXn2LHyEq4eE1lZWcyYMYNhw4YBUKtWLS5evEjfvn1NXJkQQgjx5JGAJR4pdeNGEteu5crLL+OY9wt623LgFFTy9alMZSQjccMNiwdcYK1o40ANR1fcJFj9g6IopKYaePVVe3bt8sbbWxawzV1OTg6zZs3C39+fMWPGEB8fT1FRcaMSPz8/0xYnhBBCPKHkDEs8MurKlSScOMH1fv1wvf4jPgW/oHTcBnp7VFTGMY5pTKMf/fiar+87YP2elkxNRzf8bB3Z0qxHKc3C/Jw6VYCqQnCwnnnzXNFqpT29uSsoKGDhwoVMnTqVpKQk2rVrx6RJk2jUqJGpSxNCCCGeeLKCJR4JdeFC4s6e5Xq3bnhcXYqP4bfiPa7+DFcjGck0pjGIQSxm8X2Hqx3XLtFw51Jm/HGwlGZgngwGlW7drvHaa9dRVVXClZkrKirim2++oUqVKgwbNozAwED27t3L1q1bJVwJIYQQZYSsYIlSZ/zoI2ILC0nr1AmvKwvwsriC0nYDWFhhxMgQhvAFXzCc4XzCJyjcXwjYf+MynX/5iSr25RgcUKeUZmFejEYVVQWtVmHlSnfc3bWysbKZKywsJCQkhJMnTxISEsIXX3xBu3bt5HkVQgghyhgJWKJUGT/8kBi9nowWLaiQ8DEeNjnQeg1o9RRRxEAGspSljGEMU5l63+Hqt5Qknt73AxVt7NnevCfl9NK0ITvbSL9+yQQE6PjwQxfq1LE0dUniAamqym+//UbDhg3R6XT069ePwMBAnnvuOQlWQgghRBkllwiK0vPxx6Tt2EFGkzB84qfjYW+ANt+DVg/ALGaxlKVMZjLTmHbf4epEWjLt967CzdKGnS164WFlWxqzMCsJCUU0bXqFdety8PaWfa3M3bJly2jUqBG//PILAKNGjaJLly4SroQQQogyTFawROmYNw9GjqRct25YBVXFpsIIcA8FzX9P+oczHF986U3v+x7+TMYN2u79HlsLHTtb9KK8tf3DrN4sHT6cR+fO18jONrJhgydPPy1dFM1RdHQ0169fJzw8nK5du5KTk0ODBg1MXZYQQggh7pGsYImHTv3yS+ITEsie2Alm9MHG3h48m4JGi4rKAhaQQQY22DxQuIrJSqXNnu/RoLCzRS/8bB1LYRbm5fvvs2jRIglra4UDB8pLuDJDcXFxREREEBwczBtvvIGqqtjY2DBo0CD0er2pyxNCCCHEPZKAJR6uxYspevdd0lu3Jiu0Blz64R9fjiaa13mdhSx84IcYeGQL+UYDO1r0pIp9uX9bsVlTVZX330+hV69k6te35NCh8tSoISfj5iQlJYW33nqLoKAgVq5cyZtvvsmOHTvkMkAhhBDCTMklguKhUZctg4ED0bVuRfWwMLS6xqD9Z4OFmtTkEIeow4N3+1vR6FmS83Oo6ej2b0s2a/n5Ki+9dJ3ly7N48UU7vvjCDUtLOSk3F3l5ecyZM4dp06aRnp7Oiy++yKRJk6hYsaKpSxNCCCHEvyArWOKhUH/4gcvHjhH39SzU/+jQWiqgty9paPElX/IDxatZ9aiH5j6/9YqMRubHRFFkNOJlbUdtJ/eHPgdzk55u5ODBPKZOdeabbyRcmQuj0cjSpUsJCgpi9OjRhIaGcvz4cb755hsJV0IIIcRjQAKW+Pe2b+fK3r0k9+mD1v0qFNwEo6Hky9/xHYMZzDKWoaI+0ENsSophyLFtbL0W+7CqNluJiUUUFqq4u2s5caICY8c6y+VkZsRgMDB16lTc3d2JjIxk8+bN1KpVy9RlCSGEEOIhkYAl/p2oKJK//ZarERG43lhPheyfUZ7aUrx6BWxmMxFEEE44K1hx363Y/9K5fGUOtupHR6+Ah1m92UlJMVC/fiKjR98EwM5OfoTNwdmzZ3nhhRfIyspCp9MRGRnJoUOHaNmypalLE0IIIcRDJmdn4sFdukTq5MkkvP46jun78Un7HuXpbWBV3HjiOMfpSU9qUYt1rMOa+98E+KfLZzmSkgRAIxfvh1q+OSpXTsvo0Y688oqDqUsR9yE1NZVNmzZx4sQJAMqXL49GIy+/QgghxONIfsOLB3PzJlnDhhH71lvY5p2n0pWPUZ7eCjYeAFzmMh3piBNObGQj9tz/PlX7rifQ+9AGxkfve9jVm52FCzM4dCgPgDfecKJ6dekUWJbl5OQwZcoU3nzzTQAaN25MQkICTZo0MXFlQgghhChtErDE/cvNJe+ll4h5YwR60gi4+Baa9j+CvS8AmWTyDM+QSSab2IQ397/ydDbzJp1/+Ql/W0eWNXrmYc/AbPzVhn3QoBt8/nmGqcsRd2E0Gvnuu+8ICgpi/PjxJCQkYDQaAbCzszNxdUIIIYR4FCRgiftjMFD4yitcGDAA1U5H4PnX0LVYAG4hABRRRC96cZKT/MAP1OL+b95PK8jjmf0/otNo2Ny0O+X0939p4ePAYFAZOvQmEyemERFhx1dfPdlt6cu6AwcOEBoaSr9+/fDw8GDv3r2sWrVKLgUUQgghnjDym1/cO1WFESNQd+xA6+RAYOo3WNUbCX7PlhxyghNEEsk85tGe9vf9EEZVpf/hTcRmp/NTWBcq2Tk9zBmYjfx8ld69k5k/P4PRox35+ms3LCykU2BZFB8fT58+fQgLCyMhIYHFixdz+PBhmjVrZurShBBCCGECstGwuGfqrFkwbx76kW9QtUVLFLU5aP75LRRCCGc5iw8+D/QYU8/8yoakC8yp24YmrhUeRtlmJzPTSJcu19i5M5dZs8rx5ptPZsgs61RVZeLEiXzwwQcAjB8/ntGjR8ulgEIIIcQTTgKWuDdbtnD56lUKVi2kkuUKlPzUkm6BAGtZSyqpDGDAA4erzUkxTIjeTz/fGgwNqPewKjcryckGnn46iePHC1iyxI3+/e+/OYgoXaqqoigKiqJw5coVunbtyvTp0/HxebDveyGEEEI8XuQSQXF3Fy6g9umDzsICfeWKKMZc0P63i52Kytd8zQIWUETRAz1EakEeLxzaSG0ndxbUa/9Ebpybm2ukWbMrnD5dyLp1nhKuyqDY2FiaNWvGb7/9BsD8+fNZtmyZhCshhBBClJAVLHFnWVmoXbqgaBQ8Bw8Gf3+o1QaU/2ZzBYU1rCGDDCwe8FvKWW/FwvodqOfsgY2F7mFVb1asrTUMH+5A3bqWhIVZmboc8Td/rVq5uLiQlZVFcnIyAFqt1sSVCSGEEKKskRUscXuqStFrr/HHO2+TsagLFO4t/vs/w5WKyjSmcZWraNHijPMDPITKucwUAJ6vEIS/7ZN3v9Hx4/ns25cLwNChjhKuypDCwkI++ugjwsLCKCwsxMHBgaioKDp27Gjq0oQQQghRRknAErelzpxJbMOG5FapjDb7EBjy//H1OczhXd5lJSsf+DG+iv2dmlu/4mjq1X9brllSVZWhQ28wePANDAbV1OWIv/k/9u47PKpifeD4d7JpJKRB6AFCkWpMIAhS1FhAwICgeAVU4IJgA0QEK14u6E+xIKhYACmCGBCUEoQrIAQDVkpAqvRQQ0KA9LK78/sjEcVQsptNzm7yfnx4uOyZM/OSs899zsvMvLNu3TrCw8N57rnnCAoK4uLFiwAVcvmqEEIIUZEopaorpboqpfoW/m7TWTklXiKolGoNl6oaJGqtt5W0T+EEvvuOU8eOkTZkCPWOvYFvnUhoNvTS5Z/4ied4jh70YCQj7R7mgZCmJOdm0SqwhiOidjlKKRYvrkFensZkkhd3Z5CYmMhzzz3HkiVLaNiwIStWrKBHj4p72LUQQghRkSilXgZuBn4A0oBawONKqS1a6/8rTh92J1hKqUhgAaCBREAB9Qv/dbe/1nqrvX0Lgx06xIUPPuDMxIlUTV1NsPUA3PozFP7LfQop/It/UZe6fM7nuNkxEZphzsPLzUSQpzcvNW/v6L+B0/vuuyxiYjKYNasatWvLVkhnkJuby+TJk/m///s/tNa89tprjBkzBm9vWbIphBBCVCBdtda3/eOzKUqpH4DSTbCAGcBwrfW6v3+olOoMzAQqZp1tV5eZSc6TT3Jk3Dh8co5Q7+RUVO+fwN0HAAsWHuZhkknmR360a98VwONbv+NI5gV+iHoYd7eKtVJ16dJMHnooiRtv9CQ93UpgoBRKMNq6det48sknOXjwIA888ACTJ0+mfv36RoclhBBCiLK3Uyk1FdhAwQxWABAF7CxuByVJsCr/M7kC0FqvVUpNK0G/wkCWZ57h0NChuHlBoz3DcYuaAQE3XLr+Oq+zhjXMYAat7cyhFxzbzZeJe5jYslOFS65iYjJ49NGztG3rxapVNSW5chLJycmYTCa+++47unTpYnQ4QgghhDCI1nq4UqoN0BZoCVwAvtBabyluHyVJsM4qpf4NzNNaWwCUUibg30BKCfoVRvnqKxLr1SOnQSg3HHgaz+aPQoP7L11ewxomMIEBDOAxHrNriKOZF3lq2xo6VK3DS80q1tLAL75IZ+DAZG67zZvY2JpUrlyxkktnYrVaeeedd/Dx8WHEiBH07duXBx54AE9Pz+vfLIQQQohyRSn1vdb6LqXUOGArsM2WhOqfSpJgDQQ+BaYqpU4VflYb+LXwmnAlx4+T8/rrpH72GbWSY/D39Ya2b166fI5zDGAALWnJx3yMwvaCDBZtZcCvK9HAF+2iK9Ts1Z/J1e23e7NyZU18fCrO390Zubm5sXnzZgICAoCCYiOSXAkhhBAV1gOFv3sATwORSikLfyVbE2zpzO4ES2t9GOiilArm8iqCMnvlaqxWGDgQ78OHaR4QQKXGQ8B7LLj99fXwx5+neZqe9MQXX7uGeWvfL8SnnODzm++tUOddzZ9fkFzdcUfBzJUkV8Y4c+YMkyZNIiQkhMaNG/PVV19JAQshhBBCoLW+UPj7+D8/U0rVASILf9nErgRLKeWltc4tDCQFWRLo0vTkyWSmpFD5/efxadLkUrXAS9fReODBq7xq9xhbUk8zfvcm/hXSjEfrtyxpyC5j6dJMBg5M5s47K7FiRQ1JrgxgsVj49NNPefnll8nOzubXX3+lcePGklwJIYQQFZhSqhvgr7VedKXrWuuTwElgha192/S2p5SKUkodA7KUUueVUhuVUlOUUgOUUjcqpeTt0dVs307qpk3snzOHdJ9Y2PPxZZdTSKE1rdnABruHyDTn8fAvK6np7cunkfdUqINaO3b05okn/CW5MkhCQgIdOnRg+PDhtG3bltmzZ9O/f3+jwxJCCCGE8SYAt1zpglKqcWFtCbvY+sb3EZAFDAfeA84BvYC5FJQuzLA3EGGArCx4+GGCduygXpUgKt/4KNzwyGVNUknFHXeCCbZ7mDlHf+dARirz2t5LkGfFmDX4/vts8vI01aub+PjjYEmuylhGRgajR48mMjKSo0ePsmDBAtasWUNISIjRoQkhhBDCOTQHilRELzQOmGVvx7YuEWwAPKi1/vbvHyqlAik49yrC3kBE2dMvvIA1MRHT1wup1qAhMLJImyY04Vd+tauoxZ+ebtSayKCatK9apwTRuo69e/Po0uU0EycG8cor9p0TJuy3bNkyRowYwYkTJ3j88cd58803CQqS5yCEEEKIy1jhqi+4q4G37O3Y1n9W30dBdY3LaK0vaK3Xa63fszcQUcZWreKU2cyeVcsxp4yC5K2XXU4mmVGM4iIX7U6uMs15nMhKQylVYZIrgObNPVmypAajRwcYHUqFc+bMGfr160dQUBA//vgjn376qSRXQgghhLiS7cA9V7l2Bqhhb8e2JljvgZ0HIAnnkZxMxttvc2bwYPzM23E3AYFNL2synOF8zMckkmj3MK/t+ZGW383ibE5mCQN2DbGxmWzenANA796+VKokywLLgtVqJTY2Fq01NWvWJC4ujq1bt9K+fcU6Z00IIYQQNvkIeEIp1fsK124Ckuzt2NY3wNuA5kqpRUqpptdtLZyS5cUXOfLss3ha06h7eAJEzQWPypeuL2EJX/EV4xlPGGF2jzOsYQSv33gb1b3tK+vuStasyaJPnyRefTUVrbXR4VQoCxYsoGfPnmzYUFCIpV27dnh4FJloF0IIIYS4RGu9GHgf+FoptVQp9bBS6g6l1HDgv8B39vZt6x6sjhScedUA6KOUOkHhAVz8dRCX3dmeKAMbNnDaz4+8kBCa7B+K6cbHoWanS5eTSeYpniKSSF7gBbuGsGqNAhpWDmTEDTYfHeByNm7MplevpEsrImGvAAAgAElEQVRLAytSlUSj5OTksH//fsLDw+nXrx9+fn7ccccdRoclhBBCCBeitR6jlNpCQUI1/2+XNgGv2NuvTTNYWuuWQGWgLfAEsBKoCbwAfAucsjcQUQby8sh+4w2S+vcn+Pwa/NxzoM3rlzUZwxgucpG5zMXdznOopx3cSvSmJWSY8xwRtVP76acc7r33DKGh7qxZU4sqVeyu6CmKaePGjYSHh9OlSxeysrJwd3enV69ektgKIYQQ4pqUUkX2D2itF2qtmwGNgFuBRlrr2wrP+rXLdROsfwaitc7VWm/RWs/UWj+tte4A+AMtADlgxonpd98l8cEHMZFLncR3IOpzcP+rbPoWtjCPeTzLs9zIjXaNcTwrjVd2xWNF42sq38u0tm3LpVu3M9SsaWLdulpUry7JVWm6ePEiTzzxBFFRUZjNZhYsWICPj4/RYQkhhBDCdWxSSp1WSk1XSnVVSl16WdVaH9Fab9ZaHynpIMWZwbpqIH8LSGut913tJGThBA4fJvXXX8mIjKTOiam4N+kL1W++dFmjGcUoqlOdl3nZ7mFGbF+HRVv5uHWXcj2j8Gcp9oAAN9avr03t2vbN9oniiY2NpWXLlsycOZPnnnuO33//nbvvvtvosIQQQgjhWuoAE4H6wDIgpbC2RF+llL+jBilOglUmgYhSpDXWZ5/lxNNP45N7jOD0OGjz2mVNlrCEzWzmdV7HH/se69KTf7D81AEmtOxEA99ABwTunI4dy6dz59N4eCi+/74W9epJclVakpOT6d+/Pz179qRKlSr8/PPPvPvuuzJzJYQQQgibaa3PaK0/0Vp3BapRsOVJA58CZ5VS3ymlnlBK1S7JONdNsMoqEFGKvvkGtxUrCD11ivohtVC3zgDvqpc1+Z3fiSCCwQy2a4i0/FxGbF9LeEB1Rt3QxhFRO634+ByyszXffVeTxo3L9zJII61cuZLmzZuzZMkSJk6cyJYtW7j55puvf6MQQgghxHVordO11jFa674U5Di9gSPAq8BxpdQvSqkX7enb1iIXpRaIKCXp6ehRoyAigoCHH8anXnto+ECRZhOZyM/8jAn79hG9susHTmVnMLNNVzzcyvdepEce8ePAgbrcdJOX0aGUa1WqVKFZs2YkJCTw6quv4unpaXRIQgghhCiHtNb5WuvVWusntNZ1gE5AHDDAnv7sPgnVEYEopW5TSq1QSp1USmml1KDrtI9SSi0v3BOWpZTaqZSyb8qlgtDjx/PHq69yZvJj8NMIsFouu55EEr/xGwBe2Jcw7Lhwlo8ObmN440hurlKrxDE7o5wcKz17nmHLloKiIFItsHTMnTuXcePGAdChQwfi4+Np0aKFwVEJIYQQojQ5W06gtf5Ja/2C1tqulxC7EiylVJE3cTsDqQzsAp4BsovRvgPwO9AHuBH4BJihlJLqhVeSkIB1xgy8/PzwqOwG+Wnwj9mlSUyiE51IsvOwaq01Y3asJ8jTmwktO13/BheVnq45ftzM+fN2/5uEKIZt27axefNm8vPzAcp1oRQhhBBCXGJoTqCU+r7w93FKqW5KqRr29PMnm3bnK6WigM+BEKVUGrCTgkOGtxf+vkdrbS1uf1rrVcCqwr7nFqP9G//46BOl1B3AA8CXxR23QrBa4cknMfn4ENq1KwQFgX6iSLMJTOAu7qIG9n2PrGhurVaXPiHNCPL0vv4NLkZrjcUC1aqZ+O23OmzadNDokMoVrTUzZswgLCyMDh068M477+Dh4YGbmySyQgghREXhBDnBn/tnPICngUillAXYCmzTWk+wpTNby599BGQBw4FgoBXQi4JsEyAHKOvyXv7AiTIe0/ktWUJSw4b4jbwfn+ydEHQ7/G02QKOxYMEff6KJtnsYk3LjPy06OiJip/Tii6ns25fP4sU18PSU2RRHOnr0KEOGDGH9+vUMHTqUDh064OUl+9qEEEIIYRebcgKlVDfAX2u9SGt9AUBrPf5v1+sAkYW/bKK01sVvrFQW8KDW+tt/fB4ItAYitNbv2RpEYR8ZwHCt9Vwb7okGlgIdtda/XqXNMGAYgLu7e+TatWvtCc+hMjIyqFy5cqn1rywWwsaP58iUKQSdW0Wt09P5NXQeWv2VT2+uupmZDWcy6fdJ1Mypadc4cbnncENxq2dQuVzKtWSJHx99FETPnumMGnUepUr/2VUEWmtWrlzJJ598AsATTzxBjx49yuQ7JM/Pdcmzc23y/FybPD/X5SzP7o477sijYEnfn2ZorWdcqW1p5QRXuOdXYLPW+tkrXGsMHNFaW4reWYy+bUywtgETtdbL7BnsOn3b9MNUSnUEVgMvaK0/Kc49vr6+OjMz0/4gHSQuLo6oqKjSG2DuXA6dPUta1K2E/d4N9zvnQIPely7nkUdLWuKOOzvZiQf2lRq/a+NC8q0WNkb1L3cJ1tdfZ/Dgg2fp1cuHxYtrYDIV/P1K/dmVc8ePH+exxx5jzZo13HnnncyePZv69euX2fjy/FyXPDvXJs/Ptcnzc13O8uyUUllaa99iti31nKDwvnSg7z8njgqvzQXQWg8qbn9/Z+tGh/eAx+wZyJGUUp0o+EH+x5YfZIWQl0fW559z4a67qJGyEPeaN0Nor8uazGEOBznIu7xrd3IF8N2t/+Kr9veVu+QqPj6bhx9O5pZbvFiwoPql5ErYT2vNnDlzuPHGG9m0aRMfffQRa9euLdPkSgghhBDlSwlzAitwtZe81UCUvXHZmmDdBjRXSi1SSjW1d9CSUErdRsFfeoLWeqoRMTi1zz7jVHQ0Jksu1U/PhnbvXLb3yoKFd3iHNrShO93tGiI5N4uL+bm4u7lR09v4aWdH2rs3j/vuS6J+fXdiY2tSqZIUW3CEwYMHM3jwYCIiIti5cydPPfWUFLIQQgghhN0ckBNsB+65yrUzYGcFOGwvctERqAc0APoopU5QWF2Dv6psFLvet1KqMtC48I9uQD2lVASQqrVOVEq9CbTVWt9V2D4K+Bb4GFiglPpz85BFa51s49+l/MnKInPhQi5OmULtpDm4h9wFwRGXNfmarznEIZawBHXVpP3axuzYwIazxzjQbRheJlu/Qs7r9Gkz3bqdwcND8b//1aRqVTnrqqS01iiluO+++4iIiGDEiBGSWAkhhBDiMgblBB8BXyql1mutl/7j2k1g5xlG2Jhgaa1bFp6BFUZBBcGIwt9fAHwBDdjyVtoG2PC3P08o/PU5MAioBTT62/VBFFQpHFP460/HgFAbxi2fPv6YUw88gMmSQ/VTc+G+jZdd1mje4i1u4AZ60evKfVzHtvNnmHdsFy80bVeukqv0dCvdu58hJcXCxo21adDA/qWTAnJzcxk4cCCRkZGMHTuWXr3s+74JIYQQokIo85xAa71YKdUO+FoptRxYApwCWgL/LfyzXWx+Q9Za5wJbCn8BoAo24TQFwm3sK46rr30ssrGs8M+DrtS2wktLI2PZMtLef586Z2ZhqnM7VLu8quT3fM82tjGTmZhsyoMLaK15bscGgj0r8VLz9o6K3Cnk5Wn8/NxYvLgGkZFSKrykPD09UUqVu/15QgghhHA8o3ICrfUYpdQWChKq+X+7tAl4xd5+HTIFoQtKEe4r/CWMMHUqZ3r3xt2SQ7XTc6HH+iJNJjGJWtTiUR61a4iVpw8Rl5zItFadCfAoH0nInwcJV61qYuPGWpIQlEB6ejovvvgizzzzDE2aNOHLL7+Un6cQQgghnJrWeiGwUCnVAKgNnNJaHylJn7IZojxITYXJkwndto2GNzTCdNt0qHHLZU3Oc56DHORZnsUL25Mjq9a89PtGmvpVYVhDmyYqndpbb12ka9czZGZaJRkogU2bNhEeHs4nn3zChg0FM/zy8xRCCCGEq9BaH9Faby5pcgUOmsESBnv7bXR6Ou4vv4xfUE0IKjpDFUQQBziABbvOS+Obk/vZnZZCTLseeLiVn+IPtWubCAkx4eMjyYA98vLyGD9+PG+99RYNGjTghx9+oFOnTkaHJYQQQghhGJnBcnWnT5MeH8++lbHkHp8IpzYUaZJKKjnk4IEH3njbPIRVa17b8yNN/arwYN1mjojacHl5BQdsDxjgx9y51WW2xQ579uzhlltuYdKkSQwZMoSEhARJroQQQghR4UmC5erefBOrmxtuNavikX7lLXAv8iItaEE++XYNEXvqIDsvJvNK8/aYlOt/ZRITzTRrdpwVKzKNDsUlWa1WPvjgAyIjIzl+/DjLli1j5syZ+Pn5GR2aEEIIIYThZImgK0tNhc8+I6BfPwJa3wKttnOlAiz96MdN3IQH9pUer+7tQ/96LehXt0UJAzZeerqVHj3OcO6chcaNpRS7rbTW3H///Sxfvpx7772XWbNmUaOG3efwCSGEEEKUO5JgubLZsznfvj3+j3XFlJcOnleeQbij8D97ta9ah/ZV69h9v7MwmzV9+yaxe3ceq1fXpEULT6NDcjlKKbp37063bt0YNmyYLK0UQgghhPgH11/vVVFZLGStWsXht9/m3IU4WPdgkSYXuchYxnKKU3YNobXmvT9+5XR2RgmDdQ7PPXeOVauymTYtmM6dfYwOx2VkZ2czZMgQYmJiABg2bBiPP/64JFdCCCGEEFcgCZarWrWK5PbtUVYzVU7Ng5bDizT5hE94l3dJIsmuIfakpfD8zjhiTx8sabSG+/TTND74II1nnw3giSf8jQ7HpXh4eHDgwAGOHClx1VIhhBBCiHJPlgi6KMvMmaS+8AJV0uNxD7wB6t172fU88pjKVDrTmVa0smuMlgHV2N91KCGVXLt4wcaN2YwYkUL37pV4550qRofjEiwWC1OmTGHgwIFUq1aN9evX4+4u/3chhBBCCHE9MoPlivbv55yPD1Zvb6qf/AxuHAn/WK61ilUkkcQoRtk1RI7FDECjykF4mVz3xfrIkXweeCCJxo09+PLLGphMsqzteo4dO0ZUVBRjx47liy++AJDkSgghhBCimCTBckH6o49IfvBBfPJP4WM+BQ2L7r+axzxqUIMudLFrjO7xixm6ZXVJQzXcvn35eHkpli+vQUCAfN2vZ9GiRYSHh7Njxw7mz5/PqFH2JehCCCGEEBWVvHG6mvR0MhISyAkNpfqpOdC4P3j4XtYklVRWspL+9MfdjlWg8cnH2ZCcSEv/YEdFbZhu3Xw4dKguTZpIxcBryczMZMiQIfTt25fmzZuTkJDAI488IoUshBBCCCFsJAmWq5k3j+Tu3TFZcwk6twqaDS3SZBGLyCefAQywa4jX9v5IdS8fhjWMKGm0hnnjjfN89lkaAN7e8jW/lu3bt9O6dWvmzJnDK6+8wg8//EDDhg2NDksIIYQQwiXJm6cr0Zq8L77g/J13Epweh1uV5hDcukizeczjRm4knHCbh/j53EnWJh1lTNO2+Li75kG8FosmPj6H+PgctNZGh+PU3n//fW655RYyMjL4/vvvef311/HwcM3nLoQQQgjhDGTnuiv5/nssyclUzskiOG9nwezVP5ZwHeAAP/Mzb/M2CtuXd72z/1eqeHrzZCP7Kg86A5NJERtbE4sFWeJ2HWfOnKFr167MmjWL4GDXXxIqhBBCCGE0SbBcybRpVEpLo2nbW8A7Cq4wO+OBB0/yJP3pb3P3RzMvsuzkAZ5v1o7K7q63Z+ncOQtPP53ClClVqVXLHSl8d2Xr1q3D29ubTp068frrr+Pm5iaJqBBCCCGEg8gSQVdx9Cg5O3eSP+JxsJ4v+OwKL8WhhPIxH1OHOjYP8fGhbSgFT7ng7JXFounf/yxLl2Zy/LjZ6HCcltlsZvjw4UycOBEAk8kkyZUQQgghhANJguUqPvmExDFj2NftHvSCupC6q0iT/eznJ35CY/u+o0xzHjMP7+D+Ok2o6+PviIjL1H/+c541a7KZNi2Ytm29jQ7H6SQmJpKdnY27uzvffvstS5cuNTokIYQQQohySRIsV5CdDZ99Rr2EBOrXqY66+XUIalmk2RSm0JnOZJJp8xDbL5wl32pl5A1tHBFxmVq+PJM33rjAkCF+DB3qeslhaVu6dCnh4eG8+OKLADRq1AhfX9/r3CWEEEIIIewhCZYriImB1FS8H34Y/1pNIOLFKy4PfId3WM1qKlPZ5iE6BYdwqsfTdKxq+9JCI+3fn8ejj56lTRsvpk2ranQ4TiUnJ4fhw4dz//3307hxY0aOHGl0SEIIIYQQ5Z4kWC7AunAhR6ZMIav6GTj+3VXb+eHHrdxqc//p+blorfH38HKp/TgZGVbuvz8JLy/F11/XkPOu/ubAgQO0b9+ejz76iNGjR7N582YaNWpkdFhCCCGEEOWevJE6u7NnSa1UidRbb8WyewbsnXHFZmMYw1zm2jXEI7+upGv8VyUIsuxprRk8OJl9+/JZuLAG9epJycA/LVy4kNatW5OYmEhsbCyTJ0/G09P1qkIKIYQQQrgiSbCc3bJlpN5zD16WLCqnrodmjxVpcpazTGUq+9hn1xA9azemd50mJY20TH3zTSaLF2fyxhtVuOuuSkaH4xSys7N5/PHH6devHzfddBMJCQlER0cbHZYQQgghRIUiCZaTM3/7Lelt2hCU8xvKNwRCuhRpE0MMFiw8yqN2jTGkQThPuFhp9t69fVm4sDrPPx9gdChOY+LEicyYMYMXXniBuLg46tata3RIQgghhBAVjiRYziw1lYtWK5hMBCbOgaaDwc1UpNl85tOa1rSkaGXBa8kw5zHt4FbS83MdFXGpO3XKzIkTZtzcFA89VNml9oyVloyMDABeeukl1qxZw6RJk/Dw8DA4KiGEEEKIikkSLGe2YgUXbrsND0smPll7oOm/izTZwx62stWu2at5R3cxYvs6dqWlOCLaMjF0aDK33nqKvDzbz/oqj1566SU6duxIdnY2/v7+dO7c2eiQhBBCCCEqNKkM4MSsy5eTNmYMVbN+RdVoB36hRdrMZz4mTPSjn219a82HB7fSJqgmt1Sp7aCIS99771Xljz/y8fSUmSuA2267Da21zFgJIYQQTs5qtZKSksKFCxewWCxlMmZAQAB79+4t9XFMJhOBgYEEBwfj5ibzN5JgOau0NNLS0rB6exN4fDE0Lrr3CuArvqIznalBDZu6X5d0lH3pqcxvG+0Sy+yOHcunXj13mjb1pGnTil0R75tvviExMZFRo0bRrVs3unXrZnRIQgghhLiOEydOoJQiNDQUDw+PMnn/Sk9Px8/Pr1TH0FqTn59PUlISJ06coF69eqU6niuQFNNZrVzJhU6dMFnzqZz+G4QUXfp1iEMc5jDR2F4p7oODW6nh5cuDIU0dEW2pOnYsn1atTjJhwnmjQzFUXl4ezz77LA888ACLFy/GbDYbHZIQQgghiikzM5M6derg6enpEv+4XVxKKTw9PalTpw6ZmZlGh+MUJMFyVkuW4HPqFNV9s3CrdStUb1ukyVrWAtAZ2/bdHMw4z7enD/FEowi8TM49iZmXp3noobNYLJpHHindf4FxZomJidx+++1MnTqVkSNHsmHDBtzdnfvZCSGEEOJy5Xn5XHn+u9lKfhLOKCMDVq+murc3tVvcCdHrwa3oHptmNGMEI7iBG2zqftaRnZiU4vGGEY6KuNS88MI5fvkll9mzq9G4ccXcZ/S///2PVq1asXv3bhYvXsz7778vBwcLIYQQQjgpSbCc0erVZIWEYLn/XjBnXbVZFFF8wAcoij/NbNFW5h3dRbeaDalVqbIjoi0133yTydSpaYwc6c8DDzh3rKXBYrEwfvx4unfvTkhICFu3bqVPnz5GhyWEEEIIIa5BEiwnpL/+mkNTp3Ik0B0+rwIZJ4q0OcUp/uAPNLaVK1+bdJRTORkMCg1zVLil4tChfP7977O0bevFO+9UNTqcMpeSkkL37t2ZOHEiAwYM4KeffuKGG2ybqRRCCCGEEGVPEixnk50N335L6G+/UbN6EES8BL51ijT7jM9oRjNSSbWpe393T/qENKVH7caOitjhcnM1//pXEiaTYtGi6hWyJHt2djZ79uxhxowZzJkzBx8fH6NDEkIIIUQFEBMTQ2RkJAEBATRq1Ii4uDijQ3I5skve2axZg8rIwK9jR6gTWfDrCgYxiGY0oyq2ze50CA6hQ3CIIyItNS++eI5t2/JYtqwGoaEVZ9+V1poVK1bQo0cP6taty4EDB/D29jY6LCGEEEJUEJMnT2b27NnMnz+fiIgIdu/eXepl3ssjSbCczddfc2bYMPzD6uFzOh5qtAe3oo+pXuF/tth6/gw1vHwI8fF3VLQOl51tZf36HEaM8Oe++3yNDqdMrVmzhl69evHll1/Sr18/Sa6EEEKIci4qKuq6baKjoxkzZsyl9oMGDWLQoEGkpKRcd292bGxssWNJTk5mwoQJxMfHEx4eDkBYWBgXL16kbdu27Nmzh59//pkbb7yx2H1WVLJE0Jnk5ZH766+cHDaM9JO/QeztkHehSLMtbGEOc8gm26bun9y6hp6bv3FUtKWiUiU3fv65Nm+/XcXoUMpMbm4uAF26dGHp0qU89NBDBkckhBBCiIpm3bp1hIWFXUqu/uTj48O3334rhbZsIDNYzuT777nQujUAgWe+huDW4B1cpNnnfM5sZtOf/jZ1H3NLD87mXr0qoZEsFs3bb19g+PAA/PwqTt6/bNkyhg8fzrp162jWrBm9evUyOiQhhBBClBFb9zf9vX1wcPB1709PTy9236mpqQQGBhb53MPDg2rVqhW7HyEzWM5lyRIu3H03lTw98Dq1EkKufIDwGtZwO7fjhZdN3TeqHET7qkULZjiDn37KZdy483z7rXMmgI5mNpt56aWX6N27N7Vq1aJSpUpGhySEEEKICqxVq1Zs2rSJHTt2oLXmwIED7N271+iwXJIkWM7CbCY/Lo6MsDACTamgzVCnaIKVSCJ/8AeduXLydSX5VgsDf/2WX86dcmTEDtWpkze7d4fw0EPlf99VcnIyXbt2ZdKkSQwbNoz4+Hjq169vdFhCCCGEqMA6dOjAuHHjiI6Oxs/Pj969e5Odbdt2FFFAEixnER/PxZYtwc2NwIsbwVQJanYs0mwtawFsSrD+d+YI847tIik302HhOkpqqoU1awpmrZo180Sp8l2S/bfffiMyMpJNmzYxa9Yspk+fLsUshBBCCOEUxo4dy/Hjx8nIyGDXrl20Lty6ImwjCZazOHCAC3fcgaebG5WOL4Jat4Gp6BLAtaylFrVoSctidz336O9U9/KhW82Gjoy4xLTWDBmSTI8eZzh50mx0OKVu1qxZdOrUCTc3N3788UcGDx5sdEhCCCGEENfVvXt31qxZw9ChQ5k7d67R4Tg9KXLhJCwXL5LWsSPVfN1RF/ZCsyFF2lixso513Mu9KIo305OSm0XsqYOMuCESDzeTo8MukU8/TWfZsizefbcKdeqU76/iyJEj+fDDD+nSpQtffvklVavadn6ZEEIIIYRRVq1aZXQILkVmsJxEuocH2suLwPzCzYQhXYq02c52znHOpuWBCxL3kK+tDAoNc1SoDrF3bx6jR5/jnnsq8eyzAUaHU+rCwsJ46aWXWLVqlSRXQgghhBDlWPmeNnAlGRlUOnQI71o/QqWaEFT0ELc/91/dzd3F7nbu0d+JDKpJWIDzlNfMzdX073+WypUVc+ZUw82tfO67+uGHHzh37hy9e/dm6NChRocjhBBCCCHKgCRYTiIwIYHAmBjYtQtaPw9XKPZwlrNEEklNaharz4QLSSRcOMu0VsWf8SoLr76aSkJCHsuX16BWrfL5FdRaM378eNLS0rjvvvtwc5PJYiGEEEKIiqB8vt26otRUqFKlILHyrX3FJu/xHhYsxe5yzpHf8XQz0a9ec0dFWWLr12fz7rsXefxxP3r2LH8l2bOzs8nJySEoKIiFCxfi7e0tyZUQQgghRAUib35O4uQdd3Dw2YEQNxisRSvqaTQAJopXqCLPamFB4h7uq92YKp7OcYhtaqqFAQPO0qSJB5Mnl799SMeOHaNjx4707dsXrTU1atQgIKD87y8TQgghhBB/kQTLSbifPYuH5SKkHQS3ohOLL/ESnel8KdG6HrPVysvNb2HkDW0cHardEhPNeHkpvvyyOr6+5eurt2HDBtq0acOhQ4cYMWJEuT/PSwghhBBCXJksEXQSNT7/HNyHwJQfrni9HvXIIKPY5dl93D0Y3aStI0MssYgIL/bvr4u7e/lJPrTWvP/++4wZM4YmTZqwbNkymjRpYnRYQgghhBDCIOVrGsFV5edDejoEBV21yVM8xTSmFau7PKuFL47tJi0/11ERlsihQ/n85z+p5OXpcpVcZWdnM3DgQJ599ll69OjBzz//LMmVEEIIIUQFJwmWM7hwgV2rvuZE63TITi5yOYkkcsgpdndxZxN59NeVxCUnOjJKuy1dmsmHH6Zx9mzxC3Q4u8TERG699Vbmz5/PhAkT+Prrr/H39zc6LCGEEEIIYTBZIugEdGoqeVVqQUoOeBZ9SX+FV/iO70gksVhLBO+uEcqPdz5Cq8AapRGuzcaMCaR//8rUrl0+vm5//PEHnTp1Ijc3lxUrVtCjRw+jQxJCCCGEEE5CZrCcgPX8ebS7J+6WLDB5Fbm+jW20oEWx91+5KUX7qnXwNhmb0OzYkUtCQsEyxfKSXAE0bNiQXr168csvv0hyJYQQQohyJSYmhsjISAICAmjUqBFxcXFGh+RyJMFyApaLFwFw10XLs+eRx252E0FEsframJzIU9vWkJKb5dAYbZWdbaVfv7Pcf38SZnPxKh86s9zcXF588UVSU1Nxd3dnxowZNGvWzOiwhBBCCCEcZvLkybz++uvMnDmT8+fPs2zZMkJDQ40Oy+WUn2kFF2ZOT4fgYExXmKDay17yyKMVrYrV17yju1h8Yj/vhd/p4Cht88or59m7N581a2qWi8IWBw8e5MMPP+Spp57i/vvvNzocIYQQQpQDUVGnrtsmOtqHMWMCL7UfNMiPQYP8SEmx0EG3tXgAACAASURBVKdP0jXvjY31K3YsycnJTJgwgfj4eMLDwwEICwvjp59+ol+/fnh6elK7dm3mzZuHh4dHsfutiGQGywlYsgpmm9yv8GVNIAGgWDNY+VYLy04doGftxoYuD9ywIZspUy7y9NP+dO7sY1gcjpCYWFAopGXLlvzxxx/ce++9BkckhBBCCOF469atIyws7FJy9af69euzfv16Nm7cSMOGDVm+fLlBEboOmcFyAuacggqBJu9KRa5tZzs++HADN1y3n/Vnj5Gal8ODIcYtXbt40cqgQck0aeLB229XMSwOR5g/fz5Dhw5l1qxZPPzww9SpU4cDBw4YHZYQQgghyom4uNp2tw8ONl33/vT09GL3nZqaSmBgYJHPa9f+awx3d3fc3GR+5nrkJ+QEzPn5ALh7+ha5lkACN3ETJkzX7Wfxif34uXtyT80GDo+xuEaNSuHECTPz5lXDx8c1v14Wi4WxY8cyYMAA2rdvzz333GN0SEIIIYQQpapVq1Zs2rSJHTt2oLXmwIED7N2799L1I0eOsHr1aqKjow2M0jW45htwOWOxFBS3cPe+PMHSaBJIKPbywKUn/zB0eeCyZZnMnZvByy8H0q6dtyExlNSFCxeIjo7m3Xff5amnnmLNmjUEBwcbHZYQQgghRKnq0KED48aNIzo6Gj8/P3r37k12djYAaWlpDBw4kPnz5+Pp6WlwpM5Plgg6Aa/TJwg6Hodb+I2XfX6Uo1zkYrEKXGw4m2jo8sCzZy0MG5ZM69aevPpqkCExlNT+/fvp2bMnhw8fZvr06QwbNszokIQQQgghyszYsWMZO3bsZZ+ZzWb69evHf//7X5o2bWpQZK5FZrCcQFD8TzT8cBU06H3Z54EEMotZdKbzdftYfGKfocsDd+3KQynFvHnV8fR0vaqBq1atom3btpw/f57169dLciWEEEIIQcG5WL/88gsTJ04kKiqKRYsWGR2S0zM0wVJK3aaUWqGUOqmU0kqpQddp762UmquU2qmUyldKxZVNpKXs/HkIKjrrE0QQgxlMA66dNOVbLXxz8g96GLg88M47K3H0aF1atnS9aeNZs2YRHR1Nw4YN+e2337j11luNDkkIIYQQwik8+uijpKSkEBcXR1xcHA899JDDxyhvOYHRM1iVgV3AM0B2MdqbgBxgGvBtKcZVpv4YN4qDT9wG5/dc9vl61vMHf1z3/myLmSENbuLfoWGlFeJVnTxpZsaMNLTWVKpk9NfJPu3bt2fgwIFs2rSJ+vXrGx2OEEIIIURFU65yAkPfiLXWq7TWL2utlwDWYrTP1Fo/obWeAZwo/QjLgNYEbt5AQNJh8K522aWBDGQCE67bhb+HF2/fdAd31wgtpSCvbubMNEaNOsfx45YyH7skTp8+zTvvvIPWmhYtWjBnzhx8fYtWcRRCCCGEEKWrvOUErjnlUJ5kZ1P9oxiqnagFlS5PsL7jO8Yx7pq3m61W1iUdxWy97nexVIwfH8Rvv9WhXj3Xqpfy+eefM2HCBA4fPmx0KEIIIYQQohxRWmujYwBAKZUBDNdazy1m+2nAjVrrqOu0GwYMA3B3d49cu3ZtCSMtuYyMDCpXrgyAZ3IybZ8aysGBgzkT3dPmvrbkXWTsxX285n8DnbzK7mDf5GQTWkP16q41c5WWloa/vz9Wq5XTp09Tp04dm+7/+7MTrkeen+uSZ+fa5Pm5Nnl+jhEQEEDjxo3LdEyLxYLJdP2zVB3l4MGDXLx4scjnd9xxRx7w+98+mlE4+1REaeUEZcm1ph3sUPjwZgD4+vrqqKgoYwMC4uLi+DMO686dbP/f99Q+NZtmf4ttHes4whEe4zEUV6/K186ST+MzzbmnZgMqmTxKOfICWmu6dj3Drl15HDpUF29v558ItVqtvPrqq3z22Wds3bqVkJAQu/r5+7MTrkeen+uSZ+fa5Pm5Nnl+jrF37178/PzKdMz09PQyHdPb25tWra54vJBZa92mzAIxmPO/GZdzlsIs311fPhM0hzlMZOI1kyuASiYPetVpUmbJFcBnn6WzZk02r7wS6BLJVXp6Ovfffz9vvPEGPXv2pHr16kaHJIQQQgghyinnfzsu58yFCZbpH3lUAglEEHHNe3+/mMxrezZzLrc4xVYc49ixfEaPPsedd3rzxBP+ZTauvY4ePUrHjh2JjY1l6tSpzJgxQ04gF0IIIYQQpcboc7AqK6UilFIRhbHUK/xzvcLrbyqlvv/HPS0K2wcDf7/fJZkzMwFw9/jrpT+bbPax77oJ1qLje/nv7s2oMjrX12rVDB6cDMCsWdVwc3PuA4Xj4+O5+eabSUxMZPXq1TzzzDOosvphCSGEEEKIYilvOYHRe7DaABv+9ucJhb8+BwYBtYBG/7hnFfD3w4q2F/7ukm/OluyC2Sd3b59Ln/3O71ix0oorrmG9ZOWpQ3QMrkMVz0qlGuOfpk9PZ/36HKZPDyY0tOyWJNpj1qxZPPnkkzRo0IAVK1bQtGlTo0MSQgghhBBXVq5yAkMTLK11HNf4IWitB13hs9DSi6jsmfNyATD5Blz6LIEEgGvOYB3PSmPHxbO8FRZVqvH96ejRfMaOPUfnzpUYOrRsN2jaasyYMUyePJnOnTuzaNEigoKCjA5JCCGEEEJcRXnLCWQPlsEs1oIEy93rr6RlO9vxx58GNLjqfd+ePgRAdO1/JvOOp7Vm6NAUlIKZM4OdfpldlSpVGDlyJKtWrZLkSgghhBDCBjExMURGRhIQEECjRo2Ii4szOiSXY/QSwQrPrMygzbh5B1767M8CF9eqILjy9CEa+gbS3K9qqce4Y0ceGzdm8/77wdSv75xLAw8ePMiZM2fo1KkTL730ktMngUIIIYQQzmby5MnMnj2b+fPnExERwe7du8u8tHx5IAmWwczuCndzGqpSMAAWLOxkJ0MZetV7ssz5fJ90jGENw8skkYiI8GLXrhAaN3bO5ApgyJAhnD59mj179uDuLl9rIYQQQji/qLgvr9smulYjxjRtd6n9oNAwBoWGkZKbRZ+fll3z3tjIHsWOJTk5mQkTJhAfH094eDgAYWFhJCUl0aFDBzw8PDCZTCxYsIBatWoVu9+KSJYIGsx/5w5q7FkFAU0ASCSRfPKvuf9q/dlj5FjNpb48UGvNzz/nANCkiadTVg00m80AzJ07l9WrV0tyJYQQQghhh3Xr1hEWFnYpufpTcHAwmzZtYuPGjQwYMIBZs2YZFKHrkLdRgwWt2gzJN8PghgA0oAEZZGDFetV7Vp4+RGV3T24LrluqsX3zTSZ9+pxl9eqadO3qc/0bypDZbGb06NEkJSWxcOFCGjS4+n41IYQQQghnFBfV3+72wV4+170/PT292H2npqYSGBhY5HOTyXRZfy1btix2nxWVzGAZLN/dirVGIGh96TNPPPHG+6r3VHb3oG/dZniZSjc/jo725dNPg+nSpWzKwBfXhQsXuPfee/nwww8JCQnBar16MiqEEEIIIa6vVatWbNq0iR07dqC15sCBA+zduxeAhIQE2rVrx7Rp02jdurXBkTo/SbCMZLWyb9oUjnX9ax3r8zzPFKZc87Z3w+9kZptupRaW1prMTCteXorHH/d3qqWBBw4c4JZbbmHDhg189tlnTJ48+bJ/WRFCCCGEELbr0KED48aNIzo6Gj8/P3r37k124XmtERER/PLLL7z22mu8+eabBkfq/CTBMlJaGrXnf0rVpPNQWKxiL3s5zOGr3nIhLwf9t9mu0rBoUSbNmh3n0KH8Uh3HVuvXr6ddu3akpKSwdu1ahgwZYnRIQgghhBDlxtixYzl+/DgZGRns2rWL1q1bk5ube+l6QEAAPj7OtW3EGckeLCOdP0/Vz1dD1L8ufRRL7DVv6Rr/FSGV/FjSoXephJScbGHEiBQaNvQgNNR5vh7Tp09n+PDhNGnShNjYWBo2bGh0SEIIIYQQ5d62bdt44YUXMJlMeHt7M3v2bKNDcnrO8wZdAVlTU8m+tQVegapYD0JrzeAGNxHg4VVqMY0YkUJampXZs6thMhm/NPDPYhYffvgh3bt3JyYmBn9/f6PDEkIIIYSoENq3b88PP/xgdBguRZYIGijv4kX2TZlHmnsCAO/xHu1pTz5XXpqnlGJYwwgeqtu8VOJZvjyTRYsy+c9/gmjZ0rNUxrBVXl4eP/74I6NHj2bFihWSXAkhhBBCCKcmM1gGMqenQ0AAJveCZOZHfiSZZDy48oG+65KO0tI/mFqVKjs8lgsXLDz5ZArh4Z48/3zREp1l7dChQ1SrVg1/f39++OEHWe8rhBBCCCFcgsxgGciSnQWAeyVfABJIuOoBw3lWC71/XMqEPZtLJZYxY1I5e9bC7NnV8PAwdmlgeno6HTp0YPjw4QCSXAkhhBBCCJchM1gGMucWHP5mqhxIGmkc4hD/5t9XbLsxOZEMcx7RtRo5PI5167KYNSudF14IoHXr0tvfVVx+fn5MnTqVtm3bGh2KEEIIIYQQNpEZLAOZLTkAuFeuyg52AFx1BmvlqUN4u7lzZ/X6Do0hL08zbFgKTZp4MH58kEP7toXZbGbUqFEsX74cgH79+tGokeOTSSGEEEIIIUqTzGAZyIIZtBWTdyB72ANAGGFF2mmtiT19kLtq1MfH/cr7s+zl6amYMSMYX183KlUyJt++cOECffv25bvvvsPX15f77rvPkDiEEEIIIYQoKUmwDGQ2gcmSjqoUzBHi8cCDOtQp0m5f+jmOZF7k+abtHDp+Xp7G01Nx993G7XE6ePAgPXr04ODBg8ycOZPHHnvMsFiEEEIIIYQoKVkiaCCzpwfu5jTwqsphDhNKKCZMRdqtPH0IgHsduP8qJ8dKZOQJ3nvvgsP6tNWGDRto164dycnJrFu3TpIrIYQQQgjh8iTBMpDF0xuTJQ28gznCERrQ4IrtVp8+TFhANer6OO4MqPx8uPlmL8POu5o+fTpdunShRo0a/PLLL9x+++2GxCGEEEIIIYQjyRJBA9VY9g3WNiFw6yN0oAP1KVrAItOcx6aUEzxzQxuHju3n58bs2dUd2mdxmM1mRo8ezYcffki3bt2IiYkhICCgzOMQQgghhBCiNMgMloH8l20i8JgfKDfe531GM7pImx0XzqKBe2peeXbLVmazZuDAs2zfnuuQ/my1e/dupk+fzujRo4mNjZXkSgghhBBClCuSYBklP5/0do3JC/HGggWNvmKzDsEhnLtvJLdXq+uQYd999yLz5mVw5IjZIf0V1/nz5wEIDw9n9+7dTJ48GZOp6H4zIYQQQghhnJiYGCIjIwkICKBRo0bExcUZHZLLkQTLIDo1lT8mzSClsWYFK6hMZXaz+4pt/T288HAreTKyf38e//3veR54wJf77/ctcX/F9fvvv9OoUSMWLVoEQOPGjctsbCGEEEIIUTyTJ0/m9ddfZ+bMmZw/f55ly5YRGhpqdFguR/ZgGSU1lSb/fRKPRx8ilFCGMYwQQi5rcjwrjYd/ieWdm+6gXdXaJRrOatU89lgKPj6KadOqlqgvWzVt2pQ+ffrQtm3bMh1XCCGEEMKZRRF13TbRRDOGMZfaDyr8L4UU+tDnmvfGElvsWJKTk5kwYQLx8fGEh4cDEBb21/msMTExjBw5kuTk5GL3WVHJDJZB1IUL+H27Fe+AMFrRiilMIYDL9yMl5WSSac7H1wGHC3/ySRqbNuUwZUpVatYs/bw6Ly+PV199lXPnzuHp6cmMGTNo0MAx+8iEEEIIIYRjrVu3jrCwsEvJ1d9ZrVaWLFlC3bqO2bJS3skMlkHyz58n/fHO+PlmcZaTVKUq3nhf1qZNlVps7TyoxGMdO5bPiy+m0qVLJQYMqFzi/q4nJSWFPn36sHHjRkJDQxkyZEipjymEEEII4WriiLO7fTDB170/nfRi952amkpgYOAVr3355Zf06dOHyZMnF7u/ikxmsAySlZPGkaFvkms5yN3cTX/6X3bdqjW5lpIXotBa88QTKWgN06cHo5QqcZ/XsmvXLtq2bcvPP//M/PnzJbkSQgghhHABrVq1YtOmTezYsQOtNQcOHGDv3r1YLBa++uorHnroIaNDdBmSYBnEkpsGgFvlAI5ylIY0vOz6lvOnCVr+PhvOHivROPPnZ/C//2UzaVIVQkNLvtTwWlasWEH79u3Jzs5m48aNPPLII6U6nhBCCCGEcIwOHTowbtw4oqOj8fPzo3fv3mRnZ/PFF1/wr3/9Czc3SRuKS35SBjGbswHICPQmh5wiCdaaM0fJtpi5MaBaicbx9FRER/vw1FP+JernWrTWTJo0iV69etG0aVN+++032rVrV2rjCSGEEEIIxxs7dizHjx8nIyODXbt20bp1a/bs2cO8efPo2rUrBw4cYOTIkUaH6fRkD5ZBLLpg+d9p34JEqwGXF4BYk3SE1oE1qOblU6Jx+vatTN++pbfvKisri8cee4yYmBgeeughZs+ejY9PyWIWQgghhBDO4a233rr0v9u0acMHH3xgYDSuQWawDGI2gZslg6OVCpYK/n0GKy0/l5/OneKemvZX3VuxIpOPP76I1XrlA4wd5ZNPPmHhwoW88cYbxMTESHIlhBBCCFFObdmyxegQXILMYBnE7O6OuzmNP7zPAVCf+peubTibiFlb6VLD/gRr8eJMdu/OY+hQf0pjyWxubi5eXl4888wztGvXjk6dOjl+ECGEEEIIIVyMzGAZxOLphcmcxh7P09ShzmUl2tckHcHX5EGH4Dp29z9vXjXWrq2Fh4fjqwYuXLiQFi1acObMGdzd3SW5EkIIIYQQopAkWAYxe1XCPT+dw27HrrD/6ih3VK+Hp5vJ5n5//DGHxEQzSimqVrX9/uJo1qwZN910E15eXqXSvxBCCCGEEK5KEiyDWLwq427O5DCHL9t/dTjjAgczztu1PPDCBQt9+iTRv3+SI0MFIDk5mY8++giAiIgIli5dSlBQkMPHEUIIIYQQwpXJHiwjaE2D18ajou9i/D3jCSX00qW1SUcB6FIz9Iq3Xsvo0ec4e9ZCbGxNx8RZaNu2bfTu3ZukpCS6du1Ko0aNHNq/EEIIIYQQ5YXMYBnALScHn427qWStw2M8xt3cfelat1oNmRnZlSaVq9jU5//+l8WcORk8/3wgkZGOW7q3YMECOnbsiNVqZdOmTZJcCSGEEEIIcQ2SYBnAIzOTlJE9SaqbyQ52kE/+pWv1fPx5rGE4ShW/OEVampWhQ5Np3tyD//wn0CExms1mRo8ezSOPPELbtm3ZsmULbdq0cUjfQgghhBBClFeSYBnAPSuLYwP+w8ngFCKIIImCPVP70s4x7+guMs15NvX3/PPnOHXKwuzZ1fD2LvkjTUlJ4Z577mHKlCkMHz6cdevWUaNGjRL3K4QQQgghRHknCZYBTKnnuPHRaII9I/iKr6hNbQC+Prmff/+2ilyrpdh9rV+fzfTp6Tz7bAC33OJ9/RuuIyEhgTZt2rB582bmzJnDhx9+iIeHR4n7FUIIIYQQoiKQIhcG8EzPwGvvGeoF3Ew9Ii59/lKz9vQJaUoVz0rF6ic93cqQIck0buzOxIklr+hntVoZNGgQZrOZ+Ph4br755hL3KYQQQgghREUiM1gG8PDI4fQbg1jrt5ad7Lz0uZtSNPWrWux+Nm/O4cwZC3PnVsfHx/5HmZubS05ODm5ubnz11Vds27ZNkishhBBCiAooJiaGyMhIAgICaNSoEXFxcUaH5HJkBssAbkEenGoznFmeD1CFI3zMx3x35jDfnPyDN8NuL/YMVteuPhw7Vo/q1e0/UDg/P5+oqChatGjBrFmzaNKkid19CSGEEEII1zV58mRmz57N/PnziYiIYPfu3fj5+RkdlsuRBMsAqjAf2lfpDI8UHjK85MR+vjq+j2mtOl/3/pQUCz/9lEOPHr4lSq4APDw86NmzpyRWQgghhBBlLTbq+m3qRUP4mL/aNxkETQdBTgqs7XPte6Niix1KcnIyEyZMID4+nvDwcADCwsI4evQo1apVo2XLlgAsXryYatWqFbvfikgSLCN4uKOsOZz2yeX/27v7+KiqO4/jn19CHiAkQUCeVh610lpTDFFEbAgvu5RaoC3Y13bVoqBSbVNZy9a1VLpFQXBbHkqtD6BYFNb21VpqhSpY2o2AqAVpqbSRAkLBII8JJCEJIcnZP+6EDkNIJnEydyb5vnmdF5l7zr3zG36cJL+5594ZyECcc6w7tJd/7TmApISmC6b580+wcOFJ9uzpR9++zU+hc44f/OAHDB8+nLy8PGbMmNGSVyEiIiIibcT69evJyso6W1wFy8vL48UXX/QhqvikAssPycl0qDlJcSoMYhCFZcc5UFnGzF4jwtr94Ye78vnPd2pRcVVcXMzkyZNZvXo1+fn55OXlNfsYIiIiIhIB4wtaPj61e9P7l5WFfeji4mK6dGn481TfeOMNcnNzyc3N5ZFHHmnW57W2R7rJhQ/qUjuSUFNKTQIMZCDrDu0FYEzPgY3ud/hwDSdO1JKcbIwcGd51WsHeeustsrOzWbt2LYsXL+axxx5rUfwiIiIi0rZkZ2ezadMmtm/fjnOOXbt2UVhYSO/evdm9ezcbNmzgyJEjrFq1yu9QY54KLB/UpaRBXRldAn/WHdrLx9O70j8t84L7OOeYPPko1157kDNnXLOezznHokWLyM3NJSEhgU2bNjFt2jS9+yAiIiIiAIwYMYKZM2cybtw40tPTmTBhApWVlaSkpJCWloaZMXHiRLZv3+53qDFPBZYPalM6U+NKGcQgKmvP8PrRA3yu16BG91m6tIy1ayuZNi2DpKTwC6OSkhImTpzI9OnTGTduHNu2bWPYsGEf9SWIiIiISBtz//33c+DAAcrLy9mxYwdDhw6ltLT0bP/GjRu57LLLfIwwPqjA8kFtSjpVVspABrLh6AGq6moY0+vCywN37z7D9OnHGT26I1//ekbYz7N161aGDh3KmjVrWLRoEatWreKiiz76BxKLiIiISPvw+uuvk5OTQ25uLkVFRdxyyy1+hxTzdJOLaKuroyY5g9IzJxjEINYd2ktqQgfyLu7b4PDqasettx4hKcl49tmLSUgI/+zV8ePHAdi0aRPXXnttRMIXERERkfZj/PjxjB8/3u8w4orOYEXbyZN88svjuWRfIvnkMyAtkzsHfoqOiUkNDp8xo5g//vE0y5Z155JLmq6Hi4qKWLlyJQBjxozhvffeU3ElIiIiIhIlOoMVbcXFpBwo4YqaIUB/pn2s/wWHrl59ioULT5Kfn8FNN3UO6/Bz585lxYoV3HjjjXTr1o2UlJQIBS4iIiIiIk3RGawoqz66n51L7mbV5ZvZW3WU6rraBsft31/D7bcfJTs7mfnzuzZ6zFOnTrFv3z4AHn30UbZs2UK3bt0iHbqIiIiIiDRBBVaUVZ/8kPKhd7D5om1860//x1Wv/bTBca+8UkFtreMXv+hJauqF07Rt2zZycnL44he/SG1tLenp6QwePLi1whcRERERkUZoiWCUdT6RyFVjh9P73d/x7sCBHDtd2eC4e+7JYMKETvTs2XCKqqurmTNnDvPmzaNnz5488cQTJCYmtmboIiIiIiLSBBVY0VZcTGKto0+XK+jTq/d53evXV9CpUwIjRqResLjaunUrU6ZMYceOHdx2220sWrSIrl0bX0YoIiIiIiKtT0sEo+xE6lG2/Pa7LOBF3ik5dE6fc44HHyxh2rRj1NW58/atqqpixowZDB8+nJKSEtasWcNzzz2n4kpEREREJEboDFaUlaYnkXjxZ/lJ2VxWFV7EGzd89WyfmfHaa70pKak97/Ou3n77baZMmUJhYSF33nkn8+fPp0uXLtEOX0REREREGqEzWFFWlZxAQu1J9pV0ZEyvgYB35mrZslJOn3ZkZiYwYMD5n4m1c+dOysvLWbt2Lc8884yKKxERERGRGKQCK8qqU1JwdaVwqitjenoF1qxZJdx11zGef77s7DjnHEuXLmXp0qUATJo0icLCQsaMGeNL3CIiIiIi0jQVWFFWl9SJWldKlzO9ubprL5544iQPP3yCO+5I56670s+OMzN+85vfsHr1apxzmBlpaWk+Ri4iIiIibd3PfvYzcnJyyMzM5NJLL6WgoMDvkOKOCqwoc0mdqaaUz2Zm8atfVvDNbx7nC1/oxJIl3fnggw+YNGkS77//PuD9B3/55ZcxsyaOKiIiIiLy0SxYsIA5c+bw9NNPU1JSwksvvcSAAQP8Divu+H6TCzMbCXwbyAH6AFOcc8ub2CcL+AkwDCgGlgCznXPn33ovxtR1yKCqbg/9i/vx1a8e4frrU5k/v5oHHvg2Tz31FHV1dYwbN45BgwaRkZHhd7giIiIi0kp27tzZ5JjMzEx69ep1dny3bt3o3r07NTU17Nmzp9F9+/TpE3YsR48e5aGHHmLjxo0MGTIEgKysLAAKCgqYPXs2dXV1TJs2jQkTJoR93HC0tXrA9wIL6AzsAJ4PtEaZWQbwO2ADcA0wGFgOnAIWtFqUEeISMyivq+DxuzvSv38tvXt/nyuuWI5zjptvvpnZs2frnQIRERERiar169eTlZV1triqV1VVxYIFC3j11VdJTk5uradvU/WA7wWWc+4V4BUAM1sexi63Ap2A251zlcAOM/sEMN3MFsZC1XohdRXluMQ0SiuqqTt2it1V4/jww1Pce++93HffffTr18/vEEVEREQkSgYPHtzi8R06dGhy/7Kyskb7gxUXFzd4l+rNmzfTsWNHxo8fT6dOnXjyySfPnlGLlLZWD8TjNVjXARsD/5j11uGdThzgS0RhKj78V6y2gpJSIy0tn7lz7+PAgQMsXLhQxZWIiIiI+CY7O5tNmzaxfft2nHPs2rWLwsJCDh8+zO7du1m9ejVTp05l1qxZfocKMV4P+H4GqwV6AR+EbDsc1Lc3uMPMvgZ8DbxK3887oSQfP87ph37Ilj6f4oUX5pCcnMz27dt9i0ear7y8XHfTiWPKX/xS7uKbb2DP+gAAC9VJREFU8hfflL/IyMzMbNYZpUiora0N+zmzsrK4//77GTt2LCdOnKBfv34sWbKE5ORkrrnmGk6fPs2wYcN45JFHLnjMqqqqC/1f6WBmW4MeL3XOLW3u6wnSrHog2uKxwAIIPe1nF9hOIHlLAdLS0tyoUaNaN7Km3HQTVlCA73FIixQod3FN+Ytfyl18U/7im/IXGYWFhaSnpzc9MILKysqa9ZwzZ85k5syZ52w7fvw4Tz75JJ07d+Zvf/sbl19++QWPmZqaSnZ2dkNdNc65q5sRejjCrgeiLR4LrEN4lWmwHoG/DyMiIiIiIhHRrVs3JkyYQF5eHgkJCTz77LN+hwQxXg/EY4H1JvA/ZpbqnKsKbBsNHAT2+RaViIiIiEgblJ+fT35+vt9hBIvpesD3m1yYWWczu8rMrgrE0y/wuF+gf56Z/T5olxeACmC5mV1pZhOB7wC+3zFERERERESap63VA74XWMDVwJ8CrSPwUODrhwP9vYFL6wc7507iVah9gK3A43j3u18YvZBFRERERCRC2lQ94PsSQedcAf+8KK2h/skNbHsXGNl6UYmIiIiISDS0tXogFs5giYiIiIi0eTGweq3VtOXX1lwqsEREREREWllSUhKVlZVND4xTlZWVJCUl+R1GTFCBJSIiIiLSynr06EFRUREVFRVt6myPc46KigqKioro0aNH0zu0A75fgyUiIiIi0tZlZGQAcPDgQc6cOROV56yqqiI1NbXVnycpKYmePXuefY3tnQosEREREZEoyMjIiGoRUlBQQHZ2dtSeTzxaIigiIiIiIhIhKrBEREREREQiRAWWiIiIiIhIhKjAEhERERERiRBrS7eJbIqZ1QGx8AEEHYAav4OQFlHu4pvyF7+Uu/im/MU35S9+xUruOjrn2s2JnXZVYMUKM9vqnLva7zik+ZS7+Kb8xS/lLr4pf/FN+Ytfyp0/2k0lKSIiIiIi0tpUYImIiIiIiESICix/LPU7AGkx5S6+KX/xS7mLb8pffFP+4pdy5wNdgyUiIiIiIhIhOoMlIiIiIiISISqwREREREREIkQFloiIiIiISISowIoiM/uGme01syoze8fMcv2OSc5lZrPMzIW0Q0H9Fhhz0MwqzazAzD7pZ8ztmZmNNLOXzawokKvJIf1N5svMLjKzFWZ2MtBWmFmXqL6QdiqM/C1vYD6+FTImxcweM7NjZnYqcLxLovpC2iEzm2FmW8ys1MyOmtlqM7syZIzmXwwKM3eaezHKzPLN7C+B/JWa2ZtmNjaoX/MuBqjAihIz+wqwGJgLZAObgVfNrJ+vgUlDdgK9g1pWUN9/Af8J3AtcAxwBfmdm6dEOUgDoDOwA/gOobKA/nHy9AAwFbgQ+F/h6RSvGLP/UVP4A1nPufPx8SP+PgJuAm4FcIANYY2aJrRGwnDUKeAIYAdwA1ADrzaxr0BjNv9g0iqZzB5p7seoD4AG8uXI18AfgJTP7VKBf8y4WOOfUotCAt4GnQ7btAub5HZvaOTmZBey4QJ8BHwIPBm3rCJQBd/sde3tvQDkwuTn5Aj4BOOD6oDGfDmwb7Pdrak8tNH+BbcuBNY3skwlUA7cGbesL1AFj/H5N7anhFcu1wPjAY82/OGmhuQts09yLowYUA3dr3sVO0xmsKDCzZCAHeC2k6zW8d5AktgwKLFnaa2Y/N7NBge0DgV4E5dE5VwlsQHmMReHk6zq8X+w3B+33BnAK5TRWfNrMjpjZ383saTPrEdSXAyRxbo4PAIUof9GWjrcqpiTwWPMvfoTmrp7mXowzs0Qz+3e8InkzmncxQwVWdHQHEoHDIdsP400EiR1vA5PxTptPxcvPZjPrxj9zpTzGh3Dy1Qs46gJv4QEEvj6CchoL1gK3AZ/BW/IyDPiDmaUE+nvhvfN+LGQ/zcnoWwz8GXgz8FjzL36E5g4092KamWWZWTlwGngKmOCcexfNu5jRwe8A2pnQT3W2BraJj5xzrwY/DlzU+z5wO1B/ga/yGF+ayldDuVNOY4Bz7udBD981s3eAfwBjgVWN7Kr8RZGZLcRbYvRp51xtSLfmXwy7UO4092LeTuAqoAvedXDPmdmooH7NO5/pDFZ0HMN7pyf0nYEenP8ug8QQ51w58FfgY0D93QSVx/gQTr4OAT3MzOo7A19fjHIac5xzB/Eu8P5YYNMhvNUB3UOGak5GiZktwrvJwQ3OufeDujT/YlwjuTuP5l5scc5VO+d2O+e2Oudm4J2B/BaadzFDBVYUOOeqgXeA0SFdozl3DazEGDNLBT6Od9HoXrxvTKND+nNRHmNROPl6E2/t+nVB+10HpKGcxhwz6w78C958BO/76hnOzfEleBdxK3+tzMwWA7fg/YL+Xki35l8MayJ3DY3X3IttCUAKmncxQ0sEo2chsMLM/oh3MeE9QB+8tbMSI8xsPrAa2I/3js/38L7pPOecc2b2I+BBM3sP+DswE+9i0Rd8CrldM7POwGWBhwlAPzO7Cih2zu1vKl/OuUIzWwssMbOpeEskluDdPWtnlF9Ou9NY/gJtFvArvF/qBgDz8K4T+DWAc+6kmS0DfmhmR4DjeN9r/4J3i2lpJWb2ODAJ+BJQYmb175iXO+fKw/l+qfnnj6ZyF5iXs9Dci0lm9ijwW+AA3g1KbsG79f5YzbsY4vdtDNtTA74B7MO7KPEdYKTfMamdl6OfAwfxbj9bhPcD5oqgfsP7wfMhUAW8Dlzpd9ztteH9UHENtOXh5gvoCqwESgNtJdDF79fWHlpj+cO7tfA6vF/qqvGu/1gO9A05RirwGN4veBV4b5D09eP1tKd2gbw5YFbQGM2/GGxN5U5zL7ZbIBf/CPwueQSvoB0T1K95FwPNAv/QIiIiIiIi8hHpGiwREREREZEIUYElIiIiIiISISqwREREREREIkQFloiIiIiISISowBIREREREYkQFVgiIiIiIiIRogJLRESaZGYujLYvMHZ5/dd+C8RSH19BM/etCdr3rlYKUURE2pgOfgcgIiJx4bqQx78GtuN9oGW904G/ZwOLoxBTuA4BE/A+ULM5rgf6AKsiHpGIiLRZKrBERKRJzrm3gh+b2WngWOj2wNg9UQssPKcbirMpzrm3zWxA5MMREZG2TEsERUQkokKXCJrZgMAyu3vMbJ6ZHTKzMjNbaWadzOwyM1tnZuVmttvMbm/gmEPM7GUzKzGzSjN7w8xyP0KMnc3sMTPbb2anzeywma03s4+39JgiIiKgAktERKJnBt6Su9uB/wa+AjyFt9zwt3jL+P4C/NTMPlm/k5kNBTYDXYGpwE3AcWC9meW0MJZFwL8BDwGjgXuAPwNdWng8ERERQEsERUQkevY45+rPTq0LnIGaBExyzq0EMLOtwBeALwN/DYz9IbAfuME5Vx0Ytw7YAXwP+FILYrkO+F/n3LKgbb9uwXFERETOoTNYIiISLa+GPH4v8Pe6+g3OuRLgCNAXwMw6AnnAL4E6M+tgZh0AA9YDI1sYyxZgspl918yuNrPEFh5HRETkHCqwREQkWkpCHlc3sj018HVXIBHvTNWZkPZN4CIza8nPsnuBJcAdeMXWETNbZGadWnAsERGRs7REUEREYtkJoA54HHi+oQHOubrmHtQ5V453TdgMM+uPtyTxUbzi7oEWRysiIu2eCiwREYlZzrlTZrYRGAJsa0kxFcZz/ANYYGa3AldG+vgiItK+qMASEZFYNx3YgHdjjGXAh0B3YCiQ6Jz7TnMPaGZvAi8D7wLleNd5DQGei1TQIiLSPqnAEhGRmOac22Zm1wDfB34MZAJHgW14t3lviQ14t2n/Dt7PwveBbznnfvzRIxYRkfbMnHN+xyAiItIqzGw5MAq4DHDOudpm7JsIDAB2A1Odc8+0QogiItLG6C6CIiLS1vXHu+vg75u532m84kpERCRsOoMlIiJtlpkNwLteC6DMObezGfvm4H3eFsA+59yxyEYnIiJtkQosERERERGRCNESQRERERERkQhRgSUiIiIiIhIhKrBEREREREQiRAWWiIiIiIhIhKjAEhERERERiZD/B/u0c3wzLJ2DAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"\n"
]
}
],
"source": [
"plot_results(u_vec_history)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Interactive Results "
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
""
],
"text/vnd.plotly.v1+html": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"'''Create interactive plots'''\n",
"\n",
"import plotly.offline as py\n",
"py.init_notebook_mode()\n",
"import plotly.graph_objs as go\n",
"\n",
"\n",
"layout=go.Layout(title=\"Point-Reactor Model\", \n",
" xaxis={'title':'Time [s]'}, \n",
" yaxis=dict(side='left',title='HELLO'), \n",
" yaxis2=dict(overlaying='y',anchor='x',side='right',title='HELLO')\n",
" )\n",
"\n",
"\n",
"fig = go.FigureWidget(layout=layout)\n",
"\n",
"scatt = fig.add_scatter()\n",
"\n",
"fig.layout.titlefont.size = 22\n",
"fig.layout.titlefont.family = 'Rockwell'\n",
"fig.layout.xaxis.title = 'Time [s]'\n",
"fig.layout.yaxis.title = 'n/n_0'\n",
"#fig.layout.yaxis2.title = 'T [K]'"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "6b371a01ca8249bbbd00d9f6174d456f",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"interactive(children=(FloatSlider(value=0.01, description='$\\\\rho/\\\\beta=$', max=0.1, min=-0.1, readout_format…"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "993be29d3583467d888266df3c5b75e1",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"FigureWidget({\n",
" 'data': [{'line': {'color': 'red'},\n",
" 'type': 'scatter',\n",
" 'uid': '…"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"'''Vary parameters and display results interactively'''\n",
"\n",
"from ipywidgets import interact\n",
"import ipywidgets as widgets\n",
"#display(widgets.FloatSlider(readout_format='8.4e'))\n",
"@interact(rho_over_beta=widgets.FloatSlider(description=r'$\\rho/\\beta=$',value=0.01,min=-0.1,max=0.1,step=0.01,readout_format='5.3f'), \n",
" gen_time=widgets.FloatSlider(description=r'$\\ell=$',value=1e-4,min=1e-4,max=1e-3,step=1e-4,readout_format='5.3e'),\n",
" alpha_n=widgets.FloatSlider(description=r'$\\alpha_n=$',value=0.0,min=-3e-4,max=1.0e-5,step=1e-5,readout_format='5.3e'),\n",
" select=widgets.Dropdown(description='select:',value='neutron_density',options=['neutron_density', 'c_1']) \n",
" )\n",
"def update(rho_over_beta, gen_time, alpha_n, select):\n",
" with fig.batch_update():\n",
" scatt.x=time_stamps\n",
" beta = params['beta']\n",
" params['reactivity_0'] = rho_over_beta * beta\n",
" params['alpha_n'] = alpha_n\n",
" params['gen_time'] = gen_time\n",
" history = run_point_reactor( f_vec, time_stamps, params )\n",
" if select == 'neutron_density':\n",
" scatt.y=history[:,0]/params['n_0']\n",
" scatt.line.color='red'\n",
" fig.layout.yaxis.title = 'n/n_0'\n",
" elif select == 'c_1':\n",
" scatt.y=history[:,1]/params['c_vec_0'][0]\n",
" scatt.line.color='blue'\n",
" fig.layout.yaxis.title = 'c_1/c_1_0'\n",
" else:\n",
" pass\n",
"fig"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.1"
},
"latex_envs": {
"LaTeX_envs_menu_present": true,
"autoclose": false,
"autocomplete": true,
"bibliofile": "biblio.bib",
"cite_by": "apalike",
"current_citInitial": 1,
"eqLabelWithNumbers": true,
"eqNumInitial": 1,
"hotkeys": {
"equation": "Ctrl-E",
"itemize": "Ctrl-I"
},
"labels_anchors": false,
"latex_user_defs": false,
"report_style_numbering": false,
"user_envs_cfg": false
}
},
"nbformat": 4,
"nbformat_minor": 2
}