<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<meta name="generator" content="pandoc">
<meta name="author" content="Fill In Your Name" />
<meta name="dcterms.date" content="2022-03-01" />
<title>Causal Inference</title>
<meta name="apple-mobile-web-app-capable" content="yes">
<meta name="apple-mobile-web-app-status-bar-style" content="black-translucent">
<meta name="viewport" content="width=device-width, initial-scale=1.0, maximum-scale=1.0, user-scalable=no, minimal-ui">
<link rel="stylesheet" href="causalinference-slides_files/reveal.js-3.3.0.1/css/reveal.css"/>
<link rel="stylesheet" href="causalinference-slides_files/reveal.js-3.3.0.1/css/theme/simple.css" id="theme">
<!-- some tweaks to reveal css -->
<style type="text/css">
.reveal h1 { font-size: 2.0em; }
.reveal h2 { font-size: 1.5em; }
.reveal h3 { font-size: 1.25em; }
.reveal h4 { font-size: 1em; }
.reveal .slides>section,
.reveal .slides>section>section {
padding: 0px 0px;
}
.reveal table {
border-width: 1px;
border-spacing: 2px;
border-style: dotted;
border-color: gray;
border-collapse: collapse;
font-size: 0.7em;
}
.reveal table th {
border-width: 1px;
padding-left: 10px;
padding-right: 25px;
font-weight: bold;
border-style: dotted;
border-color: gray;
}
.reveal table td {
border-width: 1px;
padding-left: 10px;
padding-right: 25px;
border-style: dotted;
border-color: gray;
}
</style>
<style type="text/css">code{white-space: pre;}</style>
<!-- Printing and PDF exports -->
<script id="paper-css" type="application/dynamic-css">
/* Default Print Stylesheet Template
by Rob Glazebrook of CSSnewbie.com
Last Updated: June 4, 2008
Feel free (nay, compelled) to edit, append, and
manipulate this file as you see fit. */
@media print {
/* SECTION 1: Set default width, margin, float, and
background. This prevents elements from extending
beyond the edge of the printed page, and prevents
unnecessary background images from printing */
html {
background: #fff;
width: auto;
height: auto;
overflow: visible;
}
body {
background: #fff;
font-size: 20pt;
width: auto;
height: auto;
border: 0;
margin: 0 5%;
padding: 0;
overflow: visible;
float: none !important;
}
/* SECTION 2: Remove any elements not needed in print.
This would include navigation, ads, sidebars, etc. */
.nestedarrow,
.controls,
.fork-reveal,
.share-reveal,
.state-background,
.reveal .progress,
.reveal .backgrounds {
display: none !important;
}
/* SECTION 3: Set body font face, size, and color.
Consider using a serif font for readability. */
body, p, td, li, div {
font-size: 20pt!important;
font-family: Georgia, "Times New Roman", Times, serif !important;
color: #000;
}
/* SECTION 4: Set heading font face, sizes, and color.
Differentiate your headings from your body text.
Perhaps use a large sans-serif for distinction. */
h1,h2,h3,h4,h5,h6 {
color: #000!important;
height: auto;
line-height: normal;
font-family: Georgia, "Times New Roman", Times, serif !important;
text-shadow: 0 0 0 #000 !important;
text-align: left;
letter-spacing: normal;
}
/* Need to reduce the size of the fonts for printing */
h1 { font-size: 28pt !important; }
h2 { font-size: 24pt !important; }
h3 { font-size: 22pt !important; }
h4 { font-size: 22pt !important; font-variant: small-caps; }
h5 { font-size: 21pt !important; }
h6 { font-size: 20pt !important; font-style: italic; }
/* SECTION 5: Make hyperlinks more usable.
Ensure links are underlined, and consider appending
the URL to the end of the link for usability. */
a:link,
a:visited {
color: #000 !important;
font-weight: bold;
text-decoration: underline;
}
/*
.reveal a:link:after,
.reveal a:visited:after {
content: " (" attr(href) ") ";
color: #222 !important;
font-size: 90%;
}
*/
/* SECTION 6: more reveal.js specific additions by @skypanther */
ul, ol, div, p {
visibility: visible;
position: static;
width: auto;
height: auto;
display: block;
overflow: visible;
margin: 0;
text-align: left !important;
}
.reveal pre,
.reveal table {
margin-left: 0;
margin-right: 0;
}
.reveal pre code {
padding: 20px;
border: 1px solid #ddd;
}
.reveal blockquote {
margin: 20px 0;
}
.reveal .slides {
position: static !important;
width: auto !important;
height: auto !important;
left: 0 !important;
top: 0 !important;
margin-left: 0 !important;
margin-top: 0 !important;
padding: 0 !important;
zoom: 1 !important;
overflow: visible !important;
display: block !important;
text-align: left !important;
-webkit-perspective: none;
-moz-perspective: none;
-ms-perspective: none;
perspective: none;
-webkit-perspective-origin: 50% 50%;
-moz-perspective-origin: 50% 50%;
-ms-perspective-origin: 50% 50%;
perspective-origin: 50% 50%;
}
.reveal .slides section {
visibility: visible !important;
position: static !important;
width: auto !important;
height: auto !important;
display: block !important;
overflow: visible !important;
left: 0 !important;
top: 0 !important;
margin-left: 0 !important;
margin-top: 0 !important;
padding: 60px 20px !important;
z-index: auto !important;
opacity: 1 !important;
page-break-after: always !important;
-webkit-transform-style: flat !important;
-moz-transform-style: flat !important;
-ms-transform-style: flat !important;
transform-style: flat !important;
-webkit-transform: none !important;
-moz-transform: none !important;
-ms-transform: none !important;
transform: none !important;
-webkit-transition: none !important;
-moz-transition: none !important;
-ms-transition: none !important;
transition: none !important;
}
.reveal .slides section.stack {
padding: 0 !important;
}
.reveal section:last-of-type {
page-break-after: avoid !important;
}
.reveal section .fragment {
opacity: 1 !important;
visibility: visible !important;
-webkit-transform: none !important;
-moz-transform: none !important;
-ms-transform: none !important;
transform: none !important;
}
.reveal section img {
display: block;
margin: 15px 0px;
background: rgba(255,255,255,1);
border: 1px solid #666;
box-shadow: none;
}
.reveal section small {
font-size: 0.8em;
}
}
</script>
<script id="pdf-css" type="application/dynamic-css">
/**
* This stylesheet is used to print reveal.js
* presentations to PDF.
*
* https://github.com/hakimel/reveal.js#pdf-export
*/
* {
-webkit-print-color-adjust: exact;
}
body {
margin: 0 auto !important;
border: 0;
padding: 0;
float: none !important;
overflow: visible;
}
html {
width: 100%;
height: 100%;
overflow: visible;
}
/* Remove any elements not needed in print. */
.nestedarrow,
.reveal .controls,
.reveal .progress,
.reveal .playback,
.reveal.overview,
.fork-reveal,
.share-reveal,
.state-background {
display: none !important;
}
h1, h2, h3, h4, h5, h6 {
text-shadow: 0 0 0 #000 !important;
}
.reveal pre code {
overflow: hidden !important;
font-family: Courier, 'Courier New', monospace !important;
}
ul, ol, div, p {
visibility: visible;
position: static;
width: auto;
height: auto;
display: block;
overflow: visible;
margin: auto;
}
.reveal {
width: auto !important;
height: auto !important;
overflow: hidden !important;
}
.reveal .slides {
position: static;
width: 100%;
height: auto;
left: auto;
top: auto;
margin: 0 !important;
padding: 0 !important;
overflow: visible;
display: block;
-webkit-perspective: none;
-moz-perspective: none;
-ms-perspective: none;
perspective: none;
-webkit-perspective-origin: 50% 50%; /* there isn't a none/auto value but 50-50 is the default */
-moz-perspective-origin: 50% 50%;
-ms-perspective-origin: 50% 50%;
perspective-origin: 50% 50%;
}
.reveal .slides section {
page-break-after: always !important;
visibility: visible !important;
position: relative !important;
display: block !important;
position: relative !important;
margin: 0 !important;
padding: 0 !important;
box-sizing: border-box !important;
min-height: 1px;
opacity: 1 !important;
-webkit-transform-style: flat !important;
-moz-transform-style: flat !important;
-ms-transform-style: flat !important;
transform-style: flat !important;
-webkit-transform: none !important;
-moz-transform: none !important;
-ms-transform: none !important;
transform: none !important;
}
.reveal section.stack {
margin: 0 !important;
padding: 0 !important;
page-break-after: avoid !important;
height: auto !important;
min-height: auto !important;
}
.reveal img {
box-shadow: none;
}
.reveal .roll {
overflow: visible;
line-height: 1em;
}
/* Slide backgrounds are placed inside of their slide when exporting to PDF */
.reveal section .slide-background {
display: block !important;
position: absolute;
top: 0;
left: 0;
width: 100%;
z-index: -1;
}
/* All elements should be above the slide-background */
.reveal section>* {
position: relative;
z-index: 1;
}
/* Display slide speaker notes when 'showNotes' is enabled */
.reveal .speaker-notes-pdf {
display: block;
width: 100%;
max-height: none;
left: auto;
top: auto;
z-index: 100;
}
/* Display slide numbers when 'slideNumber' is enabled */
.reveal .slide-number-pdf {
display: block;
position: absolute;
font-size: 14px;
}
</script>
<script>
var style = document.createElement( 'style' );
style.type = 'text/css';
var style_script_id = window.location.search.match( /print-pdf/gi ) ? 'pdf-css' : 'paper-css';
var style_script = document.getElementById(style_script_id).text;
style.innerHTML = style_script;
document.getElementsByTagName('head')[0].appendChild(style);
</script>
<script src="causalinference-slides_files/header-attrs-2.10/header-attrs.js"></script>
<link href="causalinference-slides_files/font-awesome-5.1.0/css/all.css" rel="stylesheet" />
<link href="causalinference-slides_files/font-awesome-5.1.0/css/v4-shims.css" rel="stylesheet" />
</head>
<body>
<div class="reveal">
<div class="slides">
<section>
<h1 class="title">Causal Inference</h1>
<h2 class="author">Fill In Your Name</h2>
<h3 class="date">01 March 2022</h3>
</section>
<section id="TOC">
<ul>
<li><a
href="#/why-should-social-scientists-and-policymakers-care-about-causality">Why
should social scientists and policymakers care about causality?</a></li>
<li><a
href="#/counterfactual-approach-to-causal-inference">Counterfactual
Approach to Causal Inference</a>
<ul>
<li><a href="#/recent-changes-in-social-science-research">Recent changes
in social science research</a></li>
<li><a href="#/x-causes-y-is-a-claim-about-what-didnt-happen">“X causes
Y” is a claim about what didn’t happen</a></li>
<li><a href="#/how-to-interpret-x-causes-y-in-this-approach">How to
interpret “X causes Y” in this approach</a></li>
<li><a href="#/how-to-interpret-x-causes-y-in-this-approach-1">How to
interpret “X causes Y” in this approach</a></li>
<li><a href="#/exercise-echinacea">Exercise: Echinacea</a></li>
</ul></li>
<li><a href="#/potential-outcomes">Potential Outcomes</a>
<ul>
<li><a href="#/potential-outcomes-1">Potential outcomes</a></li>
<li><a href="#/definition-of-causal-effect">Definition of causal
effect</a></li>
<li><a href="#/key-features-of-this-definition-of-causal-effect">Key
features of this definition of causal effect</a></li>
<li><a
href="#/imagine-we-know-both-y_i1-and-y_i0-this-is-never-true">Imagine
we know both <span class="math inline">\(Y_i(1)\)</span> and <span
class="math inline">\(Y_i(0)\)</span> (this is never true!)</a></li>
<li><a href="#/average-causal-effect">Average causal effect</a></li>
<li><a href="#/estimands-and-causal-questions">Estimands and causal
questions</a></li>
<li><a href="#/other-types-of-estimands-you-may-be-interested-in">Other
types of estimands you may be interested in</a></li>
</ul></li>
<li><a href="#/randomization-of-treatment-assignment">Randomization of
treatment assignment</a>
<ul>
<li><a href="#/randomization-of-treatment-assignment-1">Randomization of
treatment assignment</a></li>
<li><a href="#/random-assignment-vs.-random-sampling">Random assignment
vs. random sampling</a></li>
<li><a href="#/randomization-is-powerful-1">Randomization is powerful
(1)</a></li>
<li><a href="#/randomization-is-powerful-2">Randomization is powerful
(2)</a></li>
<li><a href="#/randomization-is-powerful-3">Randomization is powerful
(3)</a></li>
<li><a href="#/random-sampling">Random sampling</a></li>
<li><a href="#/potential-outcomes-2">Potential outcomes</a></li>
<li><a href="#/random-assignment-to-red-1-or-blue-0-condition">Random
assignment to red (1) or blue (0) condition</a></li>
<li><a href="#/three-key-assumptions">Three key assumptions</a></li>
<li><a href="#/key-assumption-sutva-part-1">Key assumption: SUTVA, part
1</a></li>
<li><a href="#/key-assumption-sutva-part-2">Key assumption: SUTVA, part
2</a></li>
<li><a href="#/key-assumption-excludability">Key assumption:
Excludability</a></li>
<li><a href="#/randomization-is-powerful-4">Randomization is powerful
(4)</a></li>
</ul></li>
<li><a href="#/randomized-vs.-observational-studies">Randomized
vs. observational studies</a>
<ul>
<li><a href="#/different-types-of-studies">Different types of
studies</a></li>
<li><a href="#/exercise-learning-about-your-prior-knowledge">Exercise:
Learning about your prior knowledge</a></li>
<li><a
href="#/exercise-observational-studies-vs.-randomized-studies">Exercise:
Observational studies vs. Randomized studies</a></li>
<li><a href="#/discuss">Discuss</a></li>
<li><a href="#/generalizability-and-external-validity">Generalizability
and external validity</a></li>
<li><a href="#/references">References</a></li>
</ul></li>
</ul>
</section>
<section
id="why-should-social-scientists-and-policymakers-care-about-causality"
class="slide level2">
<h2>Why should social scientists and policymakers care about
causality?</h2>
<ul>
<li>[Discussion with your own examples.]</li>
</ul>
</section>
<section>
<section id="counterfactual-approach-to-causal-inference"
class="title-slide slide level1">
<h1>Counterfactual Approach to Causal Inference</h1>
</section>
<section id="recent-changes-in-social-science-research"
class="slide level2">
<h2>Recent changes in social science research</h2>
<ul>
<li><p>Historically, reverse causality and omitted variable bias have
been problematic for a lot of social science research aimed at making
causal claims.</p></li>
<li><p>Recently, the counterfactual approach has been embraced in the
social sciences as a framework for causal inference.</p></li>
<li><p>This represents a big shift in research:</p>
<ul>
<li><p>Being more precise about what we mean by causal effects.</p></li>
<li><p>Using randomization or designs with as-if randomization.</p></li>
<li><p>More partnerships between researchers and practitioners.</p></li>
</ul></li>
</ul>
</section>
<section id="x-causes-y-is-a-claim-about-what-didnt-happen"
class="slide level2">
<h2>“X causes Y” is a claim about what didn’t happen</h2>
<ul>
<li><p>In the counterfactual approach: “If X had not occurred, then Y
would not have occurred.”</p></li>
<li><p>Experiments help us learn about counterfactual and
manipulation-based claims about causation.</p></li>
<li><p>It’s not wrong to <em>conceptualize</em> “cause” in another way.
But it has been productive to work in this counterfactual framework
<span class="citation" data-cites="brady2008causation">(<a
href="#/ref-brady2008causation" role="doc-biblioref">Brady
2008</a>)</span>.</p></li>
</ul>
</section>
<section id="how-to-interpret-x-causes-y-in-this-approach"
class="slide level2">
<h2>How to interpret “X causes Y” in this approach</h2>
<ol type="1">
<li><p>“X causes Y” need not imply that W and V do not cause Y: X is a
part of the story, not the whole story. (The whole story is not
necessary in order to learn about whether X causes Y).</p></li>
<li><p>“X causes Y” requires a <strong>context</strong>: matches cause
flame but require oxygen; small classrooms improve test scores but
require experienced teachers and funding <span class="citation"
data-cites="cartwright2012evidence">(<a
href="#/ref-cartwright2012evidence" role="doc-biblioref">Cartwright and
Hardie 2012</a>)</span>.</p></li>
<li><p>“X causes Y” can mean “With X, the probability of Y is higher
than would be without X.” or “Without X there is no Y.” Either is
compatible with the counterfactual idea.</p></li>
</ol>
</section>
<section id="how-to-interpret-x-causes-y-in-this-approach-1"
class="slide level2">
<h2>How to interpret “X causes Y” in this approach</h2>
<ol start="4" type="1">
<li><p>It is not necessary to know the mechanism to establish that X
causes Y. The mechanism can be complex, and it can involve probability:
X causes Y sometimes because of A and sometimes because of B.</p></li>
<li><p>Counterfactual causation does not require “a spatiotemporally
continuous sequence of causal intermediates”</p>
<ul>
<li>Ex: Person A plans event Y. Person B’s action would stop Y (say, a
random bump from a stranger). Person C doesn’t know about Person A or
action Y but stops B (maybe thinks B is going to trip). So, Person A
does action Y. And Person C causes action Y (without Person C’s action,
Y would not have occurred) <span class="citation"
data-cites="holland:1986">(<a href="#/ref-holland:1986"
role="doc-biblioref">Holland 1986</a>)</span>.</li>
</ul></li>
<li><p>Correlation is not causation.</p></li>
</ol>
</section>
<section id="exercise-echinacea" class="slide level2">
<h2>Exercise: Echinacea</h2>
<ul>
<li><p>Your friend says taking echinacea (a traditional remedy) reduces
the duration of colds.</p></li>
<li><p>If we take a counterfactual approach, what does this statement
implicitly claim about the counterfactual? What other counterfactuals
might be possible and why?</p></li>
</ul>
</section></section>
<section>
<section id="potential-outcomes" class="title-slide slide level1">
<h1>Potential Outcomes</h1>
</section>
<section id="potential-outcomes-1" class="slide level2">
<h2>Potential outcomes</h2>
<ul>
<li><p>For each unit we assume that there are two
<strong>post-treatment</strong> outcomes: <span
class="math inline">\(Y_i(1)\)</span> and <span
class="math inline">\(Y_i(0)\)</span>.</p></li>
<li><p><span class="math inline">\(Y_i(1)\)</span> is the outcome that
<strong>would</strong> obtain <em>if</em> the unit received the
treatment (<span class="math inline">\(T_i=1\)</span>).</p></li>
<li><p><span class="math inline">\(Y_i(0)\)</span> is the outcome that
<strong>would</strong> obtain <em>if</em> the unit received the control
(<span class="math inline">\(T_i=0\)</span>).</p></li>
</ul>
</section>
<section id="definition-of-causal-effect" class="slide level2">
<h2>Definition of causal effect</h2>
<ul>
<li><p>The <strong>causal effect</strong> of treatment (relative to
control) is: <span class="math inline">\(\tau_i = Y_i(1) -
Y_i(0)\)</span></p></li>
<li><p>Note that we’ve moved to using <span
class="math inline">\(T\)</span> to indicate our treatment (what we want
to learn the effect of). <span class="math inline">\(X\)</span> will be
used for background variables.</p></li>
</ul>
</section>
<section id="key-features-of-this-definition-of-causal-effect"
class="slide level2">
<h2>Key features of this definition of causal effect</h2>
<ol type="1">
<li><p>You have to define the control condition to define a causal
effect.</p>
<ul>
<li>Say <span class="math inline">\(T=1\)</span> means a community
meeting to discuss public health. Is <span
class="math inline">\(T=0\)</span> no meeting at all? Is <span
class="math inline">\(T=0\)</span> a community meeting on a different
subject? Is <span class="math inline">\(T=0\)</span> a flyer on public
health?</li>
<li>The phrase ``causal effect of <span class="math inline">\(T\)</span>
on <span class="math inline">\(Y\)</span>’’ doesn’t make sense without
knowing what is means to not have <span
class="math inline">\(T\)</span>.</li>
</ul></li>
<li><p>Each individual unit <span class="math inline">\(i\)</span> has
its own causal effect <span
class="math inline">\(\tau_i\)</span>.</p></li>
<li><p>But we can’t measure the individual-level causal effect, because
we can’t observe both <span class="math inline">\(Y_i(1)\)</span> and
<span class="math inline">\(Y_i(0)\)</span> at the same time. This is
known as the <strong>fundamental problem of causal inference</strong>.
What we observe is <span class="math inline">\(Y_i\)</span>:</p></li>
</ol>
<p><span class="math inline">\(Y_i = T_iY_i(1) +
(1-T_i)Y_i(0)\)</span></p>
</section>
<section id="imagine-we-know-both-y_i1-and-y_i0-this-is-never-true"
class="slide level2">
<h2>Imagine we know both <span class="math inline">\(Y_i(1)\)</span> and
<span class="math inline">\(Y_i(0)\)</span> (this is never true!)</h2>
<table>
<thead>
<tr class="header">
<th style="text-align: right;"><span
class="math inline">\(i\)</span></th>
<th style="text-align: center;"><span
class="math inline">\(Y_i(1)\)</span></th>
<th style="text-align: center;"><span
class="math inline">\(Y_i(0)\)</span></th>
<th style="text-align: center;"><span
class="math inline">\(\tau_i\)</span></th>
</tr>
</thead>
<tbody>
<tr class="odd">
<td style="text-align: right;">Andrei</td>
<td style="text-align: center;">1</td>
<td style="text-align: center;">1</td>
<td style="text-align: center;">0</td>
</tr>
<tr class="even">
<td style="text-align: right;">Bamidele</td>
<td style="text-align: center;">1</td>
<td style="text-align: center;">0</td>
<td style="text-align: center;">1</td>
</tr>
<tr class="odd">
<td style="text-align: right;">Claire</td>
<td style="text-align: center;">0</td>
<td style="text-align: center;">0</td>
<td style="text-align: center;">0</td>
</tr>
<tr class="even">
<td style="text-align: right;">Deepal</td>
<td style="text-align: center;">0</td>
<td style="text-align: center;">1</td>
<td style="text-align: center;">-1</td>
</tr>
</tbody>
</table>
<ul>
<li><p>We have the treatment effect for each individual.</p></li>
<li><p>Note the heterogeneity in the individual-level treatment
effects.</p></li>
<li><p>But we only have at most one potential outcome for each
individual, which means we don’t know these treatment effects.</p></li>
</ul>
</section>
<section id="average-causal-effect" class="slide level2">
<h2>Average causal effect</h2>
<ul>
<li>While we can’t measure the individual causal effect, <span
class="math inline">\(\tau_i = Y_i(1)-Y_i(0)\)</span>, we can randomly
assign subjects to treatment and control conditions to estimate the
<strong>average causal effect</strong>, <span
class="math inline">\(\bar{\tau}_i\)</span>:</li>
</ul>
<p><span class="math inline">\(\overline{\tau_i} = \frac{1}{N}
\sum_{i=1}^N ( Y_i(1)-Y_i(0) ) = \overline{Y_i(1)-Y_i(0)}\)</span></p>
<ul>
<li><p>The average causal effect is also known as the average treatment
effect (ATE).</p></li>
<li><p>Further explanation on how after we discuss randomization of
treatment assignment in the next section.</p></li>
</ul>
</section>
<section id="estimands-and-causal-questions" class="slide level2">
<h2>Estimands and causal questions</h2>
<ul>
<li><p>Before we discuss randomization and how that allows us to
estimate the ATE, note that the ATE is a type of estimand.</p></li>
<li><p>An estimand is a quantity you want to learn about (from your
data). It’s the target of your research that <em>you</em> set.</p></li>
<li><p>Being precise about your research question means being precise
about your estimand. For causal questions, this means specifying:</p>
<ul>
<li>The outcome</li>
<li>The treatment and control conditions</li>
<li>The study population</li>
</ul></li>
</ul>
</section>
<section id="other-types-of-estimands-you-may-be-interested-in"
class="slide level2">
<h2>Other types of estimands you may be interested in</h2>
<ul>
<li><p>The ATE for a particular subgroup, aka conditional average
treatment effect (CATE)</p></li>
<li><p>Differences in CATEs: differences in the average treatment effect
for one group as compared with another group.</p></li>
<li><p>The ATE for just the treated units, aka ATT (average treatment
effect on the treated)</p></li>
<li><p>The local ATE (LATE). “Local” = those whose treatment status
would be changed by an encouragement in an encouragement design (aka
CACE, complier average causal effect) or those in the neighborhood of a
discontinuity for a regression discontinuity design.</p></li>
<li><p>Estimands are discussed in detail in <a
href="estimation.html">Estimands and Estimators Module</a>.</p></li>
</ul>
</section></section>
<section>
<section id="randomization-of-treatment-assignment"
class="title-slide slide level1">
<h1>Randomization of treatment assignment</h1>
</section>
<section id="randomization-of-treatment-assignment-1"
class="slide level2">
<h2>Randomization of treatment assignment</h2>
<ul>
<li><p>Randomization means that every observation has a known
probability of assignment to experimental conditions <em>between</em> 0
and 1.</p>
<ul>
<li>No unit in the experimental sample is assigned to treatment with
certainty (probability = 1) or to control with certainty (probability =
0).</li>
</ul></li>
<li><p>Units can vary in their probability of treatment assignment.</p>
<ul>
<li><p>For example, the probability might vary by group: women might
have a 25% probability of being assigned to treatment while men have a
different probability.</p></li>
<li><p>It can even vary across individuals, though that would complicate
your analysis.</p></li>
</ul></li>
</ul>
</section>
<section id="random-assignment-vs.-random-sampling"
class="slide level2">
<h2>Random assignment vs. random sampling</h2>
<ul>
<li><p>Randomization (of treatment): assigning subjects with known
probability to experimental conditions.</p>
<ul>
<li><p>This random assignment of treatment can be combined with any kind
of sample (random sample, convenience sample, etc.).</p></li>
<li><p>But the size and other characteristics of your sample will affect
your power and your ability to extrapolate from your finding to other
populations.</p></li>
</ul></li>
<li><p>Random sampling (from population): selecting subjects into your
sample from a population with known probability.</p></li>
</ul>
</section>
<section id="randomization-is-powerful-1" class="slide level2">
<h2>Randomization is powerful (1)</h2>
<ul>
<li><p>We want the ATE, <span class="math inline">\(\overline{\tau_i}=
\overline{Y_i(1)-Y_i(0)}\)</span>.</p></li>
<li><p>We will make use of the fact that the average of differences
equals the difference of averages:</p></li>
</ul>
<p>ATE <span class="math inline">\(= \overline{Y_i(1)-Y_i(0)} =
\overline{Y_i(1)}-\overline{Y_i(0)}\)</span></p>
</section>
<section id="randomization-is-powerful-2" class="slide level2">
<h2>Randomization is powerful (2)</h2>
<ul>
<li><p>Let’s <em>randomly assign</em> some of our units to the treatment
condition. For these treated units, we measure the outcome <span
class="math inline">\(Y_i|T_i=1\)</span>, which is the same as <span
class="math inline">\(Y_i(1)\)</span> for these units.</p></li>
<li><p>Because these units were randomly assigned to treatment, these
<span class="math inline">\(Y_i=Y_i(1)\)</span> for the treated units
represent the <span class="math inline">\(Y_i(1)\)</span> for all our
units.</p></li>
<li><p>In expectation (or on average across repeated experiments
(written <span class="math inline">\(E_R[]\)</span>)):</p></li>
</ul>
<p><span
class="math inline">\(E_R[\overline{Y_i}|T_i=1]=\overline{Y_i(1)}\)</span>.</p>
<ul>
<li><p><span class="math inline">\(\overline{Y}|T_i=1\)</span> is an
unbiased estimator of the population mean of potential outcomes under
treatment.</p></li>
<li><p>The same logic applies for units randomly assigned to
control:</p></li>
</ul>
<p><span
class="math inline">\(E_R[\overline{Y_i}|T_i=0]=\overline{Y_i(0)}\)</span>.</p>
</section>
<section id="randomization-is-powerful-3" class="slide level2">
<h2>Randomization is powerful (3)</h2>
<!-- - The same logic applies when we measure $Y_i$ for the control units ($Y_i|T_i=0$). So $\overline{Y_i}|T_i=0$, which we can calculate, gives us an unbiased estimate of $\overline{Y_i(0)}$. -->
<ul>
<li>So we can write down an estimator for the ATE:</li>
</ul>
<p><span class="math inline">\(\hat{\overline{\tau_i}} = (
\overline{Y_i(1)} | T_i = 1 ) - ( \overline{Y_i(0)} | T_i = 0
)\)</span></p>
<ul>
<li>In expectation, or on average across repeated experiments, <span
class="math inline">\(\hat{\overline{\tau_i}}\)</span> equals the
ATE:</li>
</ul>
<p><span class="math inline">\(E_R[Y_i| T_i = 1 ] - E_R[Y_i | T_i = 0] =
\overline{Y_i(1)} - \overline{Y_i(0)}\)</span>.</p>
<ul>
<li>So we can just take the difference of these unbiased estimators of
<span class="math inline">\(\overline{Y_i(1)}\)</span> and <span
class="math inline">\(\overline{Y_i(0)}\)</span> to get an unbiased
estimate of the ATE.</li>
</ul>
</section>
<section id="random-sampling" class="slide level2">
<h2>Random sampling</h2>
<div class="figure">
<img src="../Images/randomsampling.png" alt="Random sample of households" width="70%" />
<p class="caption">
Random sample of households
</p>
</div>
</section>
<section id="potential-outcomes-2" class="slide level2">
<h2>Potential outcomes</h2>
<p>Each household <span class="math inline">\(i\)</span> has <span
style="color: red;"><span class="math inline">\(Y_i(1)\)</span></span>
and <span style="color: blue;"><span
class="math inline">\(Y_i(0)\)</span></span>.</p>
<p><img src="../Images/randomsampling_redblue_plain.png" width="80%" /></p>
</section>
<section id="random-assignment-to-red-1-or-blue-0-condition"
class="slide level2">
<h2>Random assignment to red (1) or blue (0) condition</h2>
<div class="figure">
<img src="../Images/randomassignment.png" alt="Random assignment of this random sample of households" width="70%" />
<p class="caption">
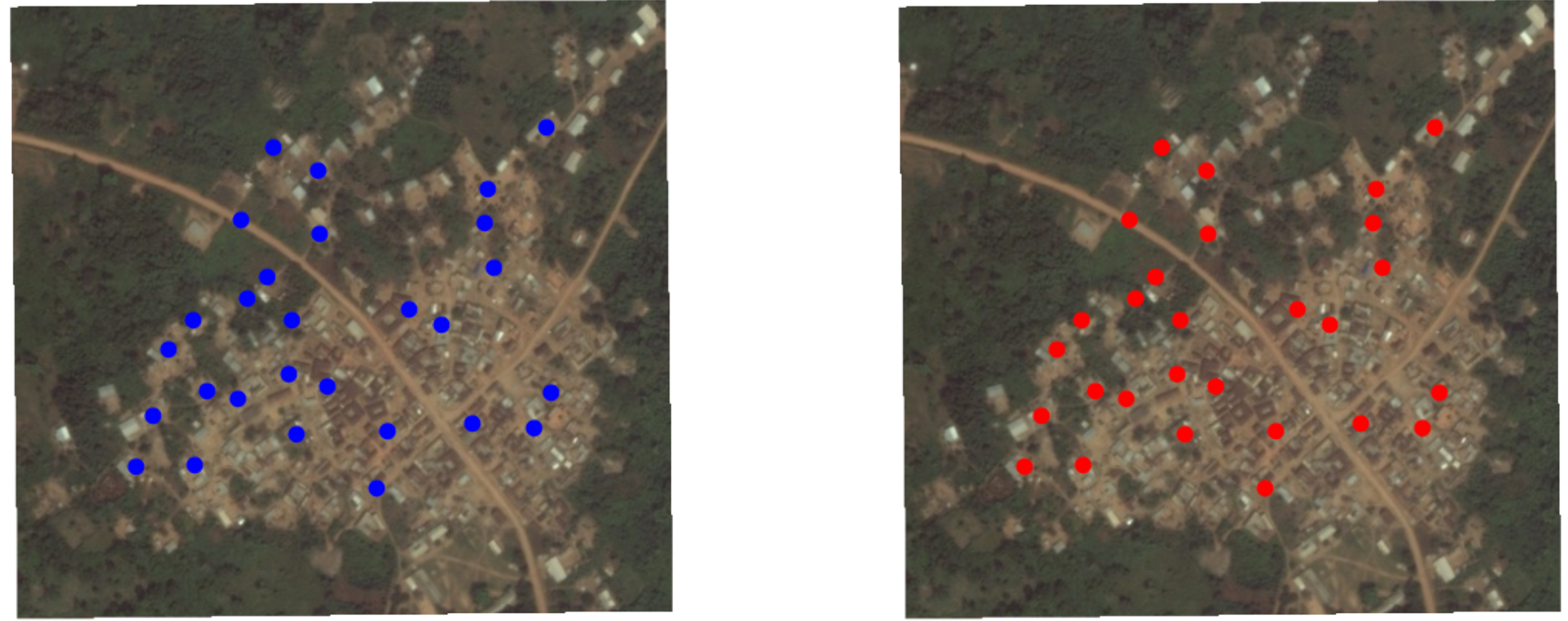
Random assignment of this random sample of households
</p>
</div>
</section>
<section id="three-key-assumptions" class="slide level2">
<h2>Three key assumptions</h2>
<p>To make causal claims with an experiment (or to judge whether we
believe a study’s claims), we need three core assumptions:</p>
<ul>
<li><p>Random assignment of subjects to treatment, which implies that
receiving the treatment is statistically independent of subjects’
potential outcomes.</p></li>
<li><p>Stable unit treatment value assumption (SUTVA).</p></li>
<li><p>Excludability, which means that a subject’s potential outcomes
respond only to the defined treatment, not other extraneous factors that
may be correlated with treatment.</p></li>
</ul>
</section>
<section id="key-assumption-sutva-part-1" class="slide level2">
<h2>Key assumption: SUTVA, part 1</h2>
<ol type="1">
<li><p>No interference – A subject’s potential outcome reflects only
whether that subject receives the treatment himself/herself. It is not
affected by how treatments happen to be allocated to other subjects.</p>
<ul>
<li><p>A classic violation is the case of vaccines and their spillover
effects.</p></li>
<li><p>Say I am in the control condition (no vaccine). If whether I get
sick (<span class="math inline">\(Y_i(0)\)</span>) depends on other
people’s treatment status (whether they take the vaccine), it’s like I
have two different <span class="math inline">\(Y_i(0)\)</span>!</p></li>
<li><p>SUTVA (= stable unit treatment value assumption)</p></li>
</ul></li>
</ol>
</section>
<section id="key-assumption-sutva-part-2" class="slide level2">
<h2>Key assumption: SUTVA, part 2</h2>
<ol start="2" type="1">
<li><p>No hidden variations of the treatment</p>
<ul>
<li><p>Say treatment is taking a vaccine, but there are two kinds of
vaccines and they have different ingredients.</p></li>
<li><p>An example of a violation is when whether I get sick when I take
the vaccine (<span class="math inline">\(Y_i(1)\)</span>) depends on
which vaccine I got. We would have two different <span
class="math inline">\(Y_i(1)\)</span>!</p></li>
</ul></li>
</ol>
</section>
<section id="key-assumption-excludability" class="slide level2">
<h2>Key assumption: Excludability</h2>
<ul>
<li><p>Treatment assignment has no effect on outcomes except through its
effect on whether treatment was received.</p>
<ul>
<li><p>Important to define the treatment precisely.</p></li>
<li><p>Important to also maintain symmetry between treatment and control
groups (e.g., through blinding, having the same data collection
procedures for all study subjects, etc.), so that treatment assignment
only affects the treatment received, not other things like interactions
with researchers that you don’t want to define as part of the
treatment.</p></li>
</ul></li>
</ul>
</section>
<section id="randomization-is-powerful-4" class="slide level2">
<h2>Randomization is powerful (4)</h2>
<ul>
<li><p>If the intervention is randomized, then who receives or doesn’t
receive the intervention is not related to the characteristics of the
potential recipients.</p></li>
<li><p>Randomization makes those who were randomly selected to not
receive the intervention to be good stand-ins for the counterfactuals
for those who were randomly selected to receive the treatment, and vice
versa.</p></li>
<li><p>We have to worry about this if the intervention were not
randomized (= an observational study).</p></li>
</ul>
</section></section>
<section>
<section id="randomized-vs.-observational-studies"
class="title-slide slide level1">
<h1>Randomized vs. observational studies</h1>
</section>
<section id="different-types-of-studies" class="slide level2">
<h2>Different types of studies</h2>
<ul>
<li><p>Randomized studies</p>
<ul>
<li>Randomize treatment, then go measure outcomes</li>
</ul></li>
<li><p>Observational studies</p>
<ul>
<li>Treatment is not randomly assigned. It is observed, but not
manipulated.</li>
</ul></li>
</ul>
</section>
<section id="exercise-learning-about-your-prior-knowledge"
class="slide level2">
<h2>Exercise: Learning about your prior knowledge</h2>
<p><strong>Discuss in small groups:</strong> Help me design the next
project to answer one of these questions (or one of your own causal
questions). Just sketch the key features of two designs — one
observational and the other randomized.</p>
<p><strong>Example research questions:</strong></p>
<ul>
<li><p>Do Community-Driven Reconstruction projects increase trust and
cooperation in Liberia? <a
href="https://egap.org/resource/brief-40-development-assistance-and-collective-action-capacity/">see
EGAP Policy Brief 40</a></p></li>
<li><p>Can community monitoring increase clinic utilization and decrease
child mortality in Uganda? <a
href="https://egap.org/resource/does-bottom-up-accountability-work-evidence-from-uganda/">see
EGAP Policy Brief 58</a></p></li>
</ul>
</section>
<section id="exercise-observational-studies-vs.-randomized-studies"
class="slide level2">
<h2>Exercise: Observational studies vs. Randomized studies</h2>
<p><strong>Tasks:</strong></p>
<ol type="1">
<li><p>Sketch an ideal observational study design (no randomization, no
researcher control but infinite resources for data collection). What
questions would critical readers ask when you claim that your results
reflect a causal relationship?</p></li>
<li><p>Sketch an ideal experimental study design (including
randomization). What questions would critical readers ask when you claim
that your results reflect a causal relationship?</p></li>
</ol>
</section>
<section id="discuss" class="slide level2">
<h2>Discuss</h2>
<ul>
<li><p>What were key components and strengths and weaknesses of the
randomized studies?</p></li>
<li><p>What were key components and strengths and weaknesses of the
observational studies?</p></li>
</ul>
</section>
<section id="generalizability-and-external-validity"
class="slide level2">
<h2>Generalizability and external validity</h2>
<ul>
<li><p>Randomization brings high internal validity to a study –
confidence that we have learned the causal effect of a treatment on an
outcome.</p></li>
<li><p>But the finding from a particular study in one particular place
and at one particular time may not hold in other settings (i.e.,
external validity).</p></li>
<li><p>This is a general concern, not just a concern for randomized
studies.</p></li>
<li><p><a
href="https://egap.org/our-work/the-metaketa-initiative/">EGAP’s
Metaketa Initiative</a> works to accumulate knowledge by pre-planning a
meta-analysis of multiple studies that have high internal validity due
to randomization.</p></li>
</ul>
</section>
<section id="references" class="slide level2">
<h2>References</h2>
<p><a
href="https://egap.org/resource/brief-40-development-assistance-and-collective-action-capacity/">EGAP
Policy Brief 40: Development Assistance and Collective Action
Capacity</a></p>
<p><a
href="https://egap.org/resource/does-bottom-up-accountability-work-evidence-from-uganda/">EGAP
Policy Brief 58: Does Bottom-Up Accountability Work?</a></p>
<div id="refs" class="references csl-bib-body hanging-indent"
role="doc-bibliography">
<div id="ref-brady2008causation" class="csl-entry"
role="doc-biblioentry">
Brady, Henry E. 2008. <span>“Causation and Explanation in Social
Science.”</span> In <em>The Oxford Handbook of Political Science</em>.
<a
href="https://www.oxfordhandbooks.com/view/10.1093/oxfordhb/9780199286546.001.0001/oxfordhb-9780199286546-e-10">https://www.oxfordhandbooks.com/view/10.1093/oxfordhb/9780199286546.001.0001/oxfordhb-9780199286546-e-10</a>.
</div>
<div id="ref-cartwright2012evidence" class="csl-entry"
role="doc-biblioentry">
Cartwright, Nancy, and Jeremy Hardie. 2012. <em><span
class="nocase">Evidence-based policy: a practical guide to doing it
better</span></em>. Oxford University Press.
</div>
<div id="ref-holland:1986" class="csl-entry" role="doc-biblioentry">
Holland, Paul W. 1986. <span>“Statistics and Causal Inference.”</span>
<em>Journal of the American Statistical Association</em> 81: 945–60.
</div>
</div>
</section></section>
</div>
</div>
<script src="causalinference-slides_files/reveal.js-3.3.0.1/lib/js/head.min.js"></script>
<script src="causalinference-slides_files/reveal.js-3.3.0.1/js/reveal.js"></script>
<script>
// Full list of configuration options available at:
// https://github.com/hakimel/reveal.js#configuration
Reveal.initialize({
// Display controls in the bottom right corner
controls: true,
// Display a presentation progress bar
progress: true,
// Display the page number of the current slide
slideNumber: true,
// Push each slide change to the browser history
history: true,
// Enable keyboard shortcuts for navigation
keyboard: true,
// Enable the slide overview mode
overview: true,
// Vertical centering of slides
center: false,
// Enables touch navigation on devices with touch input
touch: true,
// Turns fragments on and off globally
fragments: true,
// Flags if we should show a help overlay when the questionmark
// key is pressed
help: true,
// Number of milliseconds between automatically proceeding to the
// next slide, disabled when set to 0, this value can be overwritten
// by using a data-autoslide attribute on your slides
autoSlide: 0,
// Stop auto-sliding after user input
autoSlideStoppable: true,
// Opens links in an iframe preview overlay
previewLinks: true,
// Transition style
transition: 'fade', // none/fade/slide/convex/concave/zoom
// Transition speed
transitionSpeed: 'default', // default/fast/slow
// Transition style for full page slide backgrounds
backgroundTransition: 'default', // none/fade/slide/convex/concave/zoom
// Number of slides away from the current that are visible
viewDistance: 3,
chalkboard: {
toggleNotesButton: false,
theme: 'whiteboard',
},
keyboard: {
67: function() { RevealChalkboard.toggleNotesCanvas() }, // toggle notes canvas when 'c' is pressed
66: function() { RevealChalkboard.toggleChalkboard() }, // toggle chalkboard when 'b' is pressed
46: function() { RevealChalkboard.clear() }, // clear chalkboard when 'DEL' is pressed
8: function() { RevealChalkboard.reset() }, // reset chalkboard data on current slide when 'BACKSPACE' is pressed
68: function() { RevealChalkboard.download() }, // downlad recorded chalkboard drawing when 'd' is pressed
},
// Optional reveal.js plugins
dependencies: [
{ src: 'causalinference-slides_files/reveal.js-3.3.0.1/plugin/notes/notes.js', async: true },
{ src: 'causalinference-slides_files/reveal.js-3.3.0.1/plugin/search/search.js', async: true },
{ src: 'causalinference-slides_files/reveal.js-3.3.0.1/plugin/chalkboard/chalkboard.js', async: true },
]
});
</script>
<!-- dynamically load mathjax for compatibility with self-contained -->
<script>
(function () {
var script = document.createElement("script");
script.type = "text/javascript";
script.src = "https://mathjax.rstudio.com/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML";
document.getElementsByTagName("head")[0].appendChild(script);
})();
</script>
<script>
(function() {
if (window.jQuery) {
Reveal.addEventListener( 'slidechanged', function(event) {
window.jQuery(event.previousSlide).trigger('hidden');
window.jQuery(event.currentSlide).trigger('shown');
});
}
})();
</script>
</body>
</html>