Distribuciones de Probabilidad continuas
Variable aleatoria Continua
Es una variable aleatoria que puede tomar cualquier valor en un intervalo dado, son incontables y están relacionados con números reales.
Ejemplo
El tiempo que lleva completar un examen para una prueba de 60 minutos
Valores posibles = todos los números reales en el intervalo [0,60]
Edad de un fósil
Valores posibles = todos los números reales en el intervalo [edad mínima, edad máxima]
Millas por galón para un Toyota
Valores Posibles = todos los números reales del intervalo [MPG mínimo, MPG máximo]
La principal diferencia entre las variables aleatorias continuas y discretas es que la probabilidad continua se mide a lo largo de intervalos, mientras que la probabilidad discreta se calcula en puntos exactos.
Como son tantos valores posibles, ningún valor posible de la variable aleatoria tiene probabilidad positiva, esto es, P(X=c)=0 con cualquier valor posible de c
Función de densidad de probabilidad
Sea X una variable aleatoria continua Entonces, una distribución de probabilidad fdp de X es una función f(x) tal que para dos números cualesquiera a y b con a<b
\[P(a<X<b)=\int_a^bf(x)dx\]
Es decir, la probabilidad de que X asuma un valor en el intervalo [a,b] es el área sobre este intervalo y bajo la gráfica de la función de densidad
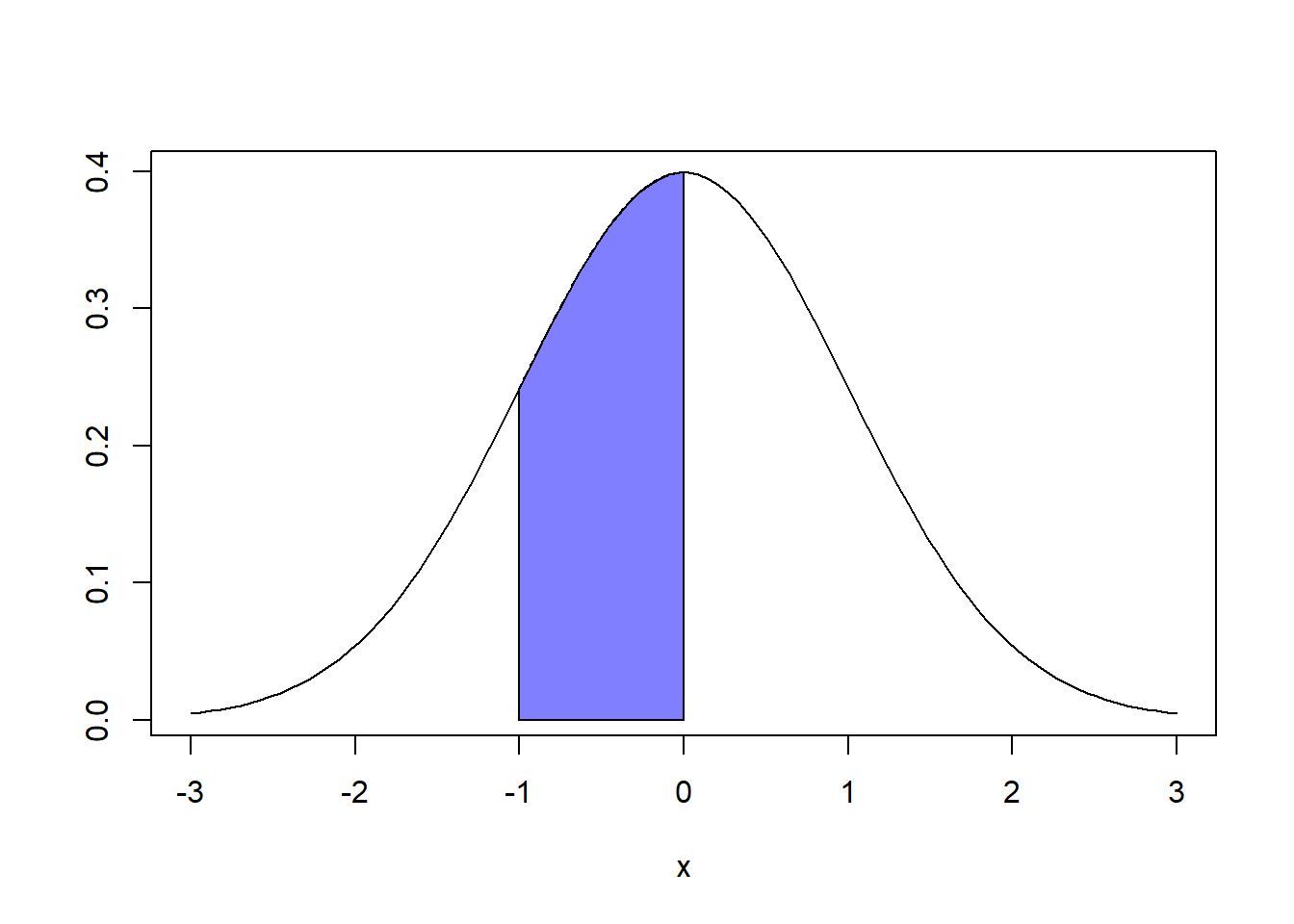
Propiedades
\[0\leq f(x) \leq 1\]
\[\int_{lim inf}^{lim sup}f(x)dx=1\]
Para cualquier valor posible de c \[P(X=c)=0\]
Función de distribución acumulada
\[F(x)=P(x\leq x)=\int_{lim inf}^{x}f(x)dx\] Proposición
Sea X una variable aleatoria continua con función de densidad de probabilidad f(x) y función acumulada F(x) entonces para un numero a:
\[P(X>a)=1-P(x\leq a) =1-F(a)\] Para dos numeros cualesquiera a y b con b>a
\[P(a\leq x \leq b)=P(x\leq b)- P(x\leq a)= F(b)-F(a)\]
Ejemplo
x denota el diámetro del agujero perforado en una hoja de metal, el diámetro objetivo es de 12.5 mm, perturbaciones aleatorias ocasionan agujeros más grandes.La distribución de x es:
\[f(x)=20e^{-20(x-12.5)}\quad x>12.5 mm\]
- Grafique la función fdp
## Warning in plot.xy(xy, type, ...): plot type 'lines' will be truncated to
## first character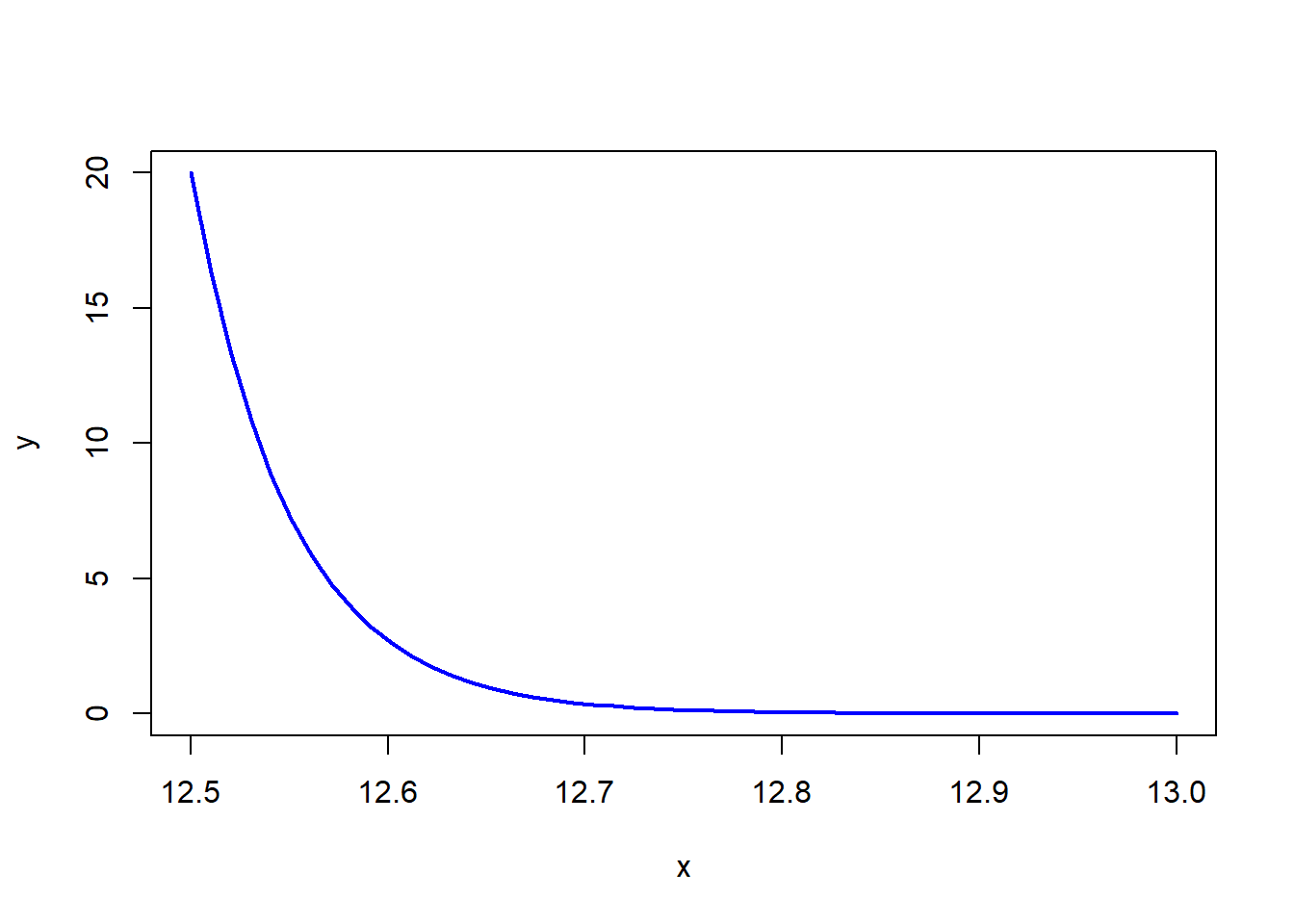
2.Obtenga la función acumulada
\[F(x)=P(x\leq x)=\int_{lim inf}^{x}f(x)dx\]
\[F(x)=\int_{12.5}^{x}20e^{-20(x-12.5)}dx\] \[F(X)= \left\{ \begin{array}{c} \displaystyle 1-e^{-20(x-12.5)} \quad x\geq12.5 \\ 0 \qquad x<12.5 \end{array} \right. \] 3. Grafique la función acumulada
## Warning in plot.xy(xy, type, ...): plot type 'lines' will be truncated to
## first character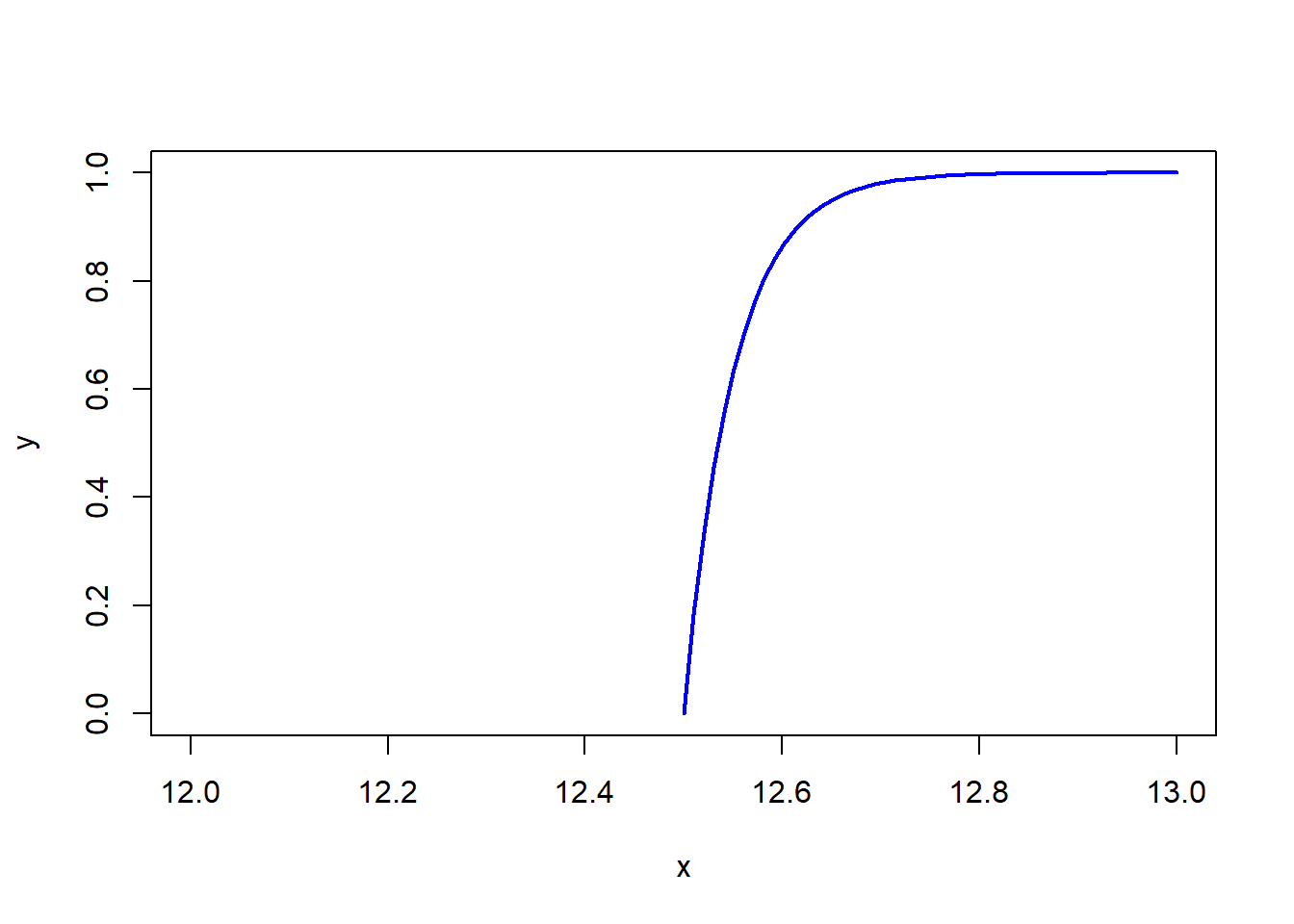
Si una parte con diámetro es más grande que 12.6 mm se desecha, ¿Qué proporción de partes se desecha?
dos caminos - Realizando la integral
\[F(x)=\int_{12.6}^{\infty}20e^{-20(x-12.5)}dx\] - Evaluando en la función acumulada \[p(x\geq12.6)=1-p(x<12.6)\] \[=1-(1-e^{-20*(x-12.5)})\] \[=e^{-2}=13.5\]
## Warning in plot.xy(xy, type, ...): plot type 'lines' will be truncated to
## first character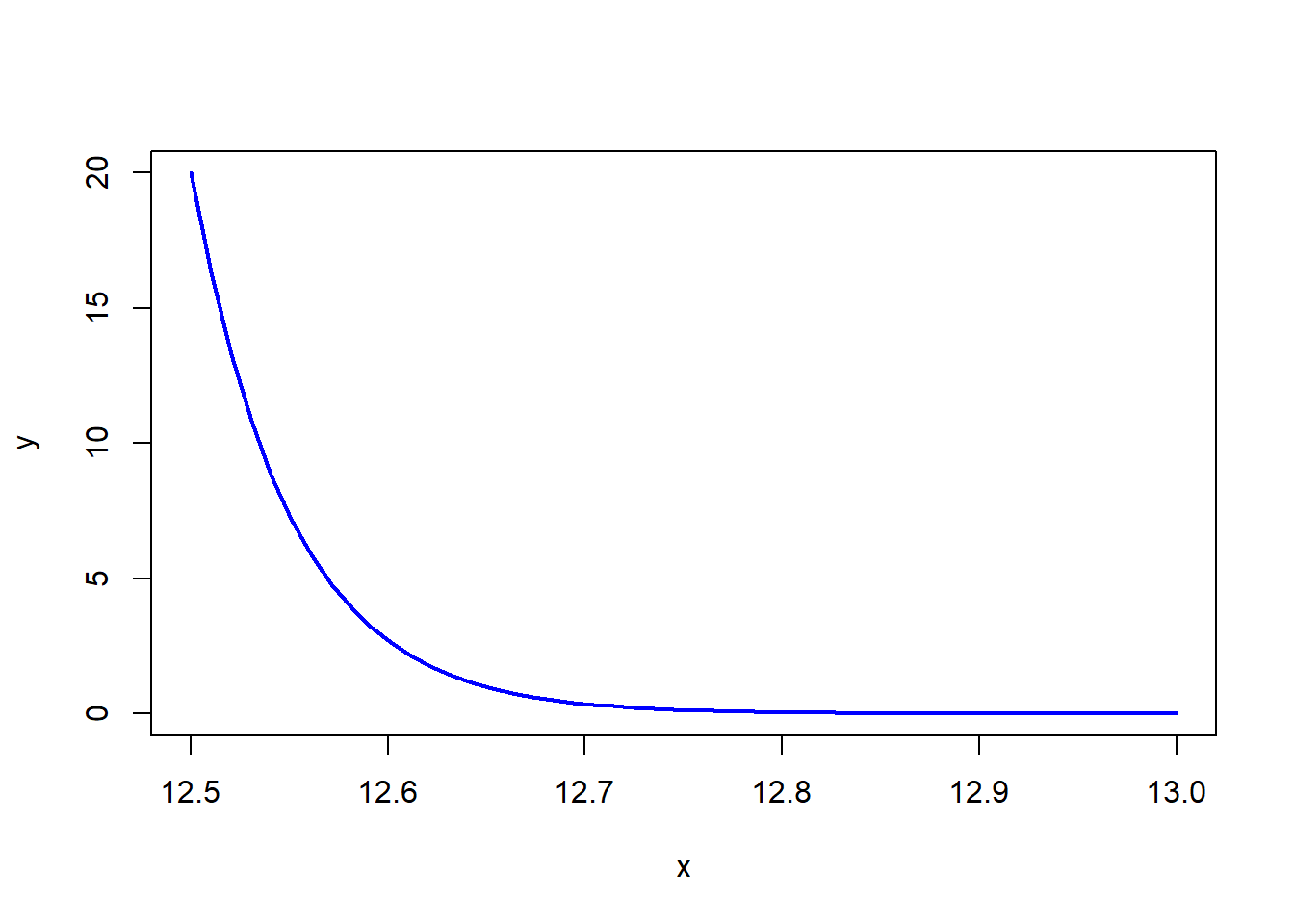
Relación entre f(x) y F(x)
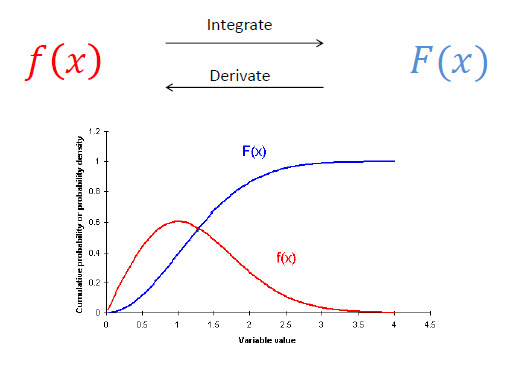
Probabilidad es un valor entre 0 y 1
Valor esperado y varianza
\[E(x)=\mu_x= \int_{lim inf}^{limsup}xf(x)dx\] \[E(x^2)= \int_{lim inf}^{limsup}x^2f(x)dx\]
\[V(x)=E(x^2)-\mu^2\]
Ejemplo
Sea x la cantidad de espacio ocupado por un artículo en un contenedor, la pdf de x es:
\[ f(x)= \left\{ \begin{array}{c} 90x^8(1-x) \quad 0<x<1 \\ 0 \quad eoc \end{array} \right. \]
- Grafique la función
## Warning in plot.xy(xy, type, ...): plot type 'lines' will be truncated to
## first character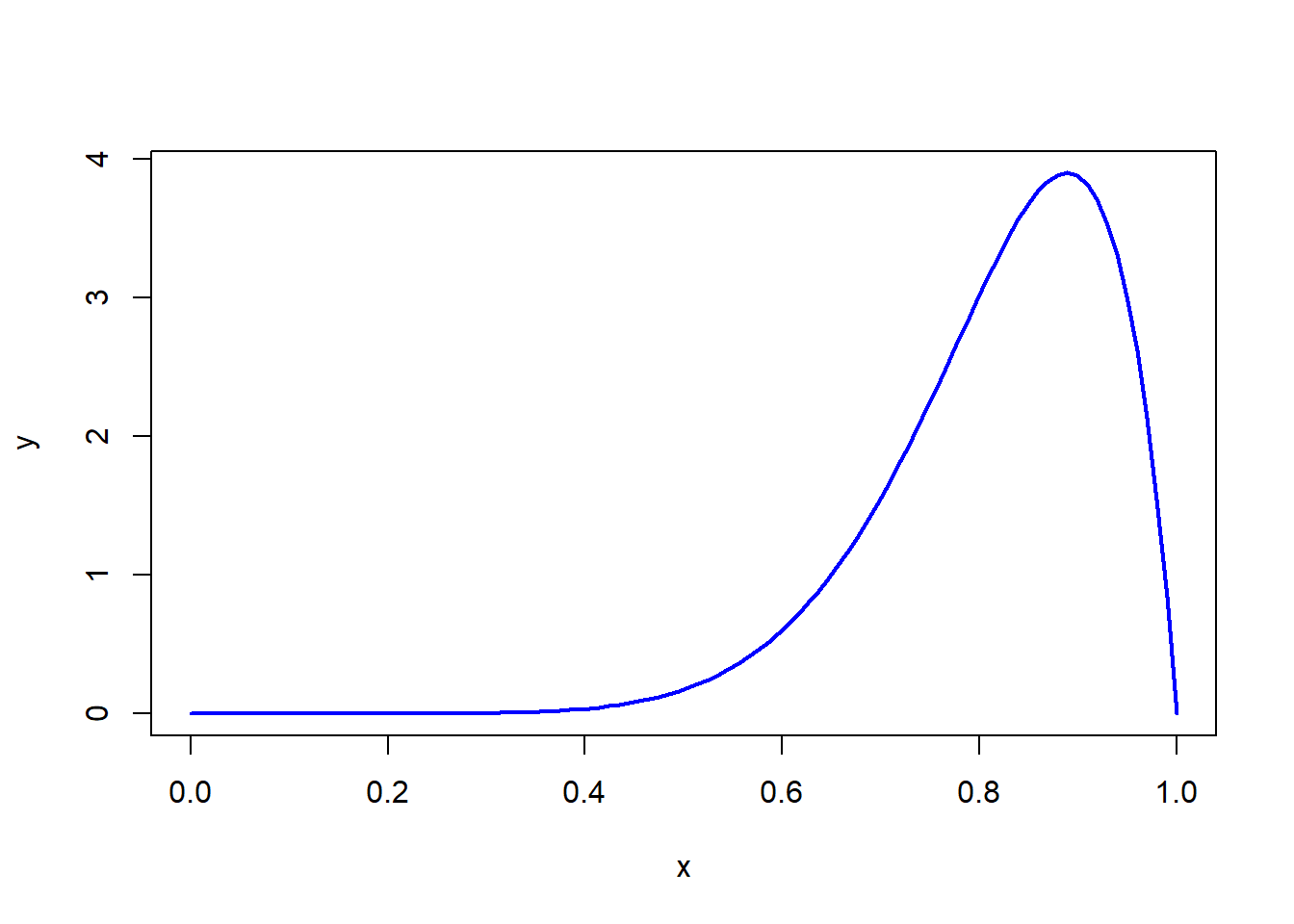
- Obtenga la función acumulada
\[ F(x)= \left\{ \begin{array}{c} 0 \quad x<0\\ x^9(10-9x) \quad 0<x<1 \\ 1 \quad x>1 \end{array} \right. \] 3. Cual es la probabilidad
\[P(x\leq 0.7)\] \[P(x>0.8)\] 4. Halle E(x), v(x)
Videos
Función de distribución de probabilidad continua
Taller
- Sea X la cantidad de tiempo durante la cual un libro puesto en reserva durante dos horas en la biblioteca de una universidad es solicitado en préstamo por un estudiante seleccionado y suponga que X tiene la función de densidad:
\[ f(x)= \left\{ \begin{array}{c} \frac{1}{2}x \quad 0\leq x\leq 2 \\ 0 \quad e.o.c \end{array} \right. \]
Grafique f(x)
Halle la función acumulada
Grafique F(x)
d.Halle las probabilidades de que:
\[p(x\leq 1)\] \[P(0.5 \leq x \leq 1.5)\] \[P(x>1.5)\]
- Halle E(x), v(x)
- Un profesor universitario nunca termina su disertación antes del final de la hora y siempre termina dentro de 2 minutos después de la hora. Sea X = el tiempo que transcurre entre el final de la hora y el final de la disertación suponga que la función de densidad de probabilidad de X es
\[ f(x)= \left\{ \begin{array}{c} kx^2 \quad 0\leq x\leq 2 \\ 0 \quad e.o.c \end{array} \right. \]
Determine el valor de la constante K
Grafique f(x)
Halle F(x)
Grafique F(x)
¿Cuál es la probabilidad de que la disertación termine dentro de un minuto final de la hora?
¿Cuál es la probabilidad de que la disertación continue entre 60 y 90 segundos?
¿Cuál es la probabilidad de que la disertación continúe durante por lo menos 90 segundos después del final de la hora?
Halle E(x), v(x)
- El error implicado al hacer una medición es una variable aleatoria continua X con función de densidad de probabilidad.
\[ f(x)= \left\{ \begin{array}{c} 0.09375(4-x^2) \quad -2\leq x\leq 2 \\ 0 \quad e.o.c \end{array} \right. \]
Grafique f(x)
Halle F(x)
Grafique F(x)
calcule
\[P(x>0)\] \[P(-1<x<1)\] \[P(-0.5<x<0.5) \] e. Halle E(x), v(x)