Técnicas de conteo
Técnica de la multiplicación
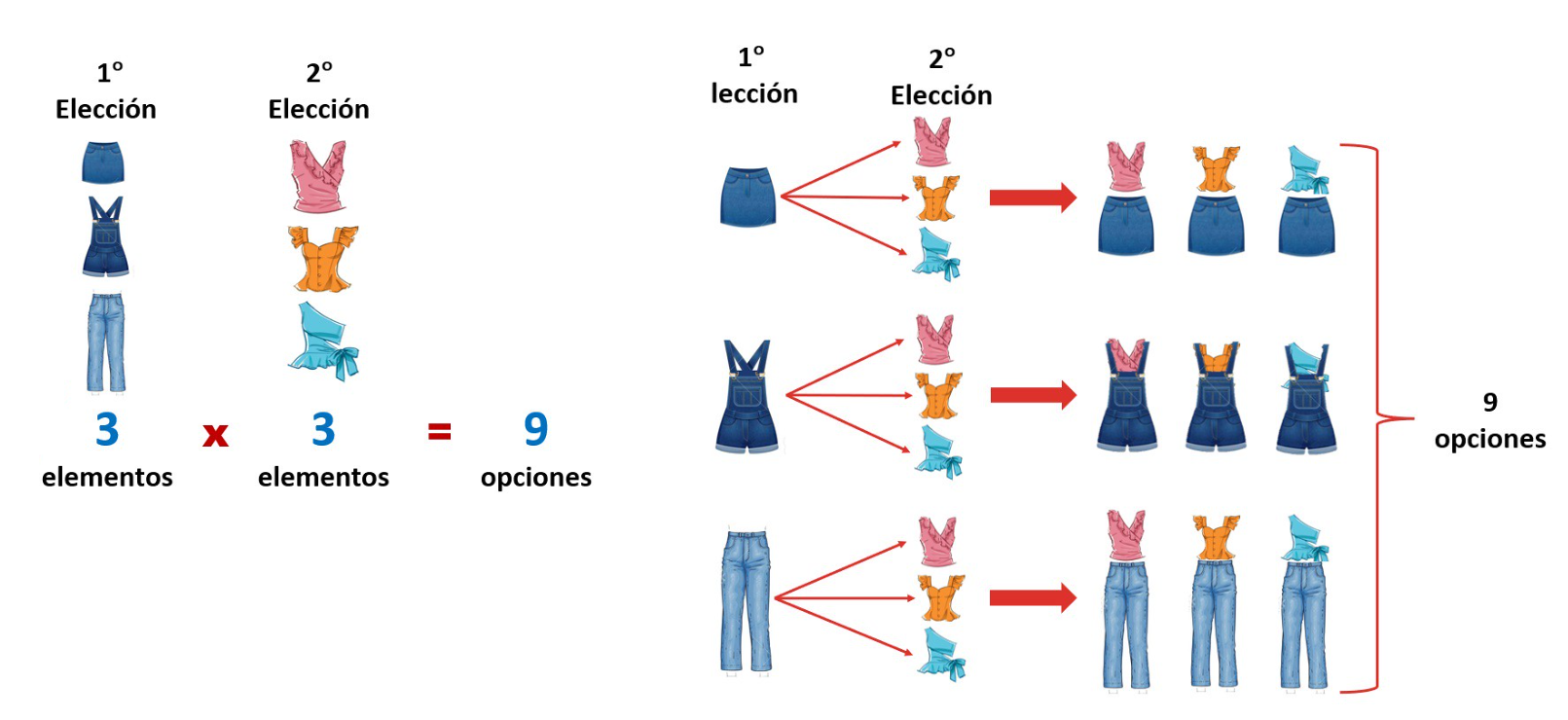
Si hay m formas de hacer una cosa y hay n formas de hacer otra cosa, hay mxn formas de hacer ambas cosas.
Número total de arreglos= m x n
imagen
Regla de la multiplicación
Permutación
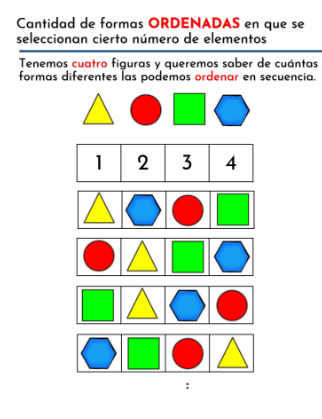
Importa el orden, por ejemplo con las letras ABC escoja pares de letras, el resultado sería:
AB BA BC CB AC CA
La fórmula usada para la estimación de los parámetros es \[nPr=\frac{n!}{(n-r)!}\]
Donde:
nPr Número de permutaciones posible
n Numero total de objetos
r numero de objetos utilizados en un mismo momento
\[n!=n*(n-1)*(n-2)*(n-3)*...*3*2*1\] \[5!=5*4*3*2*1\] Si n=r para calcular el total de permutaciones se utiliza la fórmula \(P_n=n!\)
imagen
¿CUANTAS PAREJAS ordenadas SE PUEDEN OBTENER DE LA MESA?

imagen
- Maria - Pedro
- Pedro - Maria
- Ana - Maria
- Maria - Ana
- Pedro - miguel
- Miguel - pedro
- Maria - Miguel
- Miguel - Maria
- Ana - Miguel
- Miguel - Ana
- Ana - Pedro
- Pedro - Ana
\[4P2=\frac{4!}{(4-2)!}=12\]
Vídeo de la permutación
Combinación
Considere las letras ABC, para este conjunto los posibles resultados son:
AB BC AC
Para la combinación AB es lo mismo BA
¿Cuantos subconjuntos de tamaño r se pueden obtener de un conjunto de tamaño n?
\[nCr=\binom{n}{r}=\frac{n!}{r!(n-r)!}\] ¿CUANTAS PAREJAS ordenadas SE PUEDEN OBTENER DE LA MESA?

imagen
- Maria - Pedro
- Ana - Maria
- Pedro - miguel
- Maria - Miguel
- Ana - Miguel
- Ana - Pedro
\[4C2= \binom{4}{2}=\frac{4!}{2!(4-2)!}= 6 \]
Vídeo ejemplo de la combinación
Cómo estimar combinatorias y permutaciones en la calculadora
Baloto

comprelo ganelo y disfrutelo