<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8" />
<meta name="generator" content="pandoc" />
<meta http-equiv="X-UA-Compatible" content="IE=EDGE" />
<title>Distribución gama y exponencial</title>
<script src="site_libs/header-attrs-2.14/header-attrs.js"></script>
<script src="site_libs/jquery-3.6.0/jquery-3.6.0.min.js"></script>
<meta name="viewport" content="width=device-width, initial-scale=1" />
<link href="site_libs/bootstrap-3.3.5/css/flatly.min.css" rel="stylesheet" />
<script src="site_libs/bootstrap-3.3.5/js/bootstrap.min.js"></script>
<script src="site_libs/bootstrap-3.3.5/shim/html5shiv.min.js"></script>
<script src="site_libs/bootstrap-3.3.5/shim/respond.min.js"></script>
<style>h1 {font-size: 34px;}
h1.title {font-size: 38px;}
h2 {font-size: 30px;}
h3 {font-size: 24px;}
h4 {font-size: 18px;}
h5 {font-size: 16px;}
h6 {font-size: 12px;}
code {color: inherit; background-color: rgba(0, 0, 0, 0.04);}
pre:not([class]) { background-color: white }</style>
<script src="site_libs/jqueryui-1.11.4/jquery-ui.min.js"></script>
<link href="site_libs/tocify-1.9.1/jquery.tocify.css" rel="stylesheet" />
<script src="site_libs/tocify-1.9.1/jquery.tocify.js"></script>
<script src="site_libs/navigation-1.1/tabsets.js"></script>
<link href="site_libs/highlightjs-9.12.0/textmate.css" rel="stylesheet" />
<script src="site_libs/highlightjs-9.12.0/highlight.js"></script>
<link href="site_libs/font-awesome-5.1.0/css/all.css" rel="stylesheet" />
<link href="site_libs/font-awesome-5.1.0/css/v4-shims.css" rel="stylesheet" />
<link href="site_libs/ionicons-2.0.1/css/ionicons.min.css" rel="stylesheet" />
<link rel="icon" type="image/png" href="images/favicon.png" />
<script type="text/javascript" src="js/rmarkdown.js"></script>
<link rel="stylesheet" href="https://cdnjs.cloudflare.com/ajax/libs/font-awesome/4.7.0/css/font-awesome.min.css">
<script>
(function(i,s,o,g,r,a,m){i['GoogleAnalyticsObject']=r;i[r]=i[r]||function(){
(i[r].q=i[r].q||[]).push(arguments)},i[r].l=1*new Date();a=s.createElement(o),
m=s.getElementsByTagName(o)[0];a.async=1;a.src=g;m.parentNode.insertBefore(a,m)
})(window,document,'script','https://www.google-analytics.com/analytics.js','ga');
ga('create', 'UA-88209726-1', 'auto');
ga('send', 'pageview');
</script>
<style type="text/css">
code{white-space: pre-wrap;}
span.smallcaps{font-variant: small-caps;}
span.underline{text-decoration: underline;}
div.column{display: inline-block; vertical-align: top; width: 50%;}
div.hanging-indent{margin-left: 1.5em; text-indent: -1.5em;}
ul.task-list{list-style: none;}
</style>
<style type="text/css">code{white-space: pre;}</style>
<script type="text/javascript">
if (window.hljs) {
hljs.configure({languages: []});
hljs.initHighlightingOnLoad();
if (document.readyState && document.readyState === "complete") {
window.setTimeout(function() { hljs.initHighlighting(); }, 0);
}
}
</script>
<style type = "text/css">
.main-container {
max-width: 940px;
margin-left: auto;
margin-right: auto;
}
img {
max-width:100%;
}
.tabbed-pane {
padding-top: 12px;
}
.html-widget {
margin-bottom: 20px;
}
button.code-folding-btn:focus {
outline: none;
}
summary {
display: list-item;
}
details > summary > p:only-child {
display: inline;
}
pre code {
padding: 0;
}
</style>
<style type="text/css">
.dropdown-submenu {
position: relative;
}
.dropdown-submenu>.dropdown-menu {
top: 0;
left: 100%;
margin-top: -6px;
margin-left: -1px;
border-radius: 0 6px 6px 6px;
}
.dropdown-submenu:hover>.dropdown-menu {
display: block;
}
.dropdown-submenu>a:after {
display: block;
content: " ";
float: right;
width: 0;
height: 0;
border-color: transparent;
border-style: solid;
border-width: 5px 0 5px 5px;
border-left-color: #cccccc;
margin-top: 5px;
margin-right: -10px;
}
.dropdown-submenu:hover>a:after {
border-left-color: #adb5bd;
}
.dropdown-submenu.pull-left {
float: none;
}
.dropdown-submenu.pull-left>.dropdown-menu {
left: -100%;
margin-left: 10px;
border-radius: 6px 0 6px 6px;
}
</style>
<script type="text/javascript">
// manage active state of menu based on current page
$(document).ready(function () {
// active menu anchor
href = window.location.pathname
href = href.substr(href.lastIndexOf('/') + 1)
if (href === "")
href = "index.html";
var menuAnchor = $('a[href="' + href + '"]');
// mark it active
menuAnchor.tab('show');
// if it's got a parent navbar menu mark it active as well
menuAnchor.closest('li.dropdown').addClass('active');
// Navbar adjustments
var navHeight = $(".navbar").first().height() + 15;
var style = document.createElement('style');
var pt = "padding-top: " + navHeight + "px; ";
var mt = "margin-top: -" + navHeight + "px; ";
var css = "";
// offset scroll position for anchor links (for fixed navbar)
for (var i = 1; i <= 6; i++) {
css += ".section h" + i + "{ " + pt + mt + "}\n";
}
style.innerHTML = "body {" + pt + "padding-bottom: 40px; }\n" + css;
document.head.appendChild(style);
});
</script>
<!-- tabsets -->
<style type="text/css">
.tabset-dropdown > .nav-tabs {
display: inline-table;
max-height: 500px;
min-height: 44px;
overflow-y: auto;
border: 1px solid #ddd;
border-radius: 4px;
}
.tabset-dropdown > .nav-tabs > li.active:before {
content: "";
font-family: 'Glyphicons Halflings';
display: inline-block;
padding: 10px;
border-right: 1px solid #ddd;
}
.tabset-dropdown > .nav-tabs.nav-tabs-open > li.active:before {
content: "";
border: none;
}
.tabset-dropdown > .nav-tabs.nav-tabs-open:before {
content: "";
font-family: 'Glyphicons Halflings';
display: inline-block;
padding: 10px;
border-right: 1px solid #ddd;
}
.tabset-dropdown > .nav-tabs > li.active {
display: block;
}
.tabset-dropdown > .nav-tabs > li > a,
.tabset-dropdown > .nav-tabs > li > a:focus,
.tabset-dropdown > .nav-tabs > li > a:hover {
border: none;
display: inline-block;
border-radius: 4px;
background-color: transparent;
}
.tabset-dropdown > .nav-tabs.nav-tabs-open > li {
display: block;
float: none;
}
.tabset-dropdown > .nav-tabs > li {
display: none;
}
</style>
<!-- code folding -->
<style type="text/css">
#TOC {
margin: 25px 0px 20px 0px;
}
@media (max-width: 768px) {
#TOC {
position: relative;
width: 100%;
}
}
@media print {
.toc-content {
/* see https://github.com/w3c/csswg-drafts/issues/4434 */
float: right;
}
}
.toc-content {
padding-left: 30px;
padding-right: 40px;
}
div.main-container {
max-width: 1200px;
}
div.tocify {
width: 20%;
max-width: 260px;
max-height: 85%;
}
@media (min-width: 768px) and (max-width: 991px) {
div.tocify {
width: 25%;
}
}
@media (max-width: 767px) {
div.tocify {
width: 100%;
max-width: none;
}
}
.tocify ul, .tocify li {
line-height: 20px;
}
.tocify-subheader .tocify-item {
font-size: 0.90em;
}
.tocify .list-group-item {
border-radius: 0px;
}
.tocify-subheader {
display: inline;
}
.tocify-subheader .tocify-item {
font-size: 0.95em;
}
</style>
</head>
<body>
<div class="container-fluid main-container">
<!-- setup 3col/9col grid for toc_float and main content -->
<div class="row">
<div class="col-xs-12 col-sm-4 col-md-3">
<div id="TOC" class="tocify">
</div>
</div>
<div class="toc-content col-xs-12 col-sm-8 col-md-9">
<div class="navbar navbar-default navbar-fixed-top" role="navigation">
<div class="container">
<div class="navbar-header">
<button type="button" class="navbar-toggle collapsed" data-toggle="collapse" data-bs-toggle="collapse" data-target="#navbar" data-bs-target="#navbar">
<span class="icon-bar"></span>
<span class="icon-bar"></span>
<span class="icon-bar"></span>
</button>
<a class="navbar-brand" href="index.html">Estadística ITM</a>
</div>
<div id="navbar" class="navbar-collapse collapse">
<ul class="nav navbar-nav">
</ul>
<ul class="nav navbar-nav navbar-right">
<li>
<a href="pagin1.html">
<span class="fa fa-line-chart"></span>
Est Básica
</a>
</li>
<li>
<a href="inf.html">
<span class="fa fa-bar-chart-o"></span>
Est inferencial
</a>
</li>
<li>
<a href="medi.html">
<span class="fa fa-puzzle-piece"></span>
Metrología
</a>
</li>
<li>
<a href="https://www.itm.edu.co">
<span class="ion ion-university"></span>
</a>
</li>
<li>
<a href="https://github.com/estadisticaITM">
<span class="fa fa-github"></span>
</a>
</li>
</ul>
</div><!--/.nav-collapse -->
</div><!--/.container -->
</div><!--/.navbar -->
<div id="header">
<h1 class="title toc-ignore">Distribución gama y exponencial</h1>
</div>
<div id="función-gama" class="section level2">
<h2>Función gama</h2>
<p>La distribución normal es simétrica. Existen muchas situaciones de
interés en que la distribución es asimétrica. Una familia de
distribuciones que tiene esta propiedad es la familia gama.</p>
<p>Con <span class="math inline">\(\alpha>0\)</span>, la función gama
<span class="math inline">\(\Gamma(\alpha)\)</span> se define como:</p>
<p><span class="math display">\[\Gamma(\alpha)=\int_0^\infty
x^{\alpha-1}e^{-x}dx\]</span> Las propiedades más importantes de la
función gama son las siguientes:</p>
<ol style="list-style-type: decimal">
<li><p>Con cualquier <span class="math inline">\(\alpha>1,
\Gamma(\alpha)=(\alpha-1)*\Gamma(\alpha-1)\)</span></p></li>
<li><p>Con cualquier entero positivo n, <span
class="math inline">\(\Gamma(n)=(n-1)!\)</span></p></li>
<li><p><span class="math inline">\(\Gamma(\frac{1}{2})=\sqrt
\pi\)</span></p></li>
</ol>
</div>
<div id="función-de-distribución-de-probabilidad-gama"
class="section level2">
<h2>Función de distribución de probabilidad gama</h2>
<p>Si se está interesado en la ocurrencia de un evento generado por un
proceso de Poisson de media <span
class="math inline">\(\lambda\)</span>, la variable que mide el tiempo
transcurrido hasta obtener n ocurrencias del evento, sigue una
distribución gamma, por ejemplo cuando se realiza el estudio de la
duración de elementos físicos (tiempo de vida).</p>
<p>Una variable aleatoria continua X tiene una distribución gama si la
función de densidad de probabilidad de X es:</p>
<p><span class="math display">\[
f(x;\alpha,\beta)=\left\{ \begin{array}{lc}
\\ \frac{x^{\alpha-1}e^{-x/\beta}}{\beta^\alpha\Gamma
(\alpha)} & si & x \geq 0 \\
\\ 0 & & e.o.c
\end{array}
\right.
\]</span></p>
<p>Donde <span class="math inline">\(\alpha>0\)</span> y <span
class="math inline">\(\beta>0\)</span></p>
<ul>
<li>El parámetro <span class="math inline">\(\alpha\)</span> recibe el
nombre de parámetro de forma</li>
</ul>
<p>si <span class="math inline">\(\alpha \leq 1\)</span> la función de
densidad muestra un perfil decreciente.</p>
<p>si <span class="math inline">\(\alpha>1\)</span> la función de
densidad crece</p>
<ul>
<li><p><span class="math inline">\(\beta\)</span> se llama parámetro de
escala porque los valores diferentes alargan o comprimen la función de
densidad de probabilidad en la dirección x.</p></li>
<li><p>La distribución exponencial se deriva de considerar <span
class="math inline">\(\alpha=1\)</span> y <span
class="math inline">\(\beta=1/\lambda\)</span></p></li>
<li><p>Cuando <span class="math inline">\(\beta=1\)</span> se obtiene la
<strong>Distribución gama estándar</strong></p></li>
</ul>
</div>
<div id="función-de-distribución-de-probabilidad-gama-estándar"
class="section level2">
<h2>Función de distribución de probabilidad gama estándar</h2>
<p><span class="math display">\[f(x)=\left\{ \begin{array}{lc}
\\ 0 & si & x < 0 \\
\\ \frac{x^{\alpha-1}e^{-x}}{\Gamma (\alpha)}
& si & x \geq 0
\end{array}
\right.\]</span></p>
<p>La media y la varianza de una variable aleatoria X que tiene la
distribución gama f(x,α,β) son:</p>
<p><span class="math display">\[E(x)=μ=αβ\]</span></p>
<p><span class="math display">\[V(x)=αβ^2\]</span></p>
<p>La <strong>función de distribución acumulativa de una distribución
gama estándar</strong> de X, con x>0 es:</p>
<p><span
class="math display">\[P(X≤x)=F(x;α,β)=F\left(\frac{x}{β};α\right)=
\int_0^x \frac{y^{\alpha-1}e^{-y}}{\Gamma (\alpha)} \]</span></p>
<p>donde <span class="math inline">\(F(.;\alpha)\)</span> es la función
gama incompleta</p>
<p><strong>Hallar probabilidades</strong> a partir de la tabla con <span
class="math inline">\(\beta=1\)</span>, cuya función se llama la gama
incompleta porque el integrando no posee el denominador</p>
<p><strong>Ejemplo 1:</strong></p>
<p>Suponga que el tiempo de reacción X de un individuo seleccionado al
azar a un estímulo tiene una distribución gama estándar con <span
class="math inline">\(\alpha=2\)</span></p>
<p>Como X es continua:</p>
<p><span class="math display">\[𝑷(𝒂≤𝒙≤𝒃)=𝑭(𝒃)−𝑭(𝒂)\]</span></p>
<p><span
class="math display">\[𝑷(3≤𝒙≤5)=𝑭(x=5,α=2)−𝑭(x=3,α=2)\]</span></p>
<p><span class="math display">\[= 0.960 - 0.801 = 0.159\]</span></p>
<p>La probabilidad de que el tiempo de reacción sea de más de 4 s es</p>
<p><span class="math display">\[P(x>4)=1-P(x≤4)\]</span></p>
<p><span class="math display">\[=1-F(x=4,α=2)\]</span></p>
<p><span class="math display">\[=1-0.908=0.092\]</span> <strong>Ejemplo
2:</strong> Suponga que el tiempo de sobrevivencia de un ratón macho
seleccionado al azar expuesto a 240 rads de radiación gama tiene una
distribución gama con <span class="math inline">\(\alpha=8\)</span> y
<span class="math inline">\(\beta=15\)</span>.</p>
<ol style="list-style-type: lower-alpha">
<li>Halle el tiempo de sobrevivencia esperado</li>
</ol>
<p><span class="math display">\[E(X)=8*15=120 \quad semanas\]</span> b.
halle la varianza y la sd</p>
<p><span class="math display">\[V(X)=(8)*(15)^2=1800\]</span></p>
<p><span class="math display">\[sd=\sqrt {1800}=42.43 \quad
sem\]</span></p>
<ol start="3" style="list-style-type: lower-alpha">
<li>cuál es la probabilidad de que un ratón sobreviva entre 60 y 120
semanas</li>
</ol>
<p><span class="math display">\[P(60 \leq X \leq 120)= P(X \leq 120)-
P(X\leq 60)\]</span> Estandarizando</p>
<p><span class="math display">\[F(120/15;8)- F(60/15;8)\]</span></p>
<p><span class="math display">\[ F(8; 8) - F(4; 8)= 0.547- 0.051 =
0.496\]</span> d. Cual es la probabilidad de que un ratón sobreviva por
lo menos 30 semanas</p>
<p><span class="math display">\[P(X>30)= 1 - P(X\leq 30)\]</span>
<span class="math display">\[ 1 - F(30/15;8)= 0.999\]</span></p>
</div>
<div id="función-de-distribución-de-probabilidad-exponencial"
class="section level2">
<h2>Función de distribución de probabilidad exponencial</h2>
<p>La distribución exponencial se deriva de considerar <span
class="math inline">\(\alpha=1\)</span> y <span
class="math inline">\(\beta=1/\lambda\)</span> en la distribución gama.
Esta distribución analiza el espacio entre dos eventos en un proceso de
Poisson, donde los eventos ocurren de manera continua e independiente a
una tasa constante λ.Un ejemplo es el tiempo que tarda una partícula
radiactiva en desintegrarse.</p>
<p><img src="imagen/colas.png" width="357" style="display: block; margin: auto;" /></p>
<div id="función-de-distribución-de-probabilidad"
class="section level3">
<h3>Función de distribución de probabilidad</h3>
<p>Se dice que X tiene una distribución exponencial con parámetro λ, con
λ>0, si la función de densidad de probabilidad de X es:</p>
<p><span class="math display">\[ f(x;λ)=\left\{ \begin{array}{lc}
\\ λe^{-λx} & si & x \geq 0 \\
\\ 0 & si & x < 0
\end{array}
\right. \]</span></p>
<p>El <strong>valor esperado</strong> de una variable aleatoria
exponencialmente distribuida X es:</p>
<p><span class="math display">\[
E(X)=\int_0^\infty x λe^{-λx} \,dx
\]</span></p>
<p>Después de resolver la integral por partes, se tiene que el valor
medio es <span class="math display">\[E(x)=\frac{1}{λ}\]</span></p>
<p>Mientras que la varianza se obtiene resolviendo:</p>
<p><span class="math display">\[V(X)=E(X^2)-\mu^2 \]</span> <span
class="math display">\[V(X)=\int_0^\infty x^2 λe^{-λx}-\mu^2 \]</span>
al resolver las integrales se obtiene que<br />
<span class="math display">\[Var(x)=\frac{1}{λ^2}\]</span></p>
</div>
<div id="función-de-distribución-acumulada" class="section level3">
<h3>Función de distribución acumulada</h3>
<p>La función de distribución acumulada es</p>
<p><span class="math display">\[ F(x;λ)=\left\{ \begin{array}{lc}
\\ 0 & si & x < 0 \\
\\ 1-e^{-λx} & si & x \geq 0
\end{array}
\right. \]</span></p>
<p><strong>Ejemplo 1</strong></p>
<p>En promedio un rayo mata 3 personas cada año en un país λ=3
muertes/año.</p>
<p>Así la función acumulada es</p>
<p><span class="math display">\[F(x;λ)=\left\{ \begin{array}{lc}
\\ 0 & si & x < 0 \\
\\ 1-e^{-3x} & si & x \geq 0
\end{array}
\right.\]</span></p>
<ol style="list-style-type: lower-alpha">
<li>Calcule la probabilidad de que el tiempo de muerte sea menos de un
año</li>
</ol>
<p><span class="math display">\[P(x<1)=1-e^{-3}=0.95\]</span></p>
<p>Calcule la probabilidad de que el tiempo hasta la próxima falla sea
al menos de 18 meses <span class="math display">\[P(t>1.5)=1-p(t\leq
1.5)=0.95\]</span> <span
class="math display">\[P(t>1.5)=1-F(1.5)=0.95\]</span> <span
class="math display">\[P(t>1.5)=1-(1-e^{-3*1.5})=e^{-4.5}\]</span></p>
</div>
<div id="propiedad-de-pérdida-de-memoria-de-la-distribución-exponencial"
class="section level3">
<h3>Propiedad de pérdida de memoria de la distribución exponencial</h3>
<p>En el análisis del comportamiento de las líneas de espera, se
reconoce que el proceso de llegada de los clientes al sistema ocurre de
forma totalmente aleatoria. Se entiende por aleatorio que la ocurrencia
de un evento no se ve afectado por el tiempo transcurrido desde la
ocurrencia de un evento anterior. Por ejemplo, si en estos momentos son
las 10:30 y la última llegada de un cliente fue a las 10:15, la
probabilidad de que la siguiente llegada sea a las 10:35 es función sólo
de las 10:30 a las 10:35 y en consecuencia es totalmente independiente
del tiempo transcurrido desde la ocurrencia del último evento, es decir,
de las 10:15 a las 10:30.</p>
<p>Teoricamente se traduce en la siguiente propiedad <span
class="math display">\[P(X>x+y|X>y)=P(X>x) \]</span> la
demostración de esta formula está dada por:</p>
<p><span class="math display">\[P(X>x+y|X>y)=\frac{P(X>x+y
\bigcap X>y)=}{P(X>y)}\]</span> <span
class="math display">\[\frac{P(X>x+y )}{P(X>y)}\]</span></p>
<p><span class="math display">\[\frac{e^{-\lambda(x+y)}}{e^{-\lambda
y}}\]</span> <span class="math display">\[e^{-\lambda
x}=P(X>x)\]</span></p>
</div>
<div id="relación-entre-la-distribución-exponencial-y-la-poisson"
class="section level3">
<h3>Relación entre la distribución exponencial y la poisson</h3>
<p>La distribución exponencial está estrechamente relacionada con el
proceso Poisson.</p>
<div class="figure" style="text-align: center">
<img src="imagen/REP.png" alt="Probabilidad es un valor entre 0 y 1" width="446" />
<p class="caption">
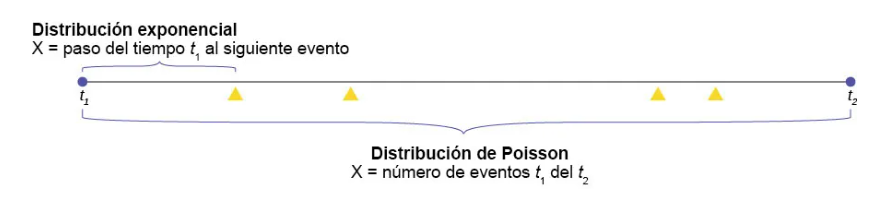
Probabilidad es un valor entre 0 y 1
</p>
</div>
<p><strong>La v.a Poisson es discreta</strong></p>
<ul>
<li><p>Cuenta los eventos durante un periodo de tiempo.</p></li>
<li><p>Calcula la probabilidad de que se produzca un número de
eventos.</p></li>
<li><p>La pregunta clásica de la distribución de Poisson es ¿cuántas
personas llegarán a la caja en la próxima hora?“.</p></li>
</ul>
<p><strong>La v.a exponencial es continua</strong></p>
<ul>
<li><p>calcula las probabilidades del paso del tiempo,</p></li>
<li><p>las preguntas clásicas de la distribución exponencial son:</p>
<ul>
<li>¿cuánto tiempo pasará hasta que llegue la siguiente persona?”</li>
<li>¿cuánto tiempo permanecerá la persona una vez que haya llegado?</li>
</ul></li>
</ul>
<p>Existe una confusión natural con µ tanto en las fórmulas de Poisson
como en las exponenciales. Tienen significados diferentes, aunque tengan
el mismo símbolo. La media de la exponencial es uno dividido entre la
media de Poisson. Si se da el número histórico de llegadas se tiene la
media de Poisson. Si se da una duración histórica entre eventos, se
tiene la media de una exponencial.</p>
<table>
<colgroup>
<col width="13%" />
<col width="37%" />
<col width="49%" />
</colgroup>
<thead>
<tr class="header">
<th>Parámetro</th>
<th align="center">Poisson</th>
<th align="center">Exponencial</th>
</tr>
</thead>
<tbody>
<tr class="odd">
<td>Media <span class="math inline">\(\mu\)</span></td>
<td align="center"><span
class="math inline">\(\lambda=\frac{evento}{tiempo}\)</span></td>
<td align="center"><span
class="math inline">\(\frac{1}{\lambda}=\frac{tiempo}{evento}\)</span></td>
</tr>
<tr class="even">
<td>tasa</td>
<td align="center"><span
class="math inline">\(\lambda=\frac{evento}{tiempo}\)</span></td>
<td align="center"><span
class="math inline">\(\lambda=\frac{evento}{tiempo}\)</span></td>
</tr>
</tbody>
</table>
<p><strong>Ejemplo</strong></p>
<p><strong>VA poisson:</strong> Cuál es la probabilidad de que en
colombia en el año sucedan 20 temblores</p>
<p><strong>VA exponencial:</strong> Cuanto tiempo transcurre entre un
temblor y otro</p>
<p>El número de eventos que ocurren en cualquier intervalo de tiempo de
duración t tiene una distribución de Poisson con parámetro <span
class="math inline">\(\alpha t\)</span> (donde <span
class="math inline">\(\alpha\)</span>,es el número esperado de eventos
que ocurren en una unidad de tiempo) y que las ocurrencias entre eventos
son independientes. Entonces la distribución del tiempo transcurrido
entre la ocurrencia de dos eventos sucesivos es exponencial con
parámetro <span class="math inline">\(\lambda=\alpha\)</span>.</p>
<p>El número de autos que corren a una alta velocidad (detectada por
cámaras) durante un lapso de una hora es una v.a. poisson con μ=8.4 .
¿Cuál es la probabilidad de esperar menos de 10 minutos entre dos autos
veloces? Solución:</p>
<p>X~p (8.4) autos / hora</p>
<p>µ=60/8.4 minuto/auto =7.1428</p>
<p>X~Exp con media de 7.1428</p>
<p>λ =1/µ donde λ =1/7.1428=0.14</p>
<p>X~Exp (0.14)</p>
<p>P(x<10)=1-e^(-0.14*10) =0.7534</p>
</div>
<div id="ejercicios" class="section level3">
<h3>Ejercicios</h3>
<p><strong>Ejercicios GAMA</strong></p>
<ol style="list-style-type: decimal">
<li>Suponga que cuando un transistor de cierto tipo se somete a una
prueba de duración acelerada, la duración X (en semanas) tiene una
distribución gama acelerada con media de 24 semanas y desviación
estándar de 12 semanas.</li>
</ol>
<ol style="list-style-type: lower-alpha">
<li><p>¿Cuál es la probabilidad de que un transistor dure entre 12 y 24
semanas?</p></li>
<li><p>¿Cuál es la probabilidad de que un transistor dure cuando mucho
24 semanas? ¿Es la mediana de la distribución de duración menor que 24?
¿Por qué si o por qué no?</p></li>
<li><p>¿Cuál es el 99o percentil de la distribución de
duración?</p></li>
<li><p>Suponga que la prueba termina en realidad después de t semanas.
¿Qué valor de t es tal que sólo el 0.5% de todos los transistores
continuarán funcionando al término de la prueba?</p></li>
<li><p>0.424 b. 0.567,$ < 24$ c. 60 d. 66</p></li>
</ol>
<ol start="2" style="list-style-type: decimal">
<li><p>En cierta ciudad el consumo diario de energía eléctrica, en
millones de kilovatios por hora, puede considerarse como una variable
aleatoria con distribución gama de parámetros α= 3 y β=2. La planta de
energía de esta ciudad tiene una capacidad diaria de 10 millones de
KW/hora ¿Cuál es la probabilidad de que este abastecimientos sea: 2.1.
Insuficiente en un día cualquiera? 2.2 Se consuman entre 3 y 8 millones
de K. W./Hora? 2.3 Encuentre E(x) y V(x)</p></li>
<li><p>Si X tiene una distribución gama estándar con <span
class="math inline">\(\alpha=7\)</span> evalúe lo siguiente: <span
class="math display">\[a. P(X \leq 5)\]</span> <span
class="math display">\[b.P(X< 5)\]</span> <span
class="math display">\[c. P(X>8)\]</span> <span
class="math display">\[d. P(3 \leq X \leq 8)\]</span> <span
class="math display">\[ e. P(3 < X < 8)\]</span> <span
class="math display">\[f. P(X <4 o X > 6)\]</span></p></li>
</ol>
<p><strong>Ejercicios exponencial</strong></p>
<ol style="list-style-type: decimal">
<li>Sea X el tiempo entre dos llegadas sucesivas a la ventanilla de
autopago de un banco local. Si X tiene una distribución exponencial con
λ=1 (la cual es idéntica a una distribución gama estándar con λ= 1),
calcule lo siguiente:</li>
</ol>
<ol style="list-style-type: lower-alpha">
<li>El tiempo esperado entre dos llegadas sucesivas</li>
<li>La desviación estándar del tiempo entre dos llegadas sucesivas</li>
<li>P(x≤4)</li>
<li><pre><code> P(2≤x≤5)</code></pre></li>
</ol>
<p>(rta/ a. 1 b. 1 c. 0.982 d. 0.129)</p>
<ol start="2" style="list-style-type: decimal">
<li>La amplia experiencia con ventiladores de un tipo utilizados en
motores diesel ha sugerido que la distribución exponencial proporciona
un buen modelo del tiempo hasta la falla. Suponga que el tiempo medio
hasta la falla es de 25000 horas. ¿Cuál es la probabilidad de que</li>
</ol>
<ol style="list-style-type: lower-alpha">
<li>¿Un ventilador seleccionado al azar dure por lo menos 20 000
horas?</li>
<li>¿Cuándo mucho 30000 horas? ¿Entre 20000 y 30000 horas?</li>
<li>¿Exceda la duración de un ventilador el valor medio por más de dos
desviaciones estándar? ¿Más de tres desviaciones estándar? (rta a.
0.449, 0.699, 0.148 b. 0.05, 0.018)</li>
</ol>
<ol start="3" style="list-style-type: decimal">
<li>El tiempo entre llegadas de mensajes electrónicos a un computador
tiene una distribución exponencial con media de 1.25 horas.</li>
</ol>
<ol style="list-style-type: lower-alpha">
<li><p>¿Cuál es la probabilidad de que el computador reciba un mensaje
en un período de 10 minutos?</p></li>
<li><p>Si son las 5 de la tarde y no ha recibido mensajes desde las 10
de la mañana, ¿Cuál es la probabilidad de recibir un mensaje antes de
las 10 de la noche?</p></li>
</ol>
<ol start="3" style="list-style-type: decimal">
<li>El tiempo entre la llegada de los clientes a un cajero automático es
una variable aleatoria exponencial con una media de cinco minutos.</li>
</ol>
<ol style="list-style-type: lower-alpha">
<li><p>¿Cuál es la probabilidad de que lleguen al cajero más de tres
clientes en un lapso de 10 minutos?</p></li>
<li><p>¿Cuál es la probabilidad de que el tiempo transcurrido hasta que
llega el quinto cliente sea menor que 15 minutos?</p></li>
</ol>
<ol start="4" style="list-style-type: decimal">
<li>La magnitud de temblores registrados en una región de América del
Norte puede modelarse como si tuviera una distribución exponencial con
media 2.4, según se mide en la escala de Richter. Encuentre la
probabilidad de que un temblor que ocurra en esta región</li>
</ol>
<p>a sea mayor que 3.0 en la escala de Richter. b caiga entre 2.0 y 3.0
en la escala de Richter. c. De los siguientes diez temblores que afecten
esta región, ¿cuál es la probabilidad de que al menos uno de ellos sea
mayor que 5.0 en la escala de Richter?</p>
<p>Suponga que la magnitud de los terremotos que afectan la región tiene
una distribución gamma con <span
class="math inline">\(\alpha=0.8\)</span> y <span
class="math inline">\(\beta = 2.4\)</span>. a ¿Cuál es la magnitud media
de los terremotos que afectan la región? b ¿Cuál es la probabilidad de
que la magnitud de un terremoto que afecte la región exceda de 3.0 en la
escala Richter? c Compare sus respuestas con el Ejercicio anterior.
¿Cuál probabilidad es mayor? Explique. d ¿Cuál es la probabilidad de que
un terremoto que afecte las regiones caiga entre 2.0 y 3.0 en la escala
Richter? (rta a E(Y) = 1.92 b P(Y > 3) =.21036 d P(2 ≤Y ≤3)
=.12943)</p>
<ol start="5" style="list-style-type: decimal">
<li><p>Si Y tiene una distribución exponencial y P(Y>2)=0.0821, ¿cuál
es <span class="math display">\[a. \beta=E(Y)?\]</span> <span
class="math display">\[b. P(Y\leq 1.7)?\]</span> (Rta/ <span
class="math inline">\(\beta=0.8\)</span>, <span
class="math inline">\(P(y\leq1.7)=0.8806\)</span>)</p></li>
<li><p>El operador de una estación de bombeo ha observado que la demanda
de agua durante las primeras horas de la tarde tiene una distribución
aproximadamente exponencial con media de 100 pes (pcs cúbicos por
segundo). a Encuentre la probabilidad de que la demanda sea mayor que
200 pcs durante las primeras horas de la tarde en un día seleccionado al
azar. b ¿Qué capacidad de bombeo de agua debe mantener la estación
durante las primeras horas de la tarde para que la probabilidad de que
la demanda sea mayor que la capacidad en un día seleccionado al azar sea
de sólo .01?</p></li>
</ol>
<p>(rta a 0.1353 b 460.52 cfs)</p>
<ol start="7" style="list-style-type: decimal">
<li><p>Una evidencia histórica indica que los tiempos entre accidentes
mortales en vuelos nacionales de horario programado en aviones de
pasajeros en Estados Unidos tienen una distribución aproximadamente
exponencial. Suponga que el tiempo medio entre accidentes es de 44 días.
a Si uno de los accidentes ocurrió el 1 de julio de un año seleccionado
al azar en el periodo de estudio, ¿cuál es la probabilidad de que ocurra
otro accidente ese mismo mes? b ¿Cuál es la varianza de los tiempos
entre accidentes? (rta a 0.5057 b. 1936)</p></li>
<li><p>Una planta de manufactura utiliza un producto específico a
granel. La cantidad de producto empleada en un día puede ser modelada
por una distribución exponencial con <span
class="math inline">\(\beta=4\)</span> (medida en toneladas). Encuentre
la probabilidad de que la planta utilice más de 4 toneladas en un día
determinado.</p></li>
</ol>
<p>(rta 0.3679) ¿Cuánto producto a granel debe tener en existencia para
que la probabilidad de que se agote el producto en la planta sea de sólo
0.05?</p>
<p>Suponga que la cantidad de producto usado en un día tiene una
distribución gamma con <span class="math inline">\(\alpha=1.5\)</span> y
<span class="math inline">\(\beta = 3\)</span>. a Encuentre la
probabilidad de que la planta use más de 4 toneladas en un día
determinado. b ¿Cuánto del producto a granel debe haber en existencia
para que la probabilidad de que la planta agote el producto sea de sólo
.05?</p>
<p><strong>Relación exponencial-poisson</strong></p>
<ol start="2" style="list-style-type: decimal">
<li><p>A una estación de servicio llegan en promedio 5 clientes por hora
¿Cuál es la probabilidad de que entre dos llegadas consecutivas:
transcurra mínimo 20 minutos? Solución: X~p (5) / hora µ=60/5
minuto/cliente<br />
µ=12 X~Exp con media de 12minutos λ =1/µ donde λ =1/12 λ =0.083 X~Exp
(1/12) a p.(x >20)= e^(-0.083*20) =0.1888</p></li>
<li><p>Suponga que las llamadas telefónicas que llegan a un conmutador
particular siguen un proceso de poisson con un promedio de 5 llamadas
que llegan por minuto. ¿Cuál es la probabilidad de que pase más de un
minuto entre dos llegadas consecutivas? Solución:</p></li>
</ol>
<p>X~p (5) / minuto Tiempo entre llamadas µ=1/5 minuto/cliente<br />
µ=0.2 X~Exp con media de 0.2 minutos λ =1/µ donde λ =1/0.2 λ =5 X~Exp
(5) a p.(x>1)= e^(-5*1) =0.006737</p>
<p>4.Se realiza un estudio de la cantidad de automóviles que llegan a un
auto lavado durante una hora se describe una distribución de poisson con
una media de 10 automóviles por hora. a. ¿Cuál es la probabilidad de que
el próximo carro en la fila tenga que esperar más de 10 minutos para ser
atendido? Solución:</p>
<p>X~p (10) / hora Tiempo entre llegadas µ=60/10 µ=6 minutos X~Exp con
media de 6 minutos. λ =1/µ donde λ =1/6 λ =0.1666 X~Exp (0.1666) a p.(x
>10)= e^(-1*10) =0.000045</p>
<p>5.El tiempo entre llegadas de barcos a un determinado puerto siguen
un proceso de poisson con un promedio de 6 barcos por minuto. ¿Cuál es
la probabilidad de que pase más de tres minutos entre dos llegadas
consecutivas de barcos?</p>
<p>Solución: X~p (6) / minuto Tiempo entre llamadas µ=1/6 minuto/barco
µ=0.166 X~Exp con media de 0.1666 minutos λ =1/µ donde λ =1/0.1666 λ =6
X~Exp (6) a p.(x>3)= e^(-6*1) =0.002478</p>
<p><strong>Selección múltiple</strong></p>
<p>Suponga que se reciben llamadas durante las 24 horas en una “línea de
emergencia para prevención del suicidio” de acuerdo con un proceso de
Poisson a razón α= 0.5 llamadas por día. Halle la probabilidad de que
transcurran más de dos días entre llamadas es</p>
<p>Solución:</p>
<p>Entonces el número de días X entre llamadas sucesivas tiene una
distribución exponencial con valor de parámetro 0.5</p>
<p>X~p (0.5 llamadas/día) El tiempo esperado entre llamadas sucesivas es
1/0.5= 2 días. µ=2 X~Exp con media de 0.5 λ =1/µ donde λ =1/2 λ =0.5
X~Exp (0.5)</p>
<p>P(X>2)=1-P(x≤2)=1-(1-e^(0.5<em>2) )= e^(0.5</em>2)=0.368</p>
<ol start="2" style="list-style-type: decimal">
<li>históricamente llegan 10 clientes a las filas de espera en las cajas
registradoras cada hora. Halle la probabilidad de que una persona tarde
9 minutos o menos en pasar por caja registradora.</li>
</ol>
<p>X~p (10 clientes) / hora Tiempo entre llegadas µ=1/10 0.1
clientes/hora µ=0.1 X~Exp con media de 0.1 minutos λ =1/µ donde λ =1/0.1
λ =10 X~Exp (10) Pasamos 9 minutos a horas 9 min*(1 hora)/(60 min)=0.15
horas</p>
<p>P(x≤0.15)=1-e^(-10*0.15)=0,7769</p>
<ol start="3" style="list-style-type: decimal">
<li>La amplia experiencia con ventiladores de un tipo utilizados en
motores diesel ha sugerido que la distribución exponencial proporciona
un buen modelo del tiempo hasta la falla. Suponga que el tiempo medio
hasta la falla es de 25000 horas. ¿Cuál es la probabilidad de que Un
ventilador seleccionado al azar dure por lo menos 20.000 horas?</li>
</ol>
<p>Tiempo entre fallas<br />
µ=25000 horas hasta la falla</p>
<p>µ=1/ λ λ=1/25000=0.00004</p>
<p>X~Exp con media de 25000 horas</p>
<p>X~Exp (0.00004)</p>
<p>P(x≥20000)=e^(-20000*0.00004)=0,449</p>
<ol start="4" style="list-style-type: decimal">
<li>Si entran llamadas a un centro policial de emergencia a razón de
diez por hora, ¿cuál es la probabilidad de que transcurran más de 15
minutos entre las dos llamadas siguientes? X~p (10) / hora Tiempo entre
llamadas µ=1/10 0.1 horas µ=0.1 X~Exp con media de 0.1 minutos λ =1/µ
donde λ =1/0.1 λ =10 X~Exp (10)</li>
</ol>
<p>Pasamos 15 minutos a horas 15 min*(1 hora)/(60 min)=0.25 horas</p>
<p>P(x≥0.25)=e^(-10*0.25)=0,082</p>
<ol start="5" style="list-style-type: decimal">
<li>Durante el año 2020, el Centro Sismológico Nacional (CSN) de la
Universidad de Chile, procesó 21 sismos por día. ¿cuál es la
probabilidad de que se reporte más de dos horas entre sismos? X~p (21
sismos) / día Tiempo medio entre sismos µ=1/21 0.0476 días µ=0.0476
X~Exp con media de 0.04762 días λ =1/µ donde λ =1/0.1 λ =10 X~Exp (21)
Pasamos 2 horas a dias 2 horas*(1 dia)/(24 horas)=0.0833 horas</li>
</ol>
<p>P(x≥0.0833)=e^(-21*0833)=0,1737</p>
</div>
</div>
<br>
<hr>
<p><center>Copyright © 2019, webpage made with Rmarkdown.</center></p>
<hr>
</div>
</div>
</div>
<script>
// add bootstrap table styles to pandoc tables
function bootstrapStylePandocTables() {
$('tr.odd').parent('tbody').parent('table').addClass('table table-condensed');
}
$(document).ready(function () {
bootstrapStylePandocTables();
});
</script>
<!-- tabsets -->
<script>
$(document).ready(function () {
window.buildTabsets("TOC");
});
$(document).ready(function () {
$('.tabset-dropdown > .nav-tabs > li').click(function () {
$(this).parent().toggleClass('nav-tabs-open');
});
});
</script>
<!-- code folding -->
<script>
$(document).ready(function () {
// temporarily add toc-ignore selector to headers for the consistency with Pandoc
$('.unlisted.unnumbered').addClass('toc-ignore')
// move toc-ignore selectors from section div to header
$('div.section.toc-ignore')
.removeClass('toc-ignore')
.children('h1,h2,h3,h4,h5').addClass('toc-ignore');
// establish options
var options = {
selectors: "h1,h2,h3,h4,h5",
theme: "bootstrap3",
context: '.toc-content',
hashGenerator: function (text) {
return text.replace(/[.\\/?&!#<>]/g, '').replace(/\s/g, '_');
},
ignoreSelector: ".toc-ignore",
scrollTo: 0
};
options.showAndHide = false;
options.smoothScroll = true;
// tocify
var toc = $("#TOC").tocify(options).data("toc-tocify");
});
</script>
<!-- dynamically load mathjax for compatibility with self-contained -->
<script>
(function () {
var script = document.createElement("script");
script.type = "text/javascript";
script.src = "https://mathjax.rstudio.com/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML";
document.getElementsByTagName("head")[0].appendChild(script);
})();
</script>
</body>
</html>