<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8" />
<meta name="generator" content="pandoc" />
<meta http-equiv="X-UA-Compatible" content="IE=EDGE" />
<title>Distribución rectangular ó uniforme</title>
<script src="site_libs/header-attrs-2.14/header-attrs.js"></script>
<script src="site_libs/jquery-3.6.0/jquery-3.6.0.min.js"></script>
<meta name="viewport" content="width=device-width, initial-scale=1" />
<link href="site_libs/bootstrap-3.3.5/css/flatly.min.css" rel="stylesheet" />
<script src="site_libs/bootstrap-3.3.5/js/bootstrap.min.js"></script>
<script src="site_libs/bootstrap-3.3.5/shim/html5shiv.min.js"></script>
<script src="site_libs/bootstrap-3.3.5/shim/respond.min.js"></script>
<style>h1 {font-size: 34px;}
h1.title {font-size: 38px;}
h2 {font-size: 30px;}
h3 {font-size: 24px;}
h4 {font-size: 18px;}
h5 {font-size: 16px;}
h6 {font-size: 12px;}
code {color: inherit; background-color: rgba(0, 0, 0, 0.04);}
pre:not([class]) { background-color: white }</style>
<script src="site_libs/jqueryui-1.11.4/jquery-ui.min.js"></script>
<link href="site_libs/tocify-1.9.1/jquery.tocify.css" rel="stylesheet" />
<script src="site_libs/tocify-1.9.1/jquery.tocify.js"></script>
<script src="site_libs/navigation-1.1/tabsets.js"></script>
<link href="site_libs/highlightjs-9.12.0/textmate.css" rel="stylesheet" />
<script src="site_libs/highlightjs-9.12.0/highlight.js"></script>
<link href="site_libs/font-awesome-5.1.0/css/all.css" rel="stylesheet" />
<link href="site_libs/font-awesome-5.1.0/css/v4-shims.css" rel="stylesheet" />
<link href="site_libs/ionicons-2.0.1/css/ionicons.min.css" rel="stylesheet" />
<link rel="icon" type="image/png" href="images/favicon.png" />
<script type="text/javascript" src="js/rmarkdown.js"></script>
<link rel="stylesheet" href="https://cdnjs.cloudflare.com/ajax/libs/font-awesome/4.7.0/css/font-awesome.min.css">
<script>
(function(i,s,o,g,r,a,m){i['GoogleAnalyticsObject']=r;i[r]=i[r]||function(){
(i[r].q=i[r].q||[]).push(arguments)},i[r].l=1*new Date();a=s.createElement(o),
m=s.getElementsByTagName(o)[0];a.async=1;a.src=g;m.parentNode.insertBefore(a,m)
})(window,document,'script','https://www.google-analytics.com/analytics.js','ga');
ga('create', 'UA-88209726-1', 'auto');
ga('send', 'pageview');
</script>
<style type="text/css">
code{white-space: pre-wrap;}
span.smallcaps{font-variant: small-caps;}
span.underline{text-decoration: underline;}
div.column{display: inline-block; vertical-align: top; width: 50%;}
div.hanging-indent{margin-left: 1.5em; text-indent: -1.5em;}
ul.task-list{list-style: none;}
</style>
<style type="text/css">code{white-space: pre;}</style>
<script type="text/javascript">
if (window.hljs) {
hljs.configure({languages: []});
hljs.initHighlightingOnLoad();
if (document.readyState && document.readyState === "complete") {
window.setTimeout(function() { hljs.initHighlighting(); }, 0);
}
}
</script>
<style type = "text/css">
.main-container {
max-width: 940px;
margin-left: auto;
margin-right: auto;
}
img {
max-width:100%;
}
.tabbed-pane {
padding-top: 12px;
}
.html-widget {
margin-bottom: 20px;
}
button.code-folding-btn:focus {
outline: none;
}
summary {
display: list-item;
}
details > summary > p:only-child {
display: inline;
}
pre code {
padding: 0;
}
</style>
<style type="text/css">
.dropdown-submenu {
position: relative;
}
.dropdown-submenu>.dropdown-menu {
top: 0;
left: 100%;
margin-top: -6px;
margin-left: -1px;
border-radius: 0 6px 6px 6px;
}
.dropdown-submenu:hover>.dropdown-menu {
display: block;
}
.dropdown-submenu>a:after {
display: block;
content: " ";
float: right;
width: 0;
height: 0;
border-color: transparent;
border-style: solid;
border-width: 5px 0 5px 5px;
border-left-color: #cccccc;
margin-top: 5px;
margin-right: -10px;
}
.dropdown-submenu:hover>a:after {
border-left-color: #adb5bd;
}
.dropdown-submenu.pull-left {
float: none;
}
.dropdown-submenu.pull-left>.dropdown-menu {
left: -100%;
margin-left: 10px;
border-radius: 6px 0 6px 6px;
}
</style>
<script type="text/javascript">
// manage active state of menu based on current page
$(document).ready(function () {
// active menu anchor
href = window.location.pathname
href = href.substr(href.lastIndexOf('/') + 1)
if (href === "")
href = "index.html";
var menuAnchor = $('a[href="' + href + '"]');
// mark it active
menuAnchor.tab('show');
// if it's got a parent navbar menu mark it active as well
menuAnchor.closest('li.dropdown').addClass('active');
// Navbar adjustments
var navHeight = $(".navbar").first().height() + 15;
var style = document.createElement('style');
var pt = "padding-top: " + navHeight + "px; ";
var mt = "margin-top: -" + navHeight + "px; ";
var css = "";
// offset scroll position for anchor links (for fixed navbar)
for (var i = 1; i <= 6; i++) {
css += ".section h" + i + "{ " + pt + mt + "}\n";
}
style.innerHTML = "body {" + pt + "padding-bottom: 40px; }\n" + css;
document.head.appendChild(style);
});
</script>
<!-- tabsets -->
<style type="text/css">
.tabset-dropdown > .nav-tabs {
display: inline-table;
max-height: 500px;
min-height: 44px;
overflow-y: auto;
border: 1px solid #ddd;
border-radius: 4px;
}
.tabset-dropdown > .nav-tabs > li.active:before {
content: "";
font-family: 'Glyphicons Halflings';
display: inline-block;
padding: 10px;
border-right: 1px solid #ddd;
}
.tabset-dropdown > .nav-tabs.nav-tabs-open > li.active:before {
content: "";
border: none;
}
.tabset-dropdown > .nav-tabs.nav-tabs-open:before {
content: "";
font-family: 'Glyphicons Halflings';
display: inline-block;
padding: 10px;
border-right: 1px solid #ddd;
}
.tabset-dropdown > .nav-tabs > li.active {
display: block;
}
.tabset-dropdown > .nav-tabs > li > a,
.tabset-dropdown > .nav-tabs > li > a:focus,
.tabset-dropdown > .nav-tabs > li > a:hover {
border: none;
display: inline-block;
border-radius: 4px;
background-color: transparent;
}
.tabset-dropdown > .nav-tabs.nav-tabs-open > li {
display: block;
float: none;
}
.tabset-dropdown > .nav-tabs > li {
display: none;
}
</style>
<!-- code folding -->
<style type="text/css">
#TOC {
margin: 25px 0px 20px 0px;
}
@media (max-width: 768px) {
#TOC {
position: relative;
width: 100%;
}
}
@media print {
.toc-content {
/* see https://github.com/w3c/csswg-drafts/issues/4434 */
float: right;
}
}
.toc-content {
padding-left: 30px;
padding-right: 40px;
}
div.main-container {
max-width: 1200px;
}
div.tocify {
width: 20%;
max-width: 260px;
max-height: 85%;
}
@media (min-width: 768px) and (max-width: 991px) {
div.tocify {
width: 25%;
}
}
@media (max-width: 767px) {
div.tocify {
width: 100%;
max-width: none;
}
}
.tocify ul, .tocify li {
line-height: 20px;
}
.tocify-subheader .tocify-item {
font-size: 0.90em;
}
.tocify .list-group-item {
border-radius: 0px;
}
.tocify-subheader {
display: inline;
}
.tocify-subheader .tocify-item {
font-size: 0.95em;
}
</style>
</head>
<body>
<div class="container-fluid main-container">
<!-- setup 3col/9col grid for toc_float and main content -->
<div class="row">
<div class="col-xs-12 col-sm-4 col-md-3">
<div id="TOC" class="tocify">
</div>
</div>
<div class="toc-content col-xs-12 col-sm-8 col-md-9">
<div class="navbar navbar-default navbar-fixed-top" role="navigation">
<div class="container">
<div class="navbar-header">
<button type="button" class="navbar-toggle collapsed" data-toggle="collapse" data-bs-toggle="collapse" data-target="#navbar" data-bs-target="#navbar">
<span class="icon-bar"></span>
<span class="icon-bar"></span>
<span class="icon-bar"></span>
</button>
<a class="navbar-brand" href="index.html">Estadística ITM</a>
</div>
<div id="navbar" class="navbar-collapse collapse">
<ul class="nav navbar-nav">
</ul>
<ul class="nav navbar-nav navbar-right">
<li>
<a href="pagin1.html">
<span class="fa fa-line-chart"></span>
Est Básica
</a>
</li>
<li>
<a href="inf.html">
<span class="fa fa-bar-chart-o"></span>
Est inferencial
</a>
</li>
<li>
<a href="medi.html">
<span class="fa fa-puzzle-piece"></span>
Metrología
</a>
</li>
<li>
<a href="https://www.itm.edu.co">
<span class="ion ion-university"></span>
</a>
</li>
<li>
<a href="https://github.com/estadisticaITM">
<span class="fa fa-github"></span>
</a>
</li>
</ul>
</div><!--/.nav-collapse -->
</div><!--/.container -->
</div><!--/.navbar -->
<div id="header">
<h1 class="title toc-ignore">Distribución rectangular ó uniforme</h1>
</div>
<p>De esta función de probabilidad se distinguen 2 formas una discreta y
otra continua:</p>
<p><strong>Ejemplo forma continua:</strong></p>
<p>Un autobús llega siempre a una parada particular entre las 8:00 y las
8:10 a.m. la probabilidad de que llegue en cualquier subintervalo dado
es proporcional sólo a la duración del subintervalo.</p>
<p>Es igual de probable que llegue entre las 8:00 y 8:02 a que llegue
entre las 8:06 y las 8:08. Denote con Y el tiempo que una persona deba
esperar para que llegue el autobús si llegó a la parada exactamente a
las 8:00.</p>
<p><span class="math display">\[P(0 ≤ Y ≤ 2) = P(6 ≤ Y ≤ 8)\]</span></p>
<p>En una distribución rectangular cada valor en un intervalo ó valor
(Continua o discreta) tiene la misma probabilidad, o sea la función de
densidad de probabilidad es constante en este intervalo o valor.</p>
<table>
<colgroup>
<col width="16%" />
<col width="36%" />
<col width="48%" />
</colgroup>
<thead>
<tr class="header">
<th align="center">Uniforme</th>
<th align="center">Discreta <span
class="math inline">\(x=1,2,3,...k\)</span></th>
<th align="center">Continua <span class="math inline">\(a,b \quad
\varepsilon \quad \mathbb{R}\)</span></th>
</tr>
</thead>
<tbody>
<tr class="odd">
<td align="center">E(x)</td>
<td align="center"><span
class="math inline">\(\frac{k+1}{2}\)</span></td>
<td align="center"><span
class="math inline">\(\frac{a+b}{2}\)</span></td>
</tr>
<tr class="even">
<td align="center"><span class="math inline">\(E(x^2)\)</span></td>
<td align="center"><span
class="math inline">\(\frac{2k^2+3k+1}{6}\)</span></td>
<td align="center"><span
class="math inline">\(\frac{(a^2+ab+b^2)}{3}\)</span></td>
</tr>
<tr class="odd">
<td align="center">V(x)</td>
<td align="center"><span
class="math display">\[\frac{k^2-1}{12}\]</span></td>
<td align="center"><span
class="math display">\[\frac{(b-a)^2}{12}\]</span></td>
</tr>
<tr class="even">
<td align="center">f(x)</td>
<td align="center"></td>
<td align="center"><span class="math display">\[\begin{cases}
\frac{1}{b-a},
& \mbox{si x $\varepsilon \quad \mathbb{R}$,}\\
0, & \mbox{e.o.c.}
\end{cases} \]</span></td>
</tr>
<tr class="odd">
<td align="center">F(x)</td>
<td align="center"></td>
<td align="center"><span class="math display">\[P(x \leq
\frac{x-a}{b-a}) \]</span></td>
</tr>
<tr class="even">
<td align="center">Notación</td>
<td align="center"><span class="math inline">\(X∼U(a,b)\)</span></td>
<td align="center"></td>
</tr>
</tbody>
</table>
<p><span class="math inline">\(a,b \quad \varepsilon \quad
\mathbb{R}\)</span>:</p>
<p><strong>Forma discreta</strong></p>
<p><strong>Demostración E(x)</strong></p>
<p><span class="math display">\[E(x)=\sum_{i=1}^n x*f(x)\]</span> <span
class="math display">\[E(x)=\sum_{i=1}^n x*\frac{1}{k}\]</span> <span
class="math display">\[E(x)=1*\frac{1}{k}+2*\frac{1}{k}+3*\frac{1}{k}+...+k*\frac{1}{k}\]</span>
en general</p>
<p><span class="math display">\[E(X)=\frac{1}{k}\sum_{i=1}^k
i\]</span></p>
<p>pero</p>
<p><span class="math display">\[\sum_{i=1}^k i=\frac{k(k+1)}{2}
\]</span> entonces: <span class="math display">\[E(x)=\frac{(k+1)}{2}
\]</span></p>
<p><strong>Demostración <span
class="math inline">\(E(x^2)\)</span></strong></p>
<p><span class="math display">\[E(x^2)=\sum_{i=1}^k x^2*f(x)\]</span>
<span class="math display">\[E(x^2)=\sum_{i=1}^n
x^2*\frac{1}{k}\]</span> pero</p>
<p><span class="math display">\[\sum_{i=1}^k x^2=\frac{k(k+1)(2k+1)}{6}
\]</span> entonces:</p>
<p><span
class="math display">\[E(x^2)=\frac{1}{k}\frac{k(k+1)(2k+1)}{6}\]</span>
<span class="math display">\[E(x^2)=\frac{(k+1)(2k+1)}{6}\]</span> <span
class="math display">\[E(x^2)=\frac{(2k^2+3k+1)}{6}\]</span></p>
<p><strong>Continua</strong></p>
<ul>
<li>El hecho de que <span class="math inline">\(P(X = c)= 0\)</span>
cuando X es continua tiene una importante consecuencia práctica: La
probabilidad de que X quede en algún intervalo entre a y b no depende
desi el límite inferior a o el límite superior b está incluido en el
cálculo de probabilidad</li>
</ul>
<p><span class="math display">\[P(a \leq X \leq b)=P(a< X
<b)=P(a\leq X < b)= P(a < X \leq b)\]</span></p>
<p><img src="uniforme_files/figure-html/unnamed-chunk-1-1.png" width="672" /></p>
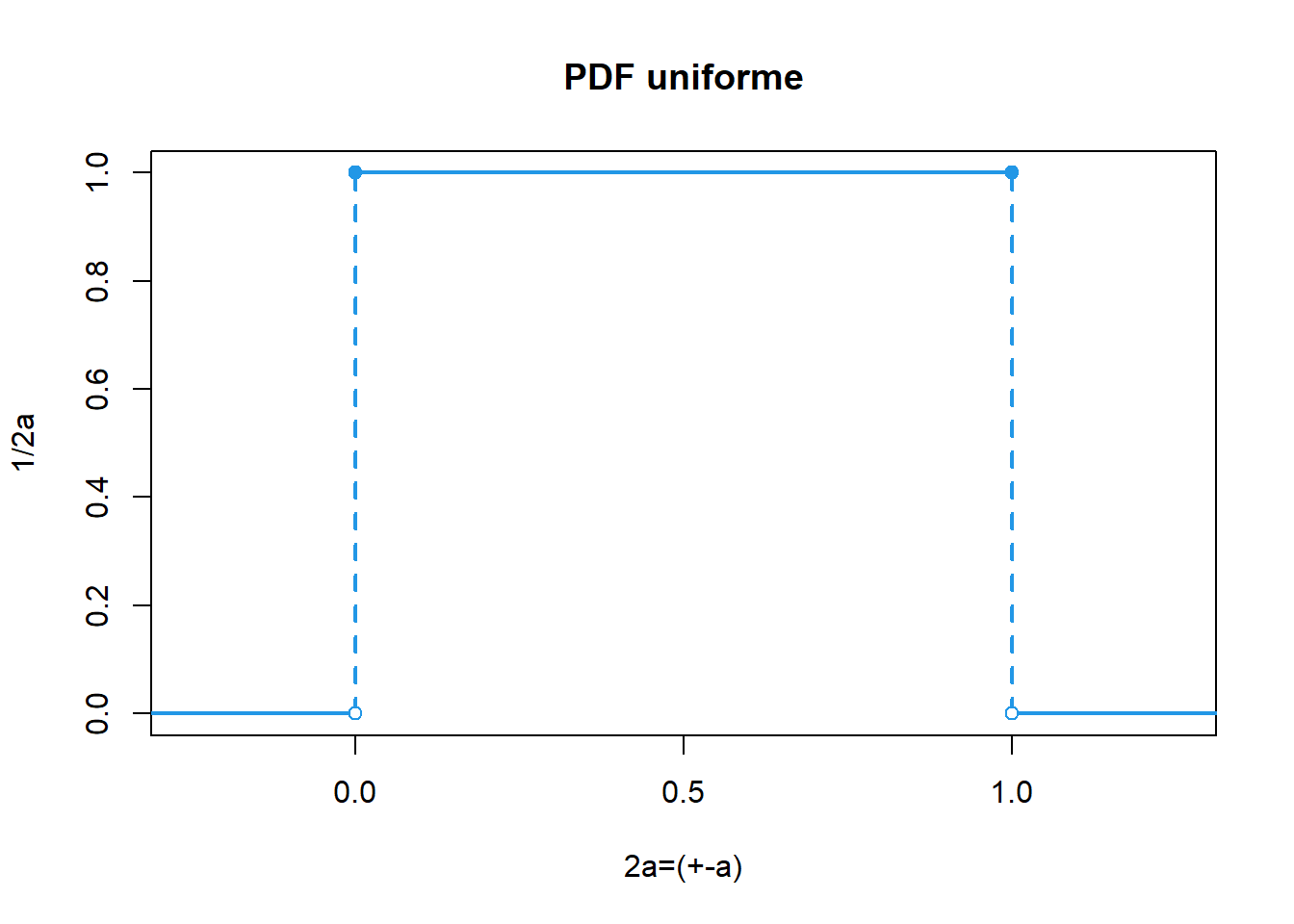
<p>Se usa para estimar la incertidumbre cuando:</p>
<ul>
<li><p>Un certificado da unos límites sin especificar el nivel de
confianza (por ejemplo, 25 mL <span class="math inline">\(\pm\)</span>
0,05 mL)</p></li>
<li><p>Se ha hecho una estimación en forma de un rango máximo (<span
class="math inline">\(\pm\)</span>a) sin conocimiento de la forma de la
distribución.</p></li>
</ul>
<p><a
href="https://huggingface.co/spaces/FreddyHernandez/discrete_uniform"
class="uri">https://huggingface.co/spaces/FreddyHernandez/discrete_uniform</a></p>
<p>El rango de una distribución de probabilidad se refiere al conjunto
de todos los posibles valores que puede tomar una variable aleatoria en
esa distribución. Es la diferencia entre el valor máximo y el valor
mínimo de esta variable.</p>
<p>Algunas variables aleatorias continuas en física, administración y
ciencias biológicas tienen distribuciones de probabilidad
aproximadamente uniformes. Por ejemplo, suponga que el número de
eventos, como las llamadas que entran en un conmutador, que se presentan
en el intervalo (0, t) tienen una distribución de Poisson. Si se sabe
que exactamente uno de estos eventos ha ocurrido en el intervalo (0, t),
entonces el tiempo real del suceso está distribuido de manera uniforme
en este intervalo.</p>
<p><strong>Ejemplo</strong> La llegada de clientes a una caja en un
establecimiento sigue una distribución de Poisson. Se sabe que durante
un periodo determinado de 30 minutos, un cliente llega a la caja.
Encuentre la probabilidad de que el cliente llegue durante los últimos 5
minutos del periodo de 30 minutos.</p>
<p><strong>Solución</strong></p>
<p>El tiempo real de llegada sigue una distribución uniforme en el
intervalo de (0, 30). Si Y denota el tiempo de llegada, entonces <span
class="math display">\[P(25 ≤Y
≤30)=\int_{25}^{30}=\frac{30-25}{30}=\frac{5}{30}=\frac{1}{6}\]</span>
La probabilidad de que la llegada ocurra en cualquier otro intervalo de
5 minutos también es 1/6.</p>
<p><strong>Ejercicios</strong></p>
<p><strong>1.</strong> Suponga que la temperatura de reacción X (en °C)
en cierto proceso químico tiene una distribución uniforme con A=-5 y B=
5.</p>
<ol style="list-style-type: lower-alpha">
<li><p>Calcule P(X < 0).</p></li>
<li><p>Calcule P(2.5 < X < 2.5)</p></li>
<li><p>Calcule <span class="math inline">\(P( -2\leq X \leq
3)\)</span></p></li>
<li><p>Para que k satisfaga -5<k< k+ 4< 5, calcule P(k < X
< k+ 4).</p></li>
</ol>
<p><strong>2.</strong> Se cree que el tiempo X (min) para que un
ayudante de laboratorio prepare el equipo para cierto experimento tiene
una distribución uniforme con A= 25 y B=35.</p>
<ol style="list-style-type: lower-alpha">
<li><p>Determine la función de densidad de probabilidad de X y trace la
curva de densidad de correspondiente.</p></li>
<li><p>¿Cuál es la probabilidad de que el tiempo de preparación exceda
de 33 min?</p></li>
<li><p>¿Cuál es la probabilidad de que el tiempo de preparación esté
dentro de dos min del tiempo medio? [Sugerencia: Identifique $$en la
gráfica de f(x).]</p></li>
<li><p>Con cualquier a de modo que 25 <a <a +2 <35, ¿cuál es la
probabilidad de que el tiempo de preparación esté entre a y a+2
min?</p></li>
<li><p>f (x) =0.1 para 25<x<35 y 0 de otro modo</p></li>
<li><p>0.20 c. 0.40 d. 0.20</p></li>
</ol>
<p><strong>3.</strong> El artículo “Modeling Sediment and Water Column
Interactions for Hidrophobic Pollutants” (Water Research, 1984:
1169-1174) sugiere la distribución uniforme en el intervalo (7.5, 20)
como modelo de profundidad (cm) de la capa de bioturbación en sedimento
en una región.</p>
<ol style="list-style-type: lower-alpha">
<li><p>¿Cuáles son la media y la varianza de la profundidad?</p></li>
<li><p>¿Cuál es la función de distribución acumulativa de la
profundidad?</p></li>
<li><p>¿Cuál es la probabilidad de que la profundidad observada sea
cuando mucho de 10? ¿Entre 10 y 15?</p></li>
</ol>
<p><strong>4.</strong> Sea X=el tiempo que una cabeza de
lectura/escritura requiere para localizar un registro deseado en un
dispositivo de memoria de disco de computadora una vez que la cabeza se
ha colocado sobre la pista correcta. Si los discos giran una vez cada 25
milisegundos, una suposición razonable es que X está uniformemente
distribuida en el intervalo [0, 25]. a. Calcule P(10<X<20). b.
Calcule P(X>10). c. Obtenga la función de distribución acumulativa
F(X). d. Calcule E(X) y sd.</p>
<ol start="5" style="list-style-type: decimal">
<li>El espesor del borde de un componente de una aeronave está
distribuido de manera uniforme entre 0.95 y 1.05 milímetros.</li>
</ol>
<ol style="list-style-type: lower-alpha">
<li><p>Obtenga la función de distribución acumulada del espesor del
borde.</p></li>
<li><p>Calcule la proporción de bordes cuyo espesor es mayor que 1.02
milímetros.</p></li>
<li><p>¿Qué espesor está excedido por el 90% de los bordes?</p></li>
<li><p>Calcule la media y la varianza del espesor del borde.</p></li>
</ol>
<br>
<hr>
<p><center>Copyright © 2019, webpage made with Rmarkdown.</center></p>
<hr>
</div>
</div>
</div>
<script>
// add bootstrap table styles to pandoc tables
function bootstrapStylePandocTables() {
$('tr.odd').parent('tbody').parent('table').addClass('table table-condensed');
}
$(document).ready(function () {
bootstrapStylePandocTables();
});
</script>
<!-- tabsets -->
<script>
$(document).ready(function () {
window.buildTabsets("TOC");
});
$(document).ready(function () {
$('.tabset-dropdown > .nav-tabs > li').click(function () {
$(this).parent().toggleClass('nav-tabs-open');
});
});
</script>
<!-- code folding -->
<script>
$(document).ready(function () {
// temporarily add toc-ignore selector to headers for the consistency with Pandoc
$('.unlisted.unnumbered').addClass('toc-ignore')
// move toc-ignore selectors from section div to header
$('div.section.toc-ignore')
.removeClass('toc-ignore')
.children('h1,h2,h3,h4,h5').addClass('toc-ignore');
// establish options
var options = {
selectors: "h1,h2,h3,h4,h5",
theme: "bootstrap3",
context: '.toc-content',
hashGenerator: function (text) {
return text.replace(/[.\\/?&!#<>]/g, '').replace(/\s/g, '_');
},
ignoreSelector: ".toc-ignore",
scrollTo: 0
};
options.showAndHide = false;
options.smoothScroll = true;
// tocify
var toc = $("#TOC").tocify(options).data("toc-tocify");
});
</script>
<!-- dynamically load mathjax for compatibility with self-contained -->
<script>
(function () {
var script = document.createElement("script");
script.type = "text/javascript";
script.src = "https://mathjax.rstudio.com/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML";
document.getElementsByTagName("head")[0].appendChild(script);
})();
</script>
</body>
</html>