{
 "cells": [
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "plVuDI_GfiiW"
   },
   "source": [
    "<font size = \"5\"> **[MSE672: Introduction to TEM](https://gduscher.github.io/MSE672-Introduction-to-TEM/)** </font>\n",
    "\n",
    "<hr style=\"height:1px;border-top:4px solid #FF8200\" />\n",
    "\n",
    "\n",
    "# Electron Optics\n",
    "\n",
    "[Download](https://raw.githubusercontent.com/gduscher/MSE672-Introduction-to-TEM//main/Introduction/CH1_07-Electron_Optics.ipynb)\n",
    "\n",
    "[![OpenInColab](https://colab.research.google.com/assets/colab-badge.svg)](\n",
    "    https://colab.research.google.com/github/gduscher/MSE672-Introduction-to-TEM/blob/main/Introduction/CH1_07-Electron_Optics.ipynb)\n",
    " \n",
    "part of\n",
    "\n",
    "<font size = \"5\"> **[MSE672:  Introduction to Transmission Electron Microscopy](../_MSE672_Intro_TEM.ipynb)**</font>\n",
    "\n",
    "**Spring 2024**\n",
    "<table style=\"margin-right:auto;margin-left:0px\">\n",
    "  <tr>\n",
    "    <td>Gerd Duscher </td>\n",
    "    <td>Khalid Hattar</td>\n",
    "  </tr>\n",
    "  <tr>\n",
    "    <td>Microscopy Facilities</td> \n",
    "    <td> Tennessee Ion Beam Materials Laboratory </td>\n",
    "  </tr>\n",
    "  \n",
    "  <tr>\n",
    "    <td>Materials Science & Engineering</td>\n",
    "    <td> Nuclear Engineering</td>\n",
    "  </tr>\n",
    "  <tr>\n",
    "    <td>Institute of Advanced Materials & Manufacturing</td>\n",
    "    <td> </td>\n",
    "  </tr>\n",
    "  <tr>\n",
    "    <td colspan=\"2\"><center> The University of Tennessee, Knoxville</center> </td>\n",
    "  </tr>\n",
    "</table>\n",
    "\n",
    "\n",
    "\n",
    "## Import packages for figures and \n",
    "### Check Installed Packages"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 1,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "installing pyTEMlib\n",
      "done\n"
     ]
    }
   ],
   "source": [
    "import sys\n",
    "import importlib.metadata\n",
    "def test_package(package_name):\n",
    "    \"\"\"Test if package exists and returns version or -1\"\"\"\n",
    "    try:\n",
    "        version = importlib.metadata.version(package_name)\n",
    "    except importlib.metadata.PackageNotFoundError:\n",
    "        version = '-1'\n",
    "    return version\n",
    "\n",
    "if test_package('pyTEMlib') < '0.2024.1.0':\n",
    "    print('installing pyTEMlib')\n",
    "    !{sys.executable} -m pip install  --upgrade pyTEMlib -q\n",
    "\n",
    "print('done')"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### Load the plotting and figure packages"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 1,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "You don't have igor2 installed.     If you wish to open igor files, you will need to install it     (pip install igor2) before attempting.\n",
      "You don't have gwyfile installed.     If you wish to open .gwy files, you will need to      install it (pip install gwyfile) before attempting.\n",
      "Symmetry functions of spglib enabled\n",
      "Using kinematic_scattering library version {_version_ }  by G.Duscher\n"
     ]
    }
   ],
   "source": [
    "%matplotlib widget\n",
    "import matplotlib.pylab as plt\n",
    "import numpy as np\n",
    "import sys\n",
    "if 'google.colab' in sys.modules:\n",
    "    from google.colab import output\n",
    "    output.enable_custom_widget_manager()\n",
    "    \n",
    "import pyTEMlib.animation as animate"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "dfb9CuuUf5qm"
   },
   "source": [
    "## Transmission Electron Microscope\n",
    "\n",
    "A TEM is a stack of electro-optical elements:\n",
    "![TEM](images/Zeiss.png)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "FsGiRUi_gGAG"
   },
   "source": [
    "- electron source\n",
    "- electrostatic lens\n",
    "- accelerator\n",
    "- magnetic lens\n",
    "- magnetic and electrostatic deflectors\n",
    "- magnetic multipoles\n",
    "- apertures\n",
    "- detectors (viewing screen,CCD)\n",
    "- sample holder\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "u-YSfinDgaFA"
   },
   "source": [
    "### Start screen on the computer of our TEM\n",
    "\n",
    "![start_screen](images/start_screen.png)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "jqsjOHmEg3p4"
   },
   "source": [
    "The big buttons on upper left, we saw already in the last notebook.\n",
    "\n",
    "You select the different modes of the TEM with those.\n",
    "\n",
    "![TEMmodes.png](images/TEMmodes.png)"
   ]
  },
  {
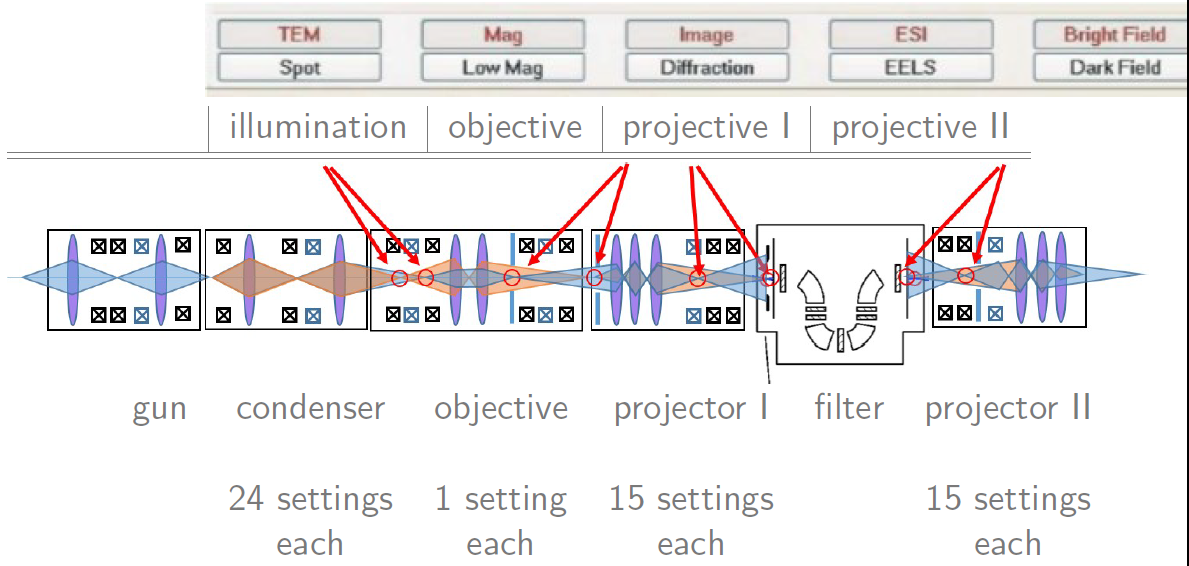   "cell_type": "markdown",
   "metadata": {
    "id": "_PEM-4gqhlWo"
   },
   "source": [
    "## Electron Optics - Overview of the Whole System\n",
    "\n",
    "We start on the top.\n",
    "\n",
    "#### The Electron Gun \n",
    "The electron gun produces the electrons, focuses them and accelerates\n",
    "them.\n",
    "\n",
    "#### The Condenser \n",
    "The condenser lens system varies the beam size, the illumination area and the convergence angle.\n",
    "\n",
    "#### The Objective Lens\n",
    "The objective lens does the maximum magnification in imaging mode.\n",
    "\n",
    "#### The Intermediate Lens\n",
    "The Intermediate lens system switches between imaging and\n",
    "diffraction mode. The objective lens does not magnify anything in diffraction mode, because the back focal plane of the objective lens is object plane of the intermediate plane. The intermediate lens does the maximum magnification.\n",
    "\n",
    "#### The Projector Lens \n",
    "The projector lens system magnifies everything roughly to the\n",
    "magnification indicated on the display/chosen on the console."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "K82oJmm3iVKj"
   },
   "source": [
    "### Electron Optics - Condenser\n",
    "\n",
    "The electron optics starts at the cross over which the gun produces in the\n",
    "differential pumping aperture.\n",
    "Then we have a condenser lens system with three lenses, three pairs of deflectors, a pair of stigmators and an aperture. \n",
    "\n",
    "This allows a very  flexible illumination of the specimen."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "WQMzs6txiq4S"
   },
   "source": [
    "### Electron Optics - Projective\n",
    "\n",
    "The projector lens system in our TEM (Zeiss Libra 200MC) is divided by the electron energy-loss filter into two parts.\n",
    "\n",
    "The first part switches from imaging to diffraction and does all the magnification. This part has three\n",
    "lenses, two pairs of deflectors, a stigmator, and an aperture. \n",
    "\n",
    "The second part switches from spectroscopy to imaging or diffraction and does only magnification in spectroscopy mode. This part has three lenses, two pairs\n",
    "of deflectors, a stigmator, and an aperture."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "HAKbBVLwjDKv"
   },
   "source": [
    "## Electron Optics - Ray Diagrams\n",
    "\n",
    "To do the optical ray diagram we only have to concern ourselves with the lenses and the apertures.\n",
    "\n",
    "Deflectors and stigmators (correcting multipoles) are only used to correct for mechanical misalignment of the optical axis.\n",
    "The correcting multipoles will be discussed in the phase contrast part of this lecture.\n",
    "The deflectors will be discussed in the STEM part in detail.\n",
    "\n",
    "### Basic Ray Diagram"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 4,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "33babba43b7841b8b088af47b736c2b9",
       "version_major": 2,
       "version_minor": 0
      },
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAoAAAAHgCAYAAAA10dzkAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjguMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8g+/7EAAAACXBIWXMAAA9hAAAPYQGoP6dpAABZxUlEQVR4nO3dd3xUVf7/8fekF8JQQjUhoIiRgBTpoIEVXEFFbCgiRXH9KUWRFVx0keIiKMUOuut3ga/LqrB+RVZstERQCV1KAiLFsIEICCQkkDr398fsDBmSSZ1kktzX8/GYR2bunLn3MyNO3jnn3nMshmEYAgAAgGn4eLsAAAAAVC0CIAAAgMkQAAEAAEyGAAgAAGAyBEAAAACTIQACAACYDAEQAADAZAiAAAAAJkMABAAAMBkCIAAAgMkQAAEAAEyGAAgAAGAyBEAAAACTIQACAACYDAEQAADAZAiAAAAAJkMABAAAMBkCIAAAgMkQAAEAAEyGAAgAAGAyBEAAAACTIQACAACYDAEQAADAZAiAAAAAJkMABAAAMBkCIAAAgMkQAAEAAEyGAAgAAGAyBEAAAACTIQACAACYDAEQAADAZAiAAAAAJkMABAAAMBkCIAAAgMkQAAEAAEyGAAgAAGAyBEAAAACTIQACAACYDAEQAADAZAiAAAAAJkMABAAAMBkCIAAAgMkQAAEAAEyGAAgAAGAyBEAAAACTIQACAACYDAEQAADAZAiAAAAAJkMABAAAMBkCIAAAgMkQAAEAAEyGAAgAAGAyBECUy5w5c9S1a1eFhYWpcePGGjJkiA4ePOjtsgAAQCkQAFEu8fHxGjdunLZs2aK1a9cqLy9Pt956qzIzM71dGgAAKIHFMAzD20Wg5jt9+rQaN26s+Ph43Xzzzd4uBwAAFIMeQHhEWlqaJKlBgwZergQAAJSEHkBUmGEYuuuuu3Tu3Dlt2rTJbbvs7GxlZ2c7H9tsNp09e1YNGzaUxWKpilIBoFYwDEMXLlxQ8+bN5eNDXw7Kzs/bBaDmGz9+vPbs2aPNmzcX227OnDmaOXNmFVUFALXf8ePHFRER4e0yUAPRA4gKmTBhglatWqVvv/1WrVq1KrbtlT2AaWlpatGihY4fP666detWdqkAUGukp6crMjJS58+fl9Vq9XY5qIHoAUS5GIahCRMm6NNPP1VcXFyJ4U+SAgMDFRgYWGh73bp1CYAAUA6cPoPyIgCiXMaNG6d//vOf+uyzzxQWFqbU1FRJktVqVXBwsJerAwAAxWEIGOXi7q/OJUuWaPTo0aXaR3p6uqxWq9LS0ugBBIAy4PsTFUUPIMqFvxsAAKi5uHYcAADAZAiAAAAAJkMABAAAMBkCIAAAgMkQAAEAAEyGAAgAAGAyBEAAAACTIQACAACYDAEQAADAZAiAAAAAJkMABAAAMBkCIAAAgMkQAAEAAEyGAAgAAGAyBEAAAACTIQACAACYDAEQAADAZAiAAAAAJkMABAAAMBkCIAAAgMkQAAGgAuLi4mSxWHT+/PkKtfGWGTNmqGPHjt4uA0AVIwACQCXr1auXTp48KavV6pH9VedACaBm8PN2AQBQ2wUEBKhp06beLgMAnOgBBFAhhmEoMTFRNpvN26VUiuzsbD311FNq3LixgoKC1KdPH23btq1Qu++++04dOnRQUFCQunfvrr179zqfK6rH7vvvv9fNN9+s4OBgRUZG6qmnnlJmZqbLcadMmaLIyEgFBgbq2muv1f/8z//o2LFj6tevnySpfv36slgsGj16dJG1L126VPXq1dOqVavUpk0bBQUFacCAATp+/Ljb97tt2zYNGDBA4eHhslqtio2N1c6dO13aWCwWvf/++7r77rsVEhKia6+9VqtXr3Zpk5iYqEGDBqlOnTpq0qSJRowYoTNnzrg9LoCqRQAEUC6GYWjNmjXq1q2bYmJilJiY6O2SKsWUKVP0ySefaNmyZdq5c6dat26t3//+9zp79qxLu8mTJ2v+/Pnatm2bGjdurMGDBys3N7fIfe7du1e///3vdc8992jPnj36+OOPtXnzZo0fP97ZZuTIkfroo4/05ptvKikpSe+++67q1KmjyMhIffLJJ5KkgwcP6uTJk3rjjTfc1n/x4kXNnj1by5Yt03fffaf09HQ9+OCDbttfuHBBo0aN0qZNm7RlyxZde+21GjRokC5cuODSbubMmRo6dKj27NmjQYMGafjw4c7P5OTJk4qNjVXHjh21fft2ffXVV/r11181dOjQ4j9sAFXHALwkLS3NkGSkpaV5uxSUICcnx9i0aZOxYcMGw2azGZ9//rnRpUsXQ5LRp08fY926dd4usVJkZGQY/v7+xvLly53bcnJyjObNmxuvvvqqYRiGsXHjRkOS8dFHHznb/Pbbb0ZwcLDx8ccfu7Q5d+6cYRiGMWLECOPxxx93OdamTZsMHx8f49KlS8bBgwcNScbatWuLrOvK/bmzZMkSQ5KxZcsW57akpCRDkpGQkGAYhmFMnz7d6NChg9t95OXlGWFhYca///1v5zZJxp///Gfn44yMDMNisRhffvmlYRiGMW3aNOPWW2912c/x48cNScbBgweLrRmlw/cnKopzAAEU69y5c2rRooUyMjLk5+cni8Wi3NxctWjRQiNHjlSrVq20efNmbd682WPHbN68uf7whz94bH/ldfjwYeXm5qp3797Obf7+/urWrZuSkpJc2vbs2dN5v0GDBrruuusKtXHYsWOHfv75Zy1fvty5zTAM2Ww2HT16VHv37pWvr69iY2Mr/B78/PzUpUsX5+Po6GjVq1dPSUlJ6tatW6H2p06d0osvvqgNGzbo119/VX5+vi5evKjk5GSXdjfccIPzfmhoqMLCwnTq1Cnn+9u4caPq1KlTaP+HDx9WmzZtKvy+AFQMARBAserXr6+rrrpKBw8eVF5eniT7OWDp6elau3atLBaLx45lGIZOnjwpSXrooYcUGhrqsX2Xtx5Jhd6jYRilet/u2thsNv2///f/9NRTTxV6rkWLFvr555/LUW3Z6nBX2+jRo3X69Gm9/vrrioqKUmBgoHr27KmcnByXdv7+/oX25zgP1Gaz6c4779Qrr7xSaP/NmjUr79sA4EEEQAAl6tixow4ePChJqlu3rvr166fPPvtMjRo10rRp0zRs2DD5+VX86yQzM7PIXiNvad26tQICArR582Y99NBDkqTc3Fxt375dEydOdGm7ZcsWtWjRQpK91/Snn35SdHR0kfvt3Lmz9u/fr9atWxf5fPv27WWz2RQfH6/+/fsXej4gIECSlJ+fX+J7yMvL0/bt2529fQcPHtT58+fd1rZp0yYtWrRIgwYNkiQdP368zBdvdO7cWZ988olatmzpkX8XADyPi0AAlCgoKMh5/9KlS1q1apV27Nihtm3bauTIkWrbtq2z5642CQ0N1ZNPPqnJkyfrq6++UmJiov7whz/o4sWLGjNmjEvbWbNmaf369dq3b59Gjx6t8PBwDRkypMj9Pvfcc/rhhx80btw47d69W4cOHdLq1as1YcIESVLLli01atQoPfroo1q1apWOHj2quLg4rVixQpIUFRUli8Wizz//XKdPn1ZGRobb9+Dv768JEyYoISFBO3fu1COPPKIePXoUOfwr2UPvBx98oKSkJCUkJGj48OEKDg4u0+c2btw4nT17VsOGDdPWrVt15MgRffPNN3r00UdLFVoBVD4CIIASOc7tkuw9Svv371fnzp2dQXDQoEHy9fX1YoWVZ+7cubr33ns1YsQIde7cWT///LO+/vpr1a9fv1C7p59+WjfeeKNOnjyp1atXO3vqrnTDDTcoPj5ehw4d0k033aROnTpp2rRpLsOjixcv1n333aexY8cqOjpaf/jDH5zTxFx11VWaOXOm/vSnP6lJkyYuVw9fKSQkRM8995weeugh9ezZU8HBwfroo4/ctv/73/+uc+fOqVOnThoxYoRzCpyyaN68ub777jvl5+fr97//vdq1a6enn35aVqtVPj782gGqA4vhOMkFqGLp6emyWq1KS0tT3bp1vV0O3MjKytIDDzygr776ynkeWGxsrNatW+fx4b2CQ8AZGRlePwfQU77++msNHDhQWVlZbkNhZVi6dKkmTpzIiiG1EN+fqCj+FANQrO+//169evVSYGCgc1ubNm00b948L1ZVc/z666/67LPPdO2111Zp+AOA4hAAARRr3bp16t+/v8t5gBcvXtSOHTu0f/9+L1ZWMwwaNEjr1q3TO++84+1SAMCJIWB4DUMYNcPAgQO1Zs0atWjRQikpKZKkpk2bavv27Xr00Ue1Zs0ajw0FZ2Vl6d5775UkffLJJy6hE8BlfH+iougBBODWuXPnijxxPzU1VefPn9fw4cM9OhQcFBSkNWvWaM2aNYQ/AKhEBEAAbm3YsEG/+93vinxu7dq1GjFiBEPBAFADEQABuOU4/8/dcxaLRW+++aYmTZrkXCUEAFD9EQABuHX06FFdffXVLtscw8FxcXHKzc1V8+bNPTYUnJmZqdDQUIWGhjrnvAMAeB4BEECRjh07pqioqELbHdPBZGZmKiEhQZI8OhR88eJFXbx4scL7AQC4RwAEUCR3w78FL85Yu3atJDEUDAA1DAEQQJHcXQBScELodevWOe97cigYAFC5CIAACrHZbDp37pwaNmxY6DlfX19FR0dLkhISEpSenu58jquCAaBmIAACKGTPnj3q0KGD2+cdQ8P5+fmKj493bmcoGABqBgIggELWrl3rdvoXSRowYIBL24IYCgaA6o8ACKCQzZs3q3fv3m6fj42Nla+vryTX8wAdyjsU7OPjo9jYWMXGxhZafQQA4Dl8wwJwkZWVJUkKDg5228Zqtapbt26SpKSkJOcawQ7lHQoODg5WXFyc4uLiij0+AKBiCIAAXHz//ffq1atXie0KDhGvX7++0PMMBQNA9UUABOCiuOXfCiruPEAHrgoGgOqJAAjAxa5du9SpU6cS23Xv3l2hoaGS7KHRMIxCbco6FJyZmalGjRqpUaNGLAUHAJWIAAjA6dy5c7JaraW6ACMgIECxsbGSpNTUVCUmJhbZrqxDwWfOnNGZM2dKXzQAoMwIgACc3K3+4U7BoWJ3w8ASQ8EAUN0QAAE4lfb8P4eC5wEWNR2MAxNEA0D1QgAE4HT06FFdffXVpW4fExOjJk2aSJLi4uKUm5vrti1XBQNA9UEABCBJOnbsmKKiosr0GovF4uwxzMzMVEJCQrHtGQoGgOqBAAhAUtmHfx1KMx2MA0PBAFA9EABRbt9++63uvPNONW/eXBaLRatWrfJ2SaiAsl4A4nDLLbc47xd3HqBDcUPBPj4+6tKli7p06cJScABQifiGRbllZmaqQ4cOevvtt71dCirIZrPp3LlzatiwYZlfGxERoejoaElSQkKC0tPTS3yNu6Hg4OBgbdu2Tdu2bWMpOACoRARAlNvAgQP1l7/8Rffcc4+3S0EF7dmzRx06dCj36x1Dx/n5+YqPjy+xPUPBAOBdBEAAWrt2bbnO/3Moy3mADlwVDADeQwBElcnOzlZ6errLDdXD5s2b1bt373K/PjY2Vr6+vpJKdx6gw5VDwRcvXlTLli3VsmVLXbx4sdz1AACKRwBElZkzZ46sVqvzFhkZ6e2SICkrK0uSKnTOndVqVbdu3SRJSUlJSklJKdXrrhwKNgxDv/zyi3755Zci1xYGAHgGARBVZurUqUpLS3Pejh8/7u2SIOmHH35Qr169KryfgkPI69evL/XrGAoGgKpHAESVCQwMVN26dV1u8L6Knv/nUJ7zAB0cQ8GJiYkVrgMAUDICIMotIyNDu3fv1u7duyXZlxHbvXu3kpOTvVsYymTXrl3q2LFjhffTvXt3hYaGSrKfB1iWIVzHUPDUqVMrXAcAoGQEQJTb9u3b1alTJ3Xq1EmSNGnSJHXq1EkvvviilytDaZ07d05Wq9V5AUdFBAQEKDY2VpKUmppa5t685s2b64EHHqhwHQCAkhEAUW59+/aVYRiFbkuXLvV2aSil8q7+4U7BoeSyDgNL0rBhwzxWCwDAPQIgYGLlXf/XnYLnAZZlOhgHHx8fXXvttQoNDVV+fr7H6gIAuCIAAiZ29OhRXX311R7bX0xMjJo0aSJJiouLU25ubpleHxISop9++kmLFi3SO++847G6AACuCICASR07dkxRUVEe3afFYnH2KGZmZiohIaFc+3G3VjAAwDMIgIBJeXr416Gi5wFKrBUMAJWNAAiYlKcvAHEoGADLeh7gxYsXFRMTo5iYGNWrV48JogGgkhAAAROy2Ww6d+6cGjZs6PF9R0REKDo6WpKUkJBQpjWfDcNQYmKiEhMTZRgGQ8EAUEkIgIAJ7dmzRx06dKi0/Tt6AfPz8xUfH1/u/TAUDACVgwAImJCnln9zpyLLwl2JtYIBwPMIgIAJbd68Wb179660/cfGxjpXFynPfIBXYigYADyLAAiYTFZWliQpODi40o5htVrVrVs3SVJSUpJSUlIqtD+GggHAswiAgMn88MMP6tWrV6Ufp+AQ8/r16yu8P4aCAcBzCICAyVT2+X8O5TkP0GKxKCoqSlFRUbJYLIWeHzFihHbu3MlQMABUEAEQMJldu3apY8eOlX6c7t27KzQ0VJL9PEDDMEp8TUhIiI4dO6Zjx44pJCSk0PMWi0VvvPEGQ8EAUEEEQMBEzp07J6vV6rxAozIFBAQoNjZWkpSamqrExESP7JehYACoOAIgYCKVtfqHOxVZFaQ4DAUDQMUQAAETqaz1f90p63mAly5dUteuXdW1a1ddunTJbTuGggGgYgiAgIkcPXpUV199dZUdLyYmRk2aNJEkxcXFKTc3t9j2NptN27dv1/bt22Wz2Ypty1AwAJQfARAwiWPHjikqKqpKj2mxWJw9jpmZmUpISPDo/hkKBoDyIQACJlHVw78OBY9Z0WXhrsRQMACUDwEQMImqvgDEobIuBHFgKBgAyo4ACJiAzWbTuXPn1LBhwyo/dkREhKKjoyVJCQkJSk9P9/gxGAoGgLIhAAImsGfPHnXo0MFrx3f0Aubn5ys+Pt7j+2coGADKhgAImEBVLf/mTlmmgwkPD1d4eHiZj8FQMACUHgEQMIHNmzerd+/eXjt+bGysc/WR4s4DDA0N1enTp3X69GnnMnJlwVAwAJQOARCo5bKysiRJwcHBXqvBarWqW7dukqSkpCSlpKRUynEYCgaA0iEAArXcDz/8oF69enm7DJch6PXr11facRgKBoCSEQCBWs7b5/85lOY8wEuXLqlv377q27dvsUvBlYShYAAoHgEQqOV27dqljh07ersMde/e3Xle37p162QYRqE2NptN8fHxio+PL3EpuOIwFAwAxSMAArXYuXPnZLVanRdgeFNAQIBiY2MlSampqUpMTKzU4zEUDADuEQCBWmzjxo1eWf3DncpeFeRKDAUDQNEIgEAtVl3O/3Moy3yAnsBQMAAUjQAI1GJHjhzR1Vdf7e0ynGJiYtSkSRNJUlxcnHJzcyv9mAwFA0BhBECgljp27Jhatmzp7TJcWCwWZ49kZmamEhISquS4DAUDgCsCIFBLrVu3rloN/zoUrKmoYeCQkBCFhIR49JgMBQOAKwIgUEtt2LChWl0A4lDchSChoaHKzMxUZmZmuZaCKw5DwQBwGQEQqIVsNpvOnTunhg0beruUQiIiIhQdHS1JSkhIUHp6epUdm6FgALAjAAK10J49e9ShQwdvl+GWoxcwPz9f8fHxVXZchoIBwI4ACNRC1W36lyu5mw4mKytLt99+u26//XZlZWVVyrEZCgYAAiBQK23evFm9e/f2dhluxcbGOlcnKXgeYH5+vr744gt98cUXys/Pr7TjMxQMwOwIgEAt4+g5Cw4O9nIl7lmtVnXr1k2SlJSUpJSUlCo9PkPBAMyOAAjUMj/88IN69erl7TJKVHCIev369VV+fIaCAZgZARCoZar7+X8OVb0sXFEYCgZgVgRAoJbZtWuXOnbs6O0yStS9e3fnXH/r1q2TYRhVXgNDwQDMigAI1CLnzp2T1Wp1XmBRnQUEBCg2NlaSlJqaqsTERK/UwVAwADMiAAK1yMaNG6vl6h/uFLcqSFViKBiA2RAAgVqkppz/53DleYChoaEyDEOGYXh8KbjiMBQMwGwIgEAtcuTIEV199dXeLqPUYmJi1KRJE0lSXFyccnNzvVYLQ8EAzIQACNQSx44dU8uWLb1dRplYLBZnj2VmZqYSEhK8Wg9DwQDMggAI1BLr1q2rUcO/DgVr/uqrr3T//ffr/vvvr7Sl4IrDUDAAsyAAArXEhg0batQFIA5XTgj9r3/9S//6178qdSm44jAUDMAM/LxdAICKs9lsOnfunBo2bOi2jWFINpuUn1/4VnC7zWa/Gcbl1xiG5OgQy8uTDhy4vL2otle+zrHPK+uxi1CLFtFKTj6grVu3OZ+Pj5dCQiSLpfB7uXKbr6/95uNjf+7Kn+7uF9xW8HHfviM0duxQxcXt1/XXxzj3X/Dm43P5PgDUNARAoBqy2ezBKTe35J/5+VJS0h41atRB335r3+Z43tHG8dgRxIq7OQJcwXmZDUNyjMhmZUlr1pTufTiCmiNguRMV1V/JyQdks13u9du3TwoMdK3BnaJqrgiLxaIuXd7QE088ov/3/9YoIMBPPj6uwdFxc4RAf//CNz+/yz8Ltiu43d3P4j4vAKgoAiBQiXJzpZwcKTvb9WfBUJadbb9dumR/7tKly89d2VOXl1d0yNm4ca0iIvpr507XcFIwtDh6rfz8VCjMFNV7dmUA8fO7/LNNG89+Tjfd1F+bNr3tsq1VKykoyLPHKS17D2ZznT07XNu3z9OQIVPdhuXcXHsovnL7lY+LUjBAFgyJvr728BsYaP8MgoPt9wMCLodEf//L2wICXJ8HgJLwVQGUUV6e/Rd+dvbln477ly5JGRn228WLRffGXcliKfzLv2AIKGro8UorVmzW6NHjXXrMapL27fvKx8fXpQfQmxyBuX//EXrllaE6dWq/WrSI8fhxHEPuBcO+499KVlbhPwCuDJKOfzsFew8DAuxD53XqSGFh9gDpCJKOUBkYaA+VRf1bAmAOBEDgCo7hzsxMe4hz3M6ds98yMlx78Qpeq2CxuA7/+flJoaGVO7SXk2Mfmw0MDPbsjqtQaKhVbdp004EDP3i7FBcWi0V/+MMbevPNR/Tii2vk6+vZr8yCw8Ll4QiPBU8LyMyU0tIuPy4YGn197QHRERStVql+ffvPkBDXm7d6XwFUDQIgTCsvTzp/3v7LMjPTHuzOnZPOnr3cq5edffkXqJ/f5V6UOnUuBz1vXwRw4MAPuv76Xt4twgM6dOhf7QKgJDVs2FyxscP1f/83T/ffP9Xb5bjw8bk8BFwaeXn2P14cpx6cPCkdO2Z/7Bj+d/QQhoTYw2H9+vY/YkJDpXr17GGRnkOg5iMAwhRsNunCBXvAO3/e/ovv11/twc9xcYPF4nreldVq/8Va3X/Z7d69Vr163evtMiqsY8cB+vjjlyRJN930oAIDQ7xc0WX9+tmHgpOTK2couKo4eqXdyc+//IdPRob022/2wGgY9v8/goPtw8rNm0uNGtnDYb169nDIRStAzUIARIUsWrRI8+bN08mTJxUTE6PXX39dN910k7fLkmQ/Hy85WUpNlVJSpPR0+1CuYdiDXWio/ZdYUFDN/uV15MguDR/+krfLqLA2bborKChUWVmZ2rcvztvluKjsoeDqwtf38hDwlWy2y+e47tljD4s+Pvbe8Hr17KGweXMpIqL8Q9oAqk7t/BZDlfj44481ceJELVq0SL1799Z7772ngQMHKjExUS1atPBKTYYhnTolHT1qn6vuzJnL5+FZrVLTpt4fsvWkjIxzCg21yrcWvCl//wC1axer7du/0LlzqTp+PLFa9bZV56HgquDjc3ko+L/LNzvPOTx7Vjp+3L6tWTPp+uulli3twRBA9UQARLktXLhQY8aM0WOPPSZJev311/X1119r8eLFmjNnTpXXY7NJu3ZJW7fafyk1aCC1bl26wJeVlSlJ8vcPcoapvLxc5eXluH2Nv3+gsyeoLG3z8/OUm5vttq2fX4D8/PxL1Xb37rVq3/53/22br9xc98un+fr6y98/oMxtbTabfv31qDIz0yRJhmE4P6+i2ubkXCpmv37y9w907ic7+6LL89HRvbR9+xeSpK1bP3cGwKLaFuTj46uAgMtXLRSsryJtLRYfl4treva8R6+9NkKHDm1TZGTbYttmZ1+U4Wb+F4vF4jLEXba2l2QYtiLbSlJQUGi52ubkZBV7FXbBtg5+fvY/rKxW++PcXOn0aWntWqlhQ+nmm+3/DwKofiyGu28doBg5OTkKCQnRypUrdffddzu3P/3009q9e7fi4+MLvSY7O1vZ2ZfDTHp6uiIjI5WWlqa6detWuKYjR6TVq+29DsUsiFGkwYPtY8CzZ29U+/Z9JUlr1ryj994b7/Y106Z9rq5db5ckrV+/VG+88YjbtlOmrFCfPvdLkjZvXqlXXx3qtu3TTy/RLbeMliRt27ZGL710h9u2UVHt9fzzn6pZs2u0d2+cXnihn9u2o0e/qnvumSxJOnRom/74x25u2z744HQ99NAMSdLOnV9pxoyBbtveffezeuQR+7Jpv/56TH/4Qyu3bQcNGqsnnnhHkpSWdlojRjR227ZBg+ZaujRFkj2kDR1ax23bXr3u05/+tNL52PHfsyhdugzSiy9ensn6/vtD3YbLdu1i9fLLcc7HDz/cSOnpZ4ps27p1Fy1ceHklk8cea6lTp34psm1kZFu9885+5+Nx42J0/HhikW0bN47S++8fcz6eNKmrfv55e5Ft69YN1z/+cdr5+Pnn+2rfvsL/L0pSYGCIVq68HH5nzbrdGb6Lsnp16X9VGIb9tAt/f+nuu8v+/yNKlp6eLqvV6rHvT5hPNT+9HdXVmTNnlJ+fryaOsaD/atKkiVJTU4t8zZw5c2S1Wp23yMjIqii1VgsJsergwS2VeozwcO/8dzp//pTy8oqYOBE1Al0LQPVGDyDK5cSJE7rqqqv0/fffq2fPns7ts2fP1gcffKADBw4Uek1l9wAWNQTcoEHNHgLOzc3RiBGN1aBBc5fepcssmj17sKZMWaGQEGulDQHHxf1Dr78+SpIUHFxXy5adcNu2IkPAWVmZGjny8h8Vc+duUtu2farNEHDBtq+8MlTPPbfCbVszDAFfyTEEnJ7OEHBlowcQFcU5gCiX8PBw+fr6FurtO3XqVKFeQYfAwEAFVuJSFT4+UufOUmSkfTj44EHp55/tAbBOHfvJ6yEhRQfCos9v8ncGsZKUpa2vr1+pryJNSPhMFy+m6eLFNJ08eVitWt1QqM1DD83SBx88r7Fj35Wvb8m/pO01+Ja6rY+Pj2JjH9Ly5dN0+nSyLl1K1+nTyYqMvL7ItqUJCpI92JTUdvfudWrbtk+p2hZUFW19fX2LfW1ZprEpW9vST/hdlrYFQ3FpOS4Ccdwk+0UgPXpIUVFcBAJUZwwBo1wCAgJ04403au3atS7b165dq169vDcpscUiNW5s/wU0dKh05532UBgaap8H8MgR6aef7JPfnj5tn9aiuvaB22w2ffTRTIWE1FVwcB19/PGsItvZJ4G2KDHxu0qrxdfXT3fe+bTz8b///UalHaug3bvXltwIVcJms08B8+uv0uHD9v+PfvnF/v9Qgwb2/+fuvlu67z6pQwfCH1Dd0QOIcps0aZJGjBihLl26qGfPnvrrX/+q5ORkPfHEE94uTZJ90trrrrPfHBNBnz9vnwz611/tk0GfPl30RNCOyaC9ORH0999/8t+Jh9spNLSevv/+Ex09uqfIXsCRI1/WK6/crxdf/MI5HOtpAwaM0YcfztClSxe0YcMyPfzwX1S3bnilHMvhp58SdPFiukJCGOKqCgUngnbcipoI+uqr7X9o1atnnww6JKRmz6UJmBEBEOX2wAMP6LffftOsWbN08uRJtWvXTl988YWioqK8XVohPj6Xp6twlOduKbhz5+yhMD298FJwjmDoWEu1spaCc/T+dep0qy5duqBmzVrr7NkUffzxLP3pT/8q1L5Onfrq3/9RffbZQt133588X5Ds6/Xeeutj+uyz15STk6Uvv3xXDzzw50o5loPNlq99++LVrdudlXocs3CsX52baw92jpDnWM/ax8d1ucPISHvAq1PHHvJYCg6oPQiAqJCxY8dq7Nix3i6jXPz8pPBw+60gw7AHwIsX7cHw4kX7LS3NvjRWRoZ9+/nz9l+k+QXOm7dY7KHQz8/9z9L0lGzZ8qmSk/dr/Pi/6e9//6N8fHw0dOif9dZbY9wuR3bzzcP08st3KzX1qJo2dT8VS0XcccdT+ve/35DNZtOaNW/rnnsmOy/q8ITAwBB98MEp7djxpfOik9271xIA3bDZ7H/I5OXZ/y0W9bPgKQ6Of4eOP2CaNbMP39ataw94jvNkQ0LsIRBA7UUABK7gGOoKDi56/rK8PHtAdPSeFLx/8aI9IDp+5uba7xf8pVzU8Xx97b+cfXzsP7OzwzRo0BQ1a9ZT+fn2kNmnzwjt2/etpKITpMVi0SOPzNff//5HTZ36iSyVMCbXpElL9ehxj77//l86f/5XffvtR7rlllEe27/FYpHV2kjdu98lHx9f2Wz5+vHHdR7bf3Xj+G9b8JaXdznYXbntyvNVLRbXUOdY9cZxCwu73KPn+Om4HxRETx5gZgRAoIz8/OxDYnXcz0vsVHCoLSfn8n3HMFxe3uXweOmS/flLl6SOHW9Vu3a3KivLHgCysqTUVH/dccdSZWXZT8CXLvcmOs7R8vFprQYNOmvVqpXq0mXof7fZb76+l+8X3O54ruA2i8V9T+WQIZP0/ff2YejPPluo3/1upMfDZmioVW3adNOBAz/o+PEk/fZbiho2vMqjxyiOI2wZhv1+UbecHPtSg+6ed+yjqODm4Pjs/fzsPx03f397gHOEtuBg+8+AgMuBLyDg8s3xnON5ACgJXxVAJXL0zISWfqYRSa5De3/7m/2k+6FDCw/x5eba2zp6iXJypOuum6znnx+k2277vQICrC5h07HfokJKfr5r8HEfWnoqKqqHfvlli44d26Mvvtiga6+9xe17cYTJkjKixSLl5WVr1apJkqSIiL46cOAHSdLatevVtetIt68tqeayctTrCMMFw7Pj5gjdBUNZwd64grcrw92VvXZX/iztqQIAUF4EQKAa8vG53KPj62vv4WnatLSvDlRo6HStXPlnvfXWW86tBYOeI+wVNQR5Zc/VlaHQZpN8fJ7RpEkPSJISExdq7NhbXJ6/8md+/uX7BV0Z2C5dytOzzy6SJM2b97XWrbOvKX369Fp16mQPgFcGo6J6Mq8McAV7NYu67+55R2hz7Lvg7dNPpZEjGUYFUDMRAIFa6Oabb9b//u//auvWrerWzb7mb8FAU1HXXHOPXn+9hZKTk7Vp0xfy90/S9dcXnhi6rByTCUvSmDFdNWNGqDIzM7V37zrdfLNRKec1lpcjdAJATcTXF1BLzZ07Vy+88ILy8vI8vm8/Pz89/fTliaHfeMPzE0MHBAQoNjZWkpSamqrExESPHwMAzIoACNRS4eHhevjhh/Xmm29Wyv7HjBmjsLAwSdKyZct05swZjx+jf//+zvvr1tXeq4EBoKoRAIFabOTIkdq4caOSk5M9vm+r1arHHntMkpSVlaV3333X48cYMGCA8/6Vyw4CAMqPAAjUYhaLRfPmzdOzzz5bKft/6qmn5PPfE+HefvttZWdne3T/MTExatKkiSQpLi5OuUVNpAgAKDMCIFDLRUdHKzo6WqtWrfL4vlu2bKl77rlHkvTrr7/qo48+8uj+LRaLcxg4MzNTCQkJHt0/AJgVARAwgeeff15vvfWWLly44PF9T5o0yXl/4cKFMiowGV9wcLCOHj2qo0ePKjg4WBLnAQJAZSAAAiYQFBSkqVOnavr06R7fd8+ePdWjRw9J0p49e7Rhw4Zy78vHx0ctW7ZUy5YtnUPLBQMg5wECgGcQAIFqxjAMPf7442rQoIEsFosyC06OVwH9+/fX2bNntXPnTo/sr6BnnnnGeX/hwoUe3XdERISio6MlSQkJCUpPT/fo/gHAjAiAQDXz1VdfaenSpfr888918uRJhYSEeGzfr776qqZOnar8/HyP7VOS7rnnHrVo0UKS9MUXXygpKalc+8nJydHkyZM1efJk5eTkOLc7egHz8/MVHx9f8YIBwOQIgEA1c/jwYTVr1ky9evVS06ZNPbr6RePGjXXfffdp0aJFHtun5LmJoXNzczV//nzNnz/f5YpfhoEBwLMIgEA1Mnr0aE2YMEHJycmyWCxq2bKlx48xZswYffnll0pJSfH4fitrYui+ffvK979r2HEhCABUHAEQqEbeeOMNzZo1SxERETp58qS2bdvm8WP4+Pjo1Vdf1eTJkz2638qcGNpqtTrXNE5KSvJ4eAUAsyEAAtWI1WpVWFiYfH191bRpUzVq1KhSjtOuXTtFRUVpzZo1Ht1vZU4MXXAYeP369R7bLwCYEQEQMKlp06ZpwYIFHrvKWKrciaFZFg4APIcACJhUSEiIJk+erFmzZnl0v56cGLqg7t27KzQ0VJL9PEBP7RcAzIgACJjYwIEDlZKSor1793psn56cGLqggIAAxcbGSpJSU1OVmJjokf0CgBkRAAGTmzdvnqZMmSKbzeaxfZZ3Yujg4GDt27dP+/btcy4FVxDLwgGAZxAAAZNr1qyZ7rjjDv3tb3/z2D7LOzG0j4+PYmJiFBMT47yYpCDOAwQAzyAAAtXMxIkTdezYsSo95hNPPKFPP/1UqampHtmfpyaGvlJMTIyaNGkiSYqLi3OZLBoAUHoEQADy9fXV3LlzNWXKFI/tszwTQ+fk5GjGjBmaMWOGy1JwDhaLxTkMnJmZqYSEBI/VCwBmQgAEIEnq2LGjGjVqpG+++cYj+yvPxNC5ubmaOXOmZs6c6bZ3j/MAAaDiCIAAnGbOnKm5c+fq0qVLHtlfZUwMzbrAAFBxBEAATnXq1NHEiRP18ssve2R/lTExdEREhKKjoyVJCQkJSk9Pr/A+AcBsCIAAXAwePFg//fRTqa/cLUllTAzt6AXMz89XfHx8hfcHAGZDAARQyPz58zV58mSPhLXKmBia8wABoGIIgAAKiYyMVP/+/bV06VKP7K+8E0O707dvX/n6+kriPEAAKA8CIIAijR8/Xh9++KFOnz5d4X2Vd2Jod6xWq7p16yZJSkpKUkpKSoVrBAAzIQACKJKfn59mz56tP/3pTx7ZV2kmhg4KCtLWrVu1detWBQUFFbvPgsPA69evr3CNAGAmBEAAbnXt2lWhoaGKi4ur8L5KMzG0r6+vunbtqq5duzqHeN1hOhgAKD8CIIBivfTSS3rppZcqPIef1WrVmDFjJJV+Yuji9OjRQ6GhoZLsF4J44oIVADALAiCAYlmtVj355JN65ZVXKryvkiaGzsnJ0bx58zRv3rwil4IrKCAgQLGxsZKk1NRUJSYmVrg+ADALAiCAEt1777368ccfdejQoQrtp1WrVsVODJ2bm6spU6ZoypQpbpeCK4jpYACgfAiAAEpksVi0YMECPfvssxUeavXkxNADBgxw3uc8QAAoPQIggFJp2bKlevfureXLl1doP56cGDomJkZNmjSRJMXFxZWq17C26du3ryZOnFipxxg9erSGDBlSptccOHBAPXr0UFBQkDp27FgpdV1p6dKlqlevXpUcC6jpCIAASu2ZZ57R0qVLdfbs2Qrvx6EiE0NbLBbnMHBmZqYSEhIqVBc8Z/r06QoNDdXBgweZpgeohgiAAErN399fs2bN0vPPP1+h/XhyYmjOA6yeDh8+rD59+igqKkoNGzb0djkArkAABFAmvXr1ksVi0XfffVfufZR2YujSYD5AKS8vT+PHj1e9evXUsGFD/fnPf3Y5t/If//iHunTporCwMDVt2lQPPfSQTp065bKP/fv36/bbb1fdunUVFhamm266SYcPHy7yeDt27FDjxo01e/bsIp+3WCzasWOHZs2aJYvFohkzZkiS9u7dq9/97ncKDg5Ww4YN9fjjjysjI8PltX//+98VExOjwMBANWvWTOPHj3c+t3DhQrVv316hoaGKjIzU2LFjC70eQOkQAAGU2csvv6zp06eXOFVLcUozMXRpREREKDo6WpKUkJCg9PT0ctdUUy1btkx+fn5KSEjQm2++qddee03vv/++8/mcnBy99NJL+vHHH7Vq1SodPXpUo0ePdj6fkpKim2++WUFBQdqwYYN27NihRx99VHl5eYWOFRcXp1tuuUUzZ87UCy+8UGQ9J0+eVExMjP74xz/q5MmTevbZZ3Xx4kXddtttql+/vrZt26aVK1dq3bp1LgFv8eLFGjdunB5//HHt3btXq1evVuvWrZ3P+/j46M0339S+ffu0bNkybdiwQVOmTPHAJwiYkAF4SVpamiHJSEtL83Yp1VrPnj2NRx991NtlFLJ8+XJjzpw5FdrHxIkTDUmGJOOll14y8vLyjI0bNxobN2408vLySr2f8ePHO/ezevXqCtVUWnfeeWeVHKcksbGxxvXXX2/YbDbntueee864/vrr3b5m69athiTjwoULhmEYxtSpU41WrVoZOTk5RbYfNWqUcddddxmrVq0ywsLCjH/+858l1tWhQwdj+vTpzsd//etfjfr16xsZGRnObWvWrDF8fHyM1NRUwzAMo3nz5sYLL7xQ4r4dVqxYYTRs2ND5eMmSJYbVai3162syvj9RUfQAAiiXYcOGacuWLTpy5Ei593HlxNB5eXnq27ev+vbtW+JScAWZ/TzAHj16yGKxOB/37NlThw4dUn5+viRp165duuuuuxQVFaWwsDD17dtXkpScnCxJ2r17t2666Sb5+/u7PUZCQoLuvfdeLVu2TMOGDStzjUlJSerQoYNz9RZJ6t27t2w2mw4ePKhTp07pxIkTuuWWW9zuY+PGjRowYICuuuoqhYWFaeTIkfrtt9+UmZlZ5noAsyMAAtVQenq6jh49Wmh7UlJShYZdPclisWj+/PkVmhuwpImhS6tgYDTreYDuZGZm6tZbb1WdOnX0j3/8Q9u2bdOnn34qSc5/S8HBwSXu55prrlF0dLT+/ve/l+vfoGEYLiG1IIvFUmINv/zyiwYNGqR27drpk08+0Y4dO/TOO+9Ikimn/wEqigAIVEPvv/++unTp4nI+24EDB9SuXbsKzZvnaa1bt1bnzp21cuXKcu+j4MTQCxYs0Ntvv6133nmnTL/UrVarunXrJskeklNSUspdT020ZcuWQo+vvfZa+fr66sCBAzpz5ozmzp2rm266SdHR0YUuALnhhhu0adOmYj/z8PBwbdiwQYcPH9YDDzxQ5tDVtm1b7d6926W37rvvvpOPj4/atGmjsLAwtWzZ0u2UMdu3b1deXp4WLFigHj16qE2bNjpx4kSZagBwGQEQqIYeeOABZWRk6K233nJu+8tf/qLmzZurX79+XqyssMmTJ+u9995TWlpauV5fcGLovXv3asKECRo/fnyZe5kKDgObbd6548ePa9KkSTp48KA+/PBDvfXWW86rrFu0aKGAgAC99dZbOnLkiFavXq2XXnrJ5fXjx49Xenq6HnzwQW3fvl2HDh3SBx98oIMHD7q0a9y4sTZs2KADBw5o2LBhRV4k4s7w4cMVFBSkUaNGad++fdq4caMmTJigESNGOCfznjFjhhYsWKA333xThw4d0s6dO53/D1xzzTXKy8tzvo8PPvhA7777bkU+NsDUCIBANXTVVVfp8ccf14IFC5SXl6fz58/rww8/1PPPP6/AwEBvl+ciMDBQ06dPd3tFaGkUnBi6vMw8HczIkSN16dIldevWTePGjdOECRP0+OOPS5IaNWqkpUuXauXKlWrbtq3mzp2r+fPnu7y+YcOG2rBhgzIyMhQbG6sbb7xRf/vb34o8J7Bp06basGGD9u7dq+HDhzvPMyxJSEiIvv76a509e1Zdu3bVfffdp1tuuUVvv/22s82oUaP0+uuva9GiRYqJidEdd9zhXH+6Y8eOWrhwoV555RW1a9dOy5cv15w5c8r7kQGmZzHKe/IOUEHp6emyWq1KS0tT3bp1vV1OtZOSkqJrrrlGjRs3VkBAgLKzs/Xzzz9XuwDo8Nhjj+nxxx93DsWWRV5enq655hrnRQmSlJGR4XLBQElycnLUoEEDZWZmqmnTpjpx4oTbc848YfDgwVq9enWl7R8oDt+fqCh6AIFqytELeOLECR05cqRa9v4VNHfuXL3wwgtlGhZ0uHJi6PIICAhQbGysJCk1NVWJiYkV2h8A1Gb0AMJr+AvWlePkeH9/fwUEBEiyn9sVFRWl4OBgHT9+vFAALNjWZrPp0qVLbvfv5+fnfL1hGLp48aJH2vr6+iooKEiSfULikydPasKECSW2LfieJSktLU3XXXedc2WHAwcO6Lrrriuy7ZV8fHwUHBys1157zXlRySuvvKJx48YVamuxWBQSEuJ8fPHiRbdXMV/Z9tKlS7LZbJKkoUOHasWKFS7tC/ZYFmxblIJts7Kyih1KLUtPKMyB709UmNdmIITpMZGpK/13IuOCk+fu27fPub2o27PPPutse/To0WLbjh071tn21KlTxbYdNWqUs21GRkaxbe+77z5nW5vNVmzbQYMGubznkJAQt21btGjh0jY8PNxt2y5duhiGYRh79+4t9viSjLZt27rst23btm7bRkVFubTt0qWL27bh4eEubWNjY922DQkJcWk7aNCgYmsGrsT3JyqKIWAAHuPJc+5Onjyp7OzsMr0mJibGeUUpAMA9hoDhNQxhuCpqCLikYd3qNgTseB8vvfSSOnbsqDvvvLPEtgXl5eXptttuc85rt3TpUo0aNarItgU5hoAl6eGHH9by5cslSd9884169erl0pYhYNQGfH+iovy8XQAAu6J+yfv4+JT6l39Z2loslkppK9nfx4wZMzRo0CDdfvvtCgsLK7btlRYuXOgMbQsXLtTIkSPLVEP//v2dAfC7777TgAEDim1fMOCVpOBqFb6+vsXWVJrVNRwKhuKqMGPGDK1atUq7d++u0uMCqD4YAka5zJ49W7169VJISIjq1avn7XJQzQQFBen555/X9OnTy/zaghND79mzp8wrn5h5PkAAKC0CIMolJydH999/v5588klvl4Jqqn///jp79qx27txZ6tfk5uZq6dKl6tSpk3PbwoULy3TciIgIRUdHS5ISEhJcltMDANgRAFEuM2fO1DPPPKP27dt7uxRUY6+++qqmTp1a6tUicnJy9Mgjj2jx4sWKjIyUJH3xxRdKSkoq03EdvYD5+fmKj48vW9E13NKlS1WvXj2tWrVKbdq0UVBQkAYMGKDjx4+7fc22bds0YMAAhYeHy2q1KjY2tlBwt1gsev/993X33XcrJCRE1157baGJsBMTEzVo0CDVqVNHTZo00YgRI3TmzJlKeZ8AKoYAiCqTnZ2t9PR0lxtqt8aNG+u+++7TokWLyvzasWPHOu+/8cYbZXptwWHgdevWlfnYNd3Fixc1e/ZsLVu2TN99951znV93Lly4oFGjRmnTpk3asmWLrr32Wg0aNEgXLlxwaTdz5kwNHTpUe/bs0aBBgzR8+HCdPXtWkv2q7djYWHXs2FHbt2/XV199pV9//VVDhw6t1PcKoJy8OgkNarwlS5YYVqu1VG2nT59e5BxnzGNVu+Xn5xsDBw40/vOf/5TYtuCcgykpKUZYWJghyQgKCjJOnz5d6mOeP3/e8PX1NSQZ119/fUXKd+vOO++slP1W1JIlSwxJxpYtW5zbkpKSDElGQkKCYRj2/xc7dOjgdh95eXlGWFiY8e9//9u5TZLx5z//2fk4IyPDsFgsxpdffmkYhmFMmzbNuPXWW132c/z4cUOScfDgQU+8NRTAPICoKHoA4TRjxgxZLJZib9u3by/3/qdOnaq0tDTnrbghKdQePj4+evXVVzV58uQyvc5qtWrMmDGS7NOkvPvuu2V6rWNN4qSkJKWkpJTp2DWdn5+funTp4nwcHR2tevXquR1KP3XqlJ544gm1adNGVqtVVqtVGRkZLmszS9INN9zgvB8aGqqwsDCdOnVKkrRjxw5t3LhRderUcd4c52IePnzY028RQAUxDQycxo8fX+wwkSS1bNmy3PsPDAys1mvZovK0a9dOUVFRWrNmjW6//fZSv+6pp57Sm2++KZvNprfffluTJ08u9b+h/v3764cffpAkrV+/XiNHjixX7TVVUZNyu5uoe/To0Tp9+rRef/11RUVFKTAwUD179lROTo5LO39//0L7c8x1aLPZdOedd+qVV14ptP9mzZqV920AqCT0AMIpPDxc0dHRxd6qer4y1B7Tpk3TggULip3Q+UqtWrXSPffcI0n69ddf9dFHH5X6tWY+DzAvL8+lt/7gwYM6f/68s0fuSps2bdJTTz2lQYMGKSYmRoGBgWW+eKNz587av3+/WrZsqdatW7vcmMgaqH4IgCiX5ORk7d69W8nJycrPz9fu3bu1e/duZWRkeLs0VFMhISGaPHmyZs2aVabXTZo0yXl/4cKFblftuFKPHj2cwWPdunWlfl1t4O/vrwkTJighIUE7d+7UI488oh49ejiHxa/UunVrffDBB0pKSlJCQoKGDx9epomsJWncuHE6e/ashg0bpq1bt+rIkSP65ptv9Oijj5b6KnAAVYcAiHJ58cUX1alTJ02fPl0ZGRnq1KmTOnXqVKFzBFH7DRw4UP/5z3+0Z8+eIp8PDAzUihUrtGLFCudQb3knhg4ICFBsbKwk+xWqiYmJHngHNUNISIiee+45PfTQQ+rZs6eCg4OL7T39+9//rnPnzqlTp04aMWKEnnrqKTVu3LhMx2zevLm+++475efn6/e//73atWunp59+WlarVT4+/KoBqhvWAobXsJalOZ08eVKPPvqo1qxZU+pgsGLFCj3wwAOSpEGDBmnNmjWlet1rr73m7EF8/fXX9fTTT5ev6CIMHjy40Dx41cHSpUs1ceJEnT9/3tuloBLx/YmK4s8yAFWqWbNmuuOOO/S3v/2t1K+555571KJFC0llmxiaZeEAoGgEQABV7oknntCnn36q1NRUl+15eXlauXKlVq5cqby8POd2Pz8/l9670k4M3a5dOzVp0kSSFBcXp9zcXA9UDwA1HwEQQJXz9fXV3LlzNWXKFJft2dnZGjp0qIYOHars7GyX58aMGaOwsDBJ0rJly0p1larFYnH2AmZmZiohIcFD76D6Gj16NMO/AEpEAATgFR07dlSjRo30zTfflKp9eSeGNvN0MADgDgEQgNfMnDlTc+fO1aVLl0rV/qmnnnJeOPL2228X6iUsCucBAkBhBEAAXlOnTh1NnDhRs2fPLlX78kwMHRER4ZwAOSEhQenp6eUvGABqCQIgAK8aPHiwDh06VOore8szMbSjFzA/P1/x8fHlKxQAahECIACvmz9/viZPnlyqMNezZ091795dUuknhuY8QABwRQAE4HWRkZHq37+//vGPf5Sq/ZW9gCXp27evfH19JXEeIABIBEAA1cT48eP1ySef6I033tCSJUsUEBDgtm1ZJ4a2Wq3OdXCTkpKUkpLiucIBoAYiAAKoFvz8/PTyyy/rxx9/1OjRo+Xv719s27JODF1wGHj9+vUVKxYAajgCIIBqo2vXrgoNDVVcXFyJbcs6MTTnAQLAZQRAANVGXl6e+vTpo6efflqZmZnFti3rxNA9evRQaGioJHsALM0FJwBQWxEAAVQb2dnZeuCBB7Rnzx7NmTOnxPZlmRg6ICBAsbGxkqSTJ08qMTHRM0UDQA1EAARQLe3du1c//fRTsW3KOjE0w8AAYEcABFAtzZkzR88++2yJQ7VlmRiaZeEAwI4ACKBaioqKUp8+fbR8+fJi25VlYuh27dqpSZMmkqS4uDjl5uZ6rmAAqEEIgACqrWeeeUZLly7V2bNni21X2omhLRaLsxcwMzNTCQkJnikUAGoYAiCAasvf31+zZs3S1KlTi21XlomhOQ8QAAiAAKq5Xr16ycfHR5s3b3bbpiwTQ3MeIAAQAAFUIwEBAXr77bf19ttvuywF9/LLL2vGjBnKyclx+9rSTgwdERGh6OhoSVJCQoLS09M9+A4AoGYgAAKoNvz9/TVu3DiNGzfOZSm4+vXr69FHHy32/L6yTAzt6AXMz89XfHy8h6oHgJqDAAigRhg2bJi2bNmiI0eOuG1T2omhOQ8QgNkRAAFUG/n5+YqLi1NcXJzy8/NdnrNYLJo/f36xcwOWdmLovn37ytfXVxLnAQIwJwIggGojKytL/fr1U79+/ZSVlVXo+datW6tz585auXKl232UZmJoq9Wqbt26SZKSkpKUkpLigeoBoOYgAAKoUSZPnqz33ntPaWlpRT5f2omhCw4Dr1+/3vOFAkA1RgAEUKMEBgZq+vTpeuGFF9y2Kc3E0JwHCMDMCIAAapybb75ZWVlZ2rp1a5HPl2Zi6B49eig0NFSSPQCWtOYwANQmBEAANdLcuXP1wgsvKC8vr9BzpZkYOiAgQLGxsZKkkydPKjExsfKKBYBqhgAIoEYKDw/Xww8/7HbVj9JMDM0wMACzIgACqLFGjhypuLg4JScnF3quNBNDsywcALMiAAKoNvz9/fXqq6/q1VdfdVkJxB2LxaJ58+bpj3/8Y5Hn8JU0MXS7du3UpEkTSVJcXJxyc3M98C4AoPojAAKoNgICAjR58mRNnjzZZS3g4kRHR6tt27ZatWpVoedKmhjaYrE4ewEzMzOVkJBQsTcAADUEARBAjTd16lS9/fbbunDhQqHnSpoYmvMAAZgRARBAtZGfn69t27Zp27ZthZaCK05QUJCmTp2q6dOnF3qupImhOQ8QgBkRAAFUG1lZWerWrZu6detW5FJwxenfv7/Onj2rnTt3FnquuImhIyIiFB0dLUlKSEhQenp6OSoHgJqFAAig1nj11Vc1derUQr2HJU0M7egFzM/PV3x8fNUUCwBeRAAEUGs0btxY9913nxYtWuSyvaSJoTkPEIDZEAAB1CpjxozRl19+qZSUlELb3U0M3bdvX/n6+kriPEAA5kAABFCr+Pj46NVXX9XkyZNdthc3MbTValW3bt0kSUlJSYXCIwDUNgRAALVOu3btFBUVpTVr1rhsL25i6ILDwOvXr6+aQgHASwiAAGqladOmacGCBcrMzHRuK25iaM4DBGAmBEAA1Ya/v7+mT5+u6dOnl2opuOKEhIRo8uTJmjVrlst2dxND9+jRQ6GhoZLsAbCopeUAoLYgAAKoNgICAjRjxgzNmDGj1EvBFWfgwIH6z3/+oz179ji3uZsYOiAgQLGxsZKkkydPKjExscLHB4DqigAIoFabP3++nnvuOdlsNuc2dxNDMwwMwCwIgACqDZvNpv3792v//v0uga0imjVrpjvuuEN/+9vfnNvcTQxNAARgFgRAANXGpUuX1K5dO7Vr106XLl3y2H6feOIJffrpp0pNTZXkfmLodu3aqUmTJpKkuLg45ebmeqwGAKhOCIAAaj1fX1/NnTtXU6ZMcW4bM2aM6tSpI+nyxNAWi8XZC5iRkaGEhASv1AsAlY0ACMAUOnbsqEaNGumbb76RZJ/8+bHHHpPkOjE0w8AAzIAACMA0Zs6cqblz5zqHl4uaGLpgAGRZOAC1FQEQgGnUqVNHEydO1OzZsyUVPTF0RESEoqOjJUkJCQlKT0/3Wr0AUFkIgABMZfDgwTp06JDzyt+iJoZ29ALm5+crPj7eK3UCQGUiAAIwnfnz5+vZZ5+VzWYrcmJozgMEUNsRAAFUG/7+/nr22Wf17LPPVngpuOJERkZqwIABWrp0qaTCvYB9+/aVr6+vJM4DBFA7WQwWvISXpKeny2q1Ki0tTXXr1vV2OTCZvLw8DRo0SMuXL1f9+vV1zTXXKDk5WZKUmJioMWPG6IcffpAk/ec//9FVV13l8vrBgwdr9erVVV43IPH9iYqjBxCAKfn5+Wn27Nl67rnnipwYuuAw8Pr1671RIgBUGgIgyuzYsWMaM2aMWrVqpeDgYF1zzTWaPn26cnJyvF0aajibzaZjx47p2LFjHlsKrjhdu3ZVnTp1tHHjxkITQ3fp0sXZjvMAAdQ2BECU2YEDB2Sz2fTee+9p//79eu211/Tuu+/q+eef93ZpqOEuXbqkVq1aqVWrVh5dCq44L730kv7yl78oKCjIZWLoXbt2KTQ0VJI9AHK2DIDahHMA4RHz5s3T4sWLdeTIkVK/hnNYcKXMzExnL1xGRoYzgFW2f/3rX0pMTNSIESPUunVr2Ww2NWnSRB07dtTXX38tSdq3b59iYmKcr+EcQHgT35+oKHoA4RFpaWlq0KBBsW2ys7OVnp7ucgOqg3vvvVc//vijcnNzXSaGLvhvmmFgALUJARAVdvjwYb311lt64oknim03Z84cWa1W5y0yMrKKKgSKZ7FYtGDBAj377LN65plnnNt37NjhvE8ABFCbEADhNGPGDFkslmJv27dvd3nNiRMndNttt+n+++93nj/lztSpU5WWlua8HT9+vDLfDlAmLVu2VJ8+fXTkyBHnxNA//fST6tWrJ0mKi4tTbm6uFysEAM/x83YBqD7Gjx+vBx98sNg2LVu2dN4/ceKE+vXrp549e+qvf/1rifsPDAxUYGBgRcsEKs0zzzyjgQMH6vHHH1dCQoIkKSQkROfPn1dGRoYSEhLUp08fL1cJABVHAIRTeHi4wsPDS9U2JSVF/fr104033qglS5bIx4fOZNR8/v7+mjVrlpYsWaIWLVooOTlZJ06ccD6/bt06AiCAWoHf2iizEydOqG/fvoqMjNT8+fN1+vRppaamKjU11duloYbz8/PT2LFjNXbsWPn5eefv0169esnPz0933nlnoedYFg5AbUEPIMrsm2++0c8//6yff/5ZERERLs8xqxAqIjAwUO+88463y9DLL7+su+++W6GhocrMzJTFYpFhGEpISFB6ejrTbgCo8egBRJmNHj1ahmEUeQNqg/r16+vxxx9Xx44dJV3+wyY/P1/x8fFerAwAPIMACKDaMAxDp0+f1unTp73+B8WwYcMUEhIii8Xisp3pYADUBgRAANXGxYsX1bhxYzVu3FgXL170ai0Wi0WLFi1Ss2bNXLZzHiCA2oAACAButG7dWrfffrvLtqSkJKWkpHipIgDwDAIgABTjrbfeKnTRx/r164t9Td++fTVx4sRKrMq7jh07JovFot27d3u7FADlRAAEgGIEBga6LA8nlXwe4P/93//ppZdeqsyyAKBCCIAAUII///nPCg0NdT7+8ssvi23foEEDhYWFVXZZAFBuBEAAKMKhQ4eUnZ0tyT5B9ZQpU5zPnTlzRhcuXHD72iuHgFu2bKm//OUvGjlypOrUqaOoqCh99tlnOn36tO666y7VqVNH7du3d1lr+7ffftOwYcMUERGhkJAQtW/fXh9++KHLcS5cuKDhw4crNDRUzZo102uvvVbo2Dk5OZoyZYquuuoqhYaGqnv37oqLiyv2vVssFi1evFgDBw5UcHCwWrVqpZUrV7ptn5+frzFjxqhVq1YKDg7WddddpzfeeMOlzejRozVkyBDNnz9fzZo1U8OGDTVu3DiX9ZXLUyuA8iEAAsAV8vLy1KNHD7Vu3VqLFy9Wdna2nn76aZfVScq68s1rr72m3r17a9euXbr99ts1YsQIjRw5Ug8//LB27typ1q1ba+TIkc7pb7KysnTjjTfq888/1759+/T4449rxIgRzjWKJWnSpEn67rvvtHr1aq1du1abNm3Szp07XY77yCOP6LvvvtNHH32kPXv26P7779dtt92mQ4cOFVvvtGnTdO+99+rHH3/Uww8/rGHDhikpKanItjabTREREVqxYoUSExP14osv6vnnn9eKFStc2m3cuFGHDx/Wxo0btWzZMi1dulRLly6tcK0AysEAvCQtLc2QZKSlpXm7FFQTWVlZxqhRo4xRo0YZWVlZXq3lwIEDxvDhww0fHx8jIiLCWLRokfHggw8akgxJRmhoqNvXxsbGGk8//bTzcVRUlPHwww87H588edKQZEybNs257YcffjAkGSdPnnS730GDBhl//OMfDcMwjPT0dMPf399YuXKl8/nz588bISEhzmP//PPPhsViMVJSUlz2c8sttxhTp051exxJxhNPPOGyrXv37saTTz5pGIZhHD161JBk7Nq1y+0+xo4da9x7773Ox6NGjTKioqKMvLw857b777/feOCBBypUq1nx/YmKYik4ANWGYym4xYsXa+7cud4uR9dee62efPJJffvttxo3bpzLeYCZmZnKyMhQnTp1SrWvG264wXm/SZMmkqT27dsX2nbq1Ck1bdpU+fn5mjt3rj7++GOlpKQoOztb2dnZzhqOHDmi3NxcdevWzbkPq9Wq6667zvl4586dMgxDbdq0caklOztbDRs2LLbenj17Fnpc3FW/7777rt5//3398ssvunTpknJycpwrqTjExMTI19fX+bhZs2bau3dvhWsFUHYEQADVyunTp/XXv/5VmZmZ3i7FKTs7W76+vsrIyJCfn5/y8vIkSXPnztVf/vKXUu3D39/fed+xukhR22w2myRpwYIFeu211/T666+rffv2Cg0N1cSJE5WTkyPp8vJ0V65UYhRYQcVms8nX11c7duxwCV6SSh1cC7ryWA4rVqzQM888owULFqhnz54KCwvTvHnzXIarr3y/jv053q+nawVQPAIggGqlZcuW+umnn7xdhiQpPj5eM2bMUFxcnDp27KgZM2boxx9/1IIFC3TnnXfqscceq7Rjb9q0SXfddZcefvhhSfaAdOjQIV1//fWSpGuuuUb+/v7aunWrIiMjJUnp6ek6dOiQYmNjJUmdOnVSfn6+Tp06pZtuuqlMx9+yZYtGjhzp8rhTp05ua+3Vq5fGjh3r3Hb48OEyHa8itQIoOwIgAFwhPz9fQ4YM0eeff66OHTtq1apVGjx4sCwWi+666y5NmzbNbW+Yp7Ru3VqffPKJvv/+e9WvX18LFy5UamqqMwCGhYVp1KhRmjx5sho0aKDGjRtr+vTp8vHxcdbWpk0bDR8+XCNHjtSCBQvUqVMnnTlzRhs2bFD79u01aNAgt8dfuXKlunTpoj59+mj58uXaunWr/ud//sdtrf/7v/+rr7/+Wq1atdIHH3ygbdu2qVWrVqV+vxWpFUDZcRUwAFzBx8dH7du316pVq7Rz507dddddLoGvssOfZL8Kt3Pnzvr973+vvn37qmnTphoyZIhLm4ULF6pnz56644471L9/f/Xu3VvXX3+9goKCnG2WLFmikSNH6o9//KOuu+46DR48WAkJCc5eQ3dmzpypjz76SDfccIOWLVum5cuXq23btkW2feKJJ3TPPffogQceUPfu3fXbb7+59AaWVnlrBVB2FqPgCSNAFUpPT5fValVaWlqhpbYAlF1mZqauuuoqLViwQGPGjCn3fiwWiz799NNCgRPVB9+fqCiGgAGghtq1a5cOHDigbt26KS0tTbNmzZIk3XXXXV6uDEB1RwAEgBps/vz5OnjwoAICAnTjjTdq06ZNCg8P93ZZAKo5AiAA1FCdOnXSjh07PL5fzgwCaj8uAgEAADAZAiAAAIDJEAABAABMhgAIAABgMgRAAAAAkyEAAgAAmAwBEAAAwGQIgAAAACZDAAQAADAZAiAAAIDJEAABAABMhgAIAABgMgRAAAAAkyEAAgAAmAwBEAAAwGQIgAAAACZDAAQAADAZAiAAAIDJEAABAABMhgAIAABgMgRAAAAAkyEAAgAAmAwBEAAAwGQIgAAAACZDAAQAADAZAiAAAIDJEAABAABMhgAIAABgMgRAAAAAkyEAAgAAmAwBEAAAwGQIgAAAACZDAAQAADAZAiAAAIDJEAABAABMhgAIAABgMgRAAAAAkyEAAgAAmAwBEOUyePBgtWjRQkFBQWrWrJlGjBihEydOeLssAABQCgRAlEu/fv20YsUKHTx4UJ988okOHz6s++67z9tlAQCAUrAYhmF4uwjUfKtXr9aQIUOUnZ0tf3//Ur0mPT1dVqtVaWlpqlu3biVXCAC1B9+fqCh6AFFhZ8+e1fLly9WrV69Shz8AAOA9BECU23PPPafQ0FA1bNhQycnJ+uyzz4ptn52drfT0dJcbAACoegRAOM2YMUMWi6XY2/bt253tJ0+erF27dumbb76Rr6+vRo4cqeLOKJgzZ46sVqvzFhkZWRVvCwAAXIFzAOF05swZnTlzptg2LVu2VFBQUKHt//nPfxQZGanvv/9ePXv2LPK12dnZys7Odj5OT09XZGQk57AAQBlxDiAqys/bBaD6CA8PV3h4eLle6/g7omDAu1JgYKACAwPLtX8AAOA5BECU2datW7V161b16dNH9evX15EjR/Tiiy/qmmuucdv7BwAAqg/OAUSZBQcH6//+7/90yy236LrrrtOjjz6qdu3aKT4+nh4+AABqAHoAUWbt27fXhg0bvF0GAAAoJ3oAAQAATIYACAAAYDIEQAAAAJMhAAIAAJgMARAAAMBkCIAAAAAmQwAEAAAwGQIgAACAyRAAAQAATIYACAAAYDIEQAAAAJMhAAIAAJgMARAAAMBkCIAAAAAmQwAEAAAwGQIgAACAyRAAAQAATIYACAAAYDIEQAAAAJMhAAIAAJgMARAAAMBkCIAAAAAmQwAEAAAwGQIgAACAyRAAAQAATIYACAAAYDJ+3i4A5mUYhiQpPT3dy5UAQM3i+N50fI8CZUUAhNf89ttvkqTIyEgvVwIANdNvv/0mq9Xq7TJQAxEA4TUNGjSQJCUnJ5v+Cyw9PV2RkZE6fvy46tat6+1yvIrPwhWfx2V8FpelpaWpRYsWzu9RoKwIgPAaHx/7KahWq9X0X+YOdevW5bP4Lz4LV3wel/FZXOb4HgXKin85AAAAJkMABAAAMBkCILwmMDBQ06dPV2BgoLdL8To+i8v4LFzxeVzGZ3EZnwUqymJwDTkAAICp0AMIAABgMgRAAAAAkyEAAgAAmAwBEAAAwGQIgPC6Y8eOacyYMWrVqpWCg4N1zTXXaPr06crJyfF2aV4xe/Zs9erVSyEhIapXr563y6lyixYtUqtWrRQUFKQbb7xRmzZt8nZJXvHtt9/qzjvvVPPmzWWxWLRq1Spvl+QVc+bMUdeuXRUWFqbGjRtryJAhOnjwoLfL8prFixfrhhtucE6G3bNnT3355ZfeLgs1EAEQXnfgwAHZbDa999572r9/v1577TW9++67ev75571dmlfk5OTo/vvv15NPPuntUqrcxx9/rIkTJ+qFF17Qrl27dNNNN2ngwIFKTk72dmlVLjMzUx06dNDbb7/t7VK8Kj4+XuPGjdOWLVu0du1a5eXl6dZbb1VmZqa3S/OKiIgIzZ07V9u3b9f27dv1u9/9TnfddZf279/v7dJQwzANDKqlefPmafHixTpy5Ii3S/GapUuXauLEiTp//ry3S6ky3bt3V+fOnbV48WLntuuvv15DhgzRnDlzvFiZd1ksFn366acaMmSIt0vxutOnT6tx48aKj4/XzTff7O1yqoUGDRpo3rx5GjNmjLdLQQ1CDyCqpbS0NBY5N5mcnBzt2LFDt956q8v2W2+9Vd9//72XqkJ1k5aWJkl8P0jKz8/XRx99pMzMTPXs2dPb5aCG8fN2AcCVDh8+rLfeeksLFizwdimoQmfOnFF+fr6aNGnisr1JkyZKTU31UlWoTgzD0KRJk9SnTx+1a9fO2+V4zd69e9WzZ09lZWWpTp06+vTTT9W2bVtvl4Uahh5AVJoZM2bIYrEUe9u+fbvLa06cOKHbbrtN999/vx577DEvVe555fkszMpisbg8Ngyj0DaY0/jx47Vnzx59+OGH3i7Fq6677jrt3r1bW7Zs0ZNPPqlRo0YpMTHR22WhhqEHEJVm/PjxevDBB4tt07JlS+f9EydOqF+/furZs6f++te/VnJ1Vausn4UZhYeHy9fXt1Bv36lTpwr1CsJ8JkyYoNWrV+vbb79VRESEt8vxqoCAALVu3VqS1KVLF23btk1vvPGG3nvvPS9XhpqEAIhKEx4ervDw8FK1TUlJUb9+/XTjjTdqyZIl8vGpXZ3TZfkszCogIEA33nij1q5dq7vvvtu5fe3atbrrrru8WBm8yTAMTZgwQZ9++qni4uLUqlUrb5dU7RiGoezsbG+XgRqGAAivO3HihPr27asWLVpo/vz5On36tPO5pk2berEy70hOTtbZs2eVnJys/Px87d69W5LUunVr1alTx7vFVbJJkyZpxIgR6tKli7MnODk5WU888YS3S6tyGRkZ+vnnn52Pjx49qt27d6tBgwZq0aKFFyurWuPGjdM///lPffbZZwoLC3P2EFutVgUHB3u5uqr3/PPPa+DAgYqMjNSFCxf00UcfKS4uTl999ZW3S0NNYwBetmTJEkNSkTczGjVqVJGfxcaNG71dWpV45513jKioKCMgIMDo3LmzER8f7+2SvGLjxo1F/jsYNWqUt0urUu6+G5YsWeLt0rzi0Ucfdf7/0ahRI+OWW24xvvnmG2+XhRqIeQABAABMpnadaAUAAIASEQABAABMhgAIAABgMgRAAAAAkyEAAgAAmAwBEAAAwGQIgAAAACZDAAQAADAZAiAAAIDJEAABAABMhgAIAABgMgRAAAAAkyEAAgAAmAwBEAAAwGQIgAAAACZDAAQAADAZAiAAAIDJEAABAABMhgAIAABgMgRAAAAAkyEAAgAAmAwBEAAAwGQIgAAAACZDAAQAADAZAiAAAIDJEAABAABMhgAIAABgMgRAAAAAkyEAAgAAmAwBEAAAwGQIgAAAACbz/wE29w7EDb2iygAAAABJRU5ErkJggg==",
      "text/html": [
       "\n",
       "            <div style=\"display: inline-block;\">\n",
       "                <div class=\"jupyter-widgets widget-label\" style=\"text-align: center;\">\n",
       "                    Figure\n",
       "                </div>\n",
       "                <img src='data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAoAAAAHgCAYAAAA10dzkAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjguMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8g+/7EAAAACXBIWXMAAA9hAAAPYQGoP6dpAABZxUlEQVR4nO3dd3xUVf7/8fekF8JQQjUhoIiRgBTpoIEVXEFFbCgiRXH9KUWRFVx0keIiKMUOuut3ga/LqrB+RVZstERQCV1KAiLFsIEICCQkkDr398fsDBmSSZ1kktzX8/GYR2bunLn3MyNO3jnn3nMshmEYAgAAgGn4eLsAAAAAVC0CIAAAgMkQAAEAAEyGAAgAAGAyBEAAAACTIQACAACYDAEQAADAZAiAAAAAJkMABAAAMBkCIAAAgMkQAAEAAEyGAAgAAGAyBEAAAACTIQACAACYDAEQAADAZAiAAAAAJkMABAAAMBkCIAAAgMkQAAEAAEyGAAgAAGAyBEAAAACTIQACAACYDAEQAADAZAiAAAAAJkMABAAAMBkCIAAAgMkQAAEAAEyGAAgAAGAyBEAAAACTIQACAACYDAEQAADAZAiAAAAAJkMABAAAMBkCIAAAgMkQAAEAAEyGAAgAAGAyBEAAAACTIQACAACYDAEQAADAZAiAAAAAJkMABAAAMBkCIAAAgMkQAAEAAEyGAAgAAGAyBEAAAACTIQACAACYDAEQAADAZAiAAAAAJkMABAAAMBkCIAAAgMkQAAEAAEyGAAgAAGAyBECUy5w5c9S1a1eFhYWpcePGGjJkiA4ePOjtsgAAQCkQAFEu8fHxGjdunLZs2aK1a9cqLy9Pt956qzIzM71dGgAAKIHFMAzD20Wg5jt9+rQaN26s+Ph43Xzzzd4uBwAAFIMeQHhEWlqaJKlBgwZergQAAJSEHkBUmGEYuuuuu3Tu3Dlt2rTJbbvs7GxlZ2c7H9tsNp09e1YNGzaUxWKpilIBoFYwDEMXLlxQ8+bN5eNDXw7Kzs/bBaDmGz9+vPbs2aPNmzcX227OnDmaOXNmFVUFALXf8ePHFRER4e0yUAPRA4gKmTBhglatWqVvv/1WrVq1KrbtlT2AaWlpatGihY4fP666detWdqkAUGukp6crMjJS58+fl9Vq9XY5qIHoAUS5GIahCRMm6NNPP1VcXFyJ4U+SAgMDFRgYWGh73bp1CYAAUA6cPoPyIgCiXMaNG6d//vOf+uyzzxQWFqbU1FRJktVqVXBwsJerAwAAxWEIGOXi7q/OJUuWaPTo0aXaR3p6uqxWq9LS0ugBBIAy4PsTFUUPIMqFvxsAAKi5uHYcAADAZAiAAAAAJkMABAAAMBkCIAAAgMkQAAEAAEyGAAgAAGAyBEAAAACTIQACAACYDAEQAADAZAiAAAAAJkMABAAAMBkCIAAAgMkQAAEAAEyGAAgAAGAyBEAAAACTIQACAACYDAEQAADAZAiAAAAAJkMABAAAMBkCIAAAgMkQAAGgAuLi4mSxWHT+/PkKtfGWGTNmqGPHjt4uA0AVIwACQCXr1auXTp48KavV6pH9VedACaBm8PN2AQBQ2wUEBKhp06beLgMAnOgBBFAhhmEoMTFRNpvN26VUiuzsbD311FNq3LixgoKC1KdPH23btq1Qu++++04dOnRQUFCQunfvrr179zqfK6rH7vvvv9fNN9+s4OBgRUZG6qmnnlJmZqbLcadMmaLIyEgFBgbq2muv1f/8z//o2LFj6tevnySpfv36slgsGj16dJG1L126VPXq1dOqVavUpk0bBQUFacCAATp+/Ljb97tt2zYNGDBA4eHhslqtio2N1c6dO13aWCwWvf/++7r77rsVEhKia6+9VqtXr3Zpk5iYqEGDBqlOnTpq0qSJRowYoTNnzrg9LoCqRQAEUC6GYWjNmjXq1q2bYmJilJiY6O2SKsWUKVP0ySefaNmyZdq5c6dat26t3//+9zp79qxLu8mTJ2v+/Pnatm2bGjdurMGDBys3N7fIfe7du1e///3vdc8992jPnj36+OOPtXnzZo0fP97ZZuTIkfroo4/05ptvKikpSe+++67q1KmjyMhIffLJJ5KkgwcP6uTJk3rjjTfc1n/x4kXNnj1by5Yt03fffaf09HQ9+OCDbttfuHBBo0aN0qZNm7RlyxZde+21GjRokC5cuODSbubMmRo6dKj27NmjQYMGafjw4c7P5OTJk4qNjVXHjh21fft2ffXVV/r11181dOjQ4j9sAFXHALwkLS3NkGSkpaV5uxSUICcnx9i0aZOxYcMGw2azGZ9//rnRpUsXQ5LRp08fY926dd4usVJkZGQY/v7+xvLly53bcnJyjObNmxuvvvqqYRiGsXHjRkOS8dFHHznb/Pbbb0ZwcLDx8ccfu7Q5d+6cYRiGMWLECOPxxx93OdamTZsMHx8f49KlS8bBgwcNScbatWuLrOvK/bmzZMkSQ5KxZcsW57akpCRDkpGQkGAYhmFMnz7d6NChg9t95OXlGWFhYca///1v5zZJxp///Gfn44yMDMNisRhffvmlYRiGMW3aNOPWW2912c/x48cNScbBgweLrRmlw/cnKopzAAEU69y5c2rRooUyMjLk5+cni8Wi3NxctWjRQiNHjlSrVq20efNmbd682WPHbN68uf7whz94bH/ldfjwYeXm5qp3797Obf7+/urWrZuSkpJc2vbs2dN5v0GDBrruuusKtXHYsWOHfv75Zy1fvty5zTAM2Ww2HT16VHv37pWvr69iY2Mr/B78/PzUpUsX5+Po6GjVq1dPSUlJ6tatW6H2p06d0osvvqgNGzbo119/VX5+vi5evKjk5GSXdjfccIPzfmhoqMLCwnTq1Cnn+9u4caPq1KlTaP+HDx9WmzZtKvy+AFQMARBAserXr6+rrrpKBw8eVF5eniT7OWDp6elau3atLBaLx45lGIZOnjwpSXrooYcUGhrqsX2Xtx5Jhd6jYRilet/u2thsNv2///f/9NRTTxV6rkWLFvr555/LUW3Z6nBX2+jRo3X69Gm9/vrrioqKUmBgoHr27KmcnByXdv7+/oX25zgP1Gaz6c4779Qrr7xSaP/NmjUr79sA4EEEQAAl6tixow4ePChJqlu3rvr166fPPvtMjRo10rRp0zRs2DD5+VX86yQzM7PIXiNvad26tQICArR582Y99NBDkqTc3Fxt375dEydOdGm7ZcsWtWjRQpK91/Snn35SdHR0kfvt3Lmz9u/fr9atWxf5fPv27WWz2RQfH6/+/fsXej4gIECSlJ+fX+J7yMvL0/bt2529fQcPHtT58+fd1rZp0yYtWrRIgwYNkiQdP368zBdvdO7cWZ988olatmzpkX8XADyPi0AAlCgoKMh5/9KlS1q1apV27Nihtm3bauTIkWrbtq2z5642CQ0N1ZNPPqnJkyfrq6++UmJiov7whz/o4sWLGjNmjEvbWbNmaf369dq3b59Gjx6t8PBwDRkypMj9Pvfcc/rhhx80btw47d69W4cOHdLq1as1YcIESVLLli01atQoPfroo1q1apWOHj2quLg4rVixQpIUFRUli8Wizz//XKdPn1ZGRobb9+Dv768JEyYoISFBO3fu1COPPKIePXoUOfwr2UPvBx98oKSkJCUkJGj48OEKDg4u0+c2btw4nT17VsOGDdPWrVt15MgRffPNN3r00UdLFVoBVD4CIIASOc7tkuw9Svv371fnzp2dQXDQoEHy9fX1YoWVZ+7cubr33ns1YsQIde7cWT///LO+/vpr1a9fv1C7p59+WjfeeKNOnjyp1atXO3vqrnTDDTcoPj5ehw4d0k033aROnTpp2rRpLsOjixcv1n333aexY8cqOjpaf/jDH5zTxFx11VWaOXOm/vSnP6lJkyYuVw9fKSQkRM8995weeugh9ezZU8HBwfroo4/ctv/73/+uc+fOqVOnThoxYoRzCpyyaN68ub777jvl5+fr97//vdq1a6enn35aVqtVPj782gGqA4vhOMkFqGLp6emyWq1KS0tT3bp1vV0O3MjKytIDDzygr776ynkeWGxsrNatW+fx4b2CQ8AZGRlePwfQU77++msNHDhQWVlZbkNhZVi6dKkmTpzIiiG1EN+fqCj+FANQrO+//169evVSYGCgc1ubNm00b948L1ZVc/z666/67LPPdO2111Zp+AOA4hAAARRr3bp16t+/v8t5gBcvXtSOHTu0f/9+L1ZWMwwaNEjr1q3TO++84+1SAMCJIWB4DUMYNcPAgQO1Zs0atWjRQikpKZKkpk2bavv27Xr00Ue1Zs0ajw0FZ2Vl6d5775UkffLJJy6hE8BlfH+iougBBODWuXPnijxxPzU1VefPn9fw4cM9OhQcFBSkNWvWaM2aNYQ/AKhEBEAAbm3YsEG/+93vinxu7dq1GjFiBEPBAFADEQABuOU4/8/dcxaLRW+++aYmTZrkXCUEAFD9EQABuHX06FFdffXVLtscw8FxcXHKzc1V8+bNPTYUnJmZqdDQUIWGhjrnvAMAeB4BEECRjh07pqioqELbHdPBZGZmKiEhQZI8OhR88eJFXbx4scL7AQC4RwAEUCR3w78FL85Yu3atJDEUDAA1DAEQQJHcXQBScELodevWOe97cigYAFC5CIAACrHZbDp37pwaNmxY6DlfX19FR0dLkhISEpSenu58jquCAaBmIAACKGTPnj3q0KGD2+cdQ8P5+fmKj493bmcoGABqBgIggELWrl3rdvoXSRowYIBL24IYCgaA6o8ACKCQzZs3q3fv3m6fj42Nla+vryTX8wAdyjsU7OPjo9jYWMXGxhZafQQA4Dl8wwJwkZWVJUkKDg5228Zqtapbt26SpKSkJOcawQ7lHQoODg5WXFyc4uLiij0+AKBiCIAAXHz//ffq1atXie0KDhGvX7++0PMMBQNA9UUABOCiuOXfCiruPEAHrgoGgOqJAAjAxa5du9SpU6cS23Xv3l2hoaGS7KHRMIxCbco6FJyZmalGjRqpUaNGLAUHAJWIAAjA6dy5c7JaraW6ACMgIECxsbGSpNTUVCUmJhbZrqxDwWfOnNGZM2dKXzQAoMwIgACc3K3+4U7BoWJ3w8ASQ8EAUN0QAAE4lfb8P4eC5wEWNR2MAxNEA0D1QgAE4HT06FFdffXVpW4fExOjJk2aSJLi4uKUm5vrti1XBQNA9UEABCBJOnbsmKKiosr0GovF4uwxzMzMVEJCQrHtGQoGgOqBAAhAUtmHfx1KMx2MA0PBAFA9EABRbt9++63uvPNONW/eXBaLRatWrfJ2SaiAsl4A4nDLLbc47xd3HqBDcUPBPj4+6tKli7p06cJScABQifiGRbllZmaqQ4cOevvtt71dCirIZrPp3LlzatiwYZlfGxERoejoaElSQkKC0tPTS3yNu6Hg4OBgbdu2Tdu2bWMpOACoRARAlNvAgQP1l7/8Rffcc4+3S0EF7dmzRx06dCj36x1Dx/n5+YqPjy+xPUPBAOBdBEAAWrt2bbnO/3Moy3mADlwVDADeQwBElcnOzlZ6errLDdXD5s2b1bt373K/PjY2Vr6+vpJKdx6gw5VDwRcvXlTLli3VsmVLXbx4sdz1AACKRwBElZkzZ46sVqvzFhkZ6e2SICkrK0uSKnTOndVqVbdu3SRJSUlJSklJKdXrrhwKNgxDv/zyi3755Zci1xYGAHgGARBVZurUqUpLS3Pejh8/7u2SIOmHH35Qr169KryfgkPI69evL/XrGAoGgKpHAESVCQwMVN26dV1u8L6Knv/nUJ7zAB0cQ8GJiYkVrgMAUDICIMotIyNDu3fv1u7duyXZlxHbvXu3kpOTvVsYymTXrl3q2LFjhffTvXt3hYaGSrKfB1iWIVzHUPDUqVMrXAcAoGQEQJTb9u3b1alTJ3Xq1EmSNGnSJHXq1EkvvviilytDaZ07d05Wq9V5AUdFBAQEKDY2VpKUmppa5t685s2b64EHHqhwHQCAkhEAUW59+/aVYRiFbkuXLvV2aSil8q7+4U7BoeSyDgNL0rBhwzxWCwDAPQIgYGLlXf/XnYLnAZZlOhgHHx8fXXvttQoNDVV+fr7H6gIAuCIAAiZ29OhRXX311R7bX0xMjJo0aSJJiouLU25ubpleHxISop9++kmLFi3SO++847G6AACuCICASR07dkxRUVEe3afFYnH2KGZmZiohIaFc+3G3VjAAwDMIgIBJeXr416Gi5wFKrBUMAJWNAAiYlKcvAHEoGADLeh7gxYsXFRMTo5iYGNWrV48JogGgkhAAAROy2Ww6d+6cGjZs6PF9R0REKDo6WpKUkJBQpjWfDcNQYmKiEhMTZRgGQ8EAUEkIgIAJ7dmzRx06dKi0/Tt6AfPz8xUfH1/u/TAUDACVgwAImJCnln9zpyLLwl2JtYIBwPMIgIAJbd68Wb179660/cfGxjpXFynPfIBXYigYADyLAAiYTFZWliQpODi40o5htVrVrVs3SVJSUpJSUlIqtD+GggHAswiAgMn88MMP6tWrV6Ufp+AQ8/r16yu8P4aCAcBzCICAyVT2+X8O5TkP0GKxKCoqSlFRUbJYLIWeHzFihHbu3MlQMABUEAEQMJldu3apY8eOlX6c7t27KzQ0VJL9PEDDMEp8TUhIiI4dO6Zjx44pJCSk0PMWi0VvvPEGQ8EAUEEEQMBEzp07J6vV6rxAozIFBAQoNjZWkpSamqrExESP7JehYACoOAIgYCKVtfqHOxVZFaQ4DAUDQMUQAAETqaz1f90p63mAly5dUteuXdW1a1ddunTJbTuGggGgYgiAgIkcPXpUV199dZUdLyYmRk2aNJEkxcXFKTc3t9j2NptN27dv1/bt22Wz2Ypty1AwAJQfARAwiWPHjikqKqpKj2mxWJw9jpmZmUpISPDo/hkKBoDyIQACJlHVw78OBY9Z0WXhrsRQMACUDwEQMImqvgDEobIuBHFgKBgAyo4ACJiAzWbTuXPn1LBhwyo/dkREhKKjoyVJCQkJSk9P9/gxGAoGgLIhAAImsGfPHnXo0MFrx3f0Aubn5ys+Pt7j+2coGADKhgAImEBVLf/mTlmmgwkPD1d4eHiZj8FQMACUHgEQMIHNmzerd+/eXjt+bGysc/WR4s4DDA0N1enTp3X69GnnMnJlwVAwAJQOARCo5bKysiRJwcHBXqvBarWqW7dukqSkpCSlpKRUynEYCgaA0iEAArXcDz/8oF69enm7DJch6PXr11facRgKBoCSEQCBWs7b5/85lOY8wEuXLqlv377q27dvsUvBlYShYAAoHgEQqOV27dqljh07ersMde/e3Xle37p162QYRqE2NptN8fHxio+PL3EpuOIwFAwAxSMAArXYuXPnZLVanRdgeFNAQIBiY2MlSampqUpMTKzU4zEUDADuEQCBWmzjxo1eWf3DncpeFeRKDAUDQNEIgEAtVl3O/3Moy3yAnsBQMAAUjQAI1GJHjhzR1Vdf7e0ynGJiYtSkSRNJUlxcnHJzcyv9mAwFA0BhBECgljp27Jhatmzp7TJcWCwWZ49kZmamEhISquS4DAUDgCsCIFBLrVu3rloN/zoUrKmoYeCQkBCFhIR49JgMBQOAKwIgUEtt2LChWl0A4lDchSChoaHKzMxUZmZmuZaCKw5DwQBwGQEQqIVsNpvOnTunhg0beruUQiIiIhQdHS1JSkhIUHp6epUdm6FgALAjAAK10J49e9ShQwdvl+GWoxcwPz9f8fHxVXZchoIBwI4ACNRC1W36lyu5mw4mKytLt99+u26//XZlZWVVyrEZCgYAAiBQK23evFm9e/f2dhluxcbGOlcnKXgeYH5+vr744gt98cUXys/Pr7TjMxQMwOwIgEAt4+g5Cw4O9nIl7lmtVnXr1k2SlJSUpJSUlCo9PkPBAMyOAAjUMj/88IN69erl7TJKVHCIev369VV+fIaCAZgZARCoZar7+X8OVb0sXFEYCgZgVgRAoJbZtWuXOnbs6O0yStS9e3fnXH/r1q2TYRhVXgNDwQDMigAI1CLnzp2T1Wp1XmBRnQUEBCg2NlaSlJqaqsTERK/UwVAwADMiAAK1yMaNG6vl6h/uFLcqSFViKBiA2RAAgVqkppz/53DleYChoaEyDEOGYXh8KbjiMBQMwGwIgEAtcuTIEV199dXeLqPUYmJi1KRJE0lSXFyccnNzvVYLQ8EAzIQACNQSx44dU8uWLb1dRplYLBZnj2VmZqYSEhK8Wg9DwQDMggAI1BLr1q2rUcO/DgVr/uqrr3T//ffr/vvvr7Sl4IrDUDAAsyAAArXEhg0batQFIA5XTgj9r3/9S//6178qdSm44jAUDMAM/LxdAICKs9lsOnfunBo2bOi2jWFINpuUn1/4VnC7zWa/Gcbl1xiG5OgQy8uTDhy4vL2otle+zrHPK+uxi1CLFtFKTj6grVu3OZ+Pj5dCQiSLpfB7uXKbr6/95uNjf+7Kn+7uF9xW8HHfviM0duxQxcXt1/XXxzj3X/Dm43P5PgDUNARAoBqy2ezBKTe35J/5+VJS0h41atRB335r3+Z43tHG8dgRxIq7OQJcwXmZDUNyjMhmZUlr1pTufTiCmiNguRMV1V/JyQdks13u9du3TwoMdK3BnaJqrgiLxaIuXd7QE088ov/3/9YoIMBPPj6uwdFxc4RAf//CNz+/yz8Ltiu43d3P4j4vAKgoAiBQiXJzpZwcKTvb9WfBUJadbb9dumR/7tKly89d2VOXl1d0yNm4ca0iIvpr507XcFIwtDh6rfz8VCjMFNV7dmUA8fO7/LNNG89+Tjfd1F+bNr3tsq1VKykoyLPHKS17D2ZznT07XNu3z9OQIVPdhuXcXHsovnL7lY+LUjBAFgyJvr728BsYaP8MgoPt9wMCLodEf//L2wICXJ8HgJLwVQGUUV6e/Rd+dvbln477ly5JGRn228WLRffGXcliKfzLv2AIKGro8UorVmzW6NHjXXrMapL27fvKx8fXpQfQmxyBuX//EXrllaE6dWq/WrSI8fhxHEPuBcO+499KVlbhPwCuDJKOfzsFew8DAuxD53XqSGFh9gDpCJKOUBkYaA+VRf1bAmAOBEDgCo7hzsxMe4hz3M6ds98yMlx78Qpeq2CxuA7/+flJoaGVO7SXk2Mfmw0MDPbsjqtQaKhVbdp004EDP3i7FBcWi0V/+MMbevPNR/Tii2vk6+vZr8yCw8Ll4QiPBU8LyMyU0tIuPy4YGn197QHRERStVql+ffvPkBDXm7d6XwFUDQIgTCsvTzp/3v7LMjPTHuzOnZPOnr3cq5edffkXqJ/f5V6UOnUuBz1vXwRw4MAPuv76Xt4twgM6dOhf7QKgJDVs2FyxscP1f/83T/ffP9Xb5bjw8bk8BFwaeXn2P14cpx6cPCkdO2Z/7Bj+d/QQhoTYw2H9+vY/YkJDpXr17GGRnkOg5iMAwhRsNunCBXvAO3/e/ovv11/twc9xcYPF4nreldVq/8Va3X/Z7d69Vr163evtMiqsY8cB+vjjlyRJN930oAIDQ7xc0WX9+tmHgpOTK2couKo4eqXdyc+//IdPRob022/2wGgY9v8/goPtw8rNm0uNGtnDYb169nDIRStAzUIARIUsWrRI8+bN08mTJxUTE6PXX39dN910k7fLkmQ/Hy85WUpNlVJSpPR0+1CuYdiDXWio/ZdYUFDN/uV15MguDR/+krfLqLA2bborKChUWVmZ2rcvztvluKjsoeDqwtf38hDwlWy2y+e47tljD4s+Pvbe8Hr17KGweXMpIqL8Q9oAqk7t/BZDlfj44481ceJELVq0SL1799Z7772ngQMHKjExUS1atPBKTYYhnTolHT1qn6vuzJnL5+FZrVLTpt4fsvWkjIxzCg21yrcWvCl//wC1axer7du/0LlzqTp+PLFa9bZV56HgquDjc3ko+L/LNzvPOTx7Vjp+3L6tWTPp+uulli3twRBA9UQARLktXLhQY8aM0WOPPSZJev311/X1119r8eLFmjNnTpXXY7NJu3ZJW7fafyk1aCC1bl26wJeVlSlJ8vcPcoapvLxc5eXluH2Nv3+gsyeoLG3z8/OUm5vttq2fX4D8/PxL1Xb37rVq3/53/22br9xc98un+fr6y98/oMxtbTabfv31qDIz0yRJhmE4P6+i2ubkXCpmv37y9w907ic7+6LL89HRvbR9+xeSpK1bP3cGwKLaFuTj46uAgMtXLRSsryJtLRYfl4treva8R6+9NkKHDm1TZGTbYttmZ1+U4Wb+F4vF4jLEXba2l2QYtiLbSlJQUGi52ubkZBV7FXbBtg5+fvY/rKxW++PcXOn0aWntWqlhQ+nmm+3/DwKofiyGu28doBg5OTkKCQnRypUrdffddzu3P/3009q9e7fi4+MLvSY7O1vZ2ZfDTHp6uiIjI5WWlqa6detWuKYjR6TVq+29DsUsiFGkwYPtY8CzZ29U+/Z9JUlr1ryj994b7/Y106Z9rq5db5ckrV+/VG+88YjbtlOmrFCfPvdLkjZvXqlXXx3qtu3TTy/RLbeMliRt27ZGL710h9u2UVHt9fzzn6pZs2u0d2+cXnihn9u2o0e/qnvumSxJOnRom/74x25u2z744HQ99NAMSdLOnV9pxoyBbtveffezeuQR+7Jpv/56TH/4Qyu3bQcNGqsnnnhHkpSWdlojRjR227ZBg+ZaujRFkj2kDR1ax23bXr3u05/+tNL52PHfsyhdugzSiy9ensn6/vtD3YbLdu1i9fLLcc7HDz/cSOnpZ4ps27p1Fy1ceHklk8cea6lTp34psm1kZFu9885+5+Nx42J0/HhikW0bN47S++8fcz6eNKmrfv55e5Ft69YN1z/+cdr5+Pnn+2rfvsL/L0pSYGCIVq68HH5nzbrdGb6Lsnp16X9VGIb9tAt/f+nuu8v+/yNKlp6eLqvV6rHvT5hPNT+9HdXVmTNnlJ+fryaOsaD/atKkiVJTU4t8zZw5c2S1Wp23yMjIqii1VgsJsergwS2VeozwcO/8dzp//pTy8oqYOBE1Al0LQPVGDyDK5cSJE7rqqqv0/fffq2fPns7ts2fP1gcffKADBw4Uek1l9wAWNQTcoEHNHgLOzc3RiBGN1aBBc5fepcssmj17sKZMWaGQEGulDQHHxf1Dr78+SpIUHFxXy5adcNu2IkPAWVmZGjny8h8Vc+duUtu2farNEHDBtq+8MlTPPbfCbVszDAFfyTEEnJ7OEHBlowcQFcU5gCiX8PBw+fr6FurtO3XqVKFeQYfAwEAFVuJSFT4+UufOUmSkfTj44EHp55/tAbBOHfvJ6yEhRQfCos9v8ncGsZKUpa2vr1+pryJNSPhMFy+m6eLFNJ08eVitWt1QqM1DD83SBx88r7Fj35Wvb8m/pO01+Ja6rY+Pj2JjH9Ly5dN0+nSyLl1K1+nTyYqMvL7ItqUJCpI92JTUdvfudWrbtk+p2hZUFW19fX2LfW1ZprEpW9vST/hdlrYFQ3FpOS4Ccdwk+0UgPXpIUVFcBAJUZwwBo1wCAgJ04403au3atS7b165dq169vDcpscUiNW5s/wU0dKh05532UBgaap8H8MgR6aef7JPfnj5tn9aiuvaB22w2ffTRTIWE1FVwcB19/PGsItvZJ4G2KDHxu0qrxdfXT3fe+bTz8b///UalHaug3bvXltwIVcJms08B8+uv0uHD9v+PfvnF/v9Qgwb2/+fuvlu67z6pQwfCH1Dd0QOIcps0aZJGjBihLl26qGfPnvrrX/+q5ORkPfHEE94uTZJ90trrrrPfHBNBnz9vnwz611/tk0GfPl30RNCOyaC9ORH0999/8t+Jh9spNLSevv/+Ex09uqfIXsCRI1/WK6/crxdf/MI5HOtpAwaM0YcfztClSxe0YcMyPfzwX1S3bnilHMvhp58SdPFiukJCGOKqCgUngnbcipoI+uqr7X9o1atnnww6JKRmz6UJmBEBEOX2wAMP6LffftOsWbN08uRJtWvXTl988YWioqK8XVohPj6Xp6twlOduKbhz5+yhMD298FJwjmDoWEu1spaCc/T+dep0qy5duqBmzVrr7NkUffzxLP3pT/8q1L5Onfrq3/9RffbZQt133588X5Ds6/Xeeutj+uyz15STk6Uvv3xXDzzw50o5loPNlq99++LVrdudlXocs3CsX52baw92jpDnWM/ax8d1ucPISHvAq1PHHvJYCg6oPQiAqJCxY8dq7Nix3i6jXPz8pPBw+60gw7AHwIsX7cHw4kX7LS3NvjRWRoZ9+/nz9l+k+QXOm7dY7KHQz8/9z9L0lGzZ8qmSk/dr/Pi/6e9//6N8fHw0dOif9dZbY9wuR3bzzcP08st3KzX1qJo2dT8VS0XcccdT+ve/35DNZtOaNW/rnnsmOy/q8ITAwBB98MEp7djxpfOik9271xIA3bDZ7H/I5OXZ/y0W9bPgKQ6Of4eOP2CaNbMP39ataw94jvNkQ0LsIRBA7UUABK7gGOoKDi56/rK8PHtAdPSeFLx/8aI9IDp+5uba7xf8pVzU8Xx97b+cfXzsP7OzwzRo0BQ1a9ZT+fn2kNmnzwjt2/etpKITpMVi0SOPzNff//5HTZ36iSyVMCbXpElL9ehxj77//l86f/5XffvtR7rlllEe27/FYpHV2kjdu98lHx9f2Wz5+vHHdR7bf3Xj+G9b8JaXdznYXbntyvNVLRbXUOdY9cZxCwu73KPn+Om4HxRETx5gZgRAoIz8/OxDYnXcz0vsVHCoLSfn8n3HMFxe3uXweOmS/flLl6SOHW9Vu3a3KivLHgCysqTUVH/dccdSZWXZT8CXLvcmOs7R8vFprQYNOmvVqpXq0mXof7fZb76+l+8X3O54ruA2i8V9T+WQIZP0/ff2YejPPluo3/1upMfDZmioVW3adNOBAz/o+PEk/fZbiho2vMqjxyiOI2wZhv1+UbecHPtSg+6ed+yjqODm4Pjs/fzsPx03f397gHOEtuBg+8+AgMuBLyDg8s3xnON5ACgJXxVAJXL0zISWfqYRSa5De3/7m/2k+6FDCw/x5eba2zp6iXJypOuum6znnx+k2277vQICrC5h07HfokJKfr5r8HEfWnoqKqqHfvlli44d26Mvvtiga6+9xe17cYTJkjKixSLl5WVr1apJkqSIiL46cOAHSdLatevVtetIt68tqeayctTrCMMFw7Pj5gjdBUNZwd64grcrw92VvXZX/iztqQIAUF4EQKAa8vG53KPj62vv4WnatLSvDlRo6HStXPlnvfXWW86tBYOeI+wVNQR5Zc/VlaHQZpN8fJ7RpEkPSJISExdq7NhbXJ6/8md+/uX7BV0Z2C5dytOzzy6SJM2b97XWrbOvKX369Fp16mQPgFcGo6J6Mq8McAV7NYu67+55R2hz7Lvg7dNPpZEjGUYFUDMRAIFa6Oabb9b//u//auvWrerWzb7mb8FAU1HXXHOPXn+9hZKTk7Vp0xfy90/S9dcXnhi6rByTCUvSmDFdNWNGqDIzM7V37zrdfLNRKec1lpcjdAJATcTXF1BLzZ07Vy+88ILy8vI8vm8/Pz89/fTliaHfeMPzE0MHBAQoNjZWkpSamqrExESPHwMAzIoACNRS4eHhevjhh/Xmm29Wyv7HjBmjsLAwSdKyZct05swZjx+jf//+zvvr1tXeq4EBoKoRAIFabOTIkdq4caOSk5M9vm+r1arHHntMkpSVlaV3333X48cYMGCA8/6Vyw4CAMqPAAjUYhaLRfPmzdOzzz5bKft/6qmn5PPfE+HefvttZWdne3T/MTExatKkiSQpLi5OuUVNpAgAKDMCIFDLRUdHKzo6WqtWrfL4vlu2bKl77rlHkvTrr7/qo48+8uj+LRaLcxg4MzNTCQkJHt0/AJgVARAwgeeff15vvfWWLly44PF9T5o0yXl/4cKFMiowGV9wcLCOHj2qo0ePKjg4WBLnAQJAZSAAAiYQFBSkqVOnavr06R7fd8+ePdWjRw9J0p49e7Rhw4Zy78vHx0ctW7ZUy5YtnUPLBQMg5wECgGcQAIFqxjAMPf7442rQoIEsFosyC06OVwH9+/fX2bNntXPnTo/sr6BnnnnGeX/hwoUe3XdERISio6MlSQkJCUpPT/fo/gHAjAiAQDXz1VdfaenSpfr888918uRJhYSEeGzfr776qqZOnar8/HyP7VOS7rnnHrVo0UKS9MUXXygpKalc+8nJydHkyZM1efJk5eTkOLc7egHz8/MVHx9f8YIBwOQIgEA1c/jwYTVr1ky9evVS06ZNPbr6RePGjXXfffdp0aJFHtun5LmJoXNzczV//nzNnz/f5YpfhoEBwLMIgEA1Mnr0aE2YMEHJycmyWCxq2bKlx48xZswYffnll0pJSfH4fitrYui+ffvK979r2HEhCABUHAEQqEbeeOMNzZo1SxERETp58qS2bdvm8WP4+Pjo1Vdf1eTJkz2638qcGNpqtTrXNE5KSvJ4eAUAsyEAAtWI1WpVWFiYfH191bRpUzVq1KhSjtOuXTtFRUVpzZo1Ht1vZU4MXXAYeP369R7bLwCYEQEQMKlp06ZpwYIFHrvKWKrciaFZFg4APIcACJhUSEiIJk+erFmzZnl0v56cGLqg7t27KzQ0VJL9PEBP7RcAzIgACJjYwIEDlZKSor1793psn56cGLqggIAAxcbGSpJSU1OVmJjokf0CgBkRAAGTmzdvnqZMmSKbzeaxfZZ3Yujg4GDt27dP+/btcy4FVxDLwgGAZxAAAZNr1qyZ7rjjDv3tb3/z2D7LOzG0j4+PYmJiFBMT47yYpCDOAwQAzyAAAtXMxIkTdezYsSo95hNPPKFPP/1UqampHtmfpyaGvlJMTIyaNGkiSYqLi3OZLBoAUHoEQADy9fXV3LlzNWXKFI/tszwTQ+fk5GjGjBmaMWOGy1JwDhaLxTkMnJmZqYSEBI/VCwBmQgAEIEnq2LGjGjVqpG+++cYj+yvPxNC5ubmaOXOmZs6c6bZ3j/MAAaDiCIAAnGbOnKm5c+fq0qVLHtlfZUwMzbrAAFBxBEAATnXq1NHEiRP18ssve2R/lTExdEREhKKjoyVJCQkJSk9Pr/A+AcBsCIAAXAwePFg//fRTqa/cLUllTAzt6AXMz89XfHx8hfcHAGZDAARQyPz58zV58mSPhLXKmBia8wABoGIIgAAKiYyMVP/+/bV06VKP7K+8E0O707dvX/n6+kriPEAAKA8CIIAijR8/Xh9++KFOnz5d4X2Vd2Jod6xWq7p16yZJSkpKUkpKSoVrBAAzIQACKJKfn59mz56tP/3pTx7ZV2kmhg4KCtLWrVu1detWBQUFFbvPgsPA69evr3CNAGAmBEAAbnXt2lWhoaGKi4ur8L5KMzG0r6+vunbtqq5duzqHeN1hOhgAKD8CIIBivfTSS3rppZcqPIef1WrVmDFjJJV+Yuji9OjRQ6GhoZLsF4J44oIVADALAiCAYlmtVj355JN65ZVXKryvkiaGzsnJ0bx58zRv3rwil4IrKCAgQLGxsZKk1NRUJSYmVrg+ADALAiCAEt1777368ccfdejQoQrtp1WrVsVODJ2bm6spU6ZoypQpbpeCK4jpYACgfAiAAEpksVi0YMECPfvssxUeavXkxNADBgxw3uc8QAAoPQIggFJp2bKlevfureXLl1doP56cGDomJkZNmjSRJMXFxZWq17C26du3ryZOnFipxxg9erSGDBlSptccOHBAPXr0UFBQkDp27FgpdV1p6dKlqlevXpUcC6jpCIAASu2ZZ57R0qVLdfbs2Qrvx6EiE0NbLBbnMHBmZqYSEhIqVBc8Z/r06QoNDdXBgweZpgeohgiAAErN399fs2bN0vPPP1+h/XhyYmjOA6yeDh8+rD59+igqKkoNGzb0djkArkAABFAmvXr1ksVi0XfffVfufZR2YujSYD5AKS8vT+PHj1e9evXUsGFD/fnPf3Y5t/If//iHunTporCwMDVt2lQPPfSQTp065bKP/fv36/bbb1fdunUVFhamm266SYcPHy7yeDt27FDjxo01e/bsIp+3WCzasWOHZs2aJYvFohkzZkiS9u7dq9/97ncKDg5Ww4YN9fjjjysjI8PltX//+98VExOjwMBANWvWTOPHj3c+t3DhQrVv316hoaGKjIzU2LFjC70eQOkQAAGU2csvv6zp06eXOFVLcUozMXRpREREKDo6WpKUkJCg9PT0ctdUUy1btkx+fn5KSEjQm2++qddee03vv/++8/mcnBy99NJL+vHHH7Vq1SodPXpUo0ePdj6fkpKim2++WUFBQdqwYYN27NihRx99VHl5eYWOFRcXp1tuuUUzZ87UCy+8UGQ9J0+eVExMjP74xz/q5MmTevbZZ3Xx4kXddtttql+/vrZt26aVK1dq3bp1LgFv8eLFGjdunB5//HHt3btXq1evVuvWrZ3P+/j46M0339S+ffu0bNkybdiwQVOmTPHAJwiYkAF4SVpamiHJSEtL83Yp1VrPnj2NRx991NtlFLJ8+XJjzpw5FdrHxIkTDUmGJOOll14y8vLyjI0bNxobN2408vLySr2f8ePHO/ezevXqCtVUWnfeeWeVHKcksbGxxvXXX2/YbDbntueee864/vrr3b5m69athiTjwoULhmEYxtSpU41WrVoZOTk5RbYfNWqUcddddxmrVq0ywsLCjH/+858l1tWhQwdj+vTpzsd//etfjfr16xsZGRnObWvWrDF8fHyM1NRUwzAMo3nz5sYLL7xQ4r4dVqxYYTRs2ND5eMmSJYbVai3162syvj9RUfQAAiiXYcOGacuWLTpy5Ei593HlxNB5eXnq27ev+vbtW+JScAWZ/TzAHj16yGKxOB/37NlThw4dUn5+viRp165duuuuuxQVFaWwsDD17dtXkpScnCxJ2r17t2666Sb5+/u7PUZCQoLuvfdeLVu2TMOGDStzjUlJSerQoYNz9RZJ6t27t2w2mw4ePKhTp07pxIkTuuWWW9zuY+PGjRowYICuuuoqhYWFaeTIkfrtt9+UmZlZ5noAsyMAAtVQenq6jh49Wmh7UlJShYZdPclisWj+/PkVmhuwpImhS6tgYDTreYDuZGZm6tZbb1WdOnX0j3/8Q9u2bdOnn34qSc5/S8HBwSXu55prrlF0dLT+/ve/l+vfoGEYLiG1IIvFUmINv/zyiwYNGqR27drpk08+0Y4dO/TOO+9Ikimn/wEqigAIVEPvv/++unTp4nI+24EDB9SuXbsKzZvnaa1bt1bnzp21cuXKcu+j4MTQCxYs0Ntvv6133nmnTL/UrVarunXrJskeklNSUspdT020ZcuWQo+vvfZa+fr66sCBAzpz5ozmzp2rm266SdHR0YUuALnhhhu0adOmYj/z8PBwbdiwQYcPH9YDDzxQ5tDVtm1b7d6926W37rvvvpOPj4/atGmjsLAwtWzZ0u2UMdu3b1deXp4WLFigHj16qE2bNjpx4kSZagBwGQEQqIYeeOABZWRk6K233nJu+8tf/qLmzZurX79+XqyssMmTJ+u9995TWlpauV5fcGLovXv3asKECRo/fnyZe5kKDgObbd6548ePa9KkSTp48KA+/PBDvfXWW86rrFu0aKGAgAC99dZbOnLkiFavXq2XXnrJ5fXjx49Xenq6HnzwQW3fvl2HDh3SBx98oIMHD7q0a9y4sTZs2KADBw5o2LBhRV4k4s7w4cMVFBSkUaNGad++fdq4caMmTJigESNGOCfznjFjhhYsWKA333xThw4d0s6dO53/D1xzzTXKy8tzvo8PPvhA7777bkU+NsDUCIBANXTVVVfp8ccf14IFC5SXl6fz58/rww8/1PPPP6/AwEBvl+ciMDBQ06dPd3tFaGkUnBi6vMw8HczIkSN16dIldevWTePGjdOECRP0+OOPS5IaNWqkpUuXauXKlWrbtq3mzp2r+fPnu7y+YcOG2rBhgzIyMhQbG6sbb7xRf/vb34o8J7Bp06basGGD9u7dq+HDhzvPMyxJSEiIvv76a509e1Zdu3bVfffdp1tuuUVvv/22s82oUaP0+uuva9GiRYqJidEdd9zhXH+6Y8eOWrhwoV555RW1a9dOy5cv15w5c8r7kQGmZzHKe/IOUEHp6emyWq1KS0tT3bp1vV1OtZOSkqJrrrlGjRs3VkBAgLKzs/Xzzz9XuwDo8Nhjj+nxxx93DsWWRV5enq655hrnRQmSlJGR4XLBQElycnLUoEEDZWZmqmnTpjpx4oTbc848YfDgwVq9enWl7R8oDt+fqCh6AIFqytELeOLECR05cqRa9v4VNHfuXL3wwgtlGhZ0uHJi6PIICAhQbGysJCk1NVWJiYkV2h8A1Gb0AMJr+AvWlePkeH9/fwUEBEiyn9sVFRWl4OBgHT9+vFAALNjWZrPp0qVLbvfv5+fnfL1hGLp48aJH2vr6+iooKEiSfULikydPasKECSW2LfieJSktLU3XXXedc2WHAwcO6Lrrriuy7ZV8fHwUHBys1157zXlRySuvvKJx48YVamuxWBQSEuJ8fPHiRbdXMV/Z9tKlS7LZbJKkoUOHasWKFS7tC/ZYFmxblIJts7Kyih1KLUtPKMyB709UmNdmIITpMZGpK/13IuOCk+fu27fPub2o27PPPutse/To0WLbjh071tn21KlTxbYdNWqUs21GRkaxbe+77z5nW5vNVmzbQYMGubznkJAQt21btGjh0jY8PNxt2y5duhiGYRh79+4t9viSjLZt27rst23btm7bRkVFubTt0qWL27bh4eEubWNjY922DQkJcWk7aNCgYmsGrsT3JyqKIWAAHuPJc+5Onjyp7OzsMr0mJibGeUUpAMA9hoDhNQxhuCpqCLikYd3qNgTseB8vvfSSOnbsqDvvvLPEtgXl5eXptttuc85rt3TpUo0aNarItgU5hoAl6eGHH9by5cslSd9884169erl0pYhYNQGfH+iovy8XQAAu6J+yfv4+JT6l39Z2loslkppK9nfx4wZMzRo0CDdfvvtCgsLK7btlRYuXOgMbQsXLtTIkSPLVEP//v2dAfC7777TgAEDim1fMOCVpOBqFb6+vsXWVJrVNRwKhuKqMGPGDK1atUq7d++u0uMCqD4YAka5zJ49W7169VJISIjq1avn7XJQzQQFBen555/X9OnTy/zaghND79mzp8wrn5h5PkAAKC0CIMolJydH999/v5588klvl4Jqqn///jp79qx27txZ6tfk5uZq6dKl6tSpk3PbwoULy3TciIgIRUdHS5ISEhJcltMDANgRAFEuM2fO1DPPPKP27dt7uxRUY6+++qqmTp1a6tUicnJy9Mgjj2jx4sWKjIyUJH3xxRdKSkoq03EdvYD5+fmKj48vW9E13NKlS1WvXj2tWrVKbdq0UVBQkAYMGKDjx4+7fc22bds0YMAAhYeHy2q1KjY2tlBwt1gsev/993X33XcrJCRE1157baGJsBMTEzVo0CDVqVNHTZo00YgRI3TmzJlKeZ8AKoYAiCqTnZ2t9PR0lxtqt8aNG+u+++7TokWLyvzasWPHOu+/8cYbZXptwWHgdevWlfnYNd3Fixc1e/ZsLVu2TN99951znV93Lly4oFGjRmnTpk3asmWLrr32Wg0aNEgXLlxwaTdz5kwNHTpUe/bs0aBBgzR8+HCdPXtWkv2q7djYWHXs2FHbt2/XV199pV9//VVDhw6t1PcKoJy8OgkNarwlS5YYVqu1VG2nT59e5BxnzGNVu+Xn5xsDBw40/vOf/5TYtuCcgykpKUZYWJghyQgKCjJOnz5d6mOeP3/e8PX1NSQZ119/fUXKd+vOO++slP1W1JIlSwxJxpYtW5zbkpKSDElGQkKCYRj2/xc7dOjgdh95eXlGWFiY8e9//9u5TZLx5z//2fk4IyPDsFgsxpdffmkYhmFMmzbNuPXWW132c/z4cUOScfDgQU+8NRTAPICoKHoA4TRjxgxZLJZib9u3by/3/qdOnaq0tDTnrbghKdQePj4+evXVVzV58uQyvc5qtWrMmDGS7NOkvPvuu2V6rWNN4qSkJKWkpJTp2DWdn5+funTp4nwcHR2tevXquR1KP3XqlJ544gm1adNGVqtVVqtVGRkZLmszS9INN9zgvB8aGqqwsDCdOnVKkrRjxw5t3LhRderUcd4c52IePnzY028RQAUxDQycxo8fX+wwkSS1bNmy3PsPDAys1mvZovK0a9dOUVFRWrNmjW6//fZSv+6pp57Sm2++KZvNprfffluTJ08u9b+h/v3764cffpAkrV+/XiNHjixX7TVVUZNyu5uoe/To0Tp9+rRef/11RUVFKTAwUD179lROTo5LO39//0L7c8x1aLPZdOedd+qVV14ptP9mzZqV920AqCT0AMIpPDxc0dHRxd6qer4y1B7Tpk3TggULip3Q+UqtWrXSPffcI0n69ddf9dFHH5X6tWY+DzAvL8+lt/7gwYM6f/68s0fuSps2bdJTTz2lQYMGKSYmRoGBgWW+eKNz587av3+/WrZsqdatW7vcmMgaqH4IgCiX5ORk7d69W8nJycrPz9fu3bu1e/duZWRkeLs0VFMhISGaPHmyZs2aVabXTZo0yXl/4cKFblftuFKPHj2cwWPdunWlfl1t4O/vrwkTJighIUE7d+7UI488oh49ejiHxa/UunVrffDBB0pKSlJCQoKGDx9epomsJWncuHE6e/ashg0bpq1bt+rIkSP65ptv9Oijj5b6KnAAVYcAiHJ58cUX1alTJ02fPl0ZGRnq1KmTOnXqVKFzBFH7DRw4UP/5z3+0Z8+eIp8PDAzUihUrtGLFCudQb3knhg4ICFBsbKwk+xWqiYmJHngHNUNISIiee+45PfTQQ+rZs6eCg4OL7T39+9//rnPnzqlTp04aMWKEnnrqKTVu3LhMx2zevLm+++475efn6/e//73atWunp59+WlarVT4+/KoBqhvWAobXsJalOZ08eVKPPvqo1qxZU+pgsGLFCj3wwAOSpEGDBmnNmjWlet1rr73m7EF8/fXX9fTTT5ev6CIMHjy40Dx41cHSpUs1ceJEnT9/3tuloBLx/YmK4s8yAFWqWbNmuuOOO/S3v/2t1K+555571KJFC0llmxiaZeEAoGgEQABV7oknntCnn36q1NRUl+15eXlauXKlVq5cqby8POd2Pz8/l9670k4M3a5dOzVp0kSSFBcXp9zcXA9UDwA1HwEQQJXz9fXV3LlzNWXKFJft2dnZGjp0qIYOHars7GyX58aMGaOwsDBJ0rJly0p1larFYnH2AmZmZiohIcFD76D6Gj16NMO/AEpEAATgFR07dlSjRo30zTfflKp9eSeGNvN0MADgDgEQgNfMnDlTc+fO1aVLl0rV/qmnnnJeOPL2228X6iUsCucBAkBhBEAAXlOnTh1NnDhRs2fPLlX78kwMHRER4ZwAOSEhQenp6eUvGABqCQIgAK8aPHiwDh06VOore8szMbSjFzA/P1/x8fHlKxQAahECIACvmz9/viZPnlyqMNezZ091795dUuknhuY8QABwRQAE4HWRkZHq37+//vGPf5Sq/ZW9gCXp27evfH19JXEeIABIBEAA1cT48eP1ySef6I033tCSJUsUEBDgtm1ZJ4a2Wq3OdXCTkpKUkpLiucIBoAYiAAKoFvz8/PTyyy/rxx9/1OjRo+Xv719s27JODF1wGHj9+vUVKxYAajgCIIBqo2vXrgoNDVVcXFyJbcs6MTTnAQLAZQRAANVGXl6e+vTpo6efflqZmZnFti3rxNA9evRQaGioJHsALM0FJwBQWxEAAVQb2dnZeuCBB7Rnzx7NmTOnxPZlmRg6ICBAsbGxkqSTJ08qMTHRM0UDQA1EAARQLe3du1c//fRTsW3KOjE0w8AAYEcABFAtzZkzR88++2yJQ7VlmRiaZeEAwI4ACKBaioqKUp8+fbR8+fJi25VlYuh27dqpSZMmkqS4uDjl5uZ6rmAAqEEIgACqrWeeeUZLly7V2bNni21X2omhLRaLsxcwMzNTCQkJnikUAGoYAiCAasvf31+zZs3S1KlTi21XlomhOQ8QAAiAAKq5Xr16ycfHR5s3b3bbpiwTQ3MeIAAQAAFUIwEBAXr77bf19ttvuywF9/LLL2vGjBnKyclx+9rSTgwdERGh6OhoSVJCQoLS09M9+A4AoGYgAAKoNvz9/TVu3DiNGzfOZSm4+vXr69FHHy32/L6yTAzt6AXMz89XfHy8h6oHgJqDAAigRhg2bJi2bNmiI0eOuG1T2omhOQ8QgNkRAAFUG/n5+YqLi1NcXJzy8/NdnrNYLJo/f36xcwOWdmLovn37ytfXVxLnAQIwJwIggGojKytL/fr1U79+/ZSVlVXo+datW6tz585auXKl232UZmJoq9Wqbt26SZKSkpKUkpLigeoBoOYgAAKoUSZPnqz33ntPaWlpRT5f2omhCw4Dr1+/3vOFAkA1RgAEUKMEBgZq+vTpeuGFF9y2Kc3E0JwHCMDMCIAAapybb75ZWVlZ2rp1a5HPl2Zi6B49eig0NFSSPQCWtOYwANQmBEAANdLcuXP1wgsvKC8vr9BzpZkYOiAgQLGxsZKkkydPKjExsfKKBYBqhgAIoEYKDw/Xww8/7HbVj9JMDM0wMACzIgACqLFGjhypuLg4JScnF3quNBNDsywcALMiAAKoNvz9/fXqq6/q1VdfdVkJxB2LxaJ58+bpj3/8Y5Hn8JU0MXS7du3UpEkTSVJcXJxyc3M98C4AoPojAAKoNgICAjR58mRNnjzZZS3g4kRHR6tt27ZatWpVoedKmhjaYrE4ewEzMzOVkJBQsTcAADUEARBAjTd16lS9/fbbunDhQqHnSpoYmvMAAZgRARBAtZGfn69t27Zp27ZthZaCK05QUJCmTp2q6dOnF3qupImhOQ8QgBkRAAFUG1lZWerWrZu6detW5FJwxenfv7/Onj2rnTt3FnquuImhIyIiFB0dLUlKSEhQenp6OSoHgJqFAAig1nj11Vc1derUQr2HJU0M7egFzM/PV3x8fNUUCwBeRAAEUGs0btxY9913nxYtWuSyvaSJoTkPEIDZEAAB1CpjxozRl19+qZSUlELb3U0M3bdvX/n6+kriPEAA5kAABFCr+Pj46NVXX9XkyZNdthc3MbTValW3bt0kSUlJSYXCIwDUNgRAALVOu3btFBUVpTVr1rhsL25i6ILDwOvXr6+aQgHASwiAAGqladOmacGCBcrMzHRuK25iaM4DBGAmBEAA1Ya/v7+mT5+u6dOnl2opuOKEhIRo8uTJmjVrlst2dxND9+jRQ6GhoZLsAbCopeUAoLYgAAKoNgICAjRjxgzNmDGj1EvBFWfgwIH6z3/+oz179ji3uZsYOiAgQLGxsZKkkydPKjExscLHB4DqigAIoFabP3++nnvuOdlsNuc2dxNDMwwMwCwIgACqDZvNpv3792v//v0uga0imjVrpjvuuEN/+9vfnNvcTQxNAARgFgRAANXGpUuX1K5dO7Vr106XLl3y2H6feOIJffrpp0pNTZXkfmLodu3aqUmTJpKkuLg45ebmeqwGAKhOCIAAaj1fX1/NnTtXU6ZMcW4bM2aM6tSpI+nyxNAWi8XZC5iRkaGEhASv1AsAlY0ACMAUOnbsqEaNGumbb76RZJ/8+bHHHpPkOjE0w8AAzIAACMA0Zs6cqblz5zqHl4uaGLpgAGRZOAC1FQEQgGnUqVNHEydO1OzZsyUVPTF0RESEoqOjJUkJCQlKT0/3Wr0AUFkIgABMZfDgwTp06JDzyt+iJoZ29ALm5+crPj7eK3UCQGUiAAIwnfnz5+vZZ5+VzWYrcmJozgMEUNsRAAFUG/7+/nr22Wf17LPPVngpuOJERkZqwIABWrp0qaTCvYB9+/aVr6+vJM4DBFA7WQwWvISXpKeny2q1Ki0tTXXr1vV2OTCZvLw8DRo0SMuXL1f9+vV1zTXXKDk5WZKUmJioMWPG6IcffpAk/ec//9FVV13l8vrBgwdr9erVVV43IPH9iYqjBxCAKfn5+Wn27Nl67rnnipwYuuAw8Pr1671RIgBUGgIgyuzYsWMaM2aMWrVqpeDgYF1zzTWaPn26cnJyvF0aajibzaZjx47p2LFjHlsKrjhdu3ZVnTp1tHHjxkITQ3fp0sXZjvMAAdQ2BECU2YEDB2Sz2fTee+9p//79eu211/Tuu+/q+eef93ZpqOEuXbqkVq1aqVWrVh5dCq44L730kv7yl78oKCjIZWLoXbt2KTQ0VJI9AHK2DIDahHMA4RHz5s3T4sWLdeTIkVK/hnNYcKXMzExnL1xGRoYzgFW2f/3rX0pMTNSIESPUunVr2Ww2NWnSRB07dtTXX38tSdq3b59iYmKcr+EcQHgT35+oKHoA4RFpaWlq0KBBsW2ys7OVnp7ucgOqg3vvvVc//vijcnNzXSaGLvhvmmFgALUJARAVdvjwYb311lt64oknim03Z84cWa1W5y0yMrKKKgSKZ7FYtGDBAj377LN65plnnNt37NjhvE8ABFCbEADhNGPGDFkslmJv27dvd3nNiRMndNttt+n+++93nj/lztSpU5WWlua8HT9+vDLfDlAmLVu2VJ8+fXTkyBHnxNA//fST6tWrJ0mKi4tTbm6uFysEAM/x83YBqD7Gjx+vBx98sNg2LVu2dN4/ceKE+vXrp549e+qvf/1rifsPDAxUYGBgRcsEKs0zzzyjgQMH6vHHH1dCQoIkKSQkROfPn1dGRoYSEhLUp08fL1cJABVHAIRTeHi4wsPDS9U2JSVF/fr104033qglS5bIx4fOZNR8/v7+mjVrlpYsWaIWLVooOTlZJ06ccD6/bt06AiCAWoHf2iizEydOqG/fvoqMjNT8+fN1+vRppaamKjU11duloYbz8/PT2LFjNXbsWPn5eefv0169esnPz0933nlnoedYFg5AbUEPIMrsm2++0c8//6yff/5ZERERLs8xqxAqIjAwUO+88463y9DLL7+su+++W6GhocrMzJTFYpFhGEpISFB6ejrTbgCo8egBRJmNHj1ahmEUeQNqg/r16+vxxx9Xx44dJV3+wyY/P1/x8fFerAwAPIMACKDaMAxDp0+f1unTp73+B8WwYcMUEhIii8Xisp3pYADUBgRAANXGxYsX1bhxYzVu3FgXL170ai0Wi0WLFi1Ss2bNXLZzHiCA2oAACAButG7dWrfffrvLtqSkJKWkpHipIgDwDAIgABTjrbfeKnTRx/r164t9Td++fTVx4sRKrMq7jh07JovFot27d3u7FADlRAAEgGIEBga6LA8nlXwe4P/93//ppZdeqsyyAKBCCIAAUII///nPCg0NdT7+8ssvi23foEEDhYWFVXZZAFBuBEAAKMKhQ4eUnZ0tyT5B9ZQpU5zPnTlzRhcuXHD72iuHgFu2bKm//OUvGjlypOrUqaOoqCh99tlnOn36tO666y7VqVNH7du3d1lr+7ffftOwYcMUERGhkJAQtW/fXh9++KHLcS5cuKDhw4crNDRUzZo102uvvVbo2Dk5OZoyZYquuuoqhYaGqnv37oqLiyv2vVssFi1evFgDBw5UcHCwWrVqpZUrV7ptn5+frzFjxqhVq1YKDg7WddddpzfeeMOlzejRozVkyBDNnz9fzZo1U8OGDTVu3DiX9ZXLUyuA8iEAAsAV8vLy1KNHD7Vu3VqLFy9Wdna2nn76aZfVScq68s1rr72m3r17a9euXbr99ts1YsQIjRw5Ug8//LB27typ1q1ba+TIkc7pb7KysnTjjTfq888/1759+/T4449rxIgRzjWKJWnSpEn67rvvtHr1aq1du1abNm3Szp07XY77yCOP6LvvvtNHH32kPXv26P7779dtt92mQ4cOFVvvtGnTdO+99+rHH3/Uww8/rGHDhikpKanItjabTREREVqxYoUSExP14osv6vnnn9eKFStc2m3cuFGHDx/Wxo0btWzZMi1dulRLly6tcK0AysEAvCQtLc2QZKSlpXm7FFQTWVlZxqhRo4xRo0YZWVlZXq3lwIEDxvDhww0fHx8jIiLCWLRokfHggw8akgxJRmhoqNvXxsbGGk8//bTzcVRUlPHwww87H588edKQZEybNs257YcffjAkGSdPnnS730GDBhl//OMfDcMwjPT0dMPf399YuXKl8/nz588bISEhzmP//PPPhsViMVJSUlz2c8sttxhTp051exxJxhNPPOGyrXv37saTTz5pGIZhHD161JBk7Nq1y+0+xo4da9x7773Ox6NGjTKioqKMvLw857b777/feOCBBypUq1nx/YmKYik4ANWGYym4xYsXa+7cud4uR9dee62efPJJffvttxo3bpzLeYCZmZnKyMhQnTp1SrWvG264wXm/SZMmkqT27dsX2nbq1Ck1bdpU+fn5mjt3rj7++GOlpKQoOztb2dnZzhqOHDmi3NxcdevWzbkPq9Wq6667zvl4586dMgxDbdq0caklOztbDRs2LLbenj17Fnpc3FW/7777rt5//3398ssvunTpknJycpwrqTjExMTI19fX+bhZs2bau3dvhWsFUHYEQADVyunTp/XXv/5VmZmZ3i7FKTs7W76+vsrIyJCfn5/y8vIkSXPnztVf/vKXUu3D39/fed+xukhR22w2myRpwYIFeu211/T666+rffv2Cg0N1cSJE5WTkyPp8vJ0V65UYhRYQcVms8nX11c7duxwCV6SSh1cC7ryWA4rVqzQM888owULFqhnz54KCwvTvHnzXIarr3y/jv053q+nawVQPAIggGqlZcuW+umnn7xdhiQpPj5eM2bMUFxcnDp27KgZM2boxx9/1IIFC3TnnXfqscceq7Rjb9q0SXfddZcefvhhSfaAdOjQIV1//fWSpGuuuUb+/v7aunWrIiMjJUnp6ek6dOiQYmNjJUmdOnVSfn6+Tp06pZtuuqlMx9+yZYtGjhzp8rhTp05ua+3Vq5fGjh3r3Hb48OEyHa8itQIoOwIgAFwhPz9fQ4YM0eeff66OHTtq1apVGjx4sCwWi+666y5NmzbNbW+Yp7Ru3VqffPKJvv/+e9WvX18LFy5UamqqMwCGhYVp1KhRmjx5sho0aKDGjRtr+vTp8vHxcdbWpk0bDR8+XCNHjtSCBQvUqVMnnTlzRhs2bFD79u01aNAgt8dfuXKlunTpoj59+mj58uXaunWr/ud//sdtrf/7v/+rr7/+Wq1atdIHH3ygbdu2qVWrVqV+vxWpFUDZcRUwAFzBx8dH7du316pVq7Rz507dddddLoGvssOfZL8Kt3Pnzvr973+vvn37qmnTphoyZIhLm4ULF6pnz56644471L9/f/Xu3VvXX3+9goKCnG2WLFmikSNH6o9//KOuu+46DR48WAkJCc5eQ3dmzpypjz76SDfccIOWLVum5cuXq23btkW2feKJJ3TPPffogQceUPfu3fXbb7+59AaWVnlrBVB2FqPgCSNAFUpPT5fValVaWlqhpbYAlF1mZqauuuoqLViwQGPGjCn3fiwWiz799NNCgRPVB9+fqCiGgAGghtq1a5cOHDigbt26KS0tTbNmzZIk3XXXXV6uDEB1RwAEgBps/vz5OnjwoAICAnTjjTdq06ZNCg8P93ZZAKo5AiAA1FCdOnXSjh07PL5fzgwCaj8uAgEAADAZAiAAAIDJEAABAABMhgAIAABgMgRAAAAAkyEAAgAAmAwBEAAAwGQIgAAAACZDAAQAADAZAiAAAIDJEAABAABMhgAIAABgMgRAAAAAkyEAAgAAmAwBEAAAwGQIgAAAACZDAAQAADAZAiAAAIDJEAABAABMhgAIAABgMgRAAAAAkyEAAgAAmAwBEAAAwGQIgAAAACZDAAQAADAZAiAAAIDJEAABAABMhgAIAABgMgRAAAAAkyEAAgAAmAwBEAAAwGQIgAAAACZDAAQAADAZAiAAAIDJEAABAABMhgAIAABgMgRAAAAAkyEAAgAAmAwBEOUyePBgtWjRQkFBQWrWrJlGjBihEydOeLssAABQCgRAlEu/fv20YsUKHTx4UJ988okOHz6s++67z9tlAQCAUrAYhmF4uwjUfKtXr9aQIUOUnZ0tf3//Ur0mPT1dVqtVaWlpqlu3biVXCAC1B9+fqCh6AFFhZ8+e1fLly9WrV69Shz8AAOA9BECU23PPPafQ0FA1bNhQycnJ+uyzz4ptn52drfT0dJcbAACoegRAOM2YMUMWi6XY2/bt253tJ0+erF27dumbb76Rr6+vRo4cqeLOKJgzZ46sVqvzFhkZWRVvCwAAXIFzAOF05swZnTlzptg2LVu2VFBQUKHt//nPfxQZGanvv/9ePXv2LPK12dnZys7Odj5OT09XZGQk57AAQBlxDiAqys/bBaD6CA8PV3h4eLle6/g7omDAu1JgYKACAwPLtX8AAOA5BECU2datW7V161b16dNH9evX15EjR/Tiiy/qmmuucdv7BwAAqg/OAUSZBQcH6//+7/90yy236LrrrtOjjz6qdu3aKT4+nh4+AABqAHoAUWbt27fXhg0bvF0GAAAoJ3oAAQAATIYACAAAYDIEQAAAAJMhAAIAAJgMARAAAMBkCIAAAAAmQwAEAAAwGQIgAACAyRAAAQAATIYACAAAYDIEQAAAAJMhAAIAAJgMARAAAMBkCIAAAAAmQwAEAAAwGQIgAACAyRAAAQAATIYACAAAYDIEQAAAAJMhAAIAAJgMARAAAMBkCIAAAAAmQwAEAAAwGQIgAACAyRAAAQAATIYACAAAYDJ+3i4A5mUYhiQpPT3dy5UAQM3i+N50fI8CZUUAhNf89ttvkqTIyEgvVwIANdNvv/0mq9Xq7TJQAxEA4TUNGjSQJCUnJ5v+Cyw9PV2RkZE6fvy46tat6+1yvIrPwhWfx2V8FpelpaWpRYsWzu9RoKwIgPAaHx/7KahWq9X0X+YOdevW5bP4Lz4LV3wel/FZXOb4HgXKin85AAAAJkMABAAAMBkCILwmMDBQ06dPV2BgoLdL8To+i8v4LFzxeVzGZ3EZnwUqymJwDTkAAICp0AMIAABgMgRAAAAAkyEAAgAAmAwBEAAAwGQIgPC6Y8eOacyYMWrVqpWCg4N1zTXXaPr06crJyfF2aV4xe/Zs9erVSyEhIapXr563y6lyixYtUqtWrRQUFKQbb7xRmzZt8nZJXvHtt9/qzjvvVPPmzWWxWLRq1Spvl+QVc+bMUdeuXRUWFqbGjRtryJAhOnjwoLfL8prFixfrhhtucE6G3bNnT3355ZfeLgs1EAEQXnfgwAHZbDa999572r9/v1577TW9++67ev75571dmlfk5OTo/vvv15NPPuntUqrcxx9/rIkTJ+qFF17Qrl27dNNNN2ngwIFKTk72dmlVLjMzUx06dNDbb7/t7VK8Kj4+XuPGjdOWLVu0du1a5eXl6dZbb1VmZqa3S/OKiIgIzZ07V9u3b9f27dv1u9/9TnfddZf279/v7dJQwzANDKqlefPmafHixTpy5Ii3S/GapUuXauLEiTp//ry3S6ky3bt3V+fOnbV48WLntuuvv15DhgzRnDlzvFiZd1ksFn366acaMmSIt0vxutOnT6tx48aKj4/XzTff7O1yqoUGDRpo3rx5GjNmjLdLQQ1CDyCqpbS0NBY5N5mcnBzt2LFDt956q8v2W2+9Vd9//72XqkJ1k5aWJkl8P0jKz8/XRx99pMzMTPXs2dPb5aCG8fN2AcCVDh8+rLfeeksLFizwdimoQmfOnFF+fr6aNGnisr1JkyZKTU31UlWoTgzD0KRJk9SnTx+1a9fO2+V4zd69e9WzZ09lZWWpTp06+vTTT9W2bVtvl4Uahh5AVJoZM2bIYrEUe9u+fbvLa06cOKHbbrtN999/vx577DEvVe555fkszMpisbg8Ngyj0DaY0/jx47Vnzx59+OGH3i7Fq6677jrt3r1bW7Zs0ZNPPqlRo0YpMTHR22WhhqEHEJVm/PjxevDBB4tt07JlS+f9EydOqF+/furZs6f++te/VnJ1Vausn4UZhYeHy9fXt1Bv36lTpwr1CsJ8JkyYoNWrV+vbb79VRESEt8vxqoCAALVu3VqS1KVLF23btk1vvPGG3nvvPS9XhpqEAIhKEx4ervDw8FK1TUlJUb9+/XTjjTdqyZIl8vGpXZ3TZfkszCogIEA33nij1q5dq7vvvtu5fe3atbrrrru8WBm8yTAMTZgwQZ9++qni4uLUqlUrb5dU7RiGoezsbG+XgRqGAAivO3HihPr27asWLVpo/vz5On36tPO5pk2berEy70hOTtbZs2eVnJys/Px87d69W5LUunVr1alTx7vFVbJJkyZpxIgR6tKli7MnODk5WU888YS3S6tyGRkZ+vnnn52Pjx49qt27d6tBgwZq0aKFFyurWuPGjdM///lPffbZZwoLC3P2EFutVgUHB3u5uqr3/PPPa+DAgYqMjNSFCxf00UcfKS4uTl999ZW3S0NNYwBetmTJEkNSkTczGjVqVJGfxcaNG71dWpV45513jKioKCMgIMDo3LmzER8f7+2SvGLjxo1F/jsYNWqUt0urUu6+G5YsWeLt0rzi0Ucfdf7/0ahRI+OWW24xvvnmG2+XhRqIeQABAABMpnadaAUAAIASEQABAABMhgAIAABgMgRAAAAAkyEAAgAAmAwBEAAAwGQIgAAAACZDAAQAADAZAiAAAIDJEAABAABMhgAIAABgMgRAAAAAkyEAAgAAmAwBEAAAwGQIgAAAACZDAAQAADAZAiAAAIDJEAABAABMhgAIAABgMgRAAAAAkyEAAgAAmAwBEAAAwGQIgAAAACZDAAQAADAZAiAAAIDJEAABAABMhgAIAABgMgRAAAAAkyEAAgAAmAwBEAAAwGQIgAAAACbz/wE29w7EDb2iygAAAABJRU5ErkJggg==' width=640.0/>\n",
       "            </div>\n",
       "        "
      ],
      "text/plain": [
       "Canvas(toolbar=Toolbar(toolitems=[('Home', 'Reset original view', 'home', 'home'), ('Back', 'Back to previous …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    }
   ],
   "source": [
    "# ---INPUT------ #\n",
    "focal_length = 0.9\n",
    "# -------------- #\n",
    "\n",
    "animate.geometric_ray_diagram(focal_length)\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "OaxKBIKfjaTd"
   },
   "source": [
    "A lens is determined by:\n",
    "- focal plane\n",
    "- object plane\n",
    "- image plane\n",
    "\n",
    "### Magnification"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 5,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "16fe75f0bfa94fea968a1b3bb18c2931",
       "version_major": 2,
       "version_minor": 0
      },
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAoAAAAHgCAYAAAA10dzkAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjguMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8g+/7EAAAACXBIWXMAAA9hAAAPYQGoP6dpAAB2RklEQVR4nO3deVxU9f4/8NewD6spCJiAmsnivoBAJqhYaIt6b3k1r0ua3kor8bZcl0C4P6JbYWqZer+VmOm1ut1MpeWCIkteBbcvLgzXVNRyRlyInWGZ8/uD74wMzAwzwwwDzOv5eMxDOPM5n/OGEl6ec97nIxIEQQARERERWQ0bSxdARERERJ2LAZCIiIjIyjAAEhEREVkZBkAiIiIiK8MASERERGRlGACJiIiIrAwDIBEREZGVYQAkIiIisjIMgERERERWhgGQiIiIyMowABIRERFZGQZAIiIiIivDAEhERERkZRgAiYiIiKwMAyARERGRlWEAJCIiIrIyDIBEREREVoYBkIiIiMjKMAASERERWRkGQCIiIiIrwwBIREREZGUYAImIiIisDAMgERERkZVhACQiIiKyMgyARERERFaGAZCIiIjIyjAAEhEREVkZBkAiIiIiK8MASERERGRlGACJiIiIrAwDIBEREZGVYQAkIiIisjIMgERERERWhgGQiIiIyMowABIRERFZGQZAIiIiIivDAEhERERkZRgAiYiIiKwMAyARERGRlWEAJCIiIrIyDIBEREREVoYBkIiIiMjKMAASERERWRkGQCIiIiIrwwBIREREZGUYAImIiIisDAMgERERkZVhACQiIiKyMgyARERERFaGAZCIiIjIyjAAEhEREVkZBkAiIiIiK8MASEZJSUlBaGgo3Nzc0LdvX8ycORPFxcWWLouIiIj0wABIRsnOzsby5ctx7NgxZGRkoLGxEY888giqq6stXRoRERG1QyQIgmDpIqj7u3XrFvr27Yvs7GxMnDjR0uUQERGRDjwDSCZRXl4OAOjdu7eFKyEiIqL28AwgdZggCJgxYwbKysqQm5urdZxcLodcLld9rlAocPfuXfTp0wcikagzSiUi6hEEQUBlZSX69esHGxueyyHD2Vm6AOr+VqxYgcLCQuTl5ekcl5KSgsTExE6qioio57t+/Tr69+9v6TKoG+IZQOqQl156Cfv27UNOTg4GDhyoc2zrM4Dl5eXw9/fH9evX4e7ubu5SiYh6jIqKCvj5+eG3336Dh4eHpcuhbohnAMkogiDgpZdewjfffIMjR460G/4AwNHREY6Ojm22u7u7MwASERmBt8+QsRgAySjLly/Hnj178O2338LNzQ0ymQwA4OHhAbFYbOHqiIiISBdeAiajaPtX544dO7Bo0SK95qioqICHhwfKy8t5BpCIyAD8+UkdxTOAZBT+u4GIiKj7Yu84ERERkZVhACQiIiKyMgyARERERFaGAZCIiIjIyjAAEhEREVkZBkAiIiIiK8MASERERGRlGACJiIiIrAwDIBEREZGVYQAkIiIisjIMgERERERWhgGQiIiIyMowABIRERFZGQZAIiIiIivDAEhERERkZRgAiYiIiKwMAyARERGRlWEAJCIiIrIyDIBEREREVoYBkIiIiMjKMAASEXXAkSNHIBKJ8Ntvv3VojKWsX78eo0aNsnQZRNTJGACJiMwsMjISUqkUHh4eJpmvKwdKIuoe7CxdABFRT+fg4AAfHx9Ll0FEpMIzgETUIYIg4MKFC1AoFJYuxSzkcjlefvll9O3bF05OTpgwYQIKCgrajPvpp58wcuRIODk5Yfz48Th79qzqPU1n7I4ePYqJEydCLBbDz88PL7/8Mqqrq9WO+/rrr8PPzw+Ojo548MEH8cknn6CkpASTJk0CANx3330QiURYtGiRxtrT0tLQq1cv7Nu3D0OGDIGTkxOmTp2K69eva/16CwoKMHXqVHh6esLDwwNRUVE4deqU2hiRSISPP/4Ys2bNgrOzMx588EHs379fbcyFCxcwffp0uLq6wtvbG/Pnz8ft27e1HpeIOhcDIBEZRRAEpKenIywsDEOHDsWFCxcsXZJZvP766/j666+xc+dOnDp1CoMHD8ajjz6Ku3fvqo177bXX8N5776GgoAB9+/bFk08+iYaGBo1znj17Fo8++ih+97vfobCwEF988QXy8vKwYsUK1ZgFCxZg79692Lx5M4qKirBt2za4urrCz88PX3/9NQCguLgYUqkUmzZt0lp/TU0NkpOTsXPnTvz000+oqKjAnDlztI6vrKzEwoULkZubi2PHjuHBBx/E9OnTUVlZqTYuMTERs2fPRmFhIaZPn4558+apvidSqRRRUVEYNWoUTpw4gR9++AE3b97E7NmzdX+ziajzCEQWUl5eLgAQysvLLV0KGUChUAgHDx4Uxo0bJwAQJkyYIGRmZlq6LLOoqqoS7O3thd27d6u21dfXC/369RPeeecdQRAEISsrSwAg7N27VzXmzp07glgsFr744gu1MWVlZYIgCML8+fOFZcuWqR0rNzdXsLGxEWpra4Xi4mIBgJCRkaGxrtbzabNjxw4BgHDs2DHVtqKiIgGAcPz4cUEQBCEhIUEYOXKk1jkaGxsFNzc34cCBA6ptAIR169apPq+qqhJEIpHw/fffC4IgCG+++abwyCOPqM1z/fp1AYBQXFyss2bSD39+UkfxHkAi0supU6fwyy+/4IUXXsCNGzfg7++PBQsWYODAgcjLy0NeXp6lSzSYQqGAq6srXnvtNY3vX7p0CQ0NDXjooYdU2+zt7REWFoaioiK1sREREaqPe/fujcDAwDZjlE6ePImff/4Zu3fvVm0TBAEKhQJXrlzB2bNnYWtri6ioqI58eQAAOzs7jBs3TvV5UFAQevXqhaKiIoSFhbUZX1paivj4eBw+fBg3b95EU1MTampqcO3aNbVxI0aMUH3s4uICNzc3lJaWqr6+rKwsuLq6tpn/0qVLGDJkSIe/LiLqGAZAImqXQqFAbGws7rvvPty4cQMikQgVFRXIyMiASCQy2XEEQYBUKgUA+Pr6mnRuTRoaGlBWVqY1AAqCAABt6hAEQa/atI1RKBT405/+hJdffrnNe/7+/vj555/bndsQmurQVtuiRYtw69YtbNy4EQEBAXB0dERERATq6+vVxtnb27eZT3kfqEKhwBNPPIG//e1vbeb39fU19ssgIhNiAKRuJT09HbNnz0ZBQQFCQkIsXY7VKCwsVJ21+cc//oGkpCR8++238PLywptvvom5c+fCzq7jP06qq6tVZ40uXrwIFxeXDs+py+bNm5GQkAC5XA5HR8c27w8ePBgODg7Iy8vDM888A6A5NJ44cQIrV65UG3vs2DH4+/sDAMrKyvDf//4XQUFBGo87ZswYnD9/HoMHD9b4/vDhw6FQKJCdnY2YmJg27zs4OAAAmpqa2v0aGxsbceLECdXZvuLiYvz2229aa8vNzcVHH32E6dOnAwCuX79ucPPGmDFj8PXXX2PAgAEm+f+CiEyPTSDUrSQlJaluaqfOk5GRgaeeegq3b9/GmDFjsG/fPpw8eRIhISFYsGABQkJCVGfuupPs7Gz07dsXR48e1fi+i4sLXnjhBbz22mv44YcfcOHCBSxduhQ1NTVYsmSJ2tikpCQcOnQI586dw6JFi+Dp6YmZM2dqnPeNN97Af/7zHyxfvhxnzpzBxYsXsX//frz00ksAgAEDBmDhwoVYvHgx9u3bhytXruDIkSP48ssvAQABAQEQiUQ4ePAgbt26haqqKq1fo729PV566SUcP34cp06dwrPPPovw8HCNl3+B5tC7a9cuFBUV4fjx45g3bx7EYnF730o1y5cvx927dzF37lzk5+fj8uXL+Pe//43FixfrFVqJyPwYAKnbOH78OPLz8wEAX331VZt7ksh88vLysHjxYpSVlam2tQyC06dPh62trQUrNFxDQwPkcjm8vb2RmZmpddzbb7+N3//+95g/fz7GjBmDn3/+GT/++CPuu+++NuNeeeUVjB07FlKpFPv371edqWttxIgRyM7OxsWLF/Hwww9j9OjRePPNN9Uuj27duhVPPfUUXnzxRQQFBWHp0qWqx8Tcf//9SExMxF/+8hd4e3urdQ+35uzsjDfeeAPPPPMMIiIiIBaLsXfvXq3jP/30U5SVlWH06NGYP3++6hE4hujXrx9++uknNDU14dFHH8WwYcPwyiuvwMPDAzY2/LVD1BWIBOVNLkSdrKKiAh4eHigvL4e7u3u746dPn44LFy7g6tWr6N27N2bPno2tW7d2QqXWra6uDn/4wx/w7bffwtfXFxcvXtR4c78ptLwEXFVVZdZLwEePHsWhQ4eQn5+PpqYmfPfdd2Y71o8//ohp06ahrq5Oayg0h7S0NKxcuZIrhvRAhv78JGqN/xSjbuH48eP4/vvvMX/+fADAc889h08++YRnATvB0aNHERkZCQDw9PREdna2hSsyjYyMDMTExEAkEsHd3V3t7KYp3bx5E99++y0efPDBTg1/RES6MABSt5CYmIjg4GDVYzH++Mc/wsPDA2+99ZaFK+v5MjMzVY0Inp6eOi+XdicFBQUIDQ0FAEyaNAlZWVlmOc706dORmZmJLVu2mGV+IiJjMABStyCVSvG3v/1NdZ+Zi4sLkpOTdS5pRaZx+vRpjB49GgDg5uam9dl2pmBra4vp06eb/Z7CyspKiMViVYfq1KlTzRZsT548if/+978au3nNbdGiRbz8S0QasT+fuoXTp08DgNpZmmXLlmHZsmWWKskqlJWVtblx39vbGzKZDD4+PiY/npOTE9LT000+b2s5OTlqD1keNGgQLl++bPbjEhF1FTwDSERaHT58GJMnT1bbFhMT0+0vAyvv/2vJ398fV69etVBFRESdiwGQiLRqef+f0pQpU7p9AJRIJAgMDFTb1hOCLRGRvhgAiUirK1euYNCgQWrb+vXrB5lMBnM8Qaq6uhouLi5wcXFRPfPO1KRSqcZl5iZPnozDhw+b5ZhERF0NAyARaVRSUoKAgACN7wUFBaG4uNgsx62pqUFNTY1Z5gaAQ4cOaWzI8PT0xN27d1Xr2RIR9WQMgESkkabLv0oxMTHIyMjo5IpMIzMzE1OmTNH43ogRI1BYWNjJFRERdT4GQCLSSFMDiFJUVFS3fCC0IAg6O5h5HyARWQsGQCJqQ6FQoKysDH369NH4vpubG2pra9HY2NjJlXWMRCJBSEiI1vcnTJiAvLy8TqyIiMgyGACJqI3CwkKMHDlS55iwsDDk5+d3UkWmoenxLy2JxWIoFArI5fJOrIqIqPMxABJRG+0FJaB7Xi7Nzs7GxIkTdY6JjIzE0aNHO6kiIiLLYAAkojby8vLw0EMP6RxjjjOANjY2iIqKQlRUlNrqI6bQ0NAAuVwOV1dXneO6Y7AlIjIUAyARqamrqwPQfDlUF3t7ezg6OqKqqspkxxaLxThy5AiOHDnS7vENVVBQgPHjx7c7bvTo0aqlB4mIeioGQCJSc/ToUURGRuo1tjt1A+tzWRsAbG1t4e7ujrKysk6oiojIMhgAiUiNruf/tdadLpcWFBQgNDRUr7GTJk1CVlaWmSsiIrIcBkAiUnP69GmMHj1ar7HBwcEoKioy2bGrq6vh5eUFLy8vky4FV1lZCbFYDDs7O73GT506tdsEWyIiYzAAEpFKWVkZPDw89G7AEIlE8Pb2hkwmM1kNt2/fxu3bt002HwDk5OQgKipK7/GDBg3C5cuXTVoDEVFXwgBIRCq6Vv/QpjtcBtb3/r+W/P39cfXqVTNVRERkWQyARKRiyP1/SlOmTOnyAVAikSAwMNCgfbpDsCUiMhYDIBGpXLlyBYMGDTJon379+kEmk0EQBDNV1TFSqRS+vr4QiUQG7Td58mQcPnzYTFUREVkWAyARAQBKSkoQEBBg1L5BQUEoLi42cUWmcejQIYPPagKAp6cn7t69C4VCYYaqiIgsiwGQiAAYd/lXKSYmBhkZGSauyDQyMzMxZcoUo/YdMWIECgsLTVwREZHlMQCS0XJycvDEE0+gX79+EIlE2Ldvn6VLog4wpgFEyVQPhLaxscG4ceMwbtw4kywFJwgCZDIZfHx8jNqf9wESUU/FAEhGq66uxsiRI/Hhhx9auhTqIIVCgbKyMvTp08eo/d3c3FBbW4vGxsYO1SEWi1FQUICCggKTLAUnkUgQEhJi9P4TJkxAXl5eh+sgIupq9HsqKpEG06ZNw7Rp0yxdBplAYWEhRo4c2aE5wsLCkJ+fr/cycp3BmMe/tCQWi6FQKCCXy+Ho6GjCyoiILItnAImow0EJ6JqXS7OzszFx4sQOzREZGYmjR4+aqCIioq6BAZA6jVwuR0VFhdqLuoa8vDw89NBDHZpDeQawI2pqajBgwAAMGDAANTU1HZqroaEBcrkcrq6uHZqnKwZbIqKOYgCkTpOSkgIPDw/Vy8/Pz9IlEYC6ujoA6PA9d/b29nB0dERVVZXRcwiCgKtXr+Lq1asdfq5gQUEBxo8f36E5AGD06NE4ffp0h+chIupKGACp06xevRrl5eWq1/Xr1y1dEgH4z3/+Y7L79kzVDWwKprisDQC2trZwd3dHWVmZCaoiIuoaGACp0zg6OsLd3V3tRZZnqqAEdK3Lpfn5+QgNDTXJXJMmTUJWVpZJ5iIi6goYAMloVVVVOHPmDM6cOQOgeRmxM2fO4Nq1a5YtjAxy+vRpjBo1yiRzBQcHo6ioyCRzdURlZSXEYjHs7EzzoIOuFGyJiEyBAZCMduLECYwePRqjR48GAKxatQqjR49GfHy8hSsjfZWVlcHDwwO2trYmmU8kEsHb2xsymcwk8xkrJycH0dHRJpvvgQcewOXLl002HxGRpTEAktGio6MhCEKbV1pamqVLIz11ZPUPbbrC2TJTXtZW8vf3x9WrV006JxGRpTAAElmxjqz/q82UKVOMDoAikQghISEICQmBSCQyugaJRILAwECj99ekKwRbIiJTYQAksmJXrlzBoEGDTDpnv379IJPJjHqMi7OzM86fP4/z58/D2dnZqONLpVL4+vp2KEBqMnnyZBw+fNikcxIRWQoDIJGVKikpQUBAgFnmDgoKQnFxsVnmbs+hQ4dMflYTADw9PXH37l0oFAqTz01E1NkYAKnHGTBgADZu3Ki2bdSoUVi/fr1F6umqzHH5VykmJgYZGRlmmbs9mZmZmDJlilnmHjFiBAoLC80yNxFRZ2IAJLJS5mgAUTL2gdA1NTUYOnQohg4datRScIIgQCaTwcfHx+B99cH7AImop2AAJLJCCoUCZWVl6NOnj1nmd3NzQ21tLRobGw3aTxAEXLhwARcuXDDqHkKJRIKQkBCD99PXhAkTkJeXZ7b5iYg6CwMgkRUqLCzEyJEjzXqMsLAw5Ofnm/UYrZnj8S8ticViKBQKyOVysx2DiKgzMABSj2NjY9Pm7FFDQ4OFqumazB2UAMtcLs3OzsbEiRPNeozIyEgcPXrUrMcgIjI3BkDqcby8vCCVSlWfV1RU4MqVKxasqOvJy8vDQw89ZNZjdPYZwIaGBsjlcri6upr1OLwPkIh6AgZA6nEmT56MXbt2ITc3F+fOncPChQtNttRZT1BXVweg+XKmOdnb28PR0RFVVVVmPY5SQUEBxo8fb/bjjB49GqdPnzb7cYiIzIkBkHqc1atXY+LEiXj88ccxffp0zJw5Ew888ICly+oy/vOf/yAyMrJTjmVsN7AxOuOyNgDY2trC3d0dZWVlZj8WEZG5MABSj+Pu7o4vvvgC5eXluHbtGhYuXIgzZ87wOYD/p7OCEmD45VKRSISAgAAEBAQYvJJHfn4+QkNDDS3RKJMmTUJWVlanHIuIyBwYAImszOnTpzFq1KhOOVZwcDCKior0Hu/s7IySkhKUlJQYtBRcZWUlxGIx7OzsjCnTYLwPkIi6OwZAIitSVlYGDw+PTrsnUiQSwdvbGzKZzKzHycnJQXR0tFmP0dIDDzyAy5cvd9rxiIhMjQGQyIqYc/UPbTrjbFlnXtZW8vf3x9WrVzv1mEREpsIASGRFzLn+rzZTpkzROwDW1tYiNDQUoaGhqK2t1fsYEokEgYGBxpZoFF4GJqLujAGQyIpcuXIFgwYN6tRj9uvXDzKZTK+l3RQKBU6cOIETJ05AoVDoNb9UKoWvr6/BTSMdNXnyZBw+fLhTj0lEZCoMgERWoqSkBAEBARY5dlBQEIqLi80y96FDhzr9rCYAeHp64u7du3oHVSKiroQBkMhKWOLyr1JMTAwyMjLMMndmZiamTJlilrnbM2LECBQWFlrk2EREHcEASGQlLNEAomSuB0ILggCZTAYfHx+Tz60P3gdIRN0VAyCRFVAoFCgrK0OfPn0scnw3NzfU1taisbHRpPNKJBKEhISYdE5DTJgwAXl5eRY7PhGRsRgAiaxAYWEhRo4cadEawsLCkJ+fb9I5LfH4l5bEYjEUCgXkcrnFaiAiMgYDIJEVsHRQAvS/XOrp6QlPT0+95szOzsbEiRM7WlqHREZG4ujRoxatgYjIUAyARFYgLy8PDz30kEVr0OcMoIuLC27duoVbt27BxcVF59iGhgbI5XK4urqaskyD8T5AIuqOGACJeri6ujoAzZcrLcne3h6Ojo6oqqoyyXwFBQUYP368SebqiNGjR+P06dOWLoOIyCAMgEQ93H/+8x9ERkZaugwApu0G7gqXtQHA1tYW7u7uKCsrs3QpRER6YwAk6uG6SlAC2r9cWltbi+joaERHR7e7FFx+fj5CQ0NNXaJRJk2ahKysLEuXQUSkNwZAoh7u9OnTGDVqlKXLAAAEBwejqKhI6/sKhQLZ2dnIzs7WucJGZWUlxGIx7OzszFGmwXgfIBF1NwyARD1YWVkZPDw8YGtra+lSAAAikQje3t6QyWQdmicnJwfR0dGmKcoEHnjgAVy+fNnSZRAR6Y0BkKgHy8rKstjqH9qY4mxZV7qsreTv74+rV69augwiIr0wABL1YF0xKE2ZMqXDAVAikSAwMNBEFZkGLwMTUXfCAEjUg12+fBmDBg2ydBlq+vXrB5lMBkEQjNpfKpXC19cXIpHIxJV1zOTJk3H48GFLl0FEpBcGQKIeqqSkBAMGDLB0GRoFBQWhuLjYqH0PHTrU5c5qAs0rmNy9e1dn8woRUVfBAEjUQ2VmZnbJoAQ0Xy7NyMjQ+J6zszOcnZ217puZmYkpU6aYq7QOGTFiBAoLCy1dBhFRuxgAiXqow4cPd7kGECVtD4R2cXFBdXU1qqurNS4FJwgCZDIZfHx8OqNMg/E+QCLqLhgAiXoghUKBsrIy9OnTx9KlaOTm5oba2lo0NjYatJ9EIkFISIiZquq4CRMmIC8vz9JlEBG1iwGQqAcqLCzEyJEjLV2GTmFhYcjPzzdon67Y1dySWCyGQqGAXC63dClERDoxABL1QF09KAGaL5fW1dXhsccew2OPPYa6uro2+2RnZ2PixImdVaJRIiMjcfToUUuXQUSkEwMgUQ+Ul5eHhx56yNJl6KTpDGBTUxO+++47fPfdd2hqalJ7r6GhAXK5HK6urp1ZpsF4HyARdQcMgEQ9jPLMmVgstnAlutnb28PR0RFVVVV6jS8oKMD48ePNXFXHjR49GqdPn7Z0GUREOjEAEvUw//nPfxAZGWnpMvSirRtYk+5wWRsAbG1t4e7ujrKyMkuXQkSkFQMgUQ/TXYISYNjl0vz8fISGhpq5ItOYNGkSsrKyLF0GEZFWDIBEPczp06cxatQoS5ehl+DgYBQVFbU7rrKyEmKxGHZ2dp1QVcfxPkAi6uoYAIl6kLKyMnh4eMDW1tbSpehFJBLB29sbMplM57icnBxER0d3TlEm8MADD+Dy5cuWLoOISCsGQKIeJCsrq8uu/qGNPmfLutNlbSV/f39cvXrV0mUQEWnEAEjUg3THoDRlyhRVAHRxcYEgCBAEQW0pOIlEgsDAQEuVaBReBiairowBkKgHuXz5MgYNGmTpMgzSr18/yGQyCIKg8X2pVApfX1+IRKJOrqxjJk+ejMOHD1u6DCIijRgAiXqIkpISDBgwwNJlGCUoKAjFxcUa3zt06FC3O6sJAJ6enrh79y4UCoWlSyEiaoMBkKiHyMzM7JZBCWi+XJqRkYG6ujo8/fTTePrpp1UPtM7MzMSUKVMsXKFxRowYgcLCQkuXQUTUBgMgUQ9x+PDhbtcAoqR8IHRTUxP++c9/4p///CeampogCAJkMhl8fHwsXaJReB8gEXVV3eOhWkSkk0KhQFlZGfr06aN1jCAACgXQ1NT21XK7QtH8EoR7+yj/rKoCiovbbm89tuXHjY335mxdzz1u+PXXWhw+3Kjakp0N3Lolgbt7CFovFtL6dkBb2+aXjU3ze63/1PaxjQ1QXQ1cuqR5P+Wcyvlbvlpu12bChAnYsmULXn31Vd3/AYmIOhkDIFEXpFA0B6eGhvb/bGoCiooK4eU1Ejk5zduU7yvHKD9XBjFdL2WAaxnQBKE5EN28CRw8qP/XoQxqyuCla1yvXmH4/vsTqm3nzgHHjmXAyysGZ860DozqNNWsL5kM2LevbT0tw6Iy8LUMiMqXMgTa27d92dmJceeOAkePyiEWO6rG2dm1/2c363khom6GAZDIjBoagPp6QC5X/7NlKJPLm1+1tc3v1dbee6/1mbrGRs0hJysrA/37x+DUKfVw0jK0KEOMnV3bMKPp7JmmAOLqCgwZYp7vVXR0DE6d+l71+cCBwL592ZgzZzHEYvMcE9D8NbU+w6krLDc0AHV1bbcrP3Z3j8SuXUcxePCkNsduGSDt7NTPMDo6Nr+cnACxuPljB4d7IdHe/t42Bwf194mI2sMfFdQtPPvss3j55ZfVtmVkZCAjIwPvvPNOp9bS2Nj8C18uv/en8uPa2ubLpFVVQE2N5rNxrYlEbX/5twwBmi49tvbll3lYtGgFHB3N//Wby5AhYfjyy/+n+ryxsQENDXKIxa6dXosyMJuCQhGDY8e+wfTpbQOg8pJ7y7Cv/H+lrq7tPwBah3/l/zstzx46OADOzs3B1s2tOUAqg6QyVDo6NodKTf8vEZF1YACkbqGwsBB//vOf8eabbwIAGhsbsXz5cgwbNszkxxKE5l++1dXNIU75KitrflVVqZ/Fa2q6t69I1PLyX/PLxcW8l/bq65u7ZR0dzXiarBPY2dnDzs5B9fmlSycxZMh4C1ZkGoMGjcaePfEa32t5+dgYyvDY8raA6mqgvPze5y1Do61tc0BUBkUPD+C++5r/dHZWfzk5GVcTEXUPDIDULcTHx2PmzJl48sknAQAHDhzAxYsXsXfvXqPnbGwEfvut+ZdldXVzsCsrA+7evXdWTy6/9wvUzu7eWRRX13tBz9LL7kok/0FwcKRlizCRkJAJyM/fDwAoLDyM0NDHLVxRx9na2sLZ2R1VVWVwdb3PpHPb2Ny7BKyPxsbmf7wobz2QSoGSkubPlZf/lWcInZ2bw+F99zX/I8bFBejVqzks8swhUffHAEjdwpNPPolRo0Zh586dAIAPP/wQTz75JMaMGaPX/goFUFnZHPB++635F9/Nm83B7/8eNweRSP2+Kw+P5l+sXf2X3ZkzGYiM/L2lyzCJsWOno7T0KhYt+hv+9rfZeOaZREuXZBLDh09CYWEWIiN/Z9E6lGeltWlquvcPn6oq4M6d5sCobAISi5svK/frB3h5NYfDXr2awyGbVoi6FwZA6pCPPvoI7777LqRSKYYOHYqNGzfi4YcfNvlxRCIR1q9fj5kzZwJoXvXi66+/1rlPbS1w7Vpzl+evvwIVFc2XcgWhOdi5uDT/EnNy6t6/vC5fPo158/5q6TJMwt8/BFLpz1AoFHB0FMPWtmf8iBo5Mgb79qVaPAC2x9b23iXg1hSKe/e4FhY2h0Ubm+az4b16NYfCfv2A/v2Nv6RNRJ2nZ/x0JYv44osvsHLlSnz00Ud46KGHsH37dkybNg0XLlyAv7+/yY/35JNPYvDgwfj5558RExOj8eyfIAClpcCVK4BEAty+fe8+PA8PwMfH8pdsTamqqgwuLh6w7SFflEgkQq9e3jh+/FsMGxZt6XJMxtf3Achkly1dRofY2Ny7FOzt3bxNec/h3bvA9evN23x9geBgYMCA5mBIRF0TAyAZbcOGDViyZAmee+45AMDGjRvx448/YuvWrUhJSTH58UQiEeLi4rB8+XKsXr26zfsKBXD6NJCf3/xLqXdvYPBg/QJfXV01AMDe3kkVphobG9DYWK91H3t7R9UZKkPGNjU1oqFBrnWsnZ0D7Ozs9Rp75kwGhg+f/H9jm9DQUKd1rK2tPeztHQweq1AoUF9fq9pP+b1qb6zmee1gb9/cqiwIAuTyGrX3GxrkkEov4syZDKxbt1+1XdPYlmxsbOHgcK9roXWNusZq+pqURCIbteYaXfO2HiuX10Bo0YHRu7cvrl8vgpeXP0QiERwdnbWOVZ+39dhaCIL29YWdnFyMGltfXweFokmvsUp2ds3/sPLwaP68oQG4dQvIyAD69AEmTmz+O0hEXY9I0PZTh0iH+vp6ODs746uvvsKsWbNU21955RWcOXMG2a2XbgAgl8shl98LMxUVFfDz80N5eTnc3d31Pvbdu3fRu3fvNtsvXwb2728+66BjQQyNnnyy+RpwcnIWhg+PBgCkp2/B9u0rtO7z5psHERr6GADg0KE0bNr0rNaxr7/+JSZMeBoAkJf3Fd55Z7bWsa+8sgNTpiwCABQUpOOvf9XeCBEQMBxr1nwDX98HcPbsEaxd2/ZRI0qLFr2D3/3uNQDAxYsF+POfw7SOnTMnAc88sx4AcO3aeaxYob3betasV/Hss+8CAG7eLMHSpQO1jp0+/UU8//wWAEB5+S3Mn99X69iJE+fi1Vf3AGgOXrNna38cTGTkU/jLX75Sfa7876nJuHHTER+fDqA5YP/ud45aQ9KwYVF4660jqs//+EcvVFTc1jh28OBx2LChQPX5c88NQGnpVY1j/fxCsGXLedXny5cPxfXrFzSO7ds3AB9/XKL6fNWqUPz88wmNY93dPfH557dUn69ZE41z59r+XQQAR0dnfPXVvUCblPQYTpz4TuNYANi/X/9fFYLQfNuFvT0wa5bhfx+pfRUVFfDw8DD45yeRUhe/vZ26qtu3b6OpqQneymtB/8fb2xsymUzjPikpKfDw8FC9/Pz8OqPUHs3JyRW//FJk6TK6rVOnfrB0CT0WTy0QdW08A0hGuXHjBu6//34cPXoUERERqu3JycnYtWsXJBJJm31McQbwo48+wvLly5GZmYkpU6aovafpEnDv3t37EnBDQz3mz++L3r37qZ1dUmpoqMc778zG+vU//N/n5rsEfO5cNoqKfsLTT69pd6z2eXVfAq6rq8aCBc3/qHj33f8gMDBc69iWjL0E/PbbT2Hx4lS4u3tqHGuqS8C//XYT27YtxxtvfAWRSNRjLgG3prwEXFHBS8DmxjOA1FG8B5CM4unpCVtb2zZn+0pLS9ucFVRydHSEYweWqhAEAe+//z4A4O23324TAG1sgDFjAD+/5svBxcXAzz83B0BX1+ab152dNQdCzfc32auCWHsMGWtra6d3d+vx49+ipqYcNTXlkEovYeDAEWrvOzm5YPz4GcjJ2YNJk+bD1rb9X9LNNdjqPdbGxgZOTi4YO3Yavv12g1pI1jZWHyKRSOfYCxfyVAGwvbGt6TP21q3rsLd3Qt++ASadV6llaNu/fyPmzEnQuqpJy7Htz6v/A78NGdsyQOtL2QSifAHNTSDh4UBAAJtAiLoyXgImozg4OGDs2LHIyMhQ256RkYHISPM8lHj//v34+eefAQCZmZk4depUmzEiEdC3b/MvoNmzgSeeaA6FLi7NzwG8fBn473+bH35761bzYy266jlwhUKBvXsT4ezsDrHYFV98kaRx3KOPLsOhQ2k6zyqagkgkwpgxsWrr9Zpay7NgFy7kme04AJCZ+SkeeeQ5sx4DAGSyy/jtt5sICgo3+7HMSaFofgTMzZvApUvNf4+uXm3+O9S7d/PfuVmzgKeeAkaOZPgj6up4BpCMtmrVKsyfPx/jxo1DREQE/v73v+PatWt4/vnnTX4sQRCwfv16jBo1CmfOnMGAAQOQmJiIb7/9Vus+YjEQGNj8Uj4I+rffmh8GffNm88Ogb93S/CBo5cOgLfkg6KNHv8a1a+fh7z8MLi69cPTo17hypbDNWUB7ewfExCzGDz9sxxNPvKxlNtOYPHkhtm59wWwrdPz6a7Hq4/r6OjQ1NZrlWYBNTY24cCEXc+ZoXqLNlPbuTcKcOQlmP44ptHwQtPKl6UHQgwY1/0OrV6/mh0E7O3fvZ2kSWSMGQDLaH/7wB9y5cwdJSUmQSqUYNmwYvvvuOwQE6H9JTV/79+/HmTNn8P777+PMmTNYsWIFXn31VZw6dUqv1UBsbO49rkJZnral4MrKmkNhRUXbpeCUwVC5lqq5loJTnv0bPfoR1NZWwtd3MO7e/RVffJGEv/zln23GT5w4FwkJj2LKlGfh7Oxm+oL+j4eHF+ztnXD79i/w9Oxv8vkLCw+rPh48eCz++998syxzd+rUDxgzJhYiM6eWK1cKYWtrB3//ELMeR1/K9asbGpqDnTLkKdeztrFRX+7Qz6854Lm6Noc8LgVH1HOwCYQsxpCbmMeOHQsPDw+8+eabmDx5MoqLi/H4449j2LBh+Ne//mXSugShOQDW1DQHw5qa5ld5efPSWFVVzb88lb9Im1rcNy8SNYdCOzvtf+qTOY4e/Rpvv/0U3nnnKD799M/o3z8YwcEP4YMPluDDD8/B339om31OnPgOFy8WYO5c855tKizMwvnzOWY5TkrK77F48XtwcnLFr78Wo7DwsFnO0r399lN48cVtWps/THmcJUs2wMvL9A9GB5rPbDc2Nr8aGjT/2fInvPL/Q+U/YDw8mi/furs3BzzlfbLOzs0hkLouNoFQR/EMIHULI0aMwMsvv4zffvsNAGBnZ4ctW7a0uQfRFJSXusRizc8va2xsDojKsyctP66paQ6Iyj8bGpo/bvlLWdPxbG2bfznb2DT/KZe7Yfr01+HrG4GmpuaQOWHCfJw7lwNAc4IcO3YavvvuI/z2Wyl69dL+fL2OGj48Gl99lYympiaTrkDS2NiAhgY5vL2bnyPo4tIL//zn2yabX0nZ/GHu8Hf+fC68vAJ0hj/lf9uWr8bGe8Gu9bbW/1wXidRDnXLVG+XLze3eGT3ln8qPnZx4Jo/ImjEAUrewY8cOAEBWVpZq29SpUzF16tROr8XOrvmSmKv25xKrtLzUVl9/72Pl2cPGxnvhsba2+f3aWmDUqEcwbNgjqKtrDgB1dYBMZo/HH09DXV3zDfjAvbOJzfdoifDQQ2vxySdv4amnNsLGpvl9G5vml63tvY9bble+13KbSKT9TGXLZhBT3gt48WIBhgwZr/rczs4e9vaOqK2t0to9awx9mj+UYUsQmj829NXUJOCzz1LwzDOf4eJF7Y1Gyu+9nV3zn8qXvX1zgFOGNrG4+U8Hh3uBz8Hh3kv5nvJ9IqL28EcFkRkpz8y46P/0EADql/b+53+ab7qfPbvtJb6GBmXgaN42blwEzpzZCHf3EvTpM0Dtnq+WZ5ZahhVlyGlqUg8+um4OCQhYiK+/fgEeHu0HQGWYbO/Sd1ZWBgYPjsY77ywHAMycuQE+PlHIzMxGSMhjOvfVp2agufnjxIlcjBkTrwrRumpWhuGW4bl1iG4ZypR/njhxAOHhkYiO9lTdJ9oy3LU+a9f6T31vFSAiMhYDIFEXpAwWDg7NocHREfDx0W/fLVvikZqahE8//VRte8ugpwx7mi5BtgyFLf9seUZMELxw4oQTRo36Bd7e/ducMWv9Z1PTvY9b16T0xRf5iI1diQ8/jAYArF37Djw9Y3Dw4P9g9Oh7AbB1MNJ0JrN1gFP+mZ39A2bMiMXjj4s0vt/6Y2VoU86t6dX6MmpTUxPef38z9u3bp9dZYiIiS2AAJOphhg4dChsbG5w9exbDhw9XbW8ZaExh1aolyMn5BAkJHW8GqaysxP33ixEdfe9H0sMPA87OwfjHP4oQFdXhQwAA1q9Pw7Zt2+Bpxtv/Pv/8c8yaNQuuTH9E1IXxFmCiHig+Ph5JSZofHG0q0dHRyM3NRVPLNmgj5eTkIDo6us12kUikc31pQ1y/fh1OTk7wNGP6k8vl+Oyzz7B06VKzHYOIyBQYAIl6IH9/f/j5+SEvz3yraYhEIsTGxuL77zu+MkhGRgZiYmI0vhcTE4PMzMwOH+PTTz/Fc8+Zd+WPrVu3YsmSJXBwcDDrcYiIOooBkKiHWrNmDVJSUmDOR30uXLgQaWlpHZ5HIpEgMDBQ43umCICNjY3Izc1FlKmuJWtQUVGB9PR0zJkzx2zHICIyFQZAoh7K09MT4eHhSE9PN9sxvLy84OTkhF9++cXoOaRSKXx9fbWuyuHr6wuZTNahIPvDDz8gNta8K3+kpqZi1apVsOHD9YioG+BPKqIeLC4uDps2bTLJfXraLFmyBJ988onR+x86dEjr5V+loKAgFBcX6xyjS1paGhYtWmT0/u25efMmTp48idjYWLMdg4jIlBgAiXowV1dXzJgxA3v27DHbMTraDJKZmYkpU6YAAMRiMa5cuYIrV65ALBarxsTExBi96ktnNH8kJydj3bp1Zl9bmIjIVBgAiXq4ZcuWIS0tDXK53Czzd6QZRBAEyGQy+PzfQw5tbGwwYMAADBgwQO1SalRUFLKzs42qz9zNH5cvX8bNmzcRHh5utmMQEZkaAyBRD+fg4IDFixdj+/btZjuGsc0gEokEwcHB7Y5zc3NDbW0tGhsbDZq/M5o/kpKSTPIsRCKizsQASGQF5s6diwMHDqCystIs8xvbDJKRkaG2nnN9fT1ee+01vPbaa6ivr1cbGxYWhvz8fIPmN3fzR2FhIezs7BASEmKW+YmIzIUBkMgK2NjYIC4uDhs2bDDbMYxpBsnOzsbEiRNVnzc0NOC9997De++9h4aGBrWxxjwOxtzNH0lJSYiPjzfb/ERE5sIASGQlpk2bhoKCApSWlpplfkObQRoaGiCXy/VeMs3QM4Dmbv7Izc1FQEAA/P39zTI/EZE5MQASdTGCIGDZsmXo3bs3RCIRqqurTTKvSCTC2rVr8dZbb5lkPk3zG9IMUlBQgPHjx+s9v729PRwdHVFVVaXXeHM2fwiCgJSUFKxevdos8xMRmRsDIFEX88MPPyAtLQ0HDx6EVCqFs7OzyeaOiIiAVCpFSUmJyeZsyZBmEF3Lv2mjbzewuZs/Dhw4gMjISLM+WoaIyJwYAIm6mEuXLsHX1xeRkZHw8fExeQNDfHw8kpKSTDqnkiHNIPn5+QgNDTVofn3vAzRn80dTUxM2b96MlStXmnxuIqLOwgBI1IUsWrQIL730Eq5duwaRSIQBAwaY/BhDhw6FSCTC2bNnTT43oF8zSGVlJcRiMezs7AyaOzg4GEVFRe2OM2fzx+eff45Zs2bpfe8iEVFXxABI1IVs2rQJSUlJ6N+/P6RSKQoKCsxyHHOeBdSnGSQnJwfR0dEGzy0SieDt7Q2ZTKZ1jDmbP+RyOT777DMsXbrU5HMTEXUmBkCiLsTDwwNubm6wtbWFj48PvLy8zHKcgIAA+Pn5IS8vz+Rz69MMou3+P7FYjHPnzuHcuXNqS8G11N5lYHM2f2zduhVLliyBg4ODWeYnIuosDIBEVmrNmjVISUmBIAgmn7u9ZhCJRILAwMA2221sbDB06FAMHTpUbSm4lnQFQHM2f1RUVCA9PR1z5swx+dxERJ2NAZDISnl6eiI8PBzp6ekmn1tXM4hUKoWvr6/RDRq+vr6QyWQag6s5mz9SU1OxatUqrcGUiKg74U8yIisWFxeHTZs26f3wZkNoawY5dOiQ1se/1NfXY/369Vi/fn2bpeBaCgoKQnFxcZvt5mr+KC0txcmTJxEbG2vyuYmILIEBkMiKubq6YsaMGdizZ4/J59bWDJKZmYkpU6Zo3KehoQGJiYlITExssxRcSzExMcjIyFDbZs7mj+TkZKxbt85sawoTEXU2BkAiK7ds2TKkpaVBLpebdF5NzSCCIEAmk8HHx6dDc2t6ILS5mj8uX74MmUyG8PBwk89NRGQpDIBEXczKlSvNtlKHJg4ODli8eDG2b99u8rlbN4NIJBIEBwd3eF43NzfU1taisbERgHmbP5KSkpCQkGDyeYmILIkBkIgwd+5cHDhwAJWVlSadt3UzSEZGBqZOnWqSucPCwpCfnw/AfM0fhYWFsLOzQ0hIiEnnJSKyNAZAIoKNjQ3i4uKwYcMGk8/dshkkOzsbEydONMm8LR8HY67mj6SkJMTHx5t8XiIiS2MAJCIAwLRp01BQUIDS0lKTzqtsBqmrq4NcLjfZEmrKM4Dmav7Izc1FQEAA/P39TTovEVFXwABIRACamzbWrl2Lt956y+TzxsbG4oMPPkBYWJjJ5rW3t4ejoyO2bdtm8uYPQRCQkpKC1atXm3ReIqKuggGQiFQiIiIglUpN3oSycOFC7Nixo937/5ycnJCfn4/8/Hw4OTm1O++ECROQnp5u8uaPAwcOIDIy0iyPlCEi6goYAIlITXx8PJKSkkw6p5eXF8rLy+Hr66tznK2tLUJDQxEaGgpbW9t253V0dIS7u7tJmz+ampqwefNmrFy50mRzEhF1NQyARKRm6NChEIlEOHv2rMnmrKysxODBg7Fz506TzQkAhw8fhp2dnUnn/PzzzzFr1iyT3atIRNQVMQASURumPguYk5ODp556Cjk5OTqXnauvr8e7776Ld999V+dScMC9lT/8/Pwgk8lMUqdcLsdnn32GpUuXmmQ+IqKuigGQiNoICAiAn58f8vLyTDKf8vl/rVcGaa2hoQGvv/46Xn/9dZ1LwQH3Vv5o+TiYjtq6dSuWLFkCBwcHk8xHRNRVMQASkUZr1qxBSkoKBEHo8FwSiQSBgYFYtGiR2sogxmq58oepAmBFRQXS09MxZ86cDs9FRNTVMQASkUaenp4IDw9Henp6h+aRSqXw9fWFSCRqszKIsVqu/OHr6wuZTNbhoJqamopVq1bBxoY/Fomo5+NPOiLSKi4uDps2bdJ53157Dh06hJiYGNXnLVcGMVbrlT+CgoJQXFxs9HylpaU4efIkYmNjO1QXEVF3wQBIRFq5urpixowZ2LNnj9FzZGZmYsqUKarPo6Oj220G0UXTyh8xMTHIyMgwusbk5GSsW7fO5GsJExF1VQyARKTTsmXLkJaWBrlcbvC+giBAJpPBx8dHtU25MoiuZhBdlM0fLUVFRSE7O9uo+S5fvgyZTIbw8HCj9ici6o4YAIlIJwcHByxevBjbt283eF+JRILg4OA2241tBmnZ/NGSm5sbamtr0djYaPCcSUlJSEhIMHg/IqLujAGQiNo1d+5cHDhwAJWVlQbtp3z8S2vamkGcnJyQlZWFrKwsjUvBtWz+aC0sLAz5+fkG1VdYWAg7OzuEhIQYtB8RUXfHAEhE7bKxsUFcXBw2bNhg0H7Z2dmYOHGixvc0NYPY2toiOjoa0dHRGpeCa9380ZIxj4NJSkpCfHy8QfsQEfUEDIBEpJdp06ahoKAApaWleo1vaGiAXC7XuqSaoc0gmpo/WjL0DGBubi4CAgLg7++v9z5dUXR0tNnXLV60aBFmzpxp0D4SiQTh4eFwcnLCqFGjzFJXa2lpaejVq1enHIuou2MAJCK9iEQirF27Fm+99ZZe4wsKChAWFqZzvtbNIA0NDdiyZQu2bNnSZiUQTc0fLdnb28PR0RFVVVXt1iYIAlJSUrB69Wo9vhIyRkJCAlxcXFBcXIxDhw5ZuhwiaoUBkIj0FhERAalUipKSknbHarv/r6XWzSD19fVYsWIFVqxYobYWsLbmj9b07QY+cOAAIiMjtZ5NpI67dOkSJkyYgICAAPTp08fS5RBRKwyARGSQ+Ph4JCUltTsuPz8foaGhOsfouzKIruaPlqZOndrufYBNTU3YvHmz2S+bdqbGxkasWLECvXr1Qp8+fbBu3Tq1lVE+//xzjBs3Dm5ubvDx8cEzzzzT5lL++fPn8dhjj8Hd3R1ubm54+OGHcenSJY3HO3nyJPr27Yvk5GSN74tEIpw8eRJJSUkQiURYv349AODs2bOYPHkyxGIx+vTpg2XLlrU5Y/vpp59i6NChcHR0hK+vL1asWKF6b8OGDRg+fDhcXFzg5+eHF198Ua8zvkTUFgMgERlk6NChEIlEOHv2rNYxlZWVEIvFsLOza3c+fVYG0dX80VJQUBCKiop0jvn8888xa9Ysrfcmdkc7d+6EnZ0djh8/js2bN+P999/Hxx9/rHq/vr4ef/3rX/G///u/2LdvH65cuaL2/fz1118xceJEODk54fDhwzh58iQWL16s8bE6R44cwZQpU5CYmIi1a9dqrEcqlWLo0KH485//DKlUildffRU1NTWIjY3Ffffdh4KCAnz11VfIzMxUC3hbt27F8uXLsWzZMpw9exb79+/H4MGDVe/b2Nhg8+bNOHfuHHbu3InDhw/j9ddfN8F3kMgKCUQWUl5eLgAQysvL9d7n8OHDAgDh0qVLZqysa4mIiBAWL15s6TLUlJSUCE899ZTW9w8ePCh88MEHes2lUCiEyZMnC42NjUJVVZUAQAAgVFVVCYIgCNeuXRPmzZund20LFiwQpFKpxvfq6uqEyZMnC3K5XO/5urqoqCghODhYUCgUqm1vvPGGEBwcrHWf/Px8AYBQWVkpCIIgrF69Whg4cKBQX1+vcfzChQuFGTNmCPv27RPc3NyEPXv2tFvXyJEjhYSEBNXnf//734X77rtP9d9VEAQhPT1dsLGxEWQymSAIgtCvXz9h7dq17c6t9OWXXwp9+vRRfb5jxw7Bw8ND7/27M2N+fhK1xDOARGSwgIAA+Pn5IS8vT+P7GRkZauv/6tLeyiDtNX+0putxMFu3bsWSJUvg4OCg93zdQXh4uNrl8YiICFy8eFHVYX369GnMmDEDAQEBcHNzQ3R0NADg2rVrAIAzZ87g4Ycfhr29vdZjHD9+HL///e+xc+dOzJ071+Aai4qKMHLkSLi4uKi2PfTQQ1AoFCguLkZpaSlu3Lihtmxga1lZWZg6dSruv/9+uLm5YcGCBbhz5w6qq6sNrofI2jEAEnVBhYWFbdbfFQQBH3zwAX799VcLVaVuzZo1SElJUbvXTEkikSAwMFDvubStDKJv80dL2gJgRUUF0tPTMWfOHL3n6gmqq6vxyCOPwNXVFZ9//jkKCgrwzTffAICq0UYsFrc7zwMPPICgoCB8+umnag06+hIEQes9nCKRqN0arl69iunTp2PYsGH4+uuvcfLkSWzZsgUA2nSME1H7GACJuqD8/HwsWLAAP//8s2rbjz/+iJdffhlXr161YGX3eHp6Ijw8HOnp6WrbpVIpfH19223YaEnZDNI63Orb/NGSr68vZDJZm2CampqKVatWwcam5/3YO3bsWJvPH3zwQdja2kIikeD27dt4++238fDDDyMoKKhNA8iIESOQm5urM0h5enri8OHDuHTpEv7whz8YHLpCQkJw5swZtbN1P/30E2xsbDBkyBC4ublhwIABWh8Zc+LECTQ2NiI1NRXh4eEYMmQIbty4YVANRHRPz/tJSNQDzJs3D15eXqouS0EQsH79ekRGRiIiIsLC1d0TFxeHTZs2qT3MOTMzU+/Lvy0tWbIEu3fvxsGDB3Hw4EE4Ojrq3fzRWlBQECQSierz0tJSnDx5ErGxsQbP1R1cv34dq1atQnFxMf7xj3/ggw8+wCuvvAIA8Pf3h4ODAz744ANcvnwZ+/fvx1//+le1/VesWIGKigrMmTMHJ06cwMWLF7Fr1y4UFxerjevbty8OHz4MiUSCuXPnGrT28rx58+Dk5ISFCxfi3LlzyMrKwksvvYT58+fD29sbALB+/XqkpqZi8+bNuHjxIk6dOoUPPvgAQPMZyMbGRtXXsWvXLmzbtq0j3zYiq8YASNQFicVi/OUvf8GuXbtQW1uLX3/9FcePH8f69esNOhtmbq6urpgxY4ba5erMzEyd93FpEx0djby8PMTGxuKxxx6DVCrVufKHLq0vAycnJ2PdunVd6ntnSgsWLEBtbS3CwsKwfPlyvPTSS1i2bBmA5rOraWlp+OqrrxASEoK3334b7733ntr+ffr0weHDh1FVVYWoqCiMHTsW//M//6PxnkAfHx8cPnwYZ8+exbx58/ReycXZ2Rk//vgj7t69i9DQUDz11FOYMmUKPvzwQ9WYhQsXYuPGjfjoo48wdOhQPP7447h48SIAYNSoUdiwYQP+9re/YdiwYdi9ezdSUlKM/ZYRWT2RoOkGHqJ2JCcnIz09HWfOnIGDgwN+++03g+eoqKiAh4cHysvL4e7urtc+WVlZmDx5Mi5duoRBgwYZfMzupLa2VnXWAwAefPBB5OXldbkQU19fj2nTpuG7776Dg4MDpk2bhh9++MGoud59910EBwfj8ccfR2JiIqKiolQNC4aorKzEs88+i3/+85+4cuUK/vKXv+CLL74wqiairsiYn59ELfEMIBmlvr4eTz/9NF544QVLl9JjKc8C3rp1C7du3epyZ/+UHBwcsHjxYmzfvh0SiQTBwcFGzzVv3jwkJibik08+QU5OjkHNHy25ubmhtrYWjY2NSExMREJCgtE1ERH1RO0/pZVIg8TERADQ2LlJxlHeHG9vb696TMmSJUvw2muv4b777kNERESbx120HKtQKFBbW6t1fjs7Ozg6OgJovqewpqbGJGNtbW0xd+5cPProo6irq8PDDz+s9bEctra2cHJyavM1tzzuiRMn8Nxzz7UJvLoe9WFjY6PWRVpTU4NRo0Zhx44dAJofW6PcXyQSwdnZWW2stgshrcfW1tZCoVBoraPlI04MGVtXV6fzUmrLsUREJmGpBxBSz2DIg1fr6uqE8vJy1ev69et8EHQL+L8HILd8eO65c+dU2zW9Xn31VdXYK1eu6Bz74osvqsaWlpbqHLtw4ULV2JYPZ9b0Uj4QOj09XQgODtY5dvr06Wpfs7Ozs9ax48ePVxvr6empdey4cePUxgYEBGgdGxISojY2JCRE69iAgAC1sePGjdM61tPTU21sVFSU1rHOzs5qY6dPn67z+0bUGh8ETR3FS8DUaVJSUuDh4aF6+fn5WbokMqGYmBjcuXPHZPPps4wcEREZhz9hSWX9+vWqS7vaFBQUYNy4cUbNv3r1aqxatUr1eUVFBUNgC8pF7Vt2XgYHB+tc7L7lWH9/f51jWwYqT09Pvcc6OzvrHGtrawug+TltTz75JBwcHPDOO+/oHKvU+nl01dXVqkeCvPjii2rvlZSUaK2h9bP9zp8/j9/97ncQiUTYuXOn2rq/re+jLCgo0HkJuKWcnBydl3Vb+v777/Ue+/XXX+vdTWsK69evx759+3DmzJlOOyYRdS0MgKSyYsWKdldJGDBggNHzOzo6qu4ro7Y03edlY2Oj9/1fhowViUQmH5uRkYHFixdj48aNuHXrll7/r7Set+Vz5b788ks888wzWsfqcujQITz88MNwd3fHiRMn8Nhjj2kd2/Iev/bos2KGMWNb3hdJRNQZGABJxdPT06hnrhEBzauXrF27FvHx8UhMTFQ1YBgiIyND9bGTkxN++eUX9O/f36A5mpqasHnzZuzbtw/Xr1/H3//+d50BkIjIGvEeQDLKtWvXcObMGVy7dg1NTU04c+YMzpw5o/NSIfVclZWVEIvFsLOzw9ChQ2FjY4OzZ88aPM/nn3+u+njBggX45JNPjJpj1qxZcHV1RVBQEIqKigyeoztLS0tDr169sG/fPgwZMgROTk6YOnUqrl+/rnWfgoICTJ06FZ6envDw8EBUVBROnTqlNkYkEuHjjz/GrFmz4OzsjAcffBD79+9XG3PhwgVMnz4drq6u8Pb2xvz583H79m2zfJ1E1DEMgGSU+Ph4jB49GgkJCaiqqsLo0aMxevRonDhxwtKlkQW0fmZffHw8kpKSDJrj+vXrcHZ2xpdffokvv/wSU6dORU5OjkH3xsnlcnz22WdYunQpgObQ4u3tDZlMZlAt3V1NTQ2Sk5Oxc+dO/PTTT6pl3rSprKzEwoULkZubq1pHePr06aisrFQbl5iYiNmzZ6OwsBDTp0/HvHnzcPfuXQDNa0BHRUVh1KhROHHiBH744QfcvHkTs2fPNuvXSkRGsnQbMlkvYx5j0JMfA9OdvfLKK0JRUZHatri4OCE3N1fvOdavXy9kZWWpbXvnnXeEAwcO6D3H+++/L+zevVtt22effSbs2rVL7zm6ux07dggAhGPHjqm2FRUVCQCE48ePC4IgCAkJCcLIkSO1ztHY2Ci4ubmpfe8BCOvWrVN9XlVVJYhEIuH7778XBEEQ3nzzTeGRRx5Rm0f5qKfi4mJTfGnUAh8DQx3FM4BE1GESiQSBgYFq29asWYOUlBStHbYtNTY2Ijc3t83KH4sWLdL7YeMVFRVIT09vc6ar9brA1sDOzk6tWz8oKAi9evXSejm8tLQUzz//PIYMGaJ6TFNVVRWuXbumNm7EiBGqj11cXODm5qbq5D558iSysrLg6uqqegUFBQEALl26ZOovkYg6iE0gRNQhUqkUvr6+bR6Z4unpifDwcKSnp+Pxxx/XOccPP/yA2NhYNDU14ZtvvgEAzJo1C15eXno3g6SmpmLVqlVtHgnj6+sLmUwGQRC65FJ65qLpa9X29S9atAi3bt3Cxo0bERAQAEdHR0RERKC+vl5tXMvHDinnUz7qRqFQ4IknnsDf/va3NvP7+voa+2UQkZnwDCARdUhmZiZiYmI0vhcXF4dNmza1ex9fWloaFi1aBLlcjtmzZ2P27NmQy+UAmpfDa68ZpLS0FCdPnkRsbKzG94OCgiCRSPT4anqGxsZGtftxi4uL8dtvv6nOyLWWm5uLl19+GdOnT8fQoUPh6OhocPPGmDFjcP78eQwYMACDBw9We3EpO6KuhwGQiDokMzMTU6ZM0fieq6srZsyYgT179mjd//r163ByctL6CKLo6Oh2m0GSk5Oxbt06rWe4rO0ysL29PV566SUcP34cp06dwrPPPovw8HCEhYVpHD948GDs2rULRUVFOH78OObNm2fQcwwBYPny5bh79y7mzp2L/Px8XL58Gf/+97+xePHiTn3INRHphwGQiIwmCAJu3rwJHx8frWOWLVuGtLQ01Rm91j799FM899xzWvcXiUSIjY3F999/r/H9K1euQCaTITw8XOscUVFRyM7O1vp+T+Ps7Iw33ngDzzzzDCIiIiAWi7F3716t4z/99FOUlZVh9OjRmD9/Pl5++WX07dvXoGP269cPP/30E5qamvDoo49i2LBheOWVV+Dh4dHmsjwRWZ5I0OcObSIzqKiogIeHB8rLy+Hu7q7XPllZWZg8eTIuXbqEQYMGmblCak9RURH+/ve/4/3339c5bvfu3bhz5w5efvllte2NjY2IjY1FRkYGRCIRqqurVcu2VVVVqS4d3rp1Cy+88AL++c9/tpl70aJFeP311xESEqKzhsceewzffvttj19jOC0tDStXrsRvv/1m6VLIjIz5+UnUEv9ZRkRGy8jIwNSpU9sdN3fuXBw4cKDNc+WUzR/tNWd4eXnB0dERv/zyi9r2wsJC2NnZtRv+ACAsLAz5+fntjiMisgYMgERktOzsbEycOLHdcTY2NoiLi8OGDRvUtiubP/ShqRkkKSkJ8fHxeu1vbfcBEhHpwgBIREZpaGiAXC5XXbJtz7Rp01BQUKB6blx7zR+tTZo0Sa0ZJDc3FwEBAfD399drf2s5A7ho0SJe/iWidjEAEpFRCgoKtHaVaiISibB27Vq89dZbADQ3fzg4OGDHjh3YsWMHHBwc2uyvbAYRBAEpKSlYvXq13se3t7eHo6Mj16smIgIDIBEZSd/7/1qKiIiAVCrFzz//rHHlD3t7eyxatAiLFi1q89Bh4N7KIAcOHEBkZKTeZw+VrK0bmIhIGwZAIjJKfn4+QkNDDd4vPj4ezz//vF7NH615eXnB3t4e7777LlauXGnwsadOncr7AImIwKXgiMgIlZWVEIvFRj1SZejQobh06ZLGy8eNjY348ccfAQCPPvqoxvn9/f1RUVGh972HLQUFBWldD5eIyJrwDCARGSwnJ6fN5Vt9Xb9+HaNGjcIHH3zQ5j25XI7HH38cjz/+uMYHR8vlcpw4cQI1NTVGrS4hEong7e0NmUxmVO1ERD0FAyARGcyY+/+UPv30U7zyyivw8/NDXl6eQftu3boVS5YswfTp07WuDNIePg6GiIgBkIiMIJFIEBgYaPB+jY2NquaPNWvWICUlBfouRlRRUYH09HTMmTNH1QxiDAZAIiIGQCIykFQqha+vr8ENHID6yh+enp4IDw9Henq6XvumpqZi1apVsLGx0boyiD58fX0hk8n0Dp5ERD0RAyARGSQzMxMxMTFG7dt65Y+4uDhs2rSp3fv5SktLcfLkScTGxqq2aVoZRF9BQUGQSCRG7UtE1BMwABKRQTIzMzFlyhSD99O08oerqytmzJiBPXv26Nw3OTkZ69atUzvr2HplEEPwMjARWTsGQOpxtm/fjvvvvx8KhUJt+5NPPomFCxdaqKqeQRAE3Lx5Ez4+Pgbvq2nlDwBYtmwZ0tLSNHb9AsCVK1cgk8kQHh6utr3lyiCG4gOhicjaMQBSj/P000/j9u3byMrKUm0rKyvDjz/+iHnz5lmwsu5PIpEgODjY4P1aNn+05uDggMWLF2P79u1wcHDAhx9+iA8//FC1FFxiYiISEhI0zmtsM4ibmxtqa2vR2Nho8L5ERD0BAyD1OL1790ZsbKzaZcWvvvoKvXv3NurSJd1j7ONfWjZ/aDJ37lwcOHAAdXV1WL58OZYvXw57e3sUFhbCzs4OISEhGvfrSDNIWFgY8vPzDd6PiKgnYACkHmnevHn4+uuvVZcVd+/ejTlz5sDW1tbClXVv2dnZmDhxosH7tW7+aM3GxgZxcXHYsGGD2vakpCTEx8frnNvYZhDeB0hE1owBkHqkJ554AgqFAunp6bh+/Tpyc3Pxxz/+0dJldWsNDQ2Qy+UGL8GmqflDk2nTpiE/Px/ffPMNjhw5giNHjiAgIAD+/v469zO2GYRnAInImnEtYOqRxGIxfve732H37t34+eefMWTIEIwdO9bSZXVrBQUFGtfvbY+25o/WRCIR/vznP6su0z/yyCPYvXu3Xvspm0Eef/xxveuyt7eHo6MjqqqqjFpXmIioO+MZQOqx5s2bh/T0dHz66ac8+2cCxtz/p6v5Q5Px48erfdzeWUMlY5tB2A1MRNaKAZB6rMmTJ6N3794oLi7GM888Y+lyur38/HyEhoYatE97zR+6LF++XO+xxjaDTJ06lfcBEpFVYgCkHsvW1hY3btyAIAgYNGiQpcvp1iorKyEWi2FnZ9hdI+01f+hSUlJi0HhjmkGCgoJQVFRk0D5ERD0BAyARtSsnJ0fvy7hK+jZ/tNTyYdBvv/22QcczphlEJBLB29sbMpnMoGMREXV3DIBE1C5j7v/Tt/mjpY8//lj1cf/+/ZGXl6f3vsauDMLHwRCRNWIAJKJ2SSQSBAYG6j3e0OYPAKioqMAPP/yg+vzVV19FSkoKBEHQew5jmkEYAInIGvExMESkk1QqhY+Pj0GNHMY0f6SmpmLlypWYNm0aAMDX1xfh4eFIT0/X+/EuLZtB+vfvr9c+vr6+kMlkEATBqGYVIqLuiGcAiUinzMxMxMTEGLSPoc0fpaWlOHnyJJ544gm89tpreO211+Dg4IC4uDhs2rTJoPv6jG0GkUgkBu1DRNSdMQASkU6GBkBjmj+Sk5Oxbt26NmfgXF1dMWPGDLV1ndtjTDMILwMTkbVhACQirQRBwM2bN+Hj46P3PoY2f1y5cgUymQzh4eFoampCQUEBCgoKVAFu2bJlSEtLU+sQ1sWYZhA+EJqIrA0DIBFpJZFIEBwcrPd4Y5o/EhMTkZCQAACoq6tDWFgYwsLCUFdXBwBwcHDA4sWLsX37dr3nNLQZxM3NDbW1tWhsbNR7HyKi7owBkIi0MvTxL4Y2fxQWFsLOzg4hISE6x82dOxcHDhxAZWWlXvMaszJIWFgY8vPz9R5PRNSdMQASkVbZ2dmYOHGi3uMNbf5ISkpCfHx8u+NsbGwQFxeHDRs26D23oc0gXBaOiKwJAyARadTQ0AC5XA5XV1e9xhva/JGbm4uAgAD4+/vrNX7atGkoKChAaWmpXuMNbQYJDQ3lGUAishoMgESkUUFBAcLCwvQeb0jzhyAISElJwerVq/WeXyQSYc2aNUhOTtZ7vCHNIPb29nB0dERVVZXeNRERdVcMgESkkSH3/xna/HHgwAFERkYa9KgYAIiMjIRUKkVJSYle4w1tBmE3MBFZCwZAItIoPz8foaGheo01pPmjqakJmzdvxsqVK42qKyEhAYmJiXqNNbQZhPcBEpG1YAAkojYqKyshFothZ6ffapGGNH98/vnnmDVrlsZ7C+3t7ZGQkICEhATY29tr3H/o0KEQiUQ4e/asXsczpBkkKCgIRUVFeo0lIurOGACJqI2cnBy9L+ca0vwhl8vx2WefYenSpRrfd3BwwPr167F+/Xo4ODhonSchIQFJSUl61WdIM4hIJIK3tzdkMplecxMRdVcMgETUhiH3/xnS/LF161YsWbJEZ7jTR0BAAPz8/JCXl9fuWEObQbgsHBFZAwZAImpDIpEgMDCw3XGGNH9UVFQgPT0dc+bM0TpGoVDg/PnzOH/+PBQKhc751qxZg5SUFAiC0O6xDWkGYQAkImvAAEhEaqRSKXx8fPRq6DCk+SM1NRWrVq2CjY32Hzu1tbUYNmwYhg0bhtraWp3zeXp6Ijw8HOnp6e0e25BmEF9fX8hkMr2CJRFRd8UASERqMjMzERMTo9dYfZs/SktLcfLkScTGxnawOnVxcXHYtGmTXvf3GdoMIpFIOloeEVGXxQBIRGr0DYCGNH8kJydj3bp1eq8RrC9XV1fMmDEDe/bsaXesIc0gvAxMRD0dAyARqQiCgJs3b8LHx6fdsfo2f1y5cgUymQzh4eGmKLGNZcuWIS0tDXK5XOc4Q5pB+EBoIurpGACJSEUikSA4OLjdcYY0fyQmJiIhIcEU5Wnk4OCAxYsXY/v27e2OXbhwoV7NIG5ubqitrUVjY6MJKiQi6noYAIlIRd/Hv+jb/FFYWAg7OzuEhISYqkSN5s6diwMHDqCyslLnuL59++rdDBIWFob8/HxTlUhE1KUwABKRSnZ2NiZOnNjuOH2bP5KSkhAfH2+CynSzsbFBXFwcUlNT2x2rbzMIl4Ujop6MAZCIAAANDQ2Qy+Ual2hrSd/mj9zcXAQEBMDf31/vGuzt7fHqq6/i1Vdf1boUnDbTpk1DQUEBSktLdY7TtxkkNDSUZwCJqMdiACQiAEBBQQHCwsLaHadP84cgCEhJScHq1asNqsHBwQHvvvsu3n33XYNXCxGJRFi7di2Sk5PbHadPM4i9vT0cHR1RVVVlUB1ERN0BAyARAdDv/j99mz8OHjyIyMhIvR4RY0qRkZGQSqUoKSnROU7fZhB2AxNRT8UASAYrKSnBkiVLMHDgQIjFYjzwwANISEhAfX29pUujDsjPz0doaKjOMfo0fzQ1NWHz5s1YuXKlwTUoFAqUlJSgpKSk3aXgtElISEBiYqLOMfo2g/A+QCLqqRgAyWASiQQKhQLbt2/H+fPn8f7772Pbtm1Ys2aNpUsjI1VWVkIsFsPOzk7nOH2aPz7//HPMnDmz3XsJNamtrcXAgQMxcODAdpeC02bo0KEQiUQ4e/asznH6NIMEBQWhqKjIqDqIiLoyBkAyWGxsLHbs2IFHHnkEgwYNwpNPPolXX30V//rXvyxdGhkpJyen3cu6+jR/yOVyfPbZZ1i6dKmpSzSIPmcB9WkGEYlE8Pb2hkwmM3WJREQWxQBIJlFeXo7evXvrHCOXy1FRUaH2oq5Bn/v/9Gn+2Lp1K5YsWWJwA4epBQQEwM/PD3l5eVrH6NsMwmXhiKgnYgCkDrt06RI++OADPP/88zrHpaSkwMPDQ/Xy8/PrpAqpPRKJBIGBgVrf16f5o6KiAunp6ZgzZ445SjTY2rVrkZKSAkEQtI7RpxmEAZCIeiIGQFJZv349RCKRzteJEyfU9rlx4wZiY2Px9NNPt3t2aPXq1SgvL1e9rl+/bs4vh/QklUrh4+Ojs7FDn+aP1NRUrFq1CjY2XePHiqenJ8LDw5Genq51jD7NIL6+vpDJZDqDJBFRd6P7jm+yKitWrGj37M2AAQNUH9+4cQOTJk1CREQE/v73v7c7v6OjIxwdHTtaJplYZmYmYmJidI5JS0vDtm3btL5fWlqKkydPYv369SaurmPi4uIwa9YsTJs2Dba2thrHKJtBdK1XHBQUpPc6yURE3QEDIKl4enrq/dy2X3/9FZMmTcLYsWOxY8eOLnPWhwyXmZmJv/3tb1rf16f5Izk5GevWrWt3beDO5urqihkzZmDPnj2YP3++xjGTJk1CcnIympqatIZE5WVgBkAi6in4W5sMduPGDURHR8PPzw/vvfcebt26BZlMxk7JbkgQBNy8eRM+Pj5ax7TX/HHlyhXIZDKEh4d3uB47Ozu8+OKLePHFF9t9JI2+li1bhrS0NMjlco3v69MMwgdCE1FPwwBIBvv3v/+Nn3/+GYcPH0b//v3h6+urelH30t5lTX2aPxITE3VePjWEo6MjtmzZgi1btpjsdgEHBwcsXrwY27dv1zqmvWYQNzc31NbWorGx0SQ1ERFZGgMgGWzRokUQBEHji7qXjIwMnff/tdf8UVhYCDs7O4SEhJirRJOYO3cuDhw4gMrKSo3v69MMEhYWhvz8fHOVSETUqRgAiaxYdna2zrN77a38kZSUhPj4eJPVIwgCbt26hVu3bpn0HxQ2NjaIi4tDamqq1jHtrQzCZeGIqCdhACSyUg0NDZDL5VqXbGuv+SM3NxcBAQHw9/c3WU01NTXo27cv+vbti5qaGpPNCwDTpk1DQUEBSktLNb7f3sogoaGhPANIRD0GAyCRlSooKEBYWJjW93U1fwiCgJSUFKxevdpc5ZmcSCTC2rVrkZycrPV9Xc0g9vb2cHR0RFVVlTnLJCLqFAyARFZK1/Jv7TV/HDx4EJGRkXo/NqiriIyMhFQqRUlJicb322sGYTcwEfUUDIBEVio/Px+hoaEa39PV/NHU1ITNmzdj5cqVZq7QPBISEpCYmKjxvfaaQXgfIBH1FAyARFaosrISYrFY67P2dDV/fP7555g5c6bWewe7uqFDh0IkEuHs2bMa39fVDBIUFISioiJzlkdE1CkYAImsUE5OjtbLu7qaP+RyOT777DMsXbrU3CWala6zgLqaQUQiEby9vfnQcyLq9hgAiayQrvv/dDV/bN26FUuWLIGDg4M5yzO7gIAA+Pn5IS8vr8177TWDKJeFIyLqzhgAiayQRCJBYGBgm+26mj8qKiqQnp6OOXPmmK0uOzs7LFy4EAsXLjTZUnDarFmzBm+99ZbG5w3qagZhACSinoABkMjKSKVS+Pj4aGzw0NX8kZqailWrVsHGxnw/NhwdHZGWloa0tDSTLQWnjZeXF8LDw5Gent7mPV3NIL6+vpDJZFz5hoi6NQZAIiuTmZmpdfk3bc0fpaWlOHnyJGJjY81cXedatWoVNm7cqPF+v/aaQSQSibnLIyIyGwZAIiujLQDqav5ITk7GunXrtK4JbCqCIKC6uhrV1dWdcobN1dUVM2bMwJ49e9q8p6sZhI+DIaLujgGQyIoIgoCbN2/Cx8enzXvamj+uXLkCmUyG8PBws9dXU1MDV1dXuLq6mnwpOG3+9Kc/IS0tDXK5XG27rmaQiRMn8oHQRNStMQASWRGJRILg4OA223U1fyQmJiIhIaEzyrMIBwcHLF68GNu2bWvznrZmEDc3N9TW1qKxsbETKiQiMj0GQCIrkpGRofHyr7bmj8LCQtjZ2SEkJKSzSrSIuXPn4uDBg6isrFTbrqsZJCwsDPn5+Z1VIhGRSTEAElmR7OxsjWf5tDV/JCUlIT4+vhMqsywbGxvExcUhNTW1zXvamkF4HyARdWcMgERWoqGhAXK5vM0SbtqaP3JzcxEQEAB/f//OLNNipk2bhoKCApSWlqpt19YMEhoayjOARNRtMQASWYmCggKEhYW12a6p+UMQBKSkpGD16tWdVZ7FiUQirF27FsnJyW22a2oGsbe3h6OjI6qqqjqzTCIik2AAJLISmpZ/09b8cfDgQURGRmp8JExPFhkZCalUipKSErXt2ppBoqKi2A1MRN0SAyCRlcjPz0doaKjaNk3NH01NTdi8eTNWrlzZyRUCtra2eOqpp/DUU0/B1ta2048PAAkJCUhMTFTbpq0ZhPcBElF3xQBIZAUqKyshFovbrK+rqflj9+7dmDlzZpt7BTuDk5MTvvrqK3z11VdwcnLq9OMDwNChQyESiXD27Fm17ZqaQYKCglBUVNSZ5RERmQQDIJEVyMnJaXOZV1Pzh1wux86dO7F06dLOLrFL0XQWMDo6uk0ziEgkgre3N2QyWWeXSETUIQyARFZA0/1/mpo/tm7diiVLlsDBwaEzy+tyAgIC4Ofnh7y8PNU2Gxsbjc0gMTExvAxMRN0OAyCRFZBIJAgMDFR9rqn5o6KiAunp6ZgzZ44lSgQAVFdXQyQSQSQSobq62mJ1AMCaNWvw1ltvqa1JrKkZhAGQiLojBkCiHk4qlcLHx0et0UNT80dqaipWrVoFGxv+WAAALy8vhIeHIz09XbVNUzOIr68vZDKZWlAkIurq+JOeqIfLzMxss/xb6+aP0tJSnDx5ErGxsZ1cXde2atUqbNy4Ue2+P23NIBKJpLPLIyIyGgMgUQ/XOgBqav5ITk7GunXr2qwFbO1cXV0xY8YM7NmzR7VNUzMIHwdDRN0NAyBRDyYIAm7evAkfHx/VttbNH1euXIFMJkN4eLglSuzy/vSnP2HHjh2Qy+UANDeDTJw4kQ+EJqJuhQGQqAeTSCQIDg5Wfa6p+SMxMREJCQmWKK9bcHBwwOLFi7Ft2zbVttbNIG5ubqitrUVjY6MFKiQiMhwDIFEPlpGRoXb5t3XzR2FhIezs7BASEmKpEruFZ555BgcPHkRlZSUAzc0gYWFhyM/Pt1SJREQGYQAk6sGys7PVzva1bv5ISkpCfHy8BSrTzNbWFtOnT8f06dMtthScJjY2NoiLi0NqaqpqW+tmEN4HSETdCQMgUQ/V0NAAuVyuWtKtdfNHbm4uAgIC4O/vb8ky1Tg5OSE9PR3p6ekWWwpOm2nTpqGgoAClpaUA2jaDhIaG8gwgEXUbDIBEPVRBQQHCwsJUn7ds/hAEASkpKVi9erWlyut2RCIR1q5di+TkZABtm0Hs7e3h6OiIqqoqS5ZJRKQXBkCiHqrl/X+tmz8OHjyIyMhItUfBUPsiIyMhlUpRUlICoG0zSFRUFLuBiahbYAAk6qHy8/NVZwBbNn80NTVh8+bNWLlypWUL1KC6uhouLi5wcXGx+FJw2iQkJCAxMRFA22YQ3gdIRN0FAyBRD1RZWQmxWAw7OzsA6s0fu3fvxsyZM1X3BnY1NTU1qKmpsXQZWg0dOhQikQhnz54FoN4MEhQUhKKiIkuWR0SkFwZAoh4oJydHdbm3ZfOHXC7Hzp07sXTpUgtX2L21PAvYshlEJBLB29sbMpnMwhUSEenGAEjUA2VkZGDq1KkA1Js/tm3bhiVLlsDBwcGS5XV7AQEB8PPzQ15eXptmkJiYGF4GJqIujwGQqAeSSCQIDAxUa/6oqKhAeno65syZY+nyeoQ1a9bgrbfegiAIas0gDIBE1B0wABL1MFKpFD4+PhCJRGrNH6mpqYiLi4ONDf/am4KXlxfCw8ORnp6u1gzi6+sLmUwGQRAsXSIRkVb8TUDUw2RmZqoe/6Js/igtLcXJkycRGxtr4ep6llWrVmHjxo1oampq0wwikUgsXB0RkXYMgEQ9jDIAtmz+SE5Oxrp161RrAHdVNjY2iIqKQlRUVLc4U+nq6ooZM2Zg9+7das0gfBwMEXV1Xf8nLBHpTRAE3Lx5Ez4+PqrmjytXrkAmkyE8PNzS5bVLLBbjyJEjOHLkCMRisaXL0cuf/vQnpKWloaGhQdUMMnHiRD4Qmoi6NAZAoh5EIpEgODhYrfkjMTERCQkJli6tx3JwcMDixYuxbds2VTOIm5sbamtr0djYaOnyiIg0YgAk6kGUy78pmz/Onj0LOzs7hISEWLq0Hu2ZZ57BgQMHIBaLVc0gYWFhyM/Pt3RpREQaMQAS9SDZ2dmIiopSNX8kJSUhPj7e0mXprbq6Gl5eXvDy8uqyS8FpYmNjg7i4OKSmpqqaQXgfIBF1ZQyARD1EQ0MD5HI5ysrK4OTkhKKiIgQEBMDf39/SpRnk9u3buH37tqXLMNj06dNRUFCAkJAQ5OTkYMyYMTwDSERdlp2lCyAi0ygoKEBYWBg+/fRTLFmyBCkpKfjss88sXZbVEIlEWLt2LVJSUhAbG4vMzEw4Ojqiqqqqy667TETWi2cAiXqIjIwMREdHIzc3F5WVlYiMjISnp6ely7IqkZGRkEqlmDRpEtLS0hAVFcVuYCLqkhgAiXqI/Px8lJWV4ZFHHsEHH3yAlStXWrokq5SQkIAtW7bA0dERw4cP532ARNQlMQAS9QCVlZUQi8XYtWsXXFxcMHPmTF52tJChQ4dCJBJh0qRJyM7ORlFRkaVLIiJqgwGQqAfIycnBiBEjYG9vj3/9619YunSppUuyagkJCfj++++Rm5sLLy8vyGQyS5dERKSGAZC6hTt37kAQBLVtCoUCd+/etVBFXUtGRgZu3bqFPn36YMmSJXBwcLB0SUaxsbHBuHHjMG7cuG6xFJw2yu7rwMBAeHl58TIwEXU53fcnLFmVoKAgfPDBB2rbXn/9dUydOtVCFXUtFy5cwNmzZ/Hf//4Xc+bMsXQ5RhOLxSgoKEBBQUG3WQpOmzVr1uC///0viouLGQCJqMthAKRuYcaMGXjrrbdQV1cHACgtLcWWLVswc+ZMyxbWBUilUjQ1NcHe3h5xcXHd+sxZT+Ll5YWJEyeiuroaJSUlbc5gaxIdHd2jm3dKSkogEolw5swZS5dCZPX4m4K6hTVr1uDOnTs4cOAAAGD79u1wcnLCyy+/bOHKLC8zMxN3796FSCRCbGyspcuhFlatWoXKykrU1tZCIpG0O/5f//oX/vrXv3ZCZURk7RgAyShPPvkk/P394eTkBF9fX8yfPx83btww2/EGDRqEhQsXYu/evQCAf/zjH1i1ahU8PDzMdszu4ttvv0VlZSWSkpIgEoksXU6H1NTUYMCAARgwYABqamosXU6Hubq6YuHChZBKpfj3v//d7vjevXvDzc2tEyojImvHAEhGmTRpEr788ksUFxfj66+/xqVLl/DUU0+Z9Zhr1qxBRUUFAMDR0ZFn/wAIgoCCggL4+fkhPDzc0uV0mCAIuHr1Kq5evarXJdOu5uOPP8YTTzyBvLw81bbnn38ednZ2qn+86NL6EvCAAQPw//7f/8OCBQvg6uqKgIAAfPvtt7h16xZmzJgBV1dXDB8+HCdOnFDtc+fOHcydOxf9+/eHs7Mzhg8fjn/84x9qx6msrMS8efPg4uICX19fvP/++22OXV9fj9dffx33338/XFxcMH78eBw5ckRn/SKRCFu3bsW0adMgFosxcOBAfPXVV1rHNzU1YcmSJRg4cCDEYjECAwOxadMmtTGLFi3CzJkz8d5778HX1xd9+vTB8uXL0dDQ0KFaiawdAyAZJS4uDuHh4QgICEBkZCT+8pe/4NixY2o/lE1t0KBBePTRRwEAixcv5tk/AOfOncPt27fx4YcfWroUAjBmzBhcu3YNDz/8MKZOnYqffvoJDg4OePXVV3H+/Hk0NjYaPOf777+Phx56CKdPn8Zjjz2G+fPnY8GCBfjjH/+IU6dOYfDgwViwYIEqMNfV1WHs2LE4ePAgzp07h2XLlmH+/Pk4fvy4as5Vq1bhp59+wv79+5GRkYHc3FycOnVK7bjPPvssfvrpJ+zduxeFhYV4+umnERsbi4sXL+qs980338Tvf/97/O///i/++Mc/Yu7cuVqfhahQKNC/f398+eWXuHDhAuLj47FmzRp8+eWXauOysrJw6dIlZGVlYefOnUhLS0NaWlqHayWyZiKhO/4zm7qUu3fv4oUXXsCvv/6qduajPRUVFfDw8EB5eTnc3d312ufs2bP4wx/+gOzsbHh5eRlbco8xY8YMnDt3Dj/99JOlSzGJmpoaPPDAAwCAS5cuwdnZ2cIVGU6hUOD7779HamoqioqKMHHiRLzxxhuYPXs2/ud//gdz587Vum90dDRGjRqFjRs3Amg+A/jwww9j165dAACZTAZfX1+8+eabSEpKAgAcO3YMERERkEql8PHx0TjvY489huDgYLz33nuorKxEnz59sGfPHtVZ+/LycvTr1w9Lly7Fxo0bcenSJTz44IP45Zdf0K9fP9U8MTExCAsLw1tvvaXxOCKRCM8//zy2bt2q2hYeHo4xY8bgo48+QklJCQYOHIjTp09j1KhRGudYvnw5bt68iX/+858Ams8AHjlyBJcuXYKtrS0AYPbs2bCxscHevXuNrrW7M+bnJ1FLdpYugLqvN954Ax9++CFqamoQHh6OgwcP6hwvl8shl8tVnysv5xpi+PDhuHDhgsH79VQHDhyAIAjw9fW1dCkmpwyC3V1OTg5ycnIQGxuLlJQUnQFQkxEjRqg+9vb2BtD896D1ttLSUvj4+KCpqQlvv/02vvjiC/z666+qv3cuLi4AgMuXL6OhoQFhYWGqOTw8PBAYGKj6/NSpUxAEAUOGDFGrRS6Xo0+fPjrrjYiIaPO5rq7fbdu24eOPP8bVq1dRW1uL+vr6NuFw6NChqvAHAL6+vjh79myHayWyZgyApLJ+/XokJibqHFNQUIBx48YBAF577TUsWbIEV69eRWJiIhYsWICDBw9qbURISUlpd34yzIkTJyCVSi1dBrVy48YNfPnllzh8+DB69eqFZ555Bhs2bDDqET329vaqj5V/tzRtUygUAIDU1FS8//772LhxI4YPHw4XFxesXLkS9fX1AKC6VNz672nLi0EKhQK2trY4efKkWvACYNQSg9p+Jnz55ZeIi4tDamoqIiIi4ObmhnfffVftcnXrr1c5n/LrNXWtRNaCAZBUVqxY0e5DhAcMGKD62NPTE56enhgyZAiCg4Ph5+enuhylyerVq7Fq1SrV5xUVFfDz8zNJ7dZqzJgxli6BWrhx4wbWrl2LXbt2oW/fvnj//fexdOnSTn2odW5uLmbMmIE//vGPAJoD0sWLFxEcHAyg+cyqvb098vPzVX//KioqcPHiRURFRQEARo8ejaamJpSWluLhhx826PjHjh3DggUL1D4fPXq01lojIyPx4osvqrZdunTJoON1pFYia8YASCrKQGcM5dmDlpd4W3N0dISjo6NR8xN1B59++in+/e9/Y8OGDZ0e/JQGDx6Mr7/+GkePHsV9992HDRs2QCaTqQKgm5sbFi5ciNdeew29e/dG3759kZCQABsbG9WZuiFDhmDevHlYsGABUlNTMXr0aNy+fRuHDx/G8OHDMX36dK3H/+qrrzBu3DhMmDABu3fvRn5+Pj755BOttX722Wf48ccfMXDgQOzatQsFBQUYOHCg3l9vR2olsmbsAiaD5efn48MPP8SZM2dw9epVZGVl4ZlnnsEDDzyg9ewfkTVYt24dfv31V7z88ssWW8ruzTffxJgxY/Doo48iOjoaPj4+bVbM2bBhAyIiIvD4448jJiYGDz30EIKDg+Hk5KQas2PHDixYsAB//vOfERgYiCeffBLHjx9v96x9YmIi9u7dixEjRmDnzp3YvXs3QkJCNI59/vnn8bvf/Q5/+MMfMH78eNy5c0ftbKC+jK2VyJqxC5gMdvbsWbzyyiv43//9X1RXV8PX1xexsbFYt24d7r//fr3nYRcbUddQXV2N+++/H6mpqViyZInR84hEInzzzTdcorET8OcndRQvAZPBhg8fjsOHD1u6DCIy0unTpyGRSBAWFoby8nLVI2VmzJhh4cqIqLMwABIRWaH33nsPxcXFcHBwwNixY5Gbm2v0PcBE1P0wABIRWZnRo0fj5MmTJp+XdxQRdR9sAiEiIiKyMgyARERERFaGAZCIiIjIyjAAEhEREVkZBkAiIiIiK8MASERERGRlGACJiIiIrAwDIBEREZGVYQAkIiIisjIMgERERERWhgGQiIiIyMowABIRERFZGQZAIiIiIivDAEhERERkZRgAiYiIiKwMAyARERGRlWEAJCIiIrIyDIBEREREVoYBkIiIiMjKMAASERERWRkGQCIiIiIrwwBIREREZGUYAImIiIisDAMgERERkZWxs3QBZL0EQQAAVFRUWLgSIqLuRflzU/lzlMhQDIBkMXfu3AEA+Pn5WbgSIqLu6c6dO/Dw8LB0GdQNMQCSxfTu3RsAcO3aNav/AVZRUQE/Pz9cv34d7u7uli7Hovi9UMfvxz38XtxTXl4Of39/1c9RIkMxAJLF2Ng034Lq4eFh9T/Mldzd3fm9+D/8Xqjj9+Mefi/uUf4cJTIU/88hIiIisjIMgERERERWhgGQLMbR0REJCQlwdHS0dCkWx+/FPfxeqOP34x5+L+7h94I6SiSwh5yIiIjIqvAMIBEREZGVYQAkIiIisjIMgERERERWhgGQiIiIyMowAJLFlZSUYMmSJRg4cCDEYjEeeOABJCQkoL6+3tKlWURycjIiIyPh7OyMXr16WbqcTvfRRx9h4MCBcHJywtixY5Gbm2vpkiwiJycHTzzxBPr16weRSIR9+/ZZuiSLSElJQWhoKNzc3NC3b1/MnDkTxcXFli7LYrZu3YoRI0aoHoYdERGB77//3tJlUTfEAEgWJ5FIoFAosH37dpw/fx7vv/8+tm3bhjVr1li6NIuor6/H008/jRdeeMHSpXS6L774AitXrsTatWtx+vRpPPzww5g2bRquXbtm6dI6XXV1NUaOHIkPP/zQ0qVYVHZ2NpYvX45jx44hIyMDjY2NeOSRR1BdXW3p0iyif//+ePvtt3HixAmcOHECkydPxowZM3D+/HlLl0bdDB8DQ13Su+++i61bt+Ly5cuWLsVi0tLSsHLlSvz222+WLqXTjB8/HmPGjMHWrVtV24KDgzFz5kykpKRYsDLLEolE+OabbzBz5kxLl2Jxt27dQt++fZGdnY2JEydaupwuoXfv3nj33XexZMkSS5dC3QjPAFKXVF5ezkXOrUx9fT1OnjyJRx55RG37I488gqNHj1qoKupqysvLAYA/HwA0NTVh7969qK6uRkREhKXLoW7GztIFELV26dIlfPDBB0hNTbV0KdSJbt++jaamJnh7e6tt9/b2hkwms1BV1JUIgoBVq1ZhwoQJGDZsmKXLsZizZ88iIiICdXV1cHV1xTfffIOQkBBLl0XdDM8AktmsX78eIpFI5+vEiRNq+9y4cQOxsbF4+umn8dxzz1moctMz5nthrUQikdrngiC02UbWacWKFSgsLMQ//vEPS5diUYGBgThz5gyOHTuGF154AQsXLsSFCxcsXRZ1MzwDSGazYsUKzJkzR+eYAQMGqD6+ceMGJk2ahIiICPz97383c3Wdy9DvhTXy9PSEra1tm7N9paWlbc4KkvV56aWXsH//fuTk5KB///6WLseiHBwcMHjwYADAuHHjUFBQgE2bNmH79u0Wroy6EwZAMhtPT094enrqNfbXX3/FpEmTMHbsWOzYsQM2Nj3r5LQh3wtr5eDggLFjxyIjIwOzZs1Sbc/IyMCMGTMsWBlZkiAIeOmll/DNN9/gyJEjGDhwoKVL6nIEQYBcLrd0GdTNMACSxd24cQPR0dHw9/fHe++9h1u3bqne8/HxsWBllnHt2jXcvXsX165dQ1NTE86cOQMAGDx4MFxdXS1bnJmtWrUK8+fPx7hx41Rngq9du4bnn3/e0qV1uqqqKvz888+qz69cuYIzZ86gd+/e8Pf3t2BlnWv58uXYs2cPvv32W7i5uanOEHt4eEAsFlu4us63Zs0aTJs2DX5+fqisrMTevXtx5MgR/PDDD5YujbobgcjCduzYIQDQ+LJGCxcu1Pi9yMrKsnRpnWLLli1CQECA4ODgIIwZM0bIzs62dEkWkZWVpfH/g4ULF1q6tE6l7WfDjh07LF2aRSxevFj198PLy0uYMmWK8O9//9vSZVE3xOcAEhEREVmZnnWjFRERERG1iwGQiIiIyMowABIRERFZGQZAIiIiIivDAEhERERkZRgAiYiIiKwMAyARERGRlWEAJCIiIrIyDIBEREREVoYBkIiIiMjKMAASERERWRkGQCIiIiIrwwBIREREZGUYAImIiIisDAMgERERkZVhACQiIiKyMgyARERERFaGAZCIiIjIyjAAEhEREVkZBkAiIiIiK8MASERERGRlGACJiIiIrAwDIBEREZGVYQAkIiIisjIMgERERERWhgGQiIiIyMowABIRERFZGQZAIiIiIivDAEhERERkZRgAiYiIiKwMAyARERGRlfn/aJl5njqFgkoAAAAASUVORK5CYII=",
      "text/html": [
       "\n",
       "            <div style=\"display: inline-block;\">\n",
       "                <div class=\"jupyter-widgets widget-label\" style=\"text-align: center;\">\n",
       "                    Figure\n",
       "                </div>\n",
       "                <img src='data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAoAAAAHgCAYAAAA10dzkAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjguMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8g+/7EAAAACXBIWXMAAA9hAAAPYQGoP6dpAAB2RklEQVR4nO3deVxU9f4/8NewD6spCJiAmsnivoBAJqhYaIt6b3k1r0ua3kor8bZcl0C4P6JbYWqZer+VmOm1ut1MpeWCIkteBbcvLgzXVNRyRlyInWGZ8/uD74wMzAwzwwwDzOv5eMxDOPM5n/OGEl6ec97nIxIEQQARERERWQ0bSxdARERERJ2LAZCIiIjIyjAAEhEREVkZBkAiIiIiK8MASERERGRlGACJiIiIrAwDIBEREZGVYQAkIiIisjIMgERERERWhgGQiIiIyMowABIRERFZGQZAIiIiIivDAEhERERkZRgAiYiIiKwMAyARERGRlWEAJCIiIrIyDIBEREREVoYBkIiIiMjKMAASERERWRkGQCIiIiIrwwBIREREZGUYAImIiIisDAMgERERkZVhACQiIiKyMgyARERERFaGAZCIiIjIyjAAEhEREVkZBkAiIiIiK8MASERERGRlGACJiIiIrAwDIBEREZGVYQAkIiIisjIMgERERERWhgGQiIiIyMowABIRERFZGQZAIiIiIivDAEhERERkZRgAiYiIiKwMAyARERGRlWEAJCIiIrIyDIBEREREVoYBkIiIiMjKMAASERERWRkGQCIiIiIrwwBIREREZGUYAImIiIisDAMgERERkZVhACQiIiKyMgyARERERFaGAZCIiIjIyjAAEhEREVkZBkAiIiIiK8MASEZJSUlBaGgo3Nzc0LdvX8ycORPFxcWWLouIiIj0wABIRsnOzsby5ctx7NgxZGRkoLGxEY888giqq6stXRoRERG1QyQIgmDpIqj7u3XrFvr27Yvs7GxMnDjR0uUQERGRDjwDSCZRXl4OAOjdu7eFKyEiIqL28AwgdZggCJgxYwbKysqQm5urdZxcLodcLld9rlAocPfuXfTp0wcikagzSiUi6hEEQUBlZSX69esHGxueyyHD2Vm6AOr+VqxYgcLCQuTl5ekcl5KSgsTExE6qioio57t+/Tr69+9v6TKoG+IZQOqQl156Cfv27UNOTg4GDhyoc2zrM4Dl5eXw9/fH9evX4e7ubu5SiYh6jIqKCvj5+eG3336Dh4eHpcuhbohnAMkogiDgpZdewjfffIMjR460G/4AwNHREY6Ojm22u7u7MwASERmBt8+QsRgAySjLly/Hnj178O2338LNzQ0ymQwA4OHhAbFYbOHqiIiISBdeAiajaPtX544dO7Bo0SK95qioqICHhwfKy8t5BpCIyAD8+UkdxTOAZBT+u4GIiKj7Yu84ERERkZVhACQiIiKyMgyARERERFaGAZCIiIjIyjAAEhEREVkZBkAiIiIiK8MASERERGRlGACJiIiIrAwDIBEREZGVYQAkIiIisjIMgERERERWhgGQiIiIyMowABIRERFZGQZAIiIiIivDAEhERERkZRgAiYiIiKwMAyARERGRlWEAJCIiIrIyDIBEREREVoYBkIiIiMjKMAASEXXAkSNHIBKJ8Ntvv3VojKWsX78eo0aNsnQZRNTJGACJiMwsMjISUqkUHh4eJpmvKwdKIuoe7CxdABFRT+fg4AAfHx9Ll0FEpMIzgETUIYIg4MKFC1AoFJYuxSzkcjlefvll9O3bF05OTpgwYQIKCgrajPvpp58wcuRIODk5Yfz48Th79qzqPU1n7I4ePYqJEydCLBbDz88PL7/8Mqqrq9WO+/rrr8PPzw+Ojo548MEH8cknn6CkpASTJk0CANx3330QiURYtGiRxtrT0tLQq1cv7Nu3D0OGDIGTkxOmTp2K69eva/16CwoKMHXqVHh6esLDwwNRUVE4deqU2hiRSISPP/4Ys2bNgrOzMx588EHs379fbcyFCxcwffp0uLq6wtvbG/Pnz8ft27e1HpeIOhcDIBEZRRAEpKenIywsDEOHDsWFCxcsXZJZvP766/j666+xc+dOnDp1CoMHD8ajjz6Ku3fvqo177bXX8N5776GgoAB9+/bFk08+iYaGBo1znj17Fo8++ih+97vfobCwEF988QXy8vKwYsUK1ZgFCxZg79692Lx5M4qKirBt2za4urrCz88PX3/9NQCguLgYUqkUmzZt0lp/TU0NkpOTsXPnTvz000+oqKjAnDlztI6vrKzEwoULkZubi2PHjuHBBx/E9OnTUVlZqTYuMTERs2fPRmFhIaZPn4558+apvidSqRRRUVEYNWoUTpw4gR9++AE3b97E7NmzdX+ziajzCEQWUl5eLgAQysvLLV0KGUChUAgHDx4Uxo0bJwAQJkyYIGRmZlq6LLOoqqoS7O3thd27d6u21dfXC/369RPeeecdQRAEISsrSwAg7N27VzXmzp07glgsFr744gu1MWVlZYIgCML8+fOFZcuWqR0rNzdXsLGxEWpra4Xi4mIBgJCRkaGxrtbzabNjxw4BgHDs2DHVtqKiIgGAcPz4cUEQBCEhIUEYOXKk1jkaGxsFNzc34cCBA6ptAIR169apPq+qqhJEIpHw/fffC4IgCG+++abwyCOPqM1z/fp1AYBQXFyss2bSD39+UkfxHkAi0supU6fwyy+/4IUXXsCNGzfg7++PBQsWYODAgcjLy0NeXp6lSzSYQqGAq6srXnvtNY3vX7p0CQ0NDXjooYdU2+zt7REWFoaioiK1sREREaqPe/fujcDAwDZjlE6ePImff/4Zu3fvVm0TBAEKhQJXrlzB2bNnYWtri6ioqI58eQAAOzs7jBs3TvV5UFAQevXqhaKiIoSFhbUZX1paivj4eBw+fBg3b95EU1MTampqcO3aNbVxI0aMUH3s4uICNzc3lJaWqr6+rKwsuLq6tpn/0qVLGDJkSIe/LiLqGAZAImqXQqFAbGws7rvvPty4cQMikQgVFRXIyMiASCQy2XEEQYBUKgUA+Pr6mnRuTRoaGlBWVqY1AAqCAABt6hAEQa/atI1RKBT405/+hJdffrnNe/7+/vj555/bndsQmurQVtuiRYtw69YtbNy4EQEBAXB0dERERATq6+vVxtnb27eZT3kfqEKhwBNPPIG//e1vbeb39fU19ssgIhNiAKRuJT09HbNnz0ZBQQFCQkIsXY7VKCwsVJ21+cc//oGkpCR8++238PLywptvvom5c+fCzq7jP06qq6tVZ40uXrwIFxeXDs+py+bNm5GQkAC5XA5HR8c27w8ePBgODg7Iy8vDM888A6A5NJ44cQIrV65UG3vs2DH4+/sDAMrKyvDf//4XQUFBGo87ZswYnD9/HoMHD9b4/vDhw6FQKJCdnY2YmJg27zs4OAAAmpqa2v0aGxsbceLECdXZvuLiYvz2229aa8vNzcVHH32E6dOnAwCuX79ucPPGmDFj8PXXX2PAgAEm+f+CiEyPTSDUrSQlJaluaqfOk5GRgaeeegq3b9/GmDFjsG/fPpw8eRIhISFYsGABQkJCVGfuupPs7Gz07dsXR48e1fi+i4sLXnjhBbz22mv44YcfcOHCBSxduhQ1NTVYsmSJ2tikpCQcOnQI586dw6JFi+Dp6YmZM2dqnPeNN97Af/7zHyxfvhxnzpzBxYsXsX//frz00ksAgAEDBmDhwoVYvHgx9u3bhytXruDIkSP48ssvAQABAQEQiUQ4ePAgbt26haqqKq1fo729PV566SUcP34cp06dwrPPPovw8HCNl3+B5tC7a9cuFBUV4fjx45g3bx7EYnF730o1y5cvx927dzF37lzk5+fj8uXL+Pe//43FixfrFVqJyPwYAKnbOH78OPLz8wEAX331VZt7ksh88vLysHjxYpSVlam2tQyC06dPh62trQUrNFxDQwPkcjm8vb2RmZmpddzbb7+N3//+95g/fz7GjBmDn3/+GT/++CPuu+++NuNeeeUVjB07FlKpFPv371edqWttxIgRyM7OxsWLF/Hwww9j9OjRePPNN9Uuj27duhVPPfUUXnzxRQQFBWHp0qWqx8Tcf//9SExMxF/+8hd4e3urdQ+35uzsjDfeeAPPPPMMIiIiIBaLsXfvXq3jP/30U5SVlWH06NGYP3++6hE4hujXrx9++uknNDU14dFHH8WwYcPwyiuvwMPDAzY2/LVD1BWIBOVNLkSdrKKiAh4eHigvL4e7u3u746dPn44LFy7g6tWr6N27N2bPno2tW7d2QqXWra6uDn/4wx/w7bffwtfXFxcvXtR4c78ptLwEXFVVZdZLwEePHsWhQ4eQn5+PpqYmfPfdd2Y71o8//ohp06ahrq5Oayg0h7S0NKxcuZIrhvRAhv78JGqN/xSjbuH48eP4/vvvMX/+fADAc889h08++YRnATvB0aNHERkZCQDw9PREdna2hSsyjYyMDMTExEAkEsHd3V3t7KYp3bx5E99++y0efPDBTg1/RES6MABSt5CYmIjg4GDVYzH++Mc/wsPDA2+99ZaFK+v5MjMzVY0Inp6eOi+XdicFBQUIDQ0FAEyaNAlZWVlmOc706dORmZmJLVu2mGV+IiJjMABStyCVSvG3v/1NdZ+Zi4sLkpOTdS5pRaZx+vRpjB49GgDg5uam9dl2pmBra4vp06eb/Z7CyspKiMViVYfq1KlTzRZsT548if/+978au3nNbdGiRbz8S0QasT+fuoXTp08DgNpZmmXLlmHZsmWWKskqlJWVtblx39vbGzKZDD4+PiY/npOTE9LT000+b2s5OTlqD1keNGgQLl++bPbjEhF1FTwDSERaHT58GJMnT1bbFhMT0+0vAyvv/2vJ398fV69etVBFRESdiwGQiLRqef+f0pQpU7p9AJRIJAgMDFTb1hOCLRGRvhgAiUirK1euYNCgQWrb+vXrB5lMBnM8Qaq6uhouLi5wcXFRPfPO1KRSqcZl5iZPnozDhw+b5ZhERF0NAyARaVRSUoKAgACN7wUFBaG4uNgsx62pqUFNTY1Z5gaAQ4cOaWzI8PT0xN27d1Xr2RIR9WQMgESkkabLv0oxMTHIyMjo5IpMIzMzE1OmTNH43ogRI1BYWNjJFRERdT4GQCLSSFMDiFJUVFS3fCC0IAg6O5h5HyARWQsGQCJqQ6FQoKysDH369NH4vpubG2pra9HY2NjJlXWMRCJBSEiI1vcnTJiAvLy8TqyIiMgyGACJqI3CwkKMHDlS55iwsDDk5+d3UkWmoenxLy2JxWIoFArI5fJOrIqIqPMxABJRG+0FJaB7Xi7Nzs7GxIkTdY6JjIzE0aNHO6kiIiLLYAAkojby8vLw0EMP6RxjjjOANjY2iIqKQlRUlNrqI6bQ0NAAuVwOV1dXneO6Y7AlIjIUAyARqamrqwPQfDlUF3t7ezg6OqKqqspkxxaLxThy5AiOHDnS7vENVVBQgPHjx7c7bvTo0aqlB4mIeioGQCJSc/ToUURGRuo1tjt1A+tzWRsAbG1t4e7ujrKysk6oiojIMhgAiUiNruf/tdadLpcWFBQgNDRUr7GTJk1CVlaWmSsiIrIcBkAiUnP69GmMHj1ar7HBwcEoKioy2bGrq6vh5eUFLy8vky4FV1lZCbFYDDs7O73GT506tdsEWyIiYzAAEpFKWVkZPDw89G7AEIlE8Pb2hkwmM1kNt2/fxu3bt002HwDk5OQgKipK7/GDBg3C5cuXTVoDEVFXwgBIRCq6Vv/QpjtcBtb3/r+W/P39cfXqVTNVRERkWQyARKRiyP1/SlOmTOnyAVAikSAwMNCgfbpDsCUiMhYDIBGpXLlyBYMGDTJon379+kEmk0EQBDNV1TFSqRS+vr4QiUQG7Td58mQcPnzYTFUREVkWAyARAQBKSkoQEBBg1L5BQUEoLi42cUWmcejQIYPPagKAp6cn7t69C4VCYYaqiIgsiwGQiAAYd/lXKSYmBhkZGSauyDQyMzMxZcoUo/YdMWIECgsLTVwREZHlMQCS0XJycvDEE0+gX79+EIlE2Ldvn6VLog4wpgFEyVQPhLaxscG4ceMwbtw4kywFJwgCZDIZfHx8jNqf9wESUU/FAEhGq66uxsiRI/Hhhx9auhTqIIVCgbKyMvTp08eo/d3c3FBbW4vGxsYO1SEWi1FQUICCggKTLAUnkUgQEhJi9P4TJkxAXl5eh+sgIupq9HsqKpEG06ZNw7Rp0yxdBplAYWEhRo4c2aE5wsLCkJ+fr/cycp3BmMe/tCQWi6FQKCCXy+Ho6GjCyoiILItnAImow0EJ6JqXS7OzszFx4sQOzREZGYmjR4+aqCIioq6BAZA6jVwuR0VFhdqLuoa8vDw89NBDHZpDeQawI2pqajBgwAAMGDAANTU1HZqroaEBcrkcrq6uHZqnKwZbIqKOYgCkTpOSkgIPDw/Vy8/Pz9IlEYC6ujoA6PA9d/b29nB0dERVVZXRcwiCgKtXr+Lq1asdfq5gQUEBxo8f36E5AGD06NE4ffp0h+chIupKGACp06xevRrl5eWq1/Xr1y1dEgH4z3/+Y7L79kzVDWwKprisDQC2trZwd3dHWVmZCaoiIuoaGACp0zg6OsLd3V3tRZZnqqAEdK3Lpfn5+QgNDTXJXJMmTUJWVpZJ5iIi6goYAMloVVVVOHPmDM6cOQOgeRmxM2fO4Nq1a5YtjAxy+vRpjBo1yiRzBQcHo6ioyCRzdURlZSXEYjHs7EzzoIOuFGyJiEyBAZCMduLECYwePRqjR48GAKxatQqjR49GfHy8hSsjfZWVlcHDwwO2trYmmU8kEsHb2xsymcwk8xkrJycH0dHRJpvvgQcewOXLl002HxGRpTEAktGio6MhCEKbV1pamqVLIz11ZPUPbbrC2TJTXtZW8vf3x9WrV006JxGRpTAAElmxjqz/q82UKVOMDoAikQghISEICQmBSCQyugaJRILAwECj99ekKwRbIiJTYQAksmJXrlzBoEGDTDpnv379IJPJjHqMi7OzM86fP4/z58/D2dnZqONLpVL4+vp2KEBqMnnyZBw+fNikcxIRWQoDIJGVKikpQUBAgFnmDgoKQnFxsVnmbs+hQ4dMflYTADw9PXH37l0oFAqTz01E1NkYAKnHGTBgADZu3Ki2bdSoUVi/fr1F6umqzHH5VykmJgYZGRlmmbs9mZmZmDJlilnmHjFiBAoLC80yNxFRZ2IAJLJS5mgAUTL2gdA1NTUYOnQohg4datRScIIgQCaTwcfHx+B99cH7AImop2AAJLJCCoUCZWVl6NOnj1nmd3NzQ21tLRobGw3aTxAEXLhwARcuXDDqHkKJRIKQkBCD99PXhAkTkJeXZ7b5iYg6CwMgkRUqLCzEyJEjzXqMsLAw5Ofnm/UYrZnj8S8ticViKBQKyOVysx2DiKgzMABSj2NjY9Pm7FFDQ4OFqumazB2UAMtcLs3OzsbEiRPNeozIyEgcPXrUrMcgIjI3BkDqcby8vCCVSlWfV1RU4MqVKxasqOvJy8vDQw89ZNZjdPYZwIaGBsjlcri6upr1OLwPkIh6AgZA6nEmT56MXbt2ITc3F+fOncPChQtNttRZT1BXVweg+XKmOdnb28PR0RFVVVVmPY5SQUEBxo8fb/bjjB49GqdPnzb7cYiIzIkBkHqc1atXY+LEiXj88ccxffp0zJw5Ew888ICly+oy/vOf/yAyMrJTjmVsN7AxOuOyNgDY2trC3d0dZWVlZj8WEZG5MABSj+Pu7o4vvvgC5eXluHbtGhYuXIgzZ87wOYD/p7OCEmD45VKRSISAgAAEBAQYvJJHfn4+QkNDDS3RKJMmTUJWVlanHIuIyBwYAImszOnTpzFq1KhOOVZwcDCKior0Hu/s7IySkhKUlJQYtBRcZWUlxGIx7OzsjCnTYLwPkIi6OwZAIitSVlYGDw+PTrsnUiQSwdvbGzKZzKzHycnJQXR0tFmP0dIDDzyAy5cvd9rxiIhMjQGQyIqYc/UPbTrjbFlnXtZW8vf3x9WrVzv1mEREpsIASGRFzLn+rzZTpkzROwDW1tYiNDQUoaGhqK2t1fsYEokEgYGBxpZoFF4GJqLujAGQyIpcuXIFgwYN6tRj9uvXDzKZTK+l3RQKBU6cOIETJ05AoVDoNb9UKoWvr6/BTSMdNXnyZBw+fLhTj0lEZCoMgERWoqSkBAEBARY5dlBQEIqLi80y96FDhzr9rCYAeHp64u7du3oHVSKiroQBkMhKWOLyr1JMTAwyMjLMMndmZiamTJlilrnbM2LECBQWFlrk2EREHcEASGQlLNEAomSuB0ILggCZTAYfHx+Tz60P3gdIRN0VAyCRFVAoFCgrK0OfPn0scnw3NzfU1taisbHRpPNKJBKEhISYdE5DTJgwAXl5eRY7PhGRsRgAiaxAYWEhRo4cadEawsLCkJ+fb9I5LfH4l5bEYjEUCgXkcrnFaiAiMgYDIJEVsHRQAvS/XOrp6QlPT0+95szOzsbEiRM7WlqHREZG4ujRoxatgYjIUAyARFYgLy8PDz30kEVr0OcMoIuLC27duoVbt27BxcVF59iGhgbI5XK4urqaskyD8T5AIuqOGACJeri6ujoAzZcrLcne3h6Ojo6oqqoyyXwFBQUYP368SebqiNGjR+P06dOWLoOIyCAMgEQ93H/+8x9ERkZaugwApu0G7gqXtQHA1tYW7u7uKCsrs3QpRER6YwAk6uG6SlAC2r9cWltbi+joaERHR7e7FFx+fj5CQ0NNXaJRJk2ahKysLEuXQUSkNwZAoh7u9OnTGDVqlKXLAAAEBwejqKhI6/sKhQLZ2dnIzs7WucJGZWUlxGIx7OzszFGmwXgfIBF1NwyARD1YWVkZPDw8YGtra+lSAAAikQje3t6QyWQdmicnJwfR0dGmKcoEHnjgAVy+fNnSZRAR6Y0BkKgHy8rKstjqH9qY4mxZV7qsreTv74+rV69augwiIr0wABL1YF0xKE2ZMqXDAVAikSAwMNBEFZkGLwMTUXfCAEjUg12+fBmDBg2ydBlq+vXrB5lMBkEQjNpfKpXC19cXIpHIxJV1zOTJk3H48GFLl0FEpBcGQKIeqqSkBAMGDLB0GRoFBQWhuLjYqH0PHTrU5c5qAs0rmNy9e1dn8woRUVfBAEjUQ2VmZnbJoAQ0Xy7NyMjQ+J6zszOcnZ217puZmYkpU6aYq7QOGTFiBAoLCy1dBhFRuxgAiXqow4cPd7kGECVtD4R2cXFBdXU1qqurNS4FJwgCZDIZfHx8OqNMg/E+QCLqLhgAiXoghUKBsrIy9OnTx9KlaOTm5oba2lo0NjYatJ9EIkFISIiZquq4CRMmIC8vz9JlEBG1iwGQqAcqLCzEyJEjLV2GTmFhYcjPzzdon67Y1dySWCyGQqGAXC63dClERDoxABL1QF09KAGaL5fW1dXhsccew2OPPYa6uro2+2RnZ2PixImdVaJRIiMjcfToUUuXQUSkEwMgUQ+Ul5eHhx56yNJl6KTpDGBTUxO+++47fPfdd2hqalJ7r6GhAXK5HK6urp1ZpsF4HyARdQcMgEQ9jPLMmVgstnAlutnb28PR0RFVVVV6jS8oKMD48ePNXFXHjR49GqdPn7Z0GUREOjEAEvUw//nPfxAZGWnpMvSirRtYk+5wWRsAbG1t4e7ujrKyMkuXQkSkFQMgUQ/TXYISYNjl0vz8fISGhpq5ItOYNGkSsrKyLF0GEZFWDIBEPczp06cxatQoS5ehl+DgYBQVFbU7rrKyEmKxGHZ2dp1QVcfxPkAi6uoYAIl6kLKyMnh4eMDW1tbSpehFJBLB29sbMplM57icnBxER0d3TlEm8MADD+Dy5cuWLoOISCsGQKIeJCsrq8uu/qGNPmfLutNlbSV/f39cvXrV0mUQEWnEAEjUg3THoDRlyhRVAHRxcYEgCBAEQW0pOIlEgsDAQEuVaBReBiairowBkKgHuXz5MgYNGmTpMgzSr18/yGQyCIKg8X2pVApfX1+IRKJOrqxjJk+ejMOHD1u6DCIijRgAiXqIkpISDBgwwNJlGCUoKAjFxcUa3zt06FC3O6sJAJ6enrh79y4UCoWlSyEiaoMBkKiHyMzM7JZBCWi+XJqRkYG6ujo8/fTTePrpp1UPtM7MzMSUKVMsXKFxRowYgcLCQkuXQUTUBgMgUQ9x+PDhbtcAoqR8IHRTUxP++c9/4p///CeampogCAJkMhl8fHwsXaJReB8gEXVV3eOhWkSkk0KhQFlZGfr06aN1jCAACgXQ1NT21XK7QtH8EoR7+yj/rKoCiovbbm89tuXHjY335mxdzz1u+PXXWhw+3Kjakp0N3Lolgbt7CFovFtL6dkBb2+aXjU3ze63/1PaxjQ1QXQ1cuqR5P+Wcyvlbvlpu12bChAnYsmULXn31Vd3/AYmIOhkDIFEXpFA0B6eGhvb/bGoCiooK4eU1Ejk5zduU7yvHKD9XBjFdL2WAaxnQBKE5EN28CRw8qP/XoQxqyuCla1yvXmH4/vsTqm3nzgHHjmXAyysGZ860DozqNNWsL5kM2LevbT0tw6Iy8LUMiMqXMgTa27d92dmJceeOAkePyiEWO6rG2dm1/2c363khom6GAZDIjBoagPp6QC5X/7NlKJPLm1+1tc3v1dbee6/1mbrGRs0hJysrA/37x+DUKfVw0jK0KEOMnV3bMKPp7JmmAOLqCgwZYp7vVXR0DE6d+l71+cCBwL592ZgzZzHEYvMcE9D8NbU+w6krLDc0AHV1bbcrP3Z3j8SuXUcxePCkNsduGSDt7NTPMDo6Nr+cnACxuPljB4d7IdHe/t42Bwf194mI2sMfFdQtPPvss3j55ZfVtmVkZCAjIwPvvPNOp9bS2Nj8C18uv/en8uPa2ubLpFVVQE2N5rNxrYlEbX/5twwBmi49tvbll3lYtGgFHB3N//Wby5AhYfjyy/+n+ryxsQENDXKIxa6dXosyMJuCQhGDY8e+wfTpbQOg8pJ7y7Cv/H+lrq7tPwBah3/l/zstzx46OADOzs3B1s2tOUAqg6QyVDo6NodKTf8vEZF1YACkbqGwsBB//vOf8eabbwIAGhsbsXz5cgwbNszkxxKE5l++1dXNIU75KitrflVVqZ/Fa2q6t69I1PLyX/PLxcW8l/bq65u7ZR0dzXiarBPY2dnDzs5B9fmlSycxZMh4C1ZkGoMGjcaePfEa32t5+dgYyvDY8raA6mqgvPze5y1Do61tc0BUBkUPD+C++5r/dHZWfzk5GVcTEXUPDIDULcTHx2PmzJl48sknAQAHDhzAxYsXsXfvXqPnbGwEfvut+ZdldXVzsCsrA+7evXdWTy6/9wvUzu7eWRRX13tBz9LL7kok/0FwcKRlizCRkJAJyM/fDwAoLDyM0NDHLVxRx9na2sLZ2R1VVWVwdb3PpHPb2Ny7BKyPxsbmf7wobz2QSoGSkubPlZf/lWcInZ2bw+F99zX/I8bFBejVqzks8swhUffHAEjdwpNPPolRo0Zh586dAIAPP/wQTz75JMaMGaPX/goFUFnZHPB++635F9/Nm83B7/8eNweRSP2+Kw+P5l+sXf2X3ZkzGYiM/L2lyzCJsWOno7T0KhYt+hv+9rfZeOaZREuXZBLDh09CYWEWIiN/Z9E6lGeltWlquvcPn6oq4M6d5sCobAISi5svK/frB3h5NYfDXr2awyGbVoi6FwZA6pCPPvoI7777LqRSKYYOHYqNGzfi4YcfNvlxRCIR1q9fj5kzZwJoXvXi66+/1rlPbS1w7Vpzl+evvwIVFc2XcgWhOdi5uDT/EnNy6t6/vC5fPo158/5q6TJMwt8/BFLpz1AoFHB0FMPWtmf8iBo5Mgb79qVaPAC2x9b23iXg1hSKe/e4FhY2h0Ubm+az4b16NYfCfv2A/v2Nv6RNRJ2nZ/x0JYv44osvsHLlSnz00Ud46KGHsH37dkybNg0XLlyAv7+/yY/35JNPYvDgwfj5558RExOj8eyfIAClpcCVK4BEAty+fe8+PA8PwMfH8pdsTamqqgwuLh6w7SFflEgkQq9e3jh+/FsMGxZt6XJMxtf3Achkly1dRofY2Ny7FOzt3bxNec/h3bvA9evN23x9geBgYMCA5mBIRF0TAyAZbcOGDViyZAmee+45AMDGjRvx448/YuvWrUhJSTH58UQiEeLi4rB8+XKsXr26zfsKBXD6NJCf3/xLqXdvYPBg/QJfXV01AMDe3kkVphobG9DYWK91H3t7R9UZKkPGNjU1oqFBrnWsnZ0D7Ozs9Rp75kwGhg+f/H9jm9DQUKd1rK2tPeztHQweq1AoUF9fq9pP+b1qb6zmee1gb9/cqiwIAuTyGrX3GxrkkEov4syZDKxbt1+1XdPYlmxsbOHgcK9roXWNusZq+pqURCIbteYaXfO2HiuX10Bo0YHRu7cvrl8vgpeXP0QiERwdnbWOVZ+39dhaCIL29YWdnFyMGltfXweFokmvsUp2ds3/sPLwaP68oQG4dQvIyAD69AEmTmz+O0hEXY9I0PZTh0iH+vp6ODs746uvvsKsWbNU21955RWcOXMG2a2XbgAgl8shl98LMxUVFfDz80N5eTnc3d31Pvbdu3fRu3fvNtsvXwb2728+66BjQQyNnnyy+RpwcnIWhg+PBgCkp2/B9u0rtO7z5psHERr6GADg0KE0bNr0rNaxr7/+JSZMeBoAkJf3Fd55Z7bWsa+8sgNTpiwCABQUpOOvf9XeCBEQMBxr1nwDX98HcPbsEaxd2/ZRI0qLFr2D3/3uNQDAxYsF+POfw7SOnTMnAc88sx4AcO3aeaxYob3betasV/Hss+8CAG7eLMHSpQO1jp0+/UU8//wWAEB5+S3Mn99X69iJE+fi1Vf3AGgOXrNna38cTGTkU/jLX75Sfa7876nJuHHTER+fDqA5YP/ud45aQ9KwYVF4660jqs//+EcvVFTc1jh28OBx2LChQPX5c88NQGnpVY1j/fxCsGXLedXny5cPxfXrFzSO7ds3AB9/XKL6fNWqUPz88wmNY93dPfH557dUn69ZE41z59r+XQQAR0dnfPXVvUCblPQYTpz4TuNYANi/X/9fFYLQfNuFvT0wa5bhfx+pfRUVFfDw8DD45yeRUhe/vZ26qtu3b6OpqQneymtB/8fb2xsymUzjPikpKfDw8FC9/Pz8OqPUHs3JyRW//FJk6TK6rVOnfrB0CT0WTy0QdW08A0hGuXHjBu6//34cPXoUERERqu3JycnYtWsXJBJJm31McQbwo48+wvLly5GZmYkpU6aovafpEnDv3t37EnBDQz3mz++L3r37qZ1dUmpoqMc778zG+vU//N/n5rsEfO5cNoqKfsLTT69pd6z2eXVfAq6rq8aCBc3/qHj33f8gMDBc69iWjL0E/PbbT2Hx4lS4u3tqHGuqS8C//XYT27YtxxtvfAWRSNRjLgG3prwEXFHBS8DmxjOA1FG8B5CM4unpCVtb2zZn+0pLS9ucFVRydHSEYweWqhAEAe+//z4A4O23324TAG1sgDFjAD+/5svBxcXAzz83B0BX1+ab152dNQdCzfc32auCWHsMGWtra6d3d+vx49+ipqYcNTXlkEovYeDAEWrvOzm5YPz4GcjJ2YNJk+bD1rb9X9LNNdjqPdbGxgZOTi4YO3Yavv12g1pI1jZWHyKRSOfYCxfyVAGwvbGt6TP21q3rsLd3Qt++ASadV6llaNu/fyPmzEnQuqpJy7Htz6v/A78NGdsyQOtL2QSifAHNTSDh4UBAAJtAiLoyXgImozg4OGDs2LHIyMhQ256RkYHISPM8lHj//v34+eefAQCZmZk4depUmzEiEdC3b/MvoNmzgSeeaA6FLi7NzwG8fBn473+bH35761bzYy266jlwhUKBvXsT4ezsDrHYFV98kaRx3KOPLsOhQ2k6zyqagkgkwpgxsWrr9Zpay7NgFy7kme04AJCZ+SkeeeQ5sx4DAGSyy/jtt5sICgo3+7HMSaFofgTMzZvApUvNf4+uXm3+O9S7d/PfuVmzgKeeAkaOZPgj6up4BpCMtmrVKsyfPx/jxo1DREQE/v73v+PatWt4/vnnTX4sQRCwfv16jBo1CmfOnMGAAQOQmJiIb7/9Vus+YjEQGNj8Uj4I+rffmh8GffNm88Ogb93S/CBo5cOgLfkg6KNHv8a1a+fh7z8MLi69cPTo17hypbDNWUB7ewfExCzGDz9sxxNPvKxlNtOYPHkhtm59wWwrdPz6a7Hq4/r6OjQ1NZrlWYBNTY24cCEXc+ZoXqLNlPbuTcKcOQlmP44ptHwQtPKl6UHQgwY1/0OrV6/mh0E7O3fvZ2kSWSMGQDLaH/7wB9y5cwdJSUmQSqUYNmwYvvvuOwQE6H9JTV/79+/HmTNn8P777+PMmTNYsWIFXn31VZw6dUqv1UBsbO49rkJZnral4MrKmkNhRUXbpeCUwVC5lqq5loJTnv0bPfoR1NZWwtd3MO7e/RVffJGEv/zln23GT5w4FwkJj2LKlGfh7Oxm+oL+j4eHF+ztnXD79i/w9Oxv8vkLCw+rPh48eCz++998syxzd+rUDxgzJhYiM6eWK1cKYWtrB3//ELMeR1/K9asbGpqDnTLkKdeztrFRX+7Qz6854Lm6Noc8LgVH1HOwCYQsxpCbmMeOHQsPDw+8+eabmDx5MoqLi/H4449j2LBh+Ne//mXSugShOQDW1DQHw5qa5ld5efPSWFVVzb88lb9Im1rcNy8SNYdCOzvtf+qTOY4e/Rpvv/0U3nnnKD799M/o3z8YwcEP4YMPluDDD8/B339om31OnPgOFy8WYO5c855tKizMwvnzOWY5TkrK77F48XtwcnLFr78Wo7DwsFnO0r399lN48cVtWps/THmcJUs2wMvL9A9GB5rPbDc2Nr8aGjT/2fInvPL/Q+U/YDw8mi/furs3BzzlfbLOzs0hkLouNoFQR/EMIHULI0aMwMsvv4zffvsNAGBnZ4ctW7a0uQfRFJSXusRizc8va2xsDojKsyctP66paQ6Iyj8bGpo/bvlLWdPxbG2bfznb2DT/KZe7Yfr01+HrG4GmpuaQOWHCfJw7lwNAc4IcO3YavvvuI/z2Wyl69dL+fL2OGj48Gl99lYympiaTrkDS2NiAhgY5vL2bnyPo4tIL//zn2yabX0nZ/GHu8Hf+fC68vAJ0hj/lf9uWr8bGe8Gu9bbW/1wXidRDnXLVG+XLze3eGT3ln8qPnZx4Jo/ImjEAUrewY8cOAEBWVpZq29SpUzF16tROr8XOrvmSmKv25xKrtLzUVl9/72Pl2cPGxnvhsba2+f3aWmDUqEcwbNgjqKtrDgB1dYBMZo/HH09DXV3zDfjAvbOJzfdoifDQQ2vxySdv4amnNsLGpvl9G5vml63tvY9bble+13KbSKT9TGXLZhBT3gt48WIBhgwZr/rczs4e9vaOqK2t0to9awx9mj+UYUsQmj829NXUJOCzz1LwzDOf4eJF7Y1Gyu+9nV3zn8qXvX1zgFOGNrG4+U8Hh3uBz8Hh3kv5nvJ9IqL28EcFkRkpz8y46P/0EADql/b+53+ab7qfPbvtJb6GBmXgaN42blwEzpzZCHf3EvTpM0Dtnq+WZ5ZahhVlyGlqUg8+um4OCQhYiK+/fgEeHu0HQGWYbO/Sd1ZWBgYPjsY77ywHAMycuQE+PlHIzMxGSMhjOvfVp2agufnjxIlcjBkTrwrRumpWhuGW4bl1iG4ZypR/njhxAOHhkYiO9lTdJ9oy3LU+a9f6T31vFSAiMhYDIFEXpAwWDg7NocHREfDx0W/fLVvikZqahE8//VRte8ugpwx7mi5BtgyFLf9seUZMELxw4oQTRo36Bd7e/ducMWv9Z1PTvY9b16T0xRf5iI1diQ8/jAYArF37Djw9Y3Dw4P9g9Oh7AbB1MNJ0JrN1gFP+mZ39A2bMiMXjj4s0vt/6Y2VoU86t6dX6MmpTUxPef38z9u3bp9dZYiIiS2AAJOphhg4dChsbG5w9exbDhw9XbW8ZaExh1aolyMn5BAkJHW8GqaysxP33ixEdfe9H0sMPA87OwfjHP4oQFdXhQwAA1q9Pw7Zt2+Bpxtv/Pv/8c8yaNQuuTH9E1IXxFmCiHig+Ph5JSZofHG0q0dHRyM3NRVPLNmgj5eTkIDo6us12kUikc31pQ1y/fh1OTk7wNGP6k8vl+Oyzz7B06VKzHYOIyBQYAIl6IH9/f/j5+SEvz3yraYhEIsTGxuL77zu+MkhGRgZiYmI0vhcTE4PMzMwOH+PTTz/Fc8+Zd+WPrVu3YsmSJXBwcDDrcYiIOooBkKiHWrNmDVJSUmDOR30uXLgQaWlpHZ5HIpEgMDBQ43umCICNjY3Izc1FlKmuJWtQUVGB9PR0zJkzx2zHICIyFQZAoh7K09MT4eHhSE9PN9sxvLy84OTkhF9++cXoOaRSKXx9fbWuyuHr6wuZTNahIPvDDz8gNta8K3+kpqZi1apVsOHD9YioG+BPKqIeLC4uDps2bTLJfXraLFmyBJ988onR+x86dEjr5V+loKAgFBcX6xyjS1paGhYtWmT0/u25efMmTp48idjYWLMdg4jIlBgAiXowV1dXzJgxA3v27DHbMTraDJKZmYkpU6YAAMRiMa5cuYIrV65ALBarxsTExBi96ktnNH8kJydj3bp1Zl9bmIjIVBgAiXq4ZcuWIS0tDXK53Czzd6QZRBAEyGQy+PzfQw5tbGwwYMAADBgwQO1SalRUFLKzs42qz9zNH5cvX8bNmzcRHh5utmMQEZkaAyBRD+fg4IDFixdj+/btZjuGsc0gEokEwcHB7Y5zc3NDbW0tGhsbDZq/M5o/kpKSTPIsRCKizsQASGQF5s6diwMHDqCystIs8xvbDJKRkaG2nnN9fT1ee+01vPbaa6ivr1cbGxYWhvz8fIPmN3fzR2FhIezs7BASEmKW+YmIzIUBkMgK2NjYIC4uDhs2bDDbMYxpBsnOzsbEiRNVnzc0NOC9997De++9h4aGBrWxxjwOxtzNH0lJSYiPjzfb/ERE5sIASGQlpk2bhoKCApSWlpplfkObQRoaGiCXy/VeMs3QM4Dmbv7Izc1FQEAA/P39zTI/EZE5MQASdTGCIGDZsmXo3bs3RCIRqqurTTKvSCTC2rVr8dZbb5lkPk3zG9IMUlBQgPHjx+s9v729PRwdHVFVVaXXeHM2fwiCgJSUFKxevdos8xMRmRsDIFEX88MPPyAtLQ0HDx6EVCqFs7OzyeaOiIiAVCpFSUmJyeZsyZBmEF3Lv2mjbzewuZs/Dhw4gMjISLM+WoaIyJwYAIm6mEuXLsHX1xeRkZHw8fExeQNDfHw8kpKSTDqnkiHNIPn5+QgNDTVofn3vAzRn80dTUxM2b96MlStXmnxuIqLOwgBI1IUsWrQIL730Eq5duwaRSIQBAwaY/BhDhw6FSCTC2bNnTT43oF8zSGVlJcRiMezs7AyaOzg4GEVFRe2OM2fzx+eff45Zs2bpfe8iEVFXxABI1IVs2rQJSUlJ6N+/P6RSKQoKCsxyHHOeBdSnGSQnJwfR0dEGzy0SieDt7Q2ZTKZ1jDmbP+RyOT777DMsXbrU5HMTEXUmBkCiLsTDwwNubm6wtbWFj48PvLy8zHKcgIAA+Pn5IS8vz+Rz69MMou3+P7FYjHPnzuHcuXNqS8G11N5lYHM2f2zduhVLliyBg4ODWeYnIuosDIBEVmrNmjVISUmBIAgmn7u9ZhCJRILAwMA2221sbDB06FAMHTpUbSm4lnQFQHM2f1RUVCA9PR1z5swx+dxERJ2NAZDISnl6eiI8PBzp6ekmn1tXM4hUKoWvr6/RDRq+vr6QyWQag6s5mz9SU1OxatUqrcGUiKg74U8yIisWFxeHTZs26f3wZkNoawY5dOiQ1se/1NfXY/369Vi/fn2bpeBaCgoKQnFxcZvt5mr+KC0txcmTJxEbG2vyuYmILIEBkMiKubq6YsaMGdizZ4/J59bWDJKZmYkpU6Zo3KehoQGJiYlITExssxRcSzExMcjIyFDbZs7mj+TkZKxbt85sawoTEXU2BkAiK7ds2TKkpaVBLpebdF5NzSCCIEAmk8HHx6dDc2t6ILS5mj8uX74MmUyG8PBwk89NRGQpDIBEXczKlSvNtlKHJg4ODli8eDG2b99u8rlbN4NIJBIEBwd3eF43NzfU1taisbERgHmbP5KSkpCQkGDyeYmILIkBkIgwd+5cHDhwAJWVlSadt3UzSEZGBqZOnWqSucPCwpCfnw/AfM0fhYWFsLOzQ0hIiEnnJSKyNAZAIoKNjQ3i4uKwYcMGk8/dshkkOzsbEydONMm8LR8HY67mj6SkJMTHx5t8XiIiS2MAJCIAwLRp01BQUIDS0lKTzqtsBqmrq4NcLjfZEmrKM4Dmav7Izc1FQEAA/P39TTovEVFXwABIRACamzbWrl2Lt956y+TzxsbG4oMPPkBYWJjJ5rW3t4ejoyO2bdtm8uYPQRCQkpKC1atXm3ReIqKuggGQiFQiIiIglUpN3oSycOFC7Nixo937/5ycnJCfn4/8/Hw4OTm1O++ECROQnp5u8uaPAwcOIDIy0iyPlCEi6goYAIlITXx8PJKSkkw6p5eXF8rLy+Hr66tznK2tLUJDQxEaGgpbW9t253V0dIS7u7tJmz+ampqwefNmrFy50mRzEhF1NQyARKRm6NChEIlEOHv2rMnmrKysxODBg7Fz506TzQkAhw8fhp2dnUnn/PzzzzFr1iyT3atIRNQVMQASURumPguYk5ODp556Cjk5OTqXnauvr8e7776Ld999V+dScMC9lT/8/Pwgk8lMUqdcLsdnn32GpUuXmmQ+IqKuigGQiNoICAiAn58f8vLyTDKf8vl/rVcGaa2hoQGvv/46Xn/9dZ1LwQH3Vv5o+TiYjtq6dSuWLFkCBwcHk8xHRNRVMQASkUZr1qxBSkoKBEHo8FwSiQSBgYFYtGiR2sogxmq58oepAmBFRQXS09MxZ86cDs9FRNTVMQASkUaenp4IDw9Henp6h+aRSqXw9fWFSCRqszKIsVqu/OHr6wuZTNbhoJqamopVq1bBxoY/Fomo5+NPOiLSKi4uDps2bdJ53157Dh06hJiYGNXnLVcGMVbrlT+CgoJQXFxs9HylpaU4efIkYmNjO1QXEVF3wQBIRFq5urpixowZ2LNnj9FzZGZmYsqUKarPo6Oj220G0UXTyh8xMTHIyMgwusbk5GSsW7fO5GsJExF1VQyARKTTsmXLkJaWBrlcbvC+giBAJpPBx8dHtU25MoiuZhBdlM0fLUVFRSE7O9uo+S5fvgyZTIbw8HCj9ici6o4YAIlIJwcHByxevBjbt283eF+JRILg4OA2241tBmnZ/NGSm5sbamtr0djYaPCcSUlJSEhIMHg/IqLujAGQiNo1d+5cHDhwAJWVlQbtp3z8S2vamkGcnJyQlZWFrKwsjUvBtWz+aC0sLAz5+fkG1VdYWAg7OzuEhIQYtB8RUXfHAEhE7bKxsUFcXBw2bNhg0H7Z2dmYOHGixvc0NYPY2toiOjoa0dHRGpeCa9380ZIxj4NJSkpCfHy8QfsQEfUEDIBEpJdp06ahoKAApaWleo1vaGiAXC7XuqSaoc0gmpo/WjL0DGBubi4CAgLg7++v9z5dUXR0tNnXLV60aBFmzpxp0D4SiQTh4eFwcnLCqFGjzFJXa2lpaejVq1enHIuou2MAJCK9iEQirF27Fm+99ZZe4wsKChAWFqZzvtbNIA0NDdiyZQu2bNnSZiUQTc0fLdnb28PR0RFVVVXt1iYIAlJSUrB69Wo9vhIyRkJCAlxcXFBcXIxDhw5ZuhwiaoUBkIj0FhERAalUipKSknbHarv/r6XWzSD19fVYsWIFVqxYobYWsLbmj9b07QY+cOAAIiMjtZ5NpI67dOkSJkyYgICAAPTp08fS5RBRKwyARGSQ+Ph4JCUltTsuPz8foaGhOsfouzKIruaPlqZOndrufYBNTU3YvHmz2S+bdqbGxkasWLECvXr1Qp8+fbBu3Tq1lVE+//xzjBs3Dm5ubvDx8cEzzzzT5lL++fPn8dhjj8Hd3R1ubm54+OGHcenSJY3HO3nyJPr27Yvk5GSN74tEIpw8eRJJSUkQiURYv349AODs2bOYPHkyxGIx+vTpg2XLlrU5Y/vpp59i6NChcHR0hK+vL1asWKF6b8OGDRg+fDhcXFzg5+eHF198Ua8zvkTUFgMgERlk6NChEIlEOHv2rNYxlZWVEIvFsLOza3c+fVYG0dX80VJQUBCKiop0jvn8888xa9Ysrfcmdkc7d+6EnZ0djh8/js2bN+P999/Hxx9/rHq/vr4ef/3rX/G///u/2LdvH65cuaL2/fz1118xceJEODk54fDhwzh58iQWL16s8bE6R44cwZQpU5CYmIi1a9dqrEcqlWLo0KH485//DKlUildffRU1NTWIjY3Ffffdh4KCAnz11VfIzMxUC3hbt27F8uXLsWzZMpw9exb79+/H4MGDVe/b2Nhg8+bNOHfuHHbu3InDhw/j9ddfN8F3kMgKCUQWUl5eLgAQysvL9d7n8OHDAgDh0qVLZqysa4mIiBAWL15s6TLUlJSUCE899ZTW9w8ePCh88MEHes2lUCiEyZMnC42NjUJVVZUAQAAgVFVVCYIgCNeuXRPmzZund20LFiwQpFKpxvfq6uqEyZMnC3K5XO/5urqoqCghODhYUCgUqm1vvPGGEBwcrHWf/Px8AYBQWVkpCIIgrF69Whg4cKBQX1+vcfzChQuFGTNmCPv27RPc3NyEPXv2tFvXyJEjhYSEBNXnf//734X77rtP9d9VEAQhPT1dsLGxEWQymSAIgtCvXz9h7dq17c6t9OWXXwp9+vRRfb5jxw7Bw8ND7/27M2N+fhK1xDOARGSwgIAA+Pn5IS8vT+P7GRkZauv/6tLeyiDtNX+0putxMFu3bsWSJUvg4OCg93zdQXh4uNrl8YiICFy8eFHVYX369GnMmDEDAQEBcHNzQ3R0NADg2rVrAIAzZ87g4Ycfhr29vdZjHD9+HL///e+xc+dOzJ071+Aai4qKMHLkSLi4uKi2PfTQQ1AoFCguLkZpaSlu3Lihtmxga1lZWZg6dSruv/9+uLm5YcGCBbhz5w6qq6sNrofI2jEAEnVBhYWFbdbfFQQBH3zwAX799VcLVaVuzZo1SElJUbvXTEkikSAwMFDvubStDKJv80dL2gJgRUUF0tPTMWfOHL3n6gmqq6vxyCOPwNXVFZ9//jkKCgrwzTffAICq0UYsFrc7zwMPPICgoCB8+umnag06+hIEQes9nCKRqN0arl69iunTp2PYsGH4+uuvcfLkSWzZsgUA2nSME1H7GACJuqD8/HwsWLAAP//8s2rbjz/+iJdffhlXr161YGX3eHp6Ijw8HOnp6WrbpVIpfH19223YaEnZDNI63Orb/NGSr68vZDJZm2CampqKVatWwcam5/3YO3bsWJvPH3zwQdja2kIikeD27dt4++238fDDDyMoKKhNA8iIESOQm5urM0h5enri8OHDuHTpEv7whz8YHLpCQkJw5swZtbN1P/30E2xsbDBkyBC4ublhwIABWh8Zc+LECTQ2NiI1NRXh4eEYMmQIbty4YVANRHRPz/tJSNQDzJs3D15eXqouS0EQsH79ekRGRiIiIsLC1d0TFxeHTZs2qT3MOTMzU+/Lvy0tWbIEu3fvxsGDB3Hw4EE4Ojrq3fzRWlBQECQSierz0tJSnDx5ErGxsQbP1R1cv34dq1atQnFxMf7xj3/ggw8+wCuvvAIA8Pf3h4ODAz744ANcvnwZ+/fvx1//+le1/VesWIGKigrMmTMHJ06cwMWLF7Fr1y4UFxerjevbty8OHz4MiUSCuXPnGrT28rx58+Dk5ISFCxfi3LlzyMrKwksvvYT58+fD29sbALB+/XqkpqZi8+bNuHjxIk6dOoUPPvgAQPMZyMbGRtXXsWvXLmzbtq0j3zYiq8YASNQFicVi/OUvf8GuXbtQW1uLX3/9FcePH8f69esNOhtmbq6urpgxY4ba5erMzEyd93FpEx0djby8PMTGxuKxxx6DVCrVufKHLq0vAycnJ2PdunVd6ntnSgsWLEBtbS3CwsKwfPlyvPTSS1i2bBmA5rOraWlp+OqrrxASEoK3334b7733ntr+ffr0weHDh1FVVYWoqCiMHTsW//M//6PxnkAfHx8cPnwYZ8+exbx58/ReycXZ2Rk//vgj7t69i9DQUDz11FOYMmUKPvzwQ9WYhQsXYuPGjfjoo48wdOhQPP7447h48SIAYNSoUdiwYQP+9re/YdiwYdi9ezdSUlKM/ZYRWT2RoOkGHqJ2JCcnIz09HWfOnIGDgwN+++03g+eoqKiAh4cHysvL4e7urtc+WVlZmDx5Mi5duoRBgwYZfMzupLa2VnXWAwAefPBB5OXldbkQU19fj2nTpuG7776Dg4MDpk2bhh9++MGoud59910EBwfj8ccfR2JiIqKiolQNC4aorKzEs88+i3/+85+4cuUK/vKXv+CLL74wqiairsiYn59ELfEMIBmlvr4eTz/9NF544QVLl9JjKc8C3rp1C7du3epyZ/+UHBwcsHjxYmzfvh0SiQTBwcFGzzVv3jwkJibik08+QU5OjkHNHy25ubmhtrYWjY2NSExMREJCgtE1ERH1RO0/pZVIg8TERADQ2LlJxlHeHG9vb696TMmSJUvw2muv4b777kNERESbx120HKtQKFBbW6t1fjs7Ozg6OgJovqewpqbGJGNtbW0xd+5cPProo6irq8PDDz+s9bEctra2cHJyavM1tzzuiRMn8Nxzz7UJvLoe9WFjY6PWRVpTU4NRo0Zhx44dAJofW6PcXyQSwdnZWW2stgshrcfW1tZCoVBoraPlI04MGVtXV6fzUmrLsUREJmGpBxBSz2DIg1fr6uqE8vJy1ev69et8EHQL+L8HILd8eO65c+dU2zW9Xn31VdXYK1eu6Bz74osvqsaWlpbqHLtw4ULV2JYPZ9b0Uj4QOj09XQgODtY5dvr06Wpfs7Ozs9ax48ePVxvr6empdey4cePUxgYEBGgdGxISojY2JCRE69iAgAC1sePGjdM61tPTU21sVFSU1rHOzs5qY6dPn67z+0bUGh8ETR3FS8DUaVJSUuDh4aF6+fn5WbokMqGYmBjcuXPHZPPps4wcEREZhz9hSWX9+vWqS7vaFBQUYNy4cUbNv3r1aqxatUr1eUVFBUNgC8pF7Vt2XgYHB+tc7L7lWH9/f51jWwYqT09Pvcc6OzvrHGtrawug+TltTz75JBwcHPDOO+/oHKvU+nl01dXVqkeCvPjii2rvlZSUaK2h9bP9zp8/j9/97ncQiUTYuXOn2rq/re+jLCgo0HkJuKWcnBydl3Vb+v777/Ue+/XXX+vdTWsK69evx759+3DmzJlOOyYRdS0MgKSyYsWKdldJGDBggNHzOzo6qu4ro7Y03edlY2Oj9/1fhowViUQmH5uRkYHFixdj48aNuHXrll7/r7Set+Vz5b788ks888wzWsfqcujQITz88MNwd3fHiRMn8Nhjj2kd2/Iev/bos2KGMWNb3hdJRNQZGABJxdPT06hnrhEBzauXrF27FvHx8UhMTFQ1YBgiIyND9bGTkxN++eUX9O/f36A5mpqasHnzZuzbtw/Xr1/H3//+d50BkIjIGvEeQDLKtWvXcObMGVy7dg1NTU04c+YMzpw5o/NSIfVclZWVEIvFsLOzw9ChQ2FjY4OzZ88aPM/nn3+u+njBggX45JNPjJpj1qxZcHV1RVBQEIqKigyeoztLS0tDr169sG/fPgwZMgROTk6YOnUqrl+/rnWfgoICTJ06FZ6envDw8EBUVBROnTqlNkYkEuHjjz/GrFmz4OzsjAcffBD79+9XG3PhwgVMnz4drq6u8Pb2xvz583H79m2zfJ1E1DEMgGSU+Ph4jB49GgkJCaiqqsLo0aMxevRonDhxwtKlkQW0fmZffHw8kpKSDJrj+vXrcHZ2xpdffokvv/wSU6dORU5OjkH3xsnlcnz22WdYunQpgObQ4u3tDZlMZlAt3V1NTQ2Sk5Oxc+dO/PTTT6pl3rSprKzEwoULkZubq1pHePr06aisrFQbl5iYiNmzZ6OwsBDTp0/HvHnzcPfuXQDNa0BHRUVh1KhROHHiBH744QfcvHkTs2fPNuvXSkRGsnQbMlkvYx5j0JMfA9OdvfLKK0JRUZHatri4OCE3N1fvOdavXy9kZWWpbXvnnXeEAwcO6D3H+++/L+zevVtt22effSbs2rVL7zm6ux07dggAhGPHjqm2FRUVCQCE48ePC4IgCAkJCcLIkSO1ztHY2Ci4ubmpfe8BCOvWrVN9XlVVJYhEIuH7778XBEEQ3nzzTeGRRx5Rm0f5qKfi4mJTfGnUAh8DQx3FM4BE1GESiQSBgYFq29asWYOUlBStHbYtNTY2Ijc3t83KH4sWLdL7YeMVFRVIT09vc6ar9brA1sDOzk6tWz8oKAi9evXSejm8tLQUzz//PIYMGaJ6TFNVVRWuXbumNm7EiBGqj11cXODm5qbq5D558iSysrLg6uqqegUFBQEALl26ZOovkYg6iE0gRNQhUqkUvr6+bR6Z4unpifDwcKSnp+Pxxx/XOccPP/yA2NhYNDU14ZtvvgEAzJo1C15eXno3g6SmpmLVqlVtHgnj6+sLmUwGQRC65FJ65qLpa9X29S9atAi3bt3Cxo0bERAQAEdHR0RERKC+vl5tXMvHDinnUz7qRqFQ4IknnsDf/va3NvP7+voa+2UQkZnwDCARdUhmZiZiYmI0vhcXF4dNmza1ex9fWloaFi1aBLlcjtmzZ2P27NmQy+UAmpfDa68ZpLS0FCdPnkRsbKzG94OCgiCRSPT4anqGxsZGtftxi4uL8dtvv6nOyLWWm5uLl19+GdOnT8fQoUPh6OhocPPGmDFjcP78eQwYMACDBw9We3EpO6KuhwGQiDokMzMTU6ZM0fieq6srZsyYgT179mjd//r163ByctL6CKLo6Oh2m0GSk5Oxbt06rWe4rO0ysL29PV566SUcP34cp06dwrPPPovw8HCEhYVpHD948GDs2rULRUVFOH78OObNm2fQcwwBYPny5bh79y7mzp2L/Px8XL58Gf/+97+xePHiTn3INRHphwGQiIwmCAJu3rwJHx8frWOWLVuGtLQ01Rm91j799FM899xzWvcXiUSIjY3F999/r/H9K1euQCaTITw8XOscUVFRyM7O1vp+T+Ps7Iw33ngDzzzzDCIiIiAWi7F3716t4z/99FOUlZVh9OjRmD9/Pl5++WX07dvXoGP269cPP/30E5qamvDoo49i2LBheOWVV+Dh4dHmsjwRWZ5I0OcObSIzqKiogIeHB8rLy+Hu7q7XPllZWZg8eTIuXbqEQYMGmblCak9RURH+/ve/4/3339c5bvfu3bhz5w5efvllte2NjY2IjY1FRkYGRCIRqqurVcu2VVVVqS4d3rp1Cy+88AL++c9/tpl70aJFeP311xESEqKzhsceewzffvttj19jOC0tDStXrsRvv/1m6VLIjIz5+UnUEv9ZRkRGy8jIwNSpU9sdN3fuXBw4cKDNc+WUzR/tNWd4eXnB0dERv/zyi9r2wsJC2NnZtRv+ACAsLAz5+fntjiMisgYMgERktOzsbEycOLHdcTY2NoiLi8OGDRvUtiubP/ShqRkkKSkJ8fHxeu1vbfcBEhHpwgBIREZpaGiAXC5XXbJtz7Rp01BQUKB6blx7zR+tTZo0Sa0ZJDc3FwEBAfD399drf2s5A7ho0SJe/iWidjEAEpFRCgoKtHaVaiISibB27Vq89dZbADQ3fzg4OGDHjh3YsWMHHBwc2uyvbAYRBAEpKSlYvXq13se3t7eHo6Mj16smIgIDIBEZSd/7/1qKiIiAVCrFzz//rHHlD3t7eyxatAiLFi1q89Bh4N7KIAcOHEBkZKTeZw+VrK0bmIhIGwZAIjJKfn4+QkNDDd4vPj4ezz//vF7NH615eXnB3t4e7777LlauXGnwsadOncr7AImIwKXgiMgIlZWVEIvFRj1SZejQobh06ZLGy8eNjY348ccfAQCPPvqoxvn9/f1RUVGh972HLQUFBWldD5eIyJrwDCARGSwnJ6fN5Vt9Xb9+HaNGjcIHH3zQ5j25XI7HH38cjz/+uMYHR8vlcpw4cQI1NTVGrS4hEong7e0NmUxmVO1ERD0FAyARGcyY+/+UPv30U7zyyivw8/NDXl6eQftu3boVS5YswfTp07WuDNIePg6GiIgBkIiMIJFIEBgYaPB+jY2NquaPNWvWICUlBfouRlRRUYH09HTMmTNH1QxiDAZAIiIGQCIykFQqha+vr8ENHID6yh+enp4IDw9Henq6XvumpqZi1apVsLGx0boyiD58fX0hk8n0Dp5ERD0RAyARGSQzMxMxMTFG7dt65Y+4uDhs2rSp3fv5SktLcfLkScTGxqq2aVoZRF9BQUGQSCRG7UtE1BMwABKRQTIzMzFlyhSD99O08oerqytmzJiBPXv26Nw3OTkZ69atUzvr2HplEEPwMjARWTsGQOpxtm/fjvvvvx8KhUJt+5NPPomFCxdaqKqeQRAE3Lx5Ez4+Pgbvq2nlDwBYtmwZ0tLSNHb9AsCVK1cgk8kQHh6utr3lyiCG4gOhicjaMQBSj/P000/j9u3byMrKUm0rKyvDjz/+iHnz5lmwsu5PIpEgODjY4P1aNn+05uDggMWLF2P79u1wcHDAhx9+iA8//FC1FFxiYiISEhI0zmtsM4ibmxtqa2vR2Nho8L5ERD0BAyD1OL1790ZsbKzaZcWvvvoKvXv3NurSJd1j7ONfWjZ/aDJ37lwcOHAAdXV1WL58OZYvXw57e3sUFhbCzs4OISEhGvfrSDNIWFgY8vPzDd6PiKgnYACkHmnevHn4+uuvVZcVd+/ejTlz5sDW1tbClXVv2dnZmDhxosH7tW7+aM3GxgZxcXHYsGGD2vakpCTEx8frnNvYZhDeB0hE1owBkHqkJ554AgqFAunp6bh+/Tpyc3Pxxz/+0dJldWsNDQ2Qy+UGL8GmqflDk2nTpiE/Px/ffPMNjhw5giNHjiAgIAD+/v469zO2GYRnAInImnEtYOqRxGIxfve732H37t34+eefMWTIEIwdO9bSZXVrBQUFGtfvbY+25o/WRCIR/vznP6su0z/yyCPYvXu3Xvspm0Eef/xxveuyt7eHo6MjqqqqjFpXmIioO+MZQOqx5s2bh/T0dHz66ac8+2cCxtz/p6v5Q5Px48erfdzeWUMlY5tB2A1MRNaKAZB6rMmTJ6N3794oLi7GM888Y+lyur38/HyEhoYatE97zR+6LF++XO+xxjaDTJ06lfcBEpFVYgCkHsvW1hY3btyAIAgYNGiQpcvp1iorKyEWi2FnZ9hdI+01f+hSUlJi0HhjmkGCgoJQVFRk0D5ERD0BAyARtSsnJ0fvy7hK+jZ/tNTyYdBvv/22QcczphlEJBLB29sbMpnMoGMREXV3DIBE1C5j7v/Tt/mjpY8//lj1cf/+/ZGXl6f3vsauDMLHwRCRNWIAJKJ2SSQSBAYG6j3e0OYPAKioqMAPP/yg+vzVV19FSkoKBEHQew5jmkEYAInIGvExMESkk1QqhY+Pj0GNHMY0f6SmpmLlypWYNm0aAMDX1xfh4eFIT0/X+/EuLZtB+vfvr9c+vr6+kMlkEATBqGYVIqLuiGcAiUinzMxMxMTEGLSPoc0fpaWlOHnyJJ544gm89tpreO211+Dg4IC4uDhs2rTJoPv6jG0GkUgkBu1DRNSdMQASkU6GBkBjmj+Sk5Oxbt26NmfgXF1dMWPGDLV1ndtjTDMILwMTkbVhACQirQRBwM2bN+Hj46P3PoY2f1y5cgUymQzh4eFoampCQUEBCgoKVAFu2bJlSEtLU+sQ1sWYZhA+EJqIrA0DIBFpJZFIEBwcrPd4Y5o/EhMTkZCQAACoq6tDWFgYwsLCUFdXBwBwcHDA4sWLsX37dr3nNLQZxM3NDbW1tWhsbNR7HyKi7owBkIi0MvTxL4Y2fxQWFsLOzg4hISE6x82dOxcHDhxAZWWlXvMaszJIWFgY8vPz9R5PRNSdMQASkVbZ2dmYOHGi3uMNbf5ISkpCfHx8u+NsbGwQFxeHDRs26D23oc0gXBaOiKwJAyARadTQ0AC5XA5XV1e9xhva/JGbm4uAgAD4+/vrNX7atGkoKChAaWmpXuMNbQYJDQ3lGUAishoMgESkUUFBAcLCwvQeb0jzhyAISElJwerVq/WeXyQSYc2aNUhOTtZ7vCHNIPb29nB0dERVVZXeNRERdVcMgESkkSH3/xna/HHgwAFERkYa9KgYAIiMjIRUKkVJSYle4w1tBmE3MBFZCwZAItIoPz8foaGheo01pPmjqakJmzdvxsqVK42qKyEhAYmJiXqNNbQZhPcBEpG1YAAkojYqKyshFothZ6ffapGGNH98/vnnmDVrlsZ7C+3t7ZGQkICEhATY29tr3H/o0KEQiUQ4e/asXsczpBkkKCgIRUVFeo0lIurOGACJqI2cnBy9L+ca0vwhl8vx2WefYenSpRrfd3BwwPr167F+/Xo4ODhonSchIQFJSUl61WdIM4hIJIK3tzdkMplecxMRdVcMgETUhiH3/xnS/LF161YsWbJEZ7jTR0BAAPz8/JCXl9fuWEObQbgsHBFZAwZAImpDIpEgMDCw3XGGNH9UVFQgPT0dc+bM0TpGoVDg/PnzOH/+PBQKhc751qxZg5SUFAiC0O6xDWkGYQAkImvAAEhEaqRSKXx8fPRq6DCk+SM1NRWrVq2CjY32Hzu1tbUYNmwYhg0bhtraWp3zeXp6Ijw8HOnp6e0e25BmEF9fX8hkMr2CJRFRd8UASERqMjMzERMTo9dYfZs/SktLcfLkScTGxnawOnVxcXHYtGmTXvf3GdoMIpFIOloeEVGXxQBIRGr0DYCGNH8kJydj3bp1eq8RrC9XV1fMmDEDe/bsaXesIc0gvAxMRD0dAyARqQiCgJs3b8LHx6fdsfo2f1y5cgUymQzh4eGmKLGNZcuWIS0tDXK5XOc4Q5pB+EBoIurpGACJSEUikSA4OLjdcYY0fyQmJiIhIcEU5Wnk4OCAxYsXY/v27e2OXbhwoV7NIG5ubqitrUVjY6MJKiQi6noYAIlIRd/Hv+jb/FFYWAg7OzuEhISYqkSN5s6diwMHDqCyslLnuL59++rdDBIWFob8/HxTlUhE1KUwABKRSnZ2NiZOnNjuOH2bP5KSkhAfH2+CynSzsbFBXFwcUlNT2x2rbzMIl4Ujop6MAZCIAAANDQ2Qy+Ual2hrSd/mj9zcXAQEBMDf31/vGuzt7fHqq6/i1Vdf1boUnDbTpk1DQUEBSktLdY7TtxkkNDSUZwCJqMdiACQiAEBBQQHCwsLaHadP84cgCEhJScHq1asNqsHBwQHvvvsu3n33XYNXCxGJRFi7di2Sk5PbHadPM4i9vT0cHR1RVVVlUB1ERN0BAyARAdDv/j99mz8OHjyIyMhIvR4RY0qRkZGQSqUoKSnROU7fZhB2AxNRT8UASAYrKSnBkiVLMHDgQIjFYjzwwANISEhAfX29pUujDsjPz0doaKjOMfo0fzQ1NWHz5s1YuXKlwTUoFAqUlJSgpKSk3aXgtElISEBiYqLOMfo2g/A+QCLqqRgAyWASiQQKhQLbt2/H+fPn8f7772Pbtm1Ys2aNpUsjI1VWVkIsFsPOzk7nOH2aPz7//HPMnDmz3XsJNamtrcXAgQMxcODAdpeC02bo0KEQiUQ4e/asznH6NIMEBQWhqKjIqDqIiLoyBkAyWGxsLHbs2IFHHnkEgwYNwpNPPolXX30V//rXvyxdGhkpJyen3cu6+jR/yOVyfPbZZ1i6dKmpSzSIPmcB9WkGEYlE8Pb2hkwmM3WJREQWxQBIJlFeXo7evXvrHCOXy1FRUaH2oq5Bn/v/9Gn+2Lp1K5YsWWJwA4epBQQEwM/PD3l5eVrH6NsMwmXhiKgnYgCkDrt06RI++OADPP/88zrHpaSkwMPDQ/Xy8/PrpAqpPRKJBIGBgVrf16f5o6KiAunp6ZgzZ445SjTY2rVrkZKSAkEQtI7RpxmEAZCIeiIGQFJZv349RCKRzteJEyfU9rlx4wZiY2Px9NNPt3t2aPXq1SgvL1e9rl+/bs4vh/QklUrh4+Ojs7FDn+aP1NRUrFq1CjY2XePHiqenJ8LDw5Genq51jD7NIL6+vpDJZDqDJBFRd6P7jm+yKitWrGj37M2AAQNUH9+4cQOTJk1CREQE/v73v7c7v6OjIxwdHTtaJplYZmYmYmJidI5JS0vDtm3btL5fWlqKkydPYv369SaurmPi4uIwa9YsTJs2Dba2thrHKJtBdK1XHBQUpPc6yURE3QEDIKl4enrq/dy2X3/9FZMmTcLYsWOxY8eOLnPWhwyXmZmJv/3tb1rf16f5Izk5GevWrWt3beDO5urqihkzZmDPnj2YP3++xjGTJk1CcnIympqatIZE5WVgBkAi6in4W5sMduPGDURHR8PPzw/vvfcebt26BZlMxk7JbkgQBNy8eRM+Pj5ax7TX/HHlyhXIZDKEh4d3uB47Ozu8+OKLePHFF9t9JI2+li1bhrS0NMjlco3v69MMwgdCE1FPwwBIBvv3v/+Nn3/+GYcPH0b//v3h6+urelH30t5lTX2aPxITE3VePjWEo6MjtmzZgi1btpjsdgEHBwcsXrwY27dv1zqmvWYQNzc31NbWorGx0SQ1ERFZGgMgGWzRokUQBEHji7qXjIwMnff/tdf8UVhYCDs7O4SEhJirRJOYO3cuDhw4gMrKSo3v69MMEhYWhvz8fHOVSETUqRgAiaxYdna2zrN77a38kZSUhPj4eJPVIwgCbt26hVu3bpn0HxQ2NjaIi4tDamqq1jHtrQzCZeGIqCdhACSyUg0NDZDL5VqXbGuv+SM3NxcBAQHw9/c3WU01NTXo27cv+vbti5qaGpPNCwDTpk1DQUEBSktLNb7f3sogoaGhPANIRD0GAyCRlSooKEBYWJjW93U1fwiCgJSUFKxevdpc5ZmcSCTC2rVrkZycrPV9Xc0g9vb2cHR0RFVVlTnLJCLqFAyARFZK1/Jv7TV/HDx4EJGRkXo/NqiriIyMhFQqRUlJicb322sGYTcwEfUUDIBEVio/Px+hoaEa39PV/NHU1ITNmzdj5cqVZq7QPBISEpCYmKjxvfaaQXgfIBH1FAyARFaosrISYrFY67P2dDV/fP7555g5c6bWewe7uqFDh0IkEuHs2bMa39fVDBIUFISioiJzlkdE1CkYAImsUE5OjtbLu7qaP+RyOT777DMsXbrU3CWala6zgLqaQUQiEby9vfnQcyLq9hgAiayQrvv/dDV/bN26FUuWLIGDg4M5yzO7gIAA+Pn5IS8vr8177TWDKJeFIyLqzhgAiayQRCJBYGBgm+26mj8qKiqQnp6OOXPmmK0uOzs7LFy4EAsXLjTZUnDarFmzBm+99ZbG5w3qagZhACSinoABkMjKSKVS+Pj4aGzw0NX8kZqailWrVsHGxnw/NhwdHZGWloa0tDSTLQWnjZeXF8LDw5Gent7mPV3NIL6+vpDJZFz5hoi6NQZAIiuTmZmpdfk3bc0fpaWlOHnyJGJjY81cXedatWoVNm7cqPF+v/aaQSQSibnLIyIyGwZAIiujLQDqav5ITk7GunXrtK4JbCqCIKC6uhrV1dWdcobN1dUVM2bMwJ49e9q8p6sZhI+DIaLujgGQyIoIgoCbN2/Cx8enzXvamj+uXLkCmUyG8PBws9dXU1MDV1dXuLq6mnwpOG3+9Kc/IS0tDXK5XG27rmaQiRMn8oHQRNStMQASWRGJRILg4OA223U1fyQmJiIhIaEzyrMIBwcHLF68GNu2bWvznrZmEDc3N9TW1qKxsbETKiQiMj0GQCIrkpGRofHyr7bmj8LCQtjZ2SEkJKSzSrSIuXPn4uDBg6isrFTbrqsZJCwsDPn5+Z1VIhGRSTEAElmR7OxsjWf5tDV/JCUlIT4+vhMqsywbGxvExcUhNTW1zXvamkF4HyARdWcMgERWoqGhAXK5vM0SbtqaP3JzcxEQEAB/f//OLNNipk2bhoKCApSWlqpt19YMEhoayjOARNRtMQASWYmCggKEhYW12a6p+UMQBKSkpGD16tWdVZ7FiUQirF27FsnJyW22a2oGsbe3h6OjI6qqqjqzTCIik2AAJLISmpZ/09b8cfDgQURGRmp8JExPFhkZCalUipKSErXt2ppBoqKi2A1MRN0SAyCRlcjPz0doaKjaNk3NH01NTdi8eTNWrlzZyRUCtra2eOqpp/DUU0/B1ta2048PAAkJCUhMTFTbpq0ZhPcBElF3xQBIZAUqKyshFovbrK+rqflj9+7dmDlzZpt7BTuDk5MTvvrqK3z11VdwcnLq9OMDwNChQyESiXD27Fm17ZqaQYKCglBUVNSZ5RERmQQDIJEVyMnJaXOZV1Pzh1wux86dO7F06dLOLrFL0XQWMDo6uk0ziEgkgre3N2QyWWeXSETUIQyARFZA0/1/mpo/tm7diiVLlsDBwaEzy+tyAgIC4Ofnh7y8PNU2Gxsbjc0gMTExvAxMRN0OAyCRFZBIJAgMDFR9rqn5o6KiAunp6ZgzZ44lSgQAVFdXQyQSQSQSobq62mJ1AMCaNWvw1ltvqa1JrKkZhAGQiLojBkCiHk4qlcLHx0et0UNT80dqaipWrVoFGxv+WAAALy8vhIeHIz09XbVNUzOIr68vZDKZWlAkIurq+JOeqIfLzMxss/xb6+aP0tJSnDx5ErGxsZ1cXde2atUqbNy4Ue2+P23NIBKJpLPLIyIyGgMgUQ/XOgBqav5ITk7GunXr2qwFbO1cXV0xY8YM7NmzR7VNUzMIHwdDRN0NAyBRDyYIAm7evAkfHx/VttbNH1euXIFMJkN4eLglSuzy/vSnP2HHjh2Qy+UANDeDTJw4kQ+EJqJuhQGQqAeTSCQIDg5Wfa6p+SMxMREJCQmWKK9bcHBwwOLFi7Ft2zbVttbNIG5ubqitrUVjY6MFKiQiMhwDIFEPlpGRoXb5t3XzR2FhIezs7BASEmKpEruFZ555BgcPHkRlZSUAzc0gYWFhyM/Pt1SJREQGYQAk6sGys7PVzva1bv5ISkpCfHy8BSrTzNbWFtOnT8f06dMtthScJjY2NoiLi0NqaqpqW+tmEN4HSETdCQMgUQ/V0NAAuVyuWtKtdfNHbm4uAgIC4O/vb8ky1Tg5OSE9PR3p6ekWWwpOm2nTpqGgoAClpaUA2jaDhIaG8gwgEXUbDIBEPVRBQQHCwsJUn7ds/hAEASkpKVi9erWlyut2RCIR1q5di+TkZABtm0Hs7e3h6OiIqqoqS5ZJRKQXBkCiHqrl/X+tmz8OHjyIyMhItUfBUPsiIyMhlUpRUlICoG0zSFRUFLuBiahbYAAk6qHy8/NVZwBbNn80NTVh8+bNWLlypWUL1KC6uhouLi5wcXGx+FJw2iQkJCAxMRFA22YQ3gdIRN0FAyBRD1RZWQmxWAw7OzsA6s0fu3fvxsyZM1X3BnY1NTU1qKmpsXQZWg0dOhQikQhnz54FoN4MEhQUhKKiIkuWR0SkFwZAoh4oJydHdbm3ZfOHXC7Hzp07sXTpUgtX2L21PAvYshlEJBLB29sbMpnMwhUSEenGAEjUA2VkZGDq1KkA1Js/tm3bhiVLlsDBwcGS5XV7AQEB8PPzQ15eXptmkJiYGF4GJqIujwGQqAeSSCQIDAxUa/6oqKhAeno65syZY+nyeoQ1a9bgrbfegiAIas0gDIBE1B0wABL1MFKpFD4+PhCJRGrNH6mpqYiLi4ONDf/am4KXlxfCw8ORnp6u1gzi6+sLmUwGQRAsXSIRkVb8TUDUw2RmZqoe/6Js/igtLcXJkycRGxtr4ep6llWrVmHjxo1oampq0wwikUgsXB0RkXYMgEQ9jDIAtmz+SE5Oxrp161RrAHdVNjY2iIqKQlRUVLc4U+nq6ooZM2Zg9+7das0gfBwMEXV1Xf8nLBHpTRAE3Lx5Ez4+PqrmjytXrkAmkyE8PNzS5bVLLBbjyJEjOHLkCMRisaXL0cuf/vQnpKWloaGhQdUMMnHiRD4Qmoi6NAZAoh5EIpEgODhYrfkjMTERCQkJli6tx3JwcMDixYuxbds2VTOIm5sbamtr0djYaOnyiIg0YgAk6kGUy78pmz/Onj0LOzs7hISEWLq0Hu2ZZ57BgQMHIBaLVc0gYWFhyM/Pt3RpREQaMQAS9SDZ2dmIiopSNX8kJSUhPj7e0mXprbq6Gl5eXvDy8uqyS8FpYmNjg7i4OKSmpqqaQXgfIBF1ZQyARD1EQ0MD5HI5ysrK4OTkhKKiIgQEBMDf39/SpRnk9u3buH37tqXLMNj06dNRUFCAkJAQ5OTkYMyYMTwDSERdlp2lCyAi0ygoKEBYWBg+/fRTLFmyBCkpKfjss88sXZbVEIlEWLt2LVJSUhAbG4vMzEw4Ojqiqqqqy667TETWi2cAiXqIjIwMREdHIzc3F5WVlYiMjISnp6ely7IqkZGRkEqlmDRpEtLS0hAVFcVuYCLqkhgAiXqI/Px8lJWV4ZFHHsEHH3yAlStXWrokq5SQkIAtW7bA0dERw4cP532ARNQlMQAS9QCVlZUQi8XYtWsXXFxcMHPmTF52tJChQ4dCJBJh0qRJyM7ORlFRkaVLIiJqgwGQqAfIycnBiBEjYG9vj3/9619YunSppUuyagkJCfj++++Rm5sLLy8vyGQyS5dERKSGAZC6hTt37kAQBLVtCoUCd+/etVBFXUtGRgZu3bqFPn36YMmSJXBwcLB0SUaxsbHBuHHjMG7cuG6xFJw2yu7rwMBAeHl58TIwEXU53fcnLFmVoKAgfPDBB2rbXn/9dUydOtVCFXUtFy5cwNmzZ/Hf//4Xc+bMsXQ5RhOLxSgoKEBBQUG3WQpOmzVr1uC///0viouLGQCJqMthAKRuYcaMGXjrrbdQV1cHACgtLcWWLVswc+ZMyxbWBUilUjQ1NcHe3h5xcXHd+sxZT+Ll5YWJEyeiuroaJSUlbc5gaxIdHd2jm3dKSkogEolw5swZS5dCZPX4m4K6hTVr1uDOnTs4cOAAAGD79u1wcnLCyy+/bOHKLC8zMxN3796FSCRCbGyspcuhFlatWoXKykrU1tZCIpG0O/5f//oX/vrXv3ZCZURk7RgAyShPPvkk/P394eTkBF9fX8yfPx83btww2/EGDRqEhQsXYu/evQCAf/zjH1i1ahU8PDzMdszu4ttvv0VlZSWSkpIgEoksXU6H1NTUYMCAARgwYABqamosXU6Hubq6YuHChZBKpfj3v//d7vjevXvDzc2tEyojImvHAEhGmTRpEr788ksUFxfj66+/xqVLl/DUU0+Z9Zhr1qxBRUUFAMDR0ZFn/wAIgoCCggL4+fkhPDzc0uV0mCAIuHr1Kq5evarXJdOu5uOPP8YTTzyBvLw81bbnn38ednZ2qn+86NL6EvCAAQPw//7f/8OCBQvg6uqKgIAAfPvtt7h16xZmzJgBV1dXDB8+HCdOnFDtc+fOHcydOxf9+/eHs7Mzhg8fjn/84x9qx6msrMS8efPg4uICX19fvP/++22OXV9fj9dffx33338/XFxcMH78eBw5ckRn/SKRCFu3bsW0adMgFosxcOBAfPXVV1rHNzU1YcmSJRg4cCDEYjECAwOxadMmtTGLFi3CzJkz8d5778HX1xd9+vTB8uXL0dDQ0KFaiawdAyAZJS4uDuHh4QgICEBkZCT+8pe/4NixY2o/lE1t0KBBePTRRwEAixcv5tk/AOfOncPt27fx4YcfWroUAjBmzBhcu3YNDz/8MKZOnYqffvoJDg4OePXVV3H+/Hk0NjYaPOf777+Phx56CKdPn8Zjjz2G+fPnY8GCBfjjH/+IU6dOYfDgwViwYIEqMNfV1WHs2LE4ePAgzp07h2XLlmH+/Pk4fvy4as5Vq1bhp59+wv79+5GRkYHc3FycOnVK7bjPPvssfvrpJ+zduxeFhYV4+umnERsbi4sXL+qs980338Tvf/97/O///i/++Mc/Yu7cuVqfhahQKNC/f398+eWXuHDhAuLj47FmzRp8+eWXauOysrJw6dIlZGVlYefOnUhLS0NaWlqHayWyZiKhO/4zm7qUu3fv4oUXXsCvv/6qduajPRUVFfDw8EB5eTnc3d312ufs2bP4wx/+gOzsbHh5eRlbco8xY8YMnDt3Dj/99JOlSzGJmpoaPPDAAwCAS5cuwdnZ2cIVGU6hUOD7779HamoqioqKMHHiRLzxxhuYPXs2/ud//gdz587Vum90dDRGjRqFjRs3Amg+A/jwww9j165dAACZTAZfX1+8+eabSEpKAgAcO3YMERERkEql8PHx0TjvY489huDgYLz33nuorKxEnz59sGfPHtVZ+/LycvTr1w9Lly7Fxo0bcenSJTz44IP45Zdf0K9fP9U8MTExCAsLw1tvvaXxOCKRCM8//zy2bt2q2hYeHo4xY8bgo48+QklJCQYOHIjTp09j1KhRGudYvnw5bt68iX/+858Ams8AHjlyBJcuXYKtrS0AYPbs2bCxscHevXuNrrW7M+bnJ1FLdpYugLqvN954Ax9++CFqamoQHh6OgwcP6hwvl8shl8tVnysv5xpi+PDhuHDhgsH79VQHDhyAIAjw9fW1dCkmpwyC3V1OTg5ycnIQGxuLlJQUnQFQkxEjRqg+9vb2BtD896D1ttLSUvj4+KCpqQlvv/02vvjiC/z666+qv3cuLi4AgMuXL6OhoQFhYWGqOTw8PBAYGKj6/NSpUxAEAUOGDFGrRS6Xo0+fPjrrjYiIaPO5rq7fbdu24eOPP8bVq1dRW1uL+vr6NuFw6NChqvAHAL6+vjh79myHayWyZgyApLJ+/XokJibqHFNQUIBx48YBAF577TUsWbIEV69eRWJiIhYsWICDBw9qbURISUlpd34yzIkTJyCVSi1dBrVy48YNfPnllzh8+DB69eqFZ555Bhs2bDDqET329vaqj5V/tzRtUygUAIDU1FS8//772LhxI4YPHw4XFxesXLkS9fX1AKC6VNz672nLi0EKhQK2trY4efKkWvACYNQSg9p+Jnz55ZeIi4tDamoqIiIi4ObmhnfffVftcnXrr1c5n/LrNXWtRNaCAZBUVqxY0e5DhAcMGKD62NPTE56enhgyZAiCg4Ph5+enuhylyerVq7Fq1SrV5xUVFfDz8zNJ7dZqzJgxli6BWrhx4wbWrl2LXbt2oW/fvnj//fexdOnSTn2odW5uLmbMmIE//vGPAJoD0sWLFxEcHAyg+cyqvb098vPzVX//KioqcPHiRURFRQEARo8ejaamJpSWluLhhx826PjHjh3DggUL1D4fPXq01lojIyPx4osvqrZdunTJoON1pFYia8YASCrKQGcM5dmDlpd4W3N0dISjo6NR8xN1B59++in+/e9/Y8OGDZ0e/JQGDx6Mr7/+GkePHsV9992HDRs2QCaTqQKgm5sbFi5ciNdeew29e/dG3759kZCQABsbG9WZuiFDhmDevHlYsGABUlNTMXr0aNy+fRuHDx/G8OHDMX36dK3H/+qrrzBu3DhMmDABu3fvRn5+Pj755BOttX722Wf48ccfMXDgQOzatQsFBQUYOHCg3l9vR2olsmbsAiaD5efn48MPP8SZM2dw9epVZGVl4ZlnnsEDDzyg9ewfkTVYt24dfv31V7z88ssWW8ruzTffxJgxY/Doo48iOjoaPj4+bVbM2bBhAyIiIvD4448jJiYGDz30EIKDg+Hk5KQas2PHDixYsAB//vOfERgYiCeffBLHjx9v96x9YmIi9u7dixEjRmDnzp3YvXs3QkJCNI59/vnn8bvf/Q5/+MMfMH78eNy5c0ftbKC+jK2VyJqxC5gMdvbsWbzyyiv43//9X1RXV8PX1xexsbFYt24d7r//fr3nYRcbUddQXV2N+++/H6mpqViyZInR84hEInzzzTdcorET8OcndRQvAZPBhg8fjsOHD1u6DCIy0unTpyGRSBAWFoby8nLVI2VmzJhh4cqIqLMwABIRWaH33nsPxcXFcHBwwNixY5Gbm2v0PcBE1P0wABIRWZnRo0fj5MmTJp+XdxQRdR9sAiEiIiKyMgyARERERFaGAZCIiIjIyjAAEhEREVkZBkAiIiIiK8MASERERGRlGACJiIiIrAwDIBEREZGVYQAkIiIisjIMgERERERWhgGQiIiIyMowABIRERFZGQZAIiIiIivDAEhERERkZRgAiYiIiKwMAyARERGRlWEAJCIiIrIyDIBEREREVoYBkIiIiMjKMAASERERWRkGQCIiIiIrwwBIREREZGUYAImIiIisDAMgERERkZWxs3QBZL0EQQAAVFRUWLgSIqLuRflzU/lzlMhQDIBkMXfu3AEA+Pn5WbgSIqLu6c6dO/Dw8LB0GdQNMQCSxfTu3RsAcO3aNav/AVZRUQE/Pz9cv34d7u7uli7Hovi9UMfvxz38XtxTXl4Of39/1c9RIkMxAJLF2Ng034Lq4eFh9T/Mldzd3fm9+D/8Xqjj9+Mefi/uUf4cJTIU/88hIiIisjIMgERERERWhgGQLMbR0REJCQlwdHS0dCkWx+/FPfxeqOP34x5+L+7h94I6SiSwh5yIiIjIqvAMIBEREZGVYQAkIiIisjIMgERERERWhgGQiIiIyMowAJLFlZSUYMmSJRg4cCDEYjEeeOABJCQkoL6+3tKlWURycjIiIyPh7OyMXr16WbqcTvfRRx9h4MCBcHJywtixY5Gbm2vpkiwiJycHTzzxBPr16weRSIR9+/ZZuiSLSElJQWhoKNzc3NC3b1/MnDkTxcXFli7LYrZu3YoRI0aoHoYdERGB77//3tJlUTfEAEgWJ5FIoFAosH37dpw/fx7vv/8+tm3bhjVr1li6NIuor6/H008/jRdeeMHSpXS6L774AitXrsTatWtx+vRpPPzww5g2bRquXbtm6dI6XXV1NUaOHIkPP/zQ0qVYVHZ2NpYvX45jx44hIyMDjY2NeOSRR1BdXW3p0iyif//+ePvtt3HixAmcOHECkydPxowZM3D+/HlLl0bdDB8DQ13Su+++i61bt+Ly5cuWLsVi0tLSsHLlSvz222+WLqXTjB8/HmPGjMHWrVtV24KDgzFz5kykpKRYsDLLEolE+OabbzBz5kxLl2Jxt27dQt++fZGdnY2JEydaupwuoXfv3nj33XexZMkSS5dC3QjPAFKXVF5ezkXOrUx9fT1OnjyJRx55RG37I488gqNHj1qoKupqysvLAYA/HwA0NTVh7969qK6uRkREhKXLoW7GztIFELV26dIlfPDBB0hNTbV0KdSJbt++jaamJnh7e6tt9/b2hkwms1BV1JUIgoBVq1ZhwoQJGDZsmKXLsZizZ88iIiICdXV1cHV1xTfffIOQkBBLl0XdDM8AktmsX78eIpFI5+vEiRNq+9y4cQOxsbF4+umn8dxzz1moctMz5nthrUQikdrngiC02UbWacWKFSgsLMQ//vEPS5diUYGBgThz5gyOHTuGF154AQsXLsSFCxcsXRZ1MzwDSGazYsUKzJkzR+eYAQMGqD6+ceMGJk2ahIiICPz97383c3Wdy9DvhTXy9PSEra1tm7N9paWlbc4KkvV56aWXsH//fuTk5KB///6WLseiHBwcMHjwYADAuHHjUFBQgE2bNmH79u0Wroy6EwZAMhtPT094enrqNfbXX3/FpEmTMHbsWOzYsQM2Nj3r5LQh3wtr5eDggLFjxyIjIwOzZs1Sbc/IyMCMGTMsWBlZkiAIeOmll/DNN9/gyJEjGDhwoKVL6nIEQYBcLrd0GdTNMACSxd24cQPR0dHw9/fHe++9h1u3bqne8/HxsWBllnHt2jXcvXsX165dQ1NTE86cOQMAGDx4MFxdXS1bnJmtWrUK8+fPx7hx41Rngq9du4bnn3/e0qV1uqqqKvz888+qz69cuYIzZ86gd+/e8Pf3t2BlnWv58uXYs2cPvv32W7i5uanOEHt4eEAsFlu4us63Zs0aTJs2DX5+fqisrMTevXtx5MgR/PDDD5YujbobgcjCduzYIQDQ+LJGCxcu1Pi9yMrKsnRpnWLLli1CQECA4ODgIIwZM0bIzs62dEkWkZWVpfH/g4ULF1q6tE6l7WfDjh07LF2aRSxevFj198PLy0uYMmWK8O9//9vSZVE3xOcAEhEREVmZnnWjFRERERG1iwGQiIiIyMowABIRERFZGQZAIiIiIivDAEhERERkZRgAiYiIiKwMAyARERGRlWEAJCIiIrIyDIBEREREVoYBkIiIiMjKMAASERERWRkGQCIiIiIrwwBIREREZGUYAImIiIisDAMgERERkZVhACQiIiKyMgyARERERFaGAZCIiIjIyjAAEhEREVkZBkAiIiIiK8MASERERGRlGACJiIiIrAwDIBEREZGVYQAkIiIisjIMgERERERWhgGQiIiIyMowABIRERFZGQZAIiIiIivDAEhERERkZRgAiYiIiKwMAyARERGRlfn/aJl5njqFgkoAAAAASUVORK5CYII=' width=640.0/>\n",
       "            </div>\n",
       "        "
      ],
      "text/plain": [
       "Canvas(toolbar=Toolbar(toolitems=[('Home', 'Reset original view', 'home', 'home'), ('Back', 'Back to previous …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    }
   ],
   "source": [
    "# ---INPUT------ #\n",
    "focal_length = 1.0\n",
    "# -------------- #\n",
    "\n",
    "animate.geometric_ray_diagram(focal_length, magnification=True)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "wZDgbEqYj1ks"
   },
   "source": [
    "The magnification of a\n",
    "lens is given by\n",
    "Newton's law:\n",
    "$$\n",
    "\\frac{1}{u}+\\frac{1}{v} =\\frac{1}{f}\n",
    "$$\n",
    "\n",
    "The magnification M is defined as\n",
    "$$ \n",
    "M = \\frac{v}{u}\n",
    "$$"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "-iSlYQSfkUXk"
   },
   "source": [
    "### Focus\n",
    "The microscope consists of a\n",
    "stack of lenses in which the\n",
    "image plane of one lens is the\n",
    "object plane of the next one.\n",
    "\n",
    "The focal length $f$ of a\n",
    "magnetic lens can be changed\n",
    "by its electric current.\n",
    "\n",
    "If the field is too weak, we call\n",
    "it underfocus, is it too strong\n",
    "we speak of overfocus.\n",
    "\n",
    "![focus](images/focus.png)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### Condenser Ray Diagram\n",
    "Below is a stack of lenses that is equivalent to the condenser lens system on the Libra 200.\n",
    "\n",
    "The objective lens focal length is usually not changed (at least not much), and the sample is in the middle of the objective lens system.\n",
    "\n",
    "Change the ``focal lengths`` parameters so that there the illumination changes from parallel to convergent. \n",
    "\n",
    "Tip: do not change the gun (first value), and the objective (last two values) values."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 13,
   "metadata": {
    "id": "pEkk_1rHfowo"
   },
   "outputs": [
    {
     "data": {
      "application/vnd.jupyter.widget-view+json": {
       "model_id": "676ecdf2d93c44e19976124bb68e6d61",
       "version_major": 2,
       "version_minor": 0
      },
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAoAAAAHgCAYAAAA10dzkAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjguMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8g+/7EAAAACXBIWXMAAA9hAAAPYQGoP6dpAAB4zElEQVR4nO3dd3hT1f8H8He6S0dKKSUdFHAgS6CUPQSUvUQURBCZKrJFURAVVLaIIAKKQoGvoiDLgQIFARllt8gU0DIKLaMtLdDdnN8f59fQ0EFHkpvkvl/PkweS3CTn3Cb3fu4Zn6MRQggQERERkWo4KF0AIiIiIrIsBoBEREREKsMAkIiIiEhlGAASERERqQwDQCIiIiKVYQBIREREpDIMAImIiIhUhgEgERERkcowACQiIiJSGQaARERERCrDAJCIiIhIZRgAEhEREakMA0AiIiIilWEASERERKQyDACJiIiIVIYBIBEREZHKMAAkIiIiUhkGgEREREQqwwCQiIiISGUYABIRERGpDANAIiIiIpVhAEhERESkMgwAiYiIiFSGASARERGRyjAAJCIiIlIZBoBEREREKsMAkIiIiEhlGAASERERqQwDQCIiIiKVYQBIREREpDIMAImIiIhUhgEgERERkcowACQiIiJSGQaARERERCrDAJCIiIhIZRgAEhEREakMA0AiIiIilWEASERERKQyDACJiIiIVIYBIBEREZHKMAAkIiIiUhkGgEREREQqwwCQiIiISGUYABIRERGpDANAIiIiIpVhAEhERESkMgwAiYiIiFSGASARERGRyjAAJCIiIlIZBoBEREREKsMAkIiIiEhlGAASERERqYzdBoAzZ85Eo0aN4OXlBX9/f/Ts2RP//POP0TZCCEydOhWBgYFwd3dHmzZtcOrUKYVKTERERGQZdhsA7t69GyNHjsSBAwcQERGB7OxsdOjQAffu3TNsM2fOHMybNw9ffvklDh8+DJ1Oh/bt2+POnTsKlpyIiIjIvDRCCKF0ISzh5s2b8Pf3x+7du/HUU09BCIHAwECMGzcO7777LgAgIyMDlSpVwuzZs/H6668rXGIiIiIi87DbFsAHJScnAwB8fX0BADExMYiPj0eHDh0M27i6uqJ169bYv3+/ImUkIiIisgQnpQtgCUIIjB8/Hi1btkSdOnUAAPHx8QCASpUqGW1bqVIlXLp0qcD3ycjIQEZGhuG+Xq9HYmIiKlSoAI1GY6bSExERkSkJIXDnzh0EBgbCwUE1bWFGVBEAjho1Cn///Tf27t2b77kHAzchRKHB3MyZM/HRRx+ZpYxERERkWVeuXEFwcLDSxVCE3QeAo0ePxi+//IK//vrL6I+s0+kAyJbAgIAAw+M3btzI1yqYa9KkSRg/frzhfnJyMkJCQnDlyhV4e3ubqQZERERkSikpKahcuTK8vLyULopi7DYAFEJg9OjR2LhxI3bt2oVq1aoZPV+tWjXodDpEREQgNDQUAJCZmYndu3dj9uzZBb6nq6srXF1d8z3u7e3NAJCIiMjGqHn4lt0GgCNHjsTq1avx888/w8vLyzDmT6vVwt3dHRqNBuPGjcOMGTPw+OOP4/HHH8eMGTNQrlw59OvXT+HSExEREZmP3QaAS5YsAQC0adPG6PHw8HAMGjQIAPDOO+8gLS0NI0aMQFJSEpo0aYJt27apukmYiIiI7J9q8gCaQ0pKCrRaLZKTk9kFTEREZCN4/lZRHkAiIiIikhgAEhEREakMA0AiIiIilWEASERERKQyDACJiIiIVIYBIJnN33//jaFDh+LRRx+Fu7s73N3d8fjjj+P111/HkSNHlC6eWfz9998YPHgwqlWrBjc3N3h6eqJBgwaYM2cOEhMTAQB79+7FsGHDEBYWBldXV2g0Gly8eFHZgpfRw+qdk5ODefPmoVOnTggODka5cuVQs2ZNTJw4Ebdv31a6+KVSnL/1F198gaZNm8LPzw+urq4ICQlB3759cerUKYVLb3sOHDiA3r17IyAgAC4uLtDpdHjhhRcQGRlptN3UqVOh0Whw69ath75nmzZt8qUKM6XVq1dj/vz5BT6n0WgwdepUs3020cPYbR5AUtbXX3+NUaNG4YknnsDYsWNRu3ZtaDQanDlzBj/88AMaNWqECxcu4NFHH1W6qCbzzTffYMSIEXjiiScwYcIE1KpVC1lZWThy5Ai++uorREZGYuPGjdixYwe2b9+O0NBQeHt7Y9euXUoXvUyKU+///e9/mDp1Kl566SUMGzYMfn5+OHbsGKZNm4Zff/0VR44cgbu7u9JVKbbi/q0TEhLQuXNn1KtXD+XLl8d///2HWbNmoUmTJjh69CieeOIJpatiExYuXIhx48ahcePGmDNnDqpUqYLLly9j0aJFaNmyJRYsWIBRo0aV+H0XL15shtLet3r1apw8eRLjxo3L91xkZKRq16AlKyGo1JKTkwUAkZycrHRRrMrevXuFg4OD6N69u8jIyChwm7Vr14qrV69auGTms3//fuHo6Cg6deok0tPT8z2fkZEhfv75ZyGEEDk5OYbHP/30UwFAxMTEWKqoJlXcemdnZ4tbt27le/6nn34SAMT//vc/SxTXJEryty7I6dOnBQDxwQcfmLOYdiP3eNKtWzeRlZVl9FxWVpbo1q2bcHBwEHv37hVCCDFlyhQBQNy8eVOJ4hrp2rWrqFKlitLFoALw/C0Eu4DJ5GbMmAFHR0d8/fXXcHFxKXCb3r17IzAwEEDh3TCDBg1C1apVDfcvXrwIjUaDuXPnYt68eahWrRo8PT3RrFkzHDhwwBxVKbYZM2ZAo9Fg6dKlBa4X7eLigh49egAAHBzs52dX3Ho7OjqiQoUK+Z5v3LgxAODKlStmL6uplORvXZCKFSsCAJyc2AFTHDNnzoRGo8GSJUvy7TMnJycsXrwYGo0Gs2bNMnruypUr6NWrF7y9vaHVavHyyy/j5s2bRtsUdOzJzMzEtGnTUKNGDbi6uqJixYoYPHhwvtcCsoWvWbNm8PT0hKenJ+rXr49ly5YZ3nvz5s24dOkSNBqN4ZYrbxfw8ePHodFoDK/N648//oBGo8Evv/xieOz8+fPo168f/P394erqipo1a2LRokUP35lEedjPmYisQk5ODnbu3ImGDRsiICDALJ+xaNEiREREYP78+fj+++9x7949dOnSBcnJyWb5vIfJycnBn3/+ibCwMFSuXFmRMijBFPX+888/AQC1a9c2ZdHMprR1zsnJQUZGBs6ePYthw4bB398fgwcPNmNJ7UPe40lh3aWVK1dGWFgY/vzzT+Tk5Bgef+655/DYY49h3bp1mDp1KjZt2oSOHTsiKyur0M/T6/V49tlnMWvWLPTr1w+bN2/GrFmzEBERgTZt2iAtLc2w7Ycffoj+/fsjMDAQK1aswMaNGzFw4EBcunQJgOxebtGiBXQ6HSIjIw23gtSrVw+hoaEIDw/P99yKFSvg7++PLl26AABOnz6NRo0a4eTJk/jss8/w22+/oWvXrhgzZgw++uijh+9Uov/HS1AyqVu3biEtLQ1VqlTJ91xOTg5EnpUHHR0dja6Ii8vLywu//fYbHB0dAQCBgYFo3Lgx/vjjD/Tt27f0hS+lW7duITU1FdWqVbP4ZyuprPW+evUqJk6ciIYNG6Jbt24mLp15lLbOHh4eyMjIAABUr14du3btUtXFQmkVd39Xq1YNhw4dQkJCguGxXr16Yc6cOQCADh06oFKlSujfvz/Wrl2L/v37F/g+a9euxZYtW7B+/Xr06tXL8Hi9evXQqFEjrFixAm+88QZiYmIwY8YM9O/fH999951hu/bt2xv+X6tWLfj4+MDV1RVNmzZ9aF0HDx6MMWPG4Ny5c6hevToAICkpCT///DNGjRplaP0cP348vLy8sHfvXsMSZu3bt0dGRgZmzZqFMWPGoHz58g/9PCK2AJLFhIWFwdnZ2XD77LPPSvU+Xbt2NQR/AFC3bl0AMFx5k/VLTExEly5dIITAmjVr7KpbvCD79+9HZGQkvvvuO3h5eaFt27acCWxCuReWeS8oHwzy+vTpAycnJ+zcubPQ9/ntt9/g4+OD7t27Izs723CrX78+dDqdYcJWREQEcnJyMHLkSJPVoX///nB1dcWKFSsMj/3www/IyMgwtBanp6djx44deO6551CuXDmjMnbp0gXp6emKD4ch22HfR12yOD8/P7i7uxcYjK1evRqHDx82GstSGg+OJcsdh5W3e8aS/Pz8UK5cOcTExCjy+Uopbb2TkpLQvn17XL16FREREXjkkUfMVELTK22dGzRogKZNm6J///7YuXMnhBB47733zFRK+1Hc/X3x4kWUK1cOvr6+hsd0Op3RNk5OTqhQoYJRK+GDrl+/jtu3b8PFxcXoYtXZ2Rnx8fGG1DK54wFNOYvX19cXPXr0wKpVqwxd2StWrEDjxo0NQyQSEhKQnZ2NhQsX5itfbhdxcdLfEAHsAiYTc3R0xNNPP41t27YhLi7OaBxgrVq1ACBfzjs3N7cCx+/ZyoHM0dERzzzzDP744w/ExsaqJrVDaeqdlJSEdu3aISYmBjt27DC03toKU/ytvby8UKNGDZw7d84MJbQvjo6OaNu2LbZs2VLo/o6NjcXRo0fRuXNno56B+Ph4BAUFGe5nZ2cjISGhwMlIufz8/FChQgVs2bKlwOe9vLwA3J/IExsba9Ku/MGDB+Onn35CREQEQkJCcPjwYSxZssTwfPny5eHo6IgBAwYU2vqotqEoVHpsASSTmzRpEnJycjB8+PAiB1znqlq1Ks6dO2cYIwXIK939+/ebs5gmNWnSJAgh8OqrryIzMzPf81lZWfj1118VKJl5laTeucHff//9h23btiE0NNTSxTWJsv6tb926hRMnTuCxxx4zZzHtRu7+HjFihNEkD0COK37jjTcghMCkSZOMnvv++++N7q9duxbZ2dlFJn7u1q0bEhISkJOTg4YNG+a75eZt7NChAxwdHY2Cs4K4urqWqGeiQ4cOCAoKQnh4OMLDw+Hm5oaXXnrJ8Hy5cuXQtm1bREVFoW7dugWWsagAlygvtgCSybVo0QKLFi3C6NGj0aBBA7z22muoXbs2HBwcEBcXh/Xr1wOAYQDzgAED8PXXX+Pll1/Gq6++ioSEBMyZM8fwvC1o1qwZlixZghEjRiAsLAxvvPEGateujaysLERFRWHp0qWoU6cOunfvjps3b2L37t0AgBMnTgCQqR4qVqyIihUronXr1kpWpUSKW+927dqhY8eOiIqKwvz585GdnW00VqlixYo2kxS8uHV+6qmn0L59e/Tr1w+PP/443N3dce7cOSxYsAAZGRmYMmWK0lWxCS1atMD8+fMxbtw4tGzZEqNGjUJISIghEfTBgwcxf/58NG/e3Oh1GzZsgJOTE9q3b49Tp07hgw8+QL169dCnT59CP6tv3774/vvv0aVLF4wdOxaNGzeGs7MzYmNjsXPnTjz77LN47rnnULVqVbz33nv45JNPkJaWhpdeeglarRanT5/GrVu3DLNxn3zySWzYsAFLlixBWFgYHBwc0LBhw0I/39HREa+88grmzZsHb29v9OrVC1qt1mibBQsWoGXLlmjVqhXeeOMNVK1aFXfu3MGFCxfw66+/GmbWEz2UYhkI7QATSRYtOjpaDB48WFSrVk24uroKNzc38dhjj4lXXnlF7Nixw2jblStXipo1awo3NzdRq1YtsWbNGjFw4ECjJKoxMTECgPj000/zfRYAMWXKFDPX6OGio6PFwIEDRUhIiHBxcREeHh4iNDRUfPjhh+LGjRtCCCF27twpABR4a926tbIVKKWH1Tv3b1fYbeDAgUpXocQeVuf09HQxbNgwUbNmTeHp6SmcnJxEcHCwePnll8WpU6eULr7NiYyMFC+88IKoVKmScHJyEv7+/qJXr15i//79RtvlJoI+evSo6N69u/D09BReXl7ipZdeEtevXzfatnXr1qJNmzZGj2VlZYm5c+eKevXqCTc3N+Hp6Slq1KghXn/9dXH+/HmjbVetWiUaNWpk2C40NFSEh4cbnk9MTBQvvPCC8PHxERqNRuQ95RZ2zDp37pzhdxEREVHgvoiJiRFDhgwRQUFBwtnZWVSsWFE0b95cTJs2rTi7kgTP30IIoREiT14OKpGUlBRotVokJyfbVGsVEREBoaGhePTRR7Fu3Tqli0IWxvM3u4CJiEhlzp07hz179uDEiRN4+eWXlS4OkSIYABIRkarMnDkTv/76K1555RWMGDFC6eIQKYIBIBERqUpBS64RqQ3TwBARERGpDANAIiIiIpVhAEhERESkMgwAiYiIiFSGASARERGRyjAAJCIiIlIZBoBEREREKsMAkIiIiEhlGAASERERqQwDQCIiIiKVYQBIREREpDIMAImIiIhUhgEgmZwQAq+99hp8fX2h0WgQHR2tdJHMjnVmncn0lNzf/FuT3RNUasnJyQKASE5OVrooVuX3338Xzs7OYt++fSIuLk5kZWWV6PWtW7cWAIxuL774otE2iYmJ4uWXXxbe3t7C29tbvPzyyyIpKcmEtSiZstQ5JiYmX31zb2vXrjVsZ091FkKI1157TTzyyCPCzc1N+Pn5iR49eogzZ84Ynt+5c2eh++XQoUOG7Q4dOiSefvppodVqhY+Pj2jfvr2IiooyVTWNlLXOX3/9tWjdurXw8vISAPL9/WJiYsSQIUNE1apVhZubm3jkkUfEhx9+KDIyMgzbhIeHF7pfrl+/bopqWg0ljyVqPI6pCc/fQthtC+Bff/2F7t27IzAwEBqNBps2bTJ6ftCgQdBoNEa3pk2bKlNYO/Pvv/8iICAAzZs3h06ng5OTU4nf49VXX0VcXJzh9vXXXxs9369fP0RHR2PLli3YsmULoqOjMWDAAFNVocTKUufKlSsb1TUuLg4fffQRPDw80LlzZ8N29lRnAAgLC0N4eDjOnDmDrVu3QgiBDh06ICcnBwDQvHnzfPtl2LBhqFq1Kho2bAgAuHPnDjp27IiQkBAcPHgQe/fuhbe3Nzp27IisrCyrq3Nqaio6deqE9957r8Dnz549C71ej6+//hqnTp3C559/jq+++spo+xdffDHffunYsSNat24Nf3//MtXP2ih5LFHjcYxURukI1Fx+//13MXnyZLF+/XoBQGzcuNHo+YEDB4pOnTqJuLg4wy0hIaFEn8EriPwGDhxodMVbpUqVEr9H69atxdixYwt9/vTp0wKAOHDggOGxyMhIAUCcPXu2FKUuG1PU+UH169cXQ4YMMdxXQ52PHz8uAIgLFy4U+HxmZqbw9/cXH3/8seGxw4cPCwDi8uXLhsf+/vvvIt+ntExZ59zWzeK09syZM0dUq1at0Odv3LghnJ2dxapVq0pdHmuk9LFEbccxteH5Wwi7DQDzKiwAfPbZZ8v0vvwC5Xf79m3x8ccfi+DgYBEXFydu3Lghpk+fLjw8PIq8/fXXX4b3aN26tfDz8xMVKlQQtWrVEm+99ZZISUkxPL9s2TKh1WrzfbZWqxXLly+3RDWNmKLOeR05ckQAEPv27TM8Zu91vnv3rhg3bpyoVq2aUXdnXuvWrRMODg5GwV5KSorw8/MTU6ZMERkZGSI1NVWMHTtW1K5du8Rddpasc0kCwMmTJ4uwsLBCn587d67QarUiNTW1LNWzOkoeS7y9vUXPnj1VdRxTG56/hSh5m7Yd2bVrF/z9/eHj44PWrVtj+vTpdteFYmlarRZeXl5wdHSETqcDAAwfPhx9+vQp8nVBQUGG//fv3x/VqlWDTqfDyZMnMWnSJBw/fhwREREAgPj4+AL/Tv7+/oiPjzdhbYrHFHXOa9myZahZsyaaN29ueMxe67x48WK88847uHfvHmrUqIGIiAi4uLgU+Nply5ahY8eOqFy5suExLy8v7Nq1C88++yw++eQTAED16tWxdevWUnXZFcXUf+fi+Pfff7Fw4UJ89tlnhW6zfPly9OvXD+7u7qX+HGuk5LGkUqVKyMrKUtVxjNRHtQFg586d0bt3b1SpUgUxMTH44IMP8PTTT+Po0aNwdXUt8DUZGRnIyMgw3E9JSbFUcW2ar68vfH19i739q6++avh/nTp18Pjjj6Nhw4Y4duwYGjRoAADQaDT5XieEKPBxJZS0zrnS0tKwevVqfPDBB/mes8c69+/fH+3bt0dcXBzmzp2LPn36YN++fXBzczPaLjY2Flu3bsXatWuNHk9LS8OQIUPQokUL/PDDD8jJycHcuXPRpUsXHD582OxBUWn/zsVx7do1dOrUCb1798awYcMK3CYyMhKnT5/GqlWrzFIGa2PJY4mSn20tv2myb3Y7CeRhXnzxRXTt2hV16tRB9+7d8ccff+DcuXPYvHlzoa+ZOXMmtFqt4Za3JYIKN2PGDHh6ehZ527NnT6Gvb9CgAZydnXH+/HkAgE6nw/Xr1/Ntd/PmTVSqVMls9SiJ0tZ53bp1SE1NxSuvvGL0uL3WWavV4vHHH8dTTz2FdevW4ezZs9i4cWO+9w4PD0eFChXQo0cPo8dXr16NixcvIjw8HI0aNULTpk2xevVqxMTE4OeffzZrfYGyf7cLc+3aNbRt2xbNmjXD0qVLC93u22+/Rf369REWFlaWatgMSx5LvLy8FPtsa/lNk31TbQvggwICAlClShXDj7MgkyZNwvjx4w33U1JSGAQWQ1m7yU6dOoWsrCwEBAQAAJo1a4bk5GQcOnQIjRs3BgAcPHgQycnJRt2mSiptnZctW4YePXqgYsWKRo/bc53zEkIYtbLnPhYeHo5XXnkFzs7ORs+lpqbCwcHBqMUk975ery9hDUrOHF3AV69eRdu2bQ2zpB0cCr5Ov3v3LtauXYuZM2eW6P1tmSWPJdWqVUNkZKQin20tv2mybwwA/19CQgKuXLli+HEWxNXVtdDuYSpcSbpO/v33X3z//ffo0qUL/Pz8cPr0abz11lsIDQ1FixYtAAA1a9ZEp06d8OqrrxrSKrz22mvo1q0bnnjiCbPVoyRK0zV44cIF/PXXX/j999/zPWdvdf7vv/+wZs0adOjQARUrVsTVq1cxe/ZsuLu7o0uXLkbb/vnnn4iJicHQoUPzvU/79u0xYcIEjBw5EqNHj4Zer8esWbPg5OSEtm3bmqReRSnp3zk+Ph7x8fG4cOECAODEiRPw8vJCSEgIfH19ce3aNbRp0wYhISGYO3cubt68aXht7li0XGvWrEF2djb69+9vmsrYAEseSx4cn6fG4xjZOSVnoJjTnTt3RFRUlIiKihIAxLx580RUVJS4dOmSuHPnjnjrrbfE/v37RUxMjNi5c6do1qyZCAoKMpql9TCcRVSwzz//vNQpMi5fviyeeuop4evrK1xcXMSjjz4qxowZky9FT0JCgujfv7/w8vISXl5eon///oomUC1LnXNNmjRJBAcHi5ycnAKft6c6X716VXTu3Fn4+/sLZ2dnERwcLPr161dg+ouXXnpJNG/evND32rZtm2jRooXQarWifPny4umnnxaRkZGlKtfDlPXvPGXKlAITOIeHhwshik7y/KBmzZqJfv36lbostkDJY4kaj2NqwvO3EBohChjtagd27dpVYAvAwIEDsWTJEvTs2RNRUVG4ffs2AgIC0LZtW3zyyScl6tJNSUmBVqtFcnIyvL29TVl8IiIiMhOevwG7DQAtgV8gIiIi28Pzt4pnARMRERGpFQNAIiIiIpVhAEhERESkMgwAiYiIiFSGASARERGRyjAAJCIiIlIZBoBEREREKsMAkIiIiEhlGAASERERqQwDQCIiIiKVYQBIREREpDIMAImIiIhUhgEgERERkcowACQiIiJSGQaARERERCrDAJDKLCUlBR07dkSbNm0wcuRIpYtjMUOGDEGbNm3QrVs3pKamKl0ci/j000/Rpk0bPPXUUzhx4oTSxbGIbdu2oXXr1mjdujVWrlypdHHs3jfffGPY37t377bY5woh8NJLL6FNmzbo1asXsrOzLfbZRErQCCGE0oWwVSkpKdBqtUhOToa3t7fSxVHMtWvXEBQUBABwcHBATk6OwiWyDHd3d6SnpwMAQkNDcezYMYVLZH5169Y1BH4hISG4dOmSwiUyv7Fjx+KLL74AAHh7eyM5Ofmhr2nYsCHi4+Oh0+lw5MgRcxfRrjzzzDP4888/AQCVKlVCfHy8xT7bycnJcPxq0KABjh49arHPJsvi+RtwUroAZPvyXimr9XrCkicpJeX9+6akpChYEsvJW+eMjIxivSY+Ph5Xr141V5HsWt79fe/ePcXKoZbfNKkXu4CpzK5du2b4v1oCQL1ebxQMqKXVMzMz0/B/tfyt8/6d1VJnJSn1Hbt7967R71iv11vss4mUwACQyiw2NtbovpJX7ZZy48YNo5OTWgLAO3fuGP6vlhPk3bt3Df9XS52VpNR37MHjmFp+06ReDACpzK5cuWJ0/8EDqT16sM5qOFkIIZCQkGC4r4Y6A8ZdgQwAzS/vd4wBIJH5MACkMnvwwKmGAFCNJ4tbt24Zdc+poc6A8d9ar9ezG9iMcnJyjAJuS37H1PibJnVjAEhlxgBQHScLNdZZCJGv3omJiQqVxv7Fx8cbfa8s+R1TY6s+qRsDQCqzBw+cD963R2o8WRRUZ3tvDUtKSsqX41EN32+lPBhsCyEslmNTjRc4pG4MAKnM2AKojpNFQSfn4uTEs2UFfZfV8P1WipL7W42/aVI3BoBUJjk5OUZpYAB1nCDVeLJQYzCkxjoriQEgkeUwAKQyuX79er4DpRpOkAW1huVNX2GP1BgMqbHOSiqoe91S+7ugIQ4MAsmeMQCkMinogG3vY6T0er3hpKTRaAyP23tgoMa/tRrrrKSCfkOW2N/37t1DUlISAOPf9I0bN8z+2URKYQBIZVLQATsxMdFiA7eVcPPmTWRlZQGQax/nsvcAUI1BL1sALUup/Z132T41/aZJ3RgAUpkUdoC053VQ89bZ0dGxwMftTd50KGo6QTIAtKzc1j5LX2TkbWXM+5tmay/ZMwaAVCaFHZzt+SSpxgAwMTER6enpAAAnJyfD4/ZcZ6DwVk97T3+jhLwTyiz9HVPjb5qIASCVSWFXyPZ85Zy3bnlPVGqps1paSIQQhvrlrXNqaqphvBiZzo0bN5CdnQ3A8t+xvIGemi5wSN0YAFKZqL0FUC0nCzW2kCQnJ+PevXsAjOsM2He9lVLYRUZCQgLS0tIs9tnOzs4FPk5kbxgAUpkUNC4s7+P2iAHg/ZPznTt3kJKSokSRzK6wOj/4HJlGUfvb3GOK1fibJmIASKWm1+sNB2Y1nSDVeLJQYzCkxjorScn9nfv+zs7OqvlNEzEApFK7fv16gWN2APvuOsmtm4+Pj1HLZ1JSkqHL0N4U1j334HP2RI11VpKS+zv3/YOCgowm/Fy9ehV6vd6sn02kFLsNAP/66y90794dgYGB0Gg02LRpk9HzQghMnToVgYGBcHd3R5s2bXDq1CllCmujCrpiz/3XXq+c86ZDCQ4Ozve8vdZbja1haqyzkpTa36mpqUhMTASQ/zedlZXFZNBkt+w2ALx37x7q1auHL7/8ssDn58yZg3nz5uHLL7/E4cOHodPp0L59e7tfzsuUigoAb926ZUgbYk9u3bqFzMxMAOoMAD09PY1aSPI+Z28YAFpW3n1qyTHFeccXquk3TWS3AWDnzp0xbdo09OrVK99zQgjMnz8fkydPRq9evVCnTh2sXLkSqampWL16tQKltU0FddnY+wzRvHWuXLlykc/bi7zpUCpXrpwvALTHOgMFf79z626vdVZS7vGiQoUK+QJAc+7vvMepgn7T9ngcIwLsOAAsSkxMDOLj49GhQwfDY66urmjdujX2799f6OsyMjKQkpJidFOzoloAH3zeXuStk1paC5KSkgxpONRSZ+B+vdzd3Q2BX94hDkwGbTp5J5RZ+juWN7gs6LMZ7JO9UmUAGB8fDwCoVKmS0eOVKlUyPFeQmTNnQqvVGm4FXS2qSUFdNgwAWWd7kXes54MB4L1795CcnKxY2ezNjRs3DOtr5/2OWWJMsVq/30ROD9/Efj3YlSWEyPdYXpMmTcL48eMN91NSUlQdBE6YMAFdunTBlStXDGMtXV1d8fnnnyM4OBhNmzZVuISm16VLF6xZswaxsbFo3ry54XFvb28sXrwYdevWVbB05hESEoJNmzYhNjYW1atXx7Zt2wAAWq0W8+bNwyOPPKJwCU1PCIG1a9fiypUrcHJywgcffAAA8PDwwPz58xEcHAw3NzeFS2k/vL298csvvyA2NhYBAQEYNWoUAMDLywuffvqpWY+zffr0waOPPoorV66gQYMGRmX66quvUL9+fbN9NpGSNEIF/RgajQYbN25Ez549AQD//fcfHn30URw7dgyhoaGG7Z599ln4+Phg5cqVxXrflJQUaLVaJCcnw9vb2xxFtxnBwcG4evUqgoKCVHXFrMZ6s84Pr7Ma95EpKbn/+LdTB56/VdoFXK1aNeh0OkRERBgey8zMxO7du41adYiIiIjskd12Ad+9excXLlww3I+JiUF0dDR8fX0REhKCcePGYcaMGXj88cfx+OOPY8aMGShXrhz69eunYKmJiIiIzM9uA8AjR46gbdu2hvu5Y/cGDhyIFStW4J133kFaWhpGjBiBpKQkNGnSBNu2bYOXl5dSRSYiIiKyCLsNANu0aVNkmgaNRoOpU6di6tSplisUERERkRVQ5RhAIiIiIjVjAEhERESkMgwAiYiIiFSGASARERGRyjAAJCIiIlIZBoBEREREKsMAkIiIiEhlGAASERERqQwDQCIiIiKVYQBIREREpDIMAImIiIhUhgEgERERkcowACQiIiJSGQaAREREpCpCKF0C5TEAJCIiItW4dAl4/nmlS6E8BoBERERk9/R6YNEioE4dYMcOpUujPAaAREREZNf++Qdo3RoYNQq4exdo0kTpEimPASARERHZpexsYNYsoF49YO9ewNMT+PJLYMsWpUumPCelC0BERERkatHRwNChwLFj8n7HjsDXXwNVqgApKYoWzSqwBZCIiIjsRno6MHky0LChDP7KlwdWrgT++EMGfySxBZCIiIjswv79stXv7Fl5/4UXZJdvpUrKlssasQWQiIiIbNrdu8CYMUDLljL40+mA9euBn35i8FcYtgASERGRzdq2DXjtNZnfDwAGDwY++0x2/VLhGAASERGRzUlKAsaPB1askPerVAGWLgU6dFC0WDaDXcBERERkUzZsAGrVksGfRiO7f0+eZPBXEmwBJCIiIpsQHy+TOa9fL+/XqAF8+y3QooWy5bJFbAEkIiIiqyYEsGqVbPVbvx5wdJSpXqKiGPyVFlsAiYiIyGpdugS8/jqwdau8HxoKLF8O1K+vaLFsHlsAiYiIyOro9cCiRUCdOjL4c3WVy7odOsTgzxTYAkhERERW5Z9/gGHD5Pq9gMzv9+23wBNPKFsue8IWQCIiIrIKWVmyla9ePRn8eXrKVsDduxn8mRpbAImIiEhxUVFyGbeoKHm/Y0fg66+5fq+5sAWQiIiIFJOeLmf0Nmokg7/y5YGVK4E//mDwZ05sASQiIiJF7N8vW/3OnpX3X3gB+PJLrt9rCWwBJCIiIou6e1eu3tGypQz+dDqZ3++nnxj8WYpqA8CpU6dCo9EY3XQ6ndLFIiIrc/kykJj4BYCNyM6upnRxiGzetm0ytcvChTLB8+DBwOnTQK9eSpdMXVQbAAJA7dq1ERcXZ7idOHFC6SIRkZXIygLmzpUrD6Sl9QLQE9evR+DTT4HsbKVLR2R7kpJksNexo0zuXLWqDAaXL5fj/siyVB0AOjk5QafTGW4VK1ZUukhEZAX27wfCwoAJE4B79wAXl0MAIgC44Z13gGbNgL//VrqURLZjwwZ5MbViBaDRyO7fEyeA9u2VLpl6qToAPH/+PAIDA1GtWjX07dsX//33X5HbZ2RkICUlxehGRPYjIQF49VW5tuiJE4CvL7BsGeDn9zyADvDxGQ8fH+DIERkgfvghkJGhdKmJrFd8vJzY8fzz8v81asj8fgsWyBx/pBzVBoBNmjTBqlWrsHXrVnzzzTeIj49H8+bNkZCQUOhrZs6cCa1Wa7hVrlzZgiUmInMRQrZM1KghVxsAgCFD5GoEQ4YAGo0AAHh4rMXp08Bzz8lu4E8+ARo0AA4cUK7sRNZICJnKpVYtObnDyUmmeomKApo3V7p0BKg4AOzcuTOef/55PPnkk2jXrh02b94MAFi5cmWhr5k0aRKSk5MNtytXrliquERkJqdOAa1by7FJt24BtWsDe/bktvzl3z4g4P5sRX9/OXi9eXPgzTdldzGR2l26BHTuDAwaJMf9NWgAHD4MTJsGuLkpXTrKpdoA8EEeHh548skncf78+UK3cXV1hbe3t9GNiGxTaiowaZJcVH7PHqBcOWD2bNlC0bJl0a/VaGS31unTwCuvyNaO+fOBJ58EduywROmJrI9eL3P41a4NbN0KuLrKZd0OHpS/M7IuDAD/X0ZGBs6cOYOAgACli0JEZvbbb7JratYs2ZXbo4cM5t55B3B2Lv77VKhwf8WCkBAgJgZo1w5ISpoDQGu28hNZm3/+AZ56Chg9WraEt2wJHD8OvPuu7P4l66PaAPDtt9/G7t27ERMTg4MHD+KFF15ASkoKBg4cqHTRiMhMLl+W4/e6d5fdVJUrA5s2AT//XLYlpzp1Ak6eBEaOlPdTU/sBOI20tA6mKDaR1crKkhdS9eoB+/bJiR2LFgG7dwNPPKF06agoqg0AY2Nj8dJLL+GJJ55Ar1694OLiggMHDqAKFx4ksjt5c/pt2iRbJCZMkK1+zz5rms/w8pLdX3/9BTg5/QsgEImJy9G3L3Djhmk+g8iaREUBTZrIoRQZGfcvhEaMABxUG13YDtU2zP74449KF4GILGD/fmD4cJnWBZApXpYskeP1zKFVK8DfvwOuXRsGYALWrHFCRIRMe9G/vxw/SGTL0tPlDPjZs4GcHJkuaf584OWX+f22JYzRicguFZbT76+/zBf85dJoMgC8h4oVu6F+fSAxERgwAOjWDWDyALJl+/bJCR0zZsjgr3dv2ZI+YACDP1vDAJCI7MrDcvpZsmvKxeUkDh0Cpk8HXFyA33+XMySXLJEzJolsxd27cvWOVq3kb0mnk6t7rF0LVKqkdOmoNBgAEpHdKGlOP0twdgbeew+IjpZLyN25I8dItW0LFJF1ishqbNsG1KkDLFwoL7CGDIEhITrZLgaARGTzCsrpN2dO8XL6WUrNmrJsX3wBeHjIrui6dWU5s7OVLh1RfomJ8mKqY0c5a75qVSAiQl5QlS+vdOmorBgAEpFNezCn37PPytaJCRNKltPPEhwdZZ60kyeB9u3lYPp33wWaNgX+/lvp0hHdt2GD/F2tWCHH9o0dK8fStmundMnIVBgAEpFNejCnX0iIzOe3aVPZcvpZQtWqcqWE8HDAxwc4ehQICwM+/FCm0yBSSny8XOXm+eeB69flWNq9e+UsX09PpUtHpsQAkKiU1q0Drl/fBuB9COGodHFUo6Ccfu+8I1v9evRQunTFp9HItVJzx1JlZ8vUGg0aAAcOKF06Uhsh5Ko2tWrJta6dnIDJk+UwiubNlS4dmQMDQKISys6W3Xa9ewPZ2bUAfIJbt37CxYtKl8z+7d8vW8omTLi/3FRUlMxH5uGhdOlKJyBAdretWydnU54+LU+4b74p60hkbpcuAZ07ywuSpCR5EXL4MDBtGuDmpnTpyFwYABKVwK1bMtv9nDnyvrv7JgApyMxsjHr1gNWrlSyd/Xowp1+FCnIg+u7dcnaitdHpdAgKCoJOpyv2a55/XgZ/AwfK1pj582W+wh07zFdOUje9Xq5eU7u2HJLg6irH0h48KCdUkX1jAEhUTLnjtHbskK1Na9YAvr6jANSHi8sRpKTIlR4GDABSUpQurX0oLKff2bOWz+lXEkeOHEFsbCyOHDlSotf5+sr6btkixzTGxMhB98OGAbdvm6WopFL//AM89ZSclHTvnszv9/ffsnfDSbVrhKmLlR4+iazLihWy9enyZeCxx+QYrT59cp+NgZ/f8/jwQxmQfPedvHqOjFSuvPbAGnP6WUrHjnKm8MiR8v6yZXJs1s8/K1susn1ZWcDMmUC9enJVD09PYNEiYNcuoHp1pUtHlsQAkKgImZkyae/gwXJ2ZrducmzMg92OGk0OPvpIdklWqSJbblq1koP6c3KUKbutsoWcfpbg5SW75/76S56Y4+KAnj2BF1+UszOJSioqCmjSRCYmz8iQw1lOnZLHOGttTSfz4Z+cqBDXrgFt2shluzQa4KOPZAuMj0/hr2nZUq748NJLMvD78EP5HpcuWabMts6WcvpZSqtWwPHjwMSJMo/g2rVyH333newiJ3qY9HQZ9DVqJINAX19g1Sq5NGFIiNKlI6UwACQqwJ49ciZcZCSg1QK//gpDF+/D+PgA338vD7BeXjKHVr16wI8/mr3YNsuWc/pZgpub7LY7dEi2jCYmyrGmXbsCV64oXTqyZvv2ye/MzJnyorRPH3lRNWCAvLAl9WIASJSHEHK9y6eflt1sdeoAR47IE21JaDTyABsdLVd5SE6WrYIDB8q1YEmyl5x+ltKggQwCp08HXFyAP/6QYyOXLJEzOoly3b0LjBkjW5D/+QfQ6YCNG+XktUqVlC4dWQMGgGTQsGFDBAcHo2HDhhZ/X3N9dknePzVVBmhjxsjux7595WSPxx4r/ec+8ohsTcxtPVy1Sl6NHzxYtrLagwdz+nl6RsHX9xns2NHQZnP6WYKzs+zOO35c5gu8c0eO4dJqj+L8+ZK/n5K/e3Pw8PCAo6MjPBT4ElnLb3fbNnnxunChvKgdMkReVPXsqWixyMowACSD+Ph4XL16FfHx8RZ/X3N9dnHfPyZGzvL93//kOKt582ROP1OcQ5ycYJggEhIC/Pef/Kxp0wqeIGLufaG0wnL6eXv3wI0bf9ptvU2tRg15caHVfgDgLu7eDUPdunLCTHZ28d9Hyd+9OaSnp0Ov1yM9Pd2inwso/9tNTJQT1jp2lEMpqlYFIiLk76t8eUWKRFaMASCp3tatsiUqOhqoWFEeMN980/TjY1q2lK02ffvKwO+DD4C2beX4NzV4WE4/jYYzGkrKwQHw9AwHUAeurruRni7zuDVtKr9rpB7r18uhFCtWyGPX2LHyAqtdO6VLRtaKASCplhDAjBlyCaSkJDlD7uhRGZSZi4+PbFlcuVLm39qzB6hbV47LsWdqzulnGZdQoUJ/hIfL79jRo0DDhvIiIyND6bKROcXHAy+8IG/XrwM1a8qJH/Pny2MMUWEYAJIqpaTIpbcmT5aB4LBhMt9a5crm/2yNBnjlFdni2KSJnCDSt69ch9PeJogwp5/laDTyO3T6tJxRnZ0thxmEhjIpuT3KbVGvVUu2/jk5Ae+/L39bzZopXTqyBQwASXXOnAEaN5Yz4lxcgKVLgW++sfyi548+KoOi99+XXXkrV8qTdWZmfcsWxEyY008ZAQHAhg3AunVytueZM3K85bhxcrIN2b6LF2US58GDZe9FWJjMVvDJJ3I9X6LiYABIqpKW1gmNG8u0CEFBstXv1VeVK4+zszxo79olJ4j8+y9w8+YmAO9BCNv8eTKnn3V4/nkZcA8cKFuLFiyQM0O3b1e6ZFRaer1cHaZOHTnT180NmD1bZiuoV0/p0pGtsc0zDFmNpCTZknb79jQA3yMzs7bSRSqQDKamIzHxW9y9K8ejHT0qu2CtQe5qDy++CABOAKbj1q21NpXklzn9rI+vr+wm3LJFBuIXLwLt2wNDhwK3bytcOCqRf/4BnnoKGD1atuTmHjPeeUf+1ohKigEglUhammxBmDRJTprw8wN69QLu3RsEoB9u3vwZ332ndCmNJSQACQn/A/AeADnDNyLC+pKh+vgAP/wA+PiMA3AHmZlNUbcu8NNPChesGPbtk0mKc3P6tWwpxyLNnm2aVDpUNh07AidPAqNGyfvLl8tA/eeflS0XPVxWllzFo149+Tvz9AQWL5a9BtWrK106smUMAKlIOTly5YEZM4BnnpG5pNq3l+O6jhyRXRI1agAeHisA/AHADQMGyGTKWVkKFx4yCGnYEMjIaA0gFeXLj8S8edY7Bk2jATw81gEIhbNzFG7flks3DRkiM/tbm4QEOYGmZUsZYOTm9Nu9W3ZTkfXw8pKJgffsAZ54AoiLk4mBExMXA/BXunhUgKgo2Uvx3ntyNnenTnJG/RtvFG9ZSqKi8CtE+WRlPYYvv5TjuCpUkAegyZOBP/+UB6HAQDmLdeVKIDZWDjL38XkfQFd4eX0O4P5yanFxytXju+/kSgkXLwKOjhcBNEW5crbS5PEvKlZ8DpMny6AwPFxOEDl8WOly3XfvXh888YQM+ADjnH48OVmvli3lDPRJk2TS87S0HgBOIzW1FwRTMVqF9HQZ9DVqJINAX1+5itDvv8uufCJT4GGacPWqPLgkJs4HEIsbN3Zh9Gg5jis5GdBqZUvBwoUy2IuNlcHfK6/IiRT3CXh7f4ZffgG8vYG9e+XstIyMMIvWJytLtkAOGCAPpJ07A/7+XQGcsGg5ykqjyca0abKrp3Jl4MIFGdDmLuqulKys6gB24/bteUhIYE4/W+TmJlv1Dx0CnJ1PAqiApKQv0LWrehKTW6t9+2TapNzfeZ8+chztgAGmT05P6sYAUIVyJ26MGiWThgYHy5mCaWkvAAgCkI5nnpEniIMHZeLe3O1r1Hj4Qah7d9lSVauWbAG8desnAG9YpHUhPl62PC5cKO9/+KFMR+LgkGz+DzeTp56Sg7379JHpVN57T3bHW3qCiF4PfPopcOPGFgBPQaNJZU4/G9egAVCxYjfI8bEZ+OMPGdAvWSL/3krR68sBqIKcHD/cuVOype1s1Z07coJHq1ZywodOJ4+7a9ZY33hlsg+cO6QC6enyqnLHDjmB4+hR44O7g4NsqTtz5kvcvbsRgYGXsH37hTJ9ZvXqMngcMgT46ScXAItx+3ZrpKUB7u5lq09hIiNl6ou4ONkC+d13Mhi1B+XLAz/+KMcAjR4tx9jVqydzGL7wgvk//+pVeZGwYwcAuAD4Ff7+0zBhwkHzfziZlUaTDWAm/P334bHHdmP/fmDECDkh6dtvLTvRICcHWLQIiI+PAuCB+Hj5WwbkTFd39/u3cuWM7+fe9PplAFKh16fj/feL3ragx4WwcEJQyOUoX3vtfuvr0KHyYovr95JZCSq15ORkAUAkJycrXRQj2dlCHDokxIwZQjzzjBBubkLITGD3b088IcTIkUJs2CBEYqJ8XVBQkAAggoKCSvyZhb1WrxfC2/sTAWQLQIgGDYS4eLH4ry8OvV6IxYuFcHaWdatVS4h//jHd+xfFHO/7sPc8f16IRo3u/y2HDBHizh2TfXw+GzcK4esrP6tcOSF8fCbYzL40FXsuW97X5+QI8cUXQnh4yL+3m5sQs2cLkZVl/nKdPi1E8+Z5j1Pp+Y5blrllC+BbERBQy+x1TkgQYuDA+59dtaoQEREl/lgqBWs9f1sSWwDtgBCyy2DHDnnbuTN/jq/AQNltmHsLDrZM2TQawMvrK6Sk7ISDw084dswXYWGyNcsUi5SnpcnWihUr5P3evWWKC3teA/Oxx2SL7tSpcpzQ8uVyDN7q1XLGs6ncuweMHy9bGQHZXbh6NfDMM6uZQ85OOTjIFubu3WWLVEQE8O67shty+XLzJBvOypLLA378MZCZKX+7jo6TkJw8G4GBgbhwIRZpafK3npoKw/8Le2zcuIkQwh1AOYwaNaFEr5XrJjsCGIrr17th40Y5Gc4c1q8HRo6U6/dqNMDYsXLpPqZNIotROgK1ZUpeQVy9KsSqVUK88ooQQUH5r2K1WiGefVaIhQvllbVe//D3NEcLYN7nKlVqLMLCZPkcHGTLQm65SvPZFy8Ko/ebM6fwetpTC2Beu3YJERws94GTkxAzZ8oW4LI6dky2Eud+nyZMECIjo+TlKwl7bmUzJ1O2AOal1wsRHi6Ej8/979f77wuRnm66ch09KkS9eve/Z507C3HpUtnq5ODgIAAIBweHEr82O1sIP7/nBHDGUKbevYWIjy/e64tT7rg4IZ5//n6da9YUYv/+EheVyogtgLa61pQK3b4tZ+WOHi0nbgQFyVm4q1bJ8VkuLnLyw/TpclmgW7fk9rkTPaxh9piT01Xs3SvXr9TrZctC795y8HNJbd8uxy0ePSpT1WzbJpMQW0M9Lal1a+Dvv+V+zM6WqT3atZMztUtDr5ereTRpIluVAwPlvp4zR37HSD00GmDQIDnzv1cv+f2aNk2mI4qMLNt7p6XJ72rjxnKCk68v8L//AZs3K5vmxNERcHU9BKA+PD0XwtFRJmKvWVMea8sykU0I2VNRq5Zs/XNyAj74QE6iatbMVDUgKj4GgFYqPV3m3XvvPXkyrlBBdkV8+aXMtabRyO6+d9+V3TS3b8vu39ztrXVpIDc3mS5kyRKZjHn9elnerKxHivV6IWQw0rGjTEKcGwQ+84yZC27Fype/30Xn4SHTxtStK/dtSVy7JvfrhAmyW+6552RwqeZ9S3I26vr1wLp1cjbqmTNAixbAuHFymEBJ7d0r05zMmmWc5uTll63pAi4DWu1sHDoky5qUJCdBdelSujQ5Fy/KCVyDB8v3CguTifQ//hhwdTV12YmKhwGglcjJkQeEWbPkShvly8sT78yZMleXXi9n440YIQ/Gt27JVCuzZskWH3PNrDUHjQYYPlzOZA0MlCeUmzd/A1D0grF37siTxbvvyv0xaJAc+1alikWKbdU0GnlyyV35JClJzg5+9dXinaR//lkGjdu3y+/S11/L71mFCuYvO9mG55+XgdrAgfJCbMECudrL9u3Fe/2dO7JHolUr4Nw520hz0qDB/ZWQXF3lmsq1a8ul2IqTJkevlymp6tSRvRRubnJ5xAMHzDOekqgkVB8ALl68GNWqVYObmxvCwsKwZ88ei3xu7sSNxYtl94qfn8z6PmmSPKCmpwMBAfKqeMUKmfPtn39kioRevWSXia1r1ky23rVqBQjhDeBnpKS8XWCS43PngKZNZSuEs7Pcb8uX21bgawmPPw7s3y+/RxqNTOPRoIG8uChIaqoMxnv2lC2qoaHAsWNyAoD1tMaQtfD1lcejLVtkV+3Fi/KCdejQ/BPP8tqyRQZBixbJ+0OHymCyZ0/zl7msnJ3l7yk6WiZiv3tXTt5o00Yelwpz9qzM4TlmjLwIa9VKdne/84719tCQuqg6AFyzZg3GjRuHyZMnIyoqCq1atULnzp1x2Uyp8OPiZG66QYPkwbNGDXkg2bhRHjy9vYEePYAvvpDrPV69KsfFDBxouVm7lqbTya5rDw+5ntidO+PQrRuQmHh/m19+kcHx6dMyKN61S66FyQClYM7OssXizz/lWNFz52SwPXu2catFVJTsivr6a3n/7bfl2K4aNZQpN9mOjh3l2s+jRsn7y5fLsW2bNj24pS8SEz9H586y67RqVTlk5dtvbS/HXY0assfhiy/kUIs9e2Sr+ezZDyaqdsKdO6NQr56cre/pKS9Yd+2ybE5FoodSehaKkho3biyGDx9u9FiNGjXExIkTi/X6h80iun1biE2bhBg9Ws70enCmrouLEG3bCjFtmhAHDpQu15YpmXsWcFHvK7fpLzSaVAEI8cgjcobgBx/c318tW8oZdKVhSzNXTfmeCQnGMw7btpWzLOfOvZ83MSCgZLnHbGlfmoo9l62sr9+zx3jGeO6sWV/f1wQQLwAhNBohxo0T4u5d85epLLOAi/vZMTFCtG9/v84NGggRHS1ExYodBHAs36xmsj6cBaziPICZmZk4evQoJk6caPR4hw4dsH///gJfk5GRgQyZKAoAkJKSkm+b1FQ5Ju3OndycUsZ8fWWrl04HVKwouwLOnJE3pSUmfgEgFYmJ5fDyy6V5bRoSE8uhf/8Hn1toeN8Hn3twGxeXSDg5PY3//pOtU7mqV5etWW+9VbJylaQM1vK+pn5PFxc50ebIEZkjsmrV+7MZg4Plc+Hh8lb88t0r1fek6Pct/ffP3Oy5bKaoW2ioPJadPi1nza5bBwghm5Y1mhS0b++NmzeB1183f5n0+lUABPR6jVn3R8WKcljKsWPyVr8+AGwBoAGQgebNXeHrKyfmkfXJylK6BMrTCGGJFVqtz7Vr1xAUFIR9+/ahefPmhsdnzJiBlStX4p9//sn3mqlTp+Kjjz7K93hycjK8/3+9orQ0ubwQERERWasUAFqj87faqLYFMJfmgYFkQoh8j+WaNGkSxo8fb7ifkpKCypUrG23j6ChTJNy4IWdi3rpl/B5OTkC1anKwfvXqsgXGwUpGYn700VQkJydDq9ViypSppXytN6ZONQ6Sp06dYnjfB597cBt395bIzn4BWVlyxlx6unz+kUfk2Ekvr1JUrJhlsJb3NfV7ZmbKWb65DduennIgOyBbMQYMAB74Gj+kfKX/nhSlLN8/c5NlS4FW622lZSv9fjPFfk9MBNauvT8pwtsbSEnJAuAMIAPPP++K5s2LP263LGV6663xhuP4Z5/NK9FrS/LZ6enA77/LtDZA7vEqDYA7AIFWrTTo0oVpXqxVWhowebLSpVCYsj3QysnIyBCOjo5iw4YNRo+PGTNGPPXUU8V6j+KMIYiNLXrFDh8fIXr2FOLLL4U4c6Z4K3aYi5JjAAMDqwhgnmG/dOggxK1bcq1iLy/5WGCgEJGRJS5asctgLe9ryveMijIef/r223Ilhz//vP99dHaWq7Lk5Fi+fJZ4X1Ow57KV5fXZ2UIsWFDw2sH+/k8JYK/hu9eqVf41us1RJkuMAdyyRYiQkPu/q6FDhUhKEiIgoLYAwg2PV60qxLZtpSoGmRnHAKp4JRAXFxeEhYUhIiLC6PGIiAijLuGyCgqSLSwrV8pULmfOyGTOzz0HaLX3V/jIXbGjcmU56/d//5OJedXg+nXg1q0fALwJQI6Z+f33+8mvDx2SM/CuXZNpFb7+umwZ+dVArwfmzZPj+86ckbOnt20DPv1Utki0bStTUvTqJcfCvPsu0KGDnHlOVBxnzsjf49ixBac5cXb+F0AraLXvG2bN1qsnE7kbz5q1HYmJsieiUyc5q7laNZm269tvAR8fwMHhNoDBqFChvyFNTocOMu1NUpKiRSfKR7UBIACMHz8e3377LZYvX44zZ87gzTffxOXLlzF8+HCzfJ5Gcz/1y4YNMu9abpLRZ56RJ+arV+WSQ6+8IoPHmjXl8m+bNhWdZ8tWHTwoJ3tkZjYDkAJf32GYPl12peeqUUPup9xgZfhwmeA4t3uYjMXFAZ07ywkzmZkytdDff8t8bXlVqCAH63/zjRy3umOHTGuRP5UH0X1ZWfKYVb++HFZQdJoTAU/PFTh5UgZC6enyYqNJExks2pL162Wqm5Ur5bF83DjgxImCV8pxc9tdYJqcjRstWmSioindBKm0RYsWiSpVqggXFxfRoEEDsXv37mK/1tRNyKmpQmzfLsTEiUI0aiSEg4Nxd7GDgxCNGwsxaZIQO3YIkZZmko81sHQX8NKlMhWOXGj+nACeKPKz9XohZs68v18aNix+igVb6rYsy3v+8osQfn5y/7i7C7FkSfGGFZw9K0RY2P3v2muvFZ6yw5b2panYc9lK8vqjR4WoX//+96RTp8J/gw++r14vRHi4HPYif/NCvP++HJJgyjqZugv42jUhevW6X+eaNYXYv794rxWi8DQ5pCx2AQuh+gCwLMz9BUpMlGPgRo40PoDk3tzchGjXTgZFhw/L8ThlYakAMD1diGHD7tfjueeECAh4otifvXWrEL6+8rV+fnI8mznrZun3Lc173rsnxBtv3N+n9eoJcfp0yT43I0OId96ROdsA+Z07dsw05SsOew6yzMkSAWBqqrwwdXSU3w1fXzm2uaiLi8LeNy7u4QGVNQSAgYFB+QLWDz4oOGB9WLnT0uSFe0n2H5kXA0AVjwG0BeXLyzFwX34plxW6ckUuwzRggFxDNz1djj+ZNEmulOHnJ9frXLxYzsazxnFyV67IcUPffiu7UWbMkF0rDg53i/0eHTrIJeRCQ+Us63btgM8+s876WsLx43L93yVL5P3x42XXes2aJXsfFxe5qsH27fL79c8/sqtu7tzirXtK9mnvXtndO2uWXLO8Tx+Z72/AgNKtxqPTyd/8unVyDeAzZ2TmhHHj7s9OV14VJCR8h8GD5dCbsDCZR/Pjj0s3q9fNTR7rDh2S+zIxUQ7z6dpVjiUkUgIDQBsSHCwniKxaBcTGyoPwwoXAs8/en1CyYYMcY/jEE3K5uUGD5PJzcXFKlx7IyGiGsDB5EPT1leuD5q5ZW1JVq8pllgYMkMHJ228Dffta0wnE/PR64PPPgcaN5UlUpwO2bpXBcFlSTzz9tBwz+NxzcrzXhAly6S+1TEoi6c4dOYatVSt5QanTyTFsa9bIwK2snn9eHsMGDpQXbwsWAE8+KZeKMzchZKL+pCT5vf73X7m03eHDwN27QwGcREZGG7i5yUkrBw7ICSxl1aCBPP5Nny4vuP74A6hdW1608yKLLE31eQBtlUYjW3hq1pQH6exs2Sq2Y4e87d0rg8SVK+UNkIOQn3lGtpi1bi2DRkuQLXNv4tatOQDkFfCGDXIGXVm4u8u6NWkiWw/WrpUnlA0bZJ5FexYXBwweLAM+QE70+PZbmdfPFCpUkK00334r9+327XKCyLJlpnl/sm5btwKvvXa/dWroUDmD3NTr9/r6yl6Nl16Sn5c7a7ZcubkAZiAzMxh79sicbWlpcqWl3P8X9phevwaAO/R6dzRrVvh2hfcYyNybLi4HcPx4U5Ov3+vsLDMd9Ool9+v+/fKi/ccf5e+N6wWTxSjdB23LrHkMQWqqXN/13XflZInccV15J5Q0aSLE5MlyDF16unnGAN69K4S7+0bD5w4YIMerFff1xbV3rxA6nfwMrVaIX3817fsXRokxgL/+WrqJHqV19qxc6zT3b1iu3CoBuNvEvjQVey5b3tcnJMicpXnz2JVkneiylCslRYhRo/Ifq8x9c3AQwtNTiIoVZW4/J6dTAhguAgODzV7nnBwhvvjifh5FV1chZs1Sfl14NbDm87elsAXQTrm7y5a+du3k/cREmaZhxw7ZmnPunBwndvCg7I5wdwf0+u8B/I7MzL+Rk2OciqU0LlyQ3YhpaT0BZEGr/QgrV04rVZfvw7RoIVtAe/eWV9TduwNTpgAffmg9K62UVVqa7OpevFjer1cP+OGHko/1K6knngAiI4H335etQKmpAwA0RXr6FPN+MFlUWlpX1KwpVzHSaGR+v2nTAA8Py3y+l5cc0vLii8DTTx9HVlYQHB0z8eijgXB3h9GtXLnC77/zzigIkQqNJh0bN64u8nXu7rJFLu8xKTi4A65evQqNJsjsdXZwkGm+uneXLaAREcDEibI3Y/ly03Q7ExVK6QjUltnyFcTlyzIlw8sv3285y3srX16I558XYvFiIc6de3gL04NXvr/9Jlvi5BV2vABaFHlVbKoWlowMOWs6tx5du8oM/bbeAnj8uBC1at2v15tvFj0b0Vy2bxfCweGaoRwvvijE1aumeW97bmUzp7KWTacLFcC6ImflWrpc1jAL2NLlLkmaHCo7Wz5/m4qdtI1QSVWuLCeI5K44cuoUoNV+AOBnaDQpSEqSY8BGjJBjUqpUkWPOvv8eiI8v/H2F0ODjj+UVbXIy0Lw54O/fBcA+i9TLxUXOml6xQs6827xZzpDNyqphkc83Nb0emD9fzvI+ffr+RI9585RZY/SZZ4BKldoC+BxADtaskYm6Fy6UM0TJdggBhIcD16//CeB5AFl4/30gKgpo1kzp0qmPRiOPyWfOyPGB2dmyBTY0VLbAE5kaA0CCRiMniHh6hgPoiYCAJxEZKQ8+bdvKoCo3Bc3LL8tlxerUkV1Ev/4KpKTkvpMWiYnLMWWKPLmMGAHs3Ak4Ol63eJ0GDpSzhKtUkTP8bt78BcCLFi9HWeTkVESXLsCbb8oVPbp1k7NzO3RQtlwyZc94VKzYBY0by9miY8bIyThHjihbNiqeixflzO4hQwAhfAAcgb9/F3zyiTIXFnSfbaTJIXvAAJDy0Why0LQpMHky8OefMlXCtm1yjc+wMBkwnjoFfPGFnH3q6wvcuPEzgCNIT28PV1fZsrBokQweldKggQxI2rUDhCgH4EckJ79vI+uQdsGNGxHYulW2ZC5aBPzyi+lm+ZqCi8sp7N8v8w/6+MgxmI0by1np9rhsoT3Q62VrbZ06cryZmxvg7T0dQFM4O59RuniUh5JpckgdGADSQ5UrJ9eRnT1bBlQ3b8qr0+HDZbqVnBwgKysMwGNwdIzFvn2yK8Ma+PnJfIOenosAAHfvDkf79nKguzVKSwNu354GYDP0ej/UrSv3+YgRpcuXaG6OjvJ7cPasbB0WQgarNWrICSpqTc5tjc6ckTn9xowB7t2T/z9+HPDyWgKA/ffWKDdNzpYtMq9rbpqcoUN5kUVlxwCQSqxCBXl1umSJnE186RLg4zMewFuoWLEzwsKULqExR0dAq50J4HloNHexaxcMCamtyYkTcqzfvXuDAAAeHktx8KBMFGvtKlWS40l37JCzhq9fB/r1kxcO584pXTp1y8qSq1DUry9nyHt6ypnku3Yx55yt6NhRJqoeNUreX75cDtvZtEnRYpGNYwBIZRYSAnh4rAUwD46OSUoXpwgbULFid1SvLpNkt2plHYmNhZDd6Y0aya51B4cbADrCx+djuLkpXbqSefpp2ao0bZrsXtyxQ3ZbTZkily4ky4qKkt3ykyfLcaSdOsnv2Btv2E96JLXITZOzZ4+8yIqLk2m2+vSRF1xEJcVDAKmKs/N5HDokl8/LzASGDQNef10uC6WE69eBLl3khJqMDDnRw9+/HYBtyhTIBFxdZcBx8qQMODIz5RqqTz4px5KS+aWn318jPDpadiWuWgX8/ru8YCPb1bKl/JtOmiR7N376SbYG/u9/HHJBJcMAkFRHq5XLxU2bJsfVLV0KPPWUbBW0pM2bZVC0ZYtsLfvySznRw9Ex0bIFMZNHH5UBx08/AYGBMjF4x45yzWauK2w+e/fKBMKzZsnxuX36yMkEAwZY5zhSKjk3N9mtf+iQ7NpPTAReeQXo2vX+8n1ED8MAkFTJwUG2Uv3+u1zf9NAhOS5w927zf3Zamsz+362bnFDz5JNyosfIkfZ3gtZogBdekBMQxo2T+525A81Dr/fAqFFyaMO5czKdyMaNcn9XqqR06cgcGjSQx67p02XGhT/+kGOGFy+WM76JisIAkFStUycZfNWrJ2cGP/OMTLxsrq6UEyfkmKwvv5T3x46VB3BbmOhRFt7ewOefy33N3IHm0AE3buzAIjnZHUOHyla/nj0VLRRZgLMz8N57cuxt8+YyV+DIkUCbNpyARUVjAEiq98gjcnZkv36yRerNN2VKk3v3TPcZeSd6nDwpW2T++EMGm7Y20aMsQkNRaO5Avd5b6eLZnMREIClpHoCtyMkJRtWqMk/ct9/Klm1Sjxo15ASRL76Q6zfv2SMvbOfMgY3kPiVLYwBIBJnr8LvvZLJVR0dg9Wp5Nf3vv2V/7+vX5dic3IkeXbrIFT06dSr7e9uiwnIHXr++C0BfDmQvpvXr5eD/1NQ+APTw8PgWJ0/KxOekTg4OcnjJyZMyBVN6OvDuu7Kl/fhxpUtH1oYBIBnodDoEBQVBp9NZ/H3N9dkleX+NRnZL/vkn4O8vg7SGDWVLXWn9/jtQt658j9yJHr/9Jt+/LGW1Bw/mDtTr/QH8gDt31rPrqghxcTIP5wsvyIsLN7f/4OfXEzVqfAUPj5K/n5K/e3Nwc3ODg4MD3BRoWreW327VqnLN8PBw2dJ+7Jg8ln3wgXIZD8gKCSq15ORkAUAkJycrXRTFBQUFCQAiKChI6aKYRGysEE2bCgEIodEI8fHHQuTk5N+usHqnpQkxZox8PSDEk08KcfKkhQpvZub4W6enCzFtmhBubnJ/ubgI8eGHcj9aA2v4fuv1QoSHC+HjI/eRk5MQ778v9529UXJ/W8Pf2pTi4oTo1ev+sahmTSH271e6VMrj+VsItgASFSAoSK6UMHy4PGx++KEcUJ+c/PDXnjwpx7V98YW8r5aJHmXB3IFFu3hRptAZPFguARYWJifPfPKJ3HdEhdHp5HCBdetkq/uZM0CLFnJWvinHOZPtYQBIVAhXVzlZYdky+f9ff72/WkdBhJBdvA0bytm+/v6yC1htEz3KgrkDjen1Ml1OnTpycoebm1yT+8ABOcCfqLief17ODB84UB6rFiyQ36vt25UuGSmFASDRQwwZImfUVa4MnD8vB1T/9JPxNjk5FdCtmxyAnXeiR+fOypTZljF3oHT2rMzpN2aMbKlp1UoO5H/nHcDJSenSkS3y9QVWrJDJ50NCZMty+/YybdDt2woXjiyOASBRMTRqJFOWPP20PBn36SNPxEI4AuiEGze24/ffZUvhF1/IiR5Mvls2as0dmJUlV3moV0+mzPH0lIl9d+0CqldXunRkDzp2lMMtRo2S95cvlzPKN21StFhkYQwAiYqpYkU5s+7tt+X9Tz8FbtzYAeAP6PUVUacOcPiwbAW0txU9lFRU7kB7a7WIipJ1mzxZjoPs1EkOOXjjDdkSSmQqXl6yRX3PHjkLPy4OeO45eXF7/brSpSNL4CGFqAScnGTgt2aNTLaanf0YAMDDYzkOHZKTFsj0CssdWKMG8MMP5lu5pbQaNmyI4OBgNGzYsFjbp6cDkybJluboaNlVt2qVHA8ZEmLespK6tWwpv3MTJ8rf2U8/ydbA//3P+n5XZFoMAIlKoU8fORC/XLkfAHSCj8+HcHdXulT278HcgdevyxVc2re3rmWv4uPjcfXqVcTHxz902717ZXfvrFlyfGOfPnKw/oABbEkmy3BzA2bOlNkK6teXK8y88opMYH/5stKlI3NhAEhUSnXqAOXLTwCwVemiqM7TT8sJEdOmyZPXjh2y9XXKFNmaZgvu3JHDBZ56SgavOh2wcaNsXeb4UVJCgwYyCJw+HXBxkQnsa9eWwy/0eqVLR6bGAJCIbJIt5w7culVeQHz5pexmGzpUtvr17Kl0yUjtnJ2B996TF1jNmwN37wIjRgBt2lhXKzuVHQNAIrJptpQ7MDERGDRIBqyXL8sluyIigG+/BcqXV7p0RPfVqCEniHzxhRzvvGePHKowZw6Qna106cgUGAASkc2zhdyB69fLwfUrV8ryjh0rE4a3a6d0yYgK5uAghymcPCnH2aanA+++K1MxHT+udOmorBgAEpHdsMbcgXFxchWGF16Qk1Zq1gT27ZMrxHh6KlMmopKoWlUOWwgPl6mYjh2TKx598IFMfE+2iQEgEdkda8kdeO9eb9SqBWzYIFMIvf++zPXXrJnlykBkChqNHL5w+rTMF5idLSdhhYYCkZFKl45KgwEgEdklJXMHZmcHA9iC27c/x+3bQFiYbIH85BM5eYXIVgUEyAuadevkbPUzZ4AWLeTQi3v3lC4dlQQDQCKya5bMHajXyzGHcoWYjgDSMXu2zBlZr55pP4tISc8/L1sDBw6UF1MLFsiZ7du3K10yKi7VBoBVq1aFRqMxuk2cOFHpYhGRmZg7d+DZszKn35gxgBAeAP6Cv397vPOO7P4lsje+vsCKFcCWLXLFmosX5YXV0KH2t0yjPVJtAAgAH3/8MeLi4gy3999/X+kiEZEZmSN3YFYWMGOGbOHbt09O7NBq3wPQBs7OMSYtP5E16thR/qZGjZL3ly+XM943bVK0WPQQqg4Avby8oNPpDDdPTskjUgVT5Q6MipKTSyZPlsFkp07AqVOAp+cqAFxIldTDy0sOf9izB6heXc5+f+454MUX5bALsj6qDgBnz56NChUqoH79+pg+fToyMzOVLhIRWUhZcgemp8vVEho1AqKjZVfYqlUyqAwJsVQNiKxPy5ZyqMXEiXIi1tq1sjXwu+/MO/GKSk61AeDYsWPx448/YufOnRg1ahTmz5+PESNGFPmajIwMpKSkGN2IyLaVNHfgvn1A/frAzJkySOzTRw6GHzBABpVEaufmJn8fhw7J30piovx9dO0qV8Ah62BXAeDUqVPzTex48Hbk/4/ob775Jlq3bo26deti2LBh+Oqrr7Bs2TIkJCQU+v4zZ86EVqs13CpXrmypqhGRmRWVO1Cv9wbgidu3P0GrVsA//wA6HbBxo2w1rFRJ6dITWZ8GDWQQOH064OIC/PEHULu2/I3p9UqXjuwqABw1ahTOnDlT5K1OnToFvrZp06YAgAsXLhT6/pMmTUJycrLhduXKFbPUg4iUUVjuwOvXdwE4iXv3BkMIYMgQ2erXs6fCBSaycs7OcrjE8eNA8+bA3bvAiBFAmzamT8NEJWNXyQn8/Pzg5+dXqtdGRUUBAAICAgrdxtXVFa7M4kpk93JzBw4eLE9W//zjDwBwdLyMLVtCuH4vUQnVqCEniCxaBEyaJP9frx7w0UfA+PFMlaQEu2oBLK7IyEh8/vnniI6ORkxMDNauXYvXX38dPXr0QAhHcBPR/8vNHejt/RGAKfD3b8fgj6iUHByA0aNlypj27eVkqnffBZo2lb8zsixVBoCurq5Ys2YN2rRpg1q1auHDDz/Eq6++ih9++EHpohGRlXF1Bby8vgHwMRwcUpUuDpHNq1oV2LoVCA+/P962YUPggw+AjAylS6ceqmx0bdCgAQ4cOKB0MYiIiFRJowEGDZL5N0eOlBOqpk0D1q8Hli0DmjVTuoT2T5UtgERERKS8gABgwwZg3To59vbMGaBFC5mb8949pUtn3xgAEhERkaKef17OrB84UM6+X7AAqFMH2L5d6ZLZLwaAREREpDhfX2DFCmDLFrmizsWLcrLIsGHA7dsKF84OMQAkIiIiq9Gxo5wpPHKkvL9smVxO7ueflS2XvWEASERERFbFywv48kvgr7+A6tWBuDiZeP3FF4Hr15UunX1gAEhERERWqVUrmSNw4kS5Us/atbI18Lvv5FhBKj0GgERERGS13NyAmTPlusL16wOJicCAAUDXrsDly0qXznYxACQiIiKr16CBDAKnTwdcXIA//gBq1waWLAH0eqVLZ3sYABIREZFNcHYG3ntPdgs3bw7cvSvX627bFjh/XunS2RYGgERERGRTatSQE0S++ALw8JD/r1sXmDMHyM5WunS2gQEgERER2RxHR2D0aJkypn17ID0dePddoGlT2UJIRWMASERERDaralVg61YgPBzw8QGOHgUaNgQ++ADIyFC6dNaLASARERHZNI0GGDRILif33HOyG3jaNCA0FDhwQOnSWScGgERERGQXAgKADRuAdeuASpWAM2fkZJE33wTu3VO6dNaFASARERHZleefl62BAwfKhNHz5wNPPgns2KF0yawHA0AiIiKyO76+wIoVMl9gSAgQEwO0awcMGwbcvq106ZTHAJCIiIjsVqdOcqbwyJHy/rJlQOPGypbJGjAAJCIiIrvm5QV8+aXMF1i9OnD9utIlUh4DQCIiIlKFVq1kjsA331S6JMpjAEhERESq4eYGTJ2qdCmUxwCQiIiISGUYABIRERGpDANAIiIiIpVhAEhERESkMgwAiYiIiFSGASARERGRyjAAJCIiIlIZBoBEREREKsMAkIiIiEhlGAASERERqQwDQCIiIiKVYQBIREREpDIMAImIiIhUhgEgERERkcowACQiIiJSGbsMAKdPn47mzZujXLly8PHxKXCby5cvo3v37vDw8ICfnx/GjBmDzMxMyxaUiIiISAFOShfAHDIzM9G7d280a9YMy5Yty/d8Tk4OunbtiooVK2Lv3r1ISEjAwIEDIYTAwoULFSgxERERkeXYZQD40UcfAQBWrFhR4PPbtm3D6dOnceXKFQQGBgIAPvvsMwwaNAjTp0+Ht7e3pYpKREREZHF2GQA+TGRkJOrUqWMI/gCgY8eOyMjIwNGjR9G2bVsFS2c7fvrpJ+zduxdXrlyBXq8HAKSnp6N///4IDg5G3759ERoaqnApTevAgQNYv349YmNjMXr0aMPjCQkJGDduHNq2bYtnn31WwRKa3tWrV7FkyRLExsaiVatWhseTkpLwxhtvoGbNmhgzZoyCJTQ9IQSmTZuGK1euQKvVGh6/c+cOhg4diuDgYLz11lu8WDSRpKQkfP7554iNjUWdOnUMj9++fRuvv/46qlSpgvfee88sn7179278+uuvuHLlCiZPnmx4PDExEePHj0fHjh3RsWNHs3w2kZJUGQDGx8ejUqVKRo+VL18eLi4uiI+PL/R1GRkZyMjIMNxPSUkxWxltwebNm7Fy5UoAgL+/PwAgKysLq1evBgCEhYXZXQB48uRJzJ07FwDQunVrw+Pp6elYsGAB9Hq93QWAd+7cwfTp0wEA2dnZhsdTU1Px1VdfITQ01O4CQI1GgwULFiAhIQFVqlQxPJ6eno7ly5cDAN555x2limd3hBD45JNPAADt27c3PJ6WloalS5ciKCjIbAHg4cOH8dlnnwEAnnvuOaPP/vzzz+Hh4cEAkOySzUwCmTp1KjQaTZG3I0eOFPv9NBpNvseEEAU+nmvmzJnQarWGW+XKlUtVF3sRHBxs+H9OTo7Rvw8+by/y1ik2NrbI5+1FUFCQ4f9qqTNwv15Xr16FEALA/e93+fLl4eHhoVjZ7E358uXh7u4OwPg7ltuzYM7vmBp/00SADbUAjho1Cn379i1ym6pVqxbrvXQ6HQ4ePGj0WFJSErKysvK1DOY1adIkjB8/3nA/JSVF1UEgA0B1nCy8vLyg1WqRnJysmjoDsl7Hjx9Hdna2IRDJ/X7ba52VotFoEBwcjPPnzyM2NjZf1zoDQCLTs5kA0M/PD35+fiZ5r2bNmmH69OmIi4tDQEAAADkxxNXVFWFhYYW+ztXVFa6uriYpgz0oKgDUaDSGfWtP1HqyCA4ONgSAFSpUyPecPSro+13Qc2QalStXxvnz53Hnzh14enoaPWfO/Z33Ir6g37SaL/LJvtlMF3BJXL58GdHR0bh8+TJycnIQHR2N6Oho3L17FwDQoUMH1KpVCwMGDEBUVBR27NiBt99+G6+++ioHdZdA3gPjgwFgQEAAnJ2dFSmXOWm1WsPJ6cqVK/met9eTRW69MjIyDK1hDz5nbwr6fhf0HJlGUQG3Ofd3QECAYehPQb9pBvtkr+wyAPzwww8RGhqKKVOm4O7duwgNDUVoaKhhjKCjoyM2b94MNzc3tGjRAn369EHPnj0Ng/upeAo6YFtizI6ScruqANlakDs2LFfemeX2RI2tYWqss5KU2t8uLi6GoT8PtgC6u7ujfPnyZvtsIiXZTBdwSaxYsaLQHIC5QkJC8Ntvv1mmQHbK19cXbm5uSE9PV9UJMjg4GGfPnkVqaqpRihB/f3+7HSKgxmBIjXVWkpL7Ozg4GPHx8UbDgnIfL2piIJEts8sWQLKMvK1hajpB5q1b3rQoaqnzg3/rvLOE7QkDQMsqqsvd3Ps797OFEEa/aXb1kz1jAEhlkvfAWdDj9ihv3dRysijs5FyhQgWUK1dOiSKZnVJj0tSqsP2t0WjMPrQi72dnZWUV+DiRvWEASGVS2AHSng+cajxZFHZytuc6e3h4GMZ/qaXVU0mFfcd0Op3ZJ5Sp8TdNxACQykTtAaDau4Dtuc4AChzioNVq4eXlpVSR7FaFChXg5uYGwPLfMTW26hMxAKQyKewAac8HzsK6Q+25zt7e3oYUSWqpM1Bw/ey9zkopbEyxJfa3Wi9wSN0YAFKZFHSAtNck0Lny1jlvTjx7P1kUdHJWS50f9hiZRu6+zTum2BL7W62/aVI3BoBUJgUdICtVqgQXFxcFSmMZPj4+hokPajpZqDEYUmOdlVRQa58l9nfeMZ15f9Ns7SV7xgCQykSNJ8i8XVV5WyrsfWKAGv/WaqyzkpTa33mTQef9Tfv6+pr9s4mUwgCQysTPzy9f8mM1XDU/WEcHBwfDAHZ7pcbxcGqss5IKCvYstb8f/GxHR0cmgSa7xgCQyiRva1guNbSQFHSysHcF/V3Z6kmmpFQXcEGfrYbfNKkbA0AqMwaA6jhZPFhnjUYDDw8PhUpjGQUFuGr4fiuloH1rqfW11fibJnVjAEhlxgBQHScLNdbZy8vLaL1nQB3fb6U8uG8dHBwsNqFMjd9vUjcGgFRmD3adqGGMlBq7i9RYZyB/vXPzIZLpPTim2JLfMQaApDYMAKnM2AKojpOFt7e30bq/aqgzYPy3VkudlaLRaKDT6Qz3Lbm/1XqBQ+rFAJDK7MFgyFJjdpSkxgBQo9EYpcVwcFDH4cPPz8/wf7XUWUlKfcfU+JsmdePRjMrswQPng2lh7JGvr6/RCUItJ4u8kz7UEgx5enoa/s+0IOaX9ztmyf394IQftfymSb3UcQQns8q77JtaTpAajQbOzs6G+2o5WeQdkK+Wv7Ua66wkpfa3q6ur0e9YLRc4pF78hlOZZWdnK10EReRdMSDv/+2ZWuqZlxrrrCQl9zf/1qQmDACpzHQ6HQIDA+Hp6YmQkBCli2MxCxcuhE6ng7e3t1ErqD2bO3cudDodPD09UaVKFaWLYxEjRoww1Llq1arFeo1Op0NQUJDRhAYqno8//hg6nQ5eXl4W/Y4JIbBgwQIEBATA29ubfzuyexrBS55SS0lJgVarRXJyMlNDEBER2Qiev9kCSERERKQ6DACJiIiIVIYBIBEREZHKMAAkIrKAv//+G4MHD0a1atXg5uYGT09PNGjQAHPmzEFiYmK+7Rs0aACNRoO5c+cqUFoisncMAImIzOybb75BWFgYDh8+jAkTJmDLli3YuHEjevfuja+++gpDhw412j46OhpRUVEAgGXLlilRZCKyc05KF4CIyJ5FRkbijTfeQPv27bFp0yajlXLat2+Pt956C1u2bDF6zbfffgsA6Nq1KzZv3oz9+/ejefPmFi03Edk3tgASEZnRjBkzoNFosHTp0gKXSXRxcUGPHj0M99PT07F69WqEhYXh888/BwAsX77cYuUlInVgAEhEZCY5OTn4888/ERYWhsqVKxfrNRs2bEBSUhKGDBmCxx9/HC1btsSaNWtw9+5dM5eWiNSEASARkZncunULqampqFatWrFfs2zZMri5uaFfv34AgKFDh+Lu3btYu3atuYpJRCrEAJCIyErExMRg586d6NWrF3x8fAAAvXv3hpeXF7uBicikGAASEZmJn58fypUrh5iYmGJtv3z5cggh8MILL+D27du4ffs2srKy0KNHD+zbtw9nz541c4mJSC0YABIRmYmjoyOeeeYZHD16FLGxsUVuq9frsWLFCgBAr169UL58ecPt+++/B8DJIERkOhohhFC6ELaKi0kT0cNERkaiVatWaN++PX7++We4uLgYPZ+VlYUtW7bAyckJXbp0wciRI/HCCy/ke59Ro0bh1q1biI2NhZMTM3gRlQXP38wDSERkVs2aNcOSJUswYsQIhIWF4Y033kDt2rWRlZWFqKgoLF26FHXq1IGjoyOcnJzw3nvvITAwMN/7vP766xgzZgw2b96MZ599VoGaEJE9YQtgGfAKgoiK6/jx4/j888+xc+dOxMfHw9nZGdWrV0f37t0xatQoBAcHo0uXLti4cWOBr799+zYCAwPRrl07/PLLLxYuPZF94fnbTgPA6dOnY/PmzYiOjoaLiwtu376dbxuNRpPvsSVLlmD48OHF/hx+gYiIiGwPz9922gWcmZmJ3r17o1mzZkWuoxkeHo5OnToZ7mu1WksUj4iIiEhRdhkAfvTRRwBgmFFXGB8fH+h0OguUiIiIiMh6qDoNzKhRo+Dn54dGjRrhq6++gl6vV7pIRERERGZnly2AxfHJJ5/gmWeegbu7O3bs2IG33noLt27dwvvvv1/oazIyMpCRkWG4n5KSYomiEhEREZmUzbQATp06FRqNpsjbkSNHiv1+77//Ppo1a4b69evjrbfewscff4xPP/20yNfMnDkTWq3WcCvu4u5ERERE1sRmZgHfunULt27dKnKbqlWrws3NzXB/xYoVGDduXIGzgB+0b98+tGzZEvHx8ahUqVKB2xTUAli5cmVVzyIiIiKyNZwFbENdwH5+fvDz8zPb+0dFRcHNzc2wAHtBXF1d4erqarYyEBEREVmCzQSAJXH58mUkJibi8uXLyMnJQXR0NADgscceg6enJ3799VfEx8ejWbNmcHd3x86dOzF58mS89tprDPCIiIjI7tllAPjhhx9i5cqVhvuhoaEAgJ07d6JNmzZwdnbG4sWLMX78eOj1ejzyyCP4+OOPMXLkSKWKTERERGQxNjMG0BpxDAEREZHt4fnbhmYBExEREZFpMAAkIiIiUhkGgEREREQqwwCQiIiISGUYABIRERGpDANAIiIiIpVhAEhERESkMgwAiYiIiFSGASARERGRyjAAJCIiIlIZBoBEREREKsMAkIiIiEhlGAASERERqQwDQCIiIiKVYQBIREREpDIMAImIiIhUhgEgERERkcowACQiIiJSGQaARERERCrDAJCIiIhIZRgAEhEREakMA0AiIiIilWEASERERKQyDACJiIiIVIYBIBEREZHKMAAkIiIiUhkGgEREREQqwwCQiIiISGUYABIRERGpDANAIiIiIpVhAEhERESkMgwAiYiIiFSGASARERGRyjAAJCIiIlIZBoBEREREKsMAkIiIiEhl7C4AvHjxIoYOHYpq1arB3d0djz76KKZMmYLMzEyj7S5fvozu3bvDw8MDfn5+GDNmTL5tiIiIiOyRk9IFMLWzZ89Cr9fj66+/xmOPPYaTJ0/i1Vdfxb179zB37lwAQE5ODrp27YqKFSti7969SEhIwMCBAyGEwMKFCxWuAREREZF5aYQQQulCmNunn36KJUuW4L///gMA/PHHH+jWrRuuXLmCwMBAAMCPP/6IQYMG4caNG/D29i7W+6akpECr1SI5ObnYryEiIiJl8fxthy2ABUlOToavr6/hfmRkJOrUqWMI/gCgY8eOyMjIwNGjR9G2bdsC3ycjIwMZGRlG7wvILxIRERHZhtzztgrawApl9wHgv//+i4ULF+Kzzz4zPBYfH49KlSoZbVe+fHm4uLggPj6+0PeaOXMmPvroo3yPV65c2XQFJiIiIotISEiAVqtVuhiKsJkAcOrUqQUGX3kdPnwYDRs2NNy/du0aOnXqhN69e2PYsGFG22o0mnyvF0IU+HiuSZMmYfz48Yb7er0eiYmJqFChgtHrUlJSULlyZVy5ckU1TctqrDOgznqzzqyzPVNjvdVY5+TkZISEhBj1DqqNzQSAo0aNQt++fYvcpmrVqob/X7t2DW3btkWzZs2wdOlSo+10Oh0OHjxo9FhSUhKysrLytQzm5erqCldXV6PHfHx8Ct3e29tbNT+mXGqsM6DOerPO6qDGOgPqrLca6+zgYHfJUIrNZgJAPz8/+Pn5FWvbq1evom3btggLC0N4eHi+P3CzZs0wffp0xMXFISAgAACwbds2uLq6IiwszORlJyIiIrImNhMAFte1a9fQpk0bhISEYO7cubh586bhOZ1OBwDo0KEDatWqhQEDBuDTTz9FYmIi3n77bbz66ququ/ohIiIi9bG7AHDbtm24cOECLly4gODgYKPncmf7ODo6YvPmzRgxYgRatGgBd3d39OvXz5AnsKxcXV0xZcqUfN3F9kyNdQbUWW/WWR3UWGdAnfVmndVJFXkAiYiIiOg+9Y5+JCIiIlIpBoBEREREKsMAkIiIiEhlGAASERERqQwDQDNYvHgxqlWrBjc3N4SFhWHPnj1KF6lUZs6ciUaNGsHLywv+/v7o2bMn/vnnH6NthBCYOnUqAgMD4e7ujjZt2uDUqVNG22RkZGD06NHw8/ODh4cHevTogdjYWEtWpdRmzpwJjUaDcePGGR6z1zpfvXoVL7/8MipUqIBy5cqhfv36OHr0qOF5e6t3dnY23n//fVSrVg3u7u545JFH8PHHH0Ov1xu2sfU6//XXX+jevTsCAwOh0WiwadMmo+dNVb+kpCQMGDAAWq0WWq0WAwYMwO3bt81cu4IVVeesrCy8++67ePLJJ+Hh4YHAwEC88soruHbtmtF72FqdgYf/rfN6/fXXodFoMH/+fKPHba3exanzmTNn0KNHD2i1Wnh5eaFp06a4fPmy4Xlbq7NJCTKpH3/8UTg7O4tvvvlGnD59WowdO1Z4eHiIS5cuKV20EuvYsaMIDw8XJ0+eFNHR0aJr164iJCRE3L1717DNrFmzhJeXl1i/fr04ceKEePHFF0VAQIBISUkxbDN8+HARFBQkIiIixLFjx0Tbtm1FvXr1RHZ2thLVKrZDhw6JqlWrirp164qxY8caHrfHOicmJooqVaqIQYMGiYMHD4qYmBixfft2ceHCBcM29lbvadOmiQoVKojffvtNxMTEiJ9++kl4enqK+fPnG7ax9Tr//vvvYvLkyWL9+vUCgNi4caPR86aqX6dOnUSdOnXE/v37xf79+0WdOnVEt27dLFVNI0XV+fbt26Jdu3ZizZo14uzZsyIyMlI0adJEhIWFGb2HrdVZiIf/rXNt3LhR1KtXTwQGBorPP//c6Dlbq/fD6nzhwgXh6+srJkyYII4dOyb+/fdf8dtvv4nr168btrG1OpsSA0ATa9y4sRg+fLjRYzVq1BATJ05UqESmc+PGDQFA7N69WwghhF6vFzqdTsyaNcuwTXp6utBqteKrr74SQsgDrrOzs/jxxx8N21y9elU4ODiILVu2WLYCJXDnzh3x+OOPi4iICNG6dWtDAGivdX733XdFy5YtC33eHuvdtWtXMWTIEKPHevXqJV5++WUhhP3V+cETpKnqd/r0aQFAHDhwwLBNZGSkACDOnj1r5loVrahAKNehQ4cEAMNFuq3XWYjC6x0bGyuCgoLEyZMnRZUqVYwCQFuvd0F1fvHFFw2/54LYep3Lil3AJpSZmYmjR4+iQ4cORo936NAB+/fvV6hUppOcnAwAhsWzY2JiEB8fb1RfV1dXtG7d2lDfo0ePIisry2ibwMBA1KlTx6r3yciRI9G1a1e0a9fO6HF7rfMvv/yChg0bonfv3vD390doaCi++eYbw/P2WO+WLVtix44dOHfuHADg+PHj2Lt3L7p06QLAPuucl6nqFxkZCa1WiyZNmhi2adq0KbRardXvA0Ae1zQajWFdd3uts16vx4ABAzBhwgTUrl073/P2Vm+9Xo/NmzejevXq6NixI/z9/dGkSROjbmJ7q3NJMQA0oVu3biEnJweVKlUyerxSpUqIj49XqFSmIYTA+PHj0bJlS9SpUwcADHUqqr7x8fFwcXFB+fLlC93G2vz44484duwYZs6cme85e63zf//9hyVLluDxxx/H1q1bMXz4cIwZMwarVq0CYJ/1fvfdd/HSSy+hRo0acHZ2RmhoKMaNG4eXXnoJgH3WOS9T1S8+Ph7+/v753t/f39/q90F6ejomTpyIfv36GZYBtdc6z549G05OThgzZkyBz9tbvW/cuIG7d+9i1qxZ6NSpE7Zt24bnnnsOvXr1wu7duwHYX51Lyu6WgrMGGo3G6L4QIt9jtmbUqFH4+++/sXfv3nzPlaa+1rpPrly5grFjx2Lbtm1wc3MrdDt7qjMgr5YbNmyIGTNmAABCQ0Nx6tQpLFmyBK+88ophO3uq95o1a/Ddd99h9erVqF27NqKjozFu3DgEBgZi4MCBhu3sqc4FMUX9Ctre2vdBVlYW+vbtC71ej8WLFz90e1uu89GjR7FgwQIcO3asxOWz1XrnTuZ69tln8eabbwIA6tevj/379+Orr75C69atC32trda5pNgCaEJ+fn5wdHTMd1Vw48aNfFfZtmT06NH45ZdfsHPnTqP1lXU6HQAUWV+dTofMzEwkJSUVuo01OXr0KG7cuIGwsDA4OTnByckJu3fvxhdffAEnJydDme2pzgAQEBCAWrVqGT1Ws2ZNw2w5e/xbT5gwARMnTkTfvn3x5JNPYsCAAXjzzTcNLb/2WOe8TFU/nU6H69ev53v/mzdvWu0+yMrKQp8+fRATE4OIiAhD6x9gn3Xes2cPbty4gZCQEMNx7dKlS3jrrbdQtWpVAPZXbz8/Pzg5OT30uGZPdS4pBoAm5OLigrCwMERERBg9HhERgebNmytUqtITQmDUqFHYsGED/vzzT1SrVs3o+WrVqkGn0xnVNzMzE7t37zbUNywsDM7OzkbbxMXF4eTJk1a5T5555hmcOHEC0dHRhlvDhg3Rv39/REdH45FHHrG7OgNAixYt8qX4OXfuHKpUqQLAPv/WqampcHAwPgQ6OjoaWg7ssc55map+zZo1Q3JyMg4dOmTY5uDBg0hOTrbKfZAb/J0/fx7bt29HhQoVjJ63xzoPGDAAf//9t9FxLTAwEBMmTMDWrVsB2F+9XVxc0KhRoyKPa/ZW5xKz7JwT+5ebBmbZsmXi9OnTYty4ccLDw0NcvHhR6aKV2BtvvCG0Wq3YtWuXiIuLM9xSU1MN28yaNUtotVqxYcMGceLECfHSSy8VmEYiODhYbN++XRw7dkw8/fTTVpMmozjyzgIWwj7rfOjQIeHk5CSmT58uzp8/L77//ntRrlw58d133xm2sbd6Dxw4UAQFBRnSwGzYsEH4+fmJd955x7CNrdf5zp07IioqSkRFRQkAYt68eSIqKsow49VU9evUqZOoW7euiIyMFJGRkeLJJ59ULE1GUXXOysoSPXr0EMHBwSI6OtrouJaRkWF4D1ursxAP/1s/6MFZwELYXr0fVucNGzYIZ2dnsXTpUnH+/HmxcOFC4ejoKPbs2WN4D1ursykxADSDRYsWiSpVqggXFxfRoEEDQ9oUWwOgwFt4eLhhG71eL6ZMmSJ0Op1wdXUVTz31lDhx4oTR+6SlpYlRo0YJX19f4e7uLrp16yYuX75s4dqU3oMBoL3W+ddffxV16tQRrq6uokaNGmLp0qVGz9tbvVNSUsTYsWNFSEiIcHNzE4888oiYPHmyUSBg63XeuXNngb/hgQMHCiFMV7+EhATRv39/4eXlJby8vET//v1FUlKShWpprKg6x8TEFHpc27lzp+E9bK3OQjz8b/2gggJAW6t3ceq8bNky8dhjjwk3NzdRr149sWnTJqP3sLU6m5JGCCHM28ZIRERERNaEYwCJiIiIVIYBIBEREZHKMAAkIiIiUhkGgEREREQqwwCQiIiISGUYABIRERGpDANAIiIiIpVhAEhERESkMgwAiYiIiFSGASARERGRyjAAJCIiIlIZBoBEREREKsMAkIiIiEhlGAASERERqQwDQCIiIiKVYQBIREREpDIMAImIiIhUhgEgERERkcowACQiIiJSGQaARERERCrDAJCIiIhIZRgAEhEREakMA0AiIiIilWEASERERKQyDACJiIiIVIYBIBEREZHKMAAkIiIiUhkGgEREREQqwwCQiIiISGUYABIRERGpDANAIiIiIpX5P3Z3v5zaj5FbAAAAAElFTkSuQmCC",
      "text/html": [
       "\n",
       "            <div style=\"display: inline-block;\">\n",
       "                <div class=\"jupyter-widgets widget-label\" style=\"text-align: center;\">\n",
       "                    Figure\n",
       "                </div>\n",
       "                <img src='data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAoAAAAHgCAYAAAA10dzkAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjguMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8g+/7EAAAACXBIWXMAAA9hAAAPYQGoP6dpAAB4zElEQVR4nO3dd3hT1f8H8He6S0dKKSUdFHAgS6CUPQSUvUQURBCZKrJFURAVVLaIIAKKQoGvoiDLgQIFARllt8gU0DIKLaMtLdDdnN8f59fQ0EFHkpvkvl/PkweS3CTn3Cb3fu4Zn6MRQggQERERkWo4KF0AIiIiIrIsBoBEREREKsMAkIiIiEhlGAASERERqQwDQCIiIiKVYQBIREREpDIMAImIiIhUhgEgERERkcowACQiIiJSGQaARERERCrDAJCIiIhIZRgAEhEREakMA0AiIiIilWEASERERKQyDACJiIiIVIYBIBEREZHKMAAkIiIiUhkGgEREREQqwwCQiIiISGUYABIRERGpDANAIiIiIpVhAEhERESkMgwAiYiIiFSGASARERGRyjAAJCIiIlIZBoBEREREKsMAkIiIiEhlGAASERERqQwDQCIiIiKVYQBIREREpDIMAImIiIhUhgEgERERkcowACQiIiJSGQaARERERCrDAJCIiIhIZRgAEhEREakMA0AiIiIilWEASERERKQyDACJiIiIVIYBIBEREZHKMAAkIiIiUhkGgEREREQqwwCQiIiISGUYABIRERGpDANAIiIiIpVhAEhERESkMgwAiYiIiFSGASARERGRyjAAJCIiIlIZBoBEREREKsMAkIiIiEhlGAASERERqYzdBoAzZ85Eo0aN4OXlBX9/f/Ts2RP//POP0TZCCEydOhWBgYFwd3dHmzZtcOrUKYVKTERERGQZdhsA7t69GyNHjsSBAwcQERGB7OxsdOjQAffu3TNsM2fOHMybNw9ffvklDh8+DJ1Oh/bt2+POnTsKlpyIiIjIvDRCCKF0ISzh5s2b8Pf3x+7du/HUU09BCIHAwECMGzcO7777LgAgIyMDlSpVwuzZs/H6668rXGIiIiIi87DbFsAHJScnAwB8fX0BADExMYiPj0eHDh0M27i6uqJ169bYv3+/ImUkIiIisgQnpQtgCUIIjB8/Hi1btkSdOnUAAPHx8QCASpUqGW1bqVIlXLp0qcD3ycjIQEZGhuG+Xq9HYmIiKlSoAI1GY6bSExERkSkJIXDnzh0EBgbCwUE1bWFGVBEAjho1Cn///Tf27t2b77kHAzchRKHB3MyZM/HRRx+ZpYxERERkWVeuXEFwcLDSxVCE3QeAo0ePxi+//IK//vrL6I+s0+kAyJbAgIAAw+M3btzI1yqYa9KkSRg/frzhfnJyMkJCQnDlyhV4e3ubqQZERERkSikpKahcuTK8vLyULopi7DYAFEJg9OjR2LhxI3bt2oVq1aoZPV+tWjXodDpEREQgNDQUAJCZmYndu3dj9uzZBb6nq6srXF1d8z3u7e3NAJCIiMjGqHn4lt0GgCNHjsTq1avx888/w8vLyzDmT6vVwt3dHRqNBuPGjcOMGTPw+OOP4/HHH8eMGTNQrlw59OvXT+HSExEREZmP3QaAS5YsAQC0adPG6PHw8HAMGjQIAPDOO+8gLS0NI0aMQFJSEpo0aYJt27apukmYiIiI7J9q8gCaQ0pKCrRaLZKTk9kFTEREZCN4/lZRHkAiIiIikhgAEhEREakMA0AiIiIilWEASERERKQyDACJiIiIVIYBIJnN33//jaFDh+LRRx+Fu7s73N3d8fjjj+P111/HkSNHlC6eWfz9998YPHgwqlWrBjc3N3h6eqJBgwaYM2cOEhMTAQB79+7FsGHDEBYWBldXV2g0Gly8eFHZgpfRw+qdk5ODefPmoVOnTggODka5cuVQs2ZNTJw4Ebdv31a6+KVSnL/1F198gaZNm8LPzw+urq4ICQlB3759cerUKYVLb3sOHDiA3r17IyAgAC4uLtDpdHjhhRcQGRlptN3UqVOh0Whw69ath75nmzZt8qUKM6XVq1dj/vz5BT6n0WgwdepUs3020cPYbR5AUtbXX3+NUaNG4YknnsDYsWNRu3ZtaDQanDlzBj/88AMaNWqECxcu4NFHH1W6qCbzzTffYMSIEXjiiScwYcIE1KpVC1lZWThy5Ai++uorREZGYuPGjdixYwe2b9+O0NBQeHt7Y9euXUoXvUyKU+///e9/mDp1Kl566SUMGzYMfn5+OHbsGKZNm4Zff/0VR44cgbu7u9JVKbbi/q0TEhLQuXNn1KtXD+XLl8d///2HWbNmoUmTJjh69CieeOIJpatiExYuXIhx48ahcePGmDNnDqpUqYLLly9j0aJFaNmyJRYsWIBRo0aV+H0XL15shtLet3r1apw8eRLjxo3L91xkZKRq16AlKyGo1JKTkwUAkZycrHRRrMrevXuFg4OD6N69u8jIyChwm7Vr14qrV69auGTms3//fuHo6Cg6deok0tPT8z2fkZEhfv75ZyGEEDk5OYbHP/30UwFAxMTEWKqoJlXcemdnZ4tbt27le/6nn34SAMT//vc/SxTXJEryty7I6dOnBQDxwQcfmLOYdiP3eNKtWzeRlZVl9FxWVpbo1q2bcHBwEHv37hVCCDFlyhQBQNy8eVOJ4hrp2rWrqFKlitLFoALw/C0Eu4DJ5GbMmAFHR0d8/fXXcHFxKXCb3r17IzAwEEDh3TCDBg1C1apVDfcvXrwIjUaDuXPnYt68eahWrRo8PT3RrFkzHDhwwBxVKbYZM2ZAo9Fg6dKlBa4X7eLigh49egAAHBzs52dX3Ho7OjqiQoUK+Z5v3LgxAODKlStmL6uplORvXZCKFSsCAJyc2AFTHDNnzoRGo8GSJUvy7TMnJycsXrwYGo0Gs2bNMnruypUr6NWrF7y9vaHVavHyyy/j5s2bRtsUdOzJzMzEtGnTUKNGDbi6uqJixYoYPHhwvtcCsoWvWbNm8PT0hKenJ+rXr49ly5YZ3nvz5s24dOkSNBqN4ZYrbxfw8ePHodFoDK/N648//oBGo8Evv/xieOz8+fPo168f/P394erqipo1a2LRokUP35lEedjPmYisQk5ODnbu3ImGDRsiICDALJ+xaNEiREREYP78+fj+++9x7949dOnSBcnJyWb5vIfJycnBn3/+ibCwMFSuXFmRMijBFPX+888/AQC1a9c2ZdHMprR1zsnJQUZGBs6ePYthw4bB398fgwcPNmNJ7UPe40lh3aWVK1dGWFgY/vzzT+Tk5Bgef+655/DYY49h3bp1mDp1KjZt2oSOHTsiKyur0M/T6/V49tlnMWvWLPTr1w+bN2/GrFmzEBERgTZt2iAtLc2w7Ycffoj+/fsjMDAQK1aswMaNGzFw4EBcunQJgOxebtGiBXQ6HSIjIw23gtSrVw+hoaEIDw/P99yKFSvg7++PLl26AABOnz6NRo0a4eTJk/jss8/w22+/oWvXrhgzZgw++uijh+9Uov/HS1AyqVu3biEtLQ1VqlTJ91xOTg5EnpUHHR0dja6Ii8vLywu//fYbHB0dAQCBgYFo3Lgx/vjjD/Tt27f0hS+lW7duITU1FdWqVbP4ZyuprPW+evUqJk6ciIYNG6Jbt24mLp15lLbOHh4eyMjIAABUr14du3btUtXFQmkVd39Xq1YNhw4dQkJCguGxXr16Yc6cOQCADh06oFKlSujfvz/Wrl2L/v37F/g+a9euxZYtW7B+/Xr06tXL8Hi9evXQqFEjrFixAm+88QZiYmIwY8YM9O/fH999951hu/bt2xv+X6tWLfj4+MDV1RVNmzZ9aF0HDx6MMWPG4Ny5c6hevToAICkpCT///DNGjRplaP0cP348vLy8sHfvXsMSZu3bt0dGRgZmzZqFMWPGoHz58g/9PCK2AJLFhIWFwdnZ2XD77LPPSvU+Xbt2NQR/AFC3bl0AMFx5k/VLTExEly5dIITAmjVr7KpbvCD79+9HZGQkvvvuO3h5eaFt27acCWxCuReWeS8oHwzy+vTpAycnJ+zcubPQ9/ntt9/g4+OD7t27Izs723CrX78+dDqdYcJWREQEcnJyMHLkSJPVoX///nB1dcWKFSsMj/3www/IyMgwtBanp6djx44deO6551CuXDmjMnbp0gXp6emKD4ch22HfR12yOD8/P7i7uxcYjK1evRqHDx82GstSGg+OJcsdh5W3e8aS/Pz8UK5cOcTExCjy+Uopbb2TkpLQvn17XL16FREREXjkkUfMVELTK22dGzRogKZNm6J///7YuXMnhBB47733zFRK+1Hc/X3x4kWUK1cOvr6+hsd0Op3RNk5OTqhQoYJRK+GDrl+/jtu3b8PFxcXoYtXZ2Rnx8fGG1DK54wFNOYvX19cXPXr0wKpVqwxd2StWrEDjxo0NQyQSEhKQnZ2NhQsX5itfbhdxcdLfEAHsAiYTc3R0xNNPP41t27YhLi7OaBxgrVq1ACBfzjs3N7cCx+/ZyoHM0dERzzzzDP744w/ExsaqJrVDaeqdlJSEdu3aISYmBjt27DC03toKU/ytvby8UKNGDZw7d84MJbQvjo6OaNu2LbZs2VLo/o6NjcXRo0fRuXNno56B+Ph4BAUFGe5nZ2cjISGhwMlIufz8/FChQgVs2bKlwOe9vLwA3J/IExsba9Ku/MGDB+Onn35CREQEQkJCcPjwYSxZssTwfPny5eHo6IgBAwYU2vqotqEoVHpsASSTmzRpEnJycjB8+PAiB1znqlq1Ks6dO2cYIwXIK939+/ebs5gmNWnSJAgh8OqrryIzMzPf81lZWfj1118VKJl5laTeucHff//9h23btiE0NNTSxTWJsv6tb926hRMnTuCxxx4zZzHtRu7+HjFihNEkD0COK37jjTcghMCkSZOMnvv++++N7q9duxbZ2dlFJn7u1q0bEhISkJOTg4YNG+a75eZt7NChAxwdHY2Cs4K4urqWqGeiQ4cOCAoKQnh4OMLDw+Hm5oaXXnrJ8Hy5cuXQtm1bREVFoW7dugWWsagAlygvtgCSybVo0QKLFi3C6NGj0aBBA7z22muoXbs2HBwcEBcXh/Xr1wOAYQDzgAED8PXXX+Pll1/Gq6++ioSEBMyZM8fwvC1o1qwZlixZghEjRiAsLAxvvPEGateujaysLERFRWHp0qWoU6cOunfvjps3b2L37t0AgBMnTgCQqR4qVqyIihUronXr1kpWpUSKW+927dqhY8eOiIqKwvz585GdnW00VqlixYo2kxS8uHV+6qmn0L59e/Tr1w+PP/443N3dce7cOSxYsAAZGRmYMmWK0lWxCS1atMD8+fMxbtw4tGzZEqNGjUJISIghEfTBgwcxf/58NG/e3Oh1GzZsgJOTE9q3b49Tp07hgw8+QL169dCnT59CP6tv3774/vvv0aVLF4wdOxaNGzeGs7MzYmNjsXPnTjz77LN47rnnULVqVbz33nv45JNPkJaWhpdeeglarRanT5/GrVu3DLNxn3zySWzYsAFLlixBWFgYHBwc0LBhw0I/39HREa+88grmzZsHb29v9OrVC1qt1mibBQsWoGXLlmjVqhXeeOMNVK1aFXfu3MGFCxfw66+/GmbWEz2UYhkI7QATSRYtOjpaDB48WFSrVk24uroKNzc38dhjj4lXXnlF7Nixw2jblStXipo1awo3NzdRq1YtsWbNGjFw4ECjJKoxMTECgPj000/zfRYAMWXKFDPX6OGio6PFwIEDRUhIiHBxcREeHh4iNDRUfPjhh+LGjRtCCCF27twpABR4a926tbIVKKWH1Tv3b1fYbeDAgUpXocQeVuf09HQxbNgwUbNmTeHp6SmcnJxEcHCwePnll8WpU6eULr7NiYyMFC+88IKoVKmScHJyEv7+/qJXr15i//79RtvlJoI+evSo6N69u/D09BReXl7ipZdeEtevXzfatnXr1qJNmzZGj2VlZYm5c+eKevXqCTc3N+Hp6Slq1KghXn/9dXH+/HmjbVetWiUaNWpk2C40NFSEh4cbnk9MTBQvvPCC8PHxERqNRuQ95RZ2zDp37pzhdxEREVHgvoiJiRFDhgwRQUFBwtnZWVSsWFE0b95cTJs2rTi7kgTP30IIoREiT14OKpGUlBRotVokJyfbVGsVEREBoaGhePTRR7Fu3Tqli0IWxvM3u4CJiEhlzp07hz179uDEiRN4+eWXlS4OkSIYABIRkarMnDkTv/76K1555RWMGDFC6eIQKYIBIBERqUpBS64RqQ3TwBARERGpDANAIiIiIpVhAEhERESkMgwAiYiIiFSGASARERGRyjAAJCIiIlIZBoBEREREKsMAkIiIiEhlGAASERERqQwDQCIiIiKVYQBIREREpDIMAImIiIhUhgEgmZwQAq+99hp8fX2h0WgQHR2tdJHMjnVmncn0lNzf/FuT3RNUasnJyQKASE5OVrooVuX3338Xzs7OYt++fSIuLk5kZWWV6PWtW7cWAIxuL774otE2iYmJ4uWXXxbe3t7C29tbvPzyyyIpKcmEtSiZstQ5JiYmX31zb2vXrjVsZ091FkKI1157TTzyyCPCzc1N+Pn5iR49eogzZ84Ynt+5c2eh++XQoUOG7Q4dOiSefvppodVqhY+Pj2jfvr2IiooyVTWNlLXOX3/9tWjdurXw8vISAPL9/WJiYsSQIUNE1apVhZubm3jkkUfEhx9+KDIyMgzbhIeHF7pfrl+/bopqWg0ljyVqPI6pCc/fQthtC+Bff/2F7t27IzAwEBqNBps2bTJ6ftCgQdBoNEa3pk2bKlNYO/Pvv/8iICAAzZs3h06ng5OTU4nf49VXX0VcXJzh9vXXXxs9369fP0RHR2PLli3YsmULoqOjMWDAAFNVocTKUufKlSsb1TUuLg4fffQRPDw80LlzZ8N29lRnAAgLC0N4eDjOnDmDrVu3QgiBDh06ICcnBwDQvHnzfPtl2LBhqFq1Kho2bAgAuHPnDjp27IiQkBAcPHgQe/fuhbe3Nzp27IisrCyrq3Nqaio6deqE9957r8Dnz549C71ej6+//hqnTp3C559/jq+++spo+xdffDHffunYsSNat24Nf3//MtXP2ih5LFHjcYxURukI1Fx+//13MXnyZLF+/XoBQGzcuNHo+YEDB4pOnTqJuLg4wy0hIaFEn8EriPwGDhxodMVbpUqVEr9H69atxdixYwt9/vTp0wKAOHDggOGxyMhIAUCcPXu2FKUuG1PU+UH169cXQ4YMMdxXQ52PHz8uAIgLFy4U+HxmZqbw9/cXH3/8seGxw4cPCwDi8uXLhsf+/vvvIt+ntExZ59zWzeK09syZM0dUq1at0Odv3LghnJ2dxapVq0pdHmuk9LFEbccxteH5Wwi7DQDzKiwAfPbZZ8v0vvwC5Xf79m3x8ccfi+DgYBEXFydu3Lghpk+fLjw8PIq8/fXXX4b3aN26tfDz8xMVKlQQtWrVEm+99ZZISUkxPL9s2TKh1WrzfbZWqxXLly+3RDWNmKLOeR05ckQAEPv27TM8Zu91vnv3rhg3bpyoVq2aUXdnXuvWrRMODg5GwV5KSorw8/MTU6ZMERkZGSI1NVWMHTtW1K5du8Rddpasc0kCwMmTJ4uwsLBCn587d67QarUiNTW1LNWzOkoeS7y9vUXPnj1VdRxTG56/hSh5m7Yd2bVrF/z9/eHj44PWrVtj+vTpdteFYmlarRZeXl5wdHSETqcDAAwfPhx9+vQp8nVBQUGG//fv3x/VqlWDTqfDyZMnMWnSJBw/fhwREREAgPj4+AL/Tv7+/oiPjzdhbYrHFHXOa9myZahZsyaaN29ueMxe67x48WK88847uHfvHmrUqIGIiAi4uLgU+Nply5ahY8eOqFy5suExLy8v7Nq1C88++yw++eQTAED16tWxdevWUnXZFcXUf+fi+Pfff7Fw4UJ89tlnhW6zfPly9OvXD+7u7qX+HGuk5LGkUqVKyMrKUtVxjNRHtQFg586d0bt3b1SpUgUxMTH44IMP8PTTT+Po0aNwdXUt8DUZGRnIyMgw3E9JSbFUcW2ar68vfH19i739q6++avh/nTp18Pjjj6Nhw4Y4duwYGjRoAADQaDT5XieEKPBxJZS0zrnS0tKwevVqfPDBB/mes8c69+/fH+3bt0dcXBzmzp2LPn36YN++fXBzczPaLjY2Flu3bsXatWuNHk9LS8OQIUPQokUL/PDDD8jJycHcuXPRpUsXHD582OxBUWn/zsVx7do1dOrUCb1798awYcMK3CYyMhKnT5/GqlWrzFIGa2PJY4mSn20tv2myb3Y7CeRhXnzxRXTt2hV16tRB9+7d8ccff+DcuXPYvHlzoa+ZOXMmtFqt4Za3JYIKN2PGDHh6ehZ527NnT6Gvb9CgAZydnXH+/HkAgE6nw/Xr1/Ntd/PmTVSqVMls9SiJ0tZ53bp1SE1NxSuvvGL0uL3WWavV4vHHH8dTTz2FdevW4ezZs9i4cWO+9w4PD0eFChXQo0cPo8dXr16NixcvIjw8HI0aNULTpk2xevVqxMTE4OeffzZrfYGyf7cLc+3aNbRt2xbNmjXD0qVLC93u22+/Rf369REWFlaWatgMSx5LvLy8FPtsa/lNk31TbQvggwICAlClShXDj7MgkyZNwvjx4w33U1JSGAQWQ1m7yU6dOoWsrCwEBAQAAJo1a4bk5GQcOnQIjRs3BgAcPHgQycnJRt2mSiptnZctW4YePXqgYsWKRo/bc53zEkIYtbLnPhYeHo5XXnkFzs7ORs+lpqbCwcHBqMUk975ery9hDUrOHF3AV69eRdu2bQ2zpB0cCr5Ov3v3LtauXYuZM2eW6P1tmSWPJdWqVUNkZKQin20tv2mybwwA/19CQgKuXLli+HEWxNXVtdDuYSpcSbpO/v33X3z//ffo0qUL/Pz8cPr0abz11lsIDQ1FixYtAAA1a9ZEp06d8OqrrxrSKrz22mvo1q0bnnjiCbPVoyRK0zV44cIF/PXXX/j999/zPWdvdf7vv/+wZs0adOjQARUrVsTVq1cxe/ZsuLu7o0uXLkbb/vnnn4iJicHQoUPzvU/79u0xYcIEjBw5EqNHj4Zer8esWbPg5OSEtm3bmqReRSnp3zk+Ph7x8fG4cOECAODEiRPw8vJCSEgIfH19ce3aNbRp0wYhISGYO3cubt68aXht7li0XGvWrEF2djb69+9vmsrYAEseSx4cn6fG4xjZOSVnoJjTnTt3RFRUlIiKihIAxLx580RUVJS4dOmSuHPnjnjrrbfE/v37RUxMjNi5c6do1qyZCAoKMpql9TCcRVSwzz//vNQpMi5fviyeeuop4evrK1xcXMSjjz4qxowZky9FT0JCgujfv7/w8vISXl5eon///oomUC1LnXNNmjRJBAcHi5ycnAKft6c6X716VXTu3Fn4+/sLZ2dnERwcLPr161dg+ouXXnpJNG/evND32rZtm2jRooXQarWifPny4umnnxaRkZGlKtfDlPXvPGXKlAITOIeHhwshik7y/KBmzZqJfv36lbostkDJY4kaj2NqwvO3EBohChjtagd27dpVYAvAwIEDsWTJEvTs2RNRUVG4ffs2AgIC0LZtW3zyyScl6tJNSUmBVqtFcnIyvL29TVl8IiIiMhOevwG7DQAtgV8gIiIi28Pzt4pnARMRERGpFQNAIiIiIpVhAEhERESkMgwAiYiIiFSGASARERGRyjAAJCIiIlIZBoBEREREKsMAkIiIiEhlGAASERERqQwDQCIiIiKVYQBIREREpDIMAImIiIhUhgEgERERkcowACQiIiJSGQaARERERCrDAJDKLCUlBR07dkSbNm0wcuRIpYtjMUOGDEGbNm3QrVs3pKamKl0ci/j000/Rpk0bPPXUUzhx4oTSxbGIbdu2oXXr1mjdujVWrlypdHHs3jfffGPY37t377bY5woh8NJLL6FNmzbo1asXsrOzLfbZRErQCCGE0oWwVSkpKdBqtUhOToa3t7fSxVHMtWvXEBQUBABwcHBATk6OwiWyDHd3d6SnpwMAQkNDcezYMYVLZH5169Y1BH4hISG4dOmSwiUyv7Fjx+KLL74AAHh7eyM5Ofmhr2nYsCHi4+Oh0+lw5MgRcxfRrjzzzDP4888/AQCVKlVCfHy8xT7bycnJcPxq0KABjh49arHPJsvi+RtwUroAZPvyXimr9XrCkicpJeX9+6akpChYEsvJW+eMjIxivSY+Ph5Xr141V5HsWt79fe/ePcXKoZbfNKkXu4CpzK5du2b4v1oCQL1ebxQMqKXVMzMz0/B/tfyt8/6d1VJnJSn1Hbt7967R71iv11vss4mUwACQyiw2NtbovpJX7ZZy48YNo5OTWgLAO3fuGP6vlhPk3bt3Df9XS52VpNR37MHjmFp+06ReDACpzK5cuWJ0/8EDqT16sM5qOFkIIZCQkGC4r4Y6A8ZdgQwAzS/vd4wBIJH5MACkMnvwwKmGAFCNJ4tbt24Zdc+poc6A8d9ar9ezG9iMcnJyjAJuS37H1PibJnVjAEhlxgBQHScLNdZZCJGv3omJiQqVxv7Fx8cbfa8s+R1TY6s+qRsDQCqzBw+cD963R2o8WRRUZ3tvDUtKSsqX41EN32+lPBhsCyEslmNTjRc4pG4MAKnM2AKojpNFQSfn4uTEs2UFfZfV8P1WipL7W42/aVI3BoBUJjk5OUZpYAB1nCDVeLJQYzCkxjoriQEgkeUwAKQyuX79er4DpRpOkAW1huVNX2GP1BgMqbHOSiqoe91S+7ugIQ4MAsmeMQCkMinogG3vY6T0er3hpKTRaAyP23tgoMa/tRrrrKSCfkOW2N/37t1DUlISAOPf9I0bN8z+2URKYQBIZVLQATsxMdFiA7eVcPPmTWRlZQGQax/nsvcAUI1BL1sALUup/Z132T41/aZJ3RgAUpkUdoC053VQ89bZ0dGxwMftTd50KGo6QTIAtKzc1j5LX2TkbWXM+5tmay/ZMwaAVCaFHZzt+SSpxgAwMTER6enpAAAnJyfD4/ZcZ6DwVk97T3+jhLwTyiz9HVPjb5qIASCVSWFXyPZ85Zy3bnlPVGqps1paSIQQhvrlrXNqaqphvBiZzo0bN5CdnQ3A8t+xvIGemi5wSN0YAFKZqL0FUC0nCzW2kCQnJ+PevXsAjOsM2He9lVLYRUZCQgLS0tIs9tnOzs4FPk5kbxgAUpkUNC4s7+P2iAHg/ZPznTt3kJKSokSRzK6wOj/4HJlGUfvb3GOK1fibJmIASKWm1+sNB2Y1nSDVeLJQYzCkxjorScn9nfv+zs7OqvlNEzEApFK7fv16gWN2APvuOsmtm4+Pj1HLZ1JSkqHL0N4U1j334HP2RI11VpKS+zv3/YOCgowm/Fy9ehV6vd6sn02kFLsNAP/66y90794dgYGB0Gg02LRpk9HzQghMnToVgYGBcHd3R5s2bXDq1CllCmujCrpiz/3XXq+c86ZDCQ4Ozve8vdZbja1haqyzkpTa36mpqUhMTASQ/zedlZXFZNBkt+w2ALx37x7q1auHL7/8ssDn58yZg3nz5uHLL7/E4cOHodPp0L59e7tfzsuUigoAb926ZUgbYk9u3bqFzMxMAOoMAD09PY1aSPI+Z28YAFpW3n1qyTHFeccXquk3TWS3AWDnzp0xbdo09OrVK99zQgjMnz8fkydPRq9evVCnTh2sXLkSqampWL16tQKltU0FddnY+wzRvHWuXLlykc/bi7zpUCpXrpwvALTHOgMFf79z626vdVZS7vGiQoUK+QJAc+7vvMepgn7T9ngcIwLsOAAsSkxMDOLj49GhQwfDY66urmjdujX2799f6OsyMjKQkpJidFOzoloAH3zeXuStk1paC5KSkgxpONRSZ+B+vdzd3Q2BX94hDkwGbTp5J5RZ+juWN7gs6LMZ7JO9UmUAGB8fDwCoVKmS0eOVKlUyPFeQmTNnQqvVGm4FXS2qSUFdNgwAWWd7kXes54MB4L1795CcnKxY2ezNjRs3DOtr5/2OWWJMsVq/30ROD9/Efj3YlSWEyPdYXpMmTcL48eMN91NSUlQdBE6YMAFdunTBlStXDGMtXV1d8fnnnyM4OBhNmzZVuISm16VLF6xZswaxsbFo3ry54XFvb28sXrwYdevWVbB05hESEoJNmzYhNjYW1atXx7Zt2wAAWq0W8+bNwyOPPKJwCU1PCIG1a9fiypUrcHJywgcffAAA8PDwwPz58xEcHAw3NzeFS2k/vL298csvvyA2NhYBAQEYNWoUAMDLywuffvqpWY+zffr0waOPPoorV66gQYMGRmX66quvUL9+fbN9NpGSNEIF/RgajQYbN25Ez549AQD//fcfHn30URw7dgyhoaGG7Z599ln4+Phg5cqVxXrflJQUaLVaJCcnw9vb2xxFtxnBwcG4evUqgoKCVHXFrMZ6s84Pr7Ma95EpKbn/+LdTB56/VdoFXK1aNeh0OkRERBgey8zMxO7du41adYiIiIjskd12Ad+9excXLlww3I+JiUF0dDR8fX0REhKCcePGYcaMGXj88cfx+OOPY8aMGShXrhz69eunYKmJiIiIzM9uA8AjR46gbdu2hvu5Y/cGDhyIFStW4J133kFaWhpGjBiBpKQkNGnSBNu2bYOXl5dSRSYiIiKyCLsNANu0aVNkmgaNRoOpU6di6tSplisUERERkRVQ5RhAIiIiIjVjAEhERESkMgwAiYiIiFSGASARERGRyjAAJCIiIlIZBoBEREREKsMAkIiIiEhlGAASERERqQwDQCIiIiKVYQBIREREpDIMAImIiIhUhgEgERERkcowACQiIiJSGQaAREREpCpCKF0C5TEAJCIiItW4dAl4/nmlS6E8BoBERERk9/R6YNEioE4dYMcOpUujPAaAREREZNf++Qdo3RoYNQq4exdo0kTpEimPASARERHZpexsYNYsoF49YO9ewNMT+PJLYMsWpUumPCelC0BERERkatHRwNChwLFj8n7HjsDXXwNVqgApKYoWzSqwBZCIiIjsRno6MHky0LChDP7KlwdWrgT++EMGfySxBZCIiIjswv79stXv7Fl5/4UXZJdvpUrKlssasQWQiIiIbNrdu8CYMUDLljL40+mA9euBn35i8FcYtgASERGRzdq2DXjtNZnfDwAGDwY++0x2/VLhGAASERGRzUlKAsaPB1askPerVAGWLgU6dFC0WDaDXcBERERkUzZsAGrVksGfRiO7f0+eZPBXEmwBJCIiIpsQHy+TOa9fL+/XqAF8+y3QooWy5bJFbAEkIiIiqyYEsGqVbPVbvx5wdJSpXqKiGPyVFlsAiYiIyGpdugS8/jqwdau8HxoKLF8O1K+vaLFsHlsAiYiIyOro9cCiRUCdOjL4c3WVy7odOsTgzxTYAkhERERW5Z9/gGHD5Pq9gMzv9+23wBNPKFsue8IWQCIiIrIKWVmyla9ePRn8eXrKVsDduxn8mRpbAImIiEhxUVFyGbeoKHm/Y0fg66+5fq+5sAWQiIiIFJOeLmf0Nmokg7/y5YGVK4E//mDwZ05sASQiIiJF7N8vW/3OnpX3X3gB+PJLrt9rCWwBJCIiIou6e1eu3tGypQz+dDqZ3++nnxj8WYpqA8CpU6dCo9EY3XQ6ndLFIiIrc/kykJj4BYCNyM6upnRxiGzetm0ytcvChTLB8+DBwOnTQK9eSpdMXVQbAAJA7dq1ERcXZ7idOHFC6SIRkZXIygLmzpUrD6Sl9QLQE9evR+DTT4HsbKVLR2R7kpJksNexo0zuXLWqDAaXL5fj/siyVB0AOjk5QafTGW4VK1ZUukhEZAX27wfCwoAJE4B79wAXl0MAIgC44Z13gGbNgL//VrqURLZjwwZ5MbViBaDRyO7fEyeA9u2VLpl6qToAPH/+PAIDA1GtWjX07dsX//33X5HbZ2RkICUlxehGRPYjIQF49VW5tuiJE4CvL7BsGeDn9zyADvDxGQ8fH+DIERkgfvghkJGhdKmJrFd8vJzY8fzz8v81asj8fgsWyBx/pBzVBoBNmjTBqlWrsHXrVnzzzTeIj49H8+bNkZCQUOhrZs6cCa1Wa7hVrlzZgiUmInMRQrZM1KghVxsAgCFD5GoEQ4YAGo0AAHh4rMXp08Bzz8lu4E8+ARo0AA4cUK7sRNZICJnKpVYtObnDyUmmeomKApo3V7p0BKg4AOzcuTOef/55PPnkk2jXrh02b94MAFi5cmWhr5k0aRKSk5MNtytXrliquERkJqdOAa1by7FJt24BtWsDe/bktvzl3z4g4P5sRX9/OXi9eXPgzTdldzGR2l26BHTuDAwaJMf9NWgAHD4MTJsGuLkpXTrKpdoA8EEeHh548skncf78+UK3cXV1hbe3t9GNiGxTaiowaZJcVH7PHqBcOWD2bNlC0bJl0a/VaGS31unTwCuvyNaO+fOBJ58EduywROmJrI9eL3P41a4NbN0KuLrKZd0OHpS/M7IuDAD/X0ZGBs6cOYOAgACli0JEZvbbb7JratYs2ZXbo4cM5t55B3B2Lv77VKhwf8WCkBAgJgZo1w5ISpoDQGu28hNZm3/+AZ56Chg9WraEt2wJHD8OvPuu7P4l66PaAPDtt9/G7t27ERMTg4MHD+KFF15ASkoKBg4cqHTRiMhMLl+W4/e6d5fdVJUrA5s2AT//XLYlpzp1Ak6eBEaOlPdTU/sBOI20tA6mKDaR1crKkhdS9eoB+/bJiR2LFgG7dwNPPKF06agoqg0AY2Nj8dJLL+GJJ55Ar1694OLiggMHDqAKFx4ksjt5c/pt2iRbJCZMkK1+zz5rms/w8pLdX3/9BTg5/QsgEImJy9G3L3Djhmk+g8iaREUBTZrIoRQZGfcvhEaMABxUG13YDtU2zP74449KF4GILGD/fmD4cJnWBZApXpYskeP1zKFVK8DfvwOuXRsGYALWrHFCRIRMe9G/vxw/SGTL0tPlDPjZs4GcHJkuaf584OWX+f22JYzRicguFZbT76+/zBf85dJoMgC8h4oVu6F+fSAxERgwAOjWDWDyALJl+/bJCR0zZsjgr3dv2ZI+YACDP1vDAJCI7MrDcvpZsmvKxeUkDh0Cpk8HXFyA33+XMySXLJEzJolsxd27cvWOVq3kb0mnk6t7rF0LVKqkdOmoNBgAEpHdKGlOP0twdgbeew+IjpZLyN25I8dItW0LFJF1ishqbNsG1KkDLFwoL7CGDIEhITrZLgaARGTzCsrpN2dO8XL6WUrNmrJsX3wBeHjIrui6dWU5s7OVLh1RfomJ8mKqY0c5a75qVSAiQl5QlS+vdOmorBgAEpFNezCn37PPytaJCRNKltPPEhwdZZ60kyeB9u3lYPp33wWaNgX+/lvp0hHdt2GD/F2tWCHH9o0dK8fStmundMnIVBgAEpFNejCnX0iIzOe3aVPZcvpZQtWqcqWE8HDAxwc4ehQICwM+/FCm0yBSSny8XOXm+eeB69flWNq9e+UsX09PpUtHpsQAkKiU1q0Drl/fBuB9COGodHFUo6Ccfu+8I1v9evRQunTFp9HItVJzx1JlZ8vUGg0aAAcOKF06Uhsh5Ko2tWrJta6dnIDJk+UwiubNlS4dmQMDQKISys6W3Xa9ewPZ2bUAfIJbt37CxYtKl8z+7d8vW8omTLi/3FRUlMxH5uGhdOlKJyBAdretWydnU54+LU+4b74p60hkbpcuAZ07ywuSpCR5EXL4MDBtGuDmpnTpyFwYABKVwK1bMtv9nDnyvrv7JgApyMxsjHr1gNWrlSyd/Xowp1+FCnIg+u7dcnaitdHpdAgKCoJOpyv2a55/XgZ/AwfK1pj582W+wh07zFdOUje9Xq5eU7u2HJLg6irH0h48KCdUkX1jAEhUTLnjtHbskK1Na9YAvr6jANSHi8sRpKTIlR4GDABSUpQurX0oLKff2bOWz+lXEkeOHEFsbCyOHDlSotf5+sr6btkixzTGxMhB98OGAbdvm6WopFL//AM89ZSclHTvnszv9/ffsnfDSbVrhKmLlR4+iazLihWy9enyZeCxx+QYrT59cp+NgZ/f8/jwQxmQfPedvHqOjFSuvPbAGnP6WUrHjnKm8MiR8v6yZXJs1s8/K1susn1ZWcDMmUC9enJVD09PYNEiYNcuoHp1pUtHlsQAkKgImZkyae/gwXJ2ZrducmzMg92OGk0OPvpIdklWqSJbblq1koP6c3KUKbutsoWcfpbg5SW75/76S56Y4+KAnj2BF1+UszOJSioqCmjSRCYmz8iQw1lOnZLHOGttTSfz4Z+cqBDXrgFt2shluzQa4KOPZAuMj0/hr2nZUq748NJLMvD78EP5HpcuWabMts6WcvpZSqtWwPHjwMSJMo/g2rVyH333newiJ3qY9HQZ9DVqJINAX19g1Sq5NGFIiNKlI6UwACQqwJ49ciZcZCSg1QK//gpDF+/D+PgA338vD7BeXjKHVr16wI8/mr3YNsuWc/pZgpub7LY7dEi2jCYmyrGmXbsCV64oXTqyZvv2ye/MzJnyorRPH3lRNWCAvLAl9WIASJSHEHK9y6eflt1sdeoAR47IE21JaDTyABsdLVd5SE6WrYIDB8q1YEmyl5x+ltKggQwCp08HXFyAP/6QYyOXLJEzOoly3b0LjBkjW5D/+QfQ6YCNG+XktUqVlC4dWQMGgGTQsGFDBAcHo2HDhhZ/X3N9dknePzVVBmhjxsjux7595WSPxx4r/ec+8ohsTcxtPVy1Sl6NHzxYtrLagwdz+nl6RsHX9xns2NHQZnP6WYKzs+zOO35c5gu8c0eO4dJqj+L8+ZK/n5K/e3Pw8PCAo6MjPBT4ElnLb3fbNnnxunChvKgdMkReVPXsqWixyMowACSD+Ph4XL16FfHx8RZ/X3N9dnHfPyZGzvL93//kOKt582ROP1OcQ5ycYJggEhIC/Pef/Kxp0wqeIGLufaG0wnL6eXv3wI0bf9ptvU2tRg15caHVfgDgLu7eDUPdunLCTHZ28d9Hyd+9OaSnp0Ov1yM9Pd2inwso/9tNTJQT1jp2lEMpqlYFIiLk76t8eUWKRFaMASCp3tatsiUqOhqoWFEeMN980/TjY1q2lK02ffvKwO+DD4C2beX4NzV4WE4/jYYzGkrKwQHw9AwHUAeurruRni7zuDVtKr9rpB7r18uhFCtWyGPX2LHyAqtdO6VLRtaKASCplhDAjBlyCaSkJDlD7uhRGZSZi4+PbFlcuVLm39qzB6hbV47LsWdqzulnGZdQoUJ/hIfL79jRo0DDhvIiIyND6bKROcXHAy+8IG/XrwM1a8qJH/Pny2MMUWEYAJIqpaTIpbcmT5aB4LBhMt9a5crm/2yNBnjlFdni2KSJnCDSt69ch9PeJogwp5/laDTyO3T6tJxRnZ0thxmEhjIpuT3KbVGvVUu2/jk5Ae+/L39bzZopXTqyBQwASXXOnAEaN5Yz4lxcgKVLgW++sfyi548+KoOi99+XXXkrV8qTdWZmfcsWxEyY008ZAQHAhg3AunVytueZM3K85bhxcrIN2b6LF2US58GDZe9FWJjMVvDJJ3I9X6LiYABIqpKW1gmNG8u0CEFBstXv1VeVK4+zszxo79olJ4j8+y9w8+YmAO9BCNv8eTKnn3V4/nkZcA8cKFuLFiyQM0O3b1e6ZFRaer1cHaZOHTnT180NmD1bZiuoV0/p0pGtsc0zDFmNpCTZknb79jQA3yMzs7bSRSqQDKamIzHxW9y9K8ejHT0qu2CtQe5qDy++CABOAKbj1q21NpXklzn9rI+vr+wm3LJFBuIXLwLt2wNDhwK3bytcOCqRf/4BnnoKGD1atuTmHjPeeUf+1ohKigEglUhammxBmDRJTprw8wN69QLu3RsEoB9u3vwZ332ndCmNJSQACQn/A/AeADnDNyLC+pKh+vgAP/wA+PiMA3AHmZlNUbcu8NNPChesGPbtk0mKc3P6tWwpxyLNnm2aVDpUNh07AidPAqNGyfvLl8tA/eeflS0XPVxWllzFo149+Tvz9AQWL5a9BtWrK106smUMAKlIOTly5YEZM4BnnpG5pNq3l+O6jhyRXRI1agAeHisA/AHADQMGyGTKWVkKFx4yCGnYEMjIaA0gFeXLj8S8edY7Bk2jATw81gEIhbNzFG7flks3DRkiM/tbm4QEOYGmZUsZYOTm9Nu9W3ZTkfXw8pKJgffsAZ54AoiLk4mBExMXA/BXunhUgKgo2Uvx3ntyNnenTnJG/RtvFG9ZSqKi8CtE+WRlPYYvv5TjuCpUkAegyZOBP/+UB6HAQDmLdeVKIDZWDjL38XkfQFd4eX0O4P5yanFxytXju+/kSgkXLwKOjhcBNEW5crbS5PEvKlZ8DpMny6AwPFxOEDl8WOly3XfvXh888YQM+ADjnH48OVmvli3lDPRJk2TS87S0HgBOIzW1FwRTMVqF9HQZ9DVqJINAX1+5itDvv8uufCJT4GGacPWqPLgkJs4HEIsbN3Zh9Gg5jis5GdBqZUvBwoUy2IuNlcHfK6/IiRT3CXh7f4ZffgG8vYG9e+XstIyMMIvWJytLtkAOGCAPpJ07A/7+XQGcsGg5ykqjyca0abKrp3Jl4MIFGdDmLuqulKys6gB24/bteUhIYE4/W+TmJlv1Dx0CnJ1PAqiApKQv0LWrehKTW6t9+2TapNzfeZ8+chztgAGmT05P6sYAUIVyJ26MGiWThgYHy5mCaWkvAAgCkI5nnpEniIMHZeLe3O1r1Hj4Qah7d9lSVauWbAG8desnAG9YpHUhPl62PC5cKO9/+KFMR+LgkGz+DzeTp56Sg7379JHpVN57T3bHW3qCiF4PfPopcOPGFgBPQaNJZU4/G9egAVCxYjfI8bEZ+OMPGdAvWSL/3krR68sBqIKcHD/cuVOype1s1Z07coJHq1ZywodOJ4+7a9ZY33hlsg+cO6QC6enyqnLHDjmB4+hR44O7g4NsqTtz5kvcvbsRgYGXsH37hTJ9ZvXqMngcMgT46ScXAItx+3ZrpKUB7u5lq09hIiNl6ou4ONkC+d13Mhi1B+XLAz/+KMcAjR4tx9jVqydzGL7wgvk//+pVeZGwYwcAuAD4Ff7+0zBhwkHzfziZlUaTDWAm/P334bHHdmP/fmDECDkh6dtvLTvRICcHWLQIiI+PAuCB+Hj5WwbkTFd39/u3cuWM7+fe9PplAFKh16fj/feL3ragx4WwcEJQyOUoX3vtfuvr0KHyYovr95JZCSq15ORkAUAkJycrXRQj2dlCHDokxIwZQjzzjBBubkLITGD3b088IcTIkUJs2CBEYqJ8XVBQkAAggoKCSvyZhb1WrxfC2/sTAWQLQIgGDYS4eLH4ry8OvV6IxYuFcHaWdatVS4h//jHd+xfFHO/7sPc8f16IRo3u/y2HDBHizh2TfXw+GzcK4esrP6tcOSF8fCbYzL40FXsuW97X5+QI8cUXQnh4yL+3m5sQs2cLkZVl/nKdPi1E8+Z5j1Pp+Y5blrllC+BbERBQy+x1TkgQYuDA+59dtaoQEREl/lgqBWs9f1sSWwDtgBCyy2DHDnnbuTN/jq/AQNltmHsLDrZM2TQawMvrK6Sk7ISDw084dswXYWGyNcsUi5SnpcnWihUr5P3evWWKC3teA/Oxx2SL7tSpcpzQ8uVyDN7q1XLGs6ncuweMHy9bGQHZXbh6NfDMM6uZQ85OOTjIFubu3WWLVEQE8O67shty+XLzJBvOypLLA378MZCZKX+7jo6TkJw8G4GBgbhwIRZpafK3npoKw/8Le2zcuIkQwh1AOYwaNaFEr5XrJjsCGIrr17th40Y5Gc4c1q8HRo6U6/dqNMDYsXLpPqZNIotROgK1ZUpeQVy9KsSqVUK88ooQQUH5r2K1WiGefVaIhQvllbVe//D3NEcLYN7nKlVqLMLCZPkcHGTLQm65SvPZFy8Ko/ebM6fwetpTC2Beu3YJERws94GTkxAzZ8oW4LI6dky2Eud+nyZMECIjo+TlKwl7bmUzJ1O2AOal1wsRHi6Ej8/979f77wuRnm66ch09KkS9eve/Z507C3HpUtnq5ODgIAAIBweHEr82O1sIP7/nBHDGUKbevYWIjy/e64tT7rg4IZ5//n6da9YUYv/+EheVyogtgLa61pQK3b4tZ+WOHi0nbgQFyVm4q1bJ8VkuLnLyw/TpclmgW7fk9rkTPaxh9piT01Xs3SvXr9TrZctC795y8HNJbd8uxy0ePSpT1WzbJpMQW0M9Lal1a+Dvv+V+zM6WqT3atZMztUtDr5ereTRpIluVAwPlvp4zR37HSD00GmDQIDnzv1cv+f2aNk2mI4qMLNt7p6XJ72rjxnKCk68v8L//AZs3K5vmxNERcHU9BKA+PD0XwtFRJmKvWVMea8sykU0I2VNRq5Zs/XNyAj74QE6iatbMVDUgKj4GgFYqPV3m3XvvPXkyrlBBdkV8+aXMtabRyO6+d9+V3TS3b8vu39ztrXVpIDc3mS5kyRKZjHn9elnerKxHivV6IWQw0rGjTEKcGwQ+84yZC27Fype/30Xn4SHTxtStK/dtSVy7JvfrhAmyW+6552RwqeZ9S3I26vr1wLp1cjbqmTNAixbAuHFymEBJ7d0r05zMmmWc5uTll63pAi4DWu1sHDoky5qUJCdBdelSujQ5Fy/KCVyDB8v3CguTifQ//hhwdTV12YmKhwGglcjJkQeEWbPkShvly8sT78yZMleXXi9n440YIQ/Gt27JVCuzZskWH3PNrDUHjQYYPlzOZA0MlCeUmzd/A1D0grF37siTxbvvyv0xaJAc+1alikWKbdU0GnlyyV35JClJzg5+9dXinaR//lkGjdu3y+/S11/L71mFCuYvO9mG55+XgdrAgfJCbMECudrL9u3Fe/2dO7JHolUr4Nw520hz0qDB/ZWQXF3lmsq1a8ul2IqTJkevlymp6tSRvRRubnJ5xAMHzDOekqgkVB8ALl68GNWqVYObmxvCwsKwZ88ei3xu7sSNxYtl94qfn8z6PmmSPKCmpwMBAfKqeMUKmfPtn39kioRevWSXia1r1ky23rVqBQjhDeBnpKS8XWCS43PngKZNZSuEs7Pcb8uX21bgawmPPw7s3y+/RxqNTOPRoIG8uChIaqoMxnv2lC2qoaHAsWNyAoD1tMaQtfD1lcejLVtkV+3Fi/KCdejQ/BPP8tqyRQZBixbJ+0OHymCyZ0/zl7msnJ3l7yk6WiZiv3tXTt5o00Yelwpz9qzM4TlmjLwIa9VKdne/84719tCQuqg6AFyzZg3GjRuHyZMnIyoqCq1atULnzp1x2Uyp8OPiZG66QYPkwbNGDXkg2bhRHjy9vYEePYAvvpDrPV69KsfFDBxouVm7lqbTya5rDw+5ntidO+PQrRuQmHh/m19+kcHx6dMyKN61S66FyQClYM7OssXizz/lWNFz52SwPXu2catFVJTsivr6a3n/7bfl2K4aNZQpN9mOjh3l2s+jRsn7y5fLsW2bNj24pS8SEz9H586y67RqVTlk5dtvbS/HXY0assfhiy/kUIs9e2Sr+ezZDyaqdsKdO6NQr56cre/pKS9Yd+2ybE5FoodSehaKkho3biyGDx9u9FiNGjXExIkTi/X6h80iun1biE2bhBg9Ws70enCmrouLEG3bCjFtmhAHDpQu15YpmXsWcFHvK7fpLzSaVAEI8cgjcobgBx/c318tW8oZdKVhSzNXTfmeCQnGMw7btpWzLOfOvZ83MSCgZLnHbGlfmoo9l62sr9+zx3jGeO6sWV/f1wQQLwAhNBohxo0T4u5d85epLLOAi/vZMTFCtG9/v84NGggRHS1ExYodBHAs36xmsj6cBaziPICZmZk4evQoJk6caPR4hw4dsH///gJfk5GRgQyZKAoAkJKSkm+b1FQ5Ju3OndycUsZ8fWWrl04HVKwouwLOnJE3pSUmfgEgFYmJ5fDyy6V5bRoSE8uhf/8Hn1toeN8Hn3twGxeXSDg5PY3//pOtU7mqV5etWW+9VbJylaQM1vK+pn5PFxc50ebIEZkjsmrV+7MZg4Plc+Hh8lb88t0r1fek6Pct/ffP3Oy5bKaoW2ioPJadPi1nza5bBwghm5Y1mhS0b++NmzeB1183f5n0+lUABPR6jVn3R8WKcljKsWPyVr8+AGwBoAGQgebNXeHrKyfmkfXJylK6BMrTCGGJFVqtz7Vr1xAUFIR9+/ahefPmhsdnzJiBlStX4p9//sn3mqlTp+Kjjz7K93hycjK8/3+9orQ0ubwQERERWasUAFqj87faqLYFMJfmgYFkQoh8j+WaNGkSxo8fb7ifkpKCypUrG23j6ChTJNy4IWdi3rpl/B5OTkC1anKwfvXqsgXGwUpGYn700VQkJydDq9ViypSppXytN6ZONQ6Sp06dYnjfB597cBt395bIzn4BWVlyxlx6unz+kUfk2Ekvr1JUrJhlsJb3NfV7ZmbKWb65DduennIgOyBbMQYMAB74Gj+kfKX/nhSlLN8/c5NlS4FW622lZSv9fjPFfk9MBNauvT8pwtsbSEnJAuAMIAPPP++K5s2LP263LGV6663xhuP4Z5/NK9FrS/LZ6enA77/LtDZA7vEqDYA7AIFWrTTo0oVpXqxVWhowebLSpVCYsj3QysnIyBCOjo5iw4YNRo+PGTNGPPXUU8V6j+KMIYiNLXrFDh8fIXr2FOLLL4U4c6Z4K3aYi5JjAAMDqwhgnmG/dOggxK1bcq1iLy/5WGCgEJGRJS5asctgLe9ryveMijIef/r223Ilhz//vP99dHaWq7Lk5Fi+fJZ4X1Ow57KV5fXZ2UIsWFDw2sH+/k8JYK/hu9eqVf41us1RJkuMAdyyRYiQkPu/q6FDhUhKEiIgoLYAwg2PV60qxLZtpSoGmRnHAKp4JRAXFxeEhYUhIiLC6PGIiAijLuGyCgqSLSwrV8pULmfOyGTOzz0HaLX3V/jIXbGjcmU56/d//5OJedXg+nXg1q0fALwJQI6Z+f33+8mvDx2SM/CuXZNpFb7+umwZ+dVArwfmzZPj+86ckbOnt20DPv1Utki0bStTUvTqJcfCvPsu0KGDnHlOVBxnzsjf49ixBac5cXb+F0AraLXvG2bN1qsnE7kbz5q1HYmJsieiUyc5q7laNZm269tvAR8fwMHhNoDBqFChvyFNTocOMu1NUpKiRSfKR7UBIACMHz8e3377LZYvX44zZ87gzTffxOXLlzF8+HCzfJ5Gcz/1y4YNMu9abpLRZ56RJ+arV+WSQ6+8IoPHmjXl8m+bNhWdZ8tWHTwoJ3tkZjYDkAJf32GYPl12peeqUUPup9xgZfhwmeA4t3uYjMXFAZ07ywkzmZkytdDff8t8bXlVqCAH63/zjRy3umOHTGuRP5UH0X1ZWfKYVb++HFZQdJoTAU/PFTh5UgZC6enyYqNJExks2pL162Wqm5Ur5bF83DjgxImCV8pxc9tdYJqcjRstWmSioindBKm0RYsWiSpVqggXFxfRoEEDsXv37mK/1tRNyKmpQmzfLsTEiUI0aiSEg4Nxd7GDgxCNGwsxaZIQO3YIkZZmko81sHQX8NKlMhWOXGj+nACeKPKz9XohZs68v18aNix+igVb6rYsy3v+8osQfn5y/7i7C7FkSfGGFZw9K0RY2P3v2muvFZ6yw5b2panYc9lK8vqjR4WoX//+96RTp8J/gw++r14vRHi4HPYif/NCvP++HJJgyjqZugv42jUhevW6X+eaNYXYv794rxWi8DQ5pCx2AQuh+gCwLMz9BUpMlGPgRo40PoDk3tzchGjXTgZFhw/L8ThlYakAMD1diGHD7tfjueeECAh4otifvXWrEL6+8rV+fnI8mznrZun3Lc173rsnxBtv3N+n9eoJcfp0yT43I0OId96ROdsA+Z07dsw05SsOew6yzMkSAWBqqrwwdXSU3w1fXzm2uaiLi8LeNy7u4QGVNQSAgYFB+QLWDz4oOGB9WLnT0uSFe0n2H5kXA0AVjwG0BeXLyzFwX34plxW6ckUuwzRggFxDNz1djj+ZNEmulOHnJ9frXLxYzsazxnFyV67IcUPffiu7UWbMkF0rDg53i/0eHTrIJeRCQ+Us63btgM8+s876WsLx43L93yVL5P3x42XXes2aJXsfFxe5qsH27fL79c8/sqtu7tzirXtK9mnvXtndO2uWXLO8Tx+Z72/AgNKtxqPTyd/8unVyDeAzZ2TmhHHj7s9OV14VJCR8h8GD5dCbsDCZR/Pjj0s3q9fNTR7rDh2S+zIxUQ7z6dpVjiUkUgIDQBsSHCwniKxaBcTGyoPwwoXAs8/en1CyYYMcY/jEE3K5uUGD5PJzcXFKlx7IyGiGsDB5EPT1leuD5q5ZW1JVq8pllgYMkMHJ228Dffta0wnE/PR64PPPgcaN5UlUpwO2bpXBcFlSTzz9tBwz+NxzcrzXhAly6S+1TEoi6c4dOYatVSt5QanTyTFsa9bIwK2snn9eHsMGDpQXbwsWAE8+KZeKMzchZKL+pCT5vf73X7m03eHDwN27QwGcREZGG7i5yUkrBw7ICSxl1aCBPP5Nny4vuP74A6hdW1608yKLLE31eQBtlUYjW3hq1pQH6exs2Sq2Y4e87d0rg8SVK+UNkIOQn3lGtpi1bi2DRkuQLXNv4tatOQDkFfCGDXIGXVm4u8u6NWkiWw/WrpUnlA0bZJ5FexYXBwweLAM+QE70+PZbmdfPFCpUkK00334r9+327XKCyLJlpnl/sm5btwKvvXa/dWroUDmD3NTr9/r6yl6Nl16Sn5c7a7ZcubkAZiAzMxh79sicbWlpcqWl3P8X9phevwaAO/R6dzRrVvh2hfcYyNybLi4HcPx4U5Ov3+vsLDMd9Ool9+v+/fKi/ccf5e+N6wWTxSjdB23LrHkMQWqqXN/13XflZInccV15J5Q0aSLE5MlyDF16unnGAN69K4S7+0bD5w4YIMerFff1xbV3rxA6nfwMrVaIX3817fsXRokxgL/+WrqJHqV19qxc6zT3b1iu3CoBuNvEvjQVey5b3tcnJMicpXnz2JVkneiylCslRYhRo/Ifq8x9c3AQwtNTiIoVZW4/J6dTAhguAgODzV7nnBwhvvjifh5FV1chZs1Sfl14NbDm87elsAXQTrm7y5a+du3k/cREmaZhxw7ZmnPunBwndvCg7I5wdwf0+u8B/I7MzL+Rk2OciqU0LlyQ3YhpaT0BZEGr/QgrV04rVZfvw7RoIVtAe/eWV9TduwNTpgAffmg9K62UVVqa7OpevFjer1cP+OGHko/1K6knngAiI4H335etQKmpAwA0RXr6FPN+MFlUWlpX1KwpVzHSaGR+v2nTAA8Py3y+l5cc0vLii8DTTx9HVlYQHB0z8eijgXB3h9GtXLnC77/zzigIkQqNJh0bN64u8nXu7rJFLu8xKTi4A65evQqNJsjsdXZwkGm+uneXLaAREcDEibI3Y/ly03Q7ExVK6QjUltnyFcTlyzIlw8sv3285y3srX16I558XYvFiIc6de3gL04NXvr/9Jlvi5BV2vABaFHlVbKoWlowMOWs6tx5du8oM/bbeAnj8uBC1at2v15tvFj0b0Vy2bxfCweGaoRwvvijE1aumeW97bmUzp7KWTacLFcC6ImflWrpc1jAL2NLlLkmaHCo7Wz5/m4qdtI1QSVWuLCeI5K44cuoUoNV+AOBnaDQpSEqSY8BGjJBjUqpUkWPOvv8eiI8v/H2F0ODjj+UVbXIy0Lw54O/fBcA+i9TLxUXOml6xQs6827xZzpDNyqphkc83Nb0emD9fzvI+ffr+RI9585RZY/SZZ4BKldoC+BxADtaskYm6Fy6UM0TJdggBhIcD16//CeB5AFl4/30gKgpo1kzp0qmPRiOPyWfOyPGB2dmyBTY0VLbAE5kaA0CCRiMniHh6hgPoiYCAJxEZKQ8+bdvKoCo3Bc3LL8tlxerUkV1Ev/4KpKTkvpMWiYnLMWWKPLmMGAHs3Ak4Ol63eJ0GDpSzhKtUkTP8bt78BcCLFi9HWeTkVESXLsCbb8oVPbp1k7NzO3RQtlwyZc94VKzYBY0by9miY8bIyThHjihbNiqeixflzO4hQwAhfAAcgb9/F3zyiTIXFnSfbaTJIXvAAJDy0Why0LQpMHky8OefMlXCtm1yjc+wMBkwnjoFfPGFnH3q6wvcuPEzgCNIT28PV1fZsrBokQweldKggQxI2rUDhCgH4EckJ79vI+uQdsGNGxHYulW2ZC5aBPzyi+lm+ZqCi8sp7N8v8w/6+MgxmI0by1np9rhsoT3Q62VrbZ06cryZmxvg7T0dQFM4O59RuniUh5JpckgdGADSQ5UrJ9eRnT1bBlQ3b8qr0+HDZbqVnBwgKysMwGNwdIzFvn2yK8Ma+PnJfIOenosAAHfvDkf79nKguzVKSwNu354GYDP0ej/UrSv3+YgRpcuXaG6OjvJ7cPasbB0WQgarNWrICSpqTc5tjc6ckTn9xowB7t2T/z9+HPDyWgKA/ffWKDdNzpYtMq9rbpqcoUN5kUVlxwCQSqxCBXl1umSJnE186RLg4zMewFuoWLEzwsKULqExR0dAq50J4HloNHexaxcMCamtyYkTcqzfvXuDAAAeHktx8KBMFGvtKlWS40l37JCzhq9fB/r1kxcO584pXTp1y8qSq1DUry9nyHt6ypnku3Yx55yt6NhRJqoeNUreX75cDtvZtEnRYpGNYwBIZRYSAnh4rAUwD46OSUoXpwgbULFid1SvLpNkt2plHYmNhZDd6Y0aya51B4cbADrCx+djuLkpXbqSefpp2ao0bZrsXtyxQ3ZbTZkily4ky4qKkt3ykyfLcaSdOsnv2Btv2E96JLXITZOzZ4+8yIqLk2m2+vSRF1xEJcVDAKmKs/N5HDokl8/LzASGDQNef10uC6WE69eBLl3khJqMDDnRw9+/HYBtyhTIBFxdZcBx8qQMODIz5RqqTz4px5KS+aWn318jPDpadiWuWgX8/ru8YCPb1bKl/JtOmiR7N376SbYG/u9/HHJBJcMAkFRHq5XLxU2bJsfVLV0KPPWUbBW0pM2bZVC0ZYtsLfvySznRw9Ex0bIFMZNHH5UBx08/AYGBMjF4x45yzWauK2w+e/fKBMKzZsnxuX36yMkEAwZY5zhSKjk3N9mtf+iQ7NpPTAReeQXo2vX+8n1ED8MAkFTJwUG2Uv3+u1zf9NAhOS5w927zf3Zamsz+362bnFDz5JNyosfIkfZ3gtZogBdekBMQxo2T+525A81Dr/fAqFFyaMO5czKdyMaNcn9XqqR06cgcGjSQx67p02XGhT/+kGOGFy+WM76JisIAkFStUycZfNWrJ2cGP/OMTLxsrq6UEyfkmKwvv5T3x46VB3BbmOhRFt7ewOefy33N3IHm0AE3buzAIjnZHUOHyla/nj0VLRRZgLMz8N57cuxt8+YyV+DIkUCbNpyARUVjAEiq98gjcnZkv36yRerNN2VKk3v3TPcZeSd6nDwpW2T++EMGm7Y20aMsQkNRaO5Avd5b6eLZnMREIClpHoCtyMkJRtWqMk/ct9/Klm1Sjxo15ASRL76Q6zfv2SMvbOfMgY3kPiVLYwBIBJnr8LvvZLJVR0dg9Wp5Nf3vv2V/7+vX5dic3IkeXbrIFT06dSr7e9uiwnIHXr++C0BfDmQvpvXr5eD/1NQ+APTw8PgWJ0/KxOekTg4OcnjJyZMyBVN6OvDuu7Kl/fhxpUtH1oYBIBnodDoEBQVBp9NZ/H3N9dkleX+NRnZL/vkn4O8vg7SGDWVLXWn9/jtQt658j9yJHr/9Jt+/LGW1Bw/mDtTr/QH8gDt31rPrqghxcTIP5wsvyIsLN7f/4OfXEzVqfAUPj5K/n5K/e3Nwc3ODg4MD3BRoWreW327VqnLN8PBw2dJ+7Jg8ln3wgXIZD8gKCSq15ORkAUAkJycrXRTFBQUFCQAiKChI6aKYRGysEE2bCgEIodEI8fHHQuTk5N+usHqnpQkxZox8PSDEk08KcfKkhQpvZub4W6enCzFtmhBubnJ/ubgI8eGHcj9aA2v4fuv1QoSHC+HjI/eRk5MQ778v9529UXJ/W8Pf2pTi4oTo1ev+sahmTSH271e6VMrj+VsItgASFSAoSK6UMHy4PGx++KEcUJ+c/PDXnjwpx7V98YW8r5aJHmXB3IFFu3hRptAZPFguARYWJifPfPKJ3HdEhdHp5HCBdetkq/uZM0CLFnJWvinHOZPtYQBIVAhXVzlZYdky+f9ff72/WkdBhJBdvA0bytm+/v6yC1htEz3KgrkDjen1Ml1OnTpycoebm1yT+8ABOcCfqLief17ODB84UB6rFiyQ36vt25UuGSmFASDRQwwZImfUVa4MnD8vB1T/9JPxNjk5FdCtmxyAnXeiR+fOypTZljF3oHT2rMzpN2aMbKlp1UoO5H/nHcDJSenSkS3y9QVWrJDJ50NCZMty+/YybdDt2woXjiyOASBRMTRqJFOWPP20PBn36SNPxEI4AuiEGze24/ffZUvhF1/IiR5Mvls2as0dmJUlV3moV0+mzPH0lIl9d+0CqldXunRkDzp2lMMtRo2S95cvlzPKN21StFhkYQwAiYqpYkU5s+7tt+X9Tz8FbtzYAeAP6PUVUacOcPiwbAW0txU9lFRU7kB7a7WIipJ1mzxZjoPs1EkOOXjjDdkSSmQqXl6yRX3PHjkLPy4OeO45eXF7/brSpSNL4CGFqAScnGTgt2aNTLaanf0YAMDDYzkOHZKTFsj0CssdWKMG8MMP5lu5pbQaNmyI4OBgNGzYsFjbp6cDkybJluboaNlVt2qVHA8ZEmLespK6tWwpv3MTJ8rf2U8/ydbA//3P+n5XZFoMAIlKoU8fORC/XLkfAHSCj8+HcHdXulT278HcgdevyxVc2re3rmWv4uPjcfXqVcTHxz902717ZXfvrFlyfGOfPnKw/oABbEkmy3BzA2bOlNkK6teXK8y88opMYH/5stKlI3NhAEhUSnXqAOXLTwCwVemiqM7TT8sJEdOmyZPXjh2y9XXKFNmaZgvu3JHDBZ56SgavOh2wcaNsXeb4UVJCgwYyCJw+HXBxkQnsa9eWwy/0eqVLR6bGAJCIbJIt5w7culVeQHz5pexmGzpUtvr17Kl0yUjtnJ2B996TF1jNmwN37wIjRgBt2lhXKzuVHQNAIrJptpQ7MDERGDRIBqyXL8sluyIigG+/BcqXV7p0RPfVqCEniHzxhRzvvGePHKowZw6Qna106cgUGAASkc2zhdyB69fLwfUrV8ryjh0rE4a3a6d0yYgK5uAghymcPCnH2aanA+++K1MxHT+udOmorBgAEpHdsMbcgXFxchWGF16Qk1Zq1gT27ZMrxHh6KlMmopKoWlUOWwgPl6mYjh2TKx598IFMfE+2iQEgEdkda8kdeO9eb9SqBWzYIFMIvf++zPXXrJnlykBkChqNHL5w+rTMF5idLSdhhYYCkZFKl45KgwEgEdklJXMHZmcHA9iC27c/x+3bQFiYbIH85BM5eYXIVgUEyAuadevkbPUzZ4AWLeTQi3v3lC4dlQQDQCKya5bMHajXyzGHcoWYjgDSMXu2zBlZr55pP4tISc8/L1sDBw6UF1MLFsiZ7du3K10yKi7VBoBVq1aFRqMxuk2cOFHpYhGRmZg7d+DZszKn35gxgBAeAP6Cv397vPOO7P4lsje+vsCKFcCWLXLFmosX5YXV0KH2t0yjPVJtAAgAH3/8MeLi4gy3999/X+kiEZEZmSN3YFYWMGOGbOHbt09O7NBq3wPQBs7OMSYtP5E16thR/qZGjZL3ly+XM943bVK0WPQQqg4Avby8oNPpDDdPTskjUgVT5Q6MipKTSyZPlsFkp07AqVOAp+cqAFxIldTDy0sOf9izB6heXc5+f+454MUX5bALsj6qDgBnz56NChUqoH79+pg+fToyMzOVLhIRWUhZcgemp8vVEho1AqKjZVfYqlUyqAwJsVQNiKxPy5ZyqMXEiXIi1tq1sjXwu+/MO/GKSk61AeDYsWPx448/YufOnRg1ahTmz5+PESNGFPmajIwMpKSkGN2IyLaVNHfgvn1A/frAzJkySOzTRw6GHzBABpVEaufmJn8fhw7J30piovx9dO0qV8Ah62BXAeDUqVPzTex48Hbk/4/ob775Jlq3bo26deti2LBh+Oqrr7Bs2TIkJCQU+v4zZ86EVqs13CpXrmypqhGRmRWVO1Cv9wbgidu3P0GrVsA//wA6HbBxo2w1rFRJ6dITWZ8GDWQQOH064OIC/PEHULu2/I3p9UqXjuwqABw1ahTOnDlT5K1OnToFvrZp06YAgAsXLhT6/pMmTUJycrLhduXKFbPUg4iUUVjuwOvXdwE4iXv3BkMIYMgQ2erXs6fCBSaycs7OcrjE8eNA8+bA3bvAiBFAmzamT8NEJWNXyQn8/Pzg5+dXqtdGRUUBAAICAgrdxtXVFa7M4kpk93JzBw4eLE9W//zjDwBwdLyMLVtCuH4vUQnVqCEniCxaBEyaJP9frx7w0UfA+PFMlaQEu2oBLK7IyEh8/vnniI6ORkxMDNauXYvXX38dPXr0QAhHcBPR/8vNHejt/RGAKfD3b8fgj6iUHByA0aNlypj27eVkqnffBZo2lb8zsixVBoCurq5Ys2YN2rRpg1q1auHDDz/Eq6++ih9++EHpohGRlXF1Bby8vgHwMRwcUpUuDpHNq1oV2LoVCA+/P962YUPggw+AjAylS6ceqmx0bdCgAQ4cOKB0MYiIiFRJowEGDZL5N0eOlBOqpk0D1q8Hli0DmjVTuoT2T5UtgERERKS8gABgwwZg3To59vbMGaBFC5mb8949pUtn3xgAEhERkaKef17OrB84UM6+X7AAqFMH2L5d6ZLZLwaAREREpDhfX2DFCmDLFrmizsWLcrLIsGHA7dsKF84OMQAkIiIiq9Gxo5wpPHKkvL9smVxO7ueflS2XvWEASERERFbFywv48kvgr7+A6tWBuDiZeP3FF4Hr15UunX1gAEhERERWqVUrmSNw4kS5Us/atbI18Lvv5FhBKj0GgERERGS13NyAmTPlusL16wOJicCAAUDXrsDly0qXznYxACQiIiKr16CBDAKnTwdcXIA//gBq1waWLAH0eqVLZ3sYABIREZFNcHYG3ntPdgs3bw7cvSvX627bFjh/XunS2RYGgERERGRTatSQE0S++ALw8JD/r1sXmDMHyM5WunS2gQEgERER2RxHR2D0aJkypn17ID0dePddoGlT2UJIRWMASERERDaralVg61YgPBzw8QGOHgUaNgQ++ADIyFC6dNaLASARERHZNI0GGDRILif33HOyG3jaNCA0FDhwQOnSWScGgERERGQXAgKADRuAdeuASpWAM2fkZJE33wTu3VO6dNaFASARERHZleefl62BAwfKhNHz5wNPPgns2KF0yawHA0AiIiKyO76+wIoVMl9gSAgQEwO0awcMGwbcvq106ZTHAJCIiIjsVqdOcqbwyJHy/rJlQOPGypbJGjAAJCIiIrvm5QV8+aXMF1i9OnD9utIlUh4DQCIiIlKFVq1kjsA331S6JMpjAEhERESq4eYGTJ2qdCmUxwCQiIiISGUYABIRERGpDANAIiIiIpVhAEhERESkMgwAiYiIiFSGASARERGRyjAAJCIiIlIZBoBEREREKsMAkIiIiEhlGAASERERqQwDQCIiIiKVYQBIREREpDIMAImIiIhUhgEgERERkcowACQiIiJSGbsMAKdPn47mzZujXLly8PHxKXCby5cvo3v37vDw8ICfnx/GjBmDzMxMyxaUiIiISAFOShfAHDIzM9G7d280a9YMy5Yty/d8Tk4OunbtiooVK2Lv3r1ISEjAwIEDIYTAwoULFSgxERERkeXYZQD40UcfAQBWrFhR4PPbtm3D6dOnceXKFQQGBgIAPvvsMwwaNAjTp0+Ht7e3pYpKREREZHF2GQA+TGRkJOrUqWMI/gCgY8eOyMjIwNGjR9G2bVsFS2c7fvrpJ+zduxdXrlyBXq8HAKSnp6N///4IDg5G3759ERoaqnApTevAgQNYv349YmNjMXr0aMPjCQkJGDduHNq2bYtnn31WwRKa3tWrV7FkyRLExsaiVatWhseTkpLwxhtvoGbNmhgzZoyCJTQ9IQSmTZuGK1euQKvVGh6/c+cOhg4diuDgYLz11lu8WDSRpKQkfP7554iNjUWdOnUMj9++fRuvv/46qlSpgvfee88sn7179278+uuvuHLlCiZPnmx4PDExEePHj0fHjh3RsWNHs3w2kZJUGQDGx8ejUqVKRo+VL18eLi4uiI+PL/R1GRkZyMjIMNxPSUkxWxltwebNm7Fy5UoAgL+/PwAgKysLq1evBgCEhYXZXQB48uRJzJ07FwDQunVrw+Pp6elYsGAB9Hq93QWAd+7cwfTp0wEA2dnZhsdTU1Px1VdfITQ01O4CQI1GgwULFiAhIQFVqlQxPJ6eno7ly5cDAN555x2limd3hBD45JNPAADt27c3PJ6WloalS5ciKCjIbAHg4cOH8dlnnwEAnnvuOaPP/vzzz+Hh4cEAkOySzUwCmTp1KjQaTZG3I0eOFPv9NBpNvseEEAU+nmvmzJnQarWGW+XKlUtVF3sRHBxs+H9OTo7Rvw8+by/y1ik2NrbI5+1FUFCQ4f9qqTNwv15Xr16FEALA/e93+fLl4eHhoVjZ7E358uXh7u4OwPg7ltuzYM7vmBp/00SADbUAjho1Cn379i1ym6pVqxbrvXQ6HQ4ePGj0WFJSErKysvK1DOY1adIkjB8/3nA/JSVF1UEgA0B1nCy8vLyg1WqRnJysmjoDsl7Hjx9Hdna2IRDJ/X7ba52VotFoEBwcjPPnzyM2NjZf1zoDQCLTs5kA0M/PD35+fiZ5r2bNmmH69OmIi4tDQEAAADkxxNXVFWFhYYW+ztXVFa6uriYpgz0oKgDUaDSGfWtP1HqyCA4ONgSAFSpUyPecPSro+13Qc2QalStXxvnz53Hnzh14enoaPWfO/Z33Ir6g37SaL/LJvtlMF3BJXL58GdHR0bh8+TJycnIQHR2N6Oho3L17FwDQoUMH1KpVCwMGDEBUVBR27NiBt99+G6+++ioHdZdA3gPjgwFgQEAAnJ2dFSmXOWm1WsPJ6cqVK/met9eTRW69MjIyDK1hDz5nbwr6fhf0HJlGUQG3Ofd3QECAYehPQb9pBvtkr+wyAPzwww8RGhqKKVOm4O7duwgNDUVoaKhhjKCjoyM2b94MNzc3tGjRAn369EHPnj0Ng/upeAo6YFtizI6ScruqANlakDs2LFfemeX2RI2tYWqss5KU2t8uLi6GoT8PtgC6u7ujfPnyZvtsIiXZTBdwSaxYsaLQHIC5QkJC8Ntvv1mmQHbK19cXbm5uSE9PV9UJMjg4GGfPnkVqaqpRihB/f3+7HSKgxmBIjXVWkpL7Ozg4GPHx8UbDgnIfL2piIJEts8sWQLKMvK1hajpB5q1b3rQoaqnzg3/rvLOE7QkDQMsqqsvd3Ps797OFEEa/aXb1kz1jAEhlkvfAWdDj9ihv3dRysijs5FyhQgWUK1dOiSKZnVJj0tSqsP2t0WjMPrQi72dnZWUV+DiRvWEASGVS2AHSng+cajxZFHZytuc6e3h4GMZ/qaXVU0mFfcd0Op3ZJ5Sp8TdNxACQykTtAaDau4Dtuc4AChzioNVq4eXlpVSR7FaFChXg5uYGwPLfMTW26hMxAKQyKewAac8HzsK6Q+25zt7e3oYUSWqpM1Bw/ey9zkopbEyxJfa3Wi9wSN0YAFKZFHSAtNck0Lny1jlvTjx7P1kUdHJWS50f9hiZRu6+zTum2BL7W62/aVI3BoBUJgUdICtVqgQXFxcFSmMZPj4+hokPajpZqDEYUmOdlVRQa58l9nfeMZ15f9Ns7SV7xgCQykSNJ8i8XVV5WyrsfWKAGv/WaqyzkpTa33mTQef9Tfv6+pr9s4mUwgCQysTPzy9f8mM1XDU/WEcHBwfDAHZ7pcbxcGqss5IKCvYstb8f/GxHR0cmgSa7xgCQyiRva1guNbSQFHSysHcF/V3Z6kmmpFQXcEGfrYbfNKkbA0AqMwaA6jhZPFhnjUYDDw8PhUpjGQUFuGr4fiuloH1rqfW11fibJnVjAEhlxgBQHScLNdbZy8vLaL1nQB3fb6U8uG8dHBwsNqFMjd9vUjcGgFRmD3adqGGMlBq7i9RYZyB/vXPzIZLpPTim2JLfMQaApDYMAKnM2AKojpOFt7e30bq/aqgzYPy3VkudlaLRaKDT6Qz3Lbm/1XqBQ+rFAJDK7MFgyFJjdpSkxgBQo9EYpcVwcFDH4cPPz8/wf7XUWUlKfcfU+JsmdePRjMrswQPng2lh7JGvr6/RCUItJ4u8kz7UEgx5enoa/s+0IOaX9ztmyf394IQftfymSb3UcQQns8q77JtaTpAajQbOzs6G+2o5WeQdkK+Wv7Ua66wkpfa3q6ur0e9YLRc4pF78hlOZZWdnK10EReRdMSDv/+2ZWuqZlxrrrCQl9zf/1qQmDACpzHQ6HQIDA+Hp6YmQkBCli2MxCxcuhE6ng7e3t1ErqD2bO3cudDodPD09UaVKFaWLYxEjRoww1Llq1arFeo1Op0NQUJDRhAYqno8//hg6nQ5eXl4W/Y4JIbBgwQIEBATA29ubfzuyexrBS55SS0lJgVarRXJyMlNDEBER2Qiev9kCSERERKQ6DACJiIiIVIYBIBEREZHKMAAkIrKAv//+G4MHD0a1atXg5uYGT09PNGjQAHPmzEFiYmK+7Rs0aACNRoO5c+cqUFoisncMAImIzOybb75BWFgYDh8+jAkTJmDLli3YuHEjevfuja+++gpDhw412j46OhpRUVEAgGXLlilRZCKyc05KF4CIyJ5FRkbijTfeQPv27bFp0yajlXLat2+Pt956C1u2bDF6zbfffgsA6Nq1KzZv3oz9+/ejefPmFi03Edk3tgASEZnRjBkzoNFosHTp0gKXSXRxcUGPHj0M99PT07F69WqEhYXh888/BwAsX77cYuUlInVgAEhEZCY5OTn4888/ERYWhsqVKxfrNRs2bEBSUhKGDBmCxx9/HC1btsSaNWtw9+5dM5eWiNSEASARkZncunULqampqFatWrFfs2zZMri5uaFfv34AgKFDh+Lu3btYu3atuYpJRCrEAJCIyErExMRg586d6NWrF3x8fAAAvXv3hpeXF7uBicikGAASEZmJn58fypUrh5iYmGJtv3z5cggh8MILL+D27du4ffs2srKy0KNHD+zbtw9nz541c4mJSC0YABIRmYmjoyOeeeYZHD16FLGxsUVuq9frsWLFCgBAr169UL58ecPt+++/B8DJIERkOhohhFC6ELaKi0kT0cNERkaiVatWaN++PX7++We4uLgYPZ+VlYUtW7bAyckJXbp0wciRI/HCCy/ke59Ro0bh1q1biI2NhZMTM3gRlQXP38wDSERkVs2aNcOSJUswYsQIhIWF4Y033kDt2rWRlZWFqKgoLF26FHXq1IGjoyOcnJzw3nvvITAwMN/7vP766xgzZgw2b96MZ599VoGaEJE9YQtgGfAKgoiK6/jx4/j888+xc+dOxMfHw9nZGdWrV0f37t0xatQoBAcHo0uXLti4cWOBr799+zYCAwPRrl07/PLLLxYuPZF94fnbTgPA6dOnY/PmzYiOjoaLiwtu376dbxuNRpPvsSVLlmD48OHF/hx+gYiIiGwPz9922gWcmZmJ3r17o1mzZkWuoxkeHo5OnToZ7mu1WksUj4iIiEhRdhkAfvTRRwBgmFFXGB8fH+h0OguUiIiIiMh6qDoNzKhRo+Dn54dGjRrhq6++gl6vV7pIRERERGZnly2AxfHJJ5/gmWeegbu7O3bs2IG33noLt27dwvvvv1/oazIyMpCRkWG4n5KSYomiEhEREZmUzbQATp06FRqNpsjbkSNHiv1+77//Ppo1a4b69evjrbfewscff4xPP/20yNfMnDkTWq3WcCvu4u5ERERE1sRmZgHfunULt27dKnKbqlWrws3NzXB/xYoVGDduXIGzgB+0b98+tGzZEvHx8ahUqVKB2xTUAli5cmVVzyIiIiKyNZwFbENdwH5+fvDz8zPb+0dFRcHNzc2wAHtBXF1d4erqarYyEBEREVmCzQSAJXH58mUkJibi8uXLyMnJQXR0NADgscceg6enJ3799VfEx8ejWbNmcHd3x86dOzF58mS89tprDPCIiIjI7tllAPjhhx9i5cqVhvuhoaEAgJ07d6JNmzZwdnbG4sWLMX78eOj1ejzyyCP4+OOPMXLkSKWKTERERGQxNjMG0BpxDAEREZHt4fnbhmYBExEREZFpMAAkIiIiUhkGgEREREQqwwCQiIiISGUYABIRERGpDANAIiIiIpVhAEhERESkMgwAiYiIiFSGASARERGRyjAAJCIiIlIZBoBEREREKsMAkIiIiEhlGAASERERqQwDQCIiIiKVYQBIREREpDIMAImIiIhUhgEgERERkcowACQiIiJSGQaARERERCrDAJCIiIhIZRgAEhEREakMA0AiIiIilWEASERERKQyDACJiIiIVIYBIBEREZHKMAAkIiIiUhkGgEREREQqwwCQiIiISGUYABIRERGpDANAIiIiIpVhAEhERESkMgwAiYiIiFSGASARERGRyjAAJCIiIlIZBoBEREREKsMAkIiIiEhl7C4AvHjxIoYOHYpq1arB3d0djz76KKZMmYLMzEyj7S5fvozu3bvDw8MDfn5+GDNmTL5tiIiIiOyRk9IFMLWzZ89Cr9fj66+/xmOPPYaTJ0/i1Vdfxb179zB37lwAQE5ODrp27YqKFSti7969SEhIwMCBAyGEwMKFCxWuAREREZF5aYQQQulCmNunn36KJUuW4L///gMA/PHHH+jWrRuuXLmCwMBAAMCPP/6IQYMG4caNG/D29i7W+6akpECr1SI5ObnYryEiIiJl8fxthy2ABUlOToavr6/hfmRkJOrUqWMI/gCgY8eOyMjIwNGjR9G2bdsC3ycjIwMZGRlG7wvILxIRERHZhtzztgrawApl9wHgv//+i4ULF+Kzzz4zPBYfH49KlSoZbVe+fHm4uLggPj6+0PeaOXMmPvroo3yPV65c2XQFJiIiIotISEiAVqtVuhiKsJkAcOrUqQUGX3kdPnwYDRs2NNy/du0aOnXqhN69e2PYsGFG22o0mnyvF0IU+HiuSZMmYfz48Yb7er0eiYmJqFChgtHrUlJSULlyZVy5ckU1TctqrDOgznqzzqyzPVNjvdVY5+TkZISEhBj1DqqNzQSAo0aNQt++fYvcpmrVqob/X7t2DW3btkWzZs2wdOlSo+10Oh0OHjxo9FhSUhKysrLytQzm5erqCldXV6PHfHx8Ct3e29tbNT+mXGqsM6DOerPO6qDGOgPqrLca6+zgYHfJUIrNZgJAPz8/+Pn5FWvbq1evom3btggLC0N4eHi+P3CzZs0wffp0xMXFISAgAACwbds2uLq6IiwszORlJyIiIrImNhMAFte1a9fQpk0bhISEYO7cubh586bhOZ1OBwDo0KEDatWqhQEDBuDTTz9FYmIi3n77bbz66ququ/ohIiIi9bG7AHDbtm24cOECLly4gODgYKPncmf7ODo6YvPmzRgxYgRatGgBd3d39OvXz5AnsKxcXV0xZcqUfN3F9kyNdQbUWW/WWR3UWGdAnfVmndVJFXkAiYiIiOg+9Y5+JCIiIlIpBoBEREREKsMAkIiIiEhlGAASERERqQwDQDNYvHgxqlWrBjc3N4SFhWHPnj1KF6lUZs6ciUaNGsHLywv+/v7o2bMn/vnnH6NthBCYOnUqAgMD4e7ujjZt2uDUqVNG22RkZGD06NHw8/ODh4cHevTogdjYWEtWpdRmzpwJjUaDcePGGR6z1zpfvXoVL7/8MipUqIBy5cqhfv36OHr0qOF5e6t3dnY23n//fVSrVg3u7u545JFH8PHHH0Ov1xu2sfU6//XXX+jevTsCAwOh0WiwadMmo+dNVb+kpCQMGDAAWq0WWq0WAwYMwO3bt81cu4IVVeesrCy8++67ePLJJ+Hh4YHAwEC88soruHbtmtF72FqdgYf/rfN6/fXXodFoMH/+fKPHba3exanzmTNn0KNHD2i1Wnh5eaFp06a4fPmy4Xlbq7NJCTKpH3/8UTg7O4tvvvlGnD59WowdO1Z4eHiIS5cuKV20EuvYsaMIDw8XJ0+eFNHR0aJr164iJCRE3L1717DNrFmzhJeXl1i/fr04ceKEePHFF0VAQIBISUkxbDN8+HARFBQkIiIixLFjx0Tbtm1FvXr1RHZ2thLVKrZDhw6JqlWrirp164qxY8caHrfHOicmJooqVaqIQYMGiYMHD4qYmBixfft2ceHCBcM29lbvadOmiQoVKojffvtNxMTEiJ9++kl4enqK+fPnG7ax9Tr//vvvYvLkyWL9+vUCgNi4caPR86aqX6dOnUSdOnXE/v37xf79+0WdOnVEt27dLFVNI0XV+fbt26Jdu3ZizZo14uzZsyIyMlI0adJEhIWFGb2HrdVZiIf/rXNt3LhR1KtXTwQGBorPP//c6Dlbq/fD6nzhwgXh6+srJkyYII4dOyb+/fdf8dtvv4nr168btrG1OpsSA0ATa9y4sRg+fLjRYzVq1BATJ05UqESmc+PGDQFA7N69WwghhF6vFzqdTsyaNcuwTXp6utBqteKrr74SQsgDrrOzs/jxxx8N21y9elU4ODiILVu2WLYCJXDnzh3x+OOPi4iICNG6dWtDAGivdX733XdFy5YtC33eHuvdtWtXMWTIEKPHevXqJV5++WUhhP3V+cETpKnqd/r0aQFAHDhwwLBNZGSkACDOnj1r5loVrahAKNehQ4cEAMNFuq3XWYjC6x0bGyuCgoLEyZMnRZUqVYwCQFuvd0F1fvHFFw2/54LYep3Lil3AJpSZmYmjR4+iQ4cORo936NAB+/fvV6hUppOcnAwAhsWzY2JiEB8fb1RfV1dXtG7d2lDfo0ePIisry2ibwMBA1KlTx6r3yciRI9G1a1e0a9fO6HF7rfMvv/yChg0bonfv3vD390doaCi++eYbw/P2WO+WLVtix44dOHfuHADg+PHj2Lt3L7p06QLAPuucl6nqFxkZCa1WiyZNmhi2adq0KbRardXvA0Ae1zQajWFdd3uts16vx4ABAzBhwgTUrl073/P2Vm+9Xo/NmzejevXq6NixI/z9/dGkSROjbmJ7q3NJMQA0oVu3biEnJweVKlUyerxSpUqIj49XqFSmIYTA+PHj0bJlS9SpUwcADHUqqr7x8fFwcXFB+fLlC93G2vz44484duwYZs6cme85e63zf//9hyVLluDxxx/H1q1bMXz4cIwZMwarVq0CYJ/1fvfdd/HSSy+hRo0acHZ2RmhoKMaNG4eXXnoJgH3WOS9T1S8+Ph7+/v753t/f39/q90F6ejomTpyIfv36GZYBtdc6z549G05OThgzZkyBz9tbvW/cuIG7d+9i1qxZ6NSpE7Zt24bnnnsOvXr1wu7duwHYX51Lyu6WgrMGGo3G6L4QIt9jtmbUqFH4+++/sXfv3nzPlaa+1rpPrly5grFjx2Lbtm1wc3MrdDt7qjMgr5YbNmyIGTNmAABCQ0Nx6tQpLFmyBK+88ophO3uq95o1a/Ddd99h9erVqF27NqKjozFu3DgEBgZi4MCBhu3sqc4FMUX9Ctre2vdBVlYW+vbtC71ej8WLFz90e1uu89GjR7FgwQIcO3asxOWz1XrnTuZ69tln8eabbwIA6tevj/379+Orr75C69atC32trda5pNgCaEJ+fn5wdHTMd1Vw48aNfFfZtmT06NH45ZdfsHPnTqP1lXU6HQAUWV+dTofMzEwkJSUVuo01OXr0KG7cuIGwsDA4OTnByckJu3fvxhdffAEnJydDme2pzgAQEBCAWrVqGT1Ws2ZNw2w5e/xbT5gwARMnTkTfvn3x5JNPYsCAAXjzzTcNLb/2WOe8TFU/nU6H69ev53v/mzdvWu0+yMrKQp8+fRATE4OIiAhD6x9gn3Xes2cPbty4gZCQEMNx7dKlS3jrrbdQtWpVAPZXbz8/Pzg5OT30uGZPdS4pBoAm5OLigrCwMERERBg9HhERgebNmytUqtITQmDUqFHYsGED/vzzT1SrVs3o+WrVqkGn0xnVNzMzE7t37zbUNywsDM7OzkbbxMXF4eTJk1a5T5555hmcOHEC0dHRhlvDhg3Rv39/REdH45FHHrG7OgNAixYt8qX4OXfuHKpUqQLAPv/WqampcHAwPgQ6OjoaWg7ssc55map+zZo1Q3JyMg4dOmTY5uDBg0hOTrbKfZAb/J0/fx7bt29HhQoVjJ63xzoPGDAAf//9t9FxLTAwEBMmTMDWrVsB2F+9XVxc0KhRoyKPa/ZW5xKz7JwT+5ebBmbZsmXi9OnTYty4ccLDw0NcvHhR6aKV2BtvvCG0Wq3YtWuXiIuLM9xSU1MN28yaNUtotVqxYcMGceLECfHSSy8VmEYiODhYbN++XRw7dkw8/fTTVpMmozjyzgIWwj7rfOjQIeHk5CSmT58uzp8/L77//ntRrlw58d133xm2sbd6Dxw4UAQFBRnSwGzYsEH4+fmJd955x7CNrdf5zp07IioqSkRFRQkAYt68eSIqKsow49VU9evUqZOoW7euiIyMFJGRkeLJJ59ULE1GUXXOysoSPXr0EMHBwSI6OtrouJaRkWF4D1ursxAP/1s/6MFZwELYXr0fVucNGzYIZ2dnsXTpUnH+/HmxcOFC4ejoKPbs2WN4D1ursykxADSDRYsWiSpVqggXFxfRoEEDQ9oUWwOgwFt4eLhhG71eL6ZMmSJ0Op1wdXUVTz31lDhx4oTR+6SlpYlRo0YJX19f4e7uLrp16yYuX75s4dqU3oMBoL3W+ddffxV16tQRrq6uokaNGmLp0qVGz9tbvVNSUsTYsWNFSEiIcHNzE4888oiYPHmyUSBg63XeuXNngb/hgQMHCiFMV7+EhATRv39/4eXlJby8vET//v1FUlKShWpprKg6x8TEFHpc27lzp+E9bK3OQjz8b/2gggJAW6t3ceq8bNky8dhjjwk3NzdRr149sWnTJqP3sLU6m5JGCCHM28ZIRERERNaEYwCJiIiIVIYBIBEREZHKMAAkIiIiUhkGgEREREQqwwCQiIiISGUYABIRERGpDANAIiIiIpVhAEhERESkMgwAiYiIiFSGASARERGRyjAAJCIiIlIZBoBEREREKsMAkIiIiEhlGAASERERqQwDQCIiIiKVYQBIREREpDIMAImIiIhUhgEgERERkcowACQiIiJSGQaARERERCrDAJCIiIhIZRgAEhEREakMA0AiIiIilWEASERERKQyDACJiIiIVIYBIBEREZHKMAAkIiIiUhkGgEREREQqwwCQiIiISGUYABIRERGpDANAIiIiIpX5P3Z3v5zaj5FbAAAAAElFTkSuQmCC' width=640.0/>\n",
       "            </div>\n",
       "        "
      ],
      "text/plain": [
       "Canvas(toolbar=Toolbar(toolitems=[('Home', 'Reset original view', 'home', 'home'), ('Back', 'Back to previous …"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    }
   ],
   "source": [
    "# ------ INPUT ------#\n",
    "focal_lengths = np.array([60.0, 70.0,  90.0,  100.0 ,  50,  50]) # Köhler Illumination\n",
    "#--------------------#\n",
    "\n",
    "# Define lenses here\n",
    "lens_labels =             ['Gun', 'C1', 'C2', 'C3' , 'Objective', '']\n",
    "lens_positions = np.array([200.0, 400.0, 600.0, 800.0, 1100,1200    ]) # lens positions\n",
    "focal_lengths = np.array([60.0, 70.0,  90.0,  100.0 ,  50,  50]) # lens focal lengths for Spot Mode in TEM# focal_lengths = np.array([50.0, 70.0,  90.0,  142.0 ,  50,  50]) # Köhler Illumination\n",
    "focal_lengths = np.array([50.0, 70.0,  378.0,  127.0 ,  50,  50]) # Slightly convergent\n",
    "\n",
    "\n",
    "animate.propagate_beam([0,],1,  3, lens_positions, focal_lengths, lens_labels,   'blue')\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "If you select any mode, magnification or brightness, the computer looks up a dataset and provides the stored values of currents to the respective lenses and other optical elements. \n",
    "\n",
    "An engineering alignment determines those values and users only have to deal with the fine-tuning of the electron optical system."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "id": "GcfSxvtik6os",
    "pycharm": {
     "name": "#%% md\n"
    }
   },
   "source": [
    "## Convergence Angle\n",
    "\n",
    "The condensor lens system defines the illumination of the sample and with it the convergence angle (even parallel illumination has ususally a convergence angle of a few $\\mu$rad).\n",
    "\n",
    "The convergence angle is set by the condenser lens system  and  can be measured with a convergent beam electron diffraction (CBED) pattern.\n",
    "\n",
    "\n",
    "Under plane wave illumination the diffraction pattern consists of points. If you imagine a second incident plane wave\n",
    "with some angle to the first one, there will be two slightly shifted diffraction patterns made out of points.\n",
    "\n",
    "\n",
    "A lot of plane waves with a conical angle distribution will result in small circles instead of a point. The radius of the circle corresponds to the convergence angle. One can easily calculate the convergence angle from a CBED pattern of a known sample."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Summary Ray Optics of TEM\n",
    "- Lenses provide illumination and magnification\n",
    "- Lenses switch modes in a TEM\n",
    "- Lenses allow to select the angles within a TEM\n",
    "- Apertures help to select the information projected in a TEM\n",
    "\n",
    "A detailed understanding of the angles within the TEM allows for a\n",
    "project oriented experimental setup.\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Navigation\n",
    "- <font size = \"3\">  **Back  [Overview](CH1_06-Overview.ipynb)** </font>\n",
    "- <font size = \"3\">  **Next: [Diffraction](../Diffraction/CH2_00-Diffraction.ipynb)** </font>\n",
    "- <font size = \"3\">  **Chapter 1: [Introduction](CH1_00-Introduction.ipynb)** </font>\n",
    "- <font size = \"3\">  **List of Content: [Front](../_MSE672_Intro_TEM.ipynb)** </font>"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Appendix:\n",
    "### Code for condenser stack ray diagram"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "# ----------------------------------------------------------------\n",
    "# Modified from Michael Fairchild :simply draws a thin-lens at the provided location parameters:\n",
    "#     - z:    location along the optical axis (in mm)\n",
    "#     - f:    focal length (in mm, can be negative if div. lens)\n",
    "#     - diam: lens diameter in mm\n",
    "#     - lens_labels:  label to identify the lens on the drawing\n",
    "# ----------------------------------------------------------------\n",
    "def add_lens(z, f, diam, lens_labels):\n",
    "    \"\"\"add lens to propagate beam plot\"\"\"\n",
    "    ww, tw, rad = diam / 10.0, diam / 3.0, diam / 2.0\n",
    "    plt.plot([z, z], [-rad, rad], 'k', linewidth=2)\n",
    "    plt.plot([z, z + tw], [-rad, -rad + np.sign(f) * ww], 'k', linewidth=2)\n",
    "    plt.plot([z, z - tw], [-rad, -rad + np.sign(f) * ww], 'k', linewidth=2)\n",
    "    plt.plot([z, z + tw], [rad, rad - np.sign(f) * ww], 'k', linewidth=2)\n",
    "    plt.plot([z, z - tw], [rad, rad - np.sign(f) * ww], 'k', linewidth=2)\n",
    "    plt.plot([z + f, z + f], [-ww, ww], 'k', linewidth=2)\n",
    "    plt.plot([z - f, z - f], [-ww, ww], 'k', linewidth=2)\n",
    "    plt.text(z, rad + 5.0, lens_labels, fontsize=12)\n",
    "    plt.text(z, rad + 2.0, 'f=' + str(int(f)), fontsize=10)\n",
    "\n",
    "\n",
    "def add_aperture(z, diam, radius, lens_labels):\n",
    "    \"\"\"add aperture to propagate beam plot\"\"\"\n",
    "\n",
    "    ww, tw, rad = diam / 10.0, diam / 3.0, diam / 2.0\n",
    "    radius = radius / 2\n",
    "    plt.plot([z, z], [-rad, -radius], 'k', linewidth=2)\n",
    "    plt.plot([z, z], [rad, radius], 'k', linewidth=2)\n",
    "    plt.text(z, -rad - 2.0, lens_labels, fontsize=12)\n",
    "\n",
    "\n",
    "def propagate_beam(source_position, numerical_aperture, number_of_rays, lens_positions, focal_lengths,\n",
    "                   lens_labels='', color='b'):\n",
    "    \"\"\"geometrical propagation of light rays from given source\n",
    "\n",
    "    Parameters\n",
    "    ----------\n",
    "    source_position:  list\n",
    "        location of the source (z0, x0) along and off axis (in mm)\n",
    "    numerical_aperture:  float\n",
    "        numerical aperture of the beam (in degrees)\n",
    "    number_of_rays:  int\n",
    "        number of rays to trace\n",
    "    lens_positions:  numpy array\n",
    "        array with the location of the lenses\n",
    "    focal_lengths:  numpy array\n",
    "        array with the focal length of lenses\n",
    "    lens_labels: list of string\n",
    "        label for the nature of lenses\n",
    "    color: str\n",
    "        color of the rays on plot\n",
    "    \"\"\"\n",
    "\n",
    "    plt.figure()\n",
    "    z_max = 1600.\n",
    "\n",
    "    # aperture (maximum angle) in radians\n",
    "    apa = numerical_aperture * np.pi / 180.0\n",
    "\n",
    "    for i in range(np.size(lens_positions)):\n",
    "        add_lens(lens_positions[i], focal_lengths[i], 25, lens_labels[i])\n",
    "\n",
    "    add_aperture(840, 25, 7, 'CA')\n",
    "\n",
    "    # position of source is z0,x0\n",
    "    z0 = source_position[0]\n",
    "    if np.size(source_position) == 2:\n",
    "        x0 = source_position[1]\n",
    "    else:\n",
    "        x0 = 0.0\n",
    "\n",
    "    # list of lens positions\n",
    "    zl1, ff1 = lens_positions[(z0 < lens_positions)], focal_lengths[(z0 < lens_positions)]\n",
    "    nl = np.size(zl1)  # number of lenses\n",
    "\n",
    "    zz, xx, tani = np.zeros(nl + 2), np.zeros(nl + 2), np.zeros(nl + 2)\n",
    "    tan0 = np.tan(apa / 2.0) - np.tan(apa) * np.arange(number_of_rays) / (number_of_rays - 1)\n",
    "\n",
    "    for i in range(number_of_rays):\n",
    "        tani[0] = tan0[i]  # initial incidence angle\n",
    "        zz[0], xx[0] = z0, x0\n",
    "        for j in range(nl):\n",
    "            zz[j + 1] = zl1[j]\n",
    "            xx[j + 1] = xx[j] + (zz[j + 1] - zz[j]) * tani[j]\n",
    "            tani[j + 1] = tani[j] - xx[j + 1] / ff1[j]\n",
    "\n",
    "        zz[nl + 1] = z_max\n",
    "        xx[nl + 1] = xx[nl] + (zz[nl + 1] - zz[nl]) * tani[nl]\n",
    "        plt.plot(zz, xx, color)\n",
    "        plt.axis([-20, z_max, -20, 20])\n"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": []
  }
 ],
 "metadata": {
  "colab": {
   "authorship_tag": "ABX9TyPpeUffxRTpGpH529V5WM6r",
   "collapsed_sections": [],
   "name": "02_ElectronOptics.ipynb",
   "provenance": [],
   "toc_visible": true
  },
  "kernelspec": {
   "display_name": "pyTEMlib",
   "language": "python",
   "name": "pytemlib"
  },
  "language_info": {
   "codemirror_mode": {
    "name": "ipython",
    "version": 3
   },
   "file_extension": ".py",
   "mimetype": "text/x-python",
   "name": "python",
   "nbconvert_exporter": "python",
   "pygments_lexer": "ipython3",
   "version": "3.11.7"
  },
  "toc": {
   "base_numbering": "8",
   "nav_menu": {},
   "number_sections": true,
   "sideBar": true,
   "skip_h1_title": false,
   "title_cell": "Table of Contents",
   "title_sidebar": "Contents",
   "toc_cell": false,
   "toc_position": {},
   "toc_section_display": true,
   "toc_window_display": true
  },
  "vscode": {
   "interpreter": {
    "hash": "838e0debddb5b6f29d3d8c39ba50ae8c51920a564d3bac000e89375a158a81de"
   }
  }
 },
 "nbformat": 4,
 "nbformat_minor": 4
}