{
 "cells": [
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "# 2.7 Statistical Considerations for geoscientific Data and Noise\n",
    "\n",
    "\n",
    "## Canonical Distributions in Geoscientific Data\n",
    "1. **Normal Distribution**: Used for variables like temperature, sea level variations, or wind speeds where values are symmetrically distributed.\n",
    "2. **Log-Normal Distribution**: Often observed in phenomena where values can’t be negative and show long tails, such as earthquake magnitudes, rainfall, and river flow.\n",
    "3. **Exponential Distribution**: Applied in modeling time intervals between events, such as the time between earthquakes.\n",
    "4. **Power-Law Distribution:** Seen in rare, large-scale events like landslides, wildfires, or large earthquakes.\n",
    "\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## 1. Statistical Features\n",
    "\n",
    "Let be $P(z)$ the distribution of the data $z$.\n",
    "\n",
    "### The mean\n",
    "\n",
    "![mean](../img/mean.png)\n",
    "\n",
    "Image taken from this [blog](https://gregorygundersen.com/blog/2020/04/11/moments).\n",
    "\n",
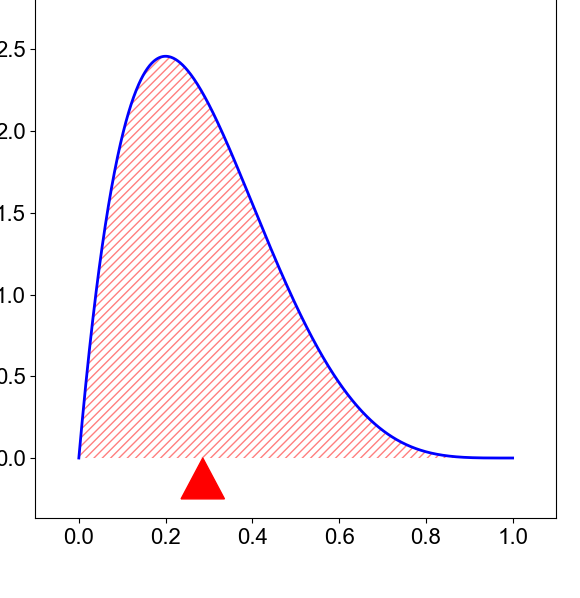
    "The mean is the sum of the values divided by the number of data points. It is the first raw moment of a distribution. \n",
    "$\\mu = \\int_{-\\infty}^\\infty zP(z)dz$, where z is the ground motion value (bin) and $P(z)$ is the distribution of the data.\n",
    "\n",
    "### The Variance\n",
    "\n",
    "![variance](../img/variance.png)\n",
    "\n",
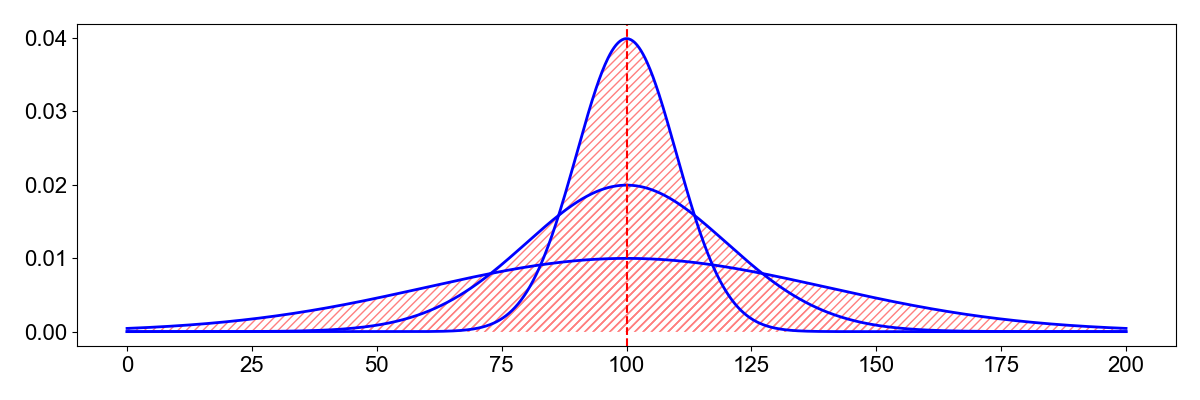
    "The variance is the second *centralized* moment. *Centralized* means that the distribution is shifted around the mean. It calculates how spread out is a distribution.\n",
    "\n",
    "$\\sigma^2 = \\int_{-\\infty}^\\infty (z-\\mu)^2P(z)dz$\n",
    "\n",
    "The standard deviation is the square root of the variance, $\\sigma$. A high variance indicates a wide distribution.\n",
    "\n",
    "### The skewness\n",
    "\n",
    "Skewness is the third *standardized* moment. The *standardized* moment is scaled by the standard deviation. It measures the relative size of the two tails of the distribution.\n",
    "\n",
    "\n",
    "$m_3= \\int_{-\\infty}^\\infty \\frac{(z - \\mu)^3}{\\sigma^3}P(z)dz$\n",
    "\n",
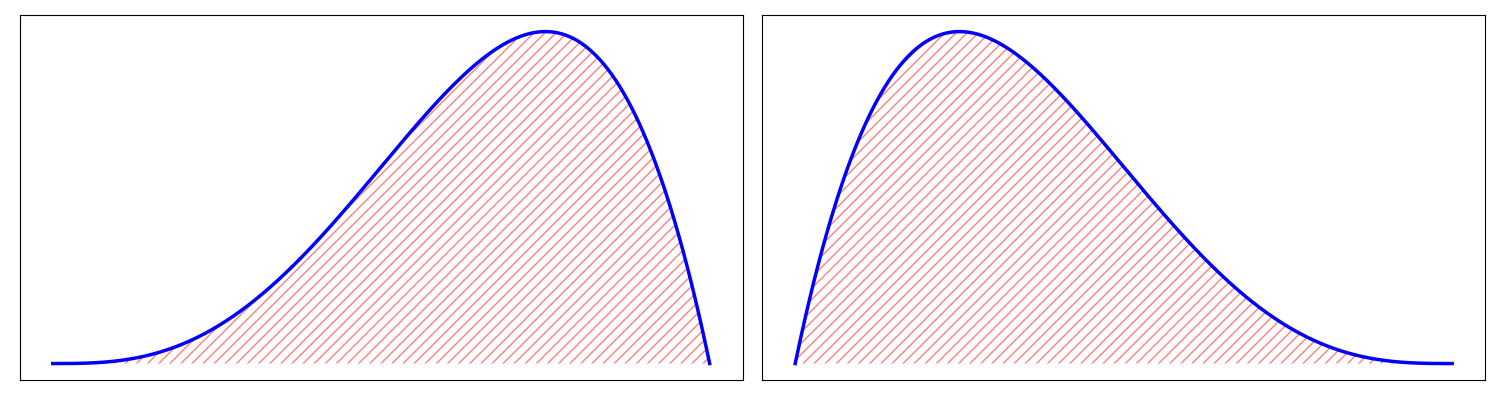
    "With the cubic exponent, it is possible that the skewness is negative.\n",
    "\n",
    "![skewness](../img/skewness.png)\n",
    "\n",
    "Image taken from this [blog](!https://gregorygundersen.com/blog/2020/04/11/moments).\n",
    "\n",
    "A **positively** skewed distribution is one where most of the weight is **at the end** of the distribution. A **negatively** skewed distribution is one where most of the weight is **at the beginning** of the distribution.\n",
    "\n",
    "\n",
    "### Kurtosis\n",
    "\n",
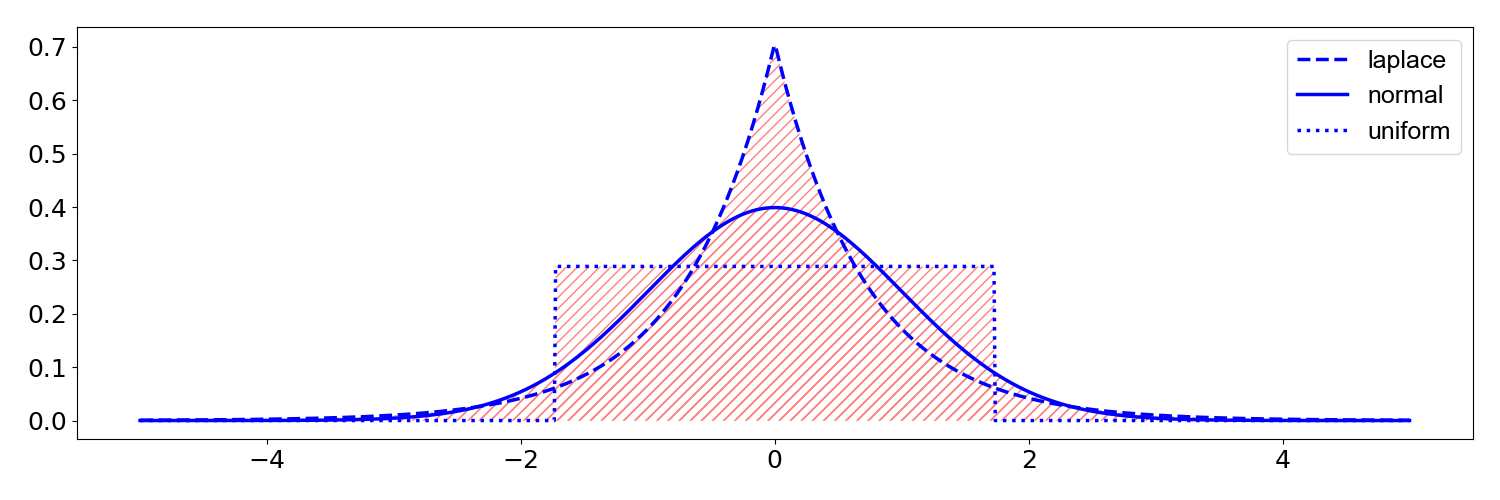
    "Kurtosis measures the combined size of the two tails relative to the whole distribution. It is the fourth centralized and standardized moment.\n",
    "\n",
    "$m_4= \\int_{-\\infty}^\\infty (\\frac{z-\\mu}{\\sigma})^4P(z)dz$\n",
    "\n",
    " ![kurtosis](../img/kurtosis.png)\n",
    "The laplace, normal, and uniform distributions have a mean of 0 and a variance of 1. But their kurtosis is 3, 0, and -1.2.\n",
    "\n",
    "\n",
    "Python functions to calculate the moments might be:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 194,
   "metadata": {},
   "outputs": [],
   "source": [
    "# Import modules for seismic data and feature extraction\n",
    "import numpy as np\n",
    "import matplotlib.pyplot as plt\n",
    "import pandas as pd\n",
    "import scipy\n",
    "import scipy.stats as st\n",
    "import scipy.signal as sig"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 195,
   "metadata": {},
   "outputs": [],
   "source": [
    "def raw_moment(X, k, c=0):\n",
    "    return ((X - c)**k).mean()\n",
    "\n",
    "def central_moment(X, k):\n",
    "    return raw_moment(X=X, k=k, c=X.mean())"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": []
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## 2. Geological data sets [Level 1]\n",
    "\n",
    "We will explore the composition of Granite in terms of Silicate and Magnesium content. The data was collected from EarthChem database."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 3,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/html": [
       "<div>\n",
       "<style scoped>\n",
       "    .dataframe tbody tr th:only-of-type {\n",
       "        vertical-align: middle;\n",
       "    }\n",
       "\n",
       "    .dataframe tbody tr th {\n",
       "        vertical-align: top;\n",
       "    }\n",
       "\n",
       "    .dataframe thead th {\n",
       "        text-align: right;\n",
       "    }\n",
       "</style>\n",
       "<table border=\"1\" class=\"dataframe\">\n",
       "  <thead>\n",
       "    <tr style=\"text-align: right;\">\n",
       "      <th></th>\n",
       "      <th>SIO2(WT%)</th>\n",
       "      <th>MGO(WT%)</th>\n",
       "    </tr>\n",
       "  </thead>\n",
       "  <tbody>\n",
       "    <tr>\n",
       "      <th>0</th>\n",
       "      <td>72.57</td>\n",
       "      <td>0.49</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>1</th>\n",
       "      <td>70.39</td>\n",
       "      <td>0.84</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>2</th>\n",
       "      <td>71.60</td>\n",
       "      <td>0.59</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>3</th>\n",
       "      <td>68.93</td>\n",
       "      <td>0.81</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>4</th>\n",
       "      <td>71.07</td>\n",
       "      <td>0.76</td>\n",
       "    </tr>\n",
       "  </tbody>\n",
       "</table>\n",
       "</div>"
      ],
      "text/plain": [
       "   SIO2(WT%)  MGO(WT%)\n",
       "0      72.57      0.49\n",
       "1      70.39      0.84\n",
       "2      71.60      0.59\n",
       "3      68.93      0.81\n",
       "4      71.07      0.76"
      ]
     },
     "execution_count": 3,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "# Load .csv data into a pandas dataframe\n",
    "import pandas as pd\n",
    "url = 'https://raw.githubusercontent.com/UW-MLGEO/MLGeo-dataset/main/data/EarthRocGranites.csv'\n",
    "df = pd.read_csv(url)\n",
    "df.head()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Data pre-processing is often necessary, and most importantly, it is critical to record any processing step to raw data. Do not change the original data file, instead record processing steps. Below, we drop the rows with NaNs (not a number)."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 197,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/html": [
       "<div>\n",
       "<style scoped>\n",
       "    .dataframe tbody tr th:only-of-type {\n",
       "        vertical-align: middle;\n",
       "    }\n",
       "\n",
       "    .dataframe tbody tr th {\n",
       "        vertical-align: top;\n",
       "    }\n",
       "\n",
       "    .dataframe thead th {\n",
       "        text-align: right;\n",
       "    }\n",
       "</style>\n",
       "<table border=\"1\" class=\"dataframe\">\n",
       "  <thead>\n",
       "    <tr style=\"text-align: right;\">\n",
       "      <th></th>\n",
       "      <th>SIO2(WT%)</th>\n",
       "      <th>MGO(WT%)</th>\n",
       "    </tr>\n",
       "  </thead>\n",
       "  <tbody>\n",
       "    <tr>\n",
       "      <th>0</th>\n",
       "      <td>72.57</td>\n",
       "      <td>0.49</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>1</th>\n",
       "      <td>70.39</td>\n",
       "      <td>0.84</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>2</th>\n",
       "      <td>71.60</td>\n",
       "      <td>0.59</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>3</th>\n",
       "      <td>68.93</td>\n",
       "      <td>0.81</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>4</th>\n",
       "      <td>71.07</td>\n",
       "      <td>0.76</td>\n",
       "    </tr>\n",
       "  </tbody>\n",
       "</table>\n",
       "</div>"
      ],
      "text/plain": [
       "   SIO2(WT%)  MGO(WT%)\n",
       "0      72.57      0.49\n",
       "1      70.39      0.84\n",
       "2      71.60      0.59\n",
       "3      68.93      0.81\n",
       "4      71.07      0.76"
      ]
     },
     "execution_count": 197,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "df = df.dropna()    # remove rows with NaN values\n",
    "df.head()   # describe the data"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Pandas python software includes methods to report basics data statistics. Use the function ``describe`` to the Pandas data frame."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 198,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/html": [
       "<div>\n",
       "<style scoped>\n",
       "    .dataframe tbody tr th:only-of-type {\n",
       "        vertical-align: middle;\n",
       "    }\n",
       "\n",
       "    .dataframe tbody tr th {\n",
       "        vertical-align: top;\n",
       "    }\n",
       "\n",
       "    .dataframe thead th {\n",
       "        text-align: right;\n",
       "    }\n",
       "</style>\n",
       "<table border=\"1\" class=\"dataframe\">\n",
       "  <thead>\n",
       "    <tr style=\"text-align: right;\">\n",
       "      <th></th>\n",
       "      <th>SIO2(WT%)</th>\n",
       "      <th>MGO(WT%)</th>\n",
       "    </tr>\n",
       "  </thead>\n",
       "  <tbody>\n",
       "    <tr>\n",
       "      <th>count</th>\n",
       "      <td>15924.000000</td>\n",
       "      <td>15924.000000</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>mean</th>\n",
       "      <td>72.113026</td>\n",
       "      <td>0.613687</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>std</th>\n",
       "      <td>4.103932</td>\n",
       "      <td>0.942135</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>min</th>\n",
       "      <td>8.710000</td>\n",
       "      <td>0.000000</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>25%</th>\n",
       "      <td>70.100000</td>\n",
       "      <td>0.170000</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>50%</th>\n",
       "      <td>72.750000</td>\n",
       "      <td>0.390000</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>75%</th>\n",
       "      <td>74.890000</td>\n",
       "      <td>0.780000</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>max</th>\n",
       "      <td>93.010000</td>\n",
       "      <td>57.000000</td>\n",
       "    </tr>\n",
       "  </tbody>\n",
       "</table>\n",
       "</div>"
      ],
      "text/plain": [
       "          SIO2(WT%)      MGO(WT%)\n",
       "count  15924.000000  15924.000000\n",
       "mean      72.113026      0.613687\n",
       "std        4.103932      0.942135\n",
       "min        8.710000      0.000000\n",
       "25%       70.100000      0.170000\n",
       "50%       72.750000      0.390000\n",
       "75%       74.890000      0.780000\n",
       "max       93.010000     57.000000"
      ]
     },
     "execution_count": 198,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "df.describe()"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 199,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAA90AAAGFCAYAAADgjJA1AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjguMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy81sbWrAAAACXBIWXMAAA9hAAAPYQGoP6dpAABHyElEQVR4nO3deXhU9d3//9eQjcUwEkIyiQQEiwgNIJsQsBIEApRIKdyiohFuLULZjIALtS1xA+VWoLdUXKqALIar34I3qI0EhGAKEQpE9sWLLSIhLsmENYHk8/uDX04dwpKEOUyW5+O6znUx57xn8jmfhPnM65wzn+MwxhgBAAAAAACvq+XrBgAAAAAAUF0RugEAAAAAsAmhGwAAAAAAmxC6AQAAAACwCaEbAAAAAACbELoBAAAAALAJoRsAAAAAAJv4+7oBVUVxcbG+++47BQcHy+Fw+Lo5AIBKzBijkydPKjIyUrVqcXy7smAsBwCUlTfHckJ3GX333XeKiorydTMAAFVIVlaWGjdu7Otm4P/HWA4AKC9vjOWE7jIKDg6WdLHT69ev7+PWAAAqs/z8fEVFRVljByoHxnIAQFl5cywndJdRyWVo9evXZ6AGAJQJlzBXLozlAIDy8sZYzhfNAAAAAACwCaEbAAAAAACbELoBAAAAALAJoRsAAAAAAJsQugEAAAAAsAmhGwAAAAAAmxC6AQAAAACwCaEbAAAAAACbELoBAAAAALAJoRsAAAAAAJsQugEAAAAAsAmhGwAAAAAAm/j7ugEAcDkOh6NMdcYYm1sCoLpxOp22vC7vRwCAy+FMNwAAAAAANiF0AwAAAABgE0I3AAAAAAA2IXQDAIDLWr9+ve677z5FRkbK4XDo448/9thujFFSUpIiIyNVp04dxcbGateuXR41BQUFGj9+vEJDQ1WvXj0NHDhQ3377rUdNbm6uEhIS5HQ65XQ6lZCQoLy8PI+ao0eP6r777lO9evUUGhqqCRMmqLCw0I7dBgDAqwjdAADgsk6fPq127dppzpw5l90+Y8YMzZw5U3PmzNHmzZvlcrnUp08fnTx50qpJTEzU8uXLlZycrPT0dJ06dUrx8fEqKiqyaoYNG6bMzEylpKQoJSVFmZmZSkhIsLYXFRVpwIABOn36tNLT05WcnKx//OMfmjRpkn07DwCAlzgMU22WSX5+vpxOp9xut+rXr+/r5gDVHrOXoyqrjmOGw+HQ8uXLNWjQIEkX/+9FRkYqMTFRzz77rKSLZ7XDw8P12muvadSoUXK73WrUqJEWLlyoBx54QJL03XffKSoqSp999pn69u2rPXv2qHXr1srIyFCXLl0kSRkZGYqJidHevXvVsmVL/fOf/1R8fLyysrIUGRkpSUpOTtaIESOUk5NT5j4u+b3YhfcjAKg+vDmWc6YbAACU26FDh5Sdna24uDhrXVBQkHr06KENGzZIkrZs2aLz58971ERGRio6Otqq2bhxo5xOpxW4Jalr165yOp0eNdHR0VbglqS+ffuqoKBAW7ZsuWIbCwoKlJ+f77EAAHCjEboBAEC5ZWdnS5LCw8M91oeHh1vbsrOzFRgYqAYNGly1JiwsrNTrh4WFedRc+nMaNGigwMBAq+Zypk+fbn1P3Ol0Kioqqpx7CQDA9SN0AwCACrv0qyDGmGt+PeTSmsvVV6TmUlOmTJHb7baWrKysq7YLAAA7ELoBAEC5uVwuSSp1pjknJ8c6K+1yuVRYWKjc3Nyr1pw4caLU63///fceNZf+nNzcXJ0/f77UGfCfCwoKUv369T0WAABuNJ+G7unTp6tz584KDg5WWFiYBg0apH379nnUjBgxQg6Hw2Pp2rWrR423bkcCAADKplmzZnK5XEpNTbXWFRYWKi0tTd26dZMkdezYUQEBAR41x48f186dO62amJgYud1ubdq0yar56quv5Ha7PWp27typ48ePWzWrVq1SUFCQOnbsaOt+AgBwvXwautPS0jR27FhlZGQoNTVVFy5cUFxcnE6fPu1R169fPx0/ftxaPvvsM4/t3rgdCYAb59IDaZdbAPjeqVOnlJmZqczMTEkXJ0/LzMzU0aNH5XA4lJiYqGnTpmn58uXauXOnRowYobp162rYsGGSJKfTqccff1yTJk3SmjVrtG3bNj3yyCNq06aNevfuLUlq1aqV+vXrp5EjRyojI0MZGRkaOXKk4uPj1bJlS0lSXFycWrdurYSEBG3btk1r1qzR5MmTNXLkSM5eAwAqP1OJ5OTkGEkmLS3NWjd8+HDzm9/85orPycvLMwEBASY5Odlad+zYMVOrVi2TkpJijDFm9+7dRpLJyMiwajZu3Ggkmb1795apbW6320gybre7nHsF4FKSvLYAlVF1GTPWrl172f93w4cPN8YYU1xcbKZOnWpcLpcJCgoy99xzj9mxY4fHa5w9e9aMGzfOhISEmDp16pj4+Hhz9OhRj5off/zRPPzwwyY4ONgEBwebhx9+2OTm5nrUHDlyxAwYMMDUqVPHhISEmHHjxplz586Va39Kfi92LQCA6sObY3mluk/3N998oxYtWmjHjh2Kjo6WdPHy8o8//liBgYG6+eab1aNHD73yyivWTKdffPGFevXqpZ9++sljdtR27dpp0KBBeuGFF/TBBx9o4sSJpS4nv/nmmzVr1iz993//d6m2FBQUqKCgwHqcn5+vqKioanXPVcBXvHkmuxK9hQGW6nif7uqA+3QDAMqqWt6n2xijiRMn6u6777YCtyT1799fixcv1hdffKE33nhDmzdv1r333msFYm/djuRS3GYEAAAAAHC9/H3dgBLjxo3T9u3blZ6e7rH+gQcesP4dHR2tTp06qWnTpvr00081ePDgK76euc5bjUyZMkUTJ060Hpec6QYAAAAAoKwqxZnu8ePHa8WKFVq7dq0aN2581dqIiAg1bdpUBw4ckOS925FcituMAAAAAACul09DtzFG48aN07Jly/TFF1+oWbNm13zOjz/+qKysLEVEREjy3u1IAAAAAADwNp9eXj527FgtWbJE//d//6fg4GDr+9VOp1N16tTRqVOnlJSUpCFDhigiIkKHDx/WH/7wB4WGhuq3v/2tVVtyO5KGDRsqJCREkydPvuLtSN555x1J0hNPPOFxOxIAAAAAALzNp6F77ty5kqTY2FiP9fPmzdOIESPk5+enHTt26MMPP1ReXp4iIiLUs2dPLV26VMHBwVb9rFmz5O/vr6FDh+rs2bPq1auX5s+fLz8/P6tm8eLFmjBhguLi4iRJAwcO1Jw5c+zfSQAAAABAjVWpbhlWmXH7F8B7uGUYqjvGjMqJW4YBAMqqWt4yDAAAAACA6obQDQAAAACATQjdAAAAAADYhNANAAAAAIBNCN0AAAAAANiE0A0AAAAAgE0I3QAAAAAA2ITQDQAAAACATQjdAAAAAADYhNANAAAAAIBNCN0AAAAAANiE0A0AAAAAgE0I3QAAAAAA2ITQDQAAAACATQjdAAAAAADYhNANAAAAAIBNCN0AAAAAANiE0A0AAAAAgE0I3QAAAAAA2ITQDQAAAACATQjdAAAAAADYhNANAAAAAIBNCN0AAAAAANiE0A0AAAAAgE0I3QAAAAAA2ITQDQAAAACATQjdAAAAAADYhNANAAAAAIBN/H3dAAC4Hg6H45o1xpgb0BIAAACgNM50AwAAAABgE0I3AAAAAAA2IXQDAAAAAGATQjcAAAAAADYhdAMAAAAAYBNCNwAAAAAANiF0AwAAAABgE0I3AAAAAAA2IXQDAAAAAGATQjcAAAAAADYhdAMAAAAAYBNCNwAAAAAANiF0AwAAAABgE0I3AACosAsXLuiPf/yjmjVrpjp16qh58+Z68cUXVVxcbNUYY5SUlKTIyEjVqVNHsbGx2rVrl8frFBQUaPz48QoNDVW9evU0cOBAffvttx41ubm5SkhIkNPplNPpVEJCgvLy8m7EbgIAUGGEbgAAUGGvvfaa3n77bc2ZM0d79uzRjBkz9D//8z968803rZoZM2Zo5syZmjNnjjZv3iyXy6U+ffro5MmTVk1iYqKWL1+u5ORkpaen69SpU4qPj1dRUZFVM2zYMGVmZiolJUUpKSnKzMxUQkLCDd1fAADKy2GMMb5uRFWQn58vp9Mpt9ut+vXr+7o5QJXmcDhu6M/jbQ43Wk0aM+Lj4xUeHq7333/fWjdkyBDVrVtXCxculDFGkZGRSkxM1LPPPivp4lnt8PBwvfbaaxo1apTcbrcaNWqkhQsX6oEHHpAkfffdd4qKitJnn32mvn37as+ePWrdurUyMjLUpUsXSVJGRoZiYmK0d+9etWzZ8pptLfm92IX3GgCoPrw5lnOmG4BXORyOay4Aqo+7775ba9as0f79+yVJX3/9tdLT0/XrX/9aknTo0CFlZ2crLi7Oek5QUJB69OihDRs2SJK2bNmi8+fPe9RERkYqOjraqtm4caOcTqcVuCWpa9eucjqdVs2lCgoKlJ+f77EAAHCj+fu6AQAAoOp69tln5Xa7dccdd8jPz09FRUV65ZVX9NBDD0mSsrOzJUnh4eEezwsPD9eRI0esmsDAQDVo0KBUTcnzs7OzFRYWVurnh4WFWTWXmj59ul544YXr20EAAK4TZ7oBAECFLV26VIsWLdKSJUu0detWLViwQK+//roWLFjgUXfpVS7GmGte+XJpzeXqr/Y6U6ZMkdvttpasrKyy7hYAAF7j09A9ffp0de7cWcHBwQoLC9OgQYO0b98+jxpmPAUAoPJ6+umn9dxzz+nBBx9UmzZtlJCQoKeeekrTp0+XJLlcLkkqdTY6JyfHOvvtcrlUWFio3Nzcq9acOHGi1M///vvvS51FLxEUFKT69et7LAAA3Gg+Dd1paWkaO3asMjIylJqaqgsXLiguLk6nT5+2apjxFACAyuvMmTOqVcvz44Sfn591y7BmzZrJ5XIpNTXV2l5YWKi0tDR169ZNktSxY0cFBAR41Bw/flw7d+60amJiYuR2u7Vp0yar5quvvpLb7bZqAAColEwlkpOTYySZtLQ0Y4wxxcXFxuVymVdffdWqOXfunHE6nebtt982xhiTl5dnAgICTHJyslVz7NgxU6tWLZOSkmKMMWb37t1GksnIyLBqNm7caCSZvXv3XrYt586dM26321qysrKMJON2u72+30B1IqnSLcCN5na7a8yYMXz4cHPLLbeYTz75xBw6dMgsW7bMhIaGmmeeecaqefXVV43T6TTLli0zO3bsMA899JCJiIgw+fn5Vs3o0aNN48aNzerVq83WrVvNvffea9q1a2cuXLhg1fTr18+0bdvWbNy40WzcuNG0adPGxMfHl7mtJb8X3msAANfizbG8Un2n2+12S5JCQkIk+XbG0+nTp1uXojudTkVFRXl3ZwEAqAbefPNN/dd//ZfGjBmjVq1aafLkyRo1apReeuklq+aZZ55RYmKixowZo06dOunYsWNatWqVgoODrZpZs2Zp0KBBGjp0qLp37666detq5cqV8vPzs2oWL16sNm3aKC4uTnFxcWrbtq0WLlx4Q/cXAIDyqjSzlxtjNHHiRN19992Kjo6W5NsZT6dMmaKJEydaj/Pz8wneAABcIjg4WLNnz9bs2bOvWONwOJSUlKSkpKQr1tSuXVtvvvmm3nzzzSvWhISEaNGiRdfRWgAAbrxKE7rHjRun7du3Kz09vdQ2X8x4GhQUpKCgoLI0HQAAAACAy6oUl5ePHz9eK1as0Nq1a9W4cWNrvS9nPAUAAAAA4Hr5NHQbYzRu3DgtW7ZMX3zxhZo1a+axnRlPAQAAAABVmU8vLx87dqyWLFmi//u//1NwcLB1RtvpdKpOnTpyOBxKTEzUtGnT1KJFC7Vo0ULTpk1T3bp1NWzYMKv28ccf16RJk9SwYUOFhIRo8uTJatOmjXr37i1JatWqlfr166eRI0fqnXfekSQ98cQTio+PV8uWLX2z8wAAAACAas+noXvu3LmSpNjYWI/18+bN04gRIyRdnPH07NmzGjNmjHJzc9WlS5fLznjq7++voUOH6uzZs+rVq5fmz59fasbTCRMmWLOcDxw4UHPmzLF3BwEAAAAANZrDGGN83YiqID8/X06nU263W/Xr1/d1c4BK61qTHPoCb3O40RgzKqeS34tdeK8BgOrDm2N5pZhIDQAAAACA6ojQDQAAAACATQjdAAAAAADYhNANAAAAAIBNCN0AAAAAANiE0A0AAAAAgE0I3QAAAAAA2ITQDQAAAACATQjdAAAAAADYhNANAAAAAIBNCN0AAAAAANiE0A0AAAAAgE0I3QAAAAAA2ITQDQAAAACATQjdAAAAAADYhNANAAAAAIBNCN0AAAAAANiE0A0AAAAAgE0I3QAAAAAA2ITQDQAAAACATQjdAAAAAADYhNANAAAAAIBNCN0AAAAAANiE0A0AAAAAgE0I3QAAAAAA2ITQDQAAAACATQjdAAAAAADYhNANAAAAAIBNCN0AAAAAANiE0A0AAAAAgE0I3QAAAAAA2ITQDQAAAACATQjdAAAAAADYhNANAAAAAIBNCN0AAAAAANiE0A0AAAAAgE0I3QAAAAAA2ITQDQAAAACATQjdAAAAAADYhNANAAAAAIBNCN0AAAAAANiE0A0AAAAAgE0I3QAAAAAA2ITQDQAArsuxY8f0yCOPqGHDhqpbt67uvPNObdmyxdpujFFSUpIiIyNVp04dxcbGateuXR6vUVBQoPHjxys0NFT16tXTwIED9e2333rU5ObmKiEhQU6nU06nUwkJCcrLy7sRuwgAQIURugGUmcPhuOYCoGbJzc1V9+7dFRAQoH/+85/avXu33njjDd18881WzYwZMzRz5kzNmTNHmzdvlsvlUp8+fXTy5EmrJjExUcuXL1dycrLS09N16tQpxcfHq6ioyKoZNmyYMjMzlZKSopSUFGVmZiohIeFG7i4AAOXmMMYYXzeiKsjPz5fT6ZTb7Vb9+vV93RzAJ6pqqOZtDjdaTRoznnvuOf3rX//Sl19+edntxhhFRkYqMTFRzz77rKSLZ7XDw8P12muvadSoUXK73WrUqJEWLlyoBx54QJL03XffKSoqSp999pn69u2rPXv2qHXr1srIyFCXLl0kSRkZGYqJidHevXvVsmXLa7a15PdiF95rAKD68OZYzpluAABQYStWrFCnTp10//33KywsTO3bt9d7771nbT906JCys7MVFxdnrQsKClKPHj20YcMGSdKWLVt0/vx5j5rIyEhFR0dbNRs3bpTT6bQCtyR17dpVTqfTqrlUQUGB8vPzPRYAAG40QjcAAKiwgwcPau7cuWrRooU+//xzjR49WhMmTNCHH34oScrOzpYkhYeHezwvPDzc2padna3AwEA1aNDgqjVhYWGlfn5YWJhVc6np06db3/92Op2Kioq6vp0FAKACKhS6mzdvrh9//LHU+ry8PDVv3rzMr7N+/Xrdd999ioyMlMPh0Mcff+yxfcSIEaW+L9q1a1ePGiZeAQDAk7fG6bIoLi5Whw4dNG3aNLVv316jRo3SyJEjNXfuXI+6S7+eYoy55ldWLq25XP3VXmfKlClyu93WkpWVVdbdAgDAayoUug8fPuwxsUmJgoICHTt2rMyvc/r0abVr105z5sy5Yk2/fv10/Phxa/nss888tjPxCgAAnrw1TpdFRESEWrdu7bGuVatWOnr0qCTJ5XJJUqmz0Tk5OdbZb5fLpcLCQuXm5l615sSJE6V+/vfff1/qLHqJoKAg1a9f32MBAOBG8y9P8YoVK6x/f/755x6TkRQVFWnNmjW69dZby/x6/fv3V//+/a9aExQUZA3Yl3K73Xr//fe1cOFC9e7dW5K0aNEiRUVFafXq1dbEKykpKR4Tr7z33nuKiYnRvn37rjjxSkFBgQoKCqzHfA8MAFDZeXucLovu3btr3759Huv279+vpk2bSpKaNWsml8ul1NRUtW/fXpJUWFiotLQ0vfbaa5Kkjh07KiAgQKmpqRo6dKgk6fjx49q5c6dmzJghSYqJiZHb7damTZt01113SZK++uorud1udevWzav7BACAV5lycDgcxuFwmFq1aln/LlkCAwPN7bffblauXFmel7RIMsuXL/dYN3z4cON0Ok2jRo1MixYtzO9+9ztz4sQJa/uaNWuMJPPTTz95PK9t27bmz3/+szHGmPfff984nc5SP8/pdJoPPvjgiu2ZOnWqkVRqcbvdFdo/oDq43P+JqrAAN5rb7fbJmGHnOH0lmzZtMv7+/uaVV14xBw4cMIsXLzZ169Y1ixYtsmpeffVV43Q6zbJly8yOHTvMQw89ZCIiIkx+fr5VM3r0aNO4cWOzevVqs3XrVnPvvfeadu3amQsXLlg1/fr1M23btjUbN240GzduNG3atDHx8fFlbmvJ74X3GgDAtXhzLC/Xme7i4mJJF49ab968WaGhoeV5ern1799f999/v5o2bapDhw7pT3/6k+69915t2bJFQUFBtk28Il38HtjEiROtx/n5+UzAAgCo1G70OC1JnTt31vLlyzVlyhS9+OKLatasmWbPnq2HH37YqnnmmWd09uxZjRkzRrm5uerSpYtWrVql4OBgq2bWrFny9/fX0KFDdfbsWfXq1Uvz58+Xn5+fVbN48WJNmDDBmuV84MCBV/2KGgAAlUG5QneJQ4cOebsdl1Vyr05Jio6OVqdOndS0aVN9+umnGjx48BWfZ65z4hXp4mXtQUFBFWw5AAC+c6PG6RLx8fGKj4+/4naHw6GkpCQlJSVdsaZ27dp688039eabb16xJiQkRIsWLbqepgIAcMNVKHRL0po1a7RmzRrl5ORYR9ZLfPDBB9fdsMuJiIhQ06ZNdeDAAUmeE6/8/Gx3Tk6O9f2uiky8AqB6udYMydLFA3FAdeKLcRoAAJRWodnLX3jhBcXFxWnNmjX64YcflJub67HY5ccff1RWVpYiIiIkeU68UqJk4pWS0P3ziVdKMPEKAKA689U4DQAASqvQme63335b8+fPv+7bbp06dUrffPON9fjQoUPKzMxUSEiIQkJClJSUpCFDhigiIkKHDx/WH/7wB4WGhuq3v/2tJMnpdOrxxx/XpEmT1LBhQ4WEhGjy5Mlq06aNNZt5q1at1K9fP40cOVLvvPOOJOmJJ55QfHz8FWcuBwCgKvPWOA0AAK5fhUJ3YWGhV84S//vf/1bPnj2txyUTlw0fPlxz587Vjh079OGHHyovL08RERHq2bOnli5dysQrAABchbfGaQAAcP0cpgJfZHz22Wd100036U9/+pMdbaqU8vPz5XQ65Xa7Vb9+fV83B/CJsnw3uqriO93wJl+PGTVxnC6Lkt+LXXgfAYDqw5tjeYXOdJ87d07vvvuuVq9erbZt2yogIMBj+8yZM6+rUQAAoOIYpwEAqDwqFLq3b9+uO++8U5K0c+dOj23V+UwYAABVAeM0AACVR4VC99q1a73dDgAA4CWM0wAAVB4VumUYAAAAAAC4tgqd6e7Zs+dVL0/74osvKtwgAABwfRinAQCoPCoUuku+J1bi/PnzyszM1M6dOzV8+HBvtAsAAFQQ4zQAAJVHhUL3rFmzLrs+KSlJp06duq4GAQCA68M4DQBA5eHV73Q/8sgj+uCDD7z5kgAAwEsYpwEAuPG8Gro3btyo2rVre/MlAQCAlzBOAwBw41Xo8vLBgwd7PDbG6Pjx4/r3v/+tP/3pT15pGAAAqBjGaQAAKo8KhW6n0+nxuFatWmrZsqVefPFFxcXFeaVhAACgYhinAQCoPCoUuufNm+ftdgAAAC9hnAYAoPKoUOgusWXLFu3Zs0cOh0OtW7dW+/btvdUuAABwnRinAQDwvQqF7pycHD344INat26dbr75Zhlj5Ha71bNnTyUnJ6tRo0bebicAACgjxmkAACqPCs1ePn78eOXn52vXrl366aeflJubq507dyo/P18TJkzwdhsBAEA5ME4DAFB5OIwxprxPcjqdWr16tTp37uyxftOmTYqLi1NeXp632ldp5Ofny+l0yu12q379+r5uDuATDofD102wTQXeCoEr8vWYURPH6bIo+b3YhfcRAKg+vDmWV+hMd3FxsQICAkqtDwgIUHFx8XU1CAAAXB/GaQAAKo8Khe57771XTz75pL777jtr3bFjx/TUU0+pV69eXmscAAAoP8ZpAAAqjwqF7jlz5ujkyZO69dZbddttt+kXv/iFmjVrppMnT+rNN9/0dhsBAEA5ME4DAFB5VGj28qioKG3dulWpqanau3evjDFq3bq1evfu7e32AQCAcmKcBgCg8ijXme4vvvhCrVu3Vn5+viSpT58+Gj9+vCZMmKDOnTvrl7/8pb788ktbGgoAAK6OcRoAgMqnXKF79uzZGjly5GVnb3M6nRo1apRmzpzptcYBAICyY5wGAKDyKVfo/vrrr9WvX78rbo+Li9OWLVuuu1EAAKD8GKcBAKh8yhW6T5w4cdlbkJTw9/fX999/f92NAgAA5cc4DQBA5VOu0H3LLbdox44dV9y+fft2RUREXHejAABA+TFOAwBQ+ZQrdP/617/Wn//8Z507d67UtrNnz2rq1KmKj4/3WuMAAEDZMU4DAFD5OIwxpqzFJ06cUIcOHeTn56dx48apZcuWcjgc2rNnj/7617+qqKhIW7duVXh4uJ1t9on8/Hw5nU653e7LTlAD1AQOh8PXTbBNOd4KgWvy1ZhRk8fpsij5vdiF9xEAqD68OZaX6z7d4eHh2rBhg37/+99rypQp1uDicDjUt29fvfXWWzV2IAcAwNcYpwEAqHzKdab753Jzc/XNN9/IGKMWLVqoQYMG3m5bpcKZboAz3UBZVYYxo6aN02XBmW4AQFn57Ez3zzVo0ECdO3e+rh8OAADswTgNAEDlUK6J1AAAAAAAQNkRugEAAAAAsAmhGwAAAAAAmxC6AQAAAACwCaEbAAAAAACbELoBAAAAALAJoRsAAAAAAJsQugEAAAAAsAmhGwAAAAAAmxC6AQAAAACwCaEbAAAAAACbELoBAAAAALCJv68bAMD3HA6Hr5sAAAAAVEuc6QYAAAAAwCaEbgAAAAAAbELoBgAAXjF9+nQ5HA4lJiZa64wxSkpKUmRkpOrUqaPY2Fjt2rXL43kFBQUaP368QkNDVa9ePQ0cOFDffvutR01ubq4SEhLkdDrldDqVkJCgvLy8G7BXAABcH0I3AAC4bps3b9a7776rtm3beqyfMWOGZs6cqTlz5mjz5s1yuVzq06ePTp48adUkJiZq+fLlSk5OVnp6uk6dOqX4+HgVFRVZNcOGDVNmZqZSUlKUkpKizMxMJSQk3LD9AwCgonwautevX6/77rtPkZGRcjgc+vjjjz22c3QcAIDK79SpU3r44Yf13nvvqUGDBtZ6Y4xmz56t559/XoMHD1Z0dLQWLFigM2fOaMmSJZIkt9ut999/X2+88YZ69+6t9u3ba9GiRdqxY4dWr14tSdqzZ49SUlL0t7/9TTExMYqJidF7772nTz75RPv27btiuwoKCpSfn++xAABwo/k0dJ8+fVrt2rXTnDlzLrudo+MAAFR+Y8eO1YABA9S7d2+P9YcOHVJ2drbi4uKsdUFBQerRo4c2bNggSdqyZYvOnz/vURMZGano6GirZuPGjXI6nerSpYtV07VrVzmdTqvmcqZPn24dcHc6nYqKivLK/gIAUB4+vWVY//791b9//8tuu/TouCQtWLBA4eHhWrJkiUaNGmUdHV+4cKE10C9atEhRUVFavXq1+vbtax0dz8jIsAbr9957TzExMdq3b59atmx5Y3YWAIBqKDk5WVu3btXmzZtLbcvOzpYkhYeHe6wPDw/XkSNHrJrAwECPM+QlNSXPz87OVlhYWKnXDwsLs2ouZ8qUKZo4caL1OD8/n+ANALjhKu13un19dJxL0gAAuLqsrCw9+eSTWrRokWrXrn3FOofD4fHYGFNq3aUurblc/bVeJygoSPXr1/dYAAC40Spt6L7a0fGfH/m26+g4l6QBAHB1W7ZsUU5Ojjp27Ch/f3/5+/srLS1N//u//yt/f39rDL90vM3JybG2uVwuFRYWKjc396o1J06cKPXzv//++1KfEwAAqGwqbegu4auj41OmTJHb7baWrKyscrYcAIDqrVevXtqxY4cyMzOtpVOnTnr44YeVmZmp5s2by+VyKTU11XpOYWGh0tLS1K1bN0lSx44dFRAQ4FFz/Phx7dy506qJiYmR2+3Wpk2brJqvvvpKbrfbqgEAoLLy6Xe6r8blckm6eHQ8IiLCWn+lo+M/P9udk5NjDcIVPToeFBSkoKAgr+wLAADVUXBwsKKjoz3W1atXTw0bNrTWJyYmatq0aWrRooVatGihadOmqW7duho2bJgkyel06vHHH9ekSZPUsGFDhYSEaPLkyWrTpo01X0urVq3Ur18/jRw5Uu+8844k6YknnlB8fDxzswAAKr1Ke6a7WbNmHB0HAKCKe+aZZ5SYmKgxY8aoU6dOOnbsmFatWqXg4GCrZtasWRo0aJCGDh2q7t27q27dulq5cqX8/PysmsWLF6tNmzaKi4tTXFyc2rZtq4ULF/pilwAAKBeHMcb46oefOnVK33zzjSSpffv2mjlzpnr27KmQkBA1adJEr732mqZPn6558+ZZR8fXrVunffv2WYP173//e33yySeaP3++dXT8xx9/1JYtW6zBun///vruu+88jo43bdpUK1euLHNb8/Pz5XQ65Xa7mYgF1c61vrJRE/jwrRDVEGNG5VTye7EL7yMAUH14cyz36eXl//73v9WzZ0/rccltPYYPH6758+frmWee0dmzZzVmzBjl5uaqS5culz067u/vr6FDh+rs2bPq1auX5s+fX+ro+IQJE6xZzgcOHHjFe4MDAAAAAOAtPj3TXZVw1gLVGWe6OUMF72LMqJw40w0AKCtvjuWV9jvdAAAAAABUdYRuAAAAAABsQugGAAAAAMAmhG4AAAAAAGxC6AYAAAAAwCaEbgAAAAAAbOLT+3QDAABUF3bdfpFbkQFA1caZbgAAAAAAbELoBgAAAADAJoRuAAAAAABsQugGAAAAAMAmhG4AAAAAAGxC6AYAAAAAwCaEbgAAAAAAbELoBgAAAADAJoRuAAAAAABsQugGAAAAAMAmhG4AAAAAAGxC6AYAAAAAwCaEbgAAAAAAbELoBgAAAADAJoRuAAAAAABsQugGAAAAAMAmhG4AAAAAAGxC6AYAAAAAwCaEbgAAAAAAbELoBgAAAADAJoRuAAAAAABsQugGAAAAAMAmhG4AAAAAAGxC6AYAAAAAwCb+vm4AAHs5HA5fNwEAAACosTjTDQAAAACATQjdAAAAAADYhNANAAAAAIBNCN0AAAAAANiE0A0AAAAAgE0I3QAAAAAA2ITQDQAAAACATQjdAAAAAADYhNANAAAAAIBNCN0AAAAAANiE0A0AAAAAgE0I3QAAAAAA2ITQDQAAAACATQjdAAAAAADYhNANAAAAAIBNCN0AAKDCpk+frs6dOys4OFhhYWEaNGiQ9u3b51FjjFFSUpIiIyNVp04dxcbGateuXR41BQUFGj9+vEJDQ1WvXj0NHDhQ3377rUdNbm6uEhIS5HQ65XQ6lZCQoLy8PLt3EQCA61KpQ3dSUpIcDofH4nK5rO3eGsQBAEDFpKWlaezYscrIyFBqaqouXLiguLg4nT592qqZMWOGZs6cqTlz5mjz5s1yuVzq06ePTp48adUkJiZq+fLlSk5OVnp6uk6dOqX4+HgVFRVZNcOGDVNmZqZSUlKUkpKizMxMJSQk3ND9BQCg3EwlNnXqVPPLX/7SHD9+3FpycnKs7a+++qoJDg42//jHP8yOHTvMAw88YCIiIkx+fr5VM3r0aHPLLbeY1NRUs3XrVtOzZ0/Trl07c+HChXK1xe12G0nG7XZ7bf+AG0ESSxkWwJtq8piRk5NjJJm0tDRjjDHFxcXG5XKZV1991ao5d+6ccTqd5u233zbGGJOXl2cCAgJMcnKyVXPs2DFTq1Ytk5KSYowxZvfu3UaSycjIsGo2btxoJJm9e/deti3nzp0zbrfbWrKysnz+XsP7EwBUDd4cyyv1mW5J8vf3l8vlspZGjRpJuniWe/bs2Xr++ec1ePBgRUdHa8GCBTpz5oyWLFkiSXK73Xr//ff1xhtvqHfv3mrfvr0WLVqkHTt2aPXq1b7cLQAAqiW32y1JCgkJkSQdOnRI2dnZiouLs2qCgoLUo0cPbdiwQZK0ZcsWnT9/3qMmMjJS0dHRVs3GjRvldDrVpUsXq6Zr165yOp1WzaWmT59uXYrudDoVFRXl3Z0FAKAMKn3oPnDggCIjI9WsWTM9+OCDOnjwoCTvDeJXUlBQoPz8fI8FAABcmTFGEydO1N13363o6GhJUnZ2tiQpPDzcozY8PNzalp2drcDAQDVo0OCqNWFhYaV+ZlhYmFVzqSlTpsjtdltLVlbW9e0gAAAV4O/rBlxNly5d9OGHH+r222/XiRMn9PLLL6tbt27atWvXVQfxI0eOSCrbIH4l06dP1wsvvODFvQEAoHobN26ctm/frvT09FLbHA6Hx2NjTKl1l7q05nL1V3udoKAgBQUFlaXpAADYplKf6e7fv7+GDBmiNm3aqHfv3vr0008lSQsWLLBqvDGIXw5HxwEAKLvx48drxYoVWrt2rRo3bmytL5kA9dKD3Tk5OdaBc5fLpcLCQuXm5l615sSJE6V+7vfff1/qADwAAJVJpQ7dl6pXr57atGmjAwcOeG0Qv5KgoCDVr1/fYwEAAJ6MMRo3bpyWLVumL774Qs2aNfPY3qxZM7lcLqWmplrrCgsLlZaWpm7dukmSOnbsqICAAI+a48ePa+fOnVZNTEyM3G63Nm3aZNV89dVXcrvdVg0AAJVRlQrdBQUF2rNnjyIiIrw2iAMAgIobO3asFi1apCVLlig4OFjZ2dnKzs7W2bNnJV28Ii0xMVHTpk3T8uXLtXPnTo0YMUJ169bVsGHDJElOp1OPP/64Jk2apDVr1mjbtm165JFHrCvdJKlVq1bq16+fRo4cqYyMDGVkZGjkyJGKj49Xy5Ytfbb/AABcS6X+TvfkyZN13333qUmTJsrJydHLL7+s/Px8DR8+3GMQb9GihVq0aKFp06ZdcRBv2LChQkJCNHnyZI9BHAAAVNzcuXMlSbGxsR7r582bpxEjRkiSnnnmGZ09e1ZjxoxRbm6uunTpolWrVik4ONiqnzVrlvz9/TV06FCdPXtWvXr10vz58+Xn52fVLF68WBMmTLAmSB04cKDmzJlj7w4CAHCdHMYY4+tGXMmDDz6o9evX64cfflCjRo3UtWtXvfTSS2rdurWki5e0vfDCC3rnnXesQfyvf/2rNWOqJJ07d05PP/20lixZYg3ib731VrlvG5Kfny+n0ym3282l5qhSrjV/AS6qxG+FqIIYMyqnkt9LVcP7EwDceN4cyyt16K5M+ACFqorQXTa8FcKbGDMqJ0I3AKCsvDmWV6nvdAMAAAAAUJUQugEAAAAAsEmlnkgNAG6Usl6Gz2WeAAAAKA/OdAMAAAAAYBPOdANVGJOkAQAAAJUbZ7oBAAAAALAJoRsAAAAAAJsQugEAAAAAsAmhGwAAAAAAmxC6AQAAAACwCaEbAAAAAACbELoBAAAAALAJoRsAAAAAAJv4+7oBAAAAuDKHw2HbaxtjbHttAMBFnOkGAAAAAMAmhG4AAAAAAGxC6AYAAAAAwCaEbgAAAAAAbELoBgAAAADAJoRuAAAAAABswi3DgErIztvDAAAAALhxONMNAAAAAIBNCN0AAAAAANiE0A0AAAAAgE0I3QAAAAAA2ITQDQAAAACATQjdAAAAAADYhNANAAAAAIBNCN0AAAAAANiE0A0AAAAAgE38fd0AoKZxOBy+bgIAAACAG4Qz3QAAAAAA2ITQDQAAAACATQjdAAAAAADYhNANAAAAAIBNCN0AAAAAANiE0A0AAAAAgE24ZRgAAEANZddtLI0xtrwuAFRFnOkGAAAAAMAmnOkGvMiuMwYAAAAAqibOdAMAAAAAYBNCNwAAAAAANuHycgAoh7J8hYAJhAAAAFCCM90AAAAAANiEM92o8Zj8DAAAAIBdCN0AAADwKjsPaPMVHgBVDZeXAwAAAABgE0I3AAAAAAA2qVGh+6233lKzZs1Uu3ZtdezYUV9++aWvmwQAAMqBsRwAUNXUmNC9dOlSJSYm6vnnn9e2bdv0q1/9Sv3799fRo0d93TRcwuFwlGnx1msB3sbfHWAPxnJIZf+cUJEFAOzgMDVkNoouXbqoQ4cOmjt3rrWuVatWGjRokKZPn16qvqCgQAUFBdZjt9utJk2aKCsrS/Xr178hba4snE6nr5sAVDtut9vXTYCN8vPzFRUVpby8PN5DvchbYzlQnTCeAPbw5lheI2YvLyws1JYtW/Tcc895rI+Li9OGDRsu+5zp06frhRdeKLU+KirKljYCqFkIYjXDjz/+yO/aS7w5lgPVCe8xgL28MZbXiND9ww8/qKioSOHh4R7rw8PDlZ2dfdnnTJkyRRMnTrQe5+XlqWnTpjp69GiNfnMrOeJTE8/4/xz9cBH98B/0xUX0w0UlZ1RDQkJ83ZRqg7Hct/i/fX3ov4qj764P/Vdx3hzLa0ToLnHpd3WMMVf8/k5QUJCCgoJKrXc6nfzBSqpfvz79IPqhBP3wH/TFRfTDRbVq1ZipU24YxnLf4v/29aH/Ko6+uz70X8V5YyyvEZ8GQkND5efnV+pIeE5OTqkj5gAAoPJhLAcAVFU1InQHBgaqY8eOSk1N9Vifmpqqbt26+ahVAACgrBjLAQBVVY25vHzixIlKSEhQp06dFBMTo3fffVdHjx7V6NGjy/T8oKAgTZ069bKXqdUk9MNF9MNF9MN/0BcX0Q8X0Q/2YCz3Hfru+tB/FUffXR/6r+K82Xc15pZhkvTWW29pxowZOn78uKKjozVr1izdc889vm4WAAAoI8ZyAEBVU6NCNwAAAAAAN1KN+E43AAAAAAC+QOgGAAAAAMAmhG4AAAAAAGxC6AYAAAAAwCaE7quYPn26HA6HEhMTrXXGGCUlJSkyMlJ16tRRbGysdu3a5btG2iApKUkOh8Njcblc1vaa0Acljh07pkceeUQNGzZU3bp1deedd2rLli3W9prSF7feemupvwmHw6GxY8dKqjn9cOHCBf3xj39Us2bNVKdOHTVv3lwvvviiiouLrZqa0hcnT55UYmKimjZtqjp16qhbt27avHmztb069sP69et13333KTIyUg6HQx9//LHH9rLsc0FBgcaPH6/Q0FDVq1dPAwcO1LfffnsD96Lmeuutt9SsWTPVrl1bHTt21JdffunrJlUJ06dPV+fOnRUcHKywsDANGjRI+/bt83WzqqTLfa7E1V3rcxguryyfV/Af3hjfr4XQfQWbN2/Wu+++q7Zt23qsnzFjhmbOnKk5c+Zo8+bNcrlc6tOnj06ePOmjltrjl7/8pY4fP24tO3bssLbVlD7Izc1V9+7dFRAQoH/+85/avXu33njjDd18881WTU3pi82bN3v8PaSmpkqS7r//fkk1px9ee+01vf3225ozZ4727NmjGTNm6H/+53/05ptvWjU1pS9+97vfKTU1VQsXLtSOHTsUFxen3r1769ixY5KqZz+cPn1a7dq105w5cy67vSz7nJiYqOXLlys5OVnp6ek6deqU4uPjVVRUdKN2o0ZaunSpEhMT9fzzz2vbtm361a9+pf79++vo0aO+blqll5aWprFjxyojI0Opqam6cOGC4uLidPr0aV83rUq50udKXFlZPofh8sryeQX/4Y3x/ZoMSjl58qRp0aKFSU1NNT169DBPPvmkMcaY4uJi43K5zKuvvmrVnjt3zjidTvP222/7qLXeN3XqVNOuXbvLbqspfWCMMc8++6y5++67r7i9JvXFpZ588klz2223meLi4hrVDwMGDDCPPfaYx7rBgwebRx55xBhTc/4mzpw5Y/z8/Mwnn3zisb5du3bm+eefrxH9IMksX77celyWfc7LyzMBAQEmOTnZqjl27JipVauWSUlJuWFtr4nuuusuM3r0aI91d9xxh3nuued81KKqKycnx0gyaWlpvm5KlXGlz5W4umt9DsOVXevzCq6sIuN7WXCm+zLGjh2rAQMGqHfv3h7rDx06pOzsbMXFxVnrgoKC1KNHD23YsOFGN9NWBw4cUGRkpJo1a6YHH3xQBw8elFSz+mDFihXq1KmT7r//foWFhal9+/Z67733rO01qS9+rrCwUIsWLdJjjz0mh8NRo/rh7rvv1po1a7R//35J0tdff6309HT9+te/llRz/iYuXLigoqIi1a5d22N9nTp1lJ6eXmP64efKss9btmzR+fPnPWoiIyMVHR1dbfulMigsLNSWLVs8+l2S4uLi6PcKcLvdkqSQkBAft6TquNLnSlzdtT6H4cqu9XkFZeetzzT+djSuKktOTtbWrVs9vptYIjs7W5IUHh7usT48PFxHjhy5Ie27Ebp06aIPP/xQt99+u06cOKGXX35Z3bp1065du2pMH0jSwYMHNXfuXE2cOFF/+MMftGnTJk2YMEFBQUF69NFHa1Rf/NzHH3+svLw8jRgxQlLN+X8hSc8++6zcbrfuuOMO+fn5qaioSK+88ooeeughSTWnL4KDgxUTE6OXXnpJrVq1Unh4uD766CN99dVXatGiRY3ph58ryz5nZ2crMDBQDRo0KFVT8nx43w8//KCioqLL/m7o9/IxxmjixIm6++67FR0d7evmVAlX+1yJq7vW5zBc2bU+r6DsvPWZhtD9M1lZWXryySe1atWqUmdwfs7hcHg8NsaUWleV9e/f3/p3mzZtFBMTo9tuu00LFixQ165dJVX/PpCk4uJiderUSdOmTZMktW/fXrt27dLcuXM93uxrQl/83Pvvv6/+/fsrMjLSY31N6IelS5dq0aJFWrJkiX75y18qMzNTiYmJioyM1PDhw626mtAXCxcu1GOPPaZbbrlFfn5+6tChg4YNG6atW7daNTWhHy5VkX2uCf1SGdTEv0dvGzdunLZv36709HRfN6VKKOvnSlxeWT+HobSyfl5B2V3vGMLl5T+zZcsW5eTkqGPHjvL395e/v7/S0tL0v//7v/L397eOcFx6ZDwnJ6fU0Y/qpF69emrTpo0OHDhgzWJeE/ogIiJCrVu39ljXqlUra+KdmtQXJY4cOaLVq1frd7/7nbWuJvXD008/reeee04PPvig2rRpo4SEBD311FOaPn26pJrVF7fddpvS0tJ06tQpZWVladOmTTp//ryaNWtWo/qhRFn22eVyqbCwULm5uVesgfeFhobKz8+vRv092mH8+PFasWKF1q5dq8aNG/u6OVXCtT5XMoHi1V3rcxiu7FqfV1B23vpMQ+j+mV69emnHjh3KzMy0lk6dOunhhx9WZmammjdvLpfLZc3cLF38rlhaWpq6devmw5bbq6CgQHv27FFERIT1gbom9EH37t1L3RZl//79atq0qSTVqL4oMW/ePIWFhWnAgAHWuprUD2fOnFGtWp5vm35+ftYtOGpSX5SoV6+eIiIilJubq88//1y/+c1vamQ/lGWfO3bsqICAAI+a48ePa+fOndW2XyqDwMBAdezY0aPfJSk1NZV+LwNjjMaNG6dly5bpiy++ULNmzXzdpCrjWp8r/fz8fN3ESu1an8NwZdf6vIKy89pnmuud4a26u3SWyVdffdU4nU6zbNkys2PHDvPQQw+ZiIgIk5+f77tGetmkSZPMunXrzMGDB01GRoaJj483wcHB5vDhw8aYmtEHxhizadMm4+/vb1555RVz4MABs3jxYlO3bl2zaNEiq6am9IUxxhQVFZkmTZqYZ599ttS2mtIPw4cPN7fccov55JNPzKFDh8yyZctMaGioeeaZZ6yamtIXKSkp5p///Kc5ePCgWbVqlWnXrp256667TGFhoTGmevbDyZMnzbZt28y2bduMJDNz5kyzbds2c+TIEWNM2fZ59OjRpnHjxmb16tVm69at5t577zXt2rUzFy5c8NVu1QjJyckmICDAvP/++2b37t0mMTHR1KtXzxrXcGW///3vjdPpNOvWrTPHjx+3ljNnzvi6aVUSs5eXXVk+h+HyyvJ5Bf/hjfH9Wgjd13Dpm2NxcbGZOnWqcblcJigoyNxzzz1mx44dvmugDR544AETERFhAgICTGRkpBk8eLDZtWuXtb0m9EGJlStXmujoaBMUFGTuuOMO8+6773psr0l98fnnnxtJZt++faW21ZR+yM/PN08++aRp0qSJqV27tmnevLl5/vnnTUFBgVVTU/pi6dKlpnnz5iYwMNC4XC4zduxYk5eXZ22vjv2wdu1aI6nUMnz4cGNM2fb57NmzZty4cSYkJMTUqVPHxMfHm6NHj/pgb2qev/71r6Zp06YmMDDQdOjQgVteldHl/uYlmXnz5vm6aVUSobt8rvU5DJdXls8r+A9vjO/X4jDGmOs97Q4AAAAAAErjO90AAAAAANiE0A0AAAAAgE0I3QAAAAAA2ITQDQAAAACATQjdAAAAAADYhNANAAAAAIBNCN0AAAAAANiE0A0AAAAAgE0I3QAAAAAA2ITQDVRjsbGxSkxM9HUzAADAZYwYMUIOh0OjR48utW3MmDFyOBwaMWJEuV93165dGjp0qBo1aqSgoCC1aNFCf/rTn3TmzBkvtPrKbr31Vs2ePdtj3eHDh3XPPffopptuUo8ePXTkyBGP7QMGDNA//vEPW9sF+BqhG6jCcnJyNGrUKDVp0kRBQUFyuVzq27evNm7cKElatmyZXnrpJY/nZGVl6fHHH1dkZKQCAwPVtGlTPfnkk/rxxx99sQuSLn9wYPHixYqKilJISIiefvppj22HDx/W7bffrvz8/BvYSgAAvC8qKkrJyck6e/aste7cuXP66KOP1KRJk3K/XkZGhrp06aLCwkJ9+umn2r9/v6ZNm6YFCxaoT58+Kiws9Gbzr2nSpEm65ZZbtG3bNrlcLk2ePNnalpycLD8/Pw0ZMuSGtgm40QjdQBU2ZMgQff3111qwYIH279+vFStWKDY2Vj/99JMkKSQkRMHBwVb9wYMH1alTJ+3fv18fffSRvvnmG7399ttas2aNYmJirOf52g8//KDf/e53ev311/X5559rwYIF+vTTT63tv//97/Xqq6+qfv36PmwlAADXr0OHDmrSpImWLVtmrVu2bJmioqLUvn17j9qTJ0/q4YcfVr169RQREaFZs2Z5HLg2xujxxx9Xq1attGzZMt11111q2rSp7r//fq1cuVIbN27UrFmzyty2jh076o033rAeDxo0SP7+/tZB7+zsbDkcDu3bt0+xsbE6cuSInnrqKTkcDjkcDknSnj17NHz4cLVo0UIjRozQ7t27JUl5eXn64x//qDlz5lSo34CqhNANVFF5eXlKT0/Xa6+9pp49e6pp06a66667NGXKFA0YMEBS6TPIY8eOVWBgoFatWqUePXqoSZMm6t+/v1avXq1jx47p+eef90rbVq5cqZtvvlnFxcWSpMzMTDkcDo8z1qNGjdJDDz2kESNGKC0tTX/5y1+sQfrgwYNyOp164IEH1LlzZ/Xs2dMapJcsWaLAwEANHjzYK20FAMDX/vu//1vz5s2zHn/wwQd67LHHStVNnDhR//rXv7RixQqlpqbqyy+/1NatW63tmZmZ2r17tyZOnKhatTw/5rdr1069e/fWRx99VOZ2xcbGat26dZIuBvovv/xSDRo0UHp6uiRp7dq1crlcatmypZYtW6bGjRvrxRdf1PHjx3X8+HHr565evVrFxcVatWqV2rZtK0maPHmyxo0bV6Gz+UBVQ+gGqqibbrpJN910kz7++GMVFBRcs/6nn37S559/rjFjxqhOnToe21wulx5++GEtXbpUxpjrbts999yjkydPatu2bZKktLQ0hYaGKi0tzapZt26devToob/85S+KiYnRyJEjrUH6tttu05kzZ7Rt2zb99NNP2rx5s9q2bauffvpJf/7znzkqDgCoVhISEpSenq7Dhw/ryJEj+te//qVHHnnEo+bkyZNasGCBXn/9dfXq1UvR0dGaN2+eioqKrJr9+/dLklq1anXZn9OqVSurpixiY2P15Zdfqri4WNu3b5efn58SEhKsIF4ylksXr67z8/NTcHCwXC6XXC6XJOn111/X3r17deutt+rAgQN6/fXXtX79en399dd69NFHNXToUDVv3lyjR4++4Ze+AzcKoRuoovz9/TV//nwtWLBAN998s7p3764//OEP2r59+2XrDxw4IGPMVQfi3Nxcff/998rKylJsbKxat26ttm3b6u9//3u52uZ0OnXnnXd6DMpPPfWUvv76a508eVLZ2dnav3+/YmNj5XQ6FRgYqLp161qDdMOGDbVgwQI9+uijuuuuu/Too4+qb9++mjx5ssaPH69Dhw6pffv2io6O1v/7f/+vXG0DAKCyCQ0N1YABA7RgwQLNmzdPAwYMUGhoqEfNwYMHdf78ed11113WOqfTqZYtW5b55xhjrMu+y+LnB9HT0tLUo0cP9ezZ0zqI/vPQfSW33HKLPvnkEx09elSffPKJQkNDNWbMGL3zzjt6+eWXFRwcrH379unAgQN65513ytw2oCohdANV2JAhQ/Tdd99pxYoV6tu3r9atW6cOHTpo/vz55X6tkjPcDodD/v7+mj17tnbv3q3Vq1frqaee0unTp8v1eiWXpJVcjvab3/xG0dHRSk9P19q1axUeHq477rjjis//7W9/qx07duibb75RUlKS1q1bpx07dmjkyJF68MEHNXv2bP3jH//Q448/rpycnHLvLwAAlcljjz1mHUy/3KXlPx+nL7dekm6//XZJsr6Sdam9e/eqRYsWZW7Tzw+ip6WlKTY2Vr/61a+UmZmpAwcOWAfQy+OVV15RXFycOnTooHXr1mnIkCEKCAjQ4MGDrYP1QHVD6AaquNq1a6tPnz7685//rA0bNmjEiBGaOnVqqbpf/OIXcjgcVx2IGzRooNDQUEVEROjOO++UJIWFhSkkJKTck6yVXJL29ddfq1atWmrdurV69OihtLS0Mh0Z/7mCggLrqPg333yjCxcuqEePHmrZsqVuv/12ffXVV+VqGwAAlU2/fv1UWFiowsJC9e3bt9T22267TQEBAdq0aZO1Lj8/XwcOHLAe33nnnbrjjjs0a9Ysa16VEl9//bVWr16thx56qFztio2N1dq1a7V+/XrFxsbq5ptvVuvWrfXyyy8rLCzM4wq6wMBAj8vdL7Vnzx599NFHevHFFyVJRUVFOn/+vCTp/PnzV30uUJURuoFqpnXr1pc9K92wYUP16dNHb731lsdtSaSLs48uXrxYDzzwQKkj6P/+979VXFysqKiocrWj5JK02bNnq0ePHnI4HOrRo4fWrVtXKnRfa5B+6aWX1L9/f3Xo0EFFRUW6cOGCtY1BGgBQHfj5+WnPnj3as2eP/Pz8Sm0PDg7W8OHD9fTTT2vt2rXatWuXHnvsMdWqVcsaux0Oh/72t79p9+7dGjJkiDZt2qSjR4/q73//u+677z7FxMSUukXntcTGxiolJUUOh0OtW7e21i1evLjUAfRbb71V69ev17Fjx/TDDz94bDPG6IknntCsWbN00003SZK6d++u9957T3v27NGHH36o7t27l6ttQFVB6AaqqB9//FH33nuvFi1apO3bt+vQoUP6+9//rhkzZug3v/nNZZ8zZ84cFRQUqG/fvlq/fr2ysrKUkpKiPn366JZbbtErr7xS6mc8+uijevfdd8vdvpJL0hYtWmRdenbPPfdo69atpS5Hu/XWW/XVV1/p8OHD+uGHHzyOzu/atUtLly61jorfcccdqlWrlt5//319+umn2rt3rzp37lzu9gEAUNnUr1//qrfDnDlzpmJiYhQfH6/evXure/fuatWqlWrXrm3VdO/eXRkZGfLz89Ovf/1r/eIXv9CUKVM0fPhwpaamKigoyKodMWLENS8Pv+eeeyTJOoBe8u+ioqJSofvFF1/U4cOHddttt6lRo0Ye2959912Fh4crPj7eWpeUlKRz586pS5cu+sUvfqGxY8devYOAqsoAqJLOnTtnnnvuOdOhQwfjdDpN3bp1TcuWLc0f//hHc+bMGWOMMT169DBPPvmkx/MOHz5sRowYYVwulwkICDBRUVFm/Pjx5ocffij1+r/61a/Mhx9+WOpnz5s3z5Tl7WPSpElGktm5c6e1rl27dqZRo0amuLjYWrdv3z7TtWtXU6dOHSPJHDp0yBhjTHFxsenWrZtZuXKlx+uuXLnSNGnSxISHh5v33nvvmu0AAKA6OnXqlHE6neZvf/tbhZ7fo0cPM3XqVO82CkApDmO8cH8gANWKMUbDhg1Ty5YtlZSUVGp7ycRmTHgCAMCNs23bNu3du1d33XWX3G63XnzxRa1bt07ffPNNqdnOr+XkyZNq3bq19uzZY13uDcAe/r5uAIDK51//+peWLl2qtm3b6uOPP5YkLVy4UG3atJEkff755/rLX/7iwxYCAFAzvf7669q3b58CAwPVsWNHffnll+UO3NLF74hnZWXZ0EIAl+JMNwAAAAAANmEiNQAAAAAAbELoBgAAAADAJoRuAAAAAABsQugGAAAAAMAmhG4AAAAAAGxC6AYAAAAAwCaEbgAAAAAAbELoBgAAAADAJoRuAAAAAABsQugGAAAAAMAmhG4AAAAAAGzy/wGcz7Q40ZRtQQAAAABJRU5ErkJggg==",
      "text/plain": [
       "<Figure size 1000x400 with 2 Axes>"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    }
   ],
   "source": [
    "# Now, let's visualize the histograms of silica and magnesium\n",
    "\n",
    "# Create a subplot with two histograms side by side\n",
    "fig, axes = plt.subplots(1, 2, figsize=(10, 4))  # 1 row, 2 columns\n",
    "\n",
    "# Plot the histograms for each column\n",
    "axes[0].hist(df['SIO2(WT%)'], bins=60, color='black')\n",
    "axes[0].set_xlabel('SiO$_2$, wt%')\n",
    "axes[0].set_ylabel('Count')\n",
    "axes[0].set_xlim([40, 100])\n",
    "\n",
    "axes[1].hist(df['MGO(WT%)'], bins=100, color='black')\n",
    "axes[1].set_xlabel('MgO, wt%')\n",
    "axes[1].set_ylabel('Count')\n",
    "# Note these xlims -> the data largely [but not completely!] sit between 0 and 10 wt%\n",
    "axes[1].set_xlim([0, 10])\n",
    "\n",
    "# Add spacing between subplots\n",
    "plt.tight_layout()\n",
    "\n",
    "# Display the plot\n",
    "plt.show()"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 200,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAcoAAAG5CAYAAAAOKnSzAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjguMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy81sbWrAAAACXBIWXMAAA9hAAAPYQGoP6dpAABB30lEQVR4nO3deXxU5b0/8M9km0zInphMAkkIGnaUzQ0oiVXgtli19lZxA19aC0XRQKtItUqtJopeoC11gdsrWEV8eQte7K+tRC1BigurYqiAEkiICSHrZJ1MMs/vj2+fOQlJjgkmmUnyeb9e88Kcc+bMk5N4Pnme8ywWpZQCERERdcjP2wUgIiLyZQxKIiIiEwxKIiIiEwxKIiIiEwxKIiIiEwxKIiIiEwxKIiIiEwxKIiIiEwxKIiIiEwxKIiIiE14Nyl27duEHP/gBEhMTYbFY8NZbb7XZr5TCypUrkZiYCJvNhoyMDOTl5bU5xul0YsmSJYiNjcWQIUNw3XXX4fTp0334XRAR0UDm1aCsq6vDJZdcgnXr1nW4f9WqVVi9ejXWrVuHvXv3wm63Y9asWaipqfEck5mZiW3btmHLli3YvXs3amtrce2116KlpaWvvg0iIhrALL4yKbrFYsG2bdtwww03AJDaZGJiIjIzM7F8+XIAUnuMj4/HM888g4ULF6K6uhoXXHAB/vSnP+Hmm28GAHz99ddISkrCX//6V8yZM8db3w4REQ0QAd4uQGfy8/NRUlKC2bNne7ZZrVakp6djz549WLhwIfbv3w+Xy9XmmMTERIwfPx579uzpNCidTiecTqfna7fbjYqKCsTExMBisfTeN0VERL1CKYWamhokJibCz69nG0t9NihLSkoAAPHx8W22x8fH49SpU55jgoKCEBUV1e4Y/f6OZGdn49e//nUPl5iIiLytsLAQw4YN69Fz+mxQaufW8JRS31jr+6ZjVqxYgWXLlnm+rq6uRnJyMgoLCxEeHv7tCkxERH3O4XAgKSkJYWFhPX5unw1Ku90OQGqNCQkJnu2lpaWeWqbdbkdTUxMqKyvb1CpLS0sxbdq0Ts9ttVphtVrbbQ8PD2dQEhH1Y73x+Mxnx1GmpqbCbrcjJyfHs62pqQm5ubmeEJwyZQoCAwPbHFNcXIzPP//cNCiJiIi6yqs1ytraWnz55Zeer/Pz83Ho0CFER0cjOTkZmZmZyMrKQlpaGtLS0pCVlYWQkBDceuutAICIiAjcfffd+PnPf46YmBhER0fjF7/4BSZMmIBrrrnGW98WERENIF4Nyn379uGqq67yfK2fGy5YsAAbN27EQw89hIaGBixevBiVlZW4/PLLsWPHjjZt0GvWrEFAQABuuukmNDQ04Oqrr8bGjRvh7+/f598PERENPD4zjtKbHA4HIiIiUF1dzWeURET9UG/ex332GSUREZEvYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZYFASERGZ8OmgbG5uxqOPPorU1FTYbDaMGDECTzzxBNxut+cYpRRWrlyJxMRE2Gw2ZGRkIC8vz4ulJiKigcSng/KZZ57Biy++iHXr1uFf//oXVq1ahWeffRa///3vPcesWrUKq1evxrp167B3717Y7XbMmjULNTU1Xiw5ERENFD4dlB9++CGuv/56zJ07F8OHD8d//ud/Yvbs2di3bx8AqU2uXbsWjzzyCG688UaMHz8emzZtQn19PTZv3uzl0hMR0UDg00E5Y8YMvPfeezh27BgA4NNPP8Xu3bvx/e9/HwCQn5+PkpISzJ492/Meq9WK9PR07Nmzp9PzOp1OOByONi8iIqKOBHi7AGaWL1+O6upqjB49Gv7+/mhpacFTTz2FW265BQBQUlICAIiPj2/zvvj4eJw6darT82ZnZ+PXv/517xWciIgGDJ+uUb7xxht49dVXsXnzZhw4cACbNm3Cc889h02bNrU5zmKxtPlaKdVuW2srVqxAdXW151VYWNgr5Sciov7Pp2uUDz74IB5++GHMmzcPADBhwgScOnUK2dnZWLBgAex2OwCpWSYkJHjeV1pa2q6W2ZrVaoXVau3dwhMR0YDg0zXK+vp6+Pm1LaK/v79neEhqairsdjtycnI8+5uampCbm4tp06b1aVmJiGhg8uka5Q9+8AM89dRTSE5Oxrhx43Dw4EGsXr0ad911FwBpcs3MzERWVhbS0tKQlpaGrKwshISE4NZbb/Vy6YmIaCDw6aD8/e9/j1/96ldYvHgxSktLkZiYiIULF+Kxxx7zHPPQQw+hoaEBixcvRmVlJS6//HLs2LEDYWFhXiw5ERENFBallPJ2IbzN4XAgIiIC1dXVCA8P93ZxiIiom3rzPu7TzyiJiIi8jUFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkgkFJRERkwueDsqioCLfffjtiYmIQEhKCiRMnYv/+/Z79SimsXLkSiYmJsNlsyMjIQF5enhdLTEREA4lPB2VlZSWmT5+OwMBA/O1vf8ORI0fwX//1X4iMjPQcs2rVKqxevRrr1q3D3r17YbfbMWvWLNTU1Hiv4ERENGBYlFLK24XozMMPP4x//vOf+OCDDzrcr5RCYmIiMjMzsXz5cgCA0+lEfHw8nnnmGSxcuLBLn+NwOBAREYHq6mqEh4f3WPmJiKhv9OZ93KdrlNu3b8fUqVPx4x//GHFxcZg0aRI2bNjg2Z+fn4+SkhLMnj3bs81qtSI9PR179uzp9LxOpxMOh6PNi4iIqCM+HZQnTpzACy+8gLS0NLzzzjtYtGgR7r//frzyyisAgJKSEgBAfHx8m/fFx8d79nUkOzsbERERnldSUlLvfRNERNSv+XRQut1uTJ48GVlZWZg0aRIWLlyIe+65By+88EKb4ywWS5uvlVLttrW2YsUKVFdXe16FhYW9Un4iIur/fDooExISMHbs2DbbxowZg4KCAgCA3W4HgHa1x9LS0na1zNasVivCw8PbvIiIiDri00E5ffp0HD16tM22Y8eOISUlBQCQmpoKu92OnJwcz/6mpibk5uZi2rRpfVpWIiIamALO943Nzc146aWXsHPnTrS0tGD69Om49957ERwc3GOFW7p0KaZNm4asrCzcdNNN+OSTT7B+/XqsX78egDS5ZmZmIisrC2lpaUhLS0NWVhZCQkJw66239lg5iIho8DrvoLz//vtx7Ngx3HjjjXC5XHjllVewb98+vP766z1WuEsvvRTbtm3DihUr8MQTTyA1NRVr167Fbbfd5jnmoYceQkNDAxYvXozKykpcfvnl2LFjB8LCwnqsHERENHh1eRzltm3b8MMf/tDz9UUXXYSjR4/C398fAPDFF1/giiuuQFVVVa8UtDdxHCURdaixEWhpAfz9gR5sLaOe15v38S4H5bXXXouAgAD84Q9/wNChQ3HTTTchIiICP/rRj+ByubBhwwY0NDS0eV7YXzAoiaiN+nqgtBSorgaam4GAACAiAoiLA0JCvF066oBPTDjwl7/8BfPmzUNGRgZ+//vfY/369QgPD8cjjzyCX/3qV0hKSsLmzZt7tHBERH2uvh7IzwfKyqQWGRUl/5aXy/b6em+XkPpYt6ewq6qqwoMPPojPPvsML730EiZOnNhLRes7rFESkcfJkxKSsbHt95WXAzExwPDhfV0q+gY+UaPUIiMjsWHDBjz77LO444478OCDD6KhoaFHC0VE5BWNjdLc2llnwNBQ2d/Y2LflIq/qclAWFhbi5ptvxoQJE3DbbbchLS0N+/fvh81mw8SJE/G3v/2tN8tJRNT7WlrkmWRgYMf7AwNlf0tL35aLvKrLQTl//nxYLBY8++yziIuLw8KFCxEUFIQnnngCb731FrKzs3HTTTf1ZlmJiHqXv7903HG5Ot7vcsn+f/f2p8Ghy+Mo9+3bh0OHDuHCCy/EnDlzkJqa6tk3ZswY7Nq1yzMRABFRvxQcLL1by8sBq7X9/tpaeUbJoSKDSpeDcvLkyXjsscewYMECvPvuu5gwYUK7Y37605/2aOGIiPpcXBxQVydhGRoqza0ul4RkcLDsp0Gly02vr7zyCpxOJ5YuXYqioiK89NJLvVkuIiLvCAkBUlOl5tjYCFRWyr8xMbKd4ygHnW4PDxmIODyEiDrEmXn6DZ8aHuLv74/S0tJ228vLyz3T2RERDQjBwcCQIQzJQa7bQdlZBdTpdCIoKOhbF4iIiMiXdLkzz+9+9zsAsrTVf//3fyM0NNSzr6WlBbt27cLo0aN7voRERERe1OWgXLNmDQCpUb744ottmlmDgoIwfPhwvPjiiz1fQiIiIi/qclDm5+cDAK666ips3boVUVFRvVYoIiIiX9HtZ5Tr169nSBIR0aDR5RqlNmrUKCQkJCA9PR3p6enIyMjAqFGjeqNsREREXtftGmVxcTGee+45hIeHY82aNRgzZgwSEhIwb948PqMkIqIB51tPOPDll1/iySefxGuvvQa3242WfjirPiccICLq33rzPt7tptfa2lrs3r0bO3fuRG5uLg4dOoQxY8ZgyZIlSE9P79HCEREReVu3gzIqKgrR0dG444478Oijj2LGjBmIiIjojbIRERF5XbeDcu7cudi9ezf+9Kc/obCwEAUFBcjIyMCYMWN6o3xERERe1e3OPG+99RbKysqQk5ODGTNm4L333kNGRgbsdjvmzZvXG2UkIiLymm7XKLWLL74YLS0tcLlccDqd+Pvf/46tW7f2ZNmIiIi8rts1yjVr1uD6669HdHQ0LrvsMrz++usYNWoUtm3bhrKyst4oIxERkdd0u0b52muvISMjA/fccw9mzpzJ4RRERDSgdTso9+3b1xvlICIi8kndbnolIiIaTBiUREREJhiUREREJhiUREREJhiUREREJno0KL/73e/iN7/5Derr63vytERERF7To0GZkpKC999/n/O+EhHRgHHeU9h15OWXXwYgS3ERERENBL3yjDI0NLQ3TktERNTnuhWUzc3NePbZZzF58mSEhoYiLCwMkydPxnPPPQeXy9VbZSQiIvKaLje9NjQ0YNasWfjwww9xzTXXYObMmVBK4YsvvsDy5cuxfft27NixA8HBwb1ZXiIioj7V5aDMzs5GYWEhDh48iIsvvrjNvk8//RTXXXcdnn76aaxcubKny0hEROQ1XW563bJlC1avXt0uJAHgkksuwXPPPYfNmzf3aOGIiIi8rctBWVBQgMsuu6zT/VdccQUKCgp6pFBERES+ostBGR4ejtLS0k73l5SUcG1KIiIacLoclFdddRWysrI63f/0008jIyOjJ8pERETkM7rcmefxxx/H5ZdfjiuuuALLli3D6NGjAQBHjhzBmjVrcOTIEXz00Ue9VlAiIiJv6HJQjh07Fjk5Obj77rsxb948WCwWAIBSCqNHj8Y777yDcePG9VpBiYiIvKFbU9hdccUVyMvLw8GDB3H8+HEAwMiRIzFx4sTeKBsREZHXnddcr5MmTcKkSZN6uixEREQ+p9tBuWzZsg63WywWBAcH46KLLsL111+P6Ojob104IiIib7MopVR33nDVVVfhwIEDaGlpwahRo6CUwvHjx+Hv74/Ro0fj6NGjsFgs2L17N8aOHdtb5e5RDocDERERqK6u5hAXIqJ+qDfv491ePeT666/HNddcg6+//hr79+/HgQMHUFRUhFmzZuGWW25BUVERZs6ciaVLl/ZoQYmIiLyh2zXKoUOHIicnp11tMS8vD7Nnz0ZRUREOHDiA2bNno6ysrEcL21tYoyQi6t98qkZZXV3d4Qw9Z8+ehcPhAABERkaiqanp25eOiIjIy86r6fWuu+7Ctm3bcPr0aRQVFWHbtm24++67ccMNNwAAPvnkE4wcObKny0pERNTnut30Wltbi6VLl+KVV15Bc3MzACAgIAALFizAmjVrMGTIEBw6dAgA+s34Sja9EhH1b715H+92UGq1tbU4ceIElFK48MILERoa2qMF60sMSiKi/q037+PnNeEAAISGhna4NiUREdFA0uWgvOuuu7p03P/8z/+cd2GIiIh8TZeDcuPGjUhJScGkSZNwnq21RERE/U6Xg3LRokXYsmULTpw4gbvuugu33347p6kjIqIBr8vDQ55//nkUFxdj+fLlePvtt5GUlISbbroJ77zzDmuYREQ0YJ13r9dTp05h48aNeOWVV+ByuXDkyJF+2/OVvV6JiPo3n5qZR7NYLLBYLFBKwe1292SZiIiIfEa3gtLpdOL111/HrFmzMGrUKBw+fBjr1q1DQUFBv61NEhERmelyUC5evBgJCQl45plncO211+L06dN488038f3vfx9+fuddMe2W7OxsWCwWZGZmerYppbBy5UokJibCZrMhIyMDeXl5fVIeIiIa+Lrc6/XFF19EcnIyUlNTkZubi9zc3A6P27p1a48VrrW9e/di/fr17SY5WLVqFVavXo2NGzdi5MiRePLJJzFr1iwcPXoUYWFhvVIWIiIaPLoclPPnz4fFYunNsnSqtrYWt912GzZs2IAnn3zSs10phbVr1+KRRx7BjTfeCADYtGkT4uPjsXnzZixcuLDD8zmdTjidTs/XetUTIiKic3VrwgFvuffeezF37lxcc801bYIyPz8fJSUlmD17tmeb1WpFeno69uzZ02lQZmdn49e//nWvl5uIiPq/vnm4+C1s2bIFBw4cQHZ2drt9JSUlAID4+Pg22+Pj4z37OrJixQpUV1d7XoWFhT1baCIiGjDOe1L0vlBYWIgHHngAO3bsQHBwcKfHndskrJQybSa2Wq2wWq09Vk4iIhq4fLpGuX//fpSWlmLKlCkICAhAQEAAcnNz8bvf/Q4BAQGemuS5tcfS0tJ2tUwiIqLz4dNBefXVV+Pw4cM4dOiQ5zV16lTcdtttOHToEEaMGAG73Y6cnBzPe5qampCbm4tp06Z5seRERDRQ+HTTa1hYGMaPH99m25AhQxATE+PZnpmZiaysLKSlpSEtLQ1ZWVkICQnBrbfe6o0iExHRAOPTQdkVDz30EBoaGrB48WJUVlbi8ssvx44dOziGkoiIesR5T4o+kHBSdCKi/s0nJ0UnIiIaDBiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJhiUREREJgK8XQAion6hsRFoaQH8/YHgYG+XhvoQg5KIyEx9PVBaClRXA83NQEAAEBEBxMUBISHeLh31AQYlEVFn6uuB/HygoQEICwMCAwGXCygvB+rqgNRUhuUgwGeURESdKS2VkIyNBaxWwM9P/o2JkabY0lJvl5D6AIOSiKgjjY3S3BoW1vH+0FDZ39jYt+WiPsegJCLqSEuLPJMMDOx4f2Cg7G9p6dtyUZ9jUBIRdcTfXzruuFwd73e5ZL+/f9+Wi/ocg5KIqCPBwdK7tba24/21tbKfQ0UGPAYlEVFn4uIkCMvLAacTcLvl3/Jy2R4X5+0SUh/g8BAios6EhMgQED2OsrZWmltjYjiOchBhUBIRmQkJAYYP58w8gxiDkoioMwxHAoOSyPfxZt33OG0dtcKgJPJVvFl7B6eto3Ow1yuRL9I367IyqUVGRRm9L/PzZT/1Dk5bR+dgUBL5It6svYPT1lEHfDoos7OzcemllyIsLAxxcXG44YYbcPTo0TbHKKWwcuVKJCYmwmazISMjA3l5eV4qMVEP4M3aezhtHXXAp4MyNzcX9957Lz766CPk5OSgubkZs2fPRl1dneeYVatWYfXq1Vi3bh327t0Lu92OWbNmoaamxoslJ/oWeLP2Hk5bRx2wKKWUtwvRVWfPnkVcXBxyc3Mxc+ZMKKWQmJiIzMxMLF++HADgdDoRHx+PZ555BgsXLuzwPE6nE06n0/O1w+FAUlISqqurER4e3iffC1GnGhuBo0flmaTV2n6/0ynHjBrFXrC94eRJeRYcE9N+n94+fHhfl4q+gcPhQERERK/cx326Rnmu6upqAEB0dDQAID8/HyUlJZg9e7bnGKvVivT0dOzZs6fT82RnZyMiIsLzSkpK6t2CE3UH5xj1Lk5bR+foN0GplMKyZcswY8YMjB8/HgBQUlICAIiPj29zbHx8vGdfR1asWIHq6mrPq7CwsPcKTnQ+eLP2Hj1tne44VVkp/8bEcGjIINVvxlHed999+Oyzz7B79+52+ywWS5uvlVLttrVmtVph7ahJi8hXcI5R7+K0ddRKvwjKJUuWYPv27di1axeGDRvm2W632wFIzTIhIcGzvbS0tF0tk6jf4c3a+3i9CT7e9KqUwn333YetW7fi/fffR2pqapv9qampsNvtyMnJ8WxrampCbm4upk2b1tfFJeodwcHAkCG8afe2xkaZeYfDbugcPl2jvPfee7F582b83//9H8LCwjzPHSMiImCz2WCxWJCZmYmsrCykpaUhLS0NWVlZCAkJwa233url0hNRv8CpAukb+HRQvvDCCwCAjIyMNttffvll3HnnnQCAhx56CA0NDVi8eDEqKytx+eWXY8eOHQjrbLA2ka9jU2vfaGwEamqAwkLpLMV5XakT/WocZW/pzfE3RF32TTUbBmjPaH2dCwokLJOSZLpAm804jmMm+5XevI/7dI2SaNAwW7GirEyeUTY1sWnw22p9na1WwGKRCeerqmRbUpIRlq2nCuQfJoOaT3fmIRo0OpsEPSQEOHECOH6cq4j0hNbX2d8fUEr+CImKknGqZWXGsZwqkP6NQUnkbWaToJeXG/OPAlxF5Ns49zr7+8tLz+s6ZIg0w+rpLTmvK/0bg5LI2zqbBN3pBBwOIDxcjjm3ZsNVRLrn3Otstcq11bXygIC215lTBdK/MSiJvK2zFSv0TdtiMWo/rbFpsHs6us4xMRKYlZXSy9XPT64ppwqkVhiURN7W2SToOhx1c+G50y6yabB7OrrONpt04NEdetxueW7JeV2pFfZ6JfIFcXFSoykvlyZV3Tyoa5Wxse3fU1srN3Q2DXZdR9fZz08Cc9QoCc2wMF5TaoNBSeQLOpsE/aKL5MZeXy83dD1spLaWTYPng5PN03lgUBL5is4mQW89QJ439m+Pk81TNzEoiXzNuTdt3th7B68hdRGDksiXmIUhb+xEXsGgJPIFXMGCyGcxKIm8zWyeV65gQeR1HEdJ5G2dzfPKaeqIfAKDksibzOZ5BThNHZEPYFASeVNn87xqnKaOyOsYlETe1Nk8rxqnqSPyOgYlkTd1Ns+rxhUsiLyOQUnkbXFxxmLMTqdMzO10cgULIh/B4SFE3sb5R4l8GoOSyBdwmjoin8WgJPIl/T0cGfQ0ADEoiejb4xR8NIAxKIno2+EUfDTAsdcrka9obJRg6W+z8HAKPhrgWKMk8rb+3GzZnSn4+MyS+ikGJZE3mTVbVlQASUmy/dyQ8ZVOM12Zgq+2llPwUb/GoCTyptbNlprbLQF6+jRQVAQkJxs1TP0eX6l9tp6Cz2ptv59T8NEAwKAk8paOmi0bGoDCQpmZJzJSamJ+flLDLCszjvOVTjN6Cr7y8o6DsrZWnlWy2ZX6MXbmIfKWjpoty8okJKOigCFDAKWkNhYTAxQXy6u3Os2cb2ciTsFHAxxrlETecm6zpdMJ1NRIQAKy3d9fXk6nBKvFIv99bu3t23Sa6WpnonOfi7b+mlPw0QDGoCTylnObLVta5BXw7/8t6+ulZmm1yn9bLLK9o44xnXWa+aZOP10ZA9nYCJSUyPn9/WW/yyXHBga2DVa73Tc6GRH1IAYlkTfFxUkglZdL6Pj5ydfNzUazKiDBo5SE5bkdY5xOCbqWFgmwujrZ5nB8cy2xdWcip1NC0d9faqiFhcDJk7Ktvl6CNCREar06xFNT5dytg1XXiIkGCAYlkTedu3KI2y0Bl5QkIWmzyXFWqxGQutm1oUECyuGQGp/FIs84g4JkW2Cg9JiNiuq404/uTBQYKD1sHQ6gqkr+dbnk/GVlwLBhwOjREognTsj7Ro+W/ZWVst9qlfOXlsrk7kQDCIOSyNtarxySmCg1OaWkdul2S2jV1gIJCXJ8ebmEVnGxUXt0uaQW2NgInD1rNIueOSPBabO1D7OWFqkd1tYa/xYWSm2xpkY+KyhIylJSIrVOPdSjokKC3OEwnpkGBUmZIiPlRTRAMCiJfIF+lhgWJrW1zjrGALLvyBEJvZgYeV9MjDwfdDqldhgbKzXJyko5btgweW/rTj/+/lJjrKiQMDx7VsI5Lk7OWV4uNcxx44CmJvm6uVnKWFcHREfLcbW18t6qKnlZLFIWduShAYJBSeRNZj1OO+sYY7fLexISZN/p08Z+t1tqkg0NEpoBARJi4eHy0p1+amokIE+flpefn4RlaKgxxEPXUKuq5LPq6owytLTIcc3NUovUnxsVJeHYupnXz+/8O/j4ygxENKgxKIm8pSs9TjvqGKODIyLCCBLdU1aPraypAb7+Ws5XXS0hGBcnn+NySRNrXZ0xPV59vcwCFBAg76+qkhpjeLjUOuPjjXPX1sq/rUMsOlpqr5GR8h5Azrd/v3zd3VmE+vP8tzTgcMIBIm/pzqobrScDaD3+Uo+zbG6W43RHn+JiCUs/PwmqkBAJsqNHZbvbbQTnkCFyLodDnmlWVMg5KyvlXEpJeLvdUmNsaJAg9fOT4wID5VirVb4Xh0NqqYWF8vLzk/fpSQny8yUIO6P/gCgrk/d0571EvYA1SiJv6OqqGxUVHQ/zCAoypocLC5PgCgqS9zY0GJ13GhqkthcUJGHY1CRBmZws+yMiJFSrq40OOFarhNPp0xKAMTFGbbekRM6XmChlKSqSEIuMlEA8fFjC9vRp+R5jY4GUFCmj1dq13rEdzX/b1fcS9QIGJZE3dGXVjbNnga++ks4x5zbNKiXHlZcbnWvOnDF6wV54oTEVnb+//HdkpITeqVNSO6yokP8+elTCODpajg8IkGDVkyF89ZV8RlSUbIuPl6DVvWlDQuR72bdPzglI0LlcwLFjUtarr5bga2mR93U2i5CuSTudEsJhYUZTLsBlu8grGJRE3tDZqht6qrrmZgmviAhg6FBjf+uaVUiIBFV1tZzL4TDGVQYESKefpCQ5h7+/UcM8dUpqhkeOGDXEsDBp0nQ4pMZZViZlcLmMQJ80SZprAwPl+WdEhLzq64EvvpCaqZ7aLjBQAvGCC+Qz3noLmDpVymyxSHgmJrYNu/p64MABYMcOKadSsn/4cOl5m5DAZbvIKxiURN5w7vR1enB/TY2EQEWF1PoSE+V4HaA68HSP1NRUqXE1NUloBgVJEAYFSSDV1EhNUs8l63DIsTk5EjihoXLeyEh5Vllfb4yLTEyUEC4tlVplUZGEqt0OXHqp/PeQIRKE//ynNL3q2m9Dg5ShpkbOcfKknHPCBNne2CjPL4cMkfCsrwc+/BDYvdsYo+lyyTUpKAC+/BKYPl2Cn8t2UR9jUBJ5i56+rqhIngXqZkm3WwLE4ZDQO3tWQkMHZViYhFRzs9Hk2tQkNU+nU4KzpkaaSCsr5fxOpwTTiRNS8ysslHPExcm+0lIJObdb3hcYaASt7lGrZ/txuWT78OEScJGRUg6LRYK3qsoYA6qHmlitckxhoXwfI0fKewsLJfz27wd27ZL3BQfLdt3LtaFBth85Iv89cqScw5vNrxy2MqgwKIm8RU9ft3+/hFBYmDQ3xsRI4OTnyys0FBgxQgKruVmCSAebXr/Sz08CMTBQbuBnz0pIBgUBH38sodXYKAGnlDGEpKZGzlFXZ8wGFBMjn1FfL6/QUNmul/2KjJTPdDik1jlsmISu7i3b0iJNs2VlxkTvLS0S6Ckpco7CQgm8kBB5b0GBlDEuTs6rn68GB0tZm5qkg1Bzs5yrvl7K05NDRnT46QnfOwpBDlsZlBiURN6kh29MmGAM9dDPLHUv1YAAI8R0jTMvTzrHjBgh73E4JKhCQ6WjTUqKhOyhQ3JjT0mRfW63hIG+0ev1Ll0uCQo/P6MpVNfYlDKGkLjdUqbAQAlCi0XKpKe90z116+uNmmh1tdQsa2vlM8eNk3DW4WizSbDX1cnLz08CuLZWAjs4WP6tqZE/JoqLjSbeiopvt2i1/uOhokKC/MwZKWtEhDxfbT3DUFfGvTIsByQGJZE36Y47UVESEJrTacx0U1kpoahvzEeOSFhZLHKjP3NGgsRmM+Z/TUmRgGlulhpbaqqcx2aT42tr5XOsVjnGZpMAqK83hoTo1UrcbuNfQPbX1koNr7xcQiYuTrYVFBjPS3XTbVOThHFTk+xvaZEQOnlSvvbzk32AnMdqlYCKiTFqumfOyH793PPsWflebTYJbD8/YMyYrl93XTMsKQGOHzeWEbNajTGnutOQDsHuDlth8+yAwaAk8qbOer/q2XYSEoweqIWF8szyq6/kmPx8GX5x9qy8d8QICcWGBgmWs2eNWqqe3NzhkCbakBCp6VVVSU0zPl4+o7xczh0fL/t0yOmlv3Qv2/JyKbNSclxdnZSzpMSo/bYOft0k63JJ+U+dku1Op9EJSe/XHZKio6VsNpuxYklpqQTluHHG89WyMvnjIT7eGOJipnXNUM9nq5+DBgTIfwNynVpaJCQLC6UM3zTuVS9J1nr9zq4uhE0+i0FJ5E3n9n7VdMA1NMiYyIAAGafY2CjHBQZKDa+szJhirqhIamKAHK8nKG+9KLRuJoyJkZBpapJgq66W99ntxk3b319u+npJLt3sq59tBgfL+/38JMB0sAJyTj3W81z6GE2f28/PCKugIDnObpcy22zyGZWVRjhHRUntLiFBvkc91EXT5QkKaruaia4ZhoXJBAmt1+6sq5NjExPlez1+XJqdm5rkMzoLSt0UnZcnNWW9fqeeBrB186wuA59z9hsMSiJva714c2ioMQmBDrfYWLmhu1xy49VhEhIiYaXHTVqtcrMeMkTeZ7fLDVuHlu6BGhQkn+d2SyhERMi5IyPl+abTaTTb6ubdqChjYeezZyVodEjW1cnXumasp9PrjtbhqZ+X6gWibTYpf0GBXKu4OKMcZ85I7fCyy+TrxkapyX36qQRWU5MEVkqKNM3qmp8eN1pebjTDBgbK9dVf69mN6urkeg4b1r7mr+np/3QzdUqKXAddy0xKkvPqyR74nLNfYVASmemL5rFzF2/WS2tddJHcPEtKpLYYGipBGBAgZdI1ndhYeV9ysrw3OVmelekajh5iUVMjN/HmZmO+17AwI4zDw2XbRRcBEyfK2MXYWOnBun+/TCpQX9+2J2tgoHGuzmYZOh863B0OeQFy/oAA41mi3S7fT3W1lLGwUI756CNjRqPgYPm+jh8H/vUvmTTB6ZQ/FpxOCajGRrkmOmR1p6GgIKPHsf4d0J997rjWwkK5BiEhxry9QUHyqqyUn0VcnJTLbBIJTs/nkxiURB3p62EArRdvbh3M9fXy/K2+Xm6+Tqc0CzY1Sbn0cliVlVKjCQ+XjjK6801UlNzoKyslNHWNZ8gQCRX9b2iofEZ4uARQQ4N8r9Ony829oEBu5E1NUoZzm1XdbiM8eoueazYgQL6HoiLj+avTKd+/n5/8a7UateiWFqOG/P778n3FxEiZjx6V8CstlUDW4aaU0eM4PFxqiMnJEqL5+UYZlDKWHEtNlcDWkyHomqde6kxP3acX4D4Xp+fzWQxKonN5cxjAuTfIkBCp4X3xhTG3qh7moZ+plZdL4MXHy81ZN12GhgLp6fKe06flhp2aKkGhmzV1M2lJiXyvCQlGr8/QUGDvXmDPHmNO2fJyKUdwsBHcbrcEhu4V29t0mV0uY1t5uTRr+vkZ11DPN9vcbAx7aR1y4eHGkBS9FJnNJtuDgyVA/fzkWulevGVlct1071z9B0l9vez7+mv57MBA2R8QIIGrpwasrgZGjer4++L0fD6LQUl0Ll9bvSIyUmo0p07Jf+s5YHXt9tNP5dnayJFyk4+NlfJbLHKjP3lS/nvSJLmh19VJcOpJCHSHl/HjgcmTZbhHUJDcuMvLJTSrquS/S0okfHTPUB0UfRWSZvSyYJqfX9ty6YWnAwONJcIsFmMBasCYfKG6WmqdISHyPZ88aUz/FxQkNfXkZNlfVyc/g5ISowOWxWLUIi+6SH5eFot8xtdfS/DabG3L63Jxej4fxaAkaq2ry1/1dfPYmDESYOXlclOvqJCbvcMhIaqbW/Wwj8JCY6yhwyEhP3Kk8QxOry6inzU2NspzszNnJGhtNgkel0uCBJAA0BMkWCwSEHqIiC/qLLxb10TPpWf90XPe2mzSxHv6tOwPCDBqpyNGSJjW1hoTJugeuM3NEnhOpzSdjx8vwTpkiJwrOFgCtDW9bBqbXX0Og5Kota4sf+WN5rHYWHle+K9/SfOhHscYHS033OHDjTled+2Sm7HVKttCQ2WO1927jdqQfr5ns0nQBgXJs88zZ+RmX1pq9EQNCzOe++mxhIGBcm5di9K1V7MQ6m/0MBhAmlUBY6FqQJ5vBgdLeF5wgdEUrZvD9fNO3cO2qkquT0WFjH/9znfkjxfdQSk4WFoJyOcwKIla62wCAM2bzWOxsXJznTBBQkz3Wm3dIzcvT2o3sbHGOEfdWUf3mE1NlfedPSuvgAAZ+uBwyNfJyVJ7dDqlBqSfxenFn8vKjM/TzYd6QveWlvZNoAOBbpptbjZq2JpuZdAB2tQk10lPuqCHtuTlyTCRyEj5g+Of/5TQHDdOaqi6FzOHh/gcBqUv4AwdvqOzCQA0X2geaz14vrWqKnmOqadhA+R3qrpatulJCYqL5XeuuLhteLrdxnbd61OPJdTNiTExRiciPQdsYqJ8tr+/1KwOH5bQ9dUm2Z6mpwPsiA5K3VNYDz2JipJrd/So/FESHGysnBIXJ021elHs1hMm8F7hFQxKb+JKBL6powkAXC7fbx5rapIbqa4V+/lJ2aur5fcqOFhqjEVF8r24XPKsMibGmNQ8KUm2WyxGUOohKCEhErZ6ujc9vV1LizT/NjdL8AYGyuvcGXgGI/2ctLlZ/l8vLZWfTXAw8NlnRhN2dLT8zjU2SqCGh0vv2JQUY4WW8HBj6EpPr5xCphiU3sKVCHxXZxMAxMT49o1JD9vQf3jpAfN6cnLd2Qcwan9JScYQD8CouegemyUlxvCKoCAjcPV0c01N8vzSbpdz6uWxBktt8nw0N8vvlFlNNChIesempRlN3yEhwJQpEp4REdJsW1EhP8OwMKOG2VO1TtZePRiU3vJthyDwl7h3dTYBgC/Tw0j27ZPfraAgo3bpcEjoOZ1S+wsKklqMHhoRGSnNgYCEnlLyPj3ZQVhY29loAgONZ3WjRsm1qqqS0AwONuaEHUide/qSXn/z9Gm53nrdzsJC+fldcIFsCwuTr0eOlJ8pYKzYEhRkTPmn5+vtyu9yRy1detxpZGT7pv/+9P/IeWJQesO3GYLA5tq+1d/+xx8zRmoi+fkSjg0N8nuk/ygLDZVmvKYm+Z3Rc7ympBiTGPj5GWtajh8P/PWv8tyyokLOVV5u3BRjY2VYiR7qEBUlN/evvzZqnQzLb6elxeiBe+qUdAqKjJTeyUOHGuuClpTIzzw+Xn4uenmyqCj5uTc2ys+4o2ZbHXZOp/ysdUtXTQ3w+ecS0IB83vDh8nsWEtK1e9EACFIGpTec7xAENtfSN4mNBa6+Gjh4UGbU0cM6LrhAbqw2m9xkT56Um19amtxYAfld0iuGJCbK7+gXX0iPzTNnpOk5MVE+o7RUbr56vCAgv492uzQF6uEl+neUek7r2YS+/lp+Rnv2SAiFhMgfOWPGyB9EtbXAhx9KbXTECPldaGiQ7XV18rOvrTXC7swZ45lzXR1w4ICEpd1utCicOiWfO3SofGZn9yJgwPxRP2CC8vnnn8ezzz6L4uJijBs3DmvXrsV3vvMdbxerY+c7BMHXZowh36SHkej5TW02+e+aGpno/OxZCcuqKqPTj65NBgbKzczPT4YvfPml0Syrp2DTf6i5XNIcN3y43ETr6+V8GRlyvkOHjGejfGbZ8/QKMHqllZQU+TlVVckfNxUVxvPpsDBjKJFeDaWxUTp2RUfLPrfbGHZUWCihWVMjwQsYS58lJEhHJIcDmDXLKE/re9EAWyVlQATlG2+8gczMTDz//POYPn06XnrpJXzve9/DkSNHkKx/yL7kfIYg+OqMMeSbWlrkRhQVZSygHBkpvz+nTskNLyZGbpIOh/zO2WxSk0hJkdVCzp6VY/Q6lDab3PgKCuR3bdIkCcqkJOMz/f3lM/z85PPef1/GVepFmTmPac9RypgY3+02puVrapJ7wJkz8vMaN05+vk1Nct/RK5royRRSUuQ+VF8v74+OlgD96qu2f3j7+8vn6efftbXyuxMe3rZcoaHyXr2up9aP/6gfEEG5evVq3H333fjJT34CAFi7di3eeecdvPDCC8jOzm53vNPphLPVoOHqfy9a69DL+fQF/df+qVPyixUQYPSGCw421hnU6urkL8XIyI673bvdsr+yUp5B0ODW2CivykqjkwcgN7vERHkOVVdnTEmXmChNYtHR8szrq68kGCsq5PfTz0/+DQqSJryiIgm+piYJzdYTD7S0SJPepElyY/znP+Xz9E1czyOra5p6cgPqPj2Ux+UyphTUC3q7XPKzqaoypuYL+PctX3cW0ku02WzGyjC6qbS8XGqPeo5al8uY57epSc6na62t6bG4eqaojhQVGeup9hB9/1a90Xqh+jmn06n8/f3V1q1b22y///771cyZMzt8z+OPP64A8MUXX3zxNcBeX331VY/nTL+vUZaVlaGlpQXxukPCv8XHx6OkpKTD96xYsQLLli3zfF1VVYWUlBQUFBQgIiKiV8vbnzkcDiQlJaGwsBDh5za3kAevU9fwOnUNr1PXVFdXIzk5GdHR0T1+7n4flJrlnOq/UqrdNs1qtcLawbPBiIgI/iJ2QXh4OK9TF/A6dQ2vU9fwOnWNn34m35Pn7PEz9rHY2Fj4+/u3qz2Wlpa2q2USERF1V78PyqCgIEyZMgU5OTlttufk5GDatGleKhUREQ0UA6LpddmyZbjjjjswdepUXHnllVi/fj0KCgqwaNGiLr3farXi8ccf77A5lgy8Tl3D69Q1vE5dw+vUNb15nSxKDYyRwM8//zxWrVqF4uJijB8/HmvWrMHMmTO9XSwiIurnBkxQEhER9YZ+/4ySiIioNzEoiYiITDAoiYiITDAoiYiITAz6oHz++eeRmpqK4OBgTJkyBR988IG3i+RV2dnZuPTSSxEWFoa4uDjccMMNOHr0aJtjlFJYuXIlEhMTYbPZkJGRgby8PC+V2DdkZ2fDYrEgMzPTs43XSRQVFeH2229HTEwMQkJCMHHiROzfv9+zn9cJaG5uxqOPPorU1FTYbDaMGDECTzzxBNxut+eYwXiddu3ahR/84AdITEyExWLBW2+91WZ/V66J0+nEkiVLEBsbiyFDhuC6667D6dOnu1eQHp89th/ZsmWLCgwMVBs2bFBHjhxRDzzwgBoyZIg6deqUt4vmNXPmzFEvv/yy+vzzz9WhQ4fU3LlzVXJysqqtrfUc8/TTT6uwsDD15z//WR0+fFjdfPPNKiEhQTkcDi+W3Hs++eQTNXz4cHXxxRerBx54wLOd10mpiooKlZKSou6880718ccfq/z8fPXuu++qL7/80nMMr5NSTz75pIqJiVF/+ctfVH5+vnrzzTdVaGioWrt2reeYwXid/vrXv6pHHnlE/fnPf1YA1LZt29rs78o1WbRokRo6dKjKyclRBw4cUFdddZW65JJLVHNzc5fLMaiD8rLLLlOLFi1qs2306NHq4Ycf9lKJfE9paakCoHJzc5VSSrndbmW329XTTz/tOaaxsVFFRESoF1980VvF9JqamhqVlpamcnJyVHp6uicoeZ3E8uXL1YwZMzrdz+sk5s6dq+66664222688UZ1++23K6V4nZRS7YKyK9ekqqpKBQYGqi1btniOKSoqUn5+furvf/97lz970Da9NjU1Yf/+/Zg9e3ab7bNnz8aePXu8VCrfo9fq1DPy5+fno6SkpM11s1qtSE9PH5TX7d5778XcuXNxzTXXtNnO6yS2b9+OqVOn4sc//jHi4uIwadIkbNiwwbOf10nMmDED7733Ho4dOwYA+PTTT7F79258//vfB8Dr1JGuXJP9+/fD5XK1OSYxMRHjx4/v1nUbEFPYnY/zWZ5rsFFKYdmyZZgxYwbGjx8PAJ5r09F1O3XqVJ+X0Zu2bNmCAwcOYO/eve328TqJEydO4IUXXsCyZcvwy1/+Ep988gnuv/9+WK1WzJ8/n9fp35YvX47q6mqMHj0a/v7+aGlpwVNPPYVbbrkFAH+fOtKVa1JSUoKgoCBERUW1O6Y79/lBG5Rad5bnGmzuu+8+fPbZZ9i9e3e7fYP9uhUWFuKBBx7Ajh07EGyySvtgv05utxtTp05FVlYWAGDSpEnIy8vDCy+8gPnz53uOG+zX6Y033sCrr76KzZs3Y9y4cTh06BAyMzORmJiIBQsWeI4b7NepI+dzTbp73QZt0yuX5zK3ZMkSbN++Hf/4xz8wbNgwz3a73Q4Ag/667d+/H6WlpZgyZQoCAgIQEBCA3Nxc/O53v0NAQIDnWgz265SQkICxY8e22TZmzBgUFBQA4O+T9uCDD+Lhhx/GvHnzMGHCBNxxxx1YunQpsrOzAfA6daQr18Rut6OpqQmVlZWdHtMVgzYouTxXx5RSuO+++7B161a8//77SE1NbbM/NTUVdru9zXVrampCbm7uoLpuV199NQ4fPoxDhw55XlOnTsVtt92GQ4cOYcSIEbxOAKZPn95ueNGxY8eQkpICgL9PWn19fbsFh/39/T3DQ3id2uvKNZkyZQoCAwPbHFNcXIzPP/+8e9ftvLsgDQB6eMgf//hHdeTIEZWZmamGDBmiTp486e2iec3PfvYzFRERoXbu3KmKi4s9r/r6es8xTz/9tIqIiFBbt25Vhw8fVrfccsuA76beFa17vSrF66SUDJ0JCAhQTz31lDp+/Lh67bXXVEhIiHr11Vc9x/A6KbVgwQI1dOhQz/CQrVu3qtjYWPXQQw95jhmM16mmpkYdPHhQHTx4UAFQq1evVgcPHvQM4evKNVm0aJEaNmyYevfdd9WBAwfUd7/7XQ4P6a4//OEPKiUlRQUFBanJkyd7hkEMVgA6fL388sueY9xut3r88ceV3W5XVqtVzZw5Ux0+fNh7hfYR5wYlr5N4++231fjx45XValWjR49W69evb7Of10kph8OhHnjgAZWcnKyCg4PViBEj1COPPKKcTqfnmMF4nf7xj390eD9asGCBUqpr16ShoUHdd999Kjo6WtlsNnXttdeqgoKCbpWDy2wRERGZGLTPKImIiLqCQUlERGSCQUlERGSCQUlERGSCQUlERGSCQUlERGSCQUlERGSCQUlERGSCQUlERGSCQUnkAzIyMpCZmentYhBRBxiURH2gtLQUCxcuRHJyMqxWK+x2O+bMmYMPP/wQALB161b85je/afOewsJC3H333UhMTERQUBBSUlLwwAMPoLy83BvfAoCOA/21115DUlISoqOj8eCDD7bZd/LkSYwcORIOh6MPS0nUswb9ws1EfeFHP/oRXC4XNm3ahBEjRuDMmTN47733UFFRAQCIjo5uc/yJEydw5ZVXYuTIkXj99deRmpqKvLw8PPjgg/jb3/6Gjz76qN17vKGsrAw/+clPsHHjRowYMQJz585FRkYG5s6dCwD42c9+hqeffhrh4eFeLinRt9Azc7wTUWcqKysVALVz585Ojzl35ZH/+I//UMOGDWuzvJlSShUXF6uQkBC1aNGiHinb9u3bVUREhGppaVFKKc9yRr/4xS88x/z0pz9V8+bNUwsWLGi3isPHH3+s4uPjPcfedNNNatWqVUoppV577TV13XXX9Ug5ibyJTa9EvSw0NBShoaF466234HQ6v/H4iooKvPPOO1i8eDFsNlubfXa7HbfddhveeOMNqB5Y+GfmzJmoqanBwYMHAQC5ubmIjY1Fbm6u55idO3ciPT0dv/3tb3HllVfinnvuQXFxMYqLi3HhhReivr4eBw8eREVFBfbu3YuLL74YFRUVeOyxx7Bu3bpvXUYib2NQEvWygIAAbNy4EZs2bUJkZCSmT5+OX/7yl/jss886PP748eNQSmHMmDEd7h8zZgwqKytx9uxZFBYWIiMjA2PHjsXFF1+MN998s1tli4iIwMSJE7Fz504AEopLly7Fp59+ipqaGpSUlODYsWPIyMhAREQEgoKCEBISArvdDrvdjpiYGGzatAnz58/HZZddhvnz52POnDn4xS9+gSVLliA/Px+TJk3C+PHj8b//+7/dKhuRr2BQEvWBH/3oR/j666+xfft2zJkzBzt37sTkyZOxcePGbp9L1yQtFgsCAgKwdu1aHDlyBO+++y6WLl2Kurq6bp0vIyMDO3fuhFIKH3zwAa6//nqMHz8eu3fvxj/+8Q/Ex8dj9OjRnb7/hz/8IQ4fPowvv/wSK1euxM6dO3H48GHcc889mDdvHtauXYs///nPuPvuu1FaWtrt75fI2xiURH0kODgYs2bNwmOPPYY9e/bgzjvvxOOPP97uuIsuuggWiwVHjhzp8DxffPEFoqKiEBsbi4SEBEycOBEAEBcXh+joaE8Hoa7KyMjABx98gE8//RR+fn4YO3Ys0tPTkZub62l27Sqn04nFixfjpZdewpdffonm5makp6dj1KhRGDlyJD7++ONulY3IFzAoibxk7NixHdb+YmJiMGvWLDz//PNoaGhos6+kpASvvfYabr75Zlgsljb79u3bB7fbjaSkpG6VQz+nXLt2LdLT02GxWJCeno6dO3e2C8qgoCC0tLR0eq7f/OY3+N73vofJkyejpaUFzc3Nnn0ul8v0vUS+ikFJ1MvKy8vx3e9+F6+++io+++wz5Ofn480338SqVatw/fXXd/iedevWwel0Ys6cOdi1axcKCwvx97//HbNmzcLQoUPx1FNPtfuM+fPnY/369d0un35O+eqrryIjIwOAhOeBAwc8zye14cOH4+OPP8bJkydRVlYGt9vt2ZeXl4c33ngDTzzxBABg9OjR8PPzwx//+Ef8v//3//DFF1/g0ksv7Xb5iLzOu51uiQa+xsZG9fDDD6vJkyeriIgIFRISokaNGqUeffRRz/CPc4eHKKXUyZMn1Z133qnsdrsKDAxUSUlJasmSJaqsrKzd+b/zne+oV155pd1nv/zyy6or/5v//Oc/VwDU559/7tl2ySWXqAsuuEC53W7PtqNHj6orrrhC2Ww2BUDl5+crpZRyu91q2rRp6u23325z3rffflslJyer+Ph4tWHDhm8sB5EvsijVA33MicgrlFK49dZbMWrUKKxcubLdft25RvdqJaLuY1AS9WO7d+/GzJkzcfHFF3u2/elPf8KECRMAAFdeeSV++9vf4rLLLvNWEYn6PQYlERGRCXbmISIiMsGgJCIiMsGgJCIiMsGgJCIiMsGgJCIiMsGgJCIiMsGgJCIiMsGgJCIiMsGgJCIiMsGgJCIiMsGgJCIiMvH/Adcd6jRKUYyUAAAAAElFTkSuQmCC",
      "text/plain": [
       "<Figure size 640x480 with 1 Axes>"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    }
   ],
   "source": [
    "# One more plot: let's look at a scatter of SiO2 vs. MgO\n",
    "plt.scatter(df['SIO2(WT%)'], df['MGO(WT%)'], c='red', alpha=0.125)\n",
    "ax = plt.gca()\n",
    "ax.set_xlim([0,100])\n",
    "ax.set_xlabel('SiO$_2$, wt%')\n",
    "ax.set_ylim([0,100])\n",
    "ax.set_ylabel('MgO, wt%')\n",
    "ax.set_aspect('equal')"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Now, let's generate *moments* for SiO$_2$\n",
    "\n"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 201,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "The mean is: 72.11\n",
      "The variance is: 16.84\n",
      "The skewness is: -1.75\n",
      "The kurtosis is: 13.67\n"
     ]
    }
   ],
   "source": [
    "# Let us first define the moment functions\n",
    "\n",
    "def raw_moment(X, k, c=0):\n",
    "    return ((X - c)**k).mean()\n",
    "\n",
    "def central_moment(X, k):\n",
    "    return raw_moment(X=X, k=k, c=X.mean())\n",
    "\n",
    "# The mean:\n",
    "print(f'The mean is: {raw_moment(df[\"SIO2(WT%)\"], 1):4.2f}')\n",
    "\n",
    "# Variance:\n",
    "print(f'The variance is: {central_moment(df[\"SIO2(WT%)\"], 2):4.2f}')\n",
    "\n",
    "# Skewness:\n",
    "skewness = central_moment(df[\"SIO2(WT%)\"], 3) / central_moment(df[\"SIO2(WT%)\"], 2) ** (3/2)\n",
    "print(f'The skewness is: {skewness:4.2f}')\n",
    "\n",
    "# Kurtosis\n",
    "kurtosis_value = central_moment(df['SIO2(WT%)'], 4) / central_moment(df['SIO2(WT%)'], 2) ** 2\n",
    "print(f'The kurtosis is: {kurtosis_value:4.2f}')"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 202,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "The mean is: 72.11, the variance is: 16.84, the skewness is: -1.75, and the kurtosis is: 10.67\n"
     ]
    }
   ],
   "source": [
    "# We can also just use pandas (or numpy or scipy):\n",
    "\n",
    "print('The mean is: %4.2f, the variance is: %4.2f, the skewness is: %4.2f, and the kurtosis is: %4.2f' % (df['SIO2(WT%)'].mean(), df['SIO2(WT%)'].var(), df['SIO2(WT%)'].skew(), df['SIO2(WT%)'].kurtosis()))\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Now in class, calculate the statistical moments between the clean data, the noise, and the noisy data. Explore what features might be discriminate between **signal** and **noise** and explore their sensitivity to noise levels."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": []
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "\n",
    "We can now calculate the mean, variance, skewness, and kurtosis of the data:\n"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 220,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "1.7763568394002505e-18\n",
      "0.07508417348193797\n",
      "0.2970118992746436\n",
      "4.060298649528828\n"
     ]
    }
   ],
   "source": [
    "# enter answers here using the functions for the moment.\n",
    "# the mean:\n",
    "print(raw_moment(news,1))\n",
    "\n",
    "# the variance:\n",
    "print(central_moment(news,2))\n",
    "\n",
    "# the skewness\n",
    "print(central_moment(news,3)/central_moment(news,2)**(3/2))\n",
    "\n",
    "# the kurtosis\n",
    "print(central_moment(news,4)/central_moment(news,2)**2)\n",
    "\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "We can also use the numpy and scipy modules to get these values"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 221,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "the mean is 0.00, the variance is 0.08, the skewness is 0.30, the kurtosis is 4.06\n"
     ]
    }
   ],
   "source": [
    "print('the mean is %4.2f, the variance is %4.2f, the skewness is %4.2f, the kurtosis is %4.2f'\n",
    " %(np.mean(news),np.std(news)**2,scipy.stats.skew(news),scipy.stats.kurtosis(news,fisher=False)))"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## 3. Geoscientific distributions\n",
    "\n",
    "**Example 1**: Sampling from the Normal Distribution\n",
    "\n",
    "Application: Simulate temperature variations at a specific location over time."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 8,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAjMAAAHFCAYAAAAHcXhbAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjguMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy81sbWrAAAACXBIWXMAAA9hAAAPYQGoP6dpAABEHElEQVR4nO3deViVdf7/8ddBWRVwQUBUlhIV1zLNUUvJknLLZSrNLJcyy6wszbJcsDFwKbJyNG1xmca0mZZpGsv8umBlNZZbKalTKOYSYSoIiAqf3x/+OHVkEQ4HDzc+H9d1rstz3/fnvt/3fT6H8/JebcYYIwAAAIvycHcBAAAAFUGYAQAAlkaYAQAAlkaYAQAAlkaYAQAAlkaYAQAAlkaYAQAAlkaYAQAAlkaYAQAAlkaYqaa+/vprDRw4UOHh4fL29lZISIg6d+6sCRMmOEwXGxur2NhYt9S4ceNG2Ww2bdy4sdxtd+/erfj4eO3fv9/ldcXHx8tms5U4vrDusrwuZwsWLNDSpUvdXUaxRowY4fA51apVS5GRkbr11lu1ZMkS5eXlFWnjzHfF2X564bL2798vm82m559/vlzzuZiEhAR98MEHRYZX5LvpKjfeeKMeeOCBIjXZbDZ9+eWXRaYfMWKEateufSlLdKni/u5069ZN48ePd09BFlPT3QXA9f7zn//o1ltvVWxsrObMmaOGDRvqyJEj+uabb7Ry5Uq98MIL9mkXLFjgxkqdt3v3bs2YMUOxsbGKjIy8pMtu3759kT+mAwcO1JVXXunyHxsrW7BggYKCgjRixAh3l1IsX19frV+/XpKUm5urgwcP6uOPP9bo0aP1wgsv6JNPPlHjxo3t0zvzXXG2n16q72VCQoJuu+02DRgwwGF4YR9v2bLlJanjQv/617/0xRdfaPny5cWOnzRpkj777LNLXNWl95e//EU9e/bUgw8+qObNm7u7nCqNMFMNzZkzR1FRUVqzZo1q1vz9Ix4yZIjmzJnjMK27/lhZWUBAgP70pz85DPP29ladOnWKDK8ujDE6ffq0fH193V2KcnJy5OfnV+H5eHh4FPm87rnnHo0cOVJ9+/bVbbfdpq+++so+7lJ8VwrXzd3fy+L6+KWUkJCggQMHqlGjRkXG3XLLLfrkk0/073//W/369au0GlzVzyqie/fuat68uV544QUtXrzYrbVUdRxmqoaOHTumoKAghyBTyMPD8SMvaXf23LlzNXv2bEVGRsrX11exsbHau3evzp49q6eeekphYWEKDAzUwIEDlZ6e7jBPm82m+Pj4IsuOjIy86P/Sv/nmGw0ZMsS+3MjISN155506cOCAfZqlS5fq9ttvlyTdcMMN9l3Pfzyk8X//93+68cYbFRAQID8/P3Xt2lXr1q0rsrz//Oc/uuqqq+Tt7a2oqCiX7lk5evSoxowZo8aNG8vLy0tRUVGaMWOGzp07Z5/GFds7MjJSffv21fvvv6+2bdvKx8dHV1xxhV5++eUiNWVmZmrixImKioqSl5eXGjVqpPHjxys7O9thOpvNpnHjxunVV19VTEyMvL29tWzZMknSjBkz1KlTJ9WrV08BAQFq37693njjDf3xmbWRkZHatWuXkpOT7Z9P4Z6JpUuXymazFTn0UtyhjdjYWLVu3VqbNm1Sly5d5Ofnp1GjRpVrXcorLi5Oo0eP1tdff61NmzY51HLhYaaFCxeqXbt2ql27tvz9/dWiRQs9/fTT9vUsrZ+Wtm4lHdIqKCjQc889p/DwcPn4+KhDhw5F+vWIESOK3Qt04WEMm82m7OxsLVu2zF5b4TJLOsz04YcfqnPnzvLz85O/v7969uxZZC9l4XJ27dqlO++8U4GBgQoJCdGoUaN08uTJYrf5H23btk3//e9/dffddxc7fsSIEWrZsqUmT56s/Pz8UudVUFCgOXPmqEWLFvL29lZwcLDuuece/fzzzw7TlfRZuOL7uWrVKsXFxalhw4by9fVVTEyMnnrqqTL307vvvlsrVqxQVlZWmaa/XLFnphrq3LmzXn/9dT3yyCO666671L59e3l6epZrHn/961/Vtm1b/fWvf9WJEyc0YcIE9evXT506dZKnp6fefPNNHThwQBMnTtR9992nDz/80CW179+/X82bN9eQIUNUr149HTlyRAsXLlTHjh21e/duBQUFqU+fPkpISNDTTz+tv/71r2rfvr0k6corr5QkvfXWW7rnnnvUv39/LVu2TJ6enlq0aJFuvvlmrVmzRjfeeKMkad26derfv786d+6slStXKj8/X3PmzNEvv/xS4fU4evSorr32Wnl4eGjatGm68sor9eWXX2rmzJnav3+/lixZ4jB9Rbf39u3bNX78eMXHxys0NFR///vf9eijj+rMmTOaOHGipPP/0+zevbt+/vlnPf3002rbtq127dqladOm6bvvvtP//d//OfzYffDBB/rss880bdo0hYaGKjg42P4ZjRkzRuHh4ZKkr776Sg8//LAOHTqkadOmSZLef/993XbbbQoMDLQfMvH29nZqWx45ckTDhg3TpEmTlJCQIA8Pj3KvS3ndeuutWrBggTZt2qRu3boVO83KlSs1duxYPfzww3r++efl4eGh//3vf9q9e7ckXbSflrRupZk/f74iIiI0b948+w91r169lJycrM6dO5drHb/88kv16NFDN9xwg6ZOnSrp/B6ZkqxYsUJ33XWX4uLi9PbbbysvL09z5sxRbGys1q1bp+uuu85h+j//+c8aPHiw7r33Xn333XeaPHmyJOnNN98sta6PPvpINWrUKHG716hRQ4mJifbvd2EALM6DDz6oxYsXa9y4cerbt6/279+vqVOnauPGjdq6dauCgoLs05b2WVTk+7lv3z717t1b48ePV61atfTDDz9o9uzZ+u9//2s/zFma2NhYPfnkk9q4cWOl7omyPINqJyMjw1x33XVGkpFkPD09TZcuXUxiYqLJyspymLZ79+6me/fu9vepqalGkmnXrp3Jz8+3D583b56RZG699VaH9uPHjzeSzMmTJ+3DJJnp06cXqSsiIsIMHz7c/n7Dhg1GktmwYUOJ63Lu3Dlz6tQpU6tWLfPSSy/Zh//jH/8otm12drapV6+e6devn8Pw/Px8065dO3Pttdfah3Xq1MmEhYWZ3Nxc+7DMzExTr149U96vRkREhOnTp4/9/ZgxY0zt2rXNgQMHHKZ7/vnnjSSza9cuY4xrtndERISx2Wxm+/btDtP27NnTBAQEmOzsbGOMMYmJicbDw8Ns2bLFYbp//vOfRpJZvXq1fZgkExgYaH777bdS1zs/P9+cPXvWPPvss6Z+/fqmoKDAPq5Vq1YOfavQkiVLjCSTmprqMLy4/tC9e3cjyaxbt85h2vKsS3GGDx9uatWqVeL4lJQUI8k8+OCDDrX8cX3GjRtn6tSpU+pySuqnhfMrbt2KW1ZhPympv950000O6xYREVFkntOnTy/Sr2vVquXwnSx04WeRn59vwsLCTJs2bRz6aVZWlgkODjZdunQpspw5c+Y4zHPs2LHGx8fHoY8Up1evXqZFixYl1vSPf/zDGGPMddddZxo3bmzfHhd+poWf4dixYx3m8/XXXxtJ5umnn7YPK+mzcMX3848KCgrM2bNnTXJyspFkduzYYR9X3OdjjDFnzpwxNpvNPPnkk8XOE+dxmKkaql+/vj777DNt2bJFs2bNUv/+/bV3715NnjxZbdq0UUZGxkXn0bt3b4f/mcTExEg6/7/NPyocnpaW5pLaT506pSeffFJNmzZVzZo1VbNmTdWuXVvZ2dlKSUm5aPvNmzfrt99+0/Dhw3Xu3Dn7q6CgQLfccou2bNmi7OxsZWdna8uWLRo0aJB8fHzs7f39/V3yv5+PPvpIN9xwg8LCwhzq6NWrlyQpOTnZYfqKbu9WrVqpXbt2DsOGDh2qzMxMbd261V5T69atddVVVznUdPPNNxd7SKFHjx6qW7dukXVbv369brrpJgUGBqpGjRry9PTUtGnTdOzYsSK72F2hbt266tGjh8Ow8q5LeZk/HDIrybXXXqsTJ07ozjvv1L/+9a8yfa8uVNy6laak/rpp06aLHnKpiD179ujw4cO6++67Hfpp7dq19ec//1lfffWVcnJyHNrceuutDu/btm2r06dPX7SPHD582L4XsDSzZ8/Wzz//rJdeeqnY8Rs2bJCkIoe2r732WsXExBQ5PFfaZ1GR7+dPP/2koUOHKjQ01P596d69uySV6W+ap6en6tSpo0OHDl102ssZh5mqsQ4dOqhDhw6SpLNnz+rJJ5/Uiy++qDlz5hQ5EfhC9erVc3jv5eVV6vDTp0+7pOahQ4dq3bp1mjp1qjp27KiAgADZbDb17t1bubm5F21feIjotttuK3Ga3377TTabTQUFBQoNDS0yvrhh5fXLL7/o3//+d4mH9y784avo9i5tPY4dO2av6X//+1+Za2rYsGGRaf773/8qLi5OsbGxeu211+znA33wwQd67rnnyvQZlVdxdZR3Xcqr8BytsLCwEqe5++67de7cOb322mv685//rIKCAnXs2FEzZ85Uz549y7Sc4tatNCV9zmfOnNGpU6cUGBhYrvmVVWEfKq7esLAwFRQU6Pjx4w4nzNavX99husLDjBfrI7m5uQoJCbloTV26dNGAAQM0a9Ys3X///eWu+Y/n4ZU0XSFnv5+nTp3S9ddfLx8fH82cOVPNmjWTn5+fDh48qEGDBpX5++Lj41Mp363qhDBzmfD09NT06dP14osv6vvvv6/UZXl7exd7n47CPy4lOXnypD766CNNnz5dTz31lH14Xl6efvvttzItu/AY+CuvvFLi1RghISE6e/asbDabjh49WmR8ccPKKygoSG3bttVzzz1X7PjSfiSdUdp6FP6oBAUFydfXt8RzFv54/oCkYs85WblypTw9PfXRRx857CEo7l4lJSlsd2EfKSmAFFdHedelvArPebjYfWVGjhypkSNHKjs7W5s2bdL06dPVt29f7d27VxERERddTnnP6ynpc/by8rLfY8XHx6fY719FAl5hHzpy5EiRcYcPH5aHh0exe/GcERQUVObve2Jiolq3bq2EhIQi4/5Y8x8vsZfO11yW/l5R69ev1+HDh7Vx40b73hhJOnHiRLnmc/z48Qr36eqOMFMNHTlypNj/ZRTu0nT1D+mFIiMjtXPnTodh69ev16lTp0ptZ7PZZIwpcqLo66+/XmQXekn/y+vatavq1Kmj3bt3a9y4cSUuy8vLS9dee63ee+89zZ071/4Dm5WVpX//+9+lr2AZ9O3bV6tXr9aVV17psj/ypdm1a5d27NjhcKhpxYoV8vf3t5942rdvXyUkJKh+/fqKiopyajk2m001a9ZUjRo17MNyc3P1t7/9rci03t7exf5vsvBKm507dzrcO6M8J5G7Yl1KsnbtWr3++uvq0qVLkZNaS1KrVi316tVLZ86c0YABA7Rr1y5FRESUeW9EWZXUX6+//nr7ZxIZGan09HT98ssv9j0cZ86c0Zo1a4rMr6TP6ELNmzdXo0aNtGLFCk2cONH+w5+dna13333XfoWTK7Ro0aLM4bhFixYaNWqUXnnlFXXp0sVhXOEho7feeksdO3a0D9+yZYtSUlL0zDPPuKTe0hRupwv/pi1atKjM8zh8+LBOnz7t9sv1qzrCTDV08803q3HjxurXr59atGihgoICbd++XS+88IJq166tRx99tFKXf/fdd2vq1KmaNm2aunfvrt27d2v+/PkX3QUeEBCgbt26ae7cuQoKClJkZKSSk5P1xhtvqE6dOg7Ttm7dWpK0ePFi+fv7y8fHR1FRUapfv75eeeUVDR8+XL/99ptuu+02BQcH69dff9WOHTv066+/auHChZLO35DqlltuUc+ePTVhwgTl5+dr9uzZqlWrVpn/Z1iSZ599VmvXrlWXLl30yCOPqHnz5jp9+rT279+v1atX69VXXy3yv8WKCAsL06233qr4+Hg1bNhQb731ltauXavZs2fbf2TGjx+vd999V926ddNjjz2mtm3bqqCgQGlpafr00081YcIEderUqdTl9OnTR0lJSRo6dKjuv/9+HTt2TM8//3yxVyq1adNGK1eu1KpVq3TFFVfIx8dHbdq0UceOHdW8eXNNnDhR586dU926dfX+++/r888/L/P6umJdCgoK7PeRycvLU1pamj7++GO98847iomJ0TvvvFNq+9GjR8vX11ddu3ZVw4YNdfToUSUmJiowMND+41laP3VGjRo11LNnTz3++OMqKCjQ7NmzlZmZqRkzZtinGTx4sKZNm6YhQ4boiSee0OnTp/Xyyy8Xe05NmzZttHHjRv373/9Ww4YN5e/vX+zN2Tw8PDRnzhzddddd6tu3r8aMGaO8vDzNnTtXJ06c0KxZs5xan+LExsbqzTff1N69e9WsWbOLTh8fH6+///3v2rBhg2rVqmUf3rx5c91///165ZVX5OHhoV69etmvZmrSpIkee+wxl9Vcki5duqhu3bp64IEHNH36dHl6eurvf/+7duzYUeZ5FPbRG264obLKrB7cfQYyXG/VqlVm6NChJjo62tSuXdt4enqa8PBwc/fdd5vdu3c7TFvSVRNz5851mO7CKwkKFV6Z8serSvLy8sykSZNMkyZNjK+vr+nevbvZvn17ma5m+vnnn82f//xnU7duXePv729uueUW8/333xdpa8z5KwqioqJMjRo1jCSzZMkS+7jk5GTTp08fU69ePePp6WkaNWpk+vTpU6T+Dz/80LRt29Z4eXmZ8PBwM2vWrBKvKijNhVczGWPMr7/+ah555BETFRVlPD09Tb169cw111xjnnnmGXPq1CljjGu2d+Gy//nPf5pWrVoZLy8vExkZaZKSkorUeerUKTNlyhTTvHlz4+XlZQIDA02bNm3MY489Zo4ePWqfTpJ56KGHil3XN9980zRv3tx4e3ubK664wiQmJpo33nijyBVK+/fvN3Fxccbf399IcrjCZu/evSYuLs4EBASYBg0amIcfftj85z//KfZqplatWhVbR1nXpTjDhw+3X+0nyfj6+prw8HDTr18/8+abb5q8vLwibS78rixbtszccMMNJiQkxHh5eZmwsDBzxx13mJ07dzq0K6mflrZuJX0vZ8+ebWbMmGEaN25svLy8zNVXX23WrFlTpP3q1avNVVddZXx9fc0VV1xh5s+fX2y/3r59u+natavx8/MzkuzLLOlKww8++MB06tTJ+Pj4mFq1apkbb7zRfPHFFw7TFC7n119/dRhe0lVsFzp58qSpXbt2kauhSvpOGGPM008/bSQVuUItPz/fzJ492zRr1sx4enqaoKAgM2zYMHPw4EGH6Ur6LFzx/dy8ebPp3Lmz8fPzMw0aNDD33Xef2bp1a5G/WSX93bn77rtNmzZtigyHI5sxZThtH0CVFRkZqdatW+ujjz5ydymASzz88MNat26ddu3adVk/4ywzM1NhYWF68cUXNXr0aHeXU6VxaTYAoEqZMmWKDh06pHfffdfdpbjViy++qPDwcI0cOdLdpVR5hBkAQJUSEhKiv//975f95cgBAQFaunRpsY+mgSMOMwEAAEtjzwwAALA0wgwAALA0wgwAALC0an9WUUFBgQ4fPix/f//L+hI/AACsxBijrKwshYWFOTzoszjVPswcPnxYTZo0cXcZAADACQcPHrzoHdOrfZjx9/eXdH5jBAQEuLkaAABQFpmZmWrSpIn9d7w01T7MFB5aCggIIMwAAGAxZTlFhBOAAQCApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApdV0dwEAqoe0tDRlZGQ41TYoKEjh4eEurgjA5YIwA6DC0tLS1CImRrk5OU619/Xz0w8pKQQaAE4hzACosIyMDOXm5OiOmQsVHBVdrrbpqfv0zpQHlZGRQZgB4BTCDACXCY6KVqOYdu4uA8BlhhOAAQCApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApRFmAACApbk1zJw7d05TpkxRVFSUfH19dcUVV+jZZ59VQUGBfRpjjOLj4xUWFiZfX1/FxsZq165dbqwaAABUJW4NM7Nnz9arr76q+fPnKyUlRXPmzNHcuXP1yiuv2KeZM2eOkpKSNH/+fG3ZskWhoaHq2bOnsrKy3Fg5AACoKtwaZr788kv1799fffr0UWRkpG677TbFxcXpm2++kXR+r8y8efP0zDPPaNCgQWrdurWWLVumnJwcrVixwp2lAwCAKsKtYea6667TunXrtHfvXknSjh079Pnnn6t3796SpNTUVB09elRxcXH2Nt7e3urevbs2b95c7Dzz8vKUmZnp8AIAANVXTXcu/Mknn9TJkyfVokUL1ahRQ/n5+Xruued05513SpKOHj0qSQoJCXFoFxISogMHDhQ7z8TERM2YMaNyCwcAAFWGW/fMrFq1Sm+99ZZWrFihrVu3atmyZXr++ee1bNkyh+lsNpvDe2NMkWGFJk+erJMnT9pfBw8erLT6AQCA+7l1z8wTTzyhp556SkOGDJEktWnTRgcOHFBiYqKGDx+u0NBQSef30DRs2NDeLj09vcjemkLe3t7y9vau/OIBAECV4NY9Mzk5OfLwcCyhRo0a9kuzo6KiFBoaqrVr19rHnzlzRsnJyerSpcslrRUAAFRNbt0z069fPz333HMKDw9Xq1attG3bNiUlJWnUqFGSzh9eGj9+vBISEhQdHa3o6GglJCTIz89PQ4cOdWfpAACginBrmHnllVc0depUjR07Vunp6QoLC9OYMWM0bdo0+zSTJk1Sbm6uxo4dq+PHj6tTp0769NNP5e/v78bKAQBAVeHWMOPv76958+Zp3rx5JU5js9kUHx+v+Pj4S1YXAACwDreGGQCwqrS0NGVkZDjVNigoSOHh4S6uCLh8EWYAoJzS0tLUIiZGuTk5TrX39fPTDykpBBrARQgzAFBOGRkZys3J0R0zFyo4KrpcbdNT9+mdKQ8qIyODMAO4CGEGAJwUHBWtRjHt3F0GcNkjzAC4bDl73ktKSkolVAPAWYQZAJelip73AqDqIMwAuCxV5LyXPV+s09oFiZVUGYDyIswAuKw5c95Leuq+SqoGgDPc+mwmAACAiiLMAAAASyPMAAAASyPMAAAASyPMAAAASyPMAAAASyPMAAAASyPMAAAASyPMAAAASyPMAAAASyPMAAAASyPMAAAAS+NBkwCqhJSUFKfaBQUFKTw83MXVALASwgwAt8rK+EU2Dw8NGzbMqfa+fn76ISWFQANcxggzANwqNytTpqBAd8xcqOCo6HK1TU/dp3emPKiMjAzCDHAZI8wAqBKCo6LVKKadu8sAYEGcAAwAACyNMAMAACyNMAMAACyNMAMAACyNMAMAACyNMAMAACyNMAMAACyNMAMAACyNMAMAACyNMAMAACyNMAMAACyNMAMAACyNMAMAACyNMAMAACyNMAMAACyNMAMAACyNMAMAACyNMAMAACyNMAMAACyNMAMAACytprsLAOBaaWlpysjIcKptUFCQwsPDXVwRAFQuwgxQjaSlpalFTIxyc3Kcau/r56cfUlIINAAshTADVCMZGRnKzcnRHTMXKjgqulxt01P36Z0pDyojI4MwA8BSCDNANRQcFa1GMe3cXQYAXBKcAAwAACyNMAMAACyNMAMAACyNMAMAACyNMAMAACyNMAMAACyNMAMAACyNMAMAACyNMAMAACyNMAMAACyNMAMAACyNMAMAACyNB00CsLyUlJRL0gZA1USYAWBZWRm/yObhoWHDhrm7FABuRJgBYFm5WZkyBQW6Y+ZCBUdFl6vtni/Wae2CxEqqDMClRJgBYHnBUdFqFNOuXG3SU/dVUjUALjVOAAYAAJZGmAEAAJZGmAEAAJZGmAEAAJbm9jBz6NAhDRs2TPXr15efn5+uuuoqffvtt/bxxhjFx8crLCxMvr6+io2N1a5du9xYMQAAqErcGmaOHz+url27ytPTUx9//LF2796tF154QXXq1LFPM2fOHCUlJWn+/PnasmWLQkND1bNnT2VlZbmvcAAAUGW49dLs2bNnq0mTJlqyZIl9WGRkpP3fxhjNmzdPzzzzjAYNGiRJWrZsmUJCQrRixQqNGTPmUpcMAACqGLfumfnwww/VoUMH3X777QoODtbVV1+t1157zT4+NTVVR48eVVxcnH2Yt7e3unfvrs2bNxc7z7y8PGVmZjq8AABA9eXWMPPTTz9p4cKFio6O1po1a/TAAw/okUce0fLlyyVJR48elSSFhIQ4tAsJCbGPu1BiYqICAwPtryZNmlTuSgAAALdya5gpKChQ+/btlZCQoKuvvlpjxozR6NGjtXDhQofpbDabw3tjTJFhhSZPnqyTJ0/aXwcPHqy0+gEAgPu5Ncw0bNhQLVu2dBgWExOjtLQ0SVJoaKgkFdkLk56eXmRvTSFvb28FBAQ4vAAAQPXl1jDTtWtX7dmzx2HY3r17FRERIUmKiopSaGio1q5dax9/5swZJScnq0uXLpe0VgAAUDW59Wqmxx57TF26dFFCQoLuuOMO/fe//9XixYu1ePFiSecPL40fP14JCQmKjo5WdHS0EhIS5Ofnp6FDh7qzdAAAUEW4Ncx07NhR77//viZPnqxnn31WUVFRmjdvnu666y77NJMmTVJubq7Gjh2r48ePq1OnTvr000/l7+/vxsoBAEBV4dYwI0l9+/ZV3759Sxxvs9kUHx+v+Pj4S1cUAACwDLc/zgAAAKAiCDMAAMDSCDMAAMDSCDMAAMDSCDMAAMDSCDMAAMDSCDMAAMDSCDMAAMDSCDMAAMDSCDMAAMDSCDMAAMDSCDMAAMDS3P6gSQBVS0pKyiVpAwCu4lSYSU1NVVRUlKtrAeBGWRm/yObhoWHDhrm7FAAoF6fCTNOmTdWtWzfde++9uu222+Tj4+PqugBcYrlZmTIFBbpj5kIFR0WXq+2eL9Zp7YLESqoMAErnVJjZsWOH3nzzTU2YMEHjxo3T4MGDde+99+raa691dX0ALrHgqGg1imlXrjbpqfsqqRoAuDinTgBu3bq1kpKSdOjQIS1ZskRHjx7Vddddp1atWikpKUm//vqrq+sEAAAoVoWuZqpZs6YGDhyod955R7Nnz9aPP/6oiRMnqnHjxrrnnnt05MgRV9UJAABQrAqFmW+++UZjx45Vw4YNlZSUpIkTJ+rHH3/U+vXrdejQIfXv399VdQIAABTLqXNmkpKStGTJEu3Zs0e9e/fW8uXL1bt3b3l4nM9GUVFRWrRokVq0aOHSYgEAAC7kVJhZuHChRo0apZEjRyo0NLTYacLDw/XGG29UqDgAgKO0tDRlZGQ41TYoKEjh4eEurghwP6fCzL59F79ywcvLS8OHD3dm9gCAYqSlpalFTIxyc3Kcau/r56cfUlIINKh2nAozS5YsUe3atXX77bc7DP/HP/6hnJwcQgwAVIKMjAzl5uQ4dS+g9NR9emfKg8rIyCDMoNpxKszMmjVLr776apHhwcHBuv/++wkzAFCJnLkXEFCdOXU104EDB4p9nEFERITS0tIqXBQAAEBZORVmgoODtXPnziLDd+zYofr161e4KAAAgLJyKswMGTJEjzzyiDZs2KD8/Hzl5+dr/fr1evTRRzVkyBBX1wgAAFAip86ZmTlzpg4cOKAbb7xRNWuen0VBQYHuueceJSQkuLRAAACA0jgVZry8vLRq1Sr95S9/0Y4dO+Tr66s2bdooIiLC1fUBAACUyqkwU6hZs2Zq1qyZq2oBAAAoN6fCTH5+vpYuXap169YpPT1dBQUFDuPXr1/vkuIAAAAuxqkw8+ijj2rp0qXq06ePWrduLZvN5uq6AAAAysSpMLNy5Uq988476t27t6vrAQBUopSUFKfa8VwnVGVOnwDctGlTV9cCAKgkWRm/yObhoWHDhjnVnuc6oSpzKsxMmDBBL730kubPn88hJgCwgNysTJmCAp7rhGrJqTDz+eefa8OGDfr444/VqlUreXp6Oox/7733XFIcAMC1eK4TqiOnwkydOnU0cOBAV9cCAABQbk6FmSVLlri6DgAAAKc49WwmSTp37pz+7//+T4sWLVJWVpYk6fDhwzp16pTLigMAALgYp/bMHDhwQLfccovS0tKUl5ennj17yt/fX3PmzNHp06f16quvurpOAACAYjl907wOHTpox44dql+/vn34wIEDdd9997msOACorpy534uz94hxFe5Rg6rK6auZvvjiC3l5eTkMj4iI0KFDh1xSGABURxW934s7cI8aVHVOhZmCggLl5+cXGf7zzz/L39+/wkUBQHVVkfu97PlindYuSKykykrGPWpQ1TkVZnr27Kl58+Zp8eLFkiSbzaZTp05p+vTpPOIAAMrAmfu9pKfuq6RqyoZ71KCqcirMvPjii7rhhhvUsmVLnT59WkOHDtW+ffsUFBSkt99+29U1ApedtLQ0ZWRklLudu8+pAAB3cCrMhIWFafv27Xr77be1detWFRQU6N5779Vdd90lX19fV9cIXFbS0tLUIiZGuTk57i4FACzBqTAjSb6+vho1apRGjRrlynqAy15GRoZyc3IsdU4FALiTU2Fm+fLlpY6/5557nCoGwO+seE4FALiD0/eZ+aOzZ88qJydHXl5e8vPzI8wA4rwXALhUnAozx48fLzJs3759evDBB/XEE09UuCjA6jjvBQAuHafPmblQdHS0Zs2apWHDhumHH35w1WwBS+K8FwC4dFwWZiSpRo0aOnz4sCtnCVga570AQOVzKsx8+OGHDu+NMTpy5Ijmz5+vrl27uqQwAACAsnAqzAwYMMDhvc1mU4MGDdSjRw+98MILrqgLAACgTJx+NhMAAEBV4OHuAgAAACrCqT0zjz/+eJmnTUpKcmYRAAAAZeJUmNm2bZu2bt2qc+fOqXnz5pKkvXv3qkaNGmrfvr19OpvN5poqAQAASuBUmOnXr5/8/f21bNky1a1bV9L5G+mNHDlS119/vSZMmODSIgEAAEri1DkzL7zwghITE+1BRpLq1q2rmTNncjUTAAC4pJwKM5mZmfrll1+KDE9PT1dWVlaFiwIAACgrp8LMwIEDNXLkSP3zn//Uzz//rJ9//ln//Oc/de+992rQoEGurhEAAKBETp0z8+qrr2rixIkaNmyYzp49e35GNWvq3nvv1dy5c11aIAAAQGmcCjN+fn5asGCB5s6dqx9//FHGGDVt2lS1atVydX0AAAClqtBN844cOaIjR46oWbNmqlWrlowxrqoLAACgTJwKM8eOHdONN96oZs2aqXfv3jpy5Igk6b777uOybAAAcEk5FWYee+wxeXp6Ki0tTX5+fvbhgwcP1ieffOKy4gAAAC7GqXNmPv30U61Zs0aNGzd2GB4dHa0DBw64pDAAAICycGrPTHZ2tsMemUIZGRny9vZ2qpDExETZbDaNHz/ePswYo/j4eIWFhcnX11exsbHatWuXU/MHAADVk1Nhplu3blq+fLn9vc1mU0FBgebOnasbbrih3PPbsmWLFi9erLZt2zoMnzNnjpKSkjR//nxt2bJFoaGh6tmzJzfmAwAAdk6Fmblz52rRokXq1auXzpw5o0mTJql169batGmTZs+eXa55nTp1SnfddZdee+01h8cjGGM0b948PfPMMxo0aJBat26tZcuWKScnRytWrHCmbAAAUA05FWZatmypnTt36tprr1XPnj2VnZ2tQYMGadu2bbryyivLNa+HHnpIffr00U033eQwPDU1VUePHlVcXJx9mLe3t7p3767Nmzc7UzYAAKiGyn0C8NmzZxUXF6dFixZpxowZFVr4ypUrtXXrVm3ZsqXIuKNHj0qSQkJCHIaHhISUepJxXl6e8vLy7O8zMzMrVCMAAKjayr1nxtPTU99//71sNluFFnzw4EE9+uijeuutt+Tj41PidBcuxxhT6rITExMVGBhofzVp0qRCdQIAgKrNqcNM99xzj954440KLfjbb79Venq6rrnmGtWsWVM1a9ZUcnKyXn75ZdWsWdO+R6ZwD02h9PT0Intr/mjy5Mk6efKk/XXw4MEK1QkAAKo2p+4zc+bMGb3++utau3atOnToUOSZTElJSRedx4033qjvvvvOYdjIkSPVokULPfnkk7riiisUGhqqtWvX6uqrr7YvNzk5udSTjL29vZ2+PBwAAFhPucLMTz/9pMjISH3//fdq3769JGnv3r0O05T18JO/v79at27tMKxWrVqqX7++ffj48eOVkJCg6OhoRUdHKyEhQX5+fho6dGh5ygYAANVYucJMdHS0jhw5og0bNkg6//iCl19+udTDPhUxadIk5ebmauzYsTp+/Lg6deqkTz/9VP7+/pWyPAAAYD3lCjMXPhX7448/VnZ2tsuK2bhxo8N7m82m+Ph4xcfHu2wZAACgenHqBOBCF4YbAACAS61cYcZmsxU5J6ail2gDAABURLkPM40YMcJ+tdDp06f1wAMPFLma6b333nNdhQAAAKUoV5gZPny4w/thw4a5tBgAAIDyKleYWbJkSWXVAQAA4JQKnQAMAADgboQZAABgaYQZAABgaYQZAABgaYQZAABgaYQZAABgaYQZAABgaYQZAABgaYQZAABgaYQZAABgaYQZAABgaeV6NhMAAM5ISUlxql1QUJDCw8NdXA2qG8IMAKDSZGX8IpuHh4YNG+ZUe18/P/2QkkKgQakIMwCASpOblSlTUKA7Zi5UcFR0udqmp+7TO1MeVEZGBmEGpSLMAAAqXXBUtBrFtHN3GaimOAEYAABYGmEGAABYGmEGAABYGmEGAABYGmEGAABYGmEGAABYGmEGAABYGmEGAABYGmEGAABYGmEGAABYGmEGAABYGmEGAABYGmEGAABYGmEGAABYGmEGAABYGmEGAABYGmEGAABYGmEGAABYGmEGAABYGmEGAABYGmEGAABYGmEGAABYGmEGAABYGmEGAABYWk13FwBUZWlpacrIyCh3u5SUlEqoBgBQHMIMUIK0tDS1iIlRbk6Ou0sBAJSCMAOUICMjQ7k5Obpj5kIFR0WXq+2eL9Zp7YLESqoMAPBHhBngIoKjotUopl252qSn7qukagAAF+IEYAAAYGmEGQAAYGmEGQAAYGmEGQAAYGmEGQAAYGmEGQAAYGmEGQAAYGmEGQAAYGmEGQAAYGmEGQAAYGmEGQAAYGmEGQAAYGmEGQAAYGmEGQAAYGmEGQAAYGmEGQAAYGk13V0AAAClSUlJcapdUFCQwsPDXVwNqiLCDACgSsrK+EU2Dw8NGzbMqfa+fn76ISWFQHMZIMwAAKqk3KxMmYIC3TFzoYKjosvVNj11n96Z8qAyMjIIM5cBwgwAoEoLjopWo5h27i4DVZhbTwBOTExUx44d5e/vr+DgYA0YMEB79uxxmMYYo/j4eIWFhcnX11exsbHatWuXmyoGAABVjVvDTHJysh566CF99dVXWrt2rc6dO6e4uDhlZ2fbp5kzZ46SkpI0f/58bdmyRaGhoerZs6eysrLcWDkAAKgq3HqY6ZNPPnF4v2TJEgUHB+vbb79Vt27dZIzRvHnz9Mwzz2jQoEGSpGXLlikkJEQrVqzQmDFj3FE2AACoQqrUfWZOnjwpSapXr54kKTU1VUePHlVcXJx9Gm9vb3Xv3l2bN292S40AAKBqqTInABtj9Pjjj+u6665T69atJUlHjx6VJIWEhDhMGxISogMHDhQ7n7y8POXl5dnfZ2ZmVlLFAACgKqgye2bGjRunnTt36u233y4yzmazObw3xhQZVigxMVGBgYH2V5MmTSqlXgAAUDVUiTDz8MMP68MPP9SGDRvUuHFj+/DQ0FBJv++hKZSenl5kb02hyZMn6+TJk/bXwYMHK69wAADgdm4NM8YYjRs3Tu+9957Wr1+vqKgoh/FRUVEKDQ3V2rVr7cPOnDmj5ORkdenSpdh5ent7KyAgwOEFAACqL7eeM/PQQw9pxYoV+te//iV/f3/7HpjAwED5+vrKZrNp/PjxSkhIUHR0tKKjo5WQkCA/Pz8NHTrUnaUDAIAqwq1hZuHChZKk2NhYh+FLlizRiBEjJEmTJk1Sbm6uxo4dq+PHj6tTp0769NNP5e/vf4mrBQAAVZFbw4wx5qLT2Gw2xcfHKz4+vvILAgAAllMlTgAGAABwVpW5zwwAAK6WkpLiVLugoCCetm0hhBkAQLWTlfGLbB4eGjZsmFPtff389ENKCoHGIggzAIBqJzcrU6agQHfMXKjgqOhytU1P3ad3pjyojIwMwoxFEGZgCWlpacrIyHCqLbuLgctXcFS0GsW0c6oth6isgzCDKi8tLU0tYmKUm5PjVHt2FwMoDw5RWQ9hBlVeRkaGcnNy2F0M4JLgEJX1EGZgGRXZXQwA5cXfHOsgzOCy4Myxb2ePlwMALi3CDKq1ih77BgBUfYQZVGsVOfa954t1WrsgsZIqAwC4CmEGlwVnjn2np+6rpGoAAK7Es5kAAIClEWYAAIClEWYAAIClEWYAAIClEWYAAIClEWYAAIClEWYAAIClEWYAAIClEWYAAIClEWYAAIClEWYAAIClEWYAAICl8aBJXDJpaWnKyMgod7uUlJRKqAYAUF0QZnBJpKWlqUVMjHJzctxdCgCgmiHM4JLIyMhQbk6O7pi5UMFR0eVqu+eLdVq7ILGSKgMAWB1hBpdUcFS0GsW0K1eb9NR9lVQNAKA64ARgAABgaYQZAABgaYQZAABgaYQZAABgaZwADABAFeHs/bgkKSgoSOHh4S6uyBoIMwAAVAEVvR+Xr5+ffkhJuSwDDWEGAIAqoCL340pP3ad3pjyojIwMwgwAAHAvZ+7HdbnjBGAAAGBphBkAAGBphBkAAGBphBkAAGBphBkAAGBphBkAAGBphBkAAGBphBkAAGBphBkAAGBphBkAAGBphBkAAGBphBkAAGBpPGgSAAAXS0lJuSRtcB5hBgAAF8nK+EU2Dw8NGzbM3aVcVggzAAC4SG5WpkxBge6YuVDBUdHlarvni3VauyCxkiqr3ggzAAC4WHBUtBrFtCtXm/TUfZVUTfVHmKmgtLQ0ZWRkONU2KChI4eHhLq6ocjm7vhwLBoCqy+q/ZYSZCkhLS1OLmBjl5uQ41d7Xz08/pKS4vROUVUXXFwBQ9VSH3zLCTAVkZGQoNyfHqWOj6an79M6UB5WRkWGZMFOR9eVYMABUTdXht4ww4wLOHBu1Mo4FA0D1Y+XfMsKMRVXk+GZeXp68vb3L3Y7zXgAAVRFhxoIqenzT5uEhU1Dg4qoAAHAPwowFueLcFc57AQBUF4QZC6vIuSuc9wIAqC4IMwAAVBOX6zOhCDMAAFjc5f5MKMIMAAAWd7k/E4owAwBANXG5ng/p4e4CAAAAKoIwAwAALI0wAwAALI0wAwAALM0SJwAvWLBAc+fO1ZEjR9SqVSvNmzdP119/vbvLconL9Z4AAAC4SpUPM6tWrdL48eO1YMECde3aVYsWLVKvXr20e/dutz5uvKIu93sCAADgKlU+zCQlJenee+/VfffdJ0maN2+e1qxZo4ULFyox0brXxV/u9wQAAMBVqnSYOXPmjL799ls99dRTDsPj4uK0efNmN1XlWpfrPQEAAHCVKh1mMjIylJ+fr5CQEIfhISEhOnr0aLFt8vLylJeXZ39/8uRJSVJmZqbL6zt16pQk6VDKTp3JyS5X21/376MtbWlLW9rS1tptD/wo6fzvoat/ZwvnZ4y5+MSmCjt06JCRZDZv3uwwfObMmaZ58+bFtpk+fbqRxIsXL168ePGqBq+DBw9eNC9U6T0zQUFBqlGjRpG9MOnp6UX21hSaPHmyHn/8cfv7goIC/fbbb6pfv75sNlul1luczMxMNWnSRAcPHlRAQMAlX76VsK3Kjm1VdmyrsmNblQ3bqewqsq2MMcrKylJYWNhFp63SYcbLy0vXXHON1q5dq4EDB9qHr127Vv379y+2jbe3t7y9vR2G1alTpzLLLJOAgAA6fRmxrcqObVV2bKuyY1uVDdup7JzdVoGBgWWarkqHGUl6/PHHdffdd6tDhw7q3LmzFi9erLS0ND3wwAPuLg0AAFQBVT7MDB48WMeOHdOzzz6rI0eOqHXr1lq9erUiIiLcXRoAAKgCqnyYkaSxY8dq7Nix7i7DKd7e3po+fXqRQ18oim1VdmyrsmNblR3bqmzYTmV3qbaVzZiyXPMEAABQNfGgSQAAYGmEGQAAYGmEGQAAYGmEGQAAYGmEmUoSHx8vm83m8AoNDXV3WVXCpk2b1K9fP4WFhclms+mDDz5wGG+MUXx8vMLCwuTr66vY2Fjt2rXLPcW60cW204gRI4r0sT/96U/uKdbNEhMT1bFjR/n7+ys4OFgDBgzQnj17HKahX51Xlm1F3zpv4cKFatu2rf2Gb507d9bHH39sH0+f+t3FtlVl9ynCTCVq1aqVjhw5Yn9999137i6pSsjOzla7du00f/78YsfPmTNHSUlJmj9/vrZs2aLQ0FD17NlTWVlZl7hS97rYdpKkW265xaGPrV69+hJWWHUkJyfroYce0ldffaW1a9fq3LlziouLU3b27w/No1+dV5ZtJdG3JKlx48aaNWuWvvnmG33zzTfq0aOH+vfvbw8s9KnfXWxbSZXcpyr4LEiUYPr06aZdu3buLqPKk2Tef/99+/uCggITGhpqZs2aZR92+vRpExgYaF599VU3VFg1XLidjDFm+PDhpn///m6pp6pLT083kkxycrIxhn5Vmgu3lTH0rdLUrVvXvP766/SpMijcVsZUfp9iz0wl2rdvn8LCwhQVFaUhQ4bop59+cndJVV5qaqqOHj2quLg4+zBvb291795dmzdvdmNlVdPGjRsVHBysZs2aafTo0UpPT3d3SVXCyZMnJUn16tWTRL8qzYXbqhB9y1F+fr5Wrlyp7Oxsde7cmT5Vigu3VaHK7FOWuAOwFXXq1EnLly9Xs2bN9Msvv2jmzJnq0qWLdu3apfr167u7vCqr8AnpFz4VPSQkRAcOHHBHSVVWr169dPvttysiIkKpqamaOnWqevTooW+//fayvjOpMUaPP/64rrvuOrVu3VoS/aokxW0rib71R9999506d+6s06dPq3bt2nr//ffVsmVLe2ChT/2upG0lVX6fIsxUkl69etn/3aZNG3Xu3FlXXnmlli1bpscff9yNlVmDzWZzeG+MKTLscjd48GD7v1u3bq0OHTooIiJC//nPfzRo0CA3VuZe48aN086dO/X5558XGUe/clTStqJv/a558+bavn27Tpw4oXfffVfDhw9XcnKyfTx96nclbauWLVtWep/iMNMlUqtWLbVp00b79u1zdylVWuEVX4X/ky6Unp5e5H9AcNSwYUNFRERc1n3s4Ycf1ocffqgNGzaocePG9uH0q6JK2lbFuZz7lpeXl5o2baoOHTooMTFR7dq100svvUSfKkZJ26o4ru5ThJlLJC8vTykpKWrYsKG7S6nSoqKiFBoaqrVr19qHnTlzRsnJyerSpYsbK6v6jh07poMHD16WfcwYo3Hjxum9997T+vXrFRUV5TCefvW7i22r4lzOfetCxhjl5eXRp8qgcFsVx+V9qtJOLb7MTZgwwWzcuNH89NNP5quvvjJ9+/Y1/v7+Zv/+/e4uze2ysrLMtm3bzLZt24wkk5SUZLZt22YOHDhgjDFm1qxZJjAw0Lz33nvmu+++M3feeadp2LChyczMdHPll1Zp2ykrK8tMmDDBbN682aSmppoNGzaYzp07m0aNGl1228kYYx588EETGBhoNm7caI4cOWJ/5eTk2KehX513sW1F3/rd5MmTzaZNm0xqaqrZuXOnefrpp42Hh4f59NNPjTH0qT8qbVtdij5FmKkkgwcPNg0bNjSenp4mLCzMDBo0yOzatcvdZVUJGzZsMJKKvIYPH26MOX8Z7fTp001oaKjx9vY23bp1M9999517i3aD0rZTTk6OiYuLMw0aNDCenp4mPDzcDB8+3KSlpbm7bLcobjtJMkuWLLFPQ78672Lbir71u1GjRpmIiAjj5eVlGjRoYG688UZ7kDGGPvVHpW2rS9GnbMYY45p9PAAAAJce58wAAABLI8wAAABLI8wAAABLI8wAAABLI8wAAABLI8wAAABLI8wAAABLI8wAgIu88cYbiouLc+k8O3bsqPfee8+l8wSqG8IMUM3YbLZSXyNGjHB3iS4XGxur8ePHu7WGvLw8TZs2TVOnTrUPy8/P19ixY9WwYUP16tWryEMJMzMz9cwzz6hFixby8fFRaGiobrrpJr333nsqvJ/p1KlT9dRTT6mgoOCSrg9gJYQZoJo5cuSI/TVv3jwFBAQ4DCvpKbZV0dmzZy2zvHfffVe1a9fW9ddfbx/29ttvKy0tTWvWrNE111zjEHROnDihLl26aPny5Zo8ebK2bt2qTZs2afDgwZo0aZJOnjwpSerTp49OnjypNWvWOL9iQDVHmAGqmdDQUPsrMDBQNpvNYdimTZt0zTXXyMfHR1dccYVmzJihc+fO2dvbbDYtWrRIffv2lZ+fn2JiYvTll1/qf//7n2JjY1WrVi117txZP/74o71NfHy8rrrqKi1atEhNmjSRn5+fbr/9dp04ccKhtiVLligmJkY+Pj5q0aKFFixYYB+3f/9+2Ww2vfPOO4qNjZWPj4/eeustHTt2THfeeacaN24sPz8/tWnTRm+//ba93YgRI5ScnKyXXnrJvvdp//79Wrp0qerUqeOw/A8++EA2m61I3W+++aauuOIKeXt7yxijkydP6v7771dwcLACAgLUo0cP7dixo9TtvnLlSt16660Ow06cOKGIiAi1bt1abdq0sQcUSXr66ae1f/9+ff311xo+fLhatmypZs2aafTo0dq+fbtq164tSapRo4Z69+7tsM4ALuCypzwBqHKWLFliAgMD7e8/+eQTExAQYJYuXWp+/PFH8+mnn5rIyEgTHx9vn0aSadSokVm1apXZs2ePGTBggImMjDQ9evQwn3zyidm9e7f505/+ZG655RZ7m+nTp5tatWqZHj16mG3btpnk5GTTtGlTM3ToUPs0ixcvNg0bNjTvvvuu+emnn8y7775r6tWrZ5YuXWqMMSY1NdVIMpGRkfZpDh06ZH7++Wczd+5cs23bNvPjjz+al19+2dSoUcN89dVXxhhjTpw4YTp37mxGjx5tfwL0uXPniqy7Mca8//775o9/9grrvvnmm83WrVvNjh07TEFBgenatavp16+f2bJli9m7d6+ZMGGCqV+/vjl27FiJ27pOnTpm5cqVDsNOnDhh2rdvb2rWrGkaNWpkdu7caYwxJj8/39StW9fcf//9ZfocFyxYYCIjI8s0LXA5IswA1diFP+jXX3+9SUhIcJjmb3/7m2nYsKH9vSQzZcoU+/svv/zSSDJvvPGGfdjbb79tfHx87O+nT59uatSoYQ4ePGgf9vHHHxsPDw9z5MgRY4wxTZo0MStWrHBY9l/+8hfTuXNnY8zvYWbevHkXXa/evXubCRMm2N93797dPProo6WuuzHFhxlPT0+Tnp5uH7Zu3ToTEBBgTp8+7dD2yiuvNIsWLSq2nuPHjxtJZtOmTcWOLwxYhX755RcjySQlJZW6noX+9a9/GQ8PD5Ofn1+m6YHLTU237RICcMl9++232rJli5577jn7sPz8fJ0+fVo5OTny8/OTJLVt29Y+PiQkRJLUpk0bh2GnT59WZmamAgICJEnh4eFq3LixfZrOnTuroKBAe/bsUY0aNXTw4EHde++9Gj16tH2ac+fOKTAw0KHGDh06OLzPz8/XrFmztGrVKh06dEh5eXnKy8tTrVq1Kro5JEkRERFq0KCB/f23336rU6dOqX79+g7T5ebmOhxau3CcJPn4+BQ7PjQ01OG9+f8n9/7xkFdpfH19VVBQoLy8PPn6+papDXA5IcwAl5GCggLNmDFDgwYNKjLujz/Enp6e9n8X/uAWN6y0K2wKp7HZbPbpXnvtNXXq1Mlhuho1aji8vzCkvPDCC3rxxRc1b948tWnTRrVq1dL48eN15syZkldUkoeHhz00FCruBN8Ll1dQUKCGDRtq48aNRaa98BycQvXr15fNZtPx48dLralQgwYNVLduXaWkpJRp+t9++01+fn4EGaAEhBngMtK+fXvt2bNHTZs2dfm809LSdPjwYYWFhUmSvvzyS3l4eKhZs2YKCQlRo0aN9NNPP+muu+4q13w/++wz9e/fX8OGDZN0Pmzs27dPMTEx9mm8vLyUn5/v0K5BgwbKyspSdna2PbBs3779ostr3769jh49qpo1ayoyMrJMNXp5eally5bavXt3me4z4+HhocGDB+tvf/ubpk+fbt9mhbKzs+Xt7a2aNc//if7+++/Vvn37MtUCXI64mgm4jEybNk3Lly9XfHy8du3apZSUFK1atUpTpkyp8Lx9fHw0fPhw7dixQ5999pkeeeQR3XHHHfZDLPHx8UpMTNRLL72kvXv36rvvvtOSJUuUlJRU6nybNm2qtWvXavPmzUpJSdGYMWOK3K8lMjJSX3/9tfbv36+MjAwVFBSoU6dO8vPz09NPP63//e9/WrFihZYuXXrR9bjpppvUuXNnDRgwQGvWrNH+/fu1efNmTZkyRd98802J7W6++WZ9/vnnF99Q/19CQoKaNGmiTp06afny5dq9e7f27dunN998U1dddZVOnTpln/azzz5z+c34gOqEMANcRm6++WZ99NFHWrt2rTp27Kg//elPSkpKUkRERIXn3bRpUw0aNEi9e/dWXFycWrdu7XDp9X333afXX39dS5cuVZs2bdS9e3ctXbpUUVFRpc536tSpat++vW6++WbFxsYqNDRUAwYMcJhm4sSJqlGjhlq2bKkGDRooLS1N9erV01tvvaXVq1fbL+eOj4+/6HrYbDatXr1a3bp106hRo9SsWTMNGTJE+/fvt58/VJzRo0dr9erVDpdfl6Zu3br66quvNGzYMM2cOVNXX321rr/+er399tuaO3eu/VyiQ4cOafPmzRo5cmSZ5gtcjmzmwoPKAFBO8fHx+uCDD8p0GKc6u+OOO3T11Vdr8uTJLpvnE088oZMnT2rx4sUumydQ3bBnBgBcZO7cufab3blKcHCw/vKXv7h0nkB1wwnAAOAiERERevjhh106zyeeeMKl8wOqIw4zAQAAS+MwEwAAsDTCDAAAsDTCDAAAsDTCDAAAsDTCDAAAsDTCDAAAsDTCDAAAsDTCDAAAsDTCDAAAsLT/B3VSGpYSHSUiAAAAAElFTkSuQmCC",
      "text/plain": [
       "<Figure size 640x480 with 1 Axes>"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    }
   ],
   "source": [
    "import numpy as np\n",
    "import matplotlib.pyplot as plt\n",
    "\n",
    "# Simulating temperatures using a normal distribution\n",
    "mean_temp = 20  # Mean temperature (°C)\n",
    "std_temp = 5    # Standard deviation (°C)\n",
    "\n",
    "temperatures = np.random.normal(loc=mean_temp, scale=std_temp, size=1000)\n",
    "\n",
    "plt.hist(temperatures, bins=30, color='skyblue', edgecolor='black')\n",
    "plt.title('Simulated Temperature Distribution (Normal)')\n",
    "plt.xlabel('Temperature (°C)')\n",
    "plt.ylabel('Frequency')\n",
    "plt.show()\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "**Example 2**: Sampling from the Log-Normal Distribution\n",
    "\n",
    "Application: Model earthquake magnitudes or river flows, which often follow a skewed log-normal distribution."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 12,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAjoAAAHFCAYAAAD7ZFORAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjguMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy81sbWrAAAACXBIWXMAAA9hAAAPYQGoP6dpAABMqUlEQVR4nO3deXxM1/8/8NdkTyRCEkJktSaxRSTUTlUssVdFNdbQJfGjSC2ldo2ltk8lllKhtlSrWqpCURSt2GliLYLEkgQhZJ3z+0NnviYzITOZMXHzej4eebRz5p5733PvLC/3nnuvTAghQERERCRBJsYugIiIiMhQGHSIiIhIshh0iIiISLIYdIiIiEiyGHSIiIhIshh0iIiISLIYdIiIiEiyGHSIiIhIshh0iIiISLIYdF7w999/o1evXnB3d4elpSWcnZ3RrFkzjB07VmW6tm3bom3btkap8Y8//oBMJsMff/yhdd/ExERMmzYN169f13td06ZNg0wme+V0gwcPhkwmK/JPn54+fYpp06ZpXFeKetPS0vS6TH1r27Yt6tWrZ9BlKNb94MGDNT4/Y8YM5TSGeO/oIjY2Vq2ejRs3YvHixQZZ3uDBg+Hp6am3+Snef4o/GxsbuLq6omPHjvj666/x+PFjvdSQkpKCadOm4fTp01r107QsmUyGESNGaDWfV4mJiUFsbKxa+/Xr1yGTyTQ+97oMHToUnTp1Uqvpq6++MlpNL1J8BqysrHDjxg2151/Hd4chFX4P5uXloUaNGjp9xhl0/vPrr7+iefPmyMzMxLx587B7924sWbIELVq0QFxcnMq0MTExiImJMVKluktMTMT06dON/mNlbW2No0ePavzTp6dPn2L69Ok6hcKyxs7ODlu2bFH7gRVCIDY2FuXLlzdSZZoFBwfj6NGjqFq1qrLNkEHHUHbt2oWjR49i165d+Oqrr+Du7o5x48ahbt26OHPmjMq0X3zxBX766Set5p+SkoLp06drHXR0WZYuigo6VatWxdGjRxEcHGzwGjQ5deoU1q5di1mzZhll+drIycnB5MmTjV2GwZmbm2PKlCmYMWMG0tPTteprZqCa3jjz5s2Dl5cX4uPjYWb2f6ulX79+mDdvnsq0vr6+r7s8STExMcFbb71lsPkLIZCdnW2w+UtRjx498OOPP2Lz5s0YPny4sn3fvn24du0ahg8fjm+++caIFaqqVKkSKlWqZOwySqxx48ZwcnJSPu7Xrx9GjBiBNm3aoHv37rh06RIsLS0BADVq1DB4PU+fPoWNjc1rWdbLWFpaGvQ74lXmzJmDJk2aICAgwGg1FFenTp2wceNGREZGomHDhgZbzrNnz2BtbW2w+RfH+++/jzFjxmDFihX4/PPPi92Pe3T+k56eDicnJ5WQo2BiorqaCh+6UuzSnD9/PubOnQtPT09YW1ujbdu2uHTpEvLy8jBhwgS4uLjA3t4evXr1wr1791TmKZPJMG3aNLVle3p6FnlIQeH48ePo16+fcrmenp54//33VXZnxsbG4r333gMAtGvXTrnL/MV/Tf3+++9o3749ypcvDxsbG7Ro0QJ79+5VW96vv/4KPz8/WFpawsvLyyC7crOzszF27Fj4+fnB3t4eDg4OaNasGX7++We1aRW71JcvXw4fHx9YWlpi7dq1yh/C6dOnF3l45u7du3j//fdhb28PZ2dnDB06FI8ePVKZJjMzE8OHD4ejoyNsbW3RqVMnXLp0SW2bFXVoQdNhvejoaLRu3RqVK1dGuXLlUL9+fcybNw95eXmvXDc//fQTbGxsMGzYMOTn5wN4/h7o3r07HBwcYGVlhUaNGuH7779/5bwUFO/Lb7/9VqX922+/RYsWLVC7dm21Pnv27EGPHj3g6uoKKysr1KxZEx999JHGw4E///wzGjRoAEtLS1SvXh1LlizRuF4U2/K7776Dj48PbGxs0LBhQ+zYsUNlusKHrtq2bYtff/0VN27cUDsUWtTh3qIOj8TGxqJOnTqwtLSEj48P1q1bp3Gd5ebmYtasWfD29oalpSUqVaqEIUOG4P79+xqnL66GDRti0qRJSE5OVtmbrOn9tWXLFjRt2hT29vawsbFB9erVMXToUOXrDgwMBAAMGTJEuU4U79nBgwfD1tYW586dQ1BQEOzs7NC+ffsil6WwYsUK1K5dG5aWlvD19cXmzZtVni/qMHbhbebp6Yl//vkHBw4cUNamWGZR2+bPP/9E+/btYWdnBxsbGzRv3hy//vqrxuXs378fn3zyCZycnODo6IjevXsjJSVF42t60d27d/HTTz9hwIABr5xWk+TkZISGhqJy5crK99CCBQsgl8tVprt16xb69OkDOzs7VKhQAR988AESEhK0PmQ3btw4ODo6Yvz48a+cNjs7GxMnToSXlxcsLCxQrVo1RERE4OHDhyrTeXp6omvXrti6dSsaNWoEKysr5d5xmUyGjRs3Yvz48ahatSpsbW3RrVs33L17F48fP8aHH34IJycnODk5YciQIXjy5InKvEvy3WdhYYGQkBCsXLkS2tyPnHt0/tOsWTOsWrUKI0eOxAcffAB/f3+Ym5trNY/o6Gg0aNAA0dHRePjwIcaOHYtu3bqhadOmMDc3x7fffosbN24gMjISw4YNwy+//KKX2q9fv446deqgX79+cHBwQGpqKpYtW4bAwEAkJibCyckJwcHB+PLLL/H5558jOjoa/v7+AP7vX4nr16/HwIED0aNHD6xduxbm5uZYsWIFOnbsiPj4eOUX4N69e9GjRw80a9YMmzdvRkFBAebNm4e7d+9qVbPiB/pFJiYmylCZk5ODjIwMREZGolq1asjNzcXvv/+O3r17Y82aNRg4cKBK323btuHQoUOYMmUKqlSpAgcHB+zatQudOnVCWFgYhg0bBgBqewHeffddhISEICwsDOfOncPEiRMBQPmDL4RAz549ceTIEUyZMgWBgYE4fPgwOnfurNXrLezq1avo37+/8gvnzJkzmD17Ni5cuKAWNl60aNEifPbZZ5g2bZpyd/X+/fvRqVMnNG3aFMuXL4e9vT02b96MkJAQPH369JVBWSEsLAzt27dHUlISfHx88PDhQ2zduhUxMTEadxVfvXoVzZo1w7Bhw2Bvb4/r169j4cKFaNmyJc6dO6f8/OzatQu9e/dG69atERcXh/z8fHz11VdFvmd+/fVXJCQkYMaMGbC1tcW8efPQq1cvXLx4EdWrV9fYJyYmBh9++CGuXr1aokMusbGxGDJkCHr06IEFCxbg0aNHmDZtGnJyclT+wSOXy9GjRw8cOnQI48aNQ/PmzXHjxg1MnToVbdu2xfHjx0v0r9/u3btj3LhxOHjwoNp7XeHo0aMICQlBSEgIpk2bphyrsW/fPgCAv78/1qxZgyFDhmDy5MnKw0Curq7KeeTm5qJ79+746KOPMGHCBI2fyxf98ssv2L9/P2bMmIFy5cohJiYG77//PszMzNCnTx+tXuNPP/2EPn36wN7eXjkUQLH3SpMDBw6gQ4cOaNCgAVavXg1LS0vExMSgW7du2LRpE0JCQlSmHzZsGIKDg7Fx40bcvHkTn332GUJDQ5Xrpyi7d+9GXl4e2rVrp9XrAYD79++jefPmyM3NxcyZM+Hp6YkdO3YgMjISV69eVb7OrKwstGvXDhkZGZg7dy5q1qyJXbt2qb2G4rCzs8PkyZMxatQo7Nu3D2+//bbG6RTfZXv37sXEiRPRqlUrnD17FlOnTlUOHXhx/Z88eRJJSUmYPHkyvLy8UK5cOWRlZQEAPv/8c7Rr1w6xsbG4fv06IiMjle+Dhg0bYtOmTTh16hQ+//xz2NnZ4X//+59yvrp+9ym0bdsWy5Ytw/nz51G/fv3irSRBQggh0tLSRMuWLQUAAUCYm5uL5s2bi6ioKPH48WOVadu0aSPatGmjfHzt2jUBQDRs2FAUFBQo2xcvXiwAiO7du6v0//TTTwUA8ejRI2UbADF16lS1ujw8PMSgQYOUj/fv3y8AiP379xf5WvLz88WTJ09EuXLlxJIlS5TtW7Zs0dg3KytLODg4iG7duqm0FxQUiIYNG4omTZoo25o2bSpcXFzEs2fPlG2ZmZnCwcFBFOftNGjQIOU6LvzXvn37l76mvLw8ERYWJho1aqTyHABhb28vMjIyVNrv379f5HqdOnWqACDmzZun0h4eHi6srKyEXC4XQgjx22+/CQAq61EIIWbPnq0270GDBgkPD48il1WUgoICkZeXJ9atWydMTU1VXkebNm1E3bp1RUFBgRgxYoSwsLAQ69evV+nv7e0tGjVqJPLy8lTau3btKqpWraryntQEgIiIiBByuVx4eXmJyMhIIYQQ0dHRwtbWVjx+/FjMnz9fABDXrl3TOA+5XC7y8vLEjRs3BADx888/K58LDAwUbm5uIicnR9n2+PFj4ejoqLZeAAhnZ2eRmZmpbLtz544wMTERUVFRyrY1a9ao1RMcHKxx/Rf1mVF8btesWSOEeL4dXFxchL+/v3L7CyHE9evXhbm5ucq8N23aJACIH3/8UWWeCQkJAoCIiYnRuJ4UFO+J+/fva3z+2bNnAoDo3Lmzsq3w++urr74SAMTDhw+LXI6iHsVrfJHis/jtt99qfK7wugQgrK2txZ07d5Rt+fn5wtvbW9SsWVPttRWmaZvVrVtX5btUofC2EUKIt956S1SuXFnl+zg/P1/Uq1dPuLq6KreZYjnh4eEq85w3b54AIFJTU9WW96JPPvlEWFtbq7wHXqxp/vz5RfadMGGCACD+/vtvtXnKZDJx8eJFIcTzzxYA8dtvv6lM99FHHxW5vQpTvM6EhASRk5MjqlevLgICApR1K747FHbt2qXxOy8uLk4AECtXrlS2eXh4CFNTU2W9CorPUuHfCsVv2siRI1Xae/bsKRwcHIp8DS/77ivq+/Ty5csCgFi2bFmR8y2Mh67+4+joiEOHDiEhIQFz5sxBjx49cOnSJUycOBH169cv1tk5Xbp0UflXn4+PDwCoDahTtCcnJ+ul9idPnmD8+PGoWbMmzMzMYGZmBltbW2RlZSEpKemV/Y8cOYKMjAwMGjQI+fn5yj+5XI5OnTohISEBWVlZyMrKQkJCAnr37g0rKytlfzs7O3Tr1q3Y9VpbWyMhIUHtr/AA7y1btqBFixawtbWFmZkZzM3NsXr1ao2v6e2330bFihWLXYNC9+7dVR43aNAA2dnZykOL+/fvBwB88MEHKtP1799f62W96NSpU+jevTscHR1hamoKc3NzDBw4EAUFBbh06ZLKtNnZ2ejZsyc2bNiA3bt3q9Ry5coVXLhwQdn24vbr0qULUlNTcfHixWLVpDi099133yE/Px+rV69G3759YWtrq3H6e/fu4eOPP4abm5ty+3h4eACAchtlZWXh+PHj6NmzJywsLJR9Fbu7NWnXrh3s7OyUj52dnVG5cmWNZ5bo08WLF5GSkoL+/furHHrx8PBA8+bNVabdsWMHKlSogG7duqmscz8/P1SpUqXEA+BFMXbLKw5L9e3bF99//z1u376t07LefffdYk/bvn17ODs7Kx+bmpoiJCQEV65cwa1bt3RafnFkZWXh77//Rp8+fVTej6amphgwYABu3bql9j7X9NkG8Mr3UUpKCipVqqTTWaD79u2Dr68vmjRpotI+ePBgCCGUe5MOHDgAOzs7lbO6gOdjUF4khFB5fxW1x83CwgKzZs3C8ePHizxkrVh24T287733HsqVK6c2TKFBgwYaD1kDQNeuXVUev+y3LiMjQ+XwlTbffZpUrlwZALR6vzPoFBIQEIDx48djy5YtSElJwejRo3H9+nW1AcmaODg4qDxWfLEX1a6vAbP9+/fH0qVLMWzYMMTHx+PYsWNISEhApUqV8OzZs1f2VxxC6NOnD8zNzVX+5s6dCyEEMjIy8ODBA8jlclSpUkVtHpraimJiYoKAgAC1vxc/VFu3bkXfvn1RrVo1rF+/HkePHkVCQgKGDh2qcb29ePaNNhwdHVUeK3bdKtZbeno6zMzM1KbT5vUWlpycjFatWuH27dtYsmSJMmBHR0erLFvh3r17iI+PR7NmzdR+cBXbLjIyUm3bhYeHA4BWp9Arxph8+eWXOHnyJMLCwjROJ5fLERQUhK1bt2LcuHHYu3cvjh07hr/++kvlNTx48ABCCJUfRwVNbYD6NgGeb5fivJdLQnF4rjjv77t37+Lhw4ewsLBQW+937twp8WULFD/GLi4uRU7TunVrbNu2Dfn5+Rg4cCBcXV1Rr149bNq0qdjLsbGx0eqMupetG23PhNGG4n2k6XOuWEeFl/+qz3ZRnj17pvIPOW2kp6cXq8b09PRifSYOHDig9v4q6qzZfv36wd/fH5MmTdI43kXxXVb48L1MJkOVKlXU1t/LvlN1/a3T9rtPE8W20eb7gGN0XsLc3BxTp07FokWLcP78eYMuy9LSEjk5OWrtr/ryePToEXbs2IGpU6diwoQJynbFGJfiUJz18fXXXxd5poOzszPy8vIgk8lw584dtec1tZXE+vXr4eXlhbi4OJV/WWlaRwD0fg0eBUdHR+Tn5yM9PV3li1PT67WystJYX+EfvW3btiErKwtbt25V7gEBUOQpwO7u7li4cCF69eqF3r17Y8uWLcoPu2LbTZw4Eb1799bYv06dOi9/kS9wc3PDO++8g+nTp6NOnTpqwUrh/PnzOHPmDGJjYzFo0CBl+5UrV1Smq1ixImQymcbxOPp+zxRFsa4Kb5vC20WxfYvz/lYMcN21a5fGZb64R0oXivF7r7peV48ePdCjRw/k5OTgr7/+QlRUFPr37w9PT080a9bslcvR9nPzsnWjWH8vru8Xx3yUJPxVrFgRJiYmSE1NVXtOMcD4xbPXSsLJyQknT57Uqa+jo2OxanR0dMSxY8fUpiu8fhs3boyEhASVtqLCr0wmw9y5c9GhQwesXLlSY235+fm4f/++StgRQuDOnTvKPYQvzk/ftP3u00Txu6bN9uYenf9oenMC/7cL/mX/stIHT09PnD17VqVt3759aiPWC5PJZBBCqA3iW7VqFQoKClTaivoXTYsWLVChQgUkJiZq3NMSEBAACwsLlCtXDk2aNMHWrVtV9qo8fvwY27dv1/o1v+p1WVhYqHzY7ty5o/Gsq6IU919wL6MYkLhhwwaV9o0bN6pN6+npiXv37qn8qOfm5iI+Pl5lOsVrenGbCSFeevp2UFAQ4uPjcfDgQXTt2lU5KLBOnTqoVasWzpw5U+S20/ZHVzGI/osvvihyGk2vAXh+Rs6LypUrh4CAAGzbtg25ubnK9idPnqidSVVSRe31UZzJU/jzVfhkgDp16qBq1arYtGmTyqGjGzdu4MiRIyrTdu3aFenp6SgoKNC4zrUJl4WdOXMGX375JTw9PdG3b99i9bG0tESbNm0wd+5cAM8PDyjagZJ9Bl60d+9elfd3QUEB4uLiUKNGDeUg56LWt6bviOLuqStXrhyaNm2KrVu3qkwvl8uxfv16uLq6FnmYRVve3t5IT09XO/uyONq3b4/ExES1oLRu3TrIZDLl90mbNm3w+PFj/PbbbyrTFT6Dzc7OTuN3cVHeeecddOjQATNmzFD77VCcULJ+/XqV9h9//BFZWVnK5w1Jl+++wv79918A2l3mhXt0/tOxY0e4urqiW7du8Pb2hlwux+nTp7FgwQLY2tpi1KhRBl3+gAED8MUXX2DKlClo06YNEhMTsXTpUtjb27+0X/ny5dG6dWvMnz8fTk5O8PT0xIEDB7B69WpUqFBBZVrFVTJXrlwJOzs7WFlZwcvLC46Ojvj6668xaNAgZGRkoE+fPqhcuTLu37+PM2fO4P79+1i2bBkAYObMmejUqRM6dOiAsWPHoqCgAHPnzkW5cuWKvQdJLpcrD3EU1qhRI1haWipPbQwPD0efPn1w8+ZNzJw5E1WrVsXly5eLtRw7Ozt4eHjg559/Rvv27eHg4KBcR8UVFBSE1q1bY9y4ccjKykJAQAAOHz6M7777Tm3akJAQTJkyBf369cNnn32G7Oxs/O9//1MLnB06dICFhQXef/99jBs3DtnZ2Vi2bBkePHjw0lpatmyJvXv3olOnTggKCsLOnTthb2+PFStWoHPnzujYsSMGDx6MatWqISMjA0lJSTh58iS2bNlS7NereM1BQUEvncbb2xs1atTAhAkTIISAg4MDtm/fjj179qhNO2PGDAQHB6Njx44YNWoUCgoKMH/+fNja2hb7PVMc9evXx9atW7Fs2TI0btxYeYi0SpUqeOeddxAVFYWKFSvCw8MDe/fuxdatW1X6m5iYYObMmRg2bBh69eqF4cOH4+HDh5g2bZraIZt+/fphw4YN6NKlC0aNGoUmTZrA3Nwct27dwv79+9GjRw/06tXrlTWfOHEC9vb2yMvLQ0pKCvbu3YvvvvsOlStXxvbt21/6ozZlyhTcunUL7du3h6urKx4+fIglS5bA3Nwcbdq0AfD8rEpra2ts2LABPj4+sLW1hYuLi87/cHNycsLbb7+NL774QnnW1YULF1R+oLt06QIHBweEhYVhxowZMDMzQ2xsLG7evKk2v/r162Pz5s2Ii4tD9erVYWVlVeSZNFFRUejQoQPatWuHyMhIWFhYICYmBufPn8emTZv0tgeibdu2EELg77//1vg5OHfuHH744Qe19sDAQIwePRrr1q1DcHAwZsyYAQ8PD/z666+IiYnBJ598ogxjgwYNwqJFixAaGopZs2ahZs2a+O2335T/KCp8SRNtzJ07F40bN8a9e/dQt25dZXuHDh3QsWNHjB8/HpmZmWjRooXyrKtGjRrpfDq9NnT97nvRX3/9BVNTU7Ru3br4Cy72sGWJi4uLE/379xe1atUStra2wtzcXLi7u4sBAwaIxMRElWmLOuuq8Gh8xQj1LVu2qLS/OFpeIScnR4wbN064ubkJa2tr0aZNG3H69OlinXV169Yt8e6774qKFSsKOzs70alTJ3H+/Hm1vkI8PxPMy8tLmJqaqo3uP3DggAgODhYODg7C3NxcVKtWTQQHB6vV/8svv4gGDRoICwsL4e7uLubMmfPKM4sUXnbWFQBx+fJl5bRz5swRnp6ewtLSUvj4+IhvvvlG43Lw31lDmvz++++iUaNGwtLSUgBQro+iznrRdGbIw4cPxdChQ0WFChWEjY2N6NChg7hw4YLGM7p27twp/Pz8hLW1tahevbpYunSpxpq3b98uGjZsKKysrES1atXEZ599pjzD68VtW/jMCSGEOH/+vKhSpYrw9/dX1n/mzBnRt29fUblyZWFubi6qVKki3n77bbF8+fIit0Vx1p+CprOuEhMTRYcOHYSdnZ2oWLGieO+990RycrLG9fLTTz+J+vXrq7xnRo4cKSpWrFisWgq/lzVtp4yMDNGnTx9RoUIFIZPJVNZ5amqq6NOnj3BwcBD29vYiNDRUHD9+XOMZLqtWrRK1atUSFhYWonbt2uLbb7/VeAZIXl6e+Oqrr5Tb0dbWVnh7e4uPPvpI5X2sieI9ofiztLQUVatWFUFBQWLJkiUqZ50pFK5hx44donPnzqJatWrCwsJCVK5cWXTp0kUcOnRIpd+mTZuEt7e3MDc3V9k2gwYNEuXKldNYX1FnXUVERIiYmBhRo0YNYW5uLry9vcWGDRvU+h87dkw0b95clCtXTlSrVk1MnTpVrFq1Sm2bXb9+XQQFBQk7OzsBQLlMTWddCSHEoUOHxNtvvy3KlSsnrK2txVtvvSW2b9+uMo2m71chinfGqhDPzwTy9PRUO2tLUVNRf4pab9y4Ifr37y8cHR2Fubm5qFOnjpg/f77a2Y/Jycmid+/ewtbWVtjZ2Yl3331X7Ny5U+2sxaIU9TqFEKJ///4CgNp3x7Nnz8T48eOFh4eHMDc3F1WrVhWffPKJePDggcp0Hh4eIjg4WG2+2vymCaH5e7a4331FnXXVqlUrtbO+XkUmhBZX3SEiJZlMhqlTp2q80CO9XF5eHvz8/FCtWjXs3r3b2OUQqViwYAFmz56N27dvv9arAX/55ZeYPHkykpOTVa53RM9dvXoVtWrVQnx8PDp06FDsfjx0RUQGFxYWhg4dOqBq1aq4c+cOli9fjqSkJCxZssTYpRGpiYiIwNKlSxEdHY3IyEiDLGPp0qUAnh8GzsvLw759+/C///0PoaGhDDlFmDVrFtq3b69VyAEYdIjoNXj8+DEiIyNx//59mJubw9/fHzt37sQ777xj7NKI1FhZWeG7775TDuo2BBsbGyxatAjXr19HTk4O3N3dMX78+DJxg05d5Ofno0aNGsqr12uDh66IiIhIsnh6OREREUkWgw4RERFJFoMOERERSVaZH4wsl8uRkpICOzs7g91GgIiIiPRLCIHHjx/DxcXlpRdZLPNBJyUlBW5ubsYug4iIiHRw8+bNl56SX+aDjuI+QDdv3tTqLr5ERERkPJmZmXBzc3vl/fzKfNBRHK4qX748gw4REdEb5lXDTjgYmYiIiCSLQYeIiIgkq8wGnejoaPj6+iIwMNDYpRAREZGBlPlbQGRmZsLe3h6PHj3iGB0iIqI3RHF/v8vsHh0iIiKSPgYdIiIikiwGHSIiIpIsBh0iIiKSLAYdIiIikiwGHSIiIpIsBh0iIiKSLAYdIiIikiwGHSIiIpKsMn/3ckNKTk5GWlqaTn2dnJzg7u6u54qIiIjKFgYdA0lOToaPdx08fZatU38bayskXbjIsENERFQCDDoGkpaWhqfPsrE+HPBx0a5vUgoQGpONtLQ0Bh0iIqISYNAxMB8XwN/L2FUQERGVTRyMTERERJJVZoNOdHQ0fH19ERgYaOxSiIiIyEDKbNCJiIhAYmIiEhISjF0KERERGUiZDTpEREQkfQw6REREJFkMOkRERCRZDDpEREQkWQw6REREJFkMOkRERCRZDDpEREQkWbwFRCmWlJSkUz/e+ZyIiOg5Bp1SKPUhYCIDQkNDderPO58TERE9x6BTCj18CsgFeOdzIiKiEmLQKcV453MiIqKS4WBkIiIikiwGHSIiIpIsBh0iIiKSLAYdIiIikiwGHSIiIpIsBh0iIiKSLAYdIiIikiwGHSIiIpIsBh0iIiKSLAYdIiIikiwGHSIiIpKsMht0oqOj4evri8DAQGOXQkRERAZSZoNOREQEEhMTkZCQYOxSiIiIyEDKbNAhIiIi6WPQISIiIsli0CEiIiLJYtAhIiIiyWLQISIiIsli0CEiIiLJYtAhIiIiyWLQISIiIsli0CEiIiLJYtAhIiIiyWLQISIiIsli0CEiIiLJYtAhIiIiyWLQISIiIskyM3YBZBhJSUk69XNycoK7u7ueqyEiIjIOBh2JSX0ImMiA0NBQnfrbWFsh6cJFhh0iIpIEBh2JefgUkAtgfTjg46Jd36QUIDQmG2lpaQw6REQkCQw6EuXjAvh7GbsKIiIi4+JgZCIiIpIsBh0iIiKSLAYdIiIikiwGHSIiIpIsBh0iIiKSLAYdIiIikiwGHSIiIpIsBh0iIiKSLAYdIiIikiwGHSIiIpIsBh0iIiKSLAYdIiIikiwGHSIiIpIsBh0iIiKSrDc+6Ny8eRNt27aFr68vGjRogC1bthi7JCIiIiolzIxdQEmZmZlh8eLF8PPzw7179+Dv748uXbqgXLlyxi6NiIiIjOyNDzpVq1ZF1apVAQCVK1eGg4MDMjIyGHSIiIjI+IeuDh48iG7dusHFxQUymQzbtm1TmyYmJgZeXl6wsrJC48aNcejQIY3zOn78OORyOdzc3AxcNREREb0JjB50srKy0LBhQyxdulTj83Fxcfj0008xadIknDp1Cq1atULnzp2RnJysMl16ejoGDhyIlStXvo6yiYiI6A1g9ENXnTt3RufOnYt8fuHChQgLC8OwYcMAAIsXL0Z8fDyWLVuGqKgoAEBOTg569eqFiRMnonnz5i9dXk5ODnJycpSPMzMz9fAqiIiIqDQy+h6dl8nNzcWJEycQFBSk0h4UFIQjR44AAIQQGDx4MN5++20MGDDglfOMioqCvb298o+HuYiIiKSrVAedtLQ0FBQUwNnZWaXd2dkZd+7cAQAcPnwYcXFx2LZtG/z8/ODn54dz584VOc+JEyfi0aNHyr+bN28a9DUQERGR8Rj90FVxyGQylcdCCGVby5YtIZfLiz0vS0tLWFpa6rU+IiIiKp1K9R4dJycnmJqaKvfeKNy7d09tLw8RERFRYaU66FhYWKBx48bYs2ePSvuePXteOeiYiIiIyOiHrp48eYIrV64oH1+7dg2nT5+Gg4MD3N3dMWbMGAwYMAABAQFo1qwZVq5cieTkZHz88cdGrJqIiIjeBEYPOsePH0e7du2Uj8eMGQMAGDRoEGJjYxESEoL09HTMmDEDqampqFevHnbu3AkPD48SLTc6OhrR0dEoKCgo0XyIiIio9DJ60Gnbti2EEC+dJjw8HOHh4XpdbkREBCIiIpCZmQl7e3u9zvtNl5SUpFM/JycnuLu767kaIiIi3Rk96FDpkfoQMJEBoaGhOvW3sbZC0oWLDDtERFRqMOiQ0sOngFwA68MBHxft+ialAKEx2UhLS2PQISKiUoNBh9T4uAD+XsaugoiIqORK9enlRERERCXBoENERESSVWaDTnR0NHx9fREYGGjsUoiIiMhAymzQiYiIQGJiIhISEoxdChERERlImQ06REREJH0MOkRERCRZDDpEREQkWQw6REREJFkMOkRERCRZDDpEREQkWWU26PA6OkRERNJXZoMOr6NDREQkfWU26BAREZH0MegQERGRZDHoEBERkWQx6BAREZFkmenSKS8vD3fu3MHTp09RqVIlODg46LsuekMlJSXp1M/JyQnu7u56roaIiMq6YgedJ0+eYMOGDdi0aROOHTuGnJwc5XOurq4ICgrChx9+yNO1y6jUh4CJDAgNDdWpv421FZIuXGTYISIivSpW0Fm0aBFmz54NT09PdO/eHRMmTEC1atVgbW2NjIwMnD9/HocOHUKHDh3w1ltv4euvv0atWrUMXTuVIg+fAnIBrA8HfFy065uUAoTGZCMtLY1Bh4iI9KpYQefIkSPYv38/6tevr/H5Jk2aYOjQoVi+fDlWr16NAwcOlPqgEx0djejoaBQUFBi7FEnxcQH8vYxdBRER0XPFCjpbtmwp1swsLS0RHh5eooJel4iICERERCAzMxP29vbGLoeIiIgMQOezrq5cuYL4+Hg8e/YMACCE0FtRRERERPqgddBJT0/HO++8g9q1a6NLly5ITU0FAAwbNgxjx47Ve4FEREREutI66IwePRpmZmZITk6GjY2Nsj0kJAS7du3Sa3FEREREJaH1dXR2796N+Ph4uLq6qrTXqlULN27c0FthRERERCWl9R6drKwslT05CmlpabC0tNRLUURERET6oHXQad26NdatW6d8LJPJIJfLMX/+fLRr106vxRERERGVhNaHrubPn4+2bdvi+PHjyM3Nxbhx4/DPP/8gIyMDhw8fNkSNRERERDrReo+Or68vzp49iyZNmqBDhw7IyspC7969cerUKdSoUcMQNRIRERHpRKebelapUgXTp0/Xdy1EREREelWsoHP27Nliz7BBgwY6F/M68RYQRERE0lesoOPn5weZTPbKqx/LZLI3JjjwFhBERETSV6ygc+3aNUPXQURERKR3xQo6Hh4ehq6DiIiISO90GowMAImJiUhOTkZubq5Ke/fu3UtcFBEREZE+aB10/v33X/Tq1Qvnzp1TGbcjk8kA4I0Zo0NERETSp/V1dEaNGgUvLy/cvXsXNjY2+Oeff3Dw4EEEBATgjz/+MECJRERERLrReo/O0aNHsW/fPlSqVAkmJiYwMTFBy5YtERUVhZEjR+LUqVOGqJOIiIhIa1rv0SkoKICtrS0AwMnJCSkpKQCeD1i+ePGifqsjIiIiKgGt9+jUq1cPZ8+eRfXq1dG0aVPMmzcPFhYWWLlyJapXr26IGomIiIh0onXQmTx5MrKysgAAs2bNQteuXdGqVSs4OjoiLi5O7wUSERER6UrroNOxY0fl/1evXh2JiYnIyMhAxYoVlWdeEREREZUGWo/RefToETIyMlTaHBwc8ODBA2RmZuqtMCIiIqKS0jro9OvXD5s3b1Zr//7779GvXz+9FPU6REdHw9fXF4GBgcYuhYiIiAxE60NXf//9NxYuXKjW3rZtW0yaNEkvRb0OvKln6ZOUlKRTPycnJ7i7u+u5GiIikgKtg05OTg7y8/PV2vPy8vDs2TO9FEVlS+pDwEQGhIaG6tTfxtoKSRcuMuwQEZEarYNOYGAgVq5cia+//lqlffny5WjcuLHeCqOy4+FTQC6A9eGAj4t2fZNSgNCYbKSlpTHoEBGRGq2DzuzZs/HOO+/gzJkzaN++PQBg7969SEhIwO7du/VeIJUdPi6Av5exqyAiIinRejByixYtcPToUbi5ueH777/H9u3bUbNmTZw9exatWrUyRI1EREREOtF6jw4A+Pn5YcOGDfquhYiIiEivtN6jc/LkSZw7d075+Oeff0bPnj3x+eefIzc3V6/FEREREZWE1kHno48+wqVLlwAA//77L0JCQmBjY4MtW7Zg3Lhxei+QiIiISFdaB51Lly7Bz88PALBlyxa0adMGGzduRGxsLH788Ud910dERESkM62DjhACcrkcAPD777+jS5cuAAA3NzekpaXptzoiIiKiEtA66AQEBGDWrFn47rvvcODAAQQHBwMArl27BmdnZ70XSERERKQrrYPO4sWLcfLkSYwYMQKTJk1CzZo1AQA//PADmjdvrvcCiYiIiHSl9enlDRo0UDnrSmH+/PkwNTXVS1FERERE+qDTdXQ0sbKy0tesiIiIiPRC60NXRERERG+KMht0oqOj4evri8DAQGOXQkRERAZSZoNOREQEEhMTkZCQYOxSiIiIyEDKbNAhIiIi6dN6MPKYMWM0tstkMlhZWaFmzZro0aMHHBwcSlwcERERUUloHXROnTqFkydPoqCgAHXq1IEQApcvX4apqSm8vb0RExODsWPH4s8//4Svr68haiYiIiIqFq2DjmJvzZo1a1C+fHkAQGZmJsLCwtCyZUsMHz4c/fv3x+jRoxEfH6/3gok0SUpK0qmfk5MT3N3d9VwNERGVFloHnfnz52PPnj3KkAMA5cuXx7Rp0xAUFIRRo0ZhypQpCAoK0muhRJqkPgRMZEBoaKhO/W2srZB04SLDDhGRRGkddB49eoR79+6pHZa6f/8+MjMzAQAVKlRAbm6ufiokeomHTwG5ANaHAz4u2vVNSgFCY7KRlpbGoENEJFE6HboaOnQoFixYgMDAQMhkMhw7dgyRkZHo2bMnAODYsWOoXbu2vmslKpKPC+DvZewqiIiotNE66KxYsQKjR49Gv379kJ+f/3wmZmYYNGgQFi1aBADw9vbGqlWr9FspERERkZa0Djq2trb45ptvsGjRIvz7778QQqBGjRqwtbVVTuPn56fPGomIiIh0ovNNPW1tbeHg4ACZTKYScoiIiIhKC62vjCyXyzFjxgzY29vDw8MD7u7uqFChAmbOnAm5XG6IGomIiIh0ovUenUmTJmH16tWYM2cOWrRoASEEDh8+jGnTpiE7OxuzZ882RJ1EREREWtM66KxduxarVq1C9+7dlW0NGzZEtWrVEB4ezqBDREREpYbWh64yMjLg7e2t1u7t7Y2MjAy9FEVERESkD1oHnYYNG2Lp0qVq7UuXLkXDhg31UhQRERGRPmh96GrevHkIDg7G77//jmbNmkEmk+HIkSO4efMmdu7caYgaiYiIiHSi9R6dNm3a4NKlS+jVqxcePnyIjIwM9O7dGxcvXkSrVq0MUSMRERGRTnS6jo6LiwsHHRMREVGpV6ygc/bs2WLPsEGDBjoXQ0RERKRPxQo6fn5+kMlkEEK8dDqZTIaCggK9FEZERERUUsUKOteuXTN0HURERER6V6yg4+HhYeg6iIiIiPSuWGddHT16tNgzzMrKwj///KNzQa9LdHQ0fH19ERgYaOxSiIiIyECKFXQGDhyIDh064Pvvv8eTJ080TpOYmIjPP/8cNWvWxMmTJ/VapCFEREQgMTERCQkJxi6FiIiIDKRYh64SExOxYsUKTJkyBR988AFq164NFxcXWFlZ4cGDB7hw4QKysrLQu3dv7NmzB/Xq1TN03URERESvVKygY25ujhEjRmDEiBE4efIkDh06hOvXr+PZs2do2LAhRo8ejXbt2sHBwcHQ9RIREREVm9YXDPT394e/v78haiEiIiLSK61vAUFERET0pmDQISIiIsli0CEiIiLJ0ummnkRSkpSUpFM/JycnuLu767kaIiLSJ62DzrVr1+Dl5WWIWoheq9SHgIkMCA0N1am/jbUVki5cZNghIirFtA46NWvWROvWrREWFoY+ffrAysrKEHURGdzDp4BcAOvDAR8X7fompQChMdlIS0tj0CEiKsW0DjpnzpzBt99+i7Fjx2LEiBEICQlBWFgYmjRpYoj6iAzOxwXw505KIiJJ0nowcr169bBw4ULcvn0ba9aswZ07d9CyZUvUrVsXCxcuxP379w1RJxEREZHWdD7ryszMDL169cL333+PuXPn4urVq4iMjISrqysGDhyI1NRUfdZJREREpDWdg87x48cRHh6OqlWrYuHChYiMjMTVq1exb98+3L59Gz169NBnnURERERa03qMzsKFC7FmzRpcvHgRXbp0wbp169ClSxeYmDzPTF5eXlixYgW8vb31XiwRERGRNrQOOsuWLcPQoUMxZMgQVKlSReM07u7uWL16dYmLIyIiIioJrYPO5cuXXzmNhYUFBg0apFNBRERERPqi9RidNWvWYMuWLWrtW7Zswdq1a/VSFBEREZE+aB105syZAycnJ7X2ypUr48svv9RLUURERET6oPWhqxs3bmi8BYSHhweSk5P1UhTRm4L3ySIiKt20DjqVK1fG2bNn4enpqdJ+5swZODo66qsuolKN98kiInozaB10+vXrh5EjR8LOzg6tW7cGABw4cACjRo1Cv3799F4gUWnE+2QREb0ZtA46s2bNwo0bN9C+fXuYmT3vLpfLMXDgQI7RoTKH98kiIirdtA46FhYWiIuLw8yZM3HmzBlYW1ujfv368PDwMER9RERERDrTOugo1K5dG7Vr19ZnLURERER6pXXQKSgoQGxsLPbu3Yt79+5BLperPL9v3z69FUdERERUEloHnVGjRiE2NhbBwcGoV68eZDKZIeoiIiIiKjGtg87mzZvx/fffo0uXLoaoh4iIiEhvtL4ysoWFBWrWrGmIWoiIiIj0SuugM3bsWCxZsgRCCEPUQ0RERKQ3Wh+6+vPPP7F//3789ttvqFu3LszNzVWe37p1q96KIyIiIioJrYNOhQoV0KtXL0PUQkRERKRXWgedNWvWGKIOIiIiIr3TeowOAOTn5+P333/HihUr8PjxYwBASkoKnjx5otfiiqtXr16oWLEi+vTpY5TlExERUemkddC5ceMG6tevjx49eiAiIgL3798HAMybNw+RkZF6L7A4Ro4ciXXr1hll2URERFR6aR10Ro0ahYCAADx48ADW1tbK9l69emHv3r16La642rVrBzs7O6Msm4iIiEovrYPOn3/+icmTJ8PCwkKl3cPDA7dv39a6gIMHD6Jbt25wcXGBTCbDtm3b1KaJiYmBl5cXrKys0LhxYxw6dEjr5RAREVHZo3XQkcvlKCgoUGu/deuWTntVsrKy0LBhQyxdulTj83Fxcfj0008xadIknDp1Cq1atULnzp2RnJys9bKIiIiobNE66HTo0AGLFy9WPpbJZHjy5AmmTp2q020hOnfujFmzZqF3794an1+4cCHCwsIwbNgw+Pj4YPHixXBzc8OyZcu0XhYA5OTkIDMzU+WPiIiIpEnroLNo0SIcOHAAvr6+yM7ORv/+/eHp6Ynbt29j7ty5ei0uNzcXJ06cQFBQkEp7UFAQjhw5otM8o6KiYG9vr/xzc3PTR6lERERUCml9HR0XFxecPn0amzZtwsmTJyGXyxEWFoYPPvhAZXCyPqSlpaGgoADOzs4q7c7Ozrhz547ycceOHXHy5ElkZWXB1dUVP/30EwIDAzXOc+LEiRgzZozycWZmJsMOERGRRGkddADA2toaQ4cOxdChQ/Vdj0YymUzlsRBCpS0+Pr7Y87K0tISlpaXeaiMiIqLSS+ug86rr1QwcOFDnYgpzcnKCqampyt4bALh3757aXh4iIiKiwrQOOqNGjVJ5nJeXh6dPn8LCwgI2NjZ6DToWFhZo3Lgx9uzZo3J/rT179qBHjx56Ww4RERFJk9ZB58GDB2ptly9fxieffILPPvtM6wKePHmCK1euKB9fu3YNp0+fhoODA9zd3TFmzBgMGDAAAQEBaNasGVauXInk5GR8/PHHWi+LiIiIyhadxugUVqtWLcyZMwehoaG4cOGCVn2PHz+Odu3aKR8rBgoPGjQIsbGxCAkJQXp6OmbMmIHU1FTUq1cPO3fuhIeHR4lqjo6ORnR0tMZrAhEREZE06CXoAICpqSlSUlK07te2bVsIIV46TXh4OMLDw3UtTaOIiAhEREQgMzMT9vb2ep03ERERlQ5aB51ffvlF5bEQAqmpqVi6dClatGiht8KIiIiISkrroNOzZ0+VxzKZDJUqVcLbb7+NBQsW6KsuIiIiohLTOujI5XJD1EFERESkd1rfAoKIiIjoTaH1Hp0Xb5/wKgsXLtR29kRERER6o3XQOXXqFE6ePIn8/HzUqVMHAHDp0iWYmprC399fOV3h2zaUNjy9nIiISPq0DjrdunWDnZ0d1q5di4oVKwJ4fhHBIUOGoFWrVhg7dqzeizQEnl5OREQkfVqP0VmwYAGioqKUIQcAKlasiFmzZvGsKyIiIipVtA46mZmZuHv3rlr7vXv38PjxY70URURERKQPWgedXr16YciQIfjhhx9w69Yt3Lp1Cz/88APCwsLQu3dvQ9RIREREpBOtx+gsX74ckZGRCA0NRV5e3vOZmJkhLCwM8+fP13uBRERERLrSOujY2NggJiYG8+fPx9WrVyGEQM2aNVGuXDlD1EdERESkM51v6pmamorU1FS0bt0a1tbWEEKU+lPKiaQgOTkZaWlpOvV1cnKCu7u7nisiIiq9tA466enp6Nu3L/bv3w+ZTIbLly+jevXqGDZsGCpUqPDGnHnF6+jQmyg5ORk+3nXw9Fm2Tv1trK2QdOEiww4RlRlaB53Ro0fD3Nz8+Reuj4+yPSQkBKNHj35jgg6vo0NvorS0NDx9lo314YCPi3Z9k1KA0JhspKWlMegQUZmhddDZvXs34uPj4erqqtJeq1Yt3LhxQ2+FEVHRfFwAfy9jV0FEVPppfXp5VlYWbGxs1NrT0tJgaWmpl6KIiIiI9EHroNO6dWusW7dO+Vgmk0Eul2P+/Plo166dXosjIiIiKgmtD13Nnz8fbdu2xfHjx5Gbm4tx48bhn3/+QUZGBg4fPmyIGomIiIh0ovUeHV9fX5w9exZNmjRBhw4dkJWVhd69e+PUqVOoUaOGIWokIiIi0olWe3Ty8vIQFBSEFStWYPr06YaqiYiIiEgvtAo65ubmOH/+PC8MSKQHSUlJr6UPEVFZpvUYnYEDB2L16tWYM2eOIep5bXjBQDKW1IeAiQwIDQ01dilERJKnddDJzc3FqlWrsGfPHgQEBKjd42rhwoV6K86QeMFAMpaHTwG5gE4X/dt5Bvhii2HqIiKSIq2Dzvnz5+Hv7w8AuHTpkspzPKRFVHy6XPQvKcUwtRARSVWxg86///4LLy8v7N+/35D1EBEREelNsU8vr1WrFu7fv698HBISgrt37xqkKCIiIiJ9KHbQEUKoPN65cyeysrL0XhARERGRvmh9wUAiIiKiN0Wxg45MJlMbbMzBx0RERFSaFXswshACgwcPVt6hPDs7Gx9//LHa6eVbt27Vb4VEREREOip20Bk0aJDKY17sjOjNpOvVlZ2cnODu7q7naoiIDKvYQWfNmjWGrOO145WRqawp6RWZbaytkHThIsMOEb1RtL5goFTwyshU1pTkisxJKUBoTDbS0tIYdIjojVJmgw5RWaXLFZmJiN5UPL2ciIiIJItBh4iIiCSLQYeIiIgki0GHiIiIJItBh4iIiCSLQYeIiIgki0GHiIiIJItBh4iIiCSLQYeIiIgki0GHiIiIJKvMBp3o6Gj4+voiMDDQ2KUQERGRgZTZoBMREYHExEQkJCQYuxQiIiIykDIbdIiIiEj6GHSIiIhIshh0iIiISLIYdIiIiEiyGHSIiIhIshh0iIiISLIYdIiIiEiyGHSIiIhIshh0iIiISLIYdIiIiEiyGHSIiIhIshh0iIiISLIYdIiIiEiyGHSIiIhIssyMXQARvTmSkpJ07puTkwNLS0ud+jo5OcHd3V3nZRNR2VVmg050dDSio6NRUFBg7FKISr3Uh4CJDAgNDdV5HqYmQIFct7421lZIunCRYYeItFZmg05ERAQiIiKQmZkJe3t7Y5dDVKo9fArIBbA+HPBx0b7/zjPAF1t065+UAoTGZCMtLY1Bh4i0VmaDDhFpz8cF8PfSvl9SSsn6ExHpioORiYiISLIYdIiIiEiyGHSIiIhIshh0iIiISLIYdIiIiEiyGHSIiIhIshh0iIiISLIYdIiIiEiyGHSIiIhIshh0iIiISLIYdIiIiEiyGHSIiIhIshh0iIiISLIYdIiIiEiyGHSIiIhIshh0iIiISLIYdIiIiEiyGHSIiIhIshh0iIiISLIYdIiIiEiyGHSIiIhIssps0ImOjoavry8CAwONXQoREREZSJkNOhEREUhMTERCQoKxSyEiIiIDKbNBh4iIiKSPQYeIiIgki0GHiIiIJItBh4iIiCSLQYeIiIgki0GHiIiIJItBh4iIiCSLQYeIiIgki0GHiIiIJItBh4iIiCSLQYeIiIgki0GHiIiIJItBh4iIiCSLQYeIiIgki0GHiIiIJItBh4iIiCSLQYeIiIgki0GHiIiIJItBh4iIiCSLQYeIiIgki0GHiIiIJItBh4iIiCSLQYeIiIgki0GHiIiIJItBh4iIiCSLQYeIiIgki0GHiIiIJItBh4iIiCSLQYeIiIgki0GHiIiIJItBh4iIiCSLQYeIiIgkSxJBZ8eOHahTpw5q1aqFVatWGbscIiIiKiXMjF1ASeXn52PMmDHYv38/ypcvD39/f/Tu3RsODg7GLo2IiIiM7I3fo3Ps2DHUrVsX1apVg52dHbp06YL4+Hhjl0VERESlgNGDzsGDB9GtWze4uLhAJpNh27ZtatPExMTAy8sLVlZWaNy4MQ4dOqR8LiUlBdWqVVM+dnV1xe3bt19H6URERFTKGT3oZGVloWHDhli6dKnG5+Pi4vDpp59i0qRJOHXqFFq1aoXOnTsjOTkZACCEUOsjk8kMWjMRERG9GYw+Rqdz587o3Llzkc8vXLgQYWFhGDZsGABg8eLFiI+Px7JlyxAVFYVq1aqp7MG5desWmjZtWuT8cnJykJOTo3ycmZmph1dBRKVVcnIy0tLSdOqbk5MDS0tLnfo6OTnB3d1dp770epTkvVHWtu+bvK6MHnReJjc3FydOnMCECRNU2oOCgnDkyBEAQJMmTXD+/Hncvn0b5cuXx86dOzFlypQi5xkVFYXp06cbtG4iKh2Sk5Ph410HT59l69Tf1AQokOu2bBtrKyRduFimfgzfJCV9b5Sl7fumr6tSHXTS0tJQUFAAZ2dnlXZnZ2fcuXMHAGBmZoYFCxagXbt2kMvlGDduHBwdHYuc58SJEzFmzBjl48zMTLi5uRnmBRCRUaWlpeHps2ysDwd8XLTru/MM8MUW6NQ3KQUIjclGWlpamfghfBOV5L1R1rbvm76uSnXQUSg85kYIodLWvXt3dO/evVjzsrS01HlXNBG9mXxcAH8v7fokpejel94c3L7F96auK6MPRn4ZJycnmJqaKvfeKNy7d09tLw8RERFRYaU66FhYWKBx48bYs2ePSvuePXvQvHlzI1VFREREbwqjH7p68uQJrly5onx87do1nD59Gg4ODnB3d8eYMWMwYMAABAQEoFmzZli5ciWSk5Px8ccfG7FqIiIiehMYPegcP34c7dq1Uz5WDBQeNGgQYmNjERISgvT0dMyYMQOpqamoV68edu7cCQ8PjxItNzo6GtHR0SgoKCjRfIiIiKj0MnrQadu2rcaL/r0oPDwc4eHhel1uREQEIiIikJmZCXt7e73Om4iIiEqHUj1Gh4iIiKgkGHSIiIhIshh0iIiISLIYdIiIiEiyGHSIiIhIssps0ImOjoavry8CAwONXQoREREZSJkNOhEREUhMTERCQoKxSyEiIiIDKbNBh4iIiKTP6BcMNDbFxQozMzP1Ot8nT548/282kPlUu75Pc8G+7CuZviXt/yT7v/8+eaL159RYn8OS1EyvR0neG2Vt+5bWdaWY36suOiwTr5pC4m7dugU3Nzdjl0FEREQ6uHnzJlxdXYt8vswHHblcjpSUFNjZ2UEmk+llnpmZmXBzc8PNmzdRvnx5vcyT9Ifbp3Tj9induH1Kt7K0fYQQePz4MVxcXGBiUvRInDJ/6MrExOSlSbAkypcvL/k32puM26d04/Yp3bh9Sreysn2Kc69KDkYmIiIiyWLQISIiIsli0DEAS0tLTJ06FZaWlsYuhTTg9induH1KN26f0o3bR12ZH4xMRERE0sU9OkRERCRZDDpEREQkWQw6REREJFkMOkRERCRZDDp6FhMTAy8vL1hZWaFx48Y4dOiQsUsiAFFRUQgMDISdnR0qV66Mnj174uLFi8Yui4oQFRUFmUyGTz/91Nil0Atu376N0NBQODo6wsbGBn5+fjhx4oSxyyIA+fn5mDx5Mry8vGBtbY3q1atjxowZkMvlxi7N6Bh09CguLg6ffvopJk2ahFOnTqFVq1bo3LkzkpOTjV1amXfgwAFERETgr7/+wp49e5Cfn4+goCBkZWUZuzQqJCEhAStXrkSDBg2MXQq94MGDB2jRogXMzc3x22+/ITExEQsWLECFChWMXRoBmDt3LpYvX46lS5ciKSkJ8+bNw/z58/H1118buzSj4+nletS0aVP4+/tj2bJlyjYfHx/07NkTUVFRRqyMCrt//z4qV66MAwcOoHXr1sYuh/7z5MkT+Pv7IyYmBrNmzYKfnx8WL15s7LIIwIQJE3D48GHupS6lunbtCmdnZ6xevVrZ9u6778LGxgbfffedESszPu7R0ZPc3FycOHECQUFBKu1BQUE4cuSIkaqiojx69AgA4ODgYORK6EUREREIDg7GO++8Y+xSqJBffvkFAQEBeO+991C5cmU0atQI33zzjbHLov+0bNkSe/fuxaVLlwAAZ86cwZ9//okuXboYuTLjK/M39dSXtLQ0FBQUwNnZWaXd2dkZd+7cMVJVpIkQAmPGjEHLli1Rr149Y5dD/9m8eTNOnjyJhIQEY5dCGvz7779YtmwZxowZg88//xzHjh3DyJEjYWlpiYEDBxq7vDJv/PjxePToEby9vWFqaoqCggLMnj0b77//vrFLMzoGHT2TyWQqj4UQam1kXCNGjMDZs2fx559/GrsU+s/NmzcxatQo7N69G1ZWVsYuhzSQy+UICAjAl19+CQBo1KgR/vnnHyxbtoxBpxSIi4vD+vXrsXHjRtStWxenT5/Gp59+ChcXFwwaNMjY5RkVg46eODk5wdTUVG3vzb1799T28pDx/L//9//wyy+/4ODBg3B1dTV2OfSfEydO4N69e2jcuLGyraCgAAcPHsTSpUuRk5MDU1NTI1ZIVatWha+vr0qbj48PfvzxRyNVRC/67LPPMGHCBPTr1w8AUL9+fdy4cQNRUVFlPuhwjI6eWFhYoHHjxtizZ49K+549e9C8eXMjVUUKQgiMGDECW7duxb59++Dl5WXskugF7du3x7lz53D69GnlX0BAAD744AOcPn2aIacUaNGihdolGS5dugQPDw8jVUQvevr0KUxMVH/STU1NeXo5uEdHr8aMGYMBAwYgICAAzZo1w8qVK5GcnIyPP/7Y2KWVeREREdi4cSN+/vln2NnZKfe82dvbw9ra2sjVkZ2dndp4qXLlysHR0ZHjqEqJ0aNHo3nz5vjyyy/Rt29fHDt2DCtXrsTKlSuNXRoB6NatG2bPng13d3fUrVsXp06dwsKFCzF06FBjl2Z0PL1cz2JiYjBv3jykpqaiXr16WLRoEU9fLgWKGie1Zs0aDB48+PUWQ8XStm1bnl5eyuzYsQMTJ07E5cuX4eXlhTFjxmD48OHGLosAPH78GF988QV++ukn3Lt3Dy4uLnj//fcxZcoUWFhYGLs8o2LQISIiIsniGB0iIiKSLAYdIiIikiwGHSIiIpIsBh0iIiKSLAYdIiIikiwGHSIiIpIsBh0iIiKSLAYdIpK8adOmwc/PzyDzjo2NRYUKFQwybyIqOQYdItKrwYMHQyaTabz1SXh4OGQy2Wu/GnVkZCT27t2rfDx48GD07NnztdZARMbBoENEeufm5obNmzfj2bNnyrbs7Gxs2rQJ7u7ur70eW1tbODo6vvblEpHxMegQkd75+/vD3d0dW7duVbZt3boVbm5uaNSokbJt165daNmyJSpUqABHR0d07doVV69eVZnXkSNH4OfnBysrKwQEBGDbtm2QyWQ4ffo0AOCPP/6ATCbD3r17ERAQABsbGzRv3lzlTtsvHrqaNm0a1q5di59//hkymQwymQx//PGHcj4PHz5U9jt9+jRkMhmuX7+ubIuNjYW7uztsbGzQq1cvpKenq73+7du3o3HjxrCyskL16tUxffp05Ofnl2CNEpGuGHSIyCCGDBmCNWvWKB9/++23andSzsrKwpgxY5CQkIC9e/fCxMQEvXr1glwuB/D8RoXdunVD/fr1cfLkScycORPjx4/XuLxJkyZhwYIFOH78OMzMzIq8a3NkZCT69u2LTp06ITU1FampqWjevHmxXtPff/+NoUOHIjw8HKdPn0a7du0wa9YslWni4+MRGhqKkSNHIjExEStWrEBsbCxmz55drGUQkX6ZGbsAIpKmAQMGYOLEibh+/TpkMhkOHz6MzZs3448//lBO8+6776r0Wb16NSpXrozExETUq1cPGzZsgEwmwzfffAMrKyv4+vri9u3bGu+YPXv2bLRp0wYAMGHCBAQHByM7OxtWVlYq09na2sLa2ho5OTmoUqWKVq9pyZIl6NixIyZMmAAAqF27No4cOYJdu3ap1DFhwgQMGjQIAFC9enXMnDkT48aNw9SpU7VaHhGVHPfoEJFBODk5ITg4GGvXrsWaNWsQHBwMJycnlWmuXr2K/v37o3r16ihfvjy8vLwAAMnJyQCAixcvokGDBiphpUmTJhqX16BBA+X/V61aFQBw7949vb6mpKQkNGvWTKWt8OMTJ05gxowZsLW1Vf4NHz4cqampePr0qV7rIaJX4x4dIjKYoUOHYsSIEQCA6Ohotee7desGNzc3fPPNN3BxcYFcLke9evWQm5sLABBCQCaTqfQRQmhclrm5ufL/FX0Uh8CKw8TERG3+eXl5xVr2i+RyOaZPn47evXurPVd47xIRGR6DDhEZTKdOnZShpWPHjirPpaenIykpCStWrECrVq0AAH/++afKNN7e3tiwYQNycnJgaWkJADh+/HiJ67KwsEBBQYFKW6VKlQAAqampqFixIgAoBzwr+Pr64q+//lJpK/zY398fFy9eRM2aNUtcJxGVHA9dEZHBmJqaIikpCUlJSTA1NVV5rmLFinB0dMTKlStx5coV7Nu3D2PGjFGZpn///pDL5fjwww+RlJSE+Ph4fPXVVwCgtqdHG56enjh79iwuXryItLQ05OXloWbNmnBzc8O0adNw6dIl/Prrr1iwYIFKv5EjR2LXrl2YN28eLl26hKVLl6qMzwGAKVOmYN26dZg2bRr++ecfJCUlIS4uDpMnT9a5XiLSHYMOERlU+fLlUb58ebV2ExMTbN68GSdOnEC9evUwevRozJ8/X63v9u3bcfr0afj5+WHSpEmYMmUKgJIdBho+fDjq1KmDgIAAVKpUCYcPH4a5uTk2bdqECxcuoGHDhpg7d67aGVVvvfUWVq1aha+//hp+fn7YvXu3WoDp2LEjduzYgT179iAwMBBvvfUWFi5cCA8PD53rJSLdyURxDjoTEZUSGzZswJAhQ/Do0SNYW1sbuxwiKuU4RoeISrV169ahevXqqFatGs6cOYPx48ejb9++DDlEVCwMOkRUqt25cwdTpkzBnTt3ULVqVbz33nu8+B4RFRsPXREREZFkcTAyERERSRaDDhEREUkWgw4RERFJFoMOERERSRaDDhEREUkWgw4RERFJFoMOERERSRaDDhEREUkWgw4RERFJ1v8Htkg6/x6I0+4AAAAASUVORK5CYII=",
      "text/plain": [
       "<Figure size 640x480 with 1 Axes>"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    }
   ],
   "source": [
    "shape, scale = 0.9, 0.5  # Shape and scale parameters for log-normal\n",
    "earthquake_magnitudes = np.random.lognormal(mean=np.log(scale), sigma=shape, size=1000)\n",
    "\n",
    "plt.hist(earthquake_magnitudes, bins=30, color='orange', edgecolor='black', log=True)\n",
    "plt.title('Simulated Earthquake Magnitude Distribution (Log-Normal)')\n",
    "plt.xlabel('Magnitude')\n",
    "plt.ylabel('Frequency (log scale)')\n",
    "plt.show()\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "This examples generates 1000 simulated earthquake magnitudes using a log-normal distribution. The long-tail property of the distribution mirrors the nature of geophysical events like earthquakes.\n",
    "\n",
    "**Example 3:** Power-Law Distributions\n",
    "\n",
    "Application in Geosciences: Power-law distributions are often observed in natural hazard occurrences like landslides or earthquakes, where small events are common, but large events are rare."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 13,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAjoAAAHFCAYAAAD7ZFORAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjguMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy81sbWrAAAACXBIWXMAAA9hAAAPYQGoP6dpAABIFElEQVR4nO3dd3xUdb7/8feQnhACIbQAoSwIRJoUXXoAQQFBsVxAQxHwrktcaSoqKkWlLoh3CSAWwIsFVGQtKNIEKUroaHLBggQhLIQWEkiAzPf3B4/MzyF1kkkmnLyej8c8dud7vnPmM1/PTN58T7MZY4wAAAAsqJynCwAAACguBB0AAGBZBB0AAGBZBB0AAGBZBB0AAGBZBB0AAGBZBB0AAGBZBB0AAGBZBB0AAGBZBB3ohx9+UP/+/RURESE/Pz9Vq1ZN7dq10/jx4536RUVFKSoqyiM1fvvtt7LZbPr2229dfm18fLwmT56s33//3e11TZ48WTabLd9+w4YNk81mczyCgoJUt25d9evXT0uWLFFGRkaha1izZo0mT55c6NfnZcWKFbr11lsVEBAgm82mffv2Fcv7uMPSpUudxtjb21u1atXSo48+quPHj3u6vCKz2Wx64oknPF1GNoXZtgvzW1LY7/GN7/X777/LZrPpn//8p0vryc+0adO0evXqbO1F+e2Ce3h7ugB41pdffql+/fopKipKs2bNUo0aNZSUlKRdu3bpww8/1Jw5cxx9FyxY4MFKCy8+Pl5TpkxRVFSU6tat67E6AgICtHHjRknS5cuXdezYMX311Vd67LHHNGfOHH399deqVauWy+tds2aNYmNj3R52Tp8+rcGDB+vuu+/WggUL5Ofnp1tuucWt71EclixZosaNG+vy5cvasmWLpk+frs2bN+vgwYMKCgrydHmW5Oq2XZjfksJ+j0vqd2vatGl68MEHdd999zm1t2rVSjt27FBkZGSJ1IHsCDpl3KxZs1SvXj2tXbtW3t7/f3MYOHCgZs2a5dSXL2rRlCtXTn/961+d2oYMGaJHH31U99xzjx588EF9//33Hqouu8OHD+vq1auKjo5Wly5d8ux76dIlBQYGllBleWvatKnatGkjSeratasyMzP18ssva/Xq1XrkkUc8XF3ujDFKT09XQECAp0txmavbdkn8lmRtk57+3apQoUK2sUHJYtdVGXfmzBmFhYU5hZws5co5bx65TQHPnj1bM2fOVN26dRUQEKCoqCjHH8lnn31W4eHhCgkJUf/+/XXq1CmnddpsthxnIurWrathw4blWfuuXbs0cOBAx/vWrVtXgwYN0tGjRx19li5dqoceekjS9T96WdPrS5cudfRZv369unfvrgoVKigwMFAdOnTQhg0bsr3fl19+qZYtW8rPz0/16tVz29R3z5499dhjj+mHH37Qli1bHO0rVqxQz549VaNGDQUEBKhJkyZ69tlnlZaW5ugzbNgwxcbGSpLT7oOs6f3Y2Fh17txZVatWVVBQkJo1a6ZZs2bp6tWredY0bNgwdezYUZI0YMAA2Ww2x3/7YcOGqXz58jp48KB69uyp4OBgde/eXZJ09uxZjRo1SjVr1pSvr6/q16+viRMnZtt9kbUbZsmSJWrUqJECAgLUpk0bff/99zLGaPbs2apXr57Kly+vbt266Zdffin0+Gb9kcnaLtLT0/Xcc8+pXr168vX1Vc2aNRUTE6Pz5887XvP0008rJCREmZmZjrZ//OMfju09y5kzZ1SuXDn961//crSlpKToqaeeclr/mDFjnP67/XkMFi1apCZNmsjPz0/Lli0r9OeUCrbNfPnll7LZbIqLi3O0ffLJJ7LZbOrTp4/T+po3b64HHnig0PXktm3ntOtq4cKFatGihcqXL6/g4GA1btxYzz//vKT8v8dRUVFq2rSptmzZovbt2yswMFDDhw/P9b0kyW6369VXX1VERIT8/f3Vpk2bbN/7YcOG5Th7dOMua5vNprS0NC1btsxRW9Z75rbr6rPPPlO7du0UGBio4OBg9ejRQzt27MjxfX766ScNGjRIISEhqlatmoYPH64LFy7kOObIjqBTxrVr104//PCDnnzySf3www/5/gHMSWxsrLZt26bY2Fi99dZb+r//+z/17dtXI0aM0OnTp/XOO+9o1qxZWr9+vUaOHOm22n///Xc1atRI8+bN09q1azVz5kwlJSWpbdu2Sk5OliT16dNH06ZNc9S5Y8cO7dixw/GDvnz5cvXs2VMVKlTQsmXLtHLlSoWGhuquu+5y+tHbsGGD7r33XgUHB+vDDz/U7NmztXLlSi1ZssQtn6Vfv36S5PTH4Oeff1bv3r319ttv6+uvv9aYMWO0cuVK9e3b19HnxRdf1IMPPihJjs+2Y8cO1ahRQ5L066+/6uGHH9b//u//6osvvtCIESM0e/Zs/e1vf8uznhdffNERoKZNm6YdO3Y47QK4cuWK+vXrp27duunf//63pkyZovT0dHXt2lXvvvuuxo0bpy+//FLR0dGaNWuW7r///mzv8cUXX+itt97SjBkz9MEHH+jixYvq06ePxo8fr23btmn+/PlavHix4uPj9cADD8gYU6ixzQpJVapUkTFG9913n/75z39q8ODB+vLLLzVu3DgtW7ZM3bp1cwSyO++8UykpKdq5c6djPevXr1dAQIDWrVvnaNuwYYOMMbrzzjslXZ9F6NKli5YtW6Ynn3xSX331lSZMmKClS5eqX79+2T7D6tWrtXDhQr300ktau3atOnXqVKjPmKUg20yXLl3k4+Oj9evXZ/tsmzdvdvwGnDp1Sj/++KPjsxVWTtv2jT788EONGjVKXbp00aeffqrVq1dr7NixjoCW3/dYkpKSkhQdHa2HH35Ya9as0ahRo/Ksa/78+fr66681b948LV++XOXKlVOvXr2yhY2C2LFjhwICAtS7d29HbXntMnv//fd17733qkKFCvrggw/09ttv69y5c4qKitLWrVuz9X/ggQd0yy236JNPPtGzzz6r999/X2PHjnW5zjLLoExLTk42HTt2NJKMJOPj42Pat29vpk+fbi5evOjUt0uXLqZLly6O50eOHDGSTIsWLUxmZqajfd68eUaS6devn9Prx4wZYySZCxcuONokmUmTJmWrq06dOmbo0KGO55s2bTKSzKZNm3L9LNeuXTOpqakmKCjIvP766472jz76KMfXpqWlmdDQUNO3b1+n9szMTNOiRQtz++23O9ruuOMOEx4ebi5fvuxoS0lJMaGhoaYgX6OhQ4eaoKCgXJcnJCQYSebvf/97jsvtdru5evWq2bx5s5Fk9u/f71gWExNToBoyMzPN1atXzbvvvmu8vLzM2bNn8+yfNeYfffRRts8iybzzzjtO7YsWLTKSzMqVK53aZ86caSSZb775xtEmyVSvXt2kpqY62lavXm0kmZYtWxq73e5oz9qeDhw4kGe9S5YsMZLM999/b65evWouXrxovvjiC1OlShUTHBxsTp48ab7++msjycyaNcvptStWrDCSzOLFi40x17cNX19fM3XqVGOMMX/88YeRZCZMmGACAgJMenq6McaYxx57zISHhzvWM336dFOuXDkTFxfntP6PP/7YSDJr1qxxGoOQkJB8/zv8uX9MTEyB+hqT9zbTsWNH061bN8fzBg0amKefftqUK1fObN682RhjzHvvvWckmcOHD+f5PoXZtm/8LXniiSdMxYoV83yf3L7HWeuTZDZs2JDjspx+t3L7Pt95551On61OnTrZ1jlp0qRs37mgoCCn36wsN/52ZWZmmvDwcNOsWTOn382LFy+aqlWrmvbt22d7nxu311GjRhl/f3+n7wlyx4xOGVe5cmV99913iouL04wZM3Tvvffq8OHDeu6559SsWTPHzEheevfu7bSbq0mTJpKUbRo8qz0xMdEttaempmrChAlq0KCBvL295e3trfLlyystLU0JCQn5vn779u06e/ashg4dqmvXrjkedrtdd999t+Li4pSWlqa0tDTFxcXp/vvvl7+/v+P1wcHBTv9SLgqTw2zFb7/9pocffljVq1eXl5eXfHx8HMfKFOTzSdLevXvVr18/Va5c2bGOIUOGKDMzU4cPHy5SzTfu0ti4caOCgoIcM0xZsnZB3rhboGvXrk4HB2dtH7169XLaLZDV/uddknn561//Kh8fHwUHB+uee+5R9erV9dVXX6latWqOA2Zv3C360EMPKSgoyFFjYGCg2rVr55j1WLdunSpWrKinn35aV65ccfyre/369U4zHl988YWaNm2qli1bOm1Td911V467L7p166ZKlSo5nmdmZmbbFl1R0G2me/fu2rZtmy5fvqyjR4/ql19+0cCBA9WyZUvHjNX69esVERGhhg0bulTDjXLatm90++236/z58xo0aJD+/e9/F+h350aVKlVSt27dCtw/t+/zli1bnHZZutuhQ4d04sQJDR482Ol3s3z58nrggQf0/fff69KlS06vyZoVy9K8eXOlp6dnOxQAOSPoQJLUpk0bTZgwQR999JFOnDihsWPH6vfff892QHJOQkNDnZ77+vrm2Z6enu6Wmh9++GHNnz9fI0eO1Nq1a7Vz507FxcWpSpUqunz5cr6v/89//iNJevDBB+Xj4+P0mDlzpowxOnv2rM6dOye73a7q1atnW0dObYWR9Uc8PDxc0vUQ16lTJ/3www965ZVX9O233youLk6rVq2SpAJ9vsTERHXq1EnHjx/X66+/7gi0WbukCrKO3AQGBqpChQpObWfOnFH16tWznW5ftWpVeXt768yZM07txbXdvPvuu4qLi9PevXt14sQJHThwQB06dHDU6O3trSpVqji9xmazqXr16k413nnnnfr++++Vlpam9evXq1u3bqpcubJat26t9evX68iRIzpy5IhT0PnPf/6jAwcOZNuegoODZYzJ9gc8axdjlr/85S9Or5s6dWqBPrPk2jZz5513KiMjQ1u3btW6desUFham2267TXfeeacj3G3YsKHIu62k7Nt2TgYPHqx33nlHR48e1QMPPKCqVavqjjvucNpNmJ8bxzI/uX2fr1y5otTUVJfW5YqsbSynesPDw2W323Xu3Dmn9sqVKzs99/Pzk1S073BZwllXyMbHx0eTJk3Sa6+9ph9//LFY38vPzy/H62zc+EfxRhcuXNAXX3yhSZMm6dlnn3W0Z2Rk6OzZswV677CwMEnSv/71r1zPiqhWrZquXr0qm82mkydPZlueU1thfPbZZ5LkOIBx48aNOnHihL799lunM57+fMBsflavXq20tDStWrVKderUcbS741o4OV07qHLlyvrhhx9kjHFafurUKV27ds0x3sWtSZMmjrOucqrx2rVrOn36tFPYMcbo5MmTatu2raOte/fuevHFF7VlyxZt2LBBkyZNcrR/8803qlevnuN5lrCwMAUEBOidd97J8f1vHIMbx/Hzzz93+j7kFQ5u5Mo2c8cdd6h8+fJav369fv/9d3Xv3l02m03du3fXnDlzFBcXp8TERLcEnRu37dw8+uijevTRR5WWlqYtW7Zo0qRJuueee3T48GGn7Tc3Bbme1Z/l9n329fVV+fLlJUn+/v45/j4VZsYpS1ZoSUpKyrbsxIkTKleunNMsH4qOGZ0yLqcvm/T/p7ld+aEtjLp16+rAgQNObRs3bsz3X1Q2m03GGMe/bLK89dZb2aadc/vXT4cOHVSxYkXFx8erTZs2OT58fX0VFBSk22+/XatWrXKaVbh48aI+//xzlz/zjdatW6e33npL7du3d5zplPWjfePne+ONN7K9PrfPl9M6jDF68803i1xzTrp3767U1NRsF0179913Hcs9LauG5cuXO7V/8sknSktLc6rx9ttvV4UKFTRv3jydPHlSPXr0kHR9NmTv3r1auXKlIiMjnb4j99xzj3799VdVrlw5x+0pv+u/NGvWzKm/K98/V7YZHx8fde7cWevWrdPGjRsdn61Tp07y9vbWCy+84Ag+RZHTtp2foKAg9erVSxMnTtSVK1f0008/OX0ud81i5PZ97tSpk7y8vCRd/306deqUY/ZXun4g/tq1a7Otz8/Pr0C1NWrUSDVr1tT777/vtFsvLS1Nn3zyieNMLLgPMzpl3F133aVatWqpb9++aty4sex2u/bt26c5c+aofPnyGj16dLG+/+DBg/Xiiy/qpZdeUpcuXRQfH6/58+crJCQkz9dVqFBBnTt31uzZsxUWFqa6detq8+bNevvtt1WxYkWnvk2bNpUkLV68WMHBwfL391e9evVUuXJl/etf/9LQoUN19uxZPfjgg6patapOnz6t/fv36/Tp01q4cKEk6eWXX9bdd9+tHj16aPz48crMzNTMmTMVFBRU4Bkku93uuJZIRkaGEhMT9dVXX2nlypVq0qSJVq5c6ejbvn17VapUSY8//rgmTZokHx8fvffee9q/f3+29TZr1kySNHPmTPXq1UteXl5q3ry5evToIV9fXw0aNEjPPPOM0tPTtXDhwmzT4u4yZMgQxcbGaujQofr999/VrFkzbd26VdOmTVPv3r3dMjtQVD169NBdd92lCRMmKCUlRR06dNCBAwc0adIk3XbbbRo8eLCjr5eXl7p06aLPP/9c9erV01/+8hdJ1wOyn5+fNmzYoCeffNJp/WPGjNEnn3yizp07a+zYsWrevLnsdrsSExP1zTffaPz48brjjjsKXf+vv/6qjz/+OFt7ZGSkS9uMdD30ZV39POu/TUBAgNq3b69vvvlGzZs3V9WqVQtUlyvbdk4ee+wxBQQEqEOHDqpRo4ZOnjyp6dOnKyQkxDHLltf3uDC8vLzUo0cPjRs3Tna7XTNnzlRKSoqmTJni6DNgwAC99NJLGjhwoJ5++mmlp6frf/7nf3I8hqdZs2b69ttv9fnnn6tGjRoKDg5Wo0aNsvUrV66cZs2apUceeUT33HOP/va3vykjI0OzZ8/W+fPnNWPGjEJ9HuTBY4dBo1RYsWKFefjhh03Dhg1N+fLljY+Pj4mIiDCDBw828fHxTn1zO3th9uzZTv1yO1sn66yYP5+RkpGRYZ555hlTu3ZtExAQYLp06WL27dtXoLOu/vjjD/PAAw+YSpUqmeDgYHP33XebH3/8Mdtrjbl+5k69evWMl5eXkWSWLFniWLZ582bTp08fExoaanx8fEzNmjVNnz59stX/2WefmebNmxtfX18TERFhZsyYkePZFznJOlMp6xEQEGAiIiJM3759zTvvvGMyMjKyvWb79u2mXbt2JjAw0FSpUsWMHDnS7NmzJ1v9GRkZZuTIkaZKlSrGZrMZSebIkSPGGGM+//xz06JFC+Pv729q1qxpnn76afPVV1/lewbbn8c8p7OucjvL5syZM+bxxx83NWrUMN7e3qZOnTrmueeec5yllEU5nEHk6vZ0o5y2r5xcvnzZTJgwwdSpU8f4+PiYGjVqmL///e/m3Llz2fq+/vrrRpJ57LHHnNp79OhhJJnPPvss22tSU1PNCy+8YBo1amR8fX1NSEiIadasmRk7dqw5efJknmOQlz9vPzc+ss5cLOg2Y4wx+/fvN5JMw4YNndpfffVVI8mMGzeuQHUVZtu+8bdk2bJlpmvXrqZatWrG19fXhIeHm//6r//KdqZdbt/jLl26mFtvvTXH+nL73Zo5c6aZMmWKqVWrlvH19TW33XabWbt2bbbXr1mzxrRs2dIEBASY+vXrm/nz5+f4vd+3b5/p0KGDCQwMNJIc75nbGaOrV682d9xxh/H39zdBQUGme/fuZtu2bU59st7n9OnTTu1Z23rW9xx5sxlTyItTAAAAlHIcowMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyrzF8w0G6368SJEwoODnb5EuIAAMAzjDG6ePGiwsPDnW6QeqMyH3ROnDih2rVre7oMAABQCMeOHVOtWrVyXV7mg05wcLCk6wN1492YAQBA6ZSSkqLatWs7/o7npswHnazdVRUqVCDoAABwk8nvsBMORgYAAJZF0AEAAJZVZoNObGysIiMj1bZtW0+XAgAAikmZv3t5SkqKQkJCdOHCBY7RAQDgJlHQv99ldkYHAABYH0EHAABYFkEHAABYFkEHAABYFkEHAABYFkEHAABYFkEHAABYFkEHAABYFkEHAABYVpm/e3lxSkxMVHJycp59wsLCFBERUUIVAQBQtpTZoBMbG6vY2FhlZmYWy/oTExPVpFEjXUpPz7NfoL+/Eg4dIuwAAFAMuNdVMd3ras+ePWrdurWWS2qSS58ESdGSdu/erVatWrntvQEAsLqC/v0uszM6JaWJJCIMAACewcHIAADAsgg6AADAsgg6AADAsgg6AADAsgg6AADAsgg6AADAsgg6AADAsgg6AADAsgg6AADAsgg6AADAsgg6AADAsgg6AADAsgg6AADAssps0ImNjVVkZKTatm3r6VIAAEAxKbNBJyYmRvHx8YqLi/N0KQAAoJiU2aADAACsj6ADAAAsi6ADAAAsi6ADAAAsi6ADAAAsi6ADAAAsi6ADAAAsi6ADAAAsi6ADAAAsi6ADAAAsi6ADAAAsi6ADAAAsi6ADAAAsi6ADAAAsi6ADAAAsi6ADAAAsi6ADAAAsi6ADAAAsi6ADAAAsi6ADAAAsy9vTBUBKSEjIc3lYWJgiIiJKqBoAAKyjzAad2NhYxcbGKjMz02M1JOn6lFp0dHSe/QL9/ZVw6BBhBwAAF5XZoBMTE6OYmBilpKQoJCTEIzWcl2SXtFxSk1z6JEiKTk9XcnIyQQcAABeV2aBTmjSR1MrTRQAAYEEcjAwAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACzL29MFoGASEhLyXB4WFqaIiIgSqgYAgJsDQaeUS9L1abfo6Og8+wX6+yvh0CHCDgAAf0LQKeXOS7JLWi6pSS59EiRFp6crOTmZoAMAwJ8QdG4STSS18nQRAADcZDgYGQAAWBZBBwAAWBZBBwAAWBZBBwAAWBZBBwAAWBZBBwAAWNZNH3SOHTumqKgoRUZGqnnz5vroo488XRIAACglbvrr6Hh7e2vevHlq2bKlTp06pVatWql3794KCgrydGkAAMDDbvqgU6NGDdWoUUOSVLVqVYWGhurs2bMEHQAA4PldV1u2bFHfvn0VHh4um82m1atXZ+uzYMEC1atXT/7+/mrdurW+++67HNe1a9cu2e121a5du5irBgAANwOPB520tDS1aNFC8+fPz3H5ihUrNGbMGE2cOFF79+5Vp06d1KtXLyUmJjr1O3PmjIYMGaLFixeXRNkAAOAm4PFdV7169VKvXr1yXT537lyNGDFCI0eOlCTNmzdPa9eu1cKFCzV9+nRJUkZGhvr376/nnntO7du3z/P9MjIylJGR4XiekpLihk8BAABKI4/P6OTlypUr2r17t3r27OnU3rNnT23fvl2SZIzRsGHD1K1bNw0ePDjfdU6fPl0hISGOB7u5AACwrlIddJKTk5WZmalq1ao5tVerVk0nT56UJG3btk0rVqzQ6tWr1bJlS7Vs2VIHDx7MdZ3PPfecLly44HgcO3asWD8DAADwHI/vuioIm83m9NwY42jr2LGj7HZ7gdfl5+cnPz8/t9YHAABKp1I9oxMWFiYvLy/H7E2WU6dOZZvlAQAAuFGpDjq+vr5q3bq11q1b59S+bt26fA86BgAA8Piuq9TUVP3yyy+O50eOHNG+ffsUGhqqiIgIjRs3ToMHD1abNm3Url07LV68WImJiXr88cc9WDUAALgZeDzo7Nq1S127dnU8HzdunCRp6NChWrp0qQYMGKAzZ85o6tSpSkpKUtOmTbVmzRrVqVOnSO8bGxur2NhYZWZmFmk9AACg9PJ40ImKipIxJs8+o0aN0qhRo9z6vjExMYqJiVFKSopCQkLcum4AAFA6lOpjdAAAAIqCoAMAACyLoAMAACyLoAMAACyrzAad2NhYRUZGqm3btp4uBQAAFJMyG3RiYmIUHx+vuLg4T5cCAACKSZkNOgAAwPoIOgAAwLIIOgAAwLIKdWXkq1ev6uTJk7p06ZKqVKmi0NBQd9cFAABQZAWe0UlNTdUbb7yhqKgohYSEqG7duoqMjFSVKlVUp04dPfbYYxzYCwAASpUCBZ3XXntNdevW1Ztvvqlu3bpp1apV2rdvnw4dOqQdO3Zo0qRJunbtmnr06KG7775bP//8c3HXDQAAkK8C7bravn27Nm3apGbNmuW4/Pbbb9fw4cO1aNEivf3229q8ebMaNmzo1kLdjbuXAwBgfQUKOh999FGBVubn5+f2u4wXFyvevTwhISHP5WFhYYqIiCihagAA8LxCHYwsSb/88ot+/fVXde7cWQEBATLGyGazubM2FFCSru+DjI6OzrNfoL+/Eg4dIuwAAMoMl4POmTNnNGDAAG3cuFE2m00///yz6tevr5EjR6pixYqaM2dOcdSJPJyXZJe0XFKTXPokSIpOT1dycjJBBwBQZrh8HZ2xY8fK29tbiYmJCgwMdLQPGDBAX3/9tVuLg2uaSGqVyyO3AAQAgJW5PKPzzTffaO3atapVq5ZTe8OGDXX06FG3FQYAAFBULs/opKWlOc3kZElOTpafn59bigIAAHAHl4NO586d9e677zqe22w22e12zZ49W127dnVrcQAAAEXh8q6r2bNnKyoqSrt27dKVK1f0zDPP6KefftLZs2e1bdu24qgRAACgUFye0YmMjNSBAwd0++23q0ePHkpLS9P999+vvXv36i9/+Utx1FgsYmNjFRkZqbZt23q6FAAAUEwKdR2d6tWra8qUKe6upURZ8YKBAADAWYGCzoEDBwq8wubNmxe6GAAAAHcqUNBp2bKlbDabjDF59rPZbNw7CgAAlBoFCjpHjhwp7joAAADcrkBBp06dOsVdBwAAgNsV+qae8fHxSkxM1JUrV5za+/XrV+SiAAAA3MHloPPbb7+pf//+OnjwoNNxO1l3LucYHQAAUFq4HHRGjx6tevXqaf369apfv7527typM2fOaPz48frnP/9ZHDXCjRISEvJcHhYWxt3NAQCW4XLQ2bFjhzZu3KgqVaqoXLlyKleunDp27Kjp06frySef1N69e4ujThRRkq5fHTI6OjrPfoH+/ko4dIiwAwCwBJevjJyZmany5ctLuv6v/xMnTki6fsDyoUOH3FtdMSprV0Y+L8kuabmk3bk8lku6lJ6u5ORkD1UJAIB7uTyj07RpUx04cED169fXHXfcoVmzZsnX11eLFy9W/fr1i6PGYlFWr4zcRFIrTxcBAEAJcTnovPDCC0pLS5MkvfLKK7rnnnvUqVMnVa5cWStWrHB7gQAAAIXlctC56667HP+/fv36io+P19mzZ1WpUiXHmVcAAAClgcvH6Fy4cEFnz551agsNDdW5c+eUkpLitsIAAACKyuWgM3DgQH344YfZ2leuXKmBAwe6pSgAAAB3cDno/PDDD+ratWu29qioKP3www9uKQoAAMAdXA46GRkZunbtWrb2q1ev6vLly24pCgAAwB1cDjpt27bV4sWLs7UvWrRIrVu3dktRAAAA7uDyWVevvvqq7rzzTu3fv1/du3eXJG3YsEFxcXH65ptv3F4gAABAYbk8o9OhQwft2LFDtWvX1sqVK/X555+rQYMGOnDggDp16lQcNQIAABSKyzM6ktSyZUu999577q4FAADArVye0dmzZ48OHjzoeP7vf/9b9913n55//nlduXLFrcUVp7J2rysAAMoil4PO3/72Nx0+fFiS9Ntvv2nAgAEKDAzURx99pGeeecbtBRaXmJgYxcfHKy4uztOlAACAYuJy0Dl8+LBatmwpSfroo4/UpUsXvf/++1q6dKk++eQTd9cHAABQaC4HHWOM7Ha7JGn9+vXq3bu3JKl27dpKTk52b3UAAABF4HLQadOmjV555RX97//+rzZv3qw+ffpIko4cOaJq1aq5vUAAAIDCcjnozJs3T3v27NETTzyhiRMnqkGDBpKkjz/+WO3bt3d7gQAAAIXl8unlzZs3dzrrKsvs2bPl5eXllqIAAADcoVDX0cmJv7+/u1YFAADgFm4LOig7EhMT8z3wPCwsTBERESVUEQAAOSPowCWJiYlq0qiRLqWn59kv0N9fCYcOEXYAAB5F0IFLkpOTdSk9XcslNcmlT4Kk6PR0JScnE3QAAB5F0EGhNJHUytNFAACQD5eDzrhx43Jst9ls8vf3V4MGDXTvvfcqNDS0yMUBAAAUhctBZ+/evdqzZ48yMzPVqFEjGWP0888/y8vLS40bN9aCBQs0fvx4bd26VZGRkcVRMwAAQIG4fMHAe++9V3feeadOnDih3bt3a8+ePTp+/Lh69OihQYMG6fjx4+rcubPGjh1bHPUCAAAUmMtBZ/bs2Xr55ZdVoUIFR1uFChU0efJkzZo1S4GBgXrppZe0e/dutxYKAADgKpeDzoULF3Tq1Kls7adPn1ZKSookqWLFirpy5UrRqytGsbGxioyMVNu2bT1dCgAAKCaF2nU1fPhwffrpp/rjjz90/PhxffrppxoxYoTuu+8+SdLOnTt1yy23uLtWt4qJiVF8fLzi4uI8XQoAACgmLh+M/MYbb2js2LEaOHCgrl27dn0l3t4aOnSoXnvtNUlS48aN9dZbb7m3UgAAABe5HHTKly+vN998U6+99pp+++03GWP0l7/8ReXLl3f0admypTtrBAAAKJRCXzCwfPnyCg0Nlc1mcwo5AAAApYXLx+jY7XZNnTpVISEhqlOnjiIiIlSxYkW9/PLLstvtxVEjAABAobg8ozNx4kS9/fbbmjFjhjp06CBjjLZt26bJkycrPT1dr776anHUCQAA4DKXg86yZcv01ltvqV+/fo62Fi1aqGbNmho1ahRBBwAAlBou77o6e/asGjdunK29cePGOnv2rFuKAgAAcAeXg06LFi00f/78bO3z589XixYt3FIUAACAO7i862rWrFnq06eP1q9fr3bt2slms2n79u06duyY1qxZUxw1AgAAFIrLMzpdunTR4cOH1b9/f50/f15nz57V/fffr0OHDqlTp07FUSMAAEChFOo6OuHh4Rx0DAAASr0CBZ0DBw4UeIXNmzcvdDEAAADuVKCg07JlS9lsNhlj8uxns9mUmZnplsIAAACKqkBB58iRI8VdBwAAgNsVKOjUqVOnuOsAAABwuwKddbVjx44CrzAtLU0//fRToQsCAABwlwIFnSFDhqhHjx5auXKlUlNTc+wTHx+v559/Xg0aNNCePXvcWiQAAEBhFGjXVXx8vN544w299NJLeuSRR3TLLbcoPDxc/v7+OnfunP7v//5PaWlpuv/++7Vu3To1bdq0uOsGAADIV4GCjo+Pj5544gk98cQT2rNnj7777jv9/vvvunz5slq0aKGxY8eqa9euCg0NLe56AQAACszlCwa2atVKrVq1Ko5aAAAA3KpQV0aGtSUkJBRqGQAApU2ZDTqxsbGKjY3lAod/kqTrR6dHR0d7uhQAANyizAadmJgYxcTEKCUlRSEhIZ4up1Q4L8kuabmkJrn0WSPpxZIqCACAIiqzQQe5ayIpt6Ow2HEFALiZFOg6On/G7SAAAMDNwuWg06BBA3Xt2lXLly9Xenp6cdQEAADgFi4Hnf379+u2227T+PHjVb16df3tb3/Tzp07i6M2AACAInE56DRt2lRz587V8ePHtWTJEp08eVIdO3bUrbfeqrlz5+r06dPFUScAAIDLXA46Wby9vdW/f3+tXLlSM2fO1K+//qqnnnpKtWrV0pAhQ5SUlOTOOgEAAFxW6KCza9cujRo1SjVq1NDcuXP11FNP6ddff9XGjRt1/Phx3Xvvve6sEwAAwGUun14+d+5cLVmyRIcOHVLv3r317rvvqnfv3ipX7npmqlevnt544w01btzY7cUCAAC4wuWgs3DhQg0fPlyPPvqoqlevnmOfiIgIvf3220UuDgAAoChcDjo///xzvn18fX01dOjQQhUEAADgLi4HnSVLlqh8+fJ66KGHnNo/+ugjXbp0iYADh/xuABoWFqaIiIgSqgYAUBa5HHRmzJihRYsWZWuvWrWq/vu//5uggwLfHDTQ318Jhw4RdgAAxcbloHP06FHVq1cvW3udOnWUmJjolqJwczuv/G8OmiApOj1dycnJBB0AQLFxOehUrVpVBw4cUN26dZ3a9+/fr8qVK7urLlhAXjcHBQCgJLh8HZ2BAwfqySef1KZNm5SZmanMzExt3LhRo0eP1sCBA4ujRgAAgEJxeUbnlVde0dGjR9W9e3d5e19/ud1u15AhQzRt2jS3FwgAAFBYLgcdX19frVixQi+//LL279+vgIAANWvWTHXq1CmO+gAAAArN5aCT5ZZbbtEtt9zizloAAADcyuWgk5mZqaVLl2rDhg06deqU7Ha70/KNGze6rTgAAICicDnojB49WkuXLlWfPn3UtGlT2Wy24qgLAACgyFwOOh9++KFWrlyp3r17F0c9AAAAbuPy6eW+vr5q0KBBcdQCAADgVi4HnfHjx+v111+XMaY46gEAAHAbl3ddbd26VZs2bdJXX32lW2+9VT4+Pk7LV61a5bbiAAAAisLloFOxYkX179+/OGoBAABwK5eDzpIlS4qjDgAAALdz+RgdSbp27ZrWr1+vN954QxcvXpQknThxQqmpqW4tDgAAoChcntE5evSo7r77biUmJiojI0M9evRQcHCwZs2apfT0dC1atKg46gQAAHCZyzM6o0ePVps2bXTu3DkFBAQ42vv3768NGza4tTgAAICiKNRZV9u2bZOvr69Te506dXT8+HG3FQYAAFBULs/o2O12ZWZmZmv/448/FBwc7JaiAAAA3MHlGZ0ePXpo3rx5Wrx4sSTJZrMpNTVVkyZN8thtIfr3769vv/1W3bt318cff+yRGlA4CQkJeS4PCwtTRERECVUDALAal4POa6+9pq5duyoyMlLp6el6+OGH9fPPPyssLEwffPBBcdSYryeffFLDhw/XsmXLPPL+cF2Srk8nRkdH59kv0N9fCYcOEXYAAIXictAJDw/Xvn379MEHH2jPnj2y2+0aMWKEHnnkEaeDk0tS165d9e2333rkvVE45yXZJS2X1CSXPgmSotPTlZycTNABABRKoa6jExAQoOHDh2v+/PlasGCBRo4cWeiQs2XLFvXt21fh4eGy2WxavXp1tj4LFixQvXr15O/vr9atW+u7774r1Huh9GkiqVUuj9wCEAAABeXyjM67776b5/IhQ4a4tL60tDS1aNFCjz76qB544IFsy1esWKExY8ZowYIF6tChg9544w316tVL8fHx/CsfAADkyeWgM3r0aKfnV69e1aVLl+Tr66vAwECXg06vXr3Uq1evXJfPnTtXI0aM0MiRIyVJ8+bN09q1a7Vw4UJNnz7d1fKVkZGhjIwMx/OUlBSX1wEAAG4OLu+6OnfunNMjNTVVhw4dUseOHd1+MPKVK1e0e/du9ezZ06m9Z8+e2r59e6HWOX36dIWEhDgetWvXdkepAACgFCrUMTo3atiwoWbMmJFttqeokpOTlZmZqWrVqjm1V6tWTSdPnnQ8v+uuu/TQQw9pzZo1qlWrluLi4nJd53PPPacLFy44HseOHXNrzQAAoPRweddVbry8vHTixAl3rc6JzWZzem6McWpbu3Ztgdfl5+cnPz8/t9UGAABKL5eDzmeffeb03BijpKQkzZ8/Xx06dHBbYdL1i8V5eXk5zd5I0qlTp7LN8gAAANzI5aBz3333OT232WyqUqWKunXrpjlz5rirLkmSr6+vWrdurXXr1ql///6O9nXr1unee+9163sBAADrcTno2O12txaQmpqqX375xfH8yJEj2rdvn0JDQxUREaFx48Zp8ODBatOmjdq1a6fFixcrMTFRjz/+uFvrQOnFbSIAAIXltmN0CmvXrl3q2rWr4/m4ceMkSUOHDtXSpUs1YMAAnTlzRlOnTlVSUpKaNm2qNWvWqE6dOkV639jYWMXGxuZ4g1KUDtwmAgBQVC4HnawgUhBz587Nt09UVJSMMXn2GTVqlEaNGlXg9y2ImJgYxcTEKCUlRSEhIW5dN9zjvLhNBACgaFwOOnv37tWePXt07do1NWrUSJJ0+PBheXl5qVWrVo5+N54pBRRW1m0iAABwlctBp2/fvgoODtayZctUqVIlSdcvIvjoo4+qU6dOGj9+vNuLBAAAKAyXLxg4Z84cTZ8+3RFyJKlSpUp65ZVX3H7WFQAAQFG4PKOTkpKi//znP7r11lud2k+dOqWLFy+6rTDAFZyZBQDIictBp3///nr00Uc1Z84c/fWvf5Ukff/993r66ad1//33u73A4sJZV9bAmVkAgLy4HHQWLVqkp556StHR0bp69er1lXh7a8SIEZo9e7bbCywunHVlDefFmVkAgNy5HHQCAwO1YMECzZ49W7/++quMMWrQoIGCgoKKoz6gQDgzCwCQk0LfvTwpKUlJSUm65ZZbFBQUlO+1cAAAAEqay0HnzJkz6t69u2655Rb17t1bSUlJkqSRI0dyajkAAChVXA46Y8eOlY+PjxITExUYGOhoHzBggL7++mu3FgcAAFAULh+j880332jt2rWqVauWU3vDhg119OhRtxUGAABQVC4HnbS0NKeZnCzJycny8/NzS1GAJyQmJio5OTnPPgW5Ho+71gMAKDqXg07nzp317rvv6uWXX5Z0/Z5Wdrtds2fPdroLeWnHdXTwZ4mJiWrSqJEupafn2S+/6/G4az0AAPdwOejMnj1bUVFR2rVrl65cuaJnnnlGP/30k86ePatt27YVR43Fguvo4M+Sk5N1KT29yNfjcdd6AADu4XLQiYyM1IEDB7Rw4UJ5eXkpLS1N999/v2JiYlSjRo3iqBEoMe66Hg/X9QGA0sGloHP16lX17NlTb7zxhqZMmVJcNQEAALiFS6eX+/j46Mcff5TNZiuuegAAANzG5evoDBkyRG+//XZx1AIAAOBWLh+jc+XKFb311ltat26d2rRpk+0eV3PnznVbcQAAAEXhctD58ccf1arV9cMsDx8+7LSMXVoAAKA0KXDQ+e2331SvXj1t2rSpOOsBAABwmwIfo9OwYUOdPn3a8XzAgAH6z3/+UyxFlYTY2FhFRkaqbdu2ni4FAAAUkwIHHWOM0/M1a9YoLS3N7QWVlJiYGMXHxysuLs7TpQAAgGLi8llXAAAAN4sCBx2bzZbtYGMOPgYAAKVZgQ9GNsZo2LBhjjuUp6en6/HHH892evmqVavcWyEAAEAhFTjoDB061Ol5dHS024sBAABwpwIHnSVLlhRnHQAAAG7HwcgAAMCyCDoAAMCyXL4FBHCzSkhIKNQyAMDNq8wGndjYWMXGxiozM9PTpaCYJen61CUH0ANA2VNmg05MTIxiYmKUkpKikJAQT5eDYnRekl3ScklNcumzRtKLJVUQAKDElNmgg7KniaRWuSxjxxUAWBMHIwMAAMsi6AAAAMsi6AAAAMsi6AAAAMsi6AAAAMsi6AAAAMsi6AAAAMsi6AAAAMvigoGAi7hnFgDcPMps0OFeV3AV98wCgJtPmQ063OsKrjov7pkFADebMht0gMLinlkAcPPgYGQAAGBZBB0AAGBZBB0AAGBZBB0AAGBZBB0AAGBZBB0AAGBZBB0AAGBZBB0AAGBZBB0AAGBZBB0AAGBZBB0AAGBZBB0AAGBZ3NQTsLjExEQlJyfn2ScsLEwRERElVFHB3Kx1AyhdymzQiY2NVWxsrDIzMz1dClBsEhMT1aRRI11KT8+zX6C/vxIOHSo1oeFmrRtA6VNmg05MTIxiYmKUkpKikJAQT5cDFIvk5GRdSk/XcklNcumTICk6PV3JycmlJjDcrHUDKH3KbNABypImklp5uohCuFnrBlB6cDAyAACwLIIOAACwLIIOAACwLIIOAACwLIIOAACwLIIOAACwLIIOAACwLIIOAACwLIIOAACwLIIOAACwLIIOAACwLIIOAACwLIIOAACwLIIOAACwLIIOAACwLIIOAACwLIIOAACwLIIOAACwLIIOAACwLG9PFwCUVQkJCXkuz8jIkJ+fX559wsLCFBER4c6ycpWYmKjk5OR8+xWkpvzWld/YoGAK8t+sJLchwBPKbNCJjY1VbGysMjMzPV0KypgkXZ9KjY6OzrOfl6T8ts5Af38lHDpU7H+oEhMT1aRRI11KT8+3b341ubIuFF5Bx7mktiHAU8ps0ImJiVFMTIxSUlIUEhLi6XJQhpyXZJe0XFKTXPqskfRiPn0SJEWnpys5ObnY/0glJyfrUnp6nvUUtKaCrCvr86PwCjLOJbkNAZ5SZoMO4GlNJLXKZVlCAfp4gjvrKcjnR9GVtm0IKGkcjAwAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACyLoAMAACzLEkHniy++UKNGjdSwYUO99dZbni4HAACUEt6eLqCorl27pnHjxmnTpk2qUKGCWrVqpfvvv1+hoaGeLg0AAHjYTT+js3PnTt16662qWbOmgoOD1bt3b61du9bTZQEAgFLA40Fny5Yt6tu3r8LDw2Wz2bR69epsfRYsWKB69erJ399frVu31nfffedYduLECdWsWdPxvFatWjp+/HhJlA4AAEo5jwedtLQ0tWjRQvPnz89x+YoVKzRmzBhNnDhRe/fuVadOndSrVy8lJiZKkowx2V5js9mKtWYAAHBz8PgxOr169VKvXr1yXT537lyNGDFCI0eOlCTNmzdPa9eu1cKFCzV9+nTVrFnTaQbnjz/+0B133JHr+jIyMpSRkeF4npKS4oZPAXhOQkJCoZYV13rcva6SkJiYqOTk5Dz7hIWFKSIiokTeKyMjQ35+fiVSD0pGadvGbsb3KiyPB528XLlyRbt379azzz7r1N6zZ09t375dknT77bfrxx9/1PHjx1WhQgWtWbNGL730Uq7rnD59uqZMmVKsdQMlIUnXp2Sjo6NLxXrcva6SkpiYqCaNGulSenqe/QL9/ZVw6FCRfrAL+l5ekjLzWZc76kHJKI3b2M32XkVRqoNOcnKyMjMzVa1aNaf2atWq6eTJk5Ikb29vzZkzR127dpXdbtczzzyjypUr57rO5557TuPGjXM8T0lJUe3atYvnAwDF6Lwku6Tlkprk0meNpBdLaD3uXldJSU5O1qX09DxrTpAUnZ6u5OTkIv1YF+S9ssanJOpBySht29jN+F5FUaqDTpYbj7kxxji19evXT/369SvQuvz8/PKdEgZuJk0ktcplmSs7idy1Hnevq6TkVXNJvldCAfrg5lRatrGb+b0Kw+MHI+clLCxMXl5ejtmbLKdOnco2ywMAAHCjUh10fH191bp1a61bt86pfd26dWrfvr2HqgIAADcLj++6Sk1N1S+//OJ4fuTIEe3bt0+hoaGKiIjQuHHjNHjwYLVp00bt2rXT4sWLlZiYqMcff9yDVQMAgJuBx4POrl271LVrV8fzrAOFhw4dqqVLl2rAgAE6c+aMpk6dqqSkJDVt2lRr1qxRnTp1ivS+sbGxio2NVWZmfuc2AACAm5XHg05UVFSOF/37s1GjRmnUqFFufd+YmBjFxMQoJSVFISEhbl03AAAoHUr1MToAAABFQdABAACWRdABAACWRdABAACWVWaDTmxsrCIjI9W2bVtPlwIAAIpJmQ06MTExio+PV1xcnKdLAQAAxaTMBh0AAGB9BB0AAGBZHr9goKdlXawwJSXFretNTU29/r+Sclvzpay+9KGPBfqU9PulZv1vamqRvr8F+a6W5Hu567OX5OdC3krbNnYzvldOstaX30WHbSa/Hhb3xx9/qHbt2p4uAwAAFMKxY8dUq1atXJeX+aBjt9t14sQJBQcHy2azebqcEpOSkqLatWvr2LFjqlChgqfLuSkxhkXD+BUdY1h0jGHReHL8jDG6ePGiwsPDVa5c7kfilPldV+XKlcszCVpdhQoV+HIXEWNYNIxf0TGGRccYFo2nxq8g96rkYGQAAGBZBB0AAGBZBJ0yys/PT5MmTZKfn5+nS7lpMYZFw/gVHWNYdIxh0dwM41fmD0YGAADWxYwOAACwLIIOAACwLIIOAACwLIIOAACwLIKOxU2fPl1t27ZVcHCwqlatqvvuu0+HDh1y6mOM0eTJkxUeHq6AgABFRUXpp59+8lDFpdv06dNls9k0ZswYRxvjl7/jx48rOjpalStXVmBgoFq2bKndu3c7ljOGubt27ZpeeOEF1atXTwEBAapfv76mTp0qu93u6MP4OduyZYv69u2r8PBw2Ww2rV692ml5QcYrIyND//jHPxQWFqagoCD169dPf/zxRwl+Cs/Ja/yuXr2qCRMmqFmzZgoKClJ4eLiGDBmiEydOOK2jNI0fQcfiNm/erJiYGH3//fdat26drl27pp49eyotLc3RZ9asWZo7d67mz5+vuLg4Va9eXT169NDFixc9WHnpExcXp8WLF6t58+ZO7Yxf3s6dO6cOHTrIx8dHX331leLj4zVnzhxVrFjR0YcxzN3MmTO1aNEizZ8/XwkJCZo1a5Zmz56tf/3rX44+jJ+ztLQ0tWjRQvPnz89xeUHGa8yYMfr000/14YcfauvWrUpNTdU999yjzMzMkvoYHpPX+F26dEl79uzRiy++qD179mjVqlU6fPiw+vXr59SvVI2fQZly6tQpI8ls3rzZGGOM3W431atXNzNmzHD0SU9PNyEhIWbRokWeKrPUuXjxomnYsKFZt26d6dKlixk9erQxhvEriAkTJpiOHTvmupwxzFufPn3M8OHDndruv/9+Ex0dbYxh/PIjyXz66aeO5wUZr/PnzxsfHx/z4YcfOvocP37clCtXznz99dclVntpcOP45WTnzp1Gkjl69KgxpvSNHzM6ZcyFCxckSaGhoZKkI0eO6OTJk+rZs6ejj5+fn7p06aLt27d7pMbSKCYmRn369NGdd97p1M745e+zzz5TmzZt9NBDD6lq1aq67bbb9OabbzqWM4Z569ixozZs2KDDhw9Lkvbv36+tW7eqd+/ekhg/VxVkvHbv3q2rV6869QkPD1fTpk0Z0xxcuHBBNpvNMUtb2savzN/UsywxxmjcuHHq2LGjmjZtKkk6efKkJKlatWpOfatVq6ajR4+WeI2l0Ycffqg9e/YoLi4u2zLGL3+//fabFi5cqHHjxun555/Xzp079eSTT8rPz09DhgxhDPMxYcIEXbhwQY0bN5aXl5cyMzP16quvatCgQZLYBl1VkPE6efKkfH19ValSpWx9sl6P69LT0/Xss8/q4YcfdtzUs7SNH0GnDHniiSd04MABbd26Ndsym83m9NwYk62tLDp27JhGjx6tb775Rv7+/rn2Y/xyZ7fb1aZNG02bNk2SdNttt+mnn37SwoULNWTIEEc/xjBnK1as0PLly/X+++/r1ltv1b59+zRmzBiFh4dr6NChjn6Mn2sKM16MqbOrV69q4MCBstvtWrBgQb79PTV+7LoqI/7xj3/os88+06ZNm1SrVi1He/Xq1SUpW8o+depUtn/xlEW7d+/WqVOn1Lp1a3l7e8vb21ubN2/W//zP/8jb29sxRoxf7mrUqKHIyEintiZNmigxMVES22B+nn76aT377LMaOHCgmjVrpsGDB2vs2LGaPn26JMbPVQUZr+rVq+vKlSs6d+5crn3KuqtXr+q//uu/dOTIEa1bt84xmyOVvvEj6FicMUZPPPGEVq1apY0bN6pevXpOy+vVq6fq1atr3bp1jrYrV65o8+bNat++fUmXW+p0795dBw8e1L59+xyPNm3a6JFHHtG+fftUv359xi8fHTp0yHZJg8OHD6tOnTqS2Abzc+nSJZUr5/xT7eXl5Ti9nPFzTUHGq3Xr1vLx8XHqk5SUpB9//JEx1f8POT///LPWr1+vypUrOy0vdeNX4oc/o0T9/e9/NyEhIebbb781SUlJjselS5ccfWbMmGFCQkLMqlWrzMGDB82gQYNMjRo1TEpKigcrL73+fNaVMYxffnbu3Gm8vb3Nq6++an7++Wfz3nvvmcDAQLN8+XJHH8Ywd0OHDjU1a9Y0X3zxhTly5IhZtWqVCQsLM88884yjD+Pn7OLFi2bv3r1m7969RpKZO3eu2bt3r+OsoIKM1+OPP25q1apl1q9fb/bs2WO6detmWrRoYa5du+apj1Vi8hq/q1evmn79+platWqZffv2Of1dycjIcKyjNI0fQcfiJOX4WLJkiaOP3W43kyZNMtWrVzd+fn6mc+fO5uDBg54rupS7Megwfvn7/PPPTdOmTY2fn59p3LixWbx4sdNyxjB3KSkpZvTo0SYiIsL4+/ub+vXrm4kTJzr9UWH8nG3atCnH372hQ4caYwo2XpcvXzZPPPGECQ0NNQEBAeaee+4xiYmJHvg0JS+v8Tty5Eiuf1c2bdrkWEdpGj+bMcaU3PwRAABAyeEYHQAAYFkEHQAAYFkEHQAAYFkEHQAAYFkEHQAAYFkEHQAAYFkEHQAAYFkEHQDIR926dTVv3jxPlwGgEAg6ANxq2LBhstls2R533313idYxefJktWzZMt9+aWlpmjBhgurXry9/f39VqVJFUVFR+uKLLxx94uLi9N///d/FWC2A4uLt6QIAWM/dd9+tJUuWOLX5+fl5qJq8Pf7449q5c6fmz5+vyMhInTlzRtu3b9eZM2ccfapUqeLBCgEUBTM6ANzOz89P1atXd3pUqlRJkjRo0CANHDjQqf/Vq1cVFhbmCEfGGM2aNUv169dXQECAWrRooY8//tjR/9tvv5XNZtOGDRvUpk0bBQYGqn379o67pC9dulRTpkzR/v37HTNKS5cuzbHWzz//XM8//7x69+6tunXrqnXr1vrHP/6hoUOHOvr8edfV0qVLc5yxmjx5sqP/kiVL1KRJE/n7+6tx48ZasGBBUYcUQCERdACUqEceeUSfffaZUlNTHW1r165VWlqaHnjgAUnSCy+8oCVLlmjhwoX66aefNHbsWEVHR2vz5s1O65o4caLmzJmjXbt2ydvbW8OHD5ckDRgwQOPHj9ett96qpKQkJSUlacCAATnWU716da1Zs0YXL14sUP0DBgxwrDMpKUkffPCBvL291aFDB0nSm2++qYkTJ+rVV19VQkKCpk2bphdffFHLli1zeawAuIFHbiUKwLKGDh1qvLy8TFBQkNNj6tSpxhhjrly5YsLCwsy7777reM2gQYPMQw89ZIwxJjU11fj7+5vt27c7rXfEiBFm0KBBxpj/f3fl9evXO5Z/+eWXRpK5fPmyMcaYSZMmmRYtWuRb7+bNm02tWrWMj4+PadOmjRkzZozZunWrU586deqY1157Ldtrf/nlF1O5cmUza9YsR1vt2rXN+++/79Tv5ZdfNu3atcu3FgDuxzE6ANyua9euWrhwoVNbaGioJMnHx0cPPfSQ3nvvPQ0ePFhpaWn697//rffff1+SFB8fr/T0dPXo0cPp9VeuXNFtt93m1Na8eXPH/69Ro4Yk6dSpU4qIiChwrZ07d9Zvv/2m77//Xtu2bdPGjRv1+uuva8qUKXrxxRdzfd2FCxd0zz33qFevXnr66aclSadPn9axY8c0YsQIPfbYY46+165dU0hISIFrAuA+BB0AbhcUFKQGDRrkuvyRRx5Rly5ddOrUKa1bt07+/v7q1auXJMlut0uSvvzyS9WsWdPpdTce0Ozj4+P4/zabzen1rvDx8VGnTp3UqVMnPfvss3rllVc0depUTZgwQb6+vtn6Z2ZmasCAAapQoYLefPNNR3vWe7/55pu64447nF7j5eXlcl0Aio6gA6DEtW/fXrVr19aKFSv01Vdf6aGHHnIEisjISPn5+SkxMVFdunQp9Hv4+voqMzOzUK+NjIzUtWvXlJ6enmPQGTt2rA4ePKi4uDj5+/s72qtVq6aaNWvqt99+0yOPPFLo2gG4D0EHgNtlZGTo5MmTTm3e3t4KCwuTdH325eGHH9aiRYt0+PBhbdq0ydEvODhYTz31lMaOHSu73a6OHTsqJSVF27dvV/ny5Z3OhspL3bp1deTIEe3bt0+1atVScHBwjqe4R0VFadCgQWrTpo0qV66s+Ph4Pf/88+ratasqVKiQrf+SJUu0YMECffrppypXrpzjc5YvX17ly5fX5MmT9eSTT6pChQrq1auXMjIytGvXLp07d07jxo0r8BgCcBNPHyQEwFqGDh1qJGV7NGrUyKnfTz/9ZCSZOnXqGLvd7rTMbreb119/3TRq1Mj4+PiYKlWqmLvuusts3rzZGPP/D0Y+d+6c4zV79+41ksyRI0eMMcakp6ebBx54wFSsWNFIMkuWLMmx3mnTppl27dqZ0NBQ4+/vb+rXr2+efPJJk5yc7Ojz54ORc/t8kyZNcvR/7733TMuWLY2vr6+pVKmS6dy5s1m1alXhBhRAkdiMMcYTAQsAAKC4cR0dAABgWQQdAABgWQQdAABgWQQdAABgWQQdAABgWQQdAABgWQQdAABgWQQdAABgWQQdAABgWQQdAABgWQQdAABgWQQdAABgWf8PAbc9t6tkoiMAAAAASUVORK5CYII=",
      "text/plain": [
       "<Figure size 640x480 with 1 Axes>"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    }
   ],
   "source": [
    "# Generating samples from a power-law distribution\n",
    "a = 2.5  # Shape parameter (the larger, the more skewed)\n",
    "size = 1000\n",
    "\n",
    "power_law_data = (np.random.pareto(a, size) + 1) * 10  # Shifted Pareto distribution\n",
    "\n",
    "plt.hist(power_law_data, bins=50, color='red', edgecolor='black', log=True)\n",
    "plt.title('Simulated Data from Power-Law Distribution')\n",
    "plt.xlabel('Event Size')\n",
    "plt.ylabel('Frequency (log scale)')\n",
    "plt.show()\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "The power-law distribution captures the tail-heavy behavior typical of geophysical processes like earthquakes or landslides."
   ]
  }
 ],
 "metadata": {
  "kernelspec": {
   "display_name": "mlgeo",
   "language": "python",
   "name": "python3"
  },
  "language_info": {
   "codemirror_mode": {
    "name": "ipython",
    "version": 3
   },
   "file_extension": ".py",
   "mimetype": "text/x-python",
   "name": "python",
   "nbconvert_exporter": "python",
   "pygments_lexer": "ipython3",
   "version": "3.9.18"
  }
 },
 "nbformat": 4,
 "nbformat_minor": 2
}