{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Feature extraction\n",
"> This chapter is a deep-dive on the most frequently used dimensionality reduction algorithm, Principal Component Analysis (PCA). You'll build intuition on how and why this algorithm is so powerful and will apply it both for data exploration and data pre-processing in a modeling pipeline. You'll end with a cool image compression use case. This is the Summary of lecture \"Dimensionality Reduction in Python\", via datacamp.\n",
"\n",
"- toc: true \n",
"- badges: true\n",
"- comments: true\n",
"- author: Chanseok Kang\n",
"- categories: [Python, Datacamp, Machine_Learning]\n",
"- image: images/mnist.png"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"import pandas as pd\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"import seaborn as sns\n",
"\n",
"plt.rcParams['figure.figsize'] = (8, 8)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Feature extraction\n",
"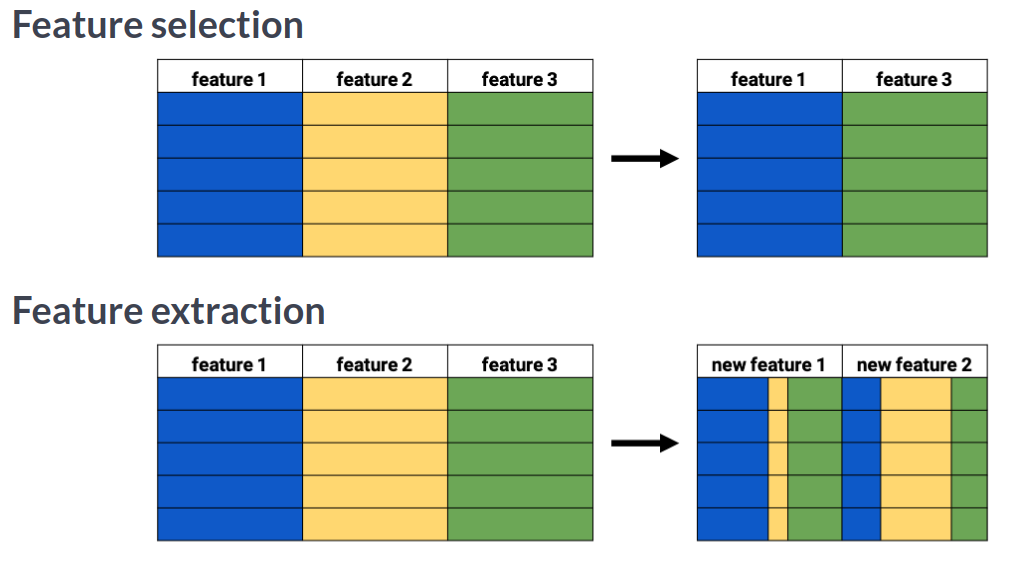"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Manual feature extraction I\n",
"You want to compare prices for specific products between stores. The features in the pre-loaded dataset `sales_df` are: `storeID`, `product`, `quantity` and `revenue`. The `quantity` and `revenue` features tell you how many items of a particular product were sold in a store and what the total revenue was. For the purpose of your analysis it's more interesting to know the average price per product."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"
\n",
"\n",
"
\n",
" \n",
"
\n",
"
\n",
"
storeID
\n",
"
product
\n",
"
quantity
\n",
"
revenue
\n",
"
\n",
" \n",
" \n",
"
\n",
"
0
\n",
"
A
\n",
"
Apples
\n",
"
1811
\n",
"
9300.6
\n",
"
\n",
"
\n",
"
1
\n",
"
A
\n",
"
Bananas
\n",
"
1003
\n",
"
3375.2
\n",
"
\n",
"
\n",
"
2
\n",
"
A
\n",
"
Oranges
\n",
"
1604
\n",
"
8528.5
\n",
"
\n",
"
\n",
"
3
\n",
"
B
\n",
"
Apples
\n",
"
1785
\n",
"
9181.0
\n",
"
\n",
"
\n",
"
4
\n",
"
B
\n",
"
Bananas
\n",
"
944
\n",
"
3680.2
\n",
"
\n",
" \n",
"
\n",
"
"
],
"text/plain": [
" storeID product quantity revenue\n",
"0 A Apples 1811 9300.6\n",
"1 A Bananas 1003 3375.2\n",
"2 A Oranges 1604 8528.5\n",
"3 B Apples 1785 9181.0\n",
"4 B Bananas 944 3680.2"
]
},
"execution_count": 2,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"sales_df = pd.read_csv('./dataset/grocery_sales.csv')\n",
"sales_df.head()"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"
\n",
"\n",
"
\n",
" \n",
"
\n",
"
\n",
"
storeID
\n",
"
product
\n",
"
price
\n",
"
\n",
" \n",
" \n",
"
\n",
"
0
\n",
"
A
\n",
"
Apples
\n",
"
5.135616
\n",
"
\n",
"
\n",
"
1
\n",
"
A
\n",
"
Bananas
\n",
"
3.365105
\n",
"
\n",
"
\n",
"
2
\n",
"
A
\n",
"
Oranges
\n",
"
5.317020
\n",
"
\n",
"
\n",
"
3
\n",
"
B
\n",
"
Apples
\n",
"
5.143417
\n",
"
\n",
"
\n",
"
4
\n",
"
B
\n",
"
Bananas
\n",
"
3.898517
\n",
"
\n",
" \n",
"
\n",
"
"
],
"text/plain": [
" storeID product price\n",
"0 A Apples 5.135616\n",
"1 A Bananas 3.365105\n",
"2 A Oranges 5.317020\n",
"3 B Apples 5.143417\n",
"4 B Bananas 3.898517"
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Calculate the price from the quantity sold and revenue\n",
"sales_df['price'] = sales_df['revenue'] / sales_df['quantity']\n",
"\n",
"# Drop the quantity and revenue features\n",
"reduced_df = sales_df.drop(['revenue', 'quantity'], axis=1)\n",
"\n",
"reduced_df.head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Manual feature extraction II\n",
"You're working on a variant of the ANSUR dataset, `height_df`, where a person's height was measured 3 times. Add a feature with the mean height to the dataset, then drop the 3 original features."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"
"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"from sklearn.preprocessing import StandardScaler\n",
"from sklearn.decomposition import PCA\n",
"\n",
"# Create the scaler and standardize the data\n",
"scaler = StandardScaler()\n",
"ansur_std = scaler.fit_transform(ansur_df)\n",
"\n",
"# Create the PCA instance and fit and transform the data with pca\n",
"pca = PCA()\n",
"pc = pca.fit_transform(ansur_std)\n",
"\n",
"# This changes the numpy array output back to a dataframe\n",
"pc_df = pd.DataFrame(pc, columns=['PC 1', 'PC 2', 'PC 3', 'PC 4'])\n",
"\n",
"# Create a pairplot of the pricipal component dataframe\n",
"sns.pairplot(pc_df);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Notice how, in contrast to the input features, none of the principal components are correlated to one another."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### PCA on a larger dataset\n",
"You'll now apply PCA on a somewhat larger ANSUR datasample with 13 dimensions. The fitted model will be used in the next exercise. Since we are not using the principal components themselves there is no need to transform the data, instead, it is sufficient to fit pca to the data."
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [],
"source": [
"df = pd.read_csv('./dataset/ANSUR_II_MALE.csv')\n",
"ansur_df = df[['stature_m', 'buttockheight', 'waistdepth', 'span', \n",
" 'waistcircumference', 'shouldercircumference', 'footlength', \n",
" 'handlength', 'functionalleglength', 'chestheight', \n",
" 'chestcircumference', 'cervicaleheight', 'sittingheight']]"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"PCA(copy=True, iterated_power='auto', n_components=None, random_state=None,\n",
" svd_solver='auto', tol=0.0, whiten=False)"
]
},
"execution_count": 12,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Scale the data\n",
"scaler = StandardScaler()\n",
"ansur_std = scaler.fit_transform(ansur_df)\n",
"\n",
"# Apply PCA\n",
"pca = PCA()\n",
"pca.fit(ansur_std)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"You've fitted PCA on our 13 feature datasample. Now let's see how the components explain the variance."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### PCA explained variance\n",
"You'll be inspecting the variance explained by the different principal components of the `pca` instance you created in the previous exercise."
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[0.57832831 0.2230137 0.06404218 0.04252456 0.0278581 0.01761021\n",
" 0.01681037 0.01014147 0.00706488 0.00607973 0.00344643 0.00228095\n",
" 0.00079911]\n"
]
}
],
"source": [
"# Inspect the explained variance ratio per component\n",
"print(pca.explained_variance_ratio_)"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[0.57832831 0.801342 0.86538419 0.90790875 0.93576684 0.95337706\n",
" 0.97018743 0.9803289 0.98739378 0.99347351 0.99691994 0.99920089\n",
" 1. ]\n"
]
}
],
"source": [
"# Print the cumulative sum of the explained variance ratio\n",
"print(pca.explained_variance_ratio_.cumsum())"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Based on the data, we can use 4 principal components if we don't want to lose more than 10% of explained variance during dimensionality reduction."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## PCA applications\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Understanding the components\n",
"You'll apply PCA to the numeric features of the Pokemon dataset, `poke_df`, using a pipeline to combine the feature scaling and PCA in one go. You'll then interpret the meanings of the first two components.\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"
"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# Use the Type feature to color the PC 1 vs. PC 2 scatterplot\n",
"sns.scatterplot(data=poke_cat_df, x='PC 1', y='PC 2', hue='Type 1');"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAfAAAAHgCAYAAABaej99AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjMsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+AADFEAAAgAElEQVR4nOzdd3zV9fX48dfn7pubmz0hQBJmIOy9RGW4cNe9t1gVt9bWb2utVn9trW0dqKi1FavWUScOwIGASNh7B0jIXjf35u77+f1x4UK4AbJvLpzn48FD7/uu9w3kns97naOoqooQQgghoosm0h0QQgghRMtJABdCCCGikARwIYQQIgpJABdCCCGikARwIYQQIgpJABdCCCGikC7SHWiJlJQUNTs7O9LdEEIIITrFypUrK1VVTW3qvqgK4NnZ2RQUFES6G0IIIUSnUBRlz9Hukyl0IYQQIgpJABdCCCGikARwIYQQIgpF1Rq4EEKIyPB6vRQVFeFyuSLdlROSyWQiKysLvV7f7OdIABdCCHFcRUVFWK1WsrOzURQl0t05oaiqSlVVFUVFReTk5DT7eTKFLoQQ4rhcLhfJyckSvDuAoigkJye3eHZDArgQQohmkeDdcVrzs5UALoQQIirExsZGugtA1+mHBHAhhBCig6iqSiAQ6JDXlgAuhBAialVUVHDxxRczevRoRo8ezZIlS0Lt06dPZ8SIEdx222306tWLyspKAN566y3GjBnDsGHDuO222/D7/UBwZP3rX/+aoUOHMm7cOMrKygDYvXs348ePZ/To0Tz22GOh97bb7UydOpURI0YwePBgPv74YwAKCwvJy8vjjjvuYMSIETzxxBPce++9oee9+uqr3HfffW3/8KqqRs2fkSNHqkIIITrfpk2bIt0F1WKxhLVdccUV6uLFi1VVVdU9e/aoAwYMUFVVVX/5y1+qTz31lKqqqjp//nwVUCsqKtRNmzapM2fOVD0ej6qqqjpr1iz1zTffVFVVVQH1k08+UVVVVR988EH1iSeeUFVVVc8999zQY55//vlQP7xer1pXV6eqqqpWVFSovXv3VgOBgLp7925VURR12bJlqqqqqt1uV3Nzc0PvOX78eHXdunVhn6WpnzFQoB4lJsoxMiGEEFFrwYIFbNq0KXTbZrNRX1/Pjz/+yEcffQTAmWeeSWJiIgALFy5k5cqVjB49GgCn00laWhoABoOBmTNnAjBy5Ei++eYbAJYsWcIHH3wAwDXXXMPDDz8MBAfAjz76KD/88AMajYbi4uLQqL1Xr16MGzcOAIvFwumnn85nn31GXl4eXq+XwYMHt/mzSwAXQggRtQKBAMuWLcNsNjdqDw5ew6mqynXXXccf//jHsPv0en1oN7hWq8Xn84Xua2qX+Lx586ioqGDlypXo9Xqys7NDR8EsFkujx95888089dRTDBgwgBtuuKFlH/IoZA1cCCFE1JoxYwbPP/986PaaNWsAmDRpEu+99x4AX3/9NTU1NQBMnTqV999/n/LycgCqq6vZs+eoBb8AmDhxIu+88w4QDNoH1dXVkZaWhl6v59tvvz3m64wdO5Z9+/bx9ttvc8UVV7Tik4aTAC6E6HSBgEog0PQISYijaWhoICsrK/Tn2Wef5e9//zsFBQUMGTKEgQMHMmfOHAB++9vf8vXXXzNixAjmz59PZmYmVquVgQMH8oc//IEZM2YwZMgQpk+fTklJyTHf929/+xsvvPACo0ePpq6uLtR+1VVXUVBQwKhRo5g3bx4DBgw45utceumlTJw4MTSd31bK0aYZuqJRo0apUg9ciOjl8wcotbn419I9OL1+bpiYTbcEMya9NtJdE8exefNm8vLyIt2NZnO73Wi1WnQ6HcuWLWPWrFmh0XmkzJw5k3vvvZepU6c2eX9TP2NFUVaqqjqqqcfLGrgQotNU1Ls587nF2N3BtcV3Vuzly9mn0DutayTGECeOvXv3cumllxIIBDAYDLz66qsR60ttbS1jxoxh6NChRw3erSEBXAjRab7YUBIK3gBev8rcH3fxxPn56LSyoifaT9++fVm9enWkuwFAQkIC27Zta/fXld8YIUSn0WvCv3IMWg1Iim0hWkwCuBCi05yRn0GSxRC6bdZruWlyLromArsQ4thkCl0I0WlSY43Mv3syn68vweX1c/6w7qRaDcd/ohAijARwIUSn0WgU0uNN3DgpJ9JdESLqybyVEEKIqKDVahk2bFjoT2Fh4VEfW1hYSH5+fud1LgJkBC6EECIqmM3miJ/l7kpkBC6EEKLd/W91MROfXkTOI58z8elF/G91cYe8T2FhIZMnT2bEiBGMGDGCpUuXhj1m48aNofKhQ4YMYfv27cDRy4pGCwngQggh2tX/Vhfzqw/XU1zrRAWKa5386sP1bQ7iTqczNH1+4YUXApCWlsY333zDqlWrePfdd7n77rvDnjdnzhxmz57NmjVrKCgoICsri82bN/Puu++yZMkS1qxZg1arbZTnPBrIFLoQQoh29aevtuL0Nh7NOr1+/vTVVi4Y3r3Vr9vUFLrX6+XOO+8MBeGmEqaMHz+eJ598kqKiIi666CL69u17zLKi0UICuBBCiHa1v9bZova2+Otf/0p6ejpr164lEAhgMpnCHnPllVcyduxYPv/8c8444wzmzp17zLKi0UKm0IUQQrSrbgnmFrW3RV1dHZmZmWg0Gv797383uY69a9cucnNzufvuuznvvPNYt25dq8qKdjURDeCKoiQoivK+oihbFEXZrCjK+Ej2RwghRNs9eEZ/zEdUmDPrtTx4Rv92f6877riDN998k3HjxrFt2zYsFkvYY959913y8/MZNmwYW7Zs4dprr21VWdGuJqLlRBVFeRNYrKrqXEVRDECMqqq1R3u8lBMVQojIaGk50f+tLuZPX21lf62TbglmHjyjf5vWv08GUVNOVFGUOOAU4HoAVVU9gCdS/RFCCNF+LhjeXQJ2B4vkFHouUAG8oSjKakVR5iqKEj73IYQQQogwkQzgOmAE8JKqqsMBB/DIkQ9SFOVWRVEKFEUpqKio6Ow+CiGEEF1SJAN4EVCkquryA7ffJxjQG1FV9RVVVUepqjoqNTW1UzsohBBCdFURC+CqqpYC+xRFObgtcSqwKVL9EUIIIaJJpBO53AXMO7ADfRdwQ4T7I4QQQkSFiAZwVVXXAE1ujxdCCCEOqqqqYurUqQCUlpai1Wo5uKz6888/YzAYItm9iIj0CFwIIYQ4ruTk5FAe9N/97nfExsbywAMPNHqMqqqoqopGc3IkGT05PqUQQojOte49+Gs+/C4h+N9173XI2+zYsYP8/Hxuv/12RowYwb59+0hISAjd/84773DzzTcDUFZWxkUXXcSoUaMYM2YMP/30U4f0qbPICFwIIUT7WvcefHo3eA8UL6nbF7wNMOTSdn+7TZs28cYbbzBnzhx8Pt9RH3f33Xfz0EMPMW7cOAoLC5k5cyYbNmxo9/50FgngQggh2tfC3x8K3gd5ncH2DgjgvXv3DpUFPZYFCxawdevW0O2amhqcTidmc/sXWekMEsCFEEK0r7qilrW30eEFTDQaDYfX+HC5XKH/V1X1hNrwJmvgQggh2ld8Vsva25FGoyExMZHt27cTCAT46KOPQvdNmzaNF154IXT74Ka4aCUBXAghRPua+n+gP2JaWm8OtneCZ555hjPPPJOpU6eSlXXoouGFF15gyZIlDBkyhIEDB/Lqq692Sn86SkTLibaUlBMVQojIaGk5Uda9F1zzrisKjryn/l+HrH+fSKKmnKgQQogT2JBLJWB3MJlCF0IIIaKQBHAhhBAiCkkAF0II0SzRtGcq2rTmZysBXAghxHGZTCaqqqokiHcAVVWpqqrCZDK16HmyiU0IIcRxZWVlUVRUREVFRaS7ckIymUyNjrw1hwRwIYQQx6XX68nJyYl0N8RhZApdCCGEiEISwIUQQogoJAFcCCGEiEISwIUQQogoJAFcCCGEiEISwIUQQogoJAFcCCGEiEISwIUQQogoJAFcCCGEiEISwIUQQogoJAFcCCGEiEISwIUQQogoJAFcCCGEiEISwIUQQogoJAFcCCGEiEISwIUQQogoJAFcCCGEiEISwIUQQogoJAFcCCGEiEISwIUQQogoJAFcCCGEiEISwIUQQogoJAFcCCGEiEISwIUQQogoJAFcCCGEiEISwIUQQogoJAFcCCGEiEISwIUQQogoJAFcCCGEiEISwIUQQogoJAFcCCGEiEISwIUQQogoJAFcCCGEiEISwIUQQogoJAFcCCHakc8foKLejc3ljXRXxAlOF+kOCCHEiaLa4eHdFXv5YFUxPZLMPHbOQHolW9BqlEh3TZyAZAQuhBDtwOML8NZPhTzz5VZ2lNv5dksFF764lCq7O9JdEycoCeBCCNEO6pwe3l9ZfESbl6IaZ4R6JE50EsCFEKId6LUaMuNNYe2JFn0EeiNOBhLAhRCiHSTEGHj8vEHEGLShtktGZpEQY4hgr8SJTDaxCSFEO+mdZuHbB05lZ7mdtDgTyRYDiRLARQeRAC6EEO1Er9WSHqclPS58Kl2I9iZT6EIIIUQUkgAuhBBCRCEJ4EIIIUQUkgAuhBBCRCEJ4EIIIUQUkgAuhBBCRKGIB3BFUbSKoqxWFOWzSPdFCCGEiBYRD+DAbGBzpDshhBBCRJOIBnBFUbKAc4C5keyHEEIIEW0iPQJ/DngICES4H0IIIURUiVgAVxRlJlCuqurK4zzuVkVRChRFKaioqOik3gkhhBBdWyRH4BOB8xRFKQTeAU5XFOWtIx+kquorqqqOUlV1VGpqamf3UQghhOiSIhbAVVX9laqqWaqqZgOXA4tUVb06Uv0RQgghokmk18CFEEII0QpdopyoqqrfAd9FuBtCCCFE1JARuBBCCBGFusQIXAghTiZ1DR6c3gAaBRJiDBh0MpYSLScBXAghOlFlvZtHPlzHwi3lxBp0PDZzIGcNzsBq0ke6ayLKyGWfEEJ0Eo8vwOtLdrNgczmqCvVuHw99sI4quyfSXRNRSAK4EEJ0Ervbx+LtlWHtm0psEeiNiHYSwIUQopNYjFrG5iSFtffPsEagNyLaSQAXQohOYtRpuW1KLmMOBHGjTsOvz8kjxWKMcM9ENJJNbEKIdlHb4MHrV0mM0aPTytjgaFKtJuZcPQKXN4BGoxBv0mM2aCPdLRGFJIALIdqkwe1lV2UDv/9sE+U2F5eN7sFlo3uSZDFEumtdVpKMuEU7kAAuhGg1j89Phd3DL+YsxeUNVgV+5sutGHUarhufjVZG4kJ0GPntEkK0ms3po6CwOhS8D3p/ZTG1Tm+EeiXEyUECuBCi1ZxeH6lWU1h7z6QYjJJdTIgOJb9hQohWM+q11Dm9nJWfEWpLiNHz0Jn9iY2mzGLOWihdD4ufhd0/gCP8rLYQXY2sgQshWi3ZYmRAhhUFuG5CNg63j7zMONLjwkflXZbfC5v+B5/OPtQ29Eo4849gTohcv4Q4DgngQohW02oU+qZbSbQYCARUDFoNCdG2+9xZDQsfb9y29m04/dcSwEWXJgFcCNFmKbFRfCxKBbyu8PaAv9O7IkRLyBq4EOLkZoqDsbc1bus5AQyWyPRHiGaSEbgQ4uSmN8OEuyA9HzZ+BD3HwZDLwJIS6Z4JcUwSwIUQ7arB7cPu8aEQ3OSm0SiR7tLxxSTD4F9A/3NAZwCNpDYVXZ8EcCFEu6myu/nL19v4YFURqVYjf7ggnzE5ScQYouSrxmCOdA+EaDZZAxdCtAuvP8B/ft7L2z/vxe0LUFTj5MZ/rqDG4Yl014Q4IUkAF0K0i3qXly83ljZqC6iwYb8tQj0S4sQmAVwI0S7Meh2DusWHteekyG5uITqCBHAhRLswG7TcM7UvvVODAVtR4NZTckmzRvEZcSG6sCjZWSKEiAaZCWbeuXUcDR4/Bq0Gi0lHXDTlRBciikgAF0K0q6aqkwkh2p9MoQshhBBRSAK4EEIIEYUkgAshhBBRSAK4EEIIEYUkgAshhBBRSAK4EEIIEYUkgAshhBBRSAK4EEIIEYUkkYsQok3sbh92lxd/IJhONcliiHSXhDgpSAAXQrRabYOHN5YU8uJ3O/D6VcbmJPH8lcNJtZrw+gMogE4rE31CdAQJ4EKIViupc/G3hdtDt5fvrmbpzioGdYtj7uLd6LUabp6cQ2a8CYNOG8GeCnHikQAuhGi1TUfU+k62GOiRGMOZzy3GF1AB+O/KfSy4bwpZiTGR6KIQJyyZ2xJCtNrwngmNbp82II0PVhaFgjeAyxvgkzX7W/0egYBKRb2LMpuL2gZPq19HiBONBHAhRKulWI08c/Fg4sw6tBqFId3jiDGGT+yZ9K2bPvf4/KzcU8OFLy5l7FMLmTVvFaV1rrZ2W4gTgkyhC3ESqHd58fgCJJj1aNtxU1mcSc+Fw7M4rX8aKhBj0FLn9PKfn/did/uA4LT62YMzW/X6NQ1ernvjZxo8fgCW7azit59s4M+XDMUqdcbFSU4CuBAnML8/wJ7qBp76YjP7a11cMiqL84d1b9ejXgadhrS4QzXAzXotX997CvM3lGDQapgxKIPUWGOrXru2wRsK3gct3VGF0+OPWAC3NXgwuitRd36LDj+avtPQWNNBI5v0ROeSAC7ECazK4eGCF5dgcwZHw49/uglfQOWGCdkddrxLp9XQLcHMTZNy2/xa8WY9eq2C139oTX1Q9zgMusis/tldXlR7GcZ/TQV7WbDRlIB6+xKUhKyI9EmcvGQNXIgT2O5KRyh4H/TOz/uodXoj1KMgjy9Ald1Nw4FpdlVVKbO5eOunQuZ8v5OimgY8Pj9xZh1/uWQo5gNr6D2SzDxz8RASYiKTLMbjD6Bs/uRQ8AZw1aKumAuqevQnCtEBZAQuxAkssYmp8vQ4I/oIJlepsrt5c1khX28sY1D3eO6f3g+dRmHmP36kot4NwHMLtvHl7FPITrEwY1AGY3OTcXv9mA06UmIjl+lNVUHrsYW1K6664J2KEoFeiZOVBHAhTmApsUbOGZzJ5+tLgOAms9+eO5B4c2TWjx1uH898uYX3CooA2FJaj9fnZ2KflFDwhuDRs5d/2MXvzxuESa9t9S729qbVKPgGXQLL/wq+A/3VaFHH3oaikQlN0bkkgAtxAkuyGHjignzuOr0P5fVu+mdYSbJEbvd2g8fH/1Y3PhNeXu/G7Q2EPdbl9aPStaalE2IM2PzpOG/6AcOy51ACXph0L5qEHpHumjgJSQAX4gSXZDGQZDEwoHUnudqZQlqckaIaZ6hl9d4a/nLJUP701VbqD6yJazUKt0/J7ZLpV+OsVvyW/vjP+St6jYKiNx3/SUJ0AJnzEUJ0mmSLgScvzEerObRWfMspvbGadMy/ZzK3TM7hitE9+HL2ZHp04dSrWo2CwWiW4C0iSlGjaOfkqFGj1IKCgkh3Q0Q5p8ePzeVFVcFi1EpCkE7W4PZR6/SyucRGdoqFZIshtKs8EFAJoKKT9WQhAFAUZaWqqqOauk+m0MVJpbbBw7+X7eGFA+UvLxzenUfPGkBSKxONiJaLMeqIMerolmAOu0+jUdAgO7mFaA65zBUnlcJKB3/5ZhsubwB/QOX9lUV8s7mMaJqJ6mwV9S4WbC7ji/UllNlcBALt87NyenxU1LtwHpFpTQjRPDICFyeVJTurwtoWbi7nvKHdMRu63oapg+pdXnQaTaf3sbzexcUvLWVfdXDTWZLFwKd3TqRbghmlDWeey2wunv1mGyt2VzM2N4l7p/VrlI5VCHF8EsDFSWVsTlJY26S+KZj0XXMyyub0smZfLXMX7yLJYmD2tH5kJZrbnIilot7F5+tK2VlRz6WjetIrOYa4Js6Gf7elIhS8AaodHl77cTezTu1NqrV1Abfa4eGOeatYuacGgF2VDnZXOnjpqpGNEs/UNnjw+ALEmnTEGKL4q8rrBFct+L2gN4MlNdI9EieIKP6tEKLleqfGctspubz24278qsoZAzM4Z3Bmm0aTHWn1vlque/3n0O1vNpWx8P4pZMSHrx83V2W9m8tfWc7OCjsA//5pL69dN4qpeelhj62wu8Paap1evtpQygXDuxPbig2ALq8/FLwP+mlXNS5fcCo9EFDZU93Aox+tZ3tZPacNSOOhM/q3+oIhotz1sOkTmP8geByQMQSueAfiu0e6Z+IE0DWHHUJ0kESLgbum9uHHh09n6SOn88zFQ0juohvY6l1eXlu8q1Gbw+Nn+e7qNr1uca0zFLwPem7Bdqoc4cH63CHd0GsPXdwoClwwrDufry/B2UTylebQahQsRywFxJl0aA5cRFU5PFz+yjKW7ayi0u7hvwVFPP7pJupdkc3f3irOWvjkl8HgDVC6Dr5+LBjYhWgjCeDipBNr1JMRbyIz3kx8TNc9QqbTaJrMZd7WUqBNTTYoCihq+B1pcUY+vnMSZwzK4LT+abxyzSh+2F7BiF6JJLQyHWuCWc/j5w8K9UNR4Pfn55N44CiZ3e2jzNb4YuKrjaU4vVG42a2uKLzISfEK8DREpj/ihCJT6KLd2ZxeGjw+FEXBeuDIkGg5s0HLPdP6sWBTGY4DO7XzMq3kZcS16XW7JZjpkxbLjvJDo/B7p/UjqYkiISa9lt4pFh6Y0Y8ftlXwj0XbGdw9nllTeqNvZUlPo17LmYMyGJebzO5KB7kpscSb9aESoWa9Fp1GwXfYbvfsZEtohB5VEnoG64QHDrv4yJ4MhtjI9UmcMCSRi2hXVXY3f/hsMx+vLUav1XDrKbncODGnyZGkOD6vP0CV3cPyXVUkWgwMzIwjxdr2Kf+KejdfbSxlR7mdS0Zl0TMp5rgJbSrtbgIBFatJh7kDN5XZ3T7eL9jH7z/bREANFmB5+5axDOuR2GHv2WHcDtj9PXx6FzgqIWcKXPQKWDMi3TMRJY6VyEUCuGg3qqryzop9/OrD9Y3aP7xjAiN6RuGXr2gTu9uLVlFaFezrXV7qXT6qHB7SrEYSY/RdMi96s/i90FAFagB0ZoiR3wXRfJKJTXQKlzfAt1vKw9qX7aySAH4SqXd52VxSz0vf7STWpGX21H70TDK3KABbTXqsJn2T2dqijlYvI27RISSAi3Zj0muY0i+VrzeVNWoflxt+9rqtqh0eXF4/Wo1CvFnfZepFC9heZufSl5eFbn+9sYxvHzj1xAjGQnQhsgtdhHF7/ZTaXKworGZfdQN1zuYd31EUhTPzMzh3SCaKAgathjtO7U1uSvtu2Cmzubj5zQImPL2I0//8HR+vKe5yR4xUVaXS7qbS7j6p0rS6vH7m/tj46JvbF2DB5rKjPEMI0VoyAhdhNu63ccWrP+H2Bc/5PjCjH9dNyG5W1a7kWCNPXjiYR8/JQ0HBatJhacdd6E6Pj798vZVVe4OJQBwePw9/sJ4JvVO6TFUxm8vLsh1V/HXBNlQV7pnWlwl9Uohv5bGrtnD7/NicPswGLbGdcBpAqyikNHGuvq1H34QQ4SI2AlcUpYeiKN8qirJZUZSNiqLMjlRfxCGVdjcPf7AuFLwBnv1mG3aXr9mvEWfWkxlvJiPe1K7BG8Du9lNQWBPWXljlaNf3aYs9VQ3c9tZKtpTWs7WsnlnzVlFY2fn9q7S7efbrbVz+yjIe+WAdxTUdf/ZYr9Nw6+Rc4syH/t5zUiyMzUnu8Pc+mtoGD9VNJKkRItpFcgTuA+5XVXWVoihWYKWiKN+oqropgn066QVUlaIa5xFtdJkkGrFGHeN7J7PrsICoKJCbYolgrxr7YGVRWNt7BfsY2iMBAK/fT7XDS0mdixSLgTizvsk85G1hd3v54xdb+GBVsC87KxysL67j/dsnkNoOx9COJSPexDf3TmH5rmosRi2DusXh8voot6kkdOJu8gaPj037bfy/r7bi8vq549Q+jO+dRLy5E2YDXDZQ/WCWzZui40QsgKuqWgKUHPj/ekVRNgPdAQngEWQx6DhncCbvrzoUhDLiTMSausZqi9mgZfbUvuyqdLBsZxVxZh1PnJ9PfEzXmaLtn2ENaxtwWNv2MjuXzFkWSs5y99Q+3Dwpt12DuNPj55O1xY3a9lQ10ODxAR0bwHVaDelxJs4enMHG/TamP/sD9W4fcSYdr103mhE9E9C2sBiLy+vH7vZhMWibfSyt3Obm0peXcTAfzO1vreTd28Z17GyAxwlV22Hh48EiJpPugx6jwRTfce8pTlpd4ltZUZRsYDiwvIn7bgVuBejZs2en9utkZDHqeOTsAVhNOr7ZXEa/9Fh+e+4gUrtQvvC0OBMvXjUCl9ePRlFIjDGEsnh1BdPy0vlXZiGbS4L5rvunWzkzP3iMqNrh5tGPNoSCN8A/Fu3g8tE923kUrpARb2pUSUyrUTB24s+p2uHhpjdXUO8OLr/YXD7u/M8qPr1rEmktKExSUe/mpe928MP2Skb0TOC+6f3JiD/+8+dvKOXI0uX/XraH4T0SOm4WwFEOc08Pnv0G2LMEbvwSeo7vmPcTJ7WIB3BFUWKBD4B7VFW1HXm/qqqvAK9AMJFLJ3fvpJQSa+ThswYw67TemHTadp/ebQ+JXWjEfaRUq5F/3zSWivrgDvS0OFNoY5fPr7LniPV6VQ1ufOtG+x2zSrYYeOaiIVz7+s+hlKR3T+3brnsSqh1uNIpCwlH+Lrx+lUq7p1Fbmc2Nz9/8X2Ob08uvPlzHgs3B/AI7yu1s3G/jXzeOOW4Rmh5J4T/PXskxaDUdmJJ1y2eHgvdBP82BbsNBF4XV1ESXFtEAriiKnmDwnqeq6oeR7ItozKTXytnqNkiJNTa5G9tq0nPOkEze+mlvqC0xRt/uu7Q1GoXhPRNY/NBp7Kiw0yMxhkSLvl126tucXpbvruaFb3eg1yo8dMYABnWLC8t5b9Rp6J1qYWfFoQuW/unWFs0COL1+Fh6RHGjjfluz9mSMzUlmULc4Nu4Pjgsy401cOy4braYDZyHiuoW3xWeBEvGxkjgBRexflRIswPwasFlV1Wcj1Q/Rdh6fn/J6N5+tK8Fq0jEtL530OBltNOVggRK9RsP8DaXkpFp44vx8ki3tv0RhNgRzlme2cwKV7eV2bvnXoZTGl72yjAX3TSE3tfF5/xSrkdeuG809765hzb5aRvRM4LnLhrWofKuiQFKMgSrHofyePCAAACAASURBVJG8UadB34w19FSrkTdvHENxjRO3L0BOiqXDN/DRayKk5UH55uBtSyqMvR3KN8Len4L3x2eBOaFj+yFOChHLha4oyiRgMbAeOHhm6VFVVb842nMkF3rXtLvCwZl/+yF09Cw9zsind04iTYL4Ubm8fmwuLwat5qhT0F2R1x/gwffX8r/V+xu13z+9H3dN7dvkc6odbnwBFZ1G0+KZBq8/wMLNZdwxb1VoPfv/zh3I5aN7ENOBBVXaxF4OlduDNcAzBsPWL+Dz+w7dP+MPMPpm0EtmOnF8XTIXuqqqPwJRWB9QHM7j8/PidzsanRsvs7lZsrOSC4dnRbBnhzR4fCgomA1dZ0kgWpcoXF4/WYkxYe09ksLbDkpqw+yCXqthct+U4FJAuZ3sFAuJFkPXDd4AsWnBPwC2/fDlw43v/+6PMPgSCeCizbrwb4GIBgE1mO3rSG5voIlHdy67y8eOinpe/HYnZoOWu07vS49EM8ZOCJwNbh+lNhcfrioiM8HM9IHpLdp5HSmBgEqVw40KJJj0+FUVnfbQlPXSHZVMy0vno1XFFNcGd7gPyLAysU9Kh/XJYtRjMerp3sSFQ5enquGb2rzOYPtJpNLuxuH2YdBqiDXpukzWxGgnAVw0m93to7bBw64KBzkpFhJigpuibj+1D5+tKwlNccaZdJzaPy2ynSWYne3CF5eGviu/3FDKwvunNDmCbG/by+1c9NJS/Ad+KC9/v4sPZnV8EpW2sLt9/Ly7msc/3cjtU3qTYNbz0epieqXEcNPEXKwmLW8t30tpnYs/XzKUaocHg04hO7kT1pajlT4G+p4B27861DboYjBE4cVIK5XWObnmtZ/ZXm5Ho8Atk3OZdWrvqFo66qokgItm8fgCLNpczux3V4cC4h8vGswFw7uRnRzD/Nmn8NqPu4k367h+Qg6psZH95fT4Arz24+5GAx23L8D8DaXcMjm3Q9+73uXl2W+2hYI3wN7qBraU2ki1pnboe7dFld3NTW+u4JS+qXh8AWbNWxW677O1JXz0y4n0SIxh2c4qXv5+Jz0SzSzfXc3j5w+ib3rj5DU1DR68/gBxppO8UlxMIpz/Aqx5G3Z/D31nwOBfnDSJXZxeP39ftIPt5XYgOGP38g+7uHhklgTwdiABXDRLTYOH33y8vlFAfOKzTZw+II30OBP9M6w8dWE+ikLHHtNpJo2m6QIaLT0/XlHvprTOiUGnJSXW0Kwd1KoKvkD4EoL/yKwiXURNgwe3N4DL62dKv1Sm5aUzb/meRo8pqXOxt6qB+2b05bLRPfhuaznVDV6eumgwPZMPjSZ9/gC7Khw89vEG9lY3MHNIN26fktuinecnnNhUGH8njL4xOCLXnDwXNE6Pnw3FdWHtO8vt9EsPz1goWkYCuGgWVVWxORsXNGnw+Bsl5dC1MD1mR9JpNNw4MYf/rtwX6ndWoplT+jV/rbbM5uIXc5aGspmNyU7kxatHNnm++3BxZj2zp/Zj6c5loQue9Dgjg7rFte7DdKAym4t73lnDsl1VpFqNPHZOHjEGLWZ9+FeDioqqwqy3VrK/zgXAv5cV8uEdE0Lr+9UOD7+YsxTbgeI3ry7ehaIEd6l3xt6DLkurBe3JF7DiTDpmDExnXdGhIK5RIL/7yTED0dG6zjeu6NJMei2T+jTOIT2iZwJmQ9f9J3SwqMZzlw1jztUj+OiwQHM8vkCAfy0rbJSK9OfCGtbuq23W8wdmWvn8rklcProH903vyye/nERqF9vEZnd7eeqLzSzbVQUEZxvu/+9a0uPNzDo1t1HGshE9E0g069m43xYK3hCcEn3um+2heuz761yh4H3QZ2v3U9fF6rWLzqHTarhiTE+uGNMDo05DZryJV64ZJeVl24mMwMVxVdrd+AMB/nzJMJ5ftJ1lu6oYlZ3IfdP7t+mIUEfTahTS40xcMLx7i5/b4Pazozy8BOjOCgdT847//FiTnoHd4nnqwsFompG60+b04vD40ByooX5kVrOWcnr8GHTKMZczGjx+lu6satTm9at4fQHyMqx8OXsyX24sJSPORLcEM8mxRoprXWGvc/jCQFNfzD2TYzB0odkZ0bmSY4385pyB3De9HxA8Vtih6WxPIhLAxTHtLLcza95KtpXZGZIVz4tXjmD2tL7EGvVd4lx1XYMHh8ePqqrEGHQktvHKvq7Bw9qiOr7dWs75wzL5amNp6D6NAtMHprfo9ZoTvKvsbn73yUY+W1+CXqPhtim53Dgxp1WfpabBQ0FhDe+vLGJgtziuGNPjqLMOZr2WoVnxoTzjELzoyUwwkRlvpqLexbjcZFweP33TYkmyGMjvHkdmvImSA6NwjQL3TOsbOhYUb9Jxy+QcXl28GwhOof7+/PwWb1jy+gP4A+rJvQHuBGIx6to1D78IilgmttaQTGydo9rhocHtQ1FgweYynvx8Cx5/cFNWjyQzH86a0CWmg6scbp78fDMfrgqWzZzSL5VnLx3apg1TX6wv4Y4Du6+fvCAft8/PvOX7iDFoeeSsAQzrEY/F2H5nWFVVZd7yvfzmfxsatX90xwSG92xZLWmfP8C/lu3h958dqsjbNy2W/9wyjpSjHPMqrnVywxs/s63MToxBy5MX5jNjYPoxP2OZzcWna/ejURROH5BGqtXY6Mu5rsGDzeWj2uEhM95EksXQ7P0RgYBKqc3F3MW7KKlzcePEHPpnWIkz6wkEVPyq2qw0qkKcKLpkJjbRNVXUu7n9rZWs3FODosBlo3rw5IX5PPj+OgD2VTsbZV3rLPUuLy6vHwUlFIw2FteFgjfA99sqmL+hlKvH9WrVe9Q4PLz6w67Q7V//bwNT89J48arhpFqNHbJcUGX38N3W8rD2n3ZVtTiAVzd4eHXxrkZt28vt1DZ4jhrAuyeYefuWcbi8fvRaDfHmYx/7sjm9VNa7mNw3laU7K9lWVo9Rr+GfS3bT4PVz5ZhepMUZiY8xHDM729FU2t3M/MePVB/IfT5/Qylv3jia/G7x/HNpIXuqGrhmfC/6p1u7ZJU8ITqTXMqKEJ8/wNvL97ByTw0QPA71zop9JMToyTxQfzk9ztjptbfL61089ME6xv1xEZe9sozVe2vw+v2sKKwJe+xPu6rw+lt3gaHRKGHTfAs3l9Pg8XdI8K52uHn+2+2M7BUeqMflJjfxjGPToGBuIvgeb/SbEmskKzGG9DjTcaes91Y3UOv0cd7zP/L4p5u49d8rufnNAgZ1j+eFb3cy46/fU1HvbnHfD1pfXBcK3gfN+W4Xn6wt5h+LdvDJ2v1cMmcZy3dXt/o9OoLfH6Dc5mJ/rZMqe+s/vxAtIQH8JOQ98GWzucTG/lpnaAexy+unYE94UNxaWk9WopmUWANzrh5JcicmYHC4fTwzfyvz15fiD6jsrHBw1dzl1DV4OX1AeLa3swdntnqKNd6s55GzBqDXHlq3HpIVT89WjCSbw+H28+ayPQzunsA5gzPRKMFKW3dP7UN2iqXFr5dkMfDIWQMatZ3aL7XZI1WvP0DtgQQsTXF5/Wwvr2fu4t2NZmE27rfhD6gMyIjF4fHz4aqiFvf9oJgm9lWY9VqqHY13sb/47Y6wQB8pbq+fFXtqOOcfPzLh6UVc89rPFFU3RLpb4iQgU+gnoe1ldi5/ZRk2V3Cd+1dn5XHFmB5YDDrOzM9g8fbKRo+fPjCdC4Z3x6ANVpPSNhEg7S4vdrcPr18lxqBttA7d4PZRYXfz/dYKclNjycu0Nnud2uH2hU0xN3j8lNrc5KRY+M05efxtwXa8gQDXT8hu1cj1cH3SYvn2gVP5fmsF3RLMDM6Kb7ckJHaXF5c3QJxZj0GnQadVUIDb31rJrFN7c92EbBSgV0pMixPOQHAGYXzvZBbcewoLtpTTP8PKkO7xzTqyU2l3M++nPSzeXsnkvilcNa4XGsCvqhh1WuLMerQahTiTHrs7/EiY1x/gd+flU+/yUVQTvnu/ufqkWembFhvK3KXXKtwzvS93/Wd1o8cZdBq6ykbmWqeXm/65AocnWBNgU4mNB95fy5yrR0q2MdGhJICfZKrsbh75cF3orK6qwtPzN3Pu0EysJj1n5WeypcTGuyuKsBi1/OqsPDLjzcccxdU2ePjn0kL+sWgH/oBKXqaVN64fQ8aBafc1RbVcPXd5KFf65L4pPHfZMBRFwajTHHN3qkGnoV+GlWWHHXfSKJBsMZAQY+Da8dmcN6wbqGA1tX1nvEmvJSsxhqtauY7elEBAZV9NA09+vpmdFQ5mDsnk2vG9iDXquH5CNq8vKeRPX20F4NlLhzC0Rzwur79VO7CtpmB++j4tyHJV2+Dh4ffXsXBL8EKpYE8Na4tqOWdwJo98uJ4p/VJ58sLBpMeZGNI9gctG92i0fJEQoyfVauLil5aS3z2Oudc2ud+mWVKtRt6+ZRwrCqsps7mYlpeOSa9ptDSgUeDBM/q3KTiqqkqF3U2Nw0uMQYvVpGv16zncvlDwPmjlnprQxk8hOooE8JOMP6Cyu6LxCCmgBit3ER+chv3V2XncdXpfUIKpR483JV1p9/Dcgu2h25tL6vn7ou08NnMgDW4fT36+mcOziC7eXklJnYvffbqRjDgTD57Rnx6JMU0euUqIMfDUhYO54pWfKLW50GsVHjtnIFZz8J+uQadpVnIWjy+ARhPM0NbZKh1ufvHSMioOrI3+beF2Gtw+7j+jP3ee3pcLhndnY7GN8X2SMem0vPT9LjaX2LhkZBYjeia2+Wjc8Ti9/lDwPmjRlgpmndoHr19lweZyNMoG/nzpUJJiDUzqk8Lr149m3vI9ZMSZuHRUj9DO9w3FNlbvreWswa0vlZlqNXL24MxGbW/dNJalOyvZW93AOUMy21zZrajGyS/mLKXMFvw7uWpsTx6Y0b9VP2uLUUeMQUvDYUF8WI8EOfsuOpwE8JOMxahjxqAMPjhsnTIxRk/8YSPsGIOuRfWWd1bYw9rW7qulwe0LXhy4fWH3V9rdbC2pp6CwhiU7KvnqnlNIi2v6Szk7OYZP75qIwx0clVpNzT9TWu/ysqvCwetLdpMWa+SGSTlkxJmadT67vVQ7PKHgfdCHq4u5ZUouadbgMashWQlU2t1c9vJPoZ/nlxtK+f15g7hybM8OTVOrKAomvQbXYSVgTXpNKHd7RpyJ0wakYWvw4vT4SYwxcPqANEb3SuTjtfu5/o2f0WoUdBoFX0BlT1Vw/bemwYPXF8Co1xBvbttFSIrVyHnDWp6QpykOt49nvtwSCt4A85bv5brx2a0K4Akxel6+ZiSz31lDtcNDn7RY/nLJMJk+Fx1OAvhJxmLU8chZ/dFq4JtNZfROjeWPFw1uU2rDQd3iUJTGJY6n5qVhNenRKHDjxBx++8nG0H09ksxoFIX6A4G9psHL3uqGowZwRVFItZpIbUUq6U37bVz2yk+h2++vKjrmxUJHiG3iYiMzwYTuiIuIaocn7GLolcW7OGtwRoeeu4836XlgRn/+8PnmUNusKb35bO1+4kw6Xrp6BE99sZlffbieWKOO3547kLPyM7Ca9YzomcAb14+muNZFtwQTn60r4dyh3dhT5eDB99exdl8tY3OTePqiIXRLaP2ovD25vP4mLzqLa530y2j5PzKjTsu43GTmz56M1x/ApNMe9dieEO1JAvhJKNVq4nfnDeKBGf3R6zSt2jB1uMQYA3OuGslvPt5AjcPDuUMzuXZ8dui42XnDupFqNfLfgiL6psdywbBu3P3Omkav0V6jFY8vuJNaBfQahblHnIuuafCyam8NZ+ZnNv0CHcB6YK37n0sLgeBO8z9cMDjsaNqRAR2Ca/KK0rGzBWaDlktGZXFKv1TWF9WR3z0ep8fHZa/8xJVje/L28r2hNW+72xc80pebjFGvYV+1kzveXoU/oKJR4OmLh2DQKlw192cKD4zEf9hWyZ1vr2LudaO6ROrdeLOec4d0Y3PJ1lCbQathQGbri43otRrSj3JRWO/yUlzj5MNVxeSmWpialy7100W7kAB+kmrpNPmxWIw6puWlMaLX5AMpTbXEHkitWdvgodrhoVu8iacvGkycSUdhtYN9hx2zOXNQRrsUN7A5vXy6dj/PfLmFBo+f84d1487T+7Joa0WjUp6dnZ4zPsbAPdP6cs34XpTUOumTZiUxJnxTYEKMnkl9Uvhxx6FTAI+cOYDkTij8EG82EG82hEo8Nnh8fP/gabh9fm7854pGj1VV2F3pwKjT8MiH60I/24AKj3+ykYn3nhIK3get2lsbkQRATdFpNVw2pgc2l5f3VxaRHmfi9+cPCl3IqqrapoummgYPW0vq+Xx9CWcMysAXCHD9G4d+hv3Sd/P2LeOOW9VOiOORAC7ahVarCRtV1Dm9vPjdTl45kN1Mr1WYd/NYhvVI4PsHT2N9cS3d4s1kJpjaJYCX2lz8+rCUpB+sKmZgZhzTBqTy1abgJq3s5JiIlPVMiAnumu+dGnvUxyRZjDx3+TDW7qtlW1k90/PSyYg3dfgIvCkHL/CcHj9jc5LYedjGR0WBnBQLflWlpqHxkTKHx48/EJx1qD9s70NmfPiSQSQlW4zcO60fN07KQasoJMcaKa938e+f9rCrws4VY3qSk2IJ5XhvLo8vwH8L9vHUF1sAyE218NHq4kaP2VZmp6TWKQFctJkEcNFhHG5fo9SeXr/Krz/awH9uHUdGvImM+Ix2fb+CwvDsXAu3lPOnXwxhZHYyqdbgDuqukMf9aFJijUzNS2dqXsuKpnQUs0HLPdP6savSwU+7qrEadTx+/iASYvT4Ayrjc5ND5UgB8rvHYTZo+etlw3jog3VUOzxYDFr+dvmwLjF9fjijXkvagdmYino3l85ZFpo5+M/P+3j9ulGc3sK/hzqnh+cX7Qjd1igKgQObQ6YPTOemSTkoBGdlvH4/eq0UaxGtJwFctJjT46O2wUu53U1ijIEEs77Jc+JOr58ja+WU1rkIBNQ2T1M2ZUhWQljbuNxk0uNM3HpKbrNew+byYnf5qHN6SbYYSD5K4prm8vkD1Lt9xBi0GHWNv6zdB/KPB1SV6oZgVrGkmGDhj0BApdLhxub0YTFqiTXqWjwabC9pcSZeunokLq8fraKQEGMI7W947vJh/OmrrSzbWcWIngn86uw8jDqFPmmxvHnDaJJjDWgUBX8gePIg8bDndiVFNQ1h0/7PLdzOsJ4JLbrwUGm8mXP+hhKun5DNp2tLuHhEFre8WUC920ecWcfr141meM9EKa0pWk0CuGgRh8fH7oPpTJ3B6dNfntabWyfnEn/ERrQ4k45u8Sb21x2qIX3B8O4s21nFzgo7V47tSZq1/Y50dU8wM2tKLq8s3o0/oDIuN4krxzT/CJbN6eWNpYU8t2Abqhpck3731vGkxxnDNtk1eHwYtJpjvnaV3c17BUV8s6mM4T0TuPWUXNLjTNQ4PPxcWM3/VhczrEcC0wemc/d/VlNp9zB7Wl9mDs6g3O7hspeXUWn3oFHg/hn9uGZ8NnERCuIH14ftbh+1Tg8xBh2xRh1pViMPndGPKoeXBo8Pm9PD3xYU8m5BEUadhrdvGcdL3+1g4ZZyYg06fjMzj7MHZx7zYsTvD1DlCG5ENOm1jY44dpSmLia1ikIwV17zxZv1/PK0Pjz9ZXAK/add1Vwysge/P38QF724NLSsYHP6uPPt1Xxy58ROPREhTizHLCeqKMoAoDuwXFVV+2HtZ6qq+mUn9K8RKScaeftrndz77pqwYhJf3XMKSRZ92PR0UU0DT8/fwtbSes4YlMH43snc/GYBTq+fZIuB+bMnt+sX2MGUrv5AcPq3JWvrRTUNTHrm20ZtY3OSuHRUD8bmJpGVGENtg4efd1fzXsE++qTFcsPEnCZ3HzvcPv789VbeXbEvlOBjULc43rppDG//vC+UeQ2C+dZvmZwbShe68L4p/ObjDY2yzwEsefh0uidG7ihWaZ2Tp77YzIrCGkZnJ/Lo2QMx6mBLqZ3nFmynuNbJuUO7MT43+Hd87tBMEmIMvPbj7kav890Dpx4113tFvZsNxXU8/ME6yuvdTOmfyp8uHtLhQa6y3s0Vr/4USuEKweQxk/qmtPi1ahweNpXY+HTtfsbmJnFK31ScXn/Yvy2ApY+c3mWO14muqVXlRBVFuRv4JbAZeE1RlNmqqn584O6ngE4P4Cc7t9dPrTMYoGKNOhLMeoydvKPa6fFRWBWe63pfTQOPfLidV68Z3egMbFZiDE9fPAS7y8tn60q44Y0VoRSTVQdGojOHdGu3/sWa9KEd8C1V4wjP8b2r0oFRr+Hed9fw8tUj+WJ9Cb/5OHimfcHmcj5fX8KHsyY22sAXCKjYXF7G5SYzfWA6JbUu/u/jDWwqseHw+MOOtq0rqgtVe4Pgz2Vnefg55fJ6F2lxxuNmxvP6A2gVpV2T1VQ7PMx6axWr99UC8MnaEopqnDx/5QhufrMglEr0pe924g+oXDo6iwuGdUev1XD24Ex+3FHJC4t24PEH2Li/rskAvr/WSZXDw63/LsDrDw4svt9awZ++3srj5w4ippnJe1ojxWrk7VvGsnBzObsqHFw8snurL5YSLQYm9klhYp9Dwb+iPpi7f3flod+d/ulWjF1wOUFEj2P9RtwCjFRV1a4oSjbwvqIo2aqq/g1aOK8k2sznD7ByTw03/6uABo+fGIOWudeOYkxOUodm6TqS1aRnel46by3fe6jNqCPerGf13jpqmqg9HWvUoVFgVRP5obvSzuS0OGPY7umpA9IoKKxhRWENbn+AuUeMJvdVOymvdzUK4KU2F7PeWsnaojoApuWl8cXdkym1uVDgwFp444uFw9dBtQrMGNj4Z2wxaFEJVobL7x7fZP9tTi/byup5a/kespMtXDGm51HPJreUy+sPBe+DDh4NOzIP+DebSnn9utE8/ukmvttWgUaBS0b14P/9Ygj3vLuGAZnhpwDqXV6e/XobUwemhYL3QT9ur6TW6e3QAA7B/AiXj+nZptewOb04PMF/PxaDLrQ3JNVq5PXrRzP7ndWsK6pjeI8Enrt8WLsVyhEnp2N982sPTpurqloInAqcpSjKs0gA73TVDg93/Wd1aDq2wePn7ndWd3pJRYtRxy2n5HLN+F6kWo2M7JXInGtG8veFwVzoR9uQE2PQcfe0vo0Cdma8qcla2JGSZDHw3u3jGd4jgcQYPZeMyuLCEd15r2Af+d2DQaepFK6Hb04rt7nYuN/G9RNzeO+28QzMjGPB5nJ2VNi58+3V/PWbbTxwRr9Gz5+Wl8am/TYgOGWfnWLhnmn9uHRkFlajjkHd4njp6pH8Y+EO7n9vLZVHqTe9fHc1768s4qLhwRzqry3eRUW9q8nHtpROoxBnbvzZ48y6Jr8Izs7PZOGWcr7bVgEEz4e/u2IfBp2GZy4aTEoTm8KcHj9LdlaSEWfiyOXowd3jqXa4CQSOvtzXoQIBcNsh4D/mw6rtbv7w+SYmPr2IiU8v4onPNlF92N9VToqFf94whp8fncpr14+iV3LLS8YKcbhjXdKWKooyTFXVNQAHRuIzgdeBwZ3SOxHiDahUHRGsK+0evJ38pWYx6tBrFe6d1perx/Zk6c4qfvfJRraX2xmbk0RCEwlKDuqVFMPC+6fwwapiUmINnDno6ClC3T4/Bq2mU89A67Ua8jLjePXaUdQ6vXy0uogb31hBksXA3y4bTma8mUfPzuOa1w5VVpvYJzm0zl5R7+aKV5eH0nSmxxl5+ZpRXP7KMkrqXCRa9Ly/qpjROUl8fvckFm0pZ3D3ePIy43D7/Hz/4KlYTbrQrufZ0/pyRn4GZTY3z3y5hY37bWg1h44lHa7a4cEfCJBqNXLHvFUowPUTs7G5fCTFBNq0kx4OFJW5YDCz312DP6Ci1Sj86qw8dlbYuWpsT+YdmC2IM+u4cmzPUHGTw+2qsHPz5NwmE+nEGLWMyk7ki/Wl/PrsPP789VZc3gB902J5+KwBfL+1ArNeR3q8qcnUtB3GUQmb/gfbvoLc02DIJWBJbfKhK/ZU817BoRoD/11ZxLSB6UzsncKeagdfrC8hv1s8o3OSOvRI3cGlNlUN1ldvbj14EX2O9ZtwLdCoCoWqqj7gWkVRXu7QXokwRp2G/ulWtpbVh9r6p1sxRWANzaDTkqTTotdqmNA7BZvTS/+MOEZlJx7zi8ls0NErWcd90xuPQCvtblbuqWFbWT0zBmZQ7/Iy98fdTOydzNmDMzt9mjHFaiTOrOPa8dlcPronJr02lA1tWI8EFt1/Kt9uLad3aiwDu8WFAvgP2ysa5dgus7n5fF0JZw7KYFC3OHYdSIbyx/lbWHDvKcGKb8eg12l45IP1jQqhnNY/tVFpzYN0muARpn8cdgb5H4t2MLJXImV1TgZnJbT6GFq9y4vD7WdEr0Q+umMCRTVOMuNNfLCqmCdWFrHwgSncekou1Q4P3RPMJFsMzBiYwVcbyxq9zin9Uo+aBS/WqOfXZw/kzrdX0SctlrduGkuSxcD+Oie3/quAnRUOFAX+ecNopvRLa9XnaDGXDb56FNa9G7y9/WvY/QNc+BKYw2eOvt9aGdb2w9YKUmONXPTS0lDbhN7JPH/l8A4J4nUNXj5eU8wzX27B6fVzVn4mvz9/kEzVn6COGsBVVS06xn1LOqY74mhSYo3MvW4U9/93Lav21DCiVyJ/uWRoh/9iqqpKpd2NyxvAoNOQZDlUXtRq0tM/Q0//VhSAOKjK4eaX81ayfHcw1/Zfvt7Gs5cOpa7By2Mfb+SHbZX86ZIhnV7ZyaDTkh4XHmwsxmAltBtScsLu21/jDGurtLu5fUpv/r5oO74Dw/apeemYm5HGNtli5D+3juXB/65jS2k9ZwxK5+GzBrCtrJ7dlQ7G5SSTFGsgxqAjzmxg8bbwAPLNxjIcHj+ZCTGtCuDVDjfPfr2N/6zYx9Cs+ANFTzZRZnOjqiqPzRwYLJupQka8CYNOg1ar4bQBaVwzrhfvrNiLQathBZ5puQAAIABJREFU9rR+9EyKOeZ7ZcSbeOXaUTR4fFTY3NhcPq6e+3PoflWFJz/fzKBu8Z2TxczjgPX/bdy2bT54GpoM4NMHpvP2z3sbtZ2el8Y/Fm1v1LZ0ZxU2p69DAnhZvYv/O6xw0OfrS8jvHs8tk3M6da+M6BxyDjyK9EiK4eVrRuL1BdqlCElz7Ci38/qS3fRNs1Lv8jK5bwqDs+LbLYNUjcMbCt4Hvfz9Lm6YlM2yXVV8s7mMBo+fhGN/93cJ5w7txnMLtzfKu37N+F6Y9Br2VDVg1muZMSidR84c0KxyqFqNQp80K69dPxrfgc1/j328ka82lobuf+umsYzKTkCv1TImJyksgAzItPLR6mIKCqvJOcrRraZ4fAF0GoXV+2pDm+lW7a3l4zXF/Pe2CeytbiDWpMNi0PLEZ5v4eO1+VBXOys/gDxfkkxxr5JGzBnDn6X2CmceaeWIiyWIgyWLAYtBRUhd+QeRwhycH6jCKAjoTeA9L8KLVE7ZIf8DQHvHcPDmHfy3dA8C1E3qR3z2OLaX1YY/1d9CHWL23Nqzt+23lXDm2J/FmCeAnGgngUebIoF1Z72b57mpK65xMH5RBaqyhydFdld2NX1WxGJpfS7vS7qbU5iIz3syHq4vokRjD5L6p2JxekmPbJ4D7AuEFLtw+f2iUr9UoR/u+BIKfyxdQ0WmUiE8TplmNfDhrAn/6auv/Z++8w6Oqszf+udN7eu8JaRASQu9VVECxYgELNmyIa11d26q7q6tr7xU7FiyAAiqidJDeQ0lCAul9er+/P24yZEgIRUB2f7zPw6NzM3fmzp0793zPOe95X9w+P9NHdaNblAGTVslH1/fHJ4rolPJjHnNrK9GX1lsDwRvA5xf5xw87eOuqPiSG6xiWGclZudEs2inpvo/KjiYlQs+G8mYen5h3VO9ldnioanHw844aBGBsj1iSw3WUt5rPDO4WybSP11FabyMjSs+UgSl8t6kysP+CbdVMGZhMdowJEfG4Rx3D9Cq8fpHUCF2QQtp1Q1I7NYI5KdCEwIj7YdHfD24bdAeoO9fSD2/VV79pmKT6Z1ArUCtk3DoiIygr7hFvIvQE9qVFUaTB6saPJF6kV8mDJgMGpkegV52RbP1fRFdz4N2AmEPL5YIgDAMqRVEsPtkHdwZdo97iYsq7awJ98acXFvHdbUPo0W7MyOXxsb3KzF9nb+FAk4PxPeN4cFzOUfsVrypu4PXfpK96W4WZ30sbmXvHUJpsbg402dlRZaF/ahiRRvVxlWgjDWoyovRBZhlTBqbw4zYpUF01IPmwpKWSOit3zNrI9koz3eNMvDq5kLRI/Z9i/gGgUysoSArltSm9EUUxqOwfYVBTb3Vhd/vwiRyXupjD3ZEF3eLwUNXiJCFMS4RBzbOTCrA4vTTb3Wze38L0WRuYOijlqGaaG20u1u5rYuG2ajKjDfRJCePBr7fw94k9Ao5k8aFatrcy5lMj9GyrMAe9xrTh6dRb3Dzw9QosTi/XDkph6pA0wvUq7C5Jotbt8yMTBLQqeZel8Cijmi9uHsSHK/dRVG3h0j6JDEqPOHWlYKUWek+VyGtlKyBpAISng/rwhjRtLZb2mNgrnrQoPbPXHyA/MZSJBfEnbLHp9PjYvL+Zv327lcpmJxML4vn29iFc0qr6NrRbBFMGpJyac+a2g0wBilPb7vr/jK5SsReBv3Wy3dH6t/NPyhH9l6DW7MTs9FJjdpAWaSBMr0SrPLUFjeI6axCpzeMTefbHXbwyuTAQTJsdHia/sxqnR8p0v95wAINazgPjczslQ7WH2+tn7ubKoG0NNjdOt4+3lxTz4aqywPaXryhkfM/YY75RRBrUzLppIF+u209RtYVJfRNJCdfhdPu4fmgaWTGGThcG9RYXryzew51jMgnRKjnQ5ODv83bw/KSCo16cnCwcGpy9Pj9F1Rb+8sUmiuusDO0WybOX5hMbog16Tp3VxcJt1chlAmd3jyXaqA4SY4kyqkkI1VLRfLC0fEnvRPY12OiTEoYgSBWaMJ0KvUpOqE7FmNxo9K1z+ofC5/fjFyX2vcfr58t1+3l6wUGFuL4pYUwZmIJRoyBEo8Dm9mFUK5DLBHx+ke2VZu4em8Unq8uI0KuY2CuO8/LjmPjqwTX/y4v3khKh5/yCOKrMTl74eTffb6kC4JweMfzzwp5dfl8xJg13j83C5fUfdeXohEIXJv2L73XcLxGqUzEsM4qB6REoZMIJXWA22d1c9d6awOz8F+v2E6ZX8uu9I3H7/GiVcsJOlh2txwGOZmm8rmEP/P42mBJgyJ3Sf2VnSvYnG139IlJFUdxy6EZRFNe1Crv8v0WtxcnLi/fwyWqpN6hTyfli2iB6JnYusHGy4PB0zMjsHl9QD/ZAkyMQvNuwaGctt4/qdsQArlXKiTaqOXAIOUulkPHR6rKgbU9+v4NBGREdLEWPBtEmDbeO7IbP70fVOlN9x5iODG2f34/PL6JSyPH6Rc7Lj+eR77ZR2eKkR7yJJy7I67Qk/2ej0eYO0o5ftqeeB7/ZyktXFAZGfGosLs59YWlAROaFn3ez4M7hxLZTaIsyavji5oG8sngv5Q12xnaX7Ea7x5k6qK5FGNREHOZ4/H6RarOTj1bto8bs4vohqUQZ1by1JFghbl1ZEw+Oz8WkUfDTXSMQAZVc4NYRGbz6615K6m04PD5evLyAxDAda0obWV3S0OH95myqYGRWFOv2NbL5QDN3j80iyqhmVXEDS/fUcXHvxC7Pn+IImvP/LTiSgt7xoLjW2kH45ucdNdwwNP3oJVodzeBsAXu9FHh1EVKvvyu4rFD0PWz8FHpdCd/devBv27+GW1eB8cS6DZ5BR3R1RXUl4fT/WrzX5vIGgjdIoiqPz9tOTcuJEc04WnSPMxFpCF5d3zYyI6h0G2PqGFCzYgxH1ZcM06v4+8QeQXKPFxTE4xfFDkQis9ODyPETc+QyIRC8D4UoilS3OPnPT7u558vNrNvXiF8UuevLTQGjlO2VZv41f+epIzgdA2ytpeP2WL63HqdXWoCJosgnq8uCFOCa7B7mbg72kQbp+7z7rExuHJaGQib1U9vLsB4N6q0uzntlOW8uKeHbjRWc/+oKHB4/ik4yJpVcwKhRIJNJ7x1uUHPjsDR+ums4r04uZFB6BIXJYUx5dw2zfi8nqROmeV5CCEq5DIvTy38mFbC+rIl3l5WQGKYlPUpPV34MZ9A1EsI6nu/sWCNa1VEuFhwtsPIVeCkf3hkNr/aD+l1H3s/ZIgXtbqNhw0fBf7M3QlWH3O8MTgK6ysDXCoJwkyiK77TfKAjCDcD6k3tYpzc608w+0OQ45dlflFHN3OlDmbm8lIoWB1MHp5FzyEiXSaPk/nOy+c9Pu/CLEGvS8NjEHkfdg82OMfLbfSPZUWkmPlRLjEmDKIrkJZiC+p+X90vCeJJKnHVWFxNfXU6tRZqHnrelioV/GYbZESRTwPqyptPSmlGrkshMLu/B6yMn1oRCOHiT7ay/3dk2pVxOTIiWaJMGUeS49M7Xlzd1UPCbv6WSv5yVyUPfbQtsG5UdhUmjZMmuOnLiTdRaXEQa1MSYNITqVGTFSNfa8z/vxuX1S78Bn8iEnnH8sFUqk2fFGJg6OBWfKHJWbgwTX1se+N5e/60YpVxG97gQVIrT73vrAEcLOBqhsQSisqVRMtWfq6YWrlNyx+huvPbrXvwiJIZp+du4XAzqo+RYuFpg2X/aPTbD93fBlZ9LmfjhYKkG0S+V0TvjBKiPf7T0T4UoHnbK4HREV3fcvwDfCoIwhYMBuy+gAi462Qd2OiMuREOoTkmz/WAgP78gvksVspMBQRCID9Xy13E5eP1ipyIZJq2SqwelcFFhAg6PD6NG2SFr7wpqpZy4EC1xIcFFl/en9mPm8lI27W/h3LxYzi+IO+Jss8XpocXhobLZQXK4jhCt8qjmoXdVWwLBuw1Ojx+DWoG1XdbaMyGk0yzyz4ZJq+A/kwq4b/ZmnB4/0UY1z19WQHjr9yAIAtcOTuXTNWWBcqhaIeOSLkrLgtA1O78raDqpdGyuaOFfF/UkLyGEBduq6JUUSrdoI+vLm1hV0shfv9kKSJatX0wbSGK45MymlMuIav0chUmhNFhdXDcklb+Oy8HvFzFoFAGi2p5aa4dF13ebKrhqYPJhFfmOB402F1aXDwGJVHYsjnSHhcsK6z+ARY9KjwWZFOQyzoITNFJ5PAjRqZg2PJ3JA5JbfxPyYzuXjo5jZzTtA5+34/b2MMWBXCXNyZ/3ApQsAV/rojC2J0RkHP0xnA5wmqXPve59CEuFgiv+K1oAXdqJAgiCMApom0HZLori4pN+VIfB6WIn6vH6KW2w8Y/vd1DeaOfcvNjD2kr+r8Dj89Fkk4wadCoFoTolAgIOjw9DK7GpK9hcXr5ct5/H50kSm0q5wMyp/RicEXnELHLtvkYmvbkqaNsdo7sxIC2cO2ZtpMnuISVCx8yp/UiPOjxD+GShyebG4fEhlwmYtMpOuQUOj5cWuxenx4dOLSdCrw46Z06Pj8pmB+8sK0Ehk3HjsDTiQjSHbSv8EdRZXFz65krKWsezlHKBedOHEh+qQQRCtCrMDjfTP9vIDUPTuHbm2qD9LypM4OqByVS3uPhhWxV3n5XFxvIm1Eo5M1eU4hdhxphM+qWGBREQS+usjHpuSdBrDUqP4I2rep8woZ56q4vbP90QsLsdnBHBy1cW/nHhF3OlVGb2tau+GeNg2hIwxvyx124Hn89Po92NKEp2uHJBoMnhYVe1mdQIPeF61YkVNbLUwOsDwNFOi6H/zTD2cYmFfzi4HVC+EubcBilDYPAMOLAWQhIhoQ8YTpFa3olCyRL4aOLBx6HJcOMiMJy47/Z4cbx2ohrgFqAbsBV4r1VK9f89lAoZWTFGnrusALfXT7i+89nr/xX4/SJbDrRw3cy1mJ1edCo5r03uTWqkHp1SjtXpxeH2EqJTEWVUY3V68PjEIParxenhqflFgccen8j9s7cwZ/qQQMbQtkhoqya0ZU5pkXqyYgzsrpFkSuUygfE944gL0fDDjGH4Wp9/LJWFE4U6i5M7Zm1kdUkjWqWcB8blcFFhQgf9aa1SgTbk8NeIRiknPcrAExfkIcAfIm35/CJen/+wPIcoo5rZtwxi6e566iwuxvWMxerycuNHUqHtrrMy6R5nondKGPs7UZcrqbOyrqwZo0ZBncXFBa+tYOGdwxj+7K8BjfjnftrF61N602z3oFLICNUq0WsUXNonkdnrJZFHvUrO3yd2P6EB6dei2iCv+pXFDSzfU8eFhV0T5Y4Irzs4eAPYauEP8D4Ohd3tZVVxA3/7div1Vjfj82K579wcxr20FJtLaqf85axMbhyadtyWuR2gi4TrF8IP90itge4XwrC7uw7eACotpI2UFjCiHxTaP8TU/1Nhb4IlTwdvay6Hul2nRQDvCl1FnQ+RPA+XAeOAXKSy+hm0on2pqm0M6ECjgyaHm16JoUQZ1X/aTPKJRIPNxR2fbcTslNZvdrePv3yxia9uGcSLS4uZ9ft+AOJDNHx200BeXrybffUOJg9IYlB6BEaNEpfX38FKtNrsxOsTEUURh9vH8r313P/1FoZnRnHjsDQarC5MWiVhOiWf3jiQ1SUNVDQ5mNgrDpvLx80fr6e4zsrZPWK5+6ysU36uXR4fby4pYXWJFDAcHh+Pzd3O8Kyo4zaQ+KNM5TqLi8/XlrOzysykPkkUJocSqlPh94s02t3IBIFwvYooo4ZL+khBbXe1mfNeWR4gAE5+dw0/3jmMK/olUWN2oZAJARlYgNG5Mawva6TJ7mFkVhS/lzay6UAz952dzRtLiokyqnns/B5c9d4a9jc6MKoVvHB5L/bVWylMCuWyvkm4vD4yow3HNA/daHNRa3HRbPeQHqlHIRMorrPh8vrJijUQbdSwvqypw34by1v+eABX6SA6F2p3HtyWOxGUJ04isNnu4aaP1gUWQfO2VBFhUHNefjxfrJV+Y68s3svl/ZJOXACXyyEqBy77RCqBa0xHDt7t9/0vKDMfEQJSS+RQyE7/pKyrI+wuimJPAEEQ3gN+7+K5/7Mwt7r6hHTR37a7vOyoMvPiIklG85rBKcz6vZwrTqAf88mCx+en0ebG0yquEWFQ4XD7aLK7abC6SQ7X4fWLAbZ3G/ytWV5b8AaobHHy7I+7SArX8s2GSjaUN/Gvi/KIMqopSAwlLVJPaf1BwZazcmOYv7WKs3vEolYI3PbpBsbkRjM6J5rL3lqF0+NHr5Lz/tR+9E0N5/yCeECawb/87RUBItZna8rx+Pw8PrEHuuOshHh9/mPOeq0ub6djU7uqLcckW3qiUGdxMfmd1eyplSoV87dW8/jE7lxUmMDiojre+K0YtVLGX8/NoSApNCCQM2vt/kDwjjKoiTCo+HztAR49vzsKQcbHNwzg8Xnbqbe6uKBXAj0TQnj5lz2M7R6D2SllpWqFjHqriw+v709xrZWn5u9kf6OUvVtcXqbP2sDHNwxg0pur0Kmk8cRPbhzQqbNaZ2i0ubhv9hZ+aVWZC9UpmTm1H7d/toFai4sYk5rv7xjGhYUJfL52f9C+5xfE/eFziyEapnwNi5+Aig2QeQ4MmSEFvBOEXTUW/IecjhV767lmUCpfIH0mn1/E4z0JZFndH7f1dbh9tDg8eHz+I4r0nFbQhsGoh+GDcQR+COHpENHtzz2uo0BXd7tAvUgURe//QiZ5LLC7veyutvCfn3bj84vcMaYbPRNCOhUVqWxxctlbqwI/vlUlDXx0fX9W7K3j4t5Jp/jIjx4uj49ai4snvt/Bop01GFQKHhiXQ3yohus+kLgGRrWCH2YMpWdCCFsrWgL79kwMCchrtkdJvZX+aeGBx3M2VTImN5rC5DA+vqE///h+ByKSq9eAtAhu+HAtWytamDEmE69f5KqBKUz/bGNgdt3W6ns+b/pQolsXQy0OTwcW9Y/bqrnv7OxjDuCNNhdLd9ezuKiW0TnRDM+K7NJkosHqwubyIpfJ0KvlDO0WGVAma0NunJEas5PfdknBZmR2NFEGdae9fpvLi8vrI0Sr+sMM+kabKxC82/DOslJGZkfzly82BbZd9d4aFt01AkO0xBdICdehVcr518U9W0Vx7AxOj8Dp8YFM0jl46+o+lDfY+WFrFbd8vB6NQsb1Q9KYMWsjvZPDAIH3Vuxj84EWnrq4Jw+0kt7a4PT4A37edrePfQ129tZaEeh8FOpQHGhyBII3SNnqO8tKuLh3Am8uKaHG7OKDlaVMLIjnb+NzeHtpCYIgMGN0N7pFnyBeREgCjH8ePDZJTlXZxeLcVi+VlrURR01yS+vEHzwvwURZ48FFb0aU4bgXqScTFqeHOZsqefL7Hbi8fnJijcyc2o+4o51F/7MR2xNuXQ2bP5NIbDkT/iv6+F1dCQWCILTdmQRA2/pYAERRFE/c0vM0RFWLk4vfWBkUlL+/Yyh5CR3FWr7ecKDDyvmHrVWc0+P07p9YXV4+WV3Gzzsk20eLy8tD323jhzuGYlQrsLi8WFxeXvxlD69N6c39szfze2kj+Ymh3D02C41SjlIuBAlJjMqODipjRhrU1FvdeH0iiWE6Hj6vO9srzaRGSDftT28cwPqyJjQKOQqZgEoh6zAzXWN2BZVwDRoFMoGgc54SoUchP7YAaHF6eHpBUcDDee7mSib1SeTR87t3ulCrs7i48cO1bD4gLWQu6Z3A/efksKvGwm+76jCqFTx8Xi4quYxzX1xKU+uUQrhexfwZw4JEWfx+kQNNDp79sYiyRjuT+iQyIT/+DzGmO1sAqBWyQOBsgyjCgm1VTG+1Mx3fM45QnYoF26oDWutKucCsmwby9foDCILADcPSiA3RcOOwNEZlR9E9PoT9jTYePb87KoWMv86W5n7XlTWhVUnGKiuLD1YnTBoFRo2S16f0psbs5PPfywnVKvmlqJZrBqUe8bNVd6KxUNXspFfSwcxxf6ODT1aX0+Lw8K+LepIdayQhVHtiRWDUeunf4eCyQcU6WPSYNGKWfznknH9UGW6YTsVfz83muZ924/WLZMUYuPfsHL7deICcWCN5CSHcMzbrT1ca7AwtDg+PzNkWSGCLqi08tWAn/7o4/9T6tx8v1AaIzoGxT/zZR3JM6MpO9P+1+v13Gys6BOWPV+3jqYvzO2RSCZ2sMiMNUtn4dIbN5WXtvo49wx1VZpIjdIHMcn1ZE3qVnDem9MHl9WNzeXjup91Em9TMnNqPf/ywkxqzk4t7JzImJ5or3lkNSNn71CGpfLl2P1qVjFqzkzs+28BDE7pz7ftrqTY7kQlw26huqJUyXp1cSLPNTXqknpJ2pfb8xJAgMRmDWsF952TzzI+7EEXp8dOX9AzKnD0+/xFlK20ub4BQ1YavNxzgnrOzOgRwn0+SGm0L3tJzK7i8XxIvXt4Lh8eHTBAI1Sl5e0kJTXYPSeFaxuXFIQC/7KxmysDUwL6Ndhfzt1ZxTl4se2qsvPTLHuxuHzcMPX7bR71KwaCMCFa1C5y3juiGTi3n5uHpvL2sJHCDbc/WjzZpyE8MCWTpUUY11w9JRQCuH5rGtooWxr+0DJfXT0KollcnF3Lt+2t47rJePDZ3R1DW32bg8eykAu74bAMbyptJDNPy4uW9WF1cz+tLikkO1/P0Jflsq2g56hZTfmIoGqUsSFVwfH4cy/cctFA9vyCef/6wg30NduZulio/L13RC8OpVHGzVsP6mTD+WWgolljZloqjCuAhOiVXD0zlosIE3F4RnUpOpFHNzcMzuLJ/MlqlHJ1agcXpQSYIf4607GFwoMnRQURp0/4WHG7ff0cA/y/FmTN7GHQmQ5gYpkMmEzA7PNjdPgRB6sWd3SOGd5aVBMZy4kI0TB6QjFFzck+vyyP1nARBckI61hKsZL4Rwoby4CCeHWtkf9PB8vjFhQkYNUq8Pj8Oj4/KFif3nZuDTikjwqjm/an9KGuw8duuOprsbt65pi8ur5/EMC3NNjd3n53FgSYHWqWcO0Zn8tqvxVSbpYzKL8Kri/dyWd8kRudEY3Z4eOfavjzw9RY272+hX2oYz1yaH0R2MmqUTBmQwsReCTTZ3EQb1QHGe7PdzY4qM1+s3U9unIlLeid0MRcrIJcJ+NtVEKRz2PE8un1+Nu3vODO7sbyZ/mkRtF+qmZ1eJvVJZGKv+FbFPknExO7yolbIaLS7cXr8ODxe/j53O31Swnjnmr78e2ERF3d5vF1Dr1bw4Lgciqot7Ku3MTQzEkT4x/c7SY/Sc+eYTF5ctIeCpBD6p4YH7dsmyxttVPPW1X146Zc9PPfTbrJjjTw0IZeCpFB+L22kotnBMz/u4or+KXy6ppxbR2Zwz1ebA/oXj53fnb21VpRyGa9P6Q1I8+rzNlfwjx+kKYR6q5tr3/+dj24Y0Oni91CYHR4ERGbfMpinFuyk3uJmyoBkRuVEsWRXLX1Twpg2Ip0dVeYg5zK/nxNJEj86VG6SZog/mADeVu2C/tNgxF9BH3nE3Q0aBYZD7htKhYwIgzTdsba0kVd/3YtKIXDX2GzSI/Wd6j+caqSE6wIa+W0Y2i3iTPA+yThzdg+Ds3KjeaudlWGsScNl/ZKot7p4ZM42Fm6rxqBS8LcJuZyfH8fsWwazp8aCzy+SHWsM9GtPFhptbmauKOWjVWUYNQoenpDLkG6Rx+QIZtIouGFoGkVVFlaVNKBWyLhzTCbhehV58SEcaHJwce8Erh6UglwmsKq4kes/XBf4kT4wLodrB6WyZHcdD7b2PN9aCsnhWt69th8yQUAhl1HZ5OCpBUVsKG/iq5sHsbeuoz9ydYuTWJOGBduqeXd5KVMHp3LH6ExA7FQ1zqRVYtIqgwKAzy/y044a7m8t587ZVMns9Qf4fNrATgk1Bo2CqYNTeWdZaWDbNYNSO9xAQVJTOz8/LtBuaMPI7GgsDg8WlzTjbdQouG5wChXNTq54Z3XgXP28o4Yf/zKcrRUtvLBoN0qZjGkj0rlqYAovLtpDjdnFrSPTabK7kctkx1VKN2mVJIbpUMpkGFRSS2JVcQPzWs1DFt8zgnN6SCYph7K/o41qYkxqrhuSxouL9rBkdx0gSdTOmLWR5y/rxTWlEo91Z5WZqYNTcXt9jM6JZtn9oyiutZIcoefLteXc13r+C5NDeeeavvhFkbeWlga9n9npRYCAdr7H58fi9KJVydEq5Xj9fuSCQIvDw1tLinlraQm5cSaevTQfpVxGVYuU8b10RSEyQUBE5JF2KnIyAe48q9uJY2sfLaJz4ZubDgZvkEw+Bs/4wy9d2mBn0lsH9RB+21XHL3ePILmT3vmpRohWydtX9+GBr7dSb3MxIiuKu8ZmoT1jY3pScSaAHwZRRg1f3TKYPbUWRBFyYg2EaFW8/lsxC7ZKfUKLy8uD32xlQFo46VGG4zLyOB6IosivRbW8sngvIPWfbvlkA4vvGXFMAVylkBNn0vD85QV4fSJymUCoVolOreCNKb1x+/yEaFWoFDLqLC4e+GZr0Ar7uZ92cXm/xA6jO3eOyeLFn/cwf5sUOEJ1St69pi/TP9vItxsrOCs3hpkr9gWer1bISInQUWeRWOxmpzcg+CKXCSy7fxQapTxQWnZ7pdTqUJGTJpubN34LdrndW2ul3urqPICrFdw6shsjs6NZtqeOYZlR5MYZD5s1DM2MYsaYTGYuL0Wrkma+w3RKXv11b6A8PSYnmn9fms/PO2qCzpVfhE/XlNNkdwfY2Q98vZWPru9PcpiOy/om0i3KSFWLA5fHj1ImYDyOUbRwvQpRFHn1172sKK4PUgtssLrplxbe6X6RBsnLvMnu4ZmFRUF/q7e6g1oYQzIiyIjU0z8tHEGApbvr8PpFPl5dFvAiB6k6sb/RTnqUntQIHXUWF1FGNdkxRvY12IhondtvsLr4bE05P+2oYcaYTEK0Cr5Yu5/0KAMXFSZa1Z6TAAAgAElEQVSwYFs1fhGu7J/MS7/sDfTpZQJ8cF1/hmVGIggCc6cP5ZsNFVSbnUwZkHxU2f1xwVYHFeuhZifkjJcEXdrY6BojmDtq2OO2ddx2DPD4/HywovSQbSLztlRx+6g/ny2tUysYkRXFDzOGIgIahYyQEyk4cwad4kwA7wJRRqksXW9xsavaSlqUniabq8PzNu1vPqUKYDaXt4PNJ8DyPfXHfBxyuayDTCrQ4ccnimIHOVOPT5rfvqgwnmijmuFZUXh9flQKWSB4w0HG8CV9Enl/eSmL7h6BxelhwdZqEsN0PHVxT3RKOWUWyS+7PXx+kUabm9nrDzClfzJmp5c3l+zF4xe5ZUQGSeHagzauAig6aSPI2/XBHW4vLQ4vlc0OYkM0mDQKhnSLZEi3I5c3w/Uqbh+ZwVUDkxEQCNMpKa6z8tZSycUrIVTL9NHd2FHZgknX8acVolUGWYECLNldxzOT8vlg5T7+9q2UQcaaNHx586DjCuAg3UwjDaqg4K1WyDo1GmmDIAgkhOlQyp1kRhuDbGrVChlqpQxBgJFZUTx6fo9A73pHlZn3lpfyxAV5JIRquWlYOg02Nx+t2sfqkkZaHB5CtCr+dVFPVhY3kBKhY11ZEzcOS0Mll2Fzefn3QolIODgjgnqri5s+Oqi2+NW6/bx1dR/Gv7yc3DgTby4p5tHzupMda2RvrZX3lpdKpj5GSaP91pEnWcLT1gBf3wQlv0qPlzwF1/4AiX2lHoI2QiKurXnz4D7GOGlU6Q9ALghEd9JaOVVJw9FAIZed9MrjGQTjTADvAo02N4/O2RbwLzaoFXx1yyBWlzays+rgDa4zZvrJhFopJy/BFChztiE3/uQNBmhVcsblxQbOhUou47aRGSBKPfN6i5unFkhuYLeO6HgTPdDkYGB6BEaNgia7i3F5cdw9NhuVQkakQU1Ni4ON5U1c0CuerzcczGAGpodTWm/jrSXFjM6J5pI3VgZMQapbnDx/WUFA4SxCr+K+c7KZ9vFBr50+yWGBcrTPL7K+rInrP1iH2+dHEOCfF/bkosIEtCr5wRExuSzgp30o1Eo50a09R7PTw65q6ToI16t446reuDx+wnQqhmZE8pGxLLDoiTKomdgrvkOFIC1Sj1wmsHBbdWBbtdnJy7/s4ckL846rBNnGNWh2eJi/tYrEMB3/vqTnUWn1h+mUPHdZAVe/twa9WsGYnGjOL4gnMVTLmgfHoFHKMWmVuL0+GqxuQjQK/nlhHmF6Nf/6YQdL9tSTGKbl0fO6kximJTvGSLPdTWKYFp/fz9R2sqzXDEzh9lHd+Haj9H2P7xnHJ4fY1O5rsGNxepnYMw6ZIPnOP/NjEf+av5OCpFAeGp97ar0nnM2B4O1LGkzdOa8xt8iGd+9eLixMJMqoQTn8Pikj3zEHIrPh7Cf/8EiSTCZwzeAUvly3n4bWEcrkcB2jsqP+8Ec6g/9enAngXaDO4goELJDGrv69oIjXJvdm7AtLkQsCd56VSXQXq+AWhwefX7qptzGi7W4vzXYPxXVWksJ1hOlUR+0OBpJa17WDUlm0ozaQKV3YK56MqJPXCzNqlPx9Yg9iQzT8VlTLM5cWsKG8CbPTy6xl5VQ0SW5oFoeHuBBNB8bwuLxYGqwuXp3cm0e+287G/c2senA04ToVzXY3v+6upXdKGIMyIugWbWDF3gb6p4VxaZ8kLn1jJYMyIvhhSxUur2Ri8vqU3uyusfDUgiLO7hHDoPRIfH6RsgYbn9wwgCW760gO19EzwYSydbys0ebi3q+2BBThRBEen7ed0TnRWF1ebvhwLVtaWeYX907g4Qm5Xc6Ei35pLlcpF3j+sgKenLcDnygytnsM8zZX8cZVfdhZZUYUpX6wTiEjPUpPUWvQ758axqjsqE7Vw0rqrTg9vuPuIUYa1fzzwjwempCLgFQiPxoth9J6O8/+WMRnNw3A7RX5YOU+5m+t4rohaehUcnZWmYk0qiips7N4Zw1xoVpcXj/76m0saWWEH2hyMOPzjSy6ewT/nL+DOoubZycV8MLPe4Le65M1ZUwbkU6EXk16lJ70KD1Du0Wwu8YSNJro8vq5fng6epWcO2ZtDJqOuG/2ZmbdNPC4ztExwd4ILgt47HDV1/DLk9Se8zrnvLc7YNDy2q/F/HjXcBLDImHYfdDvJknV7AQ5c8WaNCy4cxgb9zejVsjoER9y8jJwR3Nr2V+UxuH+YAXhDE4OzgTwLlBv7Vgur2xx0GBzsebBMXj9IkaNotNxDqfHx57WAGN1eblxaJoksalRsr6sietmrg3MNt97dhZTh6QevQUg0ujPpzcNwOryomwVFTmhJgedINKg5t6zs5k+shs/bKuiZ0II17z/eyDLXLSzlicvyGNxUS2f3jiQZxYWUWtxcXFhAuflx2N3+7j10/WUNdgpSAzB4fbxyJytTB6QwubyFiqbnLz6615GZkfTKzmUFoeki15ndeH2+tGo5PRLDeOGoWl8uqaMH7dLhLI5myq5bnAq04an8c/5RUQaVBQmh7GmtIFH57aw+sExmLRSH7rGEjxP7PL6cXl9zNlUGQjeAN9sqOCKfkn0SVZSZ3Pze0kjRo2CvISDN80QnZKKZpg5tR8NNjdry5qI0KvoER/Cvxfu4pI3VtI9zoQgQGWzA4vTw91js4g2qjFqlITqlEQY1IgiHebpLypMDFrUub1+WhxS5hWqVaFUHHk0yqBRYtAo8ftF/KIY1EroDBanh6cXFlHe6KC6xcX1H64NjAbN3nCAT24YwOR31/DDjKFM/2xDqzbAFv55UR6zfi8Pei2nx8/eWiuLi+qwuyWjljb/8zb4RTDbPXxyY39+21XHu8tKKUgKYdZNA7n10w3UWVx0jzPh8Pi46aN1/HTX8A6iOcV1tg4SvScctgb46WFJ5AMko4vLP2XhTluQu5rN7eOT1WX89dwcBIXqhAuBCIJAtEnDOT1OsnyprR5+flT6vKIoScae98JRsejP4NTiTADvAt2iDR0sKyf0jGNVcSO5saYuGa71VhcXv7EycFOe8fkm3r22L72TQnnwm61BwiQvLNrDpX2SjimAgxRQT7VcoUYpx+31s6q4nhCtskNf/It15Uzqk4QoikzIj0OrlLN0dx2PzdnOfedmU9HkYHBGBE9emMd1H6zF7vYxKD2Si/skMq1VB3pxUS2LiyQy1MW9Ezmneyzryxt5+pJ8TBoFqRH6QPBuw6dryrlxeHqrpKc7wBaPD9HQ1hbXKGSMyIrit10HWw8ZUdIYzsbyjiNiWyskB6izn18S0IHPiNIz+5bBAPhFkdRIHWE6ZWAWusHmprjOym0jM3hveSk7qsyMyIpidG40k99ZzSdryjFpFPx894gAEzzSqGbWTQN5fN4OGm1uJg9IZkJ+XEBvoMnmZs6mCmZvOEBFk4PbRnXj0j6JhB1hwebx+ahucfH+ilK8PpHrhqQSH6o97NiR1yfxDc7uHsPna8uD5nrNDi+b9zdz3aBUvD4xyNu8rN5O9zgTy/cenMluI0S2jaf9tquWy/om8emag4F+cEYELU4PC9dV8+EqqXS+uKiWZbvrefXKQnZUmekeZ+LOzzdxVm4Moghf3TKI33bVMXNFKXa3jzCdEtXJnvNuOXAweINkdLHmLTIz7+3wVNfJkDk91ajYAJs+Pfh451zIHi/19u11kqmL/MQvUM7g2HEmgHeBCL2Kr24ZxFPzd1JtdjKhZxw5cSYqmxxHdB9burs+KKMC+HR1OXnxIZLudjuDCJ9fxHVIdnI6Q6OUkxlt7FTSUa9SkByupc7i4tE52wGJWPbh9f2JC9Ww8sHR+P1wz5ebKGuwIwjSzH24XoVBowiol7VBLghcOySVR8/vzsriBuxuHz6/2EGJTSaTnvvY+d156DtJEUoll0kz5Pq2jFnFvy/J59mFu1i+t56eiSYeOU8iZJ2XH8evu2qD3ntot0jeWVYSCN4AA9Mj2FFl5rmfduP0+Jg2PJ2R2VGMyY3hHz/sxOcXefL7HUwdnMqCO4ehlMtYtLOGaR+tC1wP7VsLbeezb2o4H1zXD58oEtrK/G9Do91NepSBawalkhVt4LXfislPCGFAekSX31Ot2c3ZLywNBNHP15bz010jMKjlLNhWTb3VzcW9E4gxqtGqFOjV8sAcd1UnymdhOhXKGBmhOiU6lZzvN1dxw9A0PllTxktXFFLeaKe80Y5aIeOh8bnM2VwZWATMXLGPxfeMoFdSKD9ur6ZPShi9U8IQRTpol68rayJEp2Te5ioen7eDu87KxKBRcN4ry7G5vFzQK563ru7DbZ9u4KUrCgnTn+RRscbijtvqd1E4Uo9WKQ+cX7VCxtTBqZ23KuwNUuDThoPiNGdn71vecVvLfqjeAl9cJf1/RDe4YhZEZXV8rqNJ+rzmCojIlIh9ytOHbPe/hDMBvAso5DISQjXcPCKD8kY7y3bXsbfOyt1js3l87jbG58eTE2vstHQdF9KRjTm+Zywen59/XNiTSIOKuZsreX/FPtIj9Z0Gw0abizqLi6ZW96UIw7GLtZwMqBQyruifzO5qC72SQgMCJwqZwH3nZAMi6VEanrq4JzVmJyOyoqTZ49ZAWm91UW+VysGiCN9vkVSznr+sFzaXlwarm09WlxEfKmXP3aIM/FJUwwcr9xGiVdI/LZzHzu/OY3N3BI7plhEZhGiVTCyIZ2R2NNUtTuJDtYTqlEHKeXaXl2ijmgfG5VDWYOPBr7fw0hWFjMqJ5taRGXy0ch86tYK/jc8hyqimvPEga9yoVnBhYQKXt9O9/8sXm/jkhv70SQ3jy5sH8q/5RdhcXnLjTEQaVNjcPnJijQzKiGB+6/jh1QOTOx1V68yZq8nm5tmFRSxsrTholDLeuaYva0objxjA52yqCAQXkKYGZq4oRSmTdMsBXv91LwvuHEaYTsXqknpkMhnxrWz6H7dXBzLKxDAtGdEG6q0uft1Zy3vX9uPuLzbROyWUx87vweqSBt65pg8qhRydUo7H7+e8Vw4GgnF5sehUkp3oeflxmJ1eBj+9mHev6YtWJQ/KXAVBWgjurbW0ft8RXNmq7geSAl5unIkl947Ej7RQkckk8l6IVnniXekS+4JMDv52i+yek/CpQvju9sHM+n0/flFk6uBUYg9lYXtcULcT5t8LlmroNUUSdtF3/d39qcg6B1a+FLyt+4Xw4Xlgba18NeyFL6+SGPiGdkQ6RzMsex5Wviw9VmhgaitL/wxOOATxKN2ATgf07dtXXLdu3ZGfeILhcPswO6V+7O+ljTz63TYsrWX1R87L5eqBqUEZE0iOWdM+Xh8Ibpf1TWR4VhR3fr4pkEE+cUEePr+fsd1jOyi/Ndpc/PXrLfy8Q8oKQ7RK5tw+hNRWlyufX6TB6qK80U6IVkmkQR3kv30qUGt24vD42FFpptrsZHhmFL/srGFHlYVpw9OINKjx+UUUciGIRCWKIot21nBTq/90TqyBt67uyyu/7GX+tioSQrU8cUEeJo2C+FANv+9r4uZ2zHKVXMbCvwxjR2UL2yotjM6JJjPacMTPb3d7uX/2liBiIsAnN/RnaGYUTo/0PQtI2aZCLmPtvkYmvSmJZwztFkmflDBe+iWYjHVuXiwvXt4LjVJOk82NTxRRyAQW7azlxUW78ftFbm4defP6RPqmhgeY8c12yQnucOIte2utnPX8kqBtA9PD+dv4XPKPINX73vISnvx+Z9C2G4amUW+VyJnDM6OIDVEzMT8OjUrBwm3V/FJUS1qknkfPy6XB6ubXXXUYNQp6J4fx4DdbePuavuxvdPD+8hKuHJCMSatEq5CCvkYlD7SBfH4Rs8NNg82N1y+yr96GKMKgjAhCdSrMDg/fbKigqKqJrNhQnvj+4GLsin5JPDAuB5fXT43ZyZYDLTzcTqSl7bt4/rIC7v1qM0v31COXCUwZkMzFvRNICNWdWHKX2y7NfS+4H+z10PtafP1v5q8LKvhpew2jc2KQyeBAk52XrigMHss0V8LLheBtV9EY+wQMuv30tau0N8Lv78CKF0H0Qb9p0O966XMcirt2SCYvbWjZDy/kBT8nNh+u/vZMD/04IQjCelEUO10BnaZX0OkFrUqOViXnQJOdu9q5OoHkzzuxIL6D/GW0ScNrkwvZVWPB6vSSnxjKha+vCIh7+EV4ekERP981vFPHnoomZyB4g8Rmf+bHXTx7aT56tYL9TXYuem1FoOQ8Pi+Wf1yU1yVr+kSiwepi+mcb+H1fE1kxBmJNGgamhzO4WyQapRxNa2lRJgholPKgrEgQBAakRTB/xlC+2yhl3x+u3MfsDZIu+Z5aK1Nn/s4v94wAgQ6jRW6fn1+KaslPCOG+c+KPuirh9YtBs9FtaG41T2k77vbIjjHyxbSBvLGkmJxYIzmxHRnFaZEHjVTaFhGb9zdz71ebA895bO52Pp82kIHtsubKZgf3zd7MquIGesSH8MLlBaRHGoIqBs32YNc1gFpz58I0h2JCz3heXbw3cI3oVXKmDEhmcVEtd4zOZMG2KkrqbPhEsDq9gXn2vbVSD/+qd9fQJyUMu9vHP+fvJFynwusTeWrBTrZXmlncyiWQCTBn+lDiTGqabB4WbqtiVE4Mi3bWsKPSzOjcaOwuHw99t5UXLuvFBb3iMWmVnJsXy5jcaNxeP/NnDGVlcQMFSaFkROkDVa0YkwahE2nbS/sm8N3GCpa2Mt99fpGPVpUxLDOSVxfv5d+X5B+T13iXUOkgbRhcM7fVYSwUs0ugtG43ZqeX7zYdHHu0uw5phdVsDw7eAFu+hF6TQX+ajoDpwiWr1D7XSo/VJnCZpZ63tV2bKTIT5Ie0L1zBbngAmA+A39tx+xn8YZwJ4CcAh6thRJs0KOUytlVIzNlDg4fV5e1gmNKGGnPHHmRFkx2X14+IJH7Rvl88f1s1t4/udsQA7vOL1FmcfLepEpfHxyV9Eok2qlHIZNTbXNhdPjRKGVaXl5931JAZY6RXUmiHgLG/yc7vrUYou2us7K6xovhxN5f3TWRUTjQzZm1kY2v1YURWFP+ZlI+2XYZm0irprg2he3wItRYnP+8MJqW5vH4qWvXTO5QlgaxoA93jTUcVvK1OL1aXVEG5cVhaENnKqFbQN7VzdbK24xyQHkGP1veyuX30Sgph036JsR4fouHaQakoZMEVmLmbO6pxfb3hAAPSwhEEgSabmzs/38jafU1kxxjpEW/ilcV7eWhCbpBgR3K4jlCdMujaubxfUpeji22INqpZcOdwFm6rwu3zc15+PB6fn54JIcyYtZEdVdJ1+e3GCh6ekMs5PWIC5MBfimqZMjCFt1uDOsBdY7MQESlvCLaR9YvgdPuwuLyc++IyXr6ykOmfbQiMy83dXMkD5+Zwbo9YZq4oZXhWFJ5W5v/TC4sQRUgK0/Le1H5kxXRcICWGa7l5eDrvLi/F5xfplxrGkIyogGRue2yrMGNz+7C6vCcugLfBIFVpas0uFm6r4oLCBO4fl8O9X21mf6MDuUzoMJPuNcZ3uMmK4ekIitNc8ESplf61Qa6Wet5fXAWWKsly87KPOxLZtOFgjJXaBW3oeRloTq1Wxv8XnAngxwCdSsHwrCiWthNQmT6qG6Hazku3ylZlotEmDU02N/3Twvm9tDHw94LEEDSqzhm0eQmmDrPUl/dLIlSrpMnu5kCjo8M+1S1OesR3/UOps7g458VlAcvON5YUs/iekbi8Pq58ew0pETqu7J/MXV9uChCQBqaH8/qU3kGLgwZrx8ywyeYmwqBmzqaKQPAGSW1sbWkj2XFG9rltJIXpgpTetEo52THGgMRoG6JNaq57fy0vXNGLX4pqAx7gfVPCyDuMN/uhsLo8zF5/gCdbCWaPnpfLR9f3Z+aKfUQZVEwfk0nUUbQe2iYOtCoF713bj2qzE5fHT1K4tlPzkZ4JHcvbBYmhgUqE2+dnfVkTz1yaj0ouY8nuOrJjjEHyqyD1xb+7fQj/XlBEeavt6MReCUflWCaTCcSGaJg6JA2Qro+Jr67gzav6BIJ3Gz5ctY97xmYHAvibvxWz5L6RjMyKYkeVmfzEUNbua0SjlDO+ZxxfrDtIPIs0qIgxqXlnWSmiCCaNMhC82/Dx6jJenVzI52vLUcoFHG4x4CYHsL/JwR2fbeT9qf1ICAuuSIXpVEwf3Y3rhqTi9UsuXWE6FWO7R3cgHvZODmV1ST1KuYz1ZY2oFXLiQjQnLJiX1Nu44NXlAUJiRpSepy7K56r31nD9kLSguf16q4uiGgX98iaj3tbKYtdH4j/rceQnaDb8lEEuh/hCmLYEfC6pt91ZBcEQDdcthB8fgvpd0P1CfIPvoNEpgNNFuE6J/FS6w/2P40wAPwaE61U8f1kBy/bUsba0iYkF8eTEGTv0vztDmF7FK1cW8syPu1hT0kDflDAeGJcTIHYdigi9igUzhvHwnG3UWVxM7p/MuLw4/KKIxelhfM9YtlYcnFuWhB2OrMS2YFtVkN+20+Nnd7WFN5dKDmF3npXJG78VB40QrS5ppNHmCQRwv18kJ86ESaMIYmhfNTCF7ZUtQfaSbVhf3sy8LVUUJIYyKAMK2gVwo0bJI60+4VUtksXoTcPSkctk7Gu088S8Hbx1dR8qmx0YNUpyY41HfUO2OL088f2OQKXjie93cmnvBJ6dJPkUH4+TU4ShoxnIoRiaGcmAtDDWlEpVisLkUM5tN78rFwRuGJpGVbODFxYd7KkvLqrlrav7BF5fLhNIjdDz7KR8XB4/oTrVcRMZ1+5rxO720tnuSpkMsV0t6aHxOcgEgdRIHSkRepodLi7rm0iEXs3NI9JRK2X8tL2GjGg9D47LRaOQ4xdFRERknfwcVAoZzXYP1w5KQ6OUUd3i67BY2ddgO6yqmlGj7LBgOzdP+g3MXn8AjULOzSMyKK6z8veJeVz6xkoqW5n0BUkhvHdtv67bDn4veBwgKEDVuYa61enhuZ92BU2XFNfZcHl9zJs+BJNWSXi769rj83PDVyU8M+F2BvWbAc4WLMooDIpYYg5/JKcvZHIwHuHIBQHC0+CiN8HrpEUw8cvOel5YtAFRlBKec/NiT7pmxf8XnAngx4hIg5qLChO5qDDxmPeNMWl48oIeWF1e9KrOBWAarC6W7qljxd4GxuXF8sLlvZAJAmFaaeVaa3ZyyRsreeHyQh4Yl8OXa/cTbVLz8ITuR5wLBmnW91CYtMqANKxKIesguAESAeztpcUMyYgkwqDi49X7eH9qPz5cuY86q4uLeyfSLy2M1cUNjO0ew5xNwVrtwzIjeeDrrfy4vZq504fSZHcHHa9BJZecphQy1HIZ5U126ixOMqIMbNzfzKQ3V5EQqiU3zsh/JhUc8XO2odnu6dCmWFRUy33n5pxUG8ZIg5rXp/TB4vQiIjm/tQ/6EQYVUwamcMnrK4P2W1fWhM3lI+IQSXuDWskfTSJjTGriQrTUWV30TQljXTsFuHvOzmJgegSf3NCf5Ag9tWYnF7+xkqoWJ7lxRt6+ui9RRg0+v4jT4yM+RMNLV/ZCJZdhUMtBBtcPSeOrdQeobHYyMD2c1SUHq023jshg5opS1pU1sfiekejVCqKN6iAdgbG5MZ1q2R8O4Xrpup8xJhOPT2R7RQuJYRrmba4MBG+AzftbWF/WdFgBlBazhb21Zr7ZXEdejJqxPZOINOk5dDXhEyVC66Hw+UXSIvUddCEUMhmxIRrunFOGSi5Do5ShUliYPyOhw2v818NpAY9NKrtrQlrNXUzs29/M3V8e5II88M1W0qP09E87jVn4/0U4E8BPMXQqRacjYyARlh6Zsy0wbjR7/QFuHZHBjDGZgbKTze3F4vRh0igoq7dx84gMmu1unvx+By9fWUjMEYLShPw4XvplD1aXl4woPbeMyCAuRMOIrCjmbq7kp+01TO6fzFMLDjpSpUfqabC6+dd8adsTE3tgtnuoanFw51mZiCLUWlwIokBqpIGyBht3jc3ik1VlKOQC04ans7PKHPAANzs9pMgOMdYQBD5ZXcZFvSWBktxYE1sONPPspfm8uGg3WypayEsw8cC5Oce0eo/QqzCqFYGpAZ1Kzo1D00+6Vzt0nakLgoBWKe80mz4RU1Aujw+z04tOJUevVtDi8BBpUHPX2ExSwnU8fkEPNpY3U9Fs5/z8eBLDdZg0SoZmRlFrdnL9h2sDKmM7qyzc+fkm3ru2Lx6/n+s+WEuN+WDg7ZkQwsypfYkwqJh96yDmb63mkfO6U1pvY1tFC+N7xrF8T32AcLa9soWh6RF8euMAHp27nd3VFkZkR3H/OdnIkUh0Jo2CcL3qiK0CrVIeWAgnh+uwuryU1pd0eF5pfeduYD6Pm5931nDvt7sC2z7fVMf7VxcSERJc5g7RKrltVDdWFjcEtoXrVfRKCu1U1CnSoOKNKb0D58ukVfDW1X2Oyyr2tIa5EhY+CPuWQUJfmPAfSa0Oggh+bfhmQ8WZAH6CcCaAHyVEUcTj83ewsDzW16i3urC6fGiV8g4yrHa3LxC82/D+ilKmDkkN9NZ0SgWjcqJYvKuWWWv3M6udCMZ3GyuYOjiVFqdUIj9UEAQkYtOPfxnOgm1VDM6I4P6vt/DP+Tv56Pr+ODxeFu2sZkLPWN65pg/fbKggK8bIyOyoIPb9f37exZzbh/Lwd1tZsVe6mRUkhvDW1X2ID9Vw26frGdotivem9kUhk9Fkd/N7aSPRRjU2l5fkcF2HcmiEQc2D43O5buZaSuptKGQCd4zuhtnpYVBGBJMHpFBUbUYmCFhdHkSRo+qBh+lVzJo2kPtnb6EwOYQr+6ewqbyJjeXNZMcaT7iSXaPNzeb9zSzZXcfI7CjyE0MOSyyM0Ku4a2xWwEsdYGR2VKeVmWNBvdXFG78V82tRLXkJJv42Ppc5myp56Zc9XNw7Ea9PJDvGwMSCOPQqRYeepM3tDZIIBdhQ3oTH78fp9gUFb4CtFS14/RBpVNFoczfm1ywAACAASURBVNFodfHar3upMbsY1i2CqmYHz/woBchIg4rkcB1qtYLMGCPPTcrH5wetUsb6fY3cNksaswzXq/j8poFkdcL6B4nk+fX6A5Q32rlqYAopEdI15fL6mJAfx4J25jAyAc7K7bz022hz8vKSYCGZzQcsNDt8RHRCJ8lPCOHb2wbz/opSYk0arhuSdthrSBAEsmNNzJs+FJfXj1oh63RR0mx30+Lw0Ghzk9AqanQ0HIc/BbY6aKmQNOHDM0CugK9vgLLWStKeH+GzcrhmHhii6NmJ0VN+nBbKVkNE+hk1tz+IPzWAC4JwLvASIAfeFUXx6T/zeA6HequL+VurWF3SwLk94hiaGXlcq+iyBjtXvL2aarMThUzg4Qm5XNonMWj1LggE9Z9lQvAQjUmn4Obh6czZHDzLDFKf9Z1lJby1pARBBneOyeSS3olBGatCLiMhTMtFhQlc/d7vATLTdTPXMn10Nx4a350tB1rokxTGsMwozE4Pw/79a5DQhsvjx+/3B4I3wOYDLSzcXs3VA1L4fNrAVhtJJXtqrDz38y4Sw3S8c01flHKB8HauWGaHp7UvK/DcT7soac2UvH6RFxbtYd70IVz+9ioUMhkPjstBBO76YhNOj5/po7rRPd7UZSBXymXkJYTw2U0D2F1j4YLXDo7yDcmI4JXJhUEBVhRFye1JlIL/sfSbrU4PLy3aHZAF/WDlPq4fkso9Z2d3GpQVchnje8bRPc7Egm1VFCSF0r/djPjxwOL08Pjc7cxrnXUvqbdx/dB03lpazAfX9ee7jRW8vHgP2TFGHjmvO6ZOCJg6lSKoagGQnxiCTBBQyGV8dfMgVhbX8+6yUiwuL+mtjmoASeF67jknWzI9MagJ06mY9OZKFP/H3nlHR1Vu7/8zvSaTSe89gRAIAUKviqCAFBUEQeyIvXuv7eq193ptKBasCGIHUVB67zWhJIT03ibTy/n9cZIhk5kAelHv7yvPWqxFTs6UnJnz7nfv/eznkUp4dFI2qRE6dpU0IZOK2gCxIWIlprLZyo2f7fK2OxrMDu77ai/zr+zvdz1qTXYufnOj15p14bZSPr1uIEPTwxHaytxPTunJZ1tLUCtkzG0zQgmMLj7fLsogwRoFfRKNvBAjTiWcKtDKpJKTWmw2WRy8svIIH24sBsSpiK9uGkJGADb+X47WWvh8BpS3aXEExcC1P58I3u2oyQeX+NmMyIwgL9nI9raJldz4YMbG2uHDCyCyB8z+5mwQ/y/wlwVwiUQiA94AxgBlwDaJRPKdIAgHT/7IPxeNFgf3LN7j1c9etq+K64alcNeYTLSnkSk1mB2UNVrwCALPLz/kLSO7PAKP/XCQsdnR3gCuU8mYkhvntVcEmDsyleAOphYahZysGDFoLd9fSVyIlsLaVuKMGlptLl74+bD33Md/yKd3fEjAMSmH2+PDRK43O3j0+4P0iAnmtoW7uGFkKveNy8LicNMnMcSnnzlrYCJHOxHVMiL1DEoNY8Gm41Q22zgvK5K31xRSa7Lz70nZzHp3C0drWvni+kE021w0WpzIZFKeWnqQ7/dW8vRFvfyMKsTr72TNPecgIPYaRzy/yksiWnekju9uGXpKQRMQdcufWlbgQ5zaUFhPVbPN6xTXYnWyobCOF38+jNsjcOu56YzuHunnjd4VWu1uH61vENnX149I8wvgtSY7rXYnKrmMlAgt943LOq3XOPV7cLFsv28Vx+n2MHNgEh9vKvYG9tIGKwVVJr6+aaif6IlRq2De7H7c8vkuGswOksO0vDI9l63H6rnvq32Y7W7G9YzmnSvyuGvRbl6f2df7HAqZlKhgtdcv3O328PXNQ2kwO/h6ZzkPdhBkeXFaDpNy41DIpJhs4kjlBT2jmdYvHq1SzuaietwBjEqOVJv8fNVf/eUI2bHBhOmUxIVoeHtNIdP7J+BweThUbWJASuBRwdBgPXecm8pdX554X30SDIRoTn5vq84Qf6LZ6vQGbwCT3cXD3x3grVl9//eIXhU7TgRvEMfJzHX+8+GqIFErHZELMu/yfrRYHQi2ZgzNhwj78mIxS6k+AHVHzgbw/wJ/ZQY+ADgqCEIRgEQiWQhMBv6nArjF7vYxvwBxUZ4zIvWUAbzJInpkL95exhsz+3qtP9vhEUTSWrsKm0Gj5KEJWYzvFc2mNjJY9+hgP7KVRinHqFXwzuw8thU3kJsQQqxBzYsrDtMZP+6vChjA5VIpiaFaShpOzPQatQo/M4ZgtZzHJvfkx32VHKhoYUh6OMlhWj/701em53Lth9u9C+t764t4/6r+PPb9QdYermNMjyh+3F9Fq93FQ9/sRyKBC7Kj+a6tkrCnrIkhaeEU1p7oVcqlEjIi9US0BYM3Vx/105f/YEMxz03NQXGKTMjjERnpnVHZbCMiSEVEkJrSRgs3frLT+7u7Fu1h0dxBXfbr3G4PZocbrVLmzcQ6UwQ9Arg9Hhwut7f9UtFkZcY7m73X/sohydwxOuO/VtLzeAQazQ4ig1Q+WuZVzVZGZUZw2RpfTe+yRitmu8svgCvlMvqnhLL89uE43B7UchlWp4ubPt3lPeeHvZVkxQSz9LZhGLoYowSQtQV0jyDw3oZjPr97Ymk+wzMjiAxSE6JRcMd5GUToVfzjy7202Jxc1CcOJOIGpOPnG6gqIpNIkCBBIpGQmxDC0xfnsKe0ieRwLTEGTZfBUCaVMDorkm9uHMTXuyvoGRvEOd0iCQvWBjz/TCPQOGZpg+WPd1j7PWg87n/syE8w5S34/DJwO0R1uYmvgebEpjpMryJMZoGlN0LxWt/HO0ycxe/HX9loiQM6Np/K2o794XB7BGpMNo7Xm6lusZ3USEQi8a+mKWRSv8Jbo8VBZbOVGpMNV9vNZ3W4iQvRMP/KPAwaOcPSfecmNQqZX3ktTK9iTI9oHp6YzeC08ICLeqvdyQcbi5n8xgaeWJrP1Lc3sepQLRf39WfG908O7OMbrlfy5qy+RLT17wwaBU9fnMP7G46hUci4akgyLVYnJquTZ5bls7e8mYRQLcv2VXLVB9twuj28MDWHWIOaB8d3p6TR4pMVeQRYsPE4E3Ji2Hm8kW7RQShlUtwegY2F9fSKM/gIqnyzq4KJvWOZmBODXCohLkTD+1f1x9Ch3B4VYN46OlgdcCyqM4w6JVcPTfY5FmNQo1HKvCIp3++p8Hvcou1leAKo7dS32pm//hjXf7yd11cdpc5kR6eSMa2f72dwcd84vt5dzrojdVgdLqwONy+vPExJg2jkopJLWbCxmBqTv3DPb4XZ4eK73RU8MD7Lh83dYBE92uM6Kf7JpBLUCmnAv69dwyDeqCU8SMW2Yn/P8tWHapBKJKfVZnC5Bb+xMZPN5d3xhOqUXJgTw4Pf7Kfe7MDpFthd2kRJg4Xj9WZK6s3Y23TdUyP0pLRJCoPY4757bKb3u6JVyYkzahifE0OPWMMpN0YGnYbcpDAendyLaf2TCf+TgjeIGvNBnRKBybmxXWpL/KXIPN9f/jWuPyQOhdv3ijPid+wTz+ssVKMxwpBbfY9pQyEm9499z//H8Vdm4IHuer+VRCKRXA9cD5CYmHhGXriwppXZ72+husWOTinjlRl9GJ4RHnCsSK+Sc2lePF9sK/Meu210hk9gqWq2cdvCXWw91kCEXsUL03IYkBKKR4D8yhbeW3eM/ilGHpvcE6vTzS/5osLZazNyffrBp4tWm4t5a3yZts8uL2D5HSMYnhHOuja27/nZUfTvQmVMIpGQFR3E0tuGYXW6kUslHKs1c/eYTCKC1Djdbh75bj8xBg3je8VwT5vqlUwqoW+ikaggNfvKm3np0t4khem8DOOOEBCQSMTe/JHqVm4dnY7F4SYn3kBxnZlh6eFe4RCr0811C7bx+ZxBPDAhC7lUSphO6SMrOiIzguQwLcVtSmBhOiVXDElCFmDwuNZkZ+uxBurNdkZ3jyJcr2RsjyiUcinL9lYSb9QwtV889321j/ev6g8QUCY1KybY5z2A2Gd+7IeD3lG5zUUNbD3WwOsz+/KPC7oxPCOcVYdqGZBsJNqgYc5HYtlx7T/OQSGTcKjSxM3npHNeViQmmwu1Qkqj2V/i9XTRandicbhRSKUo5FLWHqll8Q2DKa63EG/UEKpTEBui4ZlLcrjiva3e7O6uMZlYHG4e+HofSWFaLukb77OhrGyy4hYEpBIJAwOUoPsnh6JVyrE73dSbHew43khMiJqUMJ0f+16rlNE3MYSdHWxbJ+fGev8vl0l9LF17xxt4YHwWD397gAMVLQxICeWFab0xahUYtQoWzR3EyvwaShssXNw3PqB50P8PCNUpWXLTEB759gCljRYm9Y7lmqEpp6Ut8adD1ybSsvJhcJhh8K2iSYlSI/4Ljjn54xMGwJU/wJa3IDheDOi6s+Xz/wZ/mZmJRCIZDPxbEITz236+H0AQhKe7esyZMDOpb7X7kLdAzIRX3zvK27frjAaznYMVJrYfb2BUZgTJ4Se0mlttTv65ZB9L950glSllUtbeew7/WLLHJ7D1iAnijVl90Snl2F0eVuZXE6xWMDwz3Ec+81Qob7Qy9NlffY7JpBK+vVnsZzrdHiQSCTqlzK902GRxYHO6kUgk6FVypBIJGqUMs93J+qN12J0e1AoZR2taGZEZwbojtSSH6yioNHGgvInbz8tkX3kzMqmE9Mgg5q8tZNagZFQKKbd8ttPLUJZIYP4VeawqqGHuyDTqWu38UlDDmkO1TMuL55HvDrDm3nN4fnkBS/dVIpdKmT04icm5sWTHGrrM6mpNdvIrW7A53eQmhGDUKml1iHP17YtercnOjHc2U1gr9ulVcik/3DqMjKggDle18MPeSqpaRGLizIGJ3HJOOsEaBXWtduZ8tN0bSLpHB/HxtQP9SszVLTYGP/2L33z5hvvOJS5EQ5PZTrPVye6yZpxuDzEGDfcu3sPH1w0gRKNkd2kTe8ua2VbcwG2jMxAEgXijFqNWiapNxrbj33My1JnsPLUsn6X7KkkO1/HeFXnc9NlODla0EBWsYkyPKG4clU6TxYnT5SFUr6S0wUJMiAaL3cW419Z5SZPxRg1f3zSEiCA1R6pN3PLZLg5Vm0iL0PGfy/pwvMHMrZ/txuURyEsy8tbl/YgIUnGgvJmL39robb8Mzwjn1Rm5fuz7qmYb764rYn95M4PTwuifHMoX20p44qJeBKsV7C5tYsobGwCYf2Uej3x7wKeq0ychhLvGZnKgvIVpeSI50+X2nLF+9JmEw1SPwlYH2z8Q56L7XI5bF4Vc4Xs/2p1umm1OalpsaJVyjDrlaek5/KWwNIomJ9qw3zfz6LCImfypbFUdFrA1i6V5hdbX9exvhP9VM5NtQIZEIkkByoEZwMw/+kXdguAnI2l1urEEEGhoR6hOxbAMFcMy/N10LE43W47V+xxzuD04PR6/rPRgpQmZRFygx7+2ziuTKi6c/mSiQHC43Egk+AllTOgVw8r8akZ3j6RXF6SuWpOd+7/eS79EI4NTw9Ao5bg9HpQyKVqVjMPVrZQ1WvmibTTtuZ8O8e9J2fy0v4opuXFM7RfPhNfWedXXYg1qPr52IDaXm3sX72He7DxW5lfTZHYwc2ASGqUUrTKG8kYLs9/fitMtEG/UEK5XIQjwwJK9PH1JDjeOSsPpFnB5PCQYtSctyYr9avFGrmu189aaQlYfqmVERhhXDknGqFNxqMpE/2Qjk3Jj2XW8kTVHanl5xWGenyZWC2YOTOJYXSs3jkrDqFV4SYLhehXzr8ijwezAI4hiK4FGhCSIdpcdWdoKmQRZ22JWb3Ey8T/rvd+pblGi+EyIRsmbq44ye3AyL/58iAcn9GDuxztotjqRtU0lxBs1vLW6iMFpoVw1JOWk3wmb080bq47yVRvp8VCViVnvbeHzOYNwewSRJS2V8OTSfL5taw8Y1HK+uWUoQSo5d36x22fioazRSlGtGZdb4MZPd3qJioW1Zq7/eAeL5g5m/T/Pxe3xoFGKc9rNVgdPLMv34U6sO1JHdYvdL4DbHC4aLQ6GpIdzsKKZ//x6FKkEHrqwB8FqhVhRGZzEJ5uPE6SW+xHVdpU2kWDUsDK/hq3FDSSHaXl15VHGZkcxqlvk/9R8tcJcgeSdUSdMPLbPR3b9Wl/nLuBwtYmpb2/yXr8LsqN56uJe/1N/ix+0gdtypw3labQobC2w/0txvtxlg6hsmLnY7/r93fGX1WkEQXABtwA/AfnAIkEQDvzRr6uUSRmU6lsODNUp0al+3y5erZCRm+AbMOVSCVKJKCzhe64UrVLGG6uO+miclzVa2dppE9AViussTH1rI09e1IsbR6YxOC2MO87LYMaABN5dW8SxejONZn9ijN3pZt6aQsb1jKGo1sxFb23k/FfWcv9X+zDZXZhsLoalh7Nou+9M7CsrDzOlTxxalYwPNxb7SKdWNNswO1z8uK+SS/sncvUHWymobCFMryRYI8dkc3GgooV9FS1e8tkVg5MYkGxk1T2jeH5ab8KDlKS19TT7JYWeNpGrxerk4W/389KKwwxND2NwWjhf7Sxnb5lIXFLIJGwqrGNQWhjvzM7D6nTjEQRUChnRBjWD08JJ6VBJMdtdVDRZMTtcBKkVJ50RN2gV/HNcd59jN45KI0gtx+pw8+rKI1gcbmIMah4Yn8W/LuyBUadEKZNwuLqViiYrlw9K4pkfC7yytm6PwBNL84nQq9hZ0sgbqwq584tdAd3I2mGyOVlZ4GsCc7zeQlmjhYRQLbEhGhotTm/wBrFUnV/Zgtnh4sHxWczon+DzeKlUgssj+E0ZlDVacbg8RBvUxBm13gDjcgsBv28d5XrboVbK+X5PBS+vOMxPB6pxewQyIoO8Gx+dSkbP2GAW3zCEuBANwZ3EdoamhyGTSrHYXby9upBfCmq4ckgS89YU8vaqowFV0v4KuCzNsP4VXwcucx0cWeFzXpNFnPzouPlZfqDKq/n//w3MdWCqFm1IzxRsTbD0rhNObtUHYMXDgd3O/sb4SxstgiAsEwQhUxCENEEQnvwzXjNEq+SlS3O9YyVpETo+umaAj4bxb0GwWsGjk7Lp1ja3qVfJeenSXEK1Sl6e3htt2/ypXCrh6Yt7oZRLAmb7J6sAtMNkc/LM8gIqmm08vSyfPoni3PDBihZmv7cVl0cgwajluo+2Ud/qK7bRandxqNpEsFrO4h1l3sxrT1kzy/dXsbesGYVMSueOitXhRq+SkxGpD7goN5odHK5uZW9ZEx9e3Z8HxmfRO8GIxyMwf90x9GoZcqlYMXh+ag5T+yUQHqQmJVxHTIgGjUKOSiHzGZU7HVgcbn7cX8WEXjGE61VMf2czjy/NZ9LrG3hnbRGhOhWbixp45scCth5r4J8XdO9yXrzR7GBvWRMXv7mREc+tZtb8zX4BrCNUchmTesey4s4RPHtJDstuG8Y1Q1PQqeS4PB6aLA4SQjW8Oasvaw7XcPWHW3nw6/3UmZ1cMTgJmVRCRmQQlc2+GabbI2BzebykvPVH60/6vVC3mcB0RrzxxMaxrsP3QCWXMm92PxZuLWXYs6u4/D3RvObOMZmAeC+khOmQScWqUEdE6FUBS/ohWjFr7ohQnZLUDiSzdgRr5Dx5US8UbdarIVoFL1za29svD9WpGJ0Vhdvjwe0WeOKiXt757QSjhuen5nD/V3tZvKOMw9WtxARrkEkl3HpuBuNyYmi1/34ewZmEqysCeadys9PdpjnQCSbbX/93eDxCQHIjIPa/WyqhqQxqD8GnU+HFTFh4WWCmejucVmitFoO9+xR/Y1MJfotR+Xbxtc/Ci7+lEltsiIZ3ZvfD7vJ4BSX+G8QZtXw6ZyA2pxuFTEqIVoFKLqNXnIHV94yi0eLAoFESrJajVcm5cVQayw9Ueb+fQSo5wzNO3d9xuU/4Wf9SUMNFfeLRKmUU1raSl2Tk5nPSmbe2iB3Hm6hvcwZrh04lZ1S3CD+XKBCJdoPTwpBLJX4a2ZfmJZAUpsWoU3HtsBSW7DwR/FVyKUlhOh66sAdFta0cqWlly7EGBqeGYbKp6B6j59xuUQRrFFzcJ4FgjdzHF7wdtSYbe8qa8XgEchNCiAhSBTyvI6QS0CvlTO0Xz90dfLdB9A//8oYhvPqLaBKyZGcZ1wxL7vK5WmxObv5slzfzKaw1c9vnu/j42gFdSqEGa8TSu5/ghgBXDUmmstnG4z8c9JK2dpY0cuX7W1k0dxCtdhdHqluZf2Uemwrrva5cRq0CQcDbW1fJpSdtJwSpFTwyMZuCKhNljaKd5SfXDqC8ycprvxwhKyaYC7KjeXd2P6xONw1mB0v3VXpbOxaHm2eXH+L7W4YSZ1Azslsk4UEqmix2Xp/Zhzkf7aDWZCdMp+SNWX0IC1AdkUkljO8Vg0Yp4/OtpSQYtdxxXkbAe0qrlHNhrxhGZEZgtrsIUsn9SsXt8rNuj2iM8vF1A9EqZEgksPxANTMGJDJzYBJmu4sV+dUsb5t5VyukfHnDkIDOcH8m6lvtvP5rKQ8PuwMOfnMiC9dFQPp5PucatQouG5DIU8vyvcfa59j/KtidbiqbbXywsRi5VMJVQ5KJNqhQyNoqlLYW0c/8p/th6vvw80PQWCz+rmQzLL4SZn0Juk7tRks9bHwdts4T+9nnPQrdLwRNF+6JxhTRPMXTYQObMkqcMT8LL/6WARw4qUhCk8VBdYudw9UmeseLYyinku0MtGAp5TIig/1HxVIj9Hx/yzDmryvCoFUwZ3gqEfpTVwBUcinPT80hv6qFhVtLufXznXx63UBiQ9RUNIkBo90JrH1kp8Fsx2wXWeYX5sRS2mDxe96h6eH0ijOgUch4fWYfFm0vY8fxRkZmhjOqW6R3BjcxVMt3twzjrdVHUcpkXDE4iapmK0V1Zgprzby3XpzzXby9jAm9YugVb+CzrSXcPCrdh7XfETUtNqa8scFrPhERpOL7W4YRfQpWcYhWyf3jRUOSzhmLRxCFW7znahQ4XB6qmm3eTVRHtNpdfmXLg5Utv2sW93BNK4eqTYzNjvYRLYkxqHltRi5bjzVwe4fe853nZXDDiFQ2FTXw2ORsn8X87rHdCFYrsDpcNFudlDdaiQ7RYFDLveI/7cQzs92NXi1j/ZF67ugge/v51hIeGJ/Fv78/yIvTevuIBLWjuN7C1DyxlF7VbKPWZEOvkrPkxiE4XG7vHHhXs/Yuj0BqmI57xmSSECpqBHRm7rdDq/K//oEgk4q6+gazg23FDcz9ZIf3mk3IieHGkWnc28EP3Ob08PgPomtdx3vb4xGoN9txugWUMinhp8Ez+W9gd3n4YONxxmdmk3fjJtjxYRuJbRZubYTPgiuXSZnWLx6dSsaX28tICtNy99huZ1ze97egstnG2JfXer/7n20pYeVdI09YvNqa4cd7xOxYYzwRvNtRsQu3045UEHw34Ud/gfUvif93mOHbm0R70q4CuCYEpn8G398qyremnQfnPnB6/fO/Ef62AbwrtNqcvLuuiDdWiaIXEgm8MbMvY3tEnTF9Yr1KTs84A89NzUEikZxShATEnf0rKw+zeEcZ4XoV94/rzoU5MaSE6yhvsvmYj6RF6IkIUlHXaueWz3ayuaiBl6fnYrY5yY4z8MK0HJ75sQCTzcWMAYlM6ROHUSuObNWY7ByqaiE7NphVh2p5fGk+787O47weUehUcmKD1aSG6zDZ3cz9ZAfPXZJDWoSeR7/31d9Ztr+Sq4cmc8cXu5k1MLHLzGjZviof56hak53FO0q59dyMk14PpVzKhF4xNFudXNwn3sefuk9CCMfbNipSCdxxXgb3LdnHtuIGnrkkh/E9o/EIYuAGgRCNgphgFZUdNL67t82t/xY0mh2oFVL6Jhq9s+zlTVYkEnh1Rh8sDjf//v6gT2XwjVWF/HTnCM7tHkVKuI4nL+rFvrJmsmODiQwWy9a7Shq58oOtmO0igfGpi3oxpU8sZpsbZxsJMTlcR53Jzn9+PUpquI5ZgxKJDdGw83gTGqWUMJ2CILWcASmh7Clr9nnf7Ta0da127l60mw2F9UgkcEnfeIZnhPPO2iLmDE/BqFP5BZf6Vjs3f7qD3aXNDEwJRQBuPzeDvC6Uzzqi1mSntMGCRikjMiiw8YvLI/D0jwU+12xLUT2zByX5nVtjsvsI/bjcHgqqTNz46Q5KG6xkRumZNzvPZ4b8TEMulRCuVzLtwwP0iAni3vPvwO5y01diJFLhv0k36pRc1j+R8T1jUMmlp7W5+aMgCAILNhX7bFytTjdf7yrjlvb70VR5orTtdopB3NpBIyAkkSO1VgqKKxiVGSFuphwW2L/E/wULf4GoHoHfjFInVizmrhNfT6HxEYc5CxFnA3gntNpdvN1hxloQ4JFvD9A/OfS0WOK/BadjjOJ0u2kwOzleb+aSvvEEqRW8taaQWz/fxdp7zyHaoOG8rEgWzhnE59tKyIoJ5uK+cYTplCzYWMzmogYGpoRisjl5+FuRI3hBz2ievSSHrJhgjFql1ygFYNWhGpZ2MlRZuK2EIelhaJVyBAmsOFjjVZXbfryR87MDG0VIJBKig9Un3aDUBhAwqWmxYbI5qWyyUddqJy1ST1gAgweDVonT7eGKIUnEh2rYcLSO7FgDswcl0Whx8NzUHDIi9Ww9JqrajekRxZfbSxmWHsZ/fj3Kwm2lCILAJX3jWTh3MNPe3kSNyU5ymJb/XNbntD3HQQxkD32z32uiMSU3lpen9+baD7eTFSs6q/WKM/iR0hxuD3Wt4qblmYtzSItQkBYheok2mh0cqmrhULWJj68ZyBfbS/liWylLdpSSmxDCLZ/tpLDWTGaUnrcv74dRp6RXXDCXDUjkhZ8PUd8qXgOpVMK/J2Xz+dYSpvSJo6DKxLojdWgUMv55QTfC9Co8HoFvdpWzoc1pSxBEN7xR3SIwapXIpf78CBCDpkIm44vrB7H6cC0yqTiW2GxxnFSCtqLJykVvI0Qr2wAAIABJREFUbvCOHQ5MCeWNWX39NggCAq2dFPTqWh3EGzWEaBXelhLA9P4JGDtUehosDq7+cBu1bZalh6tbuenTHXxy7cDf9Nn+Fhh1Sl6ensucj7ZzsNLEDZ/sYN7sfhh1XVfwpFLJf63Cd6YQ6F71ue8M8aJMqtsBW9+BCS/Bd7eCoxU0RhrGzeORX6vZcqyJ/1zWh4m9Y0GmgvgBcHi57xOfSsRFJoegwBawZyHibADvBGcAxagmqwPBX2PmT0F+pYnL3tmM2SFmX3eel8l1w1J5d10R+yqaiQ/VEqJVMigtjLxkIzKpBLdHoLbVjlGrJN6oYVBqGD8fOMFWXr6/iuX7q3h0UjYzB/iK4wxODeONmX3ZWtzAom2lWJ1u0iP13mw0XK/iiSk9mTl/M063wCebjzO9fzxXDknmnbUnNj4Tc2LZXtzAvydl43CJxK5AbYtL+sXz9toi7zWXSGDWwCSeXpbP4h1lbWIhMu67oDvpAQhb4UFqypps7C1tYnBqGMX1Fq76YCtLbhxMUpiWBRuLSYvQ8/6GYgBuH53OvvIWH83yxW2B6ofbhmFziJKnUcG/bYE/UtPq44D1ze4KBqSEsvD6QSjkUpbsLGNbcSNjekTz04ET5/WKM6CQSbhpVDoWpwu9Slzom60OXl5xmI82i6QgmVTCqzNyOV5v5pqhKcz5aDtljSIJ7nB1K3M+2sEX1w/i9tEZTH17E/VmB+9ekcczPxaw/XgjC68fxMJtpfy4v4pbzk3nttEZuNwCqeFiydvqdLP1mD+L+GBFC7MGJqJT+/erQRxrvHtsJpe/t7WtogHvrz/G0tuGY+ii2ulweXhnbZGPq9mWYw0cqjIRnt5Jl10jivW82EHjPz1Sj8Xh4uubhvLc8gJKGixM7RfP5Nw4n2Bjc7q9wbsd+ZUmnH+gTKlCJmVASihr7j0Hk81JkFqBQaM40UPuAIfLLTqxdWm08udCIpFwxaAkPt18HHMbedKgUfgI7qAxwqwlYgn88HJRie3mLdhsFspapTy1ppYtx8SM/KNNxQzPCBfv+76z4fAyKGvT8eh9GUSeGf3//wlYm6DuEOz6BKJ7Q49Jf4rG+9kA3glapYzs2GAfY40puXHouvDw/iNR12rn3sV7vTeTIIimDV/eMJh31xWRGq73OV8uk9JgdrBkZxlfbi8jzqjhxUt7s7e0yY9VDGJf1uJwYZCLmeyRahMPfXOAkgYz43vFsPD6Qdy1aDdXDUnxWRh7xRtYe+85FFSZiDdqCFaJffxh6eGszK9mcGoYPeMMSCViplXe5GF3aSMTe8e1kbQEtEoZQWoF0QY13908lFd+OYzLDbefl45GKaOgqpXFNwxh/ZE6PIKA0yPQYnUEdM/KjNLzz3FZLNxaQo/YYO4b150wvZoWq4PBaeHMeGez99yvdpYHDESrD9cyIefEQmW2izPL+ZUtpEboCdepuuzjgziD3Rk/H6im2erk/fXFvDIjl5s+3cm7V+QRF6Jmc1EDfRJDuHFUGs/+eIi1R2oZmRnOQxN6EBmsxmx3e4M3iJyGl34+zK2jMwjTK73Bux2Fta043B5cHpHZHG/U4HB5vIREh8uDVinzmtaAuCnY8M9zAFHM6IKe0fx80HcsbXSWqGJn0CiQSkThGA8CRq0ShUxKcpiOV1Ye8QZvEA1olu2r5OK+cZQ2WIk2qDFoFF6lQ4fLTXEAf+6SegtD032PKdpaJcFqBasO1ZAWoWdiTgxP/JDPKzNyeX5aDnanhxCtv3OcWi4jVKf04TekRehPvxVmqoajK0Sjjp4Xgz5KLOWeAiq5jChpPVEaARRq8V8HON0eKpqsvLW6kCark7kjUsmI1Af0FG+H2e7C7nJjUCv87F/PJKIMalbcNZJvd1cgk8Kk3rG+7S+FBpKHwZxfQfCAXAMaA/ubGpj67iaf54rsWH3TR8JlX4iZukQmktH+r5TEPW5xM/P13BPHdi6Ay7/6w8VnzgbwTgjTq3j/qv68tbqQ3aVNjOkRyYz+if+1R/NvgccjIJVK8AgCxfW+C53bI+Bwe7huWAqRnUr6LreHxdtLvf3wQ9Umthc3sOCaAQxICWPN4VqvycXwjHCiDWo0bRuThlYHl87b7F2IP9p0HIVUZPZ2Lu+pFTJiQjTEdGLLRgRFMCIzglabk50lTcz9eAdWpxulTMrjU3pSUNnCgk3H+SW/mvOzo3lsck8iglRkxxl4ZXofBEFAr1awuaiOhyf24KoPtnpLpPPXFbHs9uFd2l+mR+q5f1x3GixOrw54sEbJwYoWbh+dQb3Zwfd7KjhUbeKO8zK9lp/t6OgX7XZ72FhYz9yPt3sZ4XeOyeTaYcneDLnR7KC21U5Vs41uUXqGZ4T7WMFKJHBR3zhGZkYwrmcMaoWU12bk8tzyAganhfHc1ByiglTMnL+ZIzXiZ/zdnkosDjcvXZobUJ+/rtVOglFDdLCaiCCVT3YZb9SgkEnQq+VIJWLmVNthhOyb3eXcdE46z3TgSlw9JNnnez2qWyRXD03msy0lqORS7hyTSWqETlS7s7lYfaiWJ5flY7a7uGZYClP7xmPQKHAHqK1bHG4KKk3M+Wg7Lo/AB1f1Z2BqGDKpBL1aZF+vPnzCJEgulTAkPYwDFc1YHG6Sw3TelpVaIeOnA1XkJoRQ0WRjxrubuXZYCkEqBQq5lK6q4Uadknev6Mfcj3dQ1yp6bb8ZoEwfEKZqeP98aGwzYFn9lKj1HZV98se5HFC9D76+ARoKIXOcWGYOOvH9qmu1M/7Vdd6N+fL9VXx10xD6JvoLpHg8AmWNVp77qYDiejMX94lnSp+4P0zoRSGTEhui4cZRaV2fJJX6ZZcpYToGphi92XeQSs7dYzJ9101duD87/f8CLPWw9jnfY1V7xeNnA/ifj6hgNfeP647F4SZILT9j5LVTocFsZ8PRen4tqGF0ViSDUkI5PzvK69gFIks7wajlttEZfrPTjRYni7aX+RxrsbmwOt10j9Kz8PpBFNaa0ShkON0e4kI03tne8iarTxYFIhHtmmHJv7k/V9fq4B9f7sXaZj7hcIsM4YXXDyJEo8AjiC5psSEa/nF+N1QKmc+N3i06mPfXH/Ppb7bYXCzcVsrdYzJpMDuwONwcaqsARAWrQQLf765gwaZiDBol/7owSxx/0yr4taCGGIOaD6/uzyPfHSAxVMt1w1NYsLEYQYCZAxN9TF8aLA5eXXmY20dnEG/UsqesiffWFTE9Lx69SkGTxcFzPxXw+VaROKeSS1l62zDenZ3H+qO1TOodh1wmIUKvQq2QkRwuXr9og4aecSLrNkyvorjO7A3e7fi1oAaz3YVKLiMpTMvx+hNTA9PyEkiP1BOkkvPO7H5ct2A79W3uY29f3o8wnQqLw8V947J44ecCcuMNqORS7C4PX+0s5x/nd+O7W4ayu7SJnPgQkkK1PtMVoTol947txo0j00ACIRql9/tRY7JxzYJt3g3Kk0vziQsRdfKvGpLM51tLvAQyjULGiIxw3llXxBMX9eLOL3Zzz+I9fHvLUG82NzA1lGcv6cX764vRq+XcP6473+wu5+UV4uhfVLCKb24eSoxBg1Gr4JZz0rn/631UNduY0ieOa4amoDiF1KxCJqV3fAjLbhuOw+VBpZASpjvN1kjFrhPBG0TC1uqn4aJ5IsGqK1gbYMEkMdMEKPhBHJsa94z4syaUdUfqvMG7HfPWFPLK9FzvhroddWY7F725wTsvvr/8IFanmznDU/96vfSWCqjaBy4bYXF5zJ/dj6N1FhrMDnrGGQKOHf7fRYCpi98jM/sbcTaAdwGVQvanaiyb7S5WHqzms62l7C5t4utd5Vw7NIU7x2Qik0pZe7iWjCg9j0zM5oc9FVzYO5Ygte9ctVIuJdqg8mqAtyNCryJUr0av9qBVyPAIYt+t4wYg0I4+OUzX5TjQyWBzub2+5+1otbtQyqU+rYnVh2q5YWQaEZ2uc7BKHpAwZba7WJlfQ7heyYx3NnsVrP55QTeigtU8/F27kJ+ZS+dt4sfbR3DfV/u85606VMM7V+QRFazizvMymTM8FQTQqWXezBpEdaNHJ/fkjVVHWbyjjGHp4bx3VX+cbel4i9XpDd4gjg7ds3gvH13TH5Vcyqz5W7A63agVonDKkLRwbymxI3lKrZChlEl9WL9JYTq2Fjfw9uoi3r0ij/fWHyO/soUJvWKY1i/eyyPoFWfgx9uHY28LTKFtUwRIJFyYE8OYHqIgyjc3D+XZ5QU0mh3EhmhICtWe1D+9fczL4fLQZHUgAYxaJWsO1/p9Jl/uKCMnLhitUsaPtw9n/rpjyKUSLu4bz6u/HGXVoRqm5yUQoVcyNS8eh8tDSYOFFquD73ZXclHfWD68pj8ahYzj9RZ+3FflrWJUt9h5f30x/7igGxqlnMFpYXx5wxAEBHRK+WlXxORtrmq/GS57gGM20Zf2ZDDXnQje7Ti6Aqpnwy+Pwsj7CVL5M68NagXSAAt+ZZPNT+zl860lTMuL/03+CWccLRWw4EKob7Oo1UUQNGcVfRITTv64/4vQhsM5D8KXV584FtdP1Ir/g/E/aHnz18Ph8lBrEudh3X+CL2+92c6Kg9VsKmpgWr943pndD5VcyoebimkwO4kIUvH4lJ6Mzoqi0ezgvQ3HmPT6ej+CjkGj4JELs73qbwAX5sR4S4ZKuZSIYDVRBrVf9h6kkvPqjFz6JoqLe4hWwYMTsrxKWB3RbsdaVNtKZbOV1s7KUQLkJZ3IaHPiDbw2Ixe1XCT4aNoCdu94Q8Dnl8mkTO+fgKpDhqGUib3QmhYbj/+QT7xRy9D0MII1chxugcWdKg9Ot8D6I7VkdiC+1bU6cLg8RASp0ankRLVdi47BG8Dpgds+38WvBTWUNVpZuK2UjzYWo257P6ZOlYownZKMSD2tdjd3LtrtrTzYnB7uWLibxi7kUIM1ch6bnO3t3WqVMh6akMWCjcfJr2ph2tubuG5YCh9ePYBrh6UQ2iH4twemhFAtkUFq5DIpDpeH1QU1DH32V859cTUX/mc9R2taeXl6bz64uj+Tc2NPygwHsDhclDVaWLDxGB9sOEZxnYXSRouXGd8RKeE69lW0UNpoRYqEq4YmYXe5ufrDbaw9IprWRBvUfHLdIFptLkY8v5oRz63isR/yGZsdxeTXN7K5qB6H20N5k5XZg5JYcsMQ73ewuN7steaVSCREBKmIbPvs/nAkDvRfgIfeKQqzBAru7dAYQdJpWY3sIZZUy7bDp5eQF6siKewEw0+rlHHLuekBE4Zgjf/fGhl08smO3wWHRez1n47SmccNh386EbxBnNXe+g64XV0/7v8qpFJIGw3Xr4aBN4n+6Jct/FPaBWcz8E5otDhYsqOMeWuKkEkl3D02k9FZkbRYXSzdV0lciIah6eFnbKSsxerkiaX5fL1TFNj4elc50/sncN3wVN5dW4TL4/Fhd989NpPEUC3bihsprDX7ZRcpETpW3TOKI9UmIoLEXmmgErjVIQpzyGVSalps7C5tYv2ROq4YnMwr00Oob7XzS76ofBXcibdTXG9mxrzN1LbakUkl3D+uO9P7J3jLsdEGNS9N781j3x8kSC3noj7xPPNjARXNVib0imH+lXk8vSyfe8/v1uXca2SQih9vH857647hFgSuGppMUU0rIVoFd5yXQW2rneP1Zm49N4O6VjsVjVY2FfnqyccbtX4CLZ31tQPB5nT7GWksP1DFwxPFzClCryJcr6Su1cENI1MZkRnBhqN1WBwu6lp9X6/R4sTh8tBotqNXK3wWXq1SzoW9YxnZLcKrJ/7yyiPsLBH7iM1WJ0v3VXLHeZmnfM8g2ooeqGgmMVQsvducHv65ZC+/3jOK6NPMQssaRGEenUpBXauDy9/bgssjsGjuIM7tHsmvBTUApIbruHJIEq+uPMLXu8qRSiRcOSSZIekRLN5RzqszcjlS08qtn+/mgXHdvVMAAFuPNbDiYDUXZEeRHKZj2tubvK0Co1bBB1cPYNa7m5k1MNGvpPynQRcpziBvnSf2w3tfBuU7RCnQ6J4Q3sVnog6G6Z/QUlWE0lKFuvgXOPch+PZm7ykRax/iy7kvsrW4mWClwOAYkJnyoSlSFH1RnxA3CdEomdw71qtnr5JL+fekHmfWscxULbYHjq2B+P5w3r8hOLbr850W8Tp0RmuVuMGR/Q3DisYAmj6iOM2fiL/hlT459pY188TSE2pY89cdIzlcx4x3NntHnTKj9Hx23aAzoupkdrj4ppM61pIdZXw6ZyBWh4tf82u8rlJ2l4fchBA+aFsMAxmwKGRSMbPsYsFubPNt/mJ7KRmRei4flMSSHWW8uEIc01m8o4wLc2LoGWvg5ZVH2FzUwJuX9/UuGE0WBw9+vc9LkHJ7BJ5cls8FPaO9ATxEq6TV7qJPQggTesdy/strvWXsT7eUEKJV8NG1A5BJpRTVtlJQZSI7VizFNlmclDRY6BYdxPF6MxN6R1Pb4uCGj3dw3fBUesYZePGnQ6w7KsqB/ufXo7x+WV9uOTedXw/VeKsSozIjyIzSU9NhznxQamiX16Uj1AqpdxyvHfFGLWaHm6UbjzEsPZwvbxjCkh1lZETpmfnuFkBU2OsRE+zjdtctKoiqZhtPLs1neGY4VwxO9iFR6VVy9Co5MQYNi7aXsqITC3xI2qnLcG63h8pmG/PWFtFocfDIxGy2FNUzb22R2CcVxIqJRiHrUlHQ6fbgcHnYfKyOGpODnDgDD3y9z/v7q97fxufXD+LhiT2wO920WJ1sO9bAkraNp0cQeG/9Md6/Ko9rhybjdHl4/dej5CUZOdDJ/Q9gf0UzF+bEsqukyafP32hx8u3uct6/un9Anfc/DVKp6HzV4yLY9ZGoCNZUIvY1r/kZLE3gsYOAGLTb2OlNbhWbnX35+GgYcQYNt02/j9j1DyBtKPJ57giNhAk5MVC+E16fIAZFgNGPQP/rxOdEJOI9MimbuSNTqWiykR0X/Lt9GwLC2gjf3ACFbfbEDUVQWyAyqLvKIB1WkZW/9nlfw5b+c/wY92fxx+JsAO8Al8fjzYTbMSk3lpdXHPZZzA9Xt3Ks3nxGArgECVKJxIfJK5VIiApSM3dkGgcqWjg/OxqLw014kJJ9Zc00mB30SQwh9jdqJrvdHpbuq+ShNonPFQer+WFvJU9M6elz3tJ9lVw9NAWATUX12JxumiwOzA43bo/AkWrfHp8giBKckXoVTTYnggANZgff760kzqj1cVsCkXU7e1AS3+8t58m2zdK953ej1mTnw43FgMhKnje7H4u2lSGTSnh5usjgzksyeoN3+2u/vPIwi64fxNLbhlHeaEWnkhOuV6JVyll9zzlsKqwjLVJPtEGN2eHG0WxFr5J3Gcz0ajn3jO3Gs8tFxrZKLuWxydncs2iPdyzr0Yk9uGxAItd+tM37uNd/PcqL03rz4s+H2H68kb6JRh4Y3507vthDYW0ru0qbOFRl4vmpvQOat4zuHslFuXF8u6ccmVTCNcNSyIg8dRCrbXUwvoPN6w97K3n3ijx2lTTyyMRsnl1ewKbCBoakh/Hg+CxCtApkUrESYHW4KG+y8s5aseI0e1ASNqfbb5zMZHfx+qqjvDojF6fbw+6SJq/oS0dsL27k1tEZ3PeVGPyP1rZy11j/bHVQahjJYVp2lzb5/a7J7CRUq+TN1YWclxVFRqT+rxE6cVph/YuQ//2JY4IgBr3ClbDiX2A3iQF38K0I2lBWH6r1kbJdkV/NT9feReSuj8QDGiOMuFcM+K218N0tJ4I3wK+PQ+/p3gAOIj8lVKekR2wXsqP/7d/YHrzbUblHPN4V1MHQcASu+QnWPCuKugy5DYL/hv3vvxhnA3gHyKVS+iSG8M3u8g7HJH4BCMQ++ZmATiVj5oBEPu4w83vNsGQig1TYXR5+2l/JF2393ehgNR9fO4DP5wwgIyr4N2sm15sdzF9X5HOspMGCgIBeJfey0DtSacL1SiTAE0sP8uWOcq4fkcrIzAivBzWIWWSoTsnPB6t5+LsDNFocnJcVyRNTegYUwEmP1CMBXvjpkPfY0LQwpry50fuzyyPw1LICbjonjbsX7eFYnYWrhiT5aJy3w+pwY3G6CdMp6dNpFCfOqGFqXgLVLTau/mAbBytbkEpg7ohU5o5MCyguo1cpmDUwkQtzYqhqthFr1PD88gIfk5enlxdwblYUDteJ93Oszsytn+/ik+sGolPKcHkELp23yWdm++eD1TzqcAcM4GF6FY9Ozuaf47oBEoLUp0fW2lRY52PzCrBoeymPTMzmyWX5bCysZ1zPaGYOSOTFnw+3bQ6SidCrqDHZueCVdbjaNqhf7Szn5ztHMLZHlI8iIcCIjHCUMikquYyxPaNwCQLfdbAqBRieEUGwWkFOnIHl+6tosjjZXtzIgxOy+M+vR7A63EzJjeOiPnHMX1fExN5xKGQSHwnUaf3jufrDbZQ1ihuLu8dkMmdEqneO/Lei3VXrNxMyZQqI6OYbwNUhEBQDn1164tj6lyEsncaMaV4/gHY0WpwcNuuInLsOzDUQ1VM0NgEQ3P5a4oJH7Ef/WZBIxV6/pcNmTKEF6Um+dwo1hHcXA/3wu0Ghg5CE/ztz3f8f4SyJrRMm9IqhT+KJL2KNyc7NnWYio4JVZET5k3p+D4LUCu4ck8FH1/RnzvAUPr1uIHNHpKFVyalusXmDN0BVi403Vx+ld7zxNwfvBrOd4noz2gA9RYNGiasDu3ZybhybCutRyCS8NqMPlc02vtwhBuyFW0uYOTCRSb1j0ChkZMUEMW92P9HWcaHo6CUIotzqD3srMdvdPrrVkUEqHhifhUfAuzGSSMAegCxY02Lzlu53ljSSFRNMqE5FWoTvGM+MAQks2FBMZXNg0qHN6ebNVUe9pW2PAG+t8VUC64xgjYKEUC39U0KRSkRltY6wuzyoFVIuH+SrZKdWSNEoRIKZQirlmYt78cXcQbw2I5e0CD16pfyk0yXBGgXRBg3RhtMnawU6T6eUERGkYmNhPcFqOXOGpzJr/hY+21rCx5uPc8Er6zDZXCzYeNwbvNv/rs+3lhBv1PDhVf3JiglCIhHJkOdnR3unHoxaFWN7RHFpXjwyqQSlTMrckal0iw5C2sZE7xknZpEvrTiMxyPw9U1DWXPvOfx7UjbljVY+3HicBRuLWXDNAM7PjmJUZgQLrx/E2sO1PpueN1cX0hLAyvZUcLjclDRYeHzpQf79/QGK68zYnb/BM1wqh7zrIDT1xLGc6VCyyf/cA18hw0VIALEfrVpBs6G7qO0dFC26bAEo9dBjsu/JQdGgCvZ7jj8M2jCY+NoJ4p1EAuc/3bXJSDt0YZB2jjgXH5l1Nnj/RTibgXdCeJCK+Vfk0Wp3IZVI0KvkyKQSltw4hI82FZNg1HD5oOQzOsIRqlMxIjOSEZmRmO1O6lsdHKho9pvLBlGy0+Zy/ybTA4fLw3vrj7GlqIGbRqVx68Jd3pGgIalhaJUynr0kh23HGhiaEU5uQgjVLTam9jsHo07BVztPBK8Wm4trFmzj/guymDsyjf3lLYTrlGwrbvAbM9pYWMe1w5JJDU/h+hGp2JxuDFoFEXoVjRYn/ZONbCtuRBDAYncTb9T4LNwTe8ey7ogo9qFVypBKJByvN/PpdQP5dEsJh6pMjM6KQi6V8NKKwxyuNjFnRCpmh5t+SSc2OVaH28/AQ7yWJrpFiyVqT5uCmSAIqDv5k2uVcs7vEcVPHcrK43vGANAzNpjXZ/bh5wPVJIZquWxAIlHBamxON/srmrlz0W6aLE4yo/Q8PzWH8kbLmSUgAX0SQ0gM1VLSZuCikku5bXQGUolIuBuUGsr3eyt8Kkl2l4dNRXVolf57eKNWycqCGtYfqePB8VmkRejRqmQYOonoRASp+deFPbhrTDeQiJMM7ZuJcL2SVy7NpcnqRCaVcLCihR3HG5nYOwaNQu6Vbf1uTwU7SxqZmBNLRpSeOIPGL/MPVHU5HdSY7Ix9eQ02p/h3f7GtlJ/vHEFS2G8wMwmOEUvFLRWiBrg+EuqO+J8X2w+DRsX947LYemyD91r3SzJSaxIJoTeMTPNt26j0oq2mQgsFSyGiO0x44USG/mdAphAD8R37xP63MVmsMihOw/VLIjlr7/kX42wAb0Oz1YnT7SFEo/B6EndEvyQjOfEGZBLJ75qNPh04XB6W7avi3i/3opBJWDR3sF95cXLvOAynsDbtjCarg692llPZbKNnnIEvrh/MxsI6esYZ6JMQAgIMSA5lZGYEaoUUtUIkVbVjVLcI5gxPZXNRPfvKm2mxuvAIAh63QLBajksQAi6KfRONhOvVAbWeBUHg4YnZfLGtlD2lTRypMfHZnEE8v7yAo7WtjO0RRf/kMK5r6zHfM7Ybb68tZPH2Mr6/ZSiX9I3jky0lfLbluDc47yprwuJwM/fjHQxKFc0xwnQqgtRyxvSI8um3SiR456FtTje7Shq598u9VDRZGdMjiiem9PSKjhg0Cp66uBd5yaGsP1rHiMxwpuTG4fEIbCis54LsKDJGpSNIBF5acYgHx2dhc3m44ZMd3oX8cHUrL/x8iFdn5P4mAY52G9FfC6rpFR9CVkyQ3+YxIkjNkhsHs7GwniaLk/OyoogIUtJqc/KviT34+UBVwLGjknorMwYk8umWEm8JPlSnZEhaOBe/tQGnW2DZviqen5rD2B6BDWuC1IqAXAJ5m6KXTi2npN7CyG4RhGgUaBTikjMiM8JLnCxrtPLWmkJeurQ3GqWU87Oj+KmDdv8Vg5OQSMT747dcuyU7yrzBG8RNy0ebivnXhadQU+sMfWQn5TEJ5M6C3Z+KP0bnwIDrQCYnLULHL3ePZNWhWsJ1ohDOPYv30GJzcfmgJP9rpY+EMY+LfXG5+q/JZJU68Z8h/s9/7bP4r/C3D+Aut4fiejOP/3CQskYbU/vFM71/QkBhkzM+e9kJjRYHj7UQjgsZAAAgAElEQVTpVDvdAh9uLOatWf14eeVhakx2pvWLZ1h6GO9vOMbE3nFEBqlOazOhkEqJMaipbLbx4cZivtpZRs84A5fmxZ/Slam+1c7CrSUcrzdz9dBkPIJAUa2Z87OjERBICtfSbHXxS34Nd47J5M1VR7G7PPSKM3Db6IyAwdvl8fDJ5uPMW1vE5NxYJuXGcqjKRL9EK92ig+iXHEpUsGjE8vL0XCKD1Kw8WO2d9f5o83HuGdON0d0jOadbJD8frOaTzcfJSwr1uqRtLmqg2eIkTKdCLpMyo38CJQ0WvtpZRohWyWOTsr1s3markyvf3+YVVPnpQDVhOiX/urCHd4wpTK/immEpXDYwAY1CrMqUNFh4ZeURXll5xCvIolHIuGtMJmWNVj/uxK6SpoACNV3B5fbw84EqH9/r8T2jeWRSD6KCO8vYqpmcG+dzLL+qkbWHa5kzPIVgjZKFW08E6mCNnFHdI1HJpfx4xwi+2VWOTCJhXK9obl+422fTuGBTMRlRQeRqlVgdLiwONxVNViKCVARrFAHbMnBCFKbjZrAdSWFaHhifxWu/HMHh8jBzYCKjukUSqlPy1EW9GNMjivVH6hnVTdxUnv/KWm49N4OL+sQF5C0EQiC3v9NxADwldGFw/lNwzgMiC1up82bNKmczsc2HuNS9G4s0k6OeBKxOkfzpcnfx4Su1Z32uz+J34W8fwBvMDi5+c6N3YXt2eQGCIHD9iNQ/TUK1HYIg+IiEfLu7guI6M/Mu7wfAW2uOMvmNjTjcHt5cXcjyO0ac1liUUafksck9mfr2RmxODy02F8lhui4XXhDHzUobLew83sjwjAiarC7uWrSHJ6f05LbRGT6EIqvTQ3mjBbVSzsfXDkQChOqVXc7K25wedpWK2XJHRbOsmGDWH61jW3EjIRoFlw1IoHt0EDPf3ewTDGcOSOSDjcf4YEMxEglcMTiZt2b1JSJIxdyPd3jP69jbDdOr+NeFPbh7TCYSCYRqlV5TiLIGi48aGogqcXeMcfnMIcukEh/RF41Cxv9j7zzjmzrPPnwd7Wl5720MmGGWmWYGMiGTTDIJIZNmNG3TjKZt+nakGW3S7NmQUUhIICGLkMVIgLDCxmC2F962ZG2d8344smwheTFCILp+Pz74kZAlSzr389zj/0+L1jM8O5bLitIxaVUkR2t5feV+phQkoVcrA6IuAEXZMUHiNF3RYHfzz3aNfgCfbq3i12f1IdEsBanwhcOsU7JwYzkfbCjjjL6JvDlrJCt216BSKhiTF4fV4cGUaEKvUjB1YHLg83ZkZ7hOpaTWL2y0taKZLWVNjMqN48XleynKiuHMfsk9lvWMNmi4fnQWF/mdrkw6VeDzGGfScumwDHolmHj4o21s9mdY/rx4O8OyYsIGcJ9PxOryotco0fqD9EVDUnl+WSnNDvk7ZdKquGZkqI/4UaGPDj0te5yw/nUUXz2CFtACg/pfwR+mzOGtHxt/Nq5jEU4ffvEBfH+dPaSDd8H6Mi4rSg924fkJ0KmVTOiTwLKSNpMHrVrJ6r11JETpqGh0BQJNg93DF9uquHZ0drceu3eSiWW/nURptY2kKB1xJk2HJ5kmu5vHlpTwzg+y5aZCgCcuH8yeXvG8unIfZ/VPDgrgHq9IYXo02fFGDta3kJdg4tUVe5lzRn7YUTejRsm0gSl82+51gmywkmTWcN85falodJIWLc+zp0Xr2et3ryruFU+tzRVUJ31p+V7G3jiCx5aUUO2fA89PNIVkUVpnro8k2aKnuFccZ/VLxu0TWbSxnBSLLqAY1xFxRg3vzB7Jit213PLmem4ozmZC73gqGp28/t1+Hr9sEH/6aBs1NhcD0qL4xyWFXSqhtUcCnO7QpiuH24fD4+twA1Zrc1HZ6ORwk4tFt4/h6a9L2VnZjITcV6AQBNQKBQUp5oDN5ao9ck06JVrPgLQotpbLDX8KAW6ZkEtmrIHfLtgceM8EAZ6+cggL1pdRlN29+foj0aqVJHbwN3Z5fLy0Ym8geLfyzc7qECnYOpuLDzaWs2RrFYMyorl5fC5JUToSTFq+uHsCH2+uwCtKfmetjjNOHq+I0+sLTXNLkqw0JnrkOnhHNWpnI6x4ImhJs/1dpo17gMlDeve48fRni6NRFnIpXy8Ll5hTIk1sJ4lffAAPJ7ifEq07Pqm2HhJt0PD4pYN4afkeviutY3BGNJcOS+e2t2VXrxeuGcY3JdWB+x/pW94ZLS7ZFay4V9fyfi1uXyB4g9y1/eTSEn53dl9eXL6H1qx9s9ODyyPiESUeXLQVs1ZFjFFDeaMDlULgV5Pzwz6+IAicUZDEbRPymLtqP0atigenFpBg0rBdhOnPf48oySfep68awnu3jqakyorbJzI0M5q/tBPaaeWbndU8NLWA577dQ7+UKC4tSu/2BVOrFpg+NJ1XV+4LpMD7JUd1OCfeikIhoFYqePjDrUQbNIzOjeM3723m4Wn9mPXGOlpcXh69tBCTVj6pp4WxdO0Mi07NDcXZ/Ofr0sDakIxoREkKnDKPpLLRwR8+3MqXO+TPiU6tYN7sUSRG6fj9+5tZvlueoZ9WmMJDUwtI9qe3p/RLZMH6Mt5be5CXri1i7f56DtbbOad/MhWNDkQI2nBJkjz3PnNs9gnx19aoFIzIjuPTLVVB60OzgscEW1xenly6K+Dvvu5AA6v21DH3xhHEm7UkW3TcNC6XrqhqcvLyir2UVFm5ZGgak/okyrPnPh8c3grvXS+bmyQNgCveDO5Mb494xIZLkvtELEejx/5zxOOEzfPhs9+1rU35M4yYHWry4vPITXLhsFbBlveguQqGXSfX3zsziYkQll98AI81arh4SCoLN8qd1kaNkj+e3x9LmDndn4IEs5ZbxueRGq2ntNrGta+uCTgXKdulTM1aFecMSO7y8WwuL1vLm3jiixJ8osRdU/IZmhnTaXAKN+Pe2OLBpFXxyAUDiDNpabS7OFjvYG9NC/lJJvomm9lZZSXOpOGJywbRK9Eka154vIHGpfbEGjXcNSWfmWOzERCINaipbXHzh0VbAxaePlHigQ+2sPSe8Yxpt/EozosP0T4fkxdHv1QLT14+GJWiZ42Gu6ps/PrdTYGfZ89dx1f3TuzW/y1vcCBKUJhm4bvSWg7U2dl4qJFnZgzhnTUHmbtqP3dM7BX4m/p8olwrb3d6rrO5ONRgp9bmZqDfxUmlVKBVK7l2VBZZsUaW7jhM7yQT5/RPJiVaF+J9DXC4ycGBensgeINcrtha0YxY1hQI3iCLvUwrTOXsKB21Nhevf7ef9QcamNQ3kYpGB2+uOoBBo+S/3+3nvzOHB6Re29Pi9hJv1HaZqTgaBEFg2qAUlm6vCgjGXDI0jX4pwSNWLS4vC9YHfxa2VzZjd3uRk9hdU2N1ccVLbXKuK0true+cPswam4vGUQvvXCrrhIM/mN8QXqlMGwUjb4Hvngosib3Pw63QcZqEb1nE5qs/B699+3d5vK41ANvrYN9yeX4+dyL0OU9erymRO93zzoBXz4Rmv5bEmufgpq8gbehP9SpOG37xATzGqOHhaf25fWIv6lrc5MYbT47qUzsUCoGFG8uD0ofRBjVpMXpuGJONQaPkmlFZ3TphVjY6uOrl1YHmqetfW8viOcUMTI/G5fVhdch1w/azxCat3E27p6bN2ODqUZn0TTazp8bGs9+UMi4/nm3lzdy/cAsZsXqeuWooS7dXcc6AFH67YBM7Kq3o1Ur+fGF/zhuQgimMBrnHJ2LSttU+vaIUYhTS5PCEZBrG5cczdWAyn/jdqy4akhY4mfW0Fuv0+IJEdEDOOHyxrYpbJnTiiewnPUaPUiFQ0eRg2iB5tOyZr0sZkBbF2f2TGZhm4eMtFVRbXfzp/P68u/YQm8ubuGhwKmPy4hEliTve2cDqvXIK26RV8dGcYnL95iGJUTrOHZjMhD7xCIKAUhDCfj4b7W6aHPII4pEkmrV8sqUyZH3d/nrG9orjljfXs+GgXPdes6+ei4ekMSovjmf8J/9nvinlV2fkh9ibzhiRyaAMS5eNkABNdg92txdBkOfWu8puAMSbtPxnxtDAOGWt1UlZgx2vT0KvUVJrc+HxiVj06kDpBOS0f0/6Vxrs7qDXBfDf7/czfVg6iR57W/BupXKTfLo8Eo0Biu9CTB+BYseHNCaNoTJpAr97Yyev3VD0k5fkTgxSsHIcyC5tkj/z4G6BZf+ENS/IP299HwqWQv+LZbeuhL7yYzS3U7yURFj2D5j+amQsrYf84gM4yEE8xqghfML3pyfWqOHpK4dw09x1/pq1lqeuHML8tQdJMms5rzCFaIO6Wxep9zeUh7WBTLHoeXnlXr7aUU3/1CjuO6dvoF4db9by9k2jeGHZHraWNzG1MIXzBqbw9093BARNHltSwoNTCzi/MIXFmyuZ8fJq3rhxOM99u4cdlXInuMPj4/fvb2Zsr/igAN7skE03Xli2F5NOxT1T8smMNaBXKRicER3URFWUFYNWHfw640xa/nrxQB6cKpuLKBTyad3u8vZoPh5ApRTIiQ9N3WWHWWulyeGh2eGhqtlJZoyBZ2YM4f4PthBj0DA+P57lu2vZWt6M1ydR3Cued9Yc5IVrhgWU4ECWsf3jtAIGZ8YEgjfIGZPHlpTw+GWDApsqo7ZrRTa724vTK5IYpSXaoA7yUteqBM7ql8SHR4jRTC5IxObyBoJ3K4s3VfDWTSMDAdzq9LK/zsa82aN4Y9V+SqpsTB+axsjcuG6Z+tTZXPzhw618trUKhSBw7chM7pzSO+ykx5GYNUpWltZyVzvtgn9OH4jbJ/LQom1MLkjk3rP68PsPNgdun1mcE3bD2BHhGguj/PaeHm0sNbfvQVRoULnqSf7yTrn+25FSmSGOhfbBbJDS2bPNwerFcrln6fbDzDheDXQnE7UBep8HJZ+0reVOktXYAFzNsO614P+z4yMYM6fzx5Ukwog2RuiCSAD/mZIdb2TezaNweUU8XpH7F25hlT+V+PjSXXx97wSy4rp++9rbFrZyZr8k/vbpjoAcamm1jc1lTbx7y+jABTnZouP+c/tSb3ezbn89dTZ3iBrZ89/u4fHLBrF4cyUtbh82l49NR3QwixKUNdhRK2XN9ziTlpIqK1f5DUAAvtx+mK9/M5G0aD0vXDOUv326g/UHGhmRHcvvz+tLrDE4SNTaXKzb38Duaqs8RratiheX7+WK4RncPSU/5P6doVIouG50Ngs3ynPyINufDjtCkrUVq9PDG9/v50n/DHNOvIF3bhrF1/dOwO7x8Y/phTg9PlxekaomJ3f+byNeUSLZogsyOQH4eEsVqWHq4oebXbi9Iq0vo6HFjdPrQykIxPrT60ciSbCjspl9NTZeua6IV1buo6LRwfShaRSmx+DyidwyPpe5qw6gUgjcNjGPeJM20GvQPsth0qlwtuuev2lsDkP93d/3ntXH/9y6d+nw+USWbDscqGX7JIn/rjrA2QNSGJ0X5xfQceHyimiUCuKMbdMBADUtbv76yfagTWhqtIFb35KnDb7aUU1OvJH3bhnNgXo7BclmUix6onqglRClU3NO/2Q+3yY/R4UAf5jWD4NawboyD79+dxOVTU4GpVv4z1XvkCnUgCl8I5skSaw/0MA7a4M9FY484Z+y6KPh/KcgZRDs/Qayx8n1b0O774tCJeujt9LeXrVmJ8Tny25nzRVtt0/8Pegip++eEgngP2PiTVrcXpHfLNgUCN4gnzY/2VLJ7RN7dfkYUwqSeCVhH3tqZAOS9Bg9eQkmFm8ODsb7altC6oZWl5cbXltLyWEr7982JuSxnR4famVbLTY5SsfovLigmqRKIRClUzPp8W/JijPy3NVDeeUIvWiXV+SbndVcMyqLZIuev11SiN3txagJPXnW2Vzc+tZ61u2XdcmfXLqLf18xmEEZ0cxddYBeCbLDWk9q4MkWHR/NKeZAnR2tSkFKtL7D8oTN5eXfX8rB+75z+tA7ycyz35QyMN3C5IIkYg0af2rXQ7JFx3Wjs7C7fZjDnAhrrE4GpkVj1CgDfQ4gC5e0SnJWNTmY885G1h1oIN7fXzAiJzaoht5k9+D2Sby8fC/3nNmHZqeHq0dkkmzREWtUB1Lus8flcvWoTEQRGuwuDGolNVYX143OCjjcATxwXgHlDQ6mFCQya2wO/VMtAWU6tVIRoofg84nU292AvMFoX5+vt3v4rp35TCur9tYyKjeWXdVWZv13HeWNDhLNWl66bhgDUy2BIC5AUDYB5DJJi7ut1PLKin28s+Ygy3478ajS1DFGDX+9eAA3js1hT42NMXlxxJu0NDo8zJ67PpDC31TWxO8/2Mq/rxxMYgePJQgCM0ZmBjWBCgJMH3YaiaSYEmQN9BE3y2py7RvVdNEw7jdQtkYWptn7rezoVrau7T6f3AvXLZZP8c2VUDQzIiJzlEQC+M8cpQLSw4xipR2x5vL4ZGfDIxqKEsxa5t8yigN1LfhEAunipChdkGypUiGEpBIb7e6AMMr+2haKsmKCDD1uGJPNwTo7Y3vFM3t8DqnRen53dh9y4w1kxBpx+0SSzFpe/34/NpePbRXN/Pe7fcSbQlOn7acBOhr3AtmQpTV4g3zyfHHZXq4ZlckP++r5fFsVFw1JC2sW0hmyd3rXF3+H24cowRl9EzFqVcx6w39hWgNDMg7xzIwhzFt7kNe/O4Dd7eXes/pwvX/U75wBSXy+tU1h7Hfn9CXOqOGjOWP555Kd1FhdXDsqi4l9EhAEAavTwyMfbw/8zWttbmbPXc/y+yYFBfB6u5vHl+zk4fP7c9Mb60iM0pIUpeOiwalMH9p2YYw3a6m1wYrdNazcXctVIzK58uXV/On8/rwxczglh+XglRGjR69RctGQtC5P2o12N0u2VfHMN6UoBIFfn9mbSX0SidKrcbi97D5spSg7JqQGP7aX7IF+21sbAt7r1VYXs99Yzyd3jQ2ozRm1Si4rSuet1XJAzI4z4PL6uHZkFnPb9S4Mzog+Jt2GVvXFETmxgbXyRkeInPHa/fUhgixen0h9i5tam4tog4YUi2w69O8vd6NUCNx7Zu8eOwf+7FGqgk/dgXWt7KYmII+bzVoK+lj5RN6wX5ahHXINGGKh+K6f+lmfdkQC+M8cpT/Fu2B9WdCM85g8uQPW6fFR1mDn2W/2IEoSt0/MIzPOENT5HW/SBp0oRVHi75cMZObrawNiJ3dNzg8Jmq2WkwD/+Gwnz10zlO/31LG9oplphSkU94pHp1Zw/uDUQMrS6fHhk+Bvn+4g2qDmvnP6Bj3mBxsrWHRHMYs3VQTm7/MSTGTFGahvcRFr1Pp16Ak75+ztwKyktXltaFbMCRXMMOlUJEVpmVqYwn++CtbE3niokfJGJ7VWN6/PHM6sN9by+BclXDg4lfQYA3+9aCDXjMxmW0UTZ/RNJNmiQ6tWkpdo4onLB+HxSkQb1AGBFofbx5p29XEAt0+kptlJcruxpLIGO59sqUKnVvLhnGIONztJNGuJM2pDegJ2VjZzz/xNDEiLYnNZE16fxEOLthJn1JAWo2fl7hqevmoIGpWSTnR+Auw6bOW+99t8w++a9yOL54xlYLoFm9uL2yeSGWvgsqJ0Fm4oR6UUuLE4h5x42WZ2n3++X6kQuHhIGlMKknB5RERRQqEQiNJruNPfQJcTZ0IQ4Ps9dZzZP4lLhqXx9093MiwrhpnFOcddY96oUaJTK4LkWAvTo0MmAEprbFz+wiqanXKT3r1n9ua60dm8cn0RAnRbOe60oKUaXhzf5m625gW49TtI6A1n/Z/c8KY7Abaov1AiAfwUIClKyyd3jmVnlRWtSkFugikQkA83Ozn3qRUB6cuPN1fyxT3jyUvo2C1NoRAYlhXD8t/Jwi6ZsQZijGpMR9QNLXoVY3vFs7K0lhqbiytfWs38m0cye1xO2ODa0OLio00VPPGFnGKubHIy6411vH/rGD78sRynR8Tq9GDSKvj0rnF8vbMao0ZFZpyeu+f/yDUjsxjTK46/f7YTlULgnim9yYozBJ02E806cuONAWEXkDvkP99axaB0C9ePzjqhkrcJJi3v3jKafbUtYXtuREnig43lOLwiC24dzbvryqhvcZMeYyDOpGVsvpax+aGz+CatOmTqSadWMjgjmq92tnVBqxRCiA99r0QTaqXA+xvKWbixnGiDhhkjMrhzcqgPd5W/zl/Z6AxydatrcVPX4mbW2Jxub4BEUeK9I0a4AD7aVM7AdAtI4PKIzF93kH6pFt6ePRJJgjSLPjAqmJdgYk+NjX9dPohd1TYeWrQFvUbJA+cVMLZXPGadmsQoHVcOz+SFZXt49ps9gNx/ccOYbJ69eghROk2Ppw+6otbmYs2+ep6+cgi/WbCJZoeX7DgD/7y0MEi0pr7FzQMfbAlsRiUJnli6i0uGppNq0ckd7CUb5DRzcuERmuqnIbuXBluT+tzw3b9h2r9BpZX/RThuRAJ4N/CJEo12NxqVolvjL8cbQRA6TPG+t+5QkG61T5R4c9UB/nh+v06lNg0aeXyrs9RerFHLU1cOZuOhRnZWNnNW/2RSLLoOFcAONTj4csfhoDWfKLG1oon8RDPbK5t58Ly+GDVqlm4r58eDDVwzOpuqJicPT+uPx+fjsy1VfOWfY/5qRzVf3juB7HbNevFmLfNuHsX8dYcoqbJyRVEG+UkmzuqXjEGj7NZI07EgCAJZcUbijBrmTOoVpFM+MM1Cg92Nyyvy+dZKLhmShiTJY1xHQ5RezSMX9qe80cHOKitmrYq/Tx8YolEQY9Dw1qyRPLBwCxWNTs7ql8TM4pywQW1Mr3i0KgV1LW7KGx1cMzKTt384iCRBv5Qobh6f26FIzJEoFAIDUi28RxkapUK2hfWK9E+VZ7VjjVrUSoGLh8gys4fq7RSmR7Otsplb31rPlIJEnrt6CM98U4rN5Q10vQPc9tYGvrxnfOD7Znf7eGVFcO/Em6sPcOuEvOMevEHenPzt0x3cWJzDh3eMxSdKiJKEThn8nfL62rIIrUiSPKmQqmiAlybKXesAMTkwawmYwhvDHOvzPVEmSz1CCiPqI4lEWsxPDJEA3gX1LW4Wb6pg3tqDJEXpePC8ArLjjSfc2KS7hJPmtOjVXepkd0aD3Y3N6cXtFbEY1EwpSGJS7wSqbS5eXL4Xr0/k6pFZJEVpgxTrXB4fWXHGoLEogL7JZv4zYwg6lVKe+9aqGJQRTZ+UKGa/sY46v0jIxD4J3Dq+bfbaK0os2ljO3VOCT5KJUTpun9gLnyieFMU8AJNOzVn9k8lNMPH++jIyYw0MzYrhV//bAEB2nJGqZqcsPdsvKaB41lPSYgy8ddNIf8OggmiDOiTA6tRKRuTEMv/m0YhIsrGKV6Ta6iRaH3w6jTNqWHRHMf/4fCcfbCjnj+f3444zeuHxihi0qh7LfU4dmEKKRYfFoMbrk1AIAn2S5eyPUiEwIjeO+hY328ubGJQezbaKZn67QBbN+XJHNV5R4p/TC3lw0daQx/6mpIZeSf7OZClUeVCUJKQTFBgsejWXF2XwzyUlAT36VIuOD+eMDbqfyS+o1F7T36JXyz0d615vC94gK7mVLJGVx7qJKErU2Fws31WDhOzilmhqMzFqsrvZXW1j3tpD9E02c8Hg1ONqddxj8s8CfYws+AJyR/rYuyMn7xNEJIB3gk+U+HhTBX/8aBsAOyqtrN1Xz1f3TvQbW6hOukHBBYNSeWnZXmpscn08xqDmyhEZR/149S0uHv5wGx9vlpuO8hKMvDN7FKIocea/lgeael7/bj9f3TsBvVpJs8ODBGTEGrhmVCbfldYGGuTOHZBMboIxZLQrxaLjzx9vDwRvkKU6rx6ZSaJZG6j3dxRQlAoBpeLk/u0tejXDsmLon2rmyx3VXPnyKkRR9i7//bl9A6Nmy3bVMDI37qh/T3eCqiDIqfV6m4tHP9/JgvVl6DVK7ju7L9MKU7H4u9q1aiUFKVE8c9UQHG4fjQ4Pe6pt5CeZseh7fjkQBHhz1QFW+DvN8xJM/G/2yMDtrQ2JmbEGKpsc3D3/x6D//21JDQiyr/rS7cHZm4KUtrEio1bJ5UXpvNMuUJ5fmILmBG2ktWolN43LIcaoYfGmCvKTzPz6zN4hc+8GrYp7z+yDQhD4fGsVOfFG/nbJQOIMymCxklaaK0LXOqHa6mLq0ysC35MYg5rP7hpHskWPKEos21XDnfPa/qbz1h5i3uxRIWWWnwxTolzz3vgmOJth+Cwwp56c5/ILIBLAO6HR7mb+ukNBay1uHxsONPDODwfIjDVw15TeR2XkcLxINMv18ZWltfhEifG9E0g4hjTynpqWQPBu/fnVFfsoyo4J6sh1eUWsTi93z/8x0BU+OMPCK9cV8fzVw3B6fMQYNVj0qrBz2QqFENQF34rV6WXGiExeXL6XWKOmQx/qnxM6tYoJvRNY8bszKG9woFQIPP9taUBJrzP9eZ9/Dtrp9qFTK4k2qI86qyD6xwtbT4Meh5cHF22lKDs2EMBb8frkFHHrbL9Bo2T+LaPYcqiJwZnRpMXosei7br7aXN4UCN4Ae2psvPPDQWaOyabZ6aW80UFWnEEWHlIoSI/RB73vSVFakGDGyEw+21rFzip56uHs/kkUtJNNNWpVzCzOoW9KFOv2NzA4I5peiSZsLu8JK5vEGrXcOCab6UPT0asU6L2N0GKX7UTbEW/W8tDUftw1JR+1UtHWTDfyljbPcACFEgov69FzWLixPGiT22D38N66Mn41OZ/6FneQTj7Img7VVufJC+AKJVjS5LnuCCecSADvBI1KQVKUjm0VwQIcRq2SLeXNrCyto7RGtvs8WfKrgiCQGKXjkqHHZ46y9LAtZG17ZTPjjmi8KsqKYcOBhqCRrh8PNfHF9sNcUZSBT+pc1tSiV3Pl8AzWtxtL06oU5Cea2F7RzJK7x2HQKIk/ReQnzTo1Zp0avUrBI340cKIAACAASURBVB9v56ud1agUAteOygoKREey67CV61/7gWqriyi9iuevHsbw7JijCuJ2tzfkFAuwZm8dfZKDRTLqW4KFeexuH3/7dCcT8hM47+mV/PWiAVw+PKPLUtGuKisKAc4dkMIZfWVltwSzlgUbyvjLx7IKmUoh8NoNwxmTF8eL1w7jxv+u5XCziwSzlpeuLSLOpEWpEHjrppFYnV5U/pHGFreX/QfspMfo0aoU/GnxNpwekT5JZpZsq+KRj+v5+yUDyYrrWDVPkiSqrS4+2VyJzeXl4iFpIaWfzlAqFcQq7FD6Dax4ElQamPxHSB0qz0D70WuUodm4mFyY+Rksf0xOJU96UHbu6gHNzlDJ1iaHf00grCb+z6IWHuEnIRLAO8GsU/PgeQX8sK8+cPqc1CeRBrsn8CX6YV89Do+P8Lpdpx6j8+IQBIKUry4ekkZBihmzVhXQKs+MM1BaExrsN5c1MWNkFl1dHgVBYEpBEn86vz9vrTlAnFHDHZN68fyyPXy6pYryJgePTi88jq/spyHWpOWRCwdw37l9EfCnkDtofKyxurjj7Q2BckGzw8vtb2/gi3vGkxTV8wCu0ygZnhMbZFoCUJgROrYjC68EU9XkJNY/o//4FyVM6pvYYZNjs8NDi9vLOQOSGdsrnu9Ka3n6691Y9Gr+c9UQ7pq3MXBfryhx3/ub+WjOWPomR7H4V2NxeUS0agVxhjbhl9Zxxya7h6e+2sVrfnEZk1bFp3eNZUCqhReX7w3a9PVO6njaAtpS0LV+jfhnvynl87vHh5XP7ZDD22QDk1bmXgB3/ADa0C7/IHRmyBoDl/0XUByV0tgVwzN4ZcXeQKOqSiFw9ShZkjXOKCvjzZ7bJpIyIC3qmDJwEU4tIgG8C7LiDHx17wR2H7YSbdCwt7aF+99v6zw2aVVhd8GnKvFmLa9eP5z/+3g7zU4P142WhUWi9WqW3DOeBevlrvcZIzI53OwMUvAC2TGqu8QYNVw7KpPJBYl8uqWSv3y8nd3V8qZgydYq/nR+/x5JYv5ciNKruyUk45OkoHG4CwalcvWoTGwuL4LVSZxR26PPlkqh4KoRcg/C6r31KARZFzwrNjRYZcUaiNKraHa0lUWmFqaw0h/8HR4fTQ4PiVFaVIrgU3h9i5snv5D94kUJxufHc8ekXvzj850ckKC62YXHJxFv0uATJRrsHg43O5EkCaVC6LLJqtnpCQRvQZClTR9auIVHLx3ElzuqA6qCFwxK7TIQf1tSHQjeIJd+Xly2h79cNKB7jag+N6w/QttbkmDbIpjwu+C7ihJ1Nhe7q21EG9SkWHRy+egY5p6To3R8dtc43lp9AJVCweXDM0iOkgO0IAiMyo3ls7vG8eGP5fROMjM+P+GET2JEaIfHIWdXOrJNPcFEAngXqJRyGj0pSofL66OkyordrxMtCPCnC/oFZC9PB0xaFZP6JDAgdRRun8jqPXU8+tlObijOJtaoYfa43MBctkGr5MnLB/GvL3chSTBnUi96J/XslKH0S3M+/kVJ0DhcnEnL6bMtCo9OJfDStcOotbmpbnaSHqtn5utrsbt9JJq1vDVrJL2Tw/89G+xuSqttfL2zmpE5sRSmW4g1yifY564ehsPtReFvtAw3+hhn1LDo9mL++skODjXYmVqYQv9UCy98K89ZXzUik/UHGsiOM6DSBAe6XYetvLWmTSp0+e5airJjmdA7kW9KqnF4fMy/ZRTNDg8KQUAQBJZuq0LXzYbPBn924MLBqcwam0Oj3SNrwAsC824ehdXpQaNSYNKquhRJ8fhCu9Q9PjHE4KdDBBVkjYUtC4LX40JljA/V27ng2ZWBTdG4/Hj+fcXgYwqocl+EhgsGpWFzeYnWB08hmHVqClLUnZZpIpwAHI2yteyaF8GSAaNvh6g0OSj8hEQCeA/QqpSc1T+J5TmT2FfbQk68kZgwYz2nOoIg4BUlzvrXcux+je73N5bz1qyRHKpv4dyBKZh1aix6DRcOTvPXx2VP7/ZGFLU2F9VWF0pBTo+2XsiaHa3WkgJRejVmnYrfnNWHv3+2E5BPXH+7eGCQvOqxYHd50aoUQc/tp6DW5uJQvZ0Wl4/eSSYSzNrAeF+D3c3iTZW8smIfBo2S564eynlPrwioflVbXdw9/0fenDUiJAA4PT7eXn2Ax/2COc9/u4fLi9J5aGo/ovRq2eWri7+dUikLAv37ysG4vPKc7turDzK5IJExefEkW3QIECSi00r7FHYr2yqauH1iLitLa4gxqJnzv40BA48+SWbeuHFEh9kUq9NDWYODxZsq6J1kYlRuHFePzGByQTKXPr8Kt09EIcCj0wuZNiilWw5orUwpSOKfn+8MCK2oFEL3ZsftDVC7C3Z+DBkj4NqFMP9acNtkI4/s4HGyFpeXx78oCcporNhdy6EGxzEF8Fqbi1lvrGXTIbkhMtao4aM5xaTHhJoURfgJObgK/ndl289b3oVbV4I5+Sd9GpEA3kNam5UyYk/vL9CSbVWB4A1yevC99YcwqJWM650QONUpFUJYgZkaq5OrXl5DqT8lPjjDwivXD0cAHly4lSXbq9CplPz6rN5cPiyDK0dkcnb/ZPbXtZCfZCZGrz7mgNvQ4mZlaS0f/ljOoPRorhyR2aOL/7FQa3Nxw+s/sLVcboCMN8ma56015fX7G3j4w22B+9dYXUGSnSA3D/rCHBWbHR6e85+UW3lvfRn3TOndYw14s06NGTmITuyTiFqpYM3eOoZlx4RtjPT6RIrz4njsiPXReXJn9kdzivliW3WQ+1bJYSsrdtdwWVHoeKMkSazeWx9Uxx2UYeG5GUO55Pnvcfulc0UJHv5wG+Py49Fbun/ZSjBp+Pzu8by5+gA2p5cbxmSTGtNFY6TXBT++BV881LbW70K4eZkcwKPSQtzI3F6RikZnyENVNYeu9YRt5U2B4A1y+eKFZXt4eFq/k6aB8IvH3iCry7WnpUY+kUcCeIRjweM3VihrcBBv0mDRq7utxSxJEi6viFalQK8OvTjoVEpcPnl8LKWLst7CjeXsb1ff/fFQE6WHbWw81BiwbXR4fPz1kx2Mz0+gT7IZi17dqQ93T3B5fbyxaj///lLWK/9yRzWfb6ti7o2hJ9oTwY8HGwPBG2QjkpdX7OWBcwvwimLIeKLHJxFr1FDfbmRodF5c2DlniVBRk2O1Uzbr1BSmW0iL0XNZUQYxYfzmfaLElvImdlQ288B5fXn6q1LcXpFLh6WTHmPgypfXsOb+yZQ1hFpnHqlW1kpdi5vH/UIprWw61IQoybaq7XF4fCGbnK5QKhUBkx1J6maHtqNR7hxvz/YP4ay/Qnx4B8Bog5oZIzPZcLAtO6FTKxicfmy63xVNoRuA8gYnbp/ULa36CCcCqc3/vD3h1k4wPw85sQjHjb01NiY/sYzpz3/PhMe+5emvdtMYpuP4SOpsLuatPcRd837kvXWHmNAnIUgC1KCRXaFW76kjuotTXqPdzbj8BObOGsGbs0ZQ6L+I2T1elu+uCbl/+4ve8aLJ7glpsNtW0RziLnWiqGgMnXEva3DgEUXUKgV9jugVePabUl67oSigYT8qN5bHLy0M+IrbXG3jRGatimv9ncitnN0vCcMxigoJgkC8SUuCWRvW2auuRbZyfXDRVqYOTOHV64uYO2sEZp2KO97egE+U2FllZcbIzCMeFy4a0nFzo1cM3Xr4RJHiXsHz1nkJph7LptbZXByst1PZ5MTq7MF7L/bscyIIApP7JvL3SwbSPzWKCX0S+PCOYrmccQyMz08I2cRdPyarQ7e+CCeYljrY8CaMnhPcuJbUH+LyOv5/J4jIp+A0otHu5g8fbgsKUq99t58bxmR3egpvdnj40+JtLN4kC7gs2VbFHRPz+GjOWL4pqaahxU1xfjwfrC/jpeuKOr0oNdrdPPftHl5avheQhTqenTGUOe9spFeCieK8+CBvc5CtII83giBvOgIzs36O7Kg+VkRRorZFTn9rVQpijWrUSiWT+iai/mR7UBPVdaOzAjry147O4uPNFez3p5qVCoHsOCPzb5FV7yTgxeV7+O93+1EIAtePyeaOSXnE+h3Gbp/Ui6FZMXy+tYqx+fFM7pvYZaalxupie0UzHlGkMM0SVJPvDh6vGDgVW50edh228uWOalaW1lKYZmHWuByy4w0oBHjqysG8vGIvaoWCX5/VmxRL+LR1rEHDnDN6cU87hbZeiSYMGhUPnlfA89/uYfXeegakWbjvnD7E9qBhtMbq5KY31rHJL6hzWVE6959b0HVQ1VnkC/SyR9vW8qaApvOyWYxRwxVFGZzVLwm1UtGjcoZPlGhocaNQECR8FGfSsOiOMfzjs51YnV5mj885Id+XCN1AFGHHR/Dlw1B4Odzwiex3Ht8bsopPilGNIHW7HfPkU1RUJK1bt67rO/5CqbY6ueiZ70LSbovuKO70S1/Z5GDMP74O6sxVCPD97yeTbNHhcHtlgQ2lEFZVrT37am1MenxZ0NqZ/ZK4a7JsCenyivxuwSa+3lmDVqXgzsn5XD0y87hbLvp8Ip9sqeLOdvPI0wam8H8XDziuv6ukysoNr/9AZZOTaIOa568eSu8kMy6vSI3VxT+X7MTu8nHz+FzG9IoPMiKpsbqosbnQ+jXO26f2P9hQxq/f3RT0u96ZPTJgI9uK1yd2ywe72urk0udXcbBe3jAkmLUsnlPcI432WquLS1/4nqmFqYzJi+PzrVUkW3RM7JNAi8vLbxds5kCdnSEZ0Tw6vZBNZY3YXF50aiXTh6Z3eHpucngoqWpm/tpD9Ek2c/GQNBLMOupsLkoOW5EkWTwpK87YbctQryjy7Nel/OvLYMvX924dzfDs2A7+VzvsdVC2FrYuhEFXQnw+KDVgiIdwm0CPA5yN4HWDWh/2Ym53eXF4fFj0weWJRrubT7dU8urKffLGZWoBA9MsQV7szQ4PPlE6aYJREZClYd+9Vg7aAGoDpBdB0U3Q/8IT9msFQVgvSVJRuNsiJ/DTCItOzfmDUnnRf/oFiNKrZFvDThAQUCmEoNOi2u8uBXIncrhu5HCEa+TZW2MjKUobaJh68vLB2P3SoQaNAp36+H8MlUoFE/sksPSe8XxbUkP/tCj6JJmPa/Cutbq4450NVPo3TI12D7e8tZ7Xrh/OpS+sok+ymQfO7Uvf5CiSwrwHCWZt2KY6j0+UNcKPYOXu2pAA3p3gDbKzW2vwBnnz8M4Ph7hnSn63T+FxJg1v3TSSjQcbufqVNYH199eX8ZeLBgQa1zYeauSBhVs4f1Aqf168nYxYPcOzY9hX20JhejTxRk1Qg6JFr2ZEThzDsmKCPOjjTFpGGTS4fSK6MD0ZneH0iGw82BiyvrW8qXsB3BAHvc+BtOGw5T348HZQ6eCMP0DeZNC3q227bFDyKXx8N7hbIKEPXL0AottKCRWNDp74Yhc7q5o5b2AyVw7PDGzY1u6v54GFbWYuM15ezde/mRgUwHvanBjhBKDWywp8rQHcY4d9y2HywyftKUVq4KcRWrWSm8fnctvEPNJj9IzJi+P9W8d0OY5l1qmYNTYnaO3m8bmYu6izOTw+qq1OmtrV2PMSjGiPOGmdOyCF6Ha62q0Xpo83V/DpliqqrcfWqdsRUXo1+UlmZo/PZUxefI+b12qsLnZWNXOgriUwm9wenyQFuuxbaXZ4Aw1mJVVWrn99bUgavyvUSgVn9A09wY3vnRDm3t3jcJhu6KomR9gu9/ZYnR5qrE5q/WpxBo2SV1cG23rurW3B7vYSb2p7j9UqBePy45l/8yjuPbMP35XWMXvues58chllYfoDgKDg3YpCIfQ4eAMYNUqmFobKlo7tRJc+BI8DytfB5/fJJiT1e2HBTGg+wgPd2QSLbpWDN0BNCXzyG3DIqfsaq5MrXlrF+xvK2FbRzGNLdvHM16U43D5aXF7mrQ1uaBQlWYAmws8MpRpG3grJA9vWhl4vS+aeJCIn8NOMOJOWe6b0ZmZxNlqlIqzd6JEYtSpuGZ/HlIIkVu2tY0xeHLnxJgydBPBam4tnvi7l861V5CYY+ctFA8j2pzjn3Twq4E190eA0ZhZno24X1CsaHZz71IrAmFqqRceiOcUn1wbxCCoaHVz2wirK/cFmWmEKf76wP3HtSghqpcDANAtbytvGfBJMWpx+oR+lQkAAdlVbOxRk6YjxveO5YngGC9aXoRQEbhybHdL41hMuGpzGf74uDepev35Mdqc9AbVWF39evI3PtlaREWvgsUsLO/WPb2VaYQoXDk7lmlfWUNHkZEJ+PL85uw/RBjWNdg9Pf7Wb/7to4Al18hMEgckFSdwyPpe5qw5g0qp4YGrf7hsP+TzQsB82zQu9bcdiuWmplZZqEH3B96lYD14HYMHq9HKoPnjTsmB9GbdNzCPGqKFXgomvdgQH7Nz4ziViI5wkzElwzUJ5nFCpBo0J9CevJyESwE9DNCpFj4NhjFFDkTGWom6kFx1uL098URJwvapqdnL5C6v47K5xJEbpGJIZw1uzRuITJdngo92F2uMVeXH53qAZ84omJyt31x6TIYso+k0rtlTg8ohcODiNxCgNamXPg4TT4+OZr3cHgjfAx5sruWlcblAAjzVqeXbGEG57ewPbKprJjjPw+GWDePabUp64bBBZcQZ8knRUohuxRi0PTS3gnim9EQQ5S2I4hrmhxCgtH95RzBNf7GJgWhSXDE1HpRSosboQBBAgKEPhcPt48stdLN5ciVopsL+uhTve3sBbN41kZnE2d7WzsMxLMNIr0YzbK494zR6Xy+UvrvILxMCy3bVE6dXMGJHJc9/u4XCzC68oQpeK+cdGrFHD3Wf2ZtbYHAQBYgyabpccsB2G758JPzaWfIRGvylZ9rv2tht7y54AGnmsKFwGITFK9vRWKxXMLM7hky2VAZe2MXlx9E+NKKv9bDElAEefDTueRAL4aYjV6cHm8uLyihg1quMuXmJ1evl0S1XQWl2Lm0aHh0T/CaejdLUoSbSEGeUKt9YTaqwuzn1qOQ12OV39n69L+eKe8UcluOP0+AKa7O3ZX9sS0gyYGWfk5euKKGuwU2NzoVEquGtyPv9cUsL3/m77filRvHHjiB6/D62iQccDg0bFgDQLT15eyLoDDVz83Hc02D0Mzojmzxf054mlJdx7Zh/6JpvRqpVYnR7KG+zMvXEEKqWAQa3kx7JGbE4vJVVW3pw1giXbDpNq0TEuP55ovYqlv56A2+ujrsUTCN6trNpbx9kDZJGLmcXZXb4uryjidPswaFTH5K6lVyvDahp0hSSJCJvnwcxPoeQzqNoi35A7CdKHH/FLouGqebDoNrBWQfY4OPuvoJUzJiatihuLswP67iqFwF8uHBAobSVbdCy8vZjKJgc6tZI4oyaiZx6hW0QC+GlGk8PDf7/fz1Nf7kKUIDPWwDuzRx5X6UWVUiAjVk9TeVttVxDo1mxqa53+o00Vga53g0bJlIJj8/3+bGtlIHiDXJ9/7bt9PDS1IGxttTOidGouGZrG2nZWqUqFQFF2eM85jVKBUaPiie93EWfScN7AlEDwBllRbeHGMmaPy+3R2NaJwOWVuP3tDYGGxR8PNfLMN6UMzYzh8hdXsey3k0i2KNGplfz27L7Mnrsu0KR3eVEGZ/dLZsm2w7y/oYyROXHsr20hP8nEwPS2jY1K6UAhyLXcVvqnWnC4fbx4zTCGZXXu3VdrdTFv7UF+2FfPlH5JTCtMPeZ56iMfv7JJ9m1PjNIRf0SwrLW50HkETCmD4L2ZcO6joI+RT9nm1BAVNtR6+cR983KQfKDSg6HtNUbp1dw5OZ8rR2RyoK6F/qkWYozqoM9CRw2NPztEr2zeEeFnQeSdOM1otLv519JdgZ8P1tv5+6c7efTSgZi0x+c0F2vU8o9LCrn8xVWBVPjdk/O7LS6RHWfkk1+N46Xle+T6+4Q84o/x4tUqudkej1c8KnUyhULg7P4p1NrcvL36IDFGNX88v38giHh88ojY0u1VjM1P4KY31qEQBK4YnkFxXhxfhPHk3lLWhFeUECWRxhY3lc1OLDo1FoPmuAanjqhvcWF3+ai1uUMMPjYcaOCiwWm4vCKl1VaSLTqUCoGXlu8JBG+Ad9cdYtbYbObfPJKPN1exu9rK7HE5ZB2hnmfWqfnH9EL+sGgrLq9IdpyBRy7sT7RB1s/vjGqrk7v+9yOr9soboOW7a9le0cwfpvUL6so+WmqsTq54cXXABa5/ahRvzBwR+Pw1Ozz84cOtNLS4eXv6ayg+uQthwY3yqfv8f3fs561UyvXRDog2aIg2aHps9vOzwXYYNs2H6m1y41Ziv5Na+40gEwngpxmtdbT27KhsxuH2HbcADtAn2cS3v5lIeaODBJMWczctNEFumuuXGsWj0wtRCEJQg9vRMq0wlae+3E2Lf0OhVgrcODbnqIVbYo0abhmfxxXDM1AKQlBK83CTk7P/vZwLBqdSUmULyIT+7dMdJJi0vHpDEU99FTx/PH1YOmqlgtJqG9VWJ9/srCE1Wsfw7FgUAsd9Dr49tTYXd/5vI6v21vHBbWNQK4NHBgdnRlNabQUgxd+k5vT4KK0OlT8tb3DQJzmKG4qzO/x9Jq2KaYUpjM9PwO31odcow+rlh8Pu8gWCdyvvbyjjnjN7H5cA/sGG8iAL120VzSzfXRPov3C4fSzZWoUowaXzfDxx3pOknqdGpVKhik495t9/SmKrhv9Ok81dQG7su+QVGDA9/Ex8hJ+MSAA/DfB4RRweH2aditwEY8gF+sx+Scd9jlStVJIYpQzUvI8G7VHUJjsiwaxlyT3jeeP7/Ti9IjcW53So/tVdwjUDiqLEG6v20+L2kWLR811pbdDtNTbZC/s/Vw3hsSUluL0it0zIZVB6NM0ODzurmpnzTpu4zIC0KF68ZtgJDeDfllQHUvrz1h7ibxcP5C+fbKfZ4WVAWhRzJvXi5jfXc/3orEBd1qJXM60whe2VbXruaqXQbdtKg6bnTXcefxblvzOHs7msibmr9lNrc6NXK4+LtaxPFNnl36i0p/0ooCDAWQVx3DMmHovSTYsE9y2p4v5phXRpU+Hzgb0GDm+T58gt6WDswdjazxVrVVvwbmXF45A7MbScEOEnJRLAT3EONzt5ZcVetlc2c9HgNM7om8jcG0fw+w+2UNno5IJBqcwen3vaWZ4eiVqpID3GwP3nFgDdNK04SloNNTYcbGBSn0TW7KsP3KYQINGsZXBGNKNyYwEhYAxS2ejghWXBLmJby5upa3GTdgLtIde1q+XPX3uIZoeHt28aSaxBi0IAm9vLB7eNwaxr89dWKRVcOTyDRoeHBevLSDRr+ctFA06YEpgoShyqt/O7BZvZXtnMmLw4Xr6uiFveXM9tE/OOywZHqVAwY0Qm768vD1q/cHCbTnuMQc2/J6jQzT8T7PWgjeLRS96A7lR4GvfDy5PkuXCAnIlw6StgPMWDnCLMtUOp5rjsqiIcE5EAfgpTY3Vx1Utt9bzvSuu458x8bpuQx4JbxwASeo3qF2V8cCIDd+vjzyzOZt7agyzbVcPVI7OYPS6X9zeUEa1X88fz+xFr1IS1WVUqBTze0Kp8d9WMa6wu1uyt42CDnXMHpJAUpe3WKffCwalBYiGfba3ixuIc0tI6n+mONWn59Zm9uWlsDkqFXEZwe0Vq/MI7Jp26ww5vu9tLs8NLs9NDtF5NtEHdqf1lbYsrMDcOsnuc0yPy9k0jMetUPTYx6YheiSaenTGE/3xdikop8Juz+pAW3fY+qZ11qBfNkoM3gKsZ3aIb4fbVoOvkDO6ywVePtAVvgH3fQsOBUz+AmxJlBbKKDW1rZzx06r+u04BfzpX9NKTZ6Qmq5wG8ueoAV43I/FmJopxupEbrWXL3eF5ZuZfVe+q4aXwON43LQSEIxJs0HXaaJ5i03DGpV5A+e068kdTort+rOpuL61/7IZDSfnxJCe/eMrpbc/sFKVE8PK0fz3xTigDcObkX+UmyUEhHJhqt6NTKwBxzk93D4s0VgdLADWOymT0+N6QJz+HxsmRbFb99bzNeUcKoUfLmrJEMyYzu8G9jd/tCNPxXltZi0qp6pNfeFRa9PCUwMjcuZPYdkLusG/YHrzkawNuFWqDPDdaK0HVrVejaqYYxAWa8K0uIVu+AgdPBEurtHuGnJxLAT2HCeUVH6dQoIrmtE4pOrSQ3wcQjFw5AILwEaDgEQWBCnwTevWU0//vhIL2TTEwflt6tBq9DDY6gerQowT+XlPDStV3Xz6MNGq4ZlcX5g1IBiWiDBrVS4TfRqOLVlXsxalXcf25fBmVEd3iqP9Rg56FFbZrdzy/bQ/+0KKYVptLkcOPyiBi1KqxOL/d/sCVgE9ri9nHPuz+y4NYxHY5K6VVKdGpFkN93dpwBdXeFV3pAq21qWJQaSBkMlW1CNURnyqNhnaGPgWE3wqEf2tbUBkgbeuxP+OeAKQEKLzvZzyLCEURaCE9hWrt9WxEE+MO0fsSZIo5FPwUqhSIQvD0+uZGwK2Tjjlgeu6yQWyfkdTtT4vaGjsk5PT7EDvLvtTYXB+taqGh00Gh3o1Ep/LPGukBQlE00trCnpoXNZU1c/coaqq2usI8H8E0Yfe6PN1dS1eTkV//byLlPreCBhVtwuL1BgRjkccaOnitAlEHFo9MLUSvlzadJq+JfVwz+6T/Lxni4fG6bWEvyQNmYpKt0sSBA77PhwmchdQjknw2zv46kmSOcUCIn8FOYGKOGRy7szw3F2ew+bGN0XhwJpp55PEc4NkRRoqrZycsr9lLR6OSGMdn0T43qsuu/p+NtOfFGUiy6oLnsOyb2Cpv2rrY6mfn6WrZVyCf2S4el88B5wT7YnZlo3DAm2NimlXCWtMOyYnhy6U6W75K78T/8sYKrR2aSFq0PkqIdlx8fYnLTHr1axZn9klhx3xlYHR4s/rr5Sfksx2TBVfNB9MgNXN0NwoZY87AqQgAAEz9JREFUGDRDdjFTakAXkUONcGKJBPBTnFijllijlqKsblgkngBEUaLG5mLVnjoUCoFRObEkmH85m4ham4vz/7OSuhbZrWzJtipeua6IKf2OTVnuSBLMWhbdXsybq/dzoM7ONaOzKEgODRBen8hbqw8EgjfIxhlXDs8g1tj2GdGoFD020eifEsXFQ9JYuFHu4h6ZE8v5hSkUP7oz6H5/+XgHc28cwf0Lt7CtvIlx+Qn86cL+Xab6FYKAUhBIi9Z3aqTzk2CMO7r/p1CcHqNjEU4JIgE8wjFx2Opk6tMrqfcHsESzlsW/Gtt916dTnB2VzYHg3coLy/ZQlB1z3Ge7kyw67jmzNz5R6rCj2+nxselQU8j69ormoIa3cCYao3JjOzXRMGhV3HdOH+49szciYNIq8fokVAohyOWswe4mxqDhxWuG4fGJ6DXKLrXPa6wunvl6NytLaxmUHs1vz+lDynFsXgOQJAlRknosrRshws+VSACPcEzM++FQIHgDVFtdfLqlkpnF4dOwpxv6MA1fRq0K5QkaZ1MqFHTW12X090Us21UTtD4mjA92q4lGVZMDrVpJnEkT5LbWnia7hwUbDvHEF7tweUUuKEzloWkFmHVqHrmwPw8s3IpPlNCpFTx5+aAQre/OaHZ4uP+DzXzpzwbsqWlhZ5WVubNGdNxs1kMONzuZv/YgZQ0Orh2VRXa8MWhT4RXFo1btixDhZBEJ4BGOGkmSaLC7Q9brW0LXTldy440UpJjZUSkrfKmVAr87u89xcxHrKa0+2LdOyOXNVQcw6VQ8NLUfSVHhA2F3TTQqmhz85eMdgZ8X/lhOYYaF60ZnM7UwlfH5CdS1uEkwa4nW96x27fD4+GpncCp/u1/+93hQY3Vy4TPfUdUs9w+8u66Md2aPZExePHU2F1/uqGbVnjrOG5hMUXbsT6JNHyHC8SASwCMcNYIgcO3oLN5afSDgPKVWClw67Oh9vU814s1a5t44kg0HG6hscjC5b9JJd5WKNWq4e0pvbhybg4BArEGN8hjHsX5opzbXyjc7q7l0WDpmnRqTVhXQUe8pAhBn1FBra9v4aVWK4zZCtqPSGgjerfznq1J6JZr4/ftb+Nq/eVj0Yzm3T8zjV2fkB3nYR4jwc+Wk5IwEQXhMEISdgiBsFgRhoSAIEVubU5Q0i56PfzWO8wYmc8GgVD751bhfTP27lQSzlrP7J3PDmBwyYg0B4ZOTiU6tJNGsI8GsPebgDTAkM/QrOjovHsNxeK2xRg1/u3gg7asO95/blyj98TlfqMKUM5QKAZ9PCgTvVl77bh9Wpyfk/hEi/Bw5WSfwpcD9kiR5BUF4FLgfuO8kPZcIx4DB7yz2xGWDACFycjlNyYgxcMekPF5avhePT2JC73guK0o/LpsDlVJBca94Vt53BntqbGTFGYnWq3tshtIR+UlmcuKNAdc4pULgN2f3DtunEKmDRziVOCkBXJKkL9r9uBq49GQ8jwjHj3DNXBFOH2KMGm6b2ItrR2UjShIGjfK4dtkbtSqMWhWpR5mG74wEs5Z3bxnF1zurKWtwcPGQNJItOjw+iYsGp7LoxzYJ1DmTemE5Sue+GquLb0uq2X3YxsVD00iP0Z+0XogIvwwEqbtOCifqCQjCYmC+JElvdXXfoqIiad26dT/Bs4oQIcIvgTqbix8PNbJ2fz1TCpLISzQRcxQbk1qbi+te/SFI7va164s4o+D46gFE+OUhCMJ6SZKKwt12wo5NgiB8CWEtdB+UJOlD/30eBLzA2508zs3AzQCZmZkn4JlGiBDhl0qcScvkgiQmH2OgrW52BgVvgCeW7mJQRnSoYUqECMeJExbAJUma0tntgiBcD0wDJkudpAEkSXoJeAnkE/hxfZIRIkSIcBwQw1yZfKJE5IIV4URysrrQz0FuWrtAkiT7yXgOESJEiHC8SI7SkZcQLEN75+R84iIz5RFOICer8+gZQAss9Qs+rJYk6daT9FwiRIhwHGl2epAkjroZ7FQk3qxl3s2j+GhTBbuqmrlyRCZ5CaZfjCdAhJPDyepC73Uyfm+ECBFOHHa3l12HrTzxxS58osSdk/MZkBqF6RfSiZ1g1jJrbA6iKKE4QVK6ESK0JzL7EyFChONCZZOT/2/v3oPsrOs7jr+/e8lukt1NQq6EkIQ7hIRGmyoRHCgU5CZoB+y0ikxtq3GwYEfqjXbGmWpbBwfFgqPWapkWyojiwHghVRtqE0KBQLgEIQTKJYTcSXaTve/++scuuZiVHHT3PPvb5/2a2Zk8v7Nnz2fmmZzP+T3Pc57fH37t/n3ng+9/bgc/uuZMTp09qdhgVWZ5q1q8a4GGTXtXL5t2dbDy2W28uGMvuzvG/h2t9nb1srW1k61tnfT09Rcdp1B3PbLxkIu5/m31i/QPdYWXpN+aM3ANi77+xEMv7ORDtz68b2nJz1x0Mh94+zwmFr228wjZubeLLy1fz51rXqapoY7rLz6F8xfMoqVE534PNHuI5T/nTBnvjFQaIc7ANSx27u3iU99/4qB1ob+0/BnaOnsLTDVy+voT96zdxO0PvkRPX+K19h6uu/NxtrZ1FR2tMOedOpN5Uyfs257V0sgVS44uMFGeduzp4rGXd7Hi6a1sae2kt+RHdvTrjc2pkaouJdi25+Dy6ulLdI/RN5+93b0sf2rLIeMPvbCT42c0DfGMsW9GcyPfW/YOntncRl9KLDiymenN5VrY5re1Y08XV9/+CA88P7D6W3NDHff85ZkcM21iwcn0hrrboWvwRj4NLTBuwhv//jBxBq5hMX5cLRcuPPjGe8dNbxqW1apGo/H1tSyZN+WQ8YWzWwpIM3pMb27gzBOmcdaJ08dWebfvhE1r4dHbYMdz0Nl6+Of8Bl7c2b6vvAHaunq5Yfkz7O0am0eyxoT2nbDqJvjqYrjpNLjvH2Dvjqq8tDNwDYvmxno+9+5TmdnSyIqnt7LwqBY+feEpTCt4beyRUl9bwweXzmfls9t59OVd1AT86RnHMGdKdT55q4o6dsN9X4QHv75/7Ipb4eR3Q+3wfkDdNsQpmC2tnXT39eMcfJTa8iT89z/u377/qzBvKZx00Yi/tAWuYTOtuYG/ftdJLDvrWCaMqxuzF6+9bnpzA9+6agnt3X3U1QZNDXWuPjUWde+Bh75x8Ni9nxp4k24a3sVKfmfOJCaMq6W9u2/f2JWnz2NySS+MzML65YeOPXU3nHABjPDytGP7HVZV11hfS+MYPWw+lKlNDUwtOoRGVl/PwEUeB+rYxUjc6Hxq0zju+dgZfPHep9nW1s0Hl87j7JOme0e30Wz+O2H1zQePHXvOiJc3WOCS9MYaJsKsRbD5if1jb70KGpqH/aXqa2s5fkYzX37fYnr6EpMn1Fveo92cJbD4/fDY7QMf9E65DI4/tyovXfh64G+G64FLKkTbZlh9C7yyBk65FBZdDhOnFZ1Ko0XnbujaAyQY1wTjJw/bny5kPXBJGjOaZ8E5fwM97QNfE6opz2kiVaBx0sBPlVngklSJuoaBH2mU8HvgkiRlyAKXJClDFrgkSRmywCVJypAXsUkZ2drWybpXWqmJYMHsFqaP0VvVSjo8C1zKxJbWTi67eRWbWzuBgbW27/roO5jRMoYWDZFUMQ+hS5n43pqN+8obYONrHfzkyc1VzbCrvZstrZ1sa+uivz+fm0BJY5EzcCkDKSU27eo4ZPzV3Z1D/PbI2NLaySe+u5aVG3Ywe1IjN/7RYt4ydzINdd7URCqCM3ApAxHBlafP48DbYtcEXPG7c6ry+ns6e/i7Hz7Fyg0D6xxv2t3JVd9+kF3tPVV5fUmHcgYuZWLOERO48yNLuennz1IbwV+ddyJHTq7O+e/27j5Wbdh+0FhXbz/b27qYWaJz8B09fbR19FBbE0xt8gJCFcsClzLR1FDHkvlHcMv730pAVdceb6ivYdGcSfxi/f4SHyixcVXLULQde7q4ecUG7l67iSMnNfL3713EybOaaSjR8rkaXTyELmWmpbG+quUNMGn8OD7/nkXMnzoBgPH1tdxw+WlVz1GUnt5+vrPqBb6z6gV27u1m3aZW3veN1bzW4SkEFccZuKSKzD1iAncuW0pHTz/j6mqYNL6O8fXleAvZ1dHNj5949aCxrt5+/m/bHmaV6BSCRpdy/O+TNCymN5ezrBrrazl2+kSe3773oPFZk8YXlEjyELokHVZzYz1/e8mCg+589+fvPIYpE8pxCkGjkzNwSarA0VMm8KNrzuS1vT00NdTR1FjHpPEWuIpjgUtSBWpqghnNjcwo6WkEjT4eQpckKUMWuCRJGbLAJUnKkAUuSVKGLHBJkjJkgUuSlCELXJKkDFngkiRlyAKXJClDFrgkSRmywCVJypD3QpekN6NtM6y/F7raYMF7oGkm1I0rOpVKyAKXpEq1bYZvng1trw5sr/gCLFsFU48rNJbKyUPoklSp51bsL2+Ang5YdRP0dReXSaVlgUtSpXo7Dh3r6YD+VP0sKj0LXJIqdeIF0NCyfztq4Ixrob6huEwqLc+BS1KlJs6Aj66CB74Gna2w9GqYMr/oVCopC1ySKlVbB5Pnwvmfh5Sgtr7oRCoxC1yS3qwa3zpVPM+BS5KUIQtckqQMWeCSJGXIApckKUMWuCRJGbLAJUnKkAUuSVKGLHBJkjJkgUuSlCELXJKkDFngkiRlyAKXJClDFrgkSRmywCVJylChBR4R10VEiohpReaQJCk3hRV4RBwNnAe8VFQGSZJyVeQM/MvAJ4FUYAZJkrJUSIFHxKXAKymlx4p4fUmSclc3Un84In4GzBrioeuBzwLnV/h3Pgx8GGDu3LnDlk+SpJxFStU9gh0Ri4CfA+2DQ3OATcDbUkqb3+i5S5YsSQ8//PAIJ5QkaXSIiDUppSVDPTZiM/BfJ6X0BDDj9e2IeAFYklLaXu0skiTlyu+BS5KUoarPwH9VSml+0RkkScqNM3BJkjJkgUuSlCELXJKkDFngkiRlyAKXJClDFrgkSRmywCVJypAFLklShixwSZIyZIFLkpQhC1yS3ozebtizFTpbi06ikiv8XuiSlI292+HBf4Z1d8HUE+BdX4DJ86DGuZCqzwKXpEr0dMDKr8DqfxrY3r4eXnkIPrISmmcWm02l5MdGSapE5254/I6Dx/ZshfbtxeRR6VngklSJmjpoOerQ8Ybm6meRsMAlqTITp8HFN0Jd4/6xty+DhpbiMqnUPAcuSZWauRCueXTg/HfLUQOlPn5y0alUUha4JFWqvgHqZ0PL7KKTSB5ClyQpRxa4JEkZssAlScqQBS5JUoYscEmSMmSBS5KUIQtckqQMWeCSJGXIApckKUMWuCRJGbLAJUnKkAUuSVKGLHBJkjJkgUuSlCELXJKkDFngkiRlKFJKRWeoWERsA14sOkcJTQO2Fx2i5NwHo4P7YXQo036Yl1KaPtQDWRW4ihERD6eUlhSdo8zcB6OD+2F0cD8M8BC6JEkZssAlScqQBa5KfLPoAHIfjBLuh9HB/YDnwCVJypIzcEmSMmSB67Ai4oaIeDoiHo+IH0TE5KIzlUlEXBARz0TEhoj4dNF5yigijo6IFRHxy4hYFxHXFp2prCKiNiIejYgfFp2laBa4KvFTYGFK6TRgPfCZgvOURkTUArcAFwILgD+OiAXFpiqlXuATKaVTgNOBq90PhbkW+GXRIUYDC1yHlVL6z5RS7+DmA8CcIvOUzNuADSml51NK3cAdwGUFZyqdlNKrKaVHBv/dxkCBHFVsqvKJiDnAxcC3is4yGljgerM+BPyk6BAlchTw8gHbG7E4ChUR84G3AP9bbJJS+grwSaC/6CCjQV3RATQ6RMTPgFlDPHR9Sunuwd+5noFDibdVM1vJxRBjfnWkIBHRBHwf+HhKqbXoPGUSEZcAW1NKayLi7KLzjAYWuABIKf3BGz0eEVcBlwDnJr97WE0bgaMP2J4DbCooS6lFRD0D5X1bSumuovOU0BnApRFxEdAItETEv6eUPlBwrsL4PXAdVkRcANwInJVS2lZ0njKJiDoGLhw8F3gFeAj4k5TSukKDlUxEBHArsDOl9PGi85Td4Az8upTSJUVnKZLnwFWJm4Fm4KcRsTYivl50oLIYvHjwY8ByBi6c+q7lXYgzgCuBcwb/D6wdnAlKhXEGLklShpyBS5KUIQtckqQMWeCSJGXIApckKUMWuCRJGbLApRKLiL7Br0Q9GRF3RsSEwfFZEXFHRDwXEU9FxI8j4sQhnv/tiNgaEU9WP71Ubha4VG4dKaXFKaWFQDewbPCmJT8A7kspHZdSWgB8Fpg5xPP/Fbigamkl7eOtVCW97n+A04DfB3pSSvtu2JNSWjvUE1JKvxhc3ENSlTkDl/T6LVsvBJ4AFgJrik0k6XAscKncxkfEWuBh4CXgXwrOI6lCHkKXyq0jpbT4wIGIWAdcXlAeSRVyBi7pV/0X0BARf/H6QET8XkScVWAmSb/CApd0kMH13t8LnDf4NbJ1wOcYYh3yiPgPYDVwUkRsjIg/q2pYqcRcjUySpAw5A5ckKUMWuCRJGbLAJUnKkAUuSVKGLHBJkjJkgUuSlCELXJKkDFngkiRl6P8BzpZNVPj9rsAAAAAASUVORK5CYII=\n",
"text/plain": [
"
"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# Use the Legendary feature to color the PC 1 vs. PC 2 scatterplot\n",
"sns.scatterplot(data=poke_cat_df, x='PC 1', y='PC 2', hue='Legendary');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Looks like the different types are scattered all over the place while the legendary Pokemon always score high for PC 1 meaning they have high stats overall. Their spread along the PC 2 axis tells us they aren't consistently fast and vulnerable or slow and armored."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### PCA in a model pipeline\n",
"We just saw that legendary Pokemon tend to have higher stats overall. Let's see if we can add a classifier to our pipeline that detects legendary versus non-legendary Pokemon based on the principal components."
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {},
"outputs": [],
"source": [
"from sklearn.ensemble import RandomForestClassifier\n",
"from sklearn.model_selection import train_test_split\n",
"\n",
"X = poke_df\n",
"y = df['Legendary']\n",
"\n",
"X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[0.45673596 0.18599109]\n",
"92.1% test set accuracy\n"
]
}
],
"source": [
"# Build the pipeline\n",
"pipe = Pipeline([\n",
" ('scaler', StandardScaler()),\n",
" ('reducer', PCA(n_components=2)),\n",
" ('classifier', RandomForestClassifier(random_state=0))\n",
"])\n",
"\n",
"# Fit the pipeline to the training data\n",
"pipe.fit(X_train, y_train)\n",
"\n",
"# Prints the explained variance ratio\n",
"print(pipe.steps[1][1].explained_variance_ratio_)\n",
"\n",
"# Score the acuracy on the test set\n",
"accuracy = pipe.score(X_test, y_test)\n",
"\n",
"# Prints the model accuracy\n",
"print('{0:.1%} test set accuracy'.format(accuracy))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Repeat the process with 3 extracted components."
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[0.45673596 0.18599109 0.12852181]\n",
"93.8% test set accuracy\n"
]
}
],
"source": [
"# Build the pipeline\n",
"pipe = Pipeline([\n",
" ('scaler', StandardScaler()),\n",
" ('reducer', PCA(n_components=3)),\n",
" ('classifier', RandomForestClassifier(random_state=0))])\n",
"\n",
"# Fit the pipeline to the training data\n",
"pipe.fit(X_train, y_train)\n",
"\n",
"# Score the accuracy on the test set\n",
"accuracy = pipe.score(X_test, y_test)\n",
"\n",
"# Prints the explained variance ratio and accuracy\n",
"print(pipe.steps[1][1].explained_variance_ratio_)\n",
"print('{0:.1%} test set accuracy'.format(accuracy))"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[0.45673596 0.18599109 0.12852181 0.11442161]\n",
"95.0% test set accuracy\n"
]
}
],
"source": [
"# Build the pipeline\n",
"pipe = Pipeline([\n",
" ('scaler', StandardScaler()),\n",
" ('reducer', PCA(n_components=4)),\n",
" ('classifier', RandomForestClassifier(random_state=0))])\n",
"\n",
"# Fit the pipeline to the training data\n",
"pipe.fit(X_train, y_train)\n",
"\n",
"# Score the accuracy on the test set\n",
"accuracy = pipe.score(X_test, y_test)\n",
"\n",
"# Prints the explained variance ratio and accuracy\n",
"print(pipe.steps[1][1].explained_variance_ratio_)\n",
"print('{0:.1%} test set accuracy'.format(accuracy))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Principal Component Selection\n",
"- PCA operations\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Selecting the proportion of variance to keep\n",
"You'll let PCA determine the number of components to calculate based on an explained variance threshold that you decide."
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"
\n",
"\n",
"
\n",
" \n",
"
\n",
"
\n",
"
Branch
\n",
"
Component
\n",
"
Gender
\n",
"
abdominalextensiondepthsitting
\n",
"
acromialheight
\n",
"
acromionradialelength
\n",
"
anklecircumference
\n",
"
axillaheight
\n",
"
balloffootcircumference
\n",
"
balloffootlength
\n",
"
...
\n",
"
waistdepth
\n",
"
waistfrontlengthsitting
\n",
"
waistheightomphalion
\n",
"
wristcircumference
\n",
"
wristheight
\n",
"
weight_kg
\n",
"
stature_m
\n",
"
BMI
\n",
"
BMI_class
\n",
"
Height_class
\n",
"
\n",
" \n",
" \n",
"
\n",
"
0
\n",
"
Combat Support
\n",
"
Regular Army
\n",
"
Female
\n",
"
231
\n",
"
1282
\n",
"
301
\n",
"
204
\n",
"
1180
\n",
"
222
\n",
"
177
\n",
"
...
\n",
"
217
\n",
"
345
\n",
"
942
\n",
"
152
\n",
"
756
\n",
"
65.7
\n",
"
1.560
\n",
"
26.997041
\n",
"
Overweight
\n",
"
Normal
\n",
"
\n",
"
\n",
"
1
\n",
"
Combat Service Support
\n",
"
Regular Army
\n",
"
Female
\n",
"
194
\n",
"
1379
\n",
"
320
\n",
"
207
\n",
"
1292
\n",
"
225
\n",
"
178
\n",
"
...
\n",
"
168
\n",
"
329
\n",
"
1032
\n",
"
155
\n",
"
815
\n",
"
53.4
\n",
"
1.665
\n",
"
19.262506
\n",
"
Normal
\n",
"
Normal
\n",
"
\n",
"
\n",
"
2
\n",
"
Combat Service Support
\n",
"
Regular Army
\n",
"
Female
\n",
"
183
\n",
"
1369
\n",
"
329
\n",
"
233
\n",
"
1271
\n",
"
237
\n",
"
196
\n",
"
...
\n",
"
159
\n",
"
367
\n",
"
1035
\n",
"
162
\n",
"
799
\n",
"
66.3
\n",
"
1.711
\n",
"
22.647148
\n",
"
Normal
\n",
"
Tall
\n",
"
\n",
"
\n",
"
3
\n",
"
Combat Service Support
\n",
"
Regular Army
\n",
"
Female
\n",
"
261
\n",
"
1356
\n",
"
306
\n",
"
214
\n",
"
1250
\n",
"
240
\n",
"
188
\n",
"
...
\n",
"
235
\n",
"
371
\n",
"
999
\n",
"
173
\n",
"
818
\n",
"
78.2
\n",
"
1.660
\n",
"
28.378575
\n",
"
Overweight
\n",
"
Normal
\n",
"
\n",
"
\n",
"
4
\n",
"
Combat Arms
\n",
"
Regular Army
\n",
"
Female
\n",
"
309
\n",
"
1303
\n",
"
308
\n",
"
214
\n",
"
1210
\n",
"
217
\n",
"
182
\n",
"
...
\n",
"
300
\n",
"
380
\n",
"
911
\n",
"
152
\n",
"
762
\n",
"
88.6
\n",
"
1.572
\n",
"
35.853259
\n",
"
Overweight
\n",
"
Normal
\n",
"
\n",
" \n",
"
\n",
"
5 rows × 99 columns
\n",
"
"
],
"text/plain": [
" Branch Component Gender \\\n",
"0 Combat Support Regular Army Female \n",
"1 Combat Service Support Regular Army Female \n",
"2 Combat Service Support Regular Army Female \n",
"3 Combat Service Support Regular Army Female \n",
"4 Combat Arms Regular Army Female \n",
"\n",
" abdominalextensiondepthsitting acromialheight acromionradialelength \\\n",
"0 231 1282 301 \n",
"1 194 1379 320 \n",
"2 183 1369 329 \n",
"3 261 1356 306 \n",
"4 309 1303 308 \n",
"\n",
" anklecircumference axillaheight balloffootcircumference \\\n",
"0 204 1180 222 \n",
"1 207 1292 225 \n",
"2 233 1271 237 \n",
"3 214 1250 240 \n",
"4 214 1210 217 \n",
"\n",
" balloffootlength ... waistdepth waistfrontlengthsitting \\\n",
"0 177 ... 217 345 \n",
"1 178 ... 168 329 \n",
"2 196 ... 159 367 \n",
"3 188 ... 235 371 \n",
"4 182 ... 300 380 \n",
"\n",
" waistheightomphalion wristcircumference wristheight weight_kg \\\n",
"0 942 152 756 65.7 \n",
"1 1032 155 815 53.4 \n",
"2 1035 162 799 66.3 \n",
"3 999 173 818 78.2 \n",
"4 911 152 762 88.6 \n",
"\n",
" stature_m BMI BMI_class Height_class \n",
"0 1.560 26.997041 Overweight Normal \n",
"1 1.665 19.262506 Normal Normal \n",
"2 1.711 22.647148 Normal Tall \n",
"3 1.660 28.378575 Overweight Normal \n",
"4 1.572 35.853259 Overweight Normal \n",
"\n",
"[5 rows x 99 columns]"
]
},
"execution_count": 27,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"ansur_df = pd.read_csv('./dataset/ANSUR_II_FEMALE.csv')\n",
"ansur_df.head()"
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(1986, 94)"
]
},
"execution_count": 28,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"ansur_df.drop(['Gender', 'Branch', 'Component', 'BMI_class', 'Height_class'], \n",
" axis=1, inplace=True)\n",
"ansur_df.shape"
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"11 components selected\n"
]
}
],
"source": [
"# Pipe a scaler to PCA selecting 80% of the variance\n",
"pipe = Pipeline([\n",
" ('scaler', StandardScaler()),\n",
" ('reducer', PCA(n_components=0.8))\n",
"])\n",
"\n",
"# Fit the pipe to the data\n",
"pipe.fit(ansur_df)\n",
"\n",
"print('{} components selected'.format(len(pipe.steps[1][1].components_)))"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"23 components selected\n"
]
}
],
"source": [
"# Pipe a scaler to PCA selecting 90% of the variance\n",
"pipe = Pipeline([\n",
" ('scaler', StandardScaler()),\n",
" ('reducer', PCA(n_components=0.9))\n",
"])\n",
"\n",
"# Fit the pipe to the data\n",
"pipe.fit(ansur_df)\n",
"\n",
"print('{} components selected'.format(len(pipe.steps[1][1].components_)))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"From the result, we need more than 12 components to go from 80% to 90% explained variance."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Choosing the number of components\n",
"You'll now make a more informed decision on the number of principal components to reduce your data to using the \"elbow in the plot\" technique. "
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAfEAAAHwCAYAAAC2blbYAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjMsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+AADFEAAAgAElEQVR4nOzdeXxcZ3n3/881o10zlm3ZGm+JN2kcnJXEZCEpthNaAm0THpqUhAYaoA1LwlKgLe3TH1tLnxaepy2QQAhL2BMIUAhpSFgSZd/31WvsxHa827Ila9f1++McyWNZkkfyzBzNzPf9es1LM+ecOXPNkezv3Pe55z7m7oiIiEjxiUVdgIiIiEyMQlxERKRIKcRFRESKlEJcRESkSCnERUREipRCXEREpEgpxCVyZna5md2b8djNrDnKmjKZWauZ/VWBXusDZrbNzNrNrLEQrxm+7gYze2OW27ab2aI81HDI30E+mdk/mtk3C/FahZSv341MXgpxKYgwJDrD/2QGb1dHXVcumdmC8ANIxQSfXwn8B/BH7p5w912j7L992O3tuag/W2Ft6wv5mrnm7v/q7gX5YJYvI324LIXfjYzPhP6zEZmgP3X330VdxCSWAmqA546w3VR37ytAPSXJzCom+/ErhhplclBLXCart5jZejPbaWZfNLMYgJnFzOyfzGyjmW03s++ZWUO47rtm9vHw/tyw1frB8HGzme02Mxv+QmE37n1m9hUzazOzF83svJGKGuv1gbvDn3vDFvJZIzy/2sz+y8y2hLf/CpelgVUZz79jPAfLzKrM7Ekz+1D4OB6+p0+Fjz9jZj81sx+b2X4ze9zMTh5lX6eb2QNmttfMXjWzq82sKmP90OkOM/uOmV1jZv8T7vchM1ucse1xZvbb8NivMrM/z1jXaGY3m9k+M3sYWMwozOw2M7tq2LKnzOxt4f0vmdkr4b4eM7M/yNhu8L3/wMz2AZeHy36Qsc1NZrY1/P3fbWbHZ6w70ns8PuM9bjOzfwyXx8zsk2a2zsx2mdlPzGz6KO9vhZltMrO/N7OtwPVmNs3MbjGzHWa2J7w/L9z+88AfAFdbRq/WsN9NQ/j3uSP8e/0nC/8dSenQL1Qmq/8FLANOBS4E3hMuvzy8rQQWAQlgsFv+LmBFeH85sD78CfAG4B4ffZ7hM8LtZwCfBn4+yn+4Y73+G8KfU8NuzQdGeP7/Bs4ETgFOBk4H/sndVwPHZzz/3FHqHJG79wCXAZ8zs9cAnwTiwOczNrsQuAmYDvwI+IUFXfjD9QN/Q3AszgLOAz44xstfCnwWmAasHXxNM6sHfhu+VlO43VczAvIaoAuYTfD7fQ+j+1H4fMJ9LwXmA/8TLnqE4JgOvrebzKxm2Hv/KTAV+OEI+/810BLW+fgI24z2HpPA74DbgDlAM/D78DkfBt5K8Dc4B9gTvufRzArrnw9cQfD/8/Xh42OBTsK/NXf/38A9wFXh39pVI+zvK0ADwd/pcuBdwLvHeH0pRu6um255vwEbgHZgb8btr8N1lwP3ZmzrwPkZjz8I/D68/3vggxnrlgC9BKeGFof7jQHXAu8DNoXbfRf42Ci1XQ5sASxj2cPAO8P7rcBfZfH6C8LaK8Y4DuuAt2Q8fhOwIbw/5vMz1u8ddntNxjYfB14kCIyWjOWfAR7MeBwDXgX+IOP388ZRXvejwH8P+/00h/e/A3wzY91bgBfD+28n+OCUua+vE3xIiofH7biMdf+a+Xcw7HlJoAOYHz7+PPDtMY7zHuDkjPd+97D1nwF+MMpzp4bvsSGL93gp8MQo+3kBOC/j8ezBv5URtl0B9AA1Y7ynU4A9GY+H/i6H/27C49sNLM1Y9z6gNR//vnWL7qaWuBTSW919asbtG2Ns+0rG/Y0ELRnCnxuHrasAUu6+juCDwikEXY23AFvMbAlBS+SuMV5vs4f/043wmplGff0x9n2k54/0OmOZMew4vpCx7rsEYX+ru68Z9ryhY+ruA8CmkV7bzNJh1+3WsPv5Xwla5aPZmnH/AEHvBAQtyDPCbvm9ZrYX+AuCFudMguM2/Pc8InffT9DqviRcdAkZrWUz+7iZvRB2h+8laIFm1pz5OsPfb9zM/i3s9t5H8IGGYc8f7T0eQ/DBbCTzgf/OeO8vEPRyjPa3ssPduzLqqjOzr4dd4fsITtdMNbP4aO8lwwygisP/1uZm8VwpIgpxmayOybh/LEFLmfDn/GHr+oBt4eO7gIuAKnffHD5+F0E36JNjvN5cs0POl2e+ZqaxXj+bSwKO9PyRXmeivkrw4eVNZnbOsHVDxzQ8NzpvlNf+GkFrvsXdpwD/CBw2liALrwB3DfvAkXD3DwA7CI7b8N/zWG4ALrVgrEEtcGf4Xv4A+Hvgz4Fp7j4VaBtW81i/m3cQdLe/kSD8F4TLs3nPrzD6ufxXgDcPe/814d/lSIbX+HGCnp4zwt/D4OkaG2X7TDsJWv3D/9ZGe20pUgpxmaz+NhzYcwzwEeDH4fIbgL8xs4VmliBoJf7YD47kvQu4ioODzFqBDxF00/aP8XpNwIfNrNLMLgZeA9w6wnZjvf4OYIDgHORobgD+ycxmmtkM4FPAD8bYPmtm9k7gNILTAx8GvhvWOOg0M3ubBV+B+yhBd+uDI+wqCewD2s3sOOADEyzpFiBtZu8Mj2ulmb3OzF4T/i5+DnwmbHEuBf7yCPu7lSCUPkdwzAcy6h08/hUWDOabMo46kwTHYhdQR/A7zdYtwCwz+6gFAxSTZnZGuO5a4PNmNh8g/J1fOM66OgkGOk4nOA2RaRuj/K2Fx/cn4esnwxo+Ro7+1mTyUIhLIf3KDv1+83+Pse0vgccIWs//A3wrXP5t4PsEIf0SwcCoD2U87y6C//wGQ/xegv+Y72ZsDxEMbNpJcL71Ih/2Pe0jvb67Hwife1/YhXrmCM//F+BR4GngGYJBVP9yhNqG2zvsOH7MzI4F/gt4l7u3u/uPwtf5z4zn/ZLgPPUe4J3A29y9d4T9f4Kgdbof+AYHP0CNS9gF/kcEXd9bCLqk/x2oDje5iqBbeivBeefrj7C/boLgfyPB4LVBtxMMTFtN0GXcxRjd5yP4Xvi8zcDzjPzBZrSa9gN/CPwpwftYQzDoEeBLwM3Ab8xsf7jfM0bazyj+i6DHYWf43NuGrf8ScFE4cv3LIzz/QwTjCNYT/Dv4EcHfr5QQO/Q0oEj5MbPLCQYIDe9+Lhlm9hmCwWiXRV2LiOSOWuIiIiJFSiEuIiJSpNSdLiIiUqTUEhcRESlSCnEREZEiVXRXMZsxY4YvWLAgZ/vr6Oigvr4+Z/uT0elYF4aOc2HoOBeGjjM89thjO9195kjrii7EFyxYwKOPPpqz/bW2trJixYqc7U9Gp2NdGDrOhaHjXBg6zmBmo05JrO50ERGRIqUQFxERKVIKcRERkSKlEBcRESlSCnEREZEipRAXEREpUgpxERGRIqUQFxERKVIKcRERkSKlEBcRESlSCnEREZEipRAXEREpUgpxERGRIqUQFxERKVIKcRERkSKlEBcRESlSZR3i7s7ergHcPepSRERExq2sQ/wHD27ko62d7GjvjroUERGRcSvrEF80MwHAmm3tEVciIiIyfmUd4i2pIMRXbd0fcSUiIiLjV9YhPjNRTX0lrNmuEBcRkeJT1iFuZsxNxFit7nQRESlCZR3iAPMSMVZv268R6iIiUnTKPsTnJGLs7+pj676uqEsREREZl7IP8bmJ4BCoS11ERIqNQjwZHII12zS4TUREikvZh/iUKmNGoorVCnERESkyZR/iAC1NSXWni4hI0VGIA+lUgjUaoS4iIkVGIQ60pJJ09PSzeW9n1KWIiIhkTSEOLJmVBDSHuoiIFBeFOJBuCkJcg9tERKSYKMSBhrpKmpLVrFKIi4hIEVGIh9KppLrTRUSkqCjEQ+lUkrXb2xkY0Ah1EREpDgrxUDqVoLO3n017NEJdRESKg0I81JIKBrfpvLiIiBQLhXioJZUANEJdRESKh0I8NKWmkjkNNboQioiIFA2FeIaWlOZQFxGR4qEQz5BOJVi7o51+jVAXEZEioBDP0JJK0tM3wMZdHVGXIiIickQK8Qzp1OD0q+pSFxGRyU8hnqGlKRihrsFtIiJSDBTiGeqrK5g3rZbV29USFxGRyU8hPkw6lWT1VrXERURk8lOID9OSSrB+Zzu9/QNRlyIiIjImhfgwS1JJevtdI9RFRGTSU4gPoxHqIiJSLBTiwyyemcAMVum8uIiITHIK8WFqq+IcO72ONdsV4iIiMrkpxEeQ1hzqIiJSBPIa4mZ2vpmtMrO1ZvbJMba7yMzczJbls55spVMJNuzsoLuvP+pSRERERpW3EDezOHAN8GZgKXCpmS0dYbsk8GHgoXzVMl7pVJK+AeelnRqhLiIik1c+W+KnA2vdfb279wA3AheOsN0/A18AuvJYy7i0NGmEuoiITH4Vedz3XOCVjMebgDMyNzCz1wLHuPstZvaJ0XZkZlcAVwCkUilaW1tzVmR7e/th++vpd2IGv334WabsWZ2z1yp3Ix1ryT0d58LQcS4MHeex5TPEbYRlQxfqNrMY8J/A5UfakbtfB1wHsGzZMl+xYkVuKgRaW1sZaX8LnmylpybBihWT4jR9SRjtWEtu6TgXho5zYeg4jy2f3embgGMyHs8DtmQ8TgInAK1mtgE4E7h50gxua0qyRt3pIiIyieUzxB8BWsxsoZlVAZcANw+udPc2d5/h7gvcfQHwIHCBuz+ax5qylk4l2LCrg65ejVAXEZHJKW8h7u59wFXA7cALwE/c/Tkz+5yZXZCv182VllSSAYd1O9QaFxGRySmf58Rx91uBW4ct+9Qo267IZy3jtWRWMEJ9zbZ2jp/TEHE1IiIih9OMbaNY0FhPRcxYvU3Tr4qIyOSkEB9FVUWMhTPqFeIiIjJpKcTHoDnURURkMlOIjyGdSvLKngN09miEuoiITD4K8TGkUwncYe12tcZFRGTyUYiPoSUVjFBfpfPiIiIyCSnEx7CgsY6qeIw1CnEREZmEFOJjqIjHWDRTI9RFRGRyUogfgUaoi4jIZKUQP4J0KsHmvZ20d/dFXYqIiMghFOJHMDi4TefFRURkslGIH8GS1ME51EVERCYThfgRHDO9juqKmAa3iYjIpKMQP4J4zGhuSrBaE76IiMgkoxDPQjqVZPVWtcRFRGRyUYhnIZ1KsnVfF22dvVGXIiIiMkQhnoV0KgHA2u1qjYuIyOShEM9COhyhrklfRERkMlGIZ2Hu1FpqK+Os0nlxERGZRBTiWYjFjJZUgjXqThcRkUlEIZ4lzaEuIiKTjUI8S+lUgh37u9nT0RN1KSIiIoBCPGstQ4Pb1KUuIiKTg0I8S0Mj1DVzm4iITBIK8SzNaaghUV2hq5mJiMikoRDPklkwQl3d6SIiMlkoxMch3aQR6iIiMnkoxMehJZVgd0cPO9u7oy5FREREIT4eS2ZphLqIiEweCvFxGByhvkZd6iIiMgkoxMehKVnNlJoKtcRFRGRSUIiPg5mF068qxEVEJHoK8XFKzwpGqLt71KWIiEiZU4iPU7opQVtnLzv2a4S6iIhESyE+TkPTr2pwm4iIREwhPk6DF0JZpfPiIiISMYX4OM1IVDGtrlJzqIuISOQU4uOkEeoiIjJZKMQnIJ1KskYj1EVEJGIK8QlIpxLs7+7j1bauqEsREZEyphCfgJaU5lAXEZHoKcQnQHOoi4jIZKAQn4Dp9VXMSFSrJS4iIpFSiE9QOpVQiIuISKQU4hOUTiVZs72dgQGNUBcRkWgoxCconUpyoKefzXs7oy5FRETKlEJ8gtKpBABrtqtLXUREoqEQn6AWXQhFREQiphCfoIbaSlJTqlm9VS1xERGJhkL8KKRTSVarO11ERCKiED8K6VSStRqhLiIiEVGIH4V0KkFX7wCv7DkQdSkiIlKGFOJHYXBw2yqdFxcRkQgoxI9CS9Pg18w0Ql1ERApPIX4UkjWVzJ1aq+lXRUQkEgrxo9SSSui74iIiEgmF+FFKp5Ks295OX/9A1KWIiEiZUYgfpZamBD39A2zcrRHqIiJSWArxo7RkVjBCfY3Oi4uISIEpxI9SczhCXefFRUSk0BTiR6muqoJjpmuEuoiIFJ5CPAfSTUmFuIiIFJxCPAfSs5K8tLODXo1QFxGRAlKI50A6laC339mwsyPqUkREpIwoxHOgpSkYoa7BbSIiUkgK8RxobkoQM1il8+IiIlJACvEcqKmMM7+xXt8VFxGRglKI50hLU0Ij1EVEpKAU4jmSTiXZsOsA3X39UZciIiJlQiGeIy2pBP0DzvodGqEuIiKFoRDPkcE51NWlLiIihaIQz5GFM+qJx4w1+pqZiIgUiEI8R6or4ixorFNLXERECkYhnkPplOZQFxGRwlGI51BLKsnG3Qfo6tUIdRERyT+FeA4tSSVxh7XbdV5cRETyTyGeQ+lUAoA129WlLiIi+acQz6EFM+qpjJsuhCIiIgWhEM+hyniMhTPqWb1VLXEREck/hXiOpVNJVqs7XURECkAhnmPpVJJXdndyoKcv6lJERKTEKcRzbHBwm0aoi4hIvinEc6wlFcyhvkrnxUVEJM/yGuJmdr6ZrTKztWb2yRHWv9/MnjGzJ83sXjNbms96CmH+9DqqKmKsUUtcRETyLG8hbmZx4BrgzcBS4NIRQvpH7n6iu58CfAH4j3zVUygV8RiLZyY0/aqIiORdPlvipwNr3X29u/cANwIXZm7g7vsyHtYDnsd6CiadSuhqZiIiknf5DPG5wCsZjzeFyw5hZlea2TqClviH81hPwaRTSTbv7WR/V2/UpYiISAmryOO+bYRlh7W03f0a4BozewfwT8BfHrYjsyuAKwBSqRStra05K7K9vT2n+wPo2RF8vezHt91N89R4TvddzPJxrOVwOs6FoeNcGDrOY8tniG8Cjsl4PA/YMsb2NwJfG2mFu18HXAewbNkyX7FiRY5KhNbWVnK5P4CFuzr40uOtJOe2sOJ1x+Z038UsH8daDqfjXBg6zoWh4zy2fHanPwK0mNlCM6sCLgFuztzAzFoyHv4xsCaP9RTMMdPqqKmMaQ51ERHJq7y1xN29z8yuAm4H4sC33f05M/sc8Ki73wxcZWZvBHqBPYzQlV6MYjGjuUkj1EVEJL/y2Z2Ou98K3Dps2acy7n8kn68fpXQqyX1rd0ZdhoiIlDDN2JYn6VSSbfu6aevUCHUREckPhXieDM6hvkZd6iIikicK8TxpaQrmUNfgNhERyZcjhriZzTOz/zazHWa2zcx+ZmbzClFcMZs7tZa6qrgGt4mISN5k0xK/nuCrYbMJZlz7VbhMxhCLGS2ppEJcRETyJpsQn+nu17t7X3j7DjAzz3WVhHRTQt3pIiKSN9mE+E4zu8zM4uHtMmBXvgsrBelUkp3t3ezu6Im6FBERKUHZhPh7gD8HtgKvAheFy+QIWsIR6upSFxGRfDjiZC/u/jJwQQFqKTlLZgUj1Nds28+ZixojrkZERErNqCFuZn/n7l8ws68w8tXHSuKyofk0a0oNyeoKnRcXEZG8GKsl/kL489FCFFKKzIyWlOZQFxGR/Bg1xN39V+HdA+5+U+Y6M7s4r1WVkHQqye3PbcXdMRvpEusiIiITk83Atn/IcpmMIJ1KsudALzvbNUJdRERya6xz4m8G3gLMNbMvZ6yaAvTlu7BSkU4dHNw2M1kdcTUiIlJKxmqJbyE4H94FPJZxuxl4U/5LKw1pfc1MRETyZKxz4k8BT5nZj9xd19OcoJnJahpqK1mlEeoiIpJjR/yeOLDAzP4PsBSoGVzo7ovyVlUJMTOWpJK6JKmIiORcthdA+RrBefCVwPeA7+ezqFIz+DUz98O+bi8iIjJh2YR4rbv/HjB33+junwHOzW9ZpSWdSrKvq4/t+7ujLkVEREpINt3pXWYWA9aY2VXAZqApv2WVlsw51FNTao6wtYiISHayaYl/FKgDPgycBlwG/GU+iyo1g18zW7VV58VFRCR3xmyJm1kc+HN3/1ugHXh3QaoqMTMS1TTWV7FGI9RFRCSHxmyJu3s/cJppvtCj1pJKsHq7WuIiIpI72ZwTfwL4pZndBHQMLnT3n+etqhKUTiX5+eObNYe6iIjkTDYhPh3YxaEj0h1QiI9DSypJe3cfW9q6mDu1NupyRESkBBwxxN1d58FzYEk4uG31tv0KcRERyYlsRqdLDgzOoa6Z20REJFcU4gUyta6KmclqVmuEuoiI5IhCvIDS4fSrIiIiuXDEEDezlJl9y8x+HT5eambvzX9ppSedSrJmWzsDA5pDXUREjl42LfHvALcDc8LHqwlmcZNxSqeSdPb2s3lvZ9SliIhICcgmxGe4+0+AAQB37wP681pViUpnzKEuIiJytLIJ8Q4zayT4bjhmdibQlteqSlRzUziHukJcRERyIJvJXj4G3AwsNrP7gJnARXmtqkQ11FYyu6FGc6iLiEhOZDPZy+NmthxYAhiwyt17815ZiWpJJdWdLiIiOZHN6PQrgYS7P+fuzwIJM/tg/ksrTemmBGu3t9OvEeoiInKUsjkn/tfuvnfwgbvvAf46fyWVtnQqSXffAK/sPhB1KSIiUuSyCfFY5qVIw2uMV+WvpNKWnqXBbSIikhvZhPjtwE/M7DwzOxe4Abgtv2WVrpYmzaEuIiK5kc3o9L8H3gd8gGBg22+Ab+azqFJWX13B3Km1mkNdRESOWjaj0weAr4U3yQHNoS4iIrmQzej0s83st2a22szWm9lLZra+EMWVqnQqyfodHfT1D0RdioiIFLFsutO/BfwN8BiabjUn0qkkPf0DbNh1gObwHLmIiMh4ZRPibe7+67xXUkbSqWCE+ppt+xXiIiIyYdmMTr/TzL5oZmeZ2amDt7xXVsKamxKYocFtIiJyVLJpiZ8R/lyWscyBc3NfTnmorYpzzLQ6DW4TEZGjks3o9JWFKKTcpDWHuoiIHKVsWuKY2R8DxwM1g8vc/XP5KqocpFMJWldtp6dvgKqKbM5qiIiIHCqbr5hdC7wd+BDBZC8XA/PzXFfJS6eS9A04G3Z1RF2KiIgUqWyagK9393cBe9z9s8BZwDH5Lav0taSCUemrtqpLXUREJiabEO8Mfx4wszlAL7AwfyWVh8UzE8RMc6iLiMjEZXNO/BYzmwp8EXicYGS65k4/SjWVcRY01utrZiIiMmHZjE7/5/Duz8zsFqDG3dvyW1Z5aEklWL1dLXEREZmYUUPczM519zvM7G0jrMPdf57f0kpfOpXkdy9sp6u3n5rKeNTliIhIkRmrJb4cuAP40xHWOaAQP0rpVJL+AWf9jg6WzpkSdTkiIlJkRg1xd/+0mcWAX7v7TwpYU9kYmkN9+36FuIiIjNuYo9PDa4lfVaBays7CGfVUxEwzt4mIyIRk8xWz35rZJ8zsGDObPnjLe2VloKoixoIZGqEuIiITk81XzN4T/rwyY5kDi3JfTvlJpxI8t2Vf1GWIiEgRyuYrZprYJY/SqSS/fnYrnT391FZphLqIiGQv2wugnAAs5dALoHwvX0WVk3QqiTus29HOCXMboi5HRESKSDYXQPk08JXwthL4AnBBnusqG+lwDnUNbhMRkfHKZmDbRcB5wFZ3fzdwMlCd16rKyPzGeirjxiqFuIiIjFNWF0AJv2rWZ2ZTgO1oUFvOVMZjLJ6ZYI1GqIuIyDhlc0780fACKN8AHgPagYfzWlWZaUkleeLlPVGXISIiRSab0ekfDO9ea2a3AVPc/en8llVe0k0JfvXUFjq6+6ivzmqsoYiISFYD235pZu8ws3p336AAz72WcPrVtdvVpS4iItnL5pz4fwDnAM+b2U1mdpGZ1RzpSZK9JbOCENfgNhERGY9sutPvAu4yszhwLvDXwLcBXbEjR46dXkd1RYw1CnERERmHbCd7qSW4JOnbgVOB7+azqHITjxmLZyY0h7qIiIzLEUPczH4MnAHcBlwDtIZfOZMcSqcSPPzS7qjLEBGRIpLNOfHrgcXu/n53v0MBnh/pWUm2tHWxr6s36lJERKRIHDHE3f02d+8vRDHlLN0UDG7TpC8iIpKtbFriUgDp1GCIa3CbiIhkRyE+ScybVkttZVyD20REJGujDmwzs1PHeqK7P577cspXLGa0pBK6mpmIiGRtrNHp/y/8WQMsA54CDDgJeIhgAhjJoZamJPes2RF1GSIiUiRG7U5395XuvhLYCJzq7svc/TTgtcDaQhVYTtKpBNv3d9N2QCPURUTkyLI5J36cuz8z+MDdnwVOyV9J5WtwcNvq7epSFxGRI8smxF8ws2+a2QozW25m3wBeyHdh5agllQBg1VaFuIiIHFk2066+G/gA8JHw8d3A1/JWURmbO7WW+qq4vmYmIiJZyeYCKF1mdi1wq7uvKkBNZcvMaEkl9TUzERHJSjbXE78AeJJg7nTM7BQzuznfhZWrdCrBGp0TFxGRLGRzTvzTwOnAXgB3fxJYkMeaylo6lWRnew+72rujLkVERCa5bEK8z93bJrJzMzvfzFaZ2Voz++QI6z9mZs+b2dNm9nszmz+R1yklQyPU1aUuIiJHkE2IP2tm7wDiZtZiZl8B7j/Sk8wsTnDp0jcDS4FLzWzpsM2eAJa5+0nAT4EvjKv6EjQ0h7q61EVE5AiyCfEPAccD3cANwD7go1k873Rgrbuvd/ce4EbgwswN3P1Odz8QPnwQmJdt4aUqNaWaZE2Fpl8VEZEjMnfPz47NLgLOd/e/Ch+/EzjD3a8aZfurga3u/i8jrLsCuAIglUqdduONN+aszvb2dhKJRM72lwv/8mAncYN/OKM26lJyajIe61Kk41wYOs6FoeMMK1eufMzdl4207ohfMTOzNPAJgsFsQ9u7+7lHeuoIy0b8xGBmlxHMz758pPXufh1wHcCyZct8xYoVRyo7a62treRyf7lw++5n+PWzr7J8+XLMRjqMxWkyHutSpONcGDrOhaHjPLZsJnu5CbgW+CbQP459bwKOyXg8D9gyfCMzeyPwv4Hl7q4h2QRfM7vh4V52tHfTlKyJuhwREZmksgnxPnefyAxtjwAtZrYQ2AxcArwjcwMzey3wdYJu9+0TeI2SNDS4bVu7QlxEREaVzcC2X5nZB81stuT5CDMAACAASURBVJlNH7wd6Unu3gdcBdxOMNf6T9z9OTP7XDiBDMAXgQRwk5k9qUlkAoNzqGtwm4iIjCWblvhfhj//NmOZA4uO9ER3vxW4ddiyT2Xcf2MWr192ZiaqmVZXqRAXEZExZTN3+sJCFCIHaQ51ERHJxqghbmbnuvsdZva2kda7+8/zV5akUwl++eQW3L2kRqiLiEjujNUSXw7cAfzpCOscUIjnUTqVZH9XH9v2dTOrQYPbRETkcKOGuLt/Ovz57sKVI4NamoIR6qu27VeIi4jIiLIZ2IaZ/THB1KtDaeLun8tXURJ0pwOs2baf5emZEVcjIiKTUTbXE78WeDvBHOoGXAyU/dXG8q0xUc2MRJVGqIuIyKiy+Z746939XcAed/8scBaHzsQmedLSpBHqIiIyumxCvDP8ecDM5gC9gL52VgDpVII12/aTr4vUiIhIccsmxG8xs6kEs6s9DmwguKyo5Fl6VpKOnn427+088sYiIlJ2spns5Z/Duz8zs1uAGndvy29ZAofOoT5vWl3E1YiIyGQz1mQvI07yEq7TZC8FkA6/ZrZ6235WHtcUcTUiIjLZjNUSH2mSl0Ga7KUAGuoqaUpWa3CbiIiMaKzJXjTJyySwZFZSXzMTEZERZfM98UYz+7KZPW5mj5nZl8yssRDFSfA1s7Xb2xkY0Ah1ERE5VDaj028EdgB/BlwU3v9xPouSg9KpBJ29/WzaoxHqIiJyqGxCfLq7/7O7vxTe/gWYmu/CJNCSOji4TUREJFM2IX6nmV1iZrHw9ufA/+S7MAkMzqG+SiEuIiLDZBPi7wN+BHSHtxuBj5nZfjPbl8/iBJI1lcxpqGGNQlxERIbJZrKXZCEKkdG1pDSHuoiIHC6b0envHfY4bmafzl9JMlw6lWDtjnb6NUJdREQyZNOdfp6Z3Wpms83sROBBQK3zAkqnkvT0DbBxV0fUpYiIyCSSTXf6O8zs7cAzwAHgUne/L++VyZD00Aj1dhbNTERcjYiITBbZdKe3AB8BfkZwBbN3mpmuxlFAzU1BcGtwm4iIZMqmO/1XwP/n7u8DlgNrgEfyWpUcor66gnnTalm9XYPbRETkoCN2pwOnu/s+AHd34P+Z2c35LUuGS6eSaomLiMghRm2Jm9nfAbj7PjO7eNhqXRylwNKpJOt2tNPbPxB1KSIiMkmM1Z1+Scb9fxi27vw81CJjSKcS9Pa7RqiLiMiQsULcRrk/0mPJs8wR6iIiIjB2iPso90d6LHm2eGYCM10IRUREDhprYNvJ4dzoBtRmzJNuQE3eK5ND1FbFmT+9TiEuIiJDRg1xd48XshA5Ms2hLiIimbL5nrhMEulUgg07O+jp0wh1ERFRiBeVdCpJ34Dz0k6NUBcREYV4URkcob5K58VFRASFeFFZNLOeeMw0c5uIiAAK8aJSXRFnfqNGqIuISEAhXmTSTUnWaIS6iIigEC866VlJNuzqoKu3P+pSREQkYgrxIrMklWTA4ZnNbVGXIiIiEVOIF5k3pGcwpaaCb96zPupSREQkYgrxIpOsqeTysxdy+3PbNMBNRKTMKcSL0Ltfv4C6qjjX3Lk26lJERCRCCvEiNK2+isvOnM+vntrCBs3eJiJSthTiReqvzllIRTzGtXeti7oUERGJiEK8SDVNqeHty47hZ49vYsvezqjLERGRCCjEi9j7li/CHa67WyPVRUTKkUK8iM2bVsdbXzuXGx95mZ3t3VGXIyIiBaYQL3IfWLGY7r4BvnXvS1GXIiIiBaYQL3KLZyZ4y4mz+f4DG2k70Bt1OSIiUkAK8RJw5Ypm2rv7+O4DG6IuRURECkghXgKWzpnCecc18e37XqKjuy/qckREpEAU4iXiynOb2Xuglx899HLUpYiISIEoxEvEqcdO4+zmRq67Z70uUyoiUiYU4iXkypXN7NjfzU2PvhJ1KSIiUgAK8RJy1qJGTj12KtfetZ7e/oGoyxERkTxTiJcQM+Oqc5vZvLeTXzyxOepyREQkzxTiJWblkiaWzp7C11rX0T/gUZcjIiJ5pBAvMWbGlSubWb+zg18/+2rU5YiISB4pxEvQ+SfMYtHMeq65cx3uao2LiJQqhXgJiseMD65o5oVX93HHi9ujLkdERPJEIV6iLjxlDvOm1XL1nWvVGhcRKVEK8RJVGY/xvuWLeeLlvTywblfU5YiISB4oxEvYxafNoylZzdV3ro26FBERyQOFeAmrqYxzxRsWcf+6XTy2cU/U5YiISI4pxEvcO844lml1lVyj1riISMlRiJe4uqoK3nP2Qu54cTvPbWmLuhwREckhhXgZeNfrF5CsruCrd66LuhQREckhhXgZaKit5J1nzefWZ19l7fb2qMsREZEcUYiXifees5Dqihhfa1VrXESkVCjEy0RjoppLTz+WXzy5mVd2H4i6HBERyQGFeBm54g2LiBl8/W61xkVESoFCvIzMbqjlotPm8ZNHN7F9X1fU5YiIyFFSiJeZ9y9fTF//AN+4Z33UpYiIyFFSiJeZ+Y31XHDyHH740Mvs6eiJuhwRETkKCvEy9MGVzRzo6ef6+16KuhQRETkKCvEylE4ledPxKa6/fwP7unqjLkdERCZIIV6mrlrZwv6uPr7/wMaoSxERkQlSiJepE+c1sDw9k2/f+xKdPf1RlyMiIhOgEC9jV53bzK6OHm54+OWoSxERkQlQiJex1y2YzukLp3Pd3evp7lNrXESk2CjEy9xVK5vZuq+Lnz++OepSRERknBTiZe4PWmZw0rwGvta6jr7+gajLERGRcVCIlzkz48qVzby8+wC3PP1q1OWIiMg45DXEzex8M1tlZmvN7JMjrH+DmT1uZn1mdlE+a5HR/eFrUqRTCa65cy0DAx51OSIikqW8hbiZxYFrgDcDS4FLzWzpsM1eBi4HfpSvOuTIYrGgNb5mezu/eX5b1OWIiEiW8tkSPx1Y6+7r3b0HuBG4MHMDd9/g7k8DOhkbsT8+cTbzG+u45s61uKs1LiJSDPIZ4nOBVzIebwqXySRUEY/xgeWLeWZzG3et3hF1OSIikoWKPO7bRlg2oSaemV0BXAGQSqVobW09irIO1d7entP9FbMZA870GuNff/EYnFGb8/3rWBeGjnNh6DgXho7z2PIZ4puAYzIezwO2TGRH7n4dcB3AsmXLfMWKFUdd3KDW1lZyub9i96Hql/jsr56n9tgTOWNRY073rWNdGDrOhaHjXBg6zmPLZ3f6I0CLmS00syrgEuDmPL6e5MAlrzuWGYkqrr5zbdSliIjIEeQtxN29D7gKuB14AfiJuz9nZp8zswsAzOx1ZrYJuBj4upk9l696JDu1VXHee84i7lmzk6de2Rt1OSIiMoa8fk/c3W9197S7L3b3z4fLPuXuN4f3H3H3ee5e7+6N7n58PuuR7Fx25rFMqangGrXGRUQmNc3YJodJ1lRy+dkL+c3z21i1dX/U5YiIyCgU4jKid79+AXVVcb7aqta4iMhkpRCXEU2rr+KyM+fzq6e2sGFnR9TliIjICBTiMqq/OmchFfEY1961LupSRERkBApxGVXTlBrevuwYfvb4Jrbs7Yy6HBERGUYhLmN63/JFuMN1d6+PuhQRERlGIS5jmjetjre+di43PPwyO/Z3R12OiIhkUIjLEX1gxWJ6+gf41r0vRV2KiIhkUIjLES2emeAtJ87mBw9upO1Ab9TliIhISCEuWblqZTPt3X185/4NUZciIiIhhbhk5TWzp/DG1zRx/f0v0dHdF3U5IiKCQlzG4cqVzew90MsPH9oYdSkiIoJCXMbhtcdO4+zmRr5xz0t09fZHXY6ISNlTiMu4XLmymR37u7np0VeiLkVEpOwpxGVczlrUyKnHTuXau9bT2z8QdTkiImVNIS7jYmZcdW4zm/d28osnNkddjohIWVOIy7itXNLE0tlT+GrrOvoHPOpyRETKlkJcxs3MuHJlMy/t7ODWZ16NuhwRkbKlEJcJOf+EWSyaWc81d67FXa1xEZEoKMRlQuIx44Mrmnlx635+/8L2qMsRESlLCnGZsAtPmcO8abVcrda4iEgkFOIyYZXxGO9bvpgnX9nL/et2RV2OiEjZUYjLUbn4tHk0Jau5+o61UZciIlJ2FOJyVGoq41zxhkU8sH4Xj23cE3U5IiJlRSEuR+0dZxzLtLpKrrlTrXERkUJSiMtRq6uq4D1nL+SOF7fz3Ja2qMsRESkbCnHJiXe9fgHJ6gq+eue6qEsRESkbCnHJiYbaSt551nxuffZV1m5vj7ocEZGyoBCXnHnvOQuprojx1VadGxcRKQSFuORMY6KaS08/ll8+uYVXdh+IuhwRkZKnEJecuuINi4gZXHuXzo2LiOSbQlxyanZDLRedNo+bHt3Etn1dUZcjIlLSFOKSc+9fvpi+gQG+cff6qEsRESlpCnHJufmN9Vxw8hx++NDL7O7oibocEZGSpRCXvLhyZTOdvf1cf99LUZciIlKyFOKSFy2pJOcfP4vv3L+BfV29UZcjIlKSFOKSN1eubGZ/Vx/ff2Bj1KWIiJQkhbjkzYnzGliensm3732Jzp7+qMsRESk5CnHJq6vObWZXRw83PPxy1KWIiJQchbjk1esWTOf0hdP5+t3r2N/jUZcjIlJSFOKSdx85r4Vt+7r58B0H+NOv3Mu//fpF7lmzg65edbGLiByNiqgLkNJ3dvMMbr7qbK6/7WE298X55j3rufaudVRVxFg2fxpnN8/g7OYZnDi3gXjMoi5XRKRoKMSlIE6aN5ULm6tYseIsOrr7eHjDbu5bs5N71+7ki7ev4ou3r2JKTQVnLW4cCvVFM+oxU6iLiIxGIS4FV19dwcolTaxc0gTAzvZu7l+3ayjUb39uGwCzG2rCQG/k7MUzaJpSE2XZIiKTjkJcIjcjUc0FJ8/hgpPn4O68vPsA967dyX1rd/K7F7bx08c2AZBOJXj94hmc0zyDMxZNJ1lTGXHlIiLRUojLpGJmzG+sZ35jPX9xxnwGBpznX903FOo3PPwy37l/A/GYccoxUzk77H5/7bHTqKrQOE0RKS8KcZnUYjHjhLkNnDC3gfcvX0xXbz+Pv7yH+9fu4t61O7n6zrV8+Y611FbGOX3hdM4Jz6cfNytJTIPkRKTEKcSlqNRUxnn94hm8fvEMPvGmJbR19vLg+l3cvzY4n/75W18AoLG+irMWNw6F+jHT6yKuXEQk9xTiUtQaait50/GzeNPxswDY2tbFfWHX+71rd3LL068CcOz0Os5uDs6nn7W4ken1VVGWLSKSEwpxKSmzGmr4s9Pm8WenzcPdWbejnXvX7OTetbv41VNbuOHhlzGDpbOnDLXSX7dgOrVV8ahLFxEZN4W4lCwzo7kpSXNTksvPXkhf/wBPb24b+irbt+97ia/fvZ6qeIxT50/lnOYZvL55BifNbaAirkFyIjL5KcSlbFTEY5x67DROPXYaHzqvhQM9fTyyYc9Q9/v//c1q+M1qktUVnLm4kbMXN3Lq/GksmZWkukItdRGZfBTiUrbqqipYnp7J8vRMAHa1d/PA+l1hqO/it88Hk85UxWMcNzvJiXMbOGleAyfOnUpLKkGlWusiEjGFuEioMVHNn5w0hz85aQ4Am/Yc4OlNbTy9qY1nNu/l5qe28MOHgkuqVlfEWDpnCifNbeDEeVM5aV4Di2cmNPe7iBSUQlxkFPOm1TFvWh1vOXE2AAMDwWxyT29u45lNe3l6Uxs/fWwT331gIwC1lXFOmDuFE+cGoX7ivAYWNtbr++oikjcKcZEsxWLGghn1LJhRzwUnB631gQFn/c4OntkchPozm9r40cMb+fZ9AwAkqis4Ye4UTpo3dag7/tjpdbqwi4jkhEJc5CjEYkZzU4LmpgT/67XzAOjrH2Ddjg6e3rSXZzYH3fHfuX8DPX1BsE+pqQhCfV5D2B3fwNyptQp2ERk3hbhIjlXEYyyZlWTJrCQXLzsGgN7+AVZv288zm9rC7vg2vnnPenr7HYDp9VUZA+eCYJ81pUbBLiJjUoiLFEBlPMbxcxo4fk4Dl4TLuvv6WbV1/1A3/NOb2/hq6zr6B4Jgn5Go5qR5DUO3E+Y20JTU5VhF5CCFuEhEqivinDRvKifNmzq0rKu3n+df3ReEejgq/s5V2/Eg15ndUHOwxR6eZ9cUsiLlSyEuMonUVMaHJqQZ1NHdx/Ov7gtb7Ht5enMbvwm/ww4wb1rtUEv9pLlT2dk5QG//gL7HLlIGFOIik1x9dQWvWzCd1y2YPrRsX1cvz23ed3BU/OY2bn1m69D6v73718xMVDN7ai2zp9Qwe2oNcxpqmdVQw5ypNcxqqCWVrNb0siJFTiEuUoSm1FRy1uJGzlrcOLRs74Eentuyj9898ATJWfPZ2tbJq21drNm+n7vX7OBAT/8h+4gZNCVrhoJ9dkMtsxuCn4PLmpI1msBGZBJTiIuUiKl1VZzdPIPeTZWsWJE+ZJ27s6+rj61tXWxp6+TVvV1sbetkS1sXW9u6eHHrfu58cQedvYcGfTxmNCWrg3AfatUPhn0Nc6bWMiNRraAXiYhCXKQMmBkNtZU01FayZFZyxG3cnX2dfWxp6zwk7F9t6+LVtk5e2LKP37+wja7egUOeVxEzUlOCUJ8VBvusKYe27mckqjVznUgeKMRFBAiDvq6ShrpKXjN7yojbuDt7D/QOBfvQzzDsn93cxm+f30Z338hBf2i3/cFW/fT6KqbUVpKoqlDYi4yDQlxEsmZmTKuvYlp9FUvnjB70ew70smVv0KI/GPZdbNnbyVOb9nLbc11DM9hlihkkayqZUlvBlJrK4DZ4vzZ43FBbMXR/Su2h6+ur4pogR8qKQlxEcsrMmF5fxfT6Kk6Y2zDiNu7O7o6eoWDfe6CXfV297OvsZV9XX/izl32dfWzcdYC2zmBdx7DBecPFY0aypiIM+zE+DGTcb6g9uL62Uh8CpLgoxEWk4MyMxkQ1jYnqUYN+JH39A+zv6hsK+IPB3xsGfd9hHwbW7W9nX2cfbZ29hw3cG64iZmErP7O1X5ER9AfXbdzRR+OmNqbVVzK9voq6Kv13KoWnvzoRKRoV8dhQd/5E9PQNsL/r8Nb+YPC3jbBs676uoW2HD+r7j8fuHbpfUxljel1Q2/TMW7issf7QdVNrK/U9fTlqCnERKRtVFbGhHoCJ6OrtZ39X0Kq/876HWLDkBPZ09LCro4c9B3rY1R783N3Rw8ZdB9jT0cP+7r5R99dQW3louB8W+JVMr69mel0V0xNVOucvh1GIi4hkqaYyTk1lnJnJajZNi7NiaeqIz+nu62fvgV52d/QM3TIDf1dHD3s6enhl9wGeemUvew70DF3dbriqeCzsvq9men0l0+oOb+EPBv70uiqm1lVRVaHWfilTiIuI5FF1RZzUlDipKdldgc7dae/uOyT0h4I/DPzdHb3s7uhmy9597O7ooa2zd9T9JWsqmF5fxbS6KpI1FVTEjIp4jKp4jIq4URmPURk3KmKxg/eHlseoiB3cpjIeoyLzfixju2H7qqoIflbELXytjPsxIx4z9SrkgEJcRGQSMTOSNZUkayqZ31if1XN6+wcOae0fGvgHb+3dffT1O739wUVy+gac3r4Begecvv4BesN1fQM+dEnc/L1PqIyN8EGiwqiMHfxg0NnRyVdffCBYHn5gqMr4IFFVEcv4OcI2FZmPD25XFY8NrRt6PLTMDtm+YhJ/4FCIi4gUucp4jJnJamYmJ3aufyQDA07vwEBG6IcB3x8sH7ofruvrDz4M9PYN0DcwQE+4rK/f6ekfCO4PDN4P1g1u09s/wgeJ8Oe27g7iMaO7d4D2rj56+p2evv6h7Xr7B+jpO/QDSD6M/KHg4IeGyooY1fHgQ8iUmkq+dtlpealjOIW4iIgcJhYzqmNxqiNOidbWVlasODPr7Qc/fPT2Bx8oeoZC/mDQ9/QPBD0QmY8zPhD0hM8dWjb4gaFv2OOMfQ8+p7t3gH2Mfnoj1xTiIiJSMg758JG7jolJS8MWRUREipRCXEREpEgpxEVERIqUQlxERKRIKcRFRESKlEJcRESkSCnERUREilReQ9zMzjezVWa21sw+OcL6ajP7cbj+ITNbkM96RERESkneQtzM4sA1wJuBpcClZrZ02GbvBfa4ezPwn8C/56seERGRUpPPlvjpwFp3X+/uPcCNwIXDtrkQ+G54/6fAeTZZZ5kXERGZZPI57epc4JWMx5uAM0bbxt37zKwNaAR2Zm5kZlcAVwCkUilaW1tzVmR7e3tO9yej07EuDB3nwtBxLgwd57HlM8RHalEPv7xMNtvg7tcB1wEsW7bMV6xYcdTFDQom18/d/mR0OtaFoeNcGDrOhaHjPLZ8dqdvAo7JeDwP2DLaNmZWATQAu/NYk4iISMnIZ4g/ArSY2UIzqwIuAW4ets3NwF+G9y8C7nD3/F6JXkREpETkrTs9PMd9FXA7EAe+7e7PmdnngEfd/WbgW8D3zWwtQQv8knzVIyIiUmryej1xd78VuHXYsk9l3O8CLs5nDSIiIqVKM7aJiIgUKYW4iIhIkbJiG0dmZjuAjTnc5QyGfS9d8kbHujB0nAtDx7kwdJxhvrvPHGlF0YV4rpnZo+6+LOo6yoGOdWHoOBeGjnNh6DiPTd3pIiIiRUohLiIiUqQU4uF0rlIQOtaFoeNcGDrOhaHjPIayPycuIiJSrNQSFxERKVJlHeJmdr6ZrTKztWb2yajrKUVmdoyZ3WlmL5jZc2b2kahrKmVmFjezJ8zslqhrKVVmNtXMfmpmL4Z/12dFXVOpMrO/Cf/feNbMbjCzmqhrmmzKNsTNLA5cA7wZWApcamZLo62qJPUBH3f31wBnAlfqOOfVR4AXoi6ixH0JuM3djwNORsc7L8xsLvBhYJm7n0BwDQ5dX2OYsg1x4HRgrbuvd/ce4EbgwohrKjnu/qq7Px7e30/wH97caKsqTWY2D/hj4JtR11KqzGwK8AaCizfh7j3uvjfaqkpaBVAbXqq6jsMvZ132yjnE5wKvZDzehMIlr8xsAfBa4KFoKylZ/wX8HTAQdSElbBGwA7g+PG3xTTOrj7qoUuTum4H/C7wMvAq0uftvoq1q8innELcRlmmofp6YWQL4GfBRd98XdT2lxsz+BNju7o9FXUuJqwBOBb7m7q8FOgCNp8kDM5tG0Du6EJgD1JvZZdFWNfmUc4hvAo7JeDwPddXkhZlVEgT4D93951HXU6LOBi4wsw0Ep4bONbMfRFtSSdoEbHL3wd6knxKEuuTeG4GX3H2Hu/cCPwdeH3FNk045h/gjQIuZLTSzKoIBEzdHXFPJMTMjOH/4grv/R9T1lCp3/wd3n+fuCwj+lu9wd7VacszdtwKvmNmScNF5wPMRllTKXgbONLO68P+R89AgwsNURF1AVNy9z8yuAm4nGPX4bXd/LuKyStHZwDuBZ8zsyXDZP7r7rRHWJHI0PgT8MPzwvx54d8T1lCR3f8jMfgo8TvAtlyfQ7G2H0YxtIiIiRaqcu9NFRESKmkJcRESkSCnERUREipRCXEREpEgpxEVERIqUQlwkC2bWb2ZPhldTusnM6kbZ7lYzmzqB/c8Jv04z0fo2mNmMiT6/WJjZ5WY2Z5R1nzOzN45zf2Vx3KR0KcRFstPp7qeEV1PqAd6fudICMXd/y0QuiOHuW9z9olwVW8IuJ5iC8zDu/il3/11hyxGJlkJcZPzuAZrNbEF4PemvEkxIccxgyy5j3TfC6yH/xsxqAcys2cx+Z2ZPmdnjZrY43P7ZcP3lZvZLM7stvN79pwdf2Mx+YWaPhfu84kiFmtn54Ws8ZWa/D5dND/fztJk9aGYnhcs/Y2bfDWvdYGZvM7MvmNkzYS2V4XYbzOzfzezh8NYcLp9vZr8P9/t7Mzs2XP4dM/uymd1vZuvN7KKM+v7WzB4Jn/PZcNmIxy583jKCiVaeHDyeGfv6zuC+wxo/G773Z8zsuHB5Y7i/J8zs62RcQ8HMLgvfz5Nm9nULrs0+38zWhL/TmJndY2Z/NL4/F5H8UYiLjIMFl0R8M/BMuGgJ8D13f627bxy2eQtwjbsfD+wF/ixc/sNw+ckEc0G/OsJLnQ78BXAKcLGZLQuXv8fdTyMIsw+bWeMYtc4EvgH8WfhaF4erPgs84e4nAf8IfC/jaYsJLmd6IfAD4E53PxHoDJcP2ufupwNXE1w9jfD+98L9/hD4csb2s4FzgD8B/i2s74/CY3R6+D5PM7M3jHbs3P2nwKPAX4S9Ip2jvffQTnc/Ffga8Ilw2aeBe8OLl9wMDH7QeA3wduBsdz8F6A9fZyPw78C1wMeB53UlLZlMFOIi2am1YNrYRwnmdP5WuHyjuz84ynNecvfBqWYfAxaYWRKY6+7/DeDuXe5+YITn/tbdd4VB9XOCAIQguJ8CHiS4gE/LGDWfCdzt7i+Fr7U7XH4O8P1w2R1Ao5k1hOt+HV5s4hmC6YhvC5c/AyzI2PcNGT/PCu+fBfwovP/9jJoBfuHuA+7+PJAKl/1ReHuCoCfjuIz3c9ixG+N9jmbwYjuZz38DwYcT3P1/gD3h8vOA04BHwt/zeQSXHcXdvwkkCU6hDH4YEJkUynbudJFx6gxbaEPMDIJLUY6mO+N+P1DLyJfAHcnw+ZDdzFYQXNnpLHc/YGatQM0Y+7AR9jO4fLTX6wZw9wEz6/WD8zIPcOj/Fz7K/ZH2ObTfYa9vwP9x968fUlxw3fmRjt14De6jn9Frz6zpu+7+D4etCAYxzgsfJoD9E6hFJC/UEhcpoPBa6pvM7K0AZlZtI490/8Pw3HUt8FbgPqAB2BMG+HEELe2xPAAsN7OF4WtND5ffTdBVT/jBYOcErvH+9oyfD4T37ye4ghrh/u89wj5uB95jwbXmMbO59v+3d/8sXUdRHMffnxZnF9eWHoI+hIZmWwIl2wTDrU1E3XoGtWhTbj4AoSEIIpAGhcCtOd2UHCRPw72BiPJDwfSL79d4v//uvcvhgAq+XAAAAQtJREFUnPOFm0yMeOaIlhXf1Pm1PwPG+/gn4Pm/7/e9f9yvvaW1B5Zp7Qnp3jATl/6/WeB9kjXglNarPrtwzxdaSfoJ8LGqdpLsAfNJdoF9Wkn9SlV10H9+20ryCPgFPAVWgI3+nt/AyxusYSzJN1oi8KKPLQLrSd4AB4w43auqtnsv+muvahwDM7TM+SofgHdJTmgViVF98YtWgc0k34HPtNYIVfUjyRKw3ffqFFjoVYEpWq/8T5LpJK+qauOa35VuhaeYSfdMkjlgsqpe3/VcLpPkJ21+h3c9F+mhs5wuSdJAmYlLkjRQZuKSJA2UQVySpIEyiEuSNFAGcUmSBsogLknSQBnEJUkaqL9g5BTwTFat3wAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# Pipeline a scaler and PCA selecting 10 components\n",
"pipe = Pipeline([\n",
" ('scaler', StandardScaler()),\n",
" ('reducer', PCA(n_components=10))\n",
"])\n",
"\n",
"# Fit the pipe to the data\n",
"pipe.fit(ansur_df)\n",
"\n",
"# Plot the explained variance ratio\n",
"plt.plot(pipe.steps[1][1].explained_variance_ratio_);\n",
"plt.xlabel('Principal component index');\n",
"plt.ylabel('Explained variance ratio');\n",
"plt.title('Elbow plot of Explained variance ratio');\n",
"plt.grid(True);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### PCA for image compression\n",
"You'll reduce the size of 16 images with hand written digits (MNIST dataset) using PCA.\n",
"\n",
"The samples are 28 by 28 pixel gray scale images that have been flattened to arrays with 784 elements each (28 x 28 = 784) and added to the 2D numpy array `X_test`. Each of the 784 pixels has a value between 0 and 255 and can be regarded as a feature.\n",
"\n",
"A pipeline with a scaler and PCA model to select 78 components has been pre-loaded for you as `pipe`. This pipeline has already been fitted to the entire MNIST dataset except for the 16 samples in X_test."
]
},
{
"cell_type": "code",
"execution_count": 56,
"metadata": {},
"outputs": [],
"source": [
"def plot_digits(data):\n",
" fig, axes = plt.subplots(4, 4, figsize=(6, 6),\n",
" subplot_kw={'xticks':[], 'yticks':[]},\n",
" gridspec_kw=dict(hspace=0.05, wspace=0.05))\n",
" for i, ax in enumerate(axes.flat):\n",
" ax.imshow(data[i].reshape(28, 28),\n",
" cmap='binary',\n",
" clim=(0, 300))"
]
},
{
"cell_type": "code",
"execution_count": 71,
"metadata": {},
"outputs": [],
"source": [
"from sklearn.datasets import fetch_openml\n",
"\n",
"X, y = X, y = fetch_openml('mnist_784', version=1, return_X_y=True)\n",
"X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)\n",
"X_sample = X_test[:1600:100]"
]
},
{
"cell_type": "code",
"execution_count": 78,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"Pipeline(memory=None,\n",
" steps=[('scaler',\n",
" StandardScaler(copy=True, with_mean=True, with_std=True)),\n",
" ('reducer',\n",
" PCA(copy=True, iterated_power='auto', n_components=78,\n",
" random_state=None, svd_solver='auto', tol=0.0,\n",
" whiten=False))],\n",
" verbose=False)"
]
},
"execution_count": 78,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"pipe = Pipeline([\n",
" ('scaler', StandardScaler()),\n",
" ('reducer', PCA(n_components=78))\n",
"])\n",
"\n",
"pipe.fit(X_train)"
]
},
{
"cell_type": "code",
"execution_count": 79,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAV4AAAFYCAYAAAAbcpQHAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjMsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+AADFEAAAgAElEQVR4nO3deZyN5f8/8NdkTdYMQhg7JdkrSZYQhURSaNGiIjtJ6iMVEVHZRZYsUVlSobLVl8hWhEiNPRkh2Zf5/fF7XG/vY+4zZ5lzrnOfM6/nP16Pe86cc7vNXK77fV9LXHJyMoiIyJ5rIn0CRETpDRteIiLL2PASEVnGhpeIyDI2vERElrHhJSKyLGMgL46Pj09OSEgI06nErsTERCQlJcVdfZzXM3gbNmxISk5Oznf1cV7T4PGahpa333sgwIY3ISEB69evD81ZpSPVqlVzPM7rGby4uLg9Tsd5TYPHaxpa3n7vAZYaiIisY8NLRGQZG14iIsvY8BIRWcaGl4jIMja8RESWBTScjNKnadOmSR48eLDkVq1aSX7jjTesnpMbXbhwQfLatWslL1y4EAAQF3dlSOe+ffskv/7665JLly4dzlMkl2CPl4jIMja8RESWubrUMH36dMmjR4+WfPz48VS/r2DBgpI7deokWd8ak7Njx44B8CwpfPHFF46vPXLkiOTLly9Lvuaa9PP/+aBBgyQvWrRIsrmOAHDttdcCAIoVKybHdFmiXbt2kr/55hvJOXPmDO3Jkmukn98QIiKXYMNLRGSZ60oN/fr1kzxv3jzH1+inw07++usvya+++qpkXa6YPHmy5OLFiwd8nrFq4MCBAIDFixf7fO3KlSslnz9/XnLWrFlDf2IuVaFCBckNGzaUnCNHDsnZsmUDABQpUkSOnTp1SnKzZs0kL1++XHLz5s1De7LkGuzxEhFZxoaXiMgy15QaTInBW3nBm/vvvx+A563u0qVLHV+rSxDdunWTvGDBgoA+M1rpa7R69WrJK1askLxkyZIU36dLOzfffLPkF154QXJ6Ki9oukwQiOuuu07yXXfdFarTiTqbNm0CALRt21aO6REyviQnJ0vWZZ8XX3xRcp06ddJwhuHBHi8RkWVseImILHNNqWHZsmV+v/bjjz+WXKlSJQCetxy7du2SrG+HdalBv2bYsGEAgF69egVwxtFBPz1/+eWXJeuB+k5q164tuU2bNpLr1q0bwrMjAKhcubJkXfZKD6MafvzxRwCev7+6tJUpUybJ5ncdAJo2bQoA+PTTT+XYli1bJHfu3FnyiBEjJDdo0CAUp51m7PESEVnGhpeIyDLXlBoC8cknn0iuWrVqiq+XL19e8vjx4yU/99xzkg8dOiT5s88+A+C5lkOsbGdtnhpfnX3RJQWWF8JLjyTRT+bTA/277OSpp56S3LVr1xRff+ihhyQPGDDA8X179+4tedKkSZKd2g5b2OMlIrLMNT1esxj0Rx99JMd+/vlnyR07dpT82GOP+f2+ZcqUkVyuXDnJusdrVjvbuHGjHIv2Hu/JkycBXHlwCABJSUmS9UML/SDNPIzU14rCK3/+/JIzZ84cwTOxY82aNZL1Km7GTTfdJFmP7/VF39GeOXNGslmIHvD8vY8k9niJiCxjw0tEZJlrSg2NGjUCANx5551yTN8aFy5cWLK+TfZl586dkvUtjlagQAEAnqtLRaMTJ05IHj58OADgt99+k2N6xawxY8ZIrlatmoWzI02v/qYfrukV9GKVnnZufiaPHj0qx/Q07Pj4eL/f94YbbpCs2ws3Yo+XiMgyNrxERJa5ptRgZM+e3TEHQu/Jpp/qnz171vH1ZcuWTdPnuYVelW3u3Lkpvq5HhrC8EFljx46VrBfir1KlSiROxyq9l1zGjKFrgszIKMBz/zuz5x3gntFK7PESEVnGhpeIyDLXlRqCpcsLn3/+ueTvv//e8fV6C/ghQ4aE78TCTE8Dfvfdd1N8Xe9hZxaNDxU9ML1JkyaSQ3n7GEv0ymN79uyRPGHChEicjiuY0srXX3+d5vfSo0P+++8/yXq0g1umZLPHS0RkGRteIiLLYuae0GxLDvh321K6dGnJuXPnDss5hYsuq+i1LfRxMymkVq1acixPnjyS9+7dK1kvLG9GRhw+fFiO6T2wrrnG+f/ql156KcUxvQi9Xl8jV65cju8R67766ivJevHzGjVqROJ0XMGp1GAWRweAxx9/PNXvX7t2rWS9PoPbscdLRGRZ1Pd4zdRLbw/RNN2zGDx4cNjOKdzMymOA9y18Jk6cCMBzjOg777wjWfdy9e7DTrz1cn3R05L1g4/JkydL1itzxSrzb6GnrOuHnulZzZo1AXguA7B582bJ+mddT3k3W1r1799fjnkbp6/v9NyCPV4iIsvY8BIRWRaVpQZ92/rqq68C8By3p912222S9TjX66+/PkxnF356XKJeKHrGjBmSzfRJvduqLkv4Ki9o2bJlk1y9enXJK1eu9Ps9du/eLbl169aSX3zxRcktW7b0+/2iiZm2rv+t9M7N6VmJEiUAAB06dJBjersu/XDNPDAGrqxmtn//fp+foacouwV7vERElrHhJSKyLGpKDXrlLf1E+PTp0yleW7JkScmxUl7Q9BNgPU5Xlxo2bNgAAHj66afl2KVLlxzfL2/evJLNYvB16tSRY7pcoz/bW7li27ZtADxvEy9evChZjxFevXq15FgqNehdbq+77joAwH333Rep03E9vYOwXjlPj1rYvn17UO+tp2e7BXu8RESWseElIrLM1aUGPVJBryDmVF7Qq409+eSTkmOlvODNnDlzUv26t/KC2eMOAEaOHBnUZ2fNmtXxuJkGqhde97aXWN26dYP6bDfSJZQpU6ZI7tu3LwCgatWqtk8pasTFxUnW5TP9863bA1M+MJNTAM+V+tyOPV4iIsvY8BIRWea6UoOZgw0AvXr1knzw4EHH12fJkgUA8P7778sxtyx2bEOfPn0kFypUSPLs2bMBeC816Pnw7733nuR27doB8BzpECzzXgAwffp0yf/++69kvWJXqBdqt0H/XfSkCD36Q08YocDotTx0NhMv9Ip8LDUQEZFXbHiJiCxzTanBLGLcvXt3OebPUo9mEXN9S33s2DHJblwSLpT0dtV6sLm5Lt99950c27Fjh2T9BH7cuHGSzfoLZiIF4Lk+Q/ny5SXrbbP1U2mzcHrmzJnlWIYMGfz560Sdb7/9VvKhQ4ck66UvKbL0hAy3YI+XiMiyiPZ4z507J9msoqWnkPrD9Nz0g434+HjJ9evXd/w+Pb63ffv2ADxX7zLTXgHg3nvvlXz77bcHdH6RYq7no48+Kseee+45yVu2bHH8PjMt05/pmbpXrFeAMitHLV++3PH79CpT+gFctPjll18kv/HGG5J1r1/fuZnevj8LynvbZslc37lz58oxMxWZUufGLYHY4yUisowNLxGRZREtNTz//POS9X5UaZWUlCRZrxLlzdixY1Mc0zvhRvOi1bqkov+eu3btkqzLCqb8o8f2eqNXjPNFP1zr0qWLZLPnVjTRq8B52+dLj+9NTk4G4Dm219tOy0WLFpWsd782u0LrEph+6Ene6Y0D3II9XiIiy9jwEhFZFtFSg5626kvGjFdO1WnMqLepsYFo3Lix5GeffVZyuXLl0vzebqCnAeusR2qYW2e9mHyRIkUkz5s3z/G9Z86cKdkseq6vp977zUz3jFb6ei1cuFCyXjxer/5myjf65+jWW28N4xmS5safN/Z4iYgsY8NLRGRZREsN+om2mdqqp6TqAfp6ZIF+2rtv3z4AwJdffhn0eWTPnh1AdA7mDzWzuHmDBg0cv/7yyy8HdDwWtWjRwjGTOyUmJkb6FFJgj5eIyDI2vERElkW01DBq1Kg0v4d54q7XISCi9EGvzmc2RQA814HRa7D069fPynn5wh4vEZFlbHiJiCxzzULoRESBqly5suSOHTtK1nswVqpUyeo5+YM9XiIiy9jjJaKYoFc71NmN2OMlIrKMDS8RkWVseImILGPDS0RkGRteIiLL4sx+UH69OC7uCIA94TudmFUsOTk539UHeT3ThNc09HhNQ8vxegIBNrxERJR2LDUQEVnGhpeIyLKAZq7Fx8cn62XYyD+JiYlISkqKu/o4r2fwNmzYkORUP+M1DR6vaWh5+70HAmx4ExISsH79+tCcVTpSrVo1x+O8nsGLi4tzfNjDaxo8XtPQ8vZ7D7DUQERkHRteIiLL2PASEVnGhpeIyDI2vERElrHhJSKyjA0vEZFlbHiJiCzjnmvk4dixYwCAn3/+WY599913kvWiSnFxjpNy8OSTTwIASpQoEY5TJIp67PESEVnGhpeIyDKWGtKpS5cuSf7pp58kDx06FACwffv2oN87f/78AIAXX3wx6Peg9GXnzp2S58yZ4/P1X331FQDgn3/+kWPe1hbXJbG7775bcpEiRQAAVapUkWN16tSRnC1bNp/nESz2eImILGPDS0RkmetKDXv37pW8YcMGx9dUrVpVct++fVO89pprAvv/pHLlygCAhx56SI6VL19ecrly5QJ6P7c6f/68ZHPdAODrr78O6eesXbsWAEsN5Jv5mXzmmWfk2N9//+339+sygrdRNtqqVatSHJsxY4bksWPHStZlh1Bjj5eIyDI2vERElrmu1PDcc89J/vPPPx1fU7JkScm7d+8GEHh5Qdu0aZPHnwBw4403Sta3H6VKlQr6c2w6e/YsAODbb7+VY2PGjJHs7dpmz54dANCoUSM59tRTT0lu0qSJz8/euHEjAOCJJ56QY926dZNcqVIln+9hw8WLFyWfPn1a8uXLlx1f4+TgwYOSr732WskHDhyQvG7dOgCet8L79++XvHTpUsf31ueRN29eAMALL7wgx9q0aSM5Y0bX/Sr7JVOmTAA8y1L65/TIkSOpfr/+Wbrlllt8fp7+91qyZEmKr+vRPCw1EBHFEDa8RESWueb+xNwSe7sF1kx5IdRy5coluXnz5pK3bt0qOVpKDUOGDAEAzJ492+drGzduLPm1114DAOTOnVuO6YHpumTwwQcfSL7rrrskJyYmArgyugEA+vfvL7l3796S9YB22yZPnix5+fLlko8fPy7Z/F0iQZfPzBoaI0aMkGP6mhcrVszeiYWQKb+0atVKjukcCrpcZCYIeWOrZMMeLxGRZa7p8Zqebo0aNVIcA3yvdOXPqll9+vSRrHt09evXBwBkzpxZjrVo0UJy4cKFU/3sSNJ/7379+klesGBBitcWKFBAcs+ePSXff//9kp2unT7WoUMHybpnYh7+AFceVOke5ejRoyV36dJFsn6NHp9tg3kACQCbN28O2+dUr14dAHDixAk5pntW27Zt8/u99MOkaO3l2qZ7udOnT0/x9axZs0q+4447rJwTe7xERJax4SUissw1pQYzZVBPHTTjQQHPFYRCYe7cuSmO6TGD8+bNk9y5c+eQfnYo6Vv1+fPnp/h6xYoVJQ8bNkyyWZkpUGbcJeBZXtDMqk76uumSiB6nOX78eMkTJkwI6pyCpaeI63KKWfnq6teYUsisWbPkmC5DFSpUSLIeU2rKZHqs8C+//CJZ/8x7U7x4cQDA66+/7vO16ZWeEq8fQjqVF7R69epJrlChQuhPzAF7vERElrHhJSKyzDWlBiehKC/s2LFDsr6FnDhxomRz292gQQM55ubywrlz5yQ7lUyAK2OSO3XqJMeCLS+Egr6eejSBLpWsWbNGso2nywULFpSsp6y2b99esl4tz5Rtbr311qA+L2fOnJL12HB/VKtWDYDnVHby3BuwR48ekvXUYE1P6za/72+//XaYzs479niJiCxjw0tEZJmrSw3+MFMpv//+ezn26aefStarROnbjzx58kg2T9bNk2O3W7x4seQ9e/Y4vsZMFqldu7aVc/JFjxrwtrC8XpDd1kB2J3pyjc6hZFYsS41encyUGtIbvbqeHrVgfgf0173tuab16tVL8qOPPhqKUwwKe7xERJax4SUisiwqSw26fGCeRge6HbleFyBaSgyGnnSgJSQkSNYLmbuNntSh1ywwZSP6//QoiFBPIHIzXT4I9b59emLFddddB8BzJUJb2OMlIrIsanq8upertwf6/fffg3o//b9qtPnjjz8k64dW+mGB+d/cjfSqWrrHG83/Jv44deqUZL3mrze6J5aexu+aKecAkCFDBsmXLl1K83v/999/ks2WXk2bNpVjadlCLBDs8RIRWcaGl4jIsqgpNejVwoItL8Q6PTY5WuidXPX45Fg0atQoyf48DNbTvdOTmjVrSm7durVkPd23TJkyADxLMHrlPL08wLRp0yTrsb5mDLweL81SAxFRjGLDS0RkWdSUGvTqVsGuHKZ3t120aJFkMxrg/fffl2Px8fFBfYYN5jYLAHbt2iX5yy+/lNykSRMA9m6dAnHhwgXJy5Ytk+zmscdpcebMGQCeuy77IxpLR6Fmdr0OVNmyZSXr/fT0amaR5L7fSiKiGMeGl4jIsqgpNYSC3j9Llxo2bdoEAEhMTJRjbi416AXbdalhxYoVks1+dW5c1WrJkiWS9YpTpUqVisTphJ2ZOOHPSAazFTwFTk+O6Nmzp2Rv5QWzAp6epGELe7xERJax4SUisixdlRq8rQVQvnx5AJ7bc7uZHlSutxrXq3uNHDkSAPDKK6/IMfP3jITDhw9L1qur6Sf3uhQUS1atWpXq183+eADQtWvXcJ9OTNH7D06YMEGyr2sOAHXr1gXgud6JLezxEhFZxoaXiMiymC81TJ06VbK+LdfMHmDRUmooUKCAZL3VuB7VsGHDBgDAU089JcceeeQRyW3btpV8/fXXh/T8zLKVeh+8GTNmSN63b59kvVaD/nvFEr1GgxN9DfQC/eTd+vXrAXiu76F/xrzRC6u3a9cu9CfmJ/Z4iYgsi8ker37ItGDBAskXL16MxOmE1bBhwyR36dJFspmeqq/FmDFjJE+ZMkVy5syZJZsHDoGOY/7rr78kL126FIDngw+9KpR+yBerK3DpFfQOHToUwTOJbmvWrJE8c+ZMyebn++TJk47fly9fPsl6gwC9iUIkscdLRGQZG14iIsuivtRgHiLt3btXjk2cOFFy1qxZJbdo0UJyq1atJEfzDq56b7VJkyZJnj59OgBg0KBBjt93+vRpx6wXnA+WKSvUqFFDjpUoUUJy+/btJZcsWTLNn+dG/owjNfRDz1iiFxifM2eO5Hr16kk+evQoAGDcuHFybPfu3ZL1/oK6XOXETAEGgD59+kg2D8/dhD1eIiLL2PASEVlmpdSQlJQkuUePHpL1IsdmZSp926ufyGtDhw6VbFYWO3LkiBzTiyDrMZTRMk43FMztfK1ateSYGW0AeO5JtXPnTsnmds6faZS5c+eWnD9/fsktW7YE4DlO0o0LsofTunXrJJtbbn0NEhISJBctWtTaeYWDHi2kfzf1KAS9NfvAgQMl+yofeGNGLeif77feektyJKYBByJ9/TYQEbkAG14iIsuslBr0QPqffvpJ8vPPPy+5efPmKb5PT37Yv39/qp+hB+Wn1/KCk+LFi0vu2LGjY966datk/STaFz1IvWDBgsGeYsz4999/JevFt53KLHpQf7TvrWZGJgDAF198IVmXFzRf5YWKFStKzp49u2RdVjCjknLkyBHYyboEe7xERJax4SUissxKqUEPgtZ0+WD06NEAPCc86FuSIkWKSNblA3PLoW9D9NN28q1ChQqRPoWYsHz5csnHjx9P9bWxNHFEryr38ssvS37ppZccX6/3DDSjYfTkB/27nCVLlpCdp5uwx0tEZBkbXiIiy6yUGvTaCd6YfcQqVaokx/QgaD3f2o1zr4l+/fXXSJ9CxDVr1swxkyf2eImILLPS4502bZqNjyGKqJ49e0rW40vNAvR6vG7hwoXtnRi5Dnu8RESWseElIrIs6hdCJ3ILPeZU72arMxHAHi8RkXVseImILIsLZCHiuLi4IwD2hO90Ylax5OTkfFcf5PVME17T0OM1DS3H6wkE2PASEVHasdRARGQZG14iIssCGk4WHx+frDfpI/8kJiYiKSkpxe57vJ7B27BhQ5JT/YzXNHi8pqHl7fceCLDhTUhIwPr160NzVulItWrVHI/zegYvLi7O8WEPr2nweE1Dy9vvPcBSAxGRdWx4iYgsY8NLRGQZG14iIsvY8BIRWcaGl4jIMi4LSRRhq1evlrxt2zbJI0eOlGzG0X700UdyLF8+x2UAKAqwx0tEZBkbXiIiy6Km1PDdd99JPnjwoGQzo2bp0qU+3+Py5cuSr7km9f9z9Gu//fZbyUWKFPF9sjFg0qRJkkeMGCG5TJkykmfPni05c+bMdk4sCpmfnw8//FCOJSYmSj5z5ozkc+fOOb7H77//DgA4dOiQHGOpwdOFCxckjxo1SvIPP/wgWZdy8ubNCwD4+OOP5ZitqdHs8RIRWcaGl4jIMleXGmbNmiV56NChks+ePRvU+/kqLwT72mh38eJFyW+//TYAYN68eY5fP3LkiORjx45JLlCgQDhPMSrMnz9f8oQJEyTv378fAHD+/Pmg3zs+Ph4AkDNnzqDfIxatWLFC8vjx4yVv3rzZ5/cePXoUALBz50455k+p4fTp05KzZcvmx1mmlH5aFyIil2DDS0RkmetKDSdPnpQ8ceJEycGWF7y59tprJZvb5EaNGsmxqlWrSo71p8f//fefZP2E14kuNfTt21eyvrXOlClTCM/Offbt2yd5wYIFjlm/xknRokUl58mTR/Lhw4cl69LEe++9B8DeU3e3W7ZsGQCgZ8+ecsyfNsKMZACA7NmzAwC++eYbOdawYUPH7xs+fLjjcf35gWCPl4jIMja8RESWua7UoJ8M68Hioda/f3/JDz74YNg+x610eeGFF15I8fUcOXJIfvbZZyWPGzdO8po1ayQ/88wzkkePHg0AuO6660Jzsi5hJjHo66En83hzww03AADatm0rx5o2bZri64BnqeeWW26RfOuttwZxxrFryJAhADzLC2bkBwAkJSVJ1j+bDz/8sOTChQun+hl64tSMGTMk69ETwWKPl4jIMja8RESWua7UEKwWLVpIfvrppyWXKFEiEqfjevqWduPGjSm+PmjQIMkNGjSQfPPNN0vu2rWr5B9//FHyJ598AgDo0KFDaE7WMj1h5M8//5TcsWNHAN7LC3owfadOnSS3bNkSAJA7d26fn92uXbvATpaEHqmkr3/nzp39fg89wqFfv36S9Xoap06dkmzWhwh0JA97vERElrmux/vHH38E9PoHHngAADBw4EA5ljGj6/5arvDmm29KNr3Sq7Vp0wYAUKdOHcev6zuIrFmzStbjr81Ub/0AKZrGQn///feSn3/++VRfe8cdd0jWK7qlpynntsydO1eyHu9sxMXFSQ5FL1c/gNYPQKtUqSI52DHr/OkgIrKMDS8RkWWuuSc3t6d6cW1/mDF6LC8407dn3qYDFytWTPKAAQNSfT99a9WsWTPJK1eulGzGu5rxvP68bzSpXbu2ZD2umeWF0NNT1PW1dlowXi807w9T1vRWXtDeffddyaFYIY4/KURElrHhJSKyzDX353q8ZCA4Tjd1H3zwgeNx/ZRW38L5old36t27t+THHntM8t133w3Acx+8V199VXKGDBn8/rxIGDt2rOPxe+65BwDwzjvvyDGWF8LLrCAGeI7TNUqVKiVZ/0x7c+DAAclPPfUUAO/lhRtvvFGyLseFAn9qiIgsY8NLRGRZREsNn376qeTp06cH9R5ly5YF4N8tn356qdWvXx8AUKhQoaDOwY3Mbb5+KqzdfvvtkosXL57mz9MTJEypQY900CMqHn/88TR/Xjh5u/Vs3rw5AOdb3nBbv349ACBLlixyTK9eFqv0tc6cOXOKr+sJLN4mM/z000+Sx4wZI/mvv/5K9f3M4vOA52p9ocAeLxGRZWx4iYgsi2ipQT/1DlYgT5X1iluaGXjdo0cPOWZuK6PJ1q1bJZsJC8nJyXKsYsWKkvv06RPSz9b/DgULFkzx9alTp0p2e6nBNv1vtGPHDskjR46UbFZ/07fbem0I/W8bqypXrix5+/btADx/5s1KYYDnSB29d6N+jaFH/ujJMU6ljVBhj5eIyLKI9nivv/76SH68+PvvvwF4/s94+vRpyY888oj1c/KX7i3p8aX//PMPAM8Vm3QvN5zX3ozv1at86fN0oy1btkg+evRo2D/v0qVLkmfOnCn5rbfeSvX79FTZyZMnSx48eLDkSDz8s6F69eqSzTXbtGmTHNO9/suXL0v2dldsxvGa8dk2scdLRGQZG14iIssiWmp45ZVXJJvtVPSYO9t2794tWS8Ufu+990rOkyeP1XPyRe9+unbt2hRfN9vVAEC1atWsnJPZXVjf8urSjRvpMbF6TPKJEyck6y2BgqEX79ZjRD///HPH1+sy0U033QTgSgkJABYvXizZjJ0GPLfBinb6YdiqVav8/j5dXtDTjvUuw7169Urj2QWPPV4iIsvY8BIRWRbRUoOehte2bVsAQLly5eTYunXrJNeoUcPxPapWrQoAaNSokc/P03uOLViwQLLTFFEzTvDqr7ut1LBs2TLH42ZH20iOmc2fP79k/fR527Ztks0ttJv07NlTst5zzSyG3bhx46DeV5cJvJUXND2O1/x8t27dWo4dOnQoqPNwIz21XZf8JkyYIHnNmjV+v5+31ffMEgORxh4vEZFlbHiJiCxzzULo5lZKlwyOHTsmORS3+P3795esn2L37ds3xWv1U1GzhxgAFClSJM3nEUqJiYmOx82kj0iWRho2bCh59erVks2EFcCdpQZv9u/fD8BzUfc33njD7+/XpQNv9OpYr732mmTzM3r27Fm/P89N9IQGPfHDTPndvHmzHHPaut0f8fHxkvV0ajdulsAeLxGRZWx4iYgsc02pwUmob5P37Nkj+csvv/T7+7755hvJdevWDek5BUMvMO7tybZe6DxS9EgGvci8XgHKjfTt/oMPPijZjERYuHChHKtVq5ZkvS+XHp1jPPHEE5JXrFghWU+UCOTJfdGiRSXrso4bnTlzRvLw4cP9/r5cuXJJPn/+vOP7GZ07d5bsxvKCxh4vEZFlbHiJiCyLaKlh1qxZkkuXLt3K0LIAAA5sSURBVA0gNOsJ6NEQeqvuYPd104Po3UA/IdZZ37I67Sdli5lTr0s0+tbb7VuiZ82aVbJZOhC4Mlnl+PHjcqxr166S9VKbenlHs1aAGRUBeP5bBUvfTpv1MWKBHnHUpUsXyXp00ZAhQ1J8X7NmzcJ7YiHk7t8AIqIYZL3Hq1cYGjhwYKqv1Q8M9DZBTg8S/NlGyJ/FkY0yZcpI1qsbuYGePl2gQAHJenzslClTAHjuIBzO7WH0Q6Fu3boB8HygNnr06LB9djiVLFlS8rBhwwAA3bt3l2MnT56UrKcEh+suSV9T3Rt3u4wZrzQ1+iGkeeCtf04/+ugjyXpVu1GjRoXzFK1ij5eIyDI2vEREllkvNegHEHqcrn4gZngrHwS7O7Gv8kKpUqUkm1t1wH0rkukHKZ06dZKsHziY1dX0ws/6gY5e3L1evXqSK1WqBMCzvOK0ehsALFq0SLIuJZjrrM/NbdcwGGbMrr7lNWWVq+kHcIHsN6cf7OmF5J999lkAwAMPPCDHoumaZsmSRbIe+2xKDQcOHJBjeuy0niKtS2mGXvRdXzu3Y4+XiMgyNrxERJZZLzVUqFBBsl7keMyYMQA8VylyKj+khV54XY8MaNOmDQDPcZHRchunSwn6ybBZ/Hn9+vVyTE+5/OqrrxyzoZ+em/3wUlOzZk3J5vYv2AXD3e62226T7G2Krx6j7rTfnC7TFCxYULIeqWAW+Y81eh/AH3/8EYDn4ud79+71+7301PhQjI22hT1eIiLL2PASEVkW0SnDuuzQoUMHAJ5P080xwHvZwUym0CMSvJUJ9LRVW1ud26TLJybv27dPjv3www+S9a2dlpSUBAD47bff5Fj16tUl6z2r9OQCU64BouuWL1zMQvTeRNPkh1DLly+fZDNZYubMmXJMrxyof361AQMGAIiuacIae7xERJax4SUissw1C6E73frrfbooOHqPOF+3v0S2mbKDXuVN51jFHi8RkWVseImILGPDS0RkGRteIiLL2PASEVnGhpeIyDI2vERElrHhJSKyjA0vEZFlbHiJiCyLC2Q/qLi4uCMA9oTvdGJWseTk5HxXH+T1TBNe09DjNQ0tx+sJBNjwEhFR2rHUQERkGRteIiLLAloWMj4+PjkhISFMpxK7EhMTkZSUlGJbBl7P4G3YsCHJqX7Gaxo8XtPQ8vZ7DwTY8CYkJHjsWkv+8bbNEK9n8OLi4hwf9vCaBo/XNLRS216MpQYiIsvY8BIRWcaGl4jIMtfsuUZE6deOHTskd+jQQXKPHj0kt2rVyuo5hRN7vERElkV9j7dKlSoAgNOnTzt+ffr06ZKrV69u5ZyIKDDDhw+XfOzYMclxcY6jsaIee7xERJax4SUisiwqSw1Tp06VfObMGQDeb0m++uorySw1ELnL4sWLAQBr166VYwULFpRcs2ZN6+dkA3u8RESWseElIrIsakoNH374oeT58+dH8EwoPTl16pTkFi1aAAD27t0b0HuYNa91Oax48eKSK1WqJLlx48aSs2XLJjm1ef/RxpQHAWDEiBEAgAsXLsixwYMHS9Zlh1jCHi8RkWVseImILIuaUoNelm737t0RPBNKT86ePSvZ1wgaX/T3JSYmOmZvZbTKlSsDAKZNmybHMmaMml9fD/qaOpVtMmfObPN0IoI9XiIiy9jwEhFZ5up7laNHjzpmX0qXLi25e/fuIT2nWHf58mUAnuWcr7/+WvKNN94o+ZZbbnF8j1KlSgGIjXn2efPmlWxG1uhb5WCtWrVK8j///CP5xIkTkvV137RpEwDg0qVLcixaSw1Lly6VbEZ85Mt3ZcehokWLWj8n29jjJSKyjA0vEZFlrr5XefnllyVv3bo11dcWKlRI8rhx4yTnzJkz9CcWpVauXOmYdVnB3Mpu2LAh6M8xg/27du2a4lg0K1u2bMje69Zbb3U8rq/7Dz/8IPnOO+8EAGTKlClk52DT4cOHJb/33nuSTTnq0UcflWO6vBOr2OMlIrLMdT3edevWSQ6k15U9e3bJuvebnpw/f17yc889B8CzN/v3338H9b5Zs2aVfPHiRcesmTHXnTp1kmMzZsyQbB6+pWfmoRLgeffRu3dvyXpqbdu2bQEA11wTnX2lAwcOSNYLnRuPPPKIzdOJuOj8VyQiimJseImILHNdqWHz5s2Sve2jppmywtChQ8N2TtGic+fOktesWZPqa8uXLy85ISFBcq1atQAA119/vRyrU6eO5G3btknWY1H1A81z584BAP799185phek79KlS6rnFquSkpIkz5s3T/K7777r+PqHH35Yciw8nKQr2OMlIrKMDS8RkWWuKTWYqar6dswfZuHoUI6xjFb6Ft6MatD0E3G9+HYgbrrpJse8ZMkSyTt27EjxfU2aNAnq82LB9OnTAQAff/yxHPO2mLoe+9y+ffvwnpgLmIXO08OKZBp7vERElrHhJSKyzDWlBjOCwdyW+ev5558Px+lEpQoVKlj9vEOHDkl2KhHpfcX0KIn04M0335RsSgzeVmszkyMA5xJRrNGTR8qVKwfAc3+5UPM2Xfnzzz9P9dzuvfdeyQ899JBkM/InLdjjJSKyjA0vEZFlrik1/O9//wPg2dUn99HrM5iFwQHPUoNZoHvAgAFyLL2VGn7//Xe/X/vZZ59JLlKkiGS9Yle0rkrmRJdczOgOM+kGALJkyZLmz9A/p3pylZ7IY87D24gKvWD7999/73g8Pj4+qPNjj5eIyLKI9nidpp/6s13M448/Lvnaa68N6rP/+OMPyU6rJen/Bb1tcRNt9LYxixYtCuo9Nm7cKHnOnDmOr+nfvz8AoEaNGkF9Rix46aWXJJvtfE6dOiXH9LjnL774QvLbb78tWa9aNnny5LCcZ6SZ1fP0Smyh6PG+9tprknUvVzM9Yb1VmPb6669L1ksZ9OnTR3Kw/y7s8RIRWcaGl4jIsoiWGvTtxX///ZfqawsUKCBZj6nztTD0hQsXJP/222+S9fRaPR7V0It/33PPPZLNbTQA5MqVK9XPtk3vVjtq1CgAnrexmq/rHaiGDRtKbt26dUjfOxrp1d+c1K9fX/Jdd90lWW93tXr1aslz584F4PmzH00qVqwoWU81N+XGgQMHyrHBgwdLDqTscPLkScl6jK4uX+oHbffff3+Kr2sjR46UrFfo0zsiB4s9XiIiy9jwEhFZ5ppxvL7oJ4wlS5b0+/s+/fRTyfp2xpezZ89K9jYC4J133vH7/cJFL0A+fvz4FF/3dsubmJgo2WlUR6D02MZ+/foBAFq1aiXH9O1Z0aJF0/x5saRp06aS//zzT8mTJk2SPHXqVABAixYt5JgZLx0N9Lk63e5//fXXckyvyla5cmW/P2PChAmOx3PkyCG5du3akn2NoDp48KDjcV1WCxZ7vERElrHhJSKyLHruVYK0c+fOkL5f9+7dQ/p+wdCDtidOnCi5WLFiks0+XiVKlJBjCxYskKyfHDupXr265F27dkk+fvy4z/ObP3++x58AkDt3bsk33HCD5Lp160ouXLiw5JYtW/r8nFikR9ssW7ZMshmRoyfBRFOpQdOlwl69egHwLNvprd714vFO+84dOXJEsp56rZce0KNsfI1E2rNnj+Rnn33W8ftuu+22VN/DH+zxEhFZxoaXiMiyqLlXmTZtmuQyZcqk+Lpe7Fg/6V+xYoVkf9aBMDJkyCBZrxKlJ3JEin4qrP9Oen2Jjz76CIDnBAq9ApR+0qufIr/wwgspvq5vb/VaDfpWWI9qMK/XK5bpEoVeOUoPdDe3nZR+mLLCjBkz5Jie0NStWzfJZrQMADRo0ACA56QJPTpH/174Kjdu2bJFsi716MlZuk3Jnj17qu/nD/Z4iYgsY8NLRGRZREsN+im22XvJaWtwwHPeer169cJ7YvAsL+hbHDfTt0w6G7qk8MQTT0guVKhQqu+ryy633367Y9bXyJQ0zFKfVytbtqxkN06mOHDggGQ9AkNfB9tM6cfX2iTRxuy1picp6S3u9QLkPXv2lGzWfvC1Jgbg+bugR0HMmjULADBz5kw5pktiemnJSpUq+fycQMTWvyIRURSIaI9X9yamTJkCwLMn5q33Gwg9ns/bw7VSpUoB8Jxy64aHaN7o/6EXLlzo+BozbtZMyQSAhIQEyeEcA2pWlDIPQKLB+fPnJetpubp3PmjQIACe2/OEml5BT0/rbtSoEYDY2gJI07sMjx49WrLu/f7f//2f5F9++cXjz9ToXqzeOdjsbK4fJOtdy9u0aePXuQeDPV4iIsvY8BIRWeaacbxmSp4eL9e7d2/Jv/76q2Rzi+APb+WFTp06SX7wwQcB+H7I5BZVqlRxzBS8y5cvS9ZjQ9evXy/5vvvuAwD06NFDjukFzUNRgtB7tekymd5nMNbp8ehjx46VrPc9M6sO6n8rPZbcG912mFXh9BTlQFZDSwv2eImILGPDS0RkmWtKDYYeTaCnCeutrp32SPNm3bp1kvViy/oJf7SUGCh89GgB/WRbL65t9u8bMmSIHBs+fLhkvZeYHl/6wAMPALiyvxgAbN++XbK3ad36ib5+7/RKj6UN9bha29jjJSKyjA0vEZFlris1eHP33XcH9X16ELRZHJzoano6sF6hSu+9Z0pVehUsXRrQg/l1nj17NgD/VscrXbq0ZL1nHcUW9niJiCxjw0tEZFnUlBqIIqFPnz4psl5PQS+0v2TJEsl61IITXTrT24U3a9ZMcrTuqUa+scdLRGQZG14iIst4L0MUIL1UpM4dO3aMxOlQFGKPl4jIMja8RESWseElIrKMDS8RkWVseImILGPDS0RkGRteIiLL4vS+Tj5fHBd3BMCe8J1OzCqWnJyc7+qDvJ5pwmsaerymoeV4PYEAG14iIko7lhqIiCxjw0tEZBkbXiIiy9jwEhFZxoaXiMgyNrxERJax4SUisowNLxGRZWx4iYgs+3+1L5O/dbZwdwAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Plot the MNIST sample data\n",
"plot_digits(X_sample)"
]
},
{
"cell_type": "code",
"execution_count": 83,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"X_test has 784 features\n",
"pc has 78 features\n"
]
}
],
"source": [
"# Transform the input data to principal components \n",
"pc = pipe.transform(X_sample)\n",
"\n",
"# Prints the number of features per dataset\n",
"print(\"X_test has {} features\".format(X_sample.shape[1]))\n",
"print(\"pc has {} features\".format(pc.shape[1]))"
]
},
{
"cell_type": "code",
"execution_count": 84,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"X_rebuilt has 784 features\n"
]
}
],
"source": [
"# Inverse transform the components to original feature space\n",
"X_rebuilt = pipe.inverse_transform(pc)\n",
"\n",
"# Prints the number of features\n",
"print(\"X_rebuilt has {} features\".format(X_rebuilt.shape[1]))"
]
},
{
"cell_type": "code",
"execution_count": 85,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAV4AAAFYCAYAAAAbcpQHAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjMsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+AADFEAAAgAElEQVR4nO2dWbMd1XXH140djM1gBjEKpAtCaEAISQgJjQjjAeO44nJVyg+Oy18gL3nN18h3SLn8YBsnNh4CCIMECF0hIQk0TyAQ6DJDwDi28pBa6/76am9191H3Pude/X8vrGqOzunevbvv/q9pj507d86EEEKU4++GfQJCCHGpoRevEEIURi9eIYQojF68QghRGL14hRCiMHrxCiFEYb7c5sNz5sw5Nz4+3tOpzF5OnDhhk5OTY9OPazwHZ2JiYvLcuXM3TD+uMR0cjWm35J57s5Yv3vHxcdu5c2c3Z3UJsXr16uRxjefgjI2NnUwd15gOjsa0W3LPvZlcDUIIUZxWK97ZRF3F3thYUiHMaHjNg15fbtxm43gJ0Rda8QohRGH04hVCiMJcsq6GlDSmjP7b3/6W/OxMk9SDNkH6/PPPw3733XfD/uijj8L+u7+b+rv99a9/Pexrr73WzMy+8pWvDPTbs4HPPvvsPPuLL76IYxy7r33ta0mbn7lU6cI99r//+7/J7/Px5TiXer51Z4UQojAjveLlquHjjz8O+89//vN5n/3Sl74U9mWXXRb2V7/61bCvuOKKC/7eTF7ZTsf/sjcJhnF176vbgwcPxrHXXnst7Pfeey9sX9mamS1atOg8+4YbplJCeX9mKj5Of/nLX+LYp59+GvY777wT9unTp887znl79dVXh3377beHPW/evLCvu+66sP/+7//+os59ptLFc/jlL0+95jjXU3Sxwm6CVrxCCFEYvXiFEKIwI+Nq8GDO66+/Hsf27t0b9u7du8M+cuRI2JOTk2ZWlQW33HJL2KtWrQp73bp1YS9cuDBsyj4nF1wbhiN+OpRDOdvPLReg+etf/xr2m2++GfaLL75oZmZPPfVUHNu/f3/Y/L4VK1aETbeCS2qO4Ux1NXBMfY6ePXs2jp08OVXsxXF69dVXwz516pSZVYNrc+bMCXvJkiVhr1y5MuzFixeHfdNNN5lZ1XWWO08yEwN0vBaOGXF3YttnsG48+FyQnBty0HfAzLsrQggxw9GLVwghCjNUVwOjw+4+ePrpp+PYb37zm7C3b98eNjMcUlD2MtLMCPQnn3wStrsdGKVnFJnypFTU80LkIrNt5Pz7778f9q5du8L+wx/+YGZmL730UvLfUf4yGk/p7Pm7TcZnFMbzQqSyPzhvaTOb5rbbbgv7xhtvNLPq/eH8YrYNpTW/2z+fGyPOidyYjuL4Om+//XbYzAhhFg3P/6qrrjKzaubHNddcEzbdh7wvdfA3Ujm/XaEVrxBCFEYvXiGEKEynroa2svGDDz4I26PAzz77bBybmJgIm+6Fyy+/POxbb73VzMzmzp0bx+gyoIxjNgSjl16osWzZsjjm8tCsnVTpi5yUZHJ4HWfOnAmbLp3//M//DNtdOhyf+++/P+z169eHzX6jqcT/3Lnxu3NltKNYbuxziXODWQYLFiwIm3PUx4PPBOU05yVLtTk2dfeZY5qTyKPiauA1Hj9+3Myqz/orr7wS9ocffhg2x9qfcboX+KzTBcH7ctdddyU/73C86ootLgateIUQojB68QohRGGG6mpgxNKlF6UF3QeUuCyK8IwEj3KaVXs8sM/Anj17wn7rrbfC/p//+R8zq0ZCKVWakEpg71LaUfa0kUAsSPmv//qvsH/xi1+E/cILL4TtkfT77rsvjq1ZsybsDRs2hM0ilCuvvDLsNtedk8h+jV1Hk3PjyHPOZYf4ZzhPUsU3TWBWA11AdL9RCvsczfUb4Tjm+nD48WG4HHh+dLPs2LHDzMyeeOKJOMbnlC4nugz8HrH/BZ97ZoQcPXo0bHYqowstRe4562JOasUrhBCF0YtXCCEK04mroU2z7VxLPZcAdC+wF8DatWvDZvaB17BTkjAZm7/hfQjMqm0PXSazqGBQOdGljOO4UiI1+Q2Xc7/97W/j2OOPPx72vn37wr7++uvD9rH99re/Hce+9a1vhc2+AoNCKc9IdZ8J605u7HJSvcvz4PVx/h07dixsylueU11bSGY98JxHpVcD5y+fM8/oOHDgQByju/HBBx8M+7HHHgvb3Vx0L7A/Bt0VdDfSXeHvl5xriefMceS9UK8GIYSYIXSy4m3jtM8FUzwf7957741jDN7w+M033xx2Kt/Tc3vNqlvScDXhwQqzKQc9Vw1tc3f7CFhwfPhXORc84Urf83S9BHj6/1++fHnYXFW4sqDC4Iq4a0p3LcsF0QZd5VJR8X4x2Ohw/FnKzpUV5/b8+fPDrpuPnLujkq9LcvmxPn78/wx6/fSnPw37H//xH8/7XuYEU01T0XHrKgYv6+5zLrjWxfhqxSuEEIXRi1cIIQpTvDsZ5R3dBB5Uo+OaUot5unVQInBXXOYN8zMupdnVrEkpbt+dtZoESSidKK+89Jr5yszNffTRR8OmtPMm8impfCFSJdgMnLV1KfjY9imbm+Tupki5qczq9/Tjv6PNuc2S1jvuuOOC35fLQx5F+FxzrN2mi4W54t///vcv+L0szeb3cnwZrKM7om7M+mzkrxWvEEIURi9eIYQoTHFXAyUzyy09E4HR20HLUA8fPhw2ux7xOLsaefaE5wRfiFy+5yDn2QWMjrOhuecuspMWZRtzIinX3B3DXEu6VHJ5t/y8R6pZdk0pyd8bFXJ713G+ercwRtLpkqrrqMa97TheHFNm5NS5u+jm4GdLbwXf1uWWcvFwrtDdUpd5QDdCLmskd79S8Pluk0fdFq14hRCiMHrxCiFEYYaa1cBori/luaSnBKOdkh+UcdyfbevWrWEzA4AFAh7tpywnlByjsGU5I7YnTpwIm2WSLsFSxRFm1fGkLNu5c6eZVceTkWDeM44FpbO7i1gAQznKggx+3zD3B8vd47qtxnPbrRPPrGHDc0pkSmvuXZeCJbK5klZeS4k52tbVkHLPMCOkTXN/djp74403wuaeinRpcpOEFPx3fWaNaMUrhBCF0YtXCCEKM9Tt3VMNpdtKI5dxu3fvjmN0L1CKs7PWww8/HPbSpUvNrBqVpszISbphJa2zKOTUqVNhs6G2k+uzQPcCu7Z5jwc2j6aUZO8L7oNH2yPzHDe6K9iBjjYj26XHNtWEfbrt0B3WJNrthS2cixwbZjLkpHCqA2CT/h2pfh/DLrZgtpLPJxY3nT17Nuy9e/eGzUwkd9Ww89jJkyfD5nxjtlLOnejQldNnZzeteIUQojBD3fpnUMc/HeC+QuPWIc8//3zYXgJrZvaDH/wgbPab9VUXVwrM/cudM6+xTU/iQeD3c8XLlWZqdcPcxieffDJsBneY//vyyy+f9xtcMTDAxO/meLly8B1kzaorCf42AykMsJTO9c2tbni//Vw5T7iy4rUw0OO75nJMx8fHw6YSy+UC+1zj/889Y7kVbwmavAO4cvVgIreooorj+FJd+LznHGPJPOcjfy+lAHPKrM98aK14hRCiMHrxCiFEYXoLrnXduYvS7Ve/+lXYvrWNS+Tpv/fd7343bLoa2KnLZSZldK4Jed0OtH1BOcRSUUpk5sS6O2b//v1xjNurMIBBl4F/3+LFi+PYAw88EDblF+Uhz8mDZJS8zGGlq4gd4RhoG6aroc4FxuvidTOXmUEfD2QyMMmcal53m/PMwfOvK3HvmibPPYOo7nJhFz0G2hjk5fPpzc2Zx0u3Qy4X+Gtf+9p5x5psm9R1oE0rXiGEKIxevEIIUZih5vHWwbw8Zi388pe/DNvzdykFNm3aFDa7cFEyp2RQkz24hpUDmStfpHylZPWoLmUbS6Yp2xjpXb16tZlVG6Xfc889YTMyz1xgSjiPDLN0mzIwJRnNqrK9NG3ua27/MLoaODaeiXDnnXfGMboa+mRYZe1N8YwO3nu6sDimnHvuQuH/p1uFZfW5MuAUnMdt3E9t0YpXCCEKoxevEEIUplNXQxcynLKA3baY5E/57AUS3P6dMnnVqlWNzy8XuRx2ieV0WGjAAhF2uXI5nyt3ZmR55cqVYW/ZssXMql3NmLTPsV+0aFHYdHm4zH7hhRfiGKPWTFKnJBzFZP866L5hhJ2FLV4GvGzZslbfXSqZ/2K5mOfDs1r4nN5+++1hc3zpapicnDSzanEES7KZRcN/l+owR5p0myOD7g2oFa8QQhRGL14hhCjMyGQ1uARglzG6GlxamFX371qwYIGZma1ZsyaOUdKlEqbNqjLTMwDYT4ARUu4Dx+8rKf8YVc1lMvheZ2ZT2QJ0DfA6uHX48uXLw/bxpHRi5gFdFzwP4veSWSmsv6frguNc2tUwaFN7ZiwcOnQo7IMHD4bNfhQ+1uxCloNymd/h3fs499vK4r7owhXHzBrOK85pZj74nGRPBnY75DylzfmWIjc3Sep426wHrXiFEKIwevEKIURhhupqYOTXewow6Z79F5goTXnt+3qxwTGjwceOHUv+NqOb7mLgv6MsZ1tE/nZJVwPrydmTgefDa/IIO5PRKbkojXjcXTp07aQkr1l1zDkWzz77rJlVM1F4/9iHIdcGcdBocR25bdyb4LKWxSDe8tHM7PDhw2FzfN09wJ4YlNB0V9AmHumntM7tXTdMF0QXmSKc63Q7cJ66m4iuPz6znGN1+zWS1NbzTT/fBq14hRCiMEVWvPzrzpUPV2Oe8+mNzc2qK6bc6sRXfLkSXwZQ6BRnvrCvePlX8rbbbgubq7K6rUNKwNUlt4rhdfsqlatVrtQ4Fuz85nmTuTLLefPmhc17woDTH//4RzOrBuX479j4myt2rlj6yp3O7WTcZKXmK1YGwNiFjN3fUuXnVHhcvXFHZz4rzNH2vGv+f+Zzc+w4P9rs2Ns1uZxZnmsbeC1u8xi3FOJuzXxG2gTBcvOgi05lWvEKIURh9OIVQojCFNEhzL+jJGUwwoMUdC/ws2Tnzp1he7CB+Y10GVDWUF4zZ9c/wzzL+fPnh00HfknpRonfRN6kGm0zsMA9qTi2LKn0YCRdDfxeSjXKXgaOvAyYzeY9CGpmtnnz5rCZT0ypWIJc1zm6HThP/Lp43Qx28bPE85lZHs1xpGuAc5Al2d4wnI3jc4GlPnfHrSM3jnQ7MIjt87PtOfuYcew41zlnebyLDnhduMG04hVCiMLoxSuEEIUpoptze5ZRXnjmALtm5VwNlBEuZyiNCWUB3QTMR3U3BeUwZR4zGYaVI5nLwc3JHpeh7DLG62O3MHbV8kwTuh8o53LuAN63DRs2mFk1skyXAjMc+JlBo92Dkhs7Hqec93P1smqz6ryjm4DuLv93nHO5Lcdz0Xg/D96LXCbPMF0NhOeayy7yed323vuzzOeCbp/cHoW8X36cWUu5DQe6zrIZjTskhBCXEHrxCiFEYYq4Gii7KNvZuNvlM+Uwo8eUT6lSXUZQKR1y5amUzO5qYMI6JR/LMUtmNeSkDqVaE7eDQ0lLm93c3L2Tax6d6/rE8/Dxopxmsn+uTHjU8YyCjRs3xjF2duN4cI76HCy9Zf2w4TNLF13bbJ0UXojFrndnzpwJmxkkuX3W6p6XLsqfc2jFK4QQhdGLVwghClNEN1NaUsIzYuxuB0q0XKNt4nKAPQmYoE1ZnpPofh6Uw6OwLXauUxKlU076+7hQ3jaRde4KatKTguNMRnl/sC7gvWDmgWhGF1kX7v6i649FVLwvLIai+yuVScFz67Mxv1a8QghRGL14hRCiMMV7xlGmMdKZShBvgstxSogmpBKlR20b9xy5ZHmev18f3StdJ9ZT5s2UsWtLak+4JsUKuT4FTm7scvLWPzMqxRFN6DMr4M477zQzs02bNsUxugqZ1cA2pNzUYJjMnLsohBCzhOIrXv7F7qJE1AM8uVLkJucxWyjd9Hq2rnJJm2BLbpXrq+bcd7UZxz5XkV3T5Pz8egbd8Zk56MxNZ5kw1XAbZdzn+M6+t48QQow4evEKIURhhrrLcBfM9pxRMVzadKji/5+pZdGludigId1rvhOzWbkuY4OiFa8QQhRGL14hhCjMWJuyuLGxsbNmdrK/05m1zD937twN0w9qPC8KjWn3aEy7JTmeZi1fvEIIIS4euRqEEKIwevEKIURhWqWTzZkz59z4+HhPpzJ7OXHihE1OTp6Xx6LxHJyJiYnJlP9MYzo4GtNuyT33Zi1fvOPj47Zz585uzuoSYvXq1cnjGs/BGRsbSwZ7NKaDozHtltxzbzYLCijE6JEK2I5K4rq49OB8TNmcm6V6uMjHK4QQhdGLVwghCjPSrgbKglzt9aDSgN83TMkxG5FbQYwSuV4N3q4z54pQW0ghhJhFjPSKl6tS2imarFDrtlVpsgVL6t+NIqlVfBO8gTS3TuHuxewGxYbVqebV/Cy7yI26mqgLxuT+f25H69SWQRyvmTQ2s4lh7iSuuyyEEIXRi1cIIQpTxNUwqMO6Tsq2ZRQbIvdF3fV9+umnYb/55pthHz9+3MzMjh07FscmJyeT38E9rubOnRu2N6TmsWuvvTbsNm6hYdynQedJXVN+Pge+V6BZ1Y12qboaOAYcm88//zzsjz/+OGyfv5999lkc4/j6ruVmZtddd13SlqtBCCEuIfTiFUKIwvTmauiizy/lByVFSopQhnBr5yuvvDJsbu381a9+NeyUvGu7XXzfdLGHFN0LBw8eDHvv3r1h7969+7z//9Zbb4XNsf36178eNrfZXr9+vZlV9x27+uqrw26yT55f10zazrwOnv9ll11W+3lmk/ic57xs8h2jQs7N4s/1e++9F8def/31sOnyOnToUNgnTpwwM7MzZ86c911m1Tl2yy23hL1gwYKwFy5caGbVvdpuvfXWsG+++eaw6SrrYh4O/40ihBCXGHrxCiFEYXpzNbRdjnvCOWWtywkzs9OnT4dNWfLOO++c99kPP/wwbErcG26YajVKmXzFFVec9//vvvvupE13Rd8wCZ+0cX189NFHYe/YsSPsF154IWy6Fc6ePWtmZp988kkcY2T5gw8+CPv9998Pm8USnu0wZ86cOMZxo5wbFXJSmHLfoQuli8g45yvvF++Bnx9dZBzTq666Kmzei2FC99gXX3wRNl1ePt84BycmJsLes2dP2HQ7+NyjeyH3vNCVxjG74447zMxs5cqVcczdZGbVseb7oot7rhWvEEIURi9eIYQoTBFNQglA6cZMBI9kstP9888/HzZlBiOZJ0/+f9N8yuEcjEwy28EjoEuWLIljjzzySNiUlkzM7iuqnMoIaStv3DWzbdu2OLZ169awjxw5Ejbvj0eAly5dGsd4z95+++2wXSaaVeWtu4Lo/qHLh24oRpxTdJXJ4GPKa6GrhK4sLyIxq841l86XX355HKPN+0Zp7X0v6FLgb1N6M2uEUtcj7/fee28cu+eee5LnMSquBs6rnNshNTYcD3cDmlWv3d1YN954YxyjG4HuIrox6LpwNwU/y7Hj8911sYVWvEIIURi9eIUQojC9aRJKC8onRiHZA8DlHaUAo5GUtZSLlGMOI5B33nln2KzTfvfdd8N2mZOrEec5l6jvdnnd5Ld4nq+99lrY7qahu+aNN94ImxKOboW1a9ea2f9vcOjwXjKj5OjRo2FTkrvkpmSkq4hSk3ODbge6d7rAz4mZAqdOnQqbWR50d7kry2zqvtDdlHNdMDvBJTc/yzHgOXHM6A5bt26dmVWlNe/bKLoXclDC+/PLDBi6FFasWBG2ZyGYTbkF2S8kx69+9auwOWc9IyqVkWNWzRTpGq14hRCiMJ3+mcw1hebKLdcc2+Ffw7vuuits/uVjHqgHbbhC4sqWf8GYg8qVta+2uVLmyoIrnGF2NHI4tryOP/zhD2H7qo2rKa5i77///rC3bNkSNkt/U3ClRjXBYJ0H4LjqY/CKK0NeC8eZ498l/D02e+c5UQ1RBXnwhitRXiMDgamgD+d+Tg0cPnw4bM5Xv4+5QG+TMuwS5DoK5s7PV5Us273tttvCznXAq4P3bd++fWHv2rUrbL8ffOcwQNdnSbZWvEIIURi9eIUQojC9uRpY1ppzL1C2unuALoXNmzeHTbcDOwy5HMg59Sknmc/HXE3P76XEuemmm8JmDuoowLLq7du3h/3UU0+F7ddNl8J3vvOdsFkayVLpOii/eB94X12uMeBGCc2xJxz/rl0NPh8p1Skr58+fHzZlKq/XXVy8Vroo6GqgdPZr4RxlkOe3v/1t8jiDmh584vfSNVaKLrrFcUz92WIgi3ZdeTzHiMFjut0ef/zxsBkc9iCedykzq7o2+gxYasUrhBCF0YtXCCEK08laOrU/Vk4i5JpBu5RiPh+7gtVFGBm9Z/khI8MsYWVesOe0Mlti3rx5YTNLYhQac1Oq09XAzALvuPTYY4/FMdpdNHfnd1ACe7Sdso1uJbodGHFmXqrbXTehZ/4y3RmLFy8Om24HXoPbzD3mddE9VecGoIz97//+7+Rn6OLy8WBmSiqH3azfPdy6mPO89jZuPDZIP3DggJlVc7Fp+/83q2aQMGvnm9/8pplV84bZVqDPDCateIUQojB68QohRGE6Ddu1lSGU7S7nWTaa+z5KDi8g4Bbl7HrGcl9GPSnBXGYyo2LRokVhd12+OgiMtDPy/corryQ/8+CDD5qZ2Xe/+904lpOdzPzwsaNcpaslNxaUZS7hKeWZCcDyXN/jzazqgnj44Ycv+HuDwjFgVgOP5xLqHboa2pwfsxrY5Y0SmefB7mMPPPCAmVXdIDm62O9wmLCA5aWXXgr7T3/6U9jeTsDLfs2q1003DN0zHNNNmzaZWdWtyPvJ90/XLkateIUQojB68QohRGE6cTW0WXpTwjK66VHg3PKeXbZYKOCuBroRmOFA+c2INgsLvOcAXQ1N6DN6PB1Gz5nVwGIKFjRs2LDBzPKRWXY1Y6GDy2H2AehC7rOzFLNHnnnmmbApuf2+9enm4Xcze6Eumj1oDT97MrDzHo+zD8SqVavCruuhQYaVbTOd3D52fFb8M3QZ0BXFzmLM/uCcdbgdOzOiWCBE211ouSb9uWuhy2jQIguteIUQojDFm3jmVrz+F4UrsUOHDoXNfFUGlLxfKv8CMkc3ta3N9N9pUzJLSq542cuVqwP+LruFsQwyBXOdU2W0VAc5GCDiONftIsxcSa4kGBRN7e7bNVzdtMnZbBto8XFiUPTVV18Nm8Ek5gIz6FM3R4eZX87ngHZuOy4qBg9Uci4x3z61sjWbmqecS1RVVGz8Dv62Py8MlvLfEY4pr3FQtOIVQojC6MUrhBCFKb7LcG7nUYc5pZQqzCX17WnMpkop2WibUpzylQEqSnS6JtowrHxJXgfzTClT6wJAlNYs024juSmR27gacoEWyrxRCRARH/cmAZVUCXuu2TrHnEE+uhfqfjPXGbAEdAvx3vL5pjsrtXsvr/W+++4Lm889f8cDYnSJsSk9g/EMynErJ39eGGin64J0PR+14hVCiMLoxSuEEIXprRF6bpfhXPTVpRTzGJmXyhw9yhaPWDJySRcFXRfchZef9ygqXQ5NMh1KymHKUTaK5rhcfvnlYfu10I1A+cuSykG7MPE72kR6GcHm/ea1jMquuZyvbjeR8qkoON0LtHk/WarO8uDUeKTOrQldZUCkfpNjw+c0dz997rG7He020N3IDBK6G5nN420G+H5qQhddy7TiFUKIwujFK4QQhelUz+WyF3LSJtcRysmVdKZgcQTdBIyEsvyQHc480smS1SauhpJbvXN8mL3ADmDMdmBTdIdZA3Xj2YRcd68UO3bsCJslsoxa10nrYUAZ2kaW87Mubyl/6daii8W7kJlV3Q6p54PunUHP7WLw72HnuUHLqdlFMNfgvQ660tj8nO8iuuPcxZPbej6HXA1CCDED0YtXCCEK06mey/UuoMuAx/l5l8m5beEJJYXLZ0aGCWUEMxzYON2hPGlCyayGVI25WdWlwPP3rm2M4rKwIRcF9/GnPOMY8p7QTnU747n97ne/C5sym5krdBf1Rc7txbnIIoDcVu918F545zy/J2Zmk5OTYTOBn8VBc+fOPe97cwUKbeVyl1zMc+DuPWZ5sIiBTcxTsJE+u5qxgx9dYpxjXnzVhdutLVrxCiFEYfTiFUKIwvS2vXsT6cPP0w3g0O3A7ARGPesaZTOSzD2b6GrwFoqp/bUuxLBa8VGesxUepb1vm87adGYNUOrSBeFRX8pqFjnQvcDaeCave0EKWx9yPzU2nubW2rfddlvYfWWM5NwLnF85N0xdkQi/g30ZvL3p/v37k59l9gIbeBN3xdGlw+cjZ486fl0cLxY85IqvfC+2bdu2xTHOQf47NpFnc3nfLKDtc98FM+cOCSHELKHTrX8uxsGf+ivNFQZXSfysB4G4gmMD9V//+tdh79q1K2zmTq5fv97MzO66665W5zysFS9XSO+9917YXEV5s3iWSXPVydUo84I90MD82ly+Lkt/udr2YBJVDL+PwSRut8QgR4k83lxOeW7F6PORgTPOAV4vt2RK7YjrW12ZVVe5LPEmvoJrMueG2RSdgW8GaHm9xO851RODr3xmuQHC008/bWZVRcdS43Xr1oXN3OjVq1eH7buLDwOteIUQojB68QohRGGK12VSfjB3z53sqWbHZlX5R1niuXssSWVAjXKY0uLRRx8N+7HHHjOz/H5LufPvO4iRk4zMWWbeJ4OOHiRj8IHuAI4Rr9tdAnTF5JpDU3LT9sAcx5vNrWkzT5NBvNLkXBs87jm0uVxalmwzeEt3j0NZnAuoEQ825vKoUzv3mpVxNfA59qCuWdW1RTck95Jz1wqfewbXPIhmVm1o7r/DXOeHHnoo7B/+8Idhe76uWd7l4ZQaO614hRCiMHrxCiFEYXpzNXDJTrnPUr4DBw6E7VFg5uUy/47dwiiTn3nmmcq/N6tG6elSYA6fZzKY1bsMKIP42b5lXBPZQ+m0adOmsF2CsURy69atYbPUkpkRnh3Ca2ZOJO8Dv5vuCP9tSmiWOTNyz25Ro47L5Vz2DiP6nPOcmw7dLcxSyejUNF4AACAASURBVOHj1MS91cX2401IZRS9/PLLYf/iF78Im88654pnuHCu8Bq5YQGfB8+G+d73vhfHfvKTn4TdxH3jc5zPVs7uGq14hRCiMHrxCiFEYXpzNVB+eAK5mdkTTzyRtD3pntFeSudcuavLBUY0t2zZEjYjmm2S8nPuhZLlmJQ6zKZoUk7r0p4S/8EHHwyb94QN4L0IgGOV6+5Elw4LJNympCzZNH5YsJk3E/u9IID3k2XfuaIJ0mbelS4ZZnk5r5FlwCyKoO3FTps3b45jdAPSJcPjS5YsMTOzhx9+OI41uW5mpLjrgq6jUgUnWvEKIURh9OIVQojC9La9OyPhTIh2l4LZVBcrs6muSzl5csUVV4TNwgqXH5QcgzY2pnuBDKvbUy7CmiviqJNJjJ7nIukulxmh52+weGPQ/bVGhSa9DlL7mnE82J+B/S/Yicy/g/OWxSKDNlsfNj4OfN5Y0MOxY4ETMz58z8BcxpG7FKb/zqDQhVa6jwXRilcIIQqjF68QQhSmt6wGJsYz6X7jxo1hM+LuMmL58uVxjHXYlGOU2v6ZrmVIrhn2sMjV4lPOpY432cOOeL+HQbfYnm1wTFMuJ/ZnYL8KjrVnfzDDhk3fm8w1n//D3FttOi7V6X7i88sihn/+538Om+6Uut4JXTNM9wLRilcIIQrT6YqXf00YPGCD8dxuwL4qYFcswt1yueLNdc5KkdsFOcWo/GVMwXNjfmyqVLSL62gzbmbpraBmKhzf1PUw6OtbSJmZff/73w97zZo1ZlZd5TI/NbeK5Tx3htnkPAfPg53umnT76xKOF8ep7h4OA614hRCiMHrxCiFEYYoE11hmSrsNg+4EOorSrC/6Km1u+10zfZzbnD/dBHQfsAm854dzHBm8zI0vJfKlUHLt8Jmts1PuGLPhNoZvgla8QghRGL14hRCiMGNt8lXHxsbOmtnJ2g+K6cw/d+7cDdMPajwvCo1p92hMuyU5nmYtX7xCCCEuHrkahBCiMHrxCiFEYVqlk82ZM+fc+Ph4T6cyezlx4oRNTk6el8ei8RyciYmJyZT/TGM6OBrTbsk992YtX7zj4+O2c+fObs7qEmL16tXJ4xrPwRkbG0sGezSmg6Mx7Zbcc28mV4MQQhSnt8q1UqSyMkalOkUI0R11GVgz6bnXilcIIQqjF68QQhRmRroa2BjDG5CwZyy7/7fp2J/qZ2s2vM0uxcyljQuMG2ay73RqRwvu2MDe1k12F5npdO1KGKbrQm8UIYQozIz5M8nVqG8Fbza1KuAxwnZ6/AvHvbJ8PyuuGriDBlcWbHc5yivhLneB+POf/xy2Kwyz6t5Zo7QX2CjA+erj98knn8Sxt956K+zDhw+HfezYsbA5R+fNm2dmZvfee28c456Fpfcum0l8/PHHYVNF+LPBFp3cNaNPFTG6bw4hhJil6MUrhBCFGaqrgdLfA2aUtR999FHY77zzTtgnT04V2Lg0O3PmTByjpOP30aaMc6kxf/78OLZs2bKwuZsANyykC2LUdgjwsc0FEBigfO+998L2sT1+/Hgce/fdd8OmLGMZKTc09V1GKNV4Hu7amc5M33GBQTLOR5+jr732Whx78cUXw96xY0fy33Hj10ceecTMzG688cY45u6HSxF/ljlee/fuDXvfvn1hnz17Nuzrr78+bH/GuSU9Ny/tE614hRCiMHrxCiFEYYbqamCE/LPPPjMzs/fffz+OnTp1KmzKiJdeeinsV155xcyqcjmV52tWzXzg8auvvtrMqhFjSo7bb789ef6jJodTmwHyHDkulF+7du0K+5lnnjEzs/3798cxSujrrrsubEo0frePHT+by66gy4eZESXGNueGqcsE4b+jG+bIkSNhc77u2bPHzMxeffXVOMZMhjfeeCP5OzfcMNUozMeD7htm2ORgdsUws3A4ZjwnH+u25+b5ztu2bYtjP/vZz8L+05/+FDbn2Nq1a8P2+XbTTTfFMbrSaPP8U3UCnLtNMom04hVCiMLoxSuEEIUZqqshlaDMBOcTJ06Ezcjv888/H/abb75pZlXZNWfOnLCZWJ5L8ndpzMg8sxcYSb7mmmuS3zEKUOKkpDqPTU5Ohk1Z7G4HH1ezfNHIgQMHwqYsc+lGVwNh4QVlZ8ruUx63LS7xLBsWOUxMTCRtZoV88MEHZla97lWrVoX9jW98I2xmynDeuVuHGTa5CHwug8Sft1Iuspx7gccHPZe3337bzKpzlzZLr5l9w/Hz7BtmQdEdxPnBwoprr702bH/XuLvSrNk1acUrhBCF0YtXCCEKM1RXQ0rqMdpO6cCtR1hA4a4ESoh77rkn7AULFoTN6CXl81e+8hUzq7oRmMnAwoo6KKO67G6Uk22DSjWO4cGDB8N2aXrHHXfEsblz5ya/g/fKI/dmU4n/dN3QFUHobmKBi2dJDCMSz7FmxoEXPTz55JNx7IUXXgjbXQpmVTeBz8GVK1fGMW4Lw3HinOF4uKRt0pOB31HXgasLUtk0F/rMoLCgyt8NdHfxuXjggQfC/tGPfhT2P/3TP4XtY+qZUWbV9wx7PLhbwqz6rvF3RttnXSteIYQojF68QghRmE5dDbkIdZP2al4Awagi69mZnM5o7oMPPmhmZps2bYpjLIRgRJMJ6fwOjzZfjGsg1US9S1cDCxQGjQpzDJl4fvr06bDdTbBmzZo4xjFkNgSzS44ePRq2y2+2LeT9IXQlpHp3DKPdJF0ozKb5+c9/bmZmv//97+MY7/vGjRvD/s53vhP2ihUrzMxs4cKFcSznviEsJhq07SOfvRJ7kvE3ci4PFjS4zawB4oVVZlW3js89zl32Yfje974X9r/+67+GnXJdsbDq5ZdfDpuuHs5DFl/597V1iWnFK4QQhektuNbkryv/onjOLsuB2WHIA2BmZhs2bAj7H/7hH8zMbN26dXGMjnCubJuUWLah71VujjZ/XfnX+Te/+U3YXMlxXDwosWXLljjGoCSDcuwMxVWid5Jj2TE7aTFYyWvhqqJ0UI2rHpaqb9++Pexnn33WzKol1D/84Q/D/pd/+Zewcyv8OliCzFxUn8fMBW5Cnzm7bZrt81lhrr6veKnoeI1UaVyN+j3iPGFQ3bu5Tf9MCgbUGGhmgJTvEebsDvpO0YpXCCEKoxevEEIUplNXQ1t5yLy8Q4cOmVk1d5eO9SVLloRNt4I3M6ZjndCdwfNrK9nq6Fsa15UD53jiiSfC3rp1a9iU1gwKefkqcxUZoKFkZLN45jx6AI6BOJYg0xXE+0B3Um7H577gXGPurs9Lfuab3/xmHPu3f/u3sO+7774L/kaTHG+eB8fD86t57znnct/Xp+urzXfnugT6feYcY/CNri3a/plbb701jrHzGIPDOdzdxrxsukHoHmNglEF63qM2aMUrhBCF0YtXCCEKM9SSYUbCvTE0t73mMp7dwpjz53KWXZgowWiz8xMliudItt3OuWTkva1k9BJeuhoo1Vi++uijj4Z9//33X/B7mU/Ke8ISY5fUlJTcM4/Reso2UiI7hDBTgXOQ7hKXnj/+8Y/jWJ17wWxq3Dn/cp3bOB50TbhbjufGLBD+u1xObJsshK6hq4FupCuvvNLMqiXldEGyDJvzyTuE0QXAe5FzJbI8+N///d/NrPpcsLk/XRd333132GwtMOgW8FrxCiFEYfTiFUKIwhR3NTBRmpFujySzKTElEaPm3Cbb/x2lCjMZ6IJgg3R2H3O3Qy7Jv+sMiEFoIg9ff/31sD1Su3v37jhGifTQQw+FvX79+sbnwYRxl4nTv9uTzXPbnXN/vJyrobQsZjSb7gXKYpeybFyeg9kQ/t2cf01gIYcXGPE54PdxjuZcDaXJddSjCzHlcuH587o4xzyrgcUM3hzdrLrnGt8zjz/+eNjenoDuCt5bui5YTNFFIZZWvEIIURi9eIUQojCduhqaJIhTfjJ66e4B/jtGMbmHFbs2eWSXLgxGQul2oFShdPCIJSU3o7CUIrkoZt/SOPe9lJ6sZfeeF0zI5z5f3tWtLZRZHE/afk94bozG09XA+8bigBIuBs5XzkuOGbM4Fi1aZGZ5lwHnM11mPtdye6RxnNg1jsVEnhVCGZ5L6uf5DaO7m5N7H9BFlYLPGDNn6B509wGLXTwzyqxahMEOZnQjeQN6dpLjc8EOcl33edGKVwghCtNbcC33144rHP419pUFV04MyNBBzuPuqOdvMKDG3+NfO3Yh8tU0V8d06tOB36SPakn415w5in7c++uaVbebYSAxRW4sOM4cC6oM783LAFOu6xbvVandb51c/+jcjtW+UuM8Yj44v2Pp0qXJ73N43375y1+GzR7UzH32cc91zGLP5Fwf2b7IPeu0c6XhdTD4xt19/ZllDi6Da8yx5wrbeyObTXU5ZLdDzumcQukCrXiFEKIwevEKIURheguuEUoOSgAGBLwbFmUomyAzWEGp4k26KcH4GwyUMMDDrWpcOuYad3OnYp5zToL3DcfC8zvNqrLLx4AdxNixKRcs8O9mOTeDHQxw8JoprT0/kveBgVLadDXwnEqMJ10DlOSUtwyu+dhwzFkGTDdZCs7t//iP/wj717/+ddh02VDqus1AHO8R/x0Dw6R0qXCuox6fyVTOMd0wdAnSdeW7CzO4xvnGEl/afB48kMbnu9QYacUrhBCF0YtXCCEK06mrockynXIyFXGnzGP0mFKFct+7YvHfUcoymk6p8txzz4XtOa+5xt3MG85F+0vC82GZMK/VI8DsQkZ3QA4fZ0pa3lc2MacLItUFjv8/l6NbuuF5DmauMJOBbi2fE5S/3I+ObocUvmfbdJvReM5jznMfM+Ybs8yZ2TvD6D5WR2p/RbMptwIzlVKl0mbV59fnPfN1PS/XbCrn2qy6Fxt3IPddsIcxXlrxCiFEYfTiFUKIwhR3NVByMqLp3cCYncDvowRj0nodjJqz4xglm2c4MEpMqc0obC5i3Df8Xboa6B6h7PJEcEqrJrjLgFF+yu0mjZ/9XHP3mp3khimLeX50NTBRn+fn84OSlwn3HCdmJHi2iUfizaqZKUzw5zynW87dSLm5yM+WdoE1uYecpxMTE2F7wQizE/jM0hXFMfPjvId0EdElxuISdy+Yld3IYDpa8QohRGH04hVCiMIUaYRO6UC5QNtlMiUT5R+jx22gZOZ3Mwrs8o2RV9JkG+2+4RiyCxbt1F5WdZH26bh8peRt0sCbEXaPOPN8KN/pdigt91jkw99moQSvnW4AvwfMQqD7gHOK/84Ld9iVjS4bzku6DyjPPerPz/KcaY9C4/7pMEuIzfl37txpZtX5zf37OPfovkllwzBLim5FFlDUPQ/83lzfiS7QilcIIQqjF68QQhSmN1cDl+yUw7n2jp5lwMjw9ddfHzalCI97VJMyjhKN7gzu1eZFE2ZTUpASOFevP+h2zl2Sa2eY6lHBAgtGd3O4nGvbEm/79u1he48N3ksWA9CFVJpcC0OOHd1abMTtrQjZF4EZDrkG6v559gph3wZm0HC+8ri7wRitp5zmOQ8zWk+YZcNnkgUSPibsc8Hnm71BiGf28Dllo/8HHnggbGZK1ZFrW9s1o3GHhBDiEqJII3SuBLjK3bdvX9ie68gAFx3hXCUxwODlwSyX5aqBv81cQXYi879y3iHNzGz58uVhM2+4TRPnLuFfX44FVwfMj/WVxB//+Mc4xgAY8xm5GmUQLAXzn1l2vXXr1rB9NccVGX+Pq5TSW9PkOugR3m+WWbtao3JiJy2uhBlcc8V37Nix5L/jKotzm+fqY8mtabiq44qXK/km23H1Re63mXvrn+FzTzWQe65dUXAn4I0bN4bdJNfff5tzms9Qn2jFK4QQhdGLVwghCtObq4HSggEp5ilyT6kdO3aYWVXGUboNCqUb3QSU697Bq8luo8PatZVjyHxFukcYYPQOWtzDizs1L1myJGw2h3ZJSznIoJA3OTerNqqnG8MDUgx2sFsUXRulXTdNXA0ca7qcPFjEICzHlEFkSmQPLPEY3QsMxPHeUi77eWzZsiV5bjmJPMySbAb56BJj43EPtLEMnu8ABi85Zh50Y/CTgcccDPi564JzsFRgUiteIYQojF68QghRmN5cDblyTEa6KTlctrLJdBcwD5Clg5S+999/v5lVt35m2WKpSGdTmJdIOU/J5HmRlG2UutwKnl3ZPBpP1wFzMNlkntkJdFf4ONKdwXMuvY07ofRmbnjOhcS569uAU94yL52uMUpnz6bhnnj8bUpkzlHOQW/yndvzbhShy4Zjxr3/3H1AF1Yu+4O4+4/vGWYnMCOKGRP8jN/zYWQqacUrhBCF0YtXCCEKU6T+lVKdCemUqp5g73LOrBo1zzX89qwFSkImk1Oa0c3B4y6D+R2jUnaZgudGCceIuO8zxTGkTYlMt4KXqVKesUMUMzwoixcuXHjeZ9p2RisBx44ZDrnSa+JzjW4q2szYoUvGs02YxcPf5n2jPawMmq6gK4TP5Nq1a8P2DBcW2OzZsydsumdYlOLFI9xTkO4s3kO+f4aRwZBidN8uQggxS9GLVwghCjPUVlspifWNb3zjor+3z/r0Yda+15GKItMVweR7RncZgXc75c4xq7pjWITCooJhZi3UketIxvtKlwE/UydNOf6UxW7PmzdvgDNuzyjOUUp8Foa4G4uFQJs3bw47tzeduw3bdtEbFRfiaJyFEEJcQujFK4QQhRl+V+8eGBV5NcrQNUDbXT65KP+oSLUuaHItHAd3QeRaHPaJn0eTfcBGZf43cXn4/nDMnKE7i+M/rJasfTB7niIhhJghFF/x5rpD+fFRX1GNymqijrouXPz/qc9yJdf2nvj3zZSxuhCpYBzHix2z6la/FxP08s/PpDEd9FyZv5zaTThHbk6P4jtl9M5ICCFmOXrxCiFEYYq7GkY9IDDbqHMpTMdl2cXcj9l0L5sEswahrdthNo1pG+rcBLk5PYruBTLaZyeEELMQvXiFEKIwY03kZ3x4bOysmZ2s/aCYzvxz587dMP2gxvOi0Jh2j8a0W5LjadbyxSuEEOLikatBCCEKoxevEEIUplU62Zw5c86Nj4/3dCqzlxMnTtjk5OR5+UAaz8GZmJiYTPnPNKaDozHtltxzb9byxTs+Pm47d+7s5qwuIVavXp08rvEcnLGxsWSwR2M6OBrTbsk992azqDvZTKrTFrOHQYPTuflaV7Ax2wopvOMbm89/9tlnyc9y7zQ255+J6K0khBCF0YtXCCEKMyNdDZQivnU29w3j1uTck4nNlq+99tqwR3mPMDHaDCr9Uw3WzaquMc5L/x22ocydx6i71+ha+eCDD8zM7NSpU3Hs7bffDpstIrln3V133WVm+Wv9+OOPw+ZYs+k/v7s0o32HhBBiFjLUFW9d5yz+peJuo2+88UbYhw4dMrP/T91wuOLlLrv33HNP2Fwh+FYjuV1nZ9JqQvRPLqDWZvXL1WwbxTUb1Bl3uD5+/LiZmb344otx7NixY2EziLZ27dqwr7nmGjMzu/HGG+PY559/HjbfF1QUVAy+SzbHlO+cXKCziwCn3iJCCFEYvXiFEKIwQ3U11C3f6TJ46623wn7ppZfC3rp1q5mZHT16NI65DDEzW79+fdiLFy8Om072L3/5wsPQJOdyplG3b1ipa+Nv040zKmP7xRdfhP3pp5+amdmHH34Yxz766KOwKXV5XT7WnGdXXnll2Az6XnfddWHXzcuZyrvvvhv24cOHzcxsz549cezMmTNhL1y4MGx3DZiZXXXVVed9L+cPXRScSxxTv7e5gCWDb13vcKwVrxBCFEYvXiGEKMxIaxm6GuhKePbZZ8N+7rnnzKwqCXPSjfKE5Yd1NClH7lsa5yLpbcpNCSO9qXzRUoyKS4Hj6C4Fs6rs9TnomTRmU1F5M7M333wzbOaV+/elMmnMzG666aawFyxYEPaiRYvCvvPOO83MbP78+XGMc7sJqTk0DJcSXTWTk5NmVs1CYI79mjVrwqbbMCX9ed+YncDn/rLLLgvbnwG+O5pkNXSBVrxCCFEYvXiFEKIwI+1qoHRjJgNtLy9kv1CXZWZmc+fODZsRTUajGS1NkSvvpEQfVvlhm4IOum4YgU9FbylLc4npPM6xcBldN65mVQk3zIyRnBRmYc7evXvNzOzVV1+NY6dPn07+O461XxeviWPHjJ0jR46EffDgwbC9eIBjxMg9s3RyDNOtw+v1MmGzKVcO5f7dd98d9rp168JOuRdYGsxxpCsxlQFhNvU+aJs9ksoI4nPY5JnUilcIIQqjF68QQhSmN1dDE3meqjunRDtw4EDYdC8ww8ElBeXJkiVLwmbEmOf0zjvvhO1uB0pjSpWcREsVHvTVy2FQmUhZxw5Q3tXNrCrzfPw92jz9O3L3ktftWSXsjbF06dKwc8noHE+/3lLymHKTkW/Keb8uZht4lyyzaic8FvF4lJ6/wQ5c7sIwq2ZJsAuf3wP2OeC9GEX4vHG+nTw5tdGFP8t0Gdx8881hM4sjBbNO6D7kPez6meSc5DW2+T2teIUQojB68QohRGF6czVQNubq8VNQ4jJ6zAgvl/feHJny7/bbbw+b7gNGIxmB9ogrZWUuIk+5mJLGfdGkFSHHxTNCdu/eHcf27dsXNuvlmXju43/27Nk4RvcPJTRtRq1d5tGdw8yJXHtOnr/bw2iDeMMNUxvtctz9OI9xntxyyy1h180Hjj+fiVy/B/8dujNGpfiE8B5y3tDVQHeKux04l+g2zOFuFo4Xx+b6668Pu8+eFz7Xc/0ecmjFK4QQhentT0Gu3K7urw//GjLowNUTyy3vuOMOM6vm8bI5Mv/y5Vao/leL39uEvldjqRXgdDuXf+plrVzxcmz/8pe/JG0P3jAAxvH08Tar5o4yEPr666+bWbWhNQN0PH+OIeeGryq7yu1N5dI2gdfuK94uVpqpVZ9ZNUDEwLA39Gc5PFUE7yHHjEGmEnBsGPzjipf5tq62VqxYEcdYJpzD88mpUlMBzQvh58fAHud9k9xop+27QCteIYQojF68QghRmN5cDQwYNHFuey4pg2jsAkVHPd0Knud36623xrGUPJwOZYnLhC7KfkuXvVK2M9DgEo5Sk7u0MhCR6k5GmZUrx6ZkZDDOm1tT/jbZYyy391UXpFwXbfM7B72f7j5gLvqTTz4ZNoPInIMMEnvAifOc45XbV4zjWGK/wFwJOEvN6U7xecY871yJL/Hvo3sw96wTBjXdFcZ3C3+b3d/o9unCfaMVrxBCFEYvXiGEKEyRrIYmET+XrYyOcxt3uisoKdxm9kKT7ARGQ+ugZCYp10SX7oUm2SC5Uld3pbB8OrfPF/+dXxPHOCf9KGlTpay8D20zRrqWxf59ueyQNr/Hf0fZTHeLZ3aYTbleJiYm4hjL3inJly9fHva9994btpcm554lzgOeXy7/uwT8bZY/s0Td5ylzoHOwubw/k3QB5GBtwNNPPx22v3M4v2kzR5sZQ2xW32ZDBaIVrxBCFEYvXiGEKEwRV0MTvHOWyzKzatJ1LsLoNhOmm0RFiSdQM5Ga7gXKUH435XMfGQxNvpPnRteHZ3YwMk4518V21bxX7Lbl94Kdu5pEnEuQK1HO7auX2oOL2SO8bpZk79+/P2x3n7E7HLMQeF/YjWvQSHqqEGUY8BqZOUDc/cVz5r/j/eLz6W6AXCYSv4MZJM8880zY/gzQdcDzZOczuhroXvCMHxVQCCHEiKMXrxBCFGaoe65Rsnm9OvdZI5RdlGPeO4BR+hyMOvN3XEawSxclDN0YlBTMEuizA9KFyHWzcjnEbI+ceyFVhEGJStnGrJOnnnoqbEb3Fy9eXPmvWdVFk5PypTuRNWlwz3Ot26MrV7jgbgIW9vA7cv0X6GrzXhcs/MlB91PXhShtyPVGYXGOf4bPHgtz+Nk2WTJ09Wzbti1sZkqtXLnSzKqN11lgwc+yAITvIt/TUa4GIYQYcYa64mXHKu8+xnxQrtbYo5O5jsuWLTOzfPCGHbJ27dp13u+ZTeUYcnXAv6hcYfM4V4IlV7xc5TK3kX+tPTiYWxFz9c8ggq+ymHfJf8eA2o4dO8LmisY7afGe5Lqo8TjLmNvkWbch1zWP5Mq+fSVJ5cAAIleaXJl6mTVVAXNZOY84/7lq83PasGFDHGsy53hOg3ZoGxT+NleuzI/1lS7Hhnm37IZXt8rlXNq5c2fYXLly1/HNmzebWbWU/vnnnw+bz0hK0U3/zTZoxSuEEIXRi1cIIQpT3NWQ237HJS7lPnN32SGLW8cwYOEw34/N1F977bWwKWf885QN7AJFmcScy5K7vHJccgEAlqm6NKJ0ZcNtdoFjMMOviYFDSrzTp0+HzWbelIQe2Mvlu/KccnK5L1dDW+rkPIMqCxcuDJtuFp/blKsM1tDVQ1cO75GPJQM7lLxNKO1q4NjR9cJny11+HBvOMb4D6gKLzKNmZ0MGLNeuXRv2I488ct530NXAdwTdYF0891rxCiFEYfTiFUKIwhRxNeR2HmXU0Jf1jKZzeU/JQTsFJTVlOb871UmK58aSYZbdUmak9j5LRcG7gFFwugZeeeWVsJnB4dkOvE5K1xMnToRNF0tdCTZlWy7H0seIrg+eM8eW/y6139Wg3Z8uhlwHsza5mqkdqzmO/F6OI8eMmTc+ppzbzPQp0eS8LSxzpuvFs17MpuY183jpPuPYpHLoOb+ZtcTybM4rdnxLQZcHbc5TZmUMOu6jd7eEEGKWoxevEEIUpoirgVKWkW5mH3iGAyPejKxTuqVKThkZpszg9/G3KX2PHDliZlU3AbMXKHF4Hqnk9L4kH90kjPpyvy7KUD9nng8zQCjh6dLxiDOzSFKN0s2qpa6phtS8D3Qv8Ds45pSb7vYp5WrI7V3H827T9Y73y6+R/57yl79NGcvnxp8VZgJRCuci/rmua12SKzjhs8L5wbnl18C5wmc512nNx5Jl1blngdkmqfnE7AW6OXiP+H/oxwAABedJREFUWETFrIxB92nUilcIIQqjF68QQhSmiKsht203pZQv2RnFpFRhVD/VZyGXeM4uZLnPuLRhlyJG9XmcGRU8P7/GvpLTKXkpN1mYwONek84IMiO6zM6gXHKpyz4ZdDXQBZPrueBjQRnI/8/vpiuEsrJ0lJ5uDvYQyTXBryMVjc8VYzBintvzy78j1zUuR19ZNqSut4VZ1c3F4+4KpNuEzzddgpyH/hwya4mf5dyjS5PZPD7W27dvj2N8nlgUtGrVqrCZ5TRojxateIUQojB68QohRGE6cTXU1YBTWlCeMxLrkpjRQ7olGG187rnnwk65GnKSg8npjJy65GDtuzdJNqsmqtPVULIVJH+LY5jLOHCbEo8t8Rix5f3xTBJmLFAKs8iEkjDVWpLuIWao0HVDmy6IEtkMdH9wntA9lSqg4DjmaLOnHd0StFl04Pef96Jt8+1SPRrq4NxaunSpmVXdO8xEoguI98WPM8Mn1avErNoXgy5Gv+d8d/CdRNfcfffdF3Zde8omaMUrhBCF6WTJ1uYvKXNG6bz2FWaum9bRo0fDZoNoX2nxryFXWlwRcmXH5sfeWH3Lli1xbNOmTWFzFd5mt9cu4QqQ585VOldZPs4M1jDQxrxKBnF81dnknubycX2lxt/OlSDznGmXUBOcJwzAcBXFHE9XUlRDbIQ+KGxmz9UZx8PHtMlWTjn66k7G78vla+fwOblixYo4RiXCVSzvlx9nsIzBXq5Kqba4Evbz5pguWbIkbK5y+cx1gVa8QghRGL14hRCiMEPdc41BCpf5dG6z8xYbmtN2VwNdFPwOSgTa7tQ3m5I53MuNZY3D6JA1HZ4D5S1zKBcsWHDecebd5soeB4VuF46tyzxKvFEkl9dKyco56MdffvnlOOb7dpmZbdy4Mey6a2dXLTbfZvCH99ZdDQzujsK8NKu6GnKd3epyiBnAZvCY7kYGQH386JKie4FuDt/zziw9T/nvGIzms9O160srXiGEKIxevEIIUZjeXA25MsIcLqW+9a1vxTFGFbmHEht+ewQ6lzPKiCXzBxnhd5cH//+o5Dym4HkyQ4ARWZd5zCJpGwVPQZcOJRrzT2cKHA/OE9qMsLuLa9u2bXHs6aefDnvZsmVhs6zUf4dzlJkMzGHlOfF+ukSmFB7FOcrcYuZ85/LGU9AdwDxvjp/n73Mc2VWOv0GXGG1/NjiPS2UtacUrhBCF0YtXCCEK05urgRKNbgdGB+ukEmUVbUaPvXSQjacZTSWUQZTgo7KV+CDkChD6oguXQq4h9zClM8tz6eJiyapLXe7txSyE3bt3h81r9OwDymZmzbCQiNk2q1evDtuj/m06pE2nxPjyGeMYsLCC51En7XNuAncn8r4RujlyXdz8vgxjvzqteIUQojB68QohRGF6czXkmp9z2Z9yQbRd9rvLgK6DHKlm3aJ9BkrT7+O95vdy7EclMk8XGN0ALMbxQpvjx4/HMWbYsG8Aezx4Mj8zHVjswig+P8ME/pmSNcL7yTHlO4BuB++Rwf/P4odBr5tuN55TiT3omqAVrxBCFEYvXiGEKExvroactMxJ/FwmQl90La9L0uTc/TOM7qa2TzdLyzxGkHnPKB8pCVOupdz+W6M+3jxX9kZwm4UShAn8tP16m7S9HEU3zKDk3gEcX7fpBiQcR5JqcZlrAct5msq2Gsa7QCteIYQozFC7k5GZ/te9JHWrXLOpv+y5lUQbRZJbueZs/zzPZxi5kqXJbclUd+1UHJfCc8Br9NUoFUAuAJaay012ps4F/PpqDN+E2f80CCHEiKEXrxBCFOaScjXMpADPxeLXmpO/bXIYc66GXKDUPz/bx/hC1LkXcuM/k4O+g9BmrnTdjHyY46sVrxBCFEYvXiGEKMxYS8l51sxO1n5QTGf+uXPnzmujpPG8KDSm3aMx7ZbkeJq1fPEKIYS4eORqEEKIwujFK4QQhdGLVwghCqMXrxBCFEYvXiGEKIxevEIIURi9eIUQojB68QohRGH04hVCiML8H0e30iZzfs5ZAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Plot the reconstructed data\n",
"plot_digits(X_rebuilt)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"You've reduced the size of the data 10 fold but were able to reconstruct images with reasonable quality."
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.6"
}
},
"nbformat": 4,
"nbformat_minor": 4
}