{ "cells": [ { "cell_type": "markdown", "metadata": {}, "source": [ "[Table of Contents](http://nbviewer.ipython.org/github/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/table_of_contents.ipynb)" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "# Gaussian Probabilities" ] }, { "cell_type": "code", "execution_count": 1, "metadata": {}, "outputs": [ { "data": { "text/html": [ "\n", "\n" ], "text/plain": [ "" ] }, "execution_count": 1, "metadata": {}, "output_type": "execute_result" } ], "source": [ "#format the book\n", "%matplotlib inline\n", "from __future__ import division, print_function\n", "from book_format import load_style\n", "load_style()" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "## Introduction\n", "\n", "The last chapter ended by discussing some of the drawbacks of the Discrete Bayesian filter. For many tracking and filtering problems our desire is to have a filter that is *unimodal* and *continuous*. That is, we want to model our system using floating point math (continuous) and to have only one belief represented (unimodal). For example, we want to say an aircraft is at (12.34, -95.54, 2389.5) where that is latitude, longitude, and altitude. We do not want our filter to tell us \"it might be at (1.65, -78.01, 2100.45) or it might be at (34.36, -98.23, 2543.79).\" That doesn't match our physical intuition of how the world works, and as we discussed, it can be prohibitively expensive to compute the multimodal case. And, of course, multiple position estimates makes navigating impossible.\n", "\n", "We desire a unimodal, continuous way to represent probabilities that models how the real world works, and that is computationally efficient to calculate. Gaussian distributions provide all of these features." ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "## Mean, Variance, and Standard Deviations\n", "\n", "Most of you will have had exposure to at least basic statistics, but allow me to cover this material anyway. I ask that you read the material even if you are sure you know it well. I ask for two reasons. First, I want to be sure that we are using terms in the same way. Second, I strive to form an intuitive understanding of statistics that will serve you well in later chapters. It's easy to go through a stats course and only remember the formulas and calculations, and perhaps be fuzzy on the implications of what you have learned.\n", "\n", "### Random Variables\n", "\n", "Each time you roll a die the *outcome* will be between 1 and 6. If we rolled a fair die a million times we'd expect to get a one 1/6 of the time. Thus we say the *probability*, or *odds* of the outcome 1 is 1/6. Likewise, if I asked you the chance of 1 being the result of the next roll you'd reply 1/6. \n", "\n", "This combination of values and associated probabilities is called a [*random variable*](https://en.wikipedia.org/wiki/Random_variable). Here *random* does not mean the process is nondeterministic, only that we lack information. The result of a die toss is deterministic, but we lack enough information to compute the result. We don't know what will happen, except probabilistically.\n", "\n", "While we are defining terms, the range of values is called the [*sample space*](https://en.wikipedia.org/wiki/Sample_space). For a die the sample space is {1, 2, 3, 4, 5, 6}. For a coin the sample space is {H, T}. *Space* is a mathematical term which means a set with structure. The sample space for the die is a subset of the natural numbers in the range of 1 to 6.\n", "\n", "Another example of a random variable is the heights of students in a university. Here the sample space is a range of values in the real numbers between two limits defined by biology.\n", "\n", "Random variables such as coin tosses and die rolls are *discrete random variables*. This means their sample space is represented by either a finite number of values or a countably infinite number of values such as the natural numbers. Heights of humans are called *continuous random variables* since they can take on any real value between two limits.\n", "\n", "Do not confuse the *measurement* of the random variable with the actual value. If we can only measure the height of a person to 0.1 meters we would only record values from 0.1, 0.2, 0.3...2.7, yielding 27 discrete choices. Nonetheless a person's height can vary between any arbitrary real value between those ranges, and so height is a continuous random variable. \n", "\n", "In statistics capital letters are used for random variables, usually from the latter half of the alphabet. So, we might say that $X$ is the random variable representing the die toss, or $Y$ are the heights of the students in the freshmen poetry class. Later chapters use linear algebra to solve these problems, and so there we will follow the convention of using lower case for vectors, and upper case for matrices. Unfortunately these conventions clash, and you will have to determine which an author is using from context. " ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "## Probability Distribution\n", "\n", "\n", "The [*probability distribution*](https://en.wikipedia.org/wiki/Probability_distribution) gives the probability for the random variable to take any value in a sample space. For example, for a fair six sided die we might say:\n", "\n", "|Value|Probability|\n", "|-----|-----------|\n", "|1|1/6|\n", "|2|1/6|\n", "|3|1/6|\n", "|4|1/6|\n", "|5|1/6|\n", "|6|1/6|\n", "\n", "Some sources call this the *probability function*. Using ordinary function notation, we would write:\n", "\n", "$$P(X{=}4) = f(4) = \\frac{1}{6}$$\n", "\n", "This states that the probability of the die landing on 4 is $\\frac{1}{6}$. $P(X{=}x_k)$ is notation for \"the probability of $X$ being $x_k$. Some texts use $Pr$ or $Prob$ instead of $P$.\n", "\n", "\n", "Another example is a fair coin. It has the sample space {H, T}. The coin is fair, so the probability for heads (H) is 50%, and the probability for tails (T) is 50%. We write this as\n", "\n", "$$\\begin{gathered}P(X{=}H) = 0.5\\\\P(X{=}T)=0.5\\end{gathered}$$\n", "\n", "Sample spaces are not unique. One sample space for a die is {1, 2, 3, 4, 5, 6}. Another valid sample space would be {even, odd}. Another might be {dots in all corners, not dots in all corners}. A sample space is valid so long as it covers all possibilities, and any single event is described by only one element. {even, 1, 3, 4, 5} is not a valid sample space for a die since a value of 4 is matched both by 'even' and '4'.\n", "\n", "The probabilities for all values of a *discrete random value* is known as the *discrete probability distribution* and the probabilities for all values of a *continuous random value* is known as the *continuous probability distribution*.\n", "\n", "To be a probability distribution the probability of each value $x_i$ must be $x_i \\ge 0$, since no probability can be less than zero. Secondly, the sum of the probabilities for all values must equal one. This should be intuitively clear for a coin toss: if the odds of getting heads is 70%, then the odds of getting tails must be 30%. We formulize this requirement as\n", "\n", "$$\\sum\\limits_u P(X{=}u)= 1$$\n", "\n", "for discrete distributions, and as \n", "\n", "$$\\int\\limits_u P(X{=}u) \\,du= 1$$\n", "\n", "for continuous distributions." ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "### The Mean, Median, and Mode of a Random Variable\n", "\n", "Given a set of data we often want to know a representative or average value for that set. There are many measures for this, and the concept is called a [*measure of central tendency*](https://en.wikipedia.org/wiki/Central_tendency). For example we might want to know the *average* height of the students in a class. We all know how to find the average, but let me belabor the point so I can introduce more formal notation and terminology. Another word for average is the *mean*. We compute the mean by summing the values and dividing by the number of values. If the heights of the students in meters is \n", "\n", "$$X = \\{1.8, 2.0, 1.7, 1.9, 1.6\\}$$\n", "\n", "we compute the mean as\n", "\n", "$$\\mu = \\frac{1.8 + 2.0 + 1.7 + 1.9 + 1.6}{5} = 1.8$$\n", "\n", "It is traditional to use the symbol $\\mu$ (mu) to denote the mean.\n", "\n", "We can formalize this computation with the equation\n", "\n", "$$ \\mu = \\frac{1}{n}\\sum^n_{i=1} x_i$$\n", "\n", "NumPy provides `numpy.mean()` for computing the mean." ] }, { "cell_type": "code", "execution_count": 2, "metadata": { "scrolled": true }, "outputs": [ { "name": "stdout", "output_type": "stream", "text": [ "1.8\n" ] } ], "source": [ "import numpy as np\n", "x = [1.8, 2.0, 1.7, 1.9, 1.6]\n", "print(np.mean(x))" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "The *mode* of a set of numbers is the number that occurs most often. If only one number occurs most often we say it is a *unimodal* set, and if two or more numbers occur the most with equal frequency than the set is *multimodal*. For example the set {1, 2, 2, 2, 3, 4, 4, 4} has modes 2 and 4, which is multimodal, and the set {5, 7, 7, 13} has the mode 7, and so it is unimodal. We will not be computing the mode in this manner in this book, but we do use the concepts of unimodal and multimodal in a more general sense. For example, in the **Discrete Bayes** chapter we talked about our belief in the dog's position as a *multimodal distribution* because we assigned different probabilities to different positions.\n", "\n", "Finally, the *median* of a set of numbers is the middle point of the set so that half the values are below the median and half are above the median. Here, above and below is in relation to the set being sorted. If the set contains an even number of values then the two middle numbers are averaged together.\n", "\n", "Numpy provides `numpy.median()` to compute the median. As you can see the median of {1.8, 2.0, 1.7, 1.9, 1.6} is 1.8, because 1.8 is the third element of this set after being sorted." ] }, { "cell_type": "code", "execution_count": 3, "metadata": {}, "outputs": [ { "name": "stdout", "output_type": "stream", "text": [ "1.8\n" ] } ], "source": [ "print(np.median(x))" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "## Expected Value of a Random Variable\n", "\n", "The [*expected value*](https://en.wikipedia.org/wiki/Expected_value) of a random variable is the average value it would have if we took an infinite number of samples of it and then averaged those samples together. Let's say we have $x=[1,3,5]$ and each value is equally probable. What value would we *expect* $x$ to have, on average?\n", "\n", "It would be the average of 1, 3, and 5, of course, which is 3. That should make sense; we would expect equal numbers of 1, 3, and 5 to occur, so $(1+3+5)/3=3$ is clearly the average of that infinite series of samples. In other words, here the expected value is the *mean* of the sample space.\n", "\n", "Now suppose that each value has a different probability of happening. Say 1 has an 80% chance of occurring, 3 has an 15% chance, and 5 has only a 5% chance. In this case we compute the expected value by multiplying each value of $x$ by the percent chance of it occurring, and summing the result. For this case we could compute\n", "\n", "$$\\mathbb E[X] = (1)(0.8) + (3)(0.15) + (5)(0.05) = 1.5$$\n", "\n", "Here I have introduced the notation $\\mathbb E[X]$ for the expected value of $x$. Some texts use $E(x)$. The value 1.5 for $x$ makes intuitive sense because $x$ is far more likely to be 1 than 3 or 5, and 3 is more likely than 5 as well.\n", "\n", "We can formalize this by letting $x_i$ be the $i^{th}$ value of $X$, and $p_i$ be the probability of its occurrence. This gives us\n", "\n", "$$\\mathbb E[X] = \\sum_{i=1}^n p_ix_i$$\n", "\n", "A trivial bit of algebra shows that if the probabilities are all equal, the expected value is the same as the mean:\n", "\n", "$$\\mathbb E[X] = \\sum_{i=1}^n p_ix_i = \\frac{1}{n}\\sum_{i=1}^n x_i = \\mu_x$$\n", "\n", "If $x$ is continuous we substitute the sum for an integral, like so\n", "\n", "$$\\mathbb E[X] = \\int_{-\\infty}^\\infty x\\, f(x) \\,dx$$\n", "\n", "where $f(x)$ is the probability distribution function of $x$. We won't be using this equation yet, but we will be using it in the next chapter." ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "### Variance of a Random Variable\n", "\n", "The computation above tells us the average height of the students, but it doesn't tell us everything we might want to know. For example, suppose we have three classes of students, which we label $X$, $Y$, and $Z$, with these heights:" ] }, { "cell_type": "code", "execution_count": 4, "metadata": { "collapsed": true }, "outputs": [], "source": [ "X = [1.8, 2.0, 1.7, 1.9, 1.6]\n", "Y = [2.2, 1.5, 2.3, 1.7, 1.3]\n", "Z = [1.8, 1.8, 1.8, 1.8, 1.8]" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "Using NumPy we see that the mean height of each class is the same. " ] }, { "cell_type": "code", "execution_count": 5, "metadata": {}, "outputs": [ { "name": "stdout", "output_type": "stream", "text": [ "1.8\n", "1.8\n", "1.8\n" ] } ], "source": [ "print(np.mean(X))\n", "print(np.mean(Y))\n", "print(np.mean(Z))" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "The mean of each class is 1.8 meters, but notice that there is a much greater amount of variation in the heights in the second class than in the first class, and that there is no variation at all in the third class.\n", "\n", "The mean tells us something about the data, but not the whole story. We want to be able to specify how much *variation* there is between the heights of the students. You can imagine a number of reasons for this. Perhaps a school district needs to order 5,000 desks, and they want to be sure they buy sizes that accommodate the range of heights of the students. \n", "\n", "Statistics has formalized this concept of measuring variation into the notion of [*standard deviation*](https://en.wikipedia.org/wiki/Standard_deviation) and [*variance*](https://en.wikipedia.org/wiki/Variance). The equation for computing the variance is\n", "\n", "$$\\mathit{VAR}(X) = E[(X - \\mu)^2]$$\n", "\n", "Ignoring the squaring for a moment, you can see that the variance is the *expected value* for how much the sample space $X$ varies from the mean $\\mu:$ ($X-\\mu)$. I will explain the purpose of the squared term later. We have the formula for the expected value $E[X] = \\sum\\limits_{i=1}^n p_ix_i$, and we will assume that any height is equally probable, so we can substitute that into the equation above to get\n", "\n", "$$\\mathit{VAR}(X) = \\frac{1}{n}\\sum_{i=1}^n (x_i - \\mu)^2$$\n", " \n", "Let's compute the variance of the three classes to see what values we get and to become familiar with this concept.\n", "\n", "The mean of $X$ is 1.8 ($\\mu_x = 1.8$) so we compute\n", "\n", "$$ \n", "\\begin{aligned}\n", "\\mathit{VAR}(X) &=\\frac{(1.8-1.8)^2 + (2-1.8)^2 + (1.7-1.8)^2 + (1.9-1.8)^2 + (1.6-1.8)^2} {5} \\\\\n", "&= \\frac{0 + 0.04 + 0.01 + 0.01 + 0.04}{5} \\\\\n", "\\mathit{VAR}(X)&= 0.02 \\, m^2\n", "\\end{aligned}$$\n", "\n", "NumPy provides the function `var()` to compute the variance:" ] }, { "cell_type": "code", "execution_count": 6, "metadata": {}, "outputs": [ { "name": "stdout", "output_type": "stream", "text": [ "0.02 meters squared\n" ] } ], "source": [ "print(np.var(X), \"meters squared\")" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "This is perhaps a bit hard to interpret. Heights are in meters, yet the variance is meters squared. Thus we have a more commonly used measure, the *standard deviation*, which is defined as the square root of the variance:\n", "\n", "$$\\sigma = \\sqrt{\\mathit{VAR}(X)}=\\sqrt{\\frac{1}{n}\\sum_{i=1}^n(x_i - \\mu)^2}$$\n", "\n", "It is typical to use $\\sigma$ for the *standard deviation* and $\\sigma^2$ for the *variance*. In most of this book I will be using $\\sigma^2$ instead of $\\mathit{VAR}(X)$ for the variance; they symbolize the same thing.\n", "\n", "For the first class we compute the standard deviation with\n", "\n", "$$ \n", "\\begin{aligned}\n", "\\sigma_x &=\\sqrt{\\frac{(1.8-1.8)^2 + (2-1.8)^2 + (1.7-1.8)^2 + (1.9-1.8)^2 + (1.6-1.8)^2} {5}} \\\\\n", "&= \\sqrt{\\frac{0 + 0.04 + 0.01 + 0.01 + 0.04}{5}} \\\\\n", "\\sigma_x&= 0.1414\n", "\\end{aligned}$$\n", "\n", "We can verify this computation with the NumPy method `numpy.std()` which computes the standard deviation. 'std' is a common abbreviation for standard deviation." ] }, { "cell_type": "code", "execution_count": 7, "metadata": {}, "outputs": [ { "name": "stdout", "output_type": "stream", "text": [ "std 0.1414\n", "var 0.0200\n" ] } ], "source": [ "print('std {:.4f}'.format(np.std(X)))\n", "print('var {:.4f}'.format(np.std(X)**2))" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "And, of course, $0.1414^2 = 0.02$, which agrees with our earlier computation of the variance.\n", "\n", "What does the standard deviation signify? It tells us how much the heights vary amongst themselves. \"How much\" is not a mathematical term. We will be able to define it much more precisely once we introduce the concept of a Gaussian in the next section. For now I'll say that for many things 68% of all values lie within one standard deviation of the mean. In other words we can conclude that for a random class 68% of the students will have heights between 1.66 (1.8-0.1414) meters and 1.94 (1.8+0.1414) meters. \n", "\n", "We can view this in a plot:" ] }, { "cell_type": "code", "execution_count": 8, "metadata": { "scrolled": true }, "outputs": [ { "data": { "image/png": "iVBORw0KGgoAAAANSUhEUgAAAwUAAAEvCAYAAAAUzW0AAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzt3Xl4VPX59/HPLCEBkgBJCBgUEFmi\nEIJKJbGUzQ1ZHoRKVdQqoFhcfmgrUfawqKktrbEFLi2WoAhSRB5cACvIovgDrShCUOsTARUEQmLI\nQhIyy/NHyEhIJsxMZjLJnPfrunIxc+Y+Z+7hnvPNuXM2k9PpdAoAAACAYZmDnQAAAACA4KIpAAAA\nAAyOpgAAAAAwOJoCAAAAwOBoCgAAAACDoykAAAAADM4a7AQaksPhkMPhqDbNZDLJZDIFKSMAAADA\nd06nU+ffYcBsNsts9u5v/4ZrCkpKSoKdBgAAABAwLVu29Lop4PAhAAAAwOBoCgAAAACDoykAAAAA\nDM5Q5xTUdkKxL8dcoXHJzs6WzWaT1WpVz549g50O6ol6hhbqGVqoZ2ihnqGhtnNmfbmIjuGbAl/O\nzkbj4nA4ZLfbqWWIoJ6hhXqGFuoZWqhn6PKlKeAbAAAAABhc0JuC999/XxMmTFBiYqJatmypDh06\naNSoUfr00089mv/EiRO69957FRcXpxYtWig1NVVbtmwJcNYAAABA6Ah6U7BkyRIdOnRIU6ZM0YYN\nG5SZmakTJ04oJSVF77//fp3zlpeX67rrrtOWLVuUmZmp9evXq127dho6dKi2b9/eQJ8AAAAAaNqC\nfk7BokWLFB8fX23a0KFD1bVrVz399NMaMmSI23lfeukl7d+/Xx999JFSU1MlSYMHD1ZycrLS0tK0\ne/fugOYOAAAAhIKg7yk4vyGQpMjISF1xxRX6/vvv65x33bp16tGjh6shkCSr1aq77rpLH3/8sY4c\nOeL3fAEAAIBQE/SmoDanTp3Snj17Lnh5rP3796t37941pldNy87ODkh+AAAAQCgJ+uFDtXnooYdU\nUlKiGTNm1BmXl5enmJiYGtOrpuXl5V3wvbKzs+VwOHxLFI1CRUWF69+9e/cGORvUF/UMLdQztFDP\n0EI9Q4PZbFbHjh3rvZxG1xTMmjVLr776qv72t7/p6quvvmB8Xddh9eQarTabTXa73asc0XhVDXBo\n/AYNGlTjZisX0rJlS23bti0wCSHgWD9DC/UMLdSz6bJYLH5ZTqNqCubOnasFCxboqaee0sMPP3zB\n+NjY2Fr3BuTn50tSrXsRzme1WrlhRxN37kAWFhYWxEzQEKhx08L6GVqoZ2ihnqHBX9uxjaYpmDt3\nrtLT05Wenq7p06d7NE9SUpL27dtXY3rVtF69el1wGT179qQpaOL27t2riooKhYWFKTk5OdjpwEO+\nrHdms5kaNzGsn6GFeoYW6hkaHA6HioqK6r2cRrE1PH/+fKWnp2vmzJmaM2eOx/ONHj1aX331VbVL\nj9psNq1YsUL9+vVTQkJCINIFAAAAQkrQ9xQsXLhQs2fP1tChQzV8+HDt2rWr2uspKSmSpIkTJ2r5\n8uXKyclRp06dJEkTJkzQokWLNHbsWGVkZCg+Pl6LFy/W119/rc2bN3v0/qUVdplM1U80NptMigj7\n+fis02dsbuevT2zpGbucctYaa5JJzZv5FltWYZfDWXusJLVoZg16bPMwi+ucj3KbXXaH77FlNocq\nbE7ZTQ45HE6ZzZWxZ2wO2eo4iTzCavE4NtxqkcWH2Aq7QxV297HNLGZZLWavY212h87UERtmMSvM\nh1i7w6lym/tzbKxms5pZvY91OJwqOz/WGi5T2BlJktNulxxV645JprBmbhYarnKbXeHWyu+70+lU\naYX7HCxmk8exDbXeG22MOHf9rDa9AceIc3mz3jNG1Iy1O5wqO1vP2r7Lfh0jfIz1Zr03+hhRtX46\nvFw/Q2074lxNcYwwX/gUWo8EvSl46623JEmbNm3Spk2barzuPPuFsNvtstvtrueSFB4eri1btigt\nLU2PPPKITp8+rT59+mjjxo0aOHCgR+/fP+N9/VRafQUc3KOtlo2/xvX86vmb3Q4U/S6N0eoHfr5P\nQv8/blV+yZlaY3tf3EpvPtzf9fz6v2zXkYLSWmO7xUfqvd///Bn+z98/1DcnimuN7dC6uXY++fNN\n3n7zwv/qix9O1Rob07KZ9sy6wfX8nn9+rN0H82uNbR5m0Zfzh7qeT17xqbZ+nVtrrCQdyhjuevz7\nf32uDfuOuY09MO8m18o//Y39WrvnB7exn868XrGR4ZKkBW9/qVd2HXYb+8GlPXRJTAtJ0p///bVe\n3PGt29h/PzZA3dtFSZIWbf1/ytzyjdvY9Q/9UsmXtJYkLdt5UM9s/Mpt7Kr7U5R6WWzl44+/0+z1\n7i+N+897+2pIYjtJ0v/97Iimvv6F29hF467S8N4XSZLezT6uh1bucRv7p1t7a2zfSyRJO77J1YSs\n/7iNnTeqp36b2lmS9PHBfN3xj11uY6fdnKgHBl4mSdp/5JRGLdrpNnbKdd302A3dJUn/L7dYN/51\nR7XXYyZlqeqsn1O716pg2zJJkiW6rS6e/E+3y13w9peaf0vloYH5JWd09QL3fwD49VUXa+FvKneJ\nl1bYdcXsd93GDktqr8V3/nxxg7piGSMqeT1GXH2l63HQxoi0wYwR8n2MOJBbrpnvn6x8Yc3RGrH+\nHCPONWlAF00fdrkk6UhBqX717Fa3sXendGKMkHdjRHxLiz4+59ouht6OaIJjxKDubd2+7o2gNwWe\nXkkkKytLWVlZNaa3a9dOy5cv929S+l7S5+c8v0juj7T6UdKL5zxvL8ndWeC558W2k/sS/HRebLwk\ndycBFZ0X21aSm7+0qvS82DhJ4W5iK86LjZUU4SZW58XGSGpeR+wyyfUXi9aSWtYR+4qkqi65laTI\nOmJXSaoaeKMlRdURu0ZSVUMYdTbenXWq/P/Q2fdvVUfsW5KqBvSWqvx87mySVH72cQtJbeqIfU9S\n2dnHEaqshzvbJZ0++zhclXV2Z6ekf5993EyV3x93dkvacvZxmCq/l+58Kmnb2cdWVX7f/SFb0kdn\nH5tVuX6687Uqc5Ykk6S6Dik8qMqcq3SoI5YxohJjxM+MMUZER5+SdEUdsYEaI/ZK+uDsY4sq1yN3\nGCMqeT5GmM2nxRhRpSmOEZJ0Sx0xnjE5nXXsmwkxtZ2IYY1YL5OpvNo0s8mpiHPWm9Nn3O+XqU9s\n6RmTm51+lUNT82ZOn2LLKiSH030eLRpBbPMwp6quGFtuk+wO32N/+OEH2e12WSwWde3cQVXnr56x\nSbY6lhthdXocG251yuJDbIVdqrC7j21mcersnmuvYm126UwdsWEWp8J8iLU7pHKb+1ir2amqvbve\nxDocUtl5se3bT1VxceUGjKeHD0VGRij3xLMKP7tcp1MqrXCfg8Xs9Di2odZ7o40R566f3bt0qDP2\nXP4cI87lzXrPGFEz9tDh71V6ximLxaKLL764Rqw/xwhfY71Z740+RlStn1aLRd28WD9DbTviXE1x\njDCbwlVUVL0piIqK8vqCHkHfUxBszcOcMpvr7ovO/ZJeiDexzQMUWzlgeBbfGGIrB2TfY5uHOWQ3\nO2SxmHTu97+ZVWrm4XIDFRtmqfyF6u9Yq0WyBiDWYvb8O+xNrLm2WFu5nBXltUQ73UyXZDO5foFL\nksnkeQ7exEqNIzYUxohz109fl1vfMcIdxgjvYy3myppaLKYLfpfrPUb4IZYxou5Yf6yfjSHW6GOE\nv+7B2yiuPgQAAAAgeGgKAAAAAIMz/OFDAACguujoKSoqKrtw4DmioiJUWJgZoIwABBp7CgAAAACD\noykAAAAADI6mAAAAADA4mgIAAADA4GgKAAAAAIOjKQAAAAAMjqYAAAAAMDiaAgAAAMDgaAoAAAAA\ng6MpAAAAAAzOGuwEAE9FR09RUVGZV/NERUWosDAzQBkBAACEBvYUAAAAAAZHUwAAAAAYHE0BAAAA\nYHA0BQAAAIDB0RQAAAAABkdTAAAAABgcTQEAAABgcDQFAAAAgMHRFAAAAAAGR1MAAAAAGJw12AkA\nAJq+6OgpKioq82qeqKgIFRZmBigjAIA32FMAAAAAGJzh9xSUVphkMpmqTTObnIoI+/n56TMmuVOf\n2NIzJjndxJokNW/m9Cm2rEJyON3n0aIRxDYPc6rqv73cJtkdnsXKYpXJbHEb66w4I1X9T5mtkjXc\nbU0irE6Zz7bFZ2ySrY4cwq1OWXyIrbBLFXb3sc0sTlkt3sfa7NKZOmLDLE6F+RBrd0jlNvexVrNT\nzazexzocUtn5sdZwmcIqa+W02yWH7ewLJpnCmrlZaLjKbVL42eU6nZXrsDsWs9Pj2IZa70N5jJAl\nTCaz+781OSvKq8XWtX76OkZcKNab9d7QY0S19dMmOeyV001mmaxhqpU1XGds8t8Y4WOsN+u90ceI\n0gqz7HanrI7q620ob0eE4hhhdv+yV0xOp9Pd9ynkOBwOFRUVVZs26Lld+qnUVm3a4B5lWjY+z/X8\n8lkXqbSi9l90/S4t1+oHTrqeXzW/vfJLat9o7X3xGb35cK7r+S8z2ulIQe19Wbf4Cr33+xOu5zf8\nJV7fnKh9IO7Q2qadTx53Pf8/f2+rL36ofaMqpqVde2Ydcz2/7YU47T4YXmts8zCHvpz/o+v5+GWx\n2vp1RK2xknQo44jr8YOvxmjDvuZuYw/MO+pa+f/wr9Zau6el29hPZ/6o2EiHoqOnKCzlXkVdNcJt\n7A9LJsheWPn/1nrQeLXq92u3sf9+7Li6t6us/V/fi1Lmlmi3sesfOqHkSyokSS9sj9QzG1u5jV11\nf65SLzsjSXr5f1tq9vrWbmP/ee9JDUms3FBa858Wmvp6G7exi8blaXjvysMz3vkiQg+tjHUb+6db\nf9LYvqclSe9/Fa4JWXFuY+eNKtBvU0skSf+b00x3/KOt29hpN5/SAwOLJUl7vw/TqEXxbmOnXFeo\nx26oXN/+e9yqG//azm3sqd1rVbBtmSTJEh2viyf/023s3SnFmn/LKUlSXrFZVy+4yG3sr68q0cLf\nFEiq/EV7xewEt7HDkkq1+M581/POT3ZwG8sYUencMSI6eooibnpCLS77Ra2xknT4jz+vu3GjnlTL\nxP5uY30ZIyRp1v9tpVd2RbqN/SDtmC6JqdzAfXpDtF7cEeU2ljGiUt6/l6j4s3ckSeGXJKn9uGfc\nxgZqjJg0oEjThxVKkr7Pt+hXz7Z3G8sYUcmbMaJ9VLl2zfg5h1DdjpBCc4wY1F0qKrql2vSoqCiZ\n6/gjTW0Mv6egdpdIOndjcpMku5vYiySNOef5e5LOuIltK2n0Oc/fl1TqJraNpHMLvF1SsZvYKEmj\nznn+oaRTbmKbS5p0zvP/lZTvJjbsvNiPJeW6idV5sZ9KOuYuUNJ4/fz12yvphzpi75YULunxOmJ8\nMVaV/3eS9F9J39QRO1pS1UqZI+mrOmJHSqr6ZXxIUnYdsUMlVf0i/F7SF3XE3qDK75sk/ShpTx2x\nA1X5PZak45L+U0fsLyV1Pvs4T9KuOmL7Sbrs7OMCSTvriL1aUvezj4sk7agj1hs9JfU6+7hc0uY6\nYntISj772Cbp3TpiL5V06znP36kjljGi0rljhL/XT1/GCEnaL+lwHbF3SGpx9vGXkr6tI5YxwnuB\nGiOSJV1+9vFpSVvriGWMqOT5GOFwtFD19T5UtyOk0Bwj2qpyHaofw+8psEa0qOXwIZMiwn7u0k+f\nqb4nwV+xpWfscrrZ8WeSSc2b+RZbVmGXo46ytmhmDXps8zCL6/+93GaX3XHh2OjoaBWdLvXq8KGo\nVq117NiPtcZGWC0yn93ndsbmkM3hcLvccKtFFh9iK+wOVdjdxzazmGU9u4/Qm1ib3aEzdcSGWcwK\n8yHW7nCq3ObuF5dkNZvVzOp9rMPhVNl5se3bX6Ti4sr10dPDhyIjo5R74pjCzx4j4XQ6VVrhPgeL\n2eRxbEOt96E6RlSun2VeHT4UFd3K7frpyxjhSaw3672Rx4jq66dnhw9FRkbp5InjfhsjfI31Zr03\n+hixb98+VVTY1CzMqmuuvtI1PVS3IzyJbYpjhNmkGtu3vuwpMHxT4Mt/GoIjOjq6Rv0uJCoqSoWF\nhQHKCPVBPUML9Qwt1NMY9u7dq4qKCoWFhSk5OfnCM6BR8tf2LVvDAAAAgMHRFAAAAAAGR1MAAAAA\nGBxNAQAAAGBwXJIUAAAghHHiODzBngIAAADA4GgKAAAAAIOjKQAAAAAMjqYAAAAAMLhG0RQUFRUp\nLS1NN954o9q2bSuTyaT09HSP5s3KypLJZKr159ixY4FNHAAAAAgBjeLqQ3l5eXrxxReVnJysW265\nRUuXLvV6GcuWLVNiYmK1abGxsf5KEQAAAAhZjaIp6NSpk3766SeZTCadPHnSp6agV69e6tu3bwCy\nAwAAAEJbo2gKTCZTsFMAAAAADKtRnFPgDyNGjJDFYlFMTIzGjBmj/fv3BzslAAAAoEloFHsK6qN9\n+/aaMWOGUlJSFB0drX379ikjI0MpKSnauXOnkpOT65w/OztbDoejgbJFffhSJ4fDob179wYgG9QX\n9Qwt1DO0UM/QQj1Dm9lsVseOHeu9nCbfFAwdOlRDhw51PR8wYICGDx+upKQkzZ49W+vXr69zfpvN\nJrvdHug0EUQVFRXBTgF+RD1DC/UMLdQztFDPpsFisfhlOU2+KahN586d1b9/f+3ateuCsVarVWZz\nyBxFhVqEhYUFOwX4EfUMLdQztFDP0EI9mwZ/bceGZFMgSU6n06P/pJ49e9IUNBG+1MlsNl/wEDIE\nB/UMLdQztFDP0EI9Q5vD4VBRUVG9lxOSW8MHDx7Uzp07lZKSEuxUAAAAgEav0ewp2Lhxo0pKSlyd\nzoEDB/T6669LkoYNG6YWLVpo4sSJWr58uXJyctSpUydJ0vXXX68BAwaod+/erhONn332WZlMJs2f\nPz9onwcAAABoKhpNUzB58mQdPnzY9XzNmjVas2aNpMq//Hfu3Fl2u112u11Op9MVl5SUpNWrV+vP\nf/6zSktLFR8fryFDhmjWrFnq3r17g38OAAAAoKkxOc/dwg5xtR1zFRUVxTkFTUR0dLTXx8xFRUWp\nsLAwQBmhPqhnaKGeoYV6hhbqGdr8tX3L1jAAAABgcDQFAAAAgMHRFAAAAAAGR1MAAAAAGBxNAQAA\nAGBwNAUAAACAwdWrKXA4HDp9+rS/cgEAAAAQBF41BWVlZcrKytLYsWOVkJCgZs2aKSoqSi1atFDf\nvn2VlpamvXv3BipXAAAAAAHg0R2NS0tL9eyzzyozM1OnTp1SYmKirrvuOsXHxysiIkL5+fn69ttv\n9Y9//EMLFy7Utddeq2effVapqamBzh8AAABAPXnUFHTr1k0tW7bUzJkzdeedd6pdu3a1xjmdTm3d\nulXLli3T4MGD9fe//1333XefXxMGAAAA4F8eNQXz5s3TPffcI4vFUmecyWTSkCFDNGTIEM2dO1ff\nffedX5IEAAAAEDgeNQUTJkzwesFdunRRly5dvJ4PAAAAQMPikqQAAACAwXm0p+B8x44d09q1a3X4\n8GGVlZVVe81kMikzM9MvyQEAAAAIPK+bgnfffVejR4+u0QxUoSkAAAAAmhavDx+aOnWq+vTpo88/\n/1zl5eVyOBzVfux2eyDyBAAAABAgXu8pyMnJ0RtvvKHevXsHIh8AAAAADczrPQWJiYkqLCwMRC4A\nAAAAgsDrpmDevHl66qmndPz48UDkAwAAAKCBeX340PDhw7Vnzx5ddtll6tOnj2JiYqq9bjKZtH79\ner8lCAAAACCwvG4KsrKyNGfOHFksFh08eFBHjhyp9rrJZPJbcgAAAAACz+umYO7cuRo5cqSysrLU\npk2bQOQEAAAAoAF5fU7B8ePH9cgjj9AQAAAAACHC66bgyiuv1A8//BCIXAAAAAAEgddNwcKFC/Xs\ns8/q888/D0Q+AAAAABqY1+cU3H///crNzdXVV1+tiy66qNarD+3du9dvCQIAAAAILK+bgtjYWMXF\nxQUiFwAAAABB4HVTsG3btgCkAQAAACBYvD6nAAAAAEBo8agp2L17t9cLLi0tVXZ2ttfzAQAAAGhY\nHjUFAwcO1KhRo7R58+YLxh4/flx/+tOf1KVLF7399tv1ThAAAABAYHl0TkF2drYef/xx3Xjjjbro\noos0YMAAXXXVVYqPj1dERITy8/OVk5OjXbt26eOPP1abNm00d+5cTZo0KdD5AwAAAKgnj5qCyy67\nTOvWrdOXX36pJUuWaMOGDVq9enW1mObNmys1NVUvvPCCxo0bp/Dw8IAkDAAAAMC/vLr60OWXX67n\nn39ezz//vHJzc3X06FGVlpYqLi5OnTp1UlhYWKDyBAAAABAgXl+StErbtm3Vtm1bf+YCAAAAIAi4\nJCkAAABgcDQFAAAAgMHRFAAAAAAGR1MAAAAAGBxNAQAAAGBwXjcFQ4YM0VdffVXra//97381ZMiQ\neicFAAAAoOF43RRs27ZNhYWFtb5WVFSk7du31zspAAAAAA3Hr4cP/fjjj2rRooU/FwkAAAAgwDy6\nedn69eu1fv161/P58+fXuHFZaWmptm3bpiuvvNKrBIqKijR//nx9/vnn+uyzz3Ty5EnNmTNH6enp\nHs1/4sQJpaWl6e2339bp06eVnJysBQsW6LrrrvMqDwAAAMCoPGoKDhw4oDVr1kiSTCaT3n//fZnN\n1XcyhIeHKykpSZmZmV4lkJeXpxdffFHJycm65ZZbtHTpUo/nLS8v13XXXaeCggJlZmYqPj5eixYt\n0tChQ7V582YNHDjQq1wAAAAAI/KoKZg2bZqmTZsmSTKbzdq6dauuueYavyTQqVMn/fTTTzKZTDp5\n8qRXTcFLL72k/fv366OPPlJqaqokafDgwUpOTlZaWpp2797tlxwBAACAUOb1OQUOh8NvDYFUuefB\nZDL5NO+6devUo0cPV0MgSVarVXfddZc+/vhjHTlyxF9pAgAAACHLoz0F7uTm5qq0tLTG9I4dO9Zn\nsR7bv3+/fvWrX9WY3rt3b0lSdna2OnToUOcysrOz5XA4ApIf/MuXOjkcDu3duzcA2aC+qGdooZ6h\nhXqGFuoZ2sxms1+2vb1uCgoLC/X73/9eq1atUllZWa0xdru93ol5Ii8vTzExMTWmV03Ly8u74DJs\nNluD5YvgqKioCHYK8CPqGVqoZ2ihnqGFejYNFovFL8vxuil47LHHtHLlSk2cOFG9e/dWeHi4XxLx\nVV2HHnlyWJLVaq1x0jRCS1hYWLBTgB9Rz9BCPUML9Qwt1LNp8Nd2rNdNwTvvvKOMjAxNmTLFLwnU\nR2xsbK17A/Lz8yWp1r0I5+vZsydNQRPhS53MZrOSk5MDkA3qi3qGFuoZWqhnaKGeoc3hcKioqKje\ny/H6W1JWVqakpKR6v7E/JCUlad++fTWmV03r1atXQ6cEAAAANDleNwXDhg3TBx98EIhcvDZ69Gh9\n9dVX1S49arPZtGLFCvXr108JCQlBzA4AAABoGjw6fKjqcBxJmjlzpm699VZFRUVp5MiRio2NrRHv\nyWE759q4caNKSkpcuz4OHDig119/XVJlE9KiRQtNnDhRy5cvV05Ojjp16iRJmjBhghYtWqSxY8cq\nIyND8fHxWrx4sb7++mtt3rzZqxwAAAAAo/KoKYiLi6t20q7T6dTUqVM1derUWuO9vZrP5MmTdfjw\nYdfzNWvWuO6gfPDgQXXu3Fl2u112u11Op9MVFx4eri1btigtLU2PPPKITp8+rT59+mjjxo3czRgA\nAADwkEdNwezZs32+wZgnDh06dMGYrKwsZWVl1Zjerl07LV++3P9JAQAAAAbhUVOQnp4e4DQAAAAA\nBAvX4gQAAAAMzuv7FMybN8/ta2azWa1bt1bfvn2VkpJSr8QAAAAANAyvm4L09HSZTKZqJ/xWqZpu\nMpk0cOBAvfnmm4qMjPRLogAAAAACw+vDh3JyctS1a1c988wzOnTokEpLS3Xw4EE9/fTTuuyyy7R7\n92698sor+vTTTzVr1qxA5AwAAADAj7zeU/A///M/uvvuu/XEE0+4pnXq1ElPPvmkbDabZs+erY0b\nNyonJ0cvvfSS/vrXv/o1YQAAAAD+5fWegm3btik1NbXW11JTU/Xhhx+6Hv/444/1yw4AAABAwHnd\nFDRr1kyfffZZra99+umnatasmSTJ4XCoZcuW9csOAAAAQMB5ffjQLbfcojlz5qhVq1YaO3asWrdu\nrYKCAq1evVrz5s3T7bffLknat2+funbt6veEAQAAAPiX103BX/7yF/33v//VAw88oN/97neyWq2y\n2WxyOp365S9/qYULF0qSOnTooDlz5vg9YQAAAAD+5XVT0KpVK+3YsUMbN27Ujh07lJeXp9jYWA0c\nOFBDhw6VyWSSJNceAwAAAACNm9dNgVR5P4Jhw4Zp2LBh/s4HAAAAQAPz+kRjAAAAAKHFoz0FXbp0\n0bp165ScnKxLL73UdYhQbUwmk3JycvyWIAAAAIDA8qgpGDhwoKKjo12P62oKAAAAADQtHjUFy5Yt\ncz3OysoKVC4AAAAAgoBzCgAAAACD86kpyM3N1bRp05Samqpu3bopOztbkvTCCy+4vdsxAAAAgMbJ\n66bg4MGDSk5O1vPPPy+TyaRvv/1W5eXlkqQvvvhCzz//vN+TBAAAABA4XjcFaWlpat26tb755hvt\n2LFDTqfT9Vr//v21c+dOvyYIAAAAILC8vnnZli1btGTJEiUkJMhut1d77aKLLtLRo0f9lhwAAACA\nwPN6T0FZWZliYmJqfa2kpERmM+cuAwAAAE2J11vwPXr00ObNm2t9bceOHerVq1e9kwIAAADQcLw+\nfOj+++/X73//eyUkJOjOO++UJJ05c0avv/66Fi9erL///e9+TxIAAABA4HjdFDz44IP6/PPP9dhj\nj+kPf/iDpMoTjJ1Op+6//37dc889fk8SAAAAQOB43RRI0osvvqgJEybonXfe0fHjxxUXF6cRI0bo\n2muv9Xd+AAAAAALMp6ZAklJSUpSSkuLPXAAAAAAEgc9NgVR5Z+PS0tIa0zt27FifxQIAAABoQF43\nBUVFRXrssce0atUqlZWV1RpVomKJAAAWE0lEQVRz/v0LAAAAADReXjcFjz76qFauXKmJEyeqd+/e\nCg8PD0ReAAAAABqI103BO++8o4yMDE2ZMiUQ+QAAAABoYD7d0TgpKSkQuQAAAAAIAq+bgmHDhumD\nDz4IRC4AAAAAgsCjw4fy8/Ndj2fOnKlbb71VUVFRGjlypGJjY2vEx8TE+C9DAAAAAAHlUVMQFxcn\nk8nkeu50OjV16lRNnTq11niuPgQAAAA0HR41BbNnz67WFAAAAAAIHR41Benp6QFOAwAAAECweH2i\nMQAAAIDQQlMAAAAAGBxNAQAAAGBwNAUAAACAwdEUAAAAAAbXKJqC4uJiPfroo0pISFBERIT69Omj\n11577YLzZWVlyWQy1fpz7NixBsgcAAAAaPo8uiRpoI0ZM0affPKJMjIy1L17d61cuVJ33HGHHA6H\nxo0bd8H5ly1bpsTExGrTarvTMgAAAICagt4UbNiwQe+9956rEZCkwYMH6/Dhw5o6dapuu+02WSyW\nOpfRq1cv9e3btyHSBQAAAEJO0A8fWrdunSIjIzV27Nhq08ePH6+jR49q9+7dQcoMAAAAMIag7ynY\nv3+/Lr/8clmt1VPp3bu36/Vrr722zmWMGDFCubm5atWqlQYNGqR58+apV69eHr1/dna2HA6Hb8mj\nQflSJ4fDob179wYgG9QX9Qwt1DO0UM/QQj1Dm9lsVseOHeu9nKA3BXl5eerSpUuN6TExMa7X3Wnf\nvr1mzJihlJQURUdHa9++fcrIyFBKSop27typ5OTkC76/zWaT3W73/QOg0auoqAh2CvAj6hlaqGdo\noZ6hhXo2DRc6zN5TQW8KJMlkMvn02tChQzV06FDX8wEDBmj48OFKSkrS7NmztX79+gu+t9Vqldkc\n9KOoEEBhYWHBTgF+RD1DC/UMLdQztFDPpsFf27FBbwpiY2Nr3RuQn58v6ec9Bp7q3Lmz+vfvr127\ndnkU37NnT5qCJsKXOpnNZo/2GKHhUc/QQj1DC/UMLdQztDkcDhUVFdV7OUHfGk5KStKXX34pm81W\nbfq+ffskyeNzA87ldDrZ0AcAAAA8FPQt59GjR6u4uFhr166tNn358uVKSEhQv379vFrewYMHtXPn\nTqWkpPgzTQAAACBkBf3woZtvvlk33HCDJk+erMLCQnXt2lWrVq3Spk2btGLFCtfJExMnTtTy5cuV\nk5OjTp06SZKuv/56DRgwQL1793adaPzss8/KZDJp/vz5wfxYAAAAQJMR9KZAkt544w3NmDFDs2fP\nVn5+vhITE7Vq1Srdfvvtrhi73S673S6n0+malpSUpNWrV+vPf/6zSktLFR8fryFDhmjWrFnq3r17\nMD4KAAAA0OSYnOduZYe42k7EiIqK4vyDJiI6OtrrE2mioqJUWFgYoIxQH9QztFDP0EI9Qwv1DG3+\n2r5laxgAAAAwOJoCAAAAwOBoCgAAAACDoykAAAAADI6mAAAAADA4mgIAAADA4GgKAAAAAIOjKQAA\nAAAMjqYAAAAAMDiaAgAAAMDgaAoAAAAAg6MpAAAAAAyOpgAAAAAwOJoCAAAAwOBoCgAAAACDoykA\nAAAADI6mAAAAADA4mgIAAADA4GgKAAAAAIOjKQAAAAAMjqYAAAAAMDiaAgAAAMDgaAoAAAAAg6Mp\nAAAAAAyOpgAAAAAwOJoCAAAAwOBoCgAAAACDoykAAAAADI6mAAAAADA4mgIAAADA4GgKAAAAAIOj\nKQAAAAAMjqYAAAAAMDiaAgAAAMDgaAoAAAAAg6MpAAAAAAyOpgAAAAAwOJoCAAAAwOBoCgAAAACD\noykAAAAADI6mAAAAADA4mgIAAADA4BpFU1BcXKxHH31UCQkJioiIUJ8+ffTaa695NO+JEyd07733\nKi4uTi1atFBqaqq2bNkS4IwBAACA0GENdgKSNGbMGH3yySfKyMhQ9+7dtXLlSt1xxx1yOBwaN26c\n2/nKy8t13XXXqaCgQJmZmYqPj9eiRYs0dOhQbd68WQMHDmzATwEAAAA0TUFvCjZs2KD33nvP1QhI\n0uDBg3X48GFNnTpVt912mywWS63zvvTSS9q/f78++ugjpaamuuZNTk5WWlqadu/e3WCfAwAAAGiq\ngn740Lp16xQZGamxY8dWmz5+/HgdPXq0zg37devWqUePHq6GQJKsVqvuuusuffzxxzpy5EjA8gYA\nAABCRdCbgv379+vyyy+X1Vp9p0Xv3r1dr9c1b1VcbfNmZ2f7MVMAAAAgNAX98KG8vDx16dKlxvSY\nmBjX63XNWxXn7bxVsrOz5XA4PE0XQeRLnRwOh/bu3RuAbFBf1DO0UM/QQj1DC/UMbWazWR07dqz3\ncoLeFEiSyWTy6bX6zitJNptNdrv9gnEIvm3btvk0X0VFhX8TgV9Qz9BCPUML9Qwt1DO0uTv31ltB\nbwpiY2Nr/Yt+fn6+JNW6J8Af81axWq0ym4N+FBXq4dxBKywsLIiZwB+oZ2ihnqGFeoYW6hka/LUd\nG/SmICkpSatWrZLNZqt2XsG+ffskSb169apz3qq4c3kyb5WePXvSFDRxe/fuVUVFhcLCwpScnBzs\ndFBP1DO0UM/QQj1DC/UMDQ6HQ0VFRfVeTtC3hkePHq3i4mKtXbu22vTly5crISFB/fr1q3Per776\nqtoVimw2m1asWKF+/fopISEhYHkDAAAAoSLoewpuvvlm3XDDDZo8ebIKCwvVtWtXrVq1Sps2bdKK\nFStcx0lNnDhRy5cvV05Ojjp16iRJmjBhghYtWqSxY8cqIyND8fHxWrx4sb7++mtt3rw5mB8LAAAA\naDKC3hRI0htvvKEZM2Zo9uzZys/PV2JiolatWqXbb7/dFWO322W32+V0Ol3TwsPDtWXLFqWlpemR\nRx7R6dOn1adPH23cuJG7GQMAAAAeahRNQWRkpDIzM5WZmek2JisrS1lZWTWmt2vXTsuXLw9gdgAA\nAEBoC/o5BQAAAACCq1HsKWgo5x56VIUblzV9ZrNZFotFZrOZeoYA6hlaqGdooZ6hhXqGhtpqV9s2\n74WYnL7M1UTZbDaVlJQEOw0AAAAgYFq2bFntUv+e4PAhAAAAwOBoCgAAAACDoykAAAAADM5Q5xQ4\nHI4aJ2OYTCaZTKYgZQQAAAD4zul01jix2Gw2y2z27m//hmoKAAAAANTE4UMAAACAwRmqKSguLtaj\njz6qhIQERUREqE+fPnrttdeCnRZ8UFRUpLS0NN14441q27atTCaT0tPTg50WfPT+++9rwoQJSkxM\nVMuWLdWhQweNGjVKn376abBTgw8+//xzDR8+XB07dlTz5s0VExOj1NRUrVixItipwQ+WLl0qk8mk\nyMjIYKcCH2zbts116PT5P7t27Qp2evDRhx9+qGHDhqlNmzZq3ry5unXrpvnz53u1DEPdvGzMmDH6\n5JNPlJGRoe7du2vlypW644475HA4NG7cuGCnBy/k5eXpxRdfVHJysm655RYtXbo02CmhHpYsWaK8\nvDxNmTJFV1xxhXJzc7Vw4UKlpKTo3Xff1ZAhQ4KdIrxQUFCgSy65RHfccYc6dOigkpISvfrqq7r7\n7rt16NAhzZw5M9gpwkdHjhzR448/roSEBJ06dSrY6aAenn76aQ0ePLjatF69egUpG9THypUrdffd\nd+s3v/mNXn75ZUVGRionJ0dHjx71ajmGOadgw4YNGj58uKsRqHLjjTcqOztb3333nSwWSxAzhDeq\nvrYmk0knT55U27ZtNWfOHPYWNFEnTpxQfHx8tWnFxcXq2rWrevXqpc2bNwcpM/hTSkqKjh49qu++\n+y7YqcBHI0eOlMlkUkxMjF5//XUVFxcHOyV4adu2bRo8eLDWrFmjW2+9NdjpoJ6OHDmiHj166Le/\n/a0WL15cr2UZ5vChdevWKTIyUmPHjq02ffz48Tp69Kh2794dpMzgC64aFVrObwgkKTIyUldccYW+\n//77IGSEQIiLi/P6DptoPFasWKHt27fXe8MDgP8sXbpUJSUleuKJJ+q9LMM0Bfv379fll19e4xdS\n7969Xa8DaDxOnTqlPXv2qGfPnsFOBT5yOByy2WzKzc3V4sWL9e677/rlFxca3okTJ/Too48qIyND\nF198cbDTgR889NBDslqtio6O1k033aQPP/ww2CnBBzt27FBMTIy++uor9enTR1arVfHx8frd736n\nwsJCr5ZlmKYgLy9PMTExNaZXTcvLy2volADU4aGHHlJJSYlmzJgR7FTgowcffFBhYWGKj4/XY489\npueff14PPPBAsNOCDx588EH16NFDkydPDnYqqKdWrVppypQpeuGFF7R161ZlZmbq+++/16BBg/Tu\nu+8GOz146ciRIzp9+rTGjh2r2267TZs3b9bUqVP18ssva9iwYTXuX1AXQ+3HretwEw5FARqPWbNm\n6dVXX9Xf/vY3XX311cFOBz6aPn267rvvPp04cUJvvfWWHn74YZWUlOjxxx8Pdmrwwtq1a/XWW2/p\ns88+43dlCLjyyit15ZVXup7/6le/0ujRo5WUlKS0tDTddNNNQcwO3nI4HCorK9OcOXP05JNPSpIG\nDRqkZs2a6dFHH9WWLVt0/fXXe7Qsw+wpiI2NrXVvQH5+viTVuhcBQMObO3euFixYoKeeekoPP/xw\nsNNBPXTs2FF9+/bVsGHDtGTJEk2aNEnTpk1Tbm5usFODh4qLi/XQQw/pkUceUUJCggoKClRQUKAz\nZ85IqrzSVElJSZCzRH21bt1aI0aM0BdffKHS0tJgpwMvxMbGSlKNZu7mm2+WJO3Zs8fjZRmmKUhK\nStKXX34pm81Wbfq+ffskcRkuoDGYO3eu0tPTlZ6erunTpwc7HfjZNddcI5vNpm+//TbYqcBDJ0+e\n1PHjx7Vw4UK1adPG9bNq1SqVlJSoTZs2uvPOO4OdJvzg3Kv6oemoOjf2fFX1NJs939Q3TFMwevRo\nFRcXa+3atdWmL1++XAkJCerXr1+QMgMgSfPnz1d6erpmzpypOXPmBDsdBMDWrVtlNpvVpUuXYKcC\nD7Vv315bt26t8XPTTTcpIiJCW7du1YIFC4KdJurpp59+0ttvv60+ffooIiIi2OnAC7/+9a8lSRs3\nbqw2fcOGDZIqLwXtKcOcU3DzzTfrhhtu0OTJk1VYWKiuXbtq1apV2rRpk1asWME9CpqgjRs3qqSk\nREVFRZKkAwcO6PXXX5ckDRs2TC1atAhmevDCwoULNXv2bA0dOlTDhw+vcVdNbwY1BN+kSZMUHR2t\na665Ru3atdPJkye1Zs0arV69WlOnTlXbtm2DnSI8FBERoUGDBtWYnpWVJYvFUutraNzGjRvnOrQv\nLi5O33zzjRYuXKjjx48rKysr2OnBSzfeeKNGjhypefPmyeFwKCUlRf/5z380d+5cjRgxQv379/d4\nWYa5eZlUeWzkjBkz9K9//Uv5+flKTEzUtGnTdPvttwc7Nfigc+fOOnz4cK2vHTx4UJ07d27YhOCz\nQYMGafv27W5fN9AwFRKWLVumZcuW6csvv1RBQYEiIyOVnJys++67T3fddVew04Mf3Hvvvdy8rInK\nyMjQ6tWrdfDgQRUXFysmJkb9+/fXtGnT9Itf/CLY6cEHpaWlmjt3rlauXKkff/xRCQkJuvPOOzVn\nzhyFh4d7vBxDNQUAAAAAajLMOQUAAAAAakdTAAAAABgcTQEAAABgcDQFAAAAgMHRFAAAAAAGR1MA\nAAAAGBxNAQAAAGBwNAUAAEnSypUr9dxzzwVk2ffee2/Abyh44MABpaen69ChQwF9HwAIRTQFAABJ\ngW0KGsKBAwc0d+5cmgIA8AFNAQAAAGBwNAUAYBC5ubmaNGmSLrnkEoWHh6tt27b65S9/qc2bN2vQ\noEF65513dPjwYZlMJtePJG3btk0mk0nbtm2rtrxDhw7JZDIpKyur2vSsrCz16NFD4eHhuvzyy/Xy\nyy/Xms+ZM2e0YMECJSYmuvIZP368cnNzq8V17txZI0aM0KZNm3TVVVepefPmSkxM1D//+c9q7zl2\n7FhJ0uDBg135n58bAKB21mAnAABoGHfffbf27Nmjp556St27d1dBQYH27NmjvLw8LV68WJMmTVJO\nTo7WrVvn83tkZWVp/PjxGjVqlBYuXKhTp04pPT1d5eXlMpt//juUw+HQqFGj9MEHHygtLU3XXnut\nDh8+rDlz5mjQoEH6z3/+o+bNm7vi9+7dqz/84Q968skn1a5dOy1dulQTJ05U165dNWDAAA0fPlxP\nP/20pk+frkWLFumqq66SJF122WW+/4cBgIHQFACAQezcuVP33Xef7r//fte0UaNGuR63bt1a4eHh\nSklJ8Wn5DodDM2bM0FVXXaV169a59jT0799f3bp1U0JCgiv2X//6lzZt2qS1a9dqzJgxrunJycn6\nxS9+oaysLE2ePNk1/eTJk9q5c6c6duwoSRowYIC2bNmilStXasCAAWrbtq26desmSbriiit8/gwA\nYFQcPgQABnHNNdcoKytLCxYs0K5du1RRUeHX5X/99dc6evSoxo0b52oIJKlTp0669tprq8W+/fbb\nat26tUaOHCmbzeb66dOnj9q3b1/jUKU+ffq4GgJJioiIUPfu3XX48GG/fgYAMCqaAgAwiNWrV+ue\ne+7R0qVLlZqaqpiYGP32t7/VsWPH/LL8vLw8SVL79u1rvHb+tOPHj6ugoEDNmjVTWFhYtZ9jx47p\n5MmT1eJjY2NrLDM8PFylpaV+yR0AjI7DhwDAIOLi4vTcc8/pueee03fffac333xTTz75pE6cOKFN\nmza5nS8iIkKSVF5eXm26uw332pqM86fFxcUpNjbW7ftGRUVd+AMBAPyGPQUAYEAdO3bUww8/rBtu\nuEF79uyR5P4v71U3Hfviiy+qTX/zzTerPe/Ro4cuuugirVq1Sk6n0zX98OHD+uijj6rFjhgxQnl5\nebLb7erbt2+Nnx49enj9mcLDwyWJvQcA4AP2FACAAZw6dUqDBw/WuHHjlJiYqKioKH3yySfatGmT\n60TfpKQkvfHGG1qyZImuvvpqmc1m9e3bV+3bt9f111+vZ555Rm3atFGnTp20ZcsWvfHGG9Xew2w2\na/78+brvvvs0evRo3X///SooKFB6enqNw4duv/12vfrqqxo2bJimTJmia665RmFhYfrhhx+0detW\njRo1SqNHj/bqM/bq1UuS9OKLLyoqKkoRERG69NJLaz30CABQHU0BABhARESE+vXrp1deeUWHDh1S\nRUWFOnbsqCeeeEJpaWmSpClTpig7O1vTp0/XqVOn5HQ6XX/xf+WVV/TII4/oiSeekN1u18iRI7Vq\n1Sr17du32vtMnDhRkvTHP/5RY8aMUefOnTV9+nRt37692snDFotFb775pjIzM/XKK6/omWeekdVq\n1cUXX6yBAwcqKSnJ68946aWX6rnnnlNmZqYGDRoku92uZcuW6d577/XtPw0ADMTkPHcfLwAAAADD\n4ZwCAAAAwOBoCgAAAACDoykAAAAADI6mAAAAADA4mgIAAADA4GgKAAAAAIOjKQAAAAAMjqYAAAAA\nMDiaAgAAAMDgaAoAAAAAg6MpAAAAAAyOpgAAAAAwuP8PPYyoQ+KjYXUAAAAASUVORK5CYII=\n", "text/plain": [ "" ] }, "metadata": {}, "output_type": "display_data" } ], "source": [ "from kf_book.book_plots import set_figsize, figsize\n", "from kf_book.gaussian_internal import plot_height_std\n", "import matplotlib.pyplot as plt\n", "\n", "plot_height_std(X)" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "For only 5 students we obviously will not get exactly 68% within one standard deviation. We do see that 3 out of 5 students are within $\\pm1\\sigma$, or 60%, which is as close as you can get to 68% with only 5 samples. I haven't yet introduced enough math or Python for you to fully understand the next bit of code, but let's look at the results for a class with 100 students.\n", "\n", "> We write one standard deviation as $1\\sigma$, which is pronounced \"one standard deviation\", not \"one sigma\". Two standard deviations is $2\\sigma$, and so on." ] }, { "cell_type": "code", "execution_count": 9, "metadata": {}, "outputs": [ { "data": { "image/png": "iVBORw0KGgoAAAANSUhEUgAAAwgAAAEvCAYAAADhM+awAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzt3Xl4VOX9///XTFZIQEggQBICirIH\nqKIEqyAgFhG+CJbWtbJUW1yKYgEF2VHRChqt+nMlFIUqKh+sLBYQ1KLggiLErUVAArIFgRCyzpzf\nHyEnM8nMZCaZzEwyz8d1cZE59/vced8z97nnvHNmsRiGYQgAAAAAJFmDnQAAAACA0EGBAAAAAMBE\ngQAAAADARIEAAAAAwESBAAAAAMBEgQAAAADAFBnsBALJbrfLbrc7bbNYLLJYLEHKCAAAAKg5wzBU\n+VsLrFarrNaaXwcIuwIhPz8/2GkAAAAAdSYuLq5WBQIvMQIAAABgokAAAAAAYKJAAAAAAGAKq/cg\nuHozcm1fo4WGKzs7W6WlpYqMjFS3bt2CnQ5CFPME1WGOwBvME3jD1Txx9R7b2n4AT9gXCLV9lzca\nLrvdLpvNxhyBR8wTVIc5Am8wT+ANb+dJbQsEZiAAAAAAEwUCAAAAABMFAgAAAAATBQIAAAAAEwUC\nAAAAABMFAgAAAAATBQIAAAAAU1h9DwIANFSLFi3SqVOn1LRpU02aNCnY6dRr3JcAwh0FAgA0AIsW\nLdKBAweUkpLCSW0tcV8CCHe8xAgAAACAiQIBAAAAgIkCAQAAAICJ9yAAIY43TAIA4B88p3qHAgEI\ncbxhEgAA/+A51Tu8xAgAAACAKegFwvvvv69x48apc+fOiouLU0pKikaMGKEvvvjCq/2PHDmiMWPG\nqEWLFmrcuLH69u2rjRs31nHWAAAAQMMU9JcYPffcc8rNzdXEiRPVtWtXHT16VAsXLlRGRobee+89\nDRw40O2+RUVFGjRokE6cOKHMzEwlJSXpmWee0ZAhQ7Rhwwb1798/gCMBAAAILF5Tj7oQ9ALhmWee\nUVJSktO2IUOG6Pzzz9fDDz/ssUB4+eWXtWvXLn388cfq27evJGnAgAHq2bOnpkyZom3bttVp7gAA\nIDSE64kyr6lHXQh6gVC5OJCk+Ph4de3aVfv37/e478qVK9WpUyezOJCkyMhI3XzzzZo2bZp5wAAA\ngLoRKifmnCgHRqg83qhbQS8QXDl58qS2b9/u8eqBJO3atUuXX355le09evSQJGVnZ1MgAAAanFA6\nSePEPLzweIeHkCwQ7rzzTuXn52v69Oke43Jzc5WQkFBle/m23Nzcan9Xdna27HZ7zRJFg1ZSUmL+\nv2PHjrDPA67V5PFZunSpTp8+rfj4eN1yyy1BywOu+fu+rIvH5tFHH9WRI0eUlJSkQYMG+aXPmgqV\nuRcqedRUTfMP9LjD9X52py7Wc09c5W+1WpWWlubX3xNyBcKMGTP02muv6emnn9ZFF11UbbzFYqlR\nW7nS0lLZbDafckT4KT8ggy1U8oBr3j4+S5cuNU/urr/++qDlURuvvfaa8vPzFRcXp5tuuqnOf1+w\n+Pu+rIvHJpTWhVDJJVTyqKma5h/ocYfr/eyortdzT8rzj4iI8HvfIVUgzJkzR/Pnz9dDDz2ku+66\nq9r4xMREl1cJjh8/Lkkury5UFhkZKas16J/2ihDkuHBERUUFMZMKoZIHKtR2ntTFYxqIebJs2TLz\nSXHMmDF1/vuCxR/3ZV2vJaG0LoRKLqGShy/8MU8CPe76eD878nf+gbg/XM2TujiPDZkCYc6cOZo9\ne7Zmz56tadOmebVPenq6du7cWWV7+bbu3btX28d5HTtXudJgtVgUG1VRjZ0pLnW7f21iC4ptMmS4\njLXIokbRNYstLLHJbriOlaTG0ZFBj20UFWHe70WlNtns/omNjYyQ1VoWW1xqV6mHl49VF7tz506V\nlJQqKipSv0rvoQiH2CcyM3XqVJ6aNm2iu+++22m/mMgIM7bEZleJzX0O0RFWRUZYPcZGxcbJEhWj\nqOgY9ezZU5JUarOr2EO/URFWRZ3t15dYm91QUan7K2qRVquiI32PtdsNFfopNsJqUUxk2Xw3DEMF\nJf6JremxvGPHDuUVFCsqKlJdu3Tzql/zMY2N0wUO+9RmjYiKbeyyT1ex/jiWzTFERZnzsqGsERVj\nizbHVt164njcV451XEu6dunmlzXC1RxyjA3kGuGYS5du6UFbI8w8YhqZj1sorBHexu7YsUMlJSWy\nWSJcriWu+i0otrldT+rqPCIqNq7s/7PHfn07j4iKaeR2rZR8P48oP0mPiol12V85T2uEp9jKa0Tl\n9SQ6wiqrRcrLy3PbX01YDMPDvR8g8+bN08yZM/Xggw9q3rx5Xu/33HPP6Y477tDWrVvVp08fSWUv\nGerVq5fi4+O1detWp3i73V7lDrziya36pcD5wB3QqaUWj73EvN1lxjq3i0afcxP0+p8qPkXpwnnr\ndTy/2GVsj9Rz9M5dl5m3f73gfR04UeAy9oKkeK2fVPE9DoMXfaD/HjntMjalWSNtub/iDd3/7+//\n0dc5J13GJsRFa/uMwebt3z//ibbtOe4ytlFUhL6dN8S8PXbxp9r0/VGXsZK0d8E15s93vPaF1uw8\n5Db2ppgvlHhOvCZNmqT73tiht7bnuI394sErlRgfI0ma8X+7tHTrPrexH00ZoLYJjSVJD6/5Vi98\n+KPb2H/f208dWzWRJD2x/gdlbvyv29hVd/5aPds2kyQ9/8FuPbL2O7exy2/LUN8OiZKkf3yyVzNX\nZbuNfWVMbw3s3EqStOLz/Zr85tduY20fPq/9H78jSVr99c+6c9l2t7F/+20Pje7dVpL0/neHNS7r\nc7exc0d00x/6tpckfbI7Vze8uNVt7ANXd9af+neQJO3Yf0IjntniNnbioAt07+COkqQfDufpqic+\ndBt7e7/zNG1oF0nS/uNndPljm9zG3pLRTvOuLSv+c08X6aL5G9zGXndhqhb+ruxE4UxxqbrOfM9t\n7ND01nr2poqXNba/f7XbWMc1YseOHfrdGzkqcnNeEag1ot2fX5SlWbLL2LpaI+zFhbK/MVE5OWXH\nrz/XiG/m/sY8WQjWGlH6r9nKyf5MUv1YI5658UJd06ONpPBeI+zfb9ZPK/8mKTTWCMm784jyAmHc\nv47qVJHrk8dQOI8wCvP0U+YNSklJUU5OTtDOI2q6RqSNnCxrpyvcxvp6HjHwoi46cOCA2l79J1l7\nDHcbW5drxBUdW1Y5v23SpEmtriwE/QrCwoULNXPmTA0ZMkTXXHNNlZP6jIwMSdL48eO1ZMkS7d69\nW+3atZMkjRs3Ts8884xGjx6tBQsWKCkpSc8++6y+//57bdjgfkGo3n5JXzncbiP3Xzr9s6QXHG63\nluTutWBHK8W2kruHIDd3v2bPHq6mTWM1adJgSUmS3F26yqvUb0tJ0W5iCyrFtpAU4ya2pFJsoqRY\nN7GqFJsgqZHbyEceeVjJSY00aVK8pGaS4jz0u1RS+WJ5jqR4D7HLJZUvwk0lNfEQu0JSeXHY5Gy8\nOytVdn/o7O8/x0PsvySVnwDGqWx87qyTVHT258aSmnuILVLFfRyrssfDnQ8knTn7c4zKHmd3tkj6\n99mfo1U2f9zZJqn8m8qjVDYv3flC0uazP0eqbL67s0PSR2d/jlDZceROtqSPz/5sVdnx6c73KstZ\nkiySXJ9Al9mjspzLefoEtIo1IiFhvyyWi+X+uK+bNUL6pVKsp7/11NUaIUn5DvH+WyOkxaoYU7DW\nCMf7om7WiI0b90vK8BDryxqxXlLh2Z/DeY1wfO4K/hpRpvrziISE/bLZbLJYLpH75/varBH+Oo8o\nPy7Lj/3gnEfUfI2o7n0Hvp5H5HvZb12eR0jStdX8ft8E/QrCFVdcoQ8++MBte3l6Y8aM0ZIlS7Rn\nzx61b9/ebD98+LCmTJmid999V2fOnFGvXr00b948XXnllVX6cnUFITJ2lSyWIqdtVouhWIdj6Eyx\n+zc7Vxfb8YIZOvjzCSW3aab//W+uU2xBscXtU3rHCx7UgZ+OKCWlmXJyHvUYa5HUKLqitbBEshvu\nc24c5NiOF8zQgZ8Om2MrKpVsdvf9NooyVP4qsOpiYyMNlRfMxaVSaS1ic3JyZLPZFBERoQ7tUxTh\nEHteh5nm4/rDf52vesVEGmZsiU0qsbnPITrC0Nmr225jzTnUKk45+x+RJJXapGIP/UZFGCq/Cu1L\nrM0uFZW6j420Giq/Auxt7KJF63XyZKEaN43X3Xe7/uhix37tdqnQQ78RVkMxZ2MNQyoo8U9sTY/7\n/fv363ShoYiICKWmpnrVr+O64Dh/Ksf6ctyntpuhgz+fdDknn356owry8s0/OPjjWDbHkNRIOTmP\neowt9//9/d86dapQTZvG6o67BzvFVr5PfDnu/b1GVIytsXJyFniMLed43FeOdVxLUlNTnWJT207T\nwcOnXT5ukvs1wtUccowN5BrhmMuPu+f6vEZI1R/33sSaebRuopyfHpIUGmuEt7H795cVCMX2KJdr\niat+C4otusDNelJ5jfDXeUTl5/BgnXPUdI1ITZuug4fy3B5zvp5HpKVN1YEDJ5TSNlE//O8Rt7Ge\n1ghPsZXPDSqvJ9ERhqyWGOXlORcI9f4KwubNm72Ky8rKUlZWVpXtrVq10pIlS2r8+xtFGbJaPddI\njhO2OlVibUUySookW5HTQS05H4xV2JxfguAxtpKy31M1ftGi9eaTc9lVCfexvvTrc6zNuSArW5y9\n69eX2OhIKboWsY2i7LJZ7YqIsJgHanms4+PqaX5ERZQ9uXrDbWz57zIq/pISGSFFetmvL7ERVu/n\nu7exixZtKFs8U5pp6n0Dqo23+pCDxVI3sZJvsY2iyuaJ4z6ujjezXy/njy/HvWzFbvt8+on3zMdg\n0qTB/jmWy8fg8Be+6vp1nAtl94lDrIf7JOBrhIux1WY9cVxLqjzehs2ruSBVWiOqmUMBXSMccnF4\nCblP64kvx73b2PI87BWPW6isEb6uJ97GN6qj9cSX5/CgnEdU4stxL3up18ecL8e97DavHzdf+q18\nbuBqPamLT+sPeoGAwKn65AygrnC8ATXjrrgGginc5iUFAgAACBmeiuv6cJJWH3KE78Ltjz4UCAC8\nxhMfEJ78fezXtL/6cJJWH3KsCzw/NCwUCKgWBz3KhesTXyBxvCEU+fvYZy1peHhMGxYKBFSLgx4I\nHI43AECwUSAAAAAE2YsvbjWvHs6d2zbY6YQErqgGDwUC4Gf1YUGrDzkCQDh58cVtOnQoT61bN9Hc\nuaODnU5IqOkVVZ7jao8CAfCz+vASkfqQoycs/gBQOw15Ha3vz3GhgAIBqMca8gLvSaAX/3C9nwE0\nXJxEwxMKBB9wkoBQwwIfGNzPAIBwQoHgA/9/zBsFB+BvHFcAUH+wZocmCoQg4q+SaEhqssjXxRMD\nxxUA1B8Nec2uz8UPBQIAv6jJIu9pn/q8sCJwmCdVcZ8ANeP/bwyvv8UPBQLCGk+koas+L6wInPow\nTwL9+fb14T5BeKkvz7UcOxUoEBDWWAwA1LVw/Xz7+nJSiLrHc239Q4EAALXAt58CrnFSCNRfFAgA\nUAvh+tfhQOIv0WgomMuoLygQUCssdgDqGn+JRkPBXEZ9QYGAWgmVxY5CBagZT8cOx1Vwcf8DCBYK\nhAYmXJ9QQqVQQf3FsePqo2Y5roKJ+z/4KKARrigQ/CRUFgqeUFBboTKX64LnJ3uOHQDOKKARrigQ\n/ISFou415BPXUNKQ53JDHhsCo76vQ/U9fwCBQYGAeqOmJ3eh8oQYKnkAqLn6XmTW9/zhG553UFMU\nCGjwQuUJ0fOlahZxAKgr4brGhsrzH+qfsC8QCkosslgsTtusFkOxURW3zxSfbY+IkSUqRoqIMbdV\njnVsq7xPYYkqxUZX6c+xzSnPYouMsz8//fT75kJ3990DZZHUKNowYy2R0W76PJuLg8ISyW5UinPQ\n2KFfWaPc9xnhQ7+VYotKJZvd4nJsktQoypD5EEVEVjO2iu3FpVKp3eLycZOk2EjHsUVU6bOgxCqb\nzVCE3SqbXYqwVvTrrk9JksN8KrFJJTb38yc6wlBkxNlF/Oc8paS20J/vusr12CxWc1OpTSq2uR9b\nVIShqIhKsa76jIhRiU1mrM1ezdisEeaPNrtUVOp6rp8ptijSaijaXGEsnh83h37tdqmw1P3YIqyG\nUxee5mRRqRRzNgfDqG5sUU433R3HZ4otVY57S1SMFOnu2HfRr5s8rBbnsTke95VVPu59WU+cjk8X\nuTSuo/XEY2ylPJyOe2ukh7G5X09ciY00ZHU4lktdxdZgPYmJNJzWCKd+I2NkiSo254hjrCwRnsfm\ncNx7u56U9Wv1/LhZKo45l2uEg6gIh3lmsXg85opLVXHcWyyex2atOAUxj3s3Y/NtPano1zDKnucX\nZX6kgz+fUHKbZk5rbITVcFojCkrcj63qc7ib9STCzXHvZp8q5xGV1xIHlWMLPKwnlXuosp447FdQ\nbHFaT3x5Djdj3eRRm/MIT2u24xpR5biv1Xri4rh30adU/XmE4z6VzyNcrj1nOa4RTse9nM9NzhRb\nFB1hyOrdsusTi2EY7p5/Ghy73a68vDynbVc8uVW/FJQ6bRvQqVCLx+aat7vMaKOCEqtc6XNukV7/\n0zGlpk7VgQMnlDZxmSyxTV3G9kgt1jt3HTVvt7srWpb4li5jjRM5+un5PyslpZlych7V4EVJ+u+R\nKJexKc1KteX+w5Kk1NSpsg2aqZg2HV3G2s6clPH2ncrJeVSS9PvnW2jbnhiXsY2i7Pp23s/m2Nre\nPF/WlF4uYyVp74ID5s93vJagNTsbuY39adF1Sk5qpJycR3XfG8301vY4t7FfPPizEuPtSk2dqoKu\n16vJhcPcxpauvEc530+WJD28pqle+LCJ29h/33tYAy+6r2xsV4+Ttccot7Gr7jyinm1LJEnPfxCv\nR9ae4zbWtv4h5Wz/RCkpzfTwir9r5qpmbmNfGXNMAzsXKTV1qk40v0gtrrnXfb8fPqX9H18nSVr9\ndazuXJboNvZvv/1Fo3ufkSS9/12MxmW1cBs7d8QJ/aFvviTpk93RuuFF13NSkmzblytn/WtKSWmm\n1Z8s0ohnktzGThx0SvcOzlNq6lQdKWqq5PHPuo21f7NaP71TNrf2H4/Q5Y+1dht7S8ZpLb7rz2V/\nFTuvrSJHP+c29roL87XwdycklT1Bd52Z7D6Hfdu0/5/zzGOu/f0pbmMd14g2bf6qqBsWyxod6zLW\nOPyt9i2uWBMunNdax/MjXMb2SC3W9gXjzL/4tbsrSwdOuP47zgVJJVo/6Yh5u92fDVmapbrO4fRR\n/fTMWHNs/+/vLfV1TrTL2IQ4m7bPOCSpbD0p7TdVsWnpLmPtxYWyv/FHcz0ZuzhRm753fT9IUumr\nN5tj+3+Pvuhxjfhm7kHzxCJt9G5ZO/RzG7v/qRvVJsGqnJxHNeP/ztHSrfFuYz+ackhtE2ySql8j\nSv81VTnZf5EkPbG+iTI3ul7bJd/WiOW3HVXfDsWSpLYD1yvikjFuY4+smK2Eov8pJ+dRrfi8sSa/\n2dxt7DM35uqaHoVKTZ2qX+K7qeW1D7iNtX38vPZ/WLaWerNGTBt9lw4cOKHUC/sqYvB0t7EPXH1S\nf+p/WpKU2vN5RV49123sif8sU/zeNcrJeVQ/HI7UVU+0cht7e788TRt6SqmpU3UoL1qpE15xG2v/\nfr1+WtlVkpR72qqL5rdxG3vdhflKyVmhU6cK1ahJvJ47erPb2KHpBXr2puPmbU9rxJndnyn6k0zz\n2PDmPKJNm7/q0KE8n84jfr2glcc14ttFY81jrsukxV6dR0jyuEYYhaf0U+aN5noSrPMIxzXC2/MI\nSUob+Y2sndxfTcl5bpxaNylWTs6jQTuPcFwj/vFJXLXnEVd0lPLyrnXa3qRJE1mtruecN8L+CoJr\nbSVd53B7nSSbm9g2kkZJmivphKrW7I5aShrpcHuJh9jyBzVO0u2SPpB02k1sE0kjzv7sfjGuUN6n\nJH0i6bibuKizceVjc31SU+F2h5+/kHTIyzx2SMrxEHeLpBh5N7bGDnl8K+lHD7GjJc1U2dhcL5oV\nRkoqP0B3S/rOQ2z5CVKcpF9LyvYQO0RSK3k3thhVjO1nSds9xPZX2TyWpMOSPvcQ+2tJ7c/+nCtp\nq4fY8ieMOJXdJ1s8xF4kqaO8G1v5XJOkM5I2eYjtdvb3n1DZ4+1JJ0k9z/5cKuk9D7Hly2H5vFzt\nIbZijbDbZ1STg1XOx8Z6ScVuYluqYmxxKju2C9zENpfk+ITwooccytel8rH9R9JJN7GNHPL1dT35\nVNLRamLLx3auPK8RY1XxmLg/Ia2axy5J+zzE3aCKeVPdGuF4X/wg6b8eYn1ZI4ZLKi/wP/QQV658\nbPslfe0hbrDKnpN8XU+8WSPKHzv3BWCZPpI6nP3Z03NcufKx5cnzfdFTUheVja2kmj4d15MiSRs8\nxHbSokWf6MCBA0pJO1eRN7gvEMrm7G8dbntaIyTnY6P684iytSRPns4jDh2yyXk9eV+e1wjHY665\nvDuPkA4detNtDlXXk2CdRziuEd6eR0jS5GpykCrGFqzzCMc1Yq+qP49oqbK540dGGLHZbMaJEyec\n/p0uLDbyi0rMfwseX2RMnznbWLhwoblfeVtK2rmGJSrGSEk719xWUFxqGIZhpKSkGJKc2irvUx5b\nLiWtfZX+KvZrX9ZfSophGIZxpqjUbR5niir6TUlJMSyR0W76PLvf2T4NwzAKikvNcU+bOcdY8Pgi\np32cxta2nfs+0851Glt5v67+paSd6zS2whL3Y8svKjHsdntFHhGR1Ywt1cyhqMTmts/8ohLDZrM7\njC2tSp9bP99ufPTJp8bWz7cbpTa7U7/u+swvKjFSUlPN8RWX2jyOraTUVjE2a4TnsaW2NXMoKfU8\ntuKz/TrGunvcHGNLbXbPY2ubZo6t1GZ322d+UYlRVOIwNlk8j61tmsNxavc4tsKS0orHLSXF49gK\nSyqODbu9urG1c5qXnsbmeCwnJSUZlqgYIyk51c0+7Z2ODU9jKyh2HpvjcV/5n+Nx7+t64nh8usql\ntuuJ22PfYWyVYyvnUX7cG4ZhpLRt52Fs7tcTV/9slY5ld2uUr+tJ5TXCsS0pOdVpjjjGpqS29Tw2\ni9Ucm0/ricXq83ri7l9xqa3isUtNdd9n2rnmcV82tlTPY7NGmmOzOawnrsbm23rSzum499d6UvU5\n3HWfKWnnGoqIcjo2PI2tvN+kpCRDUpW1xNN6cqao1G0eZ4o8ryeO+/m2npzrcj1xl0fF4+b7eYSn\nNdtxjah83NduPbGYY3M8ll3lUt15hOM+ntaIyv8cY4tLPa8nJaU2l+e3NlvFsVgTYX8FoVFUhNMl\nmKefWFj2l4SUFE2aNEmS1Lj8hY+2YhklRZKtuGJbZZXbHPaJjapUOdtK3Pdnc/4LSaNoh32rycMo\nLXbT59n9HJTn5Djuqfe5eZmLvdR9nzbnv4hWGWulfRzFRHo/NtlKqxlbxSvmoiOtipbVu8fNbqvS\ntmL5azp16pSaNm2qPhf9yqlfj306vGovKsKqqPIXElaXh93meWyG3dwUGWFVZIR3YzNjXfVpK67I\nT1KE1eK5T7vNKdbdXK+ai+F5bA79Wsv79eZxkzzOSce5ZbFUNzbnlxp6PzaVtZW6O/adj2VfxuZ0\n3FfHh/XE6fisg/XEG1XXQ8+PjfuxeVhPqmGuEZXVcj2p0m9pses5IkmG3fPYHI57n9YTw+77euIN\nw/B4zEVHWp1iPY7N4ZizOq4n1d7H1a0nFf1aLP5bT7yes7Zi18e9V2OT63niZj1pFB1R8/XEYb+q\nbZ7WEzfP91491/p4HuHl2Koc97VaT1wc996Mz8V5hOM+EQ5vFHC79rjgdNxLLtcTu93uZu+aC/sC\nAXBn6dKlOnLkiJKSkvT4448HOx0AIWzRokXmHxTK/7gEAPUVBQIAALW0aNGiKlefAaC+okAAAABc\nBQFgokAAAABcBQFgqvkHpAIAAABocLiCAAD1BC8BAYCGLxTWegoEAKgneAmI/4TCEzAAuBIKaz0F\nAgDAb+rLiXcoPAEDqLn6stbUVxQIAAC/4cQbQCCw1tQtCgQAQIPEXxgBoGZC4lOM8vLyNGXKFF11\n1VVq2bKlLBaLZs+e7dW+WVlZslgsLv8dOnSobhMHQtiiRYs0e/ZsLVq0KNipAEGxaNEizZkzh2MA\nAHwUElcQcnNz9cILL6hnz5669tpr9dJLL/ncx+LFi9W5c2enbYmJif5KEah3uPwKAEBoCvUrnCFR\nILRr106//PKLLBaLjh07VqMCoXv37urdu3cdZAcAAAD4T6j/ES8kCgSLxRLsFAAAAAAoRN6D4A/D\nhg1TRESEEhISNGrUKO3atSvYKQEAAAD1TkhcQaiN1q1ba/r06crIyFDTpk21c+dOLViwQBkZGdqy\nZYt69uzpcf/s7GzZ7XbzdklJifn/jh07nGJr0ubv/upTmzuhlKO3+TMXGLe7NkfhNO5wfbxrMm5H\noZp/XbSFSh71ZdyOQnVsntpCJY+GPm5H5W1Wq1VpaWlu42qi3hcIQ4YM0ZAhQ8zb/fr10zXXXKP0\n9HTNnDlTq1at8rh/aWmpbDaby7byB8hfbf7uL9TbXnvtNeXn5ysuLk433XRTSOYYrLZQySPQbaGS\nR6DbQiWPQLeFSh6BbguVPEKpLVTyCHRbqOQR6LZQySPQbcHKIyIiwm1MTdX7AsGV9u3b67LLLtPW\nrVurjY2MjJTV6vqVVlFRUW73q0mbv/sL9bZly5bpyJEjSkpK0pgxY0Iyx2C1hUoegW4LlTwC3RYq\neQS6LVTyCHRbqOQRSm2hkkeg20Ilj0C3hUoegW4LVh7uzmNro1YFgt1uV2FhoRo3buyvfPzGMAyv\n7rBu3bo5xZXf2VFRUVVenlSTNn/31xDaQiWP6tochdO4w/Xx9vc8CaUcebyDO25HoZp/XbSFSh71\nZdyOQnVsntpCJY+GPm5H5W12u115eXlu42rCp5KjsLBQWVlZGj16tJKTkxUdHa0mTZqocePG6t27\nt6ZMmeL169Dr0p49e7RlyxY31wRRAAAgAElEQVRlZGQEOxUAAACgXvHqCkJBQYEee+wxZWZm6uTJ\nk+rcubMGDRqkpKQkxcbG6vjx4/rxxx/14osvauHChbr00kv12GOPqW/fvl4nsnbtWuXn55sV0Dff\nfKM333xTkjR06FA1btxY48eP15IlS7R79261a9dOknTllVeqX79+6tGjh/km5ccee0wWi0Xz5s3z\n9f4AAAAAwppXBcIFF1yguLg4Pfjgg7rpppvUqlUrl3GGYWjTpk1avHixBgwYoL///e/64x//6FUi\nEyZM0L59+8zbK1as0IoVKySVXRFo3769bDabbDabDMMw49LT0/X666/r8ccfV0FBgZKSkjRw4EDN\nmDFDHTt29Op3AwAAACjjVYEwd+5c3XrrrdW+S9pisWjgwIEaOHCg5syZo59++snrRPbu3VttTFZW\nlrKyspy2PfHEE17/DgAAAACeeVUgjBs3zueOzzvvPJ133nk+7wcAAAAgeBrMNykDAAAAqL0afczp\noUOH9NZbb2nfvn0qLCx0arNYLMrMzPRLcgAAAAACy+cC4b333tPIkSOrFAblKBAAAACA+svnlxhN\nnjxZvXr10ldffaWioiLZ7XanfzabrS7yBAAAABAAPl9B2L17t95++2316NGjLvIBAAAAEEQ+X0Ho\n3LmzTp06VRe5AAAAAAgynwuEuXPn6qGHHtLhw4frIh8AAAAAQeTzS4yuueYabd++XR06dFCvXr2U\nkJDg1G6xWLRq1Sq/JQgAAAAgcHwuELKysjRr1ixFRERoz549OnDggFO7xWLxW3IAAAAAAsvnAmHO\nnDkaPny4srKy1Lx587rICQAAAECQ+PwehMOHD+vuu++mOAAAAAAaIJ8LhF/96lfKycmpi1wAAAAA\nBJnPBcLChQv12GOP6auvvqqLfAAAAAAEkc/vQbjtttt09OhRXXTRRWrTpo3LTzHasWOH3xIEAAAA\nEDg+FwiJiYlq0aJFXeQCAAAAIMh8LhA2b95cB2kAAAAACAU+vwcBAAAAQMPlVYGwbds2nzsuKChQ\ndna2z/sBAAAACB6vCoT+/ftrxIgR2rBhQ7Wxhw8f1t/+9jedd955evfdd2udIAAAAIDA8eo9CNnZ\n2frrX/+qq666Sm3atFG/fv104YUXKikpSbGxsTp+/Lh2796trVu36tNPP1Xz5s01Z84c3X777XWd\nPwAAAAA/8qpA6NChg1auXKlvv/1Wzz33nNasWaPXX3/dKaZRo0bq27evnn/+ed14442KiYmpk4QB\nAAAA1B2fPsWoS5cueuqpp/TUU0/p6NGjOnjwoAoKCtSiRQu1a9dOUVFRdZUnAAAAgADw+WNOy7Vs\n2VItW7b0Zy4AAAAAgoyPOQUAAABgokAAAAAAYKJAAAAAAGCiQAAAAABgokAAAAAAYPK5QBg4cKC+\n++47l20//PCDBg4cWOukAAAAAASHzwXC5s2bderUKZdteXl5+uCDD2qdFAAAAIDg8OtLjH7++Wc1\nbtzYn10CAAAACCCvviht1apVWrVqlXl73rx5Vb4kraCgQJs3b9avfvUr/2YIAAAAIGC8KhC++eYb\nrVixQpJksVj0/vvvy2p1vvgQExOj9PR0ZWZm+j9LAAAAAAHhVYHwwAMP6IEHHpAkWa1Wbdq0SZdc\nckmdJgYAAAAg8LwqEBzZ7fa6yAMAAABACPC5QHB09OhRFRQUVNmelpZWm24BAAAABInPBcKpU6c0\nadIkLV++XIWFhS5jbDZbrRMDAAAAEHg+Fwj33nuvli1bpvHjx6tHjx6KiYmpi7wAAAAABIHPBcLq\n1au1YMECTZw40S8J5OXlad68efrqq6/05Zdf6tixY5o1a5Zmz57t1f5HjhzRlClT9O677+rMmTPq\n2bOn5s+fr0GDBvklPwAAACCc+PxFaYWFhUpPT/dbArm5uXrhhRdUVFSka6+91qd9i4qKNGjQIG3c\nuFGZmZlatWqVWrVqpSFDhvCNzgAAAEAN+HwFYejQofroo480cOBAvyTQrl07/fLLL7JYLDp27Jhe\neuklr/d9+eWXtWvXLn388cfq27evJGnAgAHq2bOnpkyZom3btvklRwAAACBceFUgHD9+3Pz5wQcf\n1G9/+1s1adJEw4cPV2JiYpX4hIQErxOwWCxex1a2cuVKderUySwOJCkyMlI333yzpk2bpgMHDigl\nJaXG/QMAAADhxqsCoUWLFk4n8oZhaPLkyZo8ebLL+EB9itGuXbt0+eWXV9neo0cPSVJ2dna1BUJ2\ndrbTdzuUlJSY/+/YscMptiZt/u6vIbSFSh7VtTkKp3GH6+Pt73kSSjnyeAd33I5CNf+6aAuVPOrL\nuB2F6tg8tYVKHg193I7K26xWq9+/YsCrAmHmzJm1+kt/XcnNzXV5taJ8W25ubrV9lJaWui1oyh8g\nf7X5u7+G0BYqeQS6LVTyCHRbqOQR6LZQySPQbaGSR6DbQiWPUGoLlTwC3RYqeQS6LVTyCHRbsPKI\niIhwG1NTXhUI3n6iUDB4Kly8KWoiIyNltbp+r3ZUVJTb/WrS5u/+GkJbqOQR6LZQySPQbaGSR6Db\nQiWPQLeFSh6BbguVPEKpLVTyCHRbqOQR6LZQySPQbcHKw915bG3U6puUgy0xMdHlVYLy90x4816I\nbt26Od2x5Xd2VFSUevbs6RRbkzZ/99cQ2kIlj+raHIXTuMP18fb3PAmlHHm8gztuR6Gaf120hUoe\n9WXcjkJ1bJ7aQiWPhj5uR+VtdrtdeXl5buNqwucCYe7cuW7brFarmjVrpt69eysjI6NWiXkjPT1d\nO3furLK9fFv37t3rPAcAAACgIfG5QJg9e7YsFosMw6jSVr7dYrGof//+eueddxQfH++XRF0ZOXKk\n7rjjDm3btk19+vSRVPaegldffVV9+vRRcnJynf1uAAAAoCHy+UVLu3fv1vnnn69HHnlEe/fuVUFB\ngfbs2aOHH35YHTp00LZt27R06VJ98cUXmjFjhld9rl27Vm+++ab+9a9/SZK++eYbvfnmm3rzzTd1\n5swZSdL48eMVGRmpffv2mfuNGzdO3bp10+jRo7Vs2TJt2LBBv/vd7/T999/r0Ucf9XVoAAAAQNjz\n+QrCX/7yF91yyy2aOnWqua1du3a6//77VVpaqpkzZ2rt2rXavXu3Xn75ZT3xxBPV9jlhwgSnE/8V\nK1ZoxYoVkqQ9e/aoffv2stlsstlsTlcuYmJitHHjRk2ZMkV33323zpw5o169emnt2rXq37+/r0MD\nAAAAwp7PVxA2b97s9MVkjvr27av//Oc/5s8///yzV33u3btXhmG4/Ne+fXtJUlZWltPtcq1atdKS\nJUuUm5urgoICffLJJ7ryyit9HRYAAAAA1aBAiI6O1pdffumy7YsvvlB0dLSksndUx8XF1S47AAAA\nAAHl80uMrr32Ws2aNUvnnHOORo8erWbNmunEiRN6/fXXNXfuXF1//fWSyj5J6Pzzz/d7wgAAAADq\njs8FwqJFi/TDDz/oT3/6k/785z8rMjJSpaWlMgxDv/71r7Vw4UJJUkpKimbNmuX3hAEAAADUHZ8L\nhHPOOUcffvih1q5dqw8//FC5ublKTExU//79NWTIEPPbi8uvJAAAAACoP2r0TcoWi0VDhw7V0KFD\n/Z0PAAAAgCDy+U3KAAAAABour64gnHfeeVq5cqV69uypc88913wZkSsWi0W7d+/2W4IAAAAAAser\nAqF///5q2rSp+bOnAgEAAABA/eVVgbB48WLz56ysrLrKBQAAAECQ8R4EAAAAAKYaFQhHjx7VAw88\noL59++qCCy5Qdna2JOn55593+y3LAAAAAEKfzwXCnj171LNnTz311FOyWCz68ccfVVRUJEn6+uuv\n9dRTT/k9SQAAAACB4XOBMGXKFDVr1kz//e9/9eGHH8owDLPtsssu05YtW/yaIAAAAIDA8fmL0jZu\n3KjnnntOycnJstlsTm1t2rTRwYMH/ZYcAAAAgMDy+QpCYWGhEhISXLbl5+fLauV9zwAAAEB95fPZ\nfKdOnbRhwwaXbR9++KG6d+9e66QAAAAABIfPLzG67bbbNGnSJCUnJ+umm26SJBUXF+vNN9/Us88+\nq7///e9+TxIAAABAYPhcINxxxx366quvdO+99+q+++6TVPbmZMMwdNttt+nWW2/1e5IAAAAAAsPn\nAkGSXnjhBY0bN06rV6/W4cOH1aJFCw0bNkyXXnqpv/MDAAAAEEA1KhAkKSMjQxkZGf7MBQAAAECQ\n1bhAkMq+UbmgoKDK9rS0tNp0CwAAACBIfC4Q8vLydO+992r58uUqLCx0GVP5+xEAAAAA1A8+Fwj3\n3HOPli1bpvHjx6tHjx6KiYmpi7wAAAAABIHPBcLq1au1YMECTZw4sS7yAQAAABBENfom5fT09LrI\nBQAAAECQ+VwgDB06VB999FFd5AIAAAAgyLx6idHx48fNnx988EH99re/VZMmTTR8+HAlJiZWiU9I\nSPBfhgAAAAACxqsCoUWLFrJYLOZtwzA0efJkTZ482WU8n2IEAAAA1E9eFQgzZ850KhAAAAAANExe\nFQizZ8+u4zQAAAAAhAKf36QMAAAAoOGiQAAAAABgokAAAAAAYKJAAAAAAGCiQAAAAABgokAAAAAA\nYKJAAAAAAGCiQAAAAABgCokC4fTp07rnnnuUnJys2NhY9erVS//85z+r3S8rK0sWi8Xlv0OHDgUg\ncwAAAKBh8eqblOvaqFGj9Nlnn2nBggXq2LGjli1bphtuuEF2u1033nhjtfsvXrxYnTt3dtqWmJhY\nV+kCAAAADVbQC4Q1a9Zo/fr1ZlEgSQMGDNC+ffs0efJk/f73v1dERITHPrp3767evXsHIl0AAACg\nQQv6S4xWrlyp+Ph4jR492mn72LFjdfDgQW3bti1ImQEAAADhJ+gFwq5du9SlSxdFRjpfzOjRo4fZ\nXp1hw4YpIiJCCQkJGjVqlFf7AAAAAKgq6C8xys3N1XnnnVdle0JCgtnuTuvWrTV9+nRlZGSoadOm\n2rlzpxYsWKCMjAxt2bJFPXv2rPb3Z2dny263m7dLSkrM/3fs2OEUW5M2f/fXENpCJY/q2hyF07jD\n9fH29zwJpRx5vIM7bkehmn9dtIVKHvVl3I5CdWye2kIlj4Y+bkflbVarVWlpaW7jaiLoBYIkWSyW\nGrUNGTJEQ4YMMW/369dP11xzjdLT0zVz5kytWrWq2t9dWloqm83msq38AfJXm7/7awhtoZJHoNtC\nJY9At4VKHoFuC5U8At0WKnkEui1U8giltlDJI9BtoZJHoNtCJY9AtwUrj+req1sTQS8QEhMTXV4l\nOH78uKSKKwneat++vS677DJt3brVq/jIyEhZra5faRUVFeV2v5q0+bu/htAWKnkEui1U8gh0W6jk\nEei2UMkj0G2hkkeg20Ilj1BqC5U8At0WKnkEui1U8gh0W7DycHceWxtBLxDS09O1fPlylZaWOr0P\nYefOnZLKPqHIV4ZheH1ndevWzSm2/M6Oioqq8hKlmrT5u7+G0BYqeVTX5iicxh2uj7e/50ko5cjj\nHdxxOwrV/OuiLVTyqC/jdhSqY/PUFip5NPRxOypvs9vtysvLcxtXE0F/k/LIkSN1+vRpvfXWW07b\nlyxZouTkZPXp08en/vbs2aMtW7YoIyPDn2kCAAAAYSHoVxCuvvpqDR48WBMmTNCpU6d0/vnna/ny\n5Vq3bp1effVV83VV48eP15IlS7R79261a9dOknTllVeqX79+6tGjh/km5ccee0wWi0Xz5s0L5rAA\nAACAeinoBYIkvf3225o+fbpmzpyp48ePq3Pnzlq+fLmuv/56M8Zms8lms8kwDHNbenq6Xn/9dT3+\n+OMqKChQUlKSBg4cqBkzZqhjx47BGAoAAABQr4VEgRAfH6/MzExlZma6jcnKylJWVpbTtieeeKKO\nMwMAAADCS9DfgwAAAAAgdFAgAAAAADBRIAAAAAAwUSAAAAAAMFEgAAAAADBRIAAAAAAwUSAAAAAA\nMFEgAAAAADBRIAAAAAAwUSAAAAAAMFEgAAAAADBRIAAAAAAwUSAAAAAAMFEgAAAAADBRIAAAAAAw\nUSAAAAAAMFEgAAAAADBRIAAAAAAwUSAAAAAAMFEgAAAAADBRIAAAAAAwUSAAAAAAMFEgAAAAADBR\nIAAAAAAwUSAAAAAAMFEgAAAAADBRIAAAAAAwUSAAAAAAMFEgAAAAADBRIAAAAAAwUSAAAAAAMFEg\nAAAAADBRIAAAAAAwUSAAAAAAMFEgAAAAADBRIAAAAAAwUSAAAAAAMFEgAAAAADBRIAAAAAAwhUSB\ncPr0ad1zzz1KTk5WbGysevXqpX/+859e7XvkyBGNGTNGLVq0UOPGjdW3b19t3LixjjMGAAAAGqbI\nYCcgSaNGjdJnn32mBQsWqGPHjlq2bJluuOEG2e123XjjjW73Kyoq0qBBg3TixAllZmYqKSlJzzzz\njIYMGaINGzaof//+ARwFAAAAUP8FvUBYs2aN1q9fbxYFkjRgwADt27dPkydP1u9//3tFRES43Pfl\nl1/Wrl279PHHH6tv377mvj179tSUKVO0bdu2gI0DAAAAaAiC/hKjlStXKj4+XqNHj3baPnbsWB08\neNDjSf7KlSvVqVMnsziQpMjISN1888369NNPdeDAgTrLGwAAAGiIgl4g7Nq1S126dFFkpPPFjB49\nepjtnvYtj3O1b3Z2th8zBQAAABq+oL/EKDc3V+edd16V7QkJCWa7p33L43zdt1x2drbsdrt5u6Sk\nxPx/x44dTrE1afN3fw2hLVTyqK7NUTiNO1wfb3/Pk1DKkcc7uON2FKr510VbqORRX8btKFTH5qkt\nVPJo6ON2VN5mtVqVlpbmNq4mgl4gSJLFYqlRW233laTS0lLZbDbz9o033qj8/HzFxcWZD1Bt2vzd\nX0NoC5U8GDfjZtyMm3FznzBuxl3fx+3uvbq1YTEMw/B7rz7o27evbDabPv30U6ft2dnZ6t69u55/\n/nndfvvtLvdt06aNLr/8cr3xxhtO21evXq1hw4bpvffe01VXXWVut9vtysvLc4r96aefnK4gAOUc\nD8qoqKggZoJQxjxBdZgj8AbzBN5wNU9cXUFo0qSJrNaav5Mg6FcQ0tPTtXz5cpWWljq9D2Hnzp2S\npO7du3vctzzOkTf7luvWrVut7kA0XDt27FBJSYmioqLUs2fPYKeDEMU8QXWYI/AG8wTecDVPXP0B\nvLaCfmY8cuRInT59Wm+99ZbT9iVLlig5OVl9+vTxuO93333n9ElHpaWlevXVV9WnTx8lJyfXWd4A\nAABAQxT0KwhXX321Bg8erAkTJujUqVM6//zztXz5cq1bt06vvvqq+bqq8ePHa8mSJdq9e7fatWsn\nSRo3bpyeeeYZjR49WgsWLFBSUpKeffZZff/999qwYUMwhwUAAADUS0EvECTp7bff1vTp0zVz5kwd\nP35cnTt31vLly3X99debMTabTTabTY5vmYiJidHGjRs1ZcoU3X333Tpz5ox69eqltWvX8i3KAAAA\nQA2ERIEQHx+vzMxMZWZmuo3JyspSVlZWle2tWrXSkiVL6jA7AAAAIHwE/T0IAAAAAEJHSFxBCBRX\nn+jKR5zCHavVqoiICFmtVuYJ3GKeoDrMEXiDeQJvuJonruZLbb/FIOjfgxBIpaWlys/PD3YaAAAA\nQJ2Ji4tz+voAX/ESIwAAAAAmCgQAAAAAJgoEAAAAAKaweg+C3W6v8kYOi8Uii8USpIwAAACAmjMM\no8qbkq1Wq6zWml8HCKsCAQAAAIBnvMQIAAAAgCmsCoTTp0/rnnvuUXJysmJjY9WrVy/985//DHZa\nCIL3339f48aNU+fOnRUXF6eUlBSNGDFCX3zxRZXY7du368orr1R8fLyaNWumUaNG6ccffwxC1ggF\nL730kiwWi+Lj46u0MVfC23/+8x8NHTpUzZs3V6NGjXTBBRdo3rx5TjEbNmxQ37591bhxY7Vo0UJj\nxozRkSNHgpQxAu3LL7/Utddeq+TkZDVu3FidO3fW3LlzdebMGac41pLwkJeXpylTpuiqq65Sy5Yt\nZbFYNHv2bJexvsyJp59+Wp07d1ZMTIzOPfdczZkzRyUlJT7lFlYFwqhRo7RkyRLNmjVLa9eu1cUX\nX6wbbrhBy5YtC3ZqCLDnnntOe/fu1cSJE7VmzRplZmbqyJEjysjI0Pvvv2/Gfffdd7riiitUXFys\nN954Q6+88op++OEHXX755Tp69GgQR4BgOHDggP76178qOTm5ShtzJbwtW7ZM/fv31znnnKN//OMf\nWrNmjaZOner0uuAPPvhAV199tVq1aqVVq1YpMzNTGzZs0KBBg1RUVBTE7BEI33zzjS699FLt3btX\nTz75pN59911df/31mjt3rm644QYzjrUkfOTm5uqFF15QUVGRrr32WrdxvsyJhx56SBMnTtSoUaP0\n3nvv6Y477tDDDz+sO++807fkjDCxevVqQ5KxbNkyp+2DBw82kpOTjdLS0iBlhmA4fPhwlW15eXlG\nq1atjEGDBpnbRo8ebbRo0cI4efKkuW3v3r1GVFSUMWXKlIDkitAxbNgwY/jw4catt95qxMXFObUx\nV8JXTk6OERcXZ0yYMMFj3MUXX2x07drVKCkpMbdt2bLFkGQ8++yzdZ0mgmz69OmGJON///uf0/bb\nb7/dkGQcP37cMAzWknBit9sNu91uGIZhHD161JBkzJo1q0qct3Pi2LFjRmxsrHH77bc77f/QQw8Z\nFovFyM7O9jq3sLmCsHLlSsXHx2v06NFO28eOHauDBw9q27ZtQcoMwZCUlFRlW3x8vLp27ar9+/dL\nKvvm7XfffVfXXXedmjZtasa1a9dOAwYM0MqVKwOWL4Lv1Vdf1QcffKBnn322ShtzJby99NJLys/P\n19SpU93GHDhwQJ999pluueUWp283vfTSS9WxY0fmSBiIioqSJJ1zzjlO25s1ayar1aro6GjWkjDj\nzSdp+jIn1q1bp8LCQo0dO9apj7Fjx8owDP3f//2f17mFTYGwa9cudenSpcrXTvfo0cNsR3g7efKk\ntm/frm7dukmSdu/erYKCAnOOOOrRo4f+97//qbCwMNBpIgiOHDmie+65RwsWLFBqamqVduZKePvw\nww+VkJCg7777Tr169VJkZKSSkpL05z//WadOnZJU8Rzjbo7wHNTw3XrrrWrWrJkmTJigH3/8UXl5\neXr33Xf1/PPP684771RcXBxrCarwZU6UryPp6elOcW3atFGLFi18WmfCpkDIzc1VQkJCle3l23Jz\ncwOdEkLMnXfeqfz8fE2fPl1SxZxwN28Mw9Avv/wS0BwRHHfccYc6deqkCRMmuGxnroS3AwcO6MyZ\nMxo9erR+//vfa8OGDZo8ebL+8Y9/aOjQoTIMo9o5wnNQw9e+fXt98skn2rVrlzp06KCmTZtq+PDh\nuvXWW5WZmSmJtQRV+TIncnNzFRMTo7i4OJexvqwzkdWHNByeLuPwZWnhbcaMGXrttdf09NNP66KL\nLnJqY96Et7feekv/+te/9OWXX1b7eDNXwpPdbldhYaFmzZql+++/X5J0xRVXKDo6Wvfcc482btxo\nxrqbB8yPhm/v3r0aPny4WrVqpTfffFMtW7bUtm3bNH/+fJ0+fVovv/yyGctagsq8nRP+mjthUyAk\nJia6rJyOHz8uyXVlhvAwZ84czZ8/Xw899JDuuusuc3tiYqIk11eXjh8/LovFombNmgUsTwTe6dOn\ndeedd+ruu+9WcnKyTpw4IUkqLi6WJJ04cUJRUVHMlTCXmJio//73v/rNb37jtP3qq6/WPffco+3b\nt6tnz56S3M8RnoMavvvvv1+nTp3SV199Zf6Ft1+/fmrRooXGjRunP/zhD2rdurUk1hJU8OX5JTEx\nUYWFhTpz5owaN25cJbbyH0A9CZuXGKWnp+vbb79VaWmp0/adO3dKkrp37x6MtBBkc+bM0ezZszV7\n9mxNmzbNqa1Dhw5q1KiROUcc7dy5U+eff75iY2MDlSqC4NixYzp8+LAWLlyo5s2bm/+WL1+u/Px8\nNW/eXDfddBNzJcy5em2wJPMjTq1Wq/kc426O8BzU8H311Vfq2rVrlZd/XHzxxZJkvvSItQSOfJkT\n5e89qBx76NAhHTt2zKd1JmwKhJEjR+r06dN66623nLYvWbJEycnJ6tOnT5AyQ7DMmzdPs2fP1oMP\nPqhZs2ZVaY+MjNTw4cP19ttvKy8vz9z+008/adOmTRo1alQg00UQtG7dWps2bary7ze/+Y1iY2O1\nadMmzZ8/n7kS5q677jpJ0tq1a522r1mzRpKUkZGhlJQUXXLJJXr11Vdls9nMmK1bt+r7779njoSB\n5ORkZWdn6/Tp007bP/nkE0lSamoqawmq8GVODBkyRLGxscrKynLqIysrSxaLxeN3LVTh9QeiNgCD\nBw82mjdvbrzwwgvG+++/b9x2222GJOPVV18NdmoIsMcff9yQZAwZMsT45JNPqvwr9+233xrx8fFG\nv379jDVr1hhvv/220b17dyM5Odk4cuRIEEeAYHL1PQjMlfA2fPhwIyYmxpg3b56xfv1645FHHjFi\nY2ONYcOGmTGbNm0yIiMjjZEjRxrr1683XnvtNaNt27ZG9+7djcLCwiBmj0BYtWqVYbFYjIyMDOP1\n1183Nm7caDz00ENGfHy80bVrV6OoqMgwDNaScLNmzRpjxYoVxiuvvGJIMkaPHm2sWLHCWLFihZGf\nn28Yhm9zYv78+YbFYjGmTZtmbN682fjb3/5mxMTEGLfddptPeYVVgZCXl2f85S9/MVq3bm1ER0cb\nPXr0MJYvXx7stBAE/fv3NyS5/efo888/NwYNGmQ0btzYaNq0qXHttddW+aIbhBdXBYJhMFfC2Zkz\nZ4ypU6cabdu2NSIjI420tDTjgQceqHLi/+9//9vIyMgwYmNjjYSEBOMPf/iDyy9uRMP0/vvvG1dd\ndZXRunVro1GjRkbHjvs8KiIAAAXpSURBVB2N++67zzh27JhTHGtJ+GjXrp3bc5E9e/aYcb7MiczM\nTKNjx45GdHS0kZaWZsyaNcsoLi72KS+LYTh8DzwAAACAsBY270EAAAAAUD0KBAAAAAAmCgQAAAAA\nJgoEAAAAACYKBAAAAAAmCgQAAAAAJgoEAAAAACYKBACAJGnZsmV68skn66TvMWPGqH379nXSd7lv\nvvlGs2fP1t69e+v09wBAQ0eBAACQVLcFQiB88803mjNnDgUCANQSBQIAAAAAEwUCAISJo0eP6vbb\nb1fbtm0VExOjli1b6te//rU2bNigK664QqtXr9a+fftksVjMf5K0efNmWSwWbd682am/vXv3ymKx\nKCsry2l7VlaWOnXqpJiYGHXp0kX/+Mc/XOZTXFys+fPnq3PnzmY+Y8eO1dGjR53i2rdvr2HDhmnd\nunW68MIL1ahRI3Xu3FmvvPKK0+8cPXq0JGnAgAFm/pVzAwBULzLYCQAAAuOWW27R9u3b9dBDD6lj\nx446ceKEtm/frtzcXD377LO6/fbbtXv3bq1cubLGvyMrK0tjx47ViBEjtHDhQp08eVKzZ89WUVGR\nrNaKv0nZ7XaNGDFCH330kaZMmaJLL71U+/bt06xZs3TFFVfo888/V6NGjcz4HTt26L777tP999+v\nVq1a6aWXXtL48eN1/vnnq1+/frrmmmv08MMPa9q0aXrmmWd04YUXSpI6dOhQ8zsMAMIUBQIAhIkt\nW7boj3/8o2677TZz24gRI8yfmzVrppiYGGVkZNSof7vdrunTp+vCCy/UypUrzSsQl112mS644AIl\nJyebsW+88YbWrVunt956S6NGjTK39+zZUxdffLGysrI0YcIEc/uxY8e0ZcsWpaWlSZL69eunjRs3\natmyZerXr59atmypCy64QJLUtWvXGo8BAMBLjAAgbFxyySXKysrS/PnztXXrVpWUlPi1/++//14H\nDx7UjTfeaBYHktSuXTtdeumlTrHvvvuumjVrpuHDh6u0tNT816tXL7Vu3brKy5l69eplFgeSFBsb\nq44dO2rfvn1+HQMAgAIBAMLG66+/rltvvVUvvfSS+vbtq4SEBP3hD3/QoUOH/NJ/bm6uJKl169ZV\n2ipvO3z4sE6cOKHo6GhFRUU5/Tt06JCOHTvmFJ+YmFilz5iYGBUUFPgldwBABV5iBABhokWLFnry\nySf15JNP6qefftI777yj+++/X0eOHNG6devc7hcbGytJKioqctru7iTeVcFReVuLFi2UmJjo9vc2\nadKk+gEBAOoEVxAAIAylpaXprrvu0uDBg7V9+3ZJ7v8iX/4FZ19//bXT9nfeecfpdqdOndSmTRst\nX75chmGY2/ft26ePP/7YKXbYsGHKzc2VzWZT7969q/zr1KmTz2OKiYmRJK4qAEAtcQUBAMLAyZMn\nNWDAAN14443q3LmzmjRpos8++0zr1q0z3yScnp6ut99+W88995wuuugiWa1W9e7dW61bt9aVV16p\nRx55RM2bN1e7du20ceNGvf32206/w2q1at68efrjH/+okSNH6rbbbtOJEyc0e/bsKi8xuv766/Xa\na69p6NChmjhxoi655BJFRUUpJydHmzZt0ogRIzRy5Eifxti9e3dJ0gsvvKAmTZooNjZW5557rsuX\nJwEA3KNAAIAwEBsbqz59+mjp0qXau3evSkpKlJaWpqlTp2rKlCmSpIkTJyo7O1vTpk3TyZMnZRiG\neSVg6dKluvvuuzV16lTZbDYNHz5cy5cvV+/evZ1+z/jx4yVJjz76qEaNGqX27dtr2rRp+uCDD5ze\neBwREaF33nlHmZmZWrp0qR555BFFRkYqNTVV/fv3V3p6us9jPPfcc/Xkk08qMzNTV1xxhWw2mxYv\nXqwxY8bU7E4DgDBlMRyvAwMAAAAIa7wHAQAAAICJAgEAAACAiQIBAAAAgIkCAQAAAICJAgEAAACA\niQIBAAAAgIkCAQAAAICJAgEAAACAiQIBAAAAgIkCAQAAAICJAgEAAACAiQIBAAAAgOn/B0EhQ48n\n5LpjAAAAAElFTkSuQmCC\n", "text/plain": [ "" ] }, "metadata": {}, "output_type": "display_data" }, { "name": "stdout", "output_type": "stream", "text": [ "mean = 1.821\n", "std = 0.140\n" ] } ], "source": [ "from numpy.random import randn\n", "data = [1.8 + .1414*randn() for i in range(100)]\n", "\n", "plot_height_std(data, lw=2)\n", "print('mean = {:.3f}'.format(np.mean(data)))\n", "print('std = {:.3f}'.format(np.std(data)))" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "We can see by eye that roughly 68% of the heights lie within $\\pm1\\sigma$ of the mean 1.8.\n", "\n", "We'll discuss this in greater depth soon. For now let's compute the standard deviation for \n", "\n", "$$Y = [2.2, 1.5, 2.3, 1.7, 1.3]$$\n", "\n", "The mean of $Y$ is $\\mu=1.8$ m, so \n", "\n", "$$ \n", "\\begin{aligned}\n", "\\sigma_y &=\\sqrt{\\frac{(2.2-1.8)^2 + (1.5-1.8)^2 + (2.3-1.8)^2 + (1.7-1.8)^2 + (1.3-1.8)^2} {5}} \\\\\n", "&= \\sqrt{0.152} = 0.39 \\ m\n", "\\end{aligned}$$\n", "\n", "We will verify that with NumPy with" ] }, { "cell_type": "code", "execution_count": 10, "metadata": {}, "outputs": [ { "name": "stdout", "output_type": "stream", "text": [ "std of Y is 0.39 m\n" ] } ], "source": [ "print('std of Y is {:.2f} m'.format(np.std(Y)))" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "This corresponds with what we would expect. There is more variation in the heights for $Y$, and the standard deviation is larger.\n", "\n", "Finally, let's compute the standard deviation for $Z$. There is no variation in the values, so we would expect the standard deviation to be zero. We show this to be true with\n", "\n", "$$ \n", "\\begin{aligned}\n", "\\sigma_z &=\\sqrt{\\frac{(1.8-1.8)^2 + (1.8-1.8)^2 + (1.8-1.8)^2 + (1.8-1.8)^2 + (1.8-1.8)^2} {5}} \\\\\n", "&= \\sqrt{\\frac{0+0+0+0+0}{5}} \\\\\n", "\\sigma_z&= 0.0 \\ m\n", "\\end{aligned}$$" ] }, { "cell_type": "code", "execution_count": 11, "metadata": {}, "outputs": [ { "name": "stdout", "output_type": "stream", "text": [ "0.0\n" ] } ], "source": [ "print(np.std(Z))" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "Before we continue I need to point out that I'm ignoring that on average men are taller than women. In general the height variance of a class that contains only men or women will be smaller than a class with both sexes. This is true for other factors as well. Well nourished children are taller than malnourished children. Scandinavians are taller than Italians. When designing experiments statisticians need to take these factors into account. \n", "\n", "I suggested we might be performing this analysis to order desks for a school district. For each age group there are likely to be two different means - one clustered around the mean height of the females, and a second mean clustered around the mean heights of the males. The mean of the entire class will be somewhere between the two. If we bought desks for the mean of all students we are likely to end up with desks that fit neither the males or females in the school! \n", "\n", "We will not be faced with these kinds of problems in this book. Consult any standard probability text if you need to learn techniques to deal with these issues." ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "### Why the Square of the Differences\n", "\n", "Why are we taking the *square* of the differences for the variance? I could go into a lot of math, but let's look at this in a simple way. Here is a chart of the values of $X$ plotted against the mean for $X=[3,-3,3,-3]$" ] }, { "cell_type": "code", "execution_count": 12, "metadata": {}, "outputs": [ { "data": { "image/png": "iVBORw0KGgoAAAANSUhEUgAAAukAAAEHCAYAAAATYthkAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAE0BJREFUeJzt3V+MlOW9wPHfzM54iiwkh4oeJa7G\nkEpczXKOCUIvGiCpoWCO1qRpMZoGQmipJHohJgXEJf5Je2EiVWNBEkKEWrO2vSBFOE1w0yvaRnHS\nrL2TBZM2ISDYdbq1M/vuuThxDwu7OzNY33mmfj43OzM77z6PyZNnv/v6vkNhfHx8PAAAgGQU2z0B\nAABgMpEOAACJEekAAJAYkQ4AAIkR6QAAkBiRDgAAiSm1ewKXyrIssiyb9FqhUIhCodCmGQEAwJUb\nHx+PSz/1vFgsRrE4/fnyJCO9Wq22exoAAPC5mT179oyR7nIXAABIjEgHAIDEiHQAAEhMctekT3WD\naKNrdmBoaCjq9XqUSqXo7e1t93RImLVCs6wVmmWt0MhU91w2+lCUjoj0Rne/QpZlMTY2Zq3QkLVC\ns6wVmmWtcCUaRbqVBAAAickl0t99991Ys2ZN9PT0xKxZs2LevHmxbNmyOHDgQB7DAwBAR8nlcpcL\nFy7EjTfeGGvXro0FCxZEtVqNgwcPxkMPPRTDw8Oxffv2PKYBAAAdIZdIX758eSxfvnzSa/fcc0+c\nPHky9uzZI9IBAOAibb0m/ZprrolSKbl7VwEAoK1yLeQsyyLLsjh//nwMDAzE0aNH48UXX8xzCgAA\nkLzC+Pj4eF6Dff/734/du3dHRMRVV10Vzz//fGzatGnSe7Isi5GRkUmvnT59OrIsy2uadKBarTbx\nuFwut3EmpM5aoVnWCs2yVmikWCxGT0/PpNfmzJkz40d25nomfevWrbFhw4Y4c+ZMHDp0KDZv3hzV\najUee+yxGY+r1+sxNjaW0yzpNKOjo/G1r30tIiJ++9vftnk2dJKLf7HCxewrXCn7ClPp6upq+Zhc\nI72np2fir4jVq1dHRMQPf/jD+O53vxvz58+f9rhSqeQfB2Ba9Xp90nNnMZiJM140w75CK+wrNHIl\nHdvWuzaXLFkSP/3pT+P999+fMdJ7e3tFOtO6+J/ZLZfL0dfX18bZkLpKpRK1Ws1aYUb2FVphX6GR\nqS7nbqSt5fvWW29FsViMW265pZ3TAACApORyJn3jxo0xd+7cWLJkSVx33XVx9uzZGBgYiNdffz22\nbNky41l0AAD4oskl0pctWxb79u2L/fv3x4ULF6K7uzv6+vri1VdfjQcffDCPKQAAQMfIJdLXrVsX\n69aty2MoAADoeO7GBACAxIh0AABIjEgHAIDEiHQAAEiMSAcAgMSIdAAASIxIBwCAxIh0AABIjEgH\nAIDEiHQAAEiMSAcAgMSIdAAASIxIBwCAxIh0AABIjEgHAIDEiHQAAEiMSAcAgMSIdAAASIxIBwCA\nxIh0AABIjEgHAIDEiHQAAEiMSAcAgMSIdAAASEwukX7s2LFYv359LFq0KGbPnh0LFiyIe++9N95+\n++08hgcAgI6SS6S//PLLMTw8HI888kgcPnw4du3aFWfOnImlS5fGsWPH8pgCAAB0jFIeg7z00ktx\n7bXXTnpt1apVsXDhwnj22Wdj5cqVeUwDAAA6Qi5n0i8N9IiI7u7uuO222+KDDz7IYwoAANAx2nbj\n6EcffRTvvPNO9Pb2tmsKAACQpFwud5nKww8/HNVqNbZt29bwvUNDQ5FlWQ6zohONjo5OPK7ValGp\nVNo4G1JXq9UmvlorTMe+QivsKzRSLBajp6enpWPaEulPPPFEHDx4MF544YW48847G76/Xq/H2NhY\nDjOjE326OU73HKZjrTAd+wpXylphKl1dXS0fk3uk79y5M55++ul45plnYvPmzU0dUyqVolj0ke5M\nrV6vT3peLpfbNBM6wcW/QK0VpmNfoRX2FRq5ko7NNdJ37twZ/f390d/fH1u3bm36uN7eXpHOtKrV\n6sTjcrkcfX19bZwNqatUKlGr1awVZmRfoRX2FRrJsixGRkZaOia38n3qqaeiv78/tm/fHk8++WRe\nwwIAQMfJ5Uz6c889Fzt27IhVq1bFmjVr4vjx45O+v3Tp0jymAQAAHSGXSD906FBERBw5ciSOHDly\n2ffHx8fzmAYAAHSEXCJ9cHAwj2EAAOBfgrsxAQAgMSIdAAASI9IBACAxIh0AABIj0gEAIDEiHQAA\nEiPSAQAgMSIdAAASI9IBACAxIh0AABIj0gEAIDEiHQAAEiPSAQAgMSIdAAASI9IBACAxIh0AABIj\n0gEAIDEiHQAAEiPSAQAgMSIdAAASI9IBACAxIh0AABIj0gEAIDEiHQAAEpNbpI+MjMTjjz8ed999\nd8yfPz8KhUL09/fnNTwAAHSM3CL93LlzsWfPnvjkk0/ivvvuy2tYAADoOKW8Brrpppvi/PnzUSgU\n4uzZs7F37968hgYAgI6SW6QXCoW8hgIAgI7mxlEAAEhMbmfSP4uhoaHIsqzd0yBRo6OjE49rtVpU\nKpU2zobU1Wq1ia/WCtOxr9AK+wqNFIvF6OnpaemYjoj0er0eY2Nj7Z4Gifp0c5zuOUzHWmE69hWu\nlLXCVLq6ulo+piMivVQqRbHoyhymVq/XJz0vl8ttmgmd4OJfoNYK07Gv0Ar7Co1cScd2RKT39vaK\ndKZVrVYnHpfL5ejr62vjbEhdpVKJWq1mrTAj+wqtsK/QSJZlMTIy0tIxyhcAABKT65n0N998M6rV\n6sRfEu+991688cYbERGxevXquPrqq/OcDgAAJCnXSN+0aVOcOnVq4vnAwEAMDAxERMTJkyfj5ptv\nznM6AACQpFwjfXh4OM/hAACgI7kmHQAAEiPSAQAgMSIdAAASI9IBACAxIh0AABIj0gEAIDEiHQAA\nEiPSAQAgMSIdAAASI9IBACAxIh0AABIj0gEAIDEiHQAAEiPSAQAgMSIdAAASI9IBACAxIh0AABIj\n0gEAIDEiHQAAEiPSAQAgMSIdAAASI9IBACAxIh0AABIj0gEAIDG5RfrHH38cjz76aNxwww3xpS99\nKRYvXhw///nP8xoeAAA6Rimvge6///74wx/+ED/60Y/iK1/5SvzsZz+LtWvXRpZl8cADD+Q1DQAA\nSF4ukX748OH4zW9+MxHmERErVqyIU6dOxZYtW+Lb3/52dHV15TEVAABIXi6R/qtf/Sq6u7vjW9/6\n1qTX161bFw888ED87ne/i69+9avTHj9aG4tCIfu8p0mH+ts/xqJQ/reIiPh7fTz+9o96m2dEyv5e\nz6JWH4+xQmatMC37Cq2wr9DI+Ph4y8cUxq/kqBYtW7YsxsbG4ve///2k14eGhuL222+P3bt3x8aN\nGyMiIsuyGBkZmfS+5c8fj/OjFj0AAJ3n32eVYvDRpZNemzNnThSL098emsuNo+fOnYt58+Zd9vqn\nr507dy6PaQAAQEfI7cbRQqFwRd+LiHjlv/8jxjKXuzC9Wu3//09LuZzbsqbDjI7+PVauXBEREUeP\n/k/MnTunzTMiZfYVmmFfoRldM5wxn04uu86Xv/zlKc+Wf/jhhxERU55lv9h/9d0x4/8OgEqlErVa\nLcrlcvT19bV7OiSqWq3GeO2TiIiYM+uquOvO/2zzjEiZfYVm2FdoxlSXczeSS/necccd8ac//Snq\n9cnXlf/xj3+MiIjbb789j2kAAEBHyCXSv/nNb8bHH38cv/jFLya9vn///rjhhhvirrvuymMaAADQ\nEXK53OUb3/hGfP3rX49NmzbFX//611i4cGG89tprceTIkThw4IDPSAcAgIvkdifML3/5y9i2bVvs\n2LEjPvzww1i0aFG89tpr8Z3vfCevKQAAQEfILdK7u7tj165dsWvXrryGBACAjuQjUwAAIDEiHQAA\nEiPSAQAgMSIdAAASI9IBACAxIh0AABIj0gEAIDEiHQAAEiPSAQAgMSIdAAASI9IBACAxIh0AABIj\n0gEAIDEiHQAAEiPSAQAgMSIdAAASI9IBACAxIh0AABIj0gEAIDEiHQAAEiPSAQAgMSIdAAASI9IB\nACAxuUT6yMhIPP7443H33XfH/Pnzo1AoRH9/fx5DAwBAx8kl0s+dOxd79uyJTz75JO677748hgQA\ngI5VymOQm266Kc6fPx+FQiHOnj0be/fuzWNYAADoSLlEeqFQyGMYAAD4l+DGUQAASEwuZ9I/q6Gh\nociyrN3TIGG1Wm3ia6VSafNsSNXo6OjEY2uFRuwrNMO+QjOKxWL09PS0dEzLkT44OBgrVqxo6r0n\nTpyIxYsXtzrEZer1eoyNjX3mn8MXw6e/WOFSl64Na4VmWStMx75CM7q6ulo+puVIv/XWW+OVV15p\n6r2t/sUwnVKpFMWiK3OY3sWbYrlcbuNMSFm9Xp/03FphJvYVmmFfoRlX0rEtR/r1118fGzZsaHmg\nz6K3t1ekM6NKpRK1Wi3K5XL09fW1ezokqlqtTjy2VmjEvkIz7Cs0I8uyGBkZaekY5QsAAInJ7cbR\nN998M6rV6sRfEe+991688cYbERGxevXquPrqq/OaCgAAJC23SN+0aVOcOnVq4vnAwEAMDAxERMTJ\nkyfj5ptvzmsqAACQtNwifXh4OK+hAACgo7kmHQAAEiPSAQAgMSIdAAASI9IBACAxIh0AABIj0gEA\nIDEiHQAAEiPSAQAgMSIdAAASI9IBACAxIh0AABIj0gEAIDEiHQAAEiPSAQAgMSIdAAASI9IBACAx\nIh0AABIj0gEAIDEiHQAAEiPSAQAgMSIdAAASI9IBACAxIh0AABIj0gEAIDG5RPqxY8di/fr1sWjR\nopg9e3YsWLAg7r333nj77bfzGB4AADpKLpH+8ssvx/DwcDzyyCNx+PDh2LVrV5w5cyaWLl0ax44d\ny2MKAADQMUp5DPLSSy/FtddeO+m1VatWxcKFC+PZZ5+NlStX5jENAADoCLmcSb800CMiuru747bb\nbosPPvggjykAAEDHaNuNox999FG888470dvb264pAABAknK53GUqDz/8cFSr1di2bVvD9w4NDUWW\nZTnMik5Vq9UmvlYqlTbPhlSNjo5OPLZWaMS+QjPsKzSjWCxGT09PS8e0HOmDg4OxYsWKpt574sSJ\nWLx48WWvP/HEE3Hw4MF44YUX4s4772z4c+r1eoyNjbU6Vb6gPv3FCpe6dG1YKzTLWmE69hWa0dXV\n1fIxLUf6rbfeGq+88kpT753qL4adO3fG008/Hc8880xs3ry5qZ9TKpWiWPSR7kzv4k2xXC63cSak\nrF6vT3purTAT+wrNsK/QjCvp2JYj/frrr48NGza0PFDE/wV6f39/9Pf3x9atW5s+rre3V6Qzo0ql\nErVaLcrlcvT19bV7OiSqWq1OPLZWaMS+QjPsKzQjy7IYGRlp6Zjcyvepp56K/v7+2L59ezz55JN5\nDQsAAB0nlxtHn3vuudixY0esWrUq1qxZE8ePH5/0/aVLl+YxDQAA6Ai5RPqhQ4ciIuLIkSNx5MiR\ny74/Pj6exzQAAKAj5BLpg4ODeQwDAAD/EtyNCQAAiRHpAACQGJEOAACJEekAAJAYkQ4AAIkR6QAA\nkBiRDgAAiRHpAACQGJEOAACJEekAAJAYkQ4AAIkR6QAAkBiRDgAAiRHpAACQGJEOAACJEekAAJAY\nkQ4AAIkR6QAAkBiRDgAAiRHpAACQGJEOAACJEekAAJAYkQ4AAIkR6QAAkJhcIv3dd9+NNWvWRE9P\nT8yaNSvmzZsXy5YtiwMHDuQxPAAAdJRSHoNcuHAhbrzxxli7dm0sWLAgqtVqHDx4MB566KEYHh6O\n7du35zENAADoCLlE+vLly2P58uWTXrvnnnvi5MmTsWfPHpEOAAAXaes16ddcc02USrn8nQAAAB0j\n10LOsiyyLIvz58/HwMBAHD16NF588cU8pwAAAMnLNdJ/8IMfxO7duyMi4qqrroqf/OQn8b3vfa/h\ncUNDQ5Fl2ec9PTpYrVab+FqpVNo8G1I1Ojo68dhaoRH7Cs2wr9CMYrEYPT09LR1TGB8fH2/lgMHB\nwVixYkVT7z1x4kQsXrx44vnp06fjzJkzcebMmTh06FDs2bMnfvzjH8djjz028Z4sy2JkZGTSz3n/\n/fdjbGyslWkCAEASurq64pZbbpn02pw5c6JYnP7K85Yj/S9/+Uv8+te/buq9999/f8ybN2/a72/a\ntCn27t0bf/7zn2P+/PkRMXWknz592pl0ZvTpGa+IiHK53MaZkDprhWZZKzTLWqGRqc6k/9Mj/Z9p\n3759sX79+jh+/HjcddddETF1pDf6j4BKpRK1Wi3K5XL09fW1ezokzFqhWdYKzbJWaORK+rat5fvW\nW29FsVi87PQ/AAB8keVy4+jGjRtj7ty5sWTJkrjuuuvi7NmzMTAwEK+//nps2bJl4lIXAAAgp0hf\ntmxZ7Nu3L/bv3x8XLlyI7u7u6Ovri1dffTUefPDBPKYAAAAdI5dIX7duXaxbty6PoQAAoOO5GxMA\nABKT6z9m1IypPmzGxy/SSLFYjK6urigWi9YLM7JWaJa1QrOsFRqZal00+oDFtn4E41Tq9XpUq9V2\nTwMAAD43s2fPjlJp+vPlLncBAIDEiHQAAEiMSAcAgMQkd016lmWXXVxfKBSiUCi0aUYAAHDlxsfH\nL7tRtFgsRrE4/fny5CIdAAC+6FzuAgAAiRHpAACQGJEOAACJEekAAJAYkQ4AAIkR6QAAkJj/BYV6\nxmHZ9/fCAAAAAElFTkSuQmCC\n", "text/plain": [ "" ] }, "metadata": {}, "output_type": "display_data" } ], "source": [ "X = [3, -3, 3, -3]\n", "mean = np.average(X)\n", "for i in range(len(X)):\n", " plt.plot([i ,i], [mean, X[i]], color='k')\n", "plt.axhline(mean)\n", "plt.xlim(-1, len(X))\n", "plt.tick_params(axis='x', labelbottom='off')" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "If we didn't take the square of the differences the signs would cancel everything out:\n", "\n", "$$\\frac{(3-0) + (-3-0) + (3-0) + (-3-0)}{4} = 0$$\n", "\n", "This is clearly incorrect, as there is more than 0 variance in the data. \n", "\n", "Maybe we can use the absolute value? We can see by inspection that the result is $12/4=3$ which is certainly correct — each value varies by 3 from the mean. But what if we have $Y=[6, -2, -3, 1]$? In this case we get $12/4=3$. $Y$ is clearly more spread out than $X$, but the computation yields the same variance. If we use the formula using squares we get a variance of 3.5 for $Y$, which reflects its larger variation.\n", "\n", "This is not a proof of correctness. Indeed, Carl Friedrich Gauss, the inventor of the technique, recognized that it is somewhat arbitrary. If there are outliers then squaring the difference gives disproportionate weight to that term. For example, let's see what happens if we have:" ] }, { "cell_type": "code", "execution_count": 13, "metadata": {}, "outputs": [ { "name": "stdout", "output_type": "stream", "text": [ "Variance of X = 1210.69\n" ] } ], "source": [ "X = [1, -1, 1, -2, 3, 2, 100]\n", "print('Variance of X = {:.2f}'.format(np.var(X)))" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "Is this \"correct\"? You tell me. Without the outlier of 100 we get $\\sigma^2=2.89$, which accurately reflects how $X$ is varying absent the outlier. The one outlier swamps the computation. Do we want to swamp the computation so we know there is an outlier, or robustly incorporate the outlier and still provide an estimate close to the value absent the outlier? I will not continue down this path; if you are interested you might want to look at the work that James Berger has done on this problem, in a field called *Bayesian robustness*, or the excellent publications on *robust statistics* by Peter J. Huber [3]. In this book we will always use variance and standard deviation as defined by Gauss." ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "## Gaussians\n", "\n", "We are now ready to learn about [Gaussians](https://en.wikipedia.org/wiki/Gaussian_function). Let's remind ourselves of the motivation for this chapter.\n", "\n", "> We desire a unimodal, continuous way to represent probabilities that models how the real world works, and that is computationally efficient to calculate.\n", "\n", "Let's look at a graph of a Gaussian distribution to get a sense of what we are talking about." ] }, { "cell_type": "code", "execution_count": 14, "metadata": {}, "outputs": [ { "data": { "image/png": "iVBORw0KGgoAAAANSUhEUgAAAv8AAAEvCAYAAADSLa6QAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzs3Xd4FXXaxvHvaUlIbxAglNBLSEIL\nCQioyCor7CooqIBSLdjdXfG1oLh214a9gCQ0RRDFBq6gqHQSIPROqIFUQnpyyvsHyooipE/K/bku\nrnUn5yR3Hg4590xmfmNyuVwuRERERESkzjMbHUBERERERKqHyr+IiIiISD2h8i8iIiIiUk+o/IuI\niIiI1BMq/yIiIiIi9YTKv4iIiIhIPWE1OkB1cjqdOJ3Oc7aZTCZMJpNBiUREREREys/lcvH7lfvN\nZjNm8/mP8de78p+Xl2d0DBERERGRKuPl5fWn5V+n/YiIiIiI1BMq/yIiIiIi9YTKv4iIiIhIPVGv\nzvk/34W9FzonqjJt374du92O1WolPDy8yr9eXaP5VYzmV36aXcVofhWj+ZWfZlcxml/5VffszndN\n64UWs6n35f9CV0NXJqfTicPhqLavV9dofhWj+ZWfZlcxml/FaH7lp9lVjOZXfjVhdhcq//rbFBER\nERGpJ1T+RURERETqCZV/EREREZF6QuVfRERERKSeUPkXEREREakn6tVqPyIiUjXyiuyk5xaRnltE\nRm4xRXYnRXYn+5NzcToceLhZOWI6TgObhSBvd4K93Qj2dsfDZjE6uohIvaLyLyIipZadX8Lmo6fY\ndiyb/Wm5HEjL40BaLqcL7Rd/8tqsP2wK9najdbA3rRt60baRNxGhfkQ088PTTW9PIiJVQT9dRUTk\nT6XnFrFqXzo/700n8VAWB9Pz/vSxHjYzjXw8CPRyo4HNgrvNTEFeDk6nC7sT3D29yC92kJFbTFpO\nEcUOJ+m5xaTnZrI+OfPs57GYTbQP8SE6LIB+7RoS2zoQHw9bdXy7IiJ1nsq/iIicY+/JHL7ZeoL/\n7jjB9uOn//DxsCBPIpv50z7Em1a/HLVvFtAAb3frH24sk5SURElJCTabjaioqLPbXS4X2QUlHM7M\nP/vbg10ncthyNJsTpwvZmXKanSmnmbXmEFazie4tAriqS2OujmhME78GVT4DEZG6SuVfREQ4kV3I\ngoQjfJF0nL2pued8rHMTX/q1Dya2dRBdm/kT4OVW4a9nMpnw93TD39ONyGb+f8iy6XAWq/dn8PPe\nNJIz8lmffOa3A099tYPuLfy5tlso10SF4uep3wiIiJSFyr+ISD1ldzj5YXcaH68/zA+7U3G6zmy3\nWUz0bRvM1RFNuKxDIxr6uFdrrsZ+Hvw1ogl/jWgCwJHMfJbtPMk3W1NIOJTFxsOn2Hj4FM98vZO/\ndmnMDdEtiG0deMHb2YuIyBkq/yIi9UxukZ2P1x9mxsqDpGQXnt3eKyyQ4T2bcWV4Y/wa1Jwj6s0D\nPRl3SSvGXdKKk6cL+XpLCp8kHGHXiRw+33yczzcfp3MTX27t34ohkU2xWbSKtYjIn1H5FxGpJ9Jy\niohbfZDZaw6dXZ0n0MuN67qHckN0C9o28jY44cWF+Howvm8rxl0Sxpaj2Xy84TCfbzrOjpTTPDA/\niReX7mZsnzBGxbbE211vcSIiv6efjCIidVxWXjFvr9jHrDWHKLI7AWgd7MVt/VsztHso7tbat9a+\nyWQiqrk/Uc39eWhQR+auO8zMVcmkZBfy3JJdvPfTAe68rA2jY1vqXgIiIr+h8i8iUkflFdmZsfIg\nH/x0gJyiM0f6uzb3545L23Bl5xDM5rpxjry/pxt3Xd6Wif1asXjzcd5ZsZ+D6Xk8/fVOPvj5AHcP\naMcNPZvjZtXpQCIiKv8iInWMw+nik4QjvPzf3aTnFgNnVuyZPKgDl7ZvWGcvjHW3WhjRsznDuoXy\n6cajvL58H8dOFTDl823MXHmQKX/rzOUdGhkdU0TEUCr/IiJ1yKbDWTzxxXa2HM0GzqzJ/48rOzAk\nokmdOdJ/MVaLmRuiW3Btt1A+Xn+EN77fy4H0PMbN3MCAjo2YMqQzrYK9jI4pImIIlX8RkTogPbeI\nF5bsYkHiUQB83K088Jf23Ny7Zb1d/cbdamFMnzCGdg/ljeV7mbkqme93pfLz3jRu7deae69op+sB\nRKTeUfkXEanFXC4XXyQdZ+oX28nKLwHg+h7NeGhQx2pfn7+m8vWw8ejgztwQ3YKnvtrBj3vSeHvF\nfpZuO8FzwyKIaR1kdEQRkWqj8i8iUkudyC7ksc+3smxnKgAdG/vwzNAIerQMMDhZzdS2kTdx46L5\n746TTPl8GwfS87jh/bWMjGnB//21I74eNefeBiIiVUXlX0SklnG5XCxMPMq/v9pBTqEdm8XEvQPa\nccdlbertKT6lZTKZuCq8MbGtg3h+yU4+Wn+EeesO88OuVF4eHkWftsFGRxQRqVJ6lxARqUWy80u4\ne94mHly4hZxCO1HN/Pjqnn7cc0U7Ff8y8Gtg47lhkcy7NYaWQZ6kZBcyasY6nv1mJ0V2h9HxRESq\njN4pRERqiTX7Mxg07Se+3pqC1Wziwas68OmkPnRo7GN0tFqrT5tgvrm3Hzf1ao7LBe//dIBr3lzF\nnpM5RkcTEakSKv8iIjWc3eHkxaW7GDl9LSnZhbQK9mLRnX246/K2WHW0v8K83K08NyyS92/uQaCX\nG7tO5PC3N1Yyf8Nho6OJiFQ6vWuIiNRgaTlFjJ6xjrdX7Mflghujm/PVPX2JbOZvdLQ658rwxiy9\nvx+Xtm9Ikd3JQ59u5cEFSRQU6zQgEak7VP5FRGqohORMBr/+M2sPZOLlZuHNkd14/rpIvNy1VkNV\naeTjwcyx0Tx4VQfMJliQeJShb6/iYHqe0dFERCqF4eX/+++/Z/z48XTs2BEvLy9CQ0O55pprSExM\nvOhz4+LiMJlM5/1z4sSJakgvIlL5XC4XM1Ye5Mb315KaU0S7Rt4svrsvQyKbGh2tXjCbTdx1eVvm\nTIgh2Pt/pwEt3ZZidDQRkQoz/PDRO++8Q0ZGBvfddx+dO3cmLS2Nl19+mdjYWL799lsGDBhw0c8x\nc+ZMOnbseM62oCDdtEVEap+CYgeTP93Cl0nHAfhbVFOeHxaho/0G6NM2mK/v7cc98zaxPjmTO+Zs\n5N4r2nH/Fe0wm01GxxMRKRfD303eeustGjVqdM62QYMG0bZtW5599tlSlf8uXbrQs2fPqoooIlIt\nTp4u5NZZCWw5mo3VbOKxwZ0Y0ycMk0lF0yghvh7MuzWG55fsYvrKg7y+fC97T+bw8ogoPN0MfwsV\nESkzw0/7+X3xB/D29qZz584cOXLEgEQiItVv69Fs/v7mSrYczSbA08bciTGMvaSVin8NYLWYeWxI\nZ/5zfSRuFjNLtp3g+nfWcOxUgdHRRETKzPDyfz7Z2dls3LiR8PDwUj1+yJAhWCwWAgMDGTZsGNu2\nbavihCIileebrSkMf281J0//cn7/XX2Jaa1TF2ua4T2bM+/WM9cB7Eg5zTVvriTxUKbRsUREysTk\ncrlcRof4vdGjRzN//nzWrl1Ljx49/vRxS5cuZeXKlcTGxuLr68vWrVt5/vnnycrKYtWqVURFRZ3z\neKfTSU7OuTduOXz4ME6ns0q+j98qKSk5+982m63Kv15do/lVjOZXflU5O5fLxcIdOczZchqA7k3c\n+VefILzcauRxmXKpi6+91Dw7z/6UwcFTJdjM8I8+gfRp7lklX6suzq+6aHYVo/mVX3XPzmw206JF\ni3O2+fj4YDaf/72kxpX/KVOm8PTTT/PGG29w9913l/n5ycnJREREMGDAABYvXnzOx85X/g8cOIDD\noTWcRaR6OVwuZmzK4b8Hzpw6MritJ7dEemPRhaS1QoHdybR1p0lIKcIEjI3yYXC7qtkBEBG5EIvF\nQuvWrc/ZdqHyX6OuVnryySd5+umneeaZZ8pV/AHCwsLo27cva9euLdXjrVbrnw6nMmkPumI0v4rR\n/MqvKmZXZHfxytoM1h0txARM7OHPkPbelfK5a5q6+tqz2eCR/sF8kHiKJfvymJmUQ1aRizFd/TBX\n4nUadXV+1UGzqxjNr/yMOPJfFjWm/D/55JNMnTqVqVOn8sgjj1Toc7lcrlIPIjw8vFrKf1JSEiUl\nJdhstj+cjiQXp/lVjOZXfpU9u1P5xUyITyDxaCFuVjOv3dCVqyOaVELSmqmuv/be7urinR/38+LS\n3Xy+KxeHuy8vDY/A3WqplM9f1+dXlTS7itH8yq+6Z3e+M1supEacWPrUU08xdepUHnvsMZ544okK\nfa6DBw+yatUqYmNjKymdiEjlOHaqgOveWU3ioSx8PKzMHt+rThf/+sBkMnHnZW15ZUQUVrOJL5OO\nM/bDDeQW2Y2OJiJyXoYf+X/55Zd5/PHHGTRoEIMHD/7D6Tq/lvgJEyYQHx/P/v37admyJQADBw6k\nf//+REZGnr3g98UXX8RkMvHUU09V+/ciIvJnDqTlMmr6OlKyC2ni50HcuF50aOxjdCypJMO6N6OR\njwe3z05gzYEMRk9fR9y4aPw93YyOJiJyDsPL/5dffgmcWbln6dKlf/j4r9cjOxwOHA4Hv70+OSIi\ngvnz5/PSSy9RUFBAo0aNGDBgAFOmTKF9+/bV8w2IiFzEzpTT3DxjPem5RbRp6MXsCTE09W9gdCyp\nZH3bBTP31ljGzlzP5iOnuPH9tcya0ItGPh5GRxMROcvw8r9ixYpSPS4uLo64uLhztr366quVH0hE\npBJtPnKKMR+uJ7ughM5NfJk1oRfB3u5Gx5Iq0rW5P/Nv683oGevYdSKHEe+uYc7EGJoFaCUgEakZ\nasQ5/yIiddHaAxmM+mAt2QUldGvhz0e3xar41wMdGvuw8I7eNAtoQHJGPiPeXcOBtFyjY4mIACr/\nIiJVYsXuVMZ8uJ68Ygd92gQxZ0IMfg20XF590TLIiwV39KZNQy+OZxcy4r017Dpx2uhYIiIq/yIi\nlW3ZjpPcOiuBIruTKzo24sOx0Xi5G36WpVSzJn4N+OT23oQ39SU9t5iRH6zTDoCIGE7lX0SkEi3f\neZJJcxMpcbgYHNGEd2/ugYetctZ8l9onyNudeRNjiWzmR2bemR2AnSnaARAR46j8i4hUkh92pTJp\nzsazxX/ajV2xWfRjtr7z87Qxe0LM2R2AUdO1AyAixtG7kohIJfhhdyq3z06k2OHk6ojGvHZjV6wq\n/vILvwbn7gCM/GCtdgBExBB6ZxIRqaAVvyn+f+3SmGk3dtMRf/mDX3cAopr5kZVfoh0AETGE3p1E\nRCrgpz1p3DY7kWK7k6vCQ3j9JhV/+XN+DWzM+s0OwKjp69h7MsfoWCJSj+gdSkSknFbtS+fWWQkU\n251c2TmEN27qruIvF/XrDsBvrwFITs8zOpaI1BN6lxIRKYfEQ5lMjD+znOfATiG8ObI7blb9SJXS\n8WtgY9b4XnRs7ENqThGjpq/j2KkCo2OJSD2gdyoRkTLafjybsTM3UFDioF+7YN4a1U3FX8rM39ON\n2RNiaB3sxbFTBYyevo7UnEKjY4lIHad3KxGRMtiXmsstM9aTU2gnOiyA927ugbtV6/hL+TT0cWfO\nxBhC/RtwMD2Pm6evJyuv2OhYIlKHqfyLiJTSkcx8bp6xjoy8YrqE+jJjbDSebrpzr1RMU/8GzLs1\nhhBfd3afzOGWD9dzurDE6FgiUkep/IuIlEJmgYPRM9aRkl1I20bexI/rha+HzehYUke0DPJi7sQY\nAr3c2Hosm/EzN5BfbDc6lojUQSr/IiIXkVPk5Ikf0jiUkU/zwAbMmRBDkLe70bGkjmnbyIfZE3rh\n62El4VAWd83diN3pMjqWiNQxKv8iIhdQaHfyzMosDmfbCfF1Z+6EWBr7eRgdS+qo8KZ+zBwXjYfN\nzA+703hjXRZOl3YARKTyqPyLiPyJEoeTF1dmsi/Ljo+bmTkTYmgR5Gl0LKnjerQM5O1R3bGYTaxI\nzmf2llxc2gEQkUqi8i8ich4ul4uHPt1CYkohbhaYcmkQ7UJ8jI4l9cSAjiG8eF0kAF/uzeeznbkG\nJxKRukLlX0TkPJ5fuotFG49hNsE/Y/3pEKxz/KV6XdejGeO6+gEQn5TNJwlHDE4kInWByr+IyO9M\n//kA7/14AIC7ewXQo4mKvxjj2k4+XNP+zKlmDy/ayrIdJw1OJCK1ncq/iMhvLN58jKe/3gnA5EEd\nuKK1l8GJpL4bHeHNgFaeOJwu7pq3kQ3JmUZHEpFaTOVfROQXP+9N418LkgAY2yeMSZe2MTiRCJhM\nJu7uFcAVHRtRZHcyPm4De07mGB1LRGoplX8REWDr0WzumJ1IicPFkMgmPD6kMyaTyehYIgBYzCbe\nHNmdni0DyCm0M/bD9Zw8XWh0LBGphVT+RaTeO5SRx9iZ68krdnBJ2yBeHhGF2aziLzVLAzcLH9zS\nk9bBXhzPLmTczA3kFukuwCJSNir/IlKvZeUVM3bmBjLyiglv6su7o3vgbrUYHUvkvAK83Igb14tg\nbzd2pJzmzrkbKXE4jY4lIrWIyr+I1FuFJQ5um53AwfQ8Qv0bMHNsND4eNqNjiVxQiyBPZow5cxfg\nn/ak8dhn23QTMBEpNZV/EamXnE4X/1qQxIbkLHw8rMwcF00jXw+jY4mUSlRzf968qTtmE8xPOMKb\n3+8zOpKI1BKGl//vv/+e8ePH07FjR7y8vAgNDeWaa64hMTGxVM9PTU1l7NixBAcH4+npSe/evVm+\nfHkVpxaR2u4//93NV1tSsJpNvDe6B+11916pZQZ2DuHJv4cD8PJ3e/g08ajBiUSkNjC8/L/zzjsk\nJydz33338c033zBt2jRSU1OJjY3l+++/v+Bzi4qKuOKKK1i+fDnTpk1j8eLFhISEMGjQIH788cdq\n+g5EpLaZt+4w76zYD8Dz10XSp22wwYlEyufm3mHcfmlrAB76dAur9qUbnEhEajqr0QHeeustGjVq\ndM62QYMG0bZtW5599lkGDBjwp8+dMWMG27ZtY/Xq1fTu3RuAyy+/nKioKCZPnsy6deuqNLuI1D4r\ndqcyZfE2AO67oh3X92hmcCKRinnoqo4cP1XIl0nHuWN2Igsm9aZjY1+jY4lIDWX4kf/fF38Ab29v\nOnfuzJEjRy743M8++4wOHTqcLf4AVquV0aNHs379eo4dO1bpeUWk9tpx/DR3zd2Iw+liWPdQ7h/Y\nzuhIIhVmNpt4aXgkvVoFklNkZ9zMDaRkFxgdS0RqKJOrBi4RkJ2dTcuWLRkwYACLFi3608c1adKE\nfv368cknn5yz/euvv2bIkCF8++23XHnllWe3O51OcnLOvSvi4cOHcTqrfpm0kpKSs/9ts2k1kbLS\n/CpG84P0fDuT/5tGRoGDyBB3Hr80GJvl4mv5a3YVo/lVTFnml1vs5KHvUjl62k4rfxvPDWxIA5vh\nx/gMo9dexWh+5VfdszObzbRo0eKcbT4+PpjN5//3b/hpP+dz1113kZeXx6OPPnrBx2VkZBAYGPiH\n7b9uy8jIuOjXstvtOByO8gUtp9++KKTsNL+KqY/zyy9x8u8VWWQUOGjma+GfMb7gtFNSxv3++ji7\nyqT5VczF5udugkcu8efh7zM5eKqEl1Zl8GAfPyy6U7VeexWk+ZVfdczOYinbvWlqXPmfMmUKc+fO\n5Y033qBHjx4XfbzpAj/ULvSxX1mt1j/dM6pM2oOuGM2vYurz/OxOF6+uTOdQtp0ADzNPXNYQf6/S\n/+irz7OrDJpfxZR1fqH+Nh7pH8Rjy9NISCnio+35jOvmX5URayy99ipG8ys/I478l0WNKv9PPvkk\nTz/9NM888wx33333RR8fFBR03qP7mZmZAOf9rcDvhYeHV0v5T0pKoqSkBJvNRlRUVJV/vbpG86uY\n+jo/l8vFY59vY9OJIhrYLMRPjCWyWdmKUH2dXWXR/CqmPPOLAjyDj3PPR5v4fFcuvTq1YmRMi4s+\nr67Ra69iNL/yq+7Zne+09gupMScDPvnkk0ydOpWpU6fyyCOPlOo5ERERbN269Q/bf93WpUuXSs0o\nIrVL3Opk5q47jMkEr9/UrczFX6S2+ltUU/7xl/YATFm8jZV7tQSoiJxRI8r/U089xdSpU3nsscd4\n4oknSv28oUOHsmvXrnOW9LTb7cyZM4eYmBiaNm1aFXFFpBb4YXcqT321A4BH/tqJv3QOMTiRSPW6\nZ0BbhnYLxeF0MWluIvtSS39kUETqLsPL/8svv8zjjz/OoEGDGDx4MGvXrj3nz68mTJiA1Wrl0KFD\nZ7eNHz+e8PBwhg8fzrx581i2bBkjRoxg9+7dvPDCC0Z8OyJSA+w5mcM98zbhdMENPZszsV8royOJ\nVDuTycTz10UQHRZATqGdcXEbyMgtMjqWiBjM8HP+v/zySwCWLl3K0qVL//DxX1cidTgcOBwOfrsy\nqbu7O8uXL2fy5Mncc8895Ofn07VrV5YsWcKll15aPd+AiNQoGblFTIjfQG6RnZhWgTx1bZdSXfwv\nUhe5Wy28d3NPrn1rFYcz87l9diJzJsbgYSvb6iAiUncYfuR/xYoVuFyuP/3zq7i4OFwuF2FhYec8\nPyQkhPj4eDIyMigoKGDNmjUMHDiwmr8LEakJiuwObp+dyJHMAloGefLu6B64WQ3/MSdiqEAvNz4c\nG42Ph5WEQ1k89OkWauAtfkSkmuhdUUTqBJfLxcOLtpJwKAsfDyszxkQT4OVmdCyRGqFtI2/eHd0D\nq9nE4s3HeX35PqMjiYhBVP5FpE5458f9LNp4DIvZxNujutO2kbfRkURqlEvaBvPUtWdWwXt12R4W\nbz5mcCIRMYLKv4jUeku3neDFpbsBmPq3zvRr19DgRCI10029WnBb/9YAPLhwC4mHMg1OJCLVTeVf\nRGq1bceyeWD+ZgDG9G7Jzb3DjA0kUsM9NKgjf+kcQrHdyW2zEjmSmW90JBGpRir/IlJrnTxdyMT4\nBApKHPRrF8yUIZ2NjiRS41nMJqbd2JXwpr5k5BUzIX4DOYUlRscSkWqi8i8itVJBsYNbZyVw4nQh\nbRp68ebI7lgt+pEmUhqebmcuig/xdWfPyVzu+WgTdofT6FgiUg30TikitY7T6eJfC5PYcjSbAE8b\nH46Nxq+BzehYIrVKYz8Ppt8SjYfNzIrdaTzzzU6jI4lINVD5F5Fa57Xle/l6Swo2i4l3R/egZZCX\n0ZFEaqWIZn68OqIrADNXJTN77SGDE4lIVVP5F5FaZfHmY7y+fC8AzwyNIKZ1kMGJRGq3v0Y04cGr\nOgAw9Yvt/Lw3zeBEIlKVVP5FpNbYeDiLBxduAeD2/q0Z0bO5wYlE6oY7L2vDsG6hOJwu7py7kX2p\nuUZHEpEqovIvIrXCsVMF3DYrkWK7k4GdQpg8qKPRkUTqDJPJxHPXRdCzZQA5hXYmxG8gM6/Y6Fgi\nUgVU/kWkxsstsjMhbgPpuUV0auLLtBu7YjGbjI4lUqe4Wy28d3MPmgc24FBGPnfMObOzLSJ1i8q/\niNRoDqeL+z/exK4TOQR7uzN9TE+83K1GxxKpk4K83ZkxJhofdyvrD2by6GdbcblcRscSkUqk8i8i\nNdoLS3exbGcqblYz79/Sg1D/BkZHEqnT2of48Oao7phNsCDxKO/9dMDoSCJSiVT+RaTGmr/hMO//\nUjz+c30k3VsEGJxIpH64tH1DnvhbOHBmB/zb7ScMTiQilUXlX0RqpLUHMnj0s20A3HtFO67pGmpw\nIpH6ZUyfMG7p3RKXC+7/eDPbjmUbHUlEKoHKv4jUOMnpedwxJxG708XgyCbcf0U7oyOJ1EuPD+lM\nv3bBFJQ4mBifwMnThUZHEpEKUvkXkRolu6CECfEbOJVfQlQzP14eHoVZK/uIGMJqMfPWqO60beTN\nidOFTIxPoKDYYXQsEakAlX8RqTHsDid3z9vI/rQ8Gvt68MEtPfGwWYyOJVKv+XrY+HBMNAGeNrYe\ny+afCzbjdGoFIJHaSuVfRGqMf3+1g5/3ptPAZmH6mJ408vUwOpKIAC2CPHn/lp64Wcx8s/UEr3y3\nx+hIIlJOKv8iUiPMWpPMrDWHAHj1hq50CfUzNpCInCM6LJDnhkUA8OYP+1i08ajBiUSkPFT+RcRw\nP+1J48kvdwAweVAHBnVpbHAiETmf63o0487L2gDwf59uJSE50+BEIlJWKv8iYqh9qTncNXcjDqeL\nYd1DmXRpG6MjicgF/OvKDgwKb0yxw8ltsxM5nJFvdCQRKQOVfxExTGZeMePjEsgpshMdFsBzwyIw\nmbSyj0hNZjabeOWGKLqE+pKZV8yE+A2cLiwxOpaIlJLKv4gYotju5I45iRzOzKd5YAPeHd0Dd6tW\n9hGpDTzdrEy/JZoQX3f2puZyz7xN2B1Oo2OJSCmo/ItItXO5XDz2+VbWH8zEx93KjDHRBHm7Gx1L\nRMqgsZ8H02+JxsNm5sc9aTz99U6jI4lIKdSI8p+Tk8PkyZO58soradiwISaTialTp5bquXFxcZhM\npvP+OXHiRNUGF5Fy+eDnA3yScBSzCV4f2Y32IT5GRxKRcoho5sdrN3QFIG51MrPXJBuaR0QurtTl\n/4svviA7O7tKQmRkZPD+++9TVFTEtddeW67PMXPmTNasWXPOn6CgoEpOKiIV9d2Okzy3ZBcAjw3u\nzOUdGhmcSEQqYlCXJkwe1AGAqV/u4Kc9aQYnEpELKXX5Hzp0KLt37wagdevWJCUlVVqIli1bkpWV\nxY8//shzzz1Xrs/RpUsXYmNjz/ljs9kqLaOIVNyO46e57+NNuFwwMqYF4y4JMzqSiFSCSZe2YVj3\nUBxOF3fN3cjekzlGRxKRP1Hq8t+gQQPy888s55WcnExRUVGlhfj1NB0RqbtScwqZGL+B/GIHl7QN\n4sm/h+vfvUgdYTKZeG5YBNFhAeQU2ZkQn0BmXrHRsUTkPKylfWCnTp149NFHGTp0KADz5s1j5cqV\n532syWTigQceqJyEpTRkyBDS0tLw8/Pjsssu49///jddunSp1gwicn6FJQ5um5XI8exCWgd78fbI\nHtgsNeKSIxGpJO5WC+/d3JNr31rF4cx87pidyOyJvbSKl0gNY3K5XK7SPHD58uXccMMNZGZmYjKZ\nuNDTTCYTDoejXIHS09Np2LA425+EAAAgAElEQVQhTzzxRKku+l26dCkrV64kNjYWX19ftm7dyvPP\nP09WVharVq0iKirq7GOdTic5Oef+KvLw4cM4nVW/PFlJyf/WQNbpSGWn+VWMkfNzuVy8siaTnw4V\n4O1m4j9XNqKpT+35O9Rrr2I0v4qpjfM7nF3CQ9+lkl/iYkArT+6NCTDkt3y1cXY1ieZXftU9O7PZ\nTIsWLc7Z5uPjg9l8/oNspS7/vzp27BjNmzfns88+o2vXrn/6uJYtW5bl055V1vJ/PsnJyURERDBg\nwAAWL158dvv5yv+BAwfKvaMiIhe3YEcu83fkYTHBlH4BdGnkZnQkEalim08U8eyqUzhdMKqLN0M7\nehkdSaTOslgstG7d+pxtFyr/pT7t51ehoaE88cQTREdH07Rp0/KlrGJhYWH07duXtWvXXvSxVqv1\nT4dTmbQHXTGaX8UYNb+fDuUzf0ceAHf09KdbaO0rAHrtVYzmVzG1dX7RzW1M7A7vJ55i7rZcmvu7\n07t5g2rNUFtnV1NofuVnxJH/sihz+Qd44oknyvO0auVyuUo1jPDw8Gop/0lJSZSUlGCz2c45FUlK\nR/OrGCPml5CcyRvr1wEwoW8rHhzSuVq+bmXTa69iNL+Kqc3zi4qCIrdtxK85xGvrsrikaycimvlV\n29evzbOrCTS/8qvu2Z3vzJYLKXX5Hz9+fKk/qclkYsaMGaV+fGU7ePAgq1atYuDAgYZlEKnPktPz\nuHVWAsV2J1d2DuGRqzsZHUlEDDBlSGcOZuTz0540Js7awOK7+tLYz8PoWCL1WqnL//fff3/OBTun\nTp0iOzsbq9VKUFAQGRkZ2O12/Pz8CAgIKHOQJUuWkJeXd3bPZceOHSxcuBCAq6++Gk9PTyZMmEB8\nfDz79+8/e03BwIED6d+/P5GRkWcv+H3xxRcxmUw89dRTZc4hIhWTlVfM+LgNZOWXENnMj9du7IrF\nrCU9Reojq8XMmyO7cd3bq9mbmsvEWRv45PbeeLqV68QDEakEpT7fJTk5mYMHD3Lw4EE++eQTvL29\nmTt3LgUFBaSkpFBQUMCcOXPw8vLi448/LnOQSZMmMXz48LO/YViwYAHDhw9n+PDhpKamAuBwOHA4\nHOesNBQREcH8+fO55ZZbuOqqq3jxxRcZMGAACQkJWupTpJoV2R3cPieRA+l5hPo3YPqYnnqTF6nn\nfD1szBgTTaCXG9uOneYf85NwOsu01oiIVKJyvSv/85//5F//+hc33XTT2W0Wi4WRI0dy8uRJHnjg\nAVatWlWmz5mcnHzRx8TFxREXF3fOtldffbVMX0dEqobL5eL/Pt3K+oOZ+Lhb+XBsNI189Ot9EYEW\nQZ68d3MPRn2wjqXbT/DSf3czeVBHo2OJ1EvlutI1MTHxT4+qR0REsHnz5gqFEpHaZ9ryvXy26RgW\ns4m3RnWnQ2MfoyOJSA0SHRbI89dFAPD2iv0sTDxqcCKR+qlc5d/X15dly5ad92PLli3D19e3QqFE\npHb5bNNRXlu2F4Cnr+1C//YNDU4kIjXRsO7NuOvyNgA8vGgL6w9mGpxIpP4p12k/N998M//5z3+w\n2+2MHDmSxo0bc+LECebOnctrr73GP/7xj8rOKSI11LoDGUxeuAWA2y9tzU29WlzkGSJSn/3zLx04\nkJbHkm0nuH12Ap/fdQktg2rfPUBEaqtylf9nn32W1NRUXn75ZV555ZWz210uF6NHj+bZZ5+ttIAi\nUnPtT8vlttmJlDhcXB3RmIeu0jm8InJhZrOJV0Z05WjWGrYey2ZCfAKfTuqDXwPdSEqkOpSr/Fut\nVuLi4nj44Yf54YcfyMjIICgoiMsuu4yOHfXmL1IfZOQWMT5uA9kFJXRt7s8rI7pi1pKeIlIKDdws\nTB/Tk2veXMW+1Fxun51A/PheuFstRkcTqfPKfWtbh8PBxo0bz/mzadMm7HZ7ZeYTkRqosMTBbbMT\nOZSRT7OAM0t6etj0pi0ipRfi68GMsT3xcrOw9kAmDy7YoiVARapBucp/eno6MTExjBo1iri4OFav\nXk1cXByjRo0iJiaG9PT0ys4pIjWEw+nivo83kXgoCx8PK3Hjogn2djc6lojUQuFN/XhndA+sZhNf\nJB3nhW93GR1JpM4rV/l/4IEH2L1793lv8rV3714eeOCBys4pIjWAy+XiyS+38+32k7hZzHxwS0/a\nNtKSniJSfv3bN+T56yIBeO/HA8SvTjY2kEgdV65z/r/88kuefvrp897kKzU1lalTp1ZWPhGpQd79\n8QCz1hzCZIJXbogitnWQ0ZFEpA64vkczUk4V8PJ3e5j65XZCfD0Y1KWx0bFE6qRyHfl3uVyEh4ef\n92NdunTB5dI5eyJ1zeebjvHC0jO/kn9scGeGRDY1OJGI1CV3D2jLTb1a4HLxy6mFugeASFUoV/kf\nOHDgn97k67vvvuOyyy6rSCYRqWFW7UvnwYVJAEzs24oJfVsZnEhE6hqTycRT14QzoGMjiuxOJsQn\nsD8t1+hYInVOuU77mTJlCsOGDcPhcPzhJl+LFi1i0aJFZGb+b489MDCw0gKLSPXacfw0t/+ylv+Q\nyCY8cnUnoyOJSB1ltZh5c2Q3bnp/LUlHsxk7cz2LJl1CQx8tKiBSWcpV/rt37w5w3pt8AfTo0eOc\nxzscjvLmExEDHc3KZ+zM9eQW2YltHcjLI6K0lr+IVClPNyszxkYz7O3VHM7MZ3zcBj6+LRYv93JV\nFhH5nXL9S3r88ccxmVQAROqyU/nFjJ25gdScIjqE+PDezT11Ax4RqRbB3u7Ej+/Fde+sZuuxbO6a\nt5EPbumJzVLu2xOJyC/KVf61mo9I3VZY4uC2WYnsS82liZ8HceOj8WtgMzqWiNQjrYK9mDGmJzd9\nsJYVu9N4eNFW/nN9pA4+ilSQdqFF5Bx2h5O7521ifXLmLzfx6kUTvwZGxxKReqhbiwDeuKk7FrOJ\nhYlHeW6JbgImUlEq/yJylsvl4v8WbWXZzpO4W8/cxKtDY93ES0SM85fOITw/LAKA9386wLs/7jc4\nkUjtpvIvIsCZ4v/sNztZmHgUi9nEmyO76yZeIlIjDO/ZnEeu7gjA80t2MX/DYYMTidReKv8iApy5\ne+8HPx8E4IXrIvlL5xCDE4mI/M9t/dtw+6WtAXh40VaWbjthcCKR2knlX0T4aP3h39y9txPX92hm\ncCIRkT/6v0EdGdGzGU4X3PvxJtbszzA6kkito/IvUs8t2ZrCo59tBeDOy9owsV9rgxOJiJyfyWTi\n2aERXNk5hGK7k1tnJbDtWLbRsURqFZV/kXps1b507vt4M04X3NSrOQ9e1cHoSCIiF2S1mHn9pm7E\ntAokt8jOmA/XczA9z+hYIrWGyr9IPZV05BS3zUqg2OHkr10a8/S1EVo/W0RqBQ+bheljehLe1JeM\nvGJGT1/H8VMFRscSqRVU/kXqod0nchg7cz15xQ4uaRvEazd2xWJW8ReR2sPHw0b8+F60Cvbi2KkC\nRk9fR1pOkdGxRGo8lX+ReuZAWi6jpq8jK7+EqOb+vHdzT9ytFqNjiYiUWbC3O3MmxhDq34AD6Xnc\nPGMdWXnFRscSqdFU/kXqkZO5dkZNX0d6bhGdm/gya1wvvN2tRscSESm3UP8GzJ0YQyMfd3adyGHM\nzPWcLiwxOpZIjaXyL1JPZOQ7mPJ9GinZhbRt5M3sCb3w87QZHUtEpMLCgr2YOzGGAE8bW45mM37m\nBgrtTqNjidRIhpf/nJwcJk+ezJVXXknDhg0xmUxMnTq11M9PTU1l7NixBAcH4+npSe/evVm+fHnV\nBRaphU4VOHjypyxO5jkIC/Jk3sQYgrzdjY4lIlJp2oX4MHtCDD4eVhIOZfHsTxkUO1xGxxKpcQwv\n/xkZGbz//vsUFRVx7bXXlum5RUVFXHHFFSxfvpxp06axePFiQkJCGDRoED/++GMVJRapXbLyinn8\nhzSO5zpo6Glh7q2xNPL1MDqWiEil6xLqR9y4Xni6WUg6WcQra09hd2oHQOS3DD/Zt2XLlmRlZWEy\nmUhPT2f69Omlfu6MGTPYtm0bq1evpnfv3gBcfvnlREVFMXnyZNatW1dVsUVqhdOFJdzy4XoOZdsJ\n8DDz1ICGhPo3MDqWiEiV6dEygBljohnz4VoSUop5ZXUm8ZFOrBbDj3eK1AiG/0swmUzlXlv8s88+\no0OHDmeLP4DVamX06NGsX7+eY8eOVVZMkVonp7CEsR+uZ+uxbPzczTzRP4AmPobv74uIVLnebYL4\nv75BWE2w6kgBD3yShN2hawBEoAYc+a+Ibdu20a9fvz9sj4yMBGD79u2EhoZe8HNs374dp7PqfyCU\nlJSc/d+kpKQq/3p1jeZXNvklTqauSGd3ejHebiam9POnma9V8ysHvfYqRvOrGM2v/CIbWvlHbz9e\nWZPNl0nHOZWVxQO9A3VPk1LSa6/8qnt2ZrOZFi1alPrxtbr8Z2RkEBgY+Iftv27LyMi46Oew2+04\nHI5Kz3Yhv74opHw0vwvLK3HyzM+n2JNZgrfNxOP9Agjz/9+qPppf+Wl2FaP5VYzmV3a9mnrwj97w\nyppsfj5cgNOVzr3RftoBKCO99sqvOmZnsZTtXj21uvwDFzxlqDSnE1mtVszmqj/76bd/+Tabllcs\nK82vdPKKnTyzMos9mSX4uJn59+XBtA500/wqQLOrGM2vYjS/8vt1dr2aejC5r5UXV2Ww6kgRZlOO\nfgNQCnrtlV91z66sPbZWl/+goKDzHt3PzMwEOO9vBX4vPDy8Wsp/UlISJSUl2Gw2oqKiqvzr1TWa\n38VlF5y5uHdPRjH+njbmTowhvKkfoPlVhGZXMZpfxWh+5ffb2d02uCdhYSe4a95Gfj5cgH+Ai1dH\nROoi4AvQa6/8qnt2TqeTnJycUj++Vr/qIyIi2Lp16x+2/7qtS5cu1R1JxBDZBSXcMmMdSUdO/aH4\ni4gIXBnemLdGdsdmMfFl0nFdBCz1Vq0u/0OHDmXXrl3nLOlpt9uZM2cOMTExNG3a1MB0ItXjbPE/\nmk2Ap415E2NV/EVEzuP3OwD3z99MiXYApJ6pEeV/yZIlLFy4kC+//BKAHTt2sHDhQhYuXEh+fj4A\nEyZMwGq1cujQobPPGz9+POHh4QwfPpx58+axbNkyRowYwe7du3nhhRcM+V5EqlNWXjGjp/+v+M+d\nGEvnpr5GxxIRqbF+uwPw1ZYU7py7kSJ79S78IWKkGnHO/6RJk84p9QsWLGDBggUAHDx4kLCwMBwO\nBw6HA5frf3fqc3d3Z/ny5UyePJl77rmH/Px8unbtypIlS7j00kur/fsQqU6ppwsZPWMde07mEujl\nxtyJMXRqouIvInIxV4Y35r2be3DHnI18t+MkE+MTeP/mnjRwK9uqKSK1UY048p+cnIzL5Trvn7Cw\nMADi4uLO+f+/CgkJIT4+noyMDAoKClizZg0DBw6s/m9CpBodzcpn+Htr2HMylxBfdz65PVbFX0Sk\nDAZ0DCFubDSebhZ+3pvOmA/Xk1OoJS2l7qsR5V9ESu9AWi7D313DoYx8mgU0YMHtfWjbyMfoWCIi\ntU6ftsHMntALH3cr65MzGT1jPafyi42OJVKlVP5FapGdKacZ8d5aUrILad3QiwV39KZFkKfRsURE\naq0eLQP56LZYAjxtJB05xY3vryUtp8joWCJVRuVfpJbY/MubUnpuEZ2a+PLJ7b1p4tfA6FgiIrVe\nl1A/Pr6tNw193Nl1Iocb3l/DsVMFRscSqRIq/yK1wMq96Yz6YC3ZBSV0a+HPx7fGEuztbnQsEZE6\no0NjHz65vTdN/Tw4kJbH9e+sZs/J0t84SaS2UPkXqeG+SDrOuLj15BU76NMmiDkTYvDz1K3WRUQq\nW6tgLxZO6kPbRt6kZBcy/N01JB7KNDqWSKVS+RepwT5ceZB7P9pEicPF4IgmzBwXjZd7jVihV0Sk\nTmrq34AFt/emWwt/sgtKGDV9Hct3njQ6lkilUfkXqYFcLhcvLN3Fv7/aAcCY3i15/aZuuFu1BrWI\nSFUL+OXeKZd3aEhhiZPbZieyIOGI0bFEKoXKv0gNU+Jw8q8FW3hnxX4AHryqA1P/Ho7FbDI4mYhI\n/eHpZuX9W3oyrHsoDqeLBxee+bn825uNitRGKv8iNUh+sZ3bZiXw6cajWMwmXrwukrsub4vJpOIv\nIlLdbBYzL10fxW39WwPwwtJdPPnlDhxO7QBI7aXyL1JDnDxdyIj31vDD7jTcrWbeG92DEdHNjY4l\nIlKvmc0mHrm6E49e3QmAuNXJ3DYrgbwiu8HJRMpH5V+kBthx/DTXvrWKbcdOE+jlxrxbYxjYOcTo\nWCIi8otb+7fmrZHdcbOaWb4rlRHvreHk6UKjY4mUmcq/iMF+2JXK8HdXk5JdSJuGXnx2Zx96tAw0\nOpaIiPzO4MgmfHRrLEFebmz/5aDNzpTTRscSKROVfxEDzVqTzIT4DWfX8F806RJaBnkZHUtERP5E\nj5YBfHbnJbRp6HX2XgArdqcaHUuk1FT+RQzgcLqY+sV2Hl+8HacLRvRsRty4Xrp5l4hILdAiyJNF\nky6hd+sgcovsTIhPYPbaQ0bHEikVlX+RapZdUMKE+A3ErU4GYPKgDrxwXSRuVv1zFBGpLfw8bcSP\n78V13ZvhcLqY8vk2HvlsK8V2p9HRRC5IbUOkGu1LzeHat1ax4pcVfd4a2Z07L9NSniIitZGb1cxL\nwyN5aFBHTCaYt+4wo6avJS2nyOhoIn9K5V+kmny34yTXvrWag+l5hPo34NNJfRgc2cToWCIiUgEm\nk4lJl7XhwzHR+Lhb2ZCcxTVvrmTbsWyjo4mcl8q/SBVzOl1MW7aXW2clkFtkJ6ZVIF/cfQldQv2M\njiYiIpXk8o6N+PzuS2jd0Ivj2YVc985qFm8+ZnQskT9Q+RepQrlFdibNTeTVZXsAGNO7JXMmxhDk\n7W5wMhERqWxtGnrz+V2XcHmHhhTZndz38Wae+2YndoeuA5CaQ+VfpIrsPZnD0LdW8e32k7hZzLx4\nXSRPXtMFm0X/7ERE6ipfDxvTx0Rz52VtAHjvpwOMmr6OVN0QTGoItRCRKvDZpqP8/c1V7E3NpZGP\nOx/fHsuI6OZGxxIRkWpgMZuYPKgjb43sjpebhXUHM7n69ZWs2Z9hdDQRlX+RylRY4uDhRVt4YH4S\nBSUO+rYN5pv7+tG9RYDR0UREpJoNjmzCF/f0pUOID+m5RYyavpa3ftiH0+kyOprUYyr/IpXkYHoe\nQ99ezUfrj2Aywf0D2xE/vhfBOr9fRKTe+vU6gOu6N8Ppgv98u5sJ8Rs4lV9sdDSpp1T+RSrB11tS\n+NsbK9mZcpogLzdmj4/h/oHtsZi1fr+ISH3XwM3CS8MjeeG6CNytZn7Yncbg11eSkJxpdDSph1T+\nRSogr8jOQwu3cNe8jeQW2enVKpBv7utH33bBRkcTEZEaxGQycUN0Cxbd2YeWQZ4cO1XAiPfW8Op3\ne7QakFQrlX+Rcko6coohb6xkfsKZ03zuvKwN8ybGEOLrYXQ0ERGpocKb+vHVPX0Z1i0UpwumLd/L\niPfWcCQz3+hoUk/UiPKfm5vL/fffT9OmTfHw8KBr1658/PHHF31eXFwcJpPpvH9OnDhRDcmlPnI4\nXbz1wz6ue+fM3Xqb+Hkwb2Iskwd1xKplPEVE5CJ8PGy8ckNXpt3YFR93KxsPn+Kv037ms01HjY4m\n9YDV6AAAw4YNY8OGDTz//PO0b9+eefPmcdNNN+F0Ohk5cuRFnz9z5kw6dux4zragoKCqiiv12LFT\nBTwwfzPrD545T3NwRBOeHRqBn6fN4GQiIlLbXNM1lO4tAnhg/mYSDmXxwPwkVuxO49/XdMGvgd5X\npGoYXv6/+eYbvvvuu7OFH+Dyyy/n0KFDPPjgg9xwww1YLJYLfo4uXbrQs2fP6ogr9ZTL5eLjDUd4\n5uud5BbZ8XKz8OQ1Xbiueygmky7qFRGR8mke6MnHt8Xy1g/7ef37vSzefJx1BzJ57roILu/QyOh4\nUgcZfo7CZ599hre3N8OHDz9n+7hx4zh+/Djr1q0zKJnIGcdPFTBm5gYeXrSV3CI7PVoG8M19/bi+\nRzMVfxERqTCrxcx9A9vxye29CQvy5MTpQsbN3MCDC5LILigxOp7UMYaX/23bttGpUyes1nN/CREZ\nGXn24xczZMgQLBYLgYGBDBs2rFTPEbkYl8vF/A2HuerVn/hpTxruVjOPDe7EJ7f3pmWQl9HxRESk\njunRMoAl9/Vn/CWtMJlgQeJRrnr1J37YnWp0NKlDTC6Xy9DbzLVv357WrVuzdOnSc7anpKTQtGlT\nnn32WR5++OHzPnfp0qWsXLmS2NhYfH192bp1K88//zxZWVmsWrWKqKiocx7vdDrJyck5Z9vhw4dx\nOqt+ia2Skv/tudtsOo+vrKp7fql5dt7ZkMXGlCIAOgS7cW9MAM18a+ffnV5/5afZVYzmVzGaX/nV\n9tntSCvi9bVZpOTaAbiilSfju/vj7VY9x21r+/yMVN2zM5vNtGjR4pxtPj4+mM3nf60Yfs4/cMFT\nJy70sUGDBjFo0KCz/79///4MHjyYiIgIHn/8cRYvXnzRr22323E4HGULXEG/fVFI2VXl/BxOF1/v\ny2f+9lyKHGAzw43h3gxp74nFVDf+7urC92AUza5iNL+K0fzKrzbOrp2/mZcGBjJvWy7f7Mtn+cF8\nElMKGRflQ59m7tV62mltnF9NUR2zu9i1sb9nePkPCgoiIyPjD9szM8+sphIYGFimzxcWFkbfvn1Z\nu3ZtqR5vtVr/dM+oMmkPumKqY357Mop5e30WB0+d+VrhDd24s1ftPdr/W3r9lZ9mVzGaX8VofuVX\nF2Zns8Ft0YH0C/Pi9XVZHM+x8+q6bH487M7tPQNo7F11Na4uzM8oRhz5LwvDy39ERAQfffQRdrv9\nnPP+t27dCpxZyaesXC5XqQcRHh5eLeU/KSmJkpISbDbbH05HkouryvnlFJbw0re7mbU2FZcL/D1t\nPHJ1J4bXoQt69forP82uYjS/itH8yq8uzS4KuPZSB+/+uJ+3f9jPxpQi7l2Syr1XtOPWfq1xs1Z+\nj6lL86tu1T27853WfiGGX/A7dOhQcnNz+fTTT8/ZHh8fT9OmTYmJiSnT5zt48CCrVq0iNja2MmNK\nHeR0uliYeJQBL/9I/JpDuFwwrFsoy/9xKSN6Nq8zxV9ERGo/D5uF+we2Z+n9/ejTJogiu5P/fLub\nwa//zKp96UbHk1rE8CP/f/3rX/nLX/7CpEmTOH36NG3btuWjjz5i6dKlzJkz5+x5TBMmTCA+Pp79\n+/fTsmVLAAYOHEj//v2JjIw8e8Hviy++iMlk4qmnnjLy25IaLunIKZ74Yjubj5wCICzIk6evjaBv\nu2CDk4mIiPy51g29mTsxhs83H+Ppr3ayNzWXUdPXcWXnEB4d3Emr0clFGV7+ARYtWsSjjz7K448/\nTmZmJh07duSjjz7ixhtvPPsYh8OBw+Hgt4sTRUREMH/+fF566SUKCgpo1KgRAwYMYMqUKbRv396I\nb0VquLScIl5cuosFiWduoe7lZuGeK9ox7pIw3K1lu2BGRETECCaTiaHdmnF5h0a8tmwvs9ce4r87\nTrJidxrj+7bi7gFt8XavERVPaqAa8crw9vZm2rRpTJs27U8fExcXR1xc3DnbXn311SpOJnVFQbGD\nD1cd5N0V+8kpOrNs2rDuofzfoI408vUwOJ2IiEjZ+Xu6MfXv4YyKacG/v9rBz3vTeffH/SxMPMrk\nQR24vnszzGadwirnqhHlX6Sq2B1OFiYe5dVlezh5+sya/ZHN/Jj693C6twgwOJ2IiEjFtQvxYdb4\nXny/K5Wnv97JwfQ8Ji/cwsxVyUy+qgOXdWio69jkLJV/qZNcLhff7TjJi9/uZl9qLgDNAhrwrys7\n8PeopjoSIiIidYrJZOKKTiH0a9eQ+NXJvP79XnamnGZc3AZ6hQUyeVAHeoaVbfl0qZtU/qXOWXcg\ng/98u5uEQ1kABHjauHtAO0bHttB5/SIiUqe5Wc3c2r811/doxrs/7idudTLrkzO5/t01DOzUiH9d\n1YGOjX2NjikGUvmXOmPN/gymLd/D2gNnbhDnYTMzoW8rbr+0Db4eukGJiIjUHwFebjx8dSfGXhLG\n68v38knCUZbtTGX5rlT+HtWUewa0pW0jH6NjigFU/qVWc7lcrDmQwWvL9rL+4JnSb7OYGNGzOfde\n0Y4QXcwrIiL1WBO/Bjw3LJJb+7Xm5e/28PWWFBZvPs4XSce5uksT7h7Qlk5N9JuA+kTlX2oll8vF\nqn0ZvL58L+uTz5R+N4uZG6KbM+myNjT1b2BwQhERkZqjdUNv3hrZnUmXZvPG93v5dvtJvt6awtdb\nU/hL5xDuGdCWyGb+RseUaqDyL7WK3eni803HeP+nA+xIOQ2cOb/xpujm3HFZG5r4qfSLiIj8mS6h\nfrx3c092nTjNm9/v4+utKXy34yTf7ThJ//YNub1/a/q0CTI6plQhlX+pFfJLnCzdk8fX+wpIzz8G\nQAObhRuim3PHpW1o7KfTe0REREqrY2Nf3hzZnQfScnnrh30s3nycn/ak8dOeNDo29uGqllZim9qw\n6ZK5OkflX2q0I5n5zFl7iNlrUsgvOXN352Bvd8b2acno2Jb4e7oZnFBERKT2atPQm1dGdOX+K9oz\nY+UBPkk4yq4TOew6AfEeZga396ZF22ICvPR+W1eo/EuN43S6+HFPGrPXHuKH3am4znR+Qn0sXNvJ\nl3v+FoOHTUt2ioiIVJYWQZ48eU0X/vGXDsxbf5gPftxDZoGTuVtO8+nO5fw9qimjYloS2cxPNwyr\n5VT+pcbIzCtmQcIR5qw7xJHMgrPb+7ULpn8TF1ENLbi7uan4i4iIVBE/TxuTLmtDtG8OPyXn8NXe\nAg5klfBJwlE+SThKl1BfRvZqyTVdm+LlrhpZG+lvTQzlcLpYuS+dhYlH+Xb7CYrtTgB8PawM79mc\nUTEtaN3Qm6SkJEpKSr7G5CAAACAASURBVAxOKyIiUj/YLCb6t2jAgNY+2P1bMG/dYb7amsK2Y6d5\n5LOtPPvNTq7t1pQbo1sQ3tRXvw2oRVT+xRAH0nJZmHiURRuPceJ04dntXUJ9uSU2jL9FNaWBm47w\ni4iIGMlkMtEzLJCeYYFMGdKZTzceZe66wxxMz2PO2sPMWXuY9iHeDOvejKHdQnV/nVpA5V+qzf+3\nd+9xUdX5/8BfMzAXhmG4M8hFwFCQq2UGmoauZmi6huk3b60p9nA3y8taZklcFkqki0sFbW0u+EjX\n8hearYIVaOWqq6h5wZDwAgrKbXDkMlxmmM/vD2RynAF1BpiBeT8fj3kYn/l8znmft4O9z5nP55y6\npjbkFVXhm18qcbL8pqbdQcTDrHAPzBntjRBPunpACCGEmCNHWz6WTRiG2PF+OHpJhn8fv4rvf63G\nb9VNSM27gLT9F/C4vwuefcQLU4OlEPGpzDRH9LdC+pRc0Y7vzldh79kbOHJJhg515+pdLgeYGOCG\nOaO9MHmkGwTWdJWfEEIIGQg4HA7G+btgnL8LbrUokXvuBnadqkBh2U0cKq3DodI62PCs8IeRbng6\ndAgmBbjRt/lmhIp/0uvqm9tRUFyN3HM3cKi0DqrbBT8AhHraY2b4EDwzyhNu9NUgIYQQMqDZ2/Aw\n/7GhmP/YUJTLmrHrVCV2/VKBa/Ut2Hf2BvadvUEnAmaGin/SKy7XNuGHX6uRX1yNk+U3cUe9j0B3\nO8wM98DToUPg62JruiAJIYQQ0md8nG2x5skRWD1lOM5W3ELuuRvYd+4GKm7+fiIg5HEx3t8FfwiU\nYvJIN1ojYAJU/BODtKvU+OXqTRy4UIMfiqtxubZZ6/2gIRJMDZZiRpgH/N3EJoqSEEIIIf2Nw+Eg\n3NsB4d4OWD8tUOdEIL+4BvnFNcDuzht9TL59IhDiYQ8ul9b99TUq/sl9YYzhUm0zDpXW4r+ldTh6\nWQZFe4fmfZ4VB5HDnPFkkBSTR0rh6WBjwmgJIYQQYg7uPhEovtGIAxeqkV9cgzMVchRVNqCosgHp\nBaVwEQsw3t8Z4/xdMN7fBR5US/QJKv5JtyrlLSi8Uo8jlzoX79y41ar1vpMtHxOGu+DJICmeGOEK\niZBnokgJIYQQYu44HA6CPCQI8pDg5T8MR21jGw6W1OBAcQ0OldairqkN35y+jm9OXwcADHOxxTh/\nZ4z3d0HkMGc4iPgmPoLBgYp/AgBQqxku1jbh+JV6nCirR2HZTVTKW7T68K25GOPriAnDXTHe3wVB\nQyT09RwhhBBCDOJqJ8D/PeqN/3vUG22qDpwql+PwxTr892IdzlbIcbmuGZdvP08AAAKkdhjt64gx\nvo541McJXo42dHtwA1Dxb6FuKZQ4WynH2Ypb+OWqHCfK6yFXaD9B14rLQYiHBI/5OWHCcFeM8XWi\nFfqEEEII6XUCayuMfcgZYx9yxqtPBeBWixLHLss0JwOXaptRUt2IkupG/PtY58mAu0SI0b6OGD3U\nEeHe9ggaYk91yn2g4t8CKNpVKKpswNmKzmL/bIUcZTKFTj8hj4uHvR0xxs8Jj/k64eGhDrAV0EeE\nEEIIIf3L3oaHqcHumBrsDqDzQaEnym7iZHnn7ISiyluoamjV3EUI6HyG0AipHUI97RHm7YAwT3sE\nDrGjZwndhSq7QaRDzVAua0ZJVSOKqxpRUtWAkqpGlNcrwJhu/6FOIoR52SPcywGjfR0R4mEPvjW3\n/wMnhBBCCOmBi1iA6BB3RId0ngy0tHfgTIUchVfqcaZCjjMVt1Db2IYLVY24UNWI/3eyAkDnDUke\nchUjwN0OAe52CHS3Q4C7BB72QoudMkTF/wDUpurAtXoFLtd2zoW7VNOEkupG/FbdiFalWu8YqUSA\nMC8HhHvZI8zLAWFe9rRwhhBCCCEDkg3fCpHDnBE5zFnTVt3QijPX5DhXeUsz0+GmQqk5IbiTncAa\nI26fEIxwE8PPVQw/Z1t4OtrAapCvZ6Ti30y1KjtwXd6CipstKJd1FvlX6ppxubYZFTcVWg/RupOQ\nx8UIqR0CpJ0f6JFDJAhwt4OLWNC/B0AIIYQQ0o+kEqHWVCHGGCrlLbhwo3OtQElV5+tSbRMa21Q4\nWX4TJ8tvam2Db8XFUGcRfJ1tMczVFn4utvB1toW3kw3cJUJYWw38GRJU/JsAYwxNbSpUN7RpCvyK\nmwqtP2sa23rchi3fCsNcxfBz6fxwBkjtEDhEgqFOokF/xkoIIYQQci8cDgdejiJ4OYowJUiqaW9X\nqXGlrhkXbk+PvlTbhCt1zSiTKdCuUuNiTRMu1jQBxdrbs+Jy4C4RwtPRBl6ONp3bduj8b09HG0gl\nQgh55r++wCyK/6amJsTFxWHnzp2or69HYGAg1q9fj3nz5t1zbE1NDdatW4e9e/dCoVAgPDwcKSkp\nmDx5cj9Ero0xhoYWFWTNbahpbEN1QytqGjr//O2aDHXNKsjbGOQ5N7QekNUdG54VvJ1s4O0oun32\nKcYwV1sMc7GFq53AYueqEUIIIYQYim/N1awBuFOHmuHGrRZcuWO2RedJQTOuy1ug7Oj8JqFS3oLj\nV/Rv296GBwmPwVHIhbPIGgHXL0AqEUAqEUIqEcBVLISTmA9bvpXJ6jizKP5nz56NwsJCpKamYsSI\nEfj3v/+N+fPnQ61WY8GCBd2Oa2trw+TJkyGXy5Geng43NzdkZGQgOjoa+fn5iIqKMjimNlUHGltV\naGhRorFVhVstStxUtKO+uR03m9sha27X/Nz5UkKuaIequ/k4etgJreEuEcLbSXT7DPL2WeTtPx1F\nPCrwCSGEEEL6gRX3928KJgx31XpPrWaobWq7Y6ZG56tS3jlr47q8Ba1KNW61KHGrBbjWAADtOFh2\nSe+++FZcONry4GQrgJMtD44iPpxt+XC05cPp9stRxIdEyIPExhoSIQ92QutemXZk8uI/NzcXP/zw\ng6bgB4BJkyahvLwcr732Gp577jlYWen/CmXLli0oKirCkSNHMHbsWM3Y8PBwrFu3DseOHbvn/tfn\nnMWNhjY0tKrQ2KJEQ6sKDa1KtKv0L5y9H2KBNdzsBHDTnOkJoWqUQcIH3MR8jHs4GG4SAUR8k6ef\nEEIIIYTcA5fL0dR0o31032eMoaFVhZqGVhw5/Svqmtpxqx3g2jqh9vZskOrGVtQ2tqFVqUZ7hxrV\nDW2obuh5mvfdRHwr2Al/PxmQ2PDgLhHgjSm+970Nk1efu3fvhlgsxty5c7XalyxZggULFuDYsWMY\nN25ct2MDAgI0hT8AWFtbY9GiRXjzzTdRWVkJT0/PHvf/w6/VuNmi6vZ9O0FnYu2E1nAU8eEk5sNJ\n1HlmpjlDE/1+luYg4umd73XmzBkolUrweDz4utj2GBMhhBBCCBk4OBwO7G14sLfhQeEuhFJpBR6P\nh/DwYJ2+Le0dqFe0o76pHfWKO2aUNLfrtDfevijdNV1c0d4BRXuH1kmDo431wCr+i4qKMHLkSFhb\na4cSFhameb+74r+oqAgTJkzQae8ae/78+XsW/4vC7WEFNUQ8LsR8LkQ8Dmz5XIh4XNhYc7pZPNsB\noOX2C4ACUCqA6lqgupv9KJVKzZ9nzpzpMSaii/JnHMqf4Sh3xqH8GYfyZzjKnXEof4Z7kNw5AHDg\nAn52ADRLEKxvv0Safio1g0KpRnN7159qNCsZmpVqqNmDTRE3efEvk8kwbNgwnXYnJyfN+z2N7er3\noGO7/MFHgI6OuxffMgAdUHcA6nuvy31gXR8KYhjKn3Eof4aj3BmH8mccyp/hKHfGofwZrjdzZ8MF\nbIQAhBwAv88y6W56fHdMXvwD6HFR670WvBozFuicJsTl9v09W+/8y+fxeH2+v8GG8mccyp/hKHfG\nofwZh/JnOMqdcSh/huvv3D1oHWvy4t/Z2VnvFfr6+noA0HtlvzfGdgkODu6X4v/OOf/h4eF9vr/B\nhvJnHMqf4Sh3xqH8GYfyZzjKnXEof4br79yp1Wo0Njbeu+NtJn9MWWhoKIqLi6FSaS+6PXfuHAAg\nJCSkx7Fd/R50LCGEEEIIIZbG5MV/TEwMmpqakJOTo9W+detWeHh4ICIiosexFy5c0Lqlp0qlwrZt\n2xAREQEPD48+i5sQQgghhJCBxuTTfqZNm4Ynn3wSf/nLX9DQ0AB/f3/s2LED+/fvx7Zt2zSLGGJj\nY7F161ZcunQJPj6dN1hdunQpMjIyMHfuXKSmpsLNzQ2ZmZkoKSlBfn6+KQ+LEEIIIYQQs2Py4h8A\ndu3ahQ0bNiA+Ph719fUIDAzEjh07MG/ePE2fjo4OdHR0gLHfn6ArEAhQUFCAdevW4ZVXXoFCocCo\nUaOQl5dn1NN9CSGEEEIIGYzMovgXi8VIT09Henp6t32ys7ORnZ2t0y6VSrF169b72s+dJw5d1GrD\nn+T7ILhcLqysrMDlcvttn4MJ5c84lD/DUe6MQ/kzDuXPcJQ741D+DNffudO3D301bxcO6+ndQUal\nUqG5udnUYRBCCCGEENJnbG1tdR6g28XkC34JIYQQQggh/YOKf0IIIYQQQiwEFf+EEEIIIYRYCIua\n869Wq3UWRXA4HHA4HBNFRAghhBBCiOEYYzoLfLlcLrhc/df4Lar4J4QQQgghxJLRtB9CCCGEEEIs\nBBX/RmpsbMS6deswdepUuLq6gsPhIDEx0aBtxcXFgcPhICQkpHeDNGPG5C87O1szbevuV1VVVd8G\nbgZ647O3Z88eREVFQSKRwNbWFsHBwfjss8/6JmAzY0z+Jk6c2O1njz5/9+fgwYN48skn4ebmBrFY\njLCwMHz44Yfo6Ojou6DNhLG5++677/D444/DxsYG9vb2mDlzJs6fP993AZuRAwcOYOnSpQgMDISt\nrS08PT0xa9YsnDx58r7G19TU4IUXXoCLiwtEIhHGjh2LgoKCPo7afBiTv4qKCqxevRpRUVFwcHAA\nh8PR+/ylwcqY3O3atQvz58+Hv78/bGxs4Ovri4ULF6K0tLQfItdFxb+RZDIZPvvsM7S1teGZZ54x\neDunT5/Ge++9B6lU2ovRmb/eyF9WVhaOHj2q9XJ2du7lSM2PsblLTU3F7NmzERISgp07d+Lbb7/F\nSy+9hPb29j6I1vwYk7/MzEydz1xBQQF4PB4iIyPh7u7eR1GbD2Pyl5+fjylTpkClUuGf//wnvvnm\nG0ycOBGrVq3CX//61z6K2HwYk7s9e/Zg2rRpcHNzQ05ODv7xj3+gtLQUEyZMwKVLl/ooYvPxySef\noKysDKtWrUJubi7S09NRU1ODyMhIHDhwoMexbW1tmDx5MgoKCpCeno49e/ZAKpUiOjoaP/30Uz8d\ngWkZk7+LFy9i+/bt4PP5mD59ej9FbD6Myd2mTZugUCiwYcMG7N+/HykpKfjll1/wyCOPmObEnRGj\nqNVqplarGWOM1dbWMgAsISHhgbahVCrZqFGj2MqVK1lUVBQLDg7ug0jNkzH5y8rKYgBYYWFhH0Zo\nvozJ3YkTJxiXy2WbNm3qwwjNW2/87t4pOzubAWCff/55L0Vo3ozJ38KFC5lAIGBNTU1a7VOnTmUS\niaS3QzU7xuQuICCAhYWFacYzxlhZWRnj8/lswYIFfRGuWamurtZpa2xsZFKplE2ePLnHsRkZGQwA\nO3LkiKZNqVSyoKAg9thjj/V6rObImPx1dHRo/ruwsJABYFlZWb0dotkyJnf6xlZWVjIej8diY2N7\nLcb7RVf+jdQbdwtKTU1FfX093n777V6KauCguy0ZzpjcffzxxxAIBHjllVd6OaqBo7c/e1u2bIFY\nLMZzzz3Xa9s0Z8bkj8fjgc/nw8bGRqvdwcEBQqGwN8Iza4bmTiaToaSkBNOmTdMa7+Pjg5CQEHzz\nzTeDftqUm5ubTptYLEZQUBCuXbvW49jdu3cjICAAY8eO1bRZW1tj0aJFOH78OCorK3s9XnNjTP66\nu3OMpTAmd/rGenh4wMvL655j+4Jl/02agV9//RUpKSn45JNPIBaLTR3OgDRjxgxYWVnByckJs2fP\nRlFRkalDMns///wzRo4ciZycHAQEBMDKygpeXl5Yv369xUz76U2lpaU4dOgQ5s2bR7/H9+HPf/4z\n2tvbsXLlSly/fh1yuRxffPEFdu/ejXXr1pk6PLPV9bspEAh03hMIBFAoFBYx9edut27dwqlTpxAc\nHNxjv6KiIoSFhem0d7VZyrqJu91v/oguY3J3+fJllJeXmyTv1v2+R6KhVquxdOlSzJ492yLnzxnL\n3d0dGzZsQGRkJCQSCc6dO4fU1FRERkbi8OHDCA8PN3WIZquyshK1tbVYuXIlkpOTERQUhIKCAqSm\npuLatWvYvn27qUMcULZs2QIAiI2NNXEkA0NERAQOHDiAuXPnIiMjAwBgZWWFjRs3Yu3atSaOznxJ\npVI4OTnh8OHDWu1yuVxz0UMmk5kiNJNasWIFmpubsWHDhh77yWQyODk56bR3tVli7oD7zx/RZWju\nVCoVYmNjIRaLsWbNmj6KrntU/JvQBx98gNLSUnz77bemDmVAio6ORnR0tObnJ554Ak8//TRCQ0MR\nHx+PPXv2mDA686ZWq9HY2IgdO3Zg3rx5AIBJkyahubkZf//735GUlAR/f38TRzkwqFQqbN26FcHB\nwYiMjDR1OAPCyZMnERMTg4iICHz66aewtbXFgQMHEBcXh9bWVrz11lumDtEscblcrFixAsnJyUhO\nTsby5cvR0NCA1atXQ6FQaPpYkrfeegvbt2/HRx99hNGjR9+zf0/TrSxxCuqD5o/8ztDcMcYQGxuL\nQ4cOIScnB97e3n0YpX6W9a+EGbl69Sri4+ORkJAAPp8PuVwOuVwOlUoFtVoNuVyOlpYWU4c54Pj6\n+mL8+PH43//+Z+pQzFrX3ZCeeuoprfZp06YBAE6dOtXvMQ1Uubm5qKqqwrJly0wdyoCxYsUKSKVS\n7N69GzNmzMCkSZOQnJyM9evXIzExEZcvXzZ1iGYrPj4ea9asQUpKCqRSKYYPHw4AWLJkCQDA09PT\nlOH1q6SkJKSkpODtt9/Gyy+/fM/+zs7Oeq/u19fXA4DebwUGswfNH/mdobljjGHZsmXYtm0bsrOz\nMWvWrD6MsntU/JvI5cuX0dLSglWrVsHR0VHzOnz4MIqLi+Ho6Ig33njD1GEOSIwxi7v69aD0zXsF\noHk8OOXv/m3ZsgV8Ph/PP/+8qUMZME6fPo3Ro0fDyspKq33MmDFQq9UoLi42UWTmz9raGh988AFk\nMhnOnj2L69evY+/evbh69Sr8/Pzg5eVl6hD7RVJSEhITE5GYmIg333zzvsaEhobi3LlzOu1dbZb0\njB1D8kc6GZq7rsI/KysLn3/+ORYtWtSHUfaM/g9vIqNGjcLBgwd1XuHh4fD19cXBgwfpTNwAV65c\nweHDh2n6xT08++yzAIC8vDyt9tzcXHC5XIwZM8YUYQ04VVVVyM3NxTPPPGMRz5boLR4eHjhx4oTO\nnWmOHj0KABZTwBpDLBYjNDQUQ4YMwalTp1BQUIBVq1aZOqx+kZycjMTERMTFxSEhIeG+x8XExODC\nhQs4duyYpk2lUmHbtm2IiIiAh4dHX4RrdgzNHzE8d4wxvPjii8jKysKnn36q+abOVGjOfy/Iy8tD\nc3MzGhsbAXTewefrr78GAEyfPh0ikQixsbHYunUrLl26BB8fHzg4OGDixIk623JwcIBKpdL73mBl\nSP4AYMqUKXjiiScQFhamWfCblpYGDoeD5ORkkx1PfzI0d0uWLMGnn36Kl156CXV1dQgKCkJ+fj4y\nMjLw0ksvafoNdobmr8vWrVuhUqksdsqPoflbs2YNVq5ciZkzZ2L58uUQiUQoKCjA+++/jylTpljE\nYn1Dc/fjjz+isLAQYWFhYIzh+PHj2LRpE6Kjoy3igtH777+P+Ph4REdH4+mnn9aZ4tl14Udf7pYu\nXYqMjAzMnTsXqampcHNzQ2ZmJkpKSpCfn9/vx2IKxuQPgOYz2jU178SJE5o7nM2ZM6c/DsFkjMnd\nypUrsWXLFixduhShoaFaYwUCAR5++OH+OxCAHvLVG3x8fBgAva8rV64wxhhbvHix1s/dsbSHfDFm\neP5Wr17NgoKCmJ2dHbO2tmYeHh5s0aJFrKSkxDQHYgLGfPZkMhlbvnw5k0qljMfjsREjRrB3331X\n60Eug52xv7sjRoxgvr6+Wg9csiTG5C8nJ4eNHz+eubi4MFtbWxYcHMySk5N1Hvw1WBmau8OHD7OI\niAgmkUiYQCBgISEh7L333mPt7e2mOZB+FhUV1W3e7ixpuvvcVVVVsT/96U/MycmJCYVCFhkZyX74\n4Yd+PgrTMTZ/9zN2sDImdz39vvv4+PT7sXAYuz3JlxBCCCGEEDKo0Zx/QgghhBBCLAQV/4QQQggh\nhFgIKv4JIYQQQgixEFT8E0IIIYQQYiGo+CeEEEIIIcRCUPFPCCGEEEKIhaDinxBCCCGEEAtBxT8h\nhPSjY8eOISYmBkOHDoVAIIBUKsXYsWOxdu1arX6ZmZnIzs7ukxgmTpzY508RP3LkCBITEyGXy++r\nf2JiIjgcDurq6vS+HxISYnDMxhzvCy+8oHmCaU8UCgUSExPx448/GrQfQgjpL1T8E0JIP9m3bx/G\njRuHhoYGpKWl4fvvv0d6ejoef/xxfPXVV1p9+7L47w9HjhxBUlLSfRf/fSkzMxOZmZl9ug+FQoGk\npCQq/gkhZs/a1AEQQoilSEtLg5+fH7777jtYW//+z++8efOQlpZmwsgGt6CgIFOHQAghZoOu/BNC\nSD+RyWRwcXHRKvy7cLm//3Ps6+uL8+fP46effgKHwwGHw4Gvry8AIDs7GxwOB2VlZVrjf/zxR3A4\nHK0rz4wxpKWlwcfHB0KhEI888gjy8vL0xtbQ0IBXX30Vfn5+4PP58PT0xOrVq9Hc3KzVj8Ph4OWX\nX8YXX3yBkSNHQiQSITw8HHv37tX0SUxMxGuvvQYA8PPz0xxDb18Vb29vR0pKCgIDAyEQCODq6ool\nS5agtrZWq5++aT8VFRWYM2cO7Ozs4ODggIULF6KwsBAcDkfvNy4XL17E9OnTIRaL4e3tjbVr16Kt\nrQ0AUFZWBldXVwBAUlKS5nhfeOGFXj1eQgjpDXTlnxBC+snYsWPx+eefY+XKlVi4cCEeeeQR8Hg8\nnX67d+/GnDlzYG9vr5muIhAIHnh/SUlJSEpKQmxsLObMmYNr167hxRdfREdHBwICAjT9FAoFoqKi\nUFFRgTfffBNhYWE4f/484uPjce7cOeTn54PD4Wj679u3D4WFhfjb3/4GsViMtLQ0xMTEoKSkBMOG\nDcOyZctQX1+Pjz76CLt27cKQIUMA3N8V+I6ODqhUqnv2U6vVmDVrFg4dOoR169Zh3LhxKC8vR0JC\nAiZOnIgTJ07AxsZG79jm5mZMmjQJ9fX12LRpE/z9/bF//34899xzevsrlUr88Y9/RGxsLNauXYuf\nf/4ZycnJsLe3R3x8PIYMGYL9+/cjOjoasbGxWLZsGQBoTggIIcSsMEIIIf2irq6OjR8/ngFgABiP\nx2Pjxo1jGzduZI2NjVp9g4ODWVRUlM42srKyGAB25coVrfaDBw8yAOzgwYOMMcZu3rzJhEIhi4mJ\n0ep3+PBhBkBr2xs3bmRcLpcVFhZq9f36668ZAJabm6tpA8CkUilraGjQtFVVVTEul8s2btyoaXv3\n3Xf1xtmdhIQETV66e90Z844dOxgAlpOTo7WdwsJCBoBlZmZq2qKiorTGZmRkMAAsLy9Pa+zy5csZ\nAJaVlaVpW7x4MQPAdu7cqdV3+vTpLCAgQPNzbW0tA8ASEhLu63gJIcRUaNoPIYT0E2dnZxw6dAiF\nhYVITU3FrFmz8Ntvv+GNN95AaGhot3e6McTRo0fR2tqKhQsXarWPGzcOPj4+Wm179+5FSEgIRo0a\nBZVKpXk99dRTeqfrTJo0CXZ2dpqfpVIp3NzcUF5ebnTc+fn5KCws1Hk99NBDOjE7ODhg5syZWjGP\nGjUK7u7uPU4x+umnn2BnZ4fo6Git9vnz5+vtz+FwMHPmTK22sLCwXjleQgjpbzTthxBC+tmjjz6K\nRx99FEDnlJLXX38dmzdvRlpaWq8t/JXJZAAAd3d3nffubquursbFixf1TkECoHNS4uzsrNNHIBCg\npaXF0HA1wsPD4eLiotMuFAq1fq6uroZcLgefz9e7nZ5OpGQyGaRSqU67vjYAEIlEOvsXCARobW3t\ndh+EEGKuqPgnhBAT4vF4SEhIwObNm1FUVHTP/l1FaNdi0y7dFehVVVU626iqqtIsIAYAFxcX2NjY\n4F//+pfefeorxk3NxcUFzs7O2L9/v9737/xm4m7Ozs44fvy4Tru+XBFCyGBDxT8hhPSTGzduaBa/\n3qm4uBgA4OHhoWnr7kp6V9F+9uxZrUW73377rVa/yMhICIVCbN++Hc8++6ym/ciRIygvL9cq/mfM\nmIF33nkHzs7O8PPzM+jY7ta1QLk3vg3QZ8aMGfjyyy/R0dGBiIiIBxobFRWFnTt3Ii8vD9OmTdO0\nf/nllwbH09fHSwghvYWKf0II6SdPPfUUvLy8MHPmTAQGBkKtVuP06dN4//33IRaLsWrVKk3f0NBQ\nfPnll/jqq68wbNgwCIVChIaGYsyYMQgICMCrr74KlUoFR0dH7N69G//973+19uXo6IhXX30VKSkp\nWLZsGebOnYtr164hMTFRZ9rP6tWrkZOTgyeeeAJr1qxBWFgY1Go1rl69iu+//x5r16594AI7NDQU\nAJCeno7FixeDx+MhICCgxyvyD2LevHnYvn07pk+fjlWrVuGxxx4Dj8dDRUUFDh48iFmzZiEmJkbv\n2MWLF2Pz5s1YtGgRUlJS4O/vj7y8PHz33XcAtG+7er/s7Ozg4+ODPXv2YPLkyXBycoKLi4vWSRYh\nhJgFU684JoQQS/HVV1+xBQsWsOHDhzOxWMx4PB4bOnQoe/7559mvv/6q1besrIxNnTqV2dnZMQDM\nx8dH895vv/3GJIFk/wAAAbNJREFUpk6dyiQSCXN1dWWvvPIK27dvn9bdfhhjTK1Ws40bNzJvb2/G\n5/NZWFgY+89//qNz9xvGGGtqamJxcXEsICCA8fl8Zm9vz0JDQ9maNWtYVVWVph8AtmLFCp1j8/Hx\nYYsXL9Zqe+ONN5iHhwfjcrk6sd2t624/tbW1et/Xd/cjpVLJ3nvvPRYeHs6EQiETi8UsMDCQLV++\nnJWWlmr66Tveq1evstmzZzOxWMzs7OzYs88+y3JzcxkAtmfPHk2/xYsXM1tb227jvVN+fj57+OGH\nmUAgYAB08kEIIeaAwxhjpjv1IIQQQszDO++8g7i4OFy9ehVeXl6mDocQQvoETfshhBBicT7++GMA\nQGBgIJRKJQ4cOIAPP/wQixYtosKfEDKoUfFPCCHE4ohEImzevBllZWVoa2vD0KFD8frrryMuLs7U\noRFCSJ+iaT+EEEIIIYRYCHrCLyGEEEIIIRaCin9CCCGEEEIsBBX/hBBCCCGEWAgq/gkhhBBCCLEQ\nVPwTQgghhBBiIaj4J4QQQgghxEJQ8U8IIYQQQoiFoOKfEEIIIYQQC0HFPyGEEEIIIRbi/wPacJ7y\nMrRUegAAAABJRU5ErkJggg==\n", "text/plain": [ "" ] }, "metadata": {}, "output_type": "display_data" } ], "source": [ "from filterpy.stats import plot_gaussian_pdf\n", "plt.figure()\n", "plot_gaussian_pdf(mean=1.8, variance=0.1414**2, \n", " xlabel='Student Height', ylabel='pdf');" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "This curve is a [*probability density function*](https://en.wikipedia.org/wiki/Probability_density_function) or *pdf* for short. It shows the relative likelihood for the random variable to take on a value. In the chart above, a student is somewhat more likely to have a height near 1.8 m than 1.7 m, and far more likely to have a height of 1.9 m vs 1.4 m.\n", "\n", "> I explain how to plot Gaussians, and much more, in the Notebook *Computing_and_Plotting_PDFs* in the \n", "Supporting_Notebooks folder. You can read it online [here](https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/Supporting_Notebooks/Computing_and_plotting_PDFs.ipynb) [1].\n", "\n", "This may be recognizable to you as a 'bell curve'. This curve is ubiquitous because under real world conditions many observations are distributed in such a manner. I will not use the term 'bell curve' to refer to a Gaussian because many probability distributions have a similar bell curve shape. Non-mathematical sources might not be as precise, so be judicious in what you conclude when you see the term used without definition.\n", "\n", "This curve is not unique to heights — a vast amount of natural phenomena exhibits this sort of distribution, including the sensors that we use in filtering problems. As we will see, it also has all the attributes that we are looking for — it represents a unimodal belief or value as a probability, it is continuous, and it is computationally efficient. We will soon discover that it also has other desirable qualities which we may not realize we desire.\n", "\n", "To further motivate you, recall the shapes of the probability distributions in the *Discrete Bayes* chapter:" ] }, { "cell_type": "code", "execution_count": 15, "metadata": {}, "outputs": [ { "data": { "image/png": "iVBORw0KGgoAAAANSUhEUgAAAusAAAEgCAYAAAANPj3XAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzt3X1wVNX9x/FPNgkJSVBIeLALEkrT\niCSBWKtpOlVIMSAoU4OTIlFHIYiNiIb2BxZCeRAraae0pq22VNCkRjYdDdRiAQcQbKsSwAckCI6N\nJVCxComQB3xgd+/vD4fImgTYaPYe9r5fM8zEs3t2v+c7G/ns5dx7IyzLsgQAAADAOC67CwAAAADQ\nMcI6AAAAYCjCOgAAAGAowjoAAABgKMI6AAAAYCjCOgAAAGAowjoAAABgKMI6AAAAYCjCOgAAAGCo\noMN6c3Oz5s6dq7Fjx6pfv36KiIjQ4sWLz3n+Bx98oNtvv119+/ZVXFycsrOztWXLlmDLAAAAAMJe\n0GG9oaFBf/rTn/TJJ5/ohhtuCGruJ598ojFjxmjLli0qKyvTM888owEDBujaa6/VCy+8EGwpAAAA\nQFiLCnZCcnKyPvzwQ0VEROjo0aNauXLlOc9dtWqVamtr9dJLLyk7O1uSlJOTo5EjR2ru3Lmqqalp\ne67f75ff7w+YHxERoYiIiGBLBgAAAGxnWZYsywoYc7lccrk6P34edFj/MmF57dq1uuSSS9qCuiRF\nRUXplltu0fz58/Xuu+9q4MCBkj4L662trV1+LwAAAMB08fHxZwzrIT3BtLa2ViNGjGg3fmps7969\noSwHAAAAMFpIw3pDQ4MSExPbjZ8aa2hoCGU5AAAAgNFCfunGM22jYT86AAAA8Lmg96x/GUlJSR0e\nPW9sbJSkgKPuHQX3s+3pOZ/t3btXXq9XUVFRSktLs7uckHP6+iV6INEDp69fogdOX79ED5y+fim8\ne9DROZlnO1gd0rCekZGhPXv2tBs/NZaent421lHhZztb9nzm9/vl8/nCeo1n4vT1S/RAogdOX79E\nD5y+fokeOH39kvN6cLawHtIO5OXlaf/+/QGXaPR6vaqsrFRWVpbcbncoywEAAACM1qUj6xs2bFBr\na6uam5slSW+++aaefvppSdKECRMUFxenwsJCVVRUqK6uTsnJyZKkadOm6eGHH1Z+fr5KS0vVv39/\nPfLII3rrrbe0efPmr2hJAAAAQHjoUlgvKipSfX19238/9dRTeuqppyRJ//nPfzRkyBD5fD75fL6A\nC7/HxMRoy5Ytmjt3rmbNmqUTJ04oMzNTGzZs0KhRo77kUgAAAIDw0qWwfuDAgbM+p7y8XOXl5e3G\nBwwYoIqKiq68LQAAAOAo4b9rHwAAADhPEdYBAAAAQxHWAQAAAEMR1gEAAABDEdYBAAAAQxHWAQAA\nAEMR1gEAAABDEdYBAAAAQxHWAQAAAEMR1gEAAABDEdYBAAAAQxHWAQAAAEMR1gEAAABDEdYBAAAA\nQxHWAQAAAEMR1gEAAABDEdYBAAAAQxHWAQAAAEMR1gEAAABDEdYBAAAAQxHWAQAAAEMR1gEAAABD\nEdYBAAAAQxHWAQAAAEMR1gEAAABDEdYBAAAAQxHWAQAAAEMR1gEAAABDEdYBAAAAQxHWAQAAAEMR\n1gEAAABDEdYBAAAAQxHWAQAAAEMR1gEAAABDEdYBAAAAQxHWAQAAAEMFHdZbWlpUXFwst9ut2NhY\nZWZmqqqq6pzmbt26Vbm5uerfv78SEhI0YsQI/fa3v5XP5wu6cAAAACDcRQU7YdKkSdq5c6dKS0uV\nmpqq1atXa8qUKfL7/SooKOh03ubNmzVu3DhdffXVevTRRxUfH6+//e1vuvfee1VXV6eysrIvtRAA\nAAAg3AQV1tevX69Nmza1BXRJysnJUX19vebMmaPJkycrMjKyw7nl5eWKjo7Ws88+q/j4eEnSNddc\no7feekvl5eWEdQAAAOALgtoGs3btWiUkJCg/Pz9gfOrUqTp8+LBqamo6nRsdHa0ePXqoZ8+eAeO9\ne/dWbGxsMGUAAAAAjhBhWZZ1rk/Ozs6Wz+fTjh07Asb37t2r9PR0rVixQjNmzOhwbk1NjUaNGqXp\n06dr/vz5iouL07p161RYWKhly5bpJz/5ScDz/X6/mpubA8YOHjwov99/ruWeV06ePNn2c3R0tI2V\n2MPp65fogUQPnL5+iR44ff0SPXD6+qXw7oHL5dLgwYMDxnr16iWXq/Pj50Ftg2loaNDQoUPbjScm\nJrY93pmsrCw9//zzys/P18MPPyxJioyM7DCod8br9TriZNTTP6RO5PT1S/RAogdOX79ED5y+foke\nOH39Uvj1oLPt4mcS9AmmERERXXrslVdeUV5enrKysrRixQrFx8fr+eef14IFC/Txxx/rZz/72dmL\njYo64zeP81k4f4s8F05fv0QPJHrg9PVL9MDp65fogdPXL4V3D7qSY4MK60lJSR0ePW9sbJT0+RH2\njsycOVMDBgzQ2rVr275V5OTkyOVyafHixbr55ps7PGp/urS0tLAN67t379bJkycVHR2tkSNH2l1O\nyDl9/RI9kOiB09cv0QOnr1+iB05fvxTePehom/fZBJV8MzIytG/fPnm93oDxPXv2SJLS09M7nfv6\n66/r8ssvb3f4/4orrpDf79e+ffuCKQUAAAAIe0GF9by8PLW0tKi6ujpgvKKiQm63W1lZWZ3Odbvd\n2rVrV7s95y+//LIkadCgQcGUAgAAAIS9oLbBjB8/Xrm5uSoqKlJTU5NSUlLk8Xi0ceNGVVZWth01\nLywsVEVFherq6pScnCxJmj17tu655x5NnDhRd955p+Li4rRlyxYtX75c11xzTdj9MwcAAADwZQV9\ngumaNWtUUlKihQsXqrGxUcOGDZPH49FNN93U9hyfzyefz6fTrwo5a9YsDRw4UL/5zW80ffp0ffTR\nRxoyZIgWLVqk2bNnfzWrAQAAAMJI0GE9ISFBZWVlZ7zjaHl5ucrLy9uNT5o0SZMmTQr2LQEAAABH\nCs9LqwAAAABhgLAOAAAAGIqwDgAAABiKsA4AAAAYirAOAAAAGIqwDgAAABiKsA4AAAAYirAOAAAA\nGIqwDgAAABiKsA4AAAAYirAOAAAAGIqwDgAAABiKsA4AAAAYirAOAAAAGIqwDgAAABiKsA4AAAAY\nirAOAAAAGIqwDgAAABiKsA4AAAAYirAOAAAAGIqwDgAAABiKsA4AAAAYirAOAAAAGIqwDgAAABiK\nsA4AAAAYirAOAAAAGIqwDgAAABiKsA4AAAAYirAOAAAAGIqwDgAAABiKsA4AAAAYirAOAAAAGIqw\nDgAAABiKsA4AAAAYirAOAAAAGCrosN7S0qLi4mK53W7FxsYqMzNTVVVV5zz/mWee0ahRo3TBBRco\nPj5eaWlp+tOf/hRsGQAAAEDYiwp2wqRJk7Rz506VlpYqNTVVq1ev1pQpU+T3+1VQUHDGuaWlpSop\nKdGPfvQjzZs3T9HR0dq/f78+/fTTLi8AAAAACFdBhfX169dr06ZNbQFdknJyclRfX685c+Zo8uTJ\nioyM7HDuK6+8opKSEi1btkxz585tGx8zZsyXKB8AAAAIX0Ftg1m7dq0SEhKUn58fMD516lQdPnxY\nNTU1nc79/e9/r5iYGM2aNatrlQIAAAAOE2FZlnWuT87OzpbP59OOHTsCxvfu3av09HStWLFCM2bM\n6HDuN77xDfXu3VuzZ8/W0qVL9e9//1tf+9rXdMstt+j+++9Xjx49Ap7v9/vV3NwcMHbw4EH5/f5z\nLfe8cvLkybafo6OjbazEHk5fv0QPJHrg9PVL9MDp65fogdPXL4V3D1wulwYPHhww1qtXL7lcnR8/\nD2obTENDg4YOHdpuPDExse3xzrz77rs6cuSI7rnnHi1dulTDhw/Xli1bVFpaqkOHDunJJ5886/t7\nvV75fL5gSj4vnf4hdSKnr1+iBxI9cPr6JXrg9PVL9MDp65fCrwedbRc/k6BPMI2IiOjSY6eOlHs8\nHt10002SPtvv3traqoceekhLlixRSkrKmYuNijrjN4/zWTh/izwXTl+/RA8keuD09Uv0wOnrl+iB\n09cvhXcPupJjgwrrSUlJHR49b2xslPT5EfbO5v7vf//TuHHjAsbHjx+vhx56SK+++upZw3paWlrY\nhvXdu3fr5MmTio6O1siRI+0uJ+Scvn6JHkj0wOnrl+iB09cv0QOnr18K7x50tM37bIJKvhkZGdq3\nb5+8Xm/A+J49eyRJ6enpnc4dMWJEh+OntsyHawgHAAAAuiqohJyXl6eWlhZVV1cHjFdUVMjtdisr\nK6vTuTfeeKMkacOGDQHj69evl8vl0hVXXBFMKQAAAEDYC2obzPjx45Wbm6uioiI1NTUpJSVFHo9H\nGzduVGVlZdum+cLCQlVUVKiurk7JycmSPru844oVK3TXXXfp6NGjGj58uDZv3qyHH35Yd911V9vz\nAAAAAHwm6BNM16xZo5KSEi1cuFCNjY0aNmxYwEmjkuTz+eTz+XT6VSGjo6O1adMmzZ8/Xw8++KAa\nGxv19a9/XaWlpfrxj3/81awGAAAACCNBh/WEhASVlZWprKys0+eUl5ervLy83XhiYqL++Mc/6o9/\n/GOwbwsAAAA4Dmd1AgAAAIYirAMAAACGIqwDAAAAhiKsAwAAAIYirAMAAACGIqwDAAAAhiKsAwAA\nAIYirAMAAACGIqwDAAAAhiKsAwAAAIYirAMAAACGIqwDAAAAhiKsAwAAAIYirAMAAACGIqwDAAAA\nhiKsAwAAAIYirAMAAACGirK7AADA+eGyJ94OwbvEff7jG933fq/d+s1ue20A+CpxZB0AAAAwFGEd\nAAAAMBRhHQAAADAUYR0AAAAwFGEdAAAAMBRhHQAAADAUYR0AAAAwFGEdAAAAMBRhHQAAADAUYR0A\nAAAwFGEdAAAAMBRhHQAAADAUYR0AAAAwFGEdAAAAMBRhHQAAADAUYR0AAAAwFGEdAAAAMBRhHQAA\nADBU0GG9paVFxcXFcrvdio2NVWZmpqqqqoJ+4wULFigiIkLp6elBzwUAAACcICrYCZMmTdLOnTtV\nWlqq1NRUrV69WlOmTJHf71dBQcE5vcbrr7+uX/3qVxowYEDQBQMAAABOEVRYX79+vTZt2tQW0CUp\nJydH9fX1mjNnjiZPnqzIyMgzvobX69XUqVN15513avfu3Tp69GjXqwcAAADCWFDbYNauXauEhATl\n5+cHjE+dOlWHDx9WTU3NWV+jtLRUjY2N+vnPfx5cpQAAAIDDRFiWZZ3rk7Ozs+Xz+bRjx46A8b17\n9yo9PV0rVqzQjBkzOp3/5ptv6lvf+pbWrFmjCRMmaPTo0Tp69Khqa2vbPdfv96u5uTlg7ODBg/L7\n/eda7nnl5MmTbT9HR0fbWIk9nL5+iR5I9MD09d/+RpzdJXxlykecsLuEDpn+GQgFp/fA6euXwrsH\nLpdLgwcPDhjr1auXXK7Oj58HtQ2moaFBQ4cObTeemJjY9nhn/H6/pk2bpkmTJmnChAnBvG0br9cr\nn8/Xpbnnk9M/pE7k9PVL9ECiB05ff3c7H/p7PtTY3ZzeA6evXwq/Hpxtu3hHgj7BNCIiokuP/frX\nv9bbb7+tv/3tb8G+ZZuoqKgzfvM4n4Xzt8hz4fT1S/RAogdOX38omdpfPgP0wOnrl8K7B13JsUGF\n9aSkpA6Pnjc2Nkr6/Aj7Fx08eFALFy5UaWmpevTooWPHjkn67Ei53+/XsWPHFBMTo549e57x/dPS\n0sI2rO/evVsnT55UdHS0Ro4caXc5Ief09Uv0QKIHxq//jbftruArY2R/dR58BkLA6T1w+vql8O5B\nR9u8zyao5JuRkaF9+/bJ6/UGjO/Zs0eSOr1m+jvvvKOPPvpI9957r/r06dP258UXX9S+ffvUp08f\nzZs3L6jCAQAAgHAX1JH1vLw8Pfroo6qurtbkyZPbxisqKuR2u5WVldXhvMzMTG3durXdeHFxsY4f\nP67HH39cgwYNCrJ0AAAAILwFFdbHjx+v3NxcFRUVqampSSkpKfJ4PNq4caMqKyvbNs0XFhaqoqJC\ndXV1Sk5OVu/evTV69Oh2r9e7d295vd4OHwMAAACcLugTTNesWaOSkhItXLhQjY2NGjZsmDwej266\n6aa25/h8Pvl8PgVxVUgAAAAAXxB0WE9ISFBZWZnKyso6fU55ebnKy8vP+lrbtm0L9u0BAAAAxwjP\nS6sAAAAAYYCwDgAAABiKsA4AAAAYirAOAAAAGIqwDgAAABiKsA4AAAAYirAOAAAAGIqwDgAAABiK\nsA4AAAAYirAOAAAAGIqwDgAAABiKsA4AAAAYirAOAAAAGIqwDgAAABiKsA4AAAAYirAOAAAAGIqw\nDgAAABiKsA4AAAAYirAOAAAAGIqwDgAAABiKsA4AAAAYirAOAAAAGIqwDgAAABiKsA4AAAAYirAO\nAAAAGIqwDgAAABiKsA4AAAAYirAOAAAAGIqwDgAAABiKsA4AAAAYirAOAAAAGIqwDgAAABiKsA4A\nAAAYirAOAAAAGIqwDgAAABgq6LDe0tKi4uJiud1uxcbGKjMzU1VVVWedt2bNGk2ZMkUpKSnq2bOn\nhgwZoptvvllvv/12lwoHAAAAwl1UsBMmTZqknTt3qrS0VKmpqVq9erWmTJkiv9+vgoKCTuf94he/\n0EUXXaSSkhINHTpUhw4d0oMPPqhvfetb2r59u9LS0r7UQgAAAIBwE1RYX79+vTZt2tQW0CUpJydH\n9fX1mjNnjiZPnqzIyMgO565bt079+/cPGPv+97+vIUOG6De/+Y1WrlzZxSUAAAAA4SmobTBr165V\nQkKC8vPzA8anTp2qw4cPq6amptO5XwzqkuR2uzVo0CAdOnQomDIAAAAARwgqrNfW1urSSy9VVFTg\nAfkRI0a0PR6Md955R/X19WyBAQAAADoQYVmWda5PTk1N1dChQ7Vx48aA8ffee09ut1sPPvig5s2b\nd06v5fV6lZubq1dffVW1tbW6+OKLAx73+/1qbm4OGDt48KD8fv+5lnteOXnyZNvP0dHRNlZiD6ev\nX6IHEj0wff23vxFndwlfmfIRJ+wuoUOmfwZCwek9cPr6pfDugcvl0uDBgwPGevXqJZer8+PnQZ9g\nGhER0aXHTmdZlgoLC/XPf/5T1dXV7YJ6Z7xer3w+3zk993x2+ofUiZy+fokeSPTA6evvbl3p7x37\nLuyGSuzz6KXH7S7hrJz+e+D09Uvh14POzu08k6DCelJSkhoaGtqNNzY2SpISExPP+hqWZWn69Omq\nrKxURUWFfvCDH5zz+0dFRZ3xm8f5LJy/RZ4Lp69fogcSPXD6+kOJ/prbA6f/Hjh9/VJ496ArOTao\nsJ6RkSGPxyOv1xuwb33Pnj2SpPT09DPOPxXUH3/8ca1atUq33HJLUMWmpaWFbVjfvXu3Tp48qejo\naI0cOdLuckLO6euX6IFED4xf/xvhc1+MLvU3jNYvdbEHIWD870E3c/r6pfDuQUfbvM8mqOSbl5en\nlpYWVVdXB4xXVFTI7XYrKyur07mWZemOO+7Q448/rhUrVmjq1KlBFQoAAAA4TVBH1sePH6/c3FwV\nFRWpqalJKSkp8ng82rhxoyorK9v24RQWFqqiokJ1dXVKTk6WJN1zzz1atWqVpk2bpoyMDG3fvr3t\ndWNiYnTZZZd9hcsCAAAAzn9Bn2C6Zs0alZSUaOHChWpsbNSwYcPk8Xh00003tT3H5/PJ5/Pp9AvN\nrFu3TpL02GOP6bHHHgt4zeTkZB04cKCLSwAAAADCU9BhPSEhQWVlZSorK+v0OeXl5SovLw8YI4wD\nAAAAwQnPszUBAACAMEBYBwAAAAxFWAcAAAAMRVgHAAAADEVYBwAAAAwV9NVgAMCJLnsiFHevjPv8\nx26+W+Zrt36zW18f4YnfAyD0OLIOAAAAGIqwDgAAABiKsA4AAAAYirAOAAAAGIqwDgAAABiKsA4A\nAAAYirAOAAAAGIqwDgAAABiKsA4AAAAYirAOAAAAGIqwDgAAABgqyu4CAJwfLnvi7RC8S9znP77R\nfe/32q3f7LbXBgDgq8SRdQAAAMBQhHUAAADAUIR1AAAAwFCEdQAAAMBQhHUAAADAUIR1AAAAwFCE\ndQAAAMBQhHUAAADAUIR1AAAAwFCEdQAAAMBQhHUAAADAUIR1AAAAwFCEdQAAAMBQhHUAAADAUIR1\nAAAAwFCEdQAAAMBQhHUAAADAUIR1AAAAwFBBh/WWlhYVFxfL7XYrNjZWmZmZqqqqOqe5H3zwgW6/\n/Xb17dtXcXFxys7O1pYtW4IuGgAAAHCCqGAnTJo0STt37lRpaalSU1O1evVqTZkyRX6/XwUFBZ3O\n++STTzRmzBgdO3ZMZWVl6t+/vx5++GFde+212rx5s0aNGvWlFgIAAACEm6DC+vr167Vp06a2gC5J\nOTk5qq+v15w5czR58mRFRkZ2OHfVqlWqra3VSy+9pOzs7La5I0eO1Ny5c1VTUxPwfMuy2r2G3+8P\nptzzisvlUmRkpFwuV1ivszNOX79kfg8u7BFhdwlfma70N5zWL9EDp69fogeSmbnC9L8LQiGce9DR\nejrKvKeLsM72jNPccccdqqqq0ocffqioqM9zvsfjUUFBgV588UV997vf7XBubm6uDh06pP379weM\nL1u2TPPnz9d///tfDRw4sG3c6/WqtbX1XEsDAAAAzjvx8fEBufqLgtqzXltbq0svvbTdC44YMaLt\n8TPNPfW8jubu3bs3mFIAAACAsBdUWG9oaFBiYmK78VNjDQ0N3TIXAAAAcKKgrwYTEdH5frUzPfZl\n5wIAAABOE9QJpklJSR0eAW9sbJSkDo+cd3Wuy+VSfHx8wFhERAShHgAAAOcly7LanVDqcp352HlQ\nYT0jI0Mej0derzdg3/qePXskSenp6Wece+p5p+tsrsvlOmvxAAAAQDgLKg3n5eWppaVF1dXVAeMV\nFRVyu93Kyso649z9+/cHXKLR6/WqsrJSWVlZcrvdQZYOAAAAhLegLt0oSWPHjtWuXbv0i1/8Qikp\nKfJ4PHr00UdVWVmpm2++WZJUWFioiooK1dXVKTk5WdJnN0W6/PLL1dTUpNLSUvXv31+PPPKI1q1b\nx02RAAAAgA4Evc9kzZo1uvXWW7Vw4UJde+21qqmpkcfjaQvqkuTz+eTz+QL25MTExGjLli3KycnR\nrFmzNHHiRL333nvasGGDo4N6S0uLiouL5Xa7FRsbq8zMTFVVVdldVsg0Nzdr7ty5Gjt2rPr166eI\niAgtXrzY7rJC5vnnn9e0adM0bNgwxcfHa+DAgfrBD36gV155xe7SQub111/Xddddp8GDB6tnz55K\nTExUdna2Kisr7S7NNitXrlRERIQSEhLsLiUktm3b1nZO0hf/bN++3e7yQuZf//qXJkyYoD59+qhn\nz5765je/qaVLl9pdVkjcfvvtnX4GnPI5eO2113TDDTfI7XYrLi5Ow4YN0/33368TJ07YXVrI7Nix\nQ+PGjVOvXr2UkJCgnJwcvfjii3aXZbugj6zjqzV27Fjt3LlTpaWlSk1N1erVq7Vy5Uo9+eSTKigo\nsLu8bnfgwAFlZmZq5MiRSk1N1cqVK7Vo0SLHBPb8/Hw1NDQoPz9fw4cP15EjR7R8+XLt2rVLzz33\nnL7//e/bXWK327Ztm6qqqvS9731PAwcOVGtrq5588klVVVVp6dKlWrBggd0lhtS7776rtLQ0xcfH\n6/jx42ppabG7pG63bds25eTk6MEHH1ROTk7AY+np6Y740rJ69Wrdeuut+uEPf6iCggIlJCSorq5O\nhw8f1sKFC+0ur9vV1dXpyJEj7cYnTpyomJgY1dfXd3qH9HDw5ptv6vLLL9cll1yi+fPnq2/fvvrH\nP/6hBx54QNddd52eeeYZu0vsdjt37tRVV12lK6+8Uj/+8Y9lWZZ++ctf6rXXXtPWrVuVnZ1td4n2\nsWCbv//975Yka/Xq1QHjubm5ltvttrxer02VhY7f77f8fr9lWZZ15MgRS5K1aNEie4sKoffff7/d\nWHNzszVgwABrzJgxNlRkjqysLOviiy+2u4yQu/76662JEydat912mxUfH293OSGxdetWS5L11FNP\n2V2KLf773/9a8fHxVlFRkd2lGGXbtm2WJGvBggV2l9LtSkpKLEnWv//974DxGTNmWJKsxsZGmyoL\nnXHjxlkDBgywWltb28aampqsvn37Wt/97ndtrMx+XG7FRmvXrlVCQoLy8/MDxqdOnarDhw8HnIwb\nrpx+Oc7+/fu3G0tISNDw4cN16NAhGyoyR9++fc94++VwVFlZqRdeeEGPPPKI3aUghFauXKnW1lbd\nd999dpdilFWrVikiIkLTpk2zu5RuFx0dLUm68MILA8Z79+4tl8ulHj162FFWSL344osaPXq04uLi\n2sZ69eqlq6++Wi+99JLee+89G6uzF2HdRrW1tbr00kvbBZIRI0a0PQ7nOX78uF599VWlpaXZXUpI\n+f1+eb1eHTlyRI888oiee+45R4WXDz74QMXFxSotLdWgQYPsLscWM2fOVFRUlC644AKNGzdO//rX\nv+wuKST+8Y9/KDExUfv371dmZqaioqLUv39//ehHP1JTU5Pd5dni+PHjevrppzVmzBh9/etft7uc\nbnfbbbepd+/eKioq0jvvvKPm5mY9++yzWrFihWbOnNnuvjPh6NNPP1VMTEy78VNjHV3+2ykI6zZq\naGjo8EZSp8Y6uokUwt/MmTPV2tqqkpISu0sJqbvuukvR0dHq37+/Zs+erd/+9re688477S4rZO66\n6y5dcsklKioqsruUkLvwwgt17733asWKFdq6davKysp06NAhjR49Ws8995zd5XW7d999VydOnFB+\nfr4mT56szZs3a86cOfrzn/+sCRMmtLuBihN4PB599NFHKiwstLuUkBgyZIhefvll1dbW6hvf+IYu\nuOACTZw4UbfddpvKysrsLi8khg8fru3bt8vv97eNeb3etl0GTs5Ezvo3ZgOdaQuIk7eHONXPfvYz\nPfnkk/rd736nyy+/3O5yQmr+/PmaPn26PvjgA61bt0533323Wltb9X//9392l9btqqurtW7dOr32\n2muO/L2/7LLLdNlll7X991VPDStCAAAFVElEQVRXXaW8vDxlZGRo7ty5GjdunI3VdT+/36+PP/5Y\nixYt0k9/+lNJ0ujRo9WjRw8VFxdry5Ytuuaaa2yuMrRWrVqlpKQk5eXl2V1KSBw4cEATJ07UgAED\n9PTTT6tfv36qqanRAw88oJaWFq1atcruErvdrFmzVFhYqLvvvlslJSXy+/1asmSJ6uvrJZ39Lp/h\nzLkrN0BSUlKH3xQbGxslqcOj7ghfS5Ys0QMPPKCf//znuvvuu+0uJ+QGDx6sb3/725owYYL+8Ic/\naMaMGZo3b16HV4gIJy0tLZo5c6ZmzZolt9utY8eO6dixY/r0008lSceOHVNra6vNVYZe7969df31\n1+uNN97QRx99ZHc53SopKUmS2n0pGT9+vCTp1VdfDXlNdnrjjTe0a9cu3XLLLR1uiwhHP/3pT9XU\n1KTnnntON954o66++mrNmTNHDz30kB577DG98MILdpfY7aZNm6bS0lI98cQTGjRokAYPHqw333yz\n7YDNwIEDba7QPoR1G2VkZGjfvn3yer0B46f2ZaWnp9tRFmywZMkSLV68WIsXL9b8+fPtLscIV155\npbxer9555x27S+lWR48e1fvvv6/ly5erT58+bX88Ho9aW1vVp0+fgPtYOMmp7R/h/q8Np85T+qJT\n63faEcVTR5GnT59ucyWh8/rrr2v48OHt9qZfccUVkpxzDtt9992no0ePas+ePTpw4IBeeuklffjh\nh4qPj3fcvzafzln/BzBMXl6eWlpaVF1dHTBeUVEht9utrKwsmypDKC1dulSLFy/WggULtGjRIrvL\nMcbWrVvlcrk0dOhQu0vpVhdddJG2bt3a7s+4ceMUGxurrVu36oEHHrC7zJD78MMP9eyzzyozM1Ox\nsbF2l9OtbrzxRknShg0bAsbXr18vSfrOd74T8prs8sknn6iyslJXXnmlow5Yud1u7d27t919FV5+\n+WVJctRJ5zExMUpPT1dycrIOHjyov/zlL7rjjjvUs2dPu0uzDXvWbTR+/Hjl5uaqqKhITU1NSklJ\nkcfj0caNG1VZWRnWN4A43YYNG9Ta2qrm5mZJn90c4umnn5YkTZgwIeAyTuFm+fLlbXcDvu6669rd\npc8Jf0nPmDFDF1xwga688koNGDBAR48e1VNPPaW//OUvmjNnjvr162d3id0qNjZWo0ePbjdeXl6u\nyMjIDh8LNwUFBW3boPr27au3335by5cv1/vvv6/y8nK7y+t2Y8eO1cSJE3X//ffL7/frO9/5jnbt\n2qUlS5bo+uuv1/e+9z27SwyZv/71r2psbHTUUXVJKi4u1g033KDc3FzNnj1bffv21fbt27Vs2TIN\nHz68bUtUOKutrVV1dbW+/e1vKyYmRrt371Zpaamj7uTbKZuv8+54zc3N1j333GNddNFFVo8ePawR\nI0ZYHo/H7rJCKjk52ZLU4Z///Oc/dpfXrUaNGtXp2p3y6/nYY49ZV111ldW3b18rKirK6t27tzVq\n1CjriSeesLs0WznppkjLli2zMjMzrQsvvNCKjIy0+vXrZ+Xl5Vk7duywu7SQOXHihHXfffdZF198\nsRUVFWUNHjzYmjdvnvXxxx/bXVpI5ebmWvHx8VZTU5PdpYTc888/b40dO9a66KKLrJ49e1qpqanW\nT37yE+vo0aN2lxYSb731lnX11VdbiYmJVo8ePayUlBRrwYIFVktLi92l2S7Cshx4TSgAAADgPMCe\ndQAAAMBQhHUAAADAUIR1AAAAwFCEdQAAAMBQhHUAAADAUIR1AAAAwFCEdQAAAMBQhHUAAADAUIR1\nAAAAwFCEdQAAAMBQhHUAAADAUP8PkRZAwBPDeHoAAAAASUVORK5CYII=\n", "text/plain": [ "" ] }, "metadata": {}, "output_type": "display_data" } ], "source": [ "import kf_book.book_plots as book_plots\n", "belief = [ 0.,0., 0., 0.1, 0.15, 0.5, 0.2, .15, 0, 0]\n", "book_plots.bar_plot(belief)" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "They were not perfect Gaussian curves, but they were similar. We will be using Gaussians to replace the discrete probabilities used in that chapter!" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "## Nomenclature\n", "\n", "A bit of nomenclature before we continue - this chart depicts the *probability density* of a *random variable* having any value between ($-\\infty..\\infty)$. What does that mean? Imagine we take an infinite number of infinitely precise measurements of the speed of automobiles on a section of highway. We could then plot the results by showing the relative number of cars going past at any given speed. If the average was 120 kph, it might look like this:" ] }, { "cell_type": "code", "execution_count": 16, "metadata": {}, "outputs": [ { "data": { "image/png": "iVBORw0KGgoAAAANSUhEUgAAAwAAAAEvCAYAAADy5KZEAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzs3Xlc1NX+x/HXDMMiiwsgIu4rGiK4\nIK6ldS1tMy1TywzUFiur203zV/dm3Tar2715TSvNlDK1cskWl9LMzF1TFNxRcBcFlU2WWX5/kFxJ\nVEbRLzDv5+Phg0dfvmfmPXQYzme+53uOyeFwOBAREREREZdgNjqAiIiIiIhcPyoARERERERciAoA\nEREREREXogJARERERMSFqAAQEREREXEhKgBERERERFyIxegA15vdbsdutxc7ZjKZMJlMBiUSERER\nEblyDoeDP6/sbzabMZtL/qzfJQuA7Oxso2OIiIiIiFwzPj4+Fy0ANAVIRERERMSFqAAQEREREXEh\nKgBERERERFyIy90DUNLNvpeaIyWXl5iYiNVqxWKxEBYWZnQcMZj6g/yZ+oScT/1B/kx94uqVdI/r\npRa4UQHApe+Slsuz2+3YbDb9HAVQf5ALqU/I+dQf5M/UJ66NSxUA+imLiIiIiLgQFQAiIiIiIi5E\nBYCIiIiIiAtRASAiIiIi4kJUAIiIiIiIuBCXWwVIRETKnsPh4HROASez8jiRmUdGbgF5Vjt5BXb2\npWSBw0YVdwuHzUfx8bRQ09eTQD8PAnw8cTNffKUKEREpeyoARESk1BwOB4dOnWXLwdPsOJrBvhPZ\n7DuZRXJaDvlW++UfYO2pYv9pNkHdGt40rulD40BfQoN9iahXnWZBfioMRESuERUAIiJyUQ6Hg6QT\nWfy6+ySrk06y+cBp0rLzL3p+tSru1PTzpHoVdzzdzXha3MjJysBqs2N1mPDw8iEjt/BKQVp2PnYH\nHEjP4UB6Dr/sOlH0ON4eboTXqUbnJoF0bRZIRN1qWNw0a1VEpCyoABARkWKsNjvr9qfzw7aj/Lwj\nlWMZucW+7+5m4obaVQmrU40mNX1pXNOHJoG+1KrmiafF7YLHi4+Pp6CgAHd3dyIiIoo9z8msfPaf\nLLyKsO9ENtuPZLD10Gmy822s25/Ouv3p/Gfpbvy8LNzYrCa9w4O5uUUQ3h768yUicqX0DioiIjgc\nDrYcPM3Xmw6xOOEY6ed9yu9hMRPdyJ+uTQPp0MiflrWr4uV+4UDfWRY3M8HVvAiu5kWnJgFFx232\nwqsOG5NPsWrvSX7be5IzZwv4YdtRfth2FC93Mz1Cg7i3bV26h9bUlQERESepABARcWFncgr4Zsth\nZq0/wM5jmUXHa3i7c1tYML1aBdOxcUCZDPhLy81sonktP5rX8uOB6PrY7A62HjrNksTjLNx2lAPp\nOSxKOMaihGME+XlyX7u6DIyqT/0A7+uWUUSkIlMBICLiglLSspmych9fbzxE3h8373pYzNwRXpt+\nbevQsXEA7uXkk3U3s4k29WvQpn4NXugVSuKRDL7ZfJh5mw+TmpnHpF+S+HBFEr3CghnerTHtGtQw\nOrKISLmmAkBExIVsO3SGj1YksSjhKHZH4bHQWn4M6lCPvm3qUs3b3diAl2EymWhVpxqt6lRjdK8W\nLNtxnJnrD7Byz8miqwLtGtTg0Rsb07NlLcxaSUhE5AIqAEREXEDikTP8a8kulp+30k730Jo8dmMT\nOjb2x2SqeANlD4uZ3uG16R1em93HM/lk5T6+2XyETSmneOzzTYSFVOX5W0PpHlqzQr4+EZFrRQWA\niEgllnwym3//tJtv448AhdNp7o4I4dEbG9OydlWD05Wd5rX8eOe+CJ6/NZTpq5OJW51M4pEMYqdv\noF2DGvzt1uZ0bhJodEwRkXJBBYCISCV0JqeA/yzdzYy1KVj/mOtzV0QIz/VsTqNAH4PTXTtBVb0Y\n3asFw7o24uNf9xG3OplNKad4YMo6/tKyFv+4syUNAirv6xcRKQ0VACIilYjd7uCrjQd5Z8muoqU8\nu4fW5PlbQ2lVp5rB6a6fAF9PXry9JcO6NuKDn/cyc/0Blu44zq+7TzC8WyOe7NEUH0/9CRQR16R3\nPxGRSiL+4GleXpBA/KEzADQL8uXVu8Po3NR1p77UqurFa/e0YkinBvzz++2s3HOSSb8kMff3Q4y9\nK4zerYJ1f4CIuBwVACIiFdzZfBvv/biLqav243CAn6eFZ3s2Z0inBuVmKU+jNavlx2dDO/DT9uO8\n/sMODqTn8MQXv3PrDbV47Z5W1KrqZXREEZHrRgWAiEgFtnZfGi/M3UpKWg4A90SG8OIdLQny04D2\nz0wmE7eGBXNj85pMWr6XSb8k8eP246xJSuP/bm/JwKh6WjZURFyCCgARkQooJ9/KWwt38vnaFABq\nV/Pizb7h9GgRZHCy8s/L3Y3nbg3l9ta1eWHOVuIPneHF+dv4YdsR3usfSXA1FU8iUrnp2rCISAWT\ncPgMd074rWjw/0B0fX78640a/DupRXBV5j3Rhb/f0RIvdzOr9qZx2/u/snDbUaOjiYhcUyoAREQq\nCLvdwUcrkug7aRX7TmQTXNWLL4ZH82bfcPy8yvcOvuWVm9nE8G6N+eHpboTXqcaZswU88cXv/O2r\neDJzC4yOJyJyTagAEBGpAFIzcnno03WMW7STApuDXmHBLHqmG11ceIWfstSkpi9zR3TmqR5NMZtg\n7u+HuHPCbyQeOWN0NBGRMqcCQESknFu3L407JvzGqr1pVHF3Y1y/cD4c3JYaPh5GR6tUPCxmnr8t\nlC8f60Sd6lVIScuh76TVfLnhgNHRRETKlAoAEZFyyuFwMOXXfTzwyTpOZOYRWsuP75/uysAO9bV2\n/TUU1dCfH57uys0tgsi32nlh7jZGfR3P2Xyb0dFERMqECgARkXIoM7dwLvobC3dgszu4JzKE+U92\npklNX6OjuYTq3h58MqQ9o24LxWyCrzcdou+kVew/mW10NBGRq6YCQESknEk6kUWfD1axKOEY7m4m\nXusTxn8GROLtoZWbryez2cSTPZoyY3g0gb4e7DyWSZ8PfmPlnhNGRxMRuSoqAEREypGVe05wz8RV\n7DuZTe1qXnz5WCce6tRQU34M1LlJID883Y229auTkWslZtoG4lYn43A4jI4mInJFVACIiJQTn69J\nJmbaBjJzrbRrUINvn+pK2/o1jI4lQK2qXsx6tCP3tq2Lze5g7LeJvDg/gXyr3ehoIiJOUwEgImIw\nq83OywsS+MeCRGx2B/3a1OGL4dHU9PM0Opqcx9Pixr/6t+bF21tgMsGs9Qd4aOo60rPzjY4mIuIU\nFQAiIgbKzC0gdvoGPltTuKvv6F6hvHd/BF7ubgYnk5KYTCYevbEJUx9uj6+nhXX707n3w9WkpOnm\nYBGpOFQAiIgYJDUjlwEfr2XlnpNUcXfjo8HteKJ7U833rwBublGLeU90pk71Kuw/mc29H64m/uBp\no2OJiJSKCgAREQMkncii34er2X40g0BfD758rCO9WgUbHUuc0LyWH/Of6ExYSFVOZuUzcPJalu9M\nNTqWiMhlOV0AZGVl8eyzzxISEoKXlxeRkZHMnj27VG1TU1OJiYkhMDAQb29vOnXqxLJly4qdk5GR\nwRtvvEH37t0JDg7G19eX8PBw3n77bXJzcy94zIKCAl599VUaNmyIp6cnLVq0YMKECc6+LBGR62ZT\nyinu/XA1h06dpWGAN3NHdKZ13epGx5IrEFS1cKWmbs0COVtgY/hnG7VzsIiUe04XAP369SMuLo6x\nY8eyaNEioqKiGDRoEDNnzrxku7y8PG655RaWLVvG+PHjWbBgAbVq1aJXr16sWLGi6LwDBw7w/vvv\n07ZtWyZPnsy3337LfffdxyuvvMKdd955wbJrTzzxBG+99RZPPvkkS5YsoW/fvjzzzDO8+eabzr40\nEZFrbun24zz4yVpO5xQQUbcac0Z0pkGAj9Gx5Cr4elr4NCaqaIWgF+Zu44Of92iZUBEpt5zaVWbh\nwoX89NNPzJw5k0GDBgHQo0cPUlJSGDVqFAMGDMDNreQb16ZOnUpCQgKrV6+mU6dORW0jIiIYPXo0\n69atA6BRo0YkJyfj4/O/P4g333wzPj4+jBo1ilWrVtG1a1cAEhMTmTp1Km+88QajRo0CoHv37qSl\npfH666/z+OOP4+/v7+SPRETk2pi/+RDPf70Vm91B99CaTHygLT6e2tyrMnB3M/Ov/q2pXc2LD5bv\n5V8/7iYz18qY3i10T4eIlDtOXQGYP38+vr6+9O/fv9jx2NhYjhw5UjSIv1jb0NDQosE/gMViYfDg\nwaxfv57Dhw8D4OPjU2zwf06HDh0AOHjwYNGxb775BofDQWxs7AV5zp49y+LFi515eSIi18zMdQd4\n7qv4omU+pwxpr8F/JWMymXj+tlD+fkdLAD7+dR8vfZOAza4rASJSvjhVACQkJNCyZUssluJ/tFq3\nbl30/Uu1PXdeSW0TExMv+dw///wzAGFhYcUes2bNmgQHF79xrjR5RESulym/7uPF+dtwOOChjg34\nV/8I3N20BkNlNbxbY8b1C8dkOlf4baHApg3DRKT8cOrjp7S0NBo3bnzB8XPTbNLS0i7ZtqTpOKVp\nu3XrVt555x369u1brIi42GP6+Pjg4eFxycc8X2JiIna73pyvVEFBQdHX+Ph4g9OI0dQf/sfhcPBl\nQiazEjIA6NfSj3sbWtm2bavBya4vV+wTLT3hb538+c+adBZsOcKRE+mM7hKAh5umA7lif5BLU5+4\nemazmfr165f6fKevP19qLuPl5jleSdvk5GTuvPNO6tWrxyeffFKmec6xWq3YbLZSnSuXdu6XWARc\nuz84HA4+25rFd3tyABgU5kO/FlWwWq0GJzOWK/WJjiHujO5cnffWnGbD4VxeXX6CMV2q42VREXCO\nK/UHKR31iStzsXtwL8apAiAgIKDET9XT09MBLnnD7ZW0TUlJoUePHlgsFpYtW3bBOQEBAWzZsuWC\ndtnZ2eTn55f6BmCLxYLZrMvxV+r8X1Z3d3cDk0h5oP5QOPifvOk0C/8Y/A9vW427Qv0MTmUcV+4T\nHeu787Knhdd/TSPhRD7jVp/hHzcF4GVx3b85rtwfpGTqE1fP2XGsUwVAeHg4s2bNwmq1FrsPYNu2\nbQC0atXqkm3PnXe+i7VNSUmhe/fuOBwOfvnlF+rWrVviY86ePZtjx44Vuw+gNHnOFxYWpgLgKsTH\nx1NQUIC7uzsRERFGxxGDuXp/cDgcvPrddhbuycZkgnH9whkQVfrLspWRq/eJCKBl6Cke/nQ9Cal5\n/GdTLp/GROHt4Zo3gbt6f5ALqU9cPbvdTmZmZqnPd2rU27dvX7Kyspg7d26x43FxcYSEhBAdHX3J\ntjt37iy2UpDVamXGjBlER0cTEhJSdPzAgQN0794dm83Gzz//TIMGDUp8zD59+mAymYiLiyt2fPr0\n6VSpUoVevXo58/JERK7KucH/9NXJmEzw9r2tXX7wL4XaNahB3NAO+HpaWLsvndhpG8jJd+3pYCJi\nHKc+fujduzc9e/ZkxIgRZGRk0LRpU2bNmsXixYuZMWNG0fyjYcOGERcXR1JSUtHgfejQoUycOJH+\n/fszbtw4goKCmDRpErt27WLp0qVFz5GamkqPHj04evQoU6dOJTU1ldTU/22tXrdu3aKrAWFhYQwb\nNoyxY8fi5uZGVFQUP/74I5MnT+b111/XHgAict04HA7++X3h4B8KP/m/v309Y0NJudKuQQ0+G9aB\nh6euZ93+wiJgWqzrXgkQEeM4/a4zb948XnrpJV5++WXS09Np0aIFs2bNYuDAgUXn2Gw2bDZbsV0Q\nPT09WbZsGaNHj2bkyJHk5OQQGRnJokWLuOmmm4rO2759O/v27QNg8ODBFzz/2LFjeeWVV4r+e9Kk\nSdSpU4cJEyZw7NgxGjZsyPjx4xk5cqSzL01E5Io4HA5e/2EH01YlA5r2IxfXtn4N4s4rAmKmbWC6\nigARuc5MDhfbq7ykOVJ+fn66B+AqaO6enM/V+oPD4eDNhTuYsnI/AG/2DeeBaA3+z+dqfaI0Nh84\nxZCp68nMs9KxsT/TYzvg5e7cKh4VlfqD/Jn6xNVzdnyrUa+IyBVyOBy8vXhX0eD/jb6tNPiXUmlT\nv3A60Ll7AkbM2ES+VfvRiMj1oQJAROQKTVy+l49WJAHw2j2teDC65AULRErSpn4NPo2JwsvdzPJd\nJ3hm9mas2jFYRK4DFQAiIldg2qr9/OvH3QD8/Y6WPNRRg39xXodG/kx+qD0ebmYWJRxj9Jyt2O0u\nNTNXRAygAkBExElfbTzIq99tB+DZvzRjeLfGBieSiuzG5jX54IE2uJlNzNt8mH8sSMDFbs8TketM\nBYCIiBMWbjvKmLlbARjetRHP3NLM4ERSGdwaFsy/74/AZIIv1h3gjR92qAgQkWtGBYCISCkt35XK\nM7M3Y3fAwKh6vHRHS0wmk9GxpJLoE1mHt/u1BuCT3/bz/tI9BicSkcpKBYCISCms25fG459vosDm\n4K6IEN7oG67Bv5S5+6PqMfauGwAYv2wPcX9sLCciUpZUAIiIXEbC4TMMi9tIntXOLS2C+Pf9EbiZ\nNfiXayO2SyP++pfmALzyXSLfxR8xOJGIVDYqAERELuFAWg4x0zaQ9ceGTRMfbIu7m9465dp6+pam\nDOnUAIcDnvtqCyv3nDA6kohUIvorJiJyESez8hjy6TpOZuXRsnZVJg9p7zK7tYqxTCYTY+8K447W\ntSmwOXjs803EHzxtdCwRqSRUAIiIlCArz8rQ6RtITsuhbo0qxMVGUdXL3ehY4kLczCb+fX8EXZsG\nkpNvI3b6BpJOZBkdS0QqARUAIiJ/km+1M2LGJrYeOoO/jwefDe1AUFUvo2OJC/K0uPHRQ+1oXbca\n6dn5DJm6nmNnco2OJSIVnAoAEZHz2O0ORs2JZ+Wek3h7uDEtJorGNX2NjiUuzNfTUtgPA304fPos\nQz5dx+mcfKNjiUgFpgJAROQ8by7cwYItR7CYTXw4uB0R9aobHUmEAF9P4oZ2oFZVT3Yfz2J43EZy\nC2xGxxKRCkoFgIjIHyb/msQnv+0H4N3+rbmpeU2DE4n8Tz1/bz4bGo2fl4WNKad47qst2O3aLVhE\nnKcCQEQEmL/5EG8u3AnAi7e3oG+bugYnErlQaLAfkx9qj7ubiYXbjvHmwh1GRxKRCkgFgIi4vNVJ\nJxk9ZysAw7s24tEbmxicSOTiOjUJ4F/9IwD45Lf9TFu13+BEIlLRqAAQEZe253gmj32+iQKbgzta\n1+bF21saHUnksvpE1mF0r1AA/vn9dhYnHDM4kYhUJCoARMRlpWbmEjNtA5m5Vto3qMF7/SMwm01G\nxxIplRE3NeGB6Po4HPDM7M38fuCU0ZFEpIJQASAiLikn38rwuI0cPn2WRoE+2uVXKhyTycQ/7w7j\n5hZB5FntDI/bSPLJbKNjiUgFoAJARFyOze7g6Vlb2HroDDW83ZkWE4W/j4fRsUScZnEzM2FQG8Lr\nFG4UFjNtPWlZeUbHEpFyTgWAiLic177fztIdx/GwmPnk4fY0DPQxOpLIFfPxtDA1pj11a1QhOS2H\n4Z9pjwARuTQVACLiUj79bT/TVycD8J/7I2nXwN/YQCJlIMjPi+mxHahWxZ3NB07zzOzN2LRHgIhc\nhAoAEXEZixOO8doP24HCtf7vaF3b4EQiZadpkC9ThrTHw83MksTjjFukPQJEpGQqAETEJWw+cIpn\nv9yMwwGDO9bnkW6NjY4kUuY6NPLnX/cX7hEwZeV+Zq0/YHAiESmPVACISKV3IC2H4XEbyS2w0yO0\nJq/cFYbJpOU+pXK6OyKEv/6lOQD/+CaB3/acNDiRiJQ3KgBEpFLLyC1gaNwG0rLzCQupygcPtMXi\nprc+qdyevqUpfdvUwWp3MOKLTexNzTQ6koiUI/orKCKVltVm58kvfmdvaha1q3nxaUwUPp4Wo2OJ\nXHMmk4lx94bTvkENMnOtDJ2+kfTsfKNjiUg5oQJARCqt177fzso9J6ni7saUIe2pVdXL6Egi142n\nxY2PH2pHfX9vDqTn8OhnG8mzanlQEVEBICKV1OdrkolbkwLA+wMjaVWnmrGBRAwQ4OvJpzFR+HlZ\n2JhyijFzt+FwaHlQEVenAkBEKp2Ve07wyneFy32O7hXKbWHBBicSMU7TIF8+fLAdbmYT8zcfZsLP\ne42OJCIGUwEgIpXK3tQsnvjid2x2B/3a1mHETU2MjiRiuK7NAnn9nlYA/Pun3Xwbf8TgRCJiJBUA\nIlJpnMrOZ1jcBjJzrUQ1rMFb/cK13KfIHwZ1qM8j3RoB8PzX8WxKOWVwIhExigoAEakU8q12Hpux\niZS0HOr5V+Gjwe3wtLgZHUukXBnTuyU9b6hFvtXOo59t5GB6jtGRRMQAThcAWVlZPPvss4SEhODl\n5UVkZCSzZ88uVdvU1FRiYmIIDAzE29ubTp06sWzZsgvO+/777xkyZAjh4eG4u7tf9BO85ORkTCZT\nif9Km0lEKj6Hw8Hfv9nG+v3p+HlamPpwFAG+nkbHEil33Mwmxg+MJCykKmnZ+QydvoGM3AKjY4nI\ndeb0gtj9+vVjw4YNjBs3jubNmzNz5kwGDRqE3W7ngQceuGi7vLw8brnlFk6fPs348eMJCgpi4sSJ\n9OrVi6VLl3LTTTcVnTt//nzWrl1LmzZt8PT0ZNOmTZfMNHLkyAueu1mzZs6+NBGpoKas3MdXGw9h\nNsGEB9rQvJaf0ZFEyi1vj8Iiuc/E39iTmsWTX/zOtJgobZAn4kKcKgAWLlzITz/9VDToB+jRowcp\nKSmMGjWKAQMG4OZW8iX3qVOnkpCQwOrVq+nUqVNR24iICEaPHs26deuKzp0yZQpmc+Eb0VNPPXXZ\nAqB+/fp07NjRmZciIpXET9uP89ainQD8484b6B4aZHAikfIvuJoXUx+Oov9Ha1i55ySvfb+dV/u0\nMjqWiFwnTpX78+fPx9fXl/79+xc7Hhsby5EjR4oN4ktqGxoaWjT4B7BYLAwePJj169dz+PDh/4Uy\n61MIEbm8HUczeGb2ZhwOeCC6PjGdGxodSaTCaFWnGu8PjMRkgrg1KXy2JtnoSCJynTg10k5ISKBl\ny5ZYLMUvHLRu3bro+5dqe+68ktomJiY6E6WYcePG4eHhgbe3N127duXbb7+94scSkYrhRGYew+M2\nkpNvo0vTAF69O0wr/og46bawYEbf1gKAV7/bzordJwxOJCLXg1NTgNLS0mjcuPEFx/39/Yu+f6m2\n585ztu3FeHp68sgjj9CzZ09q167NgQMHmDBhAn369GHKlCkMHz68VI+TmJiI3W53+vmlUEFBQdHX\n+Ph4g9OI0a5Hf8i3Ofj7shMcPp1PiJ+FJyI82Z6w7Zo8l1w9vUeUb52qO7i5kTc/789hxOcbeLtn\nEPWruV+z51N/kD9Tn7h6ZrOZ+vXrl/p8p28CvtQnbJf79O1q2pakdu3aTJ48udix/v37Ex0dzZgx\nY4iJibngakVJrFYrNpvN6eeXC537JRaBa9MfHA4H49dnsCstH193E//XuRqeJhsFBfodrgj0HlE+\nPdLGl6OZBew4WcBrK07y1s3+VPO89tNx1R/kz9QnrszF7sG9GKcKgICAgBI/qU9PTwco8RP+smjr\nDHd3dwYMGMCYMWPYs2cPLVu2vGwbi8Wi+w6uwvm/rO7u1+5TI6kYrnV/+DIhg98O5uJmghe6BVDf\n36vMn0PKlt4jyj934MUbAxn1YyrHsmy8t/YM/+xRE3e3sp9Wp/4gf6Y+cfWcHcc6VQCEh4cza9Ys\nrFZrsU/Wt20rvPTeqtXFVxAIDw8vOu98pWnrLIfDAZT+hxEWFqYC4CrEx8dTUFCAu7s7ERERRscR\ng13L/vD91iPM3HYIgNf7hjOoQ+kvd4px9B5RccxomEnfSavZfiKfmXvhvf6ty/zeGvUH+TP1iatn\nt9vJzMws9flOjXr79u1LVlYWc+fOLXY8Li6OkJAQoqOjL9l2586dxVYKslqtzJgxg+joaEJCQpyJ\nclEFBQV8+eWXBAYG0rRp0zJ5TBExXvzB0/ztq8K5ocO6NtLgX+QaaBrkx6QH2+JmNjHv98NM+iXJ\n6Egicg04dQWgd+/e9OzZkxEjRpCRkUHTpk2ZNWsWixcvZsaMGUXzj4YNG0ZcXBxJSUk0aNAAgKFD\nhzJx4kT69+/PuHHjCAoKYtKkSezatYulS5cWe56UlBQ2bNgAQFJS4ZvPnDlzAGjYsCHt27cH4Lnn\nnqOgoIAuXboQHBzMwYMHmTBhAlu2bGHatGlOz4cSkfLp6JmzPPLZRvKsdnqE1uTF2y8/tU9Erky3\nZjV55e4w/vFNAu8u2UWTmj70alXb6FgiUoacvgl43rx5vPTSS7z88sukp6fTokULZs2axcCBA4vO\nsdls2Gy2oqk4ULhiz7Jlyxg9ejQjR44kJyeHyMhIFi1aVGwXYIDly5cTGxtb7Ni5vQcefvhhpk+f\nDhROG/r444+ZOXMmGRkZ+Pn50aFDB5YsWcKtt97q7EsTkXIoJ9/K8LiNpGbmEVrLj/8OaoObWct9\nilxLD3VsQFJqFtNXJ/Psl1v4uro34XWrGR1LRMqIyXH+KN0FlDRHys/PT/cAXAXN3ZPzlWV/sNsd\nPD5jEz9uP06AjwffPNmFev7eZZRUrhe9R1RMVpudYXEbWbH7BLWqerLgya4EV7v6m+7VH+TP1Ceu\nnrPjW416RaTcevfHXfy4/TgebmY+fqidBv8i15HFzcyEB9rQvJYvxzPyGP7ZBnLyrUbHEpEyoAJA\nRMqlOZsO8eEfNyC+fV847RuWzVLBIlJ6Vb3cmfpwFAE+HiQczuCvX27BbnepiQMilZIKABEpdzYm\np/PivMIlgp/s0YS+beoanEjEddXz9+bjh9rh4WZmSeJx3v1xl9GRROQqqQAQkXLlYHoOj36+iXyb\nnV5hwfytZ6jRkURcXvuG/rx9XzgAH/6SxJxNhwxOJCJXQwWAiJQbmbkFDIvbQHp2Pq3qVOXfAyIw\na8UfkXKhb5u6jLy5cH+d/5u3lfX70w1OJCJXSgWAiJQLVpudkbM2s/t4FkF+nnwyJApvD6dXKhaR\na+ivf2nO7eHBFNgcPPb5RlJK8ZsaAAAgAElEQVTSso2OJCJXQAWAiJQLbyzcwS+7TuDlbuaTh9uX\nyXKDIlK2zGYT7/WPpHXdapzKKWBY3EbOnC0wOpaIOEkFgIgY7ot1KUxblQzAv++PpHXd6sYGEpGL\nquLhxidD2hNc1Yu9qVk8NfN3rDa70bFExAkqAETEUKv2nuTlBYkA/K1nc24Pr21wIhG5nKCqXnzy\ncHuquLuxcs9JXv1uu9GRRMQJKgBExDD7TmQxYsYmbHYH90SG8NQfNxiKSPnXqk413h8YickEn69N\nIW51stGRRKSUVACIiCFO5+QzLG4jGblW2tavzrh7W2MyacUfkYrktrBgXujVAoBXv0vkl12pBicS\nkdJQASAi112Bzc4TX/zO/pPZ1KlehY8fao+Xu5vRsUTkCjx2Y2P6t6uL3QFPzdzM7uOZRkcSkctQ\nASAi15XD4eDlBYmsTkrDx8ONqTHtqennaXQsEblCJpOJN/qG06GRP1l5VoZO30BaVp7RsUTkElQA\niMh19emqZGatP4DJBP8d1IYWwVWNjiQiV8nDYubjwe1oEODNoVNnefTzTeQW2IyOJSIXoQJARK6b\n5TtTeeOHwtVCXrq9Jbe0rGVwIhEpKzV8PJj6cBR+XhY2pZzi/+Ztw+FwGB1LREqgAkBErotdxzIZ\nOWszdgcMjKrHsK6NjI4kImWsaZAvHz7YDjezifmbDzPplySjI4lICVQAiMg1dzIrj2FxG8jKs9Kx\nsT//7NNKK/6IVFJdmwXy6t1hALy7ZBcLtx01OJGI/JkKABG5pvKsNh7/fBOHTp2lYYA3Hw1uh4dF\nbz0ildngjg2I7dIQgOe+2sLWQ6eNDSQixeivsIhcMw6HgxfmbGVjyimqelmYGhNFdW8Po2OJyHXw\n9ztuoHtoTXIL7AyP28jRM2eNjiQif1ABICLXzPtL9/DNliNYzCYmPdiOJjV9jY4kIteJm9nEhEFt\naF7Ll9TMPIZN30h2ntXoWCKCCgARuUZ+3p/N+GV7AHijbyu6Ngs0OJGIXG9+Xu5MfTiKAB8Pth/N\n4Nkvt2DXykAihlMBICJlLiE1n4nrTwHwRPcmDIiqb3AiETFKPX9vJg9ph4ebmZ+2H+fz+DNGRxJx\neSoARKRMHcoo4N01p7Ha4Y7WtXn+1lCjI4mIwdo18Oed+1oDMG9HFj8n634AESOpABCRMpOWlcdr\nK06SXeAgNNCD9/pHYDZruU8RgXva1OHpm5sCMHlTBgmpeQYnEnFdKgBEpEzkFth45LONHMuyUcvH\njZe6BeDl7mZ0LBEpR579S3O61KuC1QHjVqaRfDLb6EgiLkkFgIhcNbvdwfNfx/P7gdP4uJt4sUt1\nqnlp8C8ixZnNJp7pWIOmNSxk5tsZGreBMzkFRscScTkqAETkqr330y6+33oUdzcT/9ctgDpVLUZH\nEpFyytNi5oXO1QnwdmPfiWyenPk7BTa70bFEXIoKABG5Kl9tOMjE5UkAvNWvNeG1vAxOJCLlXY0q\nbvz9xgC8Pdz4be9Jxn6biEPLg4pcNyoAROSK/bbnJC/O3wbA07c04752dQ1OJCIVReMaHrw/IBKT\nCWauO8DHv+4zOpKIy1ABICJXZNexTEZ8sQmr3UGfyBD++pdmRkcSkQrm1rBg/n7HDQCMW7STBVsO\nG5xIxDWoABARpx09c5aYaevJzLUS1bAG79zXGpNJy32KiPOGdW3EsK6NAHj+63hWJ500OJFI5acC\nQESccuZsATGfbuDomVyaBvkyZUh7PC1a8UdErtxLt7fkjvDaFNgcPPbZJnYeyzA6kkilpgJAREot\nz2rjsc83sut4JkF+nkyPjaK6t4fRsUSkgjObTbx3fwQdGvqTmWf940MG7RYscq2oABCRUilc638r\na/el4+tpYVpsFHVreBsdS0QqCS93NyYPaUfTIF+OZeQS8+kGMnK1R4DItaACQERKZdzinXwXfwSL\n2cRHg9sRFlLN6EgiUslU9/ZgemwUNf082XU8k8c+20S+VXsEiJQ1pwuArKwsnn32WUJCQvDy8iIy\nMpLZs2eXqm1qaioxMTEEBgbi7e1Np06dWLZs2QXnff/99wwZMoTw8HDc3d0veXNhQUEBr776Kg0b\nNsTT05MWLVowYcIEZ1+WiFzCp7/tZ/IfS/S92781XZsFGpxIRCqrujW8mR4bhY+HG2v2pTFqTjx2\nu/YIEClLThcA/fr1Iy4ujrFjx7Jo0SKioqIYNGgQM2fOvGS7vLw8brnlFpYtW8b48eNZsGABtWrV\nolevXqxYsaLYufPnz2ft2rXccMMNREREXPJxn3jiCd566y2efPJJlixZQt++fXnmmWd48803nX1p\nIlKChduO8toP2wEY3SuUvm201r+IXFthIdX4cHA7LGYTC7Yc4Z0lu4yOJFKpWJw5eeHChfz000/M\nnDmTQYMGAdCjRw9SUlIYNWoUAwYMwM2t5NVApk6dSkJCAqtXr6ZTp05FbSMiIhg9ejTr1q0rOnfK\nlCmYzYW1yVNPPcWmTZtKfMzExESmTp3KG2+8wahRowDo3r07aWlpvP766zz++OP4+/s78xJF5Dzr\n96fz7JdbcDhgSKcGjLipidGRRMRF3Ni8JuPubc3zX8fz0YokQqp7MaRTQ6NjiVQKTl0BmD9/Pr6+\nvvTv37/Y8djYWI4cOVJsEF9S29DQ0KLBP4DFYmHw4MGsX7+ew4f/t/nHucH/5XzzzTc4HA5iY2Mv\nyHP27FkWL15cqscRkQvtOZ7J8LgN5Fvt3BZWi7F3hWmtfxG5ru5rV5fnb20OwNhvE1m47ajBiUQq\nB6euACQkJNCyZUssluLNWrduXfT9zp07X7Rtt27dLjh+rm1iYiJ16tRxJg4JCQnUrFmT4ODgi+Yp\njcTEROx23WR0pQoKCoq+xsfHG5xGykJqtpUxP50gI9dGi0APht1gIWHb1lK1VX+QP1OfkPM52x+6\n+jtIaOrD4r3ZPD3rd04cCSQy2Otax5TrSO8RV89sNlO/fv1Sn+9UAZCWlkbjxo0vOH5umk1aWtol\n25Y0Hac0bZ19TB8fHzw8PEr9mFarFZvN5vTzy4XO/RJLxXUm187YX9JJO2ujblU3XuhUDbPDypX8\nr1V/kD9Tn5DzlbY/xEb4cPqslbWH83jr1zReuakGTf3dr3E6MYLeI67MxabgX4xTBQBwySkAl5se\ncDVtr+VjWiyWUk87kgud/8vq7q435Iosp8DOm6vSOZJlo6a3G6/2qIm/t3NvE+oP8mfqE3K+K+kP\n7sDzXQJ5bcVJ4o/n8cZvpxnXsyZ1q6o/VQZ6j7h6zo5jnfrLHhAQUOKn6unp6QCXvOH2atpe6jG3\nbNlywfHs7Gzy8/NL/ZhhYWEqAK5CfHw8BQUFuLu7X3bVJim/cgtsxExbT9KpAgJ8PPjy8U40runr\n9OOoP8ifqU/I+a6mP3wRZuXBKWuJP3SGN347w5wRnQmpXuUaJZXrRe8RV89ut5OZmVnq850a9YaH\nh7Njxw6sVmux49u2bQOgVatWl2x77jxn217qMU+cOMGxY8fK7DFFXJHVZufpWZuLdvmdHtvhigb/\nIiLXUuEu5B1oXNOHI2dyeWjqOtKz842OJVLhOFUA9O3bl6ysLObOnVvseFxcHCEhIURHR1+y7c6d\nO4utFGS1WpkxYwbR0dGEhIQ4GR369OmDyWQiLi6u2PHp06dTpUoVevXq5fRjirgah8PB/83bxo/b\nj+NhMTNlSHvC62qXXxEpn/x9PPh8WDS1q3mRdCKb2OkbyM6zXr6hiBRxagpQ79696dmzJyNGjCAj\nI4OmTZsya9YsFi9ezIwZM4puQBg2bBhxcXEkJSXRoEEDAIYOHcrEiRPp378/48aNIygoiEmTJrFr\n1y6WLl1a7HlSUlLYsGEDAElJSQDMmTMHgIYNG9K+fXugcOrOsGHDGDt2LG5ubkRFRfHjjz8yefJk\nXn/9de0BIFIK4xbt5OtNhzCbYMKgNnRqEmB0JBGRS6pTvQqfD+tA/4/WEH/wNI/P2MQnD7fH0+Lc\njZAirsrpm4DnzZvHSy+9xMsvv0x6ejotWrRg1qxZDBw4sOgcm82GzWbD4fjf1t2enp4sW7aM0aNH\nM3LkSHJycoiMjGTRokXcdNNNxZ5j+fLlF6ztf27vgYcffpjp06cXHZ80aRJ16tRhwoQJHDt2jIYN\nGzJ+/HhGjhzp7EsTcTkfrUji41/3ATDu3tbcFhZ8mRYiIuVD0yA/psV24IEpa1m55yR//XIL/x3Y\nBoub7ukTuRyT4/xRugso6SYJPz8/3QR8FXTzTsX0xboUXppfuFfGi7e34NEby2aXX/UH+TP1CTlf\nWfeHlXtOMHT6BgpsDu5tW5d372uN2axNCysSvUdcPWfHtxr1irigOZsOFQ3+R3RvUmaDfxGR661b\ns5pMGNQWN7OJub8f4uVvE3CxzzZFnKYCQMTFfL/1CKPnFO60GNO5IaNvCzU4kYjI1enVKph/3x+B\nyQQz1h7grUU7VQSIXIIKABEX8tP24zw7ewt2BwyMqsfLd95wxZvwiYiUJ30i6/BW33AAJv+6j/eX\n7jE4kUj5pQJAxEX8uvsET37xO1a7g3siQ3ijb7jmyYpIpTKwQ31evvMGAMYv28PHK5IMTiRSPqkA\nEHEB6/al8ejnG8m32ekVFsy/+kfgpsG/iFRCQ7s2YtQfUxvfWrSTz9ckG5pHpDxSASBSyW0+cIqh\n0zeQW2CnR2hN/jtIy+SJSOX2ZI+mPNmjcHGDfyxI5KuNBw1OJFK+aBQgUoltPXSahz9dT3a+jc5N\nAvhwcDs8LPq1F5HK7/lbQ4np3BCAF+ZuZc6mQ8YGEilHNBIQqaS2HjrN4E/WkZFrpX2DGkwZ0h4v\nd+2SKSKuwWQyMfauGxjcsT4OB4yaE68iQOQPTu8ELCLlX/zB0wyeuo7MPwb/04d2wMdTv+4i4lpM\nJhP/vLsVULg86Kg/lkC+r11dI2OJGE4jApFKZsvB0zz0x+A/qmENpsV2wFeDfxFxUWazigCRP9Oo\nQKQS2XLwNA99so7MPA3+RUTOUREgUpxGBiKVxOYDpxgydT2ZeVY6NPRnWmyUpv2IiPxBRYDI/+gm\nYJFK4PfzB/+NNPgXESnJuSLg/BuDv9YSoeKCVACIVHAbktOLD/5jNPgXEbmYC4uArdosTFyOCgCR\nCmzlnhM8NHUdWXlWohv5M12f/IuIXJbZbOK1Pq2K9gn4x4JEPl6RZGwoketIBYBIBbUk8RjDpm8k\nt8DOTc1rMj22A94eGvyLiJTGuX0Czu0Y/Nainfz7p904HA6Dk4lceyoARCqgbzYf5okvfiffZqd3\nq2AmD2lHFQ9t8iUi4gyTycSo21ow6rZQAP67bA9vLtyhIkAqPRUAIhXMzHUH+OtXW7DZHfRrW4cJ\ng9rgadHgX0TkSj3Zoylj77oBgCkr9/P3bxKw21UESOWlAkCkApny6z5enL8NhwMGd6zPv+6LwOKm\nX2MRkasV26URb98bjskEX6w7wN++jqfAZjc6lsg1oQnDIhWAw+HgvR9388HyvQA8dlNjxvRqgclk\nMjiZiEjlMSCqPl7ubjz3VTzzNx/mdE4+Ex9sq/urpNLRR4ci5ZzVZmfM3G1Fg//nb22uwb+IyDXS\nJ7IOU4a0w8vdzPJdJ3jwk3Wcys43OpZImVIBIFKOnc238fiMTXy58SBmE7zZN5ynbm6mwb+IyDV0\nc4tafDE8mmpV3Nl84DT3fbSaw6fPGh1LpMyoABApp07n5DN46jqW7kjFw2Lmw8HteCC6vtGxRERc\nQrsG/sx5vBO1q3mRdCKb+z5cze7jmUbHEikTKgBEyqEjp8/S/6M1bEo5RVUvCzOGRXNbWLDRsURE\nXEqzWn7MHdGZJjV9OHom94/35XSjY4lcNRUAIuXM7uOZ3PvhavakZhFc1YuvH+9Mh0b+RscSEXFJ\nIdWrMOfxzkTWq86ZswU8+Mk6FiccMzqWyFVRASBSjvy25yT3TlrN0TO5NKnpw9wnOhMa7Gd0LBER\nl1bDx4OZj0TTI7QmuQV2RnyxiSm/7tOGYVJhqQAQKSdmrz9AzLT1ZOZZiWpYgzmPd6ZO9SpGxxIR\nEcDbw8KUIe15MLo+Dge8sXAH/1iQgFV7BUgFpAJAxGB2u4O3Fu1gzLxtWO0O7okMYcbwaGr4eBgd\nTUREzmNxM/P6Pa34+x0tMZlgxtoDDP9sI1l5VqOjiThFBYCIgc7m23hy5u98vGIfAM/+pRn/GRCJ\np8XN4GQiIlISk8nE8G6N+fDBwr0Cftl1gv4freHoGS0TKhWHCgARg6Rm5jJw8hoWJRzDw83M+wMi\nefYvzbXGv4hIBdCrVTCzH+1EoK8HO45mcM/EVWw7dMboWCKlogJAxAAJh89wzweriD90hhre7swY\nHs09beoYHUtERJwQWa8685/oQrMgX45n5HHfR6tZsOWw0bFELksFgMh19s3mw9z74WqOnMmlcaAP\n857oomU+RUQqqHr+3sx9ojM9QmuSZ7XzzOwtvLVoBza7VgiS8ksFgMh1YrXZeeOH7Tz75RbyrHZ6\nhNZk/pNdaBToY3Q0ERG5ClW93Pnk4ShGdG8CwMcr9jF0+gbOnC0wOJlIyVQAiFwHp3PyiZ2+gSkr\n9wPwZI8mfPJwFNWquBucTEREyoKb2cQLvVrw30Ft8HI3s2L3Ce6ZuIq9qVlGRxO5gNMFQFZWFs8+\n+ywhISF4eXkRGRnJ7NmzS9U2NTWVmJgYAgMD8fb2plOnTixbtqzEc5cuXUqnTp3w9vYmMDCQmJgY\nUlNTi52TnJyMyWQq8V9pM4lcazuPZXD3B6tYueckVdzdmPhAW0bd1gI3s272FRGpbO6OCGHO450J\nqebF/pPZ9J24ip+2Hzc6lkgxThcA/fr1Iy4ujrFjx7Jo0SKioqIYNGgQM2fOvGS7vLw8brnlFpYt\nW8b48eNZsGABtWrVolevXqxYsaLYuStWrKB3797UqlWLBQsWMH78eJYuXcott9xCXl7eBY89cuRI\n1qxZU+xfz549nX1pImVuwZbD9Ju0mgPpOdTzr8K8JzpzR+vaRscSEZFrqFWdanw7sisdGvqTmWfl\nkc82Mm7RTm0aJuWGxZmTFy5cyE8//cTMmTMZNGgQAD169CAlJYVRo0YxYMAA3NxKXr986tSpJCQk\nsHr1ajp16lTUNiIigtGjR7Nu3bqic0eNGkXz5s2ZM2cOFkthxEaNGtGlSxc+/fRTRowYUeyx69ev\nT8eOHZ15KSLXVG6BjX9+v52Z6w4A0KVpAB8MaqvNvUREXESgryczhkfz5sIdTF+dzEcrkvj9wCk+\nGNSGoKpeRscTF+fUFYD58+fj6+tL//79ix2PjY3lyJEjxQbxJbUNDQ0tGvwDWCwWBg8ezPr16zl8\nuHDZrMOHD7NhwwYeeuihosE/QOfOnWnevDnz5893JrLIdZd8Mpt+k1Yzc90BTCZ4+uamfDZUO/uK\niLgaD4uZV+4OY+IDbfH1tLB+fzq3//c3ViedNDqauDinCoCEhARatmxZbGAO0Lp166LvX6rtufNK\napuYmFjsMS52bknPMW7cODw8PPD29qZr1658++23pXxFImVr0baj3DXhN7YfzcDfx4PpsR147tZQ\nzfcXEXFhd7SuzbdPdaFFsB8ns/IY/Mk6Ji7fi11LhYpBnJoClJaWRuPGjS847u/vX/T9S7U9d96l\n2p77erFzz38OT09PHnnkEXr27Ent2rU5cOAAEyZMoE+fPkyZMoXhw4eX6nUlJiZit2te3pUqKCgo\n+hofH29wGmMU2BzEbTnDd7sLV3toGejB8138qX72CPHxRwxOd32pP8ifqU/I+Vy5P/yzmx8fb7Sx\nbH8O7y7Zxc9bU3g6ugbVq5Q8fdpVuHKfKCtms5n69euX+nynCgAAk+nin2Re6nvOtr3Yuecfr127\nNpMnTy72/f79+xMdHc2YMWOIiYm54GpFSaxWKzab7bLnyeWd+yV2JYczrIxff4Z9p60A9GnuzaBW\nvljMDpf8eZzP1V+/XEh9Qs7nav3BDIxo50dzfwtTN2ew6WguTy86zpPtq9K2tqfR8coFV+sTZeVi\n9+BejFMFQEBAQImf8qenpwMlf2rvbNuAgACg5KsJ6enpl3wOAHd3dwYMGMCYMWPYs2cPLVu2vOT5\nUHgvgtmsLRGu1Pm/rO7urrOuvcPhYElSNlN/P0O+zYGfh5mR0TWIrlvF6GiGctX+IBenPiHnU3+A\nXs3daRlUhfdWp5Fyxsqbq05zR3NfYiKr4eHmelNG1SeunrPjWKcKgPDwcGbNmoXVai32yfq2bdsA\naNWq1SXbnjvvfH9ue+7rtm3buP322y8491LPcY7DUTinrrQ/jLCwMBUAVyE+Pp6CggLc3d2JiIgw\nOs51kZaVxwtzt7F0x2kAujUL5F/9I6illR1csj/IpalPyPnUHwpFALd2tjFu0U6mr07mh91Z7D1j\nYvygSFoEVzU63nWlPnH17HY7mZmZpT7fqVFv3759ycrKYu7cucWOx8XFERISQnR09CXb7ty5s9hK\nQVarlRkzZhAdHU1ISAgAderUoUOHDsyYMaPYtJy1a9eya9cu+vXrd8mMBQUFfPnllwQGBtK0aVNn\nXp5IqazYfYJe41eydMdxPNzM/P2OlsTFdtDgX0REnOLl7sYrd4cxLTaKQF8Pdh3P5O4PVjFt1X7d\nICzXlFNXAHr37k3Pnj0ZMWIEGRkZNG3alFmzZrF48WJmzJhRNP9o2LBhxMXFkZSURIMGDQAYOnQo\nEydOpH///owbN46goCAmTZrErl27WLp0abHnefvtt+nZsyf9+/fniSeeIDU1lTFjxtCqVStiY2OL\nznvuuecoKCigS5cuBAcHc/DgQSZMmMCWLVuYNm2a0/OhRC4lM7eANxfuZNb6wrX9mwX5Mn5gG24I\nca1PakREpGz1CA1i0TM3MnpOPMt3neDV77bzY+Jx3rmvNfX8vY2OJ5WQ0zcBz5s3j5deeomXX36Z\n9PR0WrRowaxZsxg4cGDROTabDZvNVjQVBwpX7Fm2bBmjR49m5MiR5OTkEBkZyaJFi7jpppuKPUf3\n7t1ZuHAhL7/8MnfddRfe3t7ceeedvPvuu3h6/u8mmVatWvHxxx8zc+ZMMjIy8PPzo0OHDixZsoRb\nb731Sn4eIiX6bc9JXpi7lcOnzwLwcKcG/N/tLfFyV5EpIiJXr6afJ5/GRPHZmhTeWrSDNfvSuO39\nX/m/3i14MLoBZi0nLWXI5Dh/lO4CSpoj5efnp3sArkJlnruXlWflrYU7+OKPHX3r+VfhnXsj6NQk\nwOBk5Vdl7g9yZdQn5HzqD5eXfDKb0XO2sj65cKGUTo0DKvXVAPWJq+fs+FajXpGLWLnnBLf959ei\nwf+QTg1Y/MyNGvyLiMg11TDQh9mPduSVu26girtb0dWAz9ck694AKRNOTwESqexOZuXx2vfbWbCl\ncAOvujWq8M59rencJNDgZCIi4irMZhMxXRrRo0UQo+ZsZf3+dP6xIJEFW47wZr9wmtfyMzqiVGC6\nAiDyB7vdwez1B7jlvRUs2HIEswliOjdkybM3avAvIiKGaBDgw+xHCq8GeHu4sTHlFLePX8nbi3dy\nNl+bmMqV0RUAEWDP8UxenL+NDcmnAAgLqcpb/cJpXbe6wclERMTVnbsa0DMsmFe+TeSn7cf58Jck\nvos/wmt9WtGjRZDREaWCUQEgLi0jt4AJy/YwbVUyVrsDbw83nuvZnJjODbG46QKZiIiUH3WqV2HK\nkPb8mHiMV75N5NCps8RO30DvVsG8dEdL6taonDcJS9lTASAuyW53MOf3Q7yzeCcns/IB+EvLIF7t\n04o61asYnE5EROTibg0LpkvTQN5fuptPVyWzKOEYP+9M5bEbG/N49yZ4e2h4J5emHiIuZ/OBU7zy\nbSLxh84A0DjQh3/cdQM9QnUJVUREKgYfTwsv3XED/drW5dXvElm7L53//ryXrzYeYkzvFvSJDMFk\n0t4BUjIVAOIyDqbn8O+fdjN/82EAfD0tPHNLMx7u3BAPi6b7iIhIxdOydlVmPdKRJYnHeGPhDg6m\nn+XZL7cQtyaZsXeFEVlP97LJhVQASKWXnp3PxOV7+XxNCvk2OwD3tavL6F6hBPl5GZxORETk6phM\nJnq1qk330CCm/raficv3svnAae6ZuIo7W9fmb7eG0ijQx+iYUo6oAJBK62y+jU9X7eejX5LIzLMC\n0KVpAGN6tSS8bjWD04mIiJQtL3c3nuzRlPva1eWdxbuYt/kQ3289yqKEYwyIqscztzSjVlV98CUq\nAKQSyrfambPpEOOX7eZ4Rh4AN9SuypjeLejWLFBzIkVEpFKrVdWL9+6PYHi3RvxryS6W7Uxl5roD\nzPv9EDGdGzHipiZU83Y3OqYYSAWAVBr5VjtfbzrIpOVJHD59Fijcxff5W0O5OyIEs1kDfxERcR0t\na1dlakwUG5LTeXvRTjamnOKjFUl8sS6F4V0bE9OlIdWqqBBwRSoApMLLs9r4euMhJi3fy5EzuQDU\n9PNkxE1NeLBjfTwtbgYnFBERMU5UQ3++frwTy3el8s7iXew8lsl/lu7mk5X7eLhzQ4Z2bYS/j4fR\nMeU6UgEgFVZugY2vNx5k0i9JHP1j4B/k58mI7k0Y1KE+Xu4a+IuIiEDhjcI3t6jFTc2DWLjtKB/8\nvJddxzP5YPlePl21n4c6NmB4t8bU9PM0OqpcByoApMJJz87nszXJfLYmhfTswk28alUt/MR/oAb+\nIiIiF+VmNnFXRAh3hNfmx+3HmfDzHhKPZPDxr/uYvjqZAVH1GNqlEQ21alClpgJAKoz9J7OZ+ts+\n5mw6RG5B4XKedWtU4dEbG3N/+3oa+IuIiJSS2WyiV6tgbgurxfJdqfx32V62HDzNZ2tS+HxtCj1b\n1uKRGxvTvkENLZ5RCakAkHLN4XCwbn8601cls2T7MRyOwuPhdarx6I2N6d0qGIubNvESERG5Euem\nBvUIDWJ1UhpTVu7jl5W763oAACAASURBVF0n+HH7cX7cfpyIutUY1q3w7627/t5WGioApFzKzC3g\nm82H+XxtCruPZxUd7xFak0dvbELHxv76REJERKSMmEwmujQNpEvTQPYcz+TTVfuZ+/th4g+d4elZ\nm6ldzYuBUfUZEFWP4GraS6CiUwEg5cquY5l8vjaZ+b8fJjv//9u787io6v1/4K+B2WAYZGdYBFRC\nBFErcd8KIUpNobyprVT6ze3a49ZPzXI3NbvXpNL7KL2FuWVpLtcUzCW75ZJWmphLiogg+7AMA8Ns\n5/cHMjkMIJSCMK/n4zGPgc95n3M+h3kD533O55xjAgA4SRwx5n5/JA3shDBfZSv3kIiIqH27z1eJ\nZYk98FpcV2w6noUNxzORW6bDewcu4f1Dv2N4Nx883TcYg0K9eIvtNooFALU6jc6Ar3/NxZc/ZeOn\nayWW9s7eCjzbLxiJDwTyPsVEREQtzMtFhhnD78P/De2MtHN52HQ8Cz9mqpF2Lh9p5/IR5OGMCX2D\nkHh/AHz4hOE2hQUAtQqzWcCxjGJs+ykb+9JzLRf1OjqIEBfhi2f7BaN/F08O8yEiImplcokjRvcK\nwOheAbiUr8HmE1nY/nM2stSVWL7vAlakXsDg+7zxxIOBiIvw5U052gAWANSiLuZp8N8zN7DjlxzL\n03oBINTHBU8+GMijCERERPewMF8lFjweiZnxXbHnTC62nrqOn66V4MilQhy5VAilTIzHovyQ+EAA\nokM8OEToHsUCgO66K4UV2HMmF3t+vYHfC/64oFcpF+Pxnv4Y27sjegZ24NF+IiKiNsJZKsbfojvi\nb9EdcbVIix0/Z+OrX3KQXVKFraeuY+up61C5yvFYlB9G9FDh/o7uLAbuISwA6I4TBAFXCiuQdi4f\ne37Nxfnccss0qaMDhoR54/Fe/jxNSERE1A508lLgH3Fd8erwMJzMVGP7z9nYezYPeeU6fPLDVXzy\nw1UWA/cYFgB0R5jMAi4VVOO/e37DgfP5yCyutEwTO4gw6D4vjOzhj9gIX17QS0RE1A45OIjQt7Mn\n+nb2xKLR3fHdpULsPZuLA+cLrIoBH6UMD4f7IKabLwaGerZ2t+0SCwD608oqDfj+chG+PKbGqRtV\nqNALAAoB1Bzp79/FE/HdVYiPVMFdIW3dzhIREVGLkUscERepQlykCjqDyaoYKNBU4/OT1/H5yeuQ\nih0Q5S3FAyoJ+nZUtHa37QYLAGoyvdGMX7JK8P3lInz3exHOZpfCLPwxXSl1QGykH4ZH+GJImDdc\nZEwvIiIie3drMVBtNOFEhhoHz+fjwPkC5JRW4adcHX7K1WHtLxp0PfEdBoR6YlCoF/p29uS+xF3C\nnyo1yGQWcD63HCcz1fj+9yIczyi2PJyrVqiPCyLdgQdVEnRXOeOB+3u1Um+JiIjoXicTO2JImDeG\nhHljweMCLuVXYOPh0ziZXYVLagMu5mtwMV+DT3/IhNhBhJ4d3TAw1AuDQr3Qq6MbpGKH1t6EdoEF\nAFnoDCb8ml2Gk5lq/HhVjZ+vlUBTbbSK8VBIMSjUC4Pu88Lg+7zg18EJZ86cgcFggCMv6CEiIqIm\nEolE6KpS4skIV4y+zwlVZgeUy/3w/eUiHL1ShGvFlfjpWgl+ulaC9w/+DpnYAT07uiE6xB29Qzzw\nQJA7ryv8k1gA2ClBEJBdUoVfs8vwa3YpfrpWgl+zy6A3ma3iXGRiPBjsjn6dPTH4Pi9E+Lnyyn0i\nIiK641xljhjcww8jevgBAK6rK/HD5SL8cKUYRy8XoVirx49Xaw5SAlcgEgFdfZXoHeKO+zu6o0dg\nB3T2duEBySZgAWAnCjQ6/Hq9Zmf/THYZzuaUQa3V28R5ucjQp5M7okM8EB3igW5+rvxFIiIiohbX\n0cMZ4/oEYVyfoJu3GNfip2tqnMysOStwtUiLC3kaXMjTYOPxLACAs9QR3f07ICqwA3oEdkCPQDcE\nezjz4GUdLADamSq9Cb8X1PwyXMjV4GJ+OS7maVBUYbuzL3YQIdxPiR6BbugV6IboTh4I8XTmA7mI\niIjoniISiRDq44JQHxc8FR0EACjUVOOna2qcyqwZxZB+owyVehN+zFTjx0y1ZV6lTIyuKiW6qpQI\nVynRVeWKrr5KdHC23+FDLADaqHKdAVcLtbhapEVGYQV+L6jAxTwNrhZrIQi28SIREOrtgh6BbujZ\nsaYiDlcp+SAuIiIiapO8lTLEd/dDfPeaIUMms4CMwoqakQ7Zpfg1pwy/3SiHptqIU9dKcOpaidX8\nKle5pTAI9XZBJ28FOnkp4KmQtvuDoSwA7mFlVQZkl1Qiu6QKmUVaZNTu8BdpUVRR3eB8HgrpzQr3\nj0o3zNcFzlJ+3ERERNQ+OTqIcJ+vEvf5KvHkg4EAAIPJjMsFFbiUXzM64uLNV05pFfLKdcgr1+HI\npUKr5SjlYnTyUli9QjwVCHB3ajfFAfcIW4nZLEBdqUdemQ43SquQXVKF6zd39mteldDojI0uw1sp\nQ2cvBTp7K9DF28VSxXq7yNpFchIRERH9FRJHB3Tzc0U3P1eMvqVdozPgUn7FzYKgHBlFNQdZc0qr\noNEZb94kpcxmeXKJAwLdnRHg5oRAdycEuDtZfe+pkELseO/fqrTZBUBFRQXeeustfPHFF1Cr1QgP\nD8fs2bMxbty4285bUFCAmTNnYs+ePaisrETPnj2xZMkSxMTE2MQeOHAAc+fOxZkzZ+Ds7IyRI0di\nxYoV8PHxsYozGAxYunQpPv30U+Tm5qJTp06YOnUqpk+f3txNuyOMJjNKKg0o1lYjv7wa+eU6FJTr\nkF9ejQLNzfdyHQo01TCa6xmrU4enQooAdycEeyosO/u11ahSbr9j14iIiIj+LKVcggeD3fFgsLtV\nu85gQpa6EhmFWmQWay3DrTOLtSjQVENnqDmjcLmgot7lOogATxcZfF1l8FXK4eMqh49SBl9XOXxd\nZfBRyuGtlMFdIYFM3HrDsJtdACQmJuLkyZNYvnw5wsLCsHnzZowfPx5msxkTJkxocL7q6mrExMSg\ntLQUycnJ8PHxwerVqxEfH48DBw5g6NChltgjR47g0UcfxYgRI7Br1y4UFBRg1qxZiImJwalTpyCT\nySyxU6ZMwYYNG7B48WJER0cjLS0NM2bMgEajwZw5c5q7eRaCIKBSb4JGZ4RGZ0C5zoCyKgOKK/Qo\nqdSjWKtHiVYPtdYAtbYaJZUGqLV6lFUZmrwOkejmDr5bTfUY6O508+VsqSo5bIeIiIioZcgljgjz\nVSLMV2kzrdpoQm6pDtklVcgprRm1kXNz5EZOaRVyy6pgFmouTi7UVCMd5Y2uSyF1hIeLFB7OUrgr\npPBQ/PG1p6Lm3d1ZCqVcDFcnCZRyMVyk4jtyRyORINR3yWj99u7dixEjRlh2+mvFxcXh3LlzyMrK\ngqNj/dXMmjVrMHXqVBw9ehT9+/cHABiNRvTs2RMuLi44ceKEJbZPnz7QarU4c+YMxOKaHeCjR49i\n4MCBWLNmDSZPngwAOHfuHKKiovD222/jjTfesMw/adIkbNy4EdnZ2fDw8LDqh9lshkajsWpbsC8D\neeXVKNcZoNEZLe+mJhyhr49IBLg7S60qPt+bFaCPq9zS5uUig6QNnCa6ndoHgUkkEvTs2bO1u0Ot\njPlAdTEn6FbMB6qrveSEySygWFuNgltGfeTfHPVROxokv1wHtVbfpFEg9RGJap7R5CqXWIoCV7kE\nKqUU/y8m2CpWqVTCwaH+/cxmHV7esWMHXFxcMHbsWKv2pKQkTJgwASdOnMCAAQManLdr166WnX8A\nEIvFeOaZZzBnzhzk5OQgICAAOTk5OHnyJJYtW2bZ+QeAAQMGICwsDDt27LAUADt37oQgCEhKSrLp\nz9q1a5GamtroWYla314sQElV/ePtHR1EcJWLoZRL0MFJUlOd3azIPF1q3j0UEngoZPBQSODuLIWb\ns5T3ziciIiKyI44OIvgo5fBRygF0aDBOEASU64xQa/VQW0aU6KGurPnaMsqkUo/SSkPNSJQqI/Qm\nMwQBN0enGJFTWmVZpruT2KYAaEyzCoD09HR069bNasccAHr06GGZ3lABkJ6ejsGDB9u018577tw5\nBAQEID093aq9buwPP/xgtUxvb2+oVKoG+9MUz/fqAEcIUEhFcJY4QCF1gELiAIVUBJmjqIELag03\nX1rABKAc0JYDWgDZTVpr+2EwGCzvZ86caeXeUGtjPlBdzAm6FfOB6rLnnBAD8AbgLQUgBeBWO6W2\n4Q96kwCt3gytwXzzXUDlza/NaN6IkmYVAMXFxejcubNNe+0wm+Li4kbnrTscp755a98bir11HQ0t\nU6FQQCqVNtqfWw0NksFkMtVpNQMCYGz8RjxUR+0vMRHAfCBbzAm6FfOB6mJONEwEwEVc84JT7Q5/\nzdD7hobgN6TZV5g2dnvJ2916sjnzNhTb1Lim9KeWWCxucIwU3d6tv6wSCe9MZO+YD1QXc4JuxXyg\nupgTf11z92ObVQB4enrWe1Rdra553HJ9R+ObO6+npyeA+s8mqNVqq3V4enri9OnTNnFarRZ6vb7R\n/twqMjKSBcBf0F4u3qE7g/lAdTEn6FbMB6qLOfHX1XeTm8Y0a683KioK58+fh7HOuJizZ88CALp3\n797ovLVxjc1b+95Q7K3riIqKQmFhIfLy8prdHyIiIiIie9SsAiAhIQEVFRXYvn27Vfv69evh7++P\nvn37NjrvhQsXrG73aTQasXHjRvTt2xf+/v4AgICAAPTp0wcbN260Gpd//PhxXLx4EYmJiZa20aNH\nQyQSYf369VbrSklJgZOTE+Lj45uzeURERERE7V6zhgA9+uijiI2NxeTJk1FeXo7Q0FBs2bIFqamp\n2Lhxo+UChJdeegnr16/HlStXEBxcc0uiF198EatXr8bYsWOxfPly+Pj4YM2aNbh48SIOHDhgtZ53\n3nkHsbGxGDt2LKZMmYKCggLMnj0b3bt3t7rlZ2RkJF566SXMnz8fjo6OiI6Oxv79+/Hxxx9jyZIl\nTR4CRERERERkL5p9EfBXX32FN998E/PmzYNarUZ4eDi2bNmCcePGWWJMJhNMJhNufcaYTCbDwYMH\nMXPmTEyfPh2VlZXo1asX9u3bZ/UUYAAYNmwY9u7di3nz5mHUqFFwdnbGyJEj8e6771o9BRioecBY\nQEAAPvjgA+Tl5SEkJATJycmYPn16czeNiIiIiKjda9aTgNsDk8mEiooKqzaFQsGLgP+Cc+fOwWg0\nQiwWIzIysrW7Q62M+UB1MSfoVswHqos58deZzWZotVqrNhcXlwZvD2p3BYDRaLT5ARERERERtScK\nhcLm4b21eNibiIiIiMiOsAAgIiIiIrIjLACIiIiIiOyI3V0DYDabYTabrdpEIhFEIlEr9YiIiIiI\n6M8TBAF1d+kdHBwavMmN3RUARERERET2jEOAiIiIiIjsCAsAuq1ffvkFY8aMgb+/P5ydnREeHo5F\nixahsrLSKu7nn3/G8OHD4eLiAjc3NyQmJiIjI6OVek13gkajwcyZMxEXFwdvb2+IRCIsWLCg3tjm\nfP4ffPABwsPDIZPJ0KlTJyxcuBAGg+EubgndKU3JCZPJhJUrVyI+Ph6BgYFwdnZGt27dMHv2bJSW\nlta7XOZE29ScvxG1BEHAkCFDIBKJMG3atHpjmA9tV3NywmAwYOXKlYiKioKTkxPc3NwwYMAAHD16\n1CZu4cKFCAkJgUwmQ3h4OD744IMW2Jr2iwUANeq3337DgAEDkJmZiVWrVmHPnj0YN24cFi1ahPHj\nx1viLly4gGHDhkGv1+OLL77AJ598gkuXLmHw4MEoLCxsxS2gv6K4uBgff/wxqqurMWbMmAbjmvP5\nv/3225gxYwYSExORlpaGKVOmYOnSpZg6derd3hy6A5qSE1VVVViwYAGCg4OxatUq7N27FxMnTsTH\nH3+MgQMHoqqqyiqeOdF2NfVvxK1Wr16Ny5cvNzid+dC2NTUnTCYTEhISLPsT+/btw6ZNmxAfH2/z\nvKYpU6Zg2bJlmDp1KtLS0pCQkIAZM2Zg6dKld3tz2i+BqBFvvvmmAEC4fPmyVfukSZMEAIJarRYE\nQRDGjh0reHl5CWVlZZaYzMxMQSKRCDNnzmzRPtOdYzabBbPZLAiCIBQWFgoAhPnz59vENfXzLyoq\nEuRyuTBp0iSr+d9++21BJBIJ586duzsbQndMU3LCaDQKRUVFNvN++eWXAgBhw4YNljbmRNvW1L8R\nta5evSq4uLgIX331lQBAmDp1qtV05kPb19SceO+99wQHBwfh2LFjjS4vPT1dEIlEwtKlS63aJ06c\nKDg5OQnFxcV3rO/2hGcAqFESiQQA0KFDB6t2Nzc3ODg4QCqVwmg0Ys+ePXjiiSfg6upqiQkODsZD\nDz2EHTt2tGif6c5pyh2ymvP5p6amQqfTISkpyWoZSUlJEAQBO3fuvLMbQHdcU3LC0dERnp6eNu19\n+vQBAFy/ft3Sxpxo25p7F71JkyYhNjYWCQkJ9U5nPrR9Tc2J5ORkDBkyBP369Ws0bufOnRAEod6c\nqKqqQmpq6l/qr71iAUCNev755+Hm5obJkycjIyMDGo0Ge/bswUcffYSpU6dCoVDgypUrqKqqQo8e\nPWzm79GjBy5fvgydTtcKvaeW0JzPPz09HQAQFRVlFefn5wcvLy/LdGqfDh06BACIjIy0tDEn7Me6\ndevw448/4sMPP2wwhvlgH65fv47MzExERUVhzpw58PX1hVgsRmRkJNavX28Vm56eDm9vb6hUKqv2\n2v85zIk/R9zaHaB7W0hICI4dO4aEhAR06dLF0v73v/8dq1atAlAz3g8APDw8bOb38PCAIAgoKSmB\nn59fy3SaWlRzPv/i4mLIZDIoFIp6Y2uXRe1PTk4OZs+ejd69e2PkyJGWduaEfcjJycHrr7+OFStW\nwN/fv8E45oN9yMnJAQCsX78egYGB+PDDD9GhQwesXbsWL7zwAvR6PSZOnAigJifq+/+iUCgglUqZ\nE38SCwBqVGZmJkaNGgVfX19s27YN3t7eOHHiBJYsWYKKigr85z//scQ2dsqPD1pr/5r6+TNP7I9a\nrcZjjz0GQRCwdetWmwfTMCfav1deeQU9e/a07NQ1hvnQ/tU+kFWn02Hv3r0IDg4GAMTGxqJ3795Y\ntGiRVa4wJ+48FgDUqNmzZ6O8vBynT5+2HJEZMmQIvLy88OKLL+K5556znJarrwpXq9UQiURwc3Nr\n0X5Ty6kd692Uz9/T0xM6nQ6VlZVwdna2iX3wwQfvfoepRZWUlCA2NhY5OTk4dOgQOnfubDWdOdH+\nbdu2Dampqfj+++9RVlZmNU2v16O0tBQKhQISiYT5YCdq/2+Eh4dbdv6Bmp35Rx55BMuWLUNBQQF8\nfHzg6emJ06dP2yxDq9VCr9fXe3aAbo/XAFCjTp8+jYiICJvTsdHR0QBqxt516dIFTk5OOHv2rM38\nZ8+eRWhoKORyeYv0l1pecz7/2nG9dWPz8vJQVFSE7t273/0OU4spKSnB8OHDcfXqVXzzzTf1XifC\nnGj/0tPTYTQa0a9fP7i7u1teALB27Vq4u7vj66+/BsB8sBddunSxKfBqCYIAAJYzhVFRUSgsLERe\nXp5VXG2OMCf+HBYA1Ch/f3+cO3cOFRUVVu3Hjh0DAAQGBkIsFmPUqFH46quvoNFoLDFZWVk4fPgw\nEhMTW7TP1LKa8/nHx8dDLpcjJSXFahkpKSkQiURNvo843ftqd/4zMjKwf/9+3H///fXGMSfavxde\neAGHDx+2eQHAmDFjcPjwYQwaNAgA88FeiMVijB49GufPn0dmZqalXRAEpKamokuXLvDy8gIAjB49\nGiKRyObi4JSUFDg5OSE+Pr4lu95uOC643SP7yK65u7vjk08+waFDh+Dq6or8/Hxs2bIFc+fORWho\nKP75z3/C0dERUVFRWLNmDQ4fPgyVSoX09HRMnDgRIpEIn332Wb0XdFHbsG/fPpw5cwZnz57Frl27\n4OPjA5FIhN9++w0hISGQSCRN/vydnJwgEonw7rvvQq/XQywWY9u2bZg3bx6SkpLw4osvtvLWUlPc\nLieMRiNiYmLw888/45133oGfnx+ys7Mtr+rqastpe+ZE23e7fPD29kZISIjNa+HChYiJicGUKVMs\nR4OZD+1DU/5v9OrVCykpKdi5cye8vLyQlZWF2bNn48iRI/joo48QEREBAPDx8UF2djaSk5Mhl8th\nMBiwdu1aJCcnY8GCBYiLi2vlrW2jWu0JBNRmHDp0SIiLixNUKpXg5OQkhIWFCa+99prNg35OnTol\nxMTECM7OzoKrq6swZswYmweIUdsTHBwsAKj3dfXqVUtccz7/5ORkISwsTJBKpUJQUJAwf/58Qa/X\nt9AW0V91u5y4evVqg9MBCM8//7zNMpkTbVdT/0bUhXoeBFaL+dC2NTUnzp49K4wYMUJQKpWCXC4X\n+vXrJ/z3v/+1WZ5erxfmz58vBAUFCVKpVAgLCxPef//9Ftyi9kckCDcHWxERERERUbvHawCIiIiI\niOwICwAiIiIiIjvCAoCIiIiIyI6wACAiIiIisiMsAIiIiIiI7AgLACIiIiIiO8ICgIiIiIjIjrAA\nICKiu+qFF15ASEiITfuVK1cgk8lw7NgxS9uwYcPQvXv3O7bulJQUiEQinDp16raxQ4YMwauvvnrH\n1k1EdK9iAUBERK3i9ddfR2xsLPr379/aXQEALF68GGvWrMHFixdbuytERHcVCwAiImpx58+fx86d\nOzF9+vTW7orF0KFD0bVrV/zrX/9q7a4QEd1VLACIiNqQwsJCTJo0CR07doRMJoO3tzcGDhyIAwcO\nAPhjCM3//vc/9OvXD05OTggICMDcuXNhMpmslqXX67FkyRKEh4dblpWUlITCwkKb9W7duhX9+/eH\nQqGAi4sLHnnkEfzyyy82cSkpKejatStkMhm6deuGzz77rN7t+Pe//w2VSoXY2NjbbvOOHTvg7OyM\nl19+GUajEQAgEokwbdo0fPTRRwgLC4NMJkNERAQ+//zzepeh0WgwefJkeHl5wdPTE4mJibhx44ZN\n3LPPPovNmzdDo9Hctl9ERG0VCwAiojbk2Wefxc6dOzFv3jzs378f69atw/Dhw1FcXGyJycvLw7hx\n4/D0009j165dePLJJ7FkyRLMmDHDEmM2mzF69GgsX74cEyZMwNdff43ly5fjm2++wbBhw1BVVWWJ\nXbp0KcaPH4+IiAh88cUX2LBhAzQaDQYPHozffvvNEpeSkoKkpCR069YN27dvx1tvvYXFixfj0KFD\nNtvx9ddfY8iQIXBwaPzf0HvvvYexY8dizpw5WLduHcRisWXa7t278f7772PRokXYtm0bgoODMX78\neGzbts1mOS+//DIkEgk2b96MFStW4Ntvv8UzzzxjEzds2DBotVp8++23jfaLiKhNE4iIqM1wcXER\nXn311QanDx06VAAg7Nq1y6p94sSJgoODg3Dt2jVBEARhy5YtAgBh+/btVnEnT54UAAhr1qwRBEEQ\nsrKyBLFYLEyfPt0qTqPRCCqVSvjb3/4mCIIgmEwmwd/fX3jggQcEs9lsicvMzBQkEokQHBxsacvP\nzxcACMuXL6+3/5GRkYLJZBKmTZsmSKVSYePGjTZxAAQnJychLy/P0mY0GoXw8HAhNDTU0vbpp58K\nAIQpU6ZYzb9ixQoBgJCbm2vVrtfrBZFIJMyaNctmnURE7QXPABARtSF9+vRBSkoKlixZguPHj8Ng\nMNjEKJVKPP7441ZtEyZMgNlsxnfffQcA2LNnD9zc3DBq1CgYjUbLq1evXlCpVJYj4GlpaTAajXju\nuees4uRyOYYOHWqJu3jxIm7cuIEJEyZAJBJZ1hscHIwBAwZY9aV26I2Pj0+926jT6TBmzBhs2rQJ\n+/fvx9NPP11vXExMDHx9fS3fOzo64qmnnsLly5eRnZ1tFVv359GjRw8AwLVr16zaJRIJ3NzckJOT\nU+86iYjaAxYARERtyNatW/H8889j3bp16N+/Pzw8PPDcc88hLy/PEnPrTnEtlUoFAJahQvn5+Sgt\nLYVUKoVEIrF65eXloaioyBIHANHR0TZxW7dutcTVLrd2PfWtu1bt8CK5XF7vNhYUFCAtLQ39+/e3\nKR4aW25921nL09PT6nuZTGbVl1vJ5fJ624mI2gvx7UOIiOhe4eXlhVWrVmHVqlXIysrC7t27MXv2\nbBQUFCA1NRXAHzvtt6otEGp3hGsvhq2dpy6lUmmJA2AZY9+Q2uXeWojUXfet2wAAarW63mUFBQVh\n5cqVSEhIQGJiIr788st6i4XG1lV3h785SkpKLH0kImqPWAAQEbVRQUFBmDZtGg4ePIgffvjB0q7R\naLB7926rYS+bN2+Gg4MDhgwZAgAYOXIkPv/8c5hMJvTt27fBdTzyyCMQi8W4cuUKnnjiiQbjunbt\nCj8/P2zZsgX/+Mc/LMOArl27hqNHj8Lf398SGxwcDCcnJ1y5cqXB5cXFxSEtLQ0jRozAyJEjsWvX\nLigUCquYgwcPIj8/33LGw2QyYevWrejSpQsCAwMbXHZjbty4AZ1Oh4iIiD81PxFRW8ACgIiojSgr\nK8NDDz2ECRMmIDw8HEqlEidPnkRqaioSExMtcZ6enpg8eTKysrIQFhaGvXv3Yu3atZg8eTKCgoIA\nAOPGjcOmTZvw2GOPYcaMGejTpw8kEgmys7Nx+PBhjB49GgkJCQgJCcGiRYvw5ptvIiMjA/Hx8XB3\nd0d+fj5+/PFHKBQKLFy4EA4ODli8eDFefvllJCQkYOLEiSgtLcWCBQtshupIpVL0798fx48fb3R7\nBw0ahIMHDyI+Ph5xcXHYu3cvOnToYJnu5eWFhx9+GHPnzoVCocCaNWtw4cKFBm8F2hS1fXrooYf+\n9DKIiO51LACIiNoIuVyOvn37YsOGDcjMzITBYEBQUBBmzZqFmTNnWuJUKhVWr16N119/HWfPnoWH\nhwfmzJmDhQsXrRYy9AAAAaNJREFUWmIcHR2xe/duJCcnY8OGDVi2bBnEYjECAwMxdOhQREVFWWLf\neOMNREREIDk5GVu2bEF1dTVUKhWio6PxyiuvWOJeeuklAMA777yDxMREhISEYM6cOThy5IjNbTWf\nfvppTJo0Cbm5ufDz82twm3v37o0jR45g+PDhePjhh5GWlmYZnvP4448jMjISb731FrKystClSxds\n2rQJTz311J/+Ge/cuRNRUVFW209E1N6IBEEQWrsTRER0ZwwbNgxFRUVIT09v7a40SqfTISgoCK+9\n9hpmzZrV7PlFIhGmTp2KDz/88I71qby8HP7+/njvvfcwceLEO7ZcIqJ7De8CRERELU4ul2PhwoVY\nuXIltFpta3cHQM1Dx4KCgpCUlNTaXSEiuqs4BIiIiFrFpEmTUFpaioyMjHtiyI2rqytSUlKsnjZM\nRNQecQgQEREREZEd4RAgIiIiIiI7wgKAiIiIiMiOsAAgIiIiIrIjLACIiIiIiOwICwAiIiIiIjvC\nAoCIiIiIyI6wACAiIiIisiMsAIiIiIiI7AgLACIiIiIiO/L/AYh0UDFR5gF4AAAAAElFTkSuQmCC\n", "text/plain": [ "" ] }, "metadata": {}, "output_type": "display_data" } ], "source": [ "plot_gaussian_pdf(mean=120, variance=17**2, xlabel='speed(kph)');" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "The y-axis depicts the *probability density* — the relative amount of cars that are going the speed at the corresponding x-axis.\n", "\n", "You may object that human heights or automobile speeds cannot be less than zero, let alone $-\\infty$ or $\\infty$. This is true, but this is a common limitation of mathematical modeling. “The map is not the territory” is a common expression, and it is true for Bayesian filtering and statistics. The Gaussian distribution above models the distribution of the measured automobile speeds, but being a model it is necessarily imperfect. The difference between model and reality will come up again and again in these filters. Gaussians are used in many branches of mathematics, not because they perfectly model reality, but because they are easier to use than any other relatively accurate choice. However, even in this book Gaussians will fail to model reality, forcing us to use computationally expensive alternatives. \n", "\n", "You will hear these distributions called *Gaussian distributions* or *normal distributions*. *Gaussian* and *normal* both mean the same thing in this context, and are used interchangeably. I will use both throughout this book as different sources will use either term, and I want you to be used to seeing both. Finally, as in this paragraph, it is typical to shorten the name and talk about a *Gaussian* or *normal* — these are both typical shortcut names for the *Gaussian distribution*. " ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "## Gaussian Distributions\n", "\n", "Let's explore how Gaussians work. A Gaussian is a *continuous probability distribution* that is completely described with two parameters, the mean ($\\mu$) and the variance ($\\sigma^2$). It is defined as:\n", "\n", "$$ \n", "f(x, \\mu, \\sigma) = \\frac{1}{\\sigma\\sqrt{2\\pi}} \\exp\\big [{-\\frac{(x-\\mu)^2}{2\\sigma^2} }\\big ]\n", "$$\n", "\n", "$\\exp[x]$ is notation for $e^x$.\n", "\n", "

Don't be dissuaded by the equation if you haven't seen it before; you will not need to memorize or manipulate it. The computation of this function is stored in `stats.py` with the function `gaussian(x, mean, var)`.\n", "\n", "> **Optional:** Let's remind ourselves how to look at a function stored in a file by using the *%load* magic. If you type *%load -s gaussian stats.py* into a code cell and then press CTRL-Enter, the notebook will create a new input cell and load the function into it.\n", "\n", "```python\n", "%load -s gaussian stats.py\n", "\n", "def gaussian(x, mean, var):\n", " \"\"\"returns normal distribution for x given a \n", " gaussian with the specified mean and variance. \n", " \"\"\"\n", " return (np.exp((-0.5*(np.asarray(x)-mean)**2)/var) /\n", " math.sqrt(2*math.pi*var))\n", "\n", "```\n", "\n", "

We will plot a Gaussian with a mean of 22 $(\\mu=22)$, with a variance of 4 $(\\sigma^2=4)$, and then discuss what this means. " ] }, { "cell_type": "code", "execution_count": 17, "metadata": { "scrolled": true }, "outputs": [ { "data": { "image/png": "iVBORw0KGgoAAAANSUhEUgAAAvYAAAEwCAYAAADcuDUUAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzs3Xd4VHWixvHvTHolJCFAKIHQIQk1\ndBELKigqKNKlWrDsosKud3Fx17Xu3lVZRaWaKBBUiqiUFbwugtRQQhI6oQcIJIT0ZNr9I5oVpWQg\ncDLJ+3keHh9n5pzzkh8zeXPyO79jcjgcDkRERERExKWZjQ4gIiIiIiLXT8VeRERERKQKULEXERER\nEakCVOxFRERERKoAFXsRERERkSrA3egAFcFut2O32y96zGQyYTKZDEokIiIiInLtHA4Hv1680mw2\nYzZf/rx8lSn2+fn5RscQEREREblh/Pz8rljsNRVHRERERKQKULEXEREREakCVOxFRERERKqAKjHH\n/lIXyV5pDlJqaipWqxV3d3fatGlzo+PJDaAxdG0aP9dWaLHR883/A2DW/XXo0Dba4ERyLfQ+dG0a\nP9d3tTG81DWkV1sYpsoW+ytdNWy327HZbFe9slgqL42ha9P4uTaTyc75QisANrtdY+ii9D50bRo/\n13ctY3i1Yq9/CSIiIiIiVYDTxT4vL4+JEycSHh6Ot7c37dq1Y+HChVfdbsmSJQwdOpSmTZvi4+ND\no0aNGD58OAcOHLjk69esWUO3bt3w9fUlNDSU0aNHk5GR4WxcEREREZFqweliP3DgQOLj43n55ZdZ\nuXIlsbGxDB06lAULFlxxu7feeouCggKmTJnCqlWrePXVV9mxYwcdOnQgNTX1oteuXbuWvn37Urt2\nbZYtW8a0adNYs2YNd9xxB8XFxc5GFhERERGp8pyaY79ixQpWr17NggULGDp0KAC33XYbR48eZfLk\nyQwePBg3N7dLbvv1118TFhZ20WO33347jRo14p133mH27Nllj0+ePJnmzZuzaNEi3N1LIzZu3Jge\nPXowd+5cJkyY4NRfUkRERESkqnPqjP3SpUvx9/dn0KBBFz0+ZswY0tPT2bx582W3/XWpBwgPD6d+\n/focP3687LGTJ0+ydetWRo4cWVbqAbp3707z5s1ZunSpM5FFRERERKoFp4p9SkoKrVq1uqhwA8TE\nxJQ974y0tDSOHj160RI/P+/j533++jjOHkNEREREpDpwaipOZmYmkZGRv3k8ODi47PnyslqtjBs3\nDn9/f5577rmLjvHLff76OOU9RmpqKna7/ZLPWSyWsv8mJSWVO7NUHhpD16bxq/wcDgcXiu2czbdx\nocjG+SI7F4ptlNgcFFocZa/7dOd5luz5AS83EzW83AjyNhPk40YtXzcCvcxXXZpNjKP3oWvT+Lm+\nq42h2WymYcOGTu3T6XXsr/QhXd4PcIfDwbhx41i3bh2LFy+mQYMG5d5XeY9htVqx2WxXfd3PX1Rx\nXRpD16bxM57F5uDIBSsHsiyknbdwMtdGeq6V/F8U+Mv55kDhZZ/z9zARHuBOvQA3Imt60CzYg4gg\ndzzMKvuVjd6Hrk3j5/ouNYaXu271Spwq9iEhIZc8Y56VlQVc+iz7rzkcDsaPH8+8efOIj4/ngQce\n+M0x4NJn/7Oyssp1DAB3d/fLLvb/yy+eh4dHufYnlYvG0LVp/Ixlszs4kFXCztPF7DxVxIGsEqyX\n+AWnCajpY6amtxtB3m7U8Dbj5W7CDCw/UHo3xHua+GAymymyOMgptnO+yMb5IhvZhXbyLA72Z1nY\nn2Xh+6NFALiboXmIJ+3reNOurjdNanrgpqJvCL0PXZvGz/VdbQyv5cZjThX76OhoEhISym5/+7Pk\n5GQAoqKirrj9z6X+448/Zs6cOYwYMeI3r/l5H8nJyfTr1++i55KTk696jJ+1adPmsl+QpKQkLBYL\nHh4etG3btlz7k8pFY+jaNH43X7HVxvoD51iefIo1u8+QU2S96Pmavh60axBETP0gWtQJILKWH41C\n/PD2+O0Zo4ISK8un/huAMR1q0qVj+9+8pshi4/C5fNLO5rPvTC5Jx7NJOpFNdoGF3WdL2H22hPnJ\nOQT5enBnq9rcG12XHk1D8XTXfRNvFr0PXZvGz/VdbQztdju5ublO7dOpYj9gwABmzZrF4sWLGTx4\ncNnj8fHxhIeH06VLl8tu63A4eOyxx/j444+ZMWMGY8aMueTr6tWrR+fOnZk3bx6TJk0q+zXEpk2b\n2LdvHxMnTnQmsohIteVwONh+7DwLtxxnVcppcov/W+YDvd3p2SyUW5rVoltkCBEhvhU6H97bw41W\ndQNpVTeQe6lbludIZgEbDp1j3f5z/HjoHNkFFhZtO8GibScI8HanX1RdHoltQIeGQZqfLyLiJKeK\nfd++fenTpw8TJkwgJyeHpk2bkpCQwKpVq5g3b15ZCR83bhzx8fEcOnSIiIgIAH73u98xZ84cxo4d\nS3R0NJs2bSrbr5eXF+3b//eMz1tvvUWfPn0YNGgQTz31FBkZGbz44otERUVd9gcCEREplV1QwpLt\nJ1m49Rj7z+SVPV470Iu+UXXpF12XjhE1b/oUGJPJRONQPxqH+jG8SwRWm53Eo+dZkXyKlSmnOZtb\nzGeJx/ks8TjNwvwZHNuAR2IbEOitaQYiIuXh9MWzS5YsYcqUKUydOpWsrCxatmxJQkICQ4YMKXuN\nzWbDZrPhcPz3wquvv/4agLlz5zJ37tyL9hkREcGRI0fK/r93796sWLGCqVOn0r9/f3x9fbnvvvv4\nxz/+gZeXl7ORRUSqheNZBcxel8ZniccpspROmvf2MHNfTDiPdGpAp4iamCvRfHZ3NzNdI0PoGhnC\ny/3bsPVIFl8knmB5cjoHMvJ4dfke3lm9nyGdGzKmRyPq1/Q1OrKISKXmdLH39/dn2rRpTJs27bKv\niYuLIy4u7qLHflncy6NPnz706dPH2XgiItVOavoFZqxNY3nyKWz20hMqreoGMqxLQx5oF+4SZ7zd\nzKb/lvz7W/PVznQ+2XiE/WfymLP+MHEbjtAvui7P3NaUFnUCjI4rIlIpOV3sRUSkcjiYkcc/v93H\nypTTZY/d0iyUCbc2oVuTEJedox7o7cGIrhEM79KQtfvPMmtdGj8ezOTrpHS+2ZXO/W3DmXhncxqH\n+hkdVUSkUlGxFxFxMSezC5m2Zj+Ltp3A7gCTCe6LCeeJXpFE1athdLwKYzKZ6N0ijN4twkhNv8D0\n7w+yIvk0y3am882uUzzcoT4T+zSjbg0fo6OKiFQKKvYiIi6ioMTKB98fYua6NEp+Wni+T+vaTLqr\nRZWfntImvAYfDO9IyskLvL16P/+3N4PPEo/zVVI6E3o34fFekZdcmlNEpDpRsRcRqeQcDgcrU07z\n6je7Sb9QeqOnrpHB/OGelnRoWNPgdDdXVL0azB0dy7ajWby5ci9bj5zn7dX7+TzxOC/d24q729Rx\n2SlIIiLXS8VeRKQSO3Q2j6nLUvjxYOnduOvX9GHqfa3p07p2tS6wHSOC+fyJbny96xRvrNjDifOF\nPDlvO7c0C+W1B6NpGKIVdESk+lGxFxGphKw2OzPXpfHumgOUWO14uZuZ0LsJT97aRFNOfmIymbi/\nbTh3tgrjo/8c4qMf0lh34Bx3v/sDL9zVnDE9Gt/0tfpFRIykYi8iUsnsOZXDHxbtIvnkBQBubV6L\nVx+MokGwzkJfiq+nO8/f1YKBHerz4pJdbErL4tXle/g6KZ23Ho6hZZ1AoyOKiNwUZqMDiIhIKavN\nzrQ1B+j/3nqST16gho8H/xzUlrgxsSr15dAo1I+Ex7ryxsBoArzdSTpxgf7vrWfG2kPY7Y6r70BE\nxMWp2IuIVALHswoYPHMT76zZj9Xu4O42tVn9fC8e6li/Ws+ld5bJZGJo54asef5W7mxVG4vNwRsr\n9zJs9ibSswuNjicickOp2IuIGOzLHSfpN20d246eJ8DLnXcHt+OjER0JC/A2OprLqh3ozaxHO/LW\nQ9H4erqxKS2Lu9/9ga+S0o2OJiJyw2iOvYiIQQpKrLy0NIUlO04C0CmiJu8MbqdpNxXEZDIxOLYh\nnRuHMPGznSQdz+Z3CTvYeOgcL/dvo4uQRaTK0Rl7EREDHDqbx4PTf2TJjpO4mU08d2dzFj7eVaX+\nBmgc6seiJ7vxu9ubYjJBwpbjPPThBo5lFhgdTUSkQqnYi4jcZCuTT/HA+z+y/0weYQFeJDzWld/f\n2Qx3N30k3ygebmaev6sFn4ztTLCfJ6npOdz73jpW7z5jdDQRkQqj7yIiIjeJxWbnteW7mTB/O3nF\nVro0Duab3/Wkc+Ngo6NVG7c0q8Xy3/WkQ8MgcousPPZJIm+s3INNq+aISBWgYi8ichOczy9h5JzN\nzFp3GIDHe0Uyf3wXXSBrgLo1fPjsiW6M69kYgBlr0xgbt5WcIovByUREro+KvYjIDXYwI5cHP/iR\nTWlZ+Hu589GIDvypXytNvTGQh5uZP9/XmunDOuDtYWbt/rMMmP4jR87lGx1NROSa6buKiMgNVFoY\nN3A0s4AGwT4seao790TVNTqW/OTemLoserI7dWt4c+hsPg9M/5ENB88ZHUtE5Jqo2IuI3AAOh4O4\nHw8z5uMt5BZbiW1Uky+f6kHz2gFGR5NfiapXg2VP96BdgyAuFFoYOXcLn246anQsERGnqdiLiFQw\nm93BX75K5S9f78bugIc71mfe+C6E+HsZHU0uIyzQm4WPd2VA+3rY7A7+/GUKb6zcg10X1YqIC1Gx\nFxGpQEUWG0/P3078xqOYTPA/fVvyj4dj8HLXzZAqO28PN95+pC2T7moOlF5U+9znOym22gxOJiJS\nPrrzrIhIBckuKOGxTxLZeuQ8nm5m3hncjntjNJ/elZhMJp65vRl1a/jwx8W7WLYznYycYmY82pFA\nbw+j44mIXJHO2IuIVICT2YU8/NFGth45T4C3O5+M66xS78Ie6lifuaNj8fN0Y2NaJo98tJFTFwqN\njiUickUq9iIi12nf6Vwe+mADBzPyqBPozRdPdqNrZIjRseQ69Wpei8+f7EatAC/2/jTGaWfzjI4l\nInJZKvYiItch6Xg2j8zYyOmcIpqF+bPkqe60rBNodCypIG3Ca7D0qe5E1vIj/UIRj8zYyJ5TOUbH\nEhG5JBV7EZFrtDktk+GzN3Oh0EK7BkF88WQ3woN8jI4lFax+TV8+f6IbresGci6vhMEzNrL92Hmj\nY4mI/IaKvYjINVi7/yyjPt5CXrGVbpEhzBvfhSBfT6NjyQ0S6u9FwuNd6RhRk5wiKyNmb9aNrESk\n0lGxFxFx0qqUU4yP30qRxc7tLcP4eEws/l5aZKyqq+HjwafjOtOzaSgFJTZGx21l9e4zRscSESmj\nYi8i4oSlO07w9IIdWGwO7o2uy0cjOuLtoTXqqwtfT3dmj+rEXa1rU2K18+S8bXyzK93oWCIigIq9\niEi5fZF4nOc/T8JmdzCoY33+NbQ9nu76GK1uvD3c+GB4h7K71P5+4U6+TlK5FxHj6TuSiEg5LNp2\ngj8s3oXDASO7RvDWQzG4mU1GxxKDuLuZ+d9BbRnUsf5P5X6Hyr2IGE6TQkVErmLJ9hNMXpRUVupf\neaANJpNKfXXnZjbx1kMxAHyx7QS/X7gDB3B/23Bjg4lItaUz9iIiV7B0xwle+KK01I/o2lClXi5i\n/qncD+pYH7sDJi7cwbKdJ42OJSLVlM7Yi4hcxpc7TvLC56WlfliXhrxyf5RKvfzGz+XeZILPE0/w\n3Gc7AXigXT2Dk4lIdaMz9iIil7Bs50me/3wndgcM7dyAVx+Iwqw59XIZZrOJNwfGMLhTA+wOeO6z\nnaxMPmV0LBGpZlTsRUR+ZUXyKZ77rLTUD4ltwGsPRqvUy1WZzSbeGBhdNi3ndwt38P3eDKNjiUg1\nomIvIvIL3+/L4PcLd2B3wCOd6vP6AJV6KT+z2cSbD8VwX0xdLDYHT87bxoZDukOtiNwcKvYiIj/Z\nlJbJk59uw2Jz0L9tOG8MjFGpF6e5mU28M7gdd7YKo9hqZ3x8ItuOnjc6lohUAyr2IiLArhPZjI9P\npNhq585WYbz9SFutUy/XzMPNzPvDOtCzaSgFJTZGf7yFlJMXjI4lIlWcir2IVHv7Tufy6Nwt5BVb\n6d4khPeHdcDDTR+Pcn28PdyY+WhHYhvVJLfIyqNzt3DgTK7RsUSkCtN3LhGp1o6cy2fEnM1kF1ho\n1yCIWY92wtvDzehYUkX4erozZ3QsMfVrkJVfwvDZmzmWWWB0LBGpolTsRaTaOnWhkOGzN3M2t5iW\ndQKIGxOLn5du7yEVK9Dbg/gxnWlRO4CM3GJGzi39NyciUtFU7EWkWsouKGHknC2czC6kcagfn47r\nQpCvp9GxpIqq6efJp+M6U7+mD0czCxj98RZyiyxGxxKRKkbFXkSqncISG+PiEzmYkUfdGt7MG9+F\nWgFeRseSKi4s0JtPx3UhxM+T1PQcHv9kG0UWm9GxRKQKcbrY5+XlMXHiRMLDw/H29qZdu3YsXLjw\nqtudOHGCiRMncuuttxIUFITJZCIuLu6Sr+3duzcmk+k3f+655x5n44qIXMRqs/Nswna2HT1PoLc7\n8WM7Uy/Ix+hYUk00DvUjbkxn/Dzd2JiWyXOf7cRmdxgdS0SqCKeL/cCBA4mPj+fll19m5cqVxMbG\nMnToUBYsWHDF7Q4ePMj8+fPx9PSkX79+Vz1OZGQkGzduvOjPu+++62xcEZEyDoeDPy1NZs2eDLzc\nzcwdHUvz2gFGx5JqJrp+DWY92glPNzMrU07z52UpOBwq9yJy/Zy6SmzFihWsXr2aBQsWMHToUABu\nu+02jh49yuTJkxk8eDBubpdeTaJXr16cPXsWgMTERBISEq54LB8fH7p27epMPBGRK/rnt/v5PPEE\nZhO8P6wDnRoFGx1JqqnuTUN5d0g7nl6wnQWbjxHq78XzfZobHUtEXJxTZ+yXLl2Kv78/gwYNuujx\nMWPGkJ6ezubNmy9/ILOm84uIceI3HOH97w8C8PqAaPq0rm1wIqnu+kXX5ZUHogD413cHiN9wxNhA\nIuLynGrbKSkptGrVCnf3i0/0x8TElD1fUQ4dOkRwcDDu7u40adKEKVOmUFhYWGH7F5Hq45td6fzl\n61QAXujTnCGdGxqcSKTUyK4RTLyzGQB/+TqVFcmnDE4kIq7Mqak4mZmZREZG/ubx4ODgsucrQs+e\nPRk8eDAtW7aksLCQlStX8ve//53169fz/fffl+vsf2pqKna7/ZLPWSyWsv8mJSVVSGa5uTSGru1m\njt+uM0X89T/ncDigXzM/bgnJ17+Z61Rk/e9nq8Vi1dfzOvUOdbCvqR8rD+bz+4Tt5JypRataN36V\nJn2OujaNn+u72hiazWYaNnTuRJTTd2IxmUzX9JwzXn311Yv+v1+/fjRq1IhJkyaxbNkyBgwYcNV9\nWK1WbLarLyP28xdVXJfG0LXdyPE7km3h9R/OY7VD13pejIrxw2q13rDjVRcW68UXeuo9eP1Gx/hx\nNt9C4qkSXvvhHK/dFkx4wM27WZrG0LVp/FzfpcbwctetXolTnxohISGXPCuflZUF/PfM/Y0wYsQI\nJk2axKZNm8pV7N3d3S97Zv+XXzwPD48Kyyg3j8bQtd2M8TtXYOWNHy9QaHUQFebJCz1C8XSrmJMP\n1Z3NdPFvQ/UevH4ewOSeobz03VkOZFl4/cds3uoTRpC389/Yy0ufo65N4+f6rjaG13J9qlPFPjo6\nmoSEBKxW60Xz7JOTkwGIiopyOoCzyvuXbNOmzWVfm5SUhMViwcPDg7Zt21ZkPLlJNIau7UaPX26R\nhT9+tJHMQhtNw/yZ/2R3avjqG19FKSixwhfpAHh4uOs9WIEWNC9m4Ic/cjyrkLcTC1n4WFd8PG9M\nudfnqGvT+Lm+q42h3W4nNzfXqX069aPAgAEDyMvLY/HixRc9Hh8fT3h4OF26dHHq4M6Ij48H0BKY\nInJFFpudpxfsYO/pXEL9vfh4dKxKvbiMWgFexI3pTJCvB0nHs/ndwh26gZWIlJtTZ+z79u1Lnz59\nmDBhAjk5OTRt2pSEhARWrVrFvHnzyuYCjRs3jvj4eA4dOkRERETZ9osWLQIgLS0NKF3P3t/fH4CH\nH34YgHXr1vHaa68xYMAAIiMjKSoqYuXKlcycOZPbb7+d/v37X//fWkSqJIfDwdRlKfyw/yw+Hm7M\nHd2JBsG+RscScUqTWv7MerQTw2dvZvXuM/z161T+en+bCruOTUSqLqevzFmyZAlTpkxh6tSpZGVl\n0bJlSxISEhgyZEjZa2w2Gzab7Td30vv1+vfTp09n+vTpAGWvrVu3Lm5ubvztb3/j3LlzmEwmmjVr\nxiuvvMILL7yg9fBF5LI+WptGwpbjmE3wr6HtiakfZHQkkWsS2yiYdx5pxzMJ2/lk41Hq1/Th8V5N\njI4lIpWc08Xe39+fadOmMW3atMu+Ji4ujri4uN88Xp5bZjdt2pTly5c7G0tEqrmvktJ5a9VeAF7u\n30Y3oBKXd29MXU5daMWry/fw+oq9hAf5cF9MuNGxRKQS0+lvEXF5W49kMenz0jWAx/VszKjujYwN\nJFJBxvVszOif/j0//1kSWw5nGRtIRCo1FXsRcWlpZ/N47JNESmx27m5Tmz/1a2V0JJEKYzKZ+PN9\nrbmrdW1KbHae+DSRI+fyjY4lIpWUir2IuKzMvGLGxG0lu8BCuwZBvDu4PW5mXWAoVYub2cS0Ie1p\nW78G5wssjI3byoUC3ZBIRH5LxV5EXFKRxcZjnyRyNLOABsE+zB7V6Yat9y1iNB9PN2Y92onwGt6k\nnctnwvxtWGz2q28oItWKir2IuByHw8GkL5LYfiybGj4efDy6M6H+XkbHErmhwgK9mT0qFj9PNzYc\nyuSlpSnlWpRCRKoPFXsRcTnTvjvAN7tO4eFmYsbIjjQN8zc6kshN0To8kPeGtcdsgs8SjzPzhzSj\nI4lIJaJiLyIu5eukdN5dcwCA1x6MpmtkiMGJRG6u21vW5qV7WwPw5qq9rEo5bXAiEaksVOxFxGXs\nPJ7NpC9Kl7V8vFckj8Q2MDiRiDHG9GjEyK4ROBww8bMdJJ+4YHQkEakEVOxFxCWkZxcyPj6RYqud\nO1vV5o/3tDQ6kohhTCYTL/dvTa/mtSiy2BkXv5VTFwqNjiUiBlOxF5FKL7/Yyrj4RM7lFdOyTgDv\nDmmnZS2l2nN3M/P+sPY0r+1PRm4x4+ISyS+2Gh1LRAykYi8ilZrd7mDiZzvZcyqHUH9PZo/qhL+X\nu9GxRCqFQG8P5oyKJdTfk92ncvj9wh3Y7FopR6S6UrEXkUrtrX/vZfXuM3i6m5n5aCfq1/Q1OpJI\npdIg2JcZIzvh6W5mzZ4M3lixx+hIImIQFXsRqbS+SDzOjLWly/n94+EYOjSsaXAikcqpY0RN/jmo\nLQCz1x9m/uajBicSESOo2ItIpbQ5LZM/LU0G4He3N+WBdvUMTiRSufVvG87zfZoDMHVZKusPnDM4\nkYjcbCr2IlLpHM3M58l527DYHNwbXZeJdzY3OpKIS3j29qYMaF8Pm93BhPnbOJiRZ3QkEbmJVOxF\npFLJKbIwLj6R8wUWYurX4H8HtcWsFXBEysVkMvHGwGg6RtQkt8jKuPitnM8vMTqWiNwkKvYiUmlY\nbXaenr+dgxl51An0ZtajnfDxdDM6lohL8fZwY8bIjtSv6cPRzAKemLeNEqvd6FgichOo2ItIpfG3\nb3az7sA5fDzcmD2qE7UDvY2OJOKSQv29mDs6Fn8vd7YczuKlL5NxOLQMpkhVp2IvIpXCpxuPEL+x\ndCWPdwa3JapeDWMDibi45rUDeG9Ye8wm+DzxBDN/SDM6kojcYCr2ImK4dQfO8pevdwMw+e4W3BNV\n1+BEIlXDbS3CmHpfawDeXLWXf6eeNjiRiNxIKvYiYqiDGXk8NX87NruDgR3q8VTvJkZHEqlSRnVv\nxIiuDXE4YOLCnaScvGB0JBG5QVTsRcQwOcU2xsVvJbfISqeImrwxMBqTSSvgiFQkk8nEy/3bcEuz\nUAotNsbHJ3Imp8joWCJyA6jYi4ghLHYHb63P5GhmAfVr+jBjZEe83LUCjsiN4OFm5v1hHWhSy4/T\nOUU89kkixVopR6TKUbEXkZvO4XAwe3sOKRkl+Hu5M2dULCH+XkbHEqnSavh4MHd0LDV9Pdh14gLv\nbjqPXSvliFQpKvYictMt25vHd0eKMJvgvaHtaVEnwOhIItVCRIgfH43oiIebiQ3HC/ksNd/oSCJS\ngVTsReSmWrP7DHE7Sy/eG9OuBre1DDM4kUj10iUyhNcHRAOweG8+/zmsci9SVajYi8hNs+dUDr9f\nuAMH0KexD/1b+BsdSaRaGtSpAQNblf6m7L0t50k8kmVwIhGpCCr2InJTnM0tZnx8IvklNmJqezGu\nfYBWwBEx0Mi2gXQO98Jqhyc+3cbxrAKjI4nIdVKxF5Ebrshi4/FPEzmZXUjjUD/+0CMEd7NKvYiR\nzCYTv+tcg8iaHmTml/y09KzF6Fgich1U7EXkhnI4HPxx8S52HMumho8Hc0Z1IsBLHz0ilYG3u4mX\neoUSFuDF/jN5PJuwA6tNy2CKuCp9dxWRG+r9/zvIsp3puJtNfDi8A5G1NK9epDIJ8XVj9qhOeHuY\n+c++s7y6fI/RkUTkGqnYi8gNs3zXKf65ej8Af32gDd2bhhqcSEQuJaZ+EO880g6AuA1H+HTTUYMT\nici1ULEXkRti14lsXvhiJwBjejRieJcIgxOJyJX0ja7L5LtbAPCXr1JZd+CswYlExFkq9iJS4U5f\nKGJ8fCJFFju9W9TipXtbGx1JRMrhqd5NGNi+Hja7g6fmb+dgRp7RkUTECSr2IlKhCkqsjP9kKxm5\nxTSv7c97Q9vjphVwRFyCyWTijYei6RRRk9wiK+Pit5KVX2J0LBEpJxV7EakwdruD5z9LIuVkDsF+\nnswZFUuAt4fRsUTECV7ubswY2ZEGwT4czSzgyU+3UWy1GR1LRMpBxV5EKsw/V+9jVeppPN3MzBzZ\nkQbBvkZHEpFrEOLvVfqDuZc7W45kMWVpCg6Hw+hYInIVKvYiUiGWbD/B9O8PAfDmQ9F0ahRscCIR\nuR7Nawfw/vAOmE2waNsJZvxaDLueAAAgAElEQVSQZnQkEbkKFXsRuW7bjmbx4uJk4KeL7zrUNziR\niFSEW5vX4uX+bQB4a9VeVqWcNjiRiFyJir2IXJfjWQU8/sk2Smx27m5Tm0l3tTA6kohUoFHdG/Fo\ntwgcDnjus52knLxgdCQRuQwVexG5ZrlFFsbHJ5KZX0Kb8EDeGdwOs1bAEalypt7XmluahVJosTE+\nPpEzOUVGRxKRS1CxF5FrYrM7+P3Cnew7k0tYgBezR3XC19Pd6FgicgO4u5mZPrwDTcP8OZ1Tep+K\nwhKtlCNS2ajYi8g1eX3FHv5vbwZe7mZmPdqJujV8jI4kIjdQoLcHc0fFUtPXg+STF3j+853Y7Vop\nR6QycbrY5+XlMXHiRMLDw/H29qZdu3YsXLjwqtudOHGCiRMncuuttxIUFITJZCIuLu6yr1+zZg3d\nunXD19eX0NBQRo8eTUZGhrNxReQGmLfpKHPWHwbg7Ufa0bZBkMGJRORmaBjiy8xHO+HpZmZlymne\nXr3f6Egi8gtOF/uBAwcSHx/Pyy+/zMqVK4mNjWXo0KEsWLDgitsdPHiQ+fPn4+npSb9+/a742rVr\n19K3b19q167NsmXLmDZtGmvWrOGOO+6guLjY2cgiUoH+sy+Dl79KBeCFPs25N6auwYlE5GaKbRTM\nGwOjAXj/+4Ms2X7C4EQi8jOnJsSuWLGC1atXs2DBAoYOHQrAbbfdxtGjR5k8eTKDBw/Gzc3tktv2\n6tWLs2fPApCYmEhCQsJljzN58mSaN2/OokWLcHcvjdi4cWN69OjB3LlzmTBhgjOxRaSC7E7P4en5\n27HZHTzcsT7P3N7U6EgiYoCHOtbn0Nk8PvjPIV5cnEyDYF9ide8KEcM5dcZ+6dKl+Pv7M2jQoIse\nHzNmDOnp6WzevPnyBzKX71AnT55k69atjBw5sqzUA3Tv3p3mzZuzdOlSZyKLSAU5k1PEuPit5JfY\n6BYZwusDojGZtAKOSHU16a4W3NOmDiU2O098uo1jmQVGRxKp9pwq9ikpKbRq1eqiwg0QExNT9vz1\n+nkfP+/z18epiGOIiHPyi62MjdvKqQtFNKnlx0cjOuLprmvvRaozs9nE24PbElUvkKz8EsbFbyWn\nyGJ0LJFqzampOJmZmURGRv7m8eDg4LLnr9fP+/h5n78+TnmPkZqait1uv+RzFoul7L9JSUnXmFSM\npDG8eWx2B2+szyQ1vYgaXmb+0DWAIwd2X9c+NX6urcj6389Wi8WqMXRRFfU+fL6TH5Oy8jiQkcfo\nGWt5qVcobrqfxQ2nz1HXd7UxNJvNNGzY0Kl9Or3o9JV+9V6Rv5a/3L7Kewyr1YrNdvU1dn/+oorr\n0hjeWB/vzGXrySI8zfDH7jUI8XJU6Ndc4+d6LNaLlzjUGLq+6xnDQA94sXsQf/5PFttPFTNrWxbj\n2gVWYDq5Gr0HXd+lxvBy161eiVPFPiQk5JJnzLOysoBLn2V3VkhICHDps/9ZWVnlPoa7u/tl5/X/\n8ovn4eFxDSnFaBrDm+Ob/XksP1g6b3Zit2Da1PGtkP1q/FybzXTxb0M1hq6pIt+HLcI8eK6biTfX\nZ7LyYCENg7zo18z/eiPKFehz1PVdbQzLe33qLzlV7KOjo0lISMBqtV40zz45ORmAqKgopwP82s/7\nSE5O/s2ymMnJyeU+Rps2bS77BUlKSsJiseDh4UHbtm2vL7AYQmN443235wxzticC8GLfljx5a5MK\n27fGz7UVlFjhi3QAPDzcNYYuqqLfh23bgt3/IH9ftY/Z2y/QI6Y5vZrXqoCkcin6HHV9VxtDu91O\nbm6uU/t06keBAQMGkJeXx+LFiy96PD4+nvDwcLp06eLUwS+lXr16dO7cmXnz5l00lWbTpk3s27eP\ngQMHXvcxROTKUk5e4JkFO7A7YGjnBjzR67fX1oiI/NqEW5vwUIf62OwOnp6/nQNnnCslInJ9nDpj\n37dvX/r06cOECRPIycmhadOmJCQksGrVKubNm1c2F2jcuHHEx8dz6NAhIiIiyrZftGgRAGlpaUDp\nevb+/qW/qnv44YfLXvfWW2/Rp08fBg0axFNPPUVGRgYvvvgiUVFRjBkz5vr+xiJyRenZhYyN20qh\nxcYtzUJ55YEoLWspIuViMpl4fWAUx7MK2HIki9Efb2XJU92pHehtdDSRasHpi2eXLFnClClTmDp1\nKllZWbRs2ZKEhASGDBlS9hqbzYbNZsPhuPgCq1+vfz99+nSmT58OcNFre/fuzYoVK5g6dSr9+/fH\n19eX++67j3/84x94eXk5G1lEyimnyMLYuK1k5BbTvLY/04d3wMNNy1qKSPl5ubsxY2RHHvpwA2nn\n8hn98VY+f6IrAd6aBy5yozn9Hdvf359p06Zx6tQpiouLSUpKuqjUA8TFxeFwOGjUqNFFjzscjsv+\n+bU+ffqwceNGCgsLyczMJD4+nrCwMGfjikg5lVjtPPnpNvaezqVWgBdzR8cSqG/EInINavp5Ej+2\nM6H+nuw5lcOEedspsV56CWoRqTg6FSci2O0OJi9KYsOhTPw83fh4dCz1a1bMCjgiUj01CPbl49Gd\n8fV0Y/3Bc7y4ZNclT+SJSMVRsRcR3vr3XpbtTMfdbOKjkR2JqlfD6EgiUgVE16/B9OEdcDObWLL9\nJP/8dr/RkUSqNBV7kWou7sfDzFhbekH7Ww/FcEszLU8nIhXnthZhvD6gdKnq978/yPzNRw1OJFJ1\nqdiLVGMrk0/x1292AzD57hY81LG+wYlEpCoaHNuQ39/RDIA/f5nCd3vOGJxIpGpSsRepprYeyeL3\nn+3E4YARXRvyVO+KuwGViMivTbyzGY90qo/dAc8s2MHO49lGRxKpclTsRaqhgxm5jI9PpMRqp0/r\n2vz1fq1VLyI3lslk4rUB0dzavBaFFhvj4rZy5Fy+0bFEqhQVe5Fq5kxOEaPmbuVCoYUODYP415D2\nuJlV6kXkxvNwM/PB8A5E1QskM7+E0R9vITOv2OhYIlWGir1INZJTZGH0x1s5mV1IZKgfc0bF4uPp\nZnQsEalG/LzcmTs6lvo1fTiSWcCYuK3kFVuNjiVSJajYi1QTRRYb4+MT2XMqh1B/L+LHdqamn6fR\nsUSkGgoL8CZ+bGeC/TzZdeICj3+SSLHVZnQsEZenYi9SDVhtdp5ZsIMth7MI8HInbkwsDYJ1AyoR\nMU6TWv7EjYnFz9ONDYcymbhwJza7bmAlcj1U7EWqOLvdwR8XJ7Nmzxm83M3MHtVJN6ASkUohpn4Q\nMx/thKebmZUpp3npyxTdnVbkOqjYi1RhDoeD11fsYfH2E7iZTbw/rANdIkOMjiUiUqZH01CmDWmH\n2QQJW47p7rQi10HFXqQK+3DtIWavPwzA3x+KoU/r2gYnEhH5rb7RdXltQDRQenfauT99bomIc1Ts\nRaqohC3H+PuqfQC8dG8r3VVWRCq1oZ0bMvnuFgC88s1ulu44YXAiEdejYi9SBa1IPsWUpckAPH1b\nE8bfEmlwIhGRq3uqdxPG9mgMwKQvdvF/e88YnEjEtajYi1Qx6w+cY+LCndgdpWfAJt3VwuhIIiLl\nYjKZeOneVgxoXw+b3cGEedvZlJZpdCwRl6FiL1KFJB7J4vFPEymx2ekXXYdXH4zCZNJdZUXEdZjN\nJv7+cAx3tAyj2GpnXNxWdhw7b3QsEZegYi9SRew6kc2Yj7dSUGLjlmahvDO4HW5mlXoRcT0ebmam\nD+9A9yYh5JfYGDV3C6npF4yOJVLpqdiLVAF7TuUwcs4WcoutdG4czMyRnfBydzM6lojINfP2cGPW\no53oGFGTnCIrI+ds4WBGrtGxRCo1FXsRF3cwI4+RczZzodBCuwZBzB0di4+nSr2IuD4/L3c+HhNL\nVL1AsvJLGDZrM0cz842OJVJpqdiLuLBjmQWMmL2Zc3kltK4bSPzYzvh7uRsdS0SkwgR6e/DJ2C40\nr+1PRm4xw2ZtJj270OhYIpWSir2Ii0rPLmTY7E2czimiWZg/n47rTA0fD6NjiYhUuGA/T+aN70Lj\nUD9OZhcyfPZmMnKLjI4lUumo2Iu4oIzcIobP3syJ84U0CvFl/vguhPh7GR1LROSGCQvwZv74LtQL\n8uHwuXxGzN5MZl6x0bFEKhUVexEXcza3mOGzNnP4XD71gnyY/1hXwgK9jY4lInLDhQf5sOCxLoQF\neLH/TB7DVe5FLqJiL+JCzuYWM2zWJg5k5FE70IsFj5WevRIRqS4iQvxIeLwrtQK82Hs6V+Ve5BdU\n7EVcREZuEUN/KvV1Ar357PFuRIT4GR1LROSma1LLn4Uq9yK/oWIv4gIycosYOnMTBzPyqFvDm4WP\nd6VRqEq9iFRflyr3WfklRscSMZSKvUgll5FTWuoPnc1XqRcR+YVfl/thszap3Eu1pmIvUoll5BQx\nZFZpqQ//qdRr+o2IyH+p3Iv8l4q9SCX1c6lPO1u6+s1CzakXEbmkS5X7c5pzL9WQir1IJXTifAGP\nzNj4i1LflYYhvkbHEhGptH5d7h+ZsZFTF3SHWqleVOxFKpnD5/J55KONHMksoH7N0lLfIFilXkTk\naprU8ufzJ7oRXsObtLP5DPpoI8cyC4yOJXLTqNiLVCJ7T+cw6KONpF8oIrKWH1882U2lXkTECY1D\n/fj8yW40CvHlxPlCHpmxkYMZeUbHErkpVOxFKomk49kMmVk6L7RV3UA+f6IbdWvo5lMiIs6qX9OX\nz5/oRrMwf07nFDF4xkb2nMoxOpbIDadiL1IJbE7LZPjszWQXWGjXIIiFj3Ul1N/L6FgiIi4rLNCb\nz57oRlS9QDLzSxgycxM7j2cbHUvkhlKxFzHY2v1nGfXxFvKKrXSNDGbe+C7U8PUwOpaIiMsL9vNk\nwWNd6RhRkwuFFobP2sSGQ+eMjiVyw6jYixjoq6R0xsdvpchi57YWtYgb0xl/L3ejY4mIVBmB3h58\nMrYzPZqGkF9iY/TcraxIPmV0LJEbQsVexCBz1x/mdwk7sNgc3BtTlxkjO+Ht4WZ0LBGRKsfPy505\no2LpG1WHEpudpxds59NNR42OJVLhVOxFbjKHw8GbK/fyyje7ARjdvRHvDWmPp7vejiIiN4q3hxvv\nD+vA8C4NcTjgz1+m8Pbq/TgcDqOjiVQY/c5f5Cay2Oy8uDiZxdtPADD57hY81bsJJpPJ4GQiIlWf\nm9nEqw9GUSvAi3fXHOBf3x3gXF4xf3sgCjezPofF9anYi9wkBSVWnp6/ne/3ncXNbOKNgdE80qmB\n0bFERKoVk8nExDubE+rvxZ+XpbBg8zGy8kp4d0g7TYcUl6ff/YvcBJl5xQybtZnv953F28PMzJEd\nVepFRAw0omsEHwzrgKebmVWppxk5ZzNZ+SVGxxK5Lir2IjfYwYw8BnywgZ3Hswny9WD++K7c0aq2\n0bFERKq9vtF1iRsbS4C3O1uPnGfgBz9y+Fy+0bFErpnTxT4vL4+JEycSHh6Ot7c37dq1Y+HCheXa\nNiMjg9GjRxMaGoqvry/dunXju++++83revfujclk+s2fe+65x9m4IobacPAcAz/4kWNZBTQM9mXR\nk93pGFHT6FgiIvKT7k1CWTKhO/Vr+nAks4ABH/zIlsNZRscSuSZOz7EfOHAgW7du5c0336R58+Ys\nWLCAoUOHYrfbGTZs2GW3Ky4u5o477iA7O5tp06YRFhbG9OnTueeee1izZg233nrrRa+PjIxk/vz5\nFz0WFBTkbFwRw3yeeJw/LUnGanfQMaImM0d2JER3kxURqXSa1Q5g6VM9GP9JIknHsxkxezP/GBTD\nA+3qGR1NxClOFfsVK1awevXqsjIPcNttt3H06FEmT57M4MGDcXO79IUnc+bMISUlhQ0bNtCtW7ey\nbdu2bcsf/vAHNm/efNHrfXx86Nq167X8nUQMZbc7+N9v9/HBfw4B0L9tOP94OEYXZYmIVGK1ArxY\n+FhXnvtsJ6tST/P7hTs5mlnAs7c31cpl4jKcmoqzdOlS/P39GTRo0EWPjxkzhvT09N+U819v26JF\ni7JSD+Du7s6IESPYsmULJ0+edDK6SOVTZLHxbMKOslL/u9ubMm2wVloQEXEFPp5ufDC8A4/3igTg\n7dX7eeHzJIosNoOTiZSPU2fsU1JSaNWqFe7uF28WExNT9nz37t0vu+0tt9zym8d/3jY1NZV69f77\nK69Dhw4RHBxMTk4OERERDBkyhJdeegkfH59yZU1NTcVut1/yOYvFUvbfpKSkcu1PKpfKOIZn8628\nuT6Tg1kW3M3wdOea3F67iOTkXUZHq3Qq4/hJ+RVZ//vZarFYNYYuSu/Dy7u3Hpg7BTFzWzZLdpwk\n+VgG/9MzlBDfynOSRuPn+q42hmazmYYNGzq1T6eKfWZmJpGRkb95PDg4uOz5K2378+uutm3Pnj0Z\nPHgwLVu2pLCwkJUrV/L3v/+d9evX8/3332M2X/0XDVarFZvt6j9h//xFFddVGcZwz7kS/nfjBS4U\n2wnwNDGpWxBtanlWimyVnb5GrsdivfhOnRpD16cx/K07G3kR5hPE25sucCDTwgv/PsPkbjVoHuJp\ndLTf0Pi5vkuN4eWmt1+J0xfPXmme2dXmoJV321dfffWi5/r160ejRo2YNGkSy5YtY8CAAVfN6e7u\nftkfAH75xfPw8LjqvqTyqUxjuPJAHrO2ZWNzQOMgD/7nlhBq++veb1dSmcZPnGczXfzbUI2ha9L7\n8Oo61vfgf+/25vV15zh2wcrUteeZEFuTOyP9jI6m8asCrjaG5TmR/WtOtY+QkJBLnpXPyipdFupS\nZ+QrYluAESNGMGnSJDZt2lSuYt+mTZvLfkGSkpKwWCx4eHjQtm3bq+5LKp/KMIbFVht/+Wo3CYnZ\nANwXU5e/PxyDr6dK/dVUhvGTa1dQYoUv0gHw8HDXGLoovQ/Lpy3QM9bKC5/v5N+pZ3hv83ny3Gsw\npV8r3N2Mux2Qxs/1XW0M7XY7ubm5Tu3TqX+R0dHR7NmzB6vVetHjycnJAERFRV1x259f5+y2v3Qt\nP72IVLSM3CKGzdpMwpZjmEzwx3ta8t7Q9ir1IiJVkL+XOx8O78jEO5sB8PGPR3h07hbO5RUbnEzk\nYk615AEDBpCXl8fixYsvejw+Pp7w8HC6dOlyxW337t170co5VquVefPm0aVLF8LDw6947Pj4eAAt\ngSmG25SWyb3/Ws+2o+cJ8HZn7uhYJvRuouXQRESqMLPZxMQ7m/PRiI74erqx4VAm9/5rHVuP6GZW\nUnk4dXqxb9++9OnThwkTJpCTk0PTpk1JSEhg1apVzJs3r2yS/7hx44iPj+fQoUNEREQAMHbsWKZP\nn86gQYN48803CQsL44MPPmDfvn2sWbOm7Bjr1q3jtddeY8CAAURGRlJUVMTKlSuZOXMmt99+O/37\n96/Av75I+dntDj5ce4h/frsPuwOahfkz89FONA41fq6liIjcHPdE1aFJrR48OW8bh87mM2TmJl68\npyXjb2msEzxiOKfnDSxZsoQpU6YwdepUsrKyaNmyJQkJCQwZMqTsNTabDZvNhsPx35UTvLy8+O67\n7/jDH/7As88+S0FBAe3atWPlypUX3XW2bt26uLm58be//Y1z585hMplo1qwZr7zyCi+88IKm4ogh\nzueX8NznO/nPvrMADOxQj1cfjNLUGxGRaqhZ7QC+eqYnf1qazLKd6by2Yg9bj2Txj0FtqeGjC1nF\nOE63En9/f6ZNm8a0adMu+5q4uDji4uJ+83jt2rXLptRcTtOmTVm+fLmzsURumG1Hz/Psgu2kXyjC\ny93M3x6IYlCn+jozIyJSjfl5ufPu4HbENgrmla938+3uM+x9bz0fDO9AVL0aRseTakqnv0Uuw253\nMHtdGoNnbCT9QhGNQ/1Y+lQPHoltoFIvIiKYTCZGdI1g0YRu1K/pw7GsAgZ+uIG4Hw9fNGtB5GZR\nsRe5hIycIkbHbeXV5Xuw2h3cG1OXr57pQevwQKOjiYhIJRNTP4jlz97Cna3CKLHa+cvXuxkbt5Wz\nuVo1R24uFXuRX1m9+wz3TFvHD/vPlk69eTCK94e2J8Bb8yZFROTSavh6MOvRTvylf2s83c18v+8s\nfaf9wPd7M4yOJtWIir3ITwpLbExZmsxjnySSlV9Cq7qBfPNsT0Z2jdDUGxERuSqTycToHo35+pme\ntKgdwLm8EsbEbeUvX6VSZLEZHU+qARV7ESDl5AXue28d8zcfA+CxWxrz5dPdaVY7wOBkIiLialrU\nCWDZMz0Y3b0RAHEbjvDA+z+y51SOscGkylOxl2qtxGrn7W/38cD0Hzl0Np+wAC8+HdeZKfe2xsvd\nzeh4IiLiorw93PjL/W34eEwsof6e7DuTy/3vr+df3x3AYrMbHU+qKBV7qbZSTl4o/ZD9v4PY7A76\nRddh1cRe3NKsltHRRESkiritRRirJvaiT+vaWGwO3l69nwen/8judJ29l4qnYi/VTonVXvbBuvd0\nLsF+nrw/rD0fDO9IsJ+n0fFERKSKCfX3YubIjkwb0o4gXw9S03O4//31TFujs/dSsVTspVpJOp7N\nA9N/5F/fHcBqd9A3qg7fPteL+2LCjY4mIiJVmMlk4oF29fj2uV7c1bo2VruDd9bs54H3fyQ1/YLR\n8aSKcPrOsyKuKLfIwj+/3U/8xiM4HFDT14O/PRilQi8iIjdVWIA3M0Z25Otdp3h5WQq7T+Vw//s/\nMrZHIybe2Rw/L1UzuXY6Yy9VmsPhYFXKafq8/QNxG0pL/YD29Vj9/K0q9SIiYgiTycT9bcP59rlb\n6RddB5vdwax1h+nz9lpW7z5jdDxxYfqxUKqsk9mFvLwslTV7Sj8kI0J8ee3BaHo2CzU4mYiICNQK\n8OKD4R35fm8Gf16WwonzhTz2SSJ3ta7NX+5vQ3iQj9ERxcWo2EuVU2SxMWNtGh+uPUiRxY6Hm4kn\nejXhmdub4u2hJSxFRKRyua1lGKsjb2XadweYvS6Nb3efYf3Bczx7ezPG9myk5Zel3FTspcr4edrN\nq8v3cDK7EIDOjYN59cEomutGUyIiUon5eLrxYt+WPNg+nClLU9h29DxvrdpLwpZjTLm3FXe1rq27\noMtVqdhLlbDvdC5//TqVDYcyAahbw5s/9WvFfTF19UEoIiIuo2WdQL54ohtf7jzJmyv3ciyrgCc+\n3Ub3JiFM7d+alnUCjY4olZiKvbi0zAIb/7Mkmc8Tj2OzO/B0N/Nkr0ie7N0EX0/98xYREddjNpsY\n2KE+d7epwwf/OcisdYfZcCiTftPWMaxLQ57v08LoiFJJqfmIS8ovsbM4NY+vDxRQYnMAcE+bOky5\ntxUNgn0NTiciInL9/LzcmXx3S4bENuT1FXtYmXKaeZuO8eWOdO5v7kvfJl54eBidUioTFXtxKcVW\nG/M3HeOdb0+TW1J6t74ODYP4n36tiG0UbHA6ERGRitcg2JcPR3Rk46FMXl2+m9T0HBYk57B8v5lH\nogJp2camC2wFULEXF2G12flyZzrvrtnPifOlF8aGB7gxql0Qj/fronn0IiJS5XVrEsLXz/RkefIp\nXv86mVN5VmZty2Zl2lqe79OcB9rVw82s74fVmYq9VGoWm52lO04y/fuDHM0sACAswIuHW/pwawNP\nvL08VepFRKTaMJtN9G8bTrg9g38fyOGLPfmcOF/I858n8eF/DvHM7U25LyZcBb+aUrGXSslis7N0\n+0ne//4gx7JKC32wnyeP3RLJqO4RHNiTisViMTiliIiIMdzNJu6K9OXOJgFsyw3kw/8c5EBGHr9f\nuJN31xzgqd5NeLB9PTzczEZHlZtIxV4qlSKLjSXbT/Lh2oMczyqdchPi58njvSIZ0TUCPy/9kxUR\nEfmZl7uZCb2bMKxLQz7ZcIQ5Px7m8Ll8Ji/axbTvDvBU76Y81LGe5uBXE2pJUimczy/h001H+WTj\nEc7llQAQ6u/JE72aMLxrQy1dKSIicgU1fDx49o5mjOnZmHmbjjJ7XRonzhfyp6XJ/Ou7A4zp0Ygh\nnRtSw0fL6FRlaktiqGOZBcxen8bniccpspSuclMvyIexPRszrHNDfDx1hkFERKS8/L3cefLWJozq\n1ogFW44xY+0hTucU8cbKvUz77gCPdGrA2B6NaRiipaGrIhV7uekcDgeb0rL4ZOMR/p16GnvpMvS0\nCQ/k8V6R9IuuqzmBIiIi18HH041xPRszvEtDvkpKZ866w+w7k0vchiN8svEId7Wuw/hbGtMxoqYW\noahCVOzlpskpsrB0+0k+3XSUgxl5ZY/3blGLx2+JpFuTEH24iIiIVCBvDzce6dSAQR3rs/7gOWav\nO8za/WdZlXqaVamnaV03kOFdG/JAu3r46zo2l6cRlBtuz6kcPt10lC93nKSgxAaAr6cbA9rX49Fu\njWhRJ8DghCIiIlWbyWTilma1uKVZLfafyWXu+sMs2XGS3adymLI0hTdW7OXB9uEM6xxB6/BAo+PK\nNVKxlxsiu6CEr5PSWbTtBEknLpQ93izMn5HdIhjQvh4B3rqAR0RE5GZrXjuANx+K4Y/3tGTx9hMs\n2HyMtHP5zNt0jHmbjtG+YRBDYhvQL7quvle7GBV7qTA2u4MfDpxl0bYTrE49Q4mt9GJYd7OJu9vU\nYUTXCLpGBmu6jYiISCVQ08+T8bdEMq5nYzamZTJ/8zH+nXKaHcey2XEsm6nLUrm7TR0e6lifnk1D\nddMrF6BiL9fF4XCw68QFvtmVzldJ6ZzJKS57rmWdAAZ1asCD7cIJ8fcyMKWIiIhcjslkonuTULo3\nCeVsbjGLtp1g8fYTHMzI46uk0u/vYQFePNi+HgPa16NlnQCdpKukVOzFaQ6Hg92ncvhm1ymW7zpV\ndmdYgJq+HjzQrh4Pd6xPVL0aBqYUERERZ9UK8GJC7yY8eWskyScvsHjbCb5KSicjt5iZP6Qx84c0\nIkP9uDemLv2i66rkVzIq9lIudruD5JMXWLPnDMuTT5F2Nr/sOR8PN+5oFcZ9MeHc3jIMT3ctVSki\nIuLKTP/f3r0HNXXmfTJArLUAABdVSURBVAD/JiSEJBAgYFBDvWEVUdC2itS7RVurbKtuteruzI7d\nqbOd7W5ntiu1rqvY7m5tO9ut0zq71dZZp1a32up0tkV3vL2+u1atly4FK7QoULHKLQFCCCGX5/0j\nEMFcSPpqQsL3M3MmevKc8As/D37P4Tk5Egly0pOQk56E3y3Kwv9U1OPji7U4UdGAq41mvHW8Em8d\nr8SoVDUWZrtC/rghDPnhxmBPPnXYHDh9pQlHLtfh2OW6XtNsYmVSPDRWh4KJQ/BQpo53hiUiIopS\nsTIpHh4/GA+PHwxThw3Hy+vx6Vc3cPIbV8h/+0Ql3j5RCX2SEg9l6vDQOB0eHJWCODlvMhlqTGPU\ny/fNFvzn20YcL6/H/37b4P54SgBQx8Zgzlgd5melIX+cjlfKExERDTAJca4pt49P0rtD/mddIf96\nswXvn6nB+2dqoJTHYMa9qZg3Toe5Y3XQaeLCXfqAwGA/wLVZ7ThzpQn//rYB/65s7DXFBgCGJMZh\n3rg0zMtKQ94oLRQyHn0TERFR75Bv6XTg8yuNOFZej+OX63GztQNHvq7Dka/rAABj0xIwfXQqZtyb\ngtyRKbwZ1l3C7+oAY7ba8eV3zfii2oDTVxrx5XfNsDuF+3mpBJh0TxJm3jsI87PSMH6ohvPliIiI\nyC9lbAzyx6Uhf1waxGKBS9+34tjlehwrr8NXtS2oqDOhos6EnaeqIJNKcN+wJEzLSMX00anISU/k\ntJ07hME+yhnMnThXbcC5KgPOVRtQ9n0rHD2CPAAMT1Fh5r2pmDF6EB7MSEGiklNsiIiI6IeRSCSY\noE/EBH0inpt3LwzmTpy+0oT/VDbiVGUjvjO041y1Eeeqjdh67FvExkiRnZ6IySOSMWW4Fg8MT0ay\nOjbcbyMiMdhHEavdgcs3TCitbUZJbQv+e60ZlfVtHuP0SUpMGZGM3JEpmDE6FcNSVGGoloiIiAYC\nrToWi3KGYFHOEADANUM7TlU24j+VjThbZUCDyYoLNUZcqDHiHVwFAIzWxeOBYcnIuScROfokjB2c\nwE/dCwCDfYSy2h2orG9D2fUWlNS2oLS2BeU3W2FzCI+x9+riMWWkFrkjtJgyUgt9kjIMFRMREREB\n92hVWJE7DCtyh0EI4T6Df6HGgHPVRlTWt7mXD89fAwDExkiROSQB2fpE5KQnIlufhHvT4iGPYdjv\nicG+nxNCoNZoQcVN19y0yzdaUXHThKuNZo8pNYDrqDgnPdH12bP6RP46i4iIiPotiUSC4SlqDE9R\n44kH0gG4phFfqDHiv9eM+Kq2BaXXW9DcbsNXtS34qrYFH5x1bSuPkSBjUDzGDk5wLWmuR32ScsBe\nH8hg309Y7Q5819SOq41mXG0wo6qxDVcazPjmpgkmq93rNpo4GbKGajCx6wYSOemJSE8euP+YiYiI\nKPJp1bGYn5WG+VlpAG6d5HQF+2Z8VduCsustMFntKL9pQvlNU6/t4xUyjElzBf6RqWqMTI3HyFQ1\nhmlVUT+dh8E+hNqsdtQa21FrsKDW2I4aQ3tXiDej1tgOLyfgAdw6Is0cnICxgzVdjwkYkhjHEE9E\nRERRTSKR4B6tCvdoVe55+t1h/5s6V7Cv6FquNLShzWrHxe+acfG75l6vI5W4pgGNSFF3BX417tEq\nkZ6sgj5JCXUUfARn5L+DfsLmcKKxzYq6VivqWjtwo9mCWmPX0tyOWqMFze02v68Rr5BhZKoaowbd\n+geXOViDkanqqD/CJCIiIgpUz7CfPy7Nvb7T7kRVoxnlN1tRWd+GqkbXCdTqRjPMnQ7UNLWjpqkd\nJ79p8HjNZJUc+mQl0pNUrsdkJfRJSgxOjEOaJg4p6ljI+vmc/qCDfVtbGzZs2IB9+/bBYDAgMzMT\n69atw4oVK/rctr6+HoWFhfj000/R3t6OiRMn4g9/+APy8/M9xh49ehS///3vUVJSApVKhYKCArz2\n2mvQ6XTBlvyDCSHQ2mGHwdzpXupNHahrtaK+tQN1rV1/NnWgydwJ4eOMe0/JKjnSk1VI7/oHM2pQ\nvDvMD4pX8Aw8ERER0Q8UK5O659z3JIRAg8mKq10hvzvw1xotuN5sQYvFBmO7aym73ur1taUSICVe\ngTSNAmkJcdBpFNAluEL/oAQFtOpYpKhjkayOhSZOFpZMF3SwX7p0Kc6dO4ctW7ZgzJgx2LNnD1au\nXAmn04lVq1b53M5qtSI/Px/Nzc3YunUrdDodtm3bhgULFuDo0aOYPXu2e+zJkyfx6KOPYtGiRfjk\nk09QX1+PF154Afn5+Th//jwUCkVQNTudAiarHa0WG0wddlyqt6LF0gmrsxMX26pgbLfBYLbCaLah\nqevR0N4Jo7mz182b+iKTSqBLUECnicNgTZz71zuuEO86+uOd1oiIiIhCSyKRQKeJg04Th7xRKR7P\nmzpsuN5sQa3BFfRrje1djxbUt1rR0GaFw+k6OGgwWVEG7+G/m0wqQXJ30FfFQqt2LcnqWGhVcmiU\ncjTdtEAhcSJRKZDabEFCnAzxsTJIpT/8gCColFlcXIwjR464wzwAzJ07FzU1NVi7di2efPJJxMR4\nv3PYe++9h7KyMnz++ed48MEH3dtOnDgRhYWFOHv2rHvs2rVrMWbMGHz00UeQyVwljhw5EtOnT8fO\nnTvxzDPP9Fnrk++cxvXmDpg67D4vPnUx9vla6tgYVyPUse7gnpYQ5zpi07iO2NI0cdCqYv9fzSAi\nIiKi0EuIkyNzsByZgzVen3c4BZrMVtR3TbmuN1lvzdzo+rvB3AljeyfaOx2w9zgICMjh4wAAicQ1\nNVsTJ8fQRAXeXTUhqPcRVLA/ePAg4uPjsWzZsl7rV69ejVWrVuHs2bOYNm2az23Hjh3rDvUAIJPJ\n8NOf/hTr16/H9evXodfrcf36dZw7dw6vvPKKO9QDwLRp0zBmzBgcPHgwoGBfWd8Go6V3oFfIpEiI\nk0MhcUApA+IVMdAP0iJZLYdW1eNIqseSrIrlbY6JiIiIBrAYqQS6hDjoEuIwQZ/od2yHzeGewm1s\nvzWd22juRFPXOlOHHTebWmDudMJsE7DYgU6HE0LAdVK6w452q/9rM70JKtiXlZVh3LhxvQI3AOTk\n5Lif9xXsy8rKMHPmTI/13dteunQJer0eZWVlvdbfPvbUqVMB1Vo4IwVyiYA6VgKVXAq1XAp5jOts\nus126xsll8cAcALo6FoAtAP2dqC+AagP6KtRqHX30GazoaSkJMzVULDYv8jWYXe6/2yz2dnDCMX9\nMLKxf5FBA0AjAUbEA4jvXisDIIPNduvEsVwuR6dDoL3TiTabE+02AZsz+FkgQQX7pqYmjBo1ymO9\nVqt1P+9v2+5x/rbtfvQ11t/X6ClTGwOHw9H1NyfgdMLm9BzXM+RTZGIPIxv7F3ls9t7XHrGHkY89\njGzsX+Sz2WyQAFDLXAuUEp/T2/0J+kpOf1f49nX1bzDb+hob6BXGMpkMUqn3jyTqfcZeHtDrUf/C\nHkY29i+yOSS9z5Kwh5GJ+2FkY/8iX1899JVj/Qkq2KekpHg9Y24wGAB4P8se7LYpKa4rlX2N9fc1\neho/frzPb0hJSQlsNhvkcjkmTpwY0OtR/8IeRjb2L7K1d9qB/d8DAORyGXsYobgfRjb2L/L11UOn\n0wmTyeRlS9+COhTIzs7G5cuXYbf3vii1tLQUADBhgu8rd7Ozs93j/G3b/ehrrL+vQUREREQ0UAUV\n7JcsWYK2tjZ8/PHHvdbv2rULQ4cOxdSpU/1uW15e3utjLe12O3bv3o2pU6di6NChAAC9Xo/c3Fzs\n3r27xxx54MyZM6ioqMDSpUuDKZmIiIiIaEAIKtg/+uijmD9/Pp555hns2LEDJ06cwJo1a3D48GG8\n9tpr7kn+P//5zyGTyVBTU+Pe9qmnnsL48eOxbNky7NmzB0ePHsXy5ctRUVGBV199tdfXefXVV1Fe\nXo5ly5bh6NGj2LNnD5YvX44JEyZg9erVd+BtExERERFFl6Avnj1w4AB+97vfYePGjTAYDMjMzMTe\nvXuxYsUK9xiHwwGHwwEhbn1ygkKhwLFjx1BYWIhf/epXaG9vx6RJk3Do0KFed50FgDlz5qC4uBgb\nN27Ej370I6hUKhQUFOD111/3etfZnl+nm9Pp5SNwukilUsTExEAqlfodR/0XexjZ2L/IJoRAstL1\n30cMexixuB9GNvYv8vXVQ2/rvGXeniSirxERwG63w2w2h7sMIiIiIqK7Rq1We9xPqqfgP0eHiIiI\niIj6HQZ7IiIiIqIowGBPRERERBQFomKOvdPp9LjAQCKRBHyXWiIiIiKi/kQI4XGxrFQq9XtH2qgI\n9kREREREAx2n4hARERERRQEGeyIiIiKiKBCVwd5kMqGwsBAPP/wwBg0aBIlEgqKiIq9jbTYb3njj\nDWRnZ0OpVCIpKQnTpk3D559/HtqiqZdAeyiEwI4dO/DAAw9Ao9EgJSUFs2fPxmeffRb6osnt+PHj\neOqpp5CZmQm1Wg29Xo/HH38cFy5c8Bh78eJFzJs3D/Hx8UhKSsLSpUtx9erVMFRNPQXSQ4fDgTfe\neAMLFixAeno6VCoVxo0bh3Xr1qG5uTmM1VMw+2A3IQRmzZoFiUSCZ599NoTVkjfB9JBZpv8JtH93\nOsdEZbBvamrC9u3bYbVasXjxYp/jHA4HlixZgpdeegkrV67EoUOH8MEHH2DBggW84VWYBdrDTZs2\nYc2aNcjNzcXHH3+Mv//971AoFCgoKMCBAwdCWDH19Ne//hXV1dV47rnnUFxcjK1bt6K+vh55eXk4\nfvy4e1x5eTnmzJmDzs5O7Nu3Dzt37sQ333yDmTNnoqGhIYzvgALpocViQVFREYYPH44333wTxcXF\nePrpp7F9+3ZMnz4dFoslzO9i4Ap0H+xp27ZtqKysDHGl5EugPWSW6Z8C7d8dzzEiCjmdTuF0OoUQ\nQjQ0NAgAYtOmTR7j/vKXvwipVCpOnz4d4gqpL4H2UK/XixkzZvRaZ7FYRGJionjsscdCUSp5UVdX\n57HOZDKJtLQ0kZ+f7163bNkykZqaKlpaWtzrqqurhVwuF4WFhSGplbwLpId2u100NjZ6jNu/f78A\nIN5///27Xid5F+g+2K2qqkrEx8eLAwcOCADil7/8ZSjKJD8C7SGzTP8UaP/udI6JyjP2gX7U5dat\nWzFr1izk5eWFoCoKRqA9lMvlSExM7LUuLi7OvVB46HQ6j3Xx8fHIysrCtWvXAAB2ux2ffvopfvzj\nH0Oj0bjHDR8+HHPnzsXBgwdDVi95CqSHMTExSElJ8RiXm5sLAO5xFHqB9K+nNWvWYP78+ViyZEko\nyqMABNpDZpn+KdD+3ekcE5XBPhDXrl1DdXU1srOzsX79eqSlpUEmk2H8+PHYtWtXuMujAD333HM4\nfPgw3nvvPRiNRty4cQO/+c1v0NLSgl//+tfhLo96aGlpwcWLFzF+/HgAwJUrV2CxWJCTk+MxNicn\nB5WVlejo6Ah1meTH7T30pfvXzH2No9Dy1b93330XX3zxBd5+++0wVUaBur2HzDKRxds+eMdzTPC/\nXIgsvqZxnD59WgAQGo1GZGVliX379ol//etf4oknnhAAxPbt28NTMHnwNxVHCCH+9re/CYVCIQAI\nAEKr1YojR46Etkjq009+8hMhk8nE+fPnhRBCnDp1SgAQe/fu9Rj7pz/9SQAQ33//fajLJD9u76E3\ntbW1Ii0tTUyePFk4HI4QVkd98da/2tpakZiYKN555x33OnAqTr91ew+ZZSKLr5+hdzLHDNhg3x0q\nYmNjRXV1tXu90+kU999/v0hPTw9xpeSLv2C/c+dOoVAoxPPPPy+OHj0qiouLxYoVK4RKpRKHDx8O\nfbHk1YYNGwQA8dZbb7nXde+D//jHPzzGdwf7GzduhLJM8sNbD2/X1NQkcnJyhE6nE1euXAlhddQX\nX/0rKCgQs2bNcl/TJASDfX/l7+cos0z/52sfvNM5ZsAG+/LycgFA5OTkeGzz4osvCgBeL3yg0PPV\nQ4PBIJRKpdf/gGbPni1GjBgRogrJn6KiIgFA/PGPf+y1vnsf3LZtm8c2v/3tb4VEIhEWiyVUZZIf\nvnrYk8FgEPfff79ISUkRJSUlIayO+uKrf/v37xcymUycOXNGGI1G9wJAPP3008JoNIrOzs4wVU09\n9fVzlFmmf/PVv7uRYwbsHPuMjAyoVCqvzwkhAABS6YD99kSEiooKWCwWTJkyxeO5yZMno7q6Gm1t\nbWGojLpt3rwZRUVFKCoqwvr163s9l5GRAaVSidLSUo/tSktLMXr0aF4A3Q/462E3o9GIefPmoaqq\nCkeOHPF63QSFh7/+lZWVwW63Iy8vD8nJye4FAHbs2IHk5GTeE6Qf6OvnKLNM/+avf3clx/zAg4+I\n4W8ax8qVK4VcLhdVVVXudU6nU0yaNElkZGSErkjyy1cPa2pqBADxi1/8otd6p9Mppk+fLpKTk3v9\neplC66WXXhIAxIYNG3yOWb58udDpdKK1tdW9rqamRsTGxooXXnghFGWSH4H0sPtMfVJSkjh37lwI\nq6O+9NW/qqoqceLECY8FgFi8eLE4ceKEaGhoCHHV1FMg+yCzTP/VV//uRo6RBX/sERkOHToEs9kM\nk8kEAPj666/x0UcfAQAWLlwIlUqFl19+GYcOHcKCBQtQVFQEjUaDd999FyUlJdi3b184yyf03cNh\nw4Zh6dKl2L59OxQKBRYuXAir1Ypdu3bh1KlTePnllwP6yEy68/785z9j48aNWLBgARYtWoQzZ870\ner77Y9k2b96MKVOmoKCgAOvWrUNHRwc2btyI1NRUPP/88+EonboE0kOLxYJHHnkEX375Jd58803Y\n7fZe4wYNGoSMjIxQl04IrH8jRozAiBEjvG6v1+sxZ86cu18o+RToz1Fmmf4pkP7dlRzzgw9D+rnh\nw4e7ry6+fel5VFtaWioWLVokEhISRFxcnMjLyxP//Oc/w1c4uQXSQ4vFIl5//XWRk5MjEhIShFar\nFXl5eWL37t08Wx9Gs2fP9tm723/snD9/XuTn5wuVSiU0Go1YvHixqKysDFPl1C2QHlZVVfkd87Of\n/Sy8b2IAC2YfvB148Wy/EEwPmWX6n0D7d6dzjESIrklYREREREQUsXhFBRERERFRFGCwJyIiIiKK\nAgz2RERERERRgMGeiIiIiCgKMNgTEREREUUBBnsiIiIioijAYE9EREREFAUY7ImIyKvi4mI88sgj\n2LRpE3jLEyKi/o/BnoiIPHR0dOCVV17B3r174XQ6ceDAAa/jvvjiC6xevRqjRo2CUqlEfHw8cnNz\nsWXLFphMphBXTUQ0sDHYExGRB6vVioSEBGi1WmRkZMBoNHqMefHFF5GXl4fKykqsX78excXF2LNn\nD6ZMmYLNmzdj69atYaiciGjgkoW7ACIi6n8SExORl5eHyZMnY8iQIfjwww97PV9UVIQtW7agqKgI\nmzZt6vXcY489hmeffRZmszmUJRMRDXgSwYmTREQUhAsXLmDq1KlYsmQJ9u/fH+5yiIioC4M9EREF\nZcmSJfjkk09w+fJljB07NtzlEBFRFwZ7IiIKmNlshlarRV5eHk6ePBnucoiIqAdePEtERAG7dOkS\nOjs7MWnSpHCXQkREt2GwJyKigDU3NwMAhgwZEuZKiIjodgz2REQUsMGDBwMAampqwlwJERHdjnPs\niYgoYEIIjB49Gs3Nzbh8+TJ0Op3HmGPHjiE/Pz8M1RERDWwM9kREFJTjx49j4cKF0Ol0WLt2LbKy\nsuBwOFBaWooPP/wQSqWSF9YSEYUBgz0REQWtrKwMW7ZswYkTJ9DQ0ICkpCQMGzYMc+fOxapVq3Df\nffeFu0QiogGHwZ6IiIiIKArw4lkiIiIioijAYE9EREREFAUY7ImIiIiIogCDPRERERFRFGCwJyIi\nIiKKAgz2RERERERRgMGeiIiIiCgKMNgTEREREUUBBnsiIiIioijAYE9EREREFAUY7ImIiIiIogCD\nPRERERFRFPg/ohwzm0szKW4AAAAASUVORK5CYII=\n", "text/plain": [ "" ] }, "metadata": {}, "output_type": "display_data" } ], "source": [ "plot_gaussian_pdf(22, 4, mean_line=True, xlabel='$^{\\circ}C$');" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "What does this curve *mean*? Assume we have a thermometer which reads 22°C. No thermometer is perfectly accurate, and so we expect that each reading will be slightly off the actual value. However, a theorem called [*Central Limit Theorem*](https://en.wikipedia.org/wiki/Central_limit_theorem) states that if we make many measurements that the measurements will be normally distributed. When we look at this chart we can \"sort of\" think of it as representing the probability of the thermometer reading a particular value given the actual temperature of 22°C. \n", "\n", "Recall that a Gaussian distribution is *continuous*. Think of an infinitely long straight line - what is the probability that a point you pick randomly is at 2. Clearly 0%, as there is an infinite number of choices to choose from. The same is true for normal distributions; in the graph above the probability of being *exactly* 2°C is 0% because there are an infinite number of values the reading can take.\n", "\n", "What is this curve? It is something we call the *probability density function.* The area under the curve at any region gives you the probability of those values. So, for example, if you compute the area under the curve between 20 and 22 the resulting area will be the probability of the temperature reading being between those two temperatures. \n", "\n", "We can think of this in Bayesian terms or frequentist terms. As a Bayesian, if the thermometer reads exactly 22°C, then our belief is described by the curve - our belief that the actual (system) temperature is near 22 is very high, and our belief that the actual temperature is near 18 is very low. As a frequentist we would say that if we took 1 billion temperature measurements of a system at exactly 22°C, then a histogram of the measurements would look like this curve. \n", "\n", "How do you compute the probability, or area under the curve? You integrate the equation for the Gaussian \n", "\n", "$$ \\int^{x_1}_{x_0} \\frac{1}{\\sigma\\sqrt{2\\pi}} e^{-\\frac{1}{2}{(x-\\mu)^2}/\\sigma^2 } dx$$\n", "\n", "I wrote `filterpy.stats.norm_cdf` which computes the integral for you. For example, we can compute" ] }, { "cell_type": "code", "execution_count": 18, "metadata": {}, "outputs": [ { "name": "stdout", "output_type": "stream", "text": [ "Probability of range 21.5 to 22.5 is 19.74%\n", "Probability of range 23.5 to 24.5 is 12.10%\n" ] } ], "source": [ "from filterpy.stats import norm_cdf\n", "print('Probability of range 21.5 to 22.5 is {:.2f}%'.format(\n", " norm_cdf((21.5, 22.5), 22,4)*100))\n", "print('Probability of range 23.5 to 24.5 is {:.2f}%'.format(\n", " norm_cdf((23.5, 24.5), 22,4)*100))" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "The mean ($\\mu$) is what it sounds like — the average of all possible probabilities. Because of the symmetric shape of the curve it is also the tallest part of the curve. The thermometer reads 22°C, so that is what we used for the mean. \n", "\n", "The notation for a normal distribution for a random variable $X$ is $X \\sim\\ \\mathcal{N}(\\mu,\\sigma^2)$ where $\\sim$ means *distributed according to*. This means I can express the temperature reading of our thermometer as\n", "\n", "$$\\text{temp} \\sim \\mathcal{N}(22,4)$$\n", "\n", "This is an extremely important result. Gaussians allow me to capture an infinite number of possible values with only two numbers! With the values $\\mu=22$ and $\\sigma^2=4$ I can compute the distribution of measurements for over any range.\n", "\n", "> Some sources use $\\mathcal N (\\mu, \\sigma)$ instead of $\\mathcal N (\\mu, \\sigma^2)$. Either is fine, they are both conventions. You need to keep in mind which form is being used if you see a term such as $\\mathcal{N}(22,4)$. In this book I always use $\\mathcal N (\\mu, \\sigma^2)$, so $\\sigma=2$, $\\sigma^2=4$ for this example." ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "## The Variance and Belief\n", "\n", "Since this is a probability density distribution it is required that the area under the curve always equals one. This should be intuitively clear — the area under the curve represents all possible outcomes, *something* happened, and the probability of *something happening* is one, so the density must sum to one. We can prove this ourselves with a bit of code. (If you are mathematically inclined, integrate the Gaussian equation from $-\\infty$ to $\\infty$)" ] }, { "cell_type": "code", "execution_count": 19, "metadata": {}, "outputs": [ { "name": "stdout", "output_type": "stream", "text": [ "1.0\n" ] } ], "source": [ "print(norm_cdf((-1e8, 1e8), mu=0, var=4))" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "This leads to an important insight. If the variance is small the curve will be narrow. this is because the variance is a measure of *how much* the samples vary from the mean. To keep the area equal to 1, the curve must also be tall. On the other hand if the variance is large the curve will be wide, and thus it will also have to be short to make the area equal to 1.\n", "\n", "Let's look at that graphically:" ] }, { "cell_type": "code", "execution_count": 20, "metadata": { "scrolled": true }, "outputs": [ { "data": { "image/png": "iVBORw0KGgoAAAANSUhEUgAAAusAAAEaCAYAAACo3xkcAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzs3Xl8VOXd///XbNn3DQgkLCqyhUVR\n0QqCC2Kl3qJ1w6pFv9Yf3VD7la8VS6ttrdVaa+/77tf12+ACKq53XWjVFmqhAnZBQFBUIAFCgOyT\nSTLb+f0xOZOMSUgmOZP1/Xw4jyQnZ7nmEJP3XPO5rstmGIaBiIiIiIj0O/a+boCIiIiIiLRPYV1E\nREREpJ9SWBcRERER6acU1kVERERE+imFdRERERGRfsrZ1w3oSDAYJBgMRmyz2WzYbLY+apGIiIiI\nSPcZhsGXJ2K02+3Y7R33n/frsF5fX9/XzRARERERiZnk5OTjhnWVwYiIiIiI9FMK6yIiIiIi/ZTC\nuoiIiIhIP9Vva9bbG0jaWU3PULZz5078fj9Op5PJkyf3dXMGBd1T6+meWkv303q6p9bTPbWW7qf1\nevOetjcms7PJUwZUWO9stOxQFgwGCQQCukcW0j21nu6ptXQ/rad7aj3dU2vpflqvr+9pZ2Fd/8oi\nIiIiIv2UwrqIiIiISD+lsC4iIiIi0k8prIuIiIiI9FP9doCpiIiIyEAUCASorq7G4/FYfm6Xy4XT\n6cRms1FaWmr5+Yciq++p3W4nKyuLxMREC1qnsC4iIiJimUAgwMGDB8nMzCQrK6vTmT6i5fF4MAwD\nm81GUlKSpeceqqy+pz6fj7KyMkaOHInD4ejx+VQGIyIiMbWnvI4rH/07f/30aF83RSTmqquryczM\nJDU11fKgLgODy+UiJyeHiooKS86nsC4iIjH1m3f3sGVfJfe9tQvDMPq6OSIx5fF4SElJ6etmSB9L\nTEykqanJknMprIuISMxU1nv508eHAdh9uI6PDtT0cYtEYk896mLlz4DCuoiIxMyr/zqIL9DSm/7C\nhxoQJyISDYV1ERGJCcMweGFrCQAXTx0BwP/8+xAer78vmyUiMqAorIuISEz8u7SaT8vdxDvt3Hdp\nEYVZSbib/Ly1/XBfN01EZMBQWBcRkZh486MyAL5aNIL0JBdXzhwFwBsfHerLZomIDCgK6yIiEhOf\nH3UDcNqYrIiP5nYREemcwrqIiMTE/srQ6o2js5OaPyYDcKi6EV8g2GftEpHYa2pqYsmSJRQUFJCW\nlsasWbPYtGlTXzdrQFJYFxERywWDBgcqGwAozAqF9bzUeOKddgJBg0PVDX3ZPBGJMb/fz9ixY9m4\ncSPV1dUsXbqUSy65BI/H09dNG3AU1kVExHKHaxvxBoI47TZGpCcAYLfbKGgO7vsr9AdbZDBLTk5m\n5cqVFBYWYrfbueGGGwgGg+zZs6evmzbgKKyLiIjlzDA+KjMRp6PlT81oM6xXKqyLDCW7d++moaGB\nE044wZLzud1ubr31VvLz80lISGD69Ok8//zz3To+KyuLM888k7Vr10bss379emw2W7uPDz74wJLn\n0RXOXruSiIgMGSWV9QAUNtepmwqb69dLFdZFhgyPx8N1113H3XffTUpKiiXnvOyyy9i6dSv3338/\n48ePZ/Xq1VxzzTUEg0EWL14c1fGFhYW8+OKLfPOb38TlcrU5/r777mPevHkR26ZMmWLJ8+gKhXUR\nEbGc2bNu9qSbwj3rFfW93iYR6X0+n48rr7ySSZMmcdddd1lyzrfeeot33nknHNAB5s2bx/79+7nj\njju46qqrcDgcXT7e4/EwZ84cSkpK2j3+pJNOYtasWZa0vTtUBiMiIpb78kwwJnNGGNWsy1Dk8fot\neARaPaI/3gp+v58HH3yQqVOnkpiY2KZEpLCwEIBgMMj111+Pw+HgqaeewmazWXL9V199lZSUFK64\n4oqI7UuWLOHQoUNs3ry5W8dfd911XTq+t6lnXURELGeWuRR8qWfd/Lqk0oNhGJb98RYZCCat/GNf\nN4F991/c43PcdNNNPPfcc3z/+9/ngQceoLy8nOXLl3PkyBFuu+02ioqKALjlllsoKytj3bp1OJ1t\nI6dhGAQCgS5ds/XxO3bsYOLEiW3OOXXq1PD3zzrrrA7P1dHxZmnLl4//zne+w9VXX01SUhJnnnkm\nP/rRjzj77LO71G4rKKyLiIjlwmUw2V8O64nYbODxBjjm9pKbGt8XzRORblq9ejVPP/00jz/+ODff\nfHN4u2EYLFmyhHPPPZeFCxeyf/9+nnzySRISEsjJyQnv9/bbbzN79mwANmzY0KYWvCN79+5lzJgx\nAFRUVDBu3Lg2+2RlZYW/fzwdHZ+ZmRlxfHp6OsuWLWPu3LlkZ2fz2Wef8eCDDzJ37lzefPNNLrzw\nwi61vacU1kVExFI1Hh81DT6gZY51U7zTwYi0BA7VNFJS6VFYlyHl43t7Hu48nobwu1JJSYkWtCo6\njz32GBMnTowI6gATJ04EoLKyEoDRo0djGMZxz3XqqaeydevWLl03Pz8/4uvjvSvXlXfsunL8jBkz\nmDFjRnj77NmzWbRoEUVFRSxfvlxhXUREBqb9zTPB5KbGkxTX9s9MYXZSc1iv59TRmb3dPJE+097/\nD1HzO1rCuhXni0JVVRXvv/8+t99+e5vvHThwAIBRo0Z1+XwpKSlMnz69S/u2LlnJzs5ut/fcfKFg\n9rB3pKPjq6qqOj0+IyODhQsX8uijj9LQ0EBiYuxfMGmAqYiIWKqjmWBMo7M0yFRkICotLcUwjDa9\n3ACvvfYaOTk5zJkzp8vn27BhAy6Xq0uPffv2hY8rKipi165d+P2RA2a3b98OdD6tYkfH79y5s0vH\nm+8Y9NaYG/Wsi4iIpUqaB5cWZrcf1s3tJQrrIgNKRkYGALt27YrYvmnTJtasWcOPf/zjdgeSdqS7\nZTCLFi3iiSee4OWXX+aqq64Kb1+1ahX5+fmcccYZxz1XR8c/99xznR5fVVXFG2+8wfTp00lISOhS\n23tKYV1ERCxlhvAv16ubClvNCCMiA0dhYSFz5syhuLiYsWPHcvrpp7Nlyxbuu+8+5s+fz4oVK6I6\nX2pqKjNnzoy6HRdddBEXXHABS5cupba2lhNPPJE1a9awbt06nn322fAc6Rs2bOC8885j5cqVrFy5\nssPjR40axYsvvsg777wTcfzixYspLCxk5syZ5OTksGfPHh566CHKy8spLi6Out3dpbAuIiKWOlTT\nAMCozPbDujl948Hqhl5rk4hYY+3atdx66608+OCDeDwexo8fzz333MOyZcuw23uvuvqVV15hxYoV\nrFy5ksrKSiZMmMCaNWu4+uqrw/uYU0MGg8FOjx8/fjzFxcVce+214X2mTp3KCy+8wKOPPorb7SYr\nK4uzzz6bZ555htNOO61XnicorIuIiMWO1jUBdDjTS05KHAAVbq/mWhcZYPLy8li9enVfN4OUlBQe\neeQRHnnkkQ73mTt3bocz0rQ+3uNpf92HO++8kzvvvNPSdneHBpiKiIiljrlDYd0M5V+WkxIK8d5A\nkNoGa1ZUFBEZrBTWRUTEMoGgQWW9F4DclPZ71hNcDlLjQ2/sHm0O9iIi0j6FdRERsUxlvZegATYb\nZCW337MOkNNcInNMYV1E5LgU1kVExDJm+M5MisPp6PhPjFkio7AuInJ8CusiImKZzurVTWbd+rE6\nhXURkeNRWBcREcuYYb2jmWBMueEyGG/M2yQiMpAprIuIiGWO1YXCd04Hg0tN4Z51lcGIiBxX1GG9\nrq6O5cuXM3/+fHJzc7HZbPzkJz/p0rHFxcXYbLZ2H4cPH462KSIi0s+0lMEorIuIWCHqRZEqKip4\n/PHHmTZtGpdeeilPPvlk1Bf9/e9/z4QJEyK2ZWdnR30eERHpX452OazHNe+vMhgRkeOJOqyPHj2a\nqqoqbDYbx44d61ZYnzJlCjNnzoz6OBER6d/MGvROB5imaoCpiEhXRF0GY5atiIiIfJkZvnM6G2Da\nqgymo+XARUSkGz3rVli4cCFHjx4lPT2duXPncu+99zJlypROj9u5cyfBYLAXWjjw+Hy+8Mdt27b1\ncWsGB91T6+meWqs/3s+yajcAVYf2s62xrMP9mvzB8Me/f/hvkuP6x3wH/fGeDnRD7Z66XC48Hk/M\nzm++uDUMI6bXGUpidU/r6ura/Mzb7XYKCwujOk+vhvXhw4ezYsUKZs2aRVpaGtu3b+f+++9n1qxZ\nbNy4kWnTph33eL/fTyAQ6KXWDlzmL0axju6p9XRPrdUf7mfQMKhpDIXwZGfwuG2yAwlOG41+g2Pu\nJuJS+6Tv6Lj6wz0dbIbCPXU6nb32blF/fleqqamJZcuW8Ze//IXa2lomTJjAL37xC2bNmtXXTTsu\nK++pYRhtfuYdDkfU5+nV344LFixgwYIF4a/nzJnDxRdfTFFREStXruT1118/7vFOpxO7vX/0vvQ3\nrX8YXC5XH7Zk8NA9tZ7uqbX62/2sbQoQbP47l5MSj9N+/JLJjAQ7h90B3H57v2g/9L97OhgMtXsa\n63Lh1mGyP5clBwIBxowZw3vvvcfIkSNZvXo1V111Fbt37yYpKamvmxchVvfUZrO1+ZnvTo7t866M\nMWPGcPbZZ/PBBx90uu/kyZMV1juwbds2fD4fLper03copGt0T62ne2qt/nY/Py2vA8rISHJx6ozp\nne4/clM9h91VZAwvYFrRiNg3sAv62z0dDIbaPS0tLY1pGPV4PBiGgc1m63eht7WkpCR++tOfhr/+\n1re+xZ133snBgwf73c9BrO5pamoqBQUFEduCwSB1dXVRnadfJF/DMBTCRUQGuPDg0k6mbTSZM8Zo\nrnWRwW/37t00NDRwwgkn9PhcPVnzZyDq84S8d+9eNm7c2O9rmERE5Pha5lg//rSNpvDCSJq+UWRQ\n83g8XHfdddx9992kpKT0+Hzmmj9NTU1ceumlFrSwf+tWGczbb79NfX19uBv/448/5qWXXgLgq1/9\nKklJSdx0002sWrWKzz//nNGjRwNw/vnnM2fOHKZOnRoeYPrAAw9gs9ki3ioREZGBp2WO9a72rIf2\n08JIIoOXz+fjyiuvZNKkSdx1112WnNOKNX8Gkm6F9aVLl7J///7w12vXrmXt2rVAqKd8zJgxBAIB\nAoFARNF+UVERL7zwAr/61a9oaGggLy+Pc889lx/96EeMHz++h09FRET60rEurl5qCi+MpDIYGSq8\n9aGPriQwBzL6vRD0gd0Jzvi2+zoTwSwVDvjA6wkd60rsfN+AF2wOcCVY+jT8fj8PP/wwzzzzDHv2\n7KGxsTHi+wUFBZSUlBAMBrn++utxOBw89dRTlg3e7M8Da2OhW2F93759ne5TXFxMcXFxxLaHH364\nO5cTEZEBwCxnye1kQSRTrmrWZai5Lz/08Y7PITkn9PmmR+DPP4NTrodL/rNl3wdPBJ8Hln0EmaEK\nBbY8QdIff4h/4iK8X/tdy76/KQJPBXz7A8ibGNr27+fgD8vg5IvhmtWWPo2bbrqJ5557ju9///s8\n8MADlJeXs3z5co4cOcJtt91GUVERALfccgtlZWWsW7cOp7Nt5DQMo8tTcrd3/FAxdJ+5iIhYygzd\nuVGWwSisiwwcq1ev5umnn+bxxx/n5ptvDm83DIMlS5Zw7rnnsnDhQvbv38+TTz5JQkICOTk54f3e\nfvttZs+eDcCGDRuYN29el65rVm4MRQrrIiJiCbNmPbuLA0zNHvhjdapZlyHirkOhj65W0wOetQxm\nfTtUBtPaHZ+FPjpblbucfjOeiVdi2GxEFILcur3tvtOvhaIrQmUwFnrssceYOHFiRFAHmDgx1KNf\nWVkJhOrKO1tg6NRTT2Xr1q1dum5+fn43Wjs4KKyLiIglKutDoTsruWthPbN5vwZfgEZfgASXtaFC\npN+JS267zRkHtPP/THv7OlwQlwRfDsEd7euwdhGqqqoq3n//fW6//fY23ztw4AAAo0aN6vL5UlJS\nmD698zUZYGiXwfT51I0iIjI41DSEVqrMSOpaWE+Nd4ZXOa3yqHddpL8rLS3FMIx2e7lfe+01cnJy\nmDNnTpfPt2HDBlwuV5ceXRkvOVgN3ZcpIiJiGa8/iLvJD0BmUtd682w2GxlJLo65vVTV+xiRntj5\nQSLSZzIyMgDYtWtXxPZNmzaxZs0afvzjH0fVA64ymK5RWBcRkR6rbgj1jNttkJbQ9bfeM5LiOOb2\nUq2edZF+r7CwkDlz5lBcXMzYsWM5/fTT2bJlC/fddx/z589nxYoVUZ0vNTWVmTNndqstXVnzZ7BQ\nWBcRkR6r9oRKYNITXdjtXZ8D2eyFr1RYFxkQ1q5dy6233sqDDz6Ix+Nh/Pjx3HPPPSxbtgy7vfeq\nq7uy5s9gobAuIiI9VtU8uDSzi/XqJnP/quawLyL9W15eHqtXWztve3cMpRp2DTAVEZEeq24eXJre\nxXp1kxnWq+vVsy4i0h6FdRER6TGz5jzanvWM5FC4V8+6iEj7FNZFRKTHzLCd0d2eddWsi4i0S2Fd\nRER6rKqbPevmAFPNsy4i0j6FdRER6bEas2c9Mbqe9QwNMBUROS6FdRER6TGzZzwjuXuzwagMRkSk\nfQrrIiLSY2bPeFdXLzVlNQ8wrdRsMCIi7VJYFxGRHuv2bDDN+9c2+vEHgpa3S0RkoFNYFxGRHqtq\ntYJpNFrXuNc0qG5dROTLFNZFRKRHDMMIDzDNjLJm3emwk5oQWkxbg0xFRNpSWBcRkR7xeAN4m0tY\noq1ZDx2jQaYiIh1RWBcRkR4xZ4KJc9pJdDmiPr5lrnX1rIuIfJnCuoiI9Eh1q5lgbDZb1Me3zLWu\nnnWRwaKpqYklS5ZQUFBAWloas2bNYtOmTX3drAFJYV1ERHqkOrwgUnT16qasZJXBiAw2fr+fsWPH\nsnHjRqqrq1m6dCmXXHIJHo+nr5s24Cisi4hIj4QXROpGvXrr4yrrVQYjMlgkJyezcuVKCgsLsdvt\n3HDDDQSDQfbs2dPXTRtwFNZFRKRHujvHukkDTEUGv927d9PQ0MAJJ5zQ43OtX78em83W7uODDz6w\noLX9i7OvGyAiIgNbePXS5O71rLcMMFVYFxmMPB4P1113HXfffTcpKSmWnfe+++5j3rx5EdumTJli\n2fn7C4V1ERHpETNkp3ezZr1lgKnKYEQGG5/Px5VXXsmkSZO46667LD33SSedxKxZsyw9Z3+kMhgR\nEemRmlazwXSHymBEBha/38+DDz7I1KlTSUxMbFOKUlhYCEAwGOT666/H4XDw1FNPdWu2KFFYFxGR\nHqrqYc16huZZlyHC4/N0+GgKNHVp3wZ/A42Bxi6ft9Efua8VbrrpJn74wx9y/vnn8+qrr1JcXExe\nXh4At912G/fccw8At9xyC2VlZbzwwgs4nW2LOQzDwO/3d+nRnu985zs4nU7S0tK48MIL+dvf/mb5\nc+0PVAYjIiI9Yobs7s4G03rqRsMw1Psmg9YZq8/o8HuzR87md+f/Lvz13Bfn0uBvaHffGTkzeHTe\no+GvF7y8gKqmqnb3nZw9mecXPt/NFre1evVqnn76aR5//HFuvvnm8HbDMFiyZAnnnnsuCxcuZP/+\n/Tz55JMkJCSQk5MT3u/tt99m9uzZAGzYsKFNzXlH9u7dy5gxYwBIT09n2bJlzJ07l+zsbD777DMe\nfPBB5s6dy5tvvsmFF15o2fPtDxTWRUSkR6rDUzf2bDYYX8DA3eQnNaF7oV9EYu+xxx5j4sSJEUEd\nYOLEiQBUVlYCMHr0aAzDOO65Tj31VLZu3dql6+bn54c/nzFjBjNmzAh/PXv2bBYtWkRRURHLly9X\nWBcREWmtuqFnNeuJcQ7inXaa/EGqPT6FdRm0Ni/e3OH3HHZHxNfrr1zf7n4NDW1729ddvq7D89pt\n1lU8V1VV8f7773P77be3+d6BAwcAGDVqVJfPl5KSwvTp07u0b3tlNK1lZGSwcOFCHn30URoaGkhM\nTOxyO/o7hXUREem2QNCgpsEsg+lez3roWBfltU1Ue3wUZFnVOpH+JcmV1PN9fbTpsY7mvD1RWlqK\nYRgRvdym1157jZycHObMmdPl83W3DKYj5n0ZbKV0CusiItJttQ0+zNzQ3Zp1CJXClNc2Ud2gGWFE\n+quMjAwAdu3aFbF906ZNrFmzhh//+Med9oC31t0ymPZUVVXxxhtvMH36dBISErrchoFAYV1ERLrN\nnAkmJd6Jy9H9t9s1I4xI/1dYWMicOXMoLi5m7NixnH766WzZsoX77ruP+fPns2LFiqjOl5qaysyZ\nM6Nux+LFiyksLGTmzJnk5OSwZ88eHnroIcrLyykuLo76fP2dwrqIiHRbT2eCMWUkaq51kYFg7dq1\n3HrrrTz44IN4PB7Gjx/PPffcw7Jly7Dbe2dG8KlTp/LCCy/w6KOP4na7ycrK4uyzz+aZZ57htNNO\n65U29CaFdRER6baahp7NsW7KTA6F/Wr1rIv0a3l5eaxevbpP23DnnXdy55139mkbepMWRRIRkW6r\nqremZz29uWe9Sj3rIiIRFNZFRKTberp6qcmc9rFGPesiIhEU1kVEpNuqLapZN8O+etZFRCIprIuI\nSLeZUy32ZI51gHTNBiMi0i6FdRER6TYzXHd39VKT2bNuLrAkIiIhCusiItJt1RbVrLfMs64yGBGR\n1hTWRUSk28zZYNJ7Os+6OcC0wUcwaHSyt0j/Zbfb8fn0DtFQFwgELDuXwrqIiHSbZT3rzVM3GgbU\nNiroyMCVlZVFWVkZHo8Hw9ALz6EoEAhw8OBBcnNzLTmfFkUSEZFuq26wpmY9zmknOc5BvTdAlcfX\n4wGrIn0lMTGRkSNHUlFRQUVFheXnr6urwzAMbDYbqamplp9/KIrFPc3LyyMhIcGScymsi4hItzT5\nA3i8obd6rQjXGUlx1Hsbmnvrk3t8PpG+4nA4yMvLi8m5t23bhs/nw+VyUVBQEJNrDDX9/Z6qDEZE\nRLrFnGPdboPU+J73/Zh169WavlFEJExhXUREusWcuSUjKQ673dbj85l17+bc7SIiorAuIiLdZNXq\npabwwkj16lkXETFFHdbr6upYvnw58+fPJzc3F5vNxk9+8pMuH3/kyBG++c1vkpOTQ1JSEmeeeSbv\nvfdetM0QEZE+ZtVMMCZzkGq1FkYSEQmLOqxXVFTw+OOP09TUxKWXXhrVsU1NTZx33nm89957PPLI\nI7z++usMGzaMBQsWsGHDhmibIiIifciq1UtN4TIYLYwkIhIW9Yig0aNHU1VVhc1m49ixYzz55JNd\nPvapp55ix44dbNq0iTPPPBOAefPmMW3aNJYvX87mzZujbY6IiPQRs2Y9PdGanvX0RHMVU/Wsi4iY\nou5Zt9ls2GzdG0j06quvcvLJJ4eDOoDT6eQb3/gGW7Zs4eDBg906r4iI9L5q9ayLiMRcr86zvmPH\nDmbPnt1m+9SpUwHYuXMnI0eO7PD4nTt3EgwGY9a+gcxc2tjn87Ft27Y+bs3goHtqPd1Ta/X1/fzi\nQCUAjbUVlly/qrwBgEMVNX3289HX93Qw0j21lu6n9XrzntrtdgoLC6M6plfDekVFBVlZWW22m9s6\nW+nL7/cTCARi0rbBxPyhE+vonlpP99RafXE/axpDv4+TnIYl1090hDpj6pqC/eLnoz+0YbDRPbWW\n7qf1Yn1PHQ5H1Mf0+gqmxyuh6ay8xul0Yrdrtsn2tP7hcrmseUt6qNM9tZ7uqbX6+n7W+wwAMhJd\nllw/Iyn00e0N9tnPR1/f08FI99Raup/W68172p0c26thPTs7u93e88rK0Fup7fW6tzZ58mSF9Q60\nXip32rRpfd2cQUH31Hq6p9bq6/vpfW8D4GX6xJOYdmJOj89XUO+FN9/B4zOYNKUIl6P3f9/39T0d\njHRPraX7ab3evKfBYJC6urqojunV34RFRUVs3769zXZz25QpU3qzOSIi0gMtiyJZOxsMQI3mWhcR\nAXo5rC9atIjdu3dHTNHo9/t59tlnOeOMM8jPz+/N5oiISDcZhtGyKFKyNW8bO+w20hJCb/hqRhgR\nkZBuhfW3336bl156iT/84Q8AfPzxx7z00ku89NJLeDweAG666SacTif79+8PH3fjjTcyefJkrrji\nClavXs27777LlVdeySeffMIvf/lLC56OiIj0BneTH3/QrFm3pmcdIDPZnL5RPesiItDNmvWlS5dG\nhPC1a9eydu1aAPbu3cuYMWMIBAIEAgEMwwjvFx8fz3vvvcfy5cv53ve+h8fjYfr06bz99tucc845\nPXwqIiLSW8wwHe+0kxgX/ewGHclIdLEfLYwkImLqVljft29fp/sUFxdTXFzcZvuwYcNYtWpVdy4r\nIiL9hLl6aaZF9eoms/69SmUwIiJAL9esi4jI4NAyuNTaac7M1VBr1LMuIgIorIuISDeoZ11EpHco\nrIuISNRi1bNunq9aUzeKiAAK6yIi0g1mz7dVc6ybMprnWtfUjSIiIQrrIiISNbNnPdPqmnVN3Sgi\nEkFhXUREolYd85p1hXUREVBYFxGRbjDDdLrVNesqgxERiaCwLiIiUYtVz7p5PpXBiIiEKKyLiEjU\nqmJUs2721Df4AjT6ApaeW0RkIFJYFxGRqFXHaDaYtAQnDrsNgBpN3ygiorAuIiLR8QeC1Db6Aevn\nWbfZbKQ3161rYSQREYV1ERGJUuseb3NAqJXMFwBV9epZFxFRWBcRkaiY9eqpCU6cDuv/jJiDTGsa\n1LMuIqKwLiIiUTFDtNUzwZgywmUw6lkXEVFYFxGRqJjlKVbPBGPK0PSNIiJhCusiIhIVc+Bneqx6\n1pO0MJKIiElhXUREolIdoznWTeZ5NRuMiIjCuoiIRKkqRquXmlQGIyLSQmFdRESiUt08daPVc6yb\nWspgFNZFRBTWRUQkKuHVS2Mwxzq09NhXa+pGERGFdRERiU54Npjk2JTBpGvqRhGRMIV1ERGJilmz\nnhGjmnXzRUC1x4thGDG5hojIQKGwLiIiUalpiPE86809676AgccbiMk1REQGCoV1ERGJSrhnPTE2\nPetJcQ7iHPaIa4mIDFUK6yIi0mWNvgCNviAAGcmx6Vm32WyaEUZEpJnCuoiIdJnZ0+2020iNd8bs\nOgrrIiIhCusiItJl5kwwGUkSheS+AAAgAElEQVQubDZbzK5jDl6tVBmMiAxxCusiItJlFfVNAGQn\nx8f0OjkpzWHd3RTT64iI9HcK6yIi0mUV7lBPd3ZKbAaXmswXAxX16lkXkaFNYV1ERLrMDM/ZKbHt\nWTdfDCisi8hQp7AuIiJdVuE2y2Bi3bMeF3E9EZGhSmFdRES6LFwGE+uw3txzb15PRGSoUlgXEZEu\nCw8wjXUZTLLKYEREQGFdRESi0FKz3ls96yqDEZGhTWFdRES6rNfKYJrPX9vox+sPxvRaIiL9mcK6\niIh0WXiAaYzLYNITXTjsoUWXKlUKIyJDmMK6iIh0SaMvQL03AMS+DMZut5EVrltXKYyIDF0K6yIi\n0iVmvXqcw05qvDPm12uZvlE96yIydCmsi4hIl5glMFnJcdhstphfr2VhJPWsi8jQpbAuIiJdEh5c\nGuMSGFN2suZaFxFRWBcRkS5pmbYxtoNLTS096wrrIjJ0KayLiEiXhGeCifG0jaaWmnWVwYjI0KWw\nLiIiXRLuWe+tsJ6iMhgREYV1ERHpkmO9NMe6yXxRcExlMCIyhCmsi4hIl1TW9/IA0+YXBZWaDUZE\nhjCFdRER6ZLwbDC9XrOunnURGboU1kVEpEsqersMprkH3+MN0NC8cqqIyFCjsC4iIp0yDKPXB5im\nxDuJc4b+TGlhJBEZqhTWRUSkU/XeAE3+INB7Nes2m40clcKIyBAXdVh3u93ceuut5Ofnk5CQwPTp\n03n++ec7Pa64uBibzdbu4/Dhw91qvIiI9A6zBCbR5SApztlr180KL4yknnURGZqi/o172WWXsXXr\nVu6//37Gjx/P6tWrueaaawgGgyxevLjT43//+98zYcKEiG3Z2dnRNkNERHrRMXfvzgRjyk6Oj7i+\niMhQE1VYf+utt3jnnXfCAR1g3rx57N+/nzvuuIOrrroKh8Nx3HNMmTKFmTNndr/FIiLS63p7jnVT\nTvP1jtapZ11EhqaoymBeffVVUlJSuOKKKyK2L1myhEOHDrF582ZLGyciIv1DeW0jAMPTejesD2u+\n3pHm64uIDDVR9azv2LGDiRMn4nRGHjZ16tTw988666zjnmPhwoUcPXqU9PR05s6dy7333suUKVO6\ndP2dO3cSDAajafKQ4fP5wh+3bdvWx60ZHHRPrad7aq3evJ8f7akBwOl19+q/nb/ODcAnpeVs2xb7\n6Rv1M2o93VNr6X5arzfvqd1up7CwMKpjogrrFRUVjBs3rs32rKys8Pc7Mnz4cFasWMGsWbNIS0tj\n+/bt3H///cyaNYuNGzcybdq0Tq/v9/sJBDTXbmfMHzqxju6p9XRPrRXr+3m0PnT+jHhbr/7bZcQZ\nAByr9/f6z4x+Rq2ne2ot3U/rxfqedlYu3p6oB5jabLZufW/BggUsWLAg/PWcOXO4+OKLKSoqYuXK\nlbz++uudXtvpdGK3a7bJ9rT+4XK5XH3YksFD99R6uqfW6s37Wd0YCs05Ka5e/bfLTQ1dt6rJ6JXr\n6mfUerqn1tL9tF5v3tPu5Niownp2dna7veeVlZVASw97V40ZM4azzz6bDz74oEv7T548WWG9A9u2\nbcPn8+Fyubr0LoV0TvfUerqn1urN+1n/3gagidOnjGfaiTkxvVZrw2oa4U/vUd0YZErRVBz2jjuF\nrKCfUevpnlpL99N6vXlPg8EgdXV1UR0TVfItKipi165d+P3+iO3bt28H6HLteWuGYSiAi4j0c+U1\noQGew9ISevW6OSlx2G0QCBrhud5FRIaSqFLyokWLcLvdvPzyyxHbV61aRX5+PmeccUZUF9+7dy8b\nN25k1qxZUR0nIiK9p77JT11TqJNmWC/PBuN02MlNDV2zvFZhXUSGnqjKYC666CIuuOACli5dSm1t\nLSeeeCJr1qxh3bp1PPvss+Gi+ZtuuolVq1bx+eefM3r0aADOP/985syZw9SpU8MDTB944AFsNhs/\n/elPrX9mIiJiCXPaxuQ4B6kJvV8jOywtgfLaJg7XNlJEeq9fX0SkL0U9wPSVV15hxYoVrFy5ksrK\nSiZMmMCaNWu4+uqrw/sEAgECgQCGYYS3FRUV8cILL/CrX/2KhoYG8vLyOPfcc/nRj37E+PHjrXk2\nIiJiucPNYX1Yeu+WwJhCpTc14XaIiAwlUYf1lJQUHnnkER555JEO9ykuLqa4uDhi28MPPxx140RE\npO8daS4/GZbaN2F9eHOdvBZGEpGhSCM7RUTkuMwe7eF91LNuXvdwjcK6iAw9CusiInJch/toJhhT\nXvMAU5XBiMhQpLAuIiLHZQ4w7e2ZYExmz3q5wrqIDEEK6yIiclxmSB4ebc96wA973oVdfwB/q2kX\n6yugcm/ktuMwr6upG0VkKFJYFxGR4zJD8nFng9n9Jrx4PWx5InL7c5fDC9+AhuqWbR89D7+dDi/d\nGLlv6VbwNbQ5dV5zWK9p8NHoC3TrOYiIDFQK6yIi0qFg0GhVBtMc1mvL4J9Pg9/bsuOxPfDx61Dy\nQcs2hxPGzIaCWWCztWz3N4EzEbLGtWwL+KD4YvjlGKj8IqINaQlOEl2hdTw0yFREhpqop24UEZGh\no9LjxR80sNmaB3r6vfC7M6CxJhS2x5wd2vGkC0KBfPRXIk/wzTfannT27XD2bRBoFfbdRyA5JxTa\nM8a0bN/xCramWsal5bGzIlSSMyYn2fLnKSLSXymsi4hIhypKP+EbjndYl7gQl8MOxMHky+Dw9lCw\nNg2bHHp0lc0GzlYDVtNHwm07wV0O9uY3fQ0DNvwSju7m0vTvsZMzNSOMiAw5CusiItK+mgOc9OJc\n7nUGOZA8u2X7xQ+B3WH99Ww2SB3e8nXQD9OvhR0v8VnKhVBeGyrJObwj1LM/+qzI8hoRkUFINesi\nItKisbbl8/RRlOWcxfvBIvJTWv25iEVQb4/DBV/5PtzyVzKycgA4VN0I790LxV+Fv/26d9ohItKH\nFNZFRAQaquCVb8F/nw5N7vDmZ0f/nBt8dxI3bHwfNg4KMpMAOFBRB+mjQgNUJ13asoNh9FHLRERi\nS2FdRETAlQylW6CuDD57N7z5i6pQXfro7KS+alnE9fdVNcHCX8P//gSyT2jZ4S/3wWvfhpqDfdRC\nEZHYUM26iMhQZBiw968w7pzQ1844uOQ/IS4ZRp4S3m1/hQfoB2E9KzQDTEmlh2DQwJ6Q3vLNhirY\n9J/gb4ATz4P0y/uolSIi1lPPuojIUBMMwrOXw9OXwO63WraPnR0R1A3DoKQyFNYLs/p2usT8jASc\ndhtef5Dyui/NCJOYGZoi8qzvhWaqMXk9vdtIEZEYUFgXERlq7HYYMRWcCeA+3OFux9xePN4ANhsU\nZCX2YgPbcjrsjMwMtcHs7Y8waibM/1nL7DB+LzwxD17/TuTqqSIiA4zCuojIUFD+MdQfa/l6znL4\nzmaYeWOHh5RU1gOQn55IvLOXZoA5jsKsUClOSXth/cu+WA9Hd8Mn60JTQIqIDFAK6yIig9225+Hx\nc+APy1pmTYlLgswxxz3M7ME2Q3JfM+vm9ze/iDiu8fPhxj/CosdCK6Oa/N6OjxER6YcU1kVEBru8\nSaGQHvCBr6HLh/WXwaUmc5Bpu2Uw7SmcBSed3/J1yWb47Qz49E8xaJ2ISGworIuIDDaGAVX7Wr4e\nMRW+9RdY/EKoR72LwoNL+0lYN9thtitqf/s11B6Ana9Y2CoRkdhSWBcRGUwaa+D5a+GxOZFzjg8v\nahl82UX7K0LlJqP7eCYY05jsKHvWv+zrvw/V6i/4Rcs2LaYkIv2cwrqIyGDiSg7N8OL1wIEtPTqV\n2YPdX8pgzNr5mgYfNR5f9CeIS4JzV4SmejSt+yGsuwt8jR0fJyLSh7QokojIAGf3e0I9xDYbOJxw\n2RPg84R607vJ3eTnmDs0GLO/lMEkxjnIS43nSF0T+yvrmZqU0bMTHv0ENv/f0OcnL4Cxc3reSBER\ni6lnXURkAEup+Ijx730TPvx/LRuzT+hRUIeWEpis5DjSElw9OpeVzF7+fd0thWkt92RY/CKc838U\n1EWk31JYFxEZwJJq9hDvOQxbnoBgwLLzlvSzaRtN5kqqJRVdmL6xK8ZfCPPuCn9p99Uz7h8/Jc59\n8DgHiYj0HpXBiIgMNMFgaBVS4MjYRTjtBvkL7wK7dQsX7e9n9eqm8FzrVvSst2PEzkfJKltPYn0p\nnHVR1INyRUSspp51EZGBIhiA938Nzy5q6UW32Tl60jWQkGbppT45XAfACbkplp63p07MC7Xnk/K6\nmJz/yPhrqc05hQPTb1dQF5F+QT3rIiIDRe0heP8h8Lph9xvAmJhdauehGgCmjLT2RUBPTc4PtWf3\n4Tp8gSAuh7V9Tr6k4Xx6xgO44uJaNu55NzRgd9Illl5LRKQr1LMuIjJQZBTAxb+G//gdTIxdcGz0\nBfj8aKgmfHJ+esyu0x0FmUmkxjvx+oN8ftQdm4u07lGvPwav/X/w4nWw/aXYXE9E5DgU1kVE+qua\ng7BmMRzZ1bJt2lUw49qYlmjsPlxHIGiQkxJHXmp8zK7THXa7jYnNves7DtbG/oLxqTD9Whg2BSYs\njP31RES+RGFdRKS/emclfPImvHFbr660aZbATMpPx9YP67bNUhiznTHljIcL7oGb/wyuhJbt217Q\nQkoi0isU1kVE+qsLfw4nnAdfe6RXBzuaPdZmKO4JwzAIfGlKSX/Qj9GDFx9mac7OQ73Qs25ytnqH\nYftL8Oq34KkLINCNlVRFRKKgAaYiIv2BYcCOl6GuDM76Xmhb6nC47hXLL+UL+nB73bi9bup8ddT7\n6qnz1pEal8ppw0/j4+Ye688Dz3DX+wZNgSaaAk00BhrxBrw0+hs5MeNE7pt9X/icC15eQEVDBQEj\ngGEYBAkSNIIAjM8cz8uXvBze97L/uYy9NXtx2Bw4bA6cdicOuwOX3cWolFE8d/Fz4X1XblxJaV0p\nic5EklxJJDoTaWxyEJd7jF31qQSDs7DbQy9kdlXsImAESItLIy0ujdS4VBwWTmcZFp8Gybkw4WJw\n9J8Fo0RkcFJYFxHpDw5shZdvArsTxs2D4VO6dJhhGHgCHvbV7KOqqYqqxuZH8+ejUkdxzYRrAAga\nQb6y5iu4fe0PzDxj+BnMyD2V3c3TNu6oWU/dsfZ7rx22yBBsGAaNgfbLQgwie9HNnvaAESBgBPAG\nveHvpbgip4rcUbGDPVV72pwzPgeCvjRKKj2MyQktlHT/lvv555F/RuyX4kohPT6d3MRcnvnqM+Ht\n6/ato7aplqyELLITs8lOyCYrIatrPf7j58O3P4CEVoNvq0uhoQpGTO38eBGRKCisi4j0BwWnw+RF\nkHMy5J4MQL2vnnJPOcc8xzjScCT8cVTKKBZPXAxAkCC3bL8FY3v7IfOM4WeEw7rdZsdlb+kJTnQm\nkupKJSUuhZS4FMZljOPzo/U0+YOkxDtZOm0pAcNPvDOeeEfkIzMhM+I6qy5aRdAIYrfZsWHDYXdg\nw4bdZm/Tu/38wufxBX34g378QT+BYACfEfr6yy8C7jztTiobK2nwN+Dxe0IffR5e+MfnHK012Hmo\nNhzWsxKyGJ48nNqmWjz+0KJJbp8bt8+NN+CNOO/qXav515F/tblfLpuLLFcWv5r4q/C290rew+Pz\nkJeUx7CkYeQl5ZGUnNNykGHAmz+Az96Fhb+GU7/Z7r+FiEh3KKyLiPQBf8lmjm38FWXn/ICyxkqS\nXcmc8/Xfg82GP+hn7vNnU9PU/gDK04afFg7rDpuDNGcafpufzPhMshKyyEjIIDM+k8yETE7IOCHi\n2BcWvkCSK4lkVzJOe9s/Aa/88wAAk0akcd3kC7v8fIYnD+/yvqlxqV3e9/QRp7e7vWzfR6z5vJSd\nh2q4eOoIAB6e93D4+76gj9qmWmq9oYfvS7Xlpw8/nfT4dCobK6loqAi/IPAZPrxBb8TA2lU7V7UJ\n9mlxaQxLHsbI5JH8dvYD2OKSwO5gT+Yo4mr3MyJ5BHGOOEREekphXUQkBoJGEI/PQ0pcqKzDMAzu\n+ttdHHIfoqz+EEfcZQRsNnjnZgBmDpvJOQXnAOC0O4mzh4JeiiuF3KRcchNzwx9PzDgx4loPT3qY\n02ac1qV2jUgZcdzvm4NLJ1kwuDSWJuWnA6Xs6GCQqcvuCpW3JGa3+/3vzvhum20en4eN/9qI2xtZ\nJjQ9dzrxjnjKPeWU15fj8XvCLwLcXje2uES4ohgqv+Cnm3/Cv97/FzZs5LpSyU8dxciMseQn51OQ\nWsCikxb19KmLyBCjsC4i0gMltSWU1JVQWldKSW0JB+oOUFpXygH3AablTuOpC58CwGYYbCnbwpGG\nI6EDbTac2BiWPJwRKSOZkhNZo/70RU+TmZBJsiu50zaYwd4Kmz4/BsCMwgzLzhkLpzS378N9lTT5\nA8Q7ez6QNMmVRF58Hpn2yBKf22feHvG12+sOB/fW9fZkjSPOEUeiM5EGfwNHfLUcqfyYf1d+DMCI\n5BERYf329bdT0VDByJSR5KeEwrz5yEnM6ZfTZopI71NYFxE5Do/PQ2ldafjhtDu5btJ14e/fsO4G\njjUca/fYg+6DoU++2ADrfsit0y/BlT+dEckjGJE8guyE7A5nKxmVOsry59KZspoGdh+uw26DOSfl\n9vr1ozFpRBp5qfEcqWti694qzj4pp/ODLGLW+H+5xAjgyflPYhgGVWX/4tDbP+Cgzc/B077Jofoy\nkpxJEft+dPQjyj3lbQbFAoxOG80bi94If72+dD3xjngK0woZnjQ8NrPciEi/pLAuIkOaYRjU++rD\n5SoAv9zyS3Yc20FpXSkVjRUR+49MGRkR1sdnjicjPoOC1AIKUwsjekeHpzTXcX/6Rziyk6/tToOz\n7uyV59UdGz45CsC0ggwyk/t3vbXNZuOc8bms/ccB1n9ypFfDemdsNhtZ+aeQdeOfmdJQBUlZoW8E\n/PDKLTB9MYw7h4fnPsxB98Hww3xBWFZfRk5i5PP5+eafc7j+MBAqkxqVMopRqaMoSC1gYtZEldeI\nDGIK6yIyJByuP8z+2v0RveTmIyM+g3WXrwvvu/3YdrYd3Rb+2gzjo1JHMSZtDIZhhEsUHrvgsbYX\nO7YHDBuYM6+ccwc4nPCVW2P6HHtqfXNYnzs+r49b0jVzT84LhfVPj3J3XzemPTZbS1AH+Ocq+Oj5\n0Kwxt26nKLeIotyiNof5Aj5qvS21+EEjyITMCSQ6EzlQdwBf0Me+2n3sq90HwCl5p0SE9eveuo44\nR1zEC0fz0fpFqYgMDArrIjIoeANeDrgPUFobCuB13jqWTl8a/v4P1v+Aj4591O6xTYEm/EF/eHaU\n/1X0v2gMNIYDTlpcFIMtP3gU/vhDKLoSLmsO8omZcMG93X5uvcHrD/K3z0LlPHNP7t8lMKazT8rB\nYbfx2RE3pZUeCrKSOj+oL01YCEc/gZyTIK5VW4/sgryJ4S9dDlfEwFi7zc5/nvefQGiO+iOeIy3j\nJOpKGJHcMmjYG/Cy7eg2DAy2HN7SpgmzR87md+f/Lvz1u/vfJScxh4LUArISslQnL9IPKayLyIDh\n9rojegaf3P4kmw5torSulPL68ojFd5w2JzdPvTkcwMdljKPWWxsuHWhdsjIydWTENIZzC+ZG17Bg\nEOz20OcFp4MRBK8bggEYILXF/9hfhbvJT3ZyHEUj0zs/oB9IT3RxSmEGW/dVsf7To1w3a3RfN+n4\nUofBVx+I3HbgQ3jyPDjhXLj2pU5/Xhx2ByNSRjAiZQRnjDijzfftNjtPX/Q0JXUllNSGAr056Lmq\nqYqM+JaBw76Ajx9s+EF4pdlkV3JEL/yMvBnR/78gIpZTWBeRfuVw/WH21uzlgPsAB+qaH+5Q2Gjw\nN/DhtR+GB9d9WvkpWw9vDR+b5EyiMK0wXLLiDXjDIfynX/mp9Y3d/3dY/wsYdw7M/kFo28hT4Lv/\ngJwTj39sP7P+09AsNeeMz8VuHzi9q3NPzmPrvio2fHKk/4f19hz6V2jV2tQRkUG9my/0nHYn0/Om\nMz1vepvv1XnraAo0tXztq2PmsJmU1JVQXl9Ova+e3ZW72V25G4CLx10cDuv+oJ8r/nAFI5JHhF7s\nprV6sZsyUnPKi8SQwrqI9CpPwEOlr5LyfeWU1pVy0H2QFWesCAfwhz58iHX71nV4/NGGo+EFeC4f\nfzmzR80Oh4Zefxu/5gDs3RCqUf/KrS3haoAFdV8gyB/+fQiAuRMGRr26ad7JeTz4x0/466fHOFLX\nSF5qQl83KTqn3wwnXxS5re4wPHYOTLsazv1RaLyDBVLjUkmlZUGqrISs8NSiTYGm0CDX2paxHK3r\n6cvqy/is+jM+q/6szXlt2Lh6wtXcdcZdQGhBqvf2v8eIlBGMTBmJYbS/uq6IdI3CuohYxjAMqpqq\nKHOXMSFrQjiAr9q5ije/eJOSmhLqA/WhnT9tOe5bU78VDuDj0scxNn1sqHe81YwXo1JGkZ+ST5Kr\npda3vTKAmNm3EbY+CZP+AyZfGto26RI4+r/h1BsGTLlLe97aXsahmkZyUuKZP2lYXzcnKpPy05hR\nmMG/Sqp55u/7+cH8k/u6SdFL/9I0nR+9CO7DsH9TZFBvXW5lsXhHPOPSxzEufVy7389JzOGJ+U9E\nrCVg1sw3+BsixnWU15dzx1/vCH/tsrnIdmWTG5/L+PrxnDPqHOYVzgNCvzMMDOy22DwvkcFAYV1E\nuuWf5f/kH+X/4FD9IcrcZRyqP8Th+sM0+BsAeOfr74QDeEVjBbsqd4WPTXemMyZzDKNSRzEqZVRE\nvfjS6UsjBob2GcMIPcxwVLIJdr4CdWUtYd0ZD+f9qO/aaAHDMHj8r18AcMOZo0lwDbwXHd+aPY6l\nz/2TZz7Yz7fnnkhi3MB7DhFmfRuyT4DWM7f4m+C/ZsKY2XDhz0ODlntRojORWSNmMWvErIjthmFQ\n0VgREba9AS+n5J3CQfdBjniO4DN8HPYe5rD3MNvrtpOVkBUO6wfdB7nktUsYkTyC/JT80CM59DEv\nKY+x6WPJSxpY7/aIWE1hXUTCDtcf5ouaLzjiORJ+lHvKw5+v/urq8HL16w+s5/c7ft/ueXITc6lp\nqgmH9a+N+xozh82k9kAtGbYMUhNSmTZtWq89r6j9+Wfw79Ww6DEYOzu0bepVUF8B067q27ZZ7O9f\nVLDzUC0JLjvfGIg138D8ycMpzEqipNLDS/8o5bozx/R1k3rG4YQJF0du+/wvUF0Cn/8Z4lvNTnTs\nM0jLj5xdphfZbLY2c8KPyxjHqotWAaFBrOv/sZ4yTxnVwWocWQ5OH356eN+y+jJ8QV9oQGxdSZvz\nf2vqt/jejO+F9nWXcc8H9zA8aTjDkoYxLHkYeUl54c9TXamazUYGJYV1kUGuzlvH4frDVDRWUNHQ\n/Gis4KjnKEc8R/j52T9nWHKo9OH53c/z1I6nOjxXuac8HNZn5M6g4oSKcE/YiJQR5CfnMzx5eJvB\nZidlnsRJmSexrWIbPp8vdk+2Oyr3wsF/QNHXW7bVHITag/DJ2y1hPaMQLrq/b9oYI8GgwX/9OVSD\nfMWpBf1+IaSOOOw2bjp7LD/+n5088f5evn5qwcDvXf+y8RfCknVQfySy5GrtDVDxOXzjJRhzdt+1\nrwMuh4u8+Dwy7Zm4XK42L9JPyTuFP13+Jw66D3Ko/lDoo/sQZfVlHPEcoSC1ILzvAfcBNh7c2OG1\nvj3t2+F35crryyneWUx2YjY5iTnkJOaQnRD6PDMhM+LdPJH+Tj+tIgNQdWM1ZfVlVDVWtYTwVh/v\nOeuecK/273f8nie2P9Hhucrqy8JhfXTaaE7MOJG8pLzwY1hSS+/VmPQx4ePmFc4Lv5U9YASD0FQL\nic3T13kq4bczACMUdFKbVxw945ZQbfq4uX3U0N7xxPtfsOnzCuKcdv7X7LF93ZweuWLmKP7rL59R\nUunhx/+zgwe+3o/fuekOmw1Gnxm5rbEGGmvB3wh5k1q2f/w67Hgl9AJ04td6t51Raj0VZWfGpI3h\n3rPupdxTHnrUl4c/r2mqiZibvqSuhGd3PdvueWzYuPXUW7lxyo1AKNg/u+tZshOyyUrMIiM+g4z4\nDDLjM0lPSFePvfS5qMO62+3m7rvv5sUXX6SyspIJEyZw5513cvXVV3d67JEjR1i+fDlvvPEGHo+H\nadOm8bOf/YzzzjuvW40XGciaAk04bc6WaQirPuXjio+paaqhuqma6qbqiM9/M/c3FKYVAvDc7ud4\ndNujHZ77cP3hcFjPTswmPT6d7IRsshOzw71L2YnZDEsaxqjUlsFti05aNHiWLfc1hnogHc2riO58\nFf6wLDSf9RXFoW1JWTDqtNDUeZ6KlrCe33bau8Hmw32VPPDHTwD48dcmMTo7uY9b1DNJcU4euXo6\n33hyMy9+eIAzxmZz+amjOj9wIEtIh1s/gsovIldK3fUH+Pg1yBnfEtb9TbDuhzBsMpxyg2UzzPSm\n3KTcDn8/NfobI9ZZyE3M5cYpN3Ks4RgVDRWhj40VVDZWEjSCpLhaxgOU1JVQvLO4w+t+d/p3uWXa\nLQCU1pXy0IcPhQN9RnwGGQmhj2lxaRSkFpCbNDAWFZOBI+r/Wy+77DK2bt3K/fffz/jx41m9ejXX\nXHMNwWCQxYsXd3hcU1MT5513HtXV1TzyyCPk5eXx3//93yxYsIB3332Xc845p0dPRKS3NAWacHvd\nePweGvwNNPgb8Pg8uH1u3F4388fMJ9kVCj5vffEW7+x/hzpfHXXeOtxeN26fmzpvHb6gj9f+4zVO\nyDgBgHf2v3PcAF7ZWBkO62bgzojPCAfw1h9bB/DFExZz7cRrY3hH+lAwECpXaayF4VNatj97eajG\n9/rXW8pYErNCPZGHt0ee48Z1A3oml+7466dHufWFfxMIGlwyLZ/Fpxf2dZMscdYJOSw7bzwPv/sp\nd726HX8wyJUzCwZ3r6jNFhqM2trpt0DuhNALU9PR3fDhU5CQATNvbNm++XGo3g9TLg+tETBAJTgj\np+wckz6G2069rc1+gaId0mYAAB2USURBVGCAqqYqEhwt+2cnZnP9pOs51nCMqsaqcAdJdVM1Df4G\nMhNaBvMerj/MeyXvddiO78/4PjdPvRmATyo/4aY/3USKK4W0uDRS4lJIdaWGptCMS2X2qNmclX8W\nAPW+ev5Z/k+SXEkkOZMiPiY6EzVbzhAXVVh/6623eOedd8IBHWDevHns37+fO+64g6uuugqHo/0/\nek899RQ7duxg06ZNnHnmmeFjp02bxvLly9m8eXMPn4oMVUEjiDfgpSnQRFpcWvgP80H3QY56joa/\nZ340P/+PE/8j/Av+j/v+yOayzaEA7mvA4/dQUVNBQ6ABr+FlzUlrwjMS/OYfv+nw7VWAabnTGJcR\nmv5sb+1e3i15t8N967x14c9PyDiBr+R/hfT49HCPTevPzXMCXD3haq6e0Pm7WcDACypmqYqvAdJa\nvTW+7Xko2xYa6Gn2fO/dAM8sgpyT4butllZ3xIMRCAUUM6yPmgm3/BXyJkdebwgF9bKaBp56fy9P\nbdyLYUDRyHTuu6xo4P2MHMd3zz2Rj8tq+OPOcv7Py9v522cVLDvvRE7MS+384MGi4LTQo7WE9NBa\nABihgG/6+DXYvxFGTG8J6+U7YfVVMGIaXP1cy7573w/10OdPh+TIQaUDhcPuaDsgNn0cd5x2R7v7\nt15ECqAgtYAVZ6yICPTVjaGPdd66iHPXemupaaqhpqmGgxxsc+6shKxwWC+tK+Xb7327w3a3Hmhb\n4a3gt3t/S6IzkWGVw0hyhgJ9vDOeeEc8M4fN5CsjvwKAx+fhz6V/JsGRQJwjjgRHQni/eEd8qNyn\n+cWIOR/+YPp9MFhEFdZfffVVUlJSuOKKKyK2L1myhMWLF7N582bOOuusDo89+eSTw0EdwOl08o1v\nfIO77rqLgwcPMnLkyG48hd5nzgtr/mA7Wv2x9wa84e+13secRzbRmRjet9ZbG9rP3LfVcU6bk4yE\nlmWhjzUcwx/0R16/ef8vD5Q55D7U0g4MQv+17Nu67vjTqk+p99UTCAYwMAgYAYLBIAEjgNPu5Mz8\nln+vD8o+oLKhMrSPEQw/AkYAh83B5eMvD+/7p31/orSulKARxG/48QdbHgYGy09bHt531c5VbDu6\nLfx9X9AXsf8zX30m/Bzv3/wL3il5N7RfwEdjoBFfsGXA4t+v+Xt4OfrHtz3GK5+92uG/47yCueGw\n/u/yf7L207Ud7uv2usNhPam5RybRkUBic69HojORVFcyKa4UnLaWn4c5I75CtiuNlPg0UuMzQj0r\ncamk2lykuFJIbtVjs6DgfBbkzwmFR2d8y8V9DaEpBFv3HAV8EPCCzQGuVtu99aF9XYktITTgC9W0\n2hyRM0Y0ucEIgiup5S3xgC90PZsd4ltNG+c+EtqenNtyjsZaqPgMHHGRvdoHPgR3OeTPCM1SAVBd\nCv9eTU5FLWWjW72Nvf7+0FzSZ98GJzTXvx/YCv9vPmSOgWXbWvbd+Sp8ug5yT8YY0VyPnDkW7K5Q\nqUsw2BJCLrgXvvpgaFVIc0EWVxIMnxr63Pz/0qK1Wqw4TXcWjgkEDQJBA3vQwB8ILRkfNKDBF6C+\nyc8xdxNlNY3sKqvlH/ur2PjZMYLNl/nGrELuvnjSgJyq8Xgcdhv/99pTefSvn/PQnz7lD9sO8Ydt\nhzilMIPTx2YzZWQa+RmJ5KbEkxTnIN7lIN5px2m3De6QkjkGLrin7fZTrg8F9RGtavwrv4Ca0raB\nfP0vQsH+imKY3Pz/cekWePbrod8BS95q2fdvD4cGvp66BDNqOBsrYPNjkJQdOaC77KPQu1454yG1\neZ5/XyNU7Q39LsxqNfd7Yy0E/aH/n83ffcEg+OpDv7fiWpVzBfyEXpw4uj0/fbwjPuLr4cnDu9xR\nUpRTxOv/8Tq1/3979x4eVX0uevy7LjOTe4AkxHLXUEUR6g2IKKD1RoFHwWpbdx+2u1IRd6v01BbR\nUgxYL6ecqjkKClo2VCwtVGwf5Xa00r17LG5RlINVsFyCohRCCOTC3NZa7/ljkpUMSXAiMZno+3me\necj85p3FO++sWb/f+s2atWI1/jeqzW/NrzJrYHB2r7P9b2qPO4mbJ16LPOrcOnaHdwPwbu27Lf5f\nV1x/sF4VqeKev97TZo7fPuvbzCmd48devupybNMmYAYImIGkv8efPp6ZF8wEEocd3fbybQSsQKux\nX+v9NW48MzFW9MSjfGs5lmFhGiaWaTX9bVgMzBvI1wc0fQv0wj8S/bZlJmJsw/ZjCzILkur29qG3\n8cTDauh3TcPENEwMwyDbzk4a71Qcq8DDwyTxuIlJhp3RLQ5bMqQdPcTFF1+M67q88cYbSe1///vf\nOffcc1m8eDHTp09v9blf+cpXGDNmDKtWrUpqX7t2LZMmTWLjxo1cffXVfrvnedTW1ibFfvjhh3ie\nl2q6HcJ1Hb73/25GAGllQ15Sn82OT+b697NLZhFr41Ldg8IZfPBR08aysGQWNVbrsf0iAfZ8+Av/\nfp8zZnHYbj32tJjFvooH/PtnDJrNx22c1KEwbvDx3odpHF6cNfAeKkKtrwJ5DlTuaTr7xdD+97Ir\ns/X6Z3jC0X/8T//++f1/zvtZbZ/1I7LzISDxei7qex/v5kTbjA1/MB8k8YJKv3I/2/Lq247dNQfc\nxCDziqJf8mHuQeq8XI5IASI2tmdwqfE+IRHWH5iP4yZ2iL6d+xT9Mt9hm3M2m9xSxAtieRa/th4j\nSzz+tbaceskH4A5rFXfaf+Q59yrKnO/5//eO4FQChsvF0YUcJDEIn269yGx7JX9wxzLLmeHHbgtO\nI9cI8/XYr6iQxOzxVPP/MC+wjLXuKO5wZvqxm4P/TrFxlAmxh9ghiVPr3WD+hV8GlrDJPY9pTtOO\nz6uB/8Eg8yA3xMrYKmcCMMF4nSeC/5vN7jn8S3yOH7suOJuzzQ+ZGruH/+slrlR4ufk2S4ML2Oad\nweRY0/q3JjiX881dTIvdxZ+9CwEYbb7Lb4MPssPrz/hY03v/XOABLrH+zg9jd/CSl9jZO9/4By+E\n7uNDr4ixsXI/9pnAAq603uae+DRWuonfrgw29vNKaBb/lJ6URhf6sTdaf6HE+ISN7gjelq82tAom\ngod+RZyqc3sHuW5ILiP7Zn56cDe383CU59+rZcsnEX8npS2mkbj5e15G0j+Jv/07xkke6/6yOc5X\n2Y8BvM2Zfvt8cwnDjD3c7/4bWxkCwDhjK4utBbwrp3OD+6Af+6w1jxHGDma6P2KjJC5edgE7+K09\njwo5jfHuo37sEvNhxprbmO3O4I+SOCT2bPbygn0vB6Un49xFfuxj5mOMN/+bMvcWfidXAXA6H7Pe\n/glHJZtS9xk/9mFzEZPNv/JL97sslUkAFFPFJusOogQ4313ux84x/4MbjU0s8qawWBI7IvnU8V9W\nYrb7fHeZv525y/wtU40N/IdMpNxLnMo1SIw3rO8DcIn7FPUkJjVuN9Yw3fwTv5credib6v9/b1n/\nholwlVvOYRL90PeMl7jTXM2fZAxl3vdJ7Gg4vGTfSZ5E+BfnYfZTDGaYMVlrGG/9lbeM0/kjpWDG\nwHC43nqFMeFanqj9Of+gP9hHOa14CX3NA1QZWeynF5gOGHFyjBqurz3OlsofsZ3BYB8lcPpDba4X\n19WE+fDQDN6Qc8A8TqCklZ2/BlfXRqg7eDP/KRcADoGv/qzN2LH1UewD32GjJM7hHxg8G4zWP7Aj\njsco+mQKf5Kxibqf8XPEirUaOywS48z9E/z1JHT6fDw7efyQ7ZzF4ot+nnSWskAg0GauHcE0TQYM\nSD70MDc3F/MkO5TtmlmvqqrijDNaXt2sV69e/uMne25jXHuf28hxHFzXTTXdDuG6Dt5Jt8JCxGla\nqXJOEmmIEHWbYg2E5M09SY81jw2IYAs4YiENGwwLjxAOQc8i1qwsWZ6Q6wr1ZOBigRgEcMg1wmR7\nNrFmyy1wwDPjHJReHJdMEINsopxuHMJ2g3zcbLmDoiYFHGen15/D0hMwyJfjjDJ34ngh1jYbx591\n3OZMt5o33SHslT4gFgXUcYP5GhEJscRreu0X1WRxbeQAa93RvO6eC2LRmxrut39DVIL8u9s08zfu\nSD731u5iWfwbrHauBLEpkjo2Be8Gz2RovGlW5dKqQqYee4dH46MpdxOz/nnUsSgjsUP5YjwHpyF2\nQH0ut0VreMopYoOT6FgCOIzOiAAgXoDGUiT2xxOzsm4r2xNXoLEUjbvCIiQNFhr/9Jq1e80ea21g\n0XwZ0kZsa8sVo+XjScs9YXkntgFECRCWYNLaGpEg+6WQyoadmEa7pA9ZXpRammbxD0pPnnOuoJLk\n2OXuNbzkXsxWf/ANe6QPZ0WWESV5j3O1e1kr2Rt4bXyGvuwsA/IzTHpmmPTLsynpGeBrxUH65iY2\n+2l3Cs3PwRn5Jj+9OJ+qcA5bD0TZU+2w75hDdcTlWMQj1myb5Z3wGT351yUd9JVMmoqQSRVNO8SN\nZnFrs6hE+18Yyted/4WBEGk29/esdwV/MYaz3evnt1ca2bxkjOKw5Cf1m/vtAj6gL4fdbCINb0LU\ngCorl2rJSYo1AoktcdyDSMMGOGaIP5ppHusFGh5vFhvHw7QFU5L7bsN2CdlxxPP82BBCyI77y/Ua\na2G7ZNhxcF1/GYIk2oCoI0T8WIdMIwauk/T/ZVgxLEOSYy2XTCuGmRRrU2xGyTUixNzGGmfQxy3g\nm4FjBN0Mfhsf6y93ZuhPFBm1POp6iVgnnxH7R7AgsIRX3PP5fvzHfuza4I8YaFYxxY/NZdyua5gX\nXMp/e1/lR+7tGIYLhsOjgcc5X6qZ7bqJ98gIcPbHpUwLvMQeinncvRYMDwyHf7U3cKlTy3Ou57+f\npx0ZwjXWFqrI4UWvFAwXA+FScxul8Wq2NC4XyK8bwIXWDuoJ8oZ3VsNyPQYb+zkrXkOV5/jvUVYs\nn77WJ8QNk4+kcYbco6dRS5HrQLPYkBsi36jBw6CGxGSFeIEW28LPe9vY1uHiJ9OumfUzzzyTkpIS\n1q9fn9R+4MAB+vTpw0MPPcTs2bNbfW4wGGTatGk8+eSTSe2bN29m9OjRrFy5MumMMukys+65LvsP\nvQeYRDOKwLAxDLDj9QScerBzsTKaLs8t9RWJgXaoKHGGCQwC8XoCbj1iZSKhpq8V7fABDPGIhQoR\nM4CBge2GCcRrca0Q8WDTYTChyGHAIxbsgZiJQYzlhrHjtYgZ4LjZdDxmlluDIS6xYL4fa7pRAvEa\nxAokLTcQrcYUl3ggD6/h3NiGFyMQr0UMKzk2dgxTHBw7B6/hKznDizfEmkmxdrwW04vj2NnNYh3s\neC0YJvFg06DNitdhioNrZTaLdbGdWsBIjnWOY3pxPDuE1/gDIXGx43UAOM1iTSeciLVC/nIRD9up\nx8DAsXP86TDTjSRizYC/3Hg8hu0k9sKNjB7NYmMYXgwxA03LbXgdGAaulZn4OrahlqbnIIaVHOsc\nB8CzM5rFxpvFNg1UTTcCIom2hq/6DM/FkDgG5gmxiW8oPNM+IdZBDMNfHxpzMwTEtPxYxMUQFzAQ\nsx2zCymOl5244/9tB5LnCk51yJ0uM5vGKb6S9ryOtmaDQpZBoI1v7VQTT4S4C3EvMWgSBCfu+MNT\n225aR/0d2dZ2pE/ymALHaVpPbfsUZy3Fg8aJrsYfXYqH6SVmV71mPxy13DCG5+CZwWZ9gEswdqyh\nn2461WMgXoPlRnDsrETf0BCbET0MQCTU2/9w2vFabPc4jpWN03hWGREyIgcTsRm9/dzseB22U4dr\nZxEPNF3MKiP8z4bYIn/7azt1BOJ1OFZmUr+XEf4nBhAJFSKmjePEsZ16AvFajFAOsWDT4ZQZkYMY\n4jXEJmptOccJxo/hmiFioV7JsZ5LNFTo9yOWEyYYq8azgkSbjVdCkUpML040VODX0nLDBKNH8Mxg\nYnyUFBsjFuqV6A9J9GOhaBViBhL1aYyNHsZ0o8SCPXHtrIbYGKFoJWJYRDJPaxZbhelGiAV74NqJ\niTnDi5ERqQTDItwsNhg9guWGiQfy/ffI8JyG98ggnJU4RDNoGRRkWV+smfWCgoJWZ8CPHDkC0OrM\neUc8t9HQoUNP+mI+L+fTnl/IX/i55XEy27YlLjaTuOjEqC7J4YsmUVO71Qt5qM8meT3Vmp4qrWfH\n05p2PK1px2rqmwq1nh2kM9fR1iajP027Rr7Dhg3j/fffx3GcpPbt2xOnQjv33HNbe5r/3Ma49j5X\nKaWUUkqpL6N2DdanTJlCXV0dzz//fFL78uXL6dOnD6NGtT2jO2XKFHbs2JF0ikbHcVixYgWjRo2i\nT58+7UxdKaWUUkqpL7Z2HQbzjW98g6uuuorbb7+dmpoaBg8ezMqVK9mwYQMrVqzwD5qfNm0ay5cv\nZ/fu3QwcmDh7xS233MLChQu58cYbefjhh+nduzeLFi1i586dvPJK2+ehVkoppZRS6suq3VcwXbNm\nDT/72c+YO3cuR44cYciQIS1+HOq6Lq7rJp03OBQK8ec//5lZs2Zxxx13cPz4cc477zzWr1+vVy9V\nSimllFKqFe0erOfk5FBeXk55eXmbMcuWLWPZsmUt2ouLi1m+fHnLJyillFJKKaVaaPdgvbO0dkbJ\nzj5tY3dimiaWZWGaptapg2hNO57WtGNpPTue1rTjaU07ltaz43VmTVtb/qedRb1d51nvTI7jUF/f\n9pUqlVJKKaWU6u6ys7OTrutwIr1Gt1JKKaWUUmlKB+tKKaWUUkqlKR2sK6WUUkoplabS9ph1z/Na\nHIRvGAaGYXRRRkoppZRSSn12ItLiB6WmaWKabc+fp+1gXSmllFJKqS87PQxGKaWUUkqpNKWDdaWU\nUkoppdKUDta7kdraWmbNmsXVV19NUVERhmFQVlbWamw8HueRRx5h2LBhZGZm0qNHD0aPHs3f/va3\nzk06jaVaTxHh6aef5sILLyQvL4+CggLGjRvH2rVrOz/pNPbqq69yyy23MGTIELKzs+nbty/XXXcd\nb731VovYrVu3cuWVV5KTk0OPHj24/vrr2bNnTxdknd5SqanrujzyyCOMHz+efv36kZWVxdlnn83s\n2bM5evRoF2afntqznjYSEcaOHYthGPzwhz/sxGzTX3vqqf1SalKtqfZNqXvnnXeYOHEiAwYMIDMz\nk169enHxxRezYsWKFrHp2D/pYL0bqaqqYsmSJUSjUSZPntxmnOu6TJkyhfnz53PTTTexfv16nnvu\nOcaPH68Xmmom1Xred999TJ8+nZEjR/L888+zbNkyQqEQkyZNYs2aNZ2YcXp78sknqaioYObMmaxb\nt47y8nIOHTpEaWkpr776qh+3Y8cOLrvsMmKxGKtWrWLp0qV88MEHjBkzhsrKyi58BeknlZqGw2HK\nysoYOHAgjz32GOvWrePWW29lyZIlXHLJJYTD4S5+Fekl1fW0uYULF7Jr165OzrR7SLWe2i+lLtWa\nat+UuqNHj9K/f38efPBB1q1bx29+8xsGDRrE1KlT+cUvfuHHpW3/JKrb8DxPPM8TEZHKykoB5L77\n7msR9+ijj4ppmrJ58+ZOzrB7SbWeffv2lUsvvTSpLRwOS35+vlx77bWdkWq3cPDgwRZttbW1Ulxc\nLFdccYXfduONN0phYaEcO3bMb6uoqJBAICCzZs3qlFy7i1Rq6jiOHD58uEXc6tWrBZBnn332c8+z\nO0l1PW20d+9eycnJkTVr1gggP/jBDzojzW4j1Xpqv5S6VGuqfdOpGzVqlPTv39+/n679k86sdyOp\nnrqyvLycsWPHUlpa2glZdV+p1jMQCJCfn5/UlpGR4d9UQu/evVu05eTkcM455/DRRx8B4DgOL730\nEt/85jfJy8vz4wYOHMjll1/OCy+80Gn5dgep1NSyLAoKClrEjRw5EsCPUwmp1LS56dOnc9VVVzFl\nypTOSK/bSbWe2i+lLtWaat906goLC7FtG0jv/kkH618wH330ERUVFQwbNox7772X4uJibNtm6NCh\nLF++vKvT65ZmzpzJhg0b+PWvf011dTUHDhzgxz/+MceOHePOO+/s6vTS2rFjx9i6dStDhw4FYPfu\n3YTDYYYPH94idvjw4ezatYtIJNLZaXYrJ9a0LY1fl39anGq7ps888wxvvPEGTzzxRBdl1j2dWE/t\nl05da+uo9k3t53kejuNQWVnJokWL2LhxI3fffTeQ5v1Tl83pq1PS1mEbmzdvFkDy8vLknHPOkVWr\nVsnGjRvlhhtuEECWLFnSNQmnuZMdBiMi8tRTT0koFBJAAOnVq5e8/PLLnZtkN/Td735XbNuWN998\nU0REXnvtNQFk5cqVLWIffPBBAeSTTz7p7DS7lRNr2pr9+/dLcXGxXHTRReK6bidm1z21VtP9+/dL\nfn6+LF682G9DD4NJyYn11H7p1LX1ude+qX1uu+02v1bBYFAWLVrkP5bO/ZMO1ruptgaXjStbMBiU\niooKv93zPLngggukX79+nZxp93CywfrSpUslFArJXXfdJa+88oqsW7dOvvOd70hWVpZs2LCh85Pt\nJubMmSOAPP74435b4/r5u9/9rkV848bwwIEDnZlmt9JaTU9UVVUlw4cPl969e8vu3bs7Mbvuqa2a\nTpo0ScaOHev/rkVEB+upONnnXvulz6atdVT7pvbbt2+fbNmyRdauXSszZswQ0zRlwYIFIpLe/ZMO\n1ruptgaXO3bsEECGDx/e4jn33HOPAK3+eOXLrq16HjlyRDIzM1vtoMeNGyeDBg3qpAy7l7KyMgHk\ngQceSGpvXD8XLlzY4jk/+clPxDAMCYfDnZVmt9JWTZs7cuSIXHDBBVJQUCDbtm3rxOy6p7Zqunr1\narFtW15//XWprq72b4DceuutUl1dLbFYrIuyTl+f9rnXfqn92qqp9k0dY8aMGWLbthw6dCit+yc9\nZv0LpqSkhKysrFYfExEATFPf9lTt3LmTcDjMiBEjWjx20UUXUVFRQV1dXRdklr7mzZtHWVkZZWVl\n3HvvvUmPlZSUkJmZyfbt21s8b/v27QwePFh/GNWKk9W0UXV1NVdeeSV79+7l5ZdfbvW4S9XkZDV9\n9913cRyH0tJSevbs6d8Ann76aXr27Knnsj7Bp33utV9qv5PVVPumjjFy5Egcx2HPnj3p3T91yS6C\nOmUnO2zjpptukkAgIHv37vXbPM+T8847T0pKSjovyW6krXru27dPAJkxY0ZSu+d5cskll0jPnj2T\nvib/sps/f74AMmfOnDZjvvWtb0nv3r2lpqbGb9u3b58Eg0G5++67OyPNbiWVmjbOqPfo0UO2bNnS\nidl1T59W071798qmTZta3ACZPHmybNq0SSorKzs56/SVyjqq/VL7fFpNtW/qGFOnThXTNOXQoUMi\nkr79k901uwjqs1q/fj319fXU1tYC8N577/GHP/wBgAkTJpCVlcX999/P+vXrGT9+PGVlZeTl5fHM\nM8+wbds2Vq1a1ZXpp51Pq+eAAQO4/vrrWbJkCaFQiAkTJhCNRlm+fDmvvfYa999/f0qnf/wy+NWv\nfsXcuXMZP348EydO5PXXX096vPGUbfPmzWPEiBFMmjSJ2bNnE4lEmDt3LoWFhdx1111dkXraSqWm\n4XCYa665hrfffpvHHnsMx3GS4oqKiigpKens1NNWKjUdNGgQgwYNavX5ffv25bLLLvv8E+0mUv3c\na7+UulRqqn1T+0yfPp28vDxGjhxJcXExhw8fZvXq1fz+97/npz/9KUVFRUAa909dtpugPpOBAwf6\nv2Q+8dZ8xmL79u0yceJEyc3NlYyMDCktLZUXX3yx6xJPU6nUMxwOy4IFC2T48OGSm5srvXr1ktLS\nUlmxYoXOXDQzbty4Nmt54qbmzTfflCuuuEKysrIkLy9PJk+eLLt27eqizNNXKjXdu3fvSWNuvvnm\nrn0RaaY96+mJ0B+YttCeemq/lJpUa6p9U+qWLl0qY8aMkcLCQrFtW3r06CHjxo1r9aJx6dg/GSIN\nB4wppZRSSiml0or+okMppZRSSqk0pYN1pZRSSiml0pQO1pVSSimllEpTOlhXSimllFIqTelgXSml\nlFJKqTSlg3WllFJKKaXSlA7WlVJKKaWUSlM6WFdKKaWUUipN6WBdKaWUUkqpNKWDdaWUUkoppdKU\nDtaVUkoppZRKU/8fULZXjD/Hx4UAAAAASUVORK5CYII=\n", "text/plain": [ "" ] }, "metadata": {}, "output_type": "display_data" } ], "source": [ "from filterpy.stats import gaussian\n", "\n", "xs = np.arange(15, 30, 0.05)\n", "plt.plot(xs, gaussian(xs, 23, 0.05), label='$\\sigma^2$=0.05')\n", "plt.plot(xs, gaussian(xs, 23, 1), label='$\\sigma^2$=1', ls=':')\n", "plt.plot(xs, gaussian(xs, 23, 5), label='$\\sigma^2$=5', ls='--')\n", "plt.legend()\n", "plt.show()" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "What is this telling us? The Gaussian with $\\sigma^2=0.05$ is very narrow. It is saying that we believe $x=23$, and that we are very sure about that. In contrast, the Gaussian with $\\sigma^2=5$ also believes that $x=23$, but we are much less sure about that. Our believe that $x=23$ is lower, and so our belief about the likely possible values for $x$ is spread out — we think it is quite likely that $x=20$ or $x=26$, for example. $\\sigma^2=0.05$ has almost completely eliminated $22$ or $24$ as possible values, whereas $\\sigma^2=5$ considers them nearly as likely as $23$.\n", "\n", "If we think back to the thermometer, we can consider these three curves as representing the readings from three different thermometers. The curve for $\\sigma^2=0.05$ represents a very accurate thermometer, and curve for $\\sigma^2=5$ represents a fairly inaccurate one. Note the very powerful property the Gaussian distribution affords us — we can entirely represent both the reading and the error of a thermometer with only two numbers — the mean and the variance.\n", "\n", "An equivalent formation for a Gaussian is $\\mathcal{N}(\\mu,1/\\tau)$ where $\\mu$ is the *mean* and $\\tau$ the *precision*. $1/\\tau = \\sigma^2$; it is the reciprocal of the variance. While we do not use this formulation in this book, it underscores that the variance is a measure of how precise our data is. A small variance yields large precision — our measurement is very precise. Conversely, a large variance yields low precision — our belief is spread out across a large area. You should become comfortable with thinking about Gaussians in these equivalent forms. In Bayesian terms Gaussians reflect our *belief* about a measurement, they express the *precision* of the measurement, and they express how much *variance* there is in the measurements. These are all different ways of stating the same fact.\n", "\n", "I'm getting ahead of myself, but in the next chapters we will use Gaussians to express our belief in things like the estimated position of the object we are tracking, or the accuracy of the sensors we are using." ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "## The 68-95-99.7 Rule\n", "\n", "It is worth spending a few words on standard deviation now. The standard deviation is a measure of how much variation from the mean exists. For Gaussian distributions, 68% of all the data falls within one standard deviation ($\\pm1\\sigma$) of the mean, 95% falls within two standard deviations ($\\pm2\\sigma$), and 99.7% within three ($\\pm3\\sigma$). This is often called the [68-95-99.7 rule](https://en.wikipedia.org/wiki/68%E2%80%9395%E2%80%9399.7_rule). If you were told that the average test score in a class was 71 with a standard deviation of 9.4, you could conclude that 95% of the students received a score between 52.2 and 89.8 if the distribution is normal (that is calculated with $71 \\pm (2 * 9.4)$). \n", "\n", "Finally, these are not arbitrary numbers. If the Gaussian for our position is $\\mu=22$ meters, then the standard deviation also has units meters. Thus $\\sigma=0.2$ implies that 68% of the measurements range from 21.8 to 22.2 meters. Variance is the standard deviation squared, thus $\\sigma^2 = .04$ meters$^2$.\n", "\n", "The following graph depicts the relationship between the standard deviation and the normal distribution. " ] }, { "cell_type": "code", "execution_count": 21, "metadata": {}, "outputs": [ { "data": { "image/png": "iVBORw0KGgoAAAANSUhEUgAAAswAAAEbCAYAAADOAtIQAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzs3Xd4VNXCxeHflGTSGyEBQhIIJfTe\nQQGVoogNwd4btqsCFvRaEBUUVGygfvYOIopewUZRBKUTSugBEloKCeltyvfHQK5cMbQkJzNZ7/Pk\nyWQyM1kHJpk15+yzt8nlcrkQEREREZHjMhsdQERERESkNlNhFhERERGphAqziIiIiEglVJhFRERE\nRCqhwiwiIiIiUglrZd90Op04nc5jrjOZTJhMpmoNJSIiIiJSHVwuF/87SZzZbMZs/uf9yCcszIWF\nhVWTTkRERESkFgoMDKy0MGtIhoiIiIhIJVSYRUREREQqocIsIiIiIlKJSscwH+/kvhON8RARERER\nqa2Od47eiSa0OOXCfKKzCEVEREREPMmJCrOar4iIiIhIJVSYRUREREQqocIsIiIiIlIJFWYRERER\nkUqoMIuIiIiIVEKFWURERESkEpVOKyciItXD4XSxPSOfLQfyScsuIi2niAO5JRSVOSgstVNqd+Jr\nMRNgsxDgayEq2I/YcH8aRwTQIiqINo1CsFktRm+GiEidoMIsIlIDnE4XG/fnsmBzBit2ZbN+72EK\nyxzHv22ZhbSXhwIQ+8APmH3/fjtfi5k2jULo3iScga2i6N4kAh+LDhqKiFQHk8vlcv3TN51OJ/n5\n+cdcFxwcrIVLREROgsvlImlvLrNXp/FzcjrpeaXHfD/Q10LbRqHE1QsgLiKARmH+BNmsmOwWhnau\nD8DcFek4rXYO5JaQml1EWnYRyQfyyC4sO+axQvysDGwVxWVdGtOveSQWc+WT8IuI1FWn029VmEVE\nqlhBqZ1ZK9OYtSqNLQf/+zc0wNfCWS0i6d8yii7xYbSICj5usS0shKCgI49VAIGBx37f5XKRml3E\n2tTDLNmexaKtGccU6EahflzeLZZre8YRFeJXLdsoIuKpVJhFRAyUVVDKB0t389Efu8krsQNgs5o5\nv10DLu4cQ++Eevj5nHjc8YkK8/9yOF2sS8vhu6QDfL12H7nF5YB72MaIro254+wEmkSe4EFEROoI\nFWYREQPkFpczffEOPli6m1K7E4CE+oHc1KcJF3WKIdTf55Qe71QL81+VlDv4KTmdj5btZtWeHADM\nJrikUwxjhyQSE+Z/SllERLyNCrOISA0qszv5+M89vLZwO4eL3Ht1O8aGcWf/ZgxuE435NMcRn0lh\n/quVu7N5c/FOFmzJAMDXauamvk24a0DzUy7xIiLeQoVZRKSGrNiVzfg569mZWQhAi6ggxl/QioGJ\nUZhMZ3bCXVUV5qPW7z3Mc/M282dKNgCRQTaeGN6G4R0annFWERFPo8IsIlLNcovKmTR/M1+sTAMg\nMsiXsYMTGdm1MdYqmtatqgszuE8UXLglg2fnbSblSMnv37I+z1zSjtiIgDP/ASIiHkKFWUSkGi3Z\nnsnYWUlk5Lunh7uqRyyPDG1NaEDVDm+ojsJ8VKndwZuLU3hj0Q7KHE4CfC08cWEbrugeq73NIlIn\nqDCLiFSDknIHL/ywlfeW7gLcJ/RNvqwDPZpGVMvPq87CfNTOzALGz9nAil3uYRqD20QzeUQHIgJ9\nq/6HiYjUIirMIiJVbFdWIXd+srpiPuXresXz6AWt8fetvmWpa6Iwg3v1wf9bksLUn7ZS7nBRP9jG\n61d1pmdCver5gSIitYAKs4hIFfpx00HGzUoiv9ROZJAvUy7vyMBWUdX+c2uqMB+1aX8u93+xju0Z\nBVjMJsaf34pb+jXVEA0R8UoqzCIiVcDhdDH1p63MWLwTgO5Nwnnj6i41tmpeTRdmgKIyO4/O2cA3\n6/YDMKx9Q164vAOBNmv1/3ARkRp0Ov1WzVdE5C8KS+3c8fHqirJ8S7+mfHZbL69fYjrA18rLV3Ti\n6YvbYjWb+H7DAUa++QcHcouNjiYiYjgVZhGRIw7mljDqrT/4ZXM6vlYzr1zZiccvbINPFU0XV9uZ\nTCau792EmXf0IjLIl+QDeVzyxlI27ss1OpqIiKHqxquAiMgJbD6Qx8Vv/M6m/XnUC/Tl89t6cXGn\nGKNjGaJrfARf39WXFlFBpOeVMvLNP1iwOd3oWCIihlFhFpE6b8WubEa99QfpeaW0iArim7v70jU+\n3OhYhoqNCOCru/pwVotIissd3P7xar5avdfoWCIihlBhFpE6bcHmdK57dzn5JXZ6NIlg9p19tPLd\nESF+Prx3Y3dGdGmMw+li7JdJvLMkxehYIiI1ToVZROqsb9bu4/aPV1Nqd3Je6yg+uqUHof5Vu2qf\np/OxmJlyeQdu7dcUgGe+38zUH7dSyQRLIiJeR4VZROqk2av38sCsdTicLi7rEsOMa7vi51N9i5F4\nMrPZxGPDWvPQ0EQAXl+0g8k/bFFpFpE6Q4VZROqcWSvTeHB2Ei4XXNMzjqmXd6wzM2GcLpPJxF0D\nmjPhorYAvPVrCs/N26zSLCJ1gl4hRKRO+WJFKg99tR6XC27oHc8zl7TDbNaKdifrhj5NmHhJOwD+\nb8kuJv5HpVlEvJ8Ks4jUGV+v3cv4rzcAcFPfJjx1UVst/3warusVz6TL2gPw3tJdvKAxzSLi5VSY\nRaROmL/hAGNnJVXsWX7iwjYqy2fgqh5xPHepuzTPWLyT1xfuMDiRiEj1UWEWEa+3aEsG//piLU4X\njOrWmCeHa89yVbi6Zxz/HtYagBd/3qYp50TEa6kwi4hXW7U7m9GfrKbc4WJ4x0ZMuqyDxixXoVvP\nSmDMoJaAe8q5L1elGZxIRKTqqTCLiNfalp7PzR+spNTu5JxWUbw0qiMWleUqd+85zbn97AQAHpmz\ngYVbtIy2iHgXFWYR8Ur7Dhdz/bsryCux0yUujDeu7qKp46qJyWTikaGtuKxLDA6ni7s+XcPqPTlG\nxxIRqTJ69RARr5NbVM717y7nYF4JzaOCeO/G7vj7alGS6mQ2m3h+RAcGJNanpNzJzR+sZEdGgdGx\nRESqhAqziHiVcoeTOz9dzc7MQhqG+vHRzT0IC/A1Olad4GMxM/2aLnSKDSO3uJxbPlxJTmGZ0bFE\nRM6YCrOIeA2Xy8UTczexbOchAn0tvHdjdxqF+Rsdq04J8LXyzg3daBzuz55DRdzxyWrK7E6jY4mI\nnBEVZhHxGu/+vovPV6RiMsGrV3WmdcMQoyPVSZFBNt67sTtBNisrdmXz6NcbtLCJiHg0FWYR8Qq/\nJKfz7LzNADx2QWvObR1tcKK6rWV0MK9f3RmzCWav3subv2qOZhHxXCrMIuLxkvfn8a8v1uJyuVeg\nu6VfU6MjCTAgMYonh7cF4PkftvDDxgMGJxIROT0qzCLi0TLySrj1w5UUlTno27weT1+sVfxqkxv6\nNOGG3vEA3D9zHRv25hqcSETk1Kkwi4jHKi5zcNtHq9ifW0JC/UCmX91Vcy3XQo9f2IazW7qnm7v1\no5UczC0xOpKIyCnRK4uIeCSXy8X4OetJ2ptLWIAP793QndAAH6NjyXFYLWZev7ozLaKCSM8r5Y6P\nV1FS7jA6lojISVNhFhGP9NEfe/hm3X4sZhMzrulKk8hAoyNJJUL8fHjvxu6EBfiQtDeXCd8lGx1J\nROSkqTCLiMdZtTubif9xF67x57eid7N6BieSkxEbEcArV3bGZILPV6Qya2Wa0ZFERE6KCrOIeJSM\n/BLu+nQNdqeLCzs01IwYHqZ/y/qMOa8lAP+eu5H1ew8bnEhE5MRUmEXEY5Q7nNzz6Voy8ktpGR3E\n8yM6aEYMD3T3wOac1zqKMruTOz9ZQ7aWzxaRWk6FWUQ8xqR5W1ixO5sgm5U3r+1KoM1qdCQ5DWaz\niRdHdaJJvQD2HS7mvi/W4nBqJUARqb1UmEXEI3ybtJ/3lu4C4MVRHUmoH2RwIjkTof4+vHldV/x9\nLCzZnsXLP28zOpKIyD9SYRaRWm/rwXwenr0egLsGNGNI2wYGJ5Kq0KpBCJNHtAfg9UU7+GnTQYMT\niYgcnwqziNRqhaV27vxkNcXlDvo1j2Ts4ESjI0kVurhTDDf1bQLA2FlJpB4qMjaQiMhxqDCLSK3l\ncrn49zcbSckqpGGoH69e1RmLWSf5eZtHL2hNt/hw8kvt3Pv5GsrsTqMjiYgcQ4VZRGqt2av38vXa\nfVjMJl69qjMRgb5GR5Jq4GMx88pVnQn1dy9q8sIPW4yOJCJyDBVmEamVdmTk88TcTQA8cF4LujeJ\nMDiRVKeYMH+mjuwIwDu/72LB5nSDE4mI/JcKs4jUOiXlDu7+dG3FuOU7BzQ3OpLUgEFtov87nvnL\nJA7kFhsbSETkCBVmEal1nv5PMlvT84kM8uWlKzpq3HId8sj5rWgXE8LhonLu+3wddofGM4uI8VSY\nRaRW+c/6/Xy2PBWTCV6+ohNRwX5GR5IaZLNaeP2qLgTZrKzYnc2rC7YbHUlERIVZRGqP1ENFjP9q\nA+Ceb/msFvUNTiRGaBIZyHOXuednfm3RDpbuyDI4kYjUdSrMIlIrlNmd3PP5GvJL7XSLD+eB81oa\nHUkMdFHHRlzZPRaXC+6fuY7M/FKjI4lIHabCLCK1wks/b2P93lxC/X145arOWC3681TXPTm8LS2j\ng8jML+Wh2Um4XC6jI4lIHaVXJBEx3B87D/HWbzsBeH5Ee2LC/A1OJLWBv6+F167qgq/VzKKtmXzy\n5x6jI4lIHaXCLCKGyi0qZ8ysdbhccEW3WIa2a2h0JKlFEhsE88jQVgA88/1mtqfnG5xIROoiFWYR\nMYzL5eKxbzZwILeEJvUCeGJ4G6MjSS10Y58mnNUiklK7k/u+WEep3WF0JBGpY1SYRcQwX6/dx3/W\nH8BiNjHtys4E2qxGR5JayGw28eLIjoQH+JB8II+XftpmdCQRqWNUmEXEEGnZRRVLX99/bgs6xYYZ\nnEhqs6gQP54f0QGAt5eksExTzYlIDVJhFpEaZ3c4uX/mOgpK7XRvEs5dA7X0tZzY4LYNuKqHe6q5\nMbOSOFxUZnQkEakjVJhFpMZNX7yT1XtyCLZZeWlUJy19LSft8QvbkBAZyMG8Eh79eoOmmhORGqHC\nLCI1am1qDq8cWe544iXtiI0IMDiReJIAXyvTruyE1Wxi3oaDzF691+hIIlIHqDCLSI0pLnMwdlYS\nDqeLizo24pLOMUZHEg/UoXEYDwxyrwQ54btk0rKLDE4kIt5OhVlEaswLP24hJauQ6BAbEy9uZ3Qc\n8WCj+zeja3w4BaV2HpydhNOpoRkiUn1UmEWkRvyx8xDvL90NwPMjOhAa4GNsIPFoliNTzfn7WPgz\nJZsPlu02OpKIeDEVZhGpdkf3AgJc1SOWAYlRBicSb9AkMpBHh7UG4PkftrAjo8DgRCLirVSYRaTa\nPTdvM3tziokJ8+exYVrNT6rOtT3jKlYBHDtrHXaH0+hIIuKFVJhFpFr9ui2Tz5anAjBlZAeCtJqf\nVCGTycQLl3cgxM9K0t5cpi/eaXQkEfFCKswiUm1yi8t5ePZ6AG7s04Q+zSINTiTeqGGoP08fOYn0\n1QXb2bgv1+BEIuJtVJhFpNo8/V0yB/NKaFIvgIeGJhodR7zYxZ0acX67BtidLsbMWkdJucPoSCLi\nRVSYRaRa/Jyczldr9mI2wYujOhLgq6EYUn1MJhPPXNKOyCBftqUX8NLP24yOJCJeRIVZRKpcTmEZ\n4+dsAOC2sxLoGh9hcCKpC+oF2Zh0WQcA/m9JCit2ZRucSES8hQqziFS5x+duJKuglBZRQRUrsonU\nhEFtohnZtTEuF4z7MonCUrvRkUTEC6gwi0iV+s/6/fxn/QEsZhMvjeqEn4/F6EhSxzwxvA0xYf6k\nZhfx7LzNRscRES+gwiwiVSYjv4THv9kIwN0DmtG+cajBiaQuCvbzYcpI99CMz5ansmhrhsGJRMTT\nqTCLSJVwuVw8OmcjOUXltGkYwj3ntDA6ktRhfZpFclPfJgA8PHs9h4vKjA0kIh5NhVlEqsScNfv4\nZXM6PhYTL13REV+r/ryIsR4e2oqE+oFk5Jfy1LebjI4jIh5Mr2gicsYO5Bbz1HfuQnL/eS1p1SDE\n4EQi4Odj4cWRHTGb4Jt1+/lh40GjI4mIh1JhFpEz4nK5eGj2evJL7HSMDeOOsxOMjiRSoXNcOKP7\nNwPgsa83cKig1OBEIuKJVJhF5Ix8viKNJduzsFnNvDiyI1aL/qxI7XLfeS1o1SCYQ4VlPD53Iy6X\ny+hIIuJh9MomIqctLbuIZ79PBuDBIYk0jwoyOJHI39msFqaO7IjVbGLehoN8t/6A0ZFExMOoMIvI\naXE6Xe6FIcoc9GgSwU19mxodSeQftYsJ5Z5zmgPwxNyNZOSXGJxIRDyJCrOInJYP/9jN8l3Z+PtY\nmDKyAxazyehIIpW6e2Bz2sWEcLionEfnbNDQDBE5aSrMInLKUjILeP6HLQA8Oqw18fUCDU4kcmI+\nFjMvjuyEr8XML5sz+GrNPqMjiYiHUGEWkVPiODIUo6TcSb/mkVzbM87oSCInLbFBMPcPci+qM+G7\nTRzILTY4kYh4AhVmETkl/7ckhTWphwm2WXn+8g6YTBqKIZ7l9rMS6BQbRn6JnYdmr9fQDBE5IRVm\nETlpWw/m89JP2wB4fHgbYsL8DU4kcuqsFjMvjuqIzWpmyfYsPl+RZnQkEanlVJhF5KSUO5zcN+sP\ntvtewB7/C7mgfbjRkUROW7P6QfzrvFj2+F/INT/EszU90+hIIlKLqTCLyEl5Y9EOkvfnV3ytoRji\n6a7v1aTi8mNfb8Dp1NAMETk+FWYROaGN+3J5feEOo2OIVCnzX6ZCXLE7h4/+2G1YFhGp3VSYRaRS\npXYHY2clYXe6GNwm2ug4ItVm8g9b2JVVaHQMEamFVJhFpFLTftnO1vR86gX68sTwNkbHEakWvRMi\nKCl3Mu7LJBwamiEi/0OFWUT+0ZrUHN76dScAz17annqBNoMTiVSPiZe0I8hmZfWeHN79PcXoOCJS\ny6gwi8hxFZc5GDcrCacLLunUiKHtGhgdSaTaxIQF8O9hrQGY+tM2tqfnn+AeIlKXqDCLyHFN+XEr\nKVmFRIfYmHBRO6PjiFS7K7rHMiCxPmV299AMu8NpdCQRqSVUmEXkb/5MOcT7y3YBMHlEB0IDfAxO\nJFL9TCYTky/rQIiflaS9ubx5ZDiSiIgKs4gco7DUzoOzk3C54IpusQxMjDI6kkiNaRDqx1MXtQXg\nlQXbSd6fZ3AiEakNVJhF5BjPzdtMWnYxMWH+/PvC1kbHEalxl3aOYVCbaModLsZ+mUSZXUMzROo6\nFWYRqfDbtkw+XZ4KwJTLOxDsp6EYUveYTCaeu7Q94QE+bD6Qx+sLtxsdSUQMpsIsIgDkFpfz8Ffr\nAbi+dzx9mkcanEjEOPWDbUy8xH2y6xuLd7J+72GDE4mIkVSYRQSACd9u4kBuCfH1Anjk/FZGxxEx\n3IUdGjGsQ0McThdjZyVRUu4wOpKIGESFWUT4YeMB5qzdh9kEL43qSICv1ehIIrXCxIvbERnky/aM\nAl7+ZZvRcUTEICrMInVcZn4pj369EYA7+jeja3yEwYlEao+IQF+eu7Q9AP/3Wwqr9+QYnEhEjKDC\nLFKHuVwuxs/ZQHZhGa0aBHP/eS2MjiRS6wxu24DLOsfgdMG4L5MoLtPQDJG6RoVZpA6bvXovv2xO\nx8di4uUrOmGzWoyOJFIrPTm8LdEhNnZlFfLCj1uMjiMiNUyFWaSO2ptTxITvkgF4YFBLWjcMMTiR\nSO0VGuDD8yM6APD+0t38mXLI4EQiUpNUmEXqIKfTxYNfrqeg1E7X+HDuOLuZ0ZFEar0BiVFc2T0W\ngAdnJ1FYajc4kYjUFBVmkTrog2W7+SPlEP4+Fl4c2RGL2WR0JBGP8Niw1sSE+ZOWXcxz8zYbHUdE\naogKs0gdsyOjgOd/cI/BfGxYa5pEBhqcSMRzBPv5MOVy99CMT5en8tu2TIMTiUhNUGEWqUPKHU7G\nzFpHqd3J2S3rc03POKMjiXicPs0jub53POAemnG4qMzgRCJS3VSYReqQ6Yt2sn5vLiF+Vl4Y0QGT\nSUMxRE7H+PNbk1A/kPS8Uh79egMul8voSCJSjVSYReqIDXtzeW3hdgAmXtKOBqF+BicS8Vz+vham\nXdEJq9nEvA0HmbNmn9GRRKQaqTCL1AEl5Q4emLUOu9PFsPYNuahjI6MjiXi8Do3DeGBQSwCe/HYT\nadlFBicSkeqiwixSB7zww1Z2ZBRQP9jGxEvaaSiGSBUZ3b8Z3eLDKSi188DMdTicGpoh4o1UmEW8\n3G/bMnlv6S4Anh/RnohAX4MTiXgPi9m9SmaQzcqqPTm8+etOoyOJSDVQYRbxYtmFZYz7MgmA63rF\nc06raIMTiXif2IgAJlzUFoCXf97G+r2HDU4kIlVNhVnES7lcLsbPWU9GfinN6gfy6AWtjY4k4rUu\n6xLDsPYNsTtd3D9zHcVlDqMjiUgVUmEW8VKzVqXx46Z0fCwmXrmyM/6+FqMjiXgtk8nEs5e2IzrE\nRkpmoVYBFPEyKswiXmhXViETvksGYOzgRNrFhBqcSMT7hQX48uLITgB8/OceFm3JMDiRiFQVFWYR\nL1PucHL/F2spKnPQKyGC285KMDqSSJ3Rr0Ukt/RrCrhXAcwqKDU4kYhUBRVmES/z6oLtJB1Zze+l\nUZ2wmDWFnEhNenBIIonRwWQVlPHIV1oFUMQbqDCLeJGVu7N5Y9EOAJ67rD2NwvwNTiRS9/j5WJh2\nZSd8LWZ+2ZzOFyvTjI4kImdIhVnES+QWl3P/F+twutxn7F/YQav5iRildcMQHhqaCMDT3yWzI6PA\n4EQiciZUmEW8gMvl4tE5G9h3uJjYCP+KOWFFxDg3921Kv+aRFJc7uPfztZSUa6o5EU+lwiziBT5f\nkcb3Gw5gNZt47aouBPv5GB1JpM4zm028NKoj9QJ92Xwgj8nztxgdSUROkwqziIfblp7PhO82AfDQ\n0EQ6xYYZnEhEjooK8ePFUR0B+GDZbn7adNDgRCJyOlSYRTxYcZmDez5bQ6ndydkt63NrP00hJ1Lb\nDEiM4vaz3b+bD321nv2Hiw1OJCKnSoVZxINN/D6ZbekF1A+28dKojpg1hZxIrTRucCIdG4dyuMh9\ncq7d4TQ6koicAhVmEQ/1/foDfLY8FZMJXh7Vicggm9GRROQf+FrNvHpVZ4JsVlbszubVhTuMjiQi\np0CFWcQDpWUX8cic9QDc2b8Z/VpEGpxIRE4kvl4gz17aDoDXF27nj52HDE4kIidLhVnEw5Q7nPzr\ni7Xkl9jpHBfGA4NaGh1JRE7SxZ1iGNWtMU4X3D9zLdmFZUZHEpGToMIs4mGm/LiVtamHCfaz8uqV\nnfGx6NdYxJM8dVFbmtUPJD2vlAdmrsPp1NLZIrWdXmlFPMiPmw7y9m8pAEy5vCOxEQEGJxKRUxXg\na+WNa7rg52Pm122ZFcvZi0jtpcIs4iH2HCpk3JdJANzarylD2zUwOJGInK5WDUKYeLF7PPPLv2xj\n6Y4sgxOJSGVUmEU8QEm5g7s+XUN+iZ2u8eE8fH4royOJyBka2S22YjzzfV+sJT2vxOhIIvIPVJhF\nPMCE75LZtD+PiEBfXr9a45ZFvMXTF7ejVYNgsgrKuOezNZRrfmaRWkmvuiK13Jw1e/l8hXu+5Veu\n7ETDUH+jI4lIFfHzsTDj2q4E2ays3J3D1B+3Gh1JRI5DhVmkFtt6MJ/Hvt4IwP3ntuSsFvUNTiQi\nVa1pZCBTLu8AwFu/pfDTpoMGJxKR/6XCLFJLFZTaufPT1RSXOzirRST3ntPc6EgiUk3Ob9+Qm/s2\nBWDsl0mkHioyOJGI/JUKs0gt5HK5eHj2elIyC2kY6se0KzphNpuMjiW13O+//84FF1xAeHg4/v7+\ntGjRgokTJ1Z8v7S0lClTptCuXTsCAwOJjo7m/PPPZ9myZcc8Tk5ODldddRXh4eEkJCTw9ttv/+1n\nLV++HH9/fzZv3lzt21VXPHJ+K7rEhZFfYmf0J6spLnMYHUlEjlBhFqmFZvy6k+83HMDHYuL1q7tQ\nL8hmdCSp5T777DP69+9PaGgoH330EfPmzePhhx/G5frvohi33XYbjzzyCJdccgnfffcdb7zxBpmZ\nmfTv358VK1ZU3G7s2LGsXbuWTz75hHvvvZc777yTJUuWVHzfbrdz++2389BDD9G6desa3U5v5ms1\nu3/fA31JPpDHI3PWH/P/JyLGsRodQESOtWhrBlOOnPgz4aJ2dI0PNziR1Hb79u3j9ttv54477mD6\n9OkV1w8cOLDicmlpKZ999hlXX301zzzzTMX1ffv2pVGjRnz66af06NEDgO+//55p06YxbNgwhg0b\nxvz58/n+++8566yzAJg6dSqlpaU8+uijNbSFdUejMH+mX9OFa95Zztx1+2nXKJTbzk4wOpZInac9\nzCK1yK6sQv71+VpcLri6ZxxX94wzOpJ4gHfeeYfCwkIefvjhf7yN2WzGbDYTGhp6zPUhISGYzWb8\n/PwqrispKSEwMLDi66CgIEpK3HMEp6SkMHHiRN566y1sNh35qA49E+rx+IVtAJg0fzNLtmcanEhE\nVJhFaomCUju3f7SK/BI73eLDeWp4W6MjiYf47bffiIiIYMuWLXTq1Amr1UpUVBSjR48mLy8PAB8f\nH+666y4+/PBDvvnmG/Ly8ti9eze33XYboaGh3HbbbRWP16dPH15//XUyMjJYunQpP/74I3369AHg\nzjvv5Morr6R///6GbGtdcX3veEZ2dS9qcs9na3USoIjBNCRDpBZwOl2MmbmO7RkFRIfYmH5tF3yt\nej8rJ2ffvn0UFRUxcuRIxo8fz7Rp01i5ciVPPvkkGzduZMmSJZhMJl5++WVCQ0MZMWIETqd7gYy4\nuDgWLlxI8+b/nYVl2rRpDB8+nOjoaABuvvlmRo4cySeffMK6dev4/PPPDdnOusRkMjHxknZsyygg\nKe0wt3+8ijl39SHAVy/bIkbQK7JILfD6oh38lJyOr8XMm9d2JSrY78R3EjnC6XRSUlLCo48+yvjx\n4xkwYAAPPvggkyZNYunSpSzOru6JAAAgAElEQVRYsACAZ599lqlTp/LUU0+xaNEi5s6dS2JiIoMG\nDWLt2rUVj5eYmMiWLVvYvn07mZmZvPvuu+Tk5DBmzBhefvllIiIimD59Os2aNSMyMpJrrrmGnJwc\nozbfa/n5WHjr2q5EBtnYcjCfB7/USYAiRlFhFjHYL8npvPTzNgCeuaQdneN0kp+cmnr16gEwZMiQ\nY64///zzAVizZg2bN2/miSeeYMKECTz++OMMGDCAiy66iO+//56wsDDGjBlzzH3NZjPNmzcnMjIS\ngHHjxtG5c2euvvpqFixYwMMPP8zMmTPZsWMHmZmZ3H///TWwpXVPg1A/3ry2Cz4WE99vOMCMX3ca\nHUmkTlJhFjHQ1oP53D9zHeAesziqe6zBicQTdejQ4bjXH90baTabSUpKwuVy0b1792Nu4+PjQ8eO\nHdm4ceM/Pv7ixYuZOXMmM2bMAGD+/PkMHjyYbt26ERYWxj333MO8efOqaGvkf3VrEsFTF7nPaZjy\n41Z+Tk43OJFI3aPCLGKQjPwSbv5gJQWldno2jag4K17kVI0YMQJwF9m/Olpie/XqRaNGjQD4888/\nj7lNaWkpa9asoXHjxsd97NLSUu644w6efPJJEhLc05u5XC4KCwsrblNQUKChAtXsmp7xXNMzDpcL\n7vtiLRv35RodSaRO0dkDIgYoKXdw20er2Xe4mKaRgbx1XVd8LHr/Kqdn8ODBDB8+nKeffhqn00mv\nXr1YtWoVEyZM4MILL6Rfv344nU66d+/OU089RVFREWeffTa5ubm89tpr7Nq1i48//vi4j/3ss8/i\n5+d3zJCNIUOG8Morr/Dqq6/SvHlznn76aYYOHVpTm1tnPXVRW1Kzi1iyPYtbP1zFN3f3pUGozncQ\nqQkmVyW7BZxOJ/n5+cdcFxwcjNmsF3aR0+V0urj387V8v+EAYQE+fH1XX5pGBp74jrVAYVkhQZOC\nACgYX0Cgr2fk9jSFhRDk/memoAACT+Kfubi4mAkTJvDZZ59x4MABGjVqxDXXXMOTTz5ZMV9ybm4u\nU6ZMYc6cOezZs4egoCDatGnDQw89VDHe+a82b95Mly5dWLx4MT179jzmey+//DLTpk3j8OHDDB48\nmBkzZlSMd/YUnvh8zi0uZ8SMZezIKKBtoxBm3dGbQJv2fYmcitPptyrMIjVsyo9beGPRTnwsJj6+\npSe9EuoZHemkeWLB8ESnU5jl1Hnq8zktu4hL3ljKocIyBrWJ5s1ru2Ixm4yOJeIxTqffqvmK1KDZ\nq/fyxiL3We6TLuvgUWVZRGqH2IgA3r6+K75WMz8np/P8D1uMjiTi9VSYRWrInymHGD9nPQB3D2zG\n5V2Pf5KViMiJdI2PYMrl7tlR3v4thc+WpxqcSMS7qTCL1ICdmQWM/mQ15Q4Xw9o3ZOygRKMjVb+D\nB6GszOgUUlelen+BvLhTDA+c1xKAx+du5LdtmQYnEvFeKswi1Sw9r4Tr313B4aJyOsaG8eKojpi9\nebxhairceSfce697MK5ITXM6YfJkuPJKSEoyOk21+te5zbm0cwwOp4s7P1nN+r2HjY4k4pV0aq1I\nNcotLuf6d1dUTB/33g3d8POxGB2reqSmwqRJkJUF48dDly5GJ5K6ymyG6dNh9273czI31/2c7NjR\n6GRVzmQyMXlEezLyS1i64xA3vb+S2Xf28ZiZd0Q8hfYwi1STknIHt324iq3p+UQF2/jo5h7UC7IZ\nHavqHd2jPHYs3HYbfPmlyrLUDk2awFtvufc2T5/utXucbVYLb13XjfYxoRwqLOO6d5eTkVdidCwR\nr6I9zCLVwO5w8q/P17JidzbBNisf3tyD2IgAo2NVvZwcSEyEuDho2RKeesroRF7B5oC5Ry+PArz0\noESN27cPunWDH36Ac881Ok2VCrJZef+m7lw+Yxm7DxVx/XsrmDW6NyF+PkZHE/EKKswiVczlcvHv\nbzbyU3I6vlYz/3dDN1o3DDE6VvUID4f0dHj9dVi82D1u+cILweTFY7RrQGkhXHx0HuZZYNXR9TOz\nfDk8/zycdRZ89x0cWSbc20QG2fjo5p5cNmMZWw7mc9uHq/jw5h7eOwxMpAZpSIZIFXvp5218sTIN\nswlevbKz98+1HBICjz4Ks2fDhg0wZIi7lPzzmkgiNWP5crjsMvj8c/ebumnTvLYsHxVXL4APb+5O\nsM3K8l3Z3P/FOhxO/S6KnCkVZpEq9P7SXby2cAcAz1zSnqHtGhicqAYdrzhnaporMYDTCaNG1ami\n/FdtG4Xy9vXd8LWY+WHTQf79zUYqWdRXRE6CCrNIFflseSoTvksG4IHzWnJ1zziDExnkaHH+9luo\n5+V716V2Mpvhgw/qXFH+q97N6vHKlZ0wmeDzFak8/Z9klWaRM6DCLFIFvlyVxqNfbwDg9rMT+Ne5\nzQ1OVAv4+bmLi4gRArzwJNtTdH77hrwwwr0a4PtLdzN5/haVZpHTpFczkTM0d90+HvrKveT1jX2a\nMP78Vph00puI1AIju8Xy3KXtAXjrtxRe+nmbwYlEPJMKs8gZ+H79AcbMSsLlgqt7xvHk8DYqyyJS\nq1zdM44JF7UF4LWFO3h1wXaDE4l4HhVmkdP006aD3PfFWhxOFyO7NuaZi9upLItIrXRDnyb8e1hr\nwD2Tz4zFOw1OJOJZVJhFTsOiLRnc/dka7E4Xl3aOYfKIDpjNKssiUnvdelYCDw5JBOD5H7bwzpIU\ngxOJeA4VZpFT9NOmg9zx8WrKHS6GdWjIlMs7YFFZFhEPcPfA5tx/XgsAnvl+M2/9qj3NIidDhVnk\nFMxdt487P11DmcPJ+e0aMO2KTlgt+jUSEc9x37ktuPcc90w+k+Zv4aWftmr2DJET0Cu9yEn6fEUq\n9890r5p1WecYXruqMz4qyyLiYUwmE2MHJ1YMz3h14Q6e+X6zSrNIJfRqL3IS3lmSwvg5G3C54Npe\ncUwd2VF7lkXEo909sHnF7Bnv/r6L8XM2aBltkX9gNTqASG3mcrl4dcEOXv7FPXfpHf0TeGSo5lkW\nEe9wQ58mBPhaePir9XyxMo2iMgcvjuqoo2ci/0OFWeQfuFwuJs3fwtu/uc8kHze4JXcPbK6yLCJe\nZWS3WAJtVu77Yi3fJu2nqMzB61d3xs/HYnQ0kVpDbyFFjqPM7mTcl+sryvITF7bhnnNaqCyLiFe6\noH1D3r6uGzarmV82p3P9eys4XFRmdCyRWkOFWeR/5JWUc+P7K/hqzV4sZhMvjOjAzf2aGh1LRKRa\nDWwVxQc39SDYZmXFrmxGzFhGWnaR0bFEagUVZpG/2He4mMtnLGPZzkME+lp454ZujOoea3QsEZEa\n0btZPb68szeNQv3YmVnIpdOXkpR22OhYIoZTYRY5YuO+XC59Yynb0guICrYxa3RvBiZGGR1LRKRG\ntWoQwtd396VNwxCyCsq44u0/+Dk53ehYIoZSYRYBFm3NYNRbf5CRX0pidDBf392Xto1CjY4lImKI\n6BA/Zo3uTf+W9Skpd3LHx6v4cNluo2OJGEaFWeo0l8vFx3/u4dYPV1FU5qBvc/fhyJgwf6OjiZyS\nFStWMGTIEIKDgwkKCmLgwIEsXbr0b7cbMGAAJpPpbx9Dhw495nZpaWlccMEFhISE0Lp1a+bOnfu3\nx/ryyy+pV68emZmZ1bZdYpwgm5V3b+jGVT1icbrgyW838fR3ydgdTqOjidQ4TSsndVZJuYMn525i\n5qo0AEZ0acyky9rja9X7SPEsK1eu5Oyzz6ZHjx58/PHHuFwuXnjhBc4991wWLVpE7969j7l9QkIC\nn3766THXhYWFHfP1DTfcQGlpKbNnz2bx4sWMGjWK5ORkmjVrBkBubi733XcfU6dOpX79+tW7gWIY\nq8XMc5e2p3F4AFN+3Mp7S3exNT2P167qQkSgr9HxRGqMyVXJWphOp5P8/PxjrgsODsZsVqEQz3Yg\nt5jRn6whKe0wZhOMG5LInf2badq4EygsKyRoUhAABeMLCPQNNDiRdyoshCD3PzMFBRB4gn/moUOH\nsm7dOlJSUggICAAgPz+fhIQEWrZsecye5gEDBpCVlcXGjRv/8fGKiooICgpi6dKlFWW7ZcuWjBkz\nhtGjRwMwevRotm7dyqJFi85gS42l5/OpmbfhAOO+TKKozEFMmD9vXdeVdjEauiae53T6rZqv1DnL\nUw4x/LXfSUo7TKi/Dx/c1IO7BmhBEvFcS5cuZcCAARVlGdx//M8++2yWLVvGgQMHTunxysrKcLlc\nBP6lqQcFBVFSUgLAsmXL+Oijj3jrrbeqZgPEI1zQviFf39WXJvUC2He4mBEzljFnzV6jY4nUCBVm\nqTNcLhfvL93FNe8sJ6ugjNYNQ/junn6c3VKHk8WzlZWVYbPZ/nb90es2bNhwzPU7d+4kIiICq9VK\ns2bNeOyxxyguLq74flhYGK1ateLFF18kJyeHb775hqSkJPr06UN5eTm3334748ePp2XLltW7YVLr\nJDYIZu49/RiYWJ9Su5Mxs5J46ttNlGtcs3g5jWGWOqGw1M7j32xkztp9AFzcqRGTL+uAv6+WfhXP\n16ZNG/7880+cTmfFIUW73c7y5csBOHToUMVt+/XrxxVXXEGrVq0oLi5m/vz5vPDCC/z+++8sWrSo\n4v7vvvsuI0aMICIiArPZzL///W969OjBM888g8vl4uGHH675DZVaIdTfh3dv6M60Bdt5dcF2Pli2\nm+QDebx2VWeiQ/yMjidSLVSYxett3JfLvz5fS0pWIRazifHnt+KWfk01BEO8xr333sstt9zCPffc\nw2OPPYbT6WTChAns2bMH4Jhxec8888wx973gggto0qQJ48aNY+7cuVx66aUA9OnTh9TUVFJSUmjQ\noAGhoaFs376d5557jp9++gmr1cqTTz7J+++/T1lZGZdffjlTp07Fz0+FqS4wm02MGdSSdo1CGDMr\niRW7shk67TemXN6R89pEGx1PpMppSIZ4LafTxf/9lsKl05eSklVIw1A/Pr21J7eelaCyLF7l5ptv\nZvLkyXz88cc0btyYuLg4kpOTGTduHAAxMTGV3v/aa68F4M8//zzmeh8fHxITEwkNdZ/YNXr0aK67\n7jr69evH+++/z/vvv8+CBQtYu3YtS5YsYdKkSdWwdVKbDW7bgG/v6UvbRiHkFJVz60ereGLuRkrK\nHUZHE6lSKszilTLyS7jh/RU8O28z5Q4XQ9s2YP59Z9EroZ7R0USqxcMPP0xWVhYbNmxg9+7dLFu2\njJycHAIDA+natetJPUZlZ4h/8MEHJCcn8/zzzwMwf/58Ro4cSYsWLWjYsCG33HIL8+bNq5JtEc+S\nUD+IOXf14dZ+TQH46I89XPz6UrYezD/BPUU8hwqzeJ2FW9I5f9oSlmzPws/HPYfojGu7EBagOUPF\nu9lsNtq1a0d8fDypqanMnDmT2267DX//yhfi+fDDDwHo1avXcb+flZXFuHHjeOWVVyrma3a5XBQW\nFlbcpqCggEpmKRUvZ7Na+PeFbfjgpu5EBvmyNT2fi17/nY//2K3nhXgFjWEWr5FXUs6keVv4fEUq\nAK0aBPPaVZ1pER1scDKR6rVx40a++uorunXrhs1mIykpicmTJ9OiRQsmTpxYcbslS5bw7LPPcuml\nl5KQkEBJSQnz58/n7bff5pxzzmH48OHHffwxY8bQs2dPRo0aVXHdkCFDGDt2LL179yYoKIhXX32V\nW2+9tdq3VWq3AYlRzL/vbB6cncTirZk8PncTC7Zk8Oyl7bWCqng0FWbxCgs2p/PY1xs5mOeeJ/bG\nPk145PxW+PloFgzxfr6+vixcuJBXX32VgoIC4uLiGD16NI888sgxcyk3bNgQi8XCxIkTycrKwmQy\n0aJFC55++mnGjh173CEZCxYsYM6cOWzatOmY62+55RZSUlJ45JFHKCsrY8SIETz22GPVvq1S+9UP\ntvHeDd35YNluJs/fwuKtmQx+6VceuaA11/SIw2zWOSTiebTSn3i0QwWlTPgumW+SUkjzvxyAhVfu\nYWBinMHJvJNWRqsZp7rSn5wePZ+r3/p96XR8pwEAscWz6dWkEZNHtCehfpDByaQu00p/Ume4XC7m\nrtvHoJd/49uk/fx1h0WPpjqxT0SkNmj2l2Ic4Gthxe5szn9lCW/+uhO7FjsRD6LCLB4nJbOAmz5Y\nyX1frCO7sIxWDYL54vbjn6x0XA4HOPWHWkTkjNntJ33TuXf35awWkZTanUyev4WL31jKqt3Z1RhO\npOqoMIvHyC8p57l5mxky7TcWb83Ex+KeOP/be/rRPibsxA9QVgZvvw2DBsGRBR1EROQ0lZbChRfC\nM89Abu4Jb944PICPbu7BlMs7EOJnZdP+PC5/8w/u+2ItB3KLT3h/ESOpMEut53S6mLUqjYFTf+Xt\n31Iod7gYmFifH+8/m3+d2wJf6wmexkeL8tCh4OMDP/4ITZvWTHgREW9ls8H8+dC5M4wadVLF2WQy\nMbJbLAvHDeDK7rGYTDB33X7Omforry/crgVPpNZSYZZabU1qDpdOX8pDs9eTVVBKQmQg79/Ynfdv\n6nHik0aOV5Rvusl9WUREzpzJBMOGwQ8/nFJxjgyyMXlEB769ux/d4sMpLncw9adtDHr5V37YeFBz\nN0uto1kypFbaejCfF3/ayk/J6QAE2az869zm3Nin6XH3KP/tbHezDerVc3+0aQN6zlYJu9PBvO3u\n1dwuaHEBVrOm7asOdgccXTTvggvAqn/maqHnczVwudxD3rZuhZUrKWzV7IQzkbhcLr5N2s+keVsq\npgbtEhfGuMGJ9GkeWaPxpW44nX6rwiy1yq6sQl7+eRvfrd+PywVmE4zo0pgHhyYSFez3j/c77vRQ\ne/bApEmQkwPjx0OnTjW1GV5L03DVDE0rVzP0fK5iqakweTIcOgSPPAKdO5/Sv3FRmZ3pi3byzu8p\nlJS7T8zu06we44Yk0iUuvEY2QeqG0+m3WrhEaoW9OUW8tmAHs9fsxeF0v4cb1r4hDwxqQfOo01yp\nLz4e3nxTxVlEpDodpyifjgBfK+OGJHJ973imL97JZ8tTWbbzEJdNX8Y5raIYO7glbRuFVnF4kZOj\nwiyG2pFRwDtLUpizZh9lR+bkPLdVFGOq8g/j8Yrza69BVFTVPL6ISF1UXg733w9ZWWdUlP9XVIgf\nT13UllvPasrrC3fw5eq9LNySwcItGQxqE80dZyfQrUlElfwskZOlwiyGWLU7mzd/TeGXzekV1/Vt\nXo+xg6vx0NvR4rx3LwQEVM/PEBGpKywWuO8+aNmyWh6+cXgAk0d04I7+zZj2yza+TdrPz8np/Jyc\nTtf4cG4/O4FBraO11LbUCBVmqTEOp4ufk9N5+7edrEk9DLhPsD6vdQ3vMWjcuGZ+joiINzObq60s\n/1XTyEBeubIz957TouKI5Oo9Odzx8WoSIgO59awELusSg5+PTtqU6qPCLNUuM7+UL1en8cWKNFKz\niwDwtZoZ0SWGW89KOGbpVBERkeNpHhXE5BEdGDOoJR8s280nf+4hJauQR7/ewNSftjKya2Ou6hFH\nk0idvClVT4VZqoXT6eKPlEN8tjyVn5IPUu5wn8gX4mflut7x3NCnSaWzXoiIiBxPVIgfDw1txV0D\nmzNzZRrv/b6LfYeLeeu3FN76LYW+zetxdY94BrWJPvHCViInSYVZqtTB3BLmrtvHFyvT2JVVWHF9\np9gwru4Zx/AOjfD31WEzERE5M0E2K7f0a8oNveNZuCWDz1ak8uu2TJbuOMTSHYeIDLIxsltjRnRp\nTPMoHcmUM6PCLGcst6ic+RsPMHfdfv7cdYijM3sH2axc0rkRV/eIp02jEGNDioiIV7JazAxu24DB\nbRuQll3EzJVpzFyVRmZ+KTMW72TG4p20bRTCxZ0aMbxjIxqG+hsdWTyQCrOclqIyO4u2ZDJ33T4W\nb82smBIOoHuTcC7r0piLOjYi0KanmIiI1IzYiADGDUnkvvNasGBzOrNW7eW3bZls2p/Hpv15TJq/\nhZ5NI7i4UwxD2zYgPNDX6MjiIdRm5KRl5JWwYEsGvySn8/uOLErt/y3JrRoEc1GnRgzv0IjYCE3Z\nJiIixvGxmBnariFD2zUku7CMeRsO8O26/azYnc2fKe6Px77eQLcmEQxqHc2gNtE6WVAqpcIs/8jp\ndLHlYD6Ltmbwc3I669IOH/P92Ah/hndoxEWdGtGqgYZciIhI7RMR6Mu1veK5tlc8+w4X813Sfr5d\nt5/kA3ms2JXNil3ZPDtvM82jgjivdTTnto6iU2wYPhadMCj/pcIsx0jLLmLpjiyW7jzEsh1ZHCos\nO+b7HWPDGNwmmvNaR9MyOgiTSRPGi4iIZ4gJ82d0/2aM7t+MvTlF/JKczi+bM/gz5RA7MgrYkVHA\nm7/uJNDXQq+EevRtHknf5pF6vRMV5rrM5XKRml3E6j05rNydw7KdWew5VHTMbQKO/NEY1Caac1tF\nERWiqeBERMTzNQ4P4Ma+Tbmxb1PySsr5dWsmPyens2R7JjlF5SzYksGCLRkA1A+20adZPbo3iaBr\nfDgto4OxaIXBOkWFuQ4pKXewaX8uq3bnsHpPDmtSc8gqOHYPssVsonNsGH2aR9KveSSdYsM0j6WI\niHi1ED8fhnd0z6LhdLpIPpBXcbR1xa5DZOaXMnfdfuau2w9AsM1Kp7gwusaH0zU+nI6xYYT4+Ri8\nFVKdVJi9VF5JOcn789i4L9f9eX8uOzIKcLqOvZ2vxUy7mBC6xofTK6EePZpGEKxfehERqaPMZhPt\nYkJpFxPKHf2bUWp3sGbPYf5IOcSaPTmsTc0hv9TOku1ZLNmeVXG/uIgA2sWE0LZRKG0bhdAuJpTI\nIJuBWyJVSYXZwxWU2tmZUcD2jAK2Z+SzI72AbRn5pGUXH/f2kUE2usSF0a2J+11x20ah+PloIRER\nEZHjsVkt9G5Wj97N6gFgdzjZmp7Pmj3uo7WrU3NIyy4mNbuI1Owi5m04WHHfqGAbLaODaR4VRIvo\nIFpEBdMiKkjT2XkgFeZazuVykVNUTmp2EXsOFZJ25BcyNbuI1ENF7M8t+cf7xoT5V7zLPfo5Ktim\nExdEREROk9ViPrIXOZTrejcBIKewjOQD7qO6m44c1d2VVUhGfikZ+aX8viPrmMeIDPIlvl4gcREB\nxEYEEBcRQHw99+f6QTbMGh9d66gwG6yg1E56XgnpeSVk5JWSnlfCwbwS9h8uJjW7mLTsIgpK7ZU+\nRv1gGy2igmgRFUTzaPe718ToYL2DFRERqQHhgb4VM2ocVVhqZ2u6+8jv9ox895Hg9AL2HS4mq6CM\nrIIyVu/J+dtj2azmihIdE+ZPg1A/ooJtRIf40SDUj+hgP0L8rdr5VcNUmKtYmd3J4aIysovKyC4s\n43BROdmFZeQU/ve6jLxS0vPdBflEZfioBiF+x7wTjavnT1xEAM3qBxEWoGIsIiJSmwTarHSJC6dL\nXPgx1xeW2tmZWVBxtPivR473Hy6h1O6smOLun9isZqJD/IgOsREV4kdkoC/hgb6EB7g/RwT4Eh7o\nQ8SR6zT08szV+cLscrkoczgpKXdSWu6guNxBSbmTojI7BaV2Ckrs5B/5XFDq/sgvOfq5vOL6/BI7\necXl5J9kAf6rYJuVqBDbkSe/H1EhNhqG+BFfL5DYiAAah/vryS4iIuIFAm1WOjQOo0PjsL99r9zh\n5MDhkooCve9wERl5pRw8ehQ6v4TDReWU2p0VtzkZ/j4WwgJ8CPazEmSzEuTnQ7Dt6GX35+CKzz4V\n1wX4WvDzseDvY8HPx4yfjwWb1Vwn9257RGFOySzgz5Rs7E4nZXYn5Q4X5Q4ndoeTsiOX3R//vWx3\nuIvw0a9Lyp0UlzkosTsoLXceKcbuj/+dOeJMmU1UvMsLD/AhPMDX/S7vyNfRIX5EBf/3nWGQzSP+\nG0RERKQa+VjMxNULIK5ewD/epqTcQWZ+6ZHhnO4yffQo9uEjR7JzCssrvi53uCgud1Cc6+BA7pln\nNJnce7jdJfqvH2b8rBZ8rWb3h8WMj8WEj8WMz/9+bXHfxsdiYkBiFC2jg888WDXziKa2JvUwj369\nodp/jtnEX95JWQj2sx7zbuyv78COvisL8bMSZPOpuBwR6EuIn48G7IuIiEiV8/OxEHtkiOaJuFwu\nCkrt5BSWc7i47B+PmueXlP/tqHp+abl7R+ORnYyOI3sXXS4oKXfviITyM96eyCCbRxRmk8vl+sf9\nq06nk/z8/GOuCw4Oxmyu2YUs/kw5xLu/76p4d2I9+u7kfy77WMxHvjYdeedixmp2X7ZZ3e9+/vqO\n6OghBtuRyz4WU508zCAiIiJSGffReseRsuyouPzXI/bF5Y5jjvb/dVRAucPpPvJvP/bra3rG0TU+\noka35XT6rUcUZhERERGRqnA6/VbNV0RERESkEirMIiIiIiKVUGEWEREREamECrOIiIiISCVUmEVE\nREREKqHCLCIiIiJSiUoXLjnejHNOp7PawoiIiIiIVKfjddlKZlkGTqMwFxYWnmIsEREREZHa60SF\nWUMyREREREQqocIsIiIiIlIJFWYRERERkUqYXJUM2nA6nX8bGG0ymTCZTNUeTERERESkqrlcrr+N\nWTabzZjN/7wfudLCLCIiIiJS12lIhoiIiIhIJVSYRUREREQqocIsIiIiIlIJFWbxaAsXLuTmm2+m\nVatWBAYGEhMTw8UXX8zq1auNjuZV8vPzeeihhxg8eDD169fHZDLx1FNPGR1LpFJ63tYM/R2WukCF\nWTzajBkz2L17N/fd9//t3UFIFH0Yx/GfsAiGhw1WIQkXYVHcttCS8KQgEZEeOiyBJ8kKD2ZvdatM\ndzG9aEWCh1YFCaxDgtGhLmFGEOIu4iHq4CHIgpI0JPcgCdMhlHcbnXTcHGf7fmAu//+s+/jw8PAw\nOzv7n54+faq7d+9qbm5OlZWVGhsbczq8jDE/P69YLKbl5WWdOnXK6XAyWlFRkRoaGkzrNTU1qq6u\ndiAi96JudwZ9GP8CnnmgjB8AAAQNSURBVJIBV5ubm1N+fn7K2tLSkgKBgEKhkJ4/f+5QZJlltU1k\nZWXp69evysvLU3t7O1fr0mx+fl4+n0+9vb1qaWlZWzcMQ3v37lVjY6Nu377tYITuQt3uDPow/gVc\nYYar/d6kJSk3N1fBYFCzs7OmvZWVFXV3d+vQoUPKyclZe6746lFYWLgTYbvOVp+/Tp7tSSQSkqSK\nioqU9ZmZGS0uLurIkSNOhOVaW6lbata+rfRh8gy3YmBGxllcXNTU1JQOHDhg2jt79qyuXr2qY8eO\naXR0VENDQ2vN/vLly4pGozsdbkYiz/bE43F5PB6VlZWlrK/eC8rA/PdQs+m1UR8mz3Arj9MBAOnW\n3NysZDKp69evp6w/ePBA9+/fVywW0/nz59fWDcPQmTNnVFNTo7q6up0ON+OQZ/sSiYSCwaBycnJM\n67m5uSouLnYossxGzabfen2YPMPNuMKMXWN8fNz08dxGx/T09Lp/48aNGxoeHtadO3dMV+Pu3bun\n0tLSlEYtSaWlpZKkhYWFv/OP7TLpyLMV8mxfIpHQ4cOHTevj4+MqLy+3/NlW2EfNptdGfZg8w824\nwoxdo6SkRP39/Zs6d7373KLRqG7evKnOzk5duHAhZe/bt2969eqVrly5Ynrdx48fJUn79++3EbX7\nbDfPVsizfZ8/f9anT5/k8aS25ZcvX2pqakqXLl1yKLLMRs2m10Z9mDzD7RiYsWvs27dP586ds/Xa\naDSqSCSiSCSia9eumfZnZ2dlGIYKCgpMe48fP5bP51NVVZWt93ab7eT5T8izffF4XJL06NEjBYNB\nBQIBTU9Pq6+vT9KvJxG8efNGoVDIyTAzDjWbPlZ9mDzD7fh8D67X0dGhSCSi1tZWtbe3r3uO1+uV\nJL179y5l/fXr13r48KEuXrxourKHrSPP9iUSCXk8Hg0MDKi3t1enT5/W2NiYnjx5okAgoBcvXuj7\n9+9Oh5lxqNn0+FMfJs9wO6oTrnbr1i21tbXpxIkTqq2t1cTERMp+ZWWlpF+3FlRVVWloaEhFRUU6\nevSoJicn1dXVpePHj5u+IAizZ8+eKZlMrg1tb9++1cjIiCTp5MmT2rNnD3nehng8roMHDyocDisc\nDqfszczMOBSV+/2pbqnZ7dtMHybPcD0DcLHq6mpD0obH/3358sWor683vF6vkZ2dbYRCIaOnp8f4\n8eOHQ9G7i9/v3zDP79+/XzuPPNuTn59vNDU1OR1GxtlM3VKz27PZPkye4Wb80h8AOOzDhw/y+/0a\nHBxUY2Oj0+EAAH7DwAwAAABY4Et/AAAAgAUGZgAAAMACAzMAAABggYEZAAAAsMDADAAAAFhgYAYA\nAAAsMDADAAAAFhiYAQAAAAsMzAAAAIAFBmYAAADAwk/rpsxs+mU8BQAAAABJRU5ErkJggg==\n", "text/plain": [ "" ] }, "metadata": {}, "output_type": "display_data" } ], "source": [ "from kf_book.gaussian_internal import display_stddev_plot\n", "display_stddev_plot()" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "## Interactive Gaussians\n", "\n", "For those that are reading this in a Jupyter Notebook, here is an interactive version of the Gaussian plots. Use the sliders to modify $\\mu$ and $\\sigma^2$. Adjusting $\\mu$ will move the graph to the left and right because you are adjusting the mean, and adjusting $\\sigma^2$ will make the bell curve thicker and thinner." ] }, { "cell_type": "code", "execution_count": 22, "metadata": {}, "outputs": [ { "data": { "application/vnd.jupyter.widget-view+json": { "model_id": "3e38ed0d56f045db94523a2266729107", "version_major": 2, "version_minor": 0 }, "text/plain": [ "A Jupyter Widget" ] }, "metadata": {}, "output_type": "display_data" } ], "source": [ "import math\n", "from ipywidgets import interact, interactive, fixed\n", "\n", "set_figsize(y=3)\n", "def plt_g(mu,variance):\n", " plt.figure()\n", " xs = np.arange(2, 8, 0.1)\n", " ys = gaussian(xs, mu, variance)\n", " plt.plot(xs, ys)\n", " plt.ylim((0, 1))\n", "\n", "interact (plt_g, mu=(0., 10), variance = (.2, 1.));" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "Finally, if you are reading this online, here is an animation of a Gaussian. First, the mean is shifted to the right. Then the mean is centered at $\\mu=5$ and the variance is modified.\n", "\n", "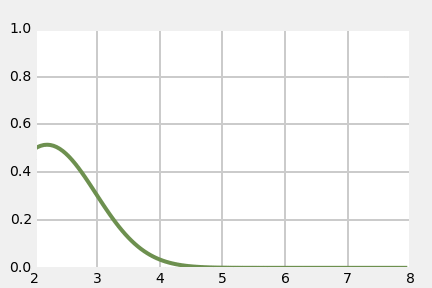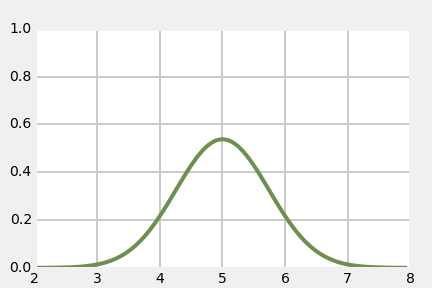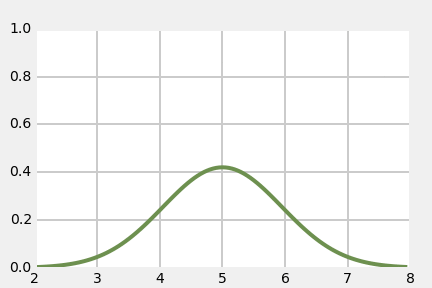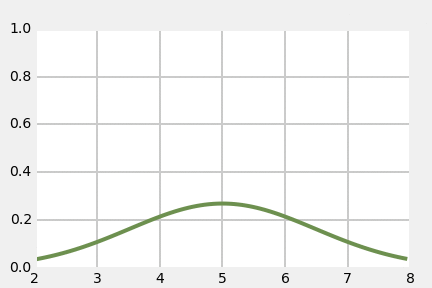" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "## Computational Properties of Gaussians\n", "\n", "A remarkable property of Gaussians is that the sum of two independent Gaussians is another Gaussian! The product is not Gaussian, but proportional to a Gaussian.\n", "\n", "The discrete Bayes filter works by multiplying and adding arbitrary probability distributions. The Kalman filter uses Gaussians instead of arbitrary distributions, but the rest of the algorithm remains the same. This means we will need to multiply and add Gaussians. \n", "\n", "The Gaussian is a nonlinear function. Typically, if you multiply a nonlinear equation with itself you end up with a different type of equation. For example, the shape of `sin(x)sin(x)` is very different from `sin(x)`. But the result of multiplying two Gaussians is yet another Gaussian. This is a key reason why Kalman filters are computationally feasible. Said another way, Kalman filters use Gaussians *because* they are computationally nice. \n", "\n", "\n", "The product of two independent Gaussians is given by:\n", "\n", "$$\\begin{aligned}\\mu &=\\frac{\\sigma_1^2\\mu_2 + \\sigma_2^2\\mu_1}{\\sigma_1^2+\\sigma_2^2}\\\\\n", "\\sigma^2 &=\\frac{\\sigma_1^2\\sigma_2^2}{\\sigma_1^2+\\sigma_2^2} \n", "\\end{aligned}$$\n", "\n", "The sum of two Gaussians is given by\n", "\n", "$$\\begin{gathered}\\mu = \\mu_1 + \\mu_2 \\\\\n", "\\sigma^2 = \\sigma^2_1 + \\sigma^2_2\n", "\\end{gathered}$$\n", "\n", "The remainder of this section is optional. I will derive the equations for the sum and product of two Gaussians. You will not need to understand this material to understand the rest of the book, so long as you accept the results. " ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "### Product of Gaussians\n", "\n", "You can find this result by multiplying the equation for two Gaussians together and combining terms. The algebra gets messy. I will derive it using Bayes theorem. We can state the problem as: let the prior be $N(\\bar\\mu, \\bar\\sigma^2)$, and measurement be $z \\propto N(z, \\sigma_z^2)$. What is the posterior x given the measurement z?\n", "\n", "Write the posterior as $P(x \\mid z)$. Now we can use Bayes Theorem to state\n", "\n", "$$P(x \\mid z) = \\frac{P(z \\mid x)P(x)}{P(z)}$$\n", "\n", "$P(z)$ is a normalizing constant, so we can create a proportinality\n", "\n", "$$P(x \\mid z) \\propto P(z|x)P(x)$$\n", "\n", "Now we subtitute in the equations for the Gaussians, which are\n", "\n", "$$P(z \\mid x) = \\frac{1}{\\sqrt{2\\pi\\sigma_z^2}}\\exp \\Big[-\\frac{(z-x)^2}{2\\sigma_z^2}\\Big]$$\n", "\n", "$$P(x) = \\frac{1}{\\sqrt{2\\pi\\bar\\sigma^2}}\\exp \\Big[-\\frac{(x-\\bar\\mu)^2}{2\\bar\\sigma^2}\\Big]$$\n", "\n", "We can drop the leading terms, as they are constants, giving us\n", "\n", "$$\\begin{aligned}\n", "P(x \\mid z) &\\propto \\exp \\Big[-\\frac{(z-x)^2}{2\\sigma_z^2}\\Big]\\exp \\Big[-\\frac{(x-\\bar\\mu)^2}{2\\bar\\sigma^2}\\Big]\\\\\n", "&\\propto \\exp \\Big[-\\frac{(z-x)^2}{2\\sigma_z^2}-\\frac{(x-\\bar\\mu)^2}{2\\bar\\sigma^2}\\Big] \\\\\n", "&\\propto \\exp \\Big[-\\frac{1}{2\\sigma_z^2\\bar\\sigma^2}[\\bar\\sigma^2(z-x)^2-\\sigma_z^2(x-\\bar\\mu)^2]\\Big]\n", "\\end{aligned}$$\n", "\n", "Now we multiply out the squared terms and group in terms of the posterior $x$.\n", "\n", "$$\\begin{aligned}\n", "P(x \\mid z) &\\propto \\exp \\Big[-\\frac{1}{2\\sigma_z^2\\bar\\sigma^2}[\\bar\\sigma^2(z^2 -2xz + x^2) + \\sigma_z^2(x^2 - 2x\\bar\\mu+\\bar\\mu^2)]\\Big ] \\\\\n", "&\\propto \\exp \\Big[-\\frac{1}{2\\sigma_z^2\\bar\\sigma^2}[x^2(\\bar\\sigma^2+\\sigma_z^2)-2x(\\sigma_z^2\\bar\\mu + \\bar\\sigma^2z) + (\\bar\\sigma^2z^2+\\sigma_z^2\\bar\\mu^2)]\\Big ]\n", "\\end{aligned}$$\n", "\n", "The last parentheses do not contain the posterior $x$, so it can be treated as a constant and discarded.\n", "\n", "$$P(x \\mid z) \\propto \\exp \\Big[-\\frac{1}{2}\\frac{x^2(\\bar\\sigma^2+\\sigma_z^2)-2x(\\sigma_z^2\\bar\\mu + \\bar\\sigma^2z)}{\\sigma_z^2\\bar\\sigma^2}\\Big ]\n", "$$\n", "\n", "Divide numerator and denominator by $\\bar\\sigma^2+\\sigma_z^2$ to get\n", "\n", "$$P(x \\mid z) \\propto \\exp \\Big[-\\frac{1}{2}\\frac{x^2-2x(\\frac{\\sigma_z^2\\bar\\mu + \\bar\\sigma^2z}{\\bar\\sigma^2+\\sigma_z^2})}{\\frac{\\sigma_z^2\\bar\\sigma^2}{\\bar\\sigma^2+\\sigma_z^2}}\\Big ]\n", "$$\n", "\n", "Proportionality allows us create or delete constants at will, so we can factor this into\n", "\n", "$$P(x \\mid z) \\propto \\exp \\Big[-\\frac{1}{2}\\frac{(x-\\frac{\\sigma_z^2\\bar\\mu + \\bar\\sigma^2z}{\\bar\\sigma^2+\\sigma_z^2})^2}{\\frac{\\sigma_z^2\\bar\\sigma^2}{\\bar\\sigma^2+\\sigma_z^2}}\\Big ]\n", "$$\n", "\n", "A Gaussian is\n", "\n", "$$N(\\mu,\\, \\sigma^2) \\propto \\exp\\Big [-\\frac{1}{2}\\frac{(x - \\mu)^2}{\\sigma^2}\\Big ]$$\n", "\n", "So we can see that $P(x \\mid z)$ has a mean of\n", "\n", "$$\\mu_\\mathtt{posterior} = \\frac{\\sigma_z^2\\bar\\mu + \\bar\\sigma^2z}{\\bar\\sigma^2+\\sigma_z^2}$$\n", "\n", "and a variance of\n", "$$\n", "\\sigma_\\mathtt{posterior} = \\frac{\\sigma_z^2\\bar\\sigma^2}{\\bar\\sigma^2+\\sigma_z^2}\n", "$$\n", "\n", "I've dropped the constants, and so the result is not a normal, but proportional to one. Bayes theorem normalizes with the $P(z)$ divisor, ensuring that the result is normal. We normalize in the update step of our filters, ensuring the filter estimate is Gaussian.\n", "\n", "$$\\mathcal N_1 = \\| \\mathcal N_2\\cdot \\mathcal N_3\\|$$" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "### Sum of Gaussians\n", "\n", "The sum of two Gaussians is given by\n", "\n", "$$\\begin{gathered}\\mu = \\mu_1 + \\mu_2 \\\\\n", "\\sigma^2 = \\sigma^2_1 + \\sigma^2_2\n", "\\end{gathered}$$\n", "\n", "There are several proofs for this. I will use convolution since we used convolution in the previous chapter for the histograms of probabilities. \n", "\n", "To find the density function of the sum of two Gaussian random variables we sum the density functions of each. They are nonlinear, continuous functions, so we need to compute the sum with an integral. If the random variables $p$ and $z$ (e.g. prior and measurement) are independent we can compute this with\n", "\n", "$p(x) = \\int\\limits_{-\\infty}^\\infty f_p(x-z)f_z(z)\\, dx$\n", "\n", "This is the equation for a convolution. Now we just do some math:\n", "\n", "\n", "$p(x) = \\int\\limits_{-\\infty}^\\infty f_2(x-x_1)f_1(x_1)\\, dx$\n", "\n", "$= \\int\\limits_{-\\infty}^\\infty \n", "\\frac{1}{\\sqrt{2\\pi}\\sigma_z}\\exp\\left[-\\frac{(x - z - \\mu_z)^2}{2\\sigma^2_z}\\right]\n", "\\frac{1}{\\sqrt{2\\pi}\\sigma_p}\\exp\\left[-\\frac{(x - \\mu_p)^2}{2\\sigma^2_p}\\right] \\, dx$\n", "\n", "$= \\int\\limits_{-\\infty}^\\infty\n", "\\frac{1}{\\sqrt{2\\pi}\\sqrt{\\sigma_p^2 + \\sigma_z^2}} \\exp\\left[ -\\frac{(x - (\\mu_p + \\mu_z)))^2}{2(\\sigma_z^2+\\sigma_p^2)}\\right]\n", "\\frac{1}{\\sqrt{2\\pi}\\frac{\\sigma_p\\sigma_z}{\\sqrt{\\sigma_p^2 + \\sigma_z^2}}} \\exp\\left[ -\\frac{(x - \\frac{\\sigma_p^2(x-\\mu_z) + \\sigma_z^2\\mu_p}{}))^2}{2\\left(\\frac{\\sigma_p\\sigma_x}{\\sqrt{\\sigma_z^2+\\sigma_p^2}}\\right)^2}\\right] \\, dx$\n", "\n", "$= \\frac{1}{\\sqrt{2\\pi}\\sqrt{\\sigma_p^2 + \\sigma_z^2}} \\exp\\left[ -\\frac{(x - (\\mu_p + \\mu_z)))^2}{2(\\sigma_z^2+\\sigma_p^2)}\\right] \\int\\limits_{-\\infty}^\\infty\n", "\\frac{1}{\\sqrt{2\\pi}\\frac{\\sigma_p\\sigma_z}{\\sqrt{\\sigma_p^2 + \\sigma_z^2}}} \\exp\\left[ -\\frac{(x - \\frac{\\sigma_p^2(x-\\mu_z) + \\sigma_z^2\\mu_p}{}))^2}{2\\left(\\frac{\\sigma_p\\sigma_x}{\\sqrt{\\sigma_z^2+\\sigma_p^2}}\\right)^2}\\right] \\, dx$\n", "\n", "The expression inside the integral is a normal distribution. The sum of a normal distribution is one, hence the integral is one. This gives us\n", "\n", "$$p(x) = \\frac{1}{\\sqrt{2\\pi}\\sqrt{\\sigma_p^2 + \\sigma_z^2}} \\exp\\left[ -\\frac{(x - (\\mu_p + \\mu_z)))^2}{2(\\sigma_z^2+\\sigma_p^2)}\\right]$$\n", "\n", "This is in the form of a normal, where\n", "\n", "$$\\begin{gathered}\\mu_x = \\mu_p + \\mu_z \\\\\n", "\\sigma_x^2 = \\sigma_z^2+\\sigma_p^2\\, \\square\\end{gathered}$$" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "## Computing Probabilities with scipy.stats\n", "\n", "In this chapter I used code from [FilterPy](https://github.com/rlabbe/filterpy) to compute and plot Gaussians. I did that to give you a chance to look at the code and see how these functions are implemented. However, Python comes with \"batteries included\" as the saying goes, and it comes with a wide range of statistics functions in the module `scipy.stats`. So let's walk through how to use scipy.stats to compute statistics and probabilities.\n", "\n", "The `scipy.stats` module contains a number of objects which you can use to compute attributes of various probability distributions. The full documentation for this module is here: http://docs.scipy.org/doc/scipy/reference/stats.html. We will focus on the norm variable, which implements the normal distribution. Let's look at some code that uses `scipy.stats.norm` to compute a Gaussian, and compare its value to the value returned by the `gaussian()` function from FilterPy." ] }, { "cell_type": "code", "execution_count": 23, "metadata": { "scrolled": true }, "outputs": [ { "name": "stdout", "output_type": "stream", "text": [ "0.131146572034\n", "0.131146572034\n" ] } ], "source": [ "from scipy.stats import norm\n", "import filterpy.stats\n", "print(norm(2, 3).pdf(1.5))\n", "print(filterpy.stats.gaussian(x=1.5, mean=2, var=3*3))" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "The call `norm(2, 3)` creates what scipy calls a 'frozen' distribution - it creates and returns an object with a mean of 2 and a standard deviation of 3. You can then use this object multiple times to get the probability density of various values, like so:" ] }, { "cell_type": "code", "execution_count": 24, "metadata": {}, "outputs": [ { "name": "stdout", "output_type": "stream", "text": [ "pdf of 1.5 is 0.1311\n", "pdf of 2.5 is also 0.1311\n", "pdf of 2 is 0.1330\n" ] } ], "source": [ "n23 = norm(2, 3)\n", "print('pdf of 1.5 is %.4f' % n23.pdf(1.5))\n", "print('pdf of 2.5 is also %.4f' % n23.pdf(2.5))\n", "print('pdf of 2 is %.4f' % n23.pdf(2))" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "The documentation for [scipy.stats.norm](http://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.norm.html#scipy.stats.normfor) [2] lists many other functions. For example, we can generate $n$ samples from the distribution with the `rvs()` function." ] }, { "cell_type": "code", "execution_count": 25, "metadata": {}, "outputs": [ { "name": "stdout", "output_type": "stream", "text": [ "[ 0.824 3.24 3.113 4.934 -3.799 -1.775 -1.02\n", " 7.542 -0.76 1.875 3.862 1.77 4.846 -0.818\n", " 5.726]\n" ] } ], "source": [ "np.set_printoptions(precision=3, linewidth=50)\n", "print(n23.rvs(size=15))" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "We can get the [*cumulative distribution function (CDF)*](https://en.wikipedia.org/wiki/Cumulative_distribution_function), which is the probability that a randomly drawn value from the distribution is less than or equal to $x$." ] }, { "cell_type": "code", "execution_count": 26, "metadata": {}, "outputs": [ { "name": "stdout", "output_type": "stream", "text": [ "0.5\n" ] } ], "source": [ "# probability that a random value is less than the mean 2\n", "print(n23.cdf(2))" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "We can get various properties of the distribution:" ] }, { "cell_type": "code", "execution_count": 27, "metadata": {}, "outputs": [ { "name": "stdout", "output_type": "stream", "text": [ "variance is 9.0\n", "standard deviation is 3.0\n", "mean is 2.0\n" ] } ], "source": [ "print('variance is', n23.var())\n", "print('standard deviation is', n23.std())\n", "print('mean is', n23.mean())" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "## Fat Tails\n", "\n", "Earlier I mentioned the *central limit theorem*, which states that under certain conditions the arithmetic sum of any independent random variable will be normally distributed, regardless of how the random variables are distributed. This is important to us because nature is full of distributions which are not normal, but when we apply the central limit theorem over large populations we end up with normal distributions. \n", "\n", "However, a key part of the proof is “under certain conditions”. These conditions often do not hold for the physical world. The resulting distributions are called *fat tailed*. Tails is a colloquial term for the far left and right side parts of the curve where the probability density is close to zero.\n", "\n", "Let's consider a trivial example. We think of things like test scores as being normally distributed. If you have ever had a professor “grade on a curve” you have been subject to this assumption. But of course test scores cannot follow a normal distribution. This is because the distribution assigns a nonzero probability distribution for *any* value, no matter how far from the mean. So, for example, say your mean is 90 and the standard deviation is 13. The normal distribution assumes that there is a large chance of somebody getting a 90, and a small chance of somebody getting a 40. However, it also implies that there is a tiny chance of somebody getting a grade of -10, or 150. It assigns an infinitesimal chance of getting a score of $-10^{300}$ or $10^{32986}$. The tails of a Gaussian distribution are infinitely long.\n", "\n", "But for a test we know this is not true. Ignoring extra credit, you cannot get less than 0, or more than 100. Let's plot this range of values using a normal distribution." ] }, { "cell_type": "code", "execution_count": 28, "metadata": {}, "outputs": [ { "data": { "image/png": "iVBORw0KGgoAAAANSUhEUgAAAxMAAAEaCAYAAABqygqxAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzt3Xt8VOW59//vTGaSkAOnhAQmHBQw\nnEKCB4hBESIiQcUKGimCFbC6Sy178+su1NoKWPWpUt0tj1ue7irdpo0JFQHxAFQIh7agQVACiYDK\nIUAAAwmQEwmZmfX7I2RKJAlJSOaUz/v1yivtmvueda25WOO6su573SbDMAwBAAAAQDOZPR0AAAAA\nAN9EMQEAAACgRSgmAAAAALQIxQQAAACAFqGYAAAAANAiFk8H4ElOp1NOp7PONpPJJJPJ5KGIAAAA\ngJYzDEPffVir2WyW2dw29xDafTFRXl7u6TAAAACANhMaGtpmxQTDnAAAAAC0CMUEAAAAgBahmAAA\nAADQIu16zkR9E63bckwZ3CMvL092u10Wi0VDhgzxdDi4RuTTv5BP/0I+/Qv59A/1zQluy4cLUUx8\nR1vOdod7OJ1OORwOcuknyKd/IZ/+hXz6F/Lpv9qymOBfCgAAAIAWoZgAAAAA0CIUEwAAAABahGIC\nAAAAQItQTAAAAABoEYoJAAAAAC1CMQEAAACgRSgmAAAAALQIxQQAAACAFqGYAAAAANAiFBMAAAAA\nWoRiAgAAAECLUEwAAAAAaBG3FRNlZWWaO3eubDabgoODNWzYMC1fvrxJfQsLCzVjxgxFRkYqJCRE\nSUlJysrKuqJdVVWVfvvb3youLk6hoaGKjo7WhAkTtH379tY+HAAAAKDdc1sxMXnyZKWlpWnhwoVa\nt26dhg8frqlTpyojI6PRflVVVRo7dqyysrK0ZMkSrVmzRtHR0UpJSdHWrVvrtH3iiSf09NNP64EH\nHtAHH3yg119/XadPn9bo0aO1Y8eOtjw8AAAAoN2xuGMna9eu1YYNG5SRkaGpU6dKkpKTk5Wfn695\n8+ZpypQpCggIqLfvsmXLlJubq+3btyspKcnVNyEhQfPnz1d2drakmqIjIyNDjzzyiF544QVX/9tu\nu002m01vv/22RowY0cZHCgAAALQfbrkzsXr1aoWFhSk1NbXO9pkzZ+rEiROugqChvgMGDHAVEpJk\nsVg0ffp07dixQwUFBZIks9kss9msTp061enfsWNHmc1mBQcHt+IRAQAAAHDLnYnc3FwNGjRIFkvd\n3cXHx7teHzlyZIN9R40adcX22r55eXmKiYmR1WrVj3/8Yy1btkx33XWX7rzzThUXF+uZZ55Rp06d\n9MQTTzQp1ry8PDmdzuYcHrxMdXW163dOTo6Ho8G1Ip/+hXz6F/LpX8infzCbzerdu7fb9ueWYqKo\nqEh9+/a9YnvXrl1drzfWt7bd1fr+7ne/U6dOnfTggw+6CoLevXtr06ZN6t+/f5NitdvtcjgcTWoL\n71f7xQj/QD79C/n0L+TTv5BP39XQ1IG24pZiQpJMJlOLXmtO3xdffFGvvPKKFi1apFGjRqmkpET/\n/d//rXHjxunjjz/WjTfeeNU4LRaLzGaemOvLLv8CtFqtHowErYF8+hfy6V/Ip38hn/7B3dexbikm\nIiIi6r37UFxcLEn13nlobt99+/ZpwYIFWrx4sX72s5+52k2YMEGDBw/WT3/6U23evPmqsQ4ZMoRi\nwsfl5OSourpaVqtVCQkJng4H14h8+hfy6V/Ip38hn/7B6XSqtLTUbftzy1Xz0KFDtW/fPtnt9jrb\n9+7dK0mKi4trtG9tu8b65uTkyDAMDR8+vE672hMiNzf3mo4BAAAAQF1uKSYmTZqksrIyrVy5ss72\ntLQ02Ww2JSYmNtp3//79dZ74ZLfblZ6ersTERNlsNkly/f7000/r9K+qqtLnn3+unj17ttbhAAAA\nAJCbhjlNmDBB48aN0+zZs1VSUqL+/fsrMzNT69evV3p6umuiyOOPP660tDQdPHhQffr0kSTNmjVL\nr7/+ulJTU/XSSy8pKipKS5cu1YEDB7Rx40bXPm6//XYNHz5cixYtUkVFhe644w6dP39er732mg4f\nPqy//OUv7jhUAAAAoN1w2wTsVatW6Ze//KUWLFig4uJiDRw4UJmZmfr+97/vauNwOORwOGQYhmtb\nUFCQsrKyNH/+fM2ZM0cVFRUaNmyY1q1bp9GjR7vamc1mbdiwQb/97W+1YsUKvfLKKwoLC9PgwYO1\ndu1aTZgwwV2HCgAAALQLJuPyK/d2pr4JKuHh4UzA9nFMIPMv5NO/kE//Qj79C/n0D+6+vuWqGQAA\nAECLUEwAAAAAaBGKCQAAAAAtQjEBAAAAoEUoJgAAAAC0CMUEAAAAgBahmAAAAADQIm5btA4AAMBX\nHDlTrrez8/WPr8/oWHGFTCaTenUN0R2xkZo2oo96R4R4OkTAK1BMAAAAXFJx0a7F6w8o7ZMj+u6y\nvvtOlmjfyRK98fdDmjHyev1sfKxCArmUQvvGGQAAACDpWHGFHvvfHTp0ulySlDygmx68uacG9+go\nQ1LeiRKt2HlM//j6jP607bC2HzyjZTOGK6ZzB88GDngQxQQAAGj3Dpwq1bQ3s3WmrErdOwZr8UPx\nuiO2W502/bqF6f4Em7Z+dVr/+U6O9p8q1QOvb9Nfn7xVfbuFeShywLOYgA0AANq1Y8UVenRZTSEx\nqEdHrfnJbVcUEpcbHdtNa35ymwZEh+t0aZWmv5mtE+cuuDFiwHtQTAAAgHar4qJdj6d9psLSKsVG\nh2n5E7cqumPwVfvFdO6gt59IVN9uoTpxvlJP/mWnKqsdbogY8C4UEwAAoN1asCZPX31bpqjwIKXN\nGqFOIdYm940MC9KfZ41Q19BA5RaUaMGa3DaMFPBOFBMAAKBdWv3Fcb2767jMJmnJ929Uj07Nn0jd\ns0uIXpt6o8wm6Z2dx7U+91QbRAp4L4oJAADQ7pwurdKi97+UJP3H2Fgl9Yto8Xvd1j9SPxrdT5L0\nq/f2qrj8YqvECPgCigkAANDuPP/hlzp/oVpDbB31VHK/a36//7jrBt0QFaYzZRf1/IdftkKEgG+g\nmAAAAO3KP74+rfdzTshskl6aHC9LwLVfDgVZAvRKaoJMJmn1FwXalV/cCpEC3o9iAgAAtBsOp6EX\nP9onSfpB0nUa2rNTq713Qq/OevjmXpKk5z74Uk6ncZUegO+jmAAAAO3Gqs+Pa/+pUnUMtmjuXTe0\n+vv/bPwAhQVZtOf4ea36oqDV3x/wNhQTAACgXbhw0aFXP/5KkvSTO/urc0hgq++jW3iQnkruL0la\nkvWVqh3OVt8H4E0oJgAAQLuQ/mm+TpVUKqZzB/0g6bo228+MkdcpMixIx4ov6N1dx9tsP4A3oJgA\nAAB+r7LaoT/+45Ak6T/G3qBga0Cb7atDYIBmj6l5QtRrWV+rys7K2PBfFBMAAMDvvbPzmE6XVimm\ncwdNuimmzfc3LbG3ojsG6cT5Sr2zk7sT8F8UEwAAwK9dtDv1hy0HJUk/Gt1X1lZ4FOzVBFsDNPvS\nQnZv/uOQHDzZCX6KYgIAAPi193YX6MT5SnULD1LqLb3ctt+Hh/dSpw5W5RdVaMOXp9y2X8CdKCYA\nAIDfMgxDf/rnYUnS47df36ZzJb4rJNCiR2/tI0n6498PuW2/gDtRTAAAAL/1yaEi7T9Vqg7WAE0d\n3tvt+//ByD4KDDDr86PnWBUbfoliAgAA+K3/3XZEkjT5phh1CrG6ff9R4cF64EabJOmNvx92+/6B\ntkYxAQAA/NLRogpt3PetJGnmbdd5LI4fjuorSfr4y1M6ef6Cx+IA2gLFBAAA8EtpnxyRYUh3xHZT\n/6hwj8URGx2uEdd3ldOQlu845rE4gLbgtmKirKxMc+fOlc1mU3BwsIYNG6bly5c3qW9hYaFmzJih\nyMhIhYSEKCkpSVlZWfW2LS8v14IFCxQbG6ugoCBFREQoOTlZX3/9dWseDgAA8GKV1Q7X6tMzR17n\n2WAkTb80EXv5Z0dldzg9HA3Qeizu2tHkyZP12Wef6aWXXlJsbKwyMjI0depUOZ1OPfLIIw32q6qq\n0tixY3Xu3DktWbJEUVFRev3115WSkqKNGzdq9OjRrrZlZWVKTk7WiRMn9PTTTys+Pl7nz5/X9u3b\nVVFR4Y7DBAAAXmB97imdv1CtmM4ddEdsN0+Ho/FDohURGqhvS6q0cV+hUuK6ezokoFW4pZhYu3at\nNmzY4CogJCk5OVn5+fmaN2+epkyZooCA+h/VtmzZMuXm5mr79u1KSkpy9U1ISND8+fOVnZ3tavur\nX/1K+/bt0549e9S3b1/X9vvvv78Njw4AAHibjB1HJUkP39JLAWaTh6ORgiwBenh4L/2/LQf1dnY+\nxQT8hluGOa1evVphYWFKTU2ts33mzJk6ceJEnYKgvr4DBgxwFRKSZLFYNH36dO3YsUMFBQWSpIqK\nCr355ptKTU2tU0gAAID25eDpMu04XCyzSXp4eE9Ph+MydXhvmUzSP74+o/yick+HA7QKt9yZyM3N\n1aBBg2Sx1N1dfHy86/WRI0c22HfUqFFXbK/tm5eXp5iYGO3atUvl5eW64YYbNHv2bC1fvlzl5eWK\nj4/Xc889p3vvvbdJsebl5cnpZCyjL6uurnb9zsnJ8XA0uFbk07+QT//irfn83y/OSZJu6hGswiNf\nqdDD8Vzuxu5B+vxklf7vh7v0g2GdPB1OHd6aTzSP2WxW797uW1PFLcVEUVFRvXcLunbt6nq9sb61\n7RrrW3uH4uWXX9bQoUP15z//WWazWa+++qomTpyodevWafz48VeN1W63y+FwXP2g4BNqvxjhH8in\nfyGf/sVb8lntNLTpcM1f/cdeF+Q1cdVK7hOsz09WafORcj08uIMCTJ4fglUfb/vc0HQNTR1oK26b\ngG1q5GRp7LWm9q29mxAYGKh169YpPLzmEXDJycm64YYb9PzzzzepmLBYLDKbeWKuL7v8C9Bqdf8C\nRWhd5NO/kE//4o35/OxYhUqqDHXtYFZirzCvmC9xuaTeFoV9XqLiC07tK3Lqxh7Bng7JxRvzieZz\n93WsW4qJiIiIeu8+FBfXLCtf352H5vaNiIiQJI0cOdJVSEhSSEiIRo8erffee69JsQ4ZMoRiwsfl\n5OSourpaVqtVCQkJng4H14h8+hfy6V+8MZ+v7d4pSZqSeL1uunGgh6Op36SjFv3l03x9cS5QM1K8\n43OTvDOfaD6n06nS0lK37c8tV81Dhw7Vvn37ZLfb62zfu3evJCkuLq7RvrXtGutbO4eiPoZhUCAA\nAODnisqqtOVAzQyJyTfGeDiahj10c82k8PW5p1RSyXAi+Da3XGFPmjRJZWVlWrlyZZ3taWlpstls\nSkxMbLTv/v376zzxyW63Kz09XYmJibLZbJKkHj16KCkpSdu2bVNJSYmrbUVFhbZu3apbb721lY8K\nAAB4kw/3nJTdaSgupqNuiPbcitdXE9+zk/pHhanK7tTaPSc9HQ5wTdxSTEyYMEHjxo3T7Nmz9cYb\nb2jz5s168skntX79ei1evNg1UeTxxx+XxWJRfn6+q++sWbM0ZMgQpaamKiMjQxs3btTDDz+sAwcO\n6OWXX66zn1deeUWlpaUaP3683nvvPa1Zs0YpKSk6c+aMnn/+eXccKgAA8JBVX9Q8jGXSjd7zONj6\nmEwm192J2lW6AV/ltrE/q1at0qOPPqoFCxYoJSVF2dnZyszM1LRp01xtHA6HHA6HDMNwbQsKClJW\nVpaSk5M1Z84cTZw4USdPntS6devqrH4t1cyXyMrKUlBQkKZNm6ZHHnlEVqtVW7ZsqbNOBQAA8C8H\nT5cp59g5BZhNuj/B5ulwrmrSjTEym6Sd+Wd1+AxrTsB3ue1pTmFhYVqyZImWLFnSYJu33npLb731\n1hXbo6OjlZaW1qT93H777dqyZUsLowQAAL7ovUt3JUbdEKlu4UEejubqojsG6/YbuunvX53Wmt0F\nmntXrKdDAlqEWckAAMCnOZ2GVruGOHnvxOvvemBYzR2U93NO1BmVAfgSigkAAODTduaf1fGzFxQW\nZNHdg7t7OpwmGzc4WkEWsw6dLlfeiZKrdwC8EMUEAADwaWt219yVSInrrg6B7l3991qEB1t158Ao\nSdIHOSc8HA3QMhQTAADAZzmchv6Wd0qSNNEHJl5/V+1k8Q9yTsjpZKgTfA/FBAAA8FnZh4t0puyi\nOodYNbJfhKfDabbkgVEKC7LoxPlK7Tp61tPhAM1GMQEAAHzW2r01i77dPTha1gDfu6wJtgbo7iHR\nkqT3dzPUCb7H9846AAAA1QxxWp/7rSTpnqE9PBxNy9UOdVq796TsDqeHowGah2ICAAD4pB2Hi3Wm\nrEqdOlh1W/9IT4fTYrf1j1TX0EAVlV/UtoNFng4HaBaKCQAA4JN8fYhTLWuAWfcMrXmkLUOd4Gt8\n98wDAADtlsNpaF1uzVOc7on33SFOte5PqFls7+MvT6nK7vBwNEDTUUwAAACfs/NIzRCnjsEW3dbP\nd4c41bqlTxdFhQeptNKubd+c8XQ4QJNRTAAAAJ9TO8Rp3ODuCrT4/uWM2WzShLiaoU5r957ycDRA\n0/n+2QcAANoV52VDnO6N7+7haFpP7ROpPs47pYt2nuoE30AxAQAAfMrO/LMqLK1SeLBFt/fv5ulw\nWs0t13VVZFiQSirt2n6QoU7wDRQTAADAp/xriFO0XwxxqhVQZ6jTSQ9HAzSN/5yBAADA79UMcaq5\n0L7Xhxeqa8iES4+I/fjLb1XNAnbwARQTAADAZ+w6elbfllQpPMii22/w/ac4fVfi9RGKCA3UuYpq\nfcICdvABFBMAAMBnXD7EKcgS4OFoWl+A2aTxl4Y61d6BAbwZxQQAAPAJTqehdZcem3qPHw5xqlU7\nfOtved/KzlAneDmKCQAA4BO+OHZWp0oqFeanQ5xqJV7fVV1DA1VcflHZh4s9HQ7QKIoJAADgEz7a\nU3NX4q5BUQq2+t8Qp1qWALPGD4mWJH3EU53g5SgmAACA17v8KU7+PMSp1oS4S0Odck/J4TQ8HA3Q\nMIoJAADg9b44dk4nz9cMcboj1n8WqmtIUr8IdQ6xqqj8orIP81QneC+KCQAA4PVqn+I01s+HONWy\nBph19+CaoU61k84Bb0QxAQAAvJphGFq3t/0McapVe6zrGOoEL0YxAQAAvNruY+d04nylQgMDNLod\nDHGqdVv/SHXqYNWZsirtPMJTneCdKCYAAIBX+9cQp+h2McSpljXArHGXhjqt5alO8FIUEwAAwGsZ\nhqG1roXquns4Gve797KhTk6GOsELUUwAAACvlXP8vArOXVBIYIDGDIjydDhud1v/SIUHW1RYWqVd\nR896OhzgChQTAADAa9UO77lzYPt4itN3BVoY6gTvRjEBAAC8kmEY+mhPzQX0ve3oKU7fdc+lBezW\n7WWoE7yP24qJsrIyzZ07VzabTcHBwRo2bJiWL1/epL6FhYWaMWOGIiMjFRISoqSkJGVlZTXa58KF\nC4qNjZXJZNIrr7zSGocAAADcaM+lIU4drO1ziFOtUbGRCguy6FRJpb44ds7T4QB1uK2YmDx5stLS\n0rRw4UKtW7dOw4cP19SpU5WRkdFov6qqKo0dO1ZZWVlasmSJ1qxZo+joaKWkpGjr1q0N9nv22WdV\nXl7e2ocBAADcZG3upSFOg6LUIbD9DXGqFWQJ0F2DaoophjrB27ilmFi7dq02bNigpUuX6t/+7d+U\nnJysN954Q+PGjdO8efPkcDga7Lts2TLl5ubqnXfe0bRp0zRu3Di9++67io2N1fz58+vts2PHDr32\n2mtasmRJWx0SAABoQzVPcWKIUy3XAnZ7TzLUCV7FLcXE6tWrFRYWptTU1DrbZ86cqRMnTig7O7vR\nvgMGDFBSUpJrm8Vi0fTp07Vjxw4VFBTUaX/x4kXNmjVLTz31lG655ZbWPRAAAOAWuQUlOlZcM8Qp\nuR0Pcap1R2w3hQYG6MT5SuUcZ6gTvIdbionc3FwNGjRIFoulzvb4+HjX6431rW1XX9+8vLw623/9\n61+rvLxczz///LWGDQAAPOSjS3clkgd2a9dDnGoFWwM0dhBPdYL3sVy9ybUrKipS3759r9jetWtX\n1+uN9a1td7W+u3fv1uLFi/XBBx8oNDRUp0+fbnaseXl5cjqdze4H71FdXe36nZOT4+FocK3Ip38h\nn/6lrfJpGIbe21WzUN2Qjhf5t3LJ4PAqvS9pzedHdW/MRZlMplZ9f85P/2A2m9W7d2+37c8txYSk\nRv/BX+1kaEpfu92uWbNmacqUKRo/fnzLgrz0Po3N4YBvqf1ihH8gn/6FfPqX1sznobPVOlXmUGCA\nlNDNwr+VS4Z2C1BwgEmF5Q7tL7yg/l2tbbYvPnPfFRDg3jt5bikmIiIi6r37UFxcLEn13nlobt/f\n//73OnTokN555x2dO1czlrCkpESSVFlZqXPnzik8PPyqH7DFYpHZzPIbvuzyL0Crte2+aOEe5NO/\nkE//0lb5/PREhSRpuK2DwjsEttr7+jqrVbo5Jljbjl7QjpMXNSg6pFXfn/PTP7j7OtYtxcTQoUOV\nmZkpu91eZ97E3r17JUlxcXGN9q1td7nv9s3NzdX58+d1ww03XNH22Wef1bPPPqsvvvhCw4YNazTW\nIUOGUEz4uJycHFVXV8tqtSohIcHT4eAakU//Qj79S1vk0zAMffa3zZKkR0YNUkI8T3K63DTzSW17\n+3N99q1Dr8bHt+pQJ85P/+B0OlVaWuq2/bnlqnnSpEkqKyvTypUr62xPS0uTzWZTYmJio333799f\n54lPdrtd6enpSkxMlM1mkyQ9/fTT2rx5c52fzMxMSdKPfvQjbd68Wf3792+DowMAAK1lb8H5fz3F\naWA3T4fjdcYM6KZgq1nHii8o70SJp8MB3HNnYsKECRo3bpxmz56tkpIS9e/fX5mZmVq/fr3S09Nd\nQ48ef/xxpaWl6eDBg+rTp48kadasWXr99deVmpqql156SVFRUVq6dKkOHDigjRs3uvYxcOBADRw4\nsM5+jxw5Iknq16+fxowZ445DBQAA16D2KU53DopSSKDbpnb6jJBAi+4cGKW1e0/po70nFRfTydMh\noZ1z23ieVatW6dFHH9WCBQuUkpKi7OxsZWZmatq0aa42DodDDodDhvGvxViCgoKUlZWl5ORkzZkz\nRxMnTtTJkye1bt06jR492l3hAwCANmYYhj7aU1NM3MdCdQ2aEPevBewuv2YCPMFtJX9YWJiWLFnS\n6KrUb731lt56660rtkdHRystLa3Z+7zuuus4yQAA8BF7jp/X8bM1Q5zGsFBdg+4cGKUgi1lHiir0\n5ckSDbFxdwKew0xjAADgFWqHOI0dFMVCdY0IDbJozICa+SQsYAdPo5gAAAAeV2eIE09wuqp7Lg0D\nW7v3FKMw4FEUEwAAwONyjp9XwbkLCglkiFNTjB0UrUCLWYfPlGv/Kfc9BhT4LooJAADgcR/tOSGp\n5iI52MoQp6sJC7JodGzNUKd1DHWCB1FMAAAAjzIMQ2v3npIk3ctTnJrsnqHdJUkf8lQneBDFBAAA\n8Kjdx86p4NwFhQYGuCYW4+ruujTU6dDpchawg8dQTAAAAI/6IKf2KU4McWqO8GCr7hpUM7/k/ZwT\nHo4G7RXFBAAA8BiH09AHl+ZL3J9g83A0vuf+hBhJ0vu7T8jpZKgT3I9iAgAAeMwnB4t0urRKnUOs\nuiOWIU7NNWZAN4UHW3SqpFI7jhR7Ohy0QxQTAADAY97bXSCpZuJ1oIXLkuYKtgZoQlzNROw1uxnq\nBPfjrAUAAB5RWe3Q+tyapzh9b1iMh6PxXbWf3dq9J3XR7vRwNGhvKCYAAIBHbNpfqLIqu2I6d9At\nfbp4OhyfdWvfCHULD9L5C9X6+1enPR0O2hmKCQAA4BHvfVEzxOn+YTaZzSYPR+O7AswmTYyvmby+\nhqc6wc0oJgAAgNudr6jWlgM1f0X/3jCe4nStaj/DDV+eUnmV3cPRoD2hmAAAAG63NvekLjqcGtg9\nXAO7d/R0OD4vvmcnXRcRospqpzZ8+a2nw0E7QjEBAADcbs3ufw1xwrUzmUy6/9JE7NrPFnAHigkA\nAOBWJ89fUPbhmjURWKiu9dQOdfr712dUWFrp4WjQXlBMAAAAt1r1eYEMQxpxXVf17BLi6XD8Rr9u\nYRrWq7McTkNrvmAiNtyDYgIAALiNYRh6d9dxSdJDN/f0cDT+p/YzXbHrmAzD8HA0aA8oJgAAgNvs\nyj+rw2fK1cEaoHvie3g6HL8zMcGmIItZX31bpr0F5z0dDtoBigkAAOA2K3bW3JW4Z2gPhQVZPByN\n/+nUwarxQ7pL+tdnDbQligkAAOAWFRft+nBPzVj+1FsY4tRWaoc6rdldoMpqh4ejgb+jmAAAAG6x\nPveUyi861LtriBKv7+rpcPzWbf0j1aNTsEoq7dq4jzUn0LYoJgAAgFvUDrt56OaeMplMHo7GfwWY\nTXrwpksTsRnqhDZGMQEAANrcseIKfXKoSCaT9CBPcWpztUOd/vH1aZ06z5oTaDsUEwAAoM2t2HlM\nknRbv0jFdO7g4Wj833WRoRp+XRc5DendXcc8HQ78GMUEAABoU9UOp5Z/VnNB+/0RvTwcTfvx/eG9\nJUmZO47J4WTNCbQNigkAANCmNn75rQpLqxQZFqS7B3f3dDjtxr3xPdQ5xKqCcxe05UChp8OBn6KY\nAAAAbert7KOSpCnDeyrQwqWHuwRbA5R6ae5E+qf5Ho4G/oozGgAAtJnDZ8r1z2/OyGT617AbuM8j\niX0kSVu+Oq1jxRUejgb+iGICAAC0mYzsmr+IJw+IUq+uIR6Opv25PjJUt/ePlGFIGTuOejoc+CGK\nCQAA0CYqqx1asatmnYNpidyV8JTpt9Z89u98dkwX7U4PRwN/47ZioqysTHPnzpXNZlNwcLCGDRum\n5cuXN6lvYWGhZsyYocjISIWEhCgpKUlZWVl12pSUlOjFF1/UmDFj1L17d4WFhWno0KF6+eWXVVnJ\n85UBAHC3D/ec1LmKasV07qAxA6I8HU67NXZQtKI7Bqmo/KLW553ydDjwM24rJiZPnqy0tDQtXLhQ\n69at0/DhwzV16lRlZGQ02q9NpUblAAAfXElEQVSqqkpjx45VVlaWlixZojVr1ig6OlopKSnaunWr\nq93Ro0f1+9//XjfddJP++Mc/6v3339dDDz2kRYsW6b777pNh8Eg0AADcxTAMLfvnYUnStFt7K8DM\niteeYg0wa8ql+SpvbTvs4Wjgbyzu2MnatWu1YcMGZWRkaOrUqZKk5ORk5efna968eZoyZYoCAgLq\n7bts2TLl5uZq+/btSkpKcvVNSEjQ/PnzlZ2dLUm6/vrrdeTIEYWGhrr63nnnnQoNDdW8efO0bds2\n3X777W18pAAAQJI+OVSkfSdL1MEaoEdGMMTJ06bf2lt/2HJQnx89p135Z3Vzny6eDgl+wi13Jlav\nXq2wsDClpqbW2T5z5kydOHHCVRA01HfAgAGuQkKSLBaLpk+frh07dqigoECSFBoaWqeQqDVixAhJ\n0rFjrP4IAIC7LPtHzV/AH7q5pzqHBHo4GkSFB+v+YTZJ0p/+yd0JtB633JnIzc3VoEGDZLHU3V18\nfLzr9ZEjRzbYd9SoUVdsr+2bl5enmJiYBve9adMmSdKQIUOaFGteXp6cTiYn+bLq6mrX75ycHA9H\ng2tFPv0L+fQvDeWzoKRaWftrFklLiqgk115iVFS13pW0LvekPt62S9Fhda/LOD/9g9lsVu/e7rsb\n6JZioqioSH379r1ie9euXV2vN9a3tl1z++7Zs0eLFy/WpEmTXMXH1djtdjkcjia1hfer/WKEfyCf\n/oV8+pfL87lmf4kk6ZYegYrqQK69RUyoFB8VqD2FF7VmX4lmDgtvsC05810NTR1oK24pJiTJZGp4\n4lVjr7W075EjR3TfffepV69eevPNN5sWpGqGUJnNPDHXl13+BWi1Wj0YCVoD+fQv5NO/1JfP0iqn\nthypeYri9wZ1JM9eZtKgjtpTeEZZRy5oWkJnhQb+65qH89M/uPs61i3FRERERL13EIqLiyWp3jsP\n19I3Pz9fycnJslgsysrKavT9v2vIkCEUEz4uJydH1dXVslqtSkhI8HQ4uEbk07+QT/9SXz5/v/Er\nVTkMDe7RUdPHjbjqHwzhXvHxhjL2/V1fF5Zpb0VH/dvwfq7XOD/9g9PpVGlpqdv255ar5qFDh2rf\nvn2y2+11tu/du1eSFBcX12jf2nZN6Zufn68xY8bIMAxt3rxZPXv2vNbwAQBAE5RWVut/tx2RJD2V\n3J9CwguZTCY9eUfN0PM3/nFYFy4ytBvXxi3FxKRJk1RWVqaVK1fW2Z6WliabzabExMRG++7fv7/O\nE5/sdrvS09OVmJgom83m2n706FGNGTNGDodDmzZtUp8+fVr/YAAAQL3SPz2q8xeq1a9bqFLiuns6\nHDTggRtj1LNLB50pq1LmjqOeDgc+zi3DnCZMmKBx48Zp9uzZKikpUf/+/ZWZman169crPT3dNVHk\n8ccfV1pamg4ePOgqBGbNmqXXX39dqampeumllxQVFaWlS5fqwIED2rhxo2sfhYWFSk5O1smTJ7Vs\n2TIVFhaqsLDQ9XrPnj25SwEAQBu5cNGhN/9xSFLNXQkWqfNe1gCzfjymv55ZvVf/8/eDeiSxt4Kt\n7p20C//htskBq1at0qOPPqoFCxYoJSVF2dnZyszM1LRp01xtHA6HHA5HndWqg4KClJWVpeTkZM2Z\nM0cTJ07UyZMntW7dOo0ePdrV7ssvv9ShQ4dUVVWl6dOnKykpqc5PcyZhAwCA5snccVRF5RfVq2sH\n3Z9gu3oHeNSDN8eoR6dgfVtSpRW7jns6HPgwk3H5lXs7U98ElfDwcCZg+zgmkPkX8ulfyKd/qc2n\n0xSgn6wvUmFplf7PpKF6JJEVr31B2vYjWvh+nmI6d9Dmn43Rvry9nJ9+wN3Xt1w1AwCAa/LBV2Uq\nLK1Szy4d9ODNDS8kC+8yZXgvRYUHqeDcBWVk53s6HPgoigkAANBiZRedWvVlzV9BfzouVkEWxt77\nimBrgP7jrhskSf930zeqqHZ6OCL4IooJAADQYu8dKFd5taEB0eH63jDuSviah2/ppb6RoSouv6j3\n9rtvbQL4D4oJAADQIkUVDq39ukKSNG/8AJ7g5IOsAWb9bPwASdKa/WU6V8m6E2geigkAANAi6XvO\n66JTGhQZqLGDojwdDlpoQlx3JfTqrCq7oZxvL3o6HPgYt6wzAQAA/Muu/LPadLjmrsTMGzux2rUP\nM5lMevGBOB365mvZQj0dDXwNxQQAAGgWh9PQovfzJEnJfYI1IDLIwxHhWsXFdJLjjFXV1dWeDgU+\nhmFOAACgWVbsPKa9BecVYjVp2tAwT4cDwIMoJgAAQJMVl1/U4r8dkCR9P66jOgfzKFigPaOYAAAA\nTfbrD/JUXH5RsdFhujeWuxJAe0cxAQAAmmTjl9/qvd0nZDZJix9KkIVHwQLtHsUEAAC4qvMXqvXL\n9/ZKkp4Y1VfDenX2cEQAvAHFBAAAaJRhGPrVe7n6tqRK10eG6v8bF+vpkAB4CYoJAADQqHd3HdcH\nOScUYDbp1YcTFGxl0jWAGhQTAACgQQdPl2nBmpo1JX46LlY39e7i4YgAeBOKCQAAUK+yKrt+nP65\nLlQ7NLJfhH40up+nQwLgZSgmAADAFZxOQz/9624d+LZUUeFB+t2UYQrg6U0AvoNiAgAAXOH3WV/r\n4y+/VWCAWX949GZFdwz2dEgAvBDFBAAAqGP5jqP6v1lfS5JenBTHPAkADaKYAAAALutzT+qZ1TXr\nScwe00+pt/TycEQAvBnFBAAAkCRtOVCof8/cLachTbmll+aPH+DpkAB4OYunAwAAAJ73t7xT+knG\n56p2GEoZ0l0vToqTycSEawCNo5gAAKCdW/3Fcf1sxR45nIbuHdpDv5syTJYABi8AuDqKCQAA2imn\n09DvNn6l1zZ9I0mafGOMFj8UTyEBoMkoJgAAaIfOX6jW0yv3aF3uKUnSj0b30/zxA2RmLQkAzUAx\nAQBAO7Mr/6z+Y/kXOn72gqwBJv2fSUN5ahOAFqGYAACgnaisdui/N32j/7f1oBxOQ726dtCS79/I\nOhIAWoxiAgAAP2cYhrYcOK0F7+fqWPEFSdL9CTa9MClOHYOtHo4OgC+jmAAAwI/tPFKs3/7tgLIP\nF0uSenQK1sKJQzR+SDSPfgVwzSgmAADwMw6noc37C/W/2w9r2zdFkqTAALMeG9lHc++KVWgQ//kH\n0Dr4NgEAwE8cLarQ+zkFemfncR0trpAkBZhNeviWnvrJnTcopnMHD0cIwN+47UHSZWVlmjt3rmw2\nm4KDgzVs2DAtX768SX0LCws1Y8YMRUZGKiQkRElJScrKyqq37caNG5WUlKSQkBBFRkZqxowZKiws\nbM1DAQDAKzidhvYcP6fXN3+jB17fpjt+u1mvfPyVjhZXqFMHq/5tdF9tnTdGv5kcTyEBoE247c7E\n5MmT9dlnn+mll15SbGysMjIyNHXqVDmdTj3yyCMN9quqqtLYsWN17tw5LVmyRFFRUXr99deVkpKi\njRs3avTo0a62W7du1YQJE3TvvfdqzZo1Kiws1M9//nONHTtWO3fuVFBQkDsOFQCANlFSWa3c4+e1\np+C8co6d06eHinS2otr1utkkjewXqfuH2XRffA+FBDIAAUDbcsu3zNq1a7VhwwZXASFJycnJys/P\n17x58zRlyhQFBATU23fZsmXKzc3V9u3blZSU5OqbkJCg+fPnKzs729V23rx5io2N1bvvviuLpebQ\nrr/+et12223605/+pNmzZ7fxkQIA0HJ2h1NF5RdVWFKlwtJK5RdV6EhRuQ6fqfk5fvbCFX3CgyxK\n6hehUbHdNH5ItKLCgz0QOYD2yi3FxOrVqxUWFqbU1NQ622fOnKlHHnlE2dnZGjlyZIN9BwwY4Cok\nJMlisWj69Ol65plnVFBQoJiYGBUUFOizzz7Tb37zG1chIUkjR45UbGysVq9e3e6LCcMwdKbsYvP6\nyGjmTtq0uYwmdCiqcKja7pC12qxT5yubfQxN2Ued9s1rLqO5O1DzY2rr92/2v4sW7aPGidJq2avt\nsliljmfKG3n/Zua5eeFc2keze7Tp+7vjGFr7/Dly9qKq7XZZLYYCT5a06N92W5/TzWUYkt3pVLXD\n0EW7U9UOpy46Lv12/X9D1XanLlQ7VFJZrbJKu8qq7CqrtKu0yq6SC9U6U3ZRReVVV423Z5cOiu/Z\nSfE9O+vmPl00rFdnWQPcNmoZAOpwSzGRm5urQYMG1bnIl6T4+HjX6w0VE7m5uRo1atQV22v75uXl\nKSYmRrm5uXW2f7fttm3bmhRrXl6enE5nk9r6GofT0OS/Fng6DPdac9LTEaA1ffitpyNAa1rPfLb6\nmE1Sp2CzugQHKDrUoh7hFsWEW2TraFHPjhZ1DKq9k18mnS/Tl+ePeSzW6upq1++cnByPxYHWQT79\ng9lsVu/evd22P7cUE0VFRerbt+8V27t27ep6vbG+te0a61v7u6G2je3jcna7XQ6Ho0ltfY3D2fw/\nzzX3CeTNfmJ5Mzu0aTzeFEsLOjQ/nmb0aEefjTfF0pL2zY+n6R3a02fT3PcOMJtkMUuWS7+t3/n/\ntb+DA0zqYDWrg8WkEKtJIVazOlhNCrGY1CnYrM7BZnUMMiugwfUfnKqu9s4/eNVeiMI/kE/f1dDU\ngbbitplZjS2Mc7VFc5rTt6G2TV2Yx2KxyGz2z9vFVklrpvb0dBht7vIvQKuVlV19Hfn0L+TTv5BP\n/0I+/YO7r2PdUkxERETUe2eguLhmNc767iY0t29ERISk+u9yFBcXN7qPyw0ZMsRvi4n2IicnR9XV\n1bJarUpISPB0OLhG5NO/kE//Qj79C/n0D06nU6WlpW7bn1uumocOHap9+/bJbrfX2b53715JUlxc\nXKN9a9s11rf2d0NtG9sHAAAAgOZzSzExadIklZWVaeXKlXW2p6WlyWazKTExsdG++/fvr/MIWLvd\nrvT0dCUmJspms0mSYmJiNGLECKWnp9eZ8/Dpp5/qwIEDmjx5cisfFQAAANC+uaWYmDBhgsaNG6fZ\ns2frjTfe0ObNm/Xkk09q/fr1Wrx4sWuiyOOPPy6LxaL8/HxX31mzZmnIkCFKTU1VRkaGNm7cqIcf\nflgHDhzQyy+/XGc/L7/8svbv36/U1FRt3LhRGRkZevjhhxUXF6eZM2e641ABAACAdsNtkwNWrVql\nRx99VAsWLFBKSoqys7OVmZmpadOmudo4HA45HI46z4sPCgpSVlaWkpOTNWfOHE2cOFEnT57UunXr\n6qx+LUljxozR2rVrdfLkSU2cOFFz5sxRcnKysrKyWP0aAAAAaGUmoyUraPmJ+iaohIeHMwHbxzGB\nzL+QT/9CPv0L+fQv5NM/uPv6lqtmAAAAAC1CMQEAAACgRSgmAAAAALQIxQQAAACAFqGYAAAAANAi\nFBMAAAAAWoRiAgAAAECLUEwAAAAAaBGKCQAAAAAtQjEBAAAAoEUoJgAAAAC0CMUEAAAAgBahmAAA\nAADQIhQTAAAAAFqEYgIAAABAi1BMAAAAAGgRigkAAAAALUIxAQAAAKBFKCYAAAAAtAjFBAAAAIAW\noZgAAAAA0CIUEwAAAABahGICAAAAQItQTAAAAABoEYoJAAAAAC1CMQEAAACgRSgmAAAAALQIxQQA\nAACAFqGYAAAAANAiFBMAAAAAWoRiAgAAAECLuK2YKCsr09y5c2Wz2RQcHKxhw4Zp+fLlTe5fWFio\nGTNmKDIyUiEhIUpKSlJWVladNiUlJXrxxRc1ZswYde/eXWFhYRo6dKhefvllVVZWtvYhAQAAAO2a\n24qJyZMnKy0tTQsXLtS6des0fPhwTZ06VRkZGVftW1VVpbFjxyorK0tLlizRmjVrFB0drZSUFG3d\nutXV7ujRo/r973+vm266SX/84x/1/vvv66GHHtKiRYt03333yTCMtjxEAAAAoF2xuGMna9eu1YYN\nG5SRkaGpU6dKkpKTk5Wfn6958+ZpypQpCggIaLD/smXLlJubq+3btyspKcnVPyEhQfPnz1d2drYk\n6frrr9eRI0cUGhrq6nvnnXcqNDRU8+bN07Zt23T77be7XquvuHA6na1yzPAcs9msgIAAmc1m8ukH\nyKd/IZ/+hXz6F/LpH+rLXVv+Qd0txcTq1asVFham1NTUOttnzpypRx55RNnZ2Ro5cmSj/QcMGOAq\nJCTJYrFo+vTpeuaZZ1RQUKCYmJg6RcTlRowYIUk6duxYne31fbDl5eVNPi54p969e7v+d2lpqQcj\nQWsgn/6FfPoX8ulfyKf/astiwi3DnHJzczVo0CBZLHVrl/j4eNfrV+tf27a+/nl5eY3237RpkyRp\nyJAhTY4ZAAAAQOPcUkwUFRWpa9euV2yv3VZUVNRm/ffs2aPFixdr0qRJ9RYkAAAAAFqm2cXEli1b\nZDKZmvSze/duVz+TydTgezb22rX0P3LkiO677z716tVLb7755lX3AQAAAKDpmj1nYsCAAXrjjTea\n1LZ27F1ERES9dw+Ki4slqd67DpdrSf/8/HwlJyfLYrEoKyur3jZms/mKeRa1hRAAAADgawzDuGKO\nhNncdoORml1M9OjRQz/84Q+b1Wfo0KHKzMyU3W6vM29i7969kqS4uLir9q9te7mG+ufn52vMmDEy\nDENbtmxRz549631fs9ncph8uAAAA4M/cciU9adIklZWVaeXKlXW2p6WlyWazKTEx8ar99+/f73oE\nrCTZ7Xalp6crMTFRNpvNtf3o0aMaM2aMHA6HNm3apD59+rTuwQAAAACQJJkMN63kdvfdd2vnzp16\n+eWX1b9/f2VmZuqNN95Qenq6pk2b5mr3+OOPKy0tTQcPHnQVAlVVVbr55ptVUlKil156SVFRUVq6\ndKk++OADbdy4UaNHj5ZUs0p2UlKSCgoKtGzZMvXr169ODD179mzwLgUAAACA5nHbGJ9Vq1bp0Ucf\n1YIFC5SSkqLs7GxlZmbWKSQkyeFwyOFw1BnrFRQUpKysLCUnJ2vOnDmaOHGiTp48qXXr1rkKCUn6\n8ssvdejQIVVVVWn69OlKSkqq8/PdSdhlZWWaO3eubDabgoODNWzYMC1fvrxtPwhcs02bNmnWrFka\nOHCgQkNDFRMTo+9973vatWvXFW0///xz3XXXXQoLC1Pnzp01efJkHTp0yANRo6nefPNNmUwmhYWF\nXfEa+fQd//znP3XPPfeoS5cu6tChg2644QY9//zzddps3LhRSUlJCgkJUWRkpGbMmKHCwkIPRYz6\nfPHFF3rggQdks9kUEhKigQMH6te//rUqKirqtOPc9D6lpaWaP3++7r77bnXr1k0mk0mLFi2qt21z\n8vfaa69p4MCBCgoK0vXXX6/nnntO1dXVbXgkkJqWT4fDof/6r/9SSkqKevbsqZCQEA0aNEhPP/20\nzp07V+/7tko+jXZs3LhxRufOnY0//OEPxqZNm4wf/vCHhiTj7bff9nRoaMRDDz1kJCcnG0uXLjW2\nbNlirFixwrj11lsNi8ViZGVludrt27fPCA8PN0aNGmV89NFHxsqVK40hQ4YYNpvNKCws9OARoCHH\njx83OnXqZNhsNiM0NLTOa+TTd7z99tuG2Ww2vv/97xvvv/++sWnTJuONN94wnnvuOVebLVu2GBaL\nxfje975nfPzxx0Z6eroRExNjxMXFGZWVlR6MHrXy8vKM4OBgIyEhwfjrX/9qZGVlGQsXLjQCAgKM\n+++/39WOc9M7HT582OjUqZNxxx13uK5vFi5ceEW75uTvhRdeMEwmk/GLX/zC2Lx5s7F48WIjMDDQ\neOKJJ9x0VO1XU/JZWlpqhIeHG08++aSxYsUKY/Pmzcarr75qdOnSxRg8eLBRUVFRp31r5bPdFhMf\nffSRIcnIyMios33cuHGGzWYz7Ha7hyLD1Xz77bdXbCstLTWio6ONsWPHuralpqYakZGRxvnz513b\njhw5YlitVmP+/PluiRXNc9999xkTJ040HnvssSuKCfLpG44fP26EhoYas2fPbrTd8OHDjcGDBxvV\n1dWubdu2bTMkGUuXLm3rMNEEv/zlLw1JxjfffFNn+5NPPmlIMoqLiw3D4Nz0Vk6n03A6nYZhGMbp\n06cbLCaamr8zZ84YwcHBxpNPPlmn/4svvmiYTCYjLy+vbQ4EhmE0LZ92u904c+bMFX1XrFhhSDL+\n8pe/uLa1Zj7b7aOMVq9erbCwMKWmptbZPnPmTJ04caLOZG94l6ioqCu2hYWFafDgwTp27Jikmgn6\nH374oR588EF17NjR1a5Pnz5KTk7W6tWr3RYvmiY9PV1bt27V0qVLr3iNfPqON998U+Xl5fr5z3/e\nYJuCggJ99tlnevTRR+s84W/kyJGKjY0ln17CarVKkjp16lRne+fOnWU2mxUYGMi56cWa8qj75uRv\n/fr1qqys1MyZM+u8x8yZM2UYht57773WPQDU0ZR8BgQEKCIi4ortI0aMkCTXNZLUuvlst8VEbm6u\nBg0aVOc/ZJJcq2Tn5uZ6Iiy00Pnz5/X5559ryJAhkqSDBw/qwoUL9a56Hh8fr2+++UaVlZXuDhMN\nKCws1Ny5c/XSSy/V+5AE8uk7/v73v6tr167av3+/hg0bJovFoqioKP3oRz9SSUmJpH99vzaUT75/\nvcNjjz2mzp07a/bs2Tp06JBKS0v14Ycf6n/+53/01FNPKTQ0lHPTxzUnf7Xn5dChQ+u069GjhyIj\nIzlvvdimTZskyXWNJLVuPtttMVFUVFTvQna12+pbJA/e66mnnlJ5ebl++ctfSvpX/hrKsWEYOnv2\nrFtjRMN+/OMfa8CAAZo9e3a9r5NP31FQUKCKigqlpqZqypQp2rhxo+bNm6c///nPuueee2QYxlXz\nyfevd7juuuv0ySefKDc3V/369VPHjh01ceJEPfbYY1qyZIkkzk1f15z8FRUVKSgo6IrFfmvbct56\np4KCAj399NO65ZZbdN9997m2t2Y+m71onT9p7HYRq2D7jmeffVZvv/22XnvtNd188811XiPH3m/l\nypX64IMP9MUXX1w1J+TT+zmdTlVWVmrhwoV6+umnJUljxoxRYGCg5s6dq6ysLFfbhnJGLr3DkSNH\nNHHiREVHR+vdd99Vt27dlJ2drRdeeEFlZWVatmyZqy3npm9rav7Is28pLi52/RHnr3/96xULNbdW\nPtttMREREVFv1VVcXCyp/iod3ue5557TCy+8oBdffFE/+clPXNtrxww2lGOTyaTOnTu7LU7Ur6ys\nTE899ZTmzJkjm83menTdxYsXJUnnzp2T1Wolnz4kIiJCX3/9tcaPH19n+4QJEzR37lx9/vnnSkhI\nkNRwPvn+9Q5PP/20SkpKtHv3btdfL++44w5FRkZq1qxZ+sEPfqDu3btL4tz0Vc35bo2IiFBlZaUq\nKioUEhJyRdvv/jEPnnX27FmNGzdOBQUF2rRpk/r27Vvn9dbMZ7sd5jR06FDt27dPdru9zva9e/dK\nkuLi4jwRFprhueee06JFi7Ro0SI988wzdV7r16+fOnTo4Mrn5fbu3av+/fsrODjYXaGiAWfOnNG3\n336rV199VV26dHH9ZGZmqry8XF26dNG0adPIpw+pb+y1JNfaQWaz2fX92lA++f71Drt379bgwYOv\nGAYxfPhwSXINf+Lc9F3NyV/t2Prvtj116pTOnDnDeetFzp49q7vuukuHDx/Whg0b6v1ebs18ttti\nYtKkSSorK9PKlSvrbE9LS5PNZlNiYqKHIkNTPP/881q0aJF+9atfaeHChVe8brFYNHHiRK1atUql\npaWu7UePHtXmzZs1efJkd4aLBnTv3l2bN2++4mf8+PEKDg7W5s2b9cILL5BPH/Lggw9KktatW1dn\n+9q1ayVJt956q2JiYjRixAilp6fL4XC42nz66ac6cOAA+fQSNptNeXl5Kisrq7P9k08+kST17NmT\nc9PHNSd/KSkpCg4O1ltvvVXnPd566y2ZTCY98MAD7gobjagtJA4dOqSPP/5YN954Y73tWjWfTX6I\nrB8aN26c0aVLF+OPf/yjsWnTJuOJJ54wJBnp6emeDg2NeOWVVwxJRkpKivHJJ59c8VNr3759RlhY\nmHHHHXcYa9euNVatWmXExcWxkJIPqG+dCfLpOyZOnGgEBQUZzz//vLFhwwbjN7/5jREcHGzcd999\nrjabN282LBaLMWnSJGPDhg3G22+/bfTq1YtF67zImjVrDJPJZNx6662uRetefPFFIywszBg8eLBR\nVVVlGAbnpjdbu3atsWLFCuNPf/qTIclITU01VqxYYaxYscIoLy83DKN5+atd5OyZZ54xtmzZYvz2\nt781goKCWLTOTa6Wz4qKCmP48OGGyWQylixZcsX10XfXjGmtfLbrYqK0tNT493//d6N79+5GYGCg\nER8fb2RmZno6LFzF6NGjDUkN/lxu586dxtixY42QkBCjY8eOxgMPPHDFyQTvU18xYRjk01dUVFQY\nP//5z41evXoZFovF6N27t/GLX/ziiiLh448/Nm699VYjODjY6Nq1q/GDH/yg3kUp4TmbNm0y7r77\nbqN79+5Ghw4djNjYWOM///M/r1gYi3PTO/Xp06fB/1YePnzY1a45+VuyZIkRGxtrBAYGGr179zYW\nLlxoXLx40U1H1L5dLZ+HDx9u9Proscceu+I9WyOfJsO4NJAVAAAAAJqh3c6ZAAAAAHBtKCYAAAAA\ntAjFBAAAAIAWoZgAAAAA0CIUEwAAAABahGICAAAAQItQTAAAAABoEYoJAAAAAC1CMQEAAACgRSgm\nAAAAALQIxQQAAACAFvn/Abiw10pmTVCWAAAAAElFTkSuQmCC\n", "text/plain": [ "" ] }, "metadata": {}, "output_type": "display_data" } ], "source": [ "xs = np.arange(10, 100, 0.05)\n", "ys = [gaussian(x, 90, 30) for x in xs]\n", "plt.plot(xs, ys, label='var=0.2')\n", "plt.xlim(0, 120)\n", "plt.ylim(-0.02, 0.09);" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "The area under the curve cannot equal 1, so it is not a probability distribution. What actually happens is that more students than predicted by a normal distribution get scores nearer the upper end of the range (for example), and that tail becomes “fat”. Also, the test is probably not able to perfectly distinguish minute differences in skill in the students, so the distribution to the left of the mean is also probably a bit bunched up in places. The resulting distribution is called a [*fat tail distribution*](https://en.wikipedia.org/wiki/Fat-tailed_distribution). \n", "\n", "Sensors measure the world. The errors in a sensor's measurements are rarely truly Gaussian. It is far too early to be talking about the difficulties that this presents to the Kalman filter designer. It is worth keeping in the back of your mind the fact that the Kalman filter math is based on an idealized model of the world. For now I will present a bit of code that I will be using later in the book to form fat tail distributions to simulate various processes and sensors. This distribution is called the [*Student's $t$-distribution*](https://en.wikipedia.org/wiki/Student%27s_t-distribution). \n", "\n", "Let's say I want to model a sensor that has some white noise in the output. For simplicity, let's say the signal is a constant 10, and the standard deviation of the noise is 2. We can use the function `numpy.random.randn()` to get a random number with a mean of 0 and a standard deviation of 1. I can simulate this with:" ] }, { "cell_type": "code", "execution_count": 29, "metadata": { "collapsed": true }, "outputs": [], "source": [ "from numpy.random import randn\n", "def sense():\n", " return 10 + randn()*2" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "Let's plot that signal and see what it looks like." ] }, { "cell_type": "code", "execution_count": 30, "metadata": {}, "outputs": [ { "data": { "image/png": "iVBORw0KGgoAAAANSUhEUgAAAuYAAAEaCAYAAABdIZKsAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzsnXecFEXax389m4AlueS8RMkLgqAC\nCoqKYkDMemc+78wZMWN4lTNgzp7nnVkwnSA5iOS85MwCS84su2ycfv+Y6Znunuruqg4zPbvP9/NR\ndma6q6q7q6ueeuoJkizLMgiCIAiCIAiCSCiBRDeAIAiCIAiCIAgSzAmCIAiCIAjCF5BgThAEQRAE\nQRA+gARzgiAIgiAIgvABJJgTBEEQBEEQhA9ITXQDACAYDCIYDGq+kyQJkiQlqEUEQRAEQRAEYR9Z\nlqEPfhgIBBAIGOvFfSOYFxYWJroZBEEQBEEQBOEZmZmZpoI5mbIQBEEQBEEQhA8gwZwgCIIgCIIg\nfAAJ5gRBEARBEAThA3xhY85y8rSywfGCNWvWoLy8HKmpqejSpUtc6yYSBz33qgs9+6oJPfeqCz37\nqksinj3Lh9IqsIlvBXMrr1UvCAaDqKioSEjdROKg5151oWdfNaHnXnWhZ1918cuztxLMqVcSBEEQ\nBEEQhA8gwZwgCIIgCIIgfAAJ5gRBEARBEAThA0gwJwiCIAiCIAgfQII5QRAEQRAEQfgAEswJgiAI\ngiAIwgeQYO5jyiqCGLtkJ2RZTnRTCIIgCIIgCI8hwdzHfDl/Ox4btxLzthxKdFMIgiAIgiAIjyHB\n3MecKCkHAJSUVyS4JQRBEARBEITXkGCeBJAlC0EQBEEQROWHBHMfY560lSAIgiAIgqhMkGDuY0hR\nThAEQRAEUXUgwZwgCIIgCIIgfAAJ5j6GTFkIgiAIgiCqDiSYEwRBEARBEIQPIMGcIAiCIAiCIHwA\nCeYEQRAEQRAE4QNIME8CKI45QRAEQRBE5YcEcx8jkfcnQRAEQRBElYEEc4IgCIIgCILwASSYEwRB\nEARBEIQPIMGcIAiCIAiCIHwACeYEQRAEQRAE4QNIMCcIgiAIgiAIH0CCOUEQBEEQBEH4ABLMkwAK\nY04QBEEQBFH5IcHcx0gUyJwgCIIgCKLKQII5QRAEQRC+YO7mgyivCCa6GQSRMEgwJwiCIAgi4Ww7\nWIgbP1uID2dtSXRTCCJhkGBOEARBEETCKSwpBwDsPV6c4JYQROIgwZwgCIIgCN9AAQ+IqgwJ5kmA\nLNMwRRAEQVRuKN4BQZBgThAE4TsOF5biZGlFoptBEARBxBkSzAmCIHzGaS9OxbWfzE90MwgiIdAm\nMVGVIcGcIAjCh6zMP5boJhAEQRBxhgRzotJSXFaBiiCpXgiCIAiCSA5IME8wxWUVmLJmb6KbUSnp\n+MwkPPj9ikQ3gyAIguBAAnl/EgQJ5glm9MT1uPPLpdhfQHFbveC33N2JbgJBEARBEAQXJJgnmAMn\nSgAAZRVkckEQBEEQFMmcqMqQYJ5geDbuaIjyN9sPFWLbwcJEN8MX7DxchJznp+BgeMFJEARB2Oe0\nF6dizNSNiW4GEUdIMPcxlGwhOTjntVkY9PqsRDfDF0xesxfHTpZh4dbDiW4KUQmRZRlBcugmqhCH\nC0vxzvRNiW5G0vHqpPVYkpec8xAJ5j6Bld1T+YrkcyLZoEVl5edYURmOnSyLa51/+ddCtHny97jW\nScQPGjcIt/hg1hbc+NnCRDfDFiSYJwGkHyIIwm/kvDAFOc9PiWudczcfimt9ROXgt9zdGPLW7EQ3\ng4gzgSRd6ZFg7mOStE8RVRi3M/Z9uWA7znh5uu3zZ67fj5X5R11sEUFUfl6fvAF//VfitI1ujyMv\njF+L9XsL3C2U8D2BJJWhUhPdgKqOFJa+KQUxURmQw/s7bo2Ho39fh8LSCtvn3/rFYgBA3uihLrWI\nICo/783cnJB6SRlFuImUpB2KNOY+hpItEMlKko6HBEEQRCUhWechEsx9jEzW5USSQTs/BEEQhB+o\nMjbmBQUFGDFiBC644AI0aNAAkiRh1KhRMcfdcsstkCQp5r+OHTu60e5KA1cc8yQUdpIxpFlphcyM\njkPwE7177gyIyboV6VeW7ziS6CYQhCU0DCeG4rKKpJy7jUjW6UNYMD906BA++eQTlJSUYNiwYabH\nVq9eHfPnz9f89/3339tubGXErOMkqynLydIKtHnyd3y/eEeimyLE1T/swtsUL5aopMzcsB9XfDAP\n09ftS3RTCILwIR2fmYQnf16V6Ga4RrJqzIWdP1u1aoUjR45AkiQcPHgQn332meGxgUAAZ5xxhqMG\nEsnHiZJyAMDUtftw7ektE9waMaas2YcHB3dIdDOSlkjs/eQcDys1+48XAwD2HaesrARBsPktdzdG\nX9k90c1whWSNyiKsMVdMUgh3qUxbd9Q9/I8ipBFVB2UHjnxXCL/iVR+lKamqkpxP3tNwiSdPnkTj\nxo1x4MABNGnSBMOGDcMLL7yArKwsy3PXrFmDYDDoZfNiKCsri/ybm5sblzqPHgnFWF63fh2O1NQ+\njj17jgMA8vLysLx8L4Dk2Jo5WhwKb3fs2PG43UczrNqgPHcg1GftttkP18pD/vEy3DNhHx7rl4X+\nLWu4Wra6z+aWOzeZqKgI9SWn99bo/ES88yK42abJy0LpqfPz85Fbzb3Y7om4b07r9Ptz9wvxvjfb\nj4aey+HDh12tu6w8VG5ubm7SPnuv27po10kAQEUwGNf7UlwexPStRbi4fabrSt+Kcu0zTsSzDwQC\naNlSzHLAM8E8JycHOTk56Nq1KwDgjz/+wJtvvonp06dj8eLFqFmzpun55eXlkUk5EaiFNS8JyqHF\nR3lZGcrKtFqCiorwbxXluOXnPaiWKuH9i+rHlDF+UyG+W12Ij4bWR830xAfaKS8LtTsoB+N2H80Q\naYMM2Xab/XCtPCimDFsOlaBvkzRXy1b6bEVFuav3w2lZPOf78fm52abp24oAAOXlFb56Nomu04/P\n3S/o783TMw9jf1EFPhnawJP6ystDZpDBoMtzR3hq1ZeZTM/ey7YeKwni/2ZHs+rG8758lVuA3zYV\noWNWClrWcVcklWB8LfG6xpSUFOFzPBPMH3roIc3n888/Hz179sRVV12FTz/9NOb3mIalpiIQiK+Q\nqX5QaWnuCixGBKTQNaakpiEtTfs4UsMPNDUlFcdKgjhWwm7XF7knAAC3/3YAP13X3OMWW5MaXlAF\npEDc7qMZVm1QP3cJku02++FaeUhJDT+fgPvPJ5AS6s+pKamulK0oUJyWZXR+It55EbxoU0pKiqvl\nJuK+6evccawMW4+UYWA23w6Q35+7X9Dfm/WHypjfu1df6F/XxybVOJKsz97Ltn624JDmczzvS5kc\nejgBF8clJbqaFNDO5wmR8WzIsXHN/HnFFVcgMzMTCxYssDy2S5cucRfMlW2utLQ05OTkxKXOU9Yt\nB7YXoVOnjmhVL1Pz27wjW4DcY8jOzgbmhF4cVruk7/Ihy0CFzP493hw6UQL8vAe1a9dObHu+zQdg\nfU/U25vVq1cXbzNnPX6hoMZBYOZBNGrUEDk57oYvnXN4M5B7HK1bt0ZO50bC58uyDFkGAmGvncBP\newGU27+3Fs8mEe88F170qXCZzZo3R05OK9fKi+t9M6jzyid/R3lQxgOXn8lVjG+fu18werYeP/Pq\n+wqA3/chKyvLUR0b9xWgoLgcvVqdAgBIG38AQAlycnKS79nH4T2b/+2EyN8pgUBc70u9rauAzYXo\n0OFUdG5a21FZpeVBvDVtI+47tz2AXcjQPeNEPPtgMIiCggKhc+Ju9yDLctwFbj+j2FSZO3/ad4TZ\ntK8Aa3Yfs32+E5LJxczv8cv3HS/GtoOFiW4GN3YtBT+evRVtnvzd1bYQlZ9yn8Zefv63Nej23ORE\nNyPpcDocX/DmbFz54Tx3GqOjuKwCe46dtH3+uj3HfT3fJHNwj99X7cEHs7bghyU7ASTvtcRVQh43\nbhyKioqqZAhFWZbxW+5uVAhMIG70qfPfnI2h78xxXpAAyfgyKE9lbdh5UU1hSbnQQHqsqAyl5e46\nLvd9eToGvT7L1TK9jJNvtwuMX7lbW44LbSF0+FgoSCZkWcY3C3eguMzYF+rfc/NQEA4fK8LMDfvx\nxE8rnTSP8IiHvl+BM1+ZYevclflHcdHbf+J/ubutD04Qfl40WBEMt11ZqCerDthWsydOnIhx48bh\nt99+AwCsXbsW48aNiwje27dvR79+/fDuu+9i4sSJmDRpEp544gncfPPN6NKlC+644w5XLyIZmL/l\nEO77djm+Wbg90U3xHEWYSuYXXKG4rAJdnpuMz+fmcZ+T88IU3P31Mu8a5WOcPvNK0GUqFSdLK7C/\nIHlCay7JO4zskROQF4fdpQ37CvDkz6vwjgdJyW77YjG+XbTT9XKTjZOlFRHtp1+Yv/WQ9UEGKI73\nOw8XudWcSoMbITIVhVDExjxJVTu2bMzvuusubN8eFTDHjh2LsWPHAgC2bduGOnXqoFGjRhgzZgz2\n7duHiooKtGrVCvfffz+efPJJZGZmGhVdKVm/9ziOF4e0JsdOaj2BI0Ksy3W+8vs6DO3exOVSQ8iy\njB+W7MTw05ojLSVJl6Q6jO6/og37c9MBFJWUo2HtDK6kSdN8nF1xt4NtWCsowZD/ERlrrv90AVbs\nPIq80UM9a4+bLNwWCgm5cV8Bsut7O88ok/7hwlJP63FKREjxwUsZDMp47n9rcPegtmhSp3rM7/oW\nvjVtIz6evRU9W9RF+0a14tNIC9y4i149i20HC9GsbnWkpzqbl/OPFCEjNQUNamW41LL4kuzzkC3B\nPC8vz/KYn376yU7RlY6jRaUY8taf6Nwk5NTghUZQQuxk+/Hsrfh5+S73K0NI+//4j6tQUFyOOwa0\niW2Psmr1pHbvWb3rGLo2qwMgOvkGZeCNqRsBIOmymeoZMS60Re7HQSumTT5sox2OF5dhxrr9GNaz\nWaKbIjQGrdgZineePXICfrmnH3q0qMt97p3/XYK/n9MGvVpZ561IRow0fKvyj6FNg0xkZtiPreDm\nPDHs/bnYsK8A61+8yL1CbbLzSBG+XLAdx4vL8PZ1PS2PVxRaZRXOboibY50TodrrXeRBr8/C9X1a\n4pXh3XDsZBk27StA72yx90+SJPT/50wASJoFuZ5kT6JWOdSdPqYkbGus2C7b6S5G73IwKGNJ3mGb\nLbNPcXlIi1xYYh5nPpnMEk6URBt7ybtzsEDZrtRtjRF8uLaFWElu+3O/rsGD36/A8WLtjllxWUXS\n9K3ZGw8IHT9l7T489fNqj1rjXy59bw4e+G55opsRITf/GIrL4pusz4gk6epJzapdocX0379cgqs+\nmp/g1iSGiMY8sc2wDQnmLpO78yimq8wY9B0jZmAyEfysOtXXC7fjqo/mw8if1KsxUBG6Vuw8go/+\n2OJRLfFl0hatzd++cMr6F35ba7tMEUffyoJfr/hkqffJyjo+MxHfLtrB/O1IUcjcQVbJR8VlFej4\nzCR8uSBkFvi/3N245d+LPG9nsiwEEoFIPzFbfG7ef8KN5gAI7Vbc/fVS18rzkilr9jqKWKKg76F+\n0oAqTz3/SGLtxI8UlqKswnjBlXfQH3bsJ0srsP94fPxU1DvcyQwJ5i5z+ftzcft/lkS/0I3ddgYY\no52z/KPmA6Bb8+/S7UewbMcRVYNC/8zccACjJ653pxKX+Hl5PgqK3cvo9eOyUAxZO/dyzNQNrrWj\nqmC0cHVKPEKGFpcF8fxva7B5v0nMWkl9fEgInLUhpIl+8Lvlkb+9JMnnLM9Yu/s4Oj07CYu2xX8X\n0orfV+1NdBO4uPPLpbjxs4W2z9fPdX42t7MTJcvNd6/ni1Px6NhoWnkrh8fyiiCKSsUjBDnlr/9a\niD4vTzf83ctn7Ae/CjuQYO4x+pfEjoBnX8B2Zxi48sN5GP4Bf0zYRCnkDp0owUPf5+J5B1puI+ws\nqOZtse+973eOFZUxNa+RrzjHw2NFZShnaH2SVatbXBbE4DGzY75nXY4yNsxYvx/DP5jrddMck5xT\nHD+bwguq1bvMF3HFZRXYesBcI263967bcxxLtx+xPtDH8DjDVoa+5MTufdvBQnR7bjKOOHQcnrl+\nf+RvqyHzrq+XofOz2pj6/f85Ay//vs5RG6xYYtGfvRjq/bTDYgcSzC3Yd7wYOw7Z3xLSL9j0Aocy\nOXvRjRIt28S7esV05PhJ9zTmCkF/mGj6guPFZch5YQq+mJeHxQY+DrwTb84LU/Di+OhCKkkVHJZE\n1iuq65NUo++yHUcdb7/Ksoz3Z272XXjDiqCcEE2dmtydRw37qigjxq3EuW/84UpZei56+0/hxDhf\nzs/jMh/5aVk+skdOQEm5t2ZdbrzCXs1dz/66GjeMcxoUwYnzZ+jf/63YjYKScqy0WAQKlR3+Nxp8\nQXsTp64Nmdj+uDQ/8l3+kZP4ZPZWwzITZY659cAJPDo2F0Gb9Sda9nEKCeYW9H15Os5+babmuzen\nbkT2yAkGZ2iJsTF3qV2ihXmpgawIypokG8n4Tli1mbUC336okLsf+BGR6eXHpfkRO8ET4UgJz/+2\nFld/NB9bVNpDO5qKWYJOhZWFgMurkCNFZXht8gb87T9LTM0x7A4Fdpv74vi1MZo6NSdsJOCx0jTe\n+aXWJvvy9+fiak5HOKvrVDTaZn09nuvLZ35dg3s48ib8uiKU1CYe/hY85B8pwudztnEd69b09d/5\n21FY5oMIL+EyxkzZEOMQbhfeOf57gbjwb0zx3hyTdT+f/20txi3NxwnBBX1sHPPkhARzG4gkPNBP\nviIDzHaHSQjUVbkpl+s7+1M/r0LHZyYBCAmr0Tr5Ki0qLedemU9ftw89XpjCdawIVk1l/T5n80HT\ncxI9KFz09p+YtjbqiPzNwh04VmRvEnhkbG4kaZL+VhQURwfPaPxY/qtnCajJrvHgwe3+obxvufnH\ncM3H4tEYissqPNGmTlptbB+959hJdH1uckzGVyv+Ocl93xbePlce3j7zUx8tNXECVIjXbpTZu6++\nZXd/vQwvjHff7FCUHYeKMHHVnjjVphUYc/OP4b0Zm10s2RqRbrDAQTIlUVjvk913TNSk0m+QYO4i\nrNTMMaYsutcnusKLLe+bhewID7yoBWO7cwhr+1c/8P4WTi88d/NBnPPaLMzbYi6w6un87GQ8pnJi\nMeO9mZtx1Mi+WahWMXw0B3Ozbs9x/F/YfvBoUSme/HkVnvlVG74ue+QEfLWALxutkWbT6W6Mujv5\nSdhxE7sanLkWiz81vIsho1vc+dlJGPjaLMfl6wmYnLb3WGgXZkmemF21l/3E6irLdbbFhaUVGPLW\nbEcmj+UVQRw8UcJ17M7DRXHVem87WIh5Av2QB0mSUFrOWkzEX5Ia/uE83KXacfh64XZXAwioYfVb\nu+YaVmXb3hlT/50g20KRau/4z2I8/MMKzXdlSR6WhQRzFbPyivDvFSYRFcIY9Znz37S2O+R9WVbm\nH42ew3dKbF2qv4M23tK8g4Vc279KyTvCGv4dNjT9EwQ1FmaXk3fIg3Tcyf2eR+yXCxnCNa9gboT6\n1swPO7yKDOfqYzfsLdCU6ea0MG5pyMbWLMSYXSat5uu/6omOp0vtOea+vbjRQiooh+pbGNaSvT3N\nfqr5v6gic3gxuQcSOHMp/Ue5javyj2L93gJ8u9i+IuWlCevQ+6VpXMcOeHUm7vxyifWBBtzw6ULk\nHSzErqMntdG2DBj0+izc4CDSih9gRSqZv/MkHh2bi2Mno2ZR2w8V4qmfV+PVScYmHO5k/nShEB28\nZoRWdSdqqrN7T6at24+flmn9Bt6Zbn/s8gMkmKt4c/5hTNhsX+ux83CsA45+DqyQZS4N42XvOY/S\noK5GX+WxojJkj5xgKlDYsf1k1cV1jovHb9znXgxhBTsLG6+YtnYfNu2zXkACsZpazVUIjoTKLTDr\nv4sEHOyUctSmLOUcmo7S8qCtGMK/rggN3qydLTUnSsqFNZL/+MrYxnfHoSL8uYlf4+iW38LPy/Nx\n42cLhM+79pPQOW9O22i7brWZlzdKN/cLNRNs3py6EV8vDC1gFbO7pdtN7PgF6xbZGQFCO5nP/LJa\n499hhXLH1u45jo9nb0G/0TOEom25Ae/uWjyiaoyecwjjluZrhHYlEZOZSVeiHdQ7PD2RuZuu3NqV\n+ccwafUeV+5gPC/Vq6zoyQgJ5nHm4z+24j/z8iKfxfRnWozO+GR2KOmPehDUC5YHToQ0cTNU4ZY6\nPDUR782IrjSNXpREdvaIgOnyW2xVmlXIp3hyx3+X4Pw3Y0PysYjx1Pdg9LNbpCKDizpBPve/NZGU\n0Wp+WpZvKnQrmlsr2b/rc5Mx4NXY8kVQm3NdoQqFOOz9uZHwkE6fxdrdx00XEI/8kIu5mxMfstPs\n8SrPxEvndHXCNx5YGv63p2+KZDFVFo/P/LrG8HhReIpQm5OUlgfx5YLteOKnVYbHbztYiI0GC/hD\nJ5yF6TPD7t34asH2iFnkT8t2IXvkBE1ZpeVBjFua735fUVWi7IakpvhXNCotD2rmaQX1bTFTFIiQ\n6EWI09UFxTGvQij2S+v2HLc8ltWvJq0RSxZhFs6Ixcu/r4+p+2//XYL/m2DuaFNaEcQ706OOKPGM\nBSr6+rBaVqQSUkQHb/3xPlKQOyKamth5WE6R/sAzHiqLRdaxZs9vGWORtGlfAR7+IddwC1OGqo9x\nXAavva8RN3wa3fo/pIogsnn/Ca44zzxc/M6fGPHjSsPfPfW5EHhBzBZedqdNM7t1hYqgjBMl5Rin\nCg/nBjyXbta87JET8PQvWoHaLIuogtqcRGmCEn3nSKGyAxqdWwa9PgsXqBbwaiHFrUggLOzKQk//\nshpvm5ggfD53Gx4dm+t6nHd1c5XdkNSAhB8W78SibYeRPXICDqnGA55nZYTb76TyTP81Z1skW7Wr\n5cdRDSfab96fuRkjTcY/IBSB6LpP5ruSjTaekGBugwMFoZf0g1nxSUe/YudR64Ms+HPTQXz6J0do\nKtXLYaRZjI3Nzj5ORLg1O3Tt7tgFEKtsdSY2N+KvGk1e2w8VanwAom3SO/YmfrUeEaZNnIzX7+Uz\ni4mUGVNGSABSXz/PgK48IzfukxKVwkzgMIrvG3dc7BYbBZ8dYH/RudNmlKiAC1pxvTMeT5d59tfV\n6PrcZG6TPPsRIPhOVHwcAOCrBVpTBNFXQF+lMif9sXE/4+gQQc0Oqlh9ZhwuLMWVH87D0SL+Baed\nV0DpA4q5iVuo770Scefn5bsw4seVuP0/iwEAWw8WMo8XRa8osYt6zCwpr8CL49fGOEAa73ib163p\nz3GcwkTfv9cmb8B3i7UR8vRzya6jJ7Fg62F8vcBZII14Q4I5J8oW+e6j0ZUXz4BsdYxZVBbHxFn+\n8MLMZO7mg7j4nT81Gc6A0CRjJoRVuNCGYgMzgXNem8X0AXhxvHkGtYqg7MoiS4Ro+MLwZ9aPOjbv\nL8DoibHh6IxuaVAOmX+8ywj7deGbs9Fv9AzTtplpP48X8wlVymSzeT/b5lZCVEAUEUp2HT0ZsU0H\nQtEzHEeh8SipmNdz6HeLd0ZMI3Yd5ddAKe2yu1jeebgI3UZNMQy7aFTulLViJiwKZoLXD0t2GoYm\nlGXzse+Hxfxhdu1i1jU1oe9c7HwTVu3B0u1HMDySGEm8J67fa737bAeed1UtqCoRd5QQsEUuRL/p\n8cIUjBjHF3XMCSXMKDfiqO9YPOTy9XtilQuJV2klFhLMOfn4j63YdfRkjLPMvuPF+N6BN76e4rIK\nPPKDOy8xz9irH7ckzW/ORm8ZMn5cmm8oLJnx1rSNuPnzRREt3W7dVtTHf2xF91FTDJ104pGpU7E5\nVRi71Hzi/Xj2Fgx7fy6X4+KKnUeZE7lZGK+Jq/Zg/pZD2HGoKGKrqcBy3DR6uvd+sxwf/RG7G2R0\nvCIYTVaZaCnCzYZ9BYZCnLJ4YsYxN6jLigVb2Q55alMWkX79188W4oHvopqodk9NjAk5mWzw7BgY\nOaDuPx7SzLJs/A0J33gzudysRUpkmuU7oyYM6j5jFdPcTaXHiHHmW+eROpnfeagp4ZBk1PfBTWd2\npeqtB+xHwxry1p/89QlIbaJrQcNdYovzzMblo0Vl+GFJyJxK6QPqa/hszjb8tEzM3Io1hvFeq2VU\nljgr9OLhv5XwXVJBSDDn5GRZBfqNnoG9Ojuue79Zhsd/NHbAEe0OszcewI+CL6lh3Yw3zEozIRv8\nrcZ6Kyz69yNjc3H5e3Nijlm6PWS7x0rVPWP9Prw1bRP+2HgAT/7MvrdzNoeyRbJj4Wo15tPX7cNW\ni+gFXry26ru0bMeRSAiu/CPW2sZh789l2g93G2WcXOmur5fh+k8X4MqP5uG+b5cDUD0LxgUabnUK\n7tUqk7xVtBOj83jsha2wavK6Pcdjdg3u+XoZRs+JahFZ7Wftyvy41FlKbzd3yTbsK8Cxk2L2wrIc\ncnLLHjkBv4uGKbXxpkR3KrTn7jtejMvfD+08rdp1DNkjJxg6K+pRP26rvAm8kUvsZ0SVwv+al2Em\nOLll9mZWvyZfgMN61uw+BlmWsWDrITz9i3ahyuOf8dPyXcImdAoi+T24drVVd0P/GFjRrPRP6rfc\n3eg2akokJj8P+jLcMIuNvVZ7T9nsfsQbtwTqZPMZI8GcE1YHkQEUlohvdakFW6+2tY3KHPLWn/hl\n+a4YEwfm+bw25rqaIrJg+I+TDIHnm4UhbXAkTrOqiNu+iMboVSYz/WLA6kVTb2/f/p8lOPeNPyIp\n5Vl4/eKqU2aP+t8aV8r8dcUuZnKK4ypBzcyp1WjQM+oSRpOc8rXa9tOojM37T+CJn1Zh8/4TkJXD\nBTJ/frdoh60wns/+ukYVAST03YRVezB/Z2iRtCD/JDo+M0ljquYVbs91r00Wz4KpvJPfLhLb7ZPl\nqD0zL8rCSy+Yq+teviNk4rV617GY80+UOHNUFI0FL+yIHr4uWTYfx82ExHjLP059cIa+Mwc/LduF\nz3j8lhzAmp9Ecl7wXKWZzTrrfP0iSknCJ/peaOpxMAFFZAgPNOYitvDjV+4WSpLlRSSmymICQ4I5\nL7Ydg8SOv/PLpaa/f794R2SdJ0eQAAAgAElEQVRQterYRj8/+P0K/Gd+HvMYnfhrWj5vvWbaIN4X\nKXYxYI7eJh0A+rw8HZNW72FO/q4Qc92qv1Xf86TP5uGB71bgN85U5ooQrhbGrRZevAMnc1vc4MEO\nHvMHvl20Aw99v0JlysJVDfYcO4mRP61imsbwaHai2q/Y9q7ZH5pQNnBobE+WVeDO/9pP8CKC0uYf\nl+bj3m/YIdDKykPXo3eEUj8WtWmKk+lQBvDXf/Enm5EkKTK588iCxWVBzWLzm4U7Igt15ToBYPam\ng6oY/eyHnwgtmVmGVy+bY3cx4YStB09wa1RlWcb7MzdHbLfjjV3Nb9T8zXkdFUEZ936zPHys+yKk\na9pl1d8izbz3m+W4+2vrMI17jp3EgFdn4htBpYATkkxhToK5EceKyjQhkvINNGnxfuCP/7gK4wWF\nMRZKmC3T8wXt7RyNNcJRCRRBk82D369gfv+Pr5bhkne1pjWyLKNUl2bbU5s0VdHHisq4wm4awXKO\nVD+H3ceK8euKXbgy7Jil1ZizCUhsDYx+J0RBkaNEJ/ugiRBz4ERJjJ2zXstnZMZkBauZyle3/nux\n7pdo69TvDK9jISvesKS3qTFBOeSRsbkYv5KtKVTu47/m8IVVDTkpch3KOFcWcvwEov1Rv4BjteHJ\nn1fhpQlRJ2q1WZ/6/G0HC207dxrhxhtvrjE3/s2pnMYTcUhtl+9GVBZJQJ+6YV8BXpu8Aa9PMc6o\naYb9/ip2vP56eJ6Lvo4/Nh5g2pwfNzE5c6Xv6cdr1ef3Z0Yd8+duPhTJpWDVGPX1T1wVVWoZhWbk\nicxzpDB0H1jR1ryCTFkqCae9NBW9VCmSJzAmxYLickuhykrAs2NvKpqVkEVZWBCNsalzwQ5Rf81s\n7ZGB1Mddh3v8vP4EJm4xFzaqpTl7VYxSsd/4rwW46G1+xyc9LFMWPQ98twJbwo5ZGsHcQmOuCEJW\nAjdPG/TIkCPnsZw/t3A4DF/67hycKCnHrA37uUQEIwGRh1v+vQiHC8W3ql+fEps90+0tXCdClqjm\njlVVMCjji7nbIslZjOrQ9xOjZn8+dxtG/W+NpbnFkXA8ePVYMlUlrLMu7dGxHI71LmgzWS03u5p4\n2PJqHPtVrfnnpPX4fM424XCYkmTc7rmbD2qEN8UZn9VHeLMYxwO9DxkLq2d18+eL8DAjgIPpebrO\ncbSolNssJLobasxrk7ULovlb+RKPzd0cCiYAhHyYLnl3DlblH0Pfl6fjj40HuMoQQZFt9GaHVQ0S\nzA3gscGb7WLHdDt5C2DeqbcdtPag530p9McpL5fp+eHfeAWDbQcL8fY082xndlm6O77JB9RXvMah\n1kDUVlRjymLR52J+NTg8IsCrvuMRlEUzf+r7yoZ9BXjyp1W45d+LI/GHzVDCiTH7jMVtnLXhANy2\nYOR553ns/X9clo8vF2y31YbZGw9gzNTYxYMhcmybpq7bh1G/rcX3jChCposQk9++mJdnaydJHY6U\nZfPLSjYUDMq2FpcszC9X+6Nau8irezZyjhW1M1a/Lh/O2oIXxq8VznZr1uIbP1uIaz6ez1XO4yZJ\nYlbmR80OWfeovCKIYyfL8ObUjcznLTKvZo+coInAxIvWPDD0987DRRj1vzV4VRUxyLRv6D73eGEq\neqsUgzy4FWlHf8++WqgdW3aGo4o5XVDpW/vujE3o9OwkAPZlK6OphKKyVFEMJyCbwq0ZvIO4na6o\nLnuHkQbFovqPBTKV8oo6n8zeijenRQUIVvg/+7A0toUap1WeagpKyjVbmAXF5cgeOYE7dvlb0zYa\nhqkzgjUYm/UPzeGGGnNtFI3IvY6cpj1RkWlEnOxkWdV2B/IuK6ObUZ8ICdfi2ky38WLb+sOZm/kX\n0roWGGVL5TkXiEazsYqoYmQaZQSvL4bTZC1nvDIdA16dyYwQJcsyNu/nF0DMBAD99fd4Yaplefrx\nQJ3JU41eIGFFGDLatbONZG7Msueo80yUasFcHzIXAJ75dTVynp+Ct6dvwovj2Zmtp6/bJ+wArMB0\nnzG4ZEmKjoXr9xbgi3l5htFWvNggEXm/Nu0z3pG0WqMqbWfNPU6mY/VuV7mbGbCApDMyJ8HcJxwo\nKMGk1Xze5m9P32QSv1ttq2BdltmLxLXtq0Lv3W46SQmVHCWyxaWU44qtZCzvzdyssVPnrebO/0ad\nd5VdCbMYtUr7Oz87CW8xdgRCxxjXLqol4bExF3F4MmoDjxK8ImLKEvsb71VFZftoIVa7CP1Gz4iJ\nJc9Tn9E1iWQ8BNSLSqHTfIFZm/87P6RZU2vS1u8tsO1DUeZSwhQr9heUYNfRk3j212i0pNLyIH5Y\nvBMTV+/F4DFsYZiFuVbU+Eej8VwUpQamYK76260dAqcZSwH+d/2nZbFhSqeujTr5MxfccijnhVPM\nxmCteaC9+8qzg62pk1F/bAQu47a8YLCIAWLHz9iM1nxttMIo7OWSvKgvj7rmDXsL8OPSfNPEgpUF\nEsxdwq7CXOnkN32+CP/4ytqjGQhl3Ru7hC3stXnyd1Xd4oMEX3QL9kHPGYQBZJUZM4hAxsr8o/zJ\niMLn292+y1VpsY2uec0ucYFCHSde7T9gdV/NMsyZzaFOArwUGoQd1Ps9WN1h1gRw3ScLLLc6ldOY\nCYY4nysr293XHHGOc3fqIvMY1GcUWUeNWqDjwcm2aiQiE7NczvplgYMZ51qZn63ezY56pK/SKu5z\nWYWMparkI1/My+NpoiU8fev1KRsw4seVXIlfeLMMsw5TYqxvNNFg8qBfTKewVrsa/yF2m0f9bw33\nGCyBX0hTTK1YCwYnzu/qXmUU3amozH4kGNb1Gc1/EiT+18oDlblR3Ub9vZ1KVhAj1mxKCZSxaf8J\nZI+cYMsURRlXrvooagL1lcpE78K3ZuORsbnobpLLw4g5mw+i+6jJjsOExgsSzF1C5HG7seIMyrKl\nxo1nO0ikLUeLSvH65A0MoZqNqMx82XtzMXjMH0Ln2H3NlMQmpmi9pbjISE1Rna5o950NBqIac9PY\n9Kq2GAmwyulXfDAX/8vdHYkmsO1gIUrKKwyjsuhRb0PHtENlysLbB1mHrWKEvjRaIDpFL5AqgzzL\nBALQLv40OOgOX4ftPXnfQbeRwQhdyln5aS9OxT2qkI9jGfbeaso8St9r1d7fV+7BJ2FzPJ405zsP\nh0wsth8qRLdRk4XqPe8NsfHOiMLwwn7aun2YtnYfM9a/RmNucA++mJdnavOtKU8Cd/jDPzeFBDWW\nAsIsjrgZa3cf11xnHPxnQ/Xo+7/qb15FkdOwkaxr3X5Iuwt4NDxu3/EfdmhXXnMR/fNhBZXqpbOH\nv+nzRSivCGKMzSg8CkaLRKOQx0aLpjW7j+N4cTlKKpJDME9NdAMqC/qJ8nhxGWpXS/N0u9rKBpOn\nbpH2vTFlI75csB2nZKbzn2RUb/jft8P2rWU2XxgnDi+yLIfjLLNRf89r75qhit5iJnDuPnoSjWpX\n4yrT7ApFNQBGhyv3AogKoOv3FuD+b5djcKdGkeNOFJfHtMeoDVYti8YxZ2jMLc7V43Sxy2XKovv8\n+pQNeHxIR8PjjRZ/su5fEQ4XlmLf8WJk6d7BUAhEgRJt3q+TZRU4WqTdSlYv9qxCWE5YuQfv38BX\n14cW2RAnrNqDN6dt5H6PFKzu0grNbhr/jZq4eq/p724555lx7GQZ7uCIse9WZCCeLMaael2pNRS6\n7y5dzOxlO47icGGp5t1YsfOoo13F0OxgrFrZdfRk1JxOMp9Pp61zN7ynUqcRSlumM3J6iPDlgu04\ns229aJ268o1o99RER/UCxu+MPuQxLymSlBT25qQx94hrPjL3SP9k9hZ0fW4ynKzzFZtONzFrjejA\nYjYRKY5BPy+3l948Itw4eMmUxUDuPvsZ2/SwtpD1piwl5UGcNXpGZFFihZnwLRyVxeCGqb/WX8EB\nVdiuXi9Ni7GHNXrO+rrU8a9l1e9uJNv4ZYW2HxWXVeDWfy/iOnfb0TJbNuaKmYVoH3TSZ8ev3IO+\nL0/nN/li1i/HTE68Do7rGWYH6usZPVE8C6kRVrkW/tx0EPuOi7+7VkIpj/lSMuK286cESVjAd+t+\nLsqL7Rs7Dhfhps+1ya+u+2SBI1MZlkiuvoZ+o2dwl/XYOL6dCBH0i2SvWKAKr6jkzlDGfaMwqaKw\n+ob7i9kkkMpBgrlr6B/3+r0F2He8GM/+upp5/BtTNtpKLe42emGjsLTCcCBTPNtjBmODvr44LyS4\n6HXSBwpKsPWgPcFCqbtUF/rOjkOIlRacZxtbj/pKlW1b/e1RBrLlO46Ah//OzzP8TSn7UpUGwcxe\n3UgIljXH6H/UXkGMxtTg+S/XmXI8pEv6pNx+3syfZugdvCav2YuZG/jsHH9eX+hovBZ2wFXiDtuY\ndBSBXG+fLQsYTMkyYt6/IW/xxdJnrQPVl7HlwAnHUVK8xuo+edH6HYeKsH5vYuN1a94zF+QTO+tp\nt8Qio1cn76BYLHZ3iJrkxcuhW13Nhjj3K31QiEs5tddfzs8z/Z1lWiNqzRaPfADxgARzl2C9kP+c\nuN4wO53jrXeXBgBWOS/8ZuyxDUCTmY8HvQB87huzcPCEWCQLhWU7QsKeMskpQtHQd8ST9NjNHGkH\ntbAi+ux57hXL1lqE3UdPRuz2rAQrvSBqJJjqve7VkSBkWY6cx4xj7vEEd6CAL3yaumX6Zu44VISC\nYj5tuxrldqkdG0VhieEiY8IVH8zTfOa1N2XWq/sc78nRzJeBhVVYRzVuXYvZ+PTDktj4715jtpjk\nveSQkYcxpRXByJiy10ipwwnvstPt5F0szHb4vFa2sa7vJMOhNh4obeFdcD4j6CQPiPtnHTPJrhoq\nLzkgwdwlZujsuFICEtcWvR9XeHY1gLw4dXzR1h2yI1QcsERY5kAwMkLJsKnGKCyUn8LlDXh1ZtRu\nz8S5CQC+1JlQHS60t8iKOH+GP1stCN18Vwp1uwp8NubaBuw9XozrP11guw13frnU8hg3rtlNYYUZ\n7s5G+WsMIrfEg8veM3f8Vo/bbnW5AhOBbYQHJg4s1NdlFklmK2foPh4N8aXvhcYU1+NSG+BlLWUV\nQcud2Zs/5zOfY5F/pAjZIydEMm2yYL9/tqt0hJ167fhELdx6CA//wJf46YmfVpn+Xljqo0nXBBLM\nXeIfX2kn2YAEpJjcXT9v93r1oh88UYKFnKmAeQkGZQzjibDCgMdJyi1YAtaczQe5zrXKniiipeER\noiwsWWI0JKI7KArKNqUiMHw+d1vkNzNzHDfQp6jm6vKMZ7h613FxG3Oxw/nKNHH+5LQ844IV/9pO\neUPfsee85QYVQRm7jpdh02G2kOXfkdkZ6usyU2TYXWiziLfQyFvf+oN816jOqPrg9yvQfdQU0/6x\n1oE9+7wtobnxz83GJnjK5WmskuJwk1n+bHZqXZx3WChLcTAo44HvVjBj2Nvhtl/5csUkGorKwmDH\nMXccKsxSjSs/sZypEo1X0QP+8tnChNtZJhu9X5qGYT2aGv7+zozNKBYwyeGxm48NB6btD3YnAn25\nt34R0i6xbMzVYfX8gtHbLJ7kyf33y6xEN2v7bM622C+TQwml4e4JIRPDX6+vEftjJZXMne6+TFip\nFWokSRLeLd1vw1kXcF/Af3qW+G7pZCXqjkG4UC+UbeMMQorKBn/Hky0HTqDvy9OsD1Rx3SdiO4xB\nWebut9MMzIaTERLMGdz3u/MHXFYhI2Dg1SZJ0XdbsZlOFGOX5mPs0nzc0b915DsvXvSdh71xforX\nFqlTtBoO/vMOniixTl3uoq38j0vz47Kbo+4LZgvYuMG4yV/Oz9PYbxo6zsYxKotpuYb16RdW3tQP\n+NM0z4z9hea7TW5EDKosTFi1O+Y70b5kZtLjBk5zRpjhdVdgmTR9t0hrBsla1CfKlOXXFbH9wW2C\nMv/88NQv5mYsyQSZsnjIEZMtQacDvtuDhFoT5iTNuxEDXp0p2iQubnRg4wu4F+pJhEQuJaye1WuT\nN1gmkHFbWOFPMOTNzDgvn734eebXNRp/iG85MorykJsvthhfwDD/0j+TAwUlhr4bK3WOwW4LL+ry\nVnNky91zTNwfxCvGzIsNu+emD4y/EH9/1MmzWO+fn/xkAHOTLltEkunI+q8iHCkqjTnGCermL9H5\nQcmMY76Yx9jFqiTsPFykCbNrhp3QqX6FBPMkxcsBcc3u47jjP4u9q8BFdluk9baiy3PGmfr8glXq\nchEsQ8VJ9jM7mmHmNCVJ1mm5eeNsKzzwHZ+zkALPJU5aw04gw5t8SuHeb5YLHc/a/hVZGw3XRWBx\nm+8WR6OKHDxRgk0W6eXPfIU/9rPXrOO0NbbDsTjFmObFznq6sCS6Y6SPHe7HzQQZcM0e2Qi9YmLy\nmtAOezwWKa9OCuUJUC8Cpq1zlkAokay0UFLwOiJXNkgw9xBTG/M4tkOU0vJgUr/sIsQrZKImuYfF\nAP7+zM2azxNWueewYiUASwC27DcfDO1opEJOU+xe//uqvbjobfNwl4PHzBauUwQnWjarRDh+w20B\nYrnOHO89Xf9NZpzE2Ncn4ko0TuecAwVajWQiAxiUGwW4lmNj9LuF1fXGQzD/9M/KpR23WsRXVUgw\n9xA/ahS8IFnsvP3CwRPmW27fLXbHZMIOkiRh73FzDX2eSTgvwv/44W11I6lUfLDfUD/cZzV25iO/\nhetU+GqBQQhaj+76wROlkZ0xo1vipX07AKzfG1Wq+M2EiHAXEsw9xNRpIWkmJsINRB53IgfdBOT6\nIWyQ7BMzreWTn1Acc+sHGc++6lVd938bNT8zmtZzd3obm583O28yQcMAGxLMPYTkcvcZ3rNZoptQ\nqck/Euto45rGy2m2Ww+H8WQTdPVmBYQ3VKZdTzvRj8zOsMr8qRDvVytRJjZW9tJukmTDlSHxiMGe\njJBg7iHmccydDR7zt7ibqCdpSNaJUqDdfhurRLO1Ed4z0iLDnSl+62CVlD82GCeKSQRuD508mT8B\nd4Qv3hLczsHBumcbDeyi3TLp5FrsVJJXuJJchuuQYO4hRgOhBAnHTjrz2DeKEFHpqQJvsujkcrTI\nu8gSAFDocexhXrycjKpAtyJsYFeYlWVgxI+xcakrE+VB2dIfBYjvuxWU4XhuVSOiPzNKBuQNNGJV\nZkgwJ5KKpB2OBBouKoAesHAmdYrTkJSEv0jadygBrN7lrd1wMrN2N1/W6nhrd0VSvltRXBb/PBdV\nifguZpIHEsw9xDATH02N3OQ0r6P5nKw2aSLxWEX7h1HkMDv0a1fPvcJ0ON1K9/LJ5+6tOjbbh00S\nnxFa7C5K/Wibbudaer0klnKdBc13YmzZbx1CMEmnwRiSLdRsvCDB3EOMhEjqjPy0b1RL87mSjEeu\nok4b75SUgH+HhBIXr1PPoZPxjTm9aR9fwiQvBLyvXcpgShA8VBYhMl58MS/P8hi6pZUb/87ClZiy\nCnqt7FIVBnlRHyI3kyTN3uidw9pChwvSh74Xy+bpZ1bs5IvgQNFXCCJ5d0q9gu5H5YYEcyKpqArD\nkeigWxXuCQDk5lcee1/eSDcv/77e45YQXkByU5RdR2NDsBLOoO5VuSHB3EPo5XGfiS6mp/crNKlX\nfsooBCVRRTjvjT8S3YRKx9Ei9yLPEP6DBHMPIQHLfdyKFVuZoG3N5KOigqI9VGZ2HC5KdBM8x2ku\nDhHmbj4Yt7oIItGQYO4hfvTMTzaqYjglUTGb5PLkgxaYBMHP61M2JroJBBE3SDAnCJ8hmmCIwpEl\nH+QAThAEQbAgwdxDSJNJ2CEoqE2lfpZ8VLgZfJ4gCIKoNJBg7iEkLxF2EO03+zjSYhP+gjTmRLIz\na8P+RDeBIColJJh7yJxN3sWEJgiF48XliW4CIchmjux+BOFnCmjcIQhPIMHcQ45QSCPCBjThVX4m\nVIGwnwRBEIQ4JJgTBEEQBEEQhA8QFswLCgowYsQIXHDBBWjQoAEkScKoUaOYxy5btgyDBw9GzZo1\nUbduXQwfPhxbt2512maCIAiCIAiCqHQIC+aHDh3CJ598gpKSEgwbNszwuPXr12PgwIEoLS3FDz/8\ngM8//xwbN27EgAEDcOAA2V4TBEEQBEEQhJpU0RNatWqFI0eOQJIkHDx4EJ999hnzuGeffRYZGRkY\nP348ateuDQDo1asX2rdvj9dffx3//Oc/nbXcA7o3ysDKfSWJbgZBEARBEARRBRHWmEuSZJmKt7y8\nHOPHj8eVV14ZEcqBkFA/aNAg/Pzzz+ItjQOnNamW6CYQBEEQBEEQVRRhjTkPW7ZswcmTJ9G9e/eY\n37p3746pU6eiuLgY1aoZC8Jr1qxBMM5JOILBirjWR/ifutUCOFpMyWAIgiAIojJQVlaG3NzcuNQV\nCATQsmVLoXM8EcwPHToEAMjKyor5LSsrC7Is48iRI2jSpIlhGeXl5aioiK+gTBkUCYIgCIIgKjdl\nZfEJZ52SkiJ8jieCuYKZyYuVOUxqaioCgfhGczx8kjSjhBbzXkoQBEG4QYoEUEJcIl6kpaXFpR47\ncqwngnm9evUARDXnag4fPgxJklC3bl3TMrp06RJ3wTxt+R9xrY/wP2lpaUAxOQQTBEF4iiTRtjUR\nF9LS0pCTkxOXuoLBIAoKCoTO8UTybdu2LapXr45Vq1bF/LZq1Sq0a9fO1L48UaQGSD9KEARBEPEm\nSEI5QQDwSDBPTU3FpZdeip9++kmzUtixYwdmzpyJ4cOHe1GtY0guJwiCIIj4Q3I5QYSwZcoyceJE\nFBYWRoTutWvXYty4cQCAiy++GDVq1MDzzz+P008/HZdccglGjhyJ4uJiPPvss6hfvz4eeeQR966A\nIDzEwhWCIAiCIAjCNWwJ5nfddRe2b98e+Tx27FiMHTsWALBt2zZkZ2ejY8eOmDVrFh5//HFcddVV\nSE1NxbnnnovXX38dDRo0cKf1BEEQBEEQBFFJsCWY5+XlcR3Xq1cvTJs2zU4VBEEQBEEQBFGliG/Y\nE4JIMiQfBUyc9vA5iW4CQRAEQRAeQoI5QSQBGakBtGtYM9HNIAiCIAjCQ0gwJzRcltM00U3wFX5x\n/qSABQRBEARR+SHBnNBw3ektEt0Egkgo/dvVT3QTCIIgiCoKCeaEFp9oiAk2Y/9xZqKbUOlZlHc4\n0U0gCIIgqigkmKvgMRc4s009z9uRSAJ+sd3wCX67GzXSUxLdhEpPaXkw0U0gCCLBpKeQeEQkBup5\ngtx8VqtEN8FT/CaIEv4lIzU6fDSslZHAlhAEQbiLenwjiHhCPY/QIJHGXINv7kd4O8dP4RvV2vta\n1WylRCCSgLYNMvHHYwMT3QxT0kmIIlwmNcU/Yy1hn/du6JnoJghDo5kgss/CY9x/bjtXy/OLHEok\njqZ1qgmf45sFDOE6bRrURKt6mYluBpNRl3ZOdBOISgqZdVYOzu6QfJnmSTAXxGdyOWpkuKuppKEo\nRJemtRPdBCbxmCtObVxL+Bw/9Jt3rk8+zQgPvVqdkugm+JZGtWMXkY0Z3xEE4R2dm/hzvgSA2tXS\nNJ9LK/wmxcVCgrkgXmjMm9Wt7uj8D288zaWWVG2NeYd66ZG/lXju+vtRFULp2dF++6HfnNuxYaKb\nUCnxwaM1JBAItU7dxskPnp2YxhCVihoZ5GjPix/Gf172F1YkugmWkGDuA5wIFLIM1NKtCAl7dG0Y\nFcyNBppXhneLU2u0yL7bq/EHP999Fga0r/yLpUTi556nmBto2iggJPylu381fQBwY9+WiW5ClSU9\nJYDVz1+Y6GYQLpMMiwgSzAUhAakyY/3G1q2RmEVQPHwbnh7aCYA9DakXTqk/3nWW5TE9WtRFt2Z1\nAACpAeM21HLZ5IvwB6wnbtINNPzr0ga4uktIME/hPYmoUlCv4ENU2L2md3NvGsJBMgi9ydBGX+E3\n50/A7RVg5RqKhp/WjPtY1pX78Xl7Re/srMjfH954Gn74u3Uyo2/u6AvAGy0Ej221JEl4+PwOmPXo\nQFRLq5xbz3ISdML6NdOtD/KAQHgGU3c/Xqe9Ohn+n/6SQbvnNn6JsCNJUpW8/wrX9ubPAi6qmHn1\nqhzR5rhGMjxTf7wBSYTfpshrT+d/eaoiZ7TmTwilfmGVgaYi6I8nHo/BpG71tEhdF3Vrgj6tsyzO\nAFpk1fC6WZakpgSQXd+fUUOqCol6TRR/CLXGOxkmXiKWL249HQBwR//WCW5JFD+Fp403+gWS0+R2\nN53pjxwwyRBBjARzQfymvcrKTE/o0HFJ9yYJrN2aUzKdafLKKrRZIO2+1HcNbOuoHV53u+ppKciM\nmHvwX2MSjHEAkqedLBI94vD0vUSNi8pjPUOVkdmOMOW3cb0qMvDUhlj81GCuXc5bzsp2tW6jAAzJ\nPG44JU2X+XTkRR0Nj+W5T34JP+mPVphDgrkJLw7rShkNLWjg8/tTMyMVgzvZd64trXAnPXuKw0HJ\na7EhJSDZ8p9QFirx0EL8/ew2ts9NpJbkjDZZETt4OySDzJhojbkE4Ky29cLfJaYtXiBBwjd/65vo\nZsQN3vkkHkJeMnYjN10l0nQJlvwiWDslGS6DBHMV+gnwr2e0ionpnMhJ8vNbems+OxFU3KIybfWx\nXthyXcxTu1ebFE7DSnZRgYuUdP+6xZltYk2QujXXCrerRl3gcq3e4fedJcCZnXiiNeahNiSkCZ5z\nVluKOqSHfHXZXNzNvXFGrzF3Q6Ad+48z8YGL4Z3tkAxCbzK00VdYCViSBGQ6sMWa+ehA5vf1a6aj\nky6If2MlQ2OSDFJmUTPcIG/00JjvZMjcE7a6dcoglFlFonlIiGrleZ9Sop2jRMKEirSzTnV3I+9Y\n9T+r1yJe8uZpLe0nMkqUUKzW4lVLsz+dxWNH5Yw21j4bepJBu+cG9w4Sy2AdiINkLkne9uv7z2vv\neplX9Woeia7FYnhP/mAIjXQZoM2UcDxPQ5KA07OzXF082CEZ3ikSzF0mIEmWg3xOc+NtbZbmqXvz\nOljy9PmMY8Xb5zb6S7aW8dEAACAASURBVDW79ES9EE5u090D2+LNa6Me5Havwe1ndUHnRrhnEJ/d\nOtccpnZ85bxGWZYjg7Vbzzb3WW+04PHsejXSU5DTvE7EbtXq0ccrVF+reuaOuk6eYUFJuf2THaC+\ndf+8qjuev6yLb6PzNKgVFXR4dzuTQIZwBdG+d2GXRnGpPzWFv2Hf3XmGS63xjjHX9uA+9sY+LfHp\nTdFdetNn5CNpN9vDcS5ekGAuiJWAlZ4SQPNTLDJ5CvaMqLkA+7xEmpPoaz6nQ4OEtMMrMtICuKJn\n4mKuKugXbPVqpuOxC42dcdQMOtXaxt5uD1K6sluDXVqqmVYmPv3cqVmGBODXe/tjzuOD0KNFXYy4\n8FQ0rB2ynbWKbLDl5YtZDXLUHoUGNc3td/2w0Bcm3CVkAA1rVcPNNp0CvTDFubqXdtwoK4/6q1wh\nEMbVbR5wWVPrxM9I8f8RebPzRg9Fr1biuw+iSJBizDmMaH5KdXQ3UbglI4GAhPM7RxdAZvoDPt1P\nfMbv8fcPMP09kATLXRLMBbEavzPSAvjqjr747Kbe5geK1OlaSdY4FbDUA9k71/fkPu/WftnoyxGe\nDxDTMGak8mvPeK7dbHC58jRjAV6G+1oeXnj7D6tvVzfRPkqSFLNoPMVhAiavBm8RUwW33jdJkvDL\nPf3QOzsLw3o0wzd39NVED4nUF64wp0VdT7XntarZM8tq29A6FKWVlsor3HJI82KM1ZvBlQfFHcm9\nMLF56PwOrpZX22a/AlRjToLVmG5W3yLLQjHnIYlycueaOy2O2fR/F7nSlppW5qf+l8tJMBfFagDP\nSA2gfs0MnNnWOH62Wb+wM0EoHf7Wftl4/rIuAID/u6JrjE26F+hftqEq+7HLcppqjzW5chGFFa/s\n8sbVOTitZd3IZzPbO8C5I5mVbfJHf+klXqgL8GgDJSkalUX9nO47z9j2k1WuU8HSKyfZRI/FkiTh\nrHZsJ74bwmnXMwwSq7h1R+zYtI6/rz8eveBUy+Nq27TLdzpGJfq5mqFfCJ0d3k20itOtj4ZRmfHz\nJo2IjCvL0XHTbLHIk83YCV46YTtVmlidnZYSqHS7DnYhwVwQq47fMGxH6MXC1arM9NRARGOdnhLw\nNA25IkToV+iiTjlKal4vBpQrezW3rUFQHGub1uHXfphduiy7o82I3iZ3O5ja0UmomQ5MWfQCiFo7\n7/b7E09FkuhzvqpXfEylenI6d6oFyq7N6nBt59vt2/Uy09FU52QmghcaQvX2vRP0igklk21Tg5jZ\nCrf3byMcxadfO/5Eam4j+gzUypugrCgDEguP0LnoqfM4yzKGJ5ux34j0xTg8JKMqjOLMV1ZIMDfA\nyEHTSnx8+7qQc4WpB7PuJ9e0hLKuLF09950r5vluhpFm1EzAZl2ncp+8jIPMK/Srn1n/dvUx4f7+\nGNRRa5/tlnNrG8FMlbERM/hvGM+REqKCcfuGNbnKDZmySJHzAWd2yr5xynHYF0Uvw+qexd3220Z9\ndh+dDBldHMR4V/oMzzt+98C23MKVG+idULs0rYOvbu9raQdfLS2A232U/dJLeJUBZjtxbRt4k/V3\n/d4CzeesGubhRJVrEDWv8jpamVOUN8vsuniuwEkknd7ZybegcQIJ5gz+2r02/nubvaQO9TJDjjDx\njN7BMsFQ2/8qPMKxJe2kblvnhwsICly46D167tIuuLZ3C6apSZY6M6jqYmSEJlIRzDRH+kVJG8HJ\n5OGwXahXwqskSTglMx0THxigMXkwu9eyLEfbY6NhrMVr9bQUDOvRFKPCJlnaNkb/Fk8aZd4+1q96\njacbsOrR32LfLFDiQDAYv4VHVmZ6ZEczHtRh+Fv0b1/f0txLgiS8NkoNJNFUrhtnQ1+Z35NzOxq/\n77f1b42NL12ERy+wbzvvZuZKUQHUTZNTT2zMFZlCsN4ndJlCnbTs1au62zpv0oPmjqB+JYne5vjR\noV46c1AFYK1N4nIgNMO4Aqui1WfGbW4XqIg1+CovtMhEJDppZdfPxD+v6s4cPJY9Ew1DqV3g2MiC\nKXwGP0aDvWKfbIbIpXRqUhupnJEIgNhrtmMGoz1fwlvX9USHRrVif3SAVbtYt1ckLrboDoia9PD9\nvjS8ZaxvitGOmpPoGjcy+k1EM2ZDs2VXtubdLWTlKPAz0x4+B7VVcfYHdzI2j9FrTNV9lfd9GtbT\n3UXk/QK7q6K9RX284jjaqLazDNLpqQE0s4qGZgKPYoj3WYi8PpMfPBv/d0VX/hMSgPKOphv4wACx\nfeCPxwbibwNsJEBk3ORmdasLBXFQqJGego6NYxc91U0if/kFEswF4UkwpP43HnRrXgddmtaOmWy9\nbIPROCYqzyqDmIgg7JWDi9ntevj8DnjNYtVuqq3wSCv48hXdLLUCvKYsokiqmP12TFn8NDyqH52S\nAMNsItLbRWviHQteWKcmtZA3eij+emZ2uC3aAoyCeTjpUnq78b+fE51EP7uZHVGqfs0M9HbZRtap\nCVuk3+m+v62ffVMQ3t0sMx8ekUXd6CvtaQPVDOvRzNVIYO1dXhgb0aNFXXxzR19c07uF7TLciORU\nt7p11ltebbSIKcupjWvZEjoTgVlYTP0lt6qXGbvAj/OAz6quZZ1UpCeBczUJ5i4T2dk3tTF3t2PU\nSE/FhPsHoFW9TMvJevZjgzQJc2LahtBgyYv6Oge0r48LuzTmPheIDmIiAt2NfVthykNnM38z+p4L\nxharwv3ntcfVvVtwL3Y6NvZmYmM5f7K0Atpz7GuD1OfeqUuKEkowZH6+mziJ+GJ1qvr36/qEhAQz\np0f9pGN3rZiVmR4zHrhxK0/PPoU7dOU5HRrgiYuiEYuMEhEteXowfvj7mS60ToUc+V+EJy/uaGq6\noCZqY679fsSQU22Hh+SJQhOq3KxdsfseRnRqoh0rJKhMEjl7gyRJGHiqezkkeLvzbf1aG777Rosj\n9b1pWrc6zmpXX/M+NeZ0uD+Ps4/wUC0twJ30iYXarM/u/H6tg8WJlyh9Mbtepu13CnBnAaXGLDyx\nEcmSq4EEcwv0D9I6vXZYg+iFjTlHmT3DQnU3A+fVlvVqWNq0iYR0Ul/nK8O7obpJAhWm86fKxpz3\nnXlxWFdDUwczEwgrAZVlqy+Cci29Wp2CFlla4UZfHE/55lF1+BvYvmH0nhiHo7LuXE9eHBtu0olA\nLnquWzGrjcqe+MAAvH61KsuryT2JV7ZOwORJW3Qio1/r6gT2WMdia051SaMalOWYy7jz7La4l9uU\ngv0cqqWlYMJ9/PalmenRd02/ILt7IF+GXetWxXJN7+Yxviyhbi6r/gZXlBY3FT5u7EoO6RpV0nxz\nR198dXvIb0vdyou6xipyLONQh7nAxbwQbgpsifDlNNvdc4raQfeKnuzEWDxCN1+eEH6Gn9bM1cWZ\nnyDBXBBLE3Nl1Wx2DGddv+szWHEMHl2b1UHe6KHo0KiWp5m2ojGvo7Amhou7RQdepo25Ul6SrGRN\nd0LC/55SIx1Biz16q5Bs6SkBXHt6VIOSXc++DTMrfnvLLOcJYdTP25YpjO4sqzJ4TN/N7DU/+stp\nJm0J2dezQhcO7d4ES58ejLzRQ9E6bEueotdyc1qyxERkYnR8NxYgEiTmOzXz0YGY/vA59ss1apos\nR3IoiFAtLQVtOaMAiSIS7Uq/WFFj592Lfc7s41jPWpJin93jQ6yz/Ho12puFquPtqu0a1mTuxLix\nmIjOudZlVU9LQaf6sWYrTqcfWVW/6CWx+ml9iyy9iUCCiS2+h4sRs/tp5hvA6lvJ4lhPgjkLM1Nh\nizeYlWRAJMasuvh2FhOWV7IsT9/lDXN13enmzonKFmZQTrzNsUZjbuPuRu+FjApdR9ELYGqhm0VG\nWiDSgh/vOisSV90OLGe+UzK1k5OdAStkyqJMRmGTJIHzJQkY9w9+0wgegfXGvq0Mz21U2/geZjAc\ngmTImPbw2Xjj6hzU002UbpmyMDEQ3vVaahkmoeIMblXr+pkx1xKtR6CJ+jYClmEAWYy5NgePXXgq\n/ndvP235nOcrIT5F436LYMcZ1q5SZOCpDTT21okeEwGtgoi1U8R1rX64EIQcbYd1Etvt+f7OMyzt\n99URv/Tj1Pd3nmF6bo200A6BMsbXqpaKJU8PFmqjl0TmQslhOFx3mqMpL0n0ecKQYM7C5GlbZXdk\nOX/qO7OZNqW5iWe5aCc0thu2dx7zWIvXrUfLumgYdhphOVUp58sCpiwseBIQWJavlczZh3DemwoL\njbmVpkgC0LVZyOSoocrpxrNwiQbfWw7EHDtEZqdmZVo7XSk4MR+xOvPl89j2ue0a1tLEo1bK8UPs\nYaukVXbNEbzcadPTsFa1cMY/rV8Lr1NoemoAeaOH4mqH9rlm75XIo74wbF7BWrjw8MWtfdCgVgZa\nhbX0vLb2rDqdoO466ghlLH8+o5Fb3f/UOzhutdONxTBPHPy+bephsMUOp1pxor+8vm3MFXMt69XA\nl7f3ETDfii/ndAj1wZoZqY7maKPnzmu6xMIoW/IVPZvhvRt62i430ZBgLsjF3RrjU5PVM8sBxGi7\n5aVh0W33NvUz8da1PVBDZevodACzOv9SF+I0W9VRu1oa/nx8EIDQtvU03TZ6JCqL45a4C0+2Qz3R\nRUbsMxedRCRJwrAezbDoyfM09upeZv4UP0dy1Efr1tBr7c0LC0gSZj82SDlauD6jR/DekHpoVjt2\nwc0UUKVoW4wQ2Z5ntcnobJHEZHa0SYrSwUwQNbo2o/4tsvBSU1ZhEIomTGpAwuU9miLbwFHVTZRn\nfUPflpj4QFR73LvVKXjsQq2jqDKmqkMlAuKLpAa1MpA3eijOaldf8/3Q7k00Guxf7umHf996ulDZ\nAJBdr0ZMiE+NMsmg98SYn0nWSgh92V5oTvV1KEx72DwYgFttkdT12xgUB7RvEJlzlLPP7iDgzBtV\nanPz7CWd8cs9/SyPu75PC2x4aQhqpKc61JizW9ewtrniyfB2SqGoZKMu7Rzz05vX9sDAU5PX/pwE\ncxYWE5OZfTCr88VozMPHqO18Zzw6EMMMHCu8sr+umcF21DQTLC7vEZp40hmCq3IWy6EnivZi7CQY\nso2lGVIUvakHD+rb9vD5zpI5SVLoOTQ0NL9wdr/cyCxoJyqL2qv/k5t6CdUXkCTUMOizPChdLE0X\nLqtxTXGNjZfOn0b3kmkz6WK9oy7rjDHXxJrtGNEiK3aX6qvb+2pCBZ5poS00wkowH3lRR7x9XU/T\nmPvK8+Z5VjUzjHdCFVOWFEmK9N+c5nXwwY29NGYnfxvQGpd0b4q80UNjnODdSiITkCR0bhotq0eL\nuhgUFkBEFoSzHhuEGY8O1Hyn2TDkHF5SUwJcuxtmmnUvadeQz2xFBiI3wGliMbfeyU9v6qUJY+o2\nt/VvzRWBTZIkVUhHowWbNV7s9tarmYFbHIRG9SskmAvwyV+tBQlW57MajowmDv23wlpXy9eFMdFb\nvD13D2yHN6/NQcdwiC/W0R/ceBq2vXIxVzuU+pzGM3YDLs9yjnJkhCKzqB22hM2QBI8XRZ850675\nQjSOOd/56gggoplVHZmySBK6NK2NPtlZuNViIDd7Vso7qLc7rlmNd6eLp49pj5ENtGFm44GdSbBW\ntTQMFwhBdu+g6Na7sh3dv319dG/GH27VCDPBfMpDZ+MOG8lLjMa2Mdfk4F8GsdsB9g5C86waqJ6e\nornP/dsbaziVzL3JAu9cc8+gdkyliv5WByS1KYs7o5utKUNviqNqS1o4e6rZMPPniEHM79WZtlmX\nN/6+/pg78ly+JoYLyEhNsTSdVWgZh50jwDingtsRV3hgzTnDerifrTkRkGAuwAUcMbqZA5rBCHKk\nqBSA1obYtGyXNA5mtn5WL096agBX9FRN3gZRBXgHXx4bv7jh2HRIMWVxfi3W9y8+piym0TslPnFc\nbW7g5M7YsC6KUFRajmppKfjhH2dy+SMA7Hui2JYrtsQdG9fCK8O74eO/iGn/FXoyNFZKvfq48cLy\njMnNzhBIgGNYvKp8jXOyC10zK9N4THR7s2L4ac3R1KRPKM+c7fjIh0g2XT9g1HX0GtaaGamGu53q\nb52asri9CI2cq/pbMSUpqzCuTB8Gl1WOhNhMtV2b1eEed9Qo122l2VaSopnB2uUWpYNBfg63/FKU\nUgKa/sJftpdhI+NJ5bgKn/DMJZ2ZHcPYOSb0L/d2m0uyqzKJmsUA5U0kMogjqYW5Y1VYmOWqTUum\nScx0Fm4sbPQC898G8G2jmT277+88A010UVfsCh92MzMaVWe1rRu1q4z97f0bQuEJeYUSq0t2Ekbw\nSFGZ7XPVKJP3rWeFnnuN9BRc36elicmROe/fGBvCUbnKkUM6YsNLQ6KhSUXsLy24/9z29k40wO2F\ndY8WdTH+vv7M33gX/W61qEvTOnj4/A54+IIOCQ/r6qUCQ31fjeo5jTG+GGamVRUhKri9cbVxEjw3\nUXclJXtvqYUZlRVOw52yTr9nENsxtHX9TMPY4vpM4Oe4kIDq1rOycc+gUFz/Ae3rC0Wc01/Y40M6\n4omLrMOAuonXO9FuQYK5BcqkqNdeqUlPCWDDS0MM7XaNxtLzOzfCv27uHdG+6XG65aec/p/b+uAD\nlQCQlZmOvNFDcV4nY1v5Pq2zTAVf5Zo6N60dsSkXbW5AQsRG086EM3vEIMOtxXihtvdUEL2Svm3q\noVszvVmHvWevLAwHtK9velysExe7vuz6xjGcX72yezRcYvg79XPsH26DW8IE74T31e198eXtfRzX\nZ1dLZ9ZK/XlqZ+/oMaGDAoGQbadRO0x3MyCZ/p6pioRgd8FqdA/0Md7t0jXmnRArXznKaQSdlICE\n+89rH+PQCWjfmxYmEbWSDZEewXL+jLnjkqpMCWhU23yX+EpGPgE9rkRlUTnsK74nVv4NzHKkaF9g\nLV7UdLbhb2DUg2c+OhBvXtuD+XvfNvViNPdOCQQkPHrBqVj2zPn48va+uHtgaMFgx5TlroFt8fdz\nrJN3JUvscTchwVyFMr6w+sGt/bINz0tNUTtHsMqN8f4EEBI0zuvUyNWMbSzaNaxpudXFWvmy2qUX\nskTtstWnPzW0cyQOsZ1Btl7NDMOtRRbWMeitMTsmEmGGUY+o8GMlWBtNnaMu64LLcpoahpFyE3UI\nMTNtrrqlToT0lAA7aY6e/u3rY0D7BvhzxCDhXRUrlOrdeGX1TqgKt9iIB65HkoCeLZ3bevOifiyv\nX+OttpN3gdaqXg08duGpzARbVqjfP3V9+qqVj71anYI2DbxJlKSpz8O5QkLI7EwoGgj4HPclKfru\nS5Dw+/0DMOUh84gpvOhzKZgfa/xFatjG3G7ytZSAhLkjz8WIC80d/x+30BKr22iVqC4RSJIUE23J\nLXOi3tlZkTr0vH1dD7x6VXdX6vQ7JJirUAYYtyMuGL1aoh3L7ivKU41i06mO2RwPu2/lVvMM7l/c\nerrh9nai8Crm8z+v7G59EIMOjWrhnet7Qnnqkx/km/zsDnI8ZkrqjutEsBDdIm6RVQOtjRLwcGCu\nFXf23L+49XT8OYLtDPbohadqNF36N+PZS0LhwWQ5th1TVcLOg4MT43DYrG51V+xZjeDtBpIk4Z5B\n7VCnhniEpS9v7xuJIR4wuRSlLTUcLgCfuKgjPjLxU1C09X2y+U3VhMwMwsx6bBD+e1sfocmG7fyp\n25HT/V6vZgY6NBJL9OMWbMUJcF7YIf5vYcdisWcausJmdat74k9g1ed5HpcX07myQ8va+dNTvyb7\nPVQ3a8SFp2LeyHOZu2KX92imiYJUmbEf2b0SoixOWXK52URs1eENFOaWWB1nJTiLCEF3ndMWQ7s1\nxqkGzh3GdfAcY3yQSFQWP8QljdGYMZxUmP6/BtdnpJ2xdmLhe7aKZqNv6yycKCmPni0gV056cIDp\njlCoNbEFur1kUS+Yedvv9mQUMaln7AZEjuFoXKcmtU0zkZqhLDZkyDH3oUnYwUySvA3pqEd/n5+7\nrDM+n7PNk7pEM3HaVTAoAqdTm2EerLb069RIQ+6zF6B2dWdT9llt+YR1kR2+07OzMHH1XgChcWbh\ntsMxx0iSuWmVHdwMvzi4Y0O0qpeJvNFDUR42ZUmUQlZj66/6vmZGqmYMZ5/rUaMM6N3qFLx8RTe0\nb1QTU9fuMzyufs103GCQlVlNakoATetWx8/3nIX5Ww7hpQnrksYu3E1IMFcRFcxd1pg7lA6UAchL\nDXbHxrWY9tJWSFCHczO/b/rWS1AJOLKMLBuarUhZHI/M6u7VynCm6TAT2lmsfeFC1/raF7eebjpo\nfx925r3svTnM382a0bGxdb9gCapmwiu7EPOf/RTYgtXUK3o2w8/Ld7leV6z5mPKD8TnxzN7J4sa+\nrXBj31a45+tlrpcdr/UGz3wQz/uszsDJg75tcx4fhAYmEcDUl2ns1xD7w5vX9sDE1ZMAhMaZ7JET\nYu6KZp5w+5ZJmn+EWf/iEMemf14JxOp7tvr5C5E9coKT0riO+nPEIJSU89nZS5KEG/q2xI5DRabH\nLXn6fOMyGN91aVoHXZrWwUsT1gmdV1nw0VSXeCKmLC4/8RiBlHsrVleOTbncqr5mdasztVD/vrWP\nqW09d/0m7VJ+k+WQ+YYSySMefKiLiHFu65D2ul1DMVtRo8gsVs+rRnqqxnTICQNPbYhLukcjqDQP\nO6IZ2THrERUweCaySMQdxo2oXU1cJ2DHDMbOhMnznrHa8ua1PazP0/3LQ48Wp4TPsbalVd9r3oW8\nPiKQHeJpCRsPDTYQvX+mCwETvxK/0fyUGpY7XwpWl/PaVd0jeT2MxjC1EO80XKJbsExsqqWlaL4X\nHWfO79wIjw/hTyinhEdua2Bmx6rdanxWxlP9tajh7aMtsmoIz4HxiqOuxmvfvERCgrmKioiGJPY3\nJ33AUPvA+aLYTv7CeZzRBN6ndRaeu7QL+xylDsEbo69JmWSDsow6NdIwtLt1PFa7KJfZpn4mPvlr\nL1wUdojt16I6WtZJ5ZrwlettXLsaclrUxcAODXF7/zaQJERsUs0Eoh/+fia+ur2vwyuxZuRFHfHt\n386ISXuvRjNZCnax3OcuABB9fm3Djm+sCA2suzHmGmshVo/a7tDJkMwrsHLIY8K/2eHl4V0xS5Wl\nMeJkzDjWjnOqkd2m3sFLz5ltog6SRvfUi2yPdgVzu89FG0ZQ/5vNQn2Ocp3PXxYd/9WZXltm1eDK\n66FG8Tuwk1WZhRuLIaYpmvIv58P99KbezJDHn97UG9MejvXx6dSkNmY8cg5XhlHe9+fms7Ix5poc\n03C5/S0DCjjjIZs+LWOu6YFrehtH4TF6DqzkS7dZZrROjheWTFlUsDKTOXn537q2B44UlWLc0nzN\n96KCdiJSGfPCcyVm45uS6EQ0C6QT/nFOW82kMqJ/PZSVReNc81xTvZrp+PWefgCAOkjDtleG4nix\nNla2dms49Az7tM6y33ABqqWl4EwLe9KFT5yHwtIKDHp9lq3ygZAt/G/39keHxjXx5YLtKC6rwJhr\ncpCeGlCZKUXPizHLEBC27dhMDzq1IVbvOi58HmCtNbyiZzPcwRnH3gkZqSmasJVm44cS5eivZ1jb\nc0bKY7ygsx4diNoWWQdb1quBP0cMwoBXZ3LVM/+Jc3HmKzO422VELcHdlux6oXvXvlFo8Xh5j6ZY\ntf2A5XmyiaJGIbLj58MxWnTRoO5XyvUoDpBLnh6MamkpeHfGJtt1t6xXA+/d0BODTcL02kHv9+G4\nPJfKOb+z8XWaRfBh1m/RprSUgGXWXjeiPZnxwOD2eHPaRuHzclrURY5FAiUWLH84HrPLZIAEcxVm\npix23tVh4cD/Y5fkM383Gswb1MrALWdluxbH3E07SLaWTtbUx4uEkDnHH48NZGZFe/Wq7mjboCau\n/HCeeEMJS9RJcXgf3cInz4s5tlvz6KKqrEKOTBCseMD6Pi3iNyHq9AeEtDjvztjM/O3a3i1wTqNS\n4TIVeExX9Ajb3ZuVIcsx9zMtJRCJ6LJsxxHbdZjFr2dhGHkq3Fuu6NkMTepE3/FPb+odyXwsiqj5\nV06Lulj01HloWCvU39++ridyc3M1i3EW0XFNbeYg2NgEUl3gPvXJzsJ1faI7J3olVf2afNmpNaij\nMYX7gdrcLlE0q+1vsUdtbuTGrsDt/Vvjp2X5hvLEuR0bYsb6/c4r8oCOjWvhkQv4zYQqC/7uoXGm\nWa2Qhigz3V0LH/27dd957bDzSJGhvd/ipwZrPnttymIHEa2VekBgRaJoVY8tBLgdGslrrZbaXj62\nbn/Duwg0iyTyzCWdNamj3dYm1qqWipIyseQfijCvvrx6YSHjom6NcUrxHkMBzdRcxUyL6rHwZtbP\njOjfzpttbOswbqFGjtDZ4JppE42ol5mOQ4X2hHlFKBeBS2PuQ0m9XmY63r2+J6YLCFs//IOd6dm2\n+U8cTAbsjCqSBLSsk4azW1bD7B3FBsck7pmOHt4NZ7SJ7nRGTNMclPnMJZ3xTDjEKotRl3bxrWA+\niRHuNyUgMU0mKxMkmKsY1qkmejRMRVZ1hsDsyMZc24nOalsfcx5nxzBmnh+JyhJuisQ3KSu2mG7E\nQNXzxtU5mLXhgLAWs071NLx9XQ888N0KG7UawzOWKtk17USf4UFZaA3q6F1YRyWqgpWZihX6+2Xk\niCSCPvOtMsGx+mpkN4dzElw56gLUrpaGinQZgzs1xGMWSTzUDO7UCJf3iGrqLuneBKfUSEe/dvWw\ncuWemOOVDI4DBBOteI1yq5Q4yYoZmBW39WuNZy81nphdIQ7z5IxHB6K4rMKz8qc+dDZ2HI5Gl+AJ\nl2hnkeQ1aSkBnNWuPqatsy9s2fFVMCrDa5QxRGQxkJHK4U9k8XuHRjVdFxCv69NS8/m8jg3xzvRN\n6GQjW2hlZfKDZ2PTvoJEN8NTSDBXEZAktKjDd0s6Nq6Fs9rWR0Cy1v64NWhHtlbBN+h5Gce4Xs0M\nrrTJLFi2/PGgalFUcAAAG8FJREFUe/O62PLyxab3ZXCnRrjz7Da2yk9PDWDDS0OYyVXc6gMNamVg\n/YtDXIvmAgA/330W2nuQ7MMsEyoLs/6gJFhJCUj47ObThdrx2c29Y+oxc4RqWLuaZSprp33XSX/o\n0aIunrmkM27o0xIz1lvbSnvBJWEn7Xi+w3WqpzEdvtyifaNamveAR+byocLcFSJZOu2rzDWkuh3q\nTID/3tYHLbJqaHxpzmlZDVO3nkR7wegjaqY8dI4LrTMnp0Vd5lg05poclLu0KEi2PtyuYU3hqDHJ\nBgnmNmFtsRjh1lZ+ZkbocXVsXBtr91g7tCkCqFVWTav38u3remDsknzM2XyQbaYheHl2bdLdwGqx\nohfiROENR+YEN4VyAOjZkj+boAgsoS0e2WQTj5mG1XmnD0ixuxPxZMvLF8eYd/jR+dEpN5+ZjUXb\nDiPNJIB+JKmYjy7fb4LW389pY3oPbcN5089m7Hxl1w0t8Lxc6HnBV7f3RbNTqqO1oA+ImkfO74DT\nVUEI7PjuEN5C4RI5cTKhurXbVb9mBqY/cg4ev6gjgFBkEDMUIdRqu82qeZf3aIaGta2df8zu0N/P\nboMx1+RYlpEsiE5+fhNc4pkYRZZlXKXbXVE7MFY2vBKMWMW2rh//+MEpASmy6KoZTsUdz6hK8WJo\n9ybIGz1Us5hXzFpYu2KVCd6kcWYo/ihdXegb9UxCLLodlSWmYB/Rv319R0I5ANx3XnuNHXuzutXx\nwuXssMiVDb8tWo0gjbkFbsgNpwhmbDOjbYOaaFM/E/++9XQMtLCBTeUUzOPBExd38rR89QQy6cEB\nwk6CIlzdqzlu9jj0VGVCRjQmth+d5dxkcKdGuPGMltYHOoA3GYpnmRZV1KmRhj9HDGJGVWIx+cGz\nsWl/8tqHNqlTDU9c1DHimO7n7tzFBV8ao+uzeo8lhEwO5j9xriYajx0++ksvDGhfH98v2emoHMKY\nm87MxrO/rnFcTqt6NXBRV+9ykdhlcKdGmLZuX9yyBjuFBHNOnAzAH9zYC4u2HcY939hLT31eR60N\nuyRJGHSqtYNhwEXB3NWQixFtjDd4Hcv0tavFNf+8C7z/3NYHJR46uCUCWQ5F2BmfuxudGtfC7I1R\nu+jKJqg7NYXiwW93rEWWtdZeGT9ObVyLGX84WZAkCX8/p23M96I7YvUyQzuQp2e7n9dA6R/DT2uG\nfu3qY8+xk6iZITbVG+1k/aVvKyzYehhdm/GNsU6FcgAY0pWdyMhWVBZnTUkqRHcj+7Wrp4mqZYc/\nHhvk6Hyv+Ozm3vh09la0SjkC/8dI81AwnzVrFgYNYj+k+fPn44wzzvCqaldxQ25oUCsDQ7s3wT3f\niJ+77oUhXOnPWaRy2pg7xQ/dXIkZn+x0blI7EnnFS+ItD7drWBPznjgPb0/TJihRTx6VTEY3xW+m\nTV5TWa/Xbp9tUCsDq0ZdgFrV3LdxjoYIldC4TjU0riMeKjIY2W3RXmCLrBqRxGpmxONdVuK0V0/3\nxq8nWYcju+3++g73ZbJf7umHuj6x4//b2W248hf4Ac815i+//HKMgN61a1evq3WNRJvAOhl0UgIh\ngd4t721LREcEl0bvba9c7Eo5XlI5xRI+WEJZPG3c/YQbXV5dxpAujTGBEfJRc7zzKgkL7MwTXgjl\nTw/thHNdCNeqJA1zErXEa4af1hzlQRlDwlmcqZ/7D6ca+KqK54J5+/btk0Y7bkYyvvT/OKcNth44\n4dhZRItzEdPtxY5fzSH82ar4Y/a8/frs/Iz6nl2a0xSX5jRF9sgJjCP9sxysqgsxr1j01HkoLY/1\no7ljgL1Qr3pOz87CuheGcCuGWtfPxLaDha7UzUtKQML1fWL9OR4f0vH/27vz4CjLPA/g3z7TuTsX\nkoSE0wC5s3JlinAsRxzBhbgizFgKNUNgRlScVQLisMDIpYxVi5TIWJY1VQSQyjD+gaFWUDq7K8dM\nCRoBYVcuJcORcCSQkJju9G//SLpJ02dC3/l+qlKpvO/T7/u87+/N27/3fZ/3efDWf571a12IvIlt\nzMPYwKRo7FnseES37gL9VCBcdd+t3MedXDVpCIXULTMxyqOuSt3p1fHAi5ig48kFhy9eOOvNSKY9\n1ZOntfteGo977Savrv+/lk3C1SbHo3O64qrDHMtFrSUmQ1OcPxHgTQMKFJ8n5kuWLMG8efMQFRWF\n4uJirFq1CuPHj3f7udOnT8Ns9l3PGo5Y2h4ZjUbU1tYCAJqbmwEA3313GnER3mnLZll2sOi+vc7c\nvn0LAHD27P+i5artI9impiYAwHenv8NVR6OmPuDHy513Vv5RV4fa2kan5R6sk6/2m6O4e8PVK/d7\nn8iOvudy2U13LPvwNPQe7MPeunevc2TDk99+69MBqLrrvl+vX+tMai9cvIDEn67iyt377f1Mpg6n\n+yhYYj9/pBIT+qf0uj6Nlv+V775DQ3TPTr8DIk2ohet90X3e9w0/AQAaGhocfuaRaBWGJmp9ej5q\nbLy/vdejXB/XY9J1UCkUDuvj7Tp663/e2NF5hdXc3Ox0OQoE3zn/Qd6qn6VRlZjFK8uMBFBbW2cz\nzdlyf7jcCgC4cuWq07ImkwlGoxFalQJvTUnE0CST0+V1dDif56oegXal63vnxx9+RK3iRoBr41/u\nYuKr73pXlEolMjN71lOXzxLz+Ph4LF26FJMmTUJSUhLOnTuHzZs3Y9KkSaiurkZpaanLz5tMJnR0\nBK53CksAzWLu+tsEo/LhLhRGpWrRcM8cdC8fCMRtnaTrIqnzxGY7z9zVht1kMsLoQTeFHabOuHZ0\ndLhcr2Xey2Pi0C9K5Zf95s11mM2d2/nauHiMTHJdf+nah0YP92FvWV62NBqNMPspMRe5v187uvZJ\nh6kz9iZj97tszo/DYIm9BkBWgrLX9bH9P+rZbfPncqPwxJAIj/5nLOsAALPZ8TnnvZ8n233G2yw3\nV4xG98d1RXG80/r4so4Ps2xLj1fxEQqny1E85Dr8wdv188U294tWob7F+XeGqaPzeO+eN9iV7fao\namiCBjCb4PSwFNfbEKwx7egwd/02BW0dfaUn2+uvfaNS9fxGm88S86KiIhQVFVn/LikpQVlZGfLy\n8lBRUeE2MVer1VAq/TuIQ/dAaTSdd4UVCmXX32poHnLExVWTHv6lHF9QQGHdXmdmZ8fj+9smpOt1\n0DwwvLKlFwCNWuPRPlKp2rt+q1yu1zJvylDfvtXtKO7eoFR27guV2vV2AsCCIj206jtIjI7w6Z1s\ny+NZjUbjtzvmgvv7VdW1T9Rd+yQ1Xo3Beg0uNhoBF8ehN+PSna9i74zlnKZWq6HR9Oz0qwEwwEmH\nPUvHJaB/jNpmG9Tqzi9olUrpl21zxLq9mp5vb3ferr+34q4B8MaEJOSkRECjcfx9pVD459h6GF6v\nnw+2eduM/jCLQOOklzK1qjMxV3ZLhOzq8EDzFFd1VChcfy8Ga0xVXW15VCp10NbRV9xtr7/P9wB6\nlcf6tY25Xq/HzJkzsX37drS2tiIy0nkfpzk5OX5PzC1d6Wg0GhQUdPZVHfu3Y0D9T8jNyUWCi9HH\nQtbuOpvtdaYAwKyJjufFffMV8I82ZOfkeNTV3/8ZLwN/u42MjAEoKBhoNz/2k2u422ZyWydvcRR3\nbzjaeB6obcKggYNQkOd60IUCAE+UeG3VTkX9z5fArSYUFBT4JzHfXQe1Wm3dr6lD2lD3Uy3mTXkM\nUV2jRhr+CRi0ohrROq39/t/d+RjbV8eCr2LvjP7UceByK0ZmZ3s8KI8nHFXdeOkW8HkDUlJSUFCQ\n7bV19cSkpvM4cvksRhXm9274cx/F35txd/nx3XVQqZR+O5f1mC/27+46ZKfF+32br6quAV/eRFpq\nKvBNZxMqmzrsroNG3Zmsuo397jqo1CrH8318TnpYlxVXgBNfoyj7URQ8mhzo6viHhzHx9/ke6Hxq\nePduzwZV8/vLn5ZH6aHyYkW49r/rXd7dR/+9bDLuhcEgO6FxhPte96OjX6wOO3491q7M+rJcFHcb\nJpq8J5Dn2vKSIfiXgvTeJeXo7P5vzGDvD8LjT32tR5rql8djQIL7Qae8LTu1c9CjsX38PDIjLxUp\niyL6/H4IZX5NzG/fvo1PP/0UhYWF0Ol8/1a5N4XIdUSveOviw1v7KCFaiwTvLIoC7GdDkzD/Z4Pc\nlnt2rP2TEwp9lkFuestb3f8FUqgMA+4tOWnxAVlvZlIULm2a4bXlhWrYFAoFk/IQ57PE/Je//CUy\nMzMxatQoJCcn4/vvv8c777yD69ev489//rOvVkshwHIZEO53ksZ1nRxHpno2fLU/+WvP7yoP/TEM\nQlVW/1joNEqUhcmouKFKGc53dYjI63yWmOfn52PPnj3Yvn07mpubkZiYiPHjx2PHjh0YPXq0r1br\nM+GeRPqVdbjnwFbD1woy9F69g0Ohz3IeET90bB+n0+Dsmz/3+XrINZ2Phoynngv37xwKDz5LzFes\nWIEVK1b4avEURDh4DhGRvbf+NQ+jB4V2G/m+KlTeg6Pww5E/PRWm/6Pp+ki8Oj3LK8sK011ERNQr\nc0f3bGARIuq5VTOzoXXSjWYoYmLexx1e8c8PvYx/fzIbyTERSIjyrDtJy8umTOQDhzeDAiNW13nK\n9Vcf8kRE4e7X4wcHugpexcTcDTbTcG9gUjTeejq/x59jckh9zRszRqIwQ4/UeO/1YU5EnvL8S4df\nTxQo4XPv38eYRBLRw4rVaTBvDJs3UHAYkMALRKJgwzvm5Hd8ChF4fLGJiD59aTxutbQHuhoh5T/m\nFmJYv5hAV4PCGBNzDzGN8T52QUlEFDj6KC30Hr4b1JdMHfkInh3r+MnWbI4LQD7GxJz8jjfMiYjI\n3zx9UPjh/FG+rQiRC2xjToHDG+ZEREREVkzMPcQ2ud5T3DVU/djBHHiDiIiIyIJNWcjvBiVHc6h6\nIiIiogfwjrmHeL+cwsFz4wYGugpERAHB73EKBbxj7gZfVKRwMmdUBuaMygh0NYiIiMgB3jH3EJuY\nExEREZEvMTEnIiIiIgoCbMpCREREYWNWYRqmZ/e3m84n3xQKmJh7iKNUEhERBb8t84oCXQWiXmNT\nFiIiIiKiIMDE3EN8BEZEREREvsTE3B32l0hERBTy2CSVQgETcyIiIiKiIMDE3B1eYBMRERGRHzAx\nd4dNWYiIiIjID5iYe4gvfxIREYUufo9TKGBiTkRERGFvYcmQQFeByC0OMOQhvs1NREQUmi5tmgEA\nqK2tDXBNiFzjHXM3hI3MiYiIiMgPmJgTEREREQUBJuZusAkLEREREfkDE3M32JSFiIiIiPyBiTkR\nERERURBgYk5EREREFASYmHuIAxMQ+V//OF2gq0BEROQ37MeciILWwX+bgHaTOdDVICIi8gveMXdj\n9ZM5mDryEaiVvGVO5G+xOg2SYiICXQ0iIiK/4B1zN3LT4/Hh/FGBrgYRERERhTneMSciIiIiCgJM\nzImIiIiIggATcyIiIiKiIMDEnIiIiIgoCDAxJyIiIiIKAkzMiYiIiIiCQFB0lygidtPMZv8PKqJU\nKqFSqaBUKgOyfgoMxr3vYuz7Jsa972Ls+65AxN7RehzlvN0pxF0JPzCZTGhpaQl0NYiIiIiIfCY6\nOhpqtfP74mzKQkREREQUBJiYExEREREFASbmRERERERBICjamJvNZrsG8gqFAgqFIkA1IiIiIiLq\nPRGxe9lTqVRCqXR+XzwoEnMiIiIior6OTVmIiIiIiIIAE3MiIiIioiDAxBxAc3MzXnnlFaSlpUGn\n06GwsBAff/xxoKtFbty9excVFRWYPn06UlJSoFAosGbNGodlT5w4galTpyImJgZ6vR5PPfUULly4\n4LDs1q1bMWLECERERGDw4MFYu3YtjEajXbn6+nosWLAAycnJiIqKQnFxMb744gtvbiI5cOjQIfzq\nV7/CiBEjEB0djfT0dMyaNQvHjx+3K8u4h5dvvvkGM2bMQGZmJiIjI5GYmIji4mJUVlbalWXsw9uH\nH34IhUKBmJgYu3mMffioqamxvnP44M+xY8dsyn7++ecoLi5GVFQUkpOTsWDBAtTX19st02g0Yu3a\ntRg0aBAiIiIwYsQIbN261eH6L1y4gKeeegp6vR4xMTGYNm0aTpw44ZNttRKSadOmiV6vl+3bt8uh\nQ4dk4cKFAkB27twZ6KqRCxcvXpT4+HiZMGGCNWarV6+2K3fmzBmJjY2VkpISqa6ulr1790pOTo6k\npaVJfX29Tdl169aJQqGQ119/XQwGg7z99tui1WqlvLzcplxbW5vk5ubKgAEDpLKyUg4cOCCzZs0S\ntVotNTU1vtzsPu/pp5+WyZMny7Zt26Smpkaqqqpk3Lhxolar5YsvvrCWY9zDj8FgkMWLF8uOHTvk\n0KFDsm/fPpk3b54AkDfffNNajrEPb3V1dRIfHy9paWkSHR1tM4+xDy8Gg0EAyIYNG+To0aM2P3fv\n3rWWq6mpEbVaLbNmzZIDBw5IZWWlpKenS25urrS1tdksc+HChRIRESFvv/22GAwGWbFihSgUClm/\nfr1Nufr6eklLS5OcnBzZu3evVFdXy/jx4yU2NlbOnj3rs23u84l5dXW1AJBdu3bZTJ82bZqkpaWJ\nyWQKUM3IHbPZLGazWUREGhoanCbmc+bMkeTkZGlqarJOu3Tpkmg0GqmoqLBOu3Hjhuh0Olm0aJHN\n59evXy8KhUJOnz5tnfbee+8JADly5Ih1mtFolOzsbBkzZoy3NpEcuH79ut20u3fvyiOPPCJTpkyx\nTmPc+46xY8dKRkaG9W/GPrzNnDlTnnzySZk/f75dYs7YhxdLYl5VVeWy3OjRoyU7O1uMRqN12uHD\nhwWAbNu2zTrt1KlTolAoZMOGDTafLy8vl8jISLl586Z12rJly0Sj0cilS5es05qamiQ5OVmeeeaZ\nh900p/p8Yr5w4UKJiYmxCaaIyK5duwSAHD58OEA1o55wlpgbjUaJjIyUxYsX231m+vTp8uijj1r/\nrqysFABy9OhRm3JXrlwRADZX01OnTpXhw4fbLXPDhg0CQOrq6h5yi6inJk+eLFlZWSLCuPc1M2bM\nkMGDB4sIYx/uduzYIbGxsXL58mW7xJyxDz+eJOZ1dXUCQDZu3Gg3LysrS6ZNm2b9e926dQJArl69\nalPuyJEjdi0lhg0bJqWlpXbLXLRokURGRtrljd7S59uYnzp1CiNHjoRarbaZnp+fb51Poev8+fNo\nbW21xrO7/Px8nDt3Dm1tbQDuxzovL8+mXGpqKpKTk22OhVOnTjldJgCcPn3aa9tA7jU1NeHEiRPI\nyckBwLiHO7PZDJPJhIaGBmzbtg2fffYZli9fDoCxD2f19fV45ZVXsGnTJgwYMMBuPmMfvpYsWQK1\nWo24uDiUlpbiyy+/tM6zxMpZjB6MZUpKCvr3729XrvuyWltbcf78eafLbG1tdfrewsPq84n5zZs3\nkZiYaDfdMu3mzZv+rhJ5kSV+zmIsIrh9+7a1bEREBKKjox2W7X4s8LgJLkuWLEFLSwveeOMNAIx7\nuHvhhReg0WjQr18//O53v8O7776LxYsXA2Dsw9kLL7yA4cOH47e//a3D+Yx9+ImPj8fSpUvxpz/9\nCQaDAVu2bMHly5cxadIkfPbZZwDcx92TWEZHR0Or1VrL3r59GyISkLir3RcJf65GGOXoo+HB0xj3\n5FjgcRMcVq1ahZ07d2Lr1q147LHHbOYx7uFp5cqVWLhwIerr67Fv3z68+OKLaGlpwWuvvWYtw9iH\nl71792Lfvn34+uuv3e5rxj58FBUVoaioyPp3SUkJysrKkJeXh4qKCpSWllrnOYvDw8QyEHHv83fM\nk5KSHF713Lp1C4DjKzAKHUlJSQAcX9neunULCoUCer3eWratrQ337t1zWLb7scDjJjisXbsW69at\nw/r16/Hiiy9apzPu4S0zMxOjRo3CE088gffffx+LFi3C66+/joaGBsY+DDU3N2PJkiV46aWXkJaW\nhsbGRjQ2NqK9vR0A0NjYiJaWFsa+j9Dr9Zg5cya+/fZbtLa2uo27J7FsaWlBe3u7tWxCQgIUCkVA\n4t7nE/O8vDycOXMGJpPJZvrJkycBALm5uYGoFnnJ0KFDERkZaY1ndydPnsSwYcOg0+kA3G9r+GDZ\na9eu4caNGzbHQl5entNlAjxu/GHt2rVYs2YN1qxZg5UrV9rMY9z7ljFjxsBkMuHChQuMfRi6ceMG\nrl+/jnfeeQcJCQnWn927d6OlpQUJCQl49tlnGfs+REQAdN61tux/ZzF6MJYNDQ24du2aXTngfiwj\nIyMxbNgwp8uMjIzEkCFDvLMxD/LJK6UhZP/+/QJAPv74Y5vpjz/+OLtLDCGuukt85plnpF+/fnLn\nzh3rtB9++EG0Wq0sX77cOu3mzZui0+nkN7/5jc3nN27caNd91rZt2wSAHDt2zDrNaDRKTk6OjB07\n1otbRo784Q9/EADy+9//3mkZxr3veO6550SpVFr7qWbsw0tra6sYDAa7n9LSUtHpdGIwGOTkyZMi\nwtj3Bbdu3ZL09HQpLCy0ThszZozk5uba5GxHjx4VAPL+++9bp1m6S9y0aZPNMhcvXmzXXWJFRYVo\ntVr58ccfrdPu3LkjKSkpMnfuXF9smoiwu0QR6eyzPCEhQT744AM5dOiQlJeXCwCprKwMdNXIjf37\n90tVVZV89NFHAkDmzJkjVVVVUlVVJS0tLSLSOeBETEyMTJgwQfbv3y9//etfJTc31+WAEytXrpSa\nmhrZvHmzREREOBxwIicnRzIyMmTnzp1y8OBBKSsr44ATfvDHP/5RAMjjjz9uN+BE967PGPfwU15e\nLq+++qrs2bNHampq5C9/+YvMnTtXAMiyZcus5Rj7vsFRP+aMfXj5xS9+IcuXL5eqqioxGAzywQcf\nyPDhw0WtVsvBgwet5QwGg6jVaikrK5ODBw/Kzp07JSMjw+UAQ5s3b5aamhpZuXKl0wGGUlNTJS8v\nTz755BPZv3+/TJgwQWJjY+XMmTM+22Ym5tI5OMnLL78s/fv3F61WK/n5+bJ79+5AV4s8MHDgQAHg\n8OfixYvWcl999ZVMmTJFoqKiJC4uTmbPni3nzp1zuMwtW7ZIVlaWaLVayczMlNWrV0t7e7tduWvX\nrsnzzz8viYmJotPpZNy4cTYnCvKNiRMnOo35gw8BGffw8tFHH0lJSYkkJyeLWq0WvV4vEydOlB07\ndtiVZezDn6PEXISxDycbN26UwsJCiY+PF5VKJSkpKVJWViZ///vf7coeOHBAxo0bJzqdThITE+X5\n5593OCBde3u7rF69WjIzM0Wr1UpWVpa8++67Dtd/7tw5mT17tsTFxUlUVJRMmTJFjh8/7vXt7E4h\n0tVQh4iIiIiIAqbPv/xJRERERBQMmJgTEREREQUBJuZEREREREGAiTkRERERURBgYk5EREREFASY\nmBMRERERBQEm5kREREREQYCJORERERFREGBiTkREREQUBJiYExEREREFASbmRERERERB4P8Bf8UW\n9j+tkgYAAAAASUVORK5CYII=\n", "text/plain": [ "" ] }, "metadata": {}, "output_type": "display_data" } ], "source": [ "zs = [sense() for i in range(5000)]\n", "plt.plot(zs, lw=1);" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "That looks like I would expect. The signal is centered around 10. A standard deviation of 2 means that 68% of the measurements will be within $\\pm$ 2 of 10, and 99% will be within $\\pm$ 6 of 10, and that looks like what is happening. \n", "\n", "Now let's look at a fat tailed distribution generated with the Student's $t$-distribution. I will not go into the math, but just give you the source code for it and then plot a distribution using it." ] }, { "cell_type": "code", "execution_count": 31, "metadata": { "collapsed": true }, "outputs": [], "source": [ "import random\n", "import math\n", "\n", "def rand_student_t(df, mu=0, std=1):\n", " \"\"\"return random number distributed by Student's t \n", " distribution with `df` degrees of freedom with the \n", " specified mean and standard deviation.\n", " \"\"\"\n", " x = random.gauss(0, std)\n", " y = 2.0*random.gammavariate(0.5*df, 2.0)\n", " return x / (math.sqrt(y / df)) + mu" ] }, { "cell_type": "code", "execution_count": 32, "metadata": {}, "outputs": [ { "data": { "image/png": "iVBORw0KGgoAAAANSUhEUgAAAuYAAAEaCAYAAABdIZKsAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzsnXecFEXax38zO7ssGZYchFVAySuC\ngiJKVkROEcN75nTGM56nGEBQ9FAxnTnhmRPieUoSJGdJS5K0sOS4LLCwcWb6/WOmZ3p6qrqre7p7\nenaf7+ejy+50V9d0paeeeoJHkiQJBEEQBEEQBEEkFW+yK0AQBEEQBEEQBAnmBEEQBEEQBOEKSDAn\nCIIgCIIgCBdAgjlBEARBEARBuAASzAmCIAiCIAjCBfiSXQEACAaDCAaDMX/zeDzweDxJqhFBEARB\nEARBmEeSJKiDH3q9Xni9fL24awTzU6dOJbsaBEEQBEEQBGEbNWvW1BTMyZSFIAiCIAiCIFwACeYE\nQRAEQRAE4QJIMCcIgiAIgiAIF+AKG3OWk6eeDY4dbNiwAX6/Hz6fD506dXL02UTyoHavulDbV02o\n3asu1PZVl2S0PcuHUi+wiWsFcz2vVTsIBoMIBAJJeTaRPKjdqy7U9lUTaveqC7V91cUtba8nmFOv\nJAiCIAiCIAgXQII5QRAEQRAEQbgAEswJgiAIgiAIwgWQYE4QBEEQBEEQLoAEc4IgCIIgCIJwASSY\nEwRBEARBEIQLIMGcIAiCcB2SJOGHFbtREQgmuyoEQRCOQYI5QRAE4TqW5BXgn5PW4vMlO5NdFYIg\nCMcgwZwgCIJwHaX+AADgVJk/yTUhCIJwDhLMCYIgCIIgCMIFkGBOEARBEARBEC6ABHOCIAiCIAiC\ncAEkmBMEQRAEQRCECyDBnCAIgiAIgiBcAAnmBEEQBEEQBOECSDAnCIIgCIIgCBdAgjlBEARBEARB\nuAASzAmCIAiCIAjCBZBgThAEQRAEQRAugARzgiAIgiAIgnABJJgTBEEQBEEQhAswJJjPnj0bt99+\nO9q3b4+aNWuiRYsWuOKKK7By5cq4a1etWoWBAweiVq1aqFevHq666ips377dsooTBEEQBEEQRGXC\nkGD+3nvvIT8/Hw899BCmTp2KN998E4cOHUKvXr0we/bsyHWbNm1C3759UV5eju+//x4TJ07Eli1b\n0KdPHxw+fNjyL0EQBEEQBEEQqY7PyMXvvPMOGjduHPO3Sy+9FG3btsWLL76I/v37AwBGjx6NatWq\n4ddff0WdOnUAAN27d0e7du0wYcIEvPTSSxZVnyAIgiAIgiAqB4Y05mqhHABq1aqFjh07Yvfu3QAA\nv9+PX3/9FSNGjIgI5QDQunVr9OvXDz/99FOCVSYIgiAIgiCIyochjTmL48ePY9WqVRFteV5eHkpK\nStC1a9e4a7t27YqZM2eitLQUmZmZmuVu2LABwWAw0eoZoqKiIvIzNzfX0WcTyYPavepCbe9eduwt\nAQAcOHAAubnFlpZN7V51obavuiSj7b1eL1q1amXonoQF8/vvvx+nTp3C008/DQAoKCgAAGRlZcVd\nm5WVBUmSUFhYiGbNmmmW6/f7EQgEEq2eaeQGJKoW1O5VF2p7d+EPz/+BQMDWtqF2r7pQ21ddnGr7\ntLQ0w/ckJJiPGjUKX331Fd566y1079495jOPx8O9T+uzSMV8Pni9zkZzVDZUenq6o88mkge1e9WF\n2t69+NL8AEILm9VtQ+1edaG2r7oko+3NyLGmBfOxY8di3LhxeOGFF/D3v/898vcGDRoAiGrOlRw9\nehQejwf16tXTLb9Tp06OC+a5ubmoqKhAeno6cnJyHH02kTyo3asu1PbupaDaQWB+AZo2bYqcnHaW\nlk3tXnWhtq+6JKPtg8EgioqKDN1jSvIdO3YsxowZgzFjxuCpp56K+axNmzaoXr061q1bF3ffunXr\n0LZtW137coIgCIIgCIKoahgWzJ9//nmMGTMGzzzzDJ599tm4z30+H4YNG4bJkyfH7BJ27dqFOXPm\n4KqrrkqsxgRBEARBEARRCTFkyvLqq69i9OjRuPTSSzF06FAsXbo05vNevXoBCGnUzz33XFx++eUY\nOXIkSktLMXr0aDRs2BD/+Mc/rKs9QRAEQRAEQVQSDAnmv/zyCwBg+vTpmD59etznkiQBANq3b4+5\nc+fiiSeewNVXXw2fz4f+/ftjwoQJaNSokQXVJgiCIAiCIIjKhSHBfO7cucLXdu/eHbNmzTJaH4Ig\nCIIgCIKokjgb9oQgCIIgCIIgCCYkmBMEQRAEQRCECyDBnCAIgqjUPPPfdViSF59bgyAIwm2QYE4Q\nBEFUar5cugt3fb4i2dUgCILQhQRzgiAIgiAIgnABJJgTBEEQlR4p2RUgCIIQgARzgiAIgiAIgnAB\nJJgTBEEQBEEQhAsgwZwgCIIgCIIgXAAJ5gRBEAThECXlAewpLE52NQiCcCkkmBMEQRCEQ9z71Upc\n+NKcZFeDIAiXQoI5QRAEUemRJHfEZVm2/Wiyq0AQhIshwZwgCIIgCIIgXAAJ5gRBEITr8MCT7CoQ\nBEE4DgnmBEEQhOuQKCUQQRBVEBLMCYIgiEoPifkEQaQCJJgTBEEQhEPQSQBBEFqQYE4QBEG4DrIx\nJwiiKkKCOUEQBOE6KqtmmTYcBEFoQYI5QRAEUelxSRhzgiAITUgwJwiCIAiCIAgXQII5QRAE4Tqs\nNvnwkAUJQRApAAnmBEEQhOuw2sa8MpuyrNpViGCwEn9BgqhCkGBOEARBEA5h9YZj++GTuOrdxfhk\n4Q5LyyUIIjmQYE64gkBQwtFT5cmuBkEQREpRVOoHAOwpLE5yTQiCsAISzAlX8PrMLTjn+ZmQKvN5\nM0EQwrBszK/9YAlu+3R5EmpjHVbbztOMSRCVC1+yK0AQALAo70iyq0AQhItgmXws33HU0vKSgVvq\nQRCEOyGNOUEQBEGkKBRshiAqFySYE66CLFkIgqjMmDVl+W3DAQx5c0Hc32nKJIjKBZmyEARBEK6D\nUtfHMm7Kn9h1lO/g6aFA7QRRKSCNOeEKSFNOEISSymqLXVm/F0EQ1kCCOeEqaMkiCIKIhxTiBFE1\nIMGccAW06BAEocTysIIu2fWTiQ5BEFqQYE64ArcsmgRBEHZCpiwEQWhBzp+EqwglGCKNEkFUdawQ\nYCtTwjKaFQmiakCCOUEQBFEpefW3LXh7zrZkVyMG6010Ks/mgyAIMmUhCIIgXIgVAuxPq/dG/u0W\n8ZVMWQiC0IIEc8JV0JJFEIRVVCZtMi9OOcUvJ4jKBQnmBEEQhOuwWrNcWcXXyrT5IAiCBHOCIAii\nkqLUJqe6+FpZNxYEQcRCgrmLOFnmRyCY6stHYlRW5c9tny7H/C2Hk10NgkgZrLAxJ20yQRCpBgnm\nLqLzszPw1OR1ya4GYQNzNh/Gk9S2BEEQBEFoQIK5y5ix8UCyq0AQBJF0Kmv0EtMnAWTLQhBVAhLM\nCVdRWRdjgiCSjEumFprjCILQggRzglCRd/gkdhw5lexqEESVxupEPJUFspsniMoNZf4kCBUDXp0H\nAMgfPzTJNSEIgghB2xSCqBqQxpxwFaQMIggCsMbkozJOJzRHEkTlxrBgXlRUhMcffxyDBw9Go0aN\n4PF4MGbMmLjrbr31Vng8nrj/2rdvb0W9CYIgiCSy6cAJZI+cgj/3n0h2VaoUlUEuX7WrEI9+tybZ\n1SAIV2JYMC8oKMCHH36IsrIyXHnllZrXVq9eHUuWLIn577vvvjNdWYIgCMId5O4+BgBYu+eYLeVb\nYWNemcw/lMmSlBgV1LceLELBybLEK5QAj32fi8mr9ya1DoR7OVnmR9cxM6rspt+wjXnr1q1RWFgI\nj8eDI0eO4OOPP+Ze6/V60atXr4QqSDjLnM2HUK96Orq1qp/sqhAEQSSEFPPvyqBrlp0/44V0jtwe\nx6DX56Nx7WpY/vRAaytGEBax9WARTpT68d0fuzHmL52SXR3HMawxl01SCGt54JvVya4CAOC2T//A\n8HcXJ7saKc+ugmJs2Hc82dUgiJQlEUH6+z92o7QiYGFt3IP6rcirsRHb80NFydWYE4QWlWMLbR5b\no7KUlJSgadOmOHz4MJo1a4Yrr7wSzz33HLKysnTv3bBhA4LBoJ3Vi6OioiLyMzc319Fn/5K7DwAQ\n8AccfzYLp+tQXFwMAFi7dh2q+WI3fkt2l6Bdg3Q0rGFPd+W1eyLv4Ipv9gAAfv5ry8jfysrLXdG2\nSoorgvjrpH14eVAjnNWwWrKr4zjJHPOpzu7dp8I/9yA3o9Dy8nfsLQEAHDhwALm5xTGfabXVruMV\neHzqQSzbuAPl4fYFQppm+b5ktnswGBI7jD63rLQ0fN9apKdF58itR0JC9pEjRwyVmcz+XlpWFqlD\nSUUQ246Wo0uTTEeebVfbPzr9IC5pWxOXtK1lWZlVlW0m+7QeyRj3Xq8XrVq1MnSPbYJ5Tk4OcnJy\n0LlzZwDAvHnz8Prrr+P333/HH3/8gVq1tDuv3+9HIJA8jUeFYkI3S3lAwlfrTuL6LrVQLU3slEGC\nZMmzE8XpOsixeSsqKuCVYt/V+IUFaFk7DW9c0tD2eii/txXvIKYMyR1tq2TvsVB9ZuadxBl1q3aQ\nJre1jdvxB/wAgEAgYMu7k+d/VvlazyspC312sswfq0aW2Pc53+7RuQ4A8o9V4MDJAHq11BZM5ROE\nCn8FEIzOkX5/qB2kYNDQd0lqf1fM928vO46Fu0vx3YjGSHP4NN7Kd5BXWIH3/ziG/q2rnoLDauQ+\nHQzaM7cAzvX/tLQ0w/fYJpg/8sgjMb8PGjQI3bp1w9VXX42PPvoo7vO4ivl88HqdFRSUDZWenp5w\neQt2n8KUbcVoVT8Dlwruoj3wWPLsRNlzUkJ2vXTnzJbCj0lP9yHdF9/uReWSbe+F1+5WPC+mDI87\n2laJzxdaIL1er+vq5gRWj3krOFYawMy8U7i6Y23Lx9+aA6UISsA5zRLXTqal+cI/02x5d2k+P7d8\nreelp0f7tNLwWlLcl9x29wCIzmePzToIAPj5r7V17gp9l3RfeozG3OcLnSwbHcNJ7e/hdklPT8fh\n4lD9M9LT4XVgvbG17T3umUdSGblPp3mtnVuSMe7NyLGOJhgaPnw4atasiaVLl+pe26lTJ8cF89zc\nXFRUVCA9PR05OTkJl7fNvwdYVojmLVoiJ6e19sVh04c0X5olzzZNuB4PTz+EF4d3wfU9jR3BmKXG\nwkVAwTF06dIV1TNUO8xv9sDn89n2XuLaPfwOEnqeuoxv9iDDon5lJen7TgDTD6FBgwbIyemS7Oo4\njtVj3gru/2oVpqw7gYeGnYdGta3Vvl3xzRQA1iTP2lS+C1heiNNOa4mcHOvniYJqB4F5BWjatCly\nctqF/igwNn37jgPTDyGrQQNkHD4EIKR593g8kfuS2e7eSfuAgIR311agd9uGAMTmm+qzjwEnTqJz\nly7ITI/OkYFdhcDMw2jYqCFycgQc5ayY3xIkc2YhUORHTk4Oqi9cBBSUI6drDrxe+wVz29r+mz0x\nfYzHvC2H8eSPa7H4yQHWPbuSYbhPC5KMcR8MBlFUVGToHsfPriVJclzgThby10zVFMr5Bc6lpY84\nMFV5tw9nIT9u8xwrLsePK/dYXm5FwBrfmpNlfuw44twYdgu8MItu6+szNhzE6J83JLsaSUdS/azs\nvDFrC/YdL01ZuYCwH0cl5EmTJqG4uLjKhFCUj+VkZx8R3LR2ODlx6D2J9fn+4yXo/+pcFJ4qt6NK\nKcmhE6VYur3A8H20RrA5WeYP2SozeOqndfjHD7kY/fN6h2slxq0Tl6PfhLnJroZpEo1jru7S1Mdd\nShVrGDNRdIiqhSnBfNq0aZg0aRJ++eUXAMDGjRsxadKkiOC9c+dO9O7dG2+99RamTZuG6dOn48kn\nn8Qtt9yCTp064c4777T0S7iViGCeogPQ7RPHr7n7sf3wKSzKO5LsqgAATpRWYMHWw0mtw4j3F+P/\nPtQ3FZOJahFd3thJovOzM9Dtud+Ynx0vCdkrfr5kp5NVEmbNbmOJf4JBCdPX7xfekLt9fqhsyBsV\ns+/90IlSC2tjHfLX6TBqesonlBHZSsp+I5V9+Ow9VmL63qo+t5gSzO+9915cc801uP322wEAP/zw\nA6655hpcc801OHToEOrUqYMmTZrgtddew4gRI3DFFVfgxx9/xIMPPohFixahZs2aln4JtxIVzCX4\nA0EcSXK2NaNYPTYkScLxYrYntBEtwgtTNuLjBdutq5hFPPpdLm76ZHlS67D7qPnJMFEOnihNekZB\nO6gIpOYqYdR0479r9uKeL1dh7pbENpelFQFc/9HShBbmRJC/tyRVjQVe5DvuKijGeS/+jp/XuC/b\nplz/8kAQk1dZbxpmJYGghN1HQ6E7n/tlIy56eY7psiqzKcvKnUfRe/zshBVVVmT/TUVMCeb5+fmQ\nJIn5X3Z2NurXr4/Jkydjx44dKC4uRllZGbZs2YKXXnoJdevWtfo7uBavYoH417RN6DFuVnIrZBCr\n541PFu5AznO/obg83jTAyKM+WrAD46b8GfndLYN3X5IEkURIVAunpOeLv6N7ivVxNxK1uU2sUYyO\ni8LwpvlkKdt0J658TvFr9xzH4rwCfLY439DzCTF4/UKrvQ8VhbTlG/a5TyOdSn5Fb8/ehj4vz8Gp\nMj8mLtqBXUeL9W9SEfWnco4TpRV49bfNhsxqE2FnQei96Pm4zNx4kBLxMagaXphJwqPQmC/OM273\nazXztxxGt+d+Q0BwcCY6YZ73wixMXLgj8vuS8DsoKTcen74yaxcI9yOf0Lw8fROenLw2ybURw6jG\nXB5jovfpDUm3jdlk1EZWWFmB8iRAWb6sZRaZr93WJkBqnWqs2xsyDyvzsx20jYw5J7/3v2dtxVuz\nt2HNHmPmbXbzt89XYOi/Fya7Gq6DBHMbkTXmAUlyhU733bnbUFhcIRz1IdGJ41BRGV6avim+XK1n\n6pSp3FSUhFNup5LGhUhNPglvMN+dm4dvlu+29VmeyM/EZg2zUUjccgIl467aGOP0J6fiBcXpntWs\n33sCXy3bZVv5Ihw4Xsp1kBYhdqPBu0ZCaUXyEg5GiSrbTJcgb7AY65ZdGye/w45uqbTZciMkmNuI\nbGMuSUptR9XtsVaEK1MK5q/N3JJ4gRaSii2bjBByWw4W4WuOMLH98EnM3HjQ4Rq5C6tMWYwma5Gn\nJreFFTT6FpQOzW7YtH+3wtqNnPIblfmjwqrIhuqjBTt0rzFKr3/9jqveXWT6fpEWenv2NrQfNd30\nM6yCdWphFnUZv+Tuw+lPTuX6YVmBy4Y2wYEEcxtJ80bDJZoZ0MGghFkWCilGNWF6WoGTZX4cK9YO\nVWjVspj85bVy4+R+cfg7i/DUT+uYn136xgL87fMVzlVGELsWtOJyP3INRk+R+f3Pg5qnX0brLAux\n6vvmbTmMvq+Yd3Kr6lg9ttyo3Nly8KTpe5Xfh/fNZv7pjs26Ffk2eOvwnM2HAABHddbURHAqk7fb\nNvepBgnmNiJ3zvfn5WH93pDTjZHh/M0fu3Dn5yuwzERcai2smtf7vjIHZz8309Ln6y06iRwhBoOS\nrQlXUnEuSkadtaKclFuUXCdVeOLHdbjinVhto4gpy9aDRbjjsxV4f24e9xqzi7D6tgkzNiO/wLiT\nW7JQOjQr36He3LL/eAl+sFi7LfJcUapKmD2ZMn/AMWdFUTxRyZz9uYEZVctsx2oi/iOWl0zYAQnm\nNiJPpKcUzo5GBMujJ0M75yLBKAlWo1fVIyeN7uwTnxa+YMSMluu5+2gxskdOwVFOwqH35+eh34S5\n3M/VGHVSddcSYgw3HPm7hZ/X7MXWg8ZSKJsl71C8plHElEX2rzisEZ7SuPOnseuVTFu3H6cSsDPW\nIpFZw0i/vvuLlfjnJOsde90gW7pZg8nrd2c9Mz0SfSsaTje5LzOy6eN8Xh4I4qFvV+sVEi5DUv1Z\nrJHu/mKF4XDBLuiCBjHmiF7ZIMHcYVx4CslFvYkorQgge+QU/LQ6ebFmD2gkyRj7y0YAwE2fLGN+\n/uf+kLDFCtfIosPo6cgeOcVgDZO/eBihqk58Wjz07Rpc8sb8ZFdDE5Ewl8ZNWeLv/P6P3Vi3Vzuc\n2fGSCtz71SqM/cWe9PJmbcyNDkO7NhZWb3pTaHrRRZIkprLqL2+HInX8unaf6npHqsXF69Wvx89r\n9vE/ROKZP2dsOBgTLlgE+VlG/U6Msu9YCR77ITdpysTKAgnmDpOIKYbTqGsqD7Ypaw8kWC7/HfA+\n0RRAwnON/G6dmBS0kkXZ1cTBoITf/zyYUoI/kxTYDKi1nE7ZZgLWRWXxehM3ZZm4KOosyOt3csQH\n+SQqVTd7sk+Q1ePLquIqa5Je5deR39XaPezNYDK/+p2frUDu7lC9rFjHnfwukkMa6AvGz8aklXsi\n0dgOF1W+hHNOQIK5gvKAhE/XFHFjlBol0TEQDatkLaIaHKvlP9FJod+EuRFHGEPlG75DnHfnbotk\neZu35TB6jJuF9TqaRKuZvHov7vhshSti4puhpDwgHEM/FbBrfyRiyqIVci1yjdHnMorS2pBsC5vh\nuDW8olFNtaxNtLqPivaTvCoYkSiUnVXp/Bn7siK/eezZNBlh1p8HI9lsE6mFXoQ2vnJKwjydrLxn\nPTMt7pQhdK+RGuojSRKe+e865HN8tuTQlm/N3mbtg6sIJJgrmL+zGFO2FWP2DvscnYzstD0GJyNJ\nkixeVNSTZOj3Mn8goQmyz0tzUM7Z/MgOmm+oQiFqPU/9kR320i9P3xzJ8rZpf8iRl5f1jff0fcdL\n0e2530wlWAIQiYBzvMT6cFpOrHcdRk/HI9+tsf9BNrD3WAk2H7DP7tzseFLeVloRQN7hqM26US0/\nLyoL61kA8HE4truZ8baz4BQOaZilKXFK7PelhZ5kdcxn0fdzyevzhSISKctTNrG6ucv9Qdc5T7JQ\n1vDTRflYubNQ6FonUY9PKzYI6hL0husva/fjlonLNa8p8wfxnsIh/Ls/duHR79ZY/t5OlPrx5dJd\nGPXzeubnvOd9OD8P3y5Pbtz9VIAEcwZ2HvfojWczR+aLth1BzxdnYcz/NqDNU1NN1iyeIOfgYMHW\nI/hPAum2y/xBrgOmfFpRLT2N+bmISQsP88KPykkngf5RWFyB3YXmNn5y39hbWGK+AvGlWliWPv/L\n1ba/tIMvluRjeAJxlmXstDtXdjEjpizKnvnk5HUY8Oq8yO9eHc0crw7KOUikd5jZaF78ylyc9+Lv\nAIDskVPw4Xx+dBkjo7bHuFm46t3FpspJS7LGXG9DwM78yX/Omc9MwzMcwcktSJH/RfmFMUfIIUXd\nYsWXSD3k8SIZPJgv0DCf5PHEj+swefXeSGx0q2UbnrzCez8vTt2EkZPX4eXpm4SUbe46i3MOEsyV\nWDToJUlCIUfwNGObpnfHO3O24eCJMnytsxO1clDO3ax9pBaBIXCwrwtdKE9a1XzsrimWdlqsaqLw\nFmrRcFfq31mROEQIK/TwwlTrMwkaeWVdxsxIKa3HqJ83YPUud6SivnnicmZEBYnxbxFTFiW5cem2\n5SyFxurIg1cM77jayDicvGqv8QoxOHKyDEUKJ04jdZBt8nkCckl5ANPW7Tdcp2TKkj+v1n6vczcf\nwm8bEvMZShQj7ydZ0aOsWlMqAkHkhu3n7fourLrKQRPcYnb27tw8zYhSMuWBYKUyfxSFBHMb+GTh\nDnR7fibTy99IF7Myy1hMHQTLS8YkKGvMM9KMd0290wazDnwBtcY8EjLLmI2gzL1frTJVDzscEJVF\nvj17KzYdOKF7T1GpH6/PMp911R1Lgz4HBU0tjDB/y2FmRAWjpzlCUVlUTtFarN97HK/M2Bwu2/2I\naOmNzpuyxpxn/vHS9E2496tVmv3icFEZ3vp9a0x7Wu3wryxNy5RFfS2LWz/9A3d9sdKKaplCkiTN\nvn+4qAw9xs1UXB/9LHvkFHyxND58rhOYadI1u4/FJATjK3aMl91j3Ez89cOl3M8jccytGtwOiQaf\nL9mJOz/7w5mHuQgSzG1g2Y6jAKKxhpXoHV8pJymPwo1J/mziwh1CNsafL8nnJtMRHVNr9xzHZW8u\ngF+eTOwcjPKiGJlAxI/I5D/phaHSWgBu+fkQHp3BdrxSm/QY3TBZtS6r67/vWAmyR07hOuCo2Xyg\nCFPWsjV+kgRM+G2Lrg2jzMETZcgeOQVFpfalj04295vcQPkDQczXcdJSh+GUEDrCn7flsJApizLt\nPPca+QqB/jfivaj5B0/YM2MK9sqMTbjugyW61206UIQDx9kCL+stzBDU8ooKIpIkYUXYtrmCY8NX\nED4F1cq2OuZ/G/DqzC04pIhGYVlUFoVp0vbDJ9F7/OxKEZZOTyGqlS/jU0XUIDtRV9HoZmtx3hFc\n+c4i/LYhusbE2ZibqNepMj/enbsNR06WY4lGIsLIGmniIdsPn0SZn70RTkjOF3yFc0RP5ysRJJgz\nEOlsG/edwP7jUVvf4nI/9oRth7Vihiaihd5TWILnft2IF6Zs1L129M8bcOPHsfG8jQ7KTQeKsHH/\nCcucDTW1O5Kk/BGH3Rv0UxUS8o6yv6daY66H8vI9Ju3JWagXsKXhiXj+1sNCsdkveWM+7v9aTNgs\nKQ/gb5+v0AwLCQC7j8bbu6d8OMcwxSaddN+fl4ebJy6PRC0RQZKAB75ZjVsmLhcyZREq08C1VmjS\nVu86Fpfg6505eRFFhR53f8F2fDT7FiSIC8W//6mIAmViYy/jDwv1/qCEj+YbSwIjigTguxW7sfdY\nCTbs0z/hcjP7OZsxHsmYWlbuLIzTRiur8b1Atlg5bKAyD4dWfwoEJSzedkS33H/P3oqXp2/m1k2N\nGVOW/q/Ow1nPTI9EWgEQiU6TCHY2ZSlDKZpKkGBuksv+vQDn/2s2HvgmlOXrlonLceFLc8Kf8o+N\n9LQDWuYK8i5dHc6RN779HM2PJEkorQjg9z/FQnNFitcY08eLK7Bmd+J2vGaEEbMyxbXvL0HfV+bo\nXmdUO6KM1iInNbICdT3kX7cdOomOo2dgkcBErodc5rIdBZi58SC+Wmrclvz0J805ILP8Mj6cn4ev\nlukfV3+5dGfMRtkKzAqr8uLLN9D1AAAgAElEQVRrZHEw2u+ZpzbcTa2EhVuPaGp6lSgVCjEac537\nZI0y71RGj5M2JfgR4ZhC+aD3PUVMyn7N3cf1BTErXMYIVbJzXCrYHYWZs/lQ3Bjv8/IcQ30/7loH\nBPVxUzZieX7s5lIpVD8ukC2W5cy4cmchZjHDY0r4dNEOXP/xMt1IUGUVYmNasqC/KM0XL/v3AgCh\nNenFqX/ihImTU61xoP6Id/rPYtOBE2g/ajqWCyoE3AgJ5gkie5D/kR8N8aQlfAd1bOqU2GZjDmD8\ntE2447MVOFRkQGOhdORUDfA7PvsDV76TQOSLSGjI2D/LphKJHtmWlAfiNP/L848ivyBWo82yL1X/\nLRLGkvOsf3wfDQkYCPKXnenrD+BRVfjARduOcB2HeciTljopx9M/rUPfV+ag4GQZZm9ib8J4MZ89\nKtMiK+EtDn//Jl6b/+LUTXj6J/3IEs/8dz3uM2l6okTLTlONlTaipqOyCDxrZ0ExbvxkGV6fyfcL\nUD5r26GTuiclvHCngD2RdyRJwvvzYiO3rMg/iuyRU7hCgdmuy+vzUw04fmq9n0SRpOQ6lJrltk//\nwM0TlyN75BRsVwhavOhfLBKZjn5du49rLqUFaxQa9UeU51flpveuL1biTkV4TOW8KJtCmTEVZMkX\nERtzw6VFOcE4OV++4yg+nL8dH8zjR1XiYWRDduunYiaWAJB3SF4P3eHwbwYSzG1AHgQPfRsfs/nT\nRTtw+pNTheLLxlqYK8tPsIJARCD3B/QLE3mebJ/JWpSDQUlfW6cyZZEnqRkbDqouY0w6cUXFXzP0\n3wuwYOuRcNn86ekNhlOjqFe4/Fzl1Vr33vPlSkxWRU244eNl3FjGPIGBZ2r01bJdyC8oxl1frMTt\n/9GPjwxE6x4JtSd0lzUcPJFYljiz8eGVKO00tbRLWpqsROw5lfcHghI3iRXLAZnXVrImep1gQqwX\npv6JHuNmYfy0TbH1Ujxgwm+bYYbHJ+XiLoFY3Uo8CNVdXZ8fV+0BIB4+NFGfEHkoizQr71FfLt2Z\ncAK7mDjmDrvq6jlr6rH1UGIniGafPPLHtfj716sNCXiLth1B9sgpKCxmza/2zoyzwqfZyuUjkXVf\nbad/qKgU787dZqotlSY2ibwFI4/eWVCM7YdjTQPX7jnGrL+8drGc7FMFEsxtQKu//Ro+5hXpk3ZG\nZbHLVm/R1nhzin9OWot2T08zVV6cKbrGtVqfbRc8Cpv5Z3zG0fioLOHnCbzEgImFjGd3qZbx5V9Z\n6auVgqOWliiySVGVHY36Ye8CtE9hq5joszbZmABIjVZMcyNfQ760/ajpcZ+9N3cbLn9rITMKiJ7Q\nf90HSyJ2rWZf6/vz8lBcxt7siPhOsDYC36/Yg98Ux/cibb48/yhTQ6l3PG/WRt+KUyLWZiGULdF8\nXPHEzFasEeDbPT0N1wo48/JIZ0TbUvcBrRwZcaFoBZ/77R8hO3BZiVEhoGyRw0iy+rpeF1ErZIx2\nqe2HQ+uVXl8UnTNlm3B5vn/6p/V4efpmnCjRPolmlX+9ynfNLEZHWX9FjoYN+47jL28vwg8r98Rd\nZ0f0MqchwdwC3pkTG8dXa6zIAzYmDTHnBqPaELmY3ZyMlMxnmOzDvNu8jB4la7ZE7rciROO+46W6\nWm4jQqDoUStrQuCdjGgdi/uD8QmYth0qigg6F7ZtqFsXo8lwtqocFe3aFCpZuPUILhg/O5Lpz4pn\nyYmEnpi0Fg99uzrxAk0hHxvrD64ShtOunJZ9R9jMimV7rRdxRelwKfd1ljN6pDzOR8oNrVFNrYjT\np0ibL2Bs9j2e6L13frYCl7+1QL8ghEwDWKd3sfOxdhkic+Z3KofA7JFT8OmifJEq6iOx569PwplY\nYy61ePz6g1KM2aZRmIK5gfut+DpL95Tgr5MPoaA4dtN56EQpZm08GDEljJx8Mfq6Xj3U/iVa7XDk\nZBnK/IHIaZ3yWl3BXKceauS+6xf0N9Hbv9hpsqWFrHTYx3BC9aa+XE6CuRKzg16O/ytSjjzOlNfo\nTdgSJOw+WqybhEMuk2cKEZlgDH7Rn9eIJ//Q2q2yJrjjJRW47M0FEYc59URgduMge8qv3FkYF5oO\nABYacJSM05jzNHSMyDI8G3OlPbQ64czBE2U45/lo7N6FW49g4GvzI051p2VVZz7/pembmH/Xeody\nnWWh/1hxecw936/YHbE3Lq0I4EULkhuVhh2Wth8JbQZ2HQ0Jf0aj37CQEwl9t2I3fl7jfJZRgK3J\n3VlwirmIaKF1MsM66OA5SAUZ9TGDJIU2iCt3Ou9Uxaq6PLL2FJZg/V6x6CRdxvyGhxkmhkqmrd+P\n3UeLsSSvANkjpxhSdGjx3K/60bREkKB/WnC4SN8szKrvxeLoqfKYDJ5aNs6GTpgskMzXHQy9myPF\nsRveC1+egzs/X4FL31QpNVjx4XXqwTPdZLXXml3H8PbsbcwIV3prtdE2NDoF2HlimkjZsuLNx5DC\n0yqBZE6COYNEm1UvDFLomujfuHakCq3l9R8vxZu/bxV6Ps+GUc4MaFQrbcRWSz0mJEjMyWjoWwsx\ndd1+LN1egI37T0Tsi/WcVDQ9uRWfnQw7iy7lxHY9yXEmZbVdnPOnQF1kRITNcVP+1PQ5uPGT2KND\n2V5QdGLjnR6s3lUYtxGqCMRqew8VleHR73NxqsyP9qOm40NVCDi5L2klXSnzB5ibI3Uba2mHFufx\nN1K88QPwI6Os3XNM875Q/czNBCyh6eJX5uKC8bMNlSOPJT2t1X9X79UU+kVMM0S/6cDX5mPEe+ZN\nGdRo1UwZCYOZPMfkuj5tffxplVKh8OLUTRjx3uKIBjPvMD/sZbk/aCoihR4sTSSrjXjtdu4LswCw\nc2nIyCdVdnDnZ3/ggW9WM5UVagytRxbIiRzrvcg7j65F4euZ1dCuSLlKMNertvKEVHmt3thnxfi2\nQpYuKQ/g+o+WYt8x65OsySRSTzk7bxrjiF55MigrvQ4V6Z+iuwkSzE2gl21Mq8PJi2TMwBZYFUWi\nkkQnQXYFlGWoLzlWXK7roCnSrb0eD9buOYazngnZlFcEJObXO1xUhud/3WjIhlwfxVG7zjs1oj1U\nDugpa/crorLo11bEyRcAShkJHCSJHQt5JjPEFh+W0LzlYBGGv7sYX3L6svL97D9WgsGva5vGXPXu\nYu5npeXa/WpvYQn2FBZrjhutEHyXv7WQ+xmvzL+8vQiXv7UQ1/2wF68tNee9z8/8KmbKEgxKmguv\nrPlhC9bRKEYPf7cGF2uE/ZRv1zZlMbgJsUgpxZurTpb58d7caKQHM+YEvAtEvuux4gqu872yLvd9\ntRJdx/ymW54Rdh8txpnPTMOcTfH+LgDQ88XfsWqXuFAtmoCMxakyv5D2Xc2usPZX7t9am0NjPhnx\nF6/fexzjDJxGyEKP6HPNbArVYQy1lChbDhWhZjUfs2zle7NDrOTNYat3F2JxXgE+X5Jv2bPUygOt\n8KiiNvw+rwfbDp3EzoJoH5+nSO4mKxXPe+F3tHnKXBjfZECCuQb7jpUwd1nvqmzK1WgJbEEBDYJZ\n5CLVIQDjrovZE4RmnbOfm4nHfshNuA5ejwffLN8Vo7WXF0LWBKcWFpR123cs9oh6zqZDmpuimO+l\nsfju0nk/apRa780HjTsYmm3rS99YwI2FbATWuzgWjjTAc+JTtsvWQye5CSXk/mMq4UT4GRN+24IL\nX5pjKK6tVZT6JSzek1g0GDV6ZgYy93+9KibmfTxhwZyxr4lq/UIPq9CIrhTdKPAxGkPc7sPiCgHb\nVV3hyB+MycApIxZVRXHSp/GcWQxn8UTZHR6T6tjZSlbtEt9MHi1mh18V2Yv95e2FEe27HsGgFFFE\nyKc9ci4NrQ2okbGtbnNJknDPlyvxMcO+nof8vfV0JlobbL3Ms0a0sy9P36zKFxC914wjspb8IVJa\n4anyyIXKr/HN8t3CiiYW6njvQ95k+4Us3nYEp3QS5kU15h4MfG0eLn5lbuQztfNwKia8I8GcQ5k/\ngAvGz8abjPB5WvNZSXlAR2Me+ilfc/BEqW6GQKVNoRVIiE5O2w6djMQfn23BIqN0ypKRJym1Q6N8\nfXztQlz08hxMVKRcfnWmdog25WO1zMz++tFS8FqRJWAqB/aKfKVTHbt8M7Fndxw5FXdkrrcJsKJL\n8L6DVY7txeV+bNzPtv9Vvyct4d7s5Cp6TH7LT/vizJ5EE/Lw0HuF09ZrL+5elfDNKlvP7wRgt/Hx\n4gqUVgR0E5jolZMoyiKVG0i1QMLUWuq07RQDccfjypbYISl5dYl8ZuGWJe59Mx6sdQqiLEcvfvfS\n7QXMhHN5h9na9kNFpVimGi+9X5odMdeSqyXP/dZpzOPRegVLtxdgocp5OGoiJvZgVvlvzNI2K1WX\nrPckZb9RbsSdFin/l7sP3Z6fiT3huVjd9w9omCz+opO/QOR9B4MSrv94GZ6avE7zukD4JfnS9Pt/\nClmwRPDpX1L1OFwcwNLtIQFspYEjQwD4YH6eWFSWcIfv8/IcrmdzxGRCJ+SerNE1s3Cq7ZdF4Wmk\nvR6PUKSIaDmxvyvv9cfZdmsPQuU70nKcUz9XOWGwTIaU8tnivAJc2rkps0zZnlN5YiFBTDgc+u+F\naN+0tu51VrBy51Fd+1L1omuWx37IxdR1bAFUnUpaCyN9W2lXLjopHysNxtnPm404ID8y0c2NbMqS\nqEDMWhBznouaX+SPH5rYAxJAWTXlWFW32y9rGYu+yfci0i5BKaox33uslDuP+LyeuHkqUeR5Tpmf\noKi0ArmMzMqszSwr4sb9X8cn31Lm2fi/cGItuS9IkqSZyfma95dgZ0FxTN9RhnmVNwwrdxaiT7tG\nOn1Y/P0xHaE11oX/YyQMi4aC1XuWfL0FmDTXcVrbuyZ8EsMLtao1dvSc7UW+inwJL2SwjNzFlXLI\nuj3H0aVl3bhr7UiSZzekMWfw/YYi3DKRn4hAy0yiIhA0ZMqiXvyPnirHhBmb8cSktTETglbfWmPg\nWDNUlsQuT2PQDf33AqGB5fUYc+ZRv0stoYaXIIWZZMCAZ7Ze5nTesSTvZMAsRsxk8o+cEjbJUb+J\nEe8t4UZwAUI2rhN+42eJNILZ2OI7C05hmkLjaWRuVcYEN7KwxTsumyP6yMSWdKXWccz/NsRoPY3U\nTe6WSzibLdF3lEgMblF+WLEbp8r8cXX6YF68r0Uio63Ur20DrPxt1H/XY5IiXrLSflhEY2cUef4M\nmQSGJid1ciUZVszvw3FZW42/qenrD2C4ht+ItglWtOff9EloHZXXvUSdeNXzidFvtv94adSURfCe\nUyYSl8X3J/GaKlPJ7z1WGpPQR+zZ5j5jX29kLTdWdqLPUzPs7YXMU3kz2V6TDQnmOizaVoDnftmI\nQFDCv6b+qZsuvSIgYYNG6C5ZI6vV/d6esw3frdit29EXbj2CQa/N467/snf5zoJTMfZc36+Ijyuu\nrBuLDfvEwpFpaczV7D9eip9UR/FWbW6NzBHlOtlP447Vwz8lhDZWxTr2cKLfych37zthLt7W8XWQ\nMTph9nl5jrEbtJ5t8r5hby3EvYqQkmbj299oIBmGepNoVtMSsU1NcKGS67Ng62H8Z3E+ev3r9+gz\nNKp2SHXcLDvGFXMEDNGvqcxHYFUSD2W77j9ein9OWovx0zbptvZD367BT6qsuWqTBR4VAQnX/bBP\ndyOt3Kj9uT8qEF79flRgTVdEhcgeOQXTdWyPtWC9Utl3oLTCvFmVmXv1NJZ6ra/sHz+t3oNOz87g\nXmtklN0QHs+yALezoFh3k6BmX1Fovj5aEsAXS/Itqdf+47EnF+p7n/hR2zRD6eg79peoI+uo/663\nLKEPEC/4Lth6JCbiVTQSnHyy7054/Y+1Fm/YJ5bx2E2QKYsAExftwFXntMAH87drhp8CEHcczsPI\nznD1rmNxA+RkmT9ihlLNp72/+mrZLvypsPNdtO2IoTjeLJQDo63C23npjqNo17iWcDn/U9mlJbJj\nZtmrcm2oFf/WE8zjFvBw2WX+AM4MR5/hmQOMn7YJw7u10Cw/mSQ68eoJzGYFuBOqTaKyCYa9tRDd\nWtXDz2v2oVPzOprl5DKyovJQR7sxfQRq0RG4bA5wjJkSnM/5qrCM6uRRasx8TzPfTZ1SGwDyj0SF\nKn94HBaVVpiqk1GzPGWfiju5k2JN2JT9XOlQmpYWNTdMFA/C/j+KtyuXy8jLw+S3DQdiolIAUWFW\nhP3HS9CsLjtPghIPy5ko5vPov/+7OnHbYzWJvO7Fu0NC9JtLCwEU4vqereNiX6/aVYivl+0SLvPR\n7xILnGAmqABvIyohZM7HiqYz6PX5yB8/NNLfH/gmlISNt37FmbLY5PY9f8thdGlRF/uOawcRGPvL\nBgzv1oK76rA220bnTzdAgrkCJ3eHIs+Sh8B/FuejZkZa5O//y90X8dwHjGvmzArlPCFMaWOZu/tY\nTOgi488wzkPfrsGQzs1i/mbknegtDHEJhsI/v/8jNrsf08muJPmTgiey5MczmxOSzbpnW4Oyjdbt\nPR4xa1qcZ40tvFUUl/sjEU4CQQn+QBA+UalKxdbwYs1W7PL7rFGTKieco5ZtL8B1DHtfXoZapx22\nWIL16wrHf70NvhUnfbKwGxuVI/RTxMkTAO76YmVCddhTWII/95/Al8tio189MWktflgZne/kPsZK\nPrd+7/GY+rJnzyjJFpwCQSlOMP+Bc6rMQ72GWG3WXBEI4mtVmzzyPT9R1iPfrdF1LtdCrr/6e+Vr\nrO16PVRLifPtH7sw5pcibOc4G8t8uigfny7Kx4Rrcpifs/w9KlLQ+5MEcwFiQhlJFtlSCZwuKpMU\nqLvWaoVdueik7RSJTLRmtZSvzNgUMxnK74RXmoe7cDDqpBrYsq0tLwxZVUJPg2JV10yG/46oc5iS\nc56fGTEdGBSO/d6odjVTzzdrn28UJ5yj9hQKhNOMmWftr5MVT5DnGSuy1kZQFCW/ByM+M4mws6CY\nGTb3uxW7GVeHHO7UXP7WQrTKqhH5ff6W+CQ4iWJl72BtZI3OW9UVirMQ7BqaPUH8dvmuuAg5WiX9\nkW8ueZS6TPWrYTnTRu5NsIvqCeUxz+L8ndUfKVxiisNrbPXfrRA2ApIUZ5empkCZDcxk33rkuzUx\nIf4SwYn+bSR8m5KPFuyINWXRuV6ZoEPve/E0kBX+1BvwTmPV0acHoQlWL36wlRw6YTy+Ocue10yC\nFiXK+ebzJfnYfVQ7GZNR3LZuSXC+TmYFJvk+KzY3St8VGbnYNIeUL0ZzWRj91kfiHFPNwRK2JElC\nRSCIqQbDZLI2VUbfdqZPLZhbixEH1G2HTmq+Z1a0nfu+ij1peXWmfFrkzEA0PXxUN7LynCQSez1Z\nkGCugNd8QSmagMOsE5qac56fifP/pZ2iOyaUmMZztSaRn1bvNZSMQrM+lpSijdLxxSjKyVrvFEGZ\nVfCuX3SSRQiEXAT4AvyY/23QLN92bFzT9W3MLXqQJ5TM5e4EjuqNak7UabWThfIVjv55g6XOuYBJ\nG3OD7Wr0CU5o8eUnlPuDppOrRZ3lEq+PXNZORbSl9+blQZLiTS3cAu97W7VOGkGSgA/m5eG+r1Zh\nPSeCF4uAjo+RCOkqPy+ruy+rPLNzq5y3RMnUdQeYjpOs5GZmWJJXEAlBbSfpjChJFjSv45BgLsgH\n8/L0L7IRrYFuJpyTuTpEK3HMZtvpGRuMpZ3nYcUEKeJAuuVgEQo5pi3f/sE+BibE2bjvRML2+m7T\nDCfCxwt2WFaWW+L8Ku21R//swGY2/LX/y7CT1qO0IoBgUIrU2RqNeai0p36KRvD4cP52TF13wDVt\npIYngJ8qs29NGvbWQuZTg5IUCfMqh5kUwc+QPnmhRXlkqPxIrG4tJzY6HUfPwAlV0reDReKhBrVO\nR0NJ/fhoZS5mwUt0lM7w5yGNeSVGblpJss8zWeT5bkEvQU3SsbCJflzJdgTapwgpNvj1+SgzmZAm\nldG3MbemITYdKMKSBB093TaGEoFn82sGM1oxvWQiakQ00vL4CUhSXGQROwiGe4SZ/APtR03HqJ/X\nRxQUieYwAMCds+7/ehU+XxJ/RO8GePsFVjxpq1i393hMZJxIXRT/HvHekriwoTxYJ6JG7J0BIIMR\nGe3nNXvx+kxr8kE4xQGV+d7czeLjsFgvIYgGsxhZZ7V4ZQY7Od0FbRrG/c1S/w+HIMFcED1nQttx\nQd9KRcHzm+XiIa94TF5tXKPmKmzsO8PfXYSDGguglVvYQwa0NyzcqnXUw+rMkmqUWUDdwEGnEoIk\n+Fp/yd0XSRBno1xOMOg9Pt4MVD2+t+mECZWxYlOVoTKheGryOjz07Rq8+fvWhMsG2BuggyZ8YGR4\n0bgScZTMP2I+GptZ1A6xrMR5qTjvk2CuRKMBlSZ+TgVBUQ6SZNjsqRnw6rxkV0ETVvPxjrwIayjz\nB/HGLP7is3G/WGIqERYIJpDhMWHGZma6crfDyu5YmdHLFWEV8nQhMp0zU8ErFoKcsYlvblwWXEsI\nN0W8UFdln+AGz2+BEfJUVWjCFW4/UeaQiKM6TwCusHHOFZkbyZSlEqNMWMPLoGcnRm2wCELG7k3d\nd3+wTyXsPM42wwfzt+OD+dtx3Ia4yb8bPIol+DgtmFt9rVkSye6ZLNy0Kl317uKY30UdepfkFXDn\nMFG0BNpSRX92+97LjhCt7Z6eZnmZRkhBXQzFMY9BQ2Uha8yPFZcnHP5MlI8sdPCqCrjhVMGN2K3U\nYikkTpX5DTlgOcUrMzbrZso1w/hpmzCgQxPLy62KWGKvLYKBx2za70xM+VTDRQpz06dzj/+41uKa\nxGJFiEg3nUzwcGsVyZQl1dE0ZQlJ5m7TAhJRFm1zVxZIt5CMaamkIpAUJ2kRSm3QyKbe1O9enFpI\njTxlOSMXRCqanljNzqPF+hcRCeN22TL/SDH2HhNIIpYESDCvxMiCOU3GqcHEhXTaIOOYBlJFVRor\nqaDRImLZVxSK27zYZLSfZKeSdwN2ZPUkUo8pBpM6OYkVASCchgRzUTzyjyokbaQwTqUzJ9jM3XwY\nD3yzOtnVYFJUFp9IwwzquPU7C5yPSlAZcWqP89SckIPe/3KNhX4kCKehbb95jpyMztO/5aXGHE2C\nuSCnLFrMCaIq8NgPuVi+w/5Mb2b4YN52S8rZcjAaji3v8Cksc+n3TTXo8IGoTLwzJ/HkhG/MSq14\n6G5lyhaxEJrJhgRzQYwE2ifcAWnCCIIgiGRihSlFCkb8cyWpYu9AgjlRaXnQpaYUROUkVSZ9t0P2\n+gRBVGVIMDfIiVJy+CEIIh5WmnDCOE5qB2kTQDhJVXKIJ8xDgrlBNuyzLpMhQRCVhxMltGm3An/Q\nuYwgpX4SzAmiqpAqGyPDgnlRUREef/xxDB48GI0aNYLH48GYMWOY165atQoDBw5ErVq1UK9ePVx1\n1VXYvt0axyuCIAg38cF8mtuswMlcEVuPUl4KgqgqpIhcblwwLygowIcffoiysjJceeWV3Os2bdqE\nvn37ory8HN9//z0mTpyILVu2oE+fPjh82J2OlKQ7IQiCSC5OmrJsPkKCOUFUGVJEMvcZvaF169Yo\nLCyEx+PBkSNH8PHHHzOvGz16NKpVq4Zff/0VderUAQB0794d7dq1w4QJE/DSSy8lVnMbIMGcIAii\n6kDRLgii6pB3tAInyoJokJ7smmhjWGPu8Xjg0THU8fv9+PXXXzFixIiIUA6EhPp+/frhp59+Ml5T\nByA/IIIgiKpDKqbrJlKXP/eTj1qyKUkBvxLDGnMR8vLyUFJSgq5du8Z91rVrV8ycOROlpaXIzMzk\nlrFhwwYEHXQCAgB/IODo8wiCIIjksbWAIukQzvH9ij3JrkKVJyMNqKioQG5uriPP83q9aNWqlaF7\nbBHMCwoKAABZWVlxn2VlZUGSJBQWFqJZs2bcMvx+PwIkKBMEQRA2sXI/2ZgTRFUiIy1k8VFR4UwU\nrbS0NMP32CKYy2iZvOiZw/h8Pni9zkZzpFNNgiAIgiCIyokvLHumpztjaG5GjrVFMG/QoAGAqOZc\nydGjR+HxeFCvXj3NMjp16uS4YH7t91MdfR5BEARBEAThDB5PSCjPyclx5HnBYBBFRUWG7rFF8m3T\npg2qV6+OdevWxX22bt06tG3bVtO+PFmUBUhlThAEQRAEURlJhYiJtgjmPp8Pw4YNw+TJk2N2Crt2\n7cKcOXNw1VVX2fFYgiAIgiAIgmCSCtk/TZmyTJs2DadOnYoI3Rs3bsSkSZMAAJdddhlq1KiBsWPH\n4txzz8Xll1+OkSNHorS0FKNHj0bDhg3xj3/8w7pvQBAEQRAEQRA6pIJg7pEk4y6P2dnZ2LlzJ/Oz\nHTt2IDs7GwCwcuVKPPHEE1iyZAl8Ph/69++PCRMmoE2bNjH3sGxwateu7biN+eBXZmJLAXnpEwRB\nEMZo3aAGdhYUJ7saBEFo8P2IxqiWkZFUG3M9+daUxjw/P1/ouu7du2PWrFlmHpEUfM7uA1xFZroX\npRXOxo0nCIKoLKSnVeEFhCBcRvumtbHpQLzTZQoozO2xMU9V/FVYLm1ax33OuERyufWC7GRXgSBS\nhlRY8AmiqqMXqtsNkGCuIFCFA5lnphsPgk9Ubi7rwk8AxiIznaYTwt0M7NDYtrLdsN43rl0t2VUg\nCFeQCgI4D1pJFQSrsMa8Cu9JCA7nnR6fuVcLD+kMCZfTrG5128p2Q/83OmYJbdK8yW9TPRrRZqzS\nQYK5guNlAeFrL2jTwMaaOI8EkszdzOT7LgAA1Mhw78lGCisoiCqClqDVsr59QjthDR2b1XH0eSZi\nYxBhfvn7hcmuQspCgrmCU+Xig/CrO3viuSs62VgbgojiDUu9xeUBfH1nzyTXBvjf33vH/Y3k8uTx\nzNAOya5CSuDV2D0mKoP50pI/ArS+nxtoWCsx7e7Ajk0sqokYwQT6hFOmfSIt/tCAdrbXQ02yu6K7\nR4I2JJgrqF9d/HV4PFI3/0QAACAASURBVB7cfH42+p7VyMYaOQcpBvTp3Vb7lMRO+06lou+Ctg1t\ne44oXVvWi/ubGZu+1g1qWFEd2+iZIqYBd1x4erKrkBJUhsApz2sohJItDClp06hmzO9vX98t4fef\nApYlriQZ81iifTHRtcFNY8EolWCaso40jwd/OdNYZ6iZYSripOsguVyfZ4dpn5BkJDHeZjIWrM4t\n6sQICdVNmNm4fUPo8upF4G2K0l2gxXUTaRqxgxM1W3BKELjp/Gx+HZypghDq8JFW2OA3t9FHIFUR\n6bV2zGNXnt1c0zQs0fbud5Z9jtpuhwRzBRJMTGxumgkN0KVF3Zjf3WRLt+Dxfo49a+ET4s+qCGh7\nB9u5MOs1T7dW9e17OIdfH+gTIyQ0r1v5Qm6m0vC+8uzmya6CrXSwwL5YlhU7NsqI+6x2ZnrC5TtF\nrWo+9G7bAJ1bxL4TN0WiUNfF4wFGDmlvurxWWTVwTY+WiVarSiKyvN+pcep210VnxP3tiSHtkffi\nZdx7Eu2KLurKjkOCuYKgJBnWPLrdpk+L/9x2buTfynE74RpnMmLxOC0r/tTiizvOs+VZLeuLn5AE\ndAwOnxnaMdHqmMYNR7x3X9xG/yIVQRdtCFm4aXhve2GIpvMvq3s69XqHGgytaYZXru6KdWMGJ1SG\nPF+r5+2aGWn4z+3nsm5xJevHXoKv7uyF/iqtoou6K4KqDun1AMO7tdR1su3UnL0B65Fd31UbD7cg\nMsZFgjt4NRaRf15yVtzfZI147WpsqwErZaNzs40rnmpy6pUKkGCuICiJdabN4y6N/Fvv6tOyQpNQ\n9fQ01Ml0T0eRIKEv56go24V2v83rRSfzKQ8mx9u7IqA9uTWoGa+Fswq9adUNG0QzmQ/Vi8ptvbOt\nqUwlxJfmRXWNfAN2yOAf39xDyNn4nRvOseHpsfjSPAlrtX1eL564tD0e7hW70A/LaW5rKEXHcGAa\nEHXgbFArdj7s117MNKF+DfY8qhb0nUBE4dGwFru+Tm2KRU67RV6d0a4jv5uc0+L9jQDzSo3aYTlJ\naQpz6wXGfWjevr6buQq4ABLMFUiSWGeq5osujqKdz+MBpjzYJ+ZvDWpmJO34OW4sq353S5SHv57X\nCjf0bIXsBlFHok7N62rcwSZ//FCh67QcOP26pizRztD3rEYY0rmpWOUswA2CuRU1qF8jI+knNlag\nNjGwCi0/BtYCbVY2qF8jHR/d3AMDOzbhLrxOY8RmlaeV9XiAe/u2QaOa4kqST29LHU263fPAjn9d\nhhaCYSXVmm/luqnF00M74M3/O9tw3exg0cj+utdcdGZyA0AI2Zgr5oYHTURoYfYqna6m3NQ82L+t\n8LPu7Wv85JVF49qpa1pJgrmCIIwLF6LX9zw9K85EIzM9DW/8XzfujttO1Gu4BCCnZd3Iv0Xixea0\nrGu7AN+kTjW8MLyLY4keHtCYtM5oVEvzXuWaGAhKeO/G7lZVS7efafi0xVEZk5AM7NAY9WuIa1Nb\n1LNXO2qXtszoKDDrO9KvfWMMCoemc8Omj8XIIe257VgjIy1yWqnEzDdxtROa2o7b9seJP8GsM3yt\naj5ccXaLuL87rS+vWz1d6BQl2YmlWGP8w5ti1x7lFbzaarUt6zN5XuCbyUTvadukNrdsIh4SzBVI\nJmzMRSeqt66PP+qNCpvWD+xnhxmzd5YkCedmRwU2ke9VGe390jS+k16GNeWdfh2zF6sRFZ7OUIUw\n43Hz+a0N18FMd1AvKl6PudHQuUVdQ5u3wZ2Mx0N+0oDj2oXtnA9paVePcyoesx7q/nXPxW0im4e4\na+ExtDm6oafx/s56ptO4eQb2GdEWCOBWd5Rk+/eoX0vOafUwuFNT7YsYXGRwzjLytY28I7mdWevJ\n45fG27ob0canCu6YcV1CUMCU5du7esX8LtrfMhnaAzkhhR3y7bAcYyYy6nErUiczE9Lf+8UPoktM\nCElWcu+50aN6pdZ1weP9cF2P04TLUQrHL1/d1ZrKhZHb57xstrZbdJP0+6MXC11nRqNsRT/2eDym\nBMzQZC5eAdFFXilsGRH8H79EXIh//0Zx++x0DS2kiA/LwA5NcGOvVsLPA9yzAWfVgnci4PGw21j5\nVe4+J6rF69KSbR6njsWthRuyJzvRVKKPqFPd2ig3Im/XyvCgRsxU7UbLr0pte//z/fHJ30Sc7Otq\nnDiyvqK83olsSM2curHuSGds9qpp+N2kKiSYK5B0nD9v652NXmdoJ5nhwVrcfDZutb0eD/owdsDn\ntAoJoaxhqqyiSM3MDLZWjIgryWbQGdHFV5lZ7rSsGniJI2CzvMSVr0NtttSiXnVMfzjWx4C1iDyg\ns/tv34x9JCjalUSFrGYqwVwkXbkZjWHyRRlxjAioaV4P8scPRTWB4/xLO4tHNNHygWBpKNXvt4eJ\n6AYAsPTJAdzPTm8oLrzK3N5b25krq2YG2jeN7eus13/VOfzweSyhXdmGg87Qn4tquDxPhfqduMXs\n6PkrOxs+dZNNX3hfQW7PWy/I5pax9QV++D41l7Q13m9Z8OY9p/JaKHt528Zsc0sRRYTRvqNnyqIs\nTr0+De1qLIqTyKZ3YIfkKvishARzBUFJWyBldVzRxZp1lZzswo6p1AN2eD9efZUDV5K0QyfJeL3s\n4+LFI/sbig/O4v/ODWmqeZOeetG2CtHIIqxkQ3qCab3qsb4EX/+tV9w1IzQEjdAz2PQ83dyGUcmV\nZzfHhzd1xw/3nI9hqokzkWNkrYyp6nLX7TnO1YJqRb1xq4BvVb0eG3wmAODt68/BqMvZZmoii5fZ\nuaapRox6dU4EADhbx2E03addk6//1hPTH75I9df4e3iOqff2beN4n0i2rTGQvPCeWTUzYhzsb+rV\n2nCUpohhJ2+NCv9MJBa6klvP1g4iIPoqee+cJyRbjqKj1+KECFSOhbNbGY+iIn/WtI5iHmBcn6M4\neVJO42rZ6e2/siOmXHxmI3QNl8Gqj1YdG9eJV1qsHjUIW8YN4d/kUkgwVyAh1sZc1orKR9iJpL1m\ndaj3wiHG+guGkTL6PC07Z7XwI0GKmRDFNOZsYaB5veqG4oOzuEQnosn//m5dyEQzi5nRSUMUntZC\nbi/eonXPxfEJILq35mhHOd3Cl+bF4E5NcW52ljnzBc4tF7Th2y6qNfHr9h6P/HvclZ1jTIs0tc+S\nBC0xeOsLsZOzqFOkltbHDi7mRHj4e/+QU3KTOpnceUjkK/FMPERoxxE0ruwWbzan23106mBEyH1H\n5b+zZdwQXHF2C0tskq0Y0xe2bRh3ejnAojlf/Z54WsNHB51pyfN46JlK8HwBlOg2l4btcTJRz5Uz\nH7kI8//Zz7LwuVee3TyuL9+iOI1oqOP7BISCKADAyyO6cp2Z5bWHpemXv6PefNiGEyBBva7x1pfP\nbj8vEhJWK0uvKPVrZiQ1I7dZUq/GNqIOl/j57T2x7KkBmPFwH7xyddeYWNpqtOILA/Edsd9ZjZAd\nPgIed2VnrB41yNLQiR54UMYI7ycLJBef1Uj196hcJUmSkGB2U69sw4ufsB2mzmVWDjar5nmjC4ae\nDayxZ8ffaHQxPrOJtRqeLeOG4NPbzuWaL13WpWmcba9a+F49WjyhjFZfNBNjXY2ppmHUSSsO9Ge3\nG0+k9dsjIc0yK9qOOroST+CtqZG4SGbmoxdj/FVd4v7ev3280KX7rhQXnH9GA/QUiBTEGxs9zwjd\n27lFHUy+74LI3CDPNUpNbjKEuvPbNMAHqigZAwUEVaPkjx+KARzBXPm1E80DoXyH/cLriJ4ZwRvX\nRcMfdlWM+UvVTorg9x25Pa06mRDdaOuFQ1SX065JbbRqUANPD+0Y813N0rpBvMlNJ8UpVROFppjX\nv7u2rIeZj1ykmTnVo/qph7zm8ObdGNNYA012Tqv6eLB/W9zfTyxsojx3NBKMr58KkGCu4LrOddCh\nYXSXWz0jDU3qZKJt49q4huMEKHc4n0GnE2Vf9qV5Ub9mBlO4GtqlmamEPwFJQoWfHXc799nBTOe0\n+/q1xZ0Xno7uresLRWIwaicGGNfWOeLMpPOQL+44Ly72K2txsGLB0DMhMvI+OhuI9/7lHT1x54Xx\nWncZkY2QumoZPi/6ndWYW+emdarH9Ydm9TL5wbd0vryRrpVM0xfZLMUqzgyHIlOHmJv16EVcsxc1\n3951vtB1ou/tb334fQkA7r6oTcTfpXOLOnGbFeaJFKcs+e+ZvjSc0yp6SmRFPhr1M5c9NUDT3p5F\nmtcTNzc4GWGkh+rkLMvCRGjyafLj4cyQi0f2x4LHtc0YX70mKqQrTZHU73ruY31jfteK1mEGVjHK\nEJvyfKPn98Orz+kNa8ZsSOxEFs6V9vffqEwl2zWpLRQSUdTWnLVU8eduoSJD5Xo9eHTwWULJxLa9\nMAQ9srPwyS09cD8jsESqQoK5giva10a7LGOe5JH+xuiRF7QxZvfL6rvZDWuga8tYmzARTWj9Gukx\nwrUc19Tj8aBu9fS4CBOSFIrb+szlHeFL86JT87p4/bqciEbEbv5h81FrIvRp10jonXs8wPSH++gu\nTFrw5HIp8rk9O5W2jWtpbgr0jqo7Na9jyvxFbVKizPqnLu75K+Pt+vUY3LEJbuoV74TG+zpapwYi\nfhdxz2FMDE5pbds2rh23oeI9W8S5FxATKH1eD4Z00d6018704anLojkQ1O+JVU2j/UsppMi+G6Kb\nZ56DYZM6mZr29kpkhYrP6xFu83ctzKBajxNlw1pbeNnEIfSzeb3qcY7voc+j/66ekYaHB7bD3Ref\ngTv7nB5niy1fm61yKhaOpCT89eIvZJ2s6T1X632KmJmIoFUHDzxY9tRA5I8fGrM5P9+g/CFPb1oh\ndT0x/w79xkukp7zWbqfkAR2apKTJCo/K802ShNzf1OPmhp6tNI+l2WYM2k4vMqx42srwdiOHtIfH\n48G7N0SPT3txBumvD/CPNYd3a6mbrU1dN1ZSD4D/nmTUiX2cDj1mNMoWq6m8Hg/aN63DXJhYsOyc\nWXHUq6enRW3MGeX0Nbh5MvJuFzzeD8ufHqApmG99YYimzb/WwqUuNRCUuJ2EZTKhLIf1Psf8pROe\nv7Iz9z4lXg8w7aFYh8NYm0prFhcjgtHdF5+BM0xEPfk8PPeIPkn0u1k1Ls2YoHM15py639+vbcSM\nRbZxZlk0sQTYSKg/k22+atQgvDA8ZPbTpE68IM97j3UEtISi1AxHlPF4zJkVaDltG0Xd5x8eeCae\nHNIB6WneOMGONz6ipizaTHuoD64waRbq4fxbi9qKMKXqTKF1MtMTDp0rAWhYO/aUw2oxt3Y1H5rX\nq44f770AX9zRU+geuR/dyFB8qGFt/K0Ibckb++rMsXrO6G6DBPME8YVnenXHy0xP07Rr1QtXGHOt\nSuAY0CHeeeNahalNs7BGR0SzI6dNNpsh0ChWPmbmI+qoDclFK2ycJEloUCtD166RNdFIkCILtjod\n9hVnN8d/bjNulxz/XPbfT8uqgca1MxFkW0UBCGmZQsf1Ie7t2warRw0Seq66P1yisDkVEWDl6D0S\nQ55/8//OZvqFDO7YBPcw0j5X86XFnSSZjWMuw+rvw3Ka4/qeYrHEnxzSAbNVR/oiyKFYhbXMHvWv\nHOHIpmmiQ1N2puEvBYSEiG2sxlcd0KEx7rm4DW7qlR3z9wmDG2NGXPQXoLmgVjymHornZ9XMQO+2\nDfHtXb1weddmusLwc1d0wqe3nZvQM7nXwIO/nhftb+p7vrqT/Y7P5eVMUPxbdjCvzvFR6BW2/7di\nTxs1ZdEurH3TOri6u3Z0K16dRLu3cq5XmjnakVG4ms+LZnWr42tFO1mVWyB//FDkjx+KdWMvQWZ6\nGrq3rq9r6iSHbJWrIFKXpowMqsO6WudTp0Zt1qdeN90OCeYMXhjQCLMeFRP6MsMa5dHDOgoLIwAn\nxi7v2vDP167NwcsjuqJx7fhFQ8+3zai2Kfo5++8Tb+0RqptNC7WIUNbOwjS/IzoY00qqhbTGtatp\nHqXtO16K9DQvpj4UimXO00bxZL92TWpj0j3n45bzsw3VUxRdDaZAQ0f8Lbwe1K/JN0mRaVY3M0Zz\n2LBWBq7sFp1QRdYeZcrsuy+KFbazGU5TAPDhzT00F9D5/+yH4eF6KOvHywpr1Ga3ekYaXhwe70Sp\nJqGQoJx3xxvv6n7H0+iKDHeRa9T1uI9jH3pOa4UNcgKySHqaFyOHtI8TINs1yGBqtP8S1rgmKv70\nOqMBPB59G/Obz8/mRstIGA/QoFY1DAwrdNSnI73bsqMmidjo333RGVj+1ABumD4zcBVU8uciZWhc\n1aK2T6iczowwoCwy09Pw030X4LkrjJvafXtXL/x4r7Z/hxyFKatWaJ6x8iTDDA3C/iB6p2zKMW7E\nHp0F18FU8P6Aw5m4E4UEcwadG1dD28bGFsVqvrQYYcQM3H4e7lPnnZ6Fa89lO6GasX9lPCKOszjC\ngZVHriycNmW5tmMt/PxXfS2LTLvGtfDM0A744+mBhp4jT2ZZNasxvyFLKytPSj2ysyLtLB+/ayXx\nkCAh91nxqCZaiCzS8mIoulm7/cLT4+LnA8baPmoiJeFehhbcDK0a1EAHRiInvhNrJtdG20gvVm/s\n7maEwBSFJ5h4ANzW+3ScpdrUCpvpCDSuchN3vkBCNo/HgzSvJyZ6T0QLrvge3O9kg/mqG2KSJ4o8\nl8h9M6JxFi1AoK29Xg8aMzY2ZtATvPWcP1kRXlho9ZdRQ6PO0kbs/bu1qo+bOUoTrffdrnEtdG8d\nPZm45+LoHPbooDOx/OkByFRFfGtZr0asyY3DXVXLrJKnwEl24quAk97WFkCCuU2Y6Qe6tnWKzj3j\n4YswTmE7K7qQ8AYOr74P9G8nZDLy6jU5mp+bHZZuXR49Hg/u7HMG095f877wT34qcbFvnBE+IlFO\n6kr+eclZqFs9HXVF02LrPFYkpbOMliOfUvhM83o0BVcjbW/FvPtYOLJEbB1CtbjrojM0TVl4zxc1\nEXv1mhxM0fD3EKVzi5BJCK8beTwhR98ZqjEdF2eY8/aNRDrJHz8ULwxn2/d7EBXE5Hek5yjL/U6y\nA6KFs4XVcoS6PCfEBNn5f8xfOsU8U9yfwBkMbxg4iEQS06OfIr58TdUpwHmnh6J/ANatS8q2aFGv\nemT8AiETGdbpeDJl3FgtuI7GPOY+myokCCvZoptxd77hSoARW02+jXnop1IuOKtpbew9Vhz53acb\nZk/7c56WMs3r0TQZke+TJ7Ea6dpdymlNuNXM/2c/psmK6LfSa4dEj/xkrA4dJaQxF5h87+vbBm/M\n2hr5nSW4GhGytR5pZDG47ey6mgnE2jWuZavWZwTDJtaMoHlh20ZYv/eE4fvEFeYWOX+6dMednuZB\nheLY2+563n3RGbhKke3XjvlRNreUN9eJfid5DlOfuiRK5Jtz6xevoOIhZHtvsM93a1WPGyfeLMo5\nRTOBmoswErbyizvOw8qdhZpz55zH+qLfhLmG6zHhmpw4S4FBHZvAz8jf4k8xwTw1ekIKYmaC1RPM\ntaNbiD3PKqeRyHMVg/SlEV3wSdj2XO960XLdRqsGNYTDpbGQ5xHe12NOYAY2cSKYebeJCGTC/oce\n/u/DcrQdhczUbusLQ/DYBTwHt/hKmwuX6Cx6kSt4f0+mFlUrUYlQNBELp7SVowZhzWhxXyFR0tO8\nsSFhw1/2rKa1meaCN/RshcWqCB+JcnnY2Y7nqKlG2R7X9miJMcNCZh73hU3Gvr9bLPa9UZxyPHZq\nb3hJ56bcyFkehQRm5Oslc2PLOsHn0addIzw88Ezm/GJmTVE+k+Xg+9HNPfApIxjCPwfHn4a6GRLM\nHUbWbLMFaW1TlvirxUen3pVmE//IGU8zfF5cd24rtKzPDhXIGsRaZiByuXrVWjdmMJ4dJpZExQ1E\n3oPEfufJtsXjYcRGz0hfYtmYq8kfPxRv/bWbeKGCpKd5IxuleFODUGUyFf2b5/wJOBfVSBedyBX8\nvwsWb9HXZEYfYgnmAnNcpCgLhk6dzHTUq2FdAh4l6pCwWmTVzNDMNG0E+f1c3b0l8scP1Q2BK6M0\nX3v56hzc2jt0ojSgQxPkjx+Kupw46UrOPyPkWKppBiYYBtHqEZZQeQb6Wp3MdG7kLOV8rzeHNKgZ\nWi9ZGX7dgvIb1FGYUWrpNLRe5fx/9sO0cMCERFBnmHY7JJjbTPN6sdrVFc/wnQW5yWV4R0cWynBm\nJ6kbe7XGc1d0wsXttGNpqyedCdfkxKWGVqYv7nlGAzzYv61ujNTamemowdAAfXJLD9yi4RiZLFht\nPEJxlM0SkGQbUbuo5vOiXnVtYSQocBQYsZ9X/f30hrUU18R+QZbtukhf1DI74T3LCHKio5vOb42x\nf+mEy7s2N5ywA0hMkE1kj6ZlY878u2C5VkVlESVWY+7cptWl+2MuIlF+WEzQ8A2SEBpnf+ujP9Z4\nPNC/LVaPGqQZOlj5PEDr5Fi7Zyk/1TRxC//khdF++equ+OGe6GlA1Ck1eoN1NubRfyuDR7DeeaPa\n1bBh7CUxpk9AMpw/9a+ZdM/5MdGqPB4Pvr/7fPi8nhgHVz1CjvjsUKqVGbIxtwm58753Q3es33c8\n8netyBWPDT4LXy3bFV9W5F795/Gwa/Bm+Lxcb3QtlNWR6/7lnT1x6EQZgJCG5VHB46fh3Voi7/Ap\nfDh/e+RvAzo0wYAOTfDZkp2G62YnkfZXLCON61RDw1oZOHKyPE5jPqB9Y+GY12bZPG6I7jVCAqZ8\nGKC6lhfZR69cI9pSqxXWI85piXo1MnBRu4a4+MzQplMrLKJL9OW69WC90WZ1M4VjtIucDFjZFh7O\nv3nXWPdcj2bZt5zfGu2a1MYz/11vw9ON04xhXicyfrTifUsSMOryxE4jvarQqSLwam31GONt9JQ5\nQYzeK4rXE/Lbkef792/sju6t62PZjgIA7KRUQNSXK9H1/P0bz8GewhJT94q0A8tp9bzTs7DtxctM\nPbOqQRpzm6lfMwN9lNpkDUFCnsAuUGnmGobjl/pUWgc9h08jGF9MzT1b6zF1MtPj0jOLkOHz4qnL\nOkSy/LkRWXuvnFCVR7jy+zeTxEaPj26Otfs3s8C1bqifzVRUkF7wePR4klUXQ86fnviNjhG4tv5e\nDwZ1bGK7ltZoVB89tEKZsUhP82DJkwMc1UabhX8KoC1E28HYKzrHneaZeX6cCZVRk0KNz0RNRPTu\ndwsNa8WOlTsFTs1YsPoR69TVTuTkTXJdLu3c1NBc0J6TkEuUSzs3w5199MOxsgId1BcwYRKZToz0\nLnf1RPshwdxhlHGXWez412VxmdhGXd4R79/YPU5j17sNOzGEOazv+o8MjDo7eVSqzRSQA4Sp5vPi\nwf78KCgXndkIY68IhY2THQiVC3DMcb0N9RvQPvHEJZ/f3hOT7hFz9tJb0E/Lih5PsgSRyP0CL0PW\nFOa01E+53L99Y256bDPvXTa9GtChsSkt8dInB2DWoxdzP9dKgvTFHWybVd2ICQkOPJGwmTf2ip7w\nGFp8GWUrN6pOxha3e34yc7LhOA5JQ7KpW8Pw+sbaJH58cw+MVZj05Y8fimdU2vxETmpuctjskWUe\nY4QOzepg6ZMDEirDLO/e0B3vXB8b471WNZ/hKD1PDumAm89vjVZZNdC5RZ2YeaOqQ4K5w+gNIY/H\nEzcx1cjw4dLO8ckTlFEi9Cd656f6hwbynZ2SIZjfekG2LeVuHjcEN3HMef587tJI7Fsgtv3PaVUf\nfdo1xE29snXtK40wQmWD6PV68Nnt5+Hjm7Uj5miRVTMDPTgpumVE6n6dKkGWWa2c/KhWWTWwetQg\nXNalme49E289V+iYWgtlrOS+ZzbCxucuwSMDzzT1PZrWzWTGmX/1mhxkpns133efdo10si1ynDzj\nfjfW4WTh566L+Nq2cVcas3fWtAf2eNCPE9FC5P5EsfskQe/9q09PncQpLeWIc1rgt0cuipi8Kd/I\n29d3w+T7LsDAjk3i4oprovFa22XFm9Y8OcTYiaten9RDNo9L5IQ0nWckbzONalfD0K6x823us4Mx\n7aE+hjZHTetm4rkrOsPr9eDXB/oIzRuu2LA6AAnmDqMVGiyZOFWfZH7tc1rXd/yZ1TPSYhyfvIr2\nz0xPwxd39IwJvygqCGgde064Jl4rfPGZjTCwo7UxeNVEaq7RyHG2kyyNucFOorRhVUZvsUOm2vT8\nEHx2e1RbXSPDl3DWXTUjurfEpuf17f5Z2D2+5PK7naZ/QqFblqqyvLqLblqtbG+7BQDRPv7133oJ\nZbTU2hia3Vw4FWnI4/HgTI629fKuzXFOK7F5m1Xb9gz/lnvPrY9/X2J+w7N2zGCMHNLB9P0AcO/F\nbbBuzGCuYJ4KpmVK0rwey+fBqgwJ5g7Di1xhlsUj+2P2P/jH4ZHn6oyZixPUAOg+P+535wexG0La\n8UyZjNZt4q3ncjXgyZrUo/be4miZRrC+xSCdzcWwnOa4wYCzbEJdIibUWQLlmH084296pixaXeP6\nnq10tXCyhr9WpvNxA2yyzjH1TMvKF3iA2e+nNcfOevQizHo0PqPzEMXJrAumy4Tp375xnAloepoH\nzWuL91/1mKqTmZ6wL5DX60HtzPjTMjP+NXb0/9euzcGTQ9pXKg31qMs7YuAZ+r5SboCisljMZ7ef\nh1smLud+bvUgkmPdStJBxTOMPWT1qEG2L7TnZmdhyfYCDO/WAqt3HcPgTk1wssxv6zPdiGjLeDyh\nSZrXlI1rZ2JgR3OJjt647mz8sHIP/v37Vv2LbYbp/Bn+yerHH9zYHUFJwvhpmyytR6Lj0i0yzL19\n2+B4SQW6tAjZvxvZEL84vAtu7306Br42j3vNtT1OQ93q6biwbeL+LaKOj5G/8zYbNogPibTnmU30\nHditVhIYfQdtG7M11Kc3rBn5t9N92tIwmw6IlIssTgDlJuSQjK/N3GLoPif6zNQH++DP/cazG99x\n4enoUfsEKioqNkpXtQAAG7pJREFUbKiVtZBgbjGyRok38XqjKlPbMDrpGw1nBRgXZD65tQcKTpaj\ndmY6Xr/ubABwXDB3hQaIE5WHt5myo86nZdXAo4PONCWY9zojCz6v9kGbkf5390Vt8POafeoCuNd7\nvR54XazHyW5QA/kFxY48i/WWGtWuhlevzeFeoz9utZ2z07weIXt+EeJNWbT7jZOnbHIyKZF4+RE8\nHix8oh/Tb0BN99Yh/4FOzWOja5gd7pqmLAL3f3VnT9zw8bLYqFFJmi+tVl5pzUcvX90VB4+XmipX\nyznbCZIxCybLwkbZhh2b10HH5pU7tjkJ5hbTOit0VHJpZ+3Fy22hqOymRoYPNbKS293c8M756aaT\nXzcRvr2LH5lFa9IecU5LHCqKXwCVE6z8BioCoX+xQnVZjVVvXW6+n/9+IU6URDUyvc7IwtLtRy16\ninNY3R3rVk/H8fB7ua13tu71RgQAO4QFr9djPPyqJHEzH6vp0rKudvkOS0ARcw3F/OSG+dJujDiD\nu1cdYB8vDu+CL5ftTHY1qhxkY24x9WtmIH/8UG6WQKMJUS4RcPwBEJOEJlUcR2StlFMxZOV3Ptbm\nTJoipES4NINE/CcYX+7Va3PwxR094z9gUOYPAgiFoTRDMsWJutXTcVpWVDj79NbzsORJe468RfpI\nvCmLFaUaR/YNuKZ7Szw7TH/8sfoQPyNkIjVzF5nhPl+rWmJzYpM6UedwsZjS0ZOS6Q+Hcgz0aO3e\n1O8yq0cNivybpdyoRF0jKYzo3hI/3dcbANCjdX3dtTOSRyEVFzAXQYK5wxg9ju0qEJ8ZCAkEWlna\nrBoot/cOHe1aUVyDWtXwwvDOGPuXzhaUJk4yJw2ucKH6XQ4NNiynuaHyz2hUU/8im7DKSqs8LJgn\nqjEXaudEKqsQBHh2xdUz0tCsrj1H3iM0sjbyUL+T3v/f3p2HR1HmeQD/VtLpdOe+CYEkHLkgB2GF\nkCjncAQVB+EBRV2RcThUdGRWCcjoAyjXA7rPo8wgOq6Ps1y6EWefB+EZQensrIrrKsq1MCOHKIMQ\nCFcIiemQ3/4RupNOd6eP9FHd/f08Dw9Pqt+qfqt+VdW/qnrrfXM630Dw3g/rgaUTsHqqjS7RHNys\ncNDEvMNi/JsNpNoY7dBVZX2TsHZaCX51R3sTmq5iYeuzzxb/ArsXOO4QoKPWDkMHFKTH4f9erLTq\nEs/b3LnAirJzAWM5kFv3qPXJga9/x95//HaMHeDdnr2oDZuy+JgPmpgHlIeG+W5gB+nw4+Nvjn6E\nIjXhOLSm0qVlHntpYvs7DH7k7h1MU80HZba9uNgvxfsXGanRbT/srvTSYMvGh2/D6Yu+aVtusvSe\ngS4Pmd4xef2fJWPttof21F3ojstx1Pba4VMkFezb9vzbI0Mc9vMPAFMH90JqnP2uThVFcal5hWmb\n6iPa999utX02P8X0X2rgygWWZdMb2xaMzcWavxxDk7G1mzUjf1PxKcCjmJj7WKDvV+7cPRjaxzP9\nh2s1Yea7qe4wd83nx6Pb8c+I+3QRvh1W2lr3tqtpi4zOT8Oxlya6vT6uJJUDUiPx+4nJyEx0PpnR\n36pXXIdEM04XgeJbI4H6iqIocDTGiNWgLB3KW/Up37mAl/W/9XTH1FxvZnk2XrnVC4TlS4jSZc3U\ncEfT2TuJ/3rrxXdXdJWoPjgsGwlRWpT3s39R4MwFjaNtrFaOVk0EmHVHX8y6oy/6LN7pm0r5iL+f\nEJH3MDH3sfYBhnz7Y+Kvg/ivC8cgOcb1Xl9s+er5cbh50/3t5uwjcW/yZe8rgcwTFxnO7vPpMa6d\nBof2ScSrM0pxtxu9k7w7t9zlebojJy0GW+cMw7c/XsHav/zNiTl810Y0OSbS4gXIp8bm4vSlG3j/\n6zM2y9urk/bWAF4zyro3qqs77shJRq6drgd9ITxMcbm5my2mbhKHOnHX31s8212iaZnBf2JV85Mk\ncg8T826aWZGNL7+vw4Cezp2cPT3AkL84ezLISvZch/5xNgZkcIcazmPBmIjbGzwp2CiKgsmlvdya\nt7yf74dYv71/Ck5eaADgv4tSV7/XleNDEx7meg8qHrJltvcvtO4sTsfOQz+5PJ8r57ns5Gh8t/JO\ni1GKA0HHVfzV7X3ap3vyJO//B60Bo6sxKMh5gXUUqlCflGh8+NQIp9vkKQrwSEU21k2zHjbdm3ic\noP0E68d75qZmELd3GqCl8xOUyaXdvwvma9G3joFkN/rFJ+8yxaTzKIiBJFQf3U8qyfDJhUegJeVA\newKYlRTlVBv/oBKah0NI4B1zH1MUBcsn+7YXEk8K5Du9rSroykmvDcehZRMQ07ntbwffrbwTmm4O\n+eysnDTHoxQ6Kz89Fn+cOQSj81Pdmn/pPa69yGifOnfSgnT/NXmYWJSOTb8u88iInb5g8xjtMK00\n07neqigAuXHq6/yUrrhXPEozE/DPPuxcwJNc2QTMz4MPE3MKOf4+kcU6aJLjqztXnzwzCinR9nuI\ncIepv2p3uNs8xB41PSX676oxSIjyTFMsdyiKghG5ji+YTM3FBvR0PLLeyLxU/PXvF7pdt47SYtv2\nx0hN+zsGnd/ZPrhsgrldOYU2e4e4XhuO/5x/h4e/y/snFFduKajp/GaSlxaLnfgJUV7qiECFq+wV\nXkvMa2pqMGbMGJuf7du3D+Xlvn0JKhR09UJpqOzQXVHnfVT/6Z/qubvl1LWOgw6pWVqcDv+1cDSy\nnKjvO7OGOnFMuXbUPT0uF0P6JNrcXqZzmKfeNSF1cadDBFcH7AsmalznJ3+Rg8qiHkgM4CZzauD1\nO+arVq2yStCLigK3KQe1CcRE33QiU0Nf3+Q9avzBCiTZyc71Hx/mheZWkZpw/KKAg5iQc3zxkiFP\nJ84LD1NQkO74aRt1zeuJeW5uLu+O+0hXJylPncDmj8nB9Z9bMDAj8A6+pOi2O21qvJrnyd/zeP0V\nXNjTA5E1HhbBhw31gogv+kZPjY3Ey9MHBeQb/JWF6fjTo2UYNyDN31WhbnpgWBYyk/QocKItNPlf\nd5IH04t9zD+CW8mtAbrceX+AT8komHj9jvn8+fMxY8YMREVFoaKiAi+88AKGDx/ucL4jR46gtdW3\nQ+gajUbz/wcOHPDpd9vjSj3Onq0HAJw+fRoHYPlSlmk5DQ0N3Vo3tWwXRzrX0/R3AoCDB89aTLcX\nd1+u682bN33+nWpxZ040cpK0Lq/77yuTceLYEavpdZcuAwD+9re/4+fzXbdHVuMxH+g6bsfGW8Og\nl8b/7Pb2ra+/DgA4fPgQdBrP3BBwNe5//GU6rv/cqop9xNk6NDY2uVTe38amCYonpePvRw+7PK/R\n2Oz0eroa+xPn2rbj+drzOHCgyeW62WLve0+fvgEAOHv2Hzhw4FqXy7je3HZs1V+rd7gegbIP2GPa\nLv84e9bhdumKP873YWFhyMrKcmkeryXm8fHxePrppzF69GgkJyfj+PHjWLduHUaPHo2dO3eisrKy\ny/lbWlrMyYo/mALob67Uw7S9bt68aTWfsaXtbxHp1rqpZbs4YrX+nf6+vXck+iZEdFnOp+sqfvhO\nlfh1adtLqJ5ad9MFfUuLEa4sMhS3vTd03I4aAO9P62E13RWmJ4EtxhYYxfP3zZ2pV6IWSNQqqthH\nnK2D6UmDGursrBSde/V193fNmXlaWloAAK03Wz22Le0tp/033PF3GW9d9Io4UzZw9gFbWm62xcBW\nbuMuX22T8HDXe6jxWmI+ePBgDB482Pz3iBEjMGXKFBQXF6OqqsphYq7RaBAW5tvmEh0DFRGhjjf/\nXamHaQfQhIdbzae99Xdhmq5b66aW7eKIqZ5rx6fi2s+tVvVeNKK96zh7cffluoaHKQAkYLavmpna\nIms0EQ63pxqP+UDn6e1oimdEhAYRHr5j3rbcwIq7s/U1de8XaOvnDkVR3FpPZ+YJ17Qly+HhYR7b\nlvaWEx5udPq7IqQtMVfCnCgb4PtA+3axzm1c4Y/j3p081qf9mCckJGDSpEnYuHEjGhsbodfr7ZYt\nLCz0eWJuatYQERGBQYMG+fS7rWw7AwAu1eN/r50EvrmKrOxsDBqUYbGcwaWl+LJ/AZKjI28lgd6v\nj190qqcztbWK+7Yz+OWgDJ+u6wfp/bDvZB0GDerjs+8MVsnfHQRO3kBBfj7yHQzqo6pjPtB56RwR\n8+UXwPmfUVxcAr3WM/0jB2TcXdy+esNfgavGwFk/d207g4gIreP1vLX9IiIiXIp9fdRFwHARPXr0\nwKBB+d2qp4m97z2Ns8Dnl5CR0QuDBvXtcnFXbjQD288iLjbW/noEyu+2A6da/wHsu4TevXp16zfS\nH8d9a2sr6uvrXZrH5wMMiXn0Rb7K42tpsTp/VyEg+GL4685ye8Qit4f/RoYkUqvOAwyRcyaV9MSx\nc64lBGSfL3c/7uuhzaeJ+eXLl/Hhhx+itLQUOh2TRG8J5WNaE6agpZWv6IeyzsNzE4Wi+WNy8Nio\n/v6uBhG5yGuJ+YMPPoisrCwMGTIEKSkp+O677/DKK6/g/PnzeOedd7z1tRTiPv6XUfjh0g1/V4OI\nPIQXWu5RFAWa8NC4TeOLroK7662ZQzD737/y2PLanySFRoxDidcS85KSErz33nvYuHEjrl+/jqSk\nJAwfPhybNm3C0KFDvfW1IW38wB5YuesoyvommadtnTMMydGRfqyVb/VJiUafFOdGLiQiIuqKpy4M\nxw3kiLbuCrWLc68l5osXL8bixYu9tXiyITs5GqdWW7aPvr1/ip9qQ+QfbJNMRJ39/sHBOHjmKoBm\n9xYQgCeUtdNKkJ0U5e9qkIsCb/hGIiIKGXcV9wTQ9v4IkS3O3E+dVJKBJXcNcHnZt2UnoqxPEh4o\ny3S9Yi5yp0lOV4fFfUMyMaxfcjdqpC4BeG3kFp/3ykJEROSsmRV98HB5NtvSkl9EaTX4j8cq/F0N\nKwlREVgwLhcPlLk2qiSpHxNzIgoqpntOTOOCB5NyIkuKomDBuDx/V4O8gIm5Sm146J9Q1+BmWzgi\nIqIQEQCdspAHhMrlORNzlTK1qyQiIiKi0MCXP4koKLH1AxERBRreMSenfPPC+BDrSZSIiIj8LdSa\nKjExJ6ckRmv9XQUip4TaSZwo1IXaADQU3NiUhYiCFNuyEBFRYOEdcyIiIpVbN60EWRzF0UrflGgs\nGJfr72oQeQwTcyIiIpWbPsT7I08GIsOzo/1dBSKPYlMWIiIiIlK3EOlqi4k5EQUVvghGRIEsNNJP\n5yVGtXU+kRQVGp1QMDEnoqBSmBEPAIjTs6UeEQWOkbmpyEmLwZ0cYNDC6PxU/OnRMtxVnO7vqvgE\nf7mIKKg8ekcfTBjYA2mxOn9XJaS88fBt+PS7i/6uBpFq/enRMiR30fVwYrQWH//LKB/WKDAoioJR\nean+robPMDEnoqCiKAoy2XuFz1UWpqOyMDTuaBG5I5SSS3Ifm7IQEREREakAE3MiIiIiIhVgYk5E\nREREpAJMzImIiIiIVICJORERERGRCjAxJyIiIiJSAVV0lyhiPVJfa2urz+sRFhaG8PBwhIWF+eX7\nyT8Y99DF2Icmxj10Mfahyx+xt/U9tnLejhRxVMIHWlpa0NDQ4O9qEBERERF5TXR0NDQa+/fF2ZSF\niIiIiEgFmJgTEREREakAE3MiIiIiIhVQRRvz1tZWqwbyiqJAURQ/1YiIiIiIyH0iYvWyZ1hYGMLC\n7N8XV0ViTkREREQU6tiUhYiIiIhIBZiYExERERGpABNzANevX8eCBQuQkZEBnU6H0tJSvPvuu/6u\nFjlQX1+PqqoqTJgwAampqVAUBcuWLbNZdv/+/Rg3bhxiYmKQkJCAqVOn4uTJkzbLrl+/HgUFBYiM\njETfvn2xfPlyGI1Gq3K1tbWYNWsWUlJSEBUVhYqKCnzyySeeXEWyYe/evXj00UdRUFCA6Oho9OrV\nC5MnT8bXX39tVZZxDy7ffvst7r77bmRlZUGv1yMpKQkVFRXYvHmzVVnGPri99dZbUBQFMTExVp8x\n9sGjpqbG/M5h539ffPGFRdmPP/4YFRUViIqKQkpKCmbNmoXa2lqrZRqNRixfvhx9+vRBZGQkCgoK\nsH79epvff/LkSUydOhUJCQmIiYnB+PHjsX//fq+sq5mQjB8/XhISEmTjxo2yd+9emT17tgCQLVu2\n+Ltq1IVTp05JfHy8jBw50hyzpUuXWpU7evSoxMbGyogRI2Tnzp2yfft2KSwslIyMDKmtrbUou2LF\nClEURZ577jkxGAyydu1a0Wq1MmfOHItyTU1NUlRUJL1795bNmzfL7t27ZfLkyaLRaKSmpsabqx3y\npk2bJmPGjJENGzZITU2NVFdXS3l5uWg0Gvnkk0/M5Rj34GMwGGTevHmyadMm2bt3r+zYsUNmzJgh\nAOSll14yl2Psg9uZM2ckPj5eMjIyJDo62uIzxj64GAwGASCrVq2Sffv2Wfyrr683l6upqRGNRiOT\nJ0+W3bt3y+bNm6VXr15SVFQkTU1NFsucPXu2REZGytq1a8VgMMjixYtFURRZuXKlRbna2lrJyMiQ\nwsJC2b59u+zcuVOGDx8usbGxcuzYMa+tc8gn5jt37hQAsnXrVovp48ePl4yMDGlpafFTzciR1tZW\naW1tFRGRCxcu2E3Mp0+fLikpKXL16lXztO+//14iIiKkqqrKPO3ixYui0+lk7ty5FvOvXLlSFEWR\nI0eOmKf94Q9/EADy+eefm6cZjUYZOHCglJWVeWoVyYbz589bTauvr5cePXrI2LFjzdMY99AxbNgw\nyczMNP/N2Ae3SZMmyT333COPPPKIVWLO2AcXU2JeXV3dZbmhQ4fKwIEDxWg0mqd99tlnAkA2bNhg\nnnb48GFRFEVWrVplMf+cOXNEr9dLXV2dedrChQslIiJCvv/+e/O0q1evSkpKitx3333dXTW7Qj4x\nnz17tsTExFgEU0Rk69atAkA+++wzP9WMXGEvMTcajaLX62XevHlW80yYMEFyc3PNf2/evFkAyL59\n+yzKnT17VgBYXE2PGzdO8vPzrZa5atUqASBnzpzp5hqRq8aMGSN5eXkiwriHmrvvvlv69u0rIox9\nsNu0aZPExsbKjz/+aJWYM/bBx5nE/MyZMwJAVq9ebfVZXl6ejB8/3vz3ihUrBID89NNPFuU+//xz\nq5YSOTk5UllZabXMuXPnil6vt8obPSXk25gfPnwYAwYMgEajsZheUlJi/pwC14kTJ9DY2GiOZ0cl\nJSU4fvw4mpqaALTHuri42KJcz549kZKSYrEvHD582O4yAeDIkSMeWwdy7OrVq9i/fz8KCwsBMO7B\nrrW1FS0tLbhw4QI2bNiAjz76CIsWLQLA2Aez2tpaLFiwAGvWrEHv3r2tPmfsg9f8+fOh0WgQFxeH\nyspKfPrpp+bPTLGyF6POsUxNTUV6erpVuY7LamxsxIkTJ+wus7Gx0e57C90V8ol5XV0dkpKSrKab\nptXV1fm6SuRBpvjZi7GI4PLly+aykZGRiI6Otlm2477A/UZd5s+fj4aGBvzud78DwLgHuyeeeAIR\nERFIS0vDb3/7W7z22muYN28eAMY+mD3xxBPIz8/H448/bvNzxj74xMfH4+mnn8Ybb7wBg8GAV199\nFT/++CNGjx6Njz76CIDjuDsTy+joaGi1WnPZy5cvQ0T8EneN4yLBr6sRRjn6aHBwNsau7Avcb9Th\nhRdewJYtW7B+/XrcdtttFp8x7sFpyZIlmD17Nmpra7Fjxw48+eSTaGhowLPPPmsuw9gHl+3bt2PH\njh345ptvHG5rxj54DB48GIMHDzb/PWLECEyZMgXFxcWoqqpCZWWl+TN7cehOLP0R95C/Y56cnGzz\nqufSpUsAbF+BUeBITk4GYPvK9tKlS1AUBQkJCeayTU1NuHHjhs2yHfcF7jfqsHz5cqxYsQIrV67E\nk08+aZ7OuAe3rKwsDBkyBHfddRdef/11zJ07F8899xwuXLjA2Aeh69evY/78+XjqqaeQkZGBK1eu\n4MqVK2hubgYAXLlyBQ0NDYx9iEhISMCkSZNw8OBBNDY2Ooy7M7FsaGhAc3OzuWxiYiIURfFL3EM+\nMS8uLsbRo0fR0tJiMf3QoUMAgKKiIn9Uizykf//+0Ov15nh2dOjQIeTk5ECn0wFob2vYuey5c+dw\n8eJFi32huLjY7jIB7je+sHz5cixbtgzLli3DkiVLLD5j3ENLWVkZWlpacPLkScY+CF28eBHnz5/H\nK6+8gsTERPO/bdu2oaGhAYmJiXjooYcY+xAiIgDa7lqbtr+9GHWO5YULF3Du3DmrckB7LPV6PXJy\ncuwuU6/Xo1+/fp5Zmc688kppANm1a5cAkHfffddi+sSJE9ldYgDpqrvE++67T9LS0uTatWvmaadP\nnxatViuLFi0yT6urqxOdTiePPfaYxfyrV6+26j5rw4YNAkC++OIL8zSj0SiFhYUybNgwD64Z2fLi\niy8KAHn++eftlmHcQ8fDDz8sYWFh5n6qGfvg0tjYKAaDwepfZWWl6HQ6MRgMcujQIRFh7EPBpUuX\npFevXlJaWmqeVlZWJkVFRRY52759+wSAvP766+Zppu4S16xZY7HMefPmWXWXWFVVJVqtVn744Qfz\ntGvXrklqaqrcf//93lg1EWF3iSLS1md5YmKivPnmm7J3716ZM2eOAJDNmzf7u2rkwK5du6S6ulre\nfvttASDTp0+X6upqqa6uloaGBhFpG3AiJiZGRo4cKbt27ZIPPvhAioqKuhxwYsmSJVJTUyPr1q2T\nyMhImwNOFBYWSmZmpmzZskX27NkjU6ZM4YATPvDyyy8LAJk4caLVgBMduz5j3IPPnDlz5JlnnpH3\n3ntPampq5P3335f7779fAMjChQvN5Rj70GCrH3PGPrg88MADsmjRIqmurhaDwSBvvvmm5Ofni0aj\nkT179pjLGQwG0Wg0MmXKFNmzZ49s2bJFMjMzuxxgaN26dVJTUyNLliyxO8BQz549pbi4WP785z/L\nrl27ZOTIkRIbGytHjx712jozMZe2wUl+85vfSHp6umi1WikpKZFt27b5u1rkhOzsbAFg89+pU6fM\n5b766isZO3asREVFSVxcnNx7771y/Phxm8t89dVXJS8vT7RarWRlZcnSpUulubnZqty5c+dk5syZ\nkpSUJDqdTsrLyy1OFOQdo0aNshvzzg8BGffg8vbbb8uIESMkJSVFNBqNJCQkyKhRo2TTpk1WZRn7\n4GcrMRdh7IPJ6tWrpbS0VOLj4yU8PFxSU1NlypQp8uWXX1qV3b17t5SXl4tOp5OkpCSZOXOmzQHp\nmpubZenSpZKVlSVarVby8vLktddes/n9x48fl3vvvVfi4uIkKipKxo4dK19//bXH17MjReRWQx0i\nIiIiIvKbkH/5k4iIiIhIDZiYExERERGpABNzIiIiIiIVYGJORERERKQCTMyJiIiIiFSAiTkRERER\nkQowMSciIiIiUgEm5kREREREKsDEnIiIiIhIBZiYExERERGpABNzIiIiIiIV+H8cKOB8ZWOTNAAA\nAABJRU5ErkJggg==\n", "text/plain": [ "" ] }, "metadata": {}, "output_type": "display_data" } ], "source": [ "def sense_t():\n", " return 10 + rand_student_t(7)*2\n", "\n", "zs = [sense_t() for i in range(5000)]\n", "plt.plot(zs, lw=1);" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "We can see from the plot that while the output is similar to the normal distribution there are outliers that go far more than 3 standard deviations from the mean (7 to 13). This is what causes the 'fat tail'.\n", "\n", "It is unlikely that the Student's $t$-distribution is an accurate model of how your sensor (say, a GPS or Doppler) performs, and this is not a book on how to model physical systems. However, it does produce reasonable data to test your filter's performance when presented with real world noise. We will be using distributions like these throughout the rest of the book in our simulations and tests. \n", "\n", "This is not an idle concern. The Kalman filter equations assume the noise is normally distributed, and perform sub-optimally if this is not true. Designers for mission critical filters, such as the filters on spacecraft, need to master a lot of theory and empirical knowledge about the performance of the sensors on their spacecraft. \n", "\n", "The code for rand_student_t is included in `filterpy.stats`. You may use it with\n", "\n", "```python\n", "from filterpy.stats import rand_student_t\n", "```" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "## Summary and Key Points\n", "\n", "This chapter is a poor introduction to statistics in general. I've only covered the concepts that needed to use Gaussians in the remainder of the book, no more. What I've covered will not get you very far if you intend to read the Kalman filter literature. If this is a new topic to you I suggest reading a statistics textbook. I've always liked the Schaum series for self study, and Alan Downey's *Think Stats* [5] is also very good. \n", "\n", "The following points **must** be understood by you before we continue:\n", "\n", "* Normals express a continuous probability distribution\n", "* They are completely described by two parameters: the mean ($\\mu$) and variance ($\\sigma^2$)\n", "* $\\mu$ is the average of all possible values\n", "* The variance $\\sigma^2$ represents how much our measurements vary from the mean\n", "* The standard deviation ($\\sigma$) is the square root of the variance ($\\sigma^2$)\n", "* Many things in nature approximate a normal distribution" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "## References" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "[1] https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/Supporting_Notebooks/Computing_and_plotting_PDFs.ipynb\n", "\n", "[2] http://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.norm.html\n", "\n", "[3] http://docs.scipy.org/doc/scipy/reference/tutorial/stats.html\n", "\n", "[4] Huber, Peter J. *Robust Statistical Procedures*, Second Edition. Society for Industrial and Applied Mathematics, 1996.\n", "\n", "[5] Downey, Alan. *Think Stats*, Second Edition. O'Reilly Media.\n", "\n", "https://github.com/AllenDowney/ThinkStats2\n", "\n", "http://greenteapress.com/thinkstats/" ] } ], "metadata": { "anaconda-cloud": {}, "kernelspec": { "display_name": "Python 3", "language": "python", "name": "python3" }, "language_info": { "codemirror_mode": { "name": "ipython", "version": 3 }, "file_extension": ".py", "mimetype": "text/x-python", "name": "python", "nbconvert_exporter": "python", "pygments_lexer": "ipython3", "version": "3.6.3" }, "widgets": { "state": { "403fcb72354342e7bc987bddee6b66e4": { "views": [ { "cell_index": 54 } ] } }, "version": "1.2.0" } }, "nbformat": 4, "nbformat_minor": 1 }