{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"[Table of Contents](http://nbviewer.ipython.org/github/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/table_of_contents.ipynb)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# One Dimensional Kalman Filters"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n"
],
"text/plain": [
""
]
},
"execution_count": 1,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"#format the book\n",
"%matplotlib inline\n",
"from __future__ import division, print_function\n",
"from book_format import load_style\n",
"load_style()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now that we understand the discrete Bayes filter and Gaussians we are prepared to implement a Kalman filter. We will do this exactly as we did the discrete Bayes filter - rather than starting with equations we will develop the code step by step based on reasoning about the problem. \n",
"\n",
"\"One dimensional\" means that the filter only tracks one variable, such as position on the x-axis. In subsequent chapters we will learn a more general form of the filter that can track many variables simultaneously, such as position, velocity, and accelerations in x, y, and z. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Problem Description\n",
"\n",
"As in the **Discrete Bayes Filter** chapter we will be tracking a moving object in a long hallway at work. Assume that in our latest hackathon someone created an RFID tracker that provides a reasonably accurate position of the dog. The sensor returns the distance of the dog from the left end of the hallway in meters. So, 23.4 would mean the dog is 23.4 meters from the left end of the hallway.\n",
"\n",
"The sensor is not perfect. A reading of 23.4 could correspond to the dog being at 23.7, or 23.0. However, it is very unlikely to correspond to a position of 47.6. Testing during the hackathon confirmed this result - the sensor is 'reasonably' accurate, and while it had errors, the errors are small. Furthermore, the errors seemed to be evenly distributed on both sides of the true position; a position of 23 m would equally likely be measured as 22.9 or 23.1. Perhaps we can model this with a Gaussian.\n",
"\n",
"We predict that the dog is moving. This prediction is not perfect. Sometimes our prediction will overshoot, sometimes it will undershoot. We are more likely to undershoot or overshoot by a little than a lot. Perhaps we can also model this with a Gaussian."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Beliefs as Gaussians\n",
"\n",
"We can express our belief in the dog's position with a Gaussian. Say we believe that our dog is at 10 meters, and the variance in that belief is 1 m$^2$, or $\\mathcal{N}(10,\\, 1)$. A plot of the pdf follows:"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"scrolled": true
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAvUAAAEgCAYAAAA0WYyMAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzt3XlcVPX+BvBnNvZ9U8cFRESQ1Vwz\nU1Ex15tahktdM9tsudktzbKstH5pt43Kui6pFIF5FSsVKS0zV9Q0BFxZVVxYhm3YZ+b8/kBJEpVh\nO3OG5/16+bLOzJl58Cvj48ezyARBEEBERERERJIlFzsAERERERE1D0s9EREREZHEsdQTEREREUkc\nSz0RERERkcSx1BMRERERSRxLPRERERGRxLHUExERERFJHEs9EREREZHEsdQTEREREUmc0aVeq9Vi\n3rx5UKvVsLKyQmhoKDZs2HDH/davXw+ZTNbgjytXrjQpPBERERERAUpjd5gyZQqOHDmCZcuWwdfX\nFzExMZg+fToMBgNmzJhxx/3XrVsHPz+/ettcXV2NjUFERERERNcYVerj4+Oxc+fOuiIPAGFhYcjO\nzsb8+fMREREBhUJx29cIDAxEv3797vheBoMBBoOh3rbrk30iIiIiIqkRBAGCINTbJpfLIZc3/4h4\no0r9li1bYGdnh6lTp9bbPnv2bMyYMQOJiYkYPHhws0MBtaW+rKysRV6LiIiIiMgU2dratkipN+oV\nUlJS4O/vD6Wy/t8FgoOD6x6/kwkTJkChUMDFxQVTpkxp1D5ERERERHRrRk3qCwoK4O3tfdN2FxeX\nusdvpWPHjli0aBEGDRoEBwcHJCcnY9myZRg0aBD279+PkJAQI6MTERERERHQhBNlb3dM++0eGzNm\nDMaMGVP3/0OHDsX48eMRFBSExYsX44cffjA2ChERERERwchS7+rq2uA0XqPRAPhrYt9YXl5eGDJk\nCA4dOnTTYw39BaGljjki8aSmpkKn00GpVCIgIEDsONRMXE/zwvU0L1xP88L1NA8NnTPaUheBMarU\nBwUFITY2tu431XXJyckAaq9sYyxBEBos6g19gS11djCJx2AwQK/Xcy3NBNfTvHA9zQvX07xwPc1X\nS5V6o35XTJ48GVqtFps3b663PSoqCmq1GgMHDjTqzTMzM7F//34MGjTIqP2IiIiIiOgvRk3qx44d\ni/DwcMydOxclJSXw8fFBbGwsEhISEB0dXXeN+jlz5iAqKgrp6enw9PQEAIwaNQpDhw5FcHBw3Ymy\n77//PmQyGZYuXdryXxkRERERUTth9ImycXFxWLRoERYvXgyNRgM/Pz/ExsZi2rRpdc/R6/XQ6/X1\nLq4fFBSE7777Dh988AEqKirg4eGBESNG4I033oCvr2/LfDVERERERO2Q0aXezs4OkZGRiIyMvOVz\n1q9fj/Xr19fb9vHHHxsdjoiIiIiI7oxnWhARERERSRxLPRERERGRxLHUExERERFJHEs9EREREZHE\nsdQTEREREUkcSz0RERERkcSx1BMRERERSRxLPRERERGRxLHUExERERFJHEs9EREREZHEsdQTERER\nEUkcSz0RERERkcSx1BMRERERSRxLPRERERGRxLHUExERERFJHEs9EREREZHEsdQTEREREUkcSz0R\nERERkcSx1BMRERERSRxLPRERERGRxLHUExERERFJHEs9EREREZHEsdQTEREREUkcSz0RERERkcSx\n1BMRERERSRxLPRERERGRxLHUExERERFJHEs9EREREZHEsdQTEREREUkcSz0RERERkcSx1BMRERER\nSRxLPRERERGRxLHUExERERFJHEs9EREREZHEsdQTEREREUkcSz0RERERkcQZXeq1Wi3mzZsHtVoN\nKysrhIaGYsOGDUa/8euvvw6ZTIbAwECj9yUiIiIior8ojd1hypQpOHLkCJYtWwZfX1/ExMRg+vTp\nMBgMmDFjRqNe488//8QHH3yADh06GB2YiIiIiIjqM6rUx8fHY+fOnXVFHgDCwsKQnZ2N+fPnIyIi\nAgqF4ravodPpMHv2bDz11FNISkpCfn5+09MTEREREZFxh99s2bIFdnZ2mDp1ar3ts2fPxqVLl5CY\nmHjH11i2bBk0Gg3effdd45ISEREREVGDjJrUp6SkwN/fH0pl/d2Cg4PrHh88ePAt9z958iTeeecd\nxMXFwc7OzuiwqampMBgMRu9HpqOmpqbu56SkJJHTUHNxPaXtqlaHk3lVyCqqwRWtDtoqPar1gLVK\nBof9v6KLowrdnVQI8LCEnQWvqyA1/P40L1xP8yCXy9GtW7dWeW2jSn1BQQG8vb1v2u7i4lL3+K0Y\nDAY89thjmDJlCsaNG2dkzFo6nQ56vb5J+5Lpuf4BReaB6ykNBRV67MqowMGcSlwsudPnaQUAQC4D\n/N1UGNrNGkO6WsFSKWv9oNSi+P1pXrie0nWnw9Sbw+gTZWWyW3+Y3+6xjz76COfOncOPP/5o7FvW\nUSqVkMs5LZKyGz+IVCqViEmoJXA9peNSaQ1ik0uw73wFDELtNrkM8HW1QA9nFTo7qGCjMMBCIUOF\nTkBpjQzni2twtqAaF0t0SM2rQWpeDb5JLsW4nnaY7G8PGxU/j00Zvz/NC9fTPLRmjzWq1Lu6ujY4\njddoNAD+mtj/3fnz57F48WIsW7YMFhYWKCoqAlA7eTcYDCgqKoKlpSWsra1v+/4BAQEs9RKXlJSE\nmpoaqFQqhISEiB2HmonrafqKK2rwwU9nEHs4B7prbX6AlwumD+yKEb06wNHmr3Jwq/U8X1CO7cmX\nEXM4Gxc0FdiYWoqdmZX4d7gvZg70hFzOyb0p4veneeF6mgeDwYDS0tJWeW2jGnJQUBBOnToFnU5X\nb3tycjIA3PKa8xkZGaioqMALL7wAZ2fnuh/79+/HqVOn4OzsjFdffbWJXwIRETVk58mrGP3xHnxz\nKBs6g4ARfh7Y9vwQbHz6bkzu06Veob+dbq42mDu8B357OQxfzrwL3u62KCyvwRs/pOKhlQeRnqdt\n5a+EiIjuxKhJ/eTJk7F69Wps3rwZERERddujoqKgVqsxcODABvcLDQ3F7t27b9o+b948FBcXY926\ndejSpYuR0YmIqCFVOj3+b/spRB3MBgB0d7PFu5MDMbiHW7NeVyGXYWxQJ4T37oBvE8/j/YTTOJpd\niAmf7sO7kwMx5S5+jhMRicWoUj927FiEh4dj7ty5KCkpgY+PD2JjY5GQkIDo6Oi6g//nzJmDqKgo\npKenw9PTE05OThg+fPhNr+fk5ASdTtfgY0REZLyrJZV48uujSLpYDAB4cqg3/h3uCytVy52cpVTI\nMWuwF0b17oAFm5KwP60A/96YhKPZhXj7HwFQKXiYJBFRWzP6RNm4uDgsWrQIixcvhkajgZ+fH2Jj\nYzFt2rS65+j1euj1egiC0KJhiYjo1tJySzFr7RHkFFXAyUaFjx8KRZifR6u9X2cna3z92EB89us5\nRP5yDjGJ53FBU44vZt4FeyueyEdE1JZkgok274ZOJLC3t+eJshLHE33MC9fTdBzJ0uDxqKMorqiB\nt5st1s8egG6uNka9RnPW89fTV/FczHGUV+vh19Ee0Y8PhJudpVGvQS2L35/mhetpHlqz37IhExFJ\n3IG0fDy8JhHFFTW4q5sTNs0dbHShb64Rfh3w3ZN3w93eEqevlGLG6kPI11a1aQYiovaMpZ6ISMIO\nZ2owJ+ooqnQGjPDzwLePD4KLrYUoWYK6OGLjU3ejo4MVzl7VYvqqQ8grZbEnImoLLPVERBJ17Hwh\nZq87jIoaPYb5uuPLh++CtUXr3a2wMbq72WLDk4PQ0cEK53K1mLnmEIorePdLIqLWxlJPRCRBGXla\nPLb+CMqq9bjHxxUrH+kLS6W4hf46r2vFvoODJc5e1eLJr4+iSqcXOxYRkVljqScikpgCbRVmrz+C\novIahHZ1wup/9mvRS1a2BC83W6x7dADsLJVIzNTg3xuTYDCY5HUZiIjMAks9EZGEVNbo8eQ3fyC7\noBxdXayxZlY/2FgYfXXiNtFb7YCVj/SFSiHD9hOXsfyn02JHIiIyWyz1REQSIQgCXo1Lxh/ZhXCw\nUmLdo/1N/rKR9/i44T8P1l5+b+WeDGxNuiRyIiIi88RST0QkEd8cysaW4zlQyGX478N94eNhL3ak\nRpnUpzOeHtYDALBg0wmculwiciIiIvPDUk9EJAHHzhdi6baTAICFY/ww2MdN5ETGmX9fL9zb0w0V\nNXo89c0fKCqvFjsSEZFZYaknIjJxBdoqPBN9DDV6AeOCOuLxe7uLHcloCrkMn03vg64u1jivKceC\nTSdgojc0JyKSJJZ6IiITJggC5m86gSsllejhbov3HwyBTCYTO1aTONlY4MuZfWGhkOPnk1cRfShb\n7EhERGaDpZ6IyIRFJ57Hr6dzYaGUY8XMu2BnaZpXummswM6OWDjWDwCwdPspnL7C4+uJiFoCSz0R\nkYlKy9Xi3e21x9G/MsYPfh0dRE7UMmbf44URfh6o1hnwXMxxVFTzxlRERM3FUk9EZIKqdQbM++44\nKmsMuLenG2YP9hI7UouRyWT4z4PB8LC3RFquFh/8fEbsSEREksdST0Rkgj7edRYpOSVwtlHhg6kh\nkMuleRz9rbjaWWL5g8EAgLX7M3EkSyNyIiIiaWOpJyIyMUkXirByTzoA4L0pQejgYCVyotYR1ssD\nU/t2gSAA8/+XxMNwiIiagaWeiMiEVOsMeGXzCRgEYFKoGmMCO4kdqVW9PqE3OjpYIaugHP/5iYfh\nEBE1FUs9EZEJWbknHaevlMLF1gKLJwaIHafVOVqr8N4DQQCAdQcycTiTh+EQETUFSz0RkYlIyy3F\nZ7+mAQDenNgbLrYWIidqG2G9PPBQv9rDcBZuPoEqHQ/DISIyFks9EZEJ0BsELNh0AtV6A0b4eeAf\nIWqxI7WpReN7w83OEhn5ZVi5J0PsOEREksNST0RkAmIOn8ex80Wws1TinUmBkr1rbFM5WqvwxgR/\nAMDnu9OQlV8mciIiImlhqSciElmBtgr/STgNAJh/Xy+onaxFTiSOf4SoMcTHDdU6A974IQWCIIgd\niYhIMljqiYhEtjzhNEoqdQhQO+DhQZ5ixxGNTCbD0kmBsFDKsfdcPraduCx2JCIiyWCpJyIS0R/Z\nhdh49CIAYMn9gVCY2U2mjNXdzRbPDvcBACzZdhIllTUiJyIikgaWeiIikegNAhb/kAIAmNq3C/p6\nOoucyDQ8Pdwb3d1skVdahRXXrgZERES3x1JPRCSSmMRspF4qgYOVEq+M9RM7jsmwVCrqTppduz8T\nmTxplojojljqiYhEUFRejQ9+PgsAePm+XnCzsxQ5kWkJ6+WBYb7uqNELeHf7KbHjEBGZPJZ6IiIR\nRP5yDsUVNfDraI+ZA9vvybG3IpPJ8MYEfyjlMuw6dRV7z+WJHYmIyKSx1BMRtbH0PC2+OZgNAHh9\nfO92f3Lsrfh42OORu2v/wrN020no9AaRExERmS6WeiKiNvZe/GnoDAJG+HlgSE83seOYtHkjfeFs\no8LZq1rEHD4vdhwiIpPFUk9E1IYOpOVj16mrUMhleG0cT469E0cbFf49uhcA4MOfz6KwrFrkRERE\npomlnoiojegNApZeO+nz4YHd4ONhL3IiaZjevyv8OtqjuKIGn+/mJS6JiBrCUk9E1EY2/3ERpy6X\nwN5KiRdG+YodRzKUCjleG1d7ictvDmbjgqZc5ERERKaHpZ6IqA2UV+vwn5/PAABeGNkTLrYWIieS\nlqG+7hji44ZqvQEfXvt1JCKiv7DUExG1gbX7MpFXWoWuLtZ1V3Qh4yy8doOu7/+8hJScYpHTEBGZ\nFqNLvVarxbx586BWq2FlZYXQ0FBs2LDhjvvt2rUL4eHhUKvVsLS0hIeHB0aMGIH4+PgmBScikorC\nsmqs3JMBAHh5dC9YKhUiJ5KmwM6OuD9UDQBYnnBa5DRERKbF6FI/ZcoUREVF4c0338SOHTvQv39/\nTJ8+HTExMbfdr6CgAAEBAfj444/x888/Y+XKlVCpVBg/fjyio6Ob/AUQEZm6L/eko7RKB/9ODpgY\nrBY7jqS9PLoXLBRy7D2XzxtSERHdQGnMk+Pj47Fz507ExMRg+vTpAICwsDBkZ2dj/vz5iIiIgELR\n8AQqIiICERER9bZNmDAB3bt3x6pVq/Dwww838UsgIjJdl4oqsP5AFgBgwZhekPNGU83S1cUGDw/y\nxNr9mVi24zTu6eHGX1MiIhg5qd+yZQvs7OwwderUettnz56NS5cuITEx0ag3V6lUcHJyglJp1N8t\niIgkI3LXOVTrDBjQ3QXDfd3FjmMWnhvhA3tLJVIvleDHpEtixyEiMglGtemUlBT4+/vfVMKDg4Pr\nHh88ePBtX8NgMMBgMCA3NxcrV67E2bNnsXz58ka9f2pqKgwG3iZcympqaup+TkpKEjkNNRfX8/Yu\nltTgf39cBQA84KPAiRMnRE50e1Jaz0m9bPDNiRIs256MrsiDktP6m0hpPenOuJ7mQS6Xo1u3bq3y\n2kaV+oKCAnh7e9+03cXFpe7xOxk3bhx++uknAICDgwO+++47jB8/vlHvr9PpoNfrjUhMpuz6BxSZ\nB67nzb7+swgGAeivtkQPR7mkfo1MPet93lb48YwWV7R6/HyuBOHeNmJHMmmmvp5kHK6ndN3qMPWW\nYPRxLzLZracht3vsus8++wxFRUW4fPkyoqOjERERgaioqLpj9G9HqVRCLudVOKXsxg8ilUolYhJq\nCVzPWztbUI3EnCrIAPwz1EkSvz5SWk+VCpgaYI81x4qx6XQ5Rvk4wELBaf2NpLSedGdcT/PQmj3W\nqFLv6ura4DReo9EA+Gtifzs9e/as++9//OMfGDt2LJ599llERETc8QsNCAhgqZe4pKQk1NTUQKVS\nISQkROw41Excz1tbvvoQAGDKXV0wcag0fm2ktp69euuxLe03XCmpREqFI2bf013sSCZFautJt8f1\nNA8GgwGlpaWt8tpGNeSgoCCcOnUKOp2u3vbk5GQAQGBgoNEBBgwYgMLCQuTl8dJkRGQeDmUU4EB6\nAVQKGV4M73nnHahJrFQKPD/SBwCwYnc6yqt1d9iDiMh8GVXqJ0+eDK1Wi82bN9fbHhUVBbVajYED\nBxr15oIgYM+ePXBycoKrq6tR+xIRmarIXecAAA/164ouzjzWuzU91K8rurnYIF9bhagD2WLHISIS\njVGH34wdOxbh4eGYO3cuSkpK4OPjg9jYWCQkJCA6Orru4P85c+YgKioK6enp8PSsvR36/fffj5CQ\nEISGhsLV1RWXLl3C+vXrsWfPHqxYsYKXtSQis3AoowAHM2qn9M+E+Ygdx+ypFHK8MLInXvpfEv67\nJx0zB3WDgxWPNyai9sfoJh0XF4dFixZh8eLF0Gg08PPzQ2xsLKZNm1b3HL1eD71eD0EQ6rbdc889\n2LRpEz7//HOUlJTAyckJ/fr1w7Zt2xp99RsiIlN345S+s5O1yGnah0l9OuOL39KQnleGr/Zm4sVw\nX7EjERG1OZlwY/M2IQ2dSGBvb88TZSWOJ/qYF65nfYkZBYhYdQgqhQy/zQ+TXKmX8npuP3EZz8Yc\ng52lEnsXhMHZ1kLsSKKT8nrSzbie5qE1+y0bMhFRC4n8hVN6sYwN7IjenRygrdLhv7+nix2HiKjN\nsdQTEbWAxBuueMNj6dueXC7DS6NrD7uJOpCFvNIqkRMREbUtlnoiohbAKb34Rvh5ILSrEyprDFjF\naT0RtTMs9UREzcQpvWmQyWR4YVTtfQG+OZTNaT0RtSss9UREzXR9Sj+VU3rRDfd1R8i1af3qvRli\nxyEiajMs9UREzVBvSj+8h9hx2j2ZTIZ516b1Xx/MQr6W03oiah9Y6omImuHGKT3vHmsahvu6I6SL\n47Vj6zmtJ6L2gaWeiKiJOKU3TbXT+tor4XxzMJvTeiJqF1jqiYiaiFN60zW8lzuCuziiokaP1ZzW\nE1E7wFJPRNQEhzM1nNKbsPrH1mejgNN6IjJzLPVERE0Q+ctZAJzSm7KwXh510/pVvBIOEZk5lnoi\nIiMdztRgfxqn9KZOJpPhhZHXrlvPaT0RmTmWeiIiI3FKLx0j/DwQ1NkR5dV6rN6bKXYcIqJWw1JP\nRGQETuml5cZp/dcHs6ApqxY3EBFRK2GpJyIywvUp/YN9OaWXipH+Hgjs7HBtWs9j64nIPLHUExE1\n0vUpvVIuw7NhnNJLhUwmw7yRtdetjzrAaT0RmSeWeiKiRuKx9NLFaT0RmTuWeiKiRjiSxSm9lNUe\nW187rf/6QBYKOa0nIjPDUk9E1AiRu3j3WKkb5e+BALUDyqr1WLOP03oiMi8s9UREd3AkS4N9afmc\n0kvcjVfCWb+f03oiMi8s9UREd8ApvfkI790BvTvVTuu/2sfr1hOR+WCpJyK6DU7pzYtMJsMLo65N\n6w9koaic03oiMg8s9UREt/HXlL4Lp/RmYnTvDvDv5ABtlY7TeiIyGyz1RES3cOOU/pnhPmLHoRZy\n47H16/ZzWk9E5oGlnojoFm6c0nd14ZTenIzu3QF+He2hrdJhLaf1RGQGWOqJiBrAKb15k8tlmDfq\nr2l9cXmNyImIiJqHpZ6IqAGc0pu/0b07wq+jPUqrdPhqP6f1RCRtLPVERH9zlFP6dkEuv+HY+n2Z\nnNYTkaSx1BMR/U3kL5zStxf3BXRErw610/q1nNYTkYSx1BMR3eBolgZ7z3FK317I5X9dt37t/kwU\nV3BaT0TSxFJPRHQDTunbnzHXp/WVOqzjtJ6IJIqlnojoGk7p2ye5XIZ/XTu2/qt9nNYTkTSx1BMR\nXfPxrrMAOKVvj8YGdoRvBzuUVuqwfn+W2HGIiIzGUk9EBCAxowD70wqgUsjwbBin9O1N/Wl9Bkoq\nOa0nImlhqSciwo1T+q7o4swpfXs0LrATenrYoYTTeiKSIJZ6Imr3DqYX4FCGBhYKOaf07diN0/o1\nezmtJyJpMbrUa7VazJs3D2q1GlZWVggNDcWGDRvuuF9cXBymT58OHx8fWFtbw8vLCzNnzsS5c+ea\nFJyIqCUIglA3pY/o3xWdnaxFTkRiGhfUCT7XpvVRnNYTkYQYXeqnTJmCqKgovPnmm9ixYwf69++P\n6dOnIyYm5rb7LV++HOXl5Vi0aBESEhLwzjvv4Pjx47jrrruQmpra5C+AiKg5DqYX4HBm7ZT+mbAe\nYschkSlunNbvy0Qpp/VEJBFKY54cHx+PnTt3IiYmBtOnTwcAhIWFITs7G/Pnz0dERAQUCkWD+27d\nuhUeHh71to0YMQJeXl74+OOPsWbNmiZ+CURETXPjlH76gK7o5MgpPQHjgzohctdZpOeVIepAFp4b\n0VPsSEREd2TUpH7Lli2ws7PD1KlT622fPXs2Ll26hMTExFvu+/dCDwBqtRpdunTBhQsXjIlBRNQi\n9qcV4EhWISyUcjzDY+npmhun9av3clpPRNJg1KQ+JSUF/v7+UCrr7xYcHFz3+ODBgxv9ehkZGcjO\nzsakSZMa9fzU1FQYDIbGByaTU1NTU/dzUlKSyGmouaS8noIgYOmuPADAfd42uJJ5BldEziQ2Ka9n\nS+sqCOjioMTFkhosjzuEqQEOYkcyGtfTvHA9zYNcLke3bt1a5bWNKvUFBQXw9va+abuLi0vd442l\n0+kwZ84c2NnZ4cUXX2z0Pnq9vtHvQabt+gcUmQepreefV6pwJr8aFnLgHz2tJJe/tfHXA3jAzwaR\nh0vw/elSjO5uCRuVdC8Yx/U0L1xP6brVYeotwahSDwAymaxJj91IEATMmTMHe/fuxebNm9G1a9dG\n7adUKiGXS/dDlep/EKlUKhGTUEuQ6noKgoCNpwoBAGN62sHDwUrkRKZBquvZWoZ1V2LTqXLklOqQ\nkFGFiEBpTeu5nuaF62keWrPHGlXqXV1dG5zGazQaAH9N7G9HEAQ8/vjjiI6ORlRUFO6///5Gv39A\nQABLvcQlJSWhpqYGKpUKISEhYsehZpLqeu4+k4uzBTmwUsnxxoOD4G5vKXYkkyDV9WxNC+WX8Hzs\ncWw9W44FkwfCycZC7EiNxvU0L1xP82AwGFBaWtoqr21UQw4KCsKpU6eg0+nqbU9OTgYABAYG3nb/\n64V+3bp1WLNmDR5++GEj4xIRNY8gCPhkZ+0Vbx4Z5MlCT7c1PqgT/Ds5oLRKh//uyRA7DhHRLRlV\n6idPngytVovNmzfX2x4VFQW1Wo2BAwfecl9BEPDEE09g3bp1WLlyJWbPnt20xEREzfDzyatIulgM\na5UCTw3jdenp9uRyGV4e7QsAWH8gE7mllSInIiJqmFGH34wdOxbh4eGYO3cuSkpK4OPjg9jYWCQk\nJCA6Orru4P85c+YgKioK6enp8PT0BAD861//wldffYXHHnsMQUFBOHToUN3rWlpaok+fPi34ZRER\n3UxvEPDBT2cAAHOGdIebHaf0dGcj/DzQp5sTjp8vwopf0/D2/bf/V2kiIjEYfaJsXFwcFi1ahMWL\nF0Oj0cDPzw+xsbGYNm1a3XP0ej30ej0EQajbtnXrVgDA2rVrsXbt2nqv6enpiaysrCZ+CUREjfPD\nnzk4l6uFo7UKTwy9+UpeRA2RyWSYP7oXZqxJRMzh83hiqDe6ONuIHYuIqB6jzzq1s7NDZGQkLl++\njKqqKiQlJdUr9ACwfv16CIIALy+vum1ZWVkQBKHBHyz0RNTaqnWGurvHPj2sBxytefUIarzBPm64\nx8cVNXoBkbvOiR2HiOgmvJQMEbUL3x05jwuaCrjbW+LRwV5ixyEJenl0LwDA5mMXkZ6nFTkNEVF9\nLPVEZPbKq3X49Nc0AMC/RvjA2qL1bv5B5qtPN2eM8u8AgwB8dO0KSkREpoKlnojM3voDWcgrrUJX\nF2tE9G+d23NT+/DSaF/IZMD2E5eReqlY7DhERHVY6onIrBVX1OC/v6UDAF4c5QsLJT/2qOn8Ozlg\nYrAaAPDhz5zWE5Hp4J9uRGTWVv2ejpJKHXw72OH+0M5ixyEz8GK4LxRyGX49nYs/sjVixyEiAsBS\nT0RmLLe0Emv3ZQEAXhrdCwq5TNxAZBa6u9liat8uAIDlO87Uu3wzEZFYWOqJyGx9/msaKmr0COnq\nhNG9O4gdh8zIC6N6wlIpx+FhVz38AAAgAElEQVQsDXaevCp2HCIilnoiMk8ZeVrEJJ4HALwyphdk\nMk7pqeV0crTGnCHdAQDLEk5DpzeInIiI2juWeiIyS8sTTkNnEDDCzwODe7iJHYfM0NPDe8DZRoWM\nvDJ8d/SC2HGIqJ1jqScis3MkS4OfUq9CLgNeHesndhwyUw5WKvxrZE8AwMc7z6GsSidyIiJqz1jq\nicisCIKAd7efAgBE9O+Knh3sRU5E5mzmQE94utogX1uF1XszxI5DRO0YSz0RmZXtyZfx54Ui2Fgo\n8OIoX7HjkJmzUMqx4L7afw1a9XsGcksrRU5ERO0VSz0RmY0qnR7vJ5wBADw51BseDlYiJ6L2YFxQ\nR4R0dUJ5tR6Ru86JHYeI2imWeiIyG9GHzuO8phzu9pZ44l5vseNQOyGTyfDatXM3Nhy5gLTcUpET\nEVF7xFJPRGahuKIGn/1aOyX9d7gvbC2VIiei9mSgtytG+XeA3vDXOR1ERG2JpZ6IzMJnv5xDUXkN\nenrY1d3tk6gtvTbODyqFDLvP5GH36Vyx4xBRO8NST0SSl5arxfoDWQCAReP9oVTwo43anre7HWbf\nU3tDqqXbT6JaxxtSEVHb4Z98RCRpgiBg6baT0BkEjPTzwPBeHmJHonbsuRE+cLOzQEZeGb4+mCV2\nHCJqR1jqiUjSdp/JxZ6zeVApZHh9Qm+x41A752Clwvz7egEAIn85h3xtlciJiKi9YKknIsmq1hmw\ndFvtSYmPDemO7m62IiciAh7s2xWBnR1QWqnDhz+fFTsOEbUTLPVEJFnr9mciM78MbnaWeC7MR+w4\nRAAAhVyGNycGAAA2HDmP1EvFIiciovaApZ6IJCm3tBKf/ZoGAHhlTC/YW6lETkT0l/5eLpgYooYg\nAG9vPQlBEMSORERmjqWeiCRp2Y7T0FbpENLFEQ/cxUtYkulZONYPVio5Dmdq8GPSJbHjEJGZY6kn\nIsk5lFGAuGM5kMmAt/4RALlcJnYkopt0drLGs8NrDwt7Z/splFTWiJyIiMwZSz0RSUq1zoDXv08B\nAMwY0A19ujmLnIjo1p4c5g1vN1vklVbhw5/OiB2HiMwYSz0RScqafRlIy9XCzc4CC+7zEzsO0W1Z\nKhV4Z1IgAOCbQ9lIvsiTZomodbDUE5FkXNCU49NfzgEAXhvnD0cbnhxLpm+wjxvuD1XDIACLvk+G\n3sCTZomo5bHUE5EkCIKAt35MRWWNAYO8XTC5T2exIxE12qLx/rC3UuLExWLEJGaLHYeIzBBLPRFJ\nws8nr+KX07lQKWR4Z1IgZDKeHEvS4WFvhQXX7jT7fsIZ5JZWipyIiMwNSz0RmbySyhq8+UMqAODJ\nod7w8bAXORGR8WYM9ERwF0eUVunw9o8nxY5DRGaGpZ6ITN578adwpaQSXq42eC6sp9hxiJpEIZfh\nvSlBUMpl2J58GTuSL4sdiYjMCEs9EZm0/Wn5iD18AQCw/IFgWFsoRE5E1HQBakc8PawHAOCNH1JR\nVF4tciIiMhcs9URkssqqdFgYdwIA8M+7PTHQ21XkRETN9/xIH/h42CFfW4Ul23gYDhG1DJZ6IjJZ\n//npDC5oKtDZyRoLxvCa9GQeLJUKvP9gMGQyIO5YDnafzhU7EhGZAZZ6IjJJR7I0iDqYBQB4b0oQ\n7CyVouYhakl3dXPGnHu6AwBe25KMksoakRMRkdQZXeq1Wi3mzZsHtVoNKysrhIaGYsOGDXfc7+LF\ni5g3bx6GDRsGJycnyGQyrF+/vimZicjMlVfrsGDTCQgCMLVvFwz1dRc7ElGLe2l0L3i62uBycSXe\n3XZK7DhEJHFGl/opU6YgKioKb775Jnbs2IH+/ftj+vTpiImJue1+aWlp+Pbbb2FhYYFx48Y1OTAR\nmb93t59CZn4ZOjhY4vXxvcWOQ9QqrC0UWP5A7WE43x29gJ9Sr4gdiYgkzKh/z46Pj8fOnTsRExOD\n6dOnAwDCwsKQnZ2N+fPnIyIiAgpFw1emGDp0KPLy8gAAR48eRWxsbDOjE5E5+uXUVXybeB4A8OHU\nUDjaqERORNR6Bnm74sl7vbHy9wy8GpeMPt2c4GFvJXYsIpIgoyb1W7ZsgZ2dHaZOnVpv++zZs3Hp\n0iUkJibe+o3kPHyfiG4vX1uFVzbXXu1mzpDuGNLTTeRERK3v36N94d/JAZqy6muHnQliRyIiCTKq\naaekpMDf3x9KZf0Bf3BwcN3jRERNIQgCFm4+gXxtNXp1sMf8+3qJHYmoTVgqFYicFgoLpRy/nclD\n9KFssSMRkQQZdfhNQUEBvL29b9ru4uJS93hrSk1NhcFgaNX3oNZVU1NT93NSUpLIaai5WnI9f0rT\nYtepIijlwDN9rHHmJIcEbY3fn+L6Z7A91hwrxtJtqXDR5aOLQ/MOPeN6mheup3mQy+Xo1q1bq7y2\n0deIk8lkTXqsJeh0Ouj1+lZ9D2o71z+gyDw0Zz0vlOjw1bEiAMDMQDt0tpPx94fI+Ovf9kZ3t8SR\nHAskXa3Gf/YX4P/CXGChaJk/V7me5oXrKV23Ove0JRhV6l1dXRucxms0GgB/Texbi1Kp5LH5Enfj\nB5FKxRMgpa4l1rNSZ8BHhwpQpQdCOlhiUm9HyFt5QEAN4/en+F4Y5Ip5CVeRVaRDVHIZnunv3OTX\n4nqaF66neWjNHmtUqQ8KCkJsbCx0Ol294+qTk5MBAIGBgS2b7m8CAgJY6iUuKSkJNTU1UKlUCAkJ\nETsONVNLrOdLG5NwoUQHd3tLrHn8XrjbW7ZwSmosfn+ahhVuefjn2sP4Ka0MY/v2xKQ+nZv0OlxP\n88L1NA8GgwGlpaWt8tpGNeTJkydDq9Vi8+bN9bZHRUVBrVZj4MCBLRqOiMzbxqMXsPnYRchlwGfT\n+7DQEwG4t6c7/jWiJwDg1bhknLvaOgWAiMyLUZP6sWPHIjw8HHPnzkVJSQl8fHwQGxuLhIQEREdH\n1x0nNGfOHERFRSE9PR2enp51+2/atAkAkJGRAaD2evV2dnYAgAcffLBFviAikobTV0rwxve1J8O+\nNLoXBnm7ipyIyHT8a2RP/JFdiH1p+Xjm22P44bl7YGNh9GlwRNSOGP0JERcXh0WLFmHx4sXQaDTw\n8/NDbGwspk2bVvccvV4PvV5/07V2/359+xUrVmDFihUAwOvyErUjReXVeOqbP1ClM2CYrzvmDush\ndiQik6KQy/DJtFCMi9yLc7lavBaXjI8jQlv9ghREJF1GH6BuZ2eHyMhIXL58GVVVVUhKSqpX6AFg\n/fr1EAQBXl5e9bYLgnDLH0TUPuj0BjwfexzZBeXo4myNjyNCIZezqBD9nZudJT6fcRcUchm+//MS\nvtqXKXYkIjJhPOuUiNrU8oTT2HsuH9YqBVY90g8uthZiRyIyWQO6u+D18f4AgP+LP4U9Z/NETkRE\npoqlnojazPfHc7B6b+208YOpIeitdhA5EZHpe3SwFyL6dYVBAJ6LOYb0PK3YkYjIBLHUE1Gb+CNb\ng1c2nwAAPBfmg/HBnURORCQNMpkMSyYFoJ+nM0ordXgi6iiKy3nzISKqj6WeiFpdZn4ZHo86iiqd\nAaP8O+Df4b5iRyKSFEulAl8+3BdqRytk5JfhqeijqNLxDutE9BeWeiJqVZqyasxedxiF5TUI7uKI\nT6fzxFiipnC3t8TqWf1ga6HAoQwNXv7fCRgMvNAEEdViqSeiVlNZo8fjUUeQde1KN1/N6s9rbRM1\nQ4DaEf99pC+Uchm2Jl3C8oTTYkciIhPBUk9EraJGb8BzMcdx7HwRHKyUWD+7P+8YS9QC7u3pjuUP\nBAMAVv6egXX7ealLImKpJ6JWoDcIePl/Sdh16ioslXKs+mc/+HjYix2LyGw80LcL5t/XCwDw9taT\n2PTHRZETEZHYWOqJqEUJgoDXv0/BD39eglIuw5cP34VB3q5ixyIyO88M74FHB3sBABZsSsK2E5fE\nDUREomKpJ6IWIwgC/i/+FGIPn4dcBnwyLRQj/DqIHYvILMlkMiye0BvT+tdew37ehj+x6+RVsWMR\nkUhY6omoRQiCgHe3n6q7udSyKcGYEKwWORWReZPLZXh3chAmhaqhMwh45ttj2H0mV+xYRCQClnoi\najaDIOCtH1OxZl9toV96fwAe6t9V5FRE7YNCLsMHU0MwNrAjqvUGPPn1USSkXBE7FhG1MZZ6ImoW\ngyDgyyNFiDqYDZkMWDYlCI/c7SV2LKJ2RamQ49PpfTA+uBNq9AKejTmG37LKxY5FRG2IpZ6ImqxG\nL+DTwyX4Ob0MchnwwYMhmDagm9ixiNollUKOT6f1wYN9u0BvEPDJQQ12ZrDYE7UXvAsMETVJSWUN\nluzJx4mrVVDIgI8iQnF/aGexYxG1awq5DO8/EAxrlQLfHMrGymOlKKwCgoMFyGS8kzOROeOknoiM\ndrWkEg/99yBOXK2ClVKGxcPcWOiJTIRcLsOS+wPwUEDtvSE2ppbipY1JqNYZRE5GRK2JpZ6IjJKS\nU4zJK/bj9JVSOFvJsWSYM0I7WYkdi4huIJPJMDPYEU/dZQ+5DIg7noNH1x1GcUWN2NGIqJWw1BNR\no/3wZw4e+PIALhVXwtvdFsvDPeDtrBI7FhHdQri3DV4f6gpbCwUOpBfg/s/34cyVUrFjEVErYKkn\nojvSGwS8t+MUXtjwJ6p0BoT1cseWZ+5BBzuelkNk6vqqrbHx6bvR2ckaWQXlmPzFfsQnXxY7FhG1\nMJZ6IrqtqyWVmLnmEFbuyQBQe2v6NbP6w9GaE3oiqQhQO2Lr80MwuIcryqv1eObbY3gv/hRq9DzO\nnshcsNQT0S3tPpOLsZF7cShDAxsLBT6d3gcLxvhBIedVNIikxsXWAl8/NgBP3NsdALDy9ww8+N+D\nyC4oEzkZEbUElnoiuklljR7vbDuJ2euOQFNWjd6dHLDt+SH4R4ha7GhE1AxKhRyLxvfGlzPvgoOV\nEkkXijD+033Ycvyi2NGIqJlY6omonj+yCzHu071Ysy8TADDrbk/EPTMY3u52IicjopYyNqgTdswb\nigFeLtBW6fDid0l4+ps/kFtSKXY0ImoilnoiAgBUVOvx7vaTePC/B5CRVwYPe0t8Nasf3r4/EFYq\nhdjxiKiFdXayRuyTg/DvcF8o5TIkpF7BqI/24H9HL0AQBLHjEZGRWOqJ2jlBEJCQUvuH+eq9mRAE\nYMpdnbHzxWEY6d9B7HhE1IoUchn+NbInfnxuCII6O6KkUof5m07g4a8Sce4qL31JJCUs9UTtWEae\nFo+uO4Kno/9ATlEFOjtZ46tZ/fDRQ6FwtOHVbYjai95qB2x5ZjBeGeMHC6Uc+9MKMCZyL5ZsPckb\nVhFJBC8yTdQOXS2pROQv5/DdkQvQGwRYKOR4cqg3ng3zgbUFD7Uhao+UCjnmDu+B8UGd8M72k/j5\n5FWs3Z+J7//MwbNhPpg5sBsPxSMyYSz1RO1IUXk1vtyTjvX7s1Clq70+9Ug/D7w+oTe6u9mKnI6I\nTEE3Vxus+mc//H42D29vTUV6XhmWbjuJNXsz8PyInpjarwtUCv5DP5GpYaknageuFFdi3f5MfJt4\nHtoqHQCgn6czXhnrh/5eLiKnIyJTNNTXHQnzhmLTHxfx6S/ncLm4Eq9tScbK39Px1NAemHJXZ07u\niUwISz2RGTt3tRSrfs/A93/moEZfezULv472WDCmF8J6eUAm402kiOjWVAo5pg/ohsl9OiMm8Ty+\n+C0N2QXleG1LMj78+QweudsTjwzyhKudpdhRido9lnoiM1NZo8dPqVcQk3geiZmauu0Du7vg6WE9\nMLyXO8s8ERnFSqXAY0O6Y9qArog9fAFr92Uip6gCn+w6hy9/S8eEYDWmDeiKfp7O/HwhEglLPZEZ\nEAQBqZdKsOV4DuKOXURhee3VKuQyYHTvjnhqmDf6dHMWOSURSZ2NhRJzhnTHrLs9kZB6Bat/z0DS\nxWJsPnYRm49dhLe7LSL6dcXkPp3h4WAldlyidoWlnkjCzl0txdakS9h64jIy88vqtqsdrRDRvxse\n6t8FnRytRUxIROZIqZBjQrAa44M64dj5Inx35Dy2nbiMjLwyvLfjNJYlnMYALxdMCO6E+wI7wsOe\nBZ+otbHUE0lIZY0ehzM12H0mF7+dyatX5C2Vcoz098CDfbtgmK8HFHL+EzgRtS6ZTIa+ns7o6+mM\nxRMDsC3pEjYevYBj54uQmKlBYqYGi39MRT9PZwzv5YFhvu7o3ckBcn4+EbU4lnoiE6bTG5B6qQRH\nsjQ4mF6AA+kFqKjR1z2uUsgwzNcdE0PUGOnfAXaW/JYmInHYWSoxbUA3TBvQDRcLy7Ej+Qq2J1/G\nnxeKcCSrEEeyCvGfn87Azc4SQ33dcE8PN/T3ckFXF2seh0/UAtgAiExIbkklUi+V4MTFYhzN1uBY\ndiHKqvX1ntPBwRJhvTwwvJcH7vFxhb0V7/xKRKali7MNnhjqjSeGeuNiYTl2n8nDnjN5OJCej3xt\nFeKO5SDuWA4AwMPeEv28nNHP0wUhXR3h19EBthxQEBnN6O8arVaL119/HRs3boRGo4Gfnx8WLlyI\nadOm3XHf3NxcLFiwANu2bUN5eTlCQkLwzjvvYOTIkU0KTyRV5dU6ZOSVITO/DGeulCLlUjFSL5Ug\nr7Tqpuc6WCnR38sF/bu74N6ebujdyYFTLSKSjC7ONnhkUO2lL6t1BhzN1mDP2TwcztQgJacYuaVV\niE++gvjkKwAAmQzo7moLf7UDeneq/eHtbovOTtZQ8qZXRLdkdKmfMmUKjhw5gmXLlsHX1xcxMTGY\nPn06DAYDZsyYccv9qqqqMHLkSBQVFSEyMhIeHh5YsWIFxowZg127dmHYsGHN+kKITIlOb0BuaRUu\nF1fgcnElLhdVIqugrK7IXympbHA/uQzwdrdDgNoBd3VzxoDuLujVwZ7HnxKRWbBQyjG4hxsG93AD\nUHueUNKFIhzNLsQf2YVIvVSMqyVVyMgvQ0Z+GbafuFy3r0ohQ1cXG3i72aK7my26utigk6M1Ojla\nQe1kDWcbFQce1K4ZVerj4+Oxc+fOuiIPAGFhYcjOzsb8+fMREREBhaLhu8t99dVXSElJwYEDB3D3\n3XfX7RsSEoIFCxYgMTGx3vMFQbjpNQwGgzFxyQTJ5XIoFArI5XJJrafBIKCsRg9tZQ2KynUoLK9G\nUXk1CstrUFxeDc21n/O0VbhaXIV8bSUMN/8WruNsrYSzrQW6udigu5st/Drao1cnB/h62MNK9fdJ\nlADD7V5MRFJdT2oY19O8SGE9LRQy9PdyRn+vvy65qymrxtmrpThzpRRnrpYiLVeLC5pyVOsMKNRW\n4Q9tFf7I0tz0WpYqOTo4WMPd3gIuNhZwsrGAs40Kzra1P9f+vwUcrFWwtVTCWimX1MBECutJd9bQ\n2jXUeZtCJhjxSk888QQ2bNiAwsJCKJV//X0gNjYWM2bMwP79+zF48OAG9w0PD8eFCxdw+vTpetvf\ne+89vPbaa7h48SI6d+5ct12n06GsrOzvL0NEREREZDZsbW3r9eqmMurgtJSUFPj7+9/0xsHBwXWP\n327f689raN/U1FRjohARERER0TVGlfqCggK4uLjctP36toKCglbZl4iIiIiIbs3o08hvdxLKnU5Q\nac6+RERERETUMKMO4HF1dW1woq7R1J6w0tAkvqn7yuVy2Nra1tsmk8lY/omIiIhIkgRBuOnEWLm8\nZS7ValSpDwoKQmxsLHQ6Xb3j6pOTkwEAgYGBt933+vNudKt95XJ5i32RRERERETmzKjWPHnyZGi1\nWmzevLne9qioKKjVagwcOPC2+54+fbrepSt1Oh2io6MxcOBAqNVqI6MTERERERFg5CUtAWD06NE4\nevQoli9fDh8fH8TGxmL16tWIjo7GzJkzAQBz5sxBVFQU0tPT4enpCaD25lN9+/ZFSUkJli1bBg8P\nD3zxxRfYunUrbz5FRERERNQMRh/fEhcXh0ceeQSLFy/GmDFjkJiYiNjY2LpCDwB6vR56vb7eMUOW\nlpb45ZdfEBYWhueffx4TJ07E5cuXsWPHjkYV+jVr1kAmk8HOzs7YyGQi9u3bh3HjxsHZ2RnW1tbo\n2bMnli5dKnYsaoLjx49j0qRJUKvVsLGxgZ+fH5YsWYLy8nKxo9EdlJaWYsGCBRg9ejTc3d0hk8nw\n1ltvNfjcY8eOYdSoUbCzs4OTkxOmTJmCjIyMtg1Mt9WY9dTr9fjoo48wZswYdOnSBTY2NvD398fC\nhQtRVFQkTnBqkDHfn9cJgoChQ4dCJpPhueeea5ug1CjGrGdNTQ0++ugjBAUFwdraGk5OThg8eDAO\nHDjQ6PczutTb2dkhMjISly9fRlVVFZKSkjBt2rR6z1m/fj0EQYCXl1e97R06dEBUVBQKCgpQUVGB\ngwcPYtSoUXd8z5ycHLz88ss8REfCYmJiMGzYMDg6OuLrr79GfHw8XnnllRa7ixq1nZMnT2Lw4MHI\nysrCJ598gm3btmHatGlYsmRJ3Z2myXQVFBRg1apVqKqqwqRJk275vNOnT2P48OGorq7Gxo0bsXbt\nWpw9exb33nsv8vLy2jAx3U5j1rOiogJvvfUWPD098cknnyA+Ph5PPPEEVq1ahXvuuQcVFRVtnJpu\npbHfnzdasWIF0tLSWjkZNUVj11Ov12Py5Ml1f47u2LED3377LcaMGWPcjVgFCZgwYYIwceJEYdas\nWYKtra3YcchIFy9eFGxtbYW5c+eKHYVawKJFiwQAQlpaWr3tTz75pABA0Gg0IiWjxjAYDILBYBAE\nQRDy8vIEAMKbb7550/OmTp0quLm5CcXFxXXbsrKyBJVKJSxYsKCt4tIdNGY9dTqdkJ+ff9O+//vf\n/wQAwjfffNMWUakRGvv9eV1mZqZgZ2cnxMXFCQCEZ599to2SUmM0dj0//vhjQS6XCwcPHmzW+5n8\n5WWio6OxZ88efPHFF2JHoSZas2YNysrK8Morr4gdhVqASqUCADg6Otbb7uTkBLlcDgsLCzFiUSM1\n5tLAOp0O27ZtwwMPPAAHB4e67Z6enggLC8OWLVtaOyY1UmPWU6FQwNXV9abtAwYMAABcuHChVbKR\n8Yy9dPeTTz6J8PBwTJ48uRVTUVM1dj0jIyMxdOhQDBo0qFnvZ9KlPjc3F/PmzcOyZcvQpUsXseNQ\nE/3+++9wcXHB6dOnERoaCqVSCQ8PDzz99NMoKSkROx4ZadasWXBycsLcuXORkZGB0tJSbNu2DStX\nrsSzzz570/0lSHrS09NRUVGB4ODgmx4LDg5GWloaKisrRUhGLenXX38FAAQEBIichJpizZo1OHz4\nMD7//HOxo1AzXLhwAVlZWQgKCsJrr72GDh06QKlUIiAgAFFRUUa9lkmX+meeeQa9evXC3LlzxY5C\nzZCTk4Py8nJMnToVERER2LVrF+bPn4+vv/4a48aN43H1EuPl5YWDBw8iJSUFPXr0gIODAyZOnIhZ\ns2YhMjJS7HjUAq7fKLChGwq6uLhAEAQUFha2dSxqQTk5OVi4cCH69euHCRMmiB2HjHT9XMP333+f\n5xtKXE5ODoDay8P/8MMP+PzzzxEfH4/evXvj0UcfxerVqxv9WkbdfKotbd68GVu3bsXx48d5F1mJ\nMxgMqKysxJtvvomFCxcCAIYPHw4LCwvMmzcPv/zyS6NOmCbTkJWVhYkTJ6JDhw7YtGkT3N3dkZiY\niHfeeQdarRZfffWV2BGphdzus5efy9Kl0WjqBirfffcdb/QoQU8//TRCQkLwxBNPiB2FmslgMAAA\nKisrER8fX3cp+PDwcPTr1w9Llixp9Dqb5HeyVqvFs88+i+effx5qtRpFRUUoKipCdXU1AKCoqMi4\ns4FJVNeP5bzvvvvqbR87diyA2svmkXQsXLgQJSUl+Omnn/DAAw9g6NChmD9/Pj755BOsXbsWe/bs\nETsiNdP179nrE/sbaTQayGQyODk5tXUsagGFhYUIDw9HTk4Odu7cCW9vb7EjkZE2bdqEhIQEvP/+\n+yguLq7rSABQXV2NoqIi1NTUiJySGuv6562fn19doQdqByf33XcfLl68iNzc3Ea9lkmW+vz8fFy9\nehUffvghnJ2d637ExsairKwMzs7O9a6LT6atoeNyAdQddsMpkbT8+eef6N27903Hzvfv3x8AkJKS\nIkYsakE9evSAtbU1kpOTb3osOTkZPj4+sLKyEiEZNUdhYSFGjRqFzMxM7Ny585afzWTaUlJSoNPp\nMGjQoHodCQBWr14NZ2dnbN++XeSU1Fg9evSAjY1Ng48Z25NM8vCbjh07Yvfu3TdtX7ZsGfbs2YMd\nO3bAzc1NhGTUFA888ABWrVqFHTt2oE+fPnXb4+PjAaDZZ3tT21Kr1UhJSYFWq613M7iDBw8CAE9q\nNwNKpRITJ05EXFwc3n//fdjb2wMAzp8/j927d+PFF18UOSEZ63qhz8jIwM6dO+t9FpO0PProoxg+\nfPhN28PCwjBp0iS88MILCAwMbPtg1CRKpRL3338/Nm3ahKysrLp7PAmCgISEBPTo0aPRndckS72V\nlVWDv2HXr18PhULR4GNkukaPHo2JEydiyZIlMBgMGDRoEI4ePYq3334bEyZMwJAhQ8SOSEaYN28e\nJk2ahPDwcLz44otwc3PDoUOH8N5776F37951h1WR6dqxYwfKyspQWloKoPaGYps2bQIAjBs3DjY2\nNnj77bfRv39/TJgwAQsXLkRlZSUWL14MNzc3vPTSS2LGp7+503pe/2f848eP45NPPoFOp8OhQ4fq\n9nd3d0ePHj1EyU43u9N6enl53XRzz+s6d+7MjmRiGvN5u3TpUuzYsQNjxozBW2+9BQcHB6xZswZJ\nSUnYuHFj49+sWVe5b2O8+ZR0lZeXC6+88orQtWtXQalUCt26dRNeffVVobKyUuxo1AS//vqrMHr0\naKFjx46CtbW14OvrK7z00ksN3uCGTI+np6cAoMEfmZmZdc87evSoMHLkSMHGxkZwcHAQJk2adNNN\nx0h8d1rPzMzMWz4OQCK5ZWYAAACeSURBVJg1a5bYXwLdoLHfn38H3nzKJDV2PZOTk4Xx48cL9vb2\ngpWVlTBo0CBh69atRr2XTBB4PUEiIiIiIinjGYpERERERBLHUk9EREREJHEs9UREREREEsdST0RE\nREQkcSz1REREREQSx1JPRERERCRxLPVERERERBLHUk9EREREJHEs9UREREREEsdST0REREQkcSz1\nREREREQS9/+MJ8pC4RMwSAAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"import filterpy.stats as stats\n",
"stats.plot_gaussian_pdf(mean=10, variance=1, \n",
" xlim=(4, 16), ylim=(0, .5));"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This plot depicts our uncertainty about the dog's position. It represents a fairly inexact belief. While we believe that it is most likely that the dog is at 10 m, any position from 9 m to 11 m or so are quite likely as well. Assume the dog is standing still, and we query the sensor again. This time it returns 10.2 m. Can we use this additional information to improve our estimate?\n",
"\n",
"Intuition suggests we can. Consider: if we read the sensor 500 times and each time it returned a value between 8 and 12, all centered around 10, we should be very confident that the dog is near 10. Of course, a different interpretation is possible. Perhaps our dog was randomly wandering back and forth in a way that exactly emulated random draws from a normal distribution. But that seems extremely unlikely - I've never seen a dog do that. Let's look at 500 draws from $\\mathcal N(10, 1)$:"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Mean of readings is 9.865\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAuYAAAEeCAYAAADGsNC6AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzsvXmcJEd1LvpVVlWvs0mj0QKSRqAF\nSQMaG8xyBRixSIDg2XpgfO+P52s/29gXecHX1766gJ9ALEbCBknIxphBgMwOo8WgZZBGo9GMdo1m\n6dn37pmepXt6eq1eqiq390dWZJ6IjMjKzFq6uie+f7q7OiszMjPixIkvvnNOxnVdFxoaGhoaGhoa\nGhoaswpjthugoaGhoaGhoaGhoaEdcw0NDQ0NDQ0NDY2WgHbMNTQ0NDQ0NDQ0NFoA2jHX0NDQ0NDQ\n0NDQaAFox1xDQ0NDQ0NDQ0OjBaAdcw0NDQ0NDQ0NDY0WgHbMNTQ0NDQ0NDQ0NFoA2jHX0NDQ0NDQ\n0NDQaAFox1xDQ0NDQ0NDQ0OjBZBL+oVCoYAvfelL2LZtG7Zu3YrTp0/j85//PG677TbuuHvuuQc/\n+clPcPDgQRQKBZx33nm49tprceutt2LFihXcsY7jwHEc7rNMJoNMJpP8jjQ0NDQ0NDQ0NDRmGa7r\nwnVd7jPDMGAYal48sWM+PDyMVatWYeXKlbjppptw7733Ko/74Ac/iJUrV+Kss87C4cOHcccdd+Ct\nb30rNm/ejNe97nX+sY7jYGpqKmlTNDQ0NDQ0NDQ0NOYMuru7Ix3zjCu68lXADs9kMjh9+jSWLVsm\nZcxl2LNnD66++mrceuut+OIXv+h/blmWdsw1NDQ0NDQ0NDTmNbq7u5HLqXnxxIx5LfKSZcuWeReN\naJCGhoaGhoaGhobGmYiGB3/ato1SqYS9e/fiE5/4BM4991z88R//caMvq6GhoaGhoaGhoTGn0HDq\nuru7G6VSCQBwxRVX4Omnn8ZFF13EHSNj4fv6+kIBoRoaGhoaGhoaGhpzAYZh4JJLLuE+q6Y8abhj\n/vzzz6NcLuPQoUO466678O53vxvr1q3jMrPIGhkljG8UTNP0f8/n802/vsbsQb/7MxP6vZ+50O/+\nzIV+92cumv3uZb7srDvmb3zjGwEAb3vb2/A7v/M7uOyyy/DZz34Wv/zlLyO/t2LFiqY75z09PTBN\nE/l8HitXrmzqtTVmF/rdn5nQ7/3MhX73Zy70uz9z0ex37zgOCoVCou801fNduHAhrrzySuzfv7+Z\nl9XQ0NDQ0NDQ0NBoeTTVMT99+jR27NiByy67rJmX1dDQ0NDQ0NDQ0Gh5pJKyrFmzBlNTUz49v3v3\nbtx///0AgBtvvBGmaeL666/Hxz/+cVx++eXo7OzE/v378Y1vfAOlUgmf//zn63cHGhoaGhoaGhoa\nGvMAqRzzm2++GUeOHPH/Xr16NVavXg0A6O3txQUXXICVK1di1apV6O/vR7FYxPnnn4/rrrsODzzw\nAK6++ur6tF5DQ0NDQ0NDQ0NjniCVY97X11f1mO985ztpTq2hoaGhoaGhoaFxRqL5OQk1NDQ0NDQ0\nNDQajt0nJvD7334Bm/pGZrspGjGhHXMNDQ0NDQ0NjXmIX+8awMu9I3i458RsN0UjJrRjrqGhoaGh\noaExD2HZXgV1y3FnuSUacaEdcw0NDQ0NDQ2NeQjmj7uudsznCrRjrqGhoaGhoaExD+FUHHLHmeWG\naMSGdsw1NDQ0NDQ0NOYh7Apl7mjGfM5AO+YaGhoaGhoaGvMQgWM+yw3RiA3tmGtoaGhoaGhozEP4\nUhbNmM8ZaMdcQ0NDQ0NDQ2MeQjvmcw/aMdfQ0NDQ0NDQmIeoZEvUUpY5BO2Ya2hoaGhoaGjMQzg6\n+HPOQTvmGhoaGhoaGhrzELafLlE75nMF2jHX0NDQ0NDQ0JiH0Iz53IN2zDU0NDQ0NDQ05iF8xlz7\n5XMG2jHX0NDQ0NDQ0JiHYA65qxnzOQPtmGtoaGhoaGhozEMwKYutKfM5A+2Ya2hoaGhoaGjMQ+jK\nn3MP2jHX0NDQ0NDQ0JiHsHWBoTkH7ZhraGhoaGhoaMxDMCmL9svnDrRjrqGhoaGhoaExD+FoxnzO\nQTvmGhoaGhoaGhrzEHbFH5/vwZ8ly8bv/uuzuO1Xu2a7KTVDO+YaGhoaGhoaGvMQZ4qU5dc7B9Bz\nbBz3Pd83202pGdox19DQ0NDQ0NCYh7DPkMqfJcuZ7SbUDdox19DQ0NDQ0NCYhzhTsrLMJ6mOdsw1\nNDQ0NDQ0NOYhWMVPe/74rVJY2jHX0NDQmN+YTwyMhobGmQnb15jPb3tm22ewlKVQKOCWW27BDTfc\ngGXLliGTyeC2227jjrFtG3feeSc+8IEP4MILL0RXVxeuuuoqfPrTn8bY2Fi92q6hoaHREBwYLOA3\nvvAE7ll3YLaboqGhoZEajCmf71KWKMa8aNo4PjbTxNbUhsSO+fDwMFatWoVSqYSbbrpJeszMzAxu\nu+02LF++HHfffTcee+wx/Nmf/RlWrVqFt7/97ZiZmTsPSEND48zD7Wv2olCycOfa/bPdFA0NDY3U\nYFlZnPlDKEsRtcN5/V0b8PY7nsK+gUITW5QeuaRfWL58OUZHR5HJZHD69Gnce++9oWM6OzvR29uL\npUuX+p9dd911uPjii/Gxj30MDzzwAP7gD/6gtpZraGhoNAj5bGa2m6ChoaFRM86UrCyUMXddF5lM\nYMP7Rzwy+PFdA3jXOU1vWmIkZswzmQx3wzJks1nOKWd4y1veAgDo7+9PelkNDQ2NpiGf1eE3Ghoa\ncx9nSuVPypiryPOsMTcIl8SMeS146qmnAAArVqyoeuyuXbvgNHnvxTRN/2dPT09Tr60xu9Dv/syE\n6r1PTYz7v+v+MD+hx/yZizPp3U9XpMPTM8V5da8DkxbO6jDQnvNIlOMnA5u9dVuPdNdzaHAA5sIO\nAM1794Zh4OKLL070naY55sePH8enP/1p/NZv/RY+/OEPVz3esizYtt2ElsnBBq5GY/DYwWlMmw5+\n76oFs92UEPS7rw7HdfEvmyZw0aIcPnJl92w3py6g7z2bcaWfa8xP6Hd85mK+v3sqZWnlez05aeH5\n/hI+eFknuvLRO5aDkxb+6tfD+I3z2/AP7zgLAGCSAkMl0wQcCTvu8j5lM55HNptN/J2mOOYjIyO4\n8cYb4boufv7zn8Mwqm8T53K5WMfVE/Ql5fP5pl77TILruviPngJsF/jQ6xZhUXvyjltv6HefDMcn\nTDxztIjufAb/9Q1LZrs5qaF67205Q/q5xvyBHvNnLs6kd++COaiZlr7Xv1s7iLINjJVcfPLNZ0Ue\nO1Ky4QI4NeUE90Qk1tlsDnmJc9+W413eZjyPNH5swx3z0dFRXH/99Th+/DieeuopvPa1r431vRUr\nVjTdMe/p6YFpmsjn81i5cmVTr30mwbId2D87DgC44sqrcd6ijllukX73SdE5WAAeHYQDY04/L9V7\nv6B/N3CgFwBwzTXXVI2r0Zh70GP+zMWZ9O5zj48AsJDLt7X0vZZ/egwA0DeVrdrOia4hYP1p5NqC\nezq7fzeASQDA1a9/PRZ1EKe7cu6LL7oQ+fxYU9+94zgoFJJlg2mo5zs6Oor3ve996O3txdq1a3HN\nNdc08nIacwQ2CULRRVzmJqxKclxrnubgooy5Od9L5mm0FI4OT2Pj/qHZbobGPMFcC/7sqCJjAYIM\nLBaxzdSvcIhfYZHCQ7k5EvzZMMecOeWHDx/GE088gd/8zd9s1KU05hioL6cd87kJZuRN252XFeVo\nVpYZc/ZiXTTOPPz2P6/HH37vZWzqG5ntpmjMAzh+5c9ZbkhMdOSqS1sdSQpI6qTT1Ill4pjP66ws\na9aswdTUlE/P7969G/fffz8A4MYbb0Qmk8H73/9+bN26FXfffTcsy8KLL77of3/ZsmW49NJL69B8\njXqhZNmYKdtY0tXW8GvNd8b81EQRyxa2z2v5AzV8tuMiN8/yflP7XTRtLO5sXW2mxvzE5iOjePMl\nZ892MzTmOOx5yJgzv4FzwEnwp6P4fK7MU6kc85tvvhlHjhzx/169ejVWr14NAOjt9XSZmzZtAgD8\nzd/8Tej7f/RHf4T77rsvzaU1GoQ//v4mbD06hmf/z7uxdEF7Q69FnXF7jhiLuFiz4yRu/vEWfPbG\nK/Hnvz1/F5/0HVqOixgkx5wCNewzZc2YazQf85G00Gg+GGE8V/pTRz4GY84WGwpmnPoV9HNjjpBl\nqRzzvr6+qsfMx+3t+Yy9AwXMmDYOnJpsuGNOB5MzR4xFXOyplPzde3JulP5NC2rkTduJZUznEigT\no6UsGrMBa47FNhwfm8FZXXl0tTW1PIpGFQQa81luSASovxhnLmG+tooxt1VMuusCc8A31+XtNAAE\nnXdkqtzwa3G6sFa2FilQrDhx0/OcZeUY8znmQMSBrR1zjVmGXSWweteJcXz9iX2YLltNapEafaen\n8PY7nsLb73hqtpuiIcD2Neata6dLxHmOF/zpHU+JvRInZQmO5R32WlrZPOilrQaAoPMON8Exb2WN\nuWm7mCxZWNCebmiwSXJ6njtzHGM+DzOz0PsrzvNFlkZrohpp8aF7ngXg2e7P3HhVM5qkxDMHvCwy\no9OtW8DmTMVcyMpSKAaLSxp4rwK7F1WQJ/UxaFatubJDrxlzDbiu63fqkckmMOYtnJXlM0+ewm//\n0/rUuuKZslP5OfssViNhK6Lh5wu0lKW1MDxZwofueQa3/WrXbDelaYhrG3efnGhwS6ojF8OZ0pgd\nBBlMZrkhEZgsBfNlnH4v082XLZv8P0LKMgegR5MGt9IcmSo1/HocY95iA6V3zMTIVBlDhXTPYcas\nMObznGWl2+zz0THXUpbWwi33b8euExO47/m+2W5K0xBX5tcKuZmTtGFgvJjavjYDJcvGU3sHW0Ii\nVA/YkkDJeqJo2vjRi0dwfGwm9TmmEjrm7F64IE+FA162icPeYv6GCtox1+C0Wc2QsrRy8CdrTtoB\nzJj2+e7MUa3evJSykPevs7LMLgYnili399RsN6PpiMuYtwJbHUd+AHjO0we+sREf/pdnWs72M3zx\n4d34k/tewed+OT92Z5h5bhRbvGbnSfx//7kTd63dn/ocVMoSp6Abs8+2E9TR4KQsKu15a3a5EGZ/\nRGvMOuhKsxnBn2KqvVaC75inbBdjyue7MzfvGXNyT8V5vshqdazZcZL7u1UdunojtmPeCow5yQ9t\nRUTYTZYsjE2bGJwotZztZ/jxS0cBAPdvPjbLLakP7AZnZRmrxBWM1RBfQBnzONWk6dhgv6qysmiN\nucacBO3Qw83QmCtK5842uHalZBfOnKwswe/mXAl1TwCtMW8diIHUsvdxdHgaX3lsDwYnis1qVsMR\n13FthWqGOSNwJcoR9oA6Xa0WXyTinIi0wa2c4UREo4M/g2I/6eeBSc4xj6Mxp+Sed9046RJbvc8x\naMdcg3fMCWPuum5DdHZOi2rM6ZjVjHk05tIEmwYOJ2WJnnBKlj2nJuq5BlvYkZEteu97vg+rNh7G\nLzb1N6tZDUe1dIkMrcCY5wljXjLV7aa3VIsj1yhQtv+yc7ulx3z6ge145z+t55zJVoXrumCmqVGO\nOXOka9k5LVDHPAbRwzHmlcM5BzyG9ryVoR1zDY7hGJ0u+yz236/ejrf84zpsPjJS1+vZnHFunYFS\nD8ecsXll24llYOYq+Fz08+8+4zLmI1NlvOG2J/CJ/3ilGc06IyEu3mWL3kLR20afmuMLYpcbV3EZ\n89mfxmlBRarpFdHKqXIBoG942v/9gsWd0mOe2nsKx0ZncOjUZLOalQi24+K+53qxd2BCKvloxPWA\n2nZOOSlLDAdfNv/weczlwZ/aMdeYMxC3eiYqk9wDW45hsmTho996Af/jh6/gVz0n6nI9frXbOgOF\nNqVWKQswvyUQ1HjGCdZpVZQsBwdHzBDjTftllMb84Z4TKFvOGRmc2CyIDty0GWYq2aQ812VV9F7j\nOq6UrZ4t0MdejnDMHSf5wqOZ2D8YVGxW7YKxPtaK7QeAn7x0BLc9vBsfuPsZbiHUMMbcDucUT4rJ\nYnopC/tdqTG36LGpm9hUaMdcI8RwMDnLkq68/9njuwbx3WcO1+V6TouyJvVoF91mn89yFo6xaLJj\nXjRt7B8s1EU+cuv60/j0UyN4qnea+5zuAkS9x1bQ9853iGNxqhR+H6VKDuO57phbMR1XuhvXCn2Q\nz4KhHi9WioVHM0Edc1XzGBHRiu0HgK39Y/7vdDPTdRujjWeSq1p2iCeTBn9K5uqSosAQ/Vwz5hpz\nBqIhZZlZuvJZ7vNihHYwCdKwQs0AHbNpBrDruhxLPp8DQGczXeIffvdl3HDXRjwqZOtIg32nvb7+\n5OEp7nPaL6OquLaCU6TCi4eHcXioNbfbk0C0EbKFUsCYt449SYO4gfGUTGkFjTl1+CKlLC3GmIuO\n6oHBYLyo5oCyz5i35iKQl68IO4ENeOSmL2WpgTEvJUyXaPM+hOu6vJZcsYPTSjv0UdCOuUZo65Fl\nZmED7tYPXw0AcFGfTt2qBYZ4jXny75csh3Pu57OUZTbTJb7c58U8/KSS1qweEH0brsBQFGOemX2n\nSIYTYzP4b6texHu+viFSWjAXEJKySALSWcDhXGfM4zqu1Pk1WsAxt2M65tyu5Cwvon64vYA/f3gA\noyThAc3q47guxmdMDIwHn7mu6/exViKVKLhdiZBj3gjGvA5ZWYoJK38KPoTozNP/mwomvZWhHfN5\nhDvX7scPX+hL/L2QY16p/sk6dEfe6ybiRNHTP4ZTKdKTuS0rZQl+T9Mu0YGb34w5lbLMjjNUTxtr\nCA427etRGnPqFLVSZhbqYKzfN7f176LdkS1454uUhfo2UTaI7nI2utvtHyxUzeVPmxopZbHpwmN2\n39XmkyWcmrKx++SE/xmnyXaAlV94Am+7fZ2/i+yxs97/W4Hxl8GOyNvdCMfc15jXiTGPM59wsQq2\nG0rRyQV/6gJDGrOFbf1juGfdAdyaolqZ2KlHKow5G2gdOU/SQieKXSfG8bvffA5v+cq6xNezY04+\nzUatecxD+ZbnsWNOJyVzlt5hPSeZSMY8wimhMoKo/M3NBm3/g1vmdqEU8T3LFryMpZ3rxa6oYxjl\n+FFZYa029F/WHcCnH9guXVi+3DuCG+7aiM/9cmfkOVSOUOi4FiJlWFdRJSOg72JvxXmnzOxsM/4q\nRGW+acQiju2e1iJpTCxlEe5R7HO242K8UvBIS1k0Zg37BwrVD1IgzJhXpCw+Y+455nTS29SbPoVi\nvTTmZcvBZx7cjke21ydbTP0Z8/rnuW0VRpAP/pwPjDn/d1wpC2XMW0kyQtvy1N5T/iQ1FyE6qDLH\nvEjSlM5l8Nkk1PdCWelamduvr92Pn23q54IGGY6NTld+zkSeQ1UCPeq42WacfcdcIa10OaLG+0n7\n12y3XwVbsbgAGsSY1yGPOXXMY0lZKLnnhh3zr6zZg5VffAJrdpzk3pmWsmg0FcfGog1nFMROPRJy\nzL1uQgdMLpu+69SjwiYA/KrnBH76cj/+6idbU5+DgnPMU7RLdODqrTG/95nDeP3nH8emvvrmlU8D\nLnvELDFH9ZxkMoKUhfb1qG18qjFvJcecZiIwbRfHxqYjjm5tiCzXjExjPofTJT645Rje8dWnsHdg\nguvTUYsMnjFPf8+0n49Nh6s+s3/LnFDTdvwFAm33XMljzvoVx5IrdnPZ/XF65RZ1zOm7Ek1kI9oc\n5DFPf26axzwO8y7uvIi29/CQF8z/pUd26wJDGrMHxmwAybWuISnLVBm24/pGuZMx5mRQ15KNol6s\nyWQxYAHroe+NmxFBBdERr7eU5cuP7kHJcvDZB3fU9bxpQJ9Ps7Oy+G1ooJQlboGhuI5UsyHb2p2r\niMOYz2XHfO3uQRwbncGLh4a5e41a6JVIn6xlYUyZd9lzlTmvgGdv3/v1DXjnV9fDtB1+HMRkzGe7\nT1aTstDmsV9NjjFvzb5mR1RlbkhWFj+PeX2kLHH6hSVkZaFFhCgymQxnl7WU5QzFvoECbv7RZi4f\najNAtxqTGjyW0eDs7jYAnpSFGqD2imNOjW9NjnmNDjDDYpJnfaJYu2ykZimL2Zzgz862bPWDGoxW\nYMzreVWxO9O+HuWYc1v4dUonWg+IzlGrbrvHAbMRrJCO1DE3WfBnc+/Tdlz86X2b8NVf7019Dj8v\nthtfq01Z6VreLWXepyX54dk4EHcQp8o2jo5M41ShhIHxIsc0RwV/tpaUpbLoUEhZHImshRaradV4\nBtFppWhsHvN053Zdt6bKn7bjKndpMhmx8FCqJjYd2jGvMx7cegxrdg7gwS3Hm3rd49QxT8mYn7+o\nAwAwPFnijKaflYUWtcikz0ZRr6ws9LJpssOIoE1Jw8aKW+yNSpfY1QKOOceYz5K1q+e8LqY9pJND\n1M4Hx3A24TmYtoN/33AIO4+PRx4nTlSt6kTEAbNnC9pzAKrlMW9uX+wbnsK6vafwoxeOpD4HYxod\nx+XsYbSUJXgGtdhQep6JYjgOgZ06XOTJEo6Lt6DgZSOzLWVh7aCfye0au73yHJCyRElFxSaXLLtm\nFpnZwLRjr2Q5XLvinEfceVE55kYmw51PS1nOUJRnYYJwXRfHicY8ad9jnfpVSzzHfHS6zAUeMSkL\nrzFPn42CHl4vtmdwopT6PAw8Yw4cGCwk0g2HGfP6B38CQFdbriHnTYK4FQobiXqyP1HBnyXLUU7C\ndNu4GRrzZw+exh1r9uKONdEMbZgxT98213Xxz4/vxQObZye7C+tfCzu8HTIx+5HrurPmmLPnXMui\nLMgD7XKkSnzGPP216XlGpmQac5drI0OB7FCWLDuVxny2pSDVgj/p7gur4cFLWVrTyYuqrkr/niia\neNOXnsQfff/lmq5H+28aiIu8pHnMLYnGnMEQGHPtmJ+hYJ2qkavpmbKN/+tfnsVtv/JSI56e5A1q\n0muzjntehTE3bRcjJBCoLRfOY27UEPQWVZksCSjbc6pQO2NOB/uveo7j+rs24m9+Fj+wVNxinyk3\nZuJpBSkLZxjnY1YW4eSq3Q/LieeQ1Assu8r4THSWlbIgJ6jFHm05OoZvrj+Ev1vdk/octYAxegFj\nzk/k1CmmUoNmgDlqtSwI2Hcd1+XYy6j+1AjGfFSSucdVOOZUE1w0+YVrlKQrymlsNmz/3uQsuMVp\nk72ffPBna+oi+PmV/x8lM9bvPYXJkoVnDpyu6XoW8XnSkCXivBlnLIk7LyofJJPJCFIW7ZifkfBT\nBzVw0K7e3I8dx8dx3/N9AICjI0I58aRSlkrHXdiR9ye/wUq1s7asgZwRzsqSrSFNHK8PS/RVDkXi\nfNSbMX981yAAYM3OgdjfD2dlqR9jTp9xdys45lyhkNkxdrQf9fSP4e9+0cMV1qkGOomIBYZC1SZL\n8ncZVxNcLzD9bpSOFwgzuPVKZTYbRZQCxtyzTeJETh3YZgciB051+kmfvRs7xJir33H9NObEMZcy\n5vDbRkFZTo8xD/6nCsQDhMIwLS9lCRNIc4Ixl7Q7+Dv4vV4xMbXGDUwJC+045xAXeGrHnLeFLfrK\nQtCOeZ1hEyPbKPSe5h3x/hE+VaKbcLwxQ9qWM/wA0MEKA53LZnwn3CIr4lqyUfD6sPTGgZey1Fdj\nngaNrPxJ9Z9MWjSb4Bnz2XLMg99/95vP4YEtx/CZBBlraD8MZ2Xh++WU4l02W2POHLJq7Hyc4E/X\ndfHrnQNcRicZ2nPBNNGMXQERThXHnDqXzZaycIuClNdmBbrsBBpzzjGvYfxRGzoqSZfo7wALDh6V\nshRNh2f6Ixw+zvbPctwDu7yqqBC1AezTssU7hK2IqMw3vOSoPvNTrYkApipBx9TPqIYQY64YK4bA\nmOusLGco2MBupLMiOuIFUaOVkjFvp455hYHOGRmuuqGMQUm68q4XY16qs5SFjlkWCAvIg6JkYHIH\nFixbT8ecShdaoUgCVwgl4eLq+UOncXS4el7tfQMFHDylzm4kY28PD03Gbgc15qGsLMItiTpIBn4c\nNL7SKxtr1cZcOF1i+PiHt5/EJ3+0Ge/46nrpOXpPT2HVxkPcPaqeQyMhaszFBTB9Fs2XstTOALN3\n40lZgs+jdmDoYqSW3Vm66yhzzFUa80mBMbdjEjWtkpXFcV3f2bYV8xGdw925xJhHpkusv/SOSn7S\n7FixWKzFnfnQ+VQQ4wKUjDlwZhQYKhQKuOWWW3DDDTdg2bJlyGQyuO2220LHPfvss/jEJz6BN73p\nTWhvb0cmk0FfX18dmtzaaIbGXGS4iuXa9KRsgLZlDSytOOYDTMqSM5AlgZ6y+6uJMa9hoFDDcqoG\nKcvYdBkP7i7g9EzwHPO54J77hB0KFZgjvrS7HUB985hTx7wVMmzYKVmS/pFpfPw7L+HmH2+OPG66\nbOH9d2/E++7cqGQiZfEJSdJ4UidOlLKIzo5qkdVsxpw5ZNXYrpIoZZHYhI37hyLP8Z6vP42vPLYX\nd63d73/WqBSgUWDvmcnspgWJWFrWeqxoo3+8toUGDZKPqtQZBSplof3OcdVOSqlOutkSx5jLNOby\na9AaEkWTz2MeyZjPYoGhmbKNlw4PV3YmSJsUMU/UyWQfz4UCQ7RZISkLue+6OeZ1YswXVXbEHLc6\nsy3uuquDPzNnRvDn8PAwVq1ahVKphJtuukl53Lp16/Dkk0/i4osvxrXXXltTI+cSAo15Ix1znjEX\nKxMmLjDEGPM8ZcwrUhbD4BhzqWOeWGMe/F6blIVozGtgzP/259vwHz3juPPFIAUdvae+GOwubQ97\nhmnTJX5z/UF8+ZHd3GfUMY+Tq9l1Xfzilf6qafXSQhUkVQ2nJ70F1FAheiFF71f1HGXdnMVDxEGJ\naGFFd57dH8udLeogxeOAZmnM40lZROdINmFWe2/s+b5yZNT/bHI2GHObl7KEGHMrnZTlSxtO4+/W\nDmNkJv1iw6yRLaTnsF035DioFntcgaFaHHPKmE+VQ3OHijGn0q6iaQtBq3HzmDdXdvRXP9mC/7rq\nRfz7hkPKlIL0d16r7f3kGPMGEiT7Bgr4k/s2pbLfsRlz0odqiR1JOxcwiIw5UL1Pi+9JJCIYxDzm\n81bKsnz5coyOjmLDhg24/faeUC6GAAAgAElEQVTblcfdeuut6Ovrw0MPPYQPfehDNTVyLoE5mo1a\nTbuuG5oci2IGhpSOeVvWwNkLeMc8n8twLKQlub+kK29VCeSk4BzziVJq47J+X5g55BzzmIz5jOCY\np2EXXdfF15/Yh3uf7cXwZOC8TlDGPMaEtm7PKdxy/3Z8+F+eTdyGOOClLPGfe9wdJcpgq2ImambM\naSEO4VysfSr5BAOdnJsb/FlFyhKDMU/y3hgalQI0Cn4e8zjBnwmcpaEpGw6A0Roccy4jTEpHjb0b\nR2ByAXWfqhdjXhQcfHFuUQV/8ukS+TzUUTtHYmGYZmLd3lMAgO8+2wv6qlSabF6m5N1TmSve07jx\n/sttx/HU3lOp6qHYkgVF8Ld83q7lXVgp5wIGtshbxDnm0c9W3OWIYsz5POaJmzcrSOyYZzIZZDLV\nJz8jAXM1nxDk9GzMoBVTIwLhtHyJ0yVWOm5bzsA5FRkG05jnDYMrviILBkqcLjGiAEIS0MClsuVU\nTSGXBGkc80DK4jnmk6Xk7TFt1zce1HDyjHn1572jQUw5Q1qWRNxRchwXm4+MhLTL1MKomEgpY55N\nImVRG2wxE4hSY15DEHQasD5vO27kc4+jMY8rvaDmfkpSHbLRCC2STJtbhHMa8wTvgL3zWiZrznlL\n+f4DKUvYdqsdc+JQ1yn4EwDGBDkLs8+inaa2rWja8dMltkA2J9Ny1FIWBaPP2s1JlxrYfmb702T2\nshz1/EqbLC7K0sLmnlMKxryUnDEXYxVU494whMqfc0TKMvuVShTYtWsXnGanvjJN/2dPT7qcvSNj\n4/7PtOeIwp6hgEU1MkBPTw+OD45yx+zevQfDC+K/2pGxCQDAyeP9ftT54IQnl7HMEnbu2O4f27Nj\nJ5Z0ZHHkaBBkt/fAQXRNxi8+Qr97cvAUenrCi404GBoZ4/7etG0Hzu2uT5emE9+u/qFY75K1Z5E7\niWzGC9J9YP0mXHZ2W+zrFokR2blrN4Yq73Hf4Qn/8+GRsartOX4ycMwb0Q9Pj4z4v586PRL7GvsH\nvJ2Ykmmhp6cHm47P4Msbh/HBy7rxyTefFZx/OpiQenbsxDld4fc6Uyzhjvufw6sXBv8rzczEbsvR\ncarbd7jvmZX3n3O9Yw70HkVPfgQiTpDn3Hf0GHq6GrsgOnkqaMMrW3vQmZcTIKdOD3N/9x7pR08b\nbyeYrQKi+0gGQVaKXfsPYvHMiWSNrhGFSW9hPDroXdd1gU1btvnZYvaeCGRsluNi27ZtscgjNkmX\na7D3h/sCW7Zj1x6MLc5HHC3HTMmz6YNDQzhwkA923rZjF86T2HLaDyanp1O3v/cof72Xtu3CyNLA\nXp044dmdUtnirnFsILh+79FjKJJ4jeGIue/I0Snye790TDUaJctGqRyM/f7jJ9DT4z0H6uAVye5Q\n35Gj6MkN4/CRoP0nBwbR01N7ml4ZTlbm9JOnhhO/W3pve/cf4P63Z+9eTJ30+uiJU4E96Nm+HR25\ndGTq5FQgrd25ew/GFiUbA4f7PTtkTQdzXM/2HVjUrs4+NjoeHNvbewQDU/IFzMzMDKaKwVw+MjoG\n01wEoDY/LwkMw8DFF1+c6Dst65hblgU7Ih9qo8Gc9KRgK0bLdlKfIwrHxgND4LheO0WNeck0YZrq\nleG63hmMzNj42NULAATbcxnXBot5ZP5hNuO9CyPjXa9UNmFmHd9xAYBi2YRpxk/hZ3Jsj536OYkS\nnpmSCbOtPitiSlQNFqxYbWTs0zkdwLUXdeCZo0U8uHscf/vWJbGvS3c/vOfq3c8E2To2Y/Qt+owb\n0Q+5SPwE77BcYYAcx4VpmhgseIuyoSmTO0eJalhLJsx8+L2enLTw76+M4dyuYELJwI3dlpkSn+mG\nfo8xZ12VATFVkvcB+pxnyun7clxQhnO6ZCKn2PQUpS6mFW4bp4+OaDcb+wAwVYw3FuoJxly2ZYL2\nFoomjHbv3mfKfHtmyibyMSRNlDFPe09Up+uN1+B/P9pRwPPHSvjKu8/Ckg61ffR3kWzbHx8MM2W5\nLRfZzqTtd10XA5N2qFjT6HQZ5iIiXazMweL4mCzxGnPa3UqW2j6ZVnC9stn8vgSE88VbZGyopDZl\ny2tribwfM+I+awVjeYtmcptC760kFuMygz4q9t2sm84xt2xxzkr2/elKX2o3XJ8EKJZMdBoRQcTk\nmmXLQlkRh5RxXT7nucCsN6P/ZbPJ0xu3rGOey+WaLoehLymfT858AIBb2YR3kUl9jihMmnyQYzaX\ng+Xwk5CRzUVe+3vbTqFku3j/5YuwtCvrG9XOfD601ZPLeveRrUzO3rlzyJB342ayie6VfhcZI/Vz\nMoX7pu1wXBeWA7QlkDaoULLdWG1kpFFnWw4fubodzxwt4oVjJXzyzUbk6p8iQxy9DHmPVAbrxOlb\nmeAZN6IfuuT8DuK/w4zhTRSW67XLqBgtV+gHBn1vVfrzJHFcctkE/YkYfsflnxPbcV9QKeZUdhXP\nnD6HTGPGPAXNBugaWeTzchNuu0K/l4wzekxUu6mPW3bTj9e0cCvtbG/LoS2bQdl2YSO4dxv85Jox\ncsgrdhIoAplGDfaevH8YQT+dNh385z4vaHzHaRvveU2H7OsAaJyN4Y8HHwrbapF3l6b9v9pbwHe3\nhnd3Ji2+DzNbLV6DkJCwXIPTnllORHuM4P4yRrJ5o16wXXAacxgGmTf444JjvLa6dCHcwPHuVB6o\npbI7Ud8VbARFlthS2oe8eT1dfQyHvPyMEW2rZShX5vHu9hyyhtd/MhU/g7tOZbwamYzvZ3nXzMLN\nyAm5jJEBp6wSdtKa0f/S+LEt65ivWLGi6Y55T08PTNNEPp/HypUrU52j6+UXAZTQ2bUg9Tmi8Nzo\nQQCBQX39G65B+7bNAILtpCuueB0uP2+h9Pum7aD0U092svyyK3DpsgUwnnwagInXXXGpl05pY7AN\nvmShdx/5B07CLNt43ZVX4aKzu/Di2CG/HRdceBFWrrww9j28UugFtnjfXXLWUqxc+YbY36Uw1m8E\nEMhgLrn0cqy8yGOn//S+TdjWP4an//d1vjZViZ9Gy3AcZGK9y9z6jQBMvO7yy/COy8/BV557EkOF\nEs6+8FKseNXiqt8HgJPjM8B/ngQAXHrZFbj6Vd62W3b7KwC8ib6jq7tqe846sguAt83eiH64oOcV\nsD7XvWBR7GsM5gYADMNxgWuuuQZbJ/sAjGHBgoXcORYMTQKPeFVXL738Clx5/qLgJML7ooZ3yaKF\nsdtSPDwMwAv8dYV3bFeucdH5S/HCsWNYsGQpVq5cEToHfc5nLT0XK1deGevaadGx5WUA3uL80suv\nxCXndEuPa9/0IoAiskYGtuPivAsuwMqVl/Lnev55AN4OnPjMPMbOewZZIwtUmNOzlp0fOk+j0faU\nN64uv/RSLNg0gZGpMi657ApcUbFx+8x+AIEk4sqrV2BJV3X5mPNz7/4y2WzqMULt8WsuvQwrl3ty\nrId7TgDwpDdvuOJSrLz6POU53AdOArCx5KyzcfHy8wAE9pfaNAr2fgEgm2tL3P7f/emj0s8HrAVY\nufIa/+91g/sAFELjAxufAes7i85airacAezx5CDZtg5le7ZO9gLwJH/nXfAqrFz5mkTtrgnEbhjZ\nwPU599zzsXLl5QAAhxzD1bWotPUFMu8tOTv93FUNC3ZvBTCN9hi2XoR7v9efAODCi5aD9qfLLr8C\nr3+1Nxd1bN0EZsOvvGoFli1sT9XW7OPDADzC5TWXXoaVF58V/QUBHXu2ApjCay9+Ndr2TcEq27ji\ndVfh4qVd/jGO4+L//rfnkDUyeODma9H10ktg/e9Vr74QpdNTAMI1LxZ0d8MiktcFCxchn8/X7Ocl\ngeM4KBTU9ThkODMjNBsItm3SqIhzMd2P7bghKUvUpWlGAxakw4LW2nNZtAtME0s/J1blqiX4k95D\nLemLxO16+veWo6MYnirj6Ei8VIdRiBsYw67PniELZpmYiR/AYyoqyyXNY97oVGSqIKlqEIN2AjmB\nEKSUIDcuDcBLm5WFy/1L/mCLumlF0GNUusRvbziE//f7L9etwh7AB9ZFZWZhbemqsGCyjCFRwWs0\nCw0f/On1Zdd18ZkHd+D2NXviNbwGMFuTNTLoquxg8CXhhe3pmMGQdQn+JOOVSoPW7Dzp/14t4Iza\nVPFYVUAxlTTVY6558yWeM7Vu76CQ8YL95K9Bg4BLFl/5M2o+4LOhND6GzHFc/K+fb8N3n+3l20Hl\nDWznJOI5suNp8Gcjs8qwviQG58ZBVMYs+h5phqVakjDYNQb0sr7kMeaesRED/k+Mz6Dn2Di2HB3D\nVNmWBH/Kr+u40XndWxXaMa8zGp2VRbTTjht2zKMMBp1wmcNAK3925PjtLJblguUy99NB1pAmTqza\nlRbifdN2BLrN2gei7bixUjHStJNAUDAhbuVQQEi/RvrQ+AyvMa+GRhchSltUgk4UthPkbRb7bNps\nJ7kEjnmZxLDQy1ucY86K2igcc66d/DG3r9mLp/cN4dHtJ8WvpQaNq4hy+H3HvCKhktmEqKwstIgP\nfR4sn/v+wUn89OWj+PaGw6mzkcQFa3vWyPhFhjjHUHg3ccaH67p1cczpO2fjoGTZWL83SMFazYFj\nz89x3JBzGCsrSx0cxHddsQwL23M4PVnGtv4gKNCvZB2VLtHkK39GLRgdwaFqNPafKuDBrcfxb+sP\ncp9Tk8XaFDUXMcevWZU/A8c8+aKe+h7iGKdNpiRdLffCpUusIY95V1sW+crcKY4Z0fEWM7uprisu\n/lq1KJSIVFKWNWvWYGpqyqfnd+/ejfvvvx8AcOONN6KrqwtDQ0PYsGEDAGDHjh3+95YtW4Zly5bh\nXe96Vz3a33KoJ2NeNG08vW8I77j8HH9CkuVbnjHFwae+Nl0ls9W471BKorKZkxnFmCfNY67KG5sU\nzGh15rOYMW3pJJnGUMhgOa5fbEYFNlkyxnyRz5jHd8xVxSEmEhYYavSkx1XIS/CMudRaEY45l1Yt\ngeNvJHHMFbsT9PdFPmOuSJcYY4Farwp7AM+YRy2I2TW723IAStL+EEUeUMeXXoftHNACUSXLQS7b\nOI6HOubdzDEvRzHm1Z+3qtpjUtCxyK47Nm1yRbGixqJDdo2kjLmqT5l0HKXfsWRY0J7Du688F7/q\nOYG1u0/hTcvP9o6ttMd1vcUMy3bDpUu0bCx0SGakiH7JB+I13klizmdoV1nCmEfNRbY0j3nj2l/2\nF3nJ3i1dcALhsUD7Ot11quVdpK0C7bej8o6623I+sSK2uyzsVIjXVI0BsT1zhTFP5ZjffPPNOHLk\niP/36tWrsXr1agBAb28vLrnkEuzatQsf+9jHuO/9xV/8BQDgXe96F55++umUTW5tsAFfq2Pkui5u\n+uZz2DtQwP+6/gp86r2Xc+cPrhdmjKIdczVj3pY1xNgInzH3HXM7bMSS5m926uaYe9dd1JnDjGlL\nJ6u0RT9EWLaLarExpRBjXnHMi+mkLNQ4FQjrHmcibjQzYEkmKNd18ZXH9qCrLYe/vf6Kqt+z7CCf\nsNhl0zr+SRhzVeEJ6hyxxZWq8icd53QSpX08X0entWTxEgIV2JjsrEg/ZKx21CSqKiQ0Wfl8dDqI\n7Siatu8wNwLUMY8nZYkxPjjGLX3bqMOgYjmjJBumo3Y4APU7pjsnSZ0qWZXk9nwWb7x4CX7VcwJH\nR4KUgHRc2o6LXDYDy3Y4iUXR5AsMRe3kcBUbm8BeFivznThHyQoMRc2brK1pGHPLdvC/79+ONy0/\nC3/wtuWxvsOY7qSMuXif4ligO7/UF6hl55p/JikY88pY7mrP+vZbtE1i9U6xWiub53NGJpLBb3IG\n7tRIZU37+vqqHnPdddfVVOZ1rqJejPkPXjiCvQPejsTmI+GtRfp3IimLGZ7YaYEhQ4xarjgVTGsu\nq9xIB80Dm4/hgsUduPayc5RtqIeUxXVdf3Ja3JnH4EQJZdvByFQZZ3Xl/YFaL0mR6TjoRLRnHmjM\nveMWdVakLAkYc2pY6TPmGLgYE3HSnYKy5WBsuoxzF6mzR1DQ98bkKXtOFvCdZ3oBAJ967+VSvXdY\nYy7fRlYZ12o2JRljTp41najJHwsV1Sb9Y0n/4phl8r6q7bQkAXXUYklZ2tRSlqgFtaqQEJtETwmM\neSPB2p7jpCzUMRelLNXHBzULNWnMJZU/ZwR7HDVeReZedA5V74gnIZLdQP/ITOizjrzh57mgO0mi\n9CSXDfeNkmXHjjmq125pXLA5IiyFCLcpmjEPO+ZxNfJ7Thbw0NbjeLl3JL5jXrlO0rElPvtyiDEO\nfucY8xrmSVW11LiYpox5xd8Q+7Qo3RLnEUY8tOcMWHTBESGRbGVojXmdwTp4rWzAg1uDUrzdJNWe\nLPhTnAiiVv4i0+SQwIm2nOEX7WDIx5CyMGMwMF7E363uwf/8+bbIe+PYyZSMdtl2fDaHMdMPbjmO\nN35pLf7x0SAgrV5SlmrtdElZ4DBjnkDKQtkHIsfhtswbwJh/5FvP4S1fWYd9A/Gix2WVP3efDIo+\nKLcWhS1IRzEpOgpjX+2+kpABPGNODX3webXKn/R+6KQ4SXZJ4hS7iQvKVEZVWAwc81yonQzUYRSf\nm4oxZ9vOA+OBc5dGB5sErO1GJuPfz5QkiJ0hOWNeX7ZQDNiL6rNi3xabrnJy6TNPOtb7JQHxHblA\n31vmxgXI794fBaGicdHkgz9LlqMch6JD1WiIVbFl1/YZ84huI2XMY85dzKlMEgSeVmMu9hdxp4zu\nbjZCY55OyuLZmu72rL9DL7abjinHdUMLPEYOtQvb2uJt1ZJsopnQjnmdUS/GnDoCNNAm5MC4rt9p\n2TZQ1KW54E/T5oxwW85Ah9Cx80Lwp89w2rwhBgIHdKwKQyzT9yUFHahMbrBhvxdwdS+JwK+XlKWa\nM0yfY1hjnkDKQto7MFHEFx7ehe3H+Aqn8RjzZPe987jnVP/ntuNVjvQg0xUeOBU49arHxU/MwRa4\n6Bzxxp4y29H3lWTccbsTdLHo58sFFrZXNOYKxpy2m55vkozfpMHRUYgrZSkJjLlMymIqdmcA3vHl\nPq/c18BE8xhz9oy94M86SVm4RUn6ttFxVlbID6KcHq5vO2HmMk7cQtJdwWOjMsY868cY0YBBWcGd\nSWGRWjTt2Ew/71A1XlegcmynzfA9RtkW1m66mxDXmWV9JMk48TXmCbOyVJOysHst207NDjWDaNOT\ngsWtdBGNufhsxYWo6JhTxpwilO1rjjDmLZvHfK4i0JjXZnRoR+Qcc0nwJ9uu62rLYqJoRTonvMbc\n4YxFW9YI6WFzImNuh40YmzzYT9N2uEAhERxblXIBwxyUTAb+9rYM1QxOXEfOst3Ie6ITKDMOaRhz\nakg/86AXNP395/qUxyjbS/pfVLtFxJ0IOA145VqHTgXlyb3rh6U/IcbcL/KiZszpZFPNriZyzKs4\nIFkj42u0VY65JVmgArzzUtd0iYmlLGrGvMyxvZ5MgUEV7Mqew+B4oFNuNGMuC/7knm8oK0v1PsDL\n6aq3wXFcqUxKlglK3MGM6pP0vXhMoHj+8LO1HZePZ3DV7ZOhfzTMmLfnDJQsGWMeHhfi7lHJciTt\ndtCeC49/ruJmMxhzRd+cKofvK/I91ZCVJXDq4/sE7Dpl20n0bmmMkvd9/m/2+MX0r2kdVleorCkb\ne88dPI2N+4fw9+9/Xci/KFuO39+84E+5lGVGdMyFfsTej+iYi7fVhHjjukAz5nWGz5jX2AMoI0wD\n/0RHtmjafudjk1aUszstaMxFhzJrZDhNLCttnfXTJYaNGHXIAW8wVMtEwJDWODMHsiOXlWaTYajm\nxMZ1Kn7xSj9WfuEJvNw7Iv2/uMAB0mnM4zjdKsfjc7/cib9f3YOy5aTWchZjOpGyrCkHiWOuuqY6\nK4twfgWbUzX1XIJ7VeUxZ9fzHEHmmCuysiikLByjmyIXsQyO43LXiBP8GaUxj3qu1RnzwDFvlsac\nOubTJfXOQfKsLNHH3rV2P37zS2vRd3oq9D8uvSnTBSdhzIVxGiePuchYV7uGiOMSxrw9n/WdGpXE\nK2DM+fvz5iD++qo+UY8aFmXLweYjI7HSdKrs+5SEMY8O/uTnOCA+429KvisDL9+LN85FiClbVYy5\nmP417Twsfk32Tv758X349sbD2CSZO+kOfmdb1vc9xPNQx9xx3VA/8qUswmJQHD9aynKGIshjXqtj\nHnREaohFw02ZPDYJR0tZaLrEQMriZWSplL4mnTusMfeOl2VlkaUOk6EeqcrY8+nIh3XxFPVyzJ/e\nN4SJooVNfdGOeVsueI6psrLESYUouadC0cQPXjiC+zcfwz88tCN1vt00jLmXpcHmijmprsk53I4T\nTIrC8VxwaaOkLFykf/A5a1POMHzG2bRdKeOlyspCd7mSZi1Stlc4j+pd0a1else8WrrEkF2JYMxd\n1+Uc82Yx5jkjg+6KjZssRwV/Vn/eYlaHKHxj3QGMz5i4c+1+AMCaHSf9gjWy4M+wxlzdHktwguPk\nMZc55kn6vSzDUEc+2C0tC2y8eA0mdWF2t2g6sdM88uM/ne1ftfEQPvqtF/CLV6IrNnttUzHmYRlX\nnJ2NNBpzdpzjym03ABwZnsIbv7zW72NUTpRkfIUWqZbYFyuOudCH0kpvRWWArGgZIzVkuxesL7Zl\nDbRViEHvvGECMrhmmDH3+6RQIDEqXWQrQzvmdUa9NOZKKYswrhmDlTUyvkMd5byIUhZZDnPq6Ob8\nrCzxGXP6mQy2hIVJCjb5UW2kDNUc3WJMNoK9DxV74RdpIlt1afKYRzkVjE2QGT/KPKzefIzL5JPE\nGMWVXXDbl46LA4OT0kkcAO5ZdwC3P7YHruvyVeLsYOtebCM9jt5vNcYjUbEjZfCn97uRCRa7gJw1\n58dB8OwawZiL51G9Kzr2uvIVKYskbRoXeCg8NyVjXrYwMlWOzdzXA+wZG0YGXdKsLPz1mQ54qmTh\n+8/1YoykdmTgJSTx2sGchpt/vAVfemQ39g5MCI6593soK0vEBczQeBAZ8/B3WWBxN+mbKulkybIx\nOMGnR5TZZmpHeekY6SMuI528/zMJYcmyQ+1W9Yl6ZGVhGvmT42HmX4SqciZ1zOPM2Wx8pMljThdm\nqvlo+7FxjE2bePbAUOg6iRhzMfhTaCN7neL4Tu2YC/cjj2VRk5V+caEKgeBnZRHOS/0hrxBX8D/H\nDfKYiwUSVQuTVod2zOuMeuQxt4TAjGlSglZ0TNiKs4OsNqOcF7HyJ5tMqHyFBoC2iXnMJUbMT7tI\nBkGUY14PKQuTXFRzzKtp/WcUDogItqCpVomPrtjTVP6McswZAy8zfqIzkCSTCUXcSYB7h7aDvmF+\nm5/2kzvX7se3Nx5Gz7Hx0NY9m/hlaUAZkpTBrkvwJ2NoKzEXrH/JnFXav1TBn/XSmIsyo2qLRIAE\nf4YcvugJXCXdcV2E3nXDGXN/ByNIl8hJWUzxXry//+3pg/jCw7vxtSf2hc7JbYXH7DJGJsM5qmPT\nJqfpZeMylL42YrEo7lqIC1RqD17pG8H1d27Ar3cOAACWdLUF31XcxF/+eAuuveMpLhOLmEoT8Owo\nmwNUO0nibjCTFZVMJ6TlVTHD9chjzvpunO+rpSzhxX6sPOaSmAIZ9g5M+EH7sgDh8Pkrc6i/+5yO\nMQ+nS1RIWerGmIuOefg8rE2ya7DUm92VnUlfyiLM2zS7ju3yBYUsOyAZRMZcdf+tDu2Y1xn1YMxl\nLC5jSUQHhnXsjnwWLD5E1flOTRR5xtx0/IFEK/fJGXMhj7kkGwUdBFHb9/TRpNV8MWPVnjOkQUYM\nVRnzmEavmmMupkoEAsZ8smRF3ufhoUk8tPVYiMUUsbhyPscN9y9VcCKQrKhC3OchasBVzojoWIgR\n/KoFpyrSv5qUJUnQdbUte7YYZcykTN5BL8elS4xgdNMizJhHLxIzGU+iAIT7S7WUflH96dAQ75g3\nkjF3SWo0I6MI/lRIWZ49OAwAePFwWH6WRk6XMzKcXcsZGZQ4m+edJwljTh0Zxwkz5tQR/MQPXsGB\nU5O460lP7sDsQdQ1Dg1NwXZcTmbG3tfSBYFj354LFqB8fv/wAp+1mb2Lsu2EKzUKfw8VSvjxS0cw\nTnYP086RPgMbQ7KkDP406T1Wb48t1ZjLj7cdFx+4+xn8zr8+h4miydmkki1vD7sn2e5zkvElzh8i\nY8yaLJIMaRdJof4qsb8yfT4DIxbZIjFryBnzUPAnt2B0/GuIvoD4POYIYa6zslTD8GQJCzvykaws\nRcAqJJ+siqaNjnyWc3LacgbKloNCycTirnzIgWHMVkc+60duywzGLzb145YHtnOflUiQIK2Y2MY5\n5nGCP1kRhxRSlhrTJXaQoCUZqulN47KZ7J2IwTWFook//8FmnL/YK8xD86iyHNiuCxRKFjeRUrzn\n6xsAABlkItvLzgd495U1gmupJiAg2TOOOwlwRSUcJ2QAZcZ4W/8YLjyrKzjG5suRK8+fILVdksle\nNcn6jnklVqCrLYfRaVPqrHKMeYOzsojnEYMMg+OCRSJbWIvvJ5zSj3/vKsYcCAcPqtohYrJk4fvP\n9uKDb7gAl527INZ36OukGvOpcnjh42UWcWBaLgpFEzuPjwPwgpJHpso4u5swzJzGPFZTkM1mUCTM\nXdbI8Ayqz5jH3z7ndpCEDBcA30fF3b2FHTm/0qHqGqaEgWXPy0sF6r3LjnzWJxWqBX+yNi4k2bCi\nduwA4L9/9yW/YB5DWmeQPfN4jHl1KUsixjxG7A4d++PTphB7Ff2eZI55IsY8bvBnWWTM0y2uRbsh\nY8zZPcv6qJ8qsdKX8oacMRfTJTqCD2EpGHMROvhzHqB/ZBpv+vKT+NA9z8T+jiw4Mg7ue64XV976\nazy+a4Bjg5kcoqBgzCd9xtzwHQmZgfnsQztCn5Us228vrdLYzklZKox5NpnGPIr5dSROkApF08bA\neLiENA3+bIsoeW5aDmCekegAACAASURBVF7uHVHKSVSGWwQzZGI6qlf6RvHC4WE8VCkI1cbtPGR9\nxjKOznxT30i0lCWCIStGMJxJFolpHHNvK1HujNB+sK1/TJmVRWwi75gnkLIkWISoGHP2bNmY6JI4\ng7L2qLKy1CuPufhulFIWktM3WFCrJzrv//KdOBnGhb4ct8/cs+4Avr52P95354ZYxwN83zVIVhba\nPvZ8KYP7ypFR7p5ozAWQLCsLQzaTCcmJZBrzRFlZqBPsSII/JVVo6d/s/arsRpDmL0yk0PN1KBhz\nOpzYWGVtpoXvxEWr2B7RKQfSO4Osf8eZY+NkZQnmNPV5/JSHnERQ4fSTsZ/JqG0EhUUYc3Hn9Nsb\nD+FOiRxLBvH8Ica40hZxfKeNTxffgVRjHrGQ8osLtTGNOevPaiJBlsfcJDYvClrKMg+wdvcgAOAA\nSQNXDWysJmUDbnt4NwDgUz/dyrHBCzsCOQQg2XIuEcbcd8zD51/QEd4cUTHmHZQxr3zOzi2T6vi6\nOKu6ARK/W8243viNZ/C229dxqfgA6phnI1fJqzcfw+9/+wX8/r+/IP1/XI05a6a4RSsyRWJbkuQy\nd6pIWdi5AGD93lPo6Q8KD0Ux5knmv7jspxgVrwo6oob62OgMTpBFFueYV376mvOUjnn64M/g80Bj\nXimupQhIYvfAwOUxL9ZfyiI6GdU05m25rLJgRzW5RRRjLiswEwe7TozHOo6C9l2PMQ8Hf7K+yOyW\nZTt48fAwd55XKtmURqbK+OLDu7H7RFClVsaijU+b+Oi3nscPX+jzP8samVB2CBkZEc5jrn7/XCyI\nG06XSM+/sIPfcVvQngsF5YuQ7VwxG0Yd8xypYcGnEQ1+H5kysetEECfSljN8TXDIMY/R59MWtQl2\nAWpwzMv8cweCZ0jjrYJrMseZf/8y0GQNlu1yNlA1L9K85eJ5H9sxgHueOohTE2GCSkQoEDrEmHs/\nxbGYmjEXpTOSZ2JGkJVTpLgQEJbMMkSlS7SdYKcpStYKpN+hbza0Yx6BuPIVCmYIXTfdtkk+a3Bs\nMAt2YrnMxRUf04p15rOo9GnpAJAV4SmZdogdBHjGPJ8Ts7KEB5lfYCimxjxJVpbDldzBj+8a4D5n\nOvyOXDaSMWfaShlj450nmcxANKyivEBsS5LqnzLmmYJOpH/906340//Y5P9di5RFFshbDdU0yQHD\nxJ9vC2EuLdshbJWLz/1yJ97x1fUYnzFDjDxDNcYjmZQlPDnTc7AdKL/vV455bMdJPLT1WOh6FmE8\nJxuRlaVK32PwMwTljIgsB9FyiyjGXHTa4+460WDFuKCMOc0rP2OSgHiXbWN7/zNtF9uOeovW//La\npQDgpzl9dMdJfO+5Xnx742H/vLIu83LfCDYfGcXPNvX7n+WMDHevpsVLuFRl1KPzmNNFZ3jOoE6d\naMMXEMa8WnrSoMZEsIgWz0ezsrj+gjn4/1/+ZAs+dM+z2DvgLWpy2SC+R+wTcVKEptWYB8GE1a+h\nLjCklrIw55Ai0JhXn7smSwEJY9ryPiKCVgdVHSPuVMkQIkgkUpaZso1fbTvBH5fyXYSDPyWMuZCV\n5fFdA779ZP2mu11kzAUCrEwZcyHGyVEXGBLRhGKzdYHWmEcgyuGTwXHc0JZ4W8yKXQy5bIZjgxeK\nUpYIjbkL3sBQSB1zjjGXB3/mDTGPuYQxT5guMY6UZWC8iHMXtvt/h9hCJvfJG6kWUMF5k41U0TkS\nvx9mzONnZvG0cur2sAIMzNCdnvTS1rXljEjmv2qKQRqcFJcxj8nAig7h2LTJHcNO47gufvDCEQDA\nz14+ysl2ygkY87QZaGSMOevzfuxGJZf5//zZNliOg/dedV7oemXbQYeRbZLGPFrK0pYzlIxqyHm0\n5XZFBnERFvf+lpB3GrcaLZ1IaYEh1saFHXn/mHbiWLLn//4V5+GFw8PYdcJLbcjqOHBF2yRdhvVn\n2kdExtx0XL56qpDHfGF7DoVSdCVmLm2jEzDmWSNT2aIP/h9yzNvz/sJLyZgLUhY65sRdVFqV0bRd\ntOUynO0YKpQAAEeGPbIjZ2TQkTcwWZJJWaqPw9Qa87pkZSE2RcKYiz5wkjzmYg0Dzr4qpSwVcqsS\nIyFDnHoY4oIoHPzo4rEdJ1EoWbjo7E5cuKQLLxweTr1IEhdHMumMT75UFnz/44ebAQBve+1SJWMe\nkmoKmbnE6uG+lEWxe25kKhVyNWM+95HPBROHzGEanCjie8/2BjKTiAC22NfMGr5h78xnCWPOHHP+\n+CmiMTciNOaiPhGoZGWRMeaS4M+QxpxmZZE55jGzssjY3O9sPIy33b4Od/x6r/+Z6Hj6i5dctur2\nVRSimGYZwkVe4jHmcdgOx3GleYsZutqyITaHORhRcoIkzmxaxnxGEUwUYj7EIB6frQqOmSrzeZGT\nMObJKn/KHX7RMaeM+dh02SuT7QJjU2boOVx/1wYcHZ7mNeZpBZwCxEVgVSlL1ggVBmOoVjZelccc\nCJfzjru4pcHPdIEWBY4xz2Q43TyzfT5jTipXsmdzxfkLsaA9h5Ll4MDgpN8/+EVZuM+wmA2aiSdr\nZLjnZtl85WQxjzlbRMTNymK7QbaJDrLIYJBpzH2pUpWgQjG4EPAcewpq99l1Zc+GLQhzRsCYi/Y5\nafXVJPDTJcZw/mcUfZMOHXFOE8vG02P44E/5ualjbtpiyfrqUhZV5pZCDHJHlBDJ0gUyie7vvfGi\n0LyeFCHGPFRwyOGOpccPjBcDxpxpzFVEQlk+b7DzBhpzuS+Qr7KAbTVoxzwCbVkS3CJxfP76J1vx\nxUd24//c72U7CQVCpNg3yRNWpp1ozNlgFw0l69jtRGMuG/s0NzmDVxjCO5jq6uSVP/ktcZnGnJuk\nYmZlEdnczUdG8I+P7QEAPLr9pP+5KodzRwLGXLa4qsYQi+cW70tMbSkaBsb6H5OUwQ61z4mWsnTm\ns74hZWD9gjFWsg0aqvf+8x+8gm88eYD7P2U50jrmofRbkqAzEaYdVP6k5yuavGOu0oLHaVfU/9XB\nn97nzAHMZoLJYpQ4lIWSGZqY+kdm8Mttx1GoImWJk+pNRIgxVzDV7HOqARafSzhAkW+PqvInEA6C\njcuYU4L8VIV9rQZmKzIZb+cikwlnZhGlLJbt+m3qyGfx+lcvAgDsPD7u2xvVu2dg9oY6WTmRMRek\nZ0xfy45hjHRkHnMx+JPp5X1ZTvD/7hBjHkdjHox9gL/vD77+fABBdhWOMbfUjjlbeOSMjM9Qin0i\njmOeZn702ha2GSrE2QFk53EjHHNL0m/UUhbqmDvcAkKpMffboI57KqRizAXH3AHGZryCW69d1q2M\nQYmLcIEh/m9R+kOf2UzZDtIlVvqgUspCCR0hFsMmUpYOBWPO5nHNmM8D0PEpGywvE90iEB6oaVZn\nuawRFM/JGT5LwnRrKoeoM5+NLDAkMwglopGkjDnt3GxiZwNY5kgxx4OyvZGMubDapfjm+kP+7zSl\nmsjKBUx/fMdcxlpXC1zrEM4t3pf4fXEr7aoLPKdgz8kJVINnYKKkLLnQpMGMNTNcSxe0h77H3tme\nkwU8sXsQ31x/kLuO6BTHQZgxlzOwURM03ZJ0BIMtW/jJrisiarL/p1/vxW988QkcrWzFc4w5OW2g\nNQ0X1xolVSQLRblMobMtG1mZ8uGeE7j6c4/j4Z4T4lcjwcYZa0/VKrQ5w19Qh7Mc8N8VF0KRjHlo\n9yqeg0Un7aG4jjkb58Sr7xaqf7LXyDHmZvAM3vDqxQCA7cfHpA6WrPWsP9MFliFozC2H1wMzZ7aY\ngDGnwXI07ZvMMXcFp2JhRw7Zin0emiyGxi7NAc9sMxtLWSODlRctwaOfegc23PJu/zPWtwLGPNxm\ndp1cNuNXWhT9HT6zi/z+0+p9AylL9RPE2REVs7KI5Ac9hqvUqnivlNk2LSde8Kci1Sp/3hiOeSgr\nS5gxZ+O3qy3r24f0Uha1Iw4gVJCJHj9dtv3dN7bYVjHbfFYWvqCV7bg+My9W/mRgO9lzhDDXjnkU\naJ+W5TAWtxbD2zppHPPA+Ms05qHgTz8rixFZYEhWtEitMZcx5hGVP4XtUvF3EVyqMkFCwIK0xPsQ\nJx32vaxRPeCDYd3eU7j3mcPcNas5Fe3CTkM4+JP/W5SyMMecZoFQwY4lZREZc28SYBPQORLHnD3v\n05OeM1S2+UqdlrDdGCe9X6jQlcCY+UxdxORp2a5vYOm7njHVUpY4jPhda/fj97/9Av7yJ1u4e3nu\n0DAKRQs7KvmtVfmaLWGxShe8VIJRKFrS+yvbjpCVhe+7f/3TrSjbDr7w8K7IexHBxgCLW1BpzP08\n5hEa86isLNVSezKbwybTuIw5XWCdKlTPMAGEZUUAQkWGmONHNeZBbvMs3nDhEgDAjuMT/vlom6X2\nUvlsKWPuCI4ac8y9nwsqAW1RQYr0fzZhzNkCn6ssKrxDjzH3jvuT+17B++/eyP1fJqFgfYbZqRWv\nWszldxerf8qcasqYqxjKOLtwaRnzJFKWOESDSDbJYstkGnPVTshkSGMu3/2TnR9QB17HkbKEgz/5\nNrouiGOe88nHJI6547j42uP78OTuwURSFpo9BfDmDJExD9J/qu1VWdDgU8ZcpTHXUpZ5BNrJZMFQ\nly4LGF1PFlI7Y543DL8T0qwsk4rgT98xzxEpS4RmkkKdlSVc+ZNu54vt8HOvEqMQJYkQiwMw7B8s\nhFJN+e1XMHyGkYnNmN9y/3Z8+dE9WL/vlP9ZNUZFdPpFwxeXMT8+NoPxKrpaL12i+rl1tWVDjDkL\nCGLv95wF4cwX7FkNTQYsJc1SUy3wr2w5+Isfb8YPX/SCMykTF3xHkZVFEcgE8AyKLSzC6N8qB1qG\n05NlfGPdAbzcO4JHt5/ElqNBFhi2rc3uL27wJ12UjnGMeaAxv++P34y3vubsSvt5xpn2GdpfLljc\nGXkvDC8cGsbuExN+e1ncQrWsLG05tcY8Ko95tXgI9q6ZVCMuY07fY2LGXOKYT4sac4mUhTLme05O\n+PdN37fMTMvsguPwFW7FPs8W1b6UJQ5jrtjqZ8xfOaLv06wsQBCUyUDHtS9lsQOZkwzMKY3HmId3\nK9vIrgWDiumtNStLHOIrCWPu75RJGHPLduAIjqWSMS/xcxg9TrWTTJ/XlIIxVzHpFCXh/OL1bNf1\nZWo0ZinJu3hi9yD+df1BfOIHr4TluxFSFpq1CvB2pdgYEvOYizvHdNyJ90S160qNeU6tJmhFaMc8\nArSTyaQslJ08XCl9zH0/jWOey/gOBM1jPqHMylKRsrRFS1lkaQE9xtzr5DlOY06zslScE3/AhB0p\nIKy3TJPH/JU+vnS26KxRsK8ZmUzi7DmniYNaVcoiMOai4xxmzPnjF3fmceFZngO2u4qcxaomZcln\nQzl2RcZ8aXfYMWcTzvBk4FTuI4652KfECeDhnhN4bMcAbv3PnZXzhdsmjo9YjLkTaMzpYaKUJU6K\nMhXoxFwSpAaidt3PoU4yY9CfjiNozImU5cKzOv1F2Dhx3ul1AXA7QqxabBRGp8r47999CX9y36bA\nMe9gjrlCysKysmQDjXnRdPCLV/pxbHTa/5uC2qqximPOCisxMHaULWwWdkQvEERQ9je2xlzmmAsa\nc9uflIMCOT5jnjew/Owu5LMZlC0HJyXFymRdVGYX7EqqOYZQn1cEf0ZmZREdc19jzrJTONJjAa9y\np7iDRkHZSrZooFVSZRAda1nb2X3nspkQUdAhccxVjmbtWVmiF4Su68ZaNLLHGvQ1efCnWG5e9V75\n4E8n1rxIj6lFyiJmdJFKWfz+mQ3thMcB3e0S5yvxemJlXJ4xt/2+EWRlUdRdIGNNjPOi9kfVr/O+\nlEU75nMeoh5KBDUM+wYKYcY8RQGFnEHymOeyPivFNOZqKUt0gSHZRFM07dC2PSBIWWLkMQc8Z4DK\nMCKlLBJ2EgBe7vPYzRWvWhT6X9gxr7Q7o95OVWEZl4axipRFGOjhdInRjDkAXB1TZy6mRxPR1Zbz\ndzAYJnyNudeuOFIWwGPMHcfFr3cOYEAoXCH29bDsIXgGbFEkSllUWVm489jB1j1dhIlSliSMuQga\n/MV+Z/ejKr4hyruiGHMa68D6ysi0ujLmMwdO+7+rHBaKkekyLMfF0GTJ72uLO6s45hxj7rXp+NgM\nbrl/O25f42U6iiqCwxjzpcLuS2dlkcqeE2OEYzPm5Br1YMwDKYv3uZ9T27S5zwwjcCBlz0wuZZHZ\ne5eTBIqSgyCPOZOyxMjK4vB9m5EqvsacOFqizV3QkZOyu/65JfaY9g0ZfMY8IviTPYOckQktDFi7\nyzEczbSMuZ/6scr8KnvX4mITCIisYEEeDqK3JLZZtTAISVlixF7RY1R2IU7K3VBlWsFRd9xgp6mr\nLQgeTsIkU9lrNfmuJUhZ6DufLFoBY87ymFfOfd/zffjXp7wkBa7Lj7socky54GRSFu2Yz31YVRxz\n2sn2DRZCAzWuho52tDzRmHe2BRrz8RmFlIVlZckZQb7lCJaDQln5k0pZJNv5smuUrXjMAMDrFul5\nWPGZt1WKgtDnLxocTsqSlW9fqa8f/J6UMQ+nS4zWmANEZy5xzMVnERU029lmqDXmTMqyUO2YDxPH\nfN9AAd9/vg+f/NFm/LdVL3LHixOpaOxot2YLERVjHrXQ8NJeVc4pOOb8lrFcchIH1GlkBnymUlxE\nnLTYddgkycZTlkjEVMGfOSKpGhMZc9LHKGM+VbLQPzKNQ0PqysKsf9lOELS1qJNpzOV91ySMudhf\nhiZK0u8+sOU4/vB7L2NsuuxrzJd2832JsVoMzDbFzeRD+0JsjTlZgDMwxpz1OXYM66eTxIFhn0UF\nzKaWsphiJpIKK52AMVdKWSTBn6JTsaA9J2V3GSibyX4vVXHM8wLjLfNj6MJVJApk2ngV05uWMS9H\nsPkUMtsuq+fB2uHHLWUy3EKQXUtkah3X+47rupwdL3AFhgQpS5VdLqA2xrxa2sqy5fjX6mrL+jbu\nxPgMfvzSkcj6BQzUpoSDP8XrUTvOZ1MpFM1AY97GMgMF5/7aE/sr5+Qd+nACBuKYS7LPASQrSzxT\nNevQBYYiQFmkGTPcYWknPDAoYcxjGh5qQGjlz/a8gUvP8XTs+wcLGJ0qQ/RzmKHNZw2wPh03+NNy\nXP/7SsY8KzLmasdcltNXBpWUhTk0F5/dVfkf1eaGt+QAz4gmLTDEOfw1aszFbXwZY/6qJZ5kYXSq\nHPqfJTyLaClLVFYW76dMyhIw5sH1j45M4zuV6ocheZTABNLn67ou5yh35rMoFK3QZBInK4tJpCz8\nYsnhGJwo1rAaihIpC3OoZKnEgMABygkyLtt2uODPiaLFxWiwRZk4gXKTLvlfoWThnf+0HgCw47Yb\nQiXXvTYH7WfnXdgezZgzZy+XzYQYVVnhHCBITfqNdQdwydJuAOF4hU6BbWROTtyiVNSxicuYy3b0\nmNMa6MUrjjlL3Uf6b7uw4ydra9wdRtvh7ZDKCWLPOA5jLgZ/ilKWqIxENI+5DDTjS1BSPli0ydAm\n7CxE7VBJGfNceEGhYoDTMOa0cqms/DuFbHG1oCMXklE5wpzG0nICPDkgs2Vl28Hv/fvzWNLZhh/+\n6VuQyWS4Me6lS6w+L/KMefzgT9d1sbV/DK87byG623OhZy1ej/6fMubff64PALDj2Dju+Og10usz\n0LEo2pGwxlzo3+T/haIVZGWpMOayhab4HkNzMPm/ql9rKcs8AjWoM+XwgKKdcEKSOi0uI0A7XtbI\nkHSJWVy8tAtXnr8QtuNi3d5ToS0n1s9y2YyywJDtqDNtMBZOWflTyGOucsyLpp1OY+6GJ49OyTau\nSspiZOJnZZFdX6a9p6ge/FmdMWcLHZkjxWWocatJWWR5zHnGnFbM9K/hMsecn5BECQtDFGNeshyO\ndRBlBQxWjO1mm0hZKGbKFjd2qAQiafAO75h7v7NA2VAGA0GmFcpj7kLIyhIEf+aMjM82TpLgKoBn\nfKijNUj0zlT/T0H7DJOzMcZcTD/m34fvmIcZc8aIqXZmJmasQMoiMOadAhuVlDG3qkhZfr1zAH/7\n822cw+svwCWO+YzvmHufs3HGgu/acoZfXTSXUMoiK0xjOw7Xn0QHyqrE2bC+u8BnzCMWp1zxrKB/\nyxxcOpZyBl9siYHbgROkLAdPFfx3q2IWmb1n7Yp0zLMRjHkMBjhNVhaeyIj+vkxitVDCmPspWwnZ\nkxWq0tq2fDdzqFDCzuMTePbgaX8s0uBP2h8A9bxIn4UoC2SQMeYb9g/hI//2PL70yG4AYSdWnE/Y\nu2A7fGL/eYTUDlGBzkHiQiBKNWA5fBXUQilgzLsljDmDOPerUhZnjYz0+/S8c0XKohnzCFBDKNvi\noSt2y3ZCk2Rsxpw4/V7ZaO9vNgG9f8X52DtQwOO7BpTnzBkZImXh/0dZt/dceS7ed9V5+OxDO7j7\nUmdlYVKWyn0KejyG4amyUPlTfe/U2LNx6rqB4etoC+sUVVkkkmRlYeAZ82jjXi34M6wxD094jP2S\nBcmJUf6ZhFlZCoLGXHSegOAZM8Z8aXcbhiXsPYPY1+nznSnb3Ptjzqdo72SOqAjTcZUyAsflnQr/\nvEk15lbgbLNJSqkxr/zps+DMqSPxFSopi8Ex5hUHuiPvL3zLloPOtiw3MdPMLYaiPD3vmPNBl/S8\nFGzyyxuZEAPFnF7VzkzOyPjO25LuvF/KGpAx5l474ua+pzahULLgOK5vswDgkz/ySnW/5pxufOq9\nlwOQa8wDxrzC6laO8aUslQUMV8GY5eeOKWWRZbGyXRcW+b64i2ravOPu5zGPLDAk7Jixe8kHizr6\nf4YFHTlkMmHG2nJc3wmhC9pnD57Gj1866v/drmLMSQAtEL31nzMyfnIABlk2mYKKMU8Rg6VaqMgg\nk28ukFTADhhz72/DyERqzNtyhv98uEqwjotcNrryp1rKEhyjWsjIPu+vFK7rrwR1V2PMWduY3RYd\n8zipcqmtCheW8haneT9Wge+/1K6PTZv+GGZjRTTvonwMCEsQmY3MGWEJEgNrj+uq8+q3EjRjHgGe\nMZdtbfLbNGnzmPNlnt2AMa84dB+oVGjbuH9Imf4paxi+IyGyHNT5vPcPfwsff+vFvvFmrA+nMSdS\nlraYjPlQocgXGIrJmDMnghryLhZAxKWZ48/HDs+mcMw5mUSE4wiEHXMx5ZPIwMkmvCjGXCz0E11g\nSJaVpZIu0Qyy84iwK0FlI1MeS/lfLl2qvAYQNu4ZBNecIakMjUx4IcDaF1QcjN7Gly00iyYfMJUk\nj7nsXAC/KJohum2uPUKxIyZhoQtempVljKQVpBpztpVN6xyw68fRmFLQbVpxUgXkrCMNSA0x5iZz\nzOXPMZvN+LsCSzrbOEZUDJxLrDHnis6omUGWOQZQOeaVuAZBysLGKnv+VJIXaMxjSlkkx3lSFnW6\nRNNxODvFtPCRWVnoHOLSyp9Mqy1flC7wKyXy9kY1bsRUitWCP5ldjGbMw1IpmTZ+so4a86i87iJk\n75DJwCjYc6V2zZAseJht7hCICr9tlf9HSVlUhBU9RiX9kTHmfkB7pR20eBBrN8WkkAUl5JhXmQ8B\nvk+Ii4Vt/WN421fW+amBxYUUbQ+VFLH2inFYluNKdgHk5Fg+G94BYKCL9JShDU2FdswjQB3vaYlD\nzEe9h7eVq221MdCOZzouly4RAK48fyFyRgYly/HlCKJkIp/NgJFj4nY/O38bCRD1MxjEZMzFNEbs\nXs9f5OmnBydK3CTC8uXKwFdZ5HWDQOBcljjHnD+fS4xoTsJwRCEOg8Egk8lEMfkyjTk7h7Q0u6Ax\nj5KydOaznOQICEtZZIy57TgYmzF9g3TtpecorwEgVPVRzE5EnSVx4cL+TpqVhUJkzKNyOVcDm5xL\nnDa4EkgtnMsP/oxgzGlgJ/2dLhDZ8+tqz/n9kvUzpWOu+JzGhkwW+UnVa5NMylJhzCWOk8/gx2DM\nF3fmOUZUJWWJy5ir2DsRdNzLHPNOojF3XZdIWXiNuYwxl+2QyXZhVEQM/b4Yi2FaAbvXkQ9kHlG7\nPHT8O044+JO+J3osy1wVZsz53VcVqqVLjMrKwpCT7Mj41VeJA11PjXmSKsCyXQ8ZY+7nMSd9TdzB\nsuygmBTdFS0KpJppO/x8bvFFqJRSFsqYK8ZFoWiG2F7WTxnZ4NcYkEh2gOBddPlZUBJMnBWYkrbS\n8wxPlfHC4WEA4aws9D6ZlC9bkWUBwPtXnMddyxFSlAISKQtjzLPh98ZAd5rnpWNeKBRwyy234IYb\nbsCyZcuQyWRw2223SY/dsmUL3ve+92HBggVYsmQJPvKRj+Dw4cO1trlpqMaYc6tBCfsXpzKZeG7L\nDow/m4AyJEqcDWyROaXGRJwIgvSLYR25rznj8pirK3+K6RIvWMIc86JQnlp976JxcVx+sPuTEmE8\nRKY6YDe8QJ0krDldMFVjCGQTGHUcQoy55Pj2CCmLLSwSVJNpW0XPqWLMZ4TFHH+NQF++pCvvT+oq\niBOpWIGVd8z5+2V9VlYpT4TlyB3zssVrEek4kq11o+YW1vfpe5qpOHThbVPvp5/b3+AZcxrsCfDB\nvDnDCC2W23NGaLdELADCEIsxr7yXzrbgOrKFHA3+lG1VixMkRdbI+FlZFnfmOUZW3I1hjnm1/Pt+\nuwT7qHTMzbDzRTW/rI+XTL40d5cggaOL5GpZWUIFTVSMOflczMoyMFH0g3k78lmIAfMycDtmruvv\nBLJdS5mm+s7fX4lvfvyN3H0F54vHKCsZ85BjrjyF1B5JGfM65jEvC3NuFGTvUOawhoI/FVlZqESM\nvVueVHOkUpI4i6U4WVlM2w31X3aPzM4FNQbkjjlzpLt9xjw5Nytj98V5Z0mXtzMhZmWh9r5AYnFY\nLMj7V5yPH3/irdx3xMW0uLihWYKqSVmAeeqYDw8PY9WqVSiVSrjpppuUx+3duxfXXXcdyuUyfvGL\nX+B73/se9u/fhz2edAAAIABJREFUj3e+850YGhqqqdHNAs8UhgcLJ8mww1KWNFlZLJtnXRh8jSRj\nwwTDSvVVIcacFCFiYA4kW2HzWVlI8KfBZzV4cMtx/D/3vug7eq9a4hXPGZwoCRrzeFIWwDOwbLDl\nSACHeA66ayEyaUmKDMUpkcwgc3RVlRwB+YTHnDMZW0evX4pwzNm7ExnzCcExl+XptR3Xf1/nLGjH\nFecthIJYqLRTHmjLrkOdJVFT3yVs38dNlxhug3wyk7GPf/nuy/DBitxLdR5OylIOV+kFaPCn9zfr\nW6zvi8GzE8SxlEmq2nMGtygTd4YoxCwWLJ0gnYjZ7kh7Ltrps/yFheGPXwovHaW8HfmsgbEZb8Gx\npCvPOV5hKUsgCxB3tw4MFiBCTDenKjFO35VY7AngpSy0b4pZbSjBwMaNbHF8ZMzEyi88gbuf3O9/\nJgv2d1x55U+Z7enMk+ItEWOAjg/XDZxvdo80hSLrIssWtvsLJpnGnCFqx1aZLlGwvVF63KyRCdmj\ndkk2GdUCLE0VRr5gTfT3Ze8wKl0i7WtRGvMckUxQO2XZriQjkxsiX2SQBX++9TVn44LFHfjTd7zG\nt9diLvOiz5RblZ8VxlyS4Qmgi3umMZceFgm6wJ4shX0VIHg3YlYW2WKsm+wAZjIZvKVSQRnw4hCq\nBX8y5CVERPA/klkMyftds5H4tSxfvhyjo6PYsGEDbr/9duVxn/vc59De3o5HHnkEN954Iz7ykY/g\n0UcfxdDQEL72ta/V1OhmgXaiHccn8M31B7kVMTWqpowxT6ExNx3HXwVTpydHghcAhIIAc4ahLDBU\nssJsKjv3lB+lTdh0afBnIGV57uCwf++vqlQvPCVqzBM45o7DF75g9yEaMfrs2XNg7VJlGWD4+sdW\nYuVFS0LXTyNlocYmJGWRlAT2pSxVGPOSZSsd2YvO9hZA4oJsopIZhN2HNPjTdbnAz862LJZXUlLK\nEGYkgt9nBCmL+Hw6FIy5rF2m7Si3+WlZeC5zhWRM/fV7Lse3/uBN0sVGScqYy68rMuasb7H+yJ6h\nzKnJGeEKtO25rP9Z0eS3tMXsEPSZv/frG/CWf1yHU4Wi4PBWxkjWCEpXyzTmzIEwMr5OnmK6bCm1\nrllBykLtgpjHvJvcAx0HN/9oM66/ayOe3D3IHZ9GymIJC3CAT5doc4453z7aN8UdR4pDoyamyjbu\nfvKA9H5oW2YkUhYmC6BoyxnxGHPh/bE+Qm11UIWT75fi7+K1ohbFynSJLHgzBmOez4azYLRLsslM\nluQLsFQac4W0R4ZAe8yTTuK9B9WHA8JBlETQ+J9cNkOkUTypJvbpUOVPxbzIS3+8c56/uAPPf/o9\nuPXDV/sLCvH87PozZRuOQ2odqBjzyrvo9h3z5J65LWHMxXlPVp3VlCTIAMLjh+6O2a4s+FMhw4uQ\nsrTlgs/nJWOeyWT8bQcVLMvCI488go9+9KNYtCjYNl++fDne/e5346GHHkre0lkA3bLZc3IC//z4\nPnzr6UPB/4XtdtHIxmXMqZTFdgJNVQfH+PDPXDQu2SwvZbEdFz9+6QgODBb8CZ2eL4ox74jIYy7i\ngsWew3hqosRJT6Ic3lA6R5KRpS0XOB3i46OOOXu2rC9WY8yvumCRnx9djA2Igszhp/cmbi1GMebS\n4E8hkFTGmD9w87X43h+9GQBCWRDKlsM5sdLgT8fFCGHMAeDK89VyFrGd1PmppjHvFBhzNoZUTL6K\nkZvgHPNoxjwvxEHI7kXUmNOhyr4W0pgLjDkr0HThWZ2h68iyA/GMucNNymcJ+eZpn2JpLF84NCxd\nzLXnDd9hlrGGrP2ydImAZ2/YexEdO1FjTiVu4rumTg7tM+v3eTui33z6IHc8e4+sTapsHfRZMGcp\np3DMaXeIcszZfcQNVJU55g6J/wEClrK7LewEHRmeJmRGfJKC3TtlIAMnJyzrEd9v3KwlslgYIBhL\nwWIgijE3JMGffLpFQJ2XWzz3xv1D+NRPt/qBgzIk0ZgzwmsxSSHbljNC49TfkWDySJnGnLC9eSKZ\nEEk1UYbiBX9WJ6xoBh12jnw2SPe5qMKAT1YyQTG7yeb2oulw0h21xpztrFaCh1NozOmcxdh9kTFn\n40ysQSF7Z+L4oVlxLMcJPTMlYz6PpCwNSZd46NAhzMzM4Jprwonqr7nmGqxduxbFYhEdHR3Kc+za\ntQtOE8s0TZUdHB0toi2bwcWLgZ6eHgwMjoWOe3HfMfSc702cRcIEzJTKOHDwEHfsgUOHcXapel7Q\nA71B5b/pmZLP/PX3HULX5DEAgOMIul+LN15He3sxMuy1a2BgEPf8agTfeNGrpPkPv7208p0ienp6\nAAB22Tt2ZGLK+3l6yP/f6engWrt3bkcmk8HJk/LqhOUxjxU7MTqF7rZgUIyMjvvnEzE9w+fP7tm+\nA0NT3jUzjo0D+/fLvoat/z97bxplyVVdCe8Y38uXY2VV1jypZtWg1IwkQEhCjDa2DLZp3GAz2S0M\nWp8x2NDuNjaf3bZx4/bUbvy1Z+tr25ihaRobAUICGwk0gJQqSTVIpZorK7Oycp7eEBH9I+Lee+4U\nES+VBVIvnbW0lPXei4gbEXc4d5999nnyEGb6U4dmYjJ9N8Nnz2BoaBJJlF+u+Pixo5iZSsPrp8+c\nxdBQmv292LAf5wAYGzmvfX7w6UOY6g2QJDrn7+RzxxBOnZY+G18QPED1mZycFNdfbLSAWF/EnPGT\nGJ50MAxgempC+/5fH32C/334qYPa98+dOMnf6eJs+l5eszHG6dEQT13QZRPPX7gotfPECaHocOTY\ncdQvpotEEkeYmRyXjo3qqXzXmXPDGBqaw5nhKQCAB/2+RscuYnrW7JyNTAgqxNRCE2/7k/vw1n3d\nOD0l/953gSeeSO/fNCWPXpzA0NAQnr4gaCjT84t4/AnxzHwXaETA04cOY+ZcgHNZmyfH0+dwcSzt\naxMz6XPw4gZCLz0GADwnnS9Ojcj9em5mCkk2Tg8dOYq588JBqDhyvzuazRV04Tp67AQuLujP7fSJ\n40CSfv7UoUOY6knPOzzTwmIrxoWxdKxeGBnG00/qlJLHDz6Nyen088CVIyLnhkf4Yn/62BFpnpka\nG5XOc/L4MfhugkYEPH7wKVzokcPnJy9MS/1ofjF9B90VBxMLCQ49exxboNMaJ2Zm+XHPnkn70+LC\nAv/s3HD6nCem5/D4kHiPZ47LG4HGwhw/pr64oF3HZENDQ5ITRu3ixASmSH9ljrkTm+eQ48+l68H8\nQt06F45ckMfP5Ez67kbOneWfPf7EQfRUPD5vHn/uGKoz6bowPSWvUU89fQjj3emyfvSc/Z6nJsaN\nbZrNznfqzDkMDc1ifsF+jrOnT2JsUr736fE06W98Usz/IxNTxuNbcSy14b/cfwGPn69je20Rt2w1\nR/SOjIlxXG80rc8VAJ47mfbx0BEd/MLIMDwojl6zlY7f0+mzn52eRqulv9PDR9P+1WwsAkl6jmMn\nhATlU08fxoV5eX4aGR3DFKlRMJbNR6rRNXEmo5LNTIrf+knanm8PHcZ7/moSewdCfOimlTg/lj7v\nRhTjO98VY6E+J6ubMNnT6ezcbB0YHdGrUec9UwA4dUYcMzqe/p205HXk2eeOYygawXMnhd8wMTWF\no8/IYxQAkuaCdk3W3oNPPoVnz8sUwgsX9TUQAKJmHUePHDZ+N5X1SwBoNJqoVFw0m/n9Z7nMdV1s\n3ry5rWMuiWN+8WL6EPr7+7Xv+vv7kSQJJiYmsG7dOus5Wq0Wohxlj+W2J8/X8VsPTGJbn493X9mN\nR87NYM7AUesNgWYzHSSy7F+ChpIM1Gi1+G/zjPLX0wSJ9G83ifjxKt7oufLCkcQREl5SPMaRC2Kg\nL7AduCPazja4C5lj6SDh33V5CTb3+ugJXbRaWdsMDiMA9IVpO2YasRRJqbdi672ru+Z6o8mjBL4L\nJJFFx3WxiWZTRqGSOL2OBQDi5sQRnGwybbTEc2XIDtVrZuY54BMwtYV6E82mWfrKSVq8jeLaIiy8\nWG/IldPIM2pECXzFu3QARK0m4uzZOgZ+HCvWUvEg3hexZqvFFQp8N33PW7odfOC6Hrzvn8e039fJ\n82HHMzs0uoD7nksnWxeAryxyYdYvm9k5moxGZaBUNKPYyjOdVVC2b59ewKHROn76ii7pc99xxBgh\nl/CcVP1nMeuHC2QTXW8lqJMNWeA6aETp+G02wduMJBsTrN8wlBlAzXfFv7Nx5SRym30nEeOs0cJC\nXbStQ3kei410rqBUiblGy6yzH0cZapqg3kjbDAC/8vULmK3H2Lc6Q+OTGLFhwzpXb3IUL/QAGh1n\nCFj6bltwHfF+fEdpSxwhdB3MI8F8NiaojS/IcwAbaz2hi4mFGDOLYn6kkZMGmTua2ZxK5ycvEfSk\nBjl/qGz+fFfMd25JXmmz2cS8pbZBK0qk5F22J68aWHQbuj0k2ZwZxfa5UI2Q8X8nEZ+TFupNdLhi\nrCSxGJ/qfLDYaKLZTD+rG6pVM/NgbpMLkZPRbDZzeeAJmVP5eR02x4rzzxvWUSC9t3qjwdFp9ru5\netP6vBYbNGoK6+8AQWPrIF6Ok8TaWhEnkOYqIDb2l3k+NhKO6NJo92KjqUUHGq1I0mu3rYs0wrCY\nocwueUcd2cLw9OgCxuYjPDa8iGazKUVwmBxu1XO0fuFlfYn12dCV5zbpPusNLTKr3hOzOUWylN9n\nMx3bkoBDpPtIaVv098guX2+0pHeeXt/cn1wHiA3rHyD6ddpW8XkZ/+z5mufl02xNdkkLDOVRXoro\nML7vw10C/2mpVgmzSTQBPv30HA6ONtDfoV9/RS1AEKTIEBUeiWLAceUX4Lge/22etRJxnSgRg7Sr\nGiIIzHqjaVKX6PSV0IfvZZ3SddFJPLyZVvp3RyDaE3Lecxae813+XQDgD9+wBg4IVcQ3d5X+zhC+\nmw746ToJWyWw3rs65XmejyRrbuC5CC3HNRPRRjgZxcZP7ym0VPxi1lEJ4DOKjpueJy0vn35U8Rws\nKEoyrusgNHHXs/daN0xqtUqg3XeNODeJ6yMgK4NDNlhxAtQVZ99zgTAUtAcakmPPfSbbCFSyd3jX\n9Svwxw8LVMFxPbQSwfVm7aPqHtRaiSPdg+MKNOSeYwJBc10HHUoYktMdnLQtcYZjq6FOAIiN24zU\nZpv6N5P1GI4yyQWeaCsdIrXAxUwjRjNO+2HsiAm7HiXwSH9OF6EEjpc9m6xvsTERcN5s+nvfc1AL\nXUzWY/4cgiBARyi3mVI9YsdD4orqdp0KtSfOntcMWcjqkQsTG6FW8XnSFmtzFCcYX0jbw8Zh6Huo\nhCHSuxPWgsfPW/VdTNfpNdOH2Bm6qIShNM/UlPB4NQxS7mY9vT/TeKefsbHWW/WAqRYWI/HuJG50\nTI5z04XTJ++5VskczxjwfHH+7g75XitkTlOTFG0WBAFiWzVgx4GB4ZLlT4j+9fPX9eGKNVXu4Edw\nrHNhrMR52HsJ/bRceiNKANdHEPiIst+GgW+9L8cT3zmu3TGvBOb3xWh3cdbmvO1MJfAR+vIvOrL1\nit1zK05wYd4OsHl+IKR4s1NFdJ5XzZUTg/PW1zhj6qZjrUXa7AKKoxYEARy2priupmOe3lP2vedy\nYKxF3p/j+WipNE04iBLxm9jSF0zjPPTFO+qqeACauDCfUVha6b03Y3HuuVbavmrgaPr2nutISZu1\nMO0noSEnqgWP1xIxWeKIc7NN/Y7+EP0dHr43XM9+42X9h1BI4Gjzd9oWvS8y4MH1fCRKdNHG0PI9\nB5XQ3B8C3+NzQ0x6dRn/7PnaUvzYS+KYr1yZUicYck5tfHwcjuOgr68v9xz79u37vjrm810XgfvH\nECUJ2Dq10NIH59o1azA4uBsAEH/mHNgyEMPBpi1bAYh73rhpMwYHNxRe+57hwwCykJDjopkhLVce\n2Ie1WXJl59cmgLk5fkxPdycwKcKYu3ftxNloFDg0g5UrV2UoRBrKm/N7AExioL8Pg4ODAIBVjz8C\nnB/lzuiGdeswOLjT2sZnW2eAh/UQ0oH9e7H2W1M4MyGHPMNqB7+Wav49FwGI3+++fC/8C7MALqC7\n1oH9+y4HvqRTSAbWb+LPs/O7DwNYxNbNmzE4uBF9334QGDeHuADgqiv2497hI8CxOQysXoPBwV1o\nRTGSf0hDxlVfd8wDz8XWzZuAR+Vw8ebLtmNw20qMTC8COCc/j317sXGFHIaN4wT4THqdXZfvQz/h\nF7dOTgAQFAEVrKv4nvQc+547CCDtB9sGunB0ZBbzYR+ACXR3VDA4OIjBQeC9r2/iQ595HPceGsWG\nDRsx480AmMXGdWt5/52cbwBf0KlW1VqXdM0jjdPAQ/qz7aiG2LppPXBQhDbXr14JnDqDlasGMDh4\nOXqz9g6s6MZRZT7o7u7FVDQPQEctFi1ymxs2bgIg2lKtBLytlS+OYq6ZbiJWdFUxMz4PL6xicHAQ\nZ91hsLHZioGdu/cCSO+drWE7duzCgY29WHn6aQCz2Vjfg/svHAWemskW+hh9PT3wwibOzaQh+jB7\nR9XzM8BXxLvcsG4NLkaTwMVxrNu4GdvXdgM4j47Qx4Y1K4EzZ/hv163fiMHBzTg+Nifa1dWH7gQA\nZBrZ/r2Xo+M7DwMLC9i2fScGN/VlyF1Gf/BDAE1s3bwJg4Ob4f/jWQmRW7dpK4JDRwA00V2rYpTM\nK2FnN4B59HWlfan7X78FTKb3uXv7Vqkf7N+7B92PPorRuTk+JgCg83PDXMt9z779IjHs8+cBxNi0\nph9PjAyjs7cfg4P7AUBqv+OJd3oiOQs8OI7enm7+WW1kBvjqKGK42Lt3H/C5dAxedeUgal84z6+9\nelU/P6bv0YeAUTkkbrIrrrgCp8cX+DugVuvqRmNUX9NW9/cCo+l7X1EL8MtveTmANC8JXxmF6/nG\nufDBZ8dwsSHTPLygAqCFbZdtReXRKTSiFnbu3oPLVnXC/dIFABEu370bezPJ064jQ2DzAQBs37ET\n+zf0AgBO4RzoekRt84b1GBzcoX2+fvgwcGQWff0DGBzci/DeCdBNB7Wd27cjGZkBhsT4v2zzBmBo\nCmElnf+HTk+iEZ1F4DnGfJ59+w/wzbxz7zcANNG/eq2xbQAwXh0FkEb5ogTWNQYAvpKtq2tX9uGJ\nkZRyuW3rZvSceg7nZgTFK3EcDA4O4uGp54DHprCyfwXOzE8Bs3PS+Vav2whgAr3dXZiNFoD5BfT2\nD4Cts5dt246F4WnQ+amrpxf+/AzYHBdWa8Y2J18YAZTo4/p16fwDAJsPP45Hz53FZBQAWEAzBvYf\nuALBg98GkPbr3jUbAYyhp1bF6lWrgGdF+yuBj0VCz9m6MV3vvzd7HHhM7oNbtu/B5pV2cYD0uab3\n3Mg2ButWD+DP79iPO+/+Lu556jwqvQP448encIEw6TpqNWzechnUPnn1jg18TWIWfmEEC60mdu7e\njRPRCADRxmqti98ztd6uLuzfvxf4X/rYXbd2LbxDs2jFCTwvABAjCILc/rNcFscxZmZ0SmGeXRLP\nd/v27ejo6MDBgzrf9eDBg9ixY0cuv/wHYSyJJYpFEoipyqako6pkiKthv6XomNebMec3Vg06vMzU\nUBMtshPFosojABw9P6OdjyGvrMm2pAl+fgsi7bkOVndXtM/zkqzU5xQRGblUzcDcLWmlPVoMAjCr\noVAzqSTQd1lROSRgcmD651947CzuOzzCEwpp8MeUy0jLtavJfEUJTCryQTPSr9mSUsUePpEuBDTx\ns7cWSMnAJglOVdmHWV7yJzXPMSR/8gJDjNLCkHqzTFkJ+WtunaGn9R2a9Ev7sFr8Rn3uLMHKdfKS\nP7PzOnLioOc6UqES9o6MyZ9E5aJO+rianMX6Ik1wHptpGItSVXwXVCVJvT9OC/MEAkhtvtHilAn1\n/THnSZVJdR19jIWey4+ncyVNtqMbdnaPK7ONKVWYoGNRUmXhVDNT8mcshdBdR0b1TZU/i2yhGRn1\nr4GUkmKa12hfWFETm+48VZaTF+fwU3/+EA6flxfsBuljWhVOntQr7kVtK+XG5yWdWgsMsVLqEaMo\nWE9h1MmvKDrm3z2Zzk0vu8xcbZi2VyQy2hF2KTE4yZdcZG2gMpqh72r3znXMSfKnKaBPK0yyuVOu\n/GkohtOSEx5tcrimOgB0fu7NdMFPXRTO9nyjJb1/JudaCz3dX1DWbzZOTONClWRUjd7PnCIewebA\n3/vaUdx7aARDZ4RDnc738n1euakPd96yXbuGR8aOSl3hktHKPfmeIyVGS9+5Do+CtFuk7gdhl8Qx\n930fb3rTm/D5z39e2imcOnUK999/P9785jdfiss+L+MdITEXMWHGZaQIFxzIqjaqDmfJ9F86EdEF\nii6a+kAzyCWSjneRFD85kmkKU8dNPz5/4bItbJ7jYHW3vsnK0wdXHb04TiSnxRYooU5LTCZRIB3g\ngedYCyuEnsulobiUH0FlK4aNh+/pqgMA8A+PnMb7/8djvMBIb0datGfbqk6s6zVvONlioHKGi4pk\nqO+JLmRXbkqRsaHTKaKvShJSXXvhmNv7gElhA7D3Y891JAUfAKgqpaDZ/02qLK04ztVJVq2r6mt9\nh07OtA8zFQOTKgsg+pLrCMeb9SmhOpM+DyY5SBcEWtrbdeRFiVnouZJUJlUeUh3zuXqErx8a4frl\nQLrQGlVZiHJRxB1zcX/zikycOrYXGkKWU+0zbNyyccWde0MxGd9zRBXOBp3DxDs6SRwJdm4WMZpW\nSpczo/Mhe9/0HipEx1yoM6W0uy7JMae0r3KO+Wy9ZSwmB8jAADX6DFlhFYBIzBrmwhSV140+fzY+\n2Zpjko6sN9WNvrhWrlxiQYEhNjfmV/50NeCgquiYf/cUc8z1fDMAGv8ayHfM1XUlr6oqe250TQg8\nV9tgqtWsPcfs4DEnmG5I6Ia0Fce8j/AKqJEsk2oDrFTfAYBEz2QbPlqVeaERSevJeLbm10JPU5VR\nN+dCLlG/T1uBI95Wcj+iuE96HhvYw37LXt+2gU7893dcg8/eeaMmw0rb1Yp0x7zJ52H5WoFnV2Wh\nSi//16qyfPnLX8bc3Bx3up9++ml89rOfBQC88Y1vRK1Ww8c//nFcd911+OEf/mF89KMfxeLiIj72\nsY9h1apV+NCHPrR8d7BMxhCi2JKRz6yuTJLU1AllKTrm1ExyX7y9aoEhsluMk4QPUkAgU3RCUifm\nIkTJthP1XEdajJjl65jL//7HR09zGb/QsyPmX3piGG+/YQuqgUeqtKXfffh1u/Hzt27Hv7v7u/jX\nZ+SERs91JCdbRcwdxxwRcB29gAazhWbEn3FH4OGLH3gFkiTRFipmlcDFTF1HbouiKip3ni5MBzbI\ndDA1csGcK1o9rSI55iqK4qExH2sToW1x9lxHkl1zCKqqPmObXGI7Zbm7Kr6GkAWFiLl5sReOOZHm\nimTkjC02at/3XHkDyH6n6ZgHQpqt3hTPNfRcSQMcAD751SPasxibraOvJssqAnL0hzl9shwkS/RN\nr60O3YWmkEtUEXOO2DpsoRXOvXp/gefyzb4kG0f66ImxVMkmIkBGP0fMzZKYTJLTcx2tkBggO8Ls\n/TJHhPYzU+XPIpuvR1bHcN4i+0efoYyYp9c39XFWxEk1kVDsIMiieKp0Ie2P6kafOk15c4tVx9yT\nHetcx9xztMgt26hPzDXwsf/1JP7piZRWcM3WFdL75G0kGwm2yTAmPGemOuatKIGNDs3uoZPoZIee\na5SKjEnEm1bRpsba5bti/Kk65lSicXSmjlYsV/60yiUWIOamNXauIffVi5n6SyfJQWGm9n9RsM7g\nmFvqCzAzgUkMvAgNkWd+HJGUXttTxWv3mYvC0XbFREqZGY2u080yRcVN5xP+kfWyLxhbkmP+vve9\nDydPnuT//sxnPoPPfOYzAIDjx49j69at2LNnD77xjW/gIx/5CH78x38cvu/jtttuwyc/+UkMDAws\nT+uX0fgOLbEnFwDCsTJ1Th1pNA/CKE4wvdDkWsYmhCb0XSlBVi0EoDpsHumUKZVFn/jz0NIlI+au\nw8Ns1NrRMf/j+4SEUuC7xk1AT9XH46cn8Yl7DuPX3rSPn4P+thb6xgWHfaZW4muQnbdvuCatQmoy\n9oyrvMqf/bdcy7yp9pE2qSxkktq5pgu+6/AN4B1XyfkM7NlEccL7Ld3sOY4jcT87Qx+T801t82AL\nF3uuq/WpgGwGAKpjrk81zShuK6zYVQ205xVaUFEWvjYVGAKEhrbrgEdomEPOUDzWXzStb8+VwuO2\n6rMV35M07MWC4mXJXMJM/WBstoFN/ea5QY3+0HdGKTemc883Io7QqUm5rH8JDXdBaVHBgMBzuZNs\nc8xPjc9rnzHnlSJzTSWnYK7RQg9536YCQwB41Ir1daqJbKr8WWSz9ZYVKLEhiZJjTvJHmLNiAmgm\nLVrdjPrluw4Hi9j4ND0LdRNB33Ve5c8iHXPumOcE9HxXTzJk552Yb+Jvv32St3dwYxrRVPsi/TdD\npG3PH9D7SboOmz1zNg7oJjjwdCoLkNX+oDrmhvWuTiJRovKn3O/ZWs4c82YrUepm6A801SXX2y9R\nWTr0NXa+0ZId84y+2hF4WvtVII6NE1OBoRlLQShmpkhMecRc78Mmo1Q9G2Kuzre+Z/Yd2PleTFSW\nJTnmJ06cKPW7a665Bvfee+9SLvF9N17UpgDFY53E1DnVsKINMf+v9z2LP/j6UfzNu67HzbsGjBOR\nOnmoyIQWxiGVP6MYEpWFGUWaNMe+oEBPHse8r0NH9YpKsdss9FytWuHWlTW8/9Yd+KXPPoHHTk1K\n51AnIFM72aQkOJ/ZOyQIpun2TSWnqTGEwsbXpEYLzVAriqqoGwP6XAPPlY5/nYJAUNSBF5lS4KXA\nc9GMWNEJy+bB0kTPlc9H3x1/xpGdykJR1DIWuI72+0LEvGV2zBkq5DkCbWVOCHum7HNTER4JMedo\nkc4xDwnktEWmAAAgAElEQVTqSZGeLgvlSmpjvSUVWmIWElqJicrCTBSLkR9aSmXJ55h7fKEVC66J\n+sQR84bZMWfROvpZEcccSN+PzTEPssJJrTjh8nRsPaZVBPMijjabb9gR87mG2THvkBBz4UDlccyn\nDO8VIPKthMqiIuZ5HHP6nPMrf5qdWbXyZx7VzHd1epMp1+dX3ng5Ois+As81UPnEpoO1N4/KUlf6\nSd5awquo+h4HIALPMbYxoog5iaJRY+2iuUf0floxqbyZOdKNKJbmaBNgZaN90o2wKXKmUlnGKGKu\nUVmU6CinsujXLUTMDe1lDn6eY06ro5d1zE15HZQSSC3MobLQKMgL3y2/RBzzF6PxSbQAMWcDyzQh\n5KEX1H7/3qNIEuA9f/OI8ThAn+CKOOae5/BBNltvGieAvMS/YsTc3FWsVJY2EHNqFQNi7roOBjKa\nhloqWuPSmRBzX0HMFZpF6LvGidhzzSXNmbFKkKbqoKoJ5FSlsrTHMVcn8fe84jIAwNuu36RNVCKC\nIhbwqgH1ZMYSglQnyYqYO450PoliwXj8DDE3lC1vRklb6EXDgLBT1IRuolhJ6maUSBEDZlyv23G4\n/jmLgrHx2BHIGzp6HeqYq4lPvG0+3SyLkGzFc43VIk12dlLmIjNaFrsme74mLjobC00F9pxvRBzF\n0x1zhWPuirGjOmGB5/AFnjnmSZJIDiG7Z/pZf1c+lQUQ6LTK92fG2s20pdnz6LRwzMtSWebqFu14\n5FFZzA4UnW+SJMHd3zmJX/z04/iHh0/xRD3VGiRiwags7DPWP+n8qEZb5doa9rnFxjFXK3+2m/yp\nRmDe84rL+BxlctrExpLogedRWTT0NA9ES88ZEtlSU/InkK5JVAghj8pCucxqpGiB5B2xz+gcPzJd\nx11//xivPcF+YzIKnvUZEHONysIQc0Pyp7ouiuRP/VlMFzjmJr+mXcS8bISecszZXEMBDqkNnvm9\nsevxnKsXgWd+SXXMX0wm+IB6QsmN21bi1Pg8zk4uCI45W8CyfhAnpsS+/B7QjNIJuwxirnHMDY41\n65Rs5xz6LlbUAoxMiwHLj2+TY24bSJ7jGCeNPI55XiZ9YJjsfVeUO1e5j+o8YCqMwCZlTZWlxSZa\nM0JCw8kmY1GJUog54RpTK0bM8x3zD75mF67ZsgKv2btGO5bmHNgRc3HjjF6hRn5sznO9FStUFodP\n9JHqmBs2LyliXn6WrDdjbVEICKeRRk8o1WSxGWnP3ajKko1H5rQzJ0+LyrgOTy4FxHP2ssmftbHi\ne1KfqxNHYeuqzlL3PDYrR75sfdnkzLCxoD7ihSZVZbFQWbJb9gliTjdBjpMl/ypUFtVRahrmS+a0\nzCy2kCQJHMfRNvIMTRe8avkeqoGL2booMe5yKgvlmFMqS0nHvGGnstjmtGrgYUUtwMR8UxqH9JrN\nKMGvf/EpRHGCzz92VpJMNZnrCMSc9UvqODJT0cSmRJvIQcwLkj85AJWLmOsRRRVQosm4plfAHXPS\nf9tK/iwR3Q79NNdjrhGlVBYDjSeKCZXFMVNZePInuW+6MWoRVRbqmKuJnf976Bwm5xu4+z0v48eZ\nrIhjPrPYlNaPcYaYG5I/O5R7ruVxzIuSP02OOYsa5gBZKce8HGIugNKEv/OOwEtpeLw4muoDFSV/\nClZEHu30hWAvIeaZ8RB8oku4ve1lm/HLr091NjmVhYcVRWZ6GSk8NTT47OiskWOuOnsax9zXnQXW\n8dhufFVniDuuFLxjqqDx/eCY28KgeZN96OuDy3Uc/jzUiIU6AZl27BWOmMu8XM5V811t4U9/7+SG\nwBmVRXV2TSbUOdrlmMvXVzXSuyo+3nhgnfG+efJnZOaYA/LzYpKGZeUSpxaaMpXFgJi3OJXFLJdY\nIEojWSOKDaosNo65uF69FWshf5786Yo+9N6/fRTv/7vv8e+YU6Eh5or6j0yzEH9XCBdclQTdtaYb\nX7rrFRxNLGvMqciTSzS1ixqlsuiqLCqVJdsIeI70rAMvzYHp4Mg1c8zNYWeaz8E2TTQp2YqYK+pL\nzFTEnFNZQhtiXm6pmyOqLLYESdU6Ag/3f/gWfO2DN2PXmm5yTdHmmcWmNNZNOUDUPIXKQo+lzvAH\nbpX1viXEPMcxL5JLZO+jXSqLutGj44TO1Wr/XZQQ8/KOeV5UgEdEPRc3bV+FNT0VbF3VaaSyxDGV\n4DVvIli7aMSKtpuqsqgRO9WoQIGVykIdcwNddELpQ0yxpRb61mRPZswxNyHMMwVyiaYob1nEXABq\n5SL0VC6RjfmmBTG3AWysfRxEzb3yC8NecswzC/gOTXeWApc4hiysyBYaV2Sma/xhw8Q4oST9fOvZ\nMWvyJzXVOTDJJbLOzsKk/V0h3nz1Rv4bigSZkkfzzOS4u06aQGiaNIB00j15cU5X+YjZPRjQbQOt\nxPcczolUqSxFITt2TnoPOmJu3mmbwvfUWOhQpYeYjKF36qJjmpQ7cpJ0//0b9uDHrtqAv/vZlxVe\nkx0aJQlHpEwcc2ZMvaARyZsqW4QjdcxlZ41zAyN586MuDEA6htqisrTi0jrmlUAgvEbEfFGnsgDA\nN45cwGxdrnSpOnUpx5xwickJaHvSTWb6N11g2Fyyf0Mvp2iVNXZ+9t5MiKNol7lfztYjPn6sVBaH\nUVlENIBG2Vg72AK/2DQ75uzfFOWqBR53pFmimYljTu9PnX+qyoaAvfvnK5c4Vxc65j2GSKDJKoGL\nvlqIncQpT68prl+EQqrmObKOOUVGKb3urddtwn0fehVu2JbKEVJHNS/5syxiXkRl0ZI/FafXtoEN\nlf5LIz42HXnaLmZ5mw+6Ef6vP3UVHvjIbeiq+MZ7bxH+s+ta5BI5lUUANotSboWIfnOOeUuP8jE7\nP5VKo5oQ6PQ6op3dVV9TVxqfMzvQJh1ztY4Eo9ItRZXFFInhHPOctbAVi0TYoo0yu/UWoQCyNaRO\nNvnUfM+B4+gRdyCb519EVJaXHPPM6EtT+53nioQRk6asTxwAaqaJcXhK5ow+emJC0iZlpvKWixxz\nj+wW2WLV31nB7rVisaB/mxz7PDOF9tgzo2E2Gkp++Pg4XvWfv4Ff+Z9yoSmGgpl216HnaYPLcwxU\nFitirrdTIOYySkOdBStiXobKssyIOXViVdRuZVcFv//WK3HT9lWF12Rtt+mYA/LzYmhjkqhatebz\nzzciLflT55in/+80cMzblUust2KtLYHF+aLqC4vNSE/+zJxvz5HRsflGxBMuGbVHlx5TOebUGZeT\nDynyUzcgPWVRWXF+uS8LjrmBymLZVNICIjbHnKuysI2Ago4yx0SlsqgONmsXO6/vpTQB5kCL5FC5\nH8xpHHMzMjtPcgUANfmz/QJDc/UWd7ZM9IH0WvK/1aiD6ZozBc6Odg2XKKQozh11Gh3HwbaBLt7v\nJAWQgiR7k3Ht9Ow8+TrmegE2lSZCN7B0rma/YxsJU4GsT9xzGD/zlw9Lm72G0k/yqIANMr87jlin\ni1RZ0uRPk2MuZEgFYk6SPyOBmDMqS57CzDePjvLjTBYqND1VmWVi3hx1qVV8ncqiACPs36YcqqK+\naopSlEPMY+tGWzWPrF3M52LjjMrOym3I5kaTwhrhn7/kmL+IjDpg6uD3PeEYcrnESDiXbAItwzFn\nu2RmUwtNvrhQWxLHXOnsTP3goV95Nf7iZ66Vijxojv0SEHN2DJ0wqMTj41nhmyNKdTuBkuiTFuMM\n0/a4lGOucB+LCikABDHXFENo8qdhMLvm3TczTmVph2OeU6mPGV3oy6pJmKyo8iegIOZk8qYOVt7i\nXFW08UXCqfyMq76nIT7NOG5rkqy3Iq0tPTmInIhSxHryp8QxlxvGqGCdFsRcLWQlFb8hfaESeDJi\nbpD5siFM6ntSz69Gf4zJn5ZNJVV6seqY84WWOeiyjjnrN2yBF1QWhWMeyf2AHcc4+gydU5P6Zgoc\nczZGdI45QczJMyzPMY+4s2XKnQF0WpaNyuY/D8ecAj7NKJEoXKY5KVD6A5CfWG6lsvB5Nqv8mTNA\nfbIRZ6Y+CxrBoMMsFzHP/v7UN47hm0cv4J4nz/Pvlsoxp2ZM/pSoLI6xyN0ij7CKDYnEMY8Fx5wh\n5qa1nRmjs9ioLFtWynkoan+00aFqZN5h1qFo+qvzCLWxApqV6ZmzcW2LxABZ5U/Luq0aBXi4Y65s\nLnT51vQY07tL8wbSv9spaveDspeSPzOjO0e133muqzmGFAFywKgsxRzzYcUxn1xoSLxOkTimOs7m\nTsiMCugzYwlGa3qqWNMjV6QsosqoZqR6GIp6LDYjuE76DEen03ulxTToRG+aUyskuY0d5Rsc89iy\nYNvoMfS3bFNVJ1QW19AWKllmMiZ5ZtMEpsYWrDKIeSVw4Tgpcp13/SJjh9LKqlpZddIP6HusNyO+\nqOaq6ChUFo1jnv0/8F0Eris5/FG7qiwtQX1581UbsG2gEz8yKHIo6CYm8F3u3C62BGJeDVLJtllD\ngSF+HVaYhGn9GgsM6Trm6TOQNwcmriR95hXL+920ooZnRme1zxkyypPPmhEePDaG6QXdAbAh5tRJ\n1JM/5YWT65grcolWKosqbabIy6oLeENx3JmpVBb1Hagcc/YKrKosJTe4c/WWoMVYJC2rgSdRU2yO\nOSvtniTFvF3VaEGnZhRLFTLzQBKqwJOX/GniWQPi/TQ5Yp7TRiOVRUXMbbkYDDHXQRp1HWVa+Gm7\nzFQpk7HNhTqHGuUSCWLuWBDzOpFLNKuyECpLNj8Yk7Iz6cbnLszhD+49ij//1+Pabyq+i62qY14L\ngYviWdgc886Kh4l5uf10M5lSyTIAzHCf56fMVWmZmZ75+r7Uv8hL/lyKKksUJ5y6olW2dtLPFgj3\nP/3cBLK5eDEVGHoJMc8sr6P4rp582OIdTFSUbAcx3z6QDjoqm0TRP3XyKKSyuPpkopb9pqaGgYoW\nLhP6xgYPRclbccIX3fPMMSe8+iJHjDvR5Jwu4Vsy/nPMd97y8WZ6jBllFCieY6SypAU0ihd0tSy9\nyWyqLKZJrhYKNY88jnuRMfS63hIc1TzEPPRF9IduIPJQKboQU0UdlcdvKtbUbFOVpUGS4HprAT5w\n205sXimSYSVKiSeKH1GOOcuHmDGosqgmEHNlE+wpVBbSVyWnOxCLQcvimNsQpk39NePnfHxkz/K3\n/vkQfurPHsJ/+udD2m9t0R6KmKvzgEploZU/5eTP9HNeYMiS/Kki5mq+B/tc45hn3HNOL7DIJTIa\noFGVhSa7l03+bLR4H1OrszJTNfltVBZA3Cdz5Ltz5mRqriPGi8oxN9EK1ZwDYGlyieo6V0Rl0SQ0\nFWWMonFi0uFXc65GphcRxwl+8dOP86JFzHIRc4veta3yJ+uCnoWnTJM/TethSmWR5RJN9oodKQ3x\n1Pg8/uDeZ4z5B7vWdGttUKlVNse8oyD5k9K96O9Y5ejRmTqaUYwTY3P4j184iNNkYwSYef1sE5EH\nJEkc84J1zTRvqmuX5zq4jKhbsaiRjXYrCgzlXvoFYS855pnlOeaeS6ksGZUiFog564xldMwZYr5j\ndRcAIm3oyVUU1clDdw4c6TvHIPGUF1YKDKoueWZLjjSeO3seTKZxZrHFw6p5iiz0WDpwKZUIkNU5\nyhQYYgu0XZXFM+6yPVeWS7Q9ozJJYjYdc1MfecWOAT7xPy/EPLsnGk7N45h7rqvlUgD5E5lDFHNC\n3+PtFoi5iEqooccyHPPfuGM/7rotVZ5IEr1kPDX6fkKCmFNVFra4USqL7RF3co65PlaqgSc2fJ7u\ncACpk0MLl5kcc9v73biiw/i5GoLOQ0Vt52abktDTiwapxZV8yTHXEU+VY64VA2GIOdmgpefN+glP\nEpbvQ8yzzDGX76GqbAjYO6otg445ewadhoRlQHfMbbQjel0Wpdi8ssYpHaEnEt1Vp0tWZSlGGj1D\nf8gbW7YNf0AAEKDIMTcoaCm8cxpZokNWjV7StXOxJWt/n59axOHzM/j8Y2e1NuRyzJVka2ZGjnmc\nSKosjmF+4cmfFsCmEcX8N6pjTh/Ty3esguPkJwTvWdutfaZSWWwc856qwTEn8z5Fz+l9rOvrQOA5\nSJLUOX/zpx7E//+dU/i1Lz4lnUvNXfBcBxuy+apYx9w+f1OT501WV0Ied67jcD+KXtvmqwiO+Qvf\nM3/JMc8sb+IOCL9SDc3SBJhFZVEyIRYs+ZN1KDZ51iqeNEh0WTuKIMsdWygnyNfKSyxrN/kzL3yq\nGms7o7IAomhBkTyeDTGnzyNV54D2O0BHgOn/baosoUVmSS0wZFsEVpdQ1min8ucPHVhXKpmmyNj7\nocnFeXKJNDJUlxxzuY237B4AALw+qzTKnKTQgJg3pVwMxQmMYmMpamqDG3vx87cISbj5puyIUaMR\no8BzeSSjThBzFkViGyRbohelEpjkEgGBBprUJgA5d4GqC1QMfVS1TSvMiLmayJxnRdEeU4EY/h1z\noMkG0SEoLnuXbJG3I+ZZP4gT6Th2npaSiyCOUx1zBTHPngPbYLFX2EXQwOoSOObzjYg7DzbEXN3c\n5smlsufHEfOqj4GudL7orQV47Fdfiwc+ehv/jJnrCBWcJgEirO9LyZ9Jj8vJDbG0mdF3ZjON+Vwq\nixJFYU2jGwJZx1xfs0z5RlGcSHPWyPQijo7IeUrMTDz6UxfncWh4WiT3a455PpUl1bzWr8V1zC0q\nXpQi1tMh9x1K+bltz2qsU6ilabvEb/as69G+V6t/mqp7A6lvoeuYU8ecIuYykMAor8OTCxyRf1ah\n1KnPfENfBxnX+Y55WR1zKtQgVFl87TfUMfdz2kCpvi8GxPwljnlmTiabZprLKMec8Z1o8ifbXauF\nWegENTXfRG8tIFSWLum3naEvobN5lT8pxw0Qk5w6GHMRc4PUUJ61g5gz52SYOOYT8w30d4aFiLnK\nBwdkJwmQucYmNJNZ1XfRaMWGyp96QlpkvD/XWLBItTKSd1QhhJopLLh/Qw8p7FLOoTAZu995hpD6\nroYESY65IckZ0JG3n7t5G37pdbuxc3WK6lQDF1MLZo45pQupG8W0IqLc5tCTeeg0WgUIeTJTuFJW\nZXH4Zogmf/LqptnGI93kaqdCZ8Xnz8pUYAhInayLcw1NDYYZLTAUJ+1RWWyIOZdLLEHNKLPZLkJg\nWf+juubNKOJOY4eCmNuQb4aYBxbEX9M/b6Wf2xBzNemUq7KEZjpgWY75rISYl6Oy5Dnm7LkxJZxa\n6GNtbxWjM3X0dQToraX/qfOY55o55rb3ZYqgqA5U6Lv423dfjzhJrJuOPlJKfqEZWRPlXEdHx1XV\nq/R+zbSJIlUhSrc6n+OYm6ICb/3v38b4XEOoIBXw4Nl5OGLu2OQSGWfdPG6o2hGNFADp+7n3l27F\nxHwD2wa6sGVlJ84p+WadFR/1VuoMmxBzFYU3Vdfe0NeB7qrcnxxHjsDTfk3vs+K7WN/bgTMTC3j0\n5AT/XG2L+sy3EDqhWl9FtboSObMZa1cUx5oqC/+NqyLm6THvv2U7Dp6dxmOnJ/DchTkA2WbrJSrL\ni9Nsm70USRQh/iRJuHOXUlkyxzzrQKyv1zOH4N6nRzD4/34Vf/Gt47iQaYyrlf9qYT5iThdZV0H5\n2CAsU2yHmcYxXwqVxTG3d2WG/tA5nfHMi6gLrF3qJO6SUDrlGqvzJ0Um2OJtQ8ypfJ2dY148RMo5\n5rbkT9lZe+dNWzO5yOWksmSKLIYFSZLAc/VcirSN4p3dunsAL7tsJfat7+Vt5oi574pCXYbNj7rJ\naBk45mrmPduEchWEpkC6tftVEi8ZYk7lEhmiSh1zU9enSJ+GmGfvhi2+EmKuUFmos2KSS7RtvNRC\nUvycrMBQCUezaPEzFfNixhYxX0G4WdvZhrUjTP8tHHN54dU45p58XrYxVZ2MRhFiriR/svvotBQY\nKo2Y1yOJY256PqqDYNLoV6/Lklk7Ao+jkpS+YnLM6XzH1hvThjT9fXqvdKyqlIOK7+KGbStzpVZr\noaBoTcw3rU6MiWpnijxRIID+zZ7Bmck0gqyCWtTJHZ2p48lz08Z2qBHHJEkwPLUozbO6eocZ5adR\niTwqi+86xrwCloBdDVzD+u1g88oaBjf1AZCdWWZ0ztm1RnfMr9ycHsvOwYw2ddea1FFV12b6bjos\nm6XAc7G2N30vXzDQhpipm+j1vQJEKFqveKSyJBAoq7LoPouEmGfHvPPll+H3fnJQo6GyW30RMFle\ncsyp2SR8VNSuEcWSUD6nsjTl6oqff+wsXvv7/4KhM6ls4FPnpviEsVIpyVyr+JLznccxVxFzG7cq\nD21tt/Jn0fcUGdnQp6N9U5kyS578FmBGzNl7oXQiG2JOs8IZeqY6+yaahWnBcx0nd7PEbHW3HpZU\nzUQRSTd4aRvedt0m3PMLr8SvvWlv1qbMgSmZtGYydk+sxLwJ2aP9QIoMKe0EgLtu24G/etf12jNn\nDrCEmGfPlkaWVB1hU4EhFY1k52PtYmPM1B11jrnumLM+IRxzM5WFtkOT5FSoLL4SDqZ/8/oIlGPu\nmX9PzbbZs9FrTKZGwVQudF4Ja3Yor/ypOGJCLjF9BmzzxxVtlMgEr5TMzyNHr9TkT4awtwiKKd1L\n9tzYdXnlT6uOeblxRBHzauDiN+/Yr1VnVR3xPLlUlWPeEXpY18sc81D7HTOX6G43W2IDa3vv4nna\nEXObEgs1xxGVnCfmGlYgheceePo8bTPa9J2ZQ/VshoSrwglTBDFPEuBfjl4wnlOli5r0/DW9a5or\nQdYEWk06z7/0PVejVQBiM9EReNr6qv5blUIEgJVdIe66bQc+/NpdxvF/6+7VGPrYa/HB23dKn1Mk\nfVeGbtP1rOLLBYdoTQm1ONq6TF3lMJE4nlMkH9XN0Jpesf4VOeZ5OULUKMecrdO6KosjKdeo1B5X\n8SH4XPwi8MxfcsyJ2fxYiiQCaefiSW2uKEIjHHPRgU5enOdyT41WLFVCpOfsDD3Jkc5TZfGURE+B\nmMvtzqey6AhNnpm+l0OWYqLaYAjDM8ScDor+Tr1iqAkx9xW0rk4KbqgDnCLczDFjmxzBw1STP/Vq\no0DGoSQL+odfuxtv2L+WJyMyW9llrnxKjcslZn3k9Pg8bvzt+/DfvnEsa6OHPWt7hIwVow4UhAbz\nTFBZsn5pSFKji5bvOTAlqRZpzzKHT6r8GSfSxoMmSbN+Hyf6JG9K8AHEu5/PobKom1XK62fPnSX0\nMUfQhpjTUL/q4LLxzhAuV7kuIIqaUPoUl6yUijKZnSVTQSaARn+Kp251keyqyNUD8zjm7J6YetT2\n1Z1Ze7N3rVBZWBEc5lCrz1mnssiRmWaLbeBkpD0m/YdaNWSqLBlint1YTzVAd9VHd9WXnPTyOuYt\ncU3Xwduu34x3vXyr9Bu1j+ZF1VRVlo7A407ZOuLQ6PUYaPJnTLi55muJZEq7mpJtE6jaiswxn5y3\nSzyy65noKUXHACLHikmCqknxJvlPk7GN/4mxOXzw04/jiTNT2m90aWAasUr/Hydyufi8TUbgmRFz\ntvmqZaoopjWMmQkxD1wXH3rtbnzgtp3ad8x6a4Gmo99PNniMdkK7ZEVZ32gVUHqfoe8aue+sVgAz\nlX65pkdsIooR85JUFiIiIFRZlLVBAUxPXJTVY2hTpAJDuVd+YdhLHHNiaWfRd1OU7wcwB1ssGOyF\nC61ouXOyjr3QiHgYJfRcdBFOWS30pN1+XoEhxzEnf2oc87zkz5zJymSm7+nE/5q9a/DXD57AQHfF\nyI/lVBauFQt86a5X4OHj4/jj+57BsYwLlouYE5oFu7QacqQDnhVVqHBnXwx2dh4gp/Kn4ris7qng\nU2+/BkdHZvDH9z0LIN1clKGbqIj5905NcDlJ9X4Bgkw+D8Sc9RGOmBsQM1vyp0xlSf9vW6yYo1nx\nhYxYRJAOdh0WzagGHk8GVsELdfJl51M5+kYqi5r8SfjPLDGbccyFXrd5Q25LWkvbxBDzQPo3IPqo\nmqQZxbAUGDI/U3XxZcY2TmVkPFm7tq3qxHNjc3j9/rX4/PfO8s1NaJF9A8SzvGX3ajzw0dv4gs0p\nLYpcIpC+G1HpNW0/QyJVKouK8LLva6GPqYUmf1aqSgwz1pfnlQJDoe/is3felF2DRoNKOuYEMWfz\nhUkus6yxkP0M55h7eOt1mxB6Dl6XJU+bruG6Dn9WTSlCa76OSS5R5fuXqbcACEnRi3N162+WMj/R\nuXpnRtVgjrmKmE+X1H1n9/vuv34Ez43N4X8aKBh6TRAVMU9kxNzVFc7k410tsgcIXjyLqASeqEui\njjOTY162mJx6bUqJYhQYtcoqffadlg1r6LtYZ4h2swTrB54dwz8dHJb4//SaQHElY5aEXxTBYo+i\nFYnkT3VOZHPUTdtX4sFjF/HmqzcYv0+vJ6gsLwaO+UuOOTFbX2FUB1YYgCK2NPmTI+bKBMhoHFQe\nKfRd1CoeLqb+KGqhz50VIL/AULobF99xYX2Lc2eytjnmhkmDop0fef0ebF1Zw6svX4NDwzofcHKe\nUVmy8zkO1vd14I6rNuCvHjiutdm08aCIub3AkLivIo65rGNudvRkDnZ6HoqmqmoKNhPorVlWTk0y\npcl2SzW2uDDnxUhl8eXJK4/KYmsKOy/VMW8RZ4x9xxHzHAdBXXRYt2ftYlzmvIWT/Z45k0+fm+Yb\nDVUCzzXIjKrtWIoqC+eC8z4Xc9kvKfnT8FCrgcsXEnURMW1cbcZ+8w8/dwO+fngUP3rlenz54Hnu\nmOch5vRzSk1TqSyUHjPfiISDTcZIM4oJ91xGzE9enMcrPnEfzkykXOPO0Esdc0VHW30HHQpiTofv\nbkPiXNkk6maUcNRZqF2pgEf5KBa7T4amVgMPXRUf77hxq/Q7UxErKl1oc/Do71n7mak0jzJUFkA4\nehM5FSDZ9agzqVIE1K5FHxtDzC/M1DE53zAg5rpjvr63qiVMMorUc2Nz1rbmCR2wfhEnso55EWJe\nNQ9dDfsAACAASURBVDnmZPPFrst56Uqf2bO2B6/btwZHR2ZxPGt72blenSMplYWJStA+W/G90hxz\nGsV57d41+OrTI3y++Ld//pB03Z+7eRtqoYdrt6zgn+VF6QEBThTdqqewENJ2ywexefsv33kdTo/P\n882e+j0ASZv+JSrLi8xsvCf2QinHmRbiCPgLT3+vToAMLaZcrcBzpUSlzopCZdGQQ3X3V4yY28p9\nA0uo/Gl4NhSd6Qg9vPPll2FTf81MZVmQEXM6aOhEYUTMDc+fJ+pY+L+ASARjjqOqGkALUNCJgjry\nlI7A3k8XeW+q/rDN1ORPNdlNRRC4XOLzoLKwczCJQZPeslw0RiQt0UJIFEkyGePYhr4rbX5kx1zI\nJeY5CCp/lzki7N0v5MglUsWf0HPxqkzW8ZuEn6qqUdioLBQxNyXmAUK/3oSYh8oG01ZgyLQYs35r\nUgVRN5k2Y30XAFb3VPG26zejFvrS5owWR1PN9q5Vx9xxRFh/sRnxMUVlCxuRiDCyOYn9/0+/eYw7\n5YB4P00VMbdswDlntWRovIw1IvmceXS5IlM55iakFdBBoRQUyCJ8UVIolyi40na5xLJUFjan2QrY\n0OvR/qs6POo4p+tTV8XH+swJfHZ0VkfMs/XislWduPcXX4Ufv2Yj/vNPDGrtiAr0d1VKCfuMmZiv\nQKgs8iZCz3txUcuhsgigQo5Gqm34/95xLX7rxw7wz8puHlXkeOeabvw/r96J3/qxA2KtU5I/aZft\ntOiYV3wXW/oFZ/u9r9wGwK63/tbrNuEXbt8lofFF98CTP0vKM89Tx9ziE1UDT3PKARNinv77ReCX\nv4SYU7PNW6wDVAIPc40oy5IXCIY6T6soGEtkYZQWx0nPSZ2EWqgkf+Yg2jSRgX6nFRjKo7K0iZib\nFnBbZbmNfXqYjnPMDdxwOuC44+HpkycrR94gSYPq+Kb39TM3bYXnOnjDgXXSeVQd88BzpfaEXiqz\nyFEhNw1JMmeChgJtC61qgophdszV57scVBZXuV+TQ0z7iOcSjjnlqlo2QczoQkQ51dQx8F2hy5xX\nkEXjmHPEnBWUsScP0Qk38BzsX9+Lge4Kr6571eY+Y+EPm1wiM1tU5vbLV+OeJ4clSoKICsiUkzhJ\njJUIqbPUU/XRXQ1w4/aVvA0zyqIoCgwVLGyWBZJufIIcVRbbu+aOtRKZWmhGWGgKxJzyWCmQwXXQ\nLdftVKhGlO8ttS+7PMMGihIPy3LMAbEpZc+wnUikauw5MiqLTcFFp7JA1jEv0H9mjg5VYtGTP8u1\ne0WNUVlyEHPDs1GjO+o4V9/RzjXdODe1iGdGZzUZWbZmBl6qvPFJg1MOmOVmqZnWwB6pGmn6fzX5\nk7a1FnocNQbSftHh2Of9GqGy8GMs45XOR2X7lSn5+IOv2SV9Rn2BauBp98NMrcbaWwvwuffdiIrv\n8dypuXrLKJtpWpsKOeZNORplM9a/aBVYFaws8lnUPDz2DAq6zAvCXnLMieWpsgAyYtsiC43qEKuh\neoYWz5KKe44jO+Za8qemoJCDmBvoH0C+pqi6sy3itwWei7vfcz2aUYx3//WjAOzSh2pxBYAg5oYF\nRkLMDffCnz/lmFt4z/S+bti2Ei/fIaTBqNMIyFJ+9BWq2s2+66BO2kYRs5pFD1g1wTGX1SuYmRAV\n9X7aNU3JogAx9ymVpRnhX5+5gH8+OMyRINv4YEm8fR2BlGBLnTHHcYwom2o2jrmqymJqCu2PTPLs\ntt2r8elHTwMAfv6WHVIVVPY70/xuK1tN/33Fxj589YOvkr5j71nlmLcigZjbCgyt6q7g67/4Ko5A\n1QwJoKaNq8lsGzq68UkT1/PnPO36PBFb31jPNyKe5FkJXE79o1QWU7VUamzTKxBzs0ygirgVUZvK\ncswBEdUyJTgCusRomevS5E+TqWPLc2wcc/P1+LjLqfyZp7dOrbcUYq5HblTnTUPMlS65baAT3zx6\nASfG5nQd80VRe4Han//0tXjk5DieGZnFfYdHcyt/mo4HgB2ru/Fje7rQFQD/cirdtEexnPzpSI6s\nD0A8C1NNBmqUysLM1t97ScS1bCRGBYNUhxXQEXP9frLfGaIH12zpByCoObTIDzXTPZWlshSOV0d2\nzAPP0ea0orWRXsJ3KZUl97AXhL3kmBOzq7LIzkG9FUkVrNTJWUUm2II8RxxzQOa7anKJOQkrKi9W\nUFnkdi8nxxwAXrlzQPq3bVI0acBOZRxzmvzJrGpAzE3JnxWyMbKFdtkzdBz7dxEvasKQZFdaNFT5\nyXTCjIyLsCmkaTI2edYtiLlt8W8nbK6aeqhpApciE4TK0ohivOMvHpZ+a5tM33fLdmxZWcNbrtmI\nkSyhtRUnHKnWpPYyiVFT//E9B44j0G82QbN25VFZaCid9cHXH1iLTz96GnvWduPVe1bjy0+el+/J\nMW84uiyLV3of9rGiVpsV1eaKqSxV35PGzuDGPl4gg5/fkk+imhUxp1SWPFUWG2LOHGsyYNjGeqEh\nkj8rnovQS4sRNVoxGiRZPv2/uV9TOctf/cKT+MpTI9n1dMdVbq/xdNzaQsxbcoKxbR4xfaddl0dM\n0n+XRcxljnmxXKJa2AsQ8xsr2tUuYp7nmLP20v7aLmLOKBWLzUhDzBmVRV2nbt+7BrfvXYM77/4u\nAFakzO5p2RzFd17Vh2aziW+dzhzzJJFAI3pZE5UlzwEVlZCpY16MmJuqmJpMXddV6WVA5ZjLwJOc\n/Gmn29C1TVVmAcxzjM3n4Pl5ZRFzhcqS5vnJvynaaKp0WLZ+5fWXF4q95JgTK0IjqLIG1WdWj7Nx\naLkaAqdEyIi5zPeSz6EqDJgQZRsP02S6jnn7DmA7/Zsh5onBoa6ZEHPDxoMj5lEkhR2p8YqZhvvR\nOOYWKotwPmTU2sTZL0tlqRLpPnpt3m4LKluU5Z5nNiULajbEfLGhT8Q2f3RNTxXvevllAICx2XQx\nn5xv4kf/5IHsGvLz89xUH97kmHtOutHlqilZ89jYywvpm5J6bt29Gn/9rutw+boeuK7uiLqOOfIj\nUVm0xLziDa+GmFs45vRv1Wn7tTftRcV38SNXrsdP/VmaeMUpMoULm7mNNGktyFFlsTn2ptLbzNl/\n2599h/OTA89N33eWENoi0SnATmVh3P56K8bd3zkp7seQHEmtiMrSDmK+2JQRcz13R58ryl7XNl/Q\n+3Od1OEVOuaxBATlXYfSC9nf1SBzzEuCCKz6Z55jbnI01XG0Y7XM+9XVbbKIQJxw1SRmjMpic4B5\nIbMolmgmqhXNn6z7xwVUFrXdtsgH/b2Uv2OjbpFzz+Xch2qem9IrN/R14E2D67XvNR1zC3WUijpo\nFY49F9UgTWCdM/DMTXOHDbSo+h6aUYtwzAs2tC5DzEXkRJ0Dijaaah4eu+SLATFf+qr/f6HZxrCJ\nStGMxc5P7YxF750NWDooO0JfGsh5iLm6o1epF8xydcxzzr8c9u9u3gYAuPNV2wGIDH+a+c7MxDE3\nJn8aEhNtUQLT/ag65o2IOubid+w67LpMFo9yE5nWL+UX55mqD65RWZTOx9AkE52hrKnOVZGOOeWY\nq5qwQHH4ETA7jMKZY2ipY3UI1WQtNfmTt8XgiNnywG7ZvZpXGlTb5zoOR3OpdeZQWWyLLCDGFXuO\nPHxqqfyZJmmmf6sIY18txO+85QrcuG0l/6yibBqt7bAi5jJav1TEnDqndEPBckkCX4T76y0TlcWG\nmKfnmlHk8ppxfoSpbMGSMsbGKEf3tfffBmKufG9D+Ux1KRiVJVVlyU9y5YmiEsc8/ZtFIconf6YI\n7MR8jmOec9//8HM34IeuWIffevN+6XM1kiqSW0WdATYGGI0itIBcbAy24gQXZ+3tLKJWsNtQqSz0\nfagJ475FLpEZe96q4pXJ6DNZaJTTbgeAX/+RffjJazfiy7/wSq19gEJl0eQSzaCDaQyxdUgtMgS0\nh5gzQEClidmMI+ZU2lVdzwpUhrS8PB69zD3sBWEvIebEbJO7Sa6vxUOzrjZJjefov9LzqIi5FH7K\n4Zir4XeB7CjXyUXMld3xMjvmH3n9Hrz9hi2ohR7+9JvHML3YwvRi06jwIfFe8xDz7Dsa9rQlZpkm\nDRtiHvpy5c9AWZD/0x37cWRkhktRAcBXPngzTozN4/rL+oseBQBdx7wIMb/r1TuxfXUXbt29utT5\nTVYOMZefM+t3TxskL4tQScA84bJFgUZD8tRAUmeccRHTz9UFtixirrVPua7rAIYobW7yZ96iwu5R\n3WBKiDkZl06mvtFoxVYUznEcTkfg5y1AAktRWdw8jrn5vIxbTu/B1G6qwpPyzEWEMa997LlTJYje\njkDanLC2Uyvqmu2osgjnwbzJXwrHnJlNn15GzNO/mePRaBVzzEUuA1FliZn+s6gzUMZY1CMv+TNv\no3PDtpW4QXlfgB5x41r2kUDM+zpCnG8u8rwW2xpGa1KM5ay3hYg5TwhUEXPxGxNinkejYL+XCxkV\nP3sTXcRm77hhC4At1u9pd6/6nlxgyCKXaAJeOis+Ls41jIh5UfJnNXBx12070RF4+MtMErldx5xR\nF9MigOomtyBaJeXhvURledGaba5hnYQWXxGqLLqT0VPNl9AzOea1ii8nfypOlI6Y66iingiZ45i7\nxY7O8zHXdbCpv4YkSbBrTReOjszin54YxoENven1SFtpeF04NK50LvrdAkXM1fAbp58YqCxsEjbq\nmJPfuXIbbtqxCjeRJFIAWN1dxepuvUqazWjfSZJES3ZSn/+Vm/pw5aa+0uc3mXpOY/InRW8zXjCQ\nSpgVnc9kJkdlbDbjmpMNj5VCYenbWgTJhJiXmG/Vfu86wGIrn8pi0zE3GUPmWTU8di9RnHClG5VS\nUMkc8zyqQejLPOFCxNxGZaGb4KWosuRQWaT20nwFgpjnUc0AgdCxd+m5Dh7/2Gs0tLWdzRKwRFWW\n7BjHkfMeKNpffF35Pq1UFnIedXOXFlTL55iztYPSSVguDa+AXFLHnHHM8/yXpQA5eqGubOMWJxwx\n76sFOD+9yKksts0EVdh6Pog5G8pxnHC1DpUqqm6mggLEnNGx1KrKRbbQLO+YF5mKmNNnL8klGiI1\n1Ng8WJZjznyTKE5Q8T28/9a0SvbffvsEAFH5uozcKyCSP0PDXFXUn3VVlvTvF4Mqy0tUFmKmjkkz\ntEMJwRALjeoE/sS1G/H2GzZjlaX4jInK0hl6ucmfdBCoyZ9l1ANUcxW0bLkRc2aO4+AtV28EAHz2\nu2eMHGGaZMK5udRRtiQA0u+YbeqvoafqY9/6Hq0tNlWWii+oLK4j0MLnQe/WjDpd9VasIebPp5CQ\nzXRVlmKOeV7xnzJdJM9RodEQW990Hblfsj/VBdbkN5ZCzAuoLGxRpYuXvvmzP6PX7luDP/vpa/HL\nr9sjXS+yIOaAuLc83qqaVNouUstMcswLIhcmYws13biYHAoZMY8lBSSgWJWFt1dRlGDWLse8nflt\n0cCDpcc/H8Tc9o7p71jhKpFTI4Agu3KYiE4wY9KJHDEvW/kzpzaDiCa2P1/pVBaB8jOggiVDqvlY\nqnF+ehTj4mxehdL89yOctYQUrYOiYmLgmJegsvSTpMwy/c+ESi/V1ORPW06Xa5hrqTEfxcwxz98k\n0nfHrq/WCLC3X17rQ09HzIv6s0rTeTGpsrzkmBMzjWETkkEnysBAZekIPPzmHQfwQwfM/GPWYWuq\njnkOYq4qAcjJiunfasctQgtMA+dS2I9dtQGuA3z35ASvckab2qEkpKXtkR1G2t46cQTUe+7tCPDt\nf/9q/PW7rtfaoXHMSfInm6BcRwzodsLfRUY3WvVmrHHML8Xz12Q8Df3BxjE3nq8ElSVvweb84pzC\nNiq/U2yKl4fKol7XdSA55uv7UsSbVsCzJeaaLPBcvGbvGqzIFmXWlxZJZUP1XkxVNFVTUdQiBM7G\n4aZjzc/hmNsQ8/e+4jLc+artuONKkXBmoj0FnishvlQhhH1vMhWdtEUR1HYXdc0yiCU7J0fGJaeF\nzrdylCn3uuraUAIx76rKiGu9KZLdbfeh1mgABK3lph2rUAs9XLd1hfFY1aqBZ+2LbGPRDmefmfqo\neHJrlHB6olpnwEZFkRDzHMpNMcdcnIdSWej7UDncgecYaYHi9+l3rB5B2t7itSQvibVdU5M/6fiw\nR230NpqoZQDLjTH3ATUBPv29vHEsdszT/zPEXN1cpJ+V55j7rnDsXwR++aV1zB9++GG87nWvQ3d3\nN7q6unDrrbfigQceuJSXfF5mmgMCqYOLiVKUmHa0yZl1cBsPjSX10OqCaeVPgpgX6Jir1BagPSoL\n/T5vkC2Hre6pclrGE2emAMiDhlbmFOi/OF6nshDH3HCLnRXfGv0AaOVPsbliP3cdcb3ljCLQrPB6\nK5I2F8t9LWbtIuaB5+QuZGU2DyqHGwDesH+tdC1TlIlew/QsQq+4uIRNVz/vONcB6sQx/9Tbr8Hd\n77kem/pFkax21I5UYw4MK4wE6BukMog5mw9EUmnR2Da/Kzmfw04psiHm2wa68NE37MFKEg28bGWn\n9rvAF1GRRhSTROv8saUi5jYqQ7tUljKb7KpyLVNUEpCd8eVCzOnczZLN2TtvSAWG8hFkSZUl69d3\nXLkeB3/9dbhtz5rctlKz0TE7OH+6/flqx+ou6d9C4jHmjnm/Iv1nR8zd7NiEU+VMZkseZcYRczX5\nkwJHhtoKJoUnZiza9oqdgv5oK8YHAD98RVoA772vvCy3re2YqmMuUVkstTdMU0YXp7Lo9R9spkb3\nTL8vqypFqSyaLHUBYi5FA1wxxuIXAWR+yTjmjzzyCG6++WZcf/31uPvuu5EkCX73d38Xr371q3H/\n/ffjxhtvvFSXXrLlOXOAWCR+76tHJedNVWmglUJNxhFzqmMe+tKutlDHXJICcrXfAMWJL3kKJstt\nG1bU8L1Tkzg7map9mFRZJE5eDmJOq4EVqTFQY+dMknRwcqUIIsVEs7eX87k4TopGLzSjlMpSoMqy\nHKY6yeYCQ9T5cHMTxJbCMf+7n30Zrs0KVkhUlpKqLMzUBdqoylIGMTc4dBQx3z7QJSX52o4pa2yB\noQnLqmPP3kFeQtk7btiCf3lmDFdsTHM08pRhTG1mpiZaFyUTlrHffssB/Lf7j+Fz3zvDPwsVxFxQ\n/1zp/6p1Koi57ZlcCipLNavsbDpGjpyaPzdeVxmDdiqL+LtbRcyVnCbjdZiTGyWYmGvgD7/+DK8a\nm/eebWZziDuCchtDk73/1h2Yq0d4Y1aJWaiyiJyb0o45v984n2NeJGdJEHPumJeQSwTAudSqMcd3\n2yqxYf3eqUlrGz75E4P4mZu24qrnmVNETRWSYPfjOPbNrmkzzu59akF2zMtIMedx7Iv6D3u/8zT5\ns0QEmBr9eVqhPXPMX/h++aVzzH/1V38VfX19uOeee1CrpejT7bffjm3btuHDH/7wCxI5N+0Y6QLC\nJglaJtv3XANizhZac8dhHbdLorJ40k5Oo7Ioi4HU6TiVhXzm6hVJVQsL0KvlNEYNODu5AECeBFj4\n2rbDZr9lUnELOVSWPKPnpCoZ6cLFzieut9wblmrgZo55VKjKshymblpMihAaxzxnsisTVdHKbq/u\n5u+1vzNF4fo6QjuVxTEj5nkbVWY5oJT1ONcBBtdUcHp6HgPd5pyQvOqyhdfLjmV91nUMG+hsrOc5\n5u995Ta895XbxHkLHXPze6SJ1nSxsrW7jG0f6MLv/eQgvntynMts6hxzlcpiQ8wVKkuBY8ZsOXTM\n1edvikqm1y5PAaQOSMXgXJjOw5MHiZKTrW6D2qZWnOBn/uphHpkElkY7sTleHUwKcAnnrIU+fv1H\n9mntakbtI+Y0+nkxR5WlrPMWE1UWR8nhUh1zqsVv2hKwqI+TqbvESX7xoGrg4bqt5dS9yhrtJ9XA\n45HlztC3zuN5yZ+qdGZen2LPhwKTeoQrp/Hk9+ydhJ6uY15YYIgqHVHEPP/SLwi7ZFSWBx54ALfc\ncgt3ygGgu7sbN998Mx588EEMDw9fqksv2UyLkYSUGAZ5GpaXj2Od2cZDY4sTdZQ6Ak/SoNU5tWQx\ncCxUFvJZmXA7LfhyqW1tplZxbjKtDCkh5qHOOzUlXomy7HZVljyji/kn7jmMU+OpE0EHveuIti23\ns8w2W4tNPfnzUrwD9ZxdhhCmWjaaqsWoCbRlnDX1mXUT7fe3XLMRn3jLAfz8rdutiCmt0EZt+RBz\n/Txv29eFO6/twxc/8HLLMc8HMZcXGNN9s3srWzI9PU97SC0zlcpie6ftjCtm3YT+EFhUWZi2s3Xj\nELi5kUPePqXdRc0tM5bVPmariuh7IqH9F27fWfq6eUoeRioLFRsoQMxZdOzx05OSU67eR1kr0sFf\njvmKtaveijmKqTnmNo559nkUJzgxptdcYFY6+TOWlYDo7amABrt3a9SHzLNf/MArsGdtN/7w31yV\n247lNjXSz/pXXtKqUce8whBzua5AXp9iz7zimcdP2r6CSIYGXpg45uWpLCnHPP27zDrxg7ZLhpg3\nGg1UKjoCxT47ePAg1q1bZz3+qaeeQlwGAltGcwxpAXHUwtDQEABgekIPR104f15bBM+fOoahyQBj\nI7rkHADMz05jaGgIEwsRHAA9FRcHDz6B0dEJ/psnDz4hHXPq/KI4fn4Ozx17lv97enICQ0NDGJ4R\nSL6LmLfbZlEz2wUnxb+1Wdnj6hmFhVWTS1p1fuzsQgTfBVZ3JPyzqUnxLM4PD2NoaBZjozMAgNHx\n9D24TvnrA3KS31986zj/+/ixZxDH6bNzAczPzWbXPYehoZnS5y+0OJ3cnjp8BJMzct84eeI5DC2c\nW75rATg+sij9e/j0CQzV5Q3xqVGBNh05dAiVejrmVnZ42NIZ4Sny29OnTmIoGW2rDUeeflL6954Q\nOHtsAs1F82J6YXQErYZoE3u/F0fl93Dq5AkMRSPSZ3ds9/DQceCHdnVZ+8WZaXmBQRyj4ju4fWsF\noyeOwnR3qu7t0cOHcbFWzok+OSlfz0WitY09i4sj5zA0pCdSGs87vJj7/cLcrPEZjJ4Tz3384gUc\nPdTAe6/uxcGROh46K845Mly+LcycFjn+3BnMzab/Pn7qNCam0uuePX0aQ+5FDJ+bM57jxHPPInAB\nxihp1ReM93FCea4z09O5c8FZ9b0r5ruQ+h0APPvMESyOpE5yFIm59fSJ43j7rgreuGktVkWjGBqy\njwk6j3k5c/LEuPjdwvQ4hoaGMEvyEo6fPA0AmJmZMp6Drg+qHTn0NM5V2nPOm3UzCh3V04jn7LS5\nHe3Mx2fOpueamBZz4cT5M9Jvxi+MYGhoQTt2bDTtm8fPjvIorMlmpyeNbWo2WX9Ix/ap06exsJg+\nw+eOPYsLo+J5XhiW23Tk0NM4G7pAbE7WPPnsUcyeE/PDJ27tBerDGBr6/oGRdJ47f+4snOlMmceJ\nrO/o7JkzGKpMSJ9Nj6fP+dTIRenzJG5Zz8P8ivrCHP/Nwrw83588nr/eDZ+T18e5mWkcOXxI+uzE\nsWfQumBXEJqcGOd/H3xiCJOTqd/QyhLxm83mkv2edsx1XWzevLmtYy6ZY75371585zvfQRzHcFmY\nrdXCQw+lpaUvXryYdzharRaiaPmylMuYaQPsIeGD2DXl8yaxFhsJnQjNZjoRm8zNztnlAx+6oRc9\nFRfNZlMuDtGUF5KETAIOEsSR/O9ms4moRSg2rqOdQzVWmMx19OvlmQtxy2WP6w3kZ7ehy+XHdvrA\nn7xhFboC8ZmTiGeRxDGazSbc7KoMMW+33dakj7glcczZBo1dd7mMMZvm6y2t2mQSRct6LQBSHwGA\nwDFcI26R37ewodPF772mHwM1D59+Snae4qjVdhttvzeOJQCIYymMZ+oPaVv0e9nZ5+LuHx1AB+lH\n2ukjmStJQZi8e6N9PolaaDbLgQaJcj3f0GdZvmPoJuWfr8UpYOY65nPROclJ0v79+m1VbO1xJcc8\nidvvj1WyV3GSCF72jhcbLU5lcZL0vI6t/XEE33HQAEOIze9FfY9A/lhV34NqrqOj7ml/z76n54oj\nRK0WeoPi+YeCPRUv5/ekf1e97N2R+Yol3zmJ+b0mOWtlEjXRbLbnmHuOeXwywJX1HdXa6jNZH1gg\ndQQ6PHlcObb3mj2vYxOpE7iqw0U9SjDTkNsdF8zh7J03W0L5Jo4iJAQU9CE/2zh7nragtIfy88Ol\nspj4Al4SYUuPjzftrOHygUB7Hv1VF+OLMfat8rTvwqwfzCzKz8CBfa5ifcd37b6Taf6WLJGv5zmJ\nPnfHEfJO4SSM/pX6k4zrSN2A5V5zTeZ55SOhzC6ZY37XXXfhPe95Dz7wgQ/gP/yH/4A4jvHxj38c\nJ0+eBADurFsb5vuFv1lus3HMgyDdlall7AEgDDwtTNNXqyDwHHSE5pdeCTx+zldeRnZ8jjg/+15c\nRwx0z3UQBuLVBVkbw5BSWRztHKoFJIml6LfUrllfxSPnFrG2yyt93Joe+RltXVGRjl2rnMcnNKAw\ne14s1M/mPNfRn1Oe+ZYQVjUM4DmEA8ySV4Ly91fG0lB5hNhxoTBZUAn9Zb0WIPcZAOiuhggCJbku\nTMjfAYLAxY5VrL/LSFQQtNdG37W/H1sYOPBdKWmVHd+hhJNt76aoeZXAToHIuzfXFRz2aiV9TmUs\nlCPzxrH21v29WN+zgJdt6ix93kqQv/AHZN6iVqtQ2UbxDAPlfIHfft/vIooqldBH6KcLaeK4vKhH\nNetDYWCeGzvCII1AZs5axTffR0X5yHPNvxPtKeLk67kNlSDg40VSkWpjrFKq2Mqa/TifLN5dlfR3\nnk80yRORNGt8HqG9P1TCUCoP3267qTEqi61/tNNnKkHaF+vEMe+ryQOmaplzWF7GuZn0HFtXhDg+\n2RShlsximJ8Xc8g4fcNxESOjTAY+Al84gV2KQk1HGGaKRuZn2l0Nvy/00DyjvkBH6KMahnjvAqzL\n6gAAIABJREFUtWYe+5++aR0WmjH6OnQHktEfZ5vy2hkl9nfNkz/p/KL0p6L1LvDVXBMPFeX3tUqA\nIIf+x9YYL/MT2L+pY77ca67JluLHXjLH/N3vfjcuXLiA3/zN38SnPvUpAMCNN96ID3/4w/jEJz6B\nDRs25B6/b9++77tjHjz8De2zWkcVg4ODAIC/OfI4ADmkvnXzprTTPZyGgCq+i+uuvhIAMBaOAA+M\nQ7W1A6swOLhf+7zvmScApCgluyaz5PQkcO+F9He9PdizezfwlTSEumb1AAYH92F4agH44nkAQGdH\nRTuHar0PPgiMT6CjEhb+ltqf7Wzgfzx0CndctQEb+jpKHdOKYrhf/DIfFK+6ahcGc8rNrz7+JPBs\n+iw2b9qIwcEteKZ1BnhkEo4fAmjC97y22g0A3j+e0zLprzywD+e/nYa0XNfBptX9+O65c9i74zIM\nDq43nWZJtiJ73hs2bYEzdAiAmPwv370LV2xcvqx8QO4zAHDtlfu1olfV8zO8H105eEDiU649dxg4\nLEKKO7Ztw+Ae+zvj9vdp6LcW+tb30//YI8B5nQKwccN6dI2fBzK6Ejv+ufgMH2MAsGP7dgzuGihu\ni2LDUwvA/z7P/x1kC3wQBLl9yf/sOS55NnjFASNf32T94/PAlwTlxjTWBgH8m7I3kFnr5Djw9fTd\ndlV8/MLtO7FjdRfe+VePAABWrlhhvJ/41ARw3xgAYPPG9Rgc3A4g6ytfE31ly+ZNGBxsL/y6+eRT\nwPETAICd27bhdHMUOH4KKwfWwh8ZBtDErp3bMbhzAMPeMPCgPjce2L8XtX+ZxHQ9Re9XrzTfx4qL\n88A/iee6st/8O2aj04t8bjRZJfDR3dUJELri/n17sT6b3zq+Og7MpeH4vXt2Y39WwbjI1pwQ89hP\n3LgTg4PmMuprzx4CjqRjbc/2rRgcTDnswWfOoRkl6O7rBzCDgZX99vdKxvqBDb04eDblml995RVt\nqz71PfQdYEyPaq8bWAWcPI3VAysxOHgg/fDvBdWjnfm43jMO3D+GRpw6kYHn4NrB/dJ7vWyLuR8+\nOnMceFxw6a/ftQEXnzyPi/NylK+7t8/YpqGhITSbTf5c1q5bD+/Z5wBE2LN7F85jFDiY0jiu2LtH\nerZXXzkI13XQ+bUJYE6+XjVwcfVVV5Z+BpfKVk7M83luz64dGFQqV5e1YW8YeGgCC5Gy0XDsa2/f\nQ98GxsaxhozdFY8/AhD63e5dOzG42a6rfyw6Azwk5vt1q1fhwIFdwBcEHejqKw9IeS2qrc7GHvMT\n2L+dzK8smvOXy+I4xsxMe5TYS+r5fuQjH8HY2BgOHjyIEydO4MEHH8TExAQ6OztxzTXXXMpLL8lM\ncxfdFc+bytK6cvInLZBg1TG3JC1EOUkJknSXkvzJdqO2Ihg2ozrm7VhfLcT7b91R2ikH0t0rLWG/\ne2137u/zkj+ZwkU7yhGm8zKjcmKuA3zotbvxG3fsx2v2ltf9LWNMd9Ukl3hJkj+V52NO/jQrTwB6\nv2j3cdv0ck3nFm3Q9WqBcjrmZcykylLqOEfvj2VM00BvE7m0GU2+Cn0X733lNtywjRQ0sSXvKaos\nzNS+0o7aEbMekugb+C5P3GtGNHnRlf6vWuA50jOyFRFRD3++qiymfqfOufzzNhRJKP+Z6fmbTE7+\nFM+RPUMm42gvMCQ/kKs2i03+UsYKvc5AdwXvu2U7PvqGPfzzpSSU2q7B5vPAc7U5o6jAELM963qM\nyYBRQZ4aT/5MFB3znKTdvDoX7SRwX0qT64Qs/V2xSOX0okwjaeXUtReIuV29qGjtLpf8WaBRr7yn\nX3vTPhz/7Tfi315RblP9g7RLDklXKhXs378fW7ZswalTp/DpT38aP/uzP4uOjvJO3ffLilRZPvia\nXbhsVScvUwukkwudpHokx9z8eG2OeZ7wPZ0o0+IGehvbdczD76MqCwCszSQTu6s+V2mxmarbDohJ\nmk3kS6mJZJpMO0IP7JX4roNN/TW844Ytyz7JMpWeukGVZTkWOtVcpY+YFi6pwJDShnaLuKiWpwBg\nooUBadhxqTrmZUxXZSl3nK08e/H1FMd8md6zqSKxpBxiUz0hi1kgzSn285e1LuqYk2JVjSgmNQMy\ndNTy/kMiswjYi4io91dY+bNEQaa8/m4CQsoYVbNQo1XytcTf3cQ5ZZJzrHaDVS5RcdhvJZGtpRSP\nkxSyHAcfef0e3Pmq7UIqcAlyido1lHcSeK6m824vMCRf//K13ca6IXkOJCDG/ye/cgRjmR56qspC\nxldBkSNqRUoh3y+TCwwtfR1jRbfUKHM9R/6RPQP63NTx167cq8kxL+qDPG+MqNZdykKKy2mXjMry\n5JNP4nOf+xyuvfZaVCoVDA0N4Xd+53ewc+dO/MZv/MaluuzzsiLEfPfabtz/4VvwX752FH/09Wey\n7+Xy4hQxtw0I28TeynPMFfTGNSB48uJR3AEFYv79mUzW9Vbx+Glg15ruwgGiypMBYsAzzdulOA/0\nmGu2rMAHb9+FauBh+4oQN22s4Kp1l27DKBBzg475Mix0qqnayKZnzp6p6+joriZx1eaklicPZyuQ\nY638qTnmbTVFOr/075L3ZHPS2r3ecr1neh6GMHuuA8dJC2hZ5e4kUCEH0Xqecompg52eo9GK0SQ1\nAwD7+w88V0JJbZKz2kaiCIGzIc1OSmf3XL0arU2vvJ3N1X/8ob342Befwsd+eG9++wxyiYDYdM03\nWlmbbIi5/PnVm1fgT37qammz1I5JmzZyalaPYm3v858n1bEQeKnOe2coCj0VFRgC0nlm66pOrXIr\nkL+mAmKjQ3/nOrJcom0slJmnflBG5/Ln0yZbkcRmjmPOdczJ2G13HlRdpNDztDFe5ENwWcsfMN9/\nKXbJHPMwDHHffffhj/7ojzA7O4vNmzfjzjvvxEc/+lF0duolnF8IZkIjTINyJdFaDRQdcxrOtSGu\ntl31tgH7c/GURcJU8II2tQyiGJIF/fth67LJfNeafBoLoJTTZYi5omO+pBAtOeaWXQO8bHLgOfjF\nG/ouaTIIm6iMlT8vMZXFxoke6K7grdduwqruUPtOdWba1bauBTlUlhwdc9N77aosD5VFL0xT7jiP\nUzDaQ13UxWS5NsH0PGwhdP5Pe2ceJUV1/v1vLb3MPgwzAwwwDA4/QBhAoqBoAEERjaDibvJzIyAq\nxuWYuKAexbhFk3Ncfi9GT/C8OeKSHxrNa/S4RAZ8zUGNG4LxjT93YyKr4DAwzPT0ff/oqepbW3dX\ndd3q6u7ncw6HmZ7q2p5bt5773O99HinlXPYmko73x6lPsuYF9+KYGxeka/Kj3v6knoVIDwY42D+q\nygZHIteIudfKn6osIdHPbKtjKoq1DwLcyZGmjKzHn5bb58c3HIu7Ht6Z1u7Fvt5+y3Y8/P2UpFTU\n/cTJzumIs2HcX/p6LziqDVNG1uMHGfTBuWIePGoF7ypjalbHnL8PR7YPRkSRbdt2JgcSAOwsaY6Y\n5zpLAWSvNBoUfL/jZobHjJOvkikVuJ2UxW2Qx9zOK6OKZQY4G5IpYl5MCHPMx44diw0bNojavRDs\n2qDdC4QvgqDKsuElUZeDlMUpmrVsVju6DyQwb4JVi8g3bNnUceiVP11G9dIvyWAa7o8Pb8XO7gNY\nfFRb1m3tymGbOwkvzgP/wGeSWohAO//uA/2WqUHRBYaqYvbXKkkSfnX6ZNu/ua2uaKbS4ZiA8zOg\nOjjm/PoEwHtna27ruV6T1g24fVbMgxs/JACA0Ta8MxAdcMyds2qkbcKnZzXfh3wj5hEl7WCnCuRo\nEfOBKJbpPlx6dDumjW4wVAwFnB0Dy1qBLL6HY9RTAdBvP1Nj1welPvff+eJvPz/A0a5fX1fjcGj+\nXKujat7OCN+m+MuNqYphLUM+mO+jJm+qjqnY3pXKox5zuGD+OZo9sAjc7n1r7mfNbNpqzf9unpF2\nupV2MyfRPGQjfmIsNui9LXiRc6Yj5t5n5MzPYjyquF7no/fZ5JgXN3ajODuj8o65okiGl0xtLos/\nHcsdK7jhRPspT8NUumTvhPPn78YxDypiPqa5OucKaJkWf2p4ccyNU6DBNn+to/q+x5oqLp+ohhNG\nx9z9tZqjFm5PMaOUxSliLtlLWZprjfpcLwt/Ae8a82yLFp2wRMx9srNTReL04jz7C+Nf0vz0vXVR\nrPv7y8/KRNX0TGJfv52UxXgfTugYhkkj6izn6NSHuj1f1dSfGCtpslS6RJMD49Qv+jW44tHkeYD5\nPuYWMefPlX8HecUQCBKky7WTsgDGIIJTxHw/lxZx1oBjbicdzTZrML+9Gr/fZKyUKsu5SdfsBulh\n0ZjzacNFRMwzMWpwqtp72+C0AsB8r7L1o+Z7XhFRXK/z0PreQqeu9AI55hx2bcXOqLxjHpGNER6j\nxtxhtO+hsVsWf9qMHu1055nwmpUlCBSbqURzJ52vxjyT4ygCTa/XZeOYi+g8+PaQa3o/nnwj5hWZ\npCwZHAy7exFTFTRURfXKsV7vl/lrue5GO13XEfMsun2vGDTm/ALeLFIRXpbAL4wzDyC83N9aQzYR\nRe//ehNJvcCQ0ywdLw/ho45OfajbtikNZLLqTzJEVRkJLcvJwO4jimxpk/w94ct4ixhE7+McTX4w\nomei0s83u5NY41FXzsO/o7wOgrMew3Qftd/5gImTY87HwUcNOIB8xPy/l83AgUQ/jmrPnCbwxLHV\nOG7aePzu/36Gzn+kUiKmpCzpbZyka3bPWFg05vGovU/iFi+O+fI5Y3B8x1D8R3O1/lm+M1yVUcVg\nh1z6YS14SY55kaPmGDHnNeaybNymNu49Yp7x3EypzfiGrTvmLjVYmqYvjA2XlwBoD6H5vnmZUeYf\n6EJJWbp6rFUIhWjM+Yi5h9mBfKOoTvIZwDnqmJIU2Bt2SG1cd8y9RvGkgYi8FjHNdco/HTHPzzH3\n68Vt1JhzTq2LwXYfl0rOfDu9tEdeyqIq6cWUvYmkfiynrB68kxbl/uaYLtHDQEJzzGOqrDvC/MJ5\nfh+SaVaSV0SIkP5pizvNxPSIeervTu2Vbw9eBuFmIqZ7IQJzG9PsbjdjYOakKS3Y/M0eHMeltOXf\nt801MbQ1Zl/LFlMlTB/TiPX/2JZ2zCUpJ1no9LZBeO3j7YbPwhIxj6kK1l09G0B+KRy9fFeRJcs6\nMnOf7iVizlPqEfNwtKKQYGdru6lDvjpZ94F+x4i53YIiwNvL2Ty1ZpCt6BWuvElZgsrK4oZcIube\nNOacYx5wztm4HjG3ccxDKGWxLNjJsYM79uDUy/K8GfbFVABn50aRJZwwKbXGYohJvsL/nk+TNabi\nzO072nZuO3nr4k+fIuYO07pOGm47+vszSFk8nCe/aFGLTAMpfbQWcNbPz5wOzSbqDziv0/GSY1/7\nDu9spCPmRgmVef+Mj5gL6C+7e601MoD07EG3i4h5pQ+OOd8fZZ+NyP8YAB8x52YMHPrFqpiKOxZN\nwtFckTrerk6Lhp3gnXjzGi7FlKVFY+msg3DjiQfjlatmpY8bEsccAA5qqsZBTdXZN8yAX9eTt8bc\n7Jjn0D/pEfMiSZHIQxFzDjtbZ0uJ9P3+PoxsSKeOqq0wlTxXZUun6y1ibpKy2LxEXEtZ1GAXf7rB\nTuNnkbLkrTEvVMTcKmURETE3Slm8RT6c9peJh889FF09CdRVZii57PAMKJKE4zuGovGiGMaZoi58\n7vt8OltVlnBg4GfRGnN5YFpci7j6pjG3iZIDfEQ6+3FmtKcX8XlNI8lTFVUwYlAFDiSSGFoX18+B\n7/8cpSx8xJzPyuKYLtF92zQvIpel9PcUk8bcfD94KYuILA/7DthHzKPcrIPdeWkY+jUfAg4RF465\nLEkZi+M5H8O+DeQSMbcjnkO7cWJUQ9oxVyRj4EuSUs+9OZNWTFWwZOZBls9KCVWRDTOMXrGmIs3c\npiwRc9O7Opd+VF97V4QRc3LMOewM6OS0Hj66Ae99vRtzxzdj58D0OmBdeBOPKFbHPN+IuWmqLS1l\nsUaZM+Fm2jto7BzzmKn6o5cXZBiysmgRc77DE9F58HaNe7jWXBfDmZFlKaNTDmRY/Cmn0hHaZX4Y\nwjnm+ThH5mcpF/Qqch4GsYosIalrrP2xMx+1NS7+zP5Mv7XiGHy5ax8Oa2vQP7OkS/QwfpAkCZ0/\nPxpJxgxZWXin02ngEHHQzGeK2Ll9frR7ojlPKcc8fUy+bzAPwPL0S7KyzyFibo78Oqd9TG+XKRtS\nrvD2yPaIKJKEfri/QU5ZWXLRmNvB59x2G+nVFiwCqevlr1mXOdmbyEBYNOZ+EuPWZHjFHLDM1n/b\nacx5cumHi1nKQo45B5+eVivU4dQRPrH0CPQk+lEZVQ1ZNniNOWCv0fKyeMhQic0kZbFrpLk03KAr\nf7rBrhy2/xHzoLOypNqCVt54SG0ct5w00aDH9RO+8/Mi2zHLuPxsJk7PVSabDvErYm6IBub4Hc0x\n9zQYlPTFj37JxpwyFER1KYvzcZpr42g2Vd41X5bX+2s8F00fzUfM7e8jv9jQKGVxbrcK55jncrpa\ne44aIubQz8cpPSJgjJiLYEb7YLz5+S5D1U/Ami4wp4i5DwEHNxFzr4+iUx5zXr7kZnY5puY2oLNj\nxKAKzJ84BL2JJOoqIhYpi6pIgHWiM+M5lAoxm+CiW+orjHUyXEfMLVKW7PdZzqPPLjTkmHPwjkzl\nQGN0Sk8ly5Lu2PEvQfMKaDutm5dRNd+2ZEkyRZSt+3M6bx4nvWcYMMwIDJynuSP38kKQfX6BuUFr\nC9pALqrKmMctXvKbfPX0lswXPnZwTo6jU4VGABhal9aY5zOY9KQxl70/K9kG0V5w1pj7s0jVj8G6\n1s/tPZCeIdIyK5jtH3WIkmfSCrud+UhHzDXHXNIXWSmmCs5WjXnW3efFxbPbMbQ2jpkDqf80cs1E\nZezX/NCYOw9SzPznEaOw+vXP9bSFuWJeiG2XUciVlGWgj0vJktw9p5Ik4aFzD9N/Ny8EzvV5KsWI\nOS8R6hhei4aqGC6fO8bVPupNM6jZNebG+2geoOeUlUXK7VhhhBxzDt7WFQNlgXN5IJPcPKdFyjIQ\nJY1HZL1ipZeHl+/EFNlUic7mHHN5/zdWpxwdPv1jWLDLo6sqskGv6+WB421VKCmLphcVXSWOd1a8\nXKsfumMnHLOy5Bgxz2eQ4CVHsx4x9yhl0fBr4WBK8pNyGKPcVJ/XomEWzbYPL7OIHjFPGH5P/SzZ\nbmv+W6YIpOLSjtr2ugMnpb9nXvxpvn7REfN4RMHZ01stn5uvP5f3kR8Bh6iLWaVrjh+Ho8YMxuGj\n3RceUhWrY85n5XHTR2p29SNqrTUnWdJSbea2z46WuryPHTZ4idC4IbX4zZlTXO+jvsKdY242O2nM\nyxjegIOrYtixt9eijbKD19OaU1VpEZ+aeAQ9faklZ14dMm3q1rz4067h5dKRnDh5GCKKjKPGZM71\nWgiMC1mNEcEDWRZCZUJzigF/Fkm5wbwwSHR0hW8CvkTMfXXMHSLmGWzKO+bJPES/XiLm2ne8Slk0\n3JRzz0ZkYEGaYfHnQJtyOwCw5DH3wdZa++6z0dcb0r+a+jM3UhaNXMyiHd8QMeeiakaNebCOuROW\nTFQBOeb89Tvl8daIqQrmjvc28xeRZfTAmEqTd7rcRL41CYwfjrnWtvSgUJb7/sylR+Ktz3fhtENH\n5H3ssMHfz6jH/su85ihb/2L2X6xSllwi5uSYlwR8EOec6SPRz4CFWSqHASld+f+57ChEVWt6xKaB\nqHRLfYVeZtirQ6ZlkzCnb7KLjuXSn8VUBQuntHg6F9EYCyqlP4+qacc82wvDDn5lvYgUhZkwT8uL\ndsz5zs9rPloePxVPTi+6TM5/A5em1Ev6R7tj5+yYO0gwcvpuhkWF+aAtSOMd2XkHN+PTbXtxWNsg\n9/vK8LsXzA6SU1TcojXOUSucKcJth3ZNbY1VaKyOYlSNrJe6jyiy4TwsGnNjQo7AMPcRuQwMK3yR\nsrhfh+HtOFx0XNVmL7w9I1rgw4/MKFo/lGuRmqmtgzC11d0zVyzwEXOvtuElvuYaAXbw7dzOr8op\njzlFzEsD3oAN1TGc5MJpnTyi3vbzmxZMwPyJQ/HN7v3Y9PVuAN4bd6qz7IcyoNVML1D1pjEPM4op\noqbBRwe9yHX5iHnQWCLmoqUseWvMc9O3esHpGcgkwZBlCX/+2Q/R1ZPIS37lVgLBn5e3arPpn/0s\n5669vPiFk+fOaMO5M9pc78t8G/yYHbHkHuZuBF+J06kCJJDZyXJrR60918RVvH7tXHz04Wbc9Oq2\ngb/Zp6DVYAWKmJuvP5d+3byA1AtGKYs4x0Y1DNasUhY36BFzlznM7dCjrfqAvPicO7/gB8deAwt8\n7ZdcHqVs7y53WVmKzxcqvjMWCD9L49dK3pENlTjt0BGGxpVPxByw6TRszrUYVyLzGBbMmUbP+jYe\nrvFAQR3zYCPm/IyCHxpzP1/QTh1rtmN0DK8z5N/2dGyZdzpy+w6vRc7neH7O0qQXRfswdW8uhOSD\nI2KZfjZNg2vPtXmAGjVIWTJozF0WVOPlSPGIMiBlSTtembOyZN29ENxEzM+eNhJjh1Tj+I6heR/X\nOGMp7l3CSxK0dux1NmxMczWiqowJw2rzPi/ttLT/DxlpH3grB/gBtlcpXpXL9082xzyXPu+gplRu\n+oNyqAAbNihizmGXG9wv+A7Wa9TMPDUjD6yEtNeYF7lj7hANc5PGy46+/sI55mYnI8gV/MPrK7Jv\nZMLsnBVaY+4XxmweuX0nXbrdi5SFa78+Xp92Ln5qajX8iZg7R8K13w8kkhlzmmeMmLvItQ3wsx7W\ngZkqy0ZtsyWPeYE05qZ7k8lJvuu0yb4dNxKYlMUaMf/RpGF49I0vMX10g9PXbBlWV4G/rTjWUIHW\nK4Z3LICVJ01Ec00Mp/6g9DTk2TBozD0GAdzKTg2OuY1Tn4t/dlhbAzZePxfNNfGs24YNcsw5+Je0\n31NXBt2k4k0Dp5oc80y6V5HTj0FgnFa2T5/l5RrDJGUJIuft/75wGnbv6zOUnM4Vc+fnr5TFfl9B\nlE/2Eg3UtvPiWBvasp8Rc+2cfOireGkc4I+trWW07R1wcxQuyj0nGbOycG3FTVYWuzUGilz8EXM/\n4duUWCkLL1NM/RyPKHjm0qM87S9bYbNcMS8crK+M4oYTJ/iy72LDDykLAEP/kg2+ndv1AbnOEg6r\ncx+QCgPkmHM4OYN+4FRy2g1ahMjcadhKWYpcE2dc2JX+3FxoyS3msspBErSUBQCOHtfs+bsWjbmf\nUhaH5yuIiLmXxZ/mQbEbnDKO5IuiO+b+7JMvre6HrS2LP81SlixVQKOKnHHg5DWPuV02l4iSOdNV\noSLm5nsY1ExovjOTOR/HlHErLKTTJRb3e9QP/JCyAKmMdVrV62xk6zOL3b/JRniehBBgiJiHUMqi\ndWJaO+WjPWaKXcoiOwySDBFzD9fYX6jQFwoTMc8HcxuS/MzK4hQxD8Qx96Axz8MJVgxSLP9nHfxy\naAwRaB92KUmSQc5iccCdNOZqbhId3o65Vf60c8zTs46FrPzphB/Vjr3Az+yIPCTfD0RC1B+a0yWW\nM35IWQBrVfRMGB1zqw3CNIgTQWlfnUuy5QbPB61By5L36WxLblWHiBMQXAcuCqeIedQwxRrkGeWP\nJV1iyDsXs/PsZ5uKOsx8BHFL3EZaAf8i5n4O+BUHx9Yr/HPmV/8Xz5Bqzan/0q4nW3YN2WV/rR3H\nLmKuypJJY27cX4H8csvgpKkm5rClv0RsBi8isNOYh4H0rHSBTyQE8AGlfPovc42XTBgysdkM2EY1\nVHo+j2KApCwcRo25v09kvjlaAWvE59Spw/H+17v11cd22xYr/MuAd54MWVmKbPBRCClLPojIba1h\ndoK0mYwgUlupHgZ3+aRNE6cxT+3Lr3akODxz+ZCqfNwHwBr5SmeVMX6u9ZHZ8lG7reCaSWOuynLG\nwEw+Ba3ywXwPRgbkkPDRa5HvEn4A4DVNogj0POZF9o4RgWHWK4++xs2iXHNRQY3fL56Olz/8Fktn\nHeT5PIoBcsw5REW2ACA6sOAzn5eoOZfyjQucF6MMrvae5zkM8A6Q00MqMo2XCCRJQlSV9QWoYXfM\nzc+An+8oQwpMvpprAC/Cglb+9DOPuc9SFtkgZfErYp5JyuKgMdekLC4i5rmc7tghNdjw8XaMaa7m\nvpcecKmGAVT4pCxVUQWDfFrcmA0v6zA8HcdQaCo8/aF2zeSYGweHbisK89S4cMz5NscHtGaPbcLs\nsU2ez6FYIMecg++L/Y4SmMtBe0GLJmbqLH512iRs+Hg7zpo20vNxwoDsoHc1Fhgqvk4zxjnmflSo\nE4klYi4oXaJTlVdRuI20AvxslfsTNDh8Pl6gFn33a4BnkIb4FTHPKGUZkOKYzl/LRz2xpS7jvt1W\n/rz+hPG4aNZBaKxOy0G0Q0cVY7pEs50LtTKFvzcjGyo9VTv2grkYVBDHCZNjnk6XWOATCQExQ8Tc\ne1twk5+eb3NhahdBQY45h7FCn7+NQXtB5aMHjejOgfPDcda0Vpw1rdXzMcKCkzMTMSz+dL/fS45u\nx4PrP8XV88bmdX5e4Velzx3vPWNKEIit/Gkv7wg6j7nbiLmXiLecIRKbDz+ePhJxVcb0Nnf5np1Q\nXDq6uWB0zM1SFvuI+fD6CvzthmOzVrB0W/lTkiSDUw4Ac9sqsLcPmD9xKLb8a0/63EzXX6hF43wg\nZ8Sg4HS1geUx52eTQjSD2Dq4EjFVxrgh+RcrKnbiqj+DJ68VacM+sywCcsw53FaSc8OEllqc0DHU\nddEEHnP+8lLG6CSkP4/lmcbrmvnjcOZhI9E2uDCLR2piKroOJHDq1OHoGJ45IlhoLFlZBEXMeZ1p\nWLOy2GX0yP14RtmOX/g9CJcF9H+5ZGWxG+zUVWSXbPihiZ/QFMWUliq0Dq7ER99+r39k9P7IAAAa\nqElEQVRu7ltqKyLY3nXA0zHywRgxDy4ns3Edhrhnkh+Uh0lj3lwTx1srjkVVLNyzmkEQi/CLP733\nXxNbvA1yKGJe5vD291tjHlFkPPifh+a1D62zLDZttRecMmfkm8dckiSMLmCJ3vvPmYpN/9yNS48e\nU7BzyJVM6ePy3rdTxDxgjXmu15VPznBRiz/9RkT/l4uUxeuLl29DfjQbwyyO6fofOX8afvHUJlx3\nwvj8D+QCfiA3MsCIOX9cke+bSEg15oB/xYqKHX5wHc1DynLO9FZs/f4Ajhwz2NX3KGJe5vBOQRgT\n2A+pjQ/8H0zKrELi5BTmW/mz0MwZ34w5IZewaPAlz/12mPnIC/+shbXAUOtANgwvWTGMjnl426xh\nXYevWVlSWAsJDWjkPTpkfp8vrytXTHaaNKIOL145K+9juIWPVgaVkQUIMGIe0gJDRJpYhmfYDaoi\n4+fzx7n+XtjTCotA6BW/9957OOWUU9DS0oLKykqMHz8et956K/bt2yfysJ4xRozC1xhuXjgRT150\nBI5qbyz0qQhHi9LIkvNCkGJ0zIsJp1zyfsBHyngrBjEb5EVjfv6MNrx05Sz8ZLp76YhhxieE/YqG\nCClLRTSDxjyPWQj++4A/52tc1xKOvoV3SkYMCk7KYlj8KfA4Yc3KQqTh1zkUwi+iiLmP/P3vf8eR\nRx6JcePG4d5770VjYyNee+013HrrrXjnnXfwpz/9SdShPSNSY+4HdRURHHGQu2mgYkV7MZo7An5V\nOPXjYnG7uM4NTi/hIBwiazQw+8I+WZYwbmiNp+MVS8Tcy4AlG5k05vriT4/T4/wgzo/mKVK65RV+\nYDM8SMec63dFporkj5OPTIIQBy9HK4SN/EwxWywIc8wff/xx9PT04Omnn0Z7ezsAYO7cufj3v/+N\nhx9+GN999x0GDRok6vCeMGZlKb/GECaqYyokCaitMDbRWJ4acyJ3+EGR71IWh+criFkQEQ5orscL\nc7+iOMxS5UOmafBIvhpzvyPmGTTmhaI6puLu0yYjokquSprnCz9YEpmRhiLm4SfmU1YWr2g1YMoJ\nYY55JJLqROrqjJkn6uvrIcsyotHwFcCJyBJqoxL6GVAZJfl9IRlcHcMD50xFQ5WxnQSVX5cwOq1+\nS0ycJB1hzcqSD0bHPLzOh/Y4+WkDQ7TNImXJT2Pu94yOQWMeIsnRmQWoSaEGFTEPaR5zIg0/uCYp\nSzAI8z7PP/983Hvvvbjkkkvwq1/9Ck1NTdiwYQMeeughLF++HFVVmTNjfPjhh0gmk6JOz5ZkfwJ3\nHTMYScbw0YebAz02YWUkAOwFNm36Rv9sx/Yu/efvdu3Epk2bfDlWX1+f/r9f+ywFFAnoZ0Cyv1/Y\nfTlwIJ2GbsvmD4RHzXft3K3/nEwkgIgi1O5de9L5sT/75H/AdoYvKAEAfQN2kMB8uxd7dqZTEO7Y\nvg2bNvXov3ftSdlh187t2LSp1/W+v9+TtuNXX36JTcltrr5vfuY/35U+h90+9i3FCOOc8e927xF2\nL3bvStvws08+Ru+2YGYFqL/Pna/29Ok/f/bJx+jbHoyNJjXHsHnbAfxHdLevNgra9rIso7XV3dok\nYY55W1sbNm7ciEWLFulSFgC4/PLLce+992b9fiKRQH9/v6jTc6S5KjU61IxHhAuZcYM1lhRiJ7J9\nGs0xlyVx90VzAiQA/YkERD/1EteG+EGAOLunj8eS/aFtX9qtkCH5do6qlL52yfS8KlLK7rLH51ji\n1gYkk4m8zrmvrw/JZIL7REzfUowk+sXdC/5ZRH8ChbjlZOfMyNxzwZLB2ejGmXU4kGCojDBhNgrC\n9ooHKY4wx/yLL77AwoULMWTIEDz11FNoamrCm2++idtuuw179+7F6tWrM5+YqkIOeNqEN5ImxSHC\nhbHYgeKbncj29siyBCQZZFncfdEkSbIUzL2PcFOzvGpD1LH5Kfp4VA1t+9LWEfhp6wpOEhiLGJ/X\nuQdVY2t3Ej9sq/Z0PGNFYPf31fzMx7ivRxT/+pZih0ES92xwz2I8FkEkEoyElPr73KmMp5+zimhw\nNooAiAuYXAza9l78WGF3+LrrrsP333+P999/X5etzJo1C42NjVi8eDHOO+88zJ492/H7EydODNwx\n37RpE/r6+hCJRDBlypRAj03kxj96vwbeTk1/DmluwpQpE3zZL9nenugz36InkUAsEvX/vjzxTwBA\nLBYDkICiyIHc+1e3fQz8PSWJikUjAPqF2r3p0w+Az1IpYjsmTAg0H7Ubql97Hdi9BxFV9e1e/L/e\nr4B3Us9rW+sITJnSpv9tCoAfz/O+7+ZPPwA+T93X9oNGY8r4Ia6+b37ma3d0Ay9sBQAMG9KMKVMO\n9n5ypcDA81lZXS3s2diw43+AD1PP4pRJHWisDqZGB/X3ubNnXx/w7L8BAJMnTURzTbzAZ5QfQds+\nmUyiq6sr+4Ycwjzf999/HxMmTLBoyadNmwYA2LJli6hDEyUMvxCEsrKIR0tpJ/JeV8dUKLKEwVXB\naK+9FBjKh2JZ/CkLXvzp98Ixvxd/hjFdYhigrCzlTYyv/Ek2CgRhEfOWlhZs2bIFe/fuRXV1tf75\nxo0bAQAjRowQdWiihDEUGKKXp3D0FHoC++PaiggeXTwd9ZXBOOYWh06c35E6XsgrCmtoz5Mox9zv\nVJGKz5U/w5guMQyIzMFgyGNOTl8oiUcUnHvEKOzv6w+sjy53hDnmV155JU455RTMmzcPV111FRob\nG/HGG2/gzjvvxIQJE3DCCSeIOjRRwvARc3p3ikdzUPzOY87DGHDkmOCq2Voi5qId8yIpO67Z2E9b\nG4uT+B0x93f2TDFEzMNrp6DpF5gu0Rgxpw49rPzylI5Cn0JZIaz3Oemkk/Dqq6+itrYWV1xxBRYs\nWIDf//73WLZsGV577bVQ5jEnwg/feYt0FokU6aIz4u61yKlyO4IuMFQszoeQiLnAct78GMeP5hkx\nOPr5769UECtlSd1oSSL5EEFoCF1eO2fOHMyZM0fkIYgywxAxp45cOKouZRHomAuMyNlhjpiLrpbA\nD2oKUaAjV7Tb4ucpCpWyGApF+RAxVyhibodIxzwip6u/UsE4gkhBvQ9RVPA6xCDKt5c7+uJPgfc6\nGXTEfOCa/Cw9nwlVLo6IuSJAtmRwzH2Wsvi9WJPfH2nM0wQRMSd9OUGkoaeBKCooK0uwaA6KSP9V\nZMlvO1QBko1M8BKRMEcFZcn/2ZEKXmPus/Ml+yxJUn3WrJcKIp9PbaAa5gErQQQNOeZEURGhiHmg\nKAE4sf3B+uWB6OZ5tIFA2KOwYiLmvMbc3+s3SpJ8jpiTo6gjNGI+MBgK86JogggaehqIosIYMS/g\niZQJQUSXWYEi5kE5ygqnow0zmnPrp635Sr1+W9nvPOayLOkzQxQxTxNEVpawPxsEEST0NBBFBWnM\ng0XRpSyll5UlqMXDacc83O1Vl7IIipj7vZbAb8ccSGdmCfvsRpAIXfw58Ez4nUqTIIoZehqIosKY\nx5xenqLRpppF+pRBO+b6NQXlmA+0UzXkUUHt9Py8L/xA2u/Iq0HK4tOtDVrmVAyIdcw1KQvdb4LQ\nEJoukSD8hp/ypHeneILQmAe9+FOEljqX40VCHoUVYWtJYKpI3nn2y5HWZU7kKOqIdMyntg7C9NEN\nOKFjqLBjEESxQY45UVTwEfOgI63liOagiIggXnJ0Ox5c/yluPHGC7/vORBC52Q3HU4ojYi5CYw4A\nP5s7Bh9v7cLhoxt83a9qyDvuzzlrucwpj3kakf1sdUzFfy+bIWz/BFGMkGNOFBX8lCc55uIRObV/\n7fHjcdmcMaiKBdsNaQ5dUBFzWSqOKKzumPt8X64+bpyv+9MwRsz92adKGnMLQc9oEUS5Q2EBoqjg\nNasJcsyFIzorS9BOORC8xlzVpSzh7m7Ti2ILfCI5wjvPfi1ODjrHfZg5ZnwzAOD8GW2FPRGCKDMo\nYk4UFfwLmCLm4gk6g0kQBO2Aavcuoob7HoqSsoiCb5N+Rfm1a6eIOfC/fvIDbP5mD37QOqjQp0IQ\nZQU55kTRQhFz8WjR5VLyU7QUfnFVybKlP6Tzpoc7FK1NRhVLRhK/CwwBaalcsQxORBKPKJjW5u+6\nAIIgskOOOVG0+J0XmbASdAaTIJg8oh4//eFoTB/dACS2Cj9eseUxLxan1JDH3Od0icVyDwiCKD3C\nHcIhiAxQxFw8QWcwCQJFlnDTggmYPzGYFG1Da+MAgGF1FYEczytykQ3CRBQYGjGoEgDQUh9uWxEE\nUbpQxJwoWvqTyUKfQslTihHzoJk+ugFPX3IkxjRXF/pUMqLZuFgGYSKkLP/146n4954etDeF21YE\nQZQu5JgTRQtFzMWj5zGnuTXPSJKEQ0eFfwFdsQ3CDOkSfWqfNfEIauIRf3ZGEAThAXrdEkULaczF\nQyXKywfNxMWir+bzwlP7JAiiVCDHnChaKGIunqBzfhOFQym6xZ/p11exRPkJgiCyQY45UXScfugI\nAMBPfzi6wGdS+lDEvHwotowkikQRc4IgSg/SmBNFxz2nT8Ztp3QgHgkmD3U5o5JjXjbIRWZrfgAh\nUYiJIIgSgbozouiQJImc8oBIR1ELfCKEcNJSlgKfSI7wjjlJWQiCKBWKpAsmCKIQUMS8fJCLbPGn\niDzmBEEQhYYcc4IgHKmtSKWOq4mT6q3U0WxdWyTpAlUBlT8JgiAKDb1tCYJw5IzDRkKSJCycPKzQ\np0II5oxDi8vWFDEnCKIUIcecIAhH6ioilP2mTKirLC5bk2NOEEQpQhOABEEQRNFhdMwLeCIEQRA+\nIswxv+CCCyBJkuO/N954Q9ShCYIgiBJHc8wlKZWpiSAIohQQJmW56aabcPHFF1s+X7hwIWKxGKZN\nmybq0ARBEESJQxmDCIIoRYQ55u3t7Whvbzd8tmHDBuzYsQM33ngjFIXyUBMEQRDe0BxyymFOEEQp\nEejiz9WrV0OSJCxevDjIwxIEQRAlRlNNDENr42ipjxf6VAiCIHxDYoyxIA60Z88eDBs2DEcddRRe\neeUVw9+SySS6uroMn3311VdIJpNBnJpOX1+f/nMkUhy5fAl/INuXJ2T34qa3n0GRvBVFItuXL2T7\n8iVo28uyjNbWVsNnNTU1kDMUXwgsYv7EE09g//79+OlPf5rT9olEAv39/YLPyhneeER5QbYvT8ju\nxYcEIAkgmeergmxfvpDty5cgbO9Fth2YY7569WoMHjwYixYtyml7VVUzjihEQKPo8oVsX56Q3csX\nsn35QrYvXwoRMXdLII75Bx98gLfffhtXXHEFYrFYTt+ZOHFi4I75pk2b0NfXh0gkgilTpgR6bKKw\nkO3LE7J7+UK2L1/I9uVL0La3k2pnIxDPd/Xq1QCAJUuWBHE4giAIgiAIgig6hDvmBw4cwJo1azB9\n+nR0dHSIPhxBEARBEARBFCXCHfNnn30Wu3btomg5QRAEQRAEQWRAuMZ89erVqKqqwtlnn+24jV3G\nxqBTJQIpkb6iKJBluSDHJwoH2b48IbuXL2T78oVsX74EbXu7Y2TLUh5YHvNMJBIJdHd3F/o0CIIg\nCIIgCEIYVVVVUFXnuHiwaU8IgiAIgiAIgrCFHHOCIAiCIAiCCAHkmBMEQRAEQRBECAiFxjyZTFoE\n8pIkQZKkAp0RQRAEQRAEQXiHMWZZ7CnLcsYCmqFwzAmCIAiCIAii3CEpC0EQBEEQBEGEAHLMCYIg\nCIIgCCIEkGMOYO/evbjyyivR0tKCeDyOQw45BE8++WShT4vwQFdXF6655hocd9xxaGpqgiRJuOWW\nW2y3fffdd3Hssceiuroa9fX1OPXUU/HZZ5/ZbvvAAw9g/PjxiMViGD16NFauXIm+vj6BV0K4Zd26\ndVi8eDHGjx+PqqoqDB8+HCeffDLeeecdy7Zk+9Li/fffx4knnojW1lZUVFSgoaEBM2bMwJo1ayzb\nku1Lm9/97neQJAnV1dWWv5HtS4f169fraxHN/9544w3Dtn/5y18wY8YMVFZWorGxERdccAG2bdtm\n2WdfXx9WrlyJtrY2xGIxjB8/Hg888EBQl5SGEWzevHmsvr6e/fa3v2Xr1q1jS5YsYQDYY489VuhT\nI1zy+eefs7q6OjZr1izdjjfffLNlu48++ojV1NSwmTNnsueff549/fTTbOLEiaylpYVt27bNsO1t\nt93GJEli119/Pevs7GR33303i0ajbOnSpQFdFZELp59+OpszZw5btWoVW79+PVu7di074ogjmKqq\n7NVXX9W3I9uXHp2dnWzZsmXs0UcfZevWrWPPPfccO/vssxkA9stf/lLfjmxf2vzzn/9kdXV1rKWl\nhVVVVRn+RrYvLTo7OxkAdscdd7CNGzca/nV1denbrV+/nqmqyk4++WT28ssvszVr1rDhw4ezjo4O\n1tPTY9jnkiVLWCwWY3fffTfr7Oxk1113HZMkid1+++2BXlvZO+bPP/88A8Aef/xxw+fz5s1jLS0t\nLJFIFOjMCC8kk0mWTCYZY4xt377d0TE/44wzWGNjI9uzZ4/+2RdffMEikQi75ppr9M927NjB4vE4\nu+iiiwzfv/3225kkSezDDz8UcyGEa7Zu3Wr5rKuriw0ZMoQdc8wx+mdk+/Lh8MMPZyNHjtR/J9uX\nNgsWLGALFy5k559/vsUxJ9uXFppjvnbt2ozbTZs2jU2YMIH19fXpn/31r39lANiqVav0z7Zs2cIk\nSWJ33HGH4ftLly5lFRUVbOfOnf5eQAbKXsryzDPPoLq6GmeccYbh8wsvvBD/+te/8OabbxbozAgv\n5JJmM5FI4M9//jNOO+001NbW6p+PGjUKc+bMwTPPPKN/9uKLL6KnpwcXXnihYR8XXnghGGN49tln\n/b0AwjPNzc2Wz6qrqzFhwgR8/fXXAMj25UZjY6Ne+ppsX9qsWbMGGzZswKpVqyx/I9uXJ9988w3+\n9re/4dxzz9X7AQA48sgjMXbsWIPdn332WTDGbO2+f/9+vPjii4Gdd9k75lu2bMHBBx9sMBoATJ48\nWf87UVp8+umn2L9/v25jnsmTJ+OTTz5BT08PgLT9J02aZNhu2LBhaGxspPYRcvbs2YN3330XEydO\nBEC2L3WSySQSiQS2b9+OVatW4aWXXsK1114LgGxfymzbtg1XXnkl7rrrLowYMcLyd7J96bJ8+XKo\nqora2lrMnz8fr7/+uv43zVZOdudtuWXLFjQ1NWHo0KGW7fh9BUHZO+Y7d+5EQ0OD5XPts507dwZ9\nSoRgNJs62Z0xhu+++07fNhaLoaqqynZbah/hZvny5eju7sYNN9wAgGxf6lx66aWIRCJobm7GVVdd\nhfvvvx/Lli0DQLYvZS699FKMGzcOl1xyie3fyfalR11dHa644go89NBD6OzsxH333Yevv/4aRx99\nNF566SUA2e3O29LJF6yqqkI0Gg3U7mr2TUqfTNIHqj5auuRqd2ofxclNN92Exx57DA888AAOPfRQ\nw9/I9qXJihUrsGTJEmzbtg3PPfccLrvsMnR3d+PnP/+5vg3ZvrR4+umn8dxzz+G9997Laheyfekw\ndepUTJ06Vf995syZWLRoESZNmoRrrrkG8+fP1//mZDPz52Gxe9lHzAcPHmw7Etq1axcA+5EWUdwM\nHjwYgP1syK5duyBJEurr6/Vte3p6sG/fPtttqX2Ek5UrV+K2227D7bffjssuu0z/nGxf2rS2tuKw\nww7Dj370Izz44IO46KKLcP3112P79u1k+xJk7969WL58OX72s5+hpaUFu3fvxu7du9Hb2wsA2L17\nN7q7u8n2ZUJ9fT0WLFiADz74APv3789qd96WTr5gd3c3ent7A7V72TvmkyZNwkcffYREImH4fPPm\nzQCAjo6OQpwWIZD29nZUVFToNubZvHkzxowZg3g8DiCtMzRv++2332LHjh3UPkLIypUrccstt+CW\nW27BihUrDH8j25cX06dPRyKRwGeffUa2L0F27NiBrVu34je/+Q0GDRqk/3viiSfQ3d2NQYMG4Sc/\n+QnZvoxgjAFIRbg1WznZnbflpEmTsH37dnz77beW7YCAfcHA8r+ElBdeeIEBYE8++aTh8+OPP57S\nJRY5mdIlnnnmmay5uZl9//33+mdffvkli0aj7Nprr9U/27lzJ4vH4+ziiy82fP/OO++k1Fkh5NZb\nb2UA2I033ui4Ddm+fDj33HOZLMt6nmqyfWmxf/9+1tnZafk3f/58Fo/HWWdnJ9u8eTNjjGxfDuza\ntYsNHz6cHXLIIfpn06dPZx0dHQZfbuPGjQwAe/DBB/XPtHSJd911l2Gfy5YtCzxdYtk75oylcpYP\nGjSIPfzww2zdunVs6dKlDABbs2ZNoU+N8MALL7zA1q5dyx555BEGgJ1xxhls7dq1bO3atay7u5sx\nlio2UV1dzWbNmsVeeOEF9sc//pF1dHRkLDaxYsUKtn79enbPPfewWCxGxSZCxq9//WsGgB1//PGW\nghMbN27UtyPblx5Lly5lV199NfvDH/7A1q9fz5566il21llnMQDsF7/4hb4d2b48sMtjTrYvLc45\n5xx27bXXsrVr17LOzk728MMPs3HjxjFVVdkrr7yib9fZ2clUVWWLFi1ir7zyCnvsscfYyJEjMxYY\nuueee9j69evZihUrqMBQoejq6mKXX345Gzp0KItGo2zy5MnsiSeeKPRpER4ZNWoUA2D77/PPP9e3\ne/vtt9kxxxzDKisrWW1tLTvllFPYJ598YrvP++67j40dO5ZFo1HW2trKbr75Ztbb2xvQFRG5MHv2\nbEe7mycHyfalxSOPPMJmzpzJGhsbmaqqrL6+ns2ePZs9+uijlm3J9qWPnWPOGNm+lLjzzjvZIYcc\nwurq6piiKKypqYktWrSIvfXWW5ZtX375ZXbEEUeweDzOGhoa2HnnnWdbkK63t5fdfPPNrLW1lUWj\nUTZ27Fh2//33B3E5BiTGBgQ5BEEQBEEQBEEUjLJf/EkQBEEQBEEQYYAcc4IgCIIgCIIIAeSYEwRB\nEARBEEQIIMecIAiCIAiCIEIAOeYEQRAEQRAEEQLIMScIgiAIgiCIEECOOUEQBEEQBEGEAHLMCYIg\nCIIgCCIEkGNOEARBEARBECGAHHOCIAiCIAiCCAHkmBMEQRAEQRBECPj/HP2AYWvQZkAAAAAASUVO\nRK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"import numpy as np\n",
"from numpy.random import randn\n",
"import matplotlib.pyplot as plt\n",
"\n",
"xs = range(500)\n",
"ys = randn(500)*1 + 10.\n",
"plt.plot(xs, ys)\n",
"print('Mean of readings is {:.3f}'.format(np.mean(ys)))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Eyeballing this confirms our intuition - no dog moves like this. However, noisy sensor data certainly looks this way. The computed mean of the readings is almost exactly 10. Assuming the dog is standing still, we say the dog is at position 10 with a variance of 1."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Tracking with Gaussian Probabilities\n",
"\n",
"The discrete Bayes filter used a histogram of probabilities to track the dog. Each bin in the histogram represents a position, and the value is the probability of the dog being in that position.\n",
"\n",
"Tracking was performed with a cycle of predictions and updates. We used the equations \n",
"\n",
"$$\\begin{aligned} \n",
"\\bar {\\mathbf x} &= \\mathbf x \\ast f_{\\mathbf x}(\\bullet)\\, \\, &\\text{Predict} \\\\\n",
"\\mathbf x &= \\mathcal L \\cdot \\bar{\\mathbf x}\\, \\, &\\text{Update}\n",
"\\end{aligned}$$\n",
"\n",
"to compute the new probability distributions. Recall that $\\bar{\\mathbf x}$ is the *prior*, $\\mathcal L$ is the *likelihood* of a measurement given the prior $\\bar{\\mathbf x}$, $f_{\\mathbf x}(\\bullet)$ is the *process model*, and $\\ast$ denotes *convolution*. $\\mathbf x$ is bold to denote that it is a histogram of numbers, or a vector.\n",
"\n",
"This method works, but led to histograms that implied the dog could be in multiple places at once. Also, the computations are very slow for large problems.\n",
"\n",
"Can we replace $\\mathbf x$, the histogram, with a Gaussian $\\mathcal N(x, \\sigma^2)$? Absolutely! We've learned how to express belief as a Gaussian. A Gaussian, which is a single number pair $\\mathcal N(\\mu, \\sigma^2),$ can replace an entire histogram of probabilities:"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"scrolled": true
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAusAAAEaCAYAAACo3xkcAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzt3XlYVeX+///nZhAHLBBTI01z6Dgi\nmlNazjiglmLmUDZpx8xO0mDZpA2ez7G+VlrW+WlOlImaYpkiKk4NDlkZqU1HTdO0VEARR4b9+2MB\nugeQrbDXAl6P61oX9F57wZtc7P1i7Xvdt81ut9sRERERERHL8TG7ARERERERcU9hXURERETEohTW\nRUREREQsSmFdRERERMSiFNZFRERERCzKz+wG8pOdnU12drZDzWazYbPZTOpIREREROTK2e12nCdi\n9PHxwccn/+vnlg7rp0+fNrsNEREREZFiU6lSpQLDuobBiIiIiIhYlMK6iIiIiIhFKayLiIiIiFiU\nZcesu7uR9HJjesqS3bt3k5mZiZ+fH02aNDG7HbEwnStSWDpXxBM6X6SwdK5c5O6ezMtNnlKiwvrl\n7pYtS7Kzs8nKytL/E7ksnStSWDpXxBM6X6SwdK4U7HJhXf/HREREREQsSmFdRERERMSiFNZFRERE\nRCxKYV1ERERExKIU1kVERERELEphXURERETEohTWRUREREQsSmFdRERERMSiLLsokoiIeF/rla2N\nTz41tw8A+0S72S2IiJhOV9ZFRERERCxKYV1ERERExKIU1kVERERELEphXURERETEohTWRUREREQs\nSmFdRERERMSiFNZFRERERCxKYV1ERERExKIU1kVERERELEphXURERETEohTWRUREREQsSmFdRERE\nRMSiFNZFRERERCxKYV1ERERExKIU1kVERERELEphXURERETEohTWRUREREQsSmFdRERERMSiFNZF\nRERERCxKYV1ERERExKIU1kVERERELEphXURERETEohTWRUREREQsSmFdRERERMSiFNZFRERERCxK\nYV1ERERExKIU1kVERERELEphXURERETEohTWRUREREQsSmFdRERERMSiFNZFRERERCxKYV1ERERE\nxKI8Duvp6elER0cTGhpK+fLlCQ8PZ+HChZc9LjExkYiICEJDQwkICKBatWp07dqV+Pj4K2pcRERE\nRKS08zisR0VFERMTw8SJE1m1ahWtW7dm6NChLFiwoMDjkpOTadKkCW+//TZr1qxhxowZ+Pv706dP\nH+bPn3/FP4CIiIiISGnl58mD4+PjWbt2LQsWLGDo0KEAdOnShQMHDjBu3DgGDx6Mr6+v22MHDx7M\n4MGDHWp9+/blpptuYubMmdx7771X+COIiIiIiJROHl1ZX7ZsGYGBgQwaNMih/uCDD3L48GG2bdvm\n0Tf39/cnKCgIPz+P/mYQERERESkTPErJu3btolGjRi7hOiwsLG9/+/btC/wa2dnZZGdnc/ToUWbM\nmMFvv/3G66+/Xqjvv3v3brKzsz1pudTKyMjI+5iUlGRyN2JlOleksHLPFavQ+Wptem6RwtK5cpGP\njw833nijR8d4FNaTk5OpW7euS71KlSp5+y8nMjKS1atXA3DNNdewaNEi+vTpU6jvn5mZSVZWlgcd\nlw1We4EV69K5IiWJzteSQ/9WUlhl/VzJb7h4QTwef2Kz2a5oX653332XEydOcOTIEebPn8/gwYOJ\niYnJGwNfED8/P3x8NNskOJ7s/v7+JnYiVqdzRQrLai+iOl+tTc8tUlg6Vy66khzrUVgPCQlxe/U8\nJSUFuHiFvSANGjTI+/yOO+6gd+/ejBkzhsGDB1/2B2jSpInCeo6kpCQyMjLw9/enefPmZrcjFqZz\nRQrLam9P63y1Nj23SGHpXLkoOzubU6dOeXSMR8m3WbNm/Pzzz2RmZjrUd+7cCUDTpk09+uYAbdq0\nITU1lWPHjnl8rIiIiIhIaeZRWB8wYADp6eksXbrUoR4TE0NoaCht27b16Jvb7XY2bdpEUFAQISEh\nHh0rIiIiIlLaeTQMpnfv3kRERDB69GjS0tKoX78+sbGxJCQkMH/+/LxB8yNGjCAmJoa9e/dSu3Zt\nAO68806aN29OeHg4ISEhHD58mHnz5rFp0ybee+89Td8oIiIiIuLE44QcFxfHCy+8wIQJE0hJSaFh\nw4bExsYyZMiQvMdkZWWRlZWF3W7Pq3Xo0IElS5Ywffp00tLSCAoKolWrVqxYsaLQs8GIiIiIiJQl\nNvulidpC3A3Ar1y5sm4wzaGbNaSwdK5IYSUlJRH+abjZbeSxT7Tky5Pk0HOLFJbOlYuuJN8q+YqI\niIiIWJQGiouIlBF2u539+/fz22+/kZqamredOHGC1NRU9u/fDweAAKB8zlbhks8rAtWASmb9BCIi\nZY/CuohIKZSVlcX//vc/vv/++7xtx44dnDhx4uq/+DXA9U5bZeDy6+KJiIiHFNZFpMyyvWKddFkU\n47OPHj3K8uXLiYuL44svvuD06dNF0JkbaTnbr5fUKgH1gcZAXaBsL1IoIlJkFNZFREqwgwcPsmzZ\nMuLi4vjyyy/Jzs42p5HTQFLOVg5oADTK+RhgTksiIqWBwrqISAmTlpbG3Llz+fjjj9m+fbvHxwcH\nB1OjRg2Cg4MJDg4mKCiI4OBgLly4wMy9M+E8cBY4l7Plfp4GZBbwhXNdAHbnbL5APaAF8A80rYGI\niIcU1kVESoj9+/fzzjvvMGvWLJepv/ITGhpKy5YtadmyJS1atKBly5bUqlULm811CFBSUhIzP52Z\n/xfLAo4DR4C/cj4ewQjnBR3zW84WDLTFCO662i4iUigK6yIiFma329myZQtvv/02cXFxlx3mUqlS\nJSIjI4mKiqJz587UqFGj6JrxBarnbLmygRRgD/Azxmwy+UkFEoANwC1AGyCo6NoTESmNFNZFRCzI\nbrezbNky3njjDbZt21bgY4ODg7njjjuIiooiIiKCChUqeKlLjGEtVXO2dkA6xo2nPwP7MMK8s/PA\nZmALxg2ptwNF+DeFiEhporAuImIxW7du5amnnmLz5s35PsZms9G/f38eeeQRunTpgr+/RaZfCcS4\nan4Lxlj3X4BvMIbLOLNzcWx7C6ALxrSQIiKSR2FdRMQifv/9d5577jkWLVqU72MCAwMZMWIEjz/+\nOHXr1vVid1egAkYID8cYHrMFx+keL7UD2AV0ANpjzCgjIiIK6yJlQeuVrY1PPjW3Dyia+cRLnbPw\nzDPPMG3aNC5ccH+35o033sjjjz/OiBEjCAoqYQO9bUCdnC0Z2IYRzjOcHpcBbAS+A7oaCzv5+vp6\nrU0RESvSJFoiImbJBrYD78D/+3//z21Qv+mmm/j444/Zu3cvTz31VMkL6s5CgEjgSaAz7hdPOgV8\nBrfccgtffvmlF5sTEbEehXURETOkADHASoyx3U6CgoKYMmUKP//8M8OGDcPPr5S9EVoBI6w/DrTE\nuPruJCkpiY4dO/L4448X32qsIiIWp7AuIuJN2RjDQP6L22kO/fz8GDt2LHv27OGpp54iIKCUT0he\nGbgDeARj8SQ33n33XcLCwti0aZMXGxMRsQaFdRERb0nGuJq+Ctfx2sCAAQP46aefmDp1KiEhIV5u\nzmTVgeHAvUA119379u2jc+fO/Otf/yI9Pd3LzYmImEdhXUSkuGUDW8n3ajrXwtq1a4mLi6NBgwbe\n7c1q6gOjgJ5Qvnx5l93Tp08nLCyMjRs3erszERFTKKyLiBSnNIyr6QlAppv9rYFHoXv37l5ty9J8\ngVvhxx9/pEOHDi67f//9d7p06cITTzyR7+w5IiKlhcK6iEhx2QfMwP3V9CDgPqAPUMqHpV+pBg0a\nsGnTJt5++223q7JOnTqVTp06cfDgQRO6ExHxDoV1EZGilg1sAj4E3E1i0hoYDVh8TSMr8PX1JTo6\nmqSkJG677TaX/Vu3bqVFixYkJCSY0J2ISPFTWBcRKUqngQXABjf7rgXuR1fTr0DuVfapU6e6zJCT\nnJxMZGQkEyZMICsry6QORUSKh8K6iEhROYgx7GWPm30NMG6cvMmrHZUqPj4+jB07li1btlC3ruPb\nEna7nddee42ePXty9OhRkzoUESl6CusiIlfLjjF3+lyMG0ovZQO6AUOBil7uq5Rq0aIF3333Hf37\n93fZt27dOsLDw/n6669N6ExEpOgprIuIXI0sYAXG3OnZTvsqYdxEejt6ti1iQUFBxMXF8eabb+Lr\n6+uw78iRI3Tt2pX58+eb1J2ISNHRy4eIyJU6C3wMfOdmX22MVTk17KXY2Gw2nnzySTZu3EhoaKjD\nvgsXLjB8+HAmTJiA3W43qUMRkaunsC4iciVSgNkY0zM6uw3jinplr3ZUZt12223s2LHD7Vz1r732\nGsOGDePcuXMmdCYicvUU1kVEPPUHMAs47lT3AwYB3TEW9hGvqVatGgkJCYwdO9Zl38KFC+natatu\nPBWREklhXUTEEzsxViQ941SvBDwANPF2Q5LL19eXqVOnMn36dHx8HF/etmzZQtu2bdm9e7dJ3YmI\nXBmFdRGRwrBjLHS0FOOm0ktVAx4Ganq7KXFnzJgxrFy5ksqVHcch7d+/n/bt27N27VqTOhMR8ZzC\nuojI5WQD8bhf6Kg+8BAQ5NWO5DJ69erF5s2bufHGGx3qaWlp9OnTh08++cSkzkREPKOwLiJSkEwg\nDtjuZl9rjPnTy3u1Iymkpk2bsm3bNtq0aeNQz8jIYPDgwcycOdOkzkRECk9hXUQkPxeAhcAuN/t6\nAX3QjaQWV6NGDTZu3Mhdd93lULfb7YwaNYrJkydrakcRsTSFdRERd84CHwF7nOo+GDO+tPN6R3KF\nKlSowKJFi3j00Udd9j333HM888wzCuwiYlkK6yIizk4B84CDTnV/YBia8aUE8vHxYfr06bz00ksu\n+6ZMmcLIkSPJzMw0oTMRkYIprIuIXCoVmAP87VQvj7HQUX2vdyRFxGaz8eqrr/L222+77JszZw53\n3323Fk8SEctRWBcRyXUcI6inOtUDgQeBWl7vSIpBdHQ0MTEx+Po63nCwbNky+vXrx5kzzpPoi4iY\nR2FdRATgGMbQl1NO9WBgBFDd2w1JcbrvvvuIi4sjICDAoZ6YmKjALiKWorAuInIUI6inO9WrY8yh\nHuzthsQb7rjjDlavXu2yeNL69evp06cPp0+fNqkzEZGLFNZFpGz7G4gBnHPZDcADQGXnA6Q06dSp\nE+vXryc42PEvso0bNxIZGUl6uvNfcCIi3qWwLiJlV0FBfThQwesdiQlatWpFYmKiS2D/4osv6N27\nN6dOOY+NEhHxHoV1ESmTkpKSjKEvzkOTa2IEda1KWqa0bNmS9evXU6VKFYf6V199Ra9evUhLSzOp\nMxEp6xTWRaTM+eGHH+jataux8NGlaqGgXoaFh4ezfv16QkJCHOqbN2+mV69enDx50qTORKQsU1gX\nkTLlxx9/pFu3bqSkpDjuuBG4Fwhwd5SUFc2bN2fDhg1cd911DvUtW7bQq1cvDYkREa9TWBeRMuOX\nX34hIiLCNajXBu5BQV0AaNasGRs2bKBatWoO9a1bt3LHHXdoWkcR8SqFdREpE/bu3Uu3bt04evSo\n4446KKiLiyZNmrBhwwaqV3ecYH/jxo1ERUVx/vx5kzoTkbJGYV1ESr2DBw/SrVs3Dh8+7LjjRmAY\nUM6MrsTqGjduzPr166latapDffXq1QwePJiMjAyTOhORskRhXURKtSNHjtC1a1cOHDjgUG/Tpo2C\nulxW48aNWbt2LUFBQQ71zz77jOHDh5OVlWVSZyJSViisi0ipdezYMbp3786ePXsc6uHh4SQkJGjW\nFymU8PBwtyudLlq0iJEjR5KdnW1SZyJSFiisi0iplJqaSo8ePfjpp58c6o0aNWLNmjUuC+CIFKRN\nmzasXLmSChUcV8qaN28ejz32GHa73aTORKS0U1gXkVInPT2dyMhIfvjhB4d6/fr1Wbduncu0fCKF\ncfvtt7N8+XICAhzvRv7vf//LuHHjFNhFpFgorItIqXL+/HkGDBjA1q1bHeq1a9dm3bp1XH/99SZ1\nJqVB9+7dWbp0Kf7+/g71N998k8mTJ5vUlYiUZn6eHpCens6LL77I4sWLSUlJoWHDhowfP54hQ4YU\neFxcXByffPIJ27dv588//6R69ep06NCBl19+mQYNGlzxDyAikisrK4t77rmHxMREh3poaCjr1q3j\nxhtvNKkzuRK2V2xmt5DHPvHiVfM+ffoQGxvL3Xff7TBe/fnnn6dKlSqMGjXKjBZFpJTy+Mp6VFQU\nMTExTJw4kVWrVtG6dWuGDh3KggULCjzu9ddf58yZM7zwwgskJCQwadIkduzYQcuWLdm9e/cV/wAi\nIgB2u51Ro0axdOlSh3pISAiJiYnUq1fPpM6kNBo4cCDz5s1zqY8ePZpFixZ5vyERKbU8urIeHx/P\n2rVrWbBgAUOHDgWgS5cuHDhwgHHjxjF48GB8fX3dHvv555+7rAbXtWtX6tSpw9tvv82sWbOu8EcQ\nEYHx48cze/Zsh1pgYCAJCQk0atTIpK6kNBs+fDgpKSlER0fn1ex2O8OHDycoKIiePXua2J2IlBYe\nXVlftmwZgYGBDBo0yKH+4IMPcvjwYbZt25bvsc5BHYy3pmvWrMnBgwc9aUNExMHrr7/OG2+84VAL\nCAhg+fLltGrVyqSupCwYO3YsEyZMcKhlZGQQFRXF5s2bTepKREoTj66s79q1i0aNGuHn53hYWFhY\n3v727dsX+uvt27ePAwcO0L9//0I9fvfu3ZrPNkfuynkZGRkkJSWZ3I1YmdVWWSzq83Xp0qW89tpr\nDjVfX18mT55MlSpVSszvhxX6tNq5YiUF/fsMGDCA3377jYULF+bVzpw5Q69evZg9ezY333yzN1r0\nOr0OSWHpXLnIx8fH4/unPArrycnJ1K1b16VepUqVvP2FlZmZyYgRIwgMDOSJJ54o9DFaLc6VXmCl\nJCnK8zUxMZFJkya51F988UVuu+22EvW7Ef5puNktSAEudy498cQTpKamsnr16rzaqVOnGD16NLNm\nzaJmzZrF3aKpStLvmpirrJ8r+Q0XL4jHs8HYbPnfnV/QvkvZ7XZGjBjBl19+ydKlS6lVq1ahjvPz\n88PHR7NNguPJ7jyFmMilrPbEWFTn6zfffMOECRNc5rZ++umnGTBgQJF8D5FchTlvJ02axJkzZ/jy\nyy/zasnJyTz++OPMmzePkJCQ4mzR6/Q6JIWlc+WiK8mxHoX1kJAQt1fPU1JSgItX2Atit9sZOXIk\n8+fPJyYmhjvvvLPQ379JkyYK6zmSkpLIyMjA39+f5s2bm92OWJjV3nIsivP1hx9+4KmnnnL5Q+TF\nF190GRJToE+vuhUpIwp73iYkJNCzZ0+++uqrvNrBgwd55pln2LBhA5UrVy6uFr1Or0NSWDpXLsrO\nzubUqVMeHeNR8m3WrBk///wzmZmZDvWdO3cC0LRp0wKPzw3qc+fOZdasWdx7770eNSsisn//fnr3\n7u3yZDd69GheffVVk7oSMVSsWJHPP/+c8HDHYU3fffcdAwcO5MKFCyZ1JiIllUdhfcCAAaSnp7vM\nYxwTE0NoaCht27bN91i73c7DDz/M3LlzmTFjBg8++OCVdSwiZdbx48fp2bMnf/31l0N94MCBvPvu\nu4UeiidSnIKCgli1ahU33XSTQ33t2rU89NBDmihBRDzi0TCY3r17ExERwejRo0lLS6N+/frExsaS\nkJDA/Pnz8wbNjxgxgpiYGPbu3Uvt2rUBePzxx5k9ezYPPfQQzZo1c1gKPCAggBYtWhThjyUipc3p\n06fp27cvv/32m0O9Y8eODs8/IlZQo0YNEhIS6NChA8ePH8+rf/zxx9SoUYMpU6aY2J2IlCQe32Aa\nFxfHCy+8wIQJE0hJSaFhw4bExsYyZMiQvMdkZWWRlZXlcOPX559/DsCcOXOYM2eOw9esXbs2+/fv\nv8IfQURKu4yMDO6++26XtRyaNm3KZ599Rvny5U3qTCR/N998M/Hx8XTu3JkzZ87k1d98802uv/56\nnnrqKRO7E5GSwuO7NQMDA5k2bRpHjhzh/PnzJCUlOQR1gHnz5mG326lTp05ebf/+/djtdrebgrqI\n5MdutzNq1Cji4+Md6rVq1SIhIYGgoCCTOhO5vNatW7N06VKX9UmefvppPv74Y5O6EpGSRFOriIil\nvfTSS8ydO9ehFhwczOrVq7nhhhtM6kqk8HIXR3L2wAMPsGbNGhM6EpGSxONhMCIiV8P2igc3gX4D\nxDvV/CB1QCqNFzcuyrZEitV9993HX3/9xbPPPptXy8zMJCoqio0bN9KqVSsTuxMRK9OVdRGxpp9w\nDeo24C7As5WaRSxh3LhxjB071qF2+vRpIiMj2bNnj0ldiYjVKayLiPXsB5a6qfcBGnq3FZGiYrPZ\neOuttxg8eLBD/dixY/Ts2ZO///7bpM5ExMoU1kXEWv4GYoEsp3pnQCMFpITz8fEhJiaGbt26OdT3\n7dtHZGSkxysbikjpp7AuItZxApgPnHeq3wJ08n47IsUhICCAuLg4l1VOv//+e6KiorTKqYg4UFgX\nEWs4gxHUnS8s/gOIxBivLlJKXHPNNW5XOU1MTOSBBx7QKqcikkdhXUTMl4Ex9OW4U70Wxg2lWpxU\nSqEaNWqwevVqqlat6lCPjY1l3LhxJnUlIlajsC4i5soClgAHnepVgaGAv9c7EvGaBg0aEB8fT6VK\nlRzqb731FlOmTDGpKxGxEoV1ETGPHWN6xl+d6pWBe4GKXu9IxOtat27NkiVLXFY5HTdunFY5FRGF\ndREx0SbgO6daAEZQD/J+OyJm6dWrF3PmzHGpa5VTEVFYFxFzfAdsdKr5Ygx9qe71bkRMN3z4cN54\n4w2HWmZmJgMHDuS775z/qhWRskJhXUS87xdghZv6QKCOd1sRsZKnn36a6Ohoh1p6ejqRkZHs3bvX\npK5ExEwK6yLiXX9g3FBqd6pHAo29346IldhsNt58802XVU6PHj1Kr169OHr0qEmdiYhZFNZFxHuO\nAQuATKf67UAb77cjYkW5q5x26dLFob5nzx769OlDenq6SZ2JiBkU1kXEO9KAj4BzTvUWQFfvtyNi\nZQEBASxbtozmzZs71L/99lvuuusuMjIyTOpMRLxNYV1Eit9ZjNVJ05zqDYC+aHVSETeuvfZaVq1a\nRe3atR3qq1evZuTIkdjtzmPJRKQ0UlgXkeKVuzqp81DbG4BBaHVSkQJcf/31rF69mpCQEIf6hx9+\nyPPPP29SVyLiTQrrIlJ8soBPMG4qvVQIMAwo5/WOREqcf/zjH6xYsYIKFSo41CdPnsw777xjUlci\n4i0K6yJSPOwY0zP+5lQPxFj0qJLLESKSj3bt2rF48WJ8fR3fioqOjmbx4sUmdSUi3qCwLiLFYx2w\nw6mWuzppsPfbESnp+vbty8yZMx1qdrud4cOHs2HDBpO6EpHiprAuIkVvK/CVU80PY+hLDe+3I1Ja\nPPTQQ0yaNMmhduHCBfr378+PP/5oUlciUpwU1kWkaP0IJDjVbMBdQG3Xh4uIZ55//nkeffRRh1pa\nWhq9evXiwIEDJnUlIsVFYV1Eis4e4FM39X5AQy/3IlJK2Ww23nnnHaKiohzqR44coWfPniQnJ5vU\nmYgUB4V1ESkah4BFQLZTvSvQ0vvtiJRmvr6+fPzxx9x+++0O9V9//VWrnIqUMgrrInL1jgMfY8yp\nfqm2wO2uDxeRq1e+fHk+++wzmjRp4lDftm0bAwcO5MKFCyZ1JiJFSWFdRK5OGvARxiqll2oK9ESr\nk4oUo+DgYBISEqhZs6ZDfc2aNdx///1kZzu/1SUiJY3CuohcubPAfOCkU70u0B89w4h4Qc2aNVmz\nZo3LKqcLFy5k7Nix2O12kzoTkaKgl1IRuTIZQCxw1KkeCgzGmKpRRLyiUaNGxMfHU6mS42pj06dP\n57XXXjOpKxEpCgrrIuK5LOAT4A+neghwD8biRyLiVW3atGHZsmX4+/s71CdOnMh///tfk7oSkaul\nsC4inrEDK4DfnOqBGKuTVnI5QkS8JCIigo8++gibzfFmkTFjxrB48WKTuhKRq6GwLiKeWQfscKoF\nYAT1YO+3IyKOBg8ezPTp0x1qdrude++9lzVr1pjUlYhcKY0qFZHC+ypnu5QfMAyo4f12RLzF9op1\npjWyT7z8DaOPPvoox44d4+WXX86rZWRkMGDAANasWUOHDh2KsUMRKUq6si4ihbMdSHSq2YC7gNre\nb0dECjZhwgQee+wxh9qZM2fo06cPO3Y4vz0mIlalK+sixcRKV+KuWhKw0k29H9DQy72ISKHYbDam\nTZtGcnIysbGxefWTJ0/Ss2dPvvjiCxo21C+wiNXpyrqIFOwX4FM39Z5ASy/3IiIe8fHxISYmhn79\n+jnUjx07RkREBAcOHDCpMxEpLIV1EcnfPowpGp2HyHYGbvV6NyJyBfz9/Vm8eDFdunRxqB86dIju\n3bvz119/mdSZiBSGwrqIuHcQY9GjLKd6O6CT99sRkStXvnx5PvvsM9q2betQ37NnDz169CAlJcWk\nzkTkchTWRcTVX8DHGKuUXqoFxvCXUjQcX6SsqFy5MvHx8TRt2tShvnPnTiIjIzl16pRJnYlIQRTW\nRcTRUeBD4JxTvQnGDaUK6iIlVpUqVVizZg316tVzqG/bto2+ffty+vRpkzoTkfworIvIRccxgvoZ\np3p9YAB6xhApBa6//noSExOpWbOmQ/2LL77gzjvv5OzZsyZ1JiLu6KVXRAwpQAyQ7lSvDdyNJnoV\nKUXq1KnD2rVrue666xzq69atIyoqivPnz5vUmYg4U1gXETiBEdSdh6zWxFidtJzXOxKRYtawYUMS\nExOpUqWKQz0hIYFBgwZx4cIFkzoTkUsprIuUdSeBeTkfLxUK3AsEeLshEfGWsLAw1q5dS1BQkEP9\n888/Z+jQoWRkON9lLiLeprAuUpadwriifsKpXgMYDpT3ekci4mUtW7Zk9erVVK5c2aEeFxfHfffd\nR2ZmpkmdiQgorIuUXekYQd15euVqGEG9gtc7EhGTtGnThoSEBCpVquRQX7hwIQ899BBZWc4LLoiI\ntyisi5RFuUH9uFO9KnAfUMno4qQyAAAdzElEQVTlCBEp5dq3b8/KlSupUMHxL/WPPvpIgV3ERArr\nImXNKYwx6sec6lUwgnqgtxsSEavo1KkTy5cvJyDA8WaVDz/8UENiREyisC5SlqRhBHXnK+pBwP3A\nNd5uSESspnv37ixbtoxy5RyngVqwYAH33nuvAruIlymsi5QVJ4G5QLJTPRh4ALjW2w2JiFX17t2b\nZcuWuVxhX7RokWaJEfEyhXWRsuAERlBPdapXwQjqQc4HiEhZFxkZyWeffeYS2JcsWcLgwYMV2EW8\nRGFdpLRLxQjqztMzhqAr6iJSoJ49e7JixQqXm06XLVvG008/rYWTRLzA47Cenp5OdHQ0oaGhlC9f\nnvDwcBYuXHjZ4w4dOkR0dDSdOnUiKCgIm83GvHnzrqRnESmsFNwveFQVI6hrjLqIXEb37t1ZuXIl\nFStWdKhv2rSJZ555hvPnz5vUmUjZ4HFYj4qKIiYmhokTJ7Jq1Spat27N0KFDWbBgQYHH7dmzh48/\n/phy5coRGRl5xQ2LSCH9DczBNahXwwjqlZ0PEBFxr0uXLqxatcplHvavv/6axx57jFOnTpnUmUjp\n51FYj4+PZ+3atbz//vuMGjWKLl268MEHHxAREcG4ceMKnIO1Y8eOHDt2jLVr1/Lkk09edeMiUoBD\nGENf0p3q1TFmfdH0jCLioY4dO7J69WoCAx2fQLZv30737t1JSXFeYU1EioJHYX3ZsmUEBgYyaNAg\nh/qDDz7I4cOH2bZtW/7fyEfD40W8Yh/wIXDOqV4DI6hrwSMRuUIdOnRg7dq1XHON4xi6b775ho4d\nO3L48GGTOhMpvfw8efCuXbto1KgRfn6Oh4WFheXtb9++fdF152T37t1kZ2cX29cvSXLvws/IyCAp\nKcnkbsQyfgE+AZzf5KoFDAMquBwhIiWM2c/5FSpUYObMmYwePZrU1ItTTO3evZu2bdsyY8YMbrjh\nBhM7FKtRZrnIx8eHG2+80aNjPArrycnJ1K1b16VepUqVvP3FKTMzU8sdu6HpswSAJOBTwO5Urw/c\nDZRzOUJESiArPOfXq1ePmTNnMmbMGI4ePZpXP3ToEPfffz/Tp0+nXr16JnYoVmWF89dMvr6+Hh/j\nUVgHsNlsV7SvKPj5+Wk4TY5LT3Z/f38TOxFL+AaId1NvDERxBb/pImJVVnnOr1OnDrNmzeKxxx7j\njz/+yKsfP36cUaNG8d5779G0aVMTOxSrUGa56EpyrEcv4SEhIW6vnufeVJJ7hb24NGnSRGE9R1JS\nEhkZGfj7+9O8eXOz2xF3PvXC97ADm4CNbva1APqh1RREShmrPOcnJSVx/fXXM3fuXJ588kmH4Q0n\nT57kkUceIS4ujoiICBO7FCtQZrkoOzvb49mTPHoZb9asGT///DOZmZkO9Z07dwLoL2gRb8oCluM+\nqN8K3IGCuogUu5CQEDZs2MCtt97qUE9PTycyMpIPP/zQpM5ESgePXsoHDBhAeno6S5cudajHxMQQ\nGhpK27Zti7Q5EcnHeSAW2OFmX1egB1C8o9JERPIEBwezdu1aevTo4VDPzMzk/vvv59///jd2u/MN\nNSJSGB4Ng+nduzcRERGMHj2atLQ06tevT2xsLAkJCcyfPz9v0PyIESOIiYlh79691K5dO+/4JUuW\nALBv3z4Avv3227z5Wu+6664i+YFESr1TwALgiFPdBkQCrb3ekYgIlSpVYvny5dx3330sXrzYYd+L\nL77IwYMHmT59usuMciJSMI9/Y+Li4njhhReYMGECKSkpNGzYkNjYWIYMGZL3mKysLLKyslz+inae\nn/29997jvffeA9Bf3CKFcRyYD5xwqvsBdwENvd6RiEiegIAAYmNjqVWrFm+++abDvhkzZvDnn3+y\ncOFCl5VQRSR/Ho9oDQwMZNq0aRw5coTz58+TlJTkENQB5s2bh91up06dOg51u92e7yYil/EHMBvX\noF4BY7EjBXURsQAfHx+mTJnC1KlTXWaJW7FiBV26dHGY7lFECqbbz0RKgl0Yq5KedaoHAyMwFj0S\nEbGQsWPH8sknnxAQEOBQ3759O7feeis///yzSZ2JlCwK6yJWlg1sAJYAmU77QjGCelVvNyUiUjgD\nBw5k3bp1BAcHO9T37dtHu3btWLVqlUmdiZQcCusiVnUB+ARjHnVnDYAHgEBvNiQi4rkOHTqwefNm\nhwknANLS0ujbty9vv/22hsOKFEBhXcSKTgJzAHfvEt8CDAHKebUjEZEr1rBhQ7Zu3UqrVq0c6tnZ\n2Tz55JOMHDmS8+fPm9SdiLUprItYzUFgJvCXU90G9Ab6Ar7ebkpE5OrUqFGDTZs2MXjwYJd9c+bM\noXv37rrxVMQNTXYqYiVJGKuSZjnVywODgHpe70hELMb2inVWPNveZ7tHj69YsSKxsbE0bdqUl156\nyWHfV199RZs2bVi+fDlhYWFF2aZIiaYr6yJWkAUkAMtwDeohwEgU1EWkVLDZbLz44ossXbqUihUr\nOuw7cOAA7du3JzY21qTuRKxHYV3EbGnAPGCrm331MIK6ZnwRkVImKiqKr7/+mlq1HOeePX36NMOG\nDeNf//oXFy5cMKk7EetQWBcx0z7g/8MYp+6sLTAMY9EjEZFSKDw8PG/edWfTp0+nU6dOHDzo7glS\npOxQWBcxQzbwJfARcMZpny9wB8bNpLqRVERKuerVq7NhwwZGjhzpsm/r1q20bNmSxMREEzoTsQaF\ndRFvOwssBNYBzlMLB2EsdNTS202JiJgnICCADz74gDlz5lC+fHmHfcePH6dHjx5MmjSJ7OxskzoU\nMY/Cuog3HQJmAL+52XczMApjZVIRkTLowQcfZMuWLdStW9ehbrfbeemll+jbt6+md5QyR2FdxBuy\ngS+A2cAJp302oCvGQkcany4iZVx4eDjfffcdd9xxh8u+VatWERYWRkJCggmdiZhDYV2kuJ3AmO1l\nPa7DXioCw4GO6LdRRCRHUFAQy5YtY/Lkyfj4OD45/v333/Tu3ZuxY8dy7tw5kzoU8R7FA5HitAv4\nL/CHm321MIa91HWzT0SkjPPx8eHZZ58lMTGR6tWru+x/5513aN26Nbt27TKhOxHvUVgXKQanTp0y\nFjhaApx32mkDOgEPANd6uTERkRKmS5cu/Pjjj/Tp08dl365du2jVqhXvvvsudrvzW5cipYPCukgR\n27RpE+Hh4ZDkZue1wINAFzQto4hIIVWrVo3PP/+c6dOnu8wWc/78eR5//HEiIyM1J7uUSgrrIkXk\n1KlTjBkzhs6dO7Nv3z7XBzQDRgM3erszEZGSz2azMWbMGL799lvCwsJc9ickJNCkSRNmzpypq+xS\nqiisixSBNWvW0LRpU95//33XneWAKGAgUN51t4iIFF6TJk3Ytm0bTzzxhMu+U6dOMWrUKLp37+7+\noolICaSwLnIVUlNTeeihh+jZsyd//OHmLtJaGFfTXS8CiYjIFSpfvjxvvfUWCQkJ1KhRw2X/+vXr\nadasGdOmTSMrK8uEDkWKjp/ZDYiUVJ999hmjR4/myJEjLvsqVKjA2Y5noS36k1hEpJj07NmTn376\niSeffJJ58+Y57Dtz5gzR0dEsXryY2bNn07BhQ6/0ZHvF5pXvUxj2iRoOVBooRoh4aN++fdxxxx30\n79/fbVDv0qULO3fuhFvRb5iISDELDg5m7ty5JCQkUKtWLZf9mzdvJiwsjOeee47Tp0+b0KHI1dGV\ndZFCOnv2LK+//jqTJ0/m/Hnn+RihcuXKTJkyhZEjR7os4iEiIsUn72r2PUAi8K3j/oyMDCZPnszk\n9ydDT6AxxjS6IiWAwrrIZdjtdj7//HOio6P5/fff3T6md+/ezJgxw+1VHRER8ZLyQF+gKfAZkOq0\nPw34BLgJiASu82p3IldEl/9ECrBnzx769u3LnXfe6TaoV69enY8++oiVK1cqqIuIWEUdjJv7O+A+\n6fyOsbr0GlwXrhOxGIV1ETeOHz9OdHQ0jRs3Jj4+3mW/r68vY8eO5ddff+Xee+/FZtP7qSIillIO\niMAI7XXd7M8GNgPvANsBTRojFqVhMCVY65WtjU8+NbcPKD13nJ85c4apU6fy+uuvk5aW5vYxt99+\nO9OnT3e7KIeIiFjMdcBw4CdgNcZQmEudBlYCW4FuQCM0nl0sRWFdBMjMzGTevHlMnDiRw4cPu31M\njRo1mDJlCsOGDdOVdBGRksQGNAEaAF9gXFHPdnpMMrAYqIlxRb62NxsUyZ+GwUiZZrfb+fTTTwkL\nC+Phhx92G9TLlSvHk08+ya+//so999yjoC4iUlKVA7oDj2IEd3cOAXOBBcDfXupLpAC6si5lUnZ2\nNkuXLmXSpEn8+OOPbh9js9m45557eO2116hTp453GxQRkeJTFWOax9+BtYC7N1R/y9kaAh2BUK91\nJ+JAYV3KlMzMTBYtWsS///1vfv7553wf16NHD15//XXCw8O92J2IiHjVTcDDwG5gHa5TPQL8krM1\nwAjtJWjiLyutprq9z3azWyixFNalTMjIyGD+/Pn83//9H3v27Mn3cS1atOCNN96ge/fuXuxORERM\nY8OYl70h8D2wETjj5nH/y9nqYoT2Ot5pT0RhXUq11NRUZs2axbvvvsvBgwfzfVyjRo146aWXGDx4\nsFYfFREpJCvNSnbV/IA2QHNgC8bsMOfcPG5fzlYTaIcxe4yvl3qUMklhXUqlX3/9lXfeeYd58+Zx\n5oy7SySGsLAwXnrpJaKiohTSRUQEAoDOGEF8O0Zwd/cycghYAlyDEfJvASp4p0UpWxTWpdSw2+0k\nJiYydepUtwsZXeqWW27hpZdeol+/fgrpIiLiqjxwO9AW+BZjusd0N49LAxKBTRhX5dtizO0uUkQU\n1qXE+/vvv/nwww+ZPXs2v/76a4GPbd++PS+++CK9evXSFIwiInJ55YD2QGuMMe1f47qwEkAGRqj/\nFuPG1ZYY4+D9vdOmlF4lKqxXm1KN5LPJpvZQWlbqLOmysrJYvXo1s2fPZvny5WRmZub7WF9fXwYN\nGsTYsWNp166dF7sUEZFSwx/jqnkr4GeMMe2H8nns7zlbeYyr7S2AGl7oUUqlEhXWRfbu3UtMTAxz\n587l0KH8niUNwcHBjBo1ijFjxlCzZk0vdSgiIqWaL8bsMU2Bg8A2jKkf3V3LO5ezfxvGPO0tMVZS\n1dh28YDCuhSJYp3L9STGE+Eu3C9c4aRhw4ZER0czfPhwKlasWHx9iYhI2VYrZ4vAuBn1O+BsPo89\nnLPFA/Uxwv4/MG5oFSmAwrpYUzrwE0ZA/6MQj/fDuFrREn6a/ZPGo4uIiPdcC3QHOmEsoPQ9xjAY\nd7K5uDqqH0Zgb4oR4DW+XdxQWBfrSAZ+xXgCO4D7txSdhWKMBWyGMTYQFNRFRMQc/hivR82AFGAH\n8ANwKp/HZ2K8c7wb40bWBsDNOR9L2RvDVpqTv6Tdf6iwLubJxrg559ec7Xghj6uIcRWiBXB98bQm\nIiJyVaoA3TDmbN+LEdx/A7LyefwFLgZ3G3AjxlX3m4GqxdyrWJrCunjXCS6u/rYP9wtNuBMANMYI\n6XXQanEiIlIy+GIE7psxbjj9BWOI517yfwfZjvEO8wFgDRAC1APqYrwGli/WjsViFNaleJ0B9nMx\nnKd4cKw/jmP5dLaKiEhJVh4Iz9lOY0wBuQvjdbIgyTnbNxhX3UMxgntdjBtc9fpYqumfV4qOHUjF\nmMrqj5yPRz38GpUwrj78A+NJqFxRNigiImIRlTDmbG+FMaY996bTvRhj2fNjB/7M2b7ESHKhGMNm\ncmenKWXj3cs6hXW5cueBvzCmosoN5+6WYr6cahjh/B8YTzg+RdWgiIhICVAZuCVnu4Axk0zuhAuX\ne13NxHgNvnTmtKpcDO6hwHVo+GgJprAuhXOOi8H8SM5W2BtCnVXg4tt3dYHgomhQRESkFCjHxQtY\n2Rivt7lDSf8g/xtUL3U8Z9uR89++GCuoXo8R3q/HCPBKgSWC/pnEUQbGL/hRp+3kVXxNP6A2F8N5\ndXT1XERE5HJ8gBtyttsxXqP/wLjyvo9CLRQIGAE/d+jMpV+7KkZor3bJFoxeoy1GYd1DxbpSp7dk\nY4TvFC7etJL7eSqFm9+8IBVxHDsXis40ERGRq+WPMStMvZz/PosxBDX3XrE/KXi8+6WyuXhBbvcl\ndT+M2WdytyqXfF4R4wZX8SpFqNLIjjHG7STGVInOWyqFexutMGwYf4nfgBHMb8T4xdYvs4iISPGq\nwMVpIcF4bT/CxQB/GON13xOZwN85m7MAjNf4oJzt2ks+D0JTShYThfWSJBtjKsQzGFM+pWPcQZ6W\n8/HSz4sqjF/KByOYXzrmrTpaHllERMQKfIGaOdutObUzXLzXLPe+s9Qr/PrnL/la7pQDrsG4YTb3\nY+7nlXK2ihihXhf1Cs3jsJ6ens6LL77I4sWLSUlJoWHDhowfP54hQ4Zc9tijR4/yzDPPsGLFCs6c\nOUPz5s2ZNGkS3bp1u6LmS7QsjJP+PMbbWKdxDOLuPj/rxf6CcBzDVg3jLTAFcxERkZKjIo5DZ8DI\nE8dwvT+tsAsV5ucCF29uLYhPTl+5W6UCPi+PcUW/HGV2LL3HYT0qKort27czefJkbr75ZhYsWMDQ\noUPJzs5m2LBh+R53/vx5unXrxokTJ5g2bRrVqlXjvffeo1evXiQmJtKpU6er+kGKjR0jWGfkbJmX\nfO5cu8DFAH7pds5NrbBjyopTOdyPSbsO4xdDRERESp8KGMNWb3Sqp2OE+GQc72lLwXh3v6hk53wv\nT6d7LoeRTy7dyrupBWBcXLx087v4uW2c7WLNy1NahlQIYe+ovR4dY7Pb7YW+nTA+Pp4+ffrkBfRc\nPXr0YPfu3fzxxx/4+rr/qd9//33GjBnD5s2bufVW472ZzMxMmjdvTmBgINu2bXN4fFZWFunpjv+K\nrZ9vTcrpFOMf2c7Fj1k5W3Y+Hy/dn+3m8c77c8N3bki/2hsuzeKD8dbTtW4+VqHU3ihy9GlPV2Iq\nHtWmVDO7BRERkauXjTHMNhXjfriTOf+dlvP5layxYhU+XAzuuZsNI8Tnbj5uPvdxekx+x/jkbDbj\nY5XAKmz/v+0OLQQGBuabn8HDsP7www+zcOFCUlNT8fO7eFE+NjaWYcOG8fXXX9O+fXu3x0ZERHDw\n4EF++eUXh/p//vMfnn/+eQ4dOsQNN9yQV8/MzOT06dOFbU1EREREpMSpVKmSQ6525tHon127dtGo\nUSOXLxgWFpa3v6Bjcx/n7tjdu3e77BMRERERKcs8CuvJyclUqVLFpZ5bS05OLpZjRURERETKIo/v\nq7XZ8h/kXNC+qz1WRERERKSs8Wg2mJCQELdXwFNSUgDcXjm/0mN9fHyoVKmSQ81msynUi4iIiEiJ\nZLfbcb5d1Men4GvnHoX1Zs2aERsbS2ZmpsO49Z07dwLQtGnTAo/Nfdyl8jvWx8fnss2LiIiIiJRm\nHqXhAQMGkJ6eztKlSx3qMTExhIaG0rZt2wKP/eWXXxymaMzMzGT+/Pm0bduW0NBQD1sXERERESnd\nPJq6EYw51b/99ltef/116tevT2xsLB988AHz58/nnnvuAWDEiBHExMSwd+9eateuDRiLIt1yyy2k\npaUxefJkqlWrxvvvv8/nn39u7UWRRERERERM4vE4k7i4OIYPH86ECRPo1asX27ZtIzY2Ni+og7Gg\nUVZWlsOYnICAANatW0eXLl3417/+Rb9+/Thy5AirVq1SUPfQV199RWRkJMHBwVSoUIEGDRrw2muv\nmd2WWMyOHTvo378/oaGhVKxYkYYNG/Lqq69y5szVrictJdmpU6d45pln6NGjB9dddx02m42XX37Z\n7WO///57unfvTmBgIEFBQURFRbFv3z7vNiymKcy5kpWVxVtvvUWvXr2oWbMmFStWpFGjRowfP54T\nJ06Y07h4nSfPK7nsdjsdO3bEZrPx2GOPeafREsrjsB4YGMi0adM4cuQI58+fJykpiSFDhjg8Zt68\nedjtdurUqeNQr169OjExMSQnJ3P27Fm2bNlC9+7dr+oHKGsWLFhAp06duPbaa/nwww+Jj4/n2Wef\ndblZQcq2n376ifbt27N//36mTp3KihUrGDJkCK+++qrD6sNS9iQnJzNz5kzOnz9P//79833cL7/8\nQufOnblw4QKLFy9mzpw5/Pbbb9x+++0cO3bMix2LWQpzrpw9e5aXX36Z2rVrM3XqVOLj43n44YeZ\nOXMmHTp04OzZs17uWsxQ2OeVS7333nvs2bOnmDsrJexSYhw6dMheqVIl++jRo81uRSzuhRdesAP2\nPXv2ONT/+c9/2gF7SkqKSZ2J2bKzs+3Z2dl2u91uP3bsmB2wT5w40eVxgwYNsletWtV+8uTJvNr+\n/fvt/v7+9meeecZb7YqJCnOuZGZm2o8fP+5y7CeffGIH7B999JE3WhWTFfZ5Jdfvv/9uDwwMtMfF\nxdkB+5gxY7zUacmk6VZKkFmzZnH69GmeffZZs1sRi/P39wfg2muvdagHBQXh4+NDuXLlzGhLLKAw\nU+BmZmayYsUKBg4cyDXXXJNXr127Nl26dGHZsmXF3aZYQGHOFV9fX0JCQlzqbdq0AeDgwYPF0ptY\ni6dTa//zn/8kIiKCAQMGFGNXpYfCegnyxRdfUKVKFX755RfCw8Px8/OjWrVqPPLII6SlpZndnljI\n/fffT1BQEKNHj2bfvn2cOnWKFStWMGPGDMaMGeOyhoHIpfbu3cvZs2cJCwtz2RcWFsaePXs4d+6c\nCZ1JSbF+/XoAmjRpYnInYjWzZs3im2++Yfr06Wa3UmIorJcgf/75J2fOnGHQoEEMHjyYxMRExo0b\nx4cffkhkZKTGrUueOnXqsGXLFnbt2kW9evW45ppr6NevH/fffz/Tpk0zuz2xuNwF7NwtdFelShXs\ndjupqanebktKiD///JPx48fTqlUr+vbta3Y7YiF//vknTz/9NG+88Yam7PaAR4siibmys7M5d+4c\nEydOZPz48QB07tyZcuXKER0dzbp163TDrgCwf/9++vXrR/Xq1VmyZAnXXXcd27ZtY9KkSaSnpzN7\n9myzW5QSoKC3tbWatLiTkpKSd/Fo0aJFWtxQHDzyyCM0b96chx9+2OxWShSF9RIkJCSE//3vf/Ts\n2dOh3rt3b6Kjo/OmWRMZP348aWlp/PDDD3lDXjp27EjVqlV56KGHuO+++zRlquQrdwxy7hX2S6Wk\npGCz2QgKCvJ2W2JxqampRERE8Oeff7J+/Xrq1q1rdktiIUuWLCEhIYGvvvqKkydPOuy7cOECJ06c\noFKlSnn3XMlF+pO3BHE3fhTIG/6iKxiS64cffqBx48YuY9Nbt24NwK5du8xoS0qIevXqUaFCBXbu\n3Omyb+fOndSvX5/y5cub0JlYVWpqKt27d+f3339n7dq1+b5eSdm1a9cuMjMzadeuHcHBwXkbwAcf\nfEBwcDArV640uUtrUrorQQYOHAjAqlWrHOrx8fEAtGvXzus9iTWFhoaye/du0tPTHepbtmwBoGbN\nmma0JSWEn58f/fr1Iy4ujlOnTuXV//jjDzZs2EBUVJSJ3YnV5Ab1ffv2sWbNGlq0aGF2S2JBDzzw\nABs2bHDZAPr378+GDRu47bbbTO7SmjQMpgTp0aMH/fr149VXXyU7O5t27drx7bff8sorr9C3b1+d\n5JInOjqa/v37ExERwRNPPEHVqlXZunUr//nPf2jcuDG9e/c2u0Ux0apVqzh9+nReEP/pp59YsmQJ\nAJGRkVSsWJFXXnmF1q1b07dvX8aPH8+5c+eYMGECVatW5amnnjKzffGiy50rNpuNnj17smPHDqZO\nnUpmZiZbt27NO/66666jXr16pvQu3nW5c6VOnToui2XmuuGGG+jcubOXOi15bHZNIVKinD17llde\neYUFCxZw5MgRQkNDueeee5g4cSIBAQFmtycWsmHDBiZPnsyPP/7IyZMnqVWrFv369eO5555zOy+y\nlB116tThwIEDbvf9/vvveS+o3333Hc8++yxbtmzBz8+Prl27MmXKFIWvMuRy5wrATTfdlO/x999/\nP/PmzSuO1sRiCvu84sxmszFmzBhN5VgAhXUREREREYvSmHUREREREYtSWBcRERERsSiFdRERERER\ni1JYFxERERGxKIV1ERERERGLUlgXEREREbEohXUREREREYtSWBcRERERsSiFdRERERERi1JYFxER\nERGxKIV1ERERERGL+v8BR2nN9z1m0usAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"import kf_book.kf_internal as kf_internal\n",
"kf_internal.gaussian_vs_histogram()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"I hope you see the power of this. We can replace hundreds to thousands of numbers with a single pair of numbers: $x = \\mathcal N(\\mu, \\sigma^2)$. \n",
"\n",
"The tails of the Gaussian extend to infinity on both sides, so it incorporates arbitrarily many bars in the histogram. If this represents our belief in the position of the dog in the hallway, this one Gaussian covers the entire hallway (and the entire universe on that axis). We think that it is likely the dog is at 10, but he could be at 8, 14, or, with infinitesimally small probability, at 10$^{80}$. \n",
"\n",
"In this chapter we replace histograms with Gaussians:\n",
"\n",
"$$\\begin{array}{l|l|c}\n",
"\\text{discrete Bayes} & \\text{Gaussian} & \\text{Step}\\\\\n",
"\\hline\n",
"\\bar {\\mathbf x} = \\mathbf x \\ast f(\\mathbf x) & \n",
"\\bar {x}_\\mathcal{N} = x_\\mathcal{N} \\, \\oplus \\, f_{x_\\mathcal{N}}(\\bullet) &\n",
"\\text{Predict} \\\\\n",
"\\mathbf x = \\|\\mathcal L \\bar{\\mathbf x}\\| & x_\\mathcal{N} = L \\, \\otimes \\, \\bar{x}_\\mathcal{N} & \\text{Update} \n",
"\\end{array}$$\n",
"\n",
"where $\\oplus$ and $\\otimes$ is meant to express some unknown operator on Gaussians. I won't do it in the rest of the book, but the subscript indicates that $x_\\mathcal{N}$ is a Gaussian. \n",
"\n",
"The discrete Bayes filter used convolution for the prediction. We showed that it used the *total probabability theorem*, computed as a sum, so maybe we can add the Gaussians. It used multiplications to incorporate the measurement into the prior, so maybe we can multiply the Gaussians. Could it be this easy:\n",
"\n",
"$$\\begin{aligned} \n",
"\\bar x &\\stackrel{?}{=} x + f_x(\\bullet) \\\\\n",
"x &\\stackrel{?}{=} \\mathcal L \\cdot \\bar x\n",
"\\end{aligned}$$\n",
"\n",
"This will only work if the sum and product of two Gaussians is another Gaussian. Otherwise after the first epoch $x$ would not be Gaussian, and this scheme falls apart."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Predictions with Gaussians\n",
"\n",
"We use Newton's equation of motion to compute current position based on the current velocity and previous position:\n",
"\n",
"$$ \\begin{aligned}\\bar{x}_k &= x_{k-1} + v_k \\Delta t \\\\\n",
" &= x_{k-1} + f_x\\end{aligned}$$\n",
"\n",
"I've dropped the notation $f_x(\\bullet)$ in favor of $f_x$ to keep the equations uncluttered. \n",
"\n",
"If the dog is at 10 m, his velocity is 15 m/s, and the epoch is 2 seconds long, we have\n",
"\n",
"$$ \\begin{aligned} f_x &= v\\Delta t = 15\\cdot 2\\\\\n",
"\\bar{x}_k &= 10 + (15\\cdot 2) = 40 \\end{aligned}$$\n",
"\n",
"We are uncertain about his current position and velocity, so this will not do. We need to express the uncertainty with a Gaussian.\n",
"\n",
"Position is easy. We define $x$ as a Gaussian. If we think the dog is at 10 m, and the standard deviation of our uncertainty is 0.2 m, we get $x=\\mathcal N(10, 0.2^2)$.\n",
"\n",
"What about our uncertainty in his movement? We define $f_x$ as a Gaussian. If the dog's velocity is 15 m/s, the epoch is 1 second, and the standard deviation of our uncertainty is 0.7 m/s, we get $f_x = \\mathcal N (15, 0.7^2)$.\n",
"\n",
"The equation for the prior is \n",
"\n",
"$$\\bar x = x + f_x$$\n",
"\n",
"What is the sum of two Gaussians? In the last chapter I proved that:\n",
"\n",
"$$\\begin{gathered}\n",
"\\mu = \\mu_1 + \\mu_2 \\\\\n",
"\\sigma^2 = \\sigma^2_1 + \\sigma^2_2\n",
"\\end{gathered}$$\n",
"\n",
"This is fantastic news; the sum of two Gaussians is another Gaussian! \n",
"\n",
"The math works, but does this make intuitive sense? Think of the physical representation of this abstract equation. We have \n",
"\n",
"$$\\begin{gathered}\n",
"x=\\mathcal N(10, 0.2^2)\\\\\n",
"f_x = \\mathcal N (15, 0.7^2)\n",
"\\end{gathered}$$\n",
"\n",
"If we add these we get:\n",
"\n",
"$$\\begin{aligned}\\bar x &= \\mu_x + \\mu_{f_x} = 10 + 15 &&= 25 \\\\\n",
"\\bar\\sigma^2 &= \\sigma_x^2 + \\sigma_{f_x}^2 = 0.2^2 + 0.7^2 &&= 0.53\\end{aligned}$$\n",
"\n",
"It makes sense that the predicted position is the previous position plus the movement. What about the variance? It is harder to form an intuition about this. However, recall that with the `predict()` function for the discrete Bayes filter we always lost information. We don't really know where the dog is moving, so the confidence should get smaller (variance gets larger). $\\mu_{f_x}^2$ is the amount of uncertainty added to the system due to the imperfect prediction about the movement, and so we would add that to the existing uncertainty. \n",
"\n",
"Here is our implementation of the predict function, where `pos` and `movement` are Gaussian tuples in the form ($\\mu$, $\\sigma^2$):"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def predict(pos, movement):\n",
" return (pos[0] + movement[0], pos[1] + movement[1])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let's test it. What is the prior if the intitial position is the Gaussian $\\mathcal N(10, 0.2^2)$ and the movement is the Gaussian $\\mathcal N (15, 0.7^2)$?"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(25, 0.530)"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"%precision 3\n",
"predict((10, .2**2), (15, .7**2))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The prior states that the dog is at 25 m with a variance of 0.53 m$^2$, which is what we computed by hand."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Updates with Gaussians\n",
"\n",
"The discrete Bayes filter encodes our belief about the position of our dog in a histogram of probabilities. The distribution is discrete and multimodal. It can express strong belief that the dog is in two positions at once, and the positions are discrete.\n",
"\n",
"We are proposing that we replace the histogram with a Gaussian. The discrete Bayes filter used this code to compute the posterior:\n",
"\n",
"\n",
"```python\n",
"def update(likelihood, prior):\n",
" posterior = likelihood * prior\n",
" return normalize(posterior)\n",
"```\n",
"\n",
"which is an implementation of the equation:\n",
"\n",
"$$x = \\| \\mathcal L\\bar x \\|$$\n",
"\n",
"We've just shown that we can represent the prior with a Gaussian. What about the likelihood? The likelihood is the probability of the measurement given the current state. We've learned how to represent measurements as a Gaussians. For example, maybe our sensor states that the dog is at 23 m, with a standard deviation of 0.4 meters. Our measurement, expressed as a likelihood, is $z = \\mathcal N (23, 0.16)$.\n",
"\n",
"Both the likelihood and prior are modeled with Gaussians. Can we multiply Gaussians? Is the product of two Gaussians another Gaussian?\n",
"\n",
"Yes to the former, and almost to the latter! In the last chapter I proved that the product of two Gaussians is proportional to another Gausian. \n",
"\n",
"$$\\begin{aligned}\n",
"\\mu &= \\frac{\\sigma_1^2 \\mu_2 + \\sigma_2^2 \\mu_1} {\\sigma_1^2 + \\sigma_2^2}, \\\\\n",
"\\sigma^2 &= \\frac{\\sigma_1^2\\sigma_2^2}{\\sigma_1^2+\\sigma_2^2}\n",
"\\end{aligned}$$\n",
"\n",
"We can immediately infer several things. If we normalize the result, the product is another Gaussian. If one Gaussian is the likelihood, and the second is the prior, then the mean is a scaled sum of the prior and the measurement. The variance is a combination of the variances of the prior and measurement. Finally, the variances are completely unaffected by the values of the mean!\n",
"\n",
"We put this in Bayesian terms like so:\n",
"\n",
"$$\\begin{aligned}\n",
"\\mathcal N(\\mu, \\sigma^2) &= \\| prior \\cdot likelihood \\|\\\\\n",
"&=\\mathcal{N}(\\bar\\mu, \\bar\\sigma^2)\\cdot \\mathcal{N}(\\mu_z, \\sigma_z^2) \\\\\n",
"&= \\mathcal N(\\frac{\\bar\\sigma^2 \\mu_z + \\sigma_z^2 \\bar\\mu}{\\bar\\sigma^2 + \\sigma_z^2},\\frac{\\bar\\sigma^2\\sigma_z^2}{\\bar\\sigma^2 + \\sigma_z^2})\n",
"\\end{aligned}$$\n",
"\n",
"If we implemented that in a function `gaussian_multiply()` we could implement our filter's update step as"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def gaussian_multiply(g1, g2):\n",
" mu1, var1 = g1\n",
" mu2, var2 = g2\n",
" mean = (var1*mu2 + var2*mu1) / (var1 + var2)\n",
" variance = (var1 * var2) / (var1 + var2)\n",
" return (mean, variance)\n",
"\n",
"\n",
"def update(prior, likelihood):\n",
" posterior = gaussian_multiply(likelihood, prior)\n",
" return posterior"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Perhaps this would be clearer if we used more specific names:\n",
"\n",
"```python\n",
"def update_dog(dog_pos, dog_var, measurement, measurement_var):\n",
" estimated_pos = gaussian_multiply(\n",
" (dog_pos, dog_var), \n",
" (measurement, measurement_var))\n",
" return estimated_pos \n",
"```\n",
"\n",
"That is less abstract, which perhaps helps with comprehension, but it is poor coding practice. We are writing a Kalman filter that works for any problem, not just tracking dogs in a hallway, so we won't use variable names with 'dog' in them. Still, the `update_dog()` function should make what we are doing very clear. \n",
"\n",
"We have the majority of our filter implemented, but I fear this step is still a bit confusing. I've asserted that we can multiply Gaussians and that it correctly performs the update step, but why is this true? Let's take a detour and spend some time multiplying Gaussians."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Understanding Gaussian Multiplication\n",
"\n",
"Let's plot the pdf of $\\mathcal{N}(10,\\, 1) \\times \\mathcal{N}(10,\\, 1)$. Can you determine its shape without looking at the result? What should the new mean be? Will the curve be wider, narrower, or the same as $\\mathcal{N}(10,\\, 1)$?"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"scrolled": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"(10.0, 0.5)\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAusAAAEaCAYAAACo3xkcAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzs3Xlc1NX+x/HXDAyboAiKivuOImDu\nuVSWdtNMkzQ165bZXtfslt3KW5Y3b4st19v2M3OhTExTs0ztWtlmuaUSiktuaEKmIDuyzHx/f0yS\nxDowMCzv5+MxD8bv93zP98M5Mn48nO85JsMwDEREREREpMYxuzoAEREREREpnpJ1EREREZEaSsm6\niIiIiEgNpWRdRERERKSGUrIuIiIiIlJDubs6gJLYbDZsNluhYyaTCZPJ5KKIREREREQqzjAM/rwQ\no9lsxmwuefy8RifrmZmZrg5DRERERKTKNGjQoNRkXdNgRERERERqKCXrIiIiIiI1lJJ1EREREZEa\nqsbOWS/uQdKy5vSI8+3bt4/8/Hzc3d0JDQ11dThSzdT/9Zv6v/5S39dv6v+qU9wzmWUtnlKrkvWy\nnpYV57PZbFitVrV9PaX+r9/U//WX+r5+U/9Xr7KSdfWAiIiIiEgNpWRdRERERKSGUrIuIiIiIlJD\nKVkXEREREamhauwDpiIiIuJ8VquVlJQUsrKySixjsVhwd3fHZDJx8uTJaoxOagL1f+WYzWYCAgLw\n9vZ2Sn1K1kVEROoJq9XKqVOnaNy4MQEBASWuQpGVlYVhGJhMJnx8fKo5SnE19X/l5OXlkZiYSMuW\nLXFzc6t0fZoGIyIiRWWn0HnzXbT56VUanNkNNqurIxInSElJoXHjxvj5+ZW5XJyIVIzFYqFJkyYk\nJSU5pT4l6yIi9Z1hwK97IWb5H8e8/QGDoBPr6PTdg/BKd9jwGJzcYS8vtVJWVha+vr6uDkOkzvP2\n9iYnJ8cpdWkajIhIfRazHL59Bc4eBDdP6DoCvBoBkBD2AI2Or6fxr9/invErbHvL/vJvA/3vgQH3\ngUZnax2NqItUPWf+nClZFxGpr7a9DRtm2N+7eULn4ZCdUpCsZzaJIKVRdxJ7PUK4z1nYuwoOfAop\nJyD1FxcGLiJSfyhZFxGpj3a880eifukDcPmjBUn6nxlmC3S9xv7KzYL4LdBpmEbVRUSqgeasi4jU\nNzsXwacP298PehCufrbERL0IDx/7CPyFRD0/B35aWTVxioiIRtZFROqf3xPtSx+AYc9UfITcZoMP\nboGfP4PkI3DFY84LUUREACXrIiL1T58p0KwHtOpTuaksZjO0H2JP1r96DkxucPkM58UpIiKaBiMi\nUi/s/wQyL1rzt3Vf58w5H/g3++g8wOZn4duXK1+nSDU7e/Ysu3fvdnUYIsVSsi4iUtcd32KfrhJ1\nHZxPdX79g6fDVU/Z338xG2I/dP49RKrIN998Q/v27enVqxezZs1ydTgiRShZFxGpy/JzYd1DgAHN\ne4Bnw6q5z5CHYdB0+/uNj9uXgBSpAU6fPl3iOcMwmD17NtHR0bRo0YKEhARmz55N9+7dsdlsBeXS\n09N59NFHufrqq2natCkmk4mnn366xHozMjKYPn06wcHBeHl50bNnT5YvX15i+ZKU974LFy6kZcuW\nZGZmOnwPqfmUrIuI1GU/vGbf8MinCYx4oWqXWxz6BAR2tq8Qc3pv1d1HxAGTJ0/m+PHjxZ7btm0b\nN9xwA6NGjeLgwYM8+eSTvPjii8yePRuz+Y8UKSkpibfffpucnByuv/76Mu8ZGRlJVFQUs2bNYsOG\nDfTt25dJkyaxbNkyh2Iv731vvfVWGjRowIsvvuhQ/VI7KFkXEamrko/B17//4/2Xf4N346q9n7sn\njF8CD+yAdoOr9l4i5bRz504WLlxY7LmPPvqIMWPGAODn58cbb7yBv78/kZGRhcq1bduWc+fO8fXX\nX/Pcc8+Ver/169ezadMm3nzzTe6++26GDh3KggULGD58ODNmzMBqtZY79vLe193dnbvvvpt58+aR\nlZVV7vqldlCyLiJSFxkGrH8E8s9D+8sg/MbquW/zHuDXrHruJU6VlZt/0ct60Su/2l7OdvToUVJT\nU1m0aBH5+UXrT0xMJDg4GIDc3FwWLlzITTfdVGhUHexbx5d3+/g1a9bg6+vL+PHjCx2fMmUKCQkJ\nbNu2rdzxO3LfyZMnk5aWVqHpNlKzaelGEZG6KG4tHP4c3Dzg2ldcs9vooc8gKxl6Tqr+e4vDuj/1\nmatD4Pjz1zq1vp07d9K+fXuOHTvG2rVrueGGGwrOHTx4kK5duxb8edu2bSQlJTF06NBK3XPv3r10\n69YNd/fCKVZ4eHjB+YEDB1bqHsVp3rw5ISEhfPrpp9x+++1Or19cRyPrIiJ1Uev+EDoWBj8ETTpX\n//0Pfw7LbrSP7qclVP/9RYCtW7fy2muvYbFYeO211wqdW7t2bcEUGIAffvgBgF69elXqnklJSQQE\nBBQ5fuFYUlJSkXPO0qtXL7Zs2VJl9YtraGRdRKQuatjCPn/8ohUtqlWHK6FVP/hlO2x8DG581zVx\nSLnFzf5LwfusrGwMw8BkMuHj4+3CqCpn9+7dzJ07l3HjxhEdHc2uXbsKkvH9+/fz6KOPFpRNSEjA\nZDLRpEmTSt+3tKkr5Z3WUhFBQUH89ttv5OfnFxnZl9pLI+siInVJ7p+WbjO76GPebIZRr9p3NY1b\nC4f+55o4pNx8PNwverld9HKvtpczJScnExAQgJubG08++SRms5lnnrFv4HX27FmCgoIKlc/OzsZi\nseDm5lap+wYGBhY7ep6cnAxQ7Ki7s3h5eWEYBufPn6+ye0j1U7IuIlJX2KywZBSsvA0yfnN1NPaH\nTS+9z/5+/SOQq1UqpPqsXr2a0aNHA9CtWzcmT57Mxx9/zObNm1m/fj2jRo0qVL5Jkybk5uZWeq3y\nsLAw9u/fX+SB1tjYWAB69OhRqfpLk5ycjKenJ76+vlV2D6l+StZFROqKH5dAwi44/AUYLpr+8meX\nPwYNW0FKPHz7squjkXpkzZo1hVZkeeGFF/Dz8+POO+/kiy++KPKQZ0hICABHjhyp1H3Hjh1LRkYG\nq1atKnQ8KiqK4OBg+vfvX6n6S3P06FG6d+9eZfWLa2hCk4hIXZCfC9+8ZH8/dCb4NXdtPBd4+sKI\n5+GDm2HrW3Dp/eBTddMApP46fPgww4YNY/HixcTFxdGnTx98fHwKzrdo0YI5c+Ywbdo0hgwZUmS6\nyxVXXAHYH0q9sHLLxTZs2EBmZibp6ekAxMXF8eGHHwIwcuTIgnuNGDGC4cOHc++995KWlkanTp2I\njo5m48aNLF26tNB9TSYTl19+OV999VWJ31d572uz2di+fTtTp051pNmkFnA4Wc/IyOCf//wnK1as\nIDk5mZCQEB577DEmTpxY6nVLlixhypQpxZ5LTEykefMa8g+LiEhtFLsS0hPAtzn0Kf6z1mVCRkHE\nTRAyErz8XR2N1FGpqanEx8dz5ZVXMmjQIDZt2lSkzAMPPMDHH39caBWYC1q3bs2QIUNYu3Ytd911\nV5Hz9957L/Hx8QV/XrlyJStXrgTg2LFjtGvXruDc6tWrmTlzJk899VRBrhQdHV0oV8rIyADs/4ko\nTXnv+9VXX5GamsrkyZNLrU9qH4eT9cjISHbs2MHzzz9Ply5dWLZsGZMmTcJms3HTTTeVef3ixYsL\nftV0QWBgoKNhiIjIBTYbbPmP/f2l99t3Eq1JTCYY+5aro5A6rnfv3nz55ZecOnWKcePG4eXlVaSM\nyWRixYoVhUbcL/bggw8yYcIETp06RcuWLQudO378eLlj8fX1Zd68ecybN6/EMt988w0mk4knnnii\n1LrKe9/FixczcODASi89KTWPQ8n6hS10LyToAEOHDiU+Pp4ZM2YwYcKEMp+i7tGjB3369Kl4xCIi\nUtjB9XD2EHg1gt63uTqashmGazZpkjqvPBsaNW7cuMRzkZGR9O3bl+eee47XX3/dmaEVsXnzZiZO\nnEhYWFil6zpy5AgffPABX375pRMik5rGoQdMnbmFroiIOMnORfavfe8Ar4aujaU0uVnw7SvwzjCw\n5rk6GpEiTCYTCxYsIDg4GFsV71Ewd+5cli1b5pS6Tpw4weuvv87gwYOdUp/ULCbDMIzyFr700kux\nWq1s37690PF9+/bRo0cP5s+fX+w8L/hjznqzZs04c+YMjRo14oorrmD27NnFLmNks9kKHqa44MSJ\nE1X+wyOF5eX98Q+qxWJxYSTiCur/2sGcn0XA8XWktBpGvpfzHt50dv+brDl0++xGLDnniO/9T1La\nXF3pOsUxFoul0NzqklycGlTlJj5SM6n/neP48eOFPkcBzGYzbdq0KXTMz88Pcyl7Yjg0DSYpKYkO\nHToUOV6eLXSbN2/OzJkzGTBgAA0bNiQ2Npbnn3+eAQMGsGXLFiIiIsq8f35+Plar1ZGQxYn+/BdO\n6hf1f01mIbHtWPvbKuon5/S/mdPtI2l1YCFBh5ZypvnlYNIKwtXJ3d0dB8boABwuL3WL+r/iDMMo\n8tlZkU23HH7AtKJb6F5zzTVcc801BX++7LLLuPbaawkLC+Opp55i7dq1Zd7b3d291P95iPNpZLV+\nU//XbOa8TGzuPlU2/7sq+v9cx0haHI7GO/04AUk/kt5iYNkXidOYTKZyjZRqZLV+U/87h8lkKvLZ\nWZE81qFk3dlb6LZr147BgwezdevWcpUPDQ1Vsl7NYmJiyMvLw2KxlOu3H1K3qP9ruJVT7A+WjnwJ\n2l7q9OqrrP9T7oQt8+hw6iO45l7n1StlOnnyZIkroVwsKysLwzAwmUzlKi91i/rfOfz8/GjdunWh\nY8VN8y6LQ5lvVWyhaxiGEnAREUclHYG4j+D0XvD0c3U0jhlwH7h5wMmtEP+Dq6MREanRHMqSnb2F\n7rFjx9iyZQsDBgxw6DoRkXrv+9fAsEHnq6G54wMlLuXXHHr+vi/Hd6+6NhYRkRrOoWkw5d1Cd+rU\nqURFRXHkyBHatm0LwLBhw7jssssIDw8veMD0xRdfxGQy8a9//cv535mISF2V/ivsed/+fvBDro2l\nogZOg7xsGPSgqyMREanRHH7AtDxb6FqtVqxWa6EHFMLCwvjggw946aWXyM7OJigoiCuvvJInn3yS\nLl26OOe7ERGpD7a+BdZcaN0f2jh/rnq1COwIkW+7OgoRkRrP4WS9PFvoLlmyhCVLlhQ69uqr+lWn\niEil5WT8sQnS4Ie0E6iISB2nJztFRGqTA+sgJw0COkLnv7g6mso7HQdrH4AtJQ8AiYjUZw6PrIuI\niAuFjQefQPs0mLqwktbpfbD7PWjYCi59AMyObxgiIlKX1YFPehGResTsBp2HQ8i1ro7EObpdB96N\nIe0XOPyFq6OReurs2bPs3r3b1WHUaWrjilOyLiJSW9TFbb8tXhD++wIFu6JcG4vUS9988w3t27en\nV69ezJo1y9Xh1Elq48pRsi4iUhvkZcMb/WDTLMjNdHU0ztX7VvvXgxvsy1KKONHp06dLPGcYBrNn\nzyY6OpoWLVqQkJDA7Nmz6d69OzabraBceno6jz76KFdffTVNmzbFZDLx9NNPl1hvRkYG06dPJzg4\nGC8vL3r27Mny5csdjr289124cCEtW7YkM9M1nw2OtjFQ6Xau7jYG17WzknURkdogbi2cPQR7V4O7\nt6ujca6gbtCqHxhW2LPM1dFIHTN58mSOHz9e7Llt27Zxww03MGrUKA4ePMiTTz7Jiy++yOzZswvt\nrp6UlMTbb79NTk4O119/fZn3jIyMJCoqilmzZrFhwwb69u3LpEmTWLbMsb/f5b3vrbfeSoMGDXjx\nxRcdqt9ZHGnjN954g4SEhEq3c3W3MbiunZWsi4jUBj/+PkWk1y1148HSP7swur7rXbhopE2ksnbu\n3MnChQuLPffRRx8xZswYAPz8/HjjjTfw9/cnMjKyULm2bdty7tw5vv76a5577rlS77d+/Xo2bdrE\nm2++yd13383QoUNZsGABw4cPZ8aMGVit1nLHXt77uru7c/fddzNv3jyysrJKrTMtLY0NGzaUeH7d\nunUOjxw70sYeHh7MmzevUu3sijYGx9rZmergJ76ISB1z5hCc+B5MZug52dXRVI3QsRAUChET7Svd\nSPXLzbzolXXRKxPyzpdS9k+vvOyKl3Wyo0ePkpqayqJFi8jPzy9yPjExkeDgYHuYubksXLiQm266\nqdBoL4DJZMJUzj0N1qxZg6+vL+PHjy90fMqUKSQkJLBt27Zyx+/IfSdPnkxaWlqZU0HeeecdRo0a\nRVRU0WdE5s+fz+jRox0anXakjcE57eyqNobyt7MzaelGEZGa7sKDl52vhkYtXRtLVfFoAPd97+oo\n6rd//5FQ+fz5XOerYfLKP/48txPklTCy2HYwTPn0jz//JwyykoovG3wJ3PVVBYItn507d9K+fXuO\nHTvG2rVrueGGGwrOHTx4kK5duxb8edu2bSQlJTF06NBK3XPv3r1069YNd/fCKVZ4eHjB+YEDB1bq\nHsVp3rw5ISEhfPrpp9x+++0llvv73//OqVOnmDJlCufPn+fuu+8GYN68eUyfPp0nnniCO++8s9Au\n9KVxpI3BOe3sqjaG8rezM2lkXUSkJsvPgZho+/tet7o2FpFaZuvWrbz22mtYLBZee+21QufWrl1b\nMD0D4IcffgCgV69elbpnUlISAQEBRY5fOJaUVMJ/XJygV69ebNmypcxyL7/8Mo8//jj33HMP8+bN\n44UXXmD69OnMnj2bOXPmOHRPR9oYnNPOrmxjKH87O4tG1kVEarIDn9pHJf1a2Ec36zprnn1VGJMZ\nuo1ydTT1yxMJBW+zsrIxDAOTyYSPjzeY/rRZ1YzDJddj+tM44PTY8pd1st27dzN37lzGjRtHdHQ0\nu3btKkgS9+/fz6OPPlpQNiEhAZPJRJMmTSp939KmVTgy5cJRQUFB/Pbbb+Tn5xcZdf6zOXPm4OXl\nxfTp0wGYO3cujzzyiMP3dKSNwXnt7Ko2Bsfa2Rk0si4iUpM1D4d+d0H/e8CtHoyv7FkGK26BL56p\nm+vK12QeDS56+Vz0amBfD7/Esn96WbwrXtaJkpOTCQgIwM3NjSeffBKz2cwzzzwD2DfoCQoKKlQ+\nOzsbi8WCm1vldtENDAwsdmQ3OTkZoNgRYWfx8vLCMAzOnz9fdmEgNTW1ILFNSUlx+H6OtjE4p51d\n2cbgeDtXVj345BcRqcWadIKRc10dRfUJHQsbH7MvU3liK7S91NURSS21evVqRo8eDUC3bt2YPHky\n7733Hps3b+bkyZOMGlX4NzdNmjQhNzeXzMxMGjRoUOH7hoWFER0dXWTUNTbW/huGHj16VLjusiQn\nJ+Pp6Ymvr2+p5QzD4G9/+xtvvfUWCxcuJCcnh/vuu4/z58/z0ksvlft+jrYxOKedXdnGUP52dhaN\nrIuISM3h1RBCf1/Obde7ro1FarU1a9YUWi3khRdewM/PjzvvvJMvvviiyAOIISEhABw5cqRS9x07\ndiwZGRmsWrWq0PGoqCiCg4Pp379/peovzdGjR+nevXupZWw2G3feeSfz58/n/fffZ8qUKdxzzz0s\nXryY//znP9x///3lfrjU0TYG57SzK9sYytfOzqSRdRGRmsiaDxv/AT1ugDaXQhXPwaxRet8Ge5bC\nvjVwzXPg7e/qiKQWOHz4MMOGDWPx4sXExcXRp08ffHz+WNemRYsWzJkzh2nTpjFkyJAi0zCuuOIK\nwP7A5IVVRS62YcMGMjMzSU9PByAuLo4PP/wQgJEjRxbca8SIEQwfPpx7772XtLQ0OnXqRHR0NBs3\nbmTp0qWF7msymbj88sv56quvSvy+yntfm83G9u3bmTp1aqnt9Morr/Dee++xcuXKQpsA3XrrrXh5\neXHzzTfTsWPHglViLlbZNgbntLMjbQxlt3N52xjK385OZdRQVqvVSElJKfSyWq2uDqve2bNnj7Fj\nxw5jz549rg5FXED970L7PzWMWQ0N44UOhpGX45IQXNb/NpthvDHA/v1ve7t6713HnThxolzlMjMz\njYyMDCMzM7OKI3KenTt3GoABGIMGDTKysrKKlLHZbMawYcOMNWvWFFvHkCFDjJEjRxZ7rm3btgX1\n//l17NixQmXT09ONadOmGc2bNzc8PDyM8PBwIzo6ukgZwJg4cWKp31d57/vFF18YgPHjjz+WWl9W\nVpbx/fffl3j+u+++M86dO1ds/zujjQ3DOe1cnja+UK6sdnakb8vbzoZR/M9bRfJbk2HUzCd4bDZb\nwf9wLvDz8yuygL5UrZiYGPLy8rBYLERERLg6HKlm6n8XWvFXiFsLlz4Af3FsKTVncWn///AmfPY4\ntOoLd3xevfeuw06ePEnr1q3LLJeVlXXRajBFVl2vsTZv3sypU6cYN24cXl5exZY5d+4cPj4+eHp6\nFjm3atUqJkyYQHx8PC1bVu2eBuvXr2fUqFHExMQQFhZW6fpuueUWjh496pQlBUvr/8q2MdSfdi7u\n560i+a2mwYiI1DTnU+HgRvv78AmujcVVetwA/5tpX8oxN9O+cohIGcqz0U7jxo1LPBcZGUnfvn15\n7rnneP31150ZWhGbN29m4sSJTkkgjxw5wgcffMCXX37phMhKV9k2BrWzo5Ssi4jUNHEfgzUHmoZA\n88r/A1Mr+TWzr8/dqJWrI5F6xGQysWDBAj7++GNsNluV/jZ/7lznrfJ04sQJXn/9dQYPHuy0OquS\n2tkxStZFRGqa2BX2r+E31q8HS/9Mibq4QI8ePap86T9nGzp0aLlGvGsStXP5aQK4iEhNkpYAx761\nvw8bX3rZ+uJ8KmSccXUUIiIuoWRdRKQmSTkBjdval2v0b+PqaFxv6//B3M7w7cuujkRExCWUrIuI\n1CRtBsC0PTDhfVdHUjM0bmefv793lX3teRGRekbJuohITWMyQYNAV0dRM3S6CrwDIPM3OPa1q6MR\nEal2StZFRGqKMwchP8fVUdQsbhboEWl//9MK18ZSB5jNZvLy8lwdhkidZ7VanVaXknURkZrAZoOl\n4+ClznBql6ujqVnCbrR/PbAOcrNcG0stFxAQQGJiYsGmNyLifFarlVOnTtG0aVOn1Ofw0o0ZGRn8\n85//ZMWKFSQnJxMSEsJjjz3GxIkTHarnn//8J3PmzCE0NJS9e/c6GoaISN1yciukngAPPwjq5upo\napbW/cC/LaTEw8H1EDbO1RHVWt7e3rRs2ZKkpCSSkpJKLJeenl6wg6Wfn181Rig1gfq/8oKCgkrc\n4dVRDifrkZGR7Nixg+eff54uXbqwbNkyJk2ahM1m46abbipXHXv27OGll16iWbNmDgcsIlInXZji\n0X00WLxdG0tNYzLZ15z/Zi7ErlSyXklubm4EBQWVWiYmJoa8vDwsFkuR7dKl7lP/1ywOJevr169n\n06ZNBQk62BeIj4+PZ8aMGUyYMAE3N7dS68jPz2fKlCncfffdxMTEcPbs2YpHLyJSF+TnQtxH9vda\nW714EZPAs6ESdRGpdxyas75mzRp8fX0ZP77wPyZTpkwhISGBbdu2lVnH888/T3JyMnPmzHEsUhGR\nuurw55B9DnybQ/vLXB1NzRTYEQZNg4bBro5ERKRaOTSyvnfvXrp164a7e+HLwsPDC84PHDiwxOvj\n4uJ49tlnWb16Nb6+vg4Hu2/fPmw2m8PXScVdWDUgLy+PmJgYF0cj1U39Xz3abn8bf+BMs8tIiK0Z\nz/Dk5Ns4k55DQ08zoP6vb/SzX7+p/6uO2WymTRvHNrxzKFlPSkqiQ4cORY4HBAQUnC+JzWbj9ttv\nJzIykpEjRzoU5AX5+flOXQpHHKPlvuo39X/VMOdn0zBxCwBngodWazsbhsGRc/kcSs7jTKaVM1l/\nvNJy/lgpxNdiokkDN4J83Gjq40YTHzMdG1sIaWLBbDJVW7wAAb98TuCpTcT3eJDcBhplrw762a/f\n1P/OVdZ08eI4/ICpqZQP5tLOvfLKK/z88898/PHHjt6ygLu7O2azVpusThf/kFosFhdGIq6g/q8G\nFguHhr5Dw9NbyQvsjqUakt/TGfl8HZ/F18ez+CWt5F1BLWbIs0FGnkFGSj7HUwqXDWrgxmVtfbii\nnQ+tG1XP34+mpzbhd2YnTX/9it9Cbq2We9ZH+tmv39T/VacieaxDyXpgYGCxo+fJycnAHyPsf3bi\nxAmeeuopnn/+eTw8PEhJSQHsI+U2m42UlBQ8PT3x9i59BYTQ0FAl69Xs4ifCIyIiXB2OVDP1f3WJ\nAMZQlePEqdl5rI9NZM2uU2w/nlxw3NPdzJDOTWgb2ICW/t60auxNy8betPL34dihfaRl53Iu14xv\nUGtOpWRz6lw28UlZbDl8lt8y8/kwLp0P49IJa9mIsZe05LqIYJr6eVbdN2JMhY920uLMt7S48WX7\nSjHidPrZr9/U/1XHZrORnp7u0DUOJethYWFER0eTn59faN56bGwsAD169Cj2uqNHj5Kdnc2DDz7I\ngw8+WOR848aNefDBB/nPf/7jSDgiIlKG83lWFnxzlDe/OkJ2nn0aockEl3YIZOwlLbmmR3P8vIof\nOTOZTPhYzDTysRDRrfBSu+fzrHy+/zRrdp3i60NniD2VSuypVP69fj9TBrVj2lWdS6y3UkJGgdt0\nOHsITu+F5mHOv4eISA3iULI+duxYFixYwKpVq5gwYULB8aioKIKDg+nfv3+x1/Xs2ZPNmzcXOT59\n+nRSU1NZvHgxrVq1cjB0EZFabvdS+0owfaZC+yFOr/6L/ad55pM4TiTbd/3s0syXyF6tGNMzmBaN\nKreWu5fFjVHhwYwKDyYpI4d1PyWyevcpYk6msODbY3y0J4HHR4Qw9pKWpU6RdPzGDaHzcPtupntX\nK1kXkTrPoWR9xIgRDB8+nHvvvZe0tDQ6depEdHQ0GzduZOnSpQWT5qdOnUpUVBRHjhyhbdu2+Pv7\nc8UVVxSpz9/fn/z8/GLPiYjUeXuWQfwWaNnbqcn6sbOZzP5kH5sPngGgWUNPnhjZjdERwc5NnH8X\n6OvJrQPbcevAdmw++BuzP4nj2NlM/r4ihve3neCZ0aH0aNnIeTfsEWlP1vethque0lQYEanTHH7A\ndPXq1cycOZOnnnqK5ORkQkKlqQhSAAAgAElEQVRCiI6OZuLEiQVlrFYrVqsVwzBKqUlEpB5LS4T4\n7+3vQ8c6pcqs3Hxe//Iw73x7jFyrDYubidsHt+dvV3bG19Phj/sKGdo1iIEdA1n43TFe++IwP8af\n47rXv+Omfm2Y8Zeu+Pt4VP4mXa4Biw+cOw4Ju6Flr8rXKSJSQzn86e3r68u8efOYN29eiWWWLFnC\nkiVLyqzrq6++cvT2IiJ1Q9xHgAGt+0Ojyk8DjE/K5K53f+TgafuDS5d1acqs67rTsanje1pUlqe7\nG/dd0Ymxl7Tk3+sP8ElMAu9vO8FXB88w/5belR9l92gAXUdCxmmwlbyajYhIXVA9Qy0iIlLY3tX2\nr6GRla7q60NnmBa9m9TsPJr6eTLn+h4M796sSqa8OKJFI29em3QJN/Vrw+Orf+J4Uhbj/u97Xrgh\nnDE9W1au8si3wez4esUiIrWN1kEUEaluKSfgl+2ACbqPqXA1hmEw/+sjTFm8ndTsPHq29mfd3wZz\ndWhzlyfqF7u0YyBrHxjMFV2bcj7PxoPL9zDn0zjyrZXYkVqJuojUE0rWRUSq27419q9tB0HDFhWq\nIis3n2nL9/DchgPYDLixTys+uHsAzRp6OTFQ52nkbWHhrX25f2hHABZ8e4zbFu/gXGZu5SrO+A3i\nf3BChCIiNZOSdRGR6ubbHJqHQ4+KPVh6MjmLG976gU9iEnA3m/jXmFBeuCEcT/eaPdrsZjYx4y8h\nvHFTL7wtbnx3+Cyj3/iO/YlpFavwxDZ4uSusvA1sVqfGKiJSUyhZFxGpbhET4J5vofftDl964Nc0\nrn9jC/sT02ji68GyOwdwy6XtatS0l7JcG96CNfcPpHWANyeTs7nhre/54UjR3bHLFNwTPPwg41c4\nodF1EamblKyLiLiK2bGP4LiENCa9vZWkzFy6t2jIxw8Mpl/7gCoKrmqFNG/IJw8MZmDHQLJyrdy+\nZAffHznrWCXuntDtOvv7Cw/siojUMUrWRUSq04FPISfd4cviEtKY/M5WzmXlEd6qEdF3DiDYv3K7\nkLqav48Hi27ry+VdmpKd93vCftjBhP3CVKK4tWDVMo4iUvcoWRcRqS5nDsHym+CV7pCbVe7L9iWk\nctPviXpEq0a8N7U/jXwsVRho9fGyuDH/lt4FK8XcHrWDLY4k7O0vB+8AyDoLx7+tukBFRFxEybqI\nSHXZ9/tUjTYDwMOnXJfsPZXKTQu2kZJlX5rxvTv608i7biTqF1xI2K8MCbIn7Et28N3P5UzY3SzQ\nfbT9/T5NhRGRukfJuohIdTAMhzdCiv0llcnvbCM1O49L2vjz7tR+NPSqW4n6BZ7ubrx1cy+uCgki\nJ9/G1KgdfHPoTPkuvtCeBzeCrRJrt4uI1EBK1kVEqsNvcXD2ILh5QMjIMotfmKOemp1Hrzb+vHt7\n3U3UL/B0d+PNm3sxrFszcvJt3PHuzvJNiWk3GMa8Cfdvc/ihXRGRmk6faiIi1eHCqHqn4eDVqNSi\nianZTFmynbTz+fRu25h3p/bHr44n6hd4urvx5uReDO/ejNx8G/e89yMHfy3jgVyzG1wyGXxq58o4\nIiKlUbIuIlLVDAP2rrK/71H6FJj083lMWbyD02k5dGnmy6Lb+uLr6V4NQdYcHu5mXr/pEvq1DyA9\nJ58pi7dzOu28q8MSEXEJJesiIlXt7M9w7hi4e0OXa0oslme1cf+y3Rz4NZ2mfp4suq1vnXuYtLw8\n3d14+5bedGjagITU80yN2kFmThlLM+6JhneGw4H11ROkiEg1ULIuIlLVmnaB6Xth3CLw9C22iGEY\nPPnRXr45dAZvixsLb+1Dq8blWzGmrvL38WDJbf0IbODB3lNp/C16N/nWUh4g/fUn+GW7VoURkTpF\nybqISHXwb13qg6VvfX2E5TtOYjbBa5MuIbyVfzUGV3O1CfRhwa198HQ38+WB33jmkzgMwyi+cMGq\nMBsgL7v6ghQRqUJK1kVEqlJJieVFPolJ4MWNBwGYdV0ow7o3q+qoapVebRrznwk9MZngva3xLPzu\nWPEFW/WBRm0gNwN+/l/1BikiUkWUrIuIVKXPn4al4+D4lmJP7zyezMMrYwC4fVB7bh3Yrvpiq0VG\nhLXgiRHdAJizfj8bYhOLFjKZIPR6+/u9mgojInWDknURkapis8FPK+DwJjifUuR0Ymo2d7/3I7n5\nNq7u3oyZ13ZzQZC1xx1D2nPLgLYYBjy0Yg8Hfk0rWujCajuHPoOcjOoNUESkCihZFxGpKr9sh/QE\n8GwIHa8qdCo338Z97+8iKTOXbi0aMm/iJbiZTS4KtHYwmUzMuq47Qzo34XyefQ32tPN5hQu16AmN\n20N+Nvz8mWsCFRFxIiXrIiJV5cJUjK4jweJV6NSzn8ax+0QKDb3cmX9zb7w93FwQYO3j7mZm3sRL\naOnvzfGkLB5eEYPNdtFzASYTREyyt7lvc9cFKiLiJErWRUSqgs0KcR/Z3/9pI6Q1u3/h3R/iAXh1\nQk/aBNbvJRodFdDAgzcn98LDzcymuNP83zdHChe44h8wKRraDXJNgCIiTqRkXUSkKpz4ATJOg1cj\n6DC04PD+xDQeXx0LwN+u7MRV3bTyS0VEtPZn1ujuALz02UG2HD7r4ohERKqGknURkapwYQpMyHXg\n7gFAanYe9y79kfN5NoZ0bsL0YV1cGGDtd1O/Nozr3QqbAdOid5OQ8qe11ZOPaVUYEan1lKyLiFSF\n1v2h7eCCKTA2m8EjK2M4npRFS39v/qsHSivNZDLx7PU96N6iIUmZudz3/i5y8q32k8lH4b89YfVd\nkF10JR4RkdpCybqISFWImABTPoVO9lVg3vr6CJviTuPhZubNyb1o3MDDxQHWDV4WN/7v5t409HJn\nz8kUnl23334ioAM07Qa2PDjwqWuDFBGpBIeT9YyMDKZPn05wcDBeXl707NmT5cuXl3nd559/zvDh\nwwkODsbT05OgoCCuvPJK1q9fX6HARURqi61Hk3j5f/YdSp8eHUpEa38XR1S3tAn04dUJPQH7Dqcf\nxyTYT1x4sHefpsKISO3lcLIeGRlJVFQUs2bNYsOGDfTt25dJkyaxbNmyUq9LSkoiNDSUV199lf/9\n73/Mnz8fi8XCtddey9KlSyv8DYiI1CjWPNi5CDLOAJCSlctDH+zBZkBkr5ZM6tfaxQHWTVd1a8YD\nQzsBMHN1LCeTsyB0rP3k0a8gK9l1wYmIVIK7I4XXr1/Ppk2bWLZsGZMmTQJg6NChxMfHM2PGDCZM\nmICbW/FrBU+YMIEJEyYUOjZq1Cjat2/P22+/zc0331zBb0FEpAY5+jWsewi+fhHjoX38Y9VPJKae\np32TBvxrTA9MJs1TryrTh3Xm+yNn2XUihQeX72bF3Zfi3iwMTsfC/o+h922uDlFExGEOjayvWbMG\nX19fxo8fX+j4lClTSEhIYNu2bQ7d3GKx4O/vj7u7Q/9nEBGpuS5MuQi5lmU7fuGzfaexuJn478RL\naOCpz7qqdGHDJD9Pd3adSGHeFz9Dj99H17UqjIjUUg4l63v37qVbt25Fkuvw8PCC82Wx2Wzk5+eT\nkJDArFmzOHToEA8//LAjYYiI1Ez5ObB/HQAng6/hX+viAHj0LyGEtWrkysjqjdYBPvw7MgyA1zcf\nZnfDK+0nEnZDToYLIxMRqRiHhnmSkpLo0KFDkeMBAQEF58sycuRIPvvsMwAaNmzIBx98wLXXXluu\n++/btw+bzeZAxFJZeXl5BV9jYmJcHI1UN/W/YxombqF9Tiq5Xk24ZYOV83k2ejb3pE/DtFrZfrW1\n/9sAV7X34YtjWdyx9jRL+r6A0fwSjANHyrxW7Gpr34tzqP+rjtlspk2bNg5d4/DvZEubb1meuZiv\nvfYaKSkpJCYmsnTpUiZMmEBUVFTBHPjS5OfnY7VaHYpXnOfCD6/UT+r/sjU88TkA37kN4HiKlUae\nZu7v44c1P5/a/slV2/r/togG7D+TQ0KGlX8d6cSMIDOmWvY91BS1re/FudT/zlXSs52lcShZDwwM\nLHb0PDnZ/pT9hRH20nTu3Lng/ejRoxkxYgT3338/EyZMwGwufVaOu7t7mWXEuS7+IbVYLC6MRFxB\n/V9+5vxs/E9/D8B/k/sB8OCAxgT5ebkyrEqpzf1vscAjgwJ5dNNvbE/I4Yv4XEZ0agCGFcx6dqAs\ntbnvpfLU/1WnInmsQ59YYWFhREdHk5+fX2jeemxsLAA9evRwOIB+/fqxceNGzpw5Q7NmzUotGxoa\nqmS9msXExJCXl4fFYiEiIsLV4Ug1U/874Ph3GEYeJ2nGHqMjUwe35/YR3V0dVaXU9v6PAJLdj/Ls\np/s5E7OekFP/w7PPLTBomqtDq/Fqe99L5aj/q47NZiM9Pd2haxzKfMeOHUtGRgarVq0qdDwqKorg\n4GD69+/v0M0Nw+Drr7/G39+fwMBAh64VEalJjLaDuK/5cu7PeYDQ4EY8ek1XV4ckwO2D2nNZl6Z4\n2bLwPHcIW+yHrg5JRMQhDo2sjxgxguHDh3PvvfeSlpZGp06diI6OZuPGjSxdurRgHs7UqVOJiori\nyJEjtG3bFoAxY8YQERFBz549CQwMJCEhgSVLlvD111/zxhtvaPlGEanV3tsaz4ajuXhZOrNu4iV4\nujs+L1Gcz2w28fL4CCa+epI8axSWX2PgzCFo2sXVoYmIlIvDGfLq1auZOXMmTz31FMnJyYSEhBAd\nHc3EiRMLylitVqxWK4ZhFBwbNGgQH374Ia+//jppaWn4+/vTp08f1q1bV+7VYEREaqIjvybx7/X7\nAXh8RDc6Bfm6OCK5WFM/Tx69YRDfLA/nKrfdnPruPVqO/ZerwxIRKReTcXFGXYMUN6fHz89Pc9ar\nmeat1W/q/7LlWW3sf/5ycnLOs7bFg8y+ezJmc93YpbSu9f/7C+Yy+dSznDS1oPE/YvH10oNzJalr\nfS+OUf9XnYrkt8p8RUQqIWrjFnrkxtLXfIhpo/rXmUS9Lho94Q7O40FrI5ElK7WjqYjUDkrWRUQq\nKOZkCr/9EI3ZZJAU2Iug1p3Lvkhcxq9hYzLaXQ2A98E1fB532sURiYiUTcm6iEgFZOdaeWjFHkaZ\n7WurBw6Y7OKIpDyaDJ5CbOA1fG7rxWOrfyIpI8fVIYmIlErJuohIBbyw8QCc/Zlw8zEMszt0H+vq\nkKQ8Og2j8z3LSG46gLMZuTyxJpYa+uiWiAigZF1ExGHf/nyGJd8fZ7SbfVTd1PFKaKC9ImoLL4sb\nr0yIwOJm4rN9p1m165SrQxIRKZGSdRERB6Rm5/Hohz8BBjc32GE/GDbepTGJgwyDUPNJojt+jgd5\nPP3xPk6lZLs6KhGRYilZFxFxwOxP4khMPU+HAC/8rvknhIyCriNdHZY4wjDg/fH0ObGQ25v9TEZO\nPv/48CdsNk2HEZGaR8m6iEg5bYo7zapdv2A2wdwJvfC8ZCJMfB88tQlSrWI2Q49IAB5oGoOXxcx3\nh8/y/rZ4FwcmIlKUknURkXI4l5nL46tjAbhzSAd6tw1wcURSKb9PXfI9vomZw1oD8O/1B4hPynRl\nVCIiRShZFxEphyfX7uVsRg6dg3z5e/d0+PYVSDnh6rCkolpEQGBnyD/P5EaxDOgQQHaelRkrf8Kq\n6TAiUoMoWRcRKcO6nxJY91MibmYTr9zYE8+f3oMvnoFvXnJ1aFJRJlPB6Lp574fMHRdBAw83th9P\nZvGWYy4OTkTkD0rWRURKcSY9hyc/2gvA/Vd0JKyZJ8SttZ/UKjC1W9g4+9cjm2ntkcHMa7sD8OJn\nBzn8W4YLAxMR+YOSdRGREhiGwRNrYjmXlUf3Fg154MrOcGgDnE+Fhi2h7UBXhyiVEdgRWvYBb384\nc5BJ/VpzWZem5ObbeHhlDPlWm6sjFBFRsi4iUpI1u0+xKe40FjcTL98YgYe7GXa/bz8ZMQnMbq4N\nUCpv/GL4+wFoPwSTycQLN4Th5+VOzMkU5n9z1NXRiYgoWRcRKU5iajazPt4HwPRhXejWoiGkJcKR\nL+wFet7kwujEafzbgLtHwR9bNPLm6etCAfjP54fYn5jmqshERAAl6yIiRRiGwT9WxZJ+Pp+I1v7c\nfVkH+4mfPgDDBq0H2KdQSN1hs0HSEQAie7VkWLdm5FkNHl4RQ26+psOIiOsoWRcR+ZPlO07yzaEz\neLibeXl8OO5uv39U5maCxUej6nVN8jGYFwHvXAX5OZhMJv4d2QN/HwtxiWm8vvmwqyMUkXpMybqI\nyEVOJmfx7Lo4AB79S1c6Bfn9cfLKmfDIIQi/0UXRSZXwbwO2PMg+B4c2AhDk58Wz1/cA4I3Nh4n9\nJdWVEYpIPaZkXUTkdzabwYwPY8jMtdK3XWOmDGpftJCnH1i8qz84qTpmN4iYaH+/Z1nB4VHhwVwb\n3gKrzeDvK/ZwPs/qogBFpD5Tsi4i8rt3fzjO1qPJeFvceGl8BG5mk/1EXjb8GuvS2KSKRfw+tenn\nTZB+uuDwv8b0oImvBz//lsGrnx9yUXAiUp8pWRcRAY6dzeT5jQcAeGJkCG0DG/xx8sCn8H+DYdlE\nF0UnVa5pF2jVFwwrxK4oOBzQwIPnIsMBWPDNUX6MP+eqCEWknlKyLiL1ntVm8MjKGM7n2RjUKZDJ\n/dsWLnBhakTzHtUfnFSfCw8O71kGhlFweHj3ZkT2aonNgEdWxpCdq+kwIlJ9lKyLSL238Dv7iKmv\npzsvjovAfGH6C0BaAhzdbH+vVWDqttBIcPeC3+Lg158KnZp1XSjNG3px7GwmL352wEUBikh9pGRd\nROq1n0+n89L/7HORnxrVnZb+f3p4NGa5fW31NgMhoIMLIpRq4+0PI16A2/8HzcMLnWrkbeGFcfZj\ni7cc54cjSa6IUETqISXrIlJv5VltPLzSvunN0K5NGd+nVeEChgF73re/16h6/dD7NmjTH0ymIqcu\n79KUSf3aADDjwxjSz+dVc3AiUh8pWReReuv1Lw/z0y+pNPK28PwN4Zj+nKD9sgOSDts3Qgq93jVB\nSo0y89putGrszS/nsnl23X5XhyMi9YCSdRGpl/acTCnYmfLZ63vQrKFX0UL71ti/dh9jX19d6odz\n8bDu77DqziKnfD3deeXGnphM8MHOk2yKO11MBSIizuNwsp6RkcH06dMJDg7Gy8uLnj17snz58jKv\nW716NZMmTaJTp054e3vTrl07Jk+ezM8//1yhwEVEKio718rfV+zBajMYHRHMdRHBxRccPhsmLYdL\n76/eAMW1rHmwcyHs/RDSfy1yul/7AO4aYn9+4fHVP5GUkVPdEYpIPeJwsh4ZGUlUVBSzZs1iw4YN\n9O3bl0mTJrFs2bJSr3vhhRfIyspi5syZbNy4kWeffZbdu3fTq1cv9u3bV+FvQETEUS9sPMDRM5k0\na+jJ7DGhJRd0s0DXEdA8rPqCE9dr0gla97c/WBwTXWyRh4Z3oWszP85m5PLEmliMi5Z6FBFxJndH\nCq9fv55NmzaxbNkyJk2aBMDQoUOJj49nxowZTJgwATc3t2Kv/eSTTwgKCip07Morr6Rdu3a8+uqr\nvPPOOxX8FkREyu+7n8+y5PvjAMwdF4G/j0fxBa354ObQR6TUJb3+Cie3wc7FMHAamAv/2+ZlceOV\nCRFc/8YWPtt3mtW7TnFD71YlVCYiUnEOjayvWbMGX19fxo8fX+j4lClTSEhIYNu2bSVe++dEHSA4\nOJhWrVpx8uRJR8IQEamQ1Ow8ZnwYA8AtA9pyWZemxRf8NRZeDYVv5lZjdFKjhEaClz+kxMPhL4ov\nEtyI6cO6APD0x/s4lZJdnRGKSD3h0LDR3r176datG+7uhS8LDw8vOD9w4MBy13f06FHi4+O5/vry\nrbKwb98+bDZb+QOWSsvLyyv4GhMT4+JopLrVtf5/5ftkElPPE+znzqjWJX9PrXbPJTDjV1IObiG+\n0dXVHGXNUdf631EtWl1N0OEVpH3xMseymxVb5lJ/g5AmHhw4m8s9i7Yw+8ommItZ9rG2qe99X9+p\n/6uO2WymTZs2Dl3jULKelJREhw5FNwUJCAgoOF9e+fn5TJ06FV9fXx566KFyX2O1aptnV7nwwyv1\nU23v/+9/Oc/X8VmYgQf6+OFmWMnLK/p54paXgf/JTQD82ua6Wv99O0t9bIfTra4l6PAK/E5vw5QS\nT26D4h9Evr+PHzM2JRP7Ww5r96cyqnODao60atXHvpc/qP+dq6Tp4qVxeEJmkXWIy3nuYoZhMHXq\nVL799ltWrVpF69aty3Wdu7s7ZrNWm6xOF/+QWiwWF0YirlBX+j8py8qCXekAjAv1I7R5yclUkxNf\n4mY9T7Zfe3Ka9cZSB0ZJK6qu9H9F2Rq3J7n1X8jzCcLNu2GJbdCmsYUpvRrx1o4U3o/NoHfLBrRp\nVLvbq773fX2n/q86FcljHUrWAwMDix09T05OBv4YYS+NYRjccccdLF26lKioKMaMGVPu+4eGhipZ\nr2YxMTHk5eVhsViIiIhwdThSzepC/9tsBn9dtJ30XBuhwQ15dtIgPNxL+BwxDPj2DgC8h9xPRM+e\n1RhpzVMX+r/SIlYAUPwkmD+EhxvsT9vBVwfP8MauLD66fxBeFsdH0GoK9X39pv6vOjabjfT0dIeu\ncSjzDQsLY//+/eTn5xc6HhsbC0CPHj1Kvf5Cor548WLeeecdbr75ZoeCFRFx1MLvjvHd4bN4WczM\nm3hJyYk6wPFv4ewh8PCF8AnVF6TUeiaTibnjIghs4MGBX9N5ceNBV4ckInWEQ8n62LFjycjIYNWq\nVYWOR0VFERwcTP/+/Uu81jAM7rzzThYvXsz8+fOZMmVKxSIWESmnvadSefGzAwA8NSqUTkG+pV+w\nfYH9a/gE8GpYxdFJrWGzwqHP4LOZpRZr6ufJ3PH2BRcWbTnGVwd/q47oRKSOc2gazIgRIxg+fDj3\n3nsvaWlpdOrUiejoaDZu3MjSpUsLJs1PnTqVqKgojhw5Qtu2bQGYNm0aCxcu5PbbbycsLIytW7cW\n1Ovp6ckll1zixG9LROq7rNx8pi3fTZ7V4C+hzZjUrxzPxlw2A7wbQ987qj5AqT2ykmH5ZLDlQdg4\nCC7536srQ5px66VtifohnkdW/sTG6UNo4utZjcGKSF3j8AOmq1evZubMmTz11FMkJycTEhJCdHQ0\nEydOLChjtVqxWq2FdnT75JNPAFi0aBGLFi0qVGfbtm05fvx4Bb8FEZGi/rVuf8Eupc9HhpfvAfgW\n4TD6v1UfnNQuvk0h9HqIXQk7FsKY10st/vjIbmw9mszB0+nMWBnDotv6lnsBBhGRP3P4aU1fX1/m\nzZtHYmIiOTk5xMTEFErUAZYsWYJhGLRr167g2PHjxzEMo9iXEnURcaaNe38levsJTCZ45caeNG5Q\nwi6lIuV14bctsR9C9rlSi3pZ3Jg3qSce7mY2HzzDuz/EV0OAIlJXaWkVEalTfk09z2OrfwLgrss6\nMKhTk7Iv2r8OProPErX5h5SgdX9oFgb52bBnWZnFQ5o35IkRIQDMWb+fg786tvqDiMgFStZFpM6w\n2QweXrmHlKw8wlo24uHhXct34da3YM/7sP+Tqg1Qai+TCfpOtb/f8Q6UYzftWwe2Y2jXpuTm25gW\nvZvzxWzCJSJSFiXrIlJnzP/mKFsOJ+FtceM/E3uWvkzjBb/th/jvwOQGvbVKlZQibDx4NoTko3B0\nc5nFTSYTc8dH0MTXg4On03lu/f5qCFJE6hol6yJSJ+w4nsxL/7Ovbf306O50bFrGMo0FF75j/9p1\nBDRqWUXRSZ3g6QsRk+zTYcqpia8nL423byoT9UM862MTqyo6EamjlKyLSK2XlJHDA8t2YbUZXN8z\nmBv7lGOZRoDMpD/mH/e7s+oClLpj+Gy451vodFW5L7miaxD3XN4RgEc//InjZzOrKjoRqYOUrItI\nrWazGTy0IobTaTl0bNqAOWPDyr9M3rb/g7wsaBEB7S+v2kClbrB42eevO+iRq7vQt11jMnLyue/9\nXZq/LiLlpmRdRGq1N786zDeHzuBlMfPm5N408Czn9hE56bD9bfv7wX+vUAIm9VhOBvzwBqT+Uq7i\n7m5mXpvUi4AGHsQlpvGvdXFVHKCI1BVK1kWk1vrhSBKvbDoEwOwxPeja3K/8F5vMMOhBaDsIul1X\nRRFKnbX6LvjsCXvCXk7NG3nx6oSemEzw/rYTrN1zqgoDFJG6Qsm6iNRKZ9JzmLZ8NzYDbujVqvzz\n1C/waABD/g5T1oPZrWqClLrrwjKOPy6xP/tQTpd3acr9V3QC4InVsRw5k1EFwYlIXaJkXURqHavN\nYPoHuzmTnkPnIF/+dX2oq0OS+qbjlfZnHfKyYPt8hy6dPqwz/dsHkJlr5X7NXxeRMihZF5Fa579f\n/Fywnvqbk3vh41HOeeoA1nxY8VeI+7hcG9uIFMtksj/rALBtvv0ZiHKyz1+/hCa+Hhz4NZ1Za/dV\nUZAiUhcoWReRWuWL/af575c/AzBnbA86N3NgnjrA/rUQtxY+mWYfFRWpqG7XQWAnOJ9inw7jgKCG\nXsybeAkmE3yw8yTLtp2omhhFpNZTsi4itcbh3zJ4cPkeDANuHtCGyF6tHKvAMODbV+3v+99j3+RG\npKLMbjBouv39D29Afo5Dlw/q1IRHru4KwKyP97LzeLKzIxSROkDJuojUCmnn87jr3Z1k5OTTr10A\nT42qwDz1w5/D6ViwNIB+dzk/SKl/widAo9bQuh+cT3X48vuu6Mi1YS3Isxrcs3QXianZVRCkiNRm\nStZFpMaz2gymL9/D0bOZBDfy4s2be+HhXoGPr29fsX/tMwV8ApwbpNRP7h5w31a48V3wDXL4cpPJ\nxNzx4YQ09+NsRg73vPejHjgVkUKUrItIjffKpoN8eeA3PN3NzL+lD018PR2v5MRWOPE9mC1w6f3O\nD1Lqr0pOp/LxcGfBX/vg72Mh5pdUnlgTi2EYTgpORGo7JesiUqN9+lMib2w+AsALN4QT1qpRxSr6\n7ve56j0nQcNgJ0Uncgz34l0AACAASURBVJHko/D1i/ZnIxzUOsCHN27qhZvZxOpdp1i05bjz4xOR\nWknJuojUWPsT03hkZQwAdw5pz/WXtKx4ZZfcDK36/vFAoIgz5WXD/Ctg8xw4uKFCVQzq1IQnRnYD\n4N/r97Pl8FknBigitZWSdRGpkZIzc7nrvZ1k51kZ0rkJ/7gmpHIVdrsO7vgcAjs6J0CRi1m8oe/t\n9vefz7Kv518Btw9qxw29WmG1Gdy/bBcnkrS8qEh9p2RdRGqc83lW7ojawcnkbNoE+PDapEtwd6vg\nx5Xm/kp1GfwQ+ATC2UOw+90KVWEymZgztgcRrRqRkpXHbUu2cy4z18mBikhtomRdRGqUCyu/7DqR\nQiNvC4tu64O/j0cFK8uHRX+xrwKTd965gYr8mVcjuPwf9veb/+3QrqaFqrG48fZf+9DS35ujZzK5\n892dWiFGpB5Tsi4iNcqcT/ezcd+veLiZefuW3nQKcnCH0ovtWQont8H3r0G+knWpBr2nQEAHyDwD\nW/5b4WqaNfRi8ZS++Hm5szP+HA+viMFm02+JROojJesiUmMs/O4Yi7YcA+ClGyPo3yGw4pXlZMCX\nc+zvL/8HePs7IUKRMrh7wLCn7e+/fw3SEipcVZdmfsy/pTcWNxOfxiby3Ib9TglRRGoXJesiUiNs\niE3k2U/jAHh8RAijIyq5vOL3r0Hmb/ZRzj63OyFCkXLqNho6XgmDp4Nnw0pVNbBjE14aHwHAgm+P\nseT3/8yKSP3h7uoARER+jE/mwQ/2YBjw10vbctdlHSpXYVoifP/7FISrZtlHO0Wqi8kEN6+2f3WC\nMT1bciolmxc3HuSZdXG08PfmL6HNnVK3iNR8GlkXEZc6eiaDO6J2kptvY1i3Zsy6LhRTZZOcr/4N\neVnQqh90H/P/7d15fBTl/cDxz+ydZHMnHAlHICBBkIhyyY2AAgUFhApoq2hREW1prUjVgqC/6qsn\ntOIFKFAEDwRrEVAu6wFyKCCnEsIZjtx3stfM748JG2ISILJHIN/367WvnZ15Zp7vZrI7333mmWd8\nE6gQdXHh/7APRiSa3C+Ze7q3QNPg18t38c3xvCvephDi6lDnZL24uJipU6eSkJCAzWbjxhtv5J13\n3rnkeqdOnWLq1Kn069ePqKgoFEVh0aJFPyVmIcQ14lReKb9YuJ28UhepzaP41/jOGA1XmKgXZ8Ke\niu+k217wWeumED/JsS9h/gA4sumKNqMoCrPu6MDAlEY43CoPLNrBgdOFPgpSCFGf1TlZHz16NIsX\nL2bmzJmsXbuWrl27Mn78eJYtW3bR9dLS0nj77bexWCwMGzbsJwcshLg2nC0oZ8L8bWTkl9E6PoyF\n93UhxGK88g3bG8HkLTD4eWjR/cq3J8SVOLgaTu+CT2eAemXDL5qMBv41oTOdW0RRUObiFwu3cfjc\nTxseUghx9ahTsr5mzRrWr1/PK6+8wsMPP8yAAQOYP38+gwcP5sknn8Tjqf2LqG/fvmRlZbF+/Xp+\n97vfXXHgQoirV1aRgwkLvuZEbiktYkJZ9qsexNmtvqsgri30+rXvtifET9VvGlgj4dzeyjM+VyDU\nYmLRxG7ckBhJTomTexZs42h2iQ8CFULUV3VK1letWoXdbmfs2LFV5k+cOJHTp0+zbdu22isySPd4\nIQTklji5d8E20rNKSIwKYdmk7jSJtF35hp2lcHLHlW9HCF8KjYG+T+jTnz4LxVlXvMnIEDNLHuhG\nSpNwMoscTJj/NSdzS694u0KI+qlOo8Hs27eP9u3bYzJVXa1Tp07e5T179vRddD+yf/9+VFX12/ZF\ndS6Xy/u8Z8+eIEcjAs3X+7/YqfLHTVmk57mICTHwx96R5Jw4TM6JK940Cd/9i7gjKzh7/SQy2917\n5RsU8vn3ESW0F20jkgkpPEL+8kkc7zbLJ9v9wy12ntlYxqmCcsbM+5w/DYonLtQ3g7zJvm/YZP/7\nj8FgoEWLFnVap06f6pycHFq3rj6kWkxMjHe5P7nd7ot2tRH+df7DKxqmK93/pS6V57/IJz3PRaTV\nwMw+0cTZNJ/8X9lz9xF3ZAUKGkX2JPlf9QP5m16Z9NQnuf7LR4nK2EzO8T7kJfS74m2GGWFGnyhm\nfJbH2RIPz27MYna/aKJDfHDtxwVk3zdssv99y2is++ezzj/BLzak2hUPt3YJJpNJutME2IUfUrPZ\nHMRIRDD4av+XulRe2pLH4VwX4RYDs2+NJynKN/9PisdBqz1/QUEjt8VQyhJ7I/+pviGff99xx11P\n5nX30vj7JcRkbqG45SCfbLex2cwLA+N5emMWZ4o9zP4in+dvjb/ihF32fcMm+99/fkoeW6dkPTY2\ntsbW89zcXKCyhd1fOnToIMl6gO3ZsweXy4XZbCY1NTXY4YgA88X+zyl2cP9bOziQ5STcZmL5pB50\nTIz0XZCfPAMlpyC8KTHjXyUmJNp3227g5PPvYx3+Cgf6En3DGKJ93Lh1XbtSfv76Vk4WljPziwKW\nPtid5jGhP3l7su8bNtn//qOqKkVFdRvFqU6Z7w033MDBgwdxu91V5u/duxeAjh071qlyIcS1LSO/\njLGvbWVvRgGxYRbfJ+ont8PXr+jTw+eAJOqiPjNZodNYv4z93yI2lHcf7kGLmFCO55Ry16tbOHRW\nxmEX4lpQp2R91KhRFBcX88EHH1SZv3jxYhISEujeXcY0FkLo0jKLGPPqFtKz9VFf3n/kFt8m6m4H\n/GcKaCp0Ggfthvhu20L4W3mhPjpMaa7PNtkyNowVj9ziHSXm569tlTudCnENqFM3mKFDhzJ48GAm\nT55MYWEhbdq0Yfny5axbt46lS5d6O80/+OCDLF68mCNHjtCyZUvv+itWrAAgPT0dgJ07d2K32wEY\nM2aMT96QECL49pzM5/639DuTJseHsfRX3WkaGeLbSowW6PUb+GouDHnRt9sWwt9WTIS0DVB0Du6a\n77PNNoqw8e5DtzBx0Xa+PZHPvQu28dovbqbfdfE+q0MIEVh1vsB05cqVPPPMM8yYMYPc3FxSUlJY\nvnw548aN85bxeDx4PB40Tauy7o/HZ583bx7z5s0DqFZWCHF12pKWzaQlOylxekhtFslbE7sRE2bx\nfUWKAp3vhdTxYPDt6BdC+F3/p+HIJtj7HnQYCSk/89mmI0PNLP1VdyYv/Zb//ZDFrxbv4O8/v5ER\nqQk+q0MIETh1vlrTbrczd+5czpw5g8PhYM+ePVUSdYBFixahaRpJSUlV5muaVutDCHH1+++e09z/\n1g5KnB56Jsfy9qQevk/UHUVQeLrytSTq4mrU7Gbo+bg+/d+pUHTWp5sPtZiY/8suDO/UFJdH49fv\n7OLNL4/K8VaIq5AMrSKEuGKqqvHndYd4fPkunB6V2zs05s37u2K3+uYGLRdUBCsfhjf6w6mdvt22\nEIHW/2mIbw8lmfDuveAq9+nmLSYDc8d15t4eLdA0mL36ANM/2IvDLfcrEeJqIsm6EOKKFJW7mLRk\nJ698dgSAh/u25pV7bsZm9kOL92d/gu8/hrJ8wL/3dRDC78w2GPc22CLh1A74+Hfg45Zvo0Hh+Ts7\n8syw9hgUeHfnSSbM30ZmkW9/GAgh/EeSdSHET3Ysu4RRr2xh46FMLCYD/7g7lT8Ma4/R4IdEev8q\n+Pwv+vQd/9S7EQhxtYtNhjFvgWKAI5uhONPnVSiKwqS+rXlrYjfCbSa+OZ7HnS9/xd5TBT6vSwjh\ne5KsCyF+ki8OZ3HnvK9IyyymcYSV9x++hVGdm/mnsjPfwYeP6tO3PAap4y5eXoirSZuBcNcCeOgz\nCG/st2r6XRfPf6b0onV8GGcKyhnz2hb+szvDb/UJIXxDknUhRJ2oqsb8z9O5783tFJS56Nwiiv8+\n1pvU5lH+qbA4C96ZAK5SSL4VBs/2Tz1CBFPHu6om6qrql2pax9v5cEovBrSLx+FW+c07u3lx7UFc\nHv/UJ4S4cpKsCyEuW2ZhOfcv2sH/rTmIqsGYm5uxfFIPGkXY/Ffppueh4CTEJMOYN2X0F3Ht++59\nmD9Av3GSH0TYzCy4ryuP9EsG4PX/pTPmta0cyy7xS31CiCsjyboQ4rKsP3COIXO/4PMfsrCaDDw/\nsiN/GdPJPxeSXuj2P+ljqY9fDiHR/q1LiGBzFMP6GXBmN6x8yG8t7EaDwvShKcybcBMRNhN7TuYz\n7J9f8N7OkzK8oxD1jCTrQoiLcrg1Xt2Rx6QlO8ktcdK+aQSrH+/NL3q0RFH8NCKLplWOimG1w6jX\nIL6df+oSoj6x2mHcUjBa4Ye18PFv/ZawA/ysU1PWTu1Lt1YxlDo9TFvxHY8t20WRQ7rFCFFfSLIu\nhKhVeq6TaRtzWJemnx6f1KcVH07pSdvG4f6rVNNg42zYOMvnw9gJcVVIvBlGvgIo8M0i+OgxUP03\nNnpiVAjLJ/Vg2pB2mAwKH+89w2/WnWNfptNvdQohLp+P71gihLgWlDk9vLz5MK//LxO3CtEhBv45\noQt92sb7t2JNg0+fha0v66/bDYPm3fxbpxD10Q1j9M/Dqodh99vgccLI18Don8O20aDwaP829EqO\nY+q7uzmaXcKsz/MY0sbJS9e5iAwx+6VeIcSlScu6EKKKTYfOMfgf/2Pe5iO4VeiWYOWfQxv7P1FX\nVVjzZGWiPuyvkqiLhq3TWBj7FhhMsPd92L/S71WmNo9i9eO9GZwchgasTSth4N8+Y9WuU9KXXYgg\nkZZ1IQQAp/PLmPXf/Xyy/xwATSNt3HdDGDc3NmKx+PkiUlWF1b+Bb5cACoyYAzff7986hbgaXH8n\n3L0UTmyFG8YGpMowq4nHukXTK9HCgt1FnCp08tt39/DejlM8P7IjbRrZAxKHEEInyboQDZzLo/LW\nV0eZs+EwpU4PRoPCg71b8ZuBbUk7tB+Xy+XfAFQP/GcK7Fmu38XxzlfgxvH+rVOIq0m7ofrjPFeZ\n/mwO8Wu1HRtZmDOkMdsK7Pxz42G2pucwdO7nPNS3NY8NaEuIv3/ECyEASdaFaLBUVeO/351mzobD\nHK0YX7lLy2heGNWRlCYRgQvk3H747l1QjHDXfP3mMEKImrkd8O69+hCPY9+CiAS/Vmc2KkwZ0IY7\nUhOY+dF+Nh3KZN7mI6z45hS/HtiWn3dpjtkoPWqF8CdJ1oVoYDRNY8PBTP726fccOlsEQGyYhaeG\npDDm5mYYDH4ajrE2TTvBwJkQmwztRwS2biGuNtmH4eR2cBTCa71h9BvQZpDfq20eE8rC+7rw6YFz\nzP7vATLyy3hm1T5e/186Uwe15c4bEzEG+rtDiAZCknUhGpCv0rL58yffs+dkPgDhNhMP923NxF6t\nCLMG6OtA02Db69BmIMS11ef1nhqYuoW42jXpCA99Bu/fD2e/g6V3QZ8noP/Tfhsp5jxFUbi9QxP6\nt4tn+bYTvLw5jRO5pfzuvT28+tkRnrjtOm7v0MR/918QooGSZF2Ia5yqamw6lMn8L9LZdjQXgBCz\nkft7JfFw39ZEhVoCF0xZHnw4Bb7/GBp1gEmbwGwLXP1CXAtik+HB9fDpM7BjAXzxNzjxNdy1ECKa\n+r16q8nI/b1a8fOuzVm05RivfXaEw5nFPLL0WzomRjCpT2uGdmyKxSTdY4TwBUnWhbhGFTvcrNh5\nkre2HON4TikAFqOBCd1b8OiAZBqFBzhJPvWN3hpYcAKMFugyEUzWwMYgxLXCbIOf/Q1a9oKPfg3H\nv4IVE+GBdQELIdRi4tH+bbine0sWfJHOwi+Psi+jkN+8s5s/RRzkl7ckMaFbC6LDAtggIMQ1SJJ1\nIa4xJ3NLWbzlGO/uOEmRww1AhM3E+G4tuK9nEglR/h1BopqSbNj8f/qdGDUVopNg7CJI6BzYOIS4\nFnUcDU1T4cPJ+r0JgiAyxMwTt7Xj/p5JvL3tBEu2HudcoYO/fPI9/9x4mNE3NeOBXkn+vfOxENcw\nSdaFuAaUONx8sv8sq3Zl8FVaNmrFvUtax4UxsXcr7ropkVBLED7u2Wkwf4B+MRzoI70M/wfYIgMf\nixDXqthkeOATuLCv+KYX9OtDev8WrIEZFz3WbuXXA9vycL/WfPzdGRZ+eZT9pwtZvv0Ey7efoEvL\naEbdlMjwGxKIDJU7ogpxuSRZF+Iq5VE1vkrLZtWuDD7Zf5ZSp8e7rE/bOB7o3Yp+beMDP7rLhWKT\nIT4F3OUw5EVI6h28WIS4ll2YqOefhC/ngOqCXf+GW/8IN04AQ2DGRbeajIy+qRmjOiey41geb355\nlE8PnGXn8Tx2Hs9j1kcHuDWlEaNuSmRAu0bSt12IS5BkXYiriNOtsv1oLhsOnmPtvjOcK3R4lyXF\nhjKqs36AbBEbGvjgNA3SN8POt+DOeWCL0BOIccsgNBYMckAWIiAim+ljsH/6R8g7Ch89Bttfh37T\n4bohfh815jxFUejWKoZurWI4V1jOf3ZnsPLbDA6dLWLd/rOs23+WqFAzQzs2YWBKY3q1iZMbLQlR\nA0nWhajnsosdbD6UyaZDmXxxOJviin7oAFGhZkZ0SmDUTYl0bh4VnCHTygtg93J9VIqcw/q82DYw\naKY+bY8PfExCNGSKot+zoO1tsP0N+N9f4OxeePceiGgGP18MzboENKTGETYe6pvMQ32TOXimkFW7\nMvhwVwaZRQ6Wbz/J8u0nsZoM9GoTx60pjbg1pVHgr68Rop6SZF2IeqagzMU3x3PZdjSXr9Nz+e5U\nPppWuTw+3Mqt7Rox6PrG9LsuPninkM/th+3z4bv3wKXfARVLOKSOgy4PBCcmIUQlkxV6Pg6p42HL\nv+DbJVCaDTGtK8uU5evXkATwh377phG0bxrBU0NS2Hokh/UHzrLhYCYZ+WVsqmiYAEhpEs4tybF0\nbxVD16QYYu0yepRomCRZFyKINE3jdEE5e07ms/1oLtuP5nLwbGGV5BygY2IEA1MaM7B9IzomRAa3\nHzro46W/0R88Tv11fAp0/ZWeqFtlxAch6pWwOBg8C/r/Ac7shtCYymVvjwFnCbQbBu2GQsJNAeuy\nZjQo9G4bR++2cTx3h8YP54rZeOgcmw5m8u2JPA6dLeLQ2SLe+uoYAG0a2enWKoburWK4sXkULWJC\n5QZMokGQZF2IAFFVjWM5Jew/Xci+0wXszyhk/+kC8kpd1cq2jgvz9vXsmRxHk8jg3DhI8TiJyPqG\nmKyv4btC+MVKfUFINHQcA85i6PaQfuGoHDSFqN/MNmjRo/J1wSk48x14HJB5AL74K4Q1gutuJ8KS\nQl50KpgDM2qLoii0axJOuybhPNq/DbklTr5Ky2bHMb0R49DZItIyi0nLLGbZthMAhFtNXJ8QQcfE\nSDpUPLeOC8NklOtjxLWlzsl6cXExzz77LO+99x65ubmkpKQwffp0xo0bd8l1MzMzmTZtGqtXr6a0\ntJTU1FReeOEFBg4c+JOCF6I+Kna4Sc8qJj2rhPSsYo5kl5CeVcLR7GLKXWq18iaDQtvG4XRLiqZb\nq1i6tooO/A2Lzis8DSe3QcY3cOobOmR8i9FTXrk8N73yFPrIVyRBF+JqFtkMnjgEh9fDD2vh8AYo\nyYRd/6YVENZyBGduelIv63ZCwUn98x+Az31MmIURqQmMSE0AIK/Eyc7jeWw/msP2Y3kcPFNIkcPN\ntqO53jszg37jt5axobSODyM53k7reLs+HWeX4SLFVavOyfro0aPZsWMHL730Etdddx3Lli1j/Pjx\nqKrKhAkTal3P4XAwcOBA8vPzmTt3Lo0aNWLevHkMGTKEDRs20K9fvyt6I0IEQrnLQ1aRg6xiB+cK\nysnIL+NUXhkZ+WVk5JVxuqCM/Bpays+zmQ2kNImgY2IEHRIi6ZgQSdvGdmzmAI6AoGn6jYpyj0BO\nGqT8TG8pB/jqn7DtVW9RI+C0xlLUtCext9wD4QmV25FEXYirX2gMpN6tP9xO/U6oP6zDsfdDSqJS\nKsud2QMLB4EtChJvhsYd9KFZY9voD3tjv34nRIdZGHx9YwZf3xgAl0clLbNYP1OZUcCB0/qZyhKn\nh8OZxRzOLAbOVdlGuNVEYnQIiVEh3ueEqBCaRtqID7cSH24Nzv0ohLiEOv1XrlmzhvXr13sTdIAB\nAwZw/PhxnnzySe6++26MxpqTjoULF7Jv3z62bNnCLbfc4l03NTWVadOmsW3btit8K0JcPpdHpbjc\nTbFDfxSVu8kvdZJf6iK/7Pyzi/xSJ9nFTrKLHGQVObx3BL2UOLuF1nF2khuF0TrO7m3laRYd4t9T\ntKoKjgIwh+oXlwGc2Ab7V0HxWcg7DjlH9DLnRbWEVn306ebd4MQWSOwCiTdzqNhOsa0pZouV2Hap\n/otbCBF8JgskD4DkARxqOh6X04G3LTr/OBitUJ4PRzbqjwsNnwNdJurTWd/DoY8hvImexIc3AXsT\nCIny2VjvZqPBe6HqmJubAXpXw4z8MtKzSziSWUx6tn6G80hWMecK9e/v8/3gaxNmMRIfbiXOrj+i\nw8xEhliICjUTFWImKlSfDreZCLeasdtM2K0mGSte+FWdkvVVq1Zht9sZO3ZslfkTJ05kwoQJbNu2\njZ49e9a6brt27byJOoDJZOLee+/l6aefJiMjg8TExJ/wFoQ/aZqGqml4VA23R0VDb5jV0LwXQaqa\nPq1qmr5c1ZerFfMuXO5RNVQVPOenK57PP9zeZ9X72u3RcHnUikfltNOt4vSoOFwqDrf+2uH24HCr\nlLk8lDs9lDo9+rRLny516om5w129O8rlspoMeiuM3UKzKBuJ0TaaRVpJiLSRGGWlaWwkESEVibKr\nTH+oHtCKoDgfVHflI7I5WCrGRC/IgOwfwOPS+5C6HfoFnK5ScJZCh5EQ1UIve2Qz7HxTP3CW5evD\nJ5bnQ3khoMEvPtQPugBZh6q0lusU/RR4bDIYLvga6Dhaf1Rw7NkDrtrPFAghrlGKUjWxvmEMtL8D\nzu2D099C9mH9zFzOET2Rv3CEmVM7YeOsmrdrjYCRr0L74ZVldywEc4j+XWgOq3iueCT1gugkvWxJ\ntv4dabSA0ax/d13wMITG0jzGTvOYUPq1jtSvqTEYQTFS4lI5U+Ago6CcjAIHp/KdnC5wkJFfxrlC\nvTGmzOWhxOmhJKeUYzmldfpzWUwGwq0mQq1GQs0mbBYjIWYDoRYTIWYjNrMRq9mA1WTAYjJgNRmx\nmipfmwwGzEalyrTZaMBoUDAZFUyGimmDgvGCh0EBg3J+uvLZoIDhgmkFBcUACnp55fw8harT6NcP\n6Mdt7VJvWwRInZL1ffv20b59e0ymqqt16tTJu7y2ZH3fvn306dOn2vzz6+7fv/+Syfr+/ftR1Z+e\nZP0UmqrS9sMhtS7/UuvEb9Tfel9/ZXwYG84ay+7UUnhYfcr7eqPxcaIorrHsflrxS88Mb0L8sen3\nNCWnamwVz0e1BO7yvOCd/4HxGVopZ2rc7mktjmHuP3u3u8w8mw7KsRrL5mnhjHTO9b5evPJxbjb8\nUGPZMix0dbzmff2q+R/0MeytsSxAR8eb3um/m1/hNsPOWst2cbxKOXry+yfTAu4wbgFAofoXSR/H\nXHKJAGCGaQnjjJurLFfQ9L4dRhjo+CvZxnhCzQpPGJZzt7rGu03lwvLAms6vY4hpRbTNSOu0N2ny\n/RIoA7Kqx/tD/zc4Gq2fPm70/VKaHnij1veW1udflMTpLdZxae+TuPdftZZNL7FR1Lg7ADHHttD8\n4Ee1lj1+8Fvyi/URH2zFYUS3HY/LFosrpDGO8OY4whLRjBU/KPKB/D01bsdVkai7XC727Km5jLh2\nyf5vuGrf90awdIWErlDRK05RXWgFClSUC8txEdNiCObyHEzl2ZjLczE5K87mOQpJP5FBkVMvG318\nPS32LKs1juNdZ5LfTL+uLTLjM5K2z6i17ImbppPXchgA4We30npr5fE2DGhT8QA4lTqVnPajgTDC\nsr6nzZdT0YwKFx5ZNBQ0FD6K/iX/td5BkVOlSdkP/K3sj3oZrbIcAG54uXwk8zwjAUhWMvjI8myt\n8b7pGcoL7p8D0EzJYp3lqVrLvuMZwAvuXwAQQyGfW6fWWvZDTy+edT8IQAjl7LA+WmW5Vhk6n6hd\neML1qHfJPqu+XtsLyhdXjCvwhdqJKe7KerdbHrlIvtOOX7mf8h5LN5t/XXu+o+n5znk15TvnpZPA\nWM//eV+vMD5NK2rOdzKI4w7PX7yv/22cxfUcq1LmgOUGLMP/VuP6/mIwGGjRokWd1qlTsp6Tk0Pr\n1q2rzY+JifEuv9i658vVdd3z3G43Ho/nkuV8SVNVwpTyWpebVSfl7sqkMdRYTohS8z+v5UdlbUZH\nrdu2qI6qZU21l7VqDi640zw2oxN7LWVDNAcXNirbqL1sOZYqr21K7WUNP/oFfrHtAoSazrcIQLji\numjZttFm3EYzJoNC0zIPdlftZe9sF4rTbMdqUrjxnIHQPEetZV8eGosa1giAZgcsWNJrb0FuFaFQ\nHgLgueQPRrfb5T3QXbAL0TCgKQY0gwlNMYJiwO3xeMuWmyIoDW+FZjCjGcyo55+NNlSjlTJjuLds\nQUQ71A6P4zHb8ZjDcVvseEx23OZwPGY7mtHibRF3hSVR1O5XVYNU0W9FXgcuaWFv0GT/N1yXt+81\n/awgkB/VkfyojlWWKqoLo6sYo6sYly0OtWKbRfbWnEqZhMFTXvXhLsfocVBmjqn84aAZKQ9rhqK6\nUDQPiuYB1eOddquKt6zHXfNx+DyPR7ugrN69UalIY3/c875rEzMtkvUhacPywrF+VfH3qKGL/u2t\nLMQlRONwa4SV5BP2fe3HoDaR0DvUhkfTiHGZsRfUfmyLtnhoYjXi0TQiVAU7tZe1KS4M6F/zwEWP\nr1aq7tuLl3WiXnBMC6P2fMequqrkGiE4at22VXPg8FxmvvOj3MhqcBJmqCXf+VFZSw1lTaoj4N9t\ntXUXvxhFq8N5juuuu47k5GTWrl1bZf6ZM2dISEjgxRdfZPr06TWua7FYePDBB3n11aqn47du3UrP\nnj1Zvnx5lRFlopdOcAAACy9JREFUVFWlqKhqv7ITJ04EpWW9MPtkrcs9RhtOa6z3dUjpaaihxRdA\nNVhw2Crv5hhSdkbvM1JBuUhZW9lZ/YvpRxQFNMVEeUjjC8qew6DV3LdaU4w4QptU1KdgLc/CoDq9\nAVS2KOtlSyxx+mkxINSTh9HjqnINkVKRcCsoOO2J3vUtjhxMajlKTd9mgNNeeRbFVJ6LwVP7F4Qz\ntAkoen9AkyMPg7vsImUbg6J/EIyOfIzu6qcyz38Vu0LivV1AjM4iDD8uW/FGNRTc1mhvWYO7FIPH\nUbktxQAoaIr+l1JNNm8MlftXuSovyLzwS8wcoCHcRP0h+7/huur3vaaB5kHRVEDTj58agAqahma0\neM8uKqoLo7OiCyHnnzRvG7vHZEc1690VFY8TkyO3aj0XUM12PJZw73bNZTWcfq3gMYXhsUZWrOjG\nUpZ5kbKheKxRFXV6sJSeq7mgpqGaQ/VjFqCpHkwlZ7xnAvSurHqXVVUDj8GG0xbrXddachoNDbfb\n413HaNKPZx6DDYct1vuWbaWnUfROsdX+FD/OYaylZ1Conr9p2uXnO6DnO2U/yneUi+Q75SFNKmO4\nMN+pYDTbsEc3/vGqflVTy3p4eDiGi9zfoE4t67GxsTW2gOfm6v+4NbWc+2Ld8zp06HDRN+M/netQ\n9ma/RREMe/bsweVyYTabSU29PdjhiACruv/lAtOGRvZ/wyX7vqG6Cbjc/X9T4MK6htTUGH0pdcp8\nb7jhBg4ePIjbXfVXzN69et/kjh071rSad93z5eq6rhBCCCGEEA1RnZL1UaNGUVxczAcffFBl/uLF\ni0lISKB79+4XXffQoUNVhmh0u90sXbqU7t27k5CQUOu6QgghhBBCNER16gYzdOhQBg8ezOTJkyks\nLKRNmzYsX76cdevWsXTpUm+n+QcffJDFixdz5MgRWrZsCcADDzzAvHnzGDt2LC+99BKNGjXilVde\n4fvvv2fDhg2+f2dCCCGEEEJc5ep8q66VK1fyzDPPMGPGDHJzc0lJSal2cajH48Hj8VQZo9NqtbJx\n40amTZvG448/TmlpKTfeeCNr166Vu5cKIYQQQghRgzon63a7nblz5zJ37txayyxatIhFixZVm9+4\ncWMWL15c1yqFEEIIIYRokOqcrAdKTSNKBnrYRqEPMWQ0GjEYDPL3b4Bk/zdssv8bLtn3DZvsf/+p\n6e95qVHU6zTOeiC53W5KSkqCHYYQQgghhBB+ExYWhslUe/t5MAYtF0IIIYQQQlwGSdaFEEIIIYSo\npyRZF0IIIYQQop6qt33WVVWt1glfURQURQlSREIIIYQQQvx0mqZVu6DUYDBgMNTefl5vk3UhhBBC\nCCEaOukGI4QQQgghRD0lyboQQgghhBD1lCTrolZffvklw4YNIzo6mpCQENq2bcvzzz8f7LBEAOza\ntYuRI0eSkJBAaGgoKSkpzJ49m9LS0mCHJnyoqKiIadOmcdtttxEfH4+iKDz33HM1lv32228ZNGgQ\ndrudqKgoRo8eTXp6emADFj51Ofvf4/Hw97//nSFDhtCsWTNCQ0Np374906dPJz8/PziBiytWl8/+\neZqm0bdvXxRF4bHHHgtMoAKQZF3UYtmyZfTr14/IyEiWLFnCmjVreOqppy55ly1x9Ttw4AA9e/bk\n2LFjzJkzh9WrVzNu3Dhmz57N+PHjgx2e8KGcnBzeeOMNHA4HI0eOrLXcoUOH6N+/P06nk/fee483\n33yTH374gT59+pCVlRXAiIUvXc7+Lysr47nnnqNly5bMmTOHNWvWMGnSJN544w169epFWVlZgKMW\nvnC5n/0LzZs3j7S0ND9HJmqkCfEjp06d0sLCwrTJkycHOxQRBM8884wGaGlpaVXmP/TQQxqg5ebm\nBiky4WuqqmqqqmqapmlZWVkaoM2cObNaubFjx2pxcXFaQUGBd96xY8c0s9msTZs2LVDhCh+7nP3v\ndru17Ozsauu+//77GqD9+9//DkSowscu97N/3tGjRzW73a6tXLlSA7QpU6YEKFKhaZomLeuimgUL\nFlBSUsJTTz0V7FBEEJjNZgAiIyOrzI+KisJgMGCxWIIRlvCDyxkO1+12s3r1au666y4iIiK881u2\nbMmAAQNYtWqVv8MUfnI5+99oNBIbG1ttfrdu3QA4efKkX2IT/lXXobAfeughBg8ezKhRo/wYlaiN\nJOuims8//5yYmBgOHTrEjTfeiMlkolGjRjzyyCMUFhYGOzzhZ/fddx9RUVFMnjyZ9PR0ioqKWL16\nNa+//jpTpkwhLCws2CGKADpy5AhlZWV06tSp2rJOnTqRlpZGeXl5ECITwbRp0yYAOnToEORIhL8t\nWLCA7du38/LLLwc7lAZLknVRTUZGBqWlpYwdO5a7776bDRs28OSTT7JkyRKGDRsm/davcUlJSWzd\nupV9+/aRnJxMREQEI0aM4L777mPu3LnBDk8EWE5ODgAxMTHVlsXExKBpGnl5eYEOSwRRRkYG06dP\np0uXLgwfPjzY4Qg/ysjI4Pe//z1//vOfSUhICHY4DZYp2AGI+kdVVcrLy5k5cybTp08HoH///lgs\nFqZOncrGjRsZNGhQkKMU/nLs2DFGjBhB48aNWbFiBfHx8Wzbto0XXniB4uJiFi5cGOwQRRBc7JS5\n3Fm64cjNzfU22rz77rsXveuiuPo98sgjpKamMmnSpGCH0qBJsi6qiY2N5fDhw9x+++1V5g8dOpSp\nU6d6h3AT16bp06dTWFjI7t27vV1e+vbtS1xcHA888AC//OUv6devX5CjFIFyvr/y+Rb2C+Xm5qIo\nClFRUYEOSwRBXl4egwcPJiMjg02bNtG6detghyT8aMWKFaxbt44vv/ySgoKCKsucTif5+fmEhYV5\nr3MS/iM/iUU1NfVNBbzdX6Ql5dq2e/durr/++mp907t27QrAvn37ghGWCJLk5GRCQkLYu3dvtWV7\n9+6lTZs22Gy2IEQmAikvL49BgwZx9OhR1q9fX+txQlw79u3bh9vtpkePHkRHR3sfAPPnzyc6OpqP\nP/44yFE2DJJ1iWruuusuANauXVtl/po1awDo0aNHwGMSgZOQkMD+/fspLi6uMn/r1q0ANGvWLBhh\niSAxmUyMGDGClStXUlRU5J1/4sQJNm/ezOjRo4MYnQiE84l6eno6n376KZ07dw52SCIA7r//fjZv\n3lztATBy5Eg2b95M7969gxxlwyDdYEQ1t912GyNGjGD27NmoqkqPHj3YuXMns2bNYvjw4fLhvMZN\nnTqVkSNHMnjwYH77298SFxfH119/zYsvvsj111/P0KFDgx2i8KG1a9dSUlLiTcQPHDjAihUrABg2\nbBihoaHMmjWLrl27Mnz4cKZPn055eTkzZswgLi6OJ554Ipjhiyt0qf2vKAq33347u3btYs6cObjd\nbr7++mvv+vHx8SQnJwcldnFlLrXvk5KSSEpKqnHdxMRE+vfvH6BIhaLJ0B6iBmVlZcyaNYtly5Zx\n5swZEhISuOeee5g5cyZWqzXY4Qk/27x5My+99BLfffcdBQUFNG/enBEjRvCHP/yhxjGXxdUrKSmJ\n48eP17js6NGj3oP1N998w1NPPcXWrVsxmUzceuut/PWvf5VE7Sp3qf0P0KpVq1rXv++++1i0aJE/\nQhN+drmf/R9TFIUpU6bIUI4BJMm6EEIIIYQQ9ZT0WRdCCCGEEKKekmRdCCGEEEKIekqSdSGEEEII\nIeopSdaFEEIIIYSopyRZF0IIIYQQop6SZF0IIYQQQoh6SpJ1IYQQQggh6ilJ1oUQQgghhKinJFkX\nQgghhBCinpJkXQghhBBCiHpKknUhhBBCCCHqqf8HiTEUJYNc1b4AAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"z = (10., 1.) # Gaussian N(10, 1)\n",
"\n",
"product = gaussian_multiply(z, z)\n",
"\n",
"xs = np.arange(5, 15, 0.1)\n",
"ys = [stats.gaussian(x, z[0], z[1]) for x in xs]\n",
"plt.plot(xs, ys, label='$\\mathcal{N}(10,1)$')\n",
"\n",
"ys = [stats.gaussian(x, product[0], product[1]) for x in xs]\n",
"plt.plot(xs, ys, label='$\\mathcal{N}(10,1) \\\\times \\mathcal{N}(10,1)$', ls='--')\n",
"plt.legend()\n",
"print(product)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The result of the multiplication is taller and narrow than the original Gaussian but the mean is unchanged. Does this match your intuition?\n",
"\n",
"Think of the Gaussians as two measurements. If I measure twice and get 10 meters each time, I should conclude that the length is close to 10 meters. Thus the mean should be 10. It would make no sense to conclude the length is actually 11, or 9.5. Also, I am more confident with two measurements than with one, so the variance of the result should be smaller. \n",
"\n",
"\"Measure twice, cut once\" is a well known saying. Gaussian multiplication is a mathematical model of this physical fact. \n",
"\n",
"I'm unlikely to get the same measurement twice in a row. Now let's plot the pdf of $\\mathcal{N}(10.2,\\, 1) \\times \\mathcal{N}(9.7,\\, 1)$. What do you think the result will be? Think about it, and then look at the graph."
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAusAAAEaCAYAAACo3xkcAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzs3XlYVGX7wPHvGWbYkVVUEMF9X3JP\nzVxCcUmTXMMWbTHbrH5pvpV7mVq+ZWZWvqamuYtbKmqJWi6ouaKmuaCouADKvsz2+2OSJNaBgUG4\nP9fF5XDOc57nHo4D95x5zv0oRqPRiBBCCCGEEKLMUVk7ACGEEEIIIUTuJFkXQgghhBCijJJkXQgh\nhBBCiDJKknUhhBBCCCHKKEnWhRBCCCGEKKPU1g4gLwaDAYPBkG2boigoimKliIQQQgghhCg6o9HI\nvwsxqlQqVKq8r5+X6WQ9JSXF2mEIIYQQQghRYpycnPJN1mUajBBCCCGEEGWUJOtCCCGEEEKUUZKs\nCyGEEEIIUUaV2Tnrud1IWtCcHmF5p0+fRqfToVarady4sbXDEaVMzn/FJue/4pJzX7HJ+S85ud2T\nWVDxlIcqWS/obllheQaDAb1eLz/7CkrOf8Um57/iknNfscn5L10FJetyBoQQQgghhCijJFkXQggh\nhBCijJJkXQghhBBCiDJKknUhhBBCCCHKqDJ7g6kQQgghhLXo9Xru3btHamqqtUMpdRqNBrVajaIo\nREdHWzuch45KpcLDwwMHBweL9CfJuhBCCCHEA/R6PdevX8fd3R0PD48Cq3WUN6mpqRiNRhRFwdHR\n0drhPHS0Wi0xMTH4+vpiY2NT7P5kGowQQlRQSZlJTDswjT6hfegT2of91/dn7dsdvZvxf45nZ9xO\nDEaDFaMUovTdu3cPd3d3XFxcKlyiLopPo9Hg5eVFXFycRfqTK+tCCFEBHYw5yIR9E7iZcjNrW5ou\nLetxijaFa+nXWH5zOceTj/NFnS/wcfaxRqhClLrU1FQ8PDysHYZ4iDk4OFgsWZcr60IIUYGk6dKY\nHjGdl3e8zM2Um/i5+DGn6xyW9lpKqyqtsto96vMoQ32GYqvYcib5DMGbgln/13qMRqMVoxei9MgV\ndVEclvz/I1fWhRCigjAajYz+ZTR/3PoDgCH1h/Buq3dx1OSck+ph70Ff7760cGzBwpiF/JXyFxP3\nT2TX1V1M6jAJLwev0g5fCCEqJLmyLoQQFYSiKDzf6Hm8Hb357onv+Kj9R7km6g+qYleFCXUm8E6r\nd9CoNOy+tpvV51aXUsRCCCHkyroQQpRzmfpMbG1sAehaoyvtfdrjoC58STGVomJkk5F08u3EwlML\neanpSyUVqhBCiH+RK+tCCFGOHYo5RN/1fTl2+1jWNnMS9QfVc6/HzM4zsxJ/ML0REEIIUXIkWRdC\niHIqNi2WcXvHEZMSw4YLGyzad6o2lQ9//5Ax4WOktKMQQpQgSdaFEKIc0hv0jN87nrj0OOq41WF8\n2/EW7f968nW2R23n9+u/syhykUX7FkKUTbGxsRw7dqzghsKiJFkXQohy6LuT3xFxMwIHtQOzu8wu\n8tSXvNR1r8t/2v4HgLnH5nL01lGL9i+EKFv27t1LzZo1admyJZMmTbJ2OBWKJOtCCFHOHIw5yLcn\nvgVgQvsJ1HKtVSLjBNcNpm+tvuiNesbuHUt8enyJjCOEKHm3bt3Kc5/RaGTq1KmsWLGCatWqcePG\nDaZOnUqjRo0wGP6ZBpeUlMS4cePo0aMHlStXRlEUJk+enGe/ycnJvP322/j4+GBvb0+LFi1YuXJl\ngbHu2rWLkSNH0qBBA5ycnPD19aV///788ccfZj1nc+NeuHAhvr6+pKSkFGmcopJkXQghypE7qXd4\nf+/7GDHydN2nebL2kyU2lqIoTGg/gZquNbmdepsPfvtA5q8L8ZAKCQkhKioq130RERE8/fTT9O3b\nl3PnzjFhwgRmzZrF1KlTUan+SSXj4uL4/vvvycjI4KmnnipwzODgYJYsWcKkSZPYtm0bbdq0Ydiw\nYSxfvjzf4+bPn09UVBRjxoxh69atzJkzh9u3b9O+fXt27dpl1vM2J+7nn38eJycnZs2aZfYYxSHJ\nuhBClCP2antaVWlFPfd6Fp+nnhtHjSOzH5+NvY09+27sY+GphSU+phDC8o4cOcLChbm/fjds2ED/\n/v0BcHFxYd68ebi5uREcHJytnb+/P3fv3mXPnj18+umn+Y63detWdu7cyTfffMOoUaPo2rUrCxYs\nIDAwkLFjx6LX6/M8dt68eezatYvRo0fz+OOPM3DgQHbu3ImnpyfTp08385kXPm61Ws2oUaOYM2cO\nqampZo9TVJKsCyFEOeJi68Lsx2fzQ88fsFfbl8qYdd3r8kG7D3C3c6exZ+NSGVMIa0nN1Fn9y9Iu\nXbpEQkICP/zwAzpdzv5jYmLw8fEBIDMzk4ULF/LMM89ku6oOpk/bFEUp1Jjr16/H2dmZQYMGZds+\nYsQIbty4QURERJ7Hent759jm7OxMo0aNiI6OLtT4DzIn7pCQEBITEws1XcdSZFEkIYQoB4xGY9Yf\nG0VRcLVzLdXxn6rzFN1qdCv1cYUobY0mbrd2CETN6GPR/o4cOULNmjW5fPkyGzdupFevXln7zp07\nR/369bO+j4iIIC4ujq5duxZrzMjISBo2bIhanT0VbdasWdb+Dh06FLq/hIQEjh49Srdu3YoVV0Gq\nVq1KgwYN2LJlCyNHjizRse6TK+tCCFEOfHbkM8btGUd0ovlXlSzBGm8QhBCWcfDgQebOnYtGo2Hu\n3LnZ9m3cuDFrCgzAgQMHAGjZsmWxxoyLi8PDwyPH9vvb4uLizOrv9ddfJyUlhQ8//LBYcRVGy5Yt\n2bdvX4mPc59cWRdCiIfcjeQbrPxzJVqDlqfqPoVfJT+rxaI1aNlwYQN7ovfwVbevUClyTUiUL2em\n9rR2CBZ37NgxPvvsMwYOHMiKFSs4duwYLVq0AODs2bOMGzcuq+2NGzdQFAUvL69ij5vf1JPCTksB\nmDBhAj/99BNz586lVatWxY6rIN7e3ty+fRudTpfjk4GSIMm6EEI85OafmI/WoKVt1bY8Wu1Rq8aS\nnJnM7COzSdGmsCNqB0E1g6wajxCW5mhbvlKn+Ph4PDw8sLGxYcKECaxatYpPP/2UVatWERsbm2N+\neFpaGhqNBhsbm2KN6+npmevV8/h4UwnY3K6652bKlCl8/PHHfPLJJ7zxxhvFiqmw7O3tMRqNpKen\n4+zsXOLjySUPIYR4iF26d4lNFzcB8FbLt8y6GlUS3O3deb7x8wB8ffxrtAatVeMRQuQvNDSUfv36\nAdCwYUNCQkLYsmULe/bsYfv27fTt2zdbey8vLzIzM4tda7xp06acPXs2xw2tp06dAqBJkyYF9jFl\nyhQmT57M5MmT+eCDD4oVjzni4+Oxs7MrlUQdJFkXQoiH2tfHv8ZgNNDVryvNKze3djgAPNfoOTzs\nPbiSeIWNFzZaOxwhRD7Wr1+frSLLzJkzcXFx4c0332T37t05bvJs0KABABcvXizWuAMGDCA5OZl1\n69Zl275kyRJ8fHxo165dvsdPmzaNyZMn89FHH5X6iqqXLl2iUaNGpTaeJOtCCPGQioyNZOeVnSgo\nvPnIm9YOJ4uTxomXmr4EmKbopOvSrRyREOK+CxcuEBAQQHh4OPPmzaN169Y4Ojpm7a9WrRqTJk3i\n0qVLqFSqHNNdunTpAphuSs3Ntm3bWLt2LZs3bwbgzJkzrF27lrVr12arTd6rVy8CAwMZPXo0CxYs\nIDw8nFdeeYWwsDBmzZqVNe6ePXtQq9VMnTo169jZs2czceJEgoKC6NOnDwcPHsz29W+KomTFnZfC\nxm0wGDh06FCxq+GYw+yJV8nJyXz00UesXr2a+Ph4GjRowPjx4xk6dGi+xy1evJgRI0bkui8mJoaq\nVauaG4oQQlRoi08vBqBvrb7Uda9r3WD+ZXD9wfx45kduptxk1blVWVNjhBDWlZCQwJUrV+jWrRsd\nO3Zk586dOdq8+uqrbNmyJccUGAA/Pz8ee+wxNm7cyCuvvJJj/+jRo7ly5UrW92vWrGHNmjUAXL58\nmYCAgKx9oaGhfPjhh0ycODErp1yxYkW2nNJoNKLX6zEY/lkd+X5CHRYWRlhYWI4YjEZj1uPk5GTA\n9CYkP4WNe/fu3SQkJBASEpJvf5ZkdrIeHBzM4cOHmTFjBvXq1WP58uUMGzYMg8HAM888U+DxixYt\nyvoI5T5PT09zwxBCiApvaoep1HOvR++ava0dSg52Nna81vw1Ju6fyMJTCxlSf0ipLdIkhMhbq1at\n2LVrF9evX2fgwIHY2+d8XSqKwo8//oiTk1OufYwZM4YhQ4Zw/fp1fH19s+2LiooqdCzOzs7MmTOH\nOXPm5NmmS5cu2ZJvMCXMhbV3714URSlwTnth4160aBEdOnQodulKc5iVrN9fGvZ+gg7QtWtXrly5\nwtixYxkyZEiBdwc3adKE1q1bFz1iIYQQADhqHHmlWc4rW2XFk7Wf5NjtYwysN1ASdSHKkMJM4XB3\nd8/zhvXg4GDatGnDp59+ytdff23p8CwqPDycoUOH0rRp02L3dfHiRVatWsWuXbssEFnhmTVnvThL\nwwohhLCM26m3MRgNBTe0MrVKzdSOU2lWuZm1QxFCWJCiKCxYsAAfH59s01PKos8++4zly5dbpK+r\nV6/y9ddf06lTJ4v0V1iK8d+fLeTj0UcfRa/Xc+jQoWzbT58+TZMmTfjuu+9ynb8E/8xZr1KlCnfu\n3MHV1ZUuXbowderUXMvzGAwGkpKSsm27evVqmf9PUd5otf+UXdNoNFaMRFiDnP+yx2A08MG5D7BR\nbHjN/zV87X0LPqiILH3+9UY9NkrxajOL0lHRX/sajSbb3OqK5sHU0NrlYB9mUVFR2V5LACqViho1\namTb5uLigkqV9/Vzs6bBxMXFUatWrRzbC7M0bNWqVfnwww9p3749lSpV4tSpU8yYMYP27duzb98+\nmjcvuOSYTqdDr9ebE7KwoH//hxMVi5z/suFk0kmupV/DQeWAM86ldl6KM06GIYPVN1dzNOko0+tM\nx8HGwYKRiZJWEV/7arU6xzzpikp+DkVnNBpzvH6KspiU2TeYFnVp2KCgIIKC/lnJrnPnzvTp04em\nTZsyceJENm4suBavWq3O952HsLyKfnWlopPzX/bsumuaK/m45+O42ruW6FiWOv9qo5o/U//knu4e\nB5MO0qNyD0uEJ0pQRX/tK4pSoa8oy5V1y1AUJcfrpyh5rFnJuqWWhr0vICCATp065Vmr898aN24s\nyXopO3HiBFqtFo1GU6hPP0T5Iue/bLmaeJUTx0+Y6qp3epMalWoUfFAxWPL8j7AfwScRn7A3aS//\n1/3/UCnyu7wsq+iv/ejo6Gy1xyua1NRUjEYjiqJU6J9Dcbm4uODn55dtW27TvAti1m9LSywN+29G\no1EScCGEKIQVf64AoJNvpxJP1C2tX+1+OGuciUqM4sCNA9YORwghHhpmZcnFXRr23y5fvsy+ffto\n3769WccJIURFk6pNZcOFDQAMazDMytGYz1HjSP86/YF/3nQIIYQomFnTYB5cGjYxMZE6deqwYsUK\nwsLCWLZsWdak+RdffJElS5Zw8eJF/P39AXjiiSfo3LkzzZo1y7rBdNasWSiKwrRp0yz/zIQQohzZ\ncWUHydpk/Cv509G3o7XDKZKh9Yfy09mf2HttL9FJ0fi5+BV8kBBCVHBm32BamKVh9Xo9er0+2w0K\nTZs2ZdWqVXz++eekpaXh7e1Nt27dmDBhAvXq1bPMsxFCiHKqX+1+eNh7oDPoHtr53gGuAXT06ci+\nG/tY+edKxrYZa+2QhBCizDM7WS/M0rCLFy9m8eLF2bZ98cUXZgcnhBDCRKWo6Fy9s7XDKLYXmrxA\nQ8+GDKk/xNqhCCHEQ8HsZF0IIUTp0hv02KjKx2JC7au1p301uU9JCCEK6+H8LFUIISqImOQYAtcG\n8tXRrzAYZQVnIYSoaCRZF0KIMmzVuVXcSbvDyTsnH9q56rk5cOMAr/3yGkduHrF2KEKIQoqNjeXY\nsWPWDqPCKT+/+YUQopxJ16Wz7i9TqdxhDR++co352XFlB79d/43lfy63dihCiELYu3cvNWvWpGXL\nlkyaNMna4VQokqwLIUQZFRYVxr2Me1Rzqsbj1R+3djgWdb9W/K6ru7iZctPK0Qghbt26lec+o9HI\n1KlTWbFiBdWqVePGjRtMnTqVRo0aYTBkn5536NAhevbsiYuLC87OznTt2pV9+/YVKoYXXngBRVHy\n/CrsivcASUlJjBs3jh49elC5cmUURWHy5Mm5tl24cCG+vr6kpKQUuv/SJMm6EEKUQUajkeVnTVed\nh9QfglpVvuoB1HOvR5uqbdAb9aw+t9ra4QhR4YWEhBAVFZXrvoiICJ5++mn69u3LuXPnmDBhArNm\nzWLq1KnZVqE/fPgwnTt3Ji0tjaVLl7J06VLS09Pp3r07Bw4UvHLxhAkTOHDgQI4vLy8vfH19adOm\nTaGfT1xcHN9//z0ZGRk89dRT+bZ9/vnncXJyYtasWYXuvzRJsi6EEGXQiTsnOBt/FluVLcF1g60d\nTom4f3V97fm1ZOgzrByNEBXbkSNHWLhwYa77NmzYQP/+phWIXVxcmDdvHm5ubgQHZ//dNGHCBNzc\n3AgLC+Opp55iwIAB7NixAxcXF957770CY6hduzbt27fP9pWRkUFsbCwjRozIWnyzMPz9/bl79y57\n9uzh008/zbetWq1m1KhRzJkzh9TU1EKPUVokWRdCiDIo9K9QAIJqBuFu727laEpGV7+uVHGswt2M\nu+yO3m3tcIQonMwU639Z2KVLl0hISOCHH35Ap9Pl2B8TE4OPj4/p6WdmsnDhQp555plsV9UB9u3b\nR5cuXXB0dMza5uLiQufOndm/fz8xMTFmx7Zw4UIURWHkyJFmHXd/6kxhhYSEkJiYyMqVK80NscSV\nr89VhRCinHim4TM4ahwJCgiydiglRq1S82TtJ/nfqf+x6eImegb0tHZIQhRsuo+1I4DJCRbt7siR\nI9SsWZPLly+zceNGevXqlbXv3Llz1K9fP+v7iIgI4uLi6Nq1a45+MjMzsbOzy7H9/rZTp05RrVq1\nQseVkJDA2rVr6d69OzVr1jTnKZmtatWqNGjQgC1btpj9xqCkyZV1IYQogxp4NGB82/G08G5h7VBK\nVL/a/Wjs2bjc3UArxMPk4MGDzJ07F41Gw9y5c7Pt27hxY9YUGCBr7nnLli1z9NOoUSMOHjyY7aZT\nnU5HREQEYJpHbo4VK1aQlpbGiy++aNZxRdWyZctC3wxbmuTKuhBCCKup6VqTlX3L3sfOQuTpgxvW\njsDijh07xmeffcbAgQNZsWIFx44do0UL04WCs2fPMm7cuKy2N27cQFEUvLy8cvTz5ptv8uKLL/LG\nG2/w4YcfYjAYmDJlCleuXAHIMW2mIAsXLsTT05MBAwYU49kVnre3N7dv30an06FWl50UWa6sCyFE\nGXIz5SYf/v4hh28etnYoQojc2DpZ/8uC4uPj8fDwwMbGhgkTJqBSqbJuyIyNjcXb2ztb+7S0NDQa\nTa43e44cOZIZM2awdOlSqlevTo0aNThz5kzWzaW+vr6FjuvkyZMcOXKE4cOH5zq1piTY29tjNBpJ\nT08vlfEKS5J1IYQoQ36+9DObLm5i3vF51g6lVCVmJrLm/Bou3btk7VCEqFBCQ0Pp168fAA0bNiQk\nJIQtW7awZ88etm/fTt++fbO19/LyIjMzM8+a5O+//z6xsbGcOnWKqKgo9u/fz927d3FycqJVq1aF\njut+ZZqXXnqpiM/MfPHx8djZ2eHs7FxqYxaGJOtCCFFGGI1GNl7YCED/2v0LaF2+fHzgY6YemMqa\n82usHYoQFcr69esZNGhQ1vczZ87ExcWFN998k927d9OhQ4ds7Rs0aADAxYsX8+zTzs6OJk2a4O/v\nz9WrV1m1ahUvv/wyDg4OhYopIyODZcuW0bZtW5o0aVKEZ1U0ly5dolGjRqU2XmFJsi6EEGXEqdhT\nRCVGYW9jT6B/oLXDKVV9a5uu3m29vBWtQWvlaIQovy5cuEBAQADh4eHMmzeP1q1bZyu1WK1aNSZN\nmsSlS5dQqVQ5prt06dIFINfVRCMjI5kyZQpbtmzhl19+Yfbs2bRq1Yq6desybdq0bG337NmDWq1m\n6tSpOfrZsGED8fHx+V5VVxQlK5a8bNu2jbVr17J582YAzpw5w9q1a1m7dm2OeuoGg4FDhw7lWuXG\n2srO7HkhhKjgNl3cBEB3/+4425atj2FLWgefDnjaexKXHsfv136na42y9wdTiPIgISGBK1eu0K1b\nNzp27MjOnTtztHn11VfZsmVLjikwAH5+fjz22GNs3LiRV155Jds+W1tbdu3axVdffUVycjI1atTg\n1VdfZfz48Tg5ZZ9rbzQa0ev12SrH3Ldw4UKcnJwYOnRors8hOTkZoMAykKNHj866uRVgzZo1rFlj\n+vTu8uXLBAQEZO3bvXs3CQkJhISE5NunNUiyLoQQZUCmPpNtl7cBpnKGFY1apaZPrT78eOZHNl3c\nJMm6ECWkVatW7Nq1i+vXrzNw4EDs7e1ztFEUhR9//DFHgn3fmDFjGDJkCNevX89202i9evXYs2dP\noeLo0qULRqMx1307duzI99i9e/eiKAoffPBBvu2ioqIKFQvAokWL6NChQ64lKa1NpsEIIUQZsDt6\nN4mZiXg7etOuajtrh2MV99+k7L62m3vp96wcjRDlV9euXRk+fHiuifp97u7ueVZhCQ4Opk2bNllV\nY0pbeHg4Q4cOpWnTphbp7+LFi6xatYqZM2dapD9Lk2RdCCHKAAMG/Fz8eLLWk9iocpZEqwjqe9Sn\ngUcDdAYd26K2WTscIUQeFEVhwYIF+Pj45DqNpaR99tlnLF++3GL9Xb16la+//ppOnTpZrE9Lkmkw\nQghRBgQFBNHTvycZ+gxrh2JV/Wr34/zd81xLumbtUIQQ+WjSpEmpVmopSV27di2TN5beJ8m6EEKU\nEYqiYK/O+2PpiuCpOk8RFBBEZcfK1g5FCCHKBJkGI4QQVvbbtd8q/BX1+1xsXSRRF0KIB0iyLoQQ\nVnQu/hyv/foaQeuCyNRnWjucMuVmyk30Br21wxBCCKuSZF0IIaxo40XTiqWPeD+CrY2tlaMpO97b\n8x491vYgIibC2qEIIYRVSbIuhBBWojfoK3Rt9fy42blhxMjmS5utHYoQQliVJOtCCGElR24dITYt\nFlc7Vzr6dLR2OGVK31qmlRPDo8NJ16VbORohhLAes5P15ORk3n77bXx8fLC3t6dFixasXLnS7IE/\n+ugjFEUpN2V/hBDCXPevqj9R4wk0NhorR1O2NKvcjGpO1UjRpvDb9d+sHY4QQliN2cl6cHAwS5Ys\nYdKkSWzbto02bdowbNgws4rTHz9+nM8//5wqVaqYO7wQQpQLWr2WnVd2AtC7Zm8rR1P2qBQVQTWD\ngH/e1AghREVkVrK+detWdu7cyTfffMOoUaPo2rUrCxYsIDAwkLFjx6LXF3zXvk6nY8SIEYwaNYoG\nDRoUOXAhhHiYHbt9jMTMRCo7VKZVlVbWDqdM6hXQC4C91/aSnJls5WiEEMI6zErW169fj7OzM4MG\nDcq2fcSIEdy4cYOIiILv2p8xYwbx8fF88skn5kUqhBDlSNtqbdn41EamdJiCjcrG2uGUSQ08GhBQ\nKYAMfQbh0eHWDkcIYSEBAQG88MILJdb/8uXL+fLLL0us/9Jm1gqmkZGRNGzYELU6+2HNmjXL2t+h\nQ4c8jz9z5gwff/wxoaGhODs7mx3s6dOnMRgMZh8nik6r1Wb9e+LECStHI0qbnP+SV4lKnIgr4s/W\naMQmMwHb1BhsU29hm3oTm8xEtPaeaB2rkvn3l0HjVKTuCzr/RqORhHQDt1P13EnRcStFT0qmAU9H\nG7wdbajspKaykw2OmqLXMujt3hudqw6vBC/5P1iKKvprX6PRkJqaau0wrMZoNGb9WxI/B6PRiE6n\nK7Gf8dKlSzlz5gyvvPJKifRfWElJSTlePyqViho1apjVj1nJelxcHLVq1cqx3cPDI2t/XgwGAyNH\njiQ4OJjevYs2P1On0xVqqo0oGfd/eYuKSc6/5RiNRhRFMfs4xaCj0p0jeFz/FcfEC9im3cZGX3Cl\nFJ3GmUyHqiR5NCWu+hOkutYHM8fXarVoDUaO3czg96vpRCXoiE3Vk1mIX8nOtgrejjY0qmxL5xr2\n1HRTF/r5t3FuY3pgAK1B/g9aQ0V87avV6qyEtaJ78OeQlpaGg4NDifRdEqx9Do1GY47Xj42N+Z+k\nmpWsA/n+gs1v33//+1/++usvNm3aZO6QWdRqNSqVVJssTQ/+J9NopFpFRSPnv2R8c+UbdEYdA6oM\nwM/BL//GRiMO9/7E/eoO3K79iibzXo4mWntPMh2qkulUFb1tJTRpsWhSb2Kbegu1NhG1Nhm19gKO\niReoErWedOca3K3Rg7vVA9E6VctzaK1Wi9Fo5Hy8lt+vZfL7lTSSMrN/uqkA7g4qvJ3UeDvZ4GSr\nIj5Vz+0UPbdTdKRojSRnGknO1HHpno6f/0qlhquaLgGOPB7giJej2X+GRCmo6K99RVHyzGnSdGl5\nHqdSVNjZ2BWqraIo2NvYF6ltcXzyySdMnz6dffv2MXPmTMLDw1EUhV69ejFz5kwqV66M0WikUaNG\nNGrUiOeee44ZM2Zw7tw5Xn/9daZNm0Z6ejrTp09n7dq13LhxAy8vL5588kkmTZqEm5tb1lharZbJ\nkyezfPlykpKSaNGiBTNmzMj2vB6MKSUlJVusS5cu5dVXX+XMmTP4+/tnbV+1ahXffvstp0+fBqBW\nrVqMHj2a559/nqCgIH77zVRB6sFZHP/uuzQoipLj9VOUPNas35Kenp65Xj2Pj48H/rnC/m9Xr15l\n4sSJzJgxA1tbW+7dM/2x0el0GAwG7t27h52dXYHv1ho3bizJeik7ceIEWq0WjUZD8+bNrR2OKGVy\n/i0vKTOJIyePkGnIZNxj46jvUT/3hukJcGgBnFwFsef/2e5UGZoMhLqB4B4ArtXRqO3QALlOdslI\ngnvREHcBzmyEP7dgn3yVamci9HZcAAAgAElEQVT+R7Uz/wP/jtAiBJoNAZt//iTcS81k5voIwi+n\ncDP5n8vn3i529G/hw+P1vPHzcKCaqwO26rx/Lyela7l+L42Lt1PYeiqGnWdvcTVBx48nEll6MpFH\na3kyuLUf/Zr7oFLlnhwlZCSw4cIGriVd48P2H+b9wxUWU9Ff+9HR0Tg6Oua6r92Sdnke95jvY3zz\nxDdZ33f5qUueSXjrKq1ZFLQo6/uglUHczbiba9vGno1Z2df8Mtm5uZ88PvPMMwwePJjXX3+d06dP\nM2HCBM6fP09ERETWm7Xjx49z/vx5PvroI2rWrImTkxMODg4EBwfz66+/8p///IfHHnuMkydPMmnS\nJA4fPsyBAwewszO9YXnhhRf48ccfee+99wgMDCQyMpJnnnmGpKQk1Gp11s/4fkz//pnf78fBwSFr\n38SJE5k2bRrBwcGMHTsWV1dXIiMjiYmJwdHRkW+//ZZXXnmFixcvsn79+qy+8jqfJcnFxQU/v+wX\nZAwGA0lJSWb1Y1ay3rRpU1asWIFOp8s2b/3UqVMAedZMv3TpEmlpaYwZM4YxY8bk2O/u7s6YMWPK\n1c0AQgiRm/DocDINmdRyrUU993o5GxgMcHIl7JwIKXdM29T20KAPNBsKtbuCOTXZ7VygSiPTV6N+\nkJ4IZzebxrj8G1zZZ/o6OB96f4berz2rDkfz2fY/uZtq+oNtZ6PQu5kPAx7xpWMdL2zySKpz42Kv\noUFVDQ2qVqJPs2okpGnZdiqG0GPXOXQ5nv0X49h/MY5F+y4zpX8TWvi55egjWZvM50c+R0Hh5WYv\n4+3oXfjnL4TIVXBwMLNmzQKgR48eVKlShZCQEFavXs2AAQMAuHPnDmfOnKFevX9+V23fvp3t27cz\na9Ysxo4dC0BgYCB+fn4MGTKEH3/8kZdffpk///yTJUuW8M4772SNExgYmDVOUVy+fJnp06cTEhLC\nsmXLsrYHBgZmPW7UqBFubm7Y2dnRvn37Io1T1piVrA8YMIAFCxawbt06hgwZkrV9yZIl+Pj40K5d\n7u82W7RoQXh4zjv53377bRISEli0aBHVq1c3M3QhhHj4bL28FYCgmkE5P2a/cRy2joVrh0zfe9aB\nTu9Aw35gX8kyAdhXgkdCTF8J101J+76v4NYpWBTEXtuufJE4kLu44++qpl89Rzr6O9O+dQuLDO/q\noGFo2xoMbVuD6PhUQo9e53+/XeLEtQSemrePwa2rMy6oAV7O/0wl8HX2pXnl5py4c4IdUTsY3mi4\nRWIRoiginsm78t2/KzvtHrw7z7YqJfsnUmFPhxW6rSX8O2EePHgwzz//POHh4VnJepMmTbIl6gC7\ndu0CyFHNZdCgQYwcOZJff/2Vl19+OSvvy2ucoti5cyd6vZ7XX3+9SMc/rMxK1nv16kVgYCCjR48m\nMTGROnXqsGLFCsLCwli2bFnWpPkXX3yRJUuWcPHiRfz9/XFzc6NLly45+nNzc0On0+W6Twghypu7\n6Xc5eOMg8E8NcQBS42HXNDiyCDCCxgm6vA/tRoPatuQCcvWFx/6P2HrDuLByHG3jf6ZrZji77Q5w\nut5o1A36YDAqaIpRzSU/fh6OjHmiLsPa+TFz2znWHb3G6iPX2BZ5k/8LrMfw9v6obUxj96rZixN3\nTrAtapsk68KqHDWFn05RUm0toWrVqtm+V6vVOaY7/7sNmIqJqNVqKleunG27oihUrVo16/j7/+Y1\nTlHcuWP6tLGiXeA1+zdwaGgozz77LBMnTiQoKIiIiAhWrFiR7Z2TXq9Hr9db/S5cIYQoS3Ze2Yne\nqKehR0MCXANMG4+vgLkt4cgPgBGaDoI3j0DHMSWbqGOqVLA84ipd559iaMww+mdO44pDI5yUdNr+\n9QWNwkfidPdMicYA4O1iz+zBzVk3+lEa+1QiKV3H5M1n6Dv3dyKvJwDQM6AnKkXFyTsnuZZ0rcRj\nEqK8u3nzZrbvdTodcXFx2RLp3G6y9fT0RKfTZSXO9xmNRm7evImXl1dWu/zGeZC9venm2YyMjGzb\nY2Njs31//w3CtWsV63eA2cm6s7Mzc+bMISYmhoyMDE6cOMHQoUOztVm8eDFGo5GAgIB8+9q9ezeR\nkZHmhiCEEA+lbZe3AdC7Zm/Qa2HL/8GGVyHtLng3hhe2wtP/g0o+JR5Lhk7P++tO8sH6UySl62ji\nW4kpo4fjP3Yf9J8Hjl7YJ1+l/oF38Yj6ucTjAWjl78GmNzrxyYAmuDlq+PNmEk/P38+GY9fxcvCi\nTVVTGcewqLynCwghCuenn37K9v3q1asLNduhe/fuANnmjAOsW7eOlJSUrP33+8lrnAfdzxdPnjyZ\nbfvmzZuzfd+jRw9sbGyYP39+vjHa2dmRlpZ3dZ2HjdTMEkKIUmA0Guni14VUXSo9vVvDj/1NN3YC\ndPkPPPZetmosJelWYjqjlv7B8eh7qBQY27MBr3Su9c+No48MhwZ9uffjcNxifsPv2CxQx0PPT0v8\nar+NSiGknT+9m1Tj3dXHCT93h7dXHef0jQR61A4iIiaCsMthvNT0pRKNQ4jyLjQ0FLVaTWBgYFY1\nmObNmzN48OAcyfSDAgMD6dmzJ++//z6JiYl07NgxqxrMI488wrPPPgtAw4YNGT58OF9++SUajYYn\nnniCyMhIPv/8cypVyn4PTu/evfHw8ODFF19k6tSpqNVqFi9eTHR0dLZ2AQEBfPDBB0ybNo20tDSG\nDRuGq6srZ86cITY2lilTpgCmgiihoaHMnz+fVq1aoVKpaN26tYV/gqVHknUhhCgFiqLwfOPned69\nGSwbAonXwNYFgr+HBkVbKK4o/rhyl1eX/cGdpAxcHTTMHfYInetVztnQwY0r7aaRcnYJvucWweH/\nwa0zMPhHcM6lvYW5O9nyv+fb8N+d55gXfpEFv13m0ZvuONo74efiR7ouHXu1ZepOC1ERhYaGMnny\nZObPn4+iKDz55JN8+eWX2Nra5pusK4rChg0bmDx5MosWLeKTTz7By8uLZ599lunTp2eVWwRYuHAh\nVapUYfHixXz11Ve0aNGCdevW5ZiRUalSJcLCwnj77bcZPnw4bm5uvPTSS/Tq1YuXXsr+xnzq1KnU\nrVuXuXPnEhISglqtpm7durz11ltZbcaMGcPp06f54IMPSEhIwGg0PtRTsxVjGY0+tzqULi4uUme9\nlFX0WrsVnZx/Czu5Gja9Cbp0U6WXoSugci7lG0vIykNXmbAxEq3eSP0qLnz/XCv8PXOtzg78c/49\nYw9R8+h0yEyCStVh6DLweaTU4t5yMob31pwgTavHz0PDgufa06CqharjiFxV9Nd+dHR0jvrY5cXk\nyZOZMmUKd+7cyZpf/m+pqalZKy1boz55eZHb/6Oi5LeS+QohRAmLSbrOpg3Pkbz+FVOiXrcHvPRr\nqSXqOr2BCRsiGR96Cq3eSFDjqoS+1iHfRP1BidU6wsu7TG8wEq/BD0Fwck0JR/2PPs2qEfpaB/w8\nHIiO1xL8zX7CImNKbXwhhLAmSdaFEKIkGfRs2fIqHyYc4z1vL9Pc9GErwSHn4j8lQac38Paq4yw9\neAVFgfd61GP+8JY42Zk5C7JyPVPCXren6Q1H6Et/l5osHQ2rVWLT653oWMeT1Ew9r6/ezpJDx0tt\nfCGEsBZJ1oUQoqQY9LDxDbYnngcgsP4g6D4B/rVwSknR6Q2MWXWcn0/GoLFRmB/Sije61c21HFuh\n2Lua3mi0e9X0/c9v/11ysnS4O9myZERbmjXbi2Pt2Uz/bSHrj1WsEm5CFNfkyZMxGo15ToERZY8k\n60IIURIMetj4OlGnV/OnnS02KHTv8H6pDa/VGxiz8jhbHkjUg5rkXODEbCoVBM2A9q+Zvv/5HTi8\nsPj9FpLaRsXo9l1Njyud5N3Vx1n3hyTsQojyS6rBCCGEpRn0sOE1OLmSHW6uALT36YCbfelMfTEl\n6sfYeupmVqL+RKMqlhtAUaDndFBUcOBr2PIuYIQ2pVNO8XG/ztjb2JNuG49id5331ioYgYGtKtaq\nhkKIikGurAshhCU9kKij2BDmY7qJtGdAz1IZXqs38NYKU6Jua6Pi2+EWTtTvUxTo8TE8+obp+y3/\nB4cWWH6cXDhqHOlcvTMAzetfwWiEsWtPsOZIdAFHClE4KpUKrVZr7TDEQ0yv11usL0nWhRDCUgx6\n2DA6K1G/1GcGf6XdQq1S061GtxIf/n6ivi3SlKh/92wrujcsgUT9vvsJe4c3Td9vfa/UEvagmkEA\npNr+QUg7P4xGGLfuJKslYRcW4OHhQUxMTFYJQyHModfruX79OpUrW2ZNCpkGI4QQlmA0mm64PLkK\nVGoY+APHNaYrK49WexRXO9cSHd5gMPLemhPZEvWuDbxLdEzAlLAHTgMU2P+VKWHXOMIjISU6bCff\nTjioHbiRfIMhvUGl+LP04BXeX3cSR1sb+jbzKdHxRfnm4OCAr68vcXFxxMXFWTucUpeUlJRVZ93F\nxcXa4TyUvL29sbe3zMJtkqwLIYQl/P5fOPqjaR73wB+gUX+CgY4+HUnWJpf48P/deZ6Nx2+gViml\nl6jfpygQOBUwwv65sPktcK0OtR4vsSEd1A50qd6FbVHb+OXKL0zt/w5GjCw7eJV3V5+gmqs9rfw9\nSmx8Uf7Z2Njg7V2Kr6My5MFFscrr4lAPE5kGI4QQxXVqLfw61fQ4aCY06p+1q4pTFWq71S7R4Vcf\njubr8AsAfBrctHQT9fsUBZ6YCk2eBoMOVj0Lt/8s0SGfbfQsX3b5ktdavIaiKEzp14QnGlYhU2fg\n5R//ICo2pUTHF0KI0iDJuhBCFMeVA6Z56mAqZ9juFQC0htK5Oe33v2L5YP0pAN7sVodBra14FUyl\ngv7fgF97yEiAnwZB0q0SG65p5aZ09++Ovdr0UbONSuGrYS1o6utKfEomIxYf5m5KZomNL4QQpUGS\ndSGEKKq4i7ByGOgzoUFf082WgNFoZPDmwYzaOYroxJK74fHczSRGL/sDncFI/xY+vBtYr8TGKjSN\nPQxdDh61IeEqrBgKmamlNryjrZqFz7fG182By7EpjFr6Bxk6y1VlEEKI0ibJuhBCFEVKHPw0ENLu\ngk9LCF6QtTLp+bvnuXDvAkduHsHd3r1Ehr+dmM7IxYdJytDRtqYHswY2K/rKpJbm5Akha8DBA24c\nhdCXTZVySkByZjLzjs/jxe0vYjAaAPCuZM+iEW1wsVNzKCqecWtPSkUPIcRDS5J1IYQwlzYdVj4D\n8ZfAtQY8swpsHbN2b4/aDkBH34442zpbfPjUTB0vLjnC9Xtp1PJy4vtnW2GntrH4OMXiWRuGrQAb\nO/jzZ9gxoUSGsbWxZdmZZRy6eYjjt49nba9XxYX5w1uhVilsPH6D/+48XyLjCyFESZNkXQghzGE0\nwsbXIPog2LmariA7ez+w28iOKzsACAoIsvjwBoORt1Yc59T1BDycbFk0og1ujrYWH8ciarSHAfNN\njw/OK5Ea7LY2tlk17O+/SbqvU10vpg9oCsDcXRdk0SQhxENJknUhhDDHgXkQuc5US33IUvBukG33\nubvnuJJ4BTsbOx73s3zpwq/DL/DL2VvYqlUseK41/p5OFh/Dopo8Dd0nmR6HjYerBy0+xP3VYXde\n2Yn+X9NtBrfx442udQD4cEMkp64lWHx8IYQoSZKsCyFEYUXtg50TTY+DZuRaRzzschgAj/k+hpPG\nson0nvN3+OIX03SO6QOa0sq/ZObDW1ynd6DJQFNJxzUvQPJti3b/aLVHcbF14U7aHY7dPpZj/7uB\n9XiioTeZOgOjf/qDe6lSIUYI8fCQZF0IIQoj6SasHQFGPTQdDG1eytHEaDRmTcW4f7XXUq7dTWXM\nymMYjfBMuxoMbFXdov2XKEWBJ+dA5QaQFANrR4JeZ7HuNTYautfoDkBYVFiO/SqVwuzBLajh4ci1\nu2m8veo4BoPccCqEeDhIsi6EEAXRa/++InwLvBvBk1+aEtB/NzPqGdFkBB19O9K5emeLDZ+u1fPa\nT0e5l6qlWXVXJvZtZLG+S42dMwxeCrbOEPUb/DrFot3nNxUGwNVBw/zhLbFTq9h97g5f7frLouML\nIURJkWRdCCEK8stkuHoA7Cr9nXDmPr1FrVIzuP5gvn3iWxw1jrm2KYopm89w8loCbo4avglpib2m\njFV+KazK9aD/PNPj/V/BmU0W67pdtXZUd67OY76PkaxNzrVNYx9XPvn7htM5v/7F7nOWnY4jhBAl\nQZJ1IYTIz+n1cOBr0+OnvgGvOqU6/Joj0aw4dBVFga+GPkJ1d8u9CbCKxk/Bo2+YHm94DWItc4Vb\no9KwNXgrH3f6GFc71zzbDWxVnWfa1cBohLdXHSc6vvQWbBJCiKKQZF0IIfJy5xxs/Dux7DgGGj6Z\nZ9Nz8edYfnY5sWmxFhv+9I0EPtoQCcA7T9Sjc73KFuvbqp6YAv4dITMJVj0LmSkW6bawi0JNerIR\nzaq7ci9Vy2s/HSVdKyucCiHKLknWhRAiNxnJfyeSyRDwGHSbmG/zDRc28OmhT5l9ZLZFhk9I1TJ6\n2VEydAa61q+cVX6wXLBRw8AfwLkK3DkLm94y1a+3AKPRyOnY01y8dzHPNnZqG74JaYmbo4ZT1xOY\nsvm0RcYWQoiSYHaynpyczNtvv42Pjw/29va0aNGClStXFnjcL7/8QmBgID4+PtjZ2eHt7U23bt3Y\nunVrkQIXQogStXUsxJ4Dl2qmxNJGnWdTvUGfVQXGEgshGY1Gxoee5Gp8KtXdHfhiSAtUqsJdNX5o\nuFSFQYtBsYHItXD0R4t0+/Xxrxm6ZSg/RP6Qb7vq7o58NfQRFAVWHIpm04kbFhlfCCEszexkPTg4\nmCVLljBp0iS2bdtGmzZtGDZsGMuXL8/3uLi4OBo3bswXX3zBjh07+O6779BoNPTp04dly5YV+QkI\nIYTFnVoLJ5aDooKnF2ZboTQ3R28f5U7aHVxsXejg06HYw688HM22yJuoVcrfV4DL6AqlxeXfAbr/\n/YlF2Hi4c77YXXb06QjArqu7yNBn5Nu2c73KvHl/waTQUzJ/XQhRJpmVrG/dupWdO3fyzTffMGrU\nKLp27cqCBQsIDAxk7Nix6PV5z/sbMmQIX375JUOGDOHxxx9nwIAB/Pzzz/j6+vL9998X+4kIIYRF\n3I2Cn98xPe48FgI6FnjItsvbAAj0D0RjoynW8BduJ2dNyxjbsz7NqrsVq78yr8NbUPNx0KbCupGg\nyz/BLkgL7xZUcaxCsjaZfdf3Fdj+re51aeXvTlKGjjErj6HTG4o1vhBCWJpZyfr69etxdnZm0KBB\n2baPGDGCGzduEBERYdbgGo0GNzc31Oq8P14WQohSo9fBupchIxH82kHncQUeojVo+eXKL0DxF0LK\n0Ol5a8Ux0rUGOtXx4uXHahWrv4eCSgUDvgMHD7h5Cn4pXv11laLKOg/3V5PNj9pGxZdDWuBip+bo\n1Xt89avUXxdClC1mZcmRkZE0bNgwR3LdrFmzrP0dOuT/EbDBYMBgMHD79m2+++47zp8/z8yZMws1\n/unTpzEY5KpHadJqtVn/njhxwsrRiNJW0c5/1TP/o8q1Q+g1zpxr+C7ayIJvPDyZeJK7GXeppK6E\n/W17Ttwp+s9p4dF7nIlJppKdihebaDh16mSR+7KE0jz/lZqPpebB/8DBeVxSBZBUpV2R+6qtqw2Y\npsJEHI3A3sa+wGNeaVWJ2fvj+Tr8AlWVBBp72xV5/PKgor32RXZy/kuOSqWiRo0aZh1jVrIeFxdH\nrVo5r/R4eHhk7S9I79692b7ddCNWpUqVWLVqFX369CnU+DqdLt+pNqJk3X/xioqpvJ9/57gTeJ9b\nCkBU07dJtfWCQjzn6NRobBQbWrm0wqAzYKBoFxSO3cxg0znTYj6vtaqEi9qAVlt2Lk6U9PmP82qL\nY8BTVInagN+RTzj9+AJ0dh5F6stP7UdlTWXuaO9w5O4R2rkWnPg/6qOhq7894VfSmb0/js8DPXGx\nlYJpUP5f+yJ/cv4ty8bG/EXtzJ5/kl8d28LUuJ07dy737t0jJiaGZcuWMWTIEJYsWcKwYcMKPFat\nVqNSyS/P0vTgi1SjKd5cXPHwqSjn3yYzkVrHP0XBSHyN3iT796Cwz7ZP1T487vU4WqO2yD+je2l6\nvj6caOqvrhOP+jsXqR9LK+3zf6vZ61SKP4FD4mVqnfycy4/ONN3kWwTt3duz+fZmIlMi6eTVqVDH\njGrjwbn429xI0vH90WTe7+RR6Nrt5U1Fee2L3Mn5LzlFyWPNStY9PT1zvXoeHx8P/HOFPT9169bN\netyvXz969erF66+/zpAhQwp8Ao0bN5ZkvZSdOHECrdaUhDRv3tza4YhSViHOv9EIq5+FtDvgWQeP\nkAV42JVesmwwGBmx+DAJGQYaVHVh9nMdsdeYf+WlJFjl/FdfAd93odKtCJqnHYBHXytSN561POmX\n3I/WVVqjVhX+T913VRMInr+PA9fSOJvpwbC25n1cXV5UiNe+yJOc/5JjMBhISkoy6xizMt+mTZty\n9uxZdDpdtu2nTp0CoEmTJmYNDtC2bVvu3r3LnTt3zD5WCCGK7Y/FcHYzqDTw9P/AjEQ9ISOh2MP/\nsO8ye87fwU6t4qthj5SZRN1qvBtCz09Mj3+ZBDFFm7df3aU67au1NytRB2ha3ZWxPesDMGXzaS7c\nNu+PqhBCWJpZyfqAAQNITk5m3bp12bYvWbIEHx8f2rUz74Ygo9HInj17cHNzw9PT06xjhRCi2OIu\nwvYPTI+7TwSfRwp9aJoujR5rexCyNYS76XeLNPy5m0nMCjsHwEd9G1GvikuR+il3Wr8I9fuAPhNC\nXwZterG6M5q5OupLnWrxWF0v0rUG3ll1Aq2UcxRCWJFZyXqvXr0IDAxk9OjRLFiwgPDwcF555RXC\nwsKYNWtW1qT5F198EbVazZUrV7KO7d+/PxMnTiQ0NJQ9e/awYsUKgoKC2LNnD5988omUbxRClC69\nDta/aqrvXbMzPPqGWYfvvbaXVF0qcWlxuNmZXws9U2fgnVXHydQb6N7Am+HtKuZ0i1wpCvSbC07e\ncOdP2DWtSN1oDVpmHppJr9Be3Eu/V+jjVCqFzwc1x81Rw6nrCczddaFI4wshhCWYPQE8NDSUZ599\nlokTJxIUFERERAQrVqwgJCQkq41er0ev12e7mtGxY0fCwsJ46aWX6N69O2+++SaKovDzzz/z2mtF\nm5MohBBFtu9LuHYI7CpB/29M9b7NcL+Gd1BAUJFuQpzz63nOxCTi7qjh06ebVtgbGfPk5GlK2AEO\nzIOo383uQqPScOTWEa4nX+fXq7+adWyVSvZ8/JRpaue88Ascjy58si+EEJZkdrLu7OzMnDlziImJ\nISMjgxMnTjB06NBsbRYvXozRaCQgICBr27hx4zh06BDx8fHodDpiY2MJCwsrdNlGIYSwmJgTsPtT\n0+Nes8DNz6zDkzOT+e36b6bDa/Yye/g/rsQzf/dFAKYPaIq3S8F1wCuk+kHQ8jnACOtHQ3qi2V0E\nBQQBsC1qm9nH9m3mQ7/mPugNRt5ddZy0TCkdLIQofVJaRQhRsWjTIXQUGHTQ8EloPrTgY/4lPDqc\nDH0GAZUCqOdez6xjUzJ0vLv6BAYjBD/iS6+m1cwev0LpOR3c/CHhKoT9x/zD/17N9PDNw8SmxZp9\n/LT+TahSyY5LsSnM2HbW7OOFEKK4JFkXQlQs4R/DnbOm+dB9vzTNjzZTWJRpCkyvmr3Mnr4yfetZ\nrsSlUs3Vnkn9Gps9doVj5wIDvgUUOL4M/txi1uHVXarTzKsZBqOBHVE7zB7e1VHDZwNNpeuWHLjC\nb39J5TIhROmSZF0IUXFE/Q77vzY97vcVOHmZ3cW99Hvsv7Ef+GeKRWGFn7vNTxFXAfh8UHNcHWSx\nkULx7wAd3zI93vQWJJuXMN+/ur7tsvlTYQA616vMc4/6AzB2zUkSUmVFRyFE6ZFkXQhRMaQnmuY9\nY4RHnoX65s81B3DQOPBpp08JaRhCLbdahT7ubkom76811Qx/oUMAHeuY/0ahQuv6IXg3htRY2DzG\ntJhVIQXVDEKlqDh+5zjRSdFFGn58rwbU9HLiZmI6EzdFFqkPIYQoCknWhRAVw/b/mOY9u/lD0KdF\n7sbOxo6gmkGMbzu+0McYjUY+2hjJ7aQMald2YnyvBkUev8JS20Hwd6bFq85tgeM/FfpQb0dvetXs\nxfCGw9GoivZphqOtmv8Obo6NSmHj8Rv8fPJGkfoRQghzSbIuhCj/zoXBsWWAYpr/bFe6iw9tPhnD\nlpMx2KgUvhjSQlYpLaqqTaHbh6bH28bDvauFPnTGYzN4v+37VHWqWuThH6nhzutdagPw0YZIbicV\nb7EmIYQoDEnWhRDlW2o8bP57vnOHN0zzn4tozfk1LDi5gJspNwt9zO2kdCZuNE2beKNrHZpVN38B\nJfGADm+BXzvITIKNb4ChdFcXfbN7XRr7VOJeqpYPQiPNXh1VCCHMJcm6EKJ82zoWkm+BV33o+lGR\nuzEajSyOXMxXx77i8M3DhT7mg9BT3EvV0tinEm90q1Pk8cXfVDbw1HxQO8DlPXBkYaEPNRgNRMRE\nsOWSeRVlHqSxUTF7cHM0Ngq/nL1F6NHrRe5LCCEKQ5J1IUT5dWYjRK4FxQYGzAdN0RcfOhV7iqtJ\nV3FQO9C9RvdCHbPu6HV+OXsbjY3yd4Inv3ItwrM2PDHZ9HjnRIi/VKjDDt44yEs7XmLW4VloDUWv\n6NKgaiXefsJUX3/y5tPEJKQVuS8hhCiI/OUQQpRPyXfg53dMjzu9Db6titXdz5d+BqBbjW44ahwL\nbB+TkMaUzacBePuJejSoWqlY44t/afsKBDwG2lTY8HqhpsO0rdYWT3tP4tPjOXDjQLGGH9W5Fs39\n3EhK1zF+3SmZDiOEKDGSrAshyh+jEba8C6lxpnJ/j79frO60Bi1hl00LIT1Z68lCDG/k/XWnSErX\n0dzPjVGdC1/iURSSSg84eycAACAASURBVAX9vwZbZ7i6HyK+LfAQtUpNr5qmkp2bL24u1vBqGxWz\nBzXDVq1iz/k7rDpctJKQQghREEnWhRDlT+Q6OLsJVGpT9Re1XbG62399P3cz7uJp70m7au0KbL/y\ncDR7z9/BTq1i9qDmqGX6S8lwD4Ae00yPf50CsX8VeEjf2n0BCI8OJzkzuVjD1/F2YWyP+gB8vOUs\n1+6mFqs/IYTIjfwFEUKUL0k3Ycv/mR53HgfVmhW7y/tTYHrX6o1apc63bXR8Kh//fAaAsT3rU8fb\nudjji3y0GgG1uoIuHTaMBoM+3+aNPBpRy7UWGfoMfrn6S7GHH9mpJq393UnO0DFu7UkMBpkOI4Sw\nLEnWhRDlh9FoWt0y/R5UawGPvWuRbp00TjioHehbq2++7QwGI+PWniQlU09rf3dGdKxpkfFFPhTF\nNB3GrhJcOwz7vyqguZJ1Hn+++HOxh7dRKXw+qDkOGhv2X4xjWcSVYvcphBAPkmRdCFF+HF8O58PA\nxtZU3s+maKtV/tvkDpPZPXg3DT0a5ttu6cErHLgUh4PGhs8HmVa7FKXAtfo/q9KGT4dbZ/Jt3rtW\nbwBupd4iXVf8hY0CvP5ZlfbTrX8SFZtS7D6FEOI+SdaFEOVDwnUIG2963OU/UKWRRbt31DiiKHkn\n31GxKczY9icA43s1IMDLyaLjiwK0CIF6QaDPNE2H0eddmtHX2ZfQfqFsemoT9uqil/N80LPt/Xm0\nlidpWj1j156Q6TBCCIuRZF0I8fAzGmHTG5CRCL6tTatcWkB8ejzn4s8V2E5vMDJ27QnStHoereXJ\ns+39LTK+MIOiwJNzwN4NYo7D71/k27yue91833yZS6VSmDWwGU62NhyOussP+y5brG8hRMUmyboQ\n4uH3x2K4uAvU9qbqLzb53wRaWP/P3n2HR1GtDxz/ztb0nhASQi+BAAGkC6gg1UJXECyIBcu9ol79\nqXjBq95rL6ioKApRBKSqKKBUBektQIAACTWEkN6zdX5/TBKIECCYXUrez/Pss5uZM3PO7mRm3z1z\nyg+HfmDY4mH8+89/XzDd9D8Ps+VINt4mPW8Pa41Omr9cGb7hMOBd7fXvb0HqrotuYnVYybPmVUv2\nUUFeTLhNu6Pzzq+JJKX/vdFmhBACJFgXQlzrso/Cby9rr3tNhJAm1bJbVVXLx+KODY2tNN2h0wW8\n/atW+/7y7S2ICrr4hEnChVoNg+Z3gNOuNYexWytNOu/APG6eezNf7vqy2rIf2TGKHk1DsdidPDs3\nHrvj4pM1CSHEhUiwLoS4djmd8OMTYC2Aul2h02PVtusD2Qc4lHMIo85In/p9zpvG7nDy7Lx4rHYn\nPZqGMqJDVLXlLy6TosBtH4BXMKTt0WrYKxHkEUS+NZ8lyUtwXGTIx0vPXuGtoa3w9TCw83gOX6xN\nrpb9CiFqLgnWhRDXri1fwpG1YPSCQVO0WS2ryQ+HfgDg5qib8TP5nTfNF2uTiT+eg6+HgbeGtqrW\nNtDib/AJhdve116v+wBStp03WffI7vib/TldfJoNqRuqLfva/p5MvF1rDvPh8oMknsqvtn0LIWoe\nCdaFENemzCRYPkl73ftVCGpYbbu2OCwsTtaawAxuPPi8aRJP5fPhcm3GzEl3xFDb37Pa8hfVIGYQ\ntBwKqgMWPQa2c4doNOlN5WOuLziwoFqzH3ZDHXpFh2F1OHlm7k5s0hxGCHGZJFgXQlx7nI7S9sjF\n0KAHtB9brbtfcXQFuZZcwr3D6RrR9Zz1ttIAzOpw0is6jKHtIqs1f1FNBrwL3mGQkQir/3veJEOa\nDAFgzfE1ZBRnVFvWiqLwxpBW+HsaSTiZx5TVh6pt30KImkWCdSHEtWfDFDi+CUy+MLB6m78ArDy2\nEtBq1fU6/Tnrp6w+RMLJPPw9jbwxRJq/XLW8grThHAHWfwzHNp2TpGlgU1qHtMau2vkp6adqzT7M\nz4NXB8YA8MmqQ+xJya3W/QshagYJ1oUQ15bT+2DV69rrvv+FgLrVnsXbPd7m454fM7TJ0HPW7T6R\nyyertFrSVwfGEOZXPZPqCBeJHgCxIwEVfhgH1nNnFx3aVDvOiw4uQlWrdzKjO2Mj6N8yHLtT5dm5\n8ZTYqqcjqxCi5pBgXQhx7bBbYeEj4LBA497Q7j6XZGPQGbg56mZqedeqsLzE5uDpuTuxO1X6twzn\nztgIl+Qvqlm/N8EvErKSYfnEc1fX78dDrR7ik16fVPtdEkVReH1QS0J8TCSm5fPB8gPVun8hxPWv\nysF6QUEB48ePJyIiAg8PD9q0acOcOXMuut3ChQsZOXIkjRs3xtPTk/r16zNq1CgOHjx4WQUXQtRA\nf7wDp3aBZyAM/EQbpq8aOZwO7E57pevf/TWRQ6cLCPEx89/B0vzlmuEZoP2/AGyZBodWVFjtZfTi\nqXZPUc/PNTPPBvuY+d/gVoA2gtDmw1kuyUcIcX2qcrA+ZMgQ4uLimDRpEkuXLqVDhw6MHDmSWbNm\nXXC7t956i6KiIiZMmMCyZct4/fXX2bFjB+3atSMhIeGy34AQooY4sRXWvqe9vu19bbbKarbmxBr6\nLujLNwnfnLNuQ1ImX5VOIf/2sFYEeZuqPX/hQo16QsdHtNc/PgnF2W7Nvk9MOMNvqIOqwrPzdlJg\nqfxHoRBCnK1Kc3IvWbKE5cuXM2vWLEaOHAnALbfcwtGjR3nuuee4++670evP7YwFsHjxYsLCwios\n69mzJ/Xr1+eDDz5g2rRpl/kWhBDXPWsRLHpUG4av5TBoOcQl2Sw4sIDTRafJKKk4Kkh+iY1/zYtH\nVbUZKntG16pkD+Kqdut/IGkVZB6CJc/B0IrfO9vTtvPt3m/pEtGFu5rdVe3ZT7yjBeuTMjmeVcx/\nf9nLG0NaV3seQojrT5Vq1hctWoSPjw/Dhw+vsHzMmDGcPHmSTZvO7Wlf5q+BOkBERAR16tTh+PHj\nVSmGEKKmWfGKFmD51oYB77gki1OFp/jz5J8ADGlc8cfAaz/vJSWnmKggTybc1sIl+Qs3MHnB4Kmg\n6GD3PNizsMLqfVn7WHFsBd8nfl/tHU0BfD2MvDs8FoDZm4+zan9atechhLj+VClY37NnD82bN8dg\nqFgh37p16/L1VZGcnMzRo0eJiYmp0nZCiBokaTVsnqq9HviJNhyfCyw6tAin6qR9rfbU969fvnz5\n3jTmbj2BosB7w9vgY67SDUlxtanTHro/q73+5RnIP1W+6vaGt2PSmTiQfYCETNc0z+zSKJix3RoA\n8Pz83WQVWl2SjxDi+lGlb53MzEwaNjx3lsCgoKDy9ZfKbrczduxYfHx8ePrppy9pm4SEBJxOmQXO\nnWw2W/lzfHz8FS6NcLcrffx11nyarXoYE5DRYBAphaHggnI4VSff7/0egPbm9uXvNbfEwb+WaLWf\ng5r5YM47Tnx8zbkTeKWPv6sogf1oHPAjXjkHyJt5P4e7vFXeWbm9f3vWZ6/ni41fMDaqeifbKtMv\nQuU3PwPH8yw8OWMdz98YdNV1Vr5ej724NHL8XUen01G3btWGHK5yFdGFLiiXerFRVZWxY8eydu1a\nFixYQFRU1CVtZ7fbcThkjNorpezkFTXTlTj+9Xd+iKk4nRKvSI41ewini8qwu2A3mbZMvHRetPVu\ni81mQ1VVPtmUS67FSV0/A8Obe9Xoc+B6e+/Jsf9Hi7Xj8EvbiH/Sj2TUuw2A7v7dWZ+9ng3ZG7gr\n9C489NU/jr4CPNnBj5dWZbH+eDGrk/PpXtez2vOpLtfbsRdVI8e/elXWt/NCqhSsBwcHn7f2PCtL\nG4aqrIb9QlRV5aGHHmLmzJnExcUxcODAS87fYDCgq+aZCsWFnX2SGo3GK1gScSVcyePvn7KGkJTl\nqOg43n4Cek8/qn6JuzTrctYBcGPQjXibvQFYlVzI5pMWDDp4umsQ3h41b/SX6/n8dwQ1IbXFI0Tu\nmULU3s8oDm+P1acOLf1bUstUizRrGtsKt3Fz8M0uyT86zMjdLe3M2p3HtB35tAr3ItT76mlidT0f\ne3Fxcvxd53Li2CpdGVq1asXs2bOx2+0V2q3v3r0bgJYtW15w+7JAffr06Xz11VeMHj26SoWNiYmR\nYN3N4uPjsdlsGI1GYmNjr3RxhJtdseOfewKWasM0Kt2fpknPUS7N7pnIZ1hwcAEjokfQNLApRzIK\nmbZgLQBP927G4JsbuzT/q9V1f/63agUFu9AfWUvzhHdh7G+gNzJSP5IPt3/I5pLNPBX7lMuyj2np\nZG/OBnYez+GL3VZmP9wOve7qaA5z3R97cUFy/F3H6XSSn59fpW2qFPkOHjyYgoICFixYUGF5XFwc\nERERdOrUqdJtVVXl4YcfZvr06UydOpUxY8ZUqaBCiBrC6YCFj0JJLkS0g5tfdHmWMSExTOwykaaB\nTbE5nDz1/U4KrQ46NQhi3E2NXJ6/uEJ0Ohj8OXj4w8ntsOYNAAY2HkjzoOYMaDAAp+q6flIGvY7J\nI9rgbdKz+XAWn/+e5LK8hBDXrirVrPfv35/evXvz2GOPkZeXR+PGjZk9ezbLli1j5syZ5e1wxo4d\nS1xcHElJSdSrp80I989//pOvvvqKBx98kFatWrFx48by/ZrNZtq2bVuNb0sIcc36czIcXQdGb20c\nbL17b8F+tPIg8cdz8PMw8MHdba6amk7hIv514I7JMO8BWPs+NOpFSP0bmXvHXLdkXy/Ym1fujOG5\n+bv4YPkBbmwcQpuoALfkLYS4NlS5TcnChQu59957mThxIv369WPTpk3Mnj2bUaPO3KZ2OBw4HI4K\n49QuXrwYgK+//pouXbpUeAwePLga3ooQ4pqXsg1W/1d7PeBtCHZtrfbaE2uZsG4CiVmJAGw+nMWU\n1YcAeGNIayICrt5Of6IaxQyGNqMBFRY+4vbZTYfdUIfbWtfG7lQZP2cHhTK7qRDiLFUO1n18fJg8\neTKpqalYLBbi4+MZMWJEhTQzZsxAVVXq169fvuzIkSOoqnrex5EjR/7u+xBCXOssBbDgYXDaocUg\naOPaduoAcQlx/JT0E78k/0JusY2nv9+JU4XhpcGTqEH6vwVBDSHvBPz8NKgqJfYSFhxYwE9JP7k0\na0VR+N+gVkT4e3Aks4hXfnLNGO9CiGuT9NYUQlwdlv0fZCWBXyTc8WH5uNeukpiVyKZTm9ArekY0\nG8GERbtJySmmXrAXk+6UidpqHLOP1uxKZ4CERbBzFr8e+ZVXNrzCR9s/wuZ07fB1/l5GPri7DYoC\n87ad4JddqS7NTwhx7ZBgXQhx5SX8ADtmAgoM+QI8A12e5bd7vwXg1nq3suGAk593pWLQKUwe0VZm\nKa2pIm8406F56fP082tKkEcQaUVprDy60uXZd2oYzOM3a02/Xly4i5M5xS7PUwhx9ZNgXQhxZeWe\ngMWlw+N1exrqd3N5lhnFGSw5vASA3pHDmfjjHgCe7t1UOvfVdN2ehnrdwFqA+ccnuLvJMODMjztX\nG39rU2KjAsgrsfP09ztxONWLbySEuK5JsC6EuHIc9tJhGnO0YRpveckt2c5NnIvNaaNVSGs+/dVO\nodVBRxmmUQDo9DBkqjacY8o27kpPwagzsitjF/Hprp923ajXMflubTjHTYez+LS0w7MQouaSYF0I\nceWseUMbptHk47ZhGi0OC98nfg+Ad3FP4o/n4O9plGEaxRn+deCOjwAI2fAZA4LbAO6rXa8f4s2r\nA7VJBj9YcYANSefOHC6EqDkkWBdCXBmHVsBabZZS7vzI5cM0lnE4HYxuPpq63s1ZvjUUgPeGxxIp\nwzSKs8UMgg4PA3Dvvt8BWHF0BakF7un4OfSGOgy7oQ5OFf45Zwfp+Ra35CuEuPpIsC6EcL+8k9p4\n1qjQfiy0HOq2rL2MXvSNHMWxPWMBPY/0aMitLWq5LX9xDen7X6gdS7P8DDo5TXSp3Zliu/s6fb42\nsCVNa/mQnm+R9utC1GASrAsh3Mthh/ljoSgTwltD3/+5NXuL3cGTs7eTX2KnXd0AnuvbzK35i2uI\nwQzDZ4DZj0+PHuIzwmgY0NBt2Xua9Ey5px2eRj3rDmXwySppvy5ETSTBuhDCvVb/F46tB5OvFggZ\nPdyW9eTtk3nyhzh2ncgmwMvIJ/e0w6iXy6C4gKCGMPATTAB/TobEZW7NvkktX14fpLVf/3DlAdYf\nynBr/kKIK0++pYQQ7nNwOax7X3s98GO3tVMHOJJ7hGm7p7Gh4EMUYxbv3xVLhLRTF5eixUDoNA6A\nUz89xrTN7+JUnW7LfugNdbirfR1UFf45Zyen80vclrcQ4sqTYF0I4R65J0rbqaN13IsZ7NbsP98x\nAwBHQTSPdO1Iz2hppy6qoPer2CLacnewJ5P3xfHH0VVuzf4/d7akWS1fMgosPDVb2q8LUZNIsC6E\ncD2HTWunXpwFtWO1jntulFaQxZIjiwGob+zHv/pIO3VRRQYzxuEzGFhsB+Cb9a+7NXtPk54po9rh\nZdKzITmTySsOuDV/IcSVI8G6EML1lr0IxzeC2U9rp24wuy1rVVV5+Mf3UBUrWCOYdtcIaacuLk9g\nfe65cSIGVWWLLZOt699za/aNw3z43+BWAHy06hDL96a5NX8hxJUh31hCCNfa/g1s+VJ7PeQLrcOe\nG322dhfJVq1T4LjWjxEZ6OXW/MX1JbzNaIb4aP/Dn+7+AlJdP6vp2Qa1jeT+LvUAePr7nRw6ne/W\n/IUQ7ifBuhDCdY5vgV+e1V7fMgGa9Xdr9uuTMvho65coOithpkY83nGgW/MX16eH+36GEYUtHiY2\nzx8Fhe4doeXl21vQsUEQBRY7D3+zjdxim1vzF0K4lwTrQgjXyEuF70eDwwrRt0P3f7k1++NZRTzx\n3XZshY3wVRowsdvTKIri1jKI61O4byTDGmsdpKeYLKjz7tf6ZbiJUa/j01HtiPD34HBGIePn7JAO\np0JcxyRYF0JUP7sF5t4LBacgtDkM/hx07rvcFFsdPPLtNrKLbDQPaM/KEQvpUaeH2/IX17+H2j6B\nv9GHVjYV+5F18Nu/3Zp/iI+Zqfe2x2zQsToxnfeXJ7o1fyGE+0iwLoSoXqqqNX05sQU8/GHEd2D2\ndWP2Ks8v2MW+1DyCvU1Mvbc9niaD1KqLahXmFcaKu1bzr14fYATY9BnsnOXWMrSq489bQ1sDMGV1\nEr/sSnVr/kII95BgXQhRvbZ+BTu+BUUHw75268RHAF/8kczi+JN4hC5nQPcEArzdN3mNqFk8DB7Q\n/A646f+0BYvHw4ltbi3DoLaRPNy9AQD/mhfPvtQ8t+YvhHA9CdaFENXnyDpYWhq49JoEjW91a/Zr\nEk/z1rL9KIZcPEL/4IejX7ErfZdbyyBqnp3N+/FGozaoDovWTyP/lFvz/79+0XRvEkKxzcEj324l\nq9Dq1vyFEK4lwboQonqkJ8Kce8Bph5ZD4can3Jp9wslcnvhuO04VWjTfgkO10S6sHZ1rd3ZrOUTN\nkmfN45GV45jlzOL3Wo0g/yR8NxwsBW4rg0Gv4+ORbakb5MXxrGIeittCic3htvyFEK4lwboQ4u/L\nT4OZw6AkF+p0gIFTwI1txFNyihkzfQuFVgc3NISTzjUAPNn2SWmrLlzKz+THyOiRAEwJr4PqFQKn\ndsG8B8Bhd1s5ArxMfP1Ae/w8DGw/lsP4OTtlhBghrhMSrAsh/h5LAcwaDrnHtAmPRs4Bo6fbss8t\ntjFm+mZO51toWsuH6OabsTvtdArvRIfwDm4rh6i5Hoh5AC+DF/vzDrPq1v8DgyccWg6/PK11uHaT\nxmG+fHlfe0x6HcsSTvG/JfvclrcQwnUkWBdCXD6HHeY/qM3i6BUMo+aDd4jbsrfanTw2cxsH0goI\n8zXzxl2RLDn8EwCPt3ncbeUQNVugRyCjmo8CYMqJZTiHTtM6WG//Bta+59aydGoYzLt3xQLw1brD\nfL3usFvzF0JUPwnWhRCXR1Vh6XNw8FcweMDI79068ouqqrywYBfrkzLxNun5+oEOLDw8Hbtqp2tE\nV9rVaue2sghxf8z9+Bh9OJh9kJ9NTuj/trZi1WsQ/71by3JnbAQv9I8G4LVf9rJsj3s7vAohqpcE\n60KIy/Pnh7D1a0CBodMgyr1NTt5ffoCFO1LQ6xSmjGpHy0h/Hm/zOD2jevLPdv90a1mE8Df7M7bV\nWADe2/oeBW1GQtd/aCt/fAIO/+HW8jzaoyGjO9dFVeGpOTvYdjTbrfkLIaqPBOtCiKrbPR9WvKK9\n7vemNta0G83ZfIyPVx0C4L+DWnJzszAAIn0imdxzMjHBMW4tjxAA97e4nxtq3cCz7Z/F2+gNt74K\nLQaB0wZzRkPaXreVRVEUXrkjhl7RYVjsTh6K28LhjEK35S+EqD5VDtYLCgoYP348EREReHh40KZN\nG+bMmXPR7U6cOMH48eO56aabCAgIQFEUZsyYcTllFkJcSYlLYdGj2uvOT0DncW7N/uddJ3lp0W4A\n/tGzMSM61iWzONOtZRDifIx6I9P7TufORndqoxDpdDB4KtTtApZc+HYwZCa5rTwGvY6P72lL6zr+\nZBfZGD1tEyk5xW7LXwhRPaocrA8ZMoS4uDgmTZrE0qVL6dChAyNHjmTWrAtPs3zo0CG+++47TCYT\nAwYMuOwCCyGuoEMrYe59pWOpD4M+r7s1+98STjF+zk6cKtzdPopnejfldNFpblt0GxPWTaDIVuTW\n8gjxV2cPFVpkK0I1mGHELAiLgYJTEHcnZB91W3m8TAa+ur8DDUO8Sckp5p4vN5KWV+K2/IUQf1+V\ngvUlS5awfPlyPv30Ux599FFuueUWvvzyS3r37s1zzz2Hw1H5JAw9evQgPT2d5cuX88wzz/ztggsh\n3OzIOpgzChxWrdnL4KlazaGb/H4gnSdn7cDuVBnUJoL/DWmFoii8u/VdCm2FHMk7ok3/LsRV4Lcj\nv3H7ottZnLwYvILgvh8gpCnknYBv7oS8k24rS6ivme8e7kRUkCdHM4u458uNZBRY3Ja/EOLvqdI3\n7aJFi/Dx8WH48OEVlo8ZM4aTJ0+yadOmyjNy45e6EKJ6eWXuge/uAnsxNOkLQ78GvcFt+a9PyuCR\nb7ZidTgZ0Cqcd4fHotcpbE7dzNLDS9EpOiZ0moBOkeuMuDqcKDhBenE67219jzxrHviEwX0/QmB9\nyD6i1bAXnHZbeWr7ezLroc7U9vcgKb2Q0dM2kVNkdVv+QojLV6Vv2z179tC8eXMMhoqbtW7dunx9\n165dq690f5GQkIDT6XTZ/sW5bDZb+XN8fPwVLo1wN5vNhlfOARpsfA7sheSHtudw83+hJrhvspV9\n6RZeWZOBxa7SIdKDB5vrSdizG7tqZ2LiRAB6BffCdsJG/An5H61Ocv5fvlhnLBHmCE6WnOQ/y//D\nfXXuA8DY8W0a//EPTJkHKf6iD0ndJuMwB7itXBO7+/PSCiv7T+Uz9JM1vHZLKN6mc3/kyrGv2eT4\nu45Op6Nu3bpV2qZKwXpmZiYNGzY8Z3lQUFD5eley2+0XbGojXKvs5BU1h2deMk03PY/BXkh+UCsO\n3vAKTqdOG93CDQ5l2Xj1j2xK7Cqtw0w83dEPnHZsTliWsYyUkhR89b4MDBko/58uJp9v1Y0KH8U7\nR99hecZybvS7kbqedbEZg0ns/A7N1j+NZ95hGvz5LAc6v4vD6OOWMoV6wMQegUxak0VSlo3/rEnn\n5e4BeBoqvyslx75mk+NfvfR6fZW3qfJ97LM7z1RlXXUwGAzSnMbNzj5JjUbjFSyJcDeP3CQabnwO\ngy2fgoDmHOn6DnqjF1W/zFyeQ1lWXl+XTZFdpWWYiZdvCsFcGlBkWbP4Mf1HAEZGjCTAw301kzWJ\nnP9/T2xgLJ1zO7MxZyMz02by78b/RqfocAbUJ7nbBzRa+0+8cw/SdPOLHO76Dg6Tr1vK1TDYyH96\nhvLyynQSM228+WcuL98UgpfxzPerHPuaTY6/61xOHFulYD04OPi8tedZWVnAmRp2V4mJiZFg3c3i\n4+Ox2WwYjUZiY2OvdHGEuxzfDEvHgzWXQr/GHL7xXVq17+K27DckZTJp4VYKrCpt6wbw7dhO+JjP\nXK62ntqKd7I30b7RPHHLE9JW3UXk/P/7Xm/8Onf8cAcHCw9yxPsIg5sMLl0TC00aQdzteGfvpeWW\n5+HeheAb7pZyxQING+UwatomEtKtvLGxkBljOhLkbQLk2Nd0cvxdx+l0kp+fX6VtqvQN16pVK/bt\n24fdbq+wfPdubczjli1bVilzIcRV6NBK+GYglORSGBTDgc7v4nRTjR/A8r1p3D99MwUWO10aBp8T\nqAO0D2/P4sGLeaP7GxKoi6taLe9aPB77OACHcw9XXBneEh74BXxqwekE+LovZB0+z15cIzYqgFkP\ndyLQy8iuE7kM/3w9J2UcdiGuOlX6lhs8eDAFBQUsWLCgwvK4uDgiIiLo1KlTtRZOCOFmexbCrLvB\nVgSNepF84/tuuzUPsGDbCcbN3IbV7qR3i1pMH9OhQqCuqmr5a1+TL3V867itbEJcrtEtRvNlny95\npv15hi2uFQMP/npmlJiv+0FagtvK1rpOAPPGdS0fJWb45xtISi9wW/5CiIurUrDev39/evfuzWOP\nPcaXX37J6tWreeSRR1i2bBlvv/12eaP5sWPHYjAYOHq04sQP8+fPZ/78+axatQqArVu3li8TQlxh\nW6fD/Ae1zqMxQ2DkHJwGT7dl/9W6wzw7Lx6HU2XYDXX4bFQ7PIxnWshbHVYe+u0hfkn+xW1lEqI6\nGHQGOtfuXP732T86AQhqoAXsYS20iZOm99eaorlJ4zAf5j/WtXzipLs+30BSlgzrKMTVosodTBcu\nXMiECROYOHEiWVlZREdHM3v2bEaMGFGexuFw4HA4zrkg/XV89ilTpjBlyhTgPBcvIYR7qCqs+wBW\n/kf7+4YxcNt7oHNPV1JVVXl/+QE+XnUIgLHdGjBhQHN0uood1j/c/iGbT20mMTuRbpHd8Df7u6V8\nQlSn00WneWndb4OfAAAAIABJREFUSzwQ8wDdIrudWeEbDmOWaPMZnNisNUW7eyY07uWWckUGeDJ3\nXBcemL6ZPSl5TFiZzgs3BtAmQjoXCnGlVbmxp4+PD5MnTyY1NRWLxUJ8fHyFQB1gxowZqKpK/fr1\nKyxXVbXShxDiCnDYYdkLZwL17v+C2z9wW6ButTt5adHu8kD9ub7NePm2cwP1P078wbd7vwXgta6v\nSaAurlkz985kU+omJqybQEZxRsWVnoHaTKeNemlN0WbdDTtnu61sIT5mZj/cmU4Ngii2q/x3bTZ/\nHityW/5CiPOTnllC1FRFWfDdMNj0ufZ3n9eh17/BxUOwlskssDB62iZmbz6OosBrg1ryxC2NzxkC\n9nTRaV5e9zIA90Tfwy11b3FL+YRwhcfbPE6TwCZklWTx4toXcap/mejP5A0j52hN0Zw2+GEc/DoB\nnO6ZY8TXw0jcgx3pGOmB1Qlv/5nFe78l4nRKpZoQV4oE60LUROmJMK0XJK8Goxfc9Q10/Yfbst97\nMo87P/mTzUey8DUb+Or+9tzbud456RxOBy+tfYlsSzbNApudv4OeENcQD4MH7/Z4Fw+9BxtTNzJ9\nz/RzExlMMPQr6PGc9veGT2DWXVCc454yGvW80C2YO5p4AfDxqkM8OnMbBRb7RbYUQriCBOtC1DQH\nfoUve0FWMvjXhbG/QYuBbst+6e5Uhn62npScYuoHe7Hoia70jK513rRf7/maTac24Wnw5J2b3sGs\nN7utnEK4SsOAhrzQ8QUAPtnxCbvSd52bSKeDni/DsOlg8IRDK7Qf2BkH3VJGvU7h/lhfnuociEmv\nY/neNIZ+up5jmdIsRgh3k2BdiJqirCPprLvBmg/1boRHVkN4K7dk73SqfLD8AI99t51im4PuTUL4\n8YluNA6rfGjIQlshAC91eokG/g3cUk4h3GFIkyH0q98Pu2rn+T+eP7f9epmWQ2Dsr+BXBzIPaT+0\nDy53Wzl7NvBmzqOdCfU1k5iWz51T1rE+qZKyCiFcQoJ1IWoCSz4seAhWvAKo0P5BuPcH8A5xS/a5\nRTYe+24bk1dqtYJjuzVg+gMd8Pe68EgT428Yz7w75jGwkftq/oVwB0VRmNhlIlG+UZj1ZuzOCzQx\nqR2r/bCO6gyWXK1JzNr3wemsfJtq1K5uIIuf7EbrOv7kFNm496vNfLXusAwOIYSbSLAuxPXuxFb4\nvBvsmQ86gzYs4+0faO1i3WBTcib9J//BrwlpmPQ63h7Wmn/f3gKD/vyXn5SClPIadYDooOhzOp0K\ncT3wNfkytfdU4vrFEe4dfuHEPmFw/2Joey+oTm0Ep28HQd5Jt5Q13N+DuY92YWCbCBxOldd+3suY\nGVtIz7e4JX8hajIJ1oW4Xjkd8Ps78FUfbWZE/yi4/2fo8JBbsrc5nLzz635GfLmRk7kl1Av2Yu64\nLtzVPqrSbdKL0hn761jG/jqWrJIst5RTiCspyjeKAI+A8r+3p23HUdnILwYT3Pkx3PGR1jH88O/w\nWVfYt9gtZfUw6vnw7ja8ckcLTAYdaxLT6T/5D1bvP+2W/IWoqSRYF+J6lHMMZtwGq18H1QEth8K4\ndVCvi1uyP5JRyLDPNzBldRKqCsNvqMMv/+xOm6iASrfJs+YxbsU4UgpSyLPmnTuknRDXubmJc3lg\n2QP8d9N/K29ioihww/3w6B9a85jibPh+NPz0T7AWnn+baqQoCg/c2IDFT3ajWS1fMgqsjJmxhVd+\nSqDE5p7hJYWoaSRYF+J6s3s+fNYNjm0Aky8MnqoNA+dZeaBcXVRVZd7W49z20Vrij+fg52Fgyj3t\neGd4LD7myidMLrGX8I+V/+BA9gFCPEOY2nsqIZ7uaU8vxNUiwKydo/MOzGPKzikXThzSBMaugBuf\nAhTYHgdTb4KTO11fUKBZuC8/PnkjD3StD8CM9UcY+MmfJJ7Kd0v+QtQkEqwLcb3ITdFq2BaM1Tqh\n1ekA49ZC7Ai3THR0PKuIsXFbeW7+LgqtDjo2CGLp+B7c1rr2BbezO7XRMLaf3o6P0YfPb/2cKN/K\nm8oIcb3qU78PL3fWJgCbumsqs/bNuvAGBhP0fhXu+xF8a0PmQW14xxWvgNX1Qyx6GPW8cmcM08d0\nIMTHRGJaPnd8vI73lx+QWnYhqpEE60Jc6xx2WP8JfNJBa7uq6KHH8zBmKQS5frhDq93JlNWH6P3B\n76zafxqjXuG5vs2Y/XBnIgM8L7ytw8pL615i9fHVmHQmPu75Mc2Cmrm8zEJcre5qdhePt3kcgDc3\nv8ncxLkX36jhTfDYemh+Jzjt2hCtUzpB4lIXl1ZzS7Mwlo3vQa/oMKwOJx+tPEi/D//gjwPpbslf\niOudBOtCXMuOb4YvboLfJoCtEKI6aW1Ze04A/YWHRawOG5IyGfDRWt75NZESm5PODYNY+lR3nril\nMXrdxWvz86x5bE/bjl7R8/ZNb9M+vL3LyyzE1W5c63GMjB6JisprG1/j/W3vX3yYRK8guPtbGDFb\n60yeewxmj4A5oyDnuMvLHOJjZtr97ZlyTztq+Zk5klnEfV9v5olZ20nLK3F5/kJczypvRCqEuHoV\nZWm3urfHaX97Bmq3w9uM1mY+dLGMAgv/W7KPhdtTAAj2NvHy7c0Z1CaySsMshniGMKXXFDKLM+ka\n2dVVxRXimqIoCi92fJFAj0A+3fkp3gbvSz+vogdoNe2/vwUbpsD+nyFpFdz8AnR+3KU/4hVF4bbW\ntenRNIT3lx8gbv0RftmVyu+J6Tzbpyn3dq5X6ZCtQojKSbAuxLXEUgCbPoc/P9LapYMWoPd+FbyD\nXZ59fomNaWsPM21tMoVWB4oC93Ssy/N9oy86wVGZ7WnbySjOoE/9PgDS7EWI81AUhcdiH6Nz7c60\nCW1TtY1N3to1ofUI+OVZOLYelk+ErdPhlpe00aF0etcUHPD1MDLpjhiGtqvDyz/sYefxHP6zeC/f\nbjzKs72b0b9lOLpLuPMmhNBIsC7EtcBWAtumw9r3oLC0HWhYDNz2LtRzfY20xe5k6u9JfPZ7EjlF\nNgBaRfrz6sAY2tYNvOT9LElewst/ah3oInwiaBnS0iXlFeJ60TasbfnrIlsRE9ZN4Mm2T9IooNHF\nN67VAsYsgZ2zYMUkyD4MCx/W2rT3fBmaDXBp5/OWkf4sfKwrs7cc491fE0lOL+SJWduJifDjX32b\ncXPTUJnwTIhLIMG6EFczhx3iZ8GatyDvhLYssAHcMqG0dsy1t5RtDpVfk4qYv7+Q7GJtpsRGod48\n26cZ/WIuvXbM4XTwxa4v+DT+UwB61e11acGGEKLch9s/ZMWxFWxK3cTbN71Nt8huF99IUaDtKGgx\nEDZPhT8nw+m9MOceiLwBek2Ehje7rMw6ncKoTvW4MzaCr9YdZtrawySczGPM9C10qB/Ic32j6dgg\nyGX5C3E9UNSL9lq5MpxOJ/n5Fcdr9fX1ReeG9rjijPj4eGw2G0ajkdjY2CtdnJrDWgjxs7U2p1nJ\n2jLfCLjpeWg72uWdRwssduZtPc5nqxI5XagNwRYZ4Mn4W5swuG1kldqdJuck8+/1/2ZX+i4AHoh5\ngKdveBqdIufy1U7O/6tLdkk241ePZ/vp7QAMazqMZ254Bl+T76XvpDgb1n8MGz8DW+nwjvVuhC5P\nQNN+5c1jXHXsswqtfP57EnHrj2CxaxOfdWscwtjuDbipSag0j7lKyLnvOpcT30qwLi5ITlg3yz0B\nm7+EbTOgJEdb5hUM3Z+F9mPB6OHS7I9nFRG3/gjfbzlOvsUOQIBZx10t/Xh2cGfMhqq1c41LiGPy\n9snYnDa8jd680PEFBjUe5IqiCxeQ8//qY3VYeWfLO8xJnANAmFcYk7pMokedHlXbUcFprVnd1q/B\nYdWWBTaATuOg7Sji9ye79Nifyi3h41UH+X7LcexOLQxpFOrNmBsbMKRdJF4mufF/Jcm57zoSrItq\nJyesmxzfAhs/hb0/glo6mUhgA+j8GLS5B8xVqDmrIlVV2Xo0m6/WHua3vaco/d6kYag3feoZ6V7H\nhI+n6bKO/4w9M3hv23t0j+zOxC4TCfcOr+bSC1eS8//qtfXUViatn8Sx/GMAvNzpZe6OvrvqO8pN\ngc1fVKwgMPtxOqofp+oORPWPcumxP18Fgb+nkZEd63Jfl3pEXGSuBuEacu67jgTrotrJCetCeamw\nex7s+h7S9pxZXr+7NsRa074uHbHhZE4xP+xMYdH2FA6eLihf3r1JCA92025J7969q0rH3+KwkF6U\nTh3fOoDWVv2PE39wc9TN0pHsGiTn/9Wt2F7MlB1T+Dn5ZxYOXEiQx99o+13W9G7j59pMqICKQkHo\nDfh2exiibwezTzWV/FxlTe9mrD/C0UyteY5ep9C9SQiD20bSp0U4nibXXQ9FRXLuu44E66LayQlb\nzayFsO9n2DUHkteAqrXZRG+CVsO1W9C1W7ss+wKLnaW7U1m0I4UNyZmUnf1mg44h7SIZc2MDmtY6\nU4t/qce/2F7MvMR5zEiYgbfRm3l3zMPD4NomO8L15Py/NhRYC/AxaYG0qqq8uvFVekT2uLwfyU4n\nJK0kf/mb+J7eema50Qua3wGt79Y6pLqoIsHhVFm1/zRfrUtmY3JW+XIfs4F+LcMZ0jaSzg2DpW27\ni8m57zqXE99KozAhXK04B5JWalN/71+izTRaJqoTxI6AFoO0GQhdIKfIyprEdJbvS2PlvjRKbM7y\ndR0bBDG0XST9W9XGz6PqnVaLbEXMSZxDXEIcWSXaF6tep+dI3hGig6Kr7T0IISpXFqgDbEzdyPwD\n85l/YD7RQdE80voRetXtdekdunU6aNKb5KIwlJyjhJ1aTXjaGq2j+67vtYdPuDa6TLN+WudUg7na\n3otep9C7RS16t6jF4YxCFm0/waKdKRzPKmb+thPM33aC2v4e9G9Zm1ubh9GhQRBGmWhJXOekZl1c\nkPy6vkyZSVpwfmAZHNsATvuZdYH1IXYktL4LghpWe9aqqpKUXsDKfadZue80W49mlbdDB2gY4s2Q\ndpEMbBNJVJDXBfdV2fEvsBYwa/8svt37LTkWrZ1rpE8kD7d6mDsb3YnRxaPVCPeQ8//ak1WSxTcJ\n3zB7/2yK7FpzksYBjXmk9SP0rtcbg+7S6ugqHPvWreHEVq2ZTMJCbUSZMiYfaNRTG0mmSR/wCa32\n91TWr2bh9hP8vCuV/JIz11Nfs4EezUK5tXkYNzcNI9DbVO3510Ry7ruONIMR1U5O2EuUmwJH18PR\nP+HwH5CVVHF9SDOtDXr07RDVsdonIjmRXcTmw1lsPpzFhuTM8jafZZrV8qVX8zD6xIQTW8f/km+N\nV3b8E7MSGbZ4GAD1/OrxcKuHGdBwAEadBOnXEzn/r105JTnM3DeTWftmkW/TvkuDPYKZc/ucS+ro\nXemxt1vh0ApIXAIHf4OCtLO2UiCyHdTvptW4R3UCz4BqfV8lNgdrEtNZsS+N1ftPk1loLV+nU6BN\nVACdGgbTsUEQ7esF4nsZdwyFnPuuJM1ghHAHpwMyDsKJLWcC9JyjFdPojFD/Rq22qWnfaq1Btzuc\nHEovYMexnPIAPSWnuEIak15H50bB9IoOo2d02EVr0CvjVJ0cKDzA5vzN1CqpxYudXgSgWVAz+tbv\nS8+onvSt3xe9CzvCCiGqLsAjgCfbPsl9Mfcxa98sZu2bhZfRi1petcrT/H78dxr6NyTKL+rSd2ww\nQfQA7eF0QuoOOPCrdifx1C5I2aY9/pwMKBDeEup21WZajmwH/lF/q7LCw6inX8tw+rUMx+lU2Xki\nh1X7TrNiXxr7T+Wz/VgO24/l8NmaJHQKtIjwo2P9YDo2CCQ2KoBwPw/p7C6uOVKzLi6oxv+6tlsh\nfR+kxp95nNoD9orBMYoOasdqtUn1umojunj4/e3sS2wODqTlk3Ayjz0puew5mcf+1LzyyUTK6HUK\nrSL96dQgiA71g+jcKBgf8+X9Fk8rTGPzqc1sObWFP47+QaYtEwBPgydr7lqDl/HyAn9x7anx5/91\nxOa0cbLgJPX86gHaeO03z72ZfGs+zYOa06l2JzqEd+CGWjfgbfS+vGOfmwJH1sKRdVpFxl/vMAJ4\nBmrXyrJHeKxWmVEN3+0pOcWsP5ShVWIcyTrnDiNAsLeJFhF+tIz0p2WEPy0j/YgK9JIOq38h577r\nuKUZTEFBAS+//DJz584lKyuL6OhoXnjhBUaMGHHRbU+fPs3zzz/Pzz//TFFREbGxsbz++uv06tWr\nWt6MqH414oRVVSjK1GrLMw5ow5ZllD6yj5wZ9/xsRm9t1JZ6pTVGdTpednCuqioZBVaS0wtISi8k\nOb2A5IxCktILOJ5VVKG9eRlvk56Y0uC8Y4Mg2tUNxPsygnOn6kRBKa9pmrBuAj8l/VQhjYfOgw7+\nHbi3/b10DO8oteg1SI04/2uoU4WnmLR+EhtTN+JUz/z41yt6YkJi6OTRia5+Xf/esc8/VXr3cT0c\n26hVfJzdf6eMwROCG0FIEwhuoj2HNIHgxn9rjolTuSVsOpzJ5sNZbDuazcHTBTjOc0H1NOppEOJN\nw1BvGoX6lD83CPG+rOvq9UDOfddxSzOYIUOGsGXLFt58802aNm3KrFmzGDlyJE6nk3vuuafS7SwW\nC7169SInJ4fJkycTFhbGlClT6NevHytWrOCmm26qalGEuDhVBUs+FKZrbStzUyD3GOQch9zjpc8n\nKo7Q8lce/mfVBLWB8NbaF8slBK2qqpJvsZOebyEj30JqbgkpOcWcyC4mJaeYlOwiTuaUUGw7zw+C\nUgFeRlpG+BMT6ac9R/hRP9i7SjVBqqqSbckmOSeZgzkHOZB9gIPZBzmYfZAfBv5AbZ/agNb+XKfo\naB7UnI7hHQkpDqGRuRE+Zh9iI+SCLcT1Itw7nKm9p5JRnMHG1I1sObWFTambSClIYVf6LpqGNy1P\neyL/BK9tfI0mAU1oEtiEpoFNqedX7+J32XzDoeUQ7QFgK4HTe7XmMmV3KtMStDuVaXsqzjdRxjNQ\nazoTULf0OUp79q0NPmHaw3j+iZPC/T0Y2EbrTA/ancr9p/JJOJnLnpQ8Ek7msj81n2Kbg72peexN\nzTtnH4FeRiIDPYkM8CQywKv8dS0/M6G+ZkJ8zHgYpQJDuFaVataXLFnCbbfdVh6gl+nTpw8JCQkc\nO3YMvf78/7SffvopTzzxBOvXr6dLly4A2O12YmNj8fHxYdOmTRXSS8361eGq+XWtqmC3aIG3Je/M\nc3E2FGVpz2c/Ck5rwXnB6XObrFTGvy6ENP5LzU4T8ItABSx2J/kldgosdgotdvKKbeQU28gpspFd\nZCW32EZOkZXsIhsZBRbS87XHX5usnI+iQJ1ATxqG+JxTuxPma75gG0urw0pWSRbZJdlkW7LJKsmi\na0TX8glSZu+fzQfbPqC4ks/hk56fcFOU9mM515KLoij4mbS7BFfN8RdXhBz/mudkwUk2n9qMOdNM\nqD4Uo9FIRkAG49eMPyetv9mfCO8IHm39KL3qaXfIs0uyOZRziEBzIIEegfib/S88Ao3DrvX5yThY\nelfzAGQc0p6LMi6t0Gb/0sC9FniHaAF+2cMrSHv2CNDufpp9wVz6rDdiczg5nlV05q5munZXMzmj\nkKyzOq9eiJ+HgVBfLXgP9jYT4GXUHp4m/L2MBHqZ8Pc04uthwMdswNfDgLfZcFUPOSnnvuu4vGZ9\n0aJF+Pj4MHz48ArLx4wZwz333MOmTZvo2rVrpds2a9asPFAHMBgMjB49mpdeeomUlBQiIyOrUhxR\nGVXVHlTyrDpLXzvPWu48s+6sh7EoDcVm1S4qGd5akxCno+Kzw67d2ix9qE47qsOG6rCB3YLqtIPd\niuqwgsMKNgvYS1DtFi0Ad5RoNS62IrAVg60YpfS1YitEsRWisxagOG2X/ZHY9N4UmYMpMoWSaw4n\nxxhOliGMDEMt0vWhnCaUPIeBYpuDouMOSpIdFFsdFFkTKbQmUFBix15++7T08wNQSj+/soeigtME\nlJ50OguKoRgfs0KQt5EgXz2hvkZCfA2E+OhpXasZjUJCqO3vQWrRMRIyE7DYLVgcFhKLLcQfLqHY\nVkyhrZDRLUbTwL8BAEuSl/DRjo/ILskuH57tbJ/f+jk3Rt4IgJfBqzxQr+1dm6aBTctrx5oGNqWu\nX93y7fzN/pf9GQshrn0RPhEMajyI+EItWANoEdyCSV0mcTC79K5czkFyLbnlD9tZ1+btadsrBPYK\nCn5mPwLNgfgYfRgXO668ciA5N5nFSYvxNHhi1psxB4ViDq2DWd8fs8FMC+861LbbIec4BVmHOJaV\niLEgHUP+KQyFmegK09E7rOjsBfhk5eFVOvOqHbAqCgqgQ0VXernWAcpZDwweGM2+NDR509DopU38\nZPQEPy8I8cKqeFDo1JNv05Nr05Fj1ZFp0ZFZopBtgZwSlWKnHpvVgC1Tjy3TQCF6ctGTjA67qseB\nDjt6HGivHehwouBAh8FgwMNkwmw0YjYZMBkNeBiNmI0GTCaD9mzQYzIYMBn1GPV6TEY9ZoMBo0GH\nUa9Hr9dh1OswGvQY9HoMeh0GvQ69TsFY+mzQKegUBb1Oe5S/VhR0OsqXKQroFO11vsWJw+7EqDrJ\nL7FVWA9aBZPWhLL081QUdArSeddFqhSs79mzh+bNm2MwVNysdevW5esrC9b37NlD9+7dz1letm1C\nQsJFg/WEhASczovXUlYnp8PBuPh7K13fqcjKG6dzy//uXy8USyX/q7ElNiafOjM+7cCoEHIr+WXd\n3GLji9RMyoLCYXXCSDOc/65FA6udOamnyv++O6IWR4znH64qwm5nUcqZtA+Eh7HPfP5xaQMdTpad\nOFn+97hdoezwOP/kFx6qyu/HUgDtxH0mLIT1npXPYLnp6Iny1y+GBrPK66zbmPrSR+nma47l4Fl6\nA+iV4CCW+HihapdaVJTSMFm7/A463BaLI5AM1Z+9ofvICThQ+gmWHZTs0sc+Cg/9C9WuDStmCv0W\nU9A6LZlZhfK3qW3tTH4arGEAeIetRBe8stL31t/zRRp5NyTQQ8e2oqUsyZoPQFbp45AFsAAZ8LLh\nZUIt0eSlwLL0ZcxMmVnpfuvZ65Hnp92mPZR5iJSClLM+Mj0+Bh/8DH74Gnw5dvgYPhnaRCmh9lDe\nbf4uwcbgikMr5kFBXgF72VtpnmVf1jabjfj4+ErTieuTHP+a6+xjfzrpNE1oQhOPJgyoPQBqQ5Gj\niExrJhnWDDwyPYjP0/4/juYepba5Nvn2fAodhaio5UE9wL6kfQRkadfdLTlbmHZkWqVlGBs1lluC\nbwFqs8ueztsZa7QVRiAACDgzpvuD/rcwxFgfgyWHvSVHeca2vdL9PpWVw0O5eWAvYa/OwT2hHkA+\nCqW1nTZQSn9/PJyTy2M52nX3sNHAMxHh4FNxf2XfLvfk5TM+W3ufp/R67qxTu9IyDMkv5IWsbHBA\njqqjb62IignspQ+gf2ERL2Rok85ZFOhRt06l+725qJi30jPL/+5Srw6VRU0diy28l5ZV/n3at24t\nis/XvHIPtCqx8fGp7LJqKgZFhZBdSfzSxGJnauqZWGdUZBCplTQVqmNzEJdyJu3YiECOmM6fNsTu\n5PsT2uegAE/UDmBfJX0K/BwqPxw/8zk8W8ufHZ7nxkVNLZ78q8tX592Hq+h0OurWrXvxhGepUrCe\nmZlJw4bnDkEXFBRUvv5C25alq+q2Zex2Ow5H5W17XcHpcFB0gVsTdp2Kt2Ip/7tYgZJK0tsVFU/l\nzG21Ep1S6b4tOjAp9ktKW/KXxSWKrtK0xX+Zxe5C+zWrKhbVgLO0NqBQMVSa1uFUSXTWKa1B0HEa\nlSJd5T+s4uy9sWDCgpHd6hGKdFmVph1ke50S/ClWPClWfgLdjvOk0kL2FT53YFB9MCgKNs9U0Nmp\n7Hf+rQ088NN7Y9RDoqrn0Pk6kpaa1COABt6heBgUfkz35qf0SpPSPtxAQy/t1Dpg02NQDOjQoVN0\n6BU9ekVbpkeP6lDLvxSDdEG08G6BUTFi0pkwKkaMOiMeOg88dB4E6gLL08Z4xvBSg5fw1fviZ/DD\nU+d5To1GWVoTJoJ1weAAm+Nv3J2wXf624tonx7/mOt+xN2Ik3BBOuCG8QprWXq1p3VirhHOoDgod\nheTb88l35FPiLKGeuV552kBdILcG3YrVacWqWrGrdqxOKzbVhtVpxUfxKU+rOlQCDYE4VAd21Y4T\nJ07ViRMnDtWBxTOC9OAeAKQV7ocjlQfrKc0eZEfATejtRRwpOogj7etK0+YEx5IaUgfFYSXDmU+J\nbn+laYs8gin0D0NRnRQrdorLqvTPo0RvwK73QFGdOBT1gnGG5S/X9gultf41raLgrKS226aASTnz\nvVd8gXjApvtL/KJUntaqo0JcZNFVXmar4sBHKTlr28o/C4vOWSGt7QKfm1F14H1WWrvO77xp7YrD\n7de2ypqLX0iV2qw3bdqURo0asXTp0grLU1NTiYiI4I033uCFF14477Ymk4mxY8fy2WefVVi+YcMG\nunbtyuzZsyuMKHO+Nj3Hjh27IjXryWm7Kl1v0pnw158ZBSTDnoWKWv5L9WxGxUCA3v+ctGec2cag\nGAg0aLUPKgpZ9mwcOM5NqyjoMRBkCCz/O9Oeg6Osd79y9n4VdIqeIFOIVj5FR449Bxt2LY2i3TQs\nS69TFPyUwPKtC8jHof7ln7r0FpgOhRBTWPnfefYcbKoVSm+TnV1qRYFa5rDyW2h5tlysqkW7hca5\nt9FCTCHlU2Xn2nKxOC1U5uy0+fZ8Shwl56Qp23+gMRC9op00hfZCSpwlpWVUKpRBQcHX4Fue1uK0\nYHVaUVDQKTot/Vmv9Yr+0qf2vsqdfREzVnK3Rly/5PjXXNfysXeqTi2gV52l38dq+WvQvrfNOu32\nqd1pJ99xJtZQVbXC97Kn3hMvvdaR1q7aybHlUFnY5Kn3xMegVbs7VAeZ1sorIT30HvgZ/MrLm2E9\nq32+qgI9AMRSAAAKBElEQVROlNImq2adGX+9LwoqTqeDdFs6qGdFGWXNWQGzzkSgwbd82Slrhrau\nvMhl95pVTDojQWfFL2nWTO3TUlVsDnv5bvUGPQYMBBr8tdHJVJV0WxZOVK31bIVyaCMKBekDypdn\n2LNx/KUyrOwz1qt6ggxnJs7KsueUxzp//ZR16Ag2BJZlQ7YjF7t6ntGF0L63QwxnKoizHXnY/hq/\nAB5Gb+qENj1nuSudr2a9WtusBwcHn7cGPCtLqxU9X815dWxbJiYm5op0MG1LO7fnebWo2Mmk05Uu\njnAz6WRUs8nxr7nk2F8fYqqQtsVZr+X4u875KqMvpkqRb6tWrdi3bx92e8VfMrt37wagZcuWF9y2\nLF1VtxVCCCGEEKImqlKwPnjwYAoKCliwYEGF5XFxcURERNCpU+U1r4MHD2b//v0Vhmi02+3MnDmT\nTp06ERERUem2QgghhBBC1ERVagbTv39/evfuzWOPPUZeXh6NGzdm9uzZLFu2jJkzZ5Y3mh87dixx\ncXEkJSVRr542tfGDDz7IlClTGD58OG+++SZhYWF8+umnJCYmsmLFiup/Z0IIIYQQQlzjqjyD6cKF\nC5kwYQITJ04kKyuL6OjoczqHOhwOHA5HhU4YZrOZlStX8vzzz/OPf/yDoqIi2rRpw9KlS2X2UiGE\nEEIIIc6jysG6j48PkydPZvLkyZWmmTFjBjNmzDhnea1atYiLi6tqlkIIIYQQQtRIVQ7W3eV8QyO5\ne9hGoQ0xpNfr0el08vnXQHL8azY5/jWXHPuaTY6/65zv87zYKOpVGmfdnex2O4WFhVe6GEIIIYQQ\nQriMt7c3BkPl9efXx8wtQgghhBBCXIckWBdCCCGEEOIqJcG6EEIIIYQQV6mrts260+k8pxG+oigo\ninKFSiSEEEIIIcTlU1X1nA6lOp0Ona7y+vOrNlgXQgghhBCippNmMEIIIYQQQlylJFgXQgghhBDi\nKiXBuqjUunXrGDBgAIGBgXh6etKkSRNee+21K10s4QY7duxg0KBBRERE4OXlRXR0NK+++ipFRUVX\numiiGuXn5/P888/Tp08fQkNDURSFV175//buLaTJP47j+Gc1rVR06ixYhiu7ycAKMkYHtXCZ4sAU\nqQgyAkWxC6ODiyBTgiIiDOoiswgDoRK7MY0ODiKYRQdJEymbdhhdmId5aCZrv/+VI//Tf/7JPb+l\nnxfs5vfsgTc8PPh1/nx2atL3vnr1CikpKQgJCYFGo0FWVhZsNpuywTSjpnP9f/78iQsXLmDHjh2I\njo5GUFAQVq1aBbPZjIGBATnh9Mf+z70/TgiBxMREqFQqHDx4UJlQAsBhnaZQU1ODpKQkhIWFobq6\nGg0NDSgpKfntt2zR36+9vR0bN25Ed3c3KioqUF9fj927d6O8vBx79uyRnUczqLe3F5WVlfjx4wcy\nMzOnfF9HRweSk5MxNjaG27dv4/r163j37h22bNmCnp4eBYtpJk3n+judTpw6dQoxMTGoqKhAQ0MD\n8vLyUFlZiU2bNsHpdCpcTTNhuvf+ry5fvozOzk4fl9GkBNG/fPnyRQQHB4vCwkLZKSTBiRMnBADR\n2dk5YT0/P18AEH19fZLKaKa53W7hdruFEEL09PQIAKK0tNTrfTk5OUKr1QqHw+FZ6+7uFgEBAeLY\nsWNK5dIMm871d7lc4tu3b17n3rlzRwAQN2/eVCKVZth07/1xXV1dIiQkRNTV1QkAoqioSKFSEkII\nfrJOXqqqqjAyMoKSkhLZKSRBQEAAACAsLGzCukajwbx58xAYGCgji3xgOo/DdblcqK+vR3Z2NkJD\nQz3rMTEx2Lp1K+7evevrTPKR6Vz/+fPnIzIy0mt9w4YNAIDPnz/7pI186/8+Cjs/Px9GoxE7d+70\nYRVNhcM6eXny5AkiIiLQ0dGBtWvXQq1WY/HixSgoKMDg4KDsPPKx3NxcaDQaFBYWwmazYWhoCPX1\n9bhy5QqKiooQHBwsO5EU9OHDBzidTsTHx3sdi4+PR2dnJ0ZHRyWUkUxNTU0AgNWrV0suIV+rqqrC\n8+fPcenSJdkpcxaHdfJit9vx/ft35OTkYNeuXXj06BGOHj2K6upqpKenc9/6LKfX62G1WtHW1obY\n2FiEhobCZDIhNzcXFy9elJ1HCuvt7QUAREREeB2LiIiAEAL9/f1KZ5FEdrsdZrMZ69evR0ZGhuwc\n8iG73Y4jR47g3Llz0Ol0snPmLLXsAPI/brcbo6OjKC0thdlsBgAkJycjMDAQxcXFePz4MVJSUiRX\nkq90d3fDZDJhyZIlqK2tRVRUFJ49e4bTp09jeHgY165dk51IEvzXn8z5zdJzR19fn+dDm1u3bv3n\nty7S36+goABr1qxBXl6e7JQ5jcM6eYmMjMT79++Rmpo6YT0tLQ3FxcWeR7jR7GQ2mzE4OIiWlhbP\nlpfExERotVocOHAA+/btQ1JSkuRKUsr4fuXxT9h/1dfXB5VKBY1Go3QWSdDf3w+j0Qi73Y6mpias\nWLFCdhL5UG1tLe7fv4+nT5/C4XBMODY2NoaBgQEEBwd7/s+JfIe/EpOXyfamAvBsf+EnKbNbS0sL\n4uLivPamJyQkAADa2tpkZJEksbGxWLRoEVpbW72Otba2YuXKlVi4cKGEMlJSf38/UlJS0NXVhYcP\nH075c4Jmj7a2NrhcLhgMBoSHh3teAHD16lWEh4fj3r17kivnBk5d5CU7OxsA0NjYOGG9oaEBAGAw\nGBRvIuXodDq8ffsWw8PDE9atVisAIDo6WkYWSaJWq2EymVBXV4ehoSHP+qdPn2CxWJCVlSWxjpQw\nPqjbbDY8ePAA69atk51ECti/fz8sFovXCwAyMzNhsViwefNmyZVzA7fBkJft27fDZDKhvLwcbrcb\nBoMBL168QFlZGTIyMnhzznLFxcXIzMyE0WjEoUOHoNVq0dzcjDNnziAuLg5paWmyE2kGNTY2YmRk\nxDOIt7e3o7a2FgCQnp6OoKAglJWVISEhARkZGTCbzRgdHcXJkyeh1Wpx+PBhmfn0h353/VUqFVJT\nU/H69WtUVFTA5XKhubnZc35UVBRiY2OltNOf+d211+v10Ov1k567dOlSJCcnK1RKKsFHe9AknE4n\nysrKUFNTg69fv0Kn02Hv3r0oLS3FggULZOeRj1ksFpw9exZv3ryBw+HAsmXLYDKZcPz48UmfuUx/\nL71ej48fP056rKury/PD+uXLlygpKYHVaoVarca2bdtw/vx5Dmp/ud9dfwBYvnz5lOfn5ubixo0b\nvkgjH5vuvf9vKpUKRUVFfJSjgjisExERERH5Ke5ZJyIiIiLyUxzWiYiIiIj8FId1IiIiIiI/xWGd\niIiIiMhPcVgnIiIiIvJTHNaJiIiIiPwUh3UiIiIiIj/FYZ2IiIiIyE9xWCciIiIi8lMc1omIiIiI\n/BSHdSIiIiIiP/UPGKpfVEWEna0AAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"def plot_products(m1, v1, m2, v2): \n",
" plt.figure()\n",
" product = gaussian_multiply((m1, v1), (m2, v2))\n",
"\n",
" xs = np.arange(5, 15, 0.1)\n",
" ys = [stats.gaussian(x, m1, v1) for x in xs]\n",
" plt.plot(xs, ys, label='$\\mathcal{N}$'+'$({},{})$'.format(m1, v1))\n",
"\n",
" ys = [stats.gaussian(x, m2, v2) for x in xs]\n",
" plt.plot(xs, ys, label='$\\mathcal{N}$'+'$({},{})$'.format(m2, v2))\n",
"\n",
" ys = [stats.gaussian(x, *product) for x in xs]\n",
" plt.plot(xs, ys, label='product', ls='--')\n",
" plt.legend();\n",
" \n",
"z1 = (10.2, 1)\n",
"z2 = (9.7, 1)\n",
" \n",
"plot_products(z1[0], z1[1], z2[0], z2[1])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"If you ask two people to measure the distance of a table from a wall, and one gets 10.2 meters, and the other got 9.7 meters, your best guess must be the average, 9.95 meters if you trust the skills of both equally.\n",
"\n",
"Recall the g-h filter. We agreed that if I weighed myself on two scales, and the first read 160 lbs while the second read 170 lbs, and both were equally accurate, the best estimate was 165 lbs. Furthermore I should be a bit more confident about 165 lbs vs 160 lbs or 170 lbs because I now have two readings, both near this estimate, increasing my confidence that neither is wildly wrong. \n",
"\n",
"This becomes counter-intuitive in more complicated situations, so let's consider it further. Perhaps a more reasonable assumption would be that one person made a mistake, and the true distance is either 10.2 or 9.7, but certainly not 9.95. Surely that is possible. But we know we have noisy measurements, so we have no reason to think one of the measurements has no noise, or that one person made a gross error that allows us to discard their measurement. Given all available information, the best estimate must be 9.95.\n",
"\n",
"In the update step of the Kalman filter we are not combining two measurements, but one measurement and the prior, our estimate before incorporating the measurement. We went through this logic for the g-h filter. It doesn't matter if we are incorporating information from two measurements, or a measurement and a prediction, the math is the same. \n",
"\n",
"Let's look at that. I'll create a fairly inaccurate prior of $\\mathcal N(8.5, 1.5)$ and a more accurate measurement of $\\mathcal N(10.2, 0.5).$ By \"accurate\" I mean the sensor variance is smaller than the prior's variance, not that I somehow know that the dog is closer to 10.2 than 8.5. Next I'll plot the reverse relationship: an accurate prior of $\\mathcal N(8.5, 0.5)$ and a inaccurate measurement of $\\mathcal N(10.2, 1.5)$."
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAusAAAEaCAYAAACo3xkcAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzs3XlcVWX+wPHP3dj3TUVR3AE3VMx9\nXzLTcqncp0lnMrPUmSnLSnNp0Wpm6qeNlVlaKVouqaWWC7jlLuJuroiCIiA7Anf5/XEDJQS9cDfg\n+369eHG455zn+70eL3zvc5/zPAqDwWBACCGEEEIIYXeUtk5ACCGEEEIIcX9SrAshhBBCCGGnpFgX\nQgghhBDCTkmxLoQQQgghhJ2SYl0IIYQQQgg7pbZ1AqXR6/Xo9fpijykUChQKhY0yEkIIIYQQovwM\nBgN/nohRqVSiVJbef27XxXp2drat0xBCCCGEEMJiXF1dyyzWZRiMEEIIIYQQdkqKdSGEEEIIIeyU\nFOtCCCGEEELYKbsds36/G0kfNKZHmN+pU6fQarWo1WqaNWtm63SElcn1r97k+ldfcu2rN7n+lnO/\nezIfNHlKpSrWH3S3rDA/vV6PTqeTf/tqSq5/9SbXv/qSa1+9yfW3rgcV63IFhBBCCCGEsFNSrAsh\nhBBCCGGnpFgXQgghhBDCTkmxLoQQQgghhJ2y2xtMhRBCCCHKS6fTkZaWRk5Ojq1TqXQ0Gg1qtRqF\nQkF8fLyt06l0lEolPj4+ODs7m6U9KdaFEEIIUaXodDquX7+Ot7c3Pj4+D5xtQxSXk5ODwWBAoVDg\n4uJi63QqnYKCAhITE6lduzYqlarC7UmxLoQQVZDBYOBa5jVibsUQkxTD76m/Ex4QzqTwSbho5I+v\nqNrS0tLw9vbG3d3d1qmIakij0eDn50dKSgoBAQEVbk+KdSGEqEI2XtzIjqs7iEmKIeVOSrF917Ku\nMa75OCnWRZWXk5ODj4+PrdMQ1ZizszMpKSkPPvAhSLEuhBBVyMEbB9l2dRsAaqWaZr7NaB3QmiD3\nIGq51sLX2bfo2AJ9ARqlxlapCmFRMvRF2JI5//9JsS6EEFXIgPoDCPYIpnVAa5r5NcNR5Xjf47Zc\n2cIXx7/g/S7v09SnqZWzFEII8bBk6kYhhKjE9AY9v1z5BYPBAEDHwI6MbzGeNjXalFqo6w16Fh1b\nxPnb5xnx8wiWnFhSdL4QQgj7IsW6EEJUYv898l9e2fkK7+x/56HPUSqUfPXoV/Su2xutXsvHRz9m\n46WNFsxSCCFEeUmxLoQQldTyM8tZemopAOEB4Sad6+vsy397/JcXWr0AwPyD80nOTTZ3ikIIISpI\ninUhhKiEfr3yK/MPzgdgSpspDGo4yOQ2FAoFz7d8nlCfUDLyM5h3cJ650xRCCFFBUqwLIUQlc+Tm\nEabvno4BAyOajmB88/Hlbkuj1DC702xUChW/XPmFQzcOmTFTIYQ9SU5OJiYmxtZpCBNJsS6EEJVI\nel46U6KmkK/Pp3fd3rz+yOsVniIs1DeUSeGTmNVxFhE1IsyUqRDCnuzatYv69evTpk0b3n77bVun\nI0wgxboQQlQi+xP3k5mfSSOvRszrOg+VsuJLWQP8veXfGdZkmMxNLUQldfPmzVL3GQwG5syZQ2Rk\nJLVq1SIhIYE5c+YQFhaGXq8vdmxMTAzDhw+nUaNG+Pn5ERISwpw5c8jJyXlgDtHR0SgUivt+7d+/\n36Tnk5mZybRp0+jXrx/+/v4oFApmzZr10OebksuSJUuoXbs22dnZJuVoLTLPuhBCVCKPBj9KY6/G\nZBVk4aR2skiMrPwsbuaU/odfCGF/Ro8ezZdffklwcHCJfQcOHGDYsGEMHDiQc+fOcfv2bcLCwli6\ndClK5d1+29OnT9OpUycaN27M/Pnz8fPz4+DBg8yZM4cjR46wfv36h8rlvffeo2fPnsUea968uUnP\nJyUlhS+++IJWrVoxePBgvvzyS5PONyWXZ599lvnz5/PBBx8we/bscsWxJCnWhRCikmng1cBibZ9L\nPcek7ZOMY9kbzEYpH8AKUSkcPnyYJUuWMHfu3BL7fvzxRyZPngyAu7s777zzDl5eXgwdOrTYcStW\nrODOnTusWLGC+vXro1AoGDBgAImJiXzxxRfcvn0bb2/vB+bSuHFjOnToUKHnU69ePW7fvo1CoSA5\nObncxfrD5KJWq5kwYQJz587ltddew8XFpVyxLMXk38JZWVlMnTqVwMBAnJycCA8PZ+XKlQ99/vr1\n6+nevTseHh64urrSrFkzvvjiC1PTEEKIaiU5N5nL6ZctHqe2W20ArmVdY03iGovHE8LacvK1Nv8y\nt0uXLpGens5XX32FVluy/cTERAIDAwHIz89nyZIljBo1qlivOoBGowHAw8Oj2ONeXl4olUocHBzM\nnntpCoesWMvo0aPJyMgwqaa1FpN71ocOHcqhQ4eYN28eTZo0YcWKFYwcORK9Xs+oUaPKPHfevHm8\n+eabvPDCC0yfPh2NRsPZs2fJz88v9xMQQojqYNGxRaw+v5qpbabyXPPnLBbHzcGNmR1nMmn7JDbf\n2kxb97Y01TS1WDwhrC1s5i+2ToEr8x43a3uHDx+mfv36XL58mfXr1zNs2LCifefOnaNp07uv4QMH\nDpCSklJiaAgYh4N8/PHHTJ06lTlz5uDv78+OHTv4/PPPmTRpEq6urg+Vz6RJkxgxYgQuLi507NiR\nGTNm0KVLl4o/0XJ42Fxq1qxJSEgIP//8M+PGjbNBpqUzqVjftGkTW7duLSrQAXr27ElcXByvvvoq\nw4cPR6W6/81OR44c4c033+T9999n2rRpRY/37t27AukLIUTVdy3zGmvPr0Vv0NPCr4XF43Wr043H\nGzzOz5d+Zu3NtUz3mG7xmEKI8tu/fz8LFixgyJAhLFiwoFixvn79ep588smin/ft2wdAmzZtSrQT\nHBzMvn37GDx4MC1a3P1dM3nyZD7++OMH5uHp6cmUKVPo0aMHvr6+XLhwgQ8//JAePXrw888/8+ij\nj1bkaZqkPLm0adOGbdu2WS3Hh2VSsb5u3Trc3Nx4+umniz3+3HPPMWrUKA4cOECnTp3ue+7ChQtx\ndHTk5ZdfLn+2QghRDX0W+xlag5ZOgZ2IqGmdqRVfCn+JTZc2cSr7FNdyr9GKVlaJK4SlnZ5jvYLR\nWmJiYvjwww956qmniIyM5OjRo0XF+JkzZ4p1kiYkJKBQKPDz8yvRzpUrVxg0aBD+/v589913+Pv7\nExsbyzvvvENWVhZLliwpM4/WrVvTunXrop+7du3KkCFDaNGiBdOmTbNqsV6eXAICAkhKSkKr1aJW\n289tnSZlcvLkSUJDQ0s8gZYtWxbtL61Y37VrF6GhoaxZs4a5c+dy4cIFatWqxZgxY5gzZ85DjYM6\ndepUiSmGhGUVFBQUfY+NjbVxNsLa5PrbXsKdBDZc3ADAo66PWvU6tHFvw5HMI2xO2kyd2DpWiyts\nr7K/9jUazUNNNWgrOVrzDf9NTU3F09OTvLw8XnnlFVatWsXMmTP5/vvvSU5Oxtvbu9i/RWZmJhqN\nhry8vBJtvfrqq6Snp7N3796iIS9dunTB3d2diRMn8swzz9C1a1eT8nNwcKB///58+eWXpKSk4Ozs\nbPJzLMy/oKCgQtf1QbmoVCoMBgOpqam4ubmVO06hzMzMEq8fpVJJ3bp1TWrHpGI9JSWFBg1KzkLg\n4+NTtL80169f59atW0yePJm5c+cSFhbG9u3bmTdvHvHx8SxfvvyB8bVaLTqdzpSUhRkV/vIW1ZNc\nf9tYnbAaAwZau7emrkNdq16Hfr79OJp5lDu6O+Tn58sc7NVUZXztq9VqDAaDrdOwivXr1zNgwAAM\nBgNNmzZl+PDhREZGEh0dzfXr1+nfv3+xfwsfHx/y8/PJysoqMQY9NjaWkJCQYo8bDIaiXvpTp06V\na+z5vR2t5bkuhecYDIYKX9eycklNTcXR0RFXV1ez/P8xGAwlXj+lDRcvi8l9/GX9si5rn16vJzMz\nk8jISEaMGAEYx7tnZ2fz8ccfM3v2bBo1alR2smp1iTuXhWXd+5+s8C5xUX3I9betq7lXOZhxEICn\nA5+2+jVo7NKYDxp/gJ+Dn1z/aqayv/atPZOILW3cuJHvvvuu6PnOnTuXn376iZdffpkOHTrw2Wef\nFfu3KLzZ9PLly8XGpQPUqlWL06dPk5WVVdSzrFAoOHToEAB16tQx+d/19u3bbNmyhZYtW5arV70w\nh8LvFbmuD8rlypUrhISEmO3/jkKhKPH6KU8da1Kx7uvre9/e89TUVOBuD3tp5964caPEGKHHHnuM\njz/+mKNHjz6wWG/WrJkU61YWGxtLQUEBGo2GVq1kzGp1I9fftm7F3cL9sjudAzszqMMgq8ePjY3F\nT+En178aquyv/fj4eLubK9tcLly4QJ8+ffj66685ffo07du3Lzb+vGHDhrz77rtMnjyZbt264e7u\nXuz8wjosNjaW9u3bF9v3r3/9i8GDB/PEE08wadIk/Pz8OHbsGO+//z5hYWEMHjy4aNjyzp076d27\nNzNnzmTmzJkAjBo1irp16xIREYGfnx/nz5/n3//+N0lJSSxbtqzYNVEoFHTv3p3o6OhSn+vmzZvJ\nzs4mMzMTgPPnz7Np0yYABgwYUNReRXMBY6fykSNHGD9+vNn+77i7uxMUFFQiTuHzeVgmFestWrQg\nMjKyxMD7EydOAGWvTtWyZUtu3LhR4vHCjxmkCBdCiOL61OvDI7UeIU9bcmyptV3Puk56XjphvmG2\nTkWIai09PZ24uDh69epF586d2bp1a4ljXnrpJTZs2FBsFphCQUFBdO3alfXr1/P8888X2/fEE0+w\nfft23n33XaZNm0ZGRgZBQUFMmDCB6dOnF7u/0GAwoNPpig0radmyJatWreKzzz4jKysLHx8funTp\nwrfffku7du2KjsvKygKMPfllmThxInFxcUU///DDD/zwww+A8ZOBwtVaK5JLoejoaNLT0xk9enSZ\nOdmCwmDCoJzNmzczYMAAVq5cyfDhw4sef+yxxzh+/DhXr14tdSzOF198wYQJE1i+fHmx+dinTJnC\nwoULuXTpEvXq1St6/H7vPNzd3aWot7LK3rsiKkauf/VWeP2PZh/l07hPae7bnOWPP/j+IlH5VfbX\nfnx8fIkezaokKiqK69ev89RTT+Hk5HTfY27fvo2LiwuOjo4l9q1Zs4bhw4cTFxdH7dq1S+zPycnB\nYDCgUCgs8gnFpk2bGDhwILGxsSWG4tjK2LFjuXTpEnv37jVbm/f7f1ie+taknvXHHnuMvn37MnHi\nRDIyMmjUqBGRkZFs2bKF7777rqhQHz9+PMuWLePixYtFBfhzzz3H559/zosvvkhycjJhYWFs27aN\nTz/9lBdffLFYoS6EENVZVn4WZ1LPEFEjwi7G3Ya4hqBSqDiefJzYW7G08q98xZsQVcn9FjT6M29v\n71L3DR06lHbt2vH++++zcOFCc6b2UKKiohgxYoTdFOoXL15k1apV7Nixw9ap3JfJ3dRr165l7Nix\nzJw5k/79+3PgwAEiIyOLfWyg0+nQ6XTF7qTVaDRs3bqVESNG8N577zFgwADWrVvHvHnz+OSTT8zz\nbIQQogrYdHkT434Zx8s77GNdCk+NJ483MK64+N3p72ycjRCiohQKBYsXLyYwMNAmU2J/+OGHrFix\nwupxS3P16lUWLlxos1VWH8SkYTDWJMNg7ENl/yhUVIxcf9sY9fMoTiSf4JWIV3i22bM2y+Pe6+8U\n5MRTG59CpVCxZdgWarrWtFlewvIq+2u/qg+DsTRLD4OpLsw1DEYqXyGEsCPnb5/nRPIJ1Ao1AxsM\ntHU6RZr6NOWRmo+gM+iIPBtp63SEEKLakGJdCCHsyNrzawHoEdQDX2dfG2dT3JjQMQCs/n01OQX2\nuzqkEEJUJVKsCyGEnSjQFfDTpZ8AGNJ4iI2zKalbnW4EuQehM+g4d/ucrdMRQohqweQVTIUQQlhG\nVHwUaXlpBDgH0Cmwk63TKUGlVPGfHv+hjlsd3Bzciu/U6+D6UUi9CHU7grfM8CWEEOYgxboQQtiJ\nPdf3APBEoydQK+3z13OIT8jdH+5kwKUoOLcFzv8KOcl39wWEQZNHoUl/qNMOlPdfg0MIIUTZ7POv\ngRBCVEOzO81mUMNBBLnb8SwWBgPErsQQG0lq/H58711d1dETfBtCYiwknTZ+7fkvOPtA437QYSIE\nhtsudyGEqISkWBdCCDuhUChoV7PkMth2Q6eFTa8QH/stk2v4kVbLj23ZDqiaDICm/Y3DX1QayEmF\nC9vh9y1wYSvkpsLxlXD6Rxi6GMKesPUzEUKISkOKdSGEsDG9QU+BvgBHVcllwe1GXhasfg7O/0pN\nFCQ5uZGhz+fQ05/RoVaH4se6+EDLp41fugKIP2DsYb+wDb7/C/R/39jLLoQQ4oFkNhghhLCxwzcO\n0+v7Xvzf0f+zdSr3pb6TAksfN45LVzuhGf4tfRsOAmDz5c1ln6zSQHAXGLkKIsYBBtjyOmyZDjZY\nOVEIISobKdaFEMLG1l1YR0Z+Bml5abZOpQSnzDga75wIicfAxRee/QlCB/F4g8cB2Bq3lXxd/oMb\nUqnh8f9An1nGn/f/D354FgpyLZa7EEJUBVKsCyGEDWXkZ7A1bisAQxrZ19zqrsnHCPltCg45N8Cn\nAYzfCkHGMfVtAtoQ4BJAZn5m0Sw2D6RQQJd/wLAloHKAMxvgmychO8WCz0IIUSg5OZmYmBhbpyFM\nJMW6EELY0OZLm8nT5dHIqxHN/ZrbOp27Lu6gwd5/oS7IJNu7mbFQ921YtFulVNE/uD/wEENh/qzF\nUzB2HTh5Gsezf9UPcm+bM3shxJ/s2rWL+vXr06ZNG95++21bpyNMIMW6EELY0PqL6wFjr7pCobBx\nNn/IugVrJ6DUF3C7Ricudv0YXP1KHDagwQAAouOjySnIMS1GcBcY9yt41IGUC7BxqnFaSCFEudy8\nebPUfQaDgTlz5hAZGUmtWrVISEhgzpw5hIWFob/n3pHMzEymTZvGoEGDqFevHq6ursyaNavUdrOy\nspg6dSqBgYE4OTkRHh7OypUrH5jrjh07GDduHCEhIbi6ulK7dm2efPJJjhw5YtJzNkcuANHR0SgU\nivt+7d+/v+i4JUuWULt2bbKzs8udZ3lIsS6EEDaSkJXAieQTKFAUFb42ZzDA+kmQnUSuR30utXkL\nQymz1IT5hDE2bCz/7vFvHFQOpscKCIHh34BSbZzW8diKCiYvRPU1evRorly5ct99Bw4cYNiwYQwc\nOJBz584xY8YMPvjgA+bMmYNSebcUTElJ4YsvviA/P59BgwY9MObQoUNZtmwZb7/9Nps3b6Zdu3aM\nHDmSFSvKfi0vWrSIK1euMGXKFDZt2sQnn3xCUlISHTp0YMeOHSY974rmcq/33nuPffv2Fftq3vzu\nJ57PPvssrq6ufPDBB+XKsbxk6kYhhLCRbXHbAGhboy1+ziV7rm3i0Jdw/hdQOXI1YmaphToY54Wf\n1m5axeLVbgs934Dtc2DzNKjbodhwGyHEwzl8+DBLlixh7ty5Jfb9+OOPTJ48GQB3d3feeecdvLy8\nGDp0aLHj6tWrx+3bt8nNzeXWrVssXbq01HibNm1i69atrFixgpEjRwLQs2dP4uLiePXVVxk+fDgq\n1f1XLv70008JCAgo9lj//v1p1KgR7733Hr169TLlqVcol3s1btyYDh06lLpfrVYzYcIE5s6dy2uv\nvYaLi4tJeZaX9KwLIYSNdK7dmb+1+BtPN3na1qkYJZ2BX98ybvedzR1PKxXNnadCvS6QnwVr/26c\nm10IS8nPtv2XmV26dIn09HS++uortFptif2JiYkEBgYan35+PkuWLGHUqFHFetWBoqEfD2PdunW4\nubnx9NPFf38999xzJCQkcODAgVLP/XOhDuDm5kZYWBjx8fEPFd9cuZhq9OjRZGRkPPQQG3OQnnUh\nhLCRhl4NmdJmiq3TMNLmwZq/gfYONOwNj0yAEyce6tRL6ZdYf2E9IT4hPFb/MdNjK1Uw9HNY1Amu\nH4Gd86HXW6a3I8TDeC/Q1hnArHSzNnf48GHq16/P5cuXWb9+PcOGDSvad+7cOZo2bVr084EDB0hJ\nSaFnz54Vinny5ElCQ0NRq4uXki1btiza36lTp4duLz09naNHj5rcq27OXCZNmsSIESNwcXGhY8eO\nzJgxgy5duhQ7pmbNmoSEhPDzzz8zbtw4k3MtD+lZF0IIYRyGcvOkcS71wYtA+fB/HnbF7+Krk1+x\n8mwFepo868DAj43bu/8Ncb+Vvy0hqpn9+/ezYMECNBoNCxYsKLZv/fr1PPnkk0U/79u3D4A2bdpU\nKGZKSgo+Pj4lHi98LCXFtClZJ02aRHZ2Nm+++abVc/H09GTKlCl8/vnnREVF8cknnxAfH0+PHj34\n5ZdfShzfpk0b9u7da3Ke5SU960IIYQNfnviShp4N6Vy7c/luzjSnC9th30Lj9pP/A/caJp3ev35/\n/n3k3xxNOsqN7BvUdK1ZvjyaD4UL2+DYclj7PLywB5y9yteWEKV5I8HWGZhdTEwMH374IU899RSR\nkZEcPXq0qBg/c+YM06bdvbckISEBhUKBn1/F75Mpa8iMKbNbzZgxg+XLl7NgwQLatm1r9Vxat25N\n69ati37u2rUrQ4YMoUWLFkybNo1HH3202PEBAQEkJSWh1WpL9OZbgvSsCyGElaXeSWVBzAImR00m\nKSfJtslkp8CPE43b7f4GTfub3ERN15q0rWH8A2vynOt/9th88A6G9Hj4+Z8ynaMwPwdX23+ZUWpq\nKj4+PqhUKmbMmIFSqWT27NmAcRGkP48Pz83NRaPRPNQNl2Xx9fW9b491amoqwH17uu9n9uzZvPPO\nO7z77ru89NJLNs3lXl5eXgwcOJDjx4+Tm1t8pWUnJycMBgN37twpV76mkmJdCCGsbMfVHegNekJ9\nQqnjXse2yfw0FbJugl9T6FtyFomHNaC+cerJChfrju7GFU4VKji5xvglhCjV2rVreeKJJwAIDQ1l\n9OjRbNiwgaioKDZt2sTAgQOLHe/n50d+fn6F5wpv0aIFZ86cKXFD64k/7nW5d8rD0syePZtZs2Yx\na9Ys3njjDZvmcj+GPzoL/twzn5qaiqOjI25ubuVq11RSrAshhJUVTtnYL7ifbROJ+w3ObDAWxsO+\nBIfyT0PWt15f1Ao1Z1LPcCn9UsXyqhMB3f/42H7r21Bgnd4rISqjdevWFZsFZf78+bi7u/P3v/+d\n7du3l7ixMiQkBICLFy9WKO6QIUPIyspizZrib6iXLVtGYGAg7du3L/P8uXPnMmvWLN56660Kr6ha\n0Vzu5/bt2/z000+Eh4fj5ORUbN+lS5cICwurUM6mkGJdCCGsKD0vnQOJxmnE+tTtY7tEDAbYOtO4\n3fZZqNWyQs15O3nTMbAjAFuvbK1odtB5CnjUhoxrcPCLircnRBVx4cIFgoODiYqK4tNPPyUiIqLY\nfN+1atXi3Xff5eLFiyiVyhLDXXr06AFQbGXOe23evJl169axebPxU7LTp0+zevVqVq9eTU7O3ZWK\nH3vsMfr27cvEiRNZvHgxUVFRPP/882zZsoUPPvigKO7OnTtRq9XMmTOn6Nx///vfzJw5k/79+/P4\n44+zf//+Yl9/plAoivK+n4rkAjBq1Chef/11Vq9eTXR0NIsXL6Zjx47cvHmTDz/8sNixer2egwcP\nVng2HVPIDaZCCGFF0fHRaA1aGnk1Itgz2HaJnP0Jrh0CjQt0f80sTfau25uTySdRKszQD6RxNi6W\ntH6ScXaYNmPB2bvi7QpRyaWnpxMXF0evXr3o3LkzW7eWfHP80ksvsWHDhmKzwBQKCgqia9eurF+/\nnueff77E/okTJxIXF1f08w8//MAPP/wAwOXLlwkODi7at3btWt58801mzpxJamoqISEhREZGMmLE\niKJjDAYDOp0OvV5f9NjGjRsB2LJlC1u2bCmRg+Gee1WysrIA45uQspQ3FzBO8bhq1So+++wzsrKy\n8PHxoUuXLnz77be0a9eu2LHR0dGkp6czevToMvMxJ4XBYJ937+j1ejIzM4s95u7uXmICf2FZsbGx\nFBQUoNFoaNWqla3TEVYm19/8Xt7+MtHXonmx1YtMDJ9omyR0WvhfB0g5D91eLXVOc1Ovf74uH5VC\nhUpZsRvXiuh1sKgz3DpjXDip72zztCseqLK/9uPj4wkKCrJ1GhYTFRXF9evXeeqpp0oM0Sh0+/Zt\nXFxccHQsuQrxmjVrGD58OHFxcdSuXbvE/pycHAwGAwqFwmqrdJamcNx9bGwsLVq0sGkuAGPHjuXS\npUsPNXXj/f4flqe+lcpXCCGsRG/QczPnJgB96tlwCEzMt8ZC3cUXOk02W7MOKgfzFepgXCypzx9j\nWQ98BunXzde2EJVYz549GTNmTKmFOoC3t/d9C3WAoUOH0q5dO95//31LpWg2UVFRjBgxwi4K9YsX\nL7Jq1Srmz59v1bhSrAshhJUoFUq+H/Q9GwdvpJFXI9skkZ8N0fOM292mgZOH2UPoDXqupF8xT2NN\n+kPdTsaVVaPtv7AQojJQKBQsXryYwMDAEkNC7M2HH37IihUrbJ0GAFevXmXhwoUlVjW1NCnWhRDC\nyoI9g01aMMSs9i+CrBvgVQ8injN782l30uj7Q1+GbBhCZn7mg094EIXi7vCXY8sh6WzF2xRC0Lx5\nc9544w0ZXmyCnj173necv6XJFRJCCCso0BWQq8198IGWlJ0Cez8xbveaAer7f0ReEV5OXrhoXNDq\ntey9bqbluIMegZCBYNDDdhm3LoSoXqRYF0IIK4i+Fk33Vd2Zf9C6Yx2L2f0R5GVAzZbQfJjFwvSs\na5zSbEf8DvM12meWcT74c5sgbp/52hVCCDsnxboQQljB1rit5GpzUSttNGPu7StwcLFxu+9ssOBH\n372CegGw59oeCvQF5mnUr7Fx+kaAbW8b54kXQohqQIp1IYSwsDxdHruu7QJsOAvMjndBXwANekDD\nXhYN1cKvBT5OPmQWZHL4xmHzNdz9dVA7Q/wBOPuz+doVQgg7JsW6EEJY2IHEA2QXZBPgEkALPxtM\nP3bzFJz43rjdx/JjvlVKFT3EPhPLAAAgAElEQVSCegAQFR9lvoY9akHHScbt7XPAzmexEEIIc5Bi\nXQghLGxn/E4Aegb1NM/qnqba+3/G72FPQmC4VUL2DDKOW4+Kj8Ksa+91ngyOnpB8Dn4vufKhEEJU\nNVKsCyGEBRkMBnZeMxbr3ep0s34C6dfh5GrjduepVgvboVYHng17lve6vIcBMxbrTp53p5z8bYH5\n2hVCCDslxboQQljQudvnuJlzE2e1M+1rtbd+AgcWgV4LwV2hdhurhXVSO/FKu1doV7Od+T9NaP8C\nKDVw9Te4ZsYx8UIIYYekWBdCCAvydfJlSpspjA4djaPK/POal+lOOhxeatzu9LJ1Y1uSRy1o+Yxx\nu3DeeCGEqKKkWBdCCAvyd/Hnby3+xpQ2U6wf/MgyyM8E/xBo1Nf68THeXPvu/ndJyEowb8OFbz7O\nbITUS+ZtWwhRpuDgYP76179arP0VK1bw8ccfW6z9ykaKdSGEqIq0+bB/kXG740sWnVe9LJ/FfsbK\ncyvNOysMQEDoH29ADLDvU/O2LYSwKSnWi5NiXQghLOTQjUP8dOkn0vPSrR/81FrITAC3GneHjNhA\n0awwV81crINxZhiAmOWQnWL+9oWoYnJzc22dgigHKdaFEMJClp9ZzvTd01lxZoV1AxsMd6drbD8B\n1FYeK3+PnnWNxfrhm4fN/6YluCvUagXaXDj0pXnbFlVWTkFOqV95uryHPvaO9k65j62IWbNmoVAo\niImJYejQoXh4eODp6cmYMWO4detW0XHBwcEMHDiQtWvX0rp1a5ycnJg927jOwp07d5g+fTr169fH\nwcGB2rVrM2nSJNLS0orFKigoYNq0adSsWRMXFxe6dOnCwYMHS83pz5YuXYpCoeDKlSvFHl+xYgUd\nO3bEzc0NNzc3wsPDWbJkCQA9evTg559/Ji4uDoVCUfRVndlo3WshhKja8nR5/JbwGwDdg7pbN/jF\nHZB0CjSuEDHOurH/JMg9iEZejbiQdoHd13czsMFA8zWuUECnybBmPBz8wtjTrnE2X/uiSmq/ovRZ\nmbrW7sr/+vyv6Oce3/cgV3v/3uiIGhF83f/rop/7r+nP7bzb9z22mW8zVg5cWc6M72/IkCE888wz\nvPDCC5w6dYoZM2Zw+vRpDhw4gEajAeDo0aOcOXOGt956i/r16+Pq6orBYGDw4MFs376d6dOn07Vr\nV44fP87bb7/Nvn372LdvX1GMSZMmsWLFCl555RX69u3LyZMnGTp0KJmZmeXOe+bMmcydO5ehQ4fy\nr3/9C09PT06ePElcXBwA//vf/3j++ee5ePEi69atq9g/UhUhxboQQljA4RuHydXmEuAcQKhPqHWD\n//ZHr3qbv4Czt3Vj30fPoJ5cSLvAjqs7zFusA4QNhm2zIf0qxEba/M2JENYydOhQPvjgAwD69etH\njRo1GD16NN9//z2jR48GICkpidOnT9OkSZOi83755Rd++eUXPvjgA1599VUA+vbtS1BQEMOHD+eb\nb75h9OjRnDt3juXLl/OPf/yjKE7fvn2L4pTH5cuXee+99xg9ejTfffdd0eN9+969AT4sLAwvLy8c\nHR3p0KFDueJUNVKsCyGEBUTHRwPQLaibdT/CTTwOl6JBoYIOE60Xtww9g3qy+MRi9iXso0BXgEal\nMV/jKjV0fBG2vA6/LYQ2f7XZzbSicjgw6kCp+1RKVbGfo5+JLvXYP68fsGVY6SvqWmLl4j8XzM88\n8wzPPvssUVFRRftatmxZrFAH2LFjB0CJ2Vyefvppxo0bx/bt2xk9ejS7du0qM055bN26FZ1Ox6RJ\nk8p1fnUlxboQQpiZwWBg1zXjH7rudaw8BKZwVc9mg8G7nnVjl6KZXzN8nHxwVDlyPes6wZ7B5g3Q\neixEvw+pF+HcJgg1c++9qFJcNC42P9YcatasWexntVqNr68vKSl3b7auVatWifNSUlJQq9X4+/sX\ne1yhUFCzZs2i81NTU8uMUx6FY+rr1KlTrvOrK+l+EEIIMzufdp6E7AQcVY7WXbU0/RqcXGPctqNF\nkJQKJasHreaXYb+Yv1AHcHSDiPHG7cI3K0JUcTdu3Cj2s1arJSUlpVghfb9P9Xx9fdFqtcVuRgVj\nJ8ONGzfw8/MDwMfHp8w493JycgIgL6/4DbrJycnFfi58g3Dt2rWyn5woRop1IYQwsxO3TgDQvlZ7\nnNVWvOFx/yIw6IyzpAS2tl7ch+Dv4m/Z4UDtJ4DKAeL3Q/why8URwk4sX7682M/ff/89Wq2WHj16\nlHle7969AYqNGQdYs2YN2dnZRfu7du1aZpx7BQcHA3D8+PFij2/cuLHYz/369UOlUrFo0aIyc3R0\ndJRpJu8hw2CEEMLMhjUZRtc6XcnKz7Je0IJciPnjj2/Hl6wX10RavRatXouT2sm8DbvXhBZPw7Hl\ncGgxBLUzb/tC2Jm1a9eiVqvp27dv0WwwrVq14plnyl5XoW/fvjz66KO89tprZGRk0Llz56LZYFq3\nbs3YsWPR6XSEhIQwYsQIPv74YzQaDX369OHkyZN89NFHeHh4FGtzwIAB+Pj4MH78eObMmYNarWbp\n0qXEx8cXOy44OJg33niDuXPnkpuby8iRI/H09OT06dMkJycXTS3ZokUL1q5dy6JFi2jbti1KpZKI\niAjz/gNWItKzLoQQFhDgEkADrwbWC3hyLdxJA8+60Ljvg4+3gS9PfEn3Vd1Zc36NZQK0+2MozKl1\nskiSqPLWrl3L2bNnGTp0KDNnzmTQoEH8+uuvODg4lHmeQqHgxx9/5J///Cdff/01AwYM4KOPPmLs\n2LHs2LEDR8e76zIsWrSIf/7znyxdupQnnniC77//njVr1uDtXXyWKQ8PD7Zs2YK7uztjxozhhRde\noHnz5rz55psl4s+ZM4dvvvmGuLg4Ro8ezeDBg/n666+pX79+0TFTpkzhqaee4o033qBDhw60a1e9\n33xLz7oQQpiRwWCwzQIeh40LihDxHPxpRgt7oVFqyMjPYNe1XYwOLd/Ub2Wq3dY4/CchBmK+hS5T\nzR9DCDtRt25dNmzYUOr+Py9EdC8nJyfmzZvHvHnzyozh4ODARx99xEcfffTAttu1a8fevXtLPD5+\n/PgSj40dO5axY8eWGtfb25sffvihzNyqE+lZF0IIM3p99+tM2DqB2Fux1guaEAPXj4BSY5wZxU51\nq9MNgEM3DpFTkGOZIIU3mh75GvR6y8QQQggrkmJdCCHMpEBXQHR8NL8l/IZKYcXe7UN/9Ko3Gwxu\n/mUfa0PBHsEEuQdRoC9gX+K+B59QHs2HgZMn3L5iXMlVCCEqOSnWhRDCTA7dPESONgc/Zz/CfMOs\nEzQ3DU6sNm5HlPy42Z4oFIqi3vXd13ZbJoiDC4T/McTm0JeWiSGEDc2aNQuDwVA0xaKo+qRYF0II\nMylcCKlbnW4WWbHwvmJXgjYXAsKgrv0vzd2t9t1i3WAwWCZIxDjj9/O/QFp82ccKIYSdk2JdCCHM\n4N5VSwt7j60Q9O6Npe3Ggy1ubDVRRM0InNXOJOUmcTb1rGWC+DWG+t3AoIcjSy0TQwghrMTkYj0r\nK4upU6cSGBiIk5MT4eHhrFy50uTAb731FgqFgubNm5t8rhBC2JsrGVeIz4xHo9TQsVZHKwXdDcm/\ng4MbtBxunZgV5KByYGTISF5o9QJejl6WC1Q4JOjoMtDmWy6OsEtKpZKCggJbpyGqMZ1OZ7a2TJ66\ncejQoRw6dIh58+bRpEkTVqxYwciRI9Hr9YwaNeqh2jh27BgfffQRNWrUMDlhIYSwR4W96hE1InDR\nuFgnaOGNpS2fAUd368Q0g3+0/Yflg4Q8Dm41IesGnN1ovPFUVBs+Pj4kJibi5+eHs7OzbaZTFdWW\nTqfj+vXrBAQEmKU9k4r1TZs2sXXr1qICHaBnz57ExcXx6quvMnz4cFSqsmdA0Gq1PPfcc0yYMIHY\n2FiSk5PLn70QQtiJOu516BTYiV5BvawTMPMGnP3JuG3nN5bahEoDbZ+FnfPh0FdSrFczzs7O1K5d\nm5SUFFJSZIEsU2VmZhatGeHuXnk6AuxJQEAATk7mWanZpGJ93bp1uLm58fTTTxd7/LnnnmPUqFEc\nOHCATp06ldnGvHnzSE1N5d1332XgwIGmZyyEEHaod93e9K7b23oBj34Dei0EdYCalW84YXZBNvsT\n9uPr7Et4QLhlgrR5FnZ9BHF7IOksBIRYJo6wSyqVymw9m9VNbGwsBQUFaDQagoKCbJ1OtWdSsX7y\n5ElCQ0NRq4uf1rJly6L9ZRXrp0+f5p133mHt2rW4ubmZnOypU6fQyyIXVlU45q+goIDYWCsu8iLs\nglx/O6XXErr/CxyAuBp9SbPQtbHk9f8h8QfW31zPI16PMDl4slnbvle9mp3wStxN8pb5XG8lK5o+\nLHntV29y/S1HqVRSt25dk84xqVhPSUmhQYMGJR738fEp2l8avV7PuHHjGDp0KAMGDDApyUJardas\nA/aFaeRmnepNrn/pzmWfI8AhAG+Nt1Xied3Yi0PuLQocvEj274TBCtfG3Ne/hUsL1rOeExknyM3P\nRa0w+Raqh5JUdyBeibvxuvoLV5uMQ692tkicqkxe+9WbXH/zetBw8fsx+bdjWTdplLXvP//5D+fP\nn2fDhg2mhiyiVqtRKmW2SWu690Wq0WhsmImwBbn+D6Y36Fl0bRHp2nRmNp5JE9cmFo9Z4+pGAG7X\nG4DaydVicSx5/Zt4NMFd5U6mLpPLeZcJc7fMIlK5tdqT51obx+zr+N/YSWr9QRaJU9XIa796k+tv\nOeWpY00q1n19fe/be56amgrc7WH/s6tXrzJz5kzmzZuHg4MDaWlpgLGnXK/Xk5aWhqOjI87OZfd4\nNGvWTIp1K7t33FqrVq1snY6wMrn+D3Yq5RTpsem4qF0Y3H4wGpWF/7ClXoakQ4CCgAGvEeAdbLFQ\nlr7+PTJ7sPHSRhKcEhjZaqTZ2y+S8yL8+iZBN38laPBblotThchrv3qT6285er2ezMxMk84xqfJt\n0aIFZ86cQavVFnv8xIkTAKXOmX7p0iVyc3OZMmUK3t7eRV979+7lzJkzeHt7M336dJMSF0IIe1A4\nZWPHwI6WL9QBYr4zfm/YCyxYqFtD4eJRhf+GFtNqJKgcIDEWEo5ZNpYQQpiZScX6kCFDyMrKYs2a\nNcUeX7ZsGYGBgbRv3/6+54WHhxMVFVXiq1WrVgQHBxMVFcVLL71U/mchhBA2svvabsBKq5bqtHBs\nuXG77bOWj2dhnWp3QqVQcSn9EvGZ8ZYL5OoLoX8Mfzn6jeXiCCGEBZg0DOaxxx6jb9++TJw4kYyM\nDBo1akRkZCRbtmzhu+++Kxo0P378eJYtW8bFixepV68eXl5e9OjRo0R7Xl5eaLXa++4TQgh7l5Kb\nwsnkkwB0rd3V8gEvbIXMRHDxgyaPWT6ehXk4eNA6oDWHbx7myM0jBLlbcIq4Nn+Bk2vgxA/Q7x1w\nsNLCVUIIUUEm32C6du1a3nzzTWbOnElqaiohISFERkYyYsSIomN0Oh06nQ6DwWDWZIUQwp7sub4H\nAwZCfULxd/G3fMAjy4zfw0eC2sHy8azg1Xav4q5xJ8jDwnM5B3czDhu6fQVO/wjhD7fithBC2JrJ\nd2u6ubnxySefkJiYSF5eHrGxscUKdYClS5diMBgIDg4us63o6GhOnjxpagpCCGEXdl+34hCYjAQ4\n/4txu03lHwJTKMw3zPKFOoBSCa3HGrdlKIwQohKRqVWEEKKcZnSYwfyu83m8weOWD3ZsORj0ULcT\n+DW2fLyqKHw0KFRwdR/cOmfrbIQQ4qFIsS6EEOXk6ejJgAYDqO9Z37KB9Ho4+q1xuwrcWPpnx5KO\nMXnHZOYdnGfZQB61oMmjxm3pXRdCVBJSrAshhL27vBPS4sDRE0KfsHU2ZpejzSEqPopfr/yK3qC3\nbLDCIUSxkaDNs2wsIYQwAynWhRCiHKbvns6XJ74kPS/d8sEKe4FbPlMlZzGJqBGBi9qFW7m3OJN6\nxrLBGvUB91qQkwLnNlk2lhBCmIEU60IIYaJrmdf46dJPLIxZiEKhsGyw7BQ4+5Nxu81fLBvLRhxU\nDnQM7AhYYYEklRpajzFuF86uI4QQdkyKdSGEMFHhLDDhAeF4OHhYNtjxlaDLh8DWUKulZWPZUPc6\n3QHYFW/hYh3uFuuXooxTOQohhB2TYl0IIUxU2Ptr8SkbDYa7Q2CqaK96oa51jItKnUw5SXJusmWD\neQdDg57G7Zjllo0lhBAVJMW6EEKYIKcgh0M3DgHQrbaFi/X4g3DrLGhcoPlTlo1lY37OfjTzbQbA\n7mu7LR+w8M1PzHeg01o+nhBClJMU60IIYYL9ifvJ0+VR2602Db0aWjZYYa96s6HgZOHhNnagZ1BP\n2gS0wcPRCs815HFw8YXMBLi43fLxhBCinKRYF0IIE+y8thMwjrG26M2ldzLg1FrjdhUfAlPo+ZbP\ns+yxZfSu29vywdSO0GqkcVtuNBVC2DEp1oUQwgQqhQpntTM9gnpYNtDJ1VCQA/4hEPSIZWPZCYvP\nrPNnhW+Cft8CmTesG1sIIR6SFOtCCGGCmR1nsnvEbtrVbGfZQIVDYFqPBWsXsTaWdieNUymnLB/I\nvykEdQCDDo6tsHw8IYQoBynWhRDCRI4qR9RKteUCJB6HhBhQOdwdqlFNHEw8SPfvu/PqzlcxGAyW\nD1jYu370G9BbePVUIYQoBynWhRDiISVkJVgnUGGveshAcPW1Tkw70cyvGUqFkvjMeK5kXLFCwMHg\n6AG3L0PcHsvHE0IIE0mxLoQQDyEhK4FH1zzKkPVDKNAVWC5QQS4c/964XU1uLL2Xq8aVdjWMQ4ws\nvpopgIMrtPhjWszCN0lCCGFHpFgXQoiHEB0fDYCHgwcalcZygU5vgLx08KoL9btbLo4d6x70x2qm\n1ijW4e6botMbICfVOjGFEOIhWXDQpRBCPFieVkdi2h0y72jJvFNAxh/fs/K0ZOdpcVArcXfS4O6k\nxs1RjbuTBg8nNf7ujni5OFgtz8IpG3sG9bRsoKIbS/8CyurZn9KtdjfmMY+jN4+SmZ+Ju4O7ZQPW\nCoeaLeDGCTjxA7SfYNl4QghhAinWhRBWodMbiEvJ5vebmZy7kWX8fjOTy8nZ6PTlu5HQ392RpjXc\naVLDnaY13WhSw53GNdxxczTvr7bsguyiVUsLe30tIvmCcdy0QgnhoywXx84FeQRR37M+l9Mv81vC\nbzwa/KhlAyoU0OZZ2PSKcc71R56vdjPwCCHslxTrQgiLSUjLZefvt9h57hZ7LySTmXf/Zd2dNSo8\nnY2958YvDW5Oatwc1OTr9EU97ll3tGTmFZB5R0taTgG3MvO4lZnHngvJRW0pFNCyjhc9mvjTvak/\nrep4oVJWrPD6LeE3CvQF1POoR33P+hVqq0wxf/SqN+oLnrUtF6cS6F6nO5fTLxMdH235Yh2M49Z/\nfQuSTsH1o1CnreVjCiHEQ5BiXQhhNlqdnv2XUtn5exLR525xPimr2H4njZImhT3hNdxpUtOdJjXc\nqOnhZPKCOFl5Ws7fzCzqqT+flMm5G5kkZeYRG59GbHwan2w/j5eLhq6N/enexJ9eIQH4uJo+dKZw\nvHr3OhbsVdcV3J3ru+2zlotTSQxqOIhgj2DLfpJxL2dvCHsSjq+Co8ukWBdC2A0p1oUQFXY5OZvv\nD8ez5sg1kjLzih5XKqB1XW+6NzEWy81re1a4l7uQm6Oa1nW9aV3Xu9jjN9LvsOv3W+z8/Ra7z98i\nLaeAjbEJbIxNQKNS0Ce0Bs+0C6JbY/+HykWn17H72m4Ay65a+vsWyL4FbjWgcT/Lxakkmng3oYl3\nE+sGbfMXY7F+cg08+h44ulk3vhBC3IcU60KIcsnN17HpRCKrDsdz8PLdGTR8XB3oHRJA96b+dGnk\nZ9WbQAFqejrxTLsgnmkXhFan51h8Gjt/v8X2M0mcTsxg88kbbD55g1qeTjzVtg7PRAQR5ONSansG\nDMzuNJu9CXtpHdDacokX3lgaPgosOduMKF29zuDTAFIvwal10GasrTMSQggp1oUQpklIy+WLXZdY\nc+Ra0Rh0pQK6NfFneEQQvUNr4KC2j1lM1ColEcE+RAT78K9+TTmTmMGqQ/H8eOw6iel3WLDjAgt2\nXKBLIz9e6N6Qzo18SwzHUSvV9Kzbk551LTgLTPo1uLDNuN1aCsRCOQU5rLuwjpikGD7s9qHJQ6VM\nplAYe9e3zTK+eZJiXQhhB6RYF0I8lKspOSzaeYHVR65RoDPO3hLk48wzbYN4KqIOtTydbZzhg4XW\n8mDWE814/bEQtp6+yapD8ey5kFz0FR7kxcu9GtErJMDyheG9jq0Agx6Cu4JvQ+vFtXNKhZJPjn5C\nrjaXcc3HEeYbZvmgrUbBjnfg2kFIOgMBoZaPKYQQZZBiXQhRpusZWtb9nsnuq9FFUyx2aODDxB6N\n6NrID6WZxqBbk5NGxaBWgQxqFUh8ag5L9lwm8uBVjsWnMX7ZYUJrefByr0Y0r6vlx4vr6FW3F839\nmlsmGb0ejn5r3K6GK5aWxUntROfAzmy7uo0dV3dYp1h3rwFN+sPZn4y96/3ft3xMIYQog318Vi2E\nsDtXkrP5YG8KU39NIfpKDjq9ge5N/PnhhY6sfL4j3Zv4V8pC/c+CfFyY9UQz9rzWiwndG+DqoOJM\nYgYvLj/K8OVfsvjEYv575L+WS+BSFKRfBScvCH3CcnEqqV51ewEQFR9lvaBt/piNJzYStHllHyuE\nEBYmPetCiGIy7hTw6Y4LfLX3ctFwl/a1nXhzSFta1vGycXaW4+/uyPTHQnmhW0O+/u0KX++9TBrH\nUANx8cGcvJ5O89qe5g9ceGNpy+GgcTJ/+5VctzrdUClU/H77d+Iz4wlyD7J80Ea9wT0QMhPgzEbj\nHOxCCGEj0rMuhACMK4xGHrxKr4+i+XzXJQp0BsJrOvJRHx/e6OZXpQv1e3m7OvDPvk3Y8s92aFzj\nALgYV49BC/fw2urj3Mo0Y09rVpJxuAXIEJhSeDp6ElEjAoCoq1bqXVeqoPUY4/aRpdaJKYQQpZBi\nXQjBvospDFywh+lrT5CclU8DP1e++msEs3r4EexVPacRjE3ejwEddd3qMyisBQYDrDocT8+PolkU\nfZE8ra7iQWK+A70W6rSDmhYaE18FFM7EsyN+h/WCtvkLKJRwZTckn7deXCGE+BMp1oWoxlKy8ng5\nMoaRi/dzJjEDDyc1MwaGsWVqN3qF1LDujCh2ZttV41SK/er35v9GtmbNxI60rONJVp6W+VvO8uh/\nd7HvYkr5A+j1cORr43bEODNkXHX1DOqJRqnBTeOGTm+GN0kPwyvo7uJU0rsuhLAhGbMuRDVkMBjY\nEJvArA2nuJ1TgFIBo9rX5Z99m+Ljat1FjOxRrjaXPdf3ANCnXh8A2tbz4ccXO7Mu5jrzt5zlSkoO\nIxfvZ+QjdZk+IAQPJxM/gbi4A9KugpMnNBti7qdQpQS6BbJnxB5cNKUvXmUREeOMK8seWw69Zsg9\nBUIIm5CedSGqmcT0XMYvO8yUlce4nVNASE13fpzUmXcGt5BC/Q9X0q/gpHKitlttwnzuTheoVCoY\n1rYO2/7VnVHt6wIQefAq/f6zix1nb5oWpLBXvdUo0Nj/HPW2ZvVCHaBRH/AMgtzbcHq99eMLIQRS\nrAtRbej1BlYcKCwsk9CoFPyzbxM2vNSl2tw8+rBCfUPZ8cwOFvdbfN+hQB5OGt4b0oLIv3egnq8L\nNzLuMG7pYaasjCE1O//BAdKvw7nNxu2I58ycfdWWmJXIHe0d6wRTqu5O43j4K+vEFEKIP5FiXYhq\nICEtlzFLDvDGuhNk5mkJD/Li58ldmdy7MQ5q+TVwP2ql+oHTBHZs6MuWKd14vlsDlApYfyyBPv/Z\nyS+nbpTdeMy3YNBBvS7g39SMWVdtU6Om0m9NP/Ze32u9oG3GgkIF8fvh5mnrxRVCiD/IX2khqrhN\nJxJ57JPd/HYxBSeNkrceD2XNxE40qeFu69TsUlZ+FnqD/qGPd3ZQ8caAUNa+2JmmNdxJzc5nwrdH\neGPdCXLz73MzpE57d2516VU3SaBbIGDlWWHca0LIAON24dAlIYSwIinWhaiicvK1vLb6OC8uP0p6\nbgEt63iyeUo3/ta1AaoqsPKopbx/8H36ru7LtrhtJp0XHuTFxpe7MKFbAwBWHLjKwAW7OZWQXvzA\n879CxnVw8YXQQeZKu1roFWRczTQ6PhqtXmu9wIWz9cSuhPxs68UVQgikWBeiSjpxLZ2B/7eHVYfj\nUSjgxR4NWTOxE/X9XG2dml0r0BUQFR9FUk4S3k7eJp/voFYyfUAo341vT4C7IxdvZTPk09/4cvcl\n9HrjarBFY59bjwG1oxmzr/rCA8LxdvQmIz+DozePWi9w/R7gXR/yMuDkGuvFFUIIpFgXokrR6w18\nvvMiQxft5VJyNjU9nFjxtw5M6x+CRiUv9wc5cOMAmfmZ+Dr5Eu4fXu52ujT2Y8vUbvQJrUG+Ts87\nP5/h2a8Pkhz/O1z4o8e+8MZF8dDUSjXdg7oDEBVvpdVMAZRKaPtX4/ZhGQojhLAu+estRBVxOzuf\nccsO8f7msxToDPRvVpMtU7vSsaGvrVOrNAqHvvSp1weVUlWhtnxcHVj8l7a8M7g5Tholu88ns+Gr\n9wEDNOgJvg3NkHH1UzgUZvvV7RgMBusFbj0GlBpIOAoJMdaLK4So9qRYF6IKiI1PY+CCPUSfu4Wj\nWsn7Q1uwaEwbvFxk3vSHpdVr2X51O3B3IaSKUigUjOlQj40vdaFZDWcG6Y3tb3EecHdYjDBJx8CO\nuKhdSMxO5HjycesFdvWDsCeN29K7LoSwIinWhajEDAYD3+6P4+nP9nE9LZdgXxfWvdiZkY/Uve/8\n4KJ0R24eIS0vDS9HLyJqRJi17cY13FnbKw1/RTpJBi9eOlKD5789THpOgVnjVAdOaidebv0yH3b/\nkCbeTawbvHD2nhOr4aDyMvoAACAASURBVE6GdWMLIaotKdaFqKRy8rX8Y9UxZvx4knydnn5hNdjw\nchfCAj1snVqltDVuKwC96vZCrVSbvX3HY0sBSGr0DEqVA9vOJDFw4W5OXk8v+0RRwpiwMfQP7o+z\n2sorv9brDH5NoCAbTnxv3dhCiGpLinUhKqGLt7IY/OlefjyWgEqp4I0BIXw+ti0eThpbp1ZpPdHw\nCUaHjmZgg4Hmbzz5AlzeCQolzQdNZs3ETtTxdiY+NZehi35j5cGr5o8pzE+huDuN46GvwJpj5oUQ\n1ZYU60JUMtvP3GTwwr38fjMLf3dHVvytPc93ayjDXiqopX9LXn/kddrVbGf+xg9+bvzeuB94BdGi\njic/vdyFXiEB5Gv1vL72BG+uO0G+9uEXY6rubmTf4IvjX7D4+GLrBm41AjQukHQKruyxbmwhRLUk\nxboQlYTBYGDhjvP87ZvDZOZpeSTYh58nd6F9A5ntxa7dSYdjK4zb7V8oetjLxYEv/xLBK/2aoFDA\n8gNXGf3lfm5l5tko0crlcvplFsQsYNnpZRTorTj239kbWg43bh/4zHpxhRDVlhTrQlQC2XlaJq04\nyke//o7BAGM61OW7v7UnwN3J1qlVenqDnv8e+S8HEg+g0+vMHyDmO8jPAv9QaNCj2C6lUsFLvRqz\n5NkI3B3VHLpymycW7uHENRnH/iDtarbDx8mH9Lx09ifst27wwjddZ3+G21esG1sIUe1IsS6EnYtP\nzWHYot/YdOIGGpWC94e24J3BLXBQy8vXHE4mn+Srk18xecdktAYzL2Gv18GBP4bAtJ9gHPN8H71C\narBuUmca+LmSmH6Hpz77jfXHrps3lypGrVTTr14/ALZc2WLd4AEh0LAXYICDVh6GI4SoduSvvRB2\n7LcLyTyxcA9nb2Ti5+ZI5N87MPKRurZOq0opXAipe53uOKoczdv471sgLa740IlSNApwY92kzvRs\n6k+eVs+Ulcd4b9MZdDIfe6kGNBgAGBdIytNZefhQ+4nG70e/hbws68YWQlQrUqwLYae+3R/3/+zd\nd3wU1drA8d9sS9v0SggQEjqBECD0LggoSBMBwVcBEbCXK3LVq6Bey71eFRUFRAUugnRRBFSESw0o\nLZDQAyEQQnrfbJ/3j4UAQoDAJpNyvnz2s5PZM2eezbCZZ8+cOYdHvvmDXIOFVnW9+fHprrQP91M6\nrBrFLttLW2WdNRHSNXZ/6Xhu+yjo3G9Z3NtNy/xHY3myl2N203nbTjNx4Z8UGMV47DcSHRhNiEcI\nxZZidpyv5Js9G/UF/0Zgyof4pZW7b0EQahWRrAtCFWO12XlzbQL/+CEBm11maJtQVkzpTKhPJY8p\nXQvsS99HWnEaeq2eHmE9nFv5xQRI3g6SGjpMuu3N1CqJaQOa8dmYGFy1Kv53PJMRX+wiJdvg3Phq\nAJWkYkD4AAA2JG+o5J2roMNkx/KeOWAXI/kIglAxRLIuCFVIfomF8Qv+ZGHcWQBe7t+Uj0e1wVWr\nVjiymunHpB8B6B/eH1eNk2/WvTxSSPPB4B1W7s0HR4eyfHJngr1cOJlRxNAvdvLHmRznxlgDDGg4\nAHeNO3qtvvJ33mYMuHhB9ilI+r3y9y8IQq0gknVBqCLOZhcz/IudbD+ZhZtWzZxxbXmqdyMxfnoF\nKbGW8GvyrwAMjhzs3MqLs+HwCsdyp6l3XE3rMB/WPtWNVnW9ySk2M3b+blbsPeekIGuGFn4t2Dpq\nKzO6zKj8nbt4QswjjuXLXZ4EQRCcTCTrglAF7D6dzZDZO0nKLCbEy5UVUzozIKqO0mHVaOcLz+Pr\n6ktdfV1igmKcW/m+b8FqhDptoF7Hu6oqxNuV5ZM7c1+rECw2mZdXHuK9DeLG08skSXL+VZHy6DAJ\nkBwt65knlItDEIQaSyTrgqCw5XvP8cjXe8gzWGgd5s3ap7sSVddb6bBqvMa+jdkwfAMLBixAJTnx\nT6HNAn9+7VjuNLXM4RrLw02n5vMxbXmmTyMA5m49zZTF+yg2OXmoyWpMlmWO5xynyFzJI7P4NYSm\njlFpxCRJgiBUBJGsC4JC7HaZDzYeY9rKQ1hsMve3rsOyJzoT7CUmOqoskiQR4hHi3EqPrIXCC+AR\nBC2HOa1alUripXubMmt0G3QaFb8dSeehuXFczDc6bR/V2Qv/e4EHf3qQ387+Vvk773RpkqT4pVCS\nW/n7FwShRit3sl5UVMTzzz9PaGgorq6utGnThu+///6W261evZoxY8bQqFEj3NzcCA8PZ+zYsZw8\nefKOAheE6sxosfH00v18+b8kAJ7t04jPRsfgphM3klaGcwXnMNvMFVP55dbV2ImgcfK47cCQNnVZ\nOqkT/h46Ei8UMHT2ThIviBlPW/i3AGDDmUoeFQYgvDsER4HF4Bh3XRAEwYnKnawPHz6chQsX8uab\nb7JhwwZiY2MZM2YMS5Ysuel2H3zwAQaDgddee42NGzfyzjvvcODAAdq2bUtiYuIdvwFBqG4yCo2M\nmre7dEbS/4yM5sV7m6JSiRtJK4Msyzy75Vn6rOjDvvR9zq38/D44/yeoddB+gnPrvkq7Br6sebIr\njYL0XCwwMnJOHL8fTa+w/VUHA8MHArDn4h6yS7Ird+eS5JihFhwzmtpE9yRBEJynXMn6+vXr+e23\n3/jiiy+YPHkyvXv35quvvqJfv368/PLL2Gy2Mrf96aefWLt2LePHj6dnz56MGzeOTZs2YTKZ+Pjj\nj+/6jQhCdXD8YiHDZu8i/lwePu5aFk/syIh25R/WT7hzx3OPcyrvFAaLgUY+jZxbedznjueoEaAP\ncm7df1Hf351VU7vQrVEABrONSYv28s2OM8hy7bzxtJ5XPaL8o7DLdtafWV/5AbQaCW5+kJ8CR3+s\n/P0LglBjlStZX7NmDXq9npEjR16zfvz48Vy4cIE9e/aUuW1Q0PUnrtDQUMLCwjh3TgxFJtR8W09k\nMuLLXaTmldAwwIM1T3alY4S/0mHVOpfHVu9VrxfeLk68kTfrFCSucSx3ftp59d6Et5uWb8fHMqZD\nPewyvLXuCG/+mIjVVjsn6BnaaCgAq06sqvwvLVo36PCEY3nHR1BLvzQJguB8mvIUTkhIoHnz5mg0\n127WunXr0te7dOly2/WdPn2as2fPMnTo0Nsqn5iYiF3MElepLBZL6XN8fLzC0VRfG04WMW9fHnYZ\nooJ0TO/mTUHqKeJTlY7s5mra8bfJNtaeWAtAK1Urp76nsP3v449MfkgXktNtkF55v69RETIuZm8W\nHsxnUdxZEpPT+VtXP9y1dzeGQHU7/vVt9XFRuZCUn8TKuJU08WhSqftX67vRXO2G+uJhTv86l8KQ\nzpW6f2eqbsdecC5x/CuOSqWifv365dqmXMl6dnY2ERER16338/Mrff12Wa1WJk6ciF6v54UXXrjt\nbW7W1UaoWJc/vMLts8kyiw8V8dNJx1TxPRu4MqWdF1qVDYulev1frgnHP74wngJrAXq1nuZuzZ32\nnnQl6fim/ALAhcgxivyuBjVyJdANZv2Rz740I6/8lsGrXX0IcHfOTcvV4fhr0RLrFcuOvB3syt5F\nQ13DSt2/RXIjs8FgQk4vJ+jYInL82jll6E6lVYdjL1QccfydS60u/9/kciXrwE1nU7zdmRZlWWbi\nxIls376dVatWUa9evdvaTqPRoFKJ0SYr09UfUq1Wq2Ak1Y/RauejuBz2pDqG1hvb2ouRLTyr1Yyk\nNe347y7YDUAX3y646dycVm+dI6tQyTYKA9tiDopGqd9Ut3AtwZ4u/HNbFin5Vv6+JYfXewTQyE93\nR/VVx+M/KHgQnfw60dqztXPHz79N2U1HE5T8A/rcRHwKjlAc0KbSY3CG6njsBecRx7/i3EkeW65k\n3d/f/4at5zk5OcCVFvabkWWZxx9/nMWLF7Nw4UKGDBly2/tv2bKlSNYrWXx8PBaLBa1WS3R0tNLh\nVBvpBUYeX7iXw6lGdBoVH46M5oHoUKXDKreadPwNFgMHDh8AYEKnCbT0b+mciosy4KefAfAc+CbR\nEcr+nqKBzm1LmLjgT45dLOT1zdl8MroN/VuWfzz56nj8o6kCcWY+Anu/plHqGrjnUaWjuSPV8dgL\nziOOf8Wx2+0UFhaWa5tyZb6tWrXi6NGjWK3XDkt1+PBhAKKiom66/eVE/dtvv2X+/PmMGzeuXMEK\nQnVwNM0x9vXh1Hz8PHQsndSxWibqNY271p1lg5bxYrsXaeHXwnkVx80GqxHqtoeGPZ1X712o6+PG\niimd6dkkkBKLjSmL9/HVttO1bqQYq92qzHvu+hxIaji9BVKdPDyoIAi1TrmS9WHDhlFUVMSqVauu\nWb9w4UJCQ0Pp2LFjmdvKssykSZP49ttvmTt3LuPHj7+ziAWhCttyPIMHv9xFWr6RiEAP1jzZhXYN\nbn3FSagckT6RjI8a77yuSCW58OfXjuXuL1Wp/smerlq+frQ94zrVR5bhn+uP8toPCVhqyUgxc+Ln\n0G9lP45kH6n8nfs2gNYPOZa3f1T5+xcEoUYpVzeYgQMH0q9fP6ZOnUpBQQGNGjVi6dKlbNy4kcWL\nF5d2mp84cSILFy4kKSmJBg0aAPDss8/y9ddfM2HCBFq1asXu3btL63VxcSEmJsaJb0sQKt+CnWd4\na90R7DJ0jvBnzrh2eLuLvn5VgSzLFXOvwB9fgbkQglpCkwHOr/8uadQq3h4SRbi/B/9cf5Qle1I4\nl2Pg84fb4u1Ws/9vnsk/Q1ZJFitOrKBlgJO6PJVHtxch/ns4tg7Sj0CwE6/mCIJQq5S7A/jq1at5\n5JFHeOONNxgwYAB79uxh6dKljB07trSMzWbDZrNdc/nxp59+AuCbb76hc+fO1zyGDRvmhLciCMqw\n2uy8sTaBGT85EvVR7euxcEIHkahXIR/v+5iX/vcSx3OOO69SUxHs/sKx3P1FqKL300iSxOPdI5j3\nSHvcdWq2n8xixJe7SMk2KB1ahXqwyYMAbDizAYNFgfca2ARaPOBY3iEm/hME4c6V++yi1+uZNWsW\naWlpmEwm4uPjGT169DVlFixYgCzLhIeHl65LTk5GluUbPpKTk+/2fQiCIgqMFiYu3MuiuLNIEvx9\nYDPeH9EKnaZqJm61kcFiYMWJFfx69lcyDBnOq3jfAkc3GL8IaFn1Gxz6tQhm+eTOhHi5ciqjiKFf\n7GRvco7SYVWY9sHtaeDVAIPVwIYzG5QJovtLjueElZBzWpkYBEGo9kRGIQh36FyOgQe/3MXWE5m4\nalV8ObYdk3tGVquhGWuDH5N+pMhSRAOvBnSt29U5lVqMsOszx3K3F0DlnLHMK1pUXW/WPt2VVnW9\nySk28/BXe1hz4LzSYVUISZIY0XgEAKtOrrpF6QpSJxoa9QPZDjs+USYGQRCqPZGsC8Id2Hc2l6Gz\nd3IivYggTxdWTO7CgKjyD40nVCy7bGfJsSUAjGk2xnnjbscvgaKL4FUXWo++dfkqJNjLlWWTO9G/\nZTBmm50XlsXzn1+PY7fXvJFiHoh8AI1Kw+Gsw87tAlUel1vXDy6BggvKxCAIQrUmknVBKKfV+88z\nZt5usovNtKjj5WipDPNWOizhBnZf2M2Z/DO4a9wZEnn7czrclNV8pZW0y7OgubMJh5TkrtPw5dh2\nTOkZCcBnm0/x9NL9GMzWW2xZvfi7+dO7Xm9Awdb1Bp2hQVewW2DnLGViEAShWhPJuiDcJptd5v0N\nx3hxeTxmm51+LYJZMaUzdbydNxOm4FzfHfsOgKGNhqLX6Z1T6b5vIe8seARB2/9zTp0KUKkkpg9s\nxr8ebI1WLbH+8EVGzonjQl6J0qE51ZhmYxjVdFRplxhF9HjZ8fzn15CbrFwcgiBUSyJZF4TbUGSy\nMvm/e5mzNQmAp3pHMndcOzxcyjX6qVCJzhacZdv5bYAjYXMKYwFs/cCx3PvvoHN3Tr0Keqh9PZZM\n6oSfh47ECwU88PlODqTkKh2W08SGxPJ6p9dp6tdUuSAie0NEb0fr+uZ3lItDEIRqSSTrgnAL53IM\njPhiF5uOZqDTqJg1ug0v92+GSiVuJK3K/F39eSX2FR5q8hDh3uHOqXTnLDBkg39jiKm+rep/FRvu\nx9qnutIsxJOsIhOj5u2usTeeKqbfTMfz4RVw4YCysQiCUK2IZF0QbmLP6WyGzN7J8fRCAj1dWD65\nM0Pa1FU6LOE26HV6xrUYxz86/8M5FRZcgLjZjuW+M0Bds66q1PNzZ+XULvRtHozZ6rjxdNHBfOxy\nzbjx9FjOMaZtncafF/9UJoA60dB6lGP5tzeghvxeBUGoeCJZF4QyfLfnLOO+3kNOsZmoul78+HRX\n2tTzUTosQSn/ew+sJVCvIzS7X+loKoTeRcO8R9oxtZfjxtNVRwv5YFcexWa7wpHdvZUnVrIheQPz\nD89XLojer4FaB2e2wanflYtDEIRqRSTrgvAXJquNv68+xGtrErDYZO5vXYcVk7uIG0mrCbts5+Wt\nL/Nj0o9YbBbnVJpxDA4sdiz3extq8Fj6KpXEKwOa8fGoaLQq2Jdm5uVfMziVUaR0aHflsZaPoZbU\n7Lqwi8TsRGWC8G0AHZ5wLG96E+w2ZeIQBKFaEcm6IFwlvcDI6Hm7WfrHOSQJXhnQjM/HxOCmqx6T\n3giO4Ro3Jm/k3T3vYrabnVPpphmOiW2aDYL6HZ1TZxU3LCaM9/oG4e+mIrXQytDZO/ntSLrSYd2x\nMM8wBjQcAMA3h79RLpDuL4GrN6QnwKFlysUhCEK1IZJ1Qbhk39lcBn22gwMpeXi5avj2sVim9hIz\nklY3l4drHNZoGB5aj7uvMHknnNgAktrRV70Waeyv41/3+NMyUEeRycqkRXv5ZNOJajuB0oSoCQD8\ndvY3kvOTlQnC3e/KREmb/+mYDVcQBOEmRLIuCMDSP1IYPS+OzEITTYL1/Ph0N3o1DVI6LKGcLg/X\nKCE5Z7hGWYbfLt2g2u5RCGh893VWM96uKt7qE8ijnRsA8Mmmk0xevI9Co5O6GFWiJr5N6BnWExmZ\nBYkLlAukw2TwCoOC8/DHXOXiEAShWhDJulCrGS2O/ul/X30Yi01mYFQIq5/sSniAE1pkhUr33yP/\nBaB7WHfqe9W/+wqP/ACp+0DrAT2n33191ZRGJTFzSBT/frA1Oo2K346kM3T2Tk6kFyodWrk93upx\nANYmrSW9WKFuPVpX6PO6Y3n7f8CQo0wcgiBUCyJZF2qtlGwDI77cVdo//W/3NuGLsW3Ri4mOqqXz\nhedLp5R/rOVjd1+h1Qy/v+VY7vIMeAbffZ3V3Mj29VgxuTMhXq4kZRYz5POdrD2YqnRY5dImqA0D\nwgfwXMxzeOo8lQuk9UMQHAXGfEfCLgiCUAaRrAu10m9H0rn/s+0kXijAz0PHogkdeLpPY9E/vRr7\nMv5LrHYrnet0JjYk9u4r/GMu5JwGjyDo8vTd11dDRNfzYd2z3ejWKIASi43nvj/I6z8cxmStPiOb\n/Lvnv3ks6jHctQrOQKtSX5ko6Y95kHVSuVgEQajSRLIu1CpWm533Nhxl0qK9FBqtxNT3Yd0z3eje\nOFDp0IS7NLTRUNoEtuGZmGfuvrLcZNjyrmP5nn+Ai4ItsFVQgN6FhRM68GyfRgAs3p3CyDlxnMsx\nKBxZNRN5DzS+F2xm+Ok5sFf/8ewFQXA+kawLtUZGgZGH5+9h7tbTAIzvGs6yJzoT6iPGT68JYkNi\nWTRwEa0CW91dRbIM614AiwHCu0PMI84JsIZRqyRevLcp346Pxcddy6Hz+Qz6bAebj1WP4R1tdhsb\nkzcy6ddJGCwKfcmQJLj/P457Is7uhAOLlIlDEIQqTSTrQq2w9UQm9326nT/O5OChUzP74ba8Obgl\nOo34CFR38lXTtjulG9Oh5ZC0GdQuMHhWjZ4AyRl6Nw1i3TPdiA7zJr/EwoQFe3lv/VHM1qrdSiwj\nM2vfLHan7WbNqTXKBeJT/8rNpr++AYUXlYtFEIQqSWQqQo1mttp5d/1RHv3mD7KKzDQN9uTHZ7px\nf+s6SocmOMm0bdP4dP+nFJgL7r6y4mz45e+O5Z7TwD/y7uusBcJ83Vk+pTP/d2l4x7nbTvPgnF0k\nZxUrHFnZNCoN46PGA7AgcQFmm5Mm0LoTHSdDaFsw5cOGacrFIQhClSSSdaHGSs4q5sE5u5i3zdHt\nZVyn+qx9uiuRgXqFIxOc5UDGATYmb+SbhG/IM+bdfYW/vAqGbAhqCV2fu/v6ahEXjZq3hkQxZ1w7\nvN0c3WLu/3Q7PxyouqPFDGk0hEC3QC4WX+S7o98pF4hKDQ986ph468haOLZeuVgEQahyRLIu1Ehr\nDpzn/k+3c+h8Pt5uWuY+0o53hrbCVatWOjTBSWRZ5tP9nwKOm0vvelz1U7/Doe8ByZE4qbV3H2Qt\nNCAqhA3PdadDuB/FZhvPLzvIi8sPUmSyKh3adVzULjzb9lkA5h6aS1ZJlnLBhLSCro5Y+PklMDrh\nSpEgCDWCSNaFGqXQaOHFZQd5YVk8xWYbHRr6seG57vRvGaJ0aIKTxaXFsTd9L1qVlinRU+6uMnMx\nrHvesdxxMoS1v/sAa7FQHzeWPtGJF/o2QSXB6v2pDPp0O/HnnHD1w8keiHyAVgGtKLYUM2v/LGWD\n6fkK+EVA4QX4faaysQiCUGWIZF2oMXadymLAJ9tZfSAVlQQv9mvC0kmdxGgvNdDVreqjmo4ixOMu\nv4xteRfyUhxTwF++2U+4K2qVxHN9G7NscmdCvV1JzjYw/MtdfPTbCSy2qnPzqUpS8UqHVwD44dQP\nnMk/o1wwWjcY9Ilj+c+vIWWPcrEIglBliGRdqPZKzDZm/JjIw/P3kJpXQn0/d5ZP7syz9zRGrRIj\nedREm89tJjE7ETeNGxNbTby7yi4cgN1fOJYHfSTGVHey2HA/NjzXg0Gt62Czy3z6+0mGzt7J8YuF\nSodWKjowmsmtJ/Nl3y9p6N1Q2WAiekKbcYAMPz0LVpOy8QiCoDiRrAvV2v6UXO7/dDsLdiUDMLZj\nfTY815324X7KBiZUqAUJCwAY13wcAW4Bd16R2QA/PAmyHVoOhyb9nROgcA1vdy2fP9yWz8bE4OOu\nJfFCAYM/28GcrUnY7PKtK6gET8c8Tbe63ZQOw+Het8EjEDKPwZZ/Kh2NIAgKE8m6UC2ZrDb+/csx\nHvxyF6ezignxcmXhhA78c1grPFw0SocnVLAPe37IoIhBPNry0TuvRJbh5xch4wh4BMHAD5wXoHBD\ng6ND+fWFHtzTLAizzc77G44xam5clRviMaskS7mJkgDc/eD+jxzLO2eJ0WEEoZYTybpQ7ew7m8vg\nz3Ywe0sSdhmGx9Tll+d70LNJoNKhCZUk2COY97q/h7eL951Xsn8RxC8FSQUPfgP6IOcFKJQpyNOV\n+Y+2518jWqN30bD3bC4DZm1j3rYkrFWgL/vaU2sZvGYw8w7NUzaQFg9Apycdyz9MgdxkRcMRBEE5\nIlkXqo0Co4V//JDAg3N2cSK9CH8PHXPGteWjUW3wdhfD7NV0NruNvRf3OqeytEOw/mXHcp/XoWF3\n59Qr3BZJkngoth4bn+9Ol0h/jBY7764/xpDZOzl0XtkRY7x0XhRZilh0ZBHnCs4pGgt9Z0JYLBjz\nYfn/gcWobDyCIChCJOtCtbAx4SL9PtrKf3efRZbhofZh/P5STwZEiZlIa4vFRxcz/pfxvLvn3bur\nqCTPkfjYTNC4P3R9wTkBCuUW5uvOd4935F8PtsbbzdGXfejsnby97gjFCo3L3qteL7qEdsFit/Dv\nvf9WJIZSGh2MXABufpAWf2V2XUEQahWRrAtVWlp+CU8s2suUxftILzAR7u/Okkkd+deD0fi465QO\nT6gkZwvO8tmBzwBo6tv0ziuSZVj7FOSeAe/6MGwOqMSfQSVJksRD7evx+0s9GdImFLsMX+84w70f\nb2PLsQxF4pkWOw21pGbLuS3sSN1R6TFcwzsMRnwFSLD3Gzi0XNl4BEGodOIsJVRJJquNOVuT6Puf\nrfx6JB2NSuLp3o3Y+HwPukTexegfQrVjl+28uetNTDYTHet0ZHjj4XdeWdxsOLYO1Dp4aIHjRj6h\nSgjQuzBrdAwLxscS5utGal4J4xf8yeT/7uVcTuXe7BnpE8mYZmMA+MfOfyg7sylAo77Qc5pj+afn\nIOOYsvEIglCpRLIuVCmyLPP70XT6f7yN9zcco9hsI6a+Dz8/252/9W+Kq1atdIhCJVtxfAX70vfh\npnFjRucZSNIdjp1/Ng5+e8Ox3P9dqNvOeUEKTtOraRC/vtCDSd0bolZJ/JKYzj0fbeXDX45jMFde\n15hn2z5LI59GZJVk8dqO17DLCt/82vMViOgFFgMsfwRMRcrGIwhCpRHJulBlJGUW8di3fzJx4V6S\nsw0Eerrw4choVk3pQtMQMVFNbXSh6AIf7XMMYfdc2+cI8wy7s4ryU2HleJBtEPUgxD7uxCgFZ3PX\naXjt/hasf7Y7XRv5Y7ba+XzLKfp8uJW1B1OR5Yofm91N48aHPT/EXeNOVEBUpezzplRqGPE1eIZC\n1glY+yTYbcrGJAhCpRDJuqC4/BIL//z5CP0/3sbWE5lo1RKTe0aw5W+9eLBdGCoxC2mtJMsyb8W9\nhcFqICYoprRbQrkVZcKiIVCYBgFNYfAsuNPWeaFSNQ3xZPHEjswZ144wXzcuFhh57vuDjJwTx+Hz\n+RW+/0ifSNYPX88zMc+gVlWBq3oeATDyW1Bp4chaxzwBSn+JEAShwonZYwTFGC02Fu5K5ov/JZFf\nYgHgnmZBvD6oBQ0DPBSOTlCaJEmMbDqS5IJkZnaZiUq6g7aFkjxYPAyyT4JXGIxbBS565wcrVBhJ\nkhgQFUKvpoHM336a2VuS2Hs2l8Gf72BQ6zq8dG/TCv174e/mX7pstpkx2Ux46hS80le/k+OG05UT\nYN8CcPGCfm+JL6CCUIOJZF2odFabnRX7zvPJphOkF5gAaByk59X7m9O7qZiYRrjinvr30DOsJxrV\nHfypMhfDkofg+VW0tQAAIABJREFU4mHH1O3/txZ86jk/SKFSuGrVPN2nMSPahfGvjcf54WAq6w6l\nsSHhIqNi6/HcPY0J9nKtsP2fKzjHS1tfIsg9iM/6fHbn9044Q8thjj7rPz4Nuz4FVy/o8bJy8QiC\nUKFEsi5UGrtdZkPCRf7z63FOX5pevK6PGy/0a8KwmLqoRXcXATiecxytWkuEdwTAnSXqVhN8PxbO\n7QFXb3jkBwho5ORIBSXU8Xbj41FtmNQ9gg9/Pc7mYxks2ZPCqn3nGd+1IVN7RlbIJGnF1mKS8pI4\nmnOUxUcX80iLR5y+j3Jp+wiYCh1jr29+B3Se0GmKsjEJglAhRJ91ocLZ7DLrD6cx6LMdPLVkP6ez\nivH30PHGoBZs/ltPHmwXJhJ1AYBMQyZP/f4U49aPIyEr4c4qsVkdXQRObwGtB4xdBSFRzg1UUFyL\nUC++eSyW5ZM7076BLyarnTlbk+j2r83859fj5BSbnbq/Zn7NeDnW0Xr90b6P7vz/pzN1fhJ6XZoo\naeMrcOA7ZeMRBKFCiGRdqDAWm52V+85z78dbefK7/RxJK8BDp+aFvk3YOq03E7o1xEVTBW7aEqqE\nEmsJz2x+hnRDOgFuAdT3ql/+Sux2R9eAy2Opj1kC9WKdH6xQZXRo6MeKKZ355rH2NAvxpNBo5bPN\np+j2wWbeWXeE9AKj0/Y1quko+jXoh9Vu5fktz3O+8LzT6r5jPV+BTk85ln982nHjqSAINYroBiM4\nndFiY8W+88zdmsT53BIAvFw1PNa1IeO7hOPrIWYeFa5ll+28uv1VErMT8XHxYXaf2XjpvMpXidUE\nPz4Lh74HSe2Ypj2iVwVEK1Q1kiTRp1kwvZoE8UviRT7fcorECwXM33GGRXFnGdk+jCk9I6nn537X\n+5nRZQan8k5xJv8Mj//6ON/2/5Y6+jpOeid3FBT0/yeYCuDAf2HlRBhSAtGjlYtJEASnEsm64DSZ\nhSaW/pHCf3efJbPQceNogF7HxG4RjOtUH09X5/cjFWqGT/d/yqaUTWhVWmb1nkU9r3LeCFqcdamP\n+m5Hoj5sLjS7v2KCFaoslUpiYKs6DIgK4X8nMpm9+RR7z+by3Z4Uvv/zHPe1qsP4ruHE1PO54xtE\nvXRezL93PhN+mcDZgrPMjJvJnH5znPxOykmSHEOSWkogYSWsmewYi73366ASF9AFoboTybpw1xJS\n8/lm5xnWxadhtjlm+Qv1dmVyz0hGxdYTs44KN7X8+HK+TvgagJldZtI2uG35Ksg46hj1JS8FXLzh\noQUQ2cf5gQrVhiRJ9G4aRK8mgew5k8PsLafYfjKLn+Iv8FP8BaLDvHmsazj3twpFpyl/MhvkHsT8\ne+czM24mMzrPcP4buBMqNQz/Cnzqw46PYPt/IOuk44ur7u6uKAiCoCyRrAt3xGKz80viRRbsTGbv\n2dzS9W3q+TC+azgDo+rc0UlQqF1kWWZH6g4Anmj9BIMjB5evgpObYMVjYC4E34bw8HIIbOL8QIVq\nSZIkOkX40ynCn4TUfBbsSubHgxeIP5/PC8vieXf9McZ2rM/DHesT5Fm+YR9DPEL4su+X16yz2q13\nNnqRs6hU0PdNCGgCPz4DR390fIkdsxS8QpWLSxCEuyKSdaFcTqYXsmLfeVbvP09WkWO0Ba1a4v5W\ndXi0Szgx9X0VjlCoTiRJ4oMeH/DDqR8Y3bQcfWxlGfbMdQxbJ9uhQVcYtRjc/SouWKFai6rrzYcj\no5k+sBnfX+qul15g4pNNJ/l88yl6Nwviofb16NU0EK26/A0N60+v59vEb5nXbx6+rgr/HWwzBnzD\nYdlYSDsIX/WBMd9DaBtl4xIE4Y5Islw15yq22+0UFhZes87T0xOV6H9XqeLj48k3mNhzwcKudDiQ\nklf6WoDehbEd6zO2Y32CKnAyEkE58fHxWCwWtFot0dHRTqmz2FLMD6d+4OFmD99Zv2FTIfzyKuxf\n5Pg5Zhzc/zFoxI3LzlYRx7+qsNjsbEy4yIJdyey76upggN6FEW3rMrJ9GI2Cbm+m0hJrCQ/88AAX\niy/S1Lcps++ZTbBHcEWFfvtyzsCSUZB1HDRuMOgjiB5zW7Od1uRjL9yaOP4V507yW9GyLtyQyWpj\nx8ksFu3KIe68AbPNsV6tkuhzly1QQu11eRz1ozlHKTIXMTl6cvkqOLUJfnoe8s8BEvSbCV2eFVOt\nC+WmVasYHB3K4OjQv1wxNDF322nmbjtNTH0fhkSHcl+rOjdtkHDTuDGv3zzGbxzP8dzjjPxpJO92\nf5dudbtV4ju6Ab+G8Phvjq5iSZvhh6mQsBoGfSxm8xWEakS0rAulzFY7O09lse5QGr8euUih0Vr6\nWpiXhke7NWZoTF0CPV0UjFKoTM5sXUnKS2LqpqmkFafh5+rH7HtmExVwm5MVGXLgl9cgfonjZ58G\n8MCnYmjGClbbWtcsNjtbjmWwfO95thzPwGZ3nB4lCTqE+zGodR0GRNUp829gSkEKL219iWM5xwCY\n1GoST7Z5Utl+7OCYKGzXp/C/98FmAp3e8UW33YQyR4upbcdeuJY4/hXnTvJbkazXcsUmKztPZbHp\naDq/JKaTX2IpfS3Yy4UOIVo619XRItiNNm1Ef8faxhl/sO2ynZUnVvLxvo8pshQR7hXOF32/oJ7n\nbbbsHVkLP/8NijMACTpOgXv+ATqPO4pHuH21+YSdUWjkp/g0fj50gf1Xdf9TSdCxoT8DW4XQu2nQ\ndWO3m2wm/v3nv1l2fBkAsSGxfNXvK9SqKjAqVuYJx42n53Y7fm7QFR74DPwjrytam4+9II5/RRLd\nYITbkpJtYPOxdH4/lsGe0zmlwy0CBHq6cF9UCIOiQ2lX35fDhw9hsVjueExioXZLzk/mjV1vcCDj\nAABtg9oyq/csfFx9br1xdhJsmuEY0QIgoCkM+Rzqdai4gAXhkiBPVyZ2a8jEbg1JzSthw+E01h1K\n4+C5POJOZxN3OhtIpHGQnj7Ng+jTNIh2DXxxUbvweqfXaR/cnhlxM4gNia0aiTo4RkoavwH+nO/4\nbJ3dCV92gR4vO74Eu+iVjlAQhBsQyXotkF9i4Y8zOcQlZbP1RAZJmcXXvF7fz50+zYIYEBVCbLgf\napVIzAXnsMt2ErIScNO48Vzb5xjddPStE5esk7DtQzi83DHSi0oD3V5wJBQa0QVLqHx1fdx4vHsE\nj3eP4FyOgQ0JaWw6msG+s7mczCjiZEYRc7eexstVQ/cmgXSNDKBzZHdWDV5FiEdIaT3Hco4R4BZA\ngFuAcm9GpYKOT0CT/vDTc3B6C2x+G+JmQ5enIXYSuJZz9mBBECqUSNZroGKTlT+THcl53OlsElLz\nsV/V2UmtkogN96VPsyD6NAsmMtBDtJwLTnOh6AKheseYzhE+Ebzb7V2iA6NvPSV7xlFHkp6wCrj0\nH7Zxf0eXl5BWFRu0INymen7uPNEjkid6RJJvsLD1ZCZbjmWw5XgGeQYLPx9K4+dDaQCEeLnSJTKT\nTpH+dGjow993/J3UolTGNR/H+KjxeOpub7SZCuHbAB5ZA4dXOPqy5yTB72/Bzk+h81Oo3LuAJEb5\nEoSqQPRZr+ZkWeZMVjEHUvLYn5LLgZQ8jqcXlt4YdVnDAA86RfjTtZE/3RsH4u2mva36Rb+12u12\nj78sy+xN38uiI4vYfn47i+9bfHs3j8oynPsDdn/h6Jt+OUlvej/0fBlCY5zzRoQ7Ij7/t89mlzl4\nLpdtJ7KIO53NwZS8a7oYSupCvMIXY9edBUCv8ebxVo8zruUYXNQKXzGyWSFxNWz7N2SdcKzSeJDe\ncBh5EUNo0fleZeMTKp347Fcc0We9hrPbZc7lGjhyoYAjaQUcTs3n4Lk88gyW68qG+brRJdKfzpH+\ndI4IIMRbtJAIzmexW/gl+RcWJS7iaM7R0vW703bfPFnPToJDy+HQMsg9c2V98wcc3V3qtK7AqAXB\n+dQqiXYN/GjXwI8XgBKzjX1nc4k7nUVcUjaHzkvkJ01Boz+CLugXisjgkwP/4bN939DSfRj96g8k\nJiyEpiGeuGoruY+7WgOtH4KoEXDkB9j6b9SZRwk9uZg6J7+D492g9ShoMUR0kREEBYhkvYrKLjKR\nlFnMqYwijl90JOdH0wopMlmvK+uiUdGqrjcx9X2Iqe9LTH0f6ni7KRC1UFuYbCYWH1nMkmNLyDBk\nAOCidmFI5BDGthhLhHfE9RsVZzta7w4tg/N/Xlmv9XAkAV2egeAWlfQOBKFiuenUdGscQLfGjv7p\nBrOVw+fz2Z/SnP1ne7I3ZxNmzw2gzeWQ8RvifnHFbqyPSoLIQD0tQr1oXseLxkF6IgP11PNzr/j7\niVRqR8LeYhjJGz/DL2kVXtnxkLzd8Vj/N2h6nyNxj+wjJiIThEoiknUFFZusnMs1cDbbQEq2gaTM\nIpIyiziVUUTuDVrLAXQaFU2DPWlRx4sWoV7E1PehWYgXOo3oHiRUrKySrNIb49SSmmXHl5FhyCDA\nLYAxzcYwssnIa6dZNxsgJQ7ObIXT/4O0Q5R2c5FUENEbokdDs/vFMIxCjeeu09Axwp+OEf5AJLLc\ngTPZTzL3wHfEZ+0loF4MRy4UklNs5qy8ipQLVn462ha7KQSQ0KlVNAzwoFGQnshADxoGelDfz516\nfu4E6l2ce9+RSkV+3V5kBXXF3ZJDC+thiF/mmAk1cbXjofWABp2hYU+I6AnBrcocs10QhLtT7mS9\nqKiI119/neXLl5OTk0OzZs2YPn06o0ePvuW2GRkZTJs2jXXr1mEwGIiOjuadd97hnnvuuaPgqzJZ\nlskpNpOWb+RivpG0/BLS8o2k5pWQkmPgXI6BrCLzTeuo6+NGoyA9jYP0tKzrRYs63kQEeohZQ4VK\nYbAYOFJ4hP15+zlYdJCChAK2j96OTq1Do9LwXNvnsNqtDGw4EJ1KC4UXIeVXuHAAzmyD83+A7S//\nx0NaO1rlWj0IniE33rEg1AKSJBER4MsH/Z4uXSfLMufy8hnx89sYbcXo/LejsntjKQ7HUtSQk7kR\nHE8PBK5NzF21Kur7uVPfz50wX3fqeLtSx8fN8eztSrCX6x2fNyzuwRB9L3R7EdIOOpL2hFWOeQ9O\nbXI8ANz8oGF3CO/u+JwHtwAXBW+gFYQapNzJ+vDhw/nzzz95//33adKkCUuWLGHMmDHY7XYefvjh\nMrczmUzcc8895OXlMWvWLIKCgpg9ezYDBgxg06ZN9OzZ867eSGWw2WXyDGZyDRbyDGayi81kFZnI\nKjSTWWQks9BEVpGZzEITFwuMmK32W9bp464tbR2JDPAg8tIlz8hAPW66KjI2r1Br7Ejdwc+nfyYx\nO5Hk/GRkrtyorFFpOJFznCj3UMhL5v7CQrh4GHZ+DekJYMi+vkKvMEerW8Oe0LAHeN1iRBhBqMUk\nSaKOtwcf9HiXH5N+ZNv5bVjIR+0Zj9ozHoCG7rG0UD3P2WwDZ3OKSTekYjT7ciK9iBPpRWXUCwF6\nF4I8XQj0dCFAf+2zv4cOX3cdvh5afN11N+4zL0mOG75DY6D/u5CRCKe3Oq6cnd0FJTmOm8SPrL2y\njW9DCIm6lLxHgV8E+NQTV9IEoZzKNRrM+vXruf/++0sT9MvuvfdeEhMTSUlJQa2+cYL5xRdf8NRT\nT7Fr1y46d+4MgNVqJTo6Gr1ez549e64pX1VGgzGYrdw3azu5Bss1s3vergC9C3W8XQnxdiX0UmtH\ng0vJeT0/99selUUp4o7w6k+WZYosReQZ87houEhqUarjUeh4frXjqzT1awpWMwvj5/Bhwlel2wZI\nrrSxu9PDDP2sJvR558B844QASQX+jR3DLDboAhG9HCdnMSxotSU+/8oyWo0czjrM3ot72Zu+l/jM\neB5t+SjPxDwDOLqm9V7eG61KR6BrGJ7qumhsgVjNXhQb3Mkv8CczR4/FVr5B39y0ajy0oNdJ6HVq\n6gT44OWqxctNg5erFk9XDZ6uGtx1GvQuGvRaGf+8w/imx+GeeRBtZgKqootl78AjEHzqg08Dx7NX\nXfAIcKy//HDzFd1qFCQ++xWnwkeDWbNmDXq9npEjR16zfvz48Tz88MPs2bOHLl26lLlt06ZNSxN1\nAI1Gw7hx43j11VdJTU2lbt265QmnUrhp1ZzLLblmKEQvVw2+l1oiLrdMBOp1BHi6EKh3IcDThRAv\nV4K8XHDRiNbx2k6WZWRkZFnGjh3ZbsdmtyLLdnQqDRpJDcgYLMUUmvKx2S3YbBasdgtWmwWLzYTZ\naiRCH4qX2hXsdlIKz3Eg5wgGSzHFlmIMFgMlVgMGq5Eiq4FJQZ1ppvUGSwkrsg/wdtauMuM7s/RB\nmhbmgzGfzlotT3m40cJkpoXJTIC9jKtDnnUutZq1crScBUdBUHPQihubBcFZXDWuxIbEEhsSC4DZ\nZsZkM5W+nlaUhovaBZPNxAXDaeD0lY11MKHXBJ6LeZ7sYjOHLp7m/QMvo8EdleyObHfFZnXFbNZh\nMmswFjagIK8eVrtMibUEs+4MuWYNmNQcKVCD7HjIshrZ7ga2y63jdlAZARXILQHHnAg+chGtNedp\npTlPS1UKjUmhjj0DPcVQnOl4pO4r873bUWPUemPW6LFoPLBqPbFq9Vi1nti0euwaN+RLDzSuyDo3\nJI2bY+I0tQ5Jc+mh1iGptUgaHSq1FkmlBrUWlVqNSqVxvKZSIanUqFRqVCoVskpyvIaESqVGUklI\nkgpJJaGSVEiShCSBhFTaFlH6zOXXHFdKLjdVSBJiPhPhjpUrWU9ISKB58+ZoNNdu1rp169LXy0rW\nExIS6N69+3XrL2+bmJh4y2Q9MTERe1nJQwWR7XYCGr983XojkAY0NFh451xB6freof6Yyvg8xpgs\nzM66UnZgHT/yy7i7v7nZyteZ+aU/Dw/x5WIZfQ7DrTaWpOeV/vxwsA/JZXxJqGOzs+pibunPEwO9\nOaq78X8DH7vM+gs5pT9PjvPmoMuNy7rKsPnClW4QL/l7Eeda9lWDXalXyr7m58kWt7JHFfj9QjZu\nl74rve2rZ4N72WMS/5yWg++lL1b/9vFgjUfZQ1auSsulzqVxkD/zduc7T/cyyy65mEOE1YaEzFwv\nD7728kCWSm+X5Op2q/+mZdHS7Oir/Y2Xnk/8vMus99u0dNobHSffNV563vf3K7PsnIsZdC0xAvCn\n3oMZgf5llu1/bAvNDCUA+Li7QXAgbnY7gTYbda1W6lqs1LXaCLNaiTGawGYDoLHVTsMSDVaXQKx6\nX7K1XpjdgjC7h2DzDMPsHoLZPRj5r+NCZ1E6PrNQc1gsltLn+Ph4haMRbuSrqK/IMmeRakwl1ZRK\nhimDPEseedY8NPkaDh8+BEC+IYmLJWevr0DjeAxpOIQHQzpSYpU5VZjKv1K+LXOfgZZe+BmGYrTa\nKbJlkx30z+vK2IADwJ7cjpguTgZAUhejb/xOaRkJkJAvPUPPQjszsnLxkYoxSXZ6hroDdqAQKLzS\nU98OffJKeD/zynmkQ4Owa+q9WpcSIx9nZJX+3KteXUrKOPfGGE3MSc8s/XlAWCi5ZZx7m5nMfJOW\niXzpXYwMCyKtjHNvA4uVhalXzqePhfqTXEZX1yCrne/PX3lvU+v4cryMc6+XTWbNuStlXwzxJr6M\nc6+LDBvOXvk9vBrkxW73m5x7k7OQgOLVMDPQk60eZZ97153Nxv1SR40PAvT8or/JuTclu/Q8PctP\nz1qvsssuPp9D6KUuxXN9PVh2k5Huvk7NpaHFcS5b6OPOQp+yz+mzL+TR3GzliK4VukH/KbNcRVCp\nVNSvX79c25QrWc/OziYi4voh2fz8/Epfv9m2l8uVd9vLrFYrtktJRWWR7XYMN7k0YcKO2lpS+nOJ\nBMYyypuRrylrlCizbpMk/6Ve37LLYr22XnzKLGu02f8Sg1eZZV1lG2rblbImPMssK9uvrdeE/qa/\nt6vLmvG4RVkj6kt/BCyy203LqqxG1Je+0Fll15uXtRtRX/r/ZJNdMN5kWDSV3YTa5hg20y67YrpJ\nWUm2IcmX/5/e/Mvl1Um+RgaNLKOWZdSAWgY1MjpZRieDStJgU7shSyqCcKGz0Yq7LOGOhJuswg3H\nwx01dT2akOfpjl3lQpRay3q7C1q1K3adGzatBzaNOzaNHpvGnRytB5kaDywuPti0no7uLDdjB+zl\n7xImVG+XE3eh6vFV+eLr7kuU+/VzG1w+boGqQF5u8DIGuwGDzUCJraR02Wg3Ul9XH6vVihbw1UED\n1waY7WZs2LDJNqyyFZvsWO5Ux5PhwY5GiEyzlWkny46tW5gb/Vv6YbTK5FvVzMu58ldP5tq/gUe9\nOjFDPw7ZZkFrzcaoerfMepNVdViviUGHGZ1sokSVVmbZAklHDl6oZDtqbBhUEiVlnSP/0vpdopLK\nPp+qJNTSlXdhlMoua5Ik3KQrN9ybVXLZZVV2PKQrV1AsNymrk23oJWPpz9abnNPtdjseV5dVlX1O\nB/CQjKVffGzSzc/THpIR90u/B7vkftOybpIJD8lxbpRVNz+nO8peOp9KNz+nu0hmPCTH/3dJ0t1G\nWTMau6nS/7aV1V38ZsrVZ71JkyZERkayYcOGa9anpaURGhrKe++9x/Tp02+4rU6nY+LEiXz55ZfX\nrI+Li6NLly4sXbr0mhFlbtSnJyUlRZGW9dz8hDJfd5G0+GquTBKRbsmmrF+oTtLgp7nSypphycFe\nRmmtpMZf41P6c6YlF1sZiZ8GFQHaK0PmZVlysZZRVo2KwKvKZlvzsMg3/gKkQsJPuvLeCijGLF8/\nzjs4WjKCtVdaenOtBZjksj8AIVeVzbMWYpTLHhknSOuH6lICmWctxGi/UvavVxUDNb6lZQtsxZTY\njZTFX+NzqQsKFNqKKbGbblhORsJP44VGcny3LbYbMdgdXzYkrvwxkC7989J4oFFpkZEw2k2Y7JZL\nlz8dl1BVkhpwPGtVOiRJdekaqQqZq5YlFSDdOnmuQFf/EdNqq/b9FYLzieNfe93usb/cvc8u20uf\nL3f7k5HRSBpc1Y6WU7tsJ9+aX7qd/Jfzn06lw1PjWVo223zjRjwZGReVC97aq86npowyY9SqtPhe\ndd67pqx8KdmW7UjIaCQ1/hpvkGVku5UMUzZ2bI5Y7Zdilh1nbg0afDXeSLLj/WZachxdHWVHjNJV\nu1BJEv4a39JvKDnWPKyX63W8qVIqVPhrfJEvncdzrflYyzz3SgRorjSE5trysdygrCxfXzbfVoC5\njHOv1WYnQO2LJElo1GrybYWlZW+Utfirr5x7C21FGOUbn08B/NQ+qK869xrlss/TV5ctshsosZeU\nWdZb5Y229DxtKD1P34iP2gutpEWtdcXTL7jMchXhRi3rTu2z7u/vf8MW8Jwcx6WdG7WcO2Pby1q2\nbFnpN5g63P6U583LUWtFlXWmq28y6SpuMql1xE1GtZs4/rWXOPa1mzj+FedGjdG3Uq7Mt1WrVhw9\nehSr9dpvbYcPHwYgKqrs6cVbtWpVWq682wqCIAiCIAhCbVSuZH3YsGEUFRWxatWqa9YvXLiQ0NBQ\nOnbseNNtjx07ds0QjVarlcWLF9OxY0dCQ0PLGbogCIIgCIIg1Gzl6gYzcOBA+vXrx9SpUykoKKBR\no0YsXbqUjRs3snjx4tJO8xMnTmThwoUkJSXRoEEDACZMmMDs2bMZOXIk77//PkFBQXzxxRccP36c\nTZs2Of+dCYIgCIIgCEI1V+4ZTFevXs1rr73GG2+8QU5ODs2aNbvu5lCbzYbNZuPqe1ddXFz4/fff\nmTZtGs888wwGg4E2bdqwYcOGajF7qSAIgiAIgiBUtnIn63q9nlmzZjFr1qwyyyxYsIAFCxZctz44\nOJiFCxeWd5eCIAiCIAiCUCuVO1mvLDcaUbKyh20UHEMMqdWOWd3E77/2Ece/dhPHv/YSx752E8e/\n4tzo93mrUdTLNc56ZbJarRQXFysdhiAIgiAIgiBUGA8PDzSastvPlZttRRAEQRAEQRCEmxLJuiAI\ngiAIgiBUUSJZFwRBEARBEIQqqsr2Wbfb7dd1wpckCUmSFIpIEARBEARBEO6cLMvX3VCqUqlQqcpu\nP6+yybogCIIgCIIg1HaiG4wgCIIgCIIgVFEiWRcEQRAEQRCEKkok60KZduzYwX333Yevry9ubm40\nbtyYt99+W+mwhEpw4MABhg4dSmhoKO7u7jRr1oy33noLg8GgdGiCExUWFjJt2jTuvfdeAgMDkSSJ\nGTNm3LDs/v376du3L3q9Hh8fH4YPH87p06crN2DBqW7n+NtsNj766CMGDBhAWFgY7u7uNG/enOnT\np5OXl6dM4MJdK89n/zJZlunRoweSJPH0009XTqACIJJ1oQxLliyhZ8+eeHt7s2jRItavX88rr7xy\ny1m2hOrvyJEjdOnSheTkZD755BPWrVvH6NGjeeuttxgzZozS4QlOlJ2dzbx58zCZTAwdOrTMcseO\nHaNXr16YzWaWL1/ON998w4kTJ+jevTuZmZmVGLHgTLdz/EtKSpgxYwYNGjTgk08+Yf369UyaNIl5\n8+bRtWtXSkpKKjlqwRlu97N/tdmzZ3Pq1KkKjky4IVkQ/uL8+fOyh4eHPHXqVKVDERTw2muvyYB8\n6tSpa9Y/8cQTMiDn5OQoFJngbHa7Xbbb7bIsy3JmZqYMyG+++eZ15UaOHCkHBATI+fn5peuSk5Nl\nrVYrT5s2rbLCFZzsdo6/1WqVs7Kyrtt2xYoVMiD/97//rYxQBSe73c/+ZWfOnJH1er28evVqGZCf\neuqpSopUkGVZFi3rwnXmz59PcXExr7zyitKhCArQarUAeHt7X7Pex8cHlUqFTqdTIiyhAtzOcLhW\nq5V169YxYsQIvLy8Stc3aNCA3r17s2bNmooOU6ggt3P81Wo1/v7+163v0KEDAOfOnauQ2ISKVd6h\nsJ944gn69evHsGHDKjAqoSwiWReus23bNvz8/Dh27Bht2rRBo9EQFBTElClTKCgoUDo8oYI9+uij\n+Pj4MHW8BeA7AAAEhUlEQVTqVE6fPk1hYSHr1q1j7ty5PPXUU3h4eCgdolCJkpKSKCkpoXXr1te9\n1rp1a06dOoXRaFQgMkFJmzdvBqBly5YKRyJUtPnz5/PHH3/w+eefKx1KrSWSdeE6qampGAwGRo4c\nyahRo9i0aRMvv/wyixYt4r777hP91mu48PBw4uLiSEhIIDIyEi8vLwYPHsyjjz7KrFmzlA5PqGTZ\n2dkA+Pn5Xfean58fsiyTm5tb2WEJCkpNTWX69Om0b9+eQYMGKR2OUIFSU1P529/+xr/+9S9CQ0OV\nDqfW0igdgFD12O12jEYjb775JtOnTwegV69e6HQ6nn/+eX7//Xf69u2rcJRCRUlOTmbw4MEEBwez\ncuVKAgMD2bNnD++88w5FRUV8/fXXSocoKOBml8zFzNK1R05OTmmjzbJly24666JQ/U2ZMoXo6Ggm\nTZqkdCi1mkjWhev4+/tz8uRJ+vfvf836gQMH8vzzz5cO4SbUTNOnT6egoICDBw+Wdnnp0aMHAQEB\nTJgwgf/7v/+jZ8+eCkcpVJbL/ZUvt7BfLScnB0mS8PHxqeywBAXk5ubSr18/UlNT2bx5MxEREUqH\nJFSglStXsnHjRnbs2EF+fv41r5nNZvLy8vDw8Ci9z0moOOIrsXCdG/VNBUq7v4iWlJrt4MGDtGjR\n4rq+6bGxsQAkJCQoEZagkMjISNzc3Dh8+PB1rx0+fJhGjRrh6uqqQGRCZcrNzaVv376cOXOG3377\nrczzhFBzJCQkYLVa6dSpE76+vqUPgK+++gpfX19+/vlnhaOsHUTWJVxnxIgRAGzYsOGa9evXrweg\nU6dOlR6TUHlCQ0NJTEykqKjomvVxcXEAhIWFKRGWoBCNRsPgwYNZvXo1hYWFpetTUlLYsmULw4cP\nVzA6oTJcTtRPnz7Nr7/+SkxMjNIhCZXgscceY8uWLdc9AIYOHcqWLVvo1q2bwlHWDqIbjHCde++9\nl8GDB/PWW29ht9vp1KkTe/fuZebMmQwaNEh8OGu4559/nqFDh9KvXz9eeOEFAgIC2L17N++99x4t\nWrRg4MCBSocoONGGDRsoLi4uTcSPHDnCypUrAbjvvvtwd3dn5syZxMbGMmjQIKZPn47RaOSNN94g\nICCAl156Scnwhbt0q+MvSRL9+/fnwIEDfPLJJ1itVnbv3l26fWBgIJGRkYrELtydWx378PBwwsPD\nb7ht3bp16dWrVyVFKkiyGNpDuIGSkhJmzpzJkiVLSEtLIzQ0lLFjx/Lmm2/i4uKidHhCBduyZQvv\nv/8+hw4dIj8/n3r16jF48GD+/ve/33DMZaH6Cg8P5+zZ/2/nDk4YBqEADL9AFskqLuIAGSBLOES2\n8eQM0k1666G0tJeUV/i+qwiCiP9BvL0cm3M+LusxRhzHEb33WNc1SinRWhNqf+7T/kdEbNv2dn6t\nNc7zvGJpXOzbs/9sWZbY991Xjj8k1gEAIClv1gEAICmxDgAASYl1AABISqwDAEBSYh0AAJIS6wAA\nkJRYBwCApMQ6AAAkJdYBACApsQ4AAEmJdQAASOoO2bbEI9XwMhwAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAusAAAEaCAYAAACo3xkcAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzs3Xd0VPW2wPHvmcwkIb2TCgkGCKEE\nkADSe1EsgBog8FS8V0Us3KfisyGCBeHeu7AXROFKVbpSvAihiBB6aAGBQAoEQioppEx5fwwJxoQy\nyZSU/VlrFs6cc357T04Sd37zK4rBYDAghBBCCCGEqHNUtk5ACCGEEEIIUT0p1oUQQgghhKijpFgX\nQgghhBCijpJiXQghhBBCiDpKinUhhBBCCCHqKLWtE7gZvV6PXq+v9JqiKCiKYqOMhBBCCCGEqDmD\nwcBfF2JUqVSoVDfvP6/TxXphYaGt0xBCCCGEEMJinJ2db1msyzAYIYQQQggh6igp1oUQQgghhKij\npFgXQgghhBCijqqzY9arm0h6uzE9wvyOHz+OVqtFrVbTtm1bW6cjrEzuf+Mm97/xknvfuMn9t5zq\n5mTebvGUelWs3262rDA/vV6PTqeTr30jJfe/cZP733jJvW/c5P5b1+2KdbkDQgghhBBC1FFSrAsh\nhBBCCFFHSbEuhBBCCCFEHSXFuhBCCCGEEHVUnZ1gKoQQQghRUzqdjtzcXIqKimydSr2j0WhQq9Uo\nikJqaqqt06l3VCoVXl5eNGnSxCztSbEuhBBCiAZFp9Nx4cIFPD098fLyuu1qG6KyoqIiDAYDiqLg\n5ORk63TqnbKyMtLT0wkKCsLOzq7W7UmxLoRotK5pr/HF4S84cPkALT1b0smvE52bdibENcTWqQkh\naiE3NxdPT09cXV1tnYpohDQaDT4+PmRlZeHn51fr9qRYF0I0SkeuHOGN397g/NXzxueZR1h5eiUD\nmw1kbv+5tk1OCFErRUVFeHl52ToN0Yg1adKErKwss7QlE0yFEI3ON0e/YcLGCZy/eh6/Jn682e1N\nnmj7BJ38OtHVv2vFeRlFGbyy/RXySvJsmK0QoiZk6IuwJXN+/0nPuhCi0fFp4oPeoOfesHt5vdvr\nuDu4VznHYDDw8vaXOZRxiIyiDL4e8jUOdg42yFYIIURjJj3rQogGz2AwcLHgYsXzB+96kAXDFvBh\nnw+rLdTB2CvyVve3cNW4cjDjIK/tfA2dXmetlIUQQghAinUhRCOw6fwmJmyYUDGcRVEU7m56922v\na+nZko8GfIRGpWFz8mZm75uNwWCwdLpCCCFEBSnWhRANWk5xDrP2ziLjWga/nP/F5Ouj/aN5v9f7\nACw5uYQFxxeYOUMhhBDi5qRYF0I0aLP3zSa7OJtwj3BGho+sURvDwobxcpeXAfj3gX/XqOgXQggh\nakImmAohGqwdaTv4OelnVIqKGT1moLHT1Litx9o+xuWiy/x+4XeifKPMmKUQQlhHZmYmqampdOrU\nydapCBNIz7oQokEqLCtk5p6ZAIxvM572vu1r3ebLXV5m0b2L8Hf2r3VbQghhTTt27CAsLIzOnTvz\n9ttv2zodYQIp1oUQDdLcA3O5VHiJYJdgJnecbJY2VYoKF3uXiucFpQVmaVcIIWrr8uXLNz1mMBiY\nMWMGS5cuJSAggIsXLzJjxgwiIyPR6/WVzj106BAxMTGEh4fj4+NDREQEM2bMoKio6LY5bNu2DUVR\nqn3s2bPH5PdUUFDAlClTCAwMxNHRkY4dO7Js2bI7utaUXObPn09QUBCFhYUm52gNMgxGCNHglOnK\nOJl9EoDpPabjpHEya/sluhJm753NhnMbWPvQWvycar+dtBBC1EZsbCzffPMNoaGhVY7Fx8czevRo\nRowYwalTp8jJySEyMpIFCxagUt3otz1x4gQ9evSgZcuWfPjhh/j4+LB3715mzJjBgQMHWLt27R3l\n8v7779O/f/9Kr7Vr187k9zRq1Cj27dvHrFmzaNWqFUuWLGHs2LHo9XrGjRtntlwee+wxPvzwQ2bP\nns0777xjcp6WJsW6EKLB0dhpWDBsAXsv7aVbQDezt2+vsud07mkKygr4+sjXvNn9TbPHEEIIU+zf\nv5/58+czc+bMKsfWrFnDCy+8AICrqyvvvvsuHh4ejBo1qtJ5S5Ysobi4mCVLlhAWFoaiKNx7772k\np6fz9ddfk5OTg6en521zadmyJd27d6/V+9mwYQObN2+uKNAB+vfvT3JyMq+88goxMTHY2dmZJRe1\nWs3TTz/NzJkzefXVV3FyMm8HT22ZPAymNh9JAKxdu5a+ffvi5uaGs7Mzbdu25euvvzY1DSGEuCU7\nlR33BN5jkbYVReH5Ts8DsPL0Si4UXLBIHCGE+RWVam3+MLekpCTy8vL49ttv0Wqrtp+enk5gYCAA\npaWlzJ8/n3HjxlXqVQfQaIyT8N3c3Cq97uHhgUqlwt7e3uy538zq1atxcXHhkUceqfT6E088wcWL\nF4mPjzdrvNjYWK5evWpSTWstJves1+YjiVmzZvHGG2/wzDPP8Nprr6HRaDh58iSlpaU1fgNCCFHu\nZPZJNiRtYFLHSTRRN7ForGj/aLoFdCM+PZ6vEr5iRs8ZFo0nhDCPyGm2X3r1/Kz7zNre/v37CQsL\n49y5c6xdu5bRo0dXHDt16hStW7eueB4fH09WVlaVoSFgHA4yd+5cpkyZwowZM/D19WXr1q189dVX\nTJ48GWdn5zvKZ/LkyYwZMwYnJyfuuece3nrrLXr16mXSezp27Bht2rRBra5cqnbo0KHieI8ePcyW\ni7+/PxEREaxfv56JEyealKulmVSs1+YjiQMHDvDGG2/wwQcfMHXq1IrXBw4cWIv0hRDihk8Pfcr2\ntO2U6Ep4rdtrFo/3fKfniU+PZ93ZdUxsN5FQ91CLxxRCiL/as2cPn3zyCSNHjuSTTz6pVKyvXbuW\nBx98sOL57t27AejcuXOVdkJDQ9m9ezcPPfQQ7dvfWEHrhRdeYO7cubfNw93dnRdffJF+/frh7e3N\nmTNnmDNnDv369WP9+vUMHTr0jt9TVlYWLVq0qPK6l5dXxXFz59K5c2d+/fXXO87RWkwq1m/1kcS4\nceOIj4+/6V85n376KQ4ODjz//PM1z1YIIW4i+Woy29O2AzCuzZ1NPKqtKN8o+gb3ZXvadj5P+JzZ\nfWZbJa4QouZOzLjzgrG+OHToEHPmzOHhhx9m6dKlHDx4sKIYT0xMrNRJevHiRRRFwcfHp0o758+f\n5/7778fX15dFixbh6+tLQkIC7777LgUFBcyfP/+WeXTq1KnSGu69e/dm5MiRtG/fnqlTp5pUrINx\nyGFNjtU0Fz8/PzIyMtBqtVV69G3JpExq85HEjh07aNOmDStXrmTmzJmcOXOGgIAAxo8fz4wZM+5o\nHNTx48erLDEkLKusrKzi34SEBBtnI6ytPt3/hWkLAejo1pHcc7nkkmuVuIOdBrOd7WxP3s6uA7tw\nUbvc/qJ6oj7df2Fe9f3eazSaO1pq0FaKtOYb/pudnY27uzslJSW8/PLLLF++nGnTpvHDDz+QmZmJ\np6dnpa9Ffn4+Go2GkpKSKm298sor5OXlsWvXroohL7169cLV1ZVJkybx6KOP0rt3b5Pys7e3Z9iw\nYXzzzTdkZWXRpMmdDVH09PTkypUrVe7jhQvGOUIuLi4m3+Pb5WJnZ4fBYCA7OxsXl9r/Ls/Pz6/y\n86NSqWjWrJlJ7ZhUrNfmI4kLFy5w5coVXnjhBWbOnElkZCRbtmxh1qxZpKamsnjx4tvG12q16HQ6\nU1IWZlT+y1s0TnX5/hfpitiRvQOAQZ6DrJprkCaIvwf9nfYu7XEwONTpr1NtNNT3JW6vPt57tVqN\nwWCwdRpWsXbtWu69914MBgOtW7cmJiaGpUuXsm3bNi5cuMCwYcMqfS28vLwoLS2loKCgyhj0hIQE\nIiIiKr1uMBgqeumPHz9u8thzoFJH653el8jISFasWEFZWVmlTuJjx44B0KZNmxrd41vlkp2djYOD\nA87Ozmb5/jEYDFV+fu5kBZu/MrmPv6YfSej1evLz81m6dCljxowBjOPdCwsLmTt3Lu+88w7h4eG3\nTlatrjJzWVjWn7/JymeJi8ajvtz/XTm7KNGXEOwYTJRH1G0/HjW3vr59rRrPWurL/RfmV9/vffnm\nN43BTz/9xKJFiyre78yZM/n55595/vnn6d69O19++WWlr0X5ZNNz585VGpcOEBAQwIkTJygoKKjo\nWVYUhX379gEQHBxs8tc1JyeHTZs20aFDhzvuVQd44IEHWLBgAWvXruXhhx+ueH3JkiUEBATQtWtX\ns+dy/vx5IiIizPa9oyhKlZ+fmtSxJhXr3t7e1faeZ2dnAzd62G927aVLl6qMERo+fDhz587l4MGD\nty3W27ZtK8W6lSUkJFBWVoZGoyEqKsrW6Qgrqw/3X6vXMnWVcTzm3zr9jY6tOtosF4PBQGJ2IpHe\nkTbLwZzqw/0XllHf731qamqdWyvbXM6cOcOgQYP47rvvOHHiBN26das0/vyuu+7ivffe44UXXqBP\nnz64urpWur68DktISKBbt8r7ULz00ks89NBDPPDAA0yePBkfHx8OHz7MBx98QGRkJA899FDFsOXt\n27czcOBApk2bxrRp0wAYN24czZo1o0uXLvj4+HD69Gn+9a9/kZGRwcKFCyvdE0VR6Nu3L9u2bav2\nfY4cOZLBgwczZcoUSkpKCA8PZ+nSpWzevJlFixZVel+1zQWMncoHDhzgySefNNv3jqurKyEhIVXi\n5Ofnm9SOScV6+/btWbp0aZWB90ePHgVuvTtVhw4duHTpUpXXyz9mkCJcCFEThWWFdG7ambL0Mu5r\nYd7l0Eyh0+t4dsuz/H7xdxYOW0jnplVXWhBCiNrKy8sjOTmZAQMG0LNnTzZv3lzlnOeee45169ZV\nWgWmXEhICL1792bt2rU89dRTlY498MADbNmyhffee4+pU6dy9epVQkJCePrpp3nttdcqzS80GAzo\ndLpKw0o6dOjA8uXL+fLLLykoKMDLy4tevXrx/fffEx0dXXFeQUEBYOzJv5VVq1bxxhtvMG3aNLKz\ns4mIiKg0QsMcuZTbtm0beXl5xMbG3jInW1AMJgzK2bhxI/feey/Lli0jJiam4vXhw4dz5MgRUlJS\nbjoW5+uvv+bpp59m8eLFldZjf/HFF/n0009JSkqiefPmFa9X95eHq6urFPVWVt97V0Tt1Kf7X6Ir\nwcHOwaY5TP99OitPr2RY6DDm9J1j01zMoT7df2Fe9f3ep6amVunRbEji4uK4cOECDz/8MI6OjtWe\nk5OTg5OTEw4OVX8vrly5kpiYGJKTkwkKCqpyvKioCIPBgKIoFvmEYsOGDYwYMYKEhIQqQ3FsZcKE\nCSQlJbFr1y6ztVnd92FN6luTetaHDx/O4MGDmTRpElevXq34SGLTpk0sWrSoolB/8sknWbhwIWfP\nnq0owJ944gm++uornn32WTIzM4mMjOTXX3/ls88+49lnn61UqAshhKlsXagDxLSOYeXplWxJ2UJe\nSR7uDu62TkkI0QBVt6HRX3l6et702KhRo4iOjuaDDz7g008/NWdqdyQuLo4xY8bUmUL97NmzLF++\nnK1bt9o6lWqZPMH0Tj6S0Ol06HS6SjNpNRoNmzdv5vXXX+f9998nOzubsLAwZs2axf/+7/+a590I\nIRqV1adX096nPeGet57vYi1tvNsQ4RXByeyT/Jz0M7Ft6t7HqUIIoSgK8+bNY926dej1equPWpgz\np2598piSksKnn35ao5VurMGkYTDWJMNg6ob6/lGoqJ26fP+vFF1hyMohaPVa1j20jjD3MFunBMCS\nxCV8sPcDWnu25sf7f6zXK1LU5fsvLKu+3/uGPgzG0iw9DKaxMNcwGKl8hRD10vJTy9HqtXTy61Rn\nCnWA+1rch73KnlM5pziRfcLW6QghhKjnpFgXQtQ7JboSfjj1AwDj24y3cTaVuTu4M7DZQAA2Jm20\ncTZCCCHqO5PHrAshhK1tSNpATkkOAc4BDGg2wNbpVPF4u8cZFjaM3sGmbcsthBBC/JUU60KIOikt\np4h957MJ8XSiUzNP7FTGsd8Gg4FFiYsAGBcxDrWq7v0ai/SObDAbIwkhhLCtuvd/OSFEo6TTGzic\nmsvWk5fZkpjByUs3JuB4Omno39qPgW2a0tQ3iz9y/sBeZc/IliNtmPGdKZ+kJYQQQtSEFOtCCJs6\ncfEq8387x7ZTGWQVlla8rlKgXZA75zMLySkqY9WhC6w6dAF7txM4BbrSwrk9bvZuNsz81gwGA58n\nfM7aM2v5dui3BLsG2zolIYQQ9ZAU60IIm9l84jLPLz1IcZlxi2hXRzV9W/kysI0f/Vr54elsT5lO\nz4HkHLYkXmbLyQySrkRSerU1++2u8ar+CO+NbI/Gru7NlVcUhYSMBNIL01lzZg3PdXrO1ikJIYSo\nh6RYF0LYxPe7z/P2uuPoDdAr3Idn+99FdKhXlcJbY6eiewtvurfw5o37IjmXWcjawxf4eMtpftif\nRnpeMZ/HdsbVUWObN3ILo1qOYnf6btacWcOkqEnYqexsnZIQQoh6pu51RwkhGjS93sAHGxN5a62x\nUI/pEsJ3T0TT4y6f2/aQp+an0ty7CVMGtWLe/3ShicaOnaczefSrPVy+Wmyld3Dn+jfrj5u9G5eL\nLrMnfY+t0xFCCFEPSbEuhLCa4jIdLyw7xFfbkwB4aXArZo2+s2EsZfoyYtfHMmTFEJKvJjOwTVOW\nP90dHxd7EtOvMvKzXZy6lH/bdqzJwc6BES1GALDq9CobZyOEEKI+kmJdCGEVuUWl/M+3e/n5SDpq\nlcK/Honi+YEt73illPj0eHJKcijTlxHkEgRAh2APVj/bkxa+zlzMK+bhL3/n9zOZlnwbJitfsWZr\n6lZyinNsnI0QojHLzMzk0KFDtk5DmEiKdSGExV0tLuORL3ez91w2rg5qFk7syui7TVsdZUPSBgCG\nhg6ttLZ6iJcTqyb1IDrUk/xiLY99t5e4kxlmzb82IrwiaOPVBq1ey/qk9bZORwjRSO3YsYOwsDA6\nd+7M22+/bet0hAmkWBdCWNy0Ncc4nVFAUzcHfpx0Dz3DfUy6/pr2GltStgBwb9i9VY57ONnz/ZPd\nuK99AGU6Ay/9mEBGHRrDPjZiLKNbjqaLfxdbpyKEaKAuX75802MGg4EZM2awdOlSAgICuHjxIjNm\nzCAyMhK9Xl9xXn5+PlOnTuX++++nefPmODs7M3369Ju2W1BQwJQpUwgMDMTR0ZGOHTuybNmy2+a6\ndetWJk6cSEREBM7OzgQFBfHggw9y4MABk97zX/MeMmQIvr6+KIpyy7z/atu2bSiKUu1jz54b843m\nz59PUFAQhYWFNcqzpqRYF0JY1JpDF1hz+CJ2KoXPY+8mwt/0tdF3pO2gSFtEkEsQUb5R1Z7jqLHj\n3zFRRAa4kV1Yyks/JqDXG2qbvlmMbDmS6T2mE+EVYetUhBANVGxsLOfPn6/2WHx8PKNHj2bEiBGc\nOnWKt956i9mzZzNjxgxUqhulYFZWFl9//TWlpaXcf//9t405atQoFi5cyNtvv83GjRuJjo5m7Nix\nLFmy5JbXffHFF5w/f54XX3yRDRs28NFHH5GRkUH37t3ZunWrSe/7z3mXlJTw0EMPmXx9uffff5/d\nu3dXerRr167i+GOPPYazszOzZ8+ucYyakKUbhRAWk5pdxFtrjgHw/IBw7m7uWaN2yofADAsddssx\n7g5qOz4e25H7Pv6Nnacz+e738zzZK6xGMYUQoj7Zv38/8+fPZ+bMmVWOrVmzhhdeeAEAV1dX3n33\nXTw8PBg1alSl85o3b05OTg7Xrl3jypUrLFiw4KbxNmzYwObNm1myZAljx44FoH///iQnJ/PKK68Q\nExODnV31y9V+9tln+Pn5VXpt2LBhhIeH8/777zNgwABT3npF3oqikJmZyTfffGPS9eVatmxJ9+7d\nb3pcrVbz9NNPM3PmTF599VWcnJxqFMdU0rMuhLAIrU7PP5YfJr9Ey93NPXmuf3iN2rlaepWdF3YC\ncG+LqkNg/ircz5U3R0QC8OHGk5y4eLVGcc1Np9dx4PIBvjv2na1TEaJxKy20/cPMkpKSyMvL49tv\nv0Wr1VY5np6eTmBgoPHtl5Yyf/58xo0bV6lXHagY+nEnVq9ejYuLC4888kil15944gkuXrxIfHz8\nTa/9a6EO4OLiQmRkJKmpqXcU/89Mybu2YmNjuXr16h0N9zEX6VkXQljE59vOsj85BxcHNXNjOqKu\n4S6jrhpXvh36LXvS99DKs9UdXTO+WzO2n8rg18QMXlx2iJ+e74WjxrYbEuWW5DLxl4noDXqGhg4l\n0CXQpvkI0Wi9Xwd+9qbnmbW5/fv3ExYWxrlz51i7di2jR4+uOHbq1Clat25d8Tw+Pp6srCz69+9f\nq5jHjh2jTZs2qNWVS8kOHTpUHO/Ro8cdt5eXl8fBgwdN7lU3p8mTJzNmzBicnJy45557eOutt+jV\nq1elc/z9/YmIiGD9+vVMnDjRKnlJz7oQwuwOpuTw0ZbTAMx8qC0hXjX/qFBRFDr6deSZqGdMuubD\n0R3wcXHgdEYBH2xIrHF8c/Fu4k1nv84A/Jr8q42zEUI0JHv27OGTTz5Bo9HwySefVDq2du1aHnzw\nwYrnu3fvBqBz5861ipmVlYWXl1eV18tfy8rKMqm9yZMnU1hYyBtvvFGrvGrC3d2dF198ka+++oq4\nuDg++ugjUlNT6devH7/88kuV8zt37syuXbuslp/0rAshzCq/uIwpyw6j0xt4sGMgIzuZtkSjuXi7\nOPCvR6N47Nu9LNydTN/WvgyIaGqTXMoNaj6I/Zf3szl5M//T9n9smosQjdbrF22dgdkdOnSIOXPm\n8PDDD7N06VIOHjxYUYwnJiYyderUinMvXryIoij4+Ji2Kld1bjX0xJRhKW+99RaLFy/mk08+4e67\n7651Xqbq1KkTnTp1qnjeu3dvRo4cSfv27Zk6dSpDhw6tdL6fnx8ZGRlotdoqnyxYgvSsCyHMavq6\nE6RkFxHk0YQZD7a7/QW3sPr0ambsnsGJrBM1ur5vK18m9jROMH3lxyNcyS+pVT61NajZIAAOXzlM\nRlHdWQteiEbF3tn2DzPKzs7Gy8sLOzs73nrrLVQqFe+88w5g3ATpr+PDr127hkajuenkzzvl7e1d\nbe95dnY2QLW97tV55513ePfdd3nvvfd47rnnapWTOXl4eDBixAiOHDnCtWvXKh1zdHTEYDBQXGyd\nJYKlWBdCmM2mY+msPJiGSoG5Yzri3kRTq/ZW/LGCH//4kUMZNd9xb+qw1kT4u5JVWMprq47UKp/a\naurctGLpyfJ144UQojZWrVrFAw88AECbNm2IjY1l3bp1xMXFsWHDBkaMGFHpfB8fH0pLS2u9Vnj7\n9u1JTEysMqH16NGjAJWWPLyZd955h+nTpzN9+nRef/31WuVjCQaDcfnfv35KkJ2djYODAy4uLlbJ\nQ4p1IYRZlGr1vHd9bPikfncRHXpnvSo3k5qfypHMI6gUFUNDh97+gptw1Njx0ZhOaOwUfk3MYNeZ\nzFrlVVuDmw8GYHPyZpvmIYRoGFavXl1pRZYPP/wQV1dX/v73v7Nly5YqkzwjIoz7PZw9e7ZWcUeO\nHElBQQErV66s9PrChQsJDAykW7dut7x+5syZTJ8+nTfffLNO7qiak5PDzz//TMeOHXF0dKx0LCkp\nicjISKvlIsW6EMIsFscnk5p9DV9XBybXcJnGPysvZqP9o/FpUruxla39XYnt1hyAWRtP2nSzpEHN\njUNh0vLTKNHZdliOEKL+OXPmDKGhocTFxfHZZ5/RpUuXSut9BwQE8N5773H27FlUKlWV4S79+vUD\nqLQz559t3LiR1atXs3HjRgBOnDjBihUrWLFiBUVFRRXnDR8+nMGDBzNp0iTmzZtHXFwcTz31FJs2\nbWL27NkVcbdv345arWbGjBkV1/7rX/9i2rRpDBs2jPvuu489e/ZUevyVoigVed/Mxo0bWbFiBT/9\n9NNN864uF4Bx48bxf//3f6xYsYJt27Yxb9487rnnHi5fvsycOXMqnavX69m7d2+tV9MxhUwwFULU\nWn5xGZ9sPQPAlEEtcbKv/a+WuJQ44MY479p6fkA4Kw6kcfRCHuuPpnN/lG2WbwtyCeLH+3+klWcr\nVIr0lwghTJOXl0dycjIDBgygZ8+ebN5c9VO65557jnXr1lVaBaZcSEgIvXv3Zu3atTz11FNVjk+a\nNInk5OSK5z/++CM//vgjAOfOnSM0NLTi2KpVq3jjjTeYNm0a2dnZREREsHTpUsaMGVNxjsFgQKfT\nodfrK14rL6g3bdrEpk2bquRQPvwEoKCgADD+EXIrd5J3dbmAcbnJ5cuX8+WXX1JQUICXlxe9evXi\n+++/Jzo6utK527ZtIy8vj9jY2FvmY06K4c9fkTpEr9eTn59f6TVXV9cqC/gLy0pISKCsrAyNRkNU\nVPXbvIuG607v/7//e4qPt56hhY8zv/yjD5oarqleLvNaJgN+GIABA5sf3oy/s3+t2iv38ZbT/Hvz\nHzT3dmLzP/pir5bfJ7ciP/+NV32/96mpqYSEhNg6DYuJi4vjwoULPPzww1WGaJTLycnByckJBweH\nKsdWrlxJTEwMycnJBAUFVTleVFSEwWBAURSr7dJ5M+Xj7hMSEmjfvr1NcwGYMGECSUlJd7R0Y3Xf\nhzWpb+X/VEKIWsnIL2beznMAvDK0da0LdYAdaTswYKCtd1uzFeoAT/YKw8fFgeSsIpbuTTFbuzWl\n1Wsp05XZOg0hRD3Tv39/xo8ff9NCHcDT07PaQh1g1KhRREdH88EHH1gqRbOJi4tjzJgxdaJQP3v2\nLMuXL+fDDz+0alwp1oUQtfLxltNcK9PRMcSDYe3MU1grKAS7BNM/xLxjAp0d1EwZ1BIw5l1QUnVb\nbmuZd2QeA34YwIZzG2yWgxCicVIUhXnz5hEYGFhlSEhdM2fOHJYsWWLrNABISUnh008/rbKrqaXJ\nmHUhRI0lXSlg6d5UAP5veIRJm2DcysiWI3ko/CG0evMX0zHRIcz/7RznMguZtyOJfwxuZfYYd0Kr\n15JTksOvyb/yYHjVcaVCCGGgr+AkAAAgAElEQVRJ7dq1u6PlFcUN/fv3t+rE0nLSsy6EqLF//vcU\nOr2BARF+dG/hbda2FUVBY1e7ddqro7FT8crQ1gDM25lERr51NrX4q/JVYXZd3EVBaYFNchBCCFH3\nSbEuhKiRQyk5bDh6CUWBV4dFmK3ds7lnLT6Oe3g7f6JCPCgq1fHJljMWjXUz4R7hhLqFUqYvY0fa\nDpvkIIQQou6TYl0IYTKDwcCsjScBGN05mNb+rmZpV6vX8vimx+m7vC9JuUlmabM6iqLw2nDjHxhL\n96ZwLrN2O/nVNIfyDZJ+TfnV6vGFEELUD1KsCyFMtu3UFeLPZWOvVpl1zPfhjMPkluSiUqlo5tbM\nbO1Wp3sLb/q39kWrN/DPX05ZNNbNlA+F2Zm2k6KyotucLYQQojGSYl0IYRKDwcDs68XtEz1CCfJo\nYra241KNGyH1CeqDWmX5+e+vDo9AUWD90XSOpuVZPN5ftfFqQ5BLEMW6YnZf3G31+EIIIeo+KdaF\nECbZ/scVEtOv4mxvx6R+d5mtXYPBUFGs929mndn2Ef5uPHh9J9Ovdpy1Ssw/UxSFMa3HMLHdRFp4\ntLB6fCGEEHWfLN0ohDDJvJ3GseRjujbDw8nebO2eyT1Dan4q9ip7egb2NFu7t/NUn7tYc/giG46m\nk5pdRIiXdXfre7zd41aNJ4QQon6RnnUhxB07diGPXWeysFMpTOwVZta2y3vVuwV0w0ljvYI5MtCN\n3i190Btg/m/nrBZXCCGEuBNSrAsh7tjXO4y96iM6BJh1rDpAXIp1h8D82VN9jENQlu9LJbeo1Orx\ni7XF7EjbwbbUbVaPLYQQom6TYl0IcUfScopYfzQdgL/3Nv/46uk9pvNsx2fpH2L9Yr1XuA9tAty4\nVqZjcXyK1eP/N/m/TN4ymc8Of2b12EIIYarQ0FAef/xxi7W/ZMkS5s6da7H26xsp1oUQd+Tb386j\n0xvoGe5NuyB3s7ff2qs1k6Im4dPEx+xt346iKDzVxzis57td5yku01k1fq+gXigonMw+yaXCS1aN\nLYQQdY0U65VJsS6EuK2CUj3L9hl7nJ/qY74VYOqSER0CCXB3JLOghLWHL1g1tpejF1G+UQCym6kQ\nwmKuXbtm6xREDUixLoS4rU1nCigq1RHh70qflubt+S4oLeD1na/zy/lf0Bv0Zm3bFBo7FRN7GnvX\nv96RhF5vsGr8viF9Adiett2qcYVobIrKim76KNGV3PG5xdriGp9bG9OnT0dRFA4dOsSoUaNwc3PD\n3d2d8ePHc+XKlYrzQkNDGTFiBKtWraJTp044OjryzjvvAFBcXMxrr71GWFgY9vb2BAUFMXnyZHJz\ncyvFKisrY+rUqfj7++Pk5ESvXr3Yu3fvTXP6qwULFqAoCufPn6/0+pIlS7jnnntwcXHBxcWFjh07\nMn/+fAD69evH+vXrSU5ORlGUikdjJks3CiFuqUxn4Oc/CgDjWHVz/9L87eJv/JT0E0cyjzCk+RCz\ntm2qMV1D+HjLac5eKSTuVAYD2zS1Wuy+wX356OBHxKfHc017jSZq807gFUIYdVvS7abHegf15vNB\nn1c87/dDP65pq++N7tK0C98N+67i+bCVw8gpyan23LbebVk2YlkNM67eyJEjefTRR3nmmWc4fvw4\nb731FidOnCA+Ph6NRgPAwYMHSUxM5M033yQsLAxnZ2cMBgMPPfQQW7Zs4bXXXqN3794cOXKEt99+\nm927d7N7940N2iZPnsySJUt4+eWXGTx4MMeOHWPUqFHk5+fXOO9p06Yxc+ZMRo0axUsvvYS7uzvH\njh0jOTkZgM8//5ynnnqKs2fPsnr16tp9kRoIKdaFELe0M7WYnGt6/N0cuf/6BkLmVL4CSv+Q/jbv\nPXF11DCuWzO+2pHEVzuSrFqsh3uEE+gcyMXCi8Snx9MvpJ/VYgsh6p9Ro0Yxe/ZsAIYMGULTpk2J\njY3lhx9+IDY2FoCMjAxOnDhBq1atKq775Zdf+OWXX5g9ezavvPIKAIMHDyYkJISYmBj+85//EBsb\ny6lTp1i8eDH/+Mc/KuIMHjy4Ik5NnDt3jvfff5/Y2FgWLVpU8frgwYMr/jsyMhIPDw8cHBzo3r17\njeI0NFKsCyFuymAwsO6PQgCe6BmKvdq8I+e0ei2/XfgNoM4Up4/3DGX+b+fYey6bw6m5dAzxsEpc\nRVHoG9KXpSeXcijjUJ35egjR0MSPi7/pMTuVXaXn2x7ddtNzVUrl34ebRm+643PN4a8F86OPPspj\njz1GXFxcxbEOHTpUKtQBtm7dClBlNZdHHnmEiRMnsmXLFmJjY9mxY8ct49TE5s2b0el0TJ48uUbX\nN1ZSrAshbupAejFpV3U0USuM7dbM7O0fuXKEvJI83OzdKiZY2lqAexMe6BjIqoMXmLcjic9iO1st\n9oTICYyJGEOYm3k3nBJC3GDKpmuWOtcc/P39Kz1Xq9V4e3uTlZVV8VpAQECV67KyslCr1fj6+lZ6\nXVEU/P39K67Pzs6+ZZyaKB9THxwcXKPrGyuZYCqEuKk1icax6kPDnXFz1Ji9/fKVT3oG9UStqjt9\nB+XryG88lk5KVpHV4oa4htDC3fzzAoQQDc+lS5WXedVqtWRlZVUqpKv7XeLt7Y1Wq600GRWMn6Re\nunQJHx/jIgJeXl63jPNnjo6OAJSUVJ6gm5mZWel5+R8IaWlpt35zohIp1oUQ1Tp2IY+jGSXYKTCi\nlYtFYuy4YCzW+wT3sUj7NdUmwI0+rXzRG+DbXedskoPBYN3VaIQQ9cvixYsrPf/hhx/QarX069fv\nltcNHDgQoNKYcYCVK1dSWFhYcbx37963jPNnoaGhABw5cqTS6z/99FOl50OGDMHOzo4vvvjiljk6\nODjIMpN/Une6soQQdcp/dp8H4J5gR3ydzf+roqisCAUFlaKiV2Avs7dfW3/rFcaOP66w4kAarwxt\njbODdX5dpl5NZe7BueSV5PHN0G+sElMIUf+sWrUKtVrN4MGDK1aDiYqK4tFHH73ldYMHD2bo0KG8\n+uqrXL16lZ49e1asBtOpUycmTJiATqcjIiKCMWPGMHfuXDQaDYMGDeLYsWP885//xM3NrVKb9957\nL15eXjz55JPMmDEDtVrNggULSE1NrXReaGgor7/+OjNnzuTatWuMHTsWd3d3Tpw4QWZmZsXSku3b\nt2fVqlV88cUX3H333ahUKrp06WLeL2A9IsW6EKKKvKIy1iVcBGDYXZZZQtBJ48TKB1aSdS0LD0fr\nTOI0Ra9wH0K9nTifVcTawxcZZ4Ex+9VpomnC5uTNGDCQUZSBn5OfVeIKIeqXVatWMX36dL744gsU\nReH+++9n7ty52Nvb3/I6RVFYs2YN06dP57vvvuO9997Dx8eHCRMm8P777+Pg4EBRkXH43xdffEFQ\nUBALFizg448/pmPHjqxcuZIxY8ZUatPNzY1NmzYxZcoUxo8fj4eHB3/7298YPnw4f/vb3yqdO2PG\nDFq2bMknn3xCbGwsarWali1b8sILL1Sc8+KLL3L8+HFef/118vLyMBgMjfrTRsVQR9+9Xq+vso6n\nq6srKpWM3LGmhIQEysrK0Gg0REXVjQmAwvLm/3aOmT+fINRDw5yBntjb2zfK+//NziTeXZ9ImwA3\nNrzQy2pjyWPXx3Ik8wjT7pnGI60esUrM6sjPf+NV3+99amoqISEhtk7DIqZPn84777zDlStXKsaX\nm1tRUREGgwFFUXBysu7E2Yakuu/DmtS3UvkKISoxGAwsjjduTjEs3NkiBWqZvuymG43UJQ/fHYyD\nWkVi+lUOpuTe/gIzKd/NdEfqDqvFFEIIUTdJsS6EqGT32SySrhTibG9H31DL9KjsubiH3st6M/33\n6RZp31w8nOwrNoJavCfZanH7BhuL9T3pe8y6TbkQQoj6R4p1IUQl318vSkd1DsZJY5lfEdvTtlOi\nK8FOsbv9yTY2vntzAH4+kk52YalVYrbybIW/sz/FumL2XtprlZhCiPph+vTpGAwGiw2BEXWPFOtC\niAqXrxbz3xOXgRtFqrkZDAZ2pu0E6t6SjdWJCnanXZAbpTo9P+5Pvf0FZqAoSkXv+rbUbVaJKYQQ\nom6SYl0IUWHZ3lR0egPRoZ609ne1SIyzuWe5WHgRBzsHugZ0tUgMc1IUhQnX/3BZHJ+CXm+dOfn9\nQvrRwacDrTxb3f5kIYQQDZbJxXpBQQFTpkwhMDAQR0dHOnbsyLJly0wO/Oabb6IoCu3atTP5WiGE\n+Wl1epbuTQEs16sONzZCivaPponaMstCmtv9UYG4OqpJyS5ix+krt7/ADHoF9WLxfYsZEzHm9icL\nISpRqVSUlZXZOg3RiOl0OrO1ZXKxPmrUKBYuXMjbb7/Nxo0biY6OZuzYsSxZsuSO2zh8+DD//Oc/\nadq0qanhhRAW8mtiBpeuFuPtbM+wdv4Wi7MjzVislw/zqA+c7NWM7hwMwKI9KTbORghxO15eXqSn\np1csQSiENel0Oi5cuICvr69Z2jNpU6QNGzawefNmlixZwtixYwHo378/ycnJvPLKK8TExGBnd+sJ\nY1qtlieeeIKnn36ahIQEMjMza569EMJsypdrfDQ6BAe1ZSZ+5pXkcTjjMFA/xqv/2fjuzVnw+3m2\nnrzMhdxrBHlY51OB/NJ8jmcdp3tAd6vEE6IhaNKkCUFBQWRlZZGVlWXrdOqd/Pz8inXWXV0tMySy\nofPz88PR0dEsbZlUrK9evRoXFxceeaTyJh1PPPEE48aNIz4+nh49etyyjVmzZpGdnc17773HiBEj\nTM9YCGF25zIL2Xk6E0WBcV0tt1Onoij84+5/cDb3LIEugRaLYwnhfi7c08Kb3UlZLNubwktDWls8\nZta1LAb9OAg9enbE7MDdwd3iMYVoKOzs7PDzkx2Aa+LPm2I11M2l6hOTivVjx47Rpk0b1OrKl3Xo\n0KHi+K2K9RMnTvDuu++yatUqXFxcTE72+PHj6PV6k68TNVc+5q+srIyEhAQbZyMs5duDxg1/7g5w\nJDv1NNnXFz2xxP3vSEc6unSsl99PvQMM7E6C739Poq/PNTR2lt/R1N/Bn7TiNJbsXkIPz1t3hpib\n/Pw3XnLvGze5/5ajUqlo1sy0TjGTivWsrCxatGhR5XUvL6+K4zej1+uZOHEio0aN4t577zUpyXJa\nrdasA/aFaWSyTsNUojOwJakQgMFhjje9z3L/oXNTNZ6OKnKK9fyeXECPEPN8xHkr7Z3bk1acxsHc\ng0S7RFs83s3I/W+85N43bnL/zet2w8WrY1KxDtxy6/FbHfv3v//N6dOnWbdunakhK6jValQqWW3S\nmv78Q6rRaGyYibCUnamFFJQZ8HO2IzrYGTvVjZ9jc97/C8UXOFN4ho5uHXHX1M/hHBpg8F3O/HA8\nn/+eK6ZvC8uP5bzb8242Zm3kWMEx7NR2qBTr/Q6Un//GS+594yb333JqUseaVKx7e3tX23uenZ0N\n3Ohh/6uUlBSmTZvGrFmzsLe3JzfX+JG7VqtFr9eTm5uLg4MDTZrcesJW27ZtpVi3sj+PW4uKirJ1\nOsICpu/aBcBjvcLp3Cm80jFz3v/tB7czL3Uew0KHMafvnFq1ZUt+oddYcWIrxzJKcA64i3A/04f0\nmaKtvi0fpXxEfmk+SqBClJ/1fg7l57/xknvfuMn9txy9Xk9+fr5J15hU+bZv357ExES0Wm2l148e\nPQpw0zXTk5KSuHbtGi+++CKenp4Vj127dpGYmIinpyevvfaaSYkLIWrv1KV8DqXkolYpPNrFspOI\nypdsrG+rwPxVgHsTBkQYJ639YIUdTdUqNT0DewI3voZCCCEaD5OK9ZEjR1JQUMDKlSsrvb5w4UIC\nAwPp1q1btdd17NiRuLi4Ko+oqChCQ0OJi4vjueeeq/m7EELUyLJ9xjXDB7Vpiq+rg8XiXCq8xKmc\nUygo9AzqabE41jIm2jg5aOWBNEq1lp/0Xv4HjhTrQgjR+Jg0DGb48OEMHjyYSZMmcfXqVcLDw1m6\ndCmbNm1i0aJFFYPmn3zySRYuXMjZs2dp3rw5Hh4e9OvXr0p7Hh4eaLXaao8JISyruEzH6kMXAIjp\nap1e9fa+7fFyrH64XH3Sr7Uvfq4OZOSX8GviZe5tH2DReL2CevFmtzfpHdzbonGEEELUPSYPAF+1\nahUTJkxg2rRpDBs2jPj4eJYuXUpsbGzFOTqdDp1OJ7uGCVGH/XL8ErlFZQS6O9KnpXl2WbuZ8mK9\nX3A/i8axFrWdike6GHc0XbrX8juaejp6EhMRU+/WphdCCFF7JhfrLi4ufPTRR6Snp1NSUkJCQgJj\nxoypdM6CBQswGAyEhobesq1t27Zx7NgxU1MQQpjB8n3G8daPdAmptAKMuRVri4lPjwfq/3j1P4vp\nYhwK89uZTFKzi2ycjRBCiIZKllYRohFKzirk97NZKAoVPcSWciLrBCW6Epo6NaWVZyuLxrKmZt5O\n9Az3xmCAH60w0bRMX8ayk8t4ceuLlOhKLB5PCCFE3SDFuhCNUHmvep+WvgR7Olk0VuemndkWs41/\n9fvXLfdiqI/KJ5r+sD8Nnd6yw/7Uipp5R+axNXUr+y/tt2gsIYQQdYcU60I0MmU6PT8eSANgTLRl\nJ5aW83L0Isq34a3VO6RtUzydNFy6Wsz2PzIsGktRlIoJprIqjBBCNB5SrAvRyMSdzOBKfgk+LvYM\nbNPU1unUaw5qO0Z1Ng4jWrbX8kNhegfdKNZlAr8QQjQOUqwL0cgsuz4EZnTnYOzVlv0VsODYAp7Y\n9ARbkrdYNI4tlX86seVkBhlXiy0aq3tgd9QqNWkFaZy/et6isYQQQtQNUqwL0Yik511j2ynjcI0Y\nKwyB2Zq6lf2X95N5LdPisWylZVNX7m7uiU5vYMXBNIvGctY406VpF0CGwgghRGMhxboQjciK/Wno\nDdA1zIsWvi4WjZVbnEvClQSgYS3ZWJ3yP3yW70u1+PCU8q/lzrSdFo0jhBCibpBiXYhGQq83sPz6\nEoPWmFj628Xf0Bv0tPJsRYCLZXf4tLURHQJwcVCTnFXE7qQsi8bqE9wHtaJGrVKjN+gtGksIIYTt\nSbEuRCOx62wmaTnXcHVUc297yxfP5cM0GnqvOoCTvZoHOhp3Fy1fFtNSmrs1Z8eYHXw5+EtUivwK\nF0KIhk5+0wvRSJSvVjKyUxCOGjuLxtLqtfx24TcA+gb3tWisuqL804qNxy6RW1Rq0Viu9q4WbV8I\nIUTdIcW6EI1AVkEJ/z1xCbixkY8lJVxJIL80Hw8HD9r7tLd4vLqgfZA7kQFulGr1rDp4wSoxM69l\notVrrRJLCCGEbUixLkQjsPrQBcp0BmNBGehm8XhqlZq+wX0Z1HwQdirL9uLXFYqiMKar9SaaPvvr\nswz4YUDFJF4hhBANkxTrQjRwBoOBpXtTACqKSUuL8o3i04Gf8vY9b1slXl3xYFQQDmoVpy7nk5CW\nZ9FY7g7uGDCwPXW7ReMIIYSwLSnWhWjgDiTncPZKIU00djwQFWjrdBo0dycN912fvLt8X4pFY/UN\nMc4F2Ja2zaJxhBBC2JYU60I0cOU7lo7oEICro8bi8f7I+YMLBdYZs10Xla+5vu7wRQpLLDeevGdg\nT9SKmnN550i+mmyxOEIIIWxLinUhGrCrxWWsP5IOWG8IzL/3/5thK4ex4o8VVolX13QN8yLMx5nC\nUh0/H7losTiu9q7c7X83ANtSt1ksjhBCCNtS2zoBIYTl/JRwkWtlOsL9XOjczNPi8YrKith7aS8A\nnf06WzxeXaQoCjHRIczaeJJl+1KJseDqO/1D+hOfHs+21G081vYxi8Wp4loO5F+GkqvGR/H1f0vy\noawYHFzAwQ0c3cDB9fp/u4NbEGgcrZenEEI0AFKsC9GAlW/QMyY6BEVRLB5vT/oeyvRlBLsEE+Ye\nZvF4ddWozkH885dTHErJ5dSlfFr7W2Zd9L7BfZm1dxaHMg6RV5KHu4O7WdtXaYtwzjmLS1EKpC+H\njBOQkQgFl2rWoGIH3neBXxvwizT+69sGvFqAnfzvSAghqiO/HYVooI5fzONIWh4aO4WRnYKsEnN7\nmnFlkj7Bfazyx0Fd5efqyMA2fvxy/DLL96Uy7f5Ii8QJdg1mfJvxtPFug0ZlhvkIeh1cPAxnfoUz\nm2mXdgAFffXnOnpc7zl3v/7v9Z50tQOUFFTtcb+WC2WFkPmH8XFi7Y227F2hRV8IHwjhg8DD8nsB\nCCFEfSHFuhANVHmv+pC2/ni7OFg8nk6vqxg7PaDZAIvHq+vGdG3GL8cvs+pQGq8Ob42D2jLrzb/a\n9dXaNVCUDaf/C6c3w9mtcC274pAClDp4UeLWAtcW0Td6xH1bGwtzUxgMkH/pRu98RqLxv6+chNJ8\nOPmz8QHg09pYtIcPhLA+YGf5idFCCFFXSbEuRANUXKZj9SHjiixjoq0zsTThSgLZxdm42bvRuWnj\nHK/+Z31a+hLg7kh6XjH/PX6Z++vSspl6PSTFwaHv4eR60JXeOObgBi36QfggTpQGUKTxQqPREBUV\nVbuYigJuAcZH+MDKuVxKuN6bvwVS90LmKeNjz2fg7Acdx0KnCeDTsnY5CCFEPSTFuhAN0MZj6eQX\nawnyaELPu3ysEjMuNQ4wDoExy5CMes5OpfBIlxA+3nKa5ftSLVqsJ19NJi4ljuiAaNp6t735ibkp\ncGgxHF4Meak3Xm/aDloNNfZmB0dX9GSXJSRAWZnF8gZApYLATsZHn1eMk1eTthuL9z82QWEG7PrI\n+Gh2j7Fob/sQ2DtbNi8hhKgjpFgXogFattdYiMVEh6BSWWfs+DNRz9Depz3+zv5WiVcfPHJ3MJ9s\nPc1vZzJJzS4ixMvJInG+OfoNa86sYXyb8VWLdYMBzu+E3+Yah7lgML7u6A4dYozFb0AHi+RVI008\njcV424dAVwZ//AIH/wNnNkPKbuNj46sQNQZ6viDj24UQDZ6ssy5EA5N0pYD4c9moFHj47mCrxXXW\nODMkdAgdfOtQ4WdjIV5O9Ao3frJRPofAEvoF9wOME3wNhuvFuMFgHIf+7VBYeD+c3QIYjGPAR30D\nL52Ce+fUrUL9r+w00GYExP4A/zgOA94CzzDjGPd98+DjTrB2MmSdtXWmQghhMVKsC9HALN9vLAr7\ntvIl0KOJjbMRY66vs/7jgVS0upusrFJL9wTeg0alITU/laScM5D4E3zdFxY/DKnxYOcA0X+HFw7B\nYz9Bh0dAU8++N9wCoc/L8PxBmLAGwvqCXguHFsGnXWDl3yHjpK2zFEIIs5NiXYgGpEynZ+WBNMC4\nGom1vPHbG3yR8AXZxdm3P7mRGRzZFC9ney5fLWH7H1csEsNJ40RX/64AbFs5BpaPh/QE0DjBPc/B\nlCNw3z+N65nXdyoV3NUfHlsHT26GlkPBoIejP8Dn3WD5BMg8Y+sshRDCbKRYF6IB2ZKYQWZBKT4u\nDgyI8LNKzEuFl1h3dh1fHP4CvcEyPcf1mb1axejOxnXul+610FCYS8fofzERgO36q8YVXXq/DFOO\nwdD3wLWBziMI6WocIvPUdmhzv/G1xHXGon3T68a13YUQop6TYl2IBmTJ3hTAOFZdY2edH+/yVWA6\n+nXEp4l1Vp6pb2KuD4WJO5VBet418zVcmAk/TYGvetM35SgAhx0dyX5mBwx8C5y9zRerLgvsCDGL\nYNJuY0+7Xmtc9vGTzrBvPui0ts5QCCFqTIp1IRqIlKwidp42DrMY29U6a6sDbE3ZCsCAENkI6WbC\n/VzoGuaFTm8wz0RTbSn8/olxguWB78Cgx7/1/US4tcBR3YTTxRm1j1EfNY009rSPX2ncWKkoC9b/\nL3zVG5K22To7IYSoEVm6UYgGYum+FAwG6N3Sh+be1lmDOq8kj/2X9gPQv1l/q8Ssr2K7NWPvuWyW\n70vluf7hqGv6yUfy77Dueci6Pi7bvwMMmwWhPfkwL4kA5wCaqOvZ5FFzCx8Ek/rC/u8g7j3jTqn/\neRAiH4Thc8C1qa0zFEKIOyY960I0AKVaPT9eXwUmtltzq8XdeWEnWoOWcI9wmrtZL259NKydP17O\n9qTnFRN3qgYTTUvyYf1L8N1wY6Hu7AcPfApPbYPQngC0cG8hhXo5Ow10e8q4Ak63Z0CxgxNr4bOu\ncHipcWlLIYSoB6RYF6IB+O+JS2QWlOLn6sDANtaZWAo3hsD0D5Fe9dtxUNvxyPV17xfHJ5t28elf\n4fN7YN83xuedJsBz+6DzBFDZVXtJsba4Nuk2HE5eMPxDeCoO/NtDcS6seca4rGWu5da+F0IIc5Fi\nXYgGYPEe48TSMdEhVptYCuBm74aLxoWBzQZaLWZ9Nvb6cprb/7hCanbR7S8oyobVz8Di0ZCXCh7N\n4X/WwoOfQhOPai/Zk76HkWtH8vpvr5sz9fovIAr+HgcDpxnXnT/zK3zeHfbOA72sYiSEqLukWBei\nnjt7pYDdSVmoFIix4trqANN7TGdHzA4ivSOtGre+CvVxpndLHwwGWLYv5dYnn9oEn3WDhKWAAt2f\nhWd3Q4t+t7zMzd6NM7ln2Jm2k6KyO/iDoDGx00Dvl+CZ3yCkO5QWwIaXYeEIyL3N/RBCCBuRYl2I\nem5pvLHI6N/ajyAb7FiqsdOgKIrV49ZX467/QbV8Xxpl1e1oWnYN1r8MS2OgMMO4qsmT/4VhH4D9\n7ScOt/FqQ5BLEMW6YnZd3GXu9BsG31bwxEYYPhs0zpC8C77oBUdX2DozIYSoQop1Ieqx4jIdKw4a\ndyyN7W69XnWdXscfOX9gkEl6JhsU2RRfVwcyC0rYfOJy5YOXj8PX/WHfPOPz7s/C0zuMm//cIUVR\nGNx8MACbz282V9oNj0oF3Z6GSbsgOBpK8mDlk7B6knEyrxBC1BFSrAtRj204mk5uURlBHk3o28p6\nE0uPZh5l9LrRxPwcIwW7iTR2KsZEG9fBr5hoajBA/FfGQv1KonGll9iVxt50jaPJMcqL9e1p2ynR\nlZgt9wbJK8zYy95nKocWLfEAACAASURBVCgqSFgCX/aGtAO2zkwIIQAp1oWo15bE35hYaqey3lCU\n8lVgwtzDZAhMDcREh6AosOtMFueTz8OSR2HjVNCVQMshMOl3aDmoxu2382lHU6emFGmL+P3C7+ZL\nvKGy08CAN+Dx9eAeAjnn4NshsOOfoNfZOjshRCMnxboQ9dTJS1fZn5yDnUohJtp6O5YaDAa2pGwB\nkFVgaijY04n+rf3oopzEe9FAOP1f4wolw2fDuB/AxbdW7asUVUXv+q8pv5oj5caheQ/j5NO2o0Cv\nha0zYdFoKMy0dWZCiEZMdjAVop4q71UfEtkUPzfTh0rUVGJ2Iin5KTjaOdIrqJfV4jYoBgOvuW8m\nzH4O6jI9ep9WqB5ZAE3bmi3EsLBhXC29yn1h95mtzUahiQc8/K1xF9QNL0NSHHzVBx5ZYNLcASGE\nMBcp1oWoh4pKtaw+eAGAcd2su1zjpnObAOgT3AcnjZNVYzcIxXmwdjItE38CBdboemDX7SPub9rK\nrGGifKOI8o0ya5uNhqJAp1gI7AQ//A9knTbuHDvkPeOkVBn6JYSwIhkGI0Q99FPCRfJLtDT3dqLn\nXT5Wi6s36Nl03lisDw8bbrW4DcalY/B1P0j8CVQa4u56lSllk/nPARlmUSc1jTTufBr5kHFYzKZX\nYcVEWS1GCGFVUqwLUc8YDAYWXx8CM65rM1RWnFh65MoR0gvTcdY4yxAYUx1eCt8MguwkcAuGiZuI\nfPB/sVOp2Hc+h1OXzF8AGgwGErMS+eLwF2j1WrO33yg4uBqHwAybBSo1HF8F8wZAxklbZyaEaCSk\nWBeinjmYksORtDzs1SoevjvYqrHb+bTjq0FfMTV6Ko5q642Tr9d0ZbDhFVjzDGivwV0DjWunB3eh\nqZsjQyKbArDg93PmD23Q8dTmp/g84XP2X95v9vYbDUWB7pPg8Q3gGgCZf8A3AyHxZ1tnJoRoBKRY\nF6Ke+XbXeQAejArE28XBqrHVKjU9gnowquUoq8attwqz4PuRsPdr4/O+/wexP4Kzd8Upj/cIBWDV\nwQvkFJaaNbxapWZAswEA/Josq8LUWrNu8PROCO0NpQWwPBbiPgB9NTvRCiGEmUixLkQ9cjH3GpuO\nXQLgiZ5hNs5G3FL6EeP49PM7wd4FYhZD/9dAZVfptK5hXkQGuFGi1bNsX6rZ06hYwjH5V/6fvfsO\nj6LcHjj+nW3pvUESeu9FOtKkI1wpYvcqoFyxXfVeBcvFXn82VLAAChZQpFgQECkKSlVqgNBDSQLp\nvWyZ+f0xEEASILDZScj5PM8+ycy+M3OSyWbPvvPOeV1SM/zK+UfAnYug83368m+vwbw7ZRy7EKLC\nSLIuRBXyxYYjuFSNzvVCaR4d6NFjv7/1fd7c/CZHc4569LhVUtxC+HQgZB+FkHpwzwpoNrTUpoqi\nMKZ7XQC+WJ+A0+XeXtrONToTYA0gvSidbanb3LrvastshcGvww1TwWyD+MUwoz+kHzQ6MiHEVUiS\ndSGqiEK7i7mb9ETZ073qTtXJ1/FfM3v3bJLzkz167CpFdcGK52H+GHAUQIPr4N5VENnsgpsNaxNN\nmJ+NpOwift510q0hWc1W+tTuA8hQGLdrd4c+jt2/BqTugel94MBKo6MSQlxlJFkXoor4blsiWQUO\nYkN86H/qpkRP2Zm7kxx7DuE+4XSI6uDRY1cZxbnwzR3w+9v6creH4LZvwTf0opt6W83cfqpe/md/\nuP9G0361+wHwc8LPMhTG3Wp1hPG/QkwHvYb+VzfChg9B04yOTAhxlZBkXYgqQNO0kiTurq51MXuw\nXCPAhqwNAAysOxDz38ZcCyDrKHw6CPYuAbMXjPgEBrwE5kufd+6OLnWwmhX+PJLJzuPZbg2ve0x3\ngryCcKpOjubKMCa3C6wJd/8Ebe8ATYVlk2Dxo3olICGEuEKSrAtRBaw7mM6+k3n42szc1LGWR49t\nV+38lf0XAIPqDvLosauEY5v0utsn48AvEsYsgTY3l3s3kYHeXN+qJuD+3nWb2cZnAz9j5U0rqRck\nNyZXCKs33PAB9H8RUOCvz+DLkVCQYXRkQogqTpJ1IaqA08nbqPaxBPlYPXrsHXk7KFKLiPaLlunr\n/27HPJg1FPJTIaqVPttl7OUPEzp9L8KPO5JIyS1yV5QANApphNXk2b+dakdRoPvDcOtcvQLQ4TX6\nRFhpB4yOTAhRhUmyLkQldyQ9n5XxKQDcfapqiCdtzN4IwMB6A1EUzw6/qbRUFVa+CAvvBVcxNLke\nxi6DoCubpKpNrWDa1w7G4dL4akPFDFdRNZX0wvQK2bc4pclgGPszBNWCjIMw4zo49KvRUQkhqihJ\n1oWo5GatS0DToFfjCBpE+Hv8+BHWCAItgQypN8Tjx66U7AXw7V2w9k19ufsjcPOX4OWec3O6d/2r\njUcodrr3ZtDNJzYzaMEgnljzhFv3K0pRo6VeCSi2o37j6Rcj4c9PjY5KCFEFSbIuRCWWW+Tg2z+P\nA5TU4va0m2rcxActPqBJSBNDjl+p5J6EWdfDnh/AZIXhH0L/58Hkvn+lg1rWoEagN2l5dhZvd2+Z\nzFj/WJLzk9l0YhNJeUlu3bcohX8k3LUYWt0Emku/6fTnp/USn0IIcYnK/Q6Tl5fHI488QnR0NN7e\n3rRt25avv/76otstXLiQW2+9lYYNG+Lj40PdunW5/fbb2b9//2UFLkR1MP+v4+QVO6kf4UfPRhGG\nxWFSTDIE5uQumNEXkraATwjc9QO0vc3th7GaTdzZtQ4An607jObGEoA1/WvSqUYnAH469JPb9isu\nwOoNIz+BPk/ry+s/gG/uBHu+sXEJIaqMcifrI0eOZPbs2Tz77LMsXbqUjh07cuuttzJnzpwLbvf6\n669TUFDA008/zbJly3jppZfYunUr7du3Z9euXZf9AwhxtVJVjdnrEgAY060uJg+Xa8yx57A7dzeq\n5t4ZNauk/Stg5kDIPgZhDeGelVCnW4Ud7rZOtfGymIhLzOHPI5lu3fewBsMA+OHgD279ICAuQFGg\n1xMwaqY+4+nen+CzwZAjE4wJIS6uXMn6kiVL+OWXX5g2bRr/+te/6NOnD9OnT6d///48/vjjuFxl\nX9r78ccf+f777xkzZgy9evXijjvuYMWKFRQXF/POO+9c8Q8ixNVmxZ6TJKQXEOBtYWT7K7tx8XIs\nObSEVw6+wttH3vb4sSuVTdNhzmiw50LdHjDuFwhrUKGHDPGzMaJdDADT1xxy67771+mPt9mbhJwE\n4tLi3LpvcRGtboS7fgTfMEjerpf8TN5hdFRCiEquXMn6okWL8Pf3Z/To0eesHzNmDElJSWzcuLHM\nbSMjI89bFx0dTWxsLMeOHStPGEJc9TRNY+qvBwF9shw/r0ufXMddx1+wfwEArQNae/TYlYbqgmVP\nwpL/6hPdtL0d7lh4STOSusM9PeqhKLB890n2n8x12379rH5cV/s6QO9dFx5Wu4t+ZSa8MeQmnZpM\na5nRUQkhKrFyZQBxcXE0a9YMi+XczVq3bl3yfLdul35p+NChQxw5coThw4dfUvtdu3ahqnJJ3pMc\nDkfJ1+3btxscTfWx7UQR249lYTNDl5ACj//uDxUcIj4jHotioVtQt2p3/k3OAmpvfoGgE+sASG4+\nnpS6t8OuPR6No0usD+uPFfLyoj95tKv7PiS0VFqyhCUsPrCYQV6DsJhKfyuQ13/FMXV+h7qbJhOQ\n+hfa3FtJav0gaQ1uNDqsEnLuqzc5/xXHZDJRu3btcm1TrmQ9PT2d+vXrn7c+NDS05PlL5XQ6GTdu\nHP7+/jz66KOXvM2FhtqIinX6xSsq3rw4fbr5vvV88DOrOBye/ZC6MnUlAB0CO+Bv0UsSVpfzby1M\npf7mZ/DLOYBqsnG47UQyo3uD0+nxWIY31pP1NUcKGN3Uhyh/91xhaeLdhIFhA7km8BpUp4pDufi5\nrS7n32MUb/Z1fIXaO6cQcWwJMTvew5JzjGMtJoBiNjq6c8i5r97k/LuX2Vz+13e5//NfqCLEpVaL\n0DSNcePGsXbtWhYsWECtWpc2fbrFYsHkxhJp4uLOfpFarTL7oSfsSS1mV6oDiwlGNQ/CavXsEJgi\nV1HJREi9QnqVrK8O5987az/11k/CVpSKwyuEhC6vUBDaAqN+8qaRVtrXzGdLcjE/HCji/o4hbtv3\nnbXuvGgbef1XNCtJ10zEEVib6F0fEZWwCJ/CExzp+Cyq1dfQyOTcV29y/ivO5eSx5coCwsLCSu09\nz8jIAM70sF+Ipmncc889fPnll8yePZsbbrjhko/fokULSdY9bPv27TgcDqxWK23ayFTznjBl1mYA\nRrWvRb9unh8vvnD/QorUIuoE1qFlUEucTmf1OP/7fobFD4MjH8KbYL19Ho1C6hodFZMCM7jp4/Ws\nPlzI86O7UCPI22PHlte/h7RtCy26wcLxBJ5cT6vNj8Nt30BQjGEhybmv3uT8VxxVVcnNLd99SOXK\nfFu1asWePXtw/u1y8M6dOwFo2bLlBbc/nah/9tlnzJgxgzvuuKNcwQpxtduVlM2q+BRMCtzXu2Ir\njpRlY7Leqz6y0cjqU1t948cw9xY9Ua/XC8Yth0qQqAN0qhdKp7qh2F0q09e6tzJMfEY8L65/ke8P\nfO/W/YrL0PwGuPsn8IuAkzv1SjFJ24yOSghRCZQrWR8xYgR5eXksWLDgnPWzZ88mOjqazp07l7mt\npmnce++9fPbZZ3z88ceMGTPm8iIW4io27VQFmOtbR1Mv3M+QGF7r8RqfD/6cEQ1HGHJ8j3I5YckT\nsPQJveJL+3/CHQvAJ9joyM5xfx/9g9ucjUfJyLe7bb+bkjcxb9885u2d57Z9iisQ20GvFBPRFPJO\n6LXY42XyKiGqu3Il64MHD6Z///5MmDCB6dOns3r1asaPH8+yZct44403SgbNjxs3DovFwpEjR0q2\nffjhh5k5cyZjxoyhVatWbNiwoeSxdetW9/5UQlRBB1PzWLJTnyTlfoN61UG/96RdZDtCvN03PrpS\nKsrRe9M3fawv93sehr0H5so3PrNX4whaxQRR6HDx2R+H3bbfIfWHYFbM7EjbwaEs9/bai8sUUke/\nslO/DzgK4OvbYd37IBNYCVFtlXsA+MKFC7nzzjuZPHkygwYNYuPGjcydO5fbb7+9pI3L5cLlcp0z\nO96PP/4IwKeffkrXrl3PeYwYUQ168IS4iI9+PYimQb9mkTSrGejx49tddgqdhR4/riGyjsKnA+HA\nL2DxgZs+h2sf0WearIQUReGBU73rs9YlkFvknuoM4T7h9IztCcDc+Llu2adwA+8guP1b6DAW0GD5\nM/Djv8ElVTmEqI7Knaz7+/szZcoUkpOTKS4uZvv27dxyyy3ntJk1axaaplG3bt2SdQkJCWiaVuoj\nISHhSn8OIaq045kFLNqaCMADfRoaEsPPCT9z3bzr+Hj7x4Yc32OObdbHA6fsBv8oGLNEHy9cyQ1o\nXoOGkf7kFjn5YsORi29wiW5vpne0fH/we3Lt7pt8SVwhsxWufxsGvgoosGU2fDkKCjONjkwI4WFS\nWkWISuCTNYdwqhrdG4bRrrYxw0/m75tPniPPkGN7TNwCmHU95KdCVCu4dxXEtDc6qktiMiklw6Nm\nrj1Mod09c050qtGJhsENKXQW8t2B79yyT+EmigJd74db54LVDw7/BjP6Q4YMWRKiOpFkXQiDpeQW\n8fXmYwA80NuYXvVDWYfYkrIFs2JmeMNLm1G4StE0+O0NmD8WXMXQeBCMXQZBsUZHVi7D2kQTG+JD\ner6dbzYfdcs+FUXhtma3ATBnzxxcqkw8V+k0Gaz/vQbGQPp+mN4XjqwzOiohhIdIsi6EwWasPYzd\nqdKudjBdG4QZEsOC/XqFpx6xPYjyizIkhgrjKIQF42D1y/pylwfgljng5W9sXJfBajZxXy+9d/3j\nNYcocrgnsb6+3vU0CGrAPxr+A4cq46IrpZqt9StB0e2gMANm/wO2fGF0VEIID5BkXQgDJWUVMmtd\nAgAPX9fIkLrmdpedHw7+AMCNjW70+PErVE6yXv4ubgGYLDD0XRj0Cpgq13Tu5XHjNbHUCPQmObuI\nL9a7Z+y6r9WXRTcsYkKbCXhbPDfpkiingBpw96l7LFQH/PAg/Pw0yNUQIa5qkqwLYaC3f9mH3anS\nuV4ovZtEGBLDqqOryCrOItI3ku4x3Q2JoUIkboHpfSBpK/iEwJ3fQYeqP7+Dt9XMYwMaA/DB6gNk\nF7inJ7zaTIBV1dl84cZZ0GuSvrz+A5hzExRlGxqWEKLiSLIuhEH2JOewYMtxAJ4c0sywZGn+vvkA\njGg4AovJYkgMbhe3QO9Rz03WJ5i5dxXU62F0VG4zqn0sTaICyC50MO3XA27br0t1seroKinjWNmZ\nTNDnSbjxM7306IEV+o2n6QeNjkwIUQEkWRfCIK8vi0fT4PrWNWlby7gZM1+69iXubH4noxuPNiwG\nt1FVWPWyfiOpswgaDYBxv0BofaMjcyuzSWHS4KYAfLYugcQs99TH35KyhX+v/jfv/PUOOfYct+xT\nVKCWI2HsUgiIhrS9MKMvHF5jdFRCCDeTZF0IA6w7kMave1OxmBQeH9DE0Fhq+NXgiY5PVP0bS4tz\nYd6dsOYNfbnrg3Dr1+Dt+QmmPKF3kwi61A/F7lR5a/let+yzQ1SHM2Uc90sZxyohuh2MXw3R7fUa\n7J8Ph42fyIynQlxFJFkXwsNUVePVpfEA3NGlDnXD/QyJw6k6DTluhUg/CDP6QfxiMNvghqkw8OUq\nfSPpxSiKwpODmwGwaGsiu5OuvCf87DKOc+PnomrqFe9TeEBADX1yr1ajQXPB0sfh+wfAUWR0ZEII\nN5BkXQgP+3FHEjsTs/H3svDQdcbUVQf43x//44GVD7A/c79hMbjFvuXwSR9IjYeAmjBmKbS7w+io\nPKJNrWCGtq6JpsFry+Ldss/r611PoC2Q43nH2ZazzS37FB5g9YGR02HAS6CYYNtX+n0b2YlGRyaE\nuEKSrAvhQcVOF2+eGrJwX6/6hPl7GRLH8dzjLD28lDXH11TdutqaBmve1CthFGdDrc4w/jeI7WB0\nZB71+MAmWM0Ka/al8vv+tCven6/Vl1GNRgGwPHX5Fe9PeJCiQLeH4I6FegWkpC3wSS+ZQEmIKk6S\ndSE86KsNRzmWUUhkgBdjr61nWByzds3CpbnoFt2N5mHNDYvjshXnwbx/wqoXAQ06jIW7FkNAFR93\nfxnqhPlxe+c6ALy6dA+qeuVjlW9uejMmxURcXhyJRdIzW+U06APjf4WolpCfCrOHwabpMo5diCpK\nknUhPCSnyMH7q/QhJ4/1b4yvzZgyiWmFaXx3QL95cFzLcYbEcEXS9uvj0/f8ACYrDJsCQ98Bi83o\nyAzz0HUNCfCysCsphx+2J13x/mL8Y+hTqw/1fOrh0mTCnSoppC6MWw4tRoLqhCX/1cex2wuMjkwI\nUU6SrAvhIR/9epDMAgcNI/258ZpYw+L4as9XFLuKaR3emo41OhoWx2WJWwif9IbUPeB/6qa6a+42\nOirDhfl7cV/vBgD83897KXZeeYL9fLfneaHxC9T2qX3F+xIGsfnBjZ9C/xfOjGOfKfXYhahqJFkX\nwgOOpOcz8/fDAEwa1BSL2ZiXXq49l6/jvwZgbKuxVWfWSqcdlk6E+WPAngd1e8C/1kCtTkZHVmmM\n7V6PqEAvErMKmbH28BXvL8grqOr8fYiyKQp0/7c+g69fBJyMg497we7vjY5MCHGJJFkXooJpmsZT\ni3ZS7FTp3jCMvs0iDYtl0f5F5DnyqB9Unz61+hgWR7lkH9erWmz8SF++9jE98aiG49MvxMdmLpko\nacrK/RxOy3fLfgtdhSw6sYi9Ge6p5S4MUr8X/Gst1O4K9lz9no9lT4Grit5gLkQ1Ism6EBVswZZE\n/jiQjrfVxCsjWhnaW3lTk5v4X5f/8XD7hzEpVeDlf2AFfNQDEv8E7yB9kqN+z4LZmPH+ld3wtjH0\naBSO3any1MKdaG64oXDuibksOLGAD7Z94IYIhaECa8JdP+oVYwA2TIVZQyHnyu9zEEJUnCrwbi1E\n1ZWWV8xLP+0G4JF+jakTZswESKd5W7y5qclN9K3d19A4LsrlgJUvwJc3QmEG1GyjD3tpMtjoyCo1\nRVF4eXgrvK0m1h9K59s/j1/xPgeHD0ZB4ddjv7IjdYcbohSGMlv1Wuw3fwlegXBsA3x0rT5fgRCi\nUpJkXYgK9OLi3WQVOGheM5B7DCzV6FAdFLuKDTt+uWQm6MNe1r4FaPoNpGOX69UtxEXVDvPlsf6N\nAXh5yR5Sc6/svNf0qkmP0B4AvLf1vSuOT1QSzYbp5R1rtIKCdJgzGpY9Cc4q8n9CiGpEknUhKsjq\nvSl8vy0JkwKvj2pt2E2lAN/Ef8Pw74az9vhaw2K4JHEL9GEvxzeDVxCMnqWXZrR6Gx1ZlTK2ez1a\nxgSSXejg+R93XfH+RkSNwGKysDF5I5uSN7khQlEphDWAcSug83368oZpMKOvXh5VCFFpSLIuRAXI\nL3byzKI4QE+cWsUGGRZLRlEG07ZN43jecU4WnDQsjguy5+s1oOePheIcfTbSCb9DixFGR1YlWcwm\nXhvZGrNJYfGOZFbuubLzHuEVwY2NbgT03nV3jIUXlYTVGwa/Drd+Az6hcGInfNyTkCNLZBIlISoJ\nSdaFqABvLd9HYlYhsSE+PDagsaGxvL/1fXIduTQLbcaIhpUw+U3erpeS2/oloEDPx+HuJRAs9b2v\nRMuYIMadGnr1zHdx5BU7r2h/41uPx9vszfbU7axNrORXaET5NRkEE9bpZVEdBdTe8hr1tr6MyZ5r\ndGRCVHuSrAvhZtuPZTFrnV7n+uURrQybqRQgPiOeBfsWADCx00TMJrNhsZzH5YTf3oDp10H6fgiI\n1itVXPeMVHtxk0f7NaZWqA/J2UW8+fOVlV6M8I3gtma3MaTeEOoFGnf/hahAgTXhn99D38loipmw\npNU0WXU3HFxldGRCVGuSrAvhRg6XysQFO1A1GN42ml6NIwyLRdM0Xt34Khoag+sO5pqoawyL5Typ\ne/WZFFe/rE+F3mwYTPgD6vUwOrKrio/NzCsjWgEwe30CW45mXtH+Hmn/CK/3fJ1agbXcEJ2olExm\n6PEfDvT8gCLfGGyFqfDFCFj8mD5cTQjhcZKsC+FG763cT/yJXEJ8rfxvaHNDY/k54We2pGzB2+zN\nYx0eMzSWEqoK66fCxz0haYteO33kdLjpC/ANNTq6q1KPRhGMbBeDpsF/v91O/hUMhzl7jgBN03Cp\nLneEKCqhgtAW7O75MWn1R+or/pwJH3aHoxuMDUyIakiSdSHcZPXeFN5fdQCA529oSZi/l6HxbDqh\nV+0Y22osNfxqGBoLoJdknD0Mfn4KnEXQsB/cvwFa36RPiS4qzDNDmxMV6MWh1HwmuWGypLTCNB79\n9VGmbZ/mpghFZaRafEhs84g+Y3BgLGQehk8HwS+TwVFkdHhCVBuSrAvhBolZhTz6zTYA7uxSh3+0\niTY4IpjcdTIf9/uYMS3GGBuI6oL102BaNzjyO1j9YOi7cPt8CDT+91QdhPrZmHpbe8wmhR+3J/Hl\nhiNXtL9tKdtYeXQln+78lPiMeDdFKSqtBn3g/nXQ9g5Agz+mwMc94Mg6oyMTolqQZF2IK2R3qjzw\n1RayChy0jg3imaHNjA6pRLeYbnhbDKxRnrxDr9v885PgyIc63fWx6R3GSG+6h3WoG8qTg5sC8OLi\nPWw/lnXZ++pXpx/96/THqTmZ/MdkHKrDXWGKyso7CIZPhVvmgl8kpO3TJy/78d9QePl/S0KIi5Nk\nXYgr9MqSPWw7lkWQj5Wpt7XHy2JsxZV5e+eRXphuaAzYC2D5/+CT3pC0VZ/gaNgUuGsxhEolEaOM\nu7YeA1tEYXep3P/VFrIK7Je9r6c6P0WgLZA9GXuYvWu2G6MUlVrTIfDgJmh/l7781yyY2gl2LZK6\n7EJUEEnWhbgCP+1IZta6BADevqkNtUJ9DY1nY/JGXtzwIjd8fwM59hxjgjiwAqZ1gXXvgebSJzZ6\ncBNcczeY5F+OkRRF4Y0b21AnzJfErEIem7cdVb28BCvcJ5xJnSYB8OG2DzmUdcidoYrKzCcE/vGe\nPh9CWCPIOwnf3g1zb4GsY0ZHJ8RVR945hbhMB1PzeGL+dgAm9G5A32ZRhsaTWZTJU78/BcCguoMI\ntAV6NoCsozDvLvhyFGQd0W9Iu/UbGD0LAirBDa4CgCAfK9Nub4/NYmJVfAofrTl42fsaWn8o18Zc\ni121M3ndZKkOU93UPTWsrdckMFlh3zKY2hnWvCk3oArhRpKsC3EZCu0u7v9yC/l2F53rhfKf/sbO\nUqpqKs/88QwpBSnUDazLY9d4sFSjvQBWvwofdITd34Figs4T4IGN+qyIotJpER3Eize0AODNn/ey\n/uDlDZtSFIVnuz6Ln9WP1IJUThSccGeYoiqweEGfJ+G+36F2V/3elFUvwrTOsGexDI0Rwg0kWRei\nnFRVY9LCHew9mUtEgBfv39YOi9nYl9IXu79gzfE12Ew23uz1Jr5WDwzH0TSIW6gn6b+9ppdjrNsD\n/rUWBr8GXv4VH4O4bDd1qMWN18SiavDQ3K0cyyi4rP3U8KvBtL7TWHTDImL8Y9wcpagyIpvCmKX6\nvAkBNfVSrd/crk+olCIVg4S4EpKsC1EOmqbx/I+7+H5bEmaTwnu3tCMywMBqK8CO1B28+9e7AEzs\nNJEmoU0q/qDJO2DWUJg/BnKOQ1AtGD0b7voRarSs+OOLK6YoCi/e0JKmNQJIyyvmzpkbScm9vKEL\n7aPae+YDoqjcFEWfN+HBP6HHf8Bsg0Or4cNusHQiFGQYHaEQVZIk60KUw1vL9zF7/REUBd4a3Yau\nDcKMDokPt3+IU3MyoM4ARjceXbEHyzgEC+7RZyA98jtYfKD3k/DAJmgxXMoxVjE+NjOzxnSiVqgP\nCekF3Dlj0xVVPazv0wAAIABJREFUiFE1lXl75/HF7i/cGKWocrz8oe/kU0PhrtdvNN/4EUxpC2vf\nAnu+0REKUaVIsi7EJfr4t4N8sFqfofTFG1oyvF3luOT/Vq+3GNNiDM91e+6c6eDdyVKUBj/9Rx/y\nsvNbQIOWo+DBzdB7EtikV7WqqhHkzVfjuhAZ4MXek7nc9dlm8oqdl7Wv1cdW8+KGF3lj8xusOLLC\nzZGKKie0Ptw6B+5cBJEtoDgbVr4A77WDzTPAJfX5hbgUkqwLcQm+2niEV5fq4y4nDmrKHV3qGBzR\nGb5WXx7r8BgBtgC379tkzyUmfiZNl9+mv7mqTmjYD/61Bm78FIJruf2YwvNqh/ny5T2dCfG1sv1Y\nFvfO/pMiR/kru/St3ZdbmtwCwJNrn2RX2i53hyqqogbXwX1r9fHswXX0Uo8lH/7ng6oaHaEQlZok\n60JcxPfbEnnmuzgAHujTgAm9GxgcEexJ38OsuFmoWgW9yRVkwK+v0Wz5LdQ8MAezqwhiO+qTGt2x\nAGq2qZjjCsM0jgpg9thO+HtZWH8onQfnbMF5GTXYJ3aaSPeY7hS5inho1UOcyJcKMQIwmc+MZx/y\nJvhFQOZhWDAOProW4haAlP4UolSSrAtxASt2n+SxedvRNLirax3+O8ADN29eRHJeMo/++ihv/fUW\nM3bOcO/Oc0/qM4++2wp+fRWLI5dC/zoc7vwyjPsF6vVw7/FEpdI6NpiZd3XAy2JixZ4UpmzIwFXO\n0nsWk4X/6/l/NAxuSGphKg+teogCx+VVmhFXIYsNOt0LD2+D654Br0BI2QXzx+o97Vu+AOfl3zch\nxNVIknUhyvDD9iTun7MFl6oxsn0Mzw5rUWFjwi/VyfyTjFs+jsS8RGoH1Oamxje5Z8dZR+Gn/+pJ\n+rr3wJ4HUa1I6Pgcu3pNJye6h9w8Wk10rh/GR3dcg8WksOZIIVM2ZlPsLF/CHmAL4IO+HxDqHUp8\nRjwT10ysuKtAomry8oeej8MjO6D3U/qsqBkH4YcH9THtGz8BR6HRUQpRKUiyLsTfaJrGO7/s4+G5\nW7E7VQa3rMEbo1pjMhmbrKYWpHLP8ns4lnuMGP8YZg6cSbB38JXtNPEvWHDvqRu+poOrWB/ucus3\ncN9asmOvA8Xsnh9AVBl9mkYy5ZZ2mBVYd7yYZ1allrusY4x/DO9d9x4+Fh+6RHfBpMjbjSiFTwj0\nngiPxEH/F8E/Si8Hu/RxvfNg9av6FT8hqjGL0QEIUZkUOVw8Pn8HP25PAmB8z/pMHNQUs8GJenph\nOvcsv4eEnARq+tXk04GfUsOvxuXtzGmHPT/opdSObz6zvl4vvTZyvZ7Siy64vnVNMk6E8/radPal\n2xn+wR/MvLsjzWoGXvI+2kS0YenIpYT5GF/iVFRyXv7Q/WHoNB62fQm/T4Hso/qEa2vfghYjoMt9\nEHON0ZEK4XHS1SHEKSm5RdzyyQZ+3J6ExaTw+qhWPDWkmeGJulN1ct+K+ziUfYgo3yhmDpxJtH90\n+XeUlwq//Z/eW7VgnJ6om23Q+ha4dzXc9QPU7yWJuijROsqbV68LJTrAQlJ2EaM+XMeK3eXr5Tw7\nUU8pSOGzuM/QZAp6URarN3S8Bx7eolecqtUZVAfsnAfTr4MZ/fQKMjKuXVQj0rMuBLA7KYd7Zm8m\nKbuIYF8rH95+TaWY8Aj0G/bGtBjDO1veYcaAGdQKKEe5RJcTDq6ErV/A3qV66UXQLzV3GAcdxoB/\nZMUELq4KNQMs/N+ASKZuK2bdwXTu/eJPnhrcjHt61CvXPRwO1cGDKx9kT8Ye9mfu5/luz2M1Wysw\nclGlma36XA4tR0HiFtj0iV4x5vhm/eEbDq1vhnZ3QFRzo6MVokKZn3vuueeMDqI0mqZht5/7ydnL\ny8vwG/yqm5MnT6KqKmazmRo1LnPYRSWmaRo/bE/iX1/8RUaBg/rhfsy5twutYoOMDg1VU0v+3huF\nNOKmxjcR7hN+aRun7Yc/3oPv7oe/PoO0faCpENMB+r8Aw97Te9FtfhfczdV+/sWFnT7/PjYL4we2\nJy3Pzs7EbNbuT+N4ZiFdG4ThZbm0exrMihmzycza42uJz4xnW+o2+tTqg5fZq4J/CnE5KtVrP7Am\nNBsK19wNtgD9/1t+ip60/zkT9i3Xyz6G1td75sUVq1Tn/ypzOfmtDIMR1daJ7CLumf0n//56GwV2\nF90ahLHo/u7UC79wAusJG5I3MOqHUefUqPa2XORNKPckbJoOMwfABx3gj3ch7wT4hkGXB2DCOrh3\nJbQerZdPE6IcrGYTr4xoyf+GNsekwIItxxn4zhpWx6dc8j5GNhrJ+9e9j4/Fh43JG7lr2V1Sh11c\nOv9I/WbUR3fpN8E3GwYmCyRtgZ8eg7ea6CUg438CR/luiBaiMpNhMKLa0TSNrzcf45Wf9pBb7MRq\nVnjoukZM6N0Aq9nYz68u1cXHOz7mo+0foaHx4fYPeb7b82VvkJeq3yy6axEc+UPvPQdQTNBogH6J\nuNFASc6FWyiKwrhr69EiOpCJC3ZwJL2AMbM2M7xtNJOHtSDU7+J/Zz1iezBr0CweWPkA+zP3c/uS\n25nWdxpNQo2fw0BUEWYLNBmkP/JS9fHsW76A1D36UJm4BXr99iZD9BtTG/QBi1zBEVWXJOuiWjmS\nns+kBTtZfygdgLa1gnnjxtY0jgowODJIK0xj4pqJbDqxCYBRjUYxqdOk8xtmHYP9P8OeH+HwmjMJ\nOujDXFoMh5Y36peOhagAXeqHsezfPXn7l73M/P0w321LYu3+NJ77RwuGtq550eGKzcOa89WQr5iw\nYgKHsg/x/tb3+aDvBx6KXlxV/COg6wPQ5X69h33nAr3zIjcJdnytP7yCoOn10HQI1O8NXsb/vxei\nPCRZF9VCgd3J7HVHmLJyH0UOFW+rif8OaMKY7vUMr/YC+rCXSWsmkV6Ujo/Fh8ldJzO0/lD9SZcT\njm+CfT/D/uWQsvvcjaPb671HzW+AkDqeD15USz42M09f35zrW0czcf4O9p7M5aG5W/lhexJPDm5K\n/Qj/C24f7R/N54M/58m1T/J4x8c9FLW4aimKXtYx5hoY8JI+nn3XQtj1nT4ccPsc/WG2QZ3u0Hig\nfvUxrIHRkQtxUZKsi6tafrGTLzYcYfqaQ6Tn6zd0dGsQxmsjW1M7zNfg6HR/nviT8cvHo6HRMLgh\nb/V6i/oq8Ncsvef8wEooyjqzgWLSy5k1HqQn6KH1jApdCNrWCubHh65l6uoDTPv1AL/sPsnKPScZ\n1iaaB/s0pNEFrloFeQUxrd+0c9a9vul1fCw+/KvNv+TmU3F5TCao3Vl/DHwVjm2A3T/AvmWQeRgO\nrdYfyyZBWENo2E+fX6JON32SJiEqGUnWxVUpt8jB5+uPMGPtITILHADUDvXl4b6NGNU+xvCqQpqm\nlcTQJqINMb5RdPKOYpLDB59Ph+kz+J3NOxga9dfHnzfsC76hBkQtROlsFhOP9m/MkFY1+b+f97Ji\nz0m+35bED9uTGNKyJg9e1/CSJlM6lHWIr/Z8hYbG8iPLebbrs3Ss0dEDP4G4aplMehJepxsMehXS\nD+hXKfctg6Pr9eX0A/okcShQs7WeuNftCXW6ypAZUSkoWiWdnUJVVXJzc89ZFxAQgMkkBWw8afv2\n7TgcDqxWK23atDE6nItKzi7k603H+OyPw+QU6TXF64X78WCfhtzQNhqLwTeQ2l125u3+ip8PfM+n\nkX2wJm6B45vJzEsmRD1r7LnJCrEdoG4P/eao2E76TVUeVtXOv3Cvyz3/cYnZfLDqAMt2nan0MrBF\nFOOurU/HuiEX/LC84sgKXtn4CqmFqQD0jO3JP5v/k041Ohn+Ibs6qRav/aJsOLgaDv8Gh9dC+v5z\nn1dMENlC/18c21F/hDXUPwBc5arF+TfI5eS3kqyLC6oKL9i8YidLdyazaGsi6w+lc/ovumGkPw9d\n15ChraONG5fuKIKU3eQn/sWyYyv5JHcPSYqelL+cms4/8vL1dooZottBvR56r06tzhetge4JVeH8\ni4pzpec//kQO7686wJKdySWvy9gQH0a0i2FEu5gyx7Xn2HN49693mb9vPhr6hk1CmvBmrzepG1T3\ncn8cUQ7V8rWfkwwJa/XhhwlrITPh/DbewXryXrMt1GilP0LqXXUJfLU8/x5yOfmtDIMRVZLDpfL7\ngTQWbUlk+e4TFDnO9Ep3qhvKnV3rMKRVTc8l6aoLso7ok3WkxsOJOFwndrAx7yg/+Puw0teHIpMJ\nFIh0OplQoDIkuhfUOtVbE90OvC58Q54QVU3TGoFMva09+0/mMn3tIX7akczxzELeX3WA91cdoE2t\nYEa2i2Fo65qE+Z8Znx5oC2Ry18n8s/k/+XLPl/xw8AdOFpwkyi+qpE2xq1jGtAv3CqwJrW/SHwA5\nSXD8zzOzpiZt1e8fOrBCf5xm84eoFnriHtUCwptAeGPwC9dvfBXiCknPurigyvLpWlU14k/ksu5g\nGn8cSGPT4Qzy7a6S5+tH+DGyXQw3tI2hVmgF3TiqaZCfqve2ZCbo4xzT9kHqPv17V/E5zY9aLFxf\nK7pkua7ZjxtrdOOmNuPxCW9SJf6JV5bzL4zh7vNfaHexfPcJFm1NZO3+NFyq/vajKNC8ZiDdG4bT\nrUEYneqF4ms705eUXZzN/sz9dKjRAdDv+Ri4YCA1/WrSq1YvetfqTb3AejJMxo3ktV8KlwNOxukJ\n/IkdcGInnNx93v/+Ej4hetJ++hFaH0Lq6lW7KvlYeDn/FccjPet5eXk888wzzJs3j4yMDJo2bcqk\nSZO45ZZbLrptSkoKTzzxBIsXL6agoIA2bdrw0ksv0bdv3/KGIa5y+cVO4k/ksjs5hw2H0ll/MJ2M\n/HOn5w3zszGsTTQj2sXQOjboyt+oXQ7ITdZ7U3ISITtR/5p19EyC7ig4ZxMNOGy18KevN3/6BKJ6\nBfBmYBuIakHtGq3pfXg+UUF1+EeDf9AqvJUkE6Ja87GZuaGt/qE6NbeYH7cnsWhrIjsTs9mVlMOu\npBw+WXMIq1mhXa0QujUMo3VsEM1rBnFN1DUl+zmYdZDk/GSS85PZkrKFd/56h9oBteldqzc9Y3vS\nMrwlflbjh5GJq4zZql8FjW53Zp3LqY91P7FTT+BT4iFtrz4fRmEmHNuoP/7ON/xU4l4XgmtBYMyp\nRzQExeozT8v7hTil3Mn6yJEj2bx5M6+99hqNGzdmzpw53Hrrraiqym233VbmdsXFxfTt25esrCym\nTJlCZGQkU6dOZdCgQaxYsYJevXpd0Q8iqqZCu4vErAIS0grYk5zDnhM57E7K4UhGAX+/5uNrM9Op\nXijdG4TTrWEYzWoEYrrYMBdHERSkQ2EGFGToPeP5qZB3Up/5Lu8k5KdA7kn9ey52oUnhr7BYdgSE\nsMtm5U81j3RXYcmzVpNC0YiP8LZ4A/B+44Hl/6UIUQ1EBHgx9tp6jL22Him5Raw/mM4fB9L440A6\niVmFbErIYFNCRkn7EF8rzWoG0qxmIM1rBvJOt/kkFGxic8rvbDqxiaO5R/l89+d8vvtzJrSZwP1t\n7wcg155LfEY8zUKb4W+ToWbCzcwWiGymP04PnwGwF5y5+pq2Tx8iebrTpzADCtL0R+KfZezXSx+W\n4xcJ/qcfUeAXoX/1DdOrgvmG6ePoDShAIDynXGd3yZIl/PLLLyUJOkCfPn04cuQIjz/+ODfffDNm\ns7nUbWfOnElcXBzr1q2ja9euJdu2adOGJ554go0bS/nkKaosVdXILnSQnl9MWp6d9Dw76fnFJGcX\ncTyzkGMZBRzPLCQtr/TLhyZU6vhDqygb7aKsdIqx0SQErM4ssB+HE3lwJBeKcvQ7+otPfS3K1scU\nFmTq/xD/1hN+IU4gw+pFamAUqX5hpPgEkGLzItEEL7cYjymsAQTFMvePp/k54WfQK0JiM9loE9mG\nDlEd6BDVAbOp9NeAEKJ0kQHeJT3umqZxNKOAPw6ks+lwOruTcziYmk9mgYN1B9NZdzD9rC1D8bWN\nIDpkJP4hh3DYdpKh7iE7K5Lf9qUS5mdjf+5GJm/8j34cn0hiAmKI8T/z6FKzCzX9ZbZf4WY2X70M\nZM3W5z9XlA2ZR/Sa75kJkH383Cu6+Sn60JrTyf2l8A7SE3efEPAK1Je9g8D71PdeQfp9UTZ/vXiB\nV4D+vZc/WP3A6qM/pDe/UirXmPV7772Xr7/+mszMTCyWM3n+3Llzue222/jjjz/o1q1bqdv279+f\nY8eOER8ff876V199laeeeorjx48TExNTsr7ajVnXNM50JZ/+/kLr9K+apqKpKhqa/lXTUE+vU1VU\nTUVVVTSXiqa6cKkuVFXF6XKhuZy4VBXV5cTlcuFyOXE6nbic+lfV5SAxMRG7w4GmqYQGB+FwOnA6\nnDidDpwOOw67HYejGKfDjtNpx+Vw4HLacTqKsWhObDiw4sSGE5uiL3udengrdrxw4KM48TM78DM5\n8KIYi1qEotrRAFVR8NI0Tv/7yFMUCk0KLhRUBRwoOBVwKgoOFJra7SWfQHfZbBy2WigyWyiy+VFk\n86XA5kOu1Ytcs5XJNXrjGxgL/pG8cnwZ3xxbhcpZ5RPPsmzUMmL89b/PeXvnsfnEZhqFNKJ9ZHta\nRbS6am90k3GL1VtlOf9FDhf7T+axJzmH3ck57EnOISE9n5M5ZYwVRoNT/zUsgdvwilyKyZpdassO\nPv+msX93vKxmkuwb+T1zBr6WQPwtQQTYgvAx++Jr8cXH6kv3Gv2pE1Afq9lEtj2Fw3n78Dbb8LLY\n8DZ74W3xxstixWa2EOETSYCXPyYFnKqDIlchZsWESTFhNZkxKSbMJhMmkwmLYql0Q+Qqy7mvlpz2\nM0My81MgL+X8K8KFGfpV46LS/64vm9UXrD7YseIy2dDMXvgGhIDFCyze5341W/UrAGbrqWUbmCz6\nssl66vmzvjeZ9edPPxTzqXXmU99bTn1vOrOu5HtTGQ/l3GWUU+uUU9+bzvq+lK+KSY/Ngyp8zHpc\nXBzNmjU7J1EHaN26dcnzZSXrcXFx9OjR47z1p7fdtWvXOcl6aXbt2oWqlp5MVRTV5eK+7XeW+XzX\ngmLeSMnk9PCJfnVqUFzGP912RcVMPZFWkngOrlWTrDLqfjcvtvPZiZSS5RtianLCUnqPbT2Hg6+T\nTpYs3xwdRYK19D++aKeTRYlnah/fXSOSPV62UtuGuFSWHU8qWb4vKoIt3n9LSm36w0fT+O1oYsnq\nh2uGs87Hm9Nptnbqhz79Frol4VhJ28ciw/nFzxf9z9HnvDg2HkvFavZBtfjyfJCFZV5l/w3MCb0V\nP1sYTlsg07NWsDJn01nPOvSHE3BCf79OhJvDoRByi71RUVFQCLYGE2wJJsQaQrA1mEivSA7GHyTN\nmgZAE5rQJLiJ/sOchPiT8aVEcnVwOBwlX7dv325wNMLTKtv5b2KDJnVgRB1fwBeHSyMl30lKvouT\n+U5O5rlIK3CSU6ySXaSSVewiO7ct+TltwZyPyZqhP2yZKNZMTNYMfjuksLr4EADWkD1418gg35VB\najGQf+7x568z4cpLBsAS9Bc+0d+WGWth4q04c/Qk1xKwE5/Yr8pum3QjruwOKAqY/fbiFTvr1DNn\nv5cooIEzdRhqdhdAQfE5jDVmZpn7VdMHoGb11Be8ErHEflR224w+qJnX6QvWFCy13z/z5Ja/tc3q\njpo+SF+wZGKp83bZ+83uhJo2TF8w5WOp91rZbXPboqaM0hcUO5b6L5bZVstrgevkmXvlLA3+V3bb\ngsa4ks+8j1vqvQgme+ltC+viShp3pm3d18CcX3rb4hhcx+8707b222DNLL2tPQLXsYdLls213kex\npZTaFkcwzqP/ObVgxRyzGMX7rInyLECACQIiwFWHgIQHCCGXYHI5Hr2UHJ9U9HT01A3cp96JrRpM\nPeKFH4X4UszrkSY2+5adBm44clT/C8yGp8LDWOnnU3JF+e9WH03E91Tn4othISz2L/uekaXHkgg9\nlcv9X2gw8wPKHp62MDGZGKdeTOL94CC+DCr7xtw5SSdo4NDnV5kRFMj04LInYvs0OYUWdjvbrW1g\n6PtltqsIJpOJ2rVrl2ubciXr6enp1K9f/7z1oaGhJc9faNvT7cq77WlOp94D7Emqy0XBBT7t2E1g\nU5wly4WKopfoK62tomBWzlzIKDQpZe676G9jsS/Y9m8fDooUU5lt8xUzuZoPGgoqCnmKpcy2Vk0h\nQamFqphQFTOZJheFptIvxGiawv6Q3ihmCyazhVzvYxSbckttC3Co7SQ0kw3VbCU3dxUUHyyz7dYB\nC/Ay6R8SchNnQNYfmDGjKAoWxYJFsWBWzFgUC6kRXSi26C/QKHsCzV152Ew2bIoNm8mGl8kLP7Mf\nviZfzC5zSTLSP6Q/fYP7EmgJxKSU/vs43ba6qu4/f3VXWc9/pA9E+phpGV56Z4aqaeQ7NHKKwsh3\nxFLg0ChwahQ6NAocKgX+GkVODbtLo8DVlbz8xhRpeRRr+djJw0VxycPHHInqY8KpgkvxQyuqDTjR\nFCeUPFwoigrq2W+vF+9k0tAvmipoKMpZV1TPpoBL03C49OfMqorNVPZ5caoqdqe+D5NFxVpGggrg\n1Jxn2pou3NalOSl2nkkEL9iWs9qaL9xW1ZwUnWqLohFwoXhxnGkLF2zr+ltbf5MdpYz2f2/rp9gx\nldFWxX7pbZVz9+uLo+y2pnP363uh/aoWkp0BJKMnsT78hsVUep5UpFoZWfxcybKPNguLqezOplvs\nT+OFE2/sHNDWU2BKKrPt587++GsurLjYx0kKTKV/wAHYrtUnRFWxoHISFwUXuPcsQwvAR3NiRiVP\nsV4wH1PP+nDrULhIW51LBdXD/9vKGi5+IeUaBtO4cWMaNGjA0qVLz1mfnJxMdHQ0r776KpMmTSp1\nW5vNxrhx4/jwww/PWb9+/Xq6devG3Llzz6koU9plgqNHjxrSs34wJY5zezjOsJlsBJn15FBDIc2Z\njoZ2Vusz31kUG8GWoJJ1ac50OKu1cvrSDGBRLARbQwAFRVFId2SgKlrJsnZWe4tiJswrQn/OpJDh\nyEBTNEwKKCgoCpjQr/iYFRMRXhElMWXYM3BqZz5snE1BIdgUXLKcRx4O1XFem9Oxh9vCS9ZnO7Jx\naI7z2p0WZgsr+T7fmY9Tc6IoCgoKJkwl+1RQ8DZ5l1wi1jSt0l0uvpqdnaBZy7haI65ecv7LT9U0\nNA1U7XQCruFSNZyaioo+dNGl6UMUXZqGpmlYFCsWkw1N04fMFKj5p9qemhLq1Nu0hoaP2Rcvk34F\n0qHayXXlcPbb+Nlv6L4mX3zMeg+nQ3OQ7Sy91xfAx+SLr1nv4XRqTtILz/T6Wqzn9ut5m3zxO9XW\npTnJdJ65EfjvGYW3yRv/U++RqqaS4UwrMwYvxYsAS9AltbUpNgItZ96f0hxl9FKX0jbdkVJmKQGr\nYiXIElKynOFIRS2jtUWxEGw50wmZ6UjDVcYHMzNmQqxn3veynOk4tdKTajMmQqzhZ7Ut+33ahEKo\n9cx7erYz85z33rMpQJg1smQ5x5mFXSvjQ4vTQaglQu8Us1gv2BYg1BJe0tGV58yhSCsqs22IJQyz\noiesea4citQLtQ3FrOh/f/muPArVsu9DCzYHY1EsgEahM48CNQ/Q0D/7avqVhlPfB1sCsWLFarEQ\nHOjZG89L61l36zCYsLCwUnvAMzL0F2ppPefu2Pa0Fi1aGDJmvR3tPX7MyuLscYu92/Q2OhzhYTJu\ntXqT8199ybmv3uT8V5zSOqMvplyZb6tWrdizZw9O57mf8Hbu3AlAy5YtL7jt6Xbl3VYIIYQQQojq\nqFzJ+ogRI8jLy2PBggXnrJ89ezbR0dF07tz5gtvGx8efU6LR6XTy5Zdf0rlzZ6Kjo8vcVgghhBBC\niOqoXMNgBg8eTP/+/ZkwYQI5OTk0bNiQuXPnsmzZMr788suSQfPjxo1j9uzZHDx4kDp16gAwduxY\npk6dyujRo3nttdeIjIxk2rRp7N27lxUrVrj/JxNCCCGEEKKKK/eUVwsXLuTpp59m8uTJZGRk0LRp\n0/NuDtVrdrvOuenFy8uLlStX8sQTT/DQQw9RUFBA27ZtWbp0qcxeKoQQQgghRCnKnaz7+/szZcoU\npkyZUmabWbNmMWvWrPPWR0VFMXv27PIeUgghhBBCiGqp3Mm6p5RWUdLTZRuFXmLIbDZjMpnk918N\nyfmv3uT8V19y7qs3Of8Vp7Tf58WqqJerzronOZ1O8vPLLqovhBBCCCFEVefn54fFUnb/ueeLlgsh\nhBBCCCEuiSTrQgghhBBCVFKSrAshhBBCCFFJVdox66qqnjcIX1EUFEUxKCIhhBBCCCEun6Zp591Q\najKZMJnK7j+vtMm6EEIIIYQQ1Z0MgxFCCCGEEKKSkmRdCCGEEEKISkqSdVGm33//nSFDhhASEoKP\njw+NGjXixRdfNDos4QFbt25l+PDhREdH4+vrS9OmTXnhhRcoKCgwOjThRrm5uTzxxBMMGDCAiIgI\nFEXhueeeK7Xtli1b6NevH/7+/gQHBzNy5EgOHTrk2YCFW13K+Xe5XLz99tsMGjSI2NhYfH19adas\nGZMmTSIrK8uYwMUVK89r/zRN0+jZsyeKovDggw96JlABSLIuyjBnzhx69epFUFAQn3/+OUuWLGHi\nxIkXnWVLVH27d++mW7duJCQk8O6777J48WJuueUWXnjhBW699VajwxNulJ6ezieffEJxcTHDhw8v\ns118fDy9e/fGbrczb948Pv30U/bt20ePHj1ITU31YMTCnS7l/BcWFvLcc89Rp04d3n33XZYsWcK9\n997LJ598Qvfu3SksLPRw1MIdLvW1f7apU6dy4MCBCo5MlEoT4m+OHz+u+fn5aRMmTDA6FGGAp59+\nWgO0AwcOnLN+/PjxGqBlZGQYFJlwN1VVNVVVNU3TtNTUVA3Qnn322fPajR49WgsPD9eys7NL1iUk\nJGhWq1WnMwBOAAAFcklEQVR74oknPBWucLNLOf9Op1NLS0s7b9tvv/1WA7QvvvjCE6EKN7vU1/5p\nhw8f1vz9/bWFCxdqgPbAAw94KFKhaZomPeviPDNmzCA/P5+JEycaHYowgNVqBSAoKOic9cHBwZhM\nJmw2mxFhiQpwKeVwnU4nixcvZtSoUQQGBpasr1OnDn369GHRokUVHaaoIJdy/s1mM2FhYeet79Sp\nEwDHjh2rkNhExSpvKezx48fTv39/RowYUYFRibJIsi7Os2bNGkJDQ4mPj6dt27ZYLBYiIyO57777\nyMnJMTo8UcHuuusugoODmTBhAocOHSI3N5fFixfz8ccf88ADD+Dn52d0iMKDDh48SGFhIa1btz7v\nudatW3PgwAGKiooMiEwYadWqVQC0aNHC4EhERZsxYwabNm3igw8+MDqUakuSdXGexMRECgoKGD16\nNDfffDMrVqzg8ccf5/PPP2fIkCEybv0qV7duXdavX09cXBwNGjQgMDCQYcOGcddddzFlyhSjwxMe\nlp6eDkBoaOh5z4WGhqJpGpmZmZ4OSxgoMTGRSZMm0aFDB4YOHWp0OKICJSYm8t///pc33niD6Oho\no8OptixGByAqH1VVKSoq4tlnn2XSpEkA9O7dG5vNxiOPPMLKlSvp16+fwVGKipKQkMCwYcOIiopi\n/vz5REREsHHjRl566SXy8vKYOXOm0SEKA1zokrnMLF19ZGRklHTafPPNNxecdVFUfffddx9t2rTh\n3nvvNTqUak2SdXGesLAw9u/fz8CBA89ZP3jwYB555JGSEm7i6jRp0iRycnLYtm1byZCXnj17Eh4e\nztixY/nnP/9Jr169DI5SeMrp8cqne9jPlpGRgaIoBAcHezosYYDMzEz69+9PYmIiq1aton79+kaH\nJCrQ/PnzWbZsGb///jvZ2dnnPGe328nKysLPz6/kPidRceQjsThPaWNTgZLhL9KTcnXbtm0bzZs3\nP29seseOHQGIi4szIixhkAYNGuDj48POnTvPe27nzp00bNgQb29vAyITnpSZmUm/fv04fPgwv/zy\nS5nvE+LqERcXh9PppEuXLoSEhJQ8AKZPn05ISAg//fSTwVFWD5J1ifOMGjUKgKVLl56zfsmSJQB0\n6dLF4zEJz4mOjmbXrl3k5eWds379+vUAxMbGGhGWMIjFYmHYsGEsXLiQ3NzckvVHjx5l9erVjBw5\n0sDohCecTtQPHTrE8uXLadeundEhCQ+4++67Wb169XkPgOHDh7N69WquvfZag6OsHmQYjDjPgAED\nGDZsGC+88AKqqtKlSxf+/PNPnn/+eYYOHSovzqvcI488wvDhw+nfvz+PPvoo4eHhbNiwgVdffZXm\nzZszePBgo0MUbrR06VLy8/NLEvHdu3czf/58AIYMGYKvry/PP/88HTt2ZOjQoUyaNImioiImT55M\neHg4//nPf4wMX1yhi51/RVEYOHAgW7du5d1338XpdLJhw4aS7SMiImjQoIEhsYsrc7FzX7duXerW\nrVvqtjExMfx/O3eMojAUhWH0DwjuQRB0J2LvCixcgAsIqcTOwkVYZRuWVjZuIFhZW6Wc6aYYHGYa\nnSec0z4CF8IjXxHubDZ70aRUH1Z78EDf99lut2nbNrfbLaPRKMvlMpvNJsPh8L/H48mOx2N2u10u\nl0vu93vG43EWi0Wapnm4c5n3NZlMcr1eH551Xff1sT6fz6nrOqfTKYPBIPP5PPv9Xqi9ud/ef5JM\np9Mfn1+tVjkcDs8YjSf7693/rqqqrNdrqxxfSKwDAECh/LMOAACFEusAAFAosQ4AAIUS6wAAUCix\nDgAAhRLrAABQKLEOAACFEusAAFAosQ4AAIUS6wAAUCixDgAAhfoE+FPbKiSBXvYAAAAASUVORK5C\nYII=\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"prior, z = (8.5, 1.5), (10.2, 0.5)\n",
"plot_products(prior[0], prior[1], z[0], z[1])\n",
"prior, z = (8.5, 0.5), (10.2, 1.5)\n",
"plot_products(prior[0], prior[1], z[0], z[1])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The result is a Gaussian that is taller than either input. This makes sense - we have incorporated information, so our variance should have been reduced. And notice how the result is far closer to the the input with the smaller variance. We have more confidence in that value, so it makes sense to weight it more heavily.\n",
"\n",
"It *seems* to work, but is it really correct? There is more to say about this, but I want to get a working filter going so you can it experience it in concrete terms. After that we will revisit Gaussian multiplication and determine why it is correct."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Interactive Example\n",
"\n",
"This interactive code provides sliders to alter the mean and variance of two Gaussians that are being multiplied together. As you move the sliders the plot is redrawn. Place your cursor inside the code cell and press CTRL+Enter to execute it."
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"scrolled": false
},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "9059fd1da4fb4d0fa87bd0db474ac9bc",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"A Jupyter Widget"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"from ipywidgets import interact\n",
"\n",
"interact(plot_products,\n",
" m1=(5, 10., .5), m2=(10, 15, .5), \n",
" v1=(.1, 2, .1), v2=(.1, 2, .1));"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## First Kalman Filter\n",
"\n",
"Let's get back to concrete terms and implement a Kalman filter. We've implemented the `update()` and `predict()` functions. We just need to write some boilerplate code to simulate a dog and create the measurements. I've put a `DogSimulation` class in `kf_internal` to avoid getting distracted with that task. The filtering is performed by 3 lines of code inside the `for` loop."
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"scrolled": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"PREDICT\t\t\tUPDATE\n",
" x var\t\t z\t x var\n",
" 1.000 401.000\t1.354\t 1.352 1.990\n",
" 2.352 2.990\t1.882\t 2.070 1.198\n",
" 3.070 2.198\t4.341\t 3.736 1.047\n",
" 4.736 2.047\t7.156\t 5.960 1.012\n",
" 6.960 2.012\t6.939\t 6.949 1.003\n",
" 7.949 2.003\t6.844\t 7.396 1.001\n",
" 8.396 2.001\t9.847\t 9.122 1.000\n",
" 10.122 2.000\t12.553\t 11.338 1.000\n",
" 12.338 2.000\t16.273\t 14.305 1.000\n",
" 15.305 2.000\t14.800\t 15.053 1.000\n",
"\n",
"final estimate: 15.053\n",
"actual final position: 14.838\n"
]
}
],
"source": [
"import kf_book.kf_internal as kf_internal\n",
"from kf_book.kf_internal import DogSimulation\n",
"\n",
"np.random.seed(13)\n",
"\n",
"process_var = 1. # variance in the dog's movement\n",
"sensor_var = 2. # variance in the sensor\n",
"\n",
"x = (0., 400.) # dog's position, N(0, 20**2)\n",
"velocity = 1\n",
"dt = 1. # time step in seconds\n",
"process_model = (velocity*dt, process_var) \n",
" \n",
"# simulate dog and get measurements\n",
"dog = DogSimulation(\n",
" x0=x[0], \n",
" velocity=process_model[0], \n",
" measurement_var=sensor_var, \n",
" process_var=process_model[1])\n",
"\n",
"# create list of measurements\n",
"zs = [dog.move_and_sense() for _ in range(10)]\n",
"\n",
"print('PREDICT\\t\\t\\tUPDATE')\n",
"print(' x var\\t\\t z\\t x var')\n",
"\n",
"# run the filter\n",
"xs, predictions = [], []\n",
"for z in zs:\n",
" # perform Kalman filter on measurement z\n",
" prior = predict(x, process_model)\n",
" likelihood = (z, sensor_var)\n",
" x = update(prior, likelihood)\n",
"\n",
" # save results\n",
" predictions.append(prior[0])\n",
" xs.append(x[0])\n",
" kf_internal.print_gh(prior, x, z)\n",
"\n",
"print()\n",
"print('final estimate: {:10.3f}'.format(x[0]))\n",
"print('actual final position: {:10.3f}'.format(dog.x))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Here is an animation of the filter. Predictions are plotted with a red triangle. After the prediction, the filter receives the next measurement, plotted as a black circle. The filter then forms an estimate part way between the two. "
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [
{
"data": {
"application/javascript": [
"/* Put everything inside the global mpl namespace */\n",
"window.mpl = {};\n",
"\n",
"\n",
"mpl.get_websocket_type = function() {\n",
" if (typeof(WebSocket) !== 'undefined') {\n",
" return WebSocket;\n",
" } else if (typeof(MozWebSocket) !== 'undefined') {\n",
" return MozWebSocket;\n",
" } else {\n",
" alert('Your browser does not have WebSocket support.' +\n",
" 'Please try Chrome, Safari or Firefox ≥ 6. ' +\n",
" 'Firefox 4 and 5 are also supported but you ' +\n",
" 'have to enable WebSockets in about:config.');\n",
" };\n",
"}\n",
"\n",
"mpl.figure = function(figure_id, websocket, ondownload, parent_element) {\n",
" this.id = figure_id;\n",
"\n",
" this.ws = websocket;\n",
"\n",
" this.supports_binary = (this.ws.binaryType != undefined);\n",
"\n",
" if (!this.supports_binary) {\n",
" var warnings = document.getElementById(\"mpl-warnings\");\n",
" if (warnings) {\n",
" warnings.style.display = 'block';\n",
" warnings.textContent = (\n",
" \"This browser does not support binary websocket messages. \" +\n",
" \"Performance may be slow.\");\n",
" }\n",
" }\n",
"\n",
" this.imageObj = new Image();\n",
"\n",
" this.context = undefined;\n",
" this.message = undefined;\n",
" this.canvas = undefined;\n",
" this.rubberband_canvas = undefined;\n",
" this.rubberband_context = undefined;\n",
" this.format_dropdown = undefined;\n",
"\n",
" this.image_mode = 'full';\n",
"\n",
" this.root = $('');\n",
" this._root_extra_style(this.root)\n",
" this.root.attr('style', 'display: inline-block');\n",
"\n",
" $(parent_element).append(this.root);\n",
"\n",
" this._init_header(this);\n",
" this._init_canvas(this);\n",
" this._init_toolbar(this);\n",
"\n",
" var fig = this;\n",
"\n",
" this.waiting = false;\n",
"\n",
" this.ws.onopen = function () {\n",
" fig.send_message(\"supports_binary\", {value: fig.supports_binary});\n",
" fig.send_message(\"send_image_mode\", {});\n",
" if (mpl.ratio != 1) {\n",
" fig.send_message(\"set_dpi_ratio\", {'dpi_ratio': mpl.ratio});\n",
" }\n",
" fig.send_message(\"refresh\", {});\n",
" }\n",
"\n",
" this.imageObj.onload = function() {\n",
" if (fig.image_mode == 'full') {\n",
" // Full images could contain transparency (where diff images\n",
" // almost always do), so we need to clear the canvas so that\n",
" // there is no ghosting.\n",
" fig.context.clearRect(0, 0, fig.canvas.width, fig.canvas.height);\n",
" }\n",
" fig.context.drawImage(fig.imageObj, 0, 0);\n",
" };\n",
"\n",
" this.imageObj.onunload = function() {\n",
" fig.ws.close();\n",
" }\n",
"\n",
" this.ws.onmessage = this._make_on_message_function(this);\n",
"\n",
" this.ondownload = ondownload;\n",
"}\n",
"\n",
"mpl.figure.prototype._init_header = function() {\n",
" var titlebar = $(\n",
" '');\n",
" var titletext = $(\n",
" '');\n",
" titlebar.append(titletext)\n",
" this.root.append(titlebar);\n",
" this.header = titletext[0];\n",
"}\n",
"\n",
"\n",
"\n",
"mpl.figure.prototype._canvas_extra_style = function(canvas_div) {\n",
"\n",
"}\n",
"\n",
"\n",
"mpl.figure.prototype._root_extra_style = function(canvas_div) {\n",
"\n",
"}\n",
"\n",
"mpl.figure.prototype._init_canvas = function() {\n",
" var fig = this;\n",
"\n",
" var canvas_div = $('');\n",
"\n",
" canvas_div.attr('style', 'position: relative; clear: both; outline: 0');\n",
"\n",
" function canvas_keyboard_event(event) {\n",
" return fig.key_event(event, event['data']);\n",
" }\n",
"\n",
" canvas_div.keydown('key_press', canvas_keyboard_event);\n",
" canvas_div.keyup('key_release', canvas_keyboard_event);\n",
" this.canvas_div = canvas_div\n",
" this._canvas_extra_style(canvas_div)\n",
" this.root.append(canvas_div);\n",
"\n",
" var canvas = $('');\n",
" canvas.addClass('mpl-canvas');\n",
" canvas.attr('style', \"left: 0; top: 0; z-index: 0; outline: 0\")\n",
"\n",
" this.canvas = canvas[0];\n",
" this.context = canvas[0].getContext(\"2d\");\n",
"\n",
" var backingStore = this.context.backingStorePixelRatio ||\n",
"\tthis.context.webkitBackingStorePixelRatio ||\n",
"\tthis.context.mozBackingStorePixelRatio ||\n",
"\tthis.context.msBackingStorePixelRatio ||\n",
"\tthis.context.oBackingStorePixelRatio ||\n",
"\tthis.context.backingStorePixelRatio || 1;\n",
"\n",
" mpl.ratio = (window.devicePixelRatio || 1) / backingStore;\n",
"\n",
" var rubberband = $('');\n",
" rubberband.attr('style', \"position: absolute; left: 0; top: 0; z-index: 1;\")\n",
"\n",
" var pass_mouse_events = true;\n",
"\n",
" canvas_div.resizable({\n",
" start: function(event, ui) {\n",
" pass_mouse_events = false;\n",
" },\n",
" resize: function(event, ui) {\n",
" fig.request_resize(ui.size.width, ui.size.height);\n",
" },\n",
" stop: function(event, ui) {\n",
" pass_mouse_events = true;\n",
" fig.request_resize(ui.size.width, ui.size.height);\n",
" },\n",
" });\n",
"\n",
" function mouse_event_fn(event) {\n",
" if (pass_mouse_events)\n",
" return fig.mouse_event(event, event['data']);\n",
" }\n",
"\n",
" rubberband.mousedown('button_press', mouse_event_fn);\n",
" rubberband.mouseup('button_release', mouse_event_fn);\n",
" // Throttle sequential mouse events to 1 every 20ms.\n",
" rubberband.mousemove('motion_notify', mouse_event_fn);\n",
"\n",
" rubberband.mouseenter('figure_enter', mouse_event_fn);\n",
" rubberband.mouseleave('figure_leave', mouse_event_fn);\n",
"\n",
" canvas_div.on(\"wheel\", function (event) {\n",
" event = event.originalEvent;\n",
" event['data'] = 'scroll'\n",
" if (event.deltaY < 0) {\n",
" event.step = 1;\n",
" } else {\n",
" event.step = -1;\n",
" }\n",
" mouse_event_fn(event);\n",
" });\n",
"\n",
" canvas_div.append(canvas);\n",
" canvas_div.append(rubberband);\n",
"\n",
" this.rubberband = rubberband;\n",
" this.rubberband_canvas = rubberband[0];\n",
" this.rubberband_context = rubberband[0].getContext(\"2d\");\n",
" this.rubberband_context.strokeStyle = \"#000000\";\n",
"\n",
" this._resize_canvas = function(width, height) {\n",
" // Keep the size of the canvas, canvas container, and rubber band\n",
" // canvas in synch.\n",
" canvas_div.css('width', width)\n",
" canvas_div.css('height', height)\n",
"\n",
" canvas.attr('width', width * mpl.ratio);\n",
" canvas.attr('height', height * mpl.ratio);\n",
" canvas.attr('style', 'width: ' + width + 'px; height: ' + height + 'px;');\n",
"\n",
" rubberband.attr('width', width);\n",
" rubberband.attr('height', height);\n",
" }\n",
"\n",
" // Set the figure to an initial 600x600px, this will subsequently be updated\n",
" // upon first draw.\n",
" this._resize_canvas(600, 600);\n",
"\n",
" // Disable right mouse context menu.\n",
" $(this.rubberband_canvas).bind(\"contextmenu\",function(e){\n",
" return false;\n",
" });\n",
"\n",
" function set_focus () {\n",
" canvas.focus();\n",
" canvas_div.focus();\n",
" }\n",
"\n",
" window.setTimeout(set_focus, 100);\n",
"}\n",
"\n",
"mpl.figure.prototype._init_toolbar = function() {\n",
" var fig = this;\n",
"\n",
" var nav_element = $('')\n",
" nav_element.attr('style', 'width: 100%');\n",
" this.root.append(nav_element);\n",
"\n",
" // Define a callback function for later on.\n",
" function toolbar_event(event) {\n",
" return fig.toolbar_button_onclick(event['data']);\n",
" }\n",
" function toolbar_mouse_event(event) {\n",
" return fig.toolbar_button_onmouseover(event['data']);\n",
" }\n",
"\n",
" for(var toolbar_ind in mpl.toolbar_items) {\n",
" var name = mpl.toolbar_items[toolbar_ind][0];\n",
" var tooltip = mpl.toolbar_items[toolbar_ind][1];\n",
" var image = mpl.toolbar_items[toolbar_ind][2];\n",
" var method_name = mpl.toolbar_items[toolbar_ind][3];\n",
"\n",
" if (!name) {\n",
" // put a spacer in here.\n",
" continue;\n",
" }\n",
" var button = $('');\n",
" button.addClass('ui-button ui-widget ui-state-default ui-corner-all ' +\n",
" 'ui-button-icon-only');\n",
" button.attr('role', 'button');\n",
" button.attr('aria-disabled', 'false');\n",
" button.click(method_name, toolbar_event);\n",
" button.mouseover(tooltip, toolbar_mouse_event);\n",
"\n",
" var icon_img = $('');\n",
" icon_img.addClass('ui-button-icon-primary ui-icon');\n",
" icon_img.addClass(image);\n",
" icon_img.addClass('ui-corner-all');\n",
"\n",
" var tooltip_span = $('');\n",
" tooltip_span.addClass('ui-button-text');\n",
" tooltip_span.html(tooltip);\n",
"\n",
" button.append(icon_img);\n",
" button.append(tooltip_span);\n",
"\n",
" nav_element.append(button);\n",
" }\n",
"\n",
" var fmt_picker_span = $('');\n",
"\n",
" var fmt_picker = $('');\n",
" fmt_picker.addClass('mpl-toolbar-option ui-widget ui-widget-content');\n",
" fmt_picker_span.append(fmt_picker);\n",
" nav_element.append(fmt_picker_span);\n",
" this.format_dropdown = fmt_picker[0];\n",
"\n",
" for (var ind in mpl.extensions) {\n",
" var fmt = mpl.extensions[ind];\n",
" var option = $(\n",
" '', {selected: fmt === mpl.default_extension}).html(fmt);\n",
" fmt_picker.append(option)\n",
" }\n",
"\n",
" // Add hover states to the ui-buttons\n",
" $( \".ui-button\" ).hover(\n",
" function() { $(this).addClass(\"ui-state-hover\");},\n",
" function() { $(this).removeClass(\"ui-state-hover\");}\n",
" );\n",
"\n",
" var status_bar = $('');\n",
" nav_element.append(status_bar);\n",
" this.message = status_bar[0];\n",
"}\n",
"\n",
"mpl.figure.prototype.request_resize = function(x_pixels, y_pixels) {\n",
" // Request matplotlib to resize the figure. Matplotlib will then trigger a resize in the client,\n",
" // which will in turn request a refresh of the image.\n",
" this.send_message('resize', {'width': x_pixels, 'height': y_pixels});\n",
"}\n",
"\n",
"mpl.figure.prototype.send_message = function(type, properties) {\n",
" properties['type'] = type;\n",
" properties['figure_id'] = this.id;\n",
" this.ws.send(JSON.stringify(properties));\n",
"}\n",
"\n",
"mpl.figure.prototype.send_draw_message = function() {\n",
" if (!this.waiting) {\n",
" this.waiting = true;\n",
" this.ws.send(JSON.stringify({type: \"draw\", figure_id: this.id}));\n",
" }\n",
"}\n",
"\n",
"\n",
"mpl.figure.prototype.handle_save = function(fig, msg) {\n",
" var format_dropdown = fig.format_dropdown;\n",
" var format = format_dropdown.options[format_dropdown.selectedIndex].value;\n",
" fig.ondownload(fig, format);\n",
"}\n",
"\n",
"\n",
"mpl.figure.prototype.handle_resize = function(fig, msg) {\n",
" var size = msg['size'];\n",
" if (size[0] != fig.canvas.width || size[1] != fig.canvas.height) {\n",
" fig._resize_canvas(size[0], size[1]);\n",
" fig.send_message(\"refresh\", {});\n",
" };\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_rubberband = function(fig, msg) {\n",
" var x0 = msg['x0'] / mpl.ratio;\n",
" var y0 = (fig.canvas.height - msg['y0']) / mpl.ratio;\n",
" var x1 = msg['x1'] / mpl.ratio;\n",
" var y1 = (fig.canvas.height - msg['y1']) / mpl.ratio;\n",
" x0 = Math.floor(x0) + 0.5;\n",
" y0 = Math.floor(y0) + 0.5;\n",
" x1 = Math.floor(x1) + 0.5;\n",
" y1 = Math.floor(y1) + 0.5;\n",
" var min_x = Math.min(x0, x1);\n",
" var min_y = Math.min(y0, y1);\n",
" var width = Math.abs(x1 - x0);\n",
" var height = Math.abs(y1 - y0);\n",
"\n",
" fig.rubberband_context.clearRect(\n",
" 0, 0, fig.canvas.width, fig.canvas.height);\n",
"\n",
" fig.rubberband_context.strokeRect(min_x, min_y, width, height);\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_figure_label = function(fig, msg) {\n",
" // Updates the figure title.\n",
" fig.header.textContent = msg['label'];\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_cursor = function(fig, msg) {\n",
" var cursor = msg['cursor'];\n",
" switch(cursor)\n",
" {\n",
" case 0:\n",
" cursor = 'pointer';\n",
" break;\n",
" case 1:\n",
" cursor = 'default';\n",
" break;\n",
" case 2:\n",
" cursor = 'crosshair';\n",
" break;\n",
" case 3:\n",
" cursor = 'move';\n",
" break;\n",
" }\n",
" fig.rubberband_canvas.style.cursor = cursor;\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_message = function(fig, msg) {\n",
" fig.message.textContent = msg['message'];\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_draw = function(fig, msg) {\n",
" // Request the server to send over a new figure.\n",
" fig.send_draw_message();\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_image_mode = function(fig, msg) {\n",
" fig.image_mode = msg['mode'];\n",
"}\n",
"\n",
"mpl.figure.prototype.updated_canvas_event = function() {\n",
" // Called whenever the canvas gets updated.\n",
" this.send_message(\"ack\", {});\n",
"}\n",
"\n",
"// A function to construct a web socket function for onmessage handling.\n",
"// Called in the figure constructor.\n",
"mpl.figure.prototype._make_on_message_function = function(fig) {\n",
" return function socket_on_message(evt) {\n",
" if (evt.data instanceof Blob) {\n",
" /* FIXME: We get \"Resource interpreted as Image but\n",
" * transferred with MIME type text/plain:\" errors on\n",
" * Chrome. But how to set the MIME type? It doesn't seem\n",
" * to be part of the websocket stream */\n",
" evt.data.type = \"image/png\";\n",
"\n",
" /* Free the memory for the previous frames */\n",
" if (fig.imageObj.src) {\n",
" (window.URL || window.webkitURL).revokeObjectURL(\n",
" fig.imageObj.src);\n",
" }\n",
"\n",
" fig.imageObj.src = (window.URL || window.webkitURL).createObjectURL(\n",
" evt.data);\n",
" fig.updated_canvas_event();\n",
" fig.waiting = false;\n",
" return;\n",
" }\n",
" else if (typeof evt.data === 'string' && evt.data.slice(0, 21) == \"data:image/png;base64\") {\n",
" fig.imageObj.src = evt.data;\n",
" fig.updated_canvas_event();\n",
" fig.waiting = false;\n",
" return;\n",
" }\n",
"\n",
" var msg = JSON.parse(evt.data);\n",
" var msg_type = msg['type'];\n",
"\n",
" // Call the \"handle_{type}\" callback, which takes\n",
" // the figure and JSON message as its only arguments.\n",
" try {\n",
" var callback = fig[\"handle_\" + msg_type];\n",
" } catch (e) {\n",
" console.log(\"No handler for the '\" + msg_type + \"' message type: \", msg);\n",
" return;\n",
" }\n",
"\n",
" if (callback) {\n",
" try {\n",
" // console.log(\"Handling '\" + msg_type + \"' message: \", msg);\n",
" callback(fig, msg);\n",
" } catch (e) {\n",
" console.log(\"Exception inside the 'handler_\" + msg_type + \"' callback:\", e, e.stack, msg);\n",
" }\n",
" }\n",
" };\n",
"}\n",
"\n",
"// from http://stackoverflow.com/questions/1114465/getting-mouse-location-in-canvas\n",
"mpl.findpos = function(e) {\n",
" //this section is from http://www.quirksmode.org/js/events_properties.html\n",
" var targ;\n",
" if (!e)\n",
" e = window.event;\n",
" if (e.target)\n",
" targ = e.target;\n",
" else if (e.srcElement)\n",
" targ = e.srcElement;\n",
" if (targ.nodeType == 3) // defeat Safari bug\n",
" targ = targ.parentNode;\n",
"\n",
" // jQuery normalizes the pageX and pageY\n",
" // pageX,Y are the mouse positions relative to the document\n",
" // offset() returns the position of the element relative to the document\n",
" var x = e.pageX - $(targ).offset().left;\n",
" var y = e.pageY - $(targ).offset().top;\n",
"\n",
" return {\"x\": x, \"y\": y};\n",
"};\n",
"\n",
"/*\n",
" * return a copy of an object with only non-object keys\n",
" * we need this to avoid circular references\n",
" * http://stackoverflow.com/a/24161582/3208463\n",
" */\n",
"function simpleKeys (original) {\n",
" return Object.keys(original).reduce(function (obj, key) {\n",
" if (typeof original[key] !== 'object')\n",
" obj[key] = original[key]\n",
" return obj;\n",
" }, {});\n",
"}\n",
"\n",
"mpl.figure.prototype.mouse_event = function(event, name) {\n",
" var canvas_pos = mpl.findpos(event)\n",
"\n",
" if (name === 'button_press')\n",
" {\n",
" this.canvas.focus();\n",
" this.canvas_div.focus();\n",
" }\n",
"\n",
" var x = canvas_pos.x * mpl.ratio;\n",
" var y = canvas_pos.y * mpl.ratio;\n",
"\n",
" this.send_message(name, {x: x, y: y, button: event.button,\n",
" step: event.step,\n",
" guiEvent: simpleKeys(event)});\n",
"\n",
" /* This prevents the web browser from automatically changing to\n",
" * the text insertion cursor when the button is pressed. We want\n",
" * to control all of the cursor setting manually through the\n",
" * 'cursor' event from matplotlib */\n",
" event.preventDefault();\n",
" return false;\n",
"}\n",
"\n",
"mpl.figure.prototype._key_event_extra = function(event, name) {\n",
" // Handle any extra behaviour associated with a key event\n",
"}\n",
"\n",
"mpl.figure.prototype.key_event = function(event, name) {\n",
"\n",
" // Prevent repeat events\n",
" if (name == 'key_press')\n",
" {\n",
" if (event.which === this._key)\n",
" return;\n",
" else\n",
" this._key = event.which;\n",
" }\n",
" if (name == 'key_release')\n",
" this._key = null;\n",
"\n",
" var value = '';\n",
" if (event.ctrlKey && event.which != 17)\n",
" value += \"ctrl+\";\n",
" if (event.altKey && event.which != 18)\n",
" value += \"alt+\";\n",
" if (event.shiftKey && event.which != 16)\n",
" value += \"shift+\";\n",
"\n",
" value += 'k';\n",
" value += event.which.toString();\n",
"\n",
" this._key_event_extra(event, name);\n",
"\n",
" this.send_message(name, {key: value,\n",
" guiEvent: simpleKeys(event)});\n",
" return false;\n",
"}\n",
"\n",
"mpl.figure.prototype.toolbar_button_onclick = function(name) {\n",
" if (name == 'download') {\n",
" this.handle_save(this, null);\n",
" } else {\n",
" this.send_message(\"toolbar_button\", {name: name});\n",
" }\n",
"};\n",
"\n",
"mpl.figure.prototype.toolbar_button_onmouseover = function(tooltip) {\n",
" this.message.textContent = tooltip;\n",
"};\n",
"mpl.toolbar_items = [[\"Home\", \"Reset original view\", \"fa fa-home icon-home\", \"home\"], [\"Back\", \"Back to previous view\", \"fa fa-arrow-left icon-arrow-left\", \"back\"], [\"Forward\", \"Forward to next view\", \"fa fa-arrow-right icon-arrow-right\", \"forward\"], [\"\", \"\", \"\", \"\"], [\"Pan\", \"Pan axes with left mouse, zoom with right\", \"fa fa-arrows icon-move\", \"pan\"], [\"Zoom\", \"Zoom to rectangle\", \"fa fa-square-o icon-check-empty\", \"zoom\"], [\"\", \"\", \"\", \"\"], [\"Download\", \"Download plot\", \"fa fa-floppy-o icon-save\", \"download\"]];\n",
"\n",
"mpl.extensions = [\"eps\", \"jpeg\", \"pdf\", \"png\", \"ps\", \"raw\", \"svg\", \"tif\"];\n",
"\n",
"mpl.default_extension = \"png\";var comm_websocket_adapter = function(comm) {\n",
" // Create a \"websocket\"-like object which calls the given IPython comm\n",
" // object with the appropriate methods. Currently this is a non binary\n",
" // socket, so there is still some room for performance tuning.\n",
" var ws = {};\n",
"\n",
" ws.close = function() {\n",
" comm.close()\n",
" };\n",
" ws.send = function(m) {\n",
" //console.log('sending', m);\n",
" comm.send(m);\n",
" };\n",
" // Register the callback with on_msg.\n",
" comm.on_msg(function(msg) {\n",
" //console.log('receiving', msg['content']['data'], msg);\n",
" // Pass the mpl event to the overriden (by mpl) onmessage function.\n",
" ws.onmessage(msg['content']['data'])\n",
" });\n",
" return ws;\n",
"}\n",
"\n",
"mpl.mpl_figure_comm = function(comm, msg) {\n",
" // This is the function which gets called when the mpl process\n",
" // starts-up an IPython Comm through the \"matplotlib\" channel.\n",
"\n",
" var id = msg.content.data.id;\n",
" // Get hold of the div created by the display call when the Comm\n",
" // socket was opened in Python.\n",
" var element = $(\"#\" + id);\n",
" var ws_proxy = comm_websocket_adapter(comm)\n",
"\n",
" function ondownload(figure, format) {\n",
" window.open(figure.imageObj.src);\n",
" }\n",
"\n",
" var fig = new mpl.figure(id, ws_proxy,\n",
" ondownload,\n",
" element.get(0));\n",
"\n",
" // Call onopen now - mpl needs it, as it is assuming we've passed it a real\n",
" // web socket which is closed, not our websocket->open comm proxy.\n",
" ws_proxy.onopen();\n",
"\n",
" fig.parent_element = element.get(0);\n",
" fig.cell_info = mpl.find_output_cell(\"\");\n",
" if (!fig.cell_info) {\n",
" console.error(\"Failed to find cell for figure\", id, fig);\n",
" return;\n",
" }\n",
"\n",
" var output_index = fig.cell_info[2]\n",
" var cell = fig.cell_info[0];\n",
"\n",
"};\n",
"\n",
"mpl.figure.prototype.handle_close = function(fig, msg) {\n",
" var width = fig.canvas.width/mpl.ratio\n",
" fig.root.unbind('remove')\n",
"\n",
" // Update the output cell to use the data from the current canvas.\n",
" fig.push_to_output();\n",
" var dataURL = fig.canvas.toDataURL();\n",
" // Re-enable the keyboard manager in IPython - without this line, in FF,\n",
" // the notebook keyboard shortcuts fail.\n",
" IPython.keyboard_manager.enable()\n",
" $(fig.parent_element).html(' ');\n",
" fig.close_ws(fig, msg);\n",
"}\n",
"\n",
"mpl.figure.prototype.close_ws = function(fig, msg){\n",
" fig.send_message('closing', msg);\n",
" // fig.ws.close()\n",
"}\n",
"\n",
"mpl.figure.prototype.push_to_output = function(remove_interactive) {\n",
" // Turn the data on the canvas into data in the output cell.\n",
" var width = this.canvas.width/mpl.ratio\n",
" var dataURL = this.canvas.toDataURL();\n",
" this.cell_info[1]['text/html'] = '
');\n",
" fig.close_ws(fig, msg);\n",
"}\n",
"\n",
"mpl.figure.prototype.close_ws = function(fig, msg){\n",
" fig.send_message('closing', msg);\n",
" // fig.ws.close()\n",
"}\n",
"\n",
"mpl.figure.prototype.push_to_output = function(remove_interactive) {\n",
" // Turn the data on the canvas into data in the output cell.\n",
" var width = this.canvas.width/mpl.ratio\n",
" var dataURL = this.canvas.toDataURL();\n",
" this.cell_info[1]['text/html'] = ' ';\n",
"}\n",
"\n",
"mpl.figure.prototype.updated_canvas_event = function() {\n",
" // Tell IPython that the notebook contents must change.\n",
" IPython.notebook.set_dirty(true);\n",
" this.send_message(\"ack\", {});\n",
" var fig = this;\n",
" // Wait a second, then push the new image to the DOM so\n",
" // that it is saved nicely (might be nice to debounce this).\n",
" setTimeout(function () { fig.push_to_output() }, 1000);\n",
"}\n",
"\n",
"mpl.figure.prototype._init_toolbar = function() {\n",
" var fig = this;\n",
"\n",
" var nav_element = $('')\n",
" nav_element.attr('style', 'width: 100%');\n",
" this.root.append(nav_element);\n",
"\n",
" // Define a callback function for later on.\n",
" function toolbar_event(event) {\n",
" return fig.toolbar_button_onclick(event['data']);\n",
" }\n",
" function toolbar_mouse_event(event) {\n",
" return fig.toolbar_button_onmouseover(event['data']);\n",
" }\n",
"\n",
" for(var toolbar_ind in mpl.toolbar_items){\n",
" var name = mpl.toolbar_items[toolbar_ind][0];\n",
" var tooltip = mpl.toolbar_items[toolbar_ind][1];\n",
" var image = mpl.toolbar_items[toolbar_ind][2];\n",
" var method_name = mpl.toolbar_items[toolbar_ind][3];\n",
"\n",
" if (!name) { continue; };\n",
"\n",
" var button = $('');\n",
" button.click(method_name, toolbar_event);\n",
" button.mouseover(tooltip, toolbar_mouse_event);\n",
" nav_element.append(button);\n",
" }\n",
"\n",
" // Add the status bar.\n",
" var status_bar = $('');\n",
" nav_element.append(status_bar);\n",
" this.message = status_bar[0];\n",
"\n",
" // Add the close button to the window.\n",
" var buttongrp = $('');\n",
" var button = $('');\n",
" button.click(function (evt) { fig.handle_close(fig, {}); } );\n",
" button.mouseover('Stop Interaction', toolbar_mouse_event);\n",
" buttongrp.append(button);\n",
" var titlebar = this.root.find($('.ui-dialog-titlebar'));\n",
" titlebar.prepend(buttongrp);\n",
"}\n",
"\n",
"mpl.figure.prototype._root_extra_style = function(el){\n",
" var fig = this\n",
" el.on(\"remove\", function(){\n",
"\tfig.close_ws(fig, {});\n",
" });\n",
"}\n",
"\n",
"mpl.figure.prototype._canvas_extra_style = function(el){\n",
" // this is important to make the div 'focusable\n",
" el.attr('tabindex', 0)\n",
" // reach out to IPython and tell the keyboard manager to turn it's self\n",
" // off when our div gets focus\n",
"\n",
" // location in version 3\n",
" if (IPython.notebook.keyboard_manager) {\n",
" IPython.notebook.keyboard_manager.register_events(el);\n",
" }\n",
" else {\n",
" // location in version 2\n",
" IPython.keyboard_manager.register_events(el);\n",
" }\n",
"\n",
"}\n",
"\n",
"mpl.figure.prototype._key_event_extra = function(event, name) {\n",
" var manager = IPython.notebook.keyboard_manager;\n",
" if (!manager)\n",
" manager = IPython.keyboard_manager;\n",
"\n",
" // Check for shift+enter\n",
" if (event.shiftKey && event.which == 13) {\n",
" this.canvas_div.blur();\n",
" event.shiftKey = false;\n",
" // Send a \"J\" for go to next cell\n",
" event.which = 74;\n",
" event.keyCode = 74;\n",
" manager.command_mode();\n",
" manager.handle_keydown(event);\n",
" }\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_save = function(fig, msg) {\n",
" fig.ondownload(fig, null);\n",
"}\n",
"\n",
"\n",
"mpl.find_output_cell = function(html_output) {\n",
" // Return the cell and output element which can be found *uniquely* in the notebook.\n",
" // Note - this is a bit hacky, but it is done because the \"notebook_saving.Notebook\"\n",
" // IPython event is triggered only after the cells have been serialised, which for\n",
" // our purposes (turning an active figure into a static one), is too late.\n",
" var cells = IPython.notebook.get_cells();\n",
" var ncells = cells.length;\n",
" for (var i=0; i= 3 moved mimebundle to data attribute of output\n",
" data = data.data;\n",
" }\n",
" if (data['text/html'] == html_output) {\n",
" return [cell, data, j];\n",
" }\n",
" }\n",
" }\n",
" }\n",
"}\n",
"\n",
"// Register the function which deals with the matplotlib target/channel.\n",
"// The kernel may be null if the page has been refreshed.\n",
"if (IPython.notebook.kernel != null) {\n",
" IPython.notebook.kernel.comm_manager.register_target('matplotlib', mpl.mpl_figure_comm);\n",
"}\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
"
';\n",
"}\n",
"\n",
"mpl.figure.prototype.updated_canvas_event = function() {\n",
" // Tell IPython that the notebook contents must change.\n",
" IPython.notebook.set_dirty(true);\n",
" this.send_message(\"ack\", {});\n",
" var fig = this;\n",
" // Wait a second, then push the new image to the DOM so\n",
" // that it is saved nicely (might be nice to debounce this).\n",
" setTimeout(function () { fig.push_to_output() }, 1000);\n",
"}\n",
"\n",
"mpl.figure.prototype._init_toolbar = function() {\n",
" var fig = this;\n",
"\n",
" var nav_element = $('')\n",
" nav_element.attr('style', 'width: 100%');\n",
" this.root.append(nav_element);\n",
"\n",
" // Define a callback function for later on.\n",
" function toolbar_event(event) {\n",
" return fig.toolbar_button_onclick(event['data']);\n",
" }\n",
" function toolbar_mouse_event(event) {\n",
" return fig.toolbar_button_onmouseover(event['data']);\n",
" }\n",
"\n",
" for(var toolbar_ind in mpl.toolbar_items){\n",
" var name = mpl.toolbar_items[toolbar_ind][0];\n",
" var tooltip = mpl.toolbar_items[toolbar_ind][1];\n",
" var image = mpl.toolbar_items[toolbar_ind][2];\n",
" var method_name = mpl.toolbar_items[toolbar_ind][3];\n",
"\n",
" if (!name) { continue; };\n",
"\n",
" var button = $('');\n",
" button.click(method_name, toolbar_event);\n",
" button.mouseover(tooltip, toolbar_mouse_event);\n",
" nav_element.append(button);\n",
" }\n",
"\n",
" // Add the status bar.\n",
" var status_bar = $('');\n",
" nav_element.append(status_bar);\n",
" this.message = status_bar[0];\n",
"\n",
" // Add the close button to the window.\n",
" var buttongrp = $('');\n",
" var button = $('');\n",
" button.click(function (evt) { fig.handle_close(fig, {}); } );\n",
" button.mouseover('Stop Interaction', toolbar_mouse_event);\n",
" buttongrp.append(button);\n",
" var titlebar = this.root.find($('.ui-dialog-titlebar'));\n",
" titlebar.prepend(buttongrp);\n",
"}\n",
"\n",
"mpl.figure.prototype._root_extra_style = function(el){\n",
" var fig = this\n",
" el.on(\"remove\", function(){\n",
"\tfig.close_ws(fig, {});\n",
" });\n",
"}\n",
"\n",
"mpl.figure.prototype._canvas_extra_style = function(el){\n",
" // this is important to make the div 'focusable\n",
" el.attr('tabindex', 0)\n",
" // reach out to IPython and tell the keyboard manager to turn it's self\n",
" // off when our div gets focus\n",
"\n",
" // location in version 3\n",
" if (IPython.notebook.keyboard_manager) {\n",
" IPython.notebook.keyboard_manager.register_events(el);\n",
" }\n",
" else {\n",
" // location in version 2\n",
" IPython.keyboard_manager.register_events(el);\n",
" }\n",
"\n",
"}\n",
"\n",
"mpl.figure.prototype._key_event_extra = function(event, name) {\n",
" var manager = IPython.notebook.keyboard_manager;\n",
" if (!manager)\n",
" manager = IPython.keyboard_manager;\n",
"\n",
" // Check for shift+enter\n",
" if (event.shiftKey && event.which == 13) {\n",
" this.canvas_div.blur();\n",
" event.shiftKey = false;\n",
" // Send a \"J\" for go to next cell\n",
" event.which = 74;\n",
" event.keyCode = 74;\n",
" manager.command_mode();\n",
" manager.handle_keydown(event);\n",
" }\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_save = function(fig, msg) {\n",
" fig.ondownload(fig, null);\n",
"}\n",
"\n",
"\n",
"mpl.find_output_cell = function(html_output) {\n",
" // Return the cell and output element which can be found *uniquely* in the notebook.\n",
" // Note - this is a bit hacky, but it is done because the \"notebook_saving.Notebook\"\n",
" // IPython event is triggered only after the cells have been serialised, which for\n",
" // our purposes (turning an active figure into a static one), is too late.\n",
" var cells = IPython.notebook.get_cells();\n",
" var ncells = cells.length;\n",
" for (var i=0; i= 3 moved mimebundle to data attribute of output\n",
" data = data.data;\n",
" }\n",
" if (data['text/html'] == html_output) {\n",
" return [cell, data, j];\n",
" }\n",
" }\n",
" }\n",
" }\n",
"}\n",
"\n",
"// Register the function which deals with the matplotlib target/channel.\n",
"// The kernel may be null if the page has been refreshed.\n",
"if (IPython.notebook.kernel != null) {\n",
" IPython.notebook.kernel.comm_manager.register_target('matplotlib', mpl.mpl_figure_comm);\n",
"}\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
" "
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"import time\n",
"from kf_book import book_plots as book_plots\n",
"from kf_book.book_plots import reset_figsize\n",
"\n",
"%matplotlib notebook\n",
"fig = plt.figure(figsize=(9,4))\n",
"canvas = fig.canvas\n",
"time_step = .25\n",
"for i in range(2, len(xs)+1):\n",
"\n",
" book_plots.plot_predictions(predictions[:i]) \n",
" plt.xlim(-1, 10)\n",
" plt.ylim(0,20)\n",
" fig.canvas.draw()\n",
" time.sleep(time_step)\n",
"\n",
" book_plots.plot_measurements(zs[:i])\n",
" plt.xlim(-1, 10)\n",
" plt.ylim(0,20)\n",
" fig.canvas.draw()\n",
" time.sleep(time_step)\n",
"\n",
" book_plots.plot_filter(xs[:i])\n",
" plt.xlim(-1, 10)\n",
" plt.ylim(0,20)\n",
" fig.canvas.draw()\n",
" time.sleep(time_step)\n",
" \n",
" if i == 2:\n",
" plt.legend(loc=4);\n",
"# reset to noninteractive plot settings\n",
"%matplotlib inline\n",
"reset_figsize()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Ignoring the boilerplate, the filter is:\n",
"\n",
"```python\n",
"for z in zs:\n",
" prior = predict(x, process_model)\n",
" likelihood = (z, sensor_var)\n",
" x = update(prior, likelihood)\n",
"```\n",
"\n",
"I've plotted the prior (labeled *prediction*), the measurements, and the filter output. For each iteration of the loop we form a prior, take a measurement, form a likelihood from the measurement, and then incorporate the likelihood into the prior. \n",
"\n",
"If you look at the plot you can see that the filter estimate is always between the measurement and prediction. Recall that for the g-h filter we argued that the estimate must always be between the measurement and prior. It makes no sense to choose a value outside of the two values. If I predict I am at 10, but measure that I am at 9, it would be foolish to decide that I must be at 8, or 11."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Kalman Gain\n",
"\n",
"We see that the filter works. Now let's go back to the math to understand what is happening. The posterior $x$ is computed as the likelihood times the prior ($\\mathcal L \\bar x$), where both are Gaussians.\n",
"\n",
"Therefore the mean of the posterior is given by:\n",
"\n",
"$$\n",
"\\mu=\\frac{\\bar\\sigma^2\\, \\mu_z + \\sigma_z^2 \\, \\bar\\mu} {\\bar\\sigma^2 + \\sigma_z^2}\n",
"$$\n",
"\n",
"I use the subscript $z$ to denote the measurement. We can rewrite this as:\n",
"\n",
"$$\\mu = \\left( \\frac{\\bar\\sigma^2}{\\bar\\sigma^2 + \\sigma_z^2}\\right) \\mu_z + \\left(\\frac{\\sigma_z^2}{\\bar\\sigma^2 + \\sigma_z^2}\\right)\\bar\\mu$$\n",
"\n",
"In this form it is easy to see that we are scaling the meaurement and the prior by weights: \n",
"\n",
"$$\\mu = W_1 \\mu_z + W_2 \\bar\\mu$$\n",
"\n",
"\n",
"The weights sum to one because the denominator is a normalization term. We introduce a new term, $K=W_1$, giving us:\n",
"\n",
"$$\\begin{aligned}\n",
"\\mu &= K \\mu_z + (1-K) \\bar\\mu\\\\\n",
"&= \\bar\\mu + K(\\mu_z - \\bar\\mu)\n",
"\\end{aligned}$$\n",
"\n",
"where\n",
"\n",
"$$K = \\frac {\\bar\\sigma^2}{\\bar\\sigma^2 + \\sigma_z^2}$$\n",
"\n",
"$K$ is the *Kalman gain*. It's the crux of the Kalman filter. It is a scaling term that chooses a value partway between $\\mu_z$ and $\\bar\\mu$.\n",
"\n",
"Let's work a few examples. If the measurement is nine times more accurate than the prior, then $\\bar\\sigma^2 = 9\\sigma_z^2$, and\n",
"\n",
"$$\\begin{aligned}\n",
"\\mu&=\\frac{9 \\sigma_z^2 \\mu_z + \\sigma_z^2\\, \\bar\\mu} {9 \\sigma_z^2 + \\sigma_\\mathtt{z}^2} \\\\\n",
"&= \\left(\\frac{9}{10}\\right) \\mu_z + \\left(\\frac{1}{10}\\right) \\bar\\mu\n",
"\\end{aligned}\n",
"$$\n",
"\n",
"Hence $K = \\frac 9 {10}$, and to form the posterior we take nine tenths of the measurement and one tenth of the prior. \n",
"\n",
"If the measurement and prior are equally accurate, then $\\bar\\sigma^2 = \\sigma_z^2$ and\n",
"\n",
"$$\\begin{gathered}\n",
"\\mu=\\frac{\\sigma_z^2\\, (\\bar\\mu + \\mu_z)}{2\\sigma_\\mathtt{z}^2} \\\\\n",
"= \\left(\\frac{1}{2}\\right)\\bar\\mu + \\left(\\frac{1}{2}\\right)\\mu_z\n",
"\\end{gathered}$$\n",
"\n",
"which is the average of the two means. It makes intuitive sense to take the average of two equally accurate values.\n",
"\n",
"We can also express the variance in terms of the Kalman gain:\n",
"\n",
"$$\\begin{aligned}\n",
"\\sigma^2 &= \\frac{\\bar\\sigma^2 \\sigma_z^2 } {\\bar\\sigma^2 + \\sigma_z^2} \\\\\n",
"&= K\\sigma_z^2 \\\\\n",
"&= (1-K)\\bar\\sigma^2 \n",
"\\end{aligned}$$\n",
"\n",
"We can understand this by looking at this chart:"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAugAAADQCAYAAABV7JR5AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzs3XlYlFX/P/D3gCwii6iY+wKmJlIs\niiCZK6QliaamJe6mZkpuuTw+CmmmZaiXifYYS6n9zEihxQ0ETU20VEpccsM0tyQRAXHYzu+P852B\ncWZg2Ed8v66La+Dc55z73DdJnznzuc9RCCEEiIiIiIjIKJjU9ACIiIiIiKgIA3QiIiIiIiPCAJ2I\niIiIyIgwQCciIiIiMiIM0ImIiIiIjAgDdCIiIiIiI8IAnYiIiIjIiDBAJyIiIiIyIgzQiYiIqFZI\nSQHq1AHi4sreNiYGMDcHLl6s/HERlZWCO4kSERGRsUhOlsHy2LFAmzZla+vnByiVwMGD5Tu3hwfQ\nujWwY0f52hNVFs6gExERkdFITgZCQoCrV8vW7uhROXM+a1b5zx0UBOzcCZw5U/4+iCoDA3QiIqIn\nVEEB8PBhTY/COISFAQ0bAq+8Uv4+hgwBrKyAjRsrb1xE5cEAnYiInkhRUYBCAezfD3zwgUxNqFsX\n6NYNSEqSdQ4eBF58EahXD2jaFFi6VLsfpRJYvhxwdgYsLYH69QF/f+DUKc16mZnAokWy/0aNAAsL\noF07YP587SD50SMgOBjo0EEGfPXrAy4uwNy5mvWCg+U16JotbtMG6NVL+3rj4+V1ODnJ8W7fXrbr\nqKz7Vp5zJiQAq1bJsVtYAO3bA19+qXk/xo2T3/fuLdsoFDLdpST5+TItxtcXMDPTPJaXJ3PLVX09\n/jVkSFFda2ugRw/g229LPh9RVatT0wMgIiKqiPnz5UxyUBCQmwt8+inw8ssy8JswAXj7beCtt2Qg\nu3gx0LYtMGqUbJuXB/TvD/zyCxAYCLz7LpCRAWzaBPj4AD//DHTpIuveuAF88QXw+uvAm2/KhxEP\nHgQ+/lgGpHv3Fo1p2jQgIgIYPRqYOVOO7+JFGaBW1Jw5ctyTJgG2tvJNQFmuozLuW1nvncrChUBO\nDjB5sgzQN2yQwXe7drLNkCHArVvA//4n6z73nGzn5FTyPTlxAsjKAjw9tY/l5srfxeNWrwZOnpRv\nKIrz9pa/y/PngY4dSz4vUZURRERET6DISCEAIdzchFAqi8pjY2W5qakQx48XlSuVQjRpIoSXV1FZ\naKisu2ePZt8ZGUK0bClEz56a7XNztcexaJHs49ixojJ7eyEGDCj9GpYskW1TU7WPtW6teX7V9bZv\nL0R2tmbdslxHZdy38p7T1VXznH//LYS5uRAjRmjXTUzUuiV6RUTINrGxhtWfO1fWX7VK+9jmzfJY\ndLTh5yeqbExxISKiJ9rUqTKFQaVHD/nq5QV07VpUbm4uZ1iLL6O3ZYucJfXwANLSir5yc2W6xOHD\ncsZX1V6VPpGfD6Sny7r9+smyY8eK+rWzkw8apqRUzfVaWWmWleU6ivdT3vtW3nO+847mOZs3l2ku\nFV3a8O5d+dqgQcn1hACmT5dpNuvXA7Nna9dp2FC+/vNPxcZEVBFMcSEioieao6Pmz/b28rVtW+26\n9vbAv/8W/XzunAwiHRz095+WBrRsKb8PC5MPEJ45AxQWatZLTy/6fs0amfbh4iLH17u3TKXw9wdM\nKjg11r69dllZrwOo2H2rrHMCMiD+6y/9fRhCoZCvJS0cXVgoU2siImSq0vjxuuup+lD1SVQTGKAT\nEdETzdS0bOXFCSGD6NBQ/XVUAWhoqJxx9fMDZswAmjWTs8E3bsg86uIB+6BB8sHPXbtknnp8PBAe\nLmep4+OLZpFLCgLz83WXPz57XtbrUKnIfavsc1Z0RxbVee7d0328oED+jrZtkzP/I0fq70vVR0lv\nPIiqGgN0IiJ6aj37rEyP6NOn9JntzZvlyiq7d2vW3bNHd/0GDeRDlaNGyQB0/nz5QGlsLDBsWFEd\nQAaFxTflefRIPizZrl3lX0dlqapzlmfmunNn+aorVSYvTz7U+/33wDffaK7aosulS5p9EtUE5qAT\nEdFTa/Ro4PZt/bPAd+4UfW9qKoPH4rO9+fnAihWabQoKgPv3NcsUCsDNTX5ffJZXla4SH69Zf/Vq\n7RSayrqOylJV57S2lq/6ZsN1cXOTK9qololUUSrlqjs//ih3By0tOAdkH888I1fHIaopnEEnIqKn\nVlCQ3H1y7ly5BGKfPjLQu3ZNrhNuaQkkJsq6Q4cCCxYAAwbIQO/BA+Drr7XX3c7MlGuHv/aaDBwb\nNwZSU+WSgvb2msv69esnH7RcvFjmeLdtKx+uTEqSa61XxXVUlqo6Z9euckb+ww9lXn+9evK+dOum\nv42pqfydxMbKoNzCQpaPHg388INMb0lPl+ktxb32mhyzSlYWcOiQ/vx0ourCAJ2IiJ5aZmbATz/J\nhz83bwaWLJHlzZrJlUvGjCmqO3eunD0PD5fBaZMmwBtvyI11OnUqqmdlBbz3ngxS4+Nl0KcK2Bcs\nkH2rmJrKoHLGDGDdOpmb7ucn89Z9fKrmOipLVZ2zVSv5IOfKlXKlmbw82VdJATog60ZFydny11+X\nv6vdu+WxqCj5VZyJiXwzVdx338lNpyZPLt/YiSqLQoiKPppBREREVPP69weys+UseHl4eMidVXfs\nqNxxEZUVA3QiIiKqFc6cAV54Qa6e4+dXtrYxMcDw4bKPZ5+tmvERGYoBOhERUS2WlQVER8vlIJs3\nl7n0qgcxicg4MUAnIiKqhbKzgSlTgKNHgcuXi8qdnABvb7nhUr16NTc+ItKPAToREVEtk50tV4h5\nfNnB4ry85EOsDNKJjA/XQSciIqplpkwpOTgH5PEpU6pnPERUNgzQiYiIapGsLJnWYoikJFmfiIwL\nA3QiIqJaJDpaM+e8JJcuyfpEZFwYoBMREdUiN26Urf7Nm1UzDiIqPwboREREtUjz5mWrX3xnUyIy\nDlzFhYiIqBbJygJcXQ1Lc2nXDjh1iuuiExkbzqATERHVItbWcp1zQ3h7MzgnMkacQSciIqpluA46\n0ZONM+hERES1TL16MvgeNUruHFpcu3ZAYCCDcyJjxhl0IiKiWiwrC/jf//7G1av34O7+PIYOZVoL\nkbGrU9MDICIioqqTlnYV8+Y9i/z8fGzbtg3W1m/U9JCIqBRMcSEiIqrFEhMTkZ+fDwDYt29fDY+G\niAzBAJ2IiKgWK57JyqxWoicDA3QiIiIiIiPCAJ2IiIiIyIgwQCciIiIiMiIM0ImIiIiIjAgDdCIi\nIiIiI8IAnYiIiIjIiDBAJyIiIiIyIgzQiYiIiIiMCAN0IiIiIiIjwgCdiIiIiMiIMEAnIiIiIjIi\nDNCJiJ4CBw4cgEKhQFRUVE0PpcqlpKSgTp06iIuLq7Q+Y2JiYG5ujosXL1Zan0RE+jBAJyKqJZKT\nkxEcHIyrV6/W9FD0qo4xzpo1Cz4+PvD19a20PgMCAuDi4oJ58+ZVWp9ERPowQCciqiWSk5MREhKi\nM/h96aWXkJOTg8DAwOofWDEljbEyHD16FHFxcZg1a1al9x0UFISdO3fizJkzld53VXr06JH6+4sX\nLyIrK6sGR0NEhmCATkT0FDAxMYGlpSVMTU1reihVKiwsDA0bNsQrr7xS6X0PGTIEVlZW2LhxY6X3\nXRWys7MRGBiI4OBgddnhw4fh6uqKwMBAZGdn19zgiKhEDNCJqFaJioqCQqFAQkICVq1aBScnJ1hY\nWKB9+/b48ssvteorlUosX74czs7OsLS0RP369eHv749Tp06p6/z1119QKBQagQ4A+Pn5QaFQYM2a\nNRrl3bp1Q6dOnUodqyHnVnn06BGCg4PRoUMHWFlZoX79+nBxccHcuXMBAMHBwRg3bhwAoHfv3lAo\nFFAoFBg7diwA3Tnoqnu1f/9+fPDBB2jdujXq1q2Lbt26ISkpCQBw8OBBvPjii6hXrx6aNm2KpUuX\naowrMzMTixYtQrdu3dCoUSNYWFigXbt2mD9/Ph4+fKhRt7QxlvWePC4/Px8xMTHw9fWFmZmZxrGc\nnBy0aNECrVq1glKp1Dg2ceJEmJqaYtu2bSX2b21tjR49euDbb78tdSzV5fa9LKRn5miVZ2dno1+/\nftiyZQvu3r2rcezy5cvYsmUL+vXrxyCdyFgJIqJaJDIyUgAQ3bp1E88//7xYuXKlWLNmjejQoYMA\nIA4fPqyum5ubK3r16iXMzc3FhAkTRFhYmPjoo4+Eo6OjqFu3rvj111/Vddu2bStefPFF9c9KpVJY\nWVkJExMTMXDgQHV5RkaGMDU1FdOmTStxnGU5txBCjB8/XgAQo0ePFhs2bBCfffaZCAoKEu7u7kII\nIX7//Xfx9ttvCwBi4cKFYvPmzWLz5s3il19+EUIIkZiYKACIyMhIrXvVpUsX4ebmJj799FPx0Ucf\niUaNGglbW1uxc+dO0aBBAzF//nwRFhYmevXqJQCIzZs3q/s4d+6ceOaZZ8Q777wj1qxZIz777DMx\nbNgwoVAohJ+fn8Y1lDbGst6TxyUlJQkAIjQ0VOfxL774Quv4/PnzBQCxfv36EvtWCQ4OFgDEuXPn\nDKpflZS5+cLmleWi7svLxOywveL2v5nqY6NGjRIASv0aNWpUDV4BEenDAJ2IahVV0Onq6iqUSqW6\n/O+//xbm5uZixIgR6rLQ0FABQOzZs0ejj4yMDNGyZUvRs2dPddmECROEmZmZyMrKEkIIcfDgQXWA\nY2NjI/Ly8oQQQnz//fcCgPjuu+9KHGdZzi2EEPb29mLAgAEGXXtiYqLWsZICdDc3N417FRsbKwAI\nU1NTcfz4cXW5UqkUTZo0EV5eXhplubm5WudbtGiRACCOHTtm8BjLek8eFxERIQCI2NhYncfz8/OF\ns7OzcHBwEJmZmWL16tUCgAgJCSmx3+I2b94sAIjo6GiN8vuZOeLQH39V69fB5Kui//ubBXoFC/QK\nFha+S8WID74VKZf+Fk5OTgYF6O3atROZmZl6rpaIakqdKpmWJyKqYe+88w7Mzc3VPzdv3hzt27fX\nWCZvy5Yt6NixIzw8PJCWlqbR3tfXF19++SVycnJQt25d9OnTB+Hh4Th8+DBefvllJCQkoHHjxggK\nCsKWLVvw66+/wtvbG4mJiTAxMUGvXr1KHF9Zzg0AdnZ2OHPmDFJSUtC5c+cK3h1NU6dO1bhXPXr0\nAAB4eXmha9eu6nJzc3N4enriyJEjGmUq+fn5yMzMREFBAfr164dly5bh2LFj8PT0NGgcZb0nj1Ol\ncjRo0EDncVNTU6xYsQL+/v4ICAhAQkICpk+fjsWLFxs0PgBo2LAhAOCff/7RKH8pKAp/XLljcD9V\nQZlXgG0JZxB76CxyLl82qM2lS5cQHR2tkWZERDWPAToR1UqOjo5aZQ0bNsRff/2l/vncuXPIycmB\ng4OD3n7S0tLQsmVL9OnTBwCQkJCgDtB79+4Nd3d32NvbIyEhAd7e3khISMALL7ygN0gsz7kBYM2a\nNQgMDISLiwscHR3Ru3dv+Pv7w9/fHyYmFXuc6PF7ZW9vDwBo27atVl17e3v8+++/GmVhYWHYuHEj\nzpw5g8LCQo1j6enpBo+jrPfkcQqFAgAghNDbfuDAgXB3d8f+/fsxYsQIrF27Vmc9T09PzJ49G2+8\n8YZGuapv1blURr/8PHYeOq/3vFXl4aM8XPsnA/8+yPm/cQGO9kBZ1pm5efNm1QyOiMqNAToR1Ur6\nVispHrwJIeDi4oLQ0FC9/aiCxSZNmuC5555DQkICHj58iGPHjmHdunUwMTFBz549sX//fkyZMgV/\n/PGHQUv8leXcADBo0CBcvXoVu3btwsGDBxEfH4/w8HD06NED8fHxGjPZZaXvXhmy4ktoaChmz54N\nPz8/zJgxA82aNYO5uTlu3LiBsWPHagXsJSnrPdF37N69e3rrbN++HcnJyQAAGxsbrUAbAAoKCnD6\n9Gm4urpqHVP1/fg4Zg/vjtnDu+s9b1VQ5uaj8ZBVeJCthLmZKd4e6I55I19E/E87MG674f00a9as\n6gZJROXCAJ2InlrPPvss7t69iz59+hg0C92nTx9s2LABP/zwA3Jzc9G3b18AQN++fTFnzhzs3r0b\nQgj1bHtlnhuQqRujRo3CqFGjIITA/Pnz8fHHHyM2NhbDhg3TGWxWtc2bN6NNmzbYvXu3xnXs2bNH\nZ/2Sxliee1KcKvVH326f+/btQ2BgIAYPHgwzMzNERERg5syZeO6559R1bt26BScnJyiVSnh4eKjb\nde8ug+9Lly5pnKsmmZuZYuzLL8DUxASzhnujhYMtAGDo0KFYtmwZLhuQ5tKuXTsMHTq0qodKRGXE\nZRaJ6Kk1evRo3L59W++M7Z07MqdYtXV8w4YNUVhYiJCQELRq1QpOTk4AZOCuVCrx0UcfoU6dOuoc\n7so4NyBndO/fv69xXKFQwM3NDUDRrK61tbXGzxW1Z88etGnTpsQ6pqamUCgUGp9M5OfnY8WKFTrr\nq8Z44sQJmJiY4ODBg+pjZbknuri5ucHW1la9RGRxx44dw5AhQ+Dj44OtW7di2bJlMDExwYIFCzTq\nNW3aFBEREfD09ERWVhaysrLUwTkAJCUl4ZlnnkGHDh1KHEt1UCgUWDt9AEKnvawOzgF5j729vQ3q\nw9vbW/07ISLjwRl0InpqBQUFIS4uDnPnzkVCQgL69OkDW1tbXLt2Dfv374elpSUSExPVW8e/9957\nWLZsGc6dO6fxUF2nTp3QpEkTnD17Ft7e3rCxsam0cwNyrfGmTZvitddeg5ubG+7du4ekpCSkpKTA\n3t4e/v7+AICuXbvCxMQEH374IdLT01GvXj20bdsW3bp1q5L7B8jZ2gULFmDAgAEYMmQIHjx4gK+/\n/lprHXIV1Ri//vpruLq6Yty4cfj666/h5eVVpnuii6mpKYYMGYLY2FgolUpYWFgAkLntr776Ktq3\nb4+YmBhYWFjAyckJEyZMwMaNG3HkyBH4+Pio+zl58qT6zU9xWVlZOHToEMaPH1/Bu1b1Nm7ciEuX\nLul8s6Li5eWFDRs2VOOoiMhgNbZ+DBFRFShpGb+ePXuK1q1ba5Tl5eWJtWvXii5duggrKythZWUl\n2rVrJ958802xd+9e8csvvwgAIiYmRgghhLu7uwAgvvrqK41+3nzzTQFA/Oc//zF4rKWdW0WpVIr5\n8+eLrl27igYNGggTExMBQAwdOlRcuHBBo8+oqCjx3HPPCTMzMwFAjBkzRghR8jKLuu4V/m8JyUeP\nHmmUjxkzRhT/X0d+fr5Yvny5cHJyEubm5qJVq1Zi7ty54uzZswKAWLJkiVbfqjGampoKAKJv375l\nvif6HDt2TGMZxL/++ku0aNFCODo6itu3b2vUvXnzpqhbt67o3r27Rnnfvn3Fxo0bdY4bgDh9+nSp\n4zAGWVlZYtSoUcLBwUFracXAwED1kqFEZHwUQpTwuDsR0VMuMDAQu3fvxq1bt/TOCle34OBghISE\nIDU1tdQUlLIqKCiAUqmElZVVpfarkpmZqf6EQQgBR0dHdO7cGT/88EOlnaN///7Izs7GoUOHytW+\nUaNG2LVrl9bykB4eHmjdujV27NhRGcOsNmFhYZg2bRoA4MUXX8Tu3buZ1kJk5JiDTkSkh76t46Oi\noqBQKBAfH4/g4GC0bt0aFhYWeP755/VuFx8TEwMfHx9YW1vD2toaPj4+iI2N1ar3yy+/YMCAAWjS\npAksLS3RvHlzvPLKK+pUhbFjxyIkJASAXAZRoVBAoVAgODhY3UdGRgbmzZuHdu3awcLCAg4ODhg5\nciSuXLmica7i17F06VI4OTnB0tIS27fLJUB69eql8w3Azz//DF9fX9jZ2aFu3bpwd3dHeHi4Vj1V\n+ytXrmDo0KFo0KABbG2LcqUVCgVefvll7NmzB1lZWXp+C2X36aef4ujRo9i3b1+Z2+bl5elcGjIm\nJganT5/GypUrK2OI1crS0lL9/bPPPsvgnOgJwBx0IiI9Tpw4gaysLL0b7cybNw/Z2dmYOnUqFAoF\nIiMjMXLkSDx69EgjR101g9mxY0csWrQICoUCUVFRCAgIwOeff463334bAPDnn3/C19cXTZo0QVBQ\nEJ555hncvn0bR44cwe+//w4vLy9MnjwZDx48wM6dO7F69Wo0atQIAPD8888DkMF59+7dce3aNYwf\nPx7Ozs64desWwsLC0K1bN/z2229o3bq1xnXMmTMHeXl5mDRpEmxtbUt8APKHH37A4MGD0aRJE8ye\nPRs2NjbYtm0bJk6ciCtXruDDDz/UqJ+VlYWePXvCx8cHH374odYGP97e3vj8889x+PBh9O/f37Bf\nTCmcnZ2Rn59frrZmZmaYM2cO/Pz8kJ+fjz/++AOOjo4ICAhAbm5upYyPiKhUNZxiQ0RktPRtHa/K\n3W7VqpW4f/++uvz+/fuiVatWwt7eXjx8+FAIIcS9e/dEvXr1hJOTk8jIyFDXzcjIEI6OjsLa2lqk\np6cLIYRYu3atACCOHTtW4riWLFkiAIjU1FStYzNmzBCWlpYiOTlZo/zq1avCxsZGnZNe/Drat28v\nsrOztfp6PGc/Pz9ftGrVStjZ2YkbN26oy5VKpejevbswMTHRyInv2bNnqXn5hw4dEgDEqlWrSrxm\nKr/w8HB1/vm4ceNqejhEZACmuBAR6VHa1vFTp06FnZ2d+mc7OztMmTIF6enpOHDgAAAgLi4O2dnZ\nmDFjhkZ6h62tLaZPn46srCzEx8er2wNAbGwsHj16VObxCiGwdetWvPTSS2jevDnS0tLUX/Xq1YOX\nl5fOtI+pU6calHN+4sQJ9cx88c1tzM3NMXfuXBQWFupM25kzZ47ePhs2bAgAWjPrRERPM6a4EBHp\nUdrW8cU3uFHp1KkTAKjzvVNTUwHItIvHqTa7UdUdMWIEtmzZguXLl2P16tXw8vLCyy+/jBEjRmil\npehy9+5d/Pvvv9i3b5/eHTd1bQDUvn37Uvsu67WoODg4oH79+nr7VN3bmthkiYjIWDFAJyLSo7St\n43UFlY8H8/qCe10sLCwQFxeH48ePY+/evfj555+xePFiBAcH4+uvv8bgwYNLbK86V79+/TBv3jyD\nz2voii1luRZD+1bdW31vKIiInkYM0ImI9Cht6/izZ8/itdde0yg7d+4cAMDR0REA1LuNnjlzBn37\n9tVqX7yuiqenp/rB1OvXr8PNzQ2LFi1SB+j6ZptVs9UPHjxAv379DLvIMih+LY/Tdy2luXTpEoCi\ne01ERFxmkYhIr5K2jgeADRs2ICMjQ/1zRkYGNm7ciPr166Nnz54AAF9fX9SrVw/r1q1DZmamum5m\nZibWrVsHa2tr+Pr6AgDS0tK0ztGiRQs4ODhozOKrlsl7fGbfxMQEb731Fo4fP47o6GidY65Irre7\nuztatWqFyMhI3L59W12el5eHTz75BAqFAoMGDSpTn0lJSahTp47GTp5ERE87zqATEemhb+t4lUaN\nGqFbt24YP348hBCIjIzEtWvX8MUXX6hTO+rXr4+PP/4Y06ZNQ7du3dTLL0ZFReHSpUv4/PPP1Q+H\nLlu2DPv27cPAgQPRtm1bCCHwww8/4Pz583j//ffV5/Xy8gIgl3l86623YGlpic6dO6Nz58748MMP\nceTIEQwfPhzDhw+Hl5cXzM3N8ddff2HXrl3w8PBAVFRUue/HZ599hsGDB6Nr1654++23YWNjg2++\n+QZJSUlYuHAhnn32WYP7E0Jg9+7d6N+/P9fmJiIqrqaWjyEiehI8vnW8EEXLE8bFxYnFixeLli1b\nCnNzc+Hs7Cy2bt2qs58dO3YIb29v9fb13t7eYufOnRp1EhMTxfDhw0Xr1q2FpaWlsLe3F56enmLT\npk2isLBQo+7KlStF27ZtRZ06dQQAsWTJEvWx7Oxs8cEHH4jOnTsLS0tLYW1tLTp27CgmTpwokpKS\ntK4jMTFR55gfX2ZR5cCBA6Jfv37CxsZGWFhYCFdXV7Fp0yaD2xfvB4D48ccf9dahiuMyi0RPHoUQ\n5Xjqh4joKfL41vFRUVEYN24cEhMT0atXr5od3BNs8ODBuHbtGn777Teu4lKFIiIiMGHCBADAuHHj\nEBERUcMjIqLSMMWFiKgUn376KV544QXs27cPfn5+JdYtKChQr59enIODA0xNTatqiE+c5ORkxMbG\nIjExkcE5EdFj+JAoEVEpVFvHlxacA3LVlaZNm2p9Xb9+vRpGqtuDBw9gYmKic/wXLlxAp06dYGFh\ngU2bNlXbmFxdXVFYWKh+mJaIiIpwBp2IqBI1adIEcXFxOstrysmTJyGEgLu7u0b5Dz/8gMDAQNSr\nVw8HDx5UP3xKREQ1iwE6EVEZjR07Vr0ay+MsLS2rZA1yADhw4AB69+5d5tz3kydPAoA6QBdC4IMP\nPkBISAh8fHzw7bff1ugbCCIi0sQUFyKiSpCTk4MWLVqgVatWUCqVGscmTpwIU1NTbNu2rUbGduLE\nCQCAh4cHMjIyMGjQIAQHB2Pq1KlISEjQCM6nTJkChUKBmzdvavXz559/wtzcHEFBQdU2diKipxED\ndCKiSlC3bl2EhITg+vXrCAsLU5cvWLAA4eHhWLduHUaMGFEjYzt58iTs7OygVCrh6emJuLg4REZG\nYv369TAzM9Oo6+3tDQA4fvy4Vj8zZ86Era0tgoODq2PYRERPLQboRESVZOzYsXB2dsZHH32ErKws\nrFmzBitWrEBISAjeeeedGhlTVlYWLly4AFNTU3h5eSEnJweHDh3Sm6KjykN/PED/6aefsHv3bnzw\nwQewt7ev6mETET3VmINORFRJTE1NsWLFCvj7+yMgIAAJCQmYPn06Fi9eXOa+CgsLce/ePY2yjIwM\n9WtaWprGsQYNGsDERHvOJTk5GYWFhcjPz0dmZibmzJmDLl266D1vhw4d0KBBA40APS8vD7NmzULn\nzp0xefLkMl8LERGVDWfQiYgq0cCBA+Hu7o79+/fjjTfewNq1a3XW8/T0xDfffKO3n2vXrsHBwUHj\nKyAgAAAQEBCgdezatWs6+1Hln69duxbdu3dHSEgIfvzxxxKvwcvLC7/99htU+9itXbsWFy5cwJo1\na7iWO1W6AwcOQKFQICoqyqAFdtmNAAAgAElEQVT6bdq0qbYNwkoaW0pKCurUqaNz1SZDxMTEwNzc\nHBcvXqzgKKk24gw6EVEl2r59O5KTkwEANjY2OjfhKSgowOnTp+Hq6qq3H13LNf7++++YM2cOVq1a\nhRdeeEGrvi6qFVy8vb0xYMAAdO3aFW+++SaOHDkCFxcXnW28vLywa9cu/Pnnn2jQoAGWLl2KgIAA\n9O3bV/+FEz1lZs2aBR8fH/j6+parfUBAAFxcXDBv3jzs2LGjkkdHTzoG6ERElWTfvn0IDAzE4MGD\nYWZmhoiICMycORPPPfecus6tW7fg5OQEpVIJDw8Pdbvu3btr9KVrucY6deSfbA8PD4NnEE+cOAEb\nGxu0b98eCoUC33//PV588UX4+/vj+PHjaNy4sVab4g+K/vzzz1Aqlfj0008Nvg9EZfHSSy8hJydH\n64FlY3b06FHExcUhJiamQv0EBQVhzJgxOHPmDJydnStpdFQbMMWFiKgSHDt2DEOGDIGPjw+2bt2K\nZcuWwcTEBAsWLNCo17RpU0RERMDT0xNZWVnIysrSCs4rS05ODs6fPw9XV1f1TL6rqyu+/PJLXLt2\nDQEBAVpLQgJAt27dYGJigvDwcERGRuK9996Do6NjlYyRnhwFBQV4+PBhpfdrYmICS0vLJyp9Kiws\nDA0bNsQrr7xSoX6GDBkCKysrbNy4sZJGRrUFA3Qiogo6d+4cXn31VbRv3x4xMTGwsLCAk5MTJkyY\ngNjYWBw5ckSj/smTJ+Hm5lbl40pOTkZBQYF6pl7l9ddfR3BwMI4ePYoJEyZotbOxsUGnTp3w888/\no3HjxvjPf/5T5WMl4xIVFQWFQoH4+HgsXboUTk5OsLS0xPbt2wEASqUSy5cvh7OzMywtLVG/fn34\n+/vj1KlTGv08evQIwcHB6NChA6ysrFC/fn24uLhg7ty56jr68ryvX7+O4cOHw87ODra2tvD398fl\ny5d1jjc4OBgKhQJXr17VOvZ4znpmZiYWLVqEbt26oVGjRrCwsEC7du0wf/58g96A5OfnIyYmBr6+\nvlqz/mXdR8Da2ho9evTAt99+W+p56enCAJ2IqAKuXbsGPz8/2NnZYffu3bC1tVUfW7x4MerWrYv3\n339fo83JkydLzD+vLI/vIFrc4sWLMXz4cPVs/+M8PT0BAB999BFsbGyqdqBktObMmYNt27Zh0qRJ\nWLt2LTp06IC8vDz0798fISEh8Pb2xurVqzF//nycPXsWPj4++O2339Ttp02bhpCQEHh5eSE0NBQf\nfvgh+vbti4SEhBLPe//+fbz00kvYsWMHAgMDsWLFClhZWaF3797Izs6u0DXduHEDX3zxBbp06YL/\n/ve/CA0Nhbu7Oz7++GMMHjy41PYnTpxAVlaW+t9IceXZR8Db2xt37tzB+fPny3dBZLQePnyIpUuX\nYtKkSQCAixcvlvqQvpogIqJq1bBhQ3Hs2LGaHoZeubm5wtHRUXTp0kUUFhbW9HCogsLDwwUAAUCM\nGzfOoDaRkZECgGjfvr3Izs7WOBYaGioAiD179miUZ2RkiJYtW4qePXuqy+zt7cWAAQNKPFdiYqIA\nICIjI9VlCxYsEABERESERt2goCABQOMcQgixZMkSAUCkpqZq9d+6dWuN+kqlUuTm5mrVW7RokQCg\n8W9T19giIiIEABEbG6vVx/nz5wUAsWDBAo3yH3/8UQAQ69ev12qzefNmAUBER0drHaMn2/Dhw8XK\nlSuFs7OzEEKIhw8fihdeeMGgtpxBJyKqRnl5eUhPT6/pYZRo1apVSE1Nxbp163SuQkNPj6lTp8LK\nykqjbMuWLejYsSM8PDyQlpam/srNzYWvry8OHz6MnJwcAICdnR3OnDmDlJSUMp03JiYGzzzzDEaP\nHq1RPm/evIpdEABzc3N1akp+fj7S09ORlpamfij72LFjJba/e/cuALn3wOPKs49Aw4YNAQD//PNP\n+S6IjNbly5fx/vvvq/97q1u3rnr52tJwFRciompkZmaGOXPmwM/PD/n5+fjjjz+M4gHMe/fuYe/e\nvfjjjz/wySefYNasWepdRenp1b59e62yc+fOIScnBw4ODnrbpaWloWXLllizZg0CAwPh4uICR0dH\n9O7dG/7+/vD399e5sZbKlStX0LVrV60HR5s2bYr69euX/4L+T1hYGDZu3IgzZ86gsLBQ41hpb6BV\nb1r1BVpeXl44cuQIhBBQKBTqfQTi4+N1Pgir6odvhmsfc3Nz5OTkqH+3ly9fhoWFhUFtGaATEVWz\nlStXYuXKlTU9DA179+7Fm2++icaNG2PmzJlYsWJFTQ+JjMDjs+eADChdXFwQGhqqt50qeB80aBCu\nXr2KXbt24eDBg4iPj0d4eDh69OiB+Ph4mJub6+1DX8CqKzAuKbjNz8/X+Dk0NBSzZ8+Gn58fZsyY\ngWbNmsHc3Bw3btzA2LFjtQJ2fdf2+E6/KmXdR0DVT0lveOjJFBwcjP79++P69et46623cOTIEURG\nRhrUlgE6ERFh5MiRGDlyZE0Pg54Azz77LO7evYs+ffqUOAuu0qBBA4waNQqjRo2CEALz58/Hxx9/\njNjYWAwbNkxnG0dHR1y4cAEFBQUas863bt1CRkaGznMAMtht06aNuvzRo0e4desW2rVrpy7bvHkz\n2rRpg927d2uMf8+ePaVeCwB07twZAPTuAFrWfQQuXbqk0S/VHn5+fvDw8EBSUhKEEFi7di0aNWpk\nUFvmoBMREZHBRo8ejdu3b+udQb9z5w4AuW76/fv3NY4pFAr1EqP6ZqABOfN+584dfPXVVxrl+j55\nUqXixMfHa5SvXr1aa0bc1NQUCoVCYyY+Pz/f4E+N3NzcYGtri6SkJJ3Hy7qPQFJSEp555hl06NDB\noPPTk6Nv375o2LAhXn31VQwcOBCNGjUyeEdmzqATERGRwYKCghAXF4e5c+ciISEBffr0ga2tLa5d\nu4b9+/fD0tISiYmJyMzMRNOmTfHaa6/Bzc0NjRs3RmpqKjZs2AB7e3v4+/vrPcf777+Pr7/+GpMm\nTcKJEyfg7OyMAwcO4OjRozpnIPv164eOHTti8eLF+Pfff9G2bVscPnwYSUlJWvWHDh2KBQsWYMCA\nARgyZAgePHiAr7/+2uCdTE1NTTFkyBDExsZCqVRq5RQX30egSZMmJe4jkJWVhUOHDmH8+PEGnZue\nDI8ePcLDhw+RlpaG9PR09ZvBBw8e6FwjXxcG6ERERGQwMzMz/PTTTwgLC8PmzZuxZMkSAECzZs3g\n6emJMWPGAJD56++99x7279+P+Ph4ZGVlqQP2BQsWoFmzZnrPYW9vj0OHDmHWrFn46quvIIRAr169\nkJiYqHMG0tTUFLGxsZgxYwbWrVsHc3Nz+Pn54eDBg/Dx8dGoO3fuXAghEB4ejqCgIDRp0gRvvPEG\nxo0bh06dOhl0D6ZOnYqoqCj8+OOPeP3117WOe3p6IiUlpdR9BL777js8fPhQ5+ou9OT6/PPPsWbN\nGty8eRMeHh7qAN3W1hbTpk0zqA+FMHS9FyIiInriREREqHeMHTduHCIiImp4RLVD//79kZ2djUOH\nDmmU5+XloWPHjurlFkt6gNXDwwOtW7fGjh07qnq4VAPWrVuH6dOnl6stZ9CJiIiI9CgoKFCvfV7c\nxx9/DHd3d+zbtw9+fn7qctU+Alu3bi0xOI+JicHp06exbdu2Khk31bzp06cjJSUFZ8+exaNHj9Tl\nj6/vrwsDdCIiIiI9rl+/jrZt22qVp6amqpdwLM8+AgEBAcjNza2SMZNxCAkJwYEDB3D27Fm88sor\n2L17N1588UUG6EREREQV0aRJE8TFxeksV+E+AqRLdHQ0fv/9d7i5uSEyMhJ37tzBxIkTDWrLAJ2I\niIhID0tLS/Tr16/EOtxHgHSpW7cuTExMUKdOHTx48ACNGzfGlStXDGrLddCJiIhIw5QpU6BQKHQu\nCffnn3/C3NwcQUFBVTqGvLw8mJubQ6FQ6PwaMmRIlZ07JycHLVq0QKtWraBUKjWOTZw4Eaampswd\np1J16dIF9+/fx6RJk+Dh4QF3d3d4enoa1JYz6ERERKTB29sbn3/+OY4fP46AgACNYzNnzoStrS2C\ng4O12hUWFpa4AdHjGjRooHc30tzcXJ0rzqxevRonT54scR31iqpbty5CQkIwceJEhIWFYebMmQCA\nBQsWIDw8HOvXr8eIESOq7PxUO4SFhQGQb3j79++PBw8e4PnnnzessSAiIqJaKzw8XAAQAMS4ceMM\nanP+/HkBQCxYsECj/McffxQAxPr163W2S01NVZ/LkK/U1NQyXcvcuXMFALFq1aoytSuP/Px84ezs\nLBwcHERmZqZYvXq1ACBCQkKq/NxUO/Tp08egMl04g05EREQaOnTooF7HWyUvLw+zZs1C586d9W6s\no++BSn2KP2hZEiEEZsyYgfXr12P9+vV45513dNa7f/8+1qxZY/D5Z8yYgQYNGug8ZmpqihUrVsDf\n3x8BAQFISEjA9OnTsXjxYoP7p6cTdxIlIiKiKuHl5YUjR45ACAGFQoG1a9fiwoULiI+Ph6mpqc42\nhjxQWVaFhYWYPHkyIiIi8MUXX2D8+PF6696/fx8hISEG9z1q1Ci9AToADBw4EO7u7ti/fz9GjBiB\ntWvX6q3r6emJ2bNn44033jD4/FQ76dpJVKFQwMbGBu+++65BfTBAJyIiIi1eXl7YtWsX/vzzTzRo\n0ABLly5FQEAA+vbtq7eNvk199HFwcNAb7Kv6Gzt2LLZt24YtW7aUulJKmzZt1LOVlWH79u1ITk4G\nANjY2OjdeKigoACnT5+Gq6trpZ2bnlxBQUEICgrCBx98gPfeew+2trZYunQpTp48CW9vb4P64Cou\nREREpEUVSBw/fhwLFy6EUqnEp59+WmKb69evo2nTpgZ/Xb9+XW9feXl5GDFiBLZv345vvvmm2pcx\n3LdvHwIDAzF48GCMGDECEREROHfunFa9W7duwcbGBkqlEh4eHrC2tsYvv/xSrWMl4xQdHQ1bW1sc\nPnwYcXFxGDt2LKZOnWpQW86gExERkZZu3brBxMQE4eHhOHz4MObOnQtHR8cS21RWDrpSqcSwYcMQ\nFxeHHTt24NVXXy3T2Cvq2LFjGDJkCHx8fLB161b8/fff+O6777BgwQLExMRo1G3atCkiIiKwZs0a\nJCUlVes4ybipPh366aefMGXKFAwaNEjn6ke6MEAnIiIiLTY2NujUqRN+/vlnNGnSBP/5z39KbVNZ\nOeijR4/GDz/8gLFjxyI9PR1btmzROP7aa6/B1ta2wufR5dy5c3j11VfRvn17xMTEwMLCAk5OTpgw\nYQI2btyII0eOwMfHR6PNyZMn4ebmViXjoSdX8+bNMXnyZMTHx2PevHlQKpUoLCw0qC0DdCIiItLJ\n09MTKSkp+Oijj2BjY1Mt5xRCYPfu3QCAqKgoREVFaRw3MTFBZmZmlZz72rVr8PPzg52dHXbv3q3x\nJmDx4sX48ssv8f777+PIkSMa7U6ePIlhw4ZVyZjoybV9+3bs2bMHc+bMQf369XHr1i188sknBrVl\ngE5ERERa8vLycODAAXTp0gVjxoyptvMqFAo8ePCg2s5XXKtWrfTmxTdt2hQPHz7UeSw5ORnLly+v\nyqHRE8jKykpjx1vVsxeGYIBOREREWlatWoXU1FRs3bpV7+olJN/IpKen1/QwqJZhgE5EREQAgHv3\n7mHv3r34448/8Mknn2DWrFnw8vKq6WEZNTMzM8yZMwd+fn7Iz8/HH3/8UerDtESlYYBOREREAIC9\ne/fizTffROPGjTFz5kysWLGipof0RFi5ciVWrlxZ08OgWoQBOhEREQEARo4cWe3rjRORNm5URERE\nRERkRBigExEREREZEQboRERERERGhAE6EREREZERYYBORERERGREGKATERERERkRBuhEREREREaE\nAToRERERkRFhgE5EREREZEQYoBMRERERGREG6ERERERERoQBOhERERGREWGATkRERERkRBigExER\nEREZEQboRERERERGhAE6EREREZERYYBORERERGREGKATERERERkRBuhEVL169QLatCm9rKrORURE\nZOQYoBPRk23NGiAqqqZHQUREVGnq1PQAiIiwbx8gRPnarlkjZ8nHjq3cfomIiGoIA3QiKllmJmBj\nU7XnMDd/svolIiKqQkxxIartoqIAhQKIjweCg4HWrQELC+D554Ft2zTrtmkj87ZPnQJefhmws5P1\nVJRKYPlywNkZsLQE6tcH/P1l/celpwOTJgGNGgH16sl+T5zQPUZ9ueKXLgHjxgEtWshgu1kzYNCg\non4UCuCvv4CDB+X3qq+rV0vu9+efAV9feX116wLu7kB4uP5x3bwJjBwJ2NvLa3n5ZeDCBd3XQkRE\nVEGcQSd6WsybB2RnA1OnyiA2MlIGnY8eaaaHXLsG9OkDDBsGvP46kJUly/PygP79gV9+AQIDgXff\nBTIygE2bAB8fGfR26VJU9+WXgV9/lXW9vIDkZKBfP6BhQ8PG+9tvQN++sq8JE4DOnYF792Qw/ssv\ngIcHsHkzMHOmfBPwn/8UtXVw0N/vDz8AgwcDTZoAs2fLTwe2bQMmTgSuXAE+/FCzfnY28NJL8hqW\nLwdSU4G1a+UbhZQUwNTUsOshqiHPPfeczu+JyIgJIqrdIiOFAIRo1UqI+/eLyu/fl2X29kI8fCjL\nWreWdTdt0u4nNFQe27NHszwjQ4iWLYXo2bOo7PPPZd3FizXrrl4ty1u31izv2VOzrLBQCGdnISws\nhPj9d+2xFBQUfd+6tea5S+o3P19es52dEDduFJUrlUJ07y6EiYkQFy5otgeEWLlSs9+PP9Z9L4iM\nUGFhodi8ebP45JNPRGZmZk0Ph4gMwBQXoqfF1KkypUPFzg6YMkWmohw4UFTeoIFMK3ncli1Ax45y\n5jotregrN1emixw+DOTkyLoxMXJmefZs7THY2pY+1uRk4MwZOY7iKTYqJuX803XihPyEYPx4mS6j\nYm4OzJ0LFBYCsbHa55oxQ7OsTx/5evFi+cZBVI0U2dkYlZ+POUolrKOjiz4VIyKjxRQXoqeFro+2\nO3WSr1euFJU5OelO2zh3TgbgJaWPpKUBLVvK/po21Q7GLSwAR0f5pqAkqsDXza3kemWVmipfnZ21\nj3XuLF+L3wtABvKWlpplqjSdf/+t3PERVabsbPkm/OhR4PLlovJlywBvb2DjRvlMBREZHQboRE8L\nhUK7TNcShFZWutsLAbi4AKGh+s+hCt6F0H0+fefUV0dfH+VVniUXS8ox5xKOZKyys+UzH0lJ2scu\nX5Zfly7Jh8cZpBMZHQboRE+Ls2eB117TLDt3Tr46Opbe/tlngbt3ZXpHaSkmTk5yDfIHDzRn0ZVK\nOYttb19y+w4d5Kuu1WEeV5Yg3slJvp45o33s7Fn5asi9IKpJqanARx8BrVrJh5ubNNGuM2WK7uC8\nuKQkWW/z5qoZJxGVG3PQiZ4WGzbIVVdUMjLkR9z16wM9e5befvRo4PZt/TPod+4UfT9oEFBQAHz6\nqfYYHjwo/VwvvCDTUCIidAfTxWeura3l6i6GcHeXQU1kpLwWlbw84JNPZLA/aJBhfRHVlPfek6sn\n/fe/ctnUMWOAkyeLjmdlybQWQyQlMSedyAhxBp3oadGoEdCtm3xAUggZpF67Bnzxhf60luKCgoC4\nOPkwZUKCnEm3tZV97N8v87QTE2XdceOA//0P+OADOdvn7S1nw7/9Vs5i5+eXfC7VMpB9+wKenkXL\nLN6/L5dZ7N8fmD5d1vXykmuY//e/Ms/exESuza7rY3tTU+Czz+Qyi127Am+/LZdZ/OYbGagsXCg/\nKSCqTnl5ckOwzEz5BvbBA83vH//50qWitrm5wFdfyS9HR/mpWHS0Zs55SS5dkvV17cRLRDWGATrR\n02LlSuDQIRmg3rkjA9GtW4E33zSsvZkZ8NNPQFiY/Eh8yRJZ3qyZDKLHjCmqa25eFMzHxADffScD\n4rg4YM6coo2EStK1q1xHfelSYPt2OdvfqJE8l49PUb0PP5Qz6OvXywBeCPmmQF9erb+/fEOxbJmc\nNc/NlYH9pk0yXYDIEIWFMs9bVwBdUnCt65hq9aOKunJF/hu9caNs7W7erJzzE1GlUQjBp5yIarWo\nKDmjnZgod8YkeloJITfmKmsArev7rCzje0jY1lYG59HRupdK1ScykjPoREaGM+hERGTcVCkg5Zmd\nfvz70tKraoJCIYNr1ZeNje7vVT8nJMhPlVRsbOSnVfPmyU+vhg6VnxAZkubSrp2sT0RGhQE6ERFV\nvsJCOctckdQP1fePHtX01ehWr17pwbQhx6ysyrYaUbNmMm0MACZPBkJCZPqXirW1fO7DkADd21vW\nJyKjwgCdiIgkVQpIZcxUZ2bW9NXoZmYmd9EtbzCt+t7aGqhTQ/8L9feXm3lZW+vfOGzjRvkAaElL\nLXp5yZWViMjoMAediOhJVzwFpKIPLNaGFJCSjllY1PTVVB99O4m2aydnzjds4CZFREaKAToRUU1g\nCkjVpYCQpqws+eDozZsyPWboUONMaykokJuhPc7BoeQdfYlqIQboRESGYgrIk5ECQiU7cADo3btm\nVm9JSQFcXYHduwFfX81jV68Cbdtqt0lNBdq0KbnfmBhg+HC5sRn3MqBagH89iaj2YwoIU0DIOMya\nJfcxeDw4B4AmTeReCbrKSxMQALi4yJVsduyo+DiJahhn0InIOD2NKSDlDa6ZAkJlUVgoN+gyM6ve\n1JGjR4Hu3eVs96BBld//V1/JDdNSUgBn58rvn6gaMUAnosrzNKWAVHSmmikgVN0KCgClUr6hq4m+\nAwNlasutW/LfUWXLygKeeQYYPx5Yt67y+yeqRgzQiaj2p4CYmFTOw4pMAaGapNoVOC4OOHxY5pDf\nvg106AAsXAiMGKG77tGj8udr14BNm2Q+t64c9LQ0YMkS4PvvgTt3ZLD72mvABx8ADRsa1re+nPb8\nfMDeHhg4EPh//0/zWE6OzBs3MZHLRxb/NzZxohzn1q2a16dP//5AcrK8L0RPME7fED2pmALCFBB6\nOs2bJ5dQnDpV/ncdGQmMHCn/HT8eIM+ZI9+AT5ok/y106CBnuh+XkSHTTy5dkjPQ7u7AqVNyKcaE\nBOD4cflvqrS+9TlxQv698vTUPla3rtxsaeJEICwMmDlTli9YAISHA+vXGxacA3L5yL17gfPngY4d\nDWtDZIQYoBNVp6chBcTcvHIeVmQKCJFuaWnAH3/IVCtArnX+/PPyAcw33pABr0pOjgy0i6eeHDig\n3efHH8vZ6/XrgXfeKSp3dQXefVceX7pUs42uvvU5e1a+OjnpPj52LLB6NfDRRzLg/+ILYMUKGbgX\nH09pVP2fOcMAnZ5o/L8fkSGethSQ8gbXTAEhqnpTpxYF54D8fsoUmeZy4AAwYIBmXUMC6J075Xrj\nb7+tWT55MhAcLI8/HqAb2jdQtL55gwa6j5uayoDc31+uyJKQAEyfDixebFj/KqpUnH/+KVs7IiPD\nAJ1qr6clBaSiM9VMASF6sjz3nHZZp07y9coVzfL27Q3rMzUV6NJF+1OrOnVk6srJk9ptDO0bKPr7\nUtJjbwMHytSa/ftlSsvatbrreXoCs2fLTwsep+qff8/oCccAnYzL05wCUtZA28aGu+sRPY10BZ/6\nAt+qWLGlPH07OMjXe/f019m+XT7gCci/b7qus6AAOH1apt7ooupfdT6iJxQD9DLIyspCdHQ0bty4\ngebNm2Po0KGwNsbtkmtC8RSQkoJnpoAwBYSIKubsWbm6SnHnzslXR8fy9enoCPz5p/z7W3wWPT8f\nuHCh/P2qdO4sXy9e1H183z65DOPgwXIJxogI+bBo8U8Lbt2SOeZKJeDhUdSue/eiOpcuaZ6P6AnF\nAN0A2dnZmDJlCo4ePYrLly+ry5ctWwZvb29s3LgR9erVq8ERllNhoVwJoCKz1EwBISKqXhs2aOah\nZ2QAGzcC9esDPXuWr8+AAGD5cvlw5pQpReWbNsn88cmTKzZmNzf5tzQpSfvYsWPAkCFyh9GtW4G/\n/wa++06u4hITU1SvaVMZuK9Zo7sfQJY/80zJK8oQPQEYoJciOzsb/fr1Q5KOPwaXL1/G5cuXcenS\nJcTHx1dPkK4vBaQ86SBMASEievI0agR06yaXQxRCLrN47ZoMrsub0vL++8C33wLTpsl8czc3uUJL\neLgMdt9/v2JjNjWVQXhsrJwBV32SeO4c8OqrMp89JkaWOzkBEybINx1HjsjAXUU1Nl2ysoBDh+R9\nIXrCMUAvxZQpU3QG58UlJSVhypQp2Lx5s/5KhqaAGHKMKSBERE+vlStlIPrZZ3JDoWeflTPPb75Z\n/j7t7GQwrNqoKDJSzkRPmSKXOnx8DfTymDpVbmr044/A66/LNxV+fvLcu3fL/weoLF4MfPmlfGNw\n5EhR+cmTwLBhuvv/7jvg4cOKz/YTGQHuJFqCrKwsuLq6aqS16DOoRQt827s3zO7fZwoIERFVPtUO\nnomJQK9eNT2a8unfX6ZWHjpUvvaNGgG7dune8MjDA2jdGtixo2JjJDICnEEvQXR0tEHBOQCs/ftv\nmJU0g16ZiqeAVCS4trZmCggREVWfTz8FXnhBPtzp51e2tnl5QHq67mMxMXJ1l23bKj5GIiPAAL0E\nN27cMLjuTQCtS6pgYlI5M9VMASEioieVs3P50zTNzIA5c2Rgn58vd1NVrS4TEADk5lbeOIlqGAP0\nEjRv3tzguv0AfD99Ovr27as70GYKCBERUcWsXCm/iGo55qCXoCw56O3atcOpU6e4LjoRERERVYhJ\nTQ/AmFlbW8Pb29ugut7e3gzOiYiIiKjCOINeipLWQVfx8vKqvnXQiYiIiKhW4wx6KerVq4f4+HiM\nGjUKTk5OGsfatWuHwMBABudEREREVGk4g14GWVlZiI6Oxs2bN9GsWTMMHTqUaS1EREREVKk4g/5/\nDhw4AIVCgaioKL11rPmdS48AAAstSURBVK2tMXbsWCxcuBBjx46ttOA8JSUFderUQVxcXKX0Vx1i\nYmJgbm6Oixcv1vRQiIiIiGoVow/Qk5OTERwcjKtXr9b0UKrMrFmz4OPjA19f35oeisECAgLg4uKC\nefPm1fRQiIiIiGoVo18HPTk5GSEhIejVqxfatGlTZed56aWXkJOTAzMzsyo7hy5Hjx5FXFwcYmJi\nqvW8lSEoKAhjxozBmTNn4OzsXNPDISIiIqoVjH4GvSoVFBTg4cOHAAATExNYWlrC1NS0SvrXJyws\nDA0bNsQrr7xSaeetLkOGDIGVlRU2btxY00MhIiIiqjUMCtCjoqKgUCgQHx+P4OBgtG7dGhYWFnj+\n+eexbds2rfppaWmYNm0aWrZsCXNzc7Rs2RLTpk3Dv//+q1Hv0aNHCA4ORocOHWBlZYX69evDxcUF\nc+fOBQAEBwdj3LhxAIDevXtDoVBAoVBg7Nix6j6USiWWL18OZ2dnWFpaon79+vD398epU6f0XsPS\npUvh5OQES0tLbN++HYD+HHRDr6W0/nXJz89HTEwMfH19tWbuc3Jy0KJFC7Rq1QpKpVLj2MSJE2Fq\naqrz3lcna2tr9OjRA99++22NjoOIiIioNilTisu8efOQnZ2NqVOnQqFQIDIyEiNHjsSjR4/UQXNG\nRga6d++OS5cuYfz48XB3d8epU6ewYcMGJCQk4Pjx47CxsQEATJs2DRERERg9ejRmzpyJgoICXLx4\nEQkJCQDkDO2tW7fwv//9DwsXLsRzzz0HAOrlDvPy8tC/f3/88ssvCAwMxLvvvouMjAxs2rQJPj4+\n+Pnnn9GlSxeNa5gzZw7y8vIwadIk2NraokOHDnqvtyzXUp7+T5w4gaysLHh6emodq1u3LkJCQjBx\n4kSEhYVh5syZAIAFCxYgPDwc69evx4gRI0r6dVULb29v7N27F+fPn0fHjh1rejhERERETz5hgMjI\nSAFAtGrVSty/f19dfv/+fdGqVSthb28vHj58KIQQYuHChQKAWL9+vUYfn332mQAgFi1apC6zt7cX\nAwYMMOjciYmJWsdCQ0MFALFnzx6N8oyMDNGyZUvRs2dPrX7at28vsrOztfpKTEwUAERkZKS6rCzX\nUlr/ukRERAgAIjY2Vufx/Px84ezsLBwcHERmZqZYvXq1ACBCQkIM6r86bN68WQAQ0dHRNT0UoqdO\nenq6+u/TjRs3xOuvv17DIyIiospQphz0qVOnws7OTv2znZ0dpkyZgvT0dBw4cAAAsHPnTjg4OODt\nt9/WaDt58mQ0atQIO3fu1Gh/5swZpKSklO1dxf/ZsmULOnbsCA8PD6Slpam/cnNz4evri8OHDyMn\nJ0frGqysrAzqvyzXUp7+7969CwBo0KCBzuOmpqZYsWIF7t69i4CAAMyaNQvTp0/H4sWLDeq/OjRs\n2BAA8M8//9TwSIiePvfv30dYWBgAoFmzZoiOjq7hERERUWUoU4CuSjEprlOnTgCAK1euAABSU1PR\noUMH1KmjmT1Tp04ddOjQQV0PANasWYP09HS4uLjAyckJEydORGxsLAoLCw0az7lz53D+/Hk4ODho\nfUVERKCgoABpaWkabdq3b2/w9ZblWsrTv0KhAACIEvaKGjhwINzd3bF//3688cYbWLt2rc56np6e\n+Oabbww+d0nWr18PT09PWFpaolevXiXWVY1ddS1EVH3mz5+Py5cvw9XVFcOGDUPnzp0ByGdiAgIC\n4O/vj7Zt2+Kzzz5DaGgo3Nzc4OXlhXv37gEALl++jP79+8PDwwM9evTA+fPna/JyiIjo/5QpB11X\nEFZScFmaQYMG4erVq9i1axcOHjyI+Ph4hIeHo0ePHoiPj4e5uXmJ7YUQcHFxQWhoqN46Dg4OGj8b\nOrtdXmXpXzU21f8sddm+fTuSk5MBADY2Njp/BwUFBTh9+jRcXV3LOFrdmjZtivnz5+PXX3/F0aNH\nS6yrGvvj95mIqt6KFSuQkpKC5ORkXL16FQMHDlQfS0lJwalTp/Do0SO0a9cOK1euxKlTpzBz5kx8\n9dVXeO+99/D2229j48aNePb/t3dHIU13fxzH362GrdpmJYVdFCrWhYUMKaFdSF5IEI0cjAgsyF3Y\nCiqhpG6MwC4sgoJgQrqC2EVIsUEtMMoLs9yNxYKkCITdVOxiiatc/mjPRfT7//dYz+Omz9Pg+bzg\nx3a2c347Zzf77vs7v3Nqa4nH4xw9etS8B0hERH6fggL0V69e4fF48l6bmJgAoLq62nx8/fo1hmHk\nZZ4Nw+DNmzdmvR/WrFlDW1sbbW1t5HI5zpw5w8WLF4lGo/h8vr/MzNbW1pJKpWhubsZiWfwVIwsd\nS6F+ZLt+tRvn0NAQBw8epLW1FavVSigUorOzM+9Kxrt376ipqSGbzdLQ0GC227lzZ9H98nq9ACST\nyb+t+/bt27yxiEhp2LVrF3a7HbvdjtPpZO/evQBs27aNRCJBJpPh6dOn+Hw+s82fV4wSEZHfo6Co\nNhgMMjU1ZZanpqbo6+ujvLycpqYm4PsOk6lUiv7+/ry2169fJ5VK0draCnzP+n78+DGvzpIlS3C5\nXMD/MrOrVq3KK/+/Q4cO8f79+19m0D98+FDI8OaY71iK5XK5cDgcjI2NzXkvHo/j9Xpxu92Ew2F6\nenqwWCycPXs2r15lZSWhUIgdO3aQyWTIZDILCs4LNTY2xvr16/9ytRoR+feVlZWZzy0Wi1m2WCwY\nhsG3b98oLy/nxYsX5vEj4SIiIr9XQRn0iooKGhsbaW9vJ5fLcePGDZLJJP39/ebUjq6uLgYHBzl2\n7Bjj4+O4XC6eP3/OwMAAW7ZsoaurC4Dp6WkqKyvxeDy4XC7WrVvH5OQkwWCQ1atXm9me7du3Y7FY\nuHDhAul0mpUrV1JVVUVjYyMnTpzg4cOHnD59msePH9Pc3IzD4SCZTPLo0SOWL1/O8PBw0V/OfMdS\nrKVLl+L1eolGo2SzWfMHdGJigj179rB582YikQhlZWXU1NTg9/vp6+tjdHQUt9ttnudH334mm80y\nOzv7yz7YbLaiN2fKZDKMjIzQ3t5eVHsRWRi73c709HRRbR0OB1VVVQwODuLz+cjlciQSCerr6xe5\nlyIiUqiCMui9vb3s37+fa9eu0d3dzbJlywiHw/j9frOO0+lkdHSUjo4OYrEYx48fJxaLceTIEZ48\neWKuG75ixQpOnjzJ5OQkly5dIhAIcOvWLTweD/F4nA0bNgCwceNGQqEQX758IRAIcODAAYLBIABW\nq5X79+9z9epVUqkU586do7Ozk9u3b1NdXT0n21yo+Y5lIQKBAOl0mnv37gHfp5W0tLTgdDp58OAB\nDofDrNvd3Y3NZpvzx2B8fPyX88/9fr95mftnx8jISNF9v3PnDp8/f6ajo6Poc4hI8dauXYvb7Wbr\n1q3mBm+FCIfDDAwMUF9fT11dHdFo9B/opYiIFGpJbh53ed68eZPDhw8zPDz8t6t6SOF2797Np0+f\nig6WKyoqiMViP93waCGuXLlCJBIxl9D8s4aGBjZt2sTdu3cX9XNFRERE/ssW/85KKdjly5d59uwZ\nQ0NDBbednZ0lnU4van8Mw2BmZsacpzozM8PXr1/z6kQiEV6+fElvb++ifraIiIjIf11Bc9Dln1FX\nV4dhGEW1tVqtnDp1ipaWFgzDIJFILHh1mZ6eHs6fP2+WbTYbTU1NeZn0ffv2zQnaRURERGThNMVF\nRERERKSEzCtAFxERERGRf4fmoIuIiIiIlBAF6CIiIiIiJUQBuoiIiIhICVGALiIiIiJSQhSgi4iI\niIiUEAXoIiIiIiIlRAG6iIiIiEgJUYAuIiIiIlJC/gBHU7vc5Cu7lwAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"import kf_book.book_plots as book_plots\n",
"book_plots.show_residual_chart()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The Kalman gain $K$ is a scale factor that chooses a value along the residual. This leads to an alternative but equivalent implementation for `update()` and `predict()`:"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def update(prior, measurement):\n",
" x, P = prior # mean and variance of prior\n",
" z, R = measurement # mean and variance of measurement\n",
" \n",
" y = z - x # residual\n",
" K = P / (P + R) # Kalman gain\n",
"\n",
" x = x + K*y # posterior\n",
" P = (1 - K) * P # posterior variance\n",
" return x, P\n",
"\n",
"def predict(posterior, movement):\n",
" x, P = posterior # mean and variance of posterior\n",
" dx, Q = movement # mean and variance of movement\n",
" x = x + dx\n",
" P = P + Q\n",
" return x, P"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Why have I written it in this form, and why have I chosen these terrible variable names? A few related reasons. A majority of books and papers present the Kalman filter in this form. My derivation of the filter from Bayesian principles is not unknown, but it is not used nearly as often. Alternative derivations naturally lead to this form of the equations. Also, the equations for the multivariate Kalman filter look almost exactly like these equations. So, you need to learn and understand them. \n",
"\n",
"Where do the names `P`, `Q`, and `R` come from? You will see them used in the rest of this book. In the literature $R$ is nearly universally used for the measurement noise, $Q$ for the process noise and $P$ for the variance of the state. Almost every book and paper you read will use these variable names. Get used to them.\n",
"\n",
"This is also a powerful way to think about filtering. This is the way we reasoned about the g-h filter. It emphasizes taking the residual $y = \\mu_z - \\bar\\mu$, finding the Kalman gain as a ratio of our uncertainty in the prior and measurement $K = P/(P+R)$, and computing the posterior by adding $Ky$ to the prior. \n",
"\n",
"The Bayesian aspect is obscured in this form, as is the fact that we are multiplying the likelihood by the prior. Both viewpoints are equivalent because the math is identical. I chose the Bayesian approach because I think it give a much more intuitive yet deep understanding of the probabilistic reasoning. This alternative form using $K$ gives a deep understanding of what is known as the *orthogonal projection* approach. Dr. Kalman used that derivation, not Bayesian reasoning, when he invented this filter. You will understand more about this in the next few chapters."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Code Walkthrough\n",
"\n",
"Now let's walk through the code.\n",
"\n",
"```python\n",
"process_var = 1.\n",
"sensor_var = 2.\n",
"```\n",
" \n",
"These are the variances for the process model and sensor. The meaning of sensor variance should be clear - it is how much variance there is in each measurement. The process variance is how much error there is in the process model. We are predicting that at each time step the dog moves forward one meter. Dogs rarely do what we expect, and things like hills or the whiff of a squirrel will change his progress. If this was a robot responding to digital commands the performance would be much better, and perhaps the variance would be $\\sigma^2=.05$. These are not 'magic' numbers; the square root of the variance is the distance error in meters. It is easy to get a Kalman filter working by just plugging in numbers, but if the numbers do not reflect reality the performance of the filter will be poor.\n",
"\n",
"```python\n",
"x = (0., 400.) # Gaussian N(0, 20**2)\n",
"```\n",
"\n",
"This is the dog's initial position expressed as a Gaussian. The position is 0 meters, and the variance to 400 m$^2$, which is a standard deviation of 20 meters. You can think of this as saying \"I believe with 99.7% accuracy the position is 0 plus or minus 60 meters\". This is because with Gaussians ~99.7% of values fall within $\\pm3\\sigma$ of the mean.\n",
"\n",
"```python\n",
"process_model = (velocity*dt, process_var)\n",
"```\n",
"\n",
"This is the process model - the description of how we think the dog moves. How do I know the velocity? Magic? Consider it a prediction, or perhaps we have a secondary velocity sensor. If this is a robot then this would be a control input to the robot. In subsequent chapters we will learn how to handle situations where you don't have a velocity sensor or input, so please accept this simplification for now.\n",
"\n",
"Next we initialize the simulation and create 10 measurements:\n",
"\n",
"```python\n",
"dog = DogSimulation(x[0], process_model[0], \n",
" sensor_var, process_model[1])\n",
"zs = [dog.move_and_sense() for _ in range(10)]\n",
"```\n",
"\n",
"Now we enter our `predict() ... update()` loop.\n",
"\n",
"```python\n",
"for z in zs:\n",
" prior = predict(x, process_model)\n",
" likelihood = (z, sensor_var)\n",
" x = update(prior, likelihood)\n",
"```\n",
"\n",
"The first time through the loop `prior` is `(1.0, 401.0)`, as can be seen in the printed table. After the prediction, we believe that we are at 1.0, and the variance is now 401, up from 400. The variance got worse, which is what always happens during the prediction step because it involves a loss of information.\n",
"\n",
"Then we call the update function using `prior` as the current position.\n",
"\n",
"For this I get this as the result: `pos = (1.352, 1.990), z = 1.354`.\n",
"\n",
"What is happening? The dog is actually at 1.0 but the measured position is 1.354 due to sensor noise. That is pretty far from the predicted value of 1. The variance of the prior is 401 m$^2$. A large variance implies that confidence is very low, so the filter estimates the position to be very close to the measurement: 1.352.\n",
"\n",
"Now look at the variance: 1.99 m$^2$. It has dropped tremendously from 401 m$^2$. Why? Well, the RFID has a reasonably small variance of 2.0 m$^2$, so we trust it far more than the prior. However, the previous belief does contain a bit of useful information, so our variance is now slightly smaller than 2.0.\n",
"\n",
"Now the software loops, calling `predict()` and `update()` in turn. By the end the final estimated position is 15.053 vs the actual position of 14.838. The variance has converged to 1.0 m$^2$. \n",
"\n",
"Now look at the plot. The noisy measurements are plotted with black circles, and the filter results are drawn with a solid blue line. Both are quite noisy, but notice how much noisier the measurements are. I plotted the prediction (prior) with red triangles. The estimate always lies between the prior and the measurement. This is your first Kalman filter and it seems to work!\n",
"\n",
"The filtering is implemented in only a few lines of code. Most of the code is either initialization, storing of data, simulating the dog movement, and printing results. The code that performs the filtering is very succinct:\n",
"\n",
"```python\n",
"prior = predict(x, process_model)\n",
"likelihood = (z, sensor_var)\n",
"x = update(prior, likelihood)\n",
"```\n",
"\n",
"If we didn't use the `predict` and `update` functions the code might be:\n",
"\n",
"```python\n",
"for z in zs:\n",
" # predict\n",
" dx = velocity*dt\n",
" pos = pos + dx\n",
" var = var + process_var\n",
"\n",
" # update\n",
" pos = (var*z + sensor_var*pos) / (var + sensor_var)\n",
" var = (var * sensor_var) / (var + sensor_var)\n",
"``` \n",
"\n",
"Just 5 lines of very simple math implements the entire filter!\n",
"\n",
"In this example I only plotted 10 data points so the output from the print statements would not overwhelm us. Now let's look at the filter's performance with more data. The variance is plotted as a lightly shaded yellow area between dotted lines. I've increased the size of the process and sensor variance so they are easier to see on the chart - for a real Kalman filter of course you will not be randomly changing these values."
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"\t4.4502 2.6507 2.2871 2.1955 2.1712\n",
"\t2.1647 2.1629 2.1625 2.1623 2.1623\n",
"\t2.1623 2.1623 2.1623 2.1623 2.1623\n",
"\t2.1623 2.1623 2.1623 2.1623 2.1623\n",
"\t2.1623 2.1623 2.1623 2.1623 2.1623\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAo8AAAC+CAYAAABUKeVaAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzs3Xl8TNf7wPHPnZnMTPZFJIJIRJDY\nKvZ9p5Talda+/tCFbzeqamlRaldtFVW0tBSNnaKWalAh9j0JiVgi+zr7/f1xI6g1ShPNeb9e8zJz\n5y7P3CvJM+ee8xxJlmUEQRAEQRAE4Umo8jsAQRAEQRAE4cUhkkdBEARBEAThiYnkURAEQRAEQXhi\nInkUBEEQBEEQnpgmPw+empoqRusIgiAIwn+Mq6urlN8xCM+PaHkUBEEQBEEQnphIHgVBEARBEIQn\nlq+3re928eJFAGrUqJHPkQh/Fx4eDohrUxCJa1NwiWtTcIlr88+8/fbbzJ8/H40GfHyKkJxsJCMj\ng5SUlPwOTfiXFJjkURAEQRCEgstgMDB79mzeeutNPD3NbNu2lOvXE8nIgAYNGuR3eMK/SCSPgiAI\ngiA81pgxY5g9ezaHD+9i3bppvPfe60RGJuDsHEJAQACpqan5HaLwLxHJoyAIgiAID2Sz2VCpVEA2\n77/fiQMHdvLWW10BcHJy4qWXSgAB+Rqj8O8TyaMgCIIgCPdISUlh3LhxXL4czYYNXwO3KF7cgQMH\nvs/v0IQCQCSPgiAIgiDcw2QysmzZUjIyMjl9+gAVK5bJ75CEAkSU6hEEQRAEgSNHjiDLMpCOl1ci\nS5aMJSJixUMTR5tNJiXL+u8GKRQIInkUBEEQhEJu2LBh1KhRg3XrvgEuANl06dKcKlXKPnD947Fm\nuixIYsjyuJyEUyhMRPIoCIIgCIWajSpVSmFvryc+PvaRa8anW3n/l1Q6fJVIbJKVbjVcEblj4SP6\nPAqCIAhCISLLMqtXr0av19OhQyPgKkOGNOfVV1+iZEnvB25jssh8/2cWX/6egdEi83+NHHmrmSPO\neldATGNd2IjkURAEQRAKkU2bNtGjRw+KF/eiefM1ODk5oFarH5o4/n7OwGeb0olOsNI8SMfHbZ0J\nKCrSh8JMXH1BEARBKGDi4+OJi4vDz8+Pzz77jLS0NObMmYOzszMACxYsYPfu3QwdOpSmTZsCEBYW\nxpQpU6hTpw5jx44FwJyZScuWLVGpVPz+yy+AhbbVvGjbohYdOjbB3l730Bgib1n4bFMae86bCCiq\nZml/d5oEaiDsBIRn5azlCCjTC1Ov3nM6G0JBI5JHQRCEQurGjRvEx8cTEBCAk5NTfodT6F25coUP\nPviAAwfCSEu7hrOzjE6n4fp1NdnZRj7/fBjOzp6AzF9/7WL16jW0ahVC06alALh58zibN29GozEC\n3cFsRgpuwd7Y66gBihcHlMEOmwAOnoJOTaF40XviSDPYmLczg6VhWdjbSYxt60yfug5oNRKs3AY9\nxz74A4i5rQsNkTwKgiAUMlevXmXo0KFs3rwZAAcHB4YNG8aUKVPQarX5HF3hYTabuXbtGn5+fgDY\n29tYs+YXZBmqVVNTpowf0dHRWK0WypQJwMnJACQC8H//145WrUKoVSsYUJK2unUD2LhxNsWKFQHS\nQCOjlq3sBlQ6LbgrrZZkGiA9EyxW0NnlxmOzyfxyJJvp2zNIzLTRvYY977Vyoqiz+k7Qwf53nteu\nBO4egAP88cfzOk1CASSSR0EQhEIkKyuLZs2acfHiRXQ6HX5+fly4cIGZM2eSkpLC4sWL8zvEQuHY\nsWM0b94cf/9SHDmyAUjm/Pnd+PmBr68Hq1Ytx8enGNHR0fTr15+UlCiioiKpVKkSALVrV6J27Ur3\n7LNYMU/atWt4Z4EkIX08gCbDpkJZXzj+E6hU0PkD+HU3DOsCRdwACL9sYuLGNE7GWajuZ8f3/dyp\nXNKO+4QEQftGsGEfNAyB6Z/DmVSoVOn+dYX/LFGqRxAEoRBZuXIlFy9eJDg4mCtXrnD+/Hn279+P\nnZ0d33//PTExMfkd4gNZLBbOnj3LiRMn7lkeGhrKvHnzuHnz5j3L3njjDVatWpW77OTJk/j7+9Oy\nZct7tv/000+ZNm0aiYmJeQ0I5s2DceMe/Ni+PXdVq9XK3r17+fXXX3OWZBEU5ITZbMRgSCM9PRow\nc/z4MTw8oHv3Dvj4FAOgdOnStGjRAuC+z/5E+rcHX284FQlrf4dj55XEUa+DD/twPdXKiJ9T6Log\niVvpNub2cGXNUI8HJ47AsWPnaZeUxk2Ar9ZAvB18+imiXk/hIloeBUEQCpE///wTgOHDh+PtrYyu\nrV+/Pi1btmTLli0cPHiQUqVK/aNjxMXFsXHjRry9venUqVPu8hEjRpCens7ChQvRaJQ/P2PHjmX7\n9u18/vnnuUnSihUrGDRoEK+//jpLliwGZFJS4qlQoQJFihQhISEasAE2pk2bzMGD4VSv7o+3dw3A\nyrlzB/jpp58oVcqZ7t1DABvqPT9x5coV7FOTCJgxGgDZ3ZOZS9aRZjLTr9vLUMQZ0DJz5kwiIiJ4\n8803qVu37sNOJIwY8fCTUKQIJCQAcOjQIZo0aUKpUiXo2DEQSTKh18O5c2sofld/Q0dHpd/p9evX\n79nVjRvXc953fKLzfw+dFsb0h2FTYeJCCPQFwDCsG4vP6PlqdwJWWeatpo4Ma+KIo+7RbUrjxi1k\n8/5jTC5dmnnR0TB4MGzcCKK7Q6EikkdBEIRC5PZo3djYO8WgZVnOfX37/Se1atUqli1bRv/+/enW\nrROQzYULhxk2bBiNG9ejU6e63E70liz5joyMTObO/R/Ozg6Ajaio44SHh3Pz5lGgGGBDfXYPBoOB\nzNU/w57fAHCyyZS30+CRkQ4LpsDQrgB07lyP6tVLU7SoBVCSrFdfrU6pUpOoVKkMkA5A4KxlRAHO\nKel4rNoFgAWYAVwCvE79DgFWQMW2bWvZufMAPXq8DFQA9KxevZ7JkyczYMAARowYATVrYvPywhYf\nj+aVV6B2bQBiFi1i7tWr2JUowVSygWTq1HGmUaNq1K1bmezsNBwc9AD3JI4ALVq04Kuv5rNt2zZK\nlChJ7dq12L17NwcPHkKn09K4ceM8XZtc/dvDlO/hdBTy6Si2V2zIZM8exP6WQeuKSukdX48HpwNm\ns4XMzGzc3FyAosyY8Q1lyixkfMeO0KQJbNigrDho0NPFJryQRPIoCIJQiHTv3p0vv/ySuXPn4u3t\nTa1atViyZAknT57E09OTZs2aPXTbSZMmsX37dr799lsqVAgEsoiOPs7WrVsJDHSnW7cAAHx9YfDg\nTgQH+wNxudvPnv0/JAm02gzABMD48f0YMaIrgYElASMAXdwdyQT0mdkQrWyvB87d3lHYidzk8YMP\n+twXZ8WKZe6bj1n7xsuUnvI9FC/K9QFtAPCJvsXgFVuhqDs0r5Wzpo2pU4dz7FhzatUqhpJawrFj\n2zhx4gRJSVHADXDQc3FAHypPnUGz/fvZtmkTREZimDiRWYBrdCQTjcfQ6bSoVLB378LHXRp8fUvy\nfu8BfL94Cb9+/R2rlm9HVmlxcgjktZ69iEx1QE4xYbWBTZaRZbDJYM35V5blnPeUu8i317PJIL/z\nIZZlm1lXsTlh/i9Rzl7DitecqR/48FI9R4+eo3fvcVStWpEVK1YDesqVg9mzZysrtG+vJI9aLYwe\n/djPJ/x3iORREAShEKlfvz5vvfUW8+fP57333stdrtFoWLRoETqdDovFwsCBAzl79iwHDoShVpuB\nLCIiwti/fz9HjqyjQgUlAevcuQaBgVPvGbwRGOjLwoUf33fsQYM63resfHn/+5bZDeyI3WffQWoG\nLJsADapCfDI0HKSMEB7xet4/+Ls9Yd4quHYLQwV/squUwWfgdOW9D/uAo33uqtWrB1O9evA9m3/0\nUT86dmxM0aLu3E6II2t6YwZUaWmw+TtYs4lyNhuf1wim0dz3sbPL259YecxXlF12gHrBg9lSvgE3\nnYvkvjf9MvBNUt4/d67y0LY8LtnpVEvbyCc9ahMSWOWRW3h4eBIZGYfJpCItzYSLi/7eFSZNUm7f\nv/mm8o0hNfUfxCe8SKT8nNA8NTU19+C//fYbx48fZ9KkSfkWj/Bg4eHhANSoUSOfIxH+Tlybgqsg\nXxtZlgkNDWXJkiVcuXKF1NRUgoKC2L59K5AFZOPnF0JMTBxnzqzJaUGEsLDjZGRkU7NmBdzdXe7Z\np9VqZf/+/YSFhQESDRs2oF69eqhUTzkuc8K3MHGR0iK482v4YC7M+AFebQgbZj/dPj/+CqZ8T0aD\nKiT2aoXf0BlKq2P0hnuSx7zImPo9KR99RcmypSAqTpmp7/xaCCj5RNvLssyJqxY2nchmyx8JxOGA\n1mKiybWTtIyNwNWYgTopFZUsIw3virp9Q1QSSBKoJAm1itzXakm68zxn+a1b8Xw0ehTpaWk4WGzo\nDMmkqYzY2Wn45psFhIRUvfNZMrIIDd1Dr17tAB/Amz/+2E+tWrXQ6R7eQnlb6l3Jo6urq5iz8D+s\nwCSPPj4+ZGdnExMTg6+vb77FJNyvIP8RLOzEtSm4XoxrIxMffwZv70o4OTmQmronN9nbuvVP3N1d\nCAkpj073iMEQ6ZnY6vTDcv4yNtu9f09UKhWaKmVRhS1RRvfmRUo6+L+qtD6umQa9x0G2EcJ/gL+1\nCj6xxBTwbw8ZWZiKeaC9kQTTR8D7vZ9ufwBZBgjoADdzRmsP7ACLP3nkJrIsc+a6hU0nDGw+YSAm\nyYqdGhr6qWj37VxantqH896voU5l2LgP2r8LxYpA1Hqw1z9y33/32WeTCA0NpVatmkycOBG9Xs+s\nWbPYuHETISFVc0szWSwWKlZ8jQsXYti1azvNmrXK86kQyWPhUWBuW7du3QKLxYDJZMrvUARBEP6z\nkpKSWL58OSNGDEGSLuPlZWD16qlUrBiAJN35e9+mTf0n26HVhu3CFbTWBzREWG2YzkShfZpGCjdn\nGPm60vr4+sdgtiitjn9LHGVZxmSFbJNM1l2PTKONbLNMplEm2ySTaZK5lWwitv0gPG9mo7bZKF4i\nDlsJf7pl23C1f8oWUgc9jOoD784GjVoZ2fwQ52+YcxPGqAQrahXUD9TyVjNHXq6gx9VBBZeLw9Fs\n5XNvmQsTcvpKju6X58QRICxMGV3/7rvv4uXlBcAHH3zA1q3biIg4RnZ2Nvb29mg0rvTt25/Q0C24\nuXnm+ThC4VJgksePP/4QrfYWZcqUefzKgiAIQp5ZrVYaNmzImTNncHNLpV+/dgB069bi6Xfq5sxG\nHzs6xRpJaVIVty3zAUhqNAj98WhWl/GgldEOY6YFg1m+87CA8e7XZhmDRcZgJvd1jFsDnF51waKy\nI8tOT1x5P3TzEu4kiCYlMbTY8hBvieY4F83GrNZgsNPDcZh0PB4vZxXlvDUEemko662hrJeGct4a\n3ByeIKkc2gUOn4FaFe+7XR15y8Km4wY2nTBwMd6CSoI6AVoGNXSkdSU9Ho5/2/+7PeHLVbAtDMZ+\nDUfPKa2OQzrxNG63JFss1txlVqsVk8lKbCxs23aYTp36AEX44IOPGT163NN3NRAKjQKTPAKoVFko\nJR3Ef1xBEIRnTa22MWpUXxYsWEHDhlUfv8FjyLLM1SQzM8q+RFSpAM67l+HMjCTisyVMzWdAc2W9\nCVNv5Wm/WjWoZAvGbAlX32CKGo1YbEZi469RzJZJSKXyOGhV2GslHHUSDtr7H/ZaCUetSnmtkwhd\n8xPfLZhPubKlGVuuNl6nY/mhYRWWbjmA3iuYBu36EHnLxurwbLJMd1pKPZ1UuYlk4F1J5T1Jn70e\nVk7OfXklUbklvemEgbPXLUgS1PS347MOLrSupLt3ur+/83SDt7vD598r5XXgqVsdARo2bMgvv6zh\niy+mMXbsWBwcHJgzZw63bskkJsK4cUvo2HEkkgR2dg8uDC4If/eP+zxKkuQLLOd2gS5YKMvyXEmS\nPIBVgD9wGXhNluXku7e9u8/jpUsn0WojSU31QqstQq1atRAKhhej71bhJK5NwVVQrs3JkyeJj4+n\nefNqQAyybMZms6FWPyKBeQCLVSYqwcLpaxbOXDMr/143k5Kl/BqXZBulk+KooMuiRFYS+gvRnNIb\nuVzWg0H9e6O3k9BrJPR2Ejo77nl95wE6jUR6WiqvvPIKRqOJN4cMoaPBnnBvPRO/nIvBYOC77xZT\ntWrekt8hQ4Zw5MhRZsyYnlscPTg4mHbtXuXGjRv89NNKypUrh80mcy3VxsV4C5duWrhw06I8j7eQ\nYbzz97KIo4pALzVlvZVksrSnhjPXlIEvJ+MsAFQrZUe7KnpeqaynmGsezndCCpRW+mbe7uu4cedf\nWCxW2rdvlHvt/vgjgujoOBo1qoa/f3EALly4wq5dhylb1pcWLWoTHx9Pz569OXs2EUkCLy9lUHRi\noj0tW7Zj8uTJlC1bNk/n8mFEn8fC41m0PFqA92RZPipJkjNwRJKkHUA/YJcsy1MlSRoNjAZGPWpH\noaF/MG7cd7z66qtsuF14VBAEQXgqERER1K1bF2dnR06eXEmxYp5IkvTYxDHLZOPsdQtnchLEM9cs\nnLthxqjkROg0EFTMjjaV9FQobkfCxTC2zpzAxhMGdDn5VaYK2leCUR9OoVUthzzFfeDAQYxGEzVr\n1mDA/w0BoBVw5kYcP/zwI7t378lz8nj7Vuzd/eptNhsWi/me91UqiZLuakq6q2la/s4gH1mWuZ6T\nVF68mfOIt7D+mIF0w52k8qWSdnz8ijOvVNFTwi1vCTrA6dORjBu3gKJBfiwIPwsTRoC9N927jyE7\n20BGxkkcHR0AifnzQ1m9ejM///wl/v6VAYlDh/YxfPhUevbsSIsWr+Ll5cWXX64mOLg5ykd0oXbt\nlowbN44qVR5dqkcQHuYfJ4+yLF8np6y/LMvpkiSdBUoAHYAmOastA/bwmOSxUaOX8PX1wtOzSO63\ndqHgENek4BLXpuDK32uTQUhIWXx9ixIbG0NSUvx9a6RkS0QmaYhKVhOZpCYqSUNcmgoZpeHIWWuj\njIeVtuUsBHhYKeNhpaSLMtjjNrmaD1nd2hB6I5TuN5VEak0xFa17vUbJkiU5c+ZMnqKOibkCKMnd\n3dtmZWUBEB9/M8/7LF++PIcPhzNnzhyGDBmCp2dRxowZQ0JCIt7eXhgMhifaZ1GgaBGoVwSooBTj\nTsqWiE1V4+1kw8dZ6YCZek15PI7BYCI5OR0fnyKARFRUCuvW7cbZ2Zkhv/yCzd8fwlNo0KAhZrOZ\niIgU9HoDAH5+FWjTxkZWliPh4cpUiDabB507dyYgoCLh4cp830ajjl69eqHVahk2bBigJNHP+v/m\ns2rBFAq+Z1qqR5Ikf2AfUAmIkWXZ7a73kmVZdr97/b/ftra3j0aWZYzGUthsTs8sLkEQhMJi7969\nVK9eDXd3A3Z2iZhMZrTa+9sJssyw8LAjv12607rm7WQlwN1KGY87iaKngw3pCW9AZl+KoUq3Cchq\nFadCJ6EvWeypPkNCQgLvvvsuKpWKd955h5CQEGJiYpkxYzopKamMHDmS6tWr5WmfRqORSZMmcfny\nlXuWq9UqRowYQUhIyFPF+k8cPHiat9+eS7VqwXz55RdYLE6Ahk2bNlGzZs3c2+sviruTR3Hb+r/t\nmSWPkiQ5AXuBybIsr5MkKeVpkscKFSoAnoDfM4lL+OcKSt8t4X7i2hRc+XFtPv/8c8aMGUOvXq/y\nww/jH7rekSsm/rcqlavJVgbUd6B5sI4KPnZKqZh/6my0UqG63D/7HT5t2jRWr/4FAEdHBzIzlVbH\nqlWrsnDht/fcer969SapqRmUKVMSfU49ySNHznL06Dlq1AgmJCQIgKNHzzB8+KckJFyjeHEICQmh\nX7/+eHh44+PjiVb7/AaMmM0Wdu48hCRJtG5dD3Di1i0bPj6VqVmzJn/88QcaTYEaw5pnos9j4fFM\nhjVLkmQHrAVWyLK8LmfxTUmSfHLe9wHuv1/yENnZN1m/fj1Go/FZhCcIglAodOnSDE9PN+rWrcCD\nGgbMVplZO9LptiAJmwyr/s+Dse1cqFtG92wSR4Dg0lDOj6wsA5GRV4mNvZH7ls1m49dfd/Pzz9vv\n2WTFiq2MGfMV589fzl1WsWI9rFZ/MjOVxNHeXk+rVm3ZvDmGqlXfyFlLBWho3fodKlXqzsWLCYAz\n4MratWEMGTKZrVtPoMyWUgKTqQiHDl3C3r4Uc+duYO7cVYSENKFmzb44Ojbgxo2E3OMfP36BU6cu\nYTKZH/lxT548xciRI2ncuDEvv9ya6dNnkJycct96Gzfu45VXRvDJJ0uAKkB5ihYNJjY2lgMHDrzw\niaNQuPzj/62SUlX2O+CsLMuz7nprA9AXmJrz7/on3WfTpgM5dOgUW7ZsoU2bNv80REEQhP8ks9nM\nb7/9Rtu2LwNXKFdOw+XLG3F8wFR70QkW/rcqlWOxZjpX0zOhvQsu+meTMG7cuI9Nm/6gd++2NGhQ\nFVCzY0c4HTuOpF27xmzcuABy+lB27vwBAN27v44kqQEVP/+8l02bdlKnThPKly8FqLh2bR/Hj19m\n4MDeTJ36Ka6u7iQlpTJ1qh82mxqolrvPwMBKyLIOKA2UA6BWrVYMGGCkcuUGQPGc9WqxePFiMjIy\nsFpdgRJkZGTg7OyGyWTF27shYAAMfPTRe2zdupe1a6fTuXNTAE6evMSpU5eoXbsSAQElOXz4MG+9\n9TYWizKSKCMjk59//pkdO/ZRqlQNypYtxahRbwLutGkzhFq11tCuXTtsNjW3Syn6+Pg8k2sgCP+m\nZ/FVpz7QGzgpSdKxnGVjUJLG1ZIkDQRigG5PusPWretitYpaj4IgCA9jtVpp3LgxBw4cYNu2r3n5\nZaW82d8TR1mWWXU4m083pWOnhvlvuNKuytPN4wzw1Ver2b//GHPmvIe3tydgz549Z1i48FdKlqxI\ngwb9ARXu7mkEBATg7R0IKLeNVSro0qULGo0Gi6Vkbl3Bnj0H5iSOtVGGpECrVp1Yv74MpUuXxtPT\nHwBPTyfi4uJwdHTkduIIEBoael+cHTt2pGPHjvcs8/T0ZODAgfcMFHFyciIyMhKj0Ygk6QBlZHip\nUkEEBsZRqdKrQCnAwJo1K/j009l89NEgJk8eysyZM8nKsuDuXpaBA7tTs2Y5JkyYwKFDUezYsQF/\nfz8+/HAekiRhbw+HDh166vMuCAXJsxhtvZ+7f4rv1fxp9jlu3GAmTHgHZdyNIAiC8HdqtUS7dg2I\ni4vG0fHBc08nZtgYvS6VHWeM1A/UMqObKz5PWG8wK8vAlClLiIm5wfLlnwJqwIHVq/eyb98h+vYd\nTuvWIYBEly798fWtSPPmzbndG6pRo0ZERkbet981a9bct6xHjx73LfP398ff3/9vn1lN8eLFnyj+\nvNLp7p17e8GCBX9bw57g4Fp06tSJunXbExvrSWjoJVxc7Dl16iI63W769h3OgAHO/PJLJ4oXL866\ndb8+l1gFIb8VyE4WSr0tI5ANPP03ZEEQhP+S+Ph44uPjqVQpAIhm1KiuvPlmW1xd769Osfu8kQ9+\nSSUt28bYts4MqO+ASvXg7/mRkVeZO/cnXFwcmTRpOKBFr3dhzpyfyczMYtasRXh6Kknb22+/T58+\nqVSpUpPb7Qb16tWjXr16z+lTFxw9evTITXSjo6MxGsFk0vLxx+8SEBAA+KDRKNfC29s7X0ZwC8K/\noUAmj7clJEQSHZ1NzZo18zsUQRCEf+zChQukpqby0ksvodUqrYV79uzhyJEjNG/ePLfw9eHDh5k8\neTJVq1ZlwoQJAFgsFooXL07p0qWIiFiOk5M9arX6vsQx2yTz+dZ0lh/Iory3hh8GuhPsc9co4vOX\nYdN+pUAhABoMN1L58stV+Hm4M+nD6eDigUoF06fPwNPTE3t719zNu3bt+rxOzwvF39+f8uXLc/78\neQwGA927dyc6OpoxY8YAiP76wn9agU0eT5y4SEhIT/z8/IiMjER60kJjgiAIz5HBYECj0eSOjg0P\nD2fXrl3UqFEj57YtnDhxgjZt2uDj48OJE8dRZm610rx5M65ejePKldOUKlUCsPLLL8v5+uvv+fLL\nSVSt6gnYSE4+y/r168nKiIdvJUhNQ4MNjQR+mMmcthQnZwdoURuqBeXGdirOzMhVKVyKtzKwgQMf\nvOyM3u7e353y29NZueMQB4D5OcvKo3RSr5qUjPzdMqT//Q8gt6C0cD9Jkvjiiy/o2LEjM2fOZNas\nWbkj3H19fRkxYkQ+RygIz0+BTR4rVgygePGilCsXSGpqKm5ubo/fSBAE4SnYbDYSExMpWlQZrGEw\nGJgyZQqZmZnMnDkzd72WLVuyc+dO/vjjdxo0qA2Y2bt3C6NHj2fkyIE0b14GMOPkdIOEhAQcHNTA\n0dztK1f2w9vbBZstEqVbDjRrFoRO9wZVqngByowgVav6sG7ddEqciYKhE3K3vw64X7oKk77L2eFW\nOPEzVpvMwn2ZzNqRgYejih8HutOg7L19+HL3Uacyg3ccIht47bXXaOTri+b6dUatXAmSBC1bPpNz\nWhi0b9+ebdu2MXHiRMLCwtDpdHTr1o0pU6bg5eWV3+EJwnPzTGeYyauHFwlXmM0W7Oz8gReryv5/\njShEXXCJa/PPbdq0ib59+9KoUQN+/fVHwILFYkCrLQGA2XwOtVoGzHTq9A6bN//BunXTadeuIQB/\n/nmMX3/dQ5Mm1Wl3/gocOIHFZuNCQhIedhqKued88S1WBGaMBP2Dk7oHup4AAR3AYISOTaCsr7L8\nuw2QlAof9uHq6Dd5d3UKf0WbaVNJx5ROrrg7PqJaRaYTS3xqIqenM2DTJqS2beHtt2H+fHjtNVi1\nKs/n8EXzPH5uzGYzarU6d47swkgUCS88CmzLI4CdnQZIQSSPgiA8C7///juLFi2ibdu29OrVDUjH\nz09NUlISVmsycAEAjQY+//xNXFycsFqTUKuVPoM//TQJnU57Tzea+vWrUr9+VaUPYfePIMuABqhw\n/+Ghf3uoHvzkAft4wv91hrk/KbO2fDECws/A9B/AQU9o2zf4ZE4CNhlmdHOlSzX9fV18jEYTY8d+\nQ6tW9WnZ8nVwdGHA+PHw/vsz/7v5AAAgAElEQVQwcSK89BIsXKi0On7ySZ7Op3DH7bJDglAYvABf\nkTK4dOkst27dyu9ABEF4gcTFxfHDDz/cVS7GTFTUSX7++WdCQ5cBp5Dly1y8+Cft2weQlhZBz569\nCA0NRZZlRo3qx7BhXe+Zsk6v1z28/7UkwYD2yvOKAcTOeovYWW9B15yKZVXL3dM/8YmN6qu0Vq79\nHU5chImLSNU58s5bMxm5xUK5Yhq2jihC1+r2D4zt++83MGPGDwwaNAWTSa8sHDoUvLzg8GHo0AFM\nJujWDSqJ8miCIDxegU8eR42aR9myFVi2bFl+hyIIQgEWHx+P2XxnKrnx4z+hT58+rFv3HXAaOEHr\n1mWZP/9DJk8eCsCsWbOYPHkyV69GkZ6ewblz5/jss0nMmjXrwQd5nNH9QGsHZ6IxBRQno0lVCDuR\nE9AQJcHMq9utj4C19yccOJ5Cm4Hz2aL24/1WTqwa4kGpIg+7iaRi8OCR9O7dm1WrVuWO8MbRET78\nUHl+9KhodRQEIU8K9G1rgBo1KuDi4kR2dnZ+hyIIQgHVtWtX1q5dy969m2jUqAqQziuvBHPzZkMC\nAz1QppyDkiW9efPN1wCIjr7MypU/odFo+PjjMTRo0ID9+/czefIUVq78ia5du+Ln55e3QEp4Yejz\nCvrF67n6fxM47qIi+JoBQ7Af+g6NH7iJzSaTbZbJNMlkGWUyjDJZJuV1ptFGllEmonRtvOvZiHMt\nxprWzfHOTmDJG2oaVbq/vuO1a7cYP/5b5sz5BEfHCqjVOpYvX37/gYcOhS++gPh40eooCEKeFPjk\nsUOHxnTo0AStVgwIEITCKDs7G3v7O5MFDB48mPDwcPbt24OzswSkU6KEPfb2OqKiDtOoUTEAOndu\nRufOzR6637+27aBNElSvUpH2SRJs+JP2SFiLVeDIiRMc3PIbfsMGPzY+WZZJM8gkZti4fCONWakW\nuoa0IdnBjXh7Zz4M1HOgiCNeX8ai1jrmJIV3ksUss8zjxy0GQsNAtBYzrx3fzl83FzPnqjfVf/gh\nZ6q+O3r2HMuePUdwdvZn1qzZD9+lo6MySGbOHJgy5bGfUxAE4bYCnzze6W+UCnjkZyiCIDwnZrOZ\nqKgoZFkmKEjpFxgXF0e1atXQ6/VcuXIWpfXQwIkThzl27Dj79y+nTRtlVpPx4/vzxRfD0ekePE3f\ng1Ree4Dul4HLx2HD8dzlnYBX1BoObTzNqfZmEjJsJGbYlH8zrbmvEzNtJKQr/5qtd+04YBinApSn\nzoYM7K1GEuUsUq7EU6l8AD6uKhy0Eo46CUethINOwlGrUl7rJOW9nPc1mBk2uB+ZqQl81Lc3Xdf8\nRUrLmvzfkeJERUWzfv163njjjbsOrmPevK/45JPP+eCDDx9/Erp1Ux6CIAh5UOCTx9tstiQuXIjP\n/cMiCMKL6eTJkxw8eJA6depQuXJlAH75ZTU9e/aiS5f2rFmzEDDi7Z1BcnISdnYajMbjuYnh7Nnv\nYGenoWLFMrn79PBwfdChHsm1dQOy954nvGQwuxq/zFmPAK7bdCSjJ12fczv4y8R7ttFpwNNJhaeT\nGi9nNcHF7CjipMpZpuLr2ZO5eeU8c0YOp97rY9EZjRh+mkSzeZ9iNJr45pOdeapZe+zYGbITogkM\nKM1rwwbAsAF4AAO2Fmfs2E84dOgQpUtX4tChU4wc+Q7gS+XKKkJDQ/N8PgRBEJ7UC5E8Go0mypdv\nRFzcLW7duiUKhgvCC+LgwYOsXbuWjz/+OOfn1sJ33y1g7tyvmTr1IypXdgAMlC8Pfn4+eHpqgKuA\nUi7nypVNeHt7KLXzTkfCzSTqARhMcPDknQOV94MSjy/KbLTIHIsxExZp5IBTB46ObIVFrUGyWdCk\nR+KbEkmXWynopGz8Ph2Ip4smNzks4qTCUSs9crarZemn0WTE4hlYlPipQ9DGxuPeqSnqryYDSjHy\nvLg9i43RaMRms+XWEDQYlD6c2dkWGjcegsVipW7d16hdO499NAVBEJ7CC5E86nRaSpcujtUqcenS\nJVEQWRAKKFmWc5Or+Ph42rV7hcTEZFaunEGdOmUYPLg/jRuXJjm5LZUqeaPUcYXq1YO4fHnjffvz\n8fFUnpyJgkrdH35gTzeI33HfaGaLVeZknJkDUSYORJo4fNmEwQwqCSqV0DDAK4H633yNb8I5egdk\nsfK8imIGG5YfP0NT9/7BKI9Tp04dYmJimT9/Pn379sG+cRV+nD+frKxsypUri7u7e572FxQUhJdX\nUeLirjFr1ix69uzJ5ctXWLhwIQCtWnWkWLHmmExWQkJC8hyvIAjC0yjQM8zcLTExBQ+PACSp9L8W\nn6AQs5gUXAXl2siyzNtvv01oaCgnTx5Cq82iR4+XOX48GqMRvL1V2NkprW5jxnxEly5d8naApFRk\nv1eRMrKI0Uvc1Ci/OgJNEu4mGepUhgPfY7PJnLthISxSSRYPRZvIMCrrBhXTULeMlroBWmqX1uLq\noAKrVUlKz13G2igE9b4IqBAAJ34CtTrP5+H69Rv07t2L5GQlKVarVVitNlQqiTlz5lC/fv0873PX\nrl2MHj0am00ZWJOYCPb2ULZsLdau/eNO+R3hiRWUn5v/GjHDTOFR4Os83lakiBuSlAbkX7IrCILC\naDSyd+/e3NeSlMW5c8eJi4tj+/ZlbNiwkGvXoqlZ059Dh9Zw5MifjBw5EoCvv/4ao9GYtwN6uHKm\nmdI/MkYrM69jMNMbFUe2yVzyKMmcTv0Y9mMy1SfF88q8RCZtTic6wUL7qnrmv+FK+NiibBvpyfhX\nXWhVUa8kjqAkiOMGKU/3RSjLxg16qsQRwMenGN999x1NmzbJTRwrV67EvHlfPjJxvHbtFkePniMh\nISV32YULV5g79yeysuz49ttvadCgAVlZ9sTEQHKyJz/8sF0kjoIg5IsX4rb1HRaMxkTS0mSKFi2a\n38EIQqFktVopU6YMcXFxREXtp3RpF8DElCmD0OmGU6VK2dxEcdCggfj7+wPQq1dPQkNDuXz5MufO\nneOll17K0zEnpF9kqksRVG4laPXKGMLPptHaX0e8cxFIghI2M82D9dQro6VuGS0+rk+YAL7WEj5d\nDOcuK62Ot2eEyYNr125x8WIMJUt6U6aMHzNmzGDduq0sWLAeL69g6tatk7tu+fKdiYu7xdWrW3Bz\ncwXUjBr1FT/+uIlly6bSp08XQMXx4wcZOXImXbq8wpo131GtWgeyskw0a9aVd955R/T9FgQh37xQ\nyeOvv+6mb9+JdO7chaVLl+Z3OILwn2exWFizZg179uzhm2++RpIyUauTqV+/IufPO3Lz5kVKl1Za\nBGvVulNk+vbAjr+3MJrNppz3H57YZRhtRN2yEp1gIfKWhahbVi7eMHC+2rc0r5VT7/E4eGZZqBd7\njMtZJzC53WTrL4sfOZjlodRqmPc+/N/nMOfd3FZHg8HIrl2Hycoy0K1bi9zVBw+exOHDZ/j55ykE\nBfkDGr7++lcmT17IxIkjGTfuf4AdRqMHO3aEk5hoBsqj3OhRk5FhITMzm4yMQNzcSgIQEFCNqlWv\n4uRUFggEICioEW+//XZOX0aldqWDAxw4cODpPqcgCMIz8kIlj0FB/qSnZxATE5PfoQhCvsrMzGTm\nzJls3ryZKlWqYLFYqF27NqNHjyYmJobPPvuMwEAlCdm/fz9hYWE0aNCAevWUuohpaWkcOnQIT09P\nQipUgB07ICuL5IwMNGo1zjlFuVWyjXdHjuD6zXgGD25M9erlAFi+fMIjayo2btyYffv+YOHChRQv\nXhw/Pz9WrFhBXNw1vLyKUrZceaITLETdshCdYM1JEpXn8el3RiSrJCjprqaUu5qY6ztwSotl1sUE\nAq9FUSw9kdQgX5rbx1KxeIV/lFD9kpLBxxo1LUP38lXLuoAd2dlm2rUbiYuLM9269UL5dWnHxYsJ\nHD9+gbg4J4KCqgESQUENadDgDD4+FYBSAPj4VGDy5Mk55/zO4JuIiAjs7e1xcrqzbOLEiUycOPGe\nmCpXrsy8efPui1UkjoIg5LcXKnkMDi7N5csb8fN7+KwRgvBfdXsks9VqpU+f3qxb9yuSBCkpf7Fv\n32Jat27Dnj3RnDhxjlGjegM6QMVvv63ls8/mMHHih9SrVw5QceHCcVq1akX16iGE9+sFb78HQAWU\nUtw3AS1KW9moCgHYRvXE19czN5bHFeNua++F3ujJrSPxHHh9Iit9qpDgWpKi5ceSUbwclSYmYrmr\nao2bg0SAp4ZG5XQEFFUT4KkhoKiaUh4a9HZKsjTqUhQ7d+4kQXKjYbrSN/BzbSJI0LZt2yc+j7t3\nh7Ny5Ta6dm3Oyy83BJxxdw/k4sUYypatCFRTYnKTadu2LZ6enthsPrmtqXPmfInNZqN8+fKAEluv\nXr3o1avXPcdxcnKiVatW9w3K8PJ6fEkhQRCEguyFSh5BqQUHyYBDfociCP+K2NhYPvroIzIyMggN\nXc73308nMvJXihVTU7lyIJUrl+Cvvw6wf/9WWrR4lVGjeuHv7wDEA1C/fhnef7839er5AVcA0Ovj\nad68FuXKlYLqd8rH6PU60s0WIhpXo/afx8FoYkS35vC/nnmK+cr4n7jk0owtNetzxlsp5q21mPFL\nuUaFyHO0a1iG0o3KUqaohgBPDe6Ojx+7995773L+/DnmR1+ljhYi9bBTnUXDhg3o3PnBo7cTE1PY\nu/coDRpUxcvLA1ATFnaBxYtDsbMryssvvwVAgwbFiYiIICAgIHdbSZLYtGnTffusWrVqns6FIAjC\nf80LU6rnXnpSUkrg6uoqbuH8C0RZi3+XxWLh2rVrlCql3P5MSbmKt3cZLBYLN2/+xpAhA7hyJYYv\nvpiGj48PAMnJybzzzgi8vb3YsmVL3g/68lvw20H4eABMGg5/RECjweDqBJc3gpvzIzeXZaVEztaT\nBraeMnIx3gJAtZsXaFMammlv4X/6OOoft4CzI0SvhyJ5H/CRmZnJhg0bCQ8PR6fT0rRpM5o1a4o6\np59ienomTk4Oub8X2rd/l40b97F06Vz69h0EOHD69Gk2b95MmzZtcme4eR7Ez03BJa7N8yFK9RQe\nL1zLI0C/fqNZsWIbYWFh1KxZM7/DEYRn5vTp0zRr1gwvL09OntwOJOPmZuKHHyZSvXownp5u3Lhx\nA4BatWoTG6v0/61duzYAN2/GY7Vac5OpJzZ+sJI8zlsF/3sDJi5Slo98/aGJoyzLnIyzsOWkgW2n\nDFxOtKKSoKa/HRNaaGnddyDFrsXC3oXQqBG03qNs+E73p0ocARwdHXn99R68/nqP+97r0OFdNm/+\nk1OnNhIUVBVwpnXr10hPV+Hm5sftuxUVK1akYsWKT3V8QRDy7siRIyonJ6cPtVptsCRJL0yJwMJK\nlmWbyWQ6m5GR8UX16tUfOC3WC5k8Ojs7IMsyERERInkUXliyLHPkyBHi4uLo0KEDkE3Zsg6YzQaM\nxgySki7kztn82mstc7fz9S3FpUuX2LNnN2XKKLeEd+/eA0DJkiXynjgC1HsJWtVREsg3xsKuv5RW\nx5Fv3LOazSYTEWvOTRjjUmyoVVCvjJYhjRxpVVGHp1PO8Qe3VpLQiYtg0jDYfkBpdfzfGw8IIG/G\nj/+W8PAzbNgwG7XaBXDG3l7pk3nqVCZBQUqL7PDhbzJ8+Jv/+HiCIDw9JyenD319fV9zcHDI2/yc\nQr7JysqqHBsbCzD1Qe+/kMnjRx/1Z8KEkRQpUje/QykUbDab6B7wHBw9epSaNWvi4+NNu3YBqNUm\ntFo4fnwlJUt6P/Sc9+jRnUmTJvPZZ59Ro0YNVCoVhw+H57x3f4vcE7vd+vjbQeV1TqujxSrz12UT\n204Z2X7awM00G1o1NCyrY2QLHS0r6HFzeEBjwsg3YM5P8Pth6KO0lj6u1dFstpCVZcDVVRmJHB0d\nR9++E7C317F9+9eAHtDz44+/ERV1hWPHoHr18gBMnz6HRYuW4uz86FvsgiD8u7RabbBIHF8sDg4O\nNq1WG/yw91/I5LF48dsFwk0oY0KF5+HQoUOMHz+enTt3otFo6NixI5MmTcotASM8uatXrzJr1iwc\nHByYNGkckEy1avbUq1eF6tWDycpKxtnZEQBf32KP3FfHqrWw1m3B9p27uXHSQraDF0WdGlI5KBCv\nYg05EGnEXithb6c89HYS+pzXdupHfAm4q/XR7O5KWPvX2LYuld9OG0nMtKG3gybldLSprKdZkA5n\n/WPuPrk5KwnoxEVwKfaeVsdbt5I5cyaKcuX8cuevXrZsE4MGfcaAAZ349tvPAR2urs788UcEjo6O\nyHLV3IR6/PhPcXJyoly5oNzD+fr6PjoeQRDyhbhV/WJ61HV7JsmjJElLgHZAvCzLlXKWeQCrAH/g\nMvCaLMvJz+J4d6SQleWEg4MYef2shYWF0axZs9wiz1arlVWrVvH777/z119/5c4aItwvNjaWTZs2\n4eXllTOHswVIY/bs2Tg6OjBmTBscHPRIEvz555I87duaks6hVp9ypEwdDr88gBR7l9z3TgE/bQel\nGsGDaVRgbyehs5P+lmCC3k7C/tVRUOQEB/yrkLraiKNWolmwjjaV9DQpr8VBm7e/AbZ3evDHjB/Z\nl5nN+8O6YJ/T6vjuu3P48cfNLF48lYED+wJ6ihWrhtVqIzVVze1C2R4eytzOf//C0qdPnzzFIQiC\nIDw7z6rlcSkwH1h+17LRwC5ZlqdKkjQ65/WoZ3Q8Ll6MoUePvqhU9hw+fPhZ7VbI8dFHH2E0GunT\npw+9e/fGYDAwa9Ysdu/ezdSpU1mwYEF+h1ggpKenc+jQIXx9fXPq/kF4eBjDhw+nWbN6dOkSBBgo\nWRKmTx9B1arl0Grz9mMnyzJHY8xsPG5g8wkDt7pMxMGUTcu447RMO0OF9KuoUwxk30wl28cbw+rp\nGNCQbZbJNslkm2UMOY9HLUvJkrlq0JJd8SXqllDRpZYbDcvqcuss5iXe3Fvubs68obXjWmY2Hdv3\noDJBgI5q1Zpz8WICTk7+3J49pWnTl8nMzMQ+p0D5bc2aibqugiD8M2q1unrZsmWzb79ev379pZs3\nb2qWLFlSZOnSpbHz5s0rEh4e7rh8+fKYH374wa1ChQqG6tWrG/Iz5oLsmSSPsizvkyTJ/2+LOwBN\ncp4vA/bwBMnjmTNnnuiYBoOJs2cvIkkafv/9d1xcXB6/kfBEsrOz2bdvH2q1mgEDBuDoqNxOHThw\nILt37yY0NJRBgwblc5QKi8XCjh07OH36NO+9915u0vLXX39x9epVqlWrlttKervv5kP7b8oyjmfO\noE5Le+DbmYGBXLVYcHV1zW3t/uqr+Sxduox+/brx7ruvo1Jl4+mZTLt29ahTpwJnzhzFZrOxb98+\nDh/ey2+/JfPjj8V5+eWXHzm3syxDVJKavZe17LusJT5TjZ1KpmZJMyPMEXSZ+QWqUh5Ehn6OQSVR\nuusn2CfEcH1IQ5JtV3AFUAP2OY/HMJlMrFixgn37/sBisXAYyAgOQjNwEN7eT1bU2mQy8+mnSwkP\nP8/69XOQJA+sVmc6vt6L5ORkohPNGMPPAtCwYUMaNmwI3Cmb8l/1X/98LzJxbZ6tsmXL5ncID6XT\n6Wznzp27J8EoX768qVGjRll/Xzc0NNTNYrGk5iV5NJvN2NnZPYtQXwjPs8+jtyzL1wFkWb4uSdIz\nnVZBr9eydOkYSpWqiUYjEsdn6e7k6u46oDab7b73/23Z2dnExMTktvKpVDJz5swmKSmZN96oh7+/\nH7KsZvv2UDZs2MG4ce8TEOCFLGvYvz+M0aPH0LJly9yp4Gw2G/PmzcPd3Z03y5cn6O23AbiFMj/L\n3f+zujk5sSYjg+nTx9OyZU3U6mzq1vUiPDyAEiXsUaszAChSxIVp04YCyvlbsmQJe/fuy91PYmIS\nJ0+eok+f3rRs2ZK7xaSo2HdZx97LWuLS1KglmWrFzfSumk1dXxMOWsBcGvV3zmijruOy7RCyXov9\nuRjMRd1I6drkqc7rkiVL+PPPMCQJ/PxKcfPmTc6ePce0aVOZMmUKer3+AdfCyLlzMYSEKH8w1GoX\nTp6MJTY2nkOHUqlRQ1nev3//p4pJEIT/pg7z95d/lvtb/1aD80+z3aZNm5xnzpzpvXv37ku3l+3Y\nscNx586dbgcPHnSeNm2az9q1ayMBhg4dWiopKUmj1+ttixcvvhISEmLo0qWLv7u7u+XkyZMOVapU\nyVq0aNHVZ/WZCroCN2DmyYqE372uG1DmucVTWDVt2pTdu3ezYMECevfuTXZ2Nt9++y0AnTt3zpfi\nutevX8fPzw8nJ0du3TqOWp2F2ZzGq69W49KlS6xatYgGDWrTrVs3OneuT9GiDrRtW4lq1ZSW0xMn\n0jGbzXh7a6lRwxHQkJSUyYoVK3B1deHLiN0wUg1WK10dHdmXmUlMowb4njwFySlUKOWF+3UVrq4W\nXnpJudVaqVJphgzp/tCYz6/ZTMWV+wjRqKlTpw7e3t5ERUUREXEM68yV+L7SgWSPkmw8YWDjcQPn\nblhQSVAnQMtbLfS0rqh/8OwrE4fCoEkUXRCKTat827X7ZBDBIXmf/SQuLo6wsDDs7DR8//1SgoOD\nSEtLY/DgIVy6dIno6Oicvpt3ZGRkUaJEG7KzTdy6dRZX11KAHYsXF6Vo0aJ5+jn+rxKFqAsucW2e\nj7uLhBc0RqNRFRQUVAHA19fXuGPHjsgHrdeyZcvMFi1apLRr1y61f//+yQB169Ytt3DhwiuVK1c2\n/v77747Dhg0rdfDgwQsAkZGR+j///POCRlPg0qnn6nl+2puSJPnktDr6cHuutGcuDVm2YrXKFLaL\n9zxNmzaNxo0bs2rVKlatWpW73MfHh9GjRz/341+8eJEPP/wQrVbLqlVLgTR8fDLw8ytGkSKuxMef\nxdPTlZEj/8fJk0ppmXPn4Ny5U6xbt46FCxfRt2+7e/bZv397evRohclkAZQ7FRpNBtOmvY3NJkNp\nGfq2hSUb0DjrsbdZONqvGb7D/gJg9NIJjK8elDvH8ZNQT1zMwJsAVlj7JwBVAW/nImwu1ZCu36Rw\nXqu06tXws2Nie2faVNbj5fyYWo192sGkJeiirimvfTxhcKcnjutup06dQpahbt26BAcro5ddXFzo\n0qUz06Z9QUTEMbKy9Jw4cYnp00cCLjg5+VGtWg0yM7OIizPi6qoksI0bN36qGARBKDyetqXwn3jQ\nbesnkZqaqoqIiHDq1q1bbiuVyWTKvf3WuXPn5MKYezzPT7wB6ItSYLIvsP55HGTRorVMmdKRceMm\niNtjz1DNmjUJCwtj4sSJbN++HY1GQ9euXZkwYcIzL4mSlJTE9u3bcXBwyCmWbcLFxUxoaCj29nqM\nxmPodEpJptOnV6PNaWn75ZdfOHjwIO7ubrz11lsUKeLJsmVLiYg4xhdfTOObb76571j29nruHo/h\n4uLEhx/2vbPg4wGwbDO7bqXAuTXw5SowmqBrc+xr5r017UJFHwJPxWJVq7jyyf/4U/ZiY6Ynf6m9\nAfC3S2FMS2faVtFTwi0Pxb3tNKS8+wZr3plBGvDuR/1ArwNg27YwjEYTTZvWwMVFqZeYkJBCVpaB\nIkVccXS8txPk7bqIV69ezR3sYjKZuXpVuQPj4ODM0KFTycrK5p13PsXX1x+ArVu3PfB2tiAIwn+F\n1WrF2dnZ8rDE08nJqVDWr3xWpXp+Qhkc4ylJ0lVgPErSuFqSpIFADNDtWRzr76xWK5cvx7Br1y6R\nPD5jVatWZd26dRw5cgRQbvFcunTp/9u77/iY7z+A46/v3eUyZEhCphAkRIjRqBlqrypV1VJV2qpZ\n9SuqWrWqpdXqMIpW6aBGteggdFAxGo1NIgSJLWZ2bn5/f1wSVFQSIxHv5+PhcXff7/c+3/fdN+fe\n95lMnDiR4OBgevfunXfs7NmzURSFgQMH5q1wEhUVxalTp4iIiKBChQqQkcGp48eJjY+nZkgIfjnr\nMm/5fT3PPPMMTZvWp2vXICAbb29Yvvw9Hn44NC9xBPISR4DIyHUAjBw5io4dOwBQp05tOnTowPbt\n/3Dx4kU8PT0L96KrVMirfWT4h/BHzkj+8S8Vqphsk8q+UyY2thnAYks74nxrcCnLtlpMoPkCI7d8\ni/vpKFpvm4evb5kCl3vtSObD9WvyElDVTseIlwZhm/PUyv/+9wnx8UeJjV2Dq6sPYGXatNl88MFC\n3ntvOK+/3hewsm3bXjp3fpWIiDp4enpw9Ogxxo4dy7p1xzh1KhlX13TOn4c2bV7FYqmFp6cnLi5X\nJ/iWxFEIURo5OztbUlNTNQAeHh7WChUqGBcsWOD+wgsvXLZarURHRzs2btw461bllGZ3arR1r5vs\nan0nyv8vPXq0oXbt6jRq1Odun+qBc+bMGfr06UPbts3o0KE+cIpDh7YxadIkOnRoSe/erQFbIvPK\nK69gtVoZMOAJbH9WCtOnT2X16rX8+OM3VPg5GYa+RqSq0h8YAUzPOc8jQPugANp3bwZcHdzWo0eb\n/4yv499JDEuC4De/gne/B8AF+DzOygUVMk+fK3zyCHm1j6yxNTPTvRWE/ffE6OfTLOxIMrEjyciO\nJBP7T5kwWgB88PBTaJWwnSpn41jjepQf/krAXoX5w9vim5NA30pc3DHGjv2MsmVdWLDgI8Cd+o3q\n0rnzD9QICQGHq/1+27TpSPXqJ3B3r0fuNDjOzoEEBATg6VkLqAdAWtp5Ll1KITNTx6hRC+jZ8ylm\nzFhPRoatnHPnYPTo0TRo0IgGDRoV/P0TQoj7WO/evS8NHjw4cO7cud4rVqw4smTJkqMvvfRSpfff\nf9/XbDYr3bp1u/SgJ4/KtaNp77WUlJS8kyck7MPR8dhtdLQP5vqxseJ2zZs3l0GDBhMY6MNPP71H\nWFgtDh1KYvHiSIKCKtCnz6N5xw4bNg2Lxcrs2a/n1Yx9+OG3/PNPLKNGPcvDW/fC/6azBvhYq6G6\nRsMsR3tIzclUxr4A78NR/isAACAASURBVAwpVHxprhG4pGVjUTTs9QnitGt5PDJTKZd5BY/MFJwj\np2PfvF7RXvyLb9tqHwH2LIHaV6egsFpVDiebibkmWUy6aAFAr4Pa/naEB+oJr2hHeCU9elMqpuCu\neFzMINEeAg1wNLwKlaKX3HQdaoPBSHLypZzVZhQSE1OoXLkVLi4unD9/Hnt7WxP17XT8N5vNpKSk\noKoq5cqV4+DBg8yePZtNmzZRtWpVBg0aRNu2bWVpyiKSQRkll1ybu+PaATNubm55/3EkJiZ+GxgY\neNOl7kTJlJiYGBcYGJhvzVwpSh7Lo6oB8kV3x5hQ1SNMmTKDiIgalC9f9vZG0KZnQuUucOEKrJtl\nWwZvRxzU7wOO9pD4M3h5FKgoVVVJvGhh/Xu/svOIhS2VapPu4HzDcRoFPMpo8Cyjsd06ayjnfPW+\nZ5nrH7s6XDMHZOJpaPw8dGlO5sw32H3cxI4kEzFJRnYeN5GWbfvT9SyjIbySHfUD9YRXsqOWvx32\nunz+Br/5BfpOvPp479Kb1mZGRe3iscde5eGHa/Pbb6sAd0DHd999R4sWLfDz88s7Vr4ESy65NiWX\nXJu7Q5LH0uW/ksdSMUTIaDTRv/9QoqL2Ex8fj14v610XxbFjxxg1ahRffDEdD48UFMXM2LEvFnji\n9v/k7ASv9YHXZ8LEz6FtQ5j0uW3f0KdumTheTLey5YiBLYeNbE4wcOqKFXQN8fM7z6PxW4jL3s0Z\n8wkmn3bFpHfjwvB+XK5ShQsZVi6m2/7FnjZxId1Kanb+P5jstFeTTU9nB8p+tIzEC2ZiJyZjyekS\nXc1bR+faDoRX0lO/kh2VPLUF+8HyTAeY/KVtjecnW+cljlarlc2bd5OVZaB9+8ZAGWrVak5mpoHL\nlw0YjW55K9I888wzBXqrhRBCiLupVCSPer0du3cfJDExkS1bttCyZcviDum+NGTIECIjIylXTmXe\nvLF34QQ94INvYdteeO8r+DnKVuv42o0/bLKMKv8k2hLFzYeNxJ4xA+DqoNCkqp5BLeyJCNIT+Nkv\nKJ/NJathKCmtIvCZugjqVYeBteEmSZ3RrHIpw8rF3MTyX7eXMqxcSLeSdNGEX1ktgx8pQ3ignocC\n7HBzKtzaznl0Opj/Fkz7Bqa9krc5MnIrjz76P+rUqUn79i8B9ri7Q2Ji4nU1jEIIIURJUSqSR4DP\nPhtD+fJBVK8u88wVjYE5c0YyfryGqVNfvjunuLb28c3Ztm05tY4Wq8r+U2Y2JxjYkmAkJtGI0WKr\nDQyvpGdUO2cigvWE+duh1VyTFA7vCR8vxjE6FscDibZtEwfcNHEE0OsUfNy0+LjdfGock8k2VU2Z\nMmXwKmBz+q2cqOLPZ7WDcf/+d0aPHgi407p1P+rV+5r27dtjNmvJnS5MEkchhBAlValJHiMi6mJb\nUE4UVFxcHD///DOjR/cHjhMY6M4337x9w3HZJricrcH1sgWdBjQa0GkUtApotbb7GoWcfbdows2t\nfbxwhSSfimxu/wybF11m6xEjKVm25uQQHx19mzjRNMieBpXtcNL/R22fmzOM6A3j59r6VdarDo81\nL/J7oqoqixcv5quvvuLy5SsAPPRQPcaMGUPVqgVfySg5+RIbN+7Ax8eT5s0fAhQuXDDw3ntf4e/v\nx6hRn6DRaLC3h507dxY5XiGEEOJeKzXJo40ByAIcb3XgAy81NZWmTZty+fJlatSw47GbJFwb4g0M\n/7EsqQYNthWfb02nAa0GtBol5zYn2dRgSzgHfIHxSibnXDzhdwu+birtQh2ICNbTpKqe8rdaXeXf\nXukJHy2GK2m3rHW8lW+//ZZPP50BgI+PN1eupLBz5y4GDBjI0qVLKF++/A3PMZvN7NuXgLe3J35+\ntv0rV25i0KB36NnzcZo37wWUISysNq+++mrOROhCCCHE/alUJY/R0ft5++3XqVOnAVOmTCnucEo0\nV1c7Jk4cyI4d+2jRIvyG/Uazyofr0/h8UyaBZa28EJ6Jn68fFhXMVtt0NWYrWKxgsapYrPlvN1vB\nqoLZqmK2qBw9lsjRy8fRpqbjn36O7hEBDOvXFTs7u3yiLBiDg55fRz3Lyf1HeLHVw+ROuZ2enom9\nvR47u4L9mRsMBhYuXAjA229PolOnTqSnZzBq1EhiYnawfPlyhg4dSkpKOk5ODnnlDhv2AXPn/sD0\n6W8xYsT/gDI0b+5Ehw4xNGvWFrCNBNfpdHz00UdFfp1CCFHa7dmzx37KlCk+27dvd3ZycrJ269bt\n0uuvv37excXltlZyURQlvGvXrpdWrVp1DGxdk7y8vOrUrVs3Y8OGDQl3JvqSKz4+Xr9hwwbnQYMG\nXboT5ZWq5NFkMrNmzR8cOpQkyWM+duzYgdlspmHDKsBJhg3rjqI8ecNxJy6ZeXlJCntOmHi2kSPd\nq5zCXgehoU63df7p06fzx9IlKIAV23Tgi/fDpaTdvPPOOwUux2AwcuLEOYKCbMskWq3wzOQvMRiM\n9Jv3AeAAmBk8eAKLFv3K4sXv8MwzthVooqP38/XXv9CsWV169eqQ83wr8fFJXLlygdTUNCpVqsij\nj9rmsHRxcaZPnz7ExOxg165dPP30G3z//e9s2rSIiIhHAGcaNOjA+vW7sLPzAmyTkteoUYO1a9fe\n1vslhBAPkj///LNM586dq2VlZeX1VYqNjXX69ddf3aOiouKdnZ2LPLego6OjNT4+3jE9PV1xdnZW\nV65c6ert7W26M5EXjslkuq0Kk6I4fPiw/bJlyzzuVPJYxKGjJVPjxmEsWDCezZv/KO5QSpyoqCga\nN25Mjx7duHRpH2DNd4qZNfuy6TTjIkfPm/msd1needwN+zvwE+PEiZMsWbIEnU7LO+9MZvPmzUyf\n/iGOjg6sXRvJgQMHClROXNwx3N1b8uijr2JbPaUajo6NGDr0ZYYMGYKLSxhQDQjFaCyDRqOhbNna\nQE2gGrt3X2LOnBX8+WcsUB5w5+JFM6GhPejUaTQAV65cwWAwMHTo+wQEPEpi4lkuX4aMDA88PCqi\n0+k4csQE+ANu9Ov3IkeOHGHYsGG3/0YJIcQD6pVXXqmYlZWladu27ZW//vorbtGiRQk+Pj7G3bt3\nl/n4449v7DNUSK1bt075/vvvywIsWbLEo3v37nmJVGpqqqZHjx6BtWrVqlGjRo3QRYsWlQVbjV14\neHj10NDQGqGhoTV+++23MgBJSUl29evXrx4SEhIaHBxcMzIy0hnAyckpb2WKhQsXunfv3j0QoHv3\n7oH9+/ev0LBhw2pDhgypcLPzzZgxw7NNmzZVW7VqFeTv7x82ZcqU8hMnTvSuUaNGaJ06dULOnTun\nBThw4IB9s2bNgmvWrFkjPDy8+q5duxxyz9OvX7+AevXqhVSoUCFs4cKF7gBjx471j4mJcQ4JCQmd\nNGmSV0xMjENYWFiNkJCQ0GrVqoXu27evUINGSlXNo1ar5fnnuyADZ27UsGEtHnqoBg8/HIKT041r\nEmebVCb/ksri6CzqBtgxs5cbAR537s9j69YtqCq0bt2ajh07AtCiRQu6dOnCsmXLiYqKombNmtc9\n58CBI0yZshAfH0+mTx8DuBIcXAk7O3vs7V1IS3PFxcUFsNVq/tuyZcuwWCzYJsLXAQ40a9aemTNn\nEhISAlQEICNDQ7Vq1XB3dyc7O4uoqL08++wUoqN3c/LkOYYO/YzUVBg/vg+dO3fmo49m4uh4tV+t\nTEwvhBC359ChQ/oDBw44OTs7W3788cejubWMmZmZJwcMGFBl9erV7uPGjUu+nXP06dPn0oQJE3yf\nfvrpK3FxcU4vvvjixa1btzoDvPnmm74tW7ZM/f777xMvXLigrV+/fo0uXbqk+vn5maOiog45OTmp\n+/bts+/Vq1eV/fv3xy1YsMCjdevWKe+///5Zs9lMWlraLSvjjhw54rBly5ZDOp2Ol19+2T+/8+W8\nF4579uyJzcrK0lSvXr3WuHHjTsXFxcW++OKLAfPmzfMcP358cv/+/St9/vnnSWFhYYY///yzzODB\ngyv+/fffhwDOnTtnFxMTc3D37t0O3bp1C3r++ecvv/vuu6emT5/undtE37dv34AhQ4acGzx48KXs\n7GzFbDYX6r0sVcnjVVcA77tSssFgYOnSpfj6+tKuXbu7co47JTo6mjp16uDgkIJef4qNG+fg4HBj\nYp2QbObl765w8KyZgc3LMKq9M3bae5MQ5SZeWVlGVq/eiIeHG82a1QN0WK0ufPddJH5+fnz44bco\nioJOBydOnMDVtWBLUf57+b/Q0NAbVsoJDAwkPj4egL///pu2bduyYsWveftTU1Pp2LEjzz77LDpd\nKf3ICCFEMcrIyNCArXnZyckpr3nay8vLDJCdnX3bLaUNGzbMOnnypP0XX3zh0aZNm5Rr923cuNF1\n3bp1ZWfMmOEDYDAYlISEBH2lSpVML774YqXY2FhHjUZDUlKSPUCjRo0yBg4cGGgymTRPPvnk5SZN\nmtxyresnnnjicu53yM3OB9CkSZM0d3d3q7u7u9XZ2dnSo0ePKwBhYWGZe/fudUpJSdHs2rXLuUeP\nHnlTgBiNxrwv7S5dulzRarWEh4dnX7x4Md/28caNG2d8+OGHvidPntT37NnzclhYmKEw72WparbO\nNXv2Aho1asiRI0duq5xffvmFpk2b5vTHywYucubMXvr160f//i8CGdhGeFtp3Lgx/v7+1zW/RkZG\nMmnSJKKjo/O2ZR8/zpnBgzENHAhDhlz/b+hQ+PPP24o519y5c2nSpAmvvfYScBJQb0gcVVVleUwm\nj828SHKahYXPu/NGJ5cbEsfz569w4cLVz1lKSjr79ydw8uS568o6ffo8ycnXd6cwGk2YzWYaN24C\nwB9//EFkZCRpaelERv7G6tWrAUhNtePxx0fxySergBpAHWrV6sDcuXP544/ruyEUNHEsikaNGrFr\n1y6GDh1KvXr1aNGiBfPmzWP16tWSOAohxF1Sq1atbC8vL9P58+ftJk+e7GU2mzl37px26tSpvgBN\nmzZNuxPn6dChw5UJEyYEPPfcc9d9WamqyooVKxIOHjwYe/DgwdgzZ87se+ihh7Lfffddby8vL1Nc\nXFzsvn37Yk0mkwagY8eO6Zs2bYr39/c39uvXr/KsWbM84fqWqKysrOu+TJ2dna23Oh+AXq/PS541\nGg0ODg5q7n2z2axYLBZcXFzMuc89ePBg7NGjR/OSj9zjc8+Tn0GDBl1avXp1gqOjo7Vjx47Vfvrp\nJ5fCvI+lMnncvHk30dHbWbVqVYGfs3DhQtq0aUNkZCRgBC5jNJ5h69atREWtAQ4AiWi1yTz7bEce\ne6wxcBDYD+zi1KlETp8+jbPzGeAwcIw1a5YxceJEtm37DbgMpLHtkw/wmzuX1p9/DnPm5P1rNGcO\njT/7DNNbb+XFNG3aNJ5++mm2b9+ety06OprXXnuNFStW5G3LOnuWGcOGsfD112HjRti4kfqKATut\nBpf0FFSL5YbXm26w8uqyFEavSKVugB1rh5ejZfUbayVnz15O27Yj2LQpDigDOPH777sIC+vJ8OEf\nY+sioMdk0uDv3xF//07YKrS1gIbOnf+HnV0j4uJO0qtXT8xmCwMGvIWbWwuee+4Njh3Lpm7dHvTt\nO5aIiAiaNm0F2AbmKIrCwIEDCQkJuadNw0FBQcyaNYudO3eyYcMGBgwYcM87NwshxIPEzs6OMWPG\nnAaYOHFiQLly5eoGBATUiY6Odilbtqx59OjR525VRkEMHjz4wsiRI083aNDguprCli1bpk6fPt3b\narXld1u2bHEESElJ0fr6+pq0Wi2fffaZpyXn+/TQoUN6f39/08iRIy88++yzF3bu3OkE4Onpadq5\nc6eDxWJh9erV7jeL42bnKwgPDw9rhQoVjAsWLHAH26DPbdu2/efz3dzcLOnp6XlNcbGxsfoaNWoY\n3nrrreR27dpd2b17d6HmOCxdVSlb98CcFQy/mEKPiHDaR0dD7nrAej2MHg2hoXz00Uds2LCBefPm\n5czLl8nhwzv5448/aNgwkA4dbP1yW7SoSmTkTCpWLMeUKVP466+/MJvNNGrUiP79n7ru1AcPruDi\nxSv4+roAqQB06vQQbm5aGjcOAI4CYKjvgxe2oR4MeQpqBqNarES/MhUA3TOtsSWfClFRkfzyywZ6\n926DrRleYc+eDXz44Yf079+LJ59sAmhIebIrw7dsxxt4fto0AOoDRwD/r36GDo3h6atN7PtPmXj5\nuyscv2RhRFtnhrYsc/2qLanp8PgoOJlM+qVUTCYzgZ8sg29+A8DZz4/Q0FACAmoCtQCwWrPx8fHJ\nqZ2rk1eURlMWrVaLVhvCiBGDcXRsyttvv42qnicry5mRI99i5MiR6HQ6oqKiinrlhRBC3OdeffXV\nC1qtVn3//ff9Tp8+nduEmzpz5swTVatWvSMjo6tWrWrKr+/ke++9d3rAgAEVQ0JCQlVVVSpUqGDY\nsGFDwv/+97/k7t27V121apV7REREmqOjoxVg3bp1LjNmzPDR6XSqk5OTZfHixccAJk2adKpr165B\nvr6+ppCQkKzc5viCnq+gr2PJkiVHX3rppUrvv/++r9lsVrp163apcePGN206b9CgQZZOp1OrV68e\n+swzz1zIzs7WfP/99546nU4tX768aerUqacLem4A5WZVmvdCSkpK3skTEvbh6Hjshv5ohdJnHCy6\nOj2KAfgUiAfmA8obr8OUN2nb9jF+/30TK1d+wuOPRwC2wRkJCSdo1CgMb2/PvDLOnTtH3759OX/+\nwnWnKlPGifnz51OtWrXCxzniI9SPv0Pp1hJ+/AD1xz/Z0X00xnLuNDnxC+Q0L2/ZspuTJ5OJiKiL\nv78XAHv2HGL9+r8JCwuiQwdbU/CVfhMY//WvOOm0vNc0J3FLzYBdtn58/PMN1A9FVVW+2prJ1DVp\neJTR8GnPsjSsor8hPEN8EvYh3QHblDqbgBbXHuDsDFeu2JaXKQKTyYTJZMLJ6fam/hEQExMDQP36\n9Ys5EvFvcm1KLrk2d0dKytXuTW5ubnk1EomJid8GBgbWKGg5FouFY8eO2Tk7O1t9fHxubDoT90Ri\nYmJcYGBgn/z2la5m676dbbeKAnPfQL9oJlMdHFgAnALoUx84zKuvPsGSJe/SpMnVRLVmzap07dri\nusQRYMGChZw/f4HatcNYunQJK1f+yCOPNCcjI5PZs2cXLc7Rz6E42MPKDbDrIMrb86kPNJn4Ul7i\nCNC0aV2efrpdXuIIUKdONV577bm8xBGg7IQBzNBpec+qwhdvwcbPoV0j285OTaF+KFcyrQz49gqT\nfk6jWbA9a4aXuyFxtFqtTJmygDpdR5LaqS0Amp498Vyxgn0rVsDDD9sOHDasyIkj2JonJHEUQgiR\nH61WS1BQkEkSx5KrxCSPVqv1ph07C6x1A2haB1QVLqeh9G7MpPDqLACcu7eCGpUB6NQpgp492+Pl\n5XHLIjdt+guAMWPGEBwcTMWKFRk3bjyKAlu2bMFoNBY+Tp9yMNhWs0e312DPIfD3gheLuGxdZX/o\n95httux3voTzl2HWctu+CS/xT6KRTp9eYGO8gXGdXZjftyweZW689CaTme+/30B8fCJrmrWybVy9\nGkuZMujS0uCff2y1jiNGFC1OIYQQQtz3Skyfx0ceeYR69exp164dQ4YMyXcN4VtSFNvaxm2Hwoff\nQpfmvLL9gG375MGFL89k5tOtl6iSCtqafQBbLXxZVP62wFk9qBeugJ/Xf5eTn9HPwZwfIOmM7fEb\n/a6rdSy0N5+Hr362NdtnGSAjC0unCOakB/LxqktUcNfyw2BPale4ceCHqqooioK9fSWWLVvJkSNH\nbXMx/v03rF6Nz7ff4piYaDt42DAoV67ocQohhBDivlZikkdVhexsAz/99DMxMTF88823uLuXLXxB\nubWPW/ZAq8FgMkOv9nm1joWiQAWjBpNOx5aAmmwOrEtyGQ9cDem4ZafjbMjAPU7B7VI2rg4Kro4a\n3Bxtty72ChrNf4wQzq19/Pi726t1zJVb+zh/FXz/O8llyvJqqxFsWZ/OY3UcmNLNFReH62sbzWYz\n48fPw2qF9977FHChWjWoVq267YAJE2D1aryWL0djNkutoxBCCCFKTvL422/rMRh2sWDBAg4ejGf5\n8mUMHDiw8AVdW/t47qLt8bj+hSrCalWJO2sm6rCBDa98xi6LJ0adHqwmtNkXcNCUIUtfBqtGC79Z\nsE1KfmMYLvYKbk4aXB0U3HITSwcNbk45t4/2xTXLG/tmYeiOqui0Buy0oNMo6LRgp1XQaXJuteTd\n1163TcFOi220dE7t46YKtRnxxBjSr+h57wlXnn7YMd+pbvbuTWDatG8AGDDgLapU+dc0T/XqQdeu\naHLmYpRaRyGEEEKUmORRG5/E8gveVK87iNTjXxO9aRdFyR2B62sfe7YrUK3juVQLUYeNRB02sPmw\nkYsZtrmXqnv50+f3n2gev53vHGM5TzYr4gCtlowDK0n18iYl00pKlpXUbNV2m6WSmmUlJUslNdt2\nm5JlJSHZSkqWidRsK9m5kw64tYa9wN4bE9DCUBSw02jRjVhBpmJHNVcL373oSTXvm81PqPDQQ62Z\nOXMmoaGhVKlSJf/DcmofLU5OaKXWUQghxN1iNoPJlH+Tnb29iqbEDNN44JWY5NFl7HvsfHIC65yD\noek7AIRPTibEV0d1bx0hvjpCfOwI9tLhqL/FhNGKAvPHwadLYPxL+R6SabQSfcxE1CEDmxOMHDpn\nW9exnLOGZsF6mgXbExGsx9tVC9kKRO6kWURdCPBGE7sOnu+CSzU/XAD/soUfeZyZbebPzf9w4HAS\nTi5lCa/fEHvHMpgtYLaqmCxgtqiYrWC69tYClny2ZWYb2bl7DwlHEtGkn8fL6TAnD/SimnervHMa\nDEbGjJnJs892JTy8M1CGwYNv0Re0Xj0OzZqF2dmZUKl1FEIIcTfs3OnAI4+EcM1E1tdp1CiNbdsO\nFbV4rVYbHhwcnGWxWJSgoKCs5cuXJ7q4uFhv/cwb/fLLLy6560QvXrzY7cCBA45Tpkw5m9+xFy5c\n0M6fP99jzJgx5wESExPtBg0aFBAZGXm0qK+lJCgxyWOAm4bf1r9B2rkMTpStSHStOpx5vh/xZ818\ntz0zr6ZOo0CgpzYnqbTLSSp1BLhrr+9jGBIIc97Ie2i1qsSeMbPpsIGoQ0Z2JBkxWkCvg4aV9TwZ\n7kJEkJ4QH92NfRWHPQ3TF6PZvNv2WKe1NREXUXJyMq+88gqHD1+dD3SpgwOTJk2kTZs2hS7PZDIx\nYMAwju7dhwbbmi9xwGuv7eLNN9+ge3fbyO6PPlrMJ58sYf36Pezd+2SBZ9tJbdiw0DEJIYQQBWax\nkJc4arVXaxnNZgVVhZSUos8PB9jb21sPHjwYC9ClS5fK06dPLz9x4sS8VWtyZ3zRFnIaut69e6cA\nKTfbf/HiRe2XX37plZs8BgYGmu73xBFKUPLoc/wwDarDzxkQkHqFunOex6mTGwAWq8rxSxYOnjFz\n8KyJg2fNxJ42s3a/gdzZfZz0CtW8ddTIq6m0w8tFQ0yikagEI1sSDFzKsB0c4qOjX1MnmgXb83Cg\nHge7W9RkujrDyN7w1hzb4+e7QKBfkV/r2LFjOXw4AR8fb9q0aUN8fDz//BPD2LFvUb16dQICAgpV\n3vr169m7dx/e3l5MmTKF4OBgli9fzqxZs5k1axadOj2Ko6Mjr776Otu3n+LNN98s9AdECCGEuGse\nfjibli1T2LDBjf79k5k79yTZ2QqVK9fi7Fk9I0bkW7NXFBEREel79+51jI+P13fs2DG4SZMmaTt2\n7HBevXp1wv79+x3efvttP6PRqFSqVMmwdOnSRDc3N+uKFStcX3vttQAPDw9zWFhYZm5ZM2bM8IyJ\niSnzzTffHD9x4oTuhRdeqHT8+HF7gFmzZiV9+umn3idOnLAPCQkJfeSRR1JHjBiR3Llz5+DDhw8f\nyMzMVJ577rlKe/fuddJqtUybNu3EY489ljZjxgzPX375pWxWVpbm+PHj9h07drwyd+7ck3fq9d8J\nJSZ5rKXX0zdVwdViwBRRB6dOzfL2aTUKlcvpqFxOR8cwh7ztmUYrh86ZiT9rJu6M7TZyfzZLtl8/\nX2R5Fw0tqtnTrJo9TYP0eLkUIXEa9jR8uhTSMm+r1jEhIYGdO3fh7OzMokWLcXcvi6qqjB07lnXr\n1rNq1SqGDRtWqDI3b94MwPPPP0/dunXz7q9ZE8nWrUfYsWM/ERHP4eDgyMqVK4scuxBCCHHXTJx4\nmg0b3Pj66/KMG3eW774ry9mzeqpWzeb55y/fiVOYTCbWrVvn2q5du1SAxMREhy+++CJx0aJFx8+c\nOaObMmWK76ZNmw65urpax44d6zN58mTvt99+++zLL78c+Ntvv8XXrFnT0Llz53wHCQwaNKhis2bN\n0saPH3/EbDaTkpKinT59+snOnTs75tZ6xsfH563O8f7773sBHDp0KHbXrl0OnTp1Cj5y5Mh+gNjY\nWKc9e/bEOjo6WoOCgmqNGjXqXFBQ0B1ZovFOuOvJo6IoHbCtEqgF5quq+l5+x61/qCGuO3cAYFfA\nORmd9BrqBuipG3B1pRRVVUlOtfD7jiSOnEkjIsSdlg9VzHe0caG4OsP2ryHLQKaXB//8tYNy5cpS\ns2bV6859q/OcOnUKgNq1w/KmIlIUhWbNmrFu3XpOniz8j4ubTa6+efMZzp6F2bM3EBFR1NFHQggh\nxD3QvHlmXu3juHG+rF1r+5IcM+b07axqBmAwGDQhISGhAA0bNkwbPnz4haSkJDtfX19j69atMwA2\nbtxY5siRIw4NGjQIATCZTEp4eHj67t27HSpUqGAICwszAPTu3fvi/Pnzb5iMeuvWrS4rVqw4BqDT\n6fD09LRcuHDhpoFv3brVediwYckA9erVy/bz8zPu27fPASAiIiLV09PTAhAUFJR95MgR+wcmeVQU\nRQvMBtoCJ4F/NdlXZAAAD1pJREFUFEX5SVXV2H8f674xynanRTi0KPp6o6dOnWLs2LfYv38/AKuB\nxo0bMXnyZNzd3Qtd3v79CSxY8BNNmtTmyScfAxw4si+OFi0GUrNmEPv3rwQsgJXg4C6cP3+ZvXuX\nUqmSLwCfffY969f/zaBB3enQoQl+fv4YDLBmzQ6aNVvHU0+1B2Dz5i2kpEBamnJdEpqQcIL09Eyq\nVPHH1dUZgLS0DFJS0nFxKYObmzMRERGsX/87X365kKCgYEJCqrNs2fdkZGSi0Wh49VUZJS2EEOI+\nkFv7uHChbfWNO1TreG2fx2s5OTnlDZpRVZWIiIjUn3/++di1x2zdutXxtiug8vFfq+rp9fq8nVqt\nVjXdbBR6MbnbNY8NgARVVY8CKIqyFOgK3HABcyX2bUdm7E13/yeTycQbb7zBuXPJODs7U7lyIIcP\nH2bbtr8ZPHgw48aNu2XNoKqqmExm9HrbFDc//LCZjz/+jm3bEggMbA1kcuxYJnXq1MHf35+YmOy8\n5168mE5qagaHDilcuJCNolhZv34fq1f/Re3aD+HjEwK4odNV5OjR4wwYMIm//95OUlIiu3fv4ehR\nmDv3DwYPTgJUFAWGDJlCVNQuZs9+nebN6wEqy5f/xuTJC+jRozUTJrxAQEAgfn6V+PXXJP78sz9B\nQXD0KBgMMHr0KDQaDTExMUV6T691J8oQd4dcm5JLrk3JJdfmzgoODr79Qq6tfYQ7UutYUC1atMgY\nOXJkxf3799vXqlXLkJaWpjl27Jhd3bp1s0+ePKk/cOCAfc2aNQ1Lly7Nd23jpk2bpn3wwQflx48f\nn2w2m0lNTdW4ublZMjIy8p1jKCIiIn3RokUeXbp0Sdu7d6/9mTNn9LVr186Ojo52uruv9Pbd7eTR\nHzhxzeOTQL5Dd81urmQ9VJXMBjWKfLKYmBjOnUvG19eHiRMn4uTkxOXLl/MGqBw6dJjq1avd9Plr\n1vzNJ58sp0ePtvTr1wez2YWmTX3p1SuNdu3a5R1XuXJl5s+ff8Pz165dS2ZmJs7OzqiqBlWFp59+\nlqZNW1C9enXMZlvN54svjmLcuHGkpKTw8ce2Cbj1ej3BwZXw9PTEYKiUV6aPTxDBwenY2weTnW1r\nItdoDuLl5YWTUwWysmyv57nnprF2bS8sFoiPh+rVq9O3b19at25d5PdTCCGEuOcmTTrNpk1uBAVl\n3am+jgXh5+dnnjdvXmLPnj2rGI1GBWDChAmnateubZg5c2ZS586dgzw8PMwNGzZMj4uLc/z38+fM\nmXO8X79+lapVq1ZOo9Ewa9aspDZt2mSEh4enBwcH12zVqlXKiBEjknOPHz16dHKfPn0qVatWLVSr\n1TJv3rxER0fHm1dHliDKf1Wb3nbhitIDaK+qav+cx32ABqqqDgNISUnJO/mR2B04OJ8gNKxWkc/3\nySef8O23ixg0aBAvvXR1VZnJk99h1apVjBo1il69egK2GsY9ew5RtqwLgYF+gD2rVkXTrVt/2rdv\nT2RkZJHjKAiLxcLatWvZuXMnXl5e9OjRA09PzztSdkH6XhZG7q/z+vWL3p1A3B1ybUouuTYll1yb\nuyMl5eqMNW5ubnlfQomJid8GBgYWrmZo1y4HfH1N+PhY7lyEojASExPjAgMD++S3727XPJ4Erp13\npgJwOr8DVb0etLc3e3xun8bDh6/OI6qqat7ja9fKnjx5PhMmzGPkyIF8+OFHgBMdOgTx11/BRERE\n3FYcBaHVauncuTOdO3e+42Xfjb4ZQgghxD1Tr172rQ8SxeVur/XzDxCsKEplRVH0QE/gp7t1sg4d\nOqDTafnjjz+ZPHkya9dGMnr0aHbsiOXiRTu0WjdAD3jTpk0Pypcvj4uLL2DrXuDg4EDz5s3RyBJI\nQgghhBD5uqs1j6qqmhVFeRlYh22qngWqqh64W+fz9vbmzTff5J133mHVqtWsWmXrT3j5soYzZ0ws\nWrSNtm1fBqBRIz9Onz6NTldiproUQgghSh1VVYu0DKAoXv913e565qSq6hpgzd0+T66uXbtSq1Yt\nVq9ezZEjF/HyCqN5804sXryY3r175x2n0WikhlEIIYS4y4xGY1xmZmbYtdPiiJItMzNTYzQa4262\nv1RWuwUEVCQ6+jyPP96Hp5/ujUajoWXLlsUdlhBCCPHASU9Pn3bixAn0en0NRVGk1qaEU1XVajQa\n49LT06fd7JhSmTxGRm5l+fLfiIs7S69e+Q4UEkIIIcQ9EB4ebgXyXV1O3J9KZfLYpEkdZs6ciodH\nxeIORQghhBCiVCmVyWO5cu68/PJr2MboCCGEEEKIO6WU9j1wQxJHIYQQQog7r9Qlj8OHf8inny4n\nLS2tuEMRQgghhCh1SlXyePr0eWbOXMbo0ROxWGRFIyGEEEKIO61U9Xn08HBl6dKZHDuWTtmyZW/9\nBCGEEEIIUSilKnl0cLDnqaeeA1yKOxQhhBBCiFKpVDVb29atlsRRCCGEEOJuKTXJ46efLuHNN+eR\nlJRU3KEIIYQQQpRapaLZ2mq18vHH35GUdIb27XtQqVKl4g5JCCGEEKJUKhXJo6IofP31VH76aS/N\nmjUr7nCEEEIIIUqtUpM8PvJIex55pG9xhyKEEEIIUaqVmj6P4FHcAQghhBBClHr3ffK4bt02+vd/\nj3/+2VPcoQghhBBClHr3ffL45Zer+fLLFWzYsKG4QxFCCCGEKPXu+z6PkyYNolq1h+nVq1dxhyKE\nEEIIUerd98ljjRp1eeed7sUdhhBCCCHEA+G+b7aWgTJCCCGEEPfOfZs8njqVTNeuI1m5Uvo6CiGE\nEELcK/dts/WSJev46ae/0Ok86dbtieIORwghhBDigXDfJo99+nTCzs6XOnUaFncoQgghhBAPjPs2\nefT29mX48HbFHYYQQgghxAPlvu3zCO7FHYAQQgghxAPnvkserVYrTzzxGrNmLcdoNBZ3OEIIIYQQ\nD5TbSh4VRemhKMoBRVGsiqLU/9e+NxRFSVAUJV5RlPa3F+ZVW7bsYeXKDUyb9gk63X3b6i6EEEII\ncV+63exrP/AEMO/ajYqihAI9gZqAH/C7oijVVFW13Ob5CA+vwZIlczAYHNFo7ruKUyGEEEKI+9pt\nJY+qqsYBKIry711dgaWqqhqAY4qiJAANgG23cz4AJycHevZ8AdDfblFCCCGEEKKQ7la7rz/w9zWP\nT+Zsu6XY2Nj/3G+xOGEwqEWPTBRZTExMcYcgbkKuTckl16bkkmtzZwUHBxd3COIeuWXyqCjK74BP\nPrvGqqq6+mZPy2fbbWd877+/GL2+HE8+2QdPT8/bLU4IIYQQQhTSLZNHVVXbFKHck0DANY8rAKcL\n8sTQ0NB8t6ekpLNs2QaMRhPjx08lICAg3+PEnZf767x+/fq3OFLca3JtSi65NiWXXJu7IyUlpbhD\nEPfI3Wq2/gn4TlGUj7ANmAkGtt9Ogc7OjqxZ8yUxMaclcRRCCCGEKCa3lTwqitINmAmUB35VFGW3\nqqrtVVU9oCjKciAWMANDb3ektVarpVWrR2nVSiYHF0IIIYQoLrc72nolsPIm+94F3r2d8q+nBcre\nueKEEEIIIUSh3RcTJc6b9wMDB05j//4DxR2KEEIIIcQD7b5IHufO/YHPP1/C4cOHizsUIYQQQogH\n2n2xvt+3305l2bJddOrUqbhDEUIIIYR4oN0XyWOtWg2pVeuJ4g5DCCGEEOKBd180W4NHcQcghBBC\nCCEo4cnjli276dbtddat21TcoQghhBBCCEp48vjNN7+yatUfbNiwobhDEUIIIYQQlPA+jxMmDKB6\n9UY8+mjX4g5FCCGEEEJQwpNHP78qjBjRobjDEEIIIYQQOUp0s7UMlBFCCCGEKFlKZPKYkpJOy5YD\nmTt3OaqqFnc4QgghhBAiR4lMHn/44Q82btzB8uUrUBSluMMRQgghhBA5SmSfx6eeaou9fQXKlw8s\n7lCEEEIIIcQ1SmTy6OzsQu/eLwFS6yiEEEIIUZKUyGZrcEcSRyGEEEKIkqfEJY9PPPEaEyfOJTU1\ntbhDEUIIIYQQ/1KiksfDh0+ycuUGPv10Lvb29sUdjhBCCCGE+JcS1eexcmVf1q//jlOnDJI8CiGE\nEEKUQCUqedTptLRt+zjgWNyhCCGEEEKIfJSoZmur1R5JHIUQQgghSq4SU/M4a9ZcMjNTmDq1PlWq\nVCnucIQQQgghRD6U4lz+LyUlRdYeFEIIIUoZNzc3mW+vFCtRzdZCCCGEEKJkk+RRCCGEEEIUWLE2\nWwshhBBCiPuL1DwKIYQQQogCk+RRCCGEEEIUWIlIHhVF6aAoSryiKAmKoowp7njE9RRFSVQUZZ+i\nKLsVRYkp7ngeZIqiLFAUJVlRlP3XbPNQFOU3RVEO59y6F2eMD6qbXJuJiqKcyvns7FYUpVNxxvig\nUhQlQFGUDYqixCmKckBRlOE52+WzI0QRFHvyqCiKFpgNdARCgV6KooQWb1QiHy1VVa2rqmr94g7k\nAfcV0OFf28YAf6iqGgz8kfNY3HtfceO1Afg457NTV1XVNfc4JmFjBkaqqloDaAQMzfmekc+OEEVQ\n7Mkj0ABIUFX1qKqqRmAp0LWYYxKiRFJVdRNw6V+buwJf59z/Gnj8ngYlgJteG1ECqKp6RlXVnTn3\n04A4wB/57AhRJCUhefQHTlzz+GTONlFyqMB6RVF2KIoyoLiDETfwVlX1DNi+JAGvYo5HXO9lRVH2\n5jRrS7NoMVMUJRCoB0Qjnx0hiqQkJI/5zUIv8weVLE1VVX0IW9eCoYqiNC/ugIS4T8wBqgJ1gTPA\n9OIN58GmKIoz8APwP1VVU4s7HiHuVyUheTwJBFzzuAJwuphiEflQVfV0zm0ysBJbVwNRcpxTFMUX\nIOc2uZjjETlUVT2nqqpFVVUr8AXy2Sk2iqLYYUscF6uq+mPOZvnsCFEEJSF5/AcIVhSlsqIoeqAn\n8FMxxyRyKIpSRlEUl9z7QDtg/38/S9xjPwF9c+73BVYXYyziGrmJSY5uyGenWCiKogBfAnGqqn50\nzS757AhRBCVihZmc6Ss+AbTAAlVV3y3mkEQORVGqYKttBNAB38n1KT6KoiwBWgDlgHPABGAVsByo\nCBwHeqiqKgM37rGbXJsW2JqsVSARGJjbx07cO4qiRABRwD7AmrP5TWz9HuWzI0QhlYjkUQghhBBC\n3B9KQrO1EEIIIYS4T0jyKIQQQgghCkySRyGEEEIIUWCSPAohhBBCiAKT5FEIIYQQQhSYJI9CCCGE\nEKLAJHkUQgghhBAF9n/yw25IQU/VMQAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"process_var = 2\n",
"sensor_var = 4.5\n",
"x = (0, 400) # gaussian N(0, 400)\n",
"process_model = (1., process_var)\n",
"N = 25\n",
"\n",
"dog = DogSimulation(x[0], process_model[0], sensor_var, process_var)\n",
"zs = [dog.move_and_sense() for _ in range(N)]\n",
"\n",
"xs, priors = np.zeros((N, 2)), np.zeros((N, 2))\n",
"for i, z in enumerate(zs):\n",
" prior = predict(x, process_model) \n",
" x = update(prior, (z, sensor_var))\n",
" priors[i] = prior\n",
" \n",
" xs[i] = x\n",
"plt.figure()\n",
"book_plots.plot_measurements(zs)\n",
"book_plots.plot_filter(xs[:, 0], var=priors[:, 1])\n",
"book_plots.plot_predictions(priors[:, 0])\n",
"book_plots.show_legend()\n",
"kf_internal.print_variance(xs)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Here we can see that the variance converges to 2.1623 in 9 steps. This means that we have become very confident in our position estimate. It is equal to $\\sigma=1.47$ meters. Contrast this to the sensor's $\\sigma=2.12$ meters. The first few measurements are unsure due to our uncertainty of the initial position, but the filter quickly converges to an estimate with lower variance than the sensor!\n",
"\n",
"This code fully implements a Kalman filter. If you have tried to read the literature you are perhaps surprised, because this looks nothing like the endless pages of math in those books. So long as we worry about *using* the equations rather than *deriving* them the topic is approachable. Moreover, I hope you'll agree that you have a decent intuitive grasp of what is happening. We represent beliefs with Gaussians, and they get better over time because more measurements means we have more data to work with."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Exercise: Modify Variance Values\n",
"\n",
"Modify the values of `process_var` and `sensor_var` and note the effect on the filter and on the variance. Which has a larger effect on the variance convergence? For example, which results in a smaller variance:\n",
"\n",
"```python\n",
"process_var = 40\n",
"sensor_var = 2\n",
"```\n",
" \n",
"or:\n",
"\n",
"```python\n",
"process_var = 2\n",
"sensor_var = 40\n",
"```"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### KF Animation\n",
"\n",
"If you are reading this in a browser you will be able to see an animation of the filter tracking the dog directly below this sentence.\n",
"
"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"import time\n",
"from kf_book import book_plots as book_plots\n",
"from kf_book.book_plots import reset_figsize\n",
"\n",
"%matplotlib notebook\n",
"fig = plt.figure(figsize=(9,4))\n",
"canvas = fig.canvas\n",
"time_step = .25\n",
"for i in range(2, len(xs)+1):\n",
"\n",
" book_plots.plot_predictions(predictions[:i]) \n",
" plt.xlim(-1, 10)\n",
" plt.ylim(0,20)\n",
" fig.canvas.draw()\n",
" time.sleep(time_step)\n",
"\n",
" book_plots.plot_measurements(zs[:i])\n",
" plt.xlim(-1, 10)\n",
" plt.ylim(0,20)\n",
" fig.canvas.draw()\n",
" time.sleep(time_step)\n",
"\n",
" book_plots.plot_filter(xs[:i])\n",
" plt.xlim(-1, 10)\n",
" plt.ylim(0,20)\n",
" fig.canvas.draw()\n",
" time.sleep(time_step)\n",
" \n",
" if i == 2:\n",
" plt.legend(loc=4);\n",
"# reset to noninteractive plot settings\n",
"%matplotlib inline\n",
"reset_figsize()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Ignoring the boilerplate, the filter is:\n",
"\n",
"```python\n",
"for z in zs:\n",
" prior = predict(x, process_model)\n",
" likelihood = (z, sensor_var)\n",
" x = update(prior, likelihood)\n",
"```\n",
"\n",
"I've plotted the prior (labeled *prediction*), the measurements, and the filter output. For each iteration of the loop we form a prior, take a measurement, form a likelihood from the measurement, and then incorporate the likelihood into the prior. \n",
"\n",
"If you look at the plot you can see that the filter estimate is always between the measurement and prediction. Recall that for the g-h filter we argued that the estimate must always be between the measurement and prior. It makes no sense to choose a value outside of the two values. If I predict I am at 10, but measure that I am at 9, it would be foolish to decide that I must be at 8, or 11."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Kalman Gain\n",
"\n",
"We see that the filter works. Now let's go back to the math to understand what is happening. The posterior $x$ is computed as the likelihood times the prior ($\\mathcal L \\bar x$), where both are Gaussians.\n",
"\n",
"Therefore the mean of the posterior is given by:\n",
"\n",
"$$\n",
"\\mu=\\frac{\\bar\\sigma^2\\, \\mu_z + \\sigma_z^2 \\, \\bar\\mu} {\\bar\\sigma^2 + \\sigma_z^2}\n",
"$$\n",
"\n",
"I use the subscript $z$ to denote the measurement. We can rewrite this as:\n",
"\n",
"$$\\mu = \\left( \\frac{\\bar\\sigma^2}{\\bar\\sigma^2 + \\sigma_z^2}\\right) \\mu_z + \\left(\\frac{\\sigma_z^2}{\\bar\\sigma^2 + \\sigma_z^2}\\right)\\bar\\mu$$\n",
"\n",
"In this form it is easy to see that we are scaling the meaurement and the prior by weights: \n",
"\n",
"$$\\mu = W_1 \\mu_z + W_2 \\bar\\mu$$\n",
"\n",
"\n",
"The weights sum to one because the denominator is a normalization term. We introduce a new term, $K=W_1$, giving us:\n",
"\n",
"$$\\begin{aligned}\n",
"\\mu &= K \\mu_z + (1-K) \\bar\\mu\\\\\n",
"&= \\bar\\mu + K(\\mu_z - \\bar\\mu)\n",
"\\end{aligned}$$\n",
"\n",
"where\n",
"\n",
"$$K = \\frac {\\bar\\sigma^2}{\\bar\\sigma^2 + \\sigma_z^2}$$\n",
"\n",
"$K$ is the *Kalman gain*. It's the crux of the Kalman filter. It is a scaling term that chooses a value partway between $\\mu_z$ and $\\bar\\mu$.\n",
"\n",
"Let's work a few examples. If the measurement is nine times more accurate than the prior, then $\\bar\\sigma^2 = 9\\sigma_z^2$, and\n",
"\n",
"$$\\begin{aligned}\n",
"\\mu&=\\frac{9 \\sigma_z^2 \\mu_z + \\sigma_z^2\\, \\bar\\mu} {9 \\sigma_z^2 + \\sigma_\\mathtt{z}^2} \\\\\n",
"&= \\left(\\frac{9}{10}\\right) \\mu_z + \\left(\\frac{1}{10}\\right) \\bar\\mu\n",
"\\end{aligned}\n",
"$$\n",
"\n",
"Hence $K = \\frac 9 {10}$, and to form the posterior we take nine tenths of the measurement and one tenth of the prior. \n",
"\n",
"If the measurement and prior are equally accurate, then $\\bar\\sigma^2 = \\sigma_z^2$ and\n",
"\n",
"$$\\begin{gathered}\n",
"\\mu=\\frac{\\sigma_z^2\\, (\\bar\\mu + \\mu_z)}{2\\sigma_\\mathtt{z}^2} \\\\\n",
"= \\left(\\frac{1}{2}\\right)\\bar\\mu + \\left(\\frac{1}{2}\\right)\\mu_z\n",
"\\end{gathered}$$\n",
"\n",
"which is the average of the two means. It makes intuitive sense to take the average of two equally accurate values.\n",
"\n",
"We can also express the variance in terms of the Kalman gain:\n",
"\n",
"$$\\begin{aligned}\n",
"\\sigma^2 &= \\frac{\\bar\\sigma^2 \\sigma_z^2 } {\\bar\\sigma^2 + \\sigma_z^2} \\\\\n",
"&= K\\sigma_z^2 \\\\\n",
"&= (1-K)\\bar\\sigma^2 \n",
"\\end{aligned}$$\n",
"\n",
"We can understand this by looking at this chart:"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAugAAADQCAYAAABV7JR5AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzs3XlYlFX/P/D3gCwii6iY+wKmJlIs\niiCZK6QliaamJe6mZkpuuTw+CmmmZaiXifYYS6n9zEihxQ0ETU20VEpccsM0tyQRAXHYzu+P852B\ncWZg2Ed8v66La+Dc55z73DdJnznzuc9RCCEEiIiIiIjIKJjU9ACIiIiIiKgIA3QiIiIiIiPCAJ2I\niIiIyIgwQCciIiIiMiIM0ImIiIiIjAgDdCIiIiIiI8IAnYiIiIjIiDBAJyIiIiIyIgzQiYiIqFZI\nSQHq1AHi4sreNiYGMDcHLl6s/HERlZWCO4kSERGRsUhOlsHy2LFAmzZla+vnByiVwMGD5Tu3hwfQ\nujWwY0f52hNVFs6gExERkdFITgZCQoCrV8vW7uhROXM+a1b5zx0UBOzcCZw5U/4+iCoDA3QiIqIn\nVEEB8PBhTY/COISFAQ0bAq+8Uv4+hgwBrKyAjRsrb1xE5cEAnYiInkhRUYBCAezfD3zwgUxNqFsX\n6NYNSEqSdQ4eBF58EahXD2jaFFi6VLsfpRJYvhxwdgYsLYH69QF/f+DUKc16mZnAokWy/0aNAAsL\noF07YP587SD50SMgOBjo0EEGfPXrAy4uwNy5mvWCg+U16JotbtMG6NVL+3rj4+V1ODnJ8W7fXrbr\nqKz7Vp5zJiQAq1bJsVtYAO3bA19+qXk/xo2T3/fuLdsoFDLdpST5+TItxtcXMDPTPJaXJ3PLVX09\n/jVkSFFda2ugRw/g229LPh9RVatT0wMgIiKqiPnz5UxyUBCQmwt8+inw8ssy8JswAXj7beCtt2Qg\nu3gx0LYtMGqUbJuXB/TvD/zyCxAYCLz7LpCRAWzaBPj4AD//DHTpIuveuAF88QXw+uvAm2/KhxEP\nHgQ+/lgGpHv3Fo1p2jQgIgIYPRqYOVOO7+JFGaBW1Jw5ctyTJgG2tvJNQFmuozLuW1nvncrChUBO\nDjB5sgzQN2yQwXe7drLNkCHArVvA//4n6z73nGzn5FTyPTlxAsjKAjw9tY/l5srfxeNWrwZOnpRv\nKIrz9pa/y/PngY4dSz4vUZURRERET6DISCEAIdzchFAqi8pjY2W5qakQx48XlSuVQjRpIoSXV1FZ\naKisu2ePZt8ZGUK0bClEz56a7XNztcexaJHs49ixojJ7eyEGDCj9GpYskW1TU7WPtW6teX7V9bZv\nL0R2tmbdslxHZdy38p7T1VXznH//LYS5uRAjRmjXTUzUuiV6RUTINrGxhtWfO1fWX7VK+9jmzfJY\ndLTh5yeqbExxISKiJ9rUqTKFQaVHD/nq5QV07VpUbm4uZ1iLL6O3ZYucJfXwANLSir5yc2W6xOHD\ncsZX1V6VPpGfD6Sny7r9+smyY8eK+rWzkw8apqRUzfVaWWmWleU6ivdT3vtW3nO+847mOZs3l2ku\nFV3a8O5d+dqgQcn1hACmT5dpNuvXA7Nna9dp2FC+/vNPxcZEVBFMcSEioieao6Pmz/b28rVtW+26\n9vbAv/8W/XzunAwiHRz095+WBrRsKb8PC5MPEJ45AxQWatZLTy/6fs0amfbh4iLH17u3TKXw9wdM\nKjg11r69dllZrwOo2H2rrHMCMiD+6y/9fRhCoZCvJS0cXVgoU2siImSq0vjxuuup+lD1SVQTGKAT\nEdETzdS0bOXFCSGD6NBQ/XVUAWhoqJxx9fMDZswAmjWTs8E3bsg86uIB+6BB8sHPXbtknnp8PBAe\nLmep4+OLZpFLCgLz83WXPz57XtbrUKnIfavsc1Z0RxbVee7d0328oED+jrZtkzP/I0fq70vVR0lv\nPIiqGgN0IiJ6aj37rEyP6NOn9JntzZvlyiq7d2vW3bNHd/0GDeRDlaNGyQB0/nz5QGlsLDBsWFEd\nQAaFxTflefRIPizZrl3lX0dlqapzlmfmunNn+aorVSYvTz7U+/33wDffaK7aosulS5p9EtUE5qAT\nEdFTa/Ro4PZt/bPAd+4UfW9qKoPH4rO9+fnAihWabQoKgPv3NcsUCsDNTX5ffJZXla4SH69Zf/Vq\n7RSayrqOylJV57S2lq/6ZsN1cXOTK9qololUUSrlqjs//ih3By0tOAdkH888I1fHIaopnEEnIqKn\nVlCQ3H1y7ly5BGKfPjLQu3ZNrhNuaQkkJsq6Q4cCCxYAAwbIQO/BA+Drr7XX3c7MlGuHv/aaDBwb\nNwZSU+WSgvb2msv69esnH7RcvFjmeLdtKx+uTEqSa61XxXVUlqo6Z9euckb+ww9lXn+9evK+dOum\nv42pqfydxMbKoNzCQpaPHg388INMb0lPl+ktxb32mhyzSlYWcOiQ/vx0ourCAJ2IiJ5aZmbATz/J\nhz83bwaWLJHlzZrJlUvGjCmqO3eunD0PD5fBaZMmwBtvyI11OnUqqmdlBbz3ngxS4+Nl0KcK2Bcs\nkH2rmJrKoHLGDGDdOpmb7ucn89Z9fKrmOipLVZ2zVSv5IOfKlXKlmbw82VdJATog60ZFydny11+X\nv6vdu+WxqCj5VZyJiXwzVdx338lNpyZPLt/YiSqLQoiKPppBREREVPP69weys+UseHl4eMidVXfs\nqNxxEZUVA3QiIiKqFc6cAV54Qa6e4+dXtrYxMcDw4bKPZ5+tmvERGYoBOhERUS2WlQVER8vlIJs3\nl7n0qgcxicg4MUAnIiKqhbKzgSlTgKNHgcuXi8qdnABvb7nhUr16NTc+ItKPAToREVEtk50tV4h5\nfNnB4ry85EOsDNKJjA/XQSciIqplpkwpOTgH5PEpU6pnPERUNgzQiYiIapGsLJnWYoikJFmfiIwL\nA3QiIqJaJDpaM+e8JJcuyfpEZFwYoBMREdUiN26Urf7Nm1UzDiIqPwboREREtUjz5mWrX3xnUyIy\nDlzFhYiIqBbJygJcXQ1Lc2nXDjh1iuuiExkbzqATERHVItbWcp1zQ3h7MzgnMkacQSciIqpluA46\n0ZONM+hERES1TL16MvgeNUruHFpcu3ZAYCCDcyJjxhl0IiKiWiwrC/jf//7G1av34O7+PIYOZVoL\nkbGrU9MDICIioqqTlnYV8+Y9i/z8fGzbtg3W1m/U9JCIqBRMcSEiIqrFEhMTkZ+fDwDYt29fDY+G\niAzBAJ2IiKgWK57JyqxWoicDA3QiIiIiIiPCAJ2IiIiIyIgwQCciIiIiMiIM0ImIiIiIjAgDdCIi\nIiIiI8IAnYiIiIjIiDBAJyIiIiIyIgzQiYiIiIiMCAN0IiIiIiIjwgCdiIiIiMiIMEAnIiIiIjIi\nDNCJiJ4CBw4cgEKhQFRUVE0PpcqlpKSgTp06iIuLq7Q+Y2JiYG5ujosXL1Zan0RE+jBAJyKqJZKT\nkxEcHIyrV6/W9FD0qo4xzpo1Cz4+PvD19a20PgMCAuDi4oJ58+ZVWp9ERPowQCciqiWSk5MREhKi\nM/h96aWXkJOTg8DAwOofWDEljbEyHD16FHFxcZg1a1al9x0UFISdO3fizJkzld53VXr06JH6+4sX\nLyIrK6sGR0NEhmCATkT0FDAxMYGlpSVMTU1reihVKiwsDA0bNsQrr7xS6X0PGTIEVlZW2LhxY6X3\nXRWys7MRGBiI4OBgddnhw4fh6uqKwMBAZGdn19zgiKhEDNCJqFaJioqCQqFAQkICVq1aBScnJ1hY\nWKB9+/b48ssvteorlUosX74czs7OsLS0RP369eHv749Tp06p6/z1119QKBQagQ4A+Pn5QaFQYM2a\nNRrl3bp1Q6dOnUodqyHnVnn06BGCg4PRoUMHWFlZoX79+nBxccHcuXMBAMHBwRg3bhwAoHfv3lAo\nFFAoFBg7diwA3Tnoqnu1f/9+fPDBB2jdujXq1q2Lbt26ISkpCQBw8OBBvPjii6hXrx6aNm2KpUuX\naowrMzMTixYtQrdu3dCoUSNYWFigXbt2mD9/Ph4+fKhRt7QxlvWePC4/Px8xMTHw9fWFmZmZxrGc\nnBy0aNECrVq1glKp1Dg2ceJEmJqaYtu2bSX2b21tjR49euDbb78tdSzV5fa9LKRn5miVZ2dno1+/\nftiyZQvu3r2rcezy5cvYsmUL+vXrxyCdyFgJIqJaJDIyUgAQ3bp1E88//7xYuXKlWLNmjejQoYMA\nIA4fPqyum5ubK3r16iXMzc3FhAkTRFhYmPjoo4+Eo6OjqFu3rvj111/Vddu2bStefPFF9c9KpVJY\nWVkJExMTMXDgQHV5RkaGMDU1FdOmTStxnGU5txBCjB8/XgAQo0ePFhs2bBCfffaZCAoKEu7u7kII\nIX7//Xfx9ttvCwBi4cKFYvPmzWLz5s3il19+EUIIkZiYKACIyMhIrXvVpUsX4ebmJj799FPx0Ucf\niUaNGglbW1uxc+dO0aBBAzF//nwRFhYmevXqJQCIzZs3q/s4d+6ceOaZZ8Q777wj1qxZIz777DMx\nbNgwoVAohJ+fn8Y1lDbGst6TxyUlJQkAIjQ0VOfxL774Quv4/PnzBQCxfv36EvtWCQ4OFgDEuXPn\nDKpflZS5+cLmleWi7svLxOywveL2v5nqY6NGjRIASv0aNWpUDV4BEenDAJ2IahVV0Onq6iqUSqW6\n/O+//xbm5uZixIgR6rLQ0FABQOzZs0ejj4yMDNGyZUvRs2dPddmECROEmZmZyMrKEkIIcfDgQXWA\nY2NjI/Ly8oQQQnz//fcCgPjuu+9KHGdZzi2EEPb29mLAgAEGXXtiYqLWsZICdDc3N417FRsbKwAI\nU1NTcfz4cXW5UqkUTZo0EV5eXhplubm5WudbtGiRACCOHTtm8BjLek8eFxERIQCI2NhYncfz8/OF\ns7OzcHBwEJmZmWL16tUCgAgJCSmx3+I2b94sAIjo6GiN8vuZOeLQH39V69fB5Kui//ubBXoFC/QK\nFha+S8WID74VKZf+Fk5OTgYF6O3atROZmZl6rpaIakqdKpmWJyKqYe+88w7Mzc3VPzdv3hzt27fX\nWCZvy5Yt6NixIzw8PJCWlqbR3tfXF19++SVycnJQt25d9OnTB+Hh4Th8+DBefvllJCQkoHHjxggK\nCsKWLVvw66+/wtvbG4mJiTAxMUGvXr1KHF9Zzg0AdnZ2OHPmDFJSUtC5c+cK3h1NU6dO1bhXPXr0\nAAB4eXmha9eu6nJzc3N4enriyJEjGmUq+fn5yMzMREFBAfr164dly5bh2LFj8PT0NGgcZb0nj1Ol\ncjRo0EDncVNTU6xYsQL+/v4ICAhAQkICpk+fjsWLFxs0PgBo2LAhAOCff/7RKH8pKAp/XLljcD9V\nQZlXgG0JZxB76CxyLl82qM2lS5cQHR2tkWZERDWPAToR1UqOjo5aZQ0bNsRff/2l/vncuXPIycmB\ng4OD3n7S0tLQsmVL9OnTBwCQkJCgDtB79+4Nd3d32NvbIyEhAd7e3khISMALL7ygN0gsz7kBYM2a\nNQgMDISLiwscHR3Ru3dv+Pv7w9/fHyYmFXuc6PF7ZW9vDwBo27atVl17e3v8+++/GmVhYWHYuHEj\nzpw5g8LCQo1j6enpBo+jrPfkcQqFAgAghNDbfuDAgXB3d8f+/fsxYsQIrF27Vmc9T09PzJ49G2+8\n8YZGuapv1blURr/8PHYeOq/3vFXl4aM8XPsnA/8+yPm/cQGO9kBZ1pm5efNm1QyOiMqNAToR1Ur6\nVispHrwJIeDi4oLQ0FC9/aiCxSZNmuC5555DQkICHj58iGPHjmHdunUwMTFBz549sX//fkyZMgV/\n/PGHQUv8leXcADBo0CBcvXoVu3btwsGDBxEfH4/w8HD06NED8fHxGjPZZaXvXhmy4ktoaChmz54N\nPz8/zJgxA82aNYO5uTlu3LiBsWPHagXsJSnrPdF37N69e3rrbN++HcnJyQAAGxsbrUAbAAoKCnD6\n9Gm4urpqHVP1/fg4Zg/vjtnDu+s9b1VQ5uaj8ZBVeJCthLmZKd4e6I55I19E/E87MG674f00a9as\n6gZJROXCAJ2InlrPPvss7t69iz59+hg0C92nTx9s2LABP/zwA3Jzc9G3b18AQN++fTFnzhzs3r0b\nQgj1bHtlnhuQqRujRo3CqFGjIITA/Pnz8fHHHyM2NhbDhg3TGWxWtc2bN6NNmzbYvXu3xnXs2bNH\nZ/2Sxliee1KcKvVH326f+/btQ2BgIAYPHgwzMzNERERg5syZeO6559R1bt26BScnJyiVSnh4eKjb\nde8ug+9Lly5pnKsmmZuZYuzLL8DUxASzhnujhYMtAGDo0KFYtmwZLhuQ5tKuXTsMHTq0qodKRGXE\nZRaJ6Kk1evRo3L59W++M7Z07MqdYtXV8w4YNUVhYiJCQELRq1QpOTk4AZOCuVCrx0UcfoU6dOuoc\n7so4NyBndO/fv69xXKFQwM3NDUDRrK61tbXGzxW1Z88etGnTpsQ6pqamUCgUGp9M5OfnY8WKFTrr\nq8Z44sQJmJiY4ODBg+pjZbknuri5ucHW1la9RGRxx44dw5AhQ+Dj44OtW7di2bJlMDExwYIFCzTq\nNW3aFBEREfD09ERWVhaysrLUwTkAJCUl4ZlnnkGHDh1KHEt1UCgUWDt9AEKnvawOzgF5j729vQ3q\nw9vbW/07ISLjwRl0InpqBQUFIS4uDnPnzkVCQgL69OkDW1tbXLt2Dfv374elpSUSExPVW8e/9957\nWLZsGc6dO6fxUF2nTp3QpEkTnD17Ft7e3rCxsam0cwNyrfGmTZvitddeg5ubG+7du4ekpCSkpKTA\n3t4e/v7+AICuXbvCxMQEH374IdLT01GvXj20bdsW3bp1q5L7B8jZ2gULFmDAgAEYMmQIHjx4gK+/\n/lprHXIV1Ri//vpruLq6Yty4cfj666/h5eVVpnuii6mpKYYMGYLY2FgolUpYWFgAkLntr776Ktq3\nb4+YmBhYWFjAyckJEyZMwMaNG3HkyBH4+Pio+zl58qT6zU9xWVlZOHToEMaPH1/Bu1b1Nm7ciEuX\nLul8s6Li5eWFDRs2VOOoiMhgNbZ+DBFRFShpGb+ePXuK1q1ba5Tl5eWJtWvXii5duggrKythZWUl\n2rVrJ958802xd+9e8csvvwgAIiYmRgghhLu7uwAgvvrqK41+3nzzTQFA/Oc//zF4rKWdW0WpVIr5\n8+eLrl27igYNGggTExMBQAwdOlRcuHBBo8+oqCjx3HPPCTMzMwFAjBkzRghR8jKLuu4V/m8JyUeP\nHmmUjxkzRhT/X0d+fr5Yvny5cHJyEubm5qJVq1Zi7ty54uzZswKAWLJkiVbfqjGampoKAKJv375l\nvif6HDt2TGMZxL/++ku0aNFCODo6itu3b2vUvXnzpqhbt67o3r27Rnnfvn3Fxo0bdY4bgDh9+nSp\n4zAGWVlZYtSoUcLBwUFracXAwED1kqFEZHwUQpTwuDsR0VMuMDAQu3fvxq1bt/TOCle34OBghISE\nIDU1tdQUlLIqKCiAUqmElZVVpfarkpmZqf6EQQgBR0dHdO7cGT/88EOlnaN///7Izs7GoUOHytW+\nUaNG2LVrl9bykB4eHmjdujV27NhRGcOsNmFhYZg2bRoA4MUXX8Tu3buZ1kJk5JiDTkSkh76t46Oi\noqBQKBAfH4/g4GC0bt0aFhYWeP755/VuFx8TEwMfHx9YW1vD2toaPj4+iI2N1ar3yy+/YMCAAWjS\npAksLS3RvHlzvPLKK+pUhbFjxyIkJASAXAZRoVBAoVAgODhY3UdGRgbmzZuHdu3awcLCAg4ODhg5\nciSuXLmica7i17F06VI4OTnB0tIS27fLJUB69eql8w3Azz//DF9fX9jZ2aFu3bpwd3dHeHi4Vj1V\n+ytXrmDo0KFo0KABbG2LcqUVCgVefvll7NmzB1lZWXp+C2X36aef4ujRo9i3b1+Z2+bl5elcGjIm\nJganT5/GypUrK2OI1crS0lL9/bPPPsvgnOgJwBx0IiI9Tpw4gaysLL0b7cybNw/Z2dmYOnUqFAoF\nIiMjMXLkSDx69EgjR101g9mxY0csWrQICoUCUVFRCAgIwOeff463334bAPDnn3/C19cXTZo0QVBQ\nEJ555hncvn0bR44cwe+//w4vLy9MnjwZDx48wM6dO7F69Wo0atQIAPD8888DkMF59+7dce3aNYwf\nPx7Ozs64desWwsLC0K1bN/z2229o3bq1xnXMmTMHeXl5mDRpEmxtbUt8APKHH37A4MGD0aRJE8ye\nPRs2NjbYtm0bJk6ciCtXruDDDz/UqJ+VlYWePXvCx8cHH374odYGP97e3vj8889x+PBh9O/f37Bf\nTCmcnZ2Rn59frrZmZmaYM2cO/Pz8kJ+fjz/++AOOjo4ICAhAbm5upYyPiKhUNZxiQ0RktPRtHa/K\n3W7VqpW4f/++uvz+/fuiVatWwt7eXjx8+FAIIcS9e/dEvXr1hJOTk8jIyFDXzcjIEI6OjsLa2lqk\np6cLIYRYu3atACCOHTtW4riWLFkiAIjU1FStYzNmzBCWlpYiOTlZo/zq1avCxsZGnZNe/Drat28v\nsrOztfp6PGc/Pz9ftGrVStjZ2YkbN26oy5VKpejevbswMTHRyInv2bNnqXn5hw4dEgDEqlWrSrxm\nKr/w8HB1/vm4ceNqejhEZACmuBAR6VHa1vFTp06FnZ2d+mc7OztMmTIF6enpOHDgAAAgLi4O2dnZ\nmDFjhkZ6h62tLaZPn46srCzEx8er2wNAbGwsHj16VObxCiGwdetWvPTSS2jevDnS0tLUX/Xq1YOX\nl5fOtI+pU6calHN+4sQJ9cx88c1tzM3NMXfuXBQWFupM25kzZ47ePhs2bAgAWjPrRERPM6a4EBHp\nUdrW8cU3uFHp1KkTAKjzvVNTUwHItIvHqTa7UdUdMWIEtmzZguXLl2P16tXw8vLCyy+/jBEjRmil\npehy9+5d/Pvvv9i3b5/eHTd1bQDUvn37Uvsu67WoODg4oH79+nr7VN3bmthkiYjIWDFAJyLSo7St\n43UFlY8H8/qCe10sLCwQFxeH48ePY+/evfj555+xePFiBAcH4+uvv8bgwYNLbK86V79+/TBv3jyD\nz2voii1luRZD+1bdW31vKIiInkYM0ImI9Cht6/izZ8/itdde0yg7d+4cAMDR0REA1LuNnjlzBn37\n9tVqX7yuiqenp/rB1OvXr8PNzQ2LFi1SB+j6ZptVs9UPHjxAv379DLvIMih+LY/Tdy2luXTpEoCi\ne01ERFxmkYhIr5K2jgeADRs2ICMjQ/1zRkYGNm7ciPr166Nnz54AAF9fX9SrVw/r1q1DZmamum5m\nZibWrVsHa2tr+Pr6AgDS0tK0ztGiRQs4ODhozOKrlsl7fGbfxMQEb731Fo4fP47o6GidY65Irre7\nuztatWqFyMhI3L59W12el5eHTz75BAqFAoMGDSpTn0lJSahTp47GTp5ERE87zqATEemhb+t4lUaN\nGqFbt24YP348hBCIjIzEtWvX8MUXX6hTO+rXr4+PP/4Y06ZNQ7du3dTLL0ZFReHSpUv4/PPP1Q+H\nLlu2DPv27cPAgQPRtm1bCCHwww8/4Pz583j//ffV5/Xy8gIgl3l86623YGlpic6dO6Nz58748MMP\nceTIEQwfPhzDhw+Hl5cXzM3N8ddff2HXrl3w8PBAVFRUue/HZ599hsGDB6Nr1654++23YWNjg2++\n+QZJSUlYuHAhnn32WYP7E0Jg9+7d6N+/P9fmJiIqrqaWjyEiehI8vnW8EEXLE8bFxYnFixeLli1b\nCnNzc+Hs7Cy2bt2qs58dO3YIb29v9fb13t7eYufOnRp1EhMTxfDhw0Xr1q2FpaWlsLe3F56enmLT\npk2isLBQo+7KlStF27ZtRZ06dQQAsWTJEvWx7Oxs8cEHH4jOnTsLS0tLYW1tLTp27CgmTpwokpKS\ntK4jMTFR55gfX2ZR5cCBA6Jfv37CxsZGWFhYCFdXV7Fp0yaD2xfvB4D48ccf9dahiuMyi0RPHoUQ\n5Xjqh4joKfL41vFRUVEYN24cEhMT0atXr5od3BNs8ODBuHbtGn777Teu4lKFIiIiMGHCBADAuHHj\nEBERUcMjIqLSMMWFiKgUn376KV544QXs27cPfn5+JdYtKChQr59enIODA0xNTatqiE+c5ORkxMbG\nIjExkcE5EdFj+JAoEVEpVFvHlxacA3LVlaZNm2p9Xb9+vRpGqtuDBw9gYmKic/wXLlxAp06dYGFh\ngU2bNlXbmFxdXVFYWKh+mJaIiIpwBp2IqBI1adIEcXFxOstrysmTJyGEgLu7u0b5Dz/8gMDAQNSr\nVw8HDx5UP3xKREQ1iwE6EVEZjR07Vr0ay+MsLS2rZA1yADhw4AB69+5d5tz3kydPAoA6QBdC4IMP\nPkBISAh8fHzw7bff1ugbCCIi0sQUFyKiSpCTk4MWLVqgVatWUCqVGscmTpwIU1NTbNu2rUbGduLE\nCQCAh4cHMjIyMGjQIAQHB2Pq1KlISEjQCM6nTJkChUKBmzdvavXz559/wtzcHEFBQdU2diKipxED\ndCKiSlC3bl2EhITg+vXrCAsLU5cvWLAA4eHhWLduHUaMGFEjYzt58iTs7OygVCrh6emJuLg4REZG\nYv369TAzM9Oo6+3tDQA4fvy4Vj8zZ86Era0tgoODq2PYRERPLQboRESVZOzYsXB2dsZHH32ErKws\nrFmzBitWrEBISAjeeeedGhlTVlYWLly4AFNTU3h5eSEnJweHDh3Sm6KjykN/PED/6aefsHv3bnzw\nwQewt7ev6mETET3VmINORFRJTE1NsWLFCvj7+yMgIAAJCQmYPn06Fi9eXOa+CgsLce/ePY2yjIwM\n9WtaWprGsQYNGsDERHvOJTk5GYWFhcjPz0dmZibmzJmDLl266D1vhw4d0KBBA40APS8vD7NmzULn\nzp0xefLkMl8LERGVDWfQiYgq0cCBA+Hu7o79+/fjjTfewNq1a3XW8/T0xDfffKO3n2vXrsHBwUHj\nKyAgAAAQEBCgdezatWs6+1Hln69duxbdu3dHSEgIfvzxxxKvwcvLC7/99htU+9itXbsWFy5cwJo1\na7iWO1W6AwcOQKFQICoqyqAFdtmNAAAgAElEQVT6bdq0qbYNwkoaW0pKCurUqaNz1SZDxMTEwNzc\nHBcvXqzgKKk24gw6EVEl2r59O5KTkwEANjY2OjfhKSgowOnTp+Hq6qq3H13LNf7++++YM2cOVq1a\nhRdeeEGrvi6qFVy8vb0xYMAAdO3aFW+++SaOHDkCFxcXnW28vLywa9cu/Pnnn2jQoAGWLl2KgIAA\n9O3bV/+FEz1lZs2aBR8fH/j6+parfUBAAFxcXDBv3jzs2LGjkkdHTzoG6ERElWTfvn0IDAzE4MGD\nYWZmhoiICMycORPPPfecus6tW7fg5OQEpVIJDw8Pdbvu3btr9KVrucY6deSfbA8PD4NnEE+cOAEb\nGxu0b98eCoUC33//PV588UX4+/vj+PHjaNy4sVab4g+K/vzzz1Aqlfj0008Nvg9EZfHSSy8hJydH\n64FlY3b06FHExcUhJiamQv0EBQVhzJgxOHPmDJydnStpdFQbMMWFiKgSHDt2DEOGDIGPjw+2bt2K\nZcuWwcTEBAsWLNCo17RpU0RERMDT0xNZWVnIysrSCs4rS05ODs6fPw9XV1f1TL6rqyu+/PJLXLt2\nDQEBAVpLQgJAt27dYGJigvDwcERGRuK9996Do6NjlYyRnhwFBQV4+PBhpfdrYmICS0vLJyp9Kiws\nDA0bNsQrr7xSoX6GDBkCKysrbNy4sZJGRrUFA3Qiogo6d+4cXn31VbRv3x4xMTGwsLCAk5MTJkyY\ngNjYWBw5ckSj/smTJ+Hm5lbl40pOTkZBQYF6pl7l9ddfR3BwMI4ePYoJEyZotbOxsUGnTp3w888/\no3HjxvjPf/5T5WMl4xIVFQWFQoH4+HgsXboUTk5OsLS0xPbt2wEASqUSy5cvh7OzMywtLVG/fn34\n+/vj1KlTGv08evQIwcHB6NChA6ysrFC/fn24uLhg7ty56jr68ryvX7+O4cOHw87ODra2tvD398fl\ny5d1jjc4OBgKhQJXr17VOvZ4znpmZiYWLVqEbt26oVGjRrCwsEC7du0wf/58g96A5OfnIyYmBr6+\nvlqz/mXdR8Da2ho9evTAt99+W+p56enCAJ2IqAKuXbsGPz8/2NnZYffu3bC1tVUfW7x4MerWrYv3\n339fo83JkydLzD+vLI/vIFrc4sWLMXz4cPVs/+M8PT0BAB999BFsbGyqdqBktObMmYNt27Zh0qRJ\nWLt2LTp06IC8vDz0798fISEh8Pb2xurVqzF//nycPXsWPj4++O2339Ttp02bhpCQEHh5eSE0NBQf\nfvgh+vbti4SEhBLPe//+fbz00kvYsWMHAgMDsWLFClhZWaF3797Izs6u0DXduHEDX3zxBbp06YL/\n/ve/CA0Nhbu7Oz7++GMMHjy41PYnTpxAVlaW+t9IceXZR8Db2xt37tzB+fPny3dBZLQePnyIpUuX\nYtKkSQCAixcvlvqQvpogIqJq1bBhQ3Hs2LGaHoZeubm5wtHRUXTp0kUUFhbW9HCogsLDwwUAAUCM\nGzfOoDaRkZECgGjfvr3Izs7WOBYaGioAiD179miUZ2RkiJYtW4qePXuqy+zt7cWAAQNKPFdiYqIA\nICIjI9VlCxYsEABERESERt2goCABQOMcQgixZMkSAUCkpqZq9d+6dWuN+kqlUuTm5mrVW7RokQCg\n8W9T19giIiIEABEbG6vVx/nz5wUAsWDBAo3yH3/8UQAQ69ev12qzefNmAUBER0drHaMn2/Dhw8XK\nlSuFs7OzEEKIhw8fihdeeMGgtpxBJyKqRnl5eUhPT6/pYZRo1apVSE1Nxbp163SuQkNPj6lTp8LK\nykqjbMuWLejYsSM8PDyQlpam/srNzYWvry8OHz6MnJwcAICdnR3OnDmDlJSUMp03JiYGzzzzDEaP\nHq1RPm/evIpdEABzc3N1akp+fj7S09ORlpamfij72LFjJba/e/cuALn3wOPKs49Aw4YNAQD//PNP\n+S6IjNbly5fx/vvvq/97q1u3rnr52tJwFRciompkZmaGOXPmwM/PD/n5+fjjjz+M4gHMe/fuYe/e\nvfjjjz/wySefYNasWepdRenp1b59e62yc+fOIScnBw4ODnrbpaWloWXLllizZg0CAwPh4uICR0dH\n9O7dG/7+/vD399e5sZbKlStX0LVrV60HR5s2bYr69euX/4L+T1hYGDZu3IgzZ86gsLBQ41hpb6BV\nb1r1BVpeXl44cuQIhBBQKBTqfQTi4+N1Pgir6odvhmsfc3Nz5OTkqH+3ly9fhoWFhUFtGaATEVWz\nlStXYuXKlTU9DA179+7Fm2++icaNG2PmzJlYsWJFTQ+JjMDjs+eADChdXFwQGhqqt50qeB80aBCu\nXr2KXbt24eDBg4iPj0d4eDh69OiB+Ph4mJub6+1DX8CqKzAuKbjNz8/X+Dk0NBSzZ8+Gn58fZsyY\ngWbNmsHc3Bw3btzA2LFjtQJ2fdf2+E6/KmXdR0DVT0lveOjJFBwcjP79++P69et46623cOTIEURG\nRhrUlgE6ERFh5MiRGDlyZE0Pg54Azz77LO7evYs+ffqUOAuu0qBBA4waNQqjRo2CEALz58/Hxx9/\njNjYWAwbNkxnG0dHR1y4cAEFBQUas863bt1CRkaGznMAMtht06aNuvzRo0e4desW2rVrpy7bvHkz\n2rRpg927d2uMf8+ePaVeCwB07twZAPTuAFrWfQQuXbqk0S/VHn5+fvDw8EBSUhKEEFi7di0aNWpk\nUFvmoBMREZHBRo8ejdu3b+udQb9z5w4AuW76/fv3NY4pFAr1EqP6ZqABOfN+584dfPXVVxrl+j55\nUqXixMfHa5SvXr1aa0bc1NQUCoVCYyY+Pz/f4E+N3NzcYGtri6SkJJ3Hy7qPQFJSEp555hl06NDB\noPPTk6Nv375o2LAhXn31VQwcOBCNGjUyeEdmzqATERGRwYKCghAXF4e5c+ciISEBffr0ga2tLa5d\nu4b9+/fD0tISiYmJyMzMRNOmTfHaa6/Bzc0NjRs3RmpqKjZs2AB7e3v4+/vrPcf777+Pr7/+GpMm\nTcKJEyfg7OyMAwcO4OjRozpnIPv164eOHTti8eLF+Pfff9G2bVscPnwYSUlJWvWHDh2KBQsWYMCA\nARgyZAgePHiAr7/+2uCdTE1NTTFkyBDExsZCqVRq5RQX30egSZMmJe4jkJWVhUOHDmH8+PEGnZue\nDI8ePcLDhw+RlpaG9PR09ZvBBw8e6FwjXxcG6ERERGQwMzMz/PTTTwgLC8PmzZuxZMkSAECzZs3g\n6emJMWPGAJD56++99x7279+P+Ph4ZGVlqQP2BQsWoFmzZnrPYW9vj0OHDmHWrFn46quvIIRAr169\nkJiYqHMG0tTUFLGxsZgxYwbWrVsHc3Nz+Pn54eDBg/Dx8dGoO3fuXAghEB4ejqCgIDRp0gRvvPEG\nxo0bh06dOhl0D6ZOnYqoqCj8+OOPeP3117WOe3p6IiUlpdR9BL777js8fPhQ5+ou9OT6/PPPsWbN\nGty8eRMeHh7qAN3W1hbTpk0zqA+FMHS9FyIiInriREREqHeMHTduHCIiImp4RLVD//79kZ2djUOH\nDmmU5+XloWPHjurlFkt6gNXDwwOtW7fGjh07qnq4VAPWrVuH6dOnl6stZ9CJiIiI9CgoKFCvfV7c\nxx9/DHd3d+zbtw9+fn7qctU+Alu3bi0xOI+JicHp06exbdu2Khk31bzp06cjJSUFZ8+exaNHj9Tl\nj6/vrwsDdCIiIiI9rl+/jrZt22qVp6amqpdwLM8+AgEBAcjNza2SMZNxCAkJwYEDB3D27Fm88sor\n2L17N1588UUG6EREREQV0aRJE8TFxeksV+E+AqRLdHQ0fv/9d7i5uSEyMhJ37tzBxIkTDWrLAJ2I\niIhID0tLS/Tr16/EOtxHgHSpW7cuTExMUKdOHTx48ACNGzfGlStXDGrLddCJiIhIw5QpU6BQKHQu\nCffnn3/C3NwcQUFBVTqGvLw8mJubQ6FQ6PwaMmRIlZ07JycHLVq0QKtWraBUKjWOTZw4Eaampswd\np1J16dIF9+/fx6RJk+Dh4QF3d3d4enoa1JYz6ERERKTB29sbn3/+OY4fP46AgACNYzNnzoStrS2C\ng4O12hUWFpa4AdHjGjRooHc30tzcXJ0rzqxevRonT54scR31iqpbty5CQkIwceJEhIWFYebMmQCA\nBQsWIDw8HOvXr8eIESOq7PxUO4SFhQGQb3j79++PBw8e4PnnnzessSAiIqJaKzw8XAAQAMS4ceMM\nanP+/HkBQCxYsECj/McffxQAxPr163W2S01NVZ/LkK/U1NQyXcvcuXMFALFq1aoytSuP/Px84ezs\nLBwcHERmZqZYvXq1ACBCQkKq/NxUO/Tp08egMl04g05EREQaOnTooF7HWyUvLw+zZs1C586d9W6s\no++BSn2KP2hZEiEEZsyYgfXr12P9+vV45513dNa7f/8+1qxZY/D5Z8yYgQYNGug8ZmpqihUrVsDf\n3x8BAQFISEjA9OnTsXjxYoP7p6cTdxIlIiKiKuHl5YUjR45ACAGFQoG1a9fiwoULiI+Ph6mpqc42\nhjxQWVaFhYWYPHkyIiIi8MUXX2D8+PF6696/fx8hISEG9z1q1Ci9AToADBw4EO7u7ti/fz9GjBiB\ntWvX6q3r6emJ2bNn44033jD4/FQ76dpJVKFQwMbGBu+++65BfTBAJyIiIi1eXl7YtWsX/vzzTzRo\n0ABLly5FQEAA+vbtq7eNvk199HFwcNAb7Kv6Gzt2LLZt24YtW7aUulJKmzZt1LOVlWH79u1ITk4G\nANjY2OjdeKigoACnT5+Gq6trpZ2bnlxBQUEICgrCBx98gPfeew+2trZYunQpTp48CW9vb4P64Cou\nREREpEUVSBw/fhwLFy6EUqnEp59+WmKb69evo2nTpgZ/Xb9+XW9feXl5GDFiBLZv345vvvmm2pcx\n3LdvHwIDAzF48GCMGDECEREROHfunFa9W7duwcbGBkqlEh4eHrC2tsYvv/xSrWMl4xQdHQ1bW1sc\nPnwYcXFxGDt2LKZOnWpQW86gExERkZZu3brBxMQE4eHhOHz4MObOnQtHR8cS21RWDrpSqcSwYcMQ\nFxeHHTt24NVXXy3T2Cvq2LFjGDJkCHx8fLB161b8/fff+O6777BgwQLExMRo1G3atCkiIiKwZs0a\nJCUlVes4ybipPh366aefMGXKFAwaNEjn6ke6MEAnIiIiLTY2NujUqRN+/vlnNGnSBP/5z39KbVNZ\nOeijR4/GDz/8gLFjxyI9PR1btmzROP7aa6/B1ta2wufR5dy5c3j11VfRvn17xMTEwMLCAk5OTpgw\nYQI2btyII0eOwMfHR6PNyZMn4ebmViXjoSdX8+bNMXnyZMTHx2PevHlQKpUoLCw0qC0DdCIiItLJ\n09MTKSkp+Oijj2BjY1Mt5xRCYPfu3QCAqKgoREVFaRw3MTFBZmZmlZz72rVr8PPzg52dHXbv3q3x\nJmDx4sX48ssv8f777+PIkSMa7U6ePIlhw4ZVyZjoybV9+3bs2bMHc+bMQf369XHr1i188sknBrVl\ngE5ERERa8vLycODAAXTp0gVjxoyptvMqFAo8ePCg2s5XXKtWrfTmxTdt2hQPHz7UeSw5ORnLly+v\nyqHRE8jKykpjx1vVsxeGYIBOREREWlatWoXU1FRs3bpV7+olJN/IpKen1/QwqJZhgE5EREQAgHv3\n7mHv3r34448/8Mknn2DWrFnw8vKq6WEZNTMzM8yZMwd+fn7Iz8/HH3/8UerDtESlYYBOREREAIC9\ne/fizTffROPGjTFz5kysWLGipof0RFi5ciVWrlxZ08OgWoQBOhEREQEARo4cWe3rjRORNm5URERE\nRERkRBigExEREREZEQboRERERERGhAE6EREREZERYYBORERERGREGKATERERERkRBuhEREREREaE\nAToRERERkRFhgE5EREREZEQYoBMRERERGREG6ERERERERoQBOhERERGREWGATkRERERkRBigExER\nEREZEQboRERERERGhAE6EREREZERYYBORERERGREGKATERERERkRBuhEVL169QLatCm9rKrORURE\nZOQYoBPRk23NGiAqqqZHQUREVGnq1PQAiIiwbx8gRPnarlkjZ8nHjq3cfomIiGoIA3QiKllmJmBj\nU7XnMDd/svolIiKqQkxxIartoqIAhQKIjweCg4HWrQELC+D554Ft2zTrtmkj87ZPnQJefhmws5P1\nVJRKYPlywNkZsLQE6tcH/P1l/celpwOTJgGNGgH16sl+T5zQPUZ9ueKXLgHjxgEtWshgu1kzYNCg\non4UCuCvv4CDB+X3qq+rV0vu9+efAV9feX116wLu7kB4uP5x3bwJjBwJ2NvLa3n5ZeDCBd3XQkRE\nVEGcQSd6WsybB2RnA1OnyiA2MlIGnY8eaaaHXLsG9OkDDBsGvP46kJUly/PygP79gV9+AQIDgXff\nBTIygE2bAB8fGfR26VJU9+WXgV9/lXW9vIDkZKBfP6BhQ8PG+9tvQN++sq8JE4DOnYF792Qw/ssv\ngIcHsHkzMHOmfBPwn/8UtXVw0N/vDz8AgwcDTZoAs2fLTwe2bQMmTgSuXAE+/FCzfnY28NJL8hqW\nLwdSU4G1a+UbhZQUwNTUsOshqiHPPfeczu+JyIgJIqrdIiOFAIRo1UqI+/eLyu/fl2X29kI8fCjL\nWreWdTdt0u4nNFQe27NHszwjQ4iWLYXo2bOo7PPPZd3FizXrrl4ty1u31izv2VOzrLBQCGdnISws\nhPj9d+2xFBQUfd+6tea5S+o3P19es52dEDduFJUrlUJ07y6EiYkQFy5otgeEWLlSs9+PP9Z9L4iM\nUGFhodi8ebP45JNPRGZmZk0Ph4gMwBQXoqfF1KkypUPFzg6YMkWmohw4UFTeoIFMK3ncli1Ax45y\n5jotregrN1emixw+DOTkyLoxMXJmefZs7THY2pY+1uRk4MwZOY7iKTYqJuX803XihPyEYPx4mS6j\nYm4OzJ0LFBYCsbHa55oxQ7OsTx/5evFi+cZBVI0U2dkYlZ+POUolrKOjiz4VIyKjxRQXoqeFro+2\nO3WSr1euFJU5OelO2zh3TgbgJaWPpKUBLVvK/po21Q7GLSwAR0f5pqAkqsDXza3kemWVmipfnZ21\nj3XuLF+L3wtABvKWlpplqjSdf/+t3PERVabsbPkm/OhR4PLlovJlywBvb2DjRvlMBREZHQboRE8L\nhUK7TNcShFZWutsLAbi4AKGh+s+hCt6F0H0+fefUV0dfH+VVniUXS8ox5xKOZKyys+UzH0lJ2scu\nX5Zfly7Jh8cZpBMZHQboRE+Ls2eB117TLDt3Tr46Opbe/tlngbt3ZXpHaSkmTk5yDfIHDzRn0ZVK\nOYttb19y+w4d5Kuu1WEeV5Yg3slJvp45o33s7Fn5asi9IKpJqanARx8BrVrJh5ubNNGuM2WK7uC8\nuKQkWW/z5qoZJxGVG3PQiZ4WGzbIVVdUMjLkR9z16wM9e5befvRo4PZt/TPod+4UfT9oEFBQAHz6\nqfYYHjwo/VwvvCDTUCIidAfTxWeura3l6i6GcHeXQU1kpLwWlbw84JNPZLA/aJBhfRHVlPfek6sn\n/fe/ctnUMWOAkyeLjmdlybQWQyQlMSedyAhxBp3oadGoEdCtm3xAUggZpF67Bnzxhf60luKCgoC4\nOPkwZUKCnEm3tZV97N8v87QTE2XdceOA//0P+OADOdvn7S1nw7/9Vs5i5+eXfC7VMpB9+wKenkXL\nLN6/L5dZ7N8fmD5d1vXykmuY//e/Ms/exESuza7rY3tTU+Czz+Qyi127Am+/LZdZ/OYbGagsXCg/\nKSCqTnl5ckOwzEz5BvbBA83vH//50qWitrm5wFdfyS9HR/mpWHS0Zs55SS5dkvV17cRLRDWGATrR\n02LlSuDQIRmg3rkjA9GtW4E33zSsvZkZ8NNPQFiY/Eh8yRJZ3qyZDKLHjCmqa25eFMzHxADffScD\n4rg4YM6coo2EStK1q1xHfelSYPt2OdvfqJE8l49PUb0PP5Qz6OvXywBeCPmmQF9erb+/fEOxbJmc\nNc/NlYH9pk0yXYDIEIWFMs9bVwBdUnCt65hq9aOKunJF/hu9caNs7W7erJzzE1GlUQjBp5yIarWo\nKDmjnZgod8YkeloJITfmKmsArev7rCzje0jY1lYG59HRupdK1ScykjPoREaGM+hERGTcVCkg5Zmd\nfvz70tKraoJCIYNr1ZeNje7vVT8nJMhPlVRsbOSnVfPmyU+vhg6VnxAZkubSrp2sT0RGhQE6ERFV\nvsJCOctckdQP1fePHtX01ehWr17pwbQhx6ysyrYaUbNmMm0MACZPBkJCZPqXirW1fO7DkADd21vW\nJyKjwgCdiIgkVQpIZcxUZ2bW9NXoZmYmd9EtbzCt+t7aGqhTQ/8L9feXm3lZW+vfOGzjRvkAaElL\nLXp5yZWViMjoMAediOhJVzwFpKIPLNaGFJCSjllY1PTVVB99O4m2aydnzjds4CZFREaKAToRUU1g\nCkjVpYCQpqws+eDozZsyPWboUONMaykokJuhPc7BoeQdfYlqIQboRESGYgrIk5ECQiU7cADo3btm\nVm9JSQFcXYHduwFfX81jV68Cbdtqt0lNBdq0KbnfmBhg+HC5sRn3MqBagH89iaj2YwoIU0DIOMya\nJfcxeDw4B4AmTeReCbrKSxMQALi4yJVsduyo+DiJahhn0InIOD2NKSDlDa6ZAkJlUVgoN+gyM6ve\n1JGjR4Hu3eVs96BBld//V1/JDdNSUgBn58rvn6gaMUAnosrzNKWAVHSmmikgVN0KCgClUr6hq4m+\nAwNlasutW/LfUWXLygKeeQYYPx5Yt67y+yeqRgzQiaj2p4CYmFTOw4pMAaGapNoVOC4OOHxY5pDf\nvg106AAsXAiMGKG77tGj8udr14BNm2Q+t64c9LQ0YMkS4PvvgTt3ZLD72mvABx8ADRsa1re+nPb8\nfMDeHhg4EPh//0/zWE6OzBs3MZHLRxb/NzZxohzn1q2a16dP//5AcrK8L0RPME7fED2pmALCFBB6\nOs2bJ5dQnDpV/ncdGQmMHCn/HT8eIM+ZI9+AT5ok/y106CBnuh+XkSHTTy5dkjPQ7u7AqVNyKcaE\nBOD4cflvqrS+9TlxQv698vTUPla3rtxsaeJEICwMmDlTli9YAISHA+vXGxacA3L5yL17gfPngY4d\nDWtDZIQYoBNVp6chBcTcvHIeVmQKCJFuaWnAH3/IVCtArnX+/PPyAcw33pABr0pOjgy0i6eeHDig\n3efHH8vZ6/XrgXfeKSp3dQXefVceX7pUs42uvvU5e1a+OjnpPj52LLB6NfDRRzLg/+ILYMUKGbgX\nH09pVP2fOcMAnZ5o/L8fkSGethSQ8gbXTAEhqnpTpxYF54D8fsoUmeZy4AAwYIBmXUMC6J075Xrj\nb7+tWT55MhAcLI8/HqAb2jdQtL55gwa6j5uayoDc31+uyJKQAEyfDixebFj/KqpUnH/+KVs7IiPD\nAJ1qr6clBaSiM9VMASF6sjz3nHZZp07y9coVzfL27Q3rMzUV6NJF+1OrOnVk6srJk9ptDO0bKPr7\nUtJjbwMHytSa/ftlSsvatbrreXoCs2fLTwsep+qff8/oCccAnYzL05wCUtZA28aGu+sRPY10BZ/6\nAt+qWLGlPH07OMjXe/f019m+XT7gCci/b7qus6AAOH1apt7ooupfdT6iJxQD9DLIyspCdHQ0bty4\ngebNm2Po0KGwNsbtkmtC8RSQkoJnpoAwBYSIKubsWbm6SnHnzslXR8fy9enoCPz5p/z7W3wWPT8f\nuHCh/P2qdO4sXy9e1H183z65DOPgwXIJxogI+bBo8U8Lbt2SOeZKJeDhUdSue/eiOpcuaZ6P6AnF\nAN0A2dnZmDJlCo4ePYrLly+ry5ctWwZvb29s3LgR9erVq8ERllNhoVwJoCKz1EwBISKqXhs2aOah\nZ2QAGzcC9esDPXuWr8+AAGD5cvlw5pQpReWbNsn88cmTKzZmNzf5tzQpSfvYsWPAkCFyh9GtW4G/\n/wa++06u4hITU1SvaVMZuK9Zo7sfQJY/80zJK8oQPQEYoJciOzsb/fr1Q5KOPwaXL1/G5cuXcenS\nJcTHx1dPkK4vBaQ86SBMASEievI0agR06yaXQxRCLrN47ZoMrsub0vL++8C33wLTpsl8czc3uUJL\neLgMdt9/v2JjNjWVQXhsrJwBV32SeO4c8OqrMp89JkaWOzkBEybINx1HjsjAXUU1Nl2ysoBDh+R9\nIXrCMUAvxZQpU3QG58UlJSVhypQp2Lx5s/5KhqaAGHKMKSBERE+vlStlIPrZZ3JDoWeflTPPb75Z\n/j7t7GQwrNqoKDJSzkRPmSKXOnx8DfTymDpVbmr044/A66/LNxV+fvLcu3fL/weoLF4MfPmlfGNw\n5EhR+cmTwLBhuvv/7jvg4cOKz/YTGQHuJFqCrKwsuLq6aqS16DOoRQt827s3zO7fZwoIERFVPtUO\nnomJQK9eNT2a8unfX6ZWHjpUvvaNGgG7dune8MjDA2jdGtixo2JjJDICnEEvQXR0tEHBOQCs/ftv\nmJU0g16ZiqeAVCS4trZmCggREVWfTz8FXnhBPtzp51e2tnl5QHq67mMxMXJ1l23bKj5GIiPAAL0E\nN27cMLjuTQCtS6pgYlI5M9VMASEioieVs3P50zTNzIA5c2Rgn58vd1NVrS4TEADk5lbeOIlqGAP0\nEjRv3tzguv0AfD99Ovr27as70GYKCBERUcWsXCm/iGo55qCXoCw56O3atcOpU6e4LjoRERERVYhJ\nTQ/AmFlbW8Pb29ugut7e3gzOiYiIiKjCOINeipLWQVfx8vKqvnXQiYiIiKhW4wx6KerVq4f4+HiM\nGjUKTk5OGsfatWuHwMBABudEREREVGk4g14GWVlZiI6Oxs2bN9GsWTMMHTqUaS1EREREVKk4g/5/\nDhw4AIVCgaioKL11rPmdS48AAAstSURBVK2tMXbsWCxcuBBjx46ttOA8JSUFderUQVxcXKX0Vx1i\nYmJgbm6Oixcv1vRQiIiIiGoVow/Qk5OTERwcjKtXr9b0UKrMrFmz4OPjA19f35oeisECAgLg4uKC\nefPm1fRQiIiIiGoVo18HPTk5GSEhIejVqxfatGlTZed56aWXkJOTAzMzsyo7hy5Hjx5FXFwcYmJi\nqvW8lSEoKAhjxozBmTNn4OzsXNPDISIiIqoVjH4GvSoVFBTg4cOHAAATExNYWlrC1NS0SvrXJyws\nDA0bNsQrr7xSaeetLkOGDIGVlRU2btxY00MhIiIiqjUMCtCjoqKgUCgQHx+P4OBgtG7dGhYWFnj+\n+eexbds2rfppaWmYNm0aWrZsCXNzc7Rs2RLTpk3Dv//+q1Hv0aNHCA4ORocOHWBlZYX69evDxcUF\nc+fOBQAEBwdj3LhxAIDevXtDoVBAoVBg7Nix6j6USiWWL18OZ2dnWFpaon79+vD398epU6f0XsPS\npUvh5OQES0tLbN++HYD+HHRDr6W0/nXJz89HTEwMfH19tWbuc3Jy0KJFC7Rq1QpKpVLj2MSJE2Fq\naqrz3lcna2tr9OjRA99++22NjoOIiIioNilTisu8efOQnZ2NqVOnQqFQIDIyEiNHjsSjR4/UQXNG\nRga6d++OS5cuYfz48XB3d8epU6ewYcMGJCQk4Pjx47CxsQEATJs2DRERERg9ejRmzpyJgoICXLx4\nEQkJCQDkDO2tW7fwv//9DwsXLsRzzz0HAOrlDvPy8tC/f3/88ssvCAwMxLvvvouMjAxs2rQJPj4+\n+Pnnn9GlSxeNa5gzZw7y8vIwadIk2NraokOHDnqvtyzXUp7+T5w4gaysLHh6emodq1u3LkJCQjBx\n4kSEhYVh5syZAIAFCxYgPDwc69evx4gRI0r6dVULb29v7N27F+fPn0fHjh1rejhERERETz5hgMjI\nSAFAtGrVSty/f19dfv/+fdGqVSthb28vHj58KIQQYuHChQKAWL9+vUYfn332mQAgFi1apC6zt7cX\nAwYMMOjciYmJWsdCQ0MFALFnzx6N8oyMDNGyZUvRs2dPrX7at28vsrOztfpKTEwUAERkZKS6rCzX\nUlr/ukRERAgAIjY2Vufx/Px84ezsLBwcHERmZqZYvXq1ACBCQkIM6r86bN68WQAQ0dHRNT0UoqdO\nenq6+u/TjRs3xOuvv17DIyIiospQphz0qVOnws7OTv2znZ0dpkyZgvT0dBw4cAAAsHPnTjg4OODt\nt9/WaDt58mQ0atQIO3fu1Gh/5swZpKSklO1dxf/ZsmULOnbsCA8PD6Slpam/cnNz4evri8OHDyMn\nJ0frGqysrAzqvyzXUp7+7969CwBo0KCBzuOmpqZYsWIF7t69i4CAAMyaNQvTp0/H4sWLDeq/OjRs\n2BAA8M8//9TwSIiePvfv30dYWBgAoFmzZoiOjq7hERERUWUoU4CuSjEprlOnTgCAK1euAABSU1PR\noUMH1KmjmT1Tp04ddOjQQV0PANasWYP09HS4uLjAyckJEydORGxsLAoLCw0az7lz53D+/Hk4ODho\nfUVERKCgoABpaWkabdq3b2/w9ZblWsrTv0KhAACIEvaKGjhwINzd3bF//3688cYbWLt2rc56np6e\n+Oabbww+d0nWr18PT09PWFpaolevXiXWVY1ddS1EVH3mz5+Py5cvw9XVFcOGDUPnzp0ByGdiAgIC\n4O/vj7Zt2+Kzzz5DaGgo3Nzc4OXlhXv37gEALl++jP79+8PDwwM9evTA+fPna/JyiIjo/5QpB11X\nEFZScFmaQYMG4erVq9i1axcOHjyI+Ph4hIeHo0ePHoiPj4e5uXmJ7YUQcHFxQWhoqN46Dg4OGj8b\nOrtdXmXpXzU21f8sddm+fTuSk5MBADY2Njp/BwUFBTh9+jRcXV3LOFrdmjZtivnz5+PXX3/F0aNH\nS6yrGvvj95mIqt6KFSuQkpKC5ORkXL16FQMHDlQfS0lJwalTp/Do0SO0a9cOK1euxKlTpzBz5kx8\n9dVXeO+99/D2229j48aNePb/t3dHIU13fxzH362GrdpmJYVdFCrWhYUMKaFdSF5IEI0cjAgsyF3Y\nCiqhpG6MwC4sgoJgQrqC2EVIsUEtMMoLs9yNxYKkCITdVOxiiatc/mjPRfT7//dYz+Omz9Pg+bzg\nx3a2c347Zzf77vs7v3Nqa4nH4xw9etS8B0hERH6fggL0V69e4fF48l6bmJgAoLq62nx8/fo1hmHk\nZZ4Nw+DNmzdmvR/WrFlDW1sbbW1t5HI5zpw5w8WLF4lGo/h8vr/MzNbW1pJKpWhubsZiWfwVIwsd\nS6F+ZLt+tRvn0NAQBw8epLW1FavVSigUorOzM+9Kxrt376ipqSGbzdLQ0GC227lzZ9H98nq9ACST\nyb+t+/bt27yxiEhp2LVrF3a7HbvdjtPpZO/evQBs27aNRCJBJpPh6dOn+Hw+s82fV4wSEZHfo6Co\nNhgMMjU1ZZanpqbo6+ujvLycpqYm4PsOk6lUiv7+/ry2169fJ5VK0draCnzP+n78+DGvzpIlS3C5\nXMD/MrOrVq3KK/+/Q4cO8f79+19m0D98+FDI8OaY71iK5XK5cDgcjI2NzXkvHo/j9Xpxu92Ew2F6\nenqwWCycPXs2r15lZSWhUIgdO3aQyWTIZDILCs4LNTY2xvr16/9ytRoR+feVlZWZzy0Wi1m2WCwY\nhsG3b98oLy/nxYsX5vEj4SIiIr9XQRn0iooKGhsbaW9vJ5fLcePGDZLJJP39/ebUjq6uLgYHBzl2\n7Bjj4+O4XC6eP3/OwMAAW7ZsoaurC4Dp6WkqKyvxeDy4XC7WrVvH5OQkwWCQ1atXm9me7du3Y7FY\nuHDhAul0mpUrV1JVVUVjYyMnTpzg4cOHnD59msePH9Pc3IzD4SCZTPLo0SOWL1/O8PBw0V/OfMdS\nrKVLl+L1eolGo2SzWfMHdGJigj179rB582YikQhlZWXU1NTg9/vp6+tjdHQUt9ttnudH334mm80y\nOzv7yz7YbLaiN2fKZDKMjIzQ3t5eVHsRWRi73c709HRRbR0OB1VVVQwODuLz+cjlciQSCerr6xe5\nlyIiUqiCMui9vb3s37+fa9eu0d3dzbJlywiHw/j9frOO0+lkdHSUjo4OYrEYx48fJxaLceTIEZ48\neWKuG75ixQpOnjzJ5OQkly5dIhAIcOvWLTweD/F4nA0bNgCwceNGQqEQX758IRAIcODAAYLBIABW\nq5X79+9z9epVUqkU586do7Ozk9u3b1NdXT0n21yo+Y5lIQKBAOl0mnv37gHfp5W0tLTgdDp58OAB\nDofDrNvd3Y3NZpvzx2B8fPyX88/9fr95mftnx8jISNF9v3PnDp8/f6ajo6Poc4hI8dauXYvb7Wbr\n1q3mBm+FCIfDDAwMUF9fT11dHdFo9B/opYiIFGpJbh53ed68eZPDhw8zPDz8t6t6SOF2797Np0+f\nig6WKyoqiMViP93waCGuXLlCJBIxl9D8s4aGBjZt2sTdu3cX9XNFRERE/ssW/85KKdjly5d59uwZ\nQ0NDBbednZ0lnU4van8Mw2BmZsacpzozM8PXr1/z6kQiEV6+fElvb++ifraIiIjIf11Bc9Dln1FX\nV4dhGEW1tVqtnDp1ipaWFgzDIJFILHh1mZ6eHs6fP2+WbTYbTU1NeZn0ffv2zQnaRURERGThNMVF\nRERERKSEzCtAFxERERGRf4fmoIuIiIiIlBAF6CIiIiIiJUQBuoiIiIhICVGALiIiIiJSQhSgi4iI\niIiUEAXoIiIiIiIlRAG6iIiIiEgJUYAuIiIiIlJC/gBHU7vc5Cu7lwAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"import kf_book.book_plots as book_plots\n",
"book_plots.show_residual_chart()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The Kalman gain $K$ is a scale factor that chooses a value along the residual. This leads to an alternative but equivalent implementation for `update()` and `predict()`:"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def update(prior, measurement):\n",
" x, P = prior # mean and variance of prior\n",
" z, R = measurement # mean and variance of measurement\n",
" \n",
" y = z - x # residual\n",
" K = P / (P + R) # Kalman gain\n",
"\n",
" x = x + K*y # posterior\n",
" P = (1 - K) * P # posterior variance\n",
" return x, P\n",
"\n",
"def predict(posterior, movement):\n",
" x, P = posterior # mean and variance of posterior\n",
" dx, Q = movement # mean and variance of movement\n",
" x = x + dx\n",
" P = P + Q\n",
" return x, P"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Why have I written it in this form, and why have I chosen these terrible variable names? A few related reasons. A majority of books and papers present the Kalman filter in this form. My derivation of the filter from Bayesian principles is not unknown, but it is not used nearly as often. Alternative derivations naturally lead to this form of the equations. Also, the equations for the multivariate Kalman filter look almost exactly like these equations. So, you need to learn and understand them. \n",
"\n",
"Where do the names `P`, `Q`, and `R` come from? You will see them used in the rest of this book. In the literature $R$ is nearly universally used for the measurement noise, $Q$ for the process noise and $P$ for the variance of the state. Almost every book and paper you read will use these variable names. Get used to them.\n",
"\n",
"This is also a powerful way to think about filtering. This is the way we reasoned about the g-h filter. It emphasizes taking the residual $y = \\mu_z - \\bar\\mu$, finding the Kalman gain as a ratio of our uncertainty in the prior and measurement $K = P/(P+R)$, and computing the posterior by adding $Ky$ to the prior. \n",
"\n",
"The Bayesian aspect is obscured in this form, as is the fact that we are multiplying the likelihood by the prior. Both viewpoints are equivalent because the math is identical. I chose the Bayesian approach because I think it give a much more intuitive yet deep understanding of the probabilistic reasoning. This alternative form using $K$ gives a deep understanding of what is known as the *orthogonal projection* approach. Dr. Kalman used that derivation, not Bayesian reasoning, when he invented this filter. You will understand more about this in the next few chapters."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Code Walkthrough\n",
"\n",
"Now let's walk through the code.\n",
"\n",
"```python\n",
"process_var = 1.\n",
"sensor_var = 2.\n",
"```\n",
" \n",
"These are the variances for the process model and sensor. The meaning of sensor variance should be clear - it is how much variance there is in each measurement. The process variance is how much error there is in the process model. We are predicting that at each time step the dog moves forward one meter. Dogs rarely do what we expect, and things like hills or the whiff of a squirrel will change his progress. If this was a robot responding to digital commands the performance would be much better, and perhaps the variance would be $\\sigma^2=.05$. These are not 'magic' numbers; the square root of the variance is the distance error in meters. It is easy to get a Kalman filter working by just plugging in numbers, but if the numbers do not reflect reality the performance of the filter will be poor.\n",
"\n",
"```python\n",
"x = (0., 400.) # Gaussian N(0, 20**2)\n",
"```\n",
"\n",
"This is the dog's initial position expressed as a Gaussian. The position is 0 meters, and the variance to 400 m$^2$, which is a standard deviation of 20 meters. You can think of this as saying \"I believe with 99.7% accuracy the position is 0 plus or minus 60 meters\". This is because with Gaussians ~99.7% of values fall within $\\pm3\\sigma$ of the mean.\n",
"\n",
"```python\n",
"process_model = (velocity*dt, process_var)\n",
"```\n",
"\n",
"This is the process model - the description of how we think the dog moves. How do I know the velocity? Magic? Consider it a prediction, or perhaps we have a secondary velocity sensor. If this is a robot then this would be a control input to the robot. In subsequent chapters we will learn how to handle situations where you don't have a velocity sensor or input, so please accept this simplification for now.\n",
"\n",
"Next we initialize the simulation and create 10 measurements:\n",
"\n",
"```python\n",
"dog = DogSimulation(x[0], process_model[0], \n",
" sensor_var, process_model[1])\n",
"zs = [dog.move_and_sense() for _ in range(10)]\n",
"```\n",
"\n",
"Now we enter our `predict() ... update()` loop.\n",
"\n",
"```python\n",
"for z in zs:\n",
" prior = predict(x, process_model)\n",
" likelihood = (z, sensor_var)\n",
" x = update(prior, likelihood)\n",
"```\n",
"\n",
"The first time through the loop `prior` is `(1.0, 401.0)`, as can be seen in the printed table. After the prediction, we believe that we are at 1.0, and the variance is now 401, up from 400. The variance got worse, which is what always happens during the prediction step because it involves a loss of information.\n",
"\n",
"Then we call the update function using `prior` as the current position.\n",
"\n",
"For this I get this as the result: `pos = (1.352, 1.990), z = 1.354`.\n",
"\n",
"What is happening? The dog is actually at 1.0 but the measured position is 1.354 due to sensor noise. That is pretty far from the predicted value of 1. The variance of the prior is 401 m$^2$. A large variance implies that confidence is very low, so the filter estimates the position to be very close to the measurement: 1.352.\n",
"\n",
"Now look at the variance: 1.99 m$^2$. It has dropped tremendously from 401 m$^2$. Why? Well, the RFID has a reasonably small variance of 2.0 m$^2$, so we trust it far more than the prior. However, the previous belief does contain a bit of useful information, so our variance is now slightly smaller than 2.0.\n",
"\n",
"Now the software loops, calling `predict()` and `update()` in turn. By the end the final estimated position is 15.053 vs the actual position of 14.838. The variance has converged to 1.0 m$^2$. \n",
"\n",
"Now look at the plot. The noisy measurements are plotted with black circles, and the filter results are drawn with a solid blue line. Both are quite noisy, but notice how much noisier the measurements are. I plotted the prediction (prior) with red triangles. The estimate always lies between the prior and the measurement. This is your first Kalman filter and it seems to work!\n",
"\n",
"The filtering is implemented in only a few lines of code. Most of the code is either initialization, storing of data, simulating the dog movement, and printing results. The code that performs the filtering is very succinct:\n",
"\n",
"```python\n",
"prior = predict(x, process_model)\n",
"likelihood = (z, sensor_var)\n",
"x = update(prior, likelihood)\n",
"```\n",
"\n",
"If we didn't use the `predict` and `update` functions the code might be:\n",
"\n",
"```python\n",
"for z in zs:\n",
" # predict\n",
" dx = velocity*dt\n",
" pos = pos + dx\n",
" var = var + process_var\n",
"\n",
" # update\n",
" pos = (var*z + sensor_var*pos) / (var + sensor_var)\n",
" var = (var * sensor_var) / (var + sensor_var)\n",
"``` \n",
"\n",
"Just 5 lines of very simple math implements the entire filter!\n",
"\n",
"In this example I only plotted 10 data points so the output from the print statements would not overwhelm us. Now let's look at the filter's performance with more data. The variance is plotted as a lightly shaded yellow area between dotted lines. I've increased the size of the process and sensor variance so they are easier to see on the chart - for a real Kalman filter of course you will not be randomly changing these values."
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"\t4.4502 2.6507 2.2871 2.1955 2.1712\n",
"\t2.1647 2.1629 2.1625 2.1623 2.1623\n",
"\t2.1623 2.1623 2.1623 2.1623 2.1623\n",
"\t2.1623 2.1623 2.1623 2.1623 2.1623\n",
"\t2.1623 2.1623 2.1623 2.1623 2.1623\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAo8AAAC+CAYAAABUKeVaAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzs3Xl8TNf7wPHPnZnMTPZFJIJIRJDY\nKvZ9p5Talda+/tCFbzeqamlRaldtFVW0tBSNnaKWalAh9j0JiVgi+zr7/f1xI6g1ShPNeb9e8zJz\n5y7P3CvJM+ee8xxJlmUEQRAEQRAE4Umo8jsAQRAEQRAE4cUhkkdBEARBEAThiYnkURAEQRAEQXhi\nInkUBEEQBEEQnpgmPw+empoqRusIgiAIwn+Mq6urlN8xCM+PaHkUBEEQBEEQnphIHgVBEARBEIQn\nlq+3re928eJFAGrUqJHPkQh/Fx4eDohrUxCJa1NwiWtTcIlr88+8/fbbzJ8/H40GfHyKkJxsJCMj\ng5SUlPwOTfiXFJjkURAEQRCEgstgMDB79mzeeutNPD3NbNu2lOvXE8nIgAYNGuR3eMK/SCSPgiAI\ngiA81pgxY5g9ezaHD+9i3bppvPfe60RGJuDsHEJAQACpqan5HaLwLxHJoyAIgiAID2Sz2VCpVEA2\n77/fiQMHdvLWW10BcHJy4qWXSgAB+Rqj8O8TyaMgCIIgCPdISUlh3LhxXL4czYYNXwO3KF7cgQMH\nvs/v0IQCQCSPgiAIgiDcw2QysmzZUjIyMjl9+gAVK5bJ75CEAkSU6hEEQRAEgSNHjiDLMpCOl1ci\nS5aMJSJixUMTR5tNJiXL+u8GKRQIInkUBEEQhEJu2LBh1KhRg3XrvgEuANl06dKcKlXKPnD947Fm\nuixIYsjyuJyEUyhMRPIoCIIgCIWajSpVSmFvryc+PvaRa8anW3n/l1Q6fJVIbJKVbjVcEblj4SP6\nPAqCIAhCISLLMqtXr0av19OhQyPgKkOGNOfVV1+iZEnvB25jssh8/2cWX/6egdEi83+NHHmrmSPO\neldATGNd2IjkURAEQRAKkU2bNtGjRw+KF/eiefM1ODk5oFarH5o4/n7OwGeb0olOsNI8SMfHbZ0J\nKCrSh8JMXH1BEARBKGDi4+OJi4vDz8+Pzz77jLS0NObMmYOzszMACxYsYPfu3QwdOpSmTZsCEBYW\nxpQpU6hTpw5jx44FwJyZScuWLVGpVPz+yy+AhbbVvGjbohYdOjbB3l730Bgib1n4bFMae86bCCiq\nZml/d5oEaiDsBIRn5azlCCjTC1Ov3nM6G0JBI5JHQRCEQurGjRvEx8cTEBCAk5NTfodT6F25coUP\nPviAAwfCSEu7hrOzjE6n4fp1NdnZRj7/fBjOzp6AzF9/7WL16jW0ahVC06alALh58zibN29GozEC\n3cFsRgpuwd7Y66gBihcHlMEOmwAOnoJOTaF40XviSDPYmLczg6VhWdjbSYxt60yfug5oNRKs3AY9\nxz74A4i5rQsNkTwKgiAUMlevXmXo0KFs3rwZAAcHB4YNG8aUKVPQarX5HF3hYTabuXbtGn5+fgDY\n29tYs+YXZBmqVVNTpowf0dHRWK0WypQJwMnJACQC8H//145WrUKoVSsYUJK2unUD2LhxNsWKFQHS\nQCOjlq3sBlQ6LbgrrZZkGiA9EyxW0NnlxmOzyfxyJJvp2zNIzLTRvYY977Vyoqiz+k7Qwf53nteu\nBO4egAP88cfzOk1CASSSR0EQhEIkKyuLZs2acfHiRXQ6HX5+fly4cIGZM2eSkpLC4sWL8zvEQuHY\nsWM0b94cf/9SHDmyAUjm/Pnd+PmBr68Hq1Ytx8enGNHR0fTr15+UlCiioiKpVKkSALVrV6J27Ur3\n7LNYMU/atWt4Z4EkIX08gCbDpkJZXzj+E6hU0PkD+HU3DOsCRdwACL9sYuLGNE7GWajuZ8f3/dyp\nXNKO+4QEQftGsGEfNAyB6Z/DmVSoVOn+dYX/LFGqRxAEoRBZuXIlFy9eJDg4mCtXrnD+/Hn279+P\nnZ0d33//PTExMfkd4gNZLBbOnj3LiRMn7lkeGhrKvHnzuHnz5j3L3njjDVatWpW77OTJk/j7+9Oy\nZct7tv/000+ZNm0aiYmJeQ0I5s2DceMe/Ni+PXdVq9XK3r17+fXXX3OWZBEU5ITZbMRgSCM9PRow\nc/z4MTw8oHv3Dvj4FAOgdOnStGjRAuC+z/5E+rcHX284FQlrf4dj55XEUa+DD/twPdXKiJ9T6Log\niVvpNub2cGXNUI8HJ47AsWPnaZeUxk2Ar9ZAvB18+imiXk/hIloeBUEQCpE///wTgOHDh+PtrYyu\nrV+/Pi1btmTLli0cPHiQUqVK/aNjxMXFsXHjRry9venUqVPu8hEjRpCens7ChQvRaJQ/P2PHjmX7\n9u18/vnnuUnSihUrGDRoEK+//jpLliwGZFJS4qlQoQJFihQhISEasAE2pk2bzMGD4VSv7o+3dw3A\nyrlzB/jpp58oVcqZ7t1DABvqPT9x5coV7FOTCJgxGgDZ3ZOZS9aRZjLTr9vLUMQZ0DJz5kwiIiJ4\n8803qVu37sNOJIwY8fCTUKQIJCQAcOjQIZo0aUKpUiXo2DEQSTKh18O5c2sofld/Q0dHpd/p9evX\n79nVjRvXc953fKLzfw+dFsb0h2FTYeJCCPQFwDCsG4vP6PlqdwJWWeatpo4Ma+KIo+7RbUrjxi1k\n8/5jTC5dmnnR0TB4MGzcCKK7Q6EikkdBEIRC5PZo3djYO8WgZVnOfX37/Se1atUqli1bRv/+/enW\nrROQzYULhxk2bBiNG9ejU6e63E70liz5joyMTObO/R/Ozg6Ajaio44SHh3Pz5lGgGGBDfXYPBoOB\nzNU/w57fAHCyyZS30+CRkQ4LpsDQrgB07lyP6tVLU7SoBVCSrFdfrU6pUpOoVKkMkA5A4KxlRAHO\nKel4rNoFgAWYAVwCvE79DgFWQMW2bWvZufMAPXq8DFQA9KxevZ7JkyczYMAARowYATVrYvPywhYf\nj+aVV6B2bQBiFi1i7tWr2JUowVSygWTq1HGmUaNq1K1bmezsNBwc9AD3JI4ALVq04Kuv5rNt2zZK\nlChJ7dq12L17NwcPHkKn09K4ceM8XZtc/dvDlO/hdBTy6Si2V2zIZM8exP6WQeuKSukdX48HpwNm\ns4XMzGzc3FyAosyY8Q1lyixkfMeO0KQJbNigrDho0NPFJryQRPIoCIJQiHTv3p0vv/ySuXPn4u3t\nTa1atViyZAknT57E09OTZs2aPXTbSZMmsX37dr799lsqVAgEsoiOPs7WrVsJDHSnW7cAAHx9YfDg\nTgQH+wNxudvPnv0/JAm02gzABMD48f0YMaIrgYElASMAXdwdyQT0mdkQrWyvB87d3lHYidzk8YMP\n+twXZ8WKZe6bj1n7xsuUnvI9FC/K9QFtAPCJvsXgFVuhqDs0r5Wzpo2pU4dz7FhzatUqhpJawrFj\n2zhx4gRJSVHADXDQc3FAHypPnUGz/fvZtmkTREZimDiRWYBrdCQTjcfQ6bSoVLB378LHXRp8fUvy\nfu8BfL94Cb9+/R2rlm9HVmlxcgjktZ69iEx1QE4xYbWBTZaRZbDJYM35V5blnPeUu8i317PJIL/z\nIZZlm1lXsTlh/i9Rzl7DitecqR/48FI9R4+eo3fvcVStWpEVK1YDesqVg9mzZysrtG+vJI9aLYwe\n/djPJ/x3iORREAShEKlfvz5vvfUW8+fP57333stdrtFoWLRoETqdDovFwsCBAzl79iwHDoShVpuB\nLCIiwti/fz9HjqyjQgUlAevcuQaBgVPvGbwRGOjLwoUf33fsQYM63resfHn/+5bZDeyI3WffQWoG\nLJsADapCfDI0HKSMEB7xet4/+Ls9Yd4quHYLQwV/squUwWfgdOW9D/uAo33uqtWrB1O9evA9m3/0\nUT86dmxM0aLu3E6II2t6YwZUaWmw+TtYs4lyNhuf1wim0dz3sbPL259YecxXlF12gHrBg9lSvgE3\nnYvkvjf9MvBNUt4/d67y0LY8LtnpVEvbyCc9ahMSWOWRW3h4eBIZGYfJpCItzYSLi/7eFSZNUm7f\nv/mm8o0hNfUfxCe8SKT8nNA8NTU19+C//fYbx48fZ9KkSfkWj/Bg4eHhANSoUSOfIxH+Tlybgqsg\nXxtZlgkNDWXJkiVcuXKF1NRUgoKC2L59K5AFZOPnF0JMTBxnzqzJaUGEsLDjZGRkU7NmBdzdXe7Z\np9VqZf/+/YSFhQESDRs2oF69eqhUTzkuc8K3MHGR0iK482v4YC7M+AFebQgbZj/dPj/+CqZ8T0aD\nKiT2aoXf0BlKq2P0hnuSx7zImPo9KR99RcmypSAqTpmp7/xaCCj5RNvLssyJqxY2nchmyx8JxOGA\n1mKiybWTtIyNwNWYgTopFZUsIw3virp9Q1QSSBKoJAm1itzXakm68zxn+a1b8Xw0ehTpaWk4WGzo\nDMmkqYzY2Wn45psFhIRUvfNZMrIIDd1Dr17tAB/Amz/+2E+tWrXQ6R7eQnlb6l3Jo6urq5iz8D+s\nwCSPPj4+ZGdnExMTg6+vb77FJNyvIP8RLOzEtSm4XoxrIxMffwZv70o4OTmQmronN9nbuvVP3N1d\nCAkpj073iMEQ6ZnY6vTDcv4yNtu9f09UKhWaKmVRhS1RRvfmRUo6+L+qtD6umQa9x0G2EcJ/gL+1\nCj6xxBTwbw8ZWZiKeaC9kQTTR8D7vZ9ufwBZBgjoADdzRmsP7ACLP3nkJrIsc+a6hU0nDGw+YSAm\nyYqdGhr6qWj37VxantqH896voU5l2LgP2r8LxYpA1Hqw1z9y33/32WeTCA0NpVatmkycOBG9Xs+s\nWbPYuHETISFVc0szWSwWKlZ8jQsXYti1azvNmrXK86kQyWPhUWBuW7du3QKLxYDJZMrvUARBEP6z\nkpKSWL58OSNGDEGSLuPlZWD16qlUrBiAJN35e9+mTf0n26HVhu3CFbTWBzREWG2YzkShfZpGCjdn\nGPm60vr4+sdgtiitjn9LHGVZxmSFbJNM1l2PTKONbLNMplEm2ySTaZK5lWwitv0gPG9mo7bZKF4i\nDlsJf7pl23C1f8oWUgc9jOoD784GjVoZ2fwQ52+YcxPGqAQrahXUD9TyVjNHXq6gx9VBBZeLw9Fs\n5XNvmQsTcvpKju6X58QRICxMGV3/7rvv4uXlBcAHH3zA1q3biIg4RnZ2Nvb29mg0rvTt25/Q0C24\nuXnm+ThC4VJgksePP/4QrfYWZcqUefzKgiAIQp5ZrVYaNmzImTNncHNLpV+/dgB069bi6Xfq5sxG\nHzs6xRpJaVIVty3zAUhqNAj98WhWl/GgldEOY6YFg1m+87CA8e7XZhmDRcZgJvd1jFsDnF51waKy\nI8tOT1x5P3TzEu4kiCYlMbTY8hBvieY4F83GrNZgsNPDcZh0PB4vZxXlvDUEemko662hrJeGct4a\n3ByeIKkc2gUOn4FaFe+7XR15y8Km4wY2nTBwMd6CSoI6AVoGNXSkdSU9Ho5/2/+7PeHLVbAtDMZ+\nDUfPKa2OQzrxNG63JFss1txlVqsVk8lKbCxs23aYTp36AEX44IOPGT163NN3NRAKjQKTPAKoVFko\nJR3Ef1xBEIRnTa22MWpUXxYsWEHDhlUfv8FjyLLM1SQzM8q+RFSpAM67l+HMjCTisyVMzWdAc2W9\nCVNv5Wm/WjWoZAvGbAlX32CKGo1YbEZi469RzJZJSKXyOGhV2GslHHUSDtr7H/ZaCUetSnmtkwhd\n8xPfLZhPubKlGVuuNl6nY/mhYRWWbjmA3iuYBu36EHnLxurwbLJMd1pKPZ1UuYlk4F1J5T1Jn70e\nVk7OfXklUbklvemEgbPXLUgS1PS347MOLrSupLt3ur+/83SDt7vD598r5XXgqVsdARo2bMgvv6zh\niy+mMXbsWBwcHJgzZw63bskkJsK4cUvo2HEkkgR2dg8uDC4If/eP+zxKkuQLLOd2gS5YKMvyXEmS\nPIBVgD9wGXhNluXku7e9u8/jpUsn0WojSU31QqstQq1atRAKhhej71bhJK5NwVVQrs3JkyeJj4+n\nefNqQAyybMZms6FWPyKBeQCLVSYqwcLpaxbOXDMr/143k5Kl/BqXZBulk+KooMuiRFYS+gvRnNIb\nuVzWg0H9e6O3k9BrJPR2Ejo77nl95wE6jUR6WiqvvPIKRqOJN4cMoaPBnnBvPRO/nIvBYOC77xZT\ntWrekt8hQ4Zw5MhRZsyYnlscPTg4mHbtXuXGjRv89NNKypUrh80mcy3VxsV4C5duWrhw06I8j7eQ\nYbzz97KIo4pALzVlvZVksrSnhjPXlIEvJ+MsAFQrZUe7KnpeqaynmGsezndCCpRW+mbe7uu4cedf\nWCxW2rdvlHvt/vgjgujoOBo1qoa/f3EALly4wq5dhylb1pcWLWoTHx9Pz569OXs2EUkCLy9lUHRi\noj0tW7Zj8uTJlC1bNk/n8mFEn8fC41m0PFqA92RZPipJkjNwRJKkHUA/YJcsy1MlSRoNjAZGPWpH\noaF/MG7cd7z66qtsuF14VBAEQXgqERER1K1bF2dnR06eXEmxYp5IkvTYxDHLZOPsdQtnchLEM9cs\nnLthxqjkROg0EFTMjjaV9FQobkfCxTC2zpzAxhMGdDn5VaYK2leCUR9OoVUthzzFfeDAQYxGEzVr\n1mDA/w0BoBVw5kYcP/zwI7t378lz8nj7Vuzd/eptNhsWi/me91UqiZLuakq6q2la/s4gH1mWuZ6T\nVF68mfOIt7D+mIF0w52k8qWSdnz8ijOvVNFTwi1vCTrA6dORjBu3gKJBfiwIPwsTRoC9N927jyE7\n20BGxkkcHR0AifnzQ1m9ejM///wl/v6VAYlDh/YxfPhUevbsSIsWr+Ll5cWXX64mOLg5ykd0oXbt\nlowbN44qVR5dqkcQHuYfJ4+yLF8np6y/LMvpkiSdBUoAHYAmOastA/bwmOSxUaOX8PX1wtOzSO63\ndqHgENek4BLXpuDK32uTQUhIWXx9ixIbG0NSUvx9a6RkS0QmaYhKVhOZpCYqSUNcmgoZpeHIWWuj\njIeVtuUsBHhYKeNhpaSLMtjjNrmaD1nd2hB6I5TuN5VEak0xFa17vUbJkiU5c+ZMnqKOibkCKMnd\n3dtmZWUBEB9/M8/7LF++PIcPhzNnzhyGDBmCp2dRxowZQ0JCIt7eXhgMhifaZ1GgaBGoVwSooBTj\nTsqWiE1V4+1kw8dZ6YCZek15PI7BYCI5OR0fnyKARFRUCuvW7cbZ2Zkhv/yCzd8fwlNo0KAhZrOZ\niIgU9HoDAH5+FWjTxkZWliPh4cpUiDabB507dyYgoCLh4cp830ajjl69eqHVahk2bBigJNHP+v/m\ns2rBFAq+Z1qqR5Ikf2AfUAmIkWXZ7a73kmVZdr97/b/ftra3j0aWZYzGUthsTs8sLkEQhMJi7969\nVK9eDXd3A3Z2iZhMZrTa+9sJssyw8LAjv12607rm7WQlwN1KGY87iaKngw3pCW9AZl+KoUq3Cchq\nFadCJ6EvWeypPkNCQgLvvvsuKpWKd955h5CQEGJiYpkxYzopKamMHDmS6tWr5WmfRqORSZMmcfny\nlXuWq9UqRowYQUhIyFPF+k8cPHiat9+eS7VqwXz55RdYLE6Ahk2bNlGzZs3c2+sviruTR3Hb+r/t\nmSWPkiQ5AXuBybIsr5MkKeVpkscKFSoAnoDfM4lL+OcKSt8t4X7i2hRc+XFtPv/8c8aMGUOvXq/y\nww/jH7rekSsm/rcqlavJVgbUd6B5sI4KPnZKqZh/6my0UqG63D/7HT5t2jRWr/4FAEdHBzIzlVbH\nqlWrsnDht/fcer969SapqRmUKVMSfU49ySNHznL06Dlq1AgmJCQIgKNHzzB8+KckJFyjeHEICQmh\nX7/+eHh44+PjiVb7/AaMmM0Wdu48hCRJtG5dD3Di1i0bPj6VqVmzJn/88QcaTYEaw5pnos9j4fFM\nhjVLkmQHrAVWyLK8LmfxTUmSfHLe9wHuv1/yENnZN1m/fj1Go/FZhCcIglAodOnSDE9PN+rWrcCD\nGgbMVplZO9LptiAJmwyr/s+Dse1cqFtG92wSR4Dg0lDOj6wsA5GRV4mNvZH7ls1m49dfd/Pzz9vv\n2WTFiq2MGfMV589fzl1WsWI9rFZ/MjOVxNHeXk+rVm3ZvDmGqlXfyFlLBWho3fodKlXqzsWLCYAz\n4MratWEMGTKZrVtPoMyWUgKTqQiHDl3C3r4Uc+duYO7cVYSENKFmzb44Ojbgxo2E3OMfP36BU6cu\nYTKZH/lxT548xciRI2ncuDEvv9ya6dNnkJycct96Gzfu45VXRvDJJ0uAKkB5ihYNJjY2lgMHDrzw\niaNQuPzj/62SUlX2O+CsLMuz7nprA9AXmJrz7/on3WfTpgM5dOgUW7ZsoU2bNv80REEQhP8ks9nM\nb7/9Rtu2LwNXKFdOw+XLG3F8wFR70QkW/rcqlWOxZjpX0zOhvQsu+meTMG7cuI9Nm/6gd++2NGhQ\nFVCzY0c4HTuOpF27xmzcuABy+lB27vwBAN27v44kqQEVP/+8l02bdlKnThPKly8FqLh2bR/Hj19m\n4MDeTJ36Ka6u7iQlpTJ1qh82mxqolrvPwMBKyLIOKA2UA6BWrVYMGGCkcuUGQPGc9WqxePFiMjIy\nsFpdgRJkZGTg7OyGyWTF27shYAAMfPTRe2zdupe1a6fTuXNTAE6evMSpU5eoXbsSAQElOXz4MG+9\n9TYWizKSKCMjk59//pkdO/ZRqlQNypYtxahRbwLutGkzhFq11tCuXTtsNjW3Syn6+Pg8k2sgCP+m\nZ/FVpz7QGzgpSdKxnGVjUJLG1ZIkDQRigG5PusPWretitYpaj4IgCA9jtVpp3LgxBw4cYNu2r3n5\nZaW82d8TR1mWWXU4m083pWOnhvlvuNKuytPN4wzw1Ver2b//GHPmvIe3tydgz549Z1i48FdKlqxI\ngwb9ARXu7mkEBATg7R0IKLeNVSro0qULGo0Gi6Vkbl3Bnj0H5iSOtVGGpECrVp1Yv74MpUuXxtPT\nHwBPTyfi4uJwdHTkduIIEBoael+cHTt2pGPHjvcs8/T0ZODAgfcMFHFyciIyMhKj0Ygk6QBlZHip\nUkEEBsZRqdKrQCnAwJo1K/j009l89NEgJk8eysyZM8nKsuDuXpaBA7tTs2Y5JkyYwKFDUezYsQF/\nfz8+/HAekiRhbw+HDh166vMuCAXJsxhtvZ+7f4rv1fxp9jlu3GAmTHgHZdyNIAiC8HdqtUS7dg2I\ni4vG0fHBc08nZtgYvS6VHWeM1A/UMqObKz5PWG8wK8vAlClLiIm5wfLlnwJqwIHVq/eyb98h+vYd\nTuvWIYBEly798fWtSPPmzbndG6pRo0ZERkbet981a9bct6xHjx73LfP398ff3/9vn1lN8eLFnyj+\nvNLp7p17e8GCBX9bw57g4Fp06tSJunXbExvrSWjoJVxc7Dl16iI63W769h3OgAHO/PJLJ4oXL866\ndb8+l1gFIb8VyE4WSr0tI5ANPP03ZEEQhP+S+Ph44uPjqVQpAIhm1KiuvPlmW1xd769Osfu8kQ9+\nSSUt28bYts4MqO+ASvXg7/mRkVeZO/cnXFwcmTRpOKBFr3dhzpyfyczMYtasRXh6Kknb22+/T58+\nqVSpUpPb7Qb16tWjXr16z+lTFxw9evTITXSjo6MxGsFk0vLxx+8SEBAA+KDRKNfC29s7X0ZwC8K/\noUAmj7clJEQSHZ1NzZo18zsUQRCEf+zChQukpqby0ksvodUqrYV79uzhyJEjNG/ePLfw9eHDh5k8\neTJVq1ZlwoQJAFgsFooXL07p0qWIiFiOk5M9arX6vsQx2yTz+dZ0lh/Iory3hh8GuhPsc9co4vOX\nYdN+pUAhABoMN1L58stV+Hm4M+nD6eDigUoF06fPwNPTE3t719zNu3bt+rxOzwvF39+f8uXLc/78\neQwGA927dyc6OpoxY8YAiP76wn9agU0eT5y4SEhIT/z8/IiMjER60kJjgiAIz5HBYECj0eSOjg0P\nD2fXrl3UqFEj57YtnDhxgjZt2uDj48OJE8dRZm610rx5M65ejePKldOUKlUCsPLLL8v5+uvv+fLL\nSVSt6gnYSE4+y/r168nKiIdvJUhNQ4MNjQR+mMmcthQnZwdoURuqBeXGdirOzMhVKVyKtzKwgQMf\nvOyM3u7e353y29NZueMQB4D5OcvKo3RSr5qUjPzdMqT//Q8gt6C0cD9Jkvjiiy/o2LEjM2fOZNas\nWbkj3H19fRkxYkQ+RygIz0+BTR4rVgygePGilCsXSGpqKm5ubo/fSBAE4SnYbDYSExMpWlQZrGEw\nGJgyZQqZmZnMnDkzd72WLVuyc+dO/vjjdxo0qA2Y2bt3C6NHj2fkyIE0b14GMOPkdIOEhAQcHNTA\n0dztK1f2w9vbBZstEqVbDjRrFoRO9wZVqngByowgVav6sG7ddEqciYKhE3K3vw64X7oKk77L2eFW\nOPEzVpvMwn2ZzNqRgYejih8HutOg7L19+HL3Uacyg3ccIht47bXXaOTri+b6dUatXAmSBC1bPpNz\nWhi0b9+ebdu2MXHiRMLCwtDpdHTr1o0pU6bg5eWV3+EJwnPzTGeYyauHFwlXmM0W7Oz8gReryv5/\njShEXXCJa/PPbdq0ib59+9KoUQN+/fVHwILFYkCrLQGA2XwOtVoGzHTq9A6bN//BunXTadeuIQB/\n/nmMX3/dQ5Mm1Wl3/gocOIHFZuNCQhIedhqKued88S1WBGaMBP2Dk7oHup4AAR3AYISOTaCsr7L8\nuw2QlAof9uHq6Dd5d3UKf0WbaVNJx5ROrrg7PqJaRaYTS3xqIqenM2DTJqS2beHtt2H+fHjtNVi1\nKs/n8EXzPH5uzGYzarU6d47swkgUCS88CmzLI4CdnQZIQSSPgiA8C7///juLFi2ibdu29OrVDUjH\nz09NUlISVmsycAEAjQY+//xNXFycsFqTUKuVPoM//TQJnU57Tzea+vWrUr9+VaUPYfePIMuABqhw\n/+Ghf3uoHvzkAft4wv91hrk/KbO2fDECws/A9B/AQU9o2zf4ZE4CNhlmdHOlSzX9fV18jEYTY8d+\nQ6tW9WnZ8nVwdGHA+PHw/vsz/7v5AAAgAElEQVQwcSK89BIsXKi0On7ySZ7Op3DH7bJDglAYvABf\nkTK4dOkst27dyu9ABEF4gcTFxfHDDz/cVS7GTFTUSX7++WdCQ5cBp5Dly1y8+Cft2weQlhZBz569\nCA0NRZZlRo3qx7BhXe+Zsk6v1z28/7UkwYD2yvOKAcTOeovYWW9B15yKZVXL3dM/8YmN6qu0Vq79\nHU5chImLSNU58s5bMxm5xUK5Yhq2jihC1+r2D4zt++83MGPGDwwaNAWTSa8sHDoUvLzg8GHo0AFM\nJujWDSqJ8miCIDxegU8eR42aR9myFVi2bFl+hyIIQgEWHx+P2XxnKrnx4z+hT58+rFv3HXAaOEHr\n1mWZP/9DJk8eCsCsWbOYPHkyV69GkZ6ewblz5/jss0nMmjXrwQd5nNH9QGsHZ6IxBRQno0lVCDuR\nE9AQJcHMq9utj4C19yccOJ5Cm4Hz2aL24/1WTqwa4kGpIg+7iaRi8OCR9O7dm1WrVuWO8MbRET78\nUHl+9KhodRQEIU8K9G1rgBo1KuDi4kR2dnZ+hyIIQgHVtWtX1q5dy969m2jUqAqQziuvBHPzZkMC\nAz1QppyDkiW9efPN1wCIjr7MypU/odFo+PjjMTRo0ID9+/czefIUVq78ia5du+Ln55e3QEp4Yejz\nCvrF67n6fxM47qIi+JoBQ7Af+g6NH7iJzSaTbZbJNMlkGWUyjDJZJuV1ptFGllEmonRtvOvZiHMt\nxprWzfHOTmDJG2oaVbq/vuO1a7cYP/5b5sz5BEfHCqjVOpYvX37/gYcOhS++gPh40eooCEKeFPjk\nsUOHxnTo0AStVgwIEITCKDs7G3v7O5MFDB48mPDwcPbt24OzswSkU6KEPfb2OqKiDtOoUTEAOndu\nRufOzR6637+27aBNElSvUpH2SRJs+JP2SFiLVeDIiRMc3PIbfsMGPzY+WZZJM8gkZti4fCONWakW\nuoa0IdnBjXh7Zz4M1HOgiCNeX8ai1jrmJIV3ksUss8zjxy0GQsNAtBYzrx3fzl83FzPnqjfVf/gh\nZ6q+O3r2HMuePUdwdvZn1qzZD9+lo6MySGbOHJgy5bGfUxAE4bYCnzze6W+UCnjkZyiCIDwnZrOZ\nqKgoZFkmKEjpFxgXF0e1atXQ6/VcuXIWpfXQwIkThzl27Dj79y+nTRtlVpPx4/vzxRfD0ekePE3f\ng1Ree4Dul4HLx2HD8dzlnYBX1BoObTzNqfZmEjJsJGbYlH8zrbmvEzNtJKQr/5qtd+04YBinApSn\nzoYM7K1GEuUsUq7EU6l8AD6uKhy0Eo46CUethINOwlGrUl7rJOW9nPc1mBk2uB+ZqQl81Lc3Xdf8\nRUrLmvzfkeJERUWzfv163njjjbsOrmPevK/45JPP+eCDDx9/Erp1Ux6CIAh5UOCTx9tstiQuXIjP\n/cMiCMKL6eTJkxw8eJA6depQuXJlAH75ZTU9e/aiS5f2rFmzEDDi7Z1BcnISdnYajMbjuYnh7Nnv\nYGenoWLFMrn79PBwfdChHsm1dQOy954nvGQwuxq/zFmPAK7bdCSjJ12fczv4y8R7ttFpwNNJhaeT\nGi9nNcHF7CjipMpZpuLr2ZO5eeU8c0YOp97rY9EZjRh+mkSzeZ9iNJr45pOdeapZe+zYGbITogkM\nKM1rwwbAsAF4AAO2Fmfs2E84dOgQpUtX4tChU4wc+Q7gS+XKKkJDQ/N8PgRBEJ7UC5E8Go0mypdv\nRFzcLW7duiUKhgvCC+LgwYOsXbuWjz/+OOfn1sJ33y1g7tyvmTr1IypXdgAMlC8Pfn4+eHpqgKuA\nUi7nypVNeHt7KLXzTkfCzSTqARhMcPDknQOV94MSjy/KbLTIHIsxExZp5IBTB46ObIVFrUGyWdCk\nR+KbEkmXWynopGz8Ph2Ip4smNzks4qTCUSs9crarZemn0WTE4hlYlPipQ9DGxuPeqSnqryYDSjHy\nvLg9i43RaMRms+XWEDQYlD6c2dkWGjcegsVipW7d16hdO499NAVBEJ7CC5E86nRaSpcujtUqcenS\nJVEQWRAKKFmWc5Or+Ph42rV7hcTEZFaunEGdOmUYPLg/jRuXJjm5LZUqeaPUcYXq1YO4fHnjffvz\n8fFUnpyJgkrdH35gTzeI33HfaGaLVeZknJkDUSYORJo4fNmEwQwqCSqV0DDAK4H633yNb8I5egdk\nsfK8imIGG5YfP0NT9/7BKI9Tp04dYmJimT9/Pn379sG+cRV+nD+frKxsypUri7u7e572FxQUhJdX\nUeLirjFr1ix69uzJ5ctXWLhwIQCtWnWkWLHmmExWQkJC8hyvIAjC0yjQM8zcLTExBQ+PACSp9L8W\nn6AQs5gUXAXl2siyzNtvv01oaCgnTx5Cq82iR4+XOX48GqMRvL1V2NkprW5jxnxEly5d8naApFRk\nv1eRMrKI0Uvc1Ci/OgJNEu4mGepUhgPfY7PJnLthISxSSRYPRZvIMCrrBhXTULeMlroBWmqX1uLq\noAKrVUlKz13G2igE9b4IqBAAJ34CtTrP5+H69Rv07t2L5GQlKVarVVitNlQqiTlz5lC/fv0873PX\nrl2MHj0am00ZWJOYCPb2ULZsLdau/eNO+R3hiRWUn5v/GjHDTOFR4Os83lakiBuSlAbkX7IrCILC\naDSyd+/e3NeSlMW5c8eJi4tj+/ZlbNiwkGvXoqlZ059Dh9Zw5MifjBw5EoCvv/4ao9GYtwN6uHKm\nmdI/MkYrM69jMNMbFUe2yVzyKMmcTv0Y9mMy1SfF88q8RCZtTic6wUL7qnrmv+FK+NiibBvpyfhX\nXWhVUa8kjqAkiOMGKU/3RSjLxg16qsQRwMenGN999x1NmzbJTRwrV67EvHlfPjJxvHbtFkePniMh\nISV32YULV5g79yeysuz49ttvadCgAVlZ9sTEQHKyJz/8sF0kjoIg5IsX4rb1HRaMxkTS0mSKFi2a\n38EIQqFktVopU6YMcXFxREXtp3RpF8DElCmD0OmGU6VK2dxEcdCggfj7+wPQq1dPQkNDuXz5MufO\nneOll17K0zEnpF9kqksRVG4laPXKGMLPptHaX0e8cxFIghI2M82D9dQro6VuGS0+rk+YAL7WEj5d\nDOcuK62Ot2eEyYNr125x8WIMJUt6U6aMHzNmzGDduq0sWLAeL69g6tatk7tu+fKdiYu7xdWrW3Bz\ncwXUjBr1FT/+uIlly6bSp08XQMXx4wcZOXImXbq8wpo131GtWgeyskw0a9aVd955R/T9FgQh37xQ\nyeOvv+6mb9+JdO7chaVLl+Z3OILwn2exWFizZg179uzhm2++RpIyUauTqV+/IufPO3Lz5kVKl1Za\nBGvVulNk+vbAjr+3MJrNppz3H57YZRhtRN2yEp1gIfKWhahbVi7eMHC+2rc0r5VT7/E4eGZZqBd7\njMtZJzC53WTrL4sfOZjlodRqmPc+/N/nMOfd3FZHg8HIrl2Hycoy0K1bi9zVBw+exOHDZ/j55ykE\nBfkDGr7++lcmT17IxIkjGTfuf4AdRqMHO3aEk5hoBsqj3OhRk5FhITMzm4yMQNzcSgIQEFCNqlWv\n4uRUFggEICioEW+//XZOX0aldqWDAxw4cODpPqcgCMIz8kIlj0FB/qSnZxATE5PfoQhCvsrMzGTm\nzJls3ryZKlWqYLFYqF27NqNHjyYmJobPPvuMwEAlCdm/fz9hYWE0aNCAevWUuohpaWkcOnQIT09P\nQipUgB07ICuL5IwMNGo1zjlFuVWyjXdHjuD6zXgGD25M9erlAFi+fMIjayo2btyYffv+YOHChRQv\nXhw/Pz9WrFhBXNw1vLyKUrZceaITLETdshCdYM1JEpXn8el3RiSrJCjprqaUu5qY6ztwSotl1sUE\nAq9FUSw9kdQgX5rbx1KxeIV/lFD9kpLBxxo1LUP38lXLuoAd2dlm2rUbiYuLM9269UL5dWnHxYsJ\nHD9+gbg4J4KCqgESQUENadDgDD4+FYBSAPj4VGDy5Mk55/zO4JuIiAjs7e1xcrqzbOLEiUycOPGe\nmCpXrsy8efPui1UkjoIg5LcXKnkMDi7N5csb8fN7+KwRgvBfdXsks9VqpU+f3qxb9yuSBCkpf7Fv\n32Jat27Dnj3RnDhxjlGjegM6QMVvv63ls8/mMHHih9SrVw5QceHCcVq1akX16iGE9+sFb78HQAWU\nUtw3AS1KW9moCgHYRvXE19czN5bHFeNua++F3ujJrSPxHHh9Iit9qpDgWpKi5ceSUbwclSYmYrmr\nao2bg0SAp4ZG5XQEFFUT4KkhoKiaUh4a9HZKsjTqUhQ7d+4kQXKjYbrSN/BzbSJI0LZt2yc+j7t3\nh7Ny5Ta6dm3Oyy83BJxxdw/k4sUYypatCFRTYnKTadu2LZ6enthsPrmtqXPmfInNZqN8+fKAEluv\nXr3o1avXPcdxcnKiVatW9w3K8PJ6fEkhQRCEguyFSh5BqQUHyYBDfociCP+K2NhYPvroIzIyMggN\nXc73308nMvJXihVTU7lyIJUrl+Cvvw6wf/9WWrR4lVGjeuHv7wDEA1C/fhnef7839er5AVcA0Ovj\nad68FuXKlYLqd8rH6PU60s0WIhpXo/afx8FoYkS35vC/nnmK+cr4n7jk0owtNetzxlsp5q21mPFL\nuUaFyHO0a1iG0o3KUqaohgBPDe6Ojx+7995773L+/DnmR1+ljhYi9bBTnUXDhg3o3PnBo7cTE1PY\nu/coDRpUxcvLA1ATFnaBxYtDsbMryssvvwVAgwbFiYiIICAgIHdbSZLYtGnTffusWrVqns6FIAjC\nf80LU6rnXnpSUkrg6uoqbuH8C0RZi3+XxWLh2rVrlCql3P5MSbmKt3cZLBYLN2/+xpAhA7hyJYYv\nvpiGj48PAMnJybzzzgi8vb3YsmVL3g/68lvw20H4eABMGg5/RECjweDqBJc3gpvzIzeXZaVEztaT\nBraeMnIx3gJAtZsXaFMammlv4X/6OOoft4CzI0SvhyJ5H/CRmZnJhg0bCQ8PR6fT0rRpM5o1a4o6\np59ienomTk4Oub8X2rd/l40b97F06Vz69h0EOHD69Gk2b95MmzZtcme4eR7Ez03BJa7N8yFK9RQe\nL1zLI0C/fqNZsWIbYWFh1KxZM7/DEYRn5vTp0zRr1gwvL09OntwOJOPmZuKHHyZSvXownp5u3Lhx\nA4BatWoTG6v0/61duzYAN2/GY7Vac5OpJzZ+sJI8zlsF/3sDJi5Slo98/aGJoyzLnIyzsOWkgW2n\nDFxOtKKSoKa/HRNaaGnddyDFrsXC3oXQqBG03qNs+E73p0ocARwdHXn99R68/nqP+97r0OFdNm/+\nk1OnNhIUVBVwpnXr10hPV+Hm5sftuxUVK1akYsWKT3V8QRDy7siRIyonJ6cPtVptsCRJL0yJwMJK\nlmWbyWQ6m5GR8UX16tUfOC3WC5k8Ojs7IMsyERERInkUXliyLHPkyBHi4uLo0KEDkE3Zsg6YzQaM\nxgySki7kztn82mstc7fz9S3FpUuX2LNnN2XKKLeEd+/eA0DJkiXynjgC1HsJWtVREsg3xsKuv5RW\nx5Fv3LOazSYTEWvOTRjjUmyoVVCvjJYhjRxpVVGHp1PO8Qe3VpLQiYtg0jDYfkBpdfzfGw8IIG/G\nj/+W8PAzbNgwG7XaBXDG3l7pk3nqVCZBQUqL7PDhbzJ8+Jv/+HiCIDw9JyenD319fV9zcHDI2/yc\nQr7JysqqHBsbCzD1Qe+/kMnjRx/1Z8KEkRQpUje/QykUbDab6B7wHBw9epSaNWvi4+NNu3YBqNUm\ntFo4fnwlJUt6P/Sc9+jRnUmTJvPZZ59Ro0YNVCoVhw+H57x3f4vcE7vd+vjbQeV1TqujxSrz12UT\n204Z2X7awM00G1o1NCyrY2QLHS0r6HFzeEBjwsg3YM5P8Pth6KO0lj6u1dFstpCVZcDVVRmJHB0d\nR9++E7C317F9+9eAHtDz44+/ERV1hWPHoHr18gBMnz6HRYuW4uz86FvsgiD8u7RabbBIHF8sDg4O\nNq1WG/yw91/I5LF48dsFwk0oY0KF5+HQoUOMHz+enTt3otFo6NixI5MmTcotASM8uatXrzJr1iwc\nHByYNGkckEy1avbUq1eF6tWDycpKxtnZEQBf32KP3FfHqrWw1m3B9p27uXHSQraDF0WdGlI5KBCv\nYg05EGnEXithb6c89HYS+pzXdupHfAm4q/XR7O5KWPvX2LYuld9OG0nMtKG3gybldLSprKdZkA5n\n/WPuPrk5KwnoxEVwKfaeVsdbt5I5cyaKcuX8cuevXrZsE4MGfcaAAZ349tvPAR2urs788UcEjo6O\nyHLV3IR6/PhPcXJyoly5oNzD+fr6PjoeQRDyhbhV/WJ61HV7JsmjJElLgHZAvCzLlXKWeQCrAH/g\nMvCaLMvJz+J4d6SQleWEg4MYef2shYWF0axZs9wiz1arlVWrVvH777/z119/5c4aItwvNjaWTZs2\n4eXllTOHswVIY/bs2Tg6OjBmTBscHPRIEvz555I87duaks6hVp9ypEwdDr88gBR7l9z3TgE/bQel\nGsGDaVRgbyehs5P+lmCC3k7C/tVRUOQEB/yrkLraiKNWolmwjjaV9DQpr8VBm7e/AbZ3evDHjB/Z\nl5nN+8O6YJ/T6vjuu3P48cfNLF48lYED+wJ6ihWrhtVqIzVVze1C2R4eytzOf//C0qdPnzzFIQiC\nIDw7z6rlcSkwH1h+17LRwC5ZlqdKkjQ65/WoZ3Q8Ll6MoUePvqhU9hw+fPhZ7VbI8dFHH2E0GunT\npw+9e/fGYDAwa9Ysdu/ezdSpU1mwYEF+h1ggpKenc+jQIXx9fXPq/kF4eBjDhw+nWbN6dOkSBBgo\nWRKmTx9B1arl0Grz9mMnyzJHY8xsPG5g8wkDt7pMxMGUTcu447RMO0OF9KuoUwxk30wl28cbw+rp\nGNCQbZbJNslkm2UMOY9HLUvJkrlq0JJd8SXqllDRpZYbDcvqcuss5iXe3Fvubs68obXjWmY2Hdv3\noDJBgI5q1Zpz8WICTk7+3J49pWnTl8nMzMQ+p0D5bc2aibqugiD8M2q1unrZsmWzb79ev379pZs3\nb2qWLFlSZOnSpbHz5s0rEh4e7rh8+fKYH374wa1ChQqG6tWrG/Iz5oLsmSSPsizvkyTJ/2+LOwBN\ncp4vA/bwBMnjmTNnnuiYBoOJs2cvIkkafv/9d1xcXB6/kfBEsrOz2bdvH2q1mgEDBuDoqNxOHThw\nILt37yY0NJRBgwblc5QKi8XCjh07OH36NO+9915u0vLXX39x9epVqlWrlttKervv5kP7b8oyjmfO\noE5Le+DbmYGBXLVYcHV1zW3t/uqr+Sxduox+/brx7ruvo1Jl4+mZTLt29ahTpwJnzhzFZrOxb98+\nDh/ey2+/JfPjj8V5+eWXHzm3syxDVJKavZe17LusJT5TjZ1KpmZJMyPMEXSZ+QWqUh5Ehn6OQSVR\nuusn2CfEcH1IQ5JtV3AFUAP2OY/HMJlMrFixgn37/sBisXAYyAgOQjNwEN7eT1bU2mQy8+mnSwkP\nP8/69XOQJA+sVmc6vt6L5ORkohPNGMPPAtCwYUMaNmwI3Cmb8l/1X/98LzJxbZ6tsmXL5ncID6XT\n6Wznzp27J8EoX768qVGjRll/Xzc0NNTNYrGk5iV5NJvN2NnZPYtQXwjPs8+jtyzL1wFkWb4uSdIz\nnVZBr9eydOkYSpWqiUYjEsdn6e7k6u46oDab7b73/23Z2dnExMTktvKpVDJz5swmKSmZN96oh7+/\nH7KsZvv2UDZs2MG4ce8TEOCFLGvYvz+M0aPH0LJly9yp4Gw2G/PmzcPd3Z03y5cn6O23AbiFMj/L\n3f+zujk5sSYjg+nTx9OyZU3U6mzq1vUiPDyAEiXsUaszAChSxIVp04YCyvlbsmQJe/fuy91PYmIS\nJ0+eok+f3rRs2ZK7xaSo2HdZx97LWuLS1KglmWrFzfSumk1dXxMOWsBcGvV3zmijruOy7RCyXov9\nuRjMRd1I6drkqc7rkiVL+PPPMCQJ/PxKcfPmTc6ePce0aVOZMmUKer3+AdfCyLlzMYSEKH8w1GoX\nTp6MJTY2nkOHUqlRQ1nev3//p4pJEIT/pg7z95d/lvtb/1aD80+z3aZNm5xnzpzpvXv37ku3l+3Y\nscNx586dbgcPHnSeNm2az9q1ayMBhg4dWiopKUmj1+ttixcvvhISEmLo0qWLv7u7u+XkyZMOVapU\nyVq0aNHVZ/WZCroCN2DmyYqE372uG1DmucVTWDVt2pTdu3ezYMECevfuTXZ2Nt9++y0AnTt3zpfi\nutevX8fPzw8nJ0du3TqOWp2F2ZzGq69W49KlS6xatYgGDWrTrVs3OneuT9GiDrRtW4lq1ZSW0xMn\n0jGbzXh7a6lRwxHQkJSUyYoVK3B1deHLiN0wUg1WK10dHdmXmUlMowb4njwFySlUKOWF+3UVrq4W\nXnpJudVaqVJphgzp/tCYz6/ZTMWV+wjRqKlTpw7e3t5ERUUREXEM68yV+L7SgWSPkmw8YWDjcQPn\nblhQSVAnQMtbLfS0rqh/8OwrE4fCoEkUXRCKTat827X7ZBDBIXmf/SQuLo6wsDDs7DR8//1SgoOD\nSEtLY/DgIVy6dIno6Oicvpt3ZGRkUaJEG7KzTdy6dRZX11KAHYsXF6Vo0aJ5+jn+rxKFqAsucW2e\nj7uLhBc0RqNRFRQUVAHA19fXuGPHjsgHrdeyZcvMFi1apLRr1y61f//+yQB169Ytt3DhwiuVK1c2\n/v77747Dhg0rdfDgwQsAkZGR+j///POCRlPg0qnn6nl+2puSJPnktDr6cHuutGcuDVm2YrXKFLaL\n9zxNmzaNxo0bs2rVKlatWpW73MfHh9GjRz/341+8eJEPP/wQrVbLqlVLgTR8fDLw8ytGkSKuxMef\nxdPTlZEj/8fJk0ppmXPn4Ny5U6xbt46FCxfRt2+7e/bZv397evRohclkAZQ7FRpNBtOmvY3NJkNp\nGfq2hSUb0DjrsbdZONqvGb7D/gJg9NIJjK8elDvH8ZNQT1zMwJsAVlj7JwBVAW/nImwu1ZCu36Rw\nXqu06tXws2Nie2faVNbj5fyYWo192sGkJeiirimvfTxhcKcnjutup06dQpahbt26BAcro5ddXFzo\n0qUz06Z9QUTEMbKy9Jw4cYnp00cCLjg5+VGtWg0yM7OIizPi6qoksI0bN36qGARBKDyetqXwn3jQ\nbesnkZqaqoqIiHDq1q1bbiuVyWTKvf3WuXPn5MKYezzPT7wB6ItSYLIvsP55HGTRorVMmdKRceMm\niNtjz1DNmjUJCwtj4sSJbN++HY1GQ9euXZkwYcIzL4mSlJTE9u3bcXBwyCmWbcLFxUxoaCj29nqM\nxmPodEpJptOnV6PNaWn75ZdfOHjwIO7ubrz11lsUKeLJsmVLiYg4xhdfTOObb76571j29nruHo/h\n4uLEhx/2vbPg4wGwbDO7bqXAuTXw5SowmqBrc+xr5r017UJFHwJPxWJVq7jyyf/4U/ZiY6Ynf6m9\nAfC3S2FMS2faVtFTwi0Pxb3tNKS8+wZr3plBGvDuR/1ArwNg27YwjEYTTZvWwMVFqZeYkJBCVpaB\nIkVccXS8txPk7bqIV69ezR3sYjKZuXpVuQPj4ODM0KFTycrK5p13PsXX1x+ArVu3PfB2tiAIwn+F\n1WrF2dnZ8rDE08nJqVDWr3xWpXp+Qhkc4ylJ0lVgPErSuFqSpIFADNDtWRzr76xWK5cvx7Br1y6R\nPD5jVatWZd26dRw5cgRQbvFcunTp/9u77/iY7z+A46/v3eUyZEhCphAkRIjRqBlqrypV1VJV2qpZ\n9SuqWrWqpdXqMIpW6aBGteggdFAxGo1NIgSJLWZ2bn5/f1wSVFQSIxHv5+PhcXff7/c+3/fdN+fe\n95lMnDiR4OBgevfunXfs7NmzURSFgQMH5q1wEhUVxalTp4iIiKBChQqQkcGp48eJjY+nZkgIfjnr\nMm/5fT3PPPMMTZvWp2vXICAbb29Yvvw9Hn44NC9xBPISR4DIyHUAjBw5io4dOwBQp05tOnTowPbt\n/3Dx4kU8PT0L96KrVMirfWT4h/BHzkj+8S8Vqphsk8q+UyY2thnAYks74nxrcCnLtlpMoPkCI7d8\ni/vpKFpvm4evb5kCl3vtSObD9WvyElDVTseIlwZhm/PUyv/+9wnx8UeJjV2Dq6sPYGXatNl88MFC\n3ntvOK+/3hewsm3bXjp3fpWIiDp4enpw9Ogxxo4dy7p1xzh1KhlX13TOn4c2bV7FYqmFp6cnLi5X\nJ/iWxFEIURo5OztbUlNTNQAeHh7WChUqGBcsWOD+wgsvXLZarURHRzs2btw461bllGZ3arR1r5vs\nan0nyv8vPXq0oXbt6jRq1Odun+qBc+bMGfr06UPbts3o0KE+cIpDh7YxadIkOnRoSe/erQFbIvPK\nK69gtVoZMOAJbH9WCtOnT2X16rX8+OM3VPg5GYa+RqSq0h8YAUzPOc8jQPugANp3bwZcHdzWo0eb\n/4yv499JDEuC4De/gne/B8AF+DzOygUVMk+fK3zyCHm1j6yxNTPTvRWE/ffE6OfTLOxIMrEjyciO\nJBP7T5kwWgB88PBTaJWwnSpn41jjepQf/krAXoX5w9vim5NA30pc3DHGjv2MsmVdWLDgI8Cd+o3q\n0rnzD9QICQGHq/1+27TpSPXqJ3B3r0fuNDjOzoEEBATg6VkLqAdAWtp5Ll1KITNTx6hRC+jZ8ylm\nzFhPRoatnHPnYPTo0TRo0IgGDRoV/P0TQoj7WO/evS8NHjw4cO7cud4rVqw4smTJkqMvvfRSpfff\nf9/XbDYr3bp1u/SgJ4/KtaNp77WUlJS8kyck7MPR8dhtdLQP5vqxseJ2zZs3l0GDBhMY6MNPP71H\nWFgtDh1KYvHiSIKCKtCnz6N5xw4bNg2Lxcrs2a/n1Yx9+OG3/PNPLKNGPcvDW/fC/6azBvhYq6G6\nRsMsR3tIzclUxr4A78NR/isAACAASURBVAwpVHxprhG4pGVjUTTs9QnitGt5PDJTKZd5BY/MFJwj\np2PfvF7RXvyLb9tqHwH2LIHaV6egsFpVDiebibkmWUy6aAFAr4Pa/naEB+oJr2hHeCU9elMqpuCu\neFzMINEeAg1wNLwKlaKX3HQdaoPBSHLypZzVZhQSE1OoXLkVLi4unD9/Hnt7WxP17XT8N5vNpKSk\noKoq5cqV4+DBg8yePZtNmzZRtWpVBg0aRNu2bWVpyiKSQRkll1ybu+PaATNubm55/3EkJiZ+GxgY\neNOl7kTJlJiYGBcYGJhvzVwpSh7Lo6oB8kV3x5hQ1SNMmTKDiIgalC9f9vZG0KZnQuUucOEKrJtl\nWwZvRxzU7wOO9pD4M3h5FKgoVVVJvGhh/Xu/svOIhS2VapPu4HzDcRoFPMpo8Cyjsd06ayjnfPW+\nZ5nrH7s6XDMHZOJpaPw8dGlO5sw32H3cxI4kEzFJRnYeN5GWbfvT9SyjIbySHfUD9YRXsqOWvx32\nunz+Br/5BfpOvPp479Kb1mZGRe3iscde5eGHa/Pbb6sAd0DHd999R4sWLfDz88s7Vr4ESy65NiWX\nXJu7Q5LH0uW/ksdSMUTIaDTRv/9QoqL2Ex8fj14v610XxbFjxxg1ahRffDEdD48UFMXM2LEvFnji\n9v/k7ASv9YHXZ8LEz6FtQ5j0uW3f0KdumTheTLey5YiBLYeNbE4wcOqKFXQN8fM7z6PxW4jL3s0Z\n8wkmn3bFpHfjwvB+XK5ShQsZVi6m2/7FnjZxId1Kanb+P5jstFeTTU9nB8p+tIzEC2ZiJyZjyekS\nXc1bR+faDoRX0lO/kh2VPLUF+8HyTAeY/KVtjecnW+cljlarlc2bd5OVZaB9+8ZAGWrVak5mpoHL\nlw0YjW55K9I888wzBXqrhRBCiLupVCSPer0du3cfJDExkS1bttCyZcviDum+NGTIECIjIylXTmXe\nvLF34QQ94INvYdteeO8r+DnKVuv42o0/bLKMKv8k2hLFzYeNxJ4xA+DqoNCkqp5BLeyJCNIT+Nkv\nKJ/NJathKCmtIvCZugjqVYeBteEmSZ3RrHIpw8rF3MTyX7eXMqxcSLeSdNGEX1ktgx8pQ3ignocC\n7HBzKtzaznl0Opj/Fkz7Bqa9krc5MnIrjz76P+rUqUn79i8B9ri7Q2Ji4nU1jEIIIURJUSqSR4DP\nPhtD+fJBVK8u88wVjYE5c0YyfryGqVNfvjunuLb28c3Ztm05tY4Wq8r+U2Y2JxjYkmAkJtGI0WKr\nDQyvpGdUO2cigvWE+duh1VyTFA7vCR8vxjE6FscDibZtEwfcNHEE0OsUfNy0+LjdfGock8k2VU2Z\nMmXwKmBz+q2cqOLPZ7WDcf/+d0aPHgi407p1P+rV+5r27dtjNmvJnS5MEkchhBAlValJHiMi6mJb\nUE4UVFxcHD///DOjR/cHjhMY6M4337x9w3HZJricrcH1sgWdBjQa0GkUtApotbb7GoWcfbdows2t\nfbxwhSSfimxu/wybF11m6xEjKVm25uQQHx19mzjRNMieBpXtcNL/R22fmzOM6A3j59r6VdarDo81\nL/J7oqoqixcv5quvvuLy5SsAPPRQPcaMGUPVqgVfySg5+RIbN+7Ax8eT5s0fAhQuXDDw3ntf4e/v\nx6hRn6DRaLC3h507dxY5XiGEEOJeKzXJo40ByAIcb3XgAy81NZWmTZty+fJlatSw47GbJFwb4g0M\n/7EsqQYNthWfb02nAa0GtBol5zYn2dRgSzgHfIHxSibnXDzhdwu+birtQh2ICNbTpKqe8rdaXeXf\nXukJHy2GK2m3rHW8lW+//ZZPP50BgI+PN1eupLBz5y4GDBjI0qVLKF++/A3PMZvN7NuXgLe3J35+\ntv0rV25i0KB36NnzcZo37wWUISysNq+++mrOROhCCCHE/alUJY/R0ft5++3XqVOnAVOmTCnucEo0\nV1c7Jk4cyI4d+2jRIvyG/Uazyofr0/h8UyaBZa28EJ6Jn68fFhXMVtt0NWYrWKxgsapYrPlvN1vB\nqoLZqmK2qBw9lsjRy8fRpqbjn36O7hEBDOvXFTs7u3yiLBiDg55fRz3Lyf1HeLHVw+ROuZ2enom9\nvR47u4L9mRsMBhYuXAjA229PolOnTqSnZzBq1EhiYnawfPlyhg4dSkpKOk5ODnnlDhv2AXPn/sD0\n6W8xYsT/gDI0b+5Ehw4xNGvWFrCNBNfpdHz00UdFfp1CCFHa7dmzx37KlCk+27dvd3ZycrJ269bt\n0uuvv37excXltlZyURQlvGvXrpdWrVp1DGxdk7y8vOrUrVs3Y8OGDQl3JvqSKz4+Xr9hwwbnQYMG\nXboT5ZWq5NFkMrNmzR8cOpQkyWM+duzYgdlspmHDKsBJhg3rjqI8ecNxJy6ZeXlJCntOmHi2kSPd\nq5zCXgehoU63df7p06fzx9IlKIAV23Tgi/fDpaTdvPPOOwUux2AwcuLEOYKCbMskWq3wzOQvMRiM\n9Jv3AeAAmBk8eAKLFv3K4sXv8MwzthVooqP38/XXv9CsWV169eqQ83wr8fFJXLlygdTUNCpVqsij\nj9rmsHRxcaZPnz7ExOxg165dPP30G3z//e9s2rSIiIhHAGcaNOjA+vW7sLPzAmyTkteoUYO1a9fe\n1vslhBAPkj///LNM586dq2VlZeX1VYqNjXX69ddf3aOiouKdnZ2LPLego6OjNT4+3jE9PV1xdnZW\nV65c6ert7W26M5EXjslkuq0Kk6I4fPiw/bJlyzzuVPJYxKGjJVPjxmEsWDCezZv/KO5QSpyoqCga\nN25Mjx7duHRpH2DNd4qZNfuy6TTjIkfPm/msd1needwN+zvwE+PEiZMsWbIEnU7LO+9MZvPmzUyf\n/iGOjg6sXRvJgQMHClROXNwx3N1b8uijr2JbPaUajo6NGDr0ZYYMGYKLSxhQDQjFaCyDRqOhbNna\nQE2gGrt3X2LOnBX8+WcsUB5w5+JFM6GhPejUaTQAV65cwWAwMHTo+wQEPEpi4lkuX4aMDA88PCqi\n0+k4csQE+ANu9Ov3IkeOHGHYsGG3/0YJIcQD6pVXXqmYlZWladu27ZW//vorbtGiRQk+Pj7G3bt3\nl/n4449v7DNUSK1bt075/vvvywIsWbLEo3v37nmJVGpqqqZHjx6BtWrVqlGjRo3QRYsWlQVbjV14\neHj10NDQGqGhoTV+++23MgBJSUl29evXrx4SEhIaHBxcMzIy0hnAyckpb2WKhQsXunfv3j0QoHv3\n7oH9+/ev0LBhw2pDhgypcLPzzZgxw7NNmzZVW7VqFeTv7x82ZcqU8hMnTvSuUaNGaJ06dULOnTun\nBThw4IB9s2bNgmvWrFkjPDy8+q5duxxyz9OvX7+AevXqhVSoUCFs4cKF7gBjx471j4mJcQ4JCQmd\nNGmSV0xMjENYWFiNkJCQ0GrVqoXu27evUINGSlXNo1ar5fnnuyADZ27UsGEtHnqoBg8/HIKT041r\nEmebVCb/ksri6CzqBtgxs5cbAR537s9j69YtqCq0bt2ajh07AtCiRQu6dOnCsmXLiYqKombNmtc9\n58CBI0yZshAfH0+mTx8DuBIcXAk7O3vs7V1IS3PFxcUFsNVq/tuyZcuwWCzYJsLXAQ40a9aemTNn\nEhISAlQEICNDQ7Vq1XB3dyc7O4uoqL08++wUoqN3c/LkOYYO/YzUVBg/vg+dO3fmo49m4uh4tV+t\nTEwvhBC359ChQ/oDBw44OTs7W3788cejubWMmZmZJwcMGFBl9erV7uPGjUu+nXP06dPn0oQJE3yf\nfvrpK3FxcU4vvvjixa1btzoDvPnmm74tW7ZM/f777xMvXLigrV+/fo0uXbqk+vn5maOiog45OTmp\n+/bts+/Vq1eV/fv3xy1YsMCjdevWKe+///5Zs9lMWlraLSvjjhw54rBly5ZDOp2Ol19+2T+/8+W8\nF4579uyJzcrK0lSvXr3WuHHjTsXFxcW++OKLAfPmzfMcP358cv/+/St9/vnnSWFhYYY///yzzODB\ngyv+/fffhwDOnTtnFxMTc3D37t0O3bp1C3r++ecvv/vuu6emT5/undtE37dv34AhQ4acGzx48KXs\n7GzFbDYX6r0sVcnjVVcA77tSssFgYOnSpfj6+tKuXbu7co47JTo6mjp16uDgkIJef4qNG+fg4HBj\nYp2QbObl765w8KyZgc3LMKq9M3bae5MQ5SZeWVlGVq/eiIeHG82a1QN0WK0ufPddJH5+fnz44bco\nioJOBydOnMDVtWBLUf57+b/Q0NAbVsoJDAwkPj4egL///pu2bduyYsWveftTU1Pp2LEjzz77LDpd\nKf3ICCFEMcrIyNCArXnZyckpr3nay8vLDJCdnX3bLaUNGzbMOnnypP0XX3zh0aZNm5Rr923cuNF1\n3bp1ZWfMmOEDYDAYlISEBH2lSpVML774YqXY2FhHjUZDUlKSPUCjRo0yBg4cGGgymTRPPvnk5SZN\nmtxyresnnnjicu53yM3OB9CkSZM0d3d3q7u7u9XZ2dnSo0ePKwBhYWGZe/fudUpJSdHs2rXLuUeP\nHnlTgBiNxrwv7S5dulzRarWEh4dnX7x4Md/28caNG2d8+OGHvidPntT37NnzclhYmKEw72WparbO\nNXv2Aho1asiRI0duq5xffvmFpk2b5vTHywYucubMXvr160f//i8CGdhGeFtp3Lgx/v7+1zW/RkZG\nMmnSJKKjo/O2ZR8/zpnBgzENHAhDhlz/b+hQ+PPP24o519y5c2nSpAmvvfYScBJQb0gcVVVleUwm\nj828SHKahYXPu/NGJ5cbEsfz569w4cLVz1lKSjr79ydw8uS568o6ffo8ycnXd6cwGk2YzWYaN24C\nwB9//EFkZCRpaelERv7G6tWrAUhNtePxx0fxySergBpAHWrV6sDcuXP544/ruyEUNHEsikaNGrFr\n1y6GDh1KvXr1aNGiBfPmzWP16tWSOAohxF1Sq1atbC8vL9P58+ftJk+e7GU2mzl37px26tSpvgBN\nmzZNuxPn6dChw5UJEyYEPPfcc9d9WamqyooVKxIOHjwYe/DgwdgzZ87se+ihh7Lfffddby8vL1Nc\nXFzsvn37Yk0mkwagY8eO6Zs2bYr39/c39uvXr/KsWbM84fqWqKysrOu+TJ2dna23Oh+AXq/PS541\nGg0ODg5q7n2z2axYLBZcXFzMuc89ePBg7NGjR/OSj9zjc8+Tn0GDBl1avXp1gqOjo7Vjx47Vfvrp\nJ5fCvI+lMnncvHk30dHbWbVqVYGfs3DhQtq0aUNkZCRgBC5jNJ5h69atREWtAQ4AiWi1yTz7bEce\ne6wxcBDYD+zi1KlETp8+jbPzGeAwcIw1a5YxceJEtm37DbgMpLHtkw/wmzuX1p9/DnPm5P1rNGcO\njT/7DNNbb+XFNG3aNJ5++mm2b9+ety06OprXXnuNFStW5G3LOnuWGcOGsfD112HjRti4kfqKATut\nBpf0FFSL5YbXm26w8uqyFEavSKVugB1rh5ejZfUbayVnz15O27Yj2LQpDigDOPH777sIC+vJ8OEf\nY+sioMdk0uDv3xF//07YKrS1gIbOnf+HnV0j4uJO0qtXT8xmCwMGvIWbWwuee+4Njh3Lpm7dHvTt\nO5aIiAiaNm0F2AbmKIrCwIEDCQkJuadNw0FBQcyaNYudO3eyYcMGBgwYcM87NwshxIPEzs6OMWPG\nnAaYOHFiQLly5eoGBATUiY6Odilbtqx59OjR525VRkEMHjz4wsiRI083aNDguprCli1bpk6fPt3b\narXld1u2bHEESElJ0fr6+pq0Wi2fffaZpyXn+/TQoUN6f39/08iRIy88++yzF3bu3OkE4Onpadq5\nc6eDxWJh9erV7jeL42bnKwgPDw9rhQoVjAsWLHAH26DPbdu2/efz3dzcLOnp6XlNcbGxsfoaNWoY\n3nrrreR27dpd2b17d6HmOCxdVSlb98CcFQy/mEKPiHDaR0dD7nrAej2MHg2hoXz00Uds2LCBefPm\n5czLl8nhwzv5448/aNgwkA4dbP1yW7SoSmTkTCpWLMeUKVP466+/MJvNNGrUiP79n7ru1AcPruDi\nxSv4+roAqQB06vQQbm5aGjcOAI4CYKjvgxe2oR4MeQpqBqNarES/MhUA3TOtsSWfClFRkfzyywZ6\n926DrRleYc+eDXz44Yf079+LJ59sAmhIebIrw7dsxxt4fto0AOoDRwD/r36GDo3h6atN7PtPmXj5\nuyscv2RhRFtnhrYsc/2qLanp8PgoOJlM+qVUTCYzgZ8sg29+A8DZz4/Q0FACAmoCtQCwWrPx8fHJ\nqZ2rk1eURlMWrVaLVhvCiBGDcXRsyttvv42qnicry5mRI99i5MiR6HQ6oqKiinrlhRBC3OdeffXV\nC1qtVn3//ff9Tp8+nduEmzpz5swTVatWvSMjo6tWrWrKr+/ke++9d3rAgAEVQ0JCQlVVVSpUqGDY\nsGFDwv/+97/k7t27V121apV7REREmqOjoxVg3bp1LjNmzPDR6XSqk5OTZfHixccAJk2adKpr165B\nvr6+ppCQkKzc5viCnq+gr2PJkiVHX3rppUrvv/++r9lsVrp163apcePGN206b9CgQZZOp1OrV68e\n+swzz1zIzs7WfP/99546nU4tX768aerUqacLem4A5WZVmvdCSkpK3skTEvbh6Hjshv5ohdJnHCy6\nOj2KAfgUiAfmA8obr8OUN2nb9jF+/30TK1d+wuOPRwC2wRkJCSdo1CgMb2/PvDLOnTtH3759OX/+\nwnWnKlPGifnz51OtWrXCxzniI9SPv0Pp1hJ+/AD1xz/Z0X00xnLuNDnxC+Q0L2/ZspuTJ5OJiKiL\nv78XAHv2HGL9+r8JCwuiQwdbU/CVfhMY//WvOOm0vNc0J3FLzYBdtn58/PMN1A9FVVW+2prJ1DVp\neJTR8GnPsjSsor8hPEN8EvYh3QHblDqbgBbXHuDsDFeu2JaXKQKTyYTJZMLJ6fam/hEQExMDQP36\n9Ys5EvFvcm1KLrk2d0dKytXuTW5ubnk1EomJid8GBgbWKGg5FouFY8eO2Tk7O1t9fHxubDoT90Ri\nYmJcYGBgn/z2la5m676dbbeKAnPfQL9oJlMdHFgAnALoUx84zKuvPsGSJe/SpMnVRLVmzap07dri\nusQRYMGChZw/f4HatcNYunQJK1f+yCOPNCcjI5PZs2cXLc7Rz6E42MPKDbDrIMrb86kPNJn4Ul7i\nCNC0aV2efrpdXuIIUKdONV577bm8xBGg7IQBzNBpec+qwhdvwcbPoV0j285OTaF+KFcyrQz49gqT\nfk6jWbA9a4aXuyFxtFqtTJmygDpdR5LaqS0Amp498Vyxgn0rVsDDD9sOHDasyIkj2JonJHEUQgiR\nH61WS1BQkEkSx5KrxCSPVqv1ph07C6x1A2haB1QVLqeh9G7MpPDqLACcu7eCGpUB6NQpgp492+Pl\n5XHLIjdt+guAMWPGEBwcTMWKFRk3bjyKAlu2bMFoNBY+Tp9yMNhWs0e312DPIfD3gheLuGxdZX/o\n95httux3voTzl2HWctu+CS/xT6KRTp9eYGO8gXGdXZjftyweZW689CaTme+/30B8fCJrmrWybVy9\nGkuZMujS0uCff2y1jiNGFC1OIYQQQtz3Skyfx0ceeYR69exp164dQ4YMyXcN4VtSFNvaxm2Hwoff\nQpfmvLL9gG375MGFL89k5tOtl6iSCtqafQBbLXxZVP62wFk9qBeugJ/Xf5eTn9HPwZwfIOmM7fEb\n/a6rdSy0N5+Hr362NdtnGSAjC0unCOakB/LxqktUcNfyw2BPale4ceCHqqooioK9fSWWLVvJkSNH\nbXMx/v03rF6Nz7ff4piYaDt42DAoV67ocQohhBDivlZikkdVhexsAz/99DMxMTF88823uLuXLXxB\nubWPW/ZAq8FgMkOv9nm1joWiQAWjBpNOx5aAmmwOrEtyGQ9cDem4ZafjbMjAPU7B7VI2rg4Kro4a\n3Bxtty72ChrNf4wQzq19/Pi726t1zJVb+zh/FXz/O8llyvJqqxFsWZ/OY3UcmNLNFReH62sbzWYz\n48fPw2qF9977FHChWjWoVq267YAJE2D1aryWL0djNkutoxBCCCFKTvL422/rMRh2sWDBAg4ejGf5\n8mUMHDiw8AVdW/t47qLt8bj+hSrCalWJO2sm6rCBDa98xi6LJ0adHqwmtNkXcNCUIUtfBqtGC79Z\nsE1KfmMYLvYKbk4aXB0U3HITSwcNbk45t4/2xTXLG/tmYeiOqui0Buy0oNMo6LRgp1XQaXJuteTd\n1163TcFOi220dE7t46YKtRnxxBjSr+h57wlXnn7YMd+pbvbuTWDatG8AGDDgLapU+dc0T/XqQdeu\naHLmYpRaRyGEEEKUmORRG5/E8gveVK87iNTjXxO9aRdFyR2B62sfe7YrUK3juVQLUYeNRB02sPmw\nkYsZtrmXqnv50+f3n2gev53vHGM5TzYr4gCtlowDK0n18iYl00pKlpXUbNV2m6WSmmUlJUslNdt2\nm5JlJSHZSkqWidRsK9m5kw64tYa9wN4bE9DCUBSw02jRjVhBpmJHNVcL373oSTXvm81PqPDQQ62Z\nOXMmoaGhVKlSJf/DcmofLU5OaKXWUQghxN1iNoPJlH+Tnb29iqbEDNN44JWY5NFl7HvsfHIC65yD\noek7AIRPTibEV0d1bx0hvjpCfOwI9tLhqL/FhNGKAvPHwadLYPxL+R6SabQSfcxE1CEDmxOMHDpn\nW9exnLOGZsF6mgXbExGsx9tVC9kKRO6kWURdCPBGE7sOnu+CSzU/XAD/soUfeZyZbebPzf9w4HAS\nTi5lCa/fEHvHMpgtYLaqmCxgtqiYrWC69tYClny2ZWYb2bl7DwlHEtGkn8fL6TAnD/SimnervHMa\nDEbGjJnJs892JTy8M1CGwYNv0Re0Xj0OzZqF2dmZUKl1FEIIcTfs3OnAI4+EcM1E1tdp1CiNbdsO\nFbV4rVYbHhwcnGWxWJSgoKCs5cuXJ7q4uFhv/cwb/fLLLy6560QvXrzY7cCBA45Tpkw5m9+xFy5c\n0M6fP99jzJgx5wESExPtBg0aFBAZGXm0qK+lJCgxyWOAm4bf1r9B2rkMTpStSHStOpx5vh/xZ818\ntz0zr6ZOo0CgpzYnqbTLSSp1BLhrr+9jGBIIc97Ie2i1qsSeMbPpsIGoQ0Z2JBkxWkCvg4aV9TwZ\n7kJEkJ4QH92NfRWHPQ3TF6PZvNv2WKe1NREXUXJyMq+88gqHD1+dD3SpgwOTJk2kTZs2hS7PZDIx\nYMAwju7dhwbbmi9xwGuv7eLNN9+ge3fbyO6PPlrMJ58sYf36Pezd+2SBZ9tJbdiw0DEJIYQQBWax\nkJc4arVXaxnNZgVVhZSUos8PB9jb21sPHjwYC9ClS5fK06dPLz9x4sS8VWtyZ3zRFnIaut69e6cA\nKTfbf/HiRe2XX37plZs8BgYGmu73xBFKUPLoc/wwDarDzxkQkHqFunOex6mTGwAWq8rxSxYOnjFz\n8KyJg2fNxJ42s3a/gdzZfZz0CtW8ddTIq6m0w8tFQ0yikagEI1sSDFzKsB0c4qOjX1MnmgXb83Cg\nHge7W9RkujrDyN7w1hzb4+e7QKBfkV/r2LFjOXw4AR8fb9q0aUN8fDz//BPD2LFvUb16dQICAgpV\n3vr169m7dx/e3l5MmTKF4OBgli9fzqxZs5k1axadOj2Ko6Mjr776Otu3n+LNN98s9AdECCGEuGse\nfjibli1T2LDBjf79k5k79yTZ2QqVK9fi7Fk9I0bkW7NXFBEREel79+51jI+P13fs2DG4SZMmaTt2\n7HBevXp1wv79+x3efvttP6PRqFSqVMmwdOnSRDc3N+uKFStcX3vttQAPDw9zWFhYZm5ZM2bM8IyJ\niSnzzTffHD9x4oTuhRdeqHT8+HF7gFmzZiV9+umn3idOnLAPCQkJfeSRR1JHjBiR3Llz5+DDhw8f\nyMzMVJ577rlKe/fuddJqtUybNu3EY489ljZjxgzPX375pWxWVpbm+PHj9h07drwyd+7ck3fq9d8J\nJSZ5rKXX0zdVwdViwBRRB6dOzfL2aTUKlcvpqFxOR8cwh7ztmUYrh86ZiT9rJu6M7TZyfzZLtl8/\nX2R5Fw0tqtnTrJo9TYP0eLkUIXEa9jR8uhTSMm+r1jEhIYGdO3fh7OzMokWLcXcvi6qqjB07lnXr\n1rNq1SqGDRtWqDI3b94MwPPPP0/dunXz7q9ZE8nWrUfYsWM/ERHP4eDgyMqVK4scuxBCCHHXTJx4\nmg0b3Pj66/KMG3eW774ry9mzeqpWzeb55y/fiVOYTCbWrVvn2q5du1SAxMREhy+++CJx0aJFx8+c\nOaObMmWK76ZNmw65urpax44d6zN58mTvt99+++zLL78c+Ntvv8XXrFnT0Llz53wHCQwaNKhis2bN\n0saPH3/EbDaTkpKinT59+snOnTs75tZ6xsfH563O8f7773sBHDp0KHbXrl0OnTp1Cj5y5Mh+gNjY\nWKc9e/bEOjo6WoOCgmqNGjXqXFBQ0B1ZovFOuOvJo6IoHbCtEqgF5quq+l5+x61/qCGuO3cAYFfA\nORmd9BrqBuipG3B1pRRVVUlOtfD7jiSOnEkjIsSdlg9VzHe0caG4OsP2ryHLQKaXB//8tYNy5cpS\ns2bV6859q/OcOnUKgNq1w/KmIlIUhWbNmrFu3XpOniz8j4ubTa6+efMZzp6F2bM3EBFR1NFHQggh\nxD3QvHlmXu3juHG+rF1r+5IcM+b07axqBmAwGDQhISGhAA0bNkwbPnz4haSkJDtfX19j69atMwA2\nbtxY5siRIw4NGjQIATCZTEp4eHj67t27HSpUqGAICwszAPTu3fvi/Pnzb5iMeuvWrS4rVqw4BqDT\n6fD09LRcuHDhpoFv3brVediwYckA9erVy/bz8zPu27fPASAiIiLV09PTAhAUFJR95MgR+wcmeVQU\nRQvMBtoCJ4F/NdlXZAAAD1pJREFUFEX5SVXV2H8f674xynanRTi0KPp6o6dOnWLs2LfYv38/AKuB\nxo0bMXnyZNzd3Qtd3v79CSxY8BNNmtTmyScfAxw4si+OFi0GUrNmEPv3rwQsgJXg4C6cP3+ZvXuX\nUqmSLwCfffY969f/zaBB3enQoQl+fv4YDLBmzQ6aNVvHU0+1B2Dz5i2kpEBamnJdEpqQcIL09Eyq\nVPHH1dUZgLS0DFJS0nFxKYObmzMRERGsX/87X365kKCgYEJCqrNs2fdkZGSi0Wh49VUZJS2EEOI+\nkFv7uHChbfWNO1TreG2fx2s5OTnlDZpRVZWIiIjUn3/++di1x2zdutXxtiug8vFfq+rp9fq8nVqt\nVjXdbBR6MbnbNY8NgARVVY8CKIqyFOgK3HABcyX2bUdm7E13/yeTycQbb7zBuXPJODs7U7lyIIcP\nH2bbtr8ZPHgw48aNu2XNoKqqmExm9HrbFDc//LCZjz/+jm3bEggMbA1kcuxYJnXq1MHf35+YmOy8\n5168mE5qagaHDilcuJCNolhZv34fq1f/Re3aD+HjEwK4odNV5OjR4wwYMIm//95OUlIiu3fv4ehR\nmDv3DwYPTgJUFAWGDJlCVNQuZs9+nebN6wEqy5f/xuTJC+jRozUTJrxAQEAgfn6V+PXXJP78sz9B\nQXD0KBgMMHr0KDQaDTExMUV6T691J8oQd4dcm5JLrk3JJdfmzgoODr79Qq6tfYQ7UutYUC1atMgY\nOXJkxf3799vXqlXLkJaWpjl27Jhd3bp1s0+ePKk/cOCAfc2aNQ1Lly7Nd23jpk2bpn3wwQflx48f\nn2w2m0lNTdW4ublZMjIy8p1jKCIiIn3RokUeXbp0Sdu7d6/9mTNn9LVr186Ojo52uruv9Pbd7eTR\nHzhxzeOTQL5Dd81urmQ9VJXMBjWKfLKYmBjOnUvG19eHiRMn4uTkxOXLl/MGqBw6dJjq1avd9Plr\n1vzNJ58sp0ePtvTr1wez2YWmTX3p1SuNdu3a5R1XuXJl5s+ff8Pz165dS2ZmJs7OzqiqBlWFp59+\nlqZNW1C9enXMZlvN54svjmLcuHGkpKTw8ce2Cbj1ej3BwZXw9PTEYKiUV6aPTxDBwenY2weTnW1r\nItdoDuLl5YWTUwWysmyv57nnprF2bS8sFoiPh+rVq9O3b19at25d5PdTCCGEuOcmTTrNpk1uBAVl\n3am+jgXh5+dnnjdvXmLPnj2rGI1GBWDChAmnateubZg5c2ZS586dgzw8PMwNGzZMj4uLc/z38+fM\nmXO8X79+lapVq1ZOo9Ewa9aspDZt2mSEh4enBwcH12zVqlXKiBEjknOPHz16dHKfPn0qVatWLVSr\n1TJv3rxER0fHm1dHliDKf1Wb3nbhitIDaK+qav+cx32ABqqqDgNISUnJO/mR2B04OJ8gNKxWkc/3\nySef8O23ixg0aBAvvXR1VZnJk99h1apVjBo1il69egK2GsY9ew5RtqwLgYF+gD2rVkXTrVt/2rdv\nT2RkZJHjKAiLxcLatWvZuXMnXl5e9OjRA09PzztSdkH6XhZG7q/z+vWL3p1A3B1ybUouuTYll1yb\nuyMl5eqMNW5ubnlfQomJid8GBgYWrmZo1y4HfH1N+PhY7lyEojASExPjAgMD++S3727XPJ4Erp13\npgJwOr8DVb0etLc3e3xun8bDh6/OI6qqat7ja9fKnjx5PhMmzGPkyIF8+OFHgBMdOgTx11/BRERE\n3FYcBaHVauncuTOdO3e+42Xfjb4ZQgghxD1Tr172rQ8SxeVur/XzDxCsKEplRVH0QE/gp7t1sg4d\nOqDTafnjjz+ZPHkya9dGMnr0aHbsiOXiRTu0WjdAD3jTpk0Pypcvj4uLL2DrXuDg4EDz5s3RyBJI\nQgghhBD5uqs1j6qqmhVFeRlYh22qngWqqh64W+fz9vbmzTff5J133mHVqtWsWmXrT3j5soYzZ0ws\nWrSNtm1fBqBRIz9Onz6NTldiproUQgghSh1VVYu0DKAoXv913e565qSq6hpgzd0+T66uXbtSq1Yt\nVq9ezZEjF/HyCqN5804sXryY3r175x2n0WikhlEIIYS4y4xGY1xmZmbYtdPiiJItMzNTYzQa4262\nv1RWuwUEVCQ6+jyPP96Hp5/ujUajoWXLlsUdlhBCCPHASU9Pn3bixAn0en0NRVGk1qaEU1XVajQa\n49LT06fd7JhSmTxGRm5l+fLfiIs7S69e+Q4UEkIIIcQ9EB4ebgXyXV1O3J9KZfLYpEkdZs6ciodH\nxeIORQghhBCiVCmVyWO5cu68/PJr2MboCCGEEEKIO6WU9j1wQxJHIYQQQog7r9Qlj8OHf8inny4n\nLS2tuEMRQgghhCh1SlXyePr0eWbOXMbo0ROxWGRFIyGEEEKIO61U9Xn08HBl6dKZHDuWTtmyZW/9\nBCGEEEIIUSilKnl0cLDnqaeeA1yKOxQhhBBCiFKpVDVb29atlsRRCCGEEOJuKTXJ46efLuHNN+eR\nlJRU3KEIIYQQQpRapaLZ2mq18vHH35GUdIb27XtQqVKl4g5JCCGEEKJUKhXJo6IofP31VH76aS/N\nmjUr7nCEEEIIIUqtUpM8PvJIex55pG9xhyKEEEIIUaqVmj6P4FHcAQghhBBClHr3ffK4bt02+vd/\nj3/+2VPcoQghhBBClHr3ffL45Zer+fLLFWzYsKG4QxFCCCGEKPXu+z6PkyYNolq1h+nVq1dxhyKE\nEEIIUerd98ljjRp1eeed7sUdhhBCCCHEA+G+b7aWgTJCCCGEEPfOfZs8njqVTNeuI1m5Uvo6CiGE\nEELcK/dts/WSJev46ae/0Ok86dbtieIORwghhBDigXDfJo99+nTCzs6XOnUaFncoQgghhBAPjPs2\nefT29mX48HbFHYYQQgghxAPlvu3zCO7FHYAQQgghxAPnvkserVYrTzzxGrNmLcdoNBZ3OEIIIYQQ\nD5TbSh4VRemhKMoBRVGsiqLU/9e+NxRFSVAUJV5RlPa3F+ZVW7bsYeXKDUyb9gk63X3b6i6EEEII\ncV+63exrP/AEMO/ajYqihAI9gZqAH/C7oijVVFW13Ob5CA+vwZIlczAYHNFo7ruKUyGEEEKI+9pt\nJY+qqsYBKIry711dgaWqqhqAY4qiJAANgG23cz4AJycHevZ8AdDfblFCCCGEEKKQ7la7rz/w9zWP\nT+Zsu6XY2Nj/3G+xOGEwqEWPTBRZTExMcYcgbkKuTckl16bkkmtzZwUHBxd3COIeuWXyqCjK74BP\nPrvGqqq6+mZPy2fbbWd877+/GL2+HE8+2QdPT8/bLU4IIYQQQhTSLZNHVVXbFKHck0DANY8rAKcL\n8sTQ0NB8t6ekpLNs2QaMRhPjx08lICAg3+PEnZf767x+/fq3OFLca3JtSi65NiWXXJu7IyUlpbhD\nEPfI3Wq2/gn4TlGUj7ANmAkGtt9Ogc7OjqxZ8yUxMaclcRRCCCGEKCa3lTwqitINmAmUB35VFGW3\nqqrtVVU9oCjKciAWMANDb3ektVarpVWrR2nVSiYHF0IIIYQoLrc72nolsPIm+94F3r2d8q+nBcre\nueKEEEIIIUSh3RcTJc6b9wMDB05j//4DxR2KEEIIIcQD7b5IHufO/YHPP1/C4cOHizsUIYQQQogH\n2n2xvt+3305l2bJddOrUqbhDEUIIIYR4oN0XyWOtWg2pVeuJ4g5DCCGEEOKBd180W4NHcQcghBBC\nCCEo4cnjli276dbtddat21TcoQghhBBCCEp48vjNN7+yatUfbNiwobhDEUIIIYQQlPA+jxMmDKB6\n9UY8+mjX4g5FCCGEEEJQwpNHP78qjBjRobjDEEIIIYQQOUp0s7UMlBFCCCGEKFlKZPKYkpJOy5YD\nmTt3OaqqFnc4QgghhBAiR4lMHn/44Q82btzB8uUrUBSluMMRQgghhBA5SmSfx6eeaou9fQXKlw8s\n7lCEEEIIIcQ1SmTy6OzsQu/eLwFS6yiEEEIIUZKUyGZrcEcSRyGEEEKIkqfEJY9PPPEaEyfOJTU1\ntbhDEUIIIYQQ/1KiksfDh0+ycuUGPv10Lvb29sUdjhBCCCGE+JcS1eexcmVf1q//jlOnDJI8CiGE\nEEKUQCUqedTptLRt+zjgWNyhCCGEEEKIfJSoZmur1R5JHIUQQgghSq4SU/M4a9ZcMjNTmDq1PlWq\nVCnucIQQQgghRD6U4lz+LyUlRdYeFEIIIUoZNzc3mW+vFCtRzdZCCCGEEKJkk+RRCCGEEEIUWLE2\nWwshhBBCiPuL1DwKIYQQQogCk+RRCCGEEEIUWIlIHhVF6aAoSryiKAmKoowp7njE9RRFSVQUZZ+i\nKLsVRYkp7ngeZIqiLFAUJVlRlP3XbPNQFOU3RVEO59y6F2eMD6qbXJuJiqKcyvns7FYUpVNxxvig\nUhQlQFGUDYqixCmKckBRlOE52+WzI0QRFHvyqCiKFpgNdARCgV6KooQWb1QiHy1VVa2rqmr94g7k\nAfcV0OFf28YAf6iqGgz8kfNY3HtfceO1Afg457NTV1XVNfc4JmFjBkaqqloDaAQMzfmekc+OEEVQ\n7Mkj0ABIUFX1qKqqRmAp0LWYYxKiRFJVdRNw6V+buwJf59z/Gnj8ngYlgJteG1ECqKp6RlXVnTn3\n04A4wB/57AhRJCUhefQHTlzz+GTONlFyqMB6RVF2KIoyoLiDETfwVlX1DNi+JAGvYo5HXO9lRVH2\n5jRrS7NoMVMUJRCoB0Qjnx0hiqQkJI/5zUIv8weVLE1VVX0IW9eCoYqiNC/ugIS4T8wBqgJ1gTPA\n9OIN58GmKIoz8APwP1VVU4s7HiHuVyUheTwJBFzzuAJwuphiEflQVfV0zm0ysBJbVwNRcpxTFMUX\nIOc2uZjjETlUVT2nqqpFVVUr8AXy2Sk2iqLYYUscF6uq+mPOZvnsCFEEJSF5/AcIVhSlsqIoeqAn\n8FMxxyRyKIpSRlEUl9z7QDtg/38/S9xjPwF9c+73BVYXYyziGrmJSY5uyGenWCiKogBfAnGqqn50\nzS757AhRBCVihZmc6Ss+AbTAAlVV3y3mkEQORVGqYKttBNAB38n1KT6KoiwBWgDlgHPABGAVsByo\nCBwHeqiqKgM37rGbXJsW2JqsVSARGJjbx07cO4qiRABRwD7AmrP5TWz9HuWzI0QhlYjkUQghhBBC\n3B9KQrO1EEIIIYS4T0jyKIQQQgghCkySRyGEEEIIUWCSPAohhBBCiAKT5FEIIYQQQhSYJI9CCCGE\nEKLAJHkUQgghhBAF9n/yw25IQU/VMQAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"process_var = 2\n",
"sensor_var = 4.5\n",
"x = (0, 400) # gaussian N(0, 400)\n",
"process_model = (1., process_var)\n",
"N = 25\n",
"\n",
"dog = DogSimulation(x[0], process_model[0], sensor_var, process_var)\n",
"zs = [dog.move_and_sense() for _ in range(N)]\n",
"\n",
"xs, priors = np.zeros((N, 2)), np.zeros((N, 2))\n",
"for i, z in enumerate(zs):\n",
" prior = predict(x, process_model) \n",
" x = update(prior, (z, sensor_var))\n",
" priors[i] = prior\n",
" \n",
" xs[i] = x\n",
"plt.figure()\n",
"book_plots.plot_measurements(zs)\n",
"book_plots.plot_filter(xs[:, 0], var=priors[:, 1])\n",
"book_plots.plot_predictions(priors[:, 0])\n",
"book_plots.show_legend()\n",
"kf_internal.print_variance(xs)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Here we can see that the variance converges to 2.1623 in 9 steps. This means that we have become very confident in our position estimate. It is equal to $\\sigma=1.47$ meters. Contrast this to the sensor's $\\sigma=2.12$ meters. The first few measurements are unsure due to our uncertainty of the initial position, but the filter quickly converges to an estimate with lower variance than the sensor!\n",
"\n",
"This code fully implements a Kalman filter. If you have tried to read the literature you are perhaps surprised, because this looks nothing like the endless pages of math in those books. So long as we worry about *using* the equations rather than *deriving* them the topic is approachable. Moreover, I hope you'll agree that you have a decent intuitive grasp of what is happening. We represent beliefs with Gaussians, and they get better over time because more measurements means we have more data to work with."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Exercise: Modify Variance Values\n",
"\n",
"Modify the values of `process_var` and `sensor_var` and note the effect on the filter and on the variance. Which has a larger effect on the variance convergence? For example, which results in a smaller variance:\n",
"\n",
"```python\n",
"process_var = 40\n",
"sensor_var = 2\n",
"```\n",
" \n",
"or:\n",
"\n",
"```python\n",
"process_var = 2\n",
"sensor_var = 40\n",
"```"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### KF Animation\n",
"\n",
"If you are reading this in a browser you will be able to see an animation of the filter tracking the dog directly below this sentence.\n",
"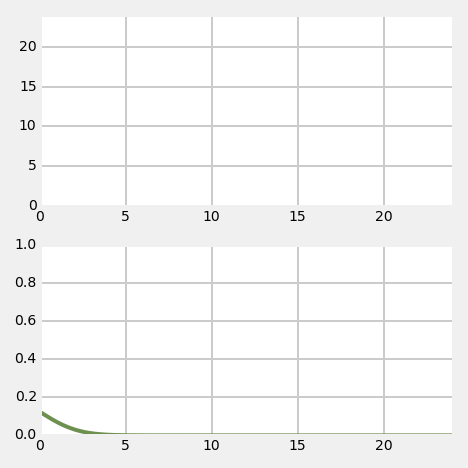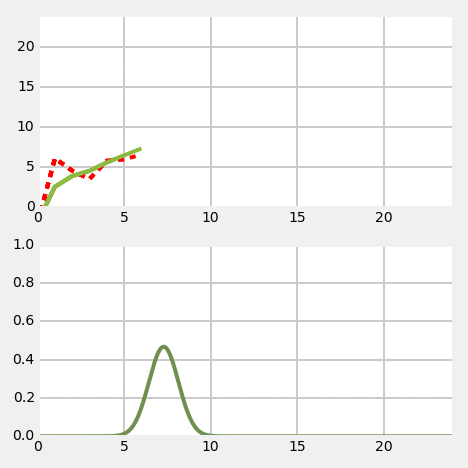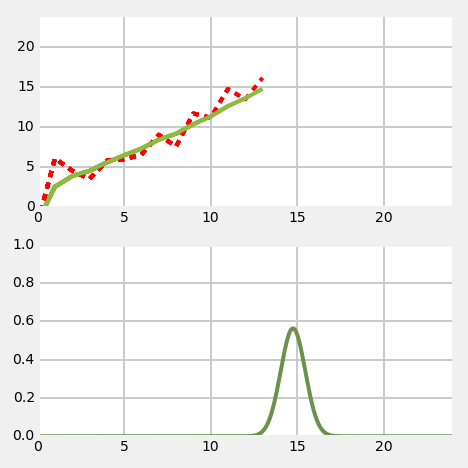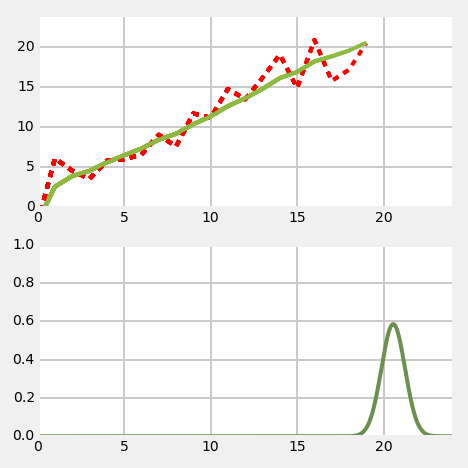 \n",
"\n",
"The top plot shows the output of the filter in green, and the measurements with a dashed red line. The bottom plot shows the Gaussian at each step. \n",
"\n",
"When the track first starts you can see that the measurements varies quite a bit from the initial prediction. At this point the Gaussian probability is small (the curve is low and wide) so the filter does not trust its prediction. As a result, the filter adjusts its estimate a large amount. As the filter innovates you can see that as the Gaussian becomes taller, indicating greater certainty in the estimate, the filter's output becomes very close to a straight line. At `x = 15` and greater you can see that there is a large amount of noise in the measurement, but the filter does not react much to it compared to how much it changed for the first noisy measurement."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Full Description of the Algorithm\n",
"\n",
"Recall the diagram we used for the g-h filter:\n",
"
\n",
"\n",
"The top plot shows the output of the filter in green, and the measurements with a dashed red line. The bottom plot shows the Gaussian at each step. \n",
"\n",
"When the track first starts you can see that the measurements varies quite a bit from the initial prediction. At this point the Gaussian probability is small (the curve is low and wide) so the filter does not trust its prediction. As a result, the filter adjusts its estimate a large amount. As the filter innovates you can see that as the Gaussian becomes taller, indicating greater certainty in the estimate, the filter's output becomes very close to a straight line. At `x = 15` and greater you can see that there is a large amount of noise in the measurement, but the filter does not react much to it compared to how much it changed for the first noisy measurement."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Full Description of the Algorithm\n",
"\n",
"Recall the diagram we used for the g-h filter:\n",
" "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We've been doing the same thing in this chapter. The Kalman filter makes a prediction, takes a measurement, and then forms a new estimate somewhere between the two.\n",
"\n",
"**This is extremely important to understand**: Every filter in this book implements the same algorithm, just with different mathematical details. The math can become challenging in later chapters, but the idea is easy to understand.\n",
"\n",
"It is important to see past the details of the equations of a specific filter and understand *what* the equations are calculating and *why*. There are a tremendous number of filters. They all use different math to implement the same algorithm. The choice of math affects the quality of results and what problems can be represented, but not the underlying ideas.\n",
"\n",
"Here is the generic algorithm:\n",
"\n",
"**Initialization**\n",
"\n",
" 1. Initialize the state of the filter\n",
" 2. Initialize our belief in the state\n",
" \n",
"**Predict**\n",
"\n",
" 1. Use system behavior to predict state at the next time step\n",
" 2. Adjust belief to account for the uncertainty in prediction\n",
" \n",
"**Update**\n",
"\n",
" 1. Get a measurement and associated belief about its accuracy\n",
" 2. Compute residual between estimated state and measurement\n",
" 3. Compute scaling factor based on whether the measurement\n",
" or prediction is more accurate\n",
" 4. set state between the prediction and measurement based \n",
" on scaling factor\n",
" 5. update belief in the state based on how certain we are \n",
" in the measurement\n",
"\n",
"You will be hard pressed to find a Bayesian filter algorithm that does not fit into this form. Some filters will not include some aspects, such as error in the prediction, and others will have very complicated methods of computation, but this is what they all do. \n",
"\n",
"The equations for the univariate Kalman filter are:\n",
"\n",
"Predict\n",
"\n",
"$\\begin{array}{|l|l|l|}\n",
"\\hline\n",
"\\text{Equation} & \\text{Implementation} & \\text{Kalman Form}\\\\\n",
"\\hline\n",
" \\bar x = x + f_x & \\bar\\mu = \\mu + \\mu_{f_x} & \\bar x = x + dx\\\\\n",
"& \\bar\\sigma^2 = \\sigma^2 + \\sigma_{f_x}^2 & \\bar P = P + Q\\\\\n",
"\\hline\n",
"\\end{array}$\n",
"\n",
"\n",
"Update\n",
"\n",
"$\\begin{array}{|l|l|l|}\n",
"\\hline\n",
"\\text{Equation} & \\text{Implementation}& \\text{Kalman Form}\\\\\n",
"\\hline\n",
" x = \\| \\mathcal L\\bar x\\| & y = z - \\bar\\mu & y = z - \\bar x\\\\\n",
" & K = \\frac {\\bar\\sigma^2} {\\bar\\sigma^2 + \\sigma_z^2} & K = \\frac {\\bar P}{\\bar P+R}\\\\\n",
" & \\mu = \\bar \\mu + Ky & x = \\bar x + Ky\\\\\n",
" & \\sigma^2 = \\frac {\\bar\\sigma^2 \\sigma_z^2} {\\bar\\sigma^2 + \\sigma_z^2} & P = (1-K)\\bar P\\\\\n",
"\\hline\n",
"\\end{array}$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Comparison with g-h and discrete Bayes Filters\n",
"\n",
"Now is a good time to understand the differences between these three filters in terms of how we model errors. For the g-h filter we modeled our measurements as shown in this graph:"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAjwAAACICAYAAADjyzHQAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAADRNJREFUeJzt3X9s1PUdx/HXuy1XwUqxU9QBo+gQ\nccosRYObThSImT9Whwkbi5sxJttMGJlGVPwVjC5hbNPItrAf0W1WJ8IkKIKTVDcXklUsoFRU0G3F\nUkBU8EYtu4PeZ3/ct3qUu/aOu95dP/d8JBe+/Xx/9PPu58q9+vl+v3fmnBMAAIDPygrdAQAAgIFG\n4AEAAN4j8AAAAO8ReAAAgPcIPAAAwHsV2R4gHA5zmxcAAJ6prq62Qvchl5jhAQAA3iPwAAAA72V9\nSitRdXV1Lg9X1FpaWiRJU6ZMKXBP8o/aS6/2Uq1bonap9Gov1bolKRwOF7oLA4YZHgAA4D0CDwAA\n8B6BBwAAeI/AAwAAvEfgAQAA3iPwAAAA7xF4AACA9wg8AADAewQeAADgPQIPAADwHoEHAAB4j8AD\nAAC8R+ABAADeI/AAAADvEXgAAID3CDwAAMB7BB4AAOA9Ag8AAPAegQcAAHiPwAMAALxH4AEAAN4j\n8AAAAO8ReAAAgPcIPAAAwHsEHgAA4D0CDwAA8B6BBwAAeI/AAwAAvEfgAQAA3iPwAAAA7xF4gIG0\nsDr+AFA4/B5CBB4AAFACCDwAAMB7BB4AAJCV2jvWuNo71rhcbTcQKgrxTQEAwOCxcePGsqqqqttC\nodBEM0s5WdLW1taYzvHS3S4TzrlYNBp9q7Ozc3F9fX2s93oCDwAA6FNVVdVtY8aMmT1s2LCjgkTc\nVklSbW3txL6PlO52x6arq+vc9vZ2SVrUex2ntAAAQJ9CodDE1GGneAwbNiwWCoWShikCDwCksmW5\nzn1xjuqfmyE9dI60ZXmhewQURF+nsYpNqr5ySgsAktmyXFo9T5WHDsa/DrdLq+fFlyfNLly/ABwT\nAg+QD3+4stA9yMqEAwfiC60nFLYj+bTzVak7cmTboYPSM3OljX8qTJ/yrCTHHUXtscceG3H99def\nsWnTpq11dXX/y2RfAg8AJNM77PTXDuBTjzfvqFny4jujPjgQCZ18QmV03vTxHddNHbsv2+MuW7as\nZvLkyZ2NjY01dXV1uzLZl8CDolR7xxpJUtuiwT0z8qkb1gzYofPxs9rW0iJJmjJlyoB9j6Lz0Dnx\n01i9VY8Z0PEsJt6MOx8rkVePN++ouf+5N8dGDsfKJGnvgUjo/ufeHJvtccPhcFlLS0tVU1PTtoaG\nhi8++OCDGQWeQXMREgDk1fR7pSFDj2wbMjTeDiCphl+tn3Df6q21PWGnR+RwrOy+1Vtrszn2E088\nMWLatGnhSZMmRUaMGNG9fv36YZnsT+ABgGQmzZauXqLI0JFysvjMztVLuGAZ6MehbmeZtKdr+fLl\nNXPmzNkvSddee+2+xsbGmkz255QWAKQyabZao6dL8uC0DpAHz8y9aNsFP2k6d++BSKj3upEnVEaT\ntadjz5495c3NzcO3b98+dO7cueru7jYzc0uXLt1ZVpbe3A0zPAAAIGfmTR/fUVlRdsSbFFZWlMXm\nTR/fcazHbGxsPHHWrFkf7dq1q7Wjo6N1z549W0aPHh1dt25dVbrHIPAAAICcuW7q2H33XHX2jpEn\nVEZN8Zmde646e0c2d2mtWLHic7Nmzdqf2NbQ0LA/k9NanNICAAA5dd3UsftycRt6jw0bNmzr3Xb3\n3XfvzeQYBB4gTas2d+iBtR/oo66YPt/0kuZfPkHX1I0qdLcAoODajvtOsBTOyXYDgcADpGHV5g4t\nWNmqg4fip6U7Pj6oBStbJYnQAwCDAIEHRe1bv/1nobsgSdr83seKdh/5QcEHD3Xrtr9s0ZMb3ku9\n42l/jf9bJHUAJWlh/mcTUHy4aBlIQ++w0187AKC4MMODovbUDy4sdBckSV9d9JI6Pj54VPuoEUML\n3seej5YAAKTGDA+QhvmXT9DQIeVHtA0dUq75l08oUI8AAJlghgdIQ8+FyQ+s3hK/S2vEUO7SAoA8\nKi8vrx8/fvxB55zKy8vdww8//N7MmTM/SXd/Ag+QpmvqRml0925JfMwAAPTp1Udq9PJPR6lzb0hV\nI6O65PYOnX9jVu/LU1lZGXv77bfflKSnn356+J133jl65syZR70/TyoEHgAAkDuvPlKjFxaM1eFI\n/LKZzvdDemHB2Fx+i3A4XF5dXX04k30IPAAAIDd+d+kE7Wk9XrFDR34y+uFImZ6/vTabQ0cikbKz\nzjrr7EgkYh9++OGQtWvXbs9kfwIPAADInd5hp7/2NCWe0mpqajr+hhtuGLd9+/atfFo6AADIr+//\nbZuqTokmXZeq/RjMmDHjk/3791fs3r077YkbAg8AAMidS27vUEXlke/KWlEZ0yW3d+TqW2zevPm4\nWCymU045Je3reDilhaLUtujKQndh0OBnBaCo9NyNlewurTW3jDvWw/ZcwyNJzjktXbq0raIi/RhD\n4AEAALl1/o37sr0Nvbfu7u6N2ezPKS0AAOA9Ag8AAPAegQcAAPTJORfrf6vikKqvBB4AANCnaDT6\nVldXV9Fnhq6urrJoNPpWsnVctAwAAPrU2dm5uL29XaFQaKKZHRV8aqV6SWpra0saNjLd7lg452LR\naPStzs7OxcnWE3gAAECf6uvrY5IWpdxgYfi7klTb34HS3W4AFP30FAAAQLYIPAAAwHsEHgAA4D0C\nDwAA8B6BBwAAeI/AAwAAvEfgAQAA3iPwAAAA7xF4AACA9wg8AADAewQeAADgPQIPAADwHoEHAAB4\nj8ADAAC8R+ABAADeI/AAAADvEXgAAID3CDwAAMB7BB4AAOA9Ag8AAPAegQcAAHiPwAMAALxH4AEA\nAN4j8AAAAO8ReAAAgPcIPAAAwHsEHgAA4D0CDwAA8B6BBwAAeI/AAwAAvEfgAQAA3iPwAAAA7xF4\nAACA9wg8AADAewQeAADgPXPOZXWAcDic3QEAAEDRqa6utkL3IZeY4QEAAN4j8AAAAO9lfUoLAACg\n2DHDAwAAvNdv4DGzR81sr5m9kWTdrWbmzOyk4OtpZhY2s9eCx70D0el8SVa7mS00s46EGq9IWLfA\nzN41s21mdnlhep0bmdRuZrVmdjCh/TeF63l2Uj3fzexHwbhuNbPFCe1ej3nQflTtPo25lPL5/lRC\nfW1m9lrCOi/GPZO6S2TMzzOz5qC+FjO7IGg3M1sSjPkWM5tcuJ5nJ8O6vXpNl3Ouz4ekr0maLOmN\nXu1jJL0gaYekk4K2aZKe6++Yg+WRrHZJCyXdmmTbsyW9LqlS0jhJ/5JUXuga8lR7be/nx2B9pKj7\nUklNkiqDr0eW0Jinqt2bMU9Ve6/1v5B0r2/jnmHd3o+5pHWSvh4sXyHp7wnLz0sySVMlvVLo/uep\nbq9e0/ud4XHO/UPSviSrHpJ0myRvLwLqo/ZkGiQtc85FnHP/kfSupAsGrHMDLMPavZGi7pskLXLO\nRYJt9gbtpTDmqWr3Sl/PdzMzSbMlPRk0eTPuGdbtlRS1O0nDg+VqSbuC5QZJj7m4ZkkjzOy0/PQ0\ntzKs2yvHdA2PmX1DUodz7vUkqy80s9fN7Hkz+1J23Stac4NpzUfN7MSgbZSk9oRtdgZtvklWuySN\nM7PNZvaymV1csN4NjDMlXWxmrwT1nR+0l8KYp6pd8nvME10s6X3n3DvB16Uw7tLRdUv+j/mPJf3M\nzNol/VzSgqDd9zFPVbfk0Wt6xoHHzIZJuktSsnN5mySNdc59WdIvJa3KrntFaamkMySdJ2m34lO+\nUnyqszffZr9S1b5b0hecc3WSbpH0ZzMbnvwQg1KFpBMVn8qeL2l58NdvKYx5qtp9H/NEc3TkLEcp\njLt0dN2lMOY3SbrZOTdG0s2SHgnafR/zVHV79Zp+LDM8Zyh+3vp1M2uTNFrSJjM71Tn3X+dcpyQ5\n59ZKGmLBBc2+cM6975zrds7FJP1en01l71T8uqYeo+XZtGCq2oOp/Y+C5Y2KX9NwZuF6mnM7Ja0M\nprM3SIpJOkklMOZKUXsJjLkkycwqJM2S9FRCs/fjnqzuEhnz6yWtDJZXqHT+f09at2+v6RkHHudc\nq3NupHOu1jlXq/gTYbJzbo+ZnRr89afgKu8ySR/ltMcF1uu87Tcl9Vzp/qykb5tZpZmNkzRe0oZ8\n928gpardzE42s/Jg+XTFa/93/ns4YFZJukySzOxMSSFJH6oExlwpai+BMe8xQ9LbzrmdCW2lMO5H\n1V0iY75L0iXB8mWSek7nPSvpe8HdWlMlhZ1zuwvRwQGStG7vXtP7u6pZ8SnN3ZIOKR5ubuy1vk2f\n3aU1V9JWxe9gaJb0lUJflZ3NI1ntkholtUraovgvwWkJ29+l+F892xRc8T5YH5nULunahHHfJOnq\nQvc/x3WHJD2ueMDbJOmyEhrzpLX7NOapag/a/yjph0m292LcM6m7FMZc0kWSNgY1viKpPtjWJP06\nGPNWSVMK3f881e3VazrvtAwAALzHOy0DAADvEXgAAID3CDwAAMB7BB4AAOA9Ag8AAPAegQcAAHiP\nwAMAALxH4AEAAN77P+xAYSvHUP+3AAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"book_plots.plot_errorbar2()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Sensor A returned a measurement of 160, and sensor B returned 170. The bars are [*error bars*](https://en.wikipedia.org/wiki/Error_bar) - they illustrate the possible range of error for the measurement. Hence, the actual value that A is measuring can be between 157 to 163, and B is measuring a value between 161 to 179.\n",
"\n",
"I did not define it at the time, but this is a [*uniform distribution*](https://en.wikipedia.org/wiki/Uniform_distribution_(continuous)). A uniform distribution assigns equal probability to any event in the range. According to this model it is equally likely for sensor A to read 157, 160, or 163. Any value outside these ranges have 0 probability. \n",
"\n",
"We can model this situation with Gaussians. I'll use $\\mathcal{N}(160, 3^2)$ for sensor A, and $\\mathcal{N}(170, 9^2)$ for sensor B. I've plotted these below with the uniform distribution error bars for comparison."
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"scrolled": true
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAh0AAADDCAYAAAAmy6ORAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzt3Xd8VFXawPHfkx4SCITea+hEOqJ0\nFGkWFDWICFbclV3dXXdXX8W67K66rmtdy2JBMSiKCtJUEESkhZ5AgEgNHQKhpee8f5wJCSEhEzLJ\nnSTPl8/95M695955JiczPHPuueeIMQallFJKqdLm43QASimllKocNOlQSimlVJnQpEMppZRSZUKT\nDqWUUkqVCU06lFJKKVUmNOlQSimlVJlwK+kQkaEisk1EEkTksQL29xORdSKSKSKjC9hfTUT2i8gb\nnghaKaWUUuVPkUmHiPgCbwLDgPbAGBFpn6/YXmAC8Gkhp3keWHr5YSqllFKqvHOnpaMnkGCM2WmM\nSQdmADfmLWCM2W2M2QRk5z9YRLoBdYHvPBCvUkoppcopPzfKNAT25XmcCPRy5+Qi4gO8DIwDBhdU\nJjk5WYdEVUoppSqYsLAwyb/NnZaOiw4C3E0UfgvMM8bsK7KkUkoppSo0d1o6EoHGeR43Ag64ef7e\nQF8R+S0QCgSIyBljzEWdUZVSSilVsbmTdKwBIkSkObAfiALucOfkxpixOesiMgHofqmEIywszJ3T\nVjoxMTEAdO/e3eFIVF5aL95H68Q7ab14n9Kqk+Tk5EvuL/LyijEmE5gELAS2Ap8bY+JE5DkRuQFA\nRHqISCJwK/COiMSVOHKllFJKVSjutHRgjJkHzMu37ak862uwl10udY4PgQ+LHaFSSimlKgS3kg6l\nlFJKlQ1jDElJSWRnXzQKhceEhoYCcPTo0cs+h4+PD+Hh4YgUdL9JwTTpUOoyZGVnkZSWhI/4YIwp\n1ptOKaUuJSkpiZCQEIKCgkrtOapUqQJASEjIZZ8jNTWVpKQkatas6fYxmnQoVQyLdi7ijTVv8MPO\nHziTfgaAWstrMSJiBA/3epgu9bs4HKFSqrzLzs4u1YTDU4KCgjh9+nSxjtGkQyk3HD5zmPvm3Me3\n27+lTkgdxkWOIzQllEyTyXH/43y59UumbZzGA90e4OUhLxMScPnfHpRSqqLSpEOpImw9upVrPr6G\npJQkXrr2JX7X83cE+gVecMvZa0Nf47mlz/HKylf4Zd8vzBs7j0bVLtm3WimlKh2d2l6pS1h/cD39\nPuxHtslm1X2rePSqRwn0C7yoXFhQGC9f9zIL7lzA7pO76fdBPw6dOeRAxEop5RlfffUVIkJ8fLzH\nzqlJh1KF2HViF9d8fA3BfsH8NOEnIutGFnnMkJZD+OGuHzhy9gjDpg/jVNqpMohUKaU8Lzo6mj59\n+jBjxgyPnVOTDqUKcC7jHKM+G0W2yWbRXYuIqBnh9rE9G/bky9u+JPZILLfOvJVsU3q3vSmlVGk4\nc+YMy5cvZ+rUqR5NOrRPh1L5GGO4f879bDq8ibl3zC1WwpHjulbX8cawN3hw7oP8e8W/efSqR0sh\nUqVUZTDgwwEePd+SCUuKLPP1118zdOhQWrduTXh4OOvWraNr164lfm5t6VAqn5lbZvLp5k95dsCz\nDIsYdtnneaDbA9zc7mb+b9H/se7gOg9GqJRSpSs6OpqoqCgAoqKiiI6O9sh5taVDqTyOnzvOpHmT\n6Fa/G4/3fbxE5xIR3rv+PSITIxn31TjWT1xPgG+AhyJVSlUW7rRMeNLx48dZvHgxsbGxiAhZWVmI\nCC+++GKJB0LUlg6l8nhk4SOcSD3B1Bum4udT8pw8PDict0e+zZajW3ht1WseiFAppUrXF198wV13\n3cWePXvYvXs3+/bto3nz5vz8888lPrcmHUq5/Lz3Zz7Z9AmPXf0YV9S7wmPnHdl6JCNbj+TZpc+y\n/9R+j51XKaVKQ3R0NKNGjbpg2y233MKnn35a4nO7lXSIyFAR2SYiCSLyWAH7+4nIOhHJFJHRebZ3\nFpEVIhInIptE5PYSR6xUKTDG8Kfv/kSDqg14rM9Ff+Il9urQV8nIyuDP3//Z4+dWSilPWrJkCUOH\nDr1g2+9//3v++9//lvjcRSYdIuILvAkMA9oDY0Skfb5ie4EJQP406BxwlzGmAzAU+I+IVC9p0Ep5\n2udxn7N6/2qmDJpSKkOYt6jRgkevepTo2GjWH1zv8fMrpVR54E5LR08gwRiz0xiTDswAbsxbwBiz\n2xizCcjOt327MWaHa/0AcASo7ZHIlfKQ9Kx0Hlv0GFfUvYJxkeNK7Xn+fNWfqRFUg8k/Ti6151BK\nKW/mTk+5hsC+PI8TgV7FfSIR6QkEAL8WViZnLgtVMP39lI6v937N7pO7ebXHq6xfV/xWiOLUy9hm\nY3kj/g2mfjeVK8I9129EXUjfK95J68U9oaGh56eeL21nz54t0fHHjx9nz5495x9HRFx6XCN3WjoK\nuj/GFCcoEakPfAzcbYwOz6i8R2Z2Jh8kfED7sPb0rt271J/vtqa3ER4Yztvb3y7151JKKW/jTktH\nItA4z+NGwAF3n0BEqgFzgSeNMSsvVbZ79+7unrZSyTubqfKsDzd8yIGUA7xz0zv0aN2jWMdebr1M\nZjJ/WPgHMutlcmWjK4t1rLo0fa94J62X4jl69CghIZ7vW5ZXTgtHSZ+nZs2atG3b9vzj5OTkS5Z3\np6VjDRAhIs1FJACIAma7E4yr/FfANGPMTHeOUaqsZGVn8fdlf6dLvS6MiBhRZs97X9f7qBFUgxeW\nv1Bmz6mUUt6gyKTDGJMJTAIWAluBz40xcSLynIjcACAiPUQkEbgVeEdE4lyH3wb0AyaIyAbX0rlU\nXolSxfTNtm/YkbSD/+v7fyUeZa84QgNCmdRzEt/Ef0P8Mc9NGa2UUp7i6+tL586dueKKK+jatSu/\n/PKLR87r1jgdxph5xpjWxpiWxpgprm1PGWNmu9bXGGMaGWNCjDE1XbfIYoz5xBjjb4zpnGfZ4JHI\nlSqhV1a+QvPqzRnVdlTRhT3sdz1/R5BfEC8tf6nMn1sppYoSHBzMhg0b2LhxI//4xz94/PGSTQuR\nQ0ckVZXS6v2r+Xnvzzzc62F8fXzL/Plrh9Tm7s5388nmTzhy9kiZP79SSrnr1KlT1KhRwyPn0gnf\nVKX0yspXqBZYjXu63ONYDJN6TuKtmLeYum5qiSeXU0pVXAMGePZ8S5YUXSYlJYXOnTuTmprKwYMH\nWbx4sUeeW1s6VKWz/9R+ZsbN5L4u91E1sKpjcbSr3Y5BzQfx9tq3ycrOciwOpZTKL+fySnx8PAsW\nLOCuu+7CmGKNllEgbelQlc7U9VPJMlk81PMhp0PhoR4Pccvnt/Dt9m+5se2NRR+glKp03GmZKE29\ne/fm2LFjHD16lDp16pToXNrSoSqVzOxM3lv3HkNaDqFFjRZOh8MNbW6gUbVGvLnmTadDUUqpAsXH\nx5OVlUXNmjVLfC5t6VCVyvwd80k8lcirQ191OhQA/Hz8mNhtIpN/nMz249tpXbO10yEppdT5Ph1g\nZ+H+6KOP8PUtead7TTpUpfLO2neoF1qP61tf73Qo593f9X6eW/ocb615i/8M/Y/T4SilFFlZpdPP\nTC+vqEpjb/Je5ifM594u9+Lv6+90OOfVDa3L6Paj+XDDh6RkpDgdjlJKlRpNOlSl8b91/8MYw/1d\n73c6lIvc1/U+ktOS+Sr+K6dDUUqpUqNJh6oUMrMzmbp+KsMihtG0elOnw7nIgGYDaFa9GR9s+MDp\nUJRSqtRo0qEqhQUJCzhw+oBXtnIA+IgPE66YwKKdi9hzco/T4SilHOTj40NqaqrTYRQpNTUVH5/i\npRHakVRVCh9t/IhaVWoxPGK406EUanzn8Tyz9Bk+2vgRT/V/yulwlFIOCQ8PJykpidOnT5facxw/\nfhygRLfB+vj4EB4eXqxjNOlQFd6JlBPM3jabB7s9SIBvgNPhFKpZ9WYMbj6YDzd8yJP9nsRHtCFS\nqcpIRDwyJsal7NljW1Tbtm1bqs+Tn36qqQrvs7jPSM9KZ3zn8U6HUqS7O9/NrpO7+GnPT06HopRS\nHudW0iEiQ0Vkm4gkiMhjBezvJyLrRCRTREbn2zdeRHa4Fu//1FcVzkcbP6JjnY50qdfF6VCKNKrd\nKKoFVtMOpUqpCqnIpENEfIE3gWFAe2CMiLTPV2wvMAH4NN+x4cDTQC+gJ/C0iHhmflyl3LDt2DZW\nJq5k/BXjERGnwylSFf8qjOk4hplxMzmTfsbpcJRSyqPc6dPRE0gwxuwEEJEZwI3AlpwCxpjdrn3Z\n+Y69DvjeGJPk2v89MBSILuiJYmJiihl+5aK/n+J7K/4tfPChY3bHUvv9efq8PQJ68E7mO/x73r8Z\n3sh7O756M32veCetF+/j6TqJiIi45H53Lq80BPbleZzo2uaOkhyrVIlkm2zm7Z9Hr9q9qBVUy+lw\n3NapRifqB9dnwYEFToeilFIe5U5LR0Ft0sbN8xfr2O7du7t52solJxPV30/xLNm9hMOph3ll+Ct0\n7+T5311p1suEUxN4cfmLNGnXhDohJZtKujLR94p30nrxPqVVJ8nJyZfc705LRyLQOM/jRsABN5+/\nJMcqVSIzYmdQxb8KN7S5welQim1sp7FkmSw+j/vc6VCUUspj3Ek61gARItJcRAKAKGC2m+dfCAwR\nkRquDqRDXNuUKlUZWRl8seULbmhzAyEBIU6HU2wd6nQgsm4k0zdPdzoUpZTymCKTDmNMJjAJmyxs\nBT43xsSJyHMicgOAiPQQkUTgVuAdEYlzHZsEPI9NXNYAz+V0KlWqNC3atYjjKceJ6hDldCiXbWyn\nsaxMXMnOEzudDkUppTzCrXE6jDHzjDGtjTEtjTFTXNueMsbMdq2vMcY0MsaEGGNqGmM65Dn2fWNM\nK9eigw+oMjEjdgZhgWEMbTXU6VAuW1RHmzB9uvnTIkoqpVT5oCOSqgonNTOVr+K/YlS7UQT6BTod\nzmVrEtaEfk37MX3zdIxxt++2Ukp5L006VIWzIGEBp9JOletLKznGdhpL/LF4Nhza4HQoSilVYpp0\nqApnRuwMalWpxaDmg5wOpcRGtx+Nv4+/dihVSlUImnSoCuVs+lnmbJ/D6Haj8ff1dzqcEgsPDmdY\nxDCiY6PJys5yOhyllCoRTTpUhTJn+xzOZZw73wmzIrij4x0cOH2AZXuXOR2KUkqViCYdqkKZETuD\nBlUb0KdJH6dD8ZiRrUcS4h/CjNgZToeilFIlokmHqjBOpp5kfsJ8bmt/G74+vk6H4zEhASHc0OYG\nvtjyBRlZGU6Ho5RSl02TDlVhfB3/NelZ6RXq0kqOMR3HcDzlOD/s/MHpUJRS6rJp0qEqjBmxM2hW\nvRk9G/Z0OhSPG9JyCNWDqhMdG+10KEopddk06VAVwtGzR/lh5w9EdYhCpKDJjcu3QL9Abml3C1/H\nf01KRorT4Sil1GXRpENVCF9u/ZIsk1UhL63kiOoYxen008zbMc/pUJRS6rJo0qEqhM/iPqNtrbZE\n1o10OpRSM7DZQOqG1GVGnN7FopQqnzTpUOXegdMHWLp7aYW9tJLD18eXW9vfyrfbv+VU2imnw1FK\nqWJzK+kQkaEisk1EEkTksQL2B4rIZ679q0SkmWu7v4h8JCKbRWSriDzu2fCVgplxMzEYbu94u9Oh\nlLoxncaQmpnK7G2znQ5FKaWKrcikQ0R8gTeBYUB7YIyItM9X7F7ghDGmFfAK8IJr+61AoDGmE9AN\nmJiTkCjlKTPiZtC5Xmfa1mrrdCil7spGV9IkrInexaKUKpfcaenoCSQYY3YaY9KBGcCN+crcCHzk\nWv8CGCy2ndsAISLiBwQD6YC2CyuP2XViFysTV1aIGWXd4SM+RHWI4rtfv+P4ueNOh6OUUsXi50aZ\nhsC+PI8TgV6FlTHGZIpIMlATm4DcCBwEqgB/MMYkFfZEMTEx7kdeCenv52If/Wpz3XbZ7Rz7/ZT1\n80b6RJKZncnLC17m5iY3l+lzlxf6XvFOWi/ex9N1EhERccn97rR0FNQzz7hZpieQBTQAmgN/EpEW\nbjynUm757sB3dKreiQZVGjgdSplpXa01TUOa8v2B750ORSmlisWdlo5EoHGex42AA4WUSXRdSgkD\nkoA7gAXGmAzgiIgsB7oDOwt6ou7duxcv+koiJxPV38+F4o/Fs33udv5z3X8c+d04WS8Tzk7guaXP\n0aBNAxpUrTwJV1H0veKdtF68T2nVSXJy8iX3u9PSsQaIEJHmIhIARAH5u87PBsa71kcDi40xBtgL\nDBIrBLgSiC9G/EoV6rPYzxCEWzvc6nQoZS6qYxQGw8y4mU6HopRSbisy6TDGZAKTgIXAVuBzY0yc\niDwnIje4ik0FaopIAvBHIOe22jeBUCAWm7x8YIzZ5OHXoCohYwwz4mbQv1n/SvlNv22ttnSu11nv\nYlFKlSvuXF7BGDMPmJdv21N51lOxt8fmP+5MQduVKqmNhzcSfyyeR3o94nQojhnTcQx//eGv7Dqx\ni+Y1mjsdjlJKFUlHJFXl0ozYGfj5+HFL+1ucDsUxt3ewg6HNiNVh0ZVS5YMmHarcMcYwI3YG17a4\nllpVajkdjmOaVm/KVY2v0rlYlFLlhiYdqtxZkbiCPcl7GNNxjNOhOC6qQxSbDm9iy9EtToeilFJF\n0qRDlTvRm6MJ8gvixrb5B8atfG7tcCs+4qOXWJRS5YImHapcyczO5PMtnzMiYgTVAqs5HY7j6oXW\nY2CzgUTHRmPvUldKKe+lSYcqV5bsXsKRs0f00koeYzqOISEpgXUH1zkdilJKXZImHapcid4cTdWA\nqgyPGO50KF7j5nY34+/jr2N2KKW8niYdqtxIy0zjy61fclPbmwj2D3Y6HK9RI7gGQ1sN5bO4z8g2\n2U6Ho5RShdKkQ5UbC39dSHJasl5aKUBUxygSTyWyfO9yp0NRSqlCadKhyo3o2GhqBtfkmhbXOB2K\n17mhzQ0E+wXrXSxKKa+mSYcqF86mn2X2ttnc2v5W/H39nQ7H64QGhHJ9m+uZuWUmmdmZToejlFIF\n0qRDlQuzt83mXMY5ojpGOR2K1xrTcQxHzx1l8a7FToeilFIF0qRDlQvRsdE0rNqQvk37Oh2K1xra\naijVAqvpXSxKKa/lVtIhIkNFZJuIJIjIYwXsDxSRz1z7V4lIszz7IkVkhYjEichmEQnyXPiqMjiR\ncoIFCQu4vcPt+IjmyYUJ8gvi5nY3M2vrLNIy05wORymlLlLkJ7iI+AJvAsOA9sAYEWmfr9i9wAlj\nTCvgFeAF17F+wCfAg8aYDsAAIMNj0atK4cutX5KRnaGXVtwQ1SGKU2mnmJ8w3+lQlFLqIu58bewJ\nJBhjdhpj0oEZQP5JL24EPnKtfwEMFhEBhgCbjDEbAYwxx40xWZ4JXVUW0zZOo03NNnRv0N3pULze\n4BaDqVWllt7FopTySn5ulGkI7MvzOBHoVVgZY0ymiCQDNYHWgBGRhUBtYIYx5sXCnigmJqYYoVc+\nlfH3k3gukWV7l/HbNr9l7dq1TodTIG+rl/61+vP11q/5aeVPVPGr4nQ4jvC2OlGW1ov38XSdRERE\nXHK/Oy0dUsC2/DNLFVbGD+gDjHX9HCUig914TqUAmL9/PoIwrOEwp0MpN65reB1p2WksO7zM6VCU\nUuoC7rR0JAKN8zxuBBwopEyiqx9HGJDk2r7UGHMMQETmAV2BRQU9Uffu2nxekJxMtLL9fowxRP0S\nxcDmAxnZd6TT4VzEW+ulq+nKc3HPsTplNU90f8LpcMqUt9ZJZaf14n1Kq06Sk5Mvud+dlo41QISI\nNBeRACAKmJ2vzGxgvGt9NLDY2Hm2FwKRIlLFlYz0B7YUI35Vif2y7xd+PfErd0Xe5XQo5YqP+HB7\nh9uZv2M+J1JOOB2OUkqdV2TSYYzJBCZhE4itwOfGmDgReU5EbnAVmwrUFJEE4I/AY65jTwD/xiYu\nG4B1xpi5nn8ZqiKatnEaVfyrcHO7m50OpdwZ03EMGdkZfB73udOhKKXUee5cXsEYMw+Yl2/bU3nW\nU4FbCzn2E+xts0q5LTUzlc/iPuPmdjdTNbCq0+GUO13rd6VjnY58sOEDJnaf6HQ4SikF6IikykvN\n2TaH5LRkvbRymUSEuzvfzar9q9h6dKvT4SilFKBJh/JS0zZNo2HVhgxqPsjpUMqtOyPvxM/Hjw82\nfOB0KEopBWjSobzQkbNHmL9jPndG3omvj6/T4ZRbdULqMCJiBB9v+lhnnlVKeQVNOpTXmb5pOlkm\ni3GR45wOpdy7u/PdHDpziAUJC5wORSmlNOlQ3sUYw3vr3qNXw150qNPB6XDKveERw6ldpbZeYlFK\neQVNOpRX+WXfL2w9tpX7u97vdCgVgr+vP3dG3smcbXM4evao0+EopSo5TTqUV3lv3XtUDajK7R1v\ndzqUCuOeLveQkZ3Bx5s+djoUpVQlp0mH8honU0/yedzn3NHpDkIDQt06Rp4V5NmCpv6puIr7mjvW\n6chVja/i7Zi3sQMFK6WUMzTpUF5j+qbppGSm6KWVUvBgtwfZkbSDH3f/6HQoSqlKTJMO5RVyOpB2\nqdeFbg26OR1OhTO6/WjCg8N5Z+07ToeilKrENOlQXiHmQAwbD2/kgW4POB1KhRTsH8z4K8Yza+ss\nDp857HQ4SqlKyq25V5Qqbf+N+S9V/KswpuMYp0OpsCZ2m8grK1/h/fXv83jfx50Op9iMgXPn4PRp\nSE3NXdLS7M/0dNi+vSo+PraMj49dfH0hOBhCQuxSpYr96e8PUrm6AynlOE06lOOOnj3Kp5s/5Z4u\n9xAWFOZ0OBVWm1ptGNhsIO+ue5e/9vkrPuJ8Q2dGBhw4kLscPJi7fuQInDhx4ZKRUdQZ27j93H5+\nULMm1KqV+zNnadAAGje2S6NGdpsmKEqVnCYdynH/W/c/0rLSmNRzktOhVHgPdn+Q27+4nQUJCxge\nMbxMnjMlBeLjYccO+PVX2Lkzd9m7F7KzLyzv5wf16kHdulCjhv2Pv0aN3KVaNdtyERgIQUG5i78/\nbN0ajzHQunVbsrNt60hmpo3h7NncJafFJCkJjh2D48dtjDnrWVkXxhQUZJOPFi0gIuLCpVkz+9xK\nqaK5lXSIyFDgVcAX+J8x5p/59gcC04BuwHHgdmPM7jz7mwBbgGeMMf/yTOiqIsjMzuStmLe4psU1\ntK/d3ulw3DZ983QeXfwoh1MO0+TnJkwZPIWxncY6HVaRbmp7Ew2qNuA/K//j8aQjLc3+xx0Xd+Gy\nc+eFiUWdOtCyJVx9NYwbB02b2paFBg2gfn3bquBzmY0wQUFnAOje/fJfR1aWbWXZtw8SE3N/7t1r\nk6aVK+HUqdzyfn42+YiMhE6d7M/ISGjSRFtHlMqvyKRDRHyBN4FrgURgjYjMNsZsyVPsXuCEMaaV\niEQBLwB5R3d6BZjvubBVRfF1/NcknkrkzeFvOh2K26Zvns4Dcx7gXMY5APYk7+GBObYDrLcnHgG+\nATzU4yGeWPwEsUdi6Vin42WdJz0dNm+GtWshJsb+3Lw59/JHzn/EnTvD2LHQoQO0aWNbCkLdG4LF\nMb6+NvmpXx969rx4vzFw9KhtuclZ4uJg9Wr47LPcctWq2SSkSxd7np497e/kchMqpSoCKWqwIBHp\njW2huM71+HEAY8w/8pRZ6CqzQkT8gENAbWOMEZGbgKuBs8CZ/C0dycnJ5wPYsWOHZ16VKjceWPEA\nh1MOM2vgLHyl+DPK9pjbA4Cu4V09HVqhNp/cTEb2xZ0L/H386VS9U6k//7qkdQCsGbHmso4/mX6S\nkYtGMrThUJ6MfNKtYw4dCmDDhlA2bAhly5YQEhKCyciw/3tWq5ZJu3ZnadfuHBER52jRIoWmTdPw\n9698A5GdOePDzp3BJCQEs2NHFRISgtm2rQopKfZvu2rVTNq3P0uHDmdp3/4snTqdJTxcZwBWFUdE\nRMT59bCwsIva+ty5vNIQ2JfncSLQq7AyxphMEUkGaopICvBXbCvJo8WKXFV425K3sT5pPY+0e+Sy\nEg6nFJRwXGq7t6keUJ0RjUbwbeK3PNTmIWoE1rhgf1YW7NwZzIYNoWzcaBONw4cDAQgJyaJdu7OM\nGXOYdu3O0a7dWRo0SNfLCC6hodlERp4lMvLs+W1ZWbBrVxBbtoQQFxdCbGwoH31Un6ws+0tr2jSF\nrl3P0KXLabp0OU29euXj70ipy+FO0lHQx0n+rzCFlXkWeMUYc0bc+FTqXpILsRVYTEwMUPF+P69/\n/TpV/Kvw1PVPUSO4RtEHFGSu/bH2d2s9F1gRmv2nGXuS91y0vWlY0zKJI2cI9JL8Pfyt6d+Y9dYs\nVmau5Inek4mNhR9+gEWLYPlySE625Ro0gAEDoE8fu3Tq5IuvbzWgWslfSCnw1vdKr3xf086dg3Xr\n4Jdf4Kefglm8OJivvqoN2I6p/frZpX9/2/+lvCd13lovlVlp1UlyzodHIdxJOhKBxnkeNwIOFFIm\n0XV5JQxIwraIjBaRF4HqQLaIpBpj3nAvfFVR7Tm5h083f8qkHpMuP+FwyJTBUy7o0wFQxb8KUwZP\ncTCq4gk+246Oif9myiPNeH2/4ehR+79a69Zw++25SUazZuX/PzxvVKVK7u/4L3+xrSGbN8NPP9ll\n/nyYNs2Wbd4crr0WhgyBQYPsHTxKlVfuJB1rgAgRaQ7sB6KAO/KVmQ2MB1YAo4HFxnYW6ZtTQESe\nwfbp0IRD8e8V/wbgj73/6HAkxZfTWfTR+a67V8K8/+6VM2dsK8b8+bZF49dfAf4AoQdp1e9XXrqt\nFYMH29tCVdnz9bWdbjt3ht//3nZWjY+HxYvh++8hOhrefdd2Qu3RwyYh114LV14JAQFOR6+U+4pM\nOlx9NCYBC7G3zL5vjIkTkeeAGGPMbGAq8LGIJGBbOKJKM2hVvh07d4z31r3HnZF30jiscdEHeKGx\nncbSJs0OROWtTcbbt8O8eXZZutTecRIaCgMH2v/YBg82jF02nGMZZ7lz3FZ8fcpPv5qKTgTatbPL\nQw/Zu4JWr7YJyHffwT/+AX/7G1StaltARo6E4cPt7chKeTO3xukwxswD5uXb9lSe9VTg1iLO8cxl\nxKcqoNdXvU5KZgp/ueovTodfdMkxAAAbJ0lEQVRSoaSm2uQiJ9FISLDb27WzScbw4XZsjNxvxsJk\neZLRM0czc8tMojrqdwVv5e9v6+7qq+GZZ2yfmx9/tC1Xc+fCl1/aRKVnTxgxwiYhnTvrpTHlfXRE\nUlWmzqSf4fXVr3NT25toV7ud0+GUe8nJ8O23MGsWLFhgOygGB9tr/3/4AwwbZvsEFGZUu1G0r92e\nKcumcFuH27xiaHRVtLAwuOkmuxgDGzfav4Nvv4Wnn4annoKGDW0CMmIEDB5s55tRymmadKgy9U7M\nO5xIPcFfr/6r06GUe8OH2/4ZGRn2LpMJE+w33AEDbOLhDh/x4Ym+TzB21li+if+GUe1GlWbIqhSI\n5PYHefJJOHw4twUkpy9IUJDtAzJqFFx/vR31VSkn6NcaVWZOp53mheUvMLj5YK5sdKXT4ZQriYnw\n+uu2P0aO+Hh4+GF72+W+ffDmm7Zlw92EI8dtHW6jVXgr/rbsbxQ1WKDyfnXr2gR05kw7l8wPP8AD\nD8CGDXDPPXZem0GD7N/Tvn1Fnk4pj9KkQ5WZV1e9ytFzR5kyqPzcWuqkhAR48UV7h0LjxrZfxtGj\nuft//RVeegl69y7Z0Np+Pn483udx1h1cx7wd84o+QJUbAQH20sqrr8KePXbI+sces60hv/+9nR+m\nRw/4+99h61ano1WVgSYdqkwkpSTxr1/+xQ1tbqBXo/wD2l4+87TBPF0xvp0bY8dqePZZO2FYRAT8\n9a92DIe//922bMTG5r5mT3YSHBc5jhY1WvB/i/+PrOysog9Q5Y4IdOtm73qJi7N/T//4h01Yn3gC\n2reHtm3h8cftnTLa6KVKgyYdqky8tPwlTqWd4vmBzzsdilcxxn7AP/aYHZgrMtImHdWrwyuvwO7d\nsGaN/Y+gTZvSi8Pf158pg6aw6fAmpm+eXnpPpLxGmzb2727VKnuZ5Y037DgtL71kR1Bt0sRevlu6\n1Ca+SnmCJh2q1B06c4hXV73KmE5jiKwb6XQ4jsvKsh/kOc3bvXrByy/bGVjffhsOHrSjUj7yiJ32\nvazc1uE2utXvxuQfJ5OamVp2T6wc16iRHQ/khx/gyBH48EPo2hXeecd2TK5f3/YLWbjQjvei1OXS\npEOVuueXPk96VjrPDnjW6VAck55ub2m9/377AT5gALz3nm3unjbNftAvXAgTJ9qOgE7wER9evPZF\n9ibv5Y3VOnBwZRUeDuPHwzff2I6on31mO55GR8PQoXYAsnHj4Ouv7S3aShWH3jKrSlXskVjeWfsO\nE7tNpFV4K6fDKVPnztlEY9YsO35CcrIdEXTkSLjlFvsBHhrqdJQXGtR8EENbDeXvy/7OvV3uLXfz\n4ijPCg2F226zS2qqHRF11iybkHzyiZ1DZvhwuPlmOx5INe+cB1B5EW3pUKXGGMMjCx6hWmA1nhv4\nnNPhlInkZJg+3SYVtWrZn/Pn2w/lb7+1d59ER8Po0d6XcOR44ZoXOJl6kmeXVt6WKXWxoCA7xscH\nH9i7X77/3raI/Pwz3HEH1K5tE+r337ctJEoVRFs6VKmZvW02i3Yt4rWhr1GzSk2nwyk1R4/ab36z\nZuUO1lW/Ptx9t006+vUDv3L0TousG8mD3R/k9dWvM/6K8XSp38XpkJSX8feHa66xyxtvwIoV9u//\nyy/toGS+vtC/v022R+l4cyoPcXowoOTk5PMBhIWFORmK14qJiQG8d2KxgpxNP0uHtzoQEhDChokb\n8Pf1dzokj9q3D157bS8//lid9eurkZ1thxu/5Rb7QdurV8nGznDaydSTtHmjDc2rN+eXe38pN8Oj\nl8f3SkViDKxfn5uAxMfb7Z06nWHQoBM8/HDjSw7Lr8pOab1XkpOTz6+HhYVddGN/+fgkUeXOM0ue\nYU/yHt4Z+U6FSTji4+14GT162LtO/vWvJiQl+fPEE/aDtrDBukTK38Rb1YOq8/KQl1m1fxXvrX3P\n6XCUl8r/ty1i73r529/sYGNbtsDzz0N6uvDqq41p0SJ3/5YtzsWtnONWS4eIDAVexU5t/z9jzD/z\n7Q8EpgHdgOPA7caY3SJyLfBPIABIB/5sjFmc91ht6Shaefv2tuHQBrq/2517utzDu9e/63Q4l80Y\nWLsWvvrKfnPL+dbWs6dtMm7VajPNmqUVWS85H8rlbbAlYwyDpw1m/aH1xD8UT91Qh26rKYby9l4p\n79z9246JiWH//gASEiKZNcsO3Q92MLKbb7ZL167lLzkvz7y2pUNEfIE3gWFAe2CMiLTPV+xe4IQx\nphXwCvCCa/sx4HpjTCdgPPDxZbwGVY6kZ6Vzzzf3ULNKTV645oWiD/AymZmwZIkdFKlpU9uq8cIL\ndkK1nLkqVq2ygyo1a5bmdLilSkR4a8RbnE0/y+/m/07nZVEl0rBhOn/6EyxfDvv327mCGja076/u\n3e3lyT/+0XZMzc52OlpVWty5vNITSDDG7DTGpAMzgBvzlbkR+Mi1/gUwWETEGLPeGHPAtT0OCHK1\niqgK6vmlz7P+0HreHfluubndMiXF3lly7712MqyBA+3MnF265PbUX7QIJk2ygyhVJm1rteXZAc8y\nc8tMZsTOcDocVUE0aAC//a3teH3okL3jpVMnm4j07WuTkd/8Jrdjtqo4iry8IiKjgaHGmPtcj8cB\nvYwxk/KUiXWVSXQ9/tVV5li+8zxojLkm7/nzXl7ZsWNHyV+RcszmE5u575f7GN5oOE9f8bTT4VzS\nkSP+/PxzGMuWVWfNmqqkpfkSEpJJnz7JDBx4kt69k6lSxTNft3r0sM2Xa9bEeOR8ZS0zO5MHVjzA\n7jO7mdF/BnWC6jgdkvISnv7bPnPGh19+CWPx4hosXx5Gaqov1apl0rfvSQYOPEnPnqcIDtZmEG8W\nERFxfr2gyyvu3MhX0FW2/JnKJcuISAfsJZchbjyfKodOZ5xm8obJ1Amuw5/a/8npcC6SnQ3x8VX4\n+efqLFsWRnx8CAANGqRx003H6NMnmW7dTuPvr5cQ8vPz8ePZzs9yx7I7mLx+Mm/2ehM/n3J0D7Aq\nN0JDsxky5ARDhpwgNVVYtSqMxYurs3RpdebOrYW/fzbdup2mT59krr76JI0a6Zjs5Y07LR29gWeM\nMde5Hj8OYIz5R54yC11lVoiIH3AIqG2MMSLSCFgM3G2MWZ7//NqRtGje3jnOGMMtn9/CnO1zWDph\nKVc1vsrpkAA7IugPP8CcOXbsgIMH7V0lvXvbQYyuv97OrHm5ndfcrZfy2pE0v483fsxdX9/FE32f\n4G+D/uZ0OAXy9vdKRVOcjqRw+fWSnm77esyda5dt2+z2tm3tSKgjRkCfPnb8EOUepzqSuvN1ZQ0Q\nISLNgf1AFHBHvjKzsR1FVwCjgcWuhKM6MBd4vKCEQ1UMr6x8ha/iv+LlIS87mnAYY6fsXrjQLj/9\nBGlpULWqHXJ85Eg7ZHOtWo6FWK6Nu2IcP+35iSnLpnBV46sYHjHc6ZAuMH06PPpoJw4fDqBJE5gy\nBcaOdToq5QkBAXb+l0GD7OSICQm5Ccjrr9tt1arBkCE2ARk2zLk5jNSlFZl0GGMyRWQSsBB7y+z7\nxpg4EXkOiDHGzAamAh+LSAKQhE1MACYBrYDJIjLZtW2IMeaIp1+Icsb8HfP58/d/ZlTbUfzhyj+U\n+fMnJdnWjAUL4LvvbK94gHbtbEe0kSNtx7SAgDIPrUJ6bdhrxByMYcyXY1hx7wra185/I5szpk+3\ns6CeO2f7qe/ZYx+DJh4VUatW9g6zhx+GM2fsZ8DcuTBvHnzxhS3TuTNce61d+vSB4GBnY1aWjkha\nDnhrk3HckTh6T+1Nixot+PmenwkNKP3JRDIyYM2a3NaMNWtsf43q1e2QzNddZ5fGjUs9lGJfXunf\nv7QjKhupgftY360nPtnBdFm7ioCM2k6HxMqVtlUrv8BAuPLKso+nsli61P4s7csr7jIGNmywX0K+\n/95eksnIsPPG9O2bm4RERpbvEYM9wZsvryh1kb3Jexn+6XBCAkKYM2ZOqSUcWVl2tM8ff7TLsmX2\nm42Pjx2ka/Jkm2T06FG+5jcpz4LSGtNh8zds7NKf2MiRRG74Ab+sqo7GVFDCcantqmISsbe6d+kC\njz8OZ8/ay6zff2+Xv/zFlqtTx35JufZaGDAAmjVzMurKRT+mVbEdOXuEaz++lpOpJ1kyfgmNwzzX\nrJCdDZs3w+LFNsn46Sc7cyvYTmPjxuVe2w0P99jTloklS5yOwJN6MnvbZ9z82c0Ejr+JuXfMJcgv\nyLFomjWzl1Tya9q0ov3evYu3jyAaEmL7dwwbZh8fOGAvxeQkIZ9+arc3aWJbIvv3t0lIixbe/9rK\nK006VLHkJBz7kvfx3bjvSjwDaVqaHWp8+XLbFLp8ORw/bve1agW33WYH6xowwM7cqrzHDW1u4MOb\nPmTcV+O45fNb+OLWLwj2d+bC+ZQpOX06crdVqWK3K5WjQQO46y675HQ8X7rUJqYLFsDHrjGzGzbM\nTUL694fWrTUJ8RRNOpTb9p/az+Bpg9mbvJdvor6hT5M+xT7H8eN23oWcJCMmJrcJPCLC3sY6cKBd\nyqJfhiqZOyPvJCUjhYnfTmTEpyOYPWZ2mfTtyS+ns+ijj6a57l4RvXtFXZIIdOxol4cesklIfLxN\nQJYuta2tOS0htWrZvkG9e8NVV9nLuSEhjoZfbmnSodyy+fBmRkaP5ETKCRbeuZC+TfsWeUx6Omza\nZDt7rlljO/tt3Wr3+fvbCZ4mTYKrr7ZvZL3FrXy6v9v9BPsHM+HrCQz4cACzx8ymQdUGZR7H2LHQ\nps1mwPs6XSvvJ2Lvesu5880Y2LHDJiArVtjl229tWV9f2xm1d+/cRKR5c20NcYcmHapIc7fPJerL\nKKoFVmPJhCV0rd/1ojJZWXbAnpwEY/Vq2LjRJh5gvyn07Al33mlvX+vRQ29hq0jujLyT6kHVifoi\nil7/68XsqNklvvSmlJNE7GWV1q3h/vvttqQk++VpxQrbYjttGrz1lt0XHg7dul24NGumiUh+mnSo\nQmVmZzJ58WT+ufyfdKnXhTlj5tCwWkNSUiA21iYVOcv69fauEoDQUPuG+/3vbXLRo4e++SqDka1H\n8vM9P3N99PX0ntqb/wz9DxO7TUS04lUFER5uBxgc7hoXLyvLfhauWGH7pq1dC//6l52tOqd83iTk\niitsJ1VfX+deg9M06VAF2nZsGxO+vpuVW/ZxXdVXuerob/jTA/5s3Ajbt+dOPR0aapsZ77rLtmT0\n6AFt2lTuN1Vl1rleZ9Y+sJZxX43jN3N/w3e/fsebw9+kflXtBawqHl9fm0hccUXuttRUewdeThKy\ndq0dMTVnttzgYOjQwc6qm7N07GgvL1eG/FyTDkVmJvz6q+1vsTkug6+WxbMhNg1zdCGkV2Uhdjja\nZs3sm+u223LfaM2b6yA76kJ1Quowf+x8/vXLv3jqx6do92Y7Xrz2Re7reh8+on8sqmILCspt4c2R\nlmYTkU2b7M/YWDt66gcf5JapVcsmIO3b2y9ubdvan40aVazPWE06KomsLNi3zyYXOUtCgu2tvWNH\nbhYO/lC1BrWbHef6kT706Gyz8shI0AFjlbt8xIe/XP0XRrUdxcRvJzLx24m8v/59pgyawuAWg50O\nT6kyFRgI3bvbJa+jR20SkneZNg1On84tExxs+5XkTUQiIuwXvpo1y1/riCYdFYQx9nbUfftg717Y\nufPCBGP37ryJhZ2LpHlzaN06m1ZXbmNj9gz2+M2nY3t/XrnxWa5pcY1jr6WiKe+zy5ZERM0IFt21\niI82fsTkHydzzcfXMLDZQJ7u/zT9mvbT/h7lXGX+2/aE2rVzBzvMYQwcOmQ75ucs8fF2eIEvvsi9\ntA328naLFvazPGfJ+7hKlbJ/TUXRpKMcMAZOn/ZlyxabVOQkFjnrOUtKyoXHhYVBy5Z24qNbbrHr\nOYtPtYPM2DKd11e/zt7kvUSER/Bh3ye4M/JOfH20Q4byHBFhQucJRHWM4t217/L3ZX9nwEcD6FSn\nE7/t8VvGdhpL1UBnh1FXyluI2IEQ69e3gyLmlZZmW6gTEmDXrtwlIcGOsJp3cDywSU3jxnZp1Mgu\nOevZ2b5UrZpVZq8rh0745hBj4NQpOHYMDh+2mW3hSzYZGRde1BOxo+vl/EHlLE2a2J8tWtie03m/\nSB46c4j5O+YTHRvNol2LyDbZ9Gvajz/1/hMjW4/U6+3F5K0T8Xm7cxnniN4czZtr3mT9ofUE+wUz\nPGI4o9uPZkTEiBIlIFon3knrpfQZYy/X7NplW7p37bIt3ImJucuJE7nlX355B/36JXvnhG8iMhR4\nFTu1/f+MMf/Mtz8QmAZ0A44Dtxtjdrv2PQ7cC2QBvzfGLLycF+Kt0tNt8pCznDhh7+U+fjx3Kehx\nUlLubVV5idjJiOrVs0v79mDMYWrWzKRHj8bnk4sGDewAW5dy8PRBVu9fzYrEFXz363esP7QegObV\nm/NE3ycY22ksbWq1KYXfilKFq+JfhXu73ss9Xe5h1f5VfLLpE77c+iVfbv0Sfx9/ejXqxaBmg+jf\nrD9d63elelB1p0NWyuvl/N9Rpw706lVwmTNnYP9+2zIOZ8syvPOKbOkQEV9gO3AtkAisAcYYY7bk\nKfNbINIY86CIRAGjjDG3i0h7IBroCTQAfgBaG2POt+mUVUtHZqZtenJ3SUmxnXnyJhQFLUXNYhkc\nbDv7hIfbn/nXa9bMTTDq1bM9mPPPlnqpbwnGGI6dO8aOpB1sP76dbce2EX88npgDMSSeSgTAz8eP\nqxpfxdCWQ7mu1XV0qddFr6V7gH5785ys7CyW71vO/B3zWbRrEWsPriXb2IvXLWq0oGv9rkTWiaRV\neCtahrekZY2WhAeHX/R3rHXinbRevI83T23fE0gwxuwEEJEZwI3AljxlbgSeca1/Abwh9tPgRmCG\nMSYN2CUiCa7zrSj2K7kMixbZvgznzl3YidJdgYFQrdqFS6NGF2/Lu4SFXZhcFDTqZrbJJj0rnbTM\nNNKz0u16Vhons9I5fMxuS81M5VTaKZLTktm0ZxNnM88yK3kWJ1NPcvDMQQ6ePsjBMwc5dOYQ6Vnp\n58/t7+NPy/CW9Gvaj54NetKzYU861+vs2ERcSrnD18eXfk370a9pPwBOpp5kZeJK1h9cz/pD61l3\ncB1fbPnigmNCA0KpF1qPuiF1qRtal7ohdclIziDEL4T1sp6qgVWpGlD1/M9Av0ACfAMKXPx9/DUR\nV6oMuNPSMRoYaoy5z/V4HNDLGDMpT5lYV5lE1+NfgV7YRGSlMeYT1/apwHxjzPlPj7wtHTt27PDQ\ny7Lmb9zJCx+cQgJSwP8c4p/nZ0C+x/7nIOBc7mO/FPDNwGDI+zvK+9i4/p3fZ8wF2woql22yyTKX\n13nHV3wJ9QulZmBNagXVonZgbWoG1aR2YG0ahzSmSUgT6gfXx89H+weriic1K5X95/aTeC6R/Wf3\ncyDlACfST5CUlsTxtOMkpSWRnJFc9IkK4Su++IovgiAiCIKP+NjHrnUgd5sIPvicL+uJpEUo2TlK\nerwnaPJWPjzZ6Um61/J8y1NERMT59ctt6SjoLyh/plJYGXeOLTURzbPpP+ErwPVmFM5/gORss2+Q\nYCAYodb5D5Dzx8BF2/K+qfJ+QOXfdn4933MH+NhvVvmXAJ8A/MTPrvsGEOoXSohfCKF+oYT6hxLo\nE6hvaFVpBfkG0bJqS1pWbVlomSyTRUpmCmczz3Iu8xznss5xJvMMKZkpZGRnkJGdQabJPL+e/3E2\n2ee/PORc3sk22ee/bOTfn3d7SZmSfjR64JO1pDGU+DWoMlPV35k7xtxJOhKBvJOMNwIOFFImUUT8\ngDAgyc1jz/P0taXudCdqUJRHz+kEvR7qnbRevE9MTAyh/qEM6D3A6VBUHvpe8T5l0aejIO7cI7kG\niBCR5iISAEQBs/OVmQ2Md62PBhYbe21hNhAlIoEi0hyIAFYXI36llFJKVRBFtnQYYzJFZBJ2+g1f\n4H1jTJyIPAfEGGNmA1OBj10dRZOwiQmucp9jO51mAg/lvXNFKaWUUpWHWz0OjTHzgHn5tj2VZz0V\nuLWQY6cAU0oQo1JKKaUqAB2CUimllFJlwquGQVdKKaVUxVDQLbPa0qGUUkqpMqFJh1JKKaXKhOOX\nV5RSSilVOWhLh1JKKaXKhCYdXkJE3heRI655bHK2PSMi+0Vkg2sZnmff4yKSICLbROQ6Z6Ku+Aqq\nF9f237l+93Ei8mKe7VovpayQ98pned4nu0VkQ559WidloJB66SwiK131EiMiPV3bRURec9XLJhHp\n6lzkFVchdXKFiKwQkc0iMkdEquXZV/rvFWOMLl6wAP2ArkBsnm3PAI8WULY9sBEIBJoDvwK+Tr+G\nirgUUi8DgR+AQNfjOlovztZJvv0vA09pnThfL8B3wDDX+nBgSZ71+dj5ua4EVjkdf0VcCqmTNUB/\n1/o9wPOu9TJ5r2hLh5cwxvyEHc3VHTcCM4wxacaYXUAC0LPUgqvECqmX3wD/NMakucoccW3XeikD\nl3qviJ0R8TYg2rVJ66SMFFIvBsj5Jh1G7txbNwLTjLUSqC4i9csm0sqjkDppA/zkWv8euMW1Xibv\nFU06vN8kV/Pj+yJSw7WtIbAvT5lE1zZVNloDfUVklYgsFZEeru1aL87rCxw2xuxwPdY6cdYjwEsi\nsg/4F/C4a7vWi3NigRtc67eSOylrmdSJJh3e7b9AS6AzcBDbbAy2STI/vQ2p7PgBNbDNwn8GPnd9\nw9Z6cd4Ycls5QOvEab8B/mCMaQz8ATtPF2i9OOke4CERWQtUBdJd28ukTtyae0U5wxhzOGddRN4D\nvnU9TCQ3OwVoRG6zpSp9icAsYy+ErhaRbKAWWi+OEhE/4GagW57NWifOGg887FqfCfzPta714hBj\nTDwwBEBEWgMjXLvKpE60pcOL5bvGOQrbLAYwG4gSkUARaQ5EAKvLOr5K7GtgEJx/0wYAx9B6cdo1\nQLwxJjHPNq0TZx0A+rvWBwE5l71mA3e57mK5Ekg2xhx0IsDKRkTquH76AE8Cb7t2lcl7RVs6vISI\nRAMDgFoikgg8DQwQkc7YJq7dwEQAY0yciHwObAEygYeMMVlOxF3RFVIv7wPvu25DSwfGu1o9tF7K\nQEF1YoyZCkRx4aUVfa+UoULeK/cDr7paoVKBB1zF52HvYEkAzgF3l3nAlUAhdRIqIg+5iswCPoCy\ne6/oiKRKKaWUKhN6eUUppZRSZUKTDqWUUkqVCU06lFJKKVUmNOlQSimlVJnQpEMppZRSZUKTDqWU\nUkqVCU06lFJKKVUmNOlQSimlVJn4f5jNvANZCp6IAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"xs = np.arange(145, 190, 0.1)\n",
"ys = [stats.gaussian(x, 160, 3**2) for x in xs]\n",
"plt.plot(xs, ys, label='A', color='g')\n",
"\n",
"ys = [stats.gaussian(x, 170, 9**2) for x in xs]\n",
"plt.plot(xs, ys, label='B', color='b')\n",
"plt.legend();\n",
"plt.errorbar(160, [0.04], xerr=[3], fmt='o', color='g', capthick=2, capsize=10) \n",
"plt.errorbar(170, [0.015], xerr=[9], fmt='o', color='b', capthick=2, capsize=10);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Using a uniform or Gaussian distribution is a modeling choice. Neither exactly describes reality. In most cases the Gaussian distribution is more realistic. Most sensors are more likely to return readings near the value being measured, and unlikely to return a reading far from that value. The Gaussian models this tendency. In contrast the uniform distribution assumes that any measurement within a range is equally likely.\n",
"\n",
"Now let's see the *discrete distribution* used in the discrete Bayes filter. This model divides the range of possible values into discrete ranges and assigns a probability to each bucket. This assignment can be entirely arbitrary so long as the probabilities sum to one.\n",
"\n",
"Let's plot the data for one sensor using a uniform distribution, a Gaussian distribution, and a discrete distribution."
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(150, 170)"
]
},
"execution_count": 19,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAisAAADDCAYAAABDJlHuAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzt3Xd4FOXax/HvnQahBQg1BAwlSFMp\ngYBSFAWCSBPQIL0ooIgFLBw9qIivggcQFI+IKCBIkSJVuoAiLSgdIVQJXcqCEEqS5/0jCyeGhGxg\nk9lyf65rr8zOPjP7ezI7mztTxRiDUkoppZSr8rE6gFJKKaXU7WixopRSSimXpsWKUkoppVyaFitK\nKaWUcmlarCillFLKpWmxopRSSimX5lCxIiJRIrJHRPaJyJtpvF5fRH4TkQQRaZvG6/lE5KiIfOaM\n0EoppZTyHhkWKyLiC4wBmgKVgPYiUilVsz+BrsB36czmfWD1ncdUSimllLdyZMtKLWCfMeaAMeYa\nMA1ombKBMeaQMWYbkJR6YhGpARQFljohr1JKKaW8jJ8DbUoAR1I8jwMiHZm5iPgAw4FOwKNptbHZ\nbHoJXaWUUsrDBAUFibPm5ciWlbTezNEC43lgkTHmSIYtlVJKKaXS4MiWlTigZIrnocAxB+dfB6gn\nIs8DeYAAEfnbGHPLQbpKKaWUUmlxpFjZBISLSGngKBANPOPIzI0xHW4Mi0hXIOJ2hUpQUJAjs/UY\nMTExAERERFicJHt5a79B+w7e13dv7Td4b9+9td8ANpstS+ab4W4gY0wC0BdYAuwGZhhjdorIYBFp\nASAiNUUkDmgHjBWRnVmSVimllFJex5EtKxhjFgGLUo0blGJ4E8m7h243jwnAhEwnVEoppZRX0yvY\nKqWUUsqlabGilFJKKZfm0G4gpZTKiDGGU5dOsePUDnb/tZu4C3Ecu3iMc1fOEX89nrO2s/iJH0Vj\ni1IgZwFC8oZQIm8JKhauSJUiVSiauygiTrssg1LKg2ixopS6Y4fOH2JR7CLWHF7DmsNrOP738Zuv\n+fv4E5I3hIKBBQn0D8RXfLmadJWjF46y/eR2jl08xvWk6zfbF8tTjPr31Kd+qfo8Hv44pQuUtqJL\nSikXpMWKUipTDp47yLfbvmXmrplsP7UdgBJ5S/Bw2MPUKlGL+4rcR6XClSiapyg+8r89zalP50wy\nSZy6dIpdp3ex/eR2Nh7byJrDa5ixcwb8CFWKVKFNxTZ0fqAzZQqUyf6OKqVchhYrSqkMJSQlMGf3\nHD6P+ZxVh1YhCHVL1eU/jf5Di3tbUK5guUzvwvERH4rlKUaxPMVoWLohkLwraf+5/czfM5+5e+Yy\nePVg3lv9HvXvqc/zEc/zZMUn8ff1z4ouKqVcmBYrSql0Xbp2ibGbx/LJ+k84cuEIZQqUYcgjQ+j0\nQCdKBZVy+vuJCOUKluOVOq/wSp1XOGI7wuRtkxn/+3iiZ0UTmi+UlyJfok9EH3IH5Hb6+yulXJOe\nDaSUusWVhCsM/3U4ZUaXof/S/pQtWJa50XPZ23cvb9V/K0sKlbSUDCrJwHoD2fviXua3n0/54PK8\ntuw1So8qzcdrPyb+eny25FBKWUuLFaXUTcYYpu2YRoXPKjBg2QDuL3o/P3f7mZ+6/ESLe1vg6+Nr\nSS4f8eGJ8k+wovMK1nZfS7Xi1Xh9+evc+9m9TNk2hSSTZEkupVT20GJFKQXA9pPbqftNXdrPak/B\nwIKs7LySZZ2WUbdUXauj/cODJR9kScclrO66miK5i9BxTkce+vohtp7YanU0pVQW0WJFKS93+fpl\nXl/2OtXGVmPvmb183eJrYp6L4ZHSj1gd7bbq31Ofjc9uZGKriRw4d4AaX9ZgwNIBXLp2yepoSikn\n02JFKS+2Pm491cZW4+NfP6Zr1a788cIfdKvW7R+nHLsyH/Gh8wOd2f3CbrpX687wdcOpOrYqvx75\n1epoSiknco9vJKWUUyUkJfDvlf/moa8f4krCFZZ3Ws5XLb4iOFew1dHuSMHAgnzZ/Et+6vIT1xOv\nU++begxcPpCEpASroymlnECLFaW8zOHzh2kwoQFDfh5C5wc6s633Nh4t86jVsZzi4bCH2d5nO92q\nduOjtR/RcGJDjl08ZnUspdRd0mJFKS/yY+yPVB1ble0ntzO1zVS+afkNQTmDrI7lVHlz5OWrFl8x\nufVkNh/fTLWx1VhxYIXVsZRSd8GhYkVEokRkj4jsE5E303i9voj8JiIJItI2xfiqIrJORHaKyDYR\nedqZ4ZVSjjHGMGztMJp914yw/GH83ut3oqtEWx0rS3W4vwObnt1EcGAwjSc3ZsiaIXqKs1JuKsNi\nRUR8gTFAU6AS0F5EKqVq9ifQFfgu1fjLQGdjTGUgCvhERPLfbWillOMuX79Mh9kdeGP5G7Sr3I5f\nuv1C2YJlrY6VLSoVrsTGZzcSXSWaf//0b5pPbc7FqxetjqWUyiQxxty+gUgd4F1jTBP784EAxpgP\n02g7AVhgjJmZzry2Am2NMbE3xtlstpsBYmNj05pMKXWHTsSf4LWY19hzYQ997u1D17JdM30PH09g\njGHm4ZkM3zWcMnnLMDJiJEUDi1odSymPEx4efnM4KCjIaV82juwGKgEcSfE8zj4uU0SkFhAA7M/s\ntEqpzNt5fidd1nbhyOUj/CfiP3Qr180rCxVIvudQu7B2jKw5kmOXj9FtbTf22PZYHUsp5SBHbmSY\n1rfb7TfHpJ6BSHHgW6CLMenvNL5x63hvERMTA2i/vUl29X3p/qW8sPQFiuQuwoJnFlCpcOo9t9nP\nFZZ7BBE0qN6AZt81o/fG3sxoO4Om4U2z9D1dod9W8da+e2u/AWw2W5bM15EtK3FAyRTPQwGHzwUU\nkXzAQuBtY8z6zMVTSmXW1O1TafZdM8oVLMfa7mtdolBxJfcXvZ8NPTcQXjCc5lObMzZmrNWRlFIZ\ncKRY2QSEi0hpEQkAooF5jszc3n4OMMkY8/2dx1RKOWL0htE8M/sZHiz5IKu7rqZ43uJWR3JJIXlD\nWNNtDVHloui9sDcfr/3Y6khKqdvIsFgxxiQAfYElwG5ghjFmp4gMFpEWACJSU0TigHbAWBHZaZ/8\nKaA+0FVEttgfVbOkJ0p5MWMMb614i5cWv0SrCq1Y0nGJx10/xdnyBORhztNziK4SzevLX+edn94h\noxMOlFLWcOSYFYwxi4BFqcYNSjG8ieTdQ6mnmwxMvsuMSqnbMMbw8uKXGb1xNM9Wf5bPm32On49D\nq7bX8/f1Z3LryeTyy8XgNYO5dP0SHzf62GsPRFbKVek3mlJuzBjDS4tf4tONn/JK7VcY3ni4/qHN\nJF8fX8a1GEfugNwMXzecS9cuMabZGLe5maNS3kCLFaXclDGGfj/247NNn9G/Tn/dInAXfMSHUVGj\nyO2fm4/WfkR8Qjxft/xaCxalXIQWK0q5IWMML/74ImM2jdFCxUlEhA8f+5Bc/rkYtGoQAb4BjH1i\nrP5elXIBWqwo5WaMMfRd1JfPYz5nQJ0BDGs0TP+gOtG/G/yba4nXGPLzEHL65WRU1Cj9/SplMS1W\nlHIjxhj6L+2vhUoWG/zIYOIT4hm+bjg5/XIy9LGh+ntWykJarCjlRoasGcLI9SN5sdaLWqhkIRHh\n40YfcyXhCh//+jGBfoG898h7VsdSymtpsaKUm/h0w6cMWjWIzg905pOoT7RQyWIiwuimo7macJXB\nawYT6B/Im3XftDqWUl5JixWl3MCkrZPot7gfrSq0YnyL8XqWSjbxER++eOIL4hPiGbhiIMGBwTxb\n41mrYynldbRYUcrFzf1jLt3ndqdh6YZMbTNVL/iWzXx9fPmm5TecjT9L74W9KZy7MK0qtLI6llJe\nRf89U8qFrTq0iqdmPkVESAQ/PP0DOf1yWh3JK/n7+vN9u++pGVKT6JnRrDm8xupISnkVLVaUclE7\nTu2g1bRWlCtYjkUdFpE3R16rI3m13AG5WfjMQkoXKE2LqS3YfnK71ZGU8hparCjlgo5eOErTKU3J\n5Z+LHzv8SMHAglZHUkBwrmCWdFxCnoA8NJnchEPnD1kdSSmvoMWKUi7GdsXG4989ju2KjUUdFlEq\nqJTVkVQKpYJKsaTjEuIT4omaHMXZ+LNWR1LK42mxopQLuZZ4jTYz2rDr9C5mPTWLqsWqWh1JpaFy\nkcrMbz+fg+cP0np6a64mXLU6klIezaFiRUSiRGSPiOwTkVsuNCAi9UXkNxFJEJG2qV7rIiKx9kcX\nZwVXytMYY+g+tzsrDq7g6xZf06hsI6sjqduoW6ouE1tNZM3hNfSY1wNjjNWRlPJYGZ4DKSK+wBig\nERAHbBKRecaYXSma/Ql0BQakmrYg8A4QARhgs33ac86Jr5TneGfVO0zZPoUPGn5Apwc6WR1HOSC6\nSjQHzh3grZVvUaZAGQY/MtjqSEp5JEcu2FAL2GeMOQAgItOAlsDNYsUYc8j+WlKqaZsAy4wxZ+2v\nLwOigKl3nVwpDzJl2xTeX/M+3at2Z2DdgVbHUZkwsO5ADpw7wPtr3qdMgTJ0rdrV6khKeRzJaNOl\nfbdOlDGmp/15JyDSGNM3jbYTgAXGmJn25wOAnMaYIfbn/wbijTH/uTGNzWa7GSA2NvauO6SUu9l2\nbht91vehSv4qfBb5Gf4+/lZHUpmUkJTAS5teYvOZzXxa61NqFqppdSSlLBEeHn5zOCgoyGn3BHHk\nmJW03szRnbN3M61SHu/45eO8FvMaRXMWZWiNoVqouCk/Hz+GVh/KPbnv4fXNr3Po70NWR1LKoziy\nGygOKJnieShwzMH5xwEPp5p2VXqNIyIiHJytZ4iJiQG0394kZd8vXr1It6+7kSiJLO22lAqFKlic\nLmt5w3JfUXEFNcfV5K0db7G+x3oKBBbwin6nx1v77q39BrDZbFkyX0e2rGwCwkWktIgEANHAPAfn\nvwRoLCIFRKQA0Ng+TimvlpiUSPtZ7dl9ejczn5rp8YWKtwjLH8bsp2Zz8NxBnp75NAlJCVZHUsoj\nZFisGGMSgL4kFxm7gRnGmJ0iMlhEWgCISE0RiQPaAWNFZKd92rPA+yQXPJuAwTcOtlXKm7227DUW\nxi7k06af8liZx6yOo5yo3j31+G+z/7LswDL6L+lvdRylPIJDt281xiwCFqUaNyjF8CaSd/GkNe3X\nwNd3kVEpjzLnzzmM3D6SF2u9SJ+afayOo7JAj+o92Hl6JyPXjyT3fbl5stSTVkdSyq3pveaVykYx\nf8UwdMdQmpRtwogmI6yOo7LQsEbD2P3XbobtGMY9ue8hAu87fkEpZ9HL7SuVTQ6cO8Abv71Bqdyl\nmN52On4++r+CJ/Pz8WNam2mUzFWSNza/wYFzB6yOpJTb0mJFqWzw97W/aTWtFQAjIkYQlDPI4kQq\nOwTlDGJ4zeEYDC2mtuDC1QtWR1LKLWmxolQWM8bQbW43dp7eyQfVPiA0d5qHdykPVSp3KT6s/iF/\n/PUHHWZ3IDEp0epISrkdLVaUymIf/fIRM3fN5KNHP6J24dpWx1EWqFWoFqObjmbB3gW8vfJtq+Mo\n5Xa0WFEqCy2KXcRbK98iuko0Ax4ckPEEymM9X/N5nqv+HB+t/Yjvd35vdRyl3IoWK0plkdgzsTwz\n6xkeKPYA41uMR8Rpt8lQbmp009HUCa1D17ld2XZym9VxlHIbWqwolQUuXr1Iy2kt8fPxY87Tc8jl\nn8vqSMoF5PDLwaynZhGUI4hW01pxNl6vkamUI7RYUcrJkkwSnX/ozN4ze5nRbgZh+cOsjqRcSPG8\nxZn99GyOXjxK+1nt9YBbpRygxYpSTjZkzRB++OMHhjceTsPSDa2Oo1xQ7dDajHl8DEv3L+VfK/5l\ndRylXJ5elUopJ5q3Zx7vrHqHzg90pl9kP6vjKBfWs3pPNh/bzLBfh1GteDWiq0RbHUkpl6VbVpRy\nkt2nd9NxdkciQiL4otkXekCtytCopqN4qORDdJ/bna0ntlodRymXpcWKUk5w/sp5Wk5rSaB/ILOf\nmk2gf6DVkZQbCPANYOZTMykYWJBW01tx5vIZqyMp5ZK0WFHqLiWZJDrO7sjB8weZ2W4mJYNKWh1J\nuZFieYox66lZHLt4jOhZ0SQkJVgdSSmX41CxIiJRIrJHRPaJyJtpvJ5DRKbbX98gImH28f4iMlFE\ntovIbhEZ6Nz4SlnvnZ/eYWHsQkZFjaLePfWsjqPcUGRoJP9t9l+WH1jOm8tv+YpVyutlWKyIiC8w\nBmgKVALai0ilVM16AOeMMeWAkcBQ+/h2QA5jzH1ADaDXjUJGKU8wa9cshvw8hB7VetAnoo/VcZQb\n616tO89HPM/wdcP5bvt3VsdRyqU4smWlFrDPGHPAGHMNmAa0TNWmJTDRPjwTeFSSjy40QG4R8QMC\ngWuA3nZUeYQdp3bQ5YcuN09D1QNq1d0aGTWSeqXq0XNeT34//rvVcZRyGWKMuX0DkbZAlDGmp/15\nJyDSGNM3RZsd9jZx9uf7gUjABnwLPArkAl4xxnyZcv42m+1mgNjYWGf0SaksZ7tmo8vaLlxJvMK3\ndb+lcM7CVkdSHuLM1TN0/qUzvuLLpLqTyB+Q3+pISjksPDz85nBQUJDT/oNzZMtKWm+WusJJr00t\nIBEIAUoD/UWkTKYSKuViEk0ib//+NifjTzKsxjAtVJRTBecIZliNYZy5eoaBvw3UA26VwrGLwsUB\nKU9vCAWOpdMmzr7LJwg4CzwDLDbGXAdOichaIAI4kNYbRUREZC69m4uJiQG03+7mjWVvsP6v9Yxr\nPo7u1btnalp37/vd8Na+30m/I4jAFDJ0m9uN6WenMzJqZFbFy1K6zL2r3wA2my1L5uvIlpVNQLiI\nlBaRACAamJeqzTygi324LbDSJO9f+hNoKMlyA7WBP5wTXansN23HNIb9OozeNXrTs3pPq+MoD9a1\nalderPUin2z4hG+3fmt1HKUslWGxYoxJAPoCS4DdwAxjzE4RGSwiLezNxgPBIrIPeBW4ce7dGCAP\nsIPkoucbY4zeF125pd+P/073ud2pW6ouo5qOsjqO8gLDGw/n4bCHeXb+s8Qci7E6jlKWcejeQMaY\nRcCiVOMGpRi+QvJpyqmn+zut8Uq5m9OXTtNqeiuCcwUzs91MAnwDrI6kvIC/rz8z2s4gYlwErae3\nJubZGIrmKWp1LKWynV7BVqkMXE+8zlMzn+LUpVPMeXqO/rFQ2apw7sL88PQPnLl8hrbft+Va4jWr\nIymV7bRYUSoD/Zf2Z9WhVXz5xJdEhHjfAXPKetWKV2N8i/H88ucvvLz4ZavjKJXtHNoNpJS3+ub3\nb/h046e8UvsVOj3Qyeo4you1v689v5/4nY9//ZhqxarxbI1nrY6kVLbRLStKpWND3AZ6L+zNY2Ue\nY1ijYVbHUYoPH/2QJmWb8MKiF/j1yK9Wx1Eq22ixolQajl88zpMznqRE3hJMazMNPx/dCKms5+vj\ny9Q2UykVVIo2M9pw9MJRqyMplS20WFEqlasJV2kzow3nr5znh+gfCM4VbHUkpW4qEFiAudFz+fva\n3zw540muJFyxOpJSWU6LFaVSMMbQd1Ff1sWtY2Kridxf9H6rIyl1i8pFKjOp1SQ2Ht1In4V9yOge\nb0q5Oy1WlErhi5gv+Or3r/hX3X/RtlJbq+Mola7WFVszqP4gJmyZwGcbP7M6jlJZSosVpezWHF5D\nv8X9aBbejMGPDLY6jlIZeufhd2hxbwteWfIKPx38yeo4SmUZLVaUAg6fP0zbGW0pU6AMU56cgq+P\nr9WRlMqQj/jwbetvKR9cnnbft+PAuTTvEauU29NiRXm9i1cv0nxqc64lXmNe9DyCcgZZHUkph+XL\nkY+50XNJMkk0n9qcC1cvWB1JKafTYkV5tcSkRDrM7sCu07v4vt333FvoXqsjKZVp4cHhzHxqJnvP\n7KX9rPYkJiVaHUkpp9JiRXm1f634F/P3zmdU1CgalW1kdRyl7ljD0g35rOlnLIpdxOvLXrc6jlJO\npVe6Ul5rwpYJDPt1GH0i+vBCrResjqPUXesV0Yudp3cyYv0IKhauSM/qPa2OpJRT6JYV5ZV++fMX\nnpv/HI+WfpRRUaOsjqOU04xoMoLGZRvTZ2EfVh9abXUcpZzCoWJFRKJEZI+I7BORN9N4PYeITLe/\nvkFEwlK8dr+IrBORnSKyXURyOi++Upl36PwhWk9vTVj+ML5v9z3+vv5WR1LKafx8/JjedjplC5Sl\nzYw27D+73+pISt21DIsVEfEFxgBNgUpAexGplKpZD+CcMaYcMBIYap/WD5gM9DbGVAYeBq47Lb1S\nmXTjzJ+EpATmt59PgcACVkdSyuny58zPgmcW3DxDyHbFZnUkpe6KZHSZZhGpA7xrjGlifz4QwBjz\nYYo2S+xt1tkLlBNAYZILnGeMMR3Tm7/NZrsZIDY29i66otTtJZpEBsQMYN3pdYyqNYrIQpFWR1Iq\nS8X8FUPfjX2pVagWIyJG6A05VZYLDw+/ORwUFCTOmq8ju4FKAEdSPI+zj0uzjTEmAbABwUB5wIjI\nEhH5TUT0EHVlmVG7R/HLqV/oX6m/FirKK0QUiuD1Kq+z7vQ6Ru4aqfcQUm7LkTI7rcoo9Sc+vTZ+\nQF2gJnAZWCEim40xK9J6o4iICAfieI6YmBhA+50dRq0fxdSDU+lXqx9Dmw7NtvdNzVuXOXhv363u\nd0REBNfyXGP4uuFE3hvJq3Vezbb3trrvVvHWfgPYbFmzy9GRLStxQMkUz0OBY+m1se8GCgLO2sev\nNsb8ZYy5DCwCqt9taKUyY87uObyy5BVaV2jNiCYjrI6jVLYb1mgYbSu1pf/S/ny/83ur4yiVaY4U\nK5uAcBEpLSIBQDQwL1WbeUAX+3BbYKVJ3t64BLhfRHLZi5gGwC7nRFcqY+vj1vPM7GeIDI1k8pOT\n9Z4/yivduIfQQyUfotOcTqz9c63VkZTKlAyLFfsxKH1JLjx2AzOMMTtFZLCItLA3Gw8Ei8g+4FXg\nTfu054ARJBc8W4DfjDELnd8NpW617+w+mk9tTom8JZgXPY9c/rmsjqSUZXL65WRu9FxKBZWixbQW\n7D2z1+pISjnMoUPDjTGLSN6Fk3LcoBTDV4B26Uw7meTTl5XKNn9d/oumU5pijOHHDj9SOHdhqyMp\nZbngXMH82OFH6oyvQ9MpTVnXYx1FchexOpZSGdIr2CqPE389nhZTWxB3IY757ecTHhye8URKeYmy\nBcsyv/18jl88TvOpzbl8/bLVkZTKkBYryqMkJiXScU5H1setZ3LrydQpWcfqSEq5nMjQSKa2mcqm\no5t4ZtYzepdm5fK0WFEewxjDgKUDmL17NiOajKBNpTZWR1LKZbWs0JLRTUczd89cXl78sl6DRbk0\nvZyh8hjD1g7jkw2f0K9WP16u/bLVcZRyeX1r9eXQ+UMMXzecYnmK8Vb9t6yOpFSatFhRHuGr377i\nzRVv0r5Ke0ZGjbQ6jlJuY1ijYZy6dIq3f3qb4FzB9I7obXUkpW6hxYpye7N3z6bXgl5ElYtiQqsJ\n+Iju3VTKUT7iw/gW4zl35RzPL3ye4MBg2lVO8+ROpSyj3+rKra08uJL2s9oTWSKSme1mEuAbYHUk\npdyOv68/M9rOoG6punSY3YFl+5dZHUmpf9BiRbmtmGMxtJzWkvLB5VnwzAJyB+S2OpJSbivQP5B5\n7edRqXAlWk9vzYa4DVZHUuom3Q2k3NKOUzuImhxFoVyFWNJxCQUDC2Z7BpHk+3fqWRSOazvzJMz8\n50WsD33UzKI0rsuqz1b+nPlZ3HExdb+uS9MpTVnVdRX3F70/WzMolRYtVpTb2XtmL49NeowA3wCW\ndVpGSN4QqyMpLxX25q13D3H34qtYnmIs67SM+hPq89ikx1jddTUVC1e0OpbyclqsKLdy4NwBGk5s\niMGwsstKyhUsZ3Uk5SSe+IffXZUuUJoVnVfQYEIDHp30KGu6rdF1TVlKj1lRbuNP2580nNiQ+IR4\nlndaToVCFayOpJTHKh9cnuWdlnM96ToNJzbk0PlDVkdSXky3rCi3cOziMRpObMj5K+dZ0XkF9xW9\nz+pISjlVWluWrFa5SGWWdVrGIxMfoeHEhqzptobQfKFWx1JeSLesKJd3/OJxHp30KCcvnWRxx8XU\nCKlhdSSlvEbVYlVZ2nEpf13+i4YTG3L0wlGrIykv5FCxIiJRIrJHRPaJyJtpvJ5DRKbbX98gImGp\nXi8lIn+LyADnxFbeIu5CHA0mNOCI7QiLnllE7dDaVkdS6o6Fvbnwloc7qFmiJos7LubE3ydoMKEB\nf9r+tDqS8jIZ7gYSEV9gDNAIiAM2icg8Y8yuFM16AOeMMeVEJBoYCjyd4vWRwI/Oi628weHzh2k4\nqSGnL51maaelPFjyQasjqTs0ZcoUBgwYwIkTJ/HNV4j89TuTp/IjVsdSmfBgyQdZ2mkpUZOjaDCh\nAT91+Ymw/GFptr2lCJu5UA+WVnfFkS0rtYB9xpgDxphrwDSgZao2LYGJ9uGZwKNiv1CAiLQCDgA7\nnRNZeYOD5w7SYEIDzlw+w/LOy7VQcWNTpkzhueee48SJE4Ah8cJpzi7+jL93/mR1NJVJtUNrs7zz\ncmxXbNT/pj77z+63OpLyEpLRRYdEpC0QZYzpaX/eCYg0xvRN0WaHvU2c/fl+IBKIB5aTvFVmAPC3\nMeY/Kedvs9luBoiNjXVGn5SbO3LpCL3X9+Zq4lU+i/yMCkGuedZPzZo1AahevbrFSVzb9u3buX79\n+q0v+PqTI+ReKhdOvkXCztPXbmly4zVXldnMt2uf8rWrR3YAsGnTpruNmCX22PbwwoYXCPAJ4PPa\nnxOWJ+wfr7edefKWaWa2LZpN6ZSVwsPDbw4HBQWJs+bryJaVtN4sdYWTXpv3gJHGmL8zG0x5p30X\n9/Hcuue4lnSNz2t/7rKFinJcmoUKQGI645XLuzfoXr6o8wWJJpFe63ux98JeqyMpD+fIlpU6wLvG\nmCb25wMBjDEfpmizxN5mnYj4ASeAwsAaoKS9WX4gCRhkjPnsxrQpt6wEBQU5o09uIyYmBoCIiAiL\nk2Sv9Pr965FfafZdM3L552Jpx6VULlLZingOu5NLojtzmbvLRdTCwsI4fPjwLeN98xUmtM83NzO7\nS39SciRzymV+u/YpXzs89Alr6z1sAAAV+klEQVTA9W/lsPv0bhpPbszFqxdZ8MwC6paqC7jnsnQm\nb/1uB7DZbDeHs3vLyiYgXERKi0gAEA3MS9VmHtDFPtwWWGmS1TPGhBljwoBPgP9LWagodcOPsT/y\n2KTHKJSrEGu7r3X5QsUTZdWZKh988AG5cuX6xzjxy0H++p2dMn9lnYqFK7K2+1qK5SlGo28bsWDv\nAqsjKQ+VYbFijEkA+gJLgN3ADGPMThEZLCIt7M3GA8Eisg94Fbjl9Gal0vPd9u9oMa0FFQpVYG33\ntemeYaDcU4cOHfjyyy8pVqwYIPjmK0zBqL56NpCHKBVUip+7/UyVIlVoNa0Vk7ZOsjqS8kAOXcHW\nGLMIWJRq3KAUw1eAdhnM4907yKc83KcbPqXf4n40uKcB89rPI1+OfFZHylI3DzxMcedhb9g83qFD\nB+699940D7x0Fd6+6+JuFM5dmJWdV9Jqeiu6/NCFAr49yZfYyupYyoPo5faVJRJNIv2X9GfE+hG0\nqtCKqW2mktMvZ5pt9Y+IcjdpfmY9/PCFvDnysuiZRXSY3YFZu78iIeEUBa73QPC1OpryAFqsqGwX\nnxDPoC2DWHVyFS/WepGRTUZS9l+Lb2mnBYlS7iWHXw6mt51OgXfacNFvLglygkLXXsOHQKujKTen\nxYrKVscvHqfX+l7sse1hVNQo+kX2szrSXUv5X7QWWMrb+fr4UvD6s/gnFees/5eczPEmha8OynhC\npW5Db2Soss32k9uJ/CqSg38f5OOIjz2iUFFKpS1v4hMUufZvrssxTuToz9YTW62OpNyYFisqW8z9\nYy4Pff0QCUkJjKszjvpF61sdSSmVxQKTalLs6lAQQ91v6jJ792yrIyk3pbuBVJZKMkm8t+o9Bq8Z\nTERIBHOensOJvSesjuUU97yRPdeU0AOMvU92fbayQ4ApQ7ErwwkN/S9tZrThrXpv8d7D7+Hrowfe\nKsfplhWVZc5fOU/LaS0ZvGYwXat25eduPxOaL9TqWEqpbOZHIVZ3XU2Paj344OcPaD61Oefiz1kd\nS7kR3bKissSu07toNa0VB88fZMzjY+gT0efm5emdRbc4eAddzp4hh18OxjUfR82Qmrz444vUHFeT\nH6J/oEqRKlZHU25At6wop5u8bTKRX0Viu2pjZeeVPF/zeacXKkop9yMi9Iroxaquq7h0/RKRX0Uy\ncctEq2MpN6DFinKav6/9TdcfutJpTieqFavGb8/9Rr176lkdSynlYh4s+SCbn9tMrRK16Dq3K53n\ndObi1YtWx1IuTIsV5RRbT2wl4ssIJm2dxKD6g1jZZSUl8pWwOpZSykWF5A1heaflvPfwe0zZPoUa\nX9bg9+O/Wx1LuSgtVtRdMcYwZuMYIr+K5MLVC6zovIL3HnkPPx89HEopdXu+Pr4MajCIlZ1Xcvn6\nZWqPr83oDaNJMklWR1MuRosVdceO2I4QNSWKvj/2pWHphmztvZVHSuuddJVSmdMgrAFbem+hcdnG\nvLT4JRp/25g/bX9aHUu5EP33V2WaMYaJWyfy0uKXSExK5PPHP6d3RG89iNYN6Jk1ylUVylWIedHz\n+HLzl/Rf2p8qn1dhZJORdK/WXb9blGPFiohEAaMAX+ArY8xHqV7PAUwCagBngKeNMYdEpBHwERAA\nXANeM8asdGJ+lc2OXzzOcwueY8HeBdS/pz7ftPyGMgXKWB3LYdn1x1qLAqUy78bZQo3LNqb7vO70\nnN+T2X/MZlzzcYTkDbE6nrJQhsWKiPgCY4BGQBywSUTmGWN2pWjWAzhnjCknItHAUOBp4C+guTHm\nmIhUAZYAetSlG0oySYz/bTxvLH+D+IR4RjYZSb/IfviI7kl0Bi1ulDPd7vPkDp+10gVKs6LzCsZs\nHMMby9+g0phKfPTYRzxX4zn9zvFSjmxZqQXsM8YcABCRaUBLIGWx0hJ41z48E/hMRMQYk/LQ7p1A\nThHJYYy5etfJVbbZdnIbvRf0Zl3cOurfU58vn/iSewvda3UsZTF3+KOn3JeP+PBi5ItElYui14Je\n9FnYhwlbJvDFE19QtVhVq+OpbOZIsVICOJLieRwQmV4bY0yCiNiAYJK3rNzQBvj9doVKTEyMI5k9\njqv2+3LCZb7c+yXTDk0jr39e3nngHZqVaMbFQxeJOXT3mTPq9+1eT++1O/ldOvP378zMrtD/zM4v\nu94/u9YZZ/bHmcv5TmT0Pm1nnrxl/My2RbPl/TMytNJQfgz6kU92f0KNsTWILh3Nc+WfI7dfbqfl\nywqu+t2elcLDw7Nkvo4UK2kd2WQy00ZEKpO8a6ix49GUVZJMEouPLmbMnjGcunKKViVb0bdCX4IC\ngqyOptxEVv/hS+89suJ9lPVEhMdDH6du0bp8/sfnTD04lWXHlvF8hed5vMTjumvICzhSrMQBJVM8\nDwWOpdMmTkT8gCDgLICIhAJzgM7GmP23e6OIiAgHY3uGG1W3K/V7zeE1vLrkVTYf30z14tWZ03QO\nD5Z80KnvkWa/Z966S+Hm6+m9drtp0nMn09zJvDKb2RX6n9n5ZXJe6XHm7+wf88ssZ/4+nbmc70R2\nfZ7u5P3vUsM6DVkft55+P/bjva3vMe/kPIY3Hu5Sl01wxe/27GKz2bJkvo6Uo5uAcBEpLSIBQDQw\nL1WbeUAX+3BbYKUxxohIfmAhMNAYs9ZZoZXzxZ6J5cnpT9JgQgNOXjrJpFaT2PTsJqcXKkopdbdq\nh9Zmfc/1TG49mb8u/0XDSQ1pOa0le/7aY3U0lUUyLFaMMQlAX5LP5NkNzDDG7BSRwSLSwt5sPBAs\nIvuAV4E37eP7AuWAf4vIFvujiNN7oe7YofOH6DmvJ5U+r8SyA8sY8sgQ9vTdQ6cHOummVaWUy/IR\nHzrc34E9fffwfw3/j58O/kTlzyvTfW53Dpw7YHU85WQOXWfFGLMIWJRq3KAUw1eAdmlMNwQYcpcZ\nVRb40/YnH6z5gK+3fI2v+NInog//qvcviuUpZnU0pe6anqnkPQL9AxlYbyA9qvfg/37+P76I+YJv\nt31L1we68lb9twjLH2Z1ROUE+q+zl9l/dj99FvSh3OhyTNg6gV41erG/335GNx2thYpSym0VyV2E\nT6I+4cBLB+gT0Ydvt31L+Kfh9Jrfi9gzsVbHU3dJL7fvJdbHrec/v/6H2btn4+/rT8/qPRlYdyAl\ng0pmPLET/eM/XvtBePofr1LKWULyhjC66WjeeOgNPvzlQ8b9No5xv42jVYVWDHhwgB6H56Z0y4oH\nS0hKYM7uOdT9ui51xtdh5cGVDKw7kEMvHeLzZp9ne6GilFLZpUS+Enz2+Gccfvkwb9V7i9WHV/PQ\n1w/x4PgHmbVrFglJCVZHVJmgW1Y8UNyFOMb/Np5xv43j6MWjhOUPY3TUaLpV60aegDxWx1PKrejx\nL+6tWJ5ivN/wfd6s+ybfbPmGEetG0Pb7toTkDaFntZ70rN5T/3FzA1qseIiEpASW7V/G2M1jmb93\nPsYYGpdtzKdNP6X5vc3x8/GeRa1/XJRSqeUOyE3fWn3pE9GHBXsXMHbzWN5f8z5Dfh5Cs/Bm9KrR\niyblmnjVd6U70aXixowx/Hb8NyZvm8zUHVM5eekkRXIX4Y2H3uDZ6s9SukBpqyMqpZRL8fXxpWWF\nlrSs0JJD5w8xbvM4xv8+nvl751MkdxGiK0fT8f6ORIREIJLWxdmVFbRYcUO7T+9m1u5ZTNk+hT/+\n+oMA3wCeKP8EHe/rSLPyzQjwDbA6olJKubyw/GF88OgHvPvwuyyKXcTk7ZMZu3ksozeOpnxweTrc\n14E2FdtQqXAlLVwspsWKG0gyScQci2HO7jnM+WMOe84kX6Wx/j31ebX2q7St1JYCgQUsTqlcie4K\nU9nBUz5n/r7+N7e2nL9ynlm7ZjF5+2TeWfUO76x6h/CC4bSu0JrWFVtTq0QtvWCmBbRYcVFn48+y\n/MByluxbwuL9izl28Rh+Pn48HPYw/SL70fLelpTIV8LqmF7BU76QlXvSz1/2yp8zPz2q96BH9R4c\nu3iMuX/MZc4fcxixfgTDfh1G8TzFiSoXRZOyTWhUthEFAwtaHdkraLHiIuKvx7Ph6AZWHVrFkv1L\n2Hh0I0kmifw58/NYmcdoUb4FT5R/QregKHUX9A9/5nnz7ywkbwh9avahT80+nIs/x8LYhczbM48f\n/viBb7Z8g4/4UDOkJk3KNuHhsIeJDI0kl38uq2N7JC1WLHIu/hy/nvqVLWe3ELs9lo1HN3It8RqC\nUKtELd6u9zZNyjWhVolaenS6UipN3lxIZLcCgQXoeH9HOt7fkcSkRDYd28TifYtZsn8JQ34ewuA1\ng/H38admiZqEB4RTrWA1wi6HUShXIaujewT9K5gN/r72NztO7WDT0U1sPLaRDXEbiD2bfPlnX/El\nIiSClyNfpv499Xmo1EPkz5nf4sTeR7/0lVKO8vXxpXZobWqH1ubdh9/FdsXG2iNrWXN4DasPr2by\ngclM3D+Rlze9TFj+MGqG1CQiJIKIkAhqFK9BUM4gq7vgdrRYcaKEpAT2nd3H9pPb2X5qO9tObmP7\nqe3/uANo8TzFiQyNpFvVbgRdCqJK/irUr13fwtRK3Z4WckrdXlDOIB4Pf5zHwx8H4Of1P7Pz/E4u\n5r3IpmObiDkWw/e7vr/ZvnxweaoWq0qlQpWoVDj5ER4crmdy3oYWK5mUZJI4euEo+87u+9/j3D5i\nz8Sy98xeriZeBZJvXx5eMJwaxWvQ9YGu3Ff0PmqG1PzHQbExMTFWdUMppVQWCfQLJKJQBBERETfH\nnbl8hphjMcQci2HTsU1sPraZ73d+j8EAyVvZw4PDqVioIhULVaRswbKUzl+a0gVKE5ov1OsPB/Du\n3qdijOHC1QvEXYjjyIUjxF2Iu/k4cuEIR2xHOHDuwM2CBCDAN4AyBcpQrmA5GpdtzH1F7uO+ovdR\nsVBFAv0DLeyNUkopVxGcK5gm5ZrQpFyTm+Pir8ez58wedp3e9Y/HvD3zSDSJN9v5+fhRKqhUcvGS\nvzT35L+HkLwh/3gEBwZ79LVgHCpWRCQKGAX4Al8ZYz5K9XoOYBJQAzgDPG2MOWR/bSDQA0gE+hlj\nljgt/W0YY7iScIULVy9gu2rjbPxZTl06xelLpzl9+fT/fqYcvnSa+IT4f8xHEIrlKUZovlAqFq5I\ns/BmlCtY7uYjNF8ovj6+2dElpZRSHiTQP5CqxapStVjVf4y/nnidIxeOcPDcQQ6cO8DB8weTH+cO\nMnfPXE5fPn3LvAJ8AyiepzjF8xanUK5CFMpViODA4Js/g3MF/2NcwcCC+Pv6Z1dX71qGxYqI+AJj\ngEZAHLBJROYZY3alaNYDOGeMKSci0cBQ4GkRqQREA5WBEGC5iJQ3JkXJmMLBcweJT4jn8vXLxF9P\n/nn5+uWb49Iaf/HaRWxXbNiu2pILE/uw7YqN60nX0+1XLv9cFM5VmMK5C1MkdxEqF6lM4VyFKZan\nGCXzlSQ0Xyih+UIJyRviVgtUKaWUe/P39adMgTKUKVCGR3n0ltevJFzhxN8nOHbxWJqPI7YjbDmx\nhTOXz9zyD3hKgX6B5M2Rl3w58pE3wP4z9fOAvAT6BxLoF3jzZ06/nP8Yl9Mv583hvOTNkt+JGGNu\n30CkDvCuMaaJ/flAAGPMhynaLLG3WScifsAJoDDwZsq2KdvdmNZms90+gFJKKaXcTlBQkNP2Szly\nzeASwJEUz+Ps49JsY4xJAGxAsIPTKqWUUkqly5FiJa3KKPXWkPTaODKtUkoppVS6HDnANg4omeJ5\nKHAsnTZx9t1AQcBZR6Z15mYipZRSSnkeR7asbALCRaS0iASQfMDsvFRt5gFd7MNtgZUm+WCYeUC0\niOQQkdJAOLDROdGVUkop5Q0yLFbsx6D0BZYAu4EZxpidIjJYRFrYm40HgkVkH/Ap0FBEdhhjdgIz\ngOPAXpJ3AW0WkcdvzF9EBorIPhHZIyJNSIO9UNogIrEiMt1eNLkUEflaRE6JyI4U494VkaMissX+\neNw+vpGIbBaR7fafDdOZZ5rTu5pM9j1MROJTjP8inXkWFJFl9mW+TERc8g6Omex7hxTjtohIkohU\nTWOeLr/c0+q3ffyL9nV5p4gMSzHeI9ZzyFzfvWFdt49Pq+8es65nst8es55Dut9x01PkPiQiW1K8\nljXrujHGqQ+gPlAd2JFi3LvAgDTaVgK2AjmA0sB+wDeNdjOAaPvwF0AfZ+fO5n5XA0Lsw1WAo+nM\nM83pXe2Ryb6HpWx3m3kOA960D78JDLW6n3fb91TT3QcccNflnk6/HwGWAznsz4vYf3rMen4HffeG\ndT29vnvMup6Zfqeazq3X8/T6nur14cAg+3CWreuO7AbKFGPMGpKPV3FES2CaMeaqMeYgsA+olbKB\niAjQEJhpHzURaOWkuE6TmX4bY343xtw4dmcnkFOSL6znljK5zB3VkuRlDS66zOGu+t4emOrkONkm\nnX73AT4yxly1tzllH+8x6zlkru9esq6nt9wd5fLr+l30263Xc7j9d5x9vX2K//Uxy9Z1pxcrt9FX\nRLbZNynd2MznyKnNwcB5k7w7Kr02riytfqfUBvj9xgf+DqZ3ZellLy0iv4vIahGpl860RY0xxwHs\nP4tkeVrnymi5Pc3tv8TccbmXB+rZN++uFpGa9vHesJ6n1/eUPHVdv13fPXldd2SZe+J6nlI94KQx\nJtb+PMvW9ewqVv4LlAWqknz8ynD7+Ls5LdodpNdvAESkMslX++11J9O7uPSyHwdKGWOqAa8C34lI\nPmsiZpmMlnskcNkYsyONaTOc3oX5AQWA2sBrwAz7f1Gevp5D+n0HPH5dT6/vnr6uZ7TMPXU9Tyn1\nlqMsW9ezpVgxxpw0xiQaY5KAcfxvs5Ajp0X/BeSX5FOi02vjkm7Tb0QkFJgDdDbG7M/s9K4uvez2\nzYNn7MObSd6nWT6NWZwUkeIA9p+Z3bRsGQeWWzS3+W/LjZd7HDDbJNsIJAGF8PD13C69vnv8uk46\nffeCdT3dZW7nqes5APZ19UlgeorRWbauZ0uxcuODaNcauFFpZnhqs0k+Aucnkk+JhuRTpOdmbWLn\nSK/fIpIfWAgMNMaszez07uA2fS8syfebQkTKkLzMD6Qxi5Snw7vNMofbLzcR8QHaAdPuZHoX9wPJ\n+6IRkfJAAMlfTB69ntul2XdvWNdJv++evq6n93n39PX8hseAP4wxcSnGZd26ntERuJl9kFxJHgeu\nk1xl9QC+BbYD2+ydKZ6i/VskV9x7gKYpxi/if0fRl7F3eB/wPfajr13pkZl+A28Dl4AtKR43jqD/\nCoiwD6f7e3OlRyb73obkAw23Ar8BzVPMJ2Xfg4EVQKz9Z0Gr++mkz/vDwPo05uNWyz2dfgcAk0n+\n0v0NaJiivUes55ntu5es6+n13WPW9Tv4vHvEep5e3+3jJwC902ifJet6hjcyVEoppZSyUnaeDaSU\nUkoplWlarCillFLKpWmxopRSSimXpsWKUkoppVyaFitKKaWUcmlarCillFLKpWmxopRSSimXpsWK\nUkoppVza/wMzmLJ74Q2kbgAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"from random import random\n",
"xs = np.arange(145, 190, 0.1)\n",
"ys = [stats.gaussian(x, 160, 3**2) for x in xs]\n",
"belief = np.array([random() for _ in range(40)])\n",
"belief = belief / sum(belief)\n",
"\n",
"x = np.linspace(155, 165, len(belief))\n",
"plt.gca().bar(x, belief, width=0.2)\n",
"plt.plot(xs, ys, label='A', color='g')\n",
"plt.errorbar(160, [0.04], xerr=[3], fmt='o', color='k', capthick=2, capsize=10) \n",
"plt.xlim(150, 170)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"I used random numbers to form the discrete distribution to illustrate that it can model any arbitrary probability distribution. This provides it with enormous power. With enough discrete buckets we can model the error characteristics of any sensor no matter how complicated. But with this power comes mathematical intractability. Multiplying or adding Gaussians takes two lines of math, and the result is another Gaussian. This regularity allows us to perform powerful analysis on the performance and behavior of our filters. Multiplying or adding a discrete distribution requires looping over the data, and we have no easy way to characterize the result. Analyzing the performance characteristics of a filter based on a discrete distribution is extremely difficult to impossible.\n",
"\n",
"There is no 'correct' choice here. Later in the book we will introduce the *particle filter* which uses a discrete distribution. It is an extremely powerful technique because it can handle arbitrarily complex situations. This comes at the cost of slow performance, and resistance to analytical analysis. \n",
"\n",
"For now we will ignore these matters and return to using Gaussians for the next several chapters. As we progress you will learn the strengths and limitations of using Gaussians in our mathematical models."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Introduction to Designing a Filter\n",
"\n",
"So far we have developed filters for a position sensor. We are used to this problem by now, and may feel ill-equipped to implement a Kalman filter for a different problem. To be honest, there is still quite a bit of information missing from this presentation. Following chapters will fill in the gaps. Still, let's get a feel for it by designing and implementing a Kalman filter for a thermometer. The sensor for the thermometer outputs a voltage that corresponds to the temperature that is being measured. We have read the manufacturer's specifications for the sensor, and it tells us that the sensor exhibits white noise with a standard deviation of 0.13 volts.\n",
"\n",
"We can simulate the temperature sensor measurement with this function:"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def volt(voltage, std):\n",
" return voltage + (randn() * std)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now we need to write the Kalman filter processing loop. As with our previous problem, we need to perform a cycle of predicting and updating. The sensing step probably seems clear - call `volt()` to get the measurement, pass the result into `update()` method, but what about the predict step? We do not have a sensor to detect 'movement' in the voltage, and for any small duration we expect the voltage to remain constant. How shall we handle this?\n",
"\n",
"As always, we will trust in the math. We have no known movement, so we will set that to zero. However, that means that we are predicting that the temperature will never change. If that is true, then over time we should become extremely confident in our results. Once the filter has enough measurements it will become very confident that it can predict the subsequent temperatures, and this will lead it to ignoring measurements that result due to an actual temperature change. This is called a *smug* filter, and is something you want to avoid. So we will add a bit of error to our prediction step to tell the filter not to discount changes in voltage over time. In the code below I set `process_var = .05**2`. This is the expected variance in the change of voltage over each time step. I chose this value merely to be able to show how the variance changes through the update and predict steps. For a real sensor you would set this value for the actual amount of change you expect. For example, this would be an extremely small number if it is a thermometer for ambient air temperature in a house, and a high number if this is a thermocouple in a chemical reaction chamber. We will say more about selecting the actual value in the later chapters.\n",
"\n",
"Let's see what happens. "
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"scrolled": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAp4AAADQCAYAAACuu2GmAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzs3Xd8zPcfwPHXJ7lEpkx700iC2KM2\nNduqTSk1O1BU6U+pWaW1Oqi2VlGU2pRSVaPUaMQWe0VCagQnO7m7z++PS1LRIEGO1vv5eNwjd9/x\n+b5z3+Tu/f18P0NprRFCCCGEECK72T3pAIQQQgghxLNBEk8hhBBCCGETkngKIYQQQgibkMRTCCGE\nEELYhCSeQgghhBDCJiTxFEIIIYQQNpFtiadSao5S6qpS6ugdy5YopQ6mPC4opQ7eY9+mSqmTSqkz\nSqkh2RWjEEIIIYSwHZVd43gqpeoAMcB8rXWZDNZ/Bhi11mPuWm4PnAIaARHAXqCj1vpYtgQqhBBC\nCCFswpBdBWuttyulima0TimlgPbACxmsrgqc0VqfS9n2R6AFkC7xNBqNMvK9EEII8R/j4eGhnnQM\nIvs8qTaetYErWuvTGawrAITf8ToiZZkQQgghhPgXe1KJZ0dg8T3WZXSlI7WbQgghhBD/ctl2q/1e\nlFIGoDVQ6R6bRACF7nhdELh8vzI9PDweT3DikYWEhABQuXLlJxyJuJucm6eTnJenk5wX2zIajU86\nBGEjT6LGsyFwQmsdcY/1ewE/pVQxpZQj0AH4yWbRCSGEEEKIbJGdwyktBnYD/kqpCKVUz5RVHbjr\nNrtSKr9Saj2A1toE9AU2AseBpVrr0OyKUwghhBBC2EZ29mrveI/l3TJYdhl46Y7X64H12RWbEEII\nIYSwPZm5SAghhBBC2IQknkIIIYQQwiYk8RRCCCGEEDYhiacQQgghhLAJSTyFEEIIIYRNSOIphBBC\nCCFsQhJPIYQQQghhE5J4CiGEEEIIm5DEUwghhBBC2IQknkIIIYQQwiYk8RRCCCGEEDYhiacQQggh\nhLAJSTyFEEIIIYRNSOIphBBCCCFsQhJPIYQQQghhE5J4CiGEEEIIm5DEUwghhBBC2IQknkIIIYQQ\nwiYk8RRCCCGEEDYhiacQQgghhLAJSTyFEEIIIYRNSOIphBBCCCFsQhJPIYQQQghhE5J4CiGEEEII\nm8i2xFMpNUcpdVUpdfSu5f2UUieVUqFKqYn32Pe9lPVHlVKLlVJO2RWnEEIIIYSwjeys8ZwHNL1z\ngVKqPtACKKu1Lg1MvnsnpVQBoD9QWWtdBrAHOmRjnEIIIYQQwgaU1jr7CleqKLAuJYFEKbUUmKm1\n/u0++xQA9gDlgNvAamCq1vrXO7czGo1pgZ8+ffqxxy6EEEII2/Dz80t77uHhoZ5gKCKb2bqNZ0mg\ntlLqT6XU70qpKndvoLW+hLUm9CIQCRjvTjqFEEIIIcS/j+EJHM8LeB6oAixVShXXd1S7KqW8sN6O\nLwbcApYppTprrRfeq9DKlStnb9Qi00JCQgA5J08jOTdPJzkvTyc5L7ZlNBqfdAjCRmxd4xkBrNRW\nwYAF8L1rm4bAea31Na11MrASqGHjOIUQQgghxGNm68RzNfACgFKqJOAIXL9rm4vA80opF6WUAhoA\nx20apRBCCCGEeOyyczilxcBuwF8pFaGU6gnMAYqnDLH0I9BVa62VUvmVUusBtNZ/AsuB/cCRlBhn\nZlecQgghhBDCNrKtjafWuuM9VnXOYNvLwEt3vB4FjMqm0IQQQgghxBMgMxcJIYQQQgibkMRTCCGE\nEELYhCSeQgghhBDCJiTxFEIIIYQQNiGJpxBCCCGEsAlJPIUQQgghhE1I4imEEEIIIWxCEk8hhBBC\nCGETkngKIYQQQgibkMRTCCGEEELYhCSeQgghhBDCJiTxFEIIIYQQNiGJpxBCCCGEsAlJPIUQQggh\nhE1I4imEEEIIIWxCEk8hhBBCCGETkngKIYQQQgibkMRTCCGEEELYhCSeQgghhBDCJiTxFEIIIYQQ\nNiGJpxBCCCGEsAlJPIUQQgghhE1I4imEEEIIIWwi2xJPpdQcpdRVpdTRu5b3U0qdVEqFKqUm3mNf\nT6XUcqXUCaXUcaVU9eyKUwghhBBC2IYhG8ueB0wD5qcuUErVB1oAZbXWiUqp3PfYdwrwi9a6rVLK\nEXDJxjiFEEIIIYQNKK119hWuVFFgnda6TMrrpcBMrfVv99knJ3AIKK7vE5zRaExbd/r06ccVshBC\nCCFszM/PL+25h4eHeoKhiGyWnTWeGSkJ1FZKjQMSgPe11nvv2qY4cA2Yq5QqB+wD3tVax9o2VCGE\nEEI8Sfv27bNzc3Mb7OjoGKiUkn4pTzmttSUpKel4TEzMxEqVKlky2sbWiacB8AKeB6oAS5VSd9ds\nGoCKQD+t9Z9KqSnAEGDEvQqtXLlyNoYssiIkJASQc/I0knPzdJLz8nSS82JbRqMxw+Vubm6DCxUq\n1N7FxSXDJEY8feLi4oLCw8MBxme03tZXDxHASm0VDFgA3wy2idBa/5nyejnWRFQIIYQQzxBHR8dA\nSTr/XVxcXCyOjo6B91pv68RzNfACgFKqJOAIXL9zA631X0C4Uso/ZVED4JgtgxRCCCHEkye31/+d\n7nfesnM4pcXAbsBfKRWhlOoJzAGKpwyx9CPQVWutlVL5lVLr79i9H/CDUuowUB74JLviFEIIIYQQ\ntpFtbTy11h3vsapzBtteBl664/VBQBrWCCGEEOKJsre3r+Tn5xef+nrNmjVnrly5YpgzZ47PvHnz\nwqdOneoTEhLiOn/+/IsLFizwLFWqVEKlSpUSnmTMTzNbdy4SQgghhPjXyJEjh+XEiRPpmvz5+/sn\n1alTJ+7ubVevXu1pMpmMWUk8k5OTcXBweByh/itI2wkhhBBCiCxYt26de/369Z+7c9mmTZtcf/vt\nN8/hw4cXDAgIKBUaGpojNDQ0R+3atf1Kly4dWKlSJf8DBw44AbRp06boG2+8UbBatWol+/TpU/DJ\n/BZPxgNrPJVSrkC81tqS0iEoANigtU7O9uiEEE+d5ORkli1bxpo1a0hOTqZx48Z06dIFFxeZYEwI\nkb1aTPvD/8FbZd6avrVOPmibxMREu4CAgFIAhQoVSty0adPZjLZr1KhRbMOGDW81a9bM2L1795sA\n1atXLzlz5sywoKCgxC1btrj27t278J49e04BnD171mnnzp2nDIZn6+ZzZn7b7VgHffcCNgMhwKtA\np+wMTAjx9ElISODll19my5YtactWrVrFtGnT2LZtG76+d4+OJoQQ/24Z3WrPDKPRaHfgwAG3du3a\nlUhdlpSUlDYrU+vWrW8+a0knZC7xVFrruJRe6V9prScqpQ5kd2BCiKfP559/zpYtW8iTJw/Dhg3D\n1dWV8ePHExoaypAhQ5g9e/aTDlEI8R+WmRrKp4XZbMbd3d10r6TVzc3tmRyfNDNtPJVSqjrWGs6f\nU5Y9eym6EIL58+cDMGfOHPr160ePHj1Yu3YtAIsWLSI5WVrgCCGeXW5ububbt2/bAXh7e1sKFiyY\nNGfOHC8Ai8XC7t27nZ9shE9eZhLPd4GhwCqtdahSqjiwNXvDEkI8jaKiogAoU6ZM2rISJUqQI0cO\n4uPjSUiQEUSEEM+uTp063Zg6dWrewMDAUqGhoTkWL158bu7cub7+/v6l/Pz8Sq9YscLzScf4pGWm\n5jKP1rp56gut9Tml1I5sjEkI8ZSqXLkyv/zyC1999RUTJ05EKcWsWbNITEykZMmSuLm5PekQhRDi\nsYqLi/tH88JmzZpFN2vWLBqgf//+UUAUQOPGjWPPnj0beue2O3bsOH33/itWrLiQPdE+/TJT4zk0\nk8uEEP9xgwcPRinF5MmTCQwMpGLFivTp0weAIUOGoJR6QAlCCCGeZfes8VRKvYh1NqECSqmpd6zK\nCZiyOzAhxNOnfv36LFq0iHfffZeTJ61t/HPmzMmoUaPo3r37E45OCCHE0+5+t9ovA/uA5ik/U0UD\n72VnUEKIp1eHDh1o3bo1e/bswWQyUbVqVbnFLoQQIlPumXhqrQ8Bh5RSC7XWUsMphEjj6OhInTp1\nHlt5W7Zs4ZtvvuH06dMUK1aM3r1706RJk8dWvhBCiKfD/W61HwF0yvN/rNdal82+sIQQz4qpU6fy\n7rvvpr0+fPgwa9as4ZNPPmHoUGlOLoQQ/yX361zUDHjlPg8hhHgkkZGRDBo0CIBhw4YRHBzMmDFj\nUEoxbNgwzp8//4QjFEII8TjdM/HUWoelPoAEICjlEZ+yTAghHsmqVaswmUw0b96csWPHUqVKFUaM\nGEGHDh3QWrN8+fInHaIQ4l8kLi5OLV682GPmzJleJ0+edHwcZSqlKrVs2bJY6uvk5GS8vLzK1a9f\n/7nHUf7T7uTJk47Tp0/3flzlPXA4JaVUeyAYaAe0B/5USrV9XAEIIZ5dsbGxAOTPnz/d8tTXqeuF\nEOJB5s+f71mgQIGyr7322nNvv/128cDAwKD27dsXSUhIeKRx3pydnS0nT550jomJUQCrVq3KmSdP\nnicyTduTmB3u9OnTOZYsWWK7xBMYBlTRWnfVWncBqgIjHlcAQohnV61atQBYuHAhoaE7gVP07v0m\n3377LcBj7cAkxNMuKiqK8ePH8/LLL9O+fXuWL1+OxfJMTuedZbt27XLu0aNH8Vu3bhn8/f3j69ev\nb7S3t9fLli3z7du3b4FHLb9BgwbGZcuWeQIsXrzYu02bNjdS192+fduuXbt2RcuUKRMYGBhYauHC\nhZ5grSmsVKmSf6lSpQJLlSoVuGnTJleAsLAwh8qVK/sHBASU8vPzK/3LL7+4Abi4uFRILXPu3Lle\nbdq0KQrQpk2bom+88UbBatWqlezTp0/Bex1v6tSpPg0bNizxwgsvPFegQIGgTz75JNfo0aPzBAYG\nlipXrlzAlStX7AFCQ0Nz1K5d26906dKBlSpV8j9w4IBT6nG6detWqEKFCgEFCxYMmjt3rhfAsGHD\nCoSEhLgFBASU+uijj3KHhIQ4BQUFBQYEBJQqWbJkqSNHjuTIynuZmZmL7LTWV+94HUXmElYhhLiv\n7du3A2CxxNC1ay3c3XOzbZv146ZSpUrUr1//SYYnhM2cOXOGevXqcenSpbRly5Yto3Xr1ixZsgSD\nITNf18+uL7/8MrfZbFbt27e/vnjx4jA7Ozs2bdrk2rhx44Affvgh16RJky57eXk9dBb/+uuv3xg1\nalS+V1999dbx48ddevbsGbVr1y43gA8//DBf/fr1by9btuzC9evX7StXrhzYvHnz2/nz5zft2LHj\nlIuLiz5y5EiOjh07Fj969OjxOXPmeDdo0MA4YcKEv0wmE9HR0Q/Mqc6ePeu0c+fOUwaDgb59+xbI\n6HgAp06dcj506NCx+Ph4O39//zIjRoy4dPz48WM9e/YsNGPGDJ+RI0defeONN4rMnDkzLCgoKHHL\nli2uvXv3Lrxnz55TAFeuXHEICQk5cfDgQadWrVo9171795vjxo279Nlnn+XZunXrGYCuXbsW6tOn\nz5XevXvfSEhIUCZT1gY+ysxf8gal1EZgccrrV4H1WTqKEEL8g4lu3RoyY0Z+goJyc+XKUW7fvoqf\nnx2BgWVZsGCNzIQknhnvvPMOly5dokqVKgwaNIjLly8zZswYVq5cyYIFC2SChgc4duyYC0CPHj2i\n7OyseVyjRo1iixQpkhgWFpbj1KlTOapVqxb/sOVXq1YtPiIiIsesWbO8GzZsaLxz3bZt23Ju3LjR\nc+rUqXkBEhMT1ZkzZxyLFCmS3LNnzyLHjh1ztrOzIywsLAfA888/H/v2228XTU5Otmvbtu3NGjVq\nPDCu1q1b30y9+LjX8QBq1KgR7eXlZfHy8rK4ubmZ27VrdwsgKCgo7vDhwy5Go9HuwIEDbu3atSuR\nWnZSUlLaB23z5s1v2dvbU6lSpYSoqCiHjGKpXr167OTJk/NFREQ4dujQ4WZQUFBiVt7LzCSefwFH\ngPKAAmZqrVdl5SBCCGE2m5k5cya///47ixdPRalI8uSB06dXYW9vT0xMDNeuXcPX1xd3d3fgCuDC\nmTNR5MmTJ2WZEP89V65c4ddff8XJyYkNGzbg4+MDgIeHBz179pTEMxNy586dHBoayq5du1ybNGkS\nA3Dx4kXD5cuXHZVS5MuX75EbRzZt2vTWqFGjCv36668nr169mpY/pXSEPFOuXLl0CdjAgQPz586d\nO3nFihXnLRYLzs7OlQBefPHFmO3bt59csWKFR7du3Yr179//St++faPuvNCOj49Pd9Xt5uaWVlt7\nr+P98ccfro6Ojjr1tZ2dHU5OTjr1uclkUmazGXd3d9OJEyeOZfQ7pm6fepyM9OrV60bt2rVjV61a\n5fHiiy+W/Oabby40b948+n7v3Z0yc8vcHRiCtW3nWWBXZgsXQohURqORYcM+ZMmSJWzbtorUmXft\n7e0BcHNzo1ixYnckmJrw8F3Ur1+X+vXrc/369ScTuBDZ7NatWwDkypULb++/+3AEBgYCcOPGjQz3\nE3/r3r37dYBPP/20wFtvvVVw7NixuevVq+efnJys6tatayxcuPAjT4TTu3fv64MGDbpctWrVdDWU\n9evXv/3ZZ5/lSW2Pu3PnTmcAo9Fony9fvmR7e3u++eYbH7PZDMCpU6ccCxQokDxo0KDrnTt3vr5/\n/34XAB8fn+T9+/c7mc1m1qxZ43WvOO51vMzw9va2FCxYMGnOnDleABaLhd27d993fw8PD3NMTIx9\n6utjx445BgYGJg4fPvxq48aNbx08eDDTx4dMJJ5a64+01qWBd4D8wO9Kqd+ychAhxL9DXFwce/bs\n4fDhw/e82r1bbGwsw4YN+8dg7126dOG5555j//79QBLe3rf46qtBLF8+gXr1KmWq7ORkEzly2OHk\nZIeLi0tWfx0h/hWKFi2Kj48P4eHhrFplvaFoMpmYOnUqAFWqVHmS4f0rdOrU6Vb37t2vJicnq1mz\nZuUZMWJEofPnzzsVKVIkcfbs2Y9lCMgSJUokjxgx4urdy8ePH3/ZZDKp1M5Cw4cPLwAwYMCAq4sX\nL/YpV65cwKlTp5ycnZ0tABs3bnQvVapU6cDAwFJr1qzxGjx48BWAjz766FKLFi2eq169uv/9es3f\n63iZtXjx4nNz58719ff3L+Xn51d6xYoVnvfbvmrVqvEGg0H7+/uX+uijj3IvWLDAu2TJkqUDAgJK\nnT592untt9+OysrxVWa/XJRSebEOqdQBcH/SMxcZjca0wD08PJ5kKALrh+SMGTP4+uuviYqKonLl\nygwaNIgXXnjhSYcmUoSEhABQuXLlf6zTWjNx4kQ+/fRTjEZr86WAgABmzJhxn57lFuAGsbG3cXMr\ngbOzE3FxxwEzYKZhw65s3ryHX3/9lkaNqpIyEVqW/fXXdXLkcMTLqwRQ+KHKeJrd77yIJ8fW5+XT\nTz/lww8/BKwd665cuUJERAROTk7s27ePUqVK2SQOW7t58yaffvopw4YNS1vm4eGRdpv5woULC4oW\nLRqY2fI2b97s+sMPP3jHxMTY1ahRI+aNN9644ebm9nAfPuKhXbhw4XjRokVfz2jdA9t4KqV6Y+1Q\nlAtYDryptc6wbYB4Nmmt6dixY7rBvtevX8/69euZO3cu3bp1s0kcsbGxWCyWe7YFTEpKYubMmSxc\nuJBbt25RtWpVBg0aRLly5WwS39NsypQpDBkyBIBSpUoRFRXFiRMnaNq0Kfv27Uu75QcQExND7969\nGTeuF4ULO+HiohkzphceHm5ofT2tQ9CMGUOwWCwULJibh006AfLm9U15dg2tkxk5ci6NGjWWoZbE\nf8oHH3xAQkICn332Gfv27QOgRIkSzJw58z+bdEZHR1O3bl2OHDmSLvF8FA0aNIht0KCBDAD8FMtM\nG88iwACtdWmt9ajMJp1KqTlKqatKqaN3Le+nlDqplApVSk28z/72SqkDSql1mTmeeHI2btzI8uXL\nyZkzJ+PGjWPlypVpScyAAQOyfRDwvXv38sILL+Dm5kbOnDmpVasWf/zxR7ptTCYTLVu2pF+/fvz5\n55+cPHmSBQsWUK1aNX77Lftbjpw6dYpu3bqRP39+ihQpQr9+/YiMjMz242ZGcnIy48ePB2D+/PmE\nhoYSHh5O+/btiY+P5/PPP0+3/fDhw1m4cCGvv94fAKUUI0a8Qf/+HdL1Qi9RoiB+foVxdnZ6bLGu\nWrWSsWPH8corr3Dz5k3A2nZ0zpw5bNy4Md22cXFxmW4uIMSTZmdnx0cffcSlS5fYunUrwcHBnDp1\n6j991+jbb7/lyJEjlCxZ8kmHImwoM208h2itDz5E2fOApncuUErVB1oAZVPajU6+z/7vAscf4rjC\nxlLbJL3//vs0btyYQoUK8emnn1KpUiWMRiPbtm3LtmMfOnSIevXqsXXrVhwcHHBwcGDnzp00aNCA\n3bt3p223ZMkSNmzYgK+vLz/++CP79+/n9ddfJzExkV69emXrIM1Hjx6latWqfP/990RGRnLx4kWm\nTZtGtWrVnorkMywsjCtXrpAvXz46d+4MgIODAwMHDgRgz5496bYfOfJ92rdvxIwZH9o81hYt6tKn\nTztmzRqFl1cMcJkLF/bRs2dPBg0aAEQD8UASpUuXxtHRkUWLFtk8TiEeloeHB/Xq1aNKlSqkDgv0\nX/XTTz8BpF34ZkRrLSPo/wvd77xl24i0WuvtSqmidy3uDYzXWiembPOPRroASqmCwMvAOGDgg46V\n2hZHPBmXL18G/u6ZCdZzklr7FRoaSp48ebLl2IMHDyYuLo6GDRsybNgw7OzsmDx5MmvXrmXAgAF8\n/fXXAMyePRuAHj16UKJECcxmM2+++SZLly7l7NmzLFq0iICAAMB6FX78+HH69OmTtuxRDBgwAKPR\nSM2aNenfvz8JCQlMmDCBY8eOMWDAAP73v/898jGy4u7/l9Qes1FRUWzevBlPT2s789QaRIPBcMc+\nJpydLzBq1OtYLHEcO2b7VjfvvPMKAMeObQMgMvIKLVrUIlcuT44dW522XVyckUKFcuHvn4N9+/ag\ntQGt9VM7Nqh8jj2d5Lxkn9T25OHhF+65TVJS0vG4uLggFxcXSUD/JeLi4uySkpLuWXFo66kQSgK1\nlVLjgATgfa313gy2+xIYjHUop6dKTEwM586dSxv65Wn7EktKSmLbtm2cPHkSb29vmjRpgq+v74N3\nfARVqlRh3bp1/Pjjj1SvXp0iRYqwefNm9u3bh4ODAxUqVHhwIQ8pODgYgHfffRc3NzfAmuitXbuW\nkJAQzGYz9vb2JCQkANbZQezsEjAYbgJJJCZah0FzdIzA0dENpeD48X3s3n2ILl0a4ODgTXJy7oeO\nLykpid27d2NnZ8eoUaPw8rKOkDFkyBC6dOnCtm3bbJ543s3b25vnn3+ePXv2MHDgQLp06UJUVBTT\np08HoGnTply/fp1t27bx2mtVUCp75go+GGngl9M5eDUogWJe5kzvV7hwHj755K1/LN+6dQomkxmD\nIQ6tzxId7U737h/wyiuv0KZNm7RhnIQQtqW1Zv78+Zw7dw5vb9i69Su6du2R4bYxMTETw8PDcXR0\nDFRK/bergP8DtNaWpKSk4zExMfdsSonWOtseQFHg6B2vjwJTsQ5EXxU4T0rP+ju2aQZ8k/K8HrAu\no7Jv3bqlUx+2YDKZ9IcffqhdXV011p4SukKFCnrfvn02OX5mnDlzRpcoUSItPkA7OjrqBQsWZOtx\nExISdPny5dOOeed7NGTIkGw9to+PjwZ0aGho2rLw8PC0391sNmuttX7vvfc0oO3tlT58eKG2WPbq\n1atH6iJF0AEBOXRc3A6tdYjWOkTv2TNP//zzl/rq1U1a6xAdGxupt23b9lDxxcbGakAbDAYdHR2d\ntvzYsWMa0Hny5HmE3z5r9u7dq/fu3ZvhulOnTum8efOm+9sB9EsvvaQTEhJ03bp1NaDHju2tU9+n\nzD7OnVuu9++frY3GLRmuvxi1R789f5Mu8sE6XeSDdTpo1M86+PyuLB/nQY9580ZrQJctW0YnJyc/\nvjf2Ed3vvIgnR85L9mrVqpkGdKlS7rpiRfRd3+nZmpvI48k+bF3jGQGs1FprIFgpZQF8gWt3bFMT\naK6UeglwAnIqpRZqrTvbONZ0Ro4cySeffAJA2bJluXTpEgcOHKBBgwYcOXKEggULPlS5kZGRrFix\ngtu3b1OjRg3q1q37ULWoWmteffVVzp49i7+/Px06dODAgQP89NNPdOvWjapVq2ZbA+4cOXKwbNky\n6taty19/XcbDIxYPj3wMGvQ+7733XrYcM1XLli357rvv6NmzJ1999RUGg4FBgwYB0KxZs5Q2UmZG\njOjBkiXfYrEk0L17Fzw9c3Lz5i18fKBfvzdxdv57/Ntq1cqkPb958zaVK7ckMjKKo0ePUrx48SzF\n5+LiktbZadCgQXz22WckJCQwePBgABo3bvzob8Jj4Ofnx6FDh5g+fTq///47rq6utG/fng4dOmCd\nG7gHkZHn6dmzRabLPHPmDGPGjCE01Ho73tHRgTZt2vDuuwNwcDAQn6T5dlsMM7bHYqcU7zd248Ug\nJ96cf5POs28w7TVPGpV6fB2TunR5GQ8PN/Lk8cZguAgUIjY2iejoaPLmzfvYjiOELWituXDhAmaz\nmeLFiz/17UF//fVX/Pz8KFYsFxDBhAk96NWrKeXKFWPatGlPOjxhS9mZ1fLPGs9ewJiU5yWBcO6q\n8bxr/3o8BTWeRqMxrRZv/fr1Wmut4+LidKNGjTSghw4d+lDlfv3119pgMKSrYapdu7a+efNmlssK\nCQnRgPb19dVGozFt+euvv64B/cEHHzxUjJmVmJigK1YM0p6ebvq77/6nzeZj+sSJo3r69OnZetyL\nFy/q/Pnz/6OmztXVVXt7e+vTp/dorQ9qrUN0RMQaPWBAbV2pErpiRXSTJr568eL3tcWyV9+vpqxD\nh8a6bNlAffjw4YeKcdu2bWnn2WAwaDs7Ow3onDlz6hMnTqTb1mKxpHt9+vRpHRISopOSkh7q2Hd6\n+BqcRK31QZ2cvEdntnbxxo1NukEDT12xIrpePXf92msBumJF6/v+6aft9NpDO3T1T9brIh+s0/0W\n/aYv3/ozbd+omGDd/KuNuviZAOlVAAAgAElEQVTQdXpJ8PZMHzPrj/36ww/7a3d3d7148eKHeF8e\nD6lZezo9zedlzZo1OigoKO3zLnfu3Hrw4ME6ISHhSYeWoYkTJ2pAd+jQTN/r/1FqPJ+dR7ZdIiml\nFgO7AX+lVIRSqicwByieMsTSj0BXrbVWSuVXSq3PrlgeVWhoKLGxsZQtW5YXX3wRAGdnZ/r3tw4n\nc3ev38zYtWsX77zzDiaTiRYtWtC/f39y5crFjh076N27d5bLu3jxIgDVqlXj1q1bDB8+nMWLF9Og\nQQPA2nP5cbt+/Trx8fFAPI6O51iyZAyrV3/C888HkZR0k2bNXqJXr17MnTv3sR87VaFChQgODqZf\nv34UKVKEwoUL89Zbb/HSSw25ceMGS5Z8T+rUjAUKFOCLL75gy5YtrFu3lnXr1tGhQ4cH1jBPn/4h\nISFzCQoq8VAx1q1bl02bNlGzZk1MJhNaa1588UV27NiBv79/2najR4+mePHiXLhwEq0vY7Gc45tv\nJlO5cuW02nawjldqiyn0Tp8+zfnz57DOlGvCYMj8DZLVq1dz8+Ytypcvx/r16/nhh4XMnj0bS85i\nfHe+En0XGfF0sWPp295M7ehJPo+/21t6u9qx6E0vapRwZPCK23yzLSb1QvSx0trMqVOhREdHU6RI\n9raDFuJxSEpKok6dOrRo0YLLl49QvXpO6tTxJCrqKhMnTuTLL7+0eUxaa1KnggTrGM7169dP+cwy\nA7G8+mot8ub1oWLF4tnyvyz+XbIt8dRad9Ra59NaO2itC2qtv9NaJ2mtO2uty2itK2qtt6Rse1lr\n/VIGZWzTWjfLrhgzK7WXb0REREqiZXXmzJl067Pi22+/BaxDEK1evZopU6awZ88eDAYDy5Yt49q1\naw8oIT0/Pz8AduzYwcSJExg3bhy7d2/ml1+WYjBAwYIFqVOnDh988EGWY83I5s2bKVOmDMOGDcA6\n6lUczz1XiFy5rO+Fk1MORo7sSY0a5Wjfvul9y3pUBQoUYPDgwfz555+EhR1jxoyBfPHF2/zyy1cM\nG9bzH9vnzJmTfPnyZTqR8vBww8HBAIQB+qE+OOvVq8cff/xBbGwscXFxrFu3jvj4+DvKSuDEiQNc\nuHCB3r3bULt2CapVe47t23+iUKHcVK+eGzgNRPLTT0vw8fHh7bffznIcmRUTE0PLli2pVKkie/dm\n1P/v/o4etQ7f27ZtO5ydnbkZa2FlWHFuVp2CybUQPctdZ20/H6oWc8xwf9ccdnzX1Yvm5ZyY+EsM\nH6+LxmJ5vF9YSimWLZvAwYOLqF7dC2uTczP79+/P1uG1ROZorQkODmbp0qUcOHDgmU1YYmJi0p47\nOpo4ezYUpaBp02r8/vtGNmxYy0svVSJnTti/fx7WG4mxDBo0iF69enHu3Llsi+3999/Hy8uLlSuX\nYR3K7BqxsWFs27aN3bs3AgeBExQu7EhY2Dr+978uT12HXGF7tm7j+a8UEBBAhQoVOHDgAM2bN+fd\nd9/lzJkzjBw5EoDXXnsty2WePXsWgJdffhmwfsgaDAYCAgI4evQoFy9eJFeuXJkqS2tNwYIFqVev\nHgcPbuPQocWUK1eI06e3cvXqOapUcaRqVR8mT96ByRQHXAecAWfq1KmHr68vs2bNwsfHJ9Px58zp\nxPXr1zl4cD/JyckpiVl6r7/+Mp06vYidXSRgwGLx4erVq4+9PV1wcDCvvPIKpUqVYNOmLzAYDBQo\nkJsCBR6+N3pG4uNvMGbMu1y5EsOcOXMeqozU+carVatGcHAwe/eup3LlwkACffq8yMWLf3DlivWL\nxSqSPHkUTk6JwG3gNpGRR8iRw5HChZ2Ai4AP4Pqov1461nZjBbFY4ggIKJrhNokmzYlIEzGJFqIT\nNNEJ1p8xiZrjTo2ICQxiakgufoy8wcHwZGISNV7XN8PR2bTq8TX2dvf/AnI0KL581QMfNzvm7Izj\nRqyFiW09cDQ83i+ucuVS2z7f4ODBfVSv3on69euzdu1aHBwcHuuxROacPXuWdu3aceDAgbRlNWrU\nYMmSJQ/dnv7fRmvNm2++yeLFizl2bCdFijgBsRQqlISPD0ycOCxt7OKlS6dQt25dzpw5QULCRZSK\n4LvvZmE0RvPee73Syjx//jy+vr73nN3tfk6fPs3ChQtp3rw5338/nTNn/iQ8PAqj0cipU9sBa+VH\nvXp+bNgwlTJl0t8hcnSU/yVhJYlnJiilmD17Ng0bNuS3335LN9NNp06daN26dZbLLF68OLt372b9\n+vXUq1edP//cQvXqL6GUwt7enkKFCmWqnMjISLp3787169dYt+4L/ve/Xhw7dhx7+5tcvQru7m6M\nHTuWoKDybNyY2oDbetvdaIxhx44dODnlwMMjHmti40K/fu8RFhbGmDFjKF++fNqxwsPDU+K6RpUq\nLuzYMYtq1crct1G7dZ0GLvLhh6OZN28Fa9eupUqVKll+z+6lUKF8KGXBYDATG5uAh4fbYyvbZPr7\nFvPly9f58suZJCYm8cEHH6S7TZ6FEoGrVKlSgsjIMP766yRgTZCPHt1LYuINSpUK4JNPPsHb25tv\nv53Ojz/+yNSpU6hduxZKKQYO7Ezfvq+SmJiEdRrJKCZMWIenZy569ep1v4NnmoeHA2vWfML16zdw\nd/9nUpuQrHl1xg0ORWQ8tFIO+7Ik5SrM6WtxGM1X8feyx/X8Eg4fXE3hwoUyPQWgnZ1iZDN3fN3s\nmLQxhhtxFqZ39sTFMXtu1ly/fhV3d2eKF8+b4cWUyH5JSUk0adKEs2fPkjt3bqpXr86OHTvYtWsX\nzZo1Y//+/U99R5rHQakk4uOjiI+PZ+vW1XTrZh2/1sfHjeTkGK5du0b+/PkB63znJpMZBwcD9vYG\nDAZ7tm+fyZYte/H3N2MdUMaL3r3fZPPm31m7di1Nm2btTtSbb77B779vZ968T/D1NaXECEFBYDSe\nxGKxYGdnR65cXjRtWuNxvhXiP0Y+WTOpYsWKHD58mFGjRnH+/Dk8Pb3o1KkTrVq1yvKHYEJCQlov\n6oULJ2E27yU8PA47O3B317Rq1YLcuXOTnJzMiRMnCAoKumdZOXO6Ehp6mJiYGKKi/mL+/PmEhOzj\n1CnrOJ5169ZNq2Vr3Pj5dPu6uTlz9OgSwsIiMRiuAFcA2LBhDWfPhjN27LukJqOffTaF999/n717\nV6bU0EH16mUz/TsnJ5sICQnh+vXrGI03M/9m3UN8fHzKexhLvny32LlzNkWL5nssYzOaTCbmz5/P\nsmXLuHr1Gnnz5uXVV9vTqVMnpk8fir9/qSwlnSaTiffff5/mzZvwwgsFgSTGj+/NV18NTHfbaefO\nXQD07duXwoWt7/GAAQNYv/5nzp+/QGRkZNoXjaOjQ1oNwh9/7GPo0JE4ODjw8ssvZ/qiJSPBwcFU\nrFgWg+EcdnaQO7d3htuN/uk2hyKSGf2KO4H5HHB3UikPO1xzKAx2MGHCfJYtW04i1laiAK6uLowe\nPTpL/zNKKd6p74aPqx0frrpNx1k3mdvNC2/Xe5ehtebIkSPs3LkLpaBOnTqZSnYbNqzG4cM/4unp\nDpwCihEZGYWnp2e6kQ9E9lm9ejVnz56lZMmShISE4O7uzo0bNyhbtiyHDh1i8+bNNGrU6EmHmS2S\nk5MxmUw4O98GIhgzphtjx3anWLECads0atSQBQsWMmbMGPr374+jYw6mT7c23WrQoEHaBVPZsn6U\nLeuXslciWkdiMkUDUKGCB/AXkJPJk79h+/btDBo0iLp16wLWHujfffcdkydPolAhdyCKN99szLlz\nIbi4xNGwYQM6dOjAhQthfPnll2zevIWtW7em9SkQ4n4k8cwkrTWTJk1i7ty5rFr1JS1aNALy0rZt\newIDAxk0aFCm23pevnyZBQsWAODra5c2pWSZMlC6dGmmTOkLHGX9+r20bNmDTp06sXDhwrQ4Vq1a\nRfPmzTEYjLi6XmL58k8pXrwAuXJZByevUqUyVapUfmAc9vb2lC5dgtKl098S2bBhCvv2HScw0A1r\nu0LYu3cT9vb2hIQEpyWeWeHgYGDDhqns2nWIunULAUlobU2cstrm5+jRo7Ru3ZqhQ/vSvXstQFOi\nxOO7/TZq1Gh++eWXtNd//fUXU6ZMJSzsIiNGDE9ZegPIOCm727x585gyZQpLlvzAuXOrcXZ2ws3N\n5R/bpb4N6duy/d2m9F7vU+3aFRg16k3Kly9PoUIP/z789NNPtG3blnbtGjN//sh7JvFL98bx4954\n3qnvSrea977F/8EHH1CrVi3WrVvHrVu3KFWqFO3atSNfvnwPFV+Hqi54udrRb/Et2k6PolcdV3I6\n2+HhrPBwtsPDxfrcUZkZMWI4v/22OW3fWbNm06xZM0aOHPHAi5P8+VObuMRgMh2mdeveREfHs2rV\nqrS21OKf4uLi2LlzJ1pratSokTahQ1YdPnwYgPbt2+Pu7k5ycjLe3t60atWKadOmcejQof9s4jlg\nwACCg3ezevU4ChTIneHnWvfu3dm1axdnz55j4MBBacvz5MlN37797lm2UorffvuGmJg43NwcgUvA\nJVav/oGdOw/yxhvtgSTAke++m8HSpSupUCEPQ4Z0BaBixaLkyhVHrly+jB07DgcHAxUqVCAuLpbP\nP/+CX3/9NV3iGRn5F/Pnf8+uXbuxt7ejdu06dOnyepaadIn/Jkk8M0kpRd68njg4GIiONgJxhIZu\nYsWKFbi7uzFo0P3Hq7x+/XrKDEKJFC9uZsqUgfj7F6F0aessPzExMZQrV47KlSunJBiJXLlyBg8P\nNypUKATcBDzp3LkzixYt4quvhtO3b0sg/biTj4OfX2H8/NInlxMn9uPLL98jb96H7/3r4GCgbt1K\nQBxwgiNH4nnttZ688847WerJv3fvn5w+fZoZM2bRtWv1x3rb7fjx4/zyyy84Ozsxfvx4atSowfbt\n2xk6dCirV6/mtdc6UqJECSCcI0fCAMN9a6QBund/mT17WtC9+ys4O997XMratWtz/PgJpkyZgo+P\nDz4+PkyfPp3o6Biee+65+7aNHT06taNROJD1CwMAX18vcuRwIF8+r3u+p0cvJTN8zW1qPufIwEb3\nTyyUUtSqVYtatWo9VDwZaVLaiQU9vHlrwU0Gr7id4TZ2WNDJPbCv9So+7o7kM1zhypYJrFu3joAA\nfzp27Jjp40VGXuHmzWvExibh45P1ToTPAqPRyFdffcXkyZNJSDBiMoG9vSNjxox5qM6MqdPr7tix\ng3bt2nHy5En27NmTNnVldk2/e6fLly8zYcIETCYT06dPt8kxb9y4wfr1P3P58mXCw6/cs426h4cH\nc+bMYdmy5fz++zbMZjPVq1enQ4cOeHs/+GL47ovexYvHsnnzXurVKwQcAex5552mlC+fj06dmqRt\nFx8fB4CPj0+6Zii5c1vfm7i4uLRl4eHh9OjRgxs3/r67FRa2kM2bf2Pu3HnkypX+eyTZ/Gx2HHtW\nqX9rT0Gj0ZgWuIeHR7YdR+vUuZ2voHU4J0+GpetssXPnQc6ejaBLl5ZAbrTOxfvvf0DHjh2pXNla\n6zh58mRGjhzJ+vXfU69eCaxtHjMnPj4Bs9mS8mFhYPXqXbz99nCmTBlEhw5NHri/raXO3f2g25rW\nD8vu7N17jEmTRvD++0MAF65cucL27dtp0qQJOXPmzGBP643befOW0r59I1xcsj7A+MUoE7+fSiLZ\nrLFoMFvAoq3Pg/fuI3jvPgJLleb56jXwcLajaw0Xxo/7iLVr1/HeewPo3LkzGzbspHnzQQQFBREc\nHPyPHvIhISGUKhWIi8sN4Gqm4jIajXTt2pXw8Ih0yw0Ge6ZMmcLzzz9/jz3TO33axLRpi/j888/T\n1e6lfnGn/l2mZwZOcf78aYoWzZ9h7aoxzkKzaVGYzJp1/XzxcXty7ewSkjXXos0Y4zW34y0Y4zXG\nlJ8z5y0iJsmeis/XQTl5s/tcEm4OJiz7p+Kf4zwrVyzL0rFiY+O5cOEypUuXAoqxffs+Vq5cSe3a\ntWnTpg1grRXv168fvr6+aSNWgHW++0KF7t+m9f7n5en266+/0qJFC0ymBIoVgypV/Dl48DrHjkUB\nsHjxYjp06JClMq9evUqRIkVISEjAzk4xYEBbwsLiWLHiZzw8PIiIiHio2tSrV68ybdo0fvvtNxwc\nHGjZsiVvvfUWrq7pa+2XLl2acnFiwdERzGYH+vbty6RJk7J5mlUz16/vYu/eA7z4Ys1sPM7DiYmJ\noWnTpsTHJzB58iTq16/P7du36d+/P0eOHOWdd/rQo4d12sshQ4awadNvVKpUkf79+2MymZg8eTLH\nj5+gbdu2DB06BLB+v/5yNJGJG6NZ/Wb1tGN5eHhI1/f/MEk872P9+vV89NFHbNw4C0/PzM1PvX79\nLl5+uT/58+cnLCwMg8HAxx8PY+TITxg2rAdjx/Z5pJi01sTGxmd4q/ZpkNnEE6zJ5+7dRyhevEDK\n7U0HZsz4mV69PqRVq1asXLkSgEuXLtG/f3+mTRtHvnwJWJOkrLsVZ2Halhi+3x1H8gOL0BjsFCYL\nvFnbhfjdE9mw4RcGDnyPTp06ERsbT9myHWja9EUmTZqS1o4WYNWqVXTo0IFXXqnP0qUfZ6lGNioq\nilmzZrFp028kJMRTsWJFevbsma6T1/2YTCYCAtpy9mwEn332GQMHDkxbl1GCs3btWnLl8ub5572x\n1kRnzGLR9Pz+Fn+cSWTp295UKJzxMEgP69q1m8TExKVry/YwTCYT1apZE/Tg4D+xt7fnSEQyw1be\n5PBlC47GE6wcXpMyBR62h63iq6/W0r//aN55pwvTpo0BNBcuhFOsWB2KFCnAhQvbAI3FYqFo0QaE\nh19i796990ws/02JZ2xsLBERESltnJOIijpFnjxlcXHRfPZZL9588w2OHz9P69YDiIu7RP785di9\n+2CmyzcajXh4eLBq1TxGj36DyEgzefJYm6GEhzvx8ceT6Nu3b5bjvnDhArVr1yYiIv1FXcWKFVm6\ndCk///wz77zzDvv376Rdu/rExlpwdHSmatVCrF9/mqQkzUcffZQ2ksnjZO3AaA+cwdqm/un17bfT\nmT17NgAFCuQnKiqKhIREfH19+PHHJXh5eWI2m6lRwzpm8fr1P6fVFp86dYqOHV/Dx8ebX3/9lb0X\nkvh0fTT7Lybjl9vA8p5/X1hL4vnfJrfa78FsNjNs2IccPHiImTNnM3hw10ztV768H//73+sULZof\ngyECSOZ//3uZevWKUbt2hUeOSyn11CadAOdu2BMc4cCQ5ywP7Hlsb29PrVp3JlTJ5M7tQO3aFWje\nvBzWLimenDhxlJUrV+LgEM2PP36a5ZgSTZoFu+P4aksMtxM07Ss506e+Kx7OdtjZgb0CezuFnYJz\nZ8/y2msdyOHowKhRo9hsrMzsHbF4hZxHYb0dDuDq6syhQ4txc/PCOrPr3/z9i+Pk5EiePDnTenpm\nlo+PD0OGDGHIkCFZ/j0BDAYDM2cO4+uvl/Pmm13uu21wcDBt2rTBycmRQ4cW3Tfpm7Y1lq0nE/m4\nRc7HnnT+/vs+WrQYRIUKQWzZshmlLpCYeAuDwT7LNUzWobTyc+nSZbZu3UrDhg0JKuhA98K7Gb5p\nN4kBPWk+LYpO1VwY1NgNT5es1tpqatf24/PP36N8eX+sQ5NB7tx2LF06Hnd3F8AIWGuImjSpQkiI\nKxUruqVs68UXX0zFy8uLtm3bPnQ7yCchJCSEBg0aUKJEUfbtW4ZS0fj4QLly9oAprWYzMLAYBw4s\noWbNWiQmHkLrCMaNm4uDgyMDBw7McIiqmzdv0qtXLw4c2M+RI6tp1SqIKlVW8NNPPxEZGUmhQoW4\neTMH/fr1w2g0MmzYsCzFPnjwYCIiIqhatSqjR48mJiaGIUOGsH//fqpXf55r165TooQjO3euwsfH\nwttvt6F58+YopRgwIIF69d7iiy++YMiQITg6Pr6//5iYGOrVq0eXLq/Qr9/LT/0Yl2+//RaOjg4s\nXLiQS5cuA9Y+BUOHDsXLy9oURWuNyWTt9X5nbXLqEE4xdr68Nf8mvx5LJLe7HRPa5KRNRWdiYxDP\niP9EjWd0dHQ2jO0Wx4UL21my5GcGD+761H8gPGkms2bG9li+2BSNyaIIKmBgdlcv8uR89FtTEybM\nY+vWfSxYMCatA1VmaK3ZcDSR8RuiuXjDTJ2Sjgx90doL+37GjRvHypWrALAYXLhV41vsEm/xdvE/\nGfz+wAz2yIPZnA87OzuUigPOcPFiBIULP+n5v50Bf8B6Du6uWTOZEuncuRUFCngzefKAe/6N/34q\nkW5zb9KyvBOft/d47P8LN29q/PyaUrlyZZYuXYqrqxPt27+CnZ2ZhQs/JkeOrH3RL1q0iM8++xyD\nwUCDBi9gNpvZunUrZrOFQUNHccqxLvN3x+HpohjcxJ32lZ2xe8CYoo/i7+Y6EB+fRJ48jYmOjuHk\nyROULOlPSEgIJpMp000pbOH06dNMmjQJb29vxo8fDySQkBBJwYIVKVmyMOvXT0np+Q8vvfQSV65c\nZdasmVSsWBGAI0eO0q1bNzw9Pfn++x8oVqwFZrOZ4ODgDGt2k5ISKFcuiIsXI9i06Wtq1Cj3j23m\nz19H9+5j+OKLifTvP+gf6+8lMTERNzc3zGYzJ0+eZM2aNfTq1YuQkO106fIy7u6elCgRxLBhPZk0\naTTnz1/ghx8Wpk0icOhQOK+9Zk10T5w48ZDDqGXsxx9/pGPHjpQsWZj9+3/A1fXfMXJCYmIiERER\n5MyZM8Pxpt966y327dtP27ZteO+99zCbzQwf+wXrL+YnqWBTXJ3s6VXXlR61XNIqKIzG59L2lxrP\n/7b/ROLp6JiEs7P1jz86OvqhBscFazutn3/+mZ49WwMXAJm9JDPOXzcxcKmRAxeTqVUkkeqFkvk6\n2B0PZ8Xsrl6Uzv9oAwff+cWdWfvCkhj3s/U2TkBeA0NfcqduyRyZ2tdisbB8+XKWL1/OpUuXcSn5\nEqfz9OCDpm70rvfPGqqjR88SFPQqo0d/wKhR7clKG96MxCdptp1MJNJopnxhB0rndyDHQw6abrG4\nM3nyajp16kRkZCSQmnha23SazdEpCXPG5UfcNNPsq+vkzWnPqj4+ODs++vfBhQuXmTVrFR9/PAA7\nu8KAJxERERQoUAClFCdOnKBatWoopfnzz7n4+xfNUvkWi4VJkyaxdOnfbTmVgi5dutCvXz+UUhy7\nnMyon26z90Iy5Qo6MKZFTsoVyv4BruPjE1i4cAP795/g229HAJ7s3x/Ga6+9RXR0NJs2bUprpnL8\n+HGMRiOBgYHZ2o59y5YtzJ49mxdeeIE33ugJxBMaup8yZWpTrFhBzp37idTPwmvXbv7j4u/rr79m\nzpy55MrlS9eu3bC3t+P777/nr7+u0LlzZ957bwAbN+5m795Qhg8fDBQEHNiyZQs1atRImRwhnAMH\nDuHj43nfC7YTJy4QEOAHlOTuOw33cvv2bTw8PMiRIwfVq1dn27ZtfPfdxzRsWJpWrVrj6+vLxo3W\nUSxSE6bhw4fj72+dWMBisaNixc7Y20NExPXH3Cs7hiVLplG+vF+W/s7NFs3WE4ksCo4nJtHCi2Wc\neDnIidyP4UL/cdi3bx99+vTBZDLj6OpJdP6XiSnYEuwcaF7azMg2BfF1Sx+rJJ7Pjv9E4unhcQZw\nwmz24rnnalKkSBGWLl1K7tz3nrnGbDYTHh5O4cKFsbOzQ2tNy5Yt+emnn1i5chKtWtW3xa+RLcwW\nzY7TSbg4KvzzGvBwzp5OIFprFu6J55P10TjYw8ctc/Kcw3nrsECefvT8/ibGeM3UDh40LJX1TkAP\nIyzKxMRfYvj5SAK53e14v7EbbSo5P3CWnAd5a/5Nfj+VyK/v+VLEJ30LlYUL1/P66yMJCnqOgwcX\nPVQv+7gkC1tOJLL+SAJbTyQRn/z3/6WjAcoWcKBSEUcqFnGgYmEHcrln7gtm7NjZjBgxnWrVqjF1\n6lT++OMPDh06yHff/Q+DIem++yYka9rPiOL8NTM/9fOhmO+jt8wxm80891wrLly4zPz583j99Yyb\nsBw6dIjo6Ghq1SoMZG362FTh4eHs3r0bpRQ1a9ZMGwM1ldaa1QcT+GR9NNdjLHSo4szwl91xzWHb\nTlPHjh2jZs0+3LoVw7Vru/H1zQfkoFevocyYMY+pU7+gX78BABw8eJDZs2dTs2bNdL3z/x7XNj2z\n2ZyuucLkyZNZvnw548aNo0GDukA88+bNpXv3d2nXrglLl34CWG+VTpu2lIoVA6hTp+J944+Pj6df\nv34cOJC+LWeZMmX45puv/9F5B+zZvz+KSpUa8tFH7zJy5OtZebtSOHD1qicrVvz8wBExzGYz5cuX\n5/z5o3Tu3Iy9e8/w+ecD2Lp1HWvXrqNhwwZMmDABsLZ5Hj36I1xcnNM6OP7++++cPRtGw4YNmTz5\nZ+DRb7VbL6aTgRNA5voPAFyLNrM0JJ5Ff8Zx6ZaF3O52eLnYcfKKCaWgWjFHmpV14sUyTjbv/GeM\nt3DmqomzV02cvmoi5FQUxy7Fk2jvCcqO3IlH+bhtfprUzLj9vySez47/UBvPBE6c+IOrV/9CKTO+\nvn/XXgQHB3P16lWaNft72vcSJUoQFhZGWFgohQvnQqkE/Px8qFmzHDVr/vM2z7/F/otJjFpzmyOX\nTGnL8nv8n72zDoj6/v/44/roEkFMBBQUUbFnd+dmzZyxGTPmXDg7f+o2a9Z0dkwFFVtBN2crBgah\nKIiChHQex919fn+cnqKggLjtO3n8Be/71MXn8369X/F8ialqL6OqvRRXeylV7aU42UrfqfVgdIqW\nb71TOBuqplkVOYs/tsDeQsKz2iKqOcg4MNaG4VuSGLktmWmdzRjW2Pi9pSxotALLT6Wz9q8MpGIR\nE9uYMrKpcbEZEXO6m9N2STw/7E9l+3CrXO9j4MBO1KjhjKOjQ6GMzoxsHadCsjl2W8Wfd7NR5UAp\nUzEf11HSqYaSyqWkBOtoFzIAACAASURBVDzO4fojNdcicth0PoNfz+j3rWgjoU4FGZ4V5TRykuNk\nm/etPGrUJ+zb9yezZn1NVlYWc+fOJTk5mXbtqjBgQMc3Xt/sQ6ncitTw6yDLdzI6c3I0iMX6jlwS\niS2zZ8/F1/cPWrVqk+8+NWu+fA/K+PPPg1SsaE/lygVPqSlfvvwbxfRFIhE9axvRxk3BspPpbDyf\nycUHapb3s/xbvJ8v89dfv2BmZo2NjZTneaPlyinx9HTFzU2Ovue1ghs3TrBq1SpSUmLo3789ICct\nTYW5uS0ODg5ERkYafptNmzbl6tWrPHp0H1tbMyCL8PBbXL58mYCAo7Rurc/Ja9XKifXrp9GwoTvP\nvfVSqZSJEwvWCtjIyIg1a9Zy6tRJzp49iyAING7cmHbt2uXTclTLpk3rMDZWYlzEdHWNJot27Xpz\n8+Y9BEFgzJjXizZDQkKYNGkSTZs2YtGiz5k+fTxXrhymdOlSzJnzHcnJKchkUoYOHWrYp3Pnzvj7\n+3PkyFH27/cxjDs5VeK77yYDYWRklCM5OYWyZYtWCHfr1i1Gjx7Njh2zqVTp7alDgiDg/zCHbZcy\nOX5HRY4WPnKSM62zMW2qKZBJRNyP03DoZhaHbqmY5pPKzIOpfOQkp6uHkvbVlVgUOpf5zaRk6jgR\npCIwSm9k3o/TEJf2IkIol0LlUma0q2NFOTMNTZwlNHbN/34v4cPiP+Tx1JOams79+5F4eroCcjIz\njSlTxhOlUkFs7A30cjwqmjUbyP37jzl4cAl16+pXYFFRcZQubf23t8pTa/RSMAX1YuVFfLqWRcfS\n8bqWRWkzMd91MMPaRExITA53YzSExGh48FRjqOaWisHJVm+EVnOQ4u6gD+lavaEbDOgfggcCVEw/\nkIpGC1M7mzGggZFhsnu1qj1TrWPS7hSOB2YzoIERs7qZI5MUr/EZn65l3M4ULoap6eWp5PsOZu8l\n5LTtUibTfVL5qbcFn9QpWi5WRraOk8F6z+bpu9lka8DWTExHd72xWa+SLF/vrCpHIPBJDtcicrgW\noTdG49N1iESwZoAlHdzz9irrC5ykXL+eQlDQeUJCwpg7d/QbFwFeVzP5xjuVUc1N+L5j3qkrr6ZA\nzJ69jrNnA5g/f4xBW3b1ai/Gjl3EunWzGTlyElD4YpqAgACaNGmMqakR/v5bKF/+/eTOXgpT89Xu\nZJ6m6ZjUzpQvmpm8s6e8IBRGCSI4OBxf30u4uJSnUye9PuqDB5FUq9ab8uXtuX//BCADJNSv3x1/\n/9ucP7/BkDN55859EhJS8PBwwcoqL7my1wkJCeHWrVuYmJjQrFmzIqcyvUpOjuadnrU7dx5n4cIt\n+Pn5YmdX6bXXT53ypU2b9pQtW5qwsAP4+fmyevVqYmL0HdoqV3bkm2++oX79+rn2EwSBy5cv4+Xl\nTU6OmpYtW9GhQweMjJSEh0fRtes3KBSmnD9/HqWy8JGc9u3b4+vry5df9uGXX77Nd7s0lQ6fGyq2\nXcrkXqwGM6WIT+oYMaCBMc6l8/7cBEEgOFrD4VsqDt1S8ThRi0wCzVwUdKqhpGkVOaWLOM9otAJn\nQrPZe02FX7AKtQZMFSKcSktxKS3FubQEZ1spLnZSyllJCn3vlHg8Pxz+c4bnq1y9GsRXXy2hUqUy\nbNo006C3+K4PveLizL1sph9IJSJBS/1KMj6pa0TnGsoCe+o0WoFtlzJZ4pdOllpgeFMTxrUywTSP\n/dUagfB4vRF6MSiOv25G8VRtjkbxQsy3nJUEdwcp7mVlVC8rw91BajCIEzN0TPNJ4ejtbOpUlPFz\nbwsqveIJy2sS1ekEFp/QeyObushZNcASc2XxrMCvP1IzZnsySZk65vUwp3fd91fxr9MJ9Pk1kftP\nNZycVOq1HKW3cScqhxFbkohJ1WFn/sLYrFMxf2PzTahUKvb5XmF1gD1Ps03ZN6YU1cvmHwYsqIET\n+CSHXqsT8KwgZ9twK6R5LBSuXLnDmDGL+P33dbi4VAHE9Or1Gfv3H8bbe/szfUsJW7ZsZ9iwEXh6\nenL58uUipSGkpaXRs2dPHBxKsXnz5PdaCJSSqeOH/akcua2iYWU5S/taUMai8BP106fxhIeHYW1t\njZOT0xuN/MIYnvmh0+lITc0wFPwAhIVFYmNjiYVF0SrnMzMz+eGHHzh79pxhTKlUMmXK97miR/8k\n+ue4EqhCRoaOy5cv06pVS/TaudGsXr2LTz5pbWj9qtFoePToEVKplPLlyxf6e0lOTsPTcyAKhTEn\nTpw0tLZ9G4IgcOXKFYKCgrCx0XD69GkWLBiLUvl63rkg6J+XWy9kkqEWcC8rZVBDY7rWVL5VKeTV\n49yK1HD4VhaHb6mITtF7JKvaSWniIqeJs4L6jrK3zjVBT3LYez2LAwEq4tN1WJuI6FbTiI89jXAv\nKy22KFaJ4fnh8J83PN8HjxM1WJuI3ymMG5eqZc7hNA7fUuFYSkIXDyVHbqkIi9diLBfRuYaS3nWN\nqFdJlu+NfSlMzayDqYTEaGjqImdmV/N8V8Ivc+fOHb74YhQqlQoAncwMjVllTMrWpkbzPoTGi3iY\n8ELo0s5cjLuDjJuROaRk6ZjU1pTP8/EGvWkS3eOfyQ/7U3EsJWXjUEvKWxfd8BcEvcE993Aa9hYS\n1g60fOcipoIQGquh04p4OtVQsrxfwTvZnAhUMXFXClbGIn7qbUHDyvJ3MqCuX7/Od999R2JiEjqF\nNcn1lyKTivAZbU01p7w9ggUxcKKStfRZm4BWB4fH2+RrXLdrNxY/v8tMnjyZH3/8EdBXzSclJVGz\nZk1DfrVWq31j8VJByc7ORiwWI5OpgAcIgua9pW0IgoDXtSxmHdTnLi/sZUHHGgXzbGVlqVi0aCFH\njx5Fq9VP9NWquTFnzhwcHR3z3Kc4DM/3wezZszl48BAmJsa0bNmKmJhorl69hlgsYsuWLf+y65Uy\nevRK1q79jUePfClfvmDtbN9Eft/LvXsRODjYY2paB3h7waKfnx+DBg0iNjYWGxuoWBEcHMqwaNGi\nPD/DlX+k85NvOl08lIxoakzNcvnPAQVFpxMIfKLh3P1szt1X4/9QjVoDMgnUriCjibOCJi5yPMrK\nkEpEPE3TciBAhfe1LEJiNMgk0NpVwcd1jGheRfFOaVr5UWJ4fjiUGJ48C08EB/Po0SMcHByoUaNG\nvjf6vutZfOudgpFcRO86RgxqZFyo/DetTmD7pUx+OpFOtlZgbAtTvmhuglImQhAErkXk4HVVv0LN\nUAtUspHQu64RvTyNDJ6XmBQtC46mcfCmirKWYqZ3Mad9dUWBH04jR47k+vUbtGnThi+//JL09HTm\nzZtHSEgIgwcPYsKECaSqdAQ90XAnKocroSnciMhEIVLzTQuBbs2r5Xuut02iFx5kM3p7MlKxiHWD\nLalTsfCJ+plqHVP3p7L/hopWrgqW9rEo9hymN7HsZDrLTqaz6TMrWlZ988QjCALrzmSy8HgaHmVl\nrB9s+c5pAElJSfTo0YP09AyqVHGhRo0a+F6N5KHTd5hrovBf3BCF7PXP423fTVSyln7rEknO1LFz\nhDU1yuVvyKemmvDjjzuYPn16seoaFoScnBR69eqGXC5h794fDeP79v2BSqWmQ4dGWFvrq8CzslQo\nFPIieVrD4zVM2JXMrUgN/eoZMaOr2Vs9TlOnTuX48RNIpRLc3d0JDw8nJSWVUqVK4e3tlWeY+p8w\nPP39/dm1azcREQ+xt7enV69etGzZ0nBfJycn0759B3Q6Lbt27XrWJhYWLVrEnj1edO3ahVmzZr12\n3Cy1gFhMkVUYikpYWCTVq/fF3d2JTZtm4O7u/Pad3sLbvxcjwJXs7BwUiryfA4IgYG1tRXJyCpUr\nK+nXrwV37twhMjISS0tLfHz25/pN+Aaq+HxbMj1qKVnat/ily56jyhG4+lDN2ftqzt/PJvCJBkEA\nM4UIZzsptyJz0OqgZjkZH9dR0tXD6K1pWO9KieH54fDBG56xsbF899133L59xzBWpYoLixYtei2M\nsv5MBvOPptGwshw7czFHb+sTvVtUlTPkIxOau7zZi3U7Mocf9qdwO0rvoZzT3TxfozVTrePo7Wy8\nrmZyOTwHsQiauMipVkbG1ouZaHQCo5qbMLq5aaEkbtLS0mjRoiVyuYyTJ08aKk5v3AhgxIgRVKxY\nwdAxSBAE1q79lQ0bfuPln0mTJo1ZtGhRnvlNBZlEHzzVMGxzEtEpWjpUV9KmmoLmVRQFqr5/GK9h\n1PZk7sZqmNTGlLEtTd5r6DUvsjUCnVfEk6UW8P2qVL6eb7VGYLpPKruvZtG5hpKf+1iglL37tW7b\ntp1ly5ZRt25dVq9ehUQiIS0tjTbDfyS28hjaOWXy6wjH1yatN303Lxud24dbv6W4xgxwAf6ZueHA\ngQP06NEDR8eKhIVdRS8NpcXdvSWBgfe4efMgHh4ugJZp05bx++/HWLXqOzp0+KjQ58rRCiz1S2fN\nXxk42khY3s8yX4M8MjKS7t17IJfL2Lp1Gy4uzmRmZvLFF18QFBTM5MmT6d//9faRf7fh6eXlxcKF\ni14bHzp0COPGjQP0Uk4DBw7C2dmJ3bt3G7a5evUqX3wxCg+PGmzatMkwficqhx2XMzkQoMJIJmJa\nFzN61FK+k+Gk0eoX6XuvZzG7uzmeb2lckJWlQqks+AL8TQiCgM/Ze+RoRfRpWSXPbXQ6HfPm/Y6X\nlx8XL17E1NSUu3fv8uuvvzJ27FicnEpx44YvvXv3ITtbzt69a6lf34OcHA0jR47g9u07fPvtN/Tt\n2xeAuzE59FqdiFNpCXu+sCmWZ8VzUlNTSUtLo3RpuzxTzBIzdFx4kM35+2qCnmho5CTnkzpGBYqg\nFRclhueHwz+f5PgPotPpmDhxIvfuhWJpaYGnpyc3b97k3r1Qxo0bh5eXF3K5HJ1OYOHxNNadyaRz\nDSVL+lqgkIqY2knLzitZ7LicyWebkqhkI2FQI2N61zXKlcOYqtKxxDedrRczsTEVs6K/BV093vxQ\nNpaL+aSOEZ/UMSIiQYP3tSz2XsvizD01bdwUzOhiRgWbwn99z0WRxWJxLpmV5yLdz8OD8ELfTywW\n0aFDeywsLDhy5Ajnzp1n5cqVTJ48udDnB31Rk88YGxafSMM3MJuDN1VIxdCgspy2bgpauynyDMP7\nBamYtCcFiRg2f2ZVYF3Ol8nOVnPx4i1atHghYj19+hr++MOfefPG0LKlfvzAgdNMm7YGhULOzp3z\nqFKlomF7hVTEwl4WfLI2kZ9905nR9fUijeRMHaO2J3MpTM24ViZ81ca02AzkR48iAGjZsoXhOzQz\nM6ONi5Z99/fgSx+2XMhkaONXZWzypqBG5+HDZ7l58wFTpvz8txv7L9O9e3du3bpFXFwcUOql8U9w\nd3+AvX0DQB/qT001IiwsipiYorUilElEfNvBjKYucr7anUKvNQmMbmFCJRspOVqBHK3eONVoIfhe\nPJmV+2FTwRHv+3YIoanUrySna/deBAXNJygosBje/buRlJTMkiVLABg27DPatGnD1atXWbFiBZs3\nb6Fjx444Oztja2uLSAQRERHExsYa2h4+b0JgZ2dHplrHoZsqdl7O4mZkDkoZdKtpRGichq92p7Dv\nehbzepi/Jj9WEK4+VDP9QCrB0RqM5SIGb0hiyzCrN0ZIjIzeXbItJVPH/htZ7PLPIiTGArFIwNFR\nTb1Kr583KyubXbt8CAl5iJ+fHz179mTBgnls3bodmSyZRYvG8ujRbSwsoGPHVtSv7wGATCalXbt2\n3L59h7CwcACSMnSM2JqMsULEukFWxWZ0RkdH8+OPP3LmzBkEAaytrRg8eDADBw7MNf9Ym4jp4qGv\nL9C38Cy+3M038eBBJDNmrGXu3HHY2Ly7l7qE/w0+aMPz8uUr3LsXip1daX7//XcsLCzIzMxk0KBB\nPHwYwenTp2nZui3feaew74aKwY2MmdnVzJDbWNpcwsQ2poxpYcKxOyq2XNDnHP7sm07P2kqGfGTM\nvVgNcw6l8TRdx+CGxnzd3rTQhTUVbaR83c6MiW1MiUvTFanY4TkWFha4ubkSHBzC8uXLGTduHBkZ\nGaxYsQKARo1edE/x9vYGYOLEiQwYMADQy40MGjSYAwcOMH78+CKHWa1MxPxfLwvm9RAIeJyDX1A2\nJ4NVzDqUxqxDabjaS2lbTUEbNyXVHKQs9Utn9ekMPMpJWT3AinJWhf8MMjNV1Kr1KeHhTwgKuoyL\nizMgIiQkgQsXbvH0qT50BiJSUq4TEhLBtm2rcXF5vYCgbiU5AxsasflCJt1rGeUy1sKeahi+JYmo\nJC1L+1rQs3bxdiN5bgT4+1+lb9++iEQisrOzCQi4iVFMLNU/6srcI+BcWkoTlzcb5wU1OlNS0hk8\neCZJSam4uDSlT58+xfqeCkuNGjVeG5s/f/5rY0uWLKFhw4b069cXvUxRNFev3sbNzbFQXWIaOSk4\nPrEUU/alsOJURj5b2YPTQO4JOiLOZyAIsO5MJgqRJ7iOJsNIWqRmCMXJuXNnUatzaNiwIWPHjgWg\natWqhIeHs3+/D6dOncLZ2ZlSpUrRvHkLTp8+zbBhw+nWrStPnkRz9OgRNCYVSa48nAbzn5KWLVDF\nTsrsbmb0qG2EhZEYrU5g5+UsFh9Po93SeMa3NmVkU5MC5QXGp2tZeCwd72tZlLEQs2aAJbUryOi/\nPpEhG99ufBaF53JFv1/J5OhtFdkaqFFWypj6GfgEK/lyZzJH8sh3NjExwtt7EY8fx9G+fTMgjLFj\n2yKXp9O/v1466HlXn8DAwFwFrTdv3nz2eilytAJjdiQTm6pl9+fW2L/D8/1l0tLS+Pzzz3nyJBqp\nVIKFhQUJCYksW7acrKwsPv/8c8O2Go2Gbdu24+W1h9jYOGxtS9G7d2+GDBliKMh9H8ybt5GdO48j\nElmzalXj93aeEv5dfNCh9m3btrFs2XL69u3Dt9++kLVYs2Ytv/32GwOHjuCmaR9O31XzdVtTvmxl\n8tZJ43ZkDlsuZnLwZhbqZ1Ka7mWlLOhpgccbcub+Ti5dusT48ePRanWIxSJ0Ov1HaWlpyfbt2yhT\npgyg9yxFRkbh7e2No2Mlw/6tW7chOTmZY8eO5hLpz8nRMGHCQs6du8Xq1T+80oe9YITHazgVnI1f\nkAr/hznoBDCWi8hUC/Svb8TMrubv4A0wZvjw/+PSpWts2rTJIKMSFBREQkICbm5ulCql96AlJSXx\n+PFjKlasiIVFApD02tFSVTraLonHyljMoXE2yCQiQw6rRAzrBllRNw9PybsSExNDz549UatzaNz4\nI2rU8ODUqZOEht6nYsUKbN6xh95rk4lO0XLgyxfC76+GdAsXXoejR+/i7X2SDRs2/M+2kE1KiqNq\n1WoolVIuXNhIuXJ2hdpfEAQik7RodSCTipCJ9V5RqQTEgpben/QkNiaGpk2b0KlLN47fSORIoJZs\n2wYgUVLeWkL3mkp61H4Rxvw7Q+3Pw+ydO3dizpw5hvHVq1ezYcNGhgwZzPjx4wFITEzkyy+/5O7d\newhiGerSjVGV64jGqjpyCXT2UPJpA2PqVsy7+CU2Vcusg6kcu5NNVTspC3qZ52s0anUCOy5n8uOJ\ndFQ5AiOeqXM8z6mNSdHSf30icak6tg4vHuMzIV3HvutZ7PLP5MFTLWYKEd1rK+lXzxj3sjKCgoJ4\nkCjh6+MW1KskZ+swq0KrT2g0Grp370FMTAw1a3rQtm07AgICOHnyJFKpFB+f/ay9YsKWi5n83NuC\nj4so05YX27dvZ+nSZVStWoUVK1ZgY2PDyZMn+f77KRgZKTl27DhmZnrFg1mzZnHo0GFA3+XruVnQ\nsWMH5s2bV2zXlJWlIjk5nTJlbAFbHj3KYfbs+cyaNQtz8xeRo5JQ+3+bD9rwPHr0KNOnz8Dd3Z3N\nmzchEukLfMaNG8f5q4GYdvqVqCxz5vc0p3/9wsn0PH+omSlF9K777p1ziht//6usXbuWgIAApFIJ\nzZo148svv6RixRch5TFjxnD58hUmTpzAoEH67iLPezCbmBhz8uTJXB5PjUZDjRr9CQkJJyBgFzVr\nvlvoJClDx+l72ZwLzaaxs4JenoV7KD94EMmUKSuZNm0UHh4tABtSU1MxNjYu5Co+h+jo02RkZODs\nnFuQ/ESgii+2JfNtB1NsTMRMfVa1v2GIZZFSIQrKH3/8wbRp08jOftF9qHRpW3755RecnZ15nKih\n28oErE3E7B9rg7lSnMvAiUrW0n9dIkkFNDrBGsi7KvvvJDExkY0bN3L58mUsLS0ZOHAgzZs3L/D+\noaGh9OvXDzMzY/78cy0aTRoHDhzA19eXjIxMatb04NNPP6VcuYIL1b/MtWvXmDBhAllZqlzjg4aN\nokKjAey/kcX5+2p0gn5B2qOWEa5Gj7A2Fv4Ww/P+/fv07dsPpVLJ2rVrqVHDnYcPH/LFF18QH5/A\n8uXLqNugMXdjNAQ+yeFOlJrLdxOJSJWjEaSUtdAxtLHeQLIuYLHJySAVMw6kEp2q49P6RnzbwSxX\nPve1CDUzDqQS+ERDE2c5s7rlrc4Rm6r/zcam6tgyrOiLOv+HajZfyMQ3UJ+jX6eijH71jOjskVuu\n6Pn9ciu9Et/vS2V8axMmtS28hmlgYCDjx48nOTnFMCaVSpk1ayZJ1s35YX8qI5saM7VzwXRVC8qk\nSZP4668zzJ07h06dOhnGBw0aRFBQMGvXrqFevXqEht6nX79+KBRyFi1aROPGjbl48SLffvsdKpWK\nHTu24+rq+s7Xc/HiLfr0mYKHhxtHjhznVUWAlJQXn0+J4fnf5oM2PDMzM+nUqRNpaek0adKEFi2a\nc+nSJU6cu0V6nbmIzcrxy6eWtK/+97R7fBOCIBAYGEhsbCwVKlR8FiZ+d9RqNWKxOE9D7M8/TzN5\n8mREIr2X09LSgmPHjpGRkcmAAZ8yadIktFotGo0WhcIIKIeX15/4+/uzePEc4D56wf5/hokTl7B8\n+U66du3CwYOHinycc+fO0aVLZ6pWLc+FCxtz5cYCjNqWhF9wNlod76xTqlJlc+LERZycyhkqc7Va\nLUlJaZQqlVu+KSEhgRMnTvD06VMqV3aiTZs2ufLcLoWpGfhbIo2d5WwcasXdkGAALByqGozObcOt\nqFU+/wncy+skHh7uVK3aEfh7W/C9SnBwMC1btiQ2NjbX+MSJE1myZEmBvbBarZbExEQsLS0YMKAd\nQUF/kZAAdnYgkYCpqQlr1qwpsiEYHR2Nt/deQkPvYW1tTbdu3fD0fNF2Mi5Ny6GbKg4EZHErUoNY\nJFDeQotLGRMq2kioYC2hgo2UCtYSyllJir1CfMqUKfj6+gFQyqES0SozNKZOmFWog3nFuoTF6z26\nAGZKEdXKSKnmIKO1q4KPnIomA5aRrWOJXzqbzuvz3Gd1NadhZTmLjqex52oW9uZ6dY5ONd5cHPSy\n8bl5mFWeuZf5cT9Ow8JjaZwMzsbSWN+1qn99I6rY5b3oem54urm58bVXCvtvqNjymRXNipBbnpqa\nypEjRwkPD8PW1pYuXbrwWGXDp+tf3J+FcU5cvRrEqlVezJz5OZUqlQO0JCamoNMJhufE8+950qSv\nDKlSOp2O7t278+RJNJs2bcTDw4OtW7eyfPkKunfvxowZMwznWLBgAXv37mPs2DEMGzas0O85O1tN\nVFScodtYXFw2zs4dcHZ25vTp07k8nFBieH5I/OcNz9jYWJKTk6lQoUKevYwvXrzI5MnfGDQtNSYV\nSfOcjcLUis3DbGlQ+e+VismLR48e8f3333P37j3DWN26dZg/f74hNPwqgiAwf/4GqlSpyMcft3rN\nWCoo69f/xrp1vxrC8QAtWjRnwYIFREcnMGTILDw83Pjll42A3FB8ULduXUDDqVPb2bhxN7/9Nq1I\nyf9Pn8YTGHgHExMTatWq/UbR/+xsNU+fJlGunD1Qivh4OdOmzWLatGlF9mCB/oFYrVo1atVyYceO\nWblEukE/GX68JpHWrgqmdzHLU3C9oEybtob58zcwZsxnrFq1DMggIOAKtWv3oG3bBvj6rjJsW5B8\nwR2XM5n6zKPS0zGSuHQxM07bFMjovH49hEaNPkOhUBIYGPjG9pN/Bw0aNODKlSs0bNiQUaNGERoa\nyo8//ohareb48eO0b9++UMdbv349n3/+OcbGSjIzVTRvXpNatcw4e/Yc1aq5sW3btvf0Tl7w4KmG\nDX6PCUuSkJxjTESClqycF/eaSAT2ZiKMtImoEsKQ5yTgVtGazq3q41rBGnsLca5mEYIgcP/+fRIT\nE6lc2Qlb21IIgsDTdB33YzXcf6rhbrSav25E8CRDjk7+Qu+ytKkI93JyqjtIqVZGRnUHKeWtJcWa\nVnE7Mocp+1O4E6VBLgWdDoY3NWF8K5MC6yLHpWrptz6RmBS95/Ntxmd8upblJzPYeSUTI5mIMS1N\nGNbY5K0pOy9HCDLVOnqsSiQ+XcuR8aXeKc8eIDJJS/eVCVgYidg/1qZAih4vM3DgTHbsOMKUKd+x\nYMECIJX58+cyc+Zy/u//xvLNN4M5efIk3333PebmZkyePJnKlZ3YvXsXhw4dxt7enoMHDyCRSAwh\n+VfTL57ruI4b92WutqKvkpWlIjAwDMDQBTAuLhEHh46Ym5uQkHANkagUYElgYCBubm55ypuVGJ4f\nDv/Z4qLHjyNZsGA+V674A2BsbETfvn0ZNWpULu9eo0aN2L9/HwcPHuRqRA5/ajtjbSRj24hSuJX5\n53Mys7OzGTt2LE+eRGNtbUX16tW5cSOAq1ev8fXXkw0pArkREx0tMH36WiwtzenduzOgD8n++ONW\nBEFgyJAu2NnZvPX8I0eOoEuXzpw+fZrs7Gzq1atH9erVAUhOTufixduEhkYzd24mlpa5JwC1Wsfw\n4bOIiIigYUN3xo17XUomP3JyNPz880/s27fPUGlfqlQpZsyYTuPGryehh4Y+olu3SVhbW3Pu3DlE\nIiNKlYK1a9cWgYhvpwAAIABJREFU+Jz5YWFhgb+/P2XKWCESBfO8n/Vz7MwlnP22VKEn6NOnr7J2\n7V4+/bQj3bp1Bqzo1etzjh27QY0a9QFzwJzwcB1GRkaULu0IVAAyyMlJwtGxAx4ezvj4/Ixcnvdv\ndUADY+7GaFh/NpOcdCXHQxVkaN5udAK4uJSne/fO2No6/ONGZ0hICFeuXMHS0hI/Pz9MTfW5aUql\nkunTp7N58+ZCG57PZYK++eY7zp49y9q1P1GunJoOHdoQFBRMZGTkOy1YCoKTrZSBtbIAqFatAoIg\nEJ+u41GilogELWGxKryOXeRRtgKtsSOCWR0eJsIxbx3Pe7qbKUTYWYixkKl5fPcaaXEPEGlV6Ezu\nYVa2BtmKMqSqXvxmzRQinOzLU89GhJ1RFp6OpnhWNi10J66iUKOcDJ8xNmy5mMn1Rzl81ca00JI9\npc0l7BppbSg42vyZFfUdX/8tq3IENpzLYM3pDLJyBAY0MGZCa1NsTAvvuTeWi1kz0JJuvyQwdkcy\nu7+wLnLr30y1jpFbk1BrBdYPsX6r0XnvXgRr1ngzaFBnPD0bALaMGzcde3tXhg0bgT4SYUlsbA4A\n1ap9BFjSsmVr3N3rcubMVaZOnclz34NMJuWHH6YYnBFNmjRh6dJlnDjhS7169WnatAkXLlzg2LFj\nADRr1iz39WeqyMnRGDpi+fpeoUePSbRr15QTJ3YDSmxtq2FhYYG1tTVpaaUN3s3nc0cJHzbvzfAU\niUQbgS5AnCAI7i+NjwO+BDTAEUEQvn1lv/LAVsAe0AHrBEFYXphzp6Wl8cUXnxMbG4dSqcTe3o6H\nDyPYtGkzKpUqlwxQtkbgZrw5t0w+4Q9BRTlrCVuGWb1TVx3QT5QXLlxAJBLRpEkTXFxcinScU6dO\n8eRJNJUrO7JlyxaMjY1JSEigX79+3Llzh4CAAGrVqoWPz2l27DjG7t2/IpFURCxOYMqUKeh0OkSi\nGug/yiyWLdvDkycxfPxxd+zsZEAOW7ceJiDgHgMGdKROHbfXrqFMmTL0798f4KXcNWNq1erBnj17\naNKkCZaWr3fxkcvlHD58mLVr1zJ27EQgpsDve/XqVXh5eSORiKlfvx6xsbFERDzi66+/ZseOHQZB\n6+eYm5uRmqpCEDKIi0vFzq54K8kdHBye/VUGePLa64X3Com4di2c3bv90Oks6NbtKwA8PW25du1a\nri179uxJSkrKM49AKcCW27cTiYqKw8TEHLm8FJDy2hmeM72LGffjNGy+ASYyHTs+f7vRCWBmVpnd\nu/eh1Wrfuu375unTpwA4OzsbjE6AmjVr5nq9MGRk6KvTGzdubBBDF4QcRCJL4uLSuXPn/ns3PF9F\nJBJhaybB1kxCnYqwYcNONOfXUNXengkTxqMwTmXtZi8Cw+OpWrsJbbp+SnSKlscJ2Zy//pBsqROC\nY10QiRGpk9EkPKKyzVMmdf0I59JSnEtLsTN/905S74JUImJ4ExOGv8MxSptL+P1za/qvS2TopiQ2\nDbUyRKd0OgGfABU/nUjjSYqOttUUfN/RDCfbd3umO9lKWfixOeN+T2HhsTSmdyl8TqZOJ/D1nhTu\nxmjYMNSqQNe0bt0Bli37ndRUBRs26EPmDRo0oEGDBrm2W7FiBTNmzMDCwgKQIZFoMTevxcOHV6le\n3RZnZxOqVatGv379cqWRVKpUif79+/H777teawrQp09vKleubPh/wwYfvvpqKZMmfcasWbMBE6pX\nt6B69Q24uHigfz7qPfUxMTHIZP+886aEfx/v0+O5GViJ3ogEQCQStQS6Ax6CIGSLRKLSeeynAb4W\nBOG6SCQyA66JRCI/QRCCCnriAwcOEBsbh5ubK6tWrcLCwoIrV64wZswYvL29GTx0GMGJJhy+qeJ4\noIo0lYCVsb4T0aS2ZkVaERsuXqNh7ty5HD58xDC2cuUqevTozg8//JAr5K3RaLh9+z61a1dD3wUj\ng9WrvfjoIw9q1aoKwL17+vB6+/btMTbWFzjZ2NjQrFlzfHx8uHv3Lq6ubowb9xNRUbF4eV2lXz9n\n7O3tn4VgniNGEIyZOXM2QUFBODq2RL9S1rB37wwOHjxK/fr1qVNHAWRz/nwAv/9+gs6dm9Cxo97D\n6O19krFjF+Pjs4lGjboCInr06PHGz8Pd3Z2VK1c++8+IzMxg/P0Dad68Tr77ZGZm4uXlBcCaNWuo\nU6cOOp2OmTNncvToMXbt2sXUqVNfaseoxM6uMX5+p6hYsaJBFP99EBsrYsKE6fTs2ZS+fdsVeD+d\nTseMGWtp3rwBbdv2Aizp08cWQSjFJ5988tb9ZTJZrrQKT09PHj16RHR0NOAE3AXylvmRSUSsHmDJ\ndzsf0bFKNrXKO+S53XNOn75Ks2bNEYvLIhKJ3qucSkGpVq0acrmca9eucfnyZRo0aIBGo2H9+vUA\nuXIoC0rTpk25dOkSixYtokGDBpiZmbFp0zb++isSgH79ZvHw4aHXUiuKk7S0NG7duoVMJsPFxeW1\nidrX1xeAH36YYvD0u7u50LFjRx7+FcSgOQMwNjZn+/btBFxYRgN3d1auXg0SJTGP0xg0aAaJGg3t\nxx8yqFX8Vyhtpjc+P12fyGeb9canVhCYfySNwCcaPMpJWdrXsljTpbrWNML/YQ4bzmVSr5KcDu6F\nSx/65Y8Mjt3J5odOZvl2PYuOjsfMzBhT09KALaNGTSM5WcaYMWPeevzcqVcSGjRoTkBACEuW/Ei9\nei5AKrt27aFr1ylMmNCf8eP1Uaivv/4aJycn9uzZQ2RkJA4OZend+xNq1qxPREQ0FSuWAYyoUKEG\naWkZBAfHoS841C8G79y58+qllBidJeTLe5tRBEE4IxKJKr0yPBpYKAhC9rNt4vLYLxqIfvZ3mkgf\n2ywL5Gt4+vn5UbZsWcP/586dA/QTS1RUFFFRURibmGLv0ZHQbEdaLk0nQ6vGWKbjowo5NKukplaZ\nHKRiiH0EsfmdqAAcOXKEw4ePoFDIady4MTqdwIUL5/HxOYCpqakhHJiRkcVnn/0fYWExeHntwM6u\nAnFxkXz55WKkUglnz67EzMyYnBy9JpO/vz8ffaTvvKLT6bh27TqCABkZKu7eTWfixK+Ji3uKo6Oj\nIc8yLzw9PfH09OT69euGsU6dulG2bEVMTZ24elUFaNm27Ty//upFamo25cvbIRbncOzYBeLiEvnp\npy1MmfJm4yWva9DpdEyZ8gOnT59l/vzP6dYtb922iIhHZGWpsLe3x8jIyJBrVbt2bY4ePcbNmzc5\nffo8kyatpGvXNnTtOgTQi3MHBwe/8breFR8fH3bvPsaFC9eoVs0BiaRgi5TDhy8wf/5GVq7cy4ED\nVQ3GcYsWLYiPjyc+Pr5I1yMWi7l69RpqdQaLFk2nZctatGtXL89tJzxr3PP888yL/fvPMG3abzRt\n2pifflpSpFaT74tu3brh7e1N48aNqV27NlFRUURHR2NkZESTJk3e+LvPi2bNmrFu3TpOnTqFvb09\nZmZmz0TpwdXVlTZtWhAZ+ZQnTx4X+3sRBAEfHx8OHz6MWq0Pka5evZrBgwdTr96L7+953lt6errh\ne9NqtcjlcrKyVNy8eQsLC3MuXboEQMOGDXkc8dCwv6urK7dv38HPz+9Z3vV/j9nNRXzva86n6xPQ\nCiJsTbR80ySL5o5qxKo43vBzLxCv3i8fV4ZL98yZtDsRaXoqDua6fPbUo9LAmXA5R+8puZcgpVXl\nbBrbJOZ5XZmZ2QwaNBetVsKSJSuwt08DYNSoUeh0ukL/xl1dXVm6dCkAV6/qxeq9vf0JC4siLCyJ\n27cfIRZnEhPzlKNHb9KpUx/q1NE7PXbs8KV374X07t2R77//AZ1OwNy8Il5eXlSqVKnQ1/I2ihoV\nLOF/j7/blVEFaCoSieYDKmCyIAj++W38zHCtDVx+00Fnz57N1KlTDVJASqUSQSTmQZwGUYSMoDgZ\nZx7KSCw9FrQqqlmk0tlDQd2yOcgLmdb05Ek8s2Ztom/fVrRu/brX7tSpUwCMHj2GOnX0XpgaNdz5\n5ZeVnDp1ymB4GhubYm9fnoQEFXFxKdjZgSDI6N27Nzk5Ochkrmg0KTRq9BE//7ybpKRryGRrcHev\nzr59f3D69CNsbRW4un6MRmNKixYtC/dGXqJOnTrUqfPye5HQtGlrFAozatSogUrlBOgYPvwbKlas\nQ8eOHYt8LkdHF/z9b1CtWt5t6ACDtlxiYgJpaWmGXsYPHz589ro5/v4h3LgRSlxcJu3bD0Re2C+y\niHTr1o3Hjx/Tt2/TAhudAO3atefcuSjatWv3Xjyyfn6nOXjwLOfO3aRpUw+MjApfeQvg6FgBExMT\n6tat/68yOgG++uorcnJyOHz4sGHSc3BwYObMmS+lQhQce3t71qxZw+LFiwkICCArKwtra2uGDh1K\nv356T5BKBTJZHCEhV8nIUNGwYfFIHp04cYJ9+/YDeo9Reno6MTExrFq1imnTpuHsrFc0cHFx4enT\neA4dOsTIkSORSqUcP37CsDAzN9ffGyYm+nsmKirScA6tVktMTMyz199fFOB9IggCT58mU7q0Vb7b\nWBkJLGyXyi+XTHCz1dDdTVXo53phkElgSvN0xh02Z8FfpvzcMRVFHjPpo2Qxx0KVnHogJ10tpryF\nllH1MuhYJZv8Mh2Sk9PIytKg0wl5FsMWB9988w1du3bF1taW7OzSgMDp0zf57bfDhIfH4enphk5n\ngodHc5RKb8Ric3Q6vWdXIpFQqVKl93JdJXw4vNeq9meG4+HnOZ4ikegO8AcwAagH7AYqC3lchEgk\nMgX+AuYLgrDv1ddfrmpv3tkNpzptadl9GPdiNQSEp/AoWQxivatfKhaw04WRcmsv5SQRHPHZU6Qq\nb0EQaNBgCP7+QYSEnKNqVUtARXBwODY2FtjaWlG3rt5bcenSJUMFdkZGBs2aNScjQ4yf30HKl68G\nlCc+PhmlUpkrZ+1VAgKuU7t2HcRi8PAAsRhiYyEqSu8BvHbt2r9KzDt3VXve6FvwlQLCyclJ4PPP\n59OuXQP69m1nMHbGjh3LpUv67kJ9+/YlJiaG7du3o1Jls2jRT7RpM5KVK7fSu3dvQyefvxcteie8\nOt8tbt++j6OjA6amLuhTlt8fgiAwZcoU+vfvTM2aeWvOvl2oXA5UISYmCXv793u978KTJ0+4fv06\nVlZWNGzYsMiKDS8TFRVFWloaTk5Or4UI09LSqFXLg/DwCA4eXEKXLk3f6VxarZZOnToTHx/P/Pnz\nqFBBX1R06NAhvLy8adOmNYsW6Xuph4aGMmTIELKz1Zibm2FkZERsrN4rO2/eXMMi8Lm+rlQqYfDg\nwbi6unLw4EHOnTuPg0MZfHx8iuVzyovU1HQWL97K1avBHDu2EZFIn0/+cqeeorJz53EGDJjGxIn9\nWbJk0t/6rJs6dTmPH8fx22+z8izeOxWsYviWZPrXN+L/elkAoNYInAhUseNyFpfC1Mgk0MFdycAG\nxtR3zFtoPzcmJCfbER+fYFh8/B0EBASwY8cOGjRokCv1JyMj429btJRUtX84/N2G53H0ofbTz/5/\nADQUBOHpK/vJgMPACUEQluR17JcNz5r/d84wXtZSTBU7KfEP/AkLOIU0PQJJRiQiXTYKhdzQQq+o\n3LqVxujRUzl69OizJO502rbtwOnTlzlw4Cd+/fVHIiOjWLx4Ea1btwbg2LHjfP75NCIjoVu3Tvj4\nHC7wAzQxMZGtW7cSExODRKIlLi6csmWrU6FCRYYMGfLeJpOiUhDD82X+/NOPVq3a4epameBgb/RF\nUHDrVhA//PAt0dF6j41Wqze2Bw7swpIl3ohERfPoFS8pnDy5g8aNa74mFXXixEU+/vhb2rRpyb59\nh/5m7+ETnmWr5CI/w3PjxgNUqeJEkyb9eFXUuQR9Lvb8+fM5dOgg589vRaFQkZKSztChszA2VrJj\nx4vOLkOHziIg4B5bt87Gw0MfOszMVKFQyAz3alxcHB07dsLCwpxTp04Z0kMUCgV9+vSlbFkHDh48\naDjm9evXWbx4MaGhetm40qVtGTVqFN27d891nWvWrOG33zbkGjM2NmLFihXUrl27+D+YZ2RnaylX\nriPx8Yn4+/tTt24dEhNDqFu3LWPH9mbixP6Fek69kAmTkpFhialpJdq1a8yhQz/lq95QHKhUes1h\npVIBSJkwYSkrVmxh2rThzJ07Os99Fh1PY83pDKZ2MiM5S8du/yzi03WUs5LwaQMj+tQ1KpBaQHx8\nMqVK2QJuwIeZG1lieH44/N2hdh+gFXBaJBJVQe9iyZXcJtI/cTYAwfkZna9iHrISUsI4uXcdpa31\n3kOdri2nTkk4fPgwyclKXF3d6NevX67WjwXlxcq9Ah4etpw/f/6l1xSYmJRCqVTSqFFn4uKi+eWX\nRUyY8AOtWjXD0tKI48d90WjA3Nycxo2bF6pfs7W1NRMnTiz0Nf+v4OrqztKlS595fWsCqaSnP6F+\n/RG4uJTn++8nERQUiK/vXeLjHxISkvMvMTph+vSfmDdvHlOmfMaCBWNzvVapUgVkMgXm5jZoNJoi\n97QvGg788ccfHD58jJ9//uqNv7U//vBn+PC5mJqacu9eu/9cAUpxIJVKmTFjBk5OTnTsOI6kpIc4\nOlbCx+c0lpYWgAsgAkSEhsZz8+Y9UlNtgWpAKkuWLGDNmt/56acJ9O/fAVNTU6RSCWlpacTEvMgo\nDw0NBcDKKndY2dPTk99//53IyEhycnKoUKFCngVfo0ePpkGDBhw6dIjExESqVKnCxx9/XKze6+xs\nNYsXb+XYsQucObMDqbQMCoUVv/yyirJlyz5L2RHh5XWG8PAoDh++wKRJAwp0bEEQ2L79KCtX7uHP\nP70xNnbGxETK+fPnqV3bA7k8kvwK6N6VNWu8mTZtDQsXTmbkyLGAJc7OdXBzu8K4cYPy3e/rtqZc\nj1Az/2gaYhG0clUwoKExzV0KLrR/+/Z9mjQZwZQp3/DddzXyDcOXUMJ/hfcpp/Q70AIoJRKJIoGZ\nwEZg47OQuxoYIgiCIBKJHIDfBEHoBDQGBgG3RSJRwLPD/SAIwtH8ziV7fBwPjxoGoxP0RRdt27ah\nbds27/Q+7t9/TMeO41m9eglt276e0ymTyfDx8THkIg4aNB9//zjWrdvEgwd/UqECPH4Mw4aNZdGi\nRf+zuVbFiVqt5tChQ4SEhFCuXDlGjBjxUrqBJYGBd1EolJib2zJgwCQglQkTRAwZ8hXLlxdKWeu9\n0qlTJ5YuXUrp0no91BcLCmOqVu3A9evXqVSp0t+eCpGUlETPnmNJTU2lSZNa9OrVKt9tmzdvwMCB\n/alVq06J0fkGJk2axLJlywz/BwToCzX69/8Uvd6qng0bNqFSqZ6FSY0AI86fv8eTJ0+xtKwIKDA2\nhrp1P+Kvv84ybtyXtG7dmvT0DI4e1SthdO7c+bXzi0SiAmmpPi8eLE4SEpKxsdHLpcnlSrZv9+Xe\nvTB8fR/RqZNeKe95TuxzvvjiC8qXL4+Tk9Mz8fBIUlKSEYtFmJnl/QzU6XQsXbqLGzeC2bLlT0aP\n1rdpfF5UCS4Iwj28vQ/yySet3+m+ysxUodFoMDc3BWSYmpYhMTGF8+fvM3Kk3vBv1KgRjRo1onTp\nakAIr+r3gl4aavUAKw7dzKJtdSVlLQsfgTp3LoDU1HRu3Qop8vspoYT/Jf4TnYvatbNh1apV76Vq\nc9q01cyfv5F27dpx/PjxAj3sMjMz6d+/P0ePHmXQoIF89933VK1atdiv7d/I20LtwcHBdO7cmfDw\ncMOYtbU1e/fupUWLFoYxtVpNdHR0rt7x/0aSkpKwstKSmHiLvn2nMH78cLp2fS7q/M/h5eXFtWtX\nmD+/PxKJ/lZ5OdSuN5LlQFUEQf6vyhP+txEQEEDt2rWRy/WpOi1atGDPnj3MmTMHhUJBVFQUNjb5\nN2MQBIFLly5Rt27dZ/mj6YwYMZwNG/ZQrhyUfklUrkWL5ixcuOidcyOLgiAIxMcnY2trZfjfze0T\n7t6NIC7uIra2ToANhw8fRalU0qpVq0KkkGgYMWIAJ078xc6d83B1LfdssW6JsbERJiZmgAOXL4cR\nEhLCoEGD8jz2pEkTWbp0OV999SlLlkwq0vtcsWIX06evYfLkEUyfPguwICtLRVBQUK4iy5efZYIQ\nx65d6+nevQXGxsXdQtkeP78gmjRp8t4Kiv4XKAm1fzj88wJ9xcCaNWuKfZX/nDlz/g8bG3dGjhxZ\n4MnZ2NiYAwcOkJ2djUwm+9dVB/9TaLVaunfvTnh4OFWrVqVr166cOXOGK1euGMatrfXacHK5/F9v\ndMKLsOjOnac5efIKERFJdOw4DKn0n/3Oe/fuTe/evYF04B4ve2s2bPDB1/cK27fvRSZTlIT23oK3\ntzcAI0aMYOxYfUrF7NmzuXjxIn5+fhw5coTBgwfnu79IJKJRo0YvjZhiZFQaIyMjhg79gvDwy5iZ\niZFIbDhw4DqVK+9j7Ng+gF52LTT0EU5O5fL1FBaF9PRM0tIyKVNGr/sYERFNzZr9sbQ05+HDvwBj\nRCJjbGwcMDVNIDxcjK2tLQBdunQp9PlUKg23boUTG5vIkiXLefToDikp8PixiGbN6uHrew6RSEaD\nBravCaO/TLt2Hdi4cTPt2xdVxUOEu3sdUlMzuH37CaD35BoZGb2i7JGbadOWs2DBAj77rCsbN84s\n4rlzo1Jlo1SWBsrStm3Zt25fQgn/Ff4TFlFxG51hYZHPEs0rIRaX5quvvnpj5Xl+KBSKEqPzJU6e\nPEloaCiVKlXixo0b/Pjjj1y8eJHmzZuTmprKjh07/ulLLDJjx85k5syZnDp16l8huP4CUzIybJg0\naQkpKRkkJ6fzzTcr2LPHl2PH/vinL+5/ApVK363rVa/m8/+zsrIKfcxffvmFuLg45sxZwsSJKxg+\nfBk6nQMPHkSi0Vijb41qx/XrkdSuPYC2bXPnEE+ZspLFi7eQnf1CVUGne11PMjExhbNnb/Dw4Ytu\nW/v2/YGZWTO+/PJn9CLg5ShXrjFqtRaVSktGRhnAAbDk4MFDpKSkUL9+/UK/x5dRKpX4+PhgamqK\nj88dkpOVWFmVQq0WOHnyCvPmLSzQcTp06MDDhw9p3/4z4O3PZJ1Ox7ZtR1iyZDtgBVSnVat+hIaG\nsmfPngJff9++fbG1taVNmyYF3udNrFu3D0/PQYSGaorleCWU8L9EiVX0CkFBYXz00XB69pyBSlWS\nj1mchIWFAdC6dWtDSEksFtOpUycAHjx48I9d27siEkmYNWvWP97TPC9Gj57O0qU7mTlzIxYWlpw4\ncZTly5fTrVu3f/rS/ido2VLvXVu/fr0hXeHMmTPs36/X4Xw5RaQwmJqa5oqiLFmylKCgIPr1GwrY\nAuVQq21xc3OjevX6gAfgikrlwMKFm5k6dQ1SqS16A0xOz57fYGvbhpMnX8gez527kWbNRvL772eB\ncoAzjo7NkMvlaLXGgCNgh0RixePHj4mJicmVh25jY1Nsi+d169aRlJREkyZNuHYtmitX4pgzZw4A\nP/30k6GF6dvQt+eVAM7cufOE77//JU+jG+DmzXsMHjyTqVPXEhkp57lqQ2Glijw8PAgPD+fTT8fz\nrtOmRqNh7dp9BAeHcelSvjLWJZTwn+Xf5Jr5V6DTCWi1oNGI8n2YlVA0HB0dAfjzzz9RqVQolUp0\nOh3Hjh0DyNUTuITiY+7cuTx48IAxYz5FpapIvXofUa9e3l2jSnidDh060LhxY86fP0/16tWxs7Mj\nNlZfjT5o0KBiy99WKpW4ubnlGmvduvUrnXNk6HQifv75Z9LS0pBIXhhQ0dGZxMcnY27ujr5XhxJP\nz/bUq3cPGxtnQK93W7NmPTIyMl7zzL8pT7U4OHv2LKBvz6g3HmH69Ons3r2bwMBAbt++XSipu+xs\nDZ06jeXx48eUL29nSE/QSxNZAgpq1+7ExIkTqV27dpGaDLzMC4O8IlFRlzEzM35WnFQ4pFIZf/11\nkr17/Rg0KP+K+RJK+K/ynygusrC4/07HEgQBnU6HRCIFKnHvXjzly5f/oBO9i8qbiou0Wi2urq7c\nv38fNzc3unXrxpkzZ7h48SJmZmaEh4e/98nvQ0UQBK5duwYUXGO1hBekpKQwefLkZ00MVFhYWDB6\n9GjmzJnzzj2pC6t9mx86nY64uDisra3/ZvmugtG9e3cOHjzIqlWrDH3H1Wo15cuXJy4ujtu3b+Pu\n7l6oY/r5+bFmzWp27pyNQqFm3LjFbNhwkJs3/6BKlUboZa6KRn7fy9mzZ+nVqwctWtRmz56FBc79\nj4iIRqGQYW9fi+eLgBJeUFJc9OHwwYfab9wIoWXLL1ixYi/gDFhTpUqVEqPzPSCRSPDx8aFChQoE\nBwf/f3v3Hlx1nd5x/P3knBWEuiFboOFqzBjEoLsol4Ego4lII2VAp4Kw7CodWCpTK1jrDttxd2mZ\nToTdWhDLjgQQtOJyiZZQ25V1XS4ykZUgI7cxclmQkkkCcieECE//OIcQssFBkpzfOSef1wyTc37n\n9zt5mO+ck+f3vTxfZs+eTUlJCR06dOCdd95R0tmCtGq9aVJTUyksLOTYsWMcPHiQiooKCgoKmpx0\nNqeUlBTS09PjMumEyDxJiPRyLlmyhE2bNjF+/HgqKyvJzs6mT58+3/g9H3roId5++x3atr0Ls29T\nUxOmtvYrNmzYRVOSzq+Tnp5OTU0tp06d59y589d1zdy5y8nMHM1LL61BSae0dq1+qP3IkeNs2LCN\nI0dOM21aAVoL1LL69OlDWVkZa9asqavjOWbMmLr92EXiWbt27ejZs2fQYSSkxx9/nBUrVlBcXMyk\nSZPqjrdr145XX321iTdHKUAvZs16iWeffeFrtoVtuqysLEpKSujd+zZCoTIi2+deraLiGOfPX+DW\nW7sA7Rk8eDih0Hyqq+NrpzmRILS6xLO8/CilpXsYOfIBIJ0RI6byq1+FGTdunFagx0hka8CxQYch\nIjEUCoX+9yvgAAAKd0lEQVQoKipi2bJlLF++nBMnTjBo0CCmTZtGr169muV3pKenN+tOTddypXc2\nA/e9nD9fU7dt7vLlv2HixJmMGzeK119/A2jHwIF3UF5erlEdEVpZ4nn4cAV33PHXmKWwd28Z6enp\nmMFTTz0VdGgiIkkvHA4zadKkq3o8E9mZM2F+9KNZHD58iA0bFpKS0p5Bgx7CfSY1NWHcb8YsMtVF\nSadIRKtKPLt3z2bYsGGEwzdx4cKfDo+IiIhcr+PHj7Nu3Yfce28f3HsBqWRmQnl5OR07dgw6PJG4\nlNRjy7t37yc392/54otzQDaQwapVRRQVFWmeloiINEmPHj1Yu3Yt3bplcvHilQWpSjpFri2pE8+f\n/exV1q8v5ac/XQxEvhTidcWniIjcGHfn5MmT1NbWxvx35+TksHTpUv1tEblOSZx43syCBUt45pln\nmD9/ftDBiIhIM3N3CgsLycrKokOHDqSmpjJ58mSOHTsWdGgicg1JlXhu3ryd6dP/DfdOwJ107tyT\nefPmqVSPiEgSmjNnDlOmTGHfvn20bduW6upqFi9eTG5uLtXV1UGHJyKNSJrE8/Tps4wc+Szz5r1F\nUdEfaKniwSKJqLS0lHfffZctW7Zw8aIW1kniO3XqFLNmzQKgsLCQM2fOsGfPHm6//XZ27NjBm2++\nGXCEItKYpEk8b7klnVdemc+MGTMYPXp00OGIxIXKykruv/9++vfvz8yZM3n66afJysqq2z5TJFF9\n9NFHnD17lgEDBjB58mRCoRC9e/fm+eefB2DdunUBRygijUmSckrdgHQmTGieIsQiycDdGTNmDBs3\nbiQtLY1+/fqxZ88eDhw4QH5+PmVlZaSlpQUdpsgNubxd6blz53D3up2Pzp49e9XrIhJfkqLHs6pK\n25CJNLRt27a6pHP37t0UFBSwevVqBg8ezNGjR3njjTeCDlHkhuXk5NCxY0d27drFjBkzOHjwIGvX\nrqWgoACARx55JOAIRaQxSZF4qmaayJ/auXMnAMOHD6/bRjAcDjN+/PirXhdJRG3atGHu3LmYGXPm\nzCEjI4NRo0ZRVVXF8OHDefTRR4MOUUQakRSJ5+UhFpEgfPnll2zcuJFdu3bh7kGHU6dLly4AbN26\n9ar6hiUlJQB07do1kLhEmsuECRN4//33yc/Pp1OnTmRnZ/Piiy9SXFxMOJwkM8lEkow+mSI3qLa2\nlueee46FCxdSU1MDQL9+/Xjttde4++67A44O8vLyyMjIYN++feTm5pKTk8Onn37Ke++9RygU4okn\nngg6RJEmy8vLIy8vL+gwROQ6KfEUuUHTp09nwYIFmBn9+/dn//79lJaW8uCDD7Jz5046d+4caHzh\ncJiVK1fy8MMPs3nzZjZv3gxAKBRi0aJFZGZmBhqfiIi0Pkkx1C4Sa5WVlRQWFpKSksKHH37Ixx9/\nzKFDhxg6dChVVVUsWrQo6BABGDBgAJ9//jlz585l9OjRTJ48mbKyMiZOnBh0aCIJr7q6mlWrVvHy\nyy/zwQcfcOnSpaBDEol7LdbjaWZLgJFApbvfVe/43wNPA18B77r7jxu5Nh+YB4SARe7+YkvFKXIj\ntm/fTm1tLffddx85OTkAtG/fnqlTp7Jp0ya2bNkScIRXpKWlMW3aNIYMGQKgnk6RZrB+/XrGjh1L\nVVVV3bF77rmH4uJiunfvHmBkIvGtJXs8lwL59Q+YWS4wGviuu/cBftnwIjMLAf8BPAxkA+PNLLsF\n4xT5xi7Xvzxw4AAXLlyoO/7ZZ59d9bqIJJ+Kioq6FfR9+/ZlypQpdOnShU8++YTHHnssrhYZisQb\na8kPiJllAP99ucfTzFYCC939/a+5ZjAw093/Mvr8JwDuXlD/vJMnT+qTLSIikmRSU1NVqiaJxXqO\nZy9gqJltMbMNZjagkXO6AV/Ue344ekxEREREElisV7WHgTRgEDAAWGlmmX51t2tjdzrq3RQRERFJ\ncLFOPA8Db0cTzT+Y2SWgI1DV4Jwe9Z53B440fCN1xYuIiIgkllgPtf8XkAdgZr2Am4CjDc75GMgy\ns9vM7CZgHFAc0yhFREREpNm1WOJpZm8BJcAdZnbYzCYBS4BMM9sJ/Bp40t3dzLqa2f8AuPtXRMot\nvQfsAVa6+66WilNEREREYqNFV7W3JNX6jA+N1Ws1s+8AK4AM4I/AWHc/HlSMrZGZ9QBeB9KBS0Sq\nScxT2wTLzNoCG4E2RKY6rXb3n5vZbURuxr8DbAN+6O4Xrv1O0hKi5fy2Av/n7iPVLiLNLyF3LlKt\nz7iylAb1WoEZwO/cPQv4XfS5xNZXwHPufieRxXx/F/2MqG2CVQPkufv3gL5AvpkNAmYD/x5tl+PA\npABjbM2mERlpu0ztItLMEjLxBAYCe919f/Tu89dECtNLjLn7RuDLBodHA8uij5cBj8Q0KMHdy919\nW/TxaSJ/TLuhtgmUR5yJPv1W9J8Tmfu+Onpc7RIAM+sO/BWwKPrcULuINLtETTxV6zO+/YW7l0Mk\nAQI6BxxPqxbdyOEeYAtqm8CZWcjMtgOVwG+BfcCJ6Px20PdZUOYCPyYyNQXgz1G7iDS7RE08VetT\n5DqY2Z8BRcB0dz8VdDwC7n7R3fsSKRU3ELizsdNiG1XrZmaX56mX1j/cyKlqF5EminUdz+ZyXbU+\nJTAVZtbF3cvNrAuRnh2JMTP7FpGk8013fzt6WG0TJ9z9hJmtJzIHt4OZhaO9a/o+i70hwCgzGwG0\nBb5NpAdU7SLSzBK1x1O1PuNbMfBk9PGTwJoAY2mVovPTFgN73P2lei+pbQJkZp3MrEP08c3AMCLz\nb38PPBY9Te0SY+7+E3fv7u4ZRP6efODuE1C7iDS7RC6nNILIHWkIWOLu/xpwSK1StF7rA0R2oKoA\nfk5ko4CVQE/gEDDG3RsuQJIWZGb3AZuAHVyZs/ZPROZ5qm0CYmbfJbJIJUTkxn+lu/+LmWVypWzP\nJ8AP3L0muEhbLzN7APjHaDkltYtIM0vYxFNEREREEkuiDrWLiIiISIJR4ikiIiIiMaHEU0RERERi\nQomniIiIiMSEEk8RERERiQklniISN8xsupm1CzoOERFpGSqnJCJxw8z+CPR396NBxyIiIs0vUbfM\nFJEEZ2btiRSz706koPoqoCvwezM76u65ZjYc+GegDbAP+Bt3PxNNUFcAudG3+7677431/0FERL4Z\nDbWLSFDygSPu/j13v4vITmRHgNxo0tkReAEY5u73AluBf6h3/Sl3Hwi8Er1WRETinBJPEQnKDmCY\nmc02s6HufrLB64OAbGCzmW0nslf2rfVef6vez8EtHq2IiDSZhtpFJBDuXmZm/YARQIGZrWtwigG/\ndffx13qLazwWEZE4pR5PEQmEmXUFzrn7fwK/BO4FTgO3RE/5CBhiZrdHz29nZr3qvcXj9X6WxCZq\nERFpCvV4ikhQ7gZ+YWaXgFpgKpEh8/81s/LoPM+JwFtm1iZ6zQtAWfRxGzPbQuQG+lq9oiIiEkdU\nTklEEo7KLomIJCYNtYuIiIhITKjHU0RERERiQj2eIiIiIhITSjxFREREJCaUeIqIiIhITCjxFBER\nEZGYUOIpIiIiIjHx/9m8IoMrnDoIAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Variance converges to 0.005\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAiMAAADOCAYAAADsbwLEAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAHZdJREFUeJzt3X2UXFWZ7/Hvr6vT1Um6Uw3pJkIS\nDJBGiCAIPQwMqPGNBFFhKcwNM6PIZY3OKPOi4gw4F+SiXGSuirpgdKngC6NeEBXbMRociTMXxZiW\nFyGBTAJiEkPIexGSdJLufu4fdbqpW+mXSqe6Tqfr91krq8/ZZ59dz9mwOk/23meXIgIzMzOztNSl\nHYCZmZnVNicjZmZmlionI2ZmZpYqJyNmZmaWKicjZmZmlionI2ZmZpYqJyNmVhWSjpX0oqRM2rGY\n2fjiZMTMBiVpiaQbBym/SNJGSfUH015ErI2IpojorVyUZjYROBkxs6F8DXiXJJWUvwv4ZkT0lNvQ\nwSYuZlZbnIyY2VDuA44EXtNfIOkI4K3ANyRdKOkRSS9IWifphqJ6cySFpCslrQUeKCqrT+pcIelJ\nSTslPSPpfUX3z5e0XtKHJW2S9JykK4quT5b0aUm/l5SX9KCkycm1syX9UtIOSY9Jmj/G/WRmh8jJ\niJkNKiL2APcA7y4q/lPgqYh4DNiVXGsBLgT+WtLFJc28DjgZWDDIR2yikNhMA64AbpV0RtH1lwE5\nYCZwJXB7kgwBfAo4E/gTCgnTPwB9kmYCPwI+kZRfDXxXUttBd4CZVY383TRmNhRJ51H4y/1lEbFH\n0i+AeyPi1kHqfhaIiPigpDnA74ATIuKZ5Hp/2aTBpngk3QcsjYjPJaMZPwaa++tK2gS8Hfg1hUTo\n7CQpKm7jH4FTIuJdRWVLgG9FxNcPpS/MbOx4ZMTMhhQRDwKbgYskHQ/8EfAtAEl/LGmppM2S8sBf\nAa0lTawbqm1JF0j6laRtknYAbym5f2tJ0rIbaErqNAJPD9Lsy4FLkymaHUm75wFHH8Rjm1mVORkx\ns5F8g8J0zLuA+yPi+aT8W0AnMDsicsAXgdLFroMOvUrKAt+lMN0yIyJagMWD3D+YLUA3cMIg19YB\nd0VES9GfqRHxyTLaNbOUOBkxs5F8A3gT8JdA8VRHM7AtIrolnQX82UG02QBkKYy69Ei6ADi/nBsj\nog+4E/iMpGMkZSSdkyQ4/wq8TdKCpLwxWQw76yBiM7MqczJiZsOKiGeBXwJTKYyE9Hs/cKOkncD1\nFBa7ltvmTuBvk3u2U0hkOoe96f93NfA4sBzYBtwC1EXEOuAi4KMUEp11wEfw7zqzcc0LWM3MzCxV\n/teCmZmZpcrJiJmZmaXKyYiZmZmlatx+X0Q+n/diFjMzswkml8sd8Aq/R0bMzMwsVU5GzMzMLFXj\ndpqmWC6Xq2h7XV1dAHR0dFS0XRua+7z63OfV5z6vPvd59Y2mz/P5/LDXPTJiZmZmqXIyYmZmZqly\nMmJmZmapcjJiZmZmqTosFrBW2hOb9rGnpw8vdzIzM0tfTY6M/HD1Lu5esSvtMMzMzIwaTUZaGjPs\n2NuXdhhmZmZGrSYj2Tpe6O6jt887zpuZmaWtNpORxjr6gO2796UdipmZWc2ryWQk11h47M0796Yc\niZmZmdVkMtKSLTz2lhedjJiZmaWtNpMRj4yYmZmNGzWdjHhkxMzMLH1lJSOSFkpaJWmNpGsGuZ6V\ndHdyfZmkOUn5dElLJb0o6baSexokfUnSf0l6StI7K/FA5ZhcLxrqPDJiZmY2Hoy4A6ukDHA78GZg\nPbBcUmdErCyqdiWwPSLmSloE3AL8N6AbuA44JflT7J+ATRFxoqQ64MhDfpoySaKlsc7JiJmZ2Tig\niOH32pB0DnBDRCxIzq8FiIibi+osSeo8JKke2Ai0RdK4pPcAHRFxVdE964CTImLQrVDz+fxAYKtX\nrx7d0w3j2ge2MbleXP/aIyretpmZmb2kvb194DiXy6n0ejnTNDOBdUXn65OyQetERA+QB6YP1aCk\nluTw45IelvQdSTPKiKViWhrr2NHtXVjNzMzSVs4X5R2QwQClwynl1Cn93FnALyLiQ5I+BHwKeNdg\nlTs6KvuVdl1dXbRk63gmHxVv2wbX1dUFVP6/pQ3NfV597vPqc59X32j6PJ/PD3u9nJGR9cDsovNZ\nwIah6iTTNDlg2zBtbgV2A99Pzr8DnFFGLBXT0ljHtt376On16IiZmVmayklGlgPtko6T1AAsAjpL\n6nQClyfHlwAPxDCLUZJrPwTmJ0VvBFYOVX8s5BrriIBtu7wlvJmZWZpGnKaJiB5JVwFLgAxwZ0Ss\nkHQj0BURncAdwF2S1lAYEVnUf7+kZ4FpQIOki4Hzkzdx/jG557PAZuCKyj7a8Pr3Gtm0cy9HTWus\n5kebmZlZkXLWjBARi4HFJWXXFx13A5cOce+cIcp/D7y23EArzVvCm5mZjQ81uQMreEt4MzOz8aJm\nk5HcwJbwXjNiZmaWpppNRibX1zGlIeORETMzs5TVbDIC0Nac9ZoRMzOzlNV0MtLalPXIiJmZWcpq\nOhlpa/LIiJmZWdpqOhlpbW5gs5MRMzOzVNV0MtLW1MiO3fvZ1+Mt4c3MzNJS08lIa3MDAFt3eXTE\nzMwsLTWdjLQ1ZQFvfGZmZpammk5GWpsLyYgXsZqZmaWnppMRj4yYmZmlr7aTkYGREW8Jb2Zmlpaa\nTkYaJ2VoztZ7ZMTMzCxFNZ2MQGHdiPcaMTMzS0/NJyNt3hLezMwsVTWfjLQ2N/htGjMzsxSVlYxI\nWihplaQ1kq4Z5HpW0t3J9WWS5iTl0yUtlfSipNuGaLtT0hOH8hCHwiMjZmZm6RoxGZGUAW4HLgDm\nAZdJmldS7Upge0TMBW4FbknKu4HrgKuHaPsdwIujC70yWpuy7OzuoXt/b5phmJmZ1SxFxPAVpHOA\nGyJiQXJ+LUBE3FxUZ0lS5yFJ9cBGoC2SxiW9B+iIiKuK7mkCfgK8F7gnIk4p/tx8Pj8Q2OrVqw/l\nGYf177/bzRd/s5MvXNBK29TMmH2OmZlZrWpvbx84zuVyKr1ezjTNTGBd0fn6pGzQOhHRA+SB6SO0\n+3Hg08DuMmIYMy3ZQgKyY6+/LM/MzCwN9WXUOSCDAUqHU8qp81Jl6XRgbkR8sH99yXA6OjpGqnJQ\nurq6BtqdtG4H/PIXtM46no55Myr6OfaS4j636nCfV5/7vPrc59U3mj7P5/PDXi9nZGQ9MLvofBaw\nYag6yTRNDtg2TJvnAGdKehZ4EDhR0s/LiKXi2vz9NGZmZqkqJxlZDrRLOk5SA7AI6Cyp0wlcnhxf\nAjwQwyxGiYgvRMQxETEHOA/4r4iYf7DBV8L0pgbA309jZmaWlhGnaSKiR9JVwBIgA9wZESsk3Qh0\nRUQncAdwl6Q1FEZEFvXfn4x+TAMaJF0MnB8RKyv/KKOTrc+QmzzJIyNmZmYpKWfNCBGxGFhcUnZ9\n0XE3cOkQ984Zoe1ngVOGqzPWWpsaPDJiZmaWkprfgRUK60Y8MmJmZpYOJyMUNj7zyIiZmVk6nIxQ\nGBlxMmJmZpYOJyMURkZ27etl976etEMxMzOrOU5GKNprZOe+lCMxMzOrPU5GKHxzL8BmL2I1MzOr\nOicjvDQy4nUjZmZm1edkhMKaEfCW8GZmZmlwMoK3hDczM0uTkxFgUqaOI6Z4S3gzM7M0OBlJeK8R\nMzOzdDgZSbQ2eUt4MzOzNDgZSbQ1Z/1qr5mZWQqcjCTamrJs2bmPiEg7FDMzs5riZCTR2pxlz/5e\ndu3rTTsUMzOzmuJkJNG/C+sWL2I1MzOrKicjidZmbwlvZmaWhrKSEUkLJa2StEbSNYNcz0q6O7m+\nTNKcpHy6pKWSXpR0W1H9KZJ+JOkpSSskfbJSDzRaHhkxMzNLx4jJiKQMcDtwATAPuEzSvJJqVwLb\nI2IucCtwS1LeDVwHXD1I05+KiJOAVwPnSrpgdI9QGa3NyS6sHhkxMzOrKo309oikc4AbImJBcn4t\nQETcXFRnSVLnIUn1wEagLZLGJb0H6IiIq4b4jM8BT0TEl/vL8vn8QGCrV68e3dMdhN4ILvvuJt5x\n8lQWvbJpzD/PzMysVrS3tw8c53I5lV4vZ5pmJrCu6Hx9UjZonYjoAfLA9HIClNQCvA34WTn1x0pG\nojlbx47uvjTDMDMzqzn1ZdQ5IIMBSodTyqlzYMOFUZRvA5+PiGeGqtfR0TFSUwelq6tr0HaPfvA/\noXFyxT/Phu5zGzvu8+pzn1ef+7z6RtPn+Xx+2OvljIysB2YXnc8CNgxVJ0kwcsC2Mtr+ErA6Ij5b\nRt0xV9iFdV/aYZiZmdWUcpKR5UC7pOMkNQCLgM6SOp3A5cnxJcADMcJiFEmfoJC0/P3BhTx2Cruw\negGrmZlZNY04TRMRPZKuApYAGeDOiFgh6UagKyI6gTuAuyStoTAisqj/fknPAtOABkkXA+cDLwD/\nBDwFPCwJ4LaI+EolH+5gtSbfTxMRJDGZmZnZGCtnzQgRsRhYXFJ2fdFxN3DpEPfOGaLZcfe3fVtT\nln09fbzQ3UNu8qS0wzEzM6sJ3oG1SP9eI1u814iZmVnVOBkp0tbUCMBmrxsxMzOrGicjRTwyYmZm\nVn1ORor0fz+NR0bMzMyqx8lIkSOmNJCpk0dGzMzMqsjJSJG6OjF9aoNHRszMzKrIyUiJtuYsW7wL\nq5mZWdU4GSnR2pT1yIiZmVkVORkpURgZcTJiZmZWLU5GSrQ2FZKREb5ax8zMzCrEyUiJtuYs+3uD\n/J79aYdiZmZWE5yMlGhtKmx85nUjZmZm1eFkpERbszc+MzMzqyYnIyUGdmH1IlYzM7OqcDJSwiMj\nZmZm1eVkpERu8iQmZeSNz8zMzKqkrGRE0kJJqyStkXTNINezku5Ori+TNCcpny5pqaQXJd1Wcs+Z\nkh5P7vm8JFXigQ6VJG98ZmZmVkUjJiOSMsDtwAXAPOAySfNKql0JbI+IucCtwC1JeTdwHXD1IE1/\nAXgv0J78WTiaBxgL/XuNmJmZ2djTSJt7SToHuCEiFiTn1wJExM1FdZYkdR6SVA9sBNoiaVzSe4CO\niLgqOT8aWBoRJyXnlwHzI+J9/W3m8/mBwFavXl2BRy3f/3pwO9u6+/jUm6ZX9XPNzMwmovb29oHj\nXC53wExIOdM0M4F1Refrk7JB60RED5AHhvubfGbSznBtpqalsY58d1/aYZiZmdWE+jLqDLaWo3Q4\npZw6o67f0dExTFMHr6ura9h2T976FP+x9hnOOONM6urGxVKWw95IfW6V5z6vPvd59bnPq280fZ7P\n54e9Xs7IyHpgdtH5LGDDUHWSaZocsG2ENmeN0GZqWpuy9PYF23f7jRozM7OxVk4yshxol3ScpAZg\nEdBZUqcTuDw5vgR4IIZZjBIRzwE7JZ2dvEXzbuAHBx39GBnYa8SLWM3MzMbciNM0EdEj6SpgCZAB\n7oyIFZJuBLoiohO4A7hL0hoKIyKL+u+X9CwwDWiQdDFwfkSsBP4a+BowGfhx8mdc6N+FdcvOffCy\nlIMxMzOb4MpZM0JELAYWl5RdX3TcDVw6xL1zhijvAk4pN9Bqah0YGelOORIzM7OJzzuwDqJ/mmbL\nTq8ZMTMzG2tORgbRnK2nob7Oa0bMzMyqwMnIICTR1pRli7eENzMzG3NORobQ2pz1yIiZmVkVOBkZ\nQpu/LM/MzKwqnIwMoa25wV+WZ2ZmVgVORobQ1pRl6659dO/vTTsUMzOzCc3JyBBe/fIjiIAHV29J\nOxQzM7MJzcnIEM49oZVpjfUsfvy5tEMxMzOb0JyMDKGhvo7zX/kyfrryefb2eKrGzMxsrDgZGcaF\npx7Nzr09nqoxMzMbQ05GhnHu3MJUzY88VWNmZjZmnIwMo6G+jjfP81SNmZnZWHIyMoILX/Uydnb3\n8Is1nqoxMzMbC05GRnDe3DaaG+v50W83ph2KmZnZhORkZASFqZoZ/HTlRvb19KUdjpmZ2YTjZKQM\nF556NC94qsbMzGxMlJWMSFooaZWkNZKuGeR6VtLdyfVlkuYUXbs2KV8laUFR+QclrZD0hKRvS2qs\nxAONhfPaW2nO+q0aMzOzsTBiMiIpA9wOXADMAy6TNK+k2pXA9oiYC9wK3JLcOw9YBLwSWAj8i6SM\npJnA3wIdEXEKkEnqjUvZ+gxvnjeD+1d4qsbMzKzSFBHDV5DOAW6IiAXJ+bUAEXFzUZ0lSZ2HJNUD\nG4E24Jriuv31gLXAr4DTgBeA+4DPR8T9/W3m8/mBwFavXn2oz3nIujbs5ZO/3MFHz23hjKOzaYdj\nZmZ22Ghvbx84zuVyKr1ezjTNTGBd0fn6pGzQOhHRA+SB6UPdGxF/AD5FISl5DsgXJyLj0WkzGphS\nLx5a3512KGZmZhNKfRl1DshggNLhlKHqDFou6QjgIuA4YAfwHUl/ERH/OlgAHR0dZYRZvq6urlG1\nu+DZR/nZk8/zqtPPoKHea38Pxmj73EbPfV597vPqc59X32j6PJ/PD3u9nL9R1wOzi85nARuGqpNM\n0+SAbcPc+ybgdxGxOSL2A98D/qSMWFL1lv63ap72WzVmZmaVUk4yshxol3ScpAYKC007S+p0Apcn\nx5cAD0RhMUonsCh52+Y4oB34NYXpmbMlTZEk4I3Ak4f+OGPrNe2tNGXrWfxbv1VjZmZWKSMmI8ka\nkKuAJRQShnsiYoWkGyW9Pal2BzBd0hrgQ7y0cHUFcA+wEvgJ8IGI6I2IZcC9wMPA40kcX6rok42B\nxkkZ3nTyUdy/8nn29/qtGjMzs0ooZ80IEbEYWFxSdn3RcTdw6RD33gTcNEj5x4CPHUyw48FbTj2a\n+x7dwC/WbGH+K45KOxwzM7PDnldhHqTXnthWmKrxBmhmZmYV4WTkIDVOyvBGT9WYmZlVjJORUXjL\nqUezY/d+fvn01rRDMTMzO+w5GRmF153YxtSGjN+qMTMzqwAnI6NQmKqZwZKVGz1VY2ZmdoicjIxS\n/1TNQ56qMTMzOyRORkZp/iuSqRq/VWNmZnZInIyMUuOkDG84eQZLVniqxszM7FA4GTkEF556NNt3\n7+eHj5V+VY+ZmZmVy8nIIXjDSUdx5suP4NrvPc5vfr897XDMzMwOS05GDkFDfR1ffncHR+ca+ctv\ndPH7rbvSDsnMzOyw42TkEB05tYGvXnEWEcEVX13O9l370g7JzMzssOJkpAKOa53Kl9/dwfode3jv\nXV107+9NOyQzM7PDhpORCumYcySfvvQ0lj+7nY/c+1v6+iLtkMzMzA4L9WkHMJG87bRj+MOOPXzy\nx09x7JGT+ciCk9IOyczMbNxzMlJh73vt8azdtpvblz7NrCOmcNlZx6YdkpmZ2bjmZKTCJHHj21/J\nH7bv4X/c9wTHtEzmdSe2pR2WmZnZuFXWmhFJCyWtkrRG0jWDXM9Kuju5vkzSnKJr1yblqyQtKCpv\nkXSvpKckPSnpnEo80HhQn6nj9j8/gxNnNPOBbz7Myg0vpB2SmZnZuDViMiIpA9wOXADMAy6TNK+k\n2pXA9oiYC9wK3JLcOw9YBLwSWAj8S9IewOeAn0TEScBpwJOH/jjjR1O2nq++549oytbz37+2nA07\n9qQdkpmZ2bikiOHf+khGLG6IiAXJ+bUAEXFzUZ0lSZ2HJNUDG4E24Jriuv31gBXAY8DxMUQA+Xx+\noHz16tWjfLz0PbtjP9f9fDsRsHDuZN7WPpVco19iMjOz2tHe3j5wnMvlVHq9nL8VZwLris7XJ2WD\n1omIHiAPTB/m3uOBzcBXJT0i6SuSppYRy2FnTsskPvnGI+k4Jkvnqt28/8eb+fpjO9ne7b1IzMzM\noLwFrAdkMEDpaMZQdYYqrwfOAP4mIpZJ+hyFUZTrBgugo6OjjDDL19XVNSbtDqUDuOj18PTmF7l9\n6Rrue+QP3P+7bv7sj4/lr153AjOmNVYljjRVu8/NfZ4G93n1uc+rbzR9ns/nh71ezsjIemB20fks\noPRragfqJNM0OWDbMPeuB9ZHxLKk/F4KycmEdkJbE5/509N54MPzeftpx/CNh37Pa/55KR/7wRM8\nl/eaEjMzq03lJCPLgXZJx0lqoLAgtbOkTidweXJ8CfBAshakE1iUvG1zHNAO/DoiNgLrJL0iueeN\nwMpDfJbDxpzWqfzvS09j6Yfn884zZvLNZWt53T//nA/e/Sjf/vVaVm3cSa93cDUzsxox4jRNRPRI\nugpYAmSAOyNihaQbga6I6ATuAO6StIbCiMii5N4Vku6hkGj0AB+IiP7FEn8DfDNJcJ4Brqjws417\nx06fws3veBUfeP1cvvgfT/Nvv32O7z/yBwCas/WcNruFM45t4dXHHsGrj22hZUpDyhGbmZlVXlmb\nnkXEYmBxSdn1RcfdwKVD3HsTcNMg5Y9SWE5R82YdMYVPXHwqH7/oFH63ZRePrN3Bw2u388jaHdy2\ndA39gyTHt07ltNktzGyZzIxpWY6a1siMaY3MmJaltSnLpIzf0jEzs8OPd2AdRyRxfFsTx7c18c4z\nZwGwa28Pv12fH0hOfvXMVjbt3HvANI4E06c2cFRzITnJTZ7ElGw9UxsyTGmoZ2r2pZ+TJ/X/zFCf\nqWNSRkzK1DEpU0d9Xf+xBq7VSWTqCj/rVIjTzMysUpyMjHNTs/Wcc8J0zjlh+kBZb1+wdddeNr2w\nl+df6Ob55Oemnd2Fsp3dPLNlF7v29rJ7Xw+791X2NWIJMhJ1dYXkJCMhqfDqlKBOQiq8StVf3tvT\nA4JJS/594BWrQh0VHfeXj5zslJMPlZszadCXvg5/e/fuBSD7wNKUI6kd7vPqc59X1qKzZvP++XOr\n/rlORg5DmTpxVHMjRzU3csrM3Ij1+/qCPft72bWvh917k5/7etmzr5eevj729wb7e/vo6Q32JT/3\n9/YVyvqC3r4gIujtg97oPw76Avqi/zoEhZ9QKC8u27RpMwCtba0AhWtJ3eL7SpftDrYlXhxQaxBl\nrv+dyMuEt27dCsD06UekHEntcJ9Xn/u8sma2TE7lc52M1IC6OjE1W8/UbD00pxPDS++lvyqdAGrQ\nS31+esqR1A73efW5zycGr3g0MzOzVDkZMTMzs1Q5GTEzM7NUORkxMzOzVCkGe11hHMjn8+MzMDMz\nMxu1XC53wH4KHhkxMzOzVDkZMTMzs1SN22kaMzMzqw0eGTEzM7NUORkxMzOzVNVcMiJpoaRVktZI\nuibteCYqSXdK2iTpiaKyIyX9VNLq5Ke/TKJCJM2WtFTSk5JWSPq7pNx9PkYkNUr6taTHkj7/n0n5\ncZKWJX1+t6SGtGOdaCRlJD0i6d+Sc/f5GJL0rKTHJT0qqSspq+jvlppKRiRlgNuBC4B5wGWS5qUb\n1YT1NWBhSdk1wM8ioh34WXJuldEDfDgiTgbOBj6Q/L/tPh87e4E3RMRpwOnAQklnA7cAtyZ9vh24\nMsUYJ6q/A54sOnefj73XR8TpEdGRnFf0d0tNJSPAWcCaiHgmIvYB/we4KOWYJqSI+E9gW0nxRcDX\nk+OvAxdXNagJLCKei4iHk+OdFH5Rz8R9Pmai4MXkdFLyJ4A3APcm5e7zCpM0C7gQ+EpyLtznaajo\n75ZaS0ZmAuuKztcnZVYdMyLiOSj85QkclXI8E5KkOcCrgWW4z8dUMl3wKLAJ+CnwNLAjInqSKv4d\nU3mfBf4B6EvOp+M+H2sB3C/pN5Lem5RV9HdL/SEGeLg5YNc3Cp1sNiFIagK+C/x9RLxQ+EejjZWI\n6AVOl9QCfB84ebBq1Y1q4pL0VmBTRPxG0vz+4kGqus8r69yI2CDpKOCnkp6q9AfU2sjIemB20fks\nYENKsdSi5yUdDZD83JRyPBOKpEkUEpFvRsT3kmL3eRVExA7g5xTW67RI6v+Hnn/HVNa5wNslPUth\nmv0NFEZK3OdjKCI2JD83UUi6z6LCv1tqLRlZDrQnK68bgEVAZ8ox1ZJO4PLk+HLgBynGMqEk8+Z3\nAE9GxGeKLrnPx4iktmREBEmTgTdRWKuzFLgkqeY+r6CIuDYiZkXEHAq/vx+IiD/HfT5mJE2V1Nx/\nDJwPPEGFf7fU3A6skt5CIZPOAHdGxE0phzQhSfo2MB9oBZ4HPgbcB9wDHAusBS6NiNJFrjYKks4D\n/i/wOC/NpX+UwroR9/kYkPQqCgv3MhT+YXdPRNwo6XgK/2o/EngE+IuI2JtepBNTMk1zdUS81X0+\ndpK+/X5yWg98KyJukjSdCv5uqblkxMzMzMaXWpumMTMzs3HGyYiZmZmlysmImZmZpcrJiJmZmaXK\nyYiZmZmlysmImZmZpcrJiJmZmaXq/wExurxBuheFkQAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"temp_change = 0\n",
"voltage_std = .13\n",
"process_var = .05**2\n",
"actual_voltage = 16.3\n",
"\n",
"x = (25, 1000) # initial state\n",
"process_model = (0., process_var)\n",
"\n",
"N = 50\n",
"zs = [volt(actual_voltage, voltage_std) for i in range(N)]\n",
"ps = []\n",
"estimates = []\n",
"\n",
"for z in zs:\n",
" prior = predict(x, process_model)\n",
" x = update(prior, (z, voltage_std**2))\n",
"\n",
" # save for latter plotting\n",
" estimates.append(x[0])\n",
" ps.append(x[1])\n",
"\n",
"# plot the filter output and the variance\n",
"book_plots.plot_measurements(zs)\n",
"book_plots.plot_filter(estimates, var=np.array(ps))\n",
"book_plots.show_legend()\n",
"plt.ylim(16, 17)\n",
"book_plots.set_labels(x='step', y='volts')\n",
"plt.show()\n",
" \n",
"plt.plot(ps)\n",
"plt.title('Variance')\n",
"print('Variance converges to {:.3f}'.format(ps[-1]))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The first plot shows the individual sensor measurements vs the filter output. Despite a lot of noise in the sensor we quickly discover the approximate voltage of the sensor. In the run I just completed at the time of authorship, the last voltage output from the filter is $16.213$, which is quite close to the $16.4$ used by the `volt()` function. On other runs I have gotten larger and smaller results.\n",
"\n",
"Spec sheets are what they sound like - specifications. Any individual sensor will exhibit different performance based on normal manufacturing variations. Values are often maximums - the spec is a guarantee that the performance will be at least that good. If you buy an expensive piece of equipment it often comes with a sheet of paper displaying the test results of your specific item; this is usually very trustworthy. On the other hand, if this is a cheap sensor it is likely it received little to no testing prior to being sold. Manufacturers typically test a small subset of their output to verify that a sample falls within the desired performance range. If you have a critical application you will need to read the specification sheet carefully to figure out exactly what they mean by their ranges. Do they guarantee their number is a maximum, or is it, say, the $3\\sigma$ error rate? Is every item tested? Is the variance normal, or some other distribution? Finally, manufacturing is not perfect. Your part might be defective and not match the performance on the sheet.\n",
"\n",
"For example, I am looking at a data sheet for an airflow sensor. There is a field *Repeatability*, with the value $\\pm 0.50\\%$. Is this a Gaussian? Is there a bias? For example, perhaps the repeatability is nearly $0.0\\%$ at low temperatures, and always nearly $+0.50\\%$ at high temperatures. Data sheets for electrical components often contain a section of \"Typical Performance Characteristics\". These are used to capture information that cannot be easily conveyed in a table. For example, I am looking at a chart showing output voltage vs current for a LM555 timer. There are three curves showing the performance at different temperatures. The response is ideally linear, but all three lines are curved. This clarifies that errors in voltage outputs are probably not Gaussian - in this chip's case higher temperatures lead to lower voltage output, and the voltage output is quite nonlinear if the input current is very high. \n",
"\n",
"As you might guess, modeling the performance of your sensors is one of the harder parts of creating a Kalman filter that performs well. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Animation\n",
"\n",
"For those reading this in a browser here is an animation showing the filter working. If you are not using a browser you can see this plot at https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/animations/05_volt_animate.gif."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"
"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We've been doing the same thing in this chapter. The Kalman filter makes a prediction, takes a measurement, and then forms a new estimate somewhere between the two.\n",
"\n",
"**This is extremely important to understand**: Every filter in this book implements the same algorithm, just with different mathematical details. The math can become challenging in later chapters, but the idea is easy to understand.\n",
"\n",
"It is important to see past the details of the equations of a specific filter and understand *what* the equations are calculating and *why*. There are a tremendous number of filters. They all use different math to implement the same algorithm. The choice of math affects the quality of results and what problems can be represented, but not the underlying ideas.\n",
"\n",
"Here is the generic algorithm:\n",
"\n",
"**Initialization**\n",
"\n",
" 1. Initialize the state of the filter\n",
" 2. Initialize our belief in the state\n",
" \n",
"**Predict**\n",
"\n",
" 1. Use system behavior to predict state at the next time step\n",
" 2. Adjust belief to account for the uncertainty in prediction\n",
" \n",
"**Update**\n",
"\n",
" 1. Get a measurement and associated belief about its accuracy\n",
" 2. Compute residual between estimated state and measurement\n",
" 3. Compute scaling factor based on whether the measurement\n",
" or prediction is more accurate\n",
" 4. set state between the prediction and measurement based \n",
" on scaling factor\n",
" 5. update belief in the state based on how certain we are \n",
" in the measurement\n",
"\n",
"You will be hard pressed to find a Bayesian filter algorithm that does not fit into this form. Some filters will not include some aspects, such as error in the prediction, and others will have very complicated methods of computation, but this is what they all do. \n",
"\n",
"The equations for the univariate Kalman filter are:\n",
"\n",
"Predict\n",
"\n",
"$\\begin{array}{|l|l|l|}\n",
"\\hline\n",
"\\text{Equation} & \\text{Implementation} & \\text{Kalman Form}\\\\\n",
"\\hline\n",
" \\bar x = x + f_x & \\bar\\mu = \\mu + \\mu_{f_x} & \\bar x = x + dx\\\\\n",
"& \\bar\\sigma^2 = \\sigma^2 + \\sigma_{f_x}^2 & \\bar P = P + Q\\\\\n",
"\\hline\n",
"\\end{array}$\n",
"\n",
"\n",
"Update\n",
"\n",
"$\\begin{array}{|l|l|l|}\n",
"\\hline\n",
"\\text{Equation} & \\text{Implementation}& \\text{Kalman Form}\\\\\n",
"\\hline\n",
" x = \\| \\mathcal L\\bar x\\| & y = z - \\bar\\mu & y = z - \\bar x\\\\\n",
" & K = \\frac {\\bar\\sigma^2} {\\bar\\sigma^2 + \\sigma_z^2} & K = \\frac {\\bar P}{\\bar P+R}\\\\\n",
" & \\mu = \\bar \\mu + Ky & x = \\bar x + Ky\\\\\n",
" & \\sigma^2 = \\frac {\\bar\\sigma^2 \\sigma_z^2} {\\bar\\sigma^2 + \\sigma_z^2} & P = (1-K)\\bar P\\\\\n",
"\\hline\n",
"\\end{array}$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Comparison with g-h and discrete Bayes Filters\n",
"\n",
"Now is a good time to understand the differences between these three filters in terms of how we model errors. For the g-h filter we modeled our measurements as shown in this graph:"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAjwAAACICAYAAADjyzHQAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAADRNJREFUeJzt3X9s1PUdx/HXuy1XwUqxU9QBo+gQ\nccosRYObThSImT9Whwkbi5sxJttMGJlGVPwVjC5hbNPItrAf0W1WJ8IkKIKTVDcXklUsoFRU0G3F\nUkBU8EYtu4PeZ3/ct3qUu/aOu95dP/d8JBe+/Xx/9PPu58q9+vl+v3fmnBMAAIDPygrdAQAAgIFG\n4AEAAN4j8AAAAO8ReAAAgPcIPAAAwHsV2R4gHA5zmxcAAJ6prq62Qvchl5jhAQAA3iPwAAAA72V9\nSitRdXV1Lg9X1FpaWiRJU6ZMKXBP8o/aS6/2Uq1bonap9Gov1bolKRwOF7oLA4YZHgAA4D0CDwAA\n8B6BBwAAeI/AAwAAvEfgAQAA3iPwAAAA7xF4AACA9wg8AADAewQeAADgPQIPAADwHoEHAAB4j8AD\nAAC8R+ABAADeI/AAAADvEXgAAID3CDwAAMB7BB4AAOA9Ag8AAPAegQcAAHiPwAMAALxH4AEAAN4j\n8AAAAO8ReAAAgPcIPAAAwHsEHgAA4D0CDwAA8B6BBwAAeI/AAwAAvEfgAQAA3iPwAAAA7xF4gIG0\nsDr+AFA4/B5CBB4AAFACCDwAAMB7BB4AAJCV2jvWuNo71rhcbTcQKgrxTQEAwOCxcePGsqqqqttC\nodBEM0s5WdLW1taYzvHS3S4TzrlYNBp9q7Ozc3F9fX2s93oCDwAA6FNVVdVtY8aMmT1s2LCjgkTc\nVklSbW3txL6PlO52x6arq+vc9vZ2SVrUex2ntAAAQJ9CodDE1GGneAwbNiwWCoWShikCDwCksmW5\nzn1xjuqfmyE9dI60ZXmhewQURF+nsYpNqr5ySgsAktmyXFo9T5WHDsa/DrdLq+fFlyfNLly/ABwT\nAg+QD3+4stA9yMqEAwfiC60nFLYj+bTzVak7cmTboYPSM3OljX8qTJ/yrCTHHUXtscceG3H99def\nsWnTpq11dXX/y2RfAg8AJNM77PTXDuBTjzfvqFny4jujPjgQCZ18QmV03vTxHddNHbsv2+MuW7as\nZvLkyZ2NjY01dXV1uzLZl8CDolR7xxpJUtuiwT0z8qkb1gzYofPxs9rW0iJJmjJlyoB9j6Lz0Dnx\n01i9VY8Z0PEsJt6MOx8rkVePN++ouf+5N8dGDsfKJGnvgUjo/ufeHJvtccPhcFlLS0tVU1PTtoaG\nhi8++OCDGQWeQXMREgDk1fR7pSFDj2wbMjTeDiCphl+tn3Df6q21PWGnR+RwrOy+1Vtrszn2E088\nMWLatGnhSZMmRUaMGNG9fv36YZnsT+ABgGQmzZauXqLI0JFysvjMztVLuGAZ6MehbmeZtKdr+fLl\nNXPmzNkvSddee+2+xsbGmkz255QWAKQyabZao6dL8uC0DpAHz8y9aNsFP2k6d++BSKj3upEnVEaT\ntadjz5495c3NzcO3b98+dO7cueru7jYzc0uXLt1ZVpbe3A0zPAAAIGfmTR/fUVlRdsSbFFZWlMXm\nTR/fcazHbGxsPHHWrFkf7dq1q7Wjo6N1z549W0aPHh1dt25dVbrHIPAAAICcuW7q2H33XHX2jpEn\nVEZN8Zmde646e0c2d2mtWLHic7Nmzdqf2NbQ0LA/k9NanNICAAA5dd3UsftycRt6jw0bNmzr3Xb3\n3XfvzeQYBB4gTas2d+iBtR/oo66YPt/0kuZfPkHX1I0qdLcAoODajvtOsBTOyXYDgcADpGHV5g4t\nWNmqg4fip6U7Pj6oBStbJYnQAwCDAIEHRe1bv/1nobsgSdr83seKdh/5QcEHD3Xrtr9s0ZMb3ku9\n42l/jf9bJHUAJWlh/mcTUHy4aBlIQ++w0187AKC4MMODovbUDy4sdBckSV9d9JI6Pj54VPuoEUML\n3seej5YAAKTGDA+QhvmXT9DQIeVHtA0dUq75l08oUI8AAJlghgdIQ8+FyQ+s3hK/S2vEUO7SAoA8\nKi8vrx8/fvxB55zKy8vdww8//N7MmTM/SXd/Ag+QpmvqRml0925JfMwAAPTp1Udq9PJPR6lzb0hV\nI6O65PYOnX9jVu/LU1lZGXv77bfflKSnn356+J133jl65syZR70/TyoEHgAAkDuvPlKjFxaM1eFI\n/LKZzvdDemHB2Fx+i3A4XF5dXX04k30IPAAAIDd+d+kE7Wk9XrFDR34y+uFImZ6/vTabQ0cikbKz\nzjrr7EgkYh9++OGQtWvXbs9kfwIPAADInd5hp7/2NCWe0mpqajr+hhtuGLd9+/atfFo6AADIr+//\nbZuqTokmXZeq/RjMmDHjk/3791fs3r077YkbAg8AAMidS27vUEXlke/KWlEZ0yW3d+TqW2zevPm4\nWCymU045Je3reDilhaLUtujKQndh0OBnBaCo9NyNlewurTW3jDvWw/ZcwyNJzjktXbq0raIi/RhD\n4AEAALl1/o37sr0Nvbfu7u6N2ezPKS0AAOA9Ag8AAPAegQcAAPTJORfrf6vikKqvBB4AANCnaDT6\nVldXV9Fnhq6urrJoNPpWsnVctAwAAPrU2dm5uL29XaFQaKKZHRV8aqV6SWpra0saNjLd7lg452LR\naPStzs7OxcnWE3gAAECf6uvrY5IWpdxgYfi7klTb34HS3W4AFP30FAAAQLYIPAAAwHsEHgAA4D0C\nDwAA8B6BBwAAeI/AAwAAvEfgAQAA3iPwAAAA7xF4AACA9wg8AADAewQeAADgPQIPAADwHoEHAAB4\nj8ADAAC8R+ABAADeI/AAAADvEXgAAID3CDwAAMB7BB4AAOA9Ag8AAPAegQcAAHiPwAMAALxH4AEA\nAN4j8AAAAO8ReAAAgPcIPAAAwHsEHgAA4D0CDwAA8B6BBwAAeI/AAwAAvEfgAQAA3iPwAAAA7xF4\nAACA9wg8AADAewQeAADgPXPOZXWAcDic3QEAAEDRqa6utkL3IZeY4QEAAN4j8AAAAO9lfUoLAACg\n2DHDAwAAvNdv4DGzR81sr5m9kWTdrWbmzOyk4OtpZhY2s9eCx70D0el8SVa7mS00s46EGq9IWLfA\nzN41s21mdnlhep0bmdRuZrVmdjCh/TeF63l2Uj3fzexHwbhuNbPFCe1ej3nQflTtPo25lPL5/lRC\nfW1m9lrCOi/GPZO6S2TMzzOz5qC+FjO7IGg3M1sSjPkWM5tcuJ5nJ8O6vXpNl3Ouz4ekr0maLOmN\nXu1jJL0gaYekk4K2aZKe6++Yg+WRrHZJCyXdmmTbsyW9LqlS0jhJ/5JUXuga8lR7be/nx2B9pKj7\nUklNkiqDr0eW0Jinqt2bMU9Ve6/1v5B0r2/jnmHd3o+5pHWSvh4sXyHp7wnLz0sySVMlvVLo/uep\nbq9e0/ud4XHO/UPSviSrHpJ0myRvLwLqo/ZkGiQtc85FnHP/kfSupAsGrHMDLMPavZGi7pskLXLO\nRYJt9gbtpTDmqWr3Sl/PdzMzSbMlPRk0eTPuGdbtlRS1O0nDg+VqSbuC5QZJj7m4ZkkjzOy0/PQ0\ntzKs2yvHdA2PmX1DUodz7vUkqy80s9fN7Hkz+1J23Stac4NpzUfN7MSgbZSk9oRtdgZtvklWuySN\nM7PNZvaymV1csN4NjDMlXWxmrwT1nR+0l8KYp6pd8nvME10s6X3n3DvB16Uw7tLRdUv+j/mPJf3M\nzNol/VzSgqDd9zFPVbfk0Wt6xoHHzIZJuktSsnN5mySNdc59WdIvJa3KrntFaamkMySdJ2m34lO+\nUnyqszffZr9S1b5b0hecc3WSbpH0ZzMbnvwQg1KFpBMVn8qeL2l58NdvKYx5qtp9H/NEc3TkLEcp\njLt0dN2lMOY3SbrZOTdG0s2SHgnafR/zVHV79Zp+LDM8Zyh+3vp1M2uTNFrSJjM71Tn3X+dcpyQ5\n59ZKGmLBBc2+cM6975zrds7FJP1en01l71T8uqYeo+XZtGCq2oOp/Y+C5Y2KX9NwZuF6mnM7Ja0M\nprM3SIpJOkklMOZKUXsJjLkkycwqJM2S9FRCs/fjnqzuEhnz6yWtDJZXqHT+f09at2+v6RkHHudc\nq3NupHOu1jlXq/gTYbJzbo+ZnRr89afgKu8ySR/ltMcF1uu87Tcl9Vzp/qykb5tZpZmNkzRe0oZ8\n928gpardzE42s/Jg+XTFa/93/ns4YFZJukySzOxMSSFJH6oExlwpai+BMe8xQ9LbzrmdCW2lMO5H\n1V0iY75L0iXB8mWSek7nPSvpe8HdWlMlhZ1zuwvRwQGStG7vXtP7u6pZ8SnN3ZIOKR5ubuy1vk2f\n3aU1V9JWxe9gaJb0lUJflZ3NI1ntkholtUraovgvwWkJ29+l+F892xRc8T5YH5nULunahHHfJOnq\nQvc/x3WHJD2ueMDbJOmyEhrzpLX7NOapag/a/yjph0m292LcM6m7FMZc0kWSNgY1viKpPtjWJP06\nGPNWSVMK3f881e3VazrvtAwAALzHOy0DAADvEXgAAID3CDwAAMB7BB4AAOA9Ag8AAPAegQcAAHiP\nwAMAALxH4AEAAN77P+xAYSvHUP+3AAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"book_plots.plot_errorbar2()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Sensor A returned a measurement of 160, and sensor B returned 170. The bars are [*error bars*](https://en.wikipedia.org/wiki/Error_bar) - they illustrate the possible range of error for the measurement. Hence, the actual value that A is measuring can be between 157 to 163, and B is measuring a value between 161 to 179.\n",
"\n",
"I did not define it at the time, but this is a [*uniform distribution*](https://en.wikipedia.org/wiki/Uniform_distribution_(continuous)). A uniform distribution assigns equal probability to any event in the range. According to this model it is equally likely for sensor A to read 157, 160, or 163. Any value outside these ranges have 0 probability. \n",
"\n",
"We can model this situation with Gaussians. I'll use $\\mathcal{N}(160, 3^2)$ for sensor A, and $\\mathcal{N}(170, 9^2)$ for sensor B. I've plotted these below with the uniform distribution error bars for comparison."
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"scrolled": true
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAh0AAADDCAYAAAAmy6ORAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzt3Xd8VFXawPHfkx4SCITea+hEOqJ0\nFGkWFDWICFbclV3dXXdXX8W67K66rmtdy2JBMSiKCtJUEESkhZ5AgEgNHQKhpee8f5wJCSEhEzLJ\nnSTPl8/95M695955JiczPHPuueeIMQallFJKqdLm43QASimllKocNOlQSimlVJnQpEMppZRSZUKT\nDqWUUkqVCU06lFJKKVUmNOlQSimlVJlwK+kQkaEisk1EEkTksQL29xORdSKSKSKjC9hfTUT2i8gb\nnghaKaWUUuVPkUmHiPgCbwLDgPbAGBFpn6/YXmAC8Gkhp3keWHr5YSqllFKqvHOnpaMnkGCM2WmM\nSQdmADfmLWCM2W2M2QRk5z9YRLoBdYHvPBCvUkoppcopPzfKNAT25XmcCPRy5+Qi4gO8DIwDBhdU\nJjk5WYdEVUoppSqYsLAwyb/NnZaOiw4C3E0UfgvMM8bsK7KkUkoppSo0d1o6EoHGeR43Ag64ef7e\nQF8R+S0QCgSIyBljzEWdUZVSSilVsbmTdKwBIkSkObAfiALucOfkxpixOesiMgHofqmEIywszJ3T\nVjoxMTEAdO/e3eFIVF5aL95H68Q7ab14n9Kqk+Tk5EvuL/LyijEmE5gELAS2Ap8bY+JE5DkRuQFA\nRHqISCJwK/COiMSVOHKllFJKVSjutHRgjJkHzMu37ak862uwl10udY4PgQ+LHaFSSimlKgS3kg6l\nlFJKlQ1jDElJSWRnXzQKhceEhoYCcPTo0cs+h4+PD+Hh4YgUdL9JwTTpUOoyZGVnkZSWhI/4YIwp\n1ptOKaUuJSkpiZCQEIKCgkrtOapUqQJASEjIZZ8jNTWVpKQkatas6fYxmnQoVQyLdi7ijTVv8MPO\nHziTfgaAWstrMSJiBA/3epgu9bs4HKFSqrzLzs4u1YTDU4KCgjh9+nSxjtGkQyk3HD5zmPvm3Me3\n27+lTkgdxkWOIzQllEyTyXH/43y59UumbZzGA90e4OUhLxMScPnfHpRSqqLSpEOpImw9upVrPr6G\npJQkXrr2JX7X83cE+gVecMvZa0Nf47mlz/HKylf4Zd8vzBs7j0bVLtm3WimlKh2d2l6pS1h/cD39\nPuxHtslm1X2rePSqRwn0C7yoXFhQGC9f9zIL7lzA7pO76fdBPw6dOeRAxEop5RlfffUVIkJ8fLzH\nzqlJh1KF2HViF9d8fA3BfsH8NOEnIutGFnnMkJZD+OGuHzhy9gjDpg/jVNqpMohUKaU8Lzo6mj59\n+jBjxgyPnVOTDqUKcC7jHKM+G0W2yWbRXYuIqBnh9rE9G/bky9u+JPZILLfOvJVsU3q3vSmlVGk4\nc+YMy5cvZ+rUqR5NOrRPh1L5GGO4f879bDq8ibl3zC1WwpHjulbX8cawN3hw7oP8e8W/efSqR0sh\nUqVUZTDgwwEePd+SCUuKLPP1118zdOhQWrduTXh4OOvWraNr164lfm5t6VAqn5lbZvLp5k95dsCz\nDIsYdtnneaDbA9zc7mb+b9H/se7gOg9GqJRSpSs6OpqoqCgAoqKiiI6O9sh5taVDqTyOnzvOpHmT\n6Fa/G4/3fbxE5xIR3rv+PSITIxn31TjWT1xPgG+AhyJVSlUW7rRMeNLx48dZvHgxsbGxiAhZWVmI\nCC+++GKJB0LUlg6l8nhk4SOcSD3B1Bum4udT8pw8PDict0e+zZajW3ht1WseiFAppUrXF198wV13\n3cWePXvYvXs3+/bto3nz5vz8888lPrcmHUq5/Lz3Zz7Z9AmPXf0YV9S7wmPnHdl6JCNbj+TZpc+y\n/9R+j51XKaVKQ3R0NKNGjbpg2y233MKnn35a4nO7lXSIyFAR2SYiCSLyWAH7+4nIOhHJFJHRebZ3\nFpEVIhInIptE5PYSR6xUKTDG8Kfv/kSDqg14rM9Ff+Il9urQV8nIyuDP3//Z4+dWSilPWrJkCUOH\nDr1g2+9//3v++9//lvjcRSYdIuILvAkMA9oDY0Skfb5ie4EJQP406BxwlzGmAzAU+I+IVC9p0Ep5\n2udxn7N6/2qmDJpSKkOYt6jRgkevepTo2GjWH1zv8fMrpVR54E5LR08gwRiz0xiTDswAbsxbwBiz\n2xizCcjOt327MWaHa/0AcASo7ZHIlfKQ9Kx0Hlv0GFfUvYJxkeNK7Xn+fNWfqRFUg8k/Ti6151BK\nKW/mTk+5hsC+PI8TgV7FfSIR6QkEAL8WViZnLgtVMP39lI6v937N7pO7ebXHq6xfV/xWiOLUy9hm\nY3kj/g2mfjeVK8I9129EXUjfK95J68U9oaGh56eeL21nz54t0fHHjx9nz5495x9HRFx6XCN3WjoK\nuj/GFCcoEakPfAzcbYwOz6i8R2Z2Jh8kfED7sPb0rt271J/vtqa3ER4Yztvb3y7151JKKW/jTktH\nItA4z+NGwAF3n0BEqgFzgSeNMSsvVbZ79+7unrZSyTubqfKsDzd8yIGUA7xz0zv0aN2jWMdebr1M\nZjJ/WPgHMutlcmWjK4t1rLo0fa94J62X4jl69CghIZ7vW5ZXTgtHSZ+nZs2atG3b9vzj5OTkS5Z3\np6VjDRAhIs1FJACIAma7E4yr/FfANGPMTHeOUaqsZGVn8fdlf6dLvS6MiBhRZs97X9f7qBFUgxeW\nv1Bmz6mUUt6gyKTDGJMJTAIWAluBz40xcSLynIjcACAiPUQkEbgVeEdE4lyH3wb0AyaIyAbX0rlU\nXolSxfTNtm/YkbSD/+v7fyUeZa84QgNCmdRzEt/Ef0P8Mc9NGa2UUp7i6+tL586dueKKK+jatSu/\n/PKLR87r1jgdxph5xpjWxpiWxpgprm1PGWNmu9bXGGMaGWNCjDE1XbfIYoz5xBjjb4zpnGfZ4JHI\nlSqhV1a+QvPqzRnVdlTRhT3sdz1/R5BfEC8tf6nMn1sppYoSHBzMhg0b2LhxI//4xz94/PGSTQuR\nQ0ckVZXS6v2r+Xnvzzzc62F8fXzL/Plrh9Tm7s5388nmTzhy9kiZP79SSrnr1KlT1KhRwyPn0gnf\nVKX0yspXqBZYjXu63ONYDJN6TuKtmLeYum5qiSeXU0pVXAMGePZ8S5YUXSYlJYXOnTuTmprKwYMH\nWbx4sUeeW1s6VKWz/9R+ZsbN5L4u91E1sKpjcbSr3Y5BzQfx9tq3ycrOciwOpZTKL+fySnx8PAsW\nLOCuu+7CmGKNllEgbelQlc7U9VPJMlk81PMhp0PhoR4Pccvnt/Dt9m+5se2NRR+glKp03GmZKE29\ne/fm2LFjHD16lDp16pToXNrSoSqVzOxM3lv3HkNaDqFFjRZOh8MNbW6gUbVGvLnmTadDUUqpAsXH\nx5OVlUXNmjVLfC5t6VCVyvwd80k8lcirQ191OhQA/Hz8mNhtIpN/nMz249tpXbO10yEppdT5Ph1g\nZ+H+6KOP8PUtead7TTpUpfLO2neoF1qP61tf73Qo593f9X6eW/ocb615i/8M/Y/T4SilFFlZpdPP\nTC+vqEpjb/Je5ifM594u9+Lv6+90OOfVDa3L6Paj+XDDh6RkpDgdjlJKlRpNOlSl8b91/8MYw/1d\n73c6lIvc1/U+ktOS+Sr+K6dDUUqpUqNJh6oUMrMzmbp+KsMihtG0elOnw7nIgGYDaFa9GR9s+MDp\nUJRSqtRo0qEqhQUJCzhw+oBXtnIA+IgPE66YwKKdi9hzco/T4SilHOTj40NqaqrTYRQpNTUVH5/i\npRHakVRVCh9t/IhaVWoxPGK406EUanzn8Tyz9Bk+2vgRT/V/yulwlFIOCQ8PJykpidOnT5facxw/\nfhygRLfB+vj4EB4eXqxjNOlQFd6JlBPM3jabB7s9SIBvgNPhFKpZ9WYMbj6YDzd8yJP9nsRHtCFS\nqcpIRDwyJsal7NljW1Tbtm1bqs+Tn36qqQrvs7jPSM9KZ3zn8U6HUqS7O9/NrpO7+GnPT06HopRS\nHudW0iEiQ0Vkm4gkiMhjBezvJyLrRCRTREbn2zdeRHa4Fu//1FcVzkcbP6JjnY50qdfF6VCKNKrd\nKKoFVtMOpUqpCqnIpENEfIE3gWFAe2CMiLTPV2wvMAH4NN+x4cDTQC+gJ/C0iHhmflyl3LDt2DZW\nJq5k/BXjERGnwylSFf8qjOk4hplxMzmTfsbpcJRSyqPc6dPRE0gwxuwEEJEZwI3AlpwCxpjdrn3Z\n+Y69DvjeGJPk2v89MBSILuiJYmJiihl+5aK/n+J7K/4tfPChY3bHUvv9efq8PQJ68E7mO/x73r8Z\n3sh7O756M32veCetF+/j6TqJiIi45H53Lq80BPbleZzo2uaOkhyrVIlkm2zm7Z9Hr9q9qBVUy+lw\n3NapRifqB9dnwYEFToeilFIe5U5LR0Ft0sbN8xfr2O7du7t52solJxPV30/xLNm9hMOph3ll+Ct0\n7+T5311p1suEUxN4cfmLNGnXhDohJZtKujLR94p30nrxPqVVJ8nJyZfc705LRyLQOM/jRsABN5+/\nJMcqVSIzYmdQxb8KN7S5welQim1sp7FkmSw+j/vc6VCUUspj3Ek61gARItJcRAKAKGC2m+dfCAwR\nkRquDqRDXNuUKlUZWRl8seULbmhzAyEBIU6HU2wd6nQgsm4k0zdPdzoUpZTymCKTDmNMJjAJmyxs\nBT43xsSJyHMicgOAiPQQkUTgVuAdEYlzHZsEPI9NXNYAz+V0KlWqNC3atYjjKceJ6hDldCiXbWyn\nsaxMXMnOEzudDkUppTzCrXE6jDHzjDGtjTEtjTFTXNueMsbMdq2vMcY0MsaEGGNqGmM65Dn2fWNM\nK9eigw+oMjEjdgZhgWEMbTXU6VAuW1RHmzB9uvnTIkoqpVT5oCOSqgonNTOVr+K/YlS7UQT6BTod\nzmVrEtaEfk37MX3zdIxxt++2Ukp5L006VIWzIGEBp9JOletLKznGdhpL/LF4Nhza4HQoSilVYpp0\nqApnRuwMalWpxaDmg5wOpcRGtx+Nv4+/dihVSlUImnSoCuVs+lnmbJ/D6Haj8ff1dzqcEgsPDmdY\nxDCiY6PJys5yOhyllCoRTTpUhTJn+xzOZZw73wmzIrij4x0cOH2AZXuXOR2KUkqViCYdqkKZETuD\nBlUb0KdJH6dD8ZiRrUcS4h/CjNgZToeilFIlokmHqjBOpp5kfsJ8bmt/G74+vk6H4zEhASHc0OYG\nvtjyBRlZGU6Ho5RSl02TDlVhfB3/NelZ6RXq0kqOMR3HcDzlOD/s/MHpUJRS6rJp0qEqjBmxM2hW\nvRk9G/Z0OhSPG9JyCNWDqhMdG+10KEopddk06VAVwtGzR/lh5w9EdYhCpKDJjcu3QL9Abml3C1/H\nf01KRorT4Sil1GXRpENVCF9u/ZIsk1UhL63kiOoYxen008zbMc/pUJRS6rJo0qEqhM/iPqNtrbZE\n1o10OpRSM7DZQOqG1GVGnN7FopQqnzTpUOXegdMHWLp7aYW9tJLD18eXW9vfyrfbv+VU2imnw1FK\nqWJzK+kQkaEisk1EEkTksQL2B4rIZ679q0SkmWu7v4h8JCKbRWSriDzu2fCVgplxMzEYbu94u9Oh\nlLoxncaQmpnK7G2znQ5FKaWKrcikQ0R8gTeBYUB7YIyItM9X7F7ghDGmFfAK8IJr+61AoDGmE9AN\nmJiTkCjlKTPiZtC5Xmfa1mrrdCil7spGV9IkrInexaKUKpfcaenoCSQYY3YaY9KBGcCN+crcCHzk\nWv8CGCy2ndsAISLiBwQD6YC2CyuP2XViFysTV1aIGWXd4SM+RHWI4rtfv+P4ueNOh6OUUsXi50aZ\nhsC+PI8TgV6FlTHGZIpIMlATm4DcCBwEqgB/MMYkFfZEMTEx7kdeCenv52If/Wpz3XbZ7Rz7/ZT1\n80b6RJKZncnLC17m5iY3l+lzlxf6XvFOWi/ex9N1EhERccn97rR0FNQzz7hZpieQBTQAmgN/EpEW\nbjynUm757sB3dKreiQZVGjgdSplpXa01TUOa8v2B750ORSmlisWdlo5EoHGex42AA4WUSXRdSgkD\nkoA7gAXGmAzgiIgsB7oDOwt6ou7duxcv+koiJxPV38+F4o/Fs33udv5z3X8c+d04WS8Tzk7guaXP\n0aBNAxpUrTwJV1H0veKdtF68T2nVSXJy8iX3u9PSsQaIEJHmIhIARAH5u87PBsa71kcDi40xBtgL\nDBIrBLgSiC9G/EoV6rPYzxCEWzvc6nQoZS6qYxQGw8y4mU6HopRSbisy6TDGZAKTgIXAVuBzY0yc\niDwnIje4ik0FaopIAvBHIOe22jeBUCAWm7x8YIzZ5OHXoCohYwwz4mbQv1n/SvlNv22ttnSu11nv\nYlFKlSvuXF7BGDMPmJdv21N51lOxt8fmP+5MQduVKqmNhzcSfyyeR3o94nQojhnTcQx//eGv7Dqx\ni+Y1mjsdjlJKFUlHJFXl0ozYGfj5+HFL+1ucDsUxt3ewg6HNiNVh0ZVS5YMmHarcMcYwI3YG17a4\nllpVajkdjmOaVm/KVY2v0rlYlFLlhiYdqtxZkbiCPcl7GNNxjNOhOC6qQxSbDm9iy9EtToeilFJF\n0qRDlTvRm6MJ8gvixrb5B8atfG7tcCs+4qOXWJRS5YImHapcyczO5PMtnzMiYgTVAqs5HY7j6oXW\nY2CzgUTHRmPvUldKKe+lSYcqV5bsXsKRs0f00koeYzqOISEpgXUH1zkdilJKXZImHapcid4cTdWA\nqgyPGO50KF7j5nY34+/jr2N2KKW8niYdqtxIy0zjy61fclPbmwj2D3Y6HK9RI7gGQ1sN5bO4z8g2\n2U6Ho5RShdKkQ5UbC39dSHJasl5aKUBUxygSTyWyfO9yp0NRSqlCadKhyo3o2GhqBtfkmhbXOB2K\n17mhzQ0E+wXrXSxKKa+mSYcqF86mn2X2ttnc2v5W/H39nQ7H64QGhHJ9m+uZuWUmmdmZToejlFIF\n0qRDlQuzt83mXMY5ojpGOR2K1xrTcQxHzx1l8a7FToeilFIF0qRDlQvRsdE0rNqQvk37Oh2K1xra\naijVAqvpXSxKKa/lVtIhIkNFZJuIJIjIYwXsDxSRz1z7V4lIszz7IkVkhYjEichmEQnyXPiqMjiR\ncoIFCQu4vcPt+IjmyYUJ8gvi5nY3M2vrLNIy05wORymlLlLkJ7iI+AJvAsOA9sAYEWmfr9i9wAlj\nTCvgFeAF17F+wCfAg8aYDsAAIMNj0atK4cutX5KRnaGXVtwQ1SGKU2mnmJ8w3+lQlFLqIu58bewJ\nJBhjdhpj0oEZQP5JL24EPnKtfwEMFhEBhgCbjDEbAYwxx40xWZ4JXVUW0zZOo03NNnRv0N3pULze\n4BaDqVWllt7FopTySn5ulGkI7MvzOBHoVVgZY0ymiCQDNYHWgBGRhUBtYIYx5sXCnigmJqYYoVc+\nlfH3k3gukWV7l/HbNr9l7dq1TodTIG+rl/61+vP11q/5aeVPVPGr4nQ4jvC2OlGW1ov38XSdRERE\nXHK/Oy0dUsC2/DNLFVbGD+gDjHX9HCUig914TqUAmL9/PoIwrOEwp0MpN65reB1p2WksO7zM6VCU\nUuoC7rR0JAKN8zxuBBwopEyiqx9HGJDk2r7UGHMMQETmAV2BRQU9Uffu2nxekJxMtLL9fowxRP0S\nxcDmAxnZd6TT4VzEW+ulq+nKc3HPsTplNU90f8LpcMqUt9ZJZaf14n1Kq06Sk5Mvud+dlo41QISI\nNBeRACAKmJ2vzGxgvGt9NLDY2Hm2FwKRIlLFlYz0B7YUI35Vif2y7xd+PfErd0Xe5XQo5YqP+HB7\nh9uZv2M+J1JOOB2OUkqdV2TSYYzJBCZhE4itwOfGmDgReU5EbnAVmwrUFJEE4I/AY65jTwD/xiYu\nG4B1xpi5nn8ZqiKatnEaVfyrcHO7m50OpdwZ03EMGdkZfB73udOhKKXUee5cXsEYMw+Yl2/bU3nW\nU4FbCzn2E+xts0q5LTUzlc/iPuPmdjdTNbCq0+GUO13rd6VjnY58sOEDJnaf6HQ4SikF6IikykvN\n2TaH5LRkvbRymUSEuzvfzar9q9h6dKvT4SilFKBJh/JS0zZNo2HVhgxqPsjpUMqtOyPvxM/Hjw82\nfOB0KEopBWjSobzQkbNHmL9jPndG3omvj6/T4ZRbdULqMCJiBB9v+lhnnlVKeQVNOpTXmb5pOlkm\ni3GR45wOpdy7u/PdHDpziAUJC5wORSmlNOlQ3sUYw3vr3qNXw150qNPB6XDKveERw6ldpbZeYlFK\neQVNOpRX+WXfL2w9tpX7u97vdCgVgr+vP3dG3smcbXM4evao0+EopSo5TTqUV3lv3XtUDajK7R1v\ndzqUCuOeLveQkZ3Bx5s+djoUpVQlp0mH8honU0/yedzn3NHpDkIDQt06Rp4V5NmCpv6puIr7mjvW\n6chVja/i7Zi3sQMFK6WUMzTpUF5j+qbppGSm6KWVUvBgtwfZkbSDH3f/6HQoSqlKTJMO5RVyOpB2\nqdeFbg26OR1OhTO6/WjCg8N5Z+07ToeilKrENOlQXiHmQAwbD2/kgW4POB1KhRTsH8z4K8Yza+ss\nDp857HQ4SqlKyq25V5Qqbf+N+S9V/KswpuMYp0OpsCZ2m8grK1/h/fXv83jfx50Op9iMgXPn4PRp\nSE3NXdLS7M/0dNi+vSo+PraMj49dfH0hOBhCQuxSpYr96e8PUrm6AynlOE06lOOOnj3Kp5s/5Z4u\n9xAWFOZ0OBVWm1ptGNhsIO+ue5e/9vkrPuJ8Q2dGBhw4kLscPJi7fuQInDhx4ZKRUdQZ27j93H5+\nULMm1KqV+zNnadAAGje2S6NGdpsmKEqVnCYdynH/W/c/0rLSmNRzktOhVHgPdn+Q27+4nQUJCxge\nMbxMnjMlBeLjYccO+PVX2Lkzd9m7F7KzLyzv5wf16kHdulCjhv2Pv0aN3KVaNdtyERgIQUG5i78/\nbN0ajzHQunVbsrNt60hmpo3h7NncJafFJCkJjh2D48dtjDnrWVkXxhQUZJOPFi0gIuLCpVkz+9xK\nqaK5lXSIyFDgVcAX+J8x5p/59gcC04BuwHHgdmPM7jz7mwBbgGeMMf/yTOiqIsjMzuStmLe4psU1\ntK/d3ulw3DZ983QeXfwoh1MO0+TnJkwZPIWxncY6HVaRbmp7Ew2qNuA/K//j8aQjLc3+xx0Xd+Gy\nc+eFiUWdOtCyJVx9NYwbB02b2paFBg2gfn3bquBzmY0wQUFnAOje/fJfR1aWbWXZtw8SE3N/7t1r\nk6aVK+HUqdzyfn42+YiMhE6d7M/ISGjSRFtHlMqvyKRDRHyBN4FrgURgjYjMNsZsyVPsXuCEMaaV\niEQBLwB5R3d6BZjvubBVRfF1/NcknkrkzeFvOh2K26Zvns4Dcx7gXMY5APYk7+GBObYDrLcnHgG+\nATzU4yGeWPwEsUdi6Vin42WdJz0dNm+GtWshJsb+3Lw59/JHzn/EnTvD2LHQoQO0aWNbCkLdG4LF\nMb6+NvmpXx969rx4vzFw9KhtuclZ4uJg9Wr47LPcctWq2SSkSxd7np497e/kchMqpSoCKWqwIBHp\njW2huM71+HEAY8w/8pRZ6CqzQkT8gENAbWOMEZGbgKuBs8CZ/C0dycnJ5wPYsWOHZ16VKjceWPEA\nh1MOM2vgLHyl+DPK9pjbA4Cu4V09HVqhNp/cTEb2xZ0L/H386VS9U6k//7qkdQCsGbHmso4/mX6S\nkYtGMrThUJ6MfNKtYw4dCmDDhlA2bAhly5YQEhKCyciw/3tWq5ZJu3ZnadfuHBER52jRIoWmTdPw\n9698A5GdOePDzp3BJCQEs2NHFRISgtm2rQopKfZvu2rVTNq3P0uHDmdp3/4snTqdJTxcZwBWFUdE\nRMT59bCwsIva+ty5vNIQ2JfncSLQq7AyxphMEUkGaopICvBXbCvJo8WKXFV425K3sT5pPY+0e+Sy\nEg6nFJRwXGq7t6keUJ0RjUbwbeK3PNTmIWoE1rhgf1YW7NwZzIYNoWzcaBONw4cDAQgJyaJdu7OM\nGXOYdu3O0a7dWRo0SNfLCC6hodlERp4lMvLs+W1ZWbBrVxBbtoQQFxdCbGwoH31Un6ws+0tr2jSF\nrl3P0KXLabp0OU29euXj70ipy+FO0lHQx0n+rzCFlXkWeMUYc0bc+FTqXpILsRVYTEwMUPF+P69/\n/TpV/Kvw1PVPUSO4RtEHFGSu/bH2d2s9F1gRmv2nGXuS91y0vWlY0zKJI2cI9JL8Pfyt6d+Y9dYs\nVmau5Inek4mNhR9+gEWLYPlySE625Ro0gAEDoE8fu3Tq5IuvbzWgWslfSCnw1vdKr3xf086dg3Xr\n4Jdf4Kefglm8OJivvqoN2I6p/frZpX9/2/+lvCd13lovlVlp1UlyzodHIdxJOhKBxnkeNwIOFFIm\n0XV5JQxIwraIjBaRF4HqQLaIpBpj3nAvfFVR7Tm5h083f8qkHpMuP+FwyJTBUy7o0wFQxb8KUwZP\ncTCq4gk+246Oif9myiPNeH2/4ehR+79a69Zw++25SUazZuX/PzxvVKVK7u/4L3+xrSGbN8NPP9ll\n/nyYNs2Wbd4crr0WhgyBQYPsHTxKlVfuJB1rgAgRaQ7sB6KAO/KVmQ2MB1YAo4HFxnYW6ZtTQESe\nwfbp0IRD8e8V/wbgj73/6HAkxZfTWfTR+a67V8K8/+6VM2dsK8b8+bZF49dfAf4AoQdp1e9XXrqt\nFYMH29tCVdnz9bWdbjt3ht//3nZWjY+HxYvh++8hOhrefdd2Qu3RwyYh114LV14JAQFOR6+U+4pM\nOlx9NCYBC7G3zL5vjIkTkeeAGGPMbGAq8LGIJGBbOKJKM2hVvh07d4z31r3HnZF30jiscdEHeKGx\nncbSJs0OROWtTcbbt8O8eXZZutTecRIaCgMH2v/YBg82jF02nGMZZ7lz3FZ8fcpPv5qKTgTatbPL\nQw/Zu4JWr7YJyHffwT/+AX/7G1StaltARo6E4cPt7chKeTO3xukwxswD5uXb9lSe9VTg1iLO8cxl\nxKcqoNdXvU5KZgp/ueovTodfdMkxAAAbJ0lEQVRSoaSm2uQiJ9FISLDb27WzScbw4XZsjNxvxsJk\neZLRM0czc8tMojrqdwVv5e9v6+7qq+GZZ2yfmx9/tC1Xc+fCl1/aRKVnTxgxwiYhnTvrpTHlfXRE\nUlWmzqSf4fXVr3NT25toV7ud0+GUe8nJ8O23MGsWLFhgOygGB9tr/3/4AwwbZvsEFGZUu1G0r92e\nKcumcFuH27xiaHRVtLAwuOkmuxgDGzfav4Nvv4Wnn4annoKGDW0CMmIEDB5s55tRymmadKgy9U7M\nO5xIPcFfr/6r06GUe8OH2/4ZGRn2LpMJE+w33AEDbOLhDh/x4Ym+TzB21li+if+GUe1GlWbIqhSI\n5PYHefJJOHw4twUkpy9IUJDtAzJqFFx/vR31VSkn6NcaVWZOp53mheUvMLj5YK5sdKXT4ZQriYnw\n+uu2P0aO+Hh4+GF72+W+ffDmm7Zlw92EI8dtHW6jVXgr/rbsbxQ1WKDyfnXr2gR05kw7l8wPP8AD\nD8CGDXDPPXZem0GD7N/Tvn1Fnk4pj9KkQ5WZV1e9ytFzR5kyqPzcWuqkhAR48UV7h0LjxrZfxtGj\nuft//RVeegl69y7Z0Np+Pn483udx1h1cx7wd84o+QJUbAQH20sqrr8KePXbI+sces60hv/+9nR+m\nRw/4+99h61ano1WVgSYdqkwkpSTxr1/+xQ1tbqBXo/wD2l4+87TBPF0xvp0bY8dqePZZO2FYRAT8\n9a92DIe//922bMTG5r5mT3YSHBc5jhY1WvB/i/+PrOysog9Q5Y4IdOtm73qJi7N/T//4h01Yn3gC\n2reHtm3h8cftnTLa6KVKgyYdqky8tPwlTqWd4vmBzzsdilcxxn7AP/aYHZgrMtImHdWrwyuvwO7d\nsGaN/Y+gTZvSi8Pf158pg6aw6fAmpm+eXnpPpLxGmzb2727VKnuZ5Y037DgtL71kR1Bt0sRevlu6\n1Ca+SnmCJh2q1B06c4hXV73KmE5jiKwb6XQ4jsvKsh/kOc3bvXrByy/bGVjffhsOHrSjUj7yiJ32\nvazc1uE2utXvxuQfJ5OamVp2T6wc16iRHQ/khx/gyBH48EPo2hXeecd2TK5f3/YLWbjQjvei1OXS\npEOVuueXPk96VjrPDnjW6VAck55ub2m9/377AT5gALz3nm3unjbNftAvXAgTJ9qOgE7wER9evPZF\n9ibv5Y3VOnBwZRUeDuPHwzff2I6on31mO55GR8PQoXYAsnHj4Ouv7S3aShWH3jKrSlXskVjeWfsO\nE7tNpFV4K6fDKVPnztlEY9YsO35CcrIdEXTkSLjlFvsBHhrqdJQXGtR8EENbDeXvy/7OvV3uLXfz\n4ijPCg2F226zS2qqHRF11iybkHzyiZ1DZvhwuPlmOx5INe+cB1B5EW3pUKXGGMMjCx6hWmA1nhv4\nnNPhlInkZJg+3SYVtWrZn/Pn2w/lb7+1d59ER8Po0d6XcOR44ZoXOJl6kmeXVt6WKXWxoCA7xscH\nH9i7X77/3raI/Pwz3HEH1K5tE+r337ctJEoVRFs6VKmZvW02i3Yt4rWhr1GzSk2nwyk1R4/ab36z\nZuUO1lW/Ptx9t006+vUDv3L0TousG8mD3R/k9dWvM/6K8XSp38XpkJSX8feHa66xyxtvwIoV9u//\nyy/toGS+vtC/v022R+l4cyoPcXowoOTk5PMBhIWFORmK14qJiQG8d2KxgpxNP0uHtzoQEhDChokb\n8Pf1dzokj9q3D157bS8//lid9eurkZ1thxu/5Rb7QdurV8nGznDaydSTtHmjDc2rN+eXe38pN8Oj\nl8f3SkViDKxfn5uAxMfb7Z06nWHQoBM8/HDjSw7Lr8pOab1XkpOTz6+HhYVddGN/+fgkUeXOM0ue\nYU/yHt4Z+U6FSTji4+14GT162LtO/vWvJiQl+fPEE/aDtrDBukTK38Rb1YOq8/KQl1m1fxXvrX3P\n6XCUl8r/ty1i73r529/sYGNbtsDzz0N6uvDqq41p0SJ3/5YtzsWtnONWS4eIDAVexU5t/z9jzD/z\n7Q8EpgHdgOPA7caY3SJyLfBPIABIB/5sjFmc91ht6Shaefv2tuHQBrq/2517utzDu9e/63Q4l80Y\nWLsWvvrKfnPL+dbWs6dtMm7VajPNmqUVWS85H8rlbbAlYwyDpw1m/aH1xD8UT91Qh26rKYby9l4p\n79z9246JiWH//gASEiKZNcsO3Q92MLKbb7ZL167lLzkvz7y2pUNEfIE3gWFAe2CMiLTPV+xe4IQx\nphXwCvCCa/sx4HpjTCdgPPDxZbwGVY6kZ6Vzzzf3ULNKTV645oWiD/AymZmwZIkdFKlpU9uq8cIL\ndkK1nLkqVq2ygyo1a5bmdLilSkR4a8RbnE0/y+/m/07nZVEl0rBhOn/6EyxfDvv327mCGja076/u\n3e3lyT/+0XZMzc52OlpVWty5vNITSDDG7DTGpAMzgBvzlbkR+Mi1/gUwWETEGLPeGHPAtT0OCHK1\niqgK6vmlz7P+0HreHfluubndMiXF3lly7712MqyBA+3MnF265PbUX7QIJk2ygyhVJm1rteXZAc8y\nc8tMZsTOcDocVUE0aAC//a3teH3okL3jpVMnm4j07WuTkd/8Jrdjtqo4iry8IiKjgaHGmPtcj8cB\nvYwxk/KUiXWVSXQ9/tVV5li+8zxojLkm7/nzXl7ZsWNHyV+RcszmE5u575f7GN5oOE9f8bTT4VzS\nkSP+/PxzGMuWVWfNmqqkpfkSEpJJnz7JDBx4kt69k6lSxTNft3r0sM2Xa9bEeOR8ZS0zO5MHVjzA\n7jO7mdF/BnWC6jgdkvISnv7bPnPGh19+CWPx4hosXx5Gaqov1apl0rfvSQYOPEnPnqcIDtZmEG8W\nERFxfr2gyyvu3MhX0FW2/JnKJcuISAfsJZchbjyfKodOZ5xm8obJ1Amuw5/a/8npcC6SnQ3x8VX4\n+efqLFsWRnx8CAANGqRx003H6NMnmW7dTuPvr5cQ8vPz8ePZzs9yx7I7mLx+Mm/2ehM/n3J0D7Aq\nN0JDsxky5ARDhpwgNVVYtSqMxYurs3RpdebOrYW/fzbdup2mT59krr76JI0a6Zjs5Y07LR29gWeM\nMde5Hj8OYIz5R54yC11lVoiIH3AIqG2MMSLSCFgM3G2MWZ7//NqRtGje3jnOGMMtn9/CnO1zWDph\nKVc1vsrpkAA7IugPP8CcOXbsgIMH7V0lvXvbQYyuv97OrHm5ndfcrZfy2pE0v483fsxdX9/FE32f\n4G+D/uZ0OAXy9vdKRVOcjqRw+fWSnm77esyda5dt2+z2tm3tSKgjRkCfPnb8EOUepzqSuvN1ZQ0Q\nISLNgf1AFHBHvjKzsR1FVwCjgcWuhKM6MBd4vKCEQ1UMr6x8ha/iv+LlIS87mnAYY6fsXrjQLj/9\nBGlpULWqHXJ85Eg7ZHOtWo6FWK6Nu2IcP+35iSnLpnBV46sYHjHc6ZAuMH06PPpoJw4fDqBJE5gy\nBcaOdToq5QkBAXb+l0GD7OSICQm5Ccjrr9tt1arBkCE2ARk2zLk5jNSlFZl0GGMyRWQSsBB7y+z7\nxpg4EXkOiDHGzAamAh+LSAKQhE1MACYBrYDJIjLZtW2IMeaIp1+Icsb8HfP58/d/ZlTbUfzhyj+U\n+fMnJdnWjAUL4LvvbK94gHbtbEe0kSNtx7SAgDIPrUJ6bdhrxByMYcyXY1hx7wra185/I5szpk+3\ns6CeO2f7qe/ZYx+DJh4VUatW9g6zhx+GM2fsZ8DcuTBvHnzxhS3TuTNce61d+vSB4GBnY1aWjkha\nDnhrk3HckTh6T+1Nixot+PmenwkNKP3JRDIyYM2a3NaMNWtsf43q1e2QzNddZ5fGjUs9lGJfXunf\nv7QjKhupgftY360nPtnBdFm7ioCM2k6HxMqVtlUrv8BAuPLKso+nsli61P4s7csr7jIGNmywX0K+\n/95eksnIsPPG9O2bm4RERpbvEYM9wZsvryh1kb3Jexn+6XBCAkKYM2ZOqSUcWVl2tM8ff7TLsmX2\nm42Pjx2ka/Jkm2T06FG+5jcpz4LSGtNh8zds7NKf2MiRRG74Ab+sqo7GVFDCcantqmISsbe6d+kC\njz8OZ8/ay6zff2+Xv/zFlqtTx35JufZaGDAAmjVzMurKRT+mVbEdOXuEaz++lpOpJ1kyfgmNwzzX\nrJCdDZs3w+LFNsn46Sc7cyvYTmPjxuVe2w0P99jTloklS5yOwJN6MnvbZ9z82c0Ejr+JuXfMJcgv\nyLFomjWzl1Tya9q0ov3evYu3jyAaEmL7dwwbZh8fOGAvxeQkIZ9+arc3aWJbIvv3t0lIixbe/9rK\nK006VLHkJBz7kvfx3bjvSjwDaVqaHWp8+XLbFLp8ORw/bve1agW33WYH6xowwM7cqrzHDW1u4MOb\nPmTcV+O45fNb+OLWLwj2d+bC+ZQpOX06crdVqWK3K5WjQQO46y675HQ8X7rUJqYLFsDHrjGzGzbM\nTUL694fWrTUJ8RRNOpTb9p/az+Bpg9mbvJdvor6hT5M+xT7H8eN23oWcJCMmJrcJPCLC3sY6cKBd\nyqJfhiqZOyPvJCUjhYnfTmTEpyOYPWZ2mfTtyS+ns+ijj6a57l4RvXtFXZIIdOxol4cesklIfLxN\nQJYuta2tOS0htWrZvkG9e8NVV9nLuSEhjoZfbmnSodyy+fBmRkaP5ETKCRbeuZC+TfsWeUx6Omza\nZDt7rlljO/tt3Wr3+fvbCZ4mTYKrr7ZvZL3FrXy6v9v9BPsHM+HrCQz4cACzx8ymQdUGZR7H2LHQ\nps1mwPs6XSvvJ2Lvesu5880Y2LHDJiArVtjl229tWV9f2xm1d+/cRKR5c20NcYcmHapIc7fPJerL\nKKoFVmPJhCV0rd/1ojJZWXbAnpwEY/Vq2LjRJh5gvyn07Al33mlvX+vRQ29hq0jujLyT6kHVifoi\nil7/68XsqNklvvSmlJNE7GWV1q3h/vvttqQk++VpxQrbYjttGrz1lt0XHg7dul24NGumiUh+mnSo\nQmVmZzJ58WT+ufyfdKnXhTlj5tCwWkNSUiA21iYVOcv69fauEoDQUPuG+/3vbXLRo4e++SqDka1H\n8vM9P3N99PX0ntqb/wz9DxO7TUS04lUFER5uBxgc7hoXLyvLfhauWGH7pq1dC//6l52tOqd83iTk\niitsJ1VfX+deg9M06VAF2nZsGxO+vpuVW/ZxXdVXuerob/jTA/5s3Ajbt+dOPR0aapsZ77rLtmT0\n6AFt2lTuN1Vl1rleZ9Y+sJZxX43jN3N/w3e/fsebw9+kflXtBawqHl9fm0hccUXuttRUewdeThKy\ndq0dMTVnttzgYOjQwc6qm7N07GgvL1eG/FyTDkVmJvz6q+1vsTkug6+WxbMhNg1zdCGkV2Uhdjja\nZs3sm+u223LfaM2b6yA76kJ1Quowf+x8/vXLv3jqx6do92Y7Xrz2Re7reh8+on8sqmILCspt4c2R\nlmYTkU2b7M/YWDt66gcf5JapVcsmIO3b2y9ubdvan40aVazPWE06KomsLNi3zyYXOUtCgu2tvWNH\nbhYO/lC1BrWbHef6kT706Gyz8shI0AFjlbt8xIe/XP0XRrUdxcRvJzLx24m8v/59pgyawuAWg50O\nT6kyFRgI3bvbJa+jR20SkneZNg1On84tExxs+5XkTUQiIuwXvpo1y1/riCYdFYQx9nbUfftg717Y\nufPCBGP37ryJhZ2LpHlzaN06m1ZXbmNj9gz2+M2nY3t/XrnxWa5pcY1jr6WiKe+zy5ZERM0IFt21\niI82fsTkHydzzcfXMLDZQJ7u/zT9mvbT/h7lXGX+2/aE2rVzBzvMYQwcOmQ75ucs8fF2eIEvvsi9\ntA328naLFvazPGfJ+7hKlbJ/TUXRpKMcMAZOn/ZlyxabVOQkFjnrOUtKyoXHhYVBy5Z24qNbbrHr\nOYtPtYPM2DKd11e/zt7kvUSER/Bh3ye4M/JOfH20Q4byHBFhQucJRHWM4t217/L3ZX9nwEcD6FSn\nE7/t8VvGdhpL1UBnh1FXyluI2IEQ69e3gyLmlZZmW6gTEmDXrtwlIcGOsJp3cDywSU3jxnZp1Mgu\nOevZ2b5UrZpVZq8rh0745hBj4NQpOHYMDh+2mW3hSzYZGRde1BOxo+vl/EHlLE2a2J8tWtie03m/\nSB46c4j5O+YTHRvNol2LyDbZ9Gvajz/1/hMjW4/U6+3F5K0T8Xm7cxnniN4czZtr3mT9ofUE+wUz\nPGI4o9uPZkTEiBIlIFon3knrpfQZYy/X7NplW7p37bIt3ImJucuJE7nlX355B/36JXvnhG8iMhR4\nFTu1/f+MMf/Mtz8QmAZ0A44Dtxtjdrv2PQ7cC2QBvzfGLLycF+Kt0tNt8pCznDhh7+U+fjx3Kehx\nUlLubVV5idjJiOrVs0v79mDMYWrWzKRHj8bnk4sGDewAW5dy8PRBVu9fzYrEFXz363esP7QegObV\nm/NE3ycY22ksbWq1KYXfilKFq+JfhXu73ss9Xe5h1f5VfLLpE77c+iVfbv0Sfx9/ejXqxaBmg+jf\nrD9d63elelB1p0NWyuvl/N9Rpw706lVwmTNnYP9+2zIOZ8syvPOKbOkQEV9gO3AtkAisAcYYY7bk\nKfNbINIY86CIRAGjjDG3i0h7IBroCTQAfgBaG2POt+mUVUtHZqZtenJ3SUmxnXnyJhQFLUXNYhkc\nbDv7hIfbn/nXa9bMTTDq1bM9mPPPlnqpbwnGGI6dO8aOpB1sP76dbce2EX88npgDMSSeSgTAz8eP\nqxpfxdCWQ7mu1XV0qddFr6V7gH5785ys7CyW71vO/B3zWbRrEWsPriXb2IvXLWq0oGv9rkTWiaRV\neCtahrekZY2WhAeHX/R3rHXinbRevI83T23fE0gwxuwEEJEZwI3AljxlbgSeca1/Abwh9tPgRmCG\nMSYN2CUiCa7zrSj2K7kMixbZvgznzl3YidJdgYFQrdqFS6NGF2/Lu4SFXZhcFDTqZrbJJj0rnbTM\nNNKz0u16Vhons9I5fMxuS81M5VTaKZLTktm0ZxNnM88yK3kWJ1NPcvDMQQ6ePsjBMwc5dOYQ6Vnp\n58/t7+NPy/CW9Gvaj54NetKzYU861+vs2ERcSrnD18eXfk370a9pPwBOpp5kZeJK1h9cz/pD61l3\ncB1fbPnigmNCA0KpF1qPuiF1qRtal7ohdclIziDEL4T1sp6qgVWpGlD1/M9Av0ACfAMKXPx9/DUR\nV6oMuNPSMRoYaoy5z/V4HNDLGDMpT5lYV5lE1+NfgV7YRGSlMeYT1/apwHxjzPlPj7wtHTt27PDQ\ny7Lmb9zJCx+cQgJSwP8c4p/nZ0C+x/7nIOBc7mO/FPDNwGDI+zvK+9i4/p3fZ8wF2woql22yyTKX\n13nHV3wJ9QulZmBNagXVonZgbWoG1aR2YG0ahzSmSUgT6gfXx89H+weriic1K5X95/aTeC6R/Wf3\ncyDlACfST5CUlsTxtOMkpSWRnJFc9IkK4Su++IovgiAiCIKP+NjHrnUgd5sIPvicL+uJpEUo2TlK\nerwnaPJWPjzZ6Um61/J8y1NERMT59ctt6SjoLyh/plJYGXeOLTURzbPpP+ErwPVmFM5/gORss2+Q\nYCAYodb5D5Dzx8BF2/K+qfJ+QOXfdn4933MH+NhvVvmXAJ8A/MTPrvsGEOoXSohfCKF+oYT6hxLo\nE6hvaFVpBfkG0bJqS1pWbVlomSyTRUpmCmczz3Iu8xznss5xJvMMKZkpZGRnkJGdQabJPL+e/3E2\n2ee/PORc3sk22ee/bOTfn3d7SZmSfjR64JO1pDGU+DWoMlPV35k7xtxJOhKBvJOMNwIOFFImUUT8\ngDAgyc1jz/P0taXudCdqUJRHz+kEvR7qnbRevE9MTAyh/qEM6D3A6VBUHvpe8T5l0aejIO7cI7kG\niBCR5iISAEQBs/OVmQ2Md62PBhYbe21hNhAlIoEi0hyIAFYXI36llFJKVRBFtnQYYzJFZBJ2+g1f\n4H1jTJyIPAfEGGNmA1OBj10dRZOwiQmucp9jO51mAg/lvXNFKaWUUpWHWz0OjTHzgHn5tj2VZz0V\nuLWQY6cAU0oQo1JKKaUqAB2CUimllFJlwquGQVdKKaVUxVDQLbPa0qGUUkqpMqFJh1JKKaXKhOOX\nV5RSSilVOWhLh1JKKaXKhCYdXkJE3heRI655bHK2PSMi+0Vkg2sZnmff4yKSICLbROQ6Z6Ku+Aqq\nF9f237l+93Ei8mKe7VovpayQ98pned4nu0VkQ559WidloJB66SwiK131EiMiPV3bRURec9XLJhHp\n6lzkFVchdXKFiKwQkc0iMkdEquXZV/rvFWOMLl6wAP2ArkBsnm3PAI8WULY9sBEIBJoDvwK+Tr+G\nirgUUi8DgR+AQNfjOlovztZJvv0vA09pnThfL8B3wDDX+nBgSZ71+dj5ua4EVjkdf0VcCqmTNUB/\n1/o9wPOu9TJ5r2hLh5cwxvyEHc3VHTcCM4wxacaYXUAC0LPUgqvECqmX3wD/NMakucoccW3XeikD\nl3qviJ0R8TYg2rVJ66SMFFIvBsj5Jh1G7txbNwLTjLUSqC4i9csm0sqjkDppA/zkWv8euMW1Xibv\nFU06vN8kV/Pj+yJSw7WtIbAvT5lE1zZVNloDfUVklYgsFZEeru1aL87rCxw2xuxwPdY6cdYjwEsi\nsg/4F/C4a7vWi3NigRtc67eSOylrmdSJJh3e7b9AS6AzcBDbbAy2STI/vQ2p7PgBNbDNwn8GPnd9\nw9Z6cd4Ycls5QOvEab8B/mCMaQz8ATtPF2i9OOke4CERWQtUBdJd28ukTtyae0U5wxhzOGddRN4D\nvnU9TCQ3OwVoRG6zpSp9icAsYy+ErhaRbKAWWi+OEhE/4GagW57NWifOGg887FqfCfzPta714hBj\nTDwwBEBEWgMjXLvKpE60pcOL5bvGOQrbLAYwG4gSkUARaQ5EAKvLOr5K7GtgEJx/0wYAx9B6cdo1\nQLwxJjHPNq0TZx0A+rvWBwE5l71mA3e57mK5Ekg2xhx0IsDKRkTquH76AE8Cb7t2lcl7RVs6vISI\nRAMDgFoikgg8DQwQkc7YJq7dwEQAY0yciHwObAEygYeMMVlOxF3RFVIv7wPvu25DSwfGu1o9tF7K\nQEF1YoyZCkRx4aUVfa+UoULeK/cDr7paoVKBB1zF52HvYEkAzgF3l3nAlUAhdRIqIg+5iswCPoCy\ne6/oiKRKKaWUKhN6eUUppZRSZUKTDqWUUkqVCU06lFJKKVUmNOlQSimlVJnQpEMppZRSZUKTDqWU\nUkqVCU06lFJKKVUmNOlQSimlVJn4f5jNvANZCp6IAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"xs = np.arange(145, 190, 0.1)\n",
"ys = [stats.gaussian(x, 160, 3**2) for x in xs]\n",
"plt.plot(xs, ys, label='A', color='g')\n",
"\n",
"ys = [stats.gaussian(x, 170, 9**2) for x in xs]\n",
"plt.plot(xs, ys, label='B', color='b')\n",
"plt.legend();\n",
"plt.errorbar(160, [0.04], xerr=[3], fmt='o', color='g', capthick=2, capsize=10) \n",
"plt.errorbar(170, [0.015], xerr=[9], fmt='o', color='b', capthick=2, capsize=10);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Using a uniform or Gaussian distribution is a modeling choice. Neither exactly describes reality. In most cases the Gaussian distribution is more realistic. Most sensors are more likely to return readings near the value being measured, and unlikely to return a reading far from that value. The Gaussian models this tendency. In contrast the uniform distribution assumes that any measurement within a range is equally likely.\n",
"\n",
"Now let's see the *discrete distribution* used in the discrete Bayes filter. This model divides the range of possible values into discrete ranges and assigns a probability to each bucket. This assignment can be entirely arbitrary so long as the probabilities sum to one.\n",
"\n",
"Let's plot the data for one sensor using a uniform distribution, a Gaussian distribution, and a discrete distribution."
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(150, 170)"
]
},
"execution_count": 19,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAisAAADDCAYAAABDJlHuAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzt3Xd4FOXax/HvnQahBQg1BAwlSFMp\ngYBSFAWCSBPQIL0ooIgFLBw9qIivggcQFI+IKCBIkSJVuoAiLSgdIVQJXcqCEEqS5/0jCyeGhGxg\nk9lyf65rr8zOPjP7ezI7mztTxRiDUkoppZSr8rE6gFJKKaXU7WixopRSSimXpsWKUkoppVyaFitK\nKaWUcmlarCillFLKpWmxopRSSimX5lCxIiJRIrJHRPaJyJtpvF5fRH4TkQQRaZvG6/lE5KiIfOaM\n0EoppZTyHhkWKyLiC4wBmgKVgPYiUilVsz+BrsB36czmfWD1ncdUSimllLdyZMtKLWCfMeaAMeYa\nMA1ombKBMeaQMWYbkJR6YhGpARQFljohr1JKKaW8jJ8DbUoAR1I8jwMiHZm5iPgAw4FOwKNptbHZ\nbHoJXaWUUsrDBAUFibPm5ciWlbTezNEC43lgkTHmSIYtlVJKKaXS4MiWlTigZIrnocAxB+dfB6gn\nIs8DeYAAEfnbGHPLQbpKKaWUUmlxpFjZBISLSGngKBANPOPIzI0xHW4Mi0hXIOJ2hUpQUJAjs/UY\nMTExAERERFicJHt5a79B+w7e13dv7Td4b9+9td8ANpstS+ab4W4gY0wC0BdYAuwGZhhjdorIYBFp\nASAiNUUkDmgHjBWRnVmSVimllFJex5EtKxhjFgGLUo0blGJ4E8m7h243jwnAhEwnVEoppZRX0yvY\nKqWUUsqlabGilFJKKZfm0G4gpZTKiDGGU5dOsePUDnb/tZu4C3Ecu3iMc1fOEX89nrO2s/iJH0Vj\ni1IgZwFC8oZQIm8JKhauSJUiVSiauygiTrssg1LKg2ixopS6Y4fOH2JR7CLWHF7DmsNrOP738Zuv\n+fv4E5I3hIKBBQn0D8RXfLmadJWjF46y/eR2jl08xvWk6zfbF8tTjPr31Kd+qfo8Hv44pQuUtqJL\nSikXpMWKUipTDp47yLfbvmXmrplsP7UdgBJ5S/Bw2MPUKlGL+4rcR6XClSiapyg+8r89zalP50wy\nSZy6dIpdp3ex/eR2Nh7byJrDa5ixcwb8CFWKVKFNxTZ0fqAzZQqUyf6OKqVchhYrSqkMJSQlMGf3\nHD6P+ZxVh1YhCHVL1eU/jf5Di3tbUK5guUzvwvERH4rlKUaxPMVoWLohkLwraf+5/czfM5+5e+Yy\nePVg3lv9HvXvqc/zEc/zZMUn8ff1z4ouKqVcmBYrSql0Xbp2ibGbx/LJ+k84cuEIZQqUYcgjQ+j0\nQCdKBZVy+vuJCOUKluOVOq/wSp1XOGI7wuRtkxn/+3iiZ0UTmi+UlyJfok9EH3IH5Hb6+yulXJOe\nDaSUusWVhCsM/3U4ZUaXof/S/pQtWJa50XPZ23cvb9V/K0sKlbSUDCrJwHoD2fviXua3n0/54PK8\ntuw1So8qzcdrPyb+eny25FBKWUuLFaXUTcYYpu2YRoXPKjBg2QDuL3o/P3f7mZ+6/ESLe1vg6+Nr\nSS4f8eGJ8k+wovMK1nZfS7Xi1Xh9+evc+9m9TNk2hSSTZEkupVT20GJFKQXA9pPbqftNXdrPak/B\nwIKs7LySZZ2WUbdUXauj/cODJR9kScclrO66miK5i9BxTkce+vohtp7YanU0pVQW0WJFKS93+fpl\nXl/2OtXGVmPvmb183eJrYp6L4ZHSj1gd7bbq31Ofjc9uZGKriRw4d4AaX9ZgwNIBXLp2yepoSikn\n02JFKS+2Pm491cZW4+NfP6Zr1a788cIfdKvW7R+nHLsyH/Gh8wOd2f3CbrpX687wdcOpOrYqvx75\n1epoSiknco9vJKWUUyUkJfDvlf/moa8f4krCFZZ3Ws5XLb4iOFew1dHuSMHAgnzZ/Et+6vIT1xOv\nU++begxcPpCEpASroymlnECLFaW8zOHzh2kwoQFDfh5C5wc6s633Nh4t86jVsZzi4bCH2d5nO92q\nduOjtR/RcGJDjl08ZnUspdRd0mJFKS/yY+yPVB1ble0ntzO1zVS+afkNQTmDrI7lVHlz5OWrFl8x\nufVkNh/fTLWx1VhxYIXVsZRSd8GhYkVEokRkj4jsE5E303i9voj8JiIJItI2xfiqIrJORHaKyDYR\nedqZ4ZVSjjHGMGztMJp914yw/GH83ut3oqtEWx0rS3W4vwObnt1EcGAwjSc3ZsiaIXqKs1JuKsNi\nRUR8gTFAU6AS0F5EKqVq9ifQFfgu1fjLQGdjTGUgCvhERPLfbWillOMuX79Mh9kdeGP5G7Sr3I5f\nuv1C2YJlrY6VLSoVrsTGZzcSXSWaf//0b5pPbc7FqxetjqWUyiQxxty+gUgd4F1jTBP784EAxpgP\n02g7AVhgjJmZzry2Am2NMbE3xtlstpsBYmNj05pMKXWHTsSf4LWY19hzYQ997u1D17JdM30PH09g\njGHm4ZkM3zWcMnnLMDJiJEUDi1odSymPEx4efnM4KCjIaV82juwGKgEcSfE8zj4uU0SkFhAA7M/s\ntEqpzNt5fidd1nbhyOUj/CfiP3Qr180rCxVIvudQu7B2jKw5kmOXj9FtbTf22PZYHUsp5SBHbmSY\n1rfb7TfHpJ6BSHHgW6CLMenvNL5x63hvERMTA2i/vUl29X3p/qW8sPQFiuQuwoJnFlCpcOo9t9nP\nFZZ7BBE0qN6AZt81o/fG3sxoO4Om4U2z9D1dod9W8da+e2u/AWw2W5bM15EtK3FAyRTPQwGHzwUU\nkXzAQuBtY8z6zMVTSmXW1O1TafZdM8oVLMfa7mtdolBxJfcXvZ8NPTcQXjCc5lObMzZmrNWRlFIZ\ncKRY2QSEi0hpEQkAooF5jszc3n4OMMkY8/2dx1RKOWL0htE8M/sZHiz5IKu7rqZ43uJWR3JJIXlD\nWNNtDVHloui9sDcfr/3Y6khKqdvIsFgxxiQAfYElwG5ghjFmp4gMFpEWACJSU0TigHbAWBHZaZ/8\nKaA+0FVEttgfVbOkJ0p5MWMMb614i5cWv0SrCq1Y0nGJx10/xdnyBORhztNziK4SzevLX+edn94h\noxMOlFLWcOSYFYwxi4BFqcYNSjG8ieTdQ6mnmwxMvsuMSqnbMMbw8uKXGb1xNM9Wf5bPm32On49D\nq7bX8/f1Z3LryeTyy8XgNYO5dP0SHzf62GsPRFbKVek3mlJuzBjDS4tf4tONn/JK7VcY3ni4/qHN\nJF8fX8a1GEfugNwMXzecS9cuMabZGLe5maNS3kCLFaXclDGGfj/247NNn9G/Tn/dInAXfMSHUVGj\nyO2fm4/WfkR8Qjxft/xaCxalXIQWK0q5IWMML/74ImM2jdFCxUlEhA8f+5Bc/rkYtGoQAb4BjH1i\nrP5elXIBWqwo5WaMMfRd1JfPYz5nQJ0BDGs0TP+gOtG/G/yba4nXGPLzEHL65WRU1Cj9/SplMS1W\nlHIjxhj6L+2vhUoWG/zIYOIT4hm+bjg5/XIy9LGh+ntWykJarCjlRoasGcLI9SN5sdaLWqhkIRHh\n40YfcyXhCh//+jGBfoG898h7VsdSymtpsaKUm/h0w6cMWjWIzg905pOoT7RQyWIiwuimo7macJXB\nawYT6B/Im3XftDqWUl5JixWl3MCkrZPot7gfrSq0YnyL8XqWSjbxER++eOIL4hPiGbhiIMGBwTxb\n41mrYynldbRYUcrFzf1jLt3ndqdh6YZMbTNVL/iWzXx9fPmm5TecjT9L74W9KZy7MK0qtLI6llJe\nRf89U8qFrTq0iqdmPkVESAQ/PP0DOf1yWh3JK/n7+vN9u++pGVKT6JnRrDm8xupISnkVLVaUclE7\nTu2g1bRWlCtYjkUdFpE3R16rI3m13AG5WfjMQkoXKE2LqS3YfnK71ZGU8hparCjlgo5eOErTKU3J\n5Z+LHzv8SMHAglZHUkBwrmCWdFxCnoA8NJnchEPnD1kdSSmvoMWKUi7GdsXG4989ju2KjUUdFlEq\nqJTVkVQKpYJKsaTjEuIT4omaHMXZ+LNWR1LK42mxopQLuZZ4jTYz2rDr9C5mPTWLqsWqWh1JpaFy\nkcrMbz+fg+cP0np6a64mXLU6klIezaFiRUSiRGSPiOwTkVsuNCAi9UXkNxFJEJG2qV7rIiKx9kcX\nZwVXytMYY+g+tzsrDq7g6xZf06hsI6sjqduoW6ouE1tNZM3hNfSY1wNjjNWRlPJYGZ4DKSK+wBig\nERAHbBKRecaYXSma/Ql0BQakmrYg8A4QARhgs33ac86Jr5TneGfVO0zZPoUPGn5Apwc6WR1HOSC6\nSjQHzh3grZVvUaZAGQY/MtjqSEp5JEcu2FAL2GeMOQAgItOAlsDNYsUYc8j+WlKqaZsAy4wxZ+2v\nLwOigKl3nVwpDzJl2xTeX/M+3at2Z2DdgVbHUZkwsO5ADpw7wPtr3qdMgTJ0rdrV6khKeRzJaNOl\nfbdOlDGmp/15JyDSGNM3jbYTgAXGmJn25wOAnMaYIfbn/wbijTH/uTGNzWa7GSA2NvauO6SUu9l2\nbht91vehSv4qfBb5Gf4+/lZHUpmUkJTAS5teYvOZzXxa61NqFqppdSSlLBEeHn5zOCgoyGn3BHHk\nmJW03szRnbN3M61SHu/45eO8FvMaRXMWZWiNoVqouCk/Hz+GVh/KPbnv4fXNr3Po70NWR1LKoziy\nGygOKJnieShwzMH5xwEPp5p2VXqNIyIiHJytZ4iJiQG0394kZd8vXr1It6+7kSiJLO22lAqFKlic\nLmt5w3JfUXEFNcfV5K0db7G+x3oKBBbwin6nx1v77q39BrDZbFkyX0e2rGwCwkWktIgEANHAPAfn\nvwRoLCIFRKQA0Ng+TimvlpiUSPtZ7dl9ejczn5rp8YWKtwjLH8bsp2Zz8NxBnp75NAlJCVZHUsoj\nZFisGGMSgL4kFxm7gRnGmJ0iMlhEWgCISE0RiQPaAWNFZKd92rPA+yQXPJuAwTcOtlXKm7227DUW\nxi7k06af8liZx6yOo5yo3j31+G+z/7LswDL6L+lvdRylPIJDt281xiwCFqUaNyjF8CaSd/GkNe3X\nwNd3kVEpjzLnzzmM3D6SF2u9SJ+afayOo7JAj+o92Hl6JyPXjyT3fbl5stSTVkdSyq3pveaVykYx\nf8UwdMdQmpRtwogmI6yOo7LQsEbD2P3XbobtGMY9ue8hAu87fkEpZ9HL7SuVTQ6cO8Abv71Bqdyl\nmN52On4++r+CJ/Pz8WNam2mUzFWSNza/wYFzB6yOpJTb0mJFqWzw97W/aTWtFQAjIkYQlDPI4kQq\nOwTlDGJ4zeEYDC2mtuDC1QtWR1LKLWmxolQWM8bQbW43dp7eyQfVPiA0d5qHdykPVSp3KT6s/iF/\n/PUHHWZ3IDEp0epISrkdLVaUymIf/fIRM3fN5KNHP6J24dpWx1EWqFWoFqObjmbB3gW8vfJtq+Mo\n5Xa0WFEqCy2KXcRbK98iuko0Ax4ckPEEymM9X/N5nqv+HB+t/Yjvd35vdRyl3IoWK0plkdgzsTwz\n6xkeKPYA41uMR8Rpt8lQbmp009HUCa1D17ld2XZym9VxlHIbWqwolQUuXr1Iy2kt8fPxY87Tc8jl\nn8vqSMoF5PDLwaynZhGUI4hW01pxNl6vkamUI7RYUcrJkkwSnX/ozN4ze5nRbgZh+cOsjqRcSPG8\nxZn99GyOXjxK+1nt9YBbpRygxYpSTjZkzRB++OMHhjceTsPSDa2Oo1xQ7dDajHl8DEv3L+VfK/5l\ndRylXJ5elUopJ5q3Zx7vrHqHzg90pl9kP6vjKBfWs3pPNh/bzLBfh1GteDWiq0RbHUkpl6VbVpRy\nkt2nd9NxdkciQiL4otkXekCtytCopqN4qORDdJ/bna0ntlodRymXpcWKUk5w/sp5Wk5rSaB/ILOf\nmk2gf6DVkZQbCPANYOZTMykYWJBW01tx5vIZqyMp5ZK0WFHqLiWZJDrO7sjB8weZ2W4mJYNKWh1J\nuZFieYox66lZHLt4jOhZ0SQkJVgdSSmX41CxIiJRIrJHRPaJyJtpvJ5DRKbbX98gImH28f4iMlFE\ntovIbhEZ6Nz4SlnvnZ/eYWHsQkZFjaLePfWsjqPcUGRoJP9t9l+WH1jOm8tv+YpVyutlWKyIiC8w\nBmgKVALai0ilVM16AOeMMeWAkcBQ+/h2QA5jzH1ADaDXjUJGKU8wa9cshvw8hB7VetAnoo/VcZQb\n616tO89HPM/wdcP5bvt3VsdRyqU4smWlFrDPGHPAGHMNmAa0TNWmJTDRPjwTeFSSjy40QG4R8QMC\ngWuA3nZUeYQdp3bQ5YcuN09D1QNq1d0aGTWSeqXq0XNeT34//rvVcZRyGWKMuX0DkbZAlDGmp/15\nJyDSGNM3RZsd9jZx9uf7gUjABnwLPArkAl4xxnyZcv42m+1mgNjYWGf0SaksZ7tmo8vaLlxJvMK3\ndb+lcM7CVkdSHuLM1TN0/qUzvuLLpLqTyB+Q3+pISjksPDz85nBQUJDT/oNzZMtKWm+WusJJr00t\nIBEIAUoD/UWkTKYSKuViEk0ib//+NifjTzKsxjAtVJRTBecIZliNYZy5eoaBvw3UA26VwrGLwsUB\nKU9vCAWOpdMmzr7LJwg4CzwDLDbGXAdOichaIAI4kNYbRUREZC69m4uJiQG03+7mjWVvsP6v9Yxr\nPo7u1btnalp37/vd8Na+30m/I4jAFDJ0m9uN6WenMzJqZFbFy1K6zL2r3wA2my1L5uvIlpVNQLiI\nlBaRACAamJeqzTygi324LbDSJO9f+hNoKMlyA7WBP5wTXansN23HNIb9OozeNXrTs3pPq+MoD9a1\nalderPUin2z4hG+3fmt1HKUslWGxYoxJAPoCS4DdwAxjzE4RGSwiLezNxgPBIrIPeBW4ce7dGCAP\nsIPkoucbY4zeF125pd+P/073ud2pW6ouo5qOsjqO8gLDGw/n4bCHeXb+s8Qci7E6jlKWcejeQMaY\nRcCiVOMGpRi+QvJpyqmn+zut8Uq5m9OXTtNqeiuCcwUzs91MAnwDrI6kvIC/rz8z2s4gYlwErae3\nJubZGIrmKWp1LKWynV7BVqkMXE+8zlMzn+LUpVPMeXqO/rFQ2apw7sL88PQPnLl8hrbft+Va4jWr\nIymV7bRYUSoD/Zf2Z9WhVXz5xJdEhHjfAXPKetWKV2N8i/H88ucvvLz4ZavjKJXtHNoNpJS3+ub3\nb/h046e8UvsVOj3Qyeo4you1v689v5/4nY9//ZhqxarxbI1nrY6kVLbRLStKpWND3AZ6L+zNY2Ue\nY1ijYVbHUYoPH/2QJmWb8MKiF/j1yK9Wx1Eq22ixolQajl88zpMznqRE3hJMazMNPx/dCKms5+vj\ny9Q2UykVVIo2M9pw9MJRqyMplS20WFEqlasJV2kzow3nr5znh+gfCM4VbHUkpW4qEFiAudFz+fva\n3zw540muJFyxOpJSWU6LFaVSMMbQd1Ff1sWtY2Kridxf9H6rIyl1i8pFKjOp1SQ2Ht1In4V9yOge\nb0q5Oy1WlErhi5gv+Or3r/hX3X/RtlJbq+Mola7WFVszqP4gJmyZwGcbP7M6jlJZSosVpezWHF5D\nv8X9aBbejMGPDLY6jlIZeufhd2hxbwteWfIKPx38yeo4SmUZLVaUAg6fP0zbGW0pU6AMU56cgq+P\nr9WRlMqQj/jwbetvKR9cnnbft+PAuTTvEauU29NiRXm9i1cv0nxqc64lXmNe9DyCcgZZHUkph+XL\nkY+50XNJMkk0n9qcC1cvWB1JKafTYkV5tcSkRDrM7sCu07v4vt333FvoXqsjKZVp4cHhzHxqJnvP\n7KX9rPYkJiVaHUkpp9JiRXm1f634F/P3zmdU1CgalW1kdRyl7ljD0g35rOlnLIpdxOvLXrc6jlJO\npVe6Ul5rwpYJDPt1GH0i+vBCrResjqPUXesV0Yudp3cyYv0IKhauSM/qPa2OpJRT6JYV5ZV++fMX\nnpv/HI+WfpRRUaOsjqOU04xoMoLGZRvTZ2EfVh9abXUcpZzCoWJFRKJEZI+I7BORN9N4PYeITLe/\nvkFEwlK8dr+IrBORnSKyXURyOi++Upl36PwhWk9vTVj+ML5v9z3+vv5WR1LKafx8/JjedjplC5Sl\nzYw27D+73+pISt21DIsVEfEFxgBNgUpAexGplKpZD+CcMaYcMBIYap/WD5gM9DbGVAYeBq47Lb1S\nmXTjzJ+EpATmt59PgcACVkdSyuny58zPgmcW3DxDyHbFZnUkpe6KZHSZZhGpA7xrjGlifz4QwBjz\nYYo2S+xt1tkLlBNAYZILnGeMMR3Tm7/NZrsZIDY29i66otTtJZpEBsQMYN3pdYyqNYrIQpFWR1Iq\nS8X8FUPfjX2pVagWIyJG6A05VZYLDw+/ORwUFCTOmq8ju4FKAEdSPI+zj0uzjTEmAbABwUB5wIjI\nEhH5TUT0EHVlmVG7R/HLqV/oX6m/FirKK0QUiuD1Kq+z7vQ6Ru4aqfcQUm7LkTI7rcoo9Sc+vTZ+\nQF2gJnAZWCEim40xK9J6o4iICAfieI6YmBhA+50dRq0fxdSDU+lXqx9Dmw7NtvdNzVuXOXhv363u\nd0REBNfyXGP4uuFE3hvJq3Vezbb3trrvVvHWfgPYbFmzy9GRLStxQMkUz0OBY+m1se8GCgLO2sev\nNsb8ZYy5DCwCqt9taKUyY87uObyy5BVaV2jNiCYjrI6jVLYb1mgYbSu1pf/S/ny/83ur4yiVaY4U\nK5uAcBEpLSIBQDQwL1WbeUAX+3BbYKVJ3t64BLhfRHLZi5gGwC7nRFcqY+vj1vPM7GeIDI1k8pOT\n9Z4/yivduIfQQyUfotOcTqz9c63VkZTKlAyLFfsxKH1JLjx2AzOMMTtFZLCItLA3Gw8Ei8g+4FXg\nTfu054ARJBc8W4DfjDELnd8NpW617+w+mk9tTom8JZgXPY9c/rmsjqSUZXL65WRu9FxKBZWixbQW\n7D2z1+pISjnMoUPDjTGLSN6Fk3LcoBTDV4B26Uw7meTTl5XKNn9d/oumU5pijOHHDj9SOHdhqyMp\nZbngXMH82OFH6oyvQ9MpTVnXYx1FchexOpZSGdIr2CqPE389nhZTWxB3IY757ecTHhye8URKeYmy\nBcsyv/18jl88TvOpzbl8/bLVkZTKkBYryqMkJiXScU5H1setZ3LrydQpWcfqSEq5nMjQSKa2mcqm\no5t4ZtYzepdm5fK0WFEewxjDgKUDmL17NiOajKBNpTZWR1LKZbWs0JLRTUczd89cXl78sl6DRbk0\nvZyh8hjD1g7jkw2f0K9WP16u/bLVcZRyeX1r9eXQ+UMMXzecYnmK8Vb9t6yOpFSatFhRHuGr377i\nzRVv0r5Ke0ZGjbQ6jlJuY1ijYZy6dIq3f3qb4FzB9I7obXUkpW6hxYpye7N3z6bXgl5ElYtiQqsJ\n+Iju3VTKUT7iw/gW4zl35RzPL3ye4MBg2lVO8+ROpSyj3+rKra08uJL2s9oTWSKSme1mEuAbYHUk\npdyOv68/M9rOoG6punSY3YFl+5dZHUmpf9BiRbmtmGMxtJzWkvLB5VnwzAJyB+S2OpJSbivQP5B5\n7edRqXAlWk9vzYa4DVZHUuom3Q2k3NKOUzuImhxFoVyFWNJxCQUDC2Z7BpHk+3fqWRSOazvzJMz8\n50WsD33UzKI0rsuqz1b+nPlZ3HExdb+uS9MpTVnVdRX3F70/WzMolRYtVpTb2XtmL49NeowA3wCW\ndVpGSN4QqyMpLxX25q13D3H34qtYnmIs67SM+hPq89ikx1jddTUVC1e0OpbyclqsKLdy4NwBGk5s\niMGwsstKyhUsZ3Uk5SSe+IffXZUuUJoVnVfQYEIDHp30KGu6rdF1TVlKj1lRbuNP2580nNiQ+IR4\nlndaToVCFayOpJTHKh9cnuWdlnM96ToNJzbk0PlDVkdSXky3rCi3cOziMRpObMj5K+dZ0XkF9xW9\nz+pISjlVWluWrFa5SGWWdVrGIxMfoeHEhqzptobQfKFWx1JeSLesKJd3/OJxHp30KCcvnWRxx8XU\nCKlhdSSlvEbVYlVZ2nEpf13+i4YTG3L0wlGrIykv5FCxIiJRIrJHRPaJyJtpvJ5DRKbbX98gImGp\nXi8lIn+LyADnxFbeIu5CHA0mNOCI7QiLnllE7dDaVkdS6o6Fvbnwloc7qFmiJos7LubE3ydoMKEB\nf9r+tDqS8jIZ7gYSEV9gDNAIiAM2icg8Y8yuFM16AOeMMeVEJBoYCjyd4vWRwI/Oi628weHzh2k4\nqSGnL51maaelPFjyQasjqTs0ZcoUBgwYwIkTJ/HNV4j89TuTp/IjVsdSmfBgyQdZ2mkpUZOjaDCh\nAT91+Ymw/GFptr2lCJu5UA+WVnfFkS0rtYB9xpgDxphrwDSgZao2LYGJ9uGZwKNiv1CAiLQCDgA7\nnRNZeYOD5w7SYEIDzlw+w/LOy7VQcWNTpkzhueee48SJE4Ah8cJpzi7+jL93/mR1NJVJtUNrs7zz\ncmxXbNT/pj77z+63OpLyEpLRRYdEpC0QZYzpaX/eCYg0xvRN0WaHvU2c/fl+IBKIB5aTvFVmAPC3\nMeY/Kedvs9luBoiNjXVGn5SbO3LpCL3X9+Zq4lU+i/yMCkGuedZPzZo1AahevbrFSVzb9u3buX79\n+q0v+PqTI+ReKhdOvkXCztPXbmly4zVXldnMt2uf8rWrR3YAsGnTpruNmCX22PbwwoYXCPAJ4PPa\nnxOWJ+wfr7edefKWaWa2LZpN6ZSVwsPDbw4HBQWJs+bryJaVtN4sdYWTXpv3gJHGmL8zG0x5p30X\n9/Hcuue4lnSNz2t/7rKFinJcmoUKQGI645XLuzfoXr6o8wWJJpFe63ux98JeqyMpD+fIlpU6wLvG\nmCb25wMBjDEfpmizxN5mnYj4ASeAwsAaoKS9WX4gCRhkjPnsxrQpt6wEBQU5o09uIyYmBoCIiAiL\nk2Sv9Pr965FfafZdM3L552Jpx6VULlLZingOu5NLojtzmbvLRdTCwsI4fPjwLeN98xUmtM83NzO7\nS39SciRzymV+u/YpXzs89Alr6z1sAAAV+klEQVTA9W/lsPv0bhpPbszFqxdZ8MwC6paqC7jnsnQm\nb/1uB7DZbDeHs3vLyiYgXERKi0gAEA3MS9VmHtDFPtwWWGmS1TPGhBljwoBPgP9LWagodcOPsT/y\n2KTHKJSrEGu7r3X5QsUTZdWZKh988AG5cuX6xzjxy0H++p2dMn9lnYqFK7K2+1qK5SlGo28bsWDv\nAqsjKQ+VYbFijEkA+gJLgN3ADGPMThEZLCIt7M3GA8Eisg94Fbjl9Gal0vPd9u9oMa0FFQpVYG33\ntemeYaDcU4cOHfjyyy8pVqwYIPjmK0zBqL56NpCHKBVUip+7/UyVIlVoNa0Vk7ZOsjqS8kAOXcHW\nGLMIWJRq3KAUw1eAdhnM4907yKc83KcbPqXf4n40uKcB89rPI1+OfFZHylI3DzxMcedhb9g83qFD\nB+699940D7x0Fd6+6+JuFM5dmJWdV9Jqeiu6/NCFAr49yZfYyupYyoPo5faVJRJNIv2X9GfE+hG0\nqtCKqW2mktMvZ5pt9Y+IcjdpfmY9/PCFvDnysuiZRXSY3YFZu78iIeEUBa73QPC1OpryAFqsqGwX\nnxDPoC2DWHVyFS/WepGRTUZS9l+Lb2mnBYlS7iWHXw6mt51OgXfacNFvLglygkLXXsOHQKujKTen\nxYrKVscvHqfX+l7sse1hVNQo+kX2szrSXUv5X7QWWMrb+fr4UvD6s/gnFees/5eczPEmha8OynhC\npW5Db2Soss32k9uJ/CqSg38f5OOIjz2iUFFKpS1v4hMUufZvrssxTuToz9YTW62OpNyYFisqW8z9\nYy4Pff0QCUkJjKszjvpF61sdSSmVxQKTalLs6lAQQ91v6jJ792yrIyk3pbuBVJZKMkm8t+o9Bq8Z\nTERIBHOensOJvSesjuUU97yRPdeU0AOMvU92fbayQ4ApQ7ErwwkN/S9tZrThrXpv8d7D7+Hrowfe\nKsfplhWVZc5fOU/LaS0ZvGYwXat25eduPxOaL9TqWEqpbOZHIVZ3XU2Paj344OcPaD61Oefiz1kd\nS7kR3bKissSu07toNa0VB88fZMzjY+gT0efm5emdRbc4eAddzp4hh18OxjUfR82Qmrz444vUHFeT\nH6J/oEqRKlZHU25At6wop5u8bTKRX0Viu2pjZeeVPF/zeacXKkop9yMi9Iroxaquq7h0/RKRX0Uy\ncctEq2MpN6DFinKav6/9TdcfutJpTieqFavGb8/9Rr176lkdSynlYh4s+SCbn9tMrRK16Dq3K53n\ndObi1YtWx1IuTIsV5RRbT2wl4ssIJm2dxKD6g1jZZSUl8pWwOpZSykWF5A1heaflvPfwe0zZPoUa\nX9bg9+O/Wx1LuSgtVtRdMcYwZuMYIr+K5MLVC6zovIL3HnkPPx89HEopdXu+Pr4MajCIlZ1Xcvn6\nZWqPr83oDaNJMklWR1MuRosVdceO2I4QNSWKvj/2pWHphmztvZVHSuuddJVSmdMgrAFbem+hcdnG\nvLT4JRp/25g/bX9aHUu5EP33V2WaMYaJWyfy0uKXSExK5PPHP6d3RG89iNYN6Jk1ylUVylWIedHz\n+HLzl/Rf2p8qn1dhZJORdK/WXb9blGPFiohEAaMAX+ArY8xHqV7PAUwCagBngKeNMYdEpBHwERAA\nXANeM8asdGJ+lc2OXzzOcwueY8HeBdS/pz7ftPyGMgXKWB3LYdn1x1qLAqUy78bZQo3LNqb7vO70\nnN+T2X/MZlzzcYTkDbE6nrJQhsWKiPgCY4BGQBywSUTmGWN2pWjWAzhnjCknItHAUOBp4C+guTHm\nmIhUAZYAetSlG0oySYz/bTxvLH+D+IR4RjYZSb/IfviI7kl0Bi1ulDPd7vPkDp+10gVKs6LzCsZs\nHMMby9+g0phKfPTYRzxX4zn9zvFSjmxZqQXsM8YcABCRaUBLIGWx0hJ41z48E/hMRMQYk/LQ7p1A\nThHJYYy5etfJVbbZdnIbvRf0Zl3cOurfU58vn/iSewvda3UsZTF3+KOn3JeP+PBi5ItElYui14Je\n9FnYhwlbJvDFE19QtVhVq+OpbOZIsVICOJLieRwQmV4bY0yCiNiAYJK3rNzQBvj9doVKTEyMI5k9\njqv2+3LCZb7c+yXTDk0jr39e3nngHZqVaMbFQxeJOXT3mTPq9+1eT++1O/ldOvP378zMrtD/zM4v\nu94/u9YZZ/bHmcv5TmT0Pm1nnrxl/My2RbPl/TMytNJQfgz6kU92f0KNsTWILh3Nc+WfI7dfbqfl\nywqu+t2elcLDw7Nkvo4UK2kd2WQy00ZEKpO8a6ix49GUVZJMEouPLmbMnjGcunKKViVb0bdCX4IC\ngqyOptxEVv/hS+89suJ9lPVEhMdDH6du0bp8/sfnTD04lWXHlvF8hed5vMTjumvICzhSrMQBJVM8\nDwWOpdMmTkT8gCDgLICIhAJzgM7GmP23e6OIiAgHY3uGG1W3K/V7zeE1vLrkVTYf30z14tWZ03QO\nD5Z80KnvkWa/Z966S+Hm6+m9drtp0nMn09zJvDKb2RX6n9n5ZXJe6XHm7+wf88ssZ/4+nbmc70R2\nfZ7u5P3vUsM6DVkft55+P/bjva3vMe/kPIY3Hu5Sl01wxe/27GKz2bJkvo6Uo5uAcBEpLSIBQDQw\nL1WbeUAX+3BbYKUxxohIfmAhMNAYs9ZZoZXzxZ6J5cnpT9JgQgNOXjrJpFaT2PTsJqcXKkopdbdq\nh9Zmfc/1TG49mb8u/0XDSQ1pOa0le/7aY3U0lUUyLFaMMQlAX5LP5NkNzDDG7BSRwSLSwt5sPBAs\nIvuAV4E37eP7AuWAf4vIFvujiNN7oe7YofOH6DmvJ5U+r8SyA8sY8sgQ9vTdQ6cHOummVaWUy/IR\nHzrc34E9fffwfw3/j58O/kTlzyvTfW53Dpw7YHU85WQOXWfFGLMIWJRq3KAUw1eAdmlMNwQYcpcZ\nVRb40/YnH6z5gK+3fI2v+NInog//qvcviuUpZnU0pe6anqnkPQL9AxlYbyA9qvfg/37+P76I+YJv\nt31L1we68lb9twjLH2Z1ROUE+q+zl9l/dj99FvSh3OhyTNg6gV41erG/335GNx2thYpSym0VyV2E\nT6I+4cBLB+gT0Ydvt31L+Kfh9Jrfi9gzsVbHU3dJL7fvJdbHrec/v/6H2btn4+/rT8/qPRlYdyAl\ng0pmPLET/eM/XvtBePofr1LKWULyhjC66WjeeOgNPvzlQ8b9No5xv42jVYVWDHhwgB6H56Z0y4oH\nS0hKYM7uOdT9ui51xtdh5cGVDKw7kEMvHeLzZp9ne6GilFLZpUS+Enz2+Gccfvkwb9V7i9WHV/PQ\n1w/x4PgHmbVrFglJCVZHVJmgW1Y8UNyFOMb/Np5xv43j6MWjhOUPY3TUaLpV60aegDxWx1PKrejx\nL+6tWJ5ivN/wfd6s+ybfbPmGEetG0Pb7toTkDaFntZ70rN5T/3FzA1qseIiEpASW7V/G2M1jmb93\nPsYYGpdtzKdNP6X5vc3x8/GeRa1/XJRSqeUOyE3fWn3pE9GHBXsXMHbzWN5f8z5Dfh5Cs/Bm9KrR\niyblmnjVd6U70aXixowx/Hb8NyZvm8zUHVM5eekkRXIX4Y2H3uDZ6s9SukBpqyMqpZRL8fXxpWWF\nlrSs0JJD5w8xbvM4xv8+nvl751MkdxGiK0fT8f6ORIREIJLWxdmVFbRYcUO7T+9m1u5ZTNk+hT/+\n+oMA3wCeKP8EHe/rSLPyzQjwDbA6olJKubyw/GF88OgHvPvwuyyKXcTk7ZMZu3ksozeOpnxweTrc\n14E2FdtQqXAlLVwspsWKG0gyScQci2HO7jnM+WMOe84kX6Wx/j31ebX2q7St1JYCgQUsTqlcie4K\nU9nBUz5n/r7+N7e2nL9ynlm7ZjF5+2TeWfUO76x6h/CC4bSu0JrWFVtTq0QtvWCmBbRYcVFn48+y\n/MByluxbwuL9izl28Rh+Pn48HPYw/SL70fLelpTIV8LqmF7BU76QlXvSz1/2yp8zPz2q96BH9R4c\nu3iMuX/MZc4fcxixfgTDfh1G8TzFiSoXRZOyTWhUthEFAwtaHdkraLHiIuKvx7Ph6AZWHVrFkv1L\n2Hh0I0kmifw58/NYmcdoUb4FT5R/QregKHUX9A9/5nnz7ywkbwh9avahT80+nIs/x8LYhczbM48f\n/viBb7Z8g4/4UDOkJk3KNuHhsIeJDI0kl38uq2N7JC1WLHIu/hy/nvqVLWe3ELs9lo1HN3It8RqC\nUKtELd6u9zZNyjWhVolaenS6UipN3lxIZLcCgQXoeH9HOt7fkcSkRDYd28TifYtZsn8JQ34ewuA1\ng/H38admiZqEB4RTrWA1wi6HUShXIaujewT9K5gN/r72NztO7WDT0U1sPLaRDXEbiD2bfPlnX/El\nIiSClyNfpv499Xmo1EPkz5nf4sTeR7/0lVKO8vXxpXZobWqH1ubdh9/FdsXG2iNrWXN4DasPr2by\ngclM3D+Rlze9TFj+MGqG1CQiJIKIkAhqFK9BUM4gq7vgdrRYcaKEpAT2nd3H9pPb2X5qO9tObmP7\nqe3/uANo8TzFiQyNpFvVbgRdCqJK/irUr13fwtRK3Z4WckrdXlDOIB4Pf5zHwx8H4Of1P7Pz/E4u\n5r3IpmObiDkWw/e7vr/ZvnxweaoWq0qlQpWoVDj5ER4crmdy3oYWK5mUZJI4euEo+87u+9/j3D5i\nz8Sy98xeriZeBZJvXx5eMJwaxWvQ9YGu3Ff0PmqG1PzHQbExMTFWdUMppVQWCfQLJKJQBBERETfH\nnbl8hphjMcQci2HTsU1sPraZ73d+j8EAyVvZw4PDqVioIhULVaRswbKUzl+a0gVKE5ov1OsPB/Du\n3qdijOHC1QvEXYjjyIUjxF2Iu/k4cuEIR2xHOHDuwM2CBCDAN4AyBcpQrmA5GpdtzH1F7uO+ovdR\nsVBFAv0DLeyNUkopVxGcK5gm5ZrQpFyTm+Pir8ez58wedp3e9Y/HvD3zSDSJN9v5+fhRKqhUcvGS\nvzT35L+HkLwh/3gEBwZ79LVgHCpWRCQKGAX4Al8ZYz5K9XoOYBJQAzgDPG2MOWR/bSDQA0gE+hlj\nljgt/W0YY7iScIULVy9gu2rjbPxZTl06xelLpzl9+fT/fqYcvnSa+IT4f8xHEIrlKUZovlAqFq5I\ns/BmlCtY7uYjNF8ovj6+2dElpZRSHiTQP5CqxapStVjVf4y/nnidIxeOcPDcQQ6cO8DB8weTH+cO\nMnfPXE5fPn3LvAJ8AyiepzjF8xanUK5CFMpViODA4Js/g3MF/2NcwcCC+Pv6Z1dX71qGxYqI+AJj\ngEZAHLBJROYZY3alaNYDOGeMKSci0cBQ4GkRqQREA5WBEGC5iJQ3JkXJmMLBcweJT4jn8vXLxF9P\n/nn5+uWb49Iaf/HaRWxXbNiu2pILE/uw7YqN60nX0+1XLv9cFM5VmMK5C1MkdxEqF6lM4VyFKZan\nGCXzlSQ0Xyih+UIJyRviVgtUKaWUe/P39adMgTKUKVCGR3n0ltevJFzhxN8nOHbxWJqPI7YjbDmx\nhTOXz9zyD3hKgX6B5M2Rl3w58pE3wP4z9fOAvAT6BxLoF3jzZ06/nP8Yl9Mv583hvOTNkt+JGGNu\n30CkDvCuMaaJ/flAAGPMhynaLLG3WScifsAJoDDwZsq2KdvdmNZms90+gFJKKaXcTlBQkNP2Szly\nzeASwJEUz+Ps49JsY4xJAGxAsIPTKqWUUkqly5FiJa3KKPXWkPTaODKtUkoppVS6HDnANg4omeJ5\nKHAsnTZx9t1AQcBZR6Z15mYipZRSSnkeR7asbALCRaS0iASQfMDsvFRt5gFd7MNtgZUm+WCYeUC0\niOQQkdJAOLDROdGVUkop5Q0yLFbsx6D0BZYAu4EZxpidIjJYRFrYm40HgkVkH/Ap0FBEdhhjdgIz\ngOPAXpJ3AW0WkcdvzF9EBorIPhHZIyJNSIO9UNogIrEiMt1eNLkUEflaRE6JyI4U494VkaMissX+\neNw+vpGIbBaR7fafDdOZZ5rTu5pM9j1MROJTjP8inXkWFJFl9mW+TERc8g6Omex7hxTjtohIkohU\nTWOeLr/c0+q3ffyL9nV5p4gMSzHeI9ZzyFzfvWFdt49Pq+8es65nst8es55Dut9x01PkPiQiW1K8\nljXrujHGqQ+gPlAd2JFi3LvAgDTaVgK2AjmA0sB+wDeNdjOAaPvwF0AfZ+fO5n5XA0Lsw1WAo+nM\nM83pXe2Ryb6HpWx3m3kOA960D78JDLW6n3fb91TT3QcccNflnk6/HwGWAznsz4vYf3rMen4HffeG\ndT29vnvMup6Zfqeazq3X8/T6nur14cAg+3CWreuO7AbKFGPMGpKPV3FES2CaMeaqMeYgsA+olbKB\niAjQEJhpHzURaOWkuE6TmX4bY343xtw4dmcnkFOSL6znljK5zB3VkuRlDS66zOGu+t4emOrkONkm\nnX73AT4yxly1tzllH+8x6zlkru9esq6nt9wd5fLr+l30263Xc7j9d5x9vX2K//Uxy9Z1pxcrt9FX\nRLbZNynd2MznyKnNwcB5k7w7Kr02riytfqfUBvj9xgf+DqZ3ZellLy0iv4vIahGpl860RY0xxwHs\nP4tkeVrnymi5Pc3tv8TccbmXB+rZN++uFpGa9vHesJ6n1/eUPHVdv13fPXldd2SZe+J6nlI94KQx\nJtb+PMvW9ewqVv4LlAWqknz8ynD7+Ls5LdodpNdvAESkMslX++11J9O7uPSyHwdKGWOqAa8C34lI\nPmsiZpmMlnskcNkYsyONaTOc3oX5AQWA2sBrwAz7f1Gevp5D+n0HPH5dT6/vnr6uZ7TMPXU9Tyn1\nlqMsW9ezpVgxxpw0xiQaY5KAcfxvs5Ajp0X/BeSX5FOi02vjkm7Tb0QkFJgDdDbG7M/s9K4uvez2\nzYNn7MObSd6nWT6NWZwUkeIA9p+Z3bRsGQeWWzS3+W/LjZd7HDDbJNsIJAGF8PD13C69vnv8uk46\nffeCdT3dZW7nqes5APZ19UlgeorRWbauZ0uxcuODaNcauFFpZnhqs0k+Aucnkk+JhuRTpOdmbWLn\nSK/fIpIfWAgMNMaszez07uA2fS8syfebQkTKkLzMD6Qxi5Snw7vNMofbLzcR8QHaAdPuZHoX9wPJ\n+6IRkfJAAMlfTB69ntul2XdvWNdJv++evq6n93n39PX8hseAP4wxcSnGZd26ntERuJl9kFxJHgeu\nk1xl9QC+BbYD2+ydKZ6i/VskV9x7gKYpxi/if0fRl7F3eB/wPfajr13pkZl+A28Dl4AtKR43jqD/\nCoiwD6f7e3OlRyb73obkAw23Ar8BzVPMJ2Xfg4EVQKz9Z0Gr++mkz/vDwPo05uNWyz2dfgcAk0n+\n0v0NaJiivUes55ntu5es6+n13WPW9Tv4vHvEep5e3+3jJwC902ifJet6hjcyVEoppZSyUnaeDaSU\nUkoplWlarCillFLKpWmxopRSSimXpsWKUkoppVyaFitKKaWUcmlarCillFLKpWmxopRSSimXpsWK\nUkoppVza/wMzmLJ74Q2kbgAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"from random import random\n",
"xs = np.arange(145, 190, 0.1)\n",
"ys = [stats.gaussian(x, 160, 3**2) for x in xs]\n",
"belief = np.array([random() for _ in range(40)])\n",
"belief = belief / sum(belief)\n",
"\n",
"x = np.linspace(155, 165, len(belief))\n",
"plt.gca().bar(x, belief, width=0.2)\n",
"plt.plot(xs, ys, label='A', color='g')\n",
"plt.errorbar(160, [0.04], xerr=[3], fmt='o', color='k', capthick=2, capsize=10) \n",
"plt.xlim(150, 170)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"I used random numbers to form the discrete distribution to illustrate that it can model any arbitrary probability distribution. This provides it with enormous power. With enough discrete buckets we can model the error characteristics of any sensor no matter how complicated. But with this power comes mathematical intractability. Multiplying or adding Gaussians takes two lines of math, and the result is another Gaussian. This regularity allows us to perform powerful analysis on the performance and behavior of our filters. Multiplying or adding a discrete distribution requires looping over the data, and we have no easy way to characterize the result. Analyzing the performance characteristics of a filter based on a discrete distribution is extremely difficult to impossible.\n",
"\n",
"There is no 'correct' choice here. Later in the book we will introduce the *particle filter* which uses a discrete distribution. It is an extremely powerful technique because it can handle arbitrarily complex situations. This comes at the cost of slow performance, and resistance to analytical analysis. \n",
"\n",
"For now we will ignore these matters and return to using Gaussians for the next several chapters. As we progress you will learn the strengths and limitations of using Gaussians in our mathematical models."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Introduction to Designing a Filter\n",
"\n",
"So far we have developed filters for a position sensor. We are used to this problem by now, and may feel ill-equipped to implement a Kalman filter for a different problem. To be honest, there is still quite a bit of information missing from this presentation. Following chapters will fill in the gaps. Still, let's get a feel for it by designing and implementing a Kalman filter for a thermometer. The sensor for the thermometer outputs a voltage that corresponds to the temperature that is being measured. We have read the manufacturer's specifications for the sensor, and it tells us that the sensor exhibits white noise with a standard deviation of 0.13 volts.\n",
"\n",
"We can simulate the temperature sensor measurement with this function:"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def volt(voltage, std):\n",
" return voltage + (randn() * std)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now we need to write the Kalman filter processing loop. As with our previous problem, we need to perform a cycle of predicting and updating. The sensing step probably seems clear - call `volt()` to get the measurement, pass the result into `update()` method, but what about the predict step? We do not have a sensor to detect 'movement' in the voltage, and for any small duration we expect the voltage to remain constant. How shall we handle this?\n",
"\n",
"As always, we will trust in the math. We have no known movement, so we will set that to zero. However, that means that we are predicting that the temperature will never change. If that is true, then over time we should become extremely confident in our results. Once the filter has enough measurements it will become very confident that it can predict the subsequent temperatures, and this will lead it to ignoring measurements that result due to an actual temperature change. This is called a *smug* filter, and is something you want to avoid. So we will add a bit of error to our prediction step to tell the filter not to discount changes in voltage over time. In the code below I set `process_var = .05**2`. This is the expected variance in the change of voltage over each time step. I chose this value merely to be able to show how the variance changes through the update and predict steps. For a real sensor you would set this value for the actual amount of change you expect. For example, this would be an extremely small number if it is a thermometer for ambient air temperature in a house, and a high number if this is a thermocouple in a chemical reaction chamber. We will say more about selecting the actual value in the later chapters.\n",
"\n",
"Let's see what happens. "
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"scrolled": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAp4AAADQCAYAAACuu2GmAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzs3Xd8zPcfwPHXJ7lEpkx700iC2KM2\nNduqTSk1O1BU6U+pWaW1Oqi2VlGU2pRSVaPUaMQWe0VCagQnO7m7z++PS1LRIEGO1vv5eNwjd9/x\n+b5z3+Tu/f18P0NprRFCCCGEECK72T3pAIQQQgghxLNBEk8hhBBCCGETkngKIYQQQgibkMRTCCGE\nEELYhCSeQgghhBDCJiTxFEIIIYQQNpFtiadSao5S6qpS6ugdy5YopQ6mPC4opQ7eY9+mSqmTSqkz\nSqkh2RWjEEIIIYSwHZVd43gqpeoAMcB8rXWZDNZ/Bhi11mPuWm4PnAIaARHAXqCj1vpYtgQqhBBC\nCCFswpBdBWuttyulima0TimlgPbACxmsrgqc0VqfS9n2R6AFkC7xNBqNMvK9EEII8R/j4eGhnnQM\nIvs8qTaetYErWuvTGawrAITf8ToiZZkQQgghhPgXe1KJZ0dg8T3WZXSlI7WbQgghhBD/ctl2q/1e\nlFIGoDVQ6R6bRACF7nhdELh8vzI9PDweT3DikYWEhABQuXLlJxyJuJucm6eTnJenk5wX2zIajU86\nBGEjT6LGsyFwQmsdcY/1ewE/pVQxpZQj0AH4yWbRCSGEEEKIbJGdwyktBnYD/kqpCKVUz5RVHbjr\nNrtSKr9Saj2A1toE9AU2AseBpVrr0OyKUwghhBBC2EZ29mrveI/l3TJYdhl46Y7X64H12RWbEEII\nIYSwPZm5SAghhBBC2IQknkIIIYQQwiYk8RRCCCGEEDYhiacQQgghhLAJSTyFEEIIIYRNSOIphBBC\nCCFsQhJPIYQQQghhE5J4CiGEEEIIm5DEUwghhBBC2IQknkIIIYQQwiYk8RRCCCGEEDYhiacQQggh\nhLAJSTyFEEIIIYRNSOIphBBCCCFsQhJPIYQQQghhE5J4CiGEEEIIm5DEUwghhBBC2IQknkIIIYQQ\nwiYk8RRCCCGEEDYhiacQQgghhLAJSTyFEEIIIYRNSOIphBBCCCFsQhJPIYQQQghhE5J4CiGEEEII\nm8i2xFMpNUcpdVUpdfSu5f2UUieVUqFKqYn32Pe9lPVHlVKLlVJO2RWnEEIIIYSwjeys8ZwHNL1z\ngVKqPtACKKu1Lg1MvnsnpVQBoD9QWWtdBrAHOmRjnEIIIYQQwgaU1jr7CleqKLAuJYFEKbUUmKm1\n/u0++xQA9gDlgNvAamCq1vrXO7czGo1pgZ8+ffqxxy6EEEII2/Dz80t77uHhoZ5gKCKb2bqNZ0mg\ntlLqT6XU70qpKndvoLW+hLUm9CIQCRjvTjqFEEIIIcS/j+EJHM8LeB6oAixVShXXd1S7KqW8sN6O\nLwbcApYppTprrRfeq9DKlStnb9Qi00JCQgA5J08jOTdPJzkvTyc5L7ZlNBqfdAjCRmxd4xkBrNRW\nwYAF8L1rm4bAea31Na11MrASqGHjOIUQQgghxGNm68RzNfACgFKqJOAIXL9rm4vA80opF6WUAhoA\nx20apRBCCCGEeOyyczilxcBuwF8pFaGU6gnMAYqnDLH0I9BVa62VUvmVUusBtNZ/AsuB/cCRlBhn\nZlecQgghhBDCNrKtjafWuuM9VnXOYNvLwEt3vB4FjMqm0IQQQgghxBMgMxcJIYQQQgibkMRTCCGE\nEELYhCSeQgghhBDCJiTxFEIIIYQQNiGJpxBCCCGEsAlJPIUQQgghhE1I4imEEEIIIWxCEk8hhBBC\nCGETkngKIYQQQgibkMRTCCGEEELYhCSeQgghhBDCJiTxFEIIIYQQNiGJpxBCCCGEsAlJPIUQQggh\nhE1I4imEEEIIIWxCEk8hhBBCCGETkngKIYQQQgibkMRTCCGEEELYhCSeQgghhBDCJiTxFEIIIYQQ\nNiGJpxBCCCGEsAlJPIUQQgghhE1I4imEEEIIIWwi2xJPpdQcpdRVpdTRu5b3U0qdVEqFKqUm3mNf\nT6XUcqXUCaXUcaVU9eyKUwghhBBC2IYhG8ueB0wD5qcuUErVB1oAZbXWiUqp3PfYdwrwi9a6rVLK\nEXDJxjiFEEIIIYQNKK119hWuVFFgnda6TMrrpcBMrfVv99knJ3AIKK7vE5zRaExbd/r06ccVshBC\nCCFszM/PL+25h4eHeoKhiGyWnTWeGSkJ1FZKjQMSgPe11nvv2qY4cA2Yq5QqB+wD3tVax9o2VCGE\nEEI8Sfv27bNzc3Mb7OjoGKiUkn4pTzmttSUpKel4TEzMxEqVKlky2sbWiacB8AKeB6oAS5VSd9ds\nGoCKQD+t9Z9KqSnAEGDEvQqtXLlyNoYssiIkJASQc/I0knPzdJLz8nSS82JbRqMxw+Vubm6DCxUq\n1N7FxSXDJEY8feLi4oLCw8MBxme03tZXDxHASm0VDFgA3wy2idBa/5nyejnWRFQIIYQQzxBHR8dA\nSTr/XVxcXCyOjo6B91pv68RzNfACgFKqJOAIXL9zA631X0C4Uso/ZVED4JgtgxRCCCHEkye31/+d\n7nfesnM4pcXAbsBfKRWhlOoJzAGKpwyx9CPQVWutlVL5lVLr79i9H/CDUuowUB74JLviFEIIIYQQ\ntpFtbTy11h3vsapzBtteBl664/VBQBrWCCGEEOKJsre3r+Tn5xef+nrNmjVnrly5YpgzZ47PvHnz\nwqdOneoTEhLiOn/+/IsLFizwLFWqVEKlSpUSnmTMTzNbdy4SQgghhPjXyJEjh+XEiRPpmvz5+/sn\n1alTJ+7ubVevXu1pMpmMWUk8k5OTcXBweByh/itI2wkhhBBCiCxYt26de/369Z+7c9mmTZtcf/vt\nN8/hw4cXDAgIKBUaGpojNDQ0R+3atf1Kly4dWKlSJf8DBw44AbRp06boG2+8UbBatWol+/TpU/DJ\n/BZPxgNrPJVSrkC81tqS0iEoANigtU7O9uiEEE+d5ORkli1bxpo1a0hOTqZx48Z06dIFFxeZYEwI\nkb1aTPvD/8FbZd6avrVOPmibxMREu4CAgFIAhQoVSty0adPZjLZr1KhRbMOGDW81a9bM2L1795sA\n1atXLzlz5sywoKCgxC1btrj27t278J49e04BnD171mnnzp2nDIZn6+ZzZn7b7VgHffcCNgMhwKtA\np+wMTAjx9ElISODll19my5YtactWrVrFtGnT2LZtG76+d4+OJoQQ/24Z3WrPDKPRaHfgwAG3du3a\nlUhdlpSUlDYrU+vWrW8+a0knZC7xVFrruJRe6V9prScqpQ5kd2BCiKfP559/zpYtW8iTJw/Dhg3D\n1dWV8ePHExoaypAhQ5g9e/aTDlEI8R+WmRrKp4XZbMbd3d10r6TVzc3tmRyfNDNtPJVSqjrWGs6f\nU5Y9eym6EIL58+cDMGfOHPr160ePHj1Yu3YtAIsWLSI5WVrgCCGeXW5ububbt2/bAXh7e1sKFiyY\nNGfOHC8Ai8XC7t27nZ9shE9eZhLPd4GhwCqtdahSqjiwNXvDEkI8jaKiogAoU6ZM2rISJUqQI0cO\n4uPjSUiQEUSEEM+uTp063Zg6dWrewMDAUqGhoTkWL158bu7cub7+/v6l/Pz8Sq9YscLzScf4pGWm\n5jKP1rp56gut9Tml1I5sjEkI8ZSqXLkyv/zyC1999RUTJ05EKcWsWbNITEykZMmSuLm5PekQhRDi\nsYqLi/tH88JmzZpFN2vWLBqgf//+UUAUQOPGjWPPnj0beue2O3bsOH33/itWrLiQPdE+/TJT4zk0\nk8uEEP9xgwcPRinF5MmTCQwMpGLFivTp0weAIUOGoJR6QAlCCCGeZfes8VRKvYh1NqECSqmpd6zK\nCZiyOzAhxNOnfv36LFq0iHfffZeTJ61t/HPmzMmoUaPo3r37E45OCCHE0+5+t9ovA/uA5ik/U0UD\n72VnUEKIp1eHDh1o3bo1e/bswWQyUbVqVbnFLoQQIlPumXhqrQ8Bh5RSC7XWUsMphEjj6OhInTp1\nHlt5W7Zs4ZtvvuH06dMUK1aM3r1706RJk8dWvhBCiKfD/W61HwF0yvN/rNdal82+sIQQz4qpU6fy\n7rvvpr0+fPgwa9as4ZNPPmHoUGlOLoQQ/yX361zUDHjlPg8hhHgkkZGRDBo0CIBhw4YRHBzMmDFj\nUEoxbNgwzp8//4QjFEII8TjdM/HUWoelPoAEICjlEZ+yTAghHsmqVaswmUw0b96csWPHUqVKFUaM\nGEGHDh3QWrN8+fInHaIQ4l8kLi5OLV682GPmzJleJ0+edHwcZSqlKrVs2bJY6uvk5GS8vLzK1a9f\n/7nHUf7T7uTJk47Tp0/3flzlPXA4JaVUeyAYaAe0B/5USrV9XAEIIZ5dsbGxAOTPnz/d8tTXqeuF\nEOJB5s+f71mgQIGyr7322nNvv/128cDAwKD27dsXSUhIeKRx3pydnS0nT550jomJUQCrVq3KmSdP\nnicyTduTmB3u9OnTOZYsWWK7xBMYBlTRWnfVWncBqgIjHlcAQohnV61atQBYuHAhoaE7gVP07v0m\n3377LcBj7cAkxNMuKiqK8ePH8/LLL9O+fXuWL1+OxfJMTuedZbt27XLu0aNH8Vu3bhn8/f3j69ev\nb7S3t9fLli3z7du3b4FHLb9BgwbGZcuWeQIsXrzYu02bNjdS192+fduuXbt2RcuUKRMYGBhYauHC\nhZ5grSmsVKmSf6lSpQJLlSoVuGnTJleAsLAwh8qVK/sHBASU8vPzK/3LL7+4Abi4uFRILXPu3Lle\nbdq0KQrQpk2bom+88UbBatWqlezTp0/Bex1v6tSpPg0bNizxwgsvPFegQIGgTz75JNfo0aPzBAYG\nlipXrlzAlStX7AFCQ0Nz1K5d26906dKBlSpV8j9w4IBT6nG6detWqEKFCgEFCxYMmjt3rhfAsGHD\nCoSEhLgFBASU+uijj3KHhIQ4BQUFBQYEBJQqWbJkqSNHjuTIynuZmZmL7LTWV+94HUXmElYhhLiv\n7du3A2CxxNC1ay3c3XOzbZv146ZSpUrUr1//SYYnhM2cOXOGevXqcenSpbRly5Yto3Xr1ixZsgSD\nITNf18+uL7/8MrfZbFbt27e/vnjx4jA7Ozs2bdrk2rhx44Affvgh16RJky57eXk9dBb/+uuv3xg1\nalS+V1999dbx48ddevbsGbVr1y43gA8//DBf/fr1by9btuzC9evX7StXrhzYvHnz2/nz5zft2LHj\nlIuLiz5y5EiOjh07Fj969OjxOXPmeDdo0MA4YcKEv0wmE9HR0Q/Mqc6ePeu0c+fOUwaDgb59+xbI\n6HgAp06dcj506NCx+Ph4O39//zIjRoy4dPz48WM9e/YsNGPGDJ+RI0defeONN4rMnDkzLCgoKHHL\nli2uvXv3Lrxnz55TAFeuXHEICQk5cfDgQadWrVo9171795vjxo279Nlnn+XZunXrGYCuXbsW6tOn\nz5XevXvfSEhIUCZT1gY+ysxf8gal1EZgccrrV4H1WTqKEEL8g4lu3RoyY0Z+goJyc+XKUW7fvoqf\nnx2BgWVZsGCNzIQknhnvvPMOly5dokqVKgwaNIjLly8zZswYVq5cyYIFC2SChgc4duyYC0CPHj2i\n7OyseVyjRo1iixQpkhgWFpbj1KlTOapVqxb/sOVXq1YtPiIiIsesWbO8GzZsaLxz3bZt23Ju3LjR\nc+rUqXkBEhMT1ZkzZxyLFCmS3LNnzyLHjh1ztrOzIywsLAfA888/H/v2228XTU5Otmvbtu3NGjVq\nPDCu1q1b30y9+LjX8QBq1KgR7eXlZfHy8rK4ubmZ27VrdwsgKCgo7vDhwy5Go9HuwIEDbu3atSuR\nWnZSUlLaB23z5s1v2dvbU6lSpYSoqCiHjGKpXr167OTJk/NFREQ4dujQ4WZQUFBiVt7LzCSefwFH\ngPKAAmZqrVdl5SBCCGE2m5k5cya///47ixdPRalI8uSB06dXYW9vT0xMDNeuXcPX1xd3d3fgCuDC\nmTNR5MmTJ2WZEP89V65c4ddff8XJyYkNGzbg4+MDgIeHBz179pTEMxNy586dHBoayq5du1ybNGkS\nA3Dx4kXD5cuXHZVS5MuX75EbRzZt2vTWqFGjCv36668nr169mpY/pXSEPFOuXLl0CdjAgQPz586d\nO3nFihXnLRYLzs7OlQBefPHFmO3bt59csWKFR7du3Yr179//St++faPuvNCOj49Pd9Xt5uaWVlt7\nr+P98ccfro6Ojjr1tZ2dHU5OTjr1uclkUmazGXd3d9OJEyeOZfQ7pm6fepyM9OrV60bt2rVjV61a\n5fHiiy+W/Oabby40b948+n7v3Z0yc8vcHRiCtW3nWWBXZgsXQohURqORYcM+ZMmSJWzbtorUmXft\n7e0BcHNzo1ixYnckmJrw8F3Ur1+X+vXrc/369ScTuBDZ7NatWwDkypULb++/+3AEBgYCcOPGjQz3\nE3/r3r37dYBPP/20wFtvvVVw7NixuevVq+efnJys6tatayxcuPAjT4TTu3fv64MGDbpctWrVdDWU\n9evXv/3ZZ5/lSW2Pu3PnTmcAo9Fony9fvmR7e3u++eYbH7PZDMCpU6ccCxQokDxo0KDrnTt3vr5/\n/34XAB8fn+T9+/c7mc1m1qxZ43WvOO51vMzw9va2FCxYMGnOnDleABaLhd27d993fw8PD3NMTIx9\n6utjx445BgYGJg4fPvxq48aNbx08eDDTx4dMJJ5a64+01qWBd4D8wO9Kqd+ychAhxL9DXFwce/bs\n4fDhw/e82r1bbGwsw4YN+8dg7126dOG5555j//79QBLe3rf46qtBLF8+gXr1KmWq7ORkEzly2OHk\nZIeLi0tWfx0h/hWKFi2Kj48P4eHhrFplvaFoMpmYOnUqAFWqVHmS4f0rdOrU6Vb37t2vJicnq1mz\nZuUZMWJEofPnzzsVKVIkcfbs2Y9lCMgSJUokjxgx4urdy8ePH3/ZZDKp1M5Cw4cPLwAwYMCAq4sX\nL/YpV65cwKlTp5ycnZ0tABs3bnQvVapU6cDAwFJr1qzxGjx48BWAjz766FKLFi2eq169uv/9es3f\n63iZtXjx4nNz58719ff3L+Xn51d6xYoVnvfbvmrVqvEGg0H7+/uX+uijj3IvWLDAu2TJkqUDAgJK\nnT592untt9+OysrxVWa/XJRSebEOqdQBcH/SMxcZjca0wD08PJ5kKALrh+SMGTP4+uuviYqKonLl\nygwaNIgXXnjhSYcmUoSEhABQuXLlf6zTWjNx4kQ+/fRTjEZr86WAgABmzJhxn57lFuAGsbG3cXMr\ngbOzE3FxxwEzYKZhw65s3ryHX3/9lkaNqpIyEVqW/fXXdXLkcMTLqwRQ+KHKeJrd77yIJ8fW5+XT\nTz/lww8/BKwd665cuUJERAROTk7s27ePUqVK2SQOW7t58yaffvopw4YNS1vm4eGRdpv5woULC4oW\nLRqY2fI2b97s+sMPP3jHxMTY1ahRI+aNN9644ebm9nAfPuKhXbhw4XjRokVfz2jdA9t4KqV6Y+1Q\nlAtYDryptc6wbYB4Nmmt6dixY7rBvtevX8/69euZO3cu3bp1s0kcsbGxWCyWe7YFTEpKYubMmSxc\nuJBbt25RtWpVBg0aRLly5WwS39NsypQpDBkyBIBSpUoRFRXFiRMnaNq0Kfv27Uu75QcQExND7969\nGTeuF4ULO+HiohkzphceHm5ofT2tQ9CMGUOwWCwULJibh006AfLm9U15dg2tkxk5ci6NGjWWoZbE\nf8oHH3xAQkICn332Gfv27QOgRIkSzJw58z+bdEZHR1O3bl2OHDmSLvF8FA0aNIht0KCBDAD8FMtM\nG88iwACtdWmt9ajMJp1KqTlKqatKqaN3Le+nlDqplApVSk28z/72SqkDSql1mTmeeHI2btzI8uXL\nyZkzJ+PGjWPlypVpScyAAQOyfRDwvXv38sILL+Dm5kbOnDmpVasWf/zxR7ptTCYTLVu2pF+/fvz5\n55+cPHmSBQsWUK1aNX77Lftbjpw6dYpu3bqRP39+ihQpQr9+/YiMjMz242ZGcnIy48ePB2D+/PmE\nhoYSHh5O+/btiY+P5/PPP0+3/fDhw1m4cCGvv94fAKUUI0a8Qf/+HdL1Qi9RoiB+foVxdnZ6bLGu\nWrWSsWPH8corr3Dz5k3A2nZ0zpw5bNy4Md22cXFxmW4uIMSTZmdnx0cffcSlS5fYunUrwcHBnDp1\n6j991+jbb7/lyJEjlCxZ8kmHImwoM208h2itDz5E2fOApncuUErVB1oAZVPajU6+z/7vAscf4rjC\nxlLbJL3//vs0btyYQoUK8emnn1KpUiWMRiPbtm3LtmMfOnSIevXqsXXrVhwcHHBwcGDnzp00aNCA\n3bt3p223ZMkSNmzYgK+vLz/++CP79+/n9ddfJzExkV69emXrIM1Hjx6latWqfP/990RGRnLx4kWm\nTZtGtWrVnorkMywsjCtXrpAvXz46d+4MgIODAwMHDgRgz5496bYfOfJ92rdvxIwZH9o81hYt6tKn\nTztmzRqFl1cMcJkLF/bRs2dPBg0aAEQD8UASpUuXxtHRkUWLFtk8TiEeloeHB/Xq1aNKlSqkDgv0\nX/XTTz8BpF34ZkRrLSPo/wvd77xl24i0WuvtSqmidy3uDYzXWiembPOPRroASqmCwMvAOGDgg46V\n2hZHPBmXL18G/u6ZCdZzklr7FRoaSp48ebLl2IMHDyYuLo6GDRsybNgw7OzsmDx5MmvXrmXAgAF8\n/fXXAMyePRuAHj16UKJECcxmM2+++SZLly7l7NmzLFq0iICAAMB6FX78+HH69OmTtuxRDBgwAKPR\nSM2aNenfvz8JCQlMmDCBY8eOMWDAAP73v/898jGy4u7/l9Qes1FRUWzevBlPT2s789QaRIPBcMc+\nJpydLzBq1OtYLHEcO2b7VjfvvPMKAMeObQMgMvIKLVrUIlcuT44dW522XVyckUKFcuHvn4N9+/ag\ntQGt9VM7Nqh8jj2d5Lxkn9T25OHhF+65TVJS0vG4uLggFxcXSUD/JeLi4uySkpLuWXFo66kQSgK1\nlVLjgATgfa313gy2+xIYjHUop6dKTEwM586dSxv65Wn7EktKSmLbtm2cPHkSb29vmjRpgq+v74N3\nfARVqlRh3bp1/Pjjj1SvXp0iRYqwefNm9u3bh4ODAxUqVHhwIQ8pODgYgHfffRc3NzfAmuitXbuW\nkJAQzGYz9vb2JCQkANbZQezsEjAYbgJJJCZah0FzdIzA0dENpeD48X3s3n2ILl0a4ODgTXJy7oeO\nLykpid27d2NnZ8eoUaPw8rKOkDFkyBC6dOnCtm3bbJ543s3b25vnn3+ePXv2MHDgQLp06UJUVBTT\np08HoGnTply/fp1t27bx2mtVUCp75go+GGngl9M5eDUogWJe5kzvV7hwHj755K1/LN+6dQomkxmD\nIQ6tzxId7U737h/wyiuv0KZNm7RhnIQQtqW1Zv78+Zw7dw5vb9i69Su6du2R4bYxMTETw8PDcXR0\nDFRK/bergP8DtNaWpKSk4zExMfdsSonWOtseQFHg6B2vjwJTsQ5EXxU4T0rP+ju2aQZ8k/K8HrAu\no7Jv3bqlUx+2YDKZ9IcffqhdXV011p4SukKFCnrfvn02OX5mnDlzRpcoUSItPkA7OjrqBQsWZOtx\nExISdPny5dOOeed7NGTIkGw9to+PjwZ0aGho2rLw8PC0391sNmuttX7vvfc0oO3tlT58eKG2WPbq\n1atH6iJF0AEBOXRc3A6tdYjWOkTv2TNP//zzl/rq1U1a6xAdGxupt23b9lDxxcbGakAbDAYdHR2d\ntvzYsWMa0Hny5HmE3z5r9u7dq/fu3ZvhulOnTum8efOm+9sB9EsvvaQTEhJ03bp1NaDHju2tU9+n\nzD7OnVuu9++frY3GLRmuvxi1R789f5Mu8sE6XeSDdTpo1M86+PyuLB/nQY9580ZrQJctW0YnJyc/\nvjf2Ed3vvIgnR85L9mrVqpkGdKlS7rpiRfRd3+nZmpvI48k+bF3jGQGs1FprIFgpZQF8gWt3bFMT\naK6UeglwAnIqpRZqrTvbONZ0Ro4cySeffAJA2bJluXTpEgcOHKBBgwYcOXKEggULPlS5kZGRrFix\ngtu3b1OjRg3q1q37ULWoWmteffVVzp49i7+/Px06dODAgQP89NNPdOvWjapVq2ZbA+4cOXKwbNky\n6taty19/XcbDIxYPj3wMGvQ+7733XrYcM1XLli357rvv6NmzJ1999RUGg4FBgwYB0KxZs5Q2UmZG\njOjBkiXfYrEk0L17Fzw9c3Lz5i18fKBfvzdxdv57/Ntq1cqkPb958zaVK7ckMjKKo0ePUrx48SzF\n5+LiktbZadCgQXz22WckJCQwePBgABo3bvzob8Jj4Ofnx6FDh5g+fTq///47rq6utG/fng4dOmCd\nG7gHkZHn6dmzRabLPHPmDGPGjCE01Ho73tHRgTZt2vDuuwNwcDAQn6T5dlsMM7bHYqcU7zd248Ug\nJ96cf5POs28w7TVPGpV6fB2TunR5GQ8PN/Lk8cZguAgUIjY2iejoaPLmzfvYjiOELWituXDhAmaz\nmeLFiz/17UF//fVX/Pz8KFYsFxDBhAk96NWrKeXKFWPatGlPOjxhS9mZ1fLPGs9ewJiU5yWBcO6q\n8bxr/3o8BTWeRqMxrRZv/fr1Wmut4+LidKNGjTSghw4d+lDlfv3119pgMKSrYapdu7a+efNmlssK\nCQnRgPb19dVGozFt+euvv64B/cEHHzxUjJmVmJigK1YM0p6ebvq77/6nzeZj+sSJo3r69OnZetyL\nFy/q/Pnz/6OmztXVVXt7e+vTp/dorQ9qrUN0RMQaPWBAbV2pErpiRXSTJr568eL3tcWyV9+vpqxD\nh8a6bNlAffjw4YeKcdu2bWnn2WAwaDs7Ow3onDlz6hMnTqTb1mKxpHt9+vRpHRISopOSkh7q2Hd6\n+BqcRK31QZ2cvEdntnbxxo1NukEDT12xIrpePXf92msBumJF6/v+6aft9NpDO3T1T9brIh+s0/0W\n/aYv3/ozbd+omGDd/KuNuviZAOlVAAAgAElEQVTQdXpJ8PZMHzPrj/36ww/7a3d3d7148eKHeF8e\nD6lZezo9zedlzZo1OigoKO3zLnfu3Hrw4ME6ISHhSYeWoYkTJ2pAd+jQTN/r/1FqPJ+dR7ZdIiml\nFgO7AX+lVIRSqicwByieMsTSj0BXrbVWSuVXSq3PrlgeVWhoKLGxsZQtW5YXX3wRAGdnZ/r3tw4n\nc3ev38zYtWsX77zzDiaTiRYtWtC/f39y5crFjh076N27d5bLu3jxIgDVqlXj1q1bDB8+nMWLF9Og\nQQPA2nP5cbt+/Trx8fFAPI6O51iyZAyrV3/C888HkZR0k2bNXqJXr17MnTv3sR87VaFChQgODqZf\nv34UKVKEwoUL89Zbb/HSSw25ceMGS5Z8T+rUjAUKFOCLL75gy5YtrFu3lnXr1tGhQ4cH1jBPn/4h\nISFzCQoq8VAx1q1bl02bNlGzZk1MJhNaa1588UV27NiBv79/2najR4+mePHiXLhwEq0vY7Gc45tv\nJlO5cuW02nawjldqiyn0Tp8+zfnz57DOlGvCYMj8DZLVq1dz8+Ytypcvx/r16/nhh4XMnj0bS85i\nfHe+En0XGfF0sWPp295M7ehJPo+/21t6u9qx6E0vapRwZPCK23yzLSb1QvSx0trMqVOhREdHU6RI\n9raDFuJxSEpKok6dOrRo0YLLl49QvXpO6tTxJCrqKhMnTuTLL7+0eUxaa1KnggTrGM7169dP+cwy\nA7G8+mot8ub1oWLF4tnyvyz+XbIt8dRad9Ra59NaO2itC2qtv9NaJ2mtO2uty2itK2qtt6Rse1lr\n/VIGZWzTWjfLrhgzK7WXb0REREqiZXXmzJl067Pi22+/BaxDEK1evZopU6awZ88eDAYDy5Yt49q1\naw8oIT0/Pz8AduzYwcSJExg3bhy7d2/ml1+WYjBAwYIFqVOnDh988EGWY83I5s2bKVOmDMOGDcA6\n6lUczz1XiFy5rO+Fk1MORo7sSY0a5Wjfvul9y3pUBQoUYPDgwfz555+EhR1jxoyBfPHF2/zyy1cM\nG9bzH9vnzJmTfPnyZTqR8vBww8HBAIQB+qE+OOvVq8cff/xBbGwscXFxrFu3jvj4+DvKSuDEiQNc\nuHCB3r3bULt2CapVe47t23+iUKHcVK+eGzgNRPLTT0vw8fHh7bffznIcmRUTE0PLli2pVKkie/dm\n1P/v/o4etQ7f27ZtO5ydnbkZa2FlWHFuVp2CybUQPctdZ20/H6oWc8xwf9ccdnzX1Yvm5ZyY+EsM\nH6+LxmJ5vF9YSimWLZvAwYOLqF7dC2uTczP79+/P1uG1ROZorQkODmbp0qUcOHDgmU1YYmJi0p47\nOpo4ezYUpaBp02r8/vtGNmxYy0svVSJnTti/fx7WG4mxDBo0iF69enHu3Llsi+3999/Hy8uLlSuX\nYR3K7BqxsWFs27aN3bs3AgeBExQu7EhY2Dr+978uT12HXGF7tm7j+a8UEBBAhQoVOHDgAM2bN+fd\nd9/lzJkzjBw5EoDXXnsty2WePXsWgJdffhmwfsgaDAYCAgI4evQoFy9eJFeuXJkqS2tNwYIFqVev\nHgcPbuPQocWUK1eI06e3cvXqOapUcaRqVR8mT96ByRQHXAecAWfq1KmHr68vs2bNwsfHJ9Px58zp\nxPXr1zl4cD/JyckpiVl6r7/+Mp06vYidXSRgwGLx4erVq4+9PV1wcDCvvPIKpUqVYNOmLzAYDBQo\nkJsCBR6+N3pG4uNvMGbMu1y5EsOcOXMeqozU+carVatGcHAwe/eup3LlwkACffq8yMWLf3DlivWL\nxSqSPHkUTk6JwG3gNpGRR8iRw5HChZ2Ai4AP4Pqov1461nZjBbFY4ggIKJrhNokmzYlIEzGJFqIT\nNNEJ1p8xiZrjTo2ICQxiakgufoy8wcHwZGISNV7XN8PR2bTq8TX2dvf/AnI0KL581QMfNzvm7Izj\nRqyFiW09cDQ83i+ucuVS2z7f4ODBfVSv3on69euzdu1aHBwcHuuxROacPXuWdu3aceDAgbRlNWrU\nYMmSJQ/dnv7fRmvNm2++yeLFizl2bCdFijgBsRQqlISPD0ycOCxt7OKlS6dQt25dzpw5QULCRZSK\n4LvvZmE0RvPee73Syjx//jy+vr73nN3tfk6fPs3ChQtp3rw5338/nTNn/iQ8PAqj0cipU9sBa+VH\nvXp+bNgwlTJl0t8hcnSU/yVhJYlnJiilmD17Ng0bNuS3335LN9NNp06daN26dZbLLF68OLt372b9\n+vXUq1edP//cQvXqL6GUwt7enkKFCmWqnMjISLp3787169dYt+4L/ve/Xhw7dhx7+5tcvQru7m6M\nHTuWoKDybNyY2oDbetvdaIxhx44dODnlwMMjHmti40K/fu8RFhbGmDFjKF++fNqxwsPDU+K6RpUq\nLuzYMYtq1crct1G7dZ0GLvLhh6OZN28Fa9eupUqVKll+z+6lUKF8KGXBYDATG5uAh4fbYyvbZPr7\nFvPly9f58suZJCYm8cEHH6S7TZ6FEoGrVKlSgsjIMP766yRgTZCPHt1LYuINSpUK4JNPPsHb25tv\nv53Ojz/+yNSpU6hduxZKKQYO7Ezfvq+SmJiEdRrJKCZMWIenZy569ep1v4NnmoeHA2vWfML16zdw\nd/9nUpuQrHl1xg0ORWQ8tFIO+7Ik5SrM6WtxGM1X8feyx/X8Eg4fXE3hwoUyPQWgnZ1iZDN3fN3s\nmLQxhhtxFqZ39sTFMXtu1ly/fhV3d2eKF8+b4cWUyH5JSUk0adKEs2fPkjt3bqpXr86OHTvYtWsX\nzZo1Y//+/U99R5rHQakk4uOjiI+PZ+vW1XTrZh2/1sfHjeTkGK5du0b+/PkB63znJpMZBwcD9vYG\nDAZ7tm+fyZYte/H3N2MdUMaL3r3fZPPm31m7di1Nm2btTtSbb77B779vZ968T/D1NaXECEFBYDSe\nxGKxYGdnR65cXjRtWuNxvhXiP0Y+WTOpYsWKHD58mFGjRnH+/Dk8Pb3o1KkTrVq1yvKHYEJCQlov\n6oULJ2E27yU8PA47O3B317Rq1YLcuXOTnJzMiRMnCAoKumdZOXO6Ehp6mJiYGKKi/mL+/PmEhOzj\n1CnrOJ5169ZNq2Vr3Pj5dPu6uTlz9OgSwsIiMRiuAFcA2LBhDWfPhjN27LukJqOffTaF999/n717\nV6bU0EH16mUz/TsnJ5sICQnh+vXrGI03M/9m3UN8fHzKexhLvny32LlzNkWL5nssYzOaTCbmz5/P\nsmXLuHr1Gnnz5uXVV9vTqVMnpk8fir9/qSwlnSaTiffff5/mzZvwwgsFgSTGj+/NV18NTHfbaefO\nXQD07duXwoWt7/GAAQNYv/5nzp+/QGRkZNoXjaOjQ1oNwh9/7GPo0JE4ODjw8ssvZ/qiJSPBwcFU\nrFgWg+EcdnaQO7d3htuN/uk2hyKSGf2KO4H5HHB3UikPO1xzKAx2MGHCfJYtW04i1laiAK6uLowe\nPTpL/zNKKd6p74aPqx0frrpNx1k3mdvNC2/Xe5ehtebIkSPs3LkLpaBOnTqZSnYbNqzG4cM/4unp\nDpwCihEZGYWnp2e6kQ9E9lm9ejVnz56lZMmShISE4O7uzo0bNyhbtiyHDh1i8+bNNGrU6EmHmS2S\nk5MxmUw4O98GIhgzphtjx3anWLECads0atSQBQsWMmbMGPr374+jYw6mT7c23WrQoEHaBVPZsn6U\nLeuXslciWkdiMkUDUKGCB/AXkJPJk79h+/btDBo0iLp16wLWHujfffcdkydPolAhdyCKN99szLlz\nIbi4xNGwYQM6dOjAhQthfPnll2zevIWtW7em9SkQ4n4k8cwkrTWTJk1i7ty5rFr1JS1aNALy0rZt\newIDAxk0aFCm23pevnyZBQsWAODra5c2pWSZMlC6dGmmTOkLHGX9+r20bNmDTp06sXDhwrQ4Vq1a\nRfPmzTEYjLi6XmL58k8pXrwAuXJZByevUqUyVapUfmAc9vb2lC5dgtKl098S2bBhCvv2HScw0A1r\nu0LYu3cT9vb2hIQEpyWeWeHgYGDDhqns2nWIunULAUlobU2cstrm5+jRo7Ru3ZqhQ/vSvXstQFOi\nxOO7/TZq1Gh++eWXtNd//fUXU6ZMJSzsIiNGDE9ZegPIOCm727x585gyZQpLlvzAuXOrcXZ2ws3N\n5R/bpb4N6duy/d2m9F7vU+3aFRg16k3Kly9PoUIP/z789NNPtG3blnbtGjN//sh7JvFL98bx4954\n3qnvSrea977F/8EHH1CrVi3WrVvHrVu3KFWqFO3atSNfvnwPFV+Hqi54udrRb/Et2k6PolcdV3I6\n2+HhrPBwtsPDxfrcUZkZMWI4v/22OW3fWbNm06xZM0aOHPHAi5P8+VObuMRgMh2mdeveREfHs2rV\nqrS21OKf4uLi2LlzJ1pratSokTahQ1YdPnwYgPbt2+Pu7k5ycjLe3t60atWKadOmcejQof9s4jlg\nwACCg3ezevU4ChTIneHnWvfu3dm1axdnz55j4MBBacvz5MlN37797lm2UorffvuGmJg43NwcgUvA\nJVav/oGdOw/yxhvtgSTAke++m8HSpSupUCEPQ4Z0BaBixaLkyhVHrly+jB07DgcHAxUqVCAuLpbP\nP/+CX3/9NV3iGRn5F/Pnf8+uXbuxt7ejdu06dOnyepaadIn/Jkk8M0kpRd68njg4GIiONgJxhIZu\nYsWKFbi7uzFo0P3Hq7x+/XrKDEKJFC9uZsqUgfj7F6F0aessPzExMZQrV47KlSunJBiJXLlyBg8P\nNypUKATcBDzp3LkzixYt4quvhtO3b0sg/biTj4OfX2H8/NInlxMn9uPLL98jb96H7/3r4GCgbt1K\nQBxwgiNH4nnttZ688847WerJv3fvn5w+fZoZM2bRtWv1x3rb7fjx4/zyyy84Ozsxfvx4atSowfbt\n2xk6dCirV6/mtdc6UqJECSCcI0fCAMN9a6QBund/mT17WtC9+ys4O997XMratWtz/PgJpkyZgo+P\nDz4+PkyfPp3o6Biee+65+7aNHT06taNROJD1CwMAX18vcuRwIF8+r3u+p0cvJTN8zW1qPufIwEb3\nTyyUUtSqVYtatWo9VDwZaVLaiQU9vHlrwU0Gr7id4TZ2WNDJPbCv9So+7o7kM1zhypYJrFu3joAA\nfzp27Jjp40VGXuHmzWvExibh45P1ToTPAqPRyFdffcXkyZNJSDBiMoG9vSNjxox5qM6MqdPr7tix\ng3bt2nHy5En27NmTNnVldk2/e6fLly8zYcIETCYT06dPt8kxb9y4wfr1P3P58mXCw6/cs426h4cH\nc+bMYdmy5fz++zbMZjPVq1enQ4cOeHs/+GL47ovexYvHsnnzXurVKwQcAex5552mlC+fj06dmqRt\nFx8fB4CPj0+6Zii5c1vfm7i4uLRl4eHh9OjRgxs3/r67FRa2kM2bf2Pu3HnkypX+eyTZ/Gx2HHtW\nqX9rT0Gj0ZgWuIeHR7YdR+vUuZ2voHU4J0+GpetssXPnQc6ejaBLl5ZAbrTOxfvvf0DHjh2pXNla\n6zh58mRGjhzJ+vXfU69eCaxtHjMnPj4Bs9mS8mFhYPXqXbz99nCmTBlEhw5NHri/raXO3f2g25rW\nD8vu7N17jEmTRvD++0MAF65cucL27dtp0qQJOXPmzGBP643befOW0r59I1xcsj7A+MUoE7+fSiLZ\nrLFoMFvAoq3Pg/fuI3jvPgJLleb56jXwcLajaw0Xxo/7iLVr1/HeewPo3LkzGzbspHnzQQQFBREc\nHPyPHvIhISGUKhWIi8sN4Gqm4jIajXTt2pXw8Ih0yw0Ge6ZMmcLzzz9/jz3TO33axLRpi/j888/T\n1e6lfnGn/l2mZwZOcf78aYoWzZ9h7aoxzkKzaVGYzJp1/XzxcXty7ewSkjXXos0Y4zW34y0Y4zXG\nlJ8z5y0iJsmeis/XQTl5s/tcEm4OJiz7p+Kf4zwrVyzL0rFiY+O5cOEypUuXAoqxffs+Vq5cSe3a\ntWnTpg1grRXv168fvr6+aSNWgHW++0KF7t+m9f7n5en266+/0qJFC0ymBIoVgypV/Dl48DrHjkUB\nsHjxYjp06JClMq9evUqRIkVISEjAzk4xYEBbwsLiWLHiZzw8PIiIiHio2tSrV68ybdo0fvvtNxwc\nHGjZsiVvvfUWrq7pa+2XLl2acnFiwdERzGYH+vbty6RJk7J5mlUz16/vYu/eA7z4Ys1sPM7DiYmJ\noWnTpsTHJzB58iTq16/P7du36d+/P0eOHOWdd/rQo4d12sshQ4awadNvVKpUkf79+2MymZg8eTLH\nj5+gbdu2DB06BLB+v/5yNJGJG6NZ/Wb1tGN5eHhI1/f/MEk872P9+vV89NFHbNw4C0/PzM1PvX79\nLl5+uT/58+cnLCwMg8HAxx8PY+TITxg2rAdjx/Z5pJi01sTGxmd4q/ZpkNnEE6zJ5+7dRyhevEDK\n7U0HZsz4mV69PqRVq1asXLkSgEuXLtG/f3+mTRtHvnwJWJOkrLsVZ2Halhi+3x1H8gOL0BjsFCYL\nvFnbhfjdE9mw4RcGDnyPTp06ERsbT9myHWja9EUmTZqS1o4WYNWqVXTo0IFXXqnP0qUfZ6lGNioq\nilmzZrFp028kJMRTsWJFevbsma6T1/2YTCYCAtpy9mwEn332GQMHDkxbl1GCs3btWnLl8ub5572x\n1kRnzGLR9Pz+Fn+cSWTp295UKJzxMEgP69q1m8TExKVry/YwTCYT1apZE/Tg4D+xt7fnSEQyw1be\n5PBlC47GE6wcXpMyBR62h63iq6/W0r//aN55pwvTpo0BNBcuhFOsWB2KFCnAhQvbAI3FYqFo0QaE\nh19i796990ws/02JZ2xsLBERESltnJOIijpFnjxlcXHRfPZZL9588w2OHz9P69YDiIu7RP785di9\n+2CmyzcajXh4eLBq1TxGj36DyEgzefJYm6GEhzvx8ceT6Nu3b5bjvnDhArVr1yYiIv1FXcWKFVm6\ndCk///wz77zzDvv376Rdu/rExlpwdHSmatVCrF9/mqQkzUcffZQ2ksnjZO3AaA+cwdqm/un17bfT\nmT17NgAFCuQnKiqKhIREfH19+PHHJXh5eWI2m6lRwzpm8fr1P6fVFp86dYqOHV/Dx8ebX3/9lb0X\nkvh0fTT7Lybjl9vA8p5/X1hL4vnfJrfa78FsNjNs2IccPHiImTNnM3hw10ztV768H//73+sULZof\ngyECSOZ//3uZevWKUbt2hUeOSyn11CadAOdu2BMc4cCQ5ywP7Hlsb29PrVp3JlTJ5M7tQO3aFWje\nvBzWLimenDhxlJUrV+LgEM2PP36a5ZgSTZoFu+P4aksMtxM07Ss506e+Kx7OdtjZgb0CezuFnYJz\nZ8/y2msdyOHowKhRo9hsrMzsHbF4hZxHYb0dDuDq6syhQ4txc/PCOrPr3/z9i+Pk5EiePDnTenpm\nlo+PD0OGDGHIkCFZ/j0BDAYDM2cO4+uvl/Pmm13uu21wcDBt2rTBycmRQ4cW3Tfpm7Y1lq0nE/m4\nRc7HnnT+/vs+WrQYRIUKQWzZshmlLpCYeAuDwT7LNUzWobTyc+nSZbZu3UrDhg0JKuhA98K7Gb5p\nN4kBPWk+LYpO1VwY1NgNT5es1tpqatf24/PP36N8eX+sQ5NB7tx2LF06Hnd3F8AIWGuImjSpQkiI\nKxUruqVs68UXX0zFy8uLtm3bPnQ7yCchJCSEBg0aUKJEUfbtW4ZS0fj4QLly9oAprWYzMLAYBw4s\noWbNWiQmHkLrCMaNm4uDgyMDBw7McIiqmzdv0qtXLw4c2M+RI6tp1SqIKlVW8NNPPxEZGUmhQoW4\neTMH/fr1w2g0MmzYsCzFPnjwYCIiIqhatSqjR48mJiaGIUOGsH//fqpXf55r165TooQjO3euwsfH\nwttvt6F58+YopRgwIIF69d7iiy++YMiQITg6Pr6//5iYGOrVq0eXLq/Qr9/LT/0Yl2+//RaOjg4s\nXLiQS5cuA9Y+BUOHDsXLy9oURWuNyWTt9X5nbXLqEE4xdr68Nf8mvx5LJLe7HRPa5KRNRWdiYxDP\niP9EjWd0dHQ2jO0Wx4UL21my5GcGD+761H8gPGkms2bG9li+2BSNyaIIKmBgdlcv8uR89FtTEybM\nY+vWfSxYMCatA1VmaK3ZcDSR8RuiuXjDTJ2Sjgx90doL+37GjRvHypWrALAYXLhV41vsEm/xdvE/\nGfz+wAz2yIPZnA87OzuUigPOcPFiBIULP+n5v50Bf8B6Du6uWTOZEuncuRUFCngzefKAe/6N/34q\nkW5zb9KyvBOft/d47P8LN29q/PyaUrlyZZYuXYqrqxPt27+CnZ2ZhQs/JkeOrH3RL1q0iM8++xyD\nwUCDBi9gNpvZunUrZrOFQUNHccqxLvN3x+HpohjcxJ32lZ2xe8CYoo/i7+Y6EB+fRJ48jYmOjuHk\nyROULOlPSEgIJpMp000pbOH06dNMmjQJb29vxo8fDySQkBBJwYIVKVmyMOvXT0np+Q8vvfQSV65c\nZdasmVSsWBGAI0eO0q1bNzw9Pfn++x8oVqwFZrOZ4ODgDGt2k5ISKFcuiIsXI9i06Wtq1Cj3j23m\nz19H9+5j+OKLifTvP+gf6+8lMTERNzc3zGYzJ0+eZM2aNfTq1YuQkO106fIy7u6elCgRxLBhPZk0\naTTnz1/ghx8Wpk0icOhQOK+9Zk10T5w48ZDDqGXsxx9/pGPHjpQsWZj9+3/A1fXfMXJCYmIiERER\n5MyZM8Pxpt966y327dtP27ZteO+99zCbzQwf+wXrL+YnqWBTXJ3s6VXXlR61XNIqKIzG59L2lxrP\n/7b/ROLp6JiEs7P1jz86OvqhBscFazutn3/+mZ49WwMXAJm9JDPOXzcxcKmRAxeTqVUkkeqFkvk6\n2B0PZ8Xsrl6Uzv9oAwff+cWdWfvCkhj3s/U2TkBeA0NfcqduyRyZ2tdisbB8+XKWL1/OpUuXcSn5\nEqfz9OCDpm70rvfPGqqjR88SFPQqo0d/wKhR7clKG96MxCdptp1MJNJopnxhB0rndyDHQw6abrG4\nM3nyajp16kRkZCSQmnha23SazdEpCXPG5UfcNNPsq+vkzWnPqj4+ODs++vfBhQuXmTVrFR9/PAA7\nu8KAJxERERQoUAClFCdOnKBatWoopfnzz7n4+xfNUvkWi4VJkyaxdOnfbTmVgi5dutCvXz+UUhy7\nnMyon26z90Iy5Qo6MKZFTsoVyv4BruPjE1i4cAP795/g229HAJ7s3x/Ga6+9RXR0NJs2bUprpnL8\n+HGMRiOBgYHZ2o59y5YtzJ49mxdeeIE33ugJxBMaup8yZWpTrFhBzp37idTPwmvXbv7j4u/rr79m\nzpy55MrlS9eu3bC3t+P777/nr7+u0LlzZ957bwAbN+5m795Qhg8fDBQEHNiyZQs1atRImRwhnAMH\nDuHj43nfC7YTJy4QEOAHlOTuOw33cvv2bTw8PMiRIwfVq1dn27ZtfPfdxzRsWJpWrVrj6+vLxo3W\nUSxSE6bhw4fj72+dWMBisaNixc7Y20NExPXH3Cs7hiVLplG+vF+W/s7NFs3WE4ksCo4nJtHCi2Wc\neDnIidyP4UL/cdi3bx99+vTBZDLj6OpJdP6XiSnYEuwcaF7azMg2BfF1Sx+rJJ7Pjv9E4unhcQZw\nwmz24rnnalKkSBGWLl1K7tz3nrnGbDYTHh5O4cKFsbOzQ2tNy5Yt+emnn1i5chKtWtW3xa+RLcwW\nzY7TSbg4KvzzGvBwzp5OIFprFu6J55P10TjYw8ctc/Kcw3nrsECefvT8/ibGeM3UDh40LJX1TkAP\nIyzKxMRfYvj5SAK53e14v7EbbSo5P3CWnAd5a/5Nfj+VyK/v+VLEJ30LlYUL1/P66yMJCnqOgwcX\nPVQv+7gkC1tOJLL+SAJbTyQRn/z3/6WjAcoWcKBSEUcqFnGgYmEHcrln7gtm7NjZjBgxnWrVqjF1\n6lT++OMPDh06yHff/Q+DIem++yYka9rPiOL8NTM/9fOhmO+jt8wxm80891wrLly4zPz583j99Yyb\nsBw6dIjo6Ghq1SoMZG362FTh4eHs3r0bpRQ1a9ZMGwM1ldaa1QcT+GR9NNdjLHSo4szwl91xzWHb\nTlPHjh2jZs0+3LoVw7Vru/H1zQfkoFevocyYMY+pU7+gX78BABw8eJDZs2dTs2bNdL3z/x7XNj2z\n2ZyuucLkyZNZvnw548aNo0GDukA88+bNpXv3d2nXrglLl34CWG+VTpu2lIoVA6hTp+J944+Pj6df\nv34cOJC+LWeZMmX45puv/9F5B+zZvz+KSpUa8tFH7zJy5OtZebtSOHD1qicrVvz8wBExzGYz5cuX\n5/z5o3Tu3Iy9e8/w+ecD2Lp1HWvXrqNhwwZMmDABsLZ5Hj36I1xcnNM6OP7++++cPRtGw4YNmTz5\nZ+DRb7VbL6aTgRNA5voPAFyLNrM0JJ5Ff8Zx6ZaF3O52eLnYcfKKCaWgWjFHmpV14sUyTjbv/GeM\nt3DmqomzV02cvmoi5FQUxy7Fk2jvCcqO3IlH+bhtfprUzLj9vySez47/UBvPBE6c+IOrV/9CKTO+\nvn/XXgQHB3P16lWaNft72vcSJUoQFhZGWFgohQvnQqkE/Px8qFmzHDVr/vM2z7/F/otJjFpzmyOX\nTGnL8nv8n72zDoj6/v/44/roEkFMBBQUUbFnd+dmzZyxGTPmXDg7f+o2a9Z0dkwFFVtBN2crBgah\nKIiChHQex919fn+cnqKggLjtO3n8Be/71MXn8369X/F8ialqL6OqvRRXeylV7aU42UrfqfVgdIqW\nb71TOBuqplkVOYs/tsDeQsKz2iKqOcg4MNaG4VuSGLktmWmdzRjW2Pi9pSxotALLT6Wz9q8MpGIR\nE9uYMrKpcbEZEXO6m9N2STw/7E9l+3CrXO9j4MBO1KjhjKOjQ6GMzoxsHadCsjl2W8Wfd7NR5UAp\nUzEf11HSqYaSyqWkBOtoFzIAACAASURBVDzO4fojNdcicth0PoNfz+j3rWgjoU4FGZ4V5TRykuNk\nm/etPGrUJ+zb9yezZn1NVlYWc+fOJTk5mXbtqjBgQMc3Xt/sQ6ncitTw6yDLdzI6c3I0iMX6jlwS\niS2zZ8/F1/cPWrVqk+8+NWu+fA/K+PPPg1SsaE/lygVPqSlfvvwbxfRFIhE9axvRxk3BspPpbDyf\nycUHapb3s/xbvJ8v89dfv2BmZo2NjZTneaPlyinx9HTFzU2Ovue1ghs3TrBq1SpSUmLo3789ICct\nTYW5uS0ODg5ERkYafptNmzbl6tWrPHp0H1tbMyCL8PBbXL58mYCAo7Rurc/Ja9XKifXrp9GwoTvP\nvfVSqZSJEwvWCtjIyIg1a9Zy6tRJzp49iyAING7cmHbt2uXTclTLpk3rMDZWYlzEdHWNJot27Xpz\n8+Y9BEFgzJjXizZDQkKYNGkSTZs2YtGiz5k+fTxXrhymdOlSzJnzHcnJKchkUoYOHWrYp3Pnzvj7\n+3PkyFH27/cxjDs5VeK77yYDYWRklCM5OYWyZYtWCHfr1i1Gjx7Njh2zqVTp7alDgiDg/zCHbZcy\nOX5HRY4WPnKSM62zMW2qKZBJRNyP03DoZhaHbqmY5pPKzIOpfOQkp6uHkvbVlVgUOpf5zaRk6jgR\npCIwSm9k3o/TEJf2IkIol0LlUma0q2NFOTMNTZwlNHbN/34v4cPiP+Tx1JOams79+5F4eroCcjIz\njSlTxhOlUkFs7A30cjwqmjUbyP37jzl4cAl16+pXYFFRcZQubf23t8pTa/RSMAX1YuVFfLqWRcfS\n8bqWRWkzMd91MMPaRExITA53YzSExGh48FRjqOaWisHJVm+EVnOQ4u6gD+lavaEbDOgfggcCVEw/\nkIpGC1M7mzGggZFhsnu1qj1TrWPS7hSOB2YzoIERs7qZI5MUr/EZn65l3M4ULoap6eWp5PsOZu8l\n5LTtUibTfVL5qbcFn9QpWi5WRraOk8F6z+bpu9lka8DWTExHd72xWa+SLF/vrCpHIPBJDtcicrgW\noTdG49N1iESwZoAlHdzz9irrC5ykXL+eQlDQeUJCwpg7d/QbFwFeVzP5xjuVUc1N+L5j3qkrr6ZA\nzJ69jrNnA5g/f4xBW3b1ai/Gjl3EunWzGTlyElD4YpqAgACaNGmMqakR/v5bKF/+/eTOXgpT89Xu\nZJ6m6ZjUzpQvmpm8s6e8IBRGCSI4OBxf30u4uJSnUye9PuqDB5FUq9ab8uXtuX//BCADJNSv3x1/\n/9ucP7/BkDN55859EhJS8PBwwcoqL7my1wkJCeHWrVuYmJjQrFmzIqcyvUpOjuadnrU7dx5n4cIt\n+Pn5YmdX6bXXT53ypU2b9pQtW5qwsAP4+fmyevVqYmL0HdoqV3bkm2++oX79+rn2EwSBy5cv4+Xl\nTU6OmpYtW9GhQweMjJSEh0fRtes3KBSmnD9/HqWy8JGc9u3b4+vry5df9uGXX77Nd7s0lQ6fGyq2\nXcrkXqwGM6WIT+oYMaCBMc6l8/7cBEEgOFrD4VsqDt1S8ThRi0wCzVwUdKqhpGkVOaWLOM9otAJn\nQrPZe02FX7AKtQZMFSKcSktxKS3FubQEZ1spLnZSyllJCn3vlHg8Pxz+c4bnq1y9GsRXXy2hUqUy\nbNo006C3+K4PveLizL1sph9IJSJBS/1KMj6pa0TnGsoCe+o0WoFtlzJZ4pdOllpgeFMTxrUywTSP\n/dUagfB4vRF6MSiOv25G8VRtjkbxQsy3nJUEdwcp7mVlVC8rw91BajCIEzN0TPNJ4ejtbOpUlPFz\nbwsqveIJy2sS1ekEFp/QeyObushZNcASc2XxrMCvP1IzZnsySZk65vUwp3fd91fxr9MJ9Pk1kftP\nNZycVOq1HKW3cScqhxFbkohJ1WFn/sLYrFMxf2PzTahUKvb5XmF1gD1Ps03ZN6YU1cvmHwYsqIET\n+CSHXqsT8KwgZ9twK6R5LBSuXLnDmDGL+P33dbi4VAHE9Or1Gfv3H8bbe/szfUsJW7ZsZ9iwEXh6\nenL58uUipSGkpaXRs2dPHBxKsXnz5PdaCJSSqeOH/akcua2iYWU5S/taUMai8BP106fxhIeHYW1t\njZOT0xuN/MIYnvmh0+lITc0wFPwAhIVFYmNjiYVF0SrnMzMz+eGHHzh79pxhTKlUMmXK97miR/8k\n+ue4EqhCRoaOy5cv06pVS/TaudGsXr2LTz5pbWj9qtFoePToEVKplPLlyxf6e0lOTsPTcyAKhTEn\nTpw0tLZ9G4IgcOXKFYKCgrCx0XD69GkWLBiLUvl63rkg6J+XWy9kkqEWcC8rZVBDY7rWVL5VKeTV\n49yK1HD4VhaHb6mITtF7JKvaSWniIqeJs4L6jrK3zjVBT3LYez2LAwEq4tN1WJuI6FbTiI89jXAv\nKy22KFaJ4fnh8J83PN8HjxM1WJuI3ymMG5eqZc7hNA7fUuFYSkIXDyVHbqkIi9diLBfRuYaS3nWN\nqFdJlu+NfSlMzayDqYTEaGjqImdmV/N8V8Ivc+fOHb74YhQqlQoAncwMjVllTMrWpkbzPoTGi3iY\n8ELo0s5cjLuDjJuROaRk6ZjU1pTP8/EGvWkS3eOfyQ/7U3EsJWXjUEvKWxfd8BcEvcE993Aa9hYS\n1g60fOcipoIQGquh04p4OtVQsrxfwTvZnAhUMXFXClbGIn7qbUHDyvJ3MqCuX7/Od999R2JiEjqF\nNcn1lyKTivAZbU01p7w9ggUxcKKStfRZm4BWB4fH2+RrXLdrNxY/v8tMnjyZH3/8EdBXzSclJVGz\nZk1DfrVWq31j8VJByc7ORiwWI5OpgAcIgua9pW0IgoDXtSxmHdTnLi/sZUHHGgXzbGVlqVi0aCFH\njx5Fq9VP9NWquTFnzhwcHR3z3Kc4DM/3wezZszl48BAmJsa0bNmKmJhorl69hlgsYsuWLf+y65Uy\nevRK1q79jUePfClfvmDtbN9Eft/LvXsRODjYY2paB3h7waKfnx+DBg0iNjYWGxuoWBEcHMqwaNGi\nPD/DlX+k85NvOl08lIxoakzNcvnPAQVFpxMIfKLh3P1szt1X4/9QjVoDMgnUriCjibOCJi5yPMrK\nkEpEPE3TciBAhfe1LEJiNMgk0NpVwcd1jGheRfFOaVr5UWJ4fjiUGJ48C08EB/Po0SMcHByoUaNG\nvjf6vutZfOudgpFcRO86RgxqZFyo/DetTmD7pUx+OpFOtlZgbAtTvmhuglImQhAErkXk4HVVv0LN\nUAtUspHQu64RvTyNDJ6XmBQtC46mcfCmirKWYqZ3Mad9dUWBH04jR47k+vUbtGnThi+//JL09HTm\nzZtHSEgIgwcPYsKECaSqdAQ90XAnKocroSnciMhEIVLzTQuBbs2r5Xuut02iFx5kM3p7MlKxiHWD\nLalTsfCJ+plqHVP3p7L/hopWrgqW9rEo9hymN7HsZDrLTqaz6TMrWlZ988QjCALrzmSy8HgaHmVl\nrB9s+c5pAElJSfTo0YP09AyqVHGhRo0a+F6N5KHTd5hrovBf3BCF7PXP423fTVSyln7rEknO1LFz\nhDU1yuVvyKemmvDjjzuYPn16seoaFoScnBR69eqGXC5h794fDeP79v2BSqWmQ4dGWFvrq8CzslQo\nFPIieVrD4zVM2JXMrUgN/eoZMaOr2Vs9TlOnTuX48RNIpRLc3d0JDw8nJSWVUqVK4e3tlWeY+p8w\nPP39/dm1azcREQ+xt7enV69etGzZ0nBfJycn0759B3Q6Lbt27XrWJhYWLVrEnj1edO3ahVmzZr12\n3Cy1gFhMkVUYikpYWCTVq/fF3d2JTZtm4O7u/Pad3sLbvxcjwJXs7BwUiryfA4IgYG1tRXJyCpUr\nK+nXrwV37twhMjISS0tLfHz25/pN+Aaq+HxbMj1qKVnat/ily56jyhG4+lDN2ftqzt/PJvCJBkEA\nM4UIZzsptyJz0OqgZjkZH9dR0tXD6K1pWO9KieH54fDBG56xsbF899133L59xzBWpYoLixYtei2M\nsv5MBvOPptGwshw7czFHb+sTvVtUlTPkIxOau7zZi3U7Mocf9qdwO0rvoZzT3TxfozVTrePo7Wy8\nrmZyOTwHsQiauMipVkbG1ouZaHQCo5qbMLq5aaEkbtLS0mjRoiVyuYyTJ08aKk5v3AhgxIgRVKxY\nwdAxSBAE1q79lQ0bfuPln0mTJo1ZtGhRnvlNBZlEHzzVMGxzEtEpWjpUV9KmmoLmVRQFqr5/GK9h\n1PZk7sZqmNTGlLEtTd5r6DUvsjUCnVfEk6UW8P2qVL6eb7VGYLpPKruvZtG5hpKf+1iglL37tW7b\ntp1ly5ZRt25dVq9ehUQiIS0tjTbDfyS28hjaOWXy6wjH1yatN303Lxud24dbv6W4xgxwAf6ZueHA\ngQP06NEDR8eKhIVdRS8NpcXdvSWBgfe4efMgHh4ugJZp05bx++/HWLXqOzp0+KjQ58rRCiz1S2fN\nXxk42khY3s8yX4M8MjKS7t17IJfL2Lp1Gy4uzmRmZvLFF18QFBTM5MmT6d//9faRf7fh6eXlxcKF\ni14bHzp0COPGjQP0Uk4DBw7C2dmJ3bt3G7a5evUqX3wxCg+PGmzatMkwficqhx2XMzkQoMJIJmJa\nFzN61FK+k+Gk0eoX6XuvZzG7uzmeb2lckJWlQqks+AL8TQiCgM/Ze+RoRfRpWSXPbXQ6HfPm/Y6X\nlx8XL17E1NSUu3fv8uuvvzJ27FicnEpx44YvvXv3ITtbzt69a6lf34OcHA0jR47g9u07fPvtN/Tt\n2xeAuzE59FqdiFNpCXu+sCmWZ8VzUlNTSUtLo3RpuzxTzBIzdFx4kM35+2qCnmho5CTnkzpGBYqg\nFRclhueHwz+f5PgPotPpmDhxIvfuhWJpaYGnpyc3b97k3r1Qxo0bh5eXF3K5HJ1OYOHxNNadyaRz\nDSVL+lqgkIqY2knLzitZ7LicyWebkqhkI2FQI2N61zXKlcOYqtKxxDedrRczsTEVs6K/BV093vxQ\nNpaL+aSOEZ/UMSIiQYP3tSz2XsvizD01bdwUzOhiRgWbwn99z0WRxWJxLpmV5yLdz8OD8ELfTywW\n0aFDeywsLDhy5Ajnzp1n5cqVTJ48udDnB31Rk88YGxafSMM3MJuDN1VIxdCgspy2bgpauynyDMP7\nBamYtCcFiRg2f2ZVYF3Ol8nOVnPx4i1atHghYj19+hr++MOfefPG0LKlfvzAgdNMm7YGhULOzp3z\nqFKlomF7hVTEwl4WfLI2kZ9905nR9fUijeRMHaO2J3MpTM24ViZ81ca02AzkR48iAGjZsoXhOzQz\nM6ONi5Z99/fgSx+2XMhkaONXZWzypqBG5+HDZ7l58wFTpvz8txv7L9O9e3du3bpFXFwcUOql8U9w\nd3+AvX0DQB/qT001IiwsipiYorUilElEfNvBjKYucr7anUKvNQmMbmFCJRspOVqBHK3eONVoIfhe\nPJmV+2FTwRHv+3YIoanUrySna/deBAXNJygosBje/buRlJTMkiVLABg27DPatGnD1atXWbFiBZs3\nb6Fjx444Oztja2uLSAQRERHExsYa2h4+b0JgZ2dHplrHoZsqdl7O4mZkDkoZdKtpRGichq92p7Dv\nehbzepi/Jj9WEK4+VDP9QCrB0RqM5SIGb0hiyzCrN0ZIjIzeXbItJVPH/htZ7PLPIiTGArFIwNFR\nTb1Kr583KyubXbt8CAl5iJ+fHz179mTBgnls3bodmSyZRYvG8ujRbSwsoGPHVtSv7wGATCalXbt2\n3L59h7CwcACSMnSM2JqMsULEukFWxWZ0RkdH8+OPP3LmzBkEAaytrRg8eDADBw7MNf9Ym4jp4qGv\nL9C38Cy+3M038eBBJDNmrGXu3HHY2Ly7l7qE/w0+aMPz8uUr3LsXip1daX7//XcsLCzIzMxk0KBB\nPHwYwenTp2nZui3feaew74aKwY2MmdnVzJDbWNpcwsQ2poxpYcKxOyq2XNDnHP7sm07P2kqGfGTM\nvVgNcw6l8TRdx+CGxnzd3rTQhTUVbaR83c6MiW1MiUvTFanY4TkWFha4ubkSHBzC8uXLGTduHBkZ\nGaxYsQKARo1edE/x9vYGYOLEiQwYMADQy40MGjSYAwcOMH78+CKHWa1MxPxfLwvm9RAIeJyDX1A2\nJ4NVzDqUxqxDabjaS2lbTUEbNyXVHKQs9Utn9ekMPMpJWT3AinJWhf8MMjNV1Kr1KeHhTwgKuoyL\nizMgIiQkgQsXbvH0qT50BiJSUq4TEhLBtm2rcXF5vYCgbiU5AxsasflCJt1rGeUy1sKeahi+JYmo\nJC1L+1rQs3bxdiN5bgT4+1+lb9++iEQisrOzCQi4iVFMLNU/6srcI+BcWkoTlzcb5wU1OlNS0hk8\neCZJSam4uDSlT58+xfqeCkuNGjVeG5s/f/5rY0uWLKFhw4b069cXvUxRNFev3sbNzbFQXWIaOSk4\nPrEUU/alsOJURj5b2YPTQO4JOiLOZyAIsO5MJgqRJ7iOJsNIWqRmCMXJuXNnUatzaNiwIWPHjgWg\natWqhIeHs3+/D6dOncLZ2ZlSpUrRvHkLTp8+zbBhw+nWrStPnkRz9OgRNCYVSa48nAbzn5KWLVDF\nTsrsbmb0qG2EhZEYrU5g5+UsFh9Po93SeMa3NmVkU5MC5QXGp2tZeCwd72tZlLEQs2aAJbUryOi/\nPpEhG99ufBaF53JFv1/J5OhtFdkaqFFWypj6GfgEK/lyZzJH8sh3NjExwtt7EY8fx9G+fTMgjLFj\n2yKXp9O/v1466HlXn8DAwFwFrTdv3nz2eilytAJjdiQTm6pl9+fW2L/D8/1l0tLS+Pzzz3nyJBqp\nVIKFhQUJCYksW7acrKwsPv/8c8O2Go2Gbdu24+W1h9jYOGxtS9G7d2+GDBliKMh9H8ybt5GdO48j\nElmzalXj93aeEv5dfNCh9m3btrFs2XL69u3Dt9++kLVYs2Ytv/32GwOHjuCmaR9O31XzdVtTvmxl\n8tZJ43ZkDlsuZnLwZhbqZ1Ka7mWlLOhpgccbcub+Ti5dusT48ePRanWIxSJ0Ov1HaWlpyfbt2yhT\npgyg9yxFRkbh7e2No2Mlw/6tW7chOTmZY8eO5hLpz8nRMGHCQs6du8Xq1T+80oe9YITHazgVnI1f\nkAr/hznoBDCWi8hUC/Svb8TMrubv4A0wZvjw/+PSpWts2rTJIKMSFBREQkICbm5ulCql96AlJSXx\n+PFjKlasiIVFApD02tFSVTraLonHyljMoXE2yCQiQw6rRAzrBllRNw9PybsSExNDz549UatzaNz4\nI2rU8ODUqZOEht6nYsUKbN6xh95rk4lO0XLgyxfC76+GdAsXXoejR+/i7X2SDRs2/M+2kE1KiqNq\n1WoolVIuXNhIuXJ2hdpfEAQik7RodSCTipCJ9V5RqQTEgpben/QkNiaGpk2b0KlLN47fSORIoJZs\n2wYgUVLeWkL3mkp61H4Rxvw7Q+3Pw+ydO3dizpw5hvHVq1ezYcNGhgwZzPjx4wFITEzkyy+/5O7d\newhiGerSjVGV64jGqjpyCXT2UPJpA2PqVsy7+CU2Vcusg6kcu5NNVTspC3qZ52s0anUCOy5n8uOJ\ndFQ5AiOeqXM8z6mNSdHSf30icak6tg4vHuMzIV3HvutZ7PLP5MFTLWYKEd1rK+lXzxj3sjKCgoJ4\nkCjh6+MW1KskZ+swq0KrT2g0Grp370FMTAw1a3rQtm07AgICOHnyJFKpFB+f/ay9YsKWi5n83NuC\nj4so05YX27dvZ+nSZVStWoUVK1ZgY2PDyZMn+f77KRgZKTl27DhmZnrFg1mzZnHo0GFA3+XruVnQ\nsWMH5s2bV2zXlJWlIjk5nTJlbAFbHj3KYfbs+cyaNQtz8xeRo5JQ+3+bD9rwPHr0KNOnz8Dd3Z3N\nmzchEukLfMaNG8f5q4GYdvqVqCxz5vc0p3/9wsn0PH+omSlF9K777p1ziht//6usXbuWgIAApFIJ\nzZo148svv6RixRch5TFjxnD58hUmTpzAoEH67iLPezCbmBhz8uTJXB5PjUZDjRr9CQkJJyBgFzVr\nvlvoJClDx+l72ZwLzaaxs4JenoV7KD94EMmUKSuZNm0UHh4tABtSU1MxNjYu5Co+h+jo02RkZODs\nnFuQ/ESgii+2JfNtB1NsTMRMfVa1v2GIZZFSIQrKH3/8wbRp08jOftF9qHRpW3755RecnZ15nKih\n28oErE3E7B9rg7lSnMvAiUrW0n9dIkkFNDrBGsi7KvvvJDExkY0bN3L58mUsLS0ZOHAgzZs3L/D+\noaGh9OvXDzMzY/78cy0aTRoHDhzA19eXjIxMatb04NNPP6VcuYIL1b/MtWvXmDBhAllZqlzjg4aN\nokKjAey/kcX5+2p0gn5B2qOWEa5Gj7A2Fv4Ww/P+/fv07dsPpVLJ2rVrqVHDnYcPH/LFF18QH5/A\n8uXLqNugMXdjNAQ+yeFOlJrLdxOJSJWjEaSUtdAxtLHeQLIuYLHJySAVMw6kEp2q49P6RnzbwSxX\nPve1CDUzDqQS+ERDE2c5s7rlrc4Rm6r/zcam6tgyrOiLOv+HajZfyMQ3UJ+jX6eijH71jOjskVuu\n6Pn9ciu9Et/vS2V8axMmtS28hmlgYCDjx48nOTnFMCaVSpk1ayZJ1s35YX8qI5saM7VzwXRVC8qk\nSZP4668zzJ07h06dOhnGBw0aRFBQMGvXrqFevXqEht6nX79+KBRyFi1aROPGjbl48SLffvsdKpWK\nHTu24+rq+s7Xc/HiLfr0mYKHhxtHjhznVUWAlJQXn0+J4fnf5oM2PDMzM+nUqRNpaek0adKEFi2a\nc+nSJU6cu0V6nbmIzcrxy6eWtK/+97R7fBOCIBAYGEhsbCwVKlR8FiZ+d9RqNWKxOE9D7M8/TzN5\n8mREIr2X09LSgmPHjpGRkcmAAZ8yadIktFotGo0WhcIIKIeX15/4+/uzePEc4D56wf5/hokTl7B8\n+U66du3CwYOHinycc+fO0aVLZ6pWLc+FCxtz5cYCjNqWhF9wNlod76xTqlJlc+LERZycyhkqc7Va\nLUlJaZQqlVu+KSEhgRMnTvD06VMqV3aiTZs2ufLcLoWpGfhbIo2d5WwcasXdkGAALByqGozObcOt\nqFU+/wncy+skHh7uVK3aEfh7W/C9SnBwMC1btiQ2NjbX+MSJE1myZEmBvbBarZbExEQsLS0YMKAd\nQUF/kZAAdnYgkYCpqQlr1qwpsiEYHR2Nt/deQkPvYW1tTbdu3fD0fNF2Mi5Ny6GbKg4EZHErUoNY\nJFDeQotLGRMq2kioYC2hgo2UCtYSyllJir1CfMqUKfj6+gFQyqES0SozNKZOmFWog3nFuoTF6z26\nAGZKEdXKSKnmIKO1q4KPnIomA5aRrWOJXzqbzuvz3Gd1NadhZTmLjqex52oW9uZ6dY5ONd5cHPSy\n8bl5mFWeuZf5cT9Ow8JjaZwMzsbSWN+1qn99I6rY5b3oem54urm58bVXCvtvqNjymRXNipBbnpqa\nypEjRwkPD8PW1pYuXbrwWGXDp+tf3J+FcU5cvRrEqlVezJz5OZUqlQO0JCamoNMJhufE8+950qSv\nDKlSOp2O7t278+RJNJs2bcTDw4OtW7eyfPkKunfvxowZMwznWLBgAXv37mPs2DEMGzas0O85O1tN\nVFScodtYXFw2zs4dcHZ25vTp07k8nFBieH5I/OcNz9jYWJKTk6lQoUKevYwvXrzI5MnfGDQtNSYV\nSfOcjcLUis3DbGlQ+e+VismLR48e8f3333P37j3DWN26dZg/f74hNPwqgiAwf/4GqlSpyMcft3rN\nWCoo69f/xrp1vxrC8QAtWjRnwYIFREcnMGTILDw83Pjll42A3FB8ULduXUDDqVPb2bhxN7/9Nq1I\nyf9Pn8YTGHgHExMTatWq/UbR/+xsNU+fJlGunD1Qivh4OdOmzWLatGlF9mCB/oFYrVo1atVyYceO\nWblEukE/GX68JpHWrgqmdzHLU3C9oEybtob58zcwZsxnrFq1DMggIOAKtWv3oG3bBvj6rjJsW5B8\nwR2XM5n6zKPS0zGSuHQxM07bFMjovH49hEaNPkOhUBIYGPjG9pN/Bw0aNODKlSs0bNiQUaNGERoa\nyo8//ohareb48eO0b9++UMdbv349n3/+OcbGSjIzVTRvXpNatcw4e/Yc1aq5sW3btvf0Tl7w4KmG\nDX6PCUuSkJxjTESClqycF/eaSAT2ZiKMtImoEsKQ5yTgVtGazq3q41rBGnsLca5mEYIgcP/+fRIT\nE6lc2Qlb21IIgsDTdB33YzXcf6rhbrSav25E8CRDjk7+Qu+ytKkI93JyqjtIqVZGRnUHKeWtJcWa\nVnE7Mocp+1O4E6VBLgWdDoY3NWF8K5MC6yLHpWrptz6RmBS95/Ntxmd8upblJzPYeSUTI5mIMS1N\nGNbY5K0pOy9HCDLVOnqsSiQ+XcuR8aXeKc8eIDJJS/eVCVgYidg/1qZAih4vM3DgTHbsOMKUKd+x\nYMECIJX58+cyc+Zy/u//xvLNN4M5efIk3333PebmZkyePJnKlZ3YvXsXhw4dxt7enoMHDyCRSAwh\n+VfTL57ruI4b92WutqKvkpWlIjAwDMDQBTAuLhEHh46Ym5uQkHANkagUYElgYCBubm55ypuVGJ4f\nDv/Z4qLHjyNZsGA+V674A2BsbETfvn0ZNWpULu9eo0aN2L9/HwcPHuRqRA5/ajtjbSRj24hSuJX5\n53Mys7OzGTt2LE+eRGNtbUX16tW5cSOAq1ev8fXXkw0pArkREx0tMH36WiwtzenduzOgD8n++ONW\nBEFgyJAu2NnZvPX8I0eOoEuXzpw+fZrs7Gzq1atH9erVAUhOTufixduEhkYzd24mlpa5JwC1Wsfw\n4bOIiIigYUN3xo17XUomP3JyNPz880/s27fPUGlfqlQpZsyYTuPGryehh4Y+olu3SVhbW3Pu3DlE\nIiNKlYK1a9cWgYhvpwAAIABJREFU+Jz5YWFhgb+/P2XKWCESBfO8n/Vz7MwlnP22VKEn6NOnr7J2\n7V4+/bQj3bp1Bqzo1etzjh27QY0a9QFzwJzwcB1GRkaULu0IVAAyyMlJwtGxAx4ezvj4/Ixcnvdv\ndUADY+7GaFh/NpOcdCXHQxVkaN5udAK4uJSne/fO2No6/ONGZ0hICFeuXMHS0hI/Pz9MTfW5aUql\nkunTp7N58+ZCG57PZYK++eY7zp49y9q1P1GunJoOHdoQFBRMZGTkOy1YCoKTrZSBtbIAqFatAoIg\nEJ+u41GilogELWGxKryOXeRRtgKtsSOCWR0eJsIxbx3Pe7qbKUTYWYixkKl5fPcaaXEPEGlV6Ezu\nYVa2BtmKMqSqXvxmzRQinOzLU89GhJ1RFp6OpnhWNi10J66iUKOcDJ8xNmy5mMn1Rzl81ca00JI9\npc0l7BppbSg42vyZFfUdX/8tq3IENpzLYM3pDLJyBAY0MGZCa1NsTAvvuTeWi1kz0JJuvyQwdkcy\nu7+wLnLr30y1jpFbk1BrBdYPsX6r0XnvXgRr1ngzaFBnPD0bALaMGzcde3tXhg0bgT4SYUlsbA4A\n1ap9BFjSsmVr3N3rcubMVaZOnclz34NMJuWHH6YYnBFNmjRh6dJlnDjhS7169WnatAkXLlzg2LFj\nADRr1iz39WeqyMnRGDpi+fpeoUePSbRr15QTJ3YDSmxtq2FhYYG1tTVpaaUN3s3nc0cJHzbvzfAU\niUQbgS5AnCAI7i+NjwO+BDTAEUEQvn1lv/LAVsAe0AHrBEFYXphzp6Wl8cUXnxMbG4dSqcTe3o6H\nDyPYtGkzKpUqlwxQtkbgZrw5t0w+4Q9BRTlrCVuGWb1TVx3QT5QXLlxAJBLRpEkTXFxcinScU6dO\n8eRJNJUrO7JlyxaMjY1JSEigX79+3Llzh4CAAGrVqoWPz2l27DjG7t2/IpFURCxOYMqUKeh0OkSi\nGug/yiyWLdvDkycxfPxxd+zsZEAOW7ceJiDgHgMGdKROHbfXrqFMmTL0798f4KXcNWNq1erBnj17\naNKkCZaWr3fxkcvlHD58mLVr1zJ27EQgpsDve/XqVXh5eSORiKlfvx6xsbFERDzi66+/ZseOHQZB\n6+eYm5uRmqpCEDKIi0vFzq54K8kdHBye/VUGePLa64X3Com4di2c3bv90Oks6NbtKwA8PW25du1a\nri179uxJSkrKM49AKcCW27cTiYqKw8TEHLm8FJDy2hmeM72LGffjNGy+ASYyHTs+f7vRCWBmVpnd\nu/eh1Wrfuu375unTpwA4OzsbjE6AmjVr5nq9MGRk6KvTGzdubBBDF4QcRCJL4uLSuXPn/ns3PF9F\nJBJhaybB1kxCnYqwYcNONOfXUNXengkTxqMwTmXtZi8Cw+OpWrsJbbp+SnSKlscJ2Zy//pBsqROC\nY10QiRGpk9EkPKKyzVMmdf0I59JSnEtLsTN/905S74JUImJ4ExOGv8MxSptL+P1za/qvS2TopiQ2\nDbUyRKd0OgGfABU/nUjjSYqOttUUfN/RDCfbd3umO9lKWfixOeN+T2HhsTSmdyl8TqZOJ/D1nhTu\nxmjYMNSqQNe0bt0Bli37ndRUBRs26EPmDRo0oEGDBrm2W7FiBTNmzMDCwgKQIZFoMTevxcOHV6le\n3RZnZxOqVatGv379cqWRVKpUif79+/H777teawrQp09vKleubPh/wwYfvvpqKZMmfcasWbMBE6pX\nt6B69Q24uHigfz7qPfUxMTHIZP+886aEfx/v0+O5GViJ3ogEQCQStQS6Ax6CIGSLRKLSeeynAb4W\nBOG6SCQyA66JRCI/QRCCCnriAwcOEBsbh5ubK6tWrcLCwoIrV64wZswYvL29GTx0GMGJJhy+qeJ4\noIo0lYCVsb4T0aS2ZkVaERsuXqNh7ty5HD58xDC2cuUqevTozg8//JAr5K3RaLh9+z61a1dD3wUj\ng9WrvfjoIw9q1aoKwL17+vB6+/btMTbWFzjZ2NjQrFlzfHx8uHv3Lq6ubowb9xNRUbF4eV2lXz9n\n7O3tn4VgniNGEIyZOXM2QUFBODq2RL9S1rB37wwOHjxK/fr1qVNHAWRz/nwAv/9+gs6dm9Cxo97D\n6O19krFjF+Pjs4lGjboCInr06PHGz8Pd3Z2VK1c++8+IzMxg/P0Dad68Tr77ZGZm4uXlBcCaNWuo\nU6cOOp2OmTNncvToMXbt2sXUqVNfaseoxM6uMX5+p6hYsaJBFP99EBsrYsKE6fTs2ZS+fdsVeD+d\nTseMGWtp3rwBbdv2Aizp08cWQSjFJ5988tb9ZTJZrrQKT09PHj16RHR0NOAE3AXylvmRSUSsHmDJ\ndzsf0bFKNrXKO+S53XNOn75Ks2bNEYvLIhKJ3qucSkGpVq0acrmca9eucfnyZRo0aIBGo2H9+vUA\nuXIoC0rTpk25dOkSixYtokGDBpiZmbFp0zb++isSgH79ZvHw4aHXUiuKk7S0NG7duoVMJsPFxeW1\nidrX1xeAH36YYvD0u7u50LFjRx7+FcSgOQMwNjZn+/btBFxYRgN3d1auXg0SJTGP0xg0aAaJGg3t\nxx8yqFX8Vyhtpjc+P12fyGeb9canVhCYfySNwCcaPMpJWdrXsljTpbrWNML/YQ4bzmVSr5KcDu6F\nSx/65Y8Mjt3J5odOZvl2PYuOjsfMzBhT09KALaNGTSM5WcaYMWPeevzcqVcSGjRoTkBACEuW/Ei9\nei5AKrt27aFr1ylMmNCf8eP1Uaivv/4aJycn9uzZQ2RkJA4OZend+xNq1qxPREQ0FSuWAYyoUKEG\naWkZBAfHoS841C8G79y58+qllBidJeTLe5tRBEE4IxKJKr0yPBpYKAhC9rNt4vLYLxqIfvZ3mkgf\n2ywL5Gt4+vn5UbZsWcP/586dA/QTS1RUFFFRURibmGLv0ZHQbEdaLk0nQ6vGWKbjowo5NKukplaZ\nHKRiiH0EsfmdqAAcOXKEw4ePoFDIady4MTqdwIUL5/HxOYCpqakhHJiRkcVnn/0fYWExeHntwM6u\nAnFxkXz55WKkUglnz67EzMyYnBy9JpO/vz8ffaTvvKLT6bh27TqCABkZKu7eTWfixK+Ji3uKo6Oj\nIc8yLzw9PfH09OT69euGsU6dulG2bEVMTZ24elUFaNm27Ty//upFamo25cvbIRbncOzYBeLiEvnp\npy1MmfJm4yWva9DpdEyZ8gOnT59l/vzP6dYtb922iIhHZGWpsLe3x8jIyJBrVbt2bY4ePcbNmzc5\nffo8kyatpGvXNnTtOgTQi3MHBwe/8breFR8fH3bvPsaFC9eoVs0BiaRgi5TDhy8wf/5GVq7cy4ED\nVQ3GcYsWLYiPjyc+Pr5I1yMWi7l69RpqdQaLFk2nZctatGtXL89tJzxr3PP888yL/fvPMG3abzRt\n2pifflpSpFaT74tu3brh7e1N48aNqV27NlFRUURHR2NkZESTJk3e+LvPi2bNmrFu3TpOnTqFvb09\nZmZmz0TpwdXVlTZtWhAZ+ZQnTx4X+3sRBAEfHx8OHz6MWq0Pka5evZrBgwdTr96L7+953lt6errh\ne9NqtcjlcrKyVNy8eQsLC3MuXboEQMOGDXkc8dCwv6urK7dv38HPz+9Z3vV/j9nNRXzva86n6xPQ\nCiJsTbR80ySL5o5qxKo43vBzLxCv3i8fV4ZL98yZtDsRaXoqDua6fPbUo9LAmXA5R+8puZcgpVXl\nbBrbJOZ5XZmZ2QwaNBetVsKSJSuwt08DYNSoUeh0ukL/xl1dXVm6dCkAV6/qxeq9vf0JC4siLCyJ\n27cfIRZnEhPzlKNHb9KpUx/q1NE7PXbs8KV374X07t2R77//AZ1OwNy8Il5eXlSqVKnQ1/I2ihoV\nLOF/j7/blVEFaCoSieYDKmCyIAj++W38zHCtDVx+00Fnz57N1KlTDVJASqUSQSTmQZwGUYSMoDgZ\nZx7KSCw9FrQqqlmk0tlDQd2yOcgLmdb05Ek8s2Ztom/fVrRu/brX7tSpUwCMHj2GOnX0XpgaNdz5\n5ZeVnDp1ymB4GhubYm9fnoQEFXFxKdjZgSDI6N27Nzk5Ochkrmg0KTRq9BE//7ybpKRryGRrcHev\nzr59f3D69CNsbRW4un6MRmNKixYtC/dGXqJOnTrUqfPye5HQtGlrFAozatSogUrlBOgYPvwbKlas\nQ8eOHYt8LkdHF/z9b1CtWt5t6ACDtlxiYgJpaWmGXsYPHz589ro5/v4h3LgRSlxcJu3bD0Re2C+y\niHTr1o3Hjx/Tt2/TAhudAO3atefcuSjatWv3Xjyyfn6nOXjwLOfO3aRpUw+MjApfeQvg6FgBExMT\n6tat/68yOgG++uorcnJyOHz4sGHSc3BwYObMmS+lQhQce3t71qxZw+LFiwkICCArKwtra2uGDh1K\nv356T5BKBTJZHCEhV8nIUNGwYfFIHp04cYJ9+/YDeo9Reno6MTExrFq1imnTpuHsrFc0cHFx4enT\neA4dOsTIkSORSqUcP37CsDAzN9ffGyYm+nsmKirScA6tVktMTMyz199fFOB9IggCT58mU7q0Vb7b\nWBkJLGyXyi+XTHCz1dDdTVXo53phkElgSvN0xh02Z8FfpvzcMRVFHjPpo2Qxx0KVnHogJ10tpryF\nllH1MuhYJZv8Mh2Sk9PIytKg0wl5FsMWB9988w1du3bF1taW7OzSgMDp0zf57bfDhIfH4enphk5n\ngodHc5RKb8Ric3Q6vWdXIpFQqVKl93JdJXw4vNeq9meG4+HnOZ4ikegO8AcwAagH7AYqC3lchEgk\nMgX+AuYLgrDv1ddfrmpv3tkNpzptadl9GPdiNQSEp/AoWQxivatfKhaw04WRcmsv5SQRHPHZU6Qq\nb0EQaNBgCP7+QYSEnKNqVUtARXBwODY2FtjaWlG3rt5bcenSJUMFdkZGBs2aNScjQ4yf30HKl68G\nlCc+PhmlUpkrZ+1VAgKuU7t2HcRi8PAAsRhiYyEqSu8BvHbt2r9KzDt3VXve6FvwlQLCyclJ4PPP\n59OuXQP69m1nMHbGjh3LpUv67kJ9+/YlJiaG7du3o1Jls2jRT7RpM5KVK7fSu3dvQyefvxcteie8\nOt8tbt++j6OjA6amLuhTlt8fgiAwZcoU+vfvTM2aeWvOvl2oXA5UISYmCXv793u978KTJ0+4fv06\nVlZWNGzYsMiKDS8TFRVFWloaTk5Or4UI09LSqFXLg/DwCA4eXEKXLk3f6VxarZZOnToTHx/P/Pnz\nqFBBX1R06NAhvLy8adOmNYsW6Xuph4aGMmTIELKz1Zibm2FkZERsrN4rO2/eXMMi8Lm+rlQqYfDg\nwbi6unLw4EHOnTuPg0MZfHx8iuVzyovU1HQWL97K1avBHDu2EZFIn0/+cqeeorJz53EGDJjGxIn9\nWbJk0t/6rJs6dTmPH8fx22+z8izeOxWsYviWZPrXN+L/elkAoNYInAhUseNyFpfC1Mgk0MFdycAG\nxtR3zFtoPzcmJCfbER+fYFh8/B0EBASwY8cOGjRokCv1JyMj429btJRUtX84/N2G53H0ofbTz/5/\nADQUBOHpK/vJgMPACUEQluR17JcNz5r/d84wXtZSTBU7KfEP/AkLOIU0PQJJRiQiXTYKhdzQQq+o\n3LqVxujRUzl69OizJO502rbtwOnTlzlw4Cd+/fVHIiOjWLx4Ea1btwbg2LHjfP75NCIjoVu3Tvj4\nHC7wAzQxMZGtW7cSExODRKIlLi6csmWrU6FCRYYMGfLeJpOiUhDD82X+/NOPVq3a4epameBgb/RF\nUHDrVhA//PAt0dF6j41Wqze2Bw7swpIl3ohERfPoFS8pnDy5g8aNa74mFXXixEU+/vhb2rRpyb59\nh/5m7+ETnmWr5CI/w3PjxgNUqeJEkyb9eFXUuQR9Lvb8+fM5dOgg589vRaFQkZKSztChszA2VrJj\nx4vOLkOHziIg4B5bt87Gw0MfOszMVKFQyAz3alxcHB07dsLCwpxTp04Z0kMUCgV9+vSlbFkHDh48\naDjm9evXWbx4MaGhetm40qVtGTVqFN27d891nWvWrOG33zbkGjM2NmLFihXUrl27+D+YZ2RnaylX\nriPx8Yn4+/tTt24dEhNDqFu3LWPH9mbixP6Fek69kAmTkpFhialpJdq1a8yhQz/lq95QHKhUes1h\npVIBSJkwYSkrVmxh2rThzJ07Os99Fh1PY83pDKZ2MiM5S8du/yzi03WUs5LwaQMj+tQ1KpBaQHx8\nMqVK2QJuwIeZG1lieH44/N2hdh+gFXBaJBJVQe9iyZXcJtI/cTYAwfkZna9iHrISUsI4uXcdpa31\n3kOdri2nTkk4fPgwyclKXF3d6NevX67WjwXlxcq9Ah4etpw/f/6l1xSYmJRCqVTSqFFn4uKi+eWX\nRUyY8AOtWjXD0tKI48d90WjA3Nycxo2bF6pfs7W1NRMnTiz0Nf+v4OrqztKlS595fWsCqaSnP6F+\n/RG4uJTn++8nERQUiK/vXeLjHxISkvMvMTph+vSfmDdvHlOmfMaCBWNzvVapUgVkMgXm5jZoNJoi\n97QvGg788ccfHD58jJ9//uqNv7U//vBn+PC5mJqacu9eu/9cAUpxIJVKmTFjBk5OTnTsOI6kpIc4\nOlbCx+c0lpYWgAsgAkSEhsZz8+Y9UlNtgWpAKkuWLGDNmt/56acJ9O/fAVNTU6RSCWlpacTEvMgo\nDw0NBcDKKndY2dPTk99//53IyEhycnKoUKFCngVfo0ePpkGDBhw6dIjExESqVKnCxx9/XKze6+xs\nNYsXb+XYsQucObMDqbQMCoUVv/yyirJlyz5L2RHh5XWG8PAoDh++wKRJAwp0bEEQ2L79KCtX7uHP\nP70xNnbGxETK+fPnqV3bA7k8kvwK6N6VNWu8mTZtDQsXTmbkyLGAJc7OdXBzu8K4cYPy3e/rtqZc\nj1Az/2gaYhG0clUwoKExzV0KLrR/+/Z9mjQZwZQp3/DddzXyDcOXUMJ/hfcpp/Q70AIoJRKJIoGZ\nwEZg47OQuxoYIgiCIBKJHIDfBEHoBDQGBgG3RSJRwLPD/SAIwtH8ziV7fBwPjxoGoxP0RRdt27ah\nbds27/Q+7t9/TMeO41m9eglt276e0ymTyfDx8THkIg4aNB9//zjWrdvEgwd/UqECPH4Mw4aNZdGi\nRf+zuVbFiVqt5tChQ4SEhFCuXDlGjBjxUrqBJYGBd1EolJib2zJgwCQglQkTRAwZ8hXLlxdKWeu9\n0qlTJ5YuXUrp0no91BcLCmOqVu3A9evXqVSp0t+eCpGUlETPnmNJTU2lSZNa9OrVKt9tmzdvwMCB\n/alVq06J0fkGJk2axLJlywz/BwToCzX69/8Uvd6qng0bNqFSqZ6FSY0AI86fv8eTJ0+xtKwIKDA2\nhrp1P+Kvv84ybtyXtG7dmvT0DI4e1SthdO7c+bXzi0SiAmmpPi8eLE4SEpKxsdHLpcnlSrZv9+Xe\nvTB8fR/RqZNeKe95TuxzvvjiC8qXL4+Tk9Mz8fBIUlKSEYtFmJnl/QzU6XQsXbqLGzeC2bLlT0aP\n1rdpfF5UCS4Iwj28vQ/yySet3+m+ysxUodFoMDc3BWSYmpYhMTGF8+fvM3Kk3vBv1KgRjRo1onTp\nakAIr+r3gl4aavUAKw7dzKJtdSVlLQsfgTp3LoDU1HRu3Qop8vspoYT/Jf4TnYvatbNh1apV76Vq\nc9q01cyfv5F27dpx/PjxAj3sMjMz6d+/P0ePHmXQoIF89933VK1atdiv7d/I20LtwcHBdO7cmfDw\ncMOYtbU1e/fupUWLFoYxtVpNdHR0rt7x/0aSkpKwstKSmHiLvn2nMH78cLp2fS7q/M/h5eXFtWtX\nmD+/PxKJ/lZ5OdSuN5LlQFUEQf6vyhP+txEQEEDt2rWRy/WpOi1atGDPnj3MmTMHhUJBVFQUNjb5\nN2MQBIFLly5Rt27dZ/mj6YwYMZwNG/ZQrhyUfklUrkWL5ixcuOidcyOLgiAIxMcnY2trZfjfze0T\n7t6NIC7uIra2ToANhw8fRalU0qpVq0KkkGgYMWIAJ078xc6d83B1LfdssW6JsbERJiZmgAOXL4cR\nEhLCoEGD8jz2pEkTWbp0OV999SlLlkwq0vtcsWIX06evYfLkEUyfPguwICtLRVBQUK4iy5efZYIQ\nx65d6+nevQXGxsXdQtkeP78gmjRp8t4Kiv4XKAm1fzj88wJ9xcCaNWuKfZX/nDlz/g8bG3dGjhxZ\n4MnZ2NiYAwcOkJ2djUwm+9dVB/9TaLVaunfvTnh4OFWrVqVr166cOXOGK1euGMatrfXacHK5/F9v\ndMKLsOjOnac5efIKERFJdOw4DKn0n/3Oe/fuTe/evYF04B4ve2s2bPDB1/cK27fvRSZTlIT23oK3\ntzcAI0aMYOxYfUrF7NmzuXjxIn5+fhw5coTBgwfnu79IJKJRo0YvjZhiZFQaIyMjhg79gvDwy5iZ\niZFIbDhw4DqVK+9j7Ng+gF52LTT0EU5O5fL1FBaF9PRM0tIyKVNGr/sYERFNzZr9sbQ05+HDvwBj\nRCJjbGwcMDVNIDxcjK2tLQBdunQp9PlUKg23boUTG5vIkiXLefToDikp8PixiGbN6uHrew6RSEaD\nBravCaO/TLt2Hdi4cTPt2xdVxUOEu3sdUlMzuH37CaD35BoZGb2i7JGbadOWs2DBAj77rCsbN84s\n4rlzo1Jlo1SWBsrStm3Zt25fQgn/Ff4TFlFxG51hYZHPEs0rIRaX5quvvnpj5Xl+KBSKEqPzJU6e\nPEloaCiVKlXixo0b/Pjjj1y8eJHmzZuTmprKjh07/ulLLDJjx85k5syZnDp16l8huP4CUzIybJg0\naQkpKRkkJ6fzzTcr2LPHl2PH/vinL+5/ApVK363rVa/m8/+zsrIKfcxffvmFuLg45sxZwsSJKxg+\nfBk6nQMPHkSi0Vijb41qx/XrkdSuPYC2bXPnEE+ZspLFi7eQnf1CVUGne11PMjExhbNnb/Dw4Ytu\nW/v2/YGZWTO+/PJn9CLg5ShXrjFqtRaVSktGRhnAAbDk4MFDpKSkUL9+/UK/x5dRKpX4+PhgamqK\nj88dkpOVWFmVQq0WOHnyCvPmLSzQcTp06MDDhw9p3/4z4O3PZJ1Ox7ZtR1iyZDtgBVSnVat+hIaG\nsmfPngJff9++fbG1taVNmyYF3udNrFu3D0/PQYSGaorleCWU8L9EiVX0CkFBYXz00XB69pyBSlWS\nj1mchIWFAdC6dWtDSEksFtOpUycAHjx48I9d27siEkmYNWvWP97TPC9Gj57O0qU7mTlzIxYWlpw4\ncZTly5fTrVu3f/rS/ido2VLvXVu/fr0hXeHMmTPs36/X4Xw5RaQwmJqa5oqiLFmylKCgIPr1GwrY\nAuVQq21xc3OjevX6gAfgikrlwMKFm5k6dQ1SqS16A0xOz57fYGvbhpMnX8gez527kWbNRvL772eB\ncoAzjo7NkMvlaLXGgCNgh0RixePHj4mJicmVh25jY1Nsi+d169aRlJREkyZNuHYtmitX4pgzZw4A\nP/30k6GF6dvQt+eVAM7cufOE77//JU+jG+DmzXsMHjyTqVPXEhkp57lqQ2Glijw8PAgPD+fTT8fz\nrtOmRqNh7dp9BAeHcelSvjLWJZTwn+Xf5Jr5V6DTCWi1oNGI8n2YlVA0HB0dAfjzzz9RqVQolUp0\nOh3Hjh0DyNUTuITiY+7cuTx48IAxYz5FpapIvXofUa9e3l2jSnidDh060LhxY86fP0/16tWxs7Mj\nNlZfjT5o0KBiy99WKpW4ubnlGmvduvUrnXNk6HQifv75Z9LS0pBIXhhQ0dGZxMcnY27ujr5XhxJP\nz/bUq3cPGxtnQK93W7NmPTIyMl7zzL8pT7U4OHv2LKBvz6g3HmH69Ons3r2bwMBAbt++XSipu+xs\nDZ06jeXx48eUL29nSE/QSxNZAgpq1+7ExIkTqV27dpGaDLzMC4O8IlFRlzEzM35WnFQ4pFIZf/11\nkr17/Rg0KP+K+RJK+K/ynygusrC4/07HEgQBnU6HRCIFKnHvXjzly5f/oBO9i8qbiou0Wi2urq7c\nv38fNzc3unXrxpkzZ7h48SJmZmaEh4e/98nvQ0UQBK5duwYUXGO1hBekpKQwefLkZ00MVFhYWDB6\n9GjmzJnzzj2pC6t9mx86nY64uDisra3/ZvmugtG9e3cOHjzIqlWrDH3H1Wo15cuXJy4ujtu3b+Pu\n7l6oY/r5+bFmzWp27pyNQqFm3LjFbNhwkJs3/6BKlUboZa6KRn7fy9mzZ+nVqwctWtRmz56FBc79\nj4iIRqGQYW9fi+eLgBJeUFJc9OHwwYfab9wIoWXLL1ixYi/gDFhTpUqVEqPzPSCRSPDx8aFChQoE\nBwf/f3v3Hlx1nd5x/P3knBWEuiFboOFqzBjEoLsol4Ego4lII2VAp4Kw7CodWCpTK1jrDttxd2mZ\nToTdWhDLjgQQtOJyiZZQ25V1XS4ykZUgI7cxclmQkkkCcieECE//OIcQssFBkpzfOSef1wyTc37n\n9zt5mO+ck+f3vTxfZs+eTUlJCR06dOCdd95R0tmCtGq9aVJTUyksLOTYsWMcPHiQiooKCgoKmpx0\nNqeUlBTS09PjMumEyDxJiPRyLlmyhE2bNjF+/HgqKyvJzs6mT58+3/g9H3roId5++x3atr0Ls29T\nUxOmtvYrNmzYRVOSzq+Tnp5OTU0tp06d59y589d1zdy5y8nMHM1LL61BSae0dq1+qP3IkeNs2LCN\nI0dOM21aAVoL1LL69OlDWVkZa9asqavjOWbMmLr92EXiWbt27ejZs2fQYSSkxx9/nBUrVlBcXMyk\nSZPqjrdr145XX321iTdHKUAvZs16iWeffeFrtoVtuqysLEpKSujd+zZCoTIi2+deraLiGOfPX+DW\nW7sA7Rk8eDih0Hyqq+NrpzmRILS6xLO8/CilpXsYOfIBIJ0RI6byq1+FGTdunFagx0hka8CxQYch\nIjEUCoX+9yvgAAAKd0lEQVQoKipi2bJlLF++nBMnTjBo0CCmTZtGr169muV3pKenN+tOTddypXc2\nA/e9nD9fU7dt7vLlv2HixJmMGzeK119/A2jHwIF3UF5erlEdEVpZ4nn4cAV33PHXmKWwd28Z6enp\nmMFTTz0VdGgiIkkvHA4zadKkq3o8E9mZM2F+9KNZHD58iA0bFpKS0p5Bgx7CfSY1NWHcb8YsMtVF\nSadIRKtKPLt3z2bYsGGEwzdx4cKfDo+IiIhcr+PHj7Nu3Yfce28f3HsBqWRmQnl5OR07dgw6PJG4\nlNRjy7t37yc392/54otzQDaQwapVRRQVFWmeloiINEmPHj1Yu3Yt3bplcvHilQWpSjpFri2pE8+f\n/exV1q8v5ac/XQxEvhTidcWniIjcGHfn5MmT1NbWxvx35+TksHTpUv1tEblOSZx43syCBUt45pln\nmD9/ftDBiIhIM3N3CgsLycrKokOHDqSmpjJ58mSOHTsWdGgicg1JlXhu3ryd6dP/DfdOwJ107tyT\nefPmqVSPiEgSmjNnDlOmTGHfvn20bduW6upqFi9eTG5uLtXV1UGHJyKNSJrE8/Tps4wc+Szz5r1F\nUdEfaKniwSKJqLS0lHfffZctW7Zw8aIW1kniO3XqFLNmzQKgsLCQM2fOsGfPHm6//XZ27NjBm2++\nGXCEItKYpEk8b7klnVdemc+MGTMYPXp00OGIxIXKykruv/9++vfvz8yZM3n66afJysqq2z5TJFF9\n9NFHnD17lgEDBjB58mRCoRC9e/fm+eefB2DdunUBRygijUmSckrdgHQmTGieIsQiycDdGTNmDBs3\nbiQtLY1+/fqxZ88eDhw4QH5+PmVlZaSlpQUdpsgNubxd6blz53D3up2Pzp49e9XrIhJfkqLHs6pK\n25CJNLRt27a6pHP37t0UFBSwevVqBg8ezNGjR3njjTeCDlHkhuXk5NCxY0d27drFjBkzOHjwIGvX\nrqWgoACARx55JOAIRaQxSZF4qmaayJ/auXMnAMOHD6/bRjAcDjN+/PirXhdJRG3atGHu3LmYGXPm\nzCEjI4NRo0ZRVVXF8OHDefTRR4MOUUQakRSJ5+UhFpEgfPnll2zcuJFdu3bh7kGHU6dLly4AbN26\n9ar6hiUlJQB07do1kLhEmsuECRN4//33yc/Pp1OnTmRnZ/Piiy9SXFxMOJwkM8lEkow+mSI3qLa2\nlueee46FCxdSU1MDQL9+/Xjttde4++67A44O8vLyyMjIYN++feTm5pKTk8Onn37Ke++9RygU4okn\nngg6RJEmy8vLIy8vL+gwROQ6KfEUuUHTp09nwYIFmBn9+/dn//79lJaW8uCDD7Jz5046d+4caHzh\ncJiVK1fy8MMPs3nzZjZv3gxAKBRi0aJFZGZmBhqfiIi0Pkkx1C4Sa5WVlRQWFpKSksKHH37Ixx9/\nzKFDhxg6dChVVVUsWrQo6BABGDBgAJ9//jlz585l9OjRTJ48mbKyMiZOnBh0aCIJr7q6mlWrVvHy\nyy/zwQcfcOnSpaBDEol7LdbjaWZLgJFApbvfVe/43wNPA18B77r7jxu5Nh+YB4SARe7+YkvFKXIj\ntm/fTm1tLffddx85OTkAtG/fnqlTp7Jp0ya2bNkScIRXpKWlMW3aNIYMGQKgnk6RZrB+/XrGjh1L\nVVVV3bF77rmH4uJiunfvHmBkIvGtJXs8lwL59Q+YWS4wGviuu/cBftnwIjMLAf8BPAxkA+PNLLsF\n4xT5xi7Xvzxw4AAXLlyoO/7ZZ59d9bqIJJ+Kioq6FfR9+/ZlypQpdOnShU8++YTHHnssrhYZisQb\na8kPiJllAP99ucfTzFYCC939/a+5ZjAw093/Mvr8JwDuXlD/vJMnT+qTLSIikmRSU1NVqiaJxXqO\nZy9gqJltMbMNZjagkXO6AV/Ue344ekxEREREElisV7WHgTRgEDAAWGlmmX51t2tjdzrq3RQRERFJ\ncLFOPA8Db0cTzT+Y2SWgI1DV4Jwe9Z53B440fCN1xYuIiIgkllgPtf8XkAdgZr2Am4CjDc75GMgy\ns9vM7CZgHFAc0yhFREREpNm1WOJpZm8BJcAdZnbYzCYBS4BMM9sJ/Bp40t3dzLqa2f8AuPtXRMot\nvQfsAVa6+66WilNEREREYqNFV7W3JNX6jA+N1Ws1s+8AK4AM4I/AWHc/HlSMrZGZ9QBeB9KBS0Sq\nScxT2wTLzNoCG4E2RKY6rXb3n5vZbURuxr8DbAN+6O4Xrv1O0hKi5fy2Av/n7iPVLiLNLyF3LlKt\nz7iylAb1WoEZwO/cPQv4XfS5xNZXwHPufieRxXx/F/2MqG2CVQPkufv3gL5AvpkNAmYD/x5tl+PA\npABjbM2mERlpu0ztItLMEjLxBAYCe919f/Tu89dECtNLjLn7RuDLBodHA8uij5cBj8Q0KMHdy919\nW/TxaSJ/TLuhtgmUR5yJPv1W9J8Tmfu+Onpc7RIAM+sO/BWwKPrcULuINLtETTxV6zO+/YW7l0Mk\nAQI6BxxPqxbdyOEeYAtqm8CZWcjMtgOVwG+BfcCJ6Px20PdZUOYCPyYyNQXgz1G7iDS7RE08VetT\n5DqY2Z8BRcB0dz8VdDwC7n7R3fsSKRU3ELizsdNiG1XrZmaX56mX1j/cyKlqF5EminUdz+ZyXbU+\nJTAVZtbF3cvNrAuRnh2JMTP7FpGk8013fzt6WG0TJ9z9hJmtJzIHt4OZhaO9a/o+i70hwCgzGwG0\nBb5NpAdU7SLSzBK1x1O1PuNbMfBk9PGTwJoAY2mVovPTFgN73P2lei+pbQJkZp3MrEP08c3AMCLz\nb38PPBY9Te0SY+7+E3fv7u4ZRP6efODuE1C7iDS7RC6nNILIHWkIWOLu/xpwSK1StF7rA0R2oKoA\nfk5ko4CVQE/gEDDG3RsuQJIWZGb3AZuAHVyZs/ZPROZ5qm0CYmbfJbJIJUTkxn+lu/+LmWVypWzP\nJ8AP3L0muEhbLzN7APjHaDkltYtIM0vYxFNEREREEkuiDrWLiIiISIJR4ikiIiIiMaHEU0RERERi\nQomniIiIiMSEEk8RERERiQklniISN8xsupm1CzoOERFpGSqnJCJxw8z+CPR396NBxyIiIs0vUbfM\nFJEEZ2btiRSz706koPoqoCvwezM76u65ZjYc+GegDbAP+Bt3PxNNUFcAudG3+7677431/0FERL4Z\nDbWLSFDygSPu/j13v4vITmRHgNxo0tkReAEY5u73AluBf6h3/Sl3Hwi8Er1WRETinBJPEQnKDmCY\nmc02s6HufrLB64OAbGCzmW0nslf2rfVef6vez8EtHq2IiDSZhtpFJBDuXmZm/YARQIGZrWtwigG/\ndffx13qLazwWEZE4pR5PEQmEmXUFzrn7fwK/BO4FTgO3RE/5CBhiZrdHz29nZr3qvcXj9X6WxCZq\nERFpCvV4ikhQ7gZ+YWaXgFpgKpEh8/81s/LoPM+JwFtm1iZ6zQtAWfRxGzPbQuQG+lq9oiIiEkdU\nTklEEo7KLomIJCYNtYuIiIhITKjHU0RERERiQj2eIiIiIhITSjxFREREJCaUeIqIiIhITCjxFBER\nEZGYUOIpIiIiIjHx/9m8IoMrnDoIAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Variance converges to 0.005\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAiMAAADOCAYAAADsbwLEAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAHZdJREFUeJzt3X2UXFWZ7/Hvr6vT1Um6Uw3pJkIS\nDJBGiCAIPQwMqPGNBFFhKcwNM6PIZY3OKPOi4gw4F+SiXGSuirpgdKngC6NeEBXbMRociTMXxZiW\nFyGBTAJiEkPIexGSdJLufu4fdbqpW+mXSqe6Tqfr91krq8/ZZ59dz9mwOk/23meXIgIzMzOztNSl\nHYCZmZnVNicjZmZmlionI2ZmZpYqJyNmZmaWKicjZmZmlionI2ZmZpYqJyNmVhWSjpX0oqRM2rGY\n2fjiZMTMBiVpiaQbBym/SNJGSfUH015ErI2IpojorVyUZjYROBkxs6F8DXiXJJWUvwv4ZkT0lNvQ\nwSYuZlZbnIyY2VDuA44EXtNfIOkI4K3ANyRdKOkRSS9IWifphqJ6cySFpCslrQUeKCqrT+pcIelJ\nSTslPSPpfUX3z5e0XtKHJW2S9JykK4quT5b0aUm/l5SX9KCkycm1syX9UtIOSY9Jmj/G/WRmh8jJ\niJkNKiL2APcA7y4q/lPgqYh4DNiVXGsBLgT+WtLFJc28DjgZWDDIR2yikNhMA64AbpV0RtH1lwE5\nYCZwJXB7kgwBfAo4E/gTCgnTPwB9kmYCPwI+kZRfDXxXUttBd4CZVY383TRmNhRJ51H4y/1lEbFH\n0i+AeyPi1kHqfhaIiPigpDnA74ATIuKZ5Hp/2aTBpngk3QcsjYjPJaMZPwaa++tK2gS8Hfg1hUTo\n7CQpKm7jH4FTIuJdRWVLgG9FxNcPpS/MbOx4ZMTMhhQRDwKbgYskHQ/8EfAtAEl/LGmppM2S8sBf\nAa0lTawbqm1JF0j6laRtknYAbym5f2tJ0rIbaErqNAJPD9Lsy4FLkymaHUm75wFHH8Rjm1mVORkx\ns5F8g8J0zLuA+yPi+aT8W0AnMDsicsAXgdLFroMOvUrKAt+lMN0yIyJagMWD3D+YLUA3cMIg19YB\nd0VES9GfqRHxyTLaNbOUOBkxs5F8A3gT8JdA8VRHM7AtIrolnQX82UG02QBkKYy69Ei6ADi/nBsj\nog+4E/iMpGMkZSSdkyQ4/wq8TdKCpLwxWQw76yBiM7MqczJiZsOKiGeBXwJTKYyE9Hs/cKOkncD1\nFBa7ltvmTuBvk3u2U0hkOoe96f93NfA4sBzYBtwC1EXEOuAi4KMUEp11wEfw7zqzcc0LWM3MzCxV\n/teCmZmZpcrJiJmZmaXKyYiZmZmlatx+X0Q+n/diFjMzswkml8sd8Aq/R0bMzMwsVU5GzMzMLFXj\ndpqmWC6Xq2h7XV1dAHR0dFS0XRua+7z63OfV5z6vPvd59Y2mz/P5/LDXPTJiZmZmqXIyYmZmZqly\nMmJmZmapcjJiZmZmqTosFrBW2hOb9rGnpw8vdzIzM0tfTY6M/HD1Lu5esSvtMMzMzIwaTUZaGjPs\n2NuXdhhmZmZGrSYj2Tpe6O6jt887zpuZmaWtNpORxjr6gO2796UdipmZWc2ryWQk11h47M0796Yc\niZmZmdVkMtKSLTz2lhedjJiZmaWtNpMRj4yYmZmNGzWdjHhkxMzMLH1lJSOSFkpaJWmNpGsGuZ6V\ndHdyfZmkOUn5dElLJb0o6baSexokfUnSf0l6StI7K/FA5ZhcLxrqPDJiZmY2Hoy4A6ukDHA78GZg\nPbBcUmdErCyqdiWwPSLmSloE3AL8N6AbuA44JflT7J+ATRFxoqQ64MhDfpoySaKlsc7JiJmZ2Tig\niOH32pB0DnBDRCxIzq8FiIibi+osSeo8JKke2Ai0RdK4pPcAHRFxVdE964CTImLQrVDz+fxAYKtX\nrx7d0w3j2ge2MbleXP/aIyretpmZmb2kvb194DiXy6n0ejnTNDOBdUXn65OyQetERA+QB6YP1aCk\nluTw45IelvQdSTPKiKViWhrr2NHtXVjNzMzSVs4X5R2QwQClwynl1Cn93FnALyLiQ5I+BHwKeNdg\nlTs6KvuVdl1dXbRk63gmHxVv2wbX1dUFVP6/pQ3NfV597vPqc59X32j6PJ/PD3u9nJGR9cDsovNZ\nwIah6iTTNDlg2zBtbgV2A99Pzr8DnFFGLBXT0ljHtt376On16IiZmVmayklGlgPtko6T1AAsAjpL\n6nQClyfHlwAPxDCLUZJrPwTmJ0VvBFYOVX8s5BrriIBtu7wlvJmZWZpGnKaJiB5JVwFLgAxwZ0Ss\nkHQj0BURncAdwF2S1lAYEVnUf7+kZ4FpQIOki4Hzkzdx/jG557PAZuCKyj7a8Pr3Gtm0cy9HTWus\n5kebmZlZkXLWjBARi4HFJWXXFx13A5cOce+cIcp/D7y23EArzVvCm5mZjQ81uQMreEt4MzOz8aJm\nk5HcwJbwXjNiZmaWpppNRibX1zGlIeORETMzs5TVbDIC0Nac9ZoRMzOzlNV0MtLalPXIiJmZWcpq\nOhlpa/LIiJmZWdpqOhlpbW5gs5MRMzOzVNV0MtLW1MiO3fvZ1+Mt4c3MzNJS08lIa3MDAFt3eXTE\nzMwsLTWdjLQ1ZQFvfGZmZpammk5GWpsLyYgXsZqZmaWnppMRj4yYmZmlr7aTkYGREW8Jb2Zmlpaa\nTkYaJ2VoztZ7ZMTMzCxFNZ2MQGHdiPcaMTMzS0/NJyNt3hLezMwsVTWfjLQ2N/htGjMzsxSVlYxI\nWihplaQ1kq4Z5HpW0t3J9WWS5iTl0yUtlfSipNuGaLtT0hOH8hCHwiMjZmZm6RoxGZGUAW4HLgDm\nAZdJmldS7Upge0TMBW4FbknKu4HrgKuHaPsdwIujC70yWpuy7OzuoXt/b5phmJmZ1SxFxPAVpHOA\nGyJiQXJ+LUBE3FxUZ0lS5yFJ9cBGoC2SxiW9B+iIiKuK7mkCfgK8F7gnIk4p/tx8Pj8Q2OrVqw/l\nGYf177/bzRd/s5MvXNBK29TMmH2OmZlZrWpvbx84zuVyKr1ezjTNTGBd0fn6pGzQOhHRA+SB6SO0\n+3Hg08DuMmIYMy3ZQgKyY6+/LM/MzCwN9WXUOSCDAUqHU8qp81Jl6XRgbkR8sH99yXA6OjpGqnJQ\nurq6BtqdtG4H/PIXtM46no55Myr6OfaS4j636nCfV5/7vPrc59U3mj7P5/PDXi9nZGQ9MLvofBaw\nYag6yTRNDtg2TJvnAGdKehZ4EDhR0s/LiKXi2vz9NGZmZqkqJxlZDrRLOk5SA7AI6Cyp0wlcnhxf\nAjwQwyxGiYgvRMQxETEHOA/4r4iYf7DBV8L0pgbA309jZmaWlhGnaSKiR9JVwBIgA9wZESsk3Qh0\nRUQncAdwl6Q1FEZEFvXfn4x+TAMaJF0MnB8RKyv/KKOTrc+QmzzJIyNmZmYpKWfNCBGxGFhcUnZ9\n0XE3cOkQ984Zoe1ngVOGqzPWWpsaPDJiZmaWkprfgRUK60Y8MmJmZpYOJyMUNj7zyIiZmVk6nIxQ\nGBlxMmJmZpYOJyMURkZ27etl976etEMxMzOrOU5GKNprZOe+lCMxMzOrPU5GKHxzL8BmL2I1MzOr\nOicjvDQy4nUjZmZm1edkhMKaEfCW8GZmZmlwMoK3hDczM0uTkxFgUqaOI6Z4S3gzM7M0OBlJeK8R\nMzOzdDgZSbQ2eUt4MzOzNDgZSbQ1Z/1qr5mZWQqcjCTamrJs2bmPiEg7FDMzs5riZCTR2pxlz/5e\ndu3rTTsUMzOzmuJkJNG/C+sWL2I1MzOrKicjidZmbwlvZmaWhrKSEUkLJa2StEbSNYNcz0q6O7m+\nTNKcpHy6pKWSXpR0W1H9KZJ+JOkpSSskfbJSDzRaHhkxMzNLx4jJiKQMcDtwATAPuEzSvJJqVwLb\nI2IucCtwS1LeDVwHXD1I05+KiJOAVwPnSrpgdI9QGa3NyS6sHhkxMzOrKo309oikc4AbImJBcn4t\nQETcXFRnSVLnIUn1wEagLZLGJb0H6IiIq4b4jM8BT0TEl/vL8vn8QGCrV68e3dMdhN4ILvvuJt5x\n8lQWvbJpzD/PzMysVrS3tw8c53I5lV4vZ5pmJrCu6Hx9UjZonYjoAfLA9HIClNQCvA34WTn1x0pG\nojlbx47uvjTDMDMzqzn1ZdQ5IIMBSodTyqlzYMOFUZRvA5+PiGeGqtfR0TFSUwelq6tr0HaPfvA/\noXFyxT/Phu5zGzvu8+pzn1ef+7z6RtPn+Xx+2OvljIysB2YXnc8CNgxVJ0kwcsC2Mtr+ErA6Ij5b\nRt0xV9iFdV/aYZiZmdWUcpKR5UC7pOMkNQCLgM6SOp3A5cnxJcADMcJiFEmfoJC0/P3BhTx2Cruw\negGrmZlZNY04TRMRPZKuApYAGeDOiFgh6UagKyI6gTuAuyStoTAisqj/fknPAtOABkkXA+cDLwD/\nBDwFPCwJ4LaI+EolH+5gtSbfTxMRJDGZmZnZGCtnzQgRsRhYXFJ2fdFxN3DpEPfOGaLZcfe3fVtT\nln09fbzQ3UNu8qS0wzEzM6sJ3oG1SP9eI1u814iZmVnVOBkp0tbUCMBmrxsxMzOrGicjRTwyYmZm\nVn1ORor0fz+NR0bMzMyqx8lIkSOmNJCpk0dGzMzMqsjJSJG6OjF9aoNHRszMzKrIyUiJtuYsW7wL\nq5mZWdU4GSnR2pT1yIiZmVkVORkpURgZcTJiZmZWLU5GSrQ2FZKREb5ax8zMzCrEyUiJtuYs+3uD\n/J79aYdiZmZWE5yMlGhtKmx85nUjZmZm1eFkpERbszc+MzMzqyYnIyUGdmH1IlYzM7OqcDJSwiMj\nZmZm1eVkpERu8iQmZeSNz8zMzKqkrGRE0kJJqyStkXTNINezku5Ori+TNCcpny5pqaQXJd1Wcs+Z\nkh5P7vm8JFXigQ6VJG98ZmZmVkUjJiOSMsDtwAXAPOAySfNKql0JbI+IucCtwC1JeTdwHXD1IE1/\nAXgv0J78WTiaBxgL/XuNmJmZ2djTSJt7SToHuCEiFiTn1wJExM1FdZYkdR6SVA9sBNoiaVzSe4CO\niLgqOT8aWBoRJyXnlwHzI+J9/W3m8/mBwFavXl2BRy3f/3pwO9u6+/jUm6ZX9XPNzMwmovb29oHj\nXC53wExIOdM0M4F1Refrk7JB60RED5AHhvubfGbSznBtpqalsY58d1/aYZiZmdWE+jLqDLaWo3Q4\npZw6o67f0dExTFMHr6ura9h2T976FP+x9hnOOONM6urGxVKWw95IfW6V5z6vPvd59bnPq280fZ7P\n54e9Xs7IyHpgdtH5LGDDUHWSaZocsG2ENmeN0GZqWpuy9PYF23f7jRozM7OxVk4yshxol3ScpAZg\nEdBZUqcTuDw5vgR4IIZZjBIRzwE7JZ2dvEXzbuAHBx39GBnYa8SLWM3MzMbciNM0EdEj6SpgCZAB\n7oyIFZJuBLoiohO4A7hL0hoKIyKL+u+X9CwwDWiQdDFwfkSsBP4a+BowGfhx8mdc6N+FdcvOffCy\nlIMxMzOb4MpZM0JELAYWl5RdX3TcDVw6xL1zhijvAk4pN9Bqah0YGelOORIzM7OJzzuwDqJ/mmbL\nTq8ZMTMzG2tORgbRnK2nob7Oa0bMzMyqwMnIICTR1pRli7eENzMzG3NORobQ2pz1yIiZmVkVOBkZ\nQpu/LM/MzKwqnIwMoa25wV+WZ2ZmVgVORobQ1pRl6659dO/vTTsUMzOzCc3JyBBe/fIjiIAHV29J\nOxQzM7MJzcnIEM49oZVpjfUsfvy5tEMxMzOb0JyMDKGhvo7zX/kyfrryefb2eKrGzMxsrDgZGcaF\npx7Nzr09nqoxMzMbQ05GhnHu3MJUzY88VWNmZjZmnIwMo6G+jjfP81SNmZnZWHIyMoILX/Uydnb3\n8Is1nqoxMzMbC05GRnDe3DaaG+v50W83ph2KmZnZhORkZASFqZoZ/HTlRvb19KUdjpmZ2YTjZKQM\nF556NC94qsbMzGxMlJWMSFooaZWkNZKuGeR6VtLdyfVlkuYUXbs2KV8laUFR+QclrZD0hKRvS2qs\nxAONhfPaW2nO+q0aMzOzsTBiMiIpA9wOXADMAy6TNK+k2pXA9oiYC9wK3JLcOw9YBLwSWAj8i6SM\npJnA3wIdEXEKkEnqjUvZ+gxvnjeD+1d4qsbMzKzSFBHDV5DOAW6IiAXJ+bUAEXFzUZ0lSZ2HJNUD\nG4E24Jriuv31gLXAr4DTgBeA+4DPR8T9/W3m8/mBwFavXn2oz3nIujbs5ZO/3MFHz23hjKOzaYdj\nZmZ22Ghvbx84zuVyKr1ezjTNTGBd0fn6pGzQOhHRA+SB6UPdGxF/AD5FISl5DsgXJyLj0WkzGphS\nLx5a3512KGZmZhNKfRl1DshggNLhlKHqDFou6QjgIuA4YAfwHUl/ERH/OlgAHR0dZYRZvq6urlG1\nu+DZR/nZk8/zqtPPoKHea38Pxmj73EbPfV597vPqc59X32j6PJ/PD3u9nL9R1wOzi85nARuGqpNM\n0+SAbcPc+ybgdxGxOSL2A98D/qSMWFL1lv63ap72WzVmZmaVUk4yshxol3ScpAYKC007S+p0Apcn\nx5cAD0RhMUonsCh52+Y4oB34NYXpmbMlTZEk4I3Ak4f+OGPrNe2tNGXrWfxbv1VjZmZWKSMmI8ka\nkKuAJRQShnsiYoWkGyW9Pal2BzBd0hrgQ7y0cHUFcA+wEvgJ8IGI6I2IZcC9wMPA40kcX6rok42B\nxkkZ3nTyUdy/8nn29/qtGjMzs0ooZ80IEbEYWFxSdn3RcTdw6RD33gTcNEj5x4CPHUyw48FbTj2a\n+x7dwC/WbGH+K45KOxwzM7PDnldhHqTXnthWmKrxBmhmZmYV4WTkIDVOyvBGT9WYmZlVjJORUXjL\nqUezY/d+fvn01rRDMTMzO+w5GRmF153YxtSGjN+qMTMzqwAnI6NQmKqZwZKVGz1VY2ZmdoicjIxS\n/1TNQ56qMTMzOyRORkZp/iuSqRq/VWNmZnZInIyMUuOkDG84eQZLVniqxszM7FA4GTkEF556NNt3\n7+eHj5V+VY+ZmZmVy8nIIXjDSUdx5suP4NrvPc5vfr897XDMzMwOS05GDkFDfR1ffncHR+ca+ctv\ndPH7rbvSDsnMzOyw42TkEB05tYGvXnEWEcEVX13O9l370g7JzMzssOJkpAKOa53Kl9/dwfode3jv\nXV107+9NOyQzM7PDhpORCumYcySfvvQ0lj+7nY/c+1v6+iLtkMzMzA4L9WkHMJG87bRj+MOOPXzy\nx09x7JGT+ciCk9IOyczMbNxzMlJh73vt8azdtpvblz7NrCOmcNlZx6YdkpmZ2bjmZKTCJHHj21/J\nH7bv4X/c9wTHtEzmdSe2pR2WmZnZuFXWmhFJCyWtkrRG0jWDXM9Kuju5vkzSnKJr1yblqyQtKCpv\nkXSvpKckPSnpnEo80HhQn6nj9j8/gxNnNPOBbz7Myg0vpB2SmZnZuDViMiIpA9wOXADMAy6TNK+k\n2pXA9oiYC9wK3JLcOw9YBLwSWAj8S9IewOeAn0TEScBpwJOH/jjjR1O2nq++549oytbz37+2nA07\n9qQdkpmZ2bikiOHf+khGLG6IiAXJ+bUAEXFzUZ0lSZ2HJNUDG4E24Jriuv31gBXAY8DxMUQA+Xx+\noHz16tWjfLz0PbtjP9f9fDsRsHDuZN7WPpVco19iMjOz2tHe3j5wnMvlVHq9nL8VZwLris7XJ2WD\n1omIHiAPTB/m3uOBzcBXJT0i6SuSppYRy2FnTsskPvnGI+k4Jkvnqt28/8eb+fpjO9ne7b1IzMzM\noLwFrAdkMEDpaMZQdYYqrwfOAP4mIpZJ+hyFUZTrBgugo6OjjDDL19XVNSbtDqUDuOj18PTmF7l9\n6Rrue+QP3P+7bv7sj4/lr153AjOmNVYljjRVu8/NfZ4G93n1uc+rbzR9ns/nh71ezsjIemB20fks\noPRragfqJNM0OWDbMPeuB9ZHxLKk/F4KycmEdkJbE5/509N54MPzeftpx/CNh37Pa/55KR/7wRM8\nl/eaEjMzq03lJCPLgXZJx0lqoLAgtbOkTidweXJ8CfBAshakE1iUvG1zHNAO/DoiNgLrJL0iueeN\nwMpDfJbDxpzWqfzvS09j6Yfn884zZvLNZWt53T//nA/e/Sjf/vVaVm3cSa93cDUzsxox4jRNRPRI\nugpYAmSAOyNihaQbga6I6ATuAO6StIbCiMii5N4Vku6hkGj0AB+IiP7FEn8DfDNJcJ4Brqjws417\nx06fws3veBUfeP1cvvgfT/Nvv32O7z/yBwCas/WcNruFM45t4dXHHsGrj22hZUpDyhGbmZlVXlmb\nnkXEYmBxSdn1RcfdwKVD3HsTcNMg5Y9SWE5R82YdMYVPXHwqH7/oFH63ZRePrN3Bw2u388jaHdy2\ndA39gyTHt07ltNktzGyZzIxpWY6a1siMaY3MmJaltSnLpIzf0jEzs8OPd2AdRyRxfFsTx7c18c4z\nZwGwa28Pv12fH0hOfvXMVjbt3HvANI4E06c2cFRzITnJTZ7ElGw9UxsyTGmoZ2r2pZ+TJ/X/zFCf\nqWNSRkzK1DEpU0d9Xf+xBq7VSWTqCj/rVIjTzMysUpyMjHNTs/Wcc8J0zjlh+kBZb1+wdddeNr2w\nl+df6Ob55Oemnd2Fsp3dPLNlF7v29rJ7Xw+791X2NWIJMhJ1dYXkJCMhqfDqlKBOQiq8StVf3tvT\nA4JJS/594BWrQh0VHfeXj5zslJMPlZszadCXvg5/e/fuBSD7wNKUI6kd7vPqc59X1qKzZvP++XOr\n/rlORg5DmTpxVHMjRzU3csrM3Ij1+/qCPft72bWvh917k5/7etmzr5eevj729wb7e/vo6Q32JT/3\n9/YVyvqC3r4gIujtg97oPw76Avqi/zoEhZ9QKC8u27RpMwCtba0AhWtJ3eL7SpftDrYlXhxQaxBl\nrv+dyMuEt27dCsD06UekHEntcJ9Xn/u8sma2TE7lc52M1IC6OjE1W8/UbD00pxPDS++lvyqdAGrQ\nS31+esqR1A73efW5zycGr3g0MzOzVDkZMTMzs1Q5GTEzM7NUORkxMzOzVCkGe11hHMjn8+MzMDMz\nMxu1XC53wH4KHhkxMzOzVDkZMTMzs1SN22kaMzMzqw0eGTEzM7NUORkxMzOzVNVcMiJpoaRVktZI\nuibteCYqSXdK2iTpiaKyIyX9VNLq5Ke/TKJCJM2WtFTSk5JWSPq7pNx9PkYkNUr6taTHkj7/n0n5\ncZKWJX1+t6SGtGOdaCRlJD0i6d+Sc/f5GJL0rKTHJT0qqSspq+jvlppKRiRlgNuBC4B5wGWS5qUb\n1YT1NWBhSdk1wM8ioh34WXJuldEDfDgiTgbOBj6Q/L/tPh87e4E3RMRpwOnAQklnA7cAtyZ9vh24\nMsUYJ6q/A54sOnefj73XR8TpEdGRnFf0d0tNJSPAWcCaiHgmIvYB/we4KOWYJqSI+E9gW0nxRcDX\nk+OvAxdXNagJLCKei4iHk+OdFH5Rz8R9Pmai4MXkdFLyJ4A3APcm5e7zCpM0C7gQ+EpyLtznaajo\n75ZaS0ZmAuuKztcnZVYdMyLiOSj85QkclXI8E5KkOcCrgWW4z8dUMl3wKLAJ+CnwNLAjInqSKv4d\nU3mfBf4B6EvOp+M+H2sB3C/pN5Lem5RV9HdL/SEGeLg5YNc3Cp1sNiFIagK+C/x9RLxQ+EejjZWI\n6AVOl9QCfB84ebBq1Y1q4pL0VmBTRPxG0vz+4kGqus8r69yI2CDpKOCnkp6q9AfU2sjIemB20fks\nYENKsdSi5yUdDZD83JRyPBOKpEkUEpFvRsT3kmL3eRVExA7g5xTW67RI6v+Hnn/HVNa5wNslPUth\nmv0NFEZK3OdjKCI2JD83UUi6z6LCv1tqLRlZDrQnK68bgEVAZ8ox1ZJO4PLk+HLgBynGMqEk8+Z3\nAE9GxGeKLrnPx4iktmREBEmTgTdRWKuzFLgkqeY+r6CIuDYiZkXEHAq/vx+IiD/HfT5mJE2V1Nx/\nDJwPPEGFf7fU3A6skt5CIZPOAHdGxE0phzQhSfo2MB9oBZ4HPgbcB9wDHAusBS6NiNJFrjYKks4D\n/i/wOC/NpX+UwroR9/kYkPQqCgv3MhT+YXdPRNwo6XgK/2o/EngE+IuI2JtepBNTMk1zdUS81X0+\ndpK+/X5yWg98KyJukjSdCv5uqblkxMzMzMaXWpumMTMzs3HGyYiZmZmlysmImZmZpcrJiJmZmaXK\nyYiZmZmlysmImZmZpcrJiJmZmaXq/wExurxBuheFkQAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"temp_change = 0\n",
"voltage_std = .13\n",
"process_var = .05**2\n",
"actual_voltage = 16.3\n",
"\n",
"x = (25, 1000) # initial state\n",
"process_model = (0., process_var)\n",
"\n",
"N = 50\n",
"zs = [volt(actual_voltage, voltage_std) for i in range(N)]\n",
"ps = []\n",
"estimates = []\n",
"\n",
"for z in zs:\n",
" prior = predict(x, process_model)\n",
" x = update(prior, (z, voltage_std**2))\n",
"\n",
" # save for latter plotting\n",
" estimates.append(x[0])\n",
" ps.append(x[1])\n",
"\n",
"# plot the filter output and the variance\n",
"book_plots.plot_measurements(zs)\n",
"book_plots.plot_filter(estimates, var=np.array(ps))\n",
"book_plots.show_legend()\n",
"plt.ylim(16, 17)\n",
"book_plots.set_labels(x='step', y='volts')\n",
"plt.show()\n",
" \n",
"plt.plot(ps)\n",
"plt.title('Variance')\n",
"print('Variance converges to {:.3f}'.format(ps[-1]))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The first plot shows the individual sensor measurements vs the filter output. Despite a lot of noise in the sensor we quickly discover the approximate voltage of the sensor. In the run I just completed at the time of authorship, the last voltage output from the filter is $16.213$, which is quite close to the $16.4$ used by the `volt()` function. On other runs I have gotten larger and smaller results.\n",
"\n",
"Spec sheets are what they sound like - specifications. Any individual sensor will exhibit different performance based on normal manufacturing variations. Values are often maximums - the spec is a guarantee that the performance will be at least that good. If you buy an expensive piece of equipment it often comes with a sheet of paper displaying the test results of your specific item; this is usually very trustworthy. On the other hand, if this is a cheap sensor it is likely it received little to no testing prior to being sold. Manufacturers typically test a small subset of their output to verify that a sample falls within the desired performance range. If you have a critical application you will need to read the specification sheet carefully to figure out exactly what they mean by their ranges. Do they guarantee their number is a maximum, or is it, say, the $3\\sigma$ error rate? Is every item tested? Is the variance normal, or some other distribution? Finally, manufacturing is not perfect. Your part might be defective and not match the performance on the sheet.\n",
"\n",
"For example, I am looking at a data sheet for an airflow sensor. There is a field *Repeatability*, with the value $\\pm 0.50\\%$. Is this a Gaussian? Is there a bias? For example, perhaps the repeatability is nearly $0.0\\%$ at low temperatures, and always nearly $+0.50\\%$ at high temperatures. Data sheets for electrical components often contain a section of \"Typical Performance Characteristics\". These are used to capture information that cannot be easily conveyed in a table. For example, I am looking at a chart showing output voltage vs current for a LM555 timer. There are three curves showing the performance at different temperatures. The response is ideally linear, but all three lines are curved. This clarifies that errors in voltage outputs are probably not Gaussian - in this chip's case higher temperatures lead to lower voltage output, and the voltage output is quite nonlinear if the input current is very high. \n",
"\n",
"As you might guess, modeling the performance of your sensors is one of the harder parts of creating a Kalman filter that performs well. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Animation\n",
"\n",
"For those reading this in a browser here is an animation showing the filter working. If you are not using a browser you can see this plot at https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/animations/05_volt_animate.gif."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"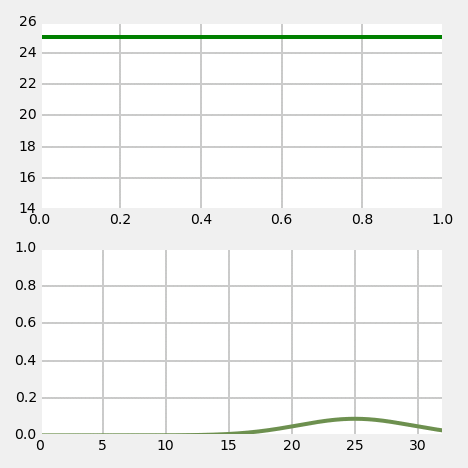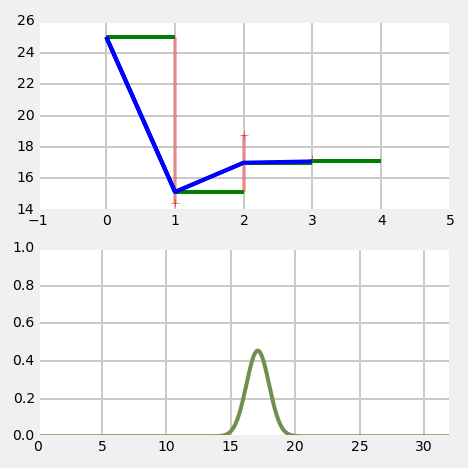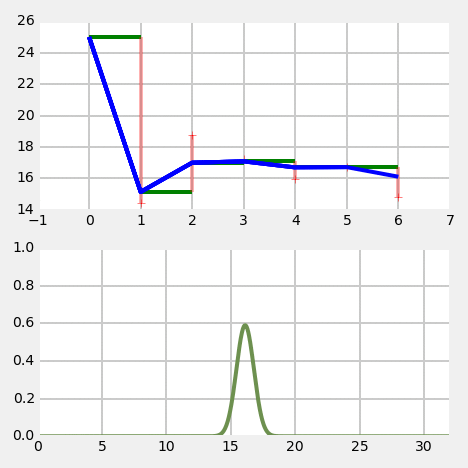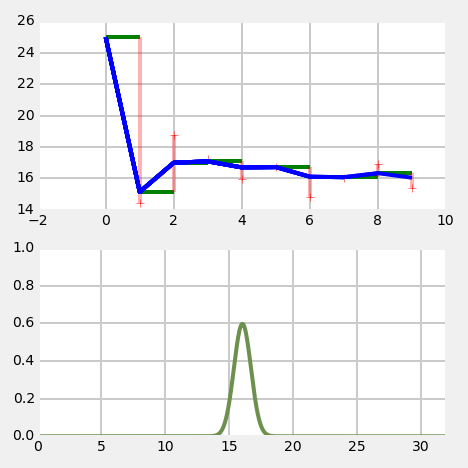 "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The top plot in the animation draws a green line for the predicted next voltage, then a red '+' for the actual measurement, draws a light red line to show the residual, and then draws a blue line to the filter's output. You can see that when the filter starts the corrections made are quite large, but after only a few updates the filter only adjusts its output by a small amount even when the measurement is far from it. \n",
"\n",
"The lower plot shows the Gaussian belief as the filter innovates. When the filter starts the Gaussian curve is centered over 25, our initial guess for the voltage, and is very wide and short due to our initial uncertainty. But as the filter innovates, the Gaussian quickly moves to about 16.0 and becomes taller, reflecting the growing confidence that the filter has in it's estimate for the voltage. You will also note that the Gaussian's height bounces up and down a little bit. If you watch closely you will see that the Gaussian becomes a bit shorter and more spread out during the prediction step, and becomes taller and narrower as the filter incorporates another measurement.\n",
"\n",
"Think of this animation in terms of the g-h filter. At each step the g-h filter makes a prediction, takes a measurement, computes the residual (the difference between the prediction and the measurement), and then selects a point on the residual line based on the scaling factor $g$. The Kalman filter is doing exactly the same thing, except that the scaling factor $g$ varies with time. As the filter becomes more confident in its state the scaling factor favors the filter's prediction over the measurement. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Example: Extreme Amounts of Noise\n",
"\n",
"With the dog filter I didn't put a lot of noise in the signal, and I 'guessed' that the dog was at position 0. How does the filter perform in real world conditions? I will start by injecting more noise in the RFID sensor while leaving the process variance at 2 m$^2$. I will inject an extreme amount of noise - noise that apparently swamps the actual measurement. What does your intuition say about the filter's performance if the sensor has a standard deviation of 300 meters? In other words, an actual position of 1.0 m might be reported as 287.9 m, or -589.6 m, or any other number in roughly that range. Think about it before you scroll down."
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAiIAAAC+CAYAAAAIj2Q7AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzsXXdcFMf7fu6OKtWGgApiRVDssZcY\nUbH3FuxGY+8RjTUae4s99i72HhsWJGoUS2KLilhRVBRFAan3/P44d3LLHYiKwu/rPp/PfMS53ZnZ\nnd19n3nnLSqSUKBAgQIFChQoyAyoM3sAChQoUKBAgYKvFwoRUaBAgQIFChRkGhQiokCBAgUKFCjI\nNChERIECBQoUKFCQaTDJ7AEYQ1RUlGJBq0CBAgUKFPyPwc7OTpWyTtGIKFCgQIECBQoyDQoRUaBA\ngQIFChRkGrLk1ow+7OzsMnsIXz3Onz8PAChfvnwmj0SBBGVOshaU+chaUOYjfTh48CAaNGgAksiX\nLx8AICwsDCqVCocOHYK3t3eG9BMVFZXm74pGRIECBQoUKPgKUb9+fWzevBkuLi4ICwtDWFgYXF1d\nsWXLlgwjIelBlteIKFCgQIECBQo+D1q3bo0WLVrg6tWrUKlU8PT0hEaj+aJjUIiIAgUKFChQ8BVD\no9GgVKlSmda/sjWjQIECBQoUKMg0KEREgQIFChQoUJBpUIiIAgUKFChQoABarRaHDh3CgAED0L9/\nfxw8eBBarfaD23n48CF69eoFR0dH5MyZ873HKzYiChQoUKBAwVeO+Ph4tGzZEvv37xd1CxYsgI+P\nD3bs2AELC4t0tRMWFoZKlSrh8ePH6e5b0YgoUKBAgQIFnwGvX7/G8ePH8ddffyE5Ofmj29Fqtbh9\n+zYePHgA8vNkQJk2bRr279+P7NmzY9y4cRg3bhxy5MiBAwcOYOrUqelu59dff8Xjx49RuXJlXL58\nGSEhIe89RyEiChQoUKDgfwJJSUmfTVB/CEhi4sSJcHZ2Ru3atVG5cmUULFgQBw4c+OC2Nm/ejMKF\nC6NIkSJwdXVFuXLlEBQUlOFjXrFiBQDA398f48ePx/jx47FlyxYAwPLly9Pdzt69ewEAixYtQsmS\nJVG4cOH3nqMQEQUKFChQ8P8a27dvR7ly5WBqago7OztMnToVr169yrTxzJ49G2PHjkVMTAzKlSuH\nAgUK4MGDB2jatCkuXbqU7nZ27NiBdu3a4e7du3BwcICdnR0uXbqEunXr4u+//87QMUtbKVWrVhV1\n0t+PHz9ON8GTND9mZmbp7lshIgoUKFCg4P8tli9fjlatWuHixYsAgDdv3mD79u348ccfERMT88XH\nk5SUhBkzZgAANm3ahPPnzyM0NBRdu3ZFYmIiZs+ena52SGLcuHEAgHHjxuHx48d48uQJ2rRpg7i4\nOHTu3Bm7du1CYmJihozb09MTALBu3TpRJ/3t6ekJlcogaa5R1KtXDwAwdOhQPH36NH2EkGSWK69e\nvaJUFGQ+goODGRwcnNnDUKAHZU6yFrLKfBw4cIANGzZk0aJF6e3tze3bt1Or1X5wO//++y+3b9/O\ns2fPftT5XwpxcXHMlSsXAXDy5Ml8+/Ytr1y5QhcXFwLg/Pnzv/iY7t69SwDMkyeP7N5duHCBAOju\n7p6udl6+fEkAtLCwYHx8PEkyMDCQ9vb2BCBKwYIF+e+//37yuFevXi3a9Pb2Zt26dcX/V65cme52\nbt26JRujSqViCpluIPPTTQ4ArATwDMBVvbrxAB4B+PtdaaD320gAtwHcBFBPr77+u7rbAPyM9aUQ\nkayFrPKRVfAflDnJWsgK8zFr1iyZgJLKqFGj0t1GREQE69WrJzvfy8uL169f/4wj/3icOnWKAFis\nWDGZ0J8wYQIBsGHDhl98TJGRkVSpVDQxMWF4eLioX79+PQGwSpUq6WonNjaWGo2GarWajx8/ZmRk\nJO3s7MS82Nvbs0iRIgTAokWLMikp6ZPGrdVqOXHiRJqZmYk+zMzMOGHChA8mo9evX2fTpk2p0WjS\nRUQ+ZGtm9TsSkRJzSJZ+V/4AAJVK5QGgHQDPd+csUqlUGpVKpQGwEIAPAA8A7d8dq0CBAgUKPhLh\n4eEYMWIEAGDChAm4fPkyZs2aBY1Gg8mTJ+PmzZvvbYMkWrdujUOHDsHa2hoNGjRAnjx5cPnyZXh7\neyM6OvpzX8YHQ63WibCkpCRZvfT/9G4nZCSyZ8+Oxo0bIykpCT4+PtiwYQPmzp2L/v37AwA6duyY\nrnYsLS3RuHFjaLVatG7dGmPHjkVUVJRwo+3bty/+/vtvFChQALdu3UJAQMAnjVulUmH06NEICwvD\nxo0bsWHDBjx8+BBjx4794PtYvHhx7Nq1C3FxcYiPj3/v8emOI0LypEqlKpDOw5sC8CcZD+CuSqW6\nDeCbd7/dJnkHAFQqlf+7Y6+n1pCUzllB5kOZi6wHZU6yFjJrPnbs2IGkpCRUr14dDRo0QHx8PGrU\nqAEfHx/s27cP8+bNQ9euXdNs49q1azhx4gRsbW2xadMmODg4IC4uDt26dUNISAimTp2KZs2afaEr\nSj9y5syJ0NBQdOnSBb6+vrh3757w8vDy8sqUOenRowfOnz+Pv//+G76+vqK+Ro0aKF26dLrH1Llz\nZwQFBeHUqVM4deoUACAuLg5FihRBnTp1cP36dZQqVQr37t3DsWPH0hU8LD0oUqQIAODBgwd48OBB\nhrWXGjIioFk/lUrVCcB5AENJvgSQF8BfeseEvasDgIcp6itmwBgUKFCg4KtFXFwcAN1qXB/S/6Xf\n08KtW7cA6DwlHBwcAAAWFhbw8fFBSEiI+D0rwcTEBIMHD8aYMWOwdu1arF27Vvzm6emJBg0aZMq4\nnJycsH79euzZswcXLlyAubk56tSpg4IFC2LKlCm4cOECzMzMULt2bXz//fewsbEx2k6+fPmwfv16\nbNq0CQcPHsSzZ8+QN29e/P7777C2tkZ8fLwgNc7Ozp/lWhISEhAYGIiwsDA4OzujZs2a6Q5ulm4Y\n269JrQAoALmNSB4AGui8b34FsPJd/UIAvnrHrQDQEkBrAMv16jsCmJ+yH8VGJGshK+x/K5BDmZOs\nhcyej0uXLhEAra2tefbsWZLklStXhCFnQEDAe9vYtWsXAbBEiRJMTk4W9R06dCAATpgw4bON/1Nx\n+PBhfvvtt7SysmK+fPnYuXNnnjhxIrOHJcPFixdpY2NjYMNTokSJdMm658+fi/OrVKnCkSNH0tPT\nUxisJiYmZviYL126xHz58snG6+joKJ6x9CLDjFVphIik9ht0hqoj9X47BKDyu3JIr152HBUikiWR\n2R9ZBYZQ5iRrISvMR8uWLYWwcHJyEn/XqlUrXcaGcXFxzJMnDwHQx8eHq1evZvfu3QmAGo2GoaGh\nX+AqMgZZYT5SombNmgTAxo0b89KlSwwICGCxYsUIgOPHj09XG0eOHJEZrAJgvnz5eOXKlQwfb1xc\nnCAhnp6eHDp0KEuVKkUAdHBwYHR0dJrnh4eH888//+S9e/c+LxEB4KT392Do7EIAnZHqPwDMAbgB\nuPNOc2Ly7m83AGbvjvFM2Y9CRLIWsuJL/bVDmZOshawwH2/fvuWgQYNobW0t3D579uzJ169fp7uN\nY8eOifOlolKp+Pvvv3/GkWc8ssJ86OPFixcEQHNzc0ZFRYn6Q4cOCc+k9OLVq1dctmwZx44dy40b\nN/Lt27efY8jcunUrAdDDw0O4DycmJrJs2bIEwDVr1qQ6vnbt2lGtVotn6H1EJN02IiqVahOAWgBy\nqVSqMADjANRSqVSl33V2D0AvACB5TaVSbYHOCDUJQF+Sye/a6fdOQ6KBbivnWnrHoECBAgUKjMPC\nwgJz5szB5MmT8fTpU+TOnRtWVlYf1Ma3336LmzdvYsWKFbh+/Try5s2Lbt26wcNDcW78FEieI+bm\n5rC0tBT19vb2ANJnwyPBzs4OPXr0yNgBGkFoaCgAXYAyKUqqiYkJ6tevj4sXL4rf9UESbdq0weHD\nh2FiYoKyZcvi2rX3i/gP8Zppb6R6RRrH/wqd3UjK+j8A/JHefhUoUKBAQfphaWmJAgUKfPT5zs7O\nGDNmTMYN6CtEcnIyAgMD8fTpUyQnJ+P48eOwtrbG69evMXToUMycORPR0dEYO3YsAOC7777L5BEb\nws3NDQAQEBCAxMREmJqaIjk5GUeOHJH9ro/z58/j8OHDsLe3R3BwMAoXLoynT5++t6+M8JpRoECB\nAgUKFAA4d+6cyA9jDPPnz8fy5cuRlJSExMRE2NvbY9iwYV94lO9HkyZN4OTkhCtXruCbb76Bj48P\njhw5gvPnzyNnzpxo1aoVAODVq1eYN28e9uzZgydPngAA6tevL5Ld5cmTB1FRUWn2pRARBQoUKPhI\nkMyUoFkKsiaeP38OHx8fREZGwtnZWSSSA4AyZcrAxMQEwcHBePv2LQDA29sbs2fPRsGCBTNryKnC\nwsICe/bsQaNGjfD333+LJHu5cuXC2rVrMX36dOzcuRMhISEGQct27NiB+/fvw9XVNV19KUnvFChQ\noOADkJCQgIkTJyJ//vzQaDTw9PTEzp07JaP9LIHQ0FD4+vrC1tYWVlZWaNGiBS5fvpzZw/qfx6pV\nqxAZGYkaNWqgbdu2AIBOnTrB2toaly5dwsqVK1G0aFEAOmF9+PBhlChRIjOHnCbKly+PO3fuYO3a\ntRg3bhxWrVqFc+fOYcCAAZg4cSKuXr0qSEiOHDmwfPlyqNVqJCQkoFq1aqhXrx6yZcv23n4UjYgC\nBQr+J/D48WMsWLAAQUFBsLKyQps2bdCxY0eYmppmWB98FwZ9z549ou769eu4fv06wsPDUaFChTTP\nT0pKwpEjR3D//n0ULVoUtWrVEmHKMwp37txBpUqV8Pz5c1G3c+dOHD58GEFBQShTpkyG9vf/CSRx\n7tw5/PXXX7Czs0PTpk0NgsB9Cq5cuQIA8PX1xenTpwEAFStWRFRUFHbv3o1r167Bw8MDt27d+iAD\n1cxEtmzZZGHpBwwYgNu3b8PLywuPHz/G8+fPUaJECVy9ehWzZ8+Gubk53r59i7CwMISFhaWvE2Ou\nNJldFPfdrIWs5gqnQJmTlLh69aoI3qVf6tWrJ1wPMwJHjx4lANrZ2fHQoUOMi4vjqlWrqFarqdFo\n+OjRo1TP/eeff+jm5iYbn6enJ2/fvp1h4yPJLl26EABr167N0NBQPnz4kC1atCAANmjQIEP7yqoI\nDg7moUOHePDgQf71119MTk5mVFQUvb29Zfff0tKSa9euzbB+hw8fTgDs0aMHFyxYQAAsU6aMiMex\nZs0aWlpaEgBv3ryZYf1+KTx58oRWVlYEwPz589Pc3JwAGBQUZDThIt4l58vQOCJfqihEJGtBEXpZ\nD8qcyCEFi6pVqxb/+OMPrlixgrlz5yYALl68OMP6GTp0KAHQz89PVl+9evU006XHxMTQ2dmZAFio\nUCF27dpVCKdixYp9cuZUfUjXrZ8xNyIiggCoVquZkJCQYX1lRSQkJLBVq1Y0MTERwrBIkSIirb29\nvT179OjB2rVri3ty4cKFDOn72rVrVKlUBEBfX19Z8DELCwuampoSAFu2bJkh/X1JPHr0iK6urkbJ\nxrfffiv+bt26tfhbmoOMzL6rQIECBVkO4eHhCAwMRLZs2bBr1y74+PigW7dumD17NgBg06ZNGdZX\naoapfGcfktrvW7duxePHj1GqVClcu3YNK1euxPXr1+Hq6oqbN2/i0KFDGTZGY2P5mgxqhw8fjm3b\ntkGr1aJatWrImzcvQkJCRGyLs2fPYtmyZTh69Ch69+4NrVaLRYsWZUjfHh4emD9/PlQqFdavXy/z\nFomLi0NycjK+//57rF69OkP6+5L45ZdfcP/+fRH7pEGDBvDy8gIAHD9+XBy3detW8XfKrMipQSEi\nChT8P8fr16/x4sWLLGUs+SXx+vVrALoEb7a2tqJeiqXxPtfBD4GURG3RokU4cOAAYmJisGLFCpw6\ndQoajQZ169Y1et6///4LAGjevDnMzc0BADY2NmjUqBEA4MaNG3j69Cn8/PxQqlQplC5dGqNHj5bZ\neQA6V8lFixZh2LBhWLhwIV6+fJnqGAcMGICHDx/i6dOn6N27NwCgbt26GWozk5GIjY3F1atXER4e\n/tFtvHz5EkuWLIFKpcLSpUsRFBSEu3fvokqVKgB0BpWSsSgAtGjRAgAyNKFf3759ce3aNYwYMQJd\nunTBrFmzEBQUhMOHD+PBgwdYv349rK2tP7r9V69e4ebNm4iJiUn1GJK4cOECdu7ciatXr350X/rY\nsWMHAGDhwoUwMzPDH3/8gTt37hg99oOJrzE1SWYXZWsma0HZBsh6CA4O5qZNm2R73l5eXtyzZ09m\nD+2LIyEhgQ4ODgTAVatWUavV8u3bt2zatCkBsHfv3hnWl1arZbNmzYyqp7t165bqefPnzxd2G1Le\nl6SkJJG7Y9GiRcyfP79Bm25ubgwPDydJnjx5kvb29rLfbW1teezYMVlfISEhzJEjh0Fb2bJl4/nz\n5zPsXnwKtFoto6OjmZSUxKSkJI4ePZq2trYy2567d+9+cLuSrYK7u7vsm7V69WqxDRMWFibqR4wY\nQQD8/vvvM+KyMgRxcXF88uSJQRK7Fy9esEOHDmK7I1u2bBw4cKBBiPfQ0FCWL19eNvdFixblzJkz\nZdeuj2fPnnHWrFns168fZ8+ezYiICJJkfHw8T58+zVOnTon5efDgAU+cOCFCvacsXl5e7Nmzp6xO\nsRFR8MlQiEjWw44dO0ROEFNTU2bLlk3kBfkaycicOXPER69w4cJCEFtbW/PWrVsZ2ld8fDx//fVX\nFihQgCYmJixZsiRHjx7Nc+fOpXrO8+fPhZFf3bp1OX36dFarVk0kEPP19SUAVqhQgceOHWNAQADL\nlClDAPzxxx8ZHR3NnDlzEgCrVq3KyZMns0aNGsLmIWU+mZs3b7Jt27bCLqFx48a8ePFiht6Hj4FW\nq+XSpUtZuHBhMT8SGcM7+xkLCwsCoKur6wfLgH///ZcAaGNjw5MnT4r6yZMniz7y58/P0aNHs337\n9qJO/1gJISEh7N27N728vFilShXOmzePcXFxJHX2Ev3792f16tXZrFkzbty48ZPtfF69esVevXoJ\nY9bcuXNz4sSJTEpKYmJioiAXarWaBQoUEGNv27ataCM+Pp6FChUiAObMmdPAOFqj0XDs2LGyJIhH\njhwxyC9kY2PDESNGCIIPgGZmZoK0vXnzhjExMezYsSMBsGbNmuL5NlYUIqLgk/H/gYhcunSJzZs3\np42NDXPmzMkePXrwwYMHmT2szwZpVe7j48PIyEjGxcXxp59+IgCWLFkyXdlW/5eg1Wo5c+ZMIawB\nsFSpUjxz5swX6T8978j+/fsFYZSKvb09g4KCxEc8JCREHH/58mUhUNatW0cALFeunBB4ycnJrFSp\nEgFwxYoVRvvUarXiWQgPD2dYWNhneTbevn3LjRs3cuTIkfztt9/47Nkzo8f9+uuv4tolw02p7N27\nl6TOsLZ06dIEwN9+++2Dx1KhQgUx/xs2bOC4ceMEuSlYsKCsT7VazZkzZxq0ce7cOdrY2BgI1Fq1\nanHUqFGyhG5SadKkiYEWI71ITExk5cqVZc+F9HefPn24a9cuArpMu1IW5LNnzwrScu3aNZKkv7+/\n0IBMnTpVGIxK3i2SIe3s2bPZp08furq6imupVq0aZ82aJYx49bUpUpZgqVhYWIhn2cTEhIGBgcL4\numLFinRxcZEZCytERMEnI6sTEf0XUr/kzZs3TXfK/8+QXnp9a//4+HjxcejQoQM7dOjAZcuWMSYm\nJhNH+mXx9u1bXrx4kTdv3vyiZCy978jTp085a9YsDhgwgPPnz2dkZCS1Wq0QBvrfvPDwcKGCl1b0\nQ4YMkbU3cuRIAuC4ceNS7fPPP//kN998I94LDw8PIfQzAjdv3pSt0CVBtW3bNtlxkZGR4j1dvnw5\nk5KSxJYVAJkb7YoVKwjo3I2HDx/O2rVrs3Xr1ty3b9975/Xq1atGt6b69OnDhIQE7t69m35+fpwy\nZQrv3LljcL5Wq2W5cuUIgI0bN+apU6fo7+9PR0dHWXtmZmaC4EgCftmyZR91D3fu3EkAdHJy4pUr\nV6jVarl//36amJhQpVKxR48eBMDx48fLzpO0OkuWLCFJ+vn5EQDHjh0rtCH+/v7s3bs3AYjtFGm8\nKUnx/v37mZSUJEhYkyZNBJmdOHGi0GJJ55QvX54BAQEkyUGDBomFUEBAAOfMmSN7rhUiouCTkNWJ\nSK1atYSK8v79+7x27ZpYKQ4YMCCzh/dZIH1k9O0DIiIijK7UihcvzidPnmTiaP/38anviPQM9+3b\nl/Hx8Xz79q0QPj4+Pty2bRsBnatvbGwsSZ0tgaenJwFw06ZNRtu9ePGiEJZWVlbCnVStVvPgwYMf\nPV4JWq2WJUuWFM/Z2LFjWa9ePSGo7927J47du3cvAd3WkoTAwEDxnOrbafzyyy9GtSaAzuZHIiNH\njx6lt7c37e3tWbBgQY4dO5bR0dE8cuQI+/Tpw6ZNm7JLly48cuRIuonpnTt3COhixUj3miRXrlwp\n0+Y8f/6c0dHR9PHxkWlMUt6fM2fOcOrUqfztt994//59o33279+fADhx4kRZvWTn1KRJEwK6bTp9\nSG6z69atI0nOnj2bANiwYUMxpsTERHp4eBjcx9RK5cqVqdFoCICjRo0SfcXExAgS8/z5c2FHIuHZ\ns2csUqSIQXtWVlYKEVHw6cjKROT169fiwxAVFSXqz549SwAsUKBAJo7u86Fbt25idXv8+HFeunRJ\nCASNRsOJEydy0aJFLFq0KAGwffv2mT3k/2l86jty/Phx8fG3s7MTK1JTU1OePn2a8fHxQutQsGBB\n9uzZU9hZ5MuXz8BgUUKrVq2EhiwmJobx8fEcMmSIUKF/Kv7880+xko+OjiapE74tW7YUK/O9e/ey\nU6dOrFq1KgFdgC8JiYmJghwVLFiQQUFBXLhwoWwLy8fHhz/++CNdXV3FSn7lypXcvHmz0ZV91apV\neerUqY+ejytXrhAAXVxcZORFn4jkz59f/KZPpkqVKiWOj4mJYaNGjWRjU6vVnDx5skGfUnyaoUOH\nyuolgqq/zTJjxgwGBwdz2LBhBHRB2SIjI0mSjx8/FrYcEgGtWLGi6D/l1mDK+5fy/1OmTBFjuXDh\nAgEwe/bsqd6758+fc/To0SxZsiSLFy/OgQMH8uHDhwoRUfDpyEwikpyczMOHD9PPz4/jx4/nlStX\nZL9HRUWJ1Zf0ISR1K0FAZ/D2v4iAgAADdbhUJk2aJI67e/cu1Wo1TUxMDAwaFWQcMuIdOXDggCCT\nAFi6dGmh9iZ1wbIkQ0SpuLm58fLly6m2KUWblewKSJ2AlEiP/or/Q3Dx4kV27dpV2FxUqVJFJrSX\nLFkixmfsGR00aBAfPXrEvXv3GrXFkIqzszO/++47g3qNRiOubdiwYXz06BGPHj0qgrnZ2tqyUKFC\nnDp1aqokLTXExsYKD5G8efOyS5cu/PPPP1mlShXZGPz9/RkaGsoxY8aIup49e1Kr1TIpKUloOezs\n7Ni7d2+2atVKCPp9+/bJ+jx16pQgFStXruStW7c4fvx4GdGQPHxSlmXLlvHq1as8cOAAb9++zfXr\n14v51S/6NhupkQ+NRiPTqmbLlo3Dhw/nqlWrxLP3MVpmhYgo+GRkFhF58+aNLGKfVIYMGSL76Ekf\niG7dujEyMpIPHjwQ5/Xq1euLj/tLIDg4mAEBARw1ahTd3d1ZoEAB8UHXJ2tarVZ8sP+XjXczGxn1\njmi1Wj58+DBVo9LExETu37+f8+bN4969e99rHCm5BP/111+iLiwsTAimj4myunXrVqOCrk+fPiR1\ni4f69euLehsbG06ePJkrVqxg3rx5jQrDqlWrsnv37ixbtizr1asnhK6k9cmTJw83btwohLNUChcu\nLO7T3r17jW5N1qpVK91h/rVarSwyaHqFuSTQu3TpIt43ScDru0xLtj4+Pj4G/UpazpQlZ86c/O23\n3xgfH8+dO3fSx8eHJUuWZOvWrbllyxahaZJKo0aN+Ndff3HIkCEimm9aBCRPnjypHpOylCpVSmhf\nPgQKEVHwycgsIiIZWOXOnZt+fn7s2bOn2DPW3xM/efKk0b3k3Llzy/ao/5dgbE4kdXj//v3Fx3nH\njh0EdC6iH2vRr+D9+Nh35Ny5c+zWrRtr167NXr168dKlSxk6rsGDBxMAS5QowcOHD/PkyZPCbbh1\n69Yf3F5MTAyzZ89OAPzhhx948uRJuri4iHeudevWwmtFIgX6Hj2PHz8W9fb29ixWrBinTp0q3GIl\nPH36VPZOr1q1im/evBFCV9p+KFKkCEldTBb98OPlypXj7NmzhYHpqlWr0nV9y5YtS1UIm5ub09/f\nXxbvJD1Ff3tD8oQqWrSoQd/Jycn85ZdfjJI8QKed0d9+jouLEzYZ9vb2/Pbbb4UxcPXq1YWRqeRN\nJ7UhaT6M9aFP5IYNG8YGDRqI/0+ePPmjDd8VIqLgk5EZROTt27diP/Pvv/8W9VIiqZo1a8qOP3Xq\nFOvUqUO1Wk1zc3O2adNG5gr5vwZjc3Lq1CnxISlRogRr1qwpVj1Tp07NpJF+HfiYd2TRokVGBUFG\nJmGLiIgQdkL6xdHRUbZdk14sX75cCL6+ffvy4sWLfPDggUHCwezZswtiIN2XBw8ecO7cuUJz9774\nLn369BHtFSpUSBCgXLlyyTxYpkyZwtOnT8s0FsOHD2dwcDB///13AjpjT1K37TJp0iS6u7vTwcGB\nDRs2ZGBgoOhTatfJyYkrV67kmDFjhOsroIs3Mm7cOAK6LZOSJUty1KhRMk3N7t27+erVK0GWzM3N\nhRZh2rRpBHQB24xBX/Cn1FwAOq8XCZs2bRJkTGr/4cOHwoX91KlT1Gq1wvVbGktqhElymQZ0BqYv\nX74k+d8CZ86cOR/8vEhQiIiCT0ZmEBFJfZwrVy5ZvRSwyM3Nzeh5ycnJX0UMjdTmZPPmzTKhYGZm\nxhEjRjA5OTkTRvnhiIuL49WrVzNsGykqKirdNgIhISE8efIknz59+sH9fOg78vDhQyE0Bw4cyL17\n97Jdu3ZCWDx//vyDx5AaXryQeCeGAAAgAElEQVR4wbFjx9LLy4uenp4cPHhwqhE208LBgweNrqTn\nzJnDmTNnEtAZRm7YsIHR0dEi2FW3bt04bdo0g3O9vb355s2bVPtLSEgwiBBaunRpg1ggKYW1h4cH\nT548KaIPA2D9+vWZkJAgkiOmJH9bt24V3xwAXLBggRjH3LlzRf2BAweEy+zy5cv59OlTzps3TxaU\nrW3btqxVq5ZMU9SwYUO2b99eLBR2795tcL1v3ryRjcva2lqQGf1y69YtarVatmnThgBYo0YN2fZP\n9+7dCYDz5s3jzz//nCrxSKsULVqUJUqUYPPmzYVXUEqPng+BQkSoE043b97kjRs3/t98kLMSMoOI\nxMfHi6A++iuWSZMmpbmi+FqQ1pzExcXx0KFD3L17d6qBpbIatFotZ8yYISNR1apVMzBOTi927twp\nhINGo2Hz5s15+/Zto8eGhoaKKKXSqrpr164fpIb+0Hdk1qxZBMAWLVpwx44dBkaoWc3tPDIy0uj2\np1Qkw+nVq1eLcy5cuJDqOdIWQs+ePdPs99GjR+KZsLCwEJ4ggC4KrTFSMn78eA4ePJg1a9YU2oEZ\nM2ZwzZo1Qttx4MAB3r17V8S+cHZ2ZnBwsIzwSIRUsuuQ3FZ//PFHAmDTpk1l40lPUalU/OWXX4xe\n64sXL4yeI8U00X829F2GpdKjRw8mJSUJLxnpGdNoNMJ7yliZNm0af/75Z5YoUSLNsf/xxx8f/fx8\n9URk7969Mt/mQoUKcfv27Z/c7teEzLIRkYLzWFpa0tfXV6a23L9//xcfT1bCl5iTGzdu0N/fn0eP\nHk0zfPXr16+5adMm/v777x9NHCT3REDn6SRFGs2ZM+cHB6XbsmWLaMvc3Fyslh0dHQ3aio6OFkLU\nxsaGFSpUECv3Nm3apLtP/fmIj49ncHAw//7771Tvm+Rp0bZtWzE+BwcHIdjUarXRsOMfA61Wy1Wr\nVrFMmTK0srKiu7s758yZw6SkJN64cYODBg1i/fr12aNHD549e9ZoG507dxYkTbIxSVnc3d0NtE97\n9uyRbQeYm5tzxIgR/Pvvv8X/jx07ZjSwmIRr164ZGK2PGzdO2EBImiRj2g6p9O/fny1atCAALl68\nWHZvJBJ49OhRWZhyMzMzmVajdOnSJHU2afptly9fXmaEa2FhwXXr1smEf/369Tlz5sw0r1Or1RqQ\ngeXLlxvkNkqZb0h6XqSxADpPHWkLqXPnztRqtRw7dqyMGJqYmIgt2+fPnxsEhUypwRoxYkSaY1+8\neDGLFy9OjUZDNzc3Tp06VdilfdVE5MSJE+Jm5s6dW1gHq1QqHjp06JPa/pqQWUQkPj6eHTp0kL0M\npqamnDVr1hcfS1bD55yTqKgog49fgQIFeOrUKYNj/f39Ddwvmzdv/kHahNjYWPFx3bBhA7VaLaOi\nokQMBf2gSu9DcnKyECyjR49mXFwcHz16JIwchw8fLjteMk4sUaKE2Ge/cuWKIAQ3b95MV7/SfCxf\nvlzmheDm5mY0iqkU3EtSvQ8bNoyhoaGyEPUZpfUbNWqUUeFcq1YtoxoLY7YAkvdNtWrVGBcXx4ED\nB8oEV758+VIljFLQtXnz5oktp4SEBIPnpkaNGkbtRqKiohgeHs7NmzcTkAdEI/8zyG7QoIFMs6RS\nqeju7i6uUQrqlfL6JJfpwMDAVF1kNRqNjGSn3DJ6X6lSpUq65koK5f4pxczMjLt37xZkd9iwYaL9\nJ0+eCMKmv9Ui2dIY2wqSip2dXarjluKgpCzt2rWjVqv9uolInTp1CID9+vVjYmIik5KSRBCYatWq\nfVLbXxMyO6DZ1atXOX/+fC5btixTIoTGxMRw7dq1nDBhAtevX//RsRcyEp9zTiTjNEtLSzZp0kSo\nv21tbfn48WNx3MWLFwXRr1KlCjt06CBWlD169Eh3f5JKvFixYrL6ffv2CQGVXoSGhhLQ2RbpayOO\nHTtG4L9VrQQpeuncuXNl9c2bNyfwX8TK9FyDfh4Ve3t7WX6PlHEjkpKSZMaB5cqVE0JAUq1ny5Yt\n1f4uXLjACRMmcPz48alqMUjy/v37VKvVVKvVXLp0KV+8eMFt27bJSET79u25a9cu4WGjVqsNtrGk\nFb+VlZVY1YeFhQltzvjx4zlmzBgWL16cBQoUYJcuXfjvv/+SJBs3bkwAsi0Jyb4BAD09PUXY8Hz5\n8onv/u3bt9moUSPRh5TWwNbWVuZCOnDgQAIQLsN2dnbctWsXg4KCSJJdunQxEJDNmzfnmzdvhPG7\nvb09Y2JimJiYyAEDBsgIWt68eQ0Wrm3btiWg00DUqFFDaIyMBVgDdMHakpOTuXr1ataoUYNFihRh\n8+bNZdvOEiS7lrSKRqPhy5cvGR4eLstRY2lpKYz0jx49SkCnVZRizZw9e1bca/0kiNKWt/74GzVq\nxOrVq8v6bdmypQE5v3PnDlUqFTUaDdeuXcvY2Fju2bNH9HPmzJmvm4hIL5v+PrkUiVOlUin2IulE\nZhORzMSZM2dEkCSpODo6fpF06pGRkbxw4YJIA6+PzzUnUnhrCwsLsTpNTEwUpF5fmEhGcfr7/Jcv\nX6ZKpaKZmRlfvHiRrj5v3LghPpj6qn1pldagQYN0j//BgwdCWOkTxj179hDQ2RXoQ1qY9O3bV9Tp\nq8hTEojUEBwcLAibMWGkUqk4ffp02Tnh4eEy9bdKpWLLli2FAHFwcDDoJykpyahgbd++vVH3bCmw\nWIsWLWT1ktB2dnaWGXdLWYBT2jFI9dKzUadOHSFo1Gq10HroF2trawYHB/PgwYPi+lq3bi2Ll9G4\ncWOS5MuXL0UelLlz5/LJkyd0cnIioNtCkKKvSqVo0aLs1q2biDOiX9RqNbt168azZ8/y7t27Qrul\nn6hNEubS3ymJ6JMnT7hv3z6uWbOGfn5+/OGHH7h48WIRFHD06NHivmq1WiYmJsq0WfXr1+e0adOE\np4+dnR27du1q9LlYs2aNwbxJx5qYmBiNjQLokgTevn1bbDkBOvsX6Xuh1WplCez0yWfz5s1l/e3f\nv192T4oUKcLg4GCjfdvb2/P69eviXMn7K6U7uEQQf/7556+biEgCRD8x2PXr18VL8jV4V2QEvlYi\nEh0dLZ6hsmXL0s/PTxhAOjk5fXDExvQiJiaGPXv2FCtklUrFZs2aybRBn2tOdu/eTUCXql4fa9eu\nJQC2atVK1EkrMf18N+R/qm5j44uJieHEiRPp7u7OPHnysHHjxgwKChL3tXHjxjxx4gQXL14sPuJL\nly7lli1buGjRIp49ezbN91ar1QqB1qFDB968eZMnTpwQLqwpw2tfunRJfIBHjx7Nffv2idWug4OD\nQXyL1KAf5ltfIOoLJwAGieAkoVykSBGuXLmS8+bNE4TGmMHqnDlzhFDp06cP+/XrJ7RQxkKHS0Ii\npb2LRCxLlCghq5e0OoMGDZLVX758OVXXT6mtokWL8ujRo/znn3/E1p6keZ46daqBULO3t5d5zUiJ\n7tq0aSMEfZUqVfj06VMmJSWJa09NMKcs3bp1E0RTuqYVK1bIts5cXFxSjTEye/ZsA1Lp4ODAsWPH\ncubMmeJ+VK1alf3795fdn2LFitHBwcFgTJaWlly6dCkvX74stjNsbW3FfThz5gzr1atHjUaTqnZF\nKqampka3UlxdXQUZefz4sUGyPmnO9L9fSUlJsqi+0ncn5XnS86xPbFMjIpIhcIYSEQArATwDcFWv\nLgeAIwBC3v2b/V29CsA8ALcBXAZQVu+czu+ODwHQ2VhfGUVEpBC7Hh4e3LVrF/fu3UsvLy8CH6Y6\n/trxIUIvMTGRO3fu5NChQzlu3DiRnvpz4vr16/T19aWjoyNdXFw4cODADNnCWb16NQGd2lxabSYk\nJIgX1t/f/5P7MAZphaNSqejh4SE+Nl5eXiIS5uciIlKOHkdHR9mHasCAAQR025wSpAiU+hlBHz9+\nLAxEU9oMxMfHG6h6JRIwffp0o6G+TU1NDfJj1K5dO83ojkFBQUa9GUqWLCkLCCVBMurTL+bm5gZe\nAgkJCZw5cyaLFStGKysrVqhQgRs3biSpEyDSalLqe8uWLTx8+LCs3apVqzI+Pl7M4+PHj42GQVer\n1Vy0aJHBWCVCpU9opC0sFxcXg+NDQ0OpUqloYmLCLVu2MCkpiUeOHBHkxdraWsQTefHihTDs37Bh\ng6ydqKgodu/eXXZfs2fPzqVLl4pv6qhRo8TW3evXrw000mvWrBHkUnq+/fz8hGZacjX94YcfRLRk\n/TnQarWyoGUajUbYrkhBxvSFrlqtFmMwNTUVW44phW2vXr1k6SHI//KqqFQqduvWjTNmzDDQyuhn\n301JNvSfI/1stX5+frJ+pKzIO3fu5MmTJ1O10UgroqtUnJychIeN9J5KeYWcnJw4atQoTpw4UXgh\npdR6hYWFGfWcMTU1NUr+JK2wtDVjYmLCdevW8datW6xXr54gMt7e3hlKRGoAKJuCiEwH4Pfubz8A\n09793QDAgXeEpBKAs/yPuNx592/2d39nT9lXRhGRiIgIuru7G9zAQoUKGVV3KzCO9Aq9iIgIA1cz\nABwzZsxnG9vFixeNCjA3N7ePigehD0lApTSWlF5uYyvQT4WUcMvKykoEcgsLCxOeHVu3biX5+YiI\nVqsVavZKlSpxyZIl7N27t9Fw1UeOHBEf/B49enDSpElCqDZq1MigbWnF6+zszIMHD/LOnTvs27cv\nAV0SsQsXLsg+9vorTGdnZ3bu3FkIsqZNm6Z5HZcuXWLbtm3p5OTEQoUKceTIkSJAkzEcO3aMvr6+\n/O677zhw4ECDfXD9uA0pyzfffMNt27bJCIVGo+GqVatkXheSQFGpVFSr1WzUqBEvX75Mf3//VIWL\nZFgZHR3N0NBQIaj08wYlJiaK441tN0sLspRFWrGbmZmxatWq4j0qWrSoTBMUFRUlyIZ+yZ49O6dN\nmyYTUiYmJhw8eDDj4uKEAXJYWBgvX74sxl6gQAGZwO3atSunTZsm5vv48ePCS0afEMXHx8s0TNOm\nTRMGzZs3bxYCX3+rQipSe+bm5kZjoXh4eHDs2LGcO3cuDx06JDR01atX58uXL2XB1QCI6LGAbsU/\nbdo0sZ1SoUKFVPPnpPxmSJ6AGzduFBrGLl268Pnz5yIOi1SqV68utkNTK5LdUb58+ajVapkjRw4C\nkNkRSVtlBQsWpFarZXx8vNAyJicns3jx4rI2pXffxMSEdevWFfWOjo7CKF36JqZW3kdEVNQRhHRB\npVIVALCPZIl3/78JoBbJcJVK5QTgBMliKpXq93d/b9I/Tioke72rlx0n4V0iMwBASEhIusdnDNHR\n0di2bRuCgoJAElWrVkWrVq1gZ2f3Se0qMMTIkSMREBAABwcHNG3aFM+ePcO+ffuQnJyMuXPnomrV\nqhneZ58+fRAcHIyaNWuiX79+iImJwZQpU3Dz5k18//33GDRo0Ee3vX//fowfPx7u7u5YtWoVTExM\nkJiYiI4dOyI0NBSTJ0+Gt7d3Bl4NsGPHDkyZMgX16tXDpEmTRP2KFSuwZMkStG/fHkOGDMnQPlMi\nJCQE/fr1Q2RkpKy+f//+6NSpk6xu2bJlWLp0qayuYMGCWLhwIXLlyiWrHzJkCIKCgvDzzz+jWbNm\nAACtVotmzZohPDwcHTp0wMaNG1GoUCHMnTsXW7Zswbp168T5lpaWqFatGgIDA5GQkIBdu3Yhb968\nGXnpqeLChQv48ccfYWJigqSkJKPHFC5cGLdv3zao12g0SE5OFv9XqVTSQg5WVlZwcnIS55UvXx6V\nKlXC5s2bERERAY1Gg8aNG+PAgQOIj48X544aNQrNmzcHAAQEBGDkyJHIly8fdu7cadC/VquFv78/\ntmzZgkePHiFXrlxo3rw5WrdujenTp+Po0aNiPGXLlsWECRPg6Ogozl+6dCmWLVsGFxcXDBkyBDY2\nNli6dCnOnj0r68fW1hZv3rwBSZQrVw4XLlyAq6srtm7diokTJ2Lv3r1o0KABxo0bh/Pnz2PQoEFI\nTEyUtdGkSRN4eXnh9OnTOHbsGBwcHODn5wdHR0esWbMGhw4dgoWFBeLi4jB//nxs27YNgYGBGDp0\nKHbv3o3bt29jyZIlGD58ON68eYOOHTti3bp14r5ZWlri7du3AHTP6bNnzxAdHZ3m3OfIkQPR0dFI\nSEiAh4cHrl+/jjlz5iA4OBgbN25E3bp18euvv+LFixdo2bIlYmJiAAC5cuVCbGwsYmNjxTNga2uL\nNWvWIG/evPjrr78wePBgkMTGjRvRrl07mJmZISAgAJaWllizZg0WLFgAADA3N0dQUBCSk5PRokUL\nhIeHi/GVKVMGVapUwZYtWxARESHGvH//flSuXBkAcObMGZiYmAAAXr16BW9vb5iYmCB79uyIiIiA\ng4MDWrVqhY4dO+LVq1cYN24czp07l+o9MTMzQ0JCAsaPH49y5cohKSkJZ86cweLFi/HmzRuYmpqi\nZcuWaNGiBRYsWIA9e/aIc+3s7FQp2zNJcwbejzwkwwHgHRlxeFefF8BDvePC3tWlVv/ZYG1tjS5d\nuqBLly6fs5uvHq9evcLx48eh0WiwfPlyODk5AQDy5s2LRYsWYefOnRlORGJiYhAcHAyNRoNx48bB\nxsYGADB8+HD06NEDgYGBn0REvvvuO8ybNw83btxAp06dULFiRZw5cwahoaHInTs3atasmVGXImBl\nZQUAePr0qaxe+vBky5Ytw/tMiSJFimDr1q3Yt28fbt68CXt7ezRq1AhFihQxOPaHH37Ad999h8OH\nDyM6OhpeXl749ttvYWpqanCsJMAtLS1FnUqlgoWFBQDg+vXrAIBOnTrB0dER58+fl53/9u1bHDly\nBObm5gCA+/fvfzEiEhQUBEB3DZJQs7CwgFqtRmxsLAAYJSEqlUpGQjw8PLBgwQIkJSVh4sSJCAoK\nEud5eXlh0aJFUKlUaNy4MerVq4fk5GTs2rULAODg4IBnz54BAKZMmYLz589DrVYjICAAANCmTRuj\nY1er1ejQoQM6dOiApKQkIZCkdp48eYKHDx/CwcEBrq6uBucfPXoUAPDTTz+hYsWKAIBff/0V3t7e\nIAkfHx+cPn0aUVFRUKvVIIkLFy4AAHr37g2VSiXmtlGjRlCr1fjmm2+wceNGdOrUCW/fvkXFihXh\n4uKCPXv2yITWs2fPZMTb3NwclStXxvHjx7Fz507UrVsXgYGBWLhwIeLi4mBiYoLly5fjzZs3KFas\nGPr16weVSoW1a9cCgCAh1tbWmDBhAvr27StrOz4+XnbtlpaWgpA7OTkhNDQUAODm5gY7Ozts3LgR\n9+/fBwDkzJkTv/zyC4YOHQoAeP78OQAdUWjYsCEmTZqE169fo0WLFsiePbtot3Xr1nBwcBB9SqTQ\nx8cHCxcuBEkkJydj06ZNOHr0qIyEADpC1bZtW+TPnx9+fn4AgG+++QYmJiZwc3PD3bt3sWfPHrRo\n0QIAsHv3bgC6ZzkiIgIqlQrPnj3DokWLcPfuXTRt2hTdunVDy5YtMXLkSGi1WoNnIiEhAQAwb948\ncR0uLi5QqXQcY8iQIUhKTkZgyHOU6TDC4HwDGFOTpFYAFIB8a+ZVit9fvvt3P4BqevVHAZQDMBzA\naL36MQCGpuxHCfGetZCebQBpS0FKQiVBygGhnyMho/Dy5UuhbtX3kJAMEF1dXT+5j7Nnzxpkp3R2\ndpa5vmUkoqKihIq5d+/eDAwMlCXCkmxu/j8aEEuRHkuUKMHQ0FAmJiaK8Nk5cuQQnhwzZsxgUlKS\nsA2Rrn316tUytfHHBk/7GEiGd9LzBujyjkiuqVJxcnIyavMhFf3Q7SEhIbLfevbsyefPn3P8+PEy\nLxQLCwuRDO/SpUtGjUb79Onz2bwAJeNZ/YR8CQkJQmV/4sQJXrt2TZZxFwB///13Jicnc9KkScId\nVq1Ws127dnzy5AmfPn1KMzMz4d4snVezZk0WK1ZMtt3j5OREX19f/vPPP7x165aww8idO7eBQTCg\nC06n73otudfql5S2R1LRD2oGGBptSh4nU6ZMIfBfHhuSvHfvnuj/999/F8bVZ86cIaDznpHuRY4c\nOThu3DjhZi7FuvH19WV4eDhv3Lhh4LEHQGZnI70bZmZm4m+VSiW8WlauXCnb2qlUqZLsuTp48CCT\nk5O5d+9eAzuU7Nmzi62dlEVlZkmTnPlonteducr70KFCQ1q4laV1aR/aVfueedpNZv7B2+g6Yh9d\nR+zLWK8ZI0TkJgCnd387Abj57u/fAbRPeRyA9gB+16uXHUeFiGRJpEfoRUVFCcMtfSEtfcA7dOjw\nWcYm7dX27duX0dHRfPr0qdjHTMsg+dWrV1y6dClHjx7NtWvXphmAKzY2lhs2bOCkSZO4adOmz+Yt\nI2H9+vVGjcP0jUL/PxKRqKgoWZRjfUO/lKG6jWU4zZYtm/gIm5mZcdq0aWlGqkwNN27c4NKlS7lu\n3bp0uxhL++pSsba25oYNGwzmydHRkVqtlkFBQcKQsm7dukJI6BtRX716lQCEYDIzMzPqaZEtWzaZ\nvVO/fv0I6Oxwfvvtt3QHXftYSJ49TZs25evXr5mYmCiiHgPy7LpSdlkTExO+fv061UBXzs7Owg6j\nQYMGInBhnz59ZM+IPhmQImIfOnTIKPkoUKAAa9asST8/P+7bt0/2fkj5YfTJjbFx6RMPfSNT/Wf2\np59+Yvfu3cWc6rt4JycnC3uuFi1asGLFinRxcRHz2rt3b75584b37t1jfHy87D6fOnXKKMmUxpM7\nd27WqlVLtC999/TJBSAP+KbVajl58mSZAa1kn9OuXTu2adOG1tbWsnfRwcGBJUqUoMrUguZ5PZjN\nvRptKjRnnrYTWXTgGroO3ESX4bsFyUhZXH7aQ6fuC1mgxTC6Vm9JjVX2z05EZkBurDr93d8NITdW\nPcf/jFXvQmeomv3d3zlS9qMQkayF9Aq93r17E+9WFL6+vsKQTKVS8fTp059lbEeOHBEfBMkQEO/Y\nfGq5RY4ePWpgAe/o6PjZtBwfg3PnzrFOnTrMnTs3XV1dOWLECNmHKysSkStXrnDUqFHs168f169f\nb9T19fHjx+zYsaP4GDo6OoqPpLW1daqr1NSKWq1OM7NwQEAAS5UqRUtLS+bIkcPAEM/S0pJLlix5\n77UlJyfLEpsZExQphYAUe2PRokVs0qSJELo3btzg5cuXRaj0tm3bppqWXSq9e/cW7UpGs7Nnz/7A\nGfo43LhxQxhfmpqaGozVwsKCY8aM4dy5c4VXi4WFBW1sbIRh7s6dO40a+7q4uPDu3bsiUmnPnj0J\n6LRmV65ckcUJcXNz48aNGwVxK1KkCCtUqCDIoL67s/77ERERQVNTU6pUKjo7O3/Qs5XyWUl5zOjR\now3ul+RtZ6ykjCUj4dy5c/zxxx9ZvXp1FipUiBYWFiL2yJYtWwyIlz5h9fT0FORErVbz+PHjBu1H\nRkZy586d3L17tzDCT+mho7a0pZVnbdpWak2n9r/S9ac9MoLh/MPvzN1sFHPU60u7ah2YrXgN5vD6\nlut2H6ZN3iK0cCtLjU1OQmW4iMpIr5lNAMIBJEJn29EdQE7otl1C3v2b492xKgALAYQCuAKgvF47\n3aBz670NoKuxvhQikrWQXqEXGxtr4CKXLVs2rly58rOO7+jRo8LiXPJGSM1tODIyUqy2q1atyjFj\nxghL8/z58wu3ysxEQkKCQYh1QLe9dfjwYZ48eVJkF80q0E+DLhV3d/dUs7zu27fPYPXftGlTET9C\nv0iRRvVLrVq12L59e0ECAgICDPr45ZdfUiUOzZs3lwV7ShkLxRiioqKMxmTQL7/99htJnfunpOK/\nfPkyr169akB+AR0Rk+JjpCwpSVmfPn04ceJEqlQqqlQqDh48mBUqVGD58uU5ZswYRkREfNokpoFj\nx44ZHX96ikql4okTJ5icnMzdu3cL0lGuXDnhySR5ukheRrt27eKdO3eo0WioVqsN8quoVCoOGDCA\niYmJYtvDwsJCtKf/zZJ+L1OmDEly+vTpRgmJ1Jexa5CEdu7cucXfbm5uXL58OV+/fi0j3ZI3mT5B\nlSLT2tnZyVyFr127JpLo6RdLS0sePnxYHBcTE8P169dz8uTJ3LVrFxMTEzl//nzZNo2zszO3bNnC\no0ePsnXr1qxYsSJ9fX155swZkmRSspax8UncceI8LQt/w2zu1VmkjR+bzD7CPN9PY/5BmwXpyNt7\nJe1rdKJlwfI0zeVKtYU1K1eubJSMGdNOpXyOv+qAZgoyBh+6+r58+TIXLVrEtWvXpukymdGIjo5+\nbwCqhQsXEtCFDZf21OPj44Wb965du77EUNOEJJjs7e05adIkzpkzx2Cv2NramoMGDcoSQfmMfXj1\nSURKhISECFWwpP6WPu5SGG+pGBMM5ubmwn117NixBOSB1sj/Qr0DOruNHj16yMY3YcIEkuTIkSMJ\ngM2aNUvXtT5//lyWqC5lUavVslV8y5Ytxbk3btygr68vc+XKxTx58rBnz548f/68LBQ8ABGQLa2S\n2tZEavleJDuAH374gV27duWmTZs+iHTr23/Y29uL/iWylSNHDuHiW7JkSV64cEFkuwV0odAlSKRV\nPyLvoUOHZNfSqlUrQRb0XUZT3vcaNWrQ09NTaEmk7L/636z79++L52bkyJGcP38+Dxw4kG4iVbFi\nRYOw6ym3dkxMTNikSROOHDlSaIVatmzJ27dvi1AREgHbs2cPQ0JCZKHZAZ1N25IlS8QiRD+g3pkz\nZ8QWn7m5Odu0bcvDZ6/ywD8P2HfuZjafsJbNfzvKSqP86dhpDvO0+5W5W45lnu+n0anrfFYbt4Ml\nxh402EbJP2Q7HTvNZp52k5mz0VCa5SlEG/scDA4ONrCVSavoa8lsbW1Zr1492e8KEVHwyciK2wAf\ni+HDhxMwDOYjbSsZS/j1pSF90KWgVadPn5YZoukHHVq2bFkmj/a/vBuATnVft25dYR8BwCAXihRz\noGXLlkJdP2TIEKPRJHm9PZAAACAASURBVGfOnMnvvvtOVtewYUPR1p9//mkg6Mj/YmeYmJgwNjZW\nEBOpfXd3d5LkP//8Q8Awz837EBkZKZuHlHv7lpaW7Nu373vzEv3222/immrUqEEAskSP0naQra2t\nGLsUFK5EiRLcv38/Dx48KMhL165dDfqIj483MKqVBKyxAG8pId0jqf9z584xOjpaaBIlEikJLl9f\nXz558oSxsbEywhQQEMCVK1cK8qm/4if/y3eiXzw9PdNMxJaymJqa8uDBg7Jv1vPnzw20OSmfs5Yt\nWxq1S6pdu7bRcRmzHzFWmjdvLoIhent7EwDXrl0rND8pCY1arWa/fv2EsfLu3XvofyCQNkUq0r5W\nVzr6zqRD24nM22u5IaHoPJd52k2mQ+vxdOw4k05d5tGh7a/M3WI0nTrN5qANZ+nVdhitPGrRLE8h\nmjq4ERpDWxlzc3MuWbJEXGPK7cy0irRw0M9GrBCRL4zXr19zypQprFChAr28vDh48GA+ePAgs4f1\nyfhfIiJLly4VH2HpAxEbGyuMJdObW+RzQvLSuXfvHsn/ErBJH63IyEixkpeCEmUmJINhtVotPCsS\nExOFXUGXLl1kx0srXH9/f1mqdGNRKvPnz2+Qx0Q/4qgUwrtdu3ayPpo2bSqEY0JCAl+/fi0TaJJH\n1bx58wiA33333Qdd8x9//EFAp6o/f/48z507xzlz5og5+ueff9I8Pzk5mYsXLxbbU46Ojhw+fLhR\nDZBGo2FgYCB/+OEHmcDX92K5efOm+E2r1fLZs2ecMWMGe/bsKVan2bNn56RJkzhr1iyhedKPlJsa\nJJsHSVAfPXqUJFPdUgJ0WqiQkBCuX7/e6O/e3t5s0aIF3dzcWLFiRS5evJiJiYlcsWJFmsQj5RYN\n8J92SMpNU7hwYZ49e5bBwcG8d++eILJp2eGo1WoDsmJlZSW2dVIjMfpbI1KRtKvSXC5dupQ7d+6i\nqZ0DLXI4cdzUOczmXo3OtTvRpkIz2pRrQpuyjWj7TXPaVmpNm/JN6dhwAHO3GMP8Azb+Rzh+2stm\n8wP53fQAuv8whzZlG9E8nyezOxdgrW9ry0iNpaUlu3fvzo4dO4rxSu+d/vhTBtxL7d6kJG7Zs2eX\n5c6Rfq9UqZKBtk6tVitE5EshKipKlk1TKrly5RJZKDMaz5494507d2RZRj8HPoWInD9/nv3792fb\ntm05depUWQLCzEBUVJR4UUqVKsUBAwYIK/1ChQoZTRyW0Th8+DCbNGlCd3d31q1bl9u3bxdkIiEh\nQYR9HjFiBEnKtitcXFyo1Wr5119/if1afZfQzIAUHdLBwUFch5T8DtDltdBHp06dCOCDDAf1i7m5\nOZs0aUIfHx9RJ2ValSClQAd0adBjYmIEOZHmvk+fPkKlv3nz5g+6ZkmrIxkrSu+IZCP1Pk2VMbsA\naX71o3Kq1WrWqVOHoaGhIqeLdF+3bNki2pOSeQI6LxZjkT1Hjhwpjpdc3C0sLOjv759mFGLJtVYK\nDe7h4cHAwEDZ/TQzMxO2PNL4PDw8hGbK1taWRYoUYbVq1dirVy+jhKtSpUpp5pGxs7NjXFycQU4U\nQLel16VLF3G+m5ubgSdW//79uWbNGvbp04dlypQh8H7NhrGkeu8rGo2GHiVL0zS3G7MVr8HczUYa\naDDeV/IP3kbnHouZs8EgWpX0pnne4uz4Q1+xnTZ58mQCusXJrVu3DKLJVqhQQeSvkTRo+hofd3d3\no9euVqtZqlSpVOehZMmSDAwM5KNHj2RbZqkVtVrNvXv3KkTkS0Ha9yxUqBB3797NwMBAEVb4Q7KH\npgfXrl2TGdrly5ePS5cuzdA+9PGxRER6WfRLjhw5vkjm2rRw+vRpg9ggbm5usoySnwuSKj5lkWwG\npFWdVPLnzy/bq5WMIaXkdKamph/sTrxz505WrVqV1tbWLFSoECdNmpTu5G7GsG3bNjG+cuXKsW3b\ntjJDy86dO8uOP3HihPjN2tqaP/74o4E2xMLCguXKlWPRokVZtGjRVENmm5mZceHChYyNjaVWq2VS\nUhL37t1rIOzSSiAm2drcvn2bvXr1YtGiRenl5cXx48eLb1BMTAyXLFnC1q1b8/vvvxdaqsGDB5P8\n7x2RtA/GMqqSOk2IZKekVqvTve2Q2nENGzZk586djWoKqlSpwnnz5gmyZWFhIRYC0hikYmpqylGj\nRhnVrsXHxwsj3dTsBtq1a5emMNq/fz9J8u3bt4LQDBgwgNeuXeP69etlQrJ///78999/hdZPv50J\nEybICBCgI8CpkdqU92306NG8deuWGIN+yZs3L+vUqcORI0fy119/TVWDIr4dahOaOrgxe6WWzF67\nB51bj6VD20l07DiLbj/9596af6A/830/mR3GL+XGs/fYcsQcWriWosrMkiqzbMyeJy/VlrY0yWZL\nlYkZ1RY2hMaELi4uMjdpQKc52759u/DIsrW1FdtyKZ/xatWq8dq1awZ2WIAuLL2UnDCtd2PYsGF8\n+vSpuF8ajYbr1q0zuN/G2ihXrhwDAwNJUiEiXwoeHh4E5PueERERwqVUPzfEp+Dhw4fiobCwsJB5\nHixevDhD+kiJjyEiwcHB4uMxYMAArlq1SuyBFytWTBZ8KTExkfPmzWPp0qXp6OhIb29vHjx4MKMv\nQ4bY2Fj6+/tz+vTp3LVr1xfxlnny5In4GKTmCgroVmEpjTYlIbBw4UKuXbuWhQoVIqBL//4hWLBg\ngdE+69ev/9GaNa1WazSIl/RxMuZOqB+wSv/4lGna//nnH2Eo6eHhwfnz59PX11cIidq1awuSUrhw\nYXFfUisWFhacOHEiBw8ezN69e7NVq1Z0d3dnsWLFUk2UFxISIt7vlMXS0pJr1qzhnj17RHwPMzMz\nIfDj4uK4bds2zp49mytXrjQaIyN37tzCkFFf6Brrr0KFCvzpp59SvT59gl2sWDEmJCQIN3pAR2Sl\nlO+ATrtUp04dMVcS0SV1ZPfbb79lnjx5WLhwYaNkKKXRcY8ePWSaKkBn5yNBSgJYokQJGemRYpXY\n2dkJEpLSziC9RX+LIuV2i6mpqSzuRrVq1ThmzBhxHfrG6keOHKFKraFpLldalfRmHu8ezOHdmw6t\nxtOp+0JZwC6XIToNRp7vp9OhzS/M13gg6/T4meZ53dmqdRvZuyUFf5RKrVq1jG7xpJVXRiKEkizI\nly+fUe8y/VK8eHExz05OTjx58iRHjBghO8bT01Mco6/VSxlHJ2VxdXUVsmjChAkyz6CIiAiFiHwp\nSH7c+nvDCQkJ4gXNqC0JaU/822+/5cuXL5mcnMz58+cT0LHlzyFQP4aISB/l/v37c8mSJaxcuTIL\nFiwoXvhTp06R1AkxfTsB/fI5tTz6ePPmDe/cufNew8JPxbJlywi8f0tC0hhJkUgdHR1FzAn9Ymtr\nKzKnpoVbt25x6tSp9PPzE9s5U6ZMYUREBA8cOCC2qnbv3v3R13b16lWjwbj8/Pz4+vVrg+eyUaNG\nBHS2GdIe9NmzZ8X+uvT7999/LwSe/jskRbWUiv7q1cbGhqNHj2b37t2NrtTc3Ny4e/duo+6otra2\nPH78OA8dOiQy3UrGw0WLFuWyZcs4c+bMNF0WZ8yYQVIXlTe9208zZ86UGZTa2tpy2bJlLFu2rHhn\nVCqV0XusXySjWUnDsH37du7du1f87uTkJNOeSPY2+s9acnJyqvYfJUuWZIsWLdivXz9euHBB5k3j\n5ubGuLg4Ll68WMwDoAu6lZCQwO3btwvD5sqVK8ueByn5oTEymPFFRfN8nrSv1fX/2Pvu8Jqy7v91\nW3rvXUQZvSQRgjDaiBIl2jDaaNEiUSPKRAuiRhmD0duIIIhuiDLCKMNog+i9J0J67v38/rj2ds69\n514x5X1/33ne/Tz7wXFP22fvtVf5rM9C5IrDmJp6FR0mrYZ9436oPnghhm76DdGbLyBgzAZ4D08W\nh02ik+DWKxHO7cbBvmkELKs0gdxS3xvFuomJiSReSKown3AOq1QqHloaO3bsJ3lmdD28ws7WwLJl\nyzB16lSjzyr8d0pKCn/ehw8fGjyPKc0s3CUsEjpnzhyYmpr+TxH5TzUW9+7QoQNycnJQXFzMeQwq\nVqz4twEKGTDw0KFD/JhGo+FZCob4M/5K+zOKCMuGYHgH3T5q1CgAHzVtW1tbJCUl4e7duzwl09ra\n2qAn6dixY+jRoweaNGnCXbmf296+fYt+/fqJrLrhw4f/Lcyp79+/x/z589G4cWN8+eWXSEhIQEJC\ngp7gkeKlYNWKi4qK+LMJKcaFvUWLFgapvTUajSQvh0KhQFhYGFJTUznzIpHWAvsr7fXr15gzZw66\ndOmCQYMGYeLEidzzYWpqil69enFmUeaZYfO2WrVqfHycnJy41c5wVyzLhTXmsjYxMcHFixfx8uVL\nLqzNzc3x9u1bZGRkcCHp6uqKyZMn8wwAZiC0aNGCW+msR0VFAfiYUsoEuZAgj4WjvL29ERgYyMnS\nFi1aBI1GI8IiffHFF6KNRCq8obvRWFpa6r0r61JzpkaNGiLGTaYEjB8/Hrm5uZIKUXR0NF6+fMkx\nPqw7Ojry54mPj8f9+/exceNG/twnTpyAWq0WgRWlNrNOnTrxP6U8YCNGjIBGo8GdO3ckPYByudwo\nZkS4CX68twxySzso7dxgWbkRbOt/A8cWw+Dx9VQ4d4yDx4Dl8I7eglIxu1E6JhXlxu1F+fF7tV6N\nkdtRZtg61Jt5GHVnHEalYatg32QAGvYaDaW9B4ikQxhsflhaWuopvsIUZWHLyckxqqSy72dhYYGk\npCS9cVAqlaIKwMIuleXSu3dvvgctWLDAYKhPmLkmk8kQHx+PhIQEPfwP+60unolI65lMSEgQAZX/\nlYrI9evXsW/fPmRkZEj+/3+jXb16lS9UKysrUQxSCCr7q61hw4YgEpfHzs3N5dbdn6G8/lT7M4qI\nEB9iY2ODdevWYdeuXVzAOTg4IC8vj4P2GK8Da2ziS1npUul0JiYm2LVrV4mfT61W87EkEnspdDkp\nnj17hjFjxqBq1aqoVq0aYmNjjXq4MjMzJUMvjF+A9a+//hpXrlzR25jGjh0L4GMmBCtdLpfLsXbt\nWhQVFWHp0qX8m+umQbKWkpLCBUbjxo0lhfrw4cMxZ84cLqz+rsa8dOz52d/Lly+P7OxsvH//XpT+\nKuzLli3jYNOOHTvycI3Qi8ZCQXXr1gWglQnCewl5KIg+hgK2bdvGhTBjoWRgPmGPjIzE8ePHRRuD\nUOG7efMmiLS4gtWrV4t4Xjw9PUXrXxc0yZ7b2AZrZWWFV69e4eXLl6J5OnDgQL3y8LpdON7+/v5c\n2WOEV2weJicn82tLUYuz52Qpviz1fcSIEVi9ejXfKHXJ90xMTPDdd9/x9xb+OXbsWFEYTwrb8qnO\nlJaKFStCZmIOE48KsKoeCtdWUfAaukGPbtxz8Fq4f7sI7n0Ww6ltDByaDYRFxQY4lHYcgFbh79BJ\nazgJs4jY+zZt2tSgQsTwN8Lu6enJ2Uvr1KljcI3cuXNHb+75+fkhICDgk9+1SpUqAD6mqbO+YcMG\n7o0WdoVCgbi4OK6MvH//HqtWreJeDGFv37695HsJlRDmWe3Zs6dBkj9mRM2aNevfpYg8evSIA0BZ\nDw0NNYr4/k+206dPi+J0fn5+2LRp0996D2ZJMqFy6tQpDt7S5VL4u9qfUURYQSsirSISGhqq5zY+\ncOAAjw0L48gAeMpdcnKy6DirzyGXyzFu3Djs2bOH8y44ODiUOLzCrF0XFxdcuXIFgPb7MaXg4sWL\nALQuSSEnBuu+vr548uSJ5LVZfY2yZcti8+bN2Lp1K09BNQYMYz0qKgpr1qzhYQoWlmndujW/x9mz\nZ/nYRUdHSz4H4y2YOXMmd90ygSqXy7mwYZvm5s2bSzR2AHD37l1cunRJEuSam5vLY94LFixAUVGR\nCGeRmJgIQBs7HjhwoKhw19dff41+/frx5zx8+DCGDx/OhWlwcLDoe9jZ2aFz5844cuSIUXp4FxcX\nfh1hN2Zx636rOnXqYNq0abhy5Qr3UAk3DTc3N72NVXh94d/d3d31gMn/ZP/iiy+4t5SFXdhcNzc3\n52tSqVRybxHDWgwePBgAMHnyZBBplTQ2J1esWAFAf0NkY8eyThwdHbk8Ly4ulsx8Yc8jHEOlUgmF\nqTnM/AJg37gfnMMnwq3HXHhFboTnoFXiTJPoJLh0nARr/9awqh4KlYsf5OY2ks/F5lOjRo24omRu\nbi6q23Pz5k3RhizkcmF/GlIKmZepatWqorXx4sULXLlyRYShuHnzJo4dO4bLly9j+/bt2LZtGyIj\nI/m9lUqlHmM1K2tgLGTCurm5OX/eDRs28PuycBzrXbt25TJat7CeLt9J69atJcNFvXr1QnJysuj7\nPnr06N+jiBQVFXELytraGo0aNeITNygo6L/OpSBsjx49wp07d/6Raph5eXkc9CnsVlZWOH36dImu\nsX//fjRs2BDm5ubw8PDAmDFjjBIb/dmsGV12PSKtm5YJsZ07d2LTpk0g0rq4r1y5ArVajc2bN0Mm\nk0GlUnEls6CgAK9eveJuaqHLU6PRcBe+MK5prI0bNw5EH1NkWevduzeIPoL2WNXOoKAgpKWl4fDh\nwxylHhERIXltZokzamUAuHbt2p/aQCpWrMiVz9DQUH69s2fP8mdlmRu6jQEjlyxZAiItEE3Km0Sk\ntXxLgi+6cOGCSNl2dHTE7NmzReuPkYxVqlSJH3v37h3fyISEZIB2vUi5kxnpXEFBgSTlve4GI0y1\ndHV1ldzoVSqVpLVnrBsqkCaTybh1P2TIEJw5c+aTgEFjz69QKNC2bVu+PlidllatWvEqqFKKkyFl\nasKECVi8eDGGDBmCQYMGISYmBjdv3kRhYaEkRoFI641iAEa2eVlYWIiqUO/atYuDgpkSX1xcjEmT\nJvFzVCoVOnbsyNdZWFgY/975+fmoWLEi5GZWUDp4wcwvAJZVm8E2MAwOoZGoPWolykQsgeeQdfAe\nsQ0+H2qeeI/YBve+S+DSJR5OYaPg0nESbOt+DfOyQVDYGMfOEBHH/EiNm7e3t2SZAIZ3EfYaNWrw\nNWWoOi3rzMPy+PFjtG3bVlRQb+TIkbhw4QK6du2q5xW1t7eXZFQm0iqx06dPx+rVqyUpI6TmAcuS\nqlWrFn839g2Z5+LOnTtISkoq8Zz18vISKY1C3A/zGBIRNm3a9O9RRFi6YqlSpXhNhSdPnnC3ECPZ\n+bubRqP5x8pr/9mWl5eH+fPno3bt2qhcuTIiIiJKXIGTbfy6PTAw0CA24s8qIgyc6e3tjaVLl+LW\nrVvYtm0biLTW78uXL1FQUCCKdQoX5NixY5GVlYVBgwZxa5f9qVs8imFSSlrXhoG2+vTpIzrOLJnl\ny5dDo9Hw57l+/TpSUlLQp08fjrq3tLTUq6AJgJ8jrLSak5NT4gXu7u6OsLAwLFq0CO/evcOzZ8/4\n5rlkyRJkZWVh3rx5XIDMnz9fco6yd2EAwZYtW+LXX38VbTJEWmWnJFld9+/f54LHxsZG5GJnAE0A\n/B6lS5dGUVERxo8fL+IssLOzw44dO7BmzRrs2LEDubm5yM/Px6ZNmzBs2DBMmDBBhHV6+vQpt9A+\nh3b6z3RdLwhTKqWsP1agzdTUFKdOncKJEyf+1D2DgoJQXFzMMytYauacOXM4rw0DqbNwnCGFR4gT\niYiIkPTAffnll3j+/LkeURzbqHStb2Fv0KABiouLuRd29OjR/Dvt3bsXJFfCoWxNtI8YA6sy/jBx\nLQMT9/IwL1Ud3i0GwqvrVPgN+hGeg9dK82dEb4FH/+UoG/E9HFtEwb5Jf9jW6wqz0v6QKU0MhpB0\nu+73klLWgoODsWvXLhw7dkySPygrK4vT1NvZ2WH69Ok4cOAA1Go1Dh8+LHlfIdhWJpPh9u3byMzM\nFCkUwneQUnJL+o4l6XZ2dlCr1Xj58iWItEY8oN3X2G9YZeKGDRtKErjVqlULcXFxIsVe6hmFoNz8\n/HwRduZfo4iwmDGLn7PGXIIJCQl6E+mvtOvXr6Njx44wMTGBQqFA8+bN9aiq/681IR9AbGwsXr16\nhZMnT/KY8bJlyyTP+5QiotFoJDfknJwc7o6Xy+WiuLnwO2ZmZiIiIoIrGV5eXpg/fz4KCwtFqXbC\nzczBwYGXcL927Ro/l1lon2rMQ6FQKDB37lz8/vvvPK6rUqnw7NkzaDQaLsCkvFBEWiWLhXFYYyGR\nqKgoFBcXQ61W8/nr7+8vacVYWlpi7dq1fKM/evSo6JqGCrixXr58eb3nYOyfQmHMxikiIoJ/m5JU\nnwU+bobOzs7w9PREjRo1eFjM0dEReXl50Gg0+O2337jgFaalGvIsODo6GsX3MKWxUaNG/H7ClFQp\nIN/AgQOxatUqJCcnl7iib0BAAH7++WfJ/2NubFdXV0RFRYFI60ViCmJqairS09NFG7+7u3uJqMAt\nLCywc+dOFBQUYMuWLTykef36dT4GWVlZBrEDnTp14uuapfZ+SmHTDTfqjpFcLhd5TaytrREZGclJ\nsnYfTIOpZ0VYVQ9FxU6jUL7jKDi3G6efZSLEa4zeCY/+y+HSJR6OLaNh36AHlh+8iJEzvofCxgVy\nC1uQXGk0fCnM5hkxYsRnpfiqVCqRB6Nbt26S802tVmPcuHF6YzJs2DCo1Wpcv35dL3vJxcVFMoR7\n5coVnnVlqLNNPT4+nv+WrU2FQmEQ9/GpdcWuAwBbtmwR/RsAD0ktWbLEYDZWpUqVUFRUBI1GI4ml\nIvqovEdGRqK4uBgajQbx8fEg+hji+dcoIomJiSASx8k1Gg3HjLBY5d/Rbt26JelyY5bP/9XGtN2y\nZcuKXOmrVq3SG1thM6SIZGZmYsiQITy+XKVKFVEMEtACPbt27coXi4uLC2bOnClpwRcUFOD169f8\n/1hmgqenJy5dugSNRiMqPmVpaYmgoCBu/bRt2/azxkOXMEko7FgTYpLYhqebYujl5SXCSqSlpfHf\nenh4iGiUd+3ahffv33MPjoODA+Li4vDmzRsAHwFyugq3RqPB+vXrUbNmTb7wTUxM0K5dOy4AXVxc\n9HBVs2bN0rMOra2tOdisdOnSePfuHbZv386ra5YqVQpxcXF6eBtd17buJrZ+/XqDAFTWhZZhpUqV\nRPVKDBHKsbDMxo0beSaGkADL0D2XLFlikGJcqisUCsk0aaGwrVmzJm7dusW/O/M2VaxYEXPmzBGl\nUfbp0wfbt28XXadx48ZYtGgRB/NKVTMl0mYRLV68GGlpaZgyZQqmTJmCkydPYunSpTxTQTfEZGNj\nI2mpmpiYwMvLS9IrEBsbK34GhQoyU0tUCgiGVZXGsA5si/bjl2LWvmuYtvsqJqRcRuel6fCL3SMC\nhPqM3gnPiBVw+GoILMrXhWXZWli5+xf0i1sIM78AmJf2h9xMrJQpFApMmjSJY6EM9Ro1avA5LOSJ\nuXTpkt5abNq0Kfbv368HEC5fvrwem60hL7qwkrS/v79IqbO1tTWoKI0ePRo3b97kHi02vuzvAwYM\nwOvXr/WwGey6Go2Gk/0xz5e1tTWKi4t5BpZQGRV6JJVKJTeWhMabqakpoqOj+Rpl+CwAHKRuZmaG\nzp07izKb2Dv6+PhgwYIFnBuGKckhISGoW7cu6tevjwEDBvDv4+XlJRr7LVu24Pjx4/8eReTp06d8\nEPr164fk5GQOFLKwsOCC/O9oLPbu6uqKli1bYt68edx91ahRo7/tPv/plp6eDiItcE2oiDD3o27s\nnjUpRSQvL09UJVS4OIWTnbV3797h4cOHn0WhzgTHjBkzRMd1AcsKhQI9e/bk1lpJW0FBAUaMGAEP\nDw/Y2tqiVq1a2Ldvn+g3x44dE92LCXO28JiCpUsRnpKSIhIUXl5eokwnVvNGt+rrsGHDQKRNu5Rq\njCjOxsaGP2t+fj4Pb33//fcAgO3bt6N+/fqwtbWFn58fwsLCUK9ePdFG1bRpU9y9e5fHu3V748aN\n+fcqKCjg669Jkya4fv06tm7dKgK1MYEt5YFQqVSIiIiAUqnkY9isWTNoNBrOFSJV9+TJkyc8VBAb\nGyt61k+ldv4dXXfTmTZtGhfgjRo1woMHD0pUr0PYnZ2d+YYaFRWFhIQEHlL5FJjZzs4OjRs3NlqI\nTFjVVWZiDrNS1WEdEAaH5kPg0e8HeA1dD9fus+HULhZ9V/yCDouOolrMFviOMOzN8B27G1+M34NK\n43fjy5kHMHv/dRy+9gzlAkJAMjl8fEph9OjRIplw4cIF7hGLiIgw+l5MgVOpVHyOMgVJqVSKModY\nZ+PeqFEjrpQ1btwYOTk5WLBgAR9LqXkSFxcnub6EGYibN282SGNubm6Obdu2iUJkMplMj/hOiG1i\nlAUAROexZ7958ybOnDkjencPDw9kZmbydSW8HgNMs/djcjExMVFSOa9SpQrCw8MxZswYPHr0CMXF\nxRzwLuz9+/fH+PHj9Y6bmZlxJUOqLo8we8bNzQ2rV6/m7/uvUUQAbfElKTfs59aJMNZyc3Mlc6wr\nV67MN59/mvjqn2r5+fncIp02bRpyc3Px+++/c1Dj4sWLJc+TUkRWrlwJIq1WfvHiRRQUFHD6chsb\nm89WCqQaC7sJCXIAcKt10aJFOH78uAiLUdL29u1bvTLcRFpeCaF3QxhLZd3f35+TRLH5OG3aNL17\n5OXl4eLFi7h48aKeAvbw4UOes79kyRK8fPkSSUlJXACdOXNG8rnZuDdv3lz0TZjLeuDAgQZp5O3t\n7dGqVSvMnTsX9+/fB6BVEJmFPWPGDFy8eBErVqzg82Tr1q3Izs7mPDlEWqtozJgxGDRokJ63hZ0n\ntXkwpYXdj6VJsxCSUMm/desWr63Culwux/Dhww26kaW4KkrSSxq6Yc/ONrjt27cD0FZ3jYiIQM2a\nNVG/fn2unFpYWBhVLCpUqMDrBL19+5YL90aNGom4PQyRWQ2OHIZF67Zi7LIU9I//EX2m/YgFO0+j\n98z1cO7wHdy/Pp+2sQAAIABJREFUXSQKlfiN3AqXzlPg2GIYXLrEw73vElSN3YY2i39B/7Vn0W3u\nDtjU6QTXBl0xeH4Stp+8hqzcQrx8nYlOnTuL3sXf359z1Hh6eiI3Nxc7duwQeZIVCgVXMITGAyMv\nk+qLFy8WYcZYoT9D3cTERJKYjnWh4i2Xy+Hv788JA4uLi3H8+HGkpKTw9cAqDZctW5Zv0vb29mjT\npo3ouuybSKWusu9fsWJF0fObmppi3rx5SE9PF+EtmEeoVKlS3OvIrmFtbY1ff/2Ve0SE+x9bT7oh\nocaNG/Nv1bp1a7Rv315vDslkMo7runTpEmbOnImEhARcvnwZgHavYGEvW1tb1K1blz+bkMBs4sSJ\nXI7a2tril19+wblz5/RC9f8qRQTQ0uNGRkYiLCwMw4cP/9sLygmzCsaMGYPly5dz60Umk0Emk/0t\nhFf/rcY2Mt1etWpVUUqZsEkpIsxFrosvYHnpQsK1P9vS0tJApMWGbNy4EXfu3OFuUwaA+rONxfk9\nPT0xZ84cTJ8+nS92XQ+MMBWtevXqKCoq4ps9UxxYSKq4uBizZ8/muBtPT09MmzZNMiNFWJhN2Lt3\n724wC4xt2j4+PqIwIfPYxcTE8I01ISEB69atk4whs0wbRhxWqVIl0QbAsA1ff/21QWyClGBmffLk\nydBoNEZrqTBByMbhm2++AQC8efOGc0UIrTBjvVq1agb5DD7FSsnWtfAYW/PW1taSKbm6iqdwjaSk\npOiFDGxsbNCjRw/UqFGDb47C1P4VK1aASIs7UavVKP1FZSgdvFCqah2YeleBVbWv0KC/NjXVvXUU\nPAb8yLNJpLrX0PVwDp8Ah2aDYFbaH97l9IGprH/55Zdo3bo132B0U+kZy62JiQnq1aun901lMhmC\ng4P5PDPmqXJ2duaZNMIxMjEx4WRwrI4PkRYnc+7cOVHtoD59+qBKlSqi5wgMDMT8+fP5HLa2tkbn\nzp3x6tUrnD17FgcPHhRx//zyyy8ij6VMJkOPHj14toeFhQVMTEwgk8lw9epV7okTvpsxHI6rqysu\nXbrEQ3OGQnDGujCMKVzDlSpVEnkipYjR5HI5Jk6cKKJRYGMuXA+6WDRhu3Tpkh73kdDLNGLECOTl\n5UGtVnNeHENs2P86ReSfbsI4eEhICP744w8cOnSIH2vWrNl//Jn+7rZt2zbuMrW1tcWQIUOMVnCV\nUkRYbHzRokX8mEaj4S7BI0eO/OXn1Gg0HJyo24Wl4D+3qdVqbkUJC/CxKqPlypXjx65fvy6KuUoJ\nIGdnZ+Tk5ACAQQtOqiaMRqPBunXrEBgYCCsrK7i6unKL0snJCePGjdNTegsLC/kmHRAQgGXLlvEQ\npUKh4Gl6ISEhIg8YI1irU6cOF0ynTp3i78yEk42NjSjUwP4uxRop7LrKzvbt2/H69WujQDpPT09E\nRETwex85cgRPnjzhnhBbW1vExMTg9OnTeuyixjYA4eZmLIQh7MxLIxTacrkcjx49wuDBg0W/FQL+\nWNNdI48fP+YeoZYtW3JgtXCOtGrVCj/99BMOHz6Mb7/9Fko7d4SPXYiuy0/BZ/ROg0qG9/BkuHSe\nAtt6XeFVPxxrdxzA5fsvMXBMHFSO3pBb2EJp8unMizlz5oiUAYVCgeHDh4vwW6wuipWVlWSVV93e\npk2bEqWUEokJ1ezt7ZGRkYH3799zI4eI8O2332Ly5Ml8HoaHh/Nny8rKQnp6ugjUy9a3MYD9gwcP\n+Pf29fXFV199xcMjffr00SM6nDNnjgiTxObG6tWrOSiTSKts9O3bF99//72IM6VevXolGg+ZTAY3\nNzcEBARg9OjRuHv3LqKiovi9pejv2ZpUKBTw9PRE9erV8e233+L27dtIT08X1Tby8fHBmTNnkJOT\nwxMHatasKTlGQnmTkpIiSXxGpE3L1mg0HOgvrPAsbP9TRD6zsY3AkPtXt9z4/+WmVqtLxL8itagZ\nCNDd3R0///wznj9/zqnZWQbF39GKi4uxZMkSBAQEwN3dHSEhIejQoQP8/f0RHByM2bNnG/TkANqF\ndOHCBc5RAmhDJmzxCkMmz58/55sxoM2s+RTzo6OjI9LT06HRaDiexNTUFCkpKVCr1di7dy9XXAyF\nWwAxIZTQ6mrZsqXeNzp58qReNVq5XI6VK1dyHoCmTZty70mVKlU40+2AAQM44dqwYcOQlZXFlYXK\nlSsjMzMTp0+f5u9dEhyGlMehZs2akoW8ZDKZ5Ji2a9cOnTp1KrHlaEgpEh4fPnw49u7dW2IsSZ06\ndXhmEOvCrBeGfyhVqpTe95NaI4yDol69enzuHTt2TEsQZesK8zK1YFm5EeybDIBH/+Vc0Wg0+wj8\n2mnLv1tUCIGZXwCUdm6QW9hCYaWVT0KgqkKhkAR86qaSOjo6ci8AY/x8/fo1fvrpJ6xbtw4PHz7k\nz/727VtMmTKFKwDlypXjGUVC5VL3G7N7st+w7yFkGpbL5UhOTsbly5c/ycMh7DVq1CgxeaUxRYTh\nH1q0aMHX/4ULFzhx1/HjxyXl/6ewQLoAc0BrbBjjlhHOL3t7e9H8NTU15YSArK7YuXPnMGPGDEyb\nNg0zZ85EZGSkpCfQ399fErhsZmYmAi7L5XKjRigAXLx4EURaLxHL3vP29uYK0tGjR7lhu3LlSslr\n/E8R+czGUi8HDRqE3r17w8HBgS+uUqVK/W3EacXFxdizZw9mzpyJNWvWGCUU+283qUVdWFhoMKW1\npFwen9tu3LghKSACAgIkeTBWrlwpisWWK1cO+/btg0aj4ZaCcOGwzTokJATAx8JULVq0QEZGBn79\n9VcORqtQoQJWrlyJ7OxspKWliTgZZDIZmjdvzgvSsZg4I+jSbXfu3IFMJoNSqURycjLUajWOHTvG\nhbyUd+ngwYMYNmwYevXqhdjYWNy8eROAVplSqVSQyWTckq9Xrx4XVtu2beMZG4zS3VAKpHDDadas\nmUHsCetSpdWFnYU7ypUrx+Pa7du3/2ywJ+u6SotQiMvlcmzatAk3b97k3jvd7ujoiMqVK6Nu3bqY\nN28ecnJyUFRUxDOahL127docJ9O5c2e97yG1Rt68eQN7r7Iw860Bv8Zd8EWrvnD4ajDces4TezhG\nbIVLJ23YRWnnBnd3dz3mUd0MGaaICrELwgq6DC8jVBKZF1Aul+PAgQOSczEvLw8XLlyQ5Bhh4y1U\ngiMjI/UwCk5OThx8K5fLoVAokJWVJQpFGgvZWVlZYefOnbh27Rri4uIwYsQIbNu27bMKehpTRBj+\nZuvWraLjzHNx6NAhvHjxgitPpqamaNOmjcF1wr6N1JguXLiQ/07Xq0KkDYsJZRRjURXio/bs2SO6\nZlpamp4CqFQqMXnyZCxatEikmAizwKTq+bB1YAxnx7J8+vTpg8LCQv5t2TMwL6Szs7NBbOD/FJHP\nbIcOHeILulKlSqL4+N+1wd67d09vodvY2GDv3r16v33x4gWOHj1qMLXxP9EMLeqcnBx899138PX1\nhZWVFRo2bKi3aP5M02g0OH/+PHbv3o27d+/y40yANGzYEEeOHMH27du5hae7yW/evJmPbalSpfji\nlMvlGDp0qIiXo0GDBiKrZefOnSJ8w+PHj/l1MzIy+PcCtJlIhsIPtra2uHnzJie+kgK0AsCyZctA\npF/jhjFcjhkzRu8cY4JWqtAdkVbBevr0KZ97LJ6rW5hQqVQiLCxMZFHVrl2bkwrq/lbXeyKkwmbd\nzc0N169fFwljc3NzNG7cGEQfUxGFG6chTwa7docOHbh351NdJpNh+fLl2LRpE+bPn4/Dhw8bNSqE\nWLEyZcrwOLxcLhcRjV26dAkduvaAQ5nqcAlojuaRMxGbdAbjtl9CrWmH9LEbUZvh2nUGnBp8AxOP\nCviqwzfw8NIqYrrg3E/1OnXqiKrfsg3xzJkzvBSCrlVcuXJlpKam6r1vTk4OevbsKQo7WltbS+KD\nhN/l6tWrehkxMTExIpZbFk559eqV5FoR/pZdW5hh9measfXBsiKFmWk5OTkcI8aIuTIzMyXTueVy\nOaKjoxEbG8tlhKWlpV4SQ3FxMVcybGxsJDNUypYtK6o+PmrUKBQXF+PQoUPcEBLCAV6/fs3XUFBQ\nkEhBLVOmDDdw2bFnz56ViMumV69eBseSKVOdOnUCoA3X6WJHHB0dJfcv1v6niPyJtn79epF1Z21t\nrQfgYu3169eIjY1FhQoV4Ofnh/79+4uqdOo2jUbDAVU+Pj6IioriQB9zc3PuHs3Ly8OAAQNEEy0o\nKOi/opB8LrPq1atX0bt3b5QtWxY1atTAjBkzjIZPdM/VLRjXsWNHPHr0iHsNhKAzVr23cuXK/JhG\no+Gb7YwZM5Cfny9p5QYHB4vc11ZWVjz9VaPRcKHZokULtG/fHitXruSF6KysrACA59cTfSTvEm7C\nderU4ZsBE3BFRUV4/vw5R5YzoGKbNm1EY8HS86Tirsa+iUajwZIlS0ScC0RaLw573zJlyuD9+/d4\n/vz5J8NPxqxX3e7p6Ynbt2/zLIk+ffpIWoJExIW0ubm5ZLrgp7q/vz8uXLhglInS3t4erVu3Rlpa\nGh8ftVqNAwcOIDY2FmPGjEFKSoqeJafRaJCYmKgXOpCb20Dl7Au/xl3QIHIuPPovkyTuKj9+Dwas\nO4u2I+fA1LsK7P2qolRFLXbCEMU8C8+ZmpryNM22bdti5syZekXyqlatqheeY7106dKcwZj1Dh06\n4NGjR5LK144dO4xmDsnlcslQmKurK4YMGWIUO6RQKDB79mykpqbyTb1p06b8+YQhHOF1hFTkf6YZ\nWx+Mq0OpVGLUqFFYtWoVz/yoWbOmaIzUajUOHTrEFV5DyrG3tzdWrFghwpzdv39fJA+kSg54e3uL\nsn5WrFihB842MTHB06dPAXwsJtmwYUNkZ2fz+cQU+b179/L7EhGePn2KtLQ0yW/k7e3N5xWTZ1Lt\n/v37vBJyYmIi7t69i8WLF4vwKWxsOnbsKBnq+Z8i8idbfn4+0tLScOjQIYP0169evZJMGbSzs+Np\nULqN0V87OTkhMzMTgFboMWQ6s+xZjROWcsYEhZOT09/KmVKS9jmKSHp6uqRQq1OnzifTnrOysvhi\ndXZ2RpMmTfgmw+rWWFtbi3Adly5dApEWdMba27dvuUAvLCzk2BX2XELkeNeuXbFy5Urs2rVL9J3f\nvHkjuYGyTZtZB8LwwM2bNyULqxER+vbti+TkZDRp0oRbKFZWVoiKisKtW7d4Ku/ixYvx4sULJCUl\n8eeVqiF09uxZ7Nu3D8uXL8eiRYtElOisaTQaZGZmIjIyUqRwffXVVzh16hTCw8O5BSxlqcpkMq6E\n1K1b95PZJ0TEuU2Yx6l27dpYunSp0XMqVKjwyWtL1dyQ+jY///wzXr9+zcNsNjY2IiX47du3kiFF\nlUqF4cOH49GrbOy7/ARr0+9i/qEb6PbDMbh/kwD3Pt+jdPQmPaXDrcc8WNdqD/NywVC5+MGrbCWQ\nXInIyEio1Wo+X86cOcM9X4Y2M/aNvL29eTVhpVKJFStW4MmTJyJlhHmxhEqkruLJuoeHBy5cuCDa\nYBl51ujRo0WblDGl9FNYG5lMhri4OPTo0QPt27eXlI2urq64fv06NyCM9YYNG6JTp07YvXv3Z4fE\nz549ixMnTmDVqlWIiIhATEyMiIJciszQxcXFoNy+evUqiLTe1Xnz5vEsLV3eECJtqvKrV6/w5s0b\nXi/oU+/KOpM5pUuXFmWxBQcHQ6PRcPkyc+ZMaDQaPsZsbixatIh7Uom09amuXbvGuXqY3Bk7dixe\nvHjByddMTEyMjicDoxqaF5UqVeIypFatWrxcAWv/U0T+wcaQ/JUrV0ZaWhp+++037ipt3ry55Dms\n1kuHDh1Ex5mQ6tWrF9dAVSoVJkyYoBcLr169+n80hbikiohGo+GAvo4dO+K3335DamoqxwBIEZ0J\nG9P2AwMDeRZKRkYG35CZ1h8fHw+1Wo3c3FyOsO/Zsye/TkFBAbc679y5wzexhIQEEOmzIyqVSkyZ\nMkUk7BixmJQlYWJiwqnkhRbzw4cPodFo9ArLjRs3TpQqqHvdZs2aGVzoPXr0kBTCw4YN09u8e/To\nYTCOnpWVhfPnz+Phw4dYunSppHBUqVTw9/dHYGAgn3NCNkpdi65ChQoIDw8XZQpNnz4dgLayLoup\nl1QQf4oKW+p5hQqWsMxDUVERz94Quoz79+8PuYUdLCvUg92X38Kp1XC49UqER78f4BGxQo/Eq/q4\nbXD9JgGVBszH8M0XsPzYbcSv2wcTt7KQqUwhk8lw8+ZNzojLvomPjw9yc3P5seLiYmRlZUlSqeu+\nF+PNMaTU6nYnJ6cSVXWuWbMmDhw4gHv37pU4s0W3s7X0xRdfwMXFhT9/vXr19FL2CwsLsXLlSoSG\nhqJBgwaYOHEit+zfvXsneuaYmBhs27bNoJdnyJAhn6WM7Nq1SxITMWnSJP6b9PR0DBo0CF26dMHs\n2bPx+vVrFBYWYsuWLYiOjsbEiRP5Os/Ly+OYiJ07dwLQcgGxzdfOzg7dunXjihyT/0I+mJJ2V1dX\nkfHADJdTp05xGdmgQQOo1WqsWbNGdK4Qr2MoJNO2bVsUFBQgPT2dy8l69eoZHU+NRoOkpCSEhITA\n3d2dZ0fa2tpyL/29e/d4CFM3RP8/ReQfbAzweOzYMX5MGAeVAu4wdlNXV1dugavVal5EKi4uDikp\nKSAikUbcuHFjURqpFAvlP9VKqojcvXuXT06h94NlclSpUgXffPMNmjZtilGjRnEwJ2vffvstiD6y\ng7LGeAWE9RZcXV259WBhYaFXY4bxarDNTalUikCRbAEyYCeRlgtk8eLFIisnLCwMLVq0gEKh4ELX\n2dmZ34fhP4i0Ftz06dNFVmVAQIAeFTP7t62tLRduhw8fxsaNGxEUFAQbGxtUrlwZCxYs0LMsAIiw\nGq1bt0b37t2558jf3x/9+/dHQkICHj16pHcuq4xLpLXAdYVVrVq1kJ+fz9/h9u3biI+P5/FzYbew\nsNAT9kKa/Vu3bkkKYlNTU1hYWOgpUnXq1BGl335uX7BgATIzMzFo0CDu6ZGbWuLryAmYf/AGWi84\nBu/opI/KxqgdCJhyACETk+DUZgyc2sbAJigce05fw8t3+cgrLMagQYNAJFaiWT0XIq0i0b59e4SG\nhoo8AJ6entBoNNxLsW7dOgAQ0X9LdZVKxeWCRqPBqlWrEBgYCAcHBwQGBiIxMRExMTF8Lvbt2xcL\nFizQc+czV7ru9eVyOX8md3d3vbCWsXRroo/GQNWqVWFpaQmFQoEmTZrgl19+kZQJP//8M1q0aAEP\nDw/UrFkTCxcu5B5NqVCFsAcHB2PGjBl8Q5aqjmuosTBpxYoVMXfuXAwaNIiPx4ABA3DkyBE9xebZ\ns2eSyvB3330HQFzvKSgoSAT+Zd6WR48e8TV17do1ZGRkSALsheFOFxcXZGRkSIZA+/fvz70ZP/74\nI968ecPvGxQUhNGjR+t5C52dnbFhwwbcuHEDPXv2hIuLC9zc3ERrWFdx9fPzQ9u2bQ2CmHUbI1Ds\n16+f6DjzNOmSUP5HFBEiukdEl4noIhGd+3DMgYgOEVHGhz/tPxyXEdFCIrpFRJeIyF/3ev9XFBG2\nsQldfnl5edyaZCGUgoICLF++HM2bN0dISAgHTpYtWxbNmzcXeTx69+7NwUZMmDJqYGZ1MWE+d+5c\nbNmyhXsP/qmmq4i8ePEC06ZNQ4sWLdClSxeeqvrHH3+ASAtMnDhxIkqVKgULCwtJBD592MhYRkhG\nRgZXHoKDgxETE4MNGzbg/fv3nNvlwIED+P7770ULLyAgACdPntR75ocPH4oqkep25rmqVasWB2MZ\nStl2cXFBdHS0Xp2UpUuX4vbt25KEQlLvSqTFLIwePZrjYFjIyRClu1RjoMYhQ4YA0FL0S6W9yuVy\n9O3bVxTKE3I0pKam8oJyws6eycnJCcnJySgsLERBQQEyMjK4S124gbm6uqJVq1Yg0pKx6TZD9VsM\ndXt7e/Tr10801/38/LjwrFWrFnx8fPQUGRsHZziUqQ6rGi3g2DIaHv1+EHg4UtFy3mHYNxkAx7qd\nYOJRAXMTFwD4GN5j623dunXYvn07vv/+ew7ELFOmDGJiYpCUlGS0ABnrffv2BQBOhCWTyVCnTh1R\nRkO7du3Qq1cvtGzZUsRjYqjduXMHS5YswZIlSziGRBc0yDqb+507d+aAUyG7qYeHB06cOFEiT0pJ\nukql0qvdsnr1asnfdujQARqNho8tw37phoUY9w4LrX777bclWh+3b98GkRZ7xPhbNmzYoKdkBQcH\n80ruGo2GG3pmZmaoX78+unbtyudYREQEwsPDUbVqVT3lTUjdDnwkgGNZOQ8ePODnBAUFYd68eXzM\niLThS+Eakclk6N+/P3799VcUFRVx+ce8DGlpaXrYJW9vb6xcuRJHjhzBzp07ERUVhREjRuDo0aNc\n4Xr37h1CQ0M/+c0N4SGFjeHavvrqK9FxxvukSwr5n1REnHSOzSKisR/+PpaIEj78vSUR7SOtQlKH\niH7Vvd7/FUWEWfCtW7dGZmYm8vPzOQ9BjRo1AGgVE6k6CcZi4sHBwSIBM3v2bMTFxfGJq7ugHBwc\n9Gqk/J1NqIhcu3ZN0mrt2rUrCgoKjG7KMpkMkyZNwq5du7ggdXNzM0r4w6whT09PjBkzRmQ12Nra\nGkXXv379GtOmTTOKGl+zZg2ePXsmekapMTbUa9WqhVu3bumBYatXr46+ffsaPI9tPMxFPnnyZMl3\n0Gg0SE9Px+jRoxEdHS0KdW3bto2zzxrrrLorAJG35+jRo8jMzPxk0bGaNWtygV1cXMyt4latWmHt\n2rVITEzkm7iuS7aoqEjPYitfvrzBcE2dOnUQExPDN1JhKEOhUKB33/6InbMMFhXqw7ZeN3h9PQWe\nA1foEYB5Dd0A5/CJqNV7Isz8AmBi7YivvvpKJISZV5Gx9TIPmxT/SUnXLutz587l3y8yMlJS+Fep\nUgUJCQmi+V+lShXJOTBy5Ei9axgC6QrHdu/evTxtdsSIEfwavXv3xtdff12iOS7Vg4ODcevWLbx+\n/ZqH5oQA0/fv33PLfcyYMbh9+zaSkpL4sbi4uE+So61ZswaANnmASJvqrduys7Mxfvx4+Pr6wt7e\nHi1atOCkfhUrVgSgVTSFY+Lp6cmNjjZt2kCj0XBMnu4aNZT63axZM77pMqUTAP744w/ueRAyH7Mw\nvpmZmUFeEV0OkcmTJ/OKt15eXqKw67t377BmzRpMnToVycnJKCgoQE5OjmTmVZcuXUS4uuzsbCQl\nJXEQ8tSpU3H+/Hm+DhQKhYhTRqq9fPmSy+bo6GgcO3YMEyZM4KBjXW/3pxQRGbTKwV9qMpnsHhEF\nAnglOHaDiL4E8FQmk7kT0VEAX8hksmUf/v6T7u/YuR/AhkRElJGR8Zef7+9oRUVFdOLECbp37x65\nuLhQ48aN6eXLl9SrVy/KyckhlUpFSqWS8vLySCaT0bx586h+/fq0fv16WrhwITk5OdHgwYPJ1taW\n1qxZQ5cvX+bXdnV1pfDwcKpRowZNmDCBXr58Sf369aNVq1aRRqMRPYdcLufHZDIZ2dnZUWZmJpma\nmtKWLVvIw8PjHx2H/v3708WLF0XPwVpsbCzduHGDtm/fTkRE5ubmVFhYSGq1moiIVCoVHT58mMzN\nzUmtVlN4eDg9efKE/zYvL0/ynjKZjNq3b8+v6+/vT+/evaOMjAySyWS0dOlS8vf3lzz3xo0b1L17\nd8nnJSIaOHAgXb58mU6ePMmPOTo6Um5ursHnadCgAZ08eZK/l4+PD1WuXJn27dtH9erVo4SEBDI1\nNaX09HQaNWoUFRUV8fcgInJxcaHnz58TEZFCoSC1Wk0//fQTlS1bVnQfjUZD06ZNo9TUVNFxS0tL\nysnJobFjx1J6ejodP35cNFZsTQvf2dTUlLZt20aTJ0+ms2fPEhGRt7c3zZs3j7Kzs6lv376ia3z5\n5Zf0xRdf0I4dO+jZs2fUtGlTmjFjBhERnTt3jqKjo6mgoED0XKGhodS7d2+ytbUlR0dH+v333+nI\nkSP0008/kUql4uMg1fz8/Oj+/ft8TIm0c6JmQCD5BjSifMfydF9tR28LiYo+fEYZQO7WSsq6d5We\n3r5Kmvz3VPz2ORU+uUHFb5/rjYdU8/HxoQcPHkg+z/PnzyknJ8fgucaaqakp7d+/n0xNTalr1650\n//59MjMzI09PT7p7967kXCQiiomJoY4dO9KbN29o06ZNdPLkScrOzqYXL16QXC6nxo0bExFRWlqa\naF2Zm5uTn58fXbx4kczMzCg/P59fk4390KFDafHixURE5OvrS9nZ2fTmzRs+Bw01qTFcsWIF+fj4\n0K5du+jmzZt0+PBhUqvVdPDgQbK3t6ddu3bR1KlT+bnVqlWjAQMG0O+//04//vjjJ8fPx8eHfvrp\nJyouLqahQ4fS5cuXKTIyknr27Ml/k5+fTxEREXTt2jXRuXK5nD/3hg0baPv27ZScnEyenp70+PFj\n6ty5M/Xs2ZM6dOhABQUFNHnyZIqLiyMiInt7e5o4cSJt376dfvnlFzIxMaHCwkIyMzOjMWPG0MuX\nL2nNmjWUl5dHw4YNo0WLFhEACgkJoXv37tHDhw/5vTt06ED29va0Z88eevXqFZmbm9Pbt28NvrOF\nhQXl5ubqHbexsaHExESqWrWq0TFbtGgRrVu3juzs7Khjx45UVFREW7dupZycHBo+fDh169aN/3bj\nxo2UmJhIzZo1o+nTp/Pjo0ePpqNHj9KoUaOoS5cuRu+3c+dOio+P15sbQ4cOpV69eomOlStXjv/d\n1tZWpnstpdE7lbyBiA5+0OiWAVhORK5MufigjLh8+K0nET0UnPvow7Gn9P9pu3v3LkVHR/NNk4ho\n/vz5lJCQQMuWLaMFCxbQ2bNnqaioiBQKBalUKtq5cyc5OzvToUOHiEgrYL788ksiIqpQoQK1atWK\nX+v58+cmCxjmAAAgAElEQVT0ww8/kJeXF4WFhdGqVavoxYsXFBsbS/Hx8SSTycjZ2ZlevHjBBZid\nnR1lZ2dTZmYmF6Y7duygwYMH/23vXVBQQA8fPiQrKytyc3OjJ0+e0MWLF4lIu0kGBgZSmTJlaPfu\n3ZSTk0NLliyh0qVLExGRlZUVvX//nmQyGTk5OdGrV6+oqKiILl68SMHBwaRQKMjExISIiDw8PKhp\n06a0bt06CgoKovPnz5NaraZatWrR1atXKTc3l37++WciIoqIiKDevXuTQqGgxMRE2rRpE23atMmg\nInLkyBEiIgoPD6d27drR/Pnz6fz583yTXrp0qd45r1+/Njgmffv2pe7du1P79u0pKyuLiIgePHjA\nNzNHR0cyNTWlDRs20IIFC0TnsgXLlBAiIrVaTV9//bWeEkJEtGPHDkpNTSUzMzMKDw8nS0tL2rZt\nG71584aIiObMmcPHUHgPJycnKiwspOzsbCIicnNzo2fPntGmTZvo3r17/LcPHz6kTp066d03MjKS\nevToQURELVq0oPDwcEpLS6OsrCyys7OjwMBA2rBhA23ZsoX++OMPsrGxIXNzc0pPT6f9+/cTEZG1\ntTW9e/eOX1NXCdHd3FxcXGjhwoW0Lmk7HbzyhDQqczL1qUYPvSrTY1MLondqquluQhWRQ9uWzSIb\nWSFtXb2E8nOyqXncGCIivjYGDx5MZ8+e5QqXrhJaoUIFun79OhGRpBJSvXp1Cg8P55sT26hbtWpF\n+/btExkChpScgoICSkxMpDp16tD9+/fJy8uL1qxZQ7a2tnTz5k3q0aOHnjLSsWNHCg8PpxcvXlDf\nvn3p2bNnov+3sbGhkSNHkpOTE+3fv58mTpxIRERfffUVTZo0iYqKiqhVq1aUmZkpOo+N/e7du4lI\nqyQJ54FQCZF6J/bvHj160Pr164mI6Pr16zR8+HDRN2b3aNGiBS1cuFB07qVLlygyMpLc3d31xopt\n9kRESqWSiouL6cGDB9SnTx96/PgxvX//nhwcHKhNmzai81JTU+natWvk4eFB3333HXl5edH69esp\nKSmJGza9e/cmS0tLIiJ6/PgxqVQq6tSpE7m6upK7uzvdu3ePf2eZTEZZWVnk6upKs2fPplatWvG1\nFhISQmFhYUSknduzZs2iM2fO0NixY2nmzJl04sQJ/lxsvmzdulX0vOwdDbXc3FxydHSkYcOGUVxc\nHFlaWtKAAQOoZcuWZGdnZ/RcALRz504i0sqF6tWrExFRpUqVKCYmhnbs2CFSRJiR5ejoKLqOk5OT\n6P+NtTZt2tDly5dp165d/DvLZDJ6+fIlaTQarhCWqEm5ST63E5HHhz9diOh3ImpARFk6v8n88Oce\nIqovOH6YiAKEv/3/KTRTXFzMQalffPEFRo0axV1rNjY2ePHiBTZu3ChZAdLc3JyD+S5evMivKUxn\n9PT0xKpVqzgKmbnO+/fvD41GI8mvYGNjg9evX+Pw4cMg+gh8ql279t9SGVij0WDGjBkiF3W1atU4\n6JRIjAXYsmWLpKuxdu3auH37Ngc2EWnDCQBw/vx57oqcOnUqJxlatmwZxxskJSVJum/d3d2RkpLC\nMSlSlNusMWAhA0/l5eWhSZMmetc0VsBK2GfPnq0XcpHL5TxcZWpqiiNHjuiFdqTqRBBpSfIMZQMw\nwB0DOgLAb7/9BiLp0BELGTCAKBtfNoaMG0cqLdnU1JQj7nXThRm4USpFGAAvYkakBTMyN7hMJkPl\nypX1wjAqlQoylRksKoTANeRrOHw1BA0n/ITOS9NRSlDILeC7XWgZtx4O1RpBZmqJpKQkDoi2sbFB\nTk4Orl27BiJxeq+9vT0fb+G6ZCGELl26cPe9VHdzcxN9Y1ZnY82aNejQoYPkOQqFgmeMsVCgSqXi\nxRUZ4PHJkyeSRfzKli3L8Qws5BsYGIgjR46IQkH9+/cHoKUXEM6t3bt347fffvskRb6LiwvWr1//\n2diQWrVqiUj+WJi4bt26orRiuVwuwvcY6qVLl0ZUVBQPY7B3vH//PoYNGyZaL3Xq1NEDowPgWKb1\n69fzY2q1mstcIdifzXFG5sayFKW6hYUFunXrJgoLCjFyJ06cAJEWGA58DO05Ojpi3rx5ePfuHWbP\nns3PXb9+Pd68eaOXGccyKIW9du3a/Prly5c3KNd0mzBDS1griJWtsLW1Ff2ecak4Ojrysb106RLH\n6Ujh7nQbK/Mhk8nQsmVLNG/enH/HefPmiX77H8+aIaJJRDSKiG4QkfuHY+5EdOPD35cRUVfB7/nv\nWP9PKyJXr15FZGQkQkNDMWDAABEpDQPn+fr68k1erVZz3Icuz7+DgwOSk5M58JLFIrt164bCwkIR\nkp71+Ph4XLhwQSSwd+/eLXo+IcLc0dERb9++xaNHj/TixI6Ojti/f/9fGg9h+qmfnx9fkA4ODnyi\nsY29sLCQ0+ITfaT7Ze8SGhqKmTNn8v+3s7NDrVq1RO86fPhwXjyqefPmHJyVnJysl+7IsDMKhYIL\ngICAAKxevRpTp07Vo4Jm38/Z2Rm//fYbNBqNCGxYt27dEjEPsi6lULi5ueHkyZNGz+vevTsnTWLf\nv27duka/A5tbQnZZjUbDn3f58uUcGCfcWIR/t7GxEcWNnZyckJWVhV9//RUjR47k4zlu3Dg+Z6Oj\no6HRaLB3716uFKpUKsksnMzMTL757dy5Ew8ePOD3l6nMoHT0gkWFENjW/wYOXw2B+7eL4DVskxjT\nMXI7vpx1GE1n/wy7kO6w96uOm49ecgWNgYlbt26N4uJintnQtm1bHDlyRPRNjAGj165dywU8E8RE\nWtDopUuXuALAvo3uN2/Xrp1BbItwDgmfh2EMWLo+U7iZ4hsZGcnn+8iRIwGA44dYMTeh4mJnZwfg\nY4HGTynQMplMlNKZkZHBDQcvLy9JPIxSqeRKMMORqFQq/PTTT3rzi3UTExMOAJfifNGVU6zqqzCL\ni4h4NfU3b97gl19+wY0bNwyuDzavt2zZIlofbLzWrVuHP/74A5MnT+bP3LZtW4wePZrLMT8/Pw6G\nNWQsEBGXqWq1mmexMKWQZUL98MMP/DmE2XQMtPrmzRt+zNraGoA+kNvDw4MrtKNHjzYqH4RNo9Fw\n7NbmzZv5cWYEBgcH6/2eGWQymUyESQwNDS1RqjRT9Bo0aMBlABtXb29vPHjwAJMmTULXrl3/eUWE\niCyJyFrw93QiCiWi2SQGq8768PdWJAarntG95n9SEdmyZYukdckmFUO9CwFJAESbKzufeU5sbW1x\n9+5dvvjYn87OziIlREjPLOyNGzcWabUA+G/ZhHFyctITiuzaZmZmos3rc1pOTg63mNkCP3r0KEfe\nCxWiwMBAvRS8ixcvGgRj6abPspRlpVKJESNGiASBhYWF6NoM0FemTBkO4GLjrmsF+vn5cQGmVqtF\n2QJCZL6QPbd69ep/KYOA1WOQyWR8McpkMrRo0YJbkbqVXT+VKsfozxk3x/nz5zFixAgQaa3+06dP\no7i42GCFYnNzc+5pYxZsu3btRPdg6Pfu3bsjPT2dj4EU+6ePjw/u3LkjOn/3gZ8ht7BDzYah2Hvp\nCeI3HoJz+/HwitosZhsdswveUZvh0mkyHEOHwjakOyxLV0fnnn3x8IOCc+7cORB9BBmydvDgQf7t\nDdXLYOPdsmVLEWC6atWqkkXBmCWuVCp5uuz9+/f5nCopWFnYhQyk7DmnT5/OrzVgwADRhmxtbY23\nb9/i1KlTIPqY8st+z7KdZs2axc9RKBSIioriis/UqVMxZcoUvbkrXGtMATY3N4dareaKuK2tLcLD\nwxEZGYmaNWtyedKxY0de4I6Nq/DarL4N43Fp2bIlTp8+zb1MTJEqU6YM5s+fL/nNunfvjh9++EFv\n8w8LCytxFiAblypVquDmzZvIz8/nRHasGCVrP/74o96cVqlUePz4sR67sPDbM2+YTCZD/fr1uZJj\namrKPQmsllRMTAy/n9ArdPDgQX5c6KFbsGAB5s6dKyl3fH19S1zgj7XExEQ+D6tWrcqVSSKtd1m3\nZWdno1+/fnxOmpmZYcCAASVmwdb1rPr6+or2JKER+Z9QRPxIG475nYiuEtH4D8cdSRt2yfjwp8OH\n4zIi+p6IbpM25TdQ95r/tCJSXFyMoqIiZGVl8QXdq1cv7Ny5k9MsKxQKPHjwAPv27QORVsObPXs2\n5syZgwsXLvBsBxsbG47wP3XqFGdtnDVrFl9kO3fuFJUjZx++X79+2LFjBxo0aMAtG0tLS8mJwGqn\nmJmZGUTLe3t7cwvZUDnmT7UzZ87obQYnT57kwkfKIhTW5gG07JXDhw/nC9/X15e7T//44w8cO3aM\n07SXpLy7ra0tnj9/zjdVYWdCg1VOZXUrSpcuzZHi7969w9ChQ/kY6y780qVLc+ZEYa9YsSIfT6lu\nYWHB3f1Mqalduza3tq2srHDmzBmkpaWJMlN8fHywa9euT36LXbt28XN0Uxvt7OywadMmAFrr5tCh\nQxg4cCAaNmyoFyYUfjMzMzPu2dBoNJyjJS4uDkePHv2gLMkgU5lBbm4Dpb0H3KuFoEpIKExcy6DO\n18OwNv0upu+5hlYLj8NXoky955B1cGg+BDa1O8Cq8pcYk7AEffp9JD27ffs23r59yynuWXv37h1f\nj4yErKCgAGFhYaL3cXZ25nNLoVCgevXqqF27tui7sv/38fExaulaW1tzD1pKSkqJFBAHBweD4QcT\nExO0adOGK8eXLl2SVBSUSiW2b98OAHj8+DGXJQC4pTpw4EDk5+fj3bt3kqypnTt3RmFhIXbs2MGP\nMa9O2bJl9VJ7e/XqxT1cuj0xMZFvHEFBQVCr1Vi1apUet4WNjQ3n07CxscGDBw8AaENFLP2VpaZb\nWVnh3LlzuHfvnihDx5DCz+41cODAEsmqrKwsUZ0a4bebOHGiHvfRkydPkJiYyNOGPT09cebMGW5A\n6vaqVasiNzcXI0eOFI2Dt7e3yIhgoRQTExPMmDEDhw4d4p4OuVyOY8eOobCwEMuXLy/R3BoyZAgn\nfvucdv78eT3lQCaTfdKzkp2djRs3bhhkEDfUmFJmZmaG8+fPA/iY4cR6q1atsHr16v8RmgnbpUuX\nEBYWxsmp2MbWoEEDkSuKFSGaNWsWioqKjKbzde7cmWvEjD2Q6CPWIygoCIBW6F+9ehXnz5/HyZMn\nRV4UZrEQidkhhe3p06eSaZZKpRJ79uzhihGrEKpr+bL29u1bLFq0CD179kRUVJReaXoWc3d0dER+\nfj6KiopERGrG+jfffCO6Dxs3IT5Gqh06dAjdunVD48aNMWTIEMybNw/z589HamoqlEol5HI57t+/\nj7y8PKxatYovcrb5N2nSBGq1GsuXLxdxgXh6eorSml+8eGGw7PjnWMAsJESkHwpgmwtLTyYikYUe\nHBys5+0y1ubNm6cnuNlm7ejoKCk8ioqKkJqaKpnKJ1OawMLFBz1GTIZ/+EDY1O4Ixyb90GN2Mtzb\nxcC9z/d6ioVULztuDzovTce8g9fh27QnrKqHwrtmQ6icS4NkxplUhZaqbhMW7AsICODeDDYG33//\nPdRqNd68ecPDo8wSvXPnDtavX4+UlBTcuXPHIFOrUqkUjem4ceNw69YtgzV1hL+dPHkyV3CZ548p\nPbphkODgYJFnws7OjivDgwYNglqtRlFREa+SHBoaCgA4fvw4n482Njbcw6BQKNC7d29MmDABp06d\n4jJLiEc4ffq0Xq0mIq2XUEim9invn4mJiciTYWJiIlpbrDqwlZUV2rRpw3/r7OysF26R6rop0NWr\nV8f58+dBpN3YSlqN/OnTp+jduzdXNqtVq4YtW7YYJWEsLi7mSppQSdWt3kxESElJAaBNV927dy+O\nHz8uSoVljWGBDM0bYY+Ojtajhjc3N8eSJUtK9M5S7f3793yt+Pr6IiQkhMvfihUrShIj/tXGjBiF\nQoHo6GjExMSIDCY3Nzcu6/7VikhOTg6OHDmCtLS0T1KeX7161WDxLd38dKZMjB07Fhs3bjS6oHx9\nfQ2Wp1epVHol3DUaDfbt24emTZuKQgpmZmYYP3685Cb15s0bkeavKzBGjx7NXfZMS5ViXr1+/bpk\nKesJEyaIno8J8LCwMD2wrKmpKd8AmLB0cHDgi65Lly6Ij4/nHqCgoCCj8UaNRoPnz58bFDyMn6Ny\n5cpYvnw5mjVrxu/FLLi5c+dy4BQTjsJvcObMGWRlZUmCBD+ns/mza9cu/PjjjyKlRi6X82q2gBY8\nNmzYML7xMLfn51odzG1vbW3NC07l5+fz8V26dKneOWq1Bhn3n8CmypewqtEC7SatReTGc6g6IVVa\nsRiVAp/RO+E5aDVcOk+BXUgP2AS1R+zan9E+ZiHMfGug7dA4lA5pD6WjF06cvYi8wo+C7fDhw0YL\nzwkFs0qlEhUt1G3FxcUYO3asaG2w2HepUqVEc+nAgQMg0nrD9MdAjbVr13LvkJubG9asWYOcnBwU\nFhbqebp03fYdOnTQY4VVKpXIz8/n92DhQnt7e4SGhvL1YGlpKbq+u7s7V5qFG7CHhweXGwqFAseP\nHxe9m1ChqFGjhh6FOmvJycn8dyEhIThz5gxiY2P587i7u4tYQY19ny+++ELP6+nv74+8vDyo1Woe\n+ihbtqxeaLl8+fI4c+aMQa8LkRZDpquENGrUiLNQfwoYbWzeCIH6n2KD3rp1q+Tz6XoTGzZsWKL7\nazQapKamIjw8HPXq1cPgwYNx7tw5xMTE8G9fqVIlrFy5ks/h27dvY+XKldi4ceNfrh+2atUqEGlD\nSczTmJ2dzRXhf4JnyhDglykjAQEB/Lf/WkVkyZIlIu3LwcEBK1asMPh7BhoLCwvD8+fP8erVK+4C\nVSgUaNu2Lbp06YLExESuLW/bto17KxYsWIAtW7ZgypQpvBIjW1DVqlVDVFSUiOirfv36OHHihOgZ\niouLJSmvvby8OEiLfbTx48ejfPny8PT05NZH1apVeW2BTwn+Cxcu8OudP38eo0aN4kKvRo0a+OGH\nH0S0x0uWLOEL5PTp0wZrPkyfPl0EuGXvHBMToydgfH19sWHDBkyZMgVz587F/fv3ReORnJwsClmx\nAk2PHz/Gli1bkJqailu3bhlUwli3sLDgG1dkZCS3zlhl3A4dOnCvlVQXPreUZ8TU1BSmpqZ8/Cwt\nLREZGYmBAwfy7xAfHy8573Jzc3Hnzp0Sx111G3PnftOjF+69eo9Ve06i0eAZ8Gj6LawD28C/7zR0\nWHIS1ScfQN0Zh1Fp4j6UitmN0jEflQ7vEdtQatgGhE3fjo7f/QjLKo1RtVknTP9+NerUb8jXj64g\nbteuHceQMFyOlZUVYmNjMXz4cM66CnwUhERabAAbU92QkpAdU61W64VnWMvMzMSxY8dw4cIFZGRk\n8GsJDQ7mBm7UqJHoXI1GI1lynYVDiouL+fydMmWKnudEmKXE1h7rrLqoELfRqVMnnD17Fmlpabh2\n7Rp+++037imrU6cOOnXqhNjYWA4GDggIEIVNypUrJwKnC9/j0aNHePz4sVFlPj8/32hRwD179ogU\nrVatWmHZsmV6HqAePXoA0BIBCssSCAvBFRUVcUX/xYsXuHr1KpKSknD8+HGo1WqOqXNwcEDr1q1F\ncsTDwwPPnz/Ho0ePuDd6wIAB/N1u3boFuVwOpVL5lzfmTykihYWFBg1TYZfJZEbL25ekaTSaf8Qj\nIWyMdZsVTWWNlSiYP3/+337PFy9e8DkUHByMHj16oF+/ftxQdHBwwLNnzwD8SxURYbpotWrVRNgB\nxiD56tUrfPfddwgICIC/vz/fMISMb8Jyybq9XLlymDNnDnfdCSe1Wq0WuWOF55mZmWHNmjUYMWIE\nfH194e7ujm+++QZXrlzh+BOp3qVLFwBaLdaQSzkhIQFFRUUikKVUF9ZqYZ4SYffz88OiRYv0skWa\nNWvGx/z27duIioriGwlz+zEmUwbiYorEoUOHcO/ePcTHxyM6OhrLli3TY5SVy+U89MQwL2xzYwqA\nsDIu23x+/PFHvqBMTEzw3XffIScnh6fvSfUKFSrwCqYODg4iK08mk6FmzZoGwzHVq1fHuHHjJFOy\npfo333zD3bWPHz9GVFQUypQpA19fX7Rv3x6DBg3C6NGjJetbAEB+UTEynr/D9afZuP3iHfZeeoIN\np+/h+9TTqPTtDHgOWg0fQVqrCAQ6MgWVY5IRvfkChm++gMm7rqD3vO1wbNIfpp6VoLJ1kQTi+fn5\ncavQ2toa0dHRHGgrBLmxdWPIzVytWjU8f/6ch/SIPlKk6yohDRo0wPv37/Hy5UtERETw+VejRg1R\n5oNu02g0fL61b98ev/76K5KTkzmYWdelzdLaLSwsOAaJPb+NjQ235H18fJCXl4f9+/fzuaRSqbhX\nMjMzkytoxkJ33t7eSExMRHx8vEHKdeFYOjg4oLi4GFeuXMEff/zxWaE6Nh6//PIL1q5di+PHj0Oj\n0eDMmTN69YBUKhXWrFnDlUlh1eenT5/yNcX66tWrAWg9pz169ODHhXiIZ8+e8UrRUrW0WLaRr68v\nlEolPDw80K9fPx4OYynKrIyFXC5H7969MX78eP49u3XrJvnO6enpWLhwITZu3Ch5b2H79ddfsXLl\nSuzdu1cSbyHEMnyKKdfb21syHPP/U2OZZU2aNOEy5tSpUzw807x5c4OVhf9KM5QGz4xBGxsbtG7d\n+t+piLD0plmzZuHx48eYPn06z+oIDAzE06dPDZbEFhaoE9Zu0RW0uv9WKBQIDQ2Fh4eHUfCbUOAI\nu7DIV3BwMA4ePIipU6dyAadQKPD27VvMmDEDRFpFKC0tTUQZXLZsWQAwSonOalpUq1ZNklpe9/10\nMRMNGjQQjfWCBQtEv6tVqxY/xrwQZmZmXMCwxtIUnZycEB0dLaJA379/P/8+kydPRmFhIe7cucNB\nvzKZDM2bN+ffVCaTcf6GuLg4AMDly5cNvptcLsf58+eNlho3MTERVZZl47tu3To8fPhQlN7Zs2dP\nvH37FuvXr+cK6NChQxEXFyfC2Dx8+FAy9CW3sIXKxQ9mfgHwa9INi1NP4+DVZ5i+9xpCEo7Ad6xh\nLIb3/2Pvu8OiuL73zxbYpUlHmqiAqFhQrCBG7FERu8YK9q7Yg71gwYi9BiWxa+zdWGPsFVuiGHtX\nFCwgfd/fH/u915mdWUDzMTH+PM9znsRhd3bmzp17zj3nPe8ZvBEOIUNhHdQOFmXqQONRBp6+fiCV\nCVQWtlBr9empyMhIhIWFyVYoGOu5YwwTIafCedq9e3dMnDiRG12W2mRhYK1WizFjxsjSZpcqVUp0\njcL3TJjaMpSTJ0/KlqrWqFFDlC4BwMGIY8aMAQDZtISlpSUWL14s6zgULVoUvXv3FuE9AgMD0a5d\nO5HRMjEx4VEyoaMr3CgoFApMmDCBV4gR6R2gj5Vbt25JOueWLl0aCQkJSElJQVxcHCIjI7FkyRK+\nfjJjIcSiqdVq0UaEgfNZFFGobm5umDlzJkaPHi1K28qJsX5NbK4Jq66EWCumVapUkawlL1++lKxl\n1tbW2Lp1q+T3k5KS8P3334s2EWq1Gj179hRF34RpJWOl76ampnwOGGvq97+SnJwcLFu2jLf3aNCg\ngajaJi9JTEzk70e9evU4fkOoKpUKa9eu/Z9f++HDh9GiRQuUKVMGISEh2LlzJ54+fcqr/oj+gaqZ\nT6GGjsiZM2cwYcIEREVFIT4+nt/c5s2bZQl82Mvi7OzMDSibYM7OzrwrIsMYBAYG4t69e5wrP7+L\ns0qlwqpVq0QLpHBBmjlzJq5duyYh5RKCN1m7eSLC3bt3+W60VKlSqFChAgYNGiT6zP79+0ULkUaj\nQf369bFixQoJ54ZwYYyOjpbkfg13rEznz5/Pr0+YZzSmwrK1lJQULFu2jO+a/vzzT2zdulWU72aL\nlb29PbZs2SJZWF1dXfn5WCt05rgw48JItJjhZ/gPtuD169dPZEiYA1GmTBmjz9jKykoWECxMc7Xv\n0AEm9oXQJWop4o7dxqbzD7D5wgNsu/gILXoOg6Vfffi2jUTQkCVwajkerl0XGnUyPCN3oeOy04ja\n+QdWHr+F6DX7MHHFHmw/nQCLgoWhtneHUmuJihUrSp4d41ERNrEzVGPAXLl3plWrVhg4cKDEyS5Z\nsiQWL17M8/6TJk3iY/HgwQOYmJhAqVTi6dOnOHfuXK6RA6ERL1iwIK5evYr09HTufDs6OkqcCqFc\nv34d3bt3h6+vL6pUqYJZs2bJYsMYKFMYKTl+/DgHDbds2RKXLl3iu0Vvb280bdo0z3dfoVDwd33y\n5Mk85M4qp4j0jnJ0dLToe4GBgdiwYQPfoISGhhq9x9wkKyuLz09nZ2d89913/J48PT2NprkY8Z9G\no8l1vjAHKi/gtkql4sRgu3btQq1ateDk5ARfX18+hhUrVkRycjIOHTrE0zO2traSyML169cxadIk\njBgxAjt37pRNYbCKPTs7O3Tt2pWD501NTXHjxg3+uVWrVknmr42NDZ93DDfHNlK5qY2NDfbu3ct/\nK79daQF9artRo0awtLSEk5MT+vTpw1MUcqLT6Yz2pRJyk+QlO3fulNgAjUaDH374gacqLSwskJyc\nnO9z/l25cuUKNm7c+N93ROQaM7EXmi0KgYGBuTIK5hV6O3LkiKiUl6nQATB2Dew7wpeNfaZ8+fIA\n9BUkwpfbzs4O3t7e6NGjB48UaLVavHnzRpZcq0CBAkaJlDZu3Ihdu3aJsCeVKlXizfeI9Ds8nU4n\nImwSqlarxcWLF3lo1N7eXkQKtmfPHtSvX1+yQFlbW2Ps2LF88di1a5ekwkjYGt0QECi8J+HuXNh0\niXVGZQuura0t9uzZIyIMMjU1RXx8vNGwuEqlEo2PXBmwMGpgaJCOnDiDEzdfYODaC/AatjnPihKv\nyJ0oMmAVnDvNgnPr8ShQuTksigei64goqK0LwrSgFyyL+uHqTX3p48qVK0W7aGFEjRlT4eKpUqkw\nZ7LLajUAACAASURBVM4c9OnTh897Nu7CcVy6dKmsc3r+/HlZDpqQkBDRe9SwYUO+GWDkRUJAJQCe\nmmPO2o0bN1C5cmXR+d3d3ZGQkICMjAw+H6ysrLjTceLECe4U9+/f/2/jAxiIrmTJknj8+DEAfWUW\nwx88fvwYM2bMAJEe+5Kamsqjb8bUxMRENC/q1KmDVq1aYc2aNTh79iw/Lmx8aQxnZdiZND+SmZmJ\nzZs38/eZgbuF3ak3bNhg9PvC6JQcR4ycEzZjxgxRybuNjQ2/J2dnZz6GxtTNzU2UZpYDFecmt27d\n4tEcrVbLMWY6nY7bBUYCd/HiRdGcc3Z25hgQFk1h743wGu3t7SVNPLVaLZKSkvh4m5mZ5XtOHjp0\nSHZ8vby88OLFC9nvMDJEMzMzxMXFISEhgZOsmZubf5Dj8OzZMw6ULl++vOi7bBxYCu6flP+8I0Kk\ndzj69u2Lnj17StIeXl5eIuNt+PJv3rwZOp2OTyoivQG1s7PjO/OxY8dixYoVIHq/K2AMhobkXOyF\nNbZwMY9ciEm5e/dunuDSZs2acUIaIj3Sfd68ebJ05ELNb3g9ISEB796947l2pra2tlizZo2E8Of0\n6dN8EjHg17t37/D8+XPcv38fly5dwp49exAVFYU5c+bg5MmT/N79/f0lzt/333/Pw75yi15wcLDo\n34MGDQLwnnArKCjIKKdHcHAwUlJScPToURH19Jw5c6BQKKBUKnHhwoVcIyGVvqkLU9fiMC9UCuYl\nguBQszMcm4+BW6847mD4RO6AY6MIWJSuhX0nLyLxbTruJKbgTmIKrj95A9tS1aG2dUXTZs0ki5FC\noUBmZqbo2KxZs7B//37+b19fXxE+g4j44st2tcaUjXelSpW4oyUsF2XKStWFIfTcOiZXqlQJGRkZ\nvCy8b9++fF7Ex8dDoVBAo9HgwoULmDx5MoYPH46tW7ciNTWVh2aFTI9CTpDTp08jMjJS8pssavmx\nkpKSwrkhTExMRA5q//79AbynUV+4cCHHKxUqVIizBAvf+y5duiA1NZUTrhmqMNp3//59XmnHonUa\njQaVK1fmz8LQmctNzp8/j/r164vmriGGguFgWNpSTjIzMzF69GjROmRubo5vv/1WhC1xd3dHnz59\ncOHCBdH9tm7dGkuWLEFMTAwH4rJzTZw4Effu3RNtfoRzin3OkBQyt+dn2PVWq9WKaMcZvikkJATA\neyZTNuYzZ87Eli1bjG5Cu3XrZpSFV6VSiVKsjEU6LxFimbp06YJHjx4hPj6ezw8WzTUUhuMbOnSo\n6DjjpBK+P/kRFi0eNWqU6DhLWRrSr/8T8kU4IsOGDcO1a9fQrl07o6RURHqPW0jfTaT3/jIzM0VA\n0aioKADA7t27jS7GNjY22LRpU66Lv1DlvOD8qkqlwps3b2SrQwx3ri4uLnmGkKtVqyZxUHx8fNCk\nSRPJ+QyBr+zcco4Ik+TkZP6SGH6vWbNmsqFGY2kjY+rs7IzRo0fz5x0XF4f09HRERETIRofMzMz4\ncUanDQD16tUDkT4cLsyRqyxsYeZdGXb1+sB34M+SqEbRETtRPGIlHBoPRYEqLaH1rAClRn8tjNpZ\nKDt27DAatSLS76CZwWO7/8jISH59I0aM4CAzIZcGK61+/vx5nn1EmOa2u/fw8MCiRYtExwYNGsSN\nBbseYX585cqVOHPmDL+/oKAgUS8OQzIxIv1ujDnRrJ07IO6zxBZgdl5ra2vuiAlbyhsTnU7HsUCP\nHj0S/e3hw4do0qQJvy5ra2uMHj2apwbYYt2xY0e+QAvBplu2bOHXyXaQQh4OlUqFzp07SzY+3t7e\nKF++vMgAenl58c9VrVo1X/TZgN7RY2NsyHFx4cIFPgbMiZcr5RaKYcqIqTB1XLZsWQ6eFVZCGZvb\n1apV4+dPSkriUdPq1avj2LFjmDt3Ll9jGCdHXsKYgjUaDa/WItJvGNhzZtwrffr0AQDOnsx2/X36\n9BEB4tn1s+sLCAjA8+fP0bVrV9F75eXlxcfawcEBU6ZMyTeY+OHDh/w6hSlDxgzs5+cn+z1W0cfs\nEhOGKxK+P/kRNncLFy6MZ8+e8U0aS9UaVnP+E/JFOCKlS5c2WsHAHICGDRvixYsXorIzIr0nzcLW\nbIIJQ6PLli2TpBNYKZyhc2Fqaioq2zNUtrPIzVGoUKGCrNPCekcQ6Z0GQ+p0ovdkWazxGdF7vIUh\nJ4kQKGSoKpVKluxKuHiycmKdToe4uDgMGjQIy5Ytw8uXL/lC4ejoiIEDB4qAUczrf/v2rWgREarh\nosoiWh4eHrJ4lE6dOvHFgEVFqlevjnXr1okiPEqlErVq18HE6bOwfOs+nPjrOVb/ehI2JQNhUboW\nrAO/g2OLsXDvu1IEBi3Y4QdYV20FrWdFaIv6w7SgF0hlInHSLCwsEBUVJcljv3r1ihsaY8++SpUq\nfHzZ/Fq/fj2fM4yhEtBjAYTfFfb4kVPmdP4dinq28LJwdq9evTgSnxHVLV++XOIMsWesUCjQoUMH\njBkzhjswbCfo4eGBQ4cO4cGDB0bLqBUKBdatW4e3b9/y9zE3Lon4+HhRik2lUiEsLEzS9DExMRHX\nrl2THL9x4wY3TixdxDYjXl5eePnyJT/3ihUrkJaWlmv00cTEJM8UcJ06dT6ItpthI1jJ8J07d/ja\n4eTkhPnz5/P3wdLSMtf0wdOnT0XrzokTJ7Bs2TLugBqW965cuVJSlRYaGopOnTqJ7rNevXqi35ED\nuxLp21bkp4T1/v37UCqVMDEx4c9f2I8lODiYp7MVCgV3yBg4nq1FpqamEsbUypUri8q62TuXkJDA\n7//evXtITEzEjRs3jGJucrt2Ir3TK/zu4cOHQaR38uSERevd3Nzwxx9/8D5PjMzx7t27H3QdWVlZ\nvOzckLzPzc3tf9IY9UPli3BEhF1FGbDNMORsbW3Nc31yWAFXV1dR+NrV1RWBgYFYuXIlkpOT0apV\nK5HXb4iHyG23m9cCVKJECW6oihYtihcvXuDUqVO4efMmd7CEaYeQkBCkpKRwT5otFEKgF7u+vICk\nhurk5IRDhw7h7t27uX6uX79+GDx4sCSlpNVqoVQqoVKpRNwnbCfr5eXFjyUnJ79vgKZQ8HyvMTCc\nmZkZB6WWL18effr0wcGDB/kO8vnz51AoFFCr1Ui4+xAHrz3FzH0JGD5/HbSF/WD7TUdRKkVOXbst\nQqmu0egRsxaWRctBoRYbFw8PD4SFhYmet7D8V1gexyQ/NPVM2Xh6e3uLMBO7du3i52OlsHKOBRs7\nVl5p6ADJVX+VKFFC4kA4Ojpi8ODBslGWhg0bIjU1lTN2duzYEWPGjJE8t8KFC/N5KwxfP3z4kBtt\nw1Qgu6YWLVqI2DCFZF0MIGhIBsjk+fPn3El0cnJChQoVRJGPCRMm5Is4bunSpZJ319LSEhs3bhSl\njAoXLiyJ3tSoUQN16tTJtTKNGTcTE5N8dTM1FDY+DOcCgDeeM3wnGXjUmCxbtgxE77FEMTExACBy\nDO3t7Y020fP29sbSpUslODOFQoH169cjJycHFy9e5CkNNzc3KBQKuLi4YNSoUfk2fixKHRwczI/d\nvXtXsjFTqVQiICcj/mPXanj9DBydkJDA50qJEiXQqVMnvgYLI6kfIzqdjqd7BgwYgDdv3uDWrVs8\nzTd8+HDZ7xmyVwtB5r179/6oa3n48KFRRvDmzZv/ndv8KPkiHBGmTZs25YvhpEmTZBdeBwcHo70D\njKkQUCmH5RgyZAguX76M0NBQST+Lbdu24cCBAyLEuFzEQ1ihkpCQgMzMTN4WulixYtwAs4XAyspK\nlKfUaDTcEbl06VK+783LywtTpkzhBsfV1RUxMTGca8HJyQkODg5QqVQIDAwU9drJ69wqlQoBAQE4\ncOCACN/SokULTJw4UTSucsbI2N9KlSqFpORk3H+Zgj9u3sPJS9fQoM8EOLedAtdui+DWc5lxZ6Pb\nPBSo1BTmJYKgLewHrWdFmLoWh9q6IBQmGigUCixdulQEeBMuxHL3+OTJEyQkJPAFgpXy6XQ6LFiw\nQBT2DQ0NzRMPVKxYMc5nw5gqnZycMGvWLCxZsoTPhWrVqmHQoEGylT6M16VevXqyue68nl/nzp35\ndZcuXVrkePXv3x979uzhkRshXb2x3zl48KBo4WEgxcOHD2P06NEoWrQobG1t0aBBA955dcSIESDS\nl4Ky3XJ8fDxUKhXUarXRSgM2ZtWrV8fBgwdlnamKFSvmi0Tur7/+wpgxYz5ozXB0dERior47sCE3\nUNu2bXHlyhWeBmSlyh8aXgfA1wK26weAO3fu8DWmW7dumDx5smxXZENh6Thh6X+DBg1E72h0dDQe\nPHiAsWPHolWrVoiIiJB9J5RKpSTVKnwGbE4olUq0adOGR4E2b96MgIAAmJmZoXDhwhg/frzEQWG4\nFCcnJ9HfWPVc2bJlMXXqVNkowdy5c2XnfeXKlZGYmAhAD+aUi2zVqVPnf1JNsmvXLtlNq7u7e66V\nM8nJyejevTt3Ph0cHDBx4sSPJkJjTQvt7OwQFxeH+/fv4/Tp0zz6LKwE/Cfki3JEmAEbPHgwbt26\nBSJ9RUlsbKzE+3N1dcW4cePg7+8Pa2tr7igoFArMnDkTFy9eFC2warWasxseOHBA5DjY29tj+vTp\n6Nu37weFv7VaLRo3bizBn5iamopY/YTevomJidEOo05OTqhXr57E0OUWrcltMWXXyGr7T506JfuS\nFipUKE8SNeHzEf67aNGifEG1sbGFjY0NFCYaKM0KQKHWoICrFzTupWDhGwzbWt3gHDYbdaP3otQo\nKR25a7dFcGwyAg6hw1GgSgt4BzbAyPFRKFm9ITQeZeBYpIQoZ5/bs4qMjJQ0U7t7965k8TU3N+cv\nEyOAmj59OoD3i6OcCsexdOnSImS+ubk5R9CnpaXlCUhm99KyZUtJyk2hUPDfCgoK4tfO5oibm5sI\n22Co33zzjVGeESL9zl84v5YsWYKEhASJgWK5euA9iFWhUGDQoEFGgad3797lc8PT0xPffvstv5cu\nXboYXdQYp8zy5ct5xKVNmzZ858nGmu365eT06dPo1asXmjZtijFjxuDevXtYunQpAgIC4O7uzudO\nvXr1ZNOp5cuXl915s9Qk65vCDPaH9BF59eoVOnToIIpyhYaG4syZM3yutG3bNt/nA/TpBzYvO3fu\nLLmf0NBQWSwES4s0adIE7du3x/DhwzlQ1MLCAj/88ANPxQnPKYxAlypVirejN9TatWuLjK1Op+Np\nhYCAACxduhQDBw7k58qtTxGgn1PR0dEIDw8XVT22bt0aY8aM4XO9Vq1aWL9+PRYtWpQrA+vHyMGD\nB1G9enUoFApotVp06NBBwiptTNLS0vD48eO/TaDGcGaGDe9YaupTMK3mJv95R6Rz5848D+3v74+z\nZ8/i2bNn3IgwRtL09HRs2LAB0dHR2LBhg4SPYP78+SDS79Zfvnwpu4ssUqQI312w3dqH9CcpWbKk\naNF3d3fH/v37cfz4cR7+E+4khGW5hvXvfzffT6Q3tuy8zBM2LFUj0u9gWrdunW8wZG6qVqsRHByM\nnr37IGbZWqw8fgvNI+fDscVYeAzZjCJDtxiNZhQZvg0F201DhWEr4BAyFJblGsA+oCUs/b6FmVdl\nWFpaSdD0QhX2uLhw4YKk4ikvZdTewrLEKlWq8DnESoAXLVrEF3b2/Aw5O9jzU6lUSE9P5wsDWwiF\nXC1ZWVlYt24d2rZty8n62JwQLu4uLi5YtGgRr2ARqvBzhvwwho6qr6+v5Jjh/PPw8MDQoUMlqT+N\nRoPVq1fLdhINDg5Gq1atZOduw4YNsXTpUglZ1W+//Sb6DYVCgY4dO+YaymcVEgxkam1tjdevX3MH\nfvLkySDSV07JybRp0yTXZ2lpyckOGQFaq1at+HcyMjI4/kz4DrPIFBtPFxcXJCQk8LJzNhasZXxe\nkpOTI8tlI1R7e3sRf0Z+RQggF6ZgAgMDjQIyWQ8nExMTdO/eHcOGDeNOKKtAYg09VSoVVCoV9u7d\nC0DvFDBnjc2v6OhoJCUlYf/+/RzftmnTJtFvXrp0SZYYbcKECfm+VwawnzdvniRKUrp0aQm4+VNI\ndnZ2voHJ/2th70B4eLjoOLObeQGb/9fyn3dEAH24Ts5IFihQIN/NkWJiYkCkN8TsJXRxceHeN9tB\nhoWFAQBv8z1u3Dhs3rwZlStXztOQ/fnnn7wXjDFt1qyZUT4POS1UqBBfcI1pgwYNEB4eLom8MDS9\noWEQknvlt9rH2K5ZbV0QGvdSsKrYBNZB7WHzTSfYfdsfhQasETkZxYdtgP23/WFbuwcKVG2FAlVa\nwqdpP9Ts8j2cywVDbe8OE42W3zORvsstMzoshCw08IbXwgyaSqXiQMv8KMvPKhQKfPvtt5ymmki/\nE/ztt984RsDU1BTPnj3j84ntyD09PWUdn+rVqyMnJ4f/hhymgsmTJ0/y1TwuLCyMvw81a9Y0CuS2\nsLAQRYhYWjMsLEz0PH/44Qfk5OSISolHjBghYfBl0QqVSsX7LRHpd7+G+BFLS0uMHDlS4viamZlh\n1apVePPmDRYuXIhOnTqhX79+WLBgATZt2pQrMC8zMxNz5szhvBlMbWxsOPi6WLFi3HgyHh+hsLSm\nUqlEREQE1q5dywGW7u7uyMrK4nNuzpw5ou+yXjELFy7EoUOHcOzYMWRmZvIKMuYAsp0wuz62WcqP\nyPEmCbVhw4aiNhUfIllZWZgwYQKPhlpZWWHgwIG5prB0Op1s5K9OnTqi77G2G/Xr1xd9X5iyZZ3I\nmTDgv6GxBPRsqjExMWjbti369+//wVELYaXf3bt3MW3aNIwYMQKbNm0ScST91yQnJwdv377N08Fh\n7S1UKhViYmJw+fJl7mCr1WpZ2vtPKV+EIwLoJ1b9+vU5UDI0NBSXL1/mf09MTDRKGANAQudtuLgy\n1Wg0mDNnDl9Y2U5GWPpJpA95Cxu2EekrYvbs2cP/XbFiRZQqVQpeXl58Z8BKsrRarWQX7ezsLNmp\nsvIxZmw8PDw4YJdpoUKFcPLkyTzTJ+z32GIXEhLCy95IoYSqgCOsXL2gti4IVQEnmNg4Q21dENqi\n/rAtVxdW/iEoENAaNt+EwaFpJAr1XyXuezJ8OzyGbYP7gDVwbDEWln710bxTTzxJTkVOjg6PHj3C\nxo0beWOs3NTc3Bxdu3bllRdCBH/79u25kZw3b94HRa2EBrhcuXI4ffo0cnJyMHLkSJExNYaxWLJk\nCV6+fCnbD6hw4cKSCIK1tTUnA7OxseG7Xdazh8m9e/dEZZRCOnlm3Ni4sGMWFhbIyMjgXCtmZmYY\nOnSoqCU5c4DKlCnDAcXTp0+XgP+KFi0qGy3TaDSi3bMcZkDunUpKSuKpT3bN7DcZiNHwe8ISZkPJ\nzs6WpNIM1dLSUsTSa2JigqFDh4oMD+O6EIIAs7OzOUZk//79nPSqWrVq/LuJiYn83k+dOiW6NiF/\njaF27tw5V7ZYody4cYN/r2bNmrh16xbmzJkjWhOmTJki+k5GRgY2btyIqVOnYt26dXl2IWf3m5iY\n+EEG+cqVK5gwYQJGjRolApAz2bFjB4j0UWuhsDJpImmEaubMmSDSV8UBwOPHjzkdfrdu3T6Ib8VQ\n8mp691+Td+/eYdiwYRyC4O7uzjcQxsSwczrTGTNm/INXrpcvxhFhkpWVJcopHjp0iC/0RHqvW9hP\nBtAv8rnhKIwZMiHBjGF3y3379uH3338XHVMoFLh+/To3Ym5ubpg2bRoPiSoUCh6BmTt3rmjnbWhw\nmJqbm4t6prRu3Ro6nU7iBIlUqYbKyhGmBb2gsrSHQmMBU2dvWPnVg2W5BihcrzOsg9qjyverUbDD\nD3DruQweQ7fmyRjKHY6hW+Ha/UcUbDIcdpVCYeZZESpLexApQAolPDw8RCRzderUQZkyZVC1alXM\nnDkThw8flq1syi/XCMNJWFhY4PXr13ynmhc1NRGJxs1w9/3kyROsXr0aa9euxYsXL3DkyBF89913\nqFq1Kjp06IATJ05Ap9OJIgWMMC2v52hqasrDzazZGqDnXmjevLnk88xZFIbpTUxMJABgPz8/+Pr6\ngohE3aeFpdOGfVAM27fLqdD5yAv4aqwcnZGdMUepfv36ovSAn58fFi5ciMGDB/NzGKPSZpw+dnZ2\n+OWXX3D9+nVJ6wShCq9Z6HSwMk9DzAbbIKxZswZJSUnc6ShWrBjat2/PnfyAgABZZ2nZsmWoVKkS\nbxxYr169DwYECqkBhBUcwijJvHnz+PFLly5JHF9nZ2dR/6N/SlJTU7mR7N+/P+Lj47FkyRL+TrMI\n0YIFC5CRkYFTp05xMP66detw+vRp2ZYTkZGRH3U9X5IjkpOTw/l9DN83lh6TE0bkWbduXfj4+KBR\no0Y8bfZPyxfniAhFuBMRtoI3MTFB+/btUbJkSZQoUYLv+lu0aIFRo0bx77AFety4cbwHg0ajQc2a\nNbFu3TrRgmNoOAMCAmR7eeS2aLN8MpF+p9yyZUvJZ4SN39gxYe076157/vx5WFhYQuNWAjbBneHc\ncQbcesXBvf/qfDsUlcbvRMG2U+HQeChsvukES7/6sPANhkXp2notUxeW5RpA4+YLta0rlObWIGXe\nxp4od7ZOY2plZSVKTeSVNvrxxx/x6NEjHi0y1jtHTo3V9OclwmojucZSRHoAaHJyMqKjoyW57uLF\ni/N0oqFTI6eGvDhCNcR1CMupX758KTt+wgggm//+/v6itAsRca6YvNTa2hpJSUk8HcKUvXNVq1bl\nvA+DBg3i2BKVSiWqUpgwYQKI9A6YnLRv3x5E4t2csaaGFhYWOH/+PI4cOcIrcFgJLEvZVapUCamp\nqQD09O/MiY2MjMTLly9x+vRpUa8idi/CUlqhMMNnuFH6EImKihK9+6NGjcKxY8d4lEepVHJsQ0ZG\nBndCSpYsiYiICL7JcXJyylfF0P9a1qxZI+uUd+7cWRaXQ6SPkqSnp3MHu3bt2li7di0iIyP5M/mY\n0ucvyRFhNA729vY4fvw4cnJysGnTJs4RcufOnX/7EvOUL84RycrKwtSpU0U7gSpVquDt27dITU3N\ntalT69atAQBHjhwR7Z7Z7l2hUGDXrl3YvHkzgoOD4erqiipVqmDZsmW59p2RU5aWMcQ0GO7a5SIb\nhgZEozWDqoATNIXK4PuffkX35Wfx7azfUDRi7f9FKLagYLtpcAgZCrt6fWAd+B0s/erDvOQ3sKrU\nFAUqN4eZTwDUtq5QWdhCobGAi6uraHft6+uLefPmiZwl4aLIek18yBgIjdXx48dlFyO5brXC3zV2\nzNbWFqGhobK9eYTPVW5htLKy+mCSICaMd6FDhw7IyspCVFSUKM1Qq1YtUcj77du36N+/P0qWLIly\n5cph6tSpfF4LSezyo8L7L1q0KI4ePSqi1WYsrMB7I21jY4PVq1dj4MCBImfaw8MD8+bNk/2dBg0a\nSKrQateuLevYCLs1C6tI2Liza9ZoNLhx4wZ3vh0cHETjKscfIRQWBatUqRKmT5+O58+fi94dljpl\njh8jLWRVJqxT66tXr/gcd3R0lAWG2tvb49y5c8jMzMTu3buxdOlSnDx5Mte8fG6GLyEhAfPnz8ei\nRYtExHWGwrgwjOGEhBFaFiEqUaIET/1kZmZysPPHlAv/L+TEiRNo3bo1SpQogeDgYCxfvpynD5Yv\nX85J6Ozt7TFkyBC8ffuW37ebm5uICGz48OEgIvTo0eODr+NLckTYO26IK2MRwdjY2H/pyvIvX5wj\nYqwUkU1WtpNTKBQ4evQojh07xncKSqUSAwcOxF9//YWZM2eKFnYHBwcsX75cgr9gGhYWlid5mBCj\nYWFhgT59+oho4uUWGLVaDYWpOUwci8LcJxAWpWrqAZ/1+8Gx2Si4dluEQoM3iru2DlwJ93aT4dBk\nBBwrNoRKa8F/s0mTJpKoTMmSJbF27VrOTyFnnG1tbVGnTh0RBiAiIgJE4oZfLi4ufIeb1xgwZaWY\nQmeOXUNevXIcHR05ONHT09MoY6ytrS2OHDmC7OxsSbtz4edUKhVnqBWKTqfDhQsXsHnzZtkKh3v3\n7klSaT4+PvDz84OtrS0vxxYCHJOTk0V9SJgWK1YMT58+5SBHlgYxMzMzWi0ldALYPc2ePVvC+Fm9\nenU0adKEf2b8+PH8et68ecPfH8ZDERcXh7p16/Ln4e3tzSmijXXvFTopGo0Gt2/fRmpqqlHQrFKp\nRKtWrUQRJIVCgfPnzwPQh57ZnBowYIBk7FkDMKEKnWIzMzPe1I1tRAICApCTk8PnjpDn5OrVq5Ln\n4uHhgRkzZvBn7Onp+UGRDTnDl52dLQGaK5VKjBkzRtap0el0nE3V8JnXqFFD9Fnm1EdERIiOs+os\noVMqPP/hw4cxaNAg9OvXD9u3b//o6M3fEcNqEoYvqVWrluhzK1euBNHHEXB9SY4Iq+AcPHiw6Dir\n4vs3mth9qHxRjggjuzE3N8f27dv5As4W4j///JMbBCsrKwD6l0/Ypjs3LVCgADfiP/zwA27fvi2i\nQf7111/Rv39/2NvbiwyGk5OTiDJdWOETGBgo+KwCFarXQcOw/rCt1hb2DQbAtcePUgzG/wE+Xbst\ngmPzMbCv3w+WZevCsXQQTKzfh/r9/Pz44q5UKqFQKHDw4EGsX79edF+jR4/GzJkzRddVsWJFji1g\njpqhstC/m5sbDh06hPv37yM7Oxvbtm0Tfa5QoUJGjRbRe8CvMNyvVCol/WrktE6dOvxzTZo04Tuq\n6OhorF+/njOMsj4is2fPNkpOxaInrq6uop3X7du3RTgjIv3OnIXhs7Ky+FhZW1vnWlot3L2xnYyX\nlxfWrVuHjRs38uvv2rUrN+hsnH/55RccOnRIck5mkNjvsnFs27atKAUjxNgoFAr06tWL8xG8fftW\ntgeNmZkZevbsyee9paWliONGqOz32Vix987CwkJCvrdz507MnDlTklpSq9Ucv2JiYoIyZcpwOQx6\ncQAAIABJREFUB8bU1BQJCQmid/7YsWN8vhibY+PGjePjxq6pRIkSfJxcXV0lwExhPyShoROW6R44\ncEB2UZUTOcPHeruYmpqiXbt2aN68OXf4Vq5cKXuetLQ0DB06VJRuHDFihATwyt7x0qVL83vLzs7m\nlVtCvBCgn8Nype81atTA27dv832fn0IePHjAad0vXrwIQD8O7L03BOjmR74kR+TEiRP8/V63bh2e\nPHnCq5FMTExyJUr7XOQ/74jMnDkTc+bMwc2bN3kOtVevXgDA+RQYkLRfv358sWSEPyz3LFwIhf8u\nV64cxowZI9rtCkvQsrKyeDi5X79+mDJlCjp27IjIyEjs3bsXly5dwrVr1/jvqm1cYOUfgrJdp8G9\nzXg4h82G+4C18BiyGR6DNrznzBixE+79VsKpzWSUbD4AFqVqwsSpKNT27rI4DOHuaPTo0bh48SJ0\nOh1feIQpKUPsgDGgrrARFzMgDMhomFIaPHgwsrOz8fjxY26IhAZ53759aN++vSgaw/4+d+5c5OTk\n8Np2pnmVJRsqM7SOjo58YWZlpMOHDzeKa/D09MTChQvx9u1bHs5nofqMjAxuRFUqFVxcXLiDW6FC\nBeTk5HDHq0iRIkhKSpLMKcNxvn79OgBwXgshCRMrq7OwsJBEj2JjY0XVXWwsa9WqhaSkJB6qZlGr\nRo0a8dLTevXq4dWrV1i/fj2WL18uST2xHXTRokURFRUlG53LDY8i1IYNG4o4W4RqbW3NiQEBvXHc\nvn07Ro8ejZiYGDx8+BBpaWlG8TWGHUPZJmL48OF48uQJ2rVrJ0kRDR8+HCkpKbLPX6PRYM+ePbKL\nI8NeLViwQHScve/GnAU5MTR8Op2OP/9t27bx46xizLCU1VAyMzPx7Nkzo8RWaWlpPCVYvnx5DB48\nmEc8bWxsJBT3zHBZWVkhMjISEydO5FVSrNP1vylsLVer1ahRowa/Nnt7+w/qz8PkS3JEdDod33AZ\n6uTJk//ty8uX/OcdEeGgM5Y/tuu8d++eUVBk69atRd0j5VSlUvHdRE5ODq+eYZ0/N23alCsuQmWi\nwZTFq1G25UA4hA6HW++fBM3UNsG12yI4tRoPu7q9YRPcGXb1+6LVyHmI+mkbKgXVlJzPzs4ODRo0\nQJ06dUS56/j4eKSlpfFyLC8vL553ZSWSU6ZMwYgRI3IFywpLQBkATuiYlSxZkhuozp07S4CWQgI2\nd3d3XmnAzi3El6hUKlEX2YIFC0ocJDmtWLFiriBVhuNh8ttvv4HofRTKwsJCBO4lEu8a2C6YEYoZ\n421gO9IDBw5g/Pjx3OAB7zlpmMPi5+eHU6dO8cWUMa8yR+/x48d48OABevfuLYocGDPmRCQZ++nT\np+Py5cuyZa/W1ta4dOmS6MXPyMjAwYMHsWvXLrx8+ZKX7jKj+NdffyE8PFzEIPrTTz/x8coNe1Og\nQAG8evUKS5cuRe3ateHr64tatWph/vz5HACal7AUm7u7O3r37o1+/frxuSjsO8Pm2Nq1a/mx1NRU\nnn6T67FjZmaGChUqoGfPnrnyDLHyUWGZrhD8/CFVL4aGLzU1lb9fwjTE06dPubPwd+Xs2bOyJddq\ntRpjx44V/S6Lem7YsIEfO3PmDJ8//0aKRijv3r1DeHi4aNNUqlQpEb39h8iX5IgAeod+3rx5KFOm\nDGxtbREQEID169f/25eVb/nPOyJhYWFo27atyGBqtVqsX78er1+/xty5c2UbfeVl8JgKm0X169eP\nG1EhuyYRgVQmMLEvBCv/EHh8NwElB62Cx5DN3PFw6xWHYp2m4tt+k2HiWERiCPN7PUR6hk8hwyYj\nMMrOzubRn5s3bwIAtm/fzn+D5clzI/0iInz//fdYs2YNiPROlxBjoFAo0K5dO7x7945fQ3h4ON/d\nKZVKNGvWDHfu3MGLFy+4gROqlZUVdxZiY2NFlPUeHh5GHRIvL6/cy5L/T4U7TJ1OlytAmRmVn3/+\nGcnJydxxPXTokIi3wVDZGM6YMYPvYuvWrQsAkmonS0tLxMXF8WjG6NGjMX78eJ7iKFu2rAQEzL5n\nrMkYW5CFmAGhWlhYwNXVFd26dcNff/0leuk3btwocmQ0Gg2fN6wC4dSpU0ad7Pr16/M0jpB3xdvb\nm0dNrly58oFL0Xu5ffs2vwch0ypz+ISVM6wfU926dbmzcOXKFZiYmECpVGLFihU8oqfVahEWFpav\n3iuAvrKIpXs8PT3RqlUrPl8M8Qp5iVxEhI05660DAKtXr+Zz4n8hK1as4M+nRIkSIgzVjz/+yD/H\nomhCRtGcnBz+7v/b6RkmDx8+xJ49e3D27Nm/xUr6pTki/3X5zzsiTFj3yNwIlaytrY3mt4n0NdcM\n4MOUUXhnZWWhQsWKUKg1IJUJ1LausPANhnOnWSg0cB08hm9/3/Ok51KEztiNyj2mwrx4Nais7LnR\nnzRpEu9ayvS3334TtbK2tLTkkQe1Ws15MBh+oEiRItwA2NnZ8fBseno6XyhZ6F2n04kqJ5gWL14c\nW7ZskQBsw8PDcfToUZ6/btmyJY+0FC9eHF26dEGlSpV4dMjU1BTz58/H+vXr8eTJE8mClZ2djZ07\nd6Jfv37o0KEDYmNj8f3336NQoULQarUICAjAxo0b8ddff4kiKLmpMG1gbW2NN2/e4N69e/zZG7I3\nCtkt1Wo1Spcujfbt24tYRQMDA7kz4Ofnh82bN0tSIyEhIdyZY7pixQokJibyiIuQn8NQmYNlDNQs\nB8w1MzOTxbQolUpUrVoVixcvxqpVq1CjRg04OjrC398fCxcuxKlTpyQLrU6nw4EDB/hcLFmypGje\nEekjHy9evBBx5zg6OmLAgAGiiBkrv507dy4nEhs0aBB/Nn+HmZHlvA2ZT1mljxCY+ejRI/5Oe3h4\noF69enwcO3ToIJoDuZE7GZMzZ85IWINr1qzJm6TlV+QMH3uvrK2tMXjwYPTt21fEp/Ehcu3aNcTE\nxCAmJkbUu4cxPgt7h7C1snjx4vwYm7csWge8Z0P18PD416jIP5V8dUQ+L/liHJHExERuxOfMmYMS\nJUqIWB979+6NjIwMI71IFNAW9kON3lNQskUE7BsNhluvZXDruRQuXeaj1LD18Ow+Hx4yfVBcuy9B\n6S7TYF2tLer3GA2No97IREREiMpRjeXXS5UqBZ1Oh2fPnvEcrlBjY2Nx/fp1fh+G0RwnJyf8/vvv\nuHnzJs8TlitXTrJwnDlzhlPHazQa7qhkZWVxbIUcLmDNmjV48OBBvtImfn5+2L9/v9Hwu9AhMFQW\nbbKyskJERISkJFqlUuGnn37CgQMHRPThVatWBQCkpKRwx8HDw0Py27/++qvRexRquXLl8PPPP8tG\nzZRKJcaPH88dHoVCwXPtv/zyi9HIljDyxEpYy5Qpgz179hjFk8ilPiwtLdG4cWNJ6WyBAgUkRF/C\nhTYnJwezZs0S8V6UKVMGr1+/BgDepMxYd+hVq1YBeB8RZM+JjQn7L3Pkvv32W9nnn5dkZGTgl19+\nQd++faFSqaBUKvHTTz8hNDQUTk5O/DcNyzVPnjwpencUCgXatm2b7zRQXpKdnY39+/djxYoVH92V\nVM7wpaeny0a0unbtmm+nKScnhzdbFGqvXr2Qk5PD321hZCkrK4t/jm1iNm/ezI/VqlULjRo14s92\n5syZH3XPn7N8dUQ+L/lsHREi+paIEojoJhF9L/ybnCPCCJPKlCnDj+l0Op6yefQsEQeOn4WJkyfM\ni1WFlX8IbGp2gVOrCfAYInYw3PuvhmeHybBvNBiOTUfCsdkoOHecCccG/WFTrS0KVG0FS7/6MHUt\nAf8KFXH8+HEQicsZIyIieAkgM+KhoaGoXLmyqHpBSMbDIh+NGzfmu2AGmjxx4gSPiLDfksMDaDQa\nrFu3DjExMZgwYYKEbpntgN3c3DBs2DAOZjSmI0eO5H1UjKmJiYmkzXeLFi0kgEiW7nFxccHhw4eR\nlJTEW7YbksgR6XeKwjH19fVFbGysqLV68eLFMXr0aBFmxtfXVzLRc3JyRDwWho5Gt27dcOTIERHA\nV9h9Wc4x0Wg0ot/466+/+PUPHDgQAwcOFKVAFAoF/7cwt82iWOw3OnbsKEn9GQKKS5cujVGjRvGd\nrKWlJRITExEfH4+xY8ciLCwM8+fPh06nw7Bhw2TvIygoCFlZWaI0gZBAzdzcHGvWrOHXyRhQ82oV\n0LBhQ1FTunv37mHEiBGoXbs2WrdujR07dkgc5UePHvHKo7y0bNmyEqrynJwcHD16FFu2bPloDphP\nKcYMn06nw++//45Ro0Zh7NixvGQ5v8II2ExNTdGpUyeEhYXxiNDs2bO5gybETbFKIwcHB9FziImJ\nETnqrGfQx0SSPnf56oh8XvJZOiJEpCKiW0TkSUSmRHSJiHzZ34UX3btPH3Tv3h0acyuo7dwwcuYy\n7LnyBCM3X8aAtRfg2iEa7v1WoogMc2ihwZvg0nUB7Gr3gKXft/rW86ZmcHZ25ka/Tp06mDZtGu8d\nolKpJJGLNm3aSGjg80vuFRQUhAULFnD+BpVKhZs3b/LUSOHChbFlyxYcP36c91OpUKEC0tPTkZSU\nhBEjRqBo0aJwcnJCy5YtMXDgQInR+uabb3D06FGeKzdUtmN3cXGBj48PAgMD+S7L0AB37txZUspq\nTB0dHfH8+XM+2Rj75ezZswHoc/D79u2TpB78/Pwk+JX84GjYAvz9999LJnpOTg53AtjOWkhoplar\nERkZibdv3/Ixef36NT+nnCPi5+cn+R32G6dPn+a/y0pHnZyceGRLyMBpSEW+fft2oxEZNhbMEOt0\nOk7KZZhmIdKnitRqNZRKJdavX89BnMz52bx5M29xoFar8ebNG14Gr9Vqeblseno6P//06dNx9OhR\nDB48mF+ng4MDKlSowJ3sPn36ANBHK+TSoT179hQZQUZR7enpifHjx8ty0VhbW3OHadGiRbksa5+f\nfCrDx0gH161bx4+xlEqxYsW4o29ra4tx48YhKiqKz9ERI0ZIzvfy5UusXbsWK1euzDeW5r8oXx2R\nz0vyckQU0DsG/6goFIoAIhoPoP7//TuSiAjAVCKi169f84vym3qMkJ1FpFCQQqXm5zBVEtmZq+jV\ni2eUmHCetLo0epv4hHJSkyn7TSJlv00kXeorMjc3p3fv3sleR6FChejHH3+kZ8+eUXh4OFlaWpKP\njw9duHDhQ+6F1Go1ZWVlkUKhIFdXV/Lw8KAKFSrQihUr6M2bN6LPFi5cmEqUKEH169enpUuX0h9/\n/CE6n5WVFS1evJh8fHyIiCghIYHWrl1LN27cIKVSSQkJCaRQKKh27drk5OREe/bsoeTkZDIxMaGs\nrCyysLCgAgUK0JMnT4iIqEaNGpScnEyXL1+m7t270+nTp+nPP/8kU1NT2XFRKpWk0+lk79XMzIzS\n0tJEx3x9fennn38mhUJBo0ePpl9//ZWGDBlCiYmJtH79esrIyBB93s7Ojt69e0fp6emS83l4eJCP\njw9pNBry9PSkxYsXU1ZWluj7rq6u9PPPP5Otra3o+Js3b6h27dpkZmZGBw4coF69etGVK1ck99Cg\nQQM6cOAAZWVl0Y4dO2jLli0UFxcn+oxCoSAAFBkZSc2bNxf9bdasWbRmzRpydXWlLl26EBFRXFwc\nPX78mNq1a0d3796lEydOUNOmTWnYsGGkVCpp0qRJtHv3btkxHTBgAM2dO5f/JpOjR4+SVqslIqIV\nK1bQvHnziIjIxMSEQkNDydLSkrZu3UqvX78mIqLAwECaM2cObdq0iaZNm0ampqaUmZlJ/v7+lJyc\nTHfu3KE6derQ1KlTiYho8ODBdPToUTI1NSV/f3+6desWJSYmko2NDW3YsIFsbGxo3LhxtHv3bmrT\npg0NHTqUiIiuX79OHTt2JI1GQ3v27KEuXbrQ3bt3KTAwkFq0aEF37tyh2NhYysjIoLlz51JAQAA9\nfvyYmjRpQlqtlrZt20Z2dnZ048YNat++PRER+fn5UXh4OFWuXJn2799P48ePp6pVq/J7/v9Zqlat\nSjk5OaL5kJGRQUFBQaRUKunYsWM0fPhwOnbsmOh7FStWpFmzZvHvfJWv8m9KsWLF+P9bW1srDP+u\nNjzwD4kbET0Q/PshEVWR+6B3WgJBqSb3Qu7kV8SOrDVK0qoV5GalJktTJSUmgtotX0mPX72S/SFD\nY+vm5kb29vZka2tL6enpNHHiRNJoNESkN4QXLlwga2trat++PZ09e5bOnj1LRHrjZGNjQ+XLl6dT\np07x87q6unKj98svv5C1tTXNnTuXiIiaNGlCu3fvphMnTtC5c+coJyeH7t69S3fv3qW9e/dSWFgY\n1a5dmw4cOEAZGRnk7+9P7du3Jzc3NyIiOnLkCI0YMYJycnLEY+LtTVOmTCGFQkHNmzenli1bUlZW\nFlWoUIFmzpxJZmZmtGfPHho3bhxdvHiRypYtS0REsbGx/BzZ2dmiczLDpdPpyNbWlpKTkyVjyZyG\nYsWKkYeHBx08eJD+/PNPmjBhAv3555/0/PlzIiJasGABpaenExGRi4sLd4qIiJKSkoiISK1W8/MV\nKFCAcnJy6P79+xQdHU3e3t5ERFSpUiWKi4ujs2fPkomJCTk6OpJOp6MhQ4ZQzZo1qWXLlvTmzRta\ns2YNnTlzhpRKJaWlpdGqVavoypUrZG9vT61bt6ZFixZR4cKF6cmTJ7Rnzx6qVq0aHT9+nEaOHEk9\ne/aky5cv07lz5/g1AqA2bdpQs2bNJGPQvXt3io+Pp2vXrlFUVBQ/XrJkSerevTvdvn2bzpw5Q1u3\nbqWDBw+SUqmk169fk0KhIFtbW37/THbs2EFEeofxt99+43ONPZ+cnByRkRk+fDg1bdqUiIhq165N\nnTp1IqL387xJkyZ09uxZOnjwIBERd6oLFy5MQ4YMoTt37tCsWbPo5MmTRESUmZlJp06dIiKiIkWK\nUFRUFNnY2BAR0Z07d4iIqG7duvz3S5QoQR4eHnT//n2KjY2lu3fvEhHR1atXqUiRItS9e3fKzs6m\nxYsX0969eykgIIDPC09PT7KzsyMi8fxTq9UUFBRERMQNp+H8/P9VXF1d6cGDB3TixAmqVasWERF/\ndq6urmRiYkIxMTF0+vRp+v333wkABQQEUFBQEKlUqn/z0r/KV8m/yIVJPrUSUSsiWir4d0cimsf+\nnd+md0zkaLTlVKlU4urVq0ZTDwwHwUp6GaaD/i/cHx8fL8JKCEPS69ev5/lX4XWnp6fzUGmbNm2w\na9cujBkzhqcmjNXJP3v2jOMnunbtilOnTomqMfbt28c/yzAqS5Ys4cd0Oh1PMbHwLZG+4mTixImi\n+2Ygx/yWPa9bt47TL3+oCstV2fjVrFmTg/p++eUXyVhcu3ZN0v2YSI+jkMMzsPuoWLEifyZLly7l\nnCFRUVGy/DMODg4YP368qHmcnKSlpSE2NhZNmjRBkyZNEBsby1Mp9+/fR0REhIgvpGTJkti+fTsS\nExNlK2QKFCiAMWPGiI55eXkhIiKCl1Cze2Kl3GfPnsWZM2dElUFTpkzBgwcPsG7dOj5Pg4ODsXjx\nYqSkpIgqj9RqtQgwO3HiRAmug1U5sb4t7P5Ysy2551uxYkVeUhoSEgJA396dMWeyUuP09HQ+b6tW\nrYrMzEzcvn2bp0inTZuW6zP43ORTpQIYZ41Wq0X37t3Ro0cP/mz/jXbu/xX5mpr5vORzxYgEENGv\ngn9HElEk+/eHOiJCzIRhKZ5Qo6Oj8f3334NIj834+eefsWrVKhHIkYiwevVqDgBUKBQcv8D4KtgC\nfuTIEV6iV6pUKQ6cFXa+ZI3NSpcuLVroWfM01sjq+fPnWLZsGWbNmiVhj6xRowZu3rwp4svo1q0b\nAODPP//kx4QtwoW9Pwwp3w31m2++kVRq5Kbdu3cXVWio1Wps374dd+7c4TgRpuXKlcOaNWs46JI5\nYL6+vhxvEBsbyysyhCykTBjgNjg4GIcPH8bmzZtFVUo1atTAb7/9hg0bNoiAwkxZhUHdunVBpOcU\nefLkCYYPHw4/Pz/4+/tjwoQJSEpKytd8kxOdToeRI0dK8DtdunQRgQFfvnzJnQtjjLeGRt7BwQHl\ny5cH0fvyy7Nnz2L+/PkS506orVu3Fs25gQMHgkhfNfHixQtkZmbyqh4hSZ7h3FWpVOjRowcmTZrE\nG+ex+alSqaBQKLBkyRL+N9bfZdKkSfxczAm0trZGeHi4pOuwsLTZ09NT1Jn3vyCfyvBlZ2fzajih\nhoeH/+skZJ+zfHVEPi/5XB0RNRHdJqKi9B6sWor93dARSU5OxtSpU/HNN9+gbNmyaNmyJXbs2MEX\nTkOyKGtra0lzNEapzAzo0aNH+SBdvXrVqNFlC6i3tzffRYeHh3Mje+TIEdEiykivmDBaem9vb+za\ntYsvHnPmzAGRPtoxf/58o83fmLHy8PAQdWt1c3NDnz59RA6Eg4MD4uLicPDgQW68K1Z8X/VjSG/P\ntFixYpxplSkbp9zKYdk1BwYG8vt9/Pgx//umTZv4cWNtwMuXL893wWXKlJHsyl+/fg2FQgG1Wo3R\no0fD29sb5ubmIudRSAG9f/9+flylUmHEiBH4448/ODGWRqPBixcv8nht9HLz5k0cOHAgX222GXcD\nI3xr0aIFd7qEDiKgrzKRIzgjIlHkx8PDAytXrkRqaipvREekjzTUr1+fj//YsWOxfft2BAcHw8HB\nAWXLlsWcOXMk9OCMXfP333/nx7Kzs3mUxLAaRafTcUdbqCzSVrp0aVGFkzBiZ29vL+qB8erVKw5Y\nZWppaYkBAwagVKlSfD61b98eu3btwq+//vqf6KHB5FMbvosXL2Ly5MmYPHky78fyVYzLV0fk85LP\n0hGB3hlpSEQ3SF89M0r4N+FFP3361GgTMx8fH/z000+8PwrTggULSnbGrq6uAMCjGcJFLi0tTbIL\ntbe3F6V8Fi9ezI3f1q1bJVU0RPr0DVskdDqdaJFmWr16ddy9e5dX7QwaNIj/LTg4WHQdSqUSSqWS\n/9aUKVNkDVjt2rUlizz9n0N27tw5pKen812zg4MDTp48iUmTJsmOqVzI3dTUVMKgKkxLTZgwQTTp\n2N+8vb2xYsUKTJ06lacQwsPDUblyZcnvuLu7i4iamDBKbGNOFBGJGtgxp9IYRbmhUyAnjx8/5tET\nofHPjeSKzRVhszHGolmsWDHJ5+/du4du3bpxR1KlUnE+j2vXrvHnLCzLjI6OloxDeHi4pKGbMWHP\nUMgmnJKSIlvpI5TLly9j1KhRGDhwIDZs2IADBw6ASB8FzMjIQEREhIiHxsbGRkI5z4RFclatWsV5\nTgB9Z+ATJ06ImHXVajV69Oghafj2OcpXw/d5ydfn8XnJZ+uI5KbCi+7WrRs3ykT6MHRufTCMqUKh\nEJVCDhs2DDqdDjqdjjdj8/f3x5IlS0RGVqvV8vx5ZGQkiPTcFqtXr0arVq34Auzu7i7CFjDeE1NT\nU0nqh4W1ixQpgpCQEBDpacE3bdoEIuI8F4YlrWwMChcujJiYGEybNg3Hjh2DTqdDZmYm7/1RuXJl\nREREiHbybNdpTE1MTDBkyBAkJSWJQsGVKlXC2rVrceLECfTo0UPieBHpOU/mz5+P9PR0xMbGGnVo\n2rZtyyNC9+7dw+TJkzFgwAAsW7YMKSkpuHXrFiZMmIBevXph4cKFeP36NXQ6HcdbaLVabNu2DQ8f\nPhR1DK5WrRouXryI1NRUXhbavn17rFmzBsHBwfDy8kKjRo1EuBpjkpWVxSM0FhYWCAoK4s84ICDA\nKAMl+4zQuGZmZvJrNMbVsGjRIhDpO+oKhfXpGTZsmOj4kydPEBsbi+HDh2PDhg3Q6XRITU3NFxcE\nwwp5e3vj119/xcWLF3lpMSOOy4+kpaXxKMqECRPw6tUr7N69m2Oh4uLi8n0uJo8ePeIl8S4uLqhe\nvTqPKLEml5+zfDV8n5d8fR6fl/znHRG5nbBhGqN27dqifiYajQbW1taoUaMGb4Dm4OCAU6dOYd++\nfdxIFi1aVBRt2bhxIwB9y/SdO3di69atIsbCpKQkWYPu6OiIGzduiAaeMYwuWrQIqamp6Ny5s+he\nqlevjlu3bvEdYHx8PN9p+vj4cOPbr18/UXqkcePGuH//fp4PPjs7W5bHwcvLC0qlEvb29hg4cCA/\nd3R0NAA9huHQoUPcqNjb22PWrFnYunUrxxjY2tpi6NChEkdJ6HyMGzcOMTExaNq0KTp06IDt27fn\nSiO9bNkyCbdIwYIFcfHiRc6vwo4Zc0TZ9Zibm390LxTWadfDw4OnfB48eMDH4/Dhw7LfMySoA96z\nvbq5uRn9vZ9//hlE0pQe60w8duxY2e+dOXMGQ4YM4ekQlUoFW1tbdO3alQNaDeXNmzeSFBxzuBgv\nSn6FkZ8ZapUqVT4qgjF27FgQ6Xl9WITr9OnTHOT6MR1Y/0n5avg+jeh0Orx48QLPnz//IL127Rqu\nXbv2wd/7qn9fX7x4IVnr//OOiHCRCwkJ4X0vhBodHY2UlBSeX1cqlQgJCRE5J0y/++47rF69WlTV\n4OTkhGXLluXrxXj16hUmTZqEChUqoEyZMoiIiMDBgwcRHx8vShEwMGVkZKSIMpxFNRiZEHMQfvjh\nBzx48EDEpqpWqzF+/HhuYIUhdWOybt06Dmy0sbFB//79kZyczBkavb29cfLkSbx48ULUcj4mJkbU\nS8SYKpVKzJw5k99HvXr1ULZsWe6EaLVa/Pjjjx/UuyIhIYE7Id999x1mzZrFK5t8fHzQp08fEL0n\n6RKOD/tNdszT01PEZvuhwqpXIiMjRccZuHj69OnYvXs3QkJC4Ovri5CQEOzZs4f3F7K0tMSgQYMw\ndOhQHlkzTF0JxyYxMZGP+ejRo3Hp0iXMnj2bP/PLly/LXifr9CunNjY2Rr/3+vVrjB8/Hr6+viha\ntCjCw8NlU2L5kW3btiEwMBCmpqZwcXHBiBEjJO3n8yusB5SwOywABAYGgkjfBflzlq/lcc8zAAAg\nAElEQVSOyKeRFy9eSFh28yMpKSmiooGv8s9JWlqaBIf3RTkiGo0GLVq0kFQbsNx6REQEN5bCv/v7\n+6Nfv348Fz5lyhRkZWXhzJkzOHny5EfnoPfv38+ZD4kIzs7OiI2NBYA8qdUZYJD1AREaernP9+3b\nF3/88UeuAD7WJdZQ/f398eLFi3yVOSsUClFjQY1Gg0KFCsHOzg4hISH4/fffeWSka9eu/LefPHnC\nUzV5lb8aCkt5derUCa9fv8bhw4dx5MgR7khOnToVRPqo1vLly0URERMTEzx69IhjXqpVq/YRT/K9\nsNbwTZs2FR1n4GdDllSmjRo1EtHQM23atCkyMjKQk5OD+fPnw8fHBwqFAoULF8bUqVORlZXFq18M\nlVVUGcqjR49E0SMfHx/MmTNHBFw2jLB87sL6KI0fP54fS0tL45Goj+0B80/JV0fk04iQuflD5Ksj\n8u+K4XP7ohwRYxoSEoKMjAy+i54zZw4KFiwIInEr7F27doFIvmnah8q5c+d4iqhgwYKictKxY8eK\n6NbVajVq1qwpSs2UKlUKAEQN3gx3+1WqVEGzZs3QunVrEW6lQYMGkgqH1NRUnmP/4YcfkJ6ejvPn\nz/PrWrp0KZKSkjB48GBRBIGVXxr+vkaj4Z09O3XqxBfZ69evcypwQ84PZqx37979QWPJOt6GhoaK\nSlEZX8KqVatQp04d2XEaPXo0AH2FC5EeqwPosR67du3CkiVLeI+Z/MijR494NKJ3797YsmULx8xo\ntVoolUooFApERUUhPj5elDZiam5ujq5du4p+V9jgT6jfffcd75obGhqK4sWLo06dOhz/ISeMw4U9\nx/379wMAhg8fLjp3y5YtPzpF9U8Lq3YyNTXFmDFjsHbtWtSoUQNE8tVUn5t8dUQ+jXx1RP6b8v+l\nI0L0vuzR2toae/fu5U6CsG29EDz4dxc2xukRHh7OG4ux8HxuyoCQbMcrdDzKly+Pjh078l3gypUr\nRQasaNGiPIxftGhRURj88OHD/PxC+fHHH/lO/vbt29izZ0+uxGX29vbo3Lkzrly5wsuFK1asiLVr\n10qI4EqUKMHTUU+ePOFOhCFeJi9hfXeY+vv7i3hK1q5di3fv3iEyMlJEYDZo0CD+HNnY16xZE+fO\nneOcFkzLly+Pe/fu5et6YmNjJWOkUql4v6DWrVsDAHbs2CFx3tj/Ozg48Egbc5LUajXWrFmD9PR0\n7Nixg4/Xh+Az3r17xwHXTIOCgnD16lVRA0GmFhYWOHPmzAc9j39DdDodj2gK1c7Ozijp3+ckXx2R\nTyNfHZH/pnxxjoixVAWRtDLDEOxIRJg/fz4fDEbs5e3t/bcHmmFMrl+/zo8lJSXx3xUaC3ZdGzZs\n4NUQxq67fPny3Ki2adOGNzRju95nz57xihHhvf32228g0kdahE4WS9cYGimVSoVff/0Vt2/fFjHI\nBgcH8++y6wgKCuJhfxsbG1EKws3NDf369ePlpvXq1QOgbwa3du1afPvtt/D390fXrl2N4hYeP37M\nn6WLiwvatWsnairYvn17/llh9ZKZmRk6derEGUCJ9GR0zCktVqwYwsLC+LWVK1cu3w5ofHw8evfu\njQYNGqB///64evUq54Tp378/AHCgMXNAoqKiOGEec6AA8NTLd999J/oN5mQaAlKzs7ORmJgoW5Yr\n1yyOSFqu7OXlhZYtW/Ln918QnU6HQ4cOITw8HKGhoZg4ceJ/hkvkqyPyaeRzcESUSiX8/Py43rlz\nB2fPnuXrwE8//YS+ffsCALZs2YI//vjjf/K7/2X54hwRY05I/fr1ce3aNclxrVaLKlWq8DSIQqFA\n69atRWyl5cuXh4WFBczMzNCsWTOjBjI3YUZo7969/NiSJUv4ddy/f587UcyoNmnSRBYM6uLigkuX\nLvFdPMMhsLC/0DkA3kc5hIZNWFI5btw4vHz5EkeOHBGBXwsUKCBKy7C0RnZ2Nr9WW1tbbNiwAVOm\nTOFcLIynJSgoiEeYxo8fL7mPSpUq4enTp9DpdLxaSaimpqYiXgwm9+7dA5EUH8NAtz4+PqLPZ2Zm\n8uiE0LGaMmUKFi9ezK+FRWuSk5P5OBiresmPHD16lI/RpUuXuAPJom/Hjx/n3X3ZcwCABQsWcMcy\nJycHly9fRnx8PAfAMkckKysLEyZM4I6UpaUl+vfvz8eczXczMzO0a9fO6LtBpCeTe/PmDX/e+SVx\n+yofJ18dkU8jn4MjYmFhkevfhY5IWFiYBHCdlxgSD34J8sU6IoYEYlevXuU7Y6E+ePAAgL4nhhzd\nt5wjYGlp+cFshQwcWahQIaxcuRLbtm3j9PKMPM0wZ5+bFilShH+eOUwsZeHj4yPayTOWUEbzziQu\nLs7o+YODg/H27VsRUZdKpcKCBQtEKSJDrVq1KseKCFuRA+Cpmm7duuHAgQOcy2Lfvn0g0mMl5s2b\nh2PHjvEqD1dXV8lOPzk5mbepX7lyJZYtW4azZ89yLpaAgADZZ3DlyhXMmTMHixYtwqNHjwC8jzKw\ncmQmDOexcOHCD3rOQtHpdCLiOGFErnLlykhPT8e5c+f4MVaJdevWLV4xJWROZd9nqZPu3bvzvwl7\nyNSsWRM5OTn8+bZq1Qpnz55FdHQ0/Pz8RA5c4cKFeRl6RkYGP8+TJ08++H4zMjJEqc2vYly+OiKf\nRuQckezsbCQlJSExMRHv3r2T/d6ndkQOHz6MRo0aAXjviBw/fhy2trYoUqQI/Pz8cPPmTdy8eRP1\n69eHv78/goKCOJA/LCwMgwYNQnBwMAYPHvw/uc7PSb5YR8RQjeEcBg4cyI02Yy1t1KgR5s6dyxur\n1atXD3fu3MHDhw/RrFkzEOn5C3r06AFnZ2c4OjqiQ4cOorSLoaSkpCAgIED2GkxNTXlVzMiRI41e\na4UKFYw6K35+foiLi+NphfDwcBw/fhwLFizgDpYcQdfOnTtRvXp1mJmZwd3dnfNM7Ny5EwAwffp0\no2Oq1WoxdOhQUVpEONZRUVH8dzIyMniUwXAB7tq1K4jEFRA5OTm8B8mhQ4ck183SK+XKlcOqVasw\ne/Zsnk5asGCB0edgKOz+GjVqxOdBVlYWTydt37493+eSk5SUFPTs2VMUWRI6ucyJ1Gg0IgyPsE+Q\noW7ZsgV//fUXnzt79+6FTqfD+fPnueOyd+9eXmFVuXJlnDlzho977969+blq1aqFp0+f4t27dxwI\n/aFgzzt37qBVq1Y8qujn54fNmzf/rXH70uWrI/JpxNCgNZ//OxrO2IcGP/zKNXT2QbRefBytF5/g\n2nLhUbRceFR0TE7zI8LUDKumk3NEAGlEpFatWhwzd+rUKdSsWZN/rlGjRl9sv6D/bxyR3JTtehs1\nagSi91gKhnMQgimfPXtm9DzW1ta5Vh2kpaVhwYIFqFOnDr755htMnDhRFDL38PDg4fvSpUvjp59+\nApG+xJRVwURGRqJFixZGr8FYp9Pq1atj7969eYb1GHMrG5Pk5GRRdEl47sWLF/NrcXR0RMOGDUUM\nphqNBtHR0di1axcf2+LFi0uMXJs2bUAkpjsHgODgYKPOwL1792QbFjZu3DjfFOaAHm/CnISQkBDM\nmDGDO4zu7u4fdK7cxLDs2tBxMzTcrJzb1tYWKpUKnp6ePLrCGH2J3gNhmbBeL0OHDkVKSgrnUmna\ntCkWL16MqKgo7jCw+S1s1KhQKLgTmh959uyZiGNHSB7IMC9fRSpfHZFPI0KDlpqaioYz9M5HyMwD\nCJ19kDslobMPfTJHJL8REUDsiLx9+xZarVaELylRogT/3M8///y3xuZzli/OETE0wr/88kuejohW\nq+UYBVNTUw54Yws1a0XOBox9LzAwEJcuXUJCQgI3tI0bN/6gB5CZmYnhw4fzkLharUabNm3w/Plz\nbNiwAUT6NEluaRRnZ2dZzg+tVivi+GDGdfXq1ejXrx8CAgLQuHFjUeknS2/Y2tpi8eLF2L9/Py+z\nZWPr6+uL1atXc9CoSqUSlQsbUysrK94t99SpUwgNDYW9vT0f51KlSvEJuX//fs6SaQyAmJycjBkz\nZiAkJAQtW7bE1P/X3pnHVVWtjf+7DogDTqkpSjkgesVEEEXRtNS84hR6IXK4mZrXvKn1ateuU4Ne\nLelWkml0zSnxqpVTds2Bur2OaT/wF+YUSopzWSoiCAjyvH+cs3fnMBgIeEDW9/PZH9hrr7PXOnud\nvdezn/UMc+fKZ599JidPnizSGKxfvz7PElzdunWLHD30dhguzC+99JJERESIj4+PKSQEBATkqW8c\nMwLZiVgFWWNZxbD76du3r8PnjHxF06dPFxGRTz/9NF+j7BkzZsgPP/wgISEh5jkDAwOL7EptCD6d\nOnWSM2fOSEZGhhn1tGnTpvfsG1xx0YJI6WA/oRlGoqdOnTKfb2lpaRIbGytxcXEOL2XOWJoRcRRE\nrl27Jh4eHvme805sScoT95wgkvuBayylGJsRayI/rYFSyuGt3EhRHxwcLKdPn5YLFy44aCMOHjwo\nR44ckblz55reDy4uLnf0Fn3jxg1JSEiQy5cvy/Llyx00C4C8++67smXLFgkKCnJY469du7apOalU\nqZIZB8Q+qqi7u7uEhoYWmAwQrMHGcnJyJDs7O881A6vh6jfffOOwfLBv3z6Ha9mxY0d5+umnzWtc\ns2ZNCQsLkx49eshLL71kxjKJiYnJE+7d2CpXrmxmawXkhRde+N1rd/jw4TyCWGhoqEMel9/j/Pnz\nEhERIRMmTJCFCxeWeFp54/saGaJFxDRUtVgsebRExhKZfdbnhIQE8zd88eJFU/sQEREhJ0+elGXL\nlpnaHftJ7rvvvpOBAweKr6+vhIWFydatWx3aSk9Pv2PbDsPuZ/v27WZZdna2GZfndsuVFRktiJQO\n9hPasWPHJDY2Ns9z4PDhwxIbG+sgeDhLEJkwYYJDrqXOnTub8ZZycnJMW0QtiJQzQSR3bgwjFLR9\ncLBGjRqZQob9Zm9bcOTIEYmKirrtm74R3TH3VhyDvYKy3ObejGy8ISEhphp/3rx5pubE3h34wIED\nImK10zCEBB8fH/nqq68kMjLStCExPHqysrJkxYoVEhwcLEFBQTJp0qR8tQwXLlww2xg4cKA5mRrL\nO/CbMbBBTk6O6UH0l7/8RZKSkmT37t15lllq1qwp06dP/92lpOTkZNP2pH79+tKrVy9zMi6qdqo0\nMWw37GN0GIaqdevWzVN/ypQpAlaj69WrV8v69etN4XTUqFEiIvL222/n+9sYO3ZsnvOV1sRnhFS3\nX1rKyMgwtVwF5bGp6GhBpHSwn9ASExMlNjbWNEwXsWqg4+LiJDY21iHFhrMEkT179oiPj4/4+/tL\nYmKinDx5UoKDg6Vt27bi4+NjpnvQgkg5E0RyP5SXLl2ap8zb29tBMDESzr3++uty/vx50zbB2OrV\nqydVqlSRypUry6BBg0zhBqxLOU899ZRDrIzXXntNjhw5Ihs2bJDY2NhCG/5dunTJfMtdtGiRpKen\ny9dff23GfFBKiYeHh8yYMUN27dolYLXNMBLrxcbGmjE+jJgQ9m+le/fuddAYGPzjH/8QQEaMGFGo\nftpjBFOrVauWTJw4MU9un9yGpsePHzcnX3vNkb1h5aFDhyQtLa1Q7RsxNzp06GB+JjEx0Qz+VVZ8\n9A1DaC8vL1mxYoVER0ebWZbz0/okJyeb7si5f7v2Hi2bNm2Snj17SqNGjaRTp06ydOnSfDPrltbE\nZ3hqeXt7y44dOyQxMdGMfFseIpw6Cy2IlA72E1pycrJ5nZOSkuTixYvy/fffS2xsbJ4gijqgmXO5\n5wWR39tGjhxpGgG+//775sO/Zs2aEhwcbHqEtGrVypw4jx075rA8YvxvCDe5s/22a9dOEhISChyE\ntLQ0SUhIMDOUPvbYYw7HDUHBPr15Tk6OBAQECPwWnMpYlnF1dTVTuCulzEHeunWr2acJEyaY54qO\njhbImy+lMOSnWXJxcTGvQe4b3oht0bBhQ4cJ0winX5DrbUEYtj32wdpExIytYuQVcjZXr17NN5Ot\nn5+fXLlyJd/PpKamynvvvSePPfaYdO/eXSIiIu54yai0Jr6UlJR87ZPc3Nzy9XbSWNGCSOmQe0I7\nd+6cea2N7dChQw7aEBEtiDibe14QUUqJt7e39OzZ0yGapIeHh/zzn/80YzFUrlzZjKTq6elpXpgr\nV66YE/zGjRtFxCoEGMalhn1Ejx49zABWYDXM7Nevn6mSb9KkSR4f9szMTHnppZfynKtbt24O9WbN\nmiWAjBs3zqE8MTHRwZ7COEenTp0chKHAwEBZuHChQ1CvDz74QESsE6Sxzv/WW2/9/i8mF/v37zfb\n9fPzkwEDBpheFLkDq4lY7QeMQGyvvvqqpKeny6lTp6RDhw6mNklE5OjRozJ16lR55pln5L333itw\nAjaWMMaMGePQhuH6ax9AztmkpaVJVFSU9OvXT/r27Svvv//+XXv4lebEd/XqVZk+fbo0b95c6tev\nL2FhYRIXF1cqbd0raEGkdMgvjkhaWpqcPXtWkpKS5Ndff81XY6gFEedyzwki8+fPl6SkJFmwYIFY\nLBaxWCxmzpCbN29KZGRknoicFotFVqxYIREREfmqyg1D1GbNmknNmjUdPj9jxgwzR4ixZm+xWMx1\nyevXr5tLJ7ndr4ygWYagYn/e+fPnS2pqqsTExJieL/l5NGRkZMjHH38s/fv3z6OJ6d+/vxlXJL/N\nx8fHXMJo2LChzJs3T7p37y4BAQEyfvx4B2+h2zFv3rw8xr+NGzcuMFfLmjVrzHr2S2SNGzeWX375\nRebPn5/nfA0aNJCDBw/mOdehQ4dMQej555+XVatWmZFdS9L9tryjJ76yhR6P0qEsRFbVFJ17ThCx\nx/BwyR0dMz4+Xp577jkJDg6WcePGmROcYU/y6KOPOqxtG8aVBW0eHh4SGhpqekbkdsc0lkkmTpxo\nlhmJzeyDmZ06dSpPcDBj69OnT76SvD3Xrl2TNWvWyJIlS8yloOTkZFmwYIGMGjVK/v73v0t8fLxM\nmTLFIWttt27dTDsZ+6169eqyb9++27ZpcOLECZk1a5ZMnDhRZs+eLXv37r1t/Y0bN5rLYG5ubjJs\n2DA5c+aMfP/992b7o0ePloULF5qRWlu3bp2vzUF+RpvVq1eXnTt35qkbHx8vERERsnjx4nKTl6Qk\n0BNf2UKPR+mgBZHyyT0tiBheLfPnzy/Uxbh69ao5Qffq1UseffRRh+ytYI3kaT+J57f5+/s7CA2G\n4egbb7xhln300UcCVvdie+bOnStgNZB1dXWVxo0by8yZM02tS0mRkpIicXFxkpSUZLr/1qtXT6Kj\no2XXrl1m5FI/P78iGxwW5SF748YNB88Yw6jT3vMjPT1dGjVqJIAZhyQ3cXFxMn78eAkNDZVXX301\nj7fOL7/8ksd92WKx5Antfq+iJ76yhR6P0kELIuWTogoirpRx9uzZw8MPP8z27dtZu3YtAL169SrU\nZ2vXrk10dDRPPvkkX331Vb51vL29iY+Pp379+ly6dMnh2MMPP0xCQgLx8fEMHDiQ8PBwduzYwbp1\n63B1deXPf/6zWdfd3R2An376yeEcxv7IkSN56623Cvel74AaNWrQvn17AD755BMA5s6dy/DhwwEI\nDAzE09OTgwcPcvz4cf7whz+USj+qVq3qsH/x4kUAgoKCzLIqVarg7+/PhQsXzOO5ad++vfl9cpOd\nnY2/vz/nz58HwM3NjZs3b5KTk8OUKVNo1aoVISEhJfF1NBqNRlPKWJzdgd+jW7duVKlShb59+5KR\nkcHIkSNp3bp1kT7v4uICQPPmzfHz83M4/t///heAAQMGmGVKKQD27dtHdHQ01apVY/PmzYwYMYLl\ny5djsVhYtGgRjRs3Nj8THBxMjRo12LdvH5MmTSIuLo758+fzwQcfAPDkk0/e2QW4A9LS0gBo1KiR\nWValShXq1asHQGpq6l3rS5s2bQBYtWoV2dnZACQlJbFjxw6H40Vh48aNphCyZMkSMjIyiImJwWKx\n/pzffPPNEui5RqMpb9y4cYPt27ezdetWrl69WiLnVEqZL3RgfRG6//77HeaMe5mkpCRWr15duo3k\npyZx9paf14ybm5u8+uqrRU6ZbOTw6NOnj4j8FnTKMJ40DErtbTl69+4tSilRSklmZqacPXtWXnvt\nNRk8eLBMnjxZjh49mm9b0dHR+UZ4LUw00ZLEyErcvXt3SU5OlpycHNOl97777iswY2VBFEftfPHi\nRTOInLe3t4SFhZneTgMGDLijcxpJ9SpXruywzGRkFr7vvvvu6LzlCb0UULbQ41E6FGVpZvny5Wbg\nPbBGLJ49e3axY9+4u7uLv7+/+dzcsmWL+Pn5mQHN7iZFnf9KAvvgbYWlqEszZV4jEhERQZ06dbh5\n8yZubm64uhZtNenatWsAeHl5AVaVf0hIiNVABsjJyQEgOTkZsC6xuLq6IiJ06dKFWbNmMXHiRK5d\nu8bLL7/MW2+9hY+PT75tDR8+nL179zJ48GDatGlD7969+fTTT3n33Xfv6LvfKRMmTKBevXrs2LGD\nRo0a0aRJE55++mkApk2blmf5pDTx8PBgy5YtPPjggyQmJrJ+/XpSU1Pp27cvK1euvKNz1qxZE4DM\nzEzi4+PN8qSkJABT86PRaCoGMTExjBo1iqtXr9KuXTs6d+5Meno6r7zyCosWLSr2+fv27csXX3wB\nwJo1axg6dKh5LC0tjWeeeYbAwEDatWvHpk2bAOvzqFu3bgQEBBAQEMA333wDWJerH3nkEfz9/WnT\npg27d+8GoHr16uY5161bx8iRIwHrsv6LL75Ijx49mDJlSoHtffTRRwwaNIjHH3+cZs2asXDhQubN\nm0e7du0ICgriypUrAPz444/06dOH9u3b061bN3744QeznRdeeIEuXbrg5eXFunXrAJg6dSq7d+/G\n39+fyMhIjhw5QseOHfH396dt27acOHGi2NfX6dqP/Lbcxqpbtmwx36iLihGxtG7dupKYmCgi1hwf\nRhj0grZKlSrlSZymlJLFixcXuQ/O4PDhww6eM/fff7+88847d/R2UBJve1lZWbJ9+3aZM2eO9OnT\nRzw8PMTLy0umTp1a5KBeRk4csMZ3efbZZ6V9+/ZmmX1o/3sV/QZettDjUToUViNiaENnzJghIlZj\n1X/9618C1ujHxdGKuLu7y8GDByUsLEzS09PFz8/PQUswbdo0WblypYhYHSRatGghqampkpaWJunp\n6SJijUDdvn17EbF6Bc6ZM0dErDGSjHxf9qHk165da0bGHjFihPTv399MOFlQe8uXL5fmzZtLSkqK\nXLp0SWrWrGnGl5o4caJERkaKiEjPnj3NwJT79++XHj16mO088cQTcuvWLTly5Ig0b95cRPJqRCZM\nmGAGlszMzMxXw35XNSJKqZlKqfNKqXjb1s/u2DSlVKJSKkEpFWxX3sdWlqiUmlqYdgICAgDyGJMW\nhq5du9K9e3cuX75Mq1ataNeuHb6+vty4cYOAgACOHj3K/v37+dOf/oSrqysWi4WePXtStWpVMjMz\nCQ0NZdWqVYwZMwYR4bnnnuPMmTNF7sfd5qGHHmLnzp2cO3eOo0ePcu7cOV588UXT/uVu4+rqSrVq\n1ZgzZw7btm3jp59+4uTJk0RERNCtWzdSUlIKfa6goCBGjRoFwPXr1/nwww85cOAAAI888gjPPfdc\nqXwHjUZTNvnuu+8AGDt2rFk2dOhQKleuzMmTJ7l+/Xqxzt+2bVuSkpJYs2YN/fr1czgWExNDREQE\n/v7+dO/enYyMDM6cOUNWVhZjxozB19eX8PBwjh49ClgdB5YvX87MmTM5dOgQNWrU+N32w8PDTVvH\ngtoD6NGjBzVq1OD++++nVq1aPP744wD4+vqSlJREamoq33zzDeHh4fj7+zN27FgHh4FBgwZhsVho\n3bo1P//8c7596dy5M2+88QZvvvkmp0+fLhENe0kszUSKiL9t2wKglGoNDAEeAvoAUUopF6WUC/A+\n0BdoDQy11b0tixcvBsDf37/InVNKsXHjRoYMGYKIEB8fT1ZWFv369eONN97g1q1b7Nmzh/r16/Pa\na69x6tQpnn32WVJSUggMDGTdunUMGzaMDz/8kPDwcLKzs0vfcKcE8fT0xMfHBzc3N6f2Q0SYOHEi\nGRkZDB06lISEBHbt2kXLli05fPgwCxcuLNL5lixZwrJly2jTpg21atWiRYsWREVFsXPnTqcJWxqN\nxjnUr18f+E0gAUhISCAzMxN3d3eqVatW7DZCQkKYPHmyw7IMWJ9t69evJz4+nvj4eM6cOYOPjw+R\nkZE0aNCAgwcPEhcXx82bNwHry9KuXbvw9PRk+PDhREdHAzg8tzIyMhzaMLwyb9ceQOXKlc16FovF\n3LdYLGRnZ5OTk0Pt2rXNz8bHx3Ps2DHzM/afF5v5Qm6GDRvG559/TtWqVQkODubrr78u/EUsgNJy\n3x0IfCwimcAppVQi0NF2LFFETgIopT621T1a0Ilat25tXqiBAwcSFxd3Rx3629/+xsiRI/nxxx9Z\nu3Yt27dvZ8uWLXnqzZkzh759+wJWrxPjTRugbt26ABw6dOiO+1GeKc53/vnnnzlw4ADu7u6MGzeO\nlJQUqlatyl//+ldefPFF/v3vf9O7d+8indPX15fly5eXWB/LIxXt+5Z19HiULNWrVy+UEDFs2DBe\nfvllRo0axaRJk6hatSoLFiwAYPDgwWRmZpKZmXnH/UhLS2PIkCFUqVIFLy8vzp07x61bt0hLS6Nn\nz57MmzePd955B6UUBw8exM/Pj19//RVPT0/S09NZuXKlWf/MmTM0atSIYcOGcfXqVb799lvCwsKo\nX78+Bw4coGXLlqxdu5YaNWqQlpZGdnY2GRkZpjdkQe1lZmaSlZVl1hMR0tLSTO1+VlYWLi4uNGnS\nhJUrVxIaGoqIcPjwYXx9ffO0Y3xvV1dXkpOTzfJTp07RtGlTRo8eTUJCAnFxcRjdD2cAAAjOSURB\nVHTq1Mnhel2+fJnTp0+b+y1atLjt9S0JjcgEpdT3SqllSqn7bGWewFm7OudsZQWVF8ixY8dwd3dn\n2rRpPPLII8XqaJ06dfjoo4/YsWMHImKqugAaNGhA165dyczMNI2Sdu7caS4Hpaamsm3bNgBatWpV\nrH5URAzXXVdXVypVqmSWGw8Z47hGo9EUlXHjxtG7d2+uXLnCK6+8wuTJkzl9+jRt27Zl5syZJdKG\np6cn48ePz1M+ZcoUsrKy6NSpE4GBgcyePRuAMWPGsGrVKnr06EFiYqKp1di9ezedO3emS5cufPbZ\nZ4wbNw6AWbNmER4eTr9+/fDw8CiwHwW1V1iWLl1KdHQ0QUFBdOjQgc2bN9+2fps2bXB1dSUoKIiF\nCxeyfv16AgMD6dy5M8ePH8+jIboj8jMcsd+Ar4DD+WwDgQaAC1aB5nVgme0z7wNP2Z1jKRAGhANL\n7MqHAwtyt2lv2PLFF1+UWIS8vXv3CiB16tSRyMhIAaRNmzbSsGFDAWTz5s2m0ZOXl5cA4u7uLn/8\n4x+lTp06ZrlhgFRRKAlDvFu3bom3t7dpUJaeni7nz5+Xrl27CiCTJ08uod5WDLRxZNlCj0fpUBT3\n3ezsbNm4caOMGDFCnnzySVm0aFGJR7DWFI4Sj6wqIoUKY6qUWgwYotU54EG7ww8AF2z/F1SeL7kN\ng4rDvn37AKvhj+G2++ijj1KjRg0iIiLYt28fXbp04csvv2TAgAEcP36cbdu28eWXXwLQsWNHVq9e\nTZUqVUqsTxUFi8XC3LlzCQ8P5/XXX+ftt9/m5s2biAgeHh5MmjTJ2V3UaDTlGBcXFwYNGsSgQYPM\nZQR7mwdN2aW4XjMN7Xb/hFVTAvA5MEQpVVkp1QxoAfw/IBZooZRqppRyw2rQ+nlx+lAUatWqBVjX\nuB566CFrRz//3PSjrlatGuvXrwesls1bt24lISGB//znP8THx7N//36aN29+t7p7z/HEE0+wadMm\n/P39yczMxGKxEBoayp49exyiwGo0Go2m4lBcY9V/KqX8scZvSALGAojIEaXUp1iNULOB8SJyC0Ap\nNQHYjnVJZ5mIHClmHwrNoEGDeP7554mJicHb25umTZuSlJTE2bNWs5WoqCjOnz/PAw88QFhYGAAt\nW7akZcuWd6uL9zwhISGEhISQkpKCm5ub1i5pNBpNBadYgoiIDL/Nsdex2o3kLt8C5HVXuQvUq1eP\nqKgoRo8eTVRUVJ7j58+fp2XLlmzYsOGuRh+tiBjRUTUajaYgLBYLGRkZ+oWlHJGRkWHm/SosZT77\nbkkzatQofH19iYqK4sSJEzRp0oQuXbpQtWpVmjRpQvfu3Yt8ETUajUZT8tSpU4crV64UOSDZ5cuX\ngd9CLmjuHhaLhTp16hTpMxVOEAHo0KEDy5Ytc3Y3Sg0RISYmhtWrV5OSkkKXLl0YPXp0kX8cGo1G\n40yUUnckTBgxLHSohfJBhRRE7mVEhDFjxrB06VKz7LPPPiMyMpIdO3ZoexeNRqPRlCn0GsQ9xoYN\nG1i6dCnVqlVj9uzZrFy5ko4dO3Lx4kXGjBnj7O5pNBqNRuOAkgLiyTuTa9eulb1OaTQajUajKRa1\natXKkwxMa0Q0Go1Go9E4DS2IaDQajUajcRplcmlGo9FoNBpNxUBrRDQajUaj0TgNLYhoNBqNRqNx\nGmVOEFFK9VFKJSilEpVSU53dn4qCUupBpdT/KqWOKaWOKKX+x1ZeRyn1pVLqhO3vfbZypZR6zzZO\n3yulApz7De5NlFIuSqnvlFKbbfvNlFLf2sbjE1vySGwJJj+xjce3Sqmmzuz3vYhSqrZSap1S6gfb\nfdJZ3x/OQyk1yfasOqyUWqOUqqLvj/JJmRJElFIuwPtAX6A1MFQp1dq5vaowZAN/ExEfIAgYb7v2\nU4H/ikgL4L+2fbCOUQvb9izwwd3vcoXgf4BjdvtvApG28bgKjLaVjwauiog3EGmrpylZ5gPbRKQV\n4Id1XPT94QSUUp7AC0AHEWmDNYnqEPT9US4pU4II0BFIFJGTInIT+BgY6OQ+VQhE5KKI/H/b/9ex\nPmQ9sV7/FbZqK4BBtv8HAtFiZT9QWynV8C53+55GKfUA0B9YYttXQE9gna1K7vEwxmkd8JitvqYE\nUErVBB4BlgKIyE0RSUbfH87EFaiqlHIFqgEX0fdHuaSsCSKewFm7/XO2Ms1dxKa2bAd8CzQQkYtg\nFVaA+rZqeqxKn3eBvwM5tv26QLKIZNv27a+5OR6249ds9TUlgxfwC7DctlS2RCnljr4/nIKInAfe\nBs5gFUCuAQfQ90e5pKwJIvlJqNq/+C6ilKoOrAcmikjK7armU6bHqoRQSg0ALonIAfvifKpKIY5p\nio8rEAB8ICLtgDR+W4bJDz0epYjNFmcg0AxoBLhjXQ7Ljb4/ygFlTRA5Bzxot/8AcMFJfalwKKUq\nYRVCVonIBlvxz4ZK2fb3kq1cj1Xp8jAQopRKwrpE2ROrhqS2TRUNjtfcHA/b8VrAlbvZ4Xucc8A5\nEfnWtr8Oq2Ci7w/n0As4JSK/iEgWsAHogr4/yiVlTRCJBVrYLJ/dsBoffe7kPlUIbOulS4FjIjLP\n7tDnwAjb/yOATXblT9u8A4KAa4aKWlN8RGSaiDwgIk2x3gdfi8ifgf8FnrBVyz0exjg9Yauv3/hK\nCBH5CTirlPqDregx4Cj6/nAWZ4AgpVQ127PLGA99f5RDylxkVaVUP6xvfi7AMhF53cldqhAopboC\nu4FD/GaTMB2rncinQGOsN3+4iFyx3fwLgT7ADWCUiMTd9Y5XAJRS3YHJIjJAKeWFVUNSB/gOeEpE\nMpVSVYCVWG17rgBDROSks/p8L6KU8sdqOOwGnARGYX2Z0/eHE1BKzQIGY/X4+w74C1ZbEH1/lDPK\nnCCi0Wg0Go2m4lDWlmY0Go1Go9FUILQgotFoNBqNxmloQUSj0Wg0Go3T0IKIRqPRaDQap6EFEY1G\no9FoNE5DCyIajUaj0WichhZENBqNRqPROI3/A5z1OcjzyxlNAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"sensor_var = 300**2\n",
"process_var = 2\n",
"process_model = (1, process_var)\n",
"pos = (0,500)\n",
"N = 1000\n",
"dog = DogSimulation(pos[0], 1, sensor_var, process_var)\n",
"zs = [dog.move_and_sense() for _ in range(N)]\n",
"ps = []\n",
"\n",
"for i in range(N):\n",
" prior = predict(pos, process_model) \n",
" pos = update(prior, (zs[i], sensor_var))\n",
" ps.append(pos[0])\n",
"\n",
"book_plots.plot_measurements(zs, lw=1)\n",
"book_plots.plot_filter(ps)\n",
"plt.legend(loc=4);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In this example the noise is extreme yet the filter still outputs a nearly straight line! This is an astonishing result! What do you think might be the cause of this performance? \n",
"\n",
"We get a nearly straight line because our process error is small. A small process error tells the filter that the prediction is very trustworthy, and the prediction is a straight line, so the filter outputs a nearly straight line. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Example: Incorrect Process Variance\n",
"\n",
"That last filter looks fantastic! Why wouldn't we set the process variance very low, as it guarantees the result will be straight and smooth?\n",
"\n",
"The process variance tells the filter how much the system is changing over time. If you lie to the filter by setting this number artificially low the filter will not be able to react to changes that are happening. Let's have the dog increase his velocity by a small amount at each time step and see how the filter performs with a process variance of 0.001 m$^2$."
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAhoAAAC+CAYAAABzq6b3AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzs3XdcVfX/wPHXuWzZCCoCIggqOXLv\nvTNnpZk7ra/91Eyz0ixNzWy4tdSyZa7U0FCzcpVbcOEAFBEBkaHsDRfu+f1x4SRZaaaC+n4+Hjy4\nnH3uYbz5fN6f90dRVRUhhBBCiPtBV9YXIIQQQohHlwQaQgghhLhvJNAQQgghxH0jgYYQQggh7hvT\nsjhpenq6ZKAKIYQQjxh7e3vlz8ukRUMIIYQQ940EGkIIIYS4b8qk6+Rm9vb2ZX0JAjhx4gQATZo0\nKeMrESXkmZQ/8kzKJ3ku99f06dOZM2cOAH5+fly9epWsrCx0Oh1Xr17F2tr6H/cv80BDCCGEEOVL\namoqYWFhuLi4MGvWLHQ6HYsWLSIsLEzbxtzcHCsrq9seS7pOhBBCCAGAXq9n4sSJVK1aldatW1Oz\nZk1at27NoEGDiI+P5/jx41y6dInOnTuTl5dHjx49bntMCTSEEEIIAcBrr73GkiVLyMvLo0GDBtjb\n23Ps2DE6depEfn4+TZo0wcfHhxUrVlC1alWCgoJue0wJNIQQQghBQkICq1atQqfTcejQIU6fPs3V\nq1dp3rw5CQkJfPXVV9q2vr6+nD17lg8//PC2x5VAQwghhBCcOnWKwsJC2rZtS+vWrQGwtbVl3Lhx\nABw7dqzU9hUrVmTq1Km3Pa4EGkIIIYTAwcEBgCtXrlBYWKgtv3TpUqn1/5aMOhFCCCEeE4WFhSQn\nJ+Pg4ICFhQXJycmsXr2ac+fOUalSJTw8PIiJieHZZ59lzJgxnD17lnnz5gEwZMiQuzqnBBpCCCHE\nI06v1zNnzhw+++wzkpOTsba2pkePHuzbt4/U1FRtO0VRsLCwYNu2bWzbtk1bPm7cODp27HhX55ZA\nQwghhHjEvfLKK3z99deAsQskLS0Nf39/ANq2bcvgwYMJCgrim2++oaCggBdffJErV67g4uLCiBEj\n6NmzJ4pyyzQmd0RyNIQQQohHWHh4OF9//TUWFhbs3r2blJQUPv/8c239W2+9pQUiI0aMQFVVqlSp\nwm+//camTZt4+umn7zrIAAk0hBBCiEfab7/9BkD//v3p0qULiqKUKht+4MAB7XXz5s0B41DXe0UC\nDSGEEOIRZmFhAUBaWpq2rF69etrrvLw8AAoKCli3bt0t6/8rydEQQgghHmE9e/bE3NycX375hblz\n5zJw4ECCgoJQFAVVVfn666+JjY3l1KlTREdHU7FiRUaMGHHPzi8tGkIIIcQjrFKlSloFz3feeQdf\nX19efvllVFXF3d2d7Oxstm7dSnR0NDVq1ODXX3/Fycnpnp1fWjSEEEKIR9zrr79OzZo1Wbp0KRcu\nXMDDw4P//e9/DB8+nPPnz3P+/HlcXV1p27YtJiYm9/TcEmgIIYQQj6D8/HySk5OpWLEiFhYW9OrV\ni169et2yXb169e5pTsafSdeJEEII8RCLiorivffe48UXX+TDDz8kKiqKyZMn4+LigpubG87Ozkya\nNInc3NwyuT5p0RBCCCHKobCwML777jtu3LhBw4YNGTp0KPb29qW22bhxI8OGDUOv12vLpk+fTlFR\nEWCc+Cw5OZnFixcTERHBtm3b/lNNjLshLRpCCCFEObNkyRLq1KnDRx99xFdffcX48eOpXbs2ISEh\n5ObmEhcXR2xsLCNGjECv1zNgwABWrlxJ8+bNKSoqQlEUfv/9d5KSkggMDMTe3p4dO3bcMgPrgyCB\nhhBCCFGOBAcHM3HiRFRVZdSoUSxbtowmTZqQkJBA27ZtcXR0xM3Njdq1a5Ofn0/Pnj3ZtGkTY8aM\noV+/fgCoqkpiYiIAzZo1Y9iwYQDs27fvgd/PbQMNRVE8FEX5TVGUMEVRQhRFea14+UxFUa4pihJc\n/NHzpn3eVhQlQlGUi4qidL+fNyCEEEI8THJycvjxxx9Zu3Ytly9fvmX9N998A8DYsWO11ow9e/Zg\nZmZGamoq+fn5ODk5kZ2dDUBycrK2r6WlpfY6Pj5ee10ycdrN6x+UO2nRKAQmq6rqB7QAximK8kTx\nukWqqjYo/tgJULxuEFAH6AEsVxTl3o6VEUIIIR5C/v7+uLu7079/f4YNG4aPjw/Dhw8nPz9f26Yk\nQGjRooW2bNeuXVoexqeffkpSUhKTJ08GIDAwkPDwcADat2+v7RMWFsbFixdZvHgxGzZsQFEUrcXj\nQVJUVf13OyhKAPAp0BrIUlV1/p/Wvw2gquqHxV//CsxUVfVoyTbp6enaSS9dunTXFy+EEEI8aCUF\nrg4dOoSqqrRu3ZpnnnkGGxubf9zv4sWLjBgxgqKiIvz8/KhcuTJHjhyhoKCA559/njfeeAOAVatW\n8cUXX9CiRQsWL16MiYkJ06dP55dffgFgy5YteHh4kJeXR5cuXcjPz8fW1pamTZty8uRJ0tPT//L8\no0eP5pVXXrm3bwbg6+urvba3t78l0/RfBRqKolQHDgB1gdeBkUAGcAJjq0eqoiifAsdUVV1bvM9X\nwM+qqv5QchwJNIQQQjyM0tLSGDNmDJGRkaWWe3p6smrVKhwdHf9239mzZ7N9+3b69evHtGnTUBSF\nkJAQRo4ciYWFBb/88gs2NjbcuHGDAQMGkJ2dTbVq1fD19WX//v0UFhbi4eHBli1btGMOHTqUixcv\nljpPvXr16NOnD7t27eLatWtUrVqVAQMG0LFjx/sy4uR2gcYdD29VFMUG8AcmqqqaoSjKCuB9QC3+\nvAAYBfzVXfxtNNOkSZM7vQRxH504cQKQ51GeyDMpf+SZlE8P8rm89tprREZGUqtWLebMmYNOp2P6\n9OmEhoayZcsWVqxY8bf7liRnTpo0iaZNm2rX/OGHH3Lx4kXs7Ozw8/PDysqKn3/+mcGDBxMTE0NM\nTIx2jOTkZM6dO0fLli1Zu3YtFy9epEKFCmzZsoXk5GRq1qxJ48aNURSFOXPm3N83o9jftaCUuKNA\nQ1EUM4xBxjpVVbcAqKqaeNP6VcCO4i9jAY+bdncH4u78koUQQojyacOGDQCsW7eOxo0bA1CzZk3q\n1avHd999R0ZGBnq9nq5duzJ06FCsrKy0fV1dXQE4duwY7dq1A4z5GCWtI61btyYvL4+6desybdo0\nIiMj2bdvH9evX6dBgwYsWrSIb775hlGjRpW6piVLltC9e/kdd3HbQEMxtrN8BYSpqrrwpuWuqqqW\npLT2B84Xv94GrFcUZSFQFfAFgu7pVQshhBBlICMjA4Dq1atry0oCiJycHNavXw/A5s2bWbZsGfv2\n7cPZ2Rkw5kgEBATw7rvvEhcXR7Vq1VixYoWW5JmXl4epqSnnz59n8ODBpKenl8qp+PLLL2nTpg1f\nffUVcXFx1KlTh4kTJ9KlS5cHcet37U5GnbQGhgGd/jSU9RNFUc4pinIW6AhMAlBVNQTYBIQCvwDj\nVFUtuj+XL4QQQtw/WVlZLFu2jN69e9OvXz+8vLwA+OCDDygqKsJgMDBgwAAATE1NWbhwIZ9//jk+\nPj6cO3eOqVOnUlhYSH5+Pr169eKNN95Ar9ezZMkSJk+eTEREBAA+Pj5cuHCB7Oxs5s83jrF49913\nycvL065Fp9MxatQoDh8+zJUrV9ixY0e5DzLgLkad3As3J4P+uZyqKBvS91z+yDMpf+SZlE/367nc\nuHGDDh06EBoa+pfrq1atiqIoXLt2DYD33nuPmTNnAnDhwgX8/PwwMTFBp9Oh1+tp2bIls2bNwtHR\nke+//57MzEwCAwM5c+YMa9euZciQIYCx2FadOnUICwvj8OHDtGrV6p7e1712c47GXyWDSmVQIYQQ\n4i9MmzaN0NBQatWqxerVq1m1ahXu7u4AODg4EBcXx7Vr19DpjH9KX3zxRW3fChUqAFBUVIRer0en\n03H06FF69OhBYmIi8+fP5/PPP8fT0xOgVMsFoNXVuNdTtpcFCTSEEEKIPykqKtLyLX788UeGDx/O\nSy+9xOrVqwFjoHHu3DnOnj1L165dAfjss88o6SV46aWXALCwsCAmJoaMjAwmTpyIwWBgypQp2nZ9\n+vQBYObMmezdu5dr164xefJkIiMjcXNz0xJOH2YSaAghhBB/otfrycnJwcTEBG9vb2157dq1AWM9\njbp161KvXj3eeustFEVh3rx51KtXj+bNm7N7924AXn31VTw8PLC2tubjjz/G3t6ekJAQ4uKMgzGH\nDh1Kq1atiI2NpUuXLri7u7No0SJ0Oh2LFi3C1PThn2RdAg0hhBDiTywtLalbty5FRUUsW7YMVVVR\nVZVFixYBaHUwADp16sSaNWtwdnYmJCSEoKAgrTulW7du2naFhYUUFhYCf3SJWFhYsGvXLmbMmIG3\ntzeOjo50796dvXv3akmmDztJBhWAJLmVR/JMyh95JuXT3T4Xg8FAfHw8FSpU+MuKnhs2bGDw4MEA\nPPHEExQUFBAREYGiKOzevZvOnTuX2j4/P5/Dhw+j1+vZu3ev1sLx1Vdf4ezszPTp01m3bh3NmjUj\nMDDwLu+2/JFkUCGEEOJP1q5di6+vL+7u7jg5OdGtWzd+/vlnXnrpJby9vfHz8+P8+fMsWLAAJycn\nQkNDiYiIoGrVqmzYsOGWIAOMrROdOnWie/fuTJkyBV9fX86dO0ezZs3w9vZm3bp1WFpasmDBgjK4\n47Lz8Hf+CCGEEP/Ct99+q40QcXBwICcnh927d7Nnzx5ubuWfO3cufn5+nDt3jsjISExMTGjSpAlm\nZma3PUfFihU5fPgwc+fOZfPmzeTm5tKhQwfeeecdGjVqdN/urTySQEMIIcQjIyIigmXLlnHy5Emc\nnZ0ZPnw43t7ezJ8/n2PHjmFnZ8eVK1cA+OSTT3j99ddJT0/Hx8eH1NRUvLy82LJlC2lpaYwbN47Q\n0FCWL19+V/OGuLi4sGjRIi2v43ElgYYQQohyRVVVjh07RkREBF5eXrRu3fqOZh3dv38/PXv2JCcn\nR1sWEBCAiYkJRUWlC1Sbm5vz6quvYmJigomJCampqQDY2NjQoEEDAJYtW0bnzp3ZsmXLA5ug7FEk\nORpCCCHKXMlojKioKJo0aUKrVq0YPnw4bdu25cknn+TSpUv/uL/BYGDUqFHk5OTQv39/du3axfz5\n81EUhaKiIjp16sSZM2f44osvACgoKOCbb77RXpewtrbWXjs4ONyyXvx7EmgIIYQoEwUFBbz//vu4\nublhZmZG9erVadGiBadOnaJSpUoMHDgQV1dXzp07R48ePf7xD35ISAiRkZFUq1aNTZs20bVrV7p1\n66blXFStWpX69evz8ssvaxOizZo1i1OnTnHs2DEt78LKyor8/HxSU1OZPn06YBy+Ku6edJ0IIYR4\n4FRVZciQIfzwww/asujoaABsbW0JDw/H3t6erKwsGjduTHh4OAEBAX9bWyIrKwsADw8PrcjVzWW9\nS2ZdBfi///s/pkyZQmJi4i2VN3/77TcqVqxIQUEBer0ee3t73nrrrXtz048padEQQgjxwB07dowf\nfvgBW1tbfv31VwoLC7VJxTIzM7l+/TpgzJl47rnnADh37tzfHq927dqYm5tz5MgR9u3bB0C1atW0\noMPExASDwUBCQgL+/v4ANG7cGF9fXxo0aMCHH37Ixo0bqV+/PtnZ2ej1erp06cKBAwfw8fG5b+/D\n40BaNIQQQjxwP//8MwCjRo3Sqmd269aNdevWAfDLL7/g6+urJYYCuLq6ljpGcHAwS5cu5dixYzg5\nOdG1a1d++uknOnfuTJ06dYiOjtZyP7Zu3YqzszOZmZkUFhbi7u7OL7/8grOzc6ljDhgwgOTkZMzN\nzbGzs7uv78HjQgINIYQQD1xJie6SQACgf//+vPTSS+j1elauXImpqSm//vor+/btw9ramkaNGvHj\njz/i7u7O1atXGThwYKn9ARo2bEh4eDghISEAtGnThq5du/L1118THR2NTqejT58+LF68+JYgA0BR\nlL9cLu6eBBpCCCEeuN69ezNr1iy+/vpr2rdvT5cuXdi6das2DDU0NJSxY8cCxoqbNWvWpEWLFtr+\npqamFBYWMmrUKFq1akVISAjLly/n9OnT7Nq1CwcHB5ydnfHy8gLg3XffJT4+HhsbG5n64gGTQEMI\nIcQD17hxY0aOHMm3337LwIEDS60bO3Ysbm5uXL58GU9PT3bu3ElgYCDW1ta0bduWI0eOkJGRgZmZ\nGUuXLiUsLIwnn3wSMzMzPvnkE7Zt28ayZctKHVOn0+Hm5vYgb1EUk0BDCCHEA6WqKoqi8OWXX9Kg\nQQM+//xzoqOj8fX15dVXX2XUqFFaga7AwEDee+89nJycOHv2LG5ubnz33XeMGDECvV7P5s2bqVu3\nLgDu7u7AHyNQRPlw21EniqJ4KIrym6IoYYqihCiK8lrxcidFUXYrinKp+LNj8XJFUZSliqJEKIpy\nVlGUx6uouxBCiFvk5+czc+ZM3N3dMTExoW7duqxevZoJEyYQGhpKdnY2wcHBjB49ulQV0ODgYMDY\n1VLSItGhQwdtmx07dgCQlJTE8uXLAWNehig/7qRFoxCYrKrqKUVRbIGTiqLsBkYCe1VV/UhRlKnA\nVGAK8BTgW/zRHFhR/FkIIcRjyGAw8Mwzz7Bz505tWUhICKNHjyY6OppZs2b97b4uLi4AnDlzBoPB\ngE6no1q1anh5eREZGYm/vz/Hjx8nPj4evV6Pr68vL7zwwn2/J3HnbtuioapqvKqqp4pfZwJhgBvQ\nF1hdvNlqoF/x677Ad6rRMcBBURRXhBBCPJJUVeXs2bP8/vvvJCcn37J+z5497Ny5E0dHR/bs2UNu\nbi6rVq1CURQ+/PBDEhMT//bYPXv2xNnZmeDgYPr27cuaNWt4+eWXiYyMRFEUKlSoQExMDIWFhfTq\n1Yt9+/ZRoUKF+3m74l9Sbp4S97YbK0p14ABQF4hRVdXhpnWpqqo6KoqyA/hIVdVDxcv3AlNUVT1R\nsm16erp20tvVrxdCCFF+XbhwgdmzZ2u/y83MzHjmmWeYOHGiVixr/vz5bNy4kdGjR/PKK69o+06Y\nMIGjR48ya9Ysevbs+bfnCAwM5I033ihV6VNRFKZOnUqPHj2Ii4vD0dGRihUr3qe7FP/E19dXe21v\nb3/L7Hd3nAyqKIoN4A9MVFU14x9m0vurFXcezQghhCgX8vLyCAoKIi8vjyeffJLKlSuXWp+UlMS4\ncePIyMjA0dGRqlWrEhoaysaNGwF44403AP525tWSf3RvNzNr8+bN2bx5MwEBAURFRVGpUiX69OlD\njRo1AKRyZ3mnquptPwAz4Ffg9ZuWXQRci1+7AheLX38OvPBX25V8pKWlqSUfonw4fvy4evz48bK+\nDHETeSblz+P0TNavX686ODioGP9RVE1MTNSxY8eqer1e2+a9995TAbVTp05qbm6uqqqqevDgQVVR\nFNXc3FxNSkpSVVVVd+3apQKqo6Oj+ssvv6hZWVnqypUrVUA1MzNTExMT/9O1Pk7PpTz609/0W2KI\nOxl1ogBfAWGqqi68adU2YETx6xFAwE3LhxePPmkBpKuqGn93YZAQQogH7ejRowwdOpS0tDQaNWrE\nU089BcDy5cuZPXu2tl1QUBBgrHthaWkJGEd8NGvWjIKCAmbMmMG0adNITk7m6aefJjU1lR49emBj\nY6N1obz77rtUqlTpAd+heJDupOukNTAMOKcoSnDxsmnAR8AmRVFGAzFAyZR6O4GeQASQA7x4T69Y\nCCHEfbV48WIMBgMTJkxgyZIlAOzevZtu3bqxbNky3nnnHSwsLHBycgKMeRol8vLyCAsLA9CGmwJ4\ne3szadIk/P39iYuLo06dOkyaNInhw4c/wDsTZeG2gYZqTOr8uw60zn+xvQqM+4/XJYQQ4l9SVZXU\n1FRMTU3/04RgJbOkjhw5UlvWtWtX3NzcuHbtGnPmzMHc3Jw6deoA8MEHHwDg5+fHggULtCnZe/Xq\nRcOGDdm4cSPh4eEcPHiQqKio2+ZkiEeLVAYVQohHwM6dO3nnnXe0AlddunRhwYIF1K9f/7b7GgwG\ntm/fztatW9Hr9VqSZlBQEA0bNgQgOjqauLg4AObMmaPtW6VKFRISEnj33XdLHfOpp55i+/btgDEp\ntEaNGpw4cYJTp07RuHHj/37D4qEhgYYQQjzkdu7cSa9evVBVFSsrKwoLC9mzZw/t2rVjz549xMXF\nYWJiQrt27bC1tS21r16v59lnn9WCgptNmjRJG+Uxf/58LQDp378/1atXZ926dSQkJNCuXTvc3d1J\nSUkhJiaG0NBQBg0apB3Hzs6O5s2b89NPPxEdHS2BxmNGAg0hhHjIvfPOO6iqyuTJk/nggw/Iyclh\n6NCh7Ny5kxYtWmgzotra2vLRRx/RtGlTtm/fjqqqpKens337dpycnHjrrbewtbVlwYIFREZGkpub\ny0cffVTqXOPGjePTTz8FYPz48dSsWZPDhw8THx+Pi4sLM2bMIDQ0lK1btzJs2DAUReHGjRscOnQI\nKF1zQTweJNAQQoiHWGpqKsHBwVhZWfHBBx9gYWGBhYUFzZo1Y+fOnRQVFdGmTRv0ej2BgYGMG/fX\nKXTLly/n+eefB6Bz587Url0bc3NzRo8eTUFBAfv37yciIoIBAwZo+3h7e+Pn58f58+eJiYnBxcWF\n0aNHM2/ePH788UdatWpFo0aN2Lp1K+np6bRv35569eo9kPdFlB+3Hd4qhBCi/CqpvqnX68nJydGW\nf/PNNwBUqlSJgwcPcuzYMZ5++mnAOGX6q6++yqRJk7TEzGPHjmn7+vr6Ym1tTUFBAe+//z5ffvkl\nzZsbp6wqmcQMICIigrCwMExMTKhWrRoAnp6e+Pv7Y29vz7Fjx1i+fDnx8fE0btyYDRs23Md3QpRX\nEmgIIcRD5syZM7zwwgu4ubnRqFEjvLy8KCwsZOjQoQQHB7N3716io6OB0iNHLl68CIC5uTlLly5l\n4cKFNGnSBIAvv/xSy8FYv3492dnZVKtWDUdHRwD+7//+DzCWE+/bty8TJkygZcuWFBUV8fzzz2uT\nn4FxfpKrV6+yZs0aFixYwJ49ewgKCsLVVaa9ehxJ14kQQjxEDh8+TNeuXcnNzS21XKfTsXPnzlIz\npIJxWGqJq1evAsaRIiXmzp1L165dycrKokGDBtja2nL48GEA3nzzTXQ64/+jrVu35rPPPmPixIls\n27ZN2799+/Z89tlnt1ynra0tQ4cO/Y93K8qzzDw9x6NSaOxq+Y/bSaAhhBDlmKqq7N+/nyNHjmBv\nb8+qVavIzc1l0KBBvPfeeyQmJvK///2P8PBwGjduTHJyMubm5tjZ2XHixAlGjhzJ5MmT0ev1FBYW\nAtCgQQPt+KmpqYAxUDl79iwAVlZWTJky5ZZ8jrFjx9K/f3/8/f3JyMigdevWtGvXTupiPCby9EWc\niErlyOUkjlxO5ty1dIoMKmfebvOP+0mgIYQQ5VRqaip9+/bl4MGDpZZbWlry9ddfY2VlRe3atVmw\nYAG9e/dGp9Nx5coVADIzM+nevTtHjx7l9ddfL7X/9u3bee655zA1NWXLli0AfPTRRzRo0ICCggJa\ntWqldZn8maurK+PHj78PdyvKmyKDSkhcOocikjgckcTxqFQKCg2Y6hSe9HBgbIcatPS+/Yy5EmgI\nIUQ59X//938cPHgQFxcXXnjhBUJCQti7dy95eXmcOnWK1q1bA2BjYwNAQUGBtq+trS379+/H39+f\nn3/+GRMTE3r37s3Ro0dZsGAB/v7+gHHm1PHjxzN58mStm0Q8ngwGlYuJmRy9nMzRyGSCrqSQnqsH\noHYVW4a38KS1jzPNvJywtvgjfEhPT//H40qgIYQQ5VBiYiKbN2/G1NSUY8eO4e3tjcFgoGLFiqSl\npTF27FiCgoJITU1lxowZQOl8DAAzMzMGDRpUqnhW//79GTduHDt37kRVVbp3765Nty4eL0UGlQsJ\nGQRdSSEwMoXAK8mk5hgDi2pOFehepzKtfZxpVcMZF1uLuz6PBBpCCFEOxcTEYDAYqFevHt7e3oAx\nj2LChAnMnj2bs2fP4uDgQEFBAQaDgcqVKzNx4sQ7Oranp6c2ikQ8PvRFBs5fSzcGFldSOB6VQmae\nMW/HzcGKzn6VaeFdkZY1KuLmYHXPziuBhhBClEPVqlVDp9MRGhrKlStX8PLyAiA7OxsAR0dHUlNT\n0el09OvXj3nz5uHm5laWlyzKmfzCIs5fS+dYZArHIpM5GZ1KToGxSqy3izW96rvS3KsiTb2c7mlg\n8WcSaAghRDlUuXJlnnvuOTZt2kSLFi0YMmQIkZGRBAQEAPDTTz/h5+eHhYUFVlb374+EeHgkZeVz\nKjqVk8UfZ6+lU1BoAKBWZVuea+xOMy8nmnk5Ucn2n4ek3ksSaAghRBmJjo7m/PnzVK5cmcaNG98y\nTHTFihXExsZy5MgRFi1aBBgrgS5ZsoSWLVuWxSWLckJVVS7fyOJEVConigOLK0nG1i5zEx313O0Z\n2ao6jT0daVrdCSdr8zK7Vgk0hBDiAcvKyuKll15i06ZNWjXOunXrsm7dulLTujs5OXHo0CH27dun\n1dF47rnnqFq1allduigjefoizlxN42RMKiejUjkZk0paceKmk7U5jao58nxTD5p4OlLXzR5LM5My\nvuI/SKAhhBAP2IsvvsgPP/yAubk5bdu25fz585w/f56OHTsyZMgQQkJCqFixIsOGDaNXr1507tyZ\nzp07l/VliwcoJbuA41EpnIhK4XhUKiFx6eiLjEGpt4s13Z6oTBNPJxpXd8Tb2bpcF02TQEMIIe6z\nH374gUWLFhEaGoqLiwuXLl3C0tKS4OBgatWqRW5uLk2bNiUkJIRly5Zp+23evJkxY8awYsWKcv2H\nRPw3qqoSmZTNqehUTsWkEnQlhcs3irtBTHU86W7P6DbeNPF0pJGnY5l2g9wNCTSEEOI++uSTT5gy\nZYr2dVpaGmDsFqlZsyZgrPSZlJQEQNWqVfn8888JDQ1l5syZfP755/Tv35/u3bs/+IsX90VOQSHB\nMWmcKA4sTsekaYWxbC1NaeKgaPZmAAAgAElEQVTpyLON3Wla3Yl65awb5G7cNtBQFOVroBdwXVXV\nusXLZgIvAzeKN5umqurO4nVvA6OBImCCqqq/3ofrFkKIcu/GjRtMnz4dgIULF/LCCy+wcuVKZs2a\nRVxcHL///jsdO3bk5MmTJCYmAvDss8/Sq1cvevXqRX5+PjNmzGDdunUSaDzEkrLyORmdyomoFIKi\nUgm5lk6hQUVRwLeSDT3qVKGRpwONqjlSw8UGne7Rar26kxaNb4FPge/+tHyRqqrzb16gKMoTwCCg\nDlAV2KMoSk1VVYvuwbUKIUS5d/36db799lsuXbpEWloaBQUFdOvWjUmTJgEwffp0Fi9eTHp6Oi++\n+CJz587VyoFD6WndS1o8SiY+E+VfYZGBCwmZnIpJLe4KSSMmJQcwdoM0cHdgTHtvmlR3olE1R+yt\nzMr4iu+/2wYaqqoeUBSl+h0ery/wvaqq+cAVRVEigGbA0b/b4cSJE3d4aPEgyPMof+SZlD9/90yC\ngoJ48803ycnJKbX82rVrpfZp164d27dvJzo6miFDhtxybIPBQG5uLh9//DEA7u7u8n1wB8riPcrR\nGwhP1nMxWU9Ykp6IFD15xUmbDpY6ajqZ0b6eDbUqmlHD0QwzEwXIgswsLoXEPPDrvR98fX3/cf1/\nydEYryjKcOAEMFlV1VTADTh20zaxxcuEEOKRlpuby7Rp08jJyaF58+a0a9eO/fv3ExQUREhICAEB\nAfTu3ZuQkBAOHToEQI8ePcjPz8fJyYn09HT27NnDmDFjqF27NnFxcWRkZODg4ED//v3L+O5Eicx8\nA2FJBYTc0BOWVEBUWiEGQAd4OpjSsboltSqaUauiOc4VdJLECyglY7j/cSNji8aOm3I0KgNJgAq8\nD7iqqjpKUZTPgKOqqq4t3u4rYKeqqv43Hy89PV07qb29/b25E/GflPwn0KRJkzK+ElFCnkn580/P\nZN26dQwdOpQmTZoQGBiITqdDVVWqV69OTIzxP1czMzP0emPSX+fOndm1a5c2Y6per+ett95i5cqV\n5OXlaef56quvStXWELe6nz8rCel5BBUPMw26ksKFhEwALEx1NKzmQLPqTjSp7kTDag7YWj763SB/\n5ebZW+3t7W+JrO6qRUNV1cSS14qirAJ2FH8ZC3jctKk7EHc35xBCiIdJfHw8AC1bttSCB0VRGD58\nOHPmzMHOzo6MjAwcHR0ZPXo0s2bNKjUtu5mZGYsWLWLGjBmEhobi5OSEn59fmdzL46rIoBKeaMyv\nOBGVyvGoFGJTcwGwNjehkaejcX4Q74rUd7fHwvThHg3yoNxVoKEoiquqqvHFX/YHzhe/3gasVxRl\nIcZkUF8g6D9fpRBClLG8vDz27t1LYmIiKSkpdOnShdDQUL744guioqIwNTX+Og0ICOD999/H3t6e\nnJwctmzZAhjLifft2xcrK6tSAcafOTo60rp16wdyT4+7tJwCTsekcbJ4mOmZq2lkF0865mxjQdPq\njoxq7UXT6k74udpiavL3z038vTsZ3roB6AA4K4oSC7wHdFAUpQHGrpMoYAyAqqohiqJsAkKBQmCc\njDgRQjzsDh8+zLPPPqsNQV20aBFubm7Ex8djMBhKbRsTE0OtWrXo2LEjhw4dIjY2Fk9PT5599lks\nLCzK4vIFfxTFOhltHA1yIjqViOtZAJjoFGpXseWZRu7aMNNqThUkv+IeuZNRJy/8xeKv/mH7D4AP\n/stFCSFEeZGSkkKvXr1IS0vDx8eHJ598kqNHj3Lt2jUARo8eTffu3QkICGDdunXodDoSExP5/vvv\nAfDz82PLli0SZDxgOQWFnLmazqkY44Rjp2NSSS2eG8TeyozGno70b+hGw2oONPBwoIK51K+8X+Sd\nFUKIf7B27VrS0tJo27Yt8+bNw8TEhN27dzNt2jQAhg0bRvv27XnuueeIjY1l//79vP3229SqVYvq\n1avTtm3bf+wqEfdGck4R28/EaVOkh8ZnUGQwjjvwqWRDtyeMRbEaezri7fzoFcUqzyTQEEKIfxAe\nHg5Av379MDExJv9lZ2eXWt++fXsURaFu3brs378fR0dHRowYUSbX+zjI0xcREpfO6Zg0Tl9NIzDi\nBkk5BiAJKzMTGng48H/ta9C4uiMNPRxwqPBwzQ3yqJFAQwjxSLp8+TL+/v7k5OTQrl07OnbseEuf\nu6qq7NmzhzVr1pCcnEyTJk0YM2ZMqWnYq1WrBsC+ffto27YtiqKUGm7q4OAAGEed/PDDD4AMSb6X\nVFUlOjmH01dTCS4OLELjMigsbq1wc7CippMZvX3N6d+2Pn6udphJ0ma5IoGGEOKRM2fOHGbMmMHN\ndYI6dOhAQEAAdnZ2gPEP2MSJE1m6dKm2zc6dO1m6dCmff/45p0+fJjExkerVq2NpaclPP/1EUlIS\nDRs25OjRP4odv/TSS6xYsYLAwECtWFeHDh0e2L0+avILizgbm07QFWPtiuCraVpuRQVzE+q72/O/\ndt408HCgQTUHKtlaanU06rs7lOWli78hgYYQ4pGyc+dOpk+fjk6nY/DgwVSpUoXVq1fz+++/07Jl\nSxISEsjIyKB27dqcP38eCwsLpk2bRp06dVi5ciV79uzh+eefL3VMW1tbAAIDAwkMDASgUqVKVKtW\njRMnTvDbb78Bxkqfq1evltEK/0JWfiEno1M5fiWFoOLAoqDQOJKnhos1XZ+oTMNqjjTwcKBmZVtM\nJLfioSOBhhDikbJixQoA3n//fS1hc9CgQTRt2pTQ0FBtu/PnjeV/evfuzYwZMwDw9vamUaNGAPTt\n25fu3buzZs0ajh49ire3N3379iUpKYlOnToxcOBAKlSoQFhYGNHR0fj4+ODj4/Mgb/WhdD0zj1PR\nqQRdMRbEColLx6Aah5jWqWrHsBaeNK3uRNPqjlS0kZE6jwIJNIQQj5QrV64AlJpWff/+/drrgIAA\nOnToQOPGjYmIiOC3336jqKgIExMT1q1bp203fvx4unTpwqhRo/Dx8SEyMpInnniCBg0alMrB8PPz\nkwqef6Og0MCFhAxtFtNTMalapc2SEt7jO/rQ1MuJhtUcsbGQP0mPInmqQohHiq+vLyEhIWzbto3G\njRsDsGnTJsBY5rtTp07Y2NgwdOhQZs6cSXJyMidPnqRZs2ZaK4eJiYmW8GlhYUHDhg2JjY0lKSmp\nbG7qIWAwqFy+kcWZ2HTOxqZxJjadsLgMCoqM3SBV7Cxp5OnAyFbVaVjNgbpuUsL7cSGBhhDioRcZ\nGUlAQAAFBQV06dKFH3/8kdmzZxMcHEyVKlU4efIkYEwItbGxAeDll19m9uzZGAwGnnrqKWrVqsWx\nY8bJpytXroyjoyNgrPS5b98+AGrUqFEGd1c+pefqOR1jbKk4HWMcEZKZXwgY5wWp62bPyNbVqe9u\nT6NqjlR1sCrjKxZlRQINIcRDS1VVpk+fzty5c0uNMKlXrx5hYWFs27at1PbR0dGcPn0aLy8vli5d\nisFgwMzMjJSUFI4ePYqpqSk6nY64uDhq165NgwYN2LVrF9nZ2fTs2RMvL68HfYvlQn5hEWHxmZy5\nmsaZ2DTOXE3j8g1jLRGdAjUr29K7QVUaehirbHq72EjSptBIoCGEKHN6vZ4tW7awd+9ezMzM6Nev\nH126dCEmJobdu3ejKAo9evTAzc2t1H6bN2/mgw8+wMTEhIEDB2Jvb8+6des4d+4c48aNo06dOmRn\nZ9OkSRPGjRtHaGioluwJxtlV165dS82aNUlJSaFevXpERkby/PPPExkZSWRkJGAcTbJ27VouX778\nQN+XspKQnqdNNHYyOpWQuHT0RcZAztnGggYeDvRr4EYjT0ee9HCQ3Arxj+S7Qwjxr2VmZrJ+/XqC\ng4OpVKkSw4YN+8sRFydPnuTjjz/m8OHD2NnZ8cILL9C/f39WrlzJ/v37sbKyolevXuzYsUOrhQCw\nfPlyatasSUREhDZpmYmJCZMnT8bJyYmffvqJoqIibb6RhQsXMmHCBACGDh1KmzZtWLduHdevX8fM\nzAyAAwcOMGvWLNavX096ejotW7bknXfeKZU0CuDi4kJERAT79+8nMTGR+vXrU7du3fvyPpYHN1fZ\nDL6axumYNK6l/ZGw+aSHA6PaeNHA3YEnPRxwtbeU4bviX1Fubm58UNLT07WT2tvbP/Dzi1uV/JKX\nioblR3l9JiEhIXTr1o24uDhtmU6n47PPPuOVV17Rlu3Zs4enn36agoKCUvubmJhQVHTrpM7u7u5M\nmDCBzMxM5s2bR15eHjqdjn79+lFYWHhLN8jNjhw5QsuWLbWvHRwcSE9PJzExkUqVKv2X2y2lvD6T\nO6WqKleSsgm+mqZ9hMVnaK0Vbg5WNPAwzgfS2NMRP1c7zE3Lf5XNh/25POzS09O11/b29rdEodKi\nIYS4Y6qqMmjQIOLi4mjUqBFDhw7l9OnTrFmzhrFjx9K2bVvq1KmDqqq8+uqrFBQUMHLkSN5++22i\noqLo06cP+fn5PPHEE3z55ZfEx8fz3HPPoaoqAwYM4M033wRg1apVJCQk4OHhgb+/PwDdunVj9+7d\nWFhYsH79eszNzRk0aBDZ2dlMmjRJS+Q8cuQI6enp2Nvbawmdj6v0XH1xK0Uqp2OM+RVpN1XZrOdm\nz+g23jSs5kBDDwcq2VmW8RWLR5EEGkKIUnJzc0lMTMTFxQVra2v8/f1ZuHAhoaGhODg4EBUVhaur\nK4cOHcLKyjiSwMLCgi+//JKvv/6aBQsWcOHCBS5cuICLiwtffPEFZmZmODg4kJ+fD4CzszMtW7Yk\nJSVFS+I8cOAAAEVFRSQkJABo28MfBbYAnnnmGQA++OADJk6cSGBgIEOGDMHBwYG1a9cC8L///U/r\nNnkcqKpKZFI2J6JSOBVtrFkRcSMLVQVFgVqVbelRp4pWutu3klTZFA+GBBpCCADy8vKYNm0aq1at\nIisrC0tLS+rXr09QUJC2TVpamvba0vKP/37btGnDl19+qXWn6PXF/zVXqICpqfHXTG5urrZ9SdeJ\ng4MDLi4u3Lhxg8TERMDYtWJjY0NWVlap5M+S5tmbl7300ktMnDgRgPXr12vL+/Xrx/vvv/9f3o5y\nryS34kRUKieKp0ZPyTZ2UzlUMKOhhwN9nqwqCZuizMl3nhCPifT0dK5fv467uzuWlpZs3bqVFStW\nEBUVRY0aNcjMzOTIkSMAuLq6Eh8frwUZ8+fPZ+jQoWzcuJHXXntNm6l0wIABFBUVsWHDBgAcHR1Z\nuXIldnZ2VKlShejoaObNm8ekSZNQFAULCwvy8/OxsrKiqKiI7OxsKlasyI0bN4iNjaV79+5kZmaS\nlZUFwIULF5gyZQpFRUVa60blypUpLCxEURTmzp0LQP369Rk+fDj5+fl07tyZZs2aPVIJi6qqci0t\nV6tZcSomjdCbRoJ4OVvTqXYlmlZ3pLGnEzVcrB+p+xcPN0kGFYAkU5VHd/tMVFXl5MmTJCQkULdu\nXezs7HjttdfYuHEjer0eGxsb6tSpo00OdjNzc3MOHDhA8+bNmTdvHm+99RYAu3btomvXroCxaFVk\nZCTm5uY8++yzBAcHExYWdkuSp5WVldaKUaFCBXJzc0vVuqhYsSI5OTnk5uZibm6OwWCgsLC44JO1\nNTVq1ODs2bOlrk9RFFRVxcXFBVNTU+Lj4wHYsWMHTz/99L96n+7Gg/o5ySko5GyscSTI6ZhUTl9N\n40amMdCyNNNR392BRtUcaVjN+NnF9vGeE0R+f5UtSQYV4hGQl5fH8uXLWbduHenp6bRo0YI333yT\nJ598stR258+fZ/DgwZw7d05b5ujoSGpqKjqdDg8PD65evUpgYCCKojB//nx69OjBlClT2LFjBwUF\nBVStWhUwtmqU+P3337VAY8CAAXz88ccUFBRoLRmWlpbk5eVhb29P3759uXDhAkFBQZiYmODp6Ulk\nZCQmJib079+fVq1asWzZMm1Oknbt2rF06VIqV67MgQMHMDc3p3PnztjY2LB//35+/vlnFEWhd+/e\npKen8/rrr3Px4kUAvLy8+Oijjx5IkHG/ZOTpCbmWQUhcOuevpXM+LoPIG1kYimMyL2dr2vo406A4\nqKhVxRYzk/I/EkSIErcNNBRF+RroBVxXVbVu8TInYCNQHYgCBqqqmqoY2+qWAD2BHGCkqqqn7s+l\nC/F4KCgooGfPntpU5ACXL1/mhx9+4KeffqJz586AMX+iS5cuJCYmUrlyZerVq8fvv/9OamoqlpaW\nnDt3Dh8fH8aNG8fy5ctRVZWePXtSu3Zt+vTpw44dOwDjpGPjx4+nU6dOWgvCpUuXMBgMHD9+nG++\n+QaAxYsXY2tri6IojB49GnNzc06dOoW3tzeqqjJkyBA2bNhA7969ee+997C0tNSSR1977TWuXr2K\nlZVVqeGnAwcOLHXvHTp0oEOHDqWWPfXUU4SHh2MwGKhZsyYmJg/PfBk5BYWExGVw5moa566lczY2\nnStJ2dr6KnaW1HWzo2c9Vxp6GOtWOFmbl+EVC/Hf3UmLxrfAp8B3Ny2bCuxVVfUjRVGmFn89BXgK\n8C3+aA6sKP4shLhDSUlJzJkzh7Vr15KXl4e3tzfnzp2jSpUqLF++nBo1ajB//nxtSGlYWBg6nY7V\nq1eTmJhI8+bN+e2337CysuLFF1/k22+/JS8vT+vWqFy5snauAwcOaIHGK6+8gsFgYNu2bbRv3549\ne/Zo223evJmtW7dqXRsdO3Zk/PjxmJiYsHfvXlRVpWnTpnh7ewPGLo7nn3+eDRs2cPHixVuGmep0\nOjw9Pe/q/VEUhVq1at3Vvg9SbkERofEZnItN49y1DM5dSyPi+h8tFa72ltRzs+fZRm7UdbOnTlX7\nx74LRDyabhtoqKp6QFGU6n9a3BfoUPx6NfA7xkCjL/CdauyIPaYoioOiKK6qqsb/3fFvrgYoyp48\nj7KVmZnJqFGjiIqK0paVdIN06tQJDw8PCgoKGDt2LDt37iQ8PJxNmzbh4+PD7t27te1CQkIASiUE\n+vv7061bt1JdIsHBwZw4cYKQkBBMTU0pKChg9+7d2sylAM2aNSM2Npa4uDjs7Ozo3bs3Y8aM4fTp\n08AfI1GCg4PZu3evlndVMmOqhYXFI/d99ef7ydEbiEorJDJNT2RqIVFphcRmFmpBhYOFDm9HU56t\nbU0NRzNqOJniaFnSEpMOmelEX4ToB3sbj5xH7fvsYeHr6/uP6+82R6NySfCgqmq8oiglbZ9uwNWb\ntostXva3gYYQ4g+bN28mKioKLy8vZs6ciYuLC8OHDycpKYm9e/cyceJEFEXBxMQEa2trkpOTef31\n18nNzdW6JcLDw7XjdezYUevqOHXqFJ6enhw8eFBbv2LFCjZu3EhKSgpgHL1hb29PdHQ0VatWpX//\n/nTs2BEw1rQwNzdHpyudH+Dp6UmjRo04deoUo0aNolevXly5coWff/4ZgP79+9+/N+wBU1WV69lF\nRKcXEpVuDCii0wtJzP4jCdbJUoeXoynN3Kyp4WiKt6MZTpY6GQUiHlt3NOqkuEVjx005Gmmqqjrc\ntD5VVVVHRVF+Aj5UVfVQ8fK9wFuqqp68+Xgy6qT8kazt8qF58+YEBQWxY8cOrYvjp59+YubMmQAE\nBgbSpEkTVq5cybhx4/7yGIqiMGHCBJo1a8bq1avZtWvXX27XsWNHgoKCyM7OxtbWltGjR/Phhx+W\nqo9xp6Kjo+natSuXLl0qdR0LFy7U6lw8bPL0RVxKzCI0Pp3QuAzC4jM5H5tKTqHx15eigFdFa/xc\n7fBztaWOmz11qtpRyVaqaz5o8vurbN2vUSeJJV0iiqK4AteLl8cCHjdt5w7E3bK3EOIvlUwgVlLk\nCmDMmDHMnj0bg8FA69atsbW1JTU1FQBbW1u+//576taty2effcYnn3yCqqosWbJE29/GxoYpU6Zw\n8OBBYmNj8fPzY8KECbRr147c3FySkpJwcXG5qwCjhKenJ+fOncPf35/jx4/j5OTECy+88JcTrZU3\n+iIDkTeyuZCQwaXELC4mZnIpMZPolBxK/g+zNjehtqsdbT0tqW5vSo8W9ahVxZYK5jJwT4jbuduf\nkm3ACOCj4s8BNy0fryjK9xiTQNP/KT9DiMeJwWBg165dbNu2jaKiIrp160bfvn1LBRVPPfUUJ06c\n4J133uHdd9+lYsWKLFiwAIPBgLW1Nbm5uaSmplKhQgVycnJ4//336dmzJwAfffQR27dvJywsjH79\n+qHT6ahfvz4vv/yyNmT1z6ysrPDw8PjLdf+WhYUFgwcPZvDgwffkePeaqqokZuRzISGDiwmZXEjI\nJCw+g8s3srTCVyY6heoVK/BEVTv6NXSjZmVbnnC1o5pTBXQ6RfvPuWG1x3sOFSH+jTsZ3roBY+Kn\ns6IoscB7GAOMTYqijAZigAHFm+/EOLQ1AuPw1hfvwzUL8dApKChg4MCBBAQEaMu++OIL2rRpw88/\n/4yNjQ0Ar776Kt999x0nT54sldugKApr166lY8eOZGVlMWHCBLZs2YK1tXWpbUryNMaPH68Ne30c\n5emLuJiQSWh8BhfiMwhLyORiQibpuXptmyp2ltR2taV9LRf8qthRs7ItNSpZY2H68AyXFeJhcCej\nTl74m1W3/BYrHm3y1x3HQjwicnJyOHPmDFZWVtSvX/+W5Mi/smTJEgICAnBwcGDSpEmYm5uzdOlS\nDh06xNSpU+nSpQv5+fm0bduWQ4cO8e677/L999+Tn59Pq1atmDFjBt27dweMeU3dunVjy5YtfPLJ\nJ7Rp0wYfHx+++uorTp06ha2tLc2bPx6jyg0GlaupOYQnZhGemKkFFzcXvLKxMKVmZRt61nOldhVb\nalWxpXYVWxwqSH0KIR4EKUEuAEmm2rVrFx9++CFBQUE4OjoydOhQpk2bhp2dnbaNqqrMnz+fDz74\nQEt+8vHxYcWKFXTp0uUfj1+7dm0uXrxIQEAAffr0AeD48eM0a9as1Hampqa8+uqrzJ8/nxMnTmAw\nGGjRosUtx8vJyaF58+bajKYlc4gAzJs3jzfeeOPu34xyqLDIwNXUXC4lZnLpehaXr2cRfj2TiOtZ\n5OkN2nZuDlb4udrxRFU7nnA1frg7WqG7R7OUPu4/J+WVPJeyJSXIhbiNDRs2lMoryMnJ4eOPP2bf\nvn0cOHBAS5L87LPPtLk/6tSpQ2pqKhEREfTq1YvAwMBbyoHfrGTa85tbGm7+4WzatClOTk7s3r2b\nRYsWUalSJbp06fK3rSUVKlTgt99+4+2332b9+vXk5OTg6+vL1KlTefHFh7fHssigEp2cTXhiFpcS\nMwm/bvwceSObgqI/AgpXe0t8KtkwpLknNSvb4FvZFt9KNthaPj7TwgvxsJBAQzzW9Ho9r7/+OgBT\np05l8uTJXLx4kSFDhnD8+HGGDh1KYWEhFSpU4NdffwXgm2++YeTIkRQWFjJq1CjWrFnDggUL+O67\nP4rnqqrKgQMHtHk6PD09OXv2LKtXr9aClTfffBMwTpVeMvdIQEAA/fr1Y/HixXTo0KFUouifOTs7\ns2rVKlasWEFubi42NjYPTa2GmxMzwxONiZnhiZlcSswiv/CPgMLd0YqalW1pX9MFn0rGgKKGi7UE\nFEI8RCTQEI+lU6dOcfr0aVJSUkhISMDHx4e5c+eiKArOzs6MGTOGadOm4e/vX2o/CwsLhg0bBhi7\nOSZNmsSaNWtKzYRaUFDA888/z48//njLeUsmL7OwsCA4OBgwzvtREiD06dMHR0dHEhMTSUtLw9nZ\n+bb3Ympqiq2t7V2/F/dbVn5h8SiPP0Z7/Dkxs5KtBbWq2DKshSc1q9hSs7iFwtpCfkUJ8bCTn2Lx\nyNi5cydLly4lPDwcDw8PXnnlFQYNGlTqv/yUlBQGDhzI3r17S+1bkt9QYs2aNYCxteHTTz8lPDyc\n2bNnk5+fz6pVq3jllVeAP6pwOjg4kJCQgJmZGcuXL+fHH3/Ezs6OMWPGYDAY+OKLL8jMzMTMzEyr\nzFkyYZmXl5d23vDwcFJTU7GwsNBGojws9EUGopOzuZSYpQ0dvZCQSUxKjrbNXyVm1qpsi6NMHCbE\nI0sCDfFIWLhwIZMnT9a+vnLlCgcOHOD48eMsXLhQWz58+HBtPo6nn36a4OBgQkNDuXr1KlOmTGH2\n7NkcPHiQsLAwAKZNm8aQIUMA2LJlC+fPn2fq1KlUrFiRpKQk3nvvPQBiY2O1OUTMzY1/NDdt2qSN\nFGnfvj19+vTBzc2NBQsWUFhYyNWrV3njjTcYP348ly5dwtHRkWXLlgEwePDg/1RA635SVZXY1P9v\n787jY7r3x4+/zixZJ3tkT2yxNE3EVqGWiqUIRVGqVPC9em9RSrWl/RV11e2S4paWam1FtdaKpUrt\nrdoiFTQRW4gsJBLZt8l8fn9MciqlWlckwef5eHjILGfOZ+bkzHnns7zfBZxOzua3lGzOXjVPyryY\nnoexbKmHRoE6rrYE+TgwsKUPjTzsaexhh4+T9QMzvCNJUuWQq04k4MGetX316lV8fX0pKSlh5syZ\n9O/fn927d/Pqq69SUlJCTEwMQUFBxMfH06hRI2xsbIiNjcXPzw+TyUTTpk3VwmU3s7CwICMjQ81V\n8c033zB48J+t9jZn6SwuLlZ7R44fP06zZs0Ac7E0e3t7LCws1MdLS0sJDw9n1apVFV6nefPm7Ny5\nkwsXLgDVe0yKjOY03LEp5hTcp5Oz+C0lm5xCcxVXjQJ1XGyp72aggZuBBu4G/GvZ4e9mwNri4ctH\n8SCfJw8zeVyql1x1Ij30tmzZQklJCWFhYbz99tuAeTnpiRMnWLRoEevXrycoKEjtpWjfvj1+fn6A\nuVz566+/zrBhw3ByciIzMxM7OzuKioooLi7mwIEDdO/eHaPRyIYNGwDzyhEHBwesra2JiYnh4sWL\nvPbaa8yaNYuioiK8vb3JyclhzJgxHDx4EDAXSwMqlDfXarWsWLGCkSNHsmHDBgoLC+ncuTP9+/fH\nwsJCDTSqSnpuEbEp2SjLtOIAACAASURBVGV1PcyBxfm0XLWXwlqvpbGnHb2DvXjcy4EAL3MvhZX+\n4QsoJEmqPDLQkB54hYWFADg7O1e4v/x2+ePe3t4AREdHk5eXp/ZU/PzzzwCEh4cTERGBRqNh2rRp\n/Pvf/6ZHjx60bt2apKQkEhMTsba2Zvny5TRq1Ijc3Fzs7OywsLDg3//+NxYWFlhYWDBhwgRmzJjB\nL7/8Qr9+/TCZTGzevBkwT/y8maIodOrUiU6dOt2nT+dWpSZBwvU8fisb+igPLq7l/D5PxdPBigBP\ne7oGuKtFw2q72KKtpHwUkiQ9OmSgIT3wysuYr1+/nn/84x889dRTxMTEsHjxYgD1It6iRQuCg4M5\nceIEbdu2ZdiwYURHR7Ny5UoURWHEiBFotea/zqdNm0ZhYSHz5s3j0KFDANStW5cvv/xS7ZXQ6XRo\nNBpKSkrIzs5W038//fTTzJgxA4CNGzcC5t6LKVOmMHLkyCr6VMwKikuJTc1Wg4rfks0rPwpKzGXN\ndRoFfzcD7Rq4mhNcednzmIe9nJwpSVKlkXM0JKDmj3GmpaWRkpJC7dq1b/s7M3ToUHWug6urK+np\n6QB07NiRXbt2qYmv4uLi6Nq1K1euXFG31Wg0zJs3j9GjR9/yuhkZGWpa7yeeeOKWBFp9+vQhMjKS\nTp06MWvWLPLy8hg/fjynTp3ipZdeomXLliiKQvfu3fHx8bmr93y3xyQjr5jTyVmcTs42T9RMzuJi\nep6aitveSleWMdM87PGYp3kuhazt8ffV9PPkQSOEICMjQ61a/L+6fv06AC4uLpXRLOkONBoNzs7O\nFSZ1yzka0gMtLS2N0aNHs2HDBkwmE5aWlgwfPpzRo0ezcuVKLl68SL169Xjrrbfw9fVl4cKFpKen\nY2NjQ3h4OFOnTmXp0qWcPn0aT09PhgwZQmxsLKtXryY6Oho3NzeGDh36p+XMnZ2d75he/MMPP+Tg\nwYPs3r27Qqrwhg0bMmvWrPvyxVdsNHEhPZe4lPKcFOb5FKnZhepzvB2tCfCy55lgL7WnwttRrviQ\napbyydb3usLKxsYGoEKRQen+KCwsJCMj466+22SPhgTUjL/UTCYTy5YtY/HixaSmphIQEEB8fDzx\n8fHodDrq169PfHw8Qgg1B0U5vV7P119/Te/evUlLS8PFxYX4+Hi6d+9OSkqK+jwLCwu++uorBg0a\nVGntvnTpEhEREezYsQO9Xk/fvn2ZOHHiLXNG7taxY8coKRXYeDXgZFIWJ69kcTIpi7PXctSy5nqt\nQv1aBhp52PG4l715kqanHPq4X2rCefIwSUtLo1atWvf8Onl5eYAMNKrKH4/bX/VoyEBDAqr/C1QI\nwYgRI1i+fPktjzk7OxMdHY2fnx979uxR51yEhYUxZMgQtmzZwurVq7GxsSExMRFnZ2dKS0t57LHH\nOHv2LM2aNWPgwIH88ssvREZGotfrOXv2LLVr167qt3lHRcZS4lJyOJmUxamkLA6fTSExy4ix7Gxx\nstET6O1AoLcDjT3saOxhT11XWyx0f109Vqoc1X2ePGxkoPFguttAQw6dSDXCvn37WL58Oba2tsyb\nN4+QkBCGDx/O0aNHycvLU3sH4uLi1G169erFCy+8wODBg7l69Sq7d+9m/fr1jBo1in379qnBxMGD\nB9Wu2QEDBrB+/Xq++uor3nnnnWp5r8ZSEwnX8zl3LUctb372am6FpaQO1npq22no1dCGp1s2Jsjb\nQSa7kiTpgSQDDalalJSUsHDhQr766ivS0tLU1R7jx49Xq4+GhYVx9OhRioqK+PHHH+nbty9paWnq\na5TX91AUheDgYHbv3s21a9cA1MmerVu3rjD+Gxoayvr167l8+XKVvM/swhLOpOaYV30kZxNbVu/j\ndoXDOj3mRpC3gxpUREVFAdAyyLNK2ipJjyKtVktQUJB6+7vvviM9PZ2vvvqKTz75hGXLlnHs2DHm\nz5/Pd999R8OGDQkICKjGFj94ZKAhVTmTycSAAQOIjIy85bHExET150GDBvHuu+8C8PXXX1OrVi2O\nHj0KmIOLJ598EoD09HQ1IVbz5s2B3xNj7dq1i4yMDHU4Zd26dYA5oVdlysgr5nxaLmev5nL2mjkl\n99mruRUmaDrZ6AnwsufF1rVp7GlPQ3cD/m4GbCzkaShJ1cXa2lotcFiuTp06tx0e++677+jVq9dd\nBRpGo/GOVZgfBY/2u5eqxaZNm4iMjMTJyYkFCxYQHBzM+PHj2bFjB6tWreLNN98kICCACxcuqJM+\n165dqwYTYJ7T0bx5c1q3bs2hQ4fIysqiSZMmPP300wC0atWKkJAQDh8+zOOPP05YWBhHjhzh1KlT\nODg4EB4e/j+1PaughN+SszmdnMW5a7mcu2Ye8sjM/70SqbVeSwN3A0/6u9DAzY5GHgYCPB1wt7eU\nQx+S9ADYu3cvERERbNmyRb3v4MGDREZGsm/fPmbOnKlWdh4zZgxpaWnY2NjwxRdf0LhxY4YPH67O\nLWvevDkff/xxdb2VGuGeAg1FURKAHKAUMAohWiqK4gx8C9QBEoCBQojMe2um9DApT+U9ZcoUdfVH\nZGQkDg4OFBUVERQUpBYtA3PpdK1WS2JiIo0bN2bgwIF8+OGH/PTTT/zwww8AdOjQga+//lodglEU\nhfXr19OnTx+ioqJYsmQJAB4eHqxdu/Yvy68LIUjNLlSzZpbnpri5EqmrwYJ6tQx0D/Skfi1zvQ//\nWga8Ha3RyAyaknTXBn3+y/+0nclkTkCn0VTMCfPtP9v85bYFBQU0bdoUMCflK0+y90dPPvkkvXv3\nplevXgwYMACAzp07s3DhQho0aMDhw4cZPXo0u3fvBsyVmH/88Uf1O+lRVhk9GqFCiPSbbk8Gdgkh\n3lcUZXLZ7TcrYT9SJcjLy+P48eNYWVnRvHnzajkJyouKOTk5qfdZWloSGBhIVFQUWq2W9PR0XF1d\nGT9+PFOmTLmlnc888wwnT55U82gEBgbesh9vb2+OHj3K/v371TwaYWFhWFpaVnieEILLGfmcuJLF\nySs3OF1W6+PmXoo6LjYEeTsw6AlfAr0deNzLHleD5R93KUnSA+Z2Qyd/R25uLgcPHuS5555T7yv/\nbgN47rnnZJBR5n4MnfQBOpb9vBzYyx0CjfLlYtL9JYRgxYoVLFmyRF0K5uXlxRtvvEHbtm3V593t\n8bh06RJ79+6luLiYli1b0qRJE/bu3cvOnTvJz8+nadOm9OvXD0dHR3Wb+vXrA/Dee+/h5uaGp6cn\nP/zwA1FRUVhaWrJhwwaEELi4uKDT6YiOjv7T/Xt5eVFYWHjHdtva2tKqVSsAYmJiSMs3cfFGCRcy\njZzPLOFcZgm5xebVHhYa8HPQ0cJdT20HK+o66vBz0GGj1wAm4AZk3yAh29xdVxXkOVLzyGNSOQwG\ng5psC2DJ0CaV+vrl33V3+7yCggJKS0vJy8ujqKiIkpIS8vLyMBqNFBYWkpeXR05ODg4ODmqtpJtf\ny2g0otVq//b+HzTXr1/n0qVL6u0GDRrc8fn3GmgIYIeiKAL4XAixCHAXQqQACCFSFEVxu8d9SJVg\n7dq1zJs3DzD/UuTk5JCcnMykSZNYsmQJjz32WIXnp6am8ssv5m7MNm3a4OHhUeFxIQQLFixg6dKl\n6n2LFi3C2dmZjIwM9b5ffvmFNWvWMHPmTH777TdycnJo0KABtWvXJiEhgb59+2IwGMjJyQFg2LBh\nuLnd+6+MEILsYkFyjpHknFKuZBtJyDJyMbOE3BJzUKFRwM9eR4i3Ff5OOuo76fFz0KGTwx6SJN2G\nwWAgNzcXAHt7e+rUqcOGDRvo168fQghOnTpVYQWLZHavgUZbIURyWTCxU1GUuL/c4g9k4pv7r7S0\nlL59+wKwZMkSRowYQWlpKaNGjWLp0qV8//33aqDRokULJk+eTEREhFp/QKPRMGnSJMaNG8f27dsp\nKSnBaDSydOlStFotQ4YMwdnZmUWLFpGRkYGFhQUffPAB3t7ezJ49m0OHDjF69OgKmTwDAgJ49tln\n2bJlCzk5OWrvyrhx4+56wqTJJLiQnkfMlRucSLzByaQszqflkVXw+9CHhU5DYw87nmnmQaC3OYNm\nTS9xLpND1TzymFSutLS0Skmyda8Ju/64nbW1NVqtFltbWywtLdHr9dja2vLiiy8yatQoPv/8c9at\nW8fq1at5+eWXiYiIoKSkhOeff57WrVuj0+mwsrJ6aBOIubi4VFi5d3PCrtuptMygiqJMB3KBUUDH\nst4MT2CvEKLRzc+VmUGrVlJSEj4+Pjg7O5OWlqYWBjt58iRNmjShXr16zJgxA51OR0ZGBqNHj0ar\n1dK7d2/AvErEZDKh0WhuKX708ccfM3HiRMCcs+Lw4cNYWFiQlZWFlZUVO3bsoFu3boB5UmdQUBAr\nVqzg8uXLhIWFsXbtWrKysnBzc/tb45nZhSWcvWpOdHUmNYczqTmcSsoip8gIgI2FlkAvBxq4G6hX\ny0C9WrbUdzXg7WT9wJU4lxe1mkcek8olM4M+mKosM6iiKLaARgiRU/bz08AMIBIIB94v+3/T/7qP\nB1FBQQGZmZm4ubnVmLXTdnZ2aDQasrKySE1NxcvLC/g9y2ZiYiJDhw4FzLVAwNzzMWzYMABGjx7N\nggULMJlMPPPMM1hbW7NmzRoAkpOT1f0YjeaLfXFxMenp6fj4+PDNN9+oj8+aNYvHH3+cMWPGUK9e\nPbZt20ZaWtptU4EbS01cTM/jt5Rs4lJziCv7PyXr97wU1notDd0N9GnmRRMfR4J9HPF3MzxwAYUk\nSdLD7F6uhO7AxrJubh3wtRBiu6IoR4E1iqL8H3AZeO4Or/HQyMzMZNKkSaxatYqioqI7rpjYuHEj\nn332GRcuXKBu3bqMHj2aZ5999r7lWLC3t6dPnz5s3LiRnj178uabb3L9+nWmTJkCmLN0enp6Ulxc\nrJZb9vPzU7c/fvw4YF4yWp5kKz4+nl9//ZUvvviCjz76CEVR8PPzIyoqCp1Op07+LP8L0GAwqJNA\nPT09CQoK4ujRoyQmJmLn6klsinmlR1xqDnGp2cRfzaW4LHtmeeGwkLrONPIwJ7pq6G4nl5FKkiQ9\nAGRRtUpQUlLCk08+qV5Ub54QOXbsWHUSJsCMGTOYNm3aLa8xbdo0pk+fXqntysrK4tdff8VgMODi\n4kJoaCgJCQm3PO/dd9+lR48elJaW8vTTT5OTk0OrVq04fPgwYA5UcnJy8PHxUTN3btq0SZ330bt3\nb9zd3Vm1ahX5+eY8E15eXri7u6srRlq0fIJtu/aTcD2fg6cvMnPeYnTOvng2bk5mgVFtSy07Sxp7\n2PGYpz2PeZoLh9WvZXgkC4fJbvqaRx6TyiWHTh5MsnprNVizZg2DBg3C19eXnTt30rBhQ77//nt6\n9+6NEIKEhAR8fX1JSEhQ/6r/4IMP6NWrF9u2beP1119HCMG5c+eoV6/ePbfHZDIxbdo0Zs+erV74\n/f39mTNnDnFxcezevRudTsfmzZvR6/Xk5uYSExMDwLfffktERASKovDaa68BMHv2bEwmEwMHDuTb\nb78F4Oeff6Zdu3YV9qvoLAnp0pO0AkgrAJ2jJxZOHmjsa6Gzd0PR/V663FSUj53Io2e7ZjR0NwcU\njT3tZG6Km8iLWs0jj0nlkoHGg0lWb60Ge/bsAcypaMtrbISFhdG9e3e2bt3K/v37GTJkCN999x0m\nk4lBgwYxadIkwFxz49ixY6xevZqNGzeqF/c/c/HiRT777DOOHz+Oq6sr4eHh9OjRo8Kwy6xZs5g5\ncyZgrv2RmprKuXPnGDhwINHR0UyaNImSkhLs7OwoKioiKSlJ3bZbt25EREQghCAiIqLCvjdv3syY\nceMRNs6s+2E/9q2epUnbLmDnRkaJjjyTnpSy5zoBBr1CbVdblLwMjuzdTkH6FYw3UilJT6R9y0A2\nbthQIb+GJEmS9PCRgUYlKM80mZlZMdN6+fDJ1KlTmThxItbW1gBqyfNyLi4uABQWFla4f+/evcye\nPZtTp07h4eFB+/bt+fTTTyskgVmzZg1jx47lk08+QVEUCgsLmT17NmAuANSnTx9KSkp44YUXWLdu\nHXPnzmXBggXo9XoGDBjAqlWr6NevH0OGDKGwsNCcqluro3/4v7Cs5Ucu1jj5NuTX80mkF8AWa1cU\nNNh0a4kNkGujp14tA0+42FDXxZY6rrbUcbHFz8UGB2u92s7MlzuyadMmMjMzCQkJoU2bNrLuhyRJ\n0iNADp3cg7i4ONLS0rhx4wa9e/fGxsaG+fPn06ZNG1asWMGsWbNuu52lpSX79++nVatWHDt2jC5d\nupCVlcXBgwdp08acm3/p0qWMHDnyttv37t2bl156iZiYGN59912KiorYvXs3oaGhnD59msDAQOrW\nrcuFCxfUbQ4cOECHDh1o0aIFx44do9QkiD5zkedGjiG9UEHv7I3OyQu9iw96Rw9Qfp8T4WJrgZ+L\nDQZRwI0r57AR+XQNacKAbh1wtLG4XROlSiC76WseeUwq190OnaSmpnLkyBFsbW1p3769ukruXoZO\nFEVh6NChrFixAjCvnvP09CQkJKRCUbWHVUJCAgcPHuSFF17429vIoZMqEBsby4gRI9TJknq9nkaN\nGnHmzJlbggOdTseXX35Jp06dWLduHRMnTqSoqIiQkBBq1apFWloaYC7O8+OPP/LZZ5/h7u7OwoUL\nAXjzzTcJDw9n5cqVauAybtw4OnfuTM+ePcnPz2fmzJm88cYb+Pj4oNebexFSU1PJzMzEycmJ7MIS\nth8/j13LPhQ1bcfTc/aRkJ5PcakJnhqLC0BpMbr8DOq5Gejcsi6NvZ2o52qgjqsNdlb6m95Rl/v6\n2UqSJP2R0Wjktdde47PPPlOX0Xt6erJo0SJ69ep1T69ta2vLqVOnKCgowNramp07d+Lt7V0Zzb5r\n1VFSPiEhga+//vquAo279dAFGufPn+fdd99l69atCCEICwtj6tSpNGzYsFJePyMjg06dOpGamoqj\noyP+/v5ERUVx5swZ2rdvT2lpKcnJyej1es6ePcs///lPtST5hAkT+PHHH9m2bRtWVlakpaVhMBjo\n2rUrO3bsYNeuXRX2Vb9+fd5//33AXDmw3KZNm+jcuTNgzmCn6CyJjr9MTFI2Ogd37Fs/h87Rg5DJ\nq7B1r01msQaohXPnUaAz4eNkQ2hjN+q62FLbxZa6rrZcjj+JRvGVf6lJklTjTJ8+nU8++QSNRkNo\naCjJycmcOXOGfv36cfToUfz9/e/p9Xv06MHWrVsZMGAAq1evZvDgwRw4cAAw95a88sornDx5EqPR\nyPTp0+nTpw8JCQm8+OKLam/K/PnzefLJJ0lJSWHQoEFkZ2djNBpZsGAB7du3r5C+fN26dWzZsoVl\ny5bdUlJ+xowZt93fsmXL+O677ygtLeXUqVO89tprFBcXs2LFCiwtLdm2bRvOzs6cP3/+T0vX29vb\nc+zYMVJTU/nwww8ZMGAAkydPJjY2lqZNmxIeHs7TTz/NiBEjKC4uxmQysX79+r+sZfKXhBBV/u/G\njRui/F9lio+PFy4uLgJzDRb1n5OTk4iNja2UfURERAhAhISEiJycHCGEEIcPHxY6nU5otVpx5coV\nIYQQkydPFoB44403Kmw/ePBgAYi5c+eKxMREkZGRIVxdXQUgevToIb788kvRrl07AQhFUUTCpcsi\nMSNPbDkSL+yadBUO7YeK4H/NEf0/+1m0/c+PwnfCWlH7zS23/PMZu0J4DI0Qrs9MEvatnxNW9VqI\nPs+/KIxG423f19GjR8XRo0cr5TOSKoc8JjWPPCaV69q1a3/5nPz8fGFvby8AsXPnTiGEECaTSQwf\nPlwAYuTIkSI3N1fk5ub+T22wtbUVJ06cEP379xcFBQUiODhY7NmzR/Ts2VMIIcSUKVPEihUrhBBC\nZGZmigYNGojc3FyRl5cnCgoKhBDma0+LFi2EEOZrxMyZM4UQQhiNRpGdna3up9zatWtFeHi4EEKI\n8PBw0bNnT/W7+c/2t3TpUlG/fn2RnZ0trl27Juzt7cWCBQuEEEK8+uqrYs6cOUIIITp16iTi4+OF\nEEIcOnRIhIaGqvsZMGCAKC0tFadPnxb169cXQogK71UIIcaOHStWrlwphBCiqKhI5Ofn3/KZ/fG4\n/eGafss1/6Hq0Zg+fTrXr1+nS5cufPrpp2g0Gl555RW2b9/O1KlT1WyW9+LIkSMA/Otf/8JgMADQ\nqlUrnnrqKXbt2kVUVBTe3t507dqV999/ny+//JJnn32WkJAQvv/+e9avXw+YI2gfHx9WfbuOG6UW\nPN6pHyNnzOVqThFNRwVw1ns3Wgd3On76K6JsvoRzj/EIUynpOenkRkeRl55MUVY6pvws/jP9LRrV\n9sTb0YZvl3zGtA8mExQUhI+PDwZfA8+//hZ9+/ZV049LkiQ9CC5cuEB2djb16tWjSxfz0K2iKIwa\nNYply5bdsbrz39WkSRMSEhJYvXo1YWFhFR7bsWMHkZGR6iq8wsJCLl++jJeXF2PHjuXXX39Fq9US\nHx8PwBNPPMHIkSMpKSmhb9++NG3a9C/3f3NJ+T/bH0BoaCh2dnbY2dnh4ODAM888A0BQUBAxMTF/\nWbq+/BoQEBDA1atXb9uWNm3a8N5773HlyhX69et3770ZPGRDJ5s3bwbg888/V/NRfPHFF/j6+rJ5\n82aEEH+50iExMZF169aRm5tL27ZtCQ0NrbBN+XLM8l8qMI+rnT9/Hvh9RUloaCjdu3dn+/bttGnT\nBmtra4o1Vlj4NaNjj4HM2J/JqW92cCPfGu+XFpELTFpnzmXhYmuBnXMtbiSdJT/uJyyNuWQlncOY\ndRUnC8jOyqzwyxMQEMDL3X7/ZW7e5HEAatWqxbZt2/6nz1KSJKkmcHV1RVEUkpKSuHbtmlrd+ddf\nfwWolGrPYJ5kP2nSJPbu3atmSAZzr//69evV1AXlpk+fjru7OydOnMBkMmFlZQVAhw4d2L9/P1u3\nbuXFF1/k9ddfZ9iwYRWuI39cYXjzJNY/29/hw4fVFY5gLnZZfluj0WA0GjGZTDg6OqqfzR/dvL34\nk4UgL7zwAiEhIWzdupVu3bqpcwzvxUMVaJQX/CqfEHnzz38sBnY7c+fOZdKkSZSWlqr3tW/fnsjI\nSDXAGDJkCIsWLeLjjz/G2tqaZs2a8cUXX5CQkECdOnVo06YNhSWlnLuWS/i0TzEF/cCpxAwUZx90\ndq4AJGoUbAuK6RHogTHrGgs+noWdtpTINSt4vK4XGItp1WoC6adPY2dnx9WcHCwtLRny/PN8/PHH\nKIpCbGwser2eDh06EBsby88//0zbtm0pKSlRJ5LK+RaSJD3o3N3d6dGjB9u2baNLly688sorJCUl\n8dFHHwEwfPjwStnPyJEjcXBwICgoiL1796r3d+vWjXnz5jFv3jwURSE6OppmzZqRlZWFj48PGo2G\n5cuXq9eNS5cu4e3tzahRo8jLy+P48eMMGzYMd3d3YmNjadSoERs3bsTOzu627fiz/f0d9vb21K1b\nl7Vr1/Lcc88hhCAmJobg4OA/3cbOzo6cnBz19oULF6hXrx7jxo3jwoULxMTEPNqBRmZmJgsXLuSH\nH35Aq9Xi7+/PiRMnGDduHJ9//jkajYaxY8cC0L179zv2Zuzdu5cJEyYA0L9/f/z8/Fi5ciUHDhxg\n7NixLF68mPz8fNq3b8+ECROYM2cOU6dONW+s0eHQoCXPvDGL/gsPEXPlBqayYNFCX4cmIY9T18WK\nFnVcaernxONe9mp5ciEEBz7/fxw+fJiuIU146qmnOHLkCKmpqfj5+XHy5ElycnJwcnLCxsZGbW/b\ntm0B+Oc//8knn3xChw4daNu2LRcvXuTKlSsYDAZGjx5d2R+5JElSlVuwYAEdO3bk5MmTvPTSS+r9\nI0aMYODAgRQUFNzzPnx8fBg/fvwt97/zzju8+uqrNGnSBCEEderUYcuWLYwePZr+/fuzdu1aQkND\n1V6JvXv38tFHH6HX6zEYDHz11VcAvP/++/Tq1QtfX18CAwPViaF/d39/16pVq3j55ZeZOXOmWrr+\nToFGkyZN0Ol0BAcHM3z4cAoLC1m5ciV6vR4PD4/fr3P3oNrzaFy9epW5c+dy6NAhHBwcGDJkCOHh\n4RV6JW4nOTmZ9u3bV8gVAdy2lLmtrS0//fTTHcfKBg0axJo1a3jrrbd47733ADh37hyNGjVCCIFe\nr6e4uBh/f39eef1tig3ubNofzXXsKHKoTamiRatRCPZxoE19Fx73cqChux11XGzQae88LyI1NZXB\ngwdXiKKDgoJYs2YNjRs3vuO2JSUlvPrqqyxatEhd9uXv78+yZcvUYOTvkPkBah55TGoeeUwq193k\n0cjJyWHFihUcOHAAg8HAoEGD6Ny5M4qiyBTkVeyBq3Xi7e1dIdMlmHsfevbsycGDB7G1tWXQoEF0\n6NCByMhIdu/ejaWlJXFxcWzfvp3g4GCmT59OYWEhb7/9NhcuXMDf35+LFy8C0K17d95+Zypnz11g\n87bvKS0uonuXUF588cUKPQStWrXi6NGjbN+9H88GQaRkFZJyPYsJb/4/sLBBY2WHhZM7Wpfa6Oxc\n1O3q17Klrb8rbf1daVPfBXurOwdIdxITE8OZM2fw9fUlJCTkrjJnXr16lejoaJycnHjiiSfuetKn\n/AKteeQxqXnkMalcstbJg+mBCzQcHR159tlnmThxIufPn2f8+PEVGl3O1dWV9PT0W+6Pj49XZ8Xu\n2befsGGv4N6sM3XbPUNiRgFG063vz1RciLYkj0D/2ng526KgsP/4aXKFJRorwy3PF6VGHG0s8HSy\nRZudwoHIr7HMv8pvB3dSy/H242wPGvkFWvPIY1LzyGNSuWSg8WB64DKDurm58c0332BhYUG7du2I\niIggKysLOzs7IiIiSE5OZubMmaSnp+Ps7Mzrr79OWloas2fPRmPjyJItPxHQWs8vF66zNy4P98Gz\nEMZi/Jxt6RHoZhz7HwAABw9JREFUyZFDB9n5w3YMNlZ07dwZrd6SPYeOkV0MV/SlFJvqYzSZaODj\nzoHtGzHeSKV5Qz98Xe1Yt3IZRbmZtA1pyYH9+9U2B675N6djTxN/OoZadzE8IUmSJEmPmmoPNFxd\nXdV89WlpaZw+fRqAwKbNCe0zmMvp2dhu/BlhaYdngwCu1evOJYd8/F4NQbG0ZfVVYNNp3O0scclL\nIGHzMp5q5MHyiE0ABEzsR3ZsLF9v2ULPnj0BOHOmGY0bNybPyooj2dnqfJD5lmeZMGEx+44ZK7Rx\nQP/+6s8mk0mdxFPebkmSJOnuaTQaCgsL1aWhUs1XWFh410Pz1R5o/PbbbyxZuZpi31YcOHkR9yEf\noXNwJ9ngRNc55l4Epx6vApBrMnLo/HV8nG1o6lzKnk2LKLmeiJtlKYnZaaSkpKDVanl76V719cvX\nQwcGBqr3+fv7Y2VlRWFhIfn5+Wpht7Fjx9K/f382bNhATk4O2dnZ/Oc//+GDDz7A39+fRo0aMWfO\nHC5duoSvry/Nmzevok9JkiTp4ePs7ExGRkaF5ZX/i/Lv+fJK2NL9o9FobqlA/leqPdBwaDeE6VFa\nNKfiMGZdxVRSRP75Iwzo3pGwp0KoZauna4fWFGReI7Rda3b9+CMA77yzjcioSKysrLhclvzE39+f\nuXPn0q5dO/X1mzdvzvbt25k/fz4ffvghiqKwePFiCgsL8fDwYMyYMRQUFNCxY0eGDx+Op6cnY8aM\nAaC4uJiDBw+yb9++CoV7tFot8+fPVzO5SZIkSXdPUZRKCQ4uXboE8Jer9KTqUe2TQYP/8xNF5w5x\nff8qStIuUrt2bS5duoRGo6Fjx44kJycTFxcHmC/wYWFhZGZm8tNPPwGwfft2PDw80Gq1BAQE3NKl\ns2fPHjp37owQgsaNG2Nra0tUVNRt21W/fn327dtXoXJfQUEB//3vf1m5ciWZmZm0atWKN954Qy3n\n/rCQk9xqHnlMah55TGomeVyq119NBq32whfJi8fwRPEJTuzbSlJSkrryRKPRsHv3buLi4nB3dycs\nLAwhBJs3b+ann37C1taWzz//nG7duhEcHExgYOBtx41CQ0NZtWoVbm5uxMXFERUVpaZhdXR05KOP\nPmLp0qUEBgaq+76ZtbU1kydP5tSpUyQlJbFx48aHLsiQJEmSpPul2ns0JEmSJEl6ONTIHg1JkiRJ\nkh5eMtCQJEmSJOm+qZahE0mSJEmSHg2yR0OSJEmSpPtGBhqSJEmSJN03VR5oKIrSXVGUM4qinFMU\nZXJV718CRVF8FUXZoyhKrKIopxVFGV92v7OiKDsVRTlb9r9Tdbf1UaMoilZRlGhFUbaU3a6rKMrh\nsmPyraIoMu99FVMUxVFRlHWKosSVnTNt5LlSvRRFmVD23XVKUZTViqJYyXOl5qrSQENRFC3wKdAD\nCAAGK4oSUJVtkAAwAq8JIR4DWgNjyo7DZGCXEKIBsKvstlS1xgOxN93+AJhTdkwygf+rllY92v4L\nbBdCNAaCMR8fea5UE0VRvIFxQEshRCCgBZ5Hnis1VlX3aLQCzgkhLgghioFvgD5V3IZHnhAiRQhx\nvOznHMxfnN6Yj8XysqctB/pWTwsfTYqi+AA9gS/LbitAJ2Bd2VPkMaliiqLYAx2AxQBCiGIhxA3k\nuVLddIC1oig6wAZIQZ4rNVZVBxreQOJNt6+U3SdVE0VR6gDNgMOAuxAiBczBCOBWfS17JM0F3gBM\nZbddgBtCiPJywvJ8qXr1gDRgadmQ1peKotgiz5VqI4RIAiKAy5gDjCwgCnmu1FhVHWjckjEMkOtr\nq4miKAZgPfCqECK7utvzKFMUpRdwTQhxcyEeeb5UPx3QHFgghGgG5CGHSapV2XyYPkBdwAuwxTwc\n/0fyXKkhqjrQuAL43nTbB0iu4jZIgKIoesxBxiohxIayu68qiuJZ9rgncK262vcIagv0VhQlAfOQ\nYifMPRyOZd3DIM+X6nAFuCKEOFx2ex3mwEOeK9WnC3BRCJEmhCgBNgBPIs+VGquqA42jQIOy2cEW\nmCfwRFZxGx55ZWP/i4FYIcTsmx6KBMLLfg4HNlV12x5VQogpQggfIUQdzOfFbiHEEGAPMKDsafKY\nVDEhRCqQqChKo7K7OgO/Ic+V6nQZaK0oik3Zd1n5MZHnSg1V5ZlBFUUJw/yXmhZYIoR4r0obIKEo\nSjvgAHCS3+cDvIV5nsYawA/zyfycECKjWhr5CFMUpSMwSQjRS1GUeph7OJyBaGCoEKKoOtv3qFEU\npSnmCboWwAVgBOY/0uS5Uk0URXkXGIR5BV008A/MczLkuVIDyRTkkiRJkiTdNzIzqCRJkiRJ940M\nNCRJkiRJum9koCFJkiRJ0n0jAw1JkiRJku4bGWhIkiRJknTfyEBDkiRJkqT7RgYakiRJkiTdN/8f\nUf7Zj7wc14sAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"sensor_var = 20\n",
"process_var = .001\n",
"process_model = (1, process_var)\n",
"pos = (0,500)\n",
"N = 100\n",
"dog = DogSimulation(pos[0], 1, sensor_var, process_var*10000)\n",
"zs, ps = [], []\n",
"for _ in range(N):\n",
" dog.velocity += 0.04\n",
" zs.append(dog.move_and_sense())\n",
"\n",
"for z in zs:\n",
" prior = predict(pos, process_model) \n",
" pos = update(prior, (z, sensor_var))\n",
" ps.append(pos[0])\n",
"\n",
"book_plots.plot_measurements(zs, lw=1)\n",
"book_plots.plot_filter(ps)\n",
"plt.legend(loc=4);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"It is easy to see that the filter is not correctly responding to the measurements. The measurements clearly indicate that the dog is changing speed but the filter has been told that it's predictions are nearly perfect so it almost entirely ignores them. I encourage you to adjust the amount of movement in the dog vs process variance. We will also be studying this topic much more in the later chapters. The key point is to recognize that math requires that the variances correctly describe your system. The filter does not 'notice' that it is diverging from the measurements and correct itself. It computes the Kalman gain from the variance of the prior and the measurement, and forms the estimate depending on which is more accurate."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Example: Bad Initial Estimate\n",
"\n",
"\n",
"Now let's look at the results when we make a bad initial estimate of position. To avoid obscuring the results I'll reduce the sensor variance to 30, but set the initial position to 1000 meters. Can the filter recover from a 1000 meter error?"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAhkAAAC+CAYAAACYnB30AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzs3XdYFMf/wPH33tE7KAgKVrD3bmJD\njVE0amLXqEk0GmMsib1ETbEQW2Ji+ZnEWCOW2HvvqICAir1QBEREQJB+N78/kP2KXcRwxnk9zz3A\n3O7s7I7nzs3OfEYRQiBJkiRJkpTfNAVdAEmSJEmS/ptkI0OSJEmSpNdCNjIkSZIkSXotZCNDkiRJ\nkqTXwqggDpqYmChHm0qSJEnSf4ytra3y8N+yJ0OSJEmSpNdCNjIkSZIkSXotCuRxycNsbW0LuggS\n4O/vD0Dt2rULuCRSDlknhkfWiWGS9fJsWVlZ1KlTh6CgIExMTChfvjwhISHodDpatWrFjh07ANDp\ndFSoUIErV65QtmxZ2rZty+HDh/H398fOzo7r169jb2/PtWvXcHd3x9zcnIsXLz7zPi57MiRJkiTp\nP8zIyIidO3fSrl07MjMzOXPmDIqi0Lt3b9asWaNut2fPHq5cuUKpUqUICgpi1qxZnDx5kkaNGpGQ\nkMDff/8NQJkyZWjbti2pqalUq1btmceWjQxJkiRJekOlpaUxZcoUPDw8sLOzw9PTk+3btz+2XZEi\nRdi0aRM3b97k1KlTREdHs3TpUqytrdVtrl27BkCLFi0wNzcHQKPR4OXllet9gKVLl9K8eXMSEhKe\nWb4Cf1wiSZIkSdLL0+l0tGvXjj179qhpBw8e5ODBg/zxxx/07dv3sX2KFi1K0aJFn5hfqVKlANi/\nfz9paWmYmZmh1+vZuXNnrvcBHBwc2Lt3r/qo6mme25OhKMpiRVFuK4py7qE0B0VR9iiKcuXBT/sH\n6YqiKHMVRbmqKMoZRVFqPi9/SZIkSZJe3oYNG9izZw+Ojo7s2LGD6OhoJk2aBMCIESNISUl5qfxa\ntmxJ6dKluXbtGrVr12bcuHE0bNiQQ4cOYWNjQ8+ePR/b53njYF7kcckSoNUjaWOAfUIID2Dfg78B\nWgMeD179gQUvkL8kSZIkSS9p8+bNAIwePZpWrVrh7OzM5MmTqVGjBgkJCRw5cuSl8jMyMmLTpk24\nubkREhLCtGnT8PX1xc7Ojg0bNuDg4PDSZXzu4xIhxGFFUUo+ktweaPrg96XAQWD0g/RlIntp1xOK\notgpiuIihIh+Wv7P62qR/l2yPgyPrBPDI+vEML1t9XL79m0AYmJicp17VlYWABcvXqRQoUIvna+P\njw8HDx4kNDSUIkWK0Lx5c6ysrJ54fS/HZdCmfqWn5pXXMRlFchoOQohoRVGcHqQXAyIe2u7mg7Sn\nNjIkSZIkSXp5DRo0YNeuXaxYsYLq1atTunRpNm/ezNmzZzE3N3/uzI+nMTExoWXLls/cRgjB7uup\n/BWURJv6T98uvwd+Kk9Ie2YIcTmv2TDIeeaGR9aJ4ZF1Ypj+K/UihEAIgUbzYhM/q1SpwtatW/H3\n96dnz55otVp0Oh0AkydPpmnTpq9Ulou3kihqa46thXGu99IydYzfcI5/Am/jWc7xmfnkdQprjKIo\nLgAPft5+kH4TcHtoO1cgKo/HkCRJkqT/lOjoaL766itcXV0pUqQIH3/8Mfv27aNXr15YWlpiZGRE\n06ZNOXjw4HPzMjU1Zc+ePQwaNAhra2t0Oh3lypXjzz//ZOTIkU/cR6cXnL2ZiF7/9O//yelZDPEJ\novUvR6jxw27a/XaUaTsucPhyLFdikui44Dj/nL7JsBYe/NmnzjPLqGQPn3i2B2MytgohKj/4ewYQ\nJ4SYrijKGMBBCDFKUZQ2wFeAF1APmCuEqPtofg8vkCYjfhqG/8o3gf8SWSeGR9aJYTKUetHpdFy6\ndAmtVkvZsmVRlNyd+9HR0dSrV4+IiIhc6Yqi8Oi9WKvVsm3bNt5///0XOrZeryc9PV2Nb/EkQgjG\nrj+Lj18EVYrZMqFNBeqVzj1m40L0PQatPE1o3H0GebqjURSOX7tDYHgCWQ8aJjZmRvzcrTrNyhcB\nIDExUd3/pRdIUxRlFeALlFMU5aaiKH2B6cB7iqJcAd578DfAduA6cBX4HfjyeflLkiRJ0ptu1apV\nlC5dmkqVKlG+fHkqVKigxpfIMW3aNCIiIqhTpw4BAQFcvHiRMmXKIITA1taW69evk5iYyJdffolO\np2PUqFGPNT6eRqPRPLOBATBr92V8/CL4oFpR7iSn03XRCb5YHkDonfsIIVjjF0GHecdISs/i78/r\nM7xlOb5+ryxrv3iH4EktWfJpHUa1KseWwQ3VBsbzvFBPRn6TPRmGx1C+CUj/I+vE8Mg6MUwFXS+b\nN2+mffv2QHawq8zMTGJjYzEyMuLw4cM0aNAAgJIlSxIWFoafn59a1goVKnDx4kUAUlJSMDc3Jz09\nHUdHR5KSkoiKisLFxeWVy/jXsRt8t+U83eq4Me2jKqRl6vnz6HXmH7xGpk5PDTd7ToXe5V33Qvzc\ntQaO1qYvnPcr9WRIkiRJkvR033//PQDffvstERERREZG0r9/f7Kyspg6daq6Xc7U0od7HLRarfq7\nXq9Xf+b8/ugjl7zYFBTJd1vO836lIvzYoTKKomBuouWrZh4cHNmUjjVdCYpIYGhzD5Z9Vu+lGhjP\nIxsZkiRJkpRHaWlpBAQEoNVqGTduHBqNBmNjYyZMmADAsWPH1G3fe+89AEaOHMnt27dJSkrC2Dh7\n5oalpSXXrl0jKiqKL7/8kvv371O7dm2cnZ1fqBxnbyYyadM5/jhynaNX7nAnOR2AQ5djGb4mmHql\nHPilWw2MtLlv+07WZkzvWJXz37/P1++VRat59UbNw+TaJZIkSZKUR8bGxpiampKenk5UVBSlS5cG\nIDw8HCDXAmTjxo1j48aN7NixA2dnZzQajTrl9P79+7niWpiYmDBjxowXKsP+izEMWhmITi/I0OnV\n9MJWpiSnZ+JRxJrf+9TGzFj71DwebXw8yblz5zh37hwuLi40atTohabayp4MSZIkScojrVZLly5d\nAOjUqRNbt27ln3/+4ZNPPgGgW7du6rYeHh4cPXqUtm3boigKOp2Ohg0bsn79er744gsKFy6MpaUl\nbdq04ciRIy8U52K1XzifLwvA3cmKY2OaETChBX/3q8e3bSviWc6R9yo6s/SzOtiYGT83r6e5e/cu\nrVq1okqVKnTv3p2mTZtSrlw5Tp8+/dx95cBPCSj4gVPS42SdGB5ZJ4apoOslMjKShg0bEhoamiu9\natWqHDp0CDs7u8f2ycjIQKfTPXdGyNMIIZi77ypz9l6mSVlH5vesiaXp63k40bJlS/bs2YO1tTXN\nmzfn9OnThIeHU7hwYXXKbo5HB37KxyWSJEmS9AqKFSuGv78/8+bNY9euXWi1Wtq3b8+AAQOwsrJ6\n4j4mJia5/k5Ky2TajoscvhyLqZEGM2Ptg5cGa1NjXOzMKGprjoudGS625qwLuMmqU+F0quXKtI+q\nYPwCjzvy4syZM2oDIyQkBDc3NzIyMvD09OT48eMsW7aMTz/99Kn7y0aGJEmSJL2iQoUKMXHiRCZO\nnPjS+564HsfwNcFEJ6bSsqIzWo1CaqaOtEwdqRk6biWmceRKLPczdLn2+8rTneEtHw/6BZCZmcmu\nXbuIjo6mUqVKNGjQIE8zVc6ePQtk92a4uWUH9DYxMaFnz54cP36cM2fOPHN/2ciQJEmSpAKQlqlj\n5q5L/HnsBsUdLFj7RQNqlfjfcupBQUH4+PiQnJxM33fepWWbdtxJ1RGdkIaFifaxaJ05fH196dKl\nCzdv3lTT6tevz/r161865kaRItlBtwIDA8nMzFRnw/j5+QE8d/aLbGRIkiRJ0r/sfNQ9hvoEcuV2\nMr3ql2CsV3ksTLJvyUIIxo0bx/Tp09Xt582bR6VKldi7dy/lyz/9xh4XF4eXlxcJCQmUL1+eOnXq\nsGPHDk6cOEGnTp04evToS/VoeHp6UrJkSa5fv06LFi3o2bMnJ06cYMmSJWg0Gvr06fPM/WUjQ5Ik\nSZLInkXx559/cuLECWxtbenZsyfNmjV74k05PT2dc+fOYWpqSqVKlV7qxn3kSiwDlgdgbWbE0s/q\n0qRs7pVMt2/fzvTp0zEyMqJ///4UL16cRYsWERISgpeXFw4ODsTHx1O3bl2GDRtGuXLl1H2XLVtG\nQkICjRs3Zt++fRgZGREbG0v58uU5fvw4AQEBjw2QvX//Prdu3aJIkSKPjSHRarWsXr2aVq1acfjw\nYQ4fPgxkBwn77bffKFeuXK6In4/JWVr233wlJCSInJdkGPz8/ISfn19BF0N6iKwTwyPrxDDlR71c\nuHBBODs7CyDX64svvhB6vT7XtvPmzROOjo7qNuXKlRN79+59oeNsDLwp3MdtE+/POSRiElOfuE2H\nDh0EIKZNm6amhYWFCUVRHiufhYWFOHTokLpdv379BCB+/fXXXHl27dpVAGLJkiVqWnJyshg4cKAw\nNzcXgDA3NxdffPGFSEpKeqxMsbGxYsaMGaJ3795i9OjR4vz58+p7j9zTc93vZZwMSZIk6a332Wef\ncevWLerVq8eyZcuYNGkSZmZmLFy4kK1bt6rb/fXXXwwaNIjY2FjKlClDkSJFuHTpEm3atCEoKOiZ\nx1h89AZDfYKoWdyeNV80wMnG7InbRUZGAtCwYUM17eTJk+piaZMmTeLIkSN06tSJlJQUPv/8c/U9\nV1dXAI4eParum56ezsmTJ3O9L4Sgc+fOLFiwgNTUVNzc3EhNTWXhwoV07NjxsYXZChcuzIgRI1i6\ndCnTp0+nQoUKz7+oOQf6t1+yJ8PwyG9ohkfWieGRdWKYXrVerly5IgBhY2Mj7t27p6Z7e3sLQHTq\n1EkIIYROpxOlSpUSgJg7d67Q6/UiIyND9OrVSwCiR48eufLNzMwUa9euFb379BENB80QJUZvFZ8v\nPSVSM7KeWZ4+ffqovSg5mjVrJgBhZGSk3jszMjKEi4uLAMTp06eFEEJcv35dGBkZCUB07NhRzJw5\nU9SpU0cAokyZMiIrK/vYx44dE4Cws7MTgYGBQgghgoODhb29vQDEkSNHXvj6yZ4MSZIkSXqKO3fu\nAFCqVKlcYcCrVKkCQGxsLAC3b9/mxo0b2Nra8uWXX6IoCsbGxowaNQqA48ePo9MLwuLusyM4grq9\nxzLgj4Ps1lcjwqoCSYHbOf/7cLLSU59ZnsGDB6PValm4cCH169enS5cuHDx4EIDmzZurQSyNjY3V\n2R/JycnqOSxZsgRjY2P++ecfRowYgZ+fH05OTqxbt04NnHXo0CEAevToQfXq1YHs4GEff/xxrvdf\nlRz4KUmSJL3Vypcvj5mZGcHBwRw9epSGDRuSlZXFokWLAKhVqxaQvYiZRqMhOTmZ2NhYdfrm9evX\nAbBxcOLD+cc4c/PBQMjiTbFySqKolRZ3s9vsP7eRY1FR/PDDD3h7ez+1PLVq1WLFihUMGDCAkydP\nqo86ABISEoiPj8fOzo7169cTFBSElZWV2lAA6NmzJ40bN2b58uVERUVRuXJlevTogY2NjbqNhYUF\nkN1welhMTAxAniORPubRro1/4yUflxge2Q1seGSdGB5ZJ4YpP+pl2LBhAhAajUY0adJElChRQh1Y\nefXqVXW7nEGZderUERs3bhR//fWXKFq0qECjFe+O9xGlx24Tvx++JlxrNBEacxuxf/9+dd+cRxRO\nTk4vVKakpCSxdu1asXjxYnH8+HF1YKq5ublaPkBMmjTppc83LCxMaDQaoSiK+OGHH0RgYKCYMmWK\nUBRFaDQaERoa+sJ5PetxiVy7RAIKPva/9DhZJ4ZH1knBuX//Pv/88w/h4eF4eHjQvn17zMyyB04+\nr150Oh07d+7kzJkzODs707Fjx1zf6iE7QuawYcNYtGgRWVlZQPajh7/++osmTZqo24WGhtKoUaNc\nga4AKn46jftOVfipU1W61HbD1NSUjIwMEhMT1WOlpaWpPQR6vf6lI3BevnyZgQMHsn//fgAcHBwY\nMWIEo0ePfqEVUR/l7e3NmDFjHkufMmUK48aNe+F8Hp7CKtcukSRJkt4oR48epUOHDsTFxalprq6u\nbNu2jSpVqpCSkqI2OB4VFhaGl5cX58+fV9OGDh3KqlWraNOmjZpmbGzMvHnzmDhxIgEBAdjZ2VGv\nXr1ci38BlCxZksDAQBYsWMC+ffswMzOjcNM+HE2wYWhzD7rUzg69Xb16dU6dOsWiRYsYMWIEgPr4\npVq1ankK8V22bFn27dtHVFQUCQkJlClTBlNT05fOJ8fo0aOpWrUq8+fP59q1a5QuXZovv/wSLy+v\nPOf5KNmTIQHyG5ohknVieGSd/Pvu3btHyZIliY+Pp3bt2jRr1oxt27YREhKCra0tZmZmxMTEYG9v\nz1dffcWECRPUxceEENSrVw8/Pz9KlCjBRx99hJ+fH0ePHsXMzIwrV66oUzrzao1fBKP+OUPnWq78\n1Kmq2nhYt24dnTt3BqBu3bpoNBpOnDgBwMqVK+nRo8crHdeQPKsnQ84ukSRJkgzW6tWriY+Pp0GD\nBpw4cQJvb28CAgKwtrYmMTGRmJgYjI2NiY+P54cffqBnz57qvv7+/vj5+VG4cGGCgoKYPXs2hw8f\npl27dqSlpbF48eLHjpel07P8RBghUc+IYvnAocuxjN1wlkYehZn6UZVcvROdOnVi7ty5WFtbc+rU\nKU6cOIGlpSWzZs36TzUwnkc+LpEkSZIMSnBwMIsXLyYqKoro6GgAWrVqpT66uHTpEklJSQD079+f\nfv364e/vz6hRo1i3bh2nTp2ibt26XLt2DYDGjRtjZ2cHZIfDbtu2LZs3b1bfz3ErMY3Bq07jFxqP\niZGGqR9WoVOtx3s6hBAsPhbK9B0XKFvEmvk9az5xqfXBgwfzySefcPjwYYQQNG7c+LGxIP91spEh\nSZIkGYzffvuNwYMHP5a+evVqxo8fj1arZceOHWq6l5cXiqJQp04d+vTpw7x589i9ezd169alVKlS\nABz1C2Te3gscuppANTdbju/NjoaZ8z5k90p8vTqItEwdUz6szNbgaEasDSY4IoFv21bExCi7ERF/\nP4OR686w90IMLSoUYUanqlibGT/1fKytrXON/XjbvFIjQ1GUr4F+ZE+jOQt8CrgAPoADcBroJYTI\neMVySpIkSf9xly9fZsiQIQAMHDiQd999l6VLl7Jnzx7Onz9PvXr1aN68OcuWLQOyYz14eXkRHBwM\nQGpqdpArrVaLEAJ94TJ49J5CumNFZuy9jg33OXXjDqJkJ4p0KUOFZh+RkaVn7r4rzDt4lbJO1szr\nWRN3Jyu61nbjp12XWHT4Ouej7zG/Z03C76YwZFUgd5LTmdi2Ip++WzJPAzjfJnke+KkoSjHgKFBR\nCJGqKMoaYDvgBawXQvgoirIQCBZCLHh4Xznw0/DIAW2GR9aJ4ZF18npNnDiRH374gd69e7N06VIg\ne6pnmTJlCA0NfWx7rVbLb/Pmk27jxsmQq+w8dALF0gG7oiXJMLVHa1sEY7LQXfPl5qHVZMaGorUq\nhH2dtri824l7mQqWJlruZ+joWtuNye0qYW6SezbJ1jNRjFp3BlMjDffSsnC1N+fX7jWo6mr3b1yS\nN8LrnMJqBJgripIJWADRQDMgZ1TLUmAysOCJe/O/D61kGGR9GB5ZJ4anoOskODiYFStWcOHCBWxt\nbWndujVdunRRZ1W8qXKmmRYqVCjXNS5XrhyhoaG0b98eZ2dnihcvzrnzF9lyLpYfTisY2+uB0ti8\nWxrd/XhSkuLQxVwn5ehKUi4eo4VnY74YMZCrV69SqFAhWrRogaW1Daci0/GNTKOOiyWNS2QQcibw\nsTI5Az82sWPuqUSqFDalXw1LMm5dxf/Wv3RR3gAeHh5PfS/PjQwhRKSiKDOBcCAV2A0EAAlCiKwH\nm90EiuX1GJIkSVJuBw4cYOzYseh0OiA7DPTly5c5efIkc+bMwcjozR1qV7ZsWQC2bdvGhx9+iLm5\nOdHR0eqKop07d6Z4aQ92X0/lfEYNCrnq0cSHk7T7F+z0iVw/H4Q+M4ORI0fS8uOWnD5tw+TJvuzZ\ns4euXbvSrFmzXMd7x82Md9yeHF/jYcVtjZj5XqH8P+G3QJ7/NSqKYg+0B0oBCcBaoPUTNn3m8xjZ\n7WgYZDew4ZF1YngKuk4yMzNp3749Op2OQYMGMWTIEEJCQhgwYAAnTpwgNDSUbt26FUjZ8kP58uVZ\ntmwZly9fplOnTtSoUYPDhw+TmppKi/few7R8EwZtCeFeWhYN3QvzZdMyNCjjRUBAHbZs2cL3wado\n06YNP/30EwAtWrTg9u3bzJo1i8uXL9O3b98CPsP/pocflzzqVZq8LYAbQohYAEVR1gPvAHaKohg9\n6M1wBaJe4RiSJEnSA6dOnSIqKgp3d3d+/fVXFEWhbNmyREREMHToUNavX28wjYzMzEyOHj3KvXv3\nqFu3Li4uLs/dx8rKij179tC9e3eCg4PZtWsXAK3bfYTrhyMZsTaYuqUcGO9VgWpuucdE6PV6gMce\nGeX8ndPzI/27XqWREQ7UVxTFguzHJc0Bf+AA0InsGSZ9gE2vWkhJkiQJMjKyJ+rZ2NjkmtWQM4A+\n5/2CtmvXLvr27UtkZCSQPUCzf//+/PLLLxgb557uGRwczLJly7h9+zbVqlXj008/JTAwkICAAKKi\notDZl2TmsTtcunyXke+X44smZdBqHp/RkRNVc/PmzaxevZrOnTtz9OhRFi5cCGTH2ZD+fXmO+CmE\nOAmsI3ua6tkHeS0CRgPfKIpyFSgE/JkP5ZQkSXrr1a5dG2tra06fPs3ixYvR6/WEhoaqjweaN29e\nwCWECxcu0L59eyIjI/Hw8FDLtGDBgscW3Zo5cybVq1dn9uzZrFixgpEjR1KuXDkCAwOpXqMm18zL\nM3x7BFqNwrovGjDI0/2JDQwAFxcXhg4dik6no1u3bhgbG9OkSRPi4+Np3bq1QVybt9ErhRUXQkwS\nQpQXQlQWQvQSQqQLIa4LIeoKIdyFEJ2FEOn5VVhJkqT8FhkZyW+//cZPP/3EiRMnKIj1nF6UtbU1\n48ePB6Bv377Y2dlRunRpzp8/j4eHB5988knBFhD49ddfSU9Pp3v37ly8eJG9e/eqq4YuWLBAjdQZ\nFBTEyJEjURSFgQMHsmjRIho2bEhcXBzd+n1Fl//z5Zd9V+hQoxjbhjSkRnH75x575syZ/Pzzz5Qq\nVQq9Xo+joyPjxo1j/fr1Mp5FAXlzhyFLkiS9olmzZjF69Ohcz+tbt27N2rVrsbS0LMCSPd2oUaOw\nsbHB29ubsLAwjI2N6dSpE7NmzcLa2rqgi0dgYPY00M8//1xdfrxx48aUL1+eixcvqouGxcfHA/Dl\nl1/y22+/AdCrVy/Kvt+btJqduRiVwC/dqtO++otPUNRoNAwdOpQhQ4aQkZGBiYnJUxsXsbGx/PHH\nHwQEBFC4cGF69+7NO++8k+fzlp5MNjIkSXor7d69W12C+8MPP6RIkSKsWrWKHTt2MGLECBYseGp4\nnwKV881/wIABxMXFYWVlhbm5eUEXS+Xk5ARkNzY8PT0BiIuL4+rVqwDqYM4chQplTw1NSMlg3IYQ\nNA36kBZ+luEflH2pBsbDFEV55hLogYGBvPfee7mWjv+///s/xo8fz48//pinY0pPJldhlSTprTR/\n/nwAJk+ezPr161mwYAGHDh0CYMmSJSQnJ+faPiMjg+PHj7Njxw4uXbr0r5f3URqNBkdHR4NqYADq\nI5vx48fz7bff8scff1C3bl2ysrLQaDRMnTqV9evXU6ZMGQBm/fIrK31v0OrnI+wOuUXysRXE+Iyn\nSZ2qr6V8Qgh69epFXFwcjRo1YtmyZYwaNQojIyOmTJmixuSQ8ofsyZAk6a2UswLnBx98oKZVq1aN\n4sWLEx4eTnR0tBrJcP/+/fTq1YuoqOwZ+RMnTuSjjz5i6dKlWFlZ/fuFN2AdOnRg4MCBLFiw4LFe\nga+//pqxY8cC4OxemTZDvbGs0oLxm85jlnqH2xt/Iin8PB06dMDd3f21lO/06dOEhIRQpEgRdu/e\njZlZdjAujUbD9OnTWbJkCQ0bNnwtx34byUaGJElvpZIlS3Lu3Dl27txJzZo1AQgJCSEiIgJTU1Oc\nnZ0BCA0N5YMPPiAlJYWSJUtSsmRJTp48yfr16zEzM2PlypUFeRoGR1EU5s2bR+fOnVm1ahVJSUmc\nOXOG8+fPU6deA3aF3MLnVDgHL8diU7sd9y8dI+n0NtJvhgDQvn17dd2S1yE2NhbIDvyV08CA7Abm\nw+9L+UM2MiRJeisNHDiQrVu3MmHCBM6ePYuzszPLly9Xu9NzBlH+3//9HykpKbRr147x48ej0Wiw\nsrKiatWq+Pj44O3tjaurawGfzasJCwvD29ubnTt3otVqadu2LaNHj1YbWi9LURQ8PT3x9PRECMFX\nE2cQXfQ6Y08I9AEBOFqb0sHdhN++7o6Sdo9169aRnp5OtWrV1NDir0uVKlXQaDQcO3aM4OBgqlWr\nRkZGBn/+mR1tIafBKeUP2ciQJOmt5OXlxY8//si3336Lj4+Pmt6sWTNmz56t/n327FkAevfurc6W\nKF++PPXr1+fIkSNcuHDhjW5kXL16lXfeeSfXN/iff/6Z9evX4+vrS9GiRfOc95bgKH7Zd4WrmZWw\nruZB0pUTaMP9wSSZX/z8EEIwZMgQ2rVrlx+n8kKKFSvGxx9/zLJly6hTpw6NGzfm4sWLREZGYmtr\nS//+/XNtn5iYyOLFizly5AhWVlZ06dKFNm3ayCmxL0g2MiRJemuNHz+eHj16sH79eu7fv0+TJk1o\n3LhxrhtIzrf5kydPUqJECQCSkpI4d+4cwAuFy35d7qVlYqzRPLY8+csYO3YssbGxNG3alJkzZ5KR\nkcHQoUPx8/OjcePGREVFIYSgdevWDBkyhA0bNrBhwwYyMzNp0aIF48ePp3z58rnyTE7PYtKmEP45\nfZOKLjZM+6gKbiKWrwZ8R3BwMDGAqakpX3zxBTNmzHjFq/DycqKArlixgn379gHZi7MtX748V32G\nhobStGlTwsLC1LTly5fTvXtYnQVDAAAgAElEQVR3li9fjlab9+v+tlAKIvBMYmKietCccLhSwSro\nhZ+kx8k6MQy+vr688847aDQaPvzwQ0qXLs3evXsJDAykaNGiaLVaYmJiqFatGiNHjlTjQLxuBy/d\npv+yAPRCULGoDTWL21OzhD01i9tRzM78hb5p63Q6zM3NyczM5ObNmxQrlj1ldPPmzbRv317dTjE2\nxbiQGyaOJTEqXByTwiUQuixSLh5BcyuEw/t2U716dQCCIxIY6hNI+N0UvvJ0Z0hzD4y02T1AQgjO\nnTvH3bt3qVKlCg4ODvlyLfL6WYmIiCAoKIjChQtTr149tacqR+vWrdm5cyc1atRg2LBhREVFMXXq\nVJKSkli6dCm9e/fOl/K/6R5eIM3W1jbXPzzZyJAAeUMzRLJODMfUqVPVSJs5TE1NSU9/PKDxnDlz\nGDZs2Gstj++1OD756xRlHK3wLO/I6bAEgiISSM3MDipW2MqUqq62D73sKGz1eNyIrKwsdS2RxMRE\nbGxsEELg1aUPRy5GYe5WiYpNPiA8Pl1dTltkZVC6sAX3M+H2/Sz0mWnYJoUxe1hPrsUmM3PXJZys\nTZnTtTr1Sv87y6O/js9KTEwMzs7OmJqaEhERgaOjIwCLFi1iwIABNG/enL179+bb8d5kz2pkyMcl\nkiRJzzFu3Djatm3LjBkzuHfvHs7OzixatAgnJydWrVpF7dq1+eOPPxg+fDgTJkzgs88+w8bG5rWU\n5XR4PH2X+lHcwYIV/erhYJm9ymiWTs/FW0mcDo8nOCKRMzcTOHDpNjnfI2uXsGeQpztNyzmqvRxG\nRkY0bdqUgwcP0n/Mjzg36srhK3HcLdOVwmVAk5VGmSK2fFTLjjmTRhB5wR+RFMuN9DRA4eC5MLqM\nmoEo+y6fL8u+0XtVcWbah1WxtTB+UvHfGHfv3gWyH5flNDAge+AowJ07dwqkXG8a2ciQJEl6AVWr\nVmXo0KEAajTQ4cOH06xZMwC++eYb1q1bh6+vLwcPHnwtgxlDohL5ZPEpHK1NWflQAwPASKuhcjFb\nKhezhQbZaffTszgXmYh/WDwrT4Tx6RI/KrjYMMizDK0ru6AXAq8vvuWiaxtO2FRA73eDtGsnSQ07\nS3rkBdYtnke7D+oAMOOTALLio9RxCBqNQn13J5IP/kncnv9jq/9VzM3N8Szn9J8YFFmqVCns7e0J\nCwtj69attG3bFr1erwZxq1WrVgGX8M0gGxmSJEkvKecxc4zOkvEbzhIQFo+jtSmJZdtgq5TgRAw4\nXoujnLN1roZAXoSHh7Nw4UJOXQwnzP0jbCzMWNmvHk42Zs/d19LUiHqlC1GvdCE+b1SaTUGRLDh0\nja/+DqRU4cukZGQRcy8dN/eKpJ7ZScjWPxAZqTg5OZF85zbz5/1GtapV0Gq1auOiUKFCxMXFYWFh\nwahRo0hPT6devXq0qVHylc7T0JiZmTFs2DAmTZrEBx98wDvvvMOtW7e4fv06JiYmr/2R2H+FHJMh\nAfL5vyGSdWJ4/P39iUnOYtOZW2w7F4uxQ1FMNFC3lANXI6KJvJuC1ir3aqFO1qaUc7amgosNZRwt\nURSFLJ0gS68nUyfQ6wXWZkbYWRhja26CrbkxlqZaIhNS2X08iAUr14N1EUyKlUdkZRDz9xjGDe7H\nd999l6dz0OkFu0JusfjoDSxMjfjknRI0LeuERqOQkJCAoijExMRQv359dRGzR2k0GjQaDVlZWWi1\nWnbt2lWgS6m/rs+KXq9n7Nix/PLLL+r4Gzc3NxYtWkSrVq3y9VhvMjnwU3oueUMzPLJOXo1er+fS\npUvodDoqVKjwytMNs3R6Bv91kB1XU1EUME0I4+bR9aRcPo7ISFW3m+Y9g+59BxJ+N4VLt5K4EJ3E\nxVv3uBKTTIZO//LnkZGGhS6Ziq72uNwN5v9mfIdOp8PPzy/Xv43du3czZcoUfH19sbW1pXv37kya\nNAkTExOCgoKwsLCgRo0aj82geJpLly4xefJkNm/erE5h7dWrF3/88Qc7duxAr9fToEEDfvzxR/WR\nUUF53Z+VuLg4/P39sbS0pH79+hgZyYcAD3tWIwMhxL/+SkhIEDkvyTD4+fkJPz+/gi6G9BBZJ3m3\nZcsW4e7uLgABiOLFi4u///47z/kl3M8QPX8/IUqM3ioGLNonbsaniOTkZDF69Gjh5OQkAFG1alWx\nfPnyp+aRkaUTYXfui/C4++JSRIzo9PGnwsjCRigmFsLY1km06tZP7Ai4KrafiRKr/cLF3DW7hda6\nsCjj7iGysrLUfIYOHSoAMWTIEDVtzZo1QlEU9XxzXo6OjsLKykr9293dXezbty/P1yFHamqqSE5O\nfuV88ov8rBSsR+7pue73chVWSZIKnBCCI0eO4O3tzYIFC4iJiclzXkeOHKFDhw5cvXqVIkWKUKxY\nMcLDw+nRowdbtmx56fyuxybz4fxjnLwRx5e1behXw4ZiduZYWloyffp0YmJi0Ov1BAcH0717dxYu\nXEjt2rVxdnamWbNmbN68GQBjrYbihSxwtTdnYJ/urFvxFyL9PlXKu0NKPDt9/uDbAd3IvOFH2AEf\nrh7dii7pDuXLlc3VC1OxYkXgf7MfdDodI0aMQAjBqFGjiI+PJyAgAEdHR2JjY0lOTqZ69eoUK1aM\nq1ev0qZNGzWQWF6ZmZlhaWmZK02v15OZmflK+Ur/QY+2Ov6Nl+zJMDzym4DheVvqJCEhQXh6eub6\nBm5iYiIWLlyYp/xatWolADFo0CCRlZUldDqdmDBhggBEnTp1nriPXq8Xt++lidSMLKHX69X0w5dv\niyqTdooa3+8Wp27EPbNO9Hq96NOnz2O9CYCYPXu2us2xY8cEIBwcHMTly5eFEEKEhYWpPSKPvkxM\nTMTZs2eFEEIkJSWJOnXqCED8/PPPQgghgoODBSBcXV2FTqcTQgiRnp4urK2tBSAqV64shBAiMzNT\ndO/eXQCib9++ebq2TxIaGip69OghTE1NBSDeffddsWfPnnzL/0W8LZ8VQ/WsngzZyJCEEPJDaoje\nljrp2bOnAEShQoXEoEGDRJs2bdQb7PHjx186v5yba1RUlJqWkpKiPk7IyMjItb1OpxcDV/iLEqO3\nihKjtwqPcdtFrR/2CM+ZB0TpsdtEy9mHRHjcfSHEs+vk6NGjAhAWFhZixYoVIjQ0VEybNk0AQqvV\nCldXV/U8ATFgwICHyqATjo6OAhC2trZi8ODBombNmup1MDIyEg0bNlT3dXFxEfHx8UIIIYKCggQg\n3Nzc1EbG5cuX1X09PT3V45w4cUIAokqVKi99XZ8kOjpaFCtWTD1WzjXWaDRi69at+XKMF/G2fFYM\nlXxcIkmSQbpz5w6rV69Gq9Xi6+vLb7/9xtatW/nmm28A1JgELyMnCNbD603cvHkTIQTm5uaPDQBd\ncOga28/eoneDEoxqVY5PG5bkvYpFqOBsw8f1ivPPl+/g5mDx3ONu3LgRgC+//JKePXtSokQJxowZ\ng7OzMzqdjps3bwLZgwgBtm/fru576NAhdYGyESNGMHfuXE6dOkXDhg2B7EcRR48eJS4ujlq1arF3\n717s7OwAqFy5Mm5ubkRERDB+/Hju3bunHgvA09NT/f3SpUsA2NvnngGTV3PmzCEyMpL69esTGhrK\nvXv3GDZsGHq9ntGjR6tTfaW3l2xkSJJUYMLDw8nKyqJChQp4eHio6TmBrK5evfrSeXbr1g3IXjV1\n7dq1bNy4kU6dOqnvPTy74siVWGbtvsQH1YryXbtKfNnUnbGtKzD1w8oMrmWBl/N9yEx7oePmjEd4\neKyCn58ft27dAmDo0KFkZGTwxx9/ANnrZvTu3Zv9+/fj7e2t7tOrVy8AtFotH374oXoue/bs4cyZ\nM/j5+anjMnK2mzlzJoqiMH36dGxtbXPN9ti0aRNr1qxh7ty5amyHjz/++IXO6Xl27twJwLRp0yhR\nogRWVlZ4e3tjZ2dHSEhIrsaO9JZ6tGvj33jJxyWGR3Y3Gp63oU5iYmKEVqsVRkZG4vr162r6mDFj\nBCB69Ojx0nnevXtXVKlS5bGxDWXKlMn1COVmfIqo/t0u8d7sgyI5LVNN9/f3F9WrV1f3s7a2FpMm\nTRI6ne6ZdbJlyxYBiCJFioiAgACh1+vVMRCACA0NVbetX7/+E8dfODg4iNTUVCFE9viNnPElM2bM\neO5579ixQzRs2FBotVphb28vPv74Y+Hi4vLYMdq2bStWrVolBgwYIAYPHiwOHDiQaxzKy8i5Trt3\n71bTUlNT1UdWkZGRecr3Zb0NnxVD9trGZAB2wDrgInCB7GC2DsAe4MqDn/aP7icbGYZHfkgNz9tS\nJ126dFFvzsOHDxedOnVSb4iHDx/OU55JSUli1qxZomnTpqJRo0ZiypQp4u7du+r7qRlZ4oNfj4hK\nE3eKa7eT1PSwsDBha2ur3vArVaqklmXy5MnPrJOsrCzRuHFjdXsLCwv195zBlzlyGh9169YV7777\nrujevbs6ZqNy5cpi4sSJ6mBYCwsLcevWrRc+94cbDHfu3BFTp04VrVq1Eh07dhR//vmnOnD04dfH\nH3+ca5rsi/r222/VMR7+/v4iPDxcHfxas2bNPDdeXtbb8lkxVK+zkbEU6Pfgd5MHjY6fgDEP0sYA\n3o/uJxsZhkd+SA3P666T2NhYMW/ePPHtt9+KtWvXivT09Nd2rGeJi4sTDRo0yHXT02q1Ys6cOfl+\nrPPnz4upU6eK98b9JUqM3ip2no3K9f6IESMEIN5//32RkpIihBBi48aNAhA2Njbi8OHDz6yTpKQk\nMXjwYPWbfOHChQUgzM3Nxbp168S9e/fEsmXLhJGRkQDE1atX1X3Pnj2rNjRyXpaWlmLbtm35dv6f\nf/65OhPF29tbjBs3To2jkZfZPHFxccLDw+OJM2IOHDiQb+V+Hvn/V8F6ViMjzxE/FUWxAYKB0uKh\nTBRFuQQ0FUJEK4riAhwUQpR7eN+HI35euXIlT8eXJCnv9u/fz6RJk0hL+994Azc3N+bOnYurq+tr\nPfadO3fYsGED58+fx8bGBi8vL2rXro2/vz/BwcFYWlrSvHlznJ2d8+V4QggS0/X8stiHg6cvYOJS\nFutq75Pou4ZKumtMnz4dM7PsdUA+//xzgoKCmDt3Lg0aNFDz6Ny5M6GhoSxdujTXeIinycrKIiUl\nBSsrK3744Qe2bt362Dbdu3dXB7jmSEtL48CBA9y4cQNHR0datmyZb1GRMzIyaNasGenp6axevZrS\npUsD2QNQJ02aRMWKFVm6dOlL5xsfH8+ff/7J3r17SU9Pp2bNmnz22WdUqlQpX8otGb6Hx1Pl51Lv\npYFY4C9FUaoBAcBQoIgQIhrgQUPD6RWOIUlSPouOjmbChAlkZmZSt25dKlWqxL59+wgPD2fMmDEs\nX778ta2ieenSJQYNGpQrDPH27dvp2rUrw4cPp169evl2rPQswZLgJHwj00jOEODUgkKtWqDoMyl0\n/wZ3gzZy7N49FixYwNdffw2AlZUVQK4Bi6mpqeqy3tbW1i90bCMjI3WWy4QJE/Dw8OCff/4hOjoa\nV1dXunbtykcfffTYfmZmZrRu3fqVzvtpkpOTSU9Px8rKilKlSqnpr7p0ub29PSNGjGDEiBH5Uk7p\nP+bRro0XfQG1gSyg3oO/fwF+ABIe2S7+0X3l4xLDI7sbDc/rqpOJEycKQHTs2FF9Zn7v3j01GJSv\nr2++H1OI7LECVatWFYBo2rSpWL16tfjuu+/UIE67du3KU76RkZHi66+/FuXLlxcVKlQQo0aNEqcu\nhomWsw+JkmO2iq9XB4pqnYcJs1I1xbS5/yd0uuxzzokZYWNjo8bO+Pvvv9VYFXPnzhVbt24VzZs3\nVwN5vcmfk6ysLFGkSBEBiI0bN6rpOeMqWrVqVYClezVvcr38Fzzrccmr9GTcBG4KIU4++Hsd2WMw\nYhRFcRH/e1xy+xWOIUlSPrtx4wYArVq1UnssrK2teffdd9mwYQOhoaHUr18/34975swZzpw5g5OT\nE9u3b8fc3Fx9b9KkSSxbtoyWLVs+M4+UlBSWL1/O3r17MTY2pmHDhvz4449ER0er24TpHVidVQc7\nG2uWfVaXRh6OuH7TlrTISDp7NUejyT7nevXqYWtrS2JiIvHx8Tg5OdGlSxc2bNjA2rVrGTJkiJqn\nvb09ixYtIisrK5+vyr9Hq9UybNgwxo4dy0cffcT7779PYmIix48fB1B7cyQpP+W5kSGEuKUoSoSi\nKOWEEJeA5sD5B68+wPQHPzflS0klScoX7u7uAGzevJm+ffuiKArx8fEcPnwYgDJlyryW4+YEoSpd\nunSuBkblypWB/63F8TSxsbF4enoSEhKipq1atQqA+vXr4z1jJivO3Wd3aCZpkReonhpJI4/3gexn\nxpGRkWzevFm9mR46dIjExETs7e1xcHAAsm/EPj4+dOzYkb///pvExETeeecdBg0aRLFixdTVPt9U\no0aNIiYmhl9//ZUdO3YA2Y+IZs2a9dwGniTlxauuVzsYWKkoiglwHfiU7ABfaxRF6QuEA51f8RiS\nJOWjzz77jOnTp7NlyxYaNmxInTp12LBhA3FxcdSrV++1LZddtWpVjI2NOXXqFL6+vjRo0ID09HQW\nLFgAPH+Z7pEjRxISEkLZsmUZOXIk9+7dY8TosZgWr4J1076MO5bOzfhM2pWz4tcZY9nmYAfz5wAw\naNAgDh48yPDhwzl+/Dg2Njb4+PgAMHDgwFxLd2s0Grp27UrXrl1fy3UoSBqNhjlz5jBixAgOHz6M\niYkJ7733njp+RJLyW55nl7yKh2eX5NfIaenV5HxDe103GOnlvc462b59O927d+fevXtqWqVKldi+\nfTvFixfP9+PlGDRoEPPnz0ej0VC/fn2uX7/OrVu3sLOz4+y5c+wNzcDCxIjmFZwoZGWq7peeno6t\nrS3p6ekcPX2eq6nm7LsQw8HzkWiMTUGXQbNKrnSvW5yKtlm4urpiZWVFUlKSmsf333/Pd999h16v\nV9O6devG0qVLMTExeaHyy8+JYZL1UrAeHsidn7NLJEl6Q3l5eXHz5k3Wr1/PrVu3qFq1Ki1btnxs\nXY/8NmdOds/C77//ro4FqFixIov/+osFp+6y8mQ4ABoFapd04P1KzrSsWIQbUbGY1e1M4bIN6Ln6\nOgClCltiFRPEjWNb0cRdZ/7tW+j1er744guAXKG1ASZOnMgnn3zC5s2bycjIoHnz5lSrVu21nq8k\nve1kT4YEyG8Chui/XCe3b9/mzJkzODg4UK1adSZsCmHVqXAGNi1Dmyou7A65xa6QGC7F/K8nAr2e\ntJshfFCrJGN7t6VUYUu6du3K2rVrgew1Q/R6PampqZiamnL06NF8v3b/5Tp5k8l6KViyJ0OSpNdu\n27ZtzJkzh/Pnz1O0aFH69evH559//sTeEScnJ1q0aIFeLxi/8SyrTkUwyLMMI1qWQ1EUKhez5ZuW\n5Qi9c5/9F29ja25MmO82hs8Yyx+r4MyauiQlJXHhwgUURcHDw4PLly8D2YNAZ8yYIW84kmQAZCND\nkqRX9uuvv+aa8hkdHU1AQAC+vr4sWbLkicG99HrBuA1n8fGL4CtPd4a3LPvYdiULW/JZw+zAUaJm\nf9LuxTF16lROnToFgKOjI3PnzqVr167ExsaiKAqOjo6v8UwlSXoZcql3SZJeSXx8PKNHjwbgxx9/\n5MaNG6xYsQILCwuWLVvGsWPHHtsnU6dn9D9n8PGLYHCzJzcwHqUoCuPGjSMyMpJdu3Zx4MABIiIi\n6NatG4qi4OTkJBsYkmRgZE+GJL0lbt26xd27dyldurS6Vkd+2LlzJ6mpqXh6ejJ+/HgASpYsSXBw\nMDNmzGDDhg00bNhQ3T7+fgaD/j7N8WtxDGnuwdctPF4qjLmtra2M6SBJbwjZkyFJ/3HXr1+nVatW\nuLi4UKlSJVxcXB6byvkqMjMzgcfX9ciJvZCRkaGmXY5JosP8Y/iHxvNTp6p8897zezAkSXpzyZ4M\nSTJAcXFx7N69G51OR7FixXBxcclTPgkJCTRt2pSIiAhMTU1xcXEhNDSUyZMnk5qayvTp01+5rE2b\nNkWj0bBt2zY2bdpEu3btOHPmDPPmzQOgRYsWAOw9H8NQn0DMTYxY1b8+tUrYPzNfIQT79+/n0KFD\nWFhY0LFjx1yrPUqSZPhkT4YkGZhZs2bh6urK+PHjmThxIsWLF2fMmDHkZbr54sWLiYiIoGbNmty8\neZMbN26wZcsWAH755ZfnhvJ+EcWLF+err75Cp9PRocOHOFSoT4MuA7ln50GNDv1JL1qDaTsu8Ply\nf0o7WrFl8LvPbWAkJSXRvHlzWrRowQ8//MDYsWMpW7YskydPfuXySpL075E9GZJkQP755x91yeza\ntWtjYmKCr68v3t7euLq68tVXX71UfkeOHAFg2LBhFC5cGIC2bdvSoEEDfH198ff3f+74Br1ez6FD\nh7hx4wbu7u40atTosUccs2fPJr1wWbZHGKFxcFXT7wKj/jmbfdwqRZjZpQZmxs8P+PXNN99w4MAB\nChcuTJ8+fYiNjWXFihV899131KxZk3bt2r3MZZAkqYDIRoYkGZDZs2cDMHPmTJo0aQLA5cuX6dmz\nJ7Nnz2bQoEEvNYbB0tISgKioKDVNp9Opq5ZaWVk9c/+LFy/y0UcfceHCBTWtatWqrF+/Xl1I7fi1\nO8zYdYnA+yUp5WFBv/pFqV7SEVNjI1b9vZI/f19EVEQYf+pSSTvQE29vbwoVKvTUYyYnJ7N8+XIA\nDh48SKVKlYDssOejR49m4cKFspEhSW8IGfFTAmTEPENhZ2dHYmIiMTExhIdnh9iuUaMGpqam6HQ6\nUlJScq1g+jxbtmyhXbt2WFtbM2PGDKpUqcL8+fNZuXIlJUqU4Nq1a08MlpWp03P+5l3af/IV97S2\nWBevgEkhNzLS7pOZkoSpRtC4QR2S03UEhMXjbGPG0BYedKrlirE2+ynspEmT+P7774HsxkxycjIA\n1atX58SJE5iamj52XIBr167h7u6Oq6srERERanpQUBA1atSgQoUKnD9//oWvQX6SnxPDJOulYMmI\nn5L0hihatCiJiYkcO3YMNzc3APz8/NDpdNjb2z/1xvw0bdu2pUePHvz999/qmh4Apqam/P7779yI\nS2HO3ivcTc4gOT2L5PQs4pPTSErXoRNAvV7YZKVTo6Qj5VxsSU3PYNP23aRkCUKjYrGwtmVCmwp8\nXL9ErscgcXFxeHt7A7By5Uq6devG5cuX8fLyIigoCB8fH/r06fPEMru4uGBhYcHNmzcJCAigVq1a\nAGzatAn431L1kiQZPtnIkCQD0q9fP4YPH84nn3xCp06dMDY2ZsOGDQD07dsXjeblxmorisKyZcto\n3bo1S5cu5c6dO9SuXZthw4ZRyqMcbX89SmxSOuWdrbHU6rh+0Z9bEaHo05LJiL1BRsx1hnzalVlf\nzfxfnqdW8Msvv/C5+3jatmiLm5vpY+Msjh07Rnp6Oo0bN6ZHjx4AlC9fnm+++YbBgwezd+/epzYy\nLCws+Oyzz/jtt9/w9PSka9eu3L59m82bNwO89LgUSZIKkBDiX38lJCSInJdkGPz8/ISfn19BF+Ot\nl5GRITp16iSAXC9PT0+RnJycr8catTZYlByzVRy7EitSU1OFh4eHAIS1tbV49913hVarFYCwt7cX\ner1eCCGETqcTNWvWFIDQaDQCEIqiiHbt2omYmBg17+3btwtA1KhRI9cxp0yZIgDx2WefPbNsKSkp\non379rmugZGRkZg1a1a+XoOXJT8nhknWS8F65J6e634vezIkyYAYGxuzZs0aDhw4wKJFi9Dr9fTq\n1QsvL698XYZ9S3AUq/2zFyV7x70wK1eu5MqVK5QrV47jx4/j4ODA6dOnqVWrFvHx8TRq1IguXbqw\nZcsWTp8+DYBGo6F69eqEhISwefNmIiIiOHXqFEZGRjRp0gR7e3sCAwMZM2YM/fv35/Tp08yYMQOA\nDz/88JnlMzc3Z+PGjQQEBHDo0CHMzc3p0KFDnuOFSJJUMGQjQ5IMjKIoNGvWTI2Ymd+D2SLupjBu\n/VlqFLdjWIuyQPa4D4A+ffrg4OAAQM2aNfH09OTAgQMcO3Ys1xok1tbWnD59Gnd3dyIjI2nQoAGB\ngYHs2LGDDz74AAsLC37++Wf69OmDt7e3Oj4DoEOHDnh5eb1QWWvVqqWOyZAk6c0jg3FJ0lskU6dn\niE8gAHO71VBngtjbZwfHunjxorqtEIKkpCQAevTowYABA/jggw8A6N69uzoAs1ixYvTu3RsAX19f\ndf/evXuzb98+WrdujYuLC9WrV+fnn39mzZo1Lz22RJKkN1OB92RkZOkxMZL/4UjSv+GXvVcIDE/g\n1+41cHOwUNN79OjBd999x7JlyyhUqBBNmjTBx8cHf39/7O3t+f3337GwsOCvv/5iy5YtXLt2LVe+\nOX8/OiW9WbNmNGvW7PWfmCRJBqnA7+5RCakFXQRJeiscuHSbeQev0qW2Kx9UK5rrPQ8PD2bNmgXA\nnDlz6NChAz4+PpiYmLBkyRIsLLIbJO3bt8fc3Jx9+/YxaNAg9uzZw+jRo/Hx8UGj0dC1a9d//bwk\nSTJcBd7ICL+bUtBFkKQnWr9+PQ0aNMDMzAw3NzcmTJhASkr+/nvNzMxk9erV9OnTh08++YR169aR\nlZWVr8cA2HchhgHLAyjvbMPkdpWeuM3XX3/NyZMn6devH61ateLrr7/m7NmzuaJrOjg4sHDhQjQa\nDfPnz+f/27vv+Jru/4Hjr3NvpoRsIWQIQglJSIkatUdtLbVn+1PEqIagqpOqr1KzaK3WHjUaHRRB\npEGJxIhNIlYSWbKTez+/P25yK4gis/V5Ph73Iffccz7nc+9xct/5jPenffv2zJkzB9BlKXVxcSny\nukuS9O9V6t0lNxNkkCGVPUuXLmXMmDH659HR0cycOZOgoCD++OMPDAwKf+ukpKTQqVMngoKC9NvW\nrl1Lq1atCAgIKHT5eXisOD4AACAASURBVH47e4exG0N5pXIFfhjeiHJGBde9UaNGNGrU6KnlDR48\nGHd3d5YuXcrly5dxdnbm//7v/2jWrFmR1VmSpP+GQv+mVBRFDfwF3BJCdFEUpRqwCbAGTgGDhBBZ\nBR0vWzKksiYlJYWpU6cCMHv2bN577z1Onz5N3759OXToED/99BN9+vQp9Hk+//xzgoKCcHBwwM/P\nD61Wy//+9z8OHjzI7NmzMa7blpN3MnG4dAozIwPKGasxMzKgpr05netVxkD95IZIIQRnz54lKSmJ\nmyp7pgdcxtPRktXDXqWCiWGh6w26mSfff/99kZQlSdJ/V1G0ZIwHIoAKuc+/AuYLITYpirIMGAF8\nW9DB0fFyTIZUtgQFBZGcnIy3tzf+/v4AvP7660yePJmJEyfy888/F0mQsXr1agC2bt3Ka6+9Bui+\nvFu3bs2akJuosh5QyUxNYk4yqVk5pGVpSMvSoNEKFvxxmYnt3XjDvTIq1d9LBRw/fpwRI0Zw9uxZ\nzOq1xabTOOyVZFYPaVNkAYYkSdKzKlSQoShKVaAzMBOYqOiWh2wN9M/dZS3wCU8JMiKiY/WL20il\nT14LuHjxIgDp6en5Po9bt24BEBcXV+jPSQhBbGys/nleeYqiYO7ZCVWDt/CpYsz7jS1Q5wYRQgiu\nXLnKmXg4kqjCd0MoLhZn6OduToNKRkRE3mPCp3PRWtbHoe/bGDp7kX79FH/9NJMJMfsZPXp0oeos\n/U3eJ2WTvC6lo2bNmgW+VtiBn98AkwFt7nMbIFEIkTdyLRqo8rQCYlI0hayCJBUNjUbD/fv3eeWV\nVyhXrhznzp1j48aNZGZmcubMGf3y402bNi30uRRF0d+YeWuTACzYfQybDmNQ3zvP+IcCjOPHj9O7\nd2/69+/Hl779ODdvII3FBTJyBF8eTWTQzlhm/KVQofMkLF/ri0vdhrxRwxT/1ywROZls2rSJ1NTU\nQtdbkiTpebzwUu+KonQB3hBCjFYUpSXgBwwD/hRC1MjdxxH4RQhR7+FjH17q3ePLIMI+bo+FqWzK\nLU0v81LJGo2Gr776igULFhATE4OpqSkeHh6EhIQ8tm+TJk0IDAzEyMio0Oddv349AwcOBMDHx4c0\nm9ok1ulJRlQ43/SqTU1XFwDUajU+Pj5kZWVhb2+Pubm5Pi/FdytXYebehnO3k/hl40rOBf3GluXz\n6N7l74ya9erV4+zZs4SEhNC4ceNC1/tl9jLfJ2WZvC6lq7iWem8KdFMU5Q3ABN2YjG8AS0VRDHJb\nM6oCt/+poJvxaVhUsfin3aRSFhkZyf79+zE0NKRjx47Y2dmVdpXyCQsL4/vvv+fmzZvUqlWLkSNH\n4urq+o/HTZw4kYULFwJgaWlJYmIiISEhuLq6Us7ehdvmbpiotLSq58KXfiOLJMAAGDBgAPfu3WPG\njBmEJ6ixbdaDnLuX8W9iSb8+b+l/cf7vf/8jKyuLQYMGsXLlSgwMDFi8eDHjxo3jy5lfcOXKUBTF\nibNrbhB6+yI3rl7WnyM1NZXo6Gjg76yekiRJJeWFgwwhxFRgKkBeS4YQYoCiKFuBt9DNMBkC7Pqn\nsqIT0nCXQUaZpdVqmThxIosWLUKr1fWMGRkZ8fnnnzN58uRSrp3OsmXLGD16NA+3zC1YsIDNmzej\nKArXr1/H1dWVTp06YWBggEajITExkeTkZBYvXoxarWbHjh106dKFiIgI2nfuTrxzC2jcE1u1mhyt\nIEgraD7/T6rZmuHlZEm7V+xp84p9oTLWdhnwLifNfTh6LQHn8rDJfziVbfMHA3mpuidPnoyhoa7F\nb/To0UyfPp1r164RExODvb09AwcOZNeuXUyfPp2cnByqV6/OwoULSUxMxNvbGzc3txeupyRJ0oso\njjwZ/sAmRVG+AEKBlf90gJzGWrbNmzePBQsWYGBgQLdu3UhPT+f333/H39+f6tWr8+abb5Zq/W7c\nuIGvry9CCEaNGkXLli3ZunUr27Zto1evXvrACMDFxYU33niDrVu3Ehsbi6mpKVqtlk6dOtG1a1dy\nNFpOJZth3ncuaq2Kypk3+enTYZgbGxAenURoVCKnohIIvBjLT6duYW1mRHdPB/p4O/JK5Qr56pWZ\nnUPYxetUMDOllksVdOOide6nZDJv3yU2Ho/CzNiA6Z1fYVATZ4wNHl9pNS9V9/Xr13F3dwcgJiaG\n1NRUVCoVZmZmAPTq1YuBAweybt06/Pz89Mfb2NjI6aaSJJWKIgkyhBCBQGDuz9eAp2fzeUgFEwMZ\nZJRhQggWLFgAwObNm+nVqxcAX3/9NX5+fnzzzTelHmRs2LABjUbD22+/zdKlSwHo2rUru3btIjs7\nm8qVK9OjRw/27dvHlStX9PuYm5uTkpICQMipM6w5ep31x6K4HJOCHSlcWzODnv26UrG8CQA+rjb4\nuNoAkKPRcuRKHFv/usm6kEhWH72Be5UK2Jkbcy85k8iYRFJzACW3lUPzF5UtTHCuaIGtuTGHLsaS\nlq1hkI8z49u6YW1WcBdMv379CAsL47333iM+Ph5LS0tmzpyJRqOhR48emJubA7ql19euXUuvXr3Y\nsGEDSUlJ+Pj4MGrUKLlEuiRJpaLUM3462ZTjpsyVUWY9ePCA6OhojI2N6dmzp35737598fPzIyIi\nohRrpxMXFwfoBjjmyQswQNfNMGHCBMLCwvD09ARg+vTpzPj4ExZvP8CsjQcoV6Mxn/x8nurWxrxd\nJZnFU/6P7LS0AgMoA7WKVrUq0qpWRRJSs9h1+ha7wm4Tm5KJJiWOuyf3o0lJwJQssrUCjXEFsqwr\nY92sNTfj0/GpboN/x9rUqGj+j+9v3Lhx7NmzhyNHjjB06FD99qpVqzJ//vx8+6pUKnr27JnvWkmS\nJJWW0g8yrMtx4c6D0q6GVAAzMzP9YMjjx4/rZyccOXJEv4+TkxMAnTt3ZurUqfrnJaVhw4YA/Pjj\nj/j6+mJhYcGJEyf0rzdp0gTQJdlCbYiJswcnqMFrXx0k9kEWFao3JCF0Dyln9hMZe50DuccNHjz4\nmVJlW5kZMbRpNYY2rYZWq6VmzZrEX7vG7NmzmTRpEqmpqfTv35+An1bTze4+e5Yte673Z2pqyr59\n+1i7di0//fQTGRkZtGnThlGjRmFra/tcZUmSJJWkF57CWhgPT2FdevQ2q4/e4MLnHfNlLpRK1tOm\ngH3wwQfMmzcPW1tbRo0aRXp6OkuWLCE9/fEWKHt7e/7880+qVatW7HXOk5GRgbu7O1evXsXS0pIG\nDRpw5MgRsrOzKV++PLfuxbL3fCwr9vxJRKKCysgUI5WgTZ3KdPesws6ln7P826XUqFGDzMxMHBwc\nGDFiBCNGjEClUj12ru3bt3PixAmsrKzo169fvgGVN2/exMnJCWtra2JiYlCrdWMsjh07ho+PD25u\nbnz99dcYGhrSokULTE1NC3xfclpe2SOvSdkkr0vpKq4prEXC0bocWRot9x5kUNmi4F+4UtF48OAB\n58+fx9LSEjc3t3yDEQvy+eefExYWxv79+/n888/zvda8eXP9mI0JEyZw+PBhOnbsSHJyMhqNhvbt\n2zN9+nRq165dLO8HwMTEhH379jFgwAD+/PNPDhzQtUWY2FRBXb8D9T8KQBiYoMrIITUiiLTLIUx7\npzeDmrlz4MAvrFmlG5u8detWfXfKk0RFRdGuXTsuXbqk3/bpp58yZ84c/UDLvKAhNTWVBw8eYGlp\nCcC9e/cAuHz5Ml27dgV0U0rnz5/PkCFDXvi9CyG4evUqqamp1K5dG2Nj4xcuS5IkqcgJIUr8kZiY\nKPIegRdjhLN/gAi5Giek4pOTkyOmTZsmzMzMBCAA4e3tLUJDQ4UQQpw4cUKcOHGiwOM1Go349ddf\nxfvvvy8mTZokTE1NBSCuXr2q3+fIkSP6sh9+VKhQQYSFhRX7exRCiPDwcDFv/R7Rb2mgcPEPEE6T\ndgnbbpOFcdW6AhAmJiZPrOOoUaP+sexWrVoJQLi5uYlZs2aJIUOGCEVRBCCCg4Mf269Dhw4iKChI\n7NixQ1hbW+vP1bRpU+Hp6al/vm/fviee75+uybFjx0SDBg305dja2or58+cLrVb7/B+c9Ez+6ZpI\npUNel9L18He6eOT7vtSDjGuxKcLZP0Bs/etmcX8OL7Vp06bpv4zc3d2FlZWVAIS1tbW4devWc9+k\nRkZGAhD37t3TbxsyZIgAhKIo4uSpUHEi7Lzo2PNtoS5vJ9r27Ccu30sWsQ8yiuPtCSGEuJWQJoat\nPi6c/QOE12d7xf9+uyAuRN4VS5cuFZMmTRLLli0TiYmJYtu2beL1118XlStXFo0bNxarVq36xy/m\ny5cvC0CYm5uLuLi/A2I/Pz8BiGHDhum3hYeHC0tLyycGM8uXL9fvN3XqVH0w8iRPuyaXL18W5ubm\nAhBWVlbC1dVVf44FCxY8z8cmPQf5ZVY2yetSup4WZJT6mAwTM3Nqf/QbY1vXZGI7mSyoOCQnJ1O5\ncmXS0tL45Zdf6NSpE2lpaXTt2pUDBw7QqlUrsrOzMTU1ZdSoUXTv3v2xsQiP6tKlC3v27GHAgAEs\nWbIEAAfX2iiV6+DUuCNGzh4kpmU/dpyiQAMnKzrWrURH90o4Wpcr8BxCCNKzNSSmZZOUno0QUKtS\nef16Hnm0WsGG41HM/vUCGq3gg/ZuDPRxxsTw8ZwTLyowMJBWrVrh4+OjT44FEBAQQNeuXWnTpg2L\nFy/G3NycqlWrcv36debPn09gYCCGhoacOnUKU1NTUlJS9J9tZGQkLi4uVKxYUd+d8rCn9TP7+vqy\nZMkSunXrxqZNmzAxMWH16tWMGDGCSpUqERUVpU/cJRUd2fdfNsnrUrrK9JgMYwM1lSuYEC1zZRSb\nM2fOkJaWhqenJ506dQKgXLlyvPnmmxw4cICDBw/q9923bx99+vRhw4YN+kGLT/LJJ5+wf/9+NmzZ\nxp6rGZjWboHdu7qET2oDQZva9rhXqYA2O4v3x49Dm5NFhfJmaMrZcj69FScjE5j5SwR1KleggbMl\nKRk5JKVnk5iWxe24JFKztWRoVeRo85/XUGTTxNWa9h7ONKthiwD8t4dz/Ho8zWrY8mWvek8NXF6U\nm5sbKpWKkydPcvnyZWrWrIkQgo0bNwIQHBzMK6+8AugWUFu6dKk+VXl2djYWFhakp6dz8eJF/X6h\noaEAVKxY8bnrExwcDMCkSZP040CGDRvGjBkzuHXrFtevX5cZPiVJKnWlHmQAVLUuJxNyFaO8jJHR\n0dFkZGRgYqJLLpWXY8HKygo/Pz9iY2NZtWoVW7ZsoUuXLgwaNKjAMuvW92Liil/YeDoOrWE5Mm9d\nIOfUDmLDA6nTsBb+41ZjbGzMe++9x4PwvQDkrQEac3At5So6MeF/q7iQqiYg/A4VTAwRWWncuHSe\njOR4tBkpaNMfYG1uQkz0dbQZKSgGRpg41+dgSgMOX9dNe1YUKG9swJy36tO7YdVnGsj6IhwcHOjT\npw+bNm3C29ubbt26cfHiRf1U2fT0dBwdHYmPj+fo0aO0bNmSsLAwHB0dMTQ0ZODAgXz33Xd07tyZ\nDz74gJSUFObMmQOQL/fFsypfvjygaw3Jm2abnJxMQkJCvtclSZJK1aP9JyXxeKT/Rnyw5bR49Ysn\nD36TCk+r1Yr69evr+//37NkjPvnkE30f/tq1a/V9msuXLxeAaNeu3RPLSsvMEd8dvioafr5XOPsH\niIHfh4igC7dESkqKuHjxorCwsNCXq1Kp9D+7ubmJ06dPi6ioKDFw4EABiCZNmujLvXDhgjA2NtaP\nGenevbswNDQUgFCr1WLWrFkiICBAdOvWTQCiWv3GYs3Ra2L2rxHiXlJ6iXyOSUlJolOnTvnGWOQN\n/Mwb15GcnCzatm0rAOHn56c/9v79+/kGe+Y9OnfuLDIzM594vqf1My9dulQAomLFimL16tXi999/\nF61btxaAaNGiRbG8f0n2/ZdV8rqUrjI98FMIIRb8cUk4+weI9KycYv0gXmbHjx8XFSpUeOxLztzc\nXGg0Gv1NevjwYQGIhg0bPlbGrYQ00WruQeHsHyAGfBciTly//9g+Z8+eFV27dtUHGOXKlROAOHTo\nkH6flJQU/eyUmJgYIYQQ48aNE4Do27evfhBmjx499MFK3n7Z2dnCyclJAOLo0aPF8VH9o1OnToll\ny5aJuXPnCkC4uLjkGzi6d+9eAYjGjRvnOy49PV2sXr1a9O/fXwwZMkTs3LlTaDSaAs/ztF+cmZmZ\nol27do9dTxsbG3HmzJmieaPSY+SXWdkkr0vpelqQUSa6SxytdX3K0Qlp1Kgom3lfhBCC5ORkzMzM\nMDB4/LK++uqrnDlzhiVLlnDs2DHKly/PwYMHSUlJISAgAAcHB3Jycli0aJF+/4dF3U+j33chJKdn\n8+OIRjSv+eRl3uvWrcvu3bvJzs5Gq9Xi4eHBxYsX89VJrVbrBz/mLV525swZQJdlM6/L4+F9Ll26\nhJ2dHQYGBlSrVo2oqCgSExML85G9MC8vL7y8vLh27Rp+fn4kJCSQnp5OuXK6sSC3bt0C0K8pksfE\nxIShQ4e+UPfIo4yMjAgICOCHH35g8+bNpKam0qJFC3x9falatWqhy5ckSSoKL75GdRFyyh2oJ9cw\neX5CCL755hucnZ2xtLTEysoKX19fkpOTH9vXycmJr776isDAQH7++Wf9Mu3du3dn8ODBdO/ena1b\nt2Jqasr48eP1x12JSaH38mBSs3LY8K5PgQHGwwwNDTE2NtYPNPX39ycqKork5GQ++OADUlNT8fLy\n0g96zFvA69ixY/oy6tevr/857ws7ODiYI0eOYGBgQIMGDZ734ypSrq6ueHt7k5SURJ8+fTh06BA/\n/vgj/v7+ALz99tvFen4jIyPeeecd9u3bR3BwMLNnz5YBhiRJZcujTRsl8Xi0u+R+SqZwmRIgvt57\nsRgbdP6b/P399U3lDyeaatKkicjOzn7qsRqNRnz44YeiQjUPYddrurDt4ieqteglft13QL/PuVtJ\nosFne0XDz/eJiDtJz12/6OhoUalSpcea9dVqtdi7d6/QarVCq9WKP/74QwDCwMBAjB07VixcuFDU\nrl1bv7+FhYXw8vLKlzwrNjZWnD9/XqSmpj53vYrKiRMnntgN1a5duwLHWjxP2bIJuGyR16Rsktel\ndD2tu6RMtGRYmxnRuJo1AWG3dQNFpGdy9+5dvv76axRFYdOmTaSmphIaGoqDgwN//vknu3bteurx\nN+6ncb92T6z6zMS21qvY1W+Btslwxgdm8M7av/j+yDX6fReCkYGKLSN9qF2pwnPXsUqVKgQHB9Ov\nXz+MjY1RFIXXX3+dLVu2sHXrViwtLTEwMOCzzz6jf//++i6bcePGceHCBRwcHPDy8iIpKYnQ0FBM\nTEwYMWIEt2/fxt7enjp16mBvb4+/v79+1dWS5O3tTWhoKOPGjaNhw4a0bNmSb7/9loCAAIyMCl6+\nXZIk6WVQJsZkAHTzqMK0HWc4dzsZ9yoWpV2df4XAwEBycnLo0KGDvmne09OTsWPHMnXqVPbu3fvE\npcpjH2SyYP8lNh6/iYmBivfbutHAPAEjlYLWxpXfz91l77m7/BFxD0drUza841Oo3BPVqlVjw4YN\naLVatFotycnJNGrUiKtXr+r3OXz4MCqViq+//ppbt26RmJhI48aNGTBgAGZmZly6dInY2FhcXV1p\n06YNERERGBoa4uzszPXr15kzZw4JCQmsWLHihev5olxdXfXrt0iSJEl/KzNBRif3SszYdZbdYbdl\nkPGM8jI6pqam5tuelpaW7/WH/Xn1PiN//Iu0LA0DGjsxtnVN7Mob6zPmNa5uQ5PqNnzctQ6XY1Jw\nsDTF3Lho/puoVCpUKhVLlizh6tWreHh4sGHDBqpWrconn3zC/PnzWbZsGRcuXHgs46ibmxtubm6s\nXbuWiIgIatasycGDB6lSpQqHDx+mTZs2rFy5kg8//BBnZ+ciqa8kSZJUOGUmyLAyM6KFmx0/h91m\nSsfactn3Z9C2bVvMzMwICgriiy++YMiQIYSEhOj/qj516hSOjo7Y2dkxZMgQHJv2YMqO8zjZlGP5\noIZUtzMvsGxFUXCzL56ZPr/88gsAM2fOpE6dOgDMmTOHdevWcfnyZa5evUrNmjWfeOyRI0cAGD16\nNFWqVAGgRYsWdOzYkYCAAIKDg2WQIUn/EkII4uPj9bPMXlTewPDY2NiiqJb0FCqVCmtr62dOfFhm\nggyAbh4OHLgQw1+RCTSqZl3a1SnzLCwsmDNnDmPGjOGjjz7io48+yvd63hob0dHRXDV0xepODRq5\nWPHd4FexKFd661rk/ed89BdL3nicp/3nNTMzA+D27dv5jito2qgkSWVXfHw8ZmZm+izELypv+nje\n7wep+GRkZBAfH4+Njc0z7V8mBn7maVfHHhNDFbvDbpV2VcqsgIAA2rdvj7OzM82aNcPc3Jyff/6Z\n1q1bY2dnh7u7u/6LdsKECURcuEi/uTuxajWM1IjD9La7V6oBBkDnzp0BmDZtGmFhYcTFxfH+++8T\nFxdHrVq1qF69eoHH5o09WbhwIQsWLODYsWOMHj2a0NBQrKysaNu2bYm8B0mSCk+r1RY6wJBKlomJ\nyXO1PJWpIMPM2IA2r9jzy5m7ZGv++U0cPHiQ1q1bY2hoiKWlJSNHjuTu3bslUNPSMW/ePLp27cq+\nffuIiori6NGjDBkyhN9++439+/cTExPDggULSElJ4ZW69ej+3lS+PJpIcKwBniZxxO3+H7t3/lTa\nb4PRo0fj5ubG2bNn8fT0xM7OjsWLF6NWq/WzZQry2muvMWbMGDIzM5kwYQI+Pj4sW7YMtVrN8uXL\n9YuFSZIkSaWvTAUZoOsyiU/N4uiVuKfuFxAQQLt27Th48CA5OTkkJSWxYsUKmjVrRnx8fAnV9sXE\nxcWxaNEipk2bxoYNG8jIyPjHY2JiYpgyZQqgG8tw6dIlVqxYgbGxMUuWLCE0NJTkjGyO3szAtttk\n0jt+zNDVJzh+PZ5Pu9XlDYdMQJCVlfWP50pISGDOnDl06tSJnj17sm7dOnJycgr7tvWsrKwICgpi\nzJgx2NjYYGxsTNu2bdm/f7++leNpFi1axJYtW+jYsSMeHh4MHDiQkJAQevfuXWR1lCRJkorAo4kz\nSuLxaDKuh2Vk5wj3j38TEzefLjDxh1arFbVq1RKAGDt2rIiPjxdnz54VHh4eAhCffvrpi2UUKQE7\nduzQr9uR93BychIRERFPPW7VqlUCEJ06dcq3ffTo0bo1P6YtELWn/yqc/QOE49h1wrrjWPHhkk0i\nNSNLXLlyRbi5uQlALF++/Inl5yWziYyMFM7Ozo8ll+rQoUOhk0tJz0cmGCp75DUpWnlrEhVWSkqK\nSElJeaFjVSqV8PDw0D+uX78uTpw4IcaOHSuEEGL16tVizJgxQgjd7+9z584VSZ3/zR69bsWSjEtR\nFEdFUQ4qihKhKMo5RVHG5263VhRln6Iol3P/tXqeco0N1HSsW4m95+6Ska154j7Xrl3j4sWL2NjY\nMG/ePKysrKhbty5ffvkloGvlKE4ZGRl88803+Pj44O7uzsiRI7l06dI/HhcdHU3fvn1JT0+nXbt2\nzJgxgzp16hAVFcWbb7751H6uzMxM4O9l2/OYWVhj03kif2qq4+Vkybb3mjDC9hrxvy1i5pi+VK5o\nS40aNbh06RJ16tRh4MCBT63j+PHjiYyMpEGDBmzatImlS5diZ2fH77//zrJly57h05EkSfr3MDU1\n5fTp0/qHi4sL3t7eLFy48LF9d+7cyfnz55+r/KJsBf43Kkx3SQ7wgRDiFcAHGKMoSh1gCrBfCFET\n2J/7/Ll083TgQWYOgRdj9NuuXLmCr68v3t7ef39Rqg0JCL/D6PUnWRt847mnQWVkZHD48GEOHTpE\nevqzrZuSmZlJx44def/99zl27Bjnzp1jxYoVNGzYkJCQkKceu2bNGjIzM+nevTu///47n376KSdO\nnKBKlSqcP39ePz3zSVq1agXAjh072L9/P0IIdgWeYFO8M2Z1Xqeri4ofRzTG28WaGR9NZ+HChTg6\nOpKcnIyRkRGDBg3i4MGD+lHYT5KSksLu3btRq9UEBATw9ttvM2rUKJYsWQLAunXrnukzkiRJ+jcL\nDAykS5cu+bYFBweze/duJk2ahKenJ1evXuXq1at07NiRhg0b0rx5cy5cuADA0KFDmThxIq1atdKv\nZfSyeuEprEKIO8Cd3J8fKIoSAVQBugMtc3dbCwQCBX7KeUmgHmakFVgYq1hz8By2GbcICwtj7Nix\n+kDAsKIrVm1HYlqnJRO2hGNqAL+cuYvqejCo1Hh5eT2x3Ift3r2bRYsW6VfytLCwYMyYMfTs2fOp\nx23bto1Dhw5ha2uLn58f9vb2rF27lsDAQIYNG8YPP/xQ4MDFvDrVqlWLkydP6rfXqVOHW7duERgY\n+NQpWF26dCEgIIC2bdti69MD09cGoVUbYR36A4Pemkzoqb/LbNKkCdu2bSMxMREzMzOMjY2Jiooi\nKiqqwPLT0tLQarVYWFgQHR2tnxaaF4nfvXv3Hz9XqejJz7zskdekaJibm+f7w2foD6FFWv6awV7/\nuE96erp+MUZnZ2c2bdpEeno6Go2G1NRUMjMzyc7OxsPDgzfeeIOOHTvqvyc6d+7MggULqFGjBidO\nnGDkyJH88ssv5OTkEBERwa5du1Cr1Y8lTPy3u3//PpGRkfrnBeU1giLKk6EoigvgBRwD7HMDEIQQ\ndxRFqfi85alVCq9VNWb/9XTi0nKY9d1mDOq0o65HU4wd3LifbYjIySLtUjAp4fvIiDqDZfOBWDTp\ng9PAL+nS8+n/sQ4fPsznn38O6FJeK4rCtWvXmDVrFubm5lSsWJGcnBzq1q2LiYkJsbGxHD58mMzM\nTH7//XcABoyZRKJDI+K08OHHn3HyZGcuXLjArVu3ClwJ08nJCYBDhw7x5ptvolKpePDggT7gcHR0\nfGq9p02bhkHVp6iu/wAAFcBJREFUepzIrIxBRVcyI0/jIy7y/kfjHsuQCX8nTXlWNjY2VKxYkZiY\nGAICAujatSsajYaNGzcC6BNnSZIk/VeYmprqcwo9j5SUFI4dO8agQYP02/K6tQF69uyJWq0ukjr+\nmxU6yFAUxRzYDkwQQiQ/axawPN7e3k8u1y6eX7/9k/d+uQ8tx2MNmJobUbeKBa1rVyTu5G988PVc\nbG1t0RioUc78jLtHLSKqeLIowpBVQ+tQ1erJXQPjxo0D4NNPP9UnsJo9ezbTpk3j448/1i+0ZWlp\nSYsWLXSRqVAwqVoH0xrNqNJ8IjszKsG5VBQFjt8rh1WNBjwIPUSNGjVwd3d/4nkdHR1ZvXo1x44d\nY+TEaVTxbk/4yRBSzRzwrOtNn/6DMDd5cg6Lk5EJfPPbBUItmuJiacKwRpXo36QNpqZFM8f8r7/+\nQq1WM2PGDHx9ffnss8/YsWMHiYmJ3Lx5EyMjI2bNmlXqy6u/TPL+Wi7oHpFKnrwmRSs2NjZf6+3W\nUc1eqJy8loIXTcb16HGmpqao1Wp9K7ChoSFmZmYYGBhgYmKCmZkZGo0GS0tLwsPDHyvPwMAAa2vr\n/2xyMBsbG2rXrq1/npSUVOC+hQoyFEUxRBdgrBdC5CVguKcoSuXcVozKQEzBJRSsgZMV77d14/bt\naBZ+OhkXCzUnTv095mF3rAMA9erV48CBA/rtwVfieG/dSXosCWbF4IY0cHp83GneL4rx48fruzby\nvjyzs7Op/kp9jCrV4FYqHNVWw27wAoxsHUFRIXIySb9+GtWFffzx4wLis9T836qj0HYiVSrWwrVG\nwc1G9vb2fLdxBxNX7iW+RlMS1AaomtalUlNIANw/2Us5IzVW5YywMDXEspwhFqaGPMjIIehKHLbm\nxnzarS59GzlibFA8EfLo0aNJTU1l1qxZnDlzBtC19ixdulQGGJIkvdTKly/PgwcPAKhQoQLVqlVj\n69at9O7dGyEE4eHheHh4lHIty5YXDjIU3bfzSiBCCDHvoZd2A0OA2bn/Pn298YLLZ3zbmqSmOrBs\n7CUuXEtm8+bN9OnTh+TkZObOnQtA8+bN8x33Wg1bfhrdlOFrTtBn2Z9M6lCLd5u75lsLxcbGhrt3\n73Lu3DmaNGnCzfh0pizfgXWHMZg6upNj40gOYAXkJMdC4i3GtG6Nl6MVSZeO89bXuq4WD7ddVKhQ\ngdjEFKzbjsTcsxv9Vv7Flz3r4WBpgpGBCiO1CgO1imuxKSw+eIVdp7MoX7cVDSzTqa6JpHpNN6q7\nNyAuJYt7yZnEPsgkMT2L5PRsEtOyuRyTQrZGy6QOtRjW1IVyRsWbCV5RFCZPnsyYMWP0S6t7eXnJ\nZj9Jkl56ffv25d1332XhwoVs27aN9evXM2rUKL744guys7Pp27evDDIeoYjc9SKe+0BFaQYcAc4A\nedM6pqEbl7EFcAKigN5CiHzZsZKSkvQnfXRK5pPMmjWLDz/8EAAXFxdiYmJIS0vDzs6O8PBwKlWq\n9NgxSenZTNkezq9n79LCzY6ve3tgV94YgMmTJzN3/kIcm7+JbdPe3M/WdVFoM1KwU6UwvOvreDpa\nMqR7G66eD8+rMxUqVADAzs6OuLi/k4VVrVqVjz76CAefLny44yxJ6dn56qJSQCvAxFDFwMbO/F8L\nVypWKFupdGUzcNkjr0nZI69J0YqNjcXOzq7Q5RS2u0R6Po9et4e7SywsLPKNmSjM7JIgoKABGG1e\ntNwnmTp1KgYGBsyZM4cbN24AupU3v/322ycGGAAWpoYsHdCADcej+Ozn83RacIT5b3tQy748Fs0H\n4pzzKsKoHLdvXiElfB+ZN8+SHRfFvK1beKtVDQDsLc25iq5/LS9ddXh4OHFxcZiamhIREYFWq8XJ\nyUn/l763szX7L9wjI1tLVo7uka3RUs5YTR9vR2zNjR+rqxCCzZs3s3z5cm7evImbmxu+vr5ERkay\ndOlSrl27RrVq1Rg9ejTvvffeEwd5SpIkSVJZU6ZWYS1IXhP++PHjuXLlChYWFgXO4Hj0uAGNnWno\nbIXvhlAGrTyOoVohRytoXd8Zx9RLhF8+DC5GCGcvdu6MZOzYscTGxlKuXDn9FB2NRsO7776Lra0t\na9asAWDIkCFPXFK8koUJAxrrtqekpDBz5kzWrFlDbGwsq7288Pf356233sp3jJ+fH/Pm/d3jdPXq\nVX799dd8+5w7d44xY8Zw7tw5fd4KSZIkSSrTHk0BWhKPp6UVLy5pmTli9q8R4pPdZ8W12MfTz6al\npYmWLVs+lk7bxsbmsW1t2rQRDx48eOr5srKyRLNmzR47FhCLFi3S7xceHi4AYWhoKBYtWiTOnTsn\nxo4dq993yZIlIiEhQaxfv14YGRkJoFjS2sp0yWWPvCZlj7wmRasspBWXnt/zpBX/V7RkFAVTIzX+\nHWsX/LqpKXv37mXTpk3s3LmT7Oxs2rdvz9ChQ7l9+zbbt28nPT2dli1b0qpVq6euFAqwdetWgoKC\ncHBwYPPmzXh6evLtt98yefJkPvzwQ4YOHYq5uTnbt28HYNiwYfj6+gJ/59MAMDY2xtLSkv79+/PH\nH3+wevVqAgICZM4KSZIkqcx7aYKMZ2FoaMigQYPyJVcBcHNzY+rUqc9V1p49ewDw9/enWTPd3O9J\nkyaxefNmTp48SVBQEB07dtSvwGpjY6M/9uH06A+v0GpgYPDY65IkSZJUVskRhCXs0RaQvDVJVq5c\nydmzZwGoWDF/klSNRkNAQIB+7ZCOHTuWQE0lSZIkqXBkkFFMOnfuDMBXX33F0aNHSU1NZe7cufz1\n119UqFBB37rRrl07WrRoQUxMDPXq1cPe3p5hw4bpy/H19cXAwICuXbuSnp7O4MGD8fT0LJX3JEmS\nVJpu3LjBzp07CQoKKrIWXUVR8rVe5+TkYGdn99gCaf9VN27cYMOGDcVWvgwyiknv3r1p2rQpt2/f\nplmzZpibmzNp0iQAZs6cibm5OaBbXyQgIICRI0diampKTEwMFhYWTJo0iZkzZ+rHZzg6OvLll1+y\ncuXKUntPkiRJpSE1NZX+/fvj6upKz549ad68ObVq1eLYsWOFLtvMzIyzZ8/qF+Dct28fVapUKXS5\nL6I0loWXQca/lKGhIb/99hv+/v5UqlQJlUqFt7c3W7Zs0Q/wzFO+fHmWLVtGXFwcUVFR3Lt3jzlz\n5jBt2jQiIyPJzs4mKiqKKVOm6MdlSJIkvSxGjhzJxo0bMTQ0pEOHDjg5OXHlyhU6dOjAnTt3Cl1+\np06d9OPoNm7cSL9+/fSvpaamMnz4cF599VW8vLzYtUuXxPrGjRs0b96cBg0a0KBBA4KDgwG4c+cO\nLVq0wNPTE3d3d44cOQKg/8MSdKt5Dx06FHh8WfiCzrdmzRp69OhB165dqVatGosXL2bevHl4eXnh\n4+NDfLwu5+XTlp8fN24cr732Gq6urmzbtg2AKVOmcOTIETw9PZk/fz7nzp2jUaNGeHp6Ur9+fS5f\nvly4D/fR6SYl8SiNKazS08mpeWWPvCZlj7wmRetZprBGRUUJRVGEoaGhOHv2rBBClyKgTZs2AhCf\nffZZoaawmpmZibCwMPHmm2+K9PR04eHhIQ4ePCg6d+4shBBi6tSp4scffxRCCJGQkCBq1qwpUlJS\nRGpqqkhPTxdCCHHp0iXRsGFDIYQQc+fOFV988YUQQoicnByRnJysP0+erVu3iiFDhgghhBgyZIjo\n3LmzyMnJeer5Vq9eLapXry6Sk5NFTEyMqFChgvj222+FEEJMmDBBzJ8/XwghROvWrcWlS5eEEEKE\nhISIVq1a6c/z1ltvCY1GI86dOyeqV68uhBD53qsQQvj6+op169YJIYTIzMwUaWlpj31mL/0U1tu3\nb3PkyBGMjY1p27ZtvghSkiRJ+vcIDw9HCEHz5s2pW7cuoGspHj58OPv37yc0NLTQ56hfvz43btxg\n48aNvPHGG/le27t3L7t379avl5WRkUFUVBQODg74+vpy+vRp1Go1ly5dAuDVV19l+PDhZGdn06NH\nj2caQ9e7d2991uiCzge6iQLly5enfPnyWFhY0LVrV0C3UGh4eDgpKSkEBwfTu3dvfdkPLz/fo0cP\nVCoVderU4d69e0+sS5MmTZg5cybR0dH06tWLmjULXvTzWfynggyNRoOfnx+LFi1Co9EAuq6IBQsW\n5BtMWVwOHz7M+vXrSUhIoFGjRgwfPhxra+tiP68kSdJ/Vd5su/Pnz5ORkYGJiW7dp9OnT+d7vbC6\ndeuGn58fgYGB3L9/X79dCMH27dupVatWvv0/+eQT7O3tCQsLQ6vV6uvVokULDh8+zJ49exg0aBCT\nJk1i8ODB+WYWPpyaAPKvuVLQ+Y4dO4ax8d/LUqhUKv1zlUpFTk4OWq0WS0tL/WfzqIePFwWsW9a/\nf38aN27Mnj176NChA99//z2tW7d+4r7P4j81JuOrr77im2++AXTTPBs3bsyDBw8YPnw4Bw8eLLbz\nCiH44IMPeP3111mxYgVbt25l0qRJ1K1bl/PnzxfbeSVJkv7rvL29qVu3Lnfv3qVdu3asWbOGiRMn\n6pdiGDJkSJGcZ/jw4cyYMYN69erl296hQwcWLVqk/1LOazlJSkqicuXKqFQqfvzxR/0ftpGRkVSs\nWJF3332XESNGcOrUKQDs7e31613t2LGjwHoUdL5n8fDy86D7bgoLC3vqMQ8vXw9w7do1XF1dGTdu\nHN26dSM8PPyZz/8k/5kgIycnhwULFgCwY8cOfv31V0JCQpgyZQoA48aNo2vXrvTo0YNVq1aRlZVV\nZOfet28f8+bNw8jIiKlTp7JmzRp8fHy4e/duibSgSJIk/VcpisKPP/6IjY0NQUFBDBs2jPnz56PR\naPj4449p0qRJkZynatWqjB8//rHtH330EdnZ2dSvXx93d3c++ugjAEaPHs3atWvx8fHh0qVL+taI\nwMBAPD098fLyYvv27foyZ8+eTZcuXWjdujWVK1cusB4Fne9ZrV+/npUrV+Lh4UHdunX1A0cLUr9+\nfQwMDPDw8GD+/Pls3rwZd3d3PD09uXDhAoMHD36u8z/qhZd6L4yHl3o/fvw47dq1K3SZd+7cwcHB\nASsrK+7fv69vmgoODqZp06aP7d+0aVN+//33IlkaeMCAAWzYsIHPPvtM/x8iJSUFJycnEhISiIiI\noHbtglOalwVyCeuyR16Tskdek6L1PEu9x8XFsWrVKk6ePImdnR2DBw+mUaNGgFzqvaQ9z1Lvpd6S\n0atXL+Li4gpdjqWlJcbGxiQkJOSbcpOXDtzExIQffviBFStWUKVKFY4ePcqcOXMKfV7QfeBAvgE+\n5ubm1KihWzI+JiamSM4jSZL0srK1tWXy5Mls3ryZxYsX6wMMqWwr9SAjJSVFny67MExNTfVzm9u3\nb8/cuXOZOnUqhw8fBnTBxqBBg3j33Xf1y7UXxXkBvLy8APjuu+/0yVROnDjBX3/9hZGRkVzMTJIk\nSXoplXqQAbov50aNGtGtWzd27txZ4KjXf/L111/j5eVFZGQkkyZNYvbs2YCuT2/y5Mn6/V555RUA\nEhISCl95YNSoUZiZmfHzzz9To0YN2rRpw2uvvYYQguHDh2Nra1sk55EkSZKkf5MyEWScP3+eEydO\n8PPPP9OzZ08mTJjwQuVYW1sTEhLChg0beOedd/D19cXFxQUhBEuXLtUnB5k/fz6gm89cFFxcXPj1\n11+pVq0akZGRHDhwACEEI0aM0M92kSRJkvJTqVSPTeeUyraMjAxUqmcPHUp94KelpSX9+/fnvffe\n4/jx40ybNo2srCyCg4OLZNTwhg0bGDBgAAB16tQhMzOTq1evoigKf/zxR6Hm/z5Ko9Hw559/kpCQ\nQIMGDUot//2LkAPayh55TcoeeU2KlhCC+Pj4Qi92lpfXwsbGpiiqJT2FSqXC2to6X96Ppw38LPVk\nXNWrV2fdunUoikLz5s25e/cuc+fOZeLEidjb22Nra8vgwYNp0aLFC5Xfv39/kpKSmD59uj5nhYOD\nA/Pnzy/SAANArVbrV1eVJEmSnk5RlCIJDCIjIwHK/Cy+l1GpBxm1a9fOFxHlCQkJ0f+8cuVK/P39\n9WMsnteoUaMYOnQoJ0+eRK1W4+3tjaGh4QvXWZIkSZKkf1bqYzL27t2rX73u7t27LFy4ENAFHxs2\nbGDatGkYGhry1Vdf6VezexGmpqY0a9aMJk2ayABDkiRJkkpAqY/JkCRJkiTpv6HMJeOSJEmSJOm/\nSQYZkiRJkiQVi1LpLpEkSZIk6b9PtmRIkiRJklQsZJAhSZIkSVKxKPEgQ1GUjoqiXFQU5YqiKFNK\n+vwSKIriqCjKQUVRIhRFOacoyvjc7daKouxTFOVy7r9WpV3Xl42iKGpFUUIVRQnIfV5NUZRjuddk\ns6IoRqVdx5eNoiiWiqJsUxTlQu4900TeK6VLUZT3c393nVUUZaOiKCbyXimbSjTIUBRFDSwBOgF1\ngH6KosglSkteDvCBEOIVwAcYk3sdpgD7hRA1gf25z6WSNR6IeOj5V8D83GuSAIwolVq93BYAvwkh\nagMe6K6PvFdKiaIoVYBxgLcQwh1QA32R90qZVNItGY2AK0KIa0KILGAT0L2E6/DSE0LcEUKcyv35\nAbpfmlXQXYu1ubutBXqUTg1fToqiVAU6A9/nPleA1sC23F3kNSlhiqJUAFoAKwGEEFlCiETkvVLa\nDABTRVEMgHLAHeS9UiaVdJBRBbj50PPo3G1SKVEUxQXwAo4B9kKIO6ALRICKpVezl9I3wGQgb7Uo\nGyBRCJGT+1zeLyXPFYgFVud2Y32vKIoZ8l4pNUKIW8BcIApdcJEEnETeK2VSSQcZjy9SAnIObSlR\nFMUc2A5MEEIkl3Z9XmaKonQBYoQQJx/e/IRd5f1SsgyABsC3QggvIBXZNVKqcse/dAeqAQ6AGbou\n+EfJe6UMKOkgIxpwfOh5VeB2CddBAhRFMUQXYKwXQvyUu/meoiiVc1+vDMSUVv1eQk2Bboqi3EDX\njdgaXcuGZW6TMMj7pTREA9FCiGO5z7ehCzrkvVJ62gLXhRCxQohs4CfgNeS9UiaVdJBxAqiZOwrY\nCN1gnd0lXIeXXm5f/0ogQggx76GXdgNDcn8eAuwq6bq9rIQQU4UQVYUQLujuiwNCiAHAQeCt3N3k\nNSlhQoi7wE1FUWrlbmoDnEfeK6UpCvBRFKVc7u+yvGsi75UyqMQzfiqK8ga6v9DUwCohxMwSrYCE\noijNgCPAGf7u/5+GblzGFsAJ3Y3cWwgRXyqVfIkpitIS8BNCdFEUxRVdy4Y1EAoMFEJklmb9XjaK\noniiG4xrBFwDhqH7A03eK6VEUZRPgbfRzZQLBd5BNwZD3itljEwrLkmSJElSsZAZPyVJkiRJKhYy\nyJAkSZIkqVjIIEOSJEmSpGIhgwxJkiRJkoqFDDIkSZIkSSoWMsiQJEmSJKlYyCBDkiRJkqRi8f/c\ngJydGcuCcgAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"sensor_var = 5**2\n",
"process_var = 2\n",
"pos = (1000, 500)\n",
"process_model = (1, process_var)\n",
"N = 100\n",
"dog = DogSimulation(0, 1, sensor_var, process_var)\n",
"zs = [dog.move_and_sense() for _ in range(N)]\n",
"ps = []\n",
"\n",
"for z in zs:\n",
" prior = predict(pos, process_model) \n",
" pos = update(prior, (z, sensor_var))\n",
" ps.append(pos[0])\n",
"\n",
"book_plots.plot_measurements(zs, lw=1)\n",
"book_plots.plot_filter(ps)\n",
"plt.legend(loc=4);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Again the answer is yes! Because we are relatively sure about our belief in the sensor ($\\sigma^2=5^2$) after only the first step we have changed our position estimate from 1000 m to roughly 50 m. After another 5-10 measurements we have converged to the correct value. This is how we get around the chicken and egg problem of initial guesses. In practice we would likely assign the first measurement from the sensor as the initial value, but you can see it doesn't matter much if we wildly guess at the initial conditions - the Kalman filter still converges so long as the filter variances are chosen to match the actual process and measurement variances."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Example: Large Noise and Bad Initial Estimate\n",
"\n",
"What about the worst of both worlds, large noise and a bad initial estimate?"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAiIAAAC+CAYAAAAIj2Q7AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzsXWdYFFcbPbO7dCmCiAUVxC6xYDdq\nVOy9xG4sxK6xxxY/Y+9GE6Mxxtg1auyixt5b7Fiwi1hQBBuIgDDn+7HOdWd3QYwaSTLned4HuDtz\n587cZd5z33YlktCgQYMGDRo0aPgY0H3sAWjQoEGDBg0a/rvQiIgGDRo0aNCg4aNBIyIaNGjQoEGD\nho8GjYho0KBBgwYNGj4aDB97ANbw9OlTLYJWgwYNGjRo+JfB1dVVMm/TLCIaNGjQoEGDho8GjYho\n0KBBgwYNGj4a0qVrxhSurq4fewj/eZw4cQIAULJkyY88Eg0KtDlJX9DmI31Bmw9LNGvWDKtXr7Zo\nz58/P2bPno0WLVogKioKwcHBqFu3rtU+SpUqhRMnTmDTpk2oV68eACAuLg5eXl6IjY1FcHAwnJyc\nULx4cZXufvr0aapj0ywiGjRo0KBBw78U58+fx9ixY5EnTx7Ur18fer1efFa7dm3s2rULVatWxVdf\nfQUA2Lp1a4p9NWnSBADQv39/7NmzB6GhoQgKCkJsbCzs7OxQr149VKlSBdmyZcOIESMgy3Kaxpju\nLSIaNGjQoEHD34GkpCQ8e/YMbm5u0On+nnX6y5cvsWXLFly/fh2+vr6oW7cubG1t37lfkujfvz9m\nzJihavf398f58+dRsWJFbNmyRTUOACqiYo6ePXtixYoVCAkJQdWqVVWfJSQkwNvbG15eXjh58iTG\njBkDe3t7DBs27I1j1SwiGjRo0KDhP43Y2Fj07dsX7u7u8PDwQPbs2TFhwgQkJye/dV/Pnz/HzJkz\nUadOHdStWxc//fQTXrx4YfXYc+fOIW/evGjUqBEGDBiAJk2awM/PD6dPn37XW8KSJUswY8YM2NjY\noHPnzujfvz8yZsyI8+fPQ6/X48CBA/j+++8RHR2NTZs2YebMmQCABg0apNini4sL9u/fj+HDhyNf\nvnzInj07/Pz8AAAtW7bEzZs3ceLECaxduxYAMG3aNCQkJLx5sCTTnTx58oSKaPj4OH78OI8fP/6x\nh6HBBNqcpC9o85G+8DbzkZyczCpVqhAAAdDR0VH83r1797e6blRUFP39/cX5ipQoUcJCn8XHxzNn\nzpwEwHz58rFXr14sWLAgATBr1qyMi4t7q2ubo1y5cgTAn3/+WbQdPXqUAGhnZ2cxRgBs1KgRZVl+\nq+sUK1aMAHjo0CHRJsuyuLfQ0FCa6XQLnZ9mi4gkSfMlSYqUJOm8SdsUSZIuSZIUIknSOkmS3F61\n+0iS9EKSpDOvZI7JOSUkSTonSdI1SZJ+kCTJIqdYgwYNGjRo+Duwbds27NmzB56enjhx4gRiY2Ox\nadMm2NjYYM6cObh582aa+xoxYgTOnz+PfPnyYenSpVi4cCF8fX1x8uRJjBs3TnXspk2bEB4ejoIF\nCyIkJAQzZ87EmTNnUKRIEURERAirwl9FWFgYAKBGjRqirXTp0nB2dkZCQgLmzp2L0qVLw8nJCXnz\n5sWkSZOwatUqmKrkU6dOYdGiRdi2bRuSkpKsXsfd3R0AcOnSJdEWHR2N+/fvAwBsbGzeONa3cc0s\nBFDLrG0HAH+SRQBcATDU5LPrJIu9km4m7T8B6AIg7ysx71ODBg0aNGj4W7Bjxw4AQLdu3VCiRAlI\nkoR69eqhfv36IIndu3enqR+SWLp0KQBg9erVaNOmDdq3by/ali1bpjr+ypUrAIA6derAzs4OAGBr\naysyVq5evfpO95UvXz4AwLp160Tbnj17EBMTAwcHB0yfPh1RUVFo3bo1tmzZgkGDBgnSEBUVhapV\nq6JEiRLo0KEDatWqBT8/Pxw9etTiOm3btgVgDGD97rvvMHr0aOTMmROJiYkAgOLFi79xrGkOViW5\nX5IkH7O27SZ/HgXweWp9SJKUFYALySOv/l4MoBGAFMN0lTQsDR8f2lykP2hzkr6gzUf6QlrmIzo6\nGgBw/fp11fH37t0DANy9ezdN/SQnJ+PZs2cAjOmqyjlxcXHiOqb9KBklwcHB+Pzzz2EwGJCcnIyN\nGzeKz9/l+1S7dm3s27cPAwYMwMaNG+Hk5CRI14sXLxAaGgoAuHHjBn777TfMnTsXefPmBQD06NED\nx48fh7OzM8qWLYtLly4hPDwcNWrUwNq1a+Hm5iauU6hQIQQGBmLXrl0YMGCAaJckCTly5EB4ePgb\nx/o+g1WDoCYUvpIknZYkaZ8kSRVftWUHcMfkmDuv2jRo0KBBg4a/HZUrVwYArFmzBlu2bMH9+/ex\nePFiHD16FDY2NihXrlya+tHr9ShUqBAAYOnSpSL+YcmSJQCM2Srm13V3d8fly5fRqVMnzJ07F507\nd8aFCxfg6uqKatWqvdN9BQYGomvXrtDpdNi7dy82b94srBQ+Pj6YPXs2lixZgvLlyyM2NlZk11y9\nehXHjx+Hk5MTVq5cifHjx2PVqlUICAhATEwMNm3aJK6RlJSEly9fYvz48Zg0aRK8vb0BALlz58aW\nLVuwZs0aTJgw4c2DtRY4kpIA8AFw3kr7NwDWAZBe/W0HwOPV7yUA3AbgAqAUgJ0m51UEsMm8Py1Y\nNX1BC8RLf9DmJH1Bm4/0BWU+EhMT+ejRIyYnJ6d4rCzL7Nixo9XgzSlTprzVddetWyfOzZs3L3Pn\nzk0AlCSJ27Ztszj+8OHD9PDwUF0zY8aM3L9//1vfc0q4ffs2Z8+ezRkzZtDX15cAuHv3bvH5o0eP\naGNjQwB88uQJly9fTgBs3Lixqp85c+YQANu3b8+bN2+yefPm4rySJUsyODiYJUqUIADu27dPnCfL\n8vsLVk0JkiS1B1APQBvSyC5IJpCMfvX7SQDXAeSD0QLibXK6N4B77zoGDRo0aNCgQUFsbCwmTpyI\njBkzwt3dHTlz5sTUqVOtFtiSJAnz5s3DnDlzUKJECXh5eaFy5cpYv349qlSpggkTJmDq1KkipiM1\nNGrUCAsWLICXlxeuXr2KGzduIFu2bFi+fLkqaFRBuXLlcPPmTcybNw9Dhw7F3LlzERYWhooVK1rp\nPXXIsowLFy7g7NmzoiYIAHh7e6N79+7o06ePaDN1rTg6OsJgMEZpTJgwAVFRUQCAkydPqlJvDx8+\nDMCYwvvpp59i1apVePnyJQwGA06cOIH69euL6167dk2c96aqqgDezSICY6DpRQCeZsd5AtC/+j03\ngLsA3F/9fRxAWQASjK6cOubX0Swi6Qvaai/9QZuT9AVtPtIPXr58yU8++cRqOu6AAQPS1EdCQgKb\nN29uYSHp379/mtJbExISePToUR47doyJiYnvektvxNatW5k3b14xzixZsnDixIl89uyZ6rhOnToR\nAOvWrcvHjx8zPj5epPmaivLMypQpwx9++IFt2rQhAOp0Onbu3JkAWLZsWYaHhzMuLo6DBg0iAGbO\nnFlYdWbOnMl169axQoUKb7SIvA0J+Q1ABICXMFo2vgRwDUa3y5lXMufVsU0BXABwFsApAPVN+ikJ\n4DyMVpIf8cqdQ42IpFtoL9n0B21O0hf+CfNx/fp1rl27lgcOHEjVVfFPx+rVq4VSPHv2LGVZ5urV\nq6nT6WgwGHj37t039vG///2PAJghQwZ269aN7dq1o8FgIAAuXLgwxfPu3r3LRYsWccmSJXzw4MH7\nvK0UcfToUTG2zJkz08XFRRAKg8HA9u3b89GjRyTJK1eu0NXVlQBoa2urqidSuXJl9u7dm25ubgRA\nBwcHFTnR6/WcPHky8+TJQwDcuXMnZVnmjz/+SB8fH3Fc9uzZLYjNeyMif6doRCR94Z/wkv2vQZuT\n9IX0PB8xMTFs1qyZSjHkyZOHx44d+9hD+yDo1q0bAbBnz56q9lq1ahEAly9fnur5cXFxdHZ2JgDW\nrl2bmzZtYnJyMufOnUsALF26tMU5sixzyJAh1Ov14hnb2Nhw7Nixbxzv+fPnOWnSJE6cOJEhISGq\ncdy4cYOxsbF89uwZ586dy6+//pozZ85kdHS0OK5Ro0YEwM6dOwvLhbmUKVOGSUlJJMkzZ84wMDBQ\n9fmXX34p+jt+/DgB0MnJidOnT2fnzp05ePBgNmzYkDqdTpzj5+fHnj17Wr2ej48P69evz8DAQI4c\nOVIjIhreHen5JftfhTYn6QvpeT5atGghqmnWqlWLOXLkIAC6ubnx/v37H3t47x1fffUVATAoKEjV\nXqFCBQLg6tWrUzz30aNHolKoqTRo0IA3b94kAGbKlMnivNmzZwvXRd26dVmzZk1x7rJly6xeKzk5\nmV27drW4Vrt27di7d286OTkJy4W9vb3qGBsbGwYFBfHu3bvCHbJjxw4CoL29PXfv3i2sHVmzZiUA\nrl+/XnX9x48fi+qnly5dUn2WKVMmAuCdO3dIUripbGxsmCtXLosxf/rppwRAX19fenp6EgDnz58v\n+tOIiIZ3Rnp+yf5Xoc1J+kJK85GUlMS1a9eyXbt2bNWqFefPn88XL16kqc/w8HB27NiRLi4utLW1\nZc2aNVVltNOCmzdvUpIk2tnZMTQ0lCSZmJgoSpqnZcX+T8OuXbvEiv63337jzZs3OXr0aBH7kJpe\nUYiBsvIPCgpixowZCYDVqlUTBG7gwIG8cuWKOE+Jz1i8eLFomzlzpsgosYYffvhBEMSgoCB26tTJ\ngnAobhLFNaJkqShib28viEb//v0JgC1atGBYWJggDoqbqV+/fhZjUO7JNDvoyJEjBEAXFxfGx8fz\n2rVr4loXLlzgkydPWKBAAQsyYmotUZ7/kSNHSGpERMN7gKb00h+0OUlfsDYfCQkJrF27tsULu2jR\nooyKikq1v4iICHp7e1uca2Njwz179qR5XBs2bCAAVq9eXdW+ePFiAuDnn3+e5r7eFqdOneKsWbO4\ndOnSv/VdLssya9SoYdVlMGvWrBTPS0xMFFYIxb3j5OQklLU1cXR0VLlDFPcHSUZHR4tjrEFR5itW\nrBBtU6dOFX0p+86YS65cuejn5yf+VuJDFCvGJ598woCAAAJgq1at2KNHDwLgsGHDLMagpBtLksTP\nP/+cXbp0EW6p/v37kyRXrlxJAKxXr57q3kwtRwqBcnR0VI3b1dWVERERGhHR8O7QlF76gzYn6QvW\n5mPy5MkEQA8PD06ePJmzZs0SdSU6d+6can8DBgwgYIxHuHTpEiMjIxkUFEQALFWqVJrHpaxus2XL\nxvj4eNHet29fAmCPHj3e7kbTgJiYGNatW1elPDNkyPDG2Iz3iSNHjvDrr79m8eLFmSVLFlarVo2b\nN29O9ZwnT54IpRofH8+WLVtakIB8+fJZ3TBOkiQC6voZCgnMnTs3Dx8+zMmTJ3PKlCm8cOECSdLW\n1pYAGBMTQ9LoqhkzZkyKpMdUevfuTQAiSFRxsZhK1qxZOWrUKGFFOX36tNX7HjNmjIU1o3HjxsJy\nt3PnTgLGuCKFaCUlJYmgVVNxd3cXVpwiRYoQAMeMGaMREQ3vDk3ppT9oc5K+YG0+ChcuTADcsGGD\naLt48aJYOaaW1qmslg8cOCDa4uLiRFplWjMykpOTRV8VK1bk/Pnz2bt3b6F4/vzzz7e80zejXbt2\nwrTfvn17VqxYUbgWUlKG7xt79+7lwIED2bhxY7Zq1YqrV69WWSusQZZlEf+wZMkSkkarjmJ98PDw\nEBauJk2asHjx4gTAQoUKCUXs4eHBESNGcOjQoaq0YXPp3r27mJdly5Zx9OjR9PLysjhOSUM2d8lk\ny5aNANiwYUMCRrfLzJkzmT9/fqvXs+aWMcWtW7f4/fffc9KkSRbf45cvXwqiExgYyB9//FEE/qYk\n9erV44IFCwiAzZo104iIhneHpvTSH7Q5SV+wNh9K0N6tW7dEW1JSkjBjp/Z+e19EhDQqU/PqncCH\niQ95+PAhDQYD9Xo9L168KNq7dOlCAOzUqdN7v6Y57ty5IwJyTaV+/fpvrOmhxHUA4GeffcaSJUuK\nv9u0aUOdTkdJkhgVFSVqcgwZMoQAhIUjNTGN8/j8888JWMZWmErDhg2Fy8Wa9SFfvnwE1CnFu3fv\nZqNGjVigQAFWq1aNK1euTFPtE2u4fv06p06dykaNGlkdZ9GiRTllyhSL+xgwYIDI5vnqq680IqLh\n3aEpvfQHbU7SF6zNh5I5MXToUNGmrBJz586dqnJQXDNlypThpUuX+PDhQ3755ZcE3s41o+Dhw4ec\nPHkyW7Zsyd69e/PEiRNv3UdacOzYMQJgsWLFVO1KRkfFihU/yHVNoSh4Pz8/LliwgNOmTaO7uzsB\n8Mcff0z1XFmW+b///U/lflHqaeTJk4eSJFGSJIaEhAhyp5REz5QpE7du3co+ffoIC4ISb7F06VIR\nS6KUQc+fP79FWjUAq5YRc1FcQYAxRsQ0zuR9YfTo0arrpCQFChQQhMia7Nu3TyMiGt4dmtJLf9Dm\nJH3B2nwoyldZOZYvX178/dNPP6Xa3/sKVv27cefOHQLGTJB79+6J9m+++YYA2Lp16w96/WfPnlGv\n11On0zE4OFi0//bbbwSs1wCxhqioKK5bt47BwcF89OiRULRKYKhSL6R06dIiMLZ9+/Ykje4w03oi\nAJiQkMC7d+8SeF211MbGRgSnFihQgFWqVGGzZs3YpEkTi3k3Ly6miGKFkCTpjTEwbwMlvkWSJGbI\nkMHCqqNk6ihExVrKsyIdOnTQiIiGd4em9NIftDlJX0hpPhYtWiRW44oSGjt2bJpM5e8jffdjQAlU\n9fHx4ahRo9i+fXuhsD40ibp9+zYBY7aGafzLuXPnhCXqryAsLEzUIUnJTXL16lWSRquKQhyUKqNr\n164V8UEKmTEYDCxTpswbLQ6mogSClitXjsHBwYyPjxfl1c0tZXFxcdy+fbsgU2nBgwcPeODAARHX\nY1ql1VS++OKLFMfo6upqYbHRiIiGd4am9NIftDlJX0htPuLi4rht2zYGBwfz8ePHf9uYZFnmwYMH\n+eOPP3LVqlV8/vz533LdiIgI1V4vysp5woQJH/zaSUlJYrWuxMDIsizqgzRv3vyd+r948SJnzpzJ\nKlWq0MbGhnZ2dmzevLkoCPbo0SO2bNnSwqVha2urIqTWxNyKYipZsmThli1bhDvoxo0bvHr1Kjdv\n3szjx48LchMXF0eSXLJkiep6Dg4OHD16dIoE+Pnz5+zYsaPox1QUi4gSIJuaKARMkiRVTRSNiGh4\nZ2hKL/1Bm5P0hfQ2H5GRkaLapSIeHh5Wt6JPCUlJSTx06BC3bNmSanDsjRs3eOrUKRXRSUxM5O+/\n/87+/ftz1KhRvHz5MpOSkhgbG/uXAyfTiunTp4t7LlWqlEgzNRgM77WsvSzL4l4ePnzIU6dOsVSp\nUoJUpEYsmjZtytOnT6foclHEdCO7kydPiiBcaxvVGQwGvnz5krt27RJEqEiRIiqXYEp1VJRYFb1e\nz5IlS6rGrgTlphZUa3p8uXLlePfuXS5cuFAjIhreH9LbS1aDNifpDeltPqpXr07AGEAZFBQkClw5\nOjoyPDz8jefv3r1btZGZjY0Ne/Xqpco6OXfunErJubi48Ntvv7XYUO/hw4fs1KmTiI0oUKAAFy1a\n9MYxJCYm/qXN+WRZZpcuXVQr8mzZslmUOI+Pj+fatWs5YcIE9u7dm0OGDOGSJUuEVSE1hIeHc8yY\nMfziiy9YtGhRlSJ2cHBgSEgIw8PDRaaNqSLfsmWL6Mdapo0pOTENmh09ejT79eun+iwgIEBcO0OG\nDIyPjxcpxoMHDxbXWbRoEQFjMTRzInj58mUCxvopyl43K1asENfx8/OzmnVlSkyU6rMKETHf80Yj\nIhreGentJatBm5P0hvQ0H0osgpOTk9grRJZl1q9fnwA4YsSIVM+/cuWKUIa5cuVipUqVhNIZMGAA\nSaP7RUkrdXZ2VmVNDB8+XPQVGxsr6qmYr5wrVqzIy5cvW1x/y5YtInbC3t6eX3zxBW/fvv1Wz+D4\n8ePcs2cPd+zYwQMHDlik7R46dEi4cMzF29ub586dS7HvNWvWWCUQpvEUtWvXFscrVVoVt0dERIT4\nzFr1VMWqYl44bfTo0dy8eXOqFonffvuNWbJkIWB03yhITk4WRFDZMC8+Pp47d+7kwIEDCYD+/v7s\n2LEjhw0bxsuXL6usMX9VMmXKRDc3N42IaHh3pKeXrAYjtDlJX/iQ8/HkyROuWLGCCxcu5M2bN1M9\n9ty5c6r4DF9fX2F9UMq6vylOQqna2bRpU1EEbO/evcKi8vTpU3777bcEwEqVKvHZs2ckyY0bNwoC\n9PTpU5KvN4PLmzevqCthvvo3DWBds2aNcCuYxlnkzJmTkZGRaX5mpvPx8uVLfvfddyxUqBDd3NxY\nunRpEfegXEMhFooVxbSKqCkePHggjlHcI8q5ptkwAIQbqE6dOgReFydr2bIlHz9+zMePHwvSYXqe\nNdIGgKdOnRJuJ3d3d7q7uzNnzpwcMGCAIBMDBw4U11m7dq0Y96VLl8T9JSQkcOXKlaLOjTXR6XQp\nBucaDAa6uroSgMpVpJBVNzc30bdSHl8jIhreGZrSS3/Q5iR94UPNx9y5c8X+J4ri7Nq1K1++fGlx\nbFhYmCpA0VSRL1iwQJSIV6waKUFRQNu3b1e1+/v7EzBWY1UUzLp161THFC1alAB48OBBkq+3qO/T\np48gKT/88IModQ8YM1mSk5OZnJwsqpgOHjyYz58/5/Xr10Xdjf/9739pfm7KfMiybLVWBwChTGvW\nrMlHjx4JS4JiKdm2bRtlWebRo0f5+++/MyQkhDNmzCAA1qpVi8OGDRNjVaqsmj7zXr16CYJga2vL\nHTt2CEuTaQxJarEXirRv354vXrywCAJWnp/iiuvSpQuHDh0qyMqkSZM4a9Ys8Vy//PJLHjx4UFyz\nYMGCKuuOt7c3q1atquq/VatWzJIlizhHqT5ragEKCQkRBNZc7Ozs3i8RATAfQCSA8yZt7gB2ALj6\n6mfGV+0SgB8AXAMQAiDA5Jz2r46/CqC9+XU0IpK+oCm99AdtTtIX/up8REdHc/r06ezUqRNHjhyp\nMqcre3zgleWhUaNGYtVszb2iKPvAwEBBCJTiWIoC1Ol0qoqn1tCgQQMC4MiRI0XbkydPhBXhxo0b\notbF9OnTxTHx8fFiS/qzZ89y27Ztwn2jKN3hw4dTlmVh9lfuJzAwkL///jsBMHPmzCprxNatWwm8\nXSE3ZT6UnXhdXFy4Zs0anj9/3iLeoXLlykxISBApqYqlY9SoUWK/FEUUC8CoUaM4YcIEAsaKq4r7\nRXl25qLUjTl27BgDAwNFe2BgIA8dOiRIkLno9XpOnDiRSUlJHDdunIrspEZgrMV0FClShFFRUWzc\nuDEB434127ZtE1YMa/0oBehkWeY333xj9ZpTp05lYmKiqErr7+8vvne2trYcPHjweycilQAEmBGR\nyQCGvPp9CIBJr36vA2DrK0JSFsAxviYuN179zPjq94zUiEi6hab00h+0Oflr+PPPPzlq1CiOHj2a\np06dem/9/pX5OHr0qEVKp8FgEPucKDEdprumbt++Xax2ExISVP0pRaX27dvHK1euiJWrad+//vpr\niuNRNl0ztcD4+flxypQpLF26tEoxKaTBxcWFs2bN4o4dO8R4CxcuzJUrV1qtypkhQwZWqVLFqtJT\nlJz5vSnFtcqWLZvmZ6vMh7JK/+abb5iQkJBi4a1WrVoJK41CnhRS5eXlxQYNGggLCmB0s1y4cEFU\nWlUqqJqWbQ8ICGDr1q2FdcgUL168EJvKnTx5MsXy8IsXLxbnKOStdevWKRIQmJDObNmysW3btmzV\nqhV//fVXEYSrfC9CQ0OFu65Zs2biHipUqCBcRp06dWJkZKTKhWQuWbJkUc11p86deSc6hlVa9aBL\nmc/p9tmbC5pJNJKDNEOSJB8AwST9X/19GUBlkhGSJGUFsJdkfkmSfn71+2+mxylCsuurdtVxAPD0\n6VMxqKtXr77V+DRo0JD+8ezZM5w/fx62trYoWrQobGxsPuj1kpKSMHLkSGzbtk3V3qBBAwwbNgx6\nvf6DXt/aeBo2bIjIyEgUK1YM1atXx5kzZ7Bjxw7o9XqsW7cOPXr0wJ07d7By5Urkzp1bnFujRg08\nfvwYmzZtQpYsWUR7UFAQzp07h0mTJqFq1aqIj4/HH3/8gYkTJyI5ORlZsmSBLMsoVqwY2rVrh/z5\n86vGNHv2bCxYsAAA4ODggBcvXqg+9/T0xOzZs+Hj4wNZljF8+HDs2LFDdYyTkxMmTZqEb7/9FtHR\n0Wjbti3OnDmD8+fPWzwDvV6P5ORkGAwG1KpVC8HBwaKtUaNG6NSpEx4+fIhRo0YhLCwMhQoVwvPn\nz+Hg4IDAwEC0aNECDg4OqT7nyZMn4/fff0e3bt2QM2dODBs2DF5eXoiMjDQqQEmCNR2YIUMGxMbG\nws/PDwsWLICDgwMePXqEli1b4vHjxwCAzJkzw9XV1aqOGjp0KJo0aZLq2BQMHDgQ+/btQ40aNfDJ\nJ5/g6NGjuHz5MqKiopA5c2YMHDgQlSpVQvXq1RETE4NixYrhzJkzAABXV1c8ffpU1V/hwoXx7Nkz\n3L59G+PGjUONGjVUn7dr1w6hoaEYN24ccuXKhbZt28LR0RFxcXEwGAzYvn07+vbti5CQEPTv3x8H\nDhzA8ePHxT3b29sjPDzc4j70LpnhkLsEXMo0hY3b6+8l5GSc/eYz8aerq6tkfq4hTU8qdXiRjACA\nV2Qk86v27ABumxx351VbSu0aNGj4l4Mk5s6diyVLliAhIQEA4O7ujkGDBiEwMPCDXXfJkiXYtm0b\nHBwcUK9ePciyjODgYGzcuBF58uRBq1atPti1reHYsWOIjIxEzpw58dNPP8FgMKB58+aQZRm7du3C\nli1b4OnpiTt37uDs2bOCiISFheHx48ewtbWFq6urqs/AwECcO3cO06dPh16vR6ZMmbBnzx4kJycD\nAO7fvw8A2L59O/bt24cffvgBAQEBAICYmBgsX74cADB16lRUqlQJu3fvxoQJE/D06VNUqFABI0eO\nFNfU6XQYM2YMKlWqhD/++AP0RSliAAAgAElEQVTPnj1D4cKFodPpMGjQIMTFxQEAzpw5AxcXF6vP\nQBlXixYt0KdPH4SEhCA8PBw6nQ7r16/H+vXrxbGSJOHixYvi70uXLmHv3r2YM2cO7O3tU3zOZcqU\nwe+//45Vq1ahePHiAIAiRYpg586dAGCVhABAbGwsAKBq1aqC7Oj1ejg6OgoiEhkZicjISACAs7Mz\n3N3dodfr4enpiYcPH+L+/fsqopgSFCVvY2ODadOmqT6LjIzEoEGDEBAQgDx58uD06dMIDQ0Vn/v7\n++PQoUNwdHREQkICkpOTceHCBXTq1Anz5s3DhQsXLIhIvXr1EBoaiokTJ6J9+/bIlSsXbt26BQDw\n8PBA27Ztce/ePbi5uaFgwYL47rvvBGGbNGkSChYsiO7du+PMhctwzFMaDnlKw867MAzOHgCAhHtX\n8PLyHnzTpysKeNrB2daCd1jCmpkkNQHgA7Vr5onZ549f/dwMoIJJ+y4AJQB8DWC4Sfv/AAww7UNz\nzaQvaG6A9Id/6px89913woRbrlw5scusTqfj4cOHP9h1Fd++6X4cq1atImCsa/GueNv5mDdvHgGw\nbdu2qnbl+XTv3l3UfrC1tWX79u05btw4sf9Mx44dLfp8/vx5iiXDs2fPzh07dvDixYvCtF+0aFFR\nU2Lp0qUELOMwlPYGDRq88Z5Gjx6tuqapuV6v14sgSlPx9/cX8SDK2KdPn8569erR1dWV2bNnF8Gj\nDRs25J9//smNGzcK98LUqVOtjkWZj6SkJFauXNnqM+nVqxenTZsmsmAyZszIYcOGccGCBcINU6hQ\nIZLG4m6mz9Z0Y7pKlSrxt99+s8h6sbe3T9P+L6buOSWWxtRVo/Rr6jIzF9N9iXQ6HVu1akXAuPPt\nmjVreOzYMTHXiYmJVjOYTMXPz48nT54U9USUMc5ftpJLj4axxKClzPn1BuYaHMzsPRax1Q/buejw\nTXbsN1z0cfXqVYaEhPDw4cPvP2vGChG5DCDrq9+zArj86vefAbQyPw5AKwA/m7SrjqNGRNId/qlK\n79+Mf+KcJCYmCr+7sluoLMvs1asXAWO66IdAUlKSeDmaBkE+efJEKIx3xdvOx5EjR0Q8gpKWmpCQ\nIJTdhAkT2LRpU6tKImvWrMydOzcdHBzo4ODAOnXq8MiRIySNZGTSpEksUaIECxQoIBTmmjVrxLXj\n4+NFcGJwcLBKwep0Ok6aNEkorTFjxhAA69evn+r9xMbGiiyKlStXCuKnXD9jxoyCdNaqVUtcLyAg\ngLIsC4Xn4OCgKoMfHh5OwJh50b17d/bs2ZO//PILly1bRiDluBHT+YiJiRF7pyji4ODAcePGsV27\ndqLtwoUL4nwldgIw7qtimhGSMWNGxsXF8fTp0yKAV6n50bJlS86fP58NGzYkYMzMUdKbU4KSzaT0\nrRC01IiCqZin+fr6+lo9rmjRogwNDSVpjAdat24d27Vrx0aNGrFly5Zs1Lgx67bswO9+/Y3Hb0Tx\n6PUoLt+8h86lGjNzs5H07rWEuQYHM9fgYPr2nE/36t1p7xvAwp8U4eDBg+nr66vaIM+0DsnfQUSm\nQB2sOvnV73WhDlb9k6+DVW/CGKia8dXv7tSISLrFP1Hp/dvxT5uTZcuWCeUEgOXLlxdb0Z8/f168\nQD8UlJfz6tWrRZticfD393/n/t92PmRZFtkZ7u7ubNmypRij6WpYkiT6+vpaFLcyFxsbG+7evdvi\nOkqQoWkqbnJyssjSUMiDs7Ozap+R7t27i/oXiuTOnZu9e/fmzp07LapzHjt2jDCxIKQUrFqoUCHe\nvXtXKFxJkkRwKKDOBvrzzz8tAm4VUc4pWrToG+dj1qxZFueZi06nU1VUvXLlSorPeceOHeK4Dh06\niM9Mi5g9e/ZMBPiaBpxag0K2zMXanFeqVEkQnLSQlAwZMrBOnTqCEHp7e3P27NksVKwU7X2KMWu1\nIHp3m0fvr5apiIa5ZP1yNj3q9KVL6aa0yawmOtb2p1Ekc+bM9Pf3f+9ZM78BiADwEsbYji8BeMDo\ndrn66qf7q2MlALMAXAdwDkBJk36CYEzrvQago/l1TAf9ItGyqIyGvxf/NKX3X8A/aU6WL19u9SXl\n7OzMy5cvi8/TukX7X4Hi8rC1tRWZBMoLdM6cOe/c/1+Zj4iICIv9YKylR0qSZGH6z5Ejh4XFJCAg\ngHfu3OGsWbM4ZcoUHjt2jEOGDBHE7969e0xMTBRWDoWE1KhRg7Gxsdy2bZuFewGAqlS6IuXLlxcV\nOsnX1Vw9PDxENsjWrVtF/QrAWPCrQ4cOwjKi3BtgzLyYNm2aIDgPHjxQlQ03Pda0fkXv3r0tnmtc\nXBzHjx/P/v37c/v27YIAz58/n4mJiaoxmZKlMmXKUJZlJiUlsXPnzgTA6tWrc8iQISKN17wYnFK/\nAzCmJpvuXJvaGM2hVKZVvpPWNphzc3PjzZs3BSGaO3cu8+fPTycnJ7q4uLBAgQKsWLGiSCHOlNuf\ne05f5arj4Ry06hR9e/zK7N0XMFvXeWqS0XEms9Try8ARv7Fip5HMUKQ6nfKU4lfjf6KLfxXaevlZ\ndQuZz09q8o8vaLby+Jv3RdDwYfFPUnr/FfxT5kSWZbHp2Lhx49iiRQuxUlPIh/JC+/HHHz/YOJKT\nk0WtB1Ml1K9fv/eyCdvbzkdSUhLHjx8vVqp2dnZi9a+Y5Rs1aiQKYpkWAAPAnTt3kiS//PJLQbCs\nrU4DAwOF9UOn04nqn8Br07mptSQkJERlXjdNFVXmSVFKn3/+uThPlmVRu6Ru3brcuXMnf/75Z+EC\nUr4D1sTFxYU5c+Zk48aNuW/fPsbExHD8+PGCcKWm4NavX8/IyEiOGjWKVapUYZkyZVTjV8TV1ZXJ\nyclcvXo1gdepuZ6eniLtGDAW61JIgOkmecp+LDqdjmPHjuWRI0fE3CjkzdvbW8yDKaGzs7PjmTNn\nUv0+/Pjjj1bnz1wUEgmAiYmJPBP+mCuPh3Px4Zv8Zf919v7tFEsMX8fsPReryIbP4GAW7fMLPer0\noWfTEWwwbhVHLwymzslNkLEpU6ZQlmWxV42pODg4sFu3buzevbuIucmRI4eF1cvJyckqmf3HE5Ea\n3+374Ls1akgd/xSl91/CP2VOlJWym5sbX758yYiICObPn9/iRdWwYUOL/UA+BC5dusQZM2bw+++/\n57Vr195bv287H0pcjCkpU2TatGkEjPU44uLirK5GlbLoP/30EwF1nEDDhg3ZtWtXYTlo3bo1Gzdu\nLKwthQoV4qpVq1i2bFkCxpiTSpUqcd68eTx//rxQJL6+vmzfvj0BY2VUJY6jcuXKtLGxoU6n4717\n90gay6gPGzbM6o6zTZo0YWJiorCE5MmTh/PmzbNaJdT8mSjujc6dO6vImFLz4scff7RqPXB0dGTD\nhg1VhcJu3brFnj17CkKRmsLPmDEja9WqxWnTpvHhw4ckyZEjR1o9dvbs2SqilSNHDkHAlLlzdXVl\n48aNBYE0R3JyMrt3727Zv05Px9wlWLbzWGas1o1Zmg6n66et6d9hLCtN3m3hQvEZuJY+HabQo3Zv\nepRvxr7fLWHdVl9SZ/vaqmVvb8/r169buN4AY9Ez82ejuIjs7OwYHh7Oli1bWn0OxYoVs0pC/hVE\nJNfgYG49dy/N/+Aa3j/+KUrvv4T0Pif3799n8+bNVS+1gQMH8uXLl4yNjRUKIWPGjFy3bt1f2mU1\nrZBlmffu3eP9+/c/2DXeZj7CwsIoSRINBgM3btxIWZZ5+vRpocRHjRolLCX169e3ukouXbo0L1y4\nIBS1IqZl0E+fPi1WszExMXz+/Dmjo6MpyzI3bdqU6jb15gp/x44dnDhxIgFj8S+lpPmRI0eYlJRk\nNQtDp9NxyJAhTEpK4o0bNwgYrR8xMTFcs2aNSlGnlBGiKPRatWoxNjZWEAulaJcSM2FNAXbv3p3R\n0dHCSpEnTx7VBnxpFTc3N65bt47Dhw9nuXLlmCdPHubPn58tWrTgqlWrOGLECFGt1FRSim/55ptv\nGBQURC8vL3p5eTEoKEhU1L1w4QJtbO1on6soK/SbRe+vljHX4GDm/HoDc/RfzRz9fjeSjoHrmLXF\naLoG1KHBLQt1Tm7U2TkROutzak4uFIsQ8JrEmj9D02OUzKUmTZoIK0i9evVUgcepyT+eiNSasZ9l\nx+9kUrJmFflYSO9K77+I9DwnL168EO4FSZJUCq9JkybcsGGDCMwcN27cBx3LH3/8oSrTXapUKe7b\nt++9X+dt5mPBggUEjK4XUyixBR4eHpw6dWqKAarWgkAVUQKAFSjK0HSX28TERGbPnl0QA2tKy7z9\ns88+E1aKefPmqSwiK1euFKRywYIFPHz4sHDB5cmTh8nJyYIU5c2blyTFNvFdunQR18iWLZvVe1Pa\nFLeSolTN42vMN7BzcnIiSdarVy/F51WyZMkUPytQoAADAgJS/DwwMNAqAerduzc3b96sUv46nS5V\n4pcpUybuP3WBQ9aEMFe/lcw1OJh5h25iyx+2M6BhJ+ozeIh+dPbOlOzUxM1092NlLqxdx3wMpjsQ\nW/u+mZIRU7G1tWViYiKvXbuW6vfxX0NENofcY67Bwdx7Oe07L2p4v0jPSu+/ivQ8J4q74E1SokQJ\nxsTEfLBx7N69W7x4nZ2dxarb1taWf/7553u91tvMh1KbIzAwUNWuWImsEYMsWbIwW7ZsFiXhFWWq\nZOAoxC4pKYlTp04VCnr48OEiTXj//v1CUVu7nr29Pbdt26aKJ1GkYMGCwlqjpFsrQbPff/+9uJeX\nL18Kl8nJkycZFxcnrBu1a9cWbhpT94yPj4/qnqxdX5FSpUqp3C6mViOFZAFGi43yt2mabErKNbXP\n9Xq91ZiVZs2ace7cuWI8BoNBuN5MlbvOwYV23oVpmzUfMxUN5KQ1hzlm1SEWbz2YGat2os+gDcw/\nfAtrjlxBh7zlaO/kwq5du7JXr15iriRJok6n46xZs8R9WbOY6XQ6QfYUyZ8/f5o22Eur/PzzzyTJ\nUaNGvfGZ/uOJSPzLJBYdtY09lp5M0z+5hveP9Kz00jtCQ0O5cuVK7t271+q24n8V6XlOlNWZk5MT\nv/76a3bo0EH1AvTz8+PEiRM/KAkhKcz2PXv2ZHx8POPi4kTMw5vqYrwt3mY+oqKiRCbKuHHjePPm\nTS5evFgo3jZt2jBPnjz09va2WPUrUqlSJe7du1fswrt582ahgFq2bKnKDFEka9asvHz5Mv/44w8L\npWV+bOXKlXn16lWxeZr5qtc0a0Yxz69atUp1n8q+Lvv37+e9e/dSXF2nxUWUKVMmtm/fnlOmTLHq\nBipfvjznzp1r0a6QH71ez88++0wobVNLhnL/itI0t6woEhQURFmWOWnSJBUBcnBwoL29PYsUKfJ6\nR10HF7pWbEvPJv+jZ9MRLDR0A/MM25xiemyuwcH0ajiIYQ8e8+eff2bOnDkt7kXZhbhx48aMj49P\nlailVZycnDhq1Cirlh9rlo6hQ4eKZ+ju7s6XL1/y6tWrqrRoa8HC/3giQpJjgy8w99DNDIuKTdM/\nuob3i/Ss9NIrnjx5oorGVxTw+1qJp9c5iY2NFS/jzp07i3YlABMAN27c+MHHkZSUJF6kpgWlbt++\nTcBoIXmfMJ0PWZZ54MAB/vrrr9y+fbtVAqpsJ28uHTp0EMH5MTExIkbDmmzYsEHV55gxYyyUR548\nebh48WIRmFqtWjUeOHDAoi9ru78uWLCAOp2OBoOB58+f58yZMzlmzBiLOiLKrrBlypQRMSjKpngZ\nMmTgs2fPxP9CxowZ31gTBYBFQLO7uztz5coliIVyn6apxTlz5nxj1okiSh0Oa8rWWrqyIv7+/iJo\nVzLY0jFfebqUbkr3mj2ZrfNcerUcx2xdfhHkInvXefTrv4LNvwum/xff0j53CTr4laJdjk84ZPQk\nrtm4mfMXL6Vk60BbW1uLmB/AWBRu+/btIrOmVatWwvWlkKy3uQdzady4sco6ZjAY6OnpmeLxBQsW\nFL+buvBMd/w1/z79K4jIg2cvmO+bLRy4KvUUKA0fBulV6aVnKC9eR0dHNmjQQPjqM2bMKEzk74KP\nPSfHjh1jjx49+Pnnn3PMmDGMiIggSRGUqNz7nDlzeOrUKZEGqtPp+Pz5c5JkZGQkR44cyUqVKrF6\n9er86aefGB8f/17Gl5ycLBTezZs3RbsSq5A5c+b3ch1Zlnn8+HGOHTuW8+bNY1hYmMXq0s/Pz2r6\n5saNGxkYGEgvLy8WKVKEP/30kypod+3ataIPJycnDh8+nNOnTxfKOH/+/BZ9Xr9+XWSXDB48WBCG\n6OhooZze5IJQRDnuiy++sHrfW7ZsYevWrVmtWjVBmOzt7VXui5EjR/LevXuUJIl2dna8d+8enzx5\nwsmTJ6eaNaPIm+IPUtsVVhnP4sWLeevWLY4dOzZNfVpT8JLBljaevnQsWImejYcxW5dfRCBprsHB\nzNF7+SsSMpdebaewfJdx9A2olOb+gdfF1nLmzMl58+Zx4cKFIhunZ8+eosiaQrbs7e1TnMu03qO5\npETkihQpwiVLloh5NrWiKVsQREREcMiQIVbJ87+CiJDkyI3nmXvoZt58qFlF/m58bKX3T8OlS5eE\nIlai4RMSEoSrYPLkye98jY85J6a1DBRxc3PjsWPHUkw3VaRYsWIkjYTF1JevSIUKFVQVLt8FCvkp\nV64c9+/fz127dolsjx49erxz/7dv3xaxGaaKDzCuYtu0aSOCcrNkycLYWPW768SJE6riVwULFuS6\ndevE56aF4ObPny/alSJlOp3OqntLqedhunePLMuq523N9G+6olWkWrVqfPr0qap/WZZFwS9TMXV3\nZMqUiRMmTOD69esZGBgo2k6ePClcDKZiGh/ytqLMqTUxrXVCvg4I7tSpExs3bsxy5crR19fXqlXB\nJlNOZihWm5kaDWXOAWsF6fDutYSejYbRo94A2ucqSsnWwUL5S5LEOXPmqPqzFgRsTQ4cOCDGe+bM\nGQJGC44syxa1cN5GUrKuTZ06VVWYrWzZsqogVoWgTJw4URV3EhgYyIiICIv/1wsXLrBDhw7CRVOv\nXr1/DxF58PQF/Uf8wcazDjIx6cOl+mmwxH+ViNy+fZuzZs3i9OnTefbs2TSfp2ymZh6HoGx01qZN\nm3ce28eak+PHj4uXar9+/bh48WJWrVqVwOsMib59+xIwBuplzZpV5TP+448/SFLsxVG6dGlu2LCB\nixYtEopy0qRJ72WsYWFhVmtM+Pr6CgvOX0VycrKIgfDw8GDVqlWFktHr9aL/+Ph4oSh//fVXcf7F\nixfFc7G3txfnSpIkXC6KGwkAf/rpJ8qyzKtXr6rSQsPDLQs+KiShefPmojaL4k4AjMXRdu3alaLC\nUla7JUuW5MyZM/ngwQNV/xs2bCDwer+WVatW8bPPPiNgXDmHhoYyPj6enTp1suhbUfje3t4qE78i\nBQsWTNUtkBapXr266MPW1pbnz5/nd999x65du7JQoUIEwGXLlon7iYqJ5+Hjp5ghez46FqxEr5bj\nmbXjTOYctNGYOjtgLTNW60rHAhVo6+VH6K3XyjCXevXqpZqVo8inn37Kfv36ib+VuiWkMQNNaU9K\nSmJSUhKbNWumOt/W1lbclzIvSnqzqZh+bxTSlDVrVvE9TW0BYS52dnbcvHkzo6KiVN+N/fv3W+3n\nX0NESHLjmbvMNTiYS4+GWfzzafhw+C8SkbFjx1qsklq1asWEhIQ3nrtv3z4CxlWn6fFdu3YlAPbv\n3/+dx/ex5uSrr74iYCxwpSAxMVGY4w8cOMAXL15YlB83GAycNm0aSeM+HEo6oykh2LhxI4GU9w/5\nK7h79y4HDBjAwoUL09/fn8OGDXsvrrGdO3cSMKacRkdH8/jx4+zTp4+436VLl4pjlRiKAQMGUJZl\nHjlyRNSzKFu2LB8/fszExESxO22hQoX4zTffsGDBgipTeebMmVWr7kyZMlktAnfx4kWhiLJmzapK\nXwaMVqfo6GgOHz7cQmGkpHQWLVok+lcUoSlhjI2NFSmjFy9eFMGzjo6OnDJlCmvWrKnq09R9pdyT\ncq/mVoOU6lyYx5q4ubmlXMFV0tHgnp0u5ZrTpVxzdp+ymF//foaVJu+m75Bg5hq06XVcR4+FzNxs\nFF0/bU29S2Y6ODlbtd6ZStWqVS1cci4uLiKjRLk3BwcHi+DgFi1a8Pnz5+LvoUOHUpZlyrIsKswG\nBASIZ/3w4UPxLBwcHLhmzRphdXpbadGiheh38+bNVl09Tk5OFjE7yvdLp9OxUaNGvHPnDpOSkoQF\nsH79+hw2bNi/k4jIsszaM/az5nSt2urfif8aEVGKLUmSxCZNmrBjx44iQn3o0KFvPD85OVm8ECtU\nqMC5c+eq6iWEhIS88xjTMifPnz/nvHnz2KlTJw4cOJCnTp166+tcvHiRQUFBzJcvHwMCAoTZ39RV\nQL7OnFi7dq1oO3XqFKdPn845c+aoCEdERAQBo7nZNJDz3LlzBIxm+vSMiIgIsRtr9+7dSRrnwzSb\n4uuvvyZJVcnsKVOmsGPHjhYv+oCAAD579ozx8fEpVqY0VdqK4h4zZkyKY9y7d6+qtoSzszMHDx5s\n0b+Xl5fVuAAHBwf269dPjF2n04nvraL0Nm3apLqmYvlZuHChcLVky5aN06ZNY3R0NKtUqWKhqBVL\nCmC0DKUUo/Cm52IuOntn2ucuQY+6/Zmj/xrm6L/aIkulwDebGbTgT45cH0L3KkF0KdmAP64/QFtH\n5xSvmdZgWMBIApVFiSLh4eEWFh9HR0cePHhQ1ZY3b17VnjymmzWStLCK/FXZu3evql9TQmNK9KzF\nnOTKlUs8o3z58gly7uPjw5cvX1KWZVEG/19FREhy+bFbzDU4mEevR1l8puHD4L9GRJQX5tSpU0Xb\n3r17CRiDTZWUydRw4sQJqz736dOnv5cxvmlObt68abE/CaCuvPkmHDlyJEVz7aeffioCS0NDQ8VL\nS4mJSQ2yLIuxff/995RlmYmJiWzbti0BY0lyU1y4cIGtW7emp6cns2XLxh49eojS4n8VCQkJXL9+\nPadPn84NGzakqbz8kydP2LJlS9WK1s3Njffv3+fx48d56NAh8Rz8/Pw4ffp0sQGZvb09p0yZIl7w\n5tY2T09PYRF5k/IzGAzs27fvG9PBlYqtBw8eZExMDO/cuaMy2ZuvzM1X/V999RXHjx8vSLiTkxMH\nDx4s6nHUqlVLfAf27NkjlLe1rJgSJUqoLEb+/v48deoUnz17lmLxLavZNZKOOkc32mTKRQe/0nQO\nqEfPKu2ZMbALMzcbxew9FjFHnxWCbOT8egMztxjDjIGd6Vy0Jp28clGydaDB1Yu16jYQ86rMUUJC\nApcvX55qSrHy3FJyISnBxL1796Ysy6xWrZr4zNRVaLovjdJer149UacFMFq9fvnlF4u5VVxtyjNS\ngplNLRpKvFJqgavly5cXwePKdgzK8QcPHuSYMWMsvn86nU7sT3T37l1BmJTaKVWrVlWN9dtvv/33\nEZHnCS9ZcuwONp51ULOK/E34rxERb29vAuDVq1dV7coLJq2lwqOiojhlyhS2bduWAwYM4Llz597b\nGN80JwqZKly4MGfMmMFevXqJl2tK+12YQpZlYWpu2rQpT5w4wQ0bNqhepNmyZWP16tXFy898Z1IF\n9+/f59q1a7l161axM6tSXRQwxiwoNSbs7Ox4+vRpce7p06etBtnlyJHjL5ORM2fOWARr+vj4pDo/\nsiyLWBi9Xq/yybu4uHDIkCEqhWOuUNesWSNiSkwlJSUhSZLVgNIFCxZYve/79+/z559/5vTp01O0\nfA0aNIiAcSVr7v6wt7cX7pTUgj/Nx50lSxaWKVNG/K2QCsUd5OPjk2IRLb1er7La5MmTh3Xq1BF9\nGDy86ZyvDO1yfkLnkg3oXusrevdebrUGR45+vzPrl7OZqeEQetTsSeeSDWmfqyh1jq6q75kSvwW8\nzpySZVm4ysaOHcslS5akeN+maanbt29P8bh8+fIJF2BMTEyagnE//fRTxsTEMCEhgYcOHeLBgwfF\n/4s5nj9/riJwI0aMsCjYptPpVEGoKYmfnx9fvHghCu0pi4Rq1arx4cOHYudqRapVq6Yay6xZswgY\nqybr9XoaDAZRpiAmJoZly5b99xERklzxp9EqsvHMXaufa3i/+K8RkQoVKhAwbmal4M8//yRgNHGn\nJU7kQyO1Obl+/ToBYw0H063aR4wYQcAY62KKxMREXrp0iXfvvv5/UtJwXV1dVVHxykrMtJiSJEls\n0aKFRQZHcnIyBwwYoDJxe3h4cMWKFSTJ2bNnq4pcFShQgLt27VL1obxIGzZsyMuXL/PUqVMiZTMt\n26ub48WLF4JM5c+fnz169BBBfI6Ojhw0aBCvX79ucZ5iOnd2dlaREGvKde7cuZwxYwa7d+/O8ePH\n886dO5RlWbVa1ev1qVa5XL58OUlaBHyePGlZ2PH777+3cCM0btzYIptBqVGxfft23rt3j2fOnFFl\nsGzdulUQpzcpL3Oxs7MTFi0vLy/evn07bdvE6wy0y/EJi3/ek1tD7rJ422H0bPwNs3efb0k2+q5i\npgaDmKF4XWPgaNZ8RqKhtyEk9bO05lapWLEiDx8+rCImCkwJiqkFQFGs5n1JkmS1VodOp+Po0aP5\n6NEj1bM/e/ZsilYWT09PLl++/K03fVTmy5ooxDA8PNyiAJxer2fr1q1VcVz9+/cXhe5y584trLkG\ng8Hi/v39/VVGACXWqGvXrmI3aEmSWKpUKfEd+FcSkaRkY6xI+Qm7+CLx/VWr1GAd/zUioqwMDAYD\ng4KC2K9fP/EP1bdv3489PJKpz8mhQ4cIGM3hplBeXJUrVyZpXAnOmDFDRQYqVarE8+fPCzNt9uzZ\nVS+dHTt2EDBmVBw9epQbN25kWFiY1XEodRt0Oh0DAwPFKlmn04nU0vj4eJ48eZIXLlywsHDev39f\nHL9w4ULxoj527BgB41WjVNUAACAASURBVMr+bbFs2TICxtLi8fHxXL16tYXSsrGx4Zo1a1TnKeXS\nFfLg4uIiLGTmUqhQIV68eFF1vkJkFWnbti3Dw8NTTKmsXbs2Dxw4YFGl0sbGRhUIq/jllTkxXbGX\nL19eRZqVeAzFpeDg4KCq+XHjxo00raBNxcnJSWRPKBlV+fLlSzHV1NHNk44FP6NXm0kqF4qKcHT/\nlXk6TGKGojWZ69OGtM9dkjYZs7Jg4U+EIn3TuKxV9yxevLiKZH377beqOVqyZInKPVWoUCHu3r2b\n4eHhqudi7q5s2rSp+C44ODgwISGB58+fZ+/evRkYGMimTZtaBOuafpcAsF27dn9pgVO3bl0CRgth\nr169uHnzZqsZM6ZiWopfIVM6nY61a9cWBKRSpUoWFrypU6eK707nzp157Ngxzpo1SyxKdu/ezfj4\neHbv3l1FukuVKvXhiQiA/ADOmMgzAH0BjARw16S9jsk5QwFcA3AZQE3zPt9EREjy0LWHzDU4mDN3\nXXnrydPwdvivERFZljlgwACLf+BatWoJf+rHRkpzIssyIyIixKZkStqxLMts1aoVAaMvl1RXO/X2\n9hYvFA8PD1Xq63fffcekpCRGRUUJZTZo0KBUx5eYmCgKNCmVVGVZFlk35vUdzLFr1y4LRZ87d25e\nunSJISEhYszm2LFjB5s2bcpSpUqxdevWqloapNFfDRiDjqOjo8U9K1kBSpEtJycn1ar2l19+EePo\n2LEjX7x4wbt376qUYs6cOQURyJEjh8oiYV5TwsHBQRULYNpPSpYSpbaDwWAQsThKGrSikMylZs2a\nIpbEtNKveXaEJEns37+/1fog5seZtx06dIik0dqkKLI5c+awTp06NLh60b1sU7rX+oq5vxgngkaz\ndZ5Lv2ZD6FbxCzrm/5Q2mXIxi/+nlGzs6eDgIFbhO3fuFO4bvV5PvV7PwYMHvxVZsia+vr4W9VFI\no8tDIaamlrFt27al+DwUcqM8m969e6focsuePbtq3k2Pq1ChwluHG5w5c0aQCUdHR4sKqTqdjtWq\nVVNl9Fy7dk31v2Au1qxJEyZMIGkM5LdmIVLK3yt4+PAh9+3bJwj532oRAaAHcB9ALhiJyEArxxQC\ncBaAHQBfANcB6E2PSQsRIcmui0+wwPCtvPfk/RRA0mAd/zUiouDixYscO3YsR4wYwX370lem1t69\ne7l161YxpsjISHbt2lWsBBWFYG9vz8aNGwsFa2try9DQUL548UJsoLZgwQLKsswnT56I2JIhQ4ao\nlK+zs7NQXp6enrxz5w5JI7nYsGEDGzVqxHLlyrFbt268cOECw8LCCBjN9KbP7ezZswRe78JqDQ8f\nPhSWAuV+lJgGPz8/1qhRQ7z8TKGkOpqLabDf/PnzCRjLkc+ePZuAMbhOiYtYsmSJiAVRNvUijfE+\nSn/t2rXjypUrrQbyenl5CcW5ZMkScb6SiWWtlHpa5fTp02zevDmB16t5xU2kPKdRo0bx3r17qr0/\nNmzYwCdPnrxxpZxm0RlocM9Oe98AOub/lNV7jOWg389yzKYLbD5mMTM1GMSsHX6gd49Fr4uA9VnB\nHL2WMFO9gcyYt4RwpaSWhWKNkGXPnl3EcFkTUwuTjY0Nvb29LVxirVu3tkpCFChFu3LkyMECBQrQ\nw8NDKPuU6oLkzJmTjRs3thi3eWCyMr6UsoB8fHx469atNLwBXuPgwYNWq9S6u7tz9+7dJMnVq1eL\n9iJFivCLL75QHevk5MSJEyeKcQUFBbFhw4bs1q0bjx07prreiRMn2LZtW37yySesVq0aly1bpqoI\nbA1vIiIGvF8EArhO8pYkSSkd0xDACpIJAG5KknQNQGkAR6wdfOLEiRQv1iBnMnaHJuPrpYfRt4zr\nu41cwxuR2lz8W1GzZk3x+8mTJwEAz549w9KlS7F7924kJiaiRIkSaN++PXx8fD74eO7evYsZM2Zg\n//79kGUZ2bJlQ5s2bbB69WrcvHlTHBcdHQ0AiI+Px7p16wAAbm5u+PbbbxEbG4s1a9bg0aNHyJEj\nBwoXLizurVGjRtizZw+2bt2KIUOGIGvWrIiIiEBMTAwAIHPmzJgxYwYiIiIQERGBqVOnYuXKleK6\nR44cwfz58zF69Gjo9Xo8fPgQwcHBsLGxwfbt23H06FEAgIODg+r7lJSUhD179uDEiRO4ceMGYmJi\nULJkSQQFBeGrr77Cs2fPAADXr1/H9evX4eLignr16ok+bt++jW+++QaSJKFTp04oXbo09uzZg+XL\nl6NXr17w8fGBm5sbcufODRcXFxw7dgy3bt0CAISEhCAqKgoZM2aEj48PsmbNCgA4ffq0aowZMmRA\nbGwsFi9ejMWLF6vmRafTwdPTEw8ePICTkxMAYMeOHShQoAAA43fGYDDg/v37f2neg4KCkJSUJL5j\nZ86cwYkTJ+Dm5gYAiI2NRaFChVCnTh0cPHgQ0dHR0Ov1SE5Oxq+//oqwsDC8ePEixf7t7Ozg7++P\nxMREhIaGIikpSZyvz+ABuxyFYZetAOyy5YetV25Iehtx7hUAYaduQwaQJLvDs2BpxEbeRVzYKSTH\nPUNc6H7ont5FfHy8xXWTkpJSHJMsy2IMCu7evQvA+F1+8uSJ+Dx//vy4fPmyOE6n0+GTTz5B69at\nUbJkSYSGhsLW1haFChWCwWDAlStXUrxumzZtsH79ety+fdvisxMnTkCn00GWZeTLlw/lypXDokWL\ncOfOHTFOWZYBGP9XFi5ciLp164rzlf+jlO47LCwMlSpVwooVK2AwGCDLMm7duoWYmBg8fPgQkiQh\nICBAzDsAGAwGPH36FACQLVs2fPbZZzhz5gxCQ0NRp04dzJo1C0WKFEG1atWwc+dOhISEICQkRHXd\nGjVqIDAwEKdPn8bKlSuRkJCA4cOHq+7bFH369FH9ferUqRSfJwDkzZs31c/fNxFpCeA3k797SZLU\nDsAJAANIPgaQHcBRk2PuvGp7a2R20qNhfif8HvocNXI7oJCn7V8dt4b/IK5du4bVq1cjLCwMXl5e\naNSoEYoXL57qOTExMejUqZNK6QcHB2PPnj2YM2eOUDwfAk+ePEGXLl0QGRkJnU4HGxsb3Lt3D1Om\nTAFgfPH98MMPyJ49O5YuXYqff/4Zrq6u6NOnD9zc3FCmTBnY2hr/R+zt7QEYFWRiYiLs7OwAAFFR\nUQCML7eePXvi0aNHcHFxQdasWXHlyhVERkZi5cqVGD58uHhp2draolu3bihYsCDWr1+Pbdu2YerU\nqahSpQp27tyJoKAgPH78WKVQwsLCcPPmTfj6+iImJga9evXCxYsXVfcbGxuLgIAAzJo1CzNmzMCl\nS5cAAJIkQa/XY+7cuWjXrh3y5s2LnTt3giRq166NLl26AACKFSuG69ev49ixY9i/fz8aNGiA6Oho\ndOjQAb/++qsgBVFRUXB2dsaUKVOQkJCAXbt2AQDy5cunGk+dOnWwatUquLi44Pnz56r7kWUZDx48\nAADcuHEDAODh4QEAuHXrFnr16pWq0tXr9dDpdHj58iVGjhyJMWPGqPrfv38/ChQoIMamEJImTZr8\nn73rDovi6t5nd+kL0nsVEI2K2AWxEI0i9m7sHRV7iQ3UqLF3RTEYG8EuUQm22EswYjcaPw12UYMN\nEJS2+/7+WO91ZneWYjT5fvlynuc+4uzuzJ07d+557ynvoeTkZCIievr0Ka1YsYJ2795NALiSvnfv\nHt24cYOfq2nTpnT69Gl68+YNP5aXl8fBKBGR3MScjD0DyKRsdTL3/4JkcgWpC3Ip/8nvlHVuDxU8\nf0CFGU9JnZdDUBdSvYDy5OjoQEoLKwpr2pg8PAIpPd2bNmzYQAl/3Na5X5lMJuqjPmGfdezYkRIS\nEphVnTIzM8nY2Jjy8vKIiCgoKIhu3rzJFb1araaLFy/SxYsXKTAwkCIjI8nJyUnvdYTy8uVLysnJ\nIYVCQW5ubmRtbU1lypShkydPEhFRw4YN6eLFi3Tr1i2SyWTk6upKaWlplJaWJupTs2bNyN7enuzt\n7Sk9PV10DXYfREQeHh6Ul5fH58/9+/fp559/JoVCQYsXL9YBREZGRtSnTx8aMGAAyWQySklJoQcP\nHpCLiwtt27aNCgoKaMaMGXTjxg3Kzc2l/v37k7+/P02fPp1sbW1FGwcmiYmJVLVqVXJ0dCQizUZm\n69atfKNVqVKlEo3dB4uUmeRDGhEZEdFzInJ8939H0rhq5EQ0i4jWvTu+koh6CH63log6CM9VUtcM\nALzJK0TQ7MNotvQkClX/Pabzf5L8E10zO3fulDQLF0cvzjJPKlSogGPHjuHKlSvcT9+wYcNP2ucZ\nM2aASEOAJZXaSfSeulqtVvNS8FIVf9VqNQ9Ga9OmDU6dOoXvv/+em/SZCdnKyooTV6WkpHA/fVpa\nGoYMGQIijRuHiUql4vEW27dvl2S6ZJVPK1asCJVKxTND3NzcMG/ePFEaLCuaJxV8SO9M7Vu3buUc\nHJMnTxbdJ4vinz59One5sFaxYkXunrKyskLz5s15XErlypV1eDr++OMPvcydtra2ouA+xrXw+PFj\nnk3SsmVLXL58WRT7wtwMzZs35/Px6tWrRWauWFpaimjAGWlUUU0YhMkq8fJ+KAygrNwITr0Ww330\nDvh8lQCPcbs0gaNjEmDTZAgMHbx1MlP0NZlMhrlz5/J5dvjwYfTu3RstW7bUm3FkbW3N70MqG6U0\n1O/CjC7WlEold1O8efOmyMDQyMhIEGkKzbHnztwu7P5atGghcn9JNV9fX6jVaowZM0bvdxwcHBAT\nE6OzFvXt27fYoFzmOmTpswMGDADwPtOMnZO5pry9vfH69WvRXFAoFPx9UygUPM1YO8aldevWf6oG\n1F8WI0Ial8tPej7zIqJreB+oOknw2UEiChJ+vzRABACSrjyG54QkxJ7QTbv7V/68/NOAyOvXr3nM\nQZ8+fbB//35MnDiRs1bevHlT72+ZL5YR+gBAZmYmVxzCdFmh5Obm4tatW3o/L4mwQFHGF+Dl5YXL\nly+LfP+urq4oKCiASqXiaan6nt0vv/yiV8FrK5a4uDj8+OOPHADFxMRwX/rq1atF52UZAjt37uSL\nuoeHB8LDw3Hw4EFkZ2fzxfDw4cO8/yywLT09nSsjc3NzHQ6Gvn37iiinLSwsePqls7Mzvv76a1Su\nXBlKpZL76xmAYGXt2W+dnJx0wEVwcLBkDRdAEysydepUDqaISp7uOnfuXFEgtHCxZzE9X3zxBS8F\nQESiwEamXE6fPq3TL8b0qt28vLxEz9isXCCUlRuhTGAnOHSZCbs2E+D6LpbDpf8q2DSNQIt5SajU\nYyqMnP1AcgM4OTlJUnxr1/EZMmQI+vTpw//PFL9QVCoVz0AyNTXFsGHD+Jz68ssvdfofHBwsyuwh\nPUCDNWHNnq5du4r6bWtry0GYQqFA27Zt8Z///EenjwwQRUZGoqCggMcPaSvnsLAwREZG8jlmYGCA\ntm3bimKHrKysSlztWDinGGATvtva84zFWTH+F29vb54xZ2lpye91zpw5vK4PuzdfX18OkNl7pv3O\nd+zYEYMHD+ZjKizrUFr5K4HIViLqK/i/s+Dv0aSJCyEiqkTiYNU79IHBqkzUajUGbDyHcpP34Vpa\nyX7zr5Rc/mlAhHFhBAYGigIpe/fuDSJN6XJ9whY2YQBXfn4+tyBoF1MrLCzEtGnT+O5TLpejXbt2\nIs4OKSksLMSZM2fw008/8cJSLEiTkS/NmjVLdG22gzp06BBfcNzd3Ytkgv39998RERGBqlWrcoZE\nBwcHDiaYVUUqC6B58+Yg0mSazJs3DzVq1OD1UGQyGR4+fMhBU0xMjOi6HTt2BBHx3RyrLspkw4YN\nkot127ZtAbwvvscW+fj4eM6T8aFNLpdj4MCBJQpKvnDhAv+d1A5eXxs3bhzS09MlCa6MjIywe/du\nEfg4efIkTp8+jejoaK6UpAj11Gq1iLnU3NIaX46YimPXHqDh5DjYt4+CY9c5ojRZtyHr4To0Dvbt\np8DE6z2JGbM8lLaUfGhoKFq2bMn/b2pqiiVLluiM57Nnz7hlLTU1Fbt27ZK8lkwmQ1RUlCgN2N7e\nHvn5+YiNjS2yL4GBgTh37hy3DjDLl3YzNzfH3bt3Rf1jae4ODg6czMvBwaFYmnnGj/Po0SMdAMnu\nx83NTYfB1sjISIeXRzute/78+ToWPSJCbm4uCgoKOAkZy6xiz9DCwgLPnz/H3LlzQUTc+tGtWzfk\n5uZi5MiRomuzOcayZID3qefm5uZ6CdaKk78EiBCRGRG9ICJLwbHviehXIrpKRIkkBiaRpMmWuUlE\nYdrnKy0QAYAX2Xmo+c0hfL7wGDJySkcM898oWVlZiI6ORrdu3TBo0CAcP378b8va+KcBkZiYGBAR\nevbsKTrOeC+K4gph7oimTZvi+fPnuHnzJq8jU7FiRZ1nxCrREmlAAduNly9fXm8q8NGjR3nxKCLN\nTmjcuHGIjo4G0XvA0a9fPx79LrUrl8lk2L59e4nHhaX3Ll26lGd5SDULCwu+CxRykGi3jRs38gWw\nadOmPLL+xYsX3AJw5swZvmizqrMAMGXKFBAR38kxRTVjxgwA4Cm8bOFctWqVTkVZQ0NDBAcHS/ZN\nOyMjJCSEX0O7jo6UXLp0SXJnrr37lVJewiJlpqamop2wsLGdtaOjI8aMGQNTa0cYWLvg5cuXOHLm\nEiJjtuOrtQex8ugtLDt8C+ErEmHbfBTKD1qBcpH7OODwnZgIl4GxcBkQgzKBnWBg5QS5mRW/X2EW\nCgNVAQEBRRKuFTWm2qBi1qxZOuPXrVs3Pn/Gjh2LBg0aiH6jLzOGPX/gfW0bAwMD/h6wd8PU1BRT\np06FTCaDgYGBDpOssAUFBYn6plKpRDVwhK1Hjx4YPny4qIgd+0yYOfLixQs+FuXKlSvWjSNsXbp0\n0QEr+jKeDh48CEBTp0nbclSmTBnOosysHyw929bWlldVfvHiBef4YQDm2rVrojFh2V76OIOKk38k\noZk++eX2c/hO3ovua375fx0vcufOHVHJZtYiIiL+FjDyTwMily5d4gqVmWbT09P57p/tbKTkzp07\nehkjmU+ZyZMnT3gu//79+wFodkvM8hAbG6tz/v/85z980fHw8EBQUBBf2PX5yI2MjLgPW6FQQKlU\nonHjxiWichcKs1LExsbyGilSbfbs2byirHYpd0NDQ74rs7CwwO3bt7nZt1q1ahg0aBD/vE6dOlCr\n1ZgzZw7ve/PmzVG3bl1+vp9++kkEJry8vHD16lVuHWKK/uLFi/j6669BpHHdXL58GS9fvoRKpRL1\nz9raWtL3vnjxYp6uXKVKlSLH6dq1a3pdWtpKmP1fCihaWlpyWvkdO3bA29tbMm5JYWEL68/787gN\n7zHSRGCeE5LgFrEBLv1XocPCH7Hr4kOsP3IVfv4aDok+ffoU60aSun7NmjVLDUqEzcTERId199Wr\nVzogUS6XIyQkBEQaN01SUhI6deokArtXrlzBy5cvkZqaysFsx44dUVBQoBd0Ct1FSqUSCQkJePr0\nKd8kyGQynXL2WVlZiIiI4PPLyMgIU6ZM4aR6DDh99913vH/Hjh1DZmYm1qxZw1lLS8tS26RJE+Tl\n5UnyGElZjczMzDiV/Nu3b7Fhwwa+frRp0wY7d+7k3D1yuRy3bt3i42RjY4Mvv/ySW1NsbW15+v6C\nBQv4WFy8eJFf60PjRP6ngAjwnv594UFd39//F2Hms4CAAMTGxmLy5Ml8p7Jr166/vD//NCACgLsV\nDAwMULNmTb67rVChQrEMh3v27BEpM+HiLSyX/sMPP4CI0LhxY9HvGX9F9+7ddc4dEREBIkKnTp24\nS0VIpuTq6or69etLKobSWkCEkpubyxdPoc9bSAPNFt+WLVvil19+KdHCam5uLmkVqFq1Kh4+fAhA\nswMdOXKkaEyVSiUPxjtx4kSRfBPNmzcH8N6KIrRoJSUlib5bvnx5LFu2TOccixYtQnZ2Nr9vJk+e\nPMHGjRuxYcMGzp3SpUsXvtDri83QbkIqdQsLC/Tt2xe3bmnIGJ8/f45y5crp/MbQ1h1laneA27B4\neIxPhF3r8fDuPBm2YSNg/3lvNO4+FJ7lKkJmaKwJJJWLx8jJyYmPqZubG6ZMmYJp06ZBLpdDJpOh\nc+fOqFKlCry8vPQWN9RuwmckpRj1PafRo0frzDmVSoVDhw7h66+/xqJFi7Bv3z7+XhJpSMdGjBjB\nAbhcLketWrV0gCQrTpmVlSVy4zBrhHD+jRkzhl9fWBmXUeprC6sILZfLMXXqVBw/fpy/oyYmJnj5\n8iWnODc3N5d00zGLl7CuTmhoqI7VJT4+nm80X758Kaq+W1TT5tPZu3evJABavnw5CgsLce3aNR3Q\n5uXlhXPnzmHXrl38frt3744RI0bwjZf2Rqs08j8HRNRqNcZuvwzPCUlYf7r4SqD/bfLgwQMQadCn\nEKWzAK82bdr85X36JwKRrKws9OjRQ7SoNW3alCubooSVcm/Tpg0ePnwoCsDz9vbmJlpWu0G7NgPL\nvAkPD9c5d506dUCk2V0xuXXrFu/jpk2bMHbsWFSpUoUrD4VCgZCQEG6mLU6ePXuGOXPmoFWrVujR\nowcSExO5haGoxgrV1ahRQ7TLZMq1qN8KF8bOnTtLEiA9evQImzdvxnfffYdZs2Zh9OjRWLNmDV6/\nfo1Tp04hKChIR+n17NkTWVlZAN5T21tYWODQoUNQqVQlLpd+/fp17Nu3jy/KarUa06dP16k7MmnS\nJL4wHzp0CGPGjCkRSZlQaYeGhnJ2SwCYMGEiDB3KomLdL9B3ylJYBneFa8/57y0dA1bAv957inAL\nCws8ePAAarWaW7GINBYz5hpiYFIul+u4Jdicl8lkqF27No+fECpRYbAja0ZGRpKF+7SbXC7XoTSX\nyWSYNm2aXuKr48ePF2k9KGp+2djYcKtAcnKyDlCRyWTcSlCxYkXcunULKSkponsZPHgwtm3bhlev\nXun0jVn/pFrVqlVx8OBBSQp39szZJkcIPJydnXlMD+uH0AoBaILqmzVrJnldYYE7pVKpM66pqan4\n6quv0LJlS05KNnv2bO4GNTMzQ4cOHRATE4ODBw+K4simTZumAzJDQ0ORnZ1dovVFSv7ngAgAFBSq\n0G99CspF7sO95x8+eH+HsCC4zz77THT86NGjINIEYf3V8k8EIkyePn2K06dP6wSsFSVs9yosQFZY\nWMgDUhmYyc3N5bu58PBwnDt3DqtXr+YAQsp1wnaEK1as4MeYZYUtOtqLkpubW4lddr/99ptkIB1T\nZN9//70oVVEul3NLCNtZamdLlKRZWVlh8+bNkMlkMDQ0FAX1FhQUYNGiRfjss89gamqqswg6OTnx\nirx5eXm4ffs2kpOT8fDhQ6SnpyM1NRURERHw9vYWuUxK6k7w9/dHWFgYBx1t27bFd999x5VJWFiY\nKIaEKcWirDTFNWsnNxxMvoRj//kDZfsuFrlXPMYnwnf4BljX7QKFuS0yMjI4eCXSFLQ7efKkjhWl\nVq1aePr0KQ9mDgsL47EJZcqUQb169TgzqFwuF1kKqlevzmnAWbyAVGNAx9bWVm9sS7du3fTGZERG\nRurMSbVaza/Zo0cP3LhxAwkJCdz10r9/fx7XZWJiAjc3N7Rp04bHdLHjQjdhy5YtER8fj3379uHe\nvXs6FWT1NWNjY/j7+6NatWro1q0bzpw5A0BT06d+/fr8e5aWlvz+jYyMeHaYs7MzJkyYwIskCpsQ\nTBkZGXEAy+j5hQGiQhHWualQoQJmzpzJj7E5WVwQ6bBhwyT7Ua9ePZ00dUADZBYsWIAZM2bg5MmT\nfzok4H8SiADAk4y3qDztAOrNO4LU9NfF/+C/RDIzMzmCPnXqFACNCZMFdw0ePPgv79P/dyCSlpaG\nYcOGwd3dHS4uLujdu3eRKbrFCdvBMH4NQGNeZwu7sEZJQkKCZExC7969JV/uLVu2gEgDOGbNmoX4\n+HgEBASIftuyZUssW7ZMtPAmJSWVqO/MJBsUFITNmzdj1qxZvH99+/bl3xNmYNSpU0ev0mnbtq1e\nThPh4s76yCobu7i4oGrVqpgxY4ZOdVBhY2NatmxZvmvLzs7G8OHDi3QnMBBS0tRJ7cZ20EOHDhWZ\n1LXPGRYWhsWLF+vNyuC/cfKFVcM+CJmyBX4j1sNj7K734GPEJljW/RKLd57AvO+2wdBEKbr3rVu3\niuKSnJ2dRcGLwvm1cuVKTJw4sci+MCA6fPhwHDt2DNeuXYNareZWsdjYWCxZskRkLdHX3Nzc+FhL\nzXOZTCYCrmZmZjpWh9TUVBBp4ndyc3P58R07dnBlyYIto6OjoVarsW/fPnTq1EkH8JiammLUqFFI\nTk4WrVmFhYW8arNUMzAwkLxXmUyGDRs2AAD//YQJE1BQUIDc3Fyeacey6aKiovg1he447eBbBiAq\nVKjA57FUZWVAYymUshaxOVC5cmWoVCpkZmZKgop79+7xtPXExESo1WpcvnyZA6ERI0agRYsWqFq1\nKqpXr4527dph9erVf8oCoi3/s0AE0ASvVpyyH51WJ/+/qtLLCHAY2QxbCI2NjXH9+vW/vD9/JxDJ\nzc3FqVOncOrUKdEiVVJJS0vTiSYn0uxotCPDSyosuNLDwwPbtm3D4cOHudnVw8MDAwcORHx8PO/v\nuXPn0L17d1SqVAmNGjVCXFycXhO1SqVCr1699CpkuVyOwYMH850tW9C6du2qt783btxAeHg4XyxN\nTExEfCZsN1q1alV+LC8vj+9IWStTpgz69evHA9qINMF1d+7c0bEOsIwGovdBtgsXLtRL0qRUKvln\nDIize2P3/uOPPyIxMbHEvvPSNLlcjg4dOiA2NlYUKF6aFFZR3JCNGyq2jYBTW03dFWbpKDtsPXp8\nexo2jQfCvEoT7Ey5iwHhg/gYFHX+Fi1a8IBqImnLlLOzs6SrhTWhQuvUqZNonrBgXUdHR2zbtg1n\nz57lrh87OzuEPW52UQAAIABJREFUhobC19e3xJYmAwMDnonl5OTEFfPRo0d5YGV4eDh38zk7O4ve\nCxYbVbt2bZ6ZNnXqVEkCNwMDA0RHR/MaMlJrFntvi2rsedeqVYuDcaVSyStBKxQKUcDm3bt3Rc+u\nevXqPKB18+bN/Lyurq46Ac7CcezSpUuRa862bdtE80xIivfll1/yAHArKyuMGzdO1EeWCq/t1mcx\nVfpahQoVdOgIPlT+p4EIAGw79wCeE5IwMeHqnz7XXyX5+fkIDw8XLWzOzs7Yt2/f39KfvwuIrF+/\nXpQpYm9vL0qtVKlU+PXXX3H16lXJnQDwPvizdu3aOH/+PK5du4awsDAQaSwLHyI5OTk6/nOpVqVK\nFe67Lo2o1Wrs3bsXPXr0QJs2bTB//nxJXg0TExMeLMkCNrXl5MmTkmmmYWFh3MLAzmFqaopbt26h\nsLCQuybMzMzw3XffYc+ePXxxY9Y5pugqVKggchPI5XJRtU+ZTAaFQsEBoUKhwJEjR7Bv3z5uaRGm\nKy9cuJAHbAvBUHE8DkU1Q0NDhISEICgoSMfCJFzgT506hZMnT5bsvAoDGBoawqVibVTrPwsew76H\na8QGnt3iOSEJrhEb4dDpa1jV7wm5qWb33rNnT66EMjIykJqaWqRy9/DwwDfffIO8vDycO3euWMZN\nbaXKFJT259pp6nl5eTytWNjMzMy4dZZJcnIyhg4dim7duqFXr14oX758ka6quLg4bhVISkrSCyZn\nzpyJ/Px8PH78mMcETZ48GYcOHRLNOQMDA84bwyxUzs7OHARor1mFhYUcuAmtS+y37BhT6C4uLgDA\n3TFxcXF8/gmL0iUnJ4NIAzRY9oy/vz++/PJLyffOysoKdevW5S4ze3t7TJ06lfe7KNm6dSvvH5Em\nNoZZGIVjQ6SJd2MWVwaIGjVqJDofy1Bi92VmZsbHiIGmL7/8sth+lUT+54EIAMzdfwOeE5KQdOXx\nRznfXyWPHj3Crl27cPjw4RJN1E8lfwcQSUxM5C9VhQoVRObxkSNHYuvWrSLl5eHhIZl2y/LxhWbP\njRs38t/Vrl0ba9euLbJ6ZEZGBr7++mv4+/vDz88PQ4YMwfXr17F06VLUr1+f98PExAQTJ07EwoUL\n+bFu3bp9lPF48eIF380OHDgQUVFRIlfHwIED8dtvv4ncPWq1mjM0duzYEYcOHRLtiOPi4pCfn69T\nQl6o6Hr06MFLzufl5aGwsBDLly8HkSYLQLgwlrQtW7aM95GlCQsX0eDgYO7+Kin4EM4FYROe18LC\nglff1deMjY1RJUArIFMmh6GtO8w+a4AydTrCunE4XAZ9B4/xiXAbsQWeE5LgNT4R9m0nw671eFg1\n7APzKk1gaOdZbL8bN27MgbG+1qNHDwDA/fv3MXny5CI5MVjT3n1rW7eISHJjk5ubi2XLliEwMBCf\nffYZ+vfvzxlvtUWlUnGLh7754+fnh0WLFvGqwT4+Pny+KZVKuLu7w9/fXwTEhHFCzs7OePLkCdRq\ntaSlkFH8M2DDGI+11yxm0WDxERYWFiKgwCwawiq7wHtunW+//ZZnSwUGBuLw4cPYu3cvd4+OHTsW\nKSkpRb4PpqamfB1SqVTIysoqtmqttuTn5yM5ORmnTp3iGT2Ghobc5ZKcnMyfNYtBe/HiBb+vmTNn\n4vbt29i4cSMfY7ZBiI+PR1paGs+qYu4c7dTrD5F/gQiA/EIV2q48jUpTD/xPMq9mZWVh48aNmD9/\nPg4cOFDqyf9XAJG3b99i27ZtmDt3Lnbs2MEtDtOnT8eJEyckd3RsoRL6X7VjJdguhfGFLFiwQPI8\ngwYNkuxXRkYGKleurPN9a2trzgHB3DLCsvF37tzhL3JRJcdLI8KaFb6+vpKmfG9vb5w/fx6Ahu+C\nSEMaxVKSJ0yYIFK6TNEbGBgU6RoQmvs7d+7MF1ylUikCAaGhoahatSpXLEqlEi4uLqJofSGoXrp0\nabFKlTV7e3u9O2l9u3EpPh4igszIDM4urjByqQDzqmGwaRoBx+7z4D5qG3ejuA39Hu6jtsPjqz2i\nYFL3Udvh2HUOrBr0hk2z4fAM6QKFUjM/nZycis0gklLYrJUvX55bAVnsjZWVFY4ePSq5w1YoFAgN\nDS0y40SKf0ahUEhmiJRGGOmdhYUFoqOj8dNPP3FLllRfTUxMOBW/vucnZAlu164dbt9+X7ZDpVJx\njhknJyd8+eWXnOGYgTmWvq69Zr1584ZbP9hYCUGU9tyPiYnB+fPneRzG9evXce/ePR2iMSJNYgHL\ncHz79i13SwYHB+PJkydIT0/ncVAdO3b8U2MulNWrV4NIk4UmFBYjNH78eH6MbR6kGls/r127BpVK\nxddaZiViafZ/Rv4FIu/kScZbBM0+jFrfHELaK42JOTMzE0+fPv3bGEv/ChGav1kLCAgo1eT61EDk\n3LlzencS8+fP1+unNzU1RWZmJlQqFY9a184qYkFun3/+OaKjo0UKq2bNmli7di3fLZw5cwaPHj0S\n+VdZtoKfnx8OHjyIs2fP8lS9Jk2aAHhP+3758mXRtdk9lSYjRyiFhYU4deoU9u3bhz/++AMFBQUY\nP358kbU22CL+448/cneOMAOroKBAh8VS2Hx8fPRSlmvXRhGCQ4VCgf79+/O4mMzMTFy/fh23b99G\nQUEB1Go1H6evv/4aBQUFyMzM5LV7/pImk8PY3R8OnaZrwMa43e/BxcitcOw2F9ZfDIZl3S9hVb8H\nbJuPgnXjcFg16AVlpUYwdvSGlZ10xhFr58+fx9WrV0tNj87aL7/8gitXruiMd0nBTXHzgv1dXExC\ncZKRkcFdXMHBwTh58qSOO9nKygo1atRA9erVMWjQIPz2229cIcpkMkRHR+P48eOiGjM1a9bEy5cv\n9RJnsZIAAQEBPCj87NmzMDAwgEwm48yfUmsWCyxlY2lpaamXWl7oahQq+qdPn2LixImoVq0aatas\niW+++UYE6NRqNV9jhG7Ze/fu8Wt/LFm7di2IdF3MjMBMO0MpKSkJX3zxBVxcXFCrVi0efMvA+tCh\nQzm4Ya4jJyenIktElFT+BSIC+c+TLFSaegAtFh1GaLP35tDy5csXyab5/1UePHjAEX1QUBCGDx/O\n0W9QUFCJAdinBCI5OTl8t1y5cmWMHj1ah62TSLObkqp8ygjEcnJy+DFhvMjp06cld8uGhoY4ceIE\nAGDo0KEgeh+FbmpqioEDByIjI4O7Ng4dOsTP+eLFC25JyMjI4KRfQrIkFminnQkAaMyrCQkJiIqK\nwvLlyznVMpOsrCxs375dlI0ik8ng6OiIkSNH4urVqyJQJZPJ0L17d0yaNEmvK2PdunVQq9V48eIF\n3/25uLggOjoa8+fP1/m+i4sLr2hL9D6w7tSpU5LkW2xM2d+mpqZcKdnZ2aFdu3Yif7aVlZVoFx8U\nFPRxlK25DRQW9jDxqgbLet3g2mwQbJuPhGOnr+E+UsNI6j56B6wa9IJ143AoK32Oxq066p6nhHEY\nCoUC8fHxfM6y6s2sIrPw+QnHVt/YeXp6YsqUKXotPEXVtRECw6LiNaysrDj3yofIzZs3JS0DbDxE\nRfbMzJCamorCwkLcvXtXlCF19uxZqNVqJCYm8v56e3tLAvf8/HzuzmCK09TUVHQtX19fvsGSWrOe\nPXtWJPAtW7YsGjZsKKKJHzp0aKnqq6jVam55EXISMS4gKyurDxt0wfnz8vKgVqvx+PFjPm5LlizB\no0eP8P333/N1TKrqtlAuXLhQrOuTkcX9WfkXiGhJ7KEr8JyQhDJBnWFoaCha/FgJ9U8tubm5iI+P\nx7BhwxAZGfnJMmEY5XWrVq046Hjx4gU3uelLF9OWTwlE4uLiQKTJsmAm+9zcXJ1UutDQUMlCYaxA\n3W+//QYijW+c3atareYBb9qKxdnZmS8wQmIjoS+9bt26nP744sWLvM95eXl8Afzjjz9w6tQprmhq\n166NFi1a8OuNHz8ey5cvR//+/TF58mQcOXJEp5KpsbExNm/ejN9//x2tWrUSKS2p9FOlUilyUTRq\n1Ah5eXl4/PixaGFmfRcqOyF4YQv+vHnzJBchBhQMDQ15psyPP/7In4O9vT3S0tKKNPsWZ71h9/Po\n0SM8e/ZMhyhNuxlYOkLp/wWsvxgMmyaDYd9hKlwHfQeXAavhNixeh/Lc46s9cBsWD7fhm2DfcgzM\nygdDZmgsuQAbGxuXqoAd0fvKw0KXX4MGDXTI17QVnvaxolJLSwvQrK2tMXv2bL2f6Yv5KKkI3SNE\nYmDFsltMTU15AbxGjRpJAhcjIyOdOcre4ZMnTwLQFKBjbloTExP06NEDp06d0st14uHhgadPn+pd\ns96+fYv169eja9euaNCgARo3boyBAwdi//79fN149uwZfv311w92qbKNSbNmzfCf//wH169f5+9P\nr169PuicjDSRbU4cHR0xbdo0zJgxQ3Ic+vfvX6LzHjhwQPIZmJiYIDIy8qN5C/4FIloyctQo2LUa\nB8/xiYjaeQHbU+5h5sxv+AJR2viJ0sqDBw90eAmINEFEH1uYW+K7774THWe7tW3btpXoPJ8SiDDX\nx+TJk0XHWbaLdtNmdhw2bBgSEhJ4HEe/fv3w3XffoU2bNnzBVCqVmDZtGicGY4o+Pj4eu3fv5uea\nNWsW1Go1rl27xt0qzOfdqlUrZGZmIj8/n1M6V6pUCWq1GtnZ2ejSpYsI7MjlcnTu3FlvUTgfHx9M\nnjyZ+7YVCsUHVz1lix5zTxWl8Fjz8vICoHH/6CswxpqhoSG/jz179vDjrFaMMA6DmXSF7J3CMRky\nZAgHOCNGjCj2Xi3dykHp3wS2zUfCJXzNe1fK6J1wH7MTzv1Wwq7NBNi3nwK7sJHoO2cjLGu0gKlv\nHciMlZAZ6MZOSMVTyOVynhLNmpubmyRLJ1OiwkySlJQUhIWF/amaLFL1a+zt7XXclv3798fhw4f1\nnqd8+fKcDTQkJAStW7dGo0aN8PXXX0tW7i2N3Lx5U/NcLC1x69YtvfWPJk+ezJlqWWPuE31zXMjI\n6uPjg4SEBMnvu7m5cQtU+/btcefOHdy6dYuDuUmTJv2tlAM3btyQrEdlb28vinkpjbBim9pj0a5d\nO2zbtg3BwcGws7NDtWrVsHr16lLpMZVKhYsXL+L48ePYu3cvkpKSdGrv/Fn5F4hoSUBAAGTGSjSf\nv58vam1XnoaDj0aRfehEKYncu3ePL9pKpRJdu3bFgAED+OIlpPX+GMIUZufOnTmyzcrK4ouHsJR9\nUfIpX2qWxVCrVi3uUsnPzxfteJhVwMXFhUffSzVfX18dZaLdhG4FobXB3t5e9PIya1KvXr14loKJ\niYkoY+GHH35Adna2ZPl5CwsLvlOsWbMmoqOj0apVK/55cnIyv1b37t358bp16/LUV+3aK9rXYCZY\nNn+EfWOLlZ+fH7fAMF88+2zr1q2iWhrFKUo/Pz9OMkWkAW73798XfYdZlIQ1P7SVjfYxmaExFGUc\nYOpbBzZNI+DUeylch8aJYjjchm+CfbtIWNRso8lGUUi7HkJDQ/n9mZiYYMmSJbhw4QL3mxMRtmzZ\nUmScTEnb559/jt9//x0AMGDAAL33W5SVZcCAAVi6dKnOd2xtbTFq1Cg8fPhQJ6W2Ro0akgRzMpmM\nz2k2F1hF49evX2PmzJmoXLkyypYti549e+Lq1dJTGrDU5lq1amHHjh061j1Wk0WlUoloyLX7KfyX\ntbFjx6KgoIBncbB/v/rqK2RnZ+POnTsiy5GlpaWoLtT+/fv5PE1JSZFcs7KysnD37t0P4iQqjdy8\neRM9e/aEnZ0d7O3t0bdvX559Vlphbh0jIyMkJCRApVLh8OHD/BmfPn36I/f+48u/QERLmNLYs2cP\n3uYXYvu5B/CfdgDuwzfByKUC0tLSPvo1Ac2OSWrH07VrV0yePBlE0kXQ/ozcuXOHm6BDQ0MRFRXF\nFXG1atU+eYyIWq3GhQsXsGvXLr3up9evX3PlVbt2bURGRnJFzJSvg4ODzsJrZmaG0aNHIyQkBA0b\nNsTcuXM50ZG7uzuvB8NauXLl+GIv3MWx3XFISIioX4zMaMKECbh48aKoTsRnn32GhIQEAOBl7r28\nvLBr1y6cPn1axKHB7mPGjBkiqvaxY8fyazH3FBFh//793KQtbMePH9fZnetT9kTvI97Xrl3L7/fK\nlSs6ikOK7K2kbciQIdwlxhq7d6FrQqhwDGxc4VI7DGafNYRty7Fw7rMc7mN2vrd0jEmAQ6evNYGi\njQbAPKAZDG3d9VpOpNJStRWj0PSsUCiQmZnJ4ync3NyKtMqYmZnp3fUzhX/s2DFRXIH2dwwMDNC6\ndWs4Ozvz75UrVw43btxAfn6+KCWXZYsICeeE4K80rX79+igsLEROTo6k68fU1FSHH6Q4efbsGQwN\nDUVjJvxboVAgJiaGr2lEGkB48eJF/PDDD5JB6SYmJoiKiuIbEeG7ZmdnJwqWFBaALFOmDHJzc6FW\nq7F8+XLRGlG2bFlRFtuLFy/Qs2dPvh5aWVkhMjLyowRifmqJjo4GkS5p4ejRo0EkZnP9b5V/gYiW\nMMXh7e2NAwcO4PLlywj7sj9cB6+F5/hELDt8C9m5H3dyCmspEGl27suXL+e+X2ZS11aGH0O2b9+u\ns9vy8fERFd0qTj4EiKSmpupYJxo3bixpGj59+rSOQnFwcMDRo0clfe2+vr6SRGEsduHYsWP82uze\nFQqFKP1VoVDg8uXLePr0Kf/OtGnTcOPGDcTGxnKAIgz4ev78OdLS0kQAjinexMREAMCVK1dElhah\nf19Y2rt9+/YAoFO4bMuWLZKKRzuAV6lU4tSpUzqgR7ux4DxGA82UckREhCSltXZMijDo0dDQUFLR\nChWSlM/awMYNlvV7wK7lOBHZl8dXe+DQeQYcWo2FRY1WMHb9DJY2dpLXlmrF0bfXq1dPVMadKSiW\nbRAYGAiVSsUzBUrSPvvsM+zatUtkoWLuQjaPqlatKmLCJNIUPMvLy+OAgCnJ/v378+84OTlxpV6z\nZk0eM6VWq0VstlLNyckJjo6OOhanwMBAns7p5eWFffv24erVq5wTo2rVqlCr1bh58yaGDh2KOnXq\noHnz5ti6date876wzyWJAbKzs+MWCFY4kT0LIo2Lj3FVJCcnQy6Xc8BmZWUlsnqwasrsugMGDNAJ\ntmafGRsb49q1a8jPz+fviUwmE4GhgQMHAtBUu129ejWioqKwadOmUgWofmphdXY6dOggOs6C7KdO\nnfo39azk8pcBESK6R0S/EtFlIjr/7pgNER0iot/f/Wv97riMiJYTUSoRXSWi6viLgMjr168lF28L\nFx+0X/ITPCckoc6swx+1Pg3jc7CxsYGBgQEUCgWuX7+OJUuWgOg9X0BERMRHu6ZQ0tPTsXz5ckRG\nRmLbtm3Flrln8vr1axw7dgzz5s1DVFQUNm/eLKqjok9yc3O5wrOzs0NYWBhXyCyuQFuysrKwbt06\nTJkyBRs2bOB1DvLy8hAXF4cuXbqgc+fO2Lhxo16zKtsRPX78mP8ttDYIW0xMDP8d23Fot379+uHX\nX39Feno6MjMz8ezZM52+s6BR5uZiKYJCtsIVK1aASAOu2E68TJkyGD58OM8kYQuvh4cHfvzxR8ld\nuHDnGRgYiKSkJE4+RKShcJaqomtmZoa9e/dyBeLo6Ij8/Hy8evUK33zzjU45cn2NKVq5XC7K0JC0\nKMjkMLT3gm2LMe/dKyM2w7b5KBg5+8HAxo0zjQpjNvQV5NPXiuLPkMlkGD58OEaNGsXnQ1RUFHe7\nTZw4EQB01oOiAE5KSgoKCgqKDC5l85zFy7DGsr4cHByQlZWF27dvc3fK0aNHAWjM8MxKtXPnTj7P\n3r59K6pdUlzz9PTkz4jdz44dO0TnY59v2rRJEmDqq4d04sQJyTkmDEht1KiR6NqdOnVCSkoKxo8f\nz7+zZMkS/rxNTEzg6urK51J4eDiP++rfvz8ePnyIlJQUnsXWp08fyYBjLy8vpKWl8aJwffr04dwl\nHh4e3JV25MgRbtnZsGGDTkCwu7v7B5eA+Nhy7949TjAWGxuL58+fY+vWrfyZMd6g/2b5q4GIndax\n+UQ08d3fE4lo3ru/mxPRftIAkkAiOiv83acEIoBG6c2YMQOVK1eGt7c3+vTpwyPJU+6+QPUZGkAy\ne99veJVTMqVdlLDy5AEBAVxRKZVKkZ/a0NDwb5n4BQUF2L9/P9atW4eUlBSo1Wqo1WrMmzdP0pVk\namqK6OjoIs/JKIXLly/PI8+fPHnCAx5Z2mxx8uLFC+zcuRM7d+4Umar1CQssdXFx4YqdKQx7e3s+\n3jY2Nvw+T548iTFjxqB169aoUaMGvLy8ULduXTRp0kRyca5SpYqo2N2gQZo6IS1btkRWVhZfKNlY\nEWmsIkKFqb1rtbCwwLZt2/TSxuuLMRAe9/b2RkZGBlQqFV/s9aWgGhsbY8iQITpumpJcs0KFCrh/\n/z7UajV27dqlmbtGxli5YQvcglrCtvlIjXVRUEnWqn4PKCx0gRWzyIhqtOixgri7uxebPcKU2Jo1\na/QWazM2NuZKslKlSnj79m2pgoM7duxYbCE4BiKlAI2npyfPVmM8L+3atRPNYxZoOmzYMNHx3Nxc\nrFy5ElWqVIG9vX2RlYY7deqErKwskVVSmIKuUql4DBMLVu7YsSOOHj2K5cuXc4vP3r17dd6zc+fO\n8XMqFArExcXh0aNHolingQMHciAmBRjKli2Lp0+f6gSfE2l4SfLy8nDo0CHJ31aoUAGvXr3Czz//\nzEG0TCZDeHg4r43y/fffg0gTL8IC37Wr27KgffZuNmzYEFFRURwA+fr66i0d8VeLMJVe2ISFKv+b\npTggYkCfVtoQUci7vzcS0XEimvDueBwAENEvMpnMSiaTOQN4on2C8+fPf5KOhYWFUVhYGP9/Tk4O\nnT9/nmRENCnInDZdy6ZvT9yhH87do55VLMjfwYgsjOQfdK38/HwyNTWlK1euUNeuXalhw4Z04sQJ\nOnnyJBERGRkZ0cyZM+nt27ef7H6Fkp2dTYmJiXT8+HG6ceMG5ebm8s+qVatGwcHBFB0dLfnbt2/f\n0rBhw6iwsJCCg4Mlv7N//34iImrYsCHdunWLHw8ODqZdu3bRnj17yMzMrMg+bty4kdasWUN5eXlE\nRGRsbEzh4eHUq1cvvb8xMjIiIqLHjx/zY+fOnSMiIm9vbz627du3p5SUFJo+fTrvK5OqVavSmzdv\nKDk5mYiIZDIZA9Ukk8no6tWr1Lp1a1qwYAE1bNiQQkNDKT4+npKSksjBwYEKCgr4ucLDw2nv3r2U\nmprKj5mZmVHZsmVJqVSSq6sr+fv70+eff07m5uY0f/582rp1Kx06dIiys7Pp7du3lJGRIXo+RERy\nuZzUajU/LpPJyMvLixYtWkRNmzbl9//FF19Qbm4unTx5kgCQXC4nCwsLyszMpJiYGCIi8vDwoJYt\nW9KZM2fo0qVL/Bq5ubm8j8Jn2KxtZ7r/+CndvP+EnhvYk2/vuZRr6UHzb1iQosFgUubl0Jt7l8nw\n8VV6dvc3qmAtI3d1Dv38+hk/h4ODA6Wnp9PLly+JiEilUvHPCgsLRffq5OREO3bsIBMTE8rIyKD2\n7dvT69evJZ8/e07bt2+nmJgY6tKlC39+MpmMXF1dKS0tjY4ePUpGRkZ0/fp18vHx4b8jIjI0NCSZ\nTEb5+fmS19i5c6fkcaE8e6a51/z8fLK2tqZXr16Rj48P9erVix4/fkxRUVHk4OBANjY2RER07949\n0Xt/7do1IiLKzMzUWQ9q165NtWvXJiKiIUOG0Pnz58nS0pIyMzOJiMjOzo5evnxJP/zwA0VERFDT\npk35OcaPH09z586lMmXK0ObNm+nx48dkbW1Njx49IicnJxo7diwZGBhQUFAQ9e7dm1atWkXR0dHk\n4OAg6kNhYSFZWVlRRkYGWVpa0sWLF6lfv36iZ7dp0ybq06cPrVq1igoKCsjQ0JC/G0qlkpYvX069\ne/emy5cvk42NDdWrV4+ePHlC586do59//pnWrl1LtWrVom+//ZbWrVtHly5dIlNTU2rSpAn169eP\nUlNTycjIiKZMmUInTpwgAwMD6tSpEz169IgePXrE3wEDAwM+Nr/++qtoPO/du0dERHl5eRQYGEgL\nFiwgmUxGzZo1o86dO1NqairFxMRQYGBgsc/8U0u7du3I0NCQtm/fTg8ePCBHR0fq0KEDdezY8S/R\nGX9WypUrV+TnHxOIgIh+ere7+BZALBE5MnAB4IlMJmMz2pWIHgp+++jdMR0g8neIl5UhRdazplsv\nCmhZSiYt/iWTzAxk1K+aBdX3MCGFTFaq85mbm1PXrl1p3bp1NHHiRPL29iYzMzN68+YNmZmZUXx8\nPLm7u3+iuxHL06dPadCgQSJlTURkb29Pubm5dOnSJbp+/ToRaRaMnJwcWrRoESUnJ1NCQgKVLVuW\n7t69S1u3btULRKytrYmIRAoMAN28eZOIiC/A+mTfvn0cCFWvXp2IiC5evEgrVqwge3t7EYAU3teB\nAwdIJpORmZkZ5eTkiD4/e/YsEWmUc79+/WjLli20f/9+kslkZGlpSe7u7vTw4UO6fPmy6HcAyNTU\nlCwsLCg9PZ3q169Pp06dom+//ZYaNGhA7u7utHr1alq0aJHot4aGhrRy5UodxfrmzRs+vkRElpaW\nZG5uTkREpqam1LdvX+rbty8RaUDf+vXracOGDQSAbG1tKS8vj96+fUsmJiYciACgo0eP0tGjR2nW\nrFmkVquJiOjIkSOi6xsaGvJFmYmjoyNt3ryZMjIy+DGmvHNycuhW6h0yKVudrIO7ksLKiXbBmnbt\nfg8qyMqT3t76hWr5uVLBs3t0ZNsasjQ3ozmrV9PgwRvowq/i6xERpaen6xwTilwuJzs7O0pPT+cL\nbUpKChkYGJC/vz8HiS4uLqJ5bGBgQIWFhXTo0CEKCAjgY6NQKMjU1JSsrKyodevWFBcXR9nZ2WRv\nb6/zHgiylG7YAAAgAElEQVSBJJOQkBA6fvx4kX3WHjsmr169IqVSSV27dqV58+bRmzdvRPdpaGhI\nly5dohUrVlBYWBhduXKFEhISiIioUaNGRV7rxYsXREQUHR1Nz58/p9GjR1NBQQGZmJjQmzdv6NWr\nV3T//n0i0gD5S5cuUfPmzcnExIS/H82bN6dNmzaRvb09GRi8VwdOTk5ERKL+MjEwMKBBgwbRvHnz\n6OXLl7R06VL+GZuXb968oStXrtCkSZNo/fr19PTpU5LJZBQcHExjxowhExMTOnz4MCkUClq7di25\nubkREdHq1atp7dq1lJCQQLVq1SJ/f39asmSJ3jGwtLSkoKAgOnPmDI0ZM4b69OlDGRkZtGrVKiIi\nCg0NJX9/f9q0aRMlJCSQu7s7BQQE0P79++nKlSt8ztSpU4dk79Z1Y2Njql69Oj1+/FhnfvxdIpPJ\nqFWrVtSqVau/uyufRqTMJB/SiMjl3b8ORHSFiBoQUYbWd169+3cvEdUTHD9CRDXY/z+1a6Y0kl+o\nwpnbz9Fs6Ul4TkhCxKYLeJNXenOdSqXClClTRObUmjVr4tKlS5+g1/qlXbt2IHpfZdLb25v7iufO\nncuj91nAl6WlJVJSUrifVWjO1SePHj3iJtXevXsjLi6Om0Gtra15/Ic+YdTRQhcQi7OoVq2a5G9W\nrVoFIk0QaFZWlqQP387ODtevX8fLly8lXQ/CwLtKlSqJAmiZf/6LL77gZnBPT0/06NED3bp1Q4cO\nHTB79mxcunQJwcHBes323t7e+OGHH0TsmcJUXm1hfBElZdQsrtnZ2UmW/65Spcp795HCAH6NO6NC\n+DJ4vMto8R27HXatxsGqYW9Y1usO86phUJYLhMzITNKdMnz4cNy9excjR47kMVAeHh4YPXo06tev\nj44dO2LmzJkYMWIEhg0bhpEjR2Ls2LFYt24dsrOzOSGXdpwFa8JgUWE8DZu/RRWGY+6AefPmca6d\notqiRYtEAcXC95fVFRHeN6vYqlAo0K1bN1y+fJnHQjRt2hSrV6/mwaf63EJDhgwp5k0GT2UfOXIk\npk+frnMOT09P/h5u375dVNzQ2dkZ69evx/Pnz2FsbAyZTIaDBw8CAF69esWzC+fPn6/3+sJ3zMjI\nCJUqVRL9n4hw7949qFQqPHz4UESFfvnyZRBp3LdCOX36NB/bksqtW7c4uZr282FBp1IZZjKZjNeb\nadiwIQ/Off36NY/TOXLkSIn78a/ol78la4aIviaicUR0k4ic3x1zJqKb7/7+loi6Cr7Pv4f/MiDC\nJLegEDN/vA7PCUmoO+cI9l19/EGsc69fv8bZs2dx69atT9DLoiUjI4MXYmOcEqtWrcKmTZtApEm5\nFFIwsxiHLVu2cPZNplTq1KlT5LU2btyoE6NgYmIiWfFTW5iiF9abyM7OBpHGF37u3Dnk5+dDrVYj\nJiYGlSpV4teqWbMmz9ywsrLSUZIsPZL9f8OGDThx4gRXHqzVqlVLxF5aUspvX19fTlLm5+eHFi1a\n8DgSIg1pFbsvlm4cERGB/Px8HD16FImJiaLMojNnzvDfVqhQAZcuXcKrV694ei6rjilFoKSz8BoY\nw9TtM3z/UwoM7Txh5OQLZaVGcK3THLEnUlGp1wzYthzLC7+5Dl4HmyaDYVouCGZligY7lpaWmDx5\nsoiWfsSIEViwYAEHStqZUV5eXujXrx9WrVqlw2L58OFDPg+MjY3RrFkzEfGasD5JcS0wMBBpaWmI\niYkRKf7atWvzTCY7O7tSxYqYmpri8OHDPE6GNQaiid5nxrDv+Pv74+bNmzqEhsbGxqhXrx78/PwQ\nEhKC+Pj4YteWH374ocR1eiZMmIDnz5/rBCXb2triwIEDomyu8uXLi0oAFBWblZaWpsNvI5fLsWjR\nIg5koqKicPPmTZ3fvnz5EoaGhpDL5SKm16+++oo/39LI06dPMXXqVDRo0AChoaGYPHmyCOCr1WrE\nx8cjJCQEfn5+aNeuHX766SeMGjWKP3djY2OEhITwQPuKFSt+coLL/xX5S4AIESmJyELwdzIRNSOi\nBSQOVp3/7u8WJA5WTRGe778RiDA5e+cFQpecgOeEJJQPXwaltT3c3d0RGRlZ7E7/7xZWeMne3p6n\nDHfv3p3vTnx9fUUsmSwoT6lU8h0522GtWbOm2OvduHED48aNQ+fOnREVFYX79++XqJ/M6iIkeGPk\nbKw5OzujWbNmkgsv66MwuFFYaVOocGbPng0AePz4sc7nzAoipaBYBgT7bMyYMXxHyK7LaOGZImIW\nBxa5z9JIGzRoIKLJNjAwwIgRI1BQUIDCwkI+9vXq1UNycjLWrFkj6pPQWsKZTc1t4FO/DcyrNIF9\n+yi4DlkP9zEJOhTooqqyI7fCbfgm2LUYBRPvGiC5LviSqgPEWnJyMh48eFBkWrCvry/q1Kmj87mD\ng4PIOlhQUFBkqrBw7EeMGIGVK1eiXbt2fCyEAFQmk2H69Ok4fPhwsZYwBtT1XUsbkEoBVBMTE8yY\nMYODCZYe3KtXLz5HypYtK7KcWVpalpjNsihKfZlMhoCAAD7GhoaGyMzM5ODYxsYGvXv35pYcU1NT\n3L59G5GRkaL3JSQkRBJAaMvAgQNBpAFgs2bNwu3bt3mwurB17NhRZ31kXD9WVlYYPHgwmjdvzr9f\nWn4TbWGUA7m5uTh//jyuXbsmAncqlUrv+kGk4Xn5OzaL/1T5q4CIN2ncMVeI6DoRRb47bksat8vv\n7/61eXdcRkQrieg2aVJ+a0IPEGnfvj1atWqFZcuW/alCTR9T1m3YCIsareAxVsOJYN8uEgY2bjza\nuyhJTU3FN998g7Fjx5YqlfZjSEFBATdhLl26lC+ibAfAdqxeXl6SBeZY69ev30fZKWRnZyMuLg7T\np0/H5s2buRmVgQ57e3vMnj1bVH/EyspKRF2uUCgwadKkIk3xLVq0QH5+vl720M8//1xktvbz8yuS\nadTMzIyngzJ+mKFDh+Lhw4cixbR06VIAwP3797kiMzAwQEZGBrKzs7myEJJchYSE8Gsz2nupzALt\nJjcxh9K/CWyaRsBt2Pc6ZevtWo2DdaMBMC0XCGP3yrCp2gTW1cNg5FIBJmWrw8jJF9bW1lizZo3o\nvIGBgbx2RnGN7WJZeqeFhQW6du3KFU79+vVx69YtrugZYGTK2dvbG/v378eECRO4tcjU1BTTp0/n\nmS78fgXPx9HRET179pR8ZsIsJmELCAjA0qVLuYtSKiOnTJkyPNNq/Pjx3JIhlU3GSPV27dqlY0VI\nTk7m5yPSuDXT09O59YSdl82XoiQjI4NbIebOnYv09HQRKd369ev5d5l1ipGAmZmZ8aJwarWau0tZ\nldbs7GxcunSpxBsGALh06RIf92bNmoneVXNzc7Rt25YDyp49e4p+m5WVpZNubmRkhFWrVpX4+vrk\n3Llz+Oqrr0SuvfLly3NXCxsTGxsbnDhxApmZmYiIiOBpsqyK77/yceT/PaGZcJL6+fnx9KxPJXl5\nedi+fTsmTZqExYsX4/Hjx6LP3759yyf34Mi5GLXpLMpPToLH2AQoK4Zgw4aNes+9ZMkSncWyYsWK\nePToEdLS0rB06VJMnToViYmJnyxtbNGiRfzaUkXk7O3tcfHiRWRmZmLJkiVo2bIl/P39ERgYiNGj\nR+Pnn3/+KIWQfv75Zx3/v7OzMy5evIg3b97o0Fqz/ubk5ECtVvOaFLa2tvw8DRs21GEKlcvliIiI\n4LtI4TWrVaumN/bCz89PVCeGLab6OCZ69eoFtVotOr+hoSG6du2Kzz//XFRsLigoiFsN2Hnr1q2L\nFStW4MqVKzwuRKlU4vHjx5x8StxkMPGqijK128FrYDQnCvMYtxv2bSfDonpLGLtVgoGNK2RGpqJ5\n5+HhIbJ8EWnA2KxZs+Dj48OPdezYEWq1Gs+fPxf9XiaTYcuWLZzZkTV/f3+kp6dzDodatWohLy+P\nU32vXLmSc3h07tyZx12sW7dO5NLRbsHBwbxfbGcfEhKiw54r7AdzDchkMsyaNQvt2rUT3QNj+j12\n7BiIiANLfbWBFi5cyFMoJ0yYgDVr1mDcuHGYN28e0tPTiyT9U6vVvO4RkSYVmVnAXF1deTyMdrqu\nlDDrWnBwMD/WunVrfu7w8HAAGoDA5tfWrVtBpIlPEQpzyWoTZZVW1q9fr8PnYm1tzatKX79+nfMn\naa+narUaZ86cwYIFC7B69WqdStQfKsK6S76+vjxGx9jYGJcvX8aoUaNApMtKysowCAHdv/Ln5f89\nEFm5ciXi4uL4zkYbVX9MuXv3rk6JcyMjI8TFxfHvHD9+nAMIppCfZr5FrSiN2dtj6EZU6TcHAyMX\niF46tisiIvTo0QMzZszgi2vFihV18uWrVKmi89J+DFGr1Zg+fbrIt1umTBk0a9YM0dHRku6wj11r\n5vXr11xh16hRA+PHj+f+bldXV+Tm5qKwsBB79uzBwIEDuQJ59uwZP4d2xdjq1atDpVJJFhQUNgZU\nGKAwMzMTgYvw8HBRvIWxsTEiIyMRGxsrOo92vYzg4GDOpung4IARI0ZIXl/oUqlRo4ZkSXhhzIs2\ncFWUcUCZwE5w7hfNLR5OvZfCKqQvjBx9QFTyOAd3d3cMGTJEb2yEsFiiNumXlEvC3Nxcp78+Pj6c\nAbJHjx68JsuSJUs4ED5y5Ah/70xNTfVao4T93L17N27fvs2fEbufxMREqFQqFBYWioJ4he+XcA15\n9eoVnw/az1TospkyZQpCQkJA9L7ibmnekadPn+pUjK1YsSKuXbvGrS5t2rTBr7/+WuS7s3PnThBp\ngCMTIe25p6cnBg8ezIHVkCFDcPHiRRBpQLjQqswq5Y4cObLoF7YEkp6ejlWrVvHnyEogMGFA7K8I\n/lSpVNzStXLlSqjVauTn5/PA5O7du3OWZUZqx4S5a4Rr/r/y5+X/PRBhkpqayheMT1GwSK1Wc0Kp\ncuXKYcqUKXynoVAocOPGDQDA0aNHOVBgolKpULtOHSgrfQ6nnovhPnqHJtiv01Qc+0UTJ8B2b8Ia\nI+np6aIded26ddGnTx++O2zSpMlHv08mGRkZOHz4MH7++edi6y18LCBy+/ZtREVF8XEOCAjglp8/\n/viD70Y/++wzzJ8/nwcwsuNCunXtIMGIiAgRQyojJRI2Br6cnZ1x+PBhUZQ/a6ampti2bRv27duH\n3bt349mzZ/j5559LVVV14cKFvH9yuRyVKlVCx44d4eTsCpmRGRq2/hI7j53HnC1HUSawE0zKVke5\n8p+hZ8+eMDKzgMxYCUNbdxg6eKNMnY6wbT4aLr2XwGf8e3p05z7LoazUCAaWRTOR6uu3oaEhNm7U\nWO9u3ryJqVOnYujQoVi/fj0HR46Ojti5c6cooK8kTSaToVmzZhwUVqxYkQMXBmiYK8Tb21tUOI8p\nsn79+mHx4sU65zYyMsKiRYsAAD/99BOI3tfVmT59umi+MdDDnjuzSi1cuJB/h1kjgoKC9FpDhKDE\n3Nxckl24JO9IYWEhf7fLli2LyMhISatkt27dOL27tjx79owDr7Vr16KgoAApKSmSrqXmzZtzCyIj\nNqtUqRJmz57NrWwymeyDit/pE+aaESp4YW0fYWDqp5K0tDQ+x4Qu5CtXrvA5xzaUFhYW3J3GMvMM\nDQ0/yDLz7NkzXL58uUTs0/9r8o8BIoWFhXwx+BQPmgVs2tjYiNLMGBMqAxA5OTn8pVq4cCFyc3NF\ntQ46deqEbQm7UKXnVI3S+GoPwuPOIbDDIJBMjqSkJH7unLwCODg66SgMS0tLvmiywMYPlYyMDKxd\nuxazZ8/Gli1bsHLlSkybNg0JCQnIz8/H/fv3cfbs2SLH9GMAka1bt+pYfQwMDHDgwAH88ccfkgty\nxYoV8fz5c+4C8PHxwffff49NmzYVafnw9PTkrKHaAY8GBgaYP38+8vPzuVIICAjAnDlzuNnfxMSE\nuwALCgpE2TNFNRMTE0yKmob0rLd8ZzV3/kKsOXkbwzdfRIXIvXoDRT3G/gCf8Xukg0hHbYNTj4Vo\nNX0z1p5MhVO59zvroijOpUCJMM1RLpfzgFqhJCYmlvic2q1WrVq8DlBWVhZX7pGRkZKBns2bN+du\nKmGWTHZ2Nt98CLNtKlWqhB07dmDjxo3cutW+fXs+X1hA5PPnz/mu+NChQ3j9+jV3RRDppt7u2rWL\nz89WrVqhbNmykllfQlbdD3lHfv31V1H2D2t169ZF7969+XxlcRtSIkzVFa4btWrVwrJlyzBv3jwk\nJyfjwoULiI2NRadOneDt7a0zVxQKhaR158/IqVOneL8iIiKwYsUKHgsTGBhY6vPl5OToBWX6JDMz\nk9erEWagsc0BK/jZqVMnyTn8zTfflOp6L1++RNeuXfl8MTIyQr9+/Xj9nH/lHwBEmPuDFf7x8fH5\nUzEKarUa+/fvR9++fdGlSxesWrUKr1+/xu7du0GkCbgSSnx8PIg0/nImK1eulJzArq6uPDUzOzsb\ntn41YNM0ApWn7tNYSCI2ouKYeNSZdRjlJu9D2YlJcB+9A/YdpsI8IBRmNk6Qm4nTJBmF7w8//ICA\ngADY2dmhfPnyWLlyZbFxJHv27JEMrGNNqKSNjY0xePBgyWJPfxaIPH36lC+CXbp0EQW0WVhY6HAA\neHh4cJ9u+fLlERsbq2PWZkpp+vTpXIEIA0L1AQX2N+PS8PPzExUXY5H7CxYsAPDefK3dFAoF5GZW\nMA8IhU3oUDi1nYAqw2PhOfadi27MTriN2MzBRN05RxARfwFOId2hrPQ5TLxrwsjJFzIjU5j61IJ1\n43BYNxqAMnU6wDKoC5T+TTB57T607f6+wBgrlCdVWE67SVkwGjRogJycHJFit7W1xaBBg3R2qosX\nL5a0puizsLC5pJ1NxQIit23bhtTUVEydOhWtW7fW4T7RLq6XmZnJC1Sy3bzUcw0MDMSzZ894zIuT\nkxPatWvHwQ1z2TFZunSpyHpgaWnJ6w4xcMtqsjx58oSb862trfHo0SO9c7w078jbt28xf/58PgYD\nBgzgaxqzuNrY2Oi1VKrVasTGxvL+WltbY8yYMVzxHTt2TMfFLGx+fn6YOXMm7t69W6L+llak5qe7\nu3upslASExO59czQ0BBdunQpVQApc3fVrl0bu3fvxrp16zgwZe92fn4+FixYAD8/PyiVStSqVQub\nNm0q1b2qVCpemFOhUKBChQr83QsLC/so8XT/BPl/D0R8fHxEuflCv3VRsn37dgQGBkKpVMLHxwez\nZs1CTk6OqB4Ca76+vjhy5AhXjAxFCyujTpo0SXT+rVu38mwGhoS3b98u+g4z/f985hfEJP0C+7aT\nYN8+Cl5dpiBw8Hw4hg6B9ReD4T5yq3gXPDwe9u0iUaZOR1gGdUFAvS+KXFD279/PQcmFCxewZMkS\nzJkzhyv/2rVri3Z3jo6OfFGXy+WoUqUKf3m6d++uM5Z/FogsXboURBpTMSCOESlpCwoKwsKFCxEa\nGoqmTZti2bJlfOG9c+eOaI6wps2tMWbMGJ6Rw6whzC8/cuRIeHp68syGHj164O7du+8VutwAZcoH\nwSqoE2ybj4Zz/5XwGJ/I015dB62Fc79o2IQOhWVwV1g3GgDbsBEInRiLIzc080kfgBUqRSGQeP78\nOQ+mZH0ODAwUgYHSuIxWr14NlUolmV5rYmKi479/+PAhj91h742NjQ26d++uk87K+hEaGsoX3xcv\nXvBrsfoqTPLz85GUlITY2FgkJydzYMjOK4ydYdatQYMGYe7cuWjUqBFCQ0MRExPDgfPNmzd1wGpw\ncLAkeHj9+jUOHDiAgwcPilJKWRFKExMTDBgwAOHh4RxgMeWlT0r6jqjVahFvB2utWrXi98LmQUnc\nA7m5uSJld/36dVFxQuE1OnXqxEHY/v37iz33n5HLly9j3Lhx6NevH2JiYkqV8cjIE7XBp6urq2T1\nbinZvXu3pKutYcOGH7Wy7v79+0GkAcC3b98GoClyyp4hK4b5vy7/74GIcJGeOnUqUlNTi00dlfIt\nE71PtTQ3N8fMmTMRGxvLwULbtm15iqCTkxOGDBnCka6xsTGuXLmCs2fP8snGpKCggC8sYWFhPH6F\nTVBzc3Pcu3ePV1mVbHIDGLlUgFVwVwT2mwb7dpFwHbzuvdl+3G7Yt4uEY90O6D3sKzi7uuuco2LF\niqICV8J7njp1Kog0hdmESogpkV9++QUXLlzgwCU1NVV0j38WiLBsA2G56jNnzuhkoNjb20tmsbAF\nVRsMCkWtVuPEiRNFEnt5enrizZs3OiZ3mbESJmWrw9S7Jqwa9EaZwE6wqtEcvaathG3zUfAYsZnH\n/XhOSILbsO9h32EqrBr2gYlHFSgMNBaZ8PBwnDlzBsuWLRO5ob744gvJNFIpUMwUsbe3Ny5duoS4\nuLgiWVVL01JTUzFnzhzRsaZNm3KGTm9vb513ixUMGzVqFN+Bjxw5sshxrlWrFoYPH85dEEFBQZI7\nwz/++ANLly7FhAkTsG7dOvTs2VPvOV1dXZGWllbkPFOr1UhOTsaWLVt0gE9JpLCwkMeVCFufPn2K\ntT6uXr0ajRo1gr+/P1q0aIHExETJ77FibAYGBlxRsuf71VdfISUlBUSaDdGHpPYzXg8WWFuxYkVs\n2bKFv1/Tpk0DkSYG579RVCoVpxOIjIzE27dv8eDBA57qzlLai5Nz587hp/9j77rDorje7tldehNE\nRUUpRhRFhdh7LLF3MSr2gj3G2Hvv0diN+sMWu8bYsSvGFhU1lthbNLEjigJK2/P9sbnXmS2ASUzQ\nj/d57gM7Oztz596Zec99y3n37uW4ceNYpUoV1q5dm2FhYf94fKFY2AwePFi1XcyDiGf6/y4fPBA5\nfvw458+fr4raz5cvH9euXWv2gqOjo+Uq5ttvv2VUVBR37typUsBK8/H9+/dpZWVFjUbDbdu2mXA2\nODs7q3LhAQOx1NWrV+UxfvvtN7mSzp49u+oYw4cPlzwM2bNnZ2hoqAkjoiU/v3dACToVq8GstXsz\nT6+VakXYZDizVGzF3NXbM2tgdWps1VkwSvO7yNUPCwtTpfoJYCbGUnxnbJ5MC4j88ssv7NWrFxs1\nasRBgwbxxo0bPHLkCEeNGsWxY8dK5efv7y+tGFFRUSbxG5a4HMT/uXLlUp33woUL7NmzJ2vWrMmu\nXbvyzJkzciVSqVIlCTiGDx9OjUZD6xy+9K7Rns4lGtAxoCqzlGvBrDW606v/pregb6A6TsNr4Fbm\nazeFbtW70v6TUqpxVgKaoKAglbJNqwKuAFiW3EjGTVgFXF1dOXXqVLOuqrSaudTjw4cPMyEhQT4f\n/v7+7Nq169tq1H8qRq1Wy/r165t1+eTJk4f79u0zm4IbGBgouSuUsmnTJpP5z5MnD7dt28aQkBB6\neHjQxsaGrq6uDA0NNXuM9yXnz5/npEmTOHHixHSVYBDlBYzbyJEjTfYV2SMLFixQgRLxHhAA7+uv\nv/5LfReWwWnTphEwWAD0er0EhSK+JCQk5C8d/33LjRs3CBgyz5TgTwQmp5f6/Z/O9LMkwn3YqlUr\n1XYRb/a///3vvffhQ5APHohcuHBBVU5dWVdi48aNJhcs0tsqV66s2q70W4obNDk5mQkJCSZxFKVL\nl+aIESO4cuVKFT13kSJFpLLMlSuXirjo5MmTqkwNBwcHDh06VJJZ2djYqHycovaBWBWZe8Ebp3bm\nLFWHzqUaM1vDQczTdZF0DQj3gEerKczTYSazB49irnYzmLPtDLrX60e/qs1ok7sgy7bqxxyffk6b\n3P6Ezor2zq7U2jpy16Gf+fOtKAYEGSwqzZs357hx4/jrr7+SNDzUp06d4i+//MJt27Zz48aN3Lhx\nIy9fvizN2cYK1nibsBC4ubmxcePGqRKQiabRaGSpdPHCFrJ69WpTy4ZGI8ds9dr1bDNoCrOUb8mc\ndXoxR4uJFoNEszUcRDufT2nrWYhaW0dq7V1okzM/rbLmobWzuwokWcoeEW4nIbNnzyZgcP1otVpq\ntdp0UXJrNBrVOdzd3aU7AngLGnfs2GHCBaJsSiVvbj40Gg2nT59OvV5v1jJjZ2cny8ZPmDDB4nna\ntWsnLRXh4eEEDHwv33zzDXfv3m3Wevn7779L8F2rVi2OHTtWjo0yZVa0Pn36pMvX/vvvv7NPnz70\n9/dnQEAAhw4dqkr5fhfR6/Uy4yQ1UWaxtG/fnpGRkZwyZYq8N0W2nRARp3Dnzh3q9XoTLhYxJnFx\ncX+p38ISMmfOHJmSvGrVKglChVXrnw5S/afk9u3bBAyAW2m92Lp1K4G0S0sI+beAyO3bt+UzO2rU\nKB49elSS8dnY2MjA7f/v8sEDEfGSbN68OePj45mcnCxJkQICAkxeFMK/WK1aNdV2pUn6s88+k6BB\nuUr09fWVLxVfX1/evn1b1kM4dOiQHFBBlmTsN9br9bxw4QKPHDki2TNF7YScOXPy3Llzct+dO3dK\n0GPOl6kEXKL5+fmpGE81Vra0c3ajbd6idK/Thx6tpvLzidtYqO8K5mg+jjmaj2Oe3qstZ2oogIyS\nhTN31zB69vyeOZqPY5mB37PyuG306f3WIpO722LmbDeT2ZuOoGPRGoTGvKLr0qWLfPFaakJJKgmf\nRFu5ciUfPnxI6KxplcWDQZ83YdjhW5y/91c65SlIK/c8DO4+mH0WbGOlft8xe9ORzN1pPj1aTjSJ\nu8ndZRGzVGhFnaMbtfYutM7mRZ2jG3Pm9iTw1uKg1WotsnSmBh6srKz4008/kTRY2cQLX3Bo1KhR\nQ4JkS4DBUsufP78MvhPgOzIykseOHVNZ+sqUKcPmzZurOGICAwN55coVnjhxgmPGjJHuxsDAQD57\n9ozbt2+X+1pbWzM8PFzWcfH29par0tOnT7N3795s2bIlBw8eTMA0oHLfvn0ELBcmTElJ4YoVKyQz\nbq5cueSYxcfHS7Dn7OzMAQMGsGvXrvL5TIvX4datWzLA2fg5atiwIVu0aMHVq1enmYGRlJTE8ePH\ny/EYfgUAACAASURBVABqDw8PjhkzxuLvBE1/2bJlVYpPpOuPGzdOtb+oaTR79my5benSpfJeOHDg\nwN8KcBTMuG5ubiakgALgFihQIMOWo9Dr9dLa1759e96+fZtHjhyRz9PkyZPTdZx/C4iQb60ixi2j\ngr3/Qj54ICJS9MTqnDSwn4qVk3F9BuUKZfHixUxKSuLx48flS8rSijZHjhxMTEzk48ePJUgRSqRS\npUqqc6xYsYIA2KRJE4sDf+vWLbMpqblz52bPnj3Zrl07AgZypbCwMNatW9dsFVUPDw+VUlRaAcT/\nSsvJ9u3beezYMQJ/VmXVaGmfryTtPylNK9dctM0TYHBLlG9J10pt6VL2CzqXbEj7fCXpUrops9Xs\nwVzBw5m98RDmbPstPbsvoWfrKczeeBhdK7VhloqtmL3JcOZoMYGePb83cFp0nMs2U9ex4dhVdKve\nhVkqtqJTUB1WC25HjY09s7jnkGMslKSYh3nz5imuT0M770A6Fv2cTp/Wo39wP3q2nqxynVhqQWP3\n0LvbQuZoPo45235L97p9aZevpIFV1N6FVlZWLFWqlCzqJwCScKMJhVerVi0575Z4Jdzc3Ni3b1+Z\nEaJsPj4+0vpTsGBBaSXw8/Pj1q1b3zneQ9y3ItU0ICCAV69e5ZEjR6QfOnv27GZjNkJCQkyU2rNn\nz+T9Ym9vrwItIgYnOTlZWlvMVQbW6/USuPXv35+xsbG8ffu2rMZqLpZHr9fL/hq31q1bc8CAAfJ+\nVro0Fi1aRMAAVFMTkYpZqVIlHjt2jNu3bzcL8kTmkCVRxqko3WYtWrSQ+yQlJXHt2rVs1aqVnJc6\ndeqoFN+wYcMImMYOCNI7rVbLL774gp07d5bvstRSdtMrSUlJZu9L8b4IDg5OM9bmv5aDBw+adSMW\nKVLEpDiiJfk3gQhpqJLdrFkzlixZkiEhITx69Oi/du4PQT54ICI4HPbv3y8v6tGjR4b0Sa3WLLI3\nVxIbMETRm7vBhSIUWS/i5ff5559Lhb5o0SLJtSEsMh06dLA48GLlExAQYDb2QTTj7zw9PdOtpIQS\nVYIrR0fHNLklcufOzQ0bNjA8PJzNmzdn+fLl06wuK7739vZmaGioHDMH/0rM1XGuoVT84K3M+/UG\ns5aW3KELmafzPNaYtI0erab+WVK+A2ftPM9u3+3mJ6GzTWqkeA/ewVydv6Nb9a5sMHA2d//6kGNn\nL6ZjHn86FKxAh0KV6V6yLid+O1flpw8KCmJwcLAqYLRNmzbygVAq33r16pnwm4h7Qrld+NjFb1ML\nrNRqtWzUqBHv37/PxMREsyXKjcfVeG5EvIUl4KzcvnLlSv7xxx8cOXIka9asyRYtWnDbtm1mV9aJ\niYlcunSpiZuoadOmKjeKsJyI0vDGsnXrVhMmUsCQpmku20PwS9jb28tYJHNuGEBt/RDsqZ6enhaf\nteTkZDlXIpakd+/e8nhZsmTh3LlzJfhUBk0rRXAJ2dvbc9euXdTr9dy7d6+c89OnTzM+Pp5Vq1Y1\nOx9iBawsSx8eHq46h16v56hRo0wsbi1btvzH6k4lJydz3bp1bNKkCWvWrMkxY8YwMjJSxY+U0SUy\nMpJNmzZltmzZ6OPjw8GDB78Tf9S/DUQyJXX54IGISOvLnz8/t27dyoiICGmmbtCggdmL1uv1DAsL\nkyAmW7ZsHDhwoFyNVKhQgQcOHOD48eMJvF35CmAhzmm8yrSysmLLli3lSmvv3r1mz3/9+nUChkBL\nYbpNTdGXKFGCbdu2lYGWBQoUUIEJnU7HVq1aqUytxoDK1tbW4mq7SJEijIyMZHh4uDSLT5kyhUeO\nHGH16tVVL0UXFxeGh4czOjo6Tbp01djYKZSKVkcrt9yGImxVO7Lu2HXM3mQ4/UJnsc6Mg8zZZjo9\nuy2WRQO9Bmw2WDHq9aNjQFXqXHJQ55SVGht7FipUiJs3b2ZKSgo3bdpkMh9KBS7+FxkLSupre3t7\nuUqxZEpVNmWV2axZs8pKvJZWm0FBQVIhu7i4qMj4zKVrKude+blAgQK8evWqWeuYsbuuUKFC3LJl\nS5ovASEHDhwwAbpijkuWLCljnoTb0NbWNtWKsLt371ZllrVu3dpiwbQ+ffoQUKeQGt+/4v88efJI\nUCSCLpWU5saSkJBAwAAAX716Rb1er0qFdnNzI0lZw8fHx8fscQQxYWhoqGq7iOeaOHGiXIR4eHhw\n1qxZnD9/vgpQ+fj4yOepXLlyFjP87ty5wzlz5nD69Okql22m/DOSCUQylnzwQOTFixdmq4/myJEj\nXQQ5SUlJcmUoGCMFw19CQoJqtVq3bl3OnTs3Xebzrl27WvTliuqj/v7+Mp5EFLQD1HwRovn7+3Pa\ntGm0traWtMs//vijCQ25RqPh1KlT+fTpU86fP5+9e/c2ywuhbPb29jKPXwR9FShQwGzGhr29PR88\neGA2jVE0rVZrNkNCmakj+qr8u3LlShNrldbehRorW5M+iHESCjlbtmxSiU6cOFHGlBhfg7u7O3ft\n2sWUlBSmpKSYWBSUMSvu7u7ye5FZJOI9lL+pVKmStI5ZynKpWLGiVLYAOHfuXHk/iEDTEiVK0M/P\nz2LhPKGMU0uNFeC6dOnSDAoKYtGiRdm1a1eToEhjuXXrljy+g4MD/fz8VJ/FuCuL3g0cODDN54s0\nWFlSS6m/c+eOBFwCkKcVF1WjRg0V6Nu0aZPqmHq9nvHx8fIZFPdD7969+erVK9VxBRHckydPCBis\nWuZEFIQU1jMhgoBvypQpEsiLQF5SXUcKMMTatGvX7oOyQJCGMT127Bhnz57NVatWZZhq539FMoFI\nxpIPHoiQBqroKVOmyJdv//7936lUtZCYmBiZIfPNN98wOjo6XSyVgME0LF6iHh4eqQaUCcuLslWt\nWlXGJ6TWxItOkEslJyczPDycw4cP55QpU0x4TEhDKqxxUTJjMLV8+XKS5NGjR1Xfd+vWjdHR0SrA\nI/L402ppuXOULV++fNKSBRjAjDlAZq4Zu06eP3/OqKgosxV6RatTp44MDvX09OSAAQNULhnlWNet\nW5d6vZ6jR49+pyBVwGCZMgdO2rdvzz/++IOxsbFpjqdxv4xbWkATMIAJS35pvV5vlvDNyclJujiV\nPDeCs+evVoCOjY3l0aNHeebMGS5ZssRkfKytrWVKu7IdPHjQJK5Kp9Nx4sSJ8tivX7/m0KFDJSGe\nl5cXp0+fzj179si5c3Z2VrHsnj17Vs4vYGBn9vf3p52dHQMCArhgwQLq9XppybSysuLixYv56NEj\nLlu2TN5/V65cke8PZTZEQkKCPN+FCxfMFo7MSKLX63ngwAF27dqVISEhnDdvHu/cuaN6PgGDZe9d\nLG4ZSTKBSMaSjwKICNHr9Vy4cKEMlPPw8JCkN+kVUQ7euHl4eDB37twmyrVevXpy5ahMtRO1SIzl\n+vXrKhBgzsdvnNUglIJyn3ehQ46Pj1fxSuTNm5cbNmxQpXc2atSI0dHRskS76IcYO2O3R3qb8fW5\nu7tz3bp1kpG2UKFCJkDC2dmZly9fNhubYa5ZWVlx48aN8lwLFy7krVu3zGYWif2FEgMMK9krV67I\nlGGdTqc6d8WKFeVY/vbbb2nWltFoNFLpWYrhEH0QHDWpHS+1zCKlu0d5XAD86quv+PPPP0ulbi6L\njHybVgsYVvtbtmyRFiBxrypdQeXLl0+zCqxSEhMT+euvv/L27ducPHmy2dTsZs2aqVwYyjERQG3B\nggUyOPfrr7/mwoULVcyoSgp+5fyK469Zs8Ysv4qwHKU2B7179yZp2Y321VdfkXxLHT5mzBjZL/FO\nyZcvX7rH7L8SvV5vtmyBmBt3d3eGhoZKl5uNjc07vYsyimQCkYwl7x2IAMgLIALAFQCXAPT5c/sY\nAPcBnPuz1VX8ZiiAmwCuAahlfExLQGTIkCFmXxK1a9dOk21VKRs3bmSZMmVobW1NOzs72tvbW1zd\n79ixg8OHDycAVf0GSxUrRfn3Jk2ayGJcaSk14TMXyjEoKCjd15KUlCRN/8ZN6YvXarXSJSCUjqOj\no6yNk5ycbBKvoPxtp06dVGOk0Wg4cOBAmTXg7OzM/fv3MyEhgS9evJAxGwcOHOCjR4+4du1aNmnS\nhAA4aNAgrlu3zuy5lCDOxcVFBomOHz9eVblVZGik1Tp27Mjk5GQZXFq5cmXu2bOHz549U/FnrF27\nlsnJyTImQTQlSFDS4qcnzsRcU16Tsjk6OprEToh50mg0EnwrmyBRevPmjQRlly5dMrlHWrVqJX8z\ndOhQPn/+nPv27TNxAeXNm1elkAQIiImJ4ffff8/p06er0kv1ej3nz59vNm22aNGi8nq0Wi0vXLgg\nM0mMmxhXcQ3Fixc3C6hEGQY3NzcePnyY9+/fV92zIpaqf//+ZjNmBECys7PjunXrGBMTw5UrV8rn\n7tq1a9Tr9Vy6dClLlChBV1dXfvrppwwLC5P92bFjhzxeYGCgis3YuPpvRhRBb2Bvb8+RI0fyf//7\nnwTeWq2W9+7dI2mYW5HGrawY/qFIJhDJWPJvAJFcAIr/+b8zgOsACsMARAaY2b8wgPMAbAH4ArgF\nQEcLQOTx48dMSkri119/LR94a2trduzYkTt27JBxCbt375YX/eDBAx48eDBVv7mSKMu4KQP67O3t\nJUueaA4ODhYrK3722Weq/ly5coWTJ09WKVih0IODg82ulo394anJ//73P/lyTo8irFKlCkeMGCHN\n/Z9//jnv37/PX3/91cS9o2zmAgyNsx7y58/PDh06SOVdrFgxpqSk8PXr1xw8eLBUDnZ2dnKchKJN\nq986nU4VQGrcsmfPbpZGvXHjxvz6669NVuk6nc6kMJiyH0I5Xr9+XRZEVF5vamRif6UdOHCAKSkp\njIyMlHOTlutLackRQOXUqVMm94gSqJqLgQEMqcb9+vXj+fPnZVbI4MGDuXXrVpOxK1WqFB89eiQL\nUQKGAFMxfnZ2drxx44asXA0YAsHv37+vAghlypQxucYiRYpYLG4m2GqHDBnCpKQkaf0Q1iljt1rF\nihVVQCUkJIQA2KVLF9VxRWG7GTNmpOuZW7Jkiep5c3Z2Zt++fT8IxScsSkoeE6Ur+cGDB3K7cG3W\nr1//v+jq35JMIJKxJC0gYoW/KSQfAnj45/+vNBrNFQCeqfykEYB1JBMA3NFoNDcBlAbws7mdc+XK\nBQ8PDzx8+BAAYGVlhaSkJCxbtgyRkZFo1KgRli5dimXLlsHBwQGTJ0/G3r17kZKSAgAoWrQoxowZ\nAy8vL3nMN2/eoHfv3gCAunXrYufOnXBxcUFycjLi4+Px8OFDBAUF4dy5c3j9+jV27dql6lPTpk1x\n9epVsxdnbW0NANi2bRvc3d0BAGXKlIFWq5X7ODk5ISYmBocOHUL58uVx7Ngx6HQ6pKSkIFu2bMiV\nKxdOnz6dyhAC9+/fx5QpU3DixAkAQFxcHJydnfHq1SvVflZWVkhOToaDgwPCwsIwdOhQHDp0SH6/\nf/9+eHqaTpe9vT1ev34tP4vjuru7IzY2FgkJCYiPj4efnx+aN2+OpUuX4ubNm7h58yYAwM/PDxMm\nTMCZM2fQr18/HD16VB7rzZs3+Omnn+RnGgCqiWg0Guh0OiQnJyMlJQVXrlyxOB5Pnz7F06dPTbZv\n2bLF7P4pKSm4ceOG/Ozh4YHHjx/Lzw4ODnj58iXmzJmD4sWLAwDi4+Pl93fv3rXYl7TE0dER8fHx\nqus+efIknJ2dodFo0KNHD0ycOFHewwBgY2ODKlWqwNnZGT/++CMAw1xERkYiPDwc165dg4uLCxIS\nEuS9k5SUhOnTpyMiIkIehySSk5NN+nTt2jVcu3YNCxcuRNeuXREREYEtW7ZgxowZSEpKQmBgIPz8\n/BAREYHIyEjUr18f9+7dAwAMHjwYZcuWRZMmTWBtbY03b95gyJAhqvvq0KFDePDgAYYMGYLRo0fL\nawaArFmzolGjRihevDhKly5tcS6fPHkCwDD2M2bMwIULF5ArVy54eXnh5MmT6NatGxYuXAiS6NCh\nA3r16gUAWLp0KRYsWCDv++joaNXz9eLFC3nctJ47AChWrBi2bduG8+fPQ6/Xo1ixYnB0dASAdP3+\nv5Q7d+4AMDzfoq8ajUZ+v2PHDnz66acAgHXr1gEA7OzsMvx1WZIPtd8fm/j5+aX6vTbVb99RNBqN\nD4BPAZz8c9OXGo3mgkajWarRaNz+3OYJ4HfFz/5AKsBFo9FIEAIAJUuWxIYNG5A9e3b8+uuvUiFo\nNBqMGTNGgoaiRYvC2dkZFy9eRM+ePREXFyePcebMGbx69QoFCxZElSpVABhehuXLlwcA6PV6nDt3\nzqQvWq0WTZs2lS84c9KgQQMAQFhYGObMmYNNmzahe/fuiI+PR2BgIAoVKoSYmBgAwLNnz3Ds2DEA\nBsWo1WoxcOBAWFmljg9jY2PRo0cPnDhxQgKcxMREExACAMnJybC2tkZ8fDymT5+Oe/fuwdfXF8OG\nDUPVqlXl73U6HWxsbAAAvr6+WL58ucnNY2NjA41Gg4SEBAAG0PXgwQOcO3cO8+fPx6xZszB06FDM\nnDkTkydPhqurK86dO4ejR4/C2dkZixcvTnXslKLT6SwqTfG9sTg5Oak+Z82aFRMmTICHh4dqe6NG\njVCvXj3VtqSkJNXnly9fAgDmzZuH0NDQVPvq7OxsMmcBAQHYt2+f2bm0sbExAV/Dhg1DmzZtcPPm\nTQlya9WqBW9vbwBAtmzZkDdvXjx69Ej+ZufOnahXrx7Gjh0LAOjQoQPs7OwAGJR2586dsWnTJpBU\nKRtzUqlSJVSqVAnx8fFYsWIFAAP4TEpKwueff46wsDAMHjwYq1evhqOjI06fPo0nT57A3d0dwcHB\ncHJygkajgV6vBwCcP38eDRo0kP15+PAhRo4ciRkzZgAAvLy80LVrV0ydOhXh4eHo2bMnypYtqwLs\nxlK5cmUAwObNm7Fjxw4Ahnv11KlT0Ol0qF27thzXrFmzyt81btwYAPD8+XMAQHh4OI4cOYLk5GRE\nRERg7969ACCf//SInZ0dypQpg3LlykkQ8iFIgQIFABgAupirZ8+eye/Hjh0rFywbN26ERqOR45cp\nmfLexJyZ5K80AE4AzgBo+udnDwA6GMDORABL/9w+H0Abxe+WAAhWHktpxpk+fbqJuXzevHkybkPE\nPSxbtoyAwZUiCnbFxMTIYFAl3a5IYS1btqzZIDZPT0+Vmbdw4cKcPXt2qoW3fvvtN06bNo3Dhw+X\nsRDKljdvXt64cYMvXrzggAEDmDNnTup0Otrb2zNLliysW7eupJFPS4SvvWjRotI8rgzcFGy0Io5D\nZJdotVrqdDru3bvXJC3YuDk4OHD58uVmYxPMtZw5c/LChQts27at9Lk7OjrKWI5+/frJ/lsqkGbc\nhKlfq9XKeAlnZ2d5fWm19evXk6TMsEirlSlTRqZYW8qeEeMh+mBcD0i0mjVrSuru9DSlW0NsW7Zs\nGWvUqGHiStHpdKrskpw5c3LWrFkyjkFZ/C+9zc3NjQcOHFC5HIRbw7gIogh0Fc+biOVSBpIWKFCA\n8+bNMxu4WrFixXSVuDcWvV4vGYmN29ixY6nX66WrRxmvISphf/LJJ9INY9yMuUPeVT4UV8DFixfl\nO7NgwYKsVq2avNeNs7N0Ot0HS1P+oczH/xf5V7JmAFgD2AOgn4XvfQD8yreBqkMV3+0BUE65v7LT\na9askQ+GuXokgCEOYNKkSfJhatq0KcPDw6nX62VEe+fOneWgREVFqQiULDGROjs788SJE2kO8syZ\nM00Ul7+/Pzt16sTWrVtz7ty5vHfvHn///Xc+evSIkydPZuPGjdmhQwfu27cv3bUlLl26JMthC+WV\nJUsWiwyV06ZN46lTp1SZG+7u7jJDJ0uWLGkWnzOXTin+79mzJ2/cuCFTP1NLM+3WrZvqWkQg7/jx\n4zly5Ei2bduWo0aNkuRRLi4ukmq9V69eEog0aNBA1u8xji8Q6ajiswjEVdbncXNzo7e3twywVM7b\nqVOnmJycbLYInDiu+CvATceOHU1igFJrGo2GAQEB1Gg01Ol0qlgZ5T6dO3c2C4YKFizIu3fvMjIy\nkrt37+b169dVdVD0er0MIAYMKcrffvutyT0iwI2lzKUSJUrILDElg/Dz588lWBGBmtWrV+f+/fs5\nY8YMs32uU6cOt27dysWLF/PkyZN/q5ZKcnIy586dq4rvadiwIffs2aMqUJk7d27OmDGDU6dOlXM1\nfvx4JiUlcfLkyRII+/j4cPr06X85VVnIh6T4duzYYRKE3bNnT8bFxXH9+vUcOHAgp0yZ8pcoEjKK\nfEjz8f9B/o1gVQ2AFQBmGW3Ppfi/LwxxIQAQAHWw6m2kEqwaHR0tX/4VKlTglClTVKvpHj16cMOG\nDWZfgIMGDWKPHj0IgAMGDFANjPKlZS7C3s3NjSdPnkxzgAV1NWAozDdkyBCp5Bo2bMg7d+6wYcOG\nFgPqxDWk9XKOioqSx01P6XidTqcizmrVqlWqVPOiWQI1/v7+vHr1qur8fn5+JA0F0dI6ro2NDZct\nW8bff/+dc+bMkRUrFyxYwB9//JHHjh0zIUQTTaksK1euLIMvU7PW6HQ6GXgnghzF9tGjR8t6QkoA\ncfbsWZJvV9DG94NY8SutDY0aNbKYRmypiXtA/E6r1XL8+PHyumrVqiWJ9r766itev36dmzdvlgp1\n/fr1Fl+0ly5dIvA248bFxYUxMTEqyyLwlrJeeT8KXhWdTsf79+/z8uXL8tlr0KABR4wYIQnPypUr\nx4sXL5oFn76+vqxRowYbN27M1atXqwrj/ZMimFCVTaPRqICnaDVr1jRJ8/+74EMpH5riS0xM5IED\nB7hlyxZVgOrHIh/afHzs8m8AkYp/PuwXoEjVBbASwMU/t2+DGpgMhyFb5hqAOsbHVHZ6woQJFrMq\nunXrxvj4eKnABKAICAiQL1Dxol2/fr1K2YuIcKHkbG1t2aRJE6kMjMu6WxKxeh48eDAvXLjAChUq\nqPqo5H9QrtZbtWrFMWPGSEU4btw4fvbZZ7S2tmaWLFno7+/PmjVrctSoUbx//z6nTp1KwOA+EMpA\nq9VKha7MSDEHdgICAlTbs2bNapbhc8yYMSaslxqNhlu2bJGMlQKIeHt7kzS4AsS+RYoUYVRUFH//\n/XfJRpoaWDC3PWvWrCZzniVLFlV/dTqdClh5eHiY8HE4OjqyRo0aZunSlU0o/WrVqkmgJL4rV66c\n5I4QY2wJrKXWqlWrxrCwMBPLiZWVlSSbE4BJ1GIpUKCA6p6dOXMmAUMBNksvWlHwMDAwUFoQS5Uq\npWJ9Nae8lZ/79Okjj7dixQqT+6RAgQK8c+cOSfLevXscMGAAS5UqxSpVqvC7775TlW9/33L48GG2\nadOGlStXZpcuXXj27FkmJCRwzZo1bNeuHTt27MjNmzf/o6DDnGQqvowlmfORseSDJzQz9+LMnj07\nlyxZQr1eL+M9goKCuGfPnlTLqpcoUULGj4h6MspmbKZu165dmoWoBPBYt26dBEROTk6ql7enp6dU\nEEKJubq6Mi4uLl18FK6urhIgiZVtWmRgefPm5Zw5c/jDDz+omD0tWR1E27Jli0xXVsYLtGrViq9f\nv1a5x0JCQnjr1i0V+AoMDOSECRN48eJFXrx4UW7v0KEDS5YsSVdXV5UrLGvWrCr3j6DXjo2NTdNt\nZK7lyJGDs2bNYq1atVTby5Qpw7FjxzJfvnwSSNnZ2TE0NJQXLlywGEeydetWPn782MSF4uPjI9NB\n7ezsJHV99erVzcaNtGvXjqQhtVxp0frss8/4ww8/cMSIEXJOZ8+eLe9XpYiYkyZNmlh80b548ULe\nY4sXLzZLlpYjRw7WqlWLtWrVUlG629nZsX///iYWjAcPHnDGjBkcOnQof/jhB5UrKFMMkqn4MpZk\nzkfGko8CiGg0GgYHB7NDhw4SaIwYMYLk25dz2bJlGRUVxVu3bnHAgAFytazRaFi5cmWpgHPnzs3d\nu3erXszmVrgCSFSoUIFDhgzh9u3b5arq9evXvHz5Mh89eiTrUAh/eZUqVXj27FnVat/BwUEW3AoK\nCpJ8Fxs3bpSrXACylLmNjY3sr/CFi1W9cCnpdDq6urqmSkmePXt2Pnv2jJs3b5bbBM21RqNho0aN\npDneGIzZ29tLBlElXfa7gAIl70dUVBS3bNli1rqlPG6pUqXkzStiRLRaLYcNG8YWLVpYDA4FDHwH\nytX41atXuX37dp4/f171ULx584Z3795VlYO/fv06v/jiC3n9AgRlz56dbdu2lcXhHB0duWXLFiYn\nJ3P16tUEDHwwe/fuJWCwFohKwEogJ6wMer1eggNz1O6DBw9WlSJYunQpU1JSeOvWLUk8NW/evFRf\ntIMHD5bHK1KkiLy/lbFCwcHBHDlypJz/EiVKZHhq8owsmYovY0nmfGQs+SiAiJJoSLAruru7c/Xq\n1aqXvbW1NYcPHy6tDwA4adIkkoYVtsgCEMF8oaGhZuuALF68mF26dDHZXqpUKQ4dOlR1znLlyqmU\na/Xq1aX5Xbl99+7dUsmZAw82NjaS/XP06NGSebRKlSqplpFPq1WtWpWHDh2Sn2vUqCGLe6WnpeaG\n0Gg0dHBwSLN/+fLl45UrV0wUrznrla2tLUkyJSVFxoCI6qmPHz+W+7Vs2ZL79+/ngAEDVH1NK9ZG\nr9czISHB4n4pKSlMSkri/fv3ZcFC0fLmzauKGxLFDfPkycOXL19KIjwRf6FkHD127Bj1er2sxpwr\nVy7evn2bI0aMYN26ddmhQwdGRETIY4vga0BNJufv789Xr16l+qJNTk7mkCFDVHMXFBTE06dPc+HC\nhSaAsnDhwqlmhGVK2pKp+DKWZM5HxpKPAogIfzRpUCRK6mgAJjEAYruSwpykXKmK/U+fPs03b95I\nlkxx3MWLF6uO161bN5OVuLe3twQWdnZ2abKDpiddVSjqtWvXSirmatWqyayU1GqSGAMHpbukVqRP\nsgAAIABJREFUUqVKEuwAhrTfhg0bSiDg4eFhthqq8XgCBkvMsGHDJPgQNWXepQkgt23bNrMukQYN\nGqgAoqgCu3DhQrnt22+/ZWBgIB0cHFSK+sKFC9y0aZMsdCYkJSWFM2bMkGm3wqLUpUsX7t+/n1On\nTuWECRN44sQJnj17lp07d2aZMmVYpUoV9unThzt27DBxSaSkpEgrRVBQELt06WIx7sXd3V0VRDln\nzhyzD+wff/zB8PBwnjx5kvPnz5f3po2NDdu0acNHjx6RTN+L9sWLFzx69Ch//fVX1Vjcu3eP33zz\nDYcMGcKNGzdmulr+AclUfBlLMucjY8lHAUQWLVpE0lDcTVl4DjDQNcfHx7Nnz54mcRP58uVTBan1\n7NmTwNuU1BkzZvDNmzcyG0LQX9evX18qYJ1Ox6ioKJ49e1Yed9WqVZw0aZJF8OHg4MAvv/wy1eqw\nqTV3d3fpCujduze1Wi2trKzkSjZfvnz09fVNd9E4AZZ8fX1NVsPFixeXWSD+/v4msRBKECKCT0NC\nQrht2zYCb105VlZWPHfuHIODg9OkJhdgKWfOnGaLlCmbt7c3o6OjSVIG7FpqxuctXbo0b9++TfJt\nDaD0NHPzKlyBxnLx4kUTkKrRaOjp6akqsqec2xkzZkhg8PLlSz558oRxcXFs3769arzFvo8ePTLJ\n+Mh80WYsyZyPjCWZ85Gx5KMAIkLhmVO82bJl44ABA0wKb4nP9evX54YNGzhgwAD5kjdOZVQq5wIF\nCqhqzTRr1owkuWfPHrlNkCopy6dbitWws7OTx3dzc5NWjSFDhkgFZalMvL29vTyuiB8x7q+y+fr6\nmtRPsdRsbGzYoEEDadFwdXWlv7+/SYDojz/+KP8XRG3e3t6yZLqy7dy5k4cOHTI5hjnFbm5b1apV\nWadOHZPr8/Ly4qlTp0wqJzs6OppYw5ycnFi3bl1VjM3Vq1dldhFgCKidOXOmKmg2T548KndcYGAg\nIyIiOH78eDlPlgodvnr1imFhYfzqq684adIkyXNifJ3FihXjy5cvSRpiUurXr29SXdfcfRQUFMSo\nqCjVOTNftBlLMucjY0nmfGQs+WiAiLK5u7ubVbhKE33BggXNBgNOnDiREydOTJeyzpYtm2SA/P77\n783uY45HQaPRSDeIjY2NVGSFChVi2bJlCUAVULhz506LReusra3ZvXt3GRj5rk2pCLVarQpkpafN\nmjVLum3E+AYEBEh+FqXiNAcu0kv0NX/+fMbFxUnrgr+/P3v37i3jRFILylW2jh07MjIykk+fPpX3\niAAYwhIjSOqUlgytVqsiz3N1dZXWNEGyNmzYsDQfuGfPnslrDgsLY1JSEk+dOiXPtX79et6/f18C\nZZ1OZxKHo9FoGBISonLnNW/eXHWezBdtxpLM+chYkjkfGUs+CiCirH4rlLpy1QkYmFOFD1682L/7\n7jsOGzaMDRo0YJcuXXj8+HFGR0fL2IiRI0dyyJAhDAkJkSvo+vXrs3HjxvK4NWrUYIcOHcxaY1JT\nwpUqVWK5cuUsKkyxGtdoNPL6ChUqJMuMFy9enPv37+fjx4+p1+vTpGRPq4n+W3KbWFtbmz1HoUKF\nTNw1AjTpdDqVWyu181sKaNVqtdL1JoBA0aJFZdq04HsBDGnQ5sjDBDmZ8fkEH4cYXzHmV69eJUl5\nn4i+ixgiMUbPnj0jSZli3atXrzQfOJGhVLlyZdX2adOmSaAkQGjZsmXZq1cvk2saOXIkSXLVqlWy\nfzqdjk+ePJHHy3zRZizJnI+MJZnzkbHkgwci1atXJ0m5Ghepr4JEyVgBubu7S26E4OBgkwERvCPK\nEuokOWPGDAJv+R4WLlxolvDrrzZz1hllc3Jy4vbt22U6pUajYZkyZbhlyxbpBkkPM6pyHJRWHGVN\nHWOOjb/S8ubNyy1btvDx48fpCqK11EqWLMnJkyfz4cOHHDNmDAGD20qIkrdk/Pjx/PXXX1V9+OOP\nP9iiRQu5zcPDw8TVNXr0aBUAq1evnirbBjDEk1y+fFl+zpIlC5OTk/nw4UMJcI1rrpgTETtTtmxZ\n1XaRBRMaGirvW2P6fNGGDh1K8m0arnA/nTt3Th4v80WbsSRzPjKWZM5HxpIPHog0bdqUJOVqXWRZ\n9OnTR7KaajQaizTbjRo1UnFLCItD6dKlVQMlVr0dO3bkgwcPVPU6lK1IkSJmV+CiBQcHm3WzVKtW\nTWUh0Wq1KrdF7ty5LcZ+jBs3jgBkoTytVsvatWubpbIWzdnZmbVr1zb7nUhjfpdmZ2fHiRMnct26\ndVy+fDmfPHnC169fc+nSpdIF4unpySZNmnDp0qWyloy5Zu46HR0dJTgoVaqUdIsowWCbNm0YFRUl\nuVvMtSZNmvD777+XxQ41Gg0fPnwoi9lZai4uLmzfvr0KsBQpUkRaUQoXLpwuxtCYmBgJOqdMmcKn\nT59y586d0uK2detWVUZTgQIFePjwYRV4cnBw4KBBg+Q4CVefCNolM1+0GU3e93xcu3aNX3/9NatX\nr87WrVvzwIED7+1cH4NkPh8ZSz54ICIUgrFFIb0VVQGwf//+ckBevXolLQsTJkzg48ePuXPnTnm8\nLVu2SBbT3Llzq9w0ANi9e3eSZMeOHc2eS0niJZpQbl5eXpI1MzUXyeLFi/ny5UuOHz+egCEORXBT\nCBDk4eFhwsOh1Wpl39PTjH9vrmKrVqtllSpVuHr1atarV0+13Rx1ep06dXjx4kUOGDDAYjFBZbOx\nsZGAydXVVcbclC1b1mylVRcXF86dO1f2QShqwHLxwsTEROr1eq5YscIkTVkQhynbJ598IgGQRqNh\n/fr1ef/+/XQ9cL/88ovFCq+1a9dmcnKyisdl9OjRvHjxImvUqGH2N+KaOnXqpDrPf/WivX//Ps+d\nO8fY2Nh//dwZWd7nfOzatcvsvS1ceJliKplAJGPJRwFELDVLAZ4AVArHycmJe/fuZa9evdipUyeL\npcQLFSok04OdnZ35+PFjRkREmOwXEhJikpqbK1cui4pw1apVLF68OAGomEzr1KnDPXv28Ntvv5XA\npFOnTty0aRMHDBjAsWPHSjfTsGHD5O9Si8fw8fFJleZe2YwtE8rgTeNzpAacJk6cqPo+rXgR4+Pe\nvHlTkoeNGDHCbACws7OzTGkWAKRv375MTEyUIO2HH37g8OHD2bx5c3bq1ImAwdKSkpIiHwjholq+\nfDmfPn1Kkty+fTsBAygShGXR0dE8ffp0ugFIVFSUyT1ha2tLBwcHfvLJJ5wwYYK0qMTGxpp11dna\n2pqNRapbty5fvXqlOt+//aK9ffu2Ciw5OTlx8ODB762g3Ycm72s+3rx5IwObmzdvzh07dnDUqFHy\neROFGjNFLZlAJGPJRwVEtFotu3fvznXr1rFZs2Yy5VGZdWCcxmupeXl5sWzZsnR2dma2bNlMsjLc\n3d356tUrvnnzJs36LOZa1qxZ2b59e/lZKEvR3NzcVNwQgk/DUpbJoUOHuGHDBrNuoeDgYF67ds2i\nO+ld+m8MYipUqKACdXZ2dmzdurVqvGbOnMm1a9eagBU7OzuLbiDl7zt27MjevXsTAL/55hu+fPlS\nul98fHwkiFM2T09PPn/+nOTbWApfX1+uWLGC69atk7FEoaGhqgdCuPDu3bsnt6WkpMhx/6s050JJ\nZ8mShc2bN5duM1dXV1WQqRBR4M7e3p6enp5s2bIlu3btKu/NsLAwzpo1y+LL9N980cbExEhiNTs7\nOwkIAQPPTaa8v/kIDw8nYMhUU5LSffnllwTU1t5MeSuZQCRjyQcPRETwn2hLly5NteaJpdW4Tqdj\n+fLl2bhxYxkkKGjCxT6NGzdm8+bN5ee2bduSfJu9YKl5enpKhk3R8ubNy4SEBI4YMUJl/hduoSJF\niqgmSihiwBALMnToUFWZ+7x583Ls2LF8+fKlJFdzc3OT19u2bVuGhoaa9C0sLMyE1VUZuAq8DQA2\nbvny5ePTp08lfwgATps2jc+fP1eNdYECBUhSldI7depUmfETFBRk9vjC7eXm5iYZT3fu3EmS0i01\ncOBAvn79mkuWLGH58uVVMSOFCxdmeHg4Y2JizAIef39/mX4tpGrVqgQMga9CBJ1+1qxZGRAQQI1G\nw7x583LcuHFpFj0kyQsXLsi5/eOPP0iSSUlJMtvom2++MfnNkydP5DWL+1P8v379+jTP+W++aAV/\nS2BgoLQiHTx4UBLtPXz48F/pR0aW9zUfIm2/UaNGqu1iToxddplikEwgkrHkgwciiYmJZoHH38lo\nsbW1lSyqDRo0IKBmzlRaFnr16iVTVM21atWq8fLly3z69KmsgyMUdPv27Xnu3DkuX75cxl8sWbJE\nApMtW7aQNJjqBb9IWq106dIyc8Td3Z1z5syxyLHh4OAg91WOobHlonDhwpKYTQl8fvrpJ+r1elll\nVvRfr9erMj7c3Nyo1+uleyV//vyqm1C4SQCwX79+MrZEWK/EeAUEBMgg1R9++IGAgQ8mPj6eR44c\nUV2DcG3odDoePHiQcXFxnD9/PmvVqsXPP/+c3377LWNiYkweCBGsDBisPTVr1kzVldSwYcM069es\nXbtWAiulLFq0iMDbTCxjuXv3Llu1aiXv5RIlSnDbtm2pnkvIv/miFVlJixcvVm0XoC69ff6Y5X3N\nh8iYs7Ozk8Ubnz9/LhcTIvX9YxW9Xs+oqCg+efLkndqVK1d45cqVd/5dZvv7LSoqyuSdmWGBCIDa\nAK4BuAlgiPI7ZaeVloZ3iT0w14KCglScJMDb4NJTp06RJCMiIqQZWtm0Wi2bNm3KU6dO8dChQ3KV\nL9xDGo2GdevWlRkk5nz9tWvXZlJSkqyACxhW7cog0axZs6oCccV5ChcuLPs1e/ZsOS49evTgzz//\nzC5dusiYmUaNGpm9fmVwqfg/rYBSf39/Fa1+/fr1efDgQVXmh6Ojo4qq3dvbW8Y0PHr0SOXaadmy\nJTds2GDCvlq0aFH+9ttv8sZNSEiQYMfHx0dFxObl5cXY2FhpRapSpco7vdzmz5+vitGwsrKSVYaX\nLFnCly9fctWqVXJe0spQEEUFvby8VJk1wr2kTEc2J0lJSSYU7mnJvwlEOnfuTMAQWCskJSVF3uvK\nYn3/X+V9zocAglqtlqVKlZJWVR8fH5PYoY9NoqKi3vnZIA2Lu8yA6v9GXr9+bcIEnSGBCAAdgFsA\n8gGwAXAeQGHxfXqDVcXDmV4g4uTkxPj4eFkEzs7OTlpExo4dyytXrqQZ6KnVajlv3jyVn9zT01OV\nZQGAO3bsYOvWrenn58fSpUtzzpw50syfkpLCsWPHqpTxp59+Ksu0CxdH9uzZZdxAx44dJeFX1apV\nuXPnTrMBpAULFuTz589VVh3RJ3OkZhMnTuS8efPMxpek5gIz19zc3CSIypEjB+vXry+vMSAgINWx\n9fDwUAERkrx8+bIJg66vry8vXbokb24xJ2lZLYzlxYsX/PHHH7lu3TqZyVSnTh2OHDlSBsuK6+/R\no0eqx1Iq5TJlynDOnDmykrJWq5UEav+k/JtAZN++fQQMFrbZs2fzp59+kqnznp6emQGrfL/zERcX\nx06dOqmex8qVK/PWrVvv5XwZSczFV6VHMoHIfyvG85ZRgUg5AHsUn4cCGCo+GwMRnU7HadOmmcQa\n2NraqvzsymYpy6N8+fISvBQrVoy7d++WylpkqAhQoQzytLe3Z8uWLeVnodRtbW05duxYzp8/XwbN\n5suXj6Qh4j08PJxLly7l+PHj2alTJ/br149nzpwhaXjBnD59mjdu3OC2bdtM3E0CQGi1WkZGRkq3\nQoUKFUiSR44cYa1atejg4MAcOXKwd+/e0od/9erVNAN3bWxsOGrUKH799deqc3/55ZcmAa4ODg4m\nsSWAgdF22LBh7NGjB7dt28YrV66YzFPVqlX58OFDRkZGqtwx1atX56ZNm6RbyJy/Ozk5mbt375YW\njF9++UV+d+3aNQkw3xWIKGX58uUEoLqXlFapXLlypalsf/nlFxMuGyVr7D8t/yYQ0ev1ZuOPbGxs\nuGvXrn+lDxld/o35ePz4MY8cOcIbN2681/NkJMkEIh+mvCsQ0dAABP5V0Wg0zQDUJhn65+e2AMqQ\n/BIAYmJiZKdcXV1RokQJLFy4EE+fPkXdunXlcaysrJCSkoK/eg1dunRB165dsXz5cixYsAB6vV5+\nlytXLjx8+BBZsmSBvb09Hj16BG9vb9y9e1fuY2dnhzdv3pgct0SJEmjbti3GjRuH6Ohos+fu3Lkz\nunfvDgC4d+8eWrZsiaSkJDg5OSE2NlY5Vhg8eDBI4vvvv8ejR48QGhqKbt26pXl9UVFR2LhxI375\n5RdoNBpYWVnh8ePHSEhIQFxcHF6+fGnyGycnJ+zfvx9JSUk4dOgQrl69itWrVyNXrlzYunUrzp49\ni1OnTsHKygqenp6YO3cuoqKi5O99fX3x7bff4uXLl3j8+DG8vLyQP39+AIBer0eFChWQnJyM8PBw\n5MiRAwBw+/ZttGjRAlmyZMH+/fvNXsuUKVPw448/ws/PD71794ZWq8X8+fNx5coVNGzYECNHjkxz\nPFIbp3r16kGv10On02H69OnQarUYOnQo4uPjAQDTp0/HZ599lupxXr16hZ07d+LGjRtwd3dHvXr1\n4OXl9Zf79b7l5s2b2LVrF2JiYlCoUCHUrl0bjo6OZvcliQMHDiA8PBzR0dEoWLAgWrRogU8++eRf\n7nWm/H8SJycn5M2b97/uRqa8o/z+++8qPebn5yf/z5Ili8Z4//8KiHwBoJYREClNsjegBiI5cuRA\nYmIiQkNDUa1aNbRu3fovAw8bGxskJiYCAGxtbbFp0yapDC9duoQuXbogKSlJ9RsfHx/cv39fbndw\ncJDKCQDq1asHAIiLi0NycjKOHj2KChUqIDIyEomJiRKsaDQakES+fPlw9+5dpKSkYMGCBShZsiRm\nzpyJNWvWoEaNGpg4cSKuXbuGsLAwHD582Ox1FCtWDDNmzECWLFnSfe2JiYkYM2YM9u3bJ7fpdDoU\nK1YMRYsWRbly5dCrVy9oNBrs2LED2bJlAwD89NNPGDBgAPz8/LBmzRr529jYWDRu3BgxMTHIly8f\ngoKCcOzYMTx+/BiffPIJ1qxZA61Wq+pDSkoKypcvD71ejwMHDsDFxQUAcP/+fTRu3BhOTk6IiIgw\n2/9nz54hNDQUf/zxh2p7rly5sHjxYjmPf1X69euHI0eOmGz38fHBb7/9hhYtWmDAgAF/6xzmJC4u\nDrt378bVq1fh5uaGunXrwsfH5x8/j7EsX74c8+fPV23z8PDA/Pnz4e3t/d7PnymZkh7JCEDExcUF\nAQEB8vO6devw7NkzrFmzBtOnT8eqVatw9uxZzJgxA9u3b0f+/PlRqFCh/7DH/728KxDJ8K4Zc/Vk\n/onWqlUrlelIyUhqbW1tls+jbt26rF+/vnRV4E/z9N69e9mhQwfpwxXpsIKJ1MXFhYcPH6ZWq6W1\ntTX79+9PwEBZTlJm5WzatEnVJ2PuEY1GI/vVoEGDd7GUsV+/frLf7dq1UwXt7t27lyRlkGvp0qW5\ndetWLl++XJKcKfkibty4IevVeHl5yZTVly9fyj5bCvAUfBtt27blixcvGBUVJdODv/jii1SvISoq\niqNHj2aJEiVYvHhxjhgx4i+bbo1FpEk6OjpSp9PRy8uLEyZMkAGxgwYN+kfOo5RLly6pSOTEHM+a\nNSvN3/4dV8Dx48el66hbt26cM2eOdKcZlz7IlPRJZrro+5GM4JpxdHRM9ftly5bJgpjt27fnDz/8\n8E7H/xhjrD6UGBErALcB+OJtsGqA+N44RsTR0VGV3dGzZ09VSqhx8/Pzk0DBysqKO3fu5O7du/nl\nl1/KbI/WrVvLQRIprs7OzqxZs6bF44rsDxsbG1XWiKUmsg3y58/PZcuWyQwdUYlVFPQTAal9+vSR\nfbpz545KOSnjFwTguXnzZrpuitevX8tI+59//lluF/VXBKi5ffu2KjtFtE8//ZRHjhwhSX7//fcm\n8Te2trZcu3YtybepupMnT+bx48e5b98+3rlzR57zxIkTci51Op2Mg3FycuLFixfTdT3vQ4yrMl++\nfJmLFi2SwE8wrv5TotfrZT2c4sWLc/bs2aqyAcpYGHPydxSfiPcYMGCA3Pby5UuZdfVfzsOHKplA\n5P1IRgUiERERrFevHsm3QOTYsWN0c3Ojj48PAwMDefPmTd68eZO1atVi8eLFWbFiRV65coWkAbD0\n7duXVapUYb9+/f6RfmYk+SCACA1gpC6A6zBkzwxXfqfstDIN1tvbm6tWrSJpeJGLQnjOzs6sXLmy\nWQZRV1dXXr16VVXFVSi+Q4cOkXxbur1OnTocOnQoAUMarTIzRql0LQEPKysrVfEyS+nGAux8/fXX\nJA0vMfFd69atOXHiRFXgY1hYGMm3lV1FsK0g/0pLbt++TcBA4a6U8+fPEzBk2ihvoLFjx7Jy5cqs\nWbMmFy5cyGPHjjEyMpJ3796VIMgcvX7fvn1NVviiNWrUiM+ePSNJ/vzzz5KDQqPRsHbt2mkq3n9D\nvvvuO7N979at2z9+LjHnOXLkYFxcnNzes2dPEwuUpd//VcUnLHUbN25UbRfZZMJClinpl0wg8n7E\nWKE1X3g8Xa3Zd0fY7Lsjae6XHtFqtQwMDGRgYKDkCjIHREhTi0i1atV4/fp1koZFWNWqVeV+9erV\nk7xJH5u8KxCxwn8kJHcC2JnWfklJSXBzc8O+ffsQFBQEnU4HADhy5AguXbqE3Llz49q1a3BycgJJ\nVKtWDYcOHULv3r0RGRmJEydOoFixYkhMTISVlRWSk5Oh0WgQGxuLBg0a4Pr169Inf/LkSTx58gQA\nsGbNGqxZswbXr19HtmzZZEBmQkICrK2tkSdPHty5c0f2U6PR4NKlSyhQoAC++OILbNy40WIsy969\ne2FnZ4eePXsCAEqWLInZs2ejb9++WL16tcn+Z8+eBQA0aNAApUqVQmRkJACk23eaI0cO2Nra4sGD\nB7h8+TIKFy4MADhw4AAAqAIqs2fPjlGjRmHUqFFy2+nTpwEAq1atQnJyMvz9/XH16lX5vRjXmTNn\nWuzD1q1b0bRpU0RERKBs2bI4ePCgjJ2xtbVN13W8b+nRowfy58+POXPm4PLly/D09ERoaCjatm37\nj5/r4cOHAIDAwEA4ODjI7eXLl8d3332HBw8e/OPnFFKkSBGEh4dj5cqVaNKkCbRaLa5du4YTJ05A\nq9X+v/dvZ0qmKMXe3h7nzp1759/Fxsbi+PHj+OKLL+S2hIQE+f8XX3wh9dn/d/nPgEh6pXTp0jh1\n6hROnz6NEiVKyO0CBHz22WdwcnICYAADwcHBOHToEN68eYNFixahSpUqeP78OQAgOTkZLi4uWLdu\nHWbOnIl9+/Zh2bJlGDJkCMqUKYOTJ0/KQNThw4fjzJkzAKDKCgEM4OjOnTuwtbWVNxZJ2NnZAQBC\nQkKwcePGVK9r+fLlqgCer776CvXq1cOaNWsQHR2NU6dO4fjx49BoNFiwYAGio6MREBCAX375BYBB\nmRQpUiTVc/z666/4/vvv8fjxYwQGBuLUqVOoWrUqOnfujKdPn2L58uUAkK4MHAB49OgRAEOWDwBM\nmjQJEyZMUAXvCsmXLx8iIiIwaNAgrF+/HjY2Nvjpp59w4sQJlCtXDgDkeGUkqVGjBmrUqPHezyPA\n4JEjR3Dnzh34+voiJSVFAtG05vbvSPfu3TFnzhxs3boVRYsWhb+/P3bv3o2kpCSEhIQgT5487+3c\nmZIpf0fWdyuXrv3i4uIAwGIW2L8her0erq6uFkHMf9m3jCbatHf5byU4OBgAcOXKFdX2fPnyAQAO\nHTqEV69eATCAgfDwcABAzpw50bx5cwlChCQkJMDFxQXNmzeXx9VoNFi7di38/PxkOu6ZM2eg0RiC\ne7NmzQrAkHVjfCylnDt3Dnq9XmXV8Pb2RqdOnTBhwgQsXbpUgo88efLg8ePHGD9+POrVq4dWrVrh\nypUrGDFiBGbOnIkhQ4bIc2q1Wqxfvx6jRo1CcnIyrKyssHnz5lTHbdasWShatCimT5+OlStXypTb\nJ0+eYPLkyVi8eDGSk5MxePBgNG3aNNVjCSlatCgAID4+Ho6OjhgyZAhOnTpl9oFq3749vLy8MGHC\nBACQGTTCuvL/XT755BM0atQIb968QWBgIJo3b44iRYpg165dcHJyQpcuXd7buX18fLBt2zbkzJkT\nly9fxqZNmxAfH49GjRph0aJF7+28mZIpH7s4OztLfeTi4gJfX1/88MMPAAz66fz58/9l9zKsZHiL\nyE8//QTAACwWL16MzZs3IzExEb6+vnB2dsbDhw/h4eGBqlWrIiYmBseOHYODgwPi4uJw7do1+Pr6\n4s6dO8iePTtKly6N8PBw9O/fHwUKFAAA6ZqJi4tDxYoV0aZNGyxYsACPHj2SrpXo6GjY2tqidu3a\n2Lp1q+ybo6MjkpKSZEpwcHAwsmXLJi0HAFC1alUsWbIEgCEFtXfv3gAMnBNFihRRWVvWrl2Ljh07\nYsmSJahfvz5CQkKwdu1a1XhYWVlh06ZNkpvDnFy4cAF9+/YFAHTt2hUlS5bEihUrcPToUeTOnRtt\n27aFg4MDmjVrJlfm6ZGQkBCMHj0aDx8+RFxcHD777DNcuHABcXFxcpyFXL58WV4zAMnRIkBdphis\nYiEhIdi9e7d8WeXKlQtr1qyBp6fnez33559/jrt372L//v2Ijo5GiRIlMl0ymZIpf1NatmyJLl26\nYM6cOdi4cSNWr16NHj16YMKECUhKSkLLli0RGBj4X3cz44m5wJH/uhlnzdja2qa7KJyLiwt37dol\nMxKUjKfpaTY2NtyxYwdHjRolsyjKly/Ps2fP8urVq+9c70akSE6fPl3Wh6lWrZosEFepUiVu2LCB\nkydPlv0UabzJyclcsWIFq1evzmLFirFSpUosVaoUixQpwnbt2lkM8BSpusogy4SEBJntWEdmAAAb\nN0lEQVR5c/jw4fTGHJFUB+JdvHjRJCjYw8PDLB18o0aNVJV/XVxc+PLly3c699+RqKgozpgxg927\nd+ekSZNkmnFGkwsXLnD58uUMDw9nYmJiun6TGRyZsSRzPt6PZISsmUx5d/lgsmZSa8pOW1lZybTX\nnDlzct68eSqOj+rVq7Nr165SEe7fv58kZUaNoAY3BhDis7+/P48dO8bbt2+zffv2BAyF5vR6PadP\nn07AkH57+PBh3rhxw+Q4Op1OlUlTvnx5Dho0iJcuXeK4ceNMlHP+/PkZEREhM3qUxeEGDRpEAGzS\npIlqElNSUlT08qJZW1tzx44d1Ov1quhrUQfEuFqq4EB51zx345dsfHy8LHGvbKGhoaoCd8Z9/fHH\nH9/pvMai1+v5008/cenSpYyIiGBKSorFfQ8fPqwqJggYagtt3rz5b/Uho0im4stYkjkf70cygciH\nKR8dEDG2VghlXaJECWo0GlpZWTE+Pl5aAfr370+Sqoqx1apV461btySZlgAQgLqE+evXr6Xy+u23\n3/jq1StpWTFulSpV4q5du/jkyRMOHDhQgpunT59Sr9fzyZMnjIuL44ULFzh06FB2796dy5cvZ3x8\nPE+cOEHAUOvm5s2bqn4BhqqaSiW7fft2AoY05cWLF/PUqVOSc8LR0VGm0hYtWpQrVqzg1KlTCYCf\nffaZXGHfvn1bWlzetQibpZfsqVOnOHHiRE6bNk2mqN27d499+vShj48Ps2bNyvz587Nbt25/u/Db\nzZs3TWrdFC5c2OxxX79+LQFRlSpVOGvWLFnc0N7eno8fP/5bfckIkqn4MpZkzsf7kUwg8mHKRwdE\nPv30U9XKVlg+qlSpQicnJwLg06dPOXnyZAIGsjOS3LNnj6oyr6VKsr6+vjx//jxJA8OdKHYmKls+\nf/6cQ4YMoa+vr0np+lq1arFr165SwefJk4cLFy6U5eutrKzYokULE5dATEyM/I04n62trcrSM3Lk\nSMbGxvLhw4ds06YNAQNJmJDXr19b5DQZO3asBCfe3t5s2LChtAy9KyMrmfpL9vnz57x27ZqKC0Mp\ner2ejx49ksX4/ookJSVJTpfcuXOzdevWksHV19dXVjUWsmHDBgJgYGCgtBTp9XrJBjtz5sy/3JeM\nIpmKL2NJ5ny8H8kEIh+mfHRA5M2bN2zWrJlczRor3bx58/LGjRsyFmHx4sWsXr26WQVtDCREc3d3\n5/379yWZWf78+c2a/Z8/fy77oCRaE01QtQvrhXDjfPLJJ4yJiVEdS1h2hFVDVKUVYESn00nwJM65\nZMkS+fuVK1fK38+aNYsJCQmcO3cuAQNZ28GDB1XkagBYv359Pn/+/B1uJ4OYe8k+e/aMrVu3ln10\ndHRk3759+ebNG7mPMlYHMLitjh9PH4mQUrZu3UrAUNVYxJjExsayYMGCBMANGzao9p81axYBsHv3\n7qrt48ePJwAOHDjwnfuQ0SRT8WUsyZyP9yOZQOTDlI8OiJAGF4AyNsP4f/H5008/lTVjsmTJwiJF\nipi4Yiw1pfUktVgGQYsuwIb4nZeXl7Tc/O9//2NKSgrv3r0r3QkzZsxQHScpKckEKPj7+3Pfvn0q\nS4eyX1mzZuXDhw+p1+tZuXJlaXWJioqSxy1TpgwBA+tqcnIyIyIiuG7dOl6+fDmte8eiGL9kk5KS\nWLJkSdk/b29v2ceQkBCS5L59+2TfnZycJJiyt7d/ZxbVSZMmEYAJFfKQIUMIgKNHj1Zt37t3r7RQ\nCeD1+vVrCYqWL1/+F0YhY0mm4stYkjkf70cygciHKR8dEHnx4gV/+eWXNEFEmzZteOjQIWn5+OOP\nPxgbG/tORfNKlizJ7du3pzrAer2e06ZNkxYMrVbLxo0b84cffiBgiPtQyqpVqwhA0gErpXnz5gTA\nHj168MyZM9Tr9Zw5c2aqfdTpdKpieNWqVVMds3jx4gTAXbt2pXod7yLGL1lBiZ8nTx5Z7+bnn3+W\nYOPy5cuSUv+rr77imzdv+OrVK4aEhBAAmzVr9k7nX758OQGwbNmy0lKlBGOLFi1S7Z+SkiIBoIeH\nB1u3bi3BUu7cuS26kT4kyVR8GUsy5+P9SCYQ+TDlowMiefLkUWVomEuf1Wg0PHTokFT6wcHBcgBi\nY2NVmRw2Nja8evUqN27cqDpGx44d32mgExMTeefOHUZHR5OkDEA1DjSdP38+AdNMGJKyD66urlyy\nZAmPHz+uAhnZs2fnli1beOPGDZOUWREf4+Hhwf379zMqKooTJ06U1qB/8iE0fsmKQOD69etz+PDh\nXLVqFV+/fi0ze+bNmydBmrIfouaNu7v7O53/5cuXdHV1JQDWqFGDs2fPltWDnZ2dzbqbfvvtNwnK\nRPPz8/toCrplKr6MJZnz8X7kXYFIYmIiDxw4wPXr18s4v78rwNtK6eTbWEJzi8uPUe7cucPVq1e/\n028+OiBiDDgAsGLFirx9+7ZcYQNguXLleODAAQkGlAGMxjwiNWrU4OrVq2ljYyO3pWUJSUuSkpIk\nT0f37t159epVbt68WYKglStXmvwmJSWFwcHBFq0fs2fPJmlY/SsBSlhYGOPi4mThOOO28P/aO/Ow\nqq5rgf82F4KKCmIdcARRY6wK4qxo1NKq0YifQ15ftagxDi8SFU1N9KVYU2ycgjGSmsY4oHEgwSZB\n0ySSvDhVUmNNnLBxHnFEirlXQYb1/rjnnl4EFEXhivv3fee7dw/n7HXu/va566y99l7vvluqe7md\n2x+yRS0lbtCggWl9io+PN31onB11HYHe6tevf88yJCcnm8qX46hSpcodA//l5+fLjh07ZPny5ZKc\nnFyhAkzpPz7XQvfHw+FeFJG//e1vBYJuuru7S2RkpOTk5JRKBi8vLwkODpYbN26Y7QQFBZWLIlLa\ne7kfnAP8lZQKp4hs2bJFFi5cWMDR9E9/+pNMmjTJVEwcPhVXrlwx/S66du0q77zzjkRERBT48ypq\n9cwTTzxhWjH2798vr732mkRFRcnGjRvvqeOTkpKKvH5YWFixG1Xl5ubKihUrpFevXhIUFGT6uIB9\nBdDevXsL+ZJUqlRJVq9eLTabTWbNmiX+/v5SpUoV6datm3zyyScllrekOD9kL1++bDrUKqUkLCxM\nAgMDTdkqV64sGRkZpoNxjx49ZNeuXfLNN9+YPhqTJk26LzkuXbok8+fPl/Hjx8vcuXPlwoULD/I2\nHyn0H59rofvj4VBSReTAgQPmi2Xz5s3l6aefNn3UXnnllVLJ4OXlJTNmzDD3X/rtb38rc+fONf+c\nrVarjB49Wtq3by/BwcHmM/jkyZMSGhoqbdu2lbZt28rf//53ERFJS0uT7t27S1BQkPz85z83N5j0\n8vIy2/zoo49k5MiRImKP1BsVFSU9e/aUqVOnFtveypUrJTw8XAYMGCD+/v6yZMkSefPNNyU4OFg6\ndepkRj8/duyY9OnTR0JCQiQ0NFQOHz5stvPSSy9Jly5dJCAgwLzfTp06SfXq1SUoKEhiY2Pl4MGD\n0qFDBwkKCpLWrVubWzc4U+EUkfz8fBGxL8ctalpm7ty5piKSkZEhe/bsKTSNUdRUjnP65Zdflvz8\nfHPVjPMREhJyT0tPU1JSZMiQIdKwYUMJCgqSBQsWFFhJcjdyc3OlZcuWxcruGFxubm6ye/fuEl+3\nNDg/ZGNjYwUo4KDqfEyePFlERI4ePVrk5maBgYEVYh+P8kb/8bkWuj8eDiVVRMaOHWtOoeTl5YnV\napXPPvvMnMYuzVS1l5eX7Nu3T4YMGWI6vTtbCWbMmGFavDMyMqRZs2ZitVrFZrPJzZs3RUTkyJEj\n0q5dOxERWbhwocTExIiI/XnvWAl4J0Wkf//+pkW3uPZWrlwpgYGBcv36dbl8+bJUr15dli5dKiIi\nU6ZMMbct6N27t6k8fPvtt9KrVy+znaFDh0peXp4cOnRIAgMDRaSwRSQyMlI++OADEbHv2O2wFDlz\nr4qIy8eaCQ8P58MPP+RXv/oVo0aNYuXKlfj4+NC3b18iIiJYt24d2dnZhIaG4uPjQ7t27Thy5Air\nV6/mwIED+Pn5MXLkSKZPn84nn3wC2JUvByEhIcyfP5/Nmzfzxhtv4O7uzpgxY6hXrx7vv/8+e/fu\nZeLEiSQkJJRI3s6dO9818u6dsFgs7Ny5kxYtWnD58uVC5XPmzOH8+fPExcURFxdHfHz8fbd1Pzji\nybz44os0bdqUZcuWce7cOaxWK6dOnaJFixYANG3alD179rBw4UK+/PJLLBYL4eHhTJ06lZ/97Gdl\nKrNGo6nYOKKSjxs3zgyw+fTTT9OsWTOOHj3K8ePHadOmzX1fv02bNpw6dYr169fzzDPPFCjbsmUL\nSUlJLFy4EICsrCzOnDlDvXr1iIyM5IcffsBisXDkyBEAOnTowPPPP09OTg6DBg0iODj4ru0PGzYM\ni8Vyx/bAHtusWrVqVKtWDW9vb5599lnAHrB0//79WK1Wdu3axbBhw8xrOwdvHTRoEG5ubrRs2ZJL\nly4VKUuXLl2YM2cO586dY/DgwQWiyN83RWknJT2ABcC/gP3Ax4CPke8P3AR+MI53nc5pBxwAjgFv\nA+r2697uI+IwraWlpRXwlXAcnp6esnPnzkJa2e3Ex8dL8+bNxcvLSxo3biyxsbHm1Itj+/N58+aZ\n9U+ePCkWi0UsFkuBJbJlwcWLF6V///7mPQYEBMi7774r+fn5sn37dgGkY8eOZSKL89ve22+/bU65\nODR0q9Vq+sckJyeXiUyPO/oN3LXQ/fFwKKlFxLGHk8Ovzmq1yqlTp8xp5LS0tPuWwWGpmD17tvj6\n+sr+/fsLWAlCQkKK3OF51qxZMm3aNMnLy5OcnByxWCxm2fnz5+W9996TVq1aSXx8vIiIVK1a1Sxf\ns2ZNAYuIc1iO4tpbuXKlTJw40Uw3btzYtOY7yjIzM6Vu3bpF3uft7TjuuygfkWPHjsnixYslICBA\nvv7660LXuleLiFsp9ZhkoJWItAGOADOcyo6LSLBxTHDKXwqMA5oZR9+7NfLee++Rl5eHn58fKSkp\njBkzBh8fH6pUqcKzzz7Lzp076dat212FjYiI4McffzTf3qOiorBYLHz11VekpKQA9mixNpsNsIdL\n9/f3Jy8vr1jtEOyRdHfv3s3x48fvKkNJqVOnDitWrMDNzQ0PDw+2bdvG+PHjUUqZEYkbNGjwwNor\nKcOHD8fb25vt27fTsWNHpkyZQps2bTh79ixPPfUUvXv3LnOZNBrN482oUaMAePXVV4mOjmbVqlUM\nGDCArKws+vTpg5+fX6nbeP7554mOjqZ169YF8vv06cOSJUtMS7vDOpOZmYmfnx9ubm6sWbOGvLw8\nAE6fPk3t2rUZO3YsY8aMYe/evYD9mX/48GHy8/P5+OOPi5WjuPZKQvXq1QkICDCjfYsI+/btu+M5\n1apV46effjLTJ06coEmTJkyaNImBAweyf//+ErdfHKWamhGRLU7Jb4Ghd6qvlPIDqotIipFeDQwC\nPi/uHE9PTzIyMti+fTvVqlUDYMKECUyYMKFAvT179hR5fnZ2Nrm5uXh5eRUqy8/PJyYmhk2bNpl5\n8+fPZ/369SxdupT09HSOHz+Op6cnV65cKdRGbm4uS5cu5aOPPuLmzZuA3QT22muv0aRJkzv9FCWm\nR48ebN26lU6dOjFw4EAuXrzI5s2bAejZs2ex9/0wcLS1YMECpk+fzt69e81B1KhRI2JiYsy0pmwo\ny/7X3B3dHw+WqlWrUqVKlbvW69evH6NGjWLVqlX88Y9/NPMbNWpEbGys+XJ5v9hsNmrUqMELL7yA\nzWbj5s2b5OXlYbPZmDp1KtOnT6dVq1aICI0bNyYxMZFRo0YxfPhwEhIS6NGjB15eXthsNr788kve\neustPDw88PLyYtmyZdhsNv7whz/Qv39/6tevT8uWLbHZbNhsNnJzc8nKyjLvobj2srOzycnJMeuJ\nCDabjcqVKxcoW7ZsGVOmTOH1118nJyeHoUOH0rRp00LtOO47MDAQpRStW7dmxIgRZGVlsWHDBjw8\nPKhTpw7Tpk0r9Pump6dz+vRpM3236Rvl0KpKi1JqE5AgIh8opfyBQ9itJNeB10Rkh1KqPTBXRMKM\nc7oDr4jIAOdrZWZmmkL5+Pjg6+vL559/bs79lYTTp0+zZMkSduzYQX5+Pi1atGD8+PGEhoaadb74\n4gt+//vfU6lSJX75y18WUEhq1arF9evXyc7O5rnnnuN3v/tdoTYWLVrEunXrAAgMDOTixYvYbDZ8\nfX3ZsGEDNWrUKLG8xXHt2jUiIyM5evRogfyxY8cybty4Ul//fsnKymLr1q1cvnwZf39/unbtiru7\ny7scaTSaR4iqVavSsGHDEtUVEbZt20ZiYiJWq5XOnTszfPhw8wVWU3acPXsWq9Vqpp0VEW9vb1Xo\nhKLma6SgH8hXwMEijnCnOv+L3UfEodh4AjXlPz4hZ4HqQAfgK6fzugObbm/zdh+R2bNnFzmnVRxn\nzpyRWrVqmatLHMu6lFIFlreGhYUJIH/+859FxD6Pdns8m+eee870fHYmPT1dPD09RSll+kVcv35d\nunXrJoDMmTPnnmS+E7du3ZLExESJioqS6OhoOXTo0AO7dknQ89+uh+4T10L3x8NB76z6aPLAfURE\nJExEWhVxfAqglBoJDACGi9i1CxHJFpF04/s/geNAc+Ac4OzY0ABIu1P7ERERzJw5825iFuDNN9/k\nypUr9OzZk7S0NDIzM5k+fToiwsyZM825NceqlJCQEMA+z5iWlmau6ti0aRMJCQlUqlSpUBvff/89\n2dnZdOzYkbCwMMA+l/bSSy8BsGvXrnuS+U54eHgwZMgQYmNjmT17Ni1btnxg19ZoNBqNpjwplbOq\nUqov8AowUERuOOXXUkpZjO9NsDulnhCRC8BPSqnOSikFRACf3qmN+Pj4ezb5JycnAxATE0OdOnWo\nVKkSMTExeHt7k5qaSlqaXfdxLJtatmyZqZzs3r2bq1ev4u3tbSoYReHt7Q3AuXPnyMnJMfNPnDhR\noFyj0Wg0Gk3xlHZSPw77NEyyXa/gW7GvkOkBvK6UygXygAkics0453+AVUBl7E6qxTqq3i8eHh4A\n3Lhh6kbcunXLVBgc5ZMnT2bdunUsX76clJQU6taty9atWwGYNGlSAUtIeno6n376KVarlW7duhES\nEkLz5s05cuQIQ4cO5cUXXyQ1NZU5c+YA8Jvf/OZB35ZGo9E8Vri5uZGVlVWkVVrjmmRlZd2TPyeU\nftVM02LyNwIbiynbA7QqTbt3Y9CgQezbt48pU6bwl7/8hVq1ahEdHc2NGzfo0qULtWvXBuxTMomJ\niYwfP57U1FRSU1Nxd3cnMjKSWbNmmddbvnw5kZGRZGVlmXn9+/cnLi6OwYMHk5SURFJSklk2evTo\nQpveaDQajebe8PX15dq1awWWj5aE9PR0AGrWrPkwxNLcATc3N3x9fe/pnAq5zGHy5MkkJCSQmppK\n9+7dzfzKlSsTGxtboG54eDj9+vVj27Zt2Gw2OnfuTN26dc3ylJQUxo4di4gQFhZGo0aNSExM5LPP\nPqNu3brs27ePuLg49uzZg6+vLxEREYSGhvLGG2/w3XffUaNGDUaMGEGvXr0wrEYajUajKQFKqftS\nJhxLRx07PWtcmwe2fPdB4rx89359LdLT05k3bx4bN27k5s2b9OzZkxkzZhTajOZujBgxgrVr1xIV\nFWUqMQcPHqRNmzZ4eHhw8eLFAst0Dxw4QO/evbl69WqB60yePJlFixY9ksqIY2+E9u3bl7MkGge6\nT1wL3R+uhe4P1yIzM9P8XtTy3dLurOqy1KxZk/nz53P8+HHS0tJYt27dPSshgBkfYPDgwWZeq1at\nePLJJ7l165a5xz/Yl0KPHDmSq1evEhoaytq1a4mOjsbT05PFixebTrQajUaj0WjsuLxFRKPRaDQa\nTcXgsbKIaDQajUajcX20IqLRaDQajabccMmpGY1Go9FoNI8H2iKi0Wg0Go2m3NCKiEaj0Wg0mnLD\nJRURpVRfpdSPSqljSqlXy1uexwGlVEOl1DdKqcNKqUNKqclGvq9SKlkpddT4rGHkK6XU20Yf7VdK\nhZTvHVRMlFIWpdT3SqnNRjpAKfUPoz8SlFJPGPmeRvqYUe5fnnJXRJRSPkqpRKXUv4xx0kWPj/JF\nKRVlPK8OKqXWK6Uq6THy6OFyiogRLO8doB/QEvhvpZQON/vwyQWmichTQGdgovG7vwp8LSLNgK+N\nNNj7p5lxjAOWlr3IjwWTgcNO6XnAIqM/MoAxRv4YIMMIu7DIqKd5sCwGvhCRFkAQ9n7R46OcUErV\nByYB7UWkFWABfo0eI48cLqeIAB2BYyJyQkRuARuA8HKWqcIjIhdEZK/x/SfsD9n62H/7eKNaPDDI\n+B4OrBY73wI+Sim/Mha7QqOUagD0B9430groDSQaVW7vD0c/JQK/UI/iNr4uilKqOvZgnssBROSW\niPwbPT7KG3egslLKHagCXECPkUcOV1RE6gNnndLnjDxNGWGYLNsC/wDqiMgFsCsrQG2jmu6nh89b\nwHQg30jXBP4tIrlG2vk3N/vDKM806mseDE2AK8BKY6rsfaWUF3p8lBsich5YCJzBroBkAv9Ej5FH\nDldURIrSUPUa4zJCKVUVe+TkKSJy/U5Vi8jT/fSAUEoNAC6LyD+ds4uoKiUo05QedyAEWCoibQEb\n/5mGKQrdHw8Zwx8nHAgA6gFe2KfEbkePERfHFRWRc0BDp3QDIK2cZHmsUEp5YFdC1orIX43sSw6T\nsvF52cjX/fRw6QYMVEqdwj492Ru7hcTHMENDwd/c7A+j3Bu4VpYCV3DOAedE5B9GOhG7YqLHR/kR\nBpwUkSsikgP8FeiKHiOPHK6oiHwHNDM8n5/A7nyUVM4yVXiMudLlwGERiXUqSgJGGt9HAp865UcY\nqwM6A5kOE7Wm9IjIDBFpICL+2MfA/4nIcOAbYKhR7fb+cPTTUKO+ftt7QIjIReCsUupJI+sXQCp6\nfJQnZ4DOSqkqxvPL0Sd6jDxiuOTOqkqpZ7C//VmAFSIyp5xFqvAopUKBHcAB/uOTMBO7n8iHQCPs\nA3+YiFwzBn4c0Be4AYwWkT1lLvhjgFKqJ/CyiAxQSjXBbiHxBb4HRohItlKqErAGu2/PNeDXInKi\nvGSuiCilgrE7Dj8BnABGY3+Z0+OjnFBKzQb+C/uqv++BF7D7gugx8gjhkoqIRqPRaDSaxwNXnJrR\naDQajUbzmKAVEY1Go9FoNOWGVkQ0Go1Go9GUG1oR0Wg0Go1GU25oRUSj0Wg0Gk25oRURjUaj0Wg0\n5YZWRDQajUaj0ZQb/w9BStFfGeAqNgAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"sensor_var = 30000\n",
"process_var = 2\n",
"pos = (1000, 500)\n",
"process_model = (1, process_var)\n",
"\n",
"N = 1000\n",
"dog = DogSimulation(0, 1, sensor_var, process_var)\n",
"zs = [dog.move_and_sense() for _ in range(N)]\n",
"ps = []\n",
"\n",
"for z in zs:\n",
" prior = predict(pos, process_model) \n",
" pos = update(prior, (z, sensor_var))\n",
" ps.append(pos[0])\n",
"\n",
"book_plots.plot_measurements(zs, lw=1)\n",
"book_plots.plot_filter(ps)\n",
"plt.legend(loc=4);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This time the filter struggles. Notice that the previous example only computed 100 updates, whereas this example uses 1000. By my eye it takes the filter 400 or so iterations to become reasonable accurate, but maybe over 600 before the results are good. Kalman filters are good, but we cannot expect miracles. If we have extremely noisy data and extremely bad initial conditions, this is as good as it gets.\n",
"\n",
"Finally, let's implement the suggestion of using the first measurement as the initial position."
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAiAAAAC+CAYAAAAMerQGAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzsXWdYFFcXfmeXDoIUURQFsURBxBZ7\n70EEa6LGihoLlqAxdlGTGDWWGGKPvSbWqDF20agpGKOxJfZeUEEUlLb7fj/WudlhdwGJBb/M+zzn\ngb07c++dubNzzj1VIgkVKlSoUKFChYpXCc3rnoAKFSpUqFCh4r8HVQBRoUKFChUqVLxyqAKIChUq\nVKhQoeKVQxVAVKhQoUKFChWvHFavewLGSExMVD1iVahQoUKFiv8zuLi4SJnbVA2IChUqVKhQoeKV\nQxVAVKhQoUKFChWvHHnKBGMMFxeX1z2F/zyOHj0KAKhSpcprnokKGeqa5C2o65G3oK7Hv8fevXvR\ntGlT6PV6FClSBBqNBtevXwcA/PDDDwgODs5xX4mJiVl+r2pAVKhQoUKFChUAgEaNGmHdunXw8fHB\nzZs3cf36dRQtWhRr1qx5LuEjJ8izGhAVKlSoUKFCxatHmzZtEBYWhtOnT4MkAgICYGX14sWFN0IA\nIYn4+Hjo9frXPZX/FJycnAAA9+7de+5zNRoN3NzcIEkmjs8qVKhQoSKPQ6vVonz58i91jDdCAImP\nj4ejoyPs7Oxe91T+U3BwcAAAODo6Pve5KSkpiI+Ph7u7+4uelgoVKlSo+D/AG+EDotfrVeHjDYOd\nnZ2qsVKhQoUKFRbxRgggKlSoUKFChYr/L6gCiAoVKlSoUKHilUMVQHIIrVaLChUqCLpy5QqOHj2K\nQYMGAQCWLl2KAQMGAAA2b96MM2fOvM7pqlChQoUKFXkab4QTal6Avb09jh8/rmjz9fU1m/Bm8+bN\nCAkJgb+/f477z8jIeClhTipUqFChQkVehKoB+ReIiYlBSEiIou3IkSPYsmULhg0bhgoVKuDixYu4\nePEimjdvjsqVK6NOnTr466+/AADdu3fHkCFD0KBBAwwfPvx1XIIKFSpUqFDxWvBGbrnfm//zC+3v\n2z41sj3m6dOnqFChAgCgePHi2LRpk9njatasidDQUISEhKBdu3YADJnl5s2bh1KlSuHXX39F//79\nsW/fPgDAuXPnsGfPHmi12hd0NSpUqFChQkXeR7YCiCRJiwGEAIgjWe5Z23gAvQHIGapGkdz+7LuR\nAHoC0AEYRHLns/bmAGYB0AL4huTkF3spLxfmTDA5QVJSEo4cOYL27duLttTUVPF/+/btVeFDhQoV\nKlS8kbhz5w50Oh0KFy783Iknc6IBWQrgawDLM7XPJDnNuEGSJH8AHQAEACgMYI8kSaWffT0bQBMA\nNwDESpK0hWSuPDVzorHIK9Dr9cifP79F4SU3Sb5UqFChQoWK14lDhw5hyJAhiI2NBQAEBARgypQp\naNGiRY77yFYAIXlQkiTfHPYXBmAtyVQAlyVJugCg6rPvLpC8BACSJK19dqxFAUSuaggYUoLLWTlf\nJ5KTkxWfnz59Cp1Oh+TkZKSmpiI9PR3Jycmws7PD/fv3kZycDK1WCx8fH6xYsQJt2rQBSZw6dQqB\ngYHIyMhASkqKSb95Dbmd34MHD3D16tUXPBsVgPL3oeL1Q12PvIU3aT1OnTqF77//Hvfu3YOfnx/a\ntGkDb2/v1z2tLHH27Fn06tULaWlpcHBwgCRJOH36NEJDQ/HVV1+hWrVqAIBSpUpl2c+/cUIdIEnS\nn5IkLZYkyfVZWxEA142OufGszVL7/yXatWuHL7/8EjVr1sSlS5ewaNEiLF++HNWrV0eVKlWwbdu2\n1z1FFSpUqFDxmrFixQr06NEDmzdvxuHDh7FixQp06NABR44ced1TyxKLFy9GWloa3nnnHezcuRO7\nd+9Gx44dodfrsWDBghz3I5HM/iCDBmSbkQ9IQQD3ARDAJwC8SIZLkjQbwM8kVz47bhGA7TAIOs1I\n9nrW3gVAVZIDjcdJTEwUk3FxcRHt9+7dQ4ECBXJ8USpeDGTNR27NROq6vXjIOztz4d8qXj3+q+tB\nEj/99BNOnjwJLy8vBAcH54lyGW/Sepw9exb+/v6QJAmRkZGoXbs2Vq1ahQ0bNqBAgQK4du3aS72n\n6enp+OGHH3D58mX4+fkhODgY1tbWOTrX3d0d8fHxuHz5Mnx9fQEY+IWzszP0ej1SU1NhY2ODxMRE\ncY6Li4uJg0iuomBI3pX/lyRpIQB5S38DQFGjQ70B3Hr2v6V2FSpUqFDxhuDWrVsICwtTmDk8PT2x\nbt061K1b9zXO7M3CqlWrAADh4eGYPn06AKBVq1aoUKEC/vzzT+zcuRNhYWEvZewTJ04gNDQU165d\nE20+Pj7YunUrAgMDsz3f3t4eAHD//n0hgMgV621sbHIcWJErE4wkSV5GH1sDOPXs/y0AOkiSZCtJ\nUnEApQD8BiAWQClJkopLkmQDg6PqltyMrUKFChUqXg9Ion379jh69CgKFiyInj17onz58oiLi0PL\nli0RFxf3uqf4xuDBgwcAoEhYKUmS+BwfH/9Sxk1JSUGLFi1w7do1vPXWW4iIiEDp0qVx9epVtGjR\nQhGlaQlyionw8HDs2bMHP/30Ezp27AgAaN26dY4FkJyE4a4BUB+AhyRJNwBEAagvSVIFGEwwVwD0\nAQCSpyVJ+g4G59IMABEkdc/6GQBgJwxhuItJns7RDFWoUKFCRZ7A77//jiNHjsDd3R2nTp2Ch4cH\ndDodmjVrhr1792Lp0qX4+OOPX9r4R44cwZo1a5CYmIgaNWqgc+fOyJcv30sb72VCNhMtWbIEPXv2\nhIuLCy5cuCB8BF+WGWnTpk24efMmypUrh6NHj8LGxgZLly5FREQErl+/jvLly2Ps2LEoU6YM5s2b\nhwsXLqB48eLo06cPqlevDgAYPXo0tm/fjpMnT6JJkyaiby8vL3z++ec5nwzJPEMPHz6kTMaIi4uj\nilePpKQkJiUl5fp8dd1ePGJjYxkbG/u6p6HiGf5r67Fy5UoCYLt27RTtc+bMIQCGh4e/lHH1ej0j\nIyMJw6ZXkI+PDy9duiSOe5PWIzk5mb6+vgTA/Pnzs3bt2rSxsSEAtmjR4qWNO2HCBALg8OHDSZLD\nhw83ua+WaPbs2aKfBw8ecOzYsSxfvjwDAgI4ZMgQ3rx5UzFWJp5uwvPVVOwqVKhQoSJHkMNDf/nl\nFzx9+lS0x8TEAACKFi1q7rR/je3bt2PmzJmwsbHBsGHDMHfuXJQvXx5Xr15Fr169XsqYLxsODg7Y\ns2cPatSogYcPH+LQoUNIT0/Hu+++i9WrV7+0cYsVKwYA2LdvH/7++29MmTIFWq1WrF2HDh3EsZ07\nd8bOnTsRGRkJABg8eDBu3rwJAHBzc8PEiRNx4sQJnDp1CtOnT4eXlxcWL16MChUqCD+RLGFOKnld\npGpA8hZUDUjew5u0w/sv4L+2HjqdjmXKlCEABgUFcdKkSQwLCyMAWltbK7QRLxJt27YlAH7++eei\n7cGDB3R0dCQAXrlyheSbux6nT5/m7t27ef369Zc+1uPHj+nu7i40SADo4eEh/n711VdC4zFt2jRx\nXuvWrQmAM2fOtNj3qFGjFBqT/6QG5MaNG1i2bBlWrlyJe/fuZX9CDiBJErp06SI+Z2RkoECBAibF\n6P5fceXKlZcqlatQoSLvQ6PRYN26dShcuDBOnDiBUaNG4fvvv4eNjQ2WLVuG4sWL56rftLQ0JCUl\nWfz+7l1D4KWxX4SbmxtKlCih+P5Nhb+/Pxo3bvxKEpA5OTlh06ZNcHV1FYki79+/Dzc3N2zevFmh\n2UpLSxP/lyxZEgDw8OFDs/1ev34dkydPhkajwcKFCy0eZ4z/KwFEr9fjo48+gq+vL7p3744uXbrA\n29sbU6ZM+dd9Ozo64tSpU2Jxdu/ejSJFXk8utYyMjFc+piqAqFChAgDKlSuHc+fOYdGiRYiMjMTU\nqVNx6dIlEQXxPLh69So6dOgAJycn5MuXD0FBQdi4caPJcUFBQQAMCbD0ej0A4LfffsOff/4JOzs7\nlC5d2uQcFZZRp04dXLlyBSNHjgQA2NraYsWKFahZsyZsbW3FcQEBAQAMm3o5bFh2RM2MHTt2QK/X\nIzQ0FL169VLk8rIIc2qR10X/1gTz5ZdfEgC1Wi1DQ0PZtGlToQr67rvvctSHJTg6OnLkyJFct24d\nSbJLly6cPHmycBZKSkpijx49WKVKFVaoUIGbN28mSV6+fJm1a9dmxYoVWbFiRR4+fJgkeevWLdap\nU4dBQUEMCAjgwYMHxTgy1q1bx27dupEku3XrxsjISNavX59DhgyxON6SJUsYFhbGkJAQ+vr6Mjo6\nmtOnT2eFChVYrVo1PnjwgCR54cIFNmvWjJUqVWLt2rV59uxZMc7AgQNZo0YN+vr6csWKFSTJatWq\n0dnZmUFBQZwxYwZPnTrFt99+m0FBQQwMDOS5c+dM7plqgnnxeFNVzP+vUNcj97h79y69vb3FO1p2\nwATA1atXK449e/YsbW1tCYBlypRh8+bNaW1tTQAcOHCgOE5dj+dH+/btxX13cHBQmFC0Wi0rVqwo\n7n2VKlWo0+nM9jN//nwCYNu2bUVbdiaY1y50GNO/EUD0er3wKF67dq1onzFjBgGwRo0a2faRFRwd\nHXnixAm2bduWT58+ZVBQEPfv3y8EkJEjRwpmnZCQwFKlSjEpKYnJycl8+vQpSfLcuXOsXLkySXLa\ntGn89NNPSZIZGRl89OiRGEdGZgGkRYsWzMjIyHK8JUuWsESJEnz06BHj4uLo7OzMuXPnkiQ//PBD\nYb9r2LChEBp++eUXNmjQQIzTrl076nQ6xsbG0s/PjyQV10qSAwYM4MqVK0mSqampfPLkick9UwWQ\nFw/1BZu3oK5H7jF27FgCYNWqVXnt2jWmpKRw/PjxwjdBftfJ+PHHH1moUCHBHDUaDXv06MGUlBRx\njKX10Ol03LFjB6OiojhjxoxX4mvxMvD48WPu2bOHBw4cYGpq6gvpMzU1laNGjRJ+IZIkmUS/SJLE\nsLCwLN/ply9fpiRJ1Gq1XL16NdPT0/87AkhycjIB0MrKSiGh3blzhwDo4uKSbR9ZQRYMKleuzMWL\nF3PkyJEKply5cmUGBAQwKCiIQUFBLFq0KM+cOcOHDx+yc+fOLFeuHIOCgmhvb0+SPHDgAEuUKMGo\nqCj+8ccfJuOQpgLI0qVLxXeWxluyZAl79eoljitatChv3LhBkly0aBEHDx7Mx48f087OTpwbFBTE\nMmXKiHFkwSIpKYlOTk4kTQWQVatW0d/fn5MnTzar/SBVAeRlQGV4eQvqeuQe1apVIwD++OOPok2n\n09HLy4sAhFbWGGlpady1axfXrVvHq1evKr47cOAAW7VqxcaNG3PatGmMj48nSd6/f1+MJZOVlRW/\n/vrrl3uBzwm9Xs8DBw5w3Lhx/PTTT3n69GnFd9OmTWO+fPnENXh6enLNmjXZ9puRkcGHDx9a1FzI\nePz4MQsWLEgArFSpEkePHs3y5csTAF1dXUVAgl6v5/79+xkZGclBgwZx+/btou/ModL/GQFEp9PR\nzc2NAHjkyBHRvn79egKgv79/tn1kBVkwmDBhAt3c3Pjnn38qmHKlSpX4119/mZwXFRXFoUOHUqfT\nMT09nVqtVnx38+ZNLliwgOXKleOyZctIUjB8klyxYoVCAJHNP1mNt2TJEkZERIjPPj4+vHfvnuK7\nxMREFipUyOx1Go+TlJQkrjuzAEIazDizZs1i8eLFuXfvXpO+VAHkxUNleHkL6nrkHrVr1yYArl+/\nXrSlpqaK9/j58+dz1I9er+fgwYNNdu1eXl48c+YM27RpIz4PGzZMfM7MK14nnjx5wuDgYJNrGDJk\nCPV6PRctWiTaKlWqxBIlSojP+/btM9tnSkoKR4wYIe6np6cnx48fz7S0NLPHr169mgBYvnx5cUxG\nRgarVKlCAFy6dCnT0tIUJhuZmjRpwidPnlCn0zE6OpolS5b8b0XBaDQa9OzZEwAQGhqKqKgojBgx\nAt27dwcA9O7d+4WMEx4ejnHjxpnky2/WrBmio6MNUh2AP/74AwCQmJgILy8vaDQarFixAjqdDoDB\n+crT0xO9e/dGz549cezYMQBAwYIFcfbsWej1emzatMniPCyNlxM4OzujePHiWLduHQCDEHrixIks\nz8mXLx8eP34sPl+6dAl+fn4YNGgQQkND8eeff+Z4fBUqVKiQ65wMHz4cBw4cwMWLF9GnTx/Ex8cj\nICBARLhkh507d2LWrFmwsbFBjx49MG7cOFStWhW3b99G586dsWnTJtjY2OCXX37B1KlTsWHDBgwd\nOhQAMG/evJd2fc+DMWPGYPv27XB1dUVkZCR69uwJa2trzJgxAytXrsTkyZMBAFOnToWvry8uX74s\nzu3WrZsoHCqDJN577z1MnjwZ8fHxsLOzQ1xcHMaPH28xb8qVK1cAAE2aNBFF6bRarch0evnyZXz1\n1VdYt24d8uXLh5EjRyIqKgoeHh7YvXs3JkyYAI1GgwEDBuD8+fM5C5YwJ5W8Lvq3TqjJycls3Lix\niXTWoUMHpqen56gPSzA2jcgw1go8efKEH3zwAcuVK8eAgADRfu7cOQYGBrJatWocMWKE6Gfp0qUM\nCAhghQoVWLt2bRE/v27dOvr5+bFevXqMiIiwqAGxNF5ONCAkeenSJTZr1ozly5dn2bJlOWHCBJNx\njDUgaWlpbNiwIcuXL88ZM2Zw0qRJ9Pf3Z1BQEJs1ayacW42hakBePNQdd96Cuh65x+PHj1mhQgWT\n97WNjQ337NmT435CQ0MJgKVKlWKzZs04c+ZMJiYm0sXFRfRZsWJFxTm7d+8mANapU+dFX9ZzIy0t\njc7OzgTAX375RbTPnTuXAIT5yMbGhhUrVhQ5V2QtAwCGhYUp+jx8+DAB0NnZmQcPHqRer+fOnTtp\nZ2dHADx58iRJMiYmhu+++y7ffvtt1qhRgwAYEBAg/EvS0tLEGi1fvlzkgNm0aZMY69ChQwRAd3d3\n6vV6xTz+MyYYGTqdjtu3b+fgwYM5ZMgQHjhwwOSmqMgZ1ERkeQ8qw8tbUNfj3+Hhw4ccNWoU/fz8\n6OnpyTZt2jzX/fz9999pZWVlIsT06tWLlSpVEs6qVlZWvHjxojhv0KBBBMDu3buLtqSkJK5Zs4bR\n0dE8cuTIK+Mbd+/eFcKCMS5evEgALFy4MO3t7cW1FS1alNeuXeMPP/wgrg8Ajx8/Ls6NiooiAA4e\nPFjRZ7du3QiAM2bMEFGj5sjf35+RkZEMDAwkABYsWJDJycnCB0Xe1JIGM43suOrv708fHx+2atWK\nV65c+e8JICpeHFQBJO9BZXh5C+p6vD7o9XoGBQUJpvn222+zX79+YpcvSRJtbW1FBk8PDw9GRESw\nefPm4vvffvuNJLl161bmz59fwYSrVq3K+/fvv/TrSE9PF34axv4c06dPJwDWr1+f4eHhYl4tW7bk\nV199JRxGZa2IcZ2WTz/9VAhixpD9NyZOnEitVksAHDlyJA8dOsQRI0aYFUa8vLzEMy5rY7788kvR\n5zfffGP2PI1GowogKnIPVQDJe1AZXt6Cuh6vDydPnhQRGnL+isKFC7NIkSKCCUZERDAhIYF169ZV\nMEdbW1suXLiQpMGZXs5zIecWkcnJycmkwNrLwOjRowmA9vb27N69O9u0aSO0Chs2bGBcXBwLFChg\nwuQbNmzIOnXqCBNJ5ntjY2PDRYsW8fr164yOjqZGo6FGo+G4ceMIgG3atFHMo3r16or+CxYsyG+/\n/VZ8v3btWoXjaYsWLRTH+/j4sH379iJFviqAqMg1VAEk70FleHkL6nq8Phw8eJAAWLlyZcbExIg8\nUDIVKVJE+DLIIa6TJ0/m3LlzFe+mjz/+mACERiAzOTs78/Hjxy/1WlJTU9mxY0cTDcLEiRPFMX/8\n8Yf4LiAggOPGjWNERIQQXJYuXcqNGzfy4cOHvHv3rogyykxjxowRGhLZRPPo0SNOnjxZHOPg4EBP\nT0+hKdq1a5eYx+eff65IGieTp6en4N2yVuT/QgC5f/++SOal4tXh3wggT58+fSXqy/8aVIaXt6Cu\nx+tDfHy80FzExMQwIyODs2fPZunSpQmAo0ePzlE/cjE9Y/+Rq1evsmzZsqJt7NixL/lqDPjzzz85\nc+ZMzp49m9euXTP5fuLEiWaFCmM/GFtbWxNNDgB6e3tz1KhR3Lt3L3fu3CnMUmPGjFHkF5GpevXq\nfO+99wiAdevWVcwjLi6OK1euZL9+/RTnuLq6sl27duJzdgKIRBJ5BYmJiWIyxnnkSSI+Pl7UAFDx\navDgwQMAgLu7+3Ofq9Fo4ObmBkmSXvS0/tM4evQoAGVRLhWvD/8P66HT6fD9999j48aNSE9PR+PG\njdG5c+eclVN/zYiMjMSXX34JSZJQpUoVXLx4EfHx8cifPz9OnTqVo3pdAwcOxNdffw3AkKLgwYMH\nSEpKQvHixUVBtYCAAJw6dUqcc+bMGSxbtgxxcXGoUKECunbtCldX1xzN+ezZs1i6dClu376NgIAA\n9OjRA56ennjy5Am2bNmCGzduICAgAE2bNoVWqzU5f/fu3Zg/fz6uX78OwFATBwAaNWqEpKQk/Prr\nr9nOwc3NDR4eHjh37lyWx0mSBFlGiIyMxLBhw+Dl5QUA2Lt3L5o0aSK+12g0JjzauCCdi4uLKTMw\nJ5W8LrKkAVHxeqDu7vIe1DXJW3jT1yM1NdVsAqxy5cq9ESbU9evXC2dMmYoXL/5ca3L8+HGFJmHC\nhAlCiyKbZcqXLy+O//LLL03SlXt6eiqiUCxh7ty5Jue6uLhw9uzZ9PDwULTnz5+fM2bMYHJystm+\n9Hq9SEgm+3/Mnj1bnC9JEr/++mvhzCrTW2+9Jf43p/lo2LChWS0Lnplm5syZw/T0dJHyokOHDoox\njY//vzDBqHg9eNNfrv+PUNfk9SA5OZmrV6/m1KlTuW3bNlGn5E1fD5k5ubu7c9q0aZw/fz5LlSpF\nQBmi+iKQkpLyQn0pFi9ebJZJlixZ0iLTtoSPPvrIpB9jP4fx48eTJE+cOKEw1cyZM0c4bpYpU4Z/\n//23KH2RGX///bcImQ0PD+fChQvZoEEDBeOWnTeNydramkOGDDGp/fLkyRMhNBnXCDOeP0mTXCuz\nZ88WNXdkkk1ZOaU6deqIqKHFixezVatWJj40zs7OqgCiIvd401+u/49Q1+TV48CBAya70zJlyvDC\nhQtvxHrcv3+fo0ePZrly5fjWW29x4MCBwr9ArvWxceNGcfzff/8tmJJxobfc4uLFi2zXrp3wU6hY\nsSK///775+rj0aNHnDt3LsPDwzls2DDGxsaKqJCJEycyOTmZx44dY9GiRQmAc+bMee55yuG5mcnL\ny0v4s3344YcEwL59+4rznj59qkh6BhiKnx49elTR/5gxYwiAXbt2FW3p6eni2ZJDcc35b2Q+jzTk\nvJLHlcdatmyZwh8jIyPDpJ8ZM2bwwYMHijYnJycCECHM5si4EKAl7Ynx+c2aNVMFEBW5x5vwcv2v\nQV2TV4v79++Ll3ylSpU4cOBAEW1Rrlw5/vrrr3l6PeLi4oRGw5gKFCjAc+fOicJvxkm6dDqd2In/\nW0fy27dvizEkSVJoFYwzO2eFv//+m97e3maZoq+vryJhmJyAK3PdKnNITExkdHQ0O3bsyD59+jAm\nJoZTp04Vgo2VlRXbt2+vqJwrmxuWLFki2ozrtOTPn18wc61WS1tbW7q6urJ3794iB0flypXZo0cP\nbtu2TWFGMdYgeHt7s1WrVuKzrCEZOnQo/fz8aG1tzcDAQDZq1IiAIfx4ypQpIpxXPickJERoXWQ6\nceIEY2JiFEKEcaKz7CizmUWSJNaoUcPsGqkCiIpcQ2V2eQ/qmrxazJw5kwBYr149UfHz0aNHLFy4\nMAFw3rx5L2U9Dh06xPfff581atTg+++/z0OHDuWqH7k6aWBgIPfu3csjR46wXr16BAw5IOQ8DkOH\nDhWMfMmSJQQMOR2yywZ669Yt7tu3z2zlWpIcPnw4AbBmzZq8ceMGnz59KphkyZIls63QSpJVq1Yl\nAJYtW9ZEEwWAX3zxhTh27NixBMCQkJAs+7x48SJ9fHxM+oqIiKBer+eTJ08U5TuuX7/OP/74Q+TP\naNiwIdPT05mRkSGeBcBQwXfbtm1mS9qboxYtWijMH7L2IyoqSjG/rEwk5hh/ZqFDpsqVK3P27Nki\nV8qwYcNEHpHsSBYeZa1ZViQLX6oAoiLXUJld3oO6Jq8W/fv3JwBOnz5d0d61a1cC4KhRo174enz9\n9ddmX+q5KR9frFgxAsoaI7du3RI7/N27dwtmGRAQoEhEZZxZMzOSkpLYtWtXxa69Ro0aPHfunOI4\nOUuncbXsjIwMIUhcuHAhy/mfOnWKgMGcINcqKVu2rAnT7NatG2fNmiW0LfPnz8+yX1lzEBQUxAUL\nFnDUqFGCyW/evFkcd/HiRXGsrCmQr7lAgQKK70JCQqjX68U1A4b6NMbZWi0JCZkFFtkckznfhp2d\nHbdu3crHjx9z8eLFIrHY/Pnz2bNnT9aoUYNFihShlZUVnZychNnLXI6TmjVr8vHjx0xLS+PatWvZ\nsmVLkdBNkiSzQpRWq1WYWWrVqiXuuTlSBRAVuYbK7PIe1DV5tZg6dSoBsHnz5kIb8PTpU2GG+frr\nr1/oety8eVMwjWHDhjEmJobDhg0TAsOtW7eeqz85mZRxafvk5GQxxpMnT7h69WqFZsHe3p6ffPJJ\nltoPOdeDlZUVa9SoIRwSixYtqnA0lbUXW7ZsEW1Pnz4VxdeuXr2a5fzlonFyXRcXFxcmJCRww4YN\nFpleqVKl+OTJE4t9Xr16lYAhosO4iOYXX3xBAGzVqhVJQ50aWYCzt7cX99KSMHHlyhUh3FnSQPj4\n+Cg0JoDBDBIZGWm2pk1mcnBw4OHDhzlnzhwuWLCATZs2JQAuXLiQXbp0MXuOl5cXvby86OLiwkKF\nCrF27dpcvny5wqn1yJEjdHd3z3Jsa2trk4ijrIQPBwcHVQBRkXuozC7vQV2TV4s7d+6IXWGDBg04\nbtw4litXTjC6X3755YWux6x8l5yjAAAgAElEQVRZsxRMUIZc8TU6Ovq5+nv33XcJgO+99x4fP37M\n1NRUYZapVq0aSUM0Ra9evYT6X5IkhoaG8vbt22b7lJ1U7e3teerUKZIGfwp5pz9lyhT279+fHh4e\nos9ixYrx4MGDPH/+PDt37kwArFChQrZOrjdu3KBGoxE7+Nq1a1On05mkVjdm+tlVuD169CgBQ+E0\nY+zdu5eAQZND/lNPxcvLi5MnT1ZoBCRJYvHixcV9AMCmTZsqolDMUUBAAHU6nRDMMms/ciKEGJN8\nbs+ePU36yooGDx7MX375hbdv32ZycrLwe6latSpHjRolBGxL/VWuXFk4/AJQVOY1JlUAUZFrqMwu\n70Fdk1ePH374QTgWyuTt7c1Tp0698PX45JNPCIAffvihol2u3vrpp5+Ktjt37nD58uVcunSpxdDP\nEydOCAZpb28vnA41Gg137NhB8h9thiRJ9Pf3F2r/cuXKmYR+kuSqVavMCknR0dFiR58dA9RoNEI4\nKVy4MHv37m1Ru9OpUyfFebLTZmbSarXUarWUJCnL+i2JiYninuzZs4ebN2/mwoULRRRMv379uGbN\nGrNajM6dO7N+/foEDE60skZA1ugYk6enp3A8lUm+Z7Vq1VK016tXz6KppnTp0uzTp4+iLTQ0VGiF\n/g1JkiT6qVSpkgjnzcjIEAKGjY0Ne/bsyRYtWog1c3Z2ZkxMjHkzTT532hQqRZfanVQBREXuoTK7\nvAd1TSxDr9fz0KFDnDRpEmfNmqWIXsgOycnJXLNmDWfMmMGdO3eaOEc+ePCAs2fP5qhRo7hy5UpR\nGuJFr4e8Cy9QoICITLlw4YIwkezfv596vZ4TJ05UhGtqtVoOHz7crNnk559/Zs2aNcWxgYGB3LZt\nG0ny9OnTBAzq8j/++IOkwQzk5+dHAFy7dq1Jf9u3bydg8MUwvk+yv4ylXbq1tTXt7OwsmiesrKwU\nBdVkPH78mG3atLHIRLVarcIXAwCPHDmS5X3u27evRcHou+++U2giqlWrJoSyfPnyibWIiYnhO++8\nQ8Dgc9KrVy/Rh6VrBGBSs8a43svQoUNNBB69Xi+ca3NK5sbPnDY9M3300UdiHjqdTvihtHnvfV66\nl8Rzdx5x+YZt1Ng7U7KypUehInTzr0nnqm3p+d6n9B6wgkUj19Fn+Db6DN/GYsO+VwUQFbmHyuzy\nHtQ1MY/Hjx8Le7gxYzKOkLCEffv2mdi/AwMDeeXKlWzPfdHrodfrhYOllZUVy5UrJ5hhnTp1qNfr\nuWLFCjHPd955RxFqmVX+i7i4ON6+fVshpMhFwzp06MD4+HiuWbOGX375pdiN29jYsHXr1kI4IQ3Z\nU+WcEG3atOHChQvZpEkTxf0rVqwYJ06cKExHlsjZ2Vk4l8prZimiJjY21kRLYGtrK4QpYx8ISxqQ\ny5cvm1RwzUyy34cs1FgyQ3To0EGY5/7++2/h/+Hk5MTdu3ezUaNGCvORObK3t+eiRYu4atUqxsfH\n86+//lIIEG+//bZCA/RvKLOPiEajYZUqVcRnDw8Pfv75588EJIk2XqXp1rQ/iw/fKoQKS+TVI5qe\nLYfSvcUQ5qsSRvtS1Wnn5qUKICpyD5XZ5T2oa2IevXv3JmCIloiIiGDbtm3Fi3Xnzp0Wz7t7964w\nr1SqVIn9+/cXYY2VK1fONgz1ZaxHQkICO3bsKBiXVqtlx44dmZCQQJJCZW4sbCxfvpyAQV1vDklJ\nSZwxYwbr1avHWrVqcfz48bx37x6//fZbsSvPKheEvb09f/75Z5KG3fGcOXOyDA3dsGGDGNu4OJk5\nH4c9e/YoSs0PHTo0y/szY8YMxfkhISH88MMPRb4We3t7jh07VpGxVr6vsnCRlYZCprlz55rNTJqZ\njHOOyAy9a9euvHr1KmNjYxkYGEjAYJJxd3dn+fLlOXr0aJM52Nvbs0ePHgRMk369CAoICFB8liNq\ngipUoNbJjVYuBelcrR3dWwyh94AVQrh4q/tkrjt6nd/FXuOQOZuYr1IIfZr3ZuuxC+lXM5j2BYtb\nHPNfCyAAFgOIA3DKqM0NwG4A55/9dX3WLgH4CsAFAH8CqGR0Trdnx58H0M3cWKoAkregMru8B3VN\nTPHo0SPa2tpSkiQuXLhQOE/K6abDwsIsnjtlyhQCYOPGjYU5ISEhQUQ8ZKfKf5nrcffuXR49etSk\nJossKMgCCWnIqCm/9I2ZLmnweTAODZWpWLFiPHPmjELwMBYEALBHjx5CgPD29ma/fv1MTAiAIbqj\ncuXK4nPBggV5/vx57t271yRLqEwyA+7Zs6dQ9wNg27ZtFfPX6/U8efIkDx8+zLlz5z5X2vBKlSrx\nzp07JA1l5OW5yiYp2ZFUkiR+8sknIj/G81DhwoU5bNgwPnjwgAcOHDA7v8KFC/Pzzz/n3r17qdfr\nFanQHR0dTZLFDRo0yGQt/g1ZF/ClXfFKdPSvz3xVwuhSswPz1+tOj1YjWaT/MoU2w3vACnq0HEa3\nik1p7WEQ2Jo2bcpOnToJs1+zZs3MjuPm5sbw8HAhPL8IAaQugEqZBJCpAEY8+38EgCnP/g8G8OMz\nQaQ6gF/5j8By6dlf12f/u2YeSxVA8hZUZpf3oK6JKbZu3ap4CVpZWTE8PJw//fQTAYM5xRJku33m\nnBdyGfJly5ZlOfbzrkdaWhqPHTvGEydOmAgKOYUccWAc2rp//37B+DNj1KhRBEA/Pz9+99133Lp1\nqxAWOnXqJKJ6zJG7u7tJ2KjMaIwdc6dPn86VK1fmijnKTqWyI2fz5s3Zu3dvjhw5kmvWrDE7v8wJ\nyYxzU1StWpXDhw8XmqwWLVpwx44dJjk1MpPs95Jb8vf358OHDxkbG8tWrVoxf/789PDwEGYaY4FD\nnq9xJElOKCcaGcnGnrbeAXSu2poeYSNYpN8Ss2aTYkM3sUjfxfRsP4HOVdswX6UQ1m7eml988QU3\nbNjAlJQUs0nH5PwvkiTxq6++4tatW1mmTBnx/dy5c3n06FHWr18/WwFEokFAyBKSJPkC2Eay3LPP\nfwOoT/K2JEleAGJIviVJ0vxn/68xPk4mkn2etSuOk5GYmCgmc/78+WznpUKFiv82EhMT0b59eyQk\nJAAASpcujYsXL0Kn06FUqVI4f/486tWrh2nTppk9f9GiRZg3bx7q16+PqVOnQpIkpKSkoG3btoiL\ni8O8efNQuXJls+empqbip59+QlxcHHx8fFC9enWz5dNlbN++HV9//TXu3bsHAChcuDAiIyNRv359\nk363b9+Ow4cPAwBq1aqF4OBg2NraAgCWL1+O6OhoODo6om3btrCyssKGDRuQmJiI8PBw9OvXT9Ff\nq1atcPPmTcW13L59G6GhobC2toaLiwvu37+Phg0b4qeffkJ6ejoGDRqEuXPnIj093ey1WFtbw9PT\nEzdv3rR4vZkhSRKsra2RlpaW43NkuLq6QqfT4dGjRwCALl264MSJE/jzzz8Vx1WvXh3R0dEAgLi4\nOLRu3RppaWmwsbER45orG58T2NnZISUlRXyW+ylSpAju3r2LjIwMtG7dGqNGjQIAPH78GC1btkRy\ncjIAwz3LfD+1Wi0aNWoEADh06BCePHmS4/lYe/jAytULVvkLwcqlEGy9SsG6gA8kKxtIkgYAkP7w\nDtJun0PKleNIf3AduieJ0D9JhD49BSABKu9DpUqVMH/+fPH5008/xffff49atWrByckJCQkJSEhI\nwPnz5xEQEIA6depg/vz5yCxHODk5wdnZGWfOnBFtLi4uUuZrsMrx1SpRkORtAHgmhHg+ay8C4LrR\ncTeetVlqV6FChYpcY+vWrUhISICrqysSEhJw9+5dNGrUCLt37xabmLZt21o8v0WLFli8eDFiYmIw\naNAglC9fHnv27EFcXBx8fX1RsWJFs+edOHECH3/8MeLj40Wbr68vZs6cCW9vb5PjDxw4gKioKACA\nl5cXdDodbt26heHDh2POnDlCMEhKSkL//v1x9uxZxbmbNm3CnDlz4OTkhE6dOuH06dPYt28fli9f\nLo6rWLEi0tPTMXLkSBQqVAhhYWHw9fUVTK1QoULiWHd3d1hZWSE9PR0eHh64f/8+6tWrBzc3N6xf\nvx4LFiywKHxUrlwZv//+OzQajaLdx8cHt27dMjlPZtQkcyR8lC5dGiEhIfj+++9x8eJFAMAXX3yB\nr7/+GsePHwcAbNy4ET/++CPOnDmDMWPG4P79+wCADh06ADAIewsWLBDjGY8rCw05EZ4kSRLM1Vj4\nkPsBoOhn06ZNqFKlCpo2bYpt27YJ4WPAgAFISkrC0qVLFX3odDrs2rULnTt3Vggf4eHhSHz0CBu3\nbIek0cCmUElo83lAsrKBVb4CcHirFqzdCv8zl9RkpMVdRtKJXdA/fYTUOxeQEXcRGUkJJoJTVjh2\n7BjWr1+P5s2b48iRI/jxxx8BGIQ5WSCWcfr0aZw+fRoA0LRpU4UAlZSUhKSkpOwHNKcWyUwAfKE0\nwTzM9H3Cs78/AKht1L4XQGUAwwCMMWofC2Bo5nFUE0zegqruf3VITU3l9evXs8zgSD7/msTFxfHq\n1as5qrnxJuHChQvs37+/8C9o164dGzZsaKIu7tKlS7Z9bdy40cQBs2jRojx9+rTZ4xMSEujq6krA\nkIysXbt2om6Hv7+/2XstOyeOHz+eer2eOp2OgwcPJp7Z12XIScK8vb0ZGRnJSZMmCZ8LY+dMvV7P\n/fv3c8iQIYyMjOSECRNMfA+0Wi2XL1/OsLAwAoZ05SkpKdTpdJw4cSIBQyryefPmETCE4vbp08di\nNVaZwsPDCRiSghm39+vXz8Tfo1SpUuzWrRsBg79FZjOIra0t27dvL5wura2tRSZV41wZ/fr1EwnM\nZH+R33//ndevX1f02aZNG1F/5kWRpUJ4lkir1fLYsWMiCZy9vT2XLVsmzCcVKlQQx8o5U2xtbal1\ndKWVuzc9arRh/U++Z5kxP1qMOvF871M6VXiHNoVKUmPnlOO5Gadal9tatmwpHGXNkew/5O7ubvHZ\nMM79It8vFxeXFxMFY0YA+RuA17P/vQD8/ez/+QA6Zj4OQEcA843aFcdRFUDyJFQB5OUjLS2NI0eO\nFKms7e3t2bt3byYmJpo9Pqdr8scff4iiY4DBzr5q1aoXPf2Xgtu3b3Pr1q08cOCAoiCYjKNHj5pN\n/FS3bl3u3r2bEyZMEALCgQMHcjRmXFwcZ82axeHDh3PFihUiz4c5yLVaatWqJTKhPnr0SLx49+zZ\nozg+LS1NvPSNBUw5bDNfvnyizZzDZrVq1QgYoijM4dGjR+K8Nm3acOXKlYLpW1tbi/9lMo5EiY6O\nZkZGRpahqTY2Nly5cqUinwfMCCAyvfXWWyZt8piZQ1onTpzIhw8fcs2aNaJNdiI2nlNYWJjw6ZGp\nX79+wmm0fv36wqn1ebOJZiZJksw+X89LmX0/AFDr4EL3sjXoGNCQHk37Mn+9bnRrPpAF35+iDGsN\n/5rNR31D56pt6FytLe18gmiVvxC1+Two2eS8cm1myuzPY29vLwQlWZCTJIl2dnYsW7Yso6Ojn8tP\npXr16qLYYJ8+fV6aAPIFlE6oU5/93wJKJ9Tf+I8T6mUYHFBdn/3vlnkcVQDJW1AFkJcPuagZoIxA\nkFNOZ0ZO1uTChQuKkETjCIO8LISkpaUxIiJCwUCKFi3Kb775huHh4SxdurQiBXRISIjYvcvUq1cv\nBgcHEzCElubW0TMryJqLKVOmKNZD1gxkzsWh1+vF7vevv/4S7YcOHSJg2DGS5Pz587N8uWu1Wu7e\nvZvz5s3jzp07xbXJIbg1atRQhA23bNkyR0wjc40TWUg4duyYCPn19va2mM9Cq9UyODiYXbp04b59\n+xQ7/KxI1jpptVqR0AsAt2/fTpKKfCdNmjTh5s2bzWZBrVSpEn/++WdGRUVlmXMjO3JwcFD0by7/\nh4uLiyK3ida5AO1LVGW+KqHMX78H3YMj6RE2gh4hHzF/ve50Dx7MAu2iWKjzVBaJWK4QMvyGb6HP\nx1voHbGCXt1nMX+9boYolaJvmR3/xx9/NBs+LG9e/g1pNBrF787GxoYTJ06kXq83EaQCAgIs5kaZ\nPn26EMTXr1//QqJg1gC4DSAdBt+NngDcYTCvnH/21+3ZsRKA2QAuAjgJoIpRP+EwhOdeANDD3Fiq\nAJK3oAogLxdnz54lYPDgj4mJIWmo/imnd/7hhx9MzsnJmshZHoODg5mYmMiMjAxOmjSJgEETklfN\nMR999JF4GdavXz/LqAStVsv79++TpNn6G05OTvzpp59yNY8DBw4wJCSEBQsWpL29PQsVKsRBgwaJ\ncM7p06cLpvjbb78xNjaWKSkpIjrF3LrJtToCAgK4bt06rl69WjC7jz/+mLdv31Ywz7Zt25pk68xs\nvihVqhRPnz4t5tOvXz/FmAMGDBCMTNYIZcV8O3TooAixbd++Pc+dO2einndycmLNmjVZp04dE4Zv\nrIo3V+5eo9EoTBqenp4mfdjY2DA4OJhly5Y1O1dnZ2dWqVKFvr6+DAoKsliH5EWRxt6ZRWuFsetX\n29nlm19YNnIFiw3dyKIffpspqmQjvQeuYuFec+k9aA2LfbSJRfotYaFuX9Lzvc/oHjyY+aqE0c4n\niLYexWjn8I/pJLsaLo6Ojpw7d67Fe5KZYmJiLCYwkyRJbHZKliwpUtDLZLxhWbJkiSLCRZ5LduNX\nrFiRUVFRaiIyFbmHKoC8XMydO5cA2LFjR0X7mDFjCChTI8vIyZrIL6mZM2dy6tSpXL58OR8+fChe\nLNeuXXuh1/Ei8OjRI7HTiomJYWJiIi9duiQ0OSVKlODvv//Or776SrzkjMvTy8mpnJ2dOXLkyGyr\nrFqCXIvFHPn5+TEuLo53794Vc61SpQo/+OADsev39fXl1atX+dtvv/HevXui3zt37pjkegAMWgBf\nX1+zTLRs2bImu08XFxd26tRJCArFihXjjh07CBiSV8lC0sOHDwWTkU0issZB9pUxDqMtUKAAdTod\nU1JS6O/vr2BGxrkxBgwYIMxI5nxujOcJGFT+jRo1shgCW6JECbOhnsb3Z9CgQWzdujUbNWrEHj16\nmK01Y21tna3vSo6EDTsnOvrXp2e78fTqEc0ifb6hz8eGTKBvjdrGGlGbGDRwHl0b9aZbk77M93Yr\n2hR+ixr7zCYbZeG6nAgZ5o7JifBo7ny5zs93332n0Kz6+fkxIiKCHTp0EMcaC4BarZb79+8X2riA\ngIAs19kc2draClOPKoCoyDVUAcQ8Ll68yJEjR/K9997jiBEjeOHChVz1s2TJEgKGpD7GkGs2jBkz\nxuScnKyJubwJLi4ugglkTmyVFyBXKC1VqhTbtm1rsiuuWrUqSYOZRlY5ly5dmnq9ng8fPmTjxo0J\ngEOGDKFer+exY8e4Y8cOi0XaMjIyeP78eUW9mJMnTyrGrFWrFkNCQhQv6WHDhpE01EPJvBP09PRk\nnTp1xItdo9Hw/fff56NHj3j37l0OHTqURYoUoaOjY5Z+CiVKlDDJc2FMfn5+vHjxohAU1qxZw7ff\nfpuAQQPRvHlzxS5WzoAp554w56MB/ON7IZelN05P7+bmxg8++EDcz+PHj4vnat++fezbty9r1Kgh\nfCdkYSBz+XaZvL29zTp3Zi76J1/Ttm3bmJ6eLq65efPmotBbTivAymTt6kWHMnVYJDiC3SYtY77K\noXQPGUrvrtNYbNj39Bm+jUX6L2OBdlEM/GA6P1y4k4UDaxFS9tlTjUl+ZoxzlFgSkmTTStu2bRUm\nrJkzZyo0EAUKFODQoUPZrVs3enl50c3NjSVKlOA777zDpUuXigRnjo6O7NevH3v16iV+9926dTMx\n1xibdEqVKsWtW7eSJJ8+ffpc1yo/f8ZUtGhRVQBRkXuoAogpNmzYYLKbs7a25rp16567r7i4OBG5\nMH78eJ45c4azZ88W/RvX35CR3Zro9XrxYtdqtQwJCVHsaOVS43kNV65cUTATrVarcMg0TjE+cOBA\n0V6oUCGxs3d1deWuXbsUL3CNRsPOnTszKSlJnL906VKRkhsAy5Qpw2+++YYff/yxaLOxsWFiYiL1\ner2iP+N53L9/n8OGDWPXrl35zTffWHTWs7GxydJOX6ZMGROnx65du5rUPWnRooWYS82aNQVzL168\nOBcuXGhSkC1zfRtzpg7jz3KUTevWrQmAn332GSMjIxVMU6PRcNCgQcI/o02bNop1NNZQWRoHMDiK\npqamcvHixQSgiELy8PAQFWeNmbccKVOwYEGmpKSwQYMGgikrmKq9M22LBtKl4jvMX7crC7QaRY+w\nEfR8dyK9B60RJpPiI/6pcVKk/1K+NWgJa/WdzM6DRrHjM/NF1apVhVBUtmxZdujQIUcmCONnWaby\n5cs/l5bGwcFB9OHs7CzukYODA0+ePGn2d5SWlsYOHTqY9BUeHm6iTZOFYFkIMS5Z8OOPP4rjypYt\nazGbbeZnq3379jx79ixPnjzJ9PR0VQBRkXuoAogS8fHx4uXz7rvvcvny5SJjpoODg/BJeB7MmjXL\n7A968ODBZo/Pbk1+++03s8xGpv79+z/3HLPDnTt3uGvXLh49etSkdkpSUhKPHj0qKrtmBdkMYWdn\nx+nTp4sMnvLLMiEhgffu3RPF2ox3y3Xr1uXBgweFQ2WBAgVYr1498cLv0KEDyX8cNgFTW7YxE7S3\ntxemBuOS6n5+foo5y+thLLxYIk9PT5MQUa1Wy02bNvHXX3/N9vy3336bMTExFr8fNWoUT58+zW++\n+cbEsTQnZG9vL9KuW1tbZ3lNsv+Kj48PU1NTuWLFClaoUCFLbURmgahNmzZCYDF+XhcvXizMk5bm\n2a1bt3/CdDVWtC/xNj1aDqN3xAplyOqw7+nVcw6L9F1Er+6z6NZsAJ2CmtGmYAna2DkYQl/zK+uu\nuLq6Ci2QrIlq1qwZ4+Pj2bx5c4XW4Hm1Lzk5Txa0ZAHBwcGBdevW5erVq8X6dOrUKcvfUmxsLD/5\n5BNOmjSJJ0+eZEREhOi/dOnSZs2BgEHT1axZM/Hb8vDwYEpKCi9fvpxt/ZyCBQua/M5VAURFrqEK\nIEosWLCAANigQQPBaPV6vbCRNmzYkIMHD+aOHTuey9Fzx44dDA4Opp+fH+vVq8dVq1ZZLIKW3Zqs\nWrWKABgaGsrPP/+clStXpr+/vwjJ7datW47npdPpGBsby/379yvqjshISUlhnz59FOYEf39/xsbG\nUqfTcezYsQp7fY0aNUx2bidOnGCXLl1YqlQps7Z9Y8qXL58QKDw9PXnt2jWeP3+et27dok6nY8eO\nHQWDat++PX/77TeeOnVK1Im5cOGCcGw1rpybeXcn79gHDBjA2NhYhWDSt29fk/VYs2aNiTBjZ2en\nCIPOijQaDTds2GCRMa1bt06YVMyFdhrTkiVLhPNqVmacrMjKyoo9evTIluHIQkNOwjSNhUVLzFfW\nEu3atSvL3Bsau3x0qfEePd/7lIV7zWXRIesNwkbktyzQdhxdanWknV8Vap09CU3Oo2JCQ0NZt25d\nsSbG3zk6Omap+ZDvhZWVlcX7Jh9j/H1mjUiPHj1MnD6NadiwYQQMvjXPAy8vLwJgvXr1qNfrqdfr\nFQK+JRo4cKDoQ9ZKAQZtTqtWrYSg6+HhoTBnylAFEBW5hiqAKPHpp58SMPgZyEhNTTXrQPjOO+9k\nmUsit8huTQ4fPkzAsIuSEzrp9XpRHTYqKipH4+zfv19xXfb29hw5cqRCsJIZnUajYe3atcXOzcXF\nRWEmKVu2rDAxeHh4CF+Dffv2mS3c5eHhwbZt27Jnz57ctWuXCSNt1qyZIpxVr9eLJFXGJEkSGzdu\nLOzTcpisMX322WeMjY0lgGxzP7i7u/Py5cti3LS0NBHya47k/B2ZyRxzlZm4zOQmTpwodvgRERHc\nvXu3ReHDmKFrNBqFpsHR0ZEfffSRMKsYt1uat7HZI/P1V69eXdGW2bwiSRKHDRtmVgPj7e2tMBMV\nK1ZMIXja2tkTGis6uBWklbs37UvXoGNgY+arHEqXOp3pEfoxvcJns9hHm+kzfBsLdZ1Jj1Yj6dqw\nF+1LvE1oss//0bBhQ8bFxfHbb78V4wYGBloUiswJV7169TJ7/8qXL2+2/d+GyY4fP15EscnCfokS\nJXL8ztDpdKKvwMBApqamkiT37t0r2uvUqcPu3buzdu3aCgEpMDCQaWlpJJmlVmrNmjVmx1YFEBW5\nxn9dANHr9UxNTRXaiG3btokX54MHD0iSY8eOFT/C9u3bc+zYsWK3as6J9N8iJz4gsu9A6dKlOWbM\nGDZp0kQwiytXrmQ7xs8//yyYUJEiRUQWTwCcMGECSUOlVmtra2o0Gv7yyy8kDdqXzE6Eq1evJkk+\nfvxY7C6joqKo1+vFTq9Tp078448/RBguAPbu3Zt//vkne/fuTcCw47t8+TLj4+OZkZHBAwcOcP36\n9bxw4QLXrl2rGPN5ckE4OzsLj385eihzVlRJkhgSEqIQesh/CtllJxRkJkuVRGWSzRoHDhwQ12Jr\na6vQNMn3uXPnzhwyZIjFvtauXcuUlBRx7/8N1apVS6xHZvLw8OC4ceOEQ7ZcedYc2XgWp41XaQa/\n25VeVYPp1iyCXj3nGEJZnzmBmqPCHyxkwU6T6droA9oXLq3o09HRkRUrVsx27Z2dnYU/kPxcBwQE\n8Mcff2StWrUU6xYVFcUTJ06Y9CGvg6xVyI5yelxWz07FihUVFY2HDx+e43eGXq9XaPmKFi3KihUr\nWvRHkX+X8nW6uLiwQ4cOFqsQOzk5KXysjKEKICpyjf+qAJKWlsZPPvlEvDi8vb05efJkpqamigiT\n/PnzMzg4WOwWihYtKrJ27tu3T7x4XjRysibnz583yaFhb2/PDRs2ZHne6dOnFTtUBwcHLliwgCS5\nZcsWcd1Pnjzh7t27CRicIUnLSbQCAwPFy0k2MzRp0oSnTp0iYDClyDusjIwME8dL+UUoV379+eef\nTa7NksrbnPOjOW2VvJwMSiQAACAASURBVBOWnfeqVq3KCxcu8ODBg7x8+bLYMRrj4MGD/5qhmyNf\nX19hptq6dWu2TovXr183G4Eg09atW4XfQFaUXaXY7EhOPy5D3rG7FStNG6/SdPKvT48WQ1h0wApT\n4WLIehbuNpOujfvSpXYnOlVsQcfAxrT29KPW2ZP5PQubRKD4+PjkOuPpBx98wOTkZKEVdHV1ZUpK\nCkmazcgqm/Yyk3F4srl1cnFxybGPSIkSJUwE34YNG5qNCvLy8hIboJzCOCeMpfV7++23s30ONBoN\nt2/fzoMHD3L37t1CKFq8eLHZcVUBREWukRcEkHPnzrFXr1708/Nj2bJlOWbMGLP+CC8Sxi8c4x9s\neHg4r1+/bjYF9alTp8T5cuptAC886VdO1yQ1NZXffvstR48ezejoaEVOCnO4du2aUN1nfknJQojM\n+E+ePMljx44RMAgQCQkJ4lw5HFZ+qQH/lLqXE2aFhIQIZ8wiRYoospXKQkq+fPlYsmRJdujQgb/9\n9htJQ4p2eSfn4+OjEACBnCVI+uGHH0ycIQGDVkvWXEVHR5u9Rzdv3uTkyZM5YMAAFi9ePMsXenZk\nHKort3l7e3PJkiVcuXIlz507JwSj0NBQTpo0SWGDN8f4svMPsUQODg4i46lMOc1mWqCILx1KVaNz\ntbb07T6N7y84wnembGeR9mPp1X2WQtAo+uG39Gg1kk7lm9ChdE06VQymo28Q+w8YKNY0N/PPvDOX\nmWjTpk3Nmt3kZ8XY56hQoUKsW7euWA+NRsOzZ8/y/PnzJj4ZXl5ewtwoU40aNQgYnMdPnz6dpXCU\n+ZmxtbVVRGUZr+369etNMtra2toyKCiIixcvtugrlhn37t3LUT4R45wfvXr14pYtW0zSt4eGhopQ\n/qioKALgyJEjzY6rCiAqco3XLYAcP37cbPiXv7//SxNCZH8AR0dH4Uy6ZcsWYZKQBY3jx49z48aN\nQm1vnH5bzu9RpkyZlzK/l7EmQ4cOFS8gObxRrhFRuHBhxsXFiR3ajRs3qNfrRYZMmVl5eHgIhmjM\nTKpVq8bo6Gjxws+8W/T19eWdO3d49+5d4WMgm3qMIScJa9SoEdPS0nj79m0TxiCvnXG7scOpzGCc\nnZ3Nak5CQkKERsYY69evt6iClulF1A+RSRbe6tatK5hMZlNTZpKFInNMTqvVWtQUTZo0yUR4MTYb\naBzy07ZYIJ2rtWOB1qNZoM0Y5q/fgx6tRrL48C3/mEh6zWWhbl+yUOdpLNx7Ad+KWMiFBy/whz+u\nMqRrf0LS0NnZmZMnT1bkB5Gfi02bNimYpLlEWZbulbE2QmbYHh4eJoJCZpIkSfGsWllZmTDcnDBt\n2Tm0fv36TE9Pz7EAZ0zGQovx/1k9d6NHjxbP6JkzZ/jll18yOjqaly5dEu1nz57NcQZVY9Lr9cJ0\nl/l5qly5MtPS0sRmbN68eWbfK6oAoiLXeN0CiCyNt2jRgseOHePevXvFbmTs2LEvZUyZyWVOa929\ne3cC4LRp0xTtxmGdzZo1Y3BwsPixWvpR/hu8rDWR7eF79+4VOR6cnZ0FU5VNIw0aNBDn/P7774qE\nVzINHjyYR44cMevMKN+b4OBgxY7e2tpavHQLFiyoeIHKkFXmK1euJEn+9ddf2b5E3dzcTHw1Mr9M\ny5Yty3fffZffffed2doxN27cEEygZcuWwryQE5KTgGUmHx8fVqtWzSQpmJ2dHUuX/se/oXnz5tyx\nYwebNWummHeJEiWeu+6JRqNh3759s3CKlGhfshrz1+1Kt0Yf0KPVSHpnMpkU7j2fRfotZrGPt7BI\n/2X0bDuWI75aSccC/+SeKVKkCMeOHasovCczql69ellkqMuWLXsujZK1tTUrVapkIli5urpmKQDI\nx8sCdenSpRkbG8sdO3bw/PnzZrURgEHbl1l4LliwIMeNG6cwn9jZ2VkURnNqNjIWmjOTq6srW7Zs\nSY1GQ61Wy6tXr4pU/8bP+PDhw/n06VOLmqWszHvOzs7CzOjh4SHef8bnyc+2XPXWHFQBREWu8ToF\nkISEBAIGdaqxtkP2PQgICPhX/V+5coX9+vWjn58fS5UqxSFDhvDOnTuCufTu3Vtx/Pvvv0/AkJnQ\nGHq9np988onix2xlZcVRo0blWD0q48GDB/z999+F7dkccrMmN2/eZFRUFFu3bs2+ffsKk4Yx5Nwa\na9euZUZGhshvYkw2NjYcOHAg7969K867ffs2x44dK5hKx44deefOHcbExIhddMmSJdmoUSMhxHzw\nwQckDfdu8uTJijGMy4U3atSIv/76qxhLzhAbGRlJ0uDYarxzN/fSz04rIUkS//rrL27cuJHt27dn\n6dKlGRgYyPHjx4v3kOxQ2bJlS7Gmz5Oe2hxTtbGxMbH5G5MsaFsSMjp37sw7d+5kWS9HHseYWR4/\nfpwDBg6kVX4v2peoSufq7elcvT3zNwinV/evhCNo0Q+/ZZH+S+kR8hGdK7ekXfFKRmXfJUJrJbQO\n8vWVLVuWer2eOp3ORJAzdqAEYDb9enYapswk/w6M/XEsCVfGjF+OXKpfv754Rg8cOMDU1FRGR0eL\n98sXX3zBrl27imdMq9Xy+PHjnD17tojyMdaWlChRwqzmqVatWmZ9OcxRdmY04+dZFpTatGkj7l+X\nLl343nvviedGjlQrU6aMEGzN/SYyh8Db29sLrWinTp1EsrfM91fOhGsJqgCiItd4nQLI3bt3CRg8\nrI2dAOWU3c8ThpYZ586dM8meCBh2pXJomq2tLVeuXMn79+9zyZIl4gV2/vx5i/NdsWIFly9fzlu3\nbj3XfJKSktizZ08hxEiSxLCwMFHXwxjPuyaHDh0ym1/j888/VxwnJ0Tz9vbmmjVruHbtWou7SNlm\nXa1aNc6ePZtpaWlctWqVWUZbtWpVdu/eXcFIPT09RfE9kiahnZk1J7Vr1+bp06dFkjWNRsOIiAiT\nImmWyNy8ChUqJEwWlsJOAwIC+PDhQ5HEyVj7dfTo0X9VedUcyQzFXL8m2T41Gl6+fNkksVlm+qcv\niXa+FegeHMmiH35n4ghabOhGFuoyg47lGmabctxYUDCe67x589i5c2dxP+vUqcO9e/eSpGCSgCGc\n94svvhB+EzlluJnJxcWFmzdvVkTcmItgAqDIBiy3ffbZZwqnZGtraxF2u2jRIrHW69evz/JZAgym\nMp1Ox7i4OBOzT3BwsKjvJPdhHLIra2Rat27N+Ph4ixoYAOzevTt37dqlECxloUB21Cb/yVkkC1ij\nR4/mnDlzcvQcWjJB1axZk8ePHxfvhXbt2mXLq1UBREWu8bzM7saNGxwxYgRr167N5s2bc8mSJWbt\n6aRBfb5gwQKuXLmS8fHxJt/r9Xqh4hs5ciRTU1MZHx8vdi/yLjo3kFX5DRo0YGxsLA8fPixMEP36\n9TOpQiqTvPPOCXQ6HRMSEnJUDj4sLEy8mAICAsTLpXz58ib373nWJD09XbzMmjVrxtWrVzMyMlK8\n8I4fPy6Offr0KWvWrGn2uh0dHTlz5kyOGDHC7As4LCyMGRkZ3LlzJxs0aEAnJycWK1aMo0aNEmGb\nVlZWCju9o6MjL126xJs3byoYmnG+CmOtkoeHB2/evMnPPvvMZHxJkiwKA5kd7woUKCCOzUnkR9++\nfTl79mwCYPXq1cV6xMfHK8xPWq2WderUUVyjOUaYFU2ZMiXbeVlZWQlH3wkTJtDL63/sXXdYFFfX\nP9uX3ouADVSwIooF7F0UW+xYsHcFG7H3hua1xhJ7VCyoMdhLjN2oMVFjSDQqauzYQAUR2P19f2zu\ndWZ3Fhb0TXzzcZ7nPOLslDt3Zu7pv1MIMqUaKicvyJRqyLW20PiUhV2lcDg3GgD3DtPg1W/V+/LW\nEdtRvncsRiz7Bj/efo7XGVnYGLcFJJMjICAAQ4YMgbe3t1lQuJIlS+Lq1auifBMiQ4muFL6JXC7P\nsUyY6L0CyNBVP5Td3Nz4fJvzKHh4ePDKEKk5HzFiBK5fv46MjAzodDqL8kIGDRqExo0bW+ztIDJ8\nl0I0ZKFCJJfLTTrVurm5ISsrywRjRi6XizyuzIBjc1u3bl3odDrExMSYfRf9/Pxw/vx5vHr1Cj17\n9hR9f46OjqLvVCaT4ffff891DSpQQAoo35QXYXf16lXJ6oJmzZqJhOi7d+/QrVs30T7Cck8h7dq1\ni+9ja2vLFwkHBweznojcKDs7m39YDx484NsvXboEIoNlrNPpsHTpUpQvXx62trYIDAzEypUrLQqp\nZGVlYerUqdxF6+zsjDFjxvAyP2NiTb1sbW15+eX9+/d53HbHjh2i/fPyTJg3x8/Pj5cIA8CgQYP4\nIvv8+XOMHDkShQsXFi0wQpe1q6srXrx4wYUr+23RokVcwEuV+D579gxqtRoymQznz5/HpUuXRItf\n5cqVRcmOxYsX56Bjq1evRkJCAn/eRAZFdOfOnZILqKOjIxYsWMDnvWvXribJqAqFAuvWrRNZo8bM\nBBYTImq1Gi9evODjKlWqFCIjI/l1HBwccg3z1KpVC9u3bxcJBClmlqz4/mSQK5RQ2LvDqlQIrP1r\nwLHaZ7Cv3h5uYUPh3n4qCo/YKYmb4RO1FZ7d5sO1xWg41u4Om3INEFKjlghMDXhvLbOuzN9++22O\n93P+/HkRtLfwvtzc3NCiRQssXLiQh8yYwidl2Xft2pXnMuSmgFiixE2fPh0XLlwQeVw+++wzE4VJ\nCDCmVqsRHh6OHTt2mIzR3t4elStX5vfGtgcGBkqC3xmz8P1m44+Li8PWrVtFlXOLFy82WT+3bdvG\n0UrNKUBNmjThCb3fffcdP9+mTZtAZPD8sHe5WbNmWLRoEc/HUavVaNeuHXr37o1du3aZGEsvX77k\n4ItSLESENkcFCkgB5ZvyIuxYDkG9evWwf/9+rFq1ii/aQuWCZYtrtVp06NBBlIgodMsz2rVrlyiR\nr0GDBrhy5Uq+74mVyMpkMrx69YpvT0pKApHBYv4Q6t69Ox+r0B3csmVLyY+VuUW7desm2j516lQQ\nmXpd8vJMWNVEixYtRNtXrFgBIkLHjh1FrmnGSqUSR48eFcXthw8fDiKDMsPyDq5cucJLa5nwEtKp\nU6dAZFA0GK1du9YkEY9hqzBlxtfXF3q9nif4snGEhITwa0uF0LRarcjiFQoscwl3QoVAuL/Qk3H0\n6FFcuHAhV8jxQoUKoXnz5nwOx48fz38zDjcIr6tQKFCufHnItbZQuRaFtngl2FZoDJemQ1Fk5C6z\nwFw+w7bAq89yODXoC5vyDWEf0gF2VVpD61sZClvT5GDm1ShZsiRXiH/77Tf+7RIRKlWqxN9b5ikz\nFvyWYoYIcTCcnJw4VoxCoeDfNLsWKwMWXkvqGRvPnTGPHj0aP/74I/bt28e3+fn5IT4+PtfKFJlM\nZlaZlMvl3PtqZWXFv2Vh2bnwXRWeU5jvEhYWBsCAZ9OnTx80b94cMTExSEpKwtu3b3Hu3DkekgwP\nDzepfBK+3wqFAk+ePMGkSZP48x02bBj69+/PjYlly5Zh7969JqEpW1tbkcJijljImyX89ujRA3Fx\ncXxtZyE2c1SggBRQvslSYXfv3j0QGdzqqampfPv69etB9L5yIj09nS+Cp0+f5vuxOLZxZ01Ger0e\nT548+WjvBSstGzBgANLS0pCamspLTtu1a5fv87J27lZWVjh06BD0ej1OnjzJF7UzZ86YHMMslVq1\naom2M/wCY+j0vCgg169f5+NhKJ7p6encfcuEZUBAAG++xaypChUqiKxcZjUxFzEDJGPPuHXr1qJr\nP3nyhGMEGL8X7HmXL18ehw4dQnZ2tqhM0MHBATt27OBKAFPqWIhIGFaxt7c38agZKxBCVigUIiGn\nUCj48xEKPGH597p16/Do0SM8fPgQY8aM4dfXaDQm7earV6/O52jNmjWYOnWqibKxeMmX2HXkFBwq\nN4dTg35w7zhTMi+jWMxuBPadC4fQTrCtGAaNlz/UHn5Q2LlCpjafwColWHfu3ImkpCQeNvL29kb3\n7t1z7XLq4+MjClUYs5eXlygPxdra2qy1bmdnJ4mkWq1aNRQrVsyiezEODcnlcu5pYc/tzJkz0Ov1\nIsWKsbOzM0+uZN/G3Llz0b9/f9F+JUqUQJ06dbjSqVKpRHgcBw4cAGAwXKQ8M6VKlZJMMl63bh0P\ntQmZrRmAoT+SJSXd8+fPB2DwKrOwspD79+/PcYgePnyI2bNno3///pg3b54okTwn+uKLL0BkqF4S\nEpvDSZMm5Xh8gQJSQPkmS4VdYmIiiAwu1rS0NDx+/Bg6nQ4nTpwAkcG6AQwInWxRExILf5QuXfq/\nch/GdPz4cW6Fa7VabtFZW1uL8iLySgsWLACRIVFMSFFRUSCS7sOSkpLCQwUDBw7EsWPHMHnyZG59\nGsdZ85qXw1zRarUa9evX56EDDw8PnveyZ88ejt5aqlQpLpSOHTvG58bY6q1Tpw5GjBjB3buFCxfG\nsGHDcOvWLaxcudLE42Bra4vFixdj7Nix/FyDBg1C9erVUapUKTRo0EDSS+Hk5MSFDptH5tKXCvkR\nEccxsZSlSomFnFvppEKhEHlHDBavDBrv0ijfZRxK9JwLrz7L4T1gDapMTkC5SQffJ3+O+hae3b6A\nc5PBsAtuBWv/GtB4B0Bh74aWrT/DmzdvEBYWJrqecQKiuZwlIoPyMXjwYFy9etWk5JdxrVq18Pvv\nv3PIfuF9nTx5EjqdTrLnzaxZs5CZmSkp6M1xSEgI9u/fz8NNffv2FUH9s/uzJI+CKZnnzp0TdXed\nNGkSNmzYwJ9rjRo10KxZM0yZMgWPHj0ShWcYW1lZid6/RYsW8W+I9eQRCnmZTIa6deuKSqZ9fHz4\nOIYPH85LaSdMmMD3Y/1UZDIZRo4ciZ07d/K8J3d3d+6ZunbtGnr06AEfHx8UL14cTZo0QXBwMAoX\nLoxGjRph7969ou9cr9fj7NmzmDx5MqZNm/ZB65iQmIe2VatWou1M6TdOZjemAgWkgPJNeUHdZMKA\nCQcvLy/uZh0yZAgAIDU1FSqVCjKZTJTDsXDhQhAZILqvX7+OEydOSFaAfEw6evSoCMK6Tp06opLP\n/BAr4Wvfvr1oO8OhmDFjhuRxmzZtkgSJmjZtmsm+eVVAXr16hY4dO4qstAoVKuDq1at84Z82bRpq\n1qxpAvw0Y8aMHEtFpdjSUkopgCilUmniws6J7ezsUL9+fRMLlHklcnKpf0zWaDT48dIVqNyKw7Z8\nQzg1HAD/0du5guHVZzkKtZ+EZtO2ofPKHzB86yVsOncHI6YYLGH27K2trU2SaaVyA4Ts7u4OvV6P\njRs3WoR0ybwxnTp14gJXiO0SHx8v2t/BwQEtWrTgSpidnR0Pme3fvx8AzCo2uXHFihVF0P/Cd0+p\nVEqGTOzt7XmeBnvXkpKSeHm+MYeHh4vynwDw41kvI+NjXF1dkZaWBsCQTM48Whs2bODvmpTXIyAg\nAHv27OHjl8lkkMvlXOFxd3fnIWhhmb9Op+Nr5Z49eyz+tv8OevjwIX/2U6ZMweXLlzF37lw+b2wd\nZwrQ+vXrcfToUe55KVBACijfZKmwS0tLE7mihR+1Wq3mDaqA95qzt7c3pk6disGDB/OFULiQKZVK\n9OjRgy8E5kin0+HIkSP4/PPPMWHCBFE/CkvoxYsXH+19u3PnDuRyOeRyOZYsWYJ79+5hzZo13GI1\nbkUvpIsXL6Jnz54ICQlBhw4dcOTIEdHvWVlZOHfuHFauXImTJ0/ma2x79+7FxYsXefzaknbcRO/j\n9M2bNzfpqirk3PqWGLNSqcSqVatw6dIlDnTk4+NjgqliybnMVW1Isb+/v9lOtTmzDGqvAFiXrg27\nKq3hWDsSTnV7wjNyIYrG7BGVtDacEo8NJ69hw5Z4TJ8+HRs2bMDz58+h0+lw/PhxrF+/XhTyKVGi\nBF69esUTr80lXFaqVMnEG8W6Lg8bNixfigDRe4TfFy9emBWySqUSP/zwA09M9PPzw759+yQ9J+xv\ne3t7fp9sXdBqtejTpw9++OEHk/UiJ1YoFBg5cqQIdKtMmTJITEzk749Go4Gnpydq1KiBFStWmFSR\nPXv2jF/P19cXO3fuRKtWrUTvnK2tLVatWoXz58/z83p7eyMrKwvr1q0zec8LFy7Mk1xVKpWk0qtW\nq7F3717069cPRKZ4Qu3btweRAYztUyOW52XMzKP7559/mvQj8vf3x6+//lqggBRQ/slSBYRl0bu6\nuprElDUajajM9vnz56hatapZAWJvb4+qVavyRaxDhw5mr5uWlmaSBEZkyO342D1YjOnt27dYuXIl\nWrVqhZYtW2LFihVIT083W2ExdOjQXM95+PBhNG/eHH5+fqhTpw7i4uKg1+uRkJAgcvHb2tpi8uTJ\nmDFjBiIiIjBq1CgkJibmev7du3ejdu3acHBwQMmSJXNsYkZkyNEYO3asSKgYW+jW1tY59mBhuTXm\nuE2bNgAM1UnGFQgXLlxAdna2SQWDMbu4uOSpmdro0aN59RG7n3r16uHs2bOwdvOBlW8wtMUrwb5a\nO7iERcGj82x4D1xnggpaZNQuFBm5C56RC+FQozOsA2oioGo9EMkQFxeHxYsXmyRMmpurAQMGADB4\nCYXCX6iATZo0CXq9HosXLxYdW7p0aXTs2FEkyHOrGFGpVKL59vDwwJUrV3hJuKenp+h8FSpU4IbE\nq1evcvRUCUNao0aNEj2bwoULc4WJNTgUshRybF69cOydMA5TAO9bLQg9dcJwj1TZLlMeGN27dw+x\nsbEYOXIkNm7ciLdv3+LBgwdo1aqVCGXV398foaGhGDBgAFfw2FpZoUIFnhf1xx9/8PfCku/4n6CD\nBw8iPDwcAQEBaNq0KRISEgAYDEAGMOju7o5OnTrx98rb27tAASmg/JOlCgiLD3t4eCAoKAjDhg3D\n5cuXeeY/c9UyysrKwq5duxAdHY2xY8dyS7xChQr82V+9epUvXM2bN8eMGTNw7949HDx4EGvXrsW5\nc+d4ToCLiwvGjBmDwYMH84VFCCRkKbGk0XHjxmH8+PE4d+6cqHLlwYMHiI6Ohp+fn2SoISgoCC9e\nvMDmzZsREhICNzc3VKlSBWvWrMGrV68wf/581K1bFzVr1sT06dNFHS2//PJLyYW0ffv2ItwKcwJM\nJpNh+fLlZu8tJxAiY48V81J16NAh114awti7JWxrayuyIGUyGe7duwcAIpe7j48Pjh8/znNWjMcr\nFZawBBhMoVDgzJkzaNu9LzQ+ZeFUqSlcwqLQLHYvGn5x1CQR1HvwBnhExMKl+Qi4thoD24phULkW\ngUxj+hxYuaatrS3vByQ1NrVazQW9kKtXr55jp9+iRYti1apVouqanJ4l+7tt27YmVrlGozHbJl6j\n0aBx48YICwvDsGHDJL2Kr169wsyZMxEUFISAgAA0adJEUngbK0JCC1+q1b2xQmBvb49nz57h7t27\nvDS9QoUKmDlzJiZPnozAwED+TVhZWaFhw4Y830KtVvPka+E3LJPJoFar0bZtW77GsJyUdu3aYf36\n9ahXrx7KlSuHyMjIPOVTPH36FL///rsIhl5Ir1+/5gLayckJtWrV4mMwrlb7X6DvvvuOKxvM0Hz7\n9i2v/ClQQAoo32SJAnL27FnJhT80NJSXeOZW7sUqPoRdSKUEshTMMRGJxrhmzRoQGTLr80Lv3r2T\nDC907doVWVlZWLZsmaSV7ejoiLlz53IrPTo6GoAh4XbhwoXo3r07KlasKBlKKF68OB48eIBnz55x\nhWbSpElITEw0ez0ha7VarFmzhruk5XI5bty4Ab1ej9OnTyM6OhoDBgzA8uXL+aI+Y8YMXL58WSSo\nAgIC8PDhQ259MndwbspHfrhEiRImYGJz5szhpYfCLrFSrnn2uzEkNEsQZPPIz2PtCKuS1WFboRHs\nglvBpdlweA9cZ9KlteF/jqHVwqPwaNATGu/ScC9XEwqb3HMqpMY3YsQIDsplZ2eHmzdv8v46wnmw\n9HxElCvkukKhMBuu6tixY46KovC7kkrI9ff3z7E9AKPU1FSzpa5FihTBxo0bRfsbw/BLMbO0AUhW\nXD169Ijf+2+//YYff/wRFy5c4B2to6KiTMbJqlmKFSuGiRMnIiIigs+BJaWpH0p//PGHKAQok8nQ\nsWNHESzA/woxELX+/fuLtrOeWgUKSAHlm3JTQPR6vcgVa29vj1GjRonyQdzc3MyCcDFiJV0sWfXa\ntWuiRXHgwIHcalYqlejUqRNPuJPL5aJwy+3bt0FkwGTIC02ZMoXfw8iRIxEVFcUtOuMYt/DeiAxV\nL6xe3tnZOVfkx+bNm/OFunv37vj6669BZGhlLyRhyWJERAROnz5tUo3w9OlTPHjwgFscpUqVMgtx\nbWVlhV27dvE8A2FoY8WKFRzx09iSlbKq88sajQZ37tzJMbEyN85JMZPJZJBb2cM3rA9KDl1nip0x\nZKPBkxHUDNpiQVA6+4DkinwrW+bKfRmzd1oq36ZIkSJmm9VJsXHJb2hoaI6YGLmxnZ0dtmzZIlnC\nKXxniAhdunQx+WYyMjKwbNky1K9fHyEhIejYsaOJx0qr1SIkJARRUVEiT0JqamqOoTv2rr1584Yf\nw3IROnXqxLexSjtmcLA1iyWDGn9TgEFpkYLxnz59ep7WjA+lX3/9FYcPH8aff/75t173YxJLWg4M\nDOTrsF6v55VbBQpIAeWbclNAbt26BSJDpnx4eLjkIrJly5Zcr/Pzzz+DyGDFjR8/nlvgRAYrfP78\n+XwxIyIcPHgQjx494kqKsGRu7ty5IDJAD+eFmDv68OHDuHXrFsaPHy9ZXnjo0CETj4+9vT3evHkj\n2maMN0FkqLRhwpMBJWm1Wl6a17FjRwCGhT09PV0kGJYtW4ZWrVqZnDMnS9qccGLARcbCwhwQ18fm\nFi1amNyHTCaDi4tLvuL9MpkMjcLCofEOgGuL0SgyygDeVaj7fNhXawu1VwAUdq5Q2Yi9JkWLFhUJ\nwbzkkbA5yq3yj4tGLgAAIABJREFUxNnZGXq9nldICdnT01PSa1G6dOlcw0lDhw6FTqfjUN1s/4YN\nG5qF1Dfm2bNnc++Z8HpKpRJ16tQReZnUajXP3QAMeDJ5Kb9lzPrpHDhwAESGcAp75nZ2diaerX79\n+uHq1avYsmUL984I0YFZab+dnR1evHjB1yyWu9S9e3fJ7z0zMxPx8fGIjo7G5MmTLYIVLyBTevv2\nLTfE6tevjyVLlnBPslarLVBACsjQ7OzSpUu4c+dOno7LTQFh+B8+Pj549+4dFi1ahEqVKvEXMi+4\nHgy0SshKpRKHDh3iOAfMa8DiyMyKUSqV6Ny5MwfWIiJ88803Fl87KyuLH7d161bJag4mMJOTkzku\nAGOVSsVdjsx7wPIo2rRpw4Wcl5cXz4KfOHEiX/R/+eUXfp6QkBDuZRAKhby0KReyVK6Ku7u7aKEP\nCQkRKSOtW7eWzA/4UO9Hflmr1ZpeW6GC2rMkHOv0QJmRmwXhlHg4NegLlWtR0f6WluM6OTnlapnn\nlevXr8+RZC1h5s1iz0Sr1YpyRoQ5GcZooV26dMGDBw/4O2P83ki9D3K5XATOtW/fPgCGEkohUm5y\ncjK/LgOo8vLywpo1a0Res0qVKpkot6GhoXwsly9f5mWzFSpUwPHjx01CREWKFJFUzlq0aGECGV6n\nTh0QGSpioqKi0KZNG/6+nDhxwuJ1oIDyR8ePHzf5vtRqNXbs2FGggPx/pV9//RXjxo1D1apVRVZl\nrVq18Ntvv1l0jtwUkMzMTC6oFi5cCJ1Oh2fPnvEFISYmJk9jPnbsGLp3785bkVeoUAHp6emYNm0a\niN5XBFy5cgWZmZmScXGlUok5c+bk6boA+LmYFdyhQwdegscWcyJCz549Rd0xicSVDWyBnzVrFogM\nFpgwbMISZ5n1yEDacipv/VCuUKGCxdZ93759OYS6JcfkVCabm9IkZeXzHASZHNpiFeFUJxLOjQfD\npclguLWdBM9u8+E9eAOKjPrWoHTE7IZP1zlwCO0E61KhkGtt4erqipYtW3J0zbx4VYTNvxQKhWTb\neHNcp04dHD16NNeqHeP5EwpfuVzOFWAGd21lZSVSBISJnOzdYyEktVqNzZs3832ZYJgxYwb27duH\nly9f8tCeg4MD2rdvj/j4eBES7dChQ3nyNatisrOzg16vh16vx+rVq7l3zcHBAe3atZN85kKh1K1b\nN45YOnz4cLx9+5Y/63HjxuHu3btYuHAhr6Lbvn07Lly4gI4dO8LPzw9Vq1bFl19+Kdnc8vbt25J9\nZBjuzk8//YSlS5di06ZNIkTe7Oxss8miBZQ3Sk5Oxrx589C3b19Mnz6dh5UKFJD/h8T6iAhZWEHh\n4eEhsmbMkSVJqKysjAkPJrTc3Nxw//59yWPevXuHK1eu8IRJY0pJSeELaqFChUTIlh4eHli0aBF3\nMxctWpQnba5evdqiZDkpYmBo7BqtW7c2sbqZwJSyIl1dXbFmzRoe02ehIK1WK4J5NhbK3377LQAg\nMjJSJNA1Gg1XxPLCxkqDTCbj5Y7GgrhYsWIoW7Ysv2bdunWh1+t5eMgST8C2bdtMckbMKSVqtZrP\nqSivxMoemsLlYFsxDE4NB8C94wx4D1pvKHUdnQCfYZvhMzQOPkM2wSMiFtWjlsGpTndYlwqFws6Q\nS+Lr68uFolKpxM2bN3HmzBl+jSJFikiWbBuP2RiB0/h52djY8L4lxty2bVsAkKxwMWapEJ2lzDx+\nrJEb+/bM5bEY9yFKTk7ONQm2VKlSvKqH6H0PE5YrZY6Fz1WY3zJq1CisXr0aRIZ8JuB9UqkxN2rU\nyAQ8LDdKT0/HunXr0LZtW/To0QNXr17Fq1evTHKm7OzssHLlSvTr14+/32XKlDFJkC2gj0MFCsj/\nM2JlUcIW5WxhatSoERfc5lA5gfeodtHR0ZgwYQKePXuW4zXXrl3LS+SICI0bN8bvv/8OvV6PI0eO\nYNKkSYiNjcXNmzexZMkSkXs2KCgIP/zwg8k5f/nlF5NGacYLtouLCy5cuPDBcwYY6tmN8UnkcjnG\njBkjsmiFVrujoyOWLFmCU6dO8URbVr2j0WhyrDxwdHSEi4sLFAoFihUrxq3Fn3/+GX/++SfS0tLw\n5s0bSWGuUqk47LuxUMtJKAgVmqCgIH7vv//+Oy9NTE1N5d4bcyyTyfi4jJUPqdwRlWtRWBcug3nx\nx1Gq7Qi4toyBW5vx8IxcaIKtUTg6Hp6RC+HRJRbWATUhUxmUPSsrK7Rr1w53796FXq9H/fr1+fmL\nFStmkoPEkj+Fln1OLAX9nZOC4OnpKQLEYixElDV+Zl27dhVhbwwdOhSDBw9Gs2bNuHJoHDZhOUJS\nSZO5saOjI8aPHy+ZBP706VOMGTMG/v7+8PX1Re/evblHQip36Nq1a0hOTuYKLgtD1q1b1yQPRur+\nf/rpJ+716969O0JCQqDVauHm5obixYvD2dkZ/v7+mDVrlijXJK8kNJpYt1p7e3tERkaahE6Nv5nF\nixfn+7oFJE3/VQWEiO4Q0VUiukxEF//a5kxER4joxl//Ov21XUZEi4noJhH9QkSVjM9XoIB8OHXs\n2BFExC3q4OBgPHr0iFvtrBMqs2iMKSUlxQQeWavVYv369TleNzs7G7dv3+bYFqmpqTwUI8XFihXj\nC5eNjY1JvT7wXhHauXMnrl27hjt37mDq1Kno378/Fi9eLAI4+xjEmkSpVCqEhobi0KFDSE5O5mEm\ntvgqFArUq1cPKSkpePz4MUaNGoWAgAD4+/ujffv2OTbWcnBwkGxLzvjMmTNYt24dAgMDTbwZTEg5\nOztL9ubIS47G4MGD8euvvyIuLg5HjhzhY7p06ZJJPLdEiRImQqVSpUo8RGCyqNu5oGLrfnBuMhje\n/VeLK1FidsOr30p49f0KXl1j4dZ8OOyqtIG2eCUo7FxF88yE2Z9//imy4M1VGcnlcu5tYgoW29fZ\n2Rm+vr4mAFqhoaG55ofUq1fPxOvFQOIsVQyYp0volWEw6ocOHeJCP6dnyCqHrK2tERISIkJ/Na6Q\nkclkuHv3bp7e/wMHDkgqH6zp2bZt20Bk6EidmJjIlc/cPDkBAQEcSE8KK4TIoMjk1eshRUwBefLk\nCRQKBRQKhWhtYQaYg4MDEhMTkZmZyUtJHR0dc0VeLqC80d+hgLgabZtLRGP++nsMEcX+9XczIjpA\nBkWkOhGdNz5fgQIipuzsbOzbtw8zZ87E8uXLcfXqVbx+/TrHY5iWzyorvLy8kJmZyWPZDK6ZVVwY\nU0REBIgMyXifffYZr1eXyWSS4ZjU1FQMHz6cW0+BgYHYvHkzz59wc3PDqFGj0KlTJ77YDBkyBElJ\nSQgLC+Pxbk9PT+zevfujzNvdu3exbt06bNq0KVfvDSNLMAmMOSgoKNcW7TmxlNVtLnxhbuG2hOVy\nOWxsbESWqpSSpFar8e233/J7i46ONhFIQuAnIoJMpYW6UCl41O6MilGr4D1g7XtvRtRWuLWdhCL1\nOsOqZAhUrkVACsug1Rm7u7uLntPJkydB9B72XaVS8fwdHx8fXtJcu3ZtvH37ljcEs5Tt7OxEAtXR\n0ZErBS1btuTbV61aBQA4deqUaF6FFjVT6mQyGbKzs/Htt9+iadOmon2E89uqVSucO3cO58+f50qY\nt7c3ihQpgkGDBvFkZSl2dnbGzz//jNevX/PqKVZxkhe6desWYmJiEB4ejv79+4s8jKzkkvWOOX36\ntCjso1AoRPdjrEz5+fnx3+3s7FC2bFkMHDiQn2Pbtm15Hq8xMQXk7NmzIHqfY8WIKSD+/v6i7Wx9\nPHbs2AePoYDeU24KiJI+PrUiorp//f01ER0nos//2r4BAIjonEwmc5TJZIUAPJI6ycWLF/8LQ8sf\nAaB3796RRqMhmUz2t1zzyZMnFB0dTTdv3hRtl8vl1LBhQxo+fDi5urqaHOfm5kZERAcPHqQiRYrQ\nn3/+SaGhoXT16lWSy+W0evVqIiIKCgqib775hmxtbcnZ2ZmIiF68eEHbtm0jhUJBa9asocKFCxMR\n0dy5c2n79u00ffp0mjhxIr9WZmYm9evXjxITE/m2K1euUEREBCkUCpLJZLRs2TIqVqwYPXjwgLZu\n3UpERIcPH6alS5cyhZWIiB4/fkwtW7akmJgYat++fb7mTK/X0/z582n79u2k1+v5fDk4OJCzszPV\nqVOHIiIiyMHBQXTcr7/+SmPGjLHoGk5OTtS7d2/auHEjXbp0iYiIypQpQ71796bPP/+csrOziYio\nWrVq5OTkRAcPHjR7rjdv3pCNjQ1VqVKFjh8/TkTEj2ek0WhILpdTeno61atXj06cOMHvLTfSaDTk\n7e1NSUlJlJaWRmlpaWRnZ0evX7+mO3fukFwuJw8PD3r8+DFfENizfPv2LXXp0oVatmxJt2/fpjM/\nnKO4A6fonW9t8qv4Gb3WKUnh5E06axfSk+GbePr8Hr17fJ1e/7Sb3t69QllP75JapaSnmZkWjVdI\nMpmMAFCpUqVEa8GCBQuIiCg0NJTu3btHSUlJ5OjoSHZ2dnT//n0aNGgQ/71nz550+PBhfi5L6PXr\n11S5cmV6+PAhPXr0iFJSUkilUlGLFi0oOjqa9u3bRzqdjs6cOUMVK1YkrVZLrVq1ovXr1xMRkU6n\nI6VSSU2bNqXWrVtTnz59CAAFBQXR1atXTa6XkZFBtra2pFAoKCEhgRISEqho0aLk4eFB9+7do+Dg\nYIqJiSEioqlTp/LjgoKCqEyZMhQXF0fu7u6UnJxMo0ePpjlz5pCdnR0REf3222/5WkeNvz92Dicn\nJ9JoNHTs2DEaOXIkhYeHk1L5XoTMnTuXQkJC6O7duxQZGUmZmZm0bt06Sk5OJmdnZzp+/DjFxcXx\neU5MTKTExETy9fUlIqL169fzvz+Unj9/TkREiYmJdPDgQb5WPnjwgIiIFAoFvy8AlJqaSkREN27c\nIFtb248yhgIiKlmyZI6/f6gCAiI6/JfF8BWAlUTkwZQKAI9kMpn7X/t6E9E9wbH3/9omqYD8U5Se\nnk7Jycnk4uJCNjY2tGXLFtq6dSs9fvyYHBwcqFWrVtS3b1/SarX/1XFMnDiRbt68STY2NpSWlsa3\n6/V6Onz4MP3xxx+0ceNGev78Oe3YsYOuXbtGDg4O5O7uTnK5nBISEsjX19fkQ0tPTyd/f3+KjY2l\nly9fEhFR9erVKSYmhlJTU0mn05G/vz85OzvTwYMH6eXLl1SoUCEiIrp3755ojEeOHKHExETy9PSk\n2NhYKlGiBO3YsYMWLFhAOp2OChUqRMWKFSMiImtra37cH3/8QURESqWSypYtS1euXOG/ffnll9Ss\nWTOysbHhY75x4wY9e/aMihcvzsciRZs2beIKVJUqVejSpUuUnZ1NL1++pJcvX9KtW7do7dq1VKxY\nMercuTO1adOG0tLSaPr06UREZG9vT61ataL4+Hh69+6d5DVevnxJR44coaFDh9KECROIiGjy5Ml0\n+fJlys7OpsqVK9NPP/1EV65coeLFi/Pj+vTpQxEREdSwYUORAtG9e3eKjIykkJAQkZB0cnKiatWq\n0WeffUbLly+nS5cuUXJyMs2fP5/mzp1LDx8+5PvKZDLq2bMnJScn03fffUcZGRnk7OxMy5YtI19f\nX7py5QrduHGDXFxcqHDhwhQREcHfpUePDJ+fo6MjpaSk0J07d8jGxoaSUnT0xab9VKpSKJ2450R3\nHMLIs2srektE6bps0qWnUtbj26R4fZ5c5W/ot9MHSffqqWiugoOD+bxbSiVLliQ/Pz86duwYvXv3\njlq0aMF/y8rKovPnzxMR0YkTJ/j2n3/+mf+dlpZGzs7OVKNGDZo3bx4RkaTyUa1aNQoODqaVK1dS\nVlYWERGVK1eObt26RT/99BMFBgbSkydPSK/XU+PGjalSpUo0ceJE0ul0RES0ceNGSkpKovT0dP59\nTZo0iXx9fcnb25scHR2JiKh06dL0+++/SyofRMSVS71eT46OjvTu3Tu6e/cu/z0hIYEOHDhAKpVK\ntA58/vnn9Pr1a4qLi6M3b94QEdGxY8do//79XOktW7asRXNuKTk6OlK/fv1oyZIlNH/+fJo/fz7/\nLTAwkGrWrElyuZyKFy9OVlZWlJmZSa6urlSuXDnKyMigqKgoIiJydXWlVatW0R9//EGzZs2ipKQk\nIpJ+TvklT09PCg0NpbNnz1Lv3r2pRYsWdP/+fT63Dx8+pPPnz5Ovry9t3bqV7t69S87OzlSuXLkP\nui4A+vXXX+nnn38mjUZDdevWJU9Pz49xS/9OknKLWMpE5PXXv+5EdIWIahNRitE+L//6dx8R1RRs\nP0pElYX7/l0hmOzsbHzzzTfo0aMHunXrhri4OKSkpGDIkCE8zq5QKERVA0J3YtOmTSWrNz4WMVer\nvb09jz3Hx8fzkjgW7hg9erSkG1+KnZyc0KRJE1FzMG9vb35+Ly8vXL16lScYSlVAVKlSRTROFlZZ\nunSpaLsQjvnKlSt8u7Hbv2XLltz9KozD16pVC7169cJXX33FW8bTX67sdu3aiUrpGOl0Onh5eYGI\nsGvXLl7WmlNJpKurq8jdnls4xVwH1bVr13JcBBZ6UigUorDJpEmTAEAy/0MKc+PVq1c4ceKESZdX\nuVyOcePGYdu2bYiJieH3LGR7e3tcunRJND+PHz/GjJmzEFKnAdSeJVG5bhgWLVuJcbFfYmnCGfT7\nYgvcO0xDmeivETh+lyhvo1CvL+FUvw+sSobAxsUTc+bEYuvWrSLEVaVSCR8fHxQuXFgyj4G53seP\nH4/U1FRRhURgYKBkiKlXr15mcz8cHR0lE0xZCIu9NzKZDKtXr8bly5dF+wcEBHBwMBZC2bx5M3bs\n2CFqCS91H+XLlxe9NxqNBgsXLpT8lt++fSv5jHr37i3K4xk+fDh27twp2sc476RUqVKi8E2DBg1M\nmj8yLl++fK45FSdOnEC7du1QtmxZNG3aFDt37sxxXbt//z6mTJmCatWqwd3dHRqNhr+fTZs2RWpq\nKrKzs3kSs5+fH0fHPHjwoGgdXbRoETIyMjB48GA+5ri4uBzHawkJk1AfPnyIcuXKmcyN1Jogk8k+\n+PppaWkiLCJ2v7Nnz/7g+/pfpb+tCoaIphDRKCK6TkSF/tpWiIiu//X3V0TUWbA/3w9/owJiLi4s\njOMao/ExDg8P58LfuF36xyQWh2dlcDVr1gQAbNiwQbSdKR9SSXKMw8LC8NNPP2Hz5s2iZm2bN2+G\nXq/Hs2fPuGCdMWOGqLpAioULLeu3IEQiBcQKiL29vQjbQ4rr1atnFu6cPZuQkBA+9vDwcJM5e/ny\nJYgMuRJv377lZY75qR6oXbt2rvsYJ4iy/iZMMJUoUUKkVE2YMAHZ2dmSvTYYC+HJV69ebVJWyRZO\nhUKB27dv8/ueOHEiypQpA19fX/Tp0wfXr1/n83I+6TkGrToKr+5foPDw7SbQ5EL26rMcQVEr0Xv9\nj4haHA8H34pQuviIxqBUKjm408uXLyUTEJ2dnbmgEVbFFC9eHHq9Hk+ePBEpHE2aNMHTp08xZ84c\ntGzZEt26dcP+/ftFwvD169dcKTZXrdG7d29cv37d5FtgKJfC/kKBgYHo06cPiN7nk3z++eeS92Nt\nbY2wsDCTd0kmk6F+/fq5rgUMhj00NBRTp07lymHPnj35uVJTU/l3+Pnnn/P7Y6i1ZcqUMWtsSI2Z\nVQGZI1YSa8yjR4+W3P/EiROS158wYQJXgrRarej93rRpEz+eQaObMwhcXFzw7t27HMdsCRlDBzDE\n0xEjRmDatGn4448/kJaWhilTpsDPzw9OTk5o1KjRR1nPmTLl4OCAgQMHol27dvzZMHC3/2/0X1NA\niMiGiOwEf58loqZENI/ESahz//q7OYmTUC8Yn/PvUEBmzJgBIoP1O3fuXCxcuJCXhapUKhw4cMDE\n8hk5ciT3hjALd9SoUfj2229Rt25duLu7IygoCEuXLjVB6csPsS6R7IMvU6YM9Ho9F/hCAenj48Nf\n/M8++wwTJ04E0fv+JdbW1pLloAsWLODXY8BajRo1EmFWSC1y9vb2uHjxItasWcMTWgsVKoTvv/8e\nz58/54igjo6OFicA7ty5U2TZzZs3T5Twx7hixYr8OURERGDkyJE4c+YM9Ho9srKyuDW2d+9eyetI\nWYt5hd+2ZPH/b56LjXfatGkAgHdZOqS/y8bV+yk4nPgYcw/+joGbLqL/hovosuqcQbkYvRue3b6A\nS9gw2FVuCevSdWBTrj7sq34G69K1ofEO4I3XtFotvv/+e7Ru3Zp/E02aNBEpkBUqVIBerxfNc4MG\nDTBz5kwT4S+8J1tbW0ydOpUnjTLrtEmTJrl+E1evXgWRQbFLTExElSpVRNcR9hxq0qSJ6DcPDw+M\nHTuWo9Oy+xR6vKRKNInee0FYiba1tTV69uwpEi6zZs3KceyHDx/mY2QggD/++KPIy/jbb79xpY1V\nyri5uSElJUU0j/Xr15f0Tmo0GqxYsYInirq6upr1Zrx48YIrgKNHj8bFixfxn//8hytixt1fMzMz\nuRenadOm2LhxIwYNGsTH9c0334gq3vz8/ETKBwA8f/6cK4wDBgzgSZ/sno29qPklSzt4f2xKS0vj\ncypEqmXypnnz5n/7mD4F+m8qIL5kCLtcIaJEIhr/13YXMoRXbvz1r/Nf22VEtJSIbpGhdDfY+Jy5\nKSBJSUkYP348IiIiMGnSJNy5cweXLl3CN998Y3HLZIaYd+DAAb4tJiaGL7bMMhAiIMbExHBhyxYi\nc54Cf39/zJw5k7cYzy+xbG32gbLFUi6Xi9zyNWvW5K7w7777DnFxcSAyZNQLXc4lS5bkiwbjc+fO\nAXhvGbZu3Zo3ETJmc+WB5rAnVq5cKQmIlhuz7pXC+TUXEmLcs2dP6HQ6/oykSgnNCfeckDxzYnMt\n4a2trUXXMjdvUuORy+UYHjMGo/6zFi5VW8EuuCXsKoWjXq8xGPnVXgT0jIVnt//AIyIWxbvPgf/o\neBSN2S3yYviO2YeK43bCb8ha+A5chWr9ZnMsjaCgICQmJuLYsWOS12dCxhyOhfDfmzdvioR2WFgY\n6tata9G7QWSowmHWcGRkJJYuXYoLFy6YFZpPnjzhWCUMbI5VbBG994plZGSIvC6WNmtj3xS7dy8v\nL5FQZc/x6NGjfEws7FaxYsUcv2WdTsfPJZPJeKdcIuL4ORUrVuQeM7ZGDR48GD/88INoXJs2beLV\nNMLxMyyd7Oxsvk0KNRQANm3aBCLTfkkMqXT8+PGi7fv37weRYW0TGljMgzNu3DgABoCzP//8U9Qc\nUkhCEDPh9xwYGPhB2B9C+qcUkKSkJBAZPH5Cunz5MogMIb//j/SvASLbvn27SY8O44UyNDQ0186C\nbKF58uQJ3yZ0R7K4sLBhVlhYGIYOHSpagJklOmfOHOzfv18SC581Yrt58yYSEhLMLrA3btzA8OHD\nUb9+fXTu3BmHDx/GnTt3TIC4hNy8eXOoVCrI5XKurMTGxvK/J0+ezDVyGxsbPHv2DDqdDqVKleLn\naNmyJb7++msefgoMDBQt3mq1Go0aNTLJW9BoNOjQoYOohbqHhwe0Wi1CQ0ORkJCAjIyMXBt1GbON\njQ10Oh0yMjJE7l5fX1+8efNGlEPStWtXjBo1intEVq5cia+++ipfzczyWqopZCEAG5HByjcWepUq\nVRJtK1KkCAYNHgwvv9Kw8g2GfeVwONTsggqfb0PxMeZDJGXH74ZH13nw7D4fXn2Ww7XFaDjW62WA\nIQ+oBY13adi7uJsdq9DNLHymffv2NYvuWaZMGdSsWVMkhIlIFI4w1y03MjIS0dHRIDKfP2OsoDVs\n2BAvX76U/HZZG3V/f38sWLCAA00REZo1a4a1a9dysKuSJUvyPBOZTCYSeFFRUbzBmVRo0N7eHmfO\nnMH58+dNnq1er8ebN28QHR0tUlpmzZqVo/czNTUVvXv35h4iGxsbDB06FLdu3ZIMS3h4eGDBggX8\nnTde6xo2bMgNDKVSydcVFqYtWbKk2bF89dVXIBJ3lQXeIyhHR0eLtrPS5vbt24u2M/yMPn36mL2W\nkFhTPvbuWVlZoXfv3haXyltC/5QC8ubNG772CPPeZs+eDSLzuEv/dvpXKCBPnz7lD7dDhw5YtWqV\nyAvQpEkTLuzKlSuX40LAFighEiizZIiINwvLCSqZLcgNGjRAdnY2X0BYzJ7BHCuVShN3cPny5XH1\n6lV+7e+++05SaMbExCArKwsJCQno06cPgoKCUKxYMVSvXh3Lly9HVlaWKIHLeAEVwiiHhoby6x07\ndszisINCoZDc18/PD15eXlAqlXzsLVq0EM3ztWvX+EJrybWYAjd79myTRlYajQZffvmlCMabxYvX\nrVsHItPOrnlhS3I+2IIpFJoODg4ihU7I1apVg9rDDzblG8KqRFW41eoE19Zj4dFxOrwHrn3fy0SY\ng9FvFZzq9YaVbzDUjh6QWztAbmUPlVMhHiJhbCkuiFDAf/3119DpdNizZ49ImR8zZgy/H3PnyWuo\nSqFQ4NmzZ/jmm29AZMjjKVy4sOS7Xr16dfTo0YPnXjFI83v37mHevHn4/PPPER8fj9u3b8Pf3z/X\na7u4uODixYt4/PgxOnbsyL1cLi4umDp1KrKzs/H27VuufBh7aooWLYoHDx5wYc7eQSLC6dOnzXo/\nBwwYYHbdYfTq1SvcvHlTBHj17NkzTJkyBZUqVZJ8rsJtjo6OfA6F4a6GDRsiLCyMr1nLli0zO4bf\nfvuNv8/Mc3Lz5k3umdm1a5dof5YUb2tri6SkJACGkANbY3K6lhTp9Xo8f/78o+R8GNM/pYAA4E0z\nnZycMGzYMHTq1Il/f3v27PlHxvRP079CAVm6dCmIDDkKer0eCQkJog9w3bp1eP78Odes9+7da3ZC\nWF8MIkOmfG6tq4ULuK2tLRYtWoS1a9eCyBDmOHToEIgMVvqECRNAZAD7ErZSt7KyQuPGjTlaoaen\nJ1JSUpCH4Y3GAAAgAElEQVSZmck9Dm3btsW+ffswdepULhx++OEH6PV6HDhwAD169ED79u2xaNEi\nXgWSmZmJ6OhoswmoWq2Wu61v3rwJwPDxs0xtJycnUQjCXPKtpdygQQO8ffsWv/32G89XkRrTh1yD\nyOC+Z8Tacf+jLJND6VgI9pXD4dp6LDy7foEiQzaYKhh9V6JQr6VwaT4CjrW7w65SODQ+ZSG3cQQp\nTDvw5oWFCnmhQoUQExMj6UGTUgjzmsdSrFgxk+oCYwVlyJAhyMrKEoUbzPHSpUuxdetW1KtXj48l\nJibGRDFwcnLCoUOHMG/ePHTp0gVRUVE4e/YsfvrpJ77gx8bG4unTp6JvPjU1Fbdv3xYJPNaHpFSp\nUnj48CE3KszNLQtPMGVAq9Xy8XXu3BkqlQoymQy3bt0yu/ZYQunp6fjqq6/QsmVLtGrVinuQ3Nzc\nJEN+arVapEwqlUqMHTs21yo9YfiqaNGifJ2rUqWKZPUMC82ytYwp/F5eXpJVaf8U/ZMKyJs3b0yS\n6WUyGc/X+v9I/woFhGWCjx07FsB7VyHTwFn3U1aml1OfEwBYsWKFKGRibW2N2bNn49ixY2jXrh3K\nlSsHf39/ntHt6OiIUaNGcavl7t27kMvlUCqV3AvRtGlTrmDs2bOHZ7KrVCq+KKWnp/PywC+//JL3\nbSlZsqQobspaYw8ePBjdu3c3WXSKFi2KpKQkrsS8fPkSp0+fxsSJEyVbyRMZrNvIyEjuClepVDxn\ngsgQstHr9dw9a7wAS5WPSgkuBweHPKF2Ms9VTqETtjiy63Xp0oXP1eTJk032t7Q0OT8sU1tBU7gc\n7CqFw7PLXBTqsVjkzfDuvxruHWfApdlw2FUKR1DtxlB7luQw4+bmLcdr5rA/y8OQEk7/bVar1Vi/\nfr1JtY5CoUBkZKQo+Zn1ajGX+5Kf6zds2NDizs7GxDrCMpjxc+fOSb6Dtra2uHLlCt6+fWvSb4bI\nkAx94cIFbnAwhNSPRaykNSoqCklJSejVqxfc3d35NzZ06FA8ffoUmzdvxsaNG/Hw4UOLzpuRkYHh\nw4fzb0WlUqFLly68lYIxvXz50qTJXoUKFZCYmPgxb/eD6Z9UQACDgXfy5ElMnz4dX3zxBfcY/X+l\nf4UCwurj/fz8kJKSwmHGmeXPSvZYEtzKlStznZjXr19j37592L17t9mYs06nQ0pKiklIJyUlxWxM\nu3bt2sjIyOCLb2BgoOhY1m+kQ4cOvPqkadOmAAwfubDTK+tbwXIxxo4dy5Nj2WJpZWWFXr164dGj\nRzm60I0FR/v27UVW344dO/gYhcqZra0tunXrlmeh2aJFC2zdujXHfXx9faFWqyGTyUQWWUREBFav\nXm22R4dcLkfjxo1z7DXzsVimsYF16dpwCRsGj4g5KDLyPUaG96D18Og8G451ImFTviHUhaTDMRZf\ny4I5ViqVIq8VC/cZ92Ux5xXL6/WE7O/vj+TkZF4ho9VqodPp8O7dOxw6dMhsSLBPnz6i5GapxF+1\nWo3Y2FgTD5mVlRViY2N5ySx7/uz+XF1dzXZdzomGDx8OIgP+BqNLly5xL6CzszOGDBmCx48f89/1\nej26dOkCIoPil5iYyAUeC7V+/fXXktc7ceIEIiIiEBoaih49eljcRJEZBI0aNRJtZxgiS5YsyfO9\nCyktLQ3Xr183uwYKSafT4auvvkL9+vXRuHFjfPXVV59c75R/WgEpIDH9KxSQzMxMLtBdXV1FGeAO\nDg5Yu3Yt2rdvzxfFwYMHY8SIEfjuu+8+OmDYixcvRCBKxot+586dRXFqPz8/HnMeNGiQyK3MEv/k\ncjkmTpxoUR4DK2Fk98r+ZsfKZDIsXLgQ+/fvF7Ufb9CgAdzc3MyeV6PRYMGCBXj37p1kKEYmk5mN\nv0tZjjNnzgQAfPbZZ7kKvG7dunHgMKL3yXF37941SfI0J5TzIkilWBhCUNi7w65yC7h3nMG9Gz5D\n4+AREQu3xgNhVbI6bD2Lg2S5W+5S1n1O45UKUW3ZssVsAzZ2PqmKE+OuquxvSzvEGjPzNCYmJvJt\nZ8+e5d/GkCFDQERo06YNFi9ezMM0O3fu5MaBVquV9NJptVquTAm9Of369UNmZqaJl+XgwYP8nDEx\nMXn+jlmCqVqtxty5c3Hq1Cmu5Dg7OyM9PV20/927d3H27FkOqGVlZYUNGzZgz549PEFdrVYjOTnZ\n5FrCHDPhs1m7dm2u43z27Bn/vnr27ImdO3fycarVapGC9N+krKwsUVhZ+C6xqqRPgQoUkE+L/hUK\nCGAocxKiYkoJNCkB16JFC1E76tu3b+PIkSO4ceNGviaUgQr5+/vj4MGDOHXqlEkbdyJDORZTCpo0\naWKCM2BOCLF7EFqwlStXxqBBg0wUg5iYGOzYsYMv3EQGhYfRmzdvuKuWeUdKly6NKVOmmE0OFSoT\nwvh9YGCgpGLC9jfOAahRowYA4M6dO2Y9GTKZDH379kVaWpoJVknbtm0xb948keAcNGgQNm/ejHr1\n6omuOWLEiHwKVRms/YLh1HAAnJsMQUCvuSjUe9l7BNDey+BYJxJqrwA0/8v9np9wgVSL+txY+C4H\nBQVxxfNDmtIxlkJezY21Wi3PrcjOzuZzX7RoUUyfPl3UbPDixYsAgGnTpoGIEBISgqioKJP7EyrT\njP39/Xl4hMgQdmUKj3BODhw4gCNHjoDIUBqfH2JeECErlUqRN/DevXuiKimlUimJq0NEmDt3rsk1\nkpKSIJfLIZPJMHbsWHz//fdcYdFqtRZVgMTFxZkomHK5PNcO1R+Tli1bBiLDOjJr1iysWLGCGySd\nO3f+28aRGxUoIJ8W/WsUEMDgAr1w4QLi4+Px008/4caNGxg3bhw6derE3fEODg4YO3Ysxo0bxwXm\n1KlT8fTpU5MYboMGDSx23+p0Ojx79owvPsKuicnJyVwwLV68GHv27EFmZiZOnjxpAqVNZEBszGmx\nl8vlohBP6dKluftTan/jkkiGiZKZmSlSNOzs7PD8+XNeGpaTxyU0NBSLFi1C586dTdqjWyKwihQp\ngoyMDF6qa44LFy4sOUfGLATy0el0IoUjt0obuY0jrPyqwqFGBFyaj4BL+Eh4dJ6NwtHxhq6t0fHw\nGRoH36Eb4N5uCuyrtoHS6T18trlKl5yuLVQgLbk/cyxVfaLRaDB58mTJuTX3fD4UME2hUODKlSt4\n/fq1CDfHeJ8vv/xS9F0wZcdcbpKQq1atinfv3onK4m1tbdGuXTvRfkqlEk+ePOGYN3Xq1LHoG5Za\nT7799lu0aNECwcHB6NGjhwhEKiMjgwtZKysrBAUF8e+8YsWKqFy5MpydnVGpUiWTyhFG7FuLiIgQ\nbWfeyTVr1lg01sTERAwbNgzNmzfHkCFD8Msvv+TrnvNLbD0SwpXfvn0bMpkMKpUKb968+VvHY44K\nFJBPi/5VCkhOxOrlN27cyMMuDIHQy8uL51VotVrUrFmTJ1+VK1cux54J2dnZmDFjhkmMvX79+rze\nOyMjg3sCJk6ciMqVK6NcuXKIiorChQsX+AJavHhxXLp0icfDWRmg0MpngsLY0i1RogQHKCIyWNWd\nOnWStIhVKhUaN25sEnKpXr26KFObJbh6e3ujdu3akkLCwcEhVyXCnKAzzkNwcnISxfKNOadESiFy\nKwDRXPBrK9VQObhDW6wiHEI6wu2zifAe+L49fJHRCfAZvBHeA9fBs9t/4NRwAGzK1AXJc/ZG5cRC\nb0JOwFvmWC6Xm1SrqNVqEwwVlUrFYaO3bNmCp0+fYu3atejXrx+aN2+O1q1b8/nTarUmYbH8KiDb\ntm0zG97ZsmULtmzZgpEjR2LmzJkcHl5If/zxhyTMvlSJt1wuz1HZY6zVatGzZ0/uWRIqPR+TNm7c\nCCJDkjgLrVy9epV/c7/++muuAm/s2LEgeg/Wxcg4CfZTJwY1IEw61ev1PFE/P3k4/w0qUEA+Lfp/\noYCwahLGFStWxJEjR5CRkSHa7ubmhj///BP379/Hzz//zCs7zFkvwPvabim2trbGuXPneFhGKn7v\n4uKCFStWgMig7Oj1eq54sI/XuKTR2KqWCmGUKVPGRDCYw2ro0qVLruicNjY2OSYuKhSKDy6hjY2N\nBQDJBN7du3dDp9Nhw4YNPPTj7e2N0aNHG+63UUesOn4dC45cR5NZu+HeYRo8u36Bwj3mw7PbfBTq\nvRRFjFBBvfosh2v4KNhVaQOnUsEICpZOHDbmEiVK5EnpyisbKwP29vbYsWOHpKfEzc0NcXFxXKn+\n8ccfMWLECJNn1aBBgzwrQMHBwfzdlOJ+/fohPT2dj8vW1hYymQw1atTAwYMH8/SNPn78GKdPnzZ5\n90qXLm1SAmtnZ4cJEybg7NmzkmEaIdeqVeujoWgaE0uqZe8to44dO4LI0K8nN4HHeqB4e3tzkMRr\n165x7yxDI/7UieVyDR06lL+L27dvB5EBVuBjtKD4GFSggHxa9K9XQE6fPi3Kp2ALM6uHJ3ofamjV\nqhWvLCF6b3FXqVIFQ4YMwe7du5GdnY2srCz8+OOP2L59O2QyGV80q1WrZpJQZpzL4efnhz179uDU\nqVNo0KABiEhUN9+lS5dchZuxJyI8PBzt27fPNf/A1tZWBCFvbW2NKVOmiJpwSQlDqfyJGjVqSCaX\n+vj4YO/evaJ8kNy6yDL+z3/+AwCi+5dbO8K1bE38+iAFfz5Pw63k11i+5wc41o5E8U4T0WvtDygy\ncLURYNdKeEYuhHvH6fDoNNPwb9d5cKgRAdvAJtAWqwiZxjQ0klPyp4eHB5o3b45169ZxvIhffvnF\nRHGbOnUqB3ISzmFePAxqtdqkl4mQPT09Ua9ePZHgZ8mGCxcu5Ps1btwYHTp0EL0vTKk1VlBY2bhw\nm5WVlaiySsihoaE4deoUTw4ODg6GXq+HTqdDWloa1q5di0GDBmHixIm4du2a5Lep0+kQHx+PVq1a\noU6dOoiJieHCW6PRoEGDBrxxoVqtxpEjR3Dp0iWRO5/lHhQrVoyD8jHIeJVKZXHZaX6IGRb9+vXj\n2/R6Pc9F27FjR64CLzs7m8MFqFQqVKhQgSuKDNfof4HOnDnD15+yZcuKlMZ58+b908PjVKCAfFr0\nr1dAWIIYQ7OUyWQmAjEyMpL/RmSwOM2VrJYrV84EPIl5FljpXK9evUyEMnOZ9+zZk7sjnz59yhf9\n+Ph4sx4Kc4qFcV8RY7axsREloBIRpk+fjuvXr+PChQt48+YN0tPTuVASQpnnxFqtlntlpLwixh4Z\nlUpltoeMkO3s7PBZ27ZQuRaBQ80IeHSejSKjEyRhx4uMTkDx4VsROvsomv3nO5Ru1gsKOzfIlLmX\nl1rCKpVKMlRBZFC+Xr9+DQAi4dytWzcA4HD9UngjSqVSlCtgjtlzY+58Ns8eHh6S8OCFChXC06dP\nufImBDdiyZ7smu7u7khJSeFCgr2D3bp1439Ljd3R0VGy6sjGxoZb6jdu3DB5j2QymUkoQafTiUqr\nhe8OU8wZu7i4ICEhQfL7ZuHL1atXi7YzL1pePTF5IdYAj1WpHTp0iDejdHR0RFpamkUCLzk5GW3a\ntOHfslKpRLdu3T4pAC9LKD4+XhTW1Wg0GD9+/CelRBUoIJ8W/asVEL1ez4V6cnIyJk2aZGLljRs3\nDs+fP+dWR4kSJbBt2zaRFa7RaEwEfdGiRU1K/1gbbXMdYxmr1Wps27YNmZmZot4ziYmJGDhwIGrW\nrGm2MkSKbW1t0bRpU5MqIKFwYffTunVr0RydPn0aRJRjG3gmRKSEdH5yB9RqNXr06IF6jZtB6ewD\nbbEg2JRvCJdmw0U5GT7DNqNU25HQ+laGe+Um8KrZDk5VWsG6ZDWQTI7g4GB07doVgwYNMnkW7Dp5\nHRsT0uPGjePoln5+fli9ejVWrFjB8womTJgA4H0fDCLTBmUMkrtFixaIjo7GokWL8OzZM97NmMhQ\nAWX83NgY/Pz8eAUVqyLJqcqlcuXKPOfk+vXr/BkLx0hk8PQBwJw5cyyel/Lly+PNmzdIS0vDF198\ngeDgYAQEBKBv374iDwd7z8qWLYt58+ahR48e/B0RLvwM48bOzg6LFi3Cvn37OFZGYGAgfv/9d3z9\n9ddISEgwKXkVEsPdEFrZer2eJ4ceP37corUiv8SUO+NvbufOnQDyJvAePnyICxcuSJbq/q9QRkYG\njhw5gj179nzUHi4fiwoUkE+L/mcVEDc3N4SGhmLz5s0mGnZmZiamTp0qEkrDhg1DVlYWHj58yDPP\nbW1t+TG5NSkzjp8fO3YMjx8/Fm2vUaMGFi5cmKN1K7RyGHZDQECAyT0IMTUcHBxMBL21tTXat29v\nETy6k5MTh2wWNoZ69eoVpk+fbvYehcxwVNjY8yrYiQgylRYq16KoOPhLBM84YuLV8BkaB9dWY2Ab\n1Ax+ZStixYoVZsGrPgaz52RjY8M9OqwctESJElw5PHbsGMaNG4dKlSrx5+Lj4wPAIOyMuwgrlUoE\nBgZyrwUrO2X7M+Redn1ra2uTd8bDw4OHvnJ6n4x/YwoSA9u7ceMGD0kI38FVq1bxe2G/e3h4YMiQ\nIVizZg3q1asHZ2dnlC5dGrGxsRb15WAeAScnJ5H1zua0f//+fBvLGRAmD799+5Ync1uKoMnay2u1\nWrRv3x579+7leCMeHh7/lX4ixvT999+jc+fOqF27NgYMGCDq5VQg8D4tKngenxb9zyogwgV18uTJ\nopsSYg4IBXe1atXw3XffcYuzd+/e/BimrHTq1AlhYWEi61kul+Pp06eiKozatWsDsMyKZBUK5n6P\nj48XjV+v13MXvJOTE9LS0vD69Wue1MXGaRzqkRT6f90/ywM4efIkAGDbtm1myz+NwzYfwgobJ9Tp\nGgWXsCgUHr7dUNY6fDvK945F4ca9YV26DqxKVIXavTgeP0mGXq9HVlYWsrOzTdq3W3qvxspAbsc5\nODhAoVBALpfz9uZCj5BUDotMJhNZqi1btjT77E+dOgXAkAwtDNlYWVmJ5jqvGB5SCZgsdKjRaDBk\nyJBcweuY4q3VanPtFJ0bHThwgI9r/fr13FPJ3tvw8HC+LwuzGIdWAgMDQUQ4c+aMyfn1ej3279+P\niIgINGnSBFFRUWZB/xQKBbZv3/5B9/MxqEDgfVpU8Dw+LfqfVUDu37+PJUuW8CRQtnhevHgRRAar\n9tChQ1i6dKmkBVmkSBGcP38ex48fx+3bt7nVVL58eRw6dEhU+sg6ubJeLozfvXvHm53JZDJRPoRQ\n4ejYsSNPThUqNvb29tiyZYvogTx8+NDEJa9SqdC9e3dRfFWI9iolUKR49OjRyMjIwOXLl/MFmNWl\nSxfMmzfPRNCrXIvAtmIYbAObwr5aWzjW7Qn3DtPgM2TTe+9G1Fa4hI+EbYVGUNiZIq4atwdnXVLZ\n/UyaNAkLFizg+5sbv3EljrW1tUl4xvg5Mh4xYgTvs9OkSRORslClShUcPnyYJ0kSGbxqjJ4/fy6a\neysrK+6NcHFxwdGjR7kSKFT8ZDIZFixYgIEDB/J5HT58OGJiYiCTyaBUKrF582YcOnTILOYH81yx\n41lbeiFXr14dAwYMkMzZsbGxwe7du/m9pKWlISEhAVu2bLFYKUlOTuYJo4xtbW2xfft27u0QIpKO\nHz8eRIbqHAbXvX//fj4e4/wHvV5v1hvm4eGBpk2bikrhP5Xy1QKB92lRwfP4tOh/VgFhxBY31vJ5\n5syZICIMHDiQL2jMIjJWQIT/b9CgAa9lN+bAwECTJEqZTIaNGzdyCywyMhLAe8EpdHu7ubnxZDkh\n5oExdgUAE0TUvDKDbxeyXC5HvXr1uDdAKKQrV64smXxqzjuiUqkgl8sht7KHbcUwePVZbpogOvIb\neEYuhEvYMNhVbgGNd2mQTJ5jiMe4QzHDA2E5ELGxsbh37x7f3xh3JS9sZ2dn4hnx9vbmIHIymQzf\nf/89Nm3axH/39/c3Sf709PTk42V5FsHBwXjw4AG6desmSuRkSlCfPn2QkZHB31NzzKqx2rRpIwp/\nCdnBwcEkvKJWq3HmzBlcvHiRKyK1a9fmzQxTUlJ46XKlSpWwcuVKvHjxgt/Hli1bRMqzXC7HgAED\ncsTCAcAVYqbgGD9rrVYr6gR7//597mVycnISlZobY2IA7zF7tFotZsyYgXXr1vH9S5QowUOYrBFl\n27Ztcxzv30UFAu/TooLn8WnR/7wC0rVrVxARFi1aBOB9SKRnz55cmIeEhEgu4HK5HCEhIdxyrVCh\nAiZOnIiKFSvCy8vLxMoWNrkScqlSpXi/g4yMDJGFbbwQC5vECRd+AJgxY8YHKR9CFl7XHBqnQqEw\nqTjgLFdAYesMtYcfbMo1gENoJ3hExKLIyG9EyoZnt/mwrRgGpZMXlE5ehvJWiR4oOYUX5HI5qlSp\nInKZMyAmVilRqFAhnDt3TvRM1Gq1yfg9PDwkPRxVq1bFkiVLRJ6tGjVqYPjw4aI8Gk9PT2zduhWA\nob+F8Xnc3NywaNEirsgwYrk00dHROUKZC8tChc345HI5GjZsiGHDhomUPyaY7ezs0KtXL7NJv0zZ\nad68OV9gd+3axY9lPVn0ej1vVDZr1izR+yec38qVK6NZs2ZcURs/fry5NYR7AW1sbHDt2jUT75yV\nlRUOHDhgctylS5d4CSq7h/Hjx0tiRjBQvKlTp/Jjhe85y7M5efIkf96fAhUIvE+LCp7Hp0X/swqI\nXq/HgQMHuELA2m6zvhDMUpdSFoT/r1KlCiIiIrg1tm/fPp6waY6tra1Rp04dNG3aFPPnzzdxFx89\nejRHgSuTybB//37RMT/++KPJPh9DERGGBUqWLIlZs2ZJKiQa7wDYV/0Mbq3HwWfIRhPQrqKf70Wh\nnkvgVL8PHGpGwCmkPVr0GGpRV1VjDg8PN3t/ixcvBgAkJCSAyBC+MAZiY+zu7m62GR07P8PTiIiI\nQPny5eHo6Ijg4GARxHVaWhqOHz+O06dP4/z585g9ezbmzp2La9eucYTcDh064Pvvv0dqair3zgjh\n35kyIVRmunTpYoI2y5Qb4P/aO/O4qMr9j38eZlgGZFFUBAQBRb2SqamJS+6glmaACy6opKWphCua\n3jSzLNzqquntpt5cgDQR8bqhqZWpuCDX5ZdZCIaC4IKhyBVk5vv7Y+Y8zmEGUCE52PN+vZ4XnGXO\nec75zjnPd77PdyFKS0vj6zdv3szXl06cB4D+/e9/0/bt28tN9mZvb08eHh7Uvn17Cg0NNfn+N2/e\nnCvlGo2GsrKyZN9ByXdq8uTJJn1xdHQsM6GXZGns2bMnX5eamsqT9Bnfp9LodDr65ZdfKDk5me7e\nvVvmfpI1R7p/eXl5simpAwcOEBHxOipSSHR1IwY8ZSHkoSxqrAJi/CIODw8nIr31ISsryyQqQWoB\nAQHc16OsZvzZ+vXr09KlS2Vz2x4eHiaF6pKTk2n27Nk0btw46tGjB9nZ2ZGlpSV5enqa+GTY2tpS\nUFAQubm5kaWlJdnZ2VHTpk1NCli9/vrrFBcXV2kFRDpurVq1KD8/n+4XPaQPv9pGtXu9TXX6TKIG\nYcvJI/KbR0m83vqS6g6YQc49wsnBfzA17DiAhr09hZha72tQWnF47733aM2aNbRw4ULavHkz7d27\nlxITE+n333+npKQkmROko6Mjvf/++7JBurQyZG9vT3fv3qWSkhJZkS9zykVFbezYseU61H7yySdc\nhsXFxWbzUgQFBfGB3NnZmffd0tKSjh8/zj//4MEDWX4YT09PruwaKyENGjSgvXv30s6dO2XOrfPm\nzeOWPa1WW66PztChQ7k/SUhIiNnwa+PvfOmQbgcHBxMFmOhR5JWTkxPZ2dnRq6++SsePH+f9/PXX\nX82+RKTEaw4ODrLQS8mKFRERYfZzT4IU7tqtWzcelmvs+Dt48GAeAs0YoxMnTlT6nFWBGPCUhZCH\nsqixCgigN7cvXLiQ8vPzKTIykpuhHRwcKDAw0KR2yPr16836DkyYMIGbmo0tJD/99BMR6SteSgXd\nGGN08eJFHtIrJR56nKbRaCoM9zUeZGfOnPlU9UMAkNpaQ9YeL1CD3m9S7V5vkfe4FfRK9CFqNneP\nPhJlWjx5zkykBmFLqU7ABKrVqi+pHV344C79Las8utQvtVpttsaHTqejEydO0I4dO2TF8Ixb7969\nSafTcUVLOufu3buJSB+W+cEHH5CnpydZWVlR27ZtaePGjXTr1i0aPnw471fdunUpMjKS96l58+Y0\nbdo0WTZGOzs7iouLo+zsbFq+fDlXInJzc4noke+Ara0tjR8/nkaPHs2PP3nyZFlYdMuWLfkvbmOM\n83sYKyJSafeKmq+vL+Xk5HDrj7u7O/c7UavV1LRpU1q2bBnFxsYSoFeG79y5w5W4d955h4YMGSJT\n6k6ePEnFxcXc50Sj0ZjNM1HaiZZ/j9RqsrDQ+++UnjI0Rkr05+3tTXPnzqWBAwcSoJ9aqorCaDk5\nOfx5rlu3rtkK05L8nmUV2IoQA56yEPJQFjVWAfnjjz+ouLiYdDpdmT4eT5uvQmqZmZmUlJRktnCX\nsYNhVU2XVKap7GqTY5fh5BG2mJrMjJdlDPWYsoXcxq2hFmMXU53e40nTuD0xSxsTXw3GmMysXV6Z\n+OjoaP7/9OnTZV+qU6dOyRw2GWPUokULk1Bk40iFV155ha8v7ZBqzJUrVygyMpJatWpF7dq1ozlz\n5tCdO3eIiGjjxo0mMpdkM3ToUNlxpKRXGzZsIJ1Ox/1GkpKS+D7r168nQO+sqdPpKD09na5cuVJu\nZkfj3B1Tp06lmzdv8ky7gN7CJlmFateuLdsG6JOPSTKIjo7mtUIAfV2TPn368Gv67LPP+NTPiy++\naDZ7aceOHXnfpGlGc+nJpdwkgN6RdNKkSbKaPIMHDy7zmomIMjMzTVL2W1paPnY118chNTWVh+kC\neh+gyZMn06lTp2j16tW0adMm/l1QCmLAUxZCHsqixiogkqOfsZVD+qVm/BL08fF5qpBT6djSoGmc\nQAdjwCkAACAASURBVMz4fJVRGtRqtdn8IKX9BoybsYVGZV+PNL4dqV7QXPKM2kmeUTvJdcznVKdv\nBDl2CiWNrz/VcSlbiZCauVovISEh9OOPP5r4sjDGaOnSpfTBBx/wdcblzq9fv86vyc3Njbp3787v\n2ejRo2UDro2NDdnb25O7uzv/1a7RaMpMQX3hwgWzGVvbtWvHU6Onp6ebLWYHyNN1SzVM1q1bR/fv\n3+fyMFYucnJyCNBPSTwu5U2bST4S0lTNsWPHSKfT0ezZs02U2Lfeeos7Y65atUomB7VaTVFRUaTT\n6ejLL7/kSkNZ501ISKCUlBQC9FNxDx48MOm3FHUjOaiWbikpKRVee3FxMcXHx9OcOXNo+fLlJj4m\nVYFOp6Nz587R999/r8hMm6URA56yEPJQFjVWASnrZevn5yeLIliyZAkP4auqJikeT+OAadx27dr1\nWMnE9I2RdUM/cnplJNUf/IEsx4ZH5Dfk1HUUqWu7mXyuUaNGtGjRIrPHLGs66IsvvqCUlBSzUy+A\nPp27sSIWFBTEv1BSNMhLL73EC6SlpqaSWq0mlUolC58014xrmEjk5OTQ9u3b+SDZu3dv+vHHHykh\nIYGHEEsRHVIeGAsLC2rUqJFJRMzcuXPp22+/5VMLkkVDCpM1rh2ybt06fi1PwuLFi2X3jjFGAwcO\n5KGw0vdTipwiIrp48SLf3ziTpsQff/xB3377LcXGxlJ2djYVFRXRjBkzTHxomjRpQsOGDZOtc3Bw\n4IpbWf4Ykp/Td999R0eOHKGIiAgaM2YMV3x+//33J7oHAj1iwFMWQh7KosYqIOaiTMzlrli5cqXJ\nAPw4hdFKWzeMf6FW1ZRLaGio+XwWzIJqufuSlWtTqv9SINXpM4nc3/k3n1JxDV9Jzv0iqVab18jK\nrRkxtfmaJ9Lga5xRVApnfPnll7kyoNFo+EDm7+9POp2OD+xqtZrGjBlj1hdFWpeQkEBE+ggkY4uO\nRqOhadOmUXFxMXcQnDJlSrl+MB9//DH/cpaUlNDUqVNNplWMLRm7du0iANS6dWsiojKn48w140Ri\nkpOjra0tvfXWW7LCbE8zjXDnzh1KSEig7du3m0wLSM61kZGRVFJSQjqdjubPn0+A3przOISFhfHr\nMJ42K89nKCAgQFZJ1hipMnT79u0pLS2N7t69S++++y4BeqVeSQXFahJiwFMWQh7KosYqIA8ePDBJ\nM/3GG29QSEiIbF1mZqasRLmlpSVptVqzxcvK+sUvtYrSWj9NY1YasqznTQ7+g6lO3whyG7qAGk7a\nJAt/9ZiyleoFzSW7Ft31vhtlHMvZ2Zmb9z/44AOzSc38/f3JysqKGGNcGQkLC+NKyowZM2T+AMuW\nLSMiohMnTpj1qfH09KTCwkK6efOm7P4Y/z9+/Hiz4aNeXl7k4eFBAwYM4Epihw4d+JdTsqZYWFjI\nroUxxiNQJIuHr6+vzAlU8hWQlJ3SSuOcOXO4RYJIP30gFTYzbqNGjaIpU6ZQUFAQzZo1i9LS0ir9\n0B0+fJgruO7u7rJQ4h07dlT4+UuXLhGgt8D99NNPlJycLOuzSqWi0NBQWWTVjh07ylUicnNzzaac\nt7CwKNcnR1A+YsBTFkIeyqLGKiAlJSUVWiKsrKzon//8p0nWybZt21bovyFZAKRzWFlZybKYPs4v\nTlNlw5Zqte5HTt1GU4OwZdQwIkamaLhP2kiuY1ZQ3dejyK5lb/LuGkyRH60g57qPp/j4+vrSxo0b\nK1SmSltdpDBNOzs7k2mlZs2a0e3bt00qqhq3t99+mxf4k3J2qNVqGjFihInlyDi0ljHGXwZJSUkE\nPLIAFBUVcf+eXbt2kVarpcaNG/PPDho0iAoKCni0xbhx42j27Nl8u2QNGzRokCzsV6pQW5ZV48yZ\nM/Tpp5/SkiVLKDo62uR7YmVl9VhKQkUkJCTIMu+6u7vTpk2bHuuzX331FQH63CREer8I4+Rn9evX\nlynYbdq0eazjXr16lUaNGkUajYYYY9S1a1c6ePDgU1+jQAx4SkPIQ1nUWAVk/fr1lfbBeJxW2Uga\nlUM9cuo2hhqM+ow8Zybqp1GidpLLiGiqEziRHDqEkG3zLqR2ejRgSL/aK7q+1q1bc0VD6uf48eOp\nR48eT9zPpk2bcmWhd+/eMsWhR48eMkWLMSabRrG0tOTZL2NiYrg5v3T7+uuvSavVynJzDBs2jDIy\nMnhYpZRxMyMjgwB93oyioiLas2cPvf3224/uq0rFp41q1apFv/zyC8/hUl70jjQtVXqw12q1tH//\nfpoxYwbNmjWLdu7cyac2wsPDKS4ujoYMGcKVm7IcZZ8ErVZLZ8+epdTU1ApTnRsTExNDgNz5NyUl\nxaxSrVKpaP/+/U/UL51OZzYbqeDJEQOeshDyUBY1VgEp/aJ1d3eX1fgYOnSo2UqZzs7O5OLiYpKc\nqawmOe9JURMVNpUlWXu8QPbt36B6IfO434bv+C+o15TPyNqtmdlU5WW1zp0705o1a8pOmW5oHTp0\nKNcaY25w+uSTT+iHH36g8+fP09ixYwkATZo0iYiI3nnnnTKPFRUVRf/3f/8nO59k2ZCcSI8cOUJv\nvvkmH8Td3Nz4ly4+Pt6s9crDw4Pn5cjPzye1Wk2MsXJTm3fs2JFOnjxJRCSLzDHXjJU14wiKwsJC\nHpZbukmFCIn0A7M0FbRhw4anfeYqzZ07d7gPVFRUFJ05c4Y+//xzfn3Sve3cubOwYFQzYsBTFkIe\nyuK5UUCMm0ajofHjxxOgn25YuHAhLVy4kJv058+fTzdv3nxsJcC4mcu1AIBsvFpTncBJsmkV93fW\nk2OXEaR2cqXx48eXm7GyrLZmzRoiIlkkz8iRIykqKoomTZrEfV7eeustSk5OpsGDB5tUTbW2tqZb\nt26ZWFTCwsJIp9PR7t27uWVg1KhRlJubSw8fPuR1dkorOpIvgbGCJ4WDajQaio6Opj179siqslpa\nWtK1a9f4Fy88PFzWv+HDh5tEWkjTK4B+WsE4JXvjxo15mOfdu3dpzpw5jx0W3bBhQ9l5oqKiCNAr\nm3PmzKFp06ZxRbZv376yfSXFbOnSpY/7jP0prF271uy1DRs2jI4fP15m2nTBs0UMeMpCyENZKE4B\nAdAXwCUAaQBmG28z7mzpX9AqlYrs7e1NfgUOHTqUpk6dSkOGDOG1Ljw8PIiIuKOktbX1U+X0sKzn\nRc6vTiHXMSu4s2jdgbNI0+Rlcm/cvEqiZTw9PamkpIQePHjA/RoaN25MycnJtHr1av5L+LvvvuNC\nLZ0l0tHRkV878Gi6pnPnzjJFQGp16tShgIAAsxYVS0tLmjVrFq1evZrfMz8/P9JqtVzpK62wSVky\nfXx8KDo6miIiIricvv322zLN/e+//775+2747NmzZ+nAgQMyHw9JCSq97Orqyuu6GFtjtFott3Id\nPXqUr5fqAVlZWfEMoNevX+eK2qFDh57wUat6fvjhBwoJCaEWLVpQYGAgbd26lU6ePClesApCDHjK\nQshDWShKAQGgAnAZgA8AKwBnAbSQtht31vjXubOzM92+fZtyc3PJx8enwkHdwsKCiOS1JCpqKpWK\n1E6upGnakeoF/53c3vrSkNJ8G9Uf+hHV6zKUoKqcv4jxuYyXMzMzqbi42OyUEqD3UZCsEhkZGWUm\n4pJaacVIrVabVUQep6nVarpw4QIR6acodu7cSSEhIdStWzeaPn06paen0/Xr180WlJs2bRp98cUX\n1L59e2rUqBENHDiQfvzxR/7llJQmNzc38vDwoJ49e9K+ffv4dNiaNWtkeTBUKhWPKDH23WncuDER\nPcr2GRgYyM9RUFDAlRrjqJjMzEz+eScnJwoICODWr5dfflmxYaniBasshDyUhZCHsqhIAWGkVwye\nCYyxjgA+IKI+huX3AICIPgGA/Px83pkePXogNTUVANCmTRv861//wqJFi5CQkGD22CqVCt7e3khL\nSwNjDAcOHEBaWhomTJhQbp8avdAef9j7wLZpR1g1aAIA0D0oQHH2Lyi8fBqFvx6DtiBP9hm1Wg1X\nV1f4+flh3759ZfZHq9XK1kVERGDVqlUofc+7dOmC9PR0ZGdnw87ODp06dcKVK1dQp04d9O/fH4GB\ngbCwsMB///tfREZGorCwsMzrYYyZHB8AmjRpgoEDB2L58uWy7X/7298QEBCAFStWmHzGwcEBK1eu\nRIsWLco8n0RxcTEOHz6M1NRU2NraolevXti4cSMOHTpk0r958+ahpKQES5YsQXFxsWx7p06dcPny\nZeTm5iIoKAgJCQlo164dTp8+DSsrKyQmJiIsLAy3bt3in7G2tkazZs1w7tw5AMCKFSvQsWNHAHoF\nu3///rhx4waio6PRs2dPAEBcXByWL18OW1tb2f3s0KEDFixYAGdn5wqvWSAQCARl4+vry/93dHRk\npbc/awVkEIC+RDTOsBwGoAMRTQbkCoiTk5PssyEhIdi7d2+5g68xrq6ucHJywqVLl6DT6WTbLJ09\noGncHjbebaHxagUAKMq+BHX2Wdz85RQe3sqEruh+mcf29fVFVFQUbG1tMWvWLFy7dk22vVmzZrh7\n9y6uX78uW29OKTHGzc0NixYtgp+fn8k2nU6H4OBgZGVloUuXLujYsSNiYmKQnZ1t9lj9+/dHVlYW\nUlNTUbduXdy6dQuzZ89GUlISV+ymTZuGoUOHwsLCAkOGDEFGRgb69u0LGxsb+Pn5oU+fPtBoNPyY\nv/32G86fPw9bW1t06dIFtWrVKvNajh49iilTpqBWrVqYPXs2mjVrhoSEBMTGxppVknx9fXH16lU8\nePAAAODp6YmXXnoJO3bswMyZM7Fv3z6cP38er732Gu7fv4/vv/8etWrVQkFBAT+GRqPBlClTEBwc\nLDv2pk2bsGLFCqhUKnTt2hXFxcU4evQoAODjjz+Gj48Prl+/Dg8PD3h5eZV5TQKBQCB4fCpSQJ71\nFMxgAGuNlsMArJSWzTmhluVnIZngS09nmEuIBYCYpTVpmrxMdfpMIs8ZO3jFWKdXwkjlUM8k5TWg\nz39x8+ZNOnv2LO3bt49P75TVF6lt2LCh3HovUnNycqJdu3ZRbGwsHTx4sNzQyKNHjxKg9xkxDumU\nfBm8vLx4VdoWLVoQEdH06dMJeJS0a+DAgeTv70+A3vdBCjUtKSnhoa1nzpzhx5bMmQUFBfTGG2/I\n+l6rVi2KiYkps79SCvqPPvqIr7t+/brs/llYWJjNmmppaUmpqak0YcIEAvS1bLZs2WI2bNnFxYVW\nr15N8fHxZYbOarVaioiIkH2XLC0tZVlZawrCxKwshDyUhZCHslCaD0hHAElGy+8BeE9aNu5sy5Yt\n6dixY7Rp0yazg77kC1BW1AqztCa1c0N9bZUhH5Ln9Hju01Gnz2SysHMy+7nSCoIUbaDT6fgA+O67\n71KTJk3I09OT3nzzTTpx4kSFWVaNm7W1NYWGhspqhVTE7t27CdCnXTdGSkwWHBxMR44cIUCfXEyn\n01FGRobs/hinUbezs6Pt27fThQsXuH+Ij4+PzE9CepjHjRvH7/XIkSOpS5cuXIE4ffq02f5KWUdX\nrVrF15VOmV+/fn3Kysriyl/v3r25T4c5/51WrVrxfS0sLGj06NFPVMMkIyODvvrqK1q/fv0T3Xsl\nIV6wykLIQ1kIeSgLpSkgagDpALzxyAnVT9pu3FnjgfD48eOPPbhbaByoTsAEWVIwt3FrqHbvCeTU\nrAPZ2JlXWKQWGBgos14MHz6ciPSZLQF9PhJzDor79u2rMKmZnZ0dzZ8//6kcHLOzs0mlUpFKpaLk\n5GQiIrp37x6vjRIdHU1FRUU88mfWrFmUnZ1N//jHP2T9srKyMpuS29LSUlaojUj/MB88eJCndj93\n7hzfJoWrhoeHm+2vVOq+SZMmlJaWRjqdjisuKpWK93PTpk1c2XjllVe4xQPQZ3B99dVXTe6rt7c3\nXbp06Ynv4fOAeMEqCyEPZSHkoSwUpYCQXgl5FcCv0EfDzDXeZtzZ//znP/wivv76az74lJmMy0JF\ntV4MII/Ib8hzZiLV7fcu9Rn/dwoaZRo66ufnR0uWLKHvv/+ePv30U75eSt8dHx8vO19QUBAfBKOj\no8u82VlZWfT666/LBkzGGA0ePJi+++47unv3Lt/38uXLtGTJEvrwww/phx9+eCylRMoUyhijtm3b\n8vBUFxcXnngrJibG7LRV69atae/evXTz5k3asmULvfjii2Rvb0+Ojo70+uuvm7VknDp1iltY/Pz8\nZNsOHz5MgD5RmDkKCwt5ZAxjTGZ9admyJX322Wd8ubSCJFk5Tpw4QUREeXl5PB/KCy+8QEVFRRXe\nq+cV8YJVFkIeykLIQ1koTgEprxl31sbGhsLDw2nkyJEypWP37t2y4l4qe2dyfnUK+c5KoEazdpHL\nsE/I0tmDNmzYQA8fPqTIyEi+r6OjI2VlZckGe+mXOgDKycmhzMxMmj9/vmzAlAbRyZMnyywzZZGf\nn0/btm2jmJgYunr1qsn2Dz/80ERJCAgIoHv37pV73KKiIpo0aZIsEVn79u15mKzE/v37qVevXuTo\n6Eje3t40f/58KigoIK1WS6NHjzZRTmrXrk0pKSkm5zt16hTt3buXGGNkZWXFE4MRPcpKOnjw4DL7\ne+PGDQoLC+P9rVevnix/S79+/WTTaz4+PhQbG8v3NUYqZ+/t7V3uPXreES9YZSHkoSyEPJRFjVVA\nyprG8PT01E+12DqRXYvu1HDyZvKYto3e/PIw9R8/hwDGlQ0pM6pxK21puHnzJh8U27VrZ9bRMTw8\nnDIyMqpEIImJifr+W1jQ8OHDKTIykifKmjBhwmMd49atW/Tjjz/SxYsXn+jc27dv51NBS5cupR07\ndvAU8G3atDG5N9LDLE2ReHl50cKFC2ns2LFccThw4ECF571//z5lZ2dTSUkJrV271sSK5ezsTN98\n8w1ptVp68OAB91uRLCBERMuWLSMA1KtXrye65ucN8YJVFkIeykLIQ1nUWAVk27ZttGjRIurRowc5\nOjrywUrj25EavbOWp0N3HbuaLJ1NfRqkZvwL28vLy+xNCgsLK/Pzkn+EOUvG09CvXz8CQJMnT6Yj\nR47QvXv3eJl5jUZDBQUFVXIecwQHBxMAWrZsGV9XWFjIFaCff/5Ztr/0MOfk5PAIG+O2YMGCp+pH\neno6LViwgCZOnEhffvmlbGqK6FFkj6OjI02cOJFCQ0O5HOPj45/qnM8L4gWrLIQ8lIWQh7KoSAFR\nQ6GMHj0GLm16ICsjFyVaNawb+qF293BYuzeH9v4dWKRuR875n1CcexnQaXluih9++AFFRUX8ODqd\nDhYWFtDpdHjnnXfMnmvDhg1IS0vD8ePHZetHjBiBgoICJCYmIjY2FlFRUZW+rgsXLgAAVq1ahVWr\nVsHe3h5z5syBu7s7srKykJubCx8fn0qfxxx//PEHAHlstkajgYeHB/Ly8nDnzh2zn3NxcUFKSgp2\n7NiBY8eOwcHBAUOHDn2sBGXm8Pb2xrx588rcvmjRIly+fBn/+c9/sHr1agD6BGbz5883yfEhEAgE\ngpqJYhUQ5wmboFVbokHnR+tKCvJwe/9qFF48At2De7CxsQF0+sRe06ZNw8KFC3Hjxg34+Pjg/v1H\nicR0Oh1GjRqFadOmmT0XYwzDhg3D8ePH0aFDBwQHByMwMBCtW7fGRx99hMTERNy4caPS13T27Fme\ntMzBwQFeXl44d+4c3nvvPQCAra0tGjRoUOnz/O9//0NSUhLu3r0Lf39/NG3aFIA+y+ehQ4ewcuVK\nBAQEwMbGBgcOHMDZs2dha2trNgGa8TH9/f0RHBwMlUpV6T6Wh0ajQWJiIk6cOIFDhw7BxsYGQUFB\n8Pb2/lPPKxAIBIJnh2IVkOJbv6MgdTdaveAH37/54dst36Dw0lHQwwd8HylrJqBPKQ4A9evXx4QJ\nE7Bs2TJ06tQJKpUKlpaWqFevHi5fvoxmzZqZPV/r1q0BAOnp6Rg9ejRcXFxQUFCAuLg42fbKYJwG\n/d69e2jSpAnq1q3L05WPGTMGtra2lTpHQkICxo0bh7y8R+njQ0NDsX79ekycOBFr1qzBgQMH4OHh\nAQ8PD54VdfLkyXB0dDQ5Xm5uLkJCQpCYmAitVgtXV1dERUUhMjISjJkmtqsMd+7cwcmTJ2FjY4NO\nnTrB398f/v7+VXoOgUAgECgEc/My1dXMOaG6uLjw7KbGzosvvviizEfj/v37fN4pICDAbMiuSqWi\nmJgYunDhAk2ePJkCAwPp7bffplOnTpFOp+NZQu3t7em1117j+UC8vLyosLCw0vNhzZs3JwAUERFh\nNpy4tA/Gk3Lu3Dke0vrSSy9RcHAwv3eSg+vp06dl987W1pZmzZplNgvr4cOHeYZUlUolc+pduHBh\npfpqjE6no/fff1+WFdXV1ZV27NhRZed4XhBz3MpCyENZCHkoixrrhFp6cJYUDXPrAdCIESMoJiaG\nZ+CUWmhoKMXGxtKoUaMI0OecMDf4r169mnJycnhUiNTatGlDv/76a5UIQ0oaFhsbS1evXqUVK1bQ\n3//+d96f27dvV+r4Up6QMWPG8IiWM2fOEGOMrK2tedl5nU5H58+fpyNHjkhfDLNMnTqVK3vXrl0j\nnU5HmzdvJkCfFbWs1OdPyuLFi/n97tixI/n6+nJZnTx5skrO8bwgXrDKQshDWQh5KIvnSgGRWteu\nXWngwIHcQlI6U6YUMdGtWzdZaKmxchEeHk47d+6kiIgIPthlZmYSEdGFCxcoPj6eTp48WaVl2b/4\n4gsedrpy5UrasmULtW3blgBQ//79K338zp07EwA6ePCgbL0UwfKkg3nXrl0JAG3cuFG2Xupz6fM8\nDQ8fPiQXFxcCQFu3biUivYIkKVOhoaGVPsfzhHjBKgshD2Uh5KEsamwUTFmoVCq0bt0a69atAwDM\nnDkTAwYMwNq1a5Geng4fHx/odDosW7YMrVq1kvkpWFtbAwAaNWqE9evXAwAGDBiA7OxsxMfHY8uW\nLZgxYwb8/PzKdch8WsaNG4fdu3djz549iIiI4Os9PDywYsWKSh/f1dUVAHDs2DFedv7GjRv47bff\nZNsfFysrKwDA7du3+TqdTsf9S2xsbCrd5+zsbOTm5qJevXoYNGgQAL1T8MSJE/Gvf/0LKSkplT6H\nQCAQCJSHRXV3oDwWLlzIIx8k50ytVosVK1bg/v37GD58OCIjI9G0aVMsXrwY27Ztw+LFixEYGAgA\n2LZtG27evAkAyMvL42G2pR1Rmzdvzvf5M7GysuIhvUFBQejbty8+/fRT/Pe//62SCI+xY8cCABYs\nWICIiAgsX74cXbt2xYMHD9CnTx80bNjwiY7Xq1cvAHo5xMXF4fz58xg/fjwyMjLg4eGBl19+udJ9\ndnJygkqlQl5eHrKysvj68+fPAwDq1q1b6XMIBAKBQIGYM4tUVys9BePi4kLz5s2jnJwcXvzMx8eH\n5s6dS8nJyWVOj2i1WmrTpg0B+oJmgYGBvG4KAKpbty6vopqbm8tTuyckJFSB0al6mTNnjsmUVdOm\nTZ8qkVpycjIvIGfc1Gq1rFZPZZHqvPj5+dG6deto8eLFXF7//Oc/q+w8zwPCxKwshDyUhZCHsqho\nCoYR0bPXesogPz+fd8bJyYmvV6lU0Gq1UKlUOHz4MF555ZUKj3X9+nWMHDmSh7gCQOfOnfHw4UOc\nPHkS1tbWaNu2Lc6ePYv79++jZcuWOHPmDNTqGjcrZUJqairi4uKQn5+PTp06YciQIdBoNE98nNOn\nT6OkpAQpKSnYuHEj8vLy0K5dO0yfPh3t2rWrsv5mZWWhe/fuSEtLk60PDg7Gli1bnguZVBWnT58G\ngCq9/4KnR8hDWQh5KIv8/Hz+v6Ojo0neBsUqIMuXL8eXX36J3NxcAHqFZPPmzXjttdee6Jg///wz\nLl++DC8vL7Rs2RJ5eXkYO3YsEhMTIV17QEAAvv76a7i5uVXh1dR8nuXDfO/ePWzYsAHff/89NBoN\nBg0ahAEDBsDCQtGzhM8c8YJVFkIeykLIQ1nUWAXE0dERDx8+xPvvv4/o6GjY2tpi165d6N69e5Uk\nwMrMzMTly5fRqFGjPy31eU1HPMzKQ8hEWQh5KAshD2VRkQKiWNv2//73PwQFBSEpKQkAUFhYiJ49\neyIkJARxcXGwtLSs1PE9PT3h6elZFV0VCAQCgUDwhCjWvr1gwQIkJSXx0FlfX184ODggPj4en3/+\neTX3TiAQCAQCQWVQrAKyePFiAEBRURGsrKwQExODTZs2AQC++uqr6uyaQCAQCASCSqJYBUTyTWnT\npg3279+P9u3bo0uXLgAgyxchEAgEAoGg5qFYBURKzDV16lR069YNABAbGwsAaNGiRbX1SyAQCAQC\nQeVRrBOqZAEZM2YMtm7diocPH3KH1KlTp1Zn1wQCgUAgEFQSxSogV65cgUqlAgDs2rULgD6V+bx5\n8zB8+PDq7JpAIBAIBIJKolgFZPjw4YiNjUW/fv0QGhoKCwsLBAYGon79+tXdNYFAIBAIBJVEsQrI\nxx9/jNjYWJw4cQJ79uyp7u4IBAKBQCCoQhTrhHrr1i0AVVPyXSAQCAQCgbJQrAIyYsQIAIC1tTVm\nzJiB3377rZp7JBAIBAKBoKpQrALy66+/AgAyMjKwbNky+Pn5Yfv27dXcK4FAIBAIBFWBYhUQABg5\nciS2bt2KYcOG4eHDhxg9erSsuI1AIBAIBIKaiWKr4QoEAoFAIHg+MFcNV9EWEIFAIBAIBM8nQgER\nCAQCgUDwzFHUFIxAIBAIBIK/BsICIhAIBAKB4JkjFBCBQCAQCATPHMUoIIyxvoyxS4yxNMbY7Oru\nz18FxpgHY+wwY+wiY+z/GGORhvV1GGMHGGO/Gf7WNqxnjLEVBjmdY4y9VL1X8HzCGFMxxlIZY7sM\ny96MsRMGeWxhjFkZ1lsbltMM272qs9/PI4wxJ8bYNsbYL4bnpKN4PqoPxthUw7vqAmMsjjFmEozp\n0AAAA4RJREFUI56PmokiFBDGmArAFwD6AWgBYBhjrEX19uovQwmA6UT0NwD+ACYZ7v1sAAeJyBfA\nQcMyoJeRr6G9DWDNs+/yX4JIABeNlqMBfGaQxx0AYw3rxwK4Q0RNAHxm2E9QtfwDwD4iag6gFfRy\nEc9HNcAYcwfwLoB2RPQCABWAUIjno0aiCAUEwMsA0ogonYiKAXwDYGA19+kvARFdJ6Izhv/vQf9y\ndYf+/m8w7LYBwBuG/wcC2Eh6kgE4McZcn3G3n2sYYw0BvAZgrWGZAegJYJthl9LykOS0DUAvw/6C\nKoAx5gCgK4B1AEBExUT0B8TzUZ2oAWgYY2oAtgCuQzwfNRKlKCDuAK4aLV8zrBM8QwzmyTYATgBw\nIaLrgF5JAVDfsJuQ1Z/P5wCiAOgMy84A/iCiEsOy8T3n8jBszzfsL6gafADcBPBvw5TYWsaYHcTz\nUS0QURaApQAyoVc88gGkQDwfNRKlKCDmNFIRH/wMYYzVAhAPYAoR3S1vVzPrhKyqCMZYfwA3iCjF\neLWZXekxtgkqjxrASwDWEFEbAPfxaLrFHEIefyIGX5uBALwBuAGwg37aqzTi+agBKEUBuQbAw2i5\nIYDsaurLXw7GmCX0ykcMEUkV/3Il07Hh7w3DeiGrP5fOAF5njF2BfiqyJ/QWESeDyRmQ33MuD8N2\nRwB5z7LDzznXAFwjohOG5W3QKyTi+ageegPIIKKbRPQQwHYAnSCejxqJUhSQUwB8DZ7MVtA7Fe2s\n5j79JTDMh64DcJGIlhtt2glgtOH/0QASjdaPMnj7+wPIl0zRgspDRO8RUUMi8oL+OThERCMAHAYw\nyLBbaXlIchpk2F/8wqsiiCgHwFXGWDPDql4AfoZ4PqqLTAD+jDFbw7tLkod4PmogismEyhh7Ffpf\neioA64no42ru0l8CxlgXAEcAnMcjn4M50PuBbAXgCf1DP5iI8gwP/SoAfQEUAggnotPPvON/ARhj\n3QHMIKL+jDEf6C0idQCkAhhJREWMMRsAm6D33ckDEEpE6dXV5+cRxlhr6B2CrQCkAwiH/sebeD6q\nAcbYAgBDoY/gSwUwDnpfD/F81DAUo4AIBAKBQCD466CUKRiBQCAQCAR/IYQCIhAIBAKB4JkjFBCB\nQCAQCATPHKGACAQCgUAgeOYIBUQgEAgEAsEzRyggAoFAIBAInjlCAREIBAKBQPDM+X/V0mbNoYFl\nwgAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"sensor_var = 30000\n",
"process_var = 2\n",
"process_model = (1, process_var)\n",
"N = 1000\n",
"dog = DogSimulation(0, 1, sensor_var, process_var)\n",
"zs = [dog.move_and_sense() for _ in range(N)]\n",
"\n",
"pos = (zs[0], 500)\n",
"ps = []\n",
"for z in zs:\n",
" prior = predict(pos, process_model) \n",
" pos = update(prior, (z, sensor_var))\n",
" ps.append(pos[0])\n",
"\n",
"book_plots.plot_measurements(zs, lw=1)\n",
"book_plots.plot_filter(ps)\n",
"plt.legend(loc='best');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This simple change significantly improves the results. On some runs it takes 200 iterations or so to settle to a good solution, but other runs it converges very rapidly. This all depends on the amount of noise in the first measurement. A large amount of noise causes the initial estimate to be far from the dog's position.\n",
"\n",
"200 iterations may seem like a lot, but the amount of noise we are injecting is truly huge. In the real world we use sensors like thermometers, laser range finders, GPS satellites, computer vision, and so on. None have the enormous errors in these examples. A reasonable variance for a cheap thermometer might be 0.2 C$^{\\circ 2}$, and our code is using 30,000 C$^{\\circ 2}$."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Exercise: Interactive Plots\n",
"\n",
"Implement the Kalman filter using Jupyter Notebook's animation features to allow you to modify the various constants in real time using sliders. Refer to the section **Interactive Gaussians** in the **Gaussians** chapter to see how to do this. You will use the `interact()` function to call a calculation and plotting function. Each parameter passed into `interact()` automatically gets a slider created for it. I have written the boilerplate for this; you fill in the required code."
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "7cdc56e40a90494cbaca4f5fb4d145e7",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"A Jupyter Widget"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"from ipywidgets import interact, FloatSlider\n",
"\n",
"def plot_kalman_filter(start_pos, \n",
" sensor_noise, \n",
" velocity, \n",
" process_noise):\n",
" plt.figure()\n",
" # your code goes here\n",
" pass;\n",
"\n",
"interact(plot_kalman_filter,\n",
" start_pos=(-10, 10), \n",
" sensor_noise=FloatSlider(value=5, min=0, max=100), \n",
" velocity=FloatSlider(value=1, min=-2., max=2.), \n",
" process_noise=FloatSlider(value=5, min=0, max=100.));"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Solution\n",
"\n",
"One possible solution follows. We have sliders for the start position, the amount of noise in the sensor, the amount we move in each time step, and how much movement error there is. Process noise is perhaps the least clear - it models how much the dog wanders off course at each time step, so we add that into the dog's position at each step. I set the random number generator seed so that each redraw uses the same random numbers, allowing us to compare the graphs as we move the sliders."
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "c60f71af532746729d0fc85ce753d6c3",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"A Jupyter Widget"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"from numpy.random import seed \n",
"from ipywidgets import interact, FloatSlider\n",
"\n",
"def plot_kalman_filter(start_pos, \n",
" sensor_noise, \n",
" velocity,\n",
" process_noise):\n",
" N = 20\n",
" zs, ps = [], [] \n",
" seed(303)\n",
" dog = DogSimulation(start_pos, velocity, sensor_noise, process_noise)\n",
" zs = [dog.move_and_sense() for _ in range(N)]\n",
" pos = (0., 1000.) # mean and variance\n",
" process_model = (velocity, process_noise)\n",
" \n",
" for z in zs: \n",
" pos = predict(pos, process_model)\n",
" pos = update(pos, (z, sensor_noise))\n",
" ps.append(pos[0])\n",
"\n",
" plt.figure()\n",
" plt.plot(zs, c='k', marker='o', linestyle='', label='measurement')\n",
" plt.plot(ps, c='#004080', alpha=0.7, label='filter')\n",
" plt.legend(loc=4);\n",
"\n",
"interact(plot_kalman_filter,\n",
" start_pos=(-10, 10), \n",
" sensor_noise=FloatSlider(value=5, min=0., max=100, continuous_update=False), \n",
" velocity=FloatSlider(value=1, min=-2., max=2., continuous_update=False), \n",
" process_noise=FloatSlider(value=.1, min=0, max=40, continuous_update=False));"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Exercise - Nonlinear Systems\n",
"\n",
"Our equations for the Kalman filter are linear:\n",
"\n",
"$$\\begin{aligned}\n",
"\\mathcal{N}(\\bar\\mu,\\, \\bar\\sigma^2) &= \\mathcal{N}(\\mu,\\, \\sigma^2) + \\mathcal{N}(\\mu_\\mathtt{move},\\, \\sigma^2_\\mathtt{move})\\\\\n",
"\\mathcal{N}(\\mu,\\, \\sigma^2) &= \\mathcal{N}(\\bar\\mu,\\, \\bar\\sigma^2) \\times \\mathcal{N}(\\mu_\\mathtt{z},\\, \\sigma^2_\\mathtt{z})\n",
"\\end{aligned}$$\n",
"\n",
"Do you suppose that this filter works well or poorly with nonlinear systems?\n",
"\n",
"Implement a Kalman filter that uses the following equation to generate the measurement value\n",
"\n",
"```python\n",
"for i in range(100):\n",
" z = math.sin(i/3.) * 2\n",
"```\n",
" \n",
"Adjust the variance and initial positions to see the effect. What is, for example, the result of a very bad initial guess?"
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"#enter your code here."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Solution"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {
"scrolled": true
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAhUAAAC+CAYAAACCoP16AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzsnXVYFGsbxu+hU9pERQUbQQUVxVaw\nxe7uPuqnxzp2t8djtxhY2BjYrYACtoKKYICECCi1O98fjyML7MLusgn7uy6uhd2dmXeH2Xee94n7\nYViWhQYNGjRo0KBBQ0HRUvYANGjQoEGDBg2FA41RoUGDBg0aNGiQCRqjQoMGDRo0aNAgEzRGhQYN\nGjRo0KBBJujI+wCJiYmaTFANGjRo0KChEGJmZsYI/q3xVGjQoEGDBg0aZILGqNCgQYMGDRo0yAS5\nhz8EMTMzk+n+AgMDAQAuLi4y3a8G4WjOt2LRnG/FojnfikVzvhWLLM93YmKiyNc0ngoNGjRo0KBB\ng0zQGBUaNGjQoEGDBpmgMSo0aNCgQYMGDTJBY1RoUCt+pWUoewgaNGjQoEEEGqNCg1qQ8isdo9ac\nhWm7ZfC99VLZw9GgQYMGDULQGBUaVJ7Hb76g7qjt2HH+MUpZmWLIytMI+xSv7GFp0AAAiPj6Hefv\nv8GPlDRlD0WDBqWj0JJSDRpE8Tk2CZcDw1HK0gQVSlmgfAkz6OpoY83Re5i96xqKmxvj6pqBqFjK\nArVHbkP3eUdxf9MwGOrrKnvoGoowUd9+wH3iHkR9+wEdbS241bCFh0sleLpWgkuV0mAYJv+daNAg\nYzJ5fBy68hRe7lVRzFhfocfWGBUalM7t0Ah0n38MMQkpf55jGMDC1BDxP36ha+Nq2D61A6zMjAAA\nB2Z1RfuZhzDh3wvYOa2TsoatoQiw9MBtaGkxmNarIbS1szt2vyenou3fB5GYkoqDs7vi+YcYXAoI\nxz+7r+Of3dfR2qUi9s/sgpKWJkoavYaiyuWAcAxafgqnFvVCZ/eqCj22xqjQoDRYlsXWM4GYuPEi\nKpQyx6lFvZDJ4+Pd5wS8//odEdGJaOpUHoM8nbKt+No1cMDs/o2x5MBtuDuWw+A2zkr8FBoKK7dC\nIjB71zUAwNXH73FwdlcUtzAGAKSmZ8Jrjg9eR8bi4or+aFGnAgBgyfCW+PY9BYevPsOMHVfgNHwr\nvGd2gYdrJaV9Dg1FD2//UFgWM0Tb+g4KP7bGqNCgFNLSMzH+Xz/sPP8E7eo74OCcrjA3MQAANK5V\nPt/tFwxuhvvPozB2/XnUcSiFWpVKyHvIGooQmTw+xv/rh/IlzPB3n0aYsvkyao/chqNzu8OtRlkM\nXHoSN0MicPifbn8MCg4bc2NM7FYfLetUQK+Fx+E5/QCm926IxcNaQFdHW0mfSENR4UdKGk7deYUh\nbZyhp6v4601jVGhQOD9TM9D6f9649zwSs/s3xoLBzXK5lvNDW1sLh+Z0Re2R29B/qS+Cd4yGlpYm\nfq1BNmw+FYCn72Lgu7AnujSuBrcaZdF93lE0/WsvmjiVx/UnH7BmjAd6t6gpch81KhRHwNYRmLL5\nElb63MOdp5G4vm6QUiZ6dSbpZxoiohMR9e3Hn59SliYY0aGu5jsvBN/bL5GanokBHrWUcny1NipY\nlkVU3E/UZVlNQpQaMXPHFdx7HolDc7qiT0tHqfdTwtIEq0d7oN8SX5y59xpeCo4daiicRMcn4589\n1+HhUunPNeVsXxJB20Zi6Moz8L39EpO7N8CUnm757stQXxdbJndAbftSGLX2HM7ee41uTavL+yMU\nGgJefULzyfuQkppbn+Zy4Dvsn+kFY0M9JYxMdfG+HAr7MpZoUN1WKcdX65LSkw8j0XXFDUREi25u\nokG1uP7kPf71fYTxXVwLZFBw9GxeAxVLW2DpwdtgWVYGI9RQ1Jm54yp+pWXg3wltsi1WzEwMcHxB\nD4TuGo01Yz0k2uewdrVR2toUey4Gy3q4hRYej4/Ra8/DzMQAPv90w92NQxHh8xfS/edg7VgPnLzz\nEk0m7UXUtx/KHqrKEPXtB64Hv0f/1o5KW2irtVFRoyx1Pb3/PFLJI9EgDj9S0jBkxWnYl7HE8hGt\nZLJPHW0tzOjTCAGvPuNK0DuZ7FND0eVpRAL2XAzGlB5uqFLOOtfrDMPAsWIJiSdsbW0tDGhdCxcf\nheFLXJKshluo2XomEI/ffsHaMR7o1aImGtYsi3K/S80n93DD2SV98CYqDvXG7EDAq0/KHq5KcPBK\nKFgW6N9KOaEPQM2NikolTWGgq437z6Pkfqz0DB66zT2KLv8cwZFrz5DyK13uxyxsTN50EZHffsjc\nZTnQwwllrE2x5MBtme1TQ9GDx2ex6tRzlLY2xZwBTWS+/yFtnMHjszjgHyrzfRc2ouOTMXvXNbSq\nWxE9m9cQ+p72bpVxf9Mw6OvqoMmkvbgcEK7gUaoWLMvC+3IoGtYoi0plLJU2DrU2KnS0tVC9rBnu\nv5C/UTF3z3X43n6Ju88+oveiEyjRdTX6LDqBs/deg8fjy/346s7Ze6+x+0IwpvduCLcaZWW6b309\nHUzr1RA3QyJw9+lHme5bHUlLz0Ricqqyh6F2XHz8CS+jErFmjAdM5BCnr1LOGm41bLH3YogmVAcg\n/GsSZh98ghcfvuV6bfq2K/iZloH/JrbN0ytUs0JxPNw8HPZlLDF4xSl8L8LXfXDYVzz/8A39Wxc8\nrFwQ1NqoAADH8hYIDvsq10ZTV4PeYaXPXYzsUAdfjk/F9XWD0L91LfgHhqPTbB/UGrYVR68/B5+v\nmSiEEZv4EyNWn0WtiiUwf1AzuRxjePs6sDYzwtKDd+Syf3WBz2fRfuYhlOy2BhP+9cNHTb6R2By5\n+wEVS5igl4iVsSwY7OmMFxHfEPDqs9yOoS7sux6Oy8GfUXfUdmw5HfDH0LodGoH9l0Pwv54NhYag\nclLcwhj7ZnghJiEF07ZelvewVZYD/qHQ1dFCz2byu37FoVAYFZk8PgJfy+dLGpv4EwOWnUSVstZY\nO9YT2tpaaOZsh61TOuDLianw+acbWLDotfA4nIZvxYmbLzTGhQCvP8ai46zDiE/6hf0zvaCvJ5+C\nI2NDPUzu3gB+D9/iydsvcjmGOvDfyUe4+vg93B3LYdvZINj3/xfDV53R9ErJh8DXn/EyKhHd3MrL\nNcGtV/MaMNTXwZ6LT+R2DHXgR0oarj39gla1SqFJrfIYu94PXnOO4Gt8Msau90O5EmaY3b+x2Pur\nU7kU/terIXaef4KrRTC3KpPHx6Grz9C+QeU/ysPKohAYFeYAIJe8CpZlMWzlGcT9+IXD/3TLlQeg\nq6ONXi1q4umuMTg0pysyMnnoPv8Yag3bgt1+T5CaninzMakL6Rk8LPa+hVrDt+J1ZCy8Z3aBk31J\nuR5znJcrzIz1i6y34vXHWPy9/Qo6uFXG5VX9EXZgIkZ1rIsD/qGoMvA/7Dr/WNlDVFm2nQ2Ega42\n2tUpI9fjmJkYoGvjajh89VmRnh+O33yBtAw++japgAsr+mHtWA9cDAhDxb4b8Ox9DNaP85Q472re\noKZwsLXEyLXnilzO29Wgd/gan4wBrZWXoMmh9kaFpYk+KpW2wIOXsjcqtpwOxJl7r7FiZCs453FD\n1NbWQp+Wjni+Zyy8Z3WBtpYWhq06g/K912Phvpv49j1F5LaFkYcvolB31Hb8s/s6vBpVxYu949Ar\nD5EgWWFmYoDxXerhxK0XeBmRO05bmOHx+Bi84jQM9XWwfWoHMAyDciXMsHFiO7w/PAktalfAuA1+\nCA77quyhqhyJyak4dPUZPGuXhomh/BvUDW7jjMTfqodFlb2XglHexhg1y5lDS4vB5B5ueLh5OBzK\nWKFH0+pSac4Y6utix9SOePc5AXP3XJfDqFWXHecfw8LUAO0bKF6WOydqb1QAgFuNsrj/PEqmyU/P\n38dg6pbLaFvfHpO61RdrG21tLfRvXQvBO0fh6pqBcK1SGvP23kDZnuuw/viDQpmcdSXoHSZtvACv\nOT6oPWIbLDutQINxu5CQ9AunF/fGkXndFdpQaVK3+jDU18VKn3sKO6YiuRr0DleD3uW6llYfvYcH\nL6KwaVI7lLIyzfZaKStTHJrTFVZmRui54BiSfmpadAvi7R+Kn6kZ6OaWvzy8LGhRuwLKlTDD3iKq\nWRH+KR63Qz+ivYtttlCTs31JhOwajSPzuksdgmrqbIfRnepi/YmHeKiABH5VIPxTPE7eeYXRHV3k\nFl6WBJkZFQzDaDMM84RhmHOy2qe4uFW3xdf4ZJmKYC05cBsGejrYM72zxBc4wzBoUacCzi3ri5f7\nxsHT1R6TN13CoGWn5JpQqmhiElLQfuYh7PJ7gvDPCShjbYrezWti7VgPvNg7Dp0aVVH4mGzMjTGi\nfR0c8A8tdEmKQa8/o83fB9Hqf95wHr4N3pdDkJ7Bw9N30Zi75wa6N60uUjbaxtwYPv90Q/jnBIxa\nc65QGrjSwDW1c6lSGtVszRRyTC0tBoM8nHA5MLxICjftvxwChoHIUFNBc1pWjGyN0lamGLLyNJ6+\niy7QvtSB9SceQFuLwfgu9ZQ9FACy9VRMAvBShvsTG7caJEcqKxGsHylpOHnnFfq2rIkSBVxlVy1n\njZOLemHR0Obw9g9F44l7Cs3Nbvu5IKRn8BC4bSSe7h6Dc8v6YvPk9pjcww3FjPWVNq6pPd3AMMDq\nI4XHW5HyKx19l/iipKUJtk5uj0weHwOXnULFvhvQde5RmJsYYPNf7fKckBvXKo9FQ5rj8LVn2KnJ\nrwAA3H0WiecfvmFMJxeFHneQpxNYFth3qWh5K/h8FvsuhaB13UooYW4ol2MUM9bH7umdEBGdiFrD\ntqLdjIO4/uR9oTSk43/8wu4Lwejb0hGlrU3z30AByMRXwjCMLYD2AJYAmCLqfYGBgbI4XC7S4iNh\noKuN09cfw8Gs4K7dM48ikZqeCZeyejIbc5tqRjAa4oK5h4LhPGwzlg2og7qVrGSyb0UTGBiITB4f\nG47fQ4PKNkiO+YDAmA/KHlY22tQuje3nAtGxVjFYmCjPwJEFgYGBWHbiKd5GxWHLqAaoWxrYM9YV\n9998w4Gb7/A4PA4rB9ZFRNhLROSzr1aVDXC2sjUmbPCDCT8RDqWLKeQzqCqLDz2BiYEOHMzTwE2H\n8pqnctKgsjWWH7yN2qW0UNzMQCHHVDaBYbGIiE7E8JZZnV3lcb4tAJye0Qwn7kfg6N0PaDElDNVs\nzTC1U3U4VVCeMJSs2XMtDD9TM+BZvZjY51EW59vBQXTuhqw8FesBTAegFBUoTgQrNCJBJvvzexyF\nctaURCRLmlQvgb0TG8HUSBdjtj3A4mOhiEtSz/j21dAviP2Rht7udsoeilAGNquE9Ew+fO58UPZQ\nCszNZ1/h++AjBjSr9McQ1dJi0KhqcWwZ1QA3FnuiaU3xKmu0tBgs6OMMUyNdzDzwGOmZPHkOXaVJ\nSE7DtdCvaF/XFoZKiEVP86qJDB4fy048LZSraGGcC4yCsYEOmtWQbyUYAJgb62FYKwecntUCM7s5\nIi4pDfOPFB7hsYxMPo7e/YD6DtYqtTgo8DeJYZgOAGJYlg1iGKZZXu91cZGti5GzuFxcXODR4DtW\nH7mPGo5OMNSXPoM74ut3BIWfx6KhzeHq6iqrof7BBYBHUzcs3H8TG048xLVn0Zg7sCkmdq2v8i2R\nBc/3hD0hcLC1xIR+bVWy/bALgK4PY3DiwTusm9xdqeEYaQkMDETsj1QsP/USdRxKYcfMPjK7RvYZ\nFEf7mYfw7JsORnasK5N9qhurfO4ig8fH3OHtUN3OJtv1rQhcACxP0cfkTZfwKkEPAzycFHJcZZH8\nKx03nl9G35a14N6wvkLPt7sbUMU+GINXnEaGYUk0rClbVV9lsO9iMGJ/pOHA7O5wcbHP9/2yPN+J\niaJD+LLwVDQC0IlhmA8AfAC0YBjmgAz2KxFu1cvKRATrwBXS5e8vx3rfYsb6WD3GA892j0GTWuUx\nbas/ag7drDbZyo9efsKDF1GY0KWeShoUHDP7uiMxJQ1bzgQoeyhSweezWHAkBCmp6Tg4p6tMjc62\n9e1Rr2oZLDt0BxkivBVp6ZnYezEYkTGFIwdIED6fxbazQWhSqzyq29kobRwTutRDwxplMXHjxULf\naOz4zRdISc3AIE/lGE9dm1SDkYEu9l8OUcrxZQnLslhz7D5qVigOD9dKwt8UHg4owStTYKOCZdmZ\nLMvasixrB6A3gGssy/Yv8MgkhOsdXxARLJZlsf9yKJo6lYddSdmGPoRRpZw1zi3rC7/lfZGanol+\nS3yRpgaCOBtPPoKpkR4GeToreyh5UrdKabR2qYh1xx6oZdWNz90PePAmFmvHeqKqGHLFksAwDOYM\naIwPX7/j0JWnQt8zf98NDFlxGhX6bECvBcdx/3lkoXEd33n6EeGfEzCiQx2ljkNbWwu7p3dCanom\nRq89X2jOrzD2XgyGfRlLpXkJTI300cW9Ko5cf672wmP+ge/w9F3M76R0IQu7qCjA3h7YvFnhYysU\nOhUA6b8XVATr0ctPeBMZh4EKdkO2re+Anf/rhPDPCfjX96FCjy0psT9SceT6MwxtW1stQgqz+jVG\ndEKK2mkCBL3+jI3nX6JpjRIYJafwRAe3ynC2L4mlh+7kaor35O0XrPK5h57NamByjwa4FBCGhuN3\no/7YnfB78FYu41EkB/xDYWygiy5SiCzJmirlrLF4WHOcufcah68+U/Zw5MK7zwm4GRKBQZ5OcpVB\nz4+BHk74npyK8/ffKG0MsmDN0fsoaWmCPqJEBR/+vo/IIYSfHzI1KliWvcGybAdZ7lMSCiqCtf9y\nCAz0dNC9aXUZjyx/PFwroYNbZSzyvoXo+GSFH19cfB98RCaPrzI10fnR1Kk8GlS3xUqfeyLd/KpG\n0s809F50Alam+vinZy25TcIMw2BO/8Z4ExmHYzdf/Hk+k8fHsFVnYG1mhK1T2mPVaA9EHZuCTZPa\n4XtyKjrP8cEDNQnVCSM1PRNHbzxH18bVJJaClhd/dWuABtVtMWHjhUIZBtl94Qm0tBgMbqNc72bL\nOhVQysoE+y+rb/v5WyERuBwYjgld6okWu2JZoHZtwEnxoaZC46kAxBfBuhL0DrvOP852k0nP4MHn\n+nN4uVdV2gp8zRgP/ErLxJzd15Ry/PxIz+ThxP2PaFffAfZl1KMsi2EY/DOgCT58/a4W2gwsy2LM\nuvN49yUBi/rUhpmRfG96XRpXQ/XyNljsfetPI7w1R+/hyduv2DSpHSxMSUvAxFAPY71c8WjLCNja\nFEPvhccR/+OXXMcmL87df4PElDQM8FB+nwQObW0t7Pm7M36lZaDfEt9cniN1JpPHx56LwWjjag9b\nG+VWKWhra6F/q1rwe/hWLdsnfE9OxYBlJ2FfxhIT81J67t4dePwY0Ff8vaxwGRViiGCl/EpHn0Un\nMHz1WTgP34bLAeEAAL+HbxH/4xcGKnGiqVzWChO61MMuvycq2WnTP/gL4pPTMLGreLLlqkLb+vZo\nUqs8Fuy7iWQVbzS0/1IIDl55ivmDmqJ2RfkbblpaDGb3b4znH77h1J1XeBMZh/l7b6JL46roJsRj\nZ25igKPzuuNzXBKGrDitljkAB/xDUcrKBC1qV8j/zQqkajlrbJrUDteffMAi71vKHo7MuPQoDJ9j\nkzCsXW1lDwUAMMCjFjJ5fPhcU79Q09h15/Hp2w8cnN0VJqK8bHw+/SiJQmVUOFYsAWMDXZzPI+a7\n8/xjxCb+xOJhzZGWkQnP6QfQcdZhbDjxECUsjNHaRUQmrYKYO6gprIoZYfKmSyo1YfN4fOy5Fgb7\nkqZo7VJR2cORCIZhsGJUK0QnpGDdsfvKHo5IXn+MxdgNfmjmbIdZ/cRv+1xQejWvAQdbSyw+cAsj\nVp+Fvq42Nk1qJ/L9rlXLYNWo1jhz7zXWH3+gsHHKgrjEn/B7+BZ9WzpCW1v1pr8hbWtjkKcTFu6/\nWWhaeO+68AQ25kbo4FZZ2UMBQPcJZ/uS8PZXrxDIQf9QHL72DPMHN0O9anl0033yBLCyAm7eVNzg\nBFC9b1UB0NHWwpjOLjh09anQlX5aeiZWHbmHpk7lMbt/EzzfMxYrR7XCzZAPuBH8Af1aOUJHyRON\nuYkBFg1tjpshEfC9pRTVc6Ecuf4cEd9SMKK1g1ITraSlQXVbdGlcFauO3FOK2zM/d/a37ynoueA4\njPR1cXB2V4Xe8LS1tTCzrzuevP2KW6ERWDPGI1dTspxM7FYfXu5V8ff2K3j08pOCRlpwjlx/joxM\nvkq0iBbFpkntUK2cDfou8VX7/Iro+GScvfcGgzydVEqHZ6BHLQS8+qw23Yw/fP2OsRv84O5YDjP7\nuuf95gcPgO/fgQrK8cQVKqMCAGb3bwJLU0NM3XI510rf2z8Un2KT/qwC9fV0MK13I7zxnoClw1tg\neu9GyhhyLoa3rwPHisUxdctl7L0YjAcvovA9OVVp4+Hx+Fi4/ybsS5qimZjKjarI0uEtkZKagSUH\nbiv0uEGvP8O47VJM3nRRaGlraHg0XEfvwJuoOByY1UUpGv79W9dC1XLW8HSthKFiuKkZhsHu6Z1Q\n2soUPRccQ0KSeuRXePuHomaF4qhVqYSyhyISY0M9HJvfA8m/0tF3sXrnV+y/HEKJv+2UW7qbkz4t\nHaGlxcBbDRI2eTw+Biw9CQDwntUl/wXHgwdAqVJAWeWU7hY6o8LcxAALBjfD9ScfcObu6z/PZ/L4\nWH7oDlx+axcIUtLSBDP7NS5w8zBZoaOthU2T2iE+6ReGrDgNt3G7YNFxBUp1W4OF+xTv0vK59gyv\nI+MworWDSotd5UfVctYY2tYZm08H4P0X2Ui6i8PxWy+QnsnD+uMPUWfk9mwCbb63XqLh+F3I4PFx\na8NgeNbLXxlPHujqaCNo20j4Le8ntifKwtQQR+f1wKfYJIxYfValwnXCCPsUjwcvojCgtfwqamRF\ndTsbbJ7UDjeCP2CBEr7zsoBlWezye4KGNcrKXGeloJS0NIGnayUcuBL6J0FZVVl84BbuPP2IzZPa\niaef9OAB0KABoKRrvNAZFQAwqpMLqpW3xrRt/kjPoAqP4zdfIPxzAmb1c1f5CQWgjpLxZ/7GG+/x\nOLOkN1aMbIXKtlZYsP+mQruc8nh8LPS+hVoVS6i1l4Jj/qBm0NbSwtw9NxR2zEsB4WjsWB6XV/VH\n0s80NBi7E/P33sCCfTfQbd5R1KxQHIFbR8C1ah5xUgVgZKArsdFYr1oZLB7WHCduvVR5LZAD/qFg\nGKBvK0dlD0UsBrVxxtC2zljkfQtHrz9X9nAk5t6zSLyOjMPw9qqRoJmTgR5OiIz5gTP3Xuf/ZiWx\n6eQjzN97EwM9nNBPnJBdbCwQFkZGhZIolEaFjrYWVo/2wNuoeGw5HQA+n8XSg7dRrbw1OjdSvtiN\nuOhoa8HB1godG1bB9D6NsG+mF1iWxbaziumiCJCX4k1kHOYNaqrWXgqOMjbFMKlbfRy8EorgsK9y\nP150fDKevP0KT9dKaO1SCc/2jEXflo5YsO/mn8nixvrB+eYwqDLTejVC89p2mPDvBbyNilP2cITC\nsiwO+IeiuXMFpZc1SsLmv9rD3bEcBi0/pTYy/hy7/J7AxFAPPZrVEP6GzEzofvsGpCunIquLe1U4\nViyOkWvOqmTuyvazQRj/7wV0blQFO6d1FG8jHg+YORPw8JDv4PKgUBoVAJURtnapiAX7b8L7cgie\nvovBzL7u4t8Y4+KA+6pVKWBX0hwd3apgx/nHCpHzFvRSeKmA8qCs+LtPI1iYGqLRhN0YvfYcnr2P\nkdux/H9n8Hv+1uc3NzHA/lldcHZpH+z5uzP2zugMAyV0yJQlWloM9s3wgp6uNvot8VVJkbEHL6IQ\n/jlBpbQpxEFfTwcnF/VCaWtTdJrjg4iv35U9JLH4kZKGIzeeo3eLGiJLH83v3IFTu3bAU+Ey8fJG\nX08HPv90R/KvdAxYelKlclf2XQzG6HXn0K6+A47M7Q5dHTGTXEuUAJYuBZyVJzJWaI0KhmGwZowH\nElPSMGzVGdiVNEeflhK4PYcMARo2BKKj5TdIKRjfxRXfvv/MpoAoLwqbl4LDwtQQdzcORZ8WNbHv\nUggch25B88n7suXgyIpLAeGwMTdCbYdS2Z7v4FYZg9s4q0UoThzKFjfD9qkdEfDqs9JzACJjEuEy\najvseq9Hia6rYdZhOZpM2gtDfR10bVwt740zVa8nhLWZEc4v64u09Ex0mHUYP1LSlD2kfDl89Sl+\npmaITtCMiID9tGn0+zflVWBUt7PBxgltcfXxe6w4fFdp4xDk0JWnGLLyNFrVrYgTC3uKVs0UxtOn\nwM+f8hucGBRaowKgeuRhbWuDx2fxd59GkpWLfv6dTHfqlHwGJyUt61RElbJW+O/kI6GvZ/L4+Bxb\ncFdeZiH1UnBULWeNndM6IeroZKwY2QrvvySg8xwfmfa14PNZXAoIQ+u6lQqVUSaK7k2rY2hbZyw9\neBu3QiKUNo4NJx4iOOwrmjrZoYt7VQxt64z/9XLD4Tnd8lTLLeHtjdqtWgEXLihwtOJRtZw1Tizo\niVcfY9Fr4XFkqtCqOicfvn7HzJ1X4Vq1NOqL0lM4fjzrdyUaFQAwtF1t9GlRE3P3XMfdpx+VOpYj\n155h4LKTaOZsh1OLekvmxeTxgEaNgP/9T34DFINCbVQAwIpRrbB6TGsMbSthslDTpvR44oTsB1UA\ntLQYjPNyxcOXnxDwKrs+QCaPjw4zD6Fi3w149TG2QMc54B9aKL0UObEyM8L0PlRWXMrKBP+dEm6s\nSUNw2Fd8+/7zT+ijKLBhQltUKm2J/kt9lSLjnfIrHbv8nqB70+rYN9MLW6d0wLpxbbBsRCt0zss4\nfvQIZTZtApORAQweDKSonoRzy7oVsWVye1x8FIZ5e64rezhCSUvPRI/5x8Dnszg8p5toT9yxY0gt\n89vgULJRwTAMtk7pgPIlzdF3iXKuWwDwvhyCvkt80ahmOZxZ0gdGBrqS7eDVKyApSalJmkARMCos\nTA0xtWdDyYVX1qwBrlwB1q6Vz8AKwCBPZ5gY6mHTqYA/z7Esi/Eb/HDpt+z4+A1+Upf4paVnYv7e\nG6hbuRS6NC58Xgph6OlqY2SNATOnAAAgAElEQVSHurj4KAzhn+Jlss9LAWEAAI8fH6gN8WvVzTKX\nFSaGejg0pyu+xidj0PJTCi/XO+Afiu/JqZJJySclAX37IsPGBs+OHwcuXgSMjeU3yAIwvH0dDGnj\njBWH7yok0VhS/tp0EYGvP2PfDC9UEtUfKCICePgQsV5e4GtrU8WCkilmrI8jc7vjS5xyyqN3+z3B\noOWn0NzZDn7L+4qW4M6LB7/VbTVGhQrTsiVQU0RrWSVSzFgfAz1qwefaM8QmUvxs7bH72HY2CDP6\nNsLasZ64+vg9jkhZhrbj/GNERCdi6fCWhSbmLw4j2teBFsNg29kgmezvUkA4nO1LouTXj0B4OPBS\ndRRS5Ylr1TJYM8YD5+6/wZqj9xR2XJZl8a/vI9RxKPWnD5BYREcDBgZ4v3Ah0kuVou6OALBsGfDv\nv/IZbAFYM9YDNubGGLrytEqFQQ74h2LrmSBM790wb6/Q79BHfKtWiJo0CWjbVkEjzBuXKqWxeGgL\n+N5+qVA1461nAjFs1Rl4utrj7NI+0nfOffAAsLAAHBxkO0AJ0RgVwmBZwMUF2LEDuHYNWL1a2SPK\nxTivekjL4GGX32P43nqJaVv90aNpdSwZ1hKjOtZF3cqlMHnTJSRKqMSZ8isdi71voZmzndr1+Cgo\nZWyKwcu9KnZfeILUAlbXJP1Mw91nkRT6iPldXRISIoNRqgfju9RD96bVMXPHVdxRUJz62uP3eBHx\nDRO71pPMGLa3B0JCkFxbIETK5wOBgcCkScC2bbIfbAGwMDXEpknt8OTtV4UabRyxiT/x+mNstu/I\ns/cxGLnmLJo6lceS4S3z3kGlSsDo0Ui3tUVMnz5AY8X1ucmPKT3dUNuhJCZsvCDx3CkN/518hDHr\nzqNjw8o4tagXDPUlDHkIomTRKw6NUSGMHz+AoCB6vHSJ6n4TFKfAKA7V7WzQonYFrD32AP2X+qJ+\nNVvsm+kFLS0G2tpa2DK5PaITkjFXwtjrv74PEZ2QgiXDWhQpLwXHmE4uiPvxC8du5PbyRMcno+WU\n/djt9yTf/Vx/8gGZPH72fAoldg5UNAzDYOf/OqJCKQv0XnhcIf1WNp58BGszI/RqIaZ3MTKSjIaU\nFEA7R3hUSws4coQ8lceOyX6wBaRrk2ro1qQa5u25gTeRitEG4fH4WH/8Aex6r0fVQZtg1GYJyvZc\nh6aT9qLdjIMwMzaAz9zu+SfEe3kBW7YAAHRjYykXQEXQ0dbC9qkdEZ2Qgjm7r8n1WC8jvmHSfxfh\n5V4Vx+dLWOUhjB07gLlzZTO4AqAxKoTBlZEWL0596TMzgTNnlDsmIYzv4oqYhBSUtDTB6cW9s1m5\nrlXLYHRHF/x3KkDsNuoJSb+w0uceOrhVRsOaytGNVzYt6lRAlbJW2Hw6u8BYegYP3ecfw7Un7zFs\n1RksO3g7z7jrpYAwGBvoolHNcllJfz9+yHPoKoeZiQGOze+B2MSf6L/kpFzzK95/ScCZe68xqmNd\n8TLmWRYYNAjYvRv4KiI3QUcHqFYNiFJN0an/JrWDob4uhq8+I/fcleCwr2gwbhcmb7qEJk7lsW+G\nF+YPaoaWdSqABQtLU0Mcm98DJfNrdRAami0xs+zatUDnznIdu6S4VCmN8V6u2HQqQK6CY3P33ICx\ngS52/K+jbJqtNWig9HwKQGNUCIdzV5coQWGQcuWyl0CpCJ0aVsGq0a1xedUAFLfInVi2ZHgLWJsZ\nYcy682JNOquP3MP35FQsHtpc/EFcvQq8lV0ZprJhGAZjOrngwYsoPH6TZYxN3nQRd55+xL4ZXujf\nuhZm7byGKZsviTyvFwPC0bx2BZosqv6OL6uYt0sRONuXxMaJbXE5MBxzdl2TWwLc5tMB0GIYjO7k\nIt4GiYnA9evAtGnkjheFrS0ZFSrY16SkpQnWjvXA7dCP2H5ONnlAOUlLz8Tf2/zhMmo7PsYkwuef\nbji/rC8Gejph7qCm2DvDC7c2DEHwztFwdyyX/w6HDwfat//zZ6a5udKrP4SxaGgLlLYyxcg15+Qi\n5hb0+jOO33yBqT3dYG1mVPAdXrsGnDxZ8P3IAI1RIQxBo4JhyFtx+TJNRCqEtrYW/terIexFZFlb\nmBpi9ejWePjyE3b5Pc5zX1/jk7H+xEP0blETTvZi9vhITQVatQLmzZN06CrNoDbOMNTXwZYzVF2z\n2+8JNp8OxP96uWGgpxP2zfDCX93rY/3xhxi47GSuSSfsUzzefU7ICn2MHAnUqlUkjQqAKhZGtK+D\nZYfuYOaOqzI3LFJ+pWPn+Sfo1qS6+BLc3Hc8v/bQHTuSS5mneiqhADC4jTNa1a2IaVv95dKC/u/t\nV7DS5x4GeTrh5d5x6NWipvRh0Q8fgIAAoFu3P09lWFjQ9yIjd/deZVLMWB8bJ7ZF6LtobDjxUOb7\nn73rGqyKGWJydzfZ7PDff4EZM2SzrwKiMSqEYWICNGlC7WMBMipKlKBGLWpG/9a10KhmWczbewM/\nU0V/cRd730JaeiYWDmkm/s5v3KDHgQMLNEZVw9zEAP1aOeLglae49CgMY9afR6u6FbFsRCsApBWy\ndqwnlg5vgYNXnqLVVG/sOv8YYZ/iwbIsLj2i6yRbPsXly8DBg8r4OEqH0wEY08kFKw7fxaSNF4V6\neKLjkxEmRTnvwStP8T05FRO61hN/I251bGOT9/uaNwemT6dQiArCMAz2/N0ZxS2M0XLqfpmKjgW8\n+oR/fR9ibGcX7JreGZbFDAu2Qy43pUePP09lmv/uuhknIi/k6VMyQl7IX0E4J10aV0PnRlUwb69s\n81ZuBn/ApYBwzOznnqcYm0QEBpJXXQXQGBXC8PAAbt6knAqA4lQREUDdusodlxQwDIPlI1vhS1wy\nNp4UbnE/ex+DrWcCMaJDHTjYWom/8/PnAUNDwN1d8oGFhqrc6kSQMZ1c8SstE+1mHkIZa1P4/NMt\nWwIawzCY2a8xdk3rhJcfv2H46rNw6L8Rtj3XYdmhO6hQyjzLg9S0KancmeQTby7EaGkx2PRXO0zp\n0QAbTz7CqLVnwePxwbIsboVEoPfC47DtuQ4O/TfCfcJueF8OEVmBw+ezCHr9GSsO30GrqfsxceMF\n1HYoiUaS5AExDODkBJTJpzMsj0fffRX2MtnaFMPtDUNQtngxtPn7wB+jtiBk8vgYueYcSlmZYml+\n1RzicuwYzaEVs6rKMi0s6BdRIZDXrwFfX6XNFRsntoWOthYch23BiNVn8LqAooIsy2L2rmsobW2K\nsZ1dZTPI6Gjg0yeVMSpU0/yWN+fPA79+kQdCHDh3H49HGfy6BSj7UQLujuXQrr4DVhy+i1EdXWBu\nYvDnNZZlMWnjRRQz1seioS3E3ynLZp1Hc3NaaZiZibctn0/iYoaGwNatEn4axVCncik0qG6L0HfR\nOLWoN6xExD2HtquNIW2d8epjLG6GROBmSATuPvuIoW1rZ7mJP38GnjwBFi0C/vlHgZ9CtWAYBqvH\neMDIQBeLvW8j6lsSPsX+wNN3MTA3McCELvVQysoEO84/xsBlp/DXpksY0LoWrIoZ4ktcMr7EJ+NL\nXBLefor/o3roWLE4xnZ2xTgvV8nc8g0bAsFitGr//Bmws6Oy0pEjpfvgCqC0tSlurh8Mj2kH0HH2\nYRyZ2x1d8utzkgfrjz9AcNhXnFjQE2YC84XUJCdT6GP+/GxPp9SsCezbB5QuLXw7rl3Cxo3Azp0F\nH4eElC1uhifbR2H1kXvYczEYu/yeoHOjqpjRpxHqV5dAC+U3Fx6G4e6zSGyd3L5g5aOCBP3Op1GV\nRS/LsnL9+f79O8v9yJqAgAA2ICBA8g3Ll2dZNzfRrw8ZwrIdOmR/LiyMZYsXZ1kfH8mPpwI8efuF\nRbP57KwdV7I9f/zGcxbN5rP/+T7Mdx/ZzvfLlywLsGyrVvT4+LFkA5o5k7Y7dUqy7RTIl7gk9vXH\n2ILvyNqaPquxsUSbSX19qwFLD9xi0Ww+6zx8K7vjXBCb8iv9z2t8Pp+9GvSO7Tn/GKvbaiGLZvNZ\ny04r2BqDN7Gt/7efHb7qNHvgcgj7JS5JpmMSer7T01lWS4tl//lH9IahoSy7cCHL8ngyHY80JCT9\nYhuM3clqt1jA7rsYLNU+3n2OZw09F7OdZh1m+Xy+bAbG47FseDjLfvny5ymxru/p0+m7Y2DAspmZ\nshmLlETHJ7P/7LrGWnRczqLZfHbB3hsSnR8ej886D9/KVuy7gU3PkOFnWbqUZRmGZX/8yPNtspxP\nctzXs93zi6anIjUVqF5d9Otv3+aOodrZkafi0iWgVy+5Dk8eONuXRO8WNbH+xENM6FofJS1N8Cst\nA1O3XIZjxeIYJW7WPIe9PXD7NnkqrlwhxcjaYvZXCQkBxo6lxk0jRlB4qUQJyT+UnClpaZJ/iVx+\nsGxWgm9KCrlx1czTJQ9m9muM4e3rwNrMKJeHgWEYtKhTAS3qVEDKr3ToaGsVvIY/J0uWUMb81at5\nv09XFyhZMu+y0sBASubs2ROoUkW245QQcxMD+K8egM6zfTBo+Sm8+5KAeYOaiu3FYVkWY9f7QVtL\nC/9Nais7rRotrWxhjz/weMC9e5S/JixplvNUpKZSKCSveVvOFLcwxsKhzTG9TyOMW++HeXtv4Nn7\nGOyd4SVWn45jN54jOOwrvGd1Eb+VuTjMmAH07QuYmspunwWg6OVU/PxJMai7d0U3DYqJycqn4NDW\nBhwd1VpqeeGQZkhLz8Ri71sAgFU+9xARnYiNE9pK1sEVIKPL3T2rLjo8XPxtBw4Ehg0DDhwg7YYR\nI1SyZE8mpKaSIcG5d79/V+54VAgbc+N8b1rGhnqyNygASvx7/16893JlpaKYOJEeg+RT1ikpJoZ6\nuLCiHwZ5OmHBvpvov+Sk2AqxR64/x8VHYVg8tDnKFhcznCkOly5RH6Wc33OWpc6ae/cK387YOKvk\n93HeFWyKwsRQD3tndMaq0a1x/NYLuE/cjciYvCsDE5NTMWXLZThVKoE+4oqziQvDAOXLy3afBaDo\nGRUfPtDjq1eib4TR0cJXztWqkVGhpjdAB1srDGtXG9vPBeFG8AcsO3QHvZrXQFNnO8l29OMHMHky\nrRxMTSmD/t078bb9/p0yut3dgRo1gOXLKTdDRSYMmZOZSQZUy9/Jbiqc8Fek+PYt98JBFHkZFQkJ\nlC8AqIxRAVCDvD1/d8aSYS1w6OpTtJq6P19V09uhERi/wY/En7pIUEkjDkeOAKtW5ZaQ1tEBLC1F\nNxXbupXmagMDlZojGIbB/3o1xNklfRD2KR6uo3fgQR5CWTN2XMHX+GTs+F9HaEu6gMuLmBhg6FCV\nagFQ9IwKwdXJRyE9CdLSyF0tzKioXp1eE6XApwbMHdgU2lpa8Jx+AAwDrBrdWvKd+PsD69dn1fpP\nngy0EDPJ8/59Msq4ipGJEymJUZwko6dPKezySfb1+HLD1JQSzLiQmcZToRp8+5Z/OSnH2LGUZCsM\nwfkkMFD4e5QEwzCY1b8xjsztjqA3X9Bg3C74PXibSyeEZVmsPnIPzSfvg5WZEQ7N6SrbGx9AIWVR\nja5sbPIWwNLRIY9oqvx7cUhKe7fKeLBpOIwN9eAxzRtBrz/nes/t0AhsPROEv7rVh2vVfKqNJCUg\nANizR6XUeoueUVG1KpX3AcKNitRUik8Jyw9wdycFPjXuiVHGphjGd3FFegYPs/o1ls7Fef48dcNz\n+y3cMnOm+Hkmd+5QKKne75WQlhYJQwFZBocoZs4k79KlS5KPWVnw+fSZPDzIYK0n4xWgME6epPCe\nBtFIYlS0bJlNsCkbnIeuYUO6caqgF7Nn8xq4vm4QeDw+2s88hLqjtsP31kvw+SwSk1PRfd4xTNvq\nDy/3qgjYMkKysnJxkcaoSEqi74uvL+W/bN4s+3HJgOp2Nri5fjAsTQ3R5u+DeCVQdpqanokRq8/C\nrqQ5Fg6RQKlYXIKC6H4kbj6bAiiwUcEwTFmGYa4zDPOSYZjnDMNMksXA5EalSsCKFZSAFRmZ+3Uz\nMxIpatcu92vOzsDKlZS4pcbMG9QMu6d3wrReDSXfmM8H/PwAT8+sZFY+nww0cVQH79wB6tShWKkg\n/v40MT99KnpbblJJSpJ83MriyhU6T0FBgJ6ULY0lpWtXMoDjJReSKjLUqyd+CV5SEl23wrxMnFFx\n5AjNJyq64GhQ3RZvvCdg17RO+JGShm7zjqLWsC1wHbMDp+++wpoxHjg2v4fsxJgE+fGDQsqSGhWf\nP9NK/NcvlT2vHLY2xeC/egC0tBh4TPPGx2jKsVhy4BZeR8Zh25QO0rc0z4ugIEoOViENHFl4KjIB\nTGVZthqABgDGMQyjvBTd/AgNpfho2bLCPRX5rTRSUtTL/S4EE0M9DGlbW6oEOKNXr2iCEDS69u+n\nRCFx8ip27qSa85zU/J28dPas6G3LlgWMjEiMSF1ITCSji2GA8ePJyJAngobd69fyPZY64+sLjBsn\n3ntDQqg996NHuV+ztiYD29Y2d6dTFUNPVxtD29XGq/3jcXB2V7AskJKagevrBmFKTzf5dSWOiKDr\nX5RRMWuWcL0arvKjdGmas93cVLKxI4eDrRUureyPxJQ0tJ7mjWuP32P5obsY6OEED9c8+ssUhKAg\nlRG94ihwWjXLsl8AfPn9exLDMC8BlAGQS1c1UE4xR0n2W71fP6Tb2CBqyRJkmpsjM8e2VmfPotya\nNXjm44MMIR6JqkOGgG9ggDe/W/cWNfS+fkWGhQWelyz559yZZGSgKoA3Fy/ihzj9UbS1hcafq9ao\nAfj44JWnZ67XTB89gunjx7C0ssKPjx/xUcXi16KwDg6GHYCnnz7BcdMmRLEsvnLSxGIiyfWtGx0N\np9+/v/P3R7ymfFVicp5vvfh41ALw/s4dxFnm6LNTqxb9BAbCdt06pJcujRg1KDmvbA7sHecKHp+F\nTvo3BAbKt6kXc/s2wDBghVzLgQAlYuZ4zfLOHVQE8DQuDun6+qgdEIDokyfxSZRQloqwZlAdjN/x\nEC2n7oeFsR4GNCwul3uf1s+fqKajg28lSiBGgv3LYiwOogxEyDingmEYOwC1Aci+A4uM0Pv8Geml\nSyPV3h6Z1ta5XteNj4d2Sgp4ItQhU+3sYMBVkBRBvrdogZCLF7PkdQGk/ZY61s+nRXSxu3dhffq0\nSG9QYuPGMH7+HDpCMsGtLl5E8aNH8ezoUXxUkcY54qD9uzIgw8oKfD096BQwdKOdlAQmLU3k6/pf\nsjqrGggL72mA8fPnqNW+PUzEUdQEkPE790IvOjrP95mEhMD8+vUCj09RMAwjeSm5lLD6+mBFhP90\nv36Fhb8/tHIkYur9Dolk2NiA1dNDaqVK5ClVcZwrWGLFgLooZqiLGV1rwtxYPmFPvpERnh8/rnpG\nbE41LGl/AJgACALQVfB5lVLUjI8ndbZVq1j2yRNSIsup0jZlSt7KhytW0D7k8HlUnYAHD9iAR49y\nv8DjkeLdlCl576BTJ5Z1cBD9enAwndudO7M/z+ezbOnSLNujh+SDVjZz5pAiI5/PsiVLsuzw4WJv\nmuv6Tkig89O3r+iNvL3pPfm9ryhz+jSdnxxzR57zSYkSuf93GRmklrphA/09ZgzLFiumEsqaKsX6\n9aQ4moM/5/vgQfp/vHqV/Q07drBskyZZfw8dyrI2NvRdUgN4PNUap6IUNWVipjIMowvgBICDLMv6\nymKfcoEr/6pQgeKjs2YBAis7AJQvkFf9erXfevpqLIIlLVZ+fqjZpUtWrJODU8vLSwCLZakiIa/m\nY7VqAUePUqKhIM+f0zE9PUmF08NDtHCZqtGgATB1KsWULSwKVlLKxewPHxb9nq5dKdm1aVNNoqYo\nuFJocXUqAMrnyemJi4oifQWj331h6talpERJhOCKAkeP5q1cylXh5EzWHD6cGjty1KlD71GTnDYt\nLTknlw4dSuXOKoYsqj8YALsAvGRZdm3BhyRHuLBFhQo0SQC5kzVjYvKWjC7CRoX16dP0C9cSXpB/\n/gFGjRK98evX1HQsL6OCYagtskBoBQBw8SI9enrSTdnfX32SNdu3p4ohgCbPTPGUDYViakqTSLFi\nohOKjYwo6dXfnwwwDbkRt+25IGvWAIsXZ3+OS0zm5Ke5ahIVEsFSCfIqJwUo2RXIW6sCoETNzp1J\nFVkDldarkD4Fhyw8FY0ADADQgmGY4N8/QuoxVQA3N7Kaq1QBypWj53IaFe3b5625UKECsGEDlT8W\nJYKCYBoSgpiePYWXd/XuDbRtK3r7O3fosVGjvI+TnEwT+P37Wc9x9eq2tllytOqS1/LjB5CeTr/f\nuEEaEpKSlkY6CY8eAZUrU0WJqAl4xw46hiwSNFkWePhQJbUXCsS3b1TSbGgo/jZNmuQuQc1pVNSo\nQXML9//WkHWt5mVUiPJUNGiQvatvnTrAqVP0HSjqfPlC3ltV6UwqQIGNCpZl77Asy7AsW4tlWeff\nP36yGJzMKVWKVsLGxlmeipzJbJMmAX/9JXof2tqkAqnkxkEKZ8MG8IyMENepk/DXk5KoMZCosMSb\nNzR55Dch6OpSe+R9+7KeW7AAePCAfueMCnXxVHTsSOEaQPpa+6VLqQQyIYHOn46O8HJogLwiR45Q\nb4tu3Sh0JC2nTtHEvn+/9PtQRWrWBPr1k2ybyEgKOwkmE757R/8L298tsHV1SVJ64EDZjVXdefuW\nHiU1KliWlHaFGWi/fslufOoK5w1TsXJSoKgpavr7Z/0zihUjoSvByZllaWWZ38rs0yfg8mX5jVPV\n+PoV8PFBbMeO4IkSWbl9m7wQojToV66kSTi/G6u+Pt2Ez56l/wOfT89z25UqRZO3uhgViYl0nQF0\nU5LwhmMQHg4sW0Y3QU9PoFUrmlSFTSZ8Pp0XOzv63dc3bzGx/OBuoGpSvvuHpCTSoPD3F/760KHA\ntm2S7fPWLVLaFbzuHB0p5Jezo7GGLBISKHclL6NCX588mcOGZT0XF0cGRZkcstaTJmk8FYBKKmly\nFC2jYuJEannM8eoVsG5d1t9xcXQD2LQp7/3s2AG0aVN0LGYbG+DoUUT36SP6PVwnwbyS1MRVfevU\niVx7jx8DU6ZQqIkz9LS0yHjhkuNUne/fAU6X4uVL6szKGUr5wefDbulSMoC561RXV/RN7MsX6ohq\nZ5flkg8Lk37svXtTiEDdtC7OnSP1VS4XJyfShHM4b4SgZ7NPH+C//7K/z9+fQqsFOe+FidatKfm9\nZj6dORs1yq5ULCh8JUi5cpQgyyXbFlXKlQP691cpJU2OomNUsCzF4StUyHquZMnsEzRXh55fAle1\narS/N29kPkyVRFsb8PJCes5VgyB2dmQ5C1PV9PMjQ0HcRmzt2tG+zp6lG4OZWXYPx/XrwNy5En0E\npSHoqTA3z/KGiYHVhQswCQ2lltGC1+SSJcIbXHF5JnZ2ZHSVKVOwmxvDkLGobtUMT57Qo6jrrWLF\nrHbl4sKFSwUrQIRpjlhbk+GhSdaUjEuXyLPGwVV45DQq6tShR+5/XFQZMkRlw5KFz6iIj6fEtpxE\nR5M7V9CouHSJyv04OOs3r+oPIKsC5EUu0dDCx4kTdAPPQ3AJALkwbW2F34AuXyZ56pxqhKKwsSFZ\n5IcPqWpEiMKmWsDnkwHBGRVcVYuY7c8TmjXD29WrgQEDsr/w8CFw7FjuDbhQnp0dPdrbF8wgWL0a\nePYM8PKSfh/KgLshCUvmZVny6BgYSLZP7ubGGRWJieRB2rAh+/tq1KAeLxqjghg0iHKi8mPjxuyG\nspkZ0KVL1rXMwbn7i7JRkZysklUfHIXPqOjZM7uhwCGoUcHx+DGtArnkQnHr1ytXJjd8YS8rZVla\nFZ84IV4zLGGr2sxM4PhxoFkzyRpqXbuWdTNr0yb7awcP0uSdn6GjbHg8mihbtaK/JTQq+MbGSGza\nNHceioMDJcDlDKP06UP75uLXderQjU9aXrwgb8eQIdLvQxlwRoVgW3KOpCS6biQpJwXICLGxyTIq\nuH1zYREOPT3SW9EYFcT587l1bYSRs6lYw4bkucjpqTA3J0/T48eyHac6sWcPedlVVK+j8GUYmZpS\nTHXjxuyTsTCjgisrjYykluhc+CM/o8LAgPZT2I2KO3doRbB1q3iVC4sX5473nzlDF7+kbYu1tcmT\nVLZs7kqbzEy64UVG0mpcVdHVJYE1DhsbugllZOS/7bVrKOnri5jevXO/Vrkyed2iorKuYQ7BviJr\nCygbEx9PhlBkJLn1JSnBVCbcjV9Hh861YE4Id+OSRPiK4+LFLI2WnOWkgtStSxU4LKvy3TXlSkIC\n5anllaTJYWNDQmLcOcvr3P39d24tm6LEvn00J+YVjlYihctTweeTqzwiIneHxg4dSPtA8CaUs6zU\nxYVuAuK46ffvB5Yvl824VZUNG+jLm9P9LopGjYD69bM/t3kz3fjat5f8+Lq6VJKZc3JRF62K1FS6\nFjmPSqNGdK3lPEfC2LkTJQ4eBF9YkiQ3SXPlehxLlwrv9igtcXEU/ihXjkIu6kLJksDChRQOynn+\npBG+4qhTRzyjon17qtYpKoncohCnnJTDxoa+J7975aBLF6BFC+HvHTmSpAGKIs+fkxds0CBlj0Qk\nhcuoCAgAxoyh33OqCRYrRjX3gi74nAJYDRuSu19LjNPSsGFWxUNhJCqKRJRGjBC/0iIujlZoXIIc\ny5KRN2eOdG2hfXyEV+Koi1ZFYCDFhG/dkmy79HTAzw/fmzQRft4qVyaDmJuAOfbsIYEtjogIMmDO\nn5d05ERcXFZinDola965k100SRBLSyo3laYsMSAgK4fi3Tval7DGgx07UlWIulQoyQtJjQogy+iL\njBSd98KyVLlXFCtsvL1pTsirEk/JFC6jQjDbO2c52f795E4XpEwZWslwPRKiosSOd+PLF2DLFvEr\nGtSNX7+oj8TIkeJv8/49lSFyQlUMA0ybRoaJNIhyf9rakuGn6kYF1waeu/GkpdEq9tChvLe7eRNI\nTMT3pk2Fv25rS4Zw59ODd7MAACAASURBVM5Zz/H59BxncAHkZXr0SHoBLCcnymvR0VG/CTwpiSqO\ncia0Vq5MN3xpwmb+/iSM9/MnVSjNmSP6vTyeJq9CX5+8v8K8OTnx8iLDlVvoff4s2r3P45HC7po1\nshurOsDnU0l6mzb5FxMokcJlVHDNwfr3p0fBevScKo0AGRQ/f9KNDwC6d6ebojh8/Eh9GNTJLSwJ\nDg40IUvijeEmj/BwWkUfPCifZEpdXTJ4cibJqRpc8zAuz0FPjwzbZ8/y3u7UKcDICD/q1RP/WF+/\nkodDMFu+WDHKHZDWIDh8mFb8FSqoj6fixg3yzkRFUdVRTuGulBTpZbS56+3TJwqnTp4s+r3z51Nb\ngMK66BCH7t3JuyNOpQ2XgKmjQzlT0dG5kzQ5dHSoh5Bgs7GigJYWzR+CWksqSOEzKhiG3MCXLmWt\ndDMzyQgQTNLkyKlTIW4CV9Wq9FgYkzXfvMmdkyIOlpY0OYSH02q8f3/5rdaOHZPMi6IMcnoqxO1U\nmpICdOwINq/JeOXK7L1WBDUqBLG3L7iXQRb7UBRhYeSdMTIir03OCpC5c8Uvbc4JZ1RERFCisKBk\nd04GDqQk0S1bpDtWUSM5GVixgoyQ6GhaEIoyKgDqwvvyZdETwapRgzyIKkzhMypsbLIMBa4jZFQU\nucyEGRW7d2d114yJEd+oMDOji74wGhULF1L+iTQrOq6sdNMmwNmZVmtFlZxGBUBGV34htr17825v\nzu3b3z+rkiQ+ntT1choVlSpJZxB8/Ej7OnWKhKLycvWrElyZXalSNP6cRsW3b1ldMSWFMyoePqTJ\n3dtb9HsdHMibsWVL3sZHYcbBgQwFcWBZYMYMErbT1gYmTMjK5xFGs2b0KGm+kirB51PFizgkJVFy\nZkFk9xVE4TIqWrakixGgC5Sz6ISVk3K8fEn5FklJFAqRJFZVrVrhMyq+fyddir59JdOV4KhYkdzO\noaEUHpJXSd369bTqL0grcXnTqhWVdQp6HCws8jYqOEMuv/NWuTIZypyHokMHEsThPGgc7u6Aq6v4\n0uAcsbFZOStt2lC4SR349IkWBnp69H0XZlRIU/kBZBkV3I0sv1yBv/6i4/n4SHc8dSYujoxZcecQ\nExPKwfj2jap3/v2XrltR1KlDjSHVOQRy/z59VlE9agTx9aX7lAqLXnEULqOiV6+sFVWZMuSiDA/P\n26goV45WElwymyT169WqURZyYWoNfegQnQ/B5j6SsGwZVcaYmZFhIi+MjMgAEkdYR1m4uuaOuzs6\n5u3WdXWlpkn5wVUvCErFM0xuY2TkSDISxaloEiQujh6trChp99499XA1f/qUleDn5ETnSdDjJok3\nMidGRmTEdelCf+dnVLRoQT0vpGl3r+5wlR/iJsQyTJYAljh5L7q6lIw/f36BhqlUTpwgr0zx4vnn\n5u3fT9dbw4aKGVsBKFxGRXR01sqVizdfugQMHkwhEMHMeA5OqyIpiVz2kvzT5s6l/RYmgZtdu2gy\nlrb7nZ0dJWcOHkwrCXnBuflVuQIkLCx3L5RduyjkJur9oaHCjd+ccGV6nFExdWrecsiSGr5cRZSV\nFZ3jRo3UozNv5cpZrvExY8gYElwtF8RTAdAcEhVFNwNu7hAFw1DfG8GeFkUFScpJOTijYulS8lzk\n511zd6frUx1hWbouWremuXL4cNHf0Y8fKSw0cKBa3GsKj1HB55N7kms0ZW9P8eQLF2iVVqaM8Jp/\nroQpOZnc9ZLUr9vYUIZ9fLzk7mVVJDKSvDvDhkl/8WprU7LVsmWyHVtO1EEAa8IE8p6Jy+nT9ChY\nKioKKytqEc8lHZ47J7wXTVIS5ResXy/+OIAsT4WlJRk5DKMeyZrr1uWtJPrXX0C3btLv/8QJyr4v\nX168ludly9J3QpXDdPLg7Vuad8UpJ+XgjIrPnykMnZ93LTmZEpbv3y/YWJXB48dkrHfrRtfks2ei\njXZvbzI4xBUhVDKFx6iIi6MvLqd4B1As+No1SjwUpQ1QrhwZHB8+0CqRx5PsuJ8/k0t71Sqph64y\nlC1Ln6egvR4YRv6SzpwxqMqeCsEOpRw7d1LtvrBVyenT1DdCHE8Fw5AXbtAgMmgjInInaQIkW5+a\nKrlBYGtLOg+WlhTrLltWPYwKQZKTyeO2Y0fWc1OmkDiVtHAT/8qV4m9z5QqdT2EdfAsr1aoBQ4dK\nlpfl40P5Kp8+5R0i5NDTo/DH0aNSD1Np+PqSsdmpEwlZlS5NDfyEYWdHCwhJDDQlUniMCk6jQtCo\n6N+fXMJr1ohOhrG2JndmSgq5/SVdUZQqRW642bPVOxOZu8lZWJDrUdUxNKSqnRo1lD0S0Xz/nr0X\nB0BeraCgrCZ2HImJwN27NMlIAstS2C8tTXh4D5CuJLRTJzJyuJtCQTueKoL372lyPnOG/jY2phUz\nly+VmkqLB2l1KoCsZE1JZOerVaNFz8aN0h9X3ejTJ7sxJw4WFpTUnJfwlSB6elRdJqgiqy6MHEk6\nPlZW9DkmTiTjMzg493v79ZNeFVcJFG6jokEDYPx4ypjNb/UXHU03AH19yY7LMLT6rFSJhLO4pmTK\ngs+XTnDqyBESDeLOozqwdWtW0pwqIsxTkVen0vXrSTBIXLZvp/1zFUjCPBWAbHQmpC1NVSSRkXT9\ncl4yhqHvPRciCwmhv8XJthcFV44aGir+NmXKUPfkXbuKRj8QPj+3hLw43L1LScrv3onnqQBIryIk\nRHwlZFWhfPnsodFRo8grGBBAf/N41N+EqxwSJ9SmIhRuowKgLptA3kbF3Lkk3SttVripKbX3Tkig\nigdJQyiyZOpUsvYlHcOJE1mxTHUiKUnZIxCNMKOC81zkFMAyM6McDEmEbYoVo8//4gVQvbpo96i9\nPYVHxOmOytGtG7lcOSZMIJetKlc6cRoVgqtcwbLSgjQT4+AalHH5L+LSvj39r1Q5B0gYwcF0Lfz8\nKf424eE0J0paSvviBZWSDh9Ost3i0KQJXZN37kh2LGVy/HhuHRpzczKKuZYGM2Zk3VPUjMJjVNSu\nTa23cxoV//1Hj3kZDFyr5ILcUB0dqSOnvn5u17Yi+fdfeuQS7cTlyxdKUpW09FCZzJ5NNwhVTZLd\nuTN3Wa0oT8WzZ5LH3Lmk4tKlycWfU6OCo1kzaqIlySr5y5fsBoSjI9C4sWpnnwszKjgBLJbNKokt\niFExYAAtQmbOlGw7QYlvdWLbNjImjxwRfxvOcyZObpAgnBdo8GDSeBGH+vXJgFEnY23RIrpX5IRr\nQLd8OeVXjBuX1SBTjVCjO0g+ODnRTSZnguB//9E/sWVL0dtySX8549+SMmQIxb6KFaOmWl5elEyn\nyJvevHn0KKmmQFyc9PLFyqJ0aQr1qKp+Qu/elJQpSOnSdHPOGWabPFmyShEgd1mpKFq2pO6axYqJ\nv++c18OvX7TyFFZhoipERVE+kODnbNiQysvT0mTjqdDXpzwtSfOOqlQhY4Sba9SFzZvJMMvZNykv\nuGtElJErCu7/EhAgfm6boSEJtXGih6oOVzYuSkxuzhwyWFu0oEomNaTwGBXh4cLzASws6B+VV0yK\n+6L37FnwcXAruchIqpFv04ZWlIqSV+U6W0qa2xEfr35GhSq3QE9JodrynB6j6tUpobd+/ezPP38u\nedKpqSkp8s2cCYwenfd7JTW+4uKyawDweJR8J6nbX5E4Ouau5e/dm1bZBgZkVBgYyFc/RRQlSpAx\nIk3LdWXCMJRUePOm+Dk1L1+S8SysLXxecEbF6NH5G8qCSKP8qyw4zRJRRsXQoSRtcPx4VqhNzSg8\nRsXgwdL3mOeMClmuInr0IMPi0CFydc+YIbt958X793TBikraE0XLltROWJ1QtFYFy5LnYeHC/N/7\n5g2tNm7fzv+9CQlkEEtTycL1rckv3FWjBtXDiwOfT2MSNCpMTMiAUeUKkGHDSMBOGCxLSb3r1ysv\nhBMbmxVqVQfu3yfRM1dXCouK6614+ZKMZ0kR9CCJm6gJ0Jzn7q4e4mwnTgB164qu1KpYka5hLkyq\nhhQeo+LLl9z5FOJSvjzFs7gGULJCX58MncmTSVlPEXXq8+fTSkySluUAGT/SSnMrC0V7KmJjqRxU\nnNJhYc3EALq5Va+evSadK3mUxqiYO5eus/yMyLp1xU9my8ig1WmDBtmfV/UKEGEu858/KVa/ejXd\nIDkjTBl4eOTvUVIlbt0ib6uTE81ff/8t3najRknXQdjCgkorjYwk83KUKEGdaa9elfyYiuTnT/Jg\nFkR8TQ0oPEbF16/SGxUODpRUx4UOZM348VT2pAjxkrg4qsdXt4QwaShWjG6qiuqEylUSiTN5cdUd\nOfN0GIaqbD5+zHquIEZFTAyFNvKr62/cmDxngscVhb4+ddfMqcWgyi3Q+Xwyphcvzv68kRG99v49\nfQeV6SmwtVUvT8W9exSusbEBPD3FzyMZNow8tZLCMHQ9ly4tmTfJyIi8rNevS35MRWJkRAnZ06Yp\neyRypXAYFUlJZAFKa1QA5FGQJJFNEszNSSkRkG9JXloa1YcfOyZZq+rgYMqnUAf3YU4WLKAbpiKQ\npKJGlKcCyN2ptFMnirVKE37jlGKFSdAL4u5Oj+J4K3g84SXJ9vZkrKqi1kJMDIlaCXMbc2WlnTpR\nMreyKFNGfYwKliWjolGjrOd2786/6iUmBnj9Wvqyeh8f6QzX5s3Jiyhrb7M8UCPNCWkoHEaFKI0K\nVYJlyYKXZ5ay4E1PkkTN2Fi6yQm26FYX0tIkEyIqCFyTLe64eZGfUSGoU1GqFMX7pYn1jx1LJWj5\nuZsdHcloFseo8PeniS9n58QRI+jmLKlAnCLgPHNc6aYgnFFR0GZiBcXWlr6jqmiU5eTtW5oXBBss\nhoaSOnFsrOjtDh2iqg/B74ok+PpSxZykNG9OHqm8ru8+fYBZs6QblywYPlz9QsxSIBOjgmGYNgzD\nvGYYJoxhGAVlJApgYwPs3ZvdqlY1GIayeXfskJ9qpbRGhWBHSnVj5UrA2ZlUU+UNd367d89fDKhT\nJ2p5LaxM2dw8u6di586s2n5JMTCgWHd+N3ptbVIgHTo0/31ynzPn2EuUoNwNVdQyEaZRwVGhAq2e\nf/1SvlEBqEdoMi2NeqQIegGHDKF8G1F9lAC6jq2spD/PXbpkF10TFzc3oEMH0ZU9iYnkBZF3o8O8\nePxY+YrLCqDAswPDMNoANgFoC6A6gD4Mw0iR+lsALCyosZKkYiuKZto0SiaTV/1xpUqkj9Gxo+Tl\ng4D6lZQCFEtlWXJ9ypu4OFrtHzuWf3a2nR3plAgLSzRvnpUEGRdHHoALF2Q+3Fz06ZNbN0MYooxM\nHo8SHq9ckf3YCgoXVhBmVLRsmZUcJ61qrixwd6dFhTp8zxwdqYdKlSpZzzk5UcLvrl2iw7gvXlCv\nE0VjaAicPZvV9j4n3Pdr4ECFDSkXBcn7UyNkEdypByCMZdl3AMAwjA+AzgByqeQEBgbK4HC5eXry\nJHQSEpBSs6ZqrqIEqNCqFcw3bUJomzb/b+/M46Kq3j/+OTOgIJsIgizu+XPDBBVzyy1Nc8tKLUOT\nNK0My/rmki2a3699M82lTbM0s/KbpZZoZVlZVpqJqKlprqgooIKQIOtwfn88c52FO/sdZjvv14vX\nMDN37j1czpzznOc8z+eBxhkxHGo14sLDEZ2Xh8x9+6xyqcccPow4APvPngW3YhXlrP+jPaj9/JAE\nIHvzZuSGhDj1Wv4DB6JOUhJKMjJogjUTxxB09ChUpaW4LjeJ33UXPWZkIDgzE20AnPD3xz8m7qtS\n95tVViL0jz9QHhuLMjMGeOzhw4gFkHHqVI103cT581Fw550476hQnMIE+/khfMwYXDh/vqYnIDIS\n9YYPR7tNm3CysBBFFu6nU/t3YiJlgbl5xVL19evQyHyfGt5xB5q+9hr++uQT3DAWt+IciYcP41r/\n/jhnwz1U8n77FRZCExAAbrSV2/yDDxAaHo5DU6cCrhi/NBp0zstDTnU1Lrl4/FTifreShPdkUGIG\njgNwQe95tva1WiPyyy/R+rHH3FtCWEvuhAlQ37iBqM8/BwCE7t2LyM2bEbtiBQL//tuhcweeOIGI\n9HQU9e6Nc3PmWK3kWdqiBa6MGAHuSSIyWjRhYShr0gRBR444/VqVjRqhpE0bJA4YgNjVq80eG71u\nHZpYUR47UDu5lNaCl41pNGj57LOIsFDxUF1UhKqQENmAsvL4eNR1w2DD4k6dcGHGDJOGXmVEBLLm\nzEGJK1bREpyj3vHjqHvhguVjXYi6qAiJd9yBhtoxSp+CwYNR1K0bmEz6rt+1a/ArKkKprRo5ChF0\n9CgSBw5EqHEsEIDCPn2Qm5qKOjk5YLbUwFEIv8JCsOpqVHriFrOtcM4d+gEwGsD7es/HA3hTel5Y\nWMilH6XZt28f37dvH+fjx3PepIni53caq1Zxnp1Nvzdtyjk5EzkfM8ax8/7nP3SesjKHmyjHzfvt\nbqSkcB4X5/zrfPop5z/8wHlsLOepqeaPHTCA8+7d5d97803OQ0Pp/zR1Kv1eXV3jMKfc727dOO/V\ny/wxmzdzPn++/Htjx3IeH69sm5QgL4/z8nL590pLOWeM83//2+wpaqV/h4Vxnpbm3Gs4ytatNI78\n9JNtnysp4fyLLzg/dcqqwxW/32VlnAcEcD59uvz7GzbQ33X4sHLXtJYLFzgfMoTGDxeh5P02mtcN\nbAIlPBXZABrrPY8HcEmB81qPI8JXrmDyZN3e79atpB8wbBjlMDtCfj7lkms0FFthLkpbH2t19t2V\n6dOBjz5yfgXNF16goMqmTS0LbhUWmq4lo1JRYOm1a6RR0a5d7XnZevUioaCyMtPH3HMP8OKL8u91\n7UrxC+4WbNinT83ibRIBAdQ31q51fZVVT9Cq2L2bvFTJyaaPyc2tmfpZrx7FEdkqvKcUdetStoqx\nXsWuXTTGNmpEz3Nza79t8fFUF6p//9q/di2jhFGxD0ArxlhzxlgdAA8ASFfgvNaTm6vrMJ5Ghw7U\n4Tp2pJQ3Ryb4q1cpuO7MGYqG/vFH6z7Xpw8wZIj913U1XbpQ8KOzJ2apyJY1RoVc2XMJKcizsJCM\nSuMyyM7k9ttJz8HcvuqVK6aNjp49acJxt8JiFy/Kp5Pq4w4S455gVPz2G1V9lqpmGlNdTd85Y4XN\nXbusk6V3Jv36kciZFHzOOTBuHCl1utKo8CEcNio451UA0gB8C+AYgM8450cdPa9NeJqnQo4XX6R0\nI3PCKKNGAevWmX5fKgIllXC3Nn2poMD2qovuxvbtzs1K0GjICIiIIKPiwgXzMSvWGBXXrlFRsNrc\ng5Z0B3bvNn1M9+6m8+k7daK/beBA5dtmL//8QwJ45lRFpaBoV8ddubtRUVFBnixz6fkqFSlmbttm\nqEcxfz7w7LPOb6M5+vWjx59/pscDB+i7evfdujnCWSn95liyhMYNS/o2XoAi0l6c868BfK3Euezi\ns89cm3+uBJZ0BvLzqRjNpk1ASop8QFp+PtU5iIigL74tRoUnpLmZ44UXaLthwADnnL+wkFY9ERGU\nMsc5DRCBgfLHb9tmevtDen3XLvJU6K+inE1kJGkJmKuWaVz2XB+12vQK1lWY06iQOHnSUHDMVcTH\n0/eyosI9q2tqNMAbb5Dn1Bzjx1Nxts8+09Uz+esv+zQmlCQ5mfRYpJTtLVtoLBw2jBZO9eq5xlNx\n/jwtItxROE5h3Dv/0lr696dtBE9n8mTgrbfk35PqTgCmYyU2bwZWraIvUcOG1hkVnHuHUdG1K7Bv\nn9UZLzajr+UxcCCwcKFpgwKgwc1U2lV8POmqHD9OYjzOarMp2rQxnXpdVaXzyJjiu+9I+8FdlCGt\nMSqiotyj7PjYsaSZ4GqPiSkCA2kcslSxOCmJYoE++oieFxaSB8Ce6qRKUqcOFTSTqpxu2UJel8hI\nuufLl7umoJePaFQAXmBU+F29SmJE9srCuhN//GFaBEnfqLhkIg42NlZXuTM62jqj4vp1mki8waj4\n5x8qOe4MmjenwLThw+n59eumVTyLi6lOgiktgvh4ChoMCCCvRW0PNmfO0OpSLoVZWs2bMyrKyyle\nx130Slq0ICPPWDfBHWndmopz+fu7uiXy7NxpnYYGY+St2LOHxiNJEdaVKbsS+fnABx9QEPSff9LW\nh8QjjxhKj9cWOTmeG/dnIx5vVAQfPQqMGUPa/p5OQoLpDBBLRkVVFbBggW6gX7rUdAS/MTNn1ixz\n7WlIKyuZHHVF8PenqPawMDIaQkOpkqccFy9STMLvv5s+H+c04LVv75pV67vvygfyWqOuKlWFNReX\nYQ9nz5JhbSstWlAflmKJ3JnSUlo9nzzp6pbUhHPaWn3pJeuOnzyZApZjY3VGhas9FQDd24kTaTvm\n0iWSF5e4eJE8mrWNJycT2IjHGxX+0laAN/zDOnSgvTe5Snvh4bTCAeSNioICiiuQJtX+/c2nhEmE\nhtIqT6pi6am0bk1Bj86S687MpDoj16/T3myDBqYzQMwVE5OIjKRJ2Z5y547SvDl5R+Qi9cPD6e80\nJ+cdGUlbCUobFZ06AbfdRvEGtnDmjHUl3d2B8nJKu0yv3QQ5q7h4kVbUt91m3fEREUBjrZrA/ffT\nZO0i4SsDOnem7+jOnTQv6BvICxe6Jsh4yBDnxXu5Gd5hVDDmGasUS0hxIXLeirffpoGoceOa7wG6\nFabktj5zhoI6LeXll5XRJOjq/H1HUatp5e+suio//0wpdFLKr7m0UmkLwZyUtRSP4AqjgjFKLZWr\n6BgVRTVq9Gs+yNGjBxkVSvYb6b7Zqnj49NMUiOcJhIVR0St3zACRDPLOna3/zNmzwNChwOHDZIia\nka6vNfz9yeu7YkVNz2WjRjTe1XY80NKl5NnxAbzDqGjY0Dtq1HfoQO5D4wqY0sBdpw6tyOQ6p+Sx\nkYyKTZsoBbW42Pw1t2yhyc/eKpnuRLNmjg1q5gb6ggIKbpS8D+aMCms8FS1b0or18cfta6uj9OxJ\nqXbGktH5+aTnoNGY//yAATSJyHnV7OHKFXpctMh0pUk58vPJmDQXpOlOMEYxNe4mHgaQUaFSUX0S\na4mMJI9A9+6u16jQR/objA1UKX6pNjNAqqtrPxjbhXi+UZGf7x1bHwDQpAkFFxm751aupEwC/XLZ\nxkieishIerRWq0IKcPX0QE2ADK7HHqNVk6189hl5geRW7wDd3/BwXdaEZFTIrdStMSrCw+n/6aqA\nve7dyQgzntzWrQNuucVyKfmUFAoqVqqwmBQz1KoVsHGjdR6Qv/+mWKBLl4C0NGXaURu4q1ZFZiYF\nWtqSMhwSotuW3b7dOe2yh0WLaGFlrLfhCgGsPXtoQWitGKGH4/HL+/MzZqC+O+zjOZP9+2kCql8f\nmDePshA+/tjwGGNPhVTiOS+PJglTSEaFpVLenoBaTQGI7dvbnmIsBVWaCjSThMUk7r2XvA3V1TW9\nI6NHU+CoOWPX1au6Ll3kg5uNPTKWUEpvITycsgmyskh2fd8+83Ed167RhKFS0UrZFRH99hIf754T\nzKpV1mvb6PPAA8CXX7pOnluO4GD6jhrjCqMiN5c8f75QTAxe4KmoiInxDo0KiSVLdOJKEgcOUBAb\nY7TCkRuQUlNpQJDcwNZ6KvLzyd3sDaIscXEUiW5PBsHhw+QyNeWxKSgwHBR69wamTZPfbgkLA269\n1bwX4ttvgffes72dSmEq48TYI2OOxx83P/HbQnIyeUnGjaN7+uWX5o8PDwdef53+155kUAAUUO1O\nq3qJ2FjSn7CVMWPISE5NVbxJinPLLcCGDdYHoyqBpODpLR51C3i2UVFdjaj162lP1Vvw9ydRJMmS\nrqigCU/6ssfEkKFgvOft50feCWmSs2X7w5ss6K5dbTcqpAJsR46QwqUc6emG71VVURyK3P397jvA\nQml03Hkn5cy7ko8+okwQ/Tofxh4Zc8TFUd9UQqny4kWdYmnv3qaNirVrgR076PcJE9wj28BWbrnF\nPVIv9cnMBBYvti9GhjHKHrPGEHU1ISFkBEniWLVBbi7dG2lr2svxgF5gGr+iIjRZulSn8+4NSF4X\nKS7gr78o2EgyKmJjyeV++bLh5z7+mFZuElFRwE8/WVaPu+++moWBPJmuXUkAy1z8iTFHj1JAa1WV\nTiHQmMBAw8n22jWaGD79tOaxH38M/PvftrXbFYSE0HZDZqbuNVuMTMlDsGePY+0oLKQtAan/3n03\n/U+MtRyuX6e+umSJY9dzNbm5pJzrTmmwW7eS1oc7ZG84m99+s8+baS+5uYYLPi/Ho40Kr9KokEhI\noEfJqAgIoBWt5K6TLGxjrYrPPzcsNubnR9VHpdgKUwwfDkyd6ni73YWuXWn1bZzVYI7GjckQaNfO\ndADdzJnkgZCIjCRDQy4DxFwxMXdCErHSNwqefhqYPdu6z3ftSiswR/UqpCBNyaCWFBB/+MHwuNde\nI2N6/nzHrudqcnJo68xZmir2kJlJacSeXljQGtLSatfoHzDAswKJHcSjAzVvGhXepKkeGUlGkqRV\n0aaN4d578+YU8W6conT1ak332jffkGvfXA7/6dMUR+ANgZoAiX5ZIzOsT3g4ZTN89x0F/RlTUUHR\n5KGhuoJJjJlOKy0qUi4rwplER1N/0jcqhgyx/vPBwVR4ylGjQvKUSN64Zs0oGFk/8C87mzwZY8da\nJ+rmzkgl2o0N2Bs3dH+jueBqZ7B/P9C3b+1e01U0alS7gZoPPFB713IDvMNT4U1GBUABT1KedXa2\noQFx6600CRgPrHJ74YsWUcEqc/ToATz3nMNNdhukAMSyMssaHRLr1pFxFR9PHiDjeBVTabfmjApP\n8FQA5K3QF7H67TfbSkNPn04GmSNkZtK91/eqGWcSvPgi/V9eecWxa7kDkZGUMWNsVKxeTRLZSUk1\ns7ucSV4exbR06lR713QlMTG1W/48L08nmucDeIdR4U3bHwAZAk89RcZE27bAv/5l+TNynoro6Jqx\nF/p4S4VSY4qKVwu5+AAAGfxJREFUaLWrH2NiisuXKeBv0yaa2DSamvfMWK1UQs6o0GjoeE/pk/fc\nQyJpFRX006sX8P771n/+oYeozoIjZGbWnNCKiykTZP16et69OzB3rmcGZhrDGAW5GhsVERH0/0hK\novTa8eMNg2idxYkTtF1qi5KmJ9OoEU30tSFIVV1N/2tr66l4AR69/ZE3diyuDRyIDrYo8HkKZWUU\nqFZcXDNlduBA8mQsWkTPq6spiM140rNUqVSqUOpN2R8AeQmSkykYbuZM8yXKJX2KHj1oMB83jgIY\n9TFlVDzyCG0XcK7zkKjVFA9jSTzKXRg1in4AnUvY1v6Qk0MZWJIIkq28/HLN7begIPKaFBYCDz4I\nTJli37ndFTkBrAcfpB+pOOD+/bWT6n377TQW+EggIWJi6B4XFDg/IyM/nxYa3uZNN4NHeyp4QADK\npf1Jb+LPP2lQ/c9/6Llx7nh+vqGstkpFRoixNRwdTYOFKZ17aypSeirPPkveG1PZHBJ79uhWaUFB\nNQ0KQJdmZzzZJidTUKFkUFRUkIEXFma6Ros7UllJ7m9pm8dWo+LJJylNz16X8pgxNVVkGSMZ86++\nIuPZ29zH//ufYYryjh2676mfH3llvvyS7kNWFmlbOLNeRUCA+5ZjV5p776Utv9BQ51/LxzQqAA83\nKryWli1p9fvZZ/RFNy46FRtbM/uDsZqDgiWtCnsnEU+gd28yFF5/3bybc/duMtoCA6mC5IwZJEyl\nz/DhNPF27Gj4+o0bFNwpZZosX07HeIqXQmLYMBpo7TUy//tfunfPPGP7tQ8fpvQ+OVnukSPpceZM\n76udEBenm9SysoDBg6mCpj6S7kN6OnkuEhNNy8g7wgMP6LaZfIG4ONpOU0IJ1hKS98+HPBUu2/7g\nnKOgoADVDgwWwdr0pytSMSJv4t13aesjPLymIM2jj5LrVPq7i4pIz6J9e0Pre9AgCkAMDNQdq09U\nFLmYY2Nl31epVGjQoAGYKfVFd4Yx8laMHUsZHXfcUfMYjYZczJIIVZ06wBtv0GBu7MqXK1h39Sod\nt3Il7X8vXkxGRW2sgJSkUycyvqQ6ILYambfcQsG+8+ZRfIUtpaWXLKEsJTkvR8+e5MWYPLl2JoDa\n5NAh8lbMnk39BwAmTZI/9sknKbZqyhQylp94ggwQW2p0mOLqVVKYVEoZ1RMoLaX6MklJuhR+W7h8\nGfjwQ0q/tlTIUjIqfMhT4TKjoqCgAEFBQQgICLD7HPW0X6ogb4yp6NeP9pNbtqy539ypE1m+kZE6\nD0VsLHVcW++FGTd9WVkZCgoKEOGpnoxRo2hV0quX/PtqNRln5eX03FQA3fr1VEJ5+XLD12Nj6Rzn\nzlHdhMuXPTMgq3t38sT4+ZHeiT3pjLNmUcbCE0+Q98HaWID9+3US9Mb4+dGE542cPk2Gwd13U2Ds\nyJHmt8wGDqT7+vzzZPgGB1vO7LIGe8qdezoaDQUYv/qqfUbF3LlkCEZGAg8/bP7YxETyMnlKFV0F\ncNn2R3V1tUMGhdcjBRfKpSYGBZGhIXl5pP1mY6tZoyFL2VRqZUUFufBNVIQMCAhwyJPkcvz8KAjN\nnKelfn3dNhEgH0C3cydtRcmdPz6eqmUuXEh5/qYMGHemWzd6zMoiQ8weT0tAAPD22ySIZe3ef2kp\nedh8JZVRHykW7PXXadvJGnGk4GAybH/6iVJslcBYI8QXCA6mH3u1KpYupceFC2umnxtz663AnDnm\ng8W9DBFT4a7Ur08Dj9yEX78+eTCkaG1TRoVUgOz6dflrXL1Kg7o1ZaY9mRdekHctL1pEE6E+8fE1\ny4Gbk65u2hTYvJkGKE/0UgC0DdayJXlb5MS/rOXOO8lbYa3w1+HDNCj7slGxaRMpudoiPNWnjzJb\nHwB5Klq29AyxNiVxRKsiIIAWGX//Tf8/c5w5UzP+zcsRRoW7EhRE2xnm0rwkY6CqigwI44I+KhV9\nvrJS/vMaDR3jCYWAHKGqCvjgA/rR5513aNWnT1wcUFJiaGjl55sOXmzalAaoLVs8W5Fw0SLaRhs7\n1vFz/fknxQpYMlalVbIvGhXR0fTdfO45ql1ka9zSm29SKq6jhIXZFgPjLdirqpmeTp6HoUNJ7XjB\nAvP9fNIk4P777W+nB+Lls4mXUlkJHDxoGFxZp478wOTvb9qoqKpCVl4e1nt75PfcuTRwTpoErFlD\nr+XkkLvfuGz2q6/Se/r30lzlztmzgW3bgBEjbJ8Y3Il77qFgQCXSi3/+mVzDzzxjfsBNSSGjrmlT\nx6/paajVugBpe7QSMjNp68TRNNPVq4EVKxw7hydiylOxbBltYZra1li7ltLUAwMprmLtWvPf+9xc\nn8r8ADxc/MrbqKqqgp+laGKAtjmqqnTGQny8zp1q6lj5C5JRsXEjHnzwQfsa7QkEBlLO/z33kGFR\nXa2bPI2NCjnPkFptOnrb3UpY20tVFblylXCDp6VRIOKyZeSmX7BA/riQEHLl+yrHj9u/jTFuHE1o\nW7dShow96Iu2+RqLFsl7aJ9+mh6vXjWMtQIooHvHDjKGGbOu7+bk+JwnyKc9FVlZWWjTpg0eeeQR\nJCQkICUlBd9//z169uyJVq1a4Y8//kBJSQkmTpyI5ORkJCUlYcuWLTc/e/vtt6NTp07o1KkTdmuL\nKuXk5KB3795ITExEQkICfvnlFwC69FcA2LhxI1JTUwEAqampeOaZZ9CvXz/MmjXL5PXWrl2LkSNH\nYvjw4WjeogXe2rQJS1asQFJSErp164YCrebE6dOnMXjwYHTu3Bm33347jp8/D1RWIjU1FU8++SR6\n9OiBFi1aYOPGjYBGg9nLluGXX35BYmIilkoBSN6IZFgMH05Brrt3U4aCcYDahQu0BaBfJOvgQd9Z\nzRUWOn4OxiiYbcoUqtUhibjpU1FBHiSpcJ4v4khcRN++tAL+5BP7z/Haa2QU14YUuLvRpEnNhdjp\n0/S4bFlNgwIAfvmFgt6HDtW9lp9PmST6FYwlSksp3d+H0kkBd/JUyO1HjxlDZblv3JCtnug3diyq\nxo0jq1KSGpYw3is3walTp/D5559j1apVSE5Oxvr16/Hrr78iPT0dr7zyCtq1a4f+/ftjzZo1KCws\nRNeuXTFgwABERUVhx44dCAgIwMmTJzF27FhkZGRg/fr1GDRoEJ5//nloNBrcuHHDYhtOnDiB77//\nHmq1GnPmzJG9HgAcOXIEBw4cQFlZGW5p0QILZ8zAgQMH8PSkSVj39tuY/uKLmDJlClauXIlWrVph\n7969mDp7Nn7UlpDOycnBr7/+iuPHj2PEiBEYlZmJV195BYvfeQfbtm2z6n55NAEBFPvAGPWP3r1r\n6h+oVMCnn1J/NPZieDN+frRP37y5MudjjAyxsjISE5s5k7biTp2i1d7XX5NaZtu29qX1+TpqNUl6\nL18uvz137hwdI+fB5JwqH7/0EpUA8MUsvJMnSavikUeAhg3pNUnhdPhw8jCo1YZF7rZto3ulr3kT\nEkJjyZkz5JHQ9/xIooPCqPAtmjdvjg7a2hrt27fHHXfcAcYYOnTogKysLGRnZyM9PR2LFy8GQNoN\n58+fR2xsLNLS0nDw4EGo1WqcOHECAJCcnIyJEyeisrISI0eORKJUbdQMo0ePhlrrdv/uu+9krwcA\n/fr1Q0hICEJCQhAWEoLh2vTFDk2a4M+zZ1FcXIzdu3dj9OjRN89dXl5+0803cuRIqFQqtGvXDnl5\neZQ6qFQUuacgfenffFN+v18KjpXSSvPyaMX9r3+REeLNWJPWaAsqFe3ZV1SQ8ZaaSqJBAMVRPPqo\n4apPYBvjxlH2lnF20qFD1FdLS0k4bM4cnU7CjRu0UPvwQxJuq81qqO7E6dN0X/r00RkV27eTgGBE\nBHmB0tLIm6PPiBGGY2adOqTRkpYG7NpluCUSHk73uWdP5/89boRDRgVjbBGA4QAqAJwG8DDn3D7/\nqTnPQr16su9XlZTQL5GRVnsmjKmrJ9KjUqluPlepVKiqqoJarcamTZvQunVrg8/NmzcP0dHROHTo\nkIHmRu/evbFr1y589dVXGD9+PGbMmIGHHnrIQJWyzMjdqC/exTmXvd7evXsN2+rnh7pRUQDnUHGO\nqupqVFdXo379+jh48KDugzdukEu/utrg85xzcnVXVNh6y7wHuf1ktZoGFMmoyMmhiO8JE2q3bd6C\nn58u1XnUKOC222hF17Kl7+7nK0ViInl8jImOpmDDuDhKE169Gpg2jSbIuXOBdetI/fSFF3yniJgx\nkvdAP1jziy9orAwLI8/46tWUYSNpTCxbJn+uiRNpi+/ll4Eff9S9HhZGWyM+hqMxFTsAJHDObwVw\nAsBzjjfJvRg0aBDefPNNmoQBHDhwAABQVFSEmJgYqFQqfPTRR9Boo4XPnTuHqKgoTJ48GZMmTUKm\nNm0uOjoax44dQ3V1Nb744gubr1cDlYq+GBoNrbhVKoSGhqJ58+b4/PPPAZDhcGj/ftNlfk+dQgjn\nuG5Kx8JX0VfV9Ob6KLXNsGHA44+TYqcwKJQjO5u2gHNzKeC2USPaWlq1isqaP/AAcO0a3fMXXqDt\np7lzfdegAHQZGfpppYGBwP/9H/0+dSp997Vjqdm4k8BAygLbudPQqDh7lgoWWhLI8jIc8lRwzvWj\nU34HMMrUsQCQkZFx8/fg4OCbMtuOUiJ5LGzkxo0bqK6uvvn5qqoqlJWVoaSk5OZ7zzzzDGbOnImE\nhARwztG0adObgZYpKSnYsGEDevfujaCgIJSUlODbb7/FsmXL4O/vj6CgILz33nsoKSnBvHnzMHTo\nUMTFxaFdu3YoKSlBSUmJwTUBmLxeeXk5Kisrbx7HOUdJcTHqaQcGDecoKSnBe++9h+nTp2P+/Pmo\nrKzE6JEj0XHUKGgqKw2uI9G6deub2z3jxo1DmpELPD8/H+fOnTN4Tf//6I00i4qCuqgIpzMyEP7H\nH2gJ4GhODkpd9Hd7+/12Nzzpfvvl56PjkCG4PHo0wnbvRnHHjsiaO9fwoLQ0WnhIf1dYmO53N8Al\n91ujQWeVCjmZmbiUkYHYFSugCQtDnpQFFxKC9s2aQfPaazjerh3+b+pUVIWE4Ixx0TctrEsXxE6Y\ngMsVFajU/j2x776LmDVrsH/3brcy4JS4361atTL5HuMKqSkyxrYC2MA5N9ikKyoqunmBkydP3nw9\nODgYjT2pPLSboS4uRsCFCyiPiYF/fj4qGjWCRqbuB6uoQL3Tp1EeE4MqvXRBVVkZAs+eRVl8PDRy\n5b61XLhwAcWmZL59gIabNqHpq6/i0Ndfo1LaexUI3IjWU6Yg5MABaAIDceLtt1GijRETmOfWu+5C\nUY8eOP/cc+g4cCAK+/VDlp4qbtSGDWi8ZAn+WrcObSdMQF5KCi5Om2b1+ZsuWID6u3bhkHHVYy9A\n36gICwszcDta9FQwxr4HIBe++jznfIv2mOcBVAEwm9/URa8S3pUrVxwuBCatur2yoJgltO7juvXq\nAXFxMBm/rY31qKtSoa7+fdK65AKCgswWIYuIiECbNm0A6CzcLr5U0fDQIaBJE3Ts16/Wo+R98n67\nEI+937NmAZMnQ/3FF2grV43XTXH5/T52DA3r10fDXbuA4mJETpyISP22tG4NpKWhfUYGoNEgZtIk\nxFhq6969JLC3YgWNsY0bu01/UvJ+FxlXztbDYkwF53wA5zxB5kcyKCYAGAYghSvl9hBYxt+fHk2p\nZUqo1RR/YbyvZ6peiIDKwffqRWlnkyZRep4vpt0JPIP776f9fw8yKNyCyEga/7ZuJc0aY5GqkBDK\nUtq2jUThrEkxP3GCYlk2b6YgUB9LJwUcDNRkjA0GMAvACM65ZUEGgXJIxkBeHhW2MRcMlJRUM189\nJARo1aqmToOAglp/+40CrQQCT0AsDmxn2zYKsExPJ4NMzmNbWkrKpdHR1t3jBx8k7ZWXXqLChD4m\n0Q04nv3xFoAQADsYYwcZYysVaJPAGhgjb0V5OVUhNVcUTIq013ck+ftTwJYbBRC5DZIBlp0NPPss\n8MQTrm2PQCBQnt9/pxo17doBeto+BgQGkufBTMaeAWo1MH8+cOwYpaU+9ZRy7fUQHM3+uEWphgjs\nQKq0Z0nDn3MSewkM1IngFBfTFoivlTy2hthYeszOppQwsfUhEHgf0tbE++/Ly3JLTJ5s23nvvZc0\nRHbu9B15fz18uvaHxxMdDQQHW3bLMUaGRX6+zltx5QqgVeoUGFG3LsnzXrxovkKpQCDwXOS0KpRA\npSIPyKOPyusDeTk+b1S88cYbaNu2LcLDw/Hqq68CILVMSSZ77dq1uHTpkiubaBqNBigpsW6vr0ED\nUs+U0kOrqsQ+rDn69aOVjLEEskAg8A5CQ+nxv/9V/tx33kn1bvRUjH0Fn59V3nnnHXzzzTdobqKQ\n0tq1a5GQkIBYySVuBVaXMHeUvDwyFMLCLB9bvz5Z0Pn5FKQpjArzfPopeXUWLNCVSRcIBN5Dr15U\nUGzePFe3xKvwaU/FY489hjNnzmDEiBFYunRpDTXJjRs3IiMjAykpKUhMTERpaSn279+PPn36oHPn\nzhg0aBBytNrxffv2xZw5c9CnTx8sX768dv4AKa3UmrQltZoK3Fy7Ri45jUYEaVqitBRITqYsGYFA\n4F0EBlK1VinOTKAIbrNU7Tt9rc2fkeptqGUmx5+WpVr8/MqVK7F9+3bs3LlTtvT3qFGj8NZbb2Hx\n4sXo0qULKisrMW3aNGzZsgUNGzbEhg0b8Pzzz2PNmjUAgMLCQvz88882/x12I6WDVlZa52Zr2JCC\nDjkXngpLfPgh1Uc4dkxXUEggEAgEZhGzig38/fffOHLkCAZqRVI0Gg1i9PKQ77///tptkGRM5eZS\nkSZLBAfTD0BqcebSUH0dxkj06uJF6+6tQCAQCNzHqLDGs2BMbct0c87Rvn177NmzR/b9WpcLl1Id\nw8Ot/0x1NZU8Dw0VngpzSFoVrVoBhw8DCQmubY9AIBB4AGKpaoGQkJCbpcFbt26NK1eu3DQqKisr\ncfToUdc1zs8P6NLFtuyEsjLgzBng+HESzhLIo69AKsWuCAQCgcAswqiwQGpqKh577DEkJiZCo9Fg\n48aNmDVrFjp27IjExETs3r3b1U20DSk+oKyMAhEF8ugHb4nsD4FAILAKn/d/Z2VlASDjITU1FQDp\nVEjcd999uO+++24+T0xMxK5du2qc56effnJiKxWEMV0WiIipMI3+VpYt20sCgUDgw4hZxRdp1oxW\n4iEhrm6JezNtGul7iNgTgUAgsAoxWvoiarVPVs+zmZYtqSiQQCAQCKxCGBUCgSl8sMKgQCAQOILL\ntj9UKhXKyspcdXmBFZSVlUEl4i4EAoFAYCUu81Q0aNAABQUFN9M17SE/Px8AECEKPjkFlUqFBiLz\nQSAQCARW4jKjgjHmsDFw7tw5AECbNm2UaJJAIBAIBAIHEL5tgUAgEAgEiiCMCoFAIBAIBIrAOOdO\nvUBRUZFzLyAQCAQCgcAlhIWFMf3nwlMhEAgEAoFAEYRRIRAIBAKBQBGcvv0hEAgEAoHANxCeCoFA\nIBAIBIogjAqBQCAQCASK4NFGBWNsMGPsb8bYKcbYbFe3x9tgjDVmjO1kjB1jjB1ljD2lfb0BY2wH\nY+yk9lHUBlcIxpiaMXaAMbZN+7w5Y2yv9l5vYIzVcXUbvQnGWH3G2EbG2HFtP+8u+rfzYIw9rR1L\njjDG/scYCxB9XDkYY2sYY5cZY0f0XpPtz4x4Qzt//skY66REGzzWqGCMqQG8DeAuAO0AjGWMtXNt\nq7yOKgD/4py3BdANwBPaezwbwA+c81YAftA+FyjDUwCO6T1fCGCp9l5fAzDJJa3yXpYD2M45bwOg\nI+jei/7tBBhjcQCeBNCFc54AQA3gAYg+riRrAQw2es1Uf74LQCvtzxQAK5RogMcaFQC6AjjFOT/D\nOa8A8CmAu13cJq+Cc57DOc/U/n4dNODGge7zh9rDPgQw0jUt9C4YY/EAhgJ4X/ucAegPYKP2EHGv\nFYQxFgqgN4DVAMA5r+CcF0L0b2fiByCQMeYHoB6AHIg+rhic810ACoxeNtWf7wawjhO/A6jPGItx\ntA2ebFTEAbig9zxb+5rACTDGmgFIArAXQDTnPAcgwwNAlOta5lUsAzATQLX2eQSAQs55lfa56OPK\n0gLAFQAfaLec3meMBUH0b6fAOb8IYDGA8yBjogjAfog+7mxM9WenzKGebFQwmddEfqwTYIwFA9gE\nYDrn/B9Xt8cbYYwNA3CZc75f/2WZQ0UfVw4/AJ0ArOCcJwEogdjqcBravfy7ATQHEAsgCOSCN0b0\n8drBKeOLJxsV2QAa6z2PB3DJRW3xWhhj/iCD4hPO+Wbty3mSm0z7eNlV7fMiegIYwRjLAm3l9Qd5\nLuprXcWA6ONKkw0gm3O+V/t8I8jIEP3bOQwAcJZzfoVzXglgM4AeEH3c2Zjqz06ZQz3ZqNgHoJU2\ncrgOKOAn3cVt8iq0e/qrARzjnC/ReysdwATt7xMAbKnttnkbnPPnOOfxnPNmoL78I+c8BcBOAKO0\nh4l7rSCc81wAFxhjrbUv3QHgL4j+7SzOA+jGGKunHVuk+y36uHMx1Z/TATykzQLpBqBI2iZxBI9W\n1GSMDQGt5tQA1nDOF7i4SV4FY6wXgF8AHIZun38OKK7iMwBNQAPFaM65cXCQwE4YY30BPMs5H8YY\nawHyXDQAcADAOM55uSvb500wxhJBgbF1AJwB8DBosSX6txNgjL0M4H5QZtkBAI+A9vFFH1cAxtj/\nAPQFEAkgD8BcAF9Cpj9rDbu3QNkiNwA8zDnPcLgNnmxUCAQCgUAgcB88eftDIBAIBAKBGyGMCoFA\nIBAIBIogjAqBQCAQCASKIIwKgUAgEAgEiiCMCoFAIBAIBIogjAqBQCAQCASKIIwKgUAgEAgEivD/\nlfk/l5oLe+gAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"import math\n",
"\n",
"sensor_var = 30\n",
"process_var = 2\n",
"pos = (100,500)\n",
"process_model = (1, process_var)\n",
"\n",
"zs, ps = [], []\n",
"\n",
"for i in range(100):\n",
" pos = predict(pos, process_model)\n",
"\n",
" z = math.sin(i/3.)*2 + randn()*1.2\n",
" zs.append(z)\n",
" \n",
" pos = update(pos, (z, sensor_var))\n",
" ps.append(pos[0])\n",
"\n",
"plt.plot(zs, c='r', linestyle='dashed', label='measurement')\n",
"plt.plot(ps, c='#004080', label='filter')\n",
"plt.legend(loc='best');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Discussion\n",
"\n",
"This is terrible! The output is not at all like a sin wave, except in the grossest way. With linear systems we could add extreme amounts of noise to our signal and still extract a very accurate result, but here even modest noise creates a very bad result.\n",
"\n",
"If we recall the **g-h Filter** chapter we can understand what is happening here. The structure of the g-h filter requires that the filter output chooses a value part way between the prediction and measurement. A varying signal like this one is always accelerating, whereas our process model assumes constant velocity, so the filter is mathematically guaranteed to always lag the input signal. \n",
"\n",
"Very shortly after practitioners began implementing Kalman filters they recognized the poor performance of them for nonlinear systems and began devising ways of dealing with it. Later chapters are devoted to this problem."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Fixed Gain Filters\n",
"\n",
"Embedded computers usually have extremely limited processors. Many do not have floating point circuitry. These simple equations can impose a heavy burden on the chip. This is less true as technology advances, but do not underestimate the value of spending one dollar less on a processor when you will be buying millions of them.\n",
"\n",
"In the example above the variance of the filter converged to a fixed value. This will always happen if the variance of the measurement and process is a constant. You can take advantage of this fact by running simulations to determine what the variance converges to. Then you can hard code this value into your filter. So long as you initialize the filter to a good starting guess (I recommend using the first measurement as your initial value) the filter will perform very well. For example, the dog tracking filter can be reduced to this:\n",
"\n",
"```python\n",
"def update(x, z):\n",
" K = .13232 # experimentally derived Kalman gain\n",
" y = z - x # residual\n",
" x = x + K*y # posterior\n",
" return x\n",
" \n",
"def predict(x):\n",
" return x + vel*dt\n",
"```\n",
"\n",
"I used the Kalman gain form of the update function to emphasize that we do not need to consider the variances at all. If the variances converge to a single value so does the Kalman gain. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## FilterPy's Implementation\n",
"\n",
"FilterPy implements `predict()` and `update()`. They work not only for the univariate case developed in this chapter, but the more general multivariate case that we learn in subsequent chapters. Because of this their interface is slightly different. They do not take Gaussians as tuples, but as two separately named variables.\n",
"\n",
"`predict()` takes several arguments, but we will only need to use these four:\n",
"\n",
"```python\n",
"predict(x, P, u, Q)\n",
"```\n",
"\n",
"`x` is the state of the system. `P` is the variance of the system. `u` is the movement due to the process, and `Q` is the noise in the process. You will need to used named arguments when you call `predict()` because most of the arguments are optional. The third argument to `predict()` is **not** `u`.\n",
"\n",
"These may strike you as terrible names. They are! As I already mentioned they come from a long history of control theory, and every paper or book you read will use these names. So, we just have to get used to it. Refusing to memorize them means you will never be able to read the literature.\n",
"\n",
"Let's try it for the state $\\mathcal N(10, 3)$ and the movement $\\mathcal N(1, 4)$. We'd expect a final position of 11 (10+1) with a variance of 7 (3+4)."
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(11, 7.000)"
]
},
"execution_count": 31,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"import filterpy.kalman as kf\n",
"kf.predict(x=10, P=3., u=1, Q=4)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"`update` also takes several arguments, but for now you will be interested in these four:\n",
" \n",
"```python\n",
"update(x, P, z, R)\n",
"```\n",
" \n",
"As before, `x` and `P` are the state and variance of the system. `z` is the measurement, and `R` is the measurement variance. Let's perform the last predict statement to get our prior, and then perform an update:"
]
},
{
"cell_type": "code",
"execution_count": 32,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(11.364, 4.455)"
]
},
"execution_count": 32,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x, P = kf.predict(x=10, P=3., u=1, Q=2**2)\n",
"x, P = kf.update(x=x, P=P, z=12, R=3.5**2)\n",
"x, P"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"I gave it a noisy measurement with a big variance, so the estimate remained close to the prior of 11.\n",
"\n",
"One final point. I did not use the variable name `prior` for the output of the predict step. I will not use that variable name in the rest of the book. The Kalman filter equations just use $\\mathbf x$. Both the prior and the posterior are the estimated state of the system, the former is the estimate before the measurement is incorporated, and the latter is after the measurement has been incorporated."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Summary\n",
"\n",
"The Kalman filter that we describe in this chapter is a special, restricted case of the more general filter we will learn next. Most texts do not discuss this one dimensional form. However, I think it is a vital stepping stone. We started the book with the g-h filter, then implemented the discrete Bayes filter, and now implemented the one dimensional Kalman filter. I have tried to show you that each of these filters use the same algorithm and reasoning. The mathematics of the Kalman filter that we will learn shortly is fairly sophisticated, and it can be difficult to understand the underlying simplicity of the filter. That sophistication comes with significant benefits: the generalized filter will markedly outperform the filters in this chapter.\n",
"\n",
"This chapter takes time to assimilate. To truly understand it you will probably have to work through this chapter several times. I encourage you to change the various constants in the code and observe the results. Convince yourself that Gaussians are a good representation of a unimodal belief of the position of a dog in a hallway, the position of an aircraft in the sky, or the temperature of a chemical reaction chamber. Then convince yourself that multiplying Gaussians truly does compute a new belief from your prior belief and the new measurement. Finally, convince yourself that if you are measuring movement, that adding the Gaussians together updates your belief. \n",
"\n",
"Most of all, spend enough time with the **Full Description of the Algorithm** section to ensure you understand the algorithm and how it relates to the g-h filter and discrete Bayes filter. There is just one 'trick' here - selecting a value somewhere between a prediction and a measurement. Each algorithm performs that trick with different math, but all use the same logic."
]
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.3"
},
"widgets": {
"state": {
"58ed37dc23fe44cc9a0e20ffc9c47414": {
"views": [
{
"cell_index": 79
}
]
},
"8b8fb12fbc4048a0af7d29dfc57d5fb9": {
"views": [
{
"cell_index": 29
}
]
},
"ec6802d3ecf14e67bbcf34b40aa0e3c4": {
"views": [
{
"cell_index": 77
}
]
}
},
"version": "1.2.0"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The top plot in the animation draws a green line for the predicted next voltage, then a red '+' for the actual measurement, draws a light red line to show the residual, and then draws a blue line to the filter's output. You can see that when the filter starts the corrections made are quite large, but after only a few updates the filter only adjusts its output by a small amount even when the measurement is far from it. \n",
"\n",
"The lower plot shows the Gaussian belief as the filter innovates. When the filter starts the Gaussian curve is centered over 25, our initial guess for the voltage, and is very wide and short due to our initial uncertainty. But as the filter innovates, the Gaussian quickly moves to about 16.0 and becomes taller, reflecting the growing confidence that the filter has in it's estimate for the voltage. You will also note that the Gaussian's height bounces up and down a little bit. If you watch closely you will see that the Gaussian becomes a bit shorter and more spread out during the prediction step, and becomes taller and narrower as the filter incorporates another measurement.\n",
"\n",
"Think of this animation in terms of the g-h filter. At each step the g-h filter makes a prediction, takes a measurement, computes the residual (the difference between the prediction and the measurement), and then selects a point on the residual line based on the scaling factor $g$. The Kalman filter is doing exactly the same thing, except that the scaling factor $g$ varies with time. As the filter becomes more confident in its state the scaling factor favors the filter's prediction over the measurement. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Example: Extreme Amounts of Noise\n",
"\n",
"With the dog filter I didn't put a lot of noise in the signal, and I 'guessed' that the dog was at position 0. How does the filter perform in real world conditions? I will start by injecting more noise in the RFID sensor while leaving the process variance at 2 m$^2$. I will inject an extreme amount of noise - noise that apparently swamps the actual measurement. What does your intuition say about the filter's performance if the sensor has a standard deviation of 300 meters? In other words, an actual position of 1.0 m might be reported as 287.9 m, or -589.6 m, or any other number in roughly that range. Think about it before you scroll down."
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAiIAAAC+CAYAAAAIj2Q7AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzsXXdcFMf7fu6OKtWGgApiRVDssZcY\nUbH3FuxGY+8RjTUae4s99i72HhsWJGoUS2KLilhRVBRFAan3/P44d3LLHYiKwu/rPp/PfMS53ZnZ\nnd19n3nnLSqSUKBAgQIFChQoyAyoM3sAChQoUKBAgYKvFwoRUaBAgQIFChRkGhQiokCBAgUKFCjI\nNChERIECBQoUKFCQaTDJ7AEYQ1RUlGJBq0CBAgUKFPyPwc7OTpWyTtGIKFCgQIECBQoyDQoRUaBA\ngQIFChRkGrLk1ow+7OzsMnsIXz3Onz8PAChfvnwmj0SBBGVOshaU+chaUOYjfTh48CAaNGgAksiX\nLx8AICwsDCqVCocOHYK3t3eG9BMVFZXm74pGRIECBQoUKPgKUb9+fWzevBkuLi4ICwtDWFgYXF1d\nsWXLlgwjIelBlteIKFCgQIECBQo+D1q3bo0WLVrg6tWrUKlU8PT0hEaj+aJjUIiIAgUKFChQ8BVD\no9GgVKlSmda/sjWjQIECBQoUKMg0KEREgQIFChQoUJBpUIiIAgUKFChQoABarRaHDh3CgAED0L9/\nfxw8eBBarfaD23n48CF69eoFR0dH5MyZ873HKzYiChQoUKBAwVeO+Ph4tGzZEvv37xd1CxYsgI+P\nD3bs2AELC4t0tRMWFoZKlSrh8ePH6e5b0YgoUKBAgQIFnwGvX7/G8ePH8ddffyE5Ofmj29Fqtbh9\n+zYePHgA8vNkQJk2bRr279+P7NmzY9y4cRg3bhxy5MiBAwcOYOrUqelu59dff8Xjx49RuXJlXL58\nGSEhIe89RyEiChQoUKDgfwJJSUmfTVB/CEhi4sSJcHZ2Ru3atVG5cmUULFgQBw4c+OC2Nm/ejMKF\nC6NIkSJwdXVFuXLlEBQUlOFjXrFiBQDA398f48ePx/jx47FlyxYAwPLly9Pdzt69ewEAixYtQsmS\nJVG4cOH3nqMQEQUKFChQ8P8a27dvR7ly5WBqago7OztMnToVr169yrTxzJ49G2PHjkVMTAzKlSuH\nAgUK4MGDB2jatCkuXbqU7nZ27NiBdu3a4e7du3BwcICdnR0uXbqEunXr4u+//87QMUtbKVWrVhV1\n0t+PHz9ON8GTND9mZmbp7lshIgoUKFCg4P8tli9fjlatWuHixYsAgDdv3mD79u348ccfERMT88XH\nk5SUhBkzZgAANm3ahPPnzyM0NBRdu3ZFYmIiZs+ena52SGLcuHEAgHHjxuHx48d48uQJ2rRpg7i4\nOHTu3Bm7du1CYmJihozb09MTALBu3TpRJ/3t6ekJlcogaa5R1KtXDwAwdOhQPH36NH2EkGSWK69e\nvaJUFGQ+goODGRwcnNnDUKAHZU6yFrLKfBw4cIANGzZk0aJF6e3tze3bt1Or1X5wO//++y+3b9/O\ns2fPftT5XwpxcXHMlSsXAXDy5Ml8+/Ytr1y5QhcXFwLg/Pnzv/iY7t69SwDMkyeP7N5duHCBAOju\n7p6udl6+fEkAtLCwYHx8PEkyMDCQ9vb2BCBKwYIF+e+//37yuFevXi3a9Pb2Zt26dcX/V65cme52\nbt26JRujSqViCpluIPPTTQ4ArATwDMBVvbrxAB4B+PtdaaD320gAtwHcBFBPr77+u7rbAPyM9aUQ\nkayFrPKRVfAflDnJWsgK8zFr1iyZgJLKqFGj0t1GREQE69WrJzvfy8uL169f/4wj/3icOnWKAFis\nWDGZ0J8wYQIBsGHDhl98TJGRkVSpVDQxMWF4eLioX79+PQGwSpUq6WonNjaWGo2GarWajx8/ZmRk\nJO3s7MS82Nvbs0iRIgTAokWLMikp6ZPGrdVqOXHiRJqZmYk+zMzMOGHChA8mo9evX2fTpk2p0WjS\nRUQ+ZGtm9TsSkRJzSJZ+V/4AAJVK5QGgHQDPd+csUqlUGpVKpQGwEIAPAA8A7d8dq0CBAgUKPhLh\n4eEYMWIEAGDChAm4fPkyZs2aBY1Gg8mTJ+PmzZvvbYMkWrdujUOHDsHa2hoNGjRAnjx5cPnyZXh7\neyM6OvpzX8YHQ63WibCkpCRZvfT/9G4nZCSyZ8+Oxo0bIykpCT4+PtiwYQPmzp2L/v37AwA6duyY\nrnYsLS3RuHFjaLVatG7dGmPHjkVUVJRwo+3bty/+/vtvFChQALdu3UJAQMAnjVulUmH06NEICwvD\nxo0bsWHDBjx8+BBjx4794PtYvHhx7Nq1C3FxcYiPj3/v8emOI0LypEqlKpDOw5sC8CcZD+CuSqW6\nDeCbd7/dJnkHAFQqlf+7Y6+n1pCUzllB5kOZi6wHZU6yFjJrPnbs2IGkpCRUr14dDRo0QHx8PGrU\nqAEfHx/s27cP8+bNQ9euXdNs49q1azhx4gRsbW2xadMmODg4IC4uDt26dUNISAimTp2KZs2afaEr\nSj9y5syJ0NBQdOnSBb6+vrh3757w8vDy8sqUOenRowfOnz+Pv//+G76+vqK+Ro0aKF26dLrH1Llz\nZwQFBeHUqVM4deoUACAuLg5FihRBnTp1cP36dZQqVQr37t3DsWPH0hU8LD0oUqQIAODBgwd48OBB\nhrWXGjIioFk/lUrVCcB5AENJvgSQF8BfeseEvasDgIcp6itmwBgUKFCg4KtFXFwcAN1qXB/S/6Xf\n08KtW7cA6DwlHBwcAAAWFhbw8fFBSEiI+D0rwcTEBIMHD8aYMWOwdu1arF27Vvzm6emJBg0aZMq4\nnJycsH79euzZswcXLlyAubk56tSpg4IFC2LKlCm4cOECzMzMULt2bXz//fewsbEx2k6+fPmwfv16\nbNq0CQcPHsSzZ8+QN29e/P7777C2tkZ8fLwgNc7Ozp/lWhISEhAYGIiwsDA4OzujZs2a6Q5ulm4Y\n269JrQAoALmNSB4AGui8b34FsPJd/UIAvnrHrQDQEkBrAMv16jsCmJ+yH8VGJGshK+x/K5BDmZOs\nhcyej0uXLhEAra2tefbsWZLklStXhCFnQEDAe9vYtWsXAbBEiRJMTk4W9R06dCAATpgw4bON/1Nx\n+PBhfvvtt7SysmK+fPnYuXNnnjhxIrOHJcPFixdpY2NjYMNTokSJdMm658+fi/OrVKnCkSNH0tPT\nUxisJiYmZviYL126xHz58snG6+joKJ6x9CLDjFVphIik9ht0hqoj9X47BKDyu3JIr152HBUikiWR\n2R9ZBYZQ5iRrISvMR8uWLYWwcHJyEn/XqlUrXcaGcXFxzJMnDwHQx8eHq1evZvfu3QmAGo2GoaGh\nX+AqMgZZYT5SombNmgTAxo0b89KlSwwICGCxYsUIgOPHj09XG0eOHJEZrAJgvnz5eOXKlQwfb1xc\nnCAhnp6eHDp0KEuVKkUAdHBwYHR0dJrnh4eH888//+S9e/c+LxEB4KT392Do7EIAnZHqPwDMAbgB\nuPNOc2Ly7m83AGbvjvFM2Y9CRLIWsuJL/bVDmZOshawwH2/fvuWgQYNobW0t3D579uzJ169fp7uN\nY8eOifOlolKp+Pvvv3/GkWc8ssJ86OPFixcEQHNzc0ZFRYn6Q4cOCc+k9OLVq1dctmwZx44dy40b\nN/Lt27efY8jcunUrAdDDw0O4DycmJrJs2bIEwDVr1qQ6vnbt2lGtVotn6H1EJN02IiqVahOAWgBy\nqVSqMADjANRSqVSl33V2D0AvACB5TaVSbYHOCDUJQF+Sye/a6fdOQ6KBbivnWnrHoECBAgUKjMPC\nwgJz5szB5MmT8fTpU+TOnRtWVlYf1Ma3336LmzdvYsWKFbh+/Try5s2Lbt26wcNDcW78FEieI+bm\n5rC0tBT19vb2ANJnwyPBzs4OPXr0yNgBGkFoaCgAXYAyKUqqiYkJ6tevj4sXL4rf9UESbdq0weHD\nh2FiYoKyZcvi2rX3i/gP8Zppb6R6RRrH/wqd3UjK+j8A/JHefhUoUKBAQfphaWmJAgUKfPT5zs7O\nGDNmTMYN6CtEcnIyAgMD8fTpUyQnJ+P48eOwtrbG69evMXToUMycORPR0dEYO3YsAOC7777L5BEb\nws3NDQAQEBCAxMREmJqaIjk5GUeOHJH9ro/z58/j8OHDsLe3R3BwMAoXLoynT5++t6+M8JpRoECB\nAgUKFAA4d+6cyA9jDPPnz8fy5cuRlJSExMRE2NvbY9iwYV94lO9HkyZN4OTkhCtXruCbb76Bj48P\njhw5gvPnzyNnzpxo1aoVAODVq1eYN28e9uzZgydPngAA6tevL5Ld5cmTB1FRUWn2pRARBQoUKPhI\nkMyUoFkKsiaeP38OHx8fREZGwtnZWSSSA4AyZcrAxMQEwcHBePv2LQDA29sbs2fPRsGCBTNryKnC\nwsICe/bsQaNGjfD333+LJHu5cuXC2rVrMX36dOzcuRMhISEGQct27NiB+/fvw9XVNV19KUnvFChQ\noOADkJCQgIkTJyJ//vzQaDTw9PTEzp07JaP9LIHQ0FD4+vrC1tYWVlZWaNGiBS5fvpzZw/qfx6pV\nqxAZGYkaNWqgbdu2AIBOnTrB2toaly5dwsqVK1G0aFEAOmF9+PBhlChRIjOHnCbKly+PO3fuYO3a\ntRg3bhxWrVqFc+fOYcCAAZg4cSKuXr0qSEiOHDmwfPlyqNVqJCQkoFq1aqhXrx6yZcv23n4UjYgC\nBQr+J/D48WMsWLAAQUFBsLKyQps2bdCxY0eYmppmWB98FwZ9z549ou769eu4fv06wsPDUaFChTTP\nT0pKwpEjR3D//n0ULVoUtWrVEmHKMwp37txBpUqV8Pz5c1G3c+dOHD58GEFBQShTpkyG9vf/CSRx\n7tw5/PXXX7Czs0PTpk0NgsB9Cq5cuQIA8PX1xenTpwEAFStWRFRUFHbv3o1r167Bw8MDt27d+iAD\n1cxEtmzZZGHpBwwYgNu3b8PLywuPHz/G8+fPUaJECVy9ehWzZ8+Gubk53r59i7CwMISFhaWvE2Ou\nNJldFPfdrIWs5gqnQJmTlLh69aoI3qVf6tWrJ1wPMwJHjx4lANrZ2fHQoUOMi4vjqlWrqFarqdFo\n+OjRo1TP/eeff+jm5iYbn6enJ2/fvp1h4yPJLl26EABr167N0NBQPnz4kC1atCAANmjQIEP7yqoI\nDg7moUOHePDgQf71119MTk5mVFQUvb29Zfff0tKSa9euzbB+hw8fTgDs0aMHFyxYQAAsU6aMiMex\nZs0aWlpaEgBv3ryZYf1+KTx58oRWVlYEwPz589Pc3JwAGBQUZDThIt4l58vQOCJfqihEJGtBEXpZ\nD8qcyCEFi6pVqxb/+OMPrlixgrlz5yYALl68OMP6GTp0KAHQz89PVl+9evU006XHxMTQ2dmZAFio\nUCF27dpVCKdixYp9cuZUfUjXrZ8xNyIiggCoVquZkJCQYX1lRSQkJLBVq1Y0MTERwrBIkSIirb29\nvT179OjB2rVri3ty4cKFDOn72rVrVKlUBEBfX19Z8DELCwuampoSAFu2bJkh/X1JPHr0iK6urkbJ\nxrfffiv+bt26tfhbmoOMzL6rQIECBVkO4eHhCAwMRLZs2bBr1y74+PigW7dumD17NgBg06ZNGdZX\naoapfGcfktrvW7duxePHj1GqVClcu3YNK1euxPXr1+Hq6oqbN2/i0KFDGTZGY2P5mgxqhw8fjm3b\ntkGr1aJatWrImzcvQkJCRGyLs2fPYtmyZTh69Ch69+4NrVaLRYsWZUjfHh4emD9/PlQqFdavXy/z\nFomLi0NycjK+//57rF69OkP6+5L45ZdfcP/+fRH7pEGDBvDy8gIAHD9+XBy3detW8XfKrMipQSEi\nChT8P8fr16/x4sWLLGUs+SXx+vVrALoEb7a2tqJeiqXxPtfBD4GURG3RokU4cOAAYmJisGLFCpw6\ndQoajQZ169Y1et6///4LAGjevDnMzc0BADY2NmjUqBEA4MaNG3j69Cn8/PxQqlQplC5dGqNHj5bZ\neQA6V8lFixZh2LBhWLhwIV6+fJnqGAcMGICHDx/i6dOn6N27NwCgbt26GWozk5GIjY3F1atXER4e\n/tFtvHz5EkuWLIFKpcLSpUsRFBSEu3fvokqVKgB0BpWSsSgAtGjRAgAyNKFf3759ce3aNYwYMQJd\nunTBrFmzEBQUhMOHD+PBgwdYv349rK2tP7r9V69e4ebNm4iJiUn1GJK4cOECdu7ciatXr350X/rY\nsWMHAGDhwoUwMzPDH3/8gTt37hg99oOJrzE1SWYXZWsma0HZBsh6CA4O5qZNm2R73l5eXtyzZ09m\nD+2LIyEhgQ4ODgTAVatWUavV8u3bt2zatCkBsHfv3hnWl1arZbNmzYyqp7t165bqefPnzxd2G1Le\nl6SkJJG7Y9GiRcyfP79Bm25ubgwPDydJnjx5kvb29rLfbW1teezYMVlfISEhzJEjh0Fb2bJl4/nz\n5zPsXnwKtFoto6OjmZSUxKSkJI4ePZq2trYy2567d+9+cLuSrYK7u7vsm7V69WqxDRMWFibqR4wY\nQQD8/vvvM+KyMgRxcXF88uSJQRK7Fy9esEOHDmK7I1u2bBw4cKBBiPfQ0FCWL19eNvdFixblzJkz\nZdeuj2fPnnHWrFns168fZ8+ezYiICJJkfHw8T58+zVOnTon5efDgAU+cOCFCvacsXl5e7Nmzp6xO\nsRFR8MlQiEjWw44dO0ROEFNTU2bLlk3kBfkaycicOXPER69w4cJCEFtbW/PWrVsZ2ld8fDx//fVX\nFihQgCYmJixZsiRHjx7Nc+fOpXrO8+fPhZFf3bp1OX36dFarVk0kEPP19SUAVqhQgceOHWNAQADL\nlClDAPzxxx8ZHR3NnDlzEgCrVq3KyZMns0aNGsLmIWU+mZs3b7Jt27bCLqFx48a8ePFiht6Hj4FW\nq+XSpUtZuHBhMT8SGcM7+xkLCwsCoKur6wfLgH///ZcAaGNjw5MnT4r6yZMniz7y58/P0aNHs337\n9qJO/1gJISEh7N27N728vFilShXOmzePcXFxJHX2Ev3792f16tXZrFkzbty48ZPtfF69esVevXoJ\nY9bcuXNz4sSJTEpKYmJioiAXarWaBQoUEGNv27ataCM+Pp6FChUiAObMmdPAOFqj0XDs2LGyJIhH\njhwxyC9kY2PDESNGCIIPgGZmZoK0vXnzhjExMezYsSMBsGbNmuL5NlYUIqLgk/H/gYhcunSJzZs3\np42NDXPmzMkePXrwwYMHmT2szwZpVe7j48PIyEjGxcXxp59+IgCWLFkyXdlW/5eg1Wo5c+ZMIawB\nsFSpUjxz5swX6T8978j+/fsFYZSKvb09g4KCxEc8JCREHH/58mUhUNatW0cALFeunBB4ycnJrFSp\nEgFwxYoVRvvUarXiWQgPD2dYWNhneTbevn3LjRs3cuTIkfztt9/47Nkzo8f9+uuv4tolw02p7N27\nl6TOsLZ06dIEwN9+++2Dx1KhQgUx/xs2bOC4ceMEuSlYsKCsT7VazZkzZxq0ce7cOdrY2BgI1Fq1\nanHUqFGyhG5SadKkiYEWI71ITExk5cqVZc+F9HefPn24a9cuArpMu1IW5LNnzwrScu3aNZKkv7+/\n0IBMnTpVGIxK3i2SIe3s2bPZp08furq6imupVq0aZ82aJYx49bUpUpZgqVhYWIhn2cTEhIGBgcL4\numLFinRxcZEZCytERMEnI6sTEf0XUr/kzZs3TXfK/8+QXnp9a//4+HjxcejQoQM7dOjAZcuWMSYm\nJhNH+mXx9u1bXrx4kTdv3vyiZCy978jTp085a9YsDhgwgPPnz2dkZCS1Wq0QBvrfvPDwcKGCl1b0\nQ4YMkbU3cuRIAuC4ceNS7fPPP//kN998I94LDw8PIfQzAjdv3pSt0CVBtW3bNtlxkZGR4j1dvnw5\nk5KSxJYVAJkb7YoVKwjo3I2HDx/O2rVrs3Xr1ty3b9975/Xq1atGt6b69OnDhIQE7t69m35+fpwy\nZQrv3LljcL5Wq2W5cuUIgI0bN+apU6fo7+9PR0dHWXtmZmaC4EgCftmyZR91D3fu3EkAdHJy4pUr\nV6jVarl//36amJhQpVKxR48eBMDx48fLzpO0OkuWLCFJ+vn5EQDHjh0rtCH+/v7s3bs3AYjtFGm8\nKUnx/v37mZSUJEhYkyZNBJmdOHGi0GJJ55QvX54BAQEkyUGDBomFUEBAAOfMmSN7rhUiouCTkNWJ\nSK1atYSK8v79+7x27ZpYKQ4YMCCzh/dZIH1k9O0DIiIijK7UihcvzidPnmTiaP/38anviPQM9+3b\nl/Hx8Xz79q0QPj4+Pty2bRsBnatvbGwsSZ0tgaenJwFw06ZNRtu9ePGiEJZWVlbCnVStVvPgwYMf\nPV4JWq2WJUuWFM/Z2LFjWa9ePSGo7927J47du3cvAd3WkoTAwEDxnOrbafzyyy9GtSaAzuZHIiNH\njx6lt7c37e3tWbBgQY4dO5bR0dE8cuQI+/Tpw6ZNm7JLly48cuRIuonpnTt3COhixUj3miRXrlwp\n0+Y8f/6c0dHR9PHxkWlMUt6fM2fOcOrUqfztt994//59o33279+fADhx4kRZvWTn1KRJEwK6bTp9\nSG6z69atI0nOnj2bANiwYUMxpsTERHp4eBjcx9RK5cqVqdFoCICjRo0SfcXExAgS8/z5c2FHIuHZ\ns2csUqSIQXtWVlYKEVHw6cjKROT169fiwxAVFSXqz549SwAsUKBAJo7u86Fbt25idXv8+HFeunRJ\nCASNRsOJEydy0aJFLFq0KAGwffv2mT3k/2l86jty/Phx8fG3s7MTK1JTU1OePn2a8fHxQutQsGBB\n9uzZU9hZ5MuXz8BgUUKrVq2EhiwmJobx8fEcMmSIUKF/Kv7880+xko+OjiapE74tW7YUK/O9e/ey\nU6dOrFq1KgFdgC8JiYmJghwVLFiQQUFBXLhwoWwLy8fHhz/++CNdXV3FSn7lypXcvHmz0ZV91apV\neerUqY+ejytXrhAAXVxcZORFn4jkz59f/KZPpkqVKiWOj4mJYaNGjWRjU6vVnDx5skGfUnyaoUOH\nyuolgqq/zTJjxgwGBwdz2LBhBHRB2SIjI0mSjx8/FrYcEgGtWLGi6D/l1mDK+5fy/1OmTBFjuXDh\nAgEwe/bsqd6758+fc/To0SxZsiSLFy/OgQMH8uHDhwoRUfDpyEwikpyczMOHD9PPz4/jx4/nlStX\nZL9HRUWJ1Zf0ISR1K0FAZ/D2v4iAgAADdbhUJk2aJI67e/cu1Wo1TUxMDAwaFWQcMuIdOXDggCCT\nAFi6dGmh9iZ1wbIkQ0SpuLm58fLly6m2KUWblewKSJ2AlEiP/or/Q3Dx4kV27dpV2FxUqVJFJrSX\nLFkixmfsGR00aBAfPXrEvXv3GrXFkIqzszO/++47g3qNRiOubdiwYXz06BGPHj0qgrnZ2tqyUKFC\nnDp1aqokLTXExsYKD5G8efOyS5cu/PPPP1mlShXZGPz9/RkaGsoxY8aIup49e1Kr1TIpKUloOezs\n7Ni7d2+2atVKCPp9+/bJ+jx16pQgFStXruStW7c4fvx4GdGQPHxSlmXLlvHq1as8cOAAb9++zfXr\n14v51S/6NhupkQ+NRiPTqmbLlo3Dhw/nqlWrxLP3MVpmhYgo+GRkFhF58+aNLGKfVIYMGSL76Ekf\niG7dujEyMpIPHjwQ5/Xq1euLj/tLIDg4mAEBARw1ahTd3d1ZoEAB8UHXJ2tarVZ8sP+XjXczGxn1\njmi1Wj58+DBVo9LExETu37+f8+bN4969e99rHCm5BP/111+iLiwsTAimj4myunXrVqOCrk+fPiR1\ni4f69euLehsbG06ePJkrVqxg3rx5jQrDqlWrsnv37ixbtizr1asnhK6k9cmTJw83btwohLNUChcu\nLO7T3r17jW5N1qpVK91h/rVarSwyaHqFuSTQu3TpIt43ScDru0xLtj4+Pj4G/UpazpQlZ86c/O23\n3xgfH8+dO3fSx8eHJUuWZOvWrbllyxahaZJKo0aN+Ndff3HIkCEimm9aBCRPnjypHpOylCpVSmhf\nPgQKEVHwycgsIiIZWOXOnZt+fn7s2bOn2DPW3xM/efKk0b3k3Llzy/ao/5dgbE4kdXj//v3Fx3nH\njh0EdC6iH2vRr+D9+Nh35Ny5c+zWrRtr167NXr168dKlSxk6rsGDBxMAS5QowcOHD/PkyZPCbbh1\n69Yf3F5MTAyzZ89OAPzhhx948uRJuri4iHeudevWwmtFIgX6Hj2PHz8W9fb29ixWrBinTp0q3GIl\nPH36VPZOr1q1im/evBFCV9p+KFKkCEldTBb98OPlypXj7NmzhYHpqlWr0nV9y5YtS1UIm5ub09/f\nXxbvJD1Ff3tD8oQqWrSoQd/Jycn85ZdfjJI8QKed0d9+jouLEzYZ9vb2/Pbbb4UxcPXq1YWRqeRN\nJ7UhaT6M9aFP5IYNG8YGDRqI/0+ePPmjDd8VIqLgk5EZROTt27diP/Pvv/8W9VIiqZo1a8qOP3Xq\nFOvUqUO1Wk1zc3O2adNG5gr5vwZjc3Lq1CnxISlRogRr1qwpVj1Tp07NpJF+HfiYd2TRokVGBUFG\nJmGLiIgQdkL6xdHRUbZdk14sX75cCL6+ffvy4sWLfPDggUHCwezZswtiIN2XBw8ecO7cuUJz9774\nLn369BHtFSpUSBCgXLlyyTxYpkyZwtOnT8s0FsOHD2dwcDB///13AjpjT1K37TJp0iS6u7vTwcGB\nDRs2ZGBgoOhTatfJyYkrV67kmDFjhOsroIs3Mm7cOAK6LZOSJUty1KhRMk3N7t27+erVK0GWzM3N\nhRZh2rRpBHQB24xBX/Cn1FwAOq8XCZs2bRJkTGr/4cOHwoX91KlT1Gq1wvVbGktqhElymQZ0BqYv\nX74k+d8CZ86cOR/8vEhQiIiCT0ZmEBFJfZwrVy5ZvRSwyM3Nzeh5ycnJX0UMjdTmZPPmzTKhYGZm\nxhEjRjA5OTkTRvnhiIuL49WrVzNsGykqKirdNgIhISE8efIknz59+sH9fOg78vDhQyE0Bw4cyL17\n97Jdu3ZCWDx//vyDx5AaXryQeCeGAAAgAElEQVR4wbFjx9LLy4uenp4cPHhwqhE208LBgweNrqTn\nzJnDmTNnEtAZRm7YsIHR0dEi2FW3bt04bdo0g3O9vb355s2bVPtLSEgwiBBaunRpg1ggKYW1h4cH\nT548KaIPA2D9+vWZkJAgkiOmJH9bt24V3xwAXLBggRjH3LlzRf2BAweEy+zy5cv59OlTzps3TxaU\nrW3btqxVq5ZMU9SwYUO2b99eLBR2795tcL1v3ryRjcva2lqQGf1y69YtarVatmnThgBYo0YN2fZP\n9+7dCYDz5s3jzz//nCrxSKsULVqUJUqUYPPmzYVXUEqPng+BQkSoE043b97kjRs3/t98kLMSMoOI\nxMfHi6A++iuWSZMmpbmi+FqQ1pzExcXx0KFD3L17d6qBpbIatFotZ8yYISNR1apVMzBOTi927twp\nhINGo2Hz5s15+/Zto8eGhoaKKKXSqrpr164fpIb+0Hdk1qxZBMAWLVpwx44dBkaoWc3tPDIy0uj2\np1Qkw+nVq1eLcy5cuJDqOdIWQs+ePdPs99GjR+KZsLCwEJ4ggC4KrTFSMn78eA4ePJg1a9YU2oEZ\nM2ZwzZo1Qttx4MAB3r17V8S+cHZ2ZnBwsIzwSIRUsuuQ3FZ//PFHAmDTpk1l40lPUalU/OWXX4xe\n64sXL4yeI8U00X829F2GpdKjRw8mJSUJLxnpGdNoNMJ7yliZNm0af/75Z5YoUSLNsf/xxx8f/fx8\n9URk7969Mt/mQoUKcfv27Z/c7teEzLIRkYLzWFpa0tfXV6a23L9//xcfT1bCl5iTGzdu0N/fn0eP\nHk0zfPXr16+5adMm/v777x9NHCT3REDn6SRFGs2ZM+cHB6XbsmWLaMvc3Fyslh0dHQ3aio6OFkLU\nxsaGFSpUECv3Nm3apLtP/fmIj49ncHAw//7771Tvm+Rp0bZtWzE+BwcHIdjUarXRsOMfA61Wy1Wr\nVrFMmTK0srKiu7s758yZw6SkJN64cYODBg1i/fr12aNHD549e9ZoG507dxYkTbIxSVnc3d0NtE97\n9uyRbQeYm5tzxIgR/Pvvv8X/jx07ZjSwmIRr164ZGK2PGzdO2EBImiRj2g6p9O/fny1atCAALl68\nWHZvJBJ49OhRWZhyMzMzmVajdOnSJHU2afptly9fXmaEa2FhwXXr1smEf/369Tlz5sw0r1Or1RqQ\ngeXLlxvkNkqZb0h6XqSxADpPHWkLqXPnztRqtRw7dqyMGJqYmIgt2+fPnxsEhUypwRoxYkSaY1+8\neDGLFy9OjUZDNzc3Tp06VdilfdVE5MSJE+Jm5s6dW1gHq1QqHjp06JPa/pqQWUQkPj6eHTp0kL0M\npqamnDVr1hcfS1bD55yTqKgog49fgQIFeOrUKYNj/f39Ddwvmzdv/kHahNjYWPFx3bBhA7VaLaOi\nokQMBf2gSu9DcnKyECyjR49mXFwcHz16JIwchw8fLjteMk4sUaKE2Ge/cuWKIAQ3b95MV7/SfCxf\nvlzmheDm5mY0iqkU3EtSvQ8bNoyhoaGyEPUZpfUbNWqUUeFcq1YtoxoLY7YAkvdNtWrVGBcXx4ED\nB8oEV758+VIljFLQtXnz5oktp4SEBIPnpkaNGkbtRqKiohgeHs7NmzcTkAdEI/8zyG7QoIFMs6RS\nqeju7i6uUQrqlfL6JJfpwMDAVF1kNRqNjGSn3DJ6X6lSpUq65koK5f4pxczMjLt37xZkd9iwYaL9\nJ0+eCMKmv9Ui2dIY2wqSip2dXarjluKgpCzt2rWjVqv9uolInTp1CID9+vVjYmIik5KSRBCYatWq\nfVLbXxMyO6DZ1atXOX/+fC5btixTIoTGxMRw7dq1nDBhAtevX//RsRcyEp9zTiTjNEtLSzZp0kSo\nv21tbfn48WNx3MWLFwXRr1KlCjt06CBWlD169Eh3f5JKvFixYrL6ffv2CQGVXoSGhhLQ2RbpayOO\nHTtG4L9VrQQpeuncuXNl9c2bNyfwX8TK9FyDfh4Ve3t7WX6PlHEjkpKSZMaB5cqVE0JAUq1ny5Yt\n1f4uXLjACRMmcPz48alqMUjy/v37VKvVVKvVXLp0KV+8eMFt27bJSET79u25a9cu4WGjVqsNtrGk\nFb+VlZVY1YeFhQltzvjx4zlmzBgWL16cBQoUYJcuXfjvv/+SJBs3bkwAsi0Jyb4BAD09PUXY8Hz5\n8onv/u3bt9moUSPRh5TWwNbWVuZCOnDgQAIQLsN2dnbctWsXg4KCSJJdunQxEJDNmzfnmzdvhPG7\nvb09Y2JimJiYyAEDBsgIWt68eQ0Wrm3btiWg00DUqFFDaIyMBVgDdMHakpOTuXr1ataoUYNFihRh\n8+bNZdvOEiS7lrSKRqPhy5cvGR4eLstRY2lpKYz0jx49SkCnVZRizZw9e1bca/0kiNKWt/74GzVq\nxOrVq8v6bdmypQE5v3PnDlUqFTUaDdeuXcvY2Fju2bNH9HPmzJmvm4hIL5v+PrkUiVOlUin2IulE\nZhORzMSZM2dEkCSpODo6fpF06pGRkbxw4YJIA6+PzzUnUnhrCwsLsTpNTEwUpF5fmEhGcfr7/Jcv\nX6ZKpaKZmRlfvHiRrj5v3LghPpj6qn1pldagQYN0j//BgwdCWOkTxj179hDQ2RXoQ1qY9O3bV9Tp\nq8hTEojUEBwcLAibMWGkUqk4ffp02Tnh4eEy9bdKpWLLli2FAHFwcDDoJykpyahgbd++vVH3bCmw\nWIsWLWT1ktB2dnaWGXdLWYBT2jFI9dKzUadOHSFo1Gq10HroF2trawYHB/PgwYPi+lq3bi2Ll9G4\ncWOS5MuXL0UelLlz5/LJkyd0cnIioNtCkKKvSqVo0aLs1q2biDOiX9RqNbt168azZ8/y7t27Qrul\nn6hNEubS3ymJ6JMnT7hv3z6uWbOGfn5+/OGHH7h48WIRFHD06NHivmq1WiYmJsq0WfXr1+e0adOE\np4+dnR27du1q9LlYs2aNwbxJx5qYmBiNjQLokgTevn1bbDkBOvsX6Xuh1WplCez0yWfz5s1l/e3f\nv192T4oUKcLg4GCjfdvb2/P69eviXMn7K6U7uEQQf/7556+biEgCRD8x2PXr18VL8jV4V2QEvlYi\nEh0dLZ6hsmXL0s/PTxhAOjk5fXDExvQiJiaGPXv2FCtklUrFZs2aybRBn2tOdu/eTUCXql4fa9eu\nJQC2atVK1EkrMf18N+R/qm5j44uJieHEiRPp7u7OPHnysHHjxgwKChL3tXHjxjxx4gQXL14sPuJL\nly7lli1buGjRIp49ezbN91ar1QqB1qFDB968eZMnTpwQLqwpw2tfunRJfIBHjx7Nffv2idWug4OD\nQXyL1KAf5ltfIOoLJwAGieAkoVykSBGuXLmS8+bNE4TGmMHqnDlzhFDp06cP+/XrJ7RQxkKHS0Ii\npb2LRCxLlCghq5e0OoMGDZLVX758OVXXT6mtokWL8ujRo/znn3/E1p6keZ46daqBULO3t5d5zUiJ\n7tq0aSMEfZUqVfj06VMmJSWJa09NMKcs3bp1E0RTuqYVK1bIts5cXFxSjTEye/ZsA1Lp4ODAsWPH\ncubMmeJ+VK1alf3795fdn2LFitHBwcFgTJaWlly6dCkvX74stjNsbW3FfThz5gzr1atHjUaTqnZF\nKqampka3UlxdXQUZefz4sUGyPmnO9L9fSUlJsqi+0ncn5XnS86xPbFMjIpIhcIYSEQArATwDcFWv\nLgeAIwBC3v2b/V29CsA8ALcBXAZQVu+czu+ODwHQ2VhfGUVEpBC7Hh4e3LVrF/fu3UsvLy8CH6Y6\n/trxIUIvMTGRO3fu5NChQzlu3DiRnvpz4vr16/T19aWjoyNdXFw4cODADNnCWb16NQGd2lxabSYk\nJIgX1t/f/5P7MAZphaNSqejh4SE+Nl5eXiIS5uciIlKOHkdHR9mHasCAAQR025wSpAiU+hlBHz9+\nLAxEU9oMxMfHG6h6JRIwffp0o6G+TU1NDfJj1K5dO83ojkFBQUa9GUqWLCkLCCVBMurTL+bm5gZe\nAgkJCZw5cyaLFStGKysrVqhQgRs3biSpEyDSalLqe8uWLTx8+LCs3apVqzI+Pl7M4+PHj42GQVer\n1Vy0aJHBWCVCpU9opC0sFxcXg+NDQ0OpUqloYmLCLVu2MCkpiUeOHBHkxdraWsQTefHihTDs37Bh\ng6ydqKgodu/eXXZfs2fPzqVLl4pv6qhRo8TW3evXrw000mvWrBHkUnq+/fz8hGZacjX94YcfRLRk\n/TnQarWyoGUajUbYrkhBxvSFrlqtFmMwNTUVW44phW2vXr1k6SHI//KqqFQqduvWjTNmzDDQyuhn\n301JNvSfI/1stX5+frJ+pKzIO3fu5MmTJ1O10UgroqtUnJychIeN9J5KeYWcnJw4atQoTpw4UXgh\npdR6hYWFGfWcMTU1NUr+JK2wtDVjYmLCdevW8datW6xXr54gMt7e3hlKRGoAKJuCiEwH4Pfubz8A\n09793QDAgXeEpBKAs/yPuNx592/2d39nT9lXRhGRiIgIuru7G9zAQoUKGVV3KzCO9Aq9iIgIA1cz\nABwzZsxnG9vFixeNCjA3N7ePigehD0lApTSWlF5uYyvQT4WUcMvKykoEcgsLCxOeHVu3biX5+YiI\nVqsVavZKlSpxyZIl7N27t9Fw1UeOHBEf/B49enDSpElCqDZq1MigbWnF6+zszIMHD/LOnTvs27cv\nAV0SsQsXLsg+9vorTGdnZ3bu3FkIsqZNm6Z5HZcuXWLbtm3p5OTEQoUKceTIkSJAkzEcO3aMvr6+\n/O677zhw4ECDfXD9uA0pyzfffMNt27bJCIVGo+GqVatkXheSQFGpVFSr1WzUqBEvX75Mf3//VIWL\nZFgZHR3N0NBQIaj08wYlJiaK441tN0sLspRFWrGbmZmxatWq4j0qWrSoTBMUFRUlyIZ+yZ49O6dN\nmyYTUiYmJhw8eDDj4uKEAXJYWBgvX74sxl6gQAGZwO3atSunTZsm5vv48ePCS0afEMXHx8s0TNOm\nTRMGzZs3bxYCX3+rQipSe+bm5kZjoXh4eHDs2LGcO3cuDx06JDR01atX58uXL2XB1QCI6LGAbsU/\nbdo0sZ1SoUKFVPPnpPxmSJ6AGzduFBrGLl268Pnz5yIOi1SqV68utkNTK5LdUb58+ajVapkjRw4C\nkNkRSVtlBQsWpFarZXx8vNAyJicns3jx4rI2pXffxMSEdevWFfWOjo7CKF36JqZW3kdEVNQRhHRB\npVIVALCPZIl3/78JoBbJcJVK5QTgBMliKpXq93d/b9I/Tioke72rlx0n4V0iMwBASEhIusdnDNHR\n0di2bRuCgoJAElWrVkWrVq1gZ2f3Se0qMMTIkSMREBAABwcHNG3aFM+ePcO+ffuQnJyMuXPnomrV\nqhneZ58+fRAcHIyaNWuiX79+iImJwZQpU3Dz5k18//33GDRo0Ee3vX//fowfPx7u7u5YtWoVTExM\nkJiYiI4dOyI0NBSTJ0+Gt7d3Bl4NsGPHDkyZMgX16tXDpEmTRP2KFSuwZMkStG/fHkOGDMnQPlMi\nJCQE/fr1Q2RkpKy+f//+6NSpk6xu2bJlWLp0qayuYMGCWLhwIXLlyiWrHzJkCIKCgvDzzz+jWbNm\nAACtVotmzZohPDwcHTp0wMaNG1GoUCHMnTsXW7Zswbp168T5lpaWqFatGgIDA5GQkIBdu3Yhb968\nGXnpqeLChQv48ccfYWJigqSkJKPHFC5cGLdv3zao12g0SE5OFv9XqVTSQg5WVlZwcnIS55UvXx6V\nKlXC5s2bERERAY1Gg8aNG+PAgQOIj48X544aNQrNmzcHAAQEBGDkyJHIly8fdu7cadC/VquFv78/\ntmzZgkePHiFXrlxo3rw5WrdujenTp+Po0aNiPGXLlsWECRPg6Ogozl+6dCmWLVsGFxcXDBkyBDY2\nNli6dCnOnj0r68fW1hZv3rwBSZQrVw4XLlyAq6srtm7diokTJ2Lv3r1o0KABxo0bh/Pnz2PQoEFI\nTEyUtdGkSRN4eXnh9OnTOHbsGBwcHODn5wdHR0esWbMGhw4dgoWFBeLi4jB//nxs27YNgYGBGDp0\nKHbv3o3bt29jyZIlGD58ON68eYOOHTti3bp14r5ZWlri7du3AHTP6bNnzxAdHZ3m3OfIkQPR0dFI\nSEiAh4cHrl+/jjlz5iA4OBgbN25E3bp18euvv+LFixdo2bIlYmJiAAC5cuVCbGwsYmNjxTNga2uL\nNWvWIG/evPjrr78wePBgkMTGjRvRrl07mJmZISAgAJaWllizZg0WLFgAADA3N0dQUBCSk5PRokUL\nhIeHi/GVKVMGVapUwZYtWxARESHGvH//flSuXBkAcObMGZiYmAAAXr16BW9vb5iYmCB79uyIiIiA\ng4MDWrVqhY4dO+LVq1cYN24czp07l+o9MTMzQ0JCAsaPH49y5cohKSkJZ86cweLFi/HmzRuYmpqi\nZcuWaNGiBRYsWIA9e/aIc+3s7FQp2zNJcwbejzwkwwHgHRlxeFefF8BDvePC3tWlVv/ZYG1tjS5d\nuqBLly6fs5uvHq9evcLx48eh0WiwfPlyODk5AQDy5s2LRYsWYefOnRlORGJiYhAcHAyNRoNx48bB\nxsYGADB8+HD06NEDgYGBn0REvvvuO8ybNw83btxAp06dULFiRZw5cwahoaHInTs3atasmVGXImBl\nZQUAePr0qaxe+vBky5Ytw/tMiSJFimDr1q3Yt28fbt68CXt7ezRq1AhFihQxOPaHH37Ad999h8OH\nDyM6OhpeXl749ttvYWpqanCsJMAtLS1FnUqlgoWFBQDg+vXrAIBOnTrB0dER58+fl53/9u1bHDly\nBObm5gCA+/fvfzEiEhQUBEB3DZJQs7CwgFqtRmxsLAAYJSEqlUpGQjw8PLBgwQIkJSVh4sSJCAoK\nEud5eXlh0aJFUKlUaNy4MerVq4fk5GTs2rULAODg4IBnz54BAKZMmYLz589DrVYjICAAANCmTRuj\nY1er1ejQoQM6dOiApKQkIZCkdp48eYKHDx/CwcEBrq6uBucfPXoUAPDTTz+hYsWKAIBff/0V3t7e\nIAkfHx+cPn0aUVFRUKvVIIkLFy4AAHr37g2VSiXmtlGjRlCr1fjmm2+wceNGdOrUCW/fvkXFihXh\n4uKCPXv2yITWs2fPZMTb3NwclStXxvHjx7Fz507UrVsXgYGBWLhwIeLi4mBiYoLly5fjzZs3KFas\nGPr16weVSoW1a9cCgCAh1tbWmDBhAvr27StrOz4+XnbtlpaWgpA7OTkhNDQUAODm5gY7Ozts3LgR\n9+/fBwDkzJkTv/zyC4YOHQoAeP78OQAdUWjYsCEmTZqE169fo0WLFsiePbtot3Xr1nBwcBB9SqTQ\nx8cHCxcuBEkkJydj06ZNOHr0qIyEADpC1bZtW+TPnx9+fn4AgG+++QYmJiZwc3PD3bt3sWfPHrRo\n0QIAsHv3bgC6ZzkiIgIqlQrPnj3DokWLcPfuXTRt2hTdunVDy5YtMXLkSGi1WoNnIiEhAQAwb948\ncR0uLi5QqXQcY8iQIUhKTkZgyHOU6TDC4HwDGFOTpFYAFIB8a+ZVit9fvvt3P4BqevVHAZQDMBzA\naL36MQCGpuxHCfGetZCebQBpS0FKQiVBygGhnyMho/Dy5UuhbtX3kJAMEF1dXT+5j7Nnzxpkp3R2\ndpa5vmUkoqKihIq5d+/eDAwMlCXCkmxu/j8aEEuRHkuUKMHQ0FAmJiaK8Nk5cuQQnhwzZsxgUlKS\nsA2Rrn316tUytfHHBk/7GEiGd9LzBujyjkiuqVJxcnIyavMhFf3Q7SEhIbLfevbsyefPn3P8+PEy\nLxQLCwuRDO/SpUtGjUb79Onz2bwAJeNZ/YR8CQkJQmV/4sQJXrt2TZZxFwB///13Jicnc9KkScId\nVq1Ws127dnzy5AmfPn1KMzMz4d4snVezZk0WK1ZMtt3j5OREX19f/vPPP7x165aww8idO7eBQTCg\nC06n73otudfql5S2R1LRD2oGGBptSh4nU6ZMIfBfHhuSvHfvnuj/999/F8bVZ86cIaDznpHuRY4c\nOThu3DjhZi7FuvH19WV4eDhv3Lhh4LEHQGZnI70bZmZm4m+VSiW8WlauXCnb2qlUqZLsuTp48CCT\nk5O5d+9eAzuU7Nmzi62dlEVlZkmTnPlonteducr70KFCQ1q4laV1aR/aVfueedpNZv7B2+g6Yh9d\nR+zLWK8ZI0TkJgCnd387Abj57u/fAbRPeRyA9gB+16uXHUeFiGRJpEfoRUVFCcMtfSEtfcA7dOjw\nWcYm7dX27duX0dHRfPr0qdjHTMsg+dWrV1y6dClHjx7NtWvXphmAKzY2lhs2bOCkSZO4adOmz+Yt\nI2H9+vVGjcP0jUL/PxKRqKgoWZRjfUO/lKG6jWU4zZYtm/gIm5mZcdq0aWlGqkwNN27c4NKlS7lu\n3bp0uxhL++pSsba25oYNGwzmydHRkVqtlkFBQcKQsm7dukJI6BtRX716lQCEYDIzMzPqaZEtWzaZ\nvVO/fv0I6Oxwfvvtt3QHXftYSJ49TZs25evXr5mYmCiiHgPy7LpSdlkTExO+fv061UBXzs7Owg6j\nQYMGInBhnz59ZM+IPhmQImIfOnTIKPkoUKAAa9asST8/P+7bt0/2fkj5YfTJjbFx6RMPfSNT/Wf2\np59+Yvfu3cWc6rt4JycnC3uuFi1asGLFinRxcRHz2rt3b75584b37t1jfHy87D6fOnXKKMmUxpM7\nd27WqlVLtC999/TJBSAP+KbVajl58mSZAa1kn9OuXTu2adOG1tbWsnfRwcGBJUqUoMrUguZ5PZjN\nvRptKjRnnrYTWXTgGroO3ESX4bsFyUhZXH7aQ6fuC1mgxTC6Vm9JjVX2z05EZkBurDr93d8NITdW\nPcf/jFXvQmeomv3d3zlS9qMQkayF9Aq93r17E+9WFL6+vsKQTKVS8fTp059lbEeOHBEfBMkQEO/Y\nfGq5RY4ePWpgAe/o6PjZtBwfg3PnzrFOnTrMnTs3XV1dOWLECNmHKysSkStXrnDUqFHs168f169f\nb9T19fHjx+zYsaP4GDo6OoqPpLW1daqr1NSKWq1OM7NwQEAAS5UqRUtLS+bIkcPAEM/S0pJLlix5\n77UlJyfLEpsZExQphYAUe2PRokVs0qSJELo3btzg5cuXRaj0tm3bppqWXSq9e/cW7UpGs7Nnz/7A\nGfo43LhxQxhfmpqaGozVwsKCY8aM4dy5c4VXi4WFBW1sbIRh7s6dO40a+7q4uPDu3bsiUmnPnj0J\n6LRmV65ckcUJcXNz48aNGwVxK1KkCCtUqCDIoL67s/77ERERQVNTU6pUKjo7O3/Qs5XyWUl5zOjR\now3ul+RtZ6ykjCUj4dy5c/zxxx9ZvXp1FipUiBYWFiL2yJYtWwyIlz5h9fT0FORErVbz+PHjBu1H\nRkZy586d3L17tzDCT+mho7a0pZVnbdpWak2n9r/S9ac9MoLh/MPvzN1sFHPU60u7ah2YrXgN5vD6\nlut2H6ZN3iK0cCtLjU1OQmW4iMpIr5lNAMIBJEJn29EdQE7otl1C3v2b492xKgALAYQCuAKgvF47\n3aBz670NoKuxvhQikrWQXqEXGxtr4CKXLVs2rly58rOO7+jRo8LiXPJGSM1tODIyUqy2q1atyjFj\nxghL8/z58wu3ysxEQkKCQYh1QLe9dfjwYZ48eVJkF80q0E+DLhV3d/dUs7zu27fPYPXftGlTET9C\nv0iRRvVLrVq12L59e0ECAgICDPr45ZdfUiUOzZs3lwV7ShkLxRiioqKMxmTQL7/99htJnfunpOK/\nfPkyr169akB+AR0Rk+JjpCwpSVmfPn04ceJEqlQqqlQqDh48mBUqVGD58uU5ZswYRkREfNokpoFj\nx44ZHX96ikql4okTJ5icnMzdu3cL0lGuXDnhySR5ukheRrt27eKdO3eo0WioVqsN8quoVCoOGDCA\niYmJYtvDwsJCtKf/zZJ+L1OmDEly+vTpRgmJ1Jexa5CEdu7cucXfbm5uXL58OV+/fi0j3ZI3mT5B\nlSLT2tnZyVyFr127JpLo6RdLS0sePnxYHBcTE8P169dz8uTJ3LVrFxMTEzl//nzZNo2zszO3bNnC\no0ePsnXr1qxYsSJ9fX155swZkmRSspax8UncceI8LQt/w2zu1VmkjR+bzD7CPN9PY/5BmwXpyNt7\nJe1rdKJlwfI0zeVKtYU1K1eubJSMGdNOpXyOv+qAZgoyBh+6+r58+TIXLVrEtWvXpukymdGIjo5+\nbwCqhQsXEtCFDZf21OPj44Wb965du77EUNOEJJjs7e05adIkzpkzx2Cv2NramoMGDcoSQfmMfXj1\nSURKhISECFWwpP6WPu5SGG+pGBMM5ubmwn117NixBOSB1sj/Qr0DOruNHj16yMY3YcIEkuTIkSMJ\ngM2aNUvXtT5//lyWqC5lUavVslV8y5Ytxbk3btygr68vc+XKxTx58rBnz548f/68LBQ8ABGQLa2S\n2tZEavleJDuAH374gV27duWmTZs+iHTr23/Y29uL/iWylSNHDuHiW7JkSV64cEFkuwV0odAlSKRV\nPyLvoUOHZNfSqlUrQRb0XUZT3vcaNWrQ09NTaEmk7L/636z79++L52bkyJGcP38+Dxw4kG4iVbFi\nRYOw6ym3dkxMTNikSROOHDlSaIVatmzJ27dvi1AREgHbs2cPQ0JCZKHZAZ1N25IlS8QiRD+g3pkz\nZ8QWn7m5Odu0bcvDZ6/ywD8P2HfuZjafsJbNfzvKSqP86dhpDvO0+5W5W45lnu+n0anrfFYbt4Ml\nxh402EbJP2Q7HTvNZp52k5mz0VCa5SlEG/scDA4ONrCVSavoa8lsbW1Zr1492e8KEVHwyciK2wAf\ni+HDhxMwDOYjbSsZS/j1pSF90KWgVadPn5YZoukHHVq2bFkmj/a/vBuATnVft25dYR8BwCAXihRz\noGXLlkJdP2TIEKPRJHm9PZAAACAASURBVGfOnMnvvvtOVtewYUPR1p9//mkg6Mj/YmeYmJgwNjZW\nEBOpfXd3d5LkP//8Q8Awz837EBkZKZuHlHv7lpaW7Nu373vzEv3222/immrUqEEAskSP0naQra2t\nGLsUFK5EiRLcv38/Dx48KMhL165dDfqIj483MKqVBKyxAG8pId0jqf9z584xOjpaaBIlEikJLl9f\nXz558oSxsbEywhQQEMCVK1cK8qm/4if/y3eiXzw9PdNMxJaymJqa8uDBg7Jv1vPnzw20OSmfs5Yt\nWxq1S6pdu7bRcRmzHzFWmjdvLoIhent7EwDXrl0rND8pCY1arWa/fv2EsfLu3XvofyCQNkUq0r5W\nVzr6zqRD24nM22u5IaHoPJd52k2mQ+vxdOw4k05d5tGh7a/M3WI0nTrN5qANZ+nVdhitPGrRLE8h\nmjq4ERpDWxlzc3MuWbJEXGPK7cy0irRw0M9GrBCRL4zXr19zypQprFChAr28vDh48GA+ePAgs4f1\nyfhfIiJLly4VH2HpAxEbGyuMJdObW+RzQvLSuXfvHsn/ErBJH63IyEixkpeCEmUmJINhtVotPCsS\nExOFXUGXLl1kx0srXH9/f1mqdGNRKvPnz2+Qx0Q/4qgUwrtdu3ayPpo2bSqEY0JCAl+/fi0TaJJH\n1bx58wiA33333Qdd8x9//EFAp6o/f/48z507xzlz5og5+ueff9I8Pzk5mYsXLxbbU46Ojhw+fLhR\nDZBGo2FgYCB/+OEHmcDX92K5efOm+E2r1fLZs2ecMWMGe/bsKVan2bNn56RJkzhr1iyhedKPlJsa\nJJsHSVAfPXqUJFPdUgJ0WqiQkBCuX7/e6O/e3t5s0aIF3dzcWLFiRS5evJiJiYlcsWJFmsQj5RYN\n8J92SMpNU7hwYZ49e5bBwcG8d++eILJp2eGo1WoDsmJlZSW2dVIjMfpbI1KRtKvSXC5dupQ7d+6i\nqZ0DLXI4cdzUOczmXo3OtTvRpkIz2pRrQpuyjWj7TXPaVmpNm/JN6dhwAHO3GMP8Azb+Rzh+2stm\n8wP53fQAuv8whzZlG9E8nyezOxdgrW9ry0iNpaUlu3fvzo4dO4rxSu+d/vhTBtxL7d6kJG7Zs2eX\n5c6Rfq9UqZKBtk6tVitE5EshKipKlk1TKrly5RJZKDMaz5494507d2RZRj8HPoWInD9/nv3792fb\ntm05depUWQLCzEBUVJR4UUqVKsUBAwYIK/1ChQoZTRyW0Th8+DCbNGlCd3d31q1bl9u3bxdkIiEh\nQYR9HjFiBEnKtitcXFyo1Wr5119/if1afZfQzIAUHdLBwUFch5T8DtDltdBHp06dCOCDDAf1i7m5\nOZs0aUIfHx9RJ2ValSClQAd0adBjYmIEOZHmvk+fPkKlv3nz5g+6ZkmrIxkrSu+IZCP1Pk2VMbsA\naX71o3Kq1WrWqVOHoaGhIqeLdF+3bNki2pOSeQI6LxZjkT1Hjhwpjpdc3C0sLOjv759mFGLJtVYK\nDe7h4cHAwEDZ/TQzMxO2PNL4PDw8hGbK1taWRYoUYbVq1dirVy+jhKtSpUpp5pGxs7NjXFycQU4U\nQLel16VLF3G+m5ubgSdW//79uWbNGvbp04dlypQh8H7NhrGkeu8rGo2GHiVL0zS3G7MVr8HczUYa\naDDeV/IP3kbnHouZs8EgWpX0pnne4uz4Q1+xnTZ58mQCusXJrVu3DKLJVqhQQeSvkTRo+hofd3d3\no9euVqtZqlSpVOehZMmSDAwM5KNHj2RbZqkVtVrNvXv3KkTkS0Ha9yxUqBB3797NwMBAEVb4Q7KH\npgfXrl2TGdrly5ePS5cuzdA+9PGxRER6WfRLjhw5vkjm2rRw+vRpg9ggbm5usoySnwuSKj5lkWwG\npFWdVPLnzy/bq5WMIaXkdKamph/sTrxz505WrVqV1tbWLFSoECdNmpTu5G7GsG3bNjG+cuXKsW3b\ntjJDy86dO8uOP3HihPjN2tqaP/74o4E2xMLCguXKlWPRokVZtGjRVENmm5mZceHChYyNjaVWq2VS\nUhL37t1rIOzSSiAm2drcvn2bvXr1YtGiRenl5cXx48eLb1BMTAyXLFnC1q1b8/vvvxdaqsGDB5P8\n7x2RtA/GMqqSOk2IZKekVqvTve2Q2nENGzZk586djWoKqlSpwnnz5gmyZWFhIRYC0hikYmpqylGj\nRhnVrsXHxwsj3dTsBtq1a5emMNq/fz9J8u3bt4LQDBgwgNeuXeP69etlQrJ///78999/hdZPv50J\nEybICBCgI8CpkdqU92306NG8deuWGIN+yZs3L+vUqcORI0fy119/TVWDIr4dahOaOrgxe6WWzF67\nB51bj6VD20l07DiLbj/9596af6A/830/mR3GL+XGs/fYcsQcWriWosrMkiqzbMyeJy/VlrY0yWZL\nlYkZ1RY2hMaELi4uMjdpQKc52759u/DIsrW1FdtyKZ/xatWq8dq1awZ2WIAuLL2UnDCtd2PYsGF8\n+vSpuF8ajYbr1q0zuN/G2ihXrhwDAwNJUiEiXwoeHh4E5PueERERwqVUPzfEp+Dhw4fiobCwsJB5\nHixevDhD+kiJjyEiwcHB4uMxYMAArlq1SuyBFytWTBZ8KTExkfPmzWPp0qXp6OhIb29vHjx4MKMv\nQ4bY2Fj6+/tz+vTp3LVr1xfxlnny5In4GKTmCgroVmEpjTYlIbBw4UKuXbuWhQoVIqBL//4hWLBg\ngdE+69ev/9GaNa1WazSIl/RxMuZOqB+wSv/4lGna//nnH2Eo6eHhwfnz59PX11cIidq1awuSUrhw\nYXFfUisWFhacOHEiBw8ezN69e7NVq1Z0d3dnsWLFUk2UFxISIt7vlMXS0pJr1qzhnj17RHwPMzMz\nIfDj4uK4bds2zp49mytXrjQaIyN37tzCkFFf6Brrr0KFCvzpp59SvT59gl2sWDEmJCQIN3pAR2Sl\nlO+ATrtUp04dMVcS0SV1ZPfbb79lnjx5WLhwYaNkKKXRcY8ePWSaKkBn5yNBSgJYokQJGemRYpXY\n2dkJEpLSziC9RX+LIuV2i6mpqSzuRrVq1ThmzBhxHfrG6keOHKFKraFpLldalfRmHu8ezOHdmw6t\nxtOp+0JZwC6XIToNRp7vp9OhzS/M13gg6/T4meZ53dmqdRvZuyUFf5RKrVq1jG7xpJVXRiKEkizI\nly+fUe8y/VK8eHExz05OTjx58iRHjBghO8bT01Mco6/VSxlHJ2VxdXUVsmjChAkyz6CIiAiFiHwp\nSH7c+nvDCQkJ4gXNqC0JaU/822+/5cuXL5mcnMz58+cT0LHlzyFQP4aISB/l/v37c8mSJaxcuTIL\nFiwoXvhTp06R1AkxfTsB/fI5tTz6ePPmDe/cufNew8JPxbJlywi8f0tC0hhJkUgdHR1FzAn9Ymtr\nKzKnpoVbt25x6tSp9PPzE9s5U6ZMYUREBA8cOCC2qnbv3v3R13b16lWjwbj8/Pz4+vVrg+eyUaNG\nBHS2GdIe9NmzZ8X+uvT7999/LwSe/jskRbWUiv7q1cbGhqNHj2b37t2NrtTc3Ny4e/duo+6otra2\nPH78OA8dOiQy3UrGw0WLFuWyZcs4c+bMNF0WZ8yYQVIXlTe9208zZ86UGZTa2tpy2bJlLFu2rHhn\nVCqV0XusXySjWUnDsH37du7du1f87uTkJNOeSPY2+s9acnJyqvYfJUuWZIsWLdivXz9euHBB5k3j\n5ubGuLg4Ll68WMwDoAu6lZCQwO3btwvD5sqVK8ueByn5oTEymPFFRfN8nrSv1fX/2Pvu8Jqy7v91\nW3rvXUQZvSQRgjDaiBIl2jDaaNEiUSPKRAuiRhmD0duIIIhuiDLCKMNog+i9J0J67v38/rj2ds69\n514x5X1/33ne/Tz7wXFP22fvtVf5rM9C5IrDmJp6FR0mrYZ9436oPnghhm76DdGbLyBgzAZ4D08W\nh02ik+DWKxHO7cbBvmkELKs0gdxS3xvFuomJiSReSKown3AOq1QqHloaO3bsJ3lmdD28ws7WwLJl\nyzB16lSjzyr8d0pKCn/ehw8fGjyPKc0s3CUsEjpnzhyYmpr+TxH5TzUW9+7QoQNycnJQXFzMeQwq\nVqz4twEKGTDw0KFD/JhGo+FZCob4M/5K+zOKCMuGYHgH3T5q1CgAHzVtW1tbJCUl4e7duzwl09ra\n2qAn6dixY+jRoweaNGnCXbmf296+fYt+/fqJrLrhw4f/Lcyp79+/x/z589G4cWN8+eWXSEhIQEJC\ngp7gkeKlYNWKi4qK+LMJKcaFvUWLFgapvTUajSQvh0KhQFhYGFJTUznzIpHWAvsr7fXr15gzZw66\ndOmCQYMGYeLEidzzYWpqil69enFmUeaZYfO2WrVqfHycnJy41c5wVyzLhTXmsjYxMcHFixfx8uVL\nLqzNzc3x9u1bZGRkcCHp6uqKyZMn8wwAZiC0aNGCW+msR0VFAfiYUsoEuZAgj4WjvL29ERgYyMnS\nFi1aBI1GI8IiffHFF6KNRCq8obvRWFpa6r0r61JzpkaNGiLGTaYEjB8/Hrm5uZIKUXR0NF6+fMkx\nPqw7Ojry54mPj8f9+/exceNG/twnTpyAWq0WgRWlNrNOnTrxP6U8YCNGjIBGo8GdO3ckPYByudwo\nZkS4CX68twxySzso7dxgWbkRbOt/A8cWw+Dx9VQ4d4yDx4Dl8I7eglIxu1E6JhXlxu1F+fF7tV6N\nkdtRZtg61Jt5GHVnHEalYatg32QAGvYaDaW9B4ikQxhsflhaWuopvsIUZWHLyckxqqSy72dhYYGk\npCS9cVAqlaIKwMIuleXSu3dvvgctWLDAYKhPmLkmk8kQHx+PhIQEPfwP+60unolI65lMSEgQAZX/\nlYrI9evXsW/fPmRkZEj+/3+jXb16lS9UKysrUQxSCCr7q61hw4YgEpfHzs3N5dbdn6G8/lT7M4qI\nEB9iY2ODdevWYdeuXVzAOTg4IC8vj4P2GK8Da2ziS1npUul0JiYm2LVrV4mfT61W87EkEnspdDkp\nnj17hjFjxqBq1aqoVq0aYmNjjXq4MjMzJUMvjF+A9a+//hpXrlzR25jGjh0L4GMmBCtdLpfLsXbt\nWhQVFWHp0qX8m+umQbKWkpLCBUbjxo0lhfrw4cMxZ84cLqz+rsa8dOz52d/Lly+P7OxsvH//XpT+\nKuzLli3jYNOOHTvycI3Qi8ZCQXXr1gWglQnCewl5KIg+hgK2bdvGhTBjoWRgPmGPjIzE8ePHRRuD\nUOG7efMmiLS4gtWrV4t4Xjw9PUXrXxc0yZ7b2AZrZWWFV69e4eXLl6J5OnDgQL3y8LpdON7+/v5c\n2WOEV2weJicn82tLUYuz52Qpviz1fcSIEVi9ejXfKHXJ90xMTPDdd9/x9xb+OXbsWFEYTwrb8qnO\nlJaKFStCZmIOE48KsKoeCtdWUfAaukGPbtxz8Fq4f7sI7n0Ww6ltDByaDYRFxQY4lHYcgFbh79BJ\nazgJs4jY+zZt2tSgQsTwN8Lu6enJ2Uvr1KljcI3cuXNHb+75+fkhICDgk9+1SpUqAD6mqbO+YcMG\n7o0WdoVCgbi4OK6MvH//HqtWreJeDGFv37695HsJlRDmWe3Zs6dBkj9mRM2aNevfpYg8evSIA0BZ\nDw0NNYr4/k+206dPi+J0fn5+2LRp0996D2ZJMqFy6tQpDt7S5VL4u9qfUURYQSsirSISGhqq5zY+\ncOAAjw0L48gAeMpdcnKy6DirzyGXyzFu3Djs2bOH8y44ODiUOLzCrF0XFxdcuXIFgPb7MaXg4sWL\nALQuSSEnBuu+vr548uSJ5LVZfY2yZcti8+bN2Lp1K09BNQYMYz0qKgpr1qzhYQoWlmndujW/x9mz\nZ/nYRUdHSz4H4y2YOXMmd90ygSqXy7mwYZvm5s2bSzR2AHD37l1cunRJEuSam5vLY94LFixAUVGR\nCGeRmJgIQBs7HjhwoKhw19dff41+/frx5zx8+DCGDx/OhWlwcLDoe9jZ2aFz5844cuSIUXp4FxcX\nfh1hN2Zx636rOnXqYNq0abhy5Qr3UAk3DTc3N72NVXh94d/d3d31gMn/ZP/iiy+4t5SFXdhcNzc3\n52tSqVRybxHDWgwePBgAMHnyZBBplTQ2J1esWAFAf0NkY8eyThwdHbk8Ly4ulsx8Yc8jHEOlUgmF\nqTnM/AJg37gfnMMnwq3HXHhFboTnoFXiTJPoJLh0nARr/9awqh4KlYsf5OY2ks/F5lOjRo24omRu\nbi6q23Pz5k3RhizkcmF/GlIKmZepatWqorXx4sULXLlyRYShuHnzJo4dO4bLly9j+/bt2LZtGyIj\nI/m9lUqlHmM1K2tgLGTCurm5OX/eDRs28PuycBzrXbt25TJat7CeLt9J69atJcNFvXr1QnJysuj7\nPnr06N+jiBQVFXELytraGo0aNeITNygo6L/OpSBsjx49wp07d/6Raph5eXkc9CnsVlZWOH36dImu\nsX//fjRs2BDm5ubw8PDAmDFjjBIb/dmsGV12PSKtm5YJsZ07d2LTpk0g0rq4r1y5ArVajc2bN0Mm\nk0GlUnEls6CgAK9eveJuaqHLU6PRcBe+MK5prI0bNw5EH1NkWevduzeIPoL2WNXOoKAgpKWl4fDh\nwxylHhERIXltZokzamUAuHbt2p/aQCpWrMiVz9DQUH69s2fP8mdlmRu6jQEjlyxZAiItEE3Km0Sk\ntXxLgi+6cOGCSNl2dHTE7NmzReuPkYxVqlSJH3v37h3fyISEZIB2vUi5kxnpXEFBgSTlve4GI0y1\ndHV1ldzoVSqVpLVnrBsqkCaTybh1P2TIEJw5c+aTgEFjz69QKNC2bVu+PlidllatWvEqqFKKkyFl\nasKECVi8eDGGDBmCQYMGISYmBjdv3kRhYaEkRoFI641iAEa2eVlYWIiqUO/atYuDgpkSX1xcjEmT\nJvFzVCoVOnbsyNdZWFgY/975+fmoWLEi5GZWUDp4wcwvAJZVm8E2MAwOoZGoPWolykQsgeeQdfAe\nsQ0+H2qeeI/YBve+S+DSJR5OYaPg0nESbOt+DfOyQVDYGMfOEBHH/EiNm7e3t2SZAIZ3EfYaNWrw\nNWWoOi3rzMPy+PFjtG3bVlRQb+TIkbhw4QK6du2q5xW1t7eXZFQm0iqx06dPx+rVqyUpI6TmAcuS\nqlWrFn839g2Z5+LOnTtISkoq8Zz18vISKY1C3A/zGBIRNm3a9O9RRFi6YqlSpXhNhSdPnnC3ECPZ\n+bubRqP5x8pr/9mWl5eH+fPno3bt2qhcuTIiIiJKXIGTbfy6PTAw0CA24s8qIgyc6e3tjaVLl+LW\nrVvYtm0biLTW78uXL1FQUCCKdQoX5NixY5GVlYVBgwZxa5f9qVs8imFSSlrXhoG2+vTpIzrOLJnl\ny5dDo9Hw57l+/TpSUlLQp08fjrq3tLTUq6AJgJ8jrLSak5NT4gXu7u6OsLAwLFq0CO/evcOzZ8/4\n5rlkyRJkZWVh3rx5XIDMnz9fco6yd2EAwZYtW+LXX38VbTJEWmWnJFld9+/f54LHxsZG5GJnAE0A\n/B6lS5dGUVERxo8fL+IssLOzw44dO7BmzRrs2LEDubm5yM/Px6ZNmzBs2DBMmDBBhHV6+vQpt9A+\nh3b6z3RdLwhTKqWsP1agzdTUFKdOncKJEyf+1D2DgoJQXFzMMytYauacOXM4rw0DqbNwnCGFR4gT\niYiIkPTAffnll3j+/LkeURzbqHStb2Fv0KABiouLuRd29OjR/Dvt3bsXJFfCoWxNtI8YA6sy/jBx\nLQMT9/IwL1Ud3i0GwqvrVPgN+hGeg9dK82dEb4FH/+UoG/E9HFtEwb5Jf9jW6wqz0v6QKU0MhpB0\nu+73klLWgoODsWvXLhw7dkySPygrK4vT1NvZ2WH69Ok4cOAA1Go1Dh8+LHlfIdhWJpPh9u3byMzM\nFCkUwneQUnJL+o4l6XZ2dlCr1Xj58iWItEY8oN3X2G9YZeKGDRtKErjVqlULcXFxIsVe6hmFoNz8\n/HwRduZfo4iwmDGLn7PGXIIJCQl6E+mvtOvXr6Njx44wMTGBQqFA8+bN9aiq/681IR9AbGwsXr16\nhZMnT/KY8bJlyyTP+5QiotFoJDfknJwc7o6Xy+WiuLnwO2ZmZiIiIoIrGV5eXpg/fz4KCwtFqXbC\nzczBwYGXcL927Ro/l1lon2rMQ6FQKDB37lz8/vvvPK6rUqnw7NkzaDQaLsCkvFBEWiWLhXFYYyGR\nqKgoFBcXQ61W8/nr7+8vacVYWlpi7dq1fKM/evSo6JqGCrixXr58eb3nYOyfQmHMxikiIoJ/m5JU\nnwU+bobOzs7w9PREjRo1eFjM0dEReXl50Gg0+O2337jgFaalGvIsODo6GsX3MKWxUaNG/H7ClFQp\nIN/AgQOxatUqJCcnl7iib0BAAH7++WfJ/2NubFdXV0RFRYFI60ViCmJqairS09NFG7+7u3uJqMAt\nLCywc+dOFBQUYMuWLTykef36dT4GWVlZBrEDnTp14uuapfZ+SmHTDTfqjpFcLhd5TaytrREZGclJ\nsnYfTIOpZ0VYVQ9FxU6jUL7jKDi3G6efZSLEa4zeCY/+y+HSJR6OLaNh36AHlh+8iJEzvofCxgVy\nC1uQXGk0fCnM5hkxYsRnpfiqVCqRB6Nbt26S802tVmPcuHF6YzJs2DCo1Wpcv35dL3vJxcVFMoR7\n5coVnnVlqLNNPT4+nv+WrU2FQmEQ9/GpdcWuAwBbtmwR/RsAD0ktWbLEYDZWpUqVUFRUBI1GI4ml\nIvqovEdGRqK4uBgajQbx8fEg+hji+dcoIomJiSASx8k1Gg3HjLBY5d/Rbt26JelyY5bP/9XGtN2y\nZcuKXOmrVq3SG1thM6SIZGZmYsiQITy+XKVKFVEMEtACPbt27coXi4uLC2bOnClpwRcUFOD169f8\n/1hmgqenJy5dugSNRiMqPmVpaYmgoCBu/bRt2/azxkOXMEko7FgTYpLYhqebYujl5SXCSqSlpfHf\nenh4iGiUd+3ahffv33MPjoODA+Li4vDmzRsAHwFyugq3RqPB+vXrUbNmTb7wTUxM0K5dOy4AXVxc\n9HBVs2bN0rMOra2tOdisdOnSePfuHbZv386ra5YqVQpxcXF6eBtd17buJrZ+/XqDAFTWhZZhpUqV\nRPVKDBHKsbDMxo0beSaGkADL0D2XLFlikGJcqisUCsk0aaGwrVmzJm7dusW/O/M2VaxYEXPmzBGl\nUfbp0wfbt28XXadx48ZYtGgRB/NKVTMl0mYRLV68GGlpaZgyZQqmTJmCkydPYunSpTxTQTfEZGNj\nI2mpmpiYwMvLS9IrEBsbK34GhQoyU0tUCgiGVZXGsA5si/bjl2LWvmuYtvsqJqRcRuel6fCL3SMC\nhPqM3gnPiBVw+GoILMrXhWXZWli5+xf0i1sIM78AmJf2h9xMrJQpFApMmjSJY6EM9Ro1avA5LOSJ\nuXTpkt5abNq0Kfbv368HEC5fvrwem60hL7qwkrS/v79IqbO1tTWoKI0ePRo3b97kHi02vuzvAwYM\nwOvXr/WwGey6Go2Gk/0xz5e1tTWKi4t5BpZQGRV6JJVKJTeWhMabqakpoqOj+Rpl+CwAHKRuZmaG\nzp07izKb2Dv6+PhgwYIFnBuGKckhISGoW7cu6tevjwEDBvDv4+XlJRr7LVu24Pjx4/8eReTp06d8\nEPr164fk5GQOFLKwsOCC/O9oLPbu6uqKli1bYt68edx91ahRo7/tPv/plp6eDiItcE2oiDD3o27s\nnjUpRSQvL09UJVS4OIWTnbV3797h4cOHn0WhzgTHjBkzRMd1AcsKhQI9e/bk1lpJW0FBAUaMGAEP\nDw/Y2tqiVq1a2Ldvn+g3x44dE92LCXO28JiCpUsRnpKSIhIUXl5eokwnVvNGt+rrsGHDQKRNu5Rq\njCjOxsaGP2t+fj4Pb33//fcAgO3bt6N+/fqwtbWFn58fwsLCUK9ePdFG1bRpU9y9e5fHu3V748aN\n+fcqKCjg669Jkya4fv06tm7dKgK1MYEt5YFQqVSIiIiAUqnkY9isWTNoNBrOFSJV9+TJkyc8VBAb\nGyt61k+ldv4dXXfTmTZtGhfgjRo1woMHD0pUr0PYnZ2d+YYaFRWFhIQEHlL5FJjZzs4OjRs3NlqI\nTFjVVWZiDrNS1WEdEAaH5kPg0e8HeA1dD9fus+HULhZ9V/yCDouOolrMFviOMOzN8B27G1+M34NK\n43fjy5kHMHv/dRy+9gzlAkJAMjl8fEph9OjRIplw4cIF7hGLiIgw+l5MgVOpVHyOMgVJqVSKModY\nZ+PeqFEjrpQ1btwYOTk5WLBgAR9LqXkSFxcnub6EGYibN282SGNubm6Obdu2iUJkMplMj/hOiG1i\nlAUAROexZ7958ybOnDkjencPDw9kZmbydSW8HgNMs/djcjExMVFSOa9SpQrCw8MxZswYPHr0CMXF\nxRzwLuz9+/fH+PHj9Y6bmZlxJUOqLo8we8bNzQ2rV6/m7/uvUUQAbfElKTfs59aJMNZyc3Mlc6wr\nV67MN59/mvjqn2r5+fncIp02bRpyc3Px+++/c1Dj4sWLJc+TUkRWrlwJIq1WfvHiRRQUFHD6chsb\nm89WCqQaC7sJCXIAcKt10aJFOH78uAiLUdL29u1bvTLcRFpeCaF3QxhLZd3f35+TRLH5OG3aNL17\n5OXl4eLFi7h48aKeAvbw4UOes79kyRK8fPkSSUlJXACdOXNG8rnZuDdv3lz0TZjLeuDAgQZp5O3t\n7dGqVSvMnTsX9+/fB6BVEJmFPWPGDFy8eBErVqzg82Tr1q3Izs7mPDlEWqtozJgxGDRokJ63hZ0n\ntXkwpYXdj6VJsxCSUMm/desWr63Culwux/Dhww26kaW4KkrSSxq6Yc/ONrjt27cD0FZ3jYiIQM2a\nNVG/fn2unFpYWBhVLCpUqMDrBL19+5YL90aNGom4PQyRWQ2OHIZF67Zi7LIU9I//EX2m/YgFO0+j\n98z1cO7wHdy/Pp+2sQAAIABJREFUXSQKlfiN3AqXzlPg2GIYXLrEw73vElSN3YY2i39B/7Vn0W3u\nDtjU6QTXBl0xeH4Stp+8hqzcQrx8nYlOnTuL3sXf359z1Hh6eiI3Nxc7duwQeZIVCgVXMITGAyMv\nk+qLFy8WYcZYoT9D3cTERJKYjnWh4i2Xy+Hv788JA4uLi3H8+HGkpKTw9cAqDZctW5Zv0vb29mjT\npo3ouuybSKWusu9fsWJF0fObmppi3rx5SE9PF+EtmEeoVKlS3OvIrmFtbY1ff/2Ve0SE+x9bT7oh\nocaNG/Nv1bp1a7Rv315vDslkMo7runTpEmbOnImEhARcvnwZgHavYGEvW1tb1K1blz+bkMBs4sSJ\nXI7a2tril19+wblz5/RC9f8qRQTQ0uNGRkYiLCwMw4cP/9sLygmzCsaMGYPly5dz60Umk0Emk/0t\nhFf/rcY2Mt1etWpVUUqZsEkpIsxFrosvYHnpQsK1P9vS0tJApMWGbNy4EXfu3OFuUwaA+rONxfk9\nPT0xZ84cTJ8+nS92XQ+MMBWtevXqKCoq4ps9UxxYSKq4uBizZ8/muBtPT09MmzZNMiNFWJhN2Lt3\n724wC4xt2j4+PqIwIfPYxcTE8I01ISEB69atk4whs0wbRhxWqVIl0QbAsA1ff/21QWyClGBmffLk\nydBoNEZrqTBByMbhm2++AQC8efOGc0UIrTBjvVq1agb5DD7FSsnWtfAYW/PW1taSKbm6iqdwjaSk\npOiFDGxsbNCjRw/UqFGDb47C1P4VK1aASIs7UavVKP1FZSgdvFCqah2YeleBVbWv0KC/NjXVvXUU\nPAb8yLNJpLrX0PVwDp8Ah2aDYFbaH97l9IGprH/55Zdo3bo132B0U+kZy62JiQnq1aun901lMhmC\ng4P5PDPmqXJ2duaZNMIxMjEx4WRwrI4PkRYnc+7cOVHtoD59+qBKlSqi5wgMDMT8+fP5HLa2tkbn\nzp3x6tUrnD17FgcPHhRx//zyyy8ij6VMJkOPHj14toeFhQVMTEwgk8lw9epV7okTvpsxHI6rqysu\nXbrEQ3OGQnDGujCMKVzDlSpVEnkipYjR5HI5Jk6cKKJRYGMuXA+6WDRhu3Tpkh73kdDLNGLECOTl\n5UGtVnNeHENs2P86ReSfbsI4eEhICP744w8cOnSIH2vWrNl//Jn+7rZt2zbuMrW1tcWQIUOMVnCV\nUkRYbHzRokX8mEaj4S7BI0eO/OXn1Gg0HJyo24Wl4D+3qdVqbkUJC/CxKqPlypXjx65fvy6KuUoJ\nIGdnZ+Tk5ACAQQtOqiaMRqPBunXrEBgYCCsrK7i6unKL0snJCePGjdNTegsLC/kmHRAQgGXLlvEQ\npUKh4Gl6ISEhIg8YI1irU6cOF0ynTp3i78yEk42NjSjUwP4uxRop7LrKzvbt2/H69WujQDpPT09E\nRETwex85cgRPnjzhnhBbW1vExMTg9OnTeuyixjYA4eZmLIQh7MxLIxTacrkcjx49wuDBg0W/FQL+\nWNNdI48fP+YeoZYtW3JgtXCOtGrVCj/99BMOHz6Mb7/9Fko7d4SPXYiuy0/BZ/ROg0qG9/BkuHSe\nAtt6XeFVPxxrdxzA5fsvMXBMHFSO3pBb2EJp8unMizlz5oiUAYVCgeHDh4vwW6wuipWVlWSVV93e\npk2bEqWUEokJ1ezt7ZGRkYH3799zI4eI8O2332Ly5Ml8HoaHh/Nny8rKQnp6ugjUy9a3MYD9gwcP\n+Pf29fXFV199xcMjffr00SM6nDNnjgiTxObG6tWrOSiTSKts9O3bF99//72IM6VevXolGg+ZTAY3\nNzcEBARg9OjRuHv3LqKiovi9pejv2ZpUKBTw9PRE9erV8e233+L27dtIT08X1Tby8fHBmTNnkJOT\nwxMHatasKTlGQnmTkpIiSXxGpE3L1mg0HOgvrPAsbP9TRD6zsY3AkPtXt9z4/+WmVqtLxL8itagZ\nCNDd3R0///wznj9/zqnZWQbF39GKi4uxZMkSBAQEwN3dHSEhIejQoQP8/f0RHByM2bNnG/TkANqF\ndOHCBc5RAmhDJmzxCkMmz58/55sxoM2s+RTzo6OjI9LT06HRaDiexNTUFCkpKVCr1di7dy9XXAyF\nWwAxIZTQ6mrZsqXeNzp58qReNVq5XI6VK1dyHoCmTZty70mVKlU40+2AAQM44dqwYcOQlZXFlYXK\nlSsjMzMTp0+f5u9dEhyGlMehZs2akoW8ZDKZ5Ji2a9cOnTp1KrHlaEgpEh4fPnw49u7dW2IsSZ06\ndXhmEOvCrBeGfyhVqpTe95NaI4yDol69enzuHTt2TEsQZesK8zK1YFm5EeybDIBH/+Vc0Wg0+wj8\n2mnLv1tUCIGZXwCUdm6QW9hCYaWVT0KgqkKhkAR86qaSOjo6ci8AY/x8/fo1fvrpJ6xbtw4PHz7k\nz/727VtMmTKFKwDlypXjGUVC5VL3G7N7st+w7yFkGpbL5UhOTsbly5c/ycMh7DVq1CgxeaUxRYTh\nH1q0aMHX/4ULFzhx1/HjxyXl/6ewQLoAc0BrbBjjlhHOL3t7e9H8NTU15YSArK7YuXPnMGPGDEyb\nNg0zZ85EZGSkpCfQ399fErhsZmYmAi7L5XKjRigAXLx4EURaLxHL3vP29uYK0tGjR7lhu3LlSslr\n/E8R+czGUi8HDRqE3r17w8HBgS+uUqVK/W3EacXFxdizZw9mzpyJNWvWGCUU+283qUVdWFhoMKW1\npFwen9tu3LghKSACAgIkeTBWrlwpisWWK1cO+/btg0aj4ZaCcOGwzTokJATAx8JULVq0QEZGBn79\n9VcORqtQoQJWrlyJ7OxspKWliTgZZDIZmjdvzgvSsZg4I+jSbXfu3IFMJoNSqURycjLUajWOHTvG\nhbyUd+ngwYMYNmwYevXqhdjYWNy8eROAVplSqVSQyWTckq9Xrx4XVtu2beMZG4zS3VAKpHDDadas\nmUHsCetSpdWFnYU7ypUrx+Pa7du3/2ywJ+u6SotQiMvlcmzatAk3b97k3jvd7ujoiMqVK6Nu3bqY\nN28ecnJyUFRUxDOahL127docJ9O5c2e97yG1Rt68eQN7r7Iw860Bv8Zd8EWrvnD4ajDces4TezhG\nbIVLJ23YRWnnBnd3dz3mUd0MGaaICrELwgq6DC8jVBKZF1Aul+PAgQOSczEvLw8XLlyQ5Bhh4y1U\ngiMjI/UwCk5OThx8K5fLoVAokJWVJQpFGgvZWVlZYefOnbh27Rri4uIwYsQIbNu27bMKehpTRBj+\nZuvWraLjzHNx6NAhvHjxgitPpqamaNOmjcF1wr6N1JguXLiQ/07Xq0KkDYsJZRRjURXio/bs2SO6\nZlpamp4CqFQqMXnyZCxatEikmAizwKTq+bB1YAxnx7J8+vTpg8LCQv5t2TMwL6Szs7NBbOD/FJHP\nbIcOHeILulKlSqL4+N+1wd67d09vodvY2GDv3r16v33x4gWOHj1qMLXxP9EMLeqcnBx899138PX1\nhZWVFRo2bKi3aP5M02g0OH/+PHbv3o27d+/y40yANGzYEEeOHMH27du5hae7yW/evJmPbalSpfji\nlMvlGDp0qIiXo0GDBiKrZefOnSJ8w+PHj/l1MzIy+PcCtJlIhsIPtra2uHnzJie+kgK0AsCyZctA\npF/jhjFcjhkzRu8cY4JWqtAdkVbBevr0KZ97LJ6rW5hQqVQiLCxMZFHVrl2bkwrq/lbXeyKkwmbd\nzc0N169fFwljc3NzNG7cGEQfUxGFG6chTwa7docOHbh351NdJpNh+fLl2LRpE+bPn4/Dhw8bNSqE\nWLEyZcrwOLxcLhcRjV26dAkduvaAQ5nqcAlojuaRMxGbdAbjtl9CrWmH9LEbUZvh2nUGnBp8AxOP\nCviqwzfw8NIqYrrg3E/1OnXqiKrfsg3xzJkzvBSCrlVcuXJlpKam6r1vTk4OevbsKQo7WltbS+KD\nhN/l6tWrehkxMTExIpZbFk559eqV5FoR/pZdW5hh9measfXBsiKFmWk5OTkcI8aIuTIzMyXTueVy\nOaKjoxEbG8tlhKWlpV4SQ3FxMVcybGxsJDNUypYtK6o+PmrUKBQXF+PQoUPcEBLCAV6/fs3XUFBQ\nkEhBLVOmDDdw2bFnz56ViMumV69eBseSKVOdOnUCoA3X6WJHHB0dJfcv1v6niPyJtn79epF1Z21t\nrQfgYu3169eIjY1FhQoV4Ofnh/79+4uqdOo2jUbDAVU+Pj6IioriQB9zc3PuHs3Ly8OAAQNEEy0o\nKOi/opB8LrPq1atX0bt3b5QtWxY1atTAjBkzjIZPdM/VLRjXsWNHPHr0iHsNhKAzVr23cuXK/JhG\no+Gb7YwZM5Cfny9p5QYHB4vc11ZWVjz9VaPRcKHZokULtG/fHitXruSF6KysrACA59cTfSTvEm7C\nderU4ZsBE3BFRUV4/vw5R5YzoGKbNm1EY8HS86Tirsa+iUajwZIlS0ScC0RaLw573zJlyuD9+/d4\n/vz5J8NPxqxX3e7p6Ynbt2/zLIk+ffpIWoJExIW0ubm5ZLrgp7q/vz8uXLhglInS3t4erVu3Rlpa\nGh8ftVqNAwcOIDY2FmPGjEFKSoqeJafRaJCYmKgXOpCb20Dl7Au/xl3QIHIuPPovkyTuKj9+Dwas\nO4u2I+fA1LsK7P2qolRFLXbCEMU8C8+ZmpryNM22bdti5syZekXyqlatqheeY7106dKcwZj1Dh06\n4NGjR5LK144dO4xmDsnlcslQmKurK4YMGWIUO6RQKDB79mykpqbyTb1p06b8+YQhHOF1hFTkf6YZ\nWx+Mq0OpVGLUqFFYtWoVz/yoWbOmaIzUajUOHTrEFV5DyrG3tzdWrFghwpzdv39fJA+kSg54e3uL\nsn5WrFihB842MTHB06dPAXwsJtmwYUNkZ2fz+cQU+b179/L7EhGePn2KtLQ0yW/k7e3N5xWTZ1Lt\n/v37vBJyYmIi7t69i8WLF4vwKWxsOnbsKBnq+Z8i8idbfn4+0tLScOjQIYP0169evZJMGbSzs+Np\nULqN0V87OTkhMzMTgFboMWQ6s+xZjROWcsYEhZOT09/KmVKS9jmKSHp6uqRQq1OnzifTnrOysvhi\ndXZ2RpMmTfgmw+rWWFtbi3Adly5dApEWdMba27dvuUAvLCzk2BX2XELkeNeuXbFy5Urs2rVL9J3f\nvHkjuYGyTZtZB8LwwM2bNyULqxER+vbti+TkZDRp0oRbKFZWVoiKisKtW7d4Ku/ixYvx4sULJCUl\n8eeVqiF09uxZ7Nu3D8uXL8eiRYtElOisaTQaZGZmIjIyUqRwffXVVzh16hTCw8O5BSxlqcpkMq6E\n1K1b95PZJ0TEuU2Yx6l27dpYunSp0XMqVKjwyWtL1dyQ+jY///wzXr9+zcNsNjY2IiX47du3kiFF\nlUqF4cOH49GrbOy7/ARr0+9i/qEb6PbDMbh/kwD3Pt+jdPQmPaXDrcc8WNdqD/NywVC5+MGrbCWQ\nXInIyEio1Wo+X86cOcM9X4Y2M/aNvL29eTVhpVKJFStW4MmTJyJlhHmxhEqkruLJuoeHBy5cuCDa\nYBl51ujRo0WblDGl9FNYG5lMhri4OPTo0QPt27eXlI2urq64fv06NyCM9YYNG6JTp07YvXv3Z4fE\nz549ixMnTmDVqlWIiIhATEyMiIJciszQxcXFoNy+evUqiLTe1Xnz5vEsLV3eECJtqvKrV6/w5s0b\nXi/oU+/KOpM5pUuXFmWxBQcHQ6PRcPkyc+ZMaDQaPsZsbixatIh7Uom09amuXbvGuXqY3Bk7dixe\nvHjByddMTEyMjicDoxqaF5UqVeIypFatWrxcAWv/U0T+wcaQ/JUrV0ZaWhp+++037ipt3ry55Dms\n1kuHDh1Ex5mQ6tWrF9dAVSoVJkyYoBcLr169+n80hbikiohGo+GAvo4dO+K3335DamoqxwBIEZ0J\nG9P2AwMDeRZKRkYG35CZ1h8fHw+1Wo3c3FyOsO/Zsye/TkFBAbc679y5wzexhIQEEOmzIyqVSkyZ\nMkUk7BixmJQlYWJiwqnkhRbzw4cPodFo9ArLjRs3TpQqqHvdZs2aGVzoPXr0kBTCw4YN09u8e/To\nYTCOnpWVhfPnz+Phw4dYunSppHBUqVTw9/dHYGAgn3NCNkpdi65ChQoIDw8XZQpNnz4dgLayLoup\nl1QQf4oKW+p5hQqWsMxDUVERz94Quoz79+8PuYUdLCvUg92X38Kp1XC49UqER78f4BGxQo/Eq/q4\nbXD9JgGVBszH8M0XsPzYbcSv2wcTt7KQqUwhk8lw8+ZNzojLvomPjw9yc3P5seLiYmRlZUlSqeu+\nF+PNMaTU6nYnJ6cSVXWuWbMmDhw4gHv37pU4s0W3s7X0xRdfwMXFhT9/vXr19FL2CwsLsXLlSoSG\nhqJBgwaYOHEit+zfvXsneuaYmBhs27bNoJdnyJAhn6WM7Nq1SxITMWnSJP6b9PR0DBo0CF26dMHs\n2bPx+vVrFBYWYsuWLYiOjsbEiRP5Os/Ly+OYiJ07dwLQcgGxzdfOzg7dunXjihyT/0I+mJJ2V1dX\nkfHADJdTp05xGdmgQQOo1WqsWbNGdK4Qr2MoJNO2bVsUFBQgPT2dy8l69eoZHU+NRoOkpCSEhITA\n3d2dZ0fa2tpyL/29e/d4CFM3RP8/ReQfbAzweOzYMX5MGAeVAu4wdlNXV1dugavVal5EKi4uDikp\nKSAikUbcuHFjURqpFAvlP9VKqojcvXuXT06h94NlclSpUgXffPMNmjZtilGjRnEwJ2vffvstiD6y\ng7LGeAWE9RZcXV259WBhYaFXY4bxarDNTalUikCRbAEyYCeRlgtk8eLFIisnLCwMLVq0gEKh4ELX\n2dmZ34fhP4i0Ftz06dNFVmVAQIAeFTP7t62tLRduhw8fxsaNGxEUFAQbGxtUrlwZCxYs0LMsAIiw\nGq1bt0b37t2558jf3x/9+/dHQkICHj16pHcuq4xLpLXAdYVVrVq1kJ+fz9/h9u3biI+P5/FzYbew\nsNAT9kKa/Vu3bkkKYlNTU1hYWOgpUnXq1BGl335uX7BgATIzMzFo0CDu6ZGbWuLryAmYf/AGWi84\nBu/opI/KxqgdCJhyACETk+DUZgyc2sbAJigce05fw8t3+cgrLMagQYNAJFaiWT0XIq0i0b59e4SG\nhoo8AJ6entBoNNxLsW7dOgAQ0X9LdZVKxeWCRqPBqlWrEBgYCAcHBwQGBiIxMRExMTF8Lvbt2xcL\nFizQc+czV7ru9eVyOX8md3d3vbCWsXRroo/GQNWqVWFpaQmFQoEmTZrgl19+kZQJP//8M1q0aAEP\nDw/UrFkTCxcu5B5NqVCFsAcHB2PGjBl8Q5aqjmuosTBpxYoVMXfuXAwaNIiPx4ABA3DkyBE9xebZ\ns2eSyvB3330HQFzvKSgoSAT+Zd6WR48e8TV17do1ZGRkSALsheFOFxcXZGRkSIZA+/fvz70ZP/74\nI968ecPvGxQUhNGjR+t5C52dnbFhwwbcuHEDPXv2hIuLC9zc3ERrWFdx9fPzQ9u2bQ2CmHUbI1Ds\n16+f6DjzNOmSUP5HFBEiukdEl4noIhGd+3DMgYgOEVHGhz/tPxyXEdFCIrpFRJeIyF/3ev9XFBG2\nsQldfnl5edyaZCGUgoICLF++HM2bN0dISAgHTpYtWxbNmzcXeTx69+7NwUZMmDJqYGZ1MWE+d+5c\nbNmyhXsP/qmmq4i8ePEC06ZNQ4sWLdClSxeeqvrHH3+ASAtMnDhxIkqVKgULCwtJBD592MhYRkhG\nRgZXHoKDgxETE4MNGzbg/fv3nNvlwIED+P7770ULLyAgACdPntR75ocPH4oqkep25rmqVasWB2MZ\nStl2cXFBdHS0Xp2UpUuX4vbt25KEQlLvSqTFLIwePZrjYFjIyRClu1RjoMYhQ4YA0FL0S6W9yuVy\n9O3bVxTKE3I0pKam8oJyws6eycnJCcnJySgsLERBQQEyMjK4S124gbm6uqJVq1Yg0pKx6TZD9VsM\ndXt7e/Tr10801/38/LjwrFWrFnx8fPQUGRsHZziUqQ6rGi3g2DIaHv1+EHg4UtFy3mHYNxkAx7qd\nYOJRAXMTFwD4GN5j623dunXYvn07vv/+ew7ELFOmDGJiYpCUlGS0ABnrffv2BQBOhCWTyVCnTh1R\nRkO7du3Qq1cvtGzZUsRjYqjduXMHS5YswZIlSziGRBc0yDqb+507d+aAUyG7qYeHB06cOFEiT0pJ\nukql0qvdsnr1asnfdujQARqNho8tw37phoUY9w4LrX777bclWh+3b98GkRZ7xPhbNmzYoKdkBQcH\n80ruGo2GG3pmZmaoX78+unbtyudYREQEwsPDUbVqVT3lTUjdDnwkgGNZOQ8ePODnBAUFYd68eXzM\niLThS+Eakclk6N+/P3799VcUFRVx+ce8DGlpaXrYJW9vb6xcuRJHjhzBzp07ERUVhREjRuDo0aNc\n4Xr37h1CQ0M/+c0N4SGFjeHavvrqK9FxxvukSwr5n1REnHSOzSKisR/+PpaIEj78vSUR7SOtQlKH\niH7Vvd7/FUWEWfCtW7dGZmYm8vPzOQ9BjRo1AGgVE6k6CcZi4sHBwSIBM3v2bMTFxfGJq7ugHBwc\n9Gqk/J1NqIhcu3ZN0mrt2rUrCgoKjG7KMpkMkyZNwq5du7ggdXNzM0r4w6whT09PjBkzRmQ12Nra\nGkXXv379GtOmTTOKGl+zZg2ePXsmekapMTbUa9WqhVu3bumBYatXr46+ffsaPI9tPMxFPnnyZMl3\n0Gg0SE9Px+jRoxEdHS0KdW3bto2zzxrrrLorAJG35+jRo8jMzPxk0bGaNWtygV1cXMyt4latWmHt\n2rVITEzkm7iuS7aoqEjPYitfvrzBcE2dOnUQExPDN1JhKEOhUKB33/6InbMMFhXqw7ZeN3h9PQWe\nA1foEYB5Dd0A5/CJqNV7Isz8AmBi7YivvvpKJISZV5Gx9TIPmxT/SUnXLutz587l3y8yMlJS+Fep\nUgUJCQmi+V+lShXJOTBy5Ei9axgC6QrHdu/evTxtdsSIEfwavXv3xtdff12iOS7Vg4ODcevWLbx+\n/ZqH5oQA0/fv33PLfcyYMbh9+zaSkpL4sbi4uE+So61ZswaANnmASJvqrduys7Mxfvx4+Pr6wt7e\nHi1atOCkfhUrVgSgVTSFY+Lp6cmNjjZt2kCj0XBMnu4aNZT63axZM77pMqUTAP744w/ueRAyH7Mw\nvpmZmUFeEV0OkcmTJ/OKt15eXqKw67t377BmzRpMnToVycnJKCgoQE5OjmTmVZcuXUS4uuzsbCQl\nJXEQ8tSpU3H+/Hm+DhQKhYhTRqq9fPmSy+bo6GgcO3YMEyZM4KBjXW/3pxQRGbTKwV9qMpnsHhEF\nAnglOHaDiL4E8FQmk7kT0VEAX8hksmUf/v6T7u/YuR/AhkRElJGR8Zef7+9oRUVFdOLECbp37x65\nuLhQ48aN6eXLl9SrVy/KyckhlUpFSqWS8vLySCaT0bx586h+/fq0fv16WrhwITk5OdHgwYPJ1taW\n1qxZQ5cvX+bXdnV1pfDwcKpRowZNmDCBXr58Sf369aNVq1aRRqMRPYdcLufHZDIZ2dnZUWZmJpma\nmtKWLVvIw8PjHx2H/v3708WLF0XPwVpsbCzduHGDtm/fTkRE5ubmVFhYSGq1moiIVCoVHT58mMzN\nzUmtVlN4eDg9efKE/zYvL0/ynjKZjNq3b8+v6+/vT+/evaOMjAySyWS0dOlS8vf3lzz3xo0b1L17\nd8nnJSIaOHAgXb58mU6ePMmPOTo6Um5ursHnadCgAZ08eZK/l4+PD1WuXJn27dtH9erVo4SEBDI1\nNaX09HQaNWoUFRUV8fcgInJxcaHnz58TEZFCoSC1Wk0//fQTlS1bVnQfjUZD06ZNo9TUVNFxS0tL\nysnJobFjx1J6ejodP35cNFZsTQvf2dTUlLZt20aTJ0+ms2fPEhGRt7c3zZs3j7Kzs6lv376ia3z5\n5Zf0xRdf0I4dO+jZs2fUtGlTmjFjBhERnTt3jqKjo6mgoED0XKGhodS7d2+ytbUlR0dH+v333+nI\nkSP0008/kUql4uMg1fz8/Oj+/ft8TIm0c6JmQCD5BjSifMfydF9tR28LiYo+fEYZQO7WSsq6d5We\n3r5Kmvz3VPz2ORU+uUHFb5/rjYdU8/HxoQcPHkg+z/PnzyknJ8fgucaaqakp7d+/n0xNTalr1650\n//59MjMzI09PT7p7967kXCQiiomJoY4dO9KbN29o06ZNdPLkScrOzqYXL16QXC6nxo0bExFRWlqa\naF2Zm5uTn58fXbx4kczMzCg/P59fk4390KFDafHixURE5OvrS9nZ2fTmzRs+Bw01qTFcsWIF+fj4\n0K5du+jmzZt0+PBhUqvVdPDgQbK3t6ddu3bR1KlT+bnVqlWjAQMG0O+//04//vjjJ8fPx8eHfvrp\nJyouLqahQ4fS5cuXKTIyknr27Ml/k5+fTxEREXTt2jXRuXK5nD/3hg0baPv27ZScnEyenp70+PFj\n6ty5M/Xs2ZM6dOhABQUFNHnyZIqLiyMiInt7e5o4cSJt376dfvnlFzIxMaHCwkIyMzOjMWPG0MuX\nL2nNmjWUl5dHw4YNo0WLFhEACgkJoXv37tHDhw/5vTt06ED29va0Z88eevXqFZmbm9Pbt28NvrOF\nhQXl5ubqHbexsaHExESqWrWq0TFbtGgRrVu3juzs7Khjx45UVFREW7dupZycHBo+fDh169aN/3bj\nxo2UmJhIzZo1o+nTp/Pjo0ePpqNHj9KoUaOoS5cuRu+3c+dOio+P15sbQ4cOpV69eomOlStXjv/d\n1tZWpnstpdE7lbyBiA5+0OiWAVhORK5MufigjLh8+K0nET0UnPvow7Gn9P9pu3v3LkVHR/NNk4ho\n/vz5lJCQQMuWLaMFCxbQ2bNnqaioiBQKBalUKtq5cyc5OzvToUOHiEgrYL788ksiIqpQoQK1atWK\nX+v58+cmCxjmAAAgAElEQVT0ww8/kJeXF4WFhdGqVavoxYsXFBsbS/Hx8SSTycjZ2ZlevHjBBZid\nnR1lZ2dTZmYmF6Y7duygwYMH/23vXVBQQA8fPiQrKytyc3OjJ0+e0MWLF4lIu0kGBgZSmTJlaPfu\n3ZSTk0NLliyh0qVLExGRlZUVvX//nmQyGTk5OdGrV6+oqKiILl68SMHBwaRQKMjExISIiDw8PKhp\n06a0bt06CgoKovPnz5NaraZatWrR1atXKTc3l37++WciIoqIiKDevXuTQqGgxMRE2rRpE23atMmg\nInLkyBEiIgoPD6d27drR/Pnz6fz583yTXrp0qd45r1+/Njgmffv2pe7du1P79u0pKyuLiIgePHjA\nNzNHR0cyNTWlDRs20IIFC0TnsgXLlBAiIrVaTV9//bWeEkJEtGPHDkpNTSUzMzMKDw8nS0tL2rZt\nG71584aIiObMmcPHUHgPJycnKiwspOzsbCIicnNzo2fPntGmTZvo3r17/LcPHz6kTp066d03MjKS\nevToQURELVq0oPDwcEpLS6OsrCyys7OjwMBA2rBhA23ZsoX++OMPsrGxIXNzc0pPT6f9+/cTEZG1\ntTW9e/eOX1NXCdHd3FxcXGjhwoW0Lmk7HbzyhDQqczL1qUYPvSrTY1MLondqquluQhWRQ9uWzSIb\nWSFtXb2E8nOyqXncGCIivjYGDx5MZ8+e5QqXrhJaoUIFun79OhGRpBJSvXp1Cg8P55sT26hbtWpF\n+/btExkChpScgoICSkxMpDp16tD9+/fJy8uL1qxZQ7a2tnTz5k3q0aOHnjLSsWNHCg8PpxcvXlDf\nvn3p2bNnov+3sbGhkSNHkpOTE+3fv58mTpxIRERfffUVTZo0iYqKiqhVq1aUmZkpOo+N/e7du4lI\nqyQJ54FQCZF6J/bvHj160Pr164mI6Pr16zR8+HDRN2b3aNGiBS1cuFB07qVLlygyMpLc3d31xopt\n9kRESqWSiouL6cGDB9SnTx96/PgxvX//nhwcHKhNmzai81JTU+natWvk4eFB3333HXl5edH69esp\nKSmJGza9e/cmS0tLIiJ6/PgxqVQq6tSpE7m6upK7uzvdu3ePf2eZTEZZWVnk6upKs2fPplatWvG1\nFhISQmFhYUSknduzZs2iM2fO0NixY2nmzJl04sQJ/lxsvmzdulX0vOwdDbXc3FxydHSkYcOGUVxc\nHFlaWtKAAQOoZcuWZGdnZ/RcALRz504i0sqF6tWrExFRpUqVKCYmhnbs2CFSRJiR5ejoKLqOk5OT\n6P+NtTZt2tDly5dp165d/DvLZDJ6+fIlaTQarhCWqEm5ST63E5HHhz9diOh3ImpARFk6v8n88Oce\nIqovOH6YiAKEv/3/KTRTXFzMQalffPEFRo0axV1rNjY2ePHiBTZu3ChZAdLc3JyD+S5evMivKUxn\n9PT0xKpVqzgKmbnO+/fvD41GI8mvYGNjg9evX+Pw4cMg+gh8ql279t9SGVij0WDGjBkiF3W1atU4\n6JRIjAXYsmWLpKuxdu3auH37Ngc2EWnDCQBw/vx57oqcOnUqJxlatmwZxxskJSVJum/d3d2RkpLC\nMSlSlNusMWAhA0/l5eWhSZMmetc0VsBK2GfPnq0XcpHL5TxcZWpqiiNHjuiFdqTqRBBpSfIMZQMw\nwB0DOgLAb7/9BiLp0BELGTCAKBtfNoaMG0cqLdnU1JQj7nXThRm4USpFGAAvYkakBTMyN7hMJkPl\nypX1wjAqlQoylRksKoTANeRrOHw1BA0n/ITOS9NRSlDILeC7XWgZtx4O1RpBZmqJpKQkDoi2sbFB\nTk4Orl27BiJxeq+9vT0fb+G6ZCGELl26cPe9VHdzcxN9Y1ZnY82aNejQoYPkOQqFgmeMsVCgSqXi\nxRUZ4PHJkyeSRfzKli3L8Qws5BsYGIgjR46IQkH9+/cHoKUXEM6t3bt347fffvskRb6LiwvWr1//\n2diQWrVqiUj+WJi4bt26orRiuVwuwvcY6qVLl0ZUVBQPY7B3vH//PoYNGyZaL3Xq1NEDowPgWKb1\n69fzY2q1mstcIdifzXFG5sayFKW6hYUFunXrJgoLCjFyJ06cAJEWGA58DO05Ojpi3rx5ePfuHWbP\nns3PXb9+Pd68eaOXGccyKIW9du3a/Prly5c3KNd0mzBDS1griJWtsLW1Ff2ecak4Ojrysb106RLH\n6Ujh7nQbK/Mhk8nQsmVLNG/enH/HefPmiX77H8+aIaJJRDSKiG4QkfuHY+5EdOPD35cRUVfB7/nv\nWP9PKyJXr15FZGQkQkNDMWDAABEpDQPn+fr68k1erVZz3Icuz7+DgwOSk5M58JLFIrt164bCwkIR\nkp71+Ph4XLhwQSSwd+/eLXo+IcLc0dERb9++xaNHj/TixI6Ojti/f/9fGg9h+qmfnx9fkA4ODnyi\nsY29sLCQ0+ITfaT7Ze8SGhqKmTNn8v+3s7NDrVq1RO86fPhwXjyqefPmHJyVnJysl+7IsDMKhYIL\ngICAAKxevRpTp07Vo4Jm38/Z2Rm//fYbNBqNCGxYt27dEjEPsi6lULi5ueHkyZNGz+vevTsnTWLf\nv27duka/A5tbQnZZjUbDn3f58uUcGCfcWIR/t7GxEcWNnZyckJWVhV9//RUjR47k4zlu3Dg+Z6Oj\no6HRaLB3716uFKpUKsksnMzMTL757dy5Ew8ePOD3l6nMoHT0gkWFENjW/wYOXw2B+7eL4DVskxjT\nMXI7vpx1GE1n/wy7kO6w96uOm49ecgWNgYlbt26N4uJintnQtm1bHDlyRPRNjAGj165dywU8E8RE\nWtDopUuXuALAvo3uN2/Xrp1BbItwDgmfh2EMWLo+U7iZ4hsZGcnn+8iRIwGA44dYMTeh4mJnZwfg\nY4HGTynQMplMlNKZkZHBDQcvLy9JPIxSqeRKMMORqFQq/PTTT3rzi3UTExMOAJfifNGVU6zqqzCL\ni4h4NfU3b97gl19+wY0bNwyuDzavt2zZIlofbLzWrVuHP/74A5MnT+bP3LZtW4wePZrLMT8/Pw6G\nNWQsEBGXqWq1mmexMKWQZUL98MMP/DmE2XQMtPrmzRt+zNraGoA+kNvDw4MrtKNHjzYqH4RNo9Fw\n7NbmzZv5cWYEBgcH6/2eGWQymUyESQwNDS1RqjRT9Bo0aMBlABtXb29vPHjwAJMmTULXrl3/eUWE\niCyJyFrw93QiCiWi2SQGq8768PdWJAarntG95n9SEdmyZYukdckmFUO9CwFJAESbKzufeU5sbW1x\n9+5dvvjYn87OziIlREjPLOyNGzcWabUA+G/ZhHFyctITiuzaZmZmos3rc1pOTg63mNkCP3r0KEfe\nCxWiwMBAvRS8ixcvGgRj6abPspRlpVKJESNGiASBhYWF6NoM0FemTBkO4GLjrmsF+vn5cQGmVqtF\n2QJCZL6QPbd69ep/KYOA1WOQyWR8McpkMrRo0YJbkbqVXT+VKsfozxk3x/nz5zFixAgQaa3+06dP\no7i42GCFYnNzc+5pYxZsu3btRPdg6Pfu3bsjPT2dj4EU+6ePjw/u3LkjOn/3gZ8ht7BDzYah2Hvp\nCeI3HoJz+/HwitosZhsdswveUZvh0mkyHEOHwjakOyxLV0fnnn3x8IOCc+7cORB9BBmydvDgQf7t\nDdXLYOPdsmVLEWC6atWqkkXBmCWuVCp5uuz9+/f5nCopWFnYhQyk7DmnT5/OrzVgwADRhmxtbY23\nb9/i1KlTIPqY8st+z7KdZs2axc9RKBSIioriis/UqVMxZcoUvbkrXGtMATY3N4dareaKuK2tLcLD\nwxEZGYmaNWtyedKxY0de4I6Nq/DarL4N43Fp2bIlTp8+zb1MTJEqU6YM5s+fL/nNunfvjh9++EFv\n8w8LCytxFiAblypVquDmzZvIz8/nRHasGCVrP/74o96cVqlUePz4sR67sPDbM2+YTCZD/fr1uZJj\namrKPQmsllRMTAy/n9ArdPDgQX5c6KFbsGAB5s6dKyl3fH19S1zgj7XExEQ+D6tWrcqVSSKtd1m3\nZWdno1+/fnxOmpmZYcCAASVmwdb1rPr6+or2JKER+Z9QRPxIG475nYiuEtH4D8cdSRt2yfjwp8OH\n4zIi+p6IbpM25TdQ95r/tCJSXFyMoqIiZGVl8QXdq1cv7Ny5k9MsKxQKPHjwAPv27QORVsObPXs2\n5syZgwsXLvBsBxsbG47wP3XqFGdtnDVrFl9kO3fuFJUjZx++X79+2LFjBxo0aMAtG0tLS8mJwGqn\nmJmZGUTLe3t7cwvZUDnmT7UzZ87obQYnT57kwkfKIhTW5gG07JXDhw/nC9/X15e7T//44w8cO3aM\n07SXpLy7ra0tnj9/zjdVYWdCg1VOZXUrSpcuzZHi7969w9ChQ/kY6y780qVLc+ZEYa9YsSIfT6lu\nYWHB3f1Mqalduza3tq2srHDmzBmkpaWJMlN8fHywa9euT36LXbt28XN0Uxvt7OywadMmAFrr5tCh\nQxg4cCAaNmyoFyYUfjMzMzPu2dBoNJyjJS4uDkePHv2gLMkgU5lBbm4Dpb0H3KuFoEpIKExcy6DO\n18OwNv0upu+5hlYLj8NXoky955B1cGg+BDa1O8Cq8pcYk7AEffp9JD27ffs23r59yynuWXv37h1f\nj4yErKCgAGFhYaL3cXZ25nNLoVCgevXqqF27tui7sv/38fExaulaW1tzD1pKSkqJFBAHBweD4QcT\nExO0adOGK8eXLl2SVBSUSiW2b98OAHj8+DGXJQC4pTpw4EDk5+fj3bt3kqypnTt3RmFhIXbs2MGP\nMa9O2bJl9VJ7e/XqxT1cuj0xMZFvHEFBQVCr1Vi1apUet4WNjQ3n07CxscGDBw8AaENFLP2VpaZb\nWVnh3LlzuHfvnihDx5DCz+41cODAEsmqrKwsUZ0a4bebOHGiHvfRkydPkJiYyNOGPT09cebMGW5A\n6vaqVasiNzcXI0eOFI2Dt7e3yIhgoRQTExPMmDEDhw4d4p4OuVyOY8eOobCwEMuXLy/R3BoyZAgn\nfvucdv78eT3lQCaTfdKzkp2djRs3bhhkEDfUmFJmZmaG8+fPA/iY4cR6q1atsHr16v8RmgnbpUuX\nEBYWxsmp2MbWoEEDkSuKFSGaNWsWioqKjKbzde7cmWvEjD2Q6CPWIygoCIBW6F+9ehXnz5/HyZMn\nRV4UZrEQidkhhe3p06eSaZZKpRJ79uzhihGrEKpr+bL29u1bLFq0CD179kRUVJReaXoWc3d0dER+\nfj6KiopERGrG+jfffCO6Dxs3IT5Gqh06dAjdunVD48aNMWTIEMybNw/z589HamoqlEol5HI57t+/\nj7y8PKxatYovcrb5N2nSBGq1GsuXLxdxgXh6eorSml+8eGGw7PjnWMAsJESkHwpgmwtLTyYikYUe\nHBys5+0y1ubNm6cnuNlm7ejoKCk8ioqKkJqaKpnKJ1OawMLFBz1GTIZ/+EDY1O4Ixyb90GN2Mtzb\nxcC9z/d6ioVULztuDzovTce8g9fh27QnrKqHwrtmQ6icS4NkxplUhZaqbhMW7AsICODeDDYG33//\nPdRqNd68ecPDo8wSvXPnDtavX4+UlBTcuXPHIFOrUqkUjem4ceNw69YtgzV1hL+dPHkyV3CZ548p\nPbphkODgYJFnws7OjivDgwYNglqtRlFREa+SHBoaCgA4fvw4n482Njbcw6BQKNC7d29MmDABp06d\n4jJLiEc4ffq0Xq0mIq2XUEim9invn4mJiciTYWJiIlpbrDqwlZUV2rRpw3/r7OysF26R6rop0NWr\nV8f58+dBpN3YSlqN/OnTp+jduzdXNqtVq4YtW7YYJWEsLi7mSppQSdWt3kxESElJAaBNV927dy+O\nHz8uSoVljWGBDM0bYY+Ojtajhjc3N8eSJUtK9M5S7f3793yt+Pr6IiQkhMvfihUrShIj/tXGjBiF\nQoHo6GjExMSIDCY3Nzcu6/7VikhOTg6OHDmCtLS0T1KeX7161WDxLd38dKZMjB07Fhs3bjS6oHx9\nfQ2Wp1epVHol3DUaDfbt24emTZuKQgpmZmYYP3685Cb15s0bkeavKzBGjx7NXfZMS5ViXr1+/bpk\nKesJEyaIno8J8LCwMD2wrKmpKd8AmLB0cHDgi65Lly6Ij4/nHqCgoCCj8UaNRoPnz58bFDyMn6Ny\n5cpYvnw5mjVrxu/FLLi5c+dy4BQTjsJvcObMGWRlZUmCBD+ns/mza9cu/PjjjyKlRi6X82q2gBY8\nNmzYML7xMLfn51odzG1vbW3NC07l5+fz8V26dKneOWq1Bhn3n8CmypewqtEC7SatReTGc6g6IVVa\nsRiVAp/RO+E5aDVcOk+BXUgP2AS1R+zan9E+ZiHMfGug7dA4lA5pD6WjF06cvYi8wo+C7fDhw0YL\nzwkFs0qlEhUt1G3FxcUYO3asaG2w2HepUqVEc+nAgQMg0nrD9MdAjbVr13LvkJubG9asWYOcnBwU\nFhbqebp03fYdOnTQY4VVKpXIz8/n92DhQnt7e4SGhvL1YGlpKbq+u7s7V5qFG7CHhweXGwqFAseP\nHxe9m1ChqFGjhh6FOmvJycn8dyEhIThz5gxiY2P587i7u4tYQY19ny+++ELP6+nv74+8vDyo1Woe\n+ihbtqxeaLl8+fI4c+aMQa8LkRZDpquENGrUiLNQfwoYbWzeCIH6n2KD3rp1q+Tz6XoTGzZsWKL7\nazQapKamIjw8HPXq1cPgwYNx7tw5xMTE8G9fqVIlrFy5ks/h27dvY+XKldi4ceNfrh+2atUqEGlD\nSczTmJ2dzRXhf4JnyhDglykjAQEB/Lf/WkVkyZIlIu3LwcEBK1asMPh7BhoLCwvD8+fP8erVK+4C\nVSgUaNu2Lbp06YLExESuLW/bto17KxYsWIAtW7ZgypQpvBIjW1DVqlVDVFSUiOirfv36OHHihOgZ\niouLJSmvvby8OEiLfbTx48ejfPny8PT05NZH1apVeW2BTwn+Cxcu8OudP38eo0aN4kKvRo0a+OGH\nH0S0x0uWLOEL5PTp0wZrPkyfPl0EuGXvHBMToydgfH19sWHDBkyZMgVz587F/fv3ReORnJwsClmx\nAk2PHz/Gli1bkJqailu3bhlUwli3sLDgG1dkZCS3zlhl3A4dOnCvlVQXPreUZ8TU1BSmpqZ8/Cwt\nLREZGYmBAwfy7xAfHy8573Jzc3Hnzp0Sx111G3PnftOjF+69eo9Ve06i0eAZ8Gj6LawD28C/7zR0\nWHIS1ScfQN0Zh1Fp4j6UitmN0jEflQ7vEdtQatgGhE3fjo7f/QjLKo1RtVknTP9+NerUb8jXj64g\nbteuHceQMFyOlZUVYmNjMXz4cM66CnwUhERabAAbU92QkpAdU61W64VnWMvMzMSxY8dw4cIFZGRk\n8GsJDQ7mBm7UqJHoXI1GI1lynYVDiouL+fydMmWKnudEmKXE1h7rrLqoELfRqVMnnD17Fmlpabh2\n7Rp+++037imrU6cOOnXqhNjYWA4GDggIEIVNypUrJwKnC9/j0aNHePz4sVFlPj8/32hRwD179ogU\nrVatWmHZsmV6HqAePXoA0BIBCssSCAvBFRUVcUX/xYsXuHr1KpKSknD8+HGo1WqOqXNwcEDr1q1F\ncsTDwwPPnz/Ho0ePuDd6wIAB/N1u3boFuVwOpVL5lzfmTykihYWFBg1TYZfJZEbL25ekaTSaf8Qj\nIWyMdZsVTWWNlSiYP3/+337PFy9e8DkUHByMHj16oF+/ftxQdHBwwLNnzwD8SxURYbpotWrVRNgB\nxiD56tUrfPfddwgICIC/vz/fMISMb8Jyybq9XLlymDNnDnfdCSe1Wq0WuWOF55mZmWHNmjUYMWIE\nfH194e7ujm+++QZXrlzh+BOp3qVLFwBaLdaQSzkhIQFFRUUikKVUF9ZqYZ4SYffz88OiRYv0skWa\nNWvGx/z27duIioriGwlz+zEmUwbiYorEoUOHcO/ePcTHxyM6OhrLli3TY5SVy+U89MQwL2xzYwqA\nsDIu23x+/PFHvqBMTEzw3XffIScnh6fvSfUKFSrwCqYODg4iK08mk6FmzZoGwzHVq1fHuHHjJFOy\npfo333zD3bWPHz9GVFQUypQpA19fX7Rv3x6DBg3C6NGjJetbAEB+UTEynr/D9afZuP3iHfZeeoIN\np+/h+9TTqPTtDHgOWg0fQVqrCAQ6MgWVY5IRvfkChm++gMm7rqD3vO1wbNIfpp6VoLJ1kQTi+fn5\ncavQ2toa0dHRHGgrBLmxdWPIzVytWjU8f/6ch/SIPlKk6yohDRo0wPv37/Hy5UtERETw+VejRg1R\n5oNu02g0fL61b98ev/76K5KTkzmYWdelzdLaLSwsOAaJPb+NjQ235H18fJCXl4f9+/fzuaRSqbhX\nMjMzkytoxkJ33t7eSExMRHx8vEHKdeFYOjg4oLi4GFeuXMEff/zxWaE6Nh6//PIL1q5di+PHj0Oj\n0eDMmTN69YBUKhXWrFnDlUlh1eenT5/yNcX66tWrAWg9pz169ODHhXiIZ8+e8UrRUrW0WLaRr68v\nlEolPDw80K9fPx4OYynKrIyFXC5H7969MX78eP49u3XrJvnO6enpWLhwITZu3Ch5b2H79ddfsXLl\nSuzdu1cSbyHEMnyKKdfb21syHPP/U2OZZU2aNOEy5tSpUzw807x5c4OVhf9KM5QGz4xBGxsbtG7d\n+t+piLD0plmzZuHx48eYPn06z+oIDAzE06dPDZbEFhaoE9Zu0RW0uv9WKBQIDQ2Fh4eHUfCbUOAI\nu7DIV3BwMA4ePIipU6dyAadQKPD27VvMmDEDRFpFKC0tTUQZXLZsWQAwSonOalpUq1ZNklpe9/10\nMRMNGjQQjfWCBQtEv6tVqxY/xrwQZmZmXMCwxtIUnZycEB0dLaJA379/P/8+kydPRmFhIe7cucNB\nvzKZDM2bN+ffVCaTcf6GuLg4AMDly5cNvptcLsf58+eNlho3MTERVZZl47tu3To8fPhQlN7Zs2dP\nvH37FuvXr+cK6NChQxEXFyfC2Dx8+FAy9CW3sIXKxQ9mfgHwa9INi1NP4+DVZ5i+9xpCEo7Ad6xh\nLIb3/2Pvu8OiuL73zxbYpUlHmqiAqFhQrCBG7FERu8YK9q7Yg71gwYi9BiWxa+zdWGPsFVuiGHtX\nFCwgfd/fH/u915mdWUDzMTH+PM9znsRhd3bmzp17zj3nPe8ZvBEOIUNhHdQOFmXqQONRBp6+fiCV\nCVQWtlBr9empyMhIhIWFyVYoGOu5YwwTIafCedq9e3dMnDiRG12W2mRhYK1WizFjxsjSZpcqVUp0\njcL3TJjaMpSTJ0/KlqrWqFFDlC4BwMGIY8aMAQDZtISlpSUWL14s6zgULVoUvXv3FuE9AgMD0a5d\nO5HRMjEx4VEyoaMr3CgoFApMmDCBV4gR6R2gj5Vbt25JOueWLl0aCQkJSElJQVxcHCIjI7FkyRK+\nfjJjIcSiqdVq0UaEgfNZFFGobm5umDlzJkaPHi1K28qJsX5NbK4Jq66EWCumVapUkawlL1++lKxl\n1tbW2Lp1q+T3k5KS8P3334s2EWq1Gj179hRF34RpJWOl76ampnwOGGvq97+SnJwcLFu2jLf3aNCg\ngajaJi9JTEzk70e9evU4fkOoKpUKa9eu/Z9f++HDh9GiRQuUKVMGISEh2LlzJ54+fcqr/oj+gaqZ\nT6GGjsiZM2cwYcIEREVFIT4+nt/c5s2bZQl82Mvi7OzMDSibYM7OzrwrIsMYBAYG4t69e5wrP7+L\ns0qlwqpVq0QLpHBBmjlzJq5duyYh5RKCN1m7eSLC3bt3+W60VKlSqFChAgYNGiT6zP79+0ULkUaj\nQf369bFixQoJ54ZwYYyOjpbkfg13rEznz5/Pr0+YZzSmwrK1lJQULFu2jO+a/vzzT2zdulWU72aL\nlb29PbZs2SJZWF1dXfn5WCt05rgw48JItJjhZ/gPtuD169dPZEiYA1GmTBmjz9jKykoWECxMc7Xv\n0AEm9oXQJWop4o7dxqbzD7D5wgNsu/gILXoOg6Vfffi2jUTQkCVwajkerl0XGnUyPCN3oeOy04ja\n+QdWHr+F6DX7MHHFHmw/nQCLgoWhtneHUmuJihUrSp4d41ERNrEzVGPAXLl3plWrVhg4cKDEyS5Z\nsiQWL17M8/6TJk3iY/HgwQOYmJhAqVTi6dOnOHfuXK6RA6ERL1iwIK5evYr09HTufDs6OkqcCqFc\nv34d3bt3h6+vL6pUqYJZs2bJYsMYKFMYKTl+/DgHDbds2RKXLl3iu0Vvb280bdo0z3dfoVDwd33y\n5Mk85M4qp4j0jnJ0dLToe4GBgdiwYQPfoISGhhq9x9wkKyuLz09nZ2d89913/J48PT2NprkY8Z9G\no8l1vjAHKi/gtkql4sRgu3btQq1ateDk5ARfX18+hhUrVkRycjIOHTrE0zO2traSyML169cxadIk\njBgxAjt37pRNYbCKPTs7O3Tt2pWD501NTXHjxg3+uVWrVknmr42NDZ93DDfHNlK5qY2NDfbu3ct/\nK79daQF9artRo0awtLSEk5MT+vTpw1MUcqLT6Yz2pRJyk+QlO3fulNgAjUaDH374gacqLSwskJyc\nnO9z/l25cuUKNm7c+N93ROQaM7EXmi0KgYGBuTIK5hV6O3LkiKiUl6nQATB2Dew7wpeNfaZ8+fIA\n9BUkwpfbzs4O3t7e6NGjB48UaLVavHnzRpZcq0CBAkaJlDZu3Ihdu3aJsCeVKlXizfeI9Ds8nU4n\nImwSqlarxcWLF3lo1N7eXkQKtmfPHtSvX1+yQFlbW2Ps2LF88di1a5ekwkjYGt0QECi8J+HuXNh0\niXVGZQuura0t9uzZIyIMMjU1RXx8vNGwuEqlEo2PXBmwMGpgaJCOnDiDEzdfYODaC/AatjnPihKv\nyJ0oMmAVnDvNgnPr8ShQuTksigei64goqK0LwrSgFyyL+uHqTX3p48qVK0W7aGFEjRlT4eKpUqkw\nZ7LLajUAACAASURBVM4c9OnTh897Nu7CcVy6dKmsc3r+/HlZDpqQkBDRe9SwYUO+GWDkRUJAJQCe\nmmPO2o0bN1C5cmXR+d3d3ZGQkICMjAw+H6ysrLjTceLECe4U9+/f/2/jAxiIrmTJknj8+DEAfWUW\nwx88fvwYM2bMAJEe+5Kamsqjb8bUxMRENC/q1KmDVq1aYc2aNTh79iw/Lmx8aQxnZdiZND+SmZmJ\nzZs38/eZgbuF3ak3bNhg9PvC6JQcR4ycEzZjxgxRybuNjQ2/J2dnZz6GxtTNzU2UZpYDFecmt27d\n4tEcrVbLMWY6nY7bBUYCd/HiRdGcc3Z25hgQFk1h743wGu3t7SVNPLVaLZKSkvh4m5mZ5XtOHjp0\nSHZ8vby88OLFC9nvMDJEMzMzxMXFISEhgZOsmZubf5Dj8OzZMw6ULl++vOi7bBxYCu6flP+8I0Kk\ndzj69u2Lnj17StIeXl5eIuNt+PJv3rwZOp2OTyoivQG1s7PjO/OxY8dixYoVIHq/K2AMhobkXOyF\nNbZwMY9ciEm5e/dunuDSZs2acUIaIj3Sfd68ebJ05ELNb3g9ISEB796947l2pra2tlizZo2E8Of0\n6dN8EjHg17t37/D8+XPcv38fly5dwp49exAVFYU5c+bg5MmT/N79/f0lzt/333/Pw75yi15wcLDo\n34MGDQLwnnArKCjIKKdHcHAwUlJScPToURH19Jw5c6BQKKBUKnHhwoVcIyGVvqkLU9fiMC9UCuYl\nguBQszMcm4+BW6847mD4RO6AY6MIWJSuhX0nLyLxbTruJKbgTmIKrj95A9tS1aG2dUXTZs0ki5FC\noUBmZqbo2KxZs7B//37+b19fXxE+g4j44st2tcaUjXelSpW4oyUsF2XKStWFIfTcOiZXqlQJGRkZ\nvCy8b9++fF7Ex8dDoVBAo9HgwoULmDx5MoYPH46tW7ciNTWVh2aFTI9CTpDTp08jMjJS8pssavmx\nkpKSwrkhTExMRA5q//79AbynUV+4cCHHKxUqVIizBAvf+y5duiA1NZUTrhmqMNp3//59XmnHonUa\njQaVK1fmz8LQmctNzp8/j/r164vmriGGguFgWNpSTjIzMzF69GjROmRubo5vv/1WhC1xd3dHnz59\ncOHCBdH9tm7dGkuWLEFMTAwH4rJzTZw4Effu3RNtfoRzin3OkBQyt+dn2PVWq9WKaMcZvikkJATA\neyZTNuYzZ87Eli1bjG5Cu3XrZpSFV6VSiVKsjEU6LxFimbp06YJHjx4hPj6ezw8WzTUUhuMbOnSo\n6DjjpBK+P/kRFi0eNWqU6DhLWRrSr/8T8kU4IsOGDcO1a9fQrl07o6RURHqPW0jfTaT3/jIzM0VA\n0aioKADA7t27jS7GNjY22LRpU66Lv1DlvOD8qkqlwps3b2SrQwx3ri4uLnmGkKtVqyZxUHx8fNCk\nSRPJ+QyBr+zcco4Ik+TkZP6SGH6vWbNmsqFGY2kjY+rs7IzRo0fz5x0XF4f09HRERETIRofMzMz4\ncUanDQD16tUDkT4cLsyRqyxsYeZdGXb1+sB34M+SqEbRETtRPGIlHBoPRYEqLaH1rAClRn8tjNpZ\nKDt27DAatSLS76CZwWO7/8jISH59I0aM4CAzIZcGK61+/vx5nn1EmOa2u/fw8MCiRYtExwYNGsSN\nBbseYX585cqVOHPmDL+/oKAgUS8OQzIxIv1ujDnRrJ07IO6zxBZgdl5ra2vuiAlbyhsTnU7HsUCP\nHj0S/e3hw4do0qQJvy5ra2uMHj2apwbYYt2xY0e+QAvBplu2bOHXyXaQQh4OlUqFzp07SzY+3t7e\nKF++vMgAenl58c9VrVo1X/TZgN7RY2NsyHFx4cIFPgbMiZcr5RaKYcqIqTB1XLZsWQ6eFVZCGZvb\n1apV4+dPSkriUdPq1avj2LFjmDt3Ll9jGCdHXsKYgjUaDa/WItJvGNhzZtwrffr0AQDOnsx2/X36\n9BEB4tn1s+sLCAjA8+fP0bVrV9F75eXlxcfawcEBU6ZMyTeY+OHDh/w6hSlDxgzs5+cn+z1W0cfs\nEhOGKxK+P/kRNncLFy6MZ8+e8U0aS9UaVnP+E/JFOCKlS5c2WsHAHICGDRvixYsXorIzIr0nzcLW\nbIIJQ6PLli2TpBNYKZyhc2Fqaioq2zNUtrPIzVGoUKGCrNPCekcQ6Z0GQ+p0ovdkWazxGdF7vIUh\nJ4kQKGSoKpVKluxKuHiycmKdToe4uDgMGjQIy5Ytw8uXL/lC4ejoiIEDB4qAUczrf/v2rWgREarh\nosoiWh4eHrJ4lE6dOvHFgEVFqlevjnXr1okiPEqlErVq18HE6bOwfOs+nPjrOVb/ehI2JQNhUboW\nrAO/g2OLsXDvu1IEBi3Y4QdYV20FrWdFaIv6w7SgF0hlInHSLCwsEBUVJcljv3r1ihsaY8++SpUq\nfHzZ/Fq/fj2fM4yhEtBjAYTfFfb4kVPmdP4dinq28LJwdq9evTgSnxHVLV++XOIMsWesUCjQoUMH\njBkzhjswbCfo4eGBQ4cO4cGDB0bLqBUKBdatW4e3b9/y9zE3Lon4+HhRik2lUiEsLEzS9DExMRHX\nrl2THL9x4wY3TixdxDYjXl5eePnyJT/3ihUrkJaWlmv00cTEJM8UcJ06dT6ItpthI1jJ8J07d/ja\n4eTkhPnz5/P3wdLSMtf0wdOnT0XrzokTJ7Bs2TLugBqW965cuVJSlRYaGopOnTqJ7rNevXqi35ED\nuxLp21bkp4T1/v37UCqVMDEx4c9f2I8lODiYp7MVCgV3yBg4nq1FpqamEsbUypUri8q62TuXkJDA\n7//evXtITEzEjRs3jGJucrt2Ir3TK/zu4cOHQaR38uSERevd3Nzwxx9/8D5PjMzx7t27H3QdWVlZ\nvOzckLzPzc3tf9IY9UPli3BEhF1FGbDNMORsbW3Nc31yWAFXV1dR+NrV1RWBgYFYuXIlkpOT0apV\nK5HXb4iHyG23m9cCVKJECW6oihYtihcvXuDUqVO4efMmd7CEaYeQkBCkpKRwT5otFEKgF7u+vICk\nhurk5IRDhw7h7t27uX6uX79+GDx4sCSlpNVqoVQqoVKpRNwnbCfr5eXFjyUnJ79vgKZQ8HyvMTCc\nmZkZB6WWL18effr0wcGDB/kO8vnz51AoFFCr1Ui4+xAHrz3FzH0JGD5/HbSF/WD7TUdRKkVOXbst\nQqmu0egRsxaWRctBoRYbFw8PD4SFhYmet7D8V1gexyQ/NPVM2Xh6e3uLMBO7du3i52OlsHKOBRs7\nVl5p6ADJVX+VKFFC4kA4Ojpi8ODBslGWhg0bIjU1lTN2duzYEWPGjJE8t8KFC/N5KwxfP3z4kBtt\nw1Qgu6YWLVqI2DCFZF0MIGhIBsjk+fPn3El0cnJChQoVRJGPCRMm5Is4bunSpZJ319LSEhs3bhSl\njAoXLiyJ3tSoUQN16tTJtTKNGTcTE5N8dTM1FDY+DOcCgDeeM3wnGXjUmCxbtgxE77FEMTExACBy\nDO3t7Y020fP29sbSpUslODOFQoH169cjJycHFy9e5CkNNzc3KBQKuLi4YNSoUfk2fixKHRwczI/d\nvXtXsjFTqVQiICcj/mPXanj9DBydkJDA50qJEiXQqVMnvgYLI6kfIzqdjqd7BgwYgDdv3uDWrVs8\nzTd8+HDZ7xmyVwtB5r179/6oa3n48KFRRvDmzZv/ndv8KPkiHBGmTZs25YvhpEmTZBdeBwcHo70D\njKkQUCmH5RgyZAguX76M0NBQST+Lbdu24cCBAyLEuFzEQ1ihkpCQgMzMTN4WulixYtwAs4XAyspK\nlKfUaDTcEbl06VK+783LywtTpkzhBsfV1RUxMTGca8HJyQkODg5QqVQIDAwU9drJ69wqlQoBAQE4\ncOCACN/SokULTJw4UTSucsbI2N9KlSqFpORk3H+Zgj9u3sPJS9fQoM8EOLedAtdui+DWc5lxZ6Pb\nPBSo1BTmJYKgLewHrWdFmLoWh9q6IBQmGigUCixdulQEeBMuxHL3+OTJEyQkJPAFgpXy6XQ6LFiw\nQBT2DQ0NzRMPVKxYMc5nw5gqnZycMGvWLCxZsoTPhWrVqmHQoEGylT6M16VevXqyue68nl/nzp35\ndZcuXVrkePXv3x979uzhkRshXb2x3zl48KBo4WEgxcOHD2P06NEoWrQobG1t0aBBA955dcSIESDS\nl4Ky3XJ8fDxUKhXUarXRSgM2ZtWrV8fBgwdlnamKFSvmi0Tur7/+wpgxYz5ozXB0dERior47sCE3\nUNu2bXHlyhWeBmSlyh8aXgfA1wK26weAO3fu8DWmW7dumDx5smxXZENh6Thh6X+DBg1E72h0dDQe\nPHiAsWPHolWrVoiIiJB9J5RKpSTVKnwGbE4olUq0adOGR4E2b96MgIAAmJmZoXDhwhg/frzEQWG4\nFCcnJ9HfWPVc2bJlMXXqVNkowdy5c2XnfeXKlZGYmAhAD+aUi2zVqVPnf1JNsmvXLtlNq7u7e66V\nM8nJyejevTt3Ph0cHDBx4sSPJkJjTQvt7OwQFxeH+/fv4/Tp0zz6LKwE/Cfki3JEmAEbPHgwbt26\nBSJ9RUlsbKzE+3N1dcW4cePg7+8Pa2tr7igoFArMnDkTFy9eFC2warWasxseOHBA5DjY29tj+vTp\n6Nu37weFv7VaLRo3bizBn5iamopY/YTevomJidEOo05OTqhXr57E0OUWrcltMWXXyGr7T506JfuS\nFipUKE8SNeHzEf67aNGifEG1sbGFjY0NFCYaKM0KQKHWoICrFzTupWDhGwzbWt3gHDYbdaP3otQo\nKR25a7dFcGwyAg6hw1GgSgt4BzbAyPFRKFm9ITQeZeBYpIQoZ5/bs4qMjJQ0U7t7965k8TU3N+cv\nEyOAmj59OoD3i6OcCsexdOnSImS+ubk5R9CnpaXlCUhm99KyZUtJyk2hUPDfCgoK4tfO5oibm5sI\n22Co33zzjVGeESL9zl84v5YsWYKEhASJgWK5euA9iFWhUGDQoEFGgad3797lc8PT0xPffvstv5cu\nXboYXdQYp8zy5ct5xKVNmzZ858nGmu365eT06dPo1asXmjZtijFjxuDevXtYunQpAgIC4O7uzudO\nvXr1ZNOp5cuXl915s9Qk65vCDPaH9BF59eoVOnToIIpyhYaG4syZM3yutG3bNt/nA/TpBzYvO3fu\nLLmf0NBQWSwES4s0adIE7du3x/DhwzlQ1MLCAj/88ANPxQnPKYxAlypVirejN9TatWuLjK1Op+Np\nhYCAACxduhQDBw7k58qtTxGgn1PR0dEIDw8XVT22bt0aY8aM4XO9Vq1aWL9+PRYtWpQrA+vHyMGD\nB1G9enUoFApotVp06NBBwiptTNLS0vD48eO/TaDGcGaGDe9YaupTMK3mJv95R6Rz5848D+3v74+z\nZ8/i2bNn3IgwRtL09HRs2LAB0dHR2LBhg4SPYP78+SDS79Zfvnwpu4ssUqQI312w3dqH9CcpWbKk\naNF3d3fH/v37cfz4cR7+E+4khGW5hvXvfzffT6Q3tuy8zBM2LFUj0u9gWrdunW8wZG6qVqsRHByM\nnr37IGbZWqw8fgvNI+fDscVYeAzZjCJDtxiNZhQZvg0F201DhWEr4BAyFJblGsA+oCUs/b6FmVdl\nWFpaSdD0QhX2uLhw4YKk4ikvZdTewrLEKlWq8DnESoAXLVrEF3b2/Aw5O9jzU6lUSE9P5wsDWwiF\nXC1ZWVlYt24d2rZty8n62JwQLu4uLi5YtGgRr2ARqvBzhvwwho6qr6+v5Jjh/PPw8MDQoUMlqT+N\nRoPVq1fLdhINDg5Gq1atZOduw4YNsXTpUglZ1W+//Sb6DYVCgY4dO+YaymcVEgxkam1tjdevX3MH\nfvLkySDSV07JybRp0yTXZ2lpyckOGQFaq1at+HcyMjI4/kz4DrPIFBtPFxcXJCQk8LJzNhasZXxe\nkpOTI8tlI1R7e3sRf0Z+RQggF6ZgAgMDjQIyWQ8nExMTdO/eHcOGDeNOKKtAYg09VSoVVCoV9u7d\nC0DvFDBnjc2v6OhoJCUlYf/+/RzftmnTJtFvXrp0SZYYbcKECfm+VwawnzdvniRKUrp0aQm4+VNI\ndnZ2voHJ/2th70B4eLjoOLObeQGb/9fyn3dEAH24Ts5IFihQIN/NkWJiYkCkN8TsJXRxceHeN9tB\nhoWFAQBv8z1u3Dhs3rwZlStXztOQ/fnnn7wXjDFt1qyZUT4POS1UqBBfcI1pgwYNEB4eLom8MDS9\noWEQknvlt9rH2K5ZbV0QGvdSsKrYBNZB7WHzTSfYfdsfhQasETkZxYdtgP23/WFbuwcKVG2FAlVa\nwqdpP9Ts8j2cywVDbe8OE42W3zORvsstMzoshCw08IbXwgyaSqXiQMv8KMvPKhQKfPvtt5ymmki/\nE/ztt984RsDU1BTPnj3j84ntyD09PWUdn+rVqyMnJ4f/hhymgsmTJ0/y1TwuLCyMvw81a9Y0CuS2\nsLAQRYhYWjMsLEz0PH/44Qfk5OSISolHjBghYfBl0QqVSsX7LRHpd7+G+BFLS0uMHDlS4viamZlh\n1apVePPmDRYuXIhOnTqhX79+WLBgATZt2pQrMC8zMxNz5szhvBlMbWxsOPi6WLFi3HgyHh+hsLSm\nUqlEREQE1q5dywGW7u7uyMrK4nNuzpw5ou+yXjELFy7EoUOHcOzYMWRmZvIKMuYAsp0wuz62WcqP\nyPEmCbVhw4aiNhUfIllZWZgwYQKPhlpZWWHgwIG5prB0Op1s5K9OnTqi77G2G/Xr1xd9X5iyZZ3I\nmTDgv6GxBPRsqjExMWjbti369+//wVELYaXf3bt3MW3aNIwYMQKbNm0ScST91yQnJwdv377N08Fh\n7S1UKhViYmJw+fJl7mCr1WpZ2vtPKV+EIwLoJ1b9+vU5UDI0NBSXL1/mf09MTDRKGANAQudtuLgy\n1Wg0mDNnDl9Y2U5GWPpJpA95Cxu2EekrYvbs2cP/XbFiRZQqVQpeXl58Z8BKsrRarWQX7ezsLNmp\nsvIxZmw8PDw4YJdpoUKFcPLkyTzTJ+z32GIXEhLCy95IoYSqgCOsXL2gti4IVQEnmNg4Q21dENqi\n/rAtVxdW/iEoENAaNt+EwaFpJAr1XyXuezJ8OzyGbYP7gDVwbDEWln710bxTTzxJTkVOjg6PHj3C\nxo0beWOs3NTc3Bxdu3bllRdCBH/79u25kZw3b94HRa2EBrhcuXI4ffo0cnJyMHLkSJExNYaxWLJk\nCV6+fCnbD6hw4cKSCIK1tTUnA7OxseG7Xdazh8m9e/dEZZRCOnlm3Ni4sGMWFhbIyMjgXCtmZmYY\nOnSoqCU5c4DKlCnDAcXTp0+XgP+KFi0qGy3TaDSi3bMcZkDunUpKSuKpT3bN7DcZiNHwe8ISZkPJ\nzs6WpNIM1dLSUsTSa2JigqFDh4oMD+O6EIIAs7OzOUZk//79nPSqWrVq/LuJiYn83k+dOiW6NiF/\njaF27tw5V7ZYody4cYN/r2bNmrh16xbmzJkjWhOmTJki+k5GRgY2btyIqVOnYt26dXl2IWf3m5iY\n+EEG+cqVK5gwYQJGjRolApAz2bFjB4j0UWuhsDJpImmEaubMmSDSV8UBwOPHjzkdfrdu3T6Ib8VQ\n8mp691+Td+/eYdiwYRyC4O7uzjcQxsSwczrTGTNm/INXrpcvxhFhkpWVJcopHjp0iC/0RHqvW9hP\nBtAv8rnhKIwZMiHBjGF3y3379uH3338XHVMoFLh+/To3Ym5ubpg2bRoPiSoUCh6BmTt3rmjnbWhw\nmJqbm4t6prRu3Ro6nU7iBIlUqYbKyhGmBb2gsrSHQmMBU2dvWPnVg2W5BihcrzOsg9qjyverUbDD\nD3DruQweQ7fmyRjKHY6hW+Ha/UcUbDIcdpVCYeZZESpLexApQAolPDw8RCRzderUQZkyZVC1alXM\nnDkThw8flq1syi/XCMNJWFhY4PXr13ynmhc1NRGJxs1w9/3kyROsXr0aa9euxYsXL3DkyBF89913\nqFq1Kjp06IATJ05Ap9OJIgWMMC2v52hqasrDzazZGqDnXmjevLnk88xZFIbpTUxMJABgPz8/+Pr6\ngohE3aeFpdOGfVAM27fLqdD5yAv4aqwcnZGdMUepfv36ovSAn58fFi5ciMGDB/NzGKPSZpw+dnZ2\n+OWXX3D9+nVJ6wShCq9Z6HSwMk9DzAbbIKxZswZJSUnc6ShWrBjat2/PnfyAgABZZ2nZsmWoVKkS\nbxxYr169DwYECqkBhBUcwijJvHnz+PFLly5JHF9nZ2dR/6N/SlJTU7mR7N+/P+Lj47FkyRL+TrMI\n0YIFC5CRkYFTp05xMP66detw+vRp2ZYTkZGRH3U9X5IjkpOTw/l9DN83lh6TE0bkWbduXfj4+KBR\no0Y8bfZPyxfniAhFuBMRtoI3MTFB+/btUbJkSZQoUYLv+lu0aIFRo0bx77AFety4cbwHg0ajQc2a\nNbFu3TrRgmNoOAMCAmR7eeS2aLN8MpF+p9yyZUvJZ4SN39gxYe076157/vx5WFhYQuNWAjbBneHc\ncQbcesXBvf/qfDsUlcbvRMG2U+HQeChsvukES7/6sPANhkXp2notUxeW5RpA4+YLta0rlObWIGXe\nxp4od7ZOY2plZSVKTeSVNvrxxx/x6NEjHi0y1jtHTo3V9OclwmojucZSRHoAaHJyMqKjoyW57uLF\ni/N0oqFTI6eGvDhCNcR1CMupX758KTt+wgggm//+/v6itAsRca6YvNTa2hpJSUk8HcKUvXNVq1bl\nvA+DBg3i2BKVSiWqUpgwYQKI9A6YnLRv3x5E4t2csaaGFhYWOH/+PI4cOcIrcFgJLEvZVapUCamp\nqQD09O/MiY2MjMTLly9x+vRpUa8idi/CUlqhMMNnuFH6EImKihK9+6NGjcKxY8d4lEepVHJsQ0ZG\nBndCSpYsiYiICL7JcXJyylfF0P9a1qxZI+uUd+7cWRaXQ6SPkqSnp3MHu3bt2li7di0iIyP5M/mY\n0ucvyRFhNA729vY4fvw4cnJysGnTJs4RcufOnX/7EvOUL84RycrKwtSpU0U7gSpVquDt27dITU3N\ntalT69atAQBHjhwR7Z7Z7l2hUGDXrl3YvHkzgoOD4erqiipVqmDZsmW59p2RU5aWMcQ0GO7a5SIb\nhgZEozWDqoATNIXK4PuffkX35Wfx7azfUDRi7f9FKLagYLtpcAgZCrt6fWAd+B0s/erDvOQ3sKrU\nFAUqN4eZTwDUtq5QWdhCobGAi6uraHft6+uLefPmiZwl4aLIek18yBgIjdXx48dlFyO5brXC3zV2\nzNbWFqGhobK9eYTPVW5htLKy+mCSICaMd6FDhw7IyspCVFSUKM1Qq1YtUcj77du36N+/P0qWLIly\n5cph6tSpfF4LSezyo8L7L1q0KI4ePSqi1WYsrMB7I21jY4PVq1dj4MCBImfaw8MD8+bNk/2dBg0a\nSKrQateuLevYCLs1C6tI2Liza9ZoNLhx4wZ3vh0cHETjKscfIRQWBatUqRKmT5+O58+fi94dljpl\njh8jLWRVJqxT66tXr/gcd3R0lAWG2tvb49y5c8jMzMTu3buxdOlSnDx5Mte8fG6GLyEhAfPnz8ei\nRYtExHWGwrgwjOGEhBFaFiEqUaIET/1kZmZysPPHlAv/L+TEiRNo3bo1SpQogeDgYCxfvpynD5Yv\nX85J6Ozt7TFkyBC8ffuW37ebm5uICGz48OEgIvTo0eODr+NLckTYO26IK2MRwdjY2H/pyvIvX5wj\nYqwUkU1WtpNTKBQ4evQojh07xncKSqUSAwcOxF9//YWZM2eKFnYHBwcsX75cgr9gGhYWlid5mBCj\nYWFhgT59+oho4uUWGLVaDYWpOUwci8LcJxAWpWrqAZ/1+8Gx2Si4dluEQoM3iru2DlwJ93aT4dBk\nBBwrNoRKa8F/s0mTJpKoTMmSJbF27VrOTyFnnG1tbVGnTh0RBiAiIgJE4oZfLi4ufIeb1xgwZaWY\nQmeOXUNevXIcHR05ONHT09MoY6ytrS2OHDmC7OxsSbtz4edUKhVnqBWKTqfDhQsXsHnzZtkKh3v3\n7klSaT4+PvDz84OtrS0vxxYCHJOTk0V9SJgWK1YMT58+5SBHlgYxMzMzWi0ldALYPc2ePVvC+Fm9\nenU0adKEf2b8+PH8et68ecPfH8ZDERcXh7p16/Ln4e3tzSmijXXvFTopGo0Gt2/fRmpqqlHQrFKp\nRKtWrUQRJIVCgfPnzwPQh57ZnBowYIBk7FkDMKEKnWIzMzPe1I1tRAICApCTk8PnjpDn5OrVq5Ln\n4uHhgRkzZvBn7Onp+UGRDTnDl52dLQGaK5VKjBkzRtap0el0nE3V8JnXqFFD9Fnm1EdERIiOs+os\noVMqPP/hw4cxaNAg9OvXD9u3b//o6M3fEcNqEoYvqVWrluhzK1euBNHHEXB9SY4Iq+AcPHiw6Dir\n4vs3mth9qHxRjggjuzE3N8f27dv5As4W4j///JMbBCsrKwD6l0/Ypjs3LVCgADfiP/zwA27fvi2i\nQf7111/Rv39/2NvbiwyGk5OTiDJdWOETGBgo+KwCFarXQcOw/rCt1hb2DQbAtcePUgzG/wE+Xbst\ngmPzMbCv3w+WZevCsXQQTKzfh/r9/Pz44q5UKqFQKHDw4EGsX79edF+jR4/GzJkzRddVsWJFji1g\njpqhstC/m5sbDh06hPv37yM7Oxvbtm0Tfa5QoUJGjRbRe8CvMNyvVCol/WrktE6dOvxzTZo04Tuq\n6OhorF+/njOMsj4is2fPNkpOxaInrq6uop3X7du3RTgjIv3OnIXhs7Ky+FhZW1vnWlot3L2xnYyX\nlxfWrVuHjRs38uvv2rUrN+hsnH/55RccOnRIck5mkNjvsnFs27atKAUjxNgoFAr06tWL8xG8fftW\ntgeNmZkZevbsyee9paWliONGqOz32Vix987CwkJCvrdz507MnDlTklpSq9Ucv2JiYoIyZcpwOQx6\ncQAAIABJREFUB8bU1BQJCQmid/7YsWN8vhibY+PGjePjxq6pRIkSfJxcXV0lwExhPyShoROW6R44\ncEB2UZUTOcPHeruYmpqiXbt2aN68OXf4Vq5cKXuetLQ0DB06VJRuHDFihATwyt7x0qVL83vLzs7m\nlVtCvBCgn8Nype81atTA27dv832fn0IePHjAad0vXrwIQD8O7L03BOjmR74kR+TEiRP8/V63bh2e\nPHnCq5FMTExyJUr7XOQ/74jMnDkTc+bMwc2bN3kOtVevXgDA+RQYkLRfv358sWSEPyz3LFwIhf8u\nV64cxowZI9rtCkvQsrKyeDi5X79+mDJlCjp27IjIyEjs3bsXly5dwrVr1/jvqm1cYOUfgrJdp8G9\nzXg4h82G+4C18BiyGR6DNrznzBixE+79VsKpzWSUbD4AFqVqwsSpKNT27rI4DOHuaPTo0bh48SJ0\nOh1feIQpKUPsgDGgrrARFzMgDMhomFIaPHgwsrOz8fjxY26IhAZ53759aN++vSgaw/4+d+5c5OTk\n8Np2pnmVJRsqM7SOjo58YWZlpMOHDzeKa/D09MTChQvx9u1bHs5nofqMjAxuRFUqFVxcXLiDW6FC\nBeTk5HDHq0iRIkhKSpLMKcNxvn79OgBwXgshCRMrq7OwsJBEj2JjY0XVXWwsa9WqhaSkJB6qZlGr\nRo0a8dLTevXq4dWrV1i/fj2WL18uST2xHXTRokURFRUlG53LDY8i1IYNG4o4W4RqbW3NiQEBvXHc\nvn07Ro8ejZiYGDx8+BBpaWlG8TWGHUPZJmL48OF48uQJ2rVrJ0kRDR8+HCkpKbLPX6PRYM+ePbKL\nI8NeLViwQHScve/GnAU5MTR8Op2OP/9t27bx46xizLCU1VAyMzPx7Nkzo8RWaWlpPCVYvnx5DB48\nmEc8bWxsJBT3zHBZWVkhMjISEydO5FVSrNP1vylsLVer1ahRowa/Nnt7+w/qz8PkS3JEdDod33AZ\n6uTJk//ty8uX/OcdEeGgM5Y/tuu8d++eUVBk69atRd0j5VSlUvHdRE5ODq+eYZ0/N23alCsuQmWi\nwZTFq1G25UA4hA6HW++fBM3UNsG12yI4tRoPu7q9YRPcGXb1+6LVyHmI+mkbKgXVlJzPzs4ODRo0\nQJ06dUS56/j4eKSlpfFyLC8vL553ZSWSU6ZMwYgRI3IFywpLQBkATuiYlSxZkhuozp07S4CWQgI2\nd3d3XmnAzi3El6hUKlEX2YIFC0ocJDmtWLFiriBVhuNh8ttvv4HofRTKwsJCBO4lEu8a2C6YEYoZ\n421gO9IDBw5g/Pjx3OAB7zlpmMPi5+eHU6dO8cWUMa8yR+/x48d48OABevfuLYocGDPmRCQZ++nT\np+Py5cuyZa/W1ta4dOmS6MXPyMjAwYMHsWvXLrx8+ZKX7jKj+NdffyE8PFzEIPrTTz/x8coNe1Og\nQAG8evUKS5cuRe3ateHr64tatWph/vz5HACal7AUm7u7O3r37o1+/frxuSjsO8Pm2Nq1a/mx1NRU\nnn6T67FjZmaGChUqoGfPnrnyDLHyUWGZrhD8/CFVL4aGLzU1lb9fwjTE06dPubPwd+Xs2bOyJddq\ntRpjx44V/S6Lem7YsIEfO3PmDJ8//0aKRijv3r1DeHi4aNNUqlQpEb39h8iX5IgAeod+3rx5KFOm\nDGxtbREQEID169f/25eVb/nPOyJhYWFo27atyGBqtVqsX78er1+/xty5c2UbfeVl8JgKm0X169eP\nG1EhuyYRgVQmMLEvBCv/EHh8NwElB62Cx5DN3PFw6xWHYp2m4tt+k2HiWERiCPN7PUR6hk8hwyYj\nMMrOzubRn5s3bwIAtm/fzn+D5clzI/0iInz//fdYs2YNiPROlxBjoFAo0K5dO7x7945fQ3h4ON/d\nKZVKNGvWDHfu3MGLFy+4gROqlZUVdxZiY2NFlPUeHh5GHRIvL6/cy5L/T4U7TJ1OlytAmRmVn3/+\nGcnJydxxPXTokIi3wVDZGM6YMYPvYuvWrQsAkmonS0tLxMXF8WjG6NGjMX78eJ7iKFu2rAQEzL5n\nrMkYW5CFmAGhWlhYwNXVFd26dcNff/0leuk3btwocmQ0Gg2fN6wC4dSpU0ad7Pr16/M0jpB3xdvb\nm0dNrly58oFL0Xu5ffs2vwch0ypz+ISVM6wfU926dbmzcOXKFZiYmECpVGLFihU8oqfVahEWFpav\n3iuAvrKIpXs8PT3RqlUrPl8M8Qp5iVxEhI05660DAKtXr+Zz4n8hK1as4M+nRIkSIgzVjz/+yD/H\nomhCRtGcnBz+7v/b6RkmDx8+xJ49e3D27Nm/xUr6pTki/3X5zzsiTFj3yNwIlaytrY3mt4n0NdcM\n4MOUUXhnZWWhQsWKUKg1IJUJ1LausPANhnOnWSg0cB08hm9/3/Ok51KEztiNyj2mwrx4Nais7LnR\nnzRpEu9ayvS3334TtbK2tLTkkQe1Ws15MBh+oEiRItwA2NnZ8fBseno6XyhZ6F2n04kqJ5gWL14c\nW7ZskQBsw8PDcfToUZ6/btmyJY+0FC9eHF26dEGlSpV4dMjU1BTz58/H+vXr8eTJE8mClZ2djZ07\nd6Jfv37o0KEDYmNj8f3336NQoULQarUICAjAxo0b8ddff4kiKLmpMG1gbW2NN2/e4N69e/zZG7I3\nCtkt1Wo1Spcujfbt24tYRQMDA7kz4Ofnh82bN0tSIyEhIdyZY7pixQokJibyiIuQn8NQmYNlDNQs\nB8w1MzOTxbQolUpUrVoVixcvxqpVq1CjRg04OjrC398fCxcuxKlTpyQLrU6nw4EDB/hcLFmypGje\nEekjHy9evBBx5zg6OmLAgAGiiBkrv507dy4nEhs0aBB/Nn+HmZHlvA2ZT1mljxCY+ejRI/5Oe3h4\noF69enwcO3ToIJoDuZE7GZMzZ85IWINr1qzJm6TlV+QMH3uvrK2tMXjwYPTt21fEp/Ehcu3aNcTE\nxCAmJkbUu4cxPgt7h7C1snjx4vwYm7csWge8Z0P18PD416jIP5V8dUQ+L/liHJHExERuxOfMmYMS\nJUqIWB979+6NjIwMI71IFNAW9kON3lNQskUE7BsNhluvZXDruRQuXeaj1LD18Ow+Hx4yfVBcuy9B\n6S7TYF2tLer3GA2No97IREREiMpRjeXXS5UqBZ1Oh2fPnvEcrlBjY2Nx/fp1fh+G0RwnJyf8/vvv\nuHnzJs8TlitXTrJwnDlzhlPHazQa7qhkZWVxbIUcLmDNmjV48OBBvtImfn5+2L9/v9Hwu9AhMFQW\nbbKyskJERISkJFqlUuGnn37CgQMHRPThVatWBQCkpKRwx8HDw0Py27/++qvRexRquXLl8PPPP8tG\nzZRKJcaPH88dHoVCwXPtv/zyi9HIljDyxEpYy5Qpgz179hjFk8ilPiwtLdG4cWNJ6WyBAgUkRF/C\nhTYnJwezZs0S8V6UKVMGr1+/BgDepMxYd+hVq1YBeB8RZM+JjQn7L3Pkvv32W9nnn5dkZGTgl19+\nQd++faFSqaBUKvHTTz8hNDQUTk5O/DcNyzVPnjwpencUCgXatm2b7zRQXpKdnY39+/djxYoVH92V\nVM7wpaeny0a0unbtmm+nKScnhzdbFGqvXr2Qk5PD321hZCkrK4t/jm1iNm/ezI/VqlULjRo14s92\n5syZH3XPn7N8dUQ+L/lsHREi+paIEojoJhF9L/ybnCPCCJPKlCnDj+l0Op6yefQsEQeOn4WJkyfM\ni1WFlX8IbGp2gVOrCfAYInYw3PuvhmeHybBvNBiOTUfCsdkoOHecCccG/WFTrS0KVG0FS7/6MHUt\nAf8KFXH8+HEQicsZIyIieAkgM+KhoaGoXLmyqHpBSMbDIh+NGzfmu2AGmjxx4gSPiLDfksMDaDQa\nrFu3DjExMZgwYYKEbpntgN3c3DBs2DAOZjSmI0eO5H1UjKmJiYmkzXeLFi0kgEiW7nFxccHhw4eR\nlJTEW7YbksgR6XeKwjH19fVFbGysqLV68eLFMXr0aBFmxtfXVzLRc3JyRDwWho5Gt27dcOTIERHA\nV9h9Wc4x0Wg0ot/466+/+PUPHDgQAwcOFKVAFAoF/7cwt82iWOw3OnbsKEn9GQKKS5cujVGjRvGd\nrKWlJRITExEfH4+xY8ciLCwM8+fPh06nw7Bhw2TvIygoCFlZWaI0gZBAzdzcHGvWrOHXyRhQ82oV\n0LBhQ1FTunv37mHEiBGoXbs2WrdujR07dkgc5UePHvHKo7y0bNmyEqrynJwcHD16FFu2bPloDphP\nKcYMn06nw++//45Ro0Zh7NixvGQ5v8II2ExNTdGpUyeEhYXxiNDs2bO5gybETbFKIwcHB9FziImJ\nETnqrGfQx0SSPnf56oh8XvJZOiJEpCKiW0TkSUSmRHSJiHzZ34UX3btPH3Tv3h0acyuo7dwwcuYy\n7LnyBCM3X8aAtRfg2iEa7v1WoogMc2ihwZvg0nUB7Gr3gKXft/rW86ZmcHZ25ka/Tp06mDZtGu8d\nolKpJJGLNm3aSGjg80vuFRQUhAULFnD+BpVKhZs3b/LUSOHChbFlyxYcP36c91OpUKEC0tPTkZSU\nhBEjRqBo0aJwcnJCy5YtMXDgQInR+uabb3D06FGeKzdUtmN3cXGBj48PAgMD+S7L0AB37txZUspq\nTB0dHfH8+XM+2Rj75ezZswHoc/D79u2TpB78/Pwk+JX84GjYAvz9999LJnpOTg53AtjOWkhoplar\nERkZibdv3/Ixef36NT+nnCPi5+cn+R32G6dPn+a/y0pHnZyceGRLyMBpSEW+fft2oxEZNhbMEOt0\nOk7KZZhmIdKnitRqNZRKJdavX89BnMz52bx5M29xoFar8ebNG14Gr9Vqeblseno6P//06dNx9OhR\nDB48mF+ng4MDKlSowJ3sPn36ANBHK+TSoT179hQZQUZR7enpifHjx8ty0VhbW3OHadGiRbksa5+f\nfCrDx0gH161bx4+xlEqxYsW4o29ra4tx48YhKiqKz9ERI0ZIzvfy5UusXbsWK1euzDeW5r8oXx2R\nz0vyckQU0DsG/6goFIoAIhoPoP7//TuSiAjAVCKi169f84vym3qMkJ1FpFCQQqXm5zBVEtmZq+jV\ni2eUmHCetLo0epv4hHJSkyn7TSJlv00kXeorMjc3p3fv3sleR6FChejHH3+kZ8+eUXh4OFlaWpKP\njw9duHDhQ+6F1Go1ZWVlkUKhIFdXV/Lw8KAKFSrQihUr6M2bN6LPFi5cmEqUKEH169enpUuX0h9/\n/CE6n5WVFS1evJh8fHyIiCghIYHWrl1LN27cIKVSSQkJCaRQKKh27drk5OREe/bsoeTkZDIxMaGs\nrCyysLCgAgUK0JMnT4iIqEaNGpScnEyXL1+m7t270+nTp+nPP/8kU1NT2XFRKpWk0+lk79XMzIzS\n0tJEx3x9fennn38mhUJBo0ePpl9//ZWGDBlCiYmJtH79esrIyBB93s7Ojt69e0fp6emS83l4eJCP\njw9pNBry9PSkxYsXU1ZWluj7rq6u9PPPP5Otra3o+Js3b6h27dpkZmZGBw4coF69etGVK1ck99Cg\nQQM6cOAAZWVl0Y4dO2jLli0UFxcn+oxCoSAAFBkZSc2bNxf9bdasWbRmzRpydXWlLl26EBFRXFwc\nPX78mNq1a0d3796lEydOUNOmTWnYsGGkVCpp0qRJtHv3btkxHTBgAM2dO5f/JpOjR4+SVqslIqIV\nK1bQvHnziIjIxMSEQkNDydLSkrZu3UqvX78mIqLAwECaM2cObdq0iaZNm0ampqaUmZlJ/v7+lJyc\nTHfu3KE6derQ1KlTiYho8ODBdPToUTI1NSV/f3+6desWJSYmko2NDW3YsIFsbGxo3LhxtHv3bmrT\npg0NHTqUiIiuX79OHTt2JI1GQ3v27KEuXbrQ3bt3KTAwkFq0aEF37tyh2NhYysjIoLlz51JAQAA9\nfvyYmjRpQlqtlrZt20Z2dnZ048YNat++PRER+fn5UXh4OFWuXJn2799P48ePp6pVq/J7/v9Zqlat\nSjk5OaL5kJGRQUFBQaRUKunYsWM0fPhwOnbsmOh7FStWpFmzZvHvfJWv8m9KsWLF+P9bW1srDP+u\nNjzwD4kbET0Q/PshEVWR+6B3WgJBqSb3Qu7kV8SOrDVK0qoV5GalJktTJSUmgtotX0mPX72S/SFD\nY+vm5kb29vZka2tL6enpNHHiRNJoNESkN4QXLlwga2trat++PZ09e5bOnj1LRHrjZGNjQ+XLl6dT\np07x87q6unKj98svv5C1tTXNnTuXiIiaNGlCu3fvphMnTtC5c+coJyeH7t69S3fv3qW9e/dSWFgY\n1a5dmw4cOEAZGRnk7+9P7du3Jzc3NyIiOnLkCI0YMYJycnLEY+LtTVOmTCGFQkHNmzenli1bUlZW\nFlWoUIFmzpxJZmZmtGfPHho3bhxdvHiRypYtS0REsbGx/BzZ2dmiczLDpdPpyNbWlpKTkyVjyZyG\nYsWKkYeHBx08eJD+/PNPmjBhAv3555/0/PlzIiJasGABpaenExGRi4sLd4qIiJKSkoiISK1W8/MV\nKFCAcnJy6P79+xQdHU3e3t5ERFSpUiWKi4ujs2fPkomJCTk6OpJOp6MhQ4ZQzZo1qWXLlvTmzRta\ns2YNnTlzhpRKJaWlpdGqVavoypUrZG9vT61bt6ZFixZR4cKF6cmTJ7Rnzx6qVq0aHT9+nEaOHEk9\ne/aky5cv07lz5/g1AqA2bdpQs2bNJGPQvXt3io+Pp2vXrlFUVBQ/XrJkSerevTvdvn2bzpw5Q1u3\nbqWDBw+SUqmk169fk0KhIFtbW37/THbs2EFEeofxt99+43ONPZ+cnByRkRk+fDg1bdqUiIhq165N\nnTp1IqL387xJkyZ09uxZOnjwIBERd6oLFy5MQ4YMoTt37tCsWbPo5MmTRESUmZlJp06dIiKiIkWK\nUFRUFNnY2BAR0Z07d4iIqG7duvz3S5QoQR4eHnT//n2KjY2lu3fvEhHR1atXqUiRItS9e3fKzs6m\nxYsX0969eykgIIDPC09PT7KzsyMi8fxTq9UUFBRERMQNp+H8/P9VXF1d6cGDB3TixAmqVasWERF/\ndq6urmRiYkIxMTF0+vRp+v333wkABQQEUFBQEKlUqn/z0r/KV8m/yIVJPrUSUSsiWir4d0cimsf+\nnd+md0zkaLTlVKlU4urVq0ZTDwwHwUp6GaaD/i/cHx8fL8JKCEPS69ev5/lX4XWnp6fzUGmbNm2w\na9cujBkzhqcmjNXJP3v2jOMnunbtilOnTomqMfbt28c/yzAqS5Ys4cd0Oh1PMbHwLZG+4mTixImi\n+2Ygx/yWPa9bt47TL3+oCstV2fjVrFmTg/p++eUXyVhcu3ZN0v2YSI+jkMMzsPuoWLEifyZLly7l\nnCFRUVGy/DMODg4YP368qHmcnKSlpSE2NhZNmjRBkyZNEBsby1Mp9+/fR0REhIgvpGTJkti+fTsS\nExNlK2QKFCiAMWPGiI55eXkhIiKCl1Cze2Kl3GfPnsWZM2dElUFTpkzBgwcPsG7dOj5Pg4ODsXjx\nYqSkpIgqj9RqtQgwO3HiRAmug1U5sb4t7P5Ysy2551uxYkVeUhoSEgJA396dMWeyUuP09HQ+b6tW\nrYrMzEzcvn2bp0inTZuW6zP43ORTpQIYZ41Wq0X37t3Ro0cP/mz/jXbu/xX5mpr5vORzxYgEENGv\ngn9HElEk+/eHOiJCzIRhKZ5Qo6Oj8f3334NIj834+eefsWrVKhHIkYiwevVqDgBUKBQcv8D4KtgC\nfuTIEV6iV6pUKQ6cFXa+ZI3NSpcuLVroWfM01sjq+fPnWLZsGWbNmiVhj6xRowZu3rwp4svo1q0b\nAODPP//kx4QtwoW9Pwwp3w31m2++kVRq5Kbdu3cXVWio1Wps374dd+7c4TgRpuXKlcOaNWs46JI5\nYL6+vhxvEBsbyysyhCykTBjgNjg4GIcPH8bmzZtFVUo1atTAb7/9hg0bNoiAwkxZhUHdunVBpOcU\nefLkCYYPHw4/Pz/4+/tjwoQJSEpKytd8kxOdToeRI0dK8DtdunQRgQFfvnzJnQtjjLeGRt7BwQHl\ny5cH0fvyy7Nnz2L+/PkS506orVu3Fs25gQMHgkhfNfHixQtkZmbyqh4hSZ7h3FWpVOjRowcmTZrE\nG+ex+alSqaBQKLBkyRL+N9bfZdKkSfxczAm0trZGeHi4pOuwsLTZ09NT1Jn3vyCfyvBlZ2fzajih\nhoeH/+skZJ+zfHVEPi/5XB0RNRHdJqKi9B6sWor93dARSU5OxtSpU/HNN9+gbNmyaNmyJXbs2MEX\nTkOyKGtra0lzNEapzAzo0aNH+SBdvXrVqNFlC6i3tzffRYeHh3Mje+TIEdEiykivmDBaem9vb+za\ntYsvHnPmzAGRPtoxf/58o83fmLHy8PAQdWt1c3NDnz59RA6Eg4MD4uLicPDgQW68K1Z8X/VjSG/P\ntFixYpxplSkbp9zKYdk1BwYG8vt9/Pgx//umTZv4cWNtwMuXL893wWXKlJHsyl+/fg2FQgG1Wo3R\no0fD29sb5ubmIudRSAG9f/9+flylUmHEiBH4448/ODGWRqPBixcv8nht9HLz5k0cOHAgX222GXcD\nI3xr0aIFd7qEDiKgrzKRIzgjIlHkx8PDAytXrkRqaipvREekjzTUr1+fj//YsWOxfft2BAcHw8HB\nAWXLlsWcOXMk9OCMXfP333/nx7Kzs3mUxLAaRafTcUdbqCzSVrp0aVGFkzBiZ29vL+qB8erVKw5Y\nZWppaYkBAwagVKlSfD61b98eu3btwq+//vqf6KHB5FMbvosXL2Ly5MmYPHky78fyVYzLV0fk85LP\n0hGB3hlpSEQ3SF89M0r4N+FFP3361GgTMx8fH/z000+8PwrTggULSnbGrq6uAMCjGcJFLi0tTbIL\ntbe3F6V8Fi9ezI3f1q1bJVU0RPr0DVskdDqdaJFmWr16ddy9e5dX7QwaNIj/LTg4WHQdSqUSSqWS\n/9aUKVNkDVjt2rUlizz9n0N27tw5pKen812zg4MDTp48iUmTJsmOqVzI3dTUVMKgKkxLTZgwQTTp\n2N+8vb2xYsUKTJ06lacQwsPDUblyZcnvuLu7i4iamDBKbGNOFBGJGtgxp9IYRbmhUyAnjx8/5tET\nofHPjeSKzRVhszHGolmsWDHJ5+/du4du3bpxR1KlUnE+j2vXrvHnLCzLjI6OloxDeHi4pKGbMWHP\nUMgmnJKSIlvpI5TLly9j1KhRGDhwIDZs2IADBw6ASB8FzMjIQEREhIiHxsbGRkI5z4RFclatWsV5\nTgB9Z+ATJ06ImHXVajV69Oghafj2OcpXw/d5ydfn8XnJZ+uI5KbCi+7WrRs3ykT6MHRufTCMqUKh\nEJVCDhs2DDqdDjqdjjdj8/f3x5IlS0RGVqvV8vx5ZGQkiPTcFqtXr0arVq34Auzu7i7CFjDeE1NT\nU0nqh4W1ixQpgpCQEBDpacE3bdoEIuI8F4YlrWwMChcujJiYGEybNg3Hjh2DTqdDZmYm7/1RuXJl\nREREiHbybNdpTE1MTDBkyBAkJSWJQsGVKlXC2rVrceLECfTo0UPieBHpOU/mz5+P9PR0xMbGGnVo\n2rZtyyNC9+7dw+TJkzFgwAAsW7YMKSkpuHXrFiZMmIBevXph4cKFeP36NXQ6HcdbaLVabNu2DQ8f\nPhR1DK5WrRouXryI1NRUXhbavn17rFmzBsHBwfDy8kKjRo1EuBpjkpWVxSM0FhYWCAoK4s84ICDA\nKAMl+4zQuGZmZvJrNMbVsGjRIhDpO+oKhfXpGTZsmOj4kydPEBsbi+HDh2PDhg3Q6XRITU3NFxcE\nwwp5e3vj119/xcWLF3lpMSOOy4+kpaXxKMqECRPw6tUr7N69m2Oh4uLi8n0uJo8ePeIl8S4uLqhe\nvTqPKLEml5+zfDV8n5d8fR6fl/znHRG5nbBhGqN27dqifiYajQbW1taoUaMGb4Dm4OCAU6dOYd++\nfdxIFi1aVBRt2bhxIwB9y/SdO3di69atIsbCpKQkWYPu6OiIGzduiAaeMYwuWrQIqamp6Ny5s+he\nqlevjlu3bvEdYHx8PN9p+vj4cOPbr18/UXqkcePGuH//fp4PPjs7W5bHwcvLC0qlEvb29hg4cCA/\nd3R0NAA9huHQoUPcqNjb22PWrFnYunUrxxjY2tpi6NChEkdJ6HyMGzcOMTExaNq0KTp06IDt27fn\nSiO9bNkyCbdIwYIFcfHiRc6vwo4Zc0TZ9Zibm390LxTWadfDw4OnfB48eMDH4/Dhw7LfMySoA96z\nvbq5uRn9vZ9//hlE0pQe60w8duxY2e+dOXMGQ4YM4ekQlUoFW1tbdO3alQNaDeXNmzeSFBxzuBgv\nSn6FkZ8ZapUqVT4qgjF27FgQ6Xl9WITr9OnTHOT6MR1Y/0n5avg+jeh0Orx48QLPnz//IL127Rqu\nXbv2wd/7qn9fX7x4IVnr//OOiHCRCwkJ4X0vhBodHY2UlBSeX1cqlQgJCRE5J0y/++47rF69WlTV\n4OTkhGXLluXrxXj16hUmTZqEChUqoEyZMoiIiMDBgwcRHx8vShEwMGVkZKSIMpxFNRiZEHMQfvjh\nBzx48EDEpqpWqzF+/HhuYIUhdWOybt06Dmy0sbFB//79kZyczBkavb29cfLkSbx48ULUcj4mJkbU\nS8SYKpVKzJw5k99HvXr1ULZsWe6EaLVa/Pjjjx/UuyIhIYE7Id999x1mzZrFK5t8fHzQp08fEL0n\n6RKOD/tNdszT01PEZvuhwqpXIiMjRccZuHj69OnYvXs3QkJC4Ovri5CQEOzZs4f3F7K0tMSgQYMw\ndOhQHlkzTF0JxyYxMZGP+ejRo3Hp0iXMnj2bP/PLly/LXifr9CunNjY2Rr/3+vVrjB8/Hr6+viha\ntCjCw8NlU2L5kW3btiEwMBCmpqZwcXHBiBEjJO3n8yusB5SwOywABAYGgkjfBflzlq/lcc8zAAAg\nAElEQVSOyKeRFy9eSFh28yMpKSmiooGv8s9JWlqaBIf3RTkiGo0GLVq0kFQbsNx6REQEN5bCv/v7\n+6Nfv348Fz5lyhRkZWXhzJkzOHny5EfnoPfv38+ZD4kIzs7OiI2NBYA8qdUZYJD1AREaernP9+3b\nF3/88UeuAD7WJdZQ/f398eLFi3yVOSsUClFjQY1Gg0KFCsHOzg4hISH4/fffeWSka9eu/LefPHnC\nUzV5lb8aCkt5derUCa9fv8bhw4dx5MgR7khOnToVRPqo1vLly0URERMTEzx69IhjXqpVq/YRT/K9\nsNbwTZs2FR1n4GdDllSmjRo1EtHQM23atCkyMjKQk5OD+fPnw8fHBwqFAoULF8bUqVORlZXFq18M\nlVVUGcqjR49E0SMfHx/MmTNHBFw2jLB87sL6KI0fP54fS0tL45Goj+0B80/JV0fk04iQuflD5Ksj\n8u+K4XP7ohwRYxoSEoKMjAy+i54zZw4KFiwIInEr7F27doFIvmnah8q5c+d4iqhgwYKictKxY8eK\n6NbVajVq1qwpSs2UKlUKAEQN3gx3+1WqVEGzZs3QunVrEW6lQYMGkgqH1NRUnmP/4YcfkJ6ejvPn\nz/PrWrp0KZKSkjB48GBRBIGVXxr+vkaj4Z09O3XqxBfZ69evcypwQ84PZqx37979QWPJOt6GhoaK\nSlEZX8KqVatQp04d2XEaPXo0AH2FC5EeqwPosR67du3CkiVLeI+Z/MijR494NKJ3797YsmULx8xo\ntVoolUooFApERUUhPj5elDZiam5ujq5du4p+V9jgT6jfffcd75obGhqK4sWLo06dOhz/ISeMw4U9\nx/379wMAhg8fLjp3y5YtPzpF9U8Lq3YyNTXFmDFjsHbtWtSoUQNE8tVUn5t8dUQ+jXx1RP6b8v+l\nI0L0vuzR2toae/fu5U6CsG29EDz4dxc2xukRHh7OG4ux8HxuyoCQbMcrdDzKly+Pjh078l3gypUr\nRQasaNGiPIxftGhRURj88OHD/PxC+fHHH/lO/vbt29izZ0+uxGX29vbo3Lkzrly5wsuFK1asiLVr\n10qI4EqUKMHTUU+ePOFOhCFeJi9hfXeY+vv7i3hK1q5di3fv3iEyMlJEYDZo0CD+HNnY16xZE+fO\nneOcFkzLly+Pe/fu5et6YmNjJWOkUql4v6DWrVsDAHbs2CFx3tj/Ozg48Egbc5LUajXWrFmD9PR0\n7Nixg4/Xh+Az3r17xwHXTIOCgnD16lVRA0GmFhYWOHPmzAc9j39DdDodj2gK1c7Ozijp3+ckXx2R\nTyNfHZH/pnxxjoixVAWRtDLDEOxIRJg/fz4fDEbs5e3t/bcHmmFMrl+/zo8lJSXx3xUaC3ZdGzZs\n4NUQxq67fPny3Ki2adOGNzRju95nz57xihHhvf32228g0kdahE4WS9cYGimVSoVff/0Vt2/fFjHI\nBgcH8++y6wgKCuJhfxsbG1EKws3NDf369ePlpvXq1QOgbwa3du1afPvtt/D390fXrl2N4hYeP37M\nn6WLiwvatWsnairYvn17/llh9ZKZmRk6derEGUCJ9GR0zCktVqwYwsLC+LWVK1cu3w5ofHw8evfu\njQYNGqB///64evUq54Tp378/AHCgMXNAoqKiOGEec6AA8NTLd999J/oN5mQaAlKzs7ORmJgoW5Yr\n1yyOSFqu7OXlhZYtW/Ln918QnU6HQ4cOITw8HKGhoZg4ceJ/hkvkqyPyaeRzcESUSiX8/Py43rlz\nB2fPnuXrwE8//YS+ffsCALZs2YI//vjjf/K7/2X54hwRY05I/fr1ce3aNclxrVaLKlWq8DSIQqFA\n69atRWyl5cuXh4WFBczMzNCsWTOjBjI3YUZo7969/NiSJUv4ddy/f587UcyoNmnSRBYM6uLigkuX\nLvFdPMMhsLC/0DkA3kc5hIZNWFI5btw4vHz5EkeOHBGBXwsUKCBKy7C0RnZ2Nr9WW1tbbNiwAVOm\nTOFcLIynJSgoiEeYxo8fL7mPSpUq4enTp9DpdLxaSaimpqYiXgwm9+7dA5EUH8NAtz4+PqLPZ2Zm\n8uiE0LGaMmUKFi9ezK+FRWuSk5P5OBiresmPHD16lI/RpUuXuAPJom/Hjx/n3X3ZcwCABQsWcMcy\nJycHly9fRnx8PAfAMkckKysLEyZM4I6UpaUl+vfvz8eczXczMzO0a9fO6LtBpCeTe/PmDX/e+SVx\n+yofJ18dkU8jn4MjYmFhkevfhY5IWFiYBHCdlxgSD34J8sU6IoYEYlevXuU7Y6E+ePAAgL4nhhzd\nt5wjYGlp+cFshQwcWahQIaxcuRLbtm3j9PKMPM0wZ5+bFilShH+eOUwsZeHj4yPayTOWUEbzziQu\nLs7o+YODg/H27VsRUZdKpcKCBQtEKSJDrVq1KseKCFuRA+Cpmm7duuHAgQOcy2Lfvn0g0mMl5s2b\nh2PHjvEqD1dXV8lOPzk5mbepX7lyJZYtW4azZ89yLpaAgADZZ3DlyhXMmTMHixYtwqNHjwC8jzKw\ncmQmDOexcOHCD3rOQtHpdCLiOGFErnLlykhPT8e5c+f4MVaJdevWLV4xJWROZd9nqZPu3bvzvwl7\nyNSsWRM5OTn8+bZq1Qpnz55FdHQ0/Pz8RA5c4cKFeRl6RkYGP8+TJ08++H4zMjJEqc2vYly+OiKf\nRuQckezsbCQlJSExMRHv3r2T/d6ndkQOHz6MRo0aAXjviBw/fhy2trYoUqQI/Pz8cPPmTdy8eRP1\n69eHv78/goKCOJA/LCwMgwYNQnBwMAYPHvw/uc7PSb5YR8RQjeEcBg4cyI02Yy1t1KgR5s6dyxur\n1atXD3fu3MHDhw/RrFkzEOn5C3r06AFnZ2c4OjqiQ4cOorSLoaSkpCAgIED2GkxNTXlVzMiRI41e\na4UKFYw6K35+foiLi+NphfDwcBw/fhwLFizgDpYcQdfOnTtRvXp1mJmZwd3dnfNM7Ny5EwAwffp0\no2Oq1WoxdOhQUVpEONZRUVH8dzIyMniUwXAB7tq1K4jEFRA5OTm8B8mhQ4ck183SK+XKlcOqVasw\ne/Zsnk5asGCB0edgKOz+GjVqxOdBVlYWTydt37493+eSk5SUFPTs2VMUWRI6ucyJ1Gg0IgyPsE+Q\noW7ZsgV//fUXnzt79+6FTqfD+fPnueOyd+9eXmFVuXJlnDlzho977969+blq1aqFp0+f4t27dxwI\n/aFgzzt37qBVq1Y8qujn54fNmzf/rXH70uWrI/JpxNCgNZ//OxrO2IcGP/zKNXT2QbRefBytF5/g\n2nLhUbRceFR0TE7zI8LUDKumk3NEAGlEpFatWhwzd+rUKdSsWZN/rlGjRl9sv6D/bxyR3JTtehs1\nagSi91gKhnMQgimfPXtm9DzW1ta5Vh2kpaVhwYIFqFOnDr755htMnDhRFDL38PDg4fvSpUvjp59+\nApG+xJRVwURGRqJFixZGr8FYp9Pq1atj7969eYb1GHMrG5Pk5GRRdEl47sWLF/NrcXR0RMOGDUUM\nphqNBtHR0di1axcf2+LFi0uMXJs2bUAkpjsHgODgYKPOwL1792QbFjZu3DjfFOaAHm/CnISQkBDM\nmDGDO4zu7u4fdK7cxLDs2tBxMzTcrJzb1tYWKpUKnp6ePLrCGH2J3gNhmbBeL0OHDkVKSgrnUmna\ntCkWL16MqKgo7jCw+S1s1KhQKLgTmh959uyZiGNHSB7IMC9fRSpfHZFPI0KDlpqaioYz9M5HyMwD\nCJ19kDslobMPfTJHJL8REUDsiLx9+xZarVaELylRogT/3M8///y3xuZzli/OETE0wr/88kuejohW\nq+UYBVNTUw54Yws1a0XOBox9LzAwEJcuXUJCQgI3tI0bN/6gB5CZmYnhw4fzkLharUabNm3w/Plz\nbNiwAUT6NEluaRRnZ2dZzg+tVivi+GDGdfXq1ejXrx8CAgLQuHFjUeknS2/Y2tpi8eLF2L9/Py+z\nZWPr6+uL1atXc9CoSqUSlQsbUysrK94t99SpUwgNDYW9vT0f51KlSvEJuX//fs6SaQyAmJycjBkz\nZiAkJAQtW7bE1P/X3pnHVVWtjf+7DogDTqkpSjkgesVEEEXRtNS84hR6IXK4mZrXvKn1ateuU4Ne\nLelWkml0zSnxqpVTds2Bur2OaT/wF+YUSopzWSoiCAjyvH+cs3fnMBgIeEDW9/PZH9hrr7PXOnud\nvdezn/UMc+fKZ599JidPnizSGKxfvz7PElzdunWLHD30dhguzC+99JJERESIj4+PKSQEBATkqW8c\nMwLZiVgFWWNZxbD76du3r8PnjHxF06dPFxGRTz/9NF+j7BkzZsgPP/wgISEh5jkDAwOL7EptCD6d\nOnWSM2fOSEZGhhn1tGnTpvfsG1xx0YJI6WA/oRlGoqdOnTKfb2lpaRIbGytxcXEOL2XOWJoRcRRE\nrl27Jh4eHvme805sScoT95wgkvuBayylGJsRayI/rYFSyuGt3EhRHxwcLKdPn5YLFy44aCMOHjwo\nR44ckblz55reDy4uLnf0Fn3jxg1JSEiQy5cvy/Llyx00C4C8++67smXLFgkKCnJY469du7apOalU\nqZIZB8Q+qqi7u7uEhoYWmAwQrMHGcnJyJDs7O881A6vh6jfffOOwfLBv3z6Ha9mxY0d5+umnzWtc\ns2ZNCQsLkx49eshLL71kxjKJiYnJE+7d2CpXrmxmawXkhRde+N1rd/jw4TyCWGhoqEMel9/j/Pnz\nEhERIRMmTJCFCxeWeFp54/saGaJFxDRUtVgsebRExhKZfdbnhIQE8zd88eJFU/sQEREhJ0+elGXL\nlpnaHftJ7rvvvpOBAweKr6+vhIWFydatWx3aSk9Pv2PbDsPuZ/v27WZZdna2GZfndsuVFRktiJQO\n9hPasWPHJDY2Ns9z4PDhwxIbG+sgeDhLEJkwYYJDrqXOnTub8ZZycnJMW0QtiJQzQSR3bgwjFLR9\ncLBGjRqZQob9Zm9bcOTIEYmKirrtm74R3TH3VhyDvYKy3ObejGy8ISEhphp/3rx5pubE3h34wIED\nImK10zCEBB8fH/nqq68kMjLStCExPHqysrJkxYoVEhwcLEFBQTJp0qR8tQwXLlww2xg4cKA5mRrL\nO/CbMbBBTk6O6UH0l7/8RZKSkmT37t15lllq1qwp06dP/92lpOTkZNP2pH79+tKrVy9zMi6qdqo0\nMWw37GN0GIaqdevWzVN/ypQpAlaj69WrV8v69etN4XTUqFEiIvL222/n+9sYO3ZsnvOV1sRnhFS3\nX1rKyMgwtVwF5bGp6GhBpHSwn9ASExMlNjbWNEwXsWqg4+LiJDY21iHFhrMEkT179oiPj4/4+/tL\nYmKinDx5UoKDg6Vt27bi4+NjpnvQgkg5E0RyP5SXLl2ap8zb29tBMDESzr3++uty/vx50zbB2OrV\nqydVqlSRypUry6BBg0zhBqxLOU899ZRDrIzXXntNjhw5Ihs2bJDY2NhCG/5dunTJfMtdtGiRpKen\ny9dff23GfFBKiYeHh8yYMUN27dolYLXNMBLrxcbGmjE+jJgQ9m+le/fuddAYGPzjH/8QQEaMGFGo\nftpjBFOrVauWTJw4MU9un9yGpsePHzcnX3vNkb1h5aFDhyQtLa1Q7RsxNzp06GB+JjEx0Qz+VVZ8\n9A1DaC8vL1mxYoVER0ebWZbz0/okJyeb7si5f7v2Hi2bNm2Snj17SqNGjaRTp06ydOnSfDPrltbE\nZ3hqeXt7y44dOyQxMdGMfFseIpw6Cy2IlA72E1pycrJ5nZOSkuTixYvy/fffS2xsbJ4gijqgmXO5\n5wWR39tGjhxpGgG+//775sO/Zs2aEhwcbHqEtGrVypw4jx075rA8YvxvCDe5s/22a9dOEhISChyE\ntLQ0SUhIMDOUPvbYYw7HDUHBPr15Tk6OBAQECPwWnMpYlnF1dTVTuCulzEHeunWr2acJEyaY54qO\njhbImy+lMOSnWXJxcTGvQe4b3oht0bBhQ4cJ0winX5DrbUEYtj32wdpExIytYuQVcjZXr17NN5Ot\nn5+fXLlyJd/PpKamynvvvSePPfaYdO/eXSIiIu54yai0Jr6UlJR87ZPc3Nzy9XbSWNGCSOmQe0I7\nd+6cea2N7dChQw7aEBEtiDibe14QUUqJt7e39OzZ0yGapIeHh/zzn/80YzFUrlzZjKTq6elpXpgr\nV66YE/zGjRtFxCoEGMalhn1Ejx49zABWYDXM7Nevn6mSb9KkSR4f9szMTHnppZfynKtbt24O9WbN\nmiWAjBs3zqE8MTHRwZ7COEenTp0chKHAwEBZuHChQ1CvDz74QESsE6Sxzv/WW2/9/i8mF/v37zfb\n9fPzkwEDBpheFLkDq4lY7QeMQGyvvvqqpKeny6lTp6RDhw6mNklE5OjRozJ16lR55pln5L333itw\nAjaWMMaMGePQhuH6ax9AztmkpaVJVFSU9OvXT/r27Svvv//+XXv4lebEd/XqVZk+fbo0b95c6tev\nL2FhYRIXF1cqbd0raEGkdMgvjkhaWpqcPXtWkpKS5Ndff81XY6gFEedyzwki8+fPl6SkJFmwYIFY\nLBaxWCxmzpCbN29KZGRknoicFotFVqxYIREREfmqyg1D1GbNmknNmjUdPj9jxgwzR4ixZm+xWMx1\nyevXr5tLJ7ndr4ygWYagYn/e+fPnS2pqqsTExJieL/l5NGRkZMjHH38s/fv3z6OJ6d+/vxlXJL/N\nx8fHXMJo2LChzJs3T7p37y4BAQEyfvx4B2+h2zFv3rw8xr+NGzcuMFfLmjVrzHr2S2SNGzeWX375\nRebPn5/nfA0aNJCDBw/mOdehQ4dMQej555+XVatWmZFdS9L9tryjJ76yhR6P0qEsRFbVFJ17ThCx\nx/BwyR0dMz4+Xp577jkJDg6WcePGmROcYU/y6KOPOqxtG8aVBW0eHh4SGhpqekbkdsc0lkkmTpxo\nlhmJzeyDmZ06dSpPcDBj69OnT76SvD3Xrl2TNWvWyJIlS8yloOTkZFmwYIGMGjVK/v73v0t8fLxM\nmTLFIWttt27dTDsZ+6169eqyb9++27ZpcOLECZk1a5ZMnDhRZs+eLXv37r1t/Y0bN5rLYG5ubjJs\n2DA5c+aMfP/992b7o0ePloULF5qRWlu3bp2vzUF+RpvVq1eXnTt35qkbHx8vERERsnjx4nKTl6Qk\n0BNf2UKPR+mgBZHyyT0tiBheLfPnzy/Uxbh69ao5Qffq1UseffRRh+ytYI3kaT+J57f5+/s7CA2G\n4egbb7xhln300UcCVvdie+bOnStgNZB1dXWVxo0by8yZM02tS0mRkpIicXFxkpSUZLr/1qtXT6Kj\no2XXrl1m5FI/P78iGxwW5SF748YNB88Yw6jT3vMjPT1dGjVqJIAZhyQ3cXFxMn78eAkNDZVXX301\nj7fOL7/8ksd92WKx5Antfq+iJ76yhR6P0kELIuWTogoirpRx9uzZw8MPP8z27dtZu3YtAL169SrU\nZ2vXrk10dDRPPvkkX331Vb51vL29iY+Pp379+ly6dMnh2MMPP0xCQgLx8fEMHDiQ8PBwduzYwbp1\n63B1deXPf/6zWdfd3R2An376yeEcxv7IkSN56623Cvel74AaNWrQvn17AD755BMA5s6dy/DhwwEI\nDAzE09OTgwcPcvz4cf7whz+USj+qVq3qsH/x4kUAgoKCzLIqVarg7+/PhQsXzOO5ad++vfl9cpOd\nnY2/vz/nz58HwM3NjZs3b5KTk8OUKVNo1aoVISEhJfF1NBqNRlPKWJzdgd+jW7duVKlShb59+5KR\nkcHIkSNp3bp1kT7v4uICQPPmzfHz83M4/t///heAAQMGmGVKKQD27dtHdHQ01apVY/PmzYwYMYLl\ny5djsVhYtGgRjRs3Nj8THBxMjRo12LdvH5MmTSIuLo758+fzwQcfAPDkk0/e2QW4A9LS0gBo1KiR\nWValShXq1asHQGpq6l3rS5s2bQBYtWoV2dnZACQlJbFjxw6H40Vh48aNphCyZMkSMjIyiImJwWKx\n/pzffPPNEui5RqMpb9y4cYPt27ezdetWrl69WiLnVEqZL3RgfRG6//77HeaMe5mkpCRWr15duo3k\npyZx9paf14ybm5u8+uqrRU6ZbOTw6NOnj4j8FnTKMJ40DErtbTl69+4tSilRSklmZqacPXtWXnvt\nNRk8eLBMnjxZjh49mm9b0dHR+UZ4LUw00ZLEyErcvXt3SU5OlpycHNOl97777iswY2VBFEftfPHi\nRTOInLe3t4SFhZneTgMGDLijcxpJ9SpXruywzGRkFr7vvvvu6LzlCb0UULbQ41E6FGVpZvny5Wbg\nPbBGLJ49e3axY9+4u7uLv7+/+dzcsmWL+Pn5mQHN7iZFnf9KAvvgbYWlqEszZV4jEhERQZ06dbh5\n8yZubm64uhZtNenatWsAeHl5AVaVf0hIiNVABsjJyQEgOTkZsC6xuLq6IiJ06dKFWbNmMXHiRK5d\nu8bLL7/MW2+9hY+PT75tDR8+nL179zJ48GDatGlD7969+fTTT3n33Xfv6LvfKRMmTKBevXrs2LGD\nRo0a0aRJE55++mkApk2blmf5pDTx8PBgy5YtPPjggyQmJrJ+/XpSU1Pp27cvK1euvKNz1qxZE4DM\nzEzi4+PN8qSkJABT86PRaCoGMTExjBo1iqtXr9KuXTs6d+5Meno6r7zyCosWLSr2+fv27csXX3wB\nwJo1axg6dKh5LC0tjWeeeYbAwEDatWvHpk2bAOvzqFu3bgQEBBAQEMA333wDWJerH3nkEfz9/WnT\npg27d+8GoHr16uY5161bx8iRIwHrsv6LL75Ijx49mDJlSoHtffTRRwwaNIjHH3+cZs2asXDhQubN\nm0e7du0ICgriypUrAPz444/06dOH9u3b061bN3744QeznRdeeIEuXbrg5eXFunXrAJg6dSq7d+/G\n39+fyMhIjhw5QseOHfH396dt27acOHGi2NfX6dqP/Lbcxqpbtmwx36iLihGxtG7dupKYmCgi1hwf\nRhj0grZKlSrlSZymlJLFixcXuQ/O4PDhww6eM/fff7+88847d/R2UBJve1lZWbJ9+3aZM2eO9OnT\nRzw8PMTLy0umTp1a5KBeRk4csMZ3efbZZ6V9+/ZmmX1o/3sV/QZettDjUToUViNiaENnzJghIlZj\n1X/9618C1ujHxdGKuLu7y8GDByUsLEzS09PFz8/PQUswbdo0WblypYhYHSRatGghqampkpaWJunp\n6SJijUDdvn17EbF6Bc6ZM0dErDGSjHxf9qHk165da0bGHjFihPTv399MOFlQe8uXL5fmzZtLSkqK\nXLp0SWrWrGnGl5o4caJERkaKiEjPnj3NwJT79++XHj16mO088cQTcuvWLTly5Ig0b95cRPJqRCZM\nmGAGlszMzMxXw35XNSJKqZlKqfNKqXjb1s/u2DSlVKJSKkEpFWxX3sdWlqiUmlqYdgICAgDyGJMW\nhq5du9K9e3cuX75Mq1ataNeuHb6+vty4cYOAgACOHj3K/v37+dOf/oSrqysWi4WePXtStWpVMjMz\nCQ0NZdWqVYwZMwYR4bnnnuPMmTNF7sfd5qGHHmLnzp2cO3eOo0ePcu7cOV588UXT/uVu4+rqSrVq\n1ZgzZw7btm3jp59+4uTJk0RERNCtWzdSUlIKfa6goCBGjRoFwPXr1/nwww85cOAAAI888gjPPfdc\nqXwHjUZTNvnuu+8AGDt2rFk2dOhQKleuzMmTJ7l+/Xqxzt+2bVuSkpJYs2YN/fr1czgWExNDREQE\n/v7+dO/enYyMDM6cOUNWVhZjxozB19eX8PBwjh49ClgdB5YvX87MmTM5dOgQNWrU+N32w8PDTVvH\ngtoD6NGjBzVq1OD++++nVq1aPP744wD4+vqSlJREamoq33zzDeHh4fj7+zN27FgHh4FBgwZhsVho\n3bo1P//8c7596dy5M2+88QZvvvkmp0+fLhENe0kszUSKiL9t2wKglGoNDAEeAvoAUUopF6WUC/A+\n0BdoDQy11b0tixcvBsDf37/InVNKsXHjRoYMGYKIEB8fT1ZWFv369eONN97g1q1b7Nmzh/r16/Pa\na69x6tQpnn32WVJSUggMDGTdunUMGzaMDz/8kPDwcLKzs0vfcKcE8fT0xMfHBzc3N6f2Q0SYOHEi\nGRkZDB06lISEBHbt2kXLli05fPgwCxcuLNL5lixZwrJly2jTpg21atWiRYsWREVFsXPnTqcJWxqN\nxjnUr18f+E0gAUhISCAzMxN3d3eqVatW7DZCQkKYPHmyw7IMWJ9t69evJz4+nvj4eM6cOYOPjw+R\nkZE0aNCAgwcPEhcXx82bNwHry9KuXbvw9PRk+PDhREdHAzg8tzIyMhzaMLwyb9ceQOXKlc16FovF\n3LdYLGRnZ5OTk0Pt2rXNz8bHx3Ps2DHzM/afF5v5Qm6GDRvG559/TtWqVQkODubrr78u/EUsgNJy\n3x0IfCwimcAppVQi0NF2LFFETgIopT621T1a0Ilat25tXqiBAwcSFxd3Rx3629/+xsiRI/nxxx9Z\nu3Yt27dvZ8uWLXnqzZkzh759+wJWrxPjTRugbt26ABw6dOiO+1GeKc53/vnnnzlw4ADu7u6MGzeO\nlJQUqlatyl//+ldefPFF/v3vf9O7d+8indPX15fly5eXWB/LIxXt+5Z19HiULNWrVy+UEDFs2DBe\nfvllRo0axaRJk6hatSoLFiwAYPDgwWRmZpKZmXnH/UhLS2PIkCFUqVIFLy8vzp07x61bt0hLS6Nn\nz57MmzePd955B6UUBw8exM/Pj19//RVPT0/S09NZuXKlWf/MmTM0atSIYcOGcfXqVb799lvCwsKo\nX78+Bw4coGXLlqxdu5YaNWqQlpZGdnY2GRkZpjdkQe1lZmaSlZVl1hMR0tLSTO1+VlYWLi4uNGnS\nhJUrVxIaGoqIcPjwYXx9ffO0Y3xvV1dXkpOTzfJTp07RtGlTRo8eTUJCAnFxcRjdD2cAAAjOSURB\nVHTq1Mnhel2+fJnTp0+b+y1atLjt9S0JjcgEpdT3SqllSqn7bGWewFm7OudsZQWVF8ixY8dwd3dn\n2rRpPPLII8XqaJ06dfjoo4/YsWMHImKqugAaNGhA165dyczMNI2Sdu7caS4Hpaamsm3bNgBatWpV\nrH5URAzXXVdXVypVqmSWGw8Z47hGo9EUlXHjxtG7d2+uXLnCK6+8wuTJkzl9+jRt27Zl5syZJdKG\np6cn48ePz1M+ZcoUsrKy6NSpE4GBgcyePRuAMWPGsGrVKnr06EFiYqKp1di9ezedO3emS5cufPbZ\nZ4wbNw6AWbNmER4eTr9+/fDw8CiwHwW1V1iWLl1KdHQ0QUFBdOjQgc2bN9+2fps2bXB1dSUoKIiF\nCxeyfv16AgMD6dy5M8ePH8+jIboj8jMcsd+Ar4DD+WwDgQaAC1aB5nVgme0z7wNP2Z1jKRAGhANL\n7MqHAwtyt2lv2PLFF1+UWIS8vXv3CiB16tSRyMhIAaRNmzbSsGFDAWTz5s2m0ZOXl5cA4u7uLn/8\n4x+lTp06ZrlhgFRRKAlDvFu3bom3t7dpUJaeni7nz5+Xrl27CiCTJ08uod5WDLRxZNlCj0fpUBT3\n3ezsbNm4caOMGDFCnnzySVm0aFGJR7DWFI4Sj6wqIoUKY6qUWgwYotU54EG7ww8AF2z/F1SeL7kN\ng4rDvn37AKvhj+G2++ijj1KjRg0iIiLYt28fXbp04csvv2TAgAEcP36cbdu28eWXXwLQsWNHVq9e\nTZUqVUqsTxUFi8XC3LlzCQ8P5/XXX+ftt9/m5s2biAgeHh5MmjTJ2V3UaDTlGBcXFwYNGsSgQYPM\nZQR7mwdN2aW4XjMN7Xb/hFVTAvA5MEQpVVkp1QxoAfw/IBZooZRqppRyw2rQ+nlx+lAUatWqBVjX\nuB566CFrRz//3PSjrlatGuvXrwesls1bt24lISGB//znP8THx7N//36aN29+t7p7z/HEE0+wadMm\n/P39yczMxGKxEBoayp49exyiwGo0Go2m4lBcY9V/KqX8scZvSALGAojIEaXUp1iNULOB8SJyC0Ap\nNQHYjnVJZ5mIHClmHwrNoEGDeP7554mJicHb25umTZuSlJTE2bNWs5WoqCjOnz/PAw88QFhYGAAt\nW7akZcuWd6uL9zwhISGEhISQkpKCm5ub1i5pNBpNBadYgoiIDL/Nsdex2o3kLt8C5HVXuQvUq1eP\nqKgoRo8eTVRUVJ7j58+fp2XLlmzYsOGuRh+tiBjRUTUajaYgLBYLGRkZ+oWlHJGRkWHm/SosZT77\nbkkzatQofH19iYqK4sSJEzRp0oQuXbpQtWpVmjRpQvfu3Yt8ETUajUZT8tSpU4crV64UOSDZ5cuX\ngd9CLmjuHhaLhTp16hTpMxVOEAHo0KEDy5Ytc3Y3Sg0RISYmhtWrV5OSkkKXLl0YPXp0kX8cGo1G\n40yUUnckTBgxLHSohfJBhRRE7mVEhDFjxrB06VKz7LPPPiMyMpIdO3ZoexeNRqPRlCn0GsQ9xoYN\nG1i6dCnVqlVj9uzZrFy5ko4dO3Lx4kXGjBnj7O5pNBqNRuOAkgLiyTuTa9eulb1OaTQajUajKRa1\natXKkwxMa0Q0Go1Go9E4DS2IaDQajUajcRplcmlGo9FoNBpNxUBrRDQajUaj0TgNLYhoNBqNRqNx\nGmVOEFFK9VFKJSilEpVSU53dn4qCUupBpdT/KqWOKaWOKKX+x1ZeRyn1pVLqhO3vfbZypZR6zzZO\n3yulApz7De5NlFIuSqnvlFKbbfvNlFLf2sbjE1vySGwJJj+xjce3Sqmmzuz3vYhSqrZSap1S6gfb\nfdJZ3x/OQyk1yfasOqyUWqOUqqLvj/JJmRJElFIuwPtAX6A1MFQp1dq5vaowZAN/ExEfIAgYb7v2\nU4H/ikgL4L+2fbCOUQvb9izwwd3vcoXgf4BjdvtvApG28bgKjLaVjwauiog3EGmrpylZ5gPbRKQV\n4Id1XPT94QSUUp7AC0AHEWmDNYnqEPT9US4pU4II0BFIFJGTInIT+BgY6OQ+VQhE5KKI/H/b/9ex\nPmQ9sV7/FbZqK4BBtv8HAtFiZT9QWynV8C53+55GKfUA0B9YYttXQE9gna1K7vEwxmkd8JitvqYE\nUErVBB4BlgKIyE0RSUbfH87EFaiqlHIFqgEX0fdHuaSsCSKewFm7/XO2Ms1dxKa2bAd8CzQQkYtg\nFVaA+rZqeqxKn3eBvwM5tv26QLKIZNv27a+5OR6249ds9TUlgxfwC7DctlS2RCnljr4/nIKInAfe\nBs5gFUCuAQfQ90e5pKwJIvlJqNq/+C6ilKoOrAcmikjK7armU6bHqoRQSg0ALonIAfvifKpKIY5p\nio8rEAB8ICLtgDR+W4bJDz0epYjNFmcg0AxoBLhjXQ7Ljb4/ygFlTRA5Bzxot/8AcMFJfalwKKUq\nYRVCVonIBlvxz4ZK2fb3kq1cj1Xp8jAQopRKwrpE2ROrhqS2TRUNjtfcHA/b8VrAlbvZ4Xucc8A5\nEfnWtr8Oq2Ci7w/n0As4JSK/iEgWsAHogr4/yiVlTRCJBVrYLJ/dsBoffe7kPlUIbOulS4FjIjLP\n7tDnwAjb/yOATXblT9u8A4KAa4aKWlN8RGSaiDwgIk2x3gdfi8ifgf8FnrBVyz0exjg9Yauv3/hK\nCBH5CTirlPqDregx4Cj6/nAWZ4AgpVQ127PLGA99f5RDylxkVaVUP6xvfi7AMhF53cldqhAopboC\nu4FD/GaTMB2rncinQGOsN3+4iFyx3fwLgT7ADWCUiMTd9Y5XAJRS3YHJIjJAKeWFVUNSB/gOeEpE\nMpVSVYCVWG17rgBDROSks/p8L6KU8sdqOOwGnARGYX2Z0/eHE1BKzQIGY/X4+w74C1ZbEH1/lDPK\nnCCi0Wg0Go2m4lDWlmY0Go1Go9FUILQgotFoNBqNxmloQUSj0Wg0Go3T0IKIRqPRaDQap6EFEY1G\no9FoNE5DCyIajUaj0WichhZENBqNRqPROI3/A5z1OcjzyxlNAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"sensor_var = 300**2\n",
"process_var = 2\n",
"process_model = (1, process_var)\n",
"pos = (0,500)\n",
"N = 1000\n",
"dog = DogSimulation(pos[0], 1, sensor_var, process_var)\n",
"zs = [dog.move_and_sense() for _ in range(N)]\n",
"ps = []\n",
"\n",
"for i in range(N):\n",
" prior = predict(pos, process_model) \n",
" pos = update(prior, (zs[i], sensor_var))\n",
" ps.append(pos[0])\n",
"\n",
"book_plots.plot_measurements(zs, lw=1)\n",
"book_plots.plot_filter(ps)\n",
"plt.legend(loc=4);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In this example the noise is extreme yet the filter still outputs a nearly straight line! This is an astonishing result! What do you think might be the cause of this performance? \n",
"\n",
"We get a nearly straight line because our process error is small. A small process error tells the filter that the prediction is very trustworthy, and the prediction is a straight line, so the filter outputs a nearly straight line. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Example: Incorrect Process Variance\n",
"\n",
"That last filter looks fantastic! Why wouldn't we set the process variance very low, as it guarantees the result will be straight and smooth?\n",
"\n",
"The process variance tells the filter how much the system is changing over time. If you lie to the filter by setting this number artificially low the filter will not be able to react to changes that are happening. Let's have the dog increase his velocity by a small amount at each time step and see how the filter performs with a process variance of 0.001 m$^2$."
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAhoAAAC+CAYAAABzq6b3AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzs3XdcVfX/wPHXuWzZCCoCIggqOXLv\nvTNnpZk7ra/91Eyz0ixNzWy4tdSyZa7U0FCzcpVbcOEAFBEBkaHsDRfu+f1x4SRZaaaC+n4+Hjy4\nnH3uYbz5fN6f90dRVRUhhBBCiPtBV9YXIIQQQohHlwQaQgghhLhvJNAQQgghxH0jgYYQQggh7hvT\nsjhpenq6ZKAKIYQQjxh7e3vlz8ukRUMIIYQQ940EGkIIIYS4b8qk6+Rm9vb2ZX0JAjhx4gQATZo0\nKeMrESXkmZQ/8kzKJ3ku99f06dOZM2cOAH5+fly9epWsrCx0Oh1Xr17F2tr6H/cv80BDCCGEEOVL\namoqYWFhuLi4MGvWLHQ6HYsWLSIsLEzbxtzcHCsrq9seS7pOhBBCCAGAXq9n4sSJVK1aldatW1Oz\nZk1at27NoEGDiI+P5/jx41y6dInOnTuTl5dHjx49bntMCTSEEEIIAcBrr73GkiVLyMvLo0GDBtjb\n23Ps2DE6depEfn4+TZo0wcfHhxUrVlC1alWCgoJue0wJNIQQQghBQkICq1atQqfTcejQIU6fPs3V\nq1dp3rw5CQkJfPXVV9q2vr6+nD17lg8//PC2x5VAQwghhBCcOnWKwsJC2rZtS+vWrQGwtbVl3Lhx\nABw7dqzU9hUrVmTq1Km3Pa4EGkIIIYTAwcEBgCtXrlBYWKgtv3TpUqn1/5aMOhFCCCEeE4WFhSQn\nJ+Pg4ICFhQXJycmsXr2ac+fOUalSJTw8PIiJieHZZ59lzJgxnD17lnnz5gEwZMiQuzqnBBpCCCHE\nI06v1zNnzhw+++wzkpOTsba2pkePHuzbt4/U1FRtO0VRsLCwYNu2bWzbtk1bPm7cODp27HhX55ZA\nQwghhHjEvfLKK3z99deAsQskLS0Nf39/ANq2bcvgwYMJCgrim2++oaCggBdffJErV67g4uLCiBEj\n6NmzJ4pyyzQmd0RyNIQQQohHWHh4OF9//TUWFhbs3r2blJQUPv/8c239W2+9pQUiI0aMQFVVqlSp\nwm+//camTZt4+umn7zrIAAk0hBBCiEfab7/9BkD//v3p0qULiqKUKht+4MAB7XXz5s0B41DXe0UC\nDSGEEOIRZmFhAUBaWpq2rF69etrrvLw8AAoKCli3bt0t6/8rydEQQgghHmE9e/bE3NycX375hblz\n5zJw4ECCgoJQFAVVVfn666+JjY3l1KlTREdHU7FiRUaMGHHPzi8tGkIIIcQjrFKlSloFz3feeQdf\nX19efvllVFXF3d2d7Oxstm7dSnR0NDVq1ODXX3/Fycnpnp1fWjSEEEKIR9zrr79OzZo1Wbp0KRcu\nXMDDw4P//e9/DB8+nPPnz3P+/HlcXV1p27YtJiYm9/TcEmgIIYQQj6D8/HySk5OpWLEiFhYW9OrV\ni169et2yXb169e5pTsafSdeJEEII8RCLiorivffe48UXX+TDDz8kKiqKyZMn4+LigpubG87Ozkya\nNInc3NwyuT5p0RBCCCHKobCwML777jtu3LhBw4YNGTp0KPb29qW22bhxI8OGDUOv12vLpk+fTlFR\nEWCc+Cw5OZnFixcTERHBtm3b/lNNjLshLRpCCCFEObNkyRLq1KnDRx99xFdffcX48eOpXbs2ISEh\n5ObmEhcXR2xsLCNGjECv1zNgwABWrlxJ8+bNKSoqQlEUfv/9d5KSkggMDMTe3p4dO3bcMgPrgyCB\nhhBCCFGOBAcHM3HiRFRVZdSoUSxbtowmTZqQkJBA27ZtcXR0xM3Njdq1a5Ofn0/Pnj3ZtGkTY8aM\noV+/fgCoqkpiYiIAzZo1Y9iwYQDs27fvgd/PbQMNRVE8FEX5TVGUMEVRQhRFea14+UxFUa4pihJc\n/NHzpn3eVhQlQlGUi4qidL+fNyCEEEI8THJycvjxxx9Zu3Ytly9fvmX9N998A8DYsWO11ow9e/Zg\nZmZGamoq+fn5ODk5kZ2dDUBycrK2r6WlpfY6Pj5ee10ycdrN6x+UO2nRKAQmq6rqB7QAximK8kTx\nukWqqjYo/tgJULxuEFAH6AEsVxTl3o6VEUIIIR5C/v7+uLu7079/f4YNG4aPjw/Dhw8nPz9f26Yk\nQGjRooW2bNeuXVoexqeffkpSUhKTJ08GIDAwkPDwcADat2+v7RMWFsbFixdZvHgxGzZsQFEUrcXj\nQVJUVf13OyhKAPAp0BrIUlV1/p/Wvw2gquqHxV//CsxUVfVoyTbp6enaSS9dunTXFy+EEEI8aCUF\nrg4dOoSqqrRu3ZpnnnkGGxubf9zv4sWLjBgxgqKiIvz8/KhcuTJHjhyhoKCA559/njfeeAOAVatW\n8cUXX9CiRQsWL16MiYkJ06dP55dffgFgy5YteHh4kJeXR5cuXcjPz8fW1pamTZty8uRJ0tPT//L8\no0eP5pVXXrm3bwbg6+urvba3t78l0/RfBRqKolQHDgB1gdeBkUAGcAJjq0eqoiifAsdUVV1bvM9X\nwM+qqv5QchwJNIQQQjyM0tLSGDNmDJGRkaWWe3p6smrVKhwdHf9239mzZ7N9+3b69evHtGnTUBSF\nkJAQRo4ciYWFBb/88gs2NjbcuHGDAQMGkJ2dTbVq1fD19WX//v0UFhbi4eHBli1btGMOHTqUixcv\nljpPvXr16NOnD7t27eLatWtUrVqVAQMG0LFjx/sy4uR2gcYdD29VFMUG8AcmqqqaoSjKCuB9QC3+\nvAAYBfzVXfxtNNOkSZM7vQRxH504cQKQ51GeyDMpf+SZlE8P8rm89tprREZGUqtWLebMmYNOp2P6\n9OmEhoayZcsWVqxY8bf7liRnTpo0iaZNm2rX/OGHH3Lx4kXs7Ozw8/PDysqKn3/+mcGDBxMTE0NM\nTIx2jOTkZM6dO0fLli1Zu3YtFy9epEKFCmzZsoXk5GRq1qxJ48aNURSFOXPm3N83o9jftaCUuKNA\nQ1EUM4xBxjpVVbcAqKqaeNP6VcCO4i9jAY+bdncH4u78koUQQojyacOGDQCsW7eOxo0bA1CzZk3q\n1avHd999R0ZGBnq9nq5duzJ06FCsrKy0fV1dXQE4duwY7dq1A4z5GCWtI61btyYvL4+6desybdo0\nIiMj2bdvH9evX6dBgwYsWrSIb775hlGjRpW6piVLltC9e/kdd3HbQEMxtrN8BYSpqrrwpuWuqqqW\npLT2B84Xv94GrFcUZSFQFfAFgu7pVQshhBBlICMjA4Dq1atry0oCiJycHNavXw/A5s2bWbZsGfv2\n7cPZ2Rkw5kgEBATw7rvvEhcXR7Vq1VixYoWW5JmXl4epqSnnz59n8ODBpKenl8qp+PLLL2nTpg1f\nffUVcXFx1KlTh4kTJ9KlS5cHcet37U5GnbQGhgGd/jSU9RNFUc4pinIW6AhMAlBVNQTYBIQCvwDj\nVFUtuj+XL4QQQtw/WVlZLFu2jN69e9OvXz+8vLwA+OCDDygqKsJgMDBgwAAATE1NWbhwIZ9//jk+\nPj6cO3eOqVOnUlhYSH5+Pr169eKNN95Ar9ezZMkSJk+eTEREBAA+Pj5cuHCB7Oxs5s83jrF49913\nycvL065Fp9MxatQoDh8+zJUrV9ixY0e5DzLgLkad3As3J4P+uZyqKBvS91z+yDMpf+SZlE/367nc\nuHGDDh06EBoa+pfrq1atiqIoXLt2DYD33nuPmTNnAnDhwgX8/PwwMTFBp9Oh1+tp2bIls2bNwtHR\nke+//57MzEwCAwM5c+YMa9euZciQIYCx2FadOnUICwvj8OHDtGrV6p7e1712c47GXyWDSmVQIYQQ\n4i9MmzaN0NBQatWqxerVq1m1ahXu7u4AODg4EBcXx7Vr19DpjH9KX3zxRW3fChUqAFBUVIRer0en\n03H06FF69OhBYmIi8+fP5/PPP8fT0xOgVMsFoNXVuNdTtpcFCTSEEEKIPykqKtLyLX788UeGDx/O\nSy+9xOrVqwFjoHHu3DnOnj1L165dAfjss88o6SV46aWXALCwsCAmJoaMjAwmTpyIwWBgypQp2nZ9\n+vQBYObMmezdu5dr164xefJkIiMjcXNz0xJOH2YSaAghhBB/otfrycnJwcTEBG9vb2157dq1AWM9\njbp161KvXj3eeustFEVh3rx51KtXj+bNm7N7924AXn31VTw8PLC2tubjjz/G3t6ekJAQ4uKMgzGH\nDh1Kq1atiI2NpUuXLri7u7No0SJ0Oh2LFi3C1PThn2RdAg0hhBDiTywtLalbty5FRUUsW7YMVVVR\nVZVFixYBaHUwADp16sSaNWtwdnYmJCSEoKAgrTulW7du2naFhYUUFhYCf3SJWFhYsGvXLmbMmIG3\ntzeOjo50796dvXv3akmmDztJBhWAJLmVR/JMyh95JuXT3T4Xg8FAfHw8FSpU+MuKnhs2bGDw4MEA\nPPHEExQUFBAREYGiKOzevZvOnTuX2j4/P5/Dhw+j1+vZu3ev1sLx1Vdf4ezszPTp01m3bh3NmjUj\nMDDwLu+2/JFkUCGEEOJP1q5di6+vL+7u7jg5OdGtWzd+/vlnXnrpJby9vfHz8+P8+fMsWLAAJycn\nQkNDiYiIoGrVqmzYsOGWIAOMrROdOnWie/fuTJkyBV9fX86dO0ezZs3w9vZm3bp1WFpasmDBgjK4\n47Lz8Hf+CCGEEP/Ct99+q40QcXBwICcnh927d7Nnzx5ubuWfO3cufn5+nDt3jsjISExMTGjSpAlm\nZma3PUfFihU5fPgwc+fOZfPmzeTm5tKhQwfeeecdGjVqdN/urTySQEMIIcQjIyIigmXLlnHy5Emc\nnZ0ZPnw43t7ezJ8/n2PHjmFnZ8eVK1cA+OSTT3j99ddJT0/Hx8eH1NRUvLy82LJlC2lpaYwbN47Q\n0FCWL19+V/OGuLi4sGjRIi2v43ElgYYQQohyRVVVjh07RkREBF5eXrRu3fqOZh3dv38/PXv2JCcn\nR1sWEBCAiYkJRUWlC1Sbm5vz6quvYmJigomJCampqQDY2NjQoEEDAJYtW0bnzp3ZsmXLA5ug7FEk\nORpCCCHKXMlojKioKJo0aUKrVq0YPnw4bdu25cknn+TSpUv/uL/BYGDUqFHk5OTQv39/du3axfz5\n81EUhaKiIjp16sSZM2f44osvACgoKOCbb77RXpewtrbWXjs4ONyyXvx7EmgIIYQoEwUFBbz//vu4\nublhZmZG9erVadGiBadOnaJSpUoMHDgQV1dXzp07R48ePf7xD35ISAiRkZFUq1aNTZs20bVrV7p1\n66blXFStWpX69evz8ssvaxOizZo1i1OnTnHs2DEt78LKyor8/HxSU1OZPn06YBy+Ku6edJ0IIYR4\n4FRVZciQIfzwww/asujoaABsbW0JDw/H3t6erKwsGjduTHh4OAEBAX9bWyIrKwsADw8PrcjVzWW9\nS2ZdBfi///s/pkyZQmJi4i2VN3/77TcqVqxIQUEBer0ee3t73nrrrXtz048padEQQgjxwB07dowf\nfvgBW1tbfv31VwoLC7VJxTIzM7l+/TpgzJl47rnnADh37tzfHq927dqYm5tz5MgR9u3bB0C1atW0\noMPExASDwUBCQgL+/v4ANG7cGF9fXxo0aMCHH37Ixo0bqV+/PtnZ2ej1erp06cKBAwfw8fG5b+/D\n40BaNIQQQjxwP//8MwCjRo3Sqmd269aNdevWAfDLL7/g6+urJYYCuLq6ljpGcHAwS5cu5dixYzg5\nOdG1a1d++uknOnfuTJ06dYiOjtZyP7Zu3YqzszOZmZkUFhbi7u7OL7/8grOzc6ljDhgwgOTkZMzN\nzbGzs7uv78HjQgINIYQQD1xJie6SQACgf//+vPTSS+j1elauXImpqSm//vor+/btw9ramkaNGvHj\njz/i7u7O1atXGThwYKn9ARo2bEh4eDghISEAtGnThq5du/L1118THR2NTqejT58+LF68+JYgA0BR\nlL9cLu6eBBpCCCEeuN69ezNr1iy+/vpr2rdvT5cuXdi6das2DDU0NJSxY8cCxoqbNWvWpEWLFtr+\npqamFBYWMmrUKFq1akVISAjLly/n9OnT7Nq1CwcHB5ydnfHy8gLg3XffJT4+HhsbG5n64gGTQEMI\nIcQD17hxY0aOHMm3337LwIEDS60bO3Ysbm5uXL58GU9PT3bu3ElgYCDW1ta0bduWI0eOkJGRgZmZ\nGUuXLiUsLIwnn3wSMzMzPvnkE7Zt28ayZctKHVOn0+Hm5vYgb1EUk0BDCCHEA6WqKoqi8OWXX9Kg\nQQM+//xzoqOj8fX15dVXX2XUqFFaga7AwEDee+89nJycOHv2LG5ubnz33XeMGDECvV7P5s2bqVu3\nLgDu7u7AHyNQRPlw21EniqJ4KIrym6IoYYqihCiK8lrxcidFUXYrinKp+LNj8XJFUZSliqJEKIpy\nVlGUx6uouxBCiFvk5+czc+ZM3N3dMTExoW7duqxevZoJEyYQGhpKdnY2wcHBjB49ulQV0ODgYMDY\n1VLSItGhQwdtmx07dgCQlJTE8uXLAWNehig/7qRFoxCYrKrqKUVRbIGTiqLsBkYCe1VV/UhRlKnA\nVGAK8BTgW/zRHFhR/FkIIcRjyGAw8Mwzz7Bz505tWUhICKNHjyY6OppZs2b97b4uLi4AnDlzBoPB\ngE6no1q1anh5eREZGYm/vz/Hjx8nPj4evV6Pr68vL7zwwn2/J3HnbtuioapqvKqqp4pfZwJhgBvQ\nF1hdvNlqoF/x677Ad6rRMcBBURRXhBBCPJJUVeXs2bP8/vvvJCcn37J+z5497Ny5E0dHR/bs2UNu\nbi6rVq1CURQ+/PBDEhMT//bYPXv2xNnZmeDgYPr27cuaNWt4+eWXiYyMRFEUKlSoQExMDIWFhfTq\n1Yt9+/ZRoUKF+3m74l9Sbp4S97YbK0p14ABQF4hRVdXhpnWpqqo6KoqyA/hIVdVDxcv3AlNUVT1R\nsm16erp20tvVrxdCCFF+XbhwgdmzZ2u/y83MzHjmmWeYOHGiVixr/vz5bNy4kdGjR/PKK69o+06Y\nMIGjR48ya9Ysevbs+bfnCAwM5I033ihV6VNRFKZOnUqPHj2Ii4vD0dGRihUr3qe7FP/E19dXe21v\nb3/L7Hd3nAyqKIoN4A9MVFU14x9m0vurFXcezQghhCgX8vLyCAoKIi8vjyeffJLKlSuXWp+UlMS4\ncePIyMjA0dGRqlWrEhoaysaNGwF44403AP525tWSf3RvNzNr8+bN2bx5MwEBAURFRVGpUiX69OlD\njRo1AKRyZ3mnquptPwAz4Ffg9ZuWXQRci1+7AheLX38OvPBX25V8pKWlqSUfonw4fvy4evz48bK+\nDHETeSblz+P0TNavX686ODioGP9RVE1MTNSxY8eqer1e2+a9995TAbVTp05qbm6uqqqqevDgQVVR\nFNXc3FxNSkpSVVVVd+3apQKqo6Oj+ssvv6hZWVnqypUrVUA1MzNTExMT/9O1Pk7PpTz609/0W2KI\nOxl1ogBfAWGqqi68adU2YETx6xFAwE3LhxePPmkBpKuqGn93YZAQQogH7ejRowwdOpS0tDQaNWrE\nU089BcDy5cuZPXu2tl1QUBBgrHthaWkJGEd8NGvWjIKCAmbMmMG0adNITk7m6aefJjU1lR49emBj\nY6N1obz77rtUqlTpAd+heJDupOukNTAMOKcoSnDxsmnAR8AmRVFGAzFAyZR6O4GeQASQA7x4T69Y\nCCHEfbV48WIMBgMTJkxgyZIlAOzevZtu3bqxbNky3nnnHSwsLHBycgKMeRol8vLyCAsLA9CGmwJ4\ne3szadIk/P39iYuLo06dOkyaNInhw4c/wDsTZeG2gYZqTOr8uw60zn+xvQqM+4/XJYQQ4l9SVZXU\n1FRMTU3/04RgJbOkjhw5UlvWtWtX3NzcuHbtGnPmzMHc3Jw6deoA8MEHHwDg5+fHggULtCnZe/Xq\nRcOGDdm4cSPh4eEcPHiQqKio2+ZkiEeLVAYVQohHwM6dO3nnnXe0AlddunRhwYIF1K9f/7b7GgwG\ntm/fztatW9Hr9VqSZlBQEA0bNgQgOjqauLg4AObMmaPtW6VKFRISEnj33XdLHfOpp55i+/btgDEp\ntEaNGpw4cYJTp07RuHHj/37D4qEhgYYQQjzkdu7cSa9evVBVFSsrKwoLC9mzZw/t2rVjz549xMXF\nYWJiQrt27bC1tS21r16v59lnn9WCgptNmjRJG+Uxf/58LQDp378/1atXZ926dSQkJNCuXTvc3d1J\nSUkhJiaG0NBQBg0apB3Hzs6O5s2b89NPPxEdHS2BxmNGAg0hhHjIvfPOO6iqyuTJk/nggw/Iyclh\n6NCh7Ny5kxYtWmgzotra2vLRRx/RtGlTtm/fjqqqpKens337dpycnHjrrbewtbVlwYIFREZGkpub\ny0cffVTqXOPGjePTTz8FYPz48dSsWZPDhw8THx+Pi4sLM2bMIDQ0lK1btzJs2DAUReHGjRscOnQI\nKF1zQTweJNAQQoiHWGpqKsHBwVhZWfHBBx9gYWGBhYUFzZo1Y+fOnRQVFdGmTRv0ej2BgYGMG/fX\nKXTLly/n+eefB6Bz587Url0bc3NzRo8eTUFBAfv37yciIoIBAwZo+3h7e+Pn58f58+eJiYnBxcWF\n0aNHM2/ePH788UdatWpFo0aN2Lp1K+np6bRv35569eo9kPdFlB+3Hd4qhBCi/CqpvqnX68nJydGW\nf/PNNwBUqlSJgwcPcuzYMZ5++mnAOGX6q6++yqRJk7TEzGPHjmn7+vr6Ym1tTUFBAe+//z5ffvkl\nzZsbp6wqmcQMICIigrCwMExMTKhWrRoAnp6e+Pv7Y29vz7Fjx1i+fDnx8fE0btyYDRs23Md3QpRX\nEmgIIcRD5syZM7zwwgu4ubnRqFEjvLy8KCwsZOjQoQQHB7N3716io6OB0iNHLl68CIC5uTlLly5l\n4cKFNGnSBIAvv/xSy8FYv3492dnZVKtWDUdHRwD+7//+DzCWE+/bty8TJkygZcuWFBUV8fzzz2uT\nn4FxfpKrV6+yZs0aFixYwJ49ewgKCsLVVaa9ehxJ14kQQjxEDh8+TNeuXcnNzS21XKfTsXPnzlIz\npIJxWGqJq1evAsaRIiXmzp1L165dycrKokGDBtja2nL48GEA3nzzTXQ64/+jrVu35rPPPmPixIls\n27ZN2799+/Z89tlnt1ynra0tQ4cO/Y93K8qzzDw9x6NSaOxq+Y/bSaAhhBDlmKqq7N+/nyNHjmBv\nb8+qVavIzc1l0KBBvPfeeyQmJvK///2P8PBwGjduTHJyMubm5tjZ2XHixAlGjhzJ5MmT0ev1FBYW\nAtCgQQPt+KmpqYAxUDl79iwAVlZWTJky5ZZ8jrFjx9K/f3/8/f3JyMigdevWtGvXTupiPCby9EWc\niErlyOUkjlxO5ty1dIoMKmfebvOP+0mgIYQQ5VRqaip9+/bl4MGDpZZbWlry9ddfY2VlRe3atVmw\nYAG9e/dGp9Nx5coVADIzM+nevTtHjx7l9ddfL7X/9u3bee655zA1NWXLli0AfPTRRzRo0ICCggJa\ntWqldZn8maurK+PHj78PdyvKmyKDSkhcOocikjgckcTxqFQKCg2Y6hSe9HBgbIcatPS+/Yy5EmgI\nIUQ59X//938cPHgQFxcXXnjhBUJCQti7dy95eXmcOnWK1q1bA2BjYwNAQUGBtq+trS379+/H39+f\nn3/+GRMTE3r37s3Ro0dZsGAB/v7+gHHm1PHjxzN58mStm0Q8ngwGlYuJmRy9nMzRyGSCrqSQnqsH\noHYVW4a38KS1jzPNvJywtvgjfEhPT//H40qgIYQQ5VBiYiKbN2/G1NSUY8eO4e3tjcFgoGLFiqSl\npTF27FiCgoJITU1lxowZQOl8DAAzMzMGDRpUqnhW//79GTduHDt37kRVVbp3765Nty4eL0UGlQsJ\nGQRdSSEwMoXAK8mk5hgDi2pOFehepzKtfZxpVcMZF1uLuz6PBBpCCFEOxcTEYDAYqFevHt7e3oAx\nj2LChAnMnj2bs2fP4uDgQEFBAQaDgcqVKzNx4sQ7Oranp6c2ikQ8PvRFBs5fSzcGFldSOB6VQmae\nMW/HzcGKzn6VaeFdkZY1KuLmYHXPziuBhhBClEPVqlVDp9MRGhrKlStX8PLyAiA7OxsAR0dHUlNT\n0el09OvXj3nz5uHm5laWlyzKmfzCIs5fS+dYZArHIpM5GZ1KToGxSqy3izW96rvS3KsiTb2c7mlg\n8WcSaAghRDlUuXJlnnvuOTZt2kSLFi0YMmQIkZGRBAQEAPDTTz/h5+eHhYUFVlb374+EeHgkZeVz\nKjqVk8UfZ6+lU1BoAKBWZVuea+xOMy8nmnk5Ucn2n4ek3ksSaAghRBmJjo7m/PnzVK5cmcaNG98y\nTHTFihXExsZy5MgRFi1aBBgrgS5ZsoSWLVuWxSWLckJVVS7fyOJEVConigOLK0nG1i5zEx313O0Z\n2ao6jT0daVrdCSdr8zK7Vgk0hBDiAcvKyuKll15i06ZNWjXOunXrsm7dulLTujs5OXHo0CH27dun\n1dF47rnnqFq1allduigjefoizlxN42RMKiejUjkZk0paceKmk7U5jao58nxTD5p4OlLXzR5LM5My\nvuI/SKAhhBAP2IsvvsgPP/yAubk5bdu25fz585w/f56OHTsyZMgQQkJCqFixIsOGDaNXr1507tyZ\nzp07l/VliwcoJbuA41EpnIhK4XhUKiFx6eiLjEGpt4s13Z6oTBNPJxpXd8Tb2bpcF02TQEMIIe6z\nH374gUWLFhEaGoqLiwuXLl3C0tKS4OBgatWqRW5uLk2bNiUkJIRly5Zp+23evJkxY8awYsWKcv2H\nRPw3qqoSmZTNqehUTsWkEnQlhcs3irtBTHU86W7P6DbeNPF0pJGnY5l2g9wNCTSEEOI++uSTT5gy\nZYr2dVpaGmDsFqlZsyZgrPSZlJQEQNWqVfn8888JDQ1l5syZfP755/Tv35/u3bs/+IsX90VOQSHB\nMWmcKA4sTsekaYWxbC1NaeKgaPZmAAAgAElEQVTpyLON3Wla3Yl65awb5G7cNtBQFOVroBdwXVXV\nusXLZgIvAzeKN5umqurO4nVvA6OBImCCqqq/3ofrFkKIcu/GjRtMnz4dgIULF/LCCy+wcuVKZs2a\nRVxcHL///jsdO3bk5MmTJCYmAvDss8/Sq1cvevXqRX5+PjNmzGDdunUSaDzEkrLyORmdyomoFIKi\nUgm5lk6hQUVRwLeSDT3qVKGRpwONqjlSw8UGne7Rar26kxaNb4FPge/+tHyRqqrzb16gKMoTwCCg\nDlAV2KMoSk1VVYvuwbUKIUS5d/36db799lsuXbpEWloaBQUFdOvWjUmTJgEwffp0Fi9eTHp6Oi++\n+CJz587VyoFD6WndS1o8SiY+E+VfYZGBCwmZnIpJLe4KSSMmJQcwdoM0cHdgTHtvmlR3olE1R+yt\nzMr4iu+/2wYaqqoeUBSl+h0ery/wvaqq+cAVRVEigGbA0b/b4cSJE3d4aPEgyPMof+SZlD9/90yC\ngoJ48803ycnJKbX82rVrpfZp164d27dvJzo6miFDhtxybIPBQG5uLh9//DEA7u7u8n1wB8riPcrR\nGwhP1nMxWU9Ykp6IFD15xUmbDpY6ajqZ0b6eDbUqmlHD0QwzEwXIgswsLoXEPPDrvR98fX3/cf1/\nydEYryjKcOAEMFlV1VTADTh20zaxxcuEEOKRlpuby7Rp08jJyaF58+a0a9eO/fv3ExQUREhICAEB\nAfTu3ZuQkBAOHToEQI8ePcjPz8fJyYn09HT27NnDmDFjqF27NnFxcWRkZODg4ED//v3L+O5Eicx8\nA2FJBYTc0BOWVEBUWiEGQAd4OpjSsboltSqaUauiOc4VdJLECyglY7j/cSNji8aOm3I0KgNJgAq8\nD7iqqjpKUZTPgKOqqq4t3u4rYKeqqv43Hy89PV07qb29/b25E/GflPwn0KRJkzK+ElFCnkn580/P\nZN26dQwdOpQmTZoQGBiITqdDVVWqV69OTIzxP1czMzP0emPSX+fOndm1a5c2Y6per+ett95i5cqV\n5OXlaef56quvStXWELe6nz8rCel5BBUPMw26ksKFhEwALEx1NKzmQLPqTjSp7kTDag7YWj763SB/\n5ebZW+3t7W+JrO6qRUNV1cSS14qirAJ2FH8ZC3jctKk7EHc35xBCiIdJfHw8AC1bttSCB0VRGD58\nOHPmzMHOzo6MjAwcHR0ZPXo0s2bNKjUtu5mZGYsWLWLGjBmEhobi5OSEn59fmdzL46rIoBKeaMyv\nOBGVyvGoFGJTcwGwNjehkaejcX4Q74rUd7fHwvThHg3yoNxVoKEoiquqqvHFX/YHzhe/3gasVxRl\nIcZkUF8g6D9fpRBClLG8vDz27t1LYmIiKSkpdOnShdDQUL744guioqIwNTX+Og0ICOD999/H3t6e\nnJwctmzZAhjLifft2xcrK6tSAcafOTo60rp16wdyT4+7tJwCTsekcbJ4mOmZq2lkF0865mxjQdPq\njoxq7UXT6k74udpiavL3z038vTsZ3roB6AA4K4oSC7wHdFAUpQHGrpMoYAyAqqohiqJsAkKBQmCc\njDgRQjzsDh8+zLPPPqsNQV20aBFubm7Ex8djMBhKbRsTE0OtWrXo2LEjhw4dIjY2Fk9PT5599lks\nLCzK4vIFfxTFOhltHA1yIjqViOtZAJjoFGpXseWZRu7aMNNqThUkv+IeuZNRJy/8xeKv/mH7D4AP\n/stFCSFEeZGSkkKvXr1IS0vDx8eHJ598kqNHj3Lt2jUARo8eTffu3QkICGDdunXodDoSExP5/vvv\nAfDz82PLli0SZDxgOQWFnLmazqkY44Rjp2NSSS2eG8TeyozGno70b+hGw2oONPBwoIK51K+8X+Sd\nFUKIf7B27VrS0tJo27Yt8+bNw8TEhN27dzNt2jQAhg0bRvv27XnuueeIjY1l//79vP3229SqVYvq\n1avTtm3bf+wqEfdGck4R28/EaVOkh8ZnUGQwjjvwqWRDtyeMRbEaezri7fzoFcUqzyTQEEKIfxAe\nHg5Av379MDExJv9lZ2eXWt++fXsURaFu3brs378fR0dHRowYUSbX+zjI0xcREpfO6Zg0Tl9NIzDi\nBkk5BiAJKzMTGng48H/ta9C4uiMNPRxwqPBwzQ3yqJFAQwjxSLp8+TL+/v7k5OTQrl07OnbseEuf\nu6qq7NmzhzVr1pCcnEyTJk0YM2ZMqWnYq1WrBsC+ffto27YtiqKUGm7q4OAAGEed/PDDD4AMSb6X\nVFUlOjmH01dTCS4OLELjMigsbq1wc7CippMZvX3N6d+2Pn6udphJ0ma5IoGGEOKRM2fOHGbMmMHN\ndYI6dOhAQEAAdnZ2gPEP2MSJE1m6dKm2zc6dO1m6dCmff/45p0+fJjExkerVq2NpaclPP/1EUlIS\nDRs25OjRP4odv/TSS6xYsYLAwECtWFeHDh0e2L0+avILizgbm07QFWPtiuCraVpuRQVzE+q72/O/\ndt408HCgQTUHKtlaanU06rs7lOWli78hgYYQ4pGyc+dOpk+fjk6nY/DgwVSpUoXVq1fz+++/07Jl\nSxISEsjIyKB27dqcP38eCwsLpk2bRp06dVi5ciV79uzh+eefL3VMW1tbAAIDAwkMDASgUqVKVKtW\njRMnTvDbb78Bxkqfq1evltEK/0JWfiEno1M5fiWFoOLAoqDQOJKnhos1XZ+oTMNqjjTwcKBmZVtM\nJLfioSOBhhDikbJixQoA3n//fS1hc9CgQTRt2pTQ0FBtu/PnjeV/evfuzYwZMwDw9vamUaNGAPTt\n25fu3buzZs0ajh49ire3N3379iUpKYlOnToxcOBAKlSoQFhYGNHR0fj4+ODj4/Mgb/WhdD0zj1PR\nqQRdMRbEColLx6Aah5jWqWrHsBaeNK3uRNPqjlS0kZE6jwIJNIQQj5QrV64AlJpWff/+/drrgIAA\nOnToQOPGjYmIiOC3336jqKgIExMT1q1bp203fvx4unTpwqhRo/Dx8SEyMpInnniCBg0alMrB8PPz\nkwqef6Og0MCFhAxtFtNTMalapc2SEt7jO/rQ1MuJhtUcsbGQP0mPInmqQohHiq+vLyEhIWzbto3G\njRsDsGnTJsBY5rtTp07Y2NgwdOhQZs6cSXJyMidPnqRZs2ZaK4eJiYmW8GlhYUHDhg2JjY0lKSmp\nbG7qIWAwqFy+kcWZ2HTOxqZxJjadsLgMCoqM3SBV7Cxp5OnAyFbVaVjNgbpuUsL7cSGBhhDioRcZ\nGUlAQAAFBQV06dKFH3/8kdmzZxMcHEyVKlU4efIkYEwItbGxAeDll19m9uzZGAwGnnrqKWrVqsWx\nY8bJpytXroyjoyNgrPS5b98+AGrUqFEGd1c+pefqOR1jbKk4HWMcEZKZXwgY5wWp62bPyNbVqe9u\nT6NqjlR1sCrjKxZlRQINIcRDS1VVpk+fzty5c0uNMKlXrx5hYWFs27at1PbR0dGcPn0aLy8vli5d\nisFgwMzMjJSUFI4ePYqpqSk6nY64uDhq165NgwYN2LVrF9nZ2fTs2RMvL68HfYvlQn5hEWHxmZy5\nmsaZ2DTOXE3j8g1jLRGdAjUr29K7QVUaehirbHq72EjSptBIoCGEKHN6vZ4tW7awd+9ezMzM6Nev\nH126dCEmJobdu3ejKAo9evTAzc2t1H6bN2/mgw8+wMTEhIEDB2Jvb8+6des4d+4c48aNo06dOmRn\nZ9OkSRPGjRtHaGioluwJxtlV165dS82aNUlJSaFevXpERkby/PPPExkZSWRkJGAcTbJ27VouX778\nQN+XspKQnqdNNHYyOpWQuHT0RcZAztnGggYeDvRr4EYjT0ee9HCQ3Arxj+S7Qwjxr2VmZrJ+/XqC\ng4OpVKkSw4YN+8sRFydPnuTjjz/m8OHD2NnZ8cILL9C/f39WrlzJ/v37sbKyolevXuzYsUOrhQCw\nfPlyatasSUREhDZpmYmJCZMnT8bJyYmffvqJoqIibb6RhQsXMmHCBACGDh1KmzZtWLduHdevX8fM\nzAyAAwcOMGvWLNavX096ejotW7bknXfeKZU0CuDi4kJERAT79+8nMTGR+vXrU7du3fvyPpYHN1fZ\nDL6axumYNK6l/ZGw+aSHA6PaeNHA3YEnPRxwtbeU4bviX1Fubm58UNLT07WT2tvbP/Dzi1uV/JKX\nioblR3l9JiEhIXTr1o24uDhtmU6n47PPPuOVV17Rlu3Zs4enn36agoKCUvubmJhQVHTrpM7u7u5M\nmDCBzMxM5s2bR15eHjqdjn79+lFYWHhLN8jNjhw5QsuWLbWvHRwcSE9PJzExkUqVKv2X2y2lvD6T\nO6WqKleSsgm+mqZ9hMVnaK0Vbg5WNPAwzgfS2NMRP1c7zE3Lf5XNh/25POzS09O11/b29rdEodKi\nIYS4Y6qqMmjQIOLi4mjUqBFDhw7l9OnTrFmzhrFjx9K2bVvq1KmDqqq8+uqrFBQUMHLkSN5++22i\noqLo06cP+fn5PPHEE3z55ZfEx8fz3HPPoaoqAwYM4M033wRg1apVJCQk4OHhgb+/PwDdunVj9+7d\nWFhYsH79eszNzRk0aBDZ2dlMmjRJS+Q8cuQI6enp2Nvbawmdj6v0XH1xK0Uqp2OM+RVpN1XZrOdm\nz+g23jSs5kBDDwcq2VmW8RWLR5EEGkKIUnJzc0lMTMTFxQVra2v8/f1ZuHAhoaGhODg4EBUVhaur\nK4cOHcLKyjiSwMLCgi+//JKvv/6aBQsWcOHCBS5cuICLiwtffPEFZmZmODg4kJ+fD4CzszMtW7Yk\nJSVFS+I8cOAAAEVFRSQkJABo28MfBbYAnnnmGQA++OADJk6cSGBgIEOGDMHBwYG1a9cC8L///U/r\nNnkcqKpKZFI2J6JSOBVtrFkRcSMLVQVFgVqVbelRp4pWutu3klTZFA+GBBpCCADy8vKYNm0aq1at\nIisrC0tLS+rXr09QUJC2TVpamvba0vKP/37btGnDl19+qXWn6PXF/zVXqICpqfHXTG5urrZ9SdeJ\ng4MDLi4u3Lhxg8TERMDYtWJjY0NWVlap5M+S5tmbl7300ktMnDgRgPXr12vL+/Xrx/vvv/9f3o5y\nryS34kRUKieKp0ZPyTZ2UzlUMKOhhwN9nqwqCZuizMl3nhCPifT0dK5fv467uzuWlpZs3bqVFStW\nEBUVRY0aNcjMzOTIkSMAuLq6Eh8frwUZ8+fPZ+jQoWzcuJHXXntNm6l0wIABFBUVsWHDBgAcHR1Z\nuXIldnZ2VKlShejoaObNm8ekSZNQFAULCwvy8/OxsrKiqKiI7OxsKlasyI0bN4iNjaV79+5kZmaS\nlZUFwIULF5gyZQpFRUVa60blypUpLCxEURTmzp0LQP369Rk+fDj5+fl07tyZZs2aPVIJi6qqci0t\nV6tZcSomjdCbRoJ4OVvTqXYlmlZ3pLGnEzVcrB+p+xcPN0kGFYAkU5VHd/tMVFXl5MmTJCQkULdu\nXezs7HjttdfYuHEjer0eGxsb6tSpo00OdjNzc3MOHDhA8+bNmTdvHm+99RYAu3btomvXroCxaFVk\nZCTm5uY8++yzBAcHExYWdkuSp5WVldaKUaFCBXJzc0vVuqhYsSI5OTnk5uZibm6OwWCgsLC44JO1\nNTVq1ODs2bOlrk9RFFRVxcXFBVNTU+Lj4wHYsWMHTz/99L96n+7Gg/o5ySko5GyscSTI6ZhUTl9N\n40amMdCyNNNR392BRtUcaVjN+NnF9vGeE0R+f5UtSQYV4hGQl5fH8uXLWbduHenp6bRo0YI333yT\nJ598stR258+fZ/DgwZw7d05b5ujoSGpqKjqdDg8PD65evUpgYCCKojB//nx69OjBlClT2LFjBwUF\nBVStWhUwtmqU+P3337VAY8CAAXz88ccUFBRoLRmWlpbk5eVhb29P3759uXDhAkFBQZiYmODp6Ulk\nZCQmJib079+fVq1asWzZMm1Oknbt2rF06VIqV67MgQMHMDc3p3PnztjY2LB//35+/vlnFEWhd+/e\npKen8/rrr3Px4kUAvLy8+Oijjx5IkHG/ZOTpCbmWQUhcOuevpXM+LoPIG1kYimMyL2dr2vo406A4\nqKhVxRYzk/I/EkSIErcNNBRF+RroBVxXVbVu8TInYCNQHYgCBqqqmqoY2+qWAD2BHGCkqqqn7s+l\nC/F4KCgooGfPntpU5ACXL1/mhx9+4KeffqJz586AMX+iS5cuJCYmUrlyZerVq8fvv/9OamoqlpaW\nnDt3Dh8fH8aNG8fy5ctRVZWePXtSu3Zt+vTpw44dOwDjpGPjx4+nU6dOWgvCpUuXMBgMHD9+nG++\n+QaAxYsXY2tri6IojB49GnNzc06dOoW3tzeqqjJkyBA2bNhA7969ee+997C0tNSSR1977TWuXr2K\nlZVVqeGnAwcOLHXvHTp0oEOHDqWWPfXUU4SHh2MwGKhZsyYmJg/PfBk5BYWExGVw5moa566lczY2\nnStJ2dr6KnaW1HWzo2c9Vxp6GOtWOFmbl+EVC/Hf3UmLxrfAp8B3Ny2bCuxVVfUjRVGmFn89BXgK\n8C3+aA6sKP4shLhDSUlJzJkzh7Vr15KXl4e3tzfnzp2jSpUqLF++nBo1ajB//nxtSGlYWBg6nY7V\nq1eTmJhI8+bN+e2337CysuLFF1/k22+/JS8vT+vWqFy5snauAwcOaIHGK6+8gsFgYNu2bbRv3549\ne/Zo223evJmtW7dqXRsdO3Zk/PjxmJiYsHfvXlRVpWnTpnh7ewPGLo7nn3+eDRs2cPHixVuGmep0\nOjw9Pe/q/VEUhVq1at3Vvg9SbkERofEZnItN49y1DM5dSyPi+h8tFa72ltRzs+fZRm7UdbOnTlX7\nx74LRDyabhtoqKp6QFGU6n9a3BfoUPx6NfA7xkCjL/CdauyIPaYoioOiKK6qqsb/3fFvrgYoyp48\nj7KVmZnJqFGjiIqK0paVdIN06tQJDw8PCgoKGDt2LDt37iQ8PJxNmzbh4+PD7t27te1CQkIASiUE\n+vv7061bt1JdIsHBwZw4cYKQkBBMTU0pKChg9+7d2sylAM2aNSM2Npa4uDjs7Ozo3bs3Y8aM4fTp\n08AfI1GCg4PZu3evlndVMmOqhYXFI/d99ef7ydEbiEorJDJNT2RqIVFphcRmFmpBhYOFDm9HU56t\nbU0NRzNqOJniaFnSEpMOmelEX4ToB3sbj5xH7fvsYeHr6/uP6+82R6NySfCgqmq8oiglbZ9uwNWb\ntostXva3gYYQ4g+bN28mKioKLy8vZs6ciYuLC8OHDycpKYm9e/cyceJEFEXBxMQEa2trkpOTef31\n18nNzdW6JcLDw7XjdezYUevqOHXqFJ6enhw8eFBbv2LFCjZu3EhKSgpgHL1hb29PdHQ0VatWpX//\n/nTs2BEw1rQwNzdHpyudH+Dp6UmjRo04deoUo0aNolevXly5coWff/4ZgP79+9+/N+wBU1WV69lF\nRKcXEpVuDCii0wtJzP4jCdbJUoeXoynN3Kyp4WiKt6MZTpY6GQUiHlt3NOqkuEVjx005Gmmqqjrc\ntD5VVVVHRVF+Aj5UVfVQ8fK9wFuqqp68+Xgy6qT8kazt8qF58+YEBQWxY8cOrYvjp59+YubMmQAE\nBgbSpEkTVq5cybhx4/7yGIqiMGHCBJo1a8bq1avZtWvXX27XsWNHgoKCyM7OxtbWltGjR/Phhx+W\nqo9xp6Kjo+natSuXLl0qdR0LFy7U6lw8bPL0RVxKzCI0Pp3QuAzC4jM5H5tKTqHx15eigFdFa/xc\n7fBztaWOmz11qtpRyVaqaz5o8vurbN2vUSeJJV0iiqK4AteLl8cCHjdt5w7E3bK3EOIvlUwgVlLk\nCmDMmDHMnj0bg8FA69atsbW1JTU1FQBbW1u+//576taty2effcYnn3yCqqosWbJE29/GxoYpU6Zw\n8OBBYmNj8fPzY8KECbRr147c3FySkpJwcXG5qwCjhKenJ+fOncPf35/jx4/j5OTECy+88JcTrZU3\n+iIDkTeyuZCQwaXELC4mZnIpMZPolBxK/g+zNjehtqsdbT0tqW5vSo8W9ahVxZYK5jJwT4jbuduf\nkm3ACOCj4s8BNy0fryjK9xiTQNP/KT9DiMeJwWBg165dbNu2jaKiIrp160bfvn1LBRVPPfUUJ06c\n4J133uHdd9+lYsWKLFiwAIPBgLW1Nbm5uaSmplKhQgVycnJ4//336dmzJwAfffQR27dvJywsjH79\n+qHT6ahfvz4vv/yyNmT1z6ysrPDw8PjLdf+WhYUFgwcPZvDgwffkePeaqqokZuRzISGDiwmZXEjI\nJCw+g8s3srTCVyY6heoVK/BEVTv6NXSjZmVbnnC1o5pTBXQ6RfvPuWG1x3sOFSH+jTsZ3roBY+Kn\ns6IoscB7GAOMTYqijAZigAHFm+/EOLQ1AuPw1hfvwzUL8dApKChg4MCBBAQEaMu++OIL2rRpw88/\n/4yNjQ0Ar776Kt999x0nT54sldugKApr166lY8eOZGVlMWHCBLZs2YK1tXWpbUryNMaPH68Ne30c\n5emLuJiQSWh8BhfiMwhLyORiQibpuXptmyp2ltR2taV9LRf8qthRs7ItNSpZY2H68AyXFeJhcCej\nTl74m1W3/BYrHm3y1x3HQjwicnJyOHPmDFZWVtSvX/+W5Mi/smTJEgICAnBwcGDSpEmYm5uzdOlS\nDh06xNSpU+nSpQv5+fm0bduWQ4cO8e677/L999+Tn59Pq1atmDFjBt27dweMeU3dunVjy5YtfPLJ\nJ7Rp0wYfHx+++uorTp06ha2tLc2bPx6jyg0GlaupOYQnZhGemKkFFzcXvLKxMKVmZRt61nOldhVb\nalWxpXYVWxwqSH0KIR4EKUEuAEmm2rVrFx9++CFBQUE4OjoydOhQpk2bhp2dnbaNqqrMnz+fDz74\nQEt+8vHxYcWKFXTp0uUfj1+7dm0uXrxIQEAAffr0AeD48eM0a9as1Hampqa8+uqrzJ8/nxMnTmAw\nGGjRosUtx8vJyaF58+bajKYlc4gAzJs3jzfeeOPu34xyqLDIwNXUXC4lZnLpehaXr2cRfj2TiOtZ\n5OkN2nZuDlb4udrxRFU7nnA1frg7WqG7R7OUPu4/J+WVPJeyJSXIhbiNDRs2lMoryMnJ4eOPP2bf\nvn0cOHBAS5L87LPPtLk/6tSpQ2pqKhEREfTq1YvAwMBbyoHfrGTa85tbGm7+4WzatClOTk7s3r2b\nRYsWUalSJbp06fK3rSUVKlTgt99+4+2332b9+vXk5OTg6+vL1KlTefHFh7fHssigEp2cTXhiFpcS\nMwm/bvwceSObgqI/AgpXe0t8KtkwpLknNSvb4FvZFt9KNthaPj7TwgvxsJBAQzzW9Ho9r7/+OgBT\np05l8uTJXLx4kSFDhnD8+HGGDh1KYWEhFSpU4NdffwXgm2++YeTIkRQWFjJq1CjWrFnDggUL+O67\nP4rnqqrKgQMHtHk6PD09OXv2LKtXr9aClTfffBMwTpVeMvdIQEAA/fr1Y/HixXTo0KFUouifOTs7\ns2rVKlasWEFubi42NjYPTa2GmxMzwxONiZnhiZlcSswiv/CPgMLd0YqalW1pX9MFn0rGgKKGi7UE\nFEI8RCTQEI+lU6dOcfr0aVJSUkhISMDHx4e5c+eiKArOzs6MGTOGadOm4e/vX2o/CwsLhg0bBhi7\nOSZNmsSaNWtKzYRaUFDA888/z48//njLeUsmL7OwsCA4OBgwzvtREiD06dMHR0dHEhMTSUtLw9nZ\n+bb3Ympqiq2t7V2/F/dbVn5h8SiPP0Z7/Dkxs5KtBbWq2DKshSc1q9hSs7iFwtpCfkUJ8bCTn2Lx\nyNi5cydLly4lPDwcDw8PXnnlFQYNGlTqv/yUlBQGDhzI3r17S+1bkt9QYs2aNYCxteHTTz8lPDyc\n2bNnk5+fz6pVq3jllVeAP6pwOjg4kJCQgJmZGcuXL+fHH3/Ezs6OMWPGYDAY+OKLL8jMzMTMzEyr\nzFkyYZmXl5d23vDwcFJTU7GwsNBGojws9EUGopOzuZSYpQ0dvZCQSUxKjrbNXyVm1qpsi6NMHCbE\nI0sCDfFIWLhwIZMnT9a+vnLlCgcOHOD48eMsXLhQWz58+HBtPo6nn36a4OBgQkNDuXr1KlOmTGH2\n7NkcPHiQsLAwAKZNm8aQIUMA2LJlC+fPn2fq1KlUrFiRpKQk3nvvPQBiY2O1OUTMzY1/NDdt2qSN\nFGnfvj19+vTBzc2NBQsWUFhYyNWrV3njjTcYP348ly5dwtHRkWXLlgEwePDg/1RA635SVZXY1P9v\n787jY7r3x4+/zixZJ3tkT2yxNE3EVqGWiqUIRVGqVPC9em9RSrWl/RV11e2S4paWam1FtdaKpUrt\nrdoiFTQRW4gsJBLZt8l8fn9MciqlWlckwef5eHjILGfOZ+bkzHnns7zfBZxOzua3lGzOXjVPyryY\nnoexbKmHRoE6rrYE+TgwsKUPjTzsaexhh4+T9QMzvCNJUuWQq04k4MGetX316lV8fX0pKSlh5syZ\n9O/fn927d/Pqq69SUlJCTEwMQUFBxMfH06hRI2xsbIiNjcXPzw+TyUTTpk3VwmU3s7CwICMjQ81V\n8c033zB48J+t9jZn6SwuLlZ7R44fP06zZs0Ac7E0e3t7LCws1MdLS0sJDw9n1apVFV6nefPm7Ny5\nkwsXLgDVe0yKjOY03LEp5hTcp5Oz+C0lm5xCcxVXjQJ1XGyp72aggZuBBu4G/GvZ4e9mwNri4ctH\n8SCfJw8zeVyql1x1Ij30tmzZQklJCWFhYbz99tuAeTnpiRMnWLRoEevXrycoKEjtpWjfvj1+fn6A\nuVz566+/zrBhw3ByciIzMxM7OzuKioooLi7mwIEDdO/eHaPRyIYNGwDzyhEHBwesra2JiYnh4sWL\nvPbaa8yaNYuioiK8vb3JyclhzJgxHDx4EDAXSwMqlDfXarWsWLGCkSNHsmHDBgoLC+ncuTP9+/fH\nwsJCDTSqSnpuEbEp2SjLtOIAACAASURBVGV1PcyBxfm0XLWXwlqvpbGnHb2DvXjcy4EAL3MvhZX+\n4QsoJEmqPDLQkB54hYWFADg7O1e4v/x2+ePe3t4AREdHk5eXp/ZU/PzzzwCEh4cTERGBRqNh2rRp\n/Pvf/6ZHjx60bt2apKQkEhMTsba2Zvny5TRq1Ijc3Fzs7OywsLDg3//+NxYWFlhYWDBhwgRmzJjB\nL7/8Qr9+/TCZTGzevBkwT/y8maIodOrUiU6dOt2nT+dWpSZBwvU8fisb+igPLq7l/D5PxdPBigBP\ne7oGuKtFw2q72KKtpHwUkiQ9OmSgIT3wysuYr1+/nn/84x889dRTxMTEsHjxYgD1It6iRQuCg4M5\nceIEbdu2ZdiwYURHR7Ny5UoURWHEiBFotea/zqdNm0ZhYSHz5s3j0KFDANStW5cvv/xS7ZXQ6XRo\nNBpKSkrIzs5W038//fTTzJgxA4CNGzcC5t6LKVOmMHLkyCr6VMwKikuJTc1Wg4rfks0rPwpKzGXN\ndRoFfzcD7Rq4mhNcednzmIe9nJwpSVKlkXM0JKDmj3GmpaWRkpJC7dq1b/s7M3ToUHWug6urK+np\n6QB07NiRXbt2qYmv4uLi6Nq1K1euXFG31Wg0zJs3j9GjR9/yuhkZGWpa7yeeeOKWBFp9+vQhMjKS\nTp06MWvWLPLy8hg/fjynTp3ipZdeomXLliiKQvfu3fHx8bmr93y3xyQjr5jTyVmcTs42T9RMzuJi\nep6aitveSleWMdM87PGYp3kuhazt8ffV9PPkQSOEICMjQ61a/L+6fv06AC4uLpXRLOkONBoNzs7O\nFSZ1yzka0gMtLS2N0aNHs2HDBkwmE5aWlgwfPpzRo0ezcuVKLl68SL169Xjrrbfw9fVl4cKFpKen\nY2NjQ3h4OFOnTmXp0qWcPn0aT09PhgwZQmxsLKtXryY6Oho3NzeGDh36p+XMnZ2d75he/MMPP+Tg\nwYPs3r27Qqrwhg0bMmvWrPvyxVdsNHEhPZe4lPKcFOb5FKnZhepzvB2tCfCy55lgL7WnwttRrviQ\napbyydb3usLKxsYGoEKRQen+KCwsJCMj466+22SPhgTUjL/UTCYTy5YtY/HixaSmphIQEEB8fDzx\n8fHodDrq169PfHw8Qgg1B0U5vV7P119/Te/evUlLS8PFxYX4+Hi6d+9OSkqK+jwLCwu++uorBg0a\nVGntvnTpEhEREezYsQO9Xk/fvn2ZOHHiLXNG7taxY8coKRXYeDXgZFIWJ69kcTIpi7PXctSy5nqt\nQv1aBhp52PG4l715kqanHPq4X2rCefIwSUtLo1atWvf8Onl5eYAMNKrKH4/bX/VoyEBDAqr/C1QI\nwYgRI1i+fPktjzk7OxMdHY2fnx979uxR51yEhYUxZMgQtmzZwurVq7GxsSExMRFnZ2dKS0t57LHH\nOHv2LM2aNWPgwIH88ssvREZGotfrOXv2LLVr167qt3lHRcZS4lJyOJmUxamkLA6fTSExy4ix7Gxx\nstET6O1AoLcDjT3saOxhT11XWyx0f109Vqoc1X2ePGxkoPFguttAQw6dSDXCvn37WL58Oba2tsyb\nN4+QkBCGDx/O0aNHycvLU3sH4uLi1G169erFCy+8wODBg7l69Sq7d+9m/fr1jBo1in379qnBxMGD\nB9Wu2QEDBrB+/Xq++uor3nnnnWp5r8ZSEwnX8zl3LUctb372am6FpaQO1npq22no1dCGp1s2Jsjb\nQSa7kiTpgSQDDalalJSUsHDhQr766ivS0tLU1R7jx49Xq4+GhYVx9OhRioqK+PHHH+nbty9paWnq\na5TX91AUheDgYHbv3s21a9cA1MmerVu3rjD+Gxoayvr167l8+XKVvM/swhLOpOaYV30kZxNbVu/j\ndoXDOj3mRpC3gxpUREVFAdAyyLNK2ipJjyKtVktQUJB6+7vvviM9PZ2vvvqKTz75hGXLlnHs2DHm\nz5/Pd999R8OGDQkICKjGFj94ZKAhVTmTycSAAQOIjIy85bHExET150GDBvHuu+8C8PXXX1OrVi2O\nHj0KmIOLJ598EoD09HQ1IVbz5s2B3xNj7dq1i4yMDHU4Zd26dYA5oVdlysgr5nxaLmev5nL2mjkl\n99mruRUmaDrZ6AnwsufF1rVp7GlPQ3cD/m4GbCzkaShJ1cXa2lotcFiuTp06tx0e++677+jVq9dd\nBRpGo/GOVZgfBY/2u5eqxaZNm4iMjMTJyYkFCxYQHBzM+PHj2bFjB6tWreLNN98kICCACxcuqJM+\n165dqwYTYJ7T0bx5c1q3bs2hQ4fIysqiSZMmPP300wC0atWKkJAQDh8+zOOPP05YWBhHjhzh1KlT\nODg4EB4e/j+1PaughN+SszmdnMW5a7mcu2Ye8sjM/70SqbVeSwN3A0/6u9DAzY5GHgYCPB1wt7eU\nQx+S9ADYu3cvERERbNmyRb3v4MGDREZGsm/fPmbOnKlWdh4zZgxpaWnY2NjwxRdf0LhxY4YPH67O\nLWvevDkff/xxdb2VGuGeAg1FURKAHKAUMAohWiqK4gx8C9QBEoCBQojMe2um9DApT+U9ZcoUdfVH\nZGQkDg4OFBUVERQUpBYtA3PpdK1WS2JiIo0bN2bgwIF8+OGH/PTTT/zwww8AdOjQga+//lodglEU\nhfXr19OnTx+ioqJYsmQJAB4eHqxdu/Yvy68LIUjNLlSzZpbnpri5EqmrwYJ6tQx0D/Skfi1zvQ//\nWga8Ha3RyAyaknTXBn3+y/+0nclkTkCn0VTMCfPtP9v85bYFBQU0bdoUMCflK0+y90dPPvkkvXv3\nplevXgwYMACAzp07s3DhQho0aMDhw4cZPXo0u3fvBsyVmH/88Uf1O+lRVhk9GqFCiPSbbk8Gdgkh\n3lcUZXLZ7TcrYT9SJcjLy+P48eNYWVnRvHnzajkJyouKOTk5qfdZWloSGBhIVFQUWq2W9PR0XF1d\nGT9+PFOmTLmlnc888wwnT55U82gEBgbesh9vb2+OHj3K/v371TwaYWFhWFpaVnieEILLGfmcuJLF\nySs3OF1W6+PmXoo6LjYEeTsw6AlfAr0deNzLHleD5R93KUnSA+Z2Qyd/R25uLgcPHuS5555T7yv/\nbgN47rnnZJBR5n4MnfQBOpb9vBzYyx0CjfLlYtL9JYRgxYoVLFmyRF0K5uXlxRtvvEHbtm3V593t\n8bh06RJ79+6luLiYli1b0qRJE/bu3cvOnTvJz8+nadOm9OvXD0dHR3Wb+vXrA/Dee+/h5uaGp6cn\nP/zwA1FRUVhaWrJhwwaEELi4uKDT6YiOjv7T/Xt5eVFYWHjHdtva2tKqVSsAYmJiSMs3cfFGCRcy\njZzPLOFcZgm5xebVHhYa8HPQ0cJdT20HK+o66vBz0GGj1wAm4AZk3yAh29xdVxXkOVLzyGNSOQwG\ng5psC2DJ0CaV+vrl33V3+7yCggJKS0vJy8ujqKiIkpIS8vLyMBqNFBYWkpeXR05ODg4ODmqtpJtf\ny2g0otVq//b+HzTXr1/n0qVL6u0GDRrc8fn3GmgIYIeiKAL4XAixCHAXQqQACCFSFEVxu8d9SJVg\n7dq1zJs3DzD/UuTk5JCcnMykSZNYsmQJjz32WIXnp6am8ssv5m7MNm3a4OHhUeFxIQQLFixg6dKl\n6n2LFi3C2dmZjIwM9b5ffvmFNWvWMHPmTH777TdycnJo0KABtWvXJiEhgb59+2IwGMjJyQFg2LBh\nuLnd+6+MEILsYkFyjpHknFKuZBtJyDJyMbOE3BJzUKFRwM9eR4i3Ff5OOuo76fFz0KGTwx6SJN2G\nwWAgNzcXAHt7e+rUqcOGDRvo168fQghOnTpVYQWLZHavgUZbIURyWTCxU1GUuL/c4g9k4pv7r7S0\nlL59+wKwZMkSRowYQWlpKaNGjWLp0qV8//33aqDRokULJk+eTEREhFp/QKPRMGnSJMaNG8f27dsp\nKSnBaDSydOlStFotQ4YMwdnZmUWLFpGRkYGFhQUffPAB3t7ezJ49m0OHDjF69OgKmTwDAgJ49tln\n2bJlCzk5OWrvyrhx4+56wqTJJLiQnkfMlRucSLzByaQszqflkVXw+9CHhU5DYw87nmnmQaC3OYNm\nTS9xLpND1TzymFSutLS0Skmyda8Ju/64nbW1NVqtFltbWywtLdHr9dja2vLiiy8yatQoPv/8c9at\nW8fq1at5+eWXiYiIoKSkhOeff57WrVuj0+mwsrJ6aBOIubi4VFi5d3PCrtuptMygiqJMB3KBUUDH\nst4MT2CvEKLRzc+VmUGrVlJSEj4+Pjg7O5OWlqYWBjt58iRNmjShXr16zJgxA51OR0ZGBqNHj0ar\n1dK7d2/AvErEZDKh0WhuKX708ccfM3HiRMCcs+Lw4cNYWFiQlZWFlZUVO3bsoFu3boB5UmdQUBAr\nVqzg8uXLhIWFsXbtWrKysnBzc/tb45nZhSWcvWpOdHUmNYczqTmcSsoip8gIgI2FlkAvBxq4G6hX\ny0C9WrbUdzXg7WT9wJU4lxe1mkcek8olM4M+mKosM6iiKLaARgiRU/bz08AMIBIIB94v+3/T/7qP\nB1FBQQGZmZm4ubnVmLXTdnZ2aDQasrKySE1NxcvLC/g9y2ZiYiJDhw4FzLVAwNzzMWzYMABGjx7N\nggULMJlMPPPMM1hbW7NmzRoAkpOT1f0YjeaLfXFxMenp6fj4+PDNN9+oj8+aNYvHH3+cMWPGUK9e\nPbZt20ZaWtptU4EbS01cTM/jt5Rs4lJziCv7PyXr97wU1notDd0N9GnmRRMfR4J9HPF3MzxwAYUk\nSdLD7F6uhO7AxrJubh3wtRBiu6IoR4E1iqL8H3AZeO4Or/HQyMzMZNKkSaxatYqioqI7rpjYuHEj\nn332GRcuXKBu3bqMHj2aZ5999r7lWLC3t6dPnz5s3LiRnj178uabb3L9+nWmTJkCmLN0enp6Ulxc\nrJZb9vPzU7c/fvw4YF4yWp5kKz4+nl9//ZUvvviCjz76CEVR8PPzIyoqCp1Op07+LP8L0GAwqJNA\nPT09CQoK4ujRoyQmJmLn6klsinmlR1xqDnGp2cRfzaW4LHtmeeGwkLrONPIwJ7pq6G4nl5FKkiQ9\nAGRRtUpQUlLCk08+qV5Ub54QOXbsWHUSJsCMGTOYNm3aLa8xbdo0pk+fXqntysrK4tdff8VgMODi\n4kJoaCgJCQm3PO/dd9+lR48elJaW8vTTT5OTk0OrVq04fPgwYA5UcnJy8PHxUTN3btq0SZ330bt3\nb9zd3Vm1ahX5+eY8E15eXri7u6srRlq0fIJtu/aTcD2fg6cvMnPeYnTOvng2bk5mgVFtSy07Sxp7\n2PGYpz2PeZoLh9WvZXgkC4fJbvqaRx6TyiWHTh5MsnprNVizZg2DBg3C19eXnTt30rBhQ77//nt6\n9+6NEIKEhAR8fX1JSEhQ/6r/4IMP6NWrF9u2beP1119HCMG5c+eoV6/ePbfHZDIxbdo0Zs+erV74\n/f39mTNnDnFxcezevRudTsfmzZvR6/Xk5uYSExMDwLfffktERASKovDaa68BMHv2bEwmEwMHDuTb\nb78F4Oeff6Zdu3YV9qvoLAnp0pO0AkgrAJ2jJxZOHmjsa6Gzd0PR/V663FSUj53Io2e7ZjR0NwcU\njT3tZG6Km8iLWs0jj0nlkoHGg0lWb60Ge/bsAcypaMtrbISFhdG9e3e2bt3K/v37GTJkCN999x0m\nk4lBgwYxadIkwFxz49ixY6xevZqNGzeqF/c/c/HiRT777DOOHz+Oq6sr4eHh9OjRo8Kwy6xZs5g5\ncyZgrv2RmprKuXPnGDhwINHR0UyaNImSkhLs7OwoKioiKSlJ3bZbt25EREQghCAiIqLCvjdv3syY\nceMRNs6s+2E/9q2epUnbLmDnRkaJjjyTnpSy5zoBBr1CbVdblLwMjuzdTkH6FYw3UilJT6R9y0A2\nbthQIb+GJEmS9PCRgUYlKM80mZlZMdN6+fDJ1KlTmThxItbW1gBqyfNyLi4uABQWFla4f+/evcye\nPZtTp07h4eFB+/bt+fTTTyskgVmzZg1jx47lk08+QVEUCgsLmT17NmAuANSnTx9KSkp44YUXWLdu\nHXPnzmXBggXo9XoGDBjAqlWr6NevH0OGDKGwsNCcqluro3/4v7Cs5Ucu1jj5NuTX80mkF8AWa1cU\nNNh0a4kNkGujp14tA0+42FDXxZY6rrbUcbHFz8UGB2u92s7MlzuyadMmMjMzCQkJoU2bNrLuhyRJ\n0iNADp3cg7i4ONLS0rhx4wa9e/fGxsaG+fPn06ZNG1asWMGsWbNuu52lpSX79++nVatWHDt2jC5d\nupCVlcXBgwdp08acm3/p0qWMHDnyttv37t2bl156iZiYGN59912KiorYvXs3oaGhnD59msDAQOrW\nrcuFCxfUbQ4cOECHDh1o0aIFx44do9QkiD5zkedGjiG9UEHv7I3OyQu9iw96Rw9Qfp8T4WJrgZ+L\nDQZRwI0r57AR+XQNacKAbh1wtLG4XROlSiC76WseeUwq190OnaSmpnLkyBFsbW1p3769ukruXoZO\nFEVh6NChrFixAjCvnvP09CQkJKRCUbWHVUJCAgcPHuSFF17429vIoZMqEBsby4gRI9TJknq9nkaN\nGnHmzJlbggOdTseXX35Jp06dWLduHRMnTqSoqIiQkBBq1apFWloaYC7O8+OPP/LZZ5/h7u7OwoUL\nAXjzzTcJDw9n5cqVauAybtw4OnfuTM+ePcnPz2fmzJm88cYb+Pj4oNebexFSU1PJzMzEycmJ7MIS\nth8/j13LPhQ1bcfTc/aRkJ5PcakJnhqLC0BpMbr8DOq5Gejcsi6NvZ2o52qgjqsNdlb6m95Rl/v6\n2UqSJP2R0Wjktdde47PPPlOX0Xt6erJo0SJ69ep1T69ta2vLqVOnKCgowNramp07d+Lt7V0Zzb5r\n1VFSPiEhga+//vquAo279dAFGufPn+fdd99l69atCCEICwtj6tSpNGzYsFJePyMjg06dOpGamoqj\noyP+/v5ERUVx5swZ2rdvT2lpKcnJyej1es6ePcs///lPtST5hAkT+PHHH9m2bRtWVlakpaVhMBjo\n2rUrO3bsYNeuXRX2Vb9+fd5//33AXDmw3KZNm+jcuTNgzmCn6CyJjr9MTFI2Ogd37Fs/h87Rg5DJ\nq7B1r01msQaohXPnUaAz4eNkQ2hjN+q62FLbxZa6rrZcjj+JRvGVf6lJklTjTJ8+nU8++QSNRkNo\naCjJycmcOXOGfv36cfToUfz9/e/p9Xv06MHWrVsZMGAAq1evZvDgwRw4cAAw95a88sornDx5EqPR\nyPTp0+nTpw8JCQm8+OKLam/K/PnzefLJJ0lJSWHQoEFkZ2djNBpZsGAB7du3r5C+fN26dWzZsoVl\ny5bdUlJ+xowZt93fsmXL+O677ygtLeXUqVO89tprFBcXs2LFCiwtLdm2bRvOzs6cP3/+T0vX29vb\nc+zYMVJTU/nwww8ZMGAAkydPJjY2lqZNmxIeHs7TTz/NiBEjKC4uxmQysX79+r+sZfKXhBBV/u/G\njRui/F9lio+PFy4uLgJzDRb1n5OTk4iNja2UfURERAhAhISEiJycHCGEEIcPHxY6nU5otVpx5coV\nIYQQkydPFoB44403Kmw/ePBgAYi5c+eKxMREkZGRIVxdXQUgevToIb788kvRrl07AQhFUUTCpcsi\nMSNPbDkSL+yadBUO7YeK4H/NEf0/+1m0/c+PwnfCWlH7zS23/PMZu0J4DI0Qrs9MEvatnxNW9VqI\nPs+/KIxG423f19GjR8XRo0cr5TOSKoc8JjWPPCaV69q1a3/5nPz8fGFvby8AsXPnTiGEECaTSQwf\nPlwAYuTIkSI3N1fk5ub+T22wtbUVJ06cEP379xcFBQUiODhY7NmzR/Ts2VMIIcSUKVPEihUrhBBC\nZGZmigYNGojc3FyRl5cnCgoKhBDma0+LFi2EEOZrxMyZM4UQQhiNRpGdna3up9zatWtFeHi4EEKI\n8PBw0bNnT/W7+c/2t3TpUlG/fn2RnZ0trl27Juzt7cWCBQuEEEK8+uqrYs6cOUIIITp16iTi4+OF\nEEIcOnRIhIaGqvsZMGCAKC0tFadPnxb169cXQogK71UIIcaOHStWrlwphBCiqKhI5Ofn3/KZ/fG4\n/eGafss1/6Hq0Zg+fTrXr1+nS5cufPrpp2g0Gl555RW2b9/O1KlT1WyW9+LIkSMA/Otf/8JgMADQ\nqlUrnnrqKXbt2kVUVBTe3t507dqV999/ny+//JJnn32WkJAQvv/+e9avXw+YI2gfHx9WfbuOG6UW\nPN6pHyNnzOVqThFNRwVw1ns3Wgd3On76K6JsvoRzj/EIUynpOenkRkeRl55MUVY6pvws/jP9LRrV\n9sTb0YZvl3zGtA8mExQUhI+PDwZfA8+//hZ9+/ZV049LkiQ9CC5cuEB2djb16tWjSxfz0K2iKIwa\nNYply5bdsbrz39WkSRMSEhJYvXo1YWFhFR7bsWMHkZGR6iq8wsJCLl++jJeXF2PHjuXXX39Fq9US\nHx8PwBNPPMHIkSMpKSmhb9++NG3a9C/3f3NJ+T/bH0BoaCh2dnbY2dnh4ODAM888A0BQUBAxMTF/\nWbq+/BoQEBDA1atXb9uWNm3a8N5773HlyhX69et3770ZPGRDJ5s3bwbg888/V/NRfPHFF/j6+rJ5\n82aEEH+50iExMZF169aRm5tL27ZtCQ0NrbBN+XLM8l8qMI+rnT9/Hvh9RUloaCjdu3dn+/bttGnT\nBmtra4o1Vlj4NaNjj4HM2J/JqW92cCPfGu+XFpELTFpnzmXhYmuBnXMtbiSdJT/uJyyNuWQlncOY\ndRUnC8jOyqzwyxMQEMDL3X7/ZW7e5HEAatWqxbZt2/6nz1KSJKkmcHV1RVEUkpKSuHbtmlrd+ddf\nfwWolGrPYJ5kP2nSJPbu3atmSAZzr//69evV1AXlpk+fjru7OydOnMBkMmFlZQVAhw4d2L9/P1u3\nbuXFF1/k9ddfZ9iwYRWuI39cYXjzJNY/29/hw4fVFY5gLnZZfluj0WA0GjGZTDg6OqqfzR/dvL34\nk4UgL7zwAiEhIWzdupVu3bqpcwzvxUMVaJQX/CqfEHnzz38sBnY7c+fOZdKkSZSWlqr3tW/fnsjI\nSDXAGDJkCIsWLeLjjz/G2tqaZs2a8cUXX5CQkECdOnVo06YNhSWlnLuWS/i0TzEF/cCpxAwUZx90\ndq4AJGoUbAuK6RHogTHrGgs+noWdtpTINSt4vK4XGItp1WoC6adPY2dnx9WcHCwtLRny/PN8/PHH\nKIpCbGwser2eDh06EBsby88//0zbtm0pKSlRJ5LK+RaSJD3o3N3d6dGjB9u2baNLly688sorJCUl\n8dFHHwEwfPjwStnPyJEjcXBwICgoiL1796r3d+vWjXnz5jFv3jwURSE6OppmzZqRlZWFj48PGo2G\n5cuXq9eNS5cu4e3tzahRo8jLy+P48eMMGzYMd3d3YmNjadSoERs3bsTOzu627fiz/f0d9vb21K1b\nl7Vr1/Lcc88hhCAmJobg4OA/3cbOzo6cnBz19oULF6hXrx7jxo3jwoULxMTEPNqBRmZmJgsXLuSH\nH35Aq9Xi7+/PiRMnGDduHJ9//jkajYaxY8cC0L179zv2Zuzdu5cJEyYA0L9/f/z8/Fi5ciUHDhxg\n7NixLF68mPz8fNq3b8+ECROYM2cOU6dONW+s0eHQoCXPvDGL/gsPEXPlBqayYNFCX4cmIY9T18WK\nFnVcaernxONe9mp5ciEEBz7/fxw+fJiuIU146qmnOHLkCKmpqfj5+XHy5ElycnJwcnLCxsZGbW/b\ntm0B+Oc//8knn3xChw4daNu2LRcvXuTKlSsYDAZGjx5d2R+5JElSlVuwYAEdO3bk5MmTvPTSS+r9\nI0aMYODAgRQUFNzzPnx8fBg/fvwt97/zzju8+uqrNGnSBCEEderUYcuWLYwePZr+/fuzdu1aQkND\n1V6JvXv38tFHH6HX6zEYDHz11VcAvP/++/Tq1QtfX18CAwPViaF/d39/16pVq3j55ZeZOXOmWrr+\nToFGkyZN0Ol0BAcHM3z4cAoLC1m5ciV6vR4PD4/fr3P3oNrzaFy9epW5c+dy6NAhHBwcGDJkCOHh\n4RV6JW4nOTmZ9u3bV8gVAdy2lLmtrS0//fTTHcfKBg0axJo1a3jrrbd47733ADh37hyNGjVCCIFe\nr6e4uBh/f39eef1tig3ubNofzXXsKHKoTamiRatRCPZxoE19Fx73cqChux11XGzQae88LyI1NZXB\ngwdXiKKDgoJYs2YNjRs3vuO2JSUlvPrqqyxatEhd9uXv78+yZcvUYOTvkPkBah55TGoeeUwq193k\n0cjJyWHFihUcOHAAg8HAoEGD6Ny5M4qiyBTkVeyBq3Xi7e1dIdMlmHsfevbsycGDB7G1tWXQoEF0\n6NCByMhIdu/ejaWlJXFxcWzfvp3g4GCmT59OYWEhb7/9NhcuXMDf35+LFy8C0K17d95+Zypnz11g\n87bvKS0uonuXUF588cUKPQStWrXi6NGjbN+9H88GQaRkFZJyPYsJb/4/sLBBY2WHhZM7Wpfa6Oxc\n1O3q17Klrb8rbf1daVPfBXurOwdIdxITE8OZM2fw9fUlJCTkrjJnXr16lejoaJycnHjiiSfuetKn\n/AKteeQxqXnkMalcstbJg+mBCzQcHR159tlnmThxIufPn2f8+PEVGl3O1dWV9PT0W+6Pj49XZ8Xu\n2befsGGv4N6sM3XbPUNiRgFG063vz1RciLYkj0D/2ng526KgsP/4aXKFJRorwy3PF6VGHG0s8HSy\nRZudwoHIr7HMv8pvB3dSy/H242wPGvkFWvPIY1LzyGNSuWSg8WB64DKDurm58c0332BhYUG7du2I\niIggKysLOzs7IiIiSE5OZubMmaSnp+Ps7Mzrr79OWloas2fPRmPjyJItPxHQWs8vF66zNy4P98Gz\nEMZi/Jxt6RHoZhz7HwAABw9JREFUyZFDB9n5w3YMNlZ07dwZrd6SPYeOkV0MV/SlFJvqYzSZaODj\nzoHtGzHeSKV5Qz98Xe1Yt3IZRbmZtA1pyYH9+9U2B675N6djTxN/OoZadzE8IUmSJEmPmmoPNFxd\nXdV89WlpaZw+fRqAwKbNCe0zmMvp2dhu/BlhaYdngwCu1evOJYd8/F4NQbG0ZfVVYNNp3O0scclL\nIGHzMp5q5MHyiE0ABEzsR3ZsLF9v2ULPnj0BOHOmGY0bNybPyooj2dnqfJD5lmeZMGEx+44ZK7Rx\nQP/+6s8mk0mdxFPebkmSJOnuaTQaCgsL1aWhUs1XWFh410Pz1R5o/PbbbyxZuZpi31YcOHkR9yEf\noXNwJ9ngRNc55l4Epx6vApBrMnLo/HV8nG1o6lzKnk2LKLmeiJtlKYnZaaSkpKDVanl76V719cvX\nQwcGBqr3+fv7Y2VlRWFhIfn5+Wpht7Fjx9K/f382bNhATk4O2dnZ/Oc//+GDDz7A39+fRo0aMWfO\nHC5duoSvry/Nmzevok9JkiTp4ePs7ExGRkaF5ZX/i/Lv+fJK2NL9o9FobqlA/leqPdBwaDeE6VFa\nNKfiMGZdxVRSRP75Iwzo3pGwp0KoZauna4fWFGReI7Rda3b9+CMA77yzjcioSKysrLhclvzE39+f\nuXPn0q5dO/X1mzdvzvbt25k/fz4ffvghiqKwePFiCgsL8fDwYMyYMRQUFNCxY0eGDx+Op6cnY8aM\nAaC4uJiDBw+yb9++CoV7tFot8+fPVzO5SZIkSXdPUZRKCQ4uXboE8Jer9KTqUe2TQYP/8xNF5w5x\nff8qStIuUrt2bS5duoRGo6Fjx44kJycTFxcHmC/wYWFhZGZm8tNPPwGwfft2PDw80Gq1BAQE3NKl\ns2fPHjp37owQgsaNG2Nra0tUVNRt21W/fn327dtXoXJfQUEB//3vf1m5ciWZmZm0atWKN954Qy3n\n/rCQk9xqHnlMah55TGomeVyq119NBq32whfJi8fwRPEJTuzbSlJSkrryRKPRsHv3buLi4nB3dycs\nLAwhBJs3b+ann37C1taWzz//nG7duhEcHExgYOBtx41CQ0NZtWoVbm5uxMXFERUVpaZhdXR05KOP\nPmLp0qUEBgaq+76ZtbU1kydP5tSpUyQlJbFx48aHLsiQJEmSpPul2ns0JEmSJEl6ONTIHg1JkiRJ\nkh5eMtCQJEmSJOm+qZahE0mSJEmSHg2yR0OSJEmSpPtGBhqSJEmSJN03VR5oKIrSXVGUM4qinFMU\nZXJV718CRVF8FUXZoyhKrKIopxVFGV92v7OiKDsVRTlb9r9Tdbf1UaMoilZRlGhFUbaU3a6rKMrh\nsmPyraIoMu99FVMUxVFRlHWKosSVnTNt5LlSvRRFmVD23XVKUZTViqJYyXOl5qrSQENRFC3wKdAD\nCAAGK4oSUJVtkAAwAq8JIR4DWgNjyo7DZGCXEKIBsKvstlS1xgOxN93+AJhTdkwygf+rllY92v4L\nbBdCNAaCMR8fea5UE0VRvIFxQEshRCCgBZ5Hnis1VlX3aLQCzgkhLgghioFvgD5V3IZHnhAiRQhx\nvOznHMxfnN6Yj8XysqctB/pWTwsfTYqi+AA9gS/LbitAJ2Bd2VPkMaliiqLYAx2AxQBCiGIhxA3k\nuVLddIC1oig6wAZIQZ4rNVZVBxreQOJNt6+U3SdVE0VR6gDNgMOAuxAiBczBCOBWfS17JM0F3gBM\nZbddgBtCiPJywvJ8qXr1gDRgadmQ1peKotgiz5VqI4RIAiKAy5gDjCwgCnmu1FhVHWjckjEMkOtr\nq4miKAZgPfCqECK7utvzKFMUpRdwTQhxcyEeeb5UPx3QHFgghGgG5CGHSapV2XyYPkBdwAuwxTwc\n/0fyXKkhqjrQuAL43nTbB0iu4jZIgKIoesxBxiohxIayu68qiuJZ9rgncK262vcIagv0VhQlAfOQ\nYifMPRyOZd3DIM+X6nAFuCKEOFx2ex3mwEOeK9WnC3BRCJEmhCgBNgBPIs+VGquqA42jQIOy2cEW\nmCfwRFZxGx55ZWP/i4FYIcTsmx6KBMLLfg4HNlV12x5VQogpQggfIUQdzOfFbiHEEGAPMKDsafKY\nVDEhRCqQqChKo7K7OgO/Ic+V6nQZaK0oik3Zd1n5MZHnSg1V5ZlBFUUJw/yXmhZYIoR4r0obIKEo\nSjvgAHCS3+cDvIV5nsYawA/zyfycECKjWhr5CFMUpSMwSQjRS1GUeph7OJyBaGCoEKKoOtv3qFEU\npSnmCboWwAVgBOY/0uS5Uk0URXkXGIR5BV008A/MczLkuVIDyRTkkiRJkiTdNzIzqCRJkiRJ940M\nNCRJkiRJum9koCFJkiRJ0n0jAw1JkiRJku4bGWhIkiRJknTfyEBDkiRJkqT7RgYakiRJkiTdN/8f\nUf7Zj7wc14sAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"sensor_var = 20\n",
"process_var = .001\n",
"process_model = (1, process_var)\n",
"pos = (0,500)\n",
"N = 100\n",
"dog = DogSimulation(pos[0], 1, sensor_var, process_var*10000)\n",
"zs, ps = [], []\n",
"for _ in range(N):\n",
" dog.velocity += 0.04\n",
" zs.append(dog.move_and_sense())\n",
"\n",
"for z in zs:\n",
" prior = predict(pos, process_model) \n",
" pos = update(prior, (z, sensor_var))\n",
" ps.append(pos[0])\n",
"\n",
"book_plots.plot_measurements(zs, lw=1)\n",
"book_plots.plot_filter(ps)\n",
"plt.legend(loc=4);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"It is easy to see that the filter is not correctly responding to the measurements. The measurements clearly indicate that the dog is changing speed but the filter has been told that it's predictions are nearly perfect so it almost entirely ignores them. I encourage you to adjust the amount of movement in the dog vs process variance. We will also be studying this topic much more in the later chapters. The key point is to recognize that math requires that the variances correctly describe your system. The filter does not 'notice' that it is diverging from the measurements and correct itself. It computes the Kalman gain from the variance of the prior and the measurement, and forms the estimate depending on which is more accurate."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Example: Bad Initial Estimate\n",
"\n",
"\n",
"Now let's look at the results when we make a bad initial estimate of position. To avoid obscuring the results I'll reduce the sensor variance to 30, but set the initial position to 1000 meters. Can the filter recover from a 1000 meter error?"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAhkAAAC+CAYAAACYnB30AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzs3XdYFMf/wPH33tE7KAgKVrD3bmJD\njVE0amLXqEk0GmMsib1ETbEQW2Ji+ZnEWCOW2HvvqICAir1QBEREQJB+N78/kP2KXcRwxnk9zz3A\n3O7s7I7nzs3OfEYRQiBJkiRJkpTfNAVdAEmSJEmS/ptkI0OSJEmSpNdCNjIkSZIkSXotZCNDkiRJ\nkqTXwqggDpqYmChHm0qSJEnSf4ytra3y8N+yJ0OSJEmSpNdCNjIkSZIkSXotCuRxycNsbW0LuggS\n4O/vD0Dt2rULuCRSDlknhkfWiWGS9fJsWVlZ1KlTh6CgIExMTChfvjwhISHodDpatWrFjh07ANDp\ndFSoUIErV65QtmxZ2rZty+HDh/H398fOzo7r169jb2/PtWvXcHd3x9zcnIsXLz7zPi57MiRJkiTp\nP8zIyIidO3fSrl07MjMzOXPmDIqi0Lt3b9asWaNut2fPHq5cuUKpUqUICgpi1qxZnDx5kkaNGpGQ\nkMDff/8NQJkyZWjbti2pqalUq1btmceWjQxJkiRJekOlpaUxZcoUPDw8sLOzw9PTk+3btz+2XZEi\nRdi0aRM3b97k1KlTREdHs3TpUqytrdVtrl27BkCLFi0wNzcHQKPR4OXllet9gKVLl9K8eXMSEhKe\nWb4Cf1wiSZIkSdLL0+l0tGvXjj179qhpBw8e5ODBg/zxxx/07dv3sX2KFi1K0aJFn5hfqVKlANi/\nfz9paWmYmZmh1+vZuXNnrvcBHBwc2Lt3r/qo6mme25OhKMpiRVFuK4py7qE0B0VR9iiKcuXBT/sH\n6YqiKHMVRbmqKMoZRVFqPi9/SZIkSZJe3oYNG9izZw+Ojo7s2LGD6OhoJk2aBMCIESNISUl5qfxa\ntmxJ6dKluXbtGrVr12bcuHE0bNiQQ4cOYWNjQ8+ePR/b53njYF7kcckSoNUjaWOAfUIID2Dfg78B\nWgMeD179gQUvkL8kSZIkSS9p8+bNAIwePZpWrVrh7OzM5MmTqVGjBgkJCRw5cuSl8jMyMmLTpk24\nubkREhLCtGnT8PX1xc7Ojg0bNuDg4PDSZXzu4xIhxGFFUUo+ktweaPrg96XAQWD0g/RlIntp1xOK\notgpiuIihIh+Wv7P62qR/l2yPgyPrBPDI+vEML1t9XL79m0AYmJicp17VlYWABcvXqRQoUIvna+P\njw8HDx4kNDSUIkWK0Lx5c6ysrJ54fS/HZdCmfqWn5pXXMRlFchoOQohoRVGcHqQXAyIe2u7mg7Sn\nNjIkSZIkSXp5DRo0YNeuXaxYsYLq1atTunRpNm/ezNmzZzE3N3/uzI+nMTExoWXLls/cRgjB7uup\n/BWURJv6T98uvwd+Kk9Ie2YIcTmv2TDIeeaGR9aJ4ZF1Ypj+K/UihEAIgUbzYhM/q1SpwtatW/H3\n96dnz55otVp0Oh0AkydPpmnTpq9Ulou3kihqa46thXGu99IydYzfcI5/Am/jWc7xmfnkdQprjKIo\nLgAPft5+kH4TcHtoO1cgKo/HkCRJkqT/lOjoaL766itcXV0pUqQIH3/8Mfv27aNXr15YWlpiZGRE\n06ZNOXjw4HPzMjU1Zc+ePQwaNAhra2t0Oh3lypXjzz//ZOTIkU/cR6cXnL2ZiF7/9O//yelZDPEJ\novUvR6jxw27a/XaUaTsucPhyLFdikui44Dj/nL7JsBYe/NmnzjPLqGQPn3i2B2MytgohKj/4ewYQ\nJ4SYrijKGMBBCDFKUZQ2wFeAF1APmCuEqPtofg8vkCYjfhqG/8o3gf8SWSeGR9aJYTKUetHpdFy6\ndAmtVkvZsmVRlNyd+9HR0dSrV4+IiIhc6Yqi8Oi9WKvVsm3bNt5///0XOrZeryc9PV2Nb/EkQgjG\nrj+Lj18EVYrZMqFNBeqVzj1m40L0PQatPE1o3H0GebqjURSOX7tDYHgCWQ8aJjZmRvzcrTrNyhcB\nIDExUd3/pRdIUxRlFeALlFMU5aaiKH2B6cB7iqJcAd578DfAduA6cBX4HfjyeflLkiRJ0ptu1apV\nlC5dmkqVKlG+fHkqVKigxpfIMW3aNCIiIqhTpw4BAQFcvHiRMmXKIITA1taW69evk5iYyJdffolO\np2PUqFGPNT6eRqPRPLOBATBr92V8/CL4oFpR7iSn03XRCb5YHkDonfsIIVjjF0GHecdISs/i78/r\nM7xlOb5+ryxrv3iH4EktWfJpHUa1KseWwQ3VBsbzvFBPRn6TPRmGx1C+CUj/I+vE8Mg6MUwFXS+b\nN2+mffv2QHawq8zMTGJjYzEyMuLw4cM0aNAAgJIlSxIWFoafn59a1goVKnDx4kUAUlJSMDc3Jz09\nHUdHR5KSkoiKisLFxeWVy/jXsRt8t+U83eq4Me2jKqRl6vnz6HXmH7xGpk5PDTd7ToXe5V33Qvzc\ntQaO1qYvnPcr9WRIkiRJkvR033//PQDffvstERERREZG0r9/f7Kyspg6daq6Xc7U0od7HLRarfq7\nXq9Xf+b8/ugjl7zYFBTJd1vO836lIvzYoTKKomBuouWrZh4cHNmUjjVdCYpIYGhzD5Z9Vu+lGhjP\nIxsZkiRJkpRHaWlpBAQEoNVqGTduHBqNBmNjYyZMmADAsWPH1G3fe+89AEaOHMnt27dJSkrC2Dh7\n5oalpSXXrl0jKiqKL7/8kvv371O7dm2cnZ1fqBxnbyYyadM5/jhynaNX7nAnOR2AQ5djGb4mmHql\nHPilWw2MtLlv+07WZkzvWJXz37/P1++VRat59UbNw+TaJZIkSZKUR8bGxpiampKenk5UVBSlS5cG\nIDw8HCDXAmTjxo1j48aN7NixA2dnZzQajTrl9P79+7niWpiYmDBjxowXKsP+izEMWhmITi/I0OnV\n9MJWpiSnZ+JRxJrf+9TGzFj71DwebXw8yblz5zh37hwuLi40atTohabayp4MSZIkScojrVZLly5d\nAOjUqRNbt27ln3/+4ZNPPgGgW7du6rYeHh4cPXqUtm3boigKOp2Ohg0bsn79er744gsKFy6MpaUl\nbdq04ciRIy8U52K1XzifLwvA3cmKY2OaETChBX/3q8e3bSviWc6R9yo6s/SzOtiYGT83r6e5e/cu\nrVq1okqVKnTv3p2mTZtSrlw5Tp8+/dx95cBPCSj4gVPS42SdGB5ZJ4apoOslMjKShg0bEhoamiu9\natWqHDp0CDs7u8f2ycjIQKfTPXdGyNMIIZi77ypz9l6mSVlH5vesiaXp63k40bJlS/bs2YO1tTXN\nmzfn9OnThIeHU7hwYXXKbo5HB37KxyWSJEmS9AqKFSuGv78/8+bNY9euXWi1Wtq3b8+AAQOwsrJ6\n4j4mJia5/k5Ky2TajoscvhyLqZEGM2Ptg5cGa1NjXOzMKGprjoudGS625qwLuMmqU+F0quXKtI+q\nYPwCjzvy4syZM2oDIyQkBDc3NzIyMvD09OT48eMsW7aMTz/99Kn7y0aGJEmSJL2iQoUKMXHiRCZO\nnPjS+564HsfwNcFEJ6bSsqIzWo1CaqaOtEwdqRk6biWmceRKLPczdLn2+8rTneEtHw/6BZCZmcmu\nXbuIjo6mUqVKNGjQIE8zVc6ePQtk92a4uWUH9DYxMaFnz54cP36cM2fOPHN/2ciQJEmSpAKQlqlj\n5q5L/HnsBsUdLFj7RQNqlfjfcupBQUH4+PiQnJxM33fepWWbdtxJ1RGdkIaFifaxaJ05fH196dKl\nCzdv3lTT6tevz/r161865kaRItlBtwIDA8nMzFRnw/j5+QE8d/aLbGRIkiRJ0r/sfNQ9hvoEcuV2\nMr3ql2CsV3ksTLJvyUIIxo0bx/Tp09Xt582bR6VKldi7dy/lyz/9xh4XF4eXlxcJCQmUL1+eOnXq\nsGPHDk6cOEGnTp04evToS/VoeHp6UrJkSa5fv06LFi3o2bMnJ06cYMmSJWg0Gvr06fPM/WUjQ5Ik\nSZLInkXx559/cuLECWxtbenZsyfNmjV74k05PT2dc+fOYWpqSqVKlV7qxn3kSiwDlgdgbWbE0s/q\n0qRs7pVMt2/fzvTp0zEyMqJ///4UL16cRYsWERISgpeXFw4ODsTHx1O3bl2GDRtGuXLl1H2XLVtG\nQkICjRs3Zt++fRgZGREbG0v58uU5fvw4AQEBjw2QvX//Prdu3aJIkSKPjSHRarWsXr2aVq1acfjw\nYQ4fPgxkBwn77bffKFeuXK6In4/JWVr233wlJCSInJdkGPz8/ISfn19BF0N6iKwTwyPrxDDlR71c\nuHBBODs7CyDX64svvhB6vT7XtvPmzROOjo7qNuXKlRN79+59oeNsDLwp3MdtE+/POSRiElOfuE2H\nDh0EIKZNm6amhYWFCUVRHiufhYWFOHTokLpdv379BCB+/fXXXHl27dpVAGLJkiVqWnJyshg4cKAw\nNzcXgDA3NxdffPGFSEpKeqxMsbGxYsaMGaJ3795i9OjR4vz58+p7j9zTc93vZZwMSZIk6a332Wef\ncevWLerVq8eyZcuYNGkSZmZmLFy4kK1bt6rb/fXXXwwaNIjY2FjKlClDkSJFuHTpEm3atCEoKOiZ\nx1h89AZDfYKoWdyeNV80wMnG7InbRUZGAtCwYUM17eTJk+piaZMmTeLIkSN06tSJlJQUPv/8c/U9\nV1dXAI4eParum56ezsmTJ3O9L4Sgc+fOLFiwgNTUVNzc3EhNTWXhwoV07NjxsYXZChcuzIgRI1i6\ndCnTp0+nQoUKz7+oOQf6t1+yJ8PwyG9ohkfWieGRdWKYXrVerly5IgBhY2Mj7t27p6Z7e3sLQHTq\n1EkIIYROpxOlSpUSgJg7d67Q6/UiIyND9OrVSwCiR48eufLNzMwUa9euFb379BENB80QJUZvFZ8v\nPSVSM7KeWZ4+ffqovSg5mjVrJgBhZGSk3jszMjKEi4uLAMTp06eFEEJcv35dGBkZCUB07NhRzJw5\nU9SpU0cAokyZMiIrK/vYx44dE4Cws7MTgYGBQgghgoODhb29vQDEkSNHXvj6yZ4MSZIkSXqKO3fu\nAFCqVKlcYcCrVKkCQGxsLAC3b9/mxo0b2Nra8uWXX6IoCsbGxowaNQqA48ePo9MLwuLusyM4grq9\nxzLgj4Ps1lcjwqoCSYHbOf/7cLLSU59ZnsGDB6PValm4cCH169enS5cuHDx4EIDmzZurQSyNjY3V\n2R/JycnqOSxZsgRjY2P++ecfRowYgZ+fH05OTqxbt04NnHXo0CEAevToQfXq1YHs4GEff/xxrvdf\nlRz4KUmSJL3Vypcvj5mZGcHBwRw9epSGDRuSlZXFokWLAKhVqxaQvYiZRqMhOTmZ2NhYdfrm9evX\nAbBxcOLD+cc4c/PBQMjiTbFySqKolRZ3s9vsP7eRY1FR/PDDD3h7ez+1PLVq1WLFihUMGDCAkydP\nqo86ABISEoiPj8fOzo7169cTFBSElZWV2lAA6NmzJ40bN2b58uVERUVRuXJlevTogY2NjbqNhYUF\nkN1welhMTAxAniORPubRro1/4yUflxge2Q1seGSdGB5ZJ4YpP+pl2LBhAhAajUY0adJElChRQh1Y\nefXqVXW7nEGZderUERs3bhR//fWXKFq0qECjFe+O9xGlx24Tvx++JlxrNBEacxuxf/9+dd+cRxRO\nTk4vVKakpCSxdu1asXjxYnH8+HF1YKq5ublaPkBMmjTppc83LCxMaDQaoSiK+OGHH0RgYKCYMmWK\nUBRFaDQaERoa+sJ5PetxiVy7RAIKPva/9DhZJ4ZH1knBuX//Pv/88w/h4eF4eHjQvn17zMyyB04+\nr150Oh07d+7kzJkzODs707Fjx1zf6iE7QuawYcNYtGgRWVlZQPajh7/++osmTZqo24WGhtKoUaNc\nga4AKn46jftOVfipU1W61HbD1NSUjIwMEhMT1WOlpaWpPQR6vf6lI3BevnyZgQMHsn//fgAcHBwY\nMWIEo0ePfqEVUR/l7e3NmDFjHkufMmUK48aNe+F8Hp7CKtcukSRJkt4oR48epUOHDsTFxalprq6u\nbNu2jSpVqpCSkqI2OB4VFhaGl5cX58+fV9OGDh3KqlWraNOmjZpmbGzMvHnzmDhxIgEBAdjZ2VGv\nXr1ci38BlCxZksDAQBYsWMC+ffswMzOjcNM+HE2wYWhzD7rUzg69Xb16dU6dOsWiRYsYMWIEgPr4\npVq1ankK8V22bFn27dtHVFQUCQkJlClTBlNT05fOJ8fo0aOpWrUq8+fP59q1a5QuXZovv/wSLy+v\nPOf5KNmTIQHyG5ohknVieGSd/Pvu3btHyZIliY+Pp3bt2jRr1oxt27YREhKCra0tZmZmxMTEYG9v\nz1dffcWECRPUxceEENSrVw8/Pz9KlCjBRx99hJ+fH0ePHsXMzIwrV66oUzrzao1fBKP+OUPnWq78\n1Kmq2nhYt24dnTt3BqBu3bpoNBpOnDgBwMqVK+nRo8crHdeQPKsnQ84ukSRJkgzW6tWriY+Pp0GD\nBpw4cQJvb28CAgKwtrYmMTGRmJgYjI2NiY+P54cffqBnz57qvv7+/vj5+VG4cGGCgoKYPXs2hw8f\npl27dqSlpbF48eLHjpel07P8RBghUc+IYvnAocuxjN1wlkYehZn6UZVcvROdOnVi7ty5WFtbc+rU\nKU6cOIGlpSWzZs36TzUwnkc+LpEkSZIMSnBwMIsXLyYqKoro6GgAWrVqpT66uHTpEklJSQD079+f\nfv364e/vz6hRo1i3bh2nTp2ibt26XLt2DYDGjRtjZ2cHZIfDbtu2LZs3b1bfz3ErMY3Bq07jFxqP\niZGGqR9WoVOtx3s6hBAsPhbK9B0XKFvEmvk9az5xqfXBgwfzySefcPjwYYQQNG7c+LGxIP91spEh\nSZIkGYzffvuNwYMHP5a+evVqxo8fj1arZceOHWq6l5cXiqJQp04d+vTpw7x589i9ezd169alVKlS\nABz1C2Te3gscuppANTdbju/NjoaZ8z5k90p8vTqItEwdUz6szNbgaEasDSY4IoFv21bExCi7ERF/\nP4OR686w90IMLSoUYUanqlibGT/1fKytrXON/XjbvFIjQ1GUr4F+ZE+jOQt8CrgAPoADcBroJYTI\neMVySpIkSf9xly9fZsiQIQAMHDiQd999l6VLl7Jnzx7Onz9PvXr1aN68OcuWLQOyYz14eXkRHBwM\nQGpqdpArrVaLEAJ94TJ49J5CumNFZuy9jg33OXXjDqJkJ4p0KUOFZh+RkaVn7r4rzDt4lbJO1szr\nWRN3Jyu61nbjp12XWHT4Ouej7zG/Z03C76YwZFUgd5LTmdi2Ip++WzJPAzjfJnke+KkoSjHgKFBR\nCJGqKMoaYDvgBawXQvgoirIQCBZCLHh4Xznw0/DIAW2GR9aJ4ZF18npNnDiRH374gd69e7N06VIg\ne6pnmTJlCA0NfWx7rVbLb/Pmk27jxsmQq+w8dALF0gG7oiXJMLVHa1sEY7LQXfPl5qHVZMaGorUq\nhH2dtri824l7mQqWJlruZ+joWtuNye0qYW6SezbJ1jNRjFp3BlMjDffSsnC1N+fX7jWo6mr3b1yS\nN8LrnMJqBJgripIJWADRQDMgZ1TLUmAysOCJe/O/D61kGGR9GB5ZJ4anoOskODiYFStWcOHCBWxt\nbWndujVdunRRZ1W8qXKmmRYqVCjXNS5XrhyhoaG0b98eZ2dnihcvzrnzF9lyLpYfTisY2+uB0ti8\nWxrd/XhSkuLQxVwn5ehKUi4eo4VnY74YMZCrV69SqFAhWrRogaW1Daci0/GNTKOOiyWNS2QQcibw\nsTI5Az82sWPuqUSqFDalXw1LMm5dxf/Wv3RR3gAeHh5PfS/PjQwhRKSiKDOBcCAV2A0EAAlCiKwH\nm90EiuX1GJIkSVJuBw4cYOzYseh0OiA7DPTly5c5efIkc+bMwcjozR1qV7ZsWQC2bdvGhx9+iLm5\nOdHR0eqKop07d6Z4aQ92X0/lfEYNCrnq0cSHk7T7F+z0iVw/H4Q+M4ORI0fS8uOWnD5tw+TJvuzZ\ns4euXbvSrFmzXMd7x82Md9yeHF/jYcVtjZj5XqH8P+G3QJ7/NSqKYg+0B0oBCcBaoPUTNn3m8xjZ\n7WgYZDew4ZF1YngKuk4yMzNp3749Op2OQYMGMWTIEEJCQhgwYAAnTpwgNDSUbt26FUjZ8kP58uVZ\ntmwZly9fplOnTtSoUYPDhw+TmppKi/few7R8EwZtCeFeWhYN3QvzZdMyNCjjRUBAHbZs2cL3wado\n06YNP/30EwAtWrTg9u3bzJo1i8uXL9O3b98CPsP/pocflzzqVZq8LYAbQohYAEVR1gPvAHaKohg9\n6M1wBaJe4RiSJEnSA6dOnSIqKgp3d3d+/fVXFEWhbNmyREREMHToUNavX28wjYzMzEyOHj3KvXv3\nqFu3Li4uLs/dx8rKij179tC9e3eCg4PZtWsXAK3bfYTrhyMZsTaYuqUcGO9VgWpuucdE6PV6gMce\nGeX8ndPzI/27XqWREQ7UVxTFguzHJc0Bf+AA0InsGSZ9gE2vWkhJkiQJMjKyJ+rZ2NjkmtWQM4A+\n5/2CtmvXLvr27UtkZCSQPUCzf//+/PLLLxgb557uGRwczLJly7h9+zbVqlXj008/JTAwkICAAKKi\notDZl2TmsTtcunyXke+X44smZdBqHp/RkRNVc/PmzaxevZrOnTtz9OhRFi5cCGTH2ZD+fXmO+CmE\nOAmsI3ua6tkHeS0CRgPfKIpyFSgE/JkP5ZQkSXrr1a5dG2tra06fPs3ixYvR6/WEhoaqjweaN29e\nwCWECxcu0L59eyIjI/Hw8FDLtGDBgscW3Zo5cybVq1dn9uzZrFixgpEjR1KuXDkCAwOpXqMm18zL\nM3x7BFqNwrovGjDI0/2JDQwAFxcXhg4dik6no1u3bhgbG9OkSRPi4+Np3bq1QVybt9ErhRUXQkwS\nQpQXQlQWQvQSQqQLIa4LIeoKIdyFEJ2FEOn5VVhJkqT8FhkZyW+//cZPP/3EiRMnKIj1nF6UtbU1\n48ePB6Bv377Y2dlRunRpzp8/j4eHB5988knBFhD49ddfSU9Pp3v37ly8eJG9e/eqq4YuWLBAjdQZ\nFBTEyJEjURSFgQMHsmjRIho2bEhcXBzd+n1Fl//z5Zd9V+hQoxjbhjSkRnH75x575syZ/Pzzz5Qq\nVQq9Xo+joyPjxo1j/fr1Mp5FAXlzhyFLkiS9olmzZjF69Ohcz+tbt27N2rVrsbS0LMCSPd2oUaOw\nsbHB29ubsLAwjI2N6dSpE7NmzcLa2rqgi0dgYPY00M8//1xdfrxx48aUL1+eixcvqouGxcfHA/Dl\nl1/y22+/AdCrVy/Kvt+btJqduRiVwC/dqtO++otPUNRoNAwdOpQhQ4aQkZGBiYnJUxsXsbGx/PHH\nHwQEBFC4cGF69+7NO++8k+fzlp5MNjIkSXor7d69W12C+8MPP6RIkSKsWrWKHTt2MGLECBYseGp4\nnwKV881/wIABxMXFYWVlhbm5eUEXS+Xk5ARkNzY8PT0BiIuL4+rVqwDqYM4chQplTw1NSMlg3IYQ\nNA36kBZ+luEflH2pBsbDFEV55hLogYGBvPfee7mWjv+///s/xo8fz48//pinY0pPJldhlSTprTR/\n/nwAJk+ezPr161mwYAGHDh0CYMmSJSQnJ+faPiMjg+PHj7Njxw4uXbr0r5f3URqNBkdHR4NqYADq\nI5vx48fz7bff8scff1C3bl2ysrLQaDRMnTqV9evXU6ZMGQBm/fIrK31v0OrnI+wOuUXysRXE+Iyn\nSZ2qr6V8Qgh69epFXFwcjRo1YtmyZYwaNQojIyOmTJmixuSQ8ofsyZAk6a2UswLnBx98oKZVq1aN\n4sWLEx4eTnR0tBrJcP/+/fTq1YuoqOwZ+RMnTuSjjz5i6dKlWFlZ/fuFN2AdOnRg4MCBLFiw4LFe\nga+//pqxY8cC4OxemTZDvbGs0oLxm85jlnqH2xt/Iin8PB06dMDd3f21lO/06dOEhIRQpEgRdu/e\njZlZdjAujUbD9OnTWbJkCQ0bNnwtx34byUaGJElvpZIlS3Lu3Dl27txJzZo1AQgJCSEiIgJTU1Oc\nnZ0BCA0N5YMPPiAlJYWSJUtSsmRJTp48yfr16zEzM2PlypUFeRoGR1EU5s2bR+fOnVm1ahVJSUmc\nOXOG8+fPU6deA3aF3MLnVDgHL8diU7sd9y8dI+n0NtJvhgDQvn17dd2S1yE2NhbIDvyV08CA7Abm\nw+9L+UM2MiRJeisNHDiQrVu3MmHCBM6ePYuzszPLly9Xu9NzBlH+3//9HykpKbRr147x48ej0Wiw\nsrKiatWq+Pj44O3tjaurawGfzasJCwvD29ubnTt3otVqadu2LaNHj1YbWi9LURQ8PT3x9PRECMFX\nE2cQXfQ6Y08I9AEBOFqb0sHdhN++7o6Sdo9169aRnp5OtWrV1NDir0uVKlXQaDQcO3aM4OBgqlWr\nRkZGBn/+mR1tIafBKeUP2ciQJOmt5OXlxY8//si3336Lj4+Pmt6sWTNmz56t/n327FkAevfurc6W\nKF++PPXr1+fIkSNcuHDhjW5kXL16lXfeeSfXN/iff/6Z9evX4+vrS9GiRfOc95bgKH7Zd4WrmZWw\nruZB0pUTaMP9wSSZX/z8EEIwZMgQ2rVrlx+n8kKKFSvGxx9/zLJly6hTpw6NGzfm4sWLREZGYmtr\nS//+/XNtn5iYyOLFizly5AhWVlZ06dKFNm3ayCmxL0g2MiRJemuNHz+eHj16sH79eu7fv0+TJk1o\n3LhxrhtIzrf5kydPUqJECQCSkpI4d+4cwAuFy35d7qVlYqzRPLY8+csYO3YssbGxNG3alJkzZ5KR\nkcHQoUPx8/OjcePGREVFIYSgdevWDBkyhA0bNrBhwwYyMzNp0aIF48ePp3z58rnyTE7PYtKmEP45\nfZOKLjZM+6gKbiKWrwZ8R3BwMDGAqakpX3zxBTNmzHjFq/DycqKArlixgn379gHZi7MtX748V32G\nhobStGlTwsLC1LTly5fTvXtYnQVDAAAgAElEQVR3li9fjlab9+v+tlAKIvBMYmKietCccLhSwSro\nhZ+kx8k6MQy+vr688847aDQaPvzwQ0qXLs3evXsJDAykaNGiaLVaYmJiqFatGiNHjlTjQLxuBy/d\npv+yAPRCULGoDTWL21OzhD01i9tRzM78hb5p63Q6zM3NyczM5ObNmxQrlj1ldPPmzbRv317dTjE2\nxbiQGyaOJTEqXByTwiUQuixSLh5BcyuEw/t2U716dQCCIxIY6hNI+N0UvvJ0Z0hzD4y02T1AQgjO\nnTvH3bt3qVKlCg4ODvlyLfL6WYmIiCAoKIjChQtTr149tacqR+vWrdm5cyc1atRg2LBhREVFMXXq\nVJKSkli6dCm9e/fOl/K/6R5eIM3W1jbXPzzZyJAAeUMzRLJODMfUqVPVSJs5TE1NSU9/PKDxnDlz\nGDZs2Gstj++1OD756xRlHK3wLO/I6bAEgiISSM3MDipW2MqUqq62D73sKGz1eNyIrKwsdS2RxMRE\nbGxsEELg1aUPRy5GYe5WiYpNPiA8Pl1dTltkZVC6sAX3M+H2/Sz0mWnYJoUxe1hPrsUmM3PXJZys\nTZnTtTr1Sv87y6O/js9KTEwMzs7OmJqaEhERgaOjIwCLFi1iwIABNG/enL179+bb8d5kz2pkyMcl\nkiRJzzFu3Djatm3LjBkzuHfvHs7OzixatAgnJydWrVpF7dq1+eOPPxg+fDgTJkzgs88+w8bG5rWU\n5XR4PH2X+lHcwYIV/erhYJm9ymiWTs/FW0mcDo8nOCKRMzcTOHDpNjnfI2uXsGeQpztNyzmqvRxG\nRkY0bdqUgwcP0n/Mjzg36srhK3HcLdOVwmVAk5VGmSK2fFTLjjmTRhB5wR+RFMuN9DRA4eC5MLqM\nmoEo+y6fL8u+0XtVcWbah1WxtTB+UvHfGHfv3gWyH5flNDAge+AowJ07dwqkXG8a2ciQJEl6AVWr\nVmXo0KEAajTQ4cOH06xZMwC++eYb1q1bh6+vLwcPHnwtgxlDohL5ZPEpHK1NWflQAwPASKuhcjFb\nKhezhQbZaffTszgXmYh/WDwrT4Tx6RI/KrjYMMizDK0ru6AXAq8vvuWiaxtO2FRA73eDtGsnSQ07\nS3rkBdYtnke7D+oAMOOTALLio9RxCBqNQn13J5IP/kncnv9jq/9VzM3N8Szn9J8YFFmqVCns7e0J\nCwtj69attG3bFr1erwZxq1WrVgGX8M0gGxmSJEkvKecxc4zOkvEbzhIQFo+jtSmJZdtgq5TgRAw4\nXoujnLN1roZAXoSHh7Nw4UJOXQwnzP0jbCzMWNmvHk42Zs/d19LUiHqlC1GvdCE+b1SaTUGRLDh0\nja/+DqRU4cukZGQRcy8dN/eKpJ7ZScjWPxAZqTg5OZF85zbz5/1GtapV0Gq1auOiUKFCxMXFYWFh\nwahRo0hPT6devXq0qVHylc7T0JiZmTFs2DAmTZrEBx98wDvvvMOtW7e4fv06JiYmr/2R2H+FHJMh\nAfL5vyGSdWJ4/P39iUnOYtOZW2w7F4uxQ1FMNFC3lANXI6KJvJuC1ir3aqFO1qaUc7amgosNZRwt\nURSFLJ0gS68nUyfQ6wXWZkbYWRhja26CrbkxlqZaIhNS2X08iAUr14N1EUyKlUdkZRDz9xjGDe7H\nd999l6dz0OkFu0JusfjoDSxMjfjknRI0LeuERqOQkJCAoijExMRQv359dRGzR2k0GjQaDVlZWWi1\nWnbt2lWgS6m/rs+KXq9n7Nix/PLLL+r4Gzc3NxYtWkSrVq3y9VhvMjnwU3oueUMzPLJOXo1er+fS\npUvodDoqVKjwytMNs3R6Bv91kB1XU1EUME0I4+bR9aRcPo7ISFW3m+Y9g+59BxJ+N4VLt5K4EJ3E\nxVv3uBKTTIZO//LnkZGGhS6Ziq72uNwN5v9mfIdOp8PPzy/Xv43du3czZcoUfH19sbW1pXv37kya\nNAkTExOCgoKwsLCgRo0aj82geJpLly4xefJkNm/erE5h7dWrF3/88Qc7duxAr9fToEEDfvzxR/WR\nUUF53Z+VuLg4/P39sbS0pH79+hgZyYcAD3tWIwMhxL/+SkhIEDkvyTD4+fkJPz+/gi6G9BBZJ3m3\nZcsW4e7uLgABiOLFi4u///47z/kl3M8QPX8/IUqM3ioGLNonbsaniOTkZDF69Gjh5OQkAFG1alWx\nfPnyp+aRkaUTYXfui/C4++JSRIzo9PGnwsjCRigmFsLY1km06tZP7Ai4KrafiRKr/cLF3DW7hda6\nsCjj7iGysrLUfIYOHSoAMWTIEDVtzZo1QlEU9XxzXo6OjsLKykr9293dXezbty/P1yFHamqqSE5O\nfuV88ov8rBSsR+7pue73chVWSZIKnBCCI0eO4O3tzYIFC4iJiclzXkeOHKFDhw5cvXqVIkWKUKxY\nMcLDw+nRowdbtmx56fyuxybz4fxjnLwRx5e1behXw4ZiduZYWloyffp0YmJi0Ov1BAcH0717dxYu\nXEjt2rVxdnamWbNmbN68GQBjrYbihSxwtTdnYJ/urFvxFyL9PlXKu0NKPDt9/uDbAd3IvOFH2AEf\nrh7dii7pDuXLlc3VC1OxYkXgf7MfdDodI0aMQAjBqFGjiI+PJyAgAEdHR2JjY0lOTqZ69eoUK1aM\nq1ev0qZNGzWQWF6ZmZlhaWmZK02v15OZmflK+Ur/QY+2Ov6Nl+zJMDzym4DheVvqJCEhQXh6eub6\nBm5iYiIWLlyYp/xatWolADFo0CCRlZUldDqdmDBhggBEnTp1nriPXq8Xt++lidSMLKHX69X0w5dv\niyqTdooa3+8Wp27EPbNO9Hq96NOnz2O9CYCYPXu2us2xY8cEIBwcHMTly5eFEEKEhYWpPSKPvkxM\nTMTZs2eFEEIkJSWJOnXqCED8/PPPQgghgoODBSBcXV2FTqcTQgiRnp4urK2tBSAqV64shBAiMzNT\ndO/eXQCib9++ebq2TxIaGip69OghTE1NBSDeffddsWfPnnzL/0W8LZ8VQ/WsngzZyJCEEPJDaoje\nljrp2bOnAEShQoXEoEGDRJs2bdQb7PHjx186v5yba1RUlJqWkpKiPk7IyMjItb1OpxcDV/iLEqO3\nihKjtwqPcdtFrR/2CM+ZB0TpsdtEy9mHRHjcfSHEs+vk6NGjAhAWFhZixYoVIjQ0VEybNk0AQqvV\nCldXV/U8ATFgwICHyqATjo6OAhC2trZi8ODBombNmup1MDIyEg0bNlT3dXFxEfHx8UIIIYKCggQg\n3Nzc1EbG5cuX1X09PT3V45w4cUIAokqVKi99XZ8kOjpaFCtWTD1WzjXWaDRi69at+XKMF/G2fFYM\nlXxcIkmSQbpz5w6rV69Gq9Xi6+vLb7/9xtatW/nmm28A1JgELyMnCNbD603cvHkTIQTm5uaPDQBd\ncOga28/eoneDEoxqVY5PG5bkvYpFqOBsw8f1ivPPl+/g5mDx3ONu3LgRgC+//JKePXtSokQJxowZ\ng7OzMzqdjps3bwLZgwgBtm/fru576NAhdYGyESNGMHfuXE6dOkXDhg2B7EcRR48eJS4ujlq1arF3\n717s7OwAqFy5Mm5ubkRERDB+/Hju3bunHgvA09NT/f3SpUsA2NvnngGTV3PmzCEyMpL69esTGhrK\nvXv3GDZsGHq9ntGjR6tTfaW3l2xkSJJUYMLDw8nKyqJChQp4eHio6TmBrK5evfrSeXbr1g3IXjV1\n7dq1bNy4kU6dOqnvPTy74siVWGbtvsQH1YryXbtKfNnUnbGtKzD1w8oMrmWBl/N9yEx7oePmjEd4\neKyCn58ft27dAmDo0KFkZGTwxx9/ANnrZvTu3Zv9+/fj7e2t7tOrVy8AtFotH374oXoue/bs4cyZ\nM/j5+anjMnK2mzlzJoqiMH36dGxtbXPN9ti0aRNr1qxh7ty5amyHjz/++IXO6Xl27twJwLRp0yhR\nogRWVlZ4e3tjZ2dHSEhIrsaO9JZ6tGvj33jJxyWGR3Y3Gp63oU5iYmKEVqsVRkZG4vr162r6mDFj\nBCB69Ojx0nnevXtXVKlS5bGxDWXKlMn1COVmfIqo/t0u8d7sgyI5LVNN9/f3F9WrV1f3s7a2FpMm\nTRI6ne6ZdbJlyxYBiCJFioiAgACh1+vVMRCACA0NVbetX7/+E8dfODg4iNTUVCFE9viNnPElM2bM\neO5579ixQzRs2FBotVphb28vPv74Y+Hi4vLYMdq2bStWrVolBgwYIAYPHiwOHDiQaxzKy8i5Trt3\n71bTUlNT1UdWkZGRecr3Zb0NnxVD9trGZAB2wDrgInCB7GC2DsAe4MqDn/aP7icbGYZHfkgNz9tS\nJ126dFFvzsOHDxedOnVSb4iHDx/OU55JSUli1qxZomnTpqJRo0ZiypQp4u7du+r7qRlZ4oNfj4hK\nE3eKa7eT1PSwsDBha2ur3vArVaqklmXy5MnPrJOsrCzRuHFjdXsLCwv195zBlzlyGh9169YV7777\nrujevbs6ZqNy5cpi4sSJ6mBYCwsLcevWrRc+94cbDHfu3BFTp04VrVq1Eh07dhR//vmnOnD04dfH\nH3+ca5rsi/r222/VMR7+/v4iPDxcHfxas2bNPDdeXtbb8lkxVK+zkbEU6Pfgd5MHjY6fgDEP0sYA\n3o/uJxsZhkd+SA3P666T2NhYMW/ePPHtt9+KtWvXivT09Nd2rGeJi4sTDRo0yHXT02q1Ys6cOfl+\nrPPnz4upU6eK98b9JUqM3ip2no3K9f6IESMEIN5//32RkpIihBBi48aNAhA2Njbi8OHDz6yTpKQk\nMXjwYPWbfOHChQUgzM3Nxbp168S9e/fEsmXLhJGRkQDE1atX1X3Pnj2rNjRyXpaWlmLbtm35dv6f\nf/65OhPF29tbjBs3To2jkZfZPHFxccLDw+OJM2IOHDiQb+V+Hvn/V8F6ViMjzxE/FUWxAYKB0uKh\nTBRFuQQ0FUJEK4riAhwUQpR7eN+HI35euXIlT8eXJCnv9u/fz6RJk0hL+994Azc3N+bOnYurq+tr\nPfadO3fYsGED58+fx8bGBi8vL2rXro2/vz/BwcFYWlrSvHlznJ2d8+V4QggS0/X8stiHg6cvYOJS\nFutq75Pou4ZKumtMnz4dM7PsdUA+//xzgoKCmDt3Lg0aNFDz6Ny5M6GhoSxdujTXeIinycrKIiUl\nBSsrK3744Qe2bt362Dbdu3dXB7jmSEtL48CBA9y4cQNHR0datmyZb1GRMzIyaNasGenp6axevZrS\npUsD2QNQJ02aRMWKFVm6dOlL5xsfH8+ff/7J3r17SU9Pp2bNmnz22WdUqlQpX8otGb6Hx1Pl51Lv\npYFY4C9FUaoBAcBQoIgQIhrgQUPD6RWOIUlSPouOjmbChAlkZmZSt25dKlWqxL59+wgPD2fMmDEs\nX778ta2ieenSJQYNGpQrDPH27dvp2rUrw4cPp169evl2rPQswZLgJHwj00jOEODUgkKtWqDoMyl0\n/wZ3gzZy7N49FixYwNdffw2AlZUVQK4Bi6mpqeqy3tbW1i90bCMjI3WWy4QJE/Dw8OCff/4hOjoa\nV1dXunbtykcfffTYfmZmZrRu3fqVzvtpkpOTSU9Px8rKilKlSqnpr7p0ub29PSNGjGDEiBH5Uk7p\nP+bRro0XfQG1gSyg3oO/fwF+ABIe2S7+0X3l4xLDI7sbDc/rqpOJEycKQHTs2FF9Zn7v3j01GJSv\nr2++H1OI7LECVatWFYBo2rSpWL16tfjuu+/UIE67du3KU76RkZHi66+/FuXLlxcVKlQQo0aNEqcu\nhomWsw+JkmO2iq9XB4pqnYcJs1I1xbS5/yd0uuxzzokZYWNjo8bO+Pvvv9VYFXPnzhVbt24VzZs3\nVwN5vcmfk6ysLFGkSBEBiI0bN6rpOeMqWrVqVYClezVvcr38Fzzrccmr9GTcBG4KIU4++Hsd2WMw\nYhRFcRH/e1xy+xWOIUlSPrtx4wYArVq1UnssrK2teffdd9mwYQOhoaHUr18/34975swZzpw5g5OT\nE9u3b8fc3Fx9b9KkSSxbtoyWLVs+M4+UlBSWL1/O3r17MTY2pmHDhvz4449ER0er24TpHVidVQc7\nG2uWfVaXRh6OuH7TlrTISDp7NUejyT7nevXqYWtrS2JiIvHx8Tg5OdGlSxc2bNjA2rVrGTJkiJqn\nvb09ixYtIisrK5+vyr9Hq9UybNgwxo4dy0cffcT7779PYmIix48fB1B7cyQpP+W5kSGEuKUoSoSi\nKOWEEJeA5sD5B68+wPQHPzflS0klScoX7u7uAGzevJm+ffuiKArx8fEcPnwYgDJlyryW4+YEoSpd\nunSuBkblypWB/63F8TSxsbF4enoSEhKipq1atQqA+vXr4z1jJivO3Wd3aCZpkReonhpJI4/3gexn\nxpGRkWzevFm9mR46dIjExETs7e1xcHAAsm/EPj4+dOzYkb///pvExETeeecdBg0aRLFixdTVPt9U\no0aNIiYmhl9//ZUdO3YA2Y+IZs2a9dwGniTlxauuVzsYWKkoiglwHfiU7ABfaxRF6QuEA51f8RiS\nJOWjzz77jOnTp7NlyxYaNmxInTp12LBhA3FxcdSrV++1LZddtWpVjI2NOXXqFL6+vjRo0ID09HQW\nLFgAPH+Z7pEjRxISEkLZsmUZOXIk9+7dY8TosZgWr4J1076MO5bOzfhM2pWz4tcZY9nmYAfz5wAw\naNAgDh48yPDhwzl+/Dg2Njb4+PgAMHDgwFxLd2s0Grp27UrXrl1fy3UoSBqNhjlz5jBixAgOHz6M\niYkJ7733njp+RJLyW55nl7yKh2eX5NfIaenV5HxDe103GOnlvc462b59O927d+fevXtqWqVKldi+\nfTvFixfP9+PlGDRoEPPnz0ej0VC/fn2uX7/OrVu3sLOz4+y5c+wNzcDCxIjmFZwoZGWq7peeno6t\nrS3p6ekcPX2eq6nm7LsQw8HzkWiMTUGXQbNKrnSvW5yKtlm4urpiZWVFUlKSmsf333/Pd999h16v\nV9O6devG0qVLMTExeaHyy8+JYZL1UrAeHsidn7NLJEl6Q3l5eXHz5k3Wr1/PrVu3qFq1Ki1btnxs\nXY/8NmdOds/C77//ro4FqFixIov/+osFp+6y8mQ4ABoFapd04P1KzrSsWIQbUbGY1e1M4bIN6Ln6\nOgClCltiFRPEjWNb0cRdZ/7tW+j1er744guAXKG1ASZOnMgnn3zC5s2bycjIoHnz5lSrVu21nq8k\nve1kT4YEyG8Chui/XCe3b9/mzJkzODg4UK1adSZsCmHVqXAGNi1Dmyou7A65xa6QGC7F/K8nAr2e\ntJshfFCrJGN7t6VUYUu6du3K2rVrgew1Q/R6PampqZiamnL06NF8v3b/5Tp5k8l6KViyJ0OSpNdu\n27ZtzJkzh/Pnz1O0aFH69evH559//sTeEScnJ1q0aIFeLxi/8SyrTkUwyLMMI1qWQ1EUKhez5ZuW\n5Qi9c5/9F29ja25MmO82hs8Yyx+r4MyauiQlJXHhwgUURcHDw4PLly8D2YNAZ8yYIW84kmQAZCND\nkqRX9uuvv+aa8hkdHU1AQAC+vr4sWbLkicG99HrBuA1n8fGL4CtPd4a3LPvYdiULW/JZw+zAUaJm\nf9LuxTF16lROnToFgKOjI3PnzqVr167ExsaiKAqOjo6v8UwlSXoZcql3SZJeSXx8PKNHjwbgxx9/\n5MaNG6xYsQILCwuWLVvGsWPHHtsnU6dn9D9n8PGLYHCzJzcwHqUoCuPGjSMyMpJdu3Zx4MABIiIi\n6NatG4qi4OTkJBsYkmRgZE+GJL0lbt26xd27dyldurS6Vkd+2LlzJ6mpqXh6ejJ+/HgASpYsSXBw\nMDNmzGDDhg00bNhQ3T7+fgaD/j7N8WtxDGnuwdctPF4qjLmtra2M6SBJbwjZkyFJ/3HXr1+nVatW\nuLi4UKlSJVxcXB6byvkqMjMzgcfX9ciJvZCRkaGmXY5JosP8Y/iHxvNTp6p8897zezAkSXpzyZ4M\nSTJAcXFx7N69G51OR7FixXBxcclTPgkJCTRt2pSIiAhMTU1xcXEhNDSUyZMnk5qayvTp01+5rE2b\nNkWj0bBt2zY2bdpEu3btOHPmDPPmzQOgRYsWAOw9H8NQn0DMTYxY1b8+tUrYPzNfIQT79+/n0KFD\nWFhY0LFjx1yrPUqSZPhkT4YkGZhZs2bh6urK+PHjmThxIsWLF2fMmDHkZbr54sWLiYiIoGbNmty8\neZMbN26wZcsWAH755ZfnhvJ+EcWLF+err75Cp9PRocOHOFSoT4MuA7ln50GNDv1JL1qDaTsu8Ply\nf0o7WrFl8LvPbWAkJSXRvHlzWrRowQ8//MDYsWMpW7YskydPfuXySpL075E9GZJkQP755x91yeza\ntWtjYmKCr68v3t7euLq68tVXX71UfkeOHAFg2LBhFC5cGIC2bdvSoEEDfH198ff3f+74Br1ez6FD\nh7hx4wbu7u40atTosUccs2fPJr1wWbZHGKFxcFXT7wKj/jmbfdwqRZjZpQZmxs8P+PXNN99w4MAB\nChcuTJ8+fYiNjWXFihV899131KxZk3bt2r3MZZAkqYDIRoYkGZDZs2cDMHPmTJo0aQLA5cuX6dmz\nJ7Nnz2bQoEEvNYbB0tISgKioKDVNp9Opq5ZaWVk9c/+LFy/y0UcfceHCBTWtatWqrF+/Xl1I7fi1\nO8zYdYnA+yUp5WFBv/pFqV7SEVNjI1b9vZI/f19EVEQYf+pSSTvQE29vbwoVKvTUYyYnJ7N8+XIA\nDh48SKVKlYDssOejR49m4cKFspEhSW8IGfFTAmTEPENhZ2dHYmIiMTExhIdnh9iuUaMGpqam6HQ6\nUlJScq1g+jxbtmyhXbt2WFtbM2PGDKpUqcL8+fNZuXIlJUqU4Nq1a08MlpWp03P+5l3af/IV97S2\nWBevgEkhNzLS7pOZkoSpRtC4QR2S03UEhMXjbGPG0BYedKrlirE2+ynspEmT+P7774HsxkxycjIA\n1atX58SJE5iamj52XIBr167h7u6Oq6srERERanpQUBA1atSgQoUKnD9//oWvQX6SnxPDJOulYMmI\nn5L0hihatCiJiYkcO3YMNzc3APz8/NDpdNjb2z/1xvw0bdu2pUePHvz999/qmh4Apqam/P7779yI\nS2HO3ivcTc4gOT2L5PQs4pPTSErXoRNAvV7YZKVTo6Qj5VxsSU3PYNP23aRkCUKjYrGwtmVCmwp8\nXL9ErscgcXFxeHt7A7By5Uq6devG5cuX8fLyIigoCB8fH/r06fPEMru4uGBhYcHNmzcJCAigVq1a\nAGzatAn431L1kiQZPtnIkCQD0q9fP4YPH84nn3xCp06dMDY2ZsOGDQD07dsXjeblxmorisKyZcto\n3bo1S5cu5c6dO9SuXZthw4ZRyqMcbX89SmxSOuWdrbHU6rh+0Z9bEaHo05LJiL1BRsx1hnzalVlf\nzfxfnqdW8Msvv/C5+3jatmiLm5vpY+Msjh07Rnp6Oo0bN6ZHjx4AlC9fnm+++YbBgwezd+/epzYy\nLCws+Oyzz/jtt9/w9PSka9eu3L59m82bNwO89LgUSZIKkBDiX38lJCSInJdkGPz8/ISfn19BF+Ot\nl5GRITp16iSAXC9PT0+RnJycr8catTZYlByzVRy7EitSU1OFh4eHAIS1tbV49913hVarFYCwt7cX\ner1eCCGETqcTNWvWFIDQaDQCEIqiiHbt2omYmBg17+3btwtA1KhRI9cxp0yZIgDx2WefPbNsKSkp\non379rmugZGRkZg1a1a+XoOXJT8nhknWS8F65J6e634vezIkyYAYGxuzZs0aDhw4wKJFi9Dr9fTq\n1QsvL698XYZ9S3AUq/2zFyV7x70wK1eu5MqVK5QrV47jx4/j4ODA6dOnqVWrFvHx8TRq1IguXbqw\nZcsWTp8+DYBGo6F69eqEhISwefNmIiIiOHXqFEZGRjRp0gR7e3sCAwMZM2YM/fv35/Tp08yYMQOA\nDz/88JnlMzc3Z+PGjQQEBHDo0CHMzc3p0KFDnuOFSJJUMGQjQ5IMjKIoNGvWTI2Ymd+D2SLupjBu\n/VlqFLdjWIuyQPa4D4A+ffrg4OAAQM2aNfH09OTAgQMcO3Ys1xok1tbWnD59Gnd3dyIjI2nQoAGB\ngYHs2LGDDz74AAsLC37++Wf69OmDt7e3Oj4DoEOHDnh5eb1QWWvVqqWOyZAk6c0jg3FJ0lskU6dn\niE8gAHO71VBngtjbZwfHunjxorqtEIKkpCQAevTowYABA/jggw8A6N69uzoAs1ixYvTu3RsAX19f\ndf/evXuzb98+WrdujYuLC9WrV+fnn39mzZo1Lz22RJKkN1OB92RkZOkxMZL/4UjSv+GXvVcIDE/g\n1+41cHOwUNN79OjBd999x7JlyyhUqBBNmjTBx8cHf39/7O3t+f3337GwsOCvv/5iy5YtXLt2LVe+\nOX8/OiW9WbNmNGvW7PWfmCRJBqnA7+5RCakFXQRJeiscuHSbeQev0qW2Kx9UK5rrPQ8PD2bNmgXA\nnDlz6NChAz4+PpiYmLBkyRIsLLIbJO3bt8fc3Jx9+/YxaNAg9uzZw+jRo/Hx8UGj0dC1a9d//bwk\nSTJcBd7ICL+bUtBFkKQnWr9+PQ0aNMDMzAw3NzcmTJhASkr+/nvNzMxk9erV9OnTh08++YR169aR\nlZWVr8cA2HchhgHLAyjvbMPkdpWeuM3XX3/NyZMn6devH61ateLrr7/m7NmzuaJrOjg4sHDhQjQa\nDfPnz+f/27vv+Jru/4Hjr3NvpoRsIWQIQglJSIkatUdtLbVn+1PEqIagqpOqr1KzaK3WHjUaHRRB\npEGJxIhNIlYSWbKTez+/P25yK4gis/V5Ph73Iffccz7nc+9xct/5jPenffv2zJkzB9BlKXVxcSny\nukuS9O9V6t0lNxNkkCGVPUuXLmXMmDH659HR0cycOZOgoCD++OMPDAwKf+ukpKTQqVMngoKC9NvW\nrl1Lq1atCAgIKHT5eXisOD4AACAASURBVH47e4exG0N5pXIFfhjeiHJGBde9UaNGNGrU6KnlDR48\nGHd3d5YuXcrly5dxdnbm//7v/2jWrFmR1VmSpP+GQv+mVBRFDfwF3BJCdFEUpRqwCbAGTgGDhBBZ\nBR0vWzKksiYlJYWpU6cCMHv2bN577z1Onz5N3759OXToED/99BN9+vQp9Hk+//xzgoKCcHBwwM/P\nD61Wy//+9z8OHjzI7NmzMa7blpN3MnG4dAozIwPKGasxMzKgpr05netVxkD95IZIIQRnz54lKSmJ\nmyp7pgdcxtPRktXDXqWCiWGh6w26mSfff/99kZQlSdJ/V1G0ZIwHIoAKuc+/AuYLITYpirIMGAF8\nW9DB0fFyTIZUtgQFBZGcnIy3tzf+/v4AvP7660yePJmJEyfy888/F0mQsXr1agC2bt3Ka6+9Bui+\nvFu3bs2akJuosh5QyUxNYk4yqVk5pGVpSMvSoNEKFvxxmYnt3XjDvTIq1d9LBRw/fpwRI0Zw9uxZ\nzOq1xabTOOyVZFYPaVNkAYYkSdKzKlSQoShKVaAzMBOYqOiWh2wN9M/dZS3wCU8JMiKiY/WL20il\nT14LuHjxIgDp6en5Po9bt24BEBcXV+jPSQhBbGys/nleeYqiYO7ZCVWDt/CpYsz7jS1Q5wYRQgiu\nXLnKmXg4kqjCd0MoLhZn6OduToNKRkRE3mPCp3PRWtbHoe/bGDp7kX79FH/9NJMJMfsZPXp0oeos\n/U3eJ2WTvC6lo2bNmgW+VtiBn98AkwFt7nMbIFEIkTdyLRqo8rQCYlI0hayCJBUNjUbD/fv3eeWV\nVyhXrhznzp1j48aNZGZmcubMGf3y402bNi30uRRF0d+YeWuTACzYfQybDmNQ3zvP+IcCjOPHj9O7\nd2/69+/Hl779ODdvII3FBTJyBF8eTWTQzlhm/KVQofMkLF/ri0vdhrxRwxT/1ywROZls2rSJ1NTU\nQtdbkiTpebzwUu+KonQB3hBCjFYUpSXgBwwD/hRC1MjdxxH4RQhR7+FjH17q3ePLIMI+bo+FqWzK\nLU0v81LJGo2Gr776igULFhATE4OpqSkeHh6EhIQ8tm+TJk0IDAzEyMio0Oddv349AwcOBMDHx4c0\nm9ok1ulJRlQ43/SqTU1XFwDUajU+Pj5kZWVhb2+Pubm5Pi/FdytXYebehnO3k/hl40rOBf3GluXz\n6N7l74ya9erV4+zZs4SEhNC4ceNC1/tl9jLfJ2WZvC6lq7iWem8KdFMU5Q3ABN2YjG8AS0VRDHJb\nM6oCt/+poJvxaVhUsfin3aRSFhkZyf79+zE0NKRjx47Y2dmVdpXyCQsL4/vvv+fmzZvUqlWLkSNH\n4urq+o/HTZw4kYULFwJgaWlJYmIiISEhuLq6Us7ehdvmbpiotLSq58KXfiOLJMAAGDBgAPfu3WPG\njBmEJ6ixbdaDnLuX8W9iSb8+b+l/cf7vf/8jKyuLQYMGsXLlSgwMDFi8eDHjxo3jy5lfcOXKUBTF\nibNrbhB6+yI3rl7WnyM1NZXo6Gjg76yekiRJJeWFgwwhxFRgKkBeS4YQYoCiKFuBt9DNMBkC7Pqn\nsqIT0nCXQUaZpdVqmThxIosWLUKr1fWMGRkZ8fnnnzN58uRSrp3OsmXLGD16NA+3zC1YsIDNmzej\nKArXr1/H1dWVTp06YWBggEajITExkeTkZBYvXoxarWbHjh106dKFiIgI2nfuTrxzC2jcE1u1mhyt\nIEgraD7/T6rZmuHlZEm7V+xp84p9oTLWdhnwLifNfTh6LQHn8rDJfziVbfMHA3mpuidPnoyhoa7F\nb/To0UyfPp1r164RExODvb09AwcOZNeuXUyfPp2cnByqV6/OwoULSUxMxNvbGzc3txeupyRJ0oso\njjwZ/sAmRVG+AEKBlf90gJzGWrbNmzePBQsWYGBgQLdu3UhPT+f333/H39+f6tWr8+abb5Zq/W7c\nuIGvry9CCEaNGkXLli3ZunUr27Zto1evXvrACMDFxYU33niDrVu3Ehsbi6mpKVqtlk6dOtG1a1dy\nNFpOJZth3ncuaq2Kypk3+enTYZgbGxAenURoVCKnohIIvBjLT6duYW1mRHdPB/p4O/JK5Qr56pWZ\nnUPYxetUMDOllksVdOOide6nZDJv3yU2Ho/CzNiA6Z1fYVATZ4wNHl9pNS9V9/Xr13F3dwcgJiaG\n1NRUVCoVZmZmAPTq1YuBAweybt06/Pz89Mfb2NjI6aaSJJWKIgkyhBCBQGDuz9eAp2fzeUgFEwMZ\nZJRhQggWLFgAwObNm+nVqxcAX3/9NX5+fnzzzTelHmRs2LABjUbD22+/zdKlSwHo2rUru3btIjs7\nm8qVK9OjRw/27dvHlStX9PuYm5uTkpICQMipM6w5ep31x6K4HJOCHSlcWzODnv26UrG8CQA+rjb4\nuNoAkKPRcuRKHFv/usm6kEhWH72Be5UK2Jkbcy85k8iYRFJzACW3lUPzF5UtTHCuaIGtuTGHLsaS\nlq1hkI8z49u6YW1WcBdMv379CAsL47333iM+Ph5LS0tmzpyJRqOhR48emJubA7ql19euXUuvXr3Y\nsGEDSUlJ+Pj4MGrUKLlEuiRJpaLUM3462ZTjpsyVUWY9ePCA6OhojI2N6dmzp35737598fPzIyIi\nohRrpxMXFwfoBjjmyQswQNfNMGHCBMLCwvD09ARg+vTpzPj4ExZvP8CsjQcoV6Mxn/x8nurWxrxd\nJZnFU/6P7LS0AgMoA7WKVrUq0qpWRRJSs9h1+ha7wm4Tm5KJJiWOuyf3o0lJwJQssrUCjXEFsqwr\nY92sNTfj0/GpboN/x9rUqGj+j+9v3Lhx7NmzhyNHjjB06FD99qpVqzJ//vx8+6pUKnr27JnvWkmS\nJJWW0g8yrMtx4c6D0q6GVAAzMzP9YMjjx4/rZyccOXJEv4+TkxMAnTt3ZurUqfrnJaVhw4YA/Pjj\nj/j6+mJhYcGJEyf0rzdp0gTQJdlCbYiJswcnqMFrXx0k9kEWFao3JCF0Dyln9hMZe50DuccNHjz4\nmVJlW5kZMbRpNYY2rYZWq6VmzZrEX7vG7NmzmTRpEqmpqfTv35+An1bTze4+e5Yte673Z2pqyr59\n+1i7di0//fQTGRkZtGnThlGjRmFra/tcZUmSJJWkF57CWhgPT2FdevQ2q4/e4MLnHfNlLpRK1tOm\ngH3wwQfMmzcPW1tbRo0aRXp6OkuWLCE9/fEWKHt7e/7880+qVatW7HXOk5GRgbu7O1evXsXS0pIG\nDRpw5MgRsrOzKV++PLfuxbL3fCwr9vxJRKKCysgUI5WgTZ3KdPesws6ln7P826XUqFGDzMxMHBwc\nGDFiBCNGjEClUj12ru3bt3PixAmsrKzo169fvgGVN2/exMnJCWtra2JiYlCrdWMsjh07ho+PD25u\nbnz99dcYGhrSokULTE1NC3xfclpe2SOvSdkkr0vpKq4prEXC0bocWRot9x5kUNmi4F+4UtF48OAB\n58+fx9LSEjc3t3yDEQvy+eefExYWxv79+/n888/zvda8eXP9mI0JEyZw+PBhOnbsSHJyMhqNhvbt\n2zN9+nRq165dLO8HwMTEhH379jFgwAD+/PNPDhzQtUWY2FRBXb8D9T8KQBiYoMrIITUiiLTLIUx7\npzeDmrlz4MAvrFmlG5u8detWfXfKk0RFRdGuXTsuXbqk3/bpp58yZ84c/UDLvKAhNTWVBw8eYGlp\nCcC9e/cAuHz5Ml27dgV0U0rnz5/PkCFDXvi9CyG4evUqqamp1K5dG2Nj4xcuS5IkqcgJIUr8kZiY\nKPIegRdjhLN/gAi5Giek4pOTkyOmTZsmzMzMBCAA4e3tLUJDQ4UQQpw4cUKcOHGiwOM1Go349ddf\nxfvvvy8mTZokTE1NBSCuXr2q3+fIkSP6sh9+VKhQQYSFhRX7exRCiPDwcDFv/R7Rb2mgcPEPEE6T\ndgnbbpOFcdW6AhAmJiZPrOOoUaP+sexWrVoJQLi5uYlZs2aJIUOGCEVRBCCCg4Mf269Dhw4iKChI\n7NixQ1hbW+vP1bRpU+Hp6al/vm/fviee75+uybFjx0SDBg305dja2or58+cLrVb7/B+c9Ez+6ZpI\npUNel9L18He6eOT7vtSDjGuxKcLZP0Bs/etmcX8OL7Vp06bpv4zc3d2FlZWVAIS1tbW4devWc9+k\nRkZGAhD37t3TbxsyZIgAhKIo4uSpUHEi7Lzo2PNtoS5vJ9r27Ccu30sWsQ8yiuPtCSGEuJWQJoat\nPi6c/QOE12d7xf9+uyAuRN4VS5cuFZMmTRLLli0TiYmJYtu2beL1118XlStXFo0bNxarVq36xy/m\ny5cvC0CYm5uLuLi/A2I/Pz8BiGHDhum3hYeHC0tLyycGM8uXL9fvN3XqVH0w8iRPuyaXL18W5ubm\nAhBWVlbC1dVVf44FCxY8z8cmPQf5ZVY2yetSup4WZJT6mAwTM3Nqf/QbY1vXZGI7mSyoOCQnJ1O5\ncmXS0tL45Zdf6NSpE2lpaXTt2pUDBw7QqlUrsrOzMTU1ZdSoUXTv3v2xsQiP6tKlC3v27GHAgAEs\nWbIEAAfX2iiV6+DUuCNGzh4kpmU/dpyiQAMnKzrWrURH90o4Wpcr8BxCCNKzNSSmZZOUno0QUKtS\nef16Hnm0WsGG41HM/vUCGq3gg/ZuDPRxxsTw8ZwTLyowMJBWrVrh4+OjT44FEBAQQNeuXWnTpg2L\nFy/G3NycqlWrcv36debPn09gYCCGhoacOnUKU1NTUlJS9J9tZGQkLi4uVKxYUd+d8rCn9TP7+vqy\nZMkSunXrxqZNmzAxMWH16tWMGDGCSpUqERUVpU/cJRUd2fdfNsnrUrrK9JgMYwM1lSuYEC1zZRSb\nM2fOkJaWhqenJ506dQKgXLlyvPnmmxw4cICDBw/q9923bx99+vRhw4YN+kGLT/LJJ5+wf/9+NmzZ\nxp6rGZjWboHdu7qET2oDQZva9rhXqYA2O4v3x49Dm5NFhfJmaMrZcj69FScjE5j5SwR1KleggbMl\nKRk5JKVnk5iWxe24JFKztWRoVeRo85/XUGTTxNWa9h7ONKthiwD8t4dz/Ho8zWrY8mWvek8NXF6U\nm5sbKpWKkydPcvnyZWrWrIkQgo0bNwIQHBzMK6+8AugWUFu6dKk+VXl2djYWFhakp6dz8eJF/X6h\noaEAVKxY8bnrExwcDMCkSZP040CGDRvGjBkzuHXrFtevX5cZPiVJKnWlHmQAVLUuJxNyFaO8jJHR\n0dFkZGRgYqJLLpWXY8HKygo/Pz9iY2NZtWoVW7ZsoUuXLgwaNKjAMuvW92Liil/YeDoOrWE5Mm9d\nIOfUDmLDA6nTsBb+41ZjbGzMe++9x4PwvQDkrQEac3At5So6MeF/q7iQqiYg/A4VTAwRWWncuHSe\njOR4tBkpaNMfYG1uQkz0dbQZKSgGRpg41+dgSgMOX9dNe1YUKG9swJy36tO7YdVnGsj6IhwcHOjT\npw+bNm3C29ubbt26cfHiRf1U2fT0dBwdHYmPj+fo0aO0bNmSsLAwHB0dMTQ0ZODAgXz33Xd07tyZ\nDz74gJSUFObMmQOQL/fFsypfvjygaw3Jm2abnJxMQkJCvtclSZJK1aP9JyXxeKT/Rnyw5bR49Ysn\nD36TCk+r1Yr69evr+//37NkjPvnkE30f/tq1a/V9msuXLxeAaNeu3RPLSsvMEd8dvioafr5XOPsH\niIHfh4igC7dESkqKuHjxorCwsNCXq1Kp9D+7ubmJ06dPi6ioKDFw4EABiCZNmujLvXDhgjA2NtaP\nGenevbswNDQUgFCr1WLWrFkiICBAdOvWTQCiWv3GYs3Ra2L2rxHiXlJ6iXyOSUlJolOnTvnGWOQN\n/Mwb15GcnCzatm0rAOHn56c/9v79+/kGe+Y9OnfuLDIzM594vqf1My9dulQAomLFimL16tXi999/\nF61btxaAaNGiRbG8f0n2/ZdV8rqUrjI98FMIIRb8cUk4+weI9KycYv0gXmbHjx8XFSpUeOxLztzc\nXGg0Gv1NevjwYQGIhg0bPlbGrYQ00WruQeHsHyAGfBciTly//9g+Z8+eFV27dtUHGOXKlROAOHTo\nkH6flJQU/eyUmJgYIYQQ48aNE4Do27evfhBmjx499MFK3n7Z2dnCyclJAOLo0aPF8VH9o1OnToll\ny5aJuXPnCkC4uLjkGzi6d+9eAYjGjRvnOy49PV2sXr1a9O/fXwwZMkTs3LlTaDSaAs/ztF+cmZmZ\nol27do9dTxsbG3HmzJmieaPSY+SXWdkkr0vpelqQUSa6SxytdX3K0Qlp1Kgom3lfhBCC5ORkzMzM\nMDB4/LK++uqrnDlzhiVLlnDs2DHKly/PwYMHSUlJISAgAAcHB3Jycli0aJF+/4dF3U+j33chJKdn\n8+OIRjSv+eRl3uvWrcvu3bvJzs5Gq9Xi4eHBxYsX89VJrVbrBz/mLV525swZQJdlM6/L4+F9Ll26\nhJ2dHQYGBlSrVo2oqCgSExML85G9MC8vL7y8vLh27Rp+fn4kJCSQnp5OuXK6sSC3bt0C0K8pksfE\nxIShQ4e+UPfIo4yMjAgICOCHH35g8+bNpKam0qJFC3x9falatWqhy5ckSSoKL75GdRFyyh2oJ9cw\neX5CCL755hucnZ2xtLTEysoKX19fkpOTH9vXycmJr776isDAQH7++Wf9Mu3du3dn8ODBdO/ena1b\nt2Jqasr48eP1x12JSaH38mBSs3LY8K5PgQHGwwwNDTE2NtYPNPX39ycqKork5GQ++OADUlNT8fLy\n0g96zFvA69ixY/oy6tevr/857ws7ODiYI0eOYGBgQIMGDZ734ypSrq6ueHt7k5SURJ8+fTh06BA/\n/vgj/v7+ALz99tvFen4jIyPeeecd9u3bR3BwMLNnz5YBhiRJZcujTRsl8Xi0u+R+SqZwmRIgvt57\nsRgbdP6b/P399U3lDyeaatKkicjOzn7qsRqNRnz44YeiQjUPYddrurDt4ieqteglft13QL/PuVtJ\nosFne0XDz/eJiDtJz12/6OhoUalSpcea9dVqtdi7d6/QarVCq9WKP/74QwDCwMBAjB07VixcuFDU\nrl1bv7+FhYXw8vLKlzwrNjZWnD9/XqSmpj53vYrKiRMnntgN1a5duwLHWjxP2bIJuGyR16Rsktel\ndD2tu6RMtGRYmxnRuJo1AWG3dQNFpGdy9+5dvv76axRFYdOmTaSmphIaGoqDgwN//vknu3bteurx\nN+6ncb92T6z6zMS21qvY1W+Btslwxgdm8M7av/j+yDX6fReCkYGKLSN9qF2pwnPXsUqVKgQHB9Ov\nXz+MjY1RFIXXX3+dLVu2sHXrViwtLTEwMOCzzz6jf//++i6bcePGceHCBRwcHPDy8iIpKYnQ0FBM\nTEwYMWIEt2/fxt7enjp16mBvb4+/v79+1dWS5O3tTWhoKOPGjaNhw4a0bNmSb7/9loCAAIyMCl6+\nXZIk6WVQJsZkAHTzqMK0HWc4dzsZ9yoWpV2df4XAwEBycnLo0KGDvmne09OTsWPHMnXqVPbu3fvE\npcpjH2SyYP8lNh6/iYmBivfbutHAPAEjlYLWxpXfz91l77m7/BFxD0drUza841Oo3BPVqlVjw4YN\naLVatFotycnJNGrUiKtXr+r3OXz4MCqViq+//ppbt26RmJhI48aNGTBgAGZmZly6dInY2FhcXV1p\n06YNERERGBoa4uzszPXr15kzZw4JCQmsWLHihev5olxdXfXrt0iSJEl/KzNBRif3SszYdZbdYbdl\nkPGM8jI6pqam5tuelpaW7/WH/Xn1PiN//Iu0LA0DGjsxtnVN7Mob6zPmNa5uQ5PqNnzctQ6XY1Jw\nsDTF3Lho/puoVCpUKhVLlizh6tWreHh4sGHDBqpWrconn3zC/PnzWbZsGRcuXHgs46ibmxtubm6s\nXbuWiIgIatasycGDB6lSpQqHDx+mTZs2rFy5kg8//BBnZ+ciqa8kSZJUOGUmyLAyM6KFmx0/h91m\nSsfactn3Z9C2bVvMzMwICgriiy++YMiQIYSEhOj/qj516hSOjo7Y2dkxZMgQHJv2YMqO8zjZlGP5\noIZUtzMvsGxFUXCzL56ZPr/88gsAM2fOpE6dOgDMmTOHdevWcfnyZa5evUrNmjWfeOyRI0cAGD16\nNFWqVAGgRYsWdOzYkYCAAIKDg2WQIUn/EkII4uPj9bPMXlTewPDY2NiiqJb0FCqVCmtr62dOfFhm\nggyAbh4OHLgQw1+RCTSqZl3a1SnzLCwsmDNnDmPGjOGjjz7io48+yvd63hob0dHRXDV0xepODRq5\nWPHd4FexKFd661rk/ed89BdL3nicp/3nNTMzA+D27dv5jito2qgkSWVXfHw8ZmZm+izELypv+nje\n7wep+GRkZBAfH4+Njc0z7V8mBn7maVfHHhNDFbvDbpV2VcqsgIAA2rdvj7OzM82aNcPc3Jyff/6Z\n1q1bY2dnh7u7u/6LdsKECURcuEi/uTuxajWM1IjD9La7V6oBBkDnzp0BmDZtGmFhYcTFxfH+++8T\nFxdHrVq1qF69eoHH5o09WbhwIQsWLODYsWOMHj2a0NBQrKysaNu2bYm8B0mSCk+r1RY6wJBKlomJ\nyXO1PJWpIMPM2IA2r9jzy5m7ZGv++U0cPHiQ1q1bY2hoiKWlJSNHjuTu3bslUNPSMW/ePLp27cq+\nffuIiori6NGjDBkyhN9++439+/cTExPDggULSElJ4ZW69ej+3lS+PJpIcKwBniZxxO3+H7t3/lTa\nb4PRo0fj5ubG2bNn8fT0xM7OjsWLF6NWq/WzZQry2muvMWbMGDIzM5kwYQI+Pj4sW7YMtVrN8uXL\n9YuFSZIkSaWvTAUZoOsyiU/N4uiVuKfuFxAQQLt27Th48CA5OTkkJSWxYsUKmjVrRnx8fAnV9sXE\nxcWxaNEipk2bxoYNG8jIyPjHY2JiYpgyZQqgG8tw6dIlVqxYgbGxMUuWLCE0NJTkjGyO3szAtttk\n0jt+zNDVJzh+PZ5Pu9XlDYdMQJCVlfWP50pISGDOnDl06tSJnj17sm7dOnJycgr7tvWsrKwICgpi\nzJgx2NjYYGxsTNu2bdm/f7++leNpFi1axJYtW+jYsSMeHh4MHDiQkJAQevfuXWR1lCRJkorAo4kz\nSuLxaDKuh2Vk5wj3j38TEzefLjDxh1arFbVq1RKAGDt2rIiPjxdnz54VHh4eAhCffvrpi2UUKQE7\nduzQr9uR93BychIRERFPPW7VqlUCEJ06dcq3ffTo0bo1P6YtELWn/yqc/QOE49h1wrrjWPHhkk0i\nNSNLXLlyRbi5uQlALF++/Inl5yWziYyMFM7Ozo8ll+rQoUOhk0tJz0cmGCp75DUpWnlrEhVWSkqK\nSElJeaFjVSqV8PDw0D+uX78uTpw4IcaOHSuEEGL16tVizJgxQgjd7+9z584VSZ3/zR69bsWSjEtR\nFEdFUQ4qihKhKMo5RVHG5263VhRln6Iol3P/tXqeco0N1HSsW4m95+6Ska154j7Xrl3j4sWL2NjY\nMG/ePKysrKhbty5ffvkloGvlKE4ZGRl88803+Pj44O7uzsiRI7l06dI/HhcdHU3fvn1JT0+nXbt2\nzJgxgzp16hAVFcWbb7751H6uzMxM4O9l2/OYWVhj03kif2qq4+Vkybb3mjDC9hrxvy1i5pi+VK5o\nS40aNbh06RJ16tRh4MCBT63j+PHjiYyMpEGDBmzatImlS5diZ2fH77//zrJly57h05EkSfr3MDU1\n5fTp0/qHi4sL3t7eLFy48LF9d+7cyfnz55+r/KJsBf43Kkx3SQ7wgRDiFcAHGKMoSh1gCrBfCFET\n2J/7/Ll083TgQWYOgRdj9NuuXLmCr68v3t7ef39Rqg0JCL/D6PUnWRt847mnQWVkZHD48GEOHTpE\nevqzrZuSmZlJx44def/99zl27Bjnzp1jxYoVNGzYkJCQkKceu2bNGjIzM+nevTu///47n376KSdO\nnKBKlSqcP39ePz3zSVq1agXAjh072L9/P0IIdgWeYFO8M2Z1Xqeri4ofRzTG28WaGR9NZ+HChTg6\nOpKcnIyRkRGDBg3i4MGD+lHYT5KSksLu3btRq9UEBATw9ttvM2rUKJYsWQLAunXrnukzkiRJ+jcL\nDAykS5cu+bYFBweze/duJk2ahKenJ1evXuXq1at07NiRhg0b0rx5cy5cuADA0KFDmThxIq1atdKv\nZfSyeuEprEKIO8Cd3J8fKIoSAVQBugMtc3dbCwQCBX7KeUmgHmakFVgYq1hz8By2GbcICwtj7Nix\n+kDAsKIrVm1HYlqnJRO2hGNqAL+cuYvqejCo1Hh5eT2x3Ift3r2bRYsW6VfytLCwYMyYMfTs2fOp\nx23bto1Dhw5ha2uLn58f9vb2rF27lsDAQIYNG8YPP/xQ4MDFvDrVqlWLkydP6rfXqVOHW7duERgY\n+NQpWF26dCEgIIC2bdti69MD09cGoVUbYR36A4Pemkzoqb/LbNKkCdu2bSMxMREzMzOMjY2Jiooi\nKiqqwPLT0tLQarVYWFgQHR2tnxaaF4nfvXv3Hz9XqejJz7zskdekaJibm+f7w2foD6FFWv6awV7/\nuE96erp+MUZnZ2c2bdpEeno6Go2G1NRUMjMzyc7OxsPDgzfeeIOOHTvqvyc6d+7MggULqFGjBidO\nnGDkyJH88ssv5OTkEBERwa5du1Cr1Y8lTPy3u3//PpGRkfrnBeU1giLKk6EoigvgBRwD7HMDEIQQ\ndxRFqfi85alVCq9VNWb/9XTi0nKY9d1mDOq0o65HU4wd3LifbYjIySLtUjAp4fvIiDqDZfOBWDTp\ng9PAL+nS8+n/sQ4fPsznn38O6FJeK4rCtWvXmDVrFubm5lSsWJGcnBzq1q2LiYkJsbGxHD58mMzM\nTH7//XcABoyZRKJDI+K08OHHn3HyZGcuXLjArVu3ClwJ08nJCYBDhw7x5ptvolKpePDggT7gcHR0\nfGq9p02bhkHVp6iu/wAAFcBJREFUepzIrIxBRVcyI0/jIy7y/kfjHsuQCX8nTXlWNjY2VKxYkZiY\nGAICAujatSsajYaNGzcC6BNnSZIk/VeYmprqcwo9j5SUFI4dO8agQYP02/K6tQF69uyJWq0ukjr+\nmxU6yFAUxRzYDkwQQiQ/axawPN7e3k8u1y6eX7/9k/d+uQ8tx2MNmJobUbeKBa1rVyTu5G988PVc\nbG1t0RioUc78jLtHLSKqeLIowpBVQ+tQ1erJXQPjxo0D4NNPP9UnsJo9ezbTpk3j448/1i+0ZWlp\nSYsWLXSRqVAwqVoH0xrNqNJ8IjszKsG5VBQFjt8rh1WNBjwIPUSNGjVwd3d/4nkdHR1ZvXo1x44d\nY+TEaVTxbk/4yRBSzRzwrOtNn/6DMDd5cg6Lk5EJfPPbBUItmuJiacKwRpXo36QNpqZFM8f8r7/+\nQq1WM2PGDHx9ffnss8/YsWMHiYmJ3Lx5EyMjI2bNmlXqy6u/TPL+Wi7oHpFKnrwmRSs2NjZf6+3W\nUc1eqJy8loIXTcb16HGmpqao1Wp9K7ChoSFmZmYYGBhgYmKCmZkZGo0GS0tLwsPDHyvPwMAAa2vr\n/2xyMBsbG2rXrq1/npSUVOC+hQoyFEUxRBdgrBdC5CVguKcoSuXcVozKQEzBJRSsgZMV77d14/bt\naBZ+OhkXCzUnTv095mF3rAMA9erV48CBA/rtwVfieG/dSXosCWbF4IY0cHp83GneL4rx48fruzby\nvjyzs7Op/kp9jCrV4FYqHNVWw27wAoxsHUFRIXIySb9+GtWFffzx4wLis9T836qj0HYiVSrWwrVG\nwc1G9vb2fLdxBxNX7iW+RlMS1AaomtalUlNIANw/2Us5IzVW5YywMDXEspwhFqaGPMjIIehKHLbm\nxnzarS59GzlibFA8EfLo0aNJTU1l1qxZnDlzBtC19ixdulQGGJIkvdTKly/PgwcPAKhQoQLVqlVj\n69at9O7dGyEE4eHheHh4lHIty5YXDjIU3bfzSiBCCDHvoZd2A0OA2bn/Pn298YLLZ3zbmqSmOrBs\n7CUuXEtm8+bN9OnTh+TkZObOnQtA8+bN8x33Wg1bfhrdlOFrTtBn2Z9M6lCLd5u75lsLxcbGhrt3\n73Lu3DmaNGnCzfh0pizfgXWHMZg6upNj40gOYAXkJMdC4i3GtG6Nl6MVSZeO89bXuq4WD7ddVKhQ\ngdjEFKzbjsTcsxv9Vv7Flz3r4WBpgpGBCiO1CgO1imuxKSw+eIVdp7MoX7cVDSzTqa6JpHpNN6q7\nNyAuJYt7yZnEPsgkMT2L5PRsEtOyuRyTQrZGy6QOtRjW1IVyRsWbCV5RFCZPnsyYMWP0S6t7eXnJ\nZj9Jkl56ffv25d1332XhwoVs27aN9evXM2rUKL744guys7Pp27evDDIeoYjc9SKe+0BFaQYcAc4A\nedM6pqEbl7EFcAKigN5CiHzZsZKSkvQnfXRK5pPMmjWLDz/8EAAXFxdiYmJIS0vDzs6O8PBwKlWq\n9NgxSenZTNkezq9n79LCzY6ve3tgV94YgMmTJzN3/kIcm7+JbdPe3M/WdVFoM1KwU6UwvOvreDpa\nMqR7G66eD8+rMxUqVADAzs6OuLi/k4VVrVqVjz76CAefLny44yxJ6dn56qJSQCvAxFDFwMbO/F8L\nVypWKFupdGUzcNkjr0nZI69J0YqNjcXOzq7Q5RS2u0R6Po9et4e7SywsLPKNmSjM7JIgoKABGG1e\ntNwnmTp1KgYGBsyZM4cbN24AupU3v/322ycGGAAWpoYsHdCADcej+Ozn83RacIT5b3tQy748Fs0H\n4pzzKsKoHLdvXiElfB+ZN8+SHRfFvK1beKtVDQDsLc25iq5/LS9ddXh4OHFxcZiamhIREYFWq8XJ\nyUn/l763szX7L9wjI1tLVo7uka3RUs5YTR9vR2zNjR+rqxCCzZs3s3z5cm7evImbmxu+vr5ERkay\ndOlSrl27RrVq1Rg9ejTvvffeEwd5SpIkSVJZU6ZWYS1IXhP++PHjuXLlChYWFgXO4Hj0uAGNnWno\nbIXvhlAGrTyOoVohRytoXd8Zx9RLhF8+DC5GCGcvdu6MZOzYscTGxlKuXDn9FB2NRsO7776Lra0t\na9asAWDIkCFPXFK8koUJAxrrtqekpDBz5kzWrFlDbGwsq7288Pf356233sp3jJ+fH/Pm/d3jdPXq\nVX799dd8+5w7d44xY8Zw7tw5fd4KSZIkSSrTHk0BWhKPp6UVLy5pmTli9q8R4pPdZ8W12MfTz6al\npYmWLVs+lk7bxsbmsW1t2rQRDx48eOr5srKyRLNmzR47FhCLFi3S7xceHi4AYWhoKBYtWiTOnTsn\nxo4dq993yZIlIiEhQaxfv14YGRkJoFjS2sp0yWWPvCZlj7wmRasspBWXnt/zpBX/V7RkFAVTIzX+\nHWsX/LqpKXv37mXTpk3s3LmT7Oxs2rdvz9ChQ7l9+zbbt28nPT2dli1b0qpVq6euFAqwdetWgoKC\ncHBwYPPmzXh6evLtt98yefJkPvzwQ4YOHYq5uTnbt28HYNiwYfj6+gJ/59MAMDY2xtLSkv79+/PH\nH3+wevVqAgICZM4KSZIkqcx7aYKMZ2FoaMigQYPyJVcBcHNzY+rUqc9V1p49ewDw9/enWTPd3O9J\nkyaxefNmTp48SVBQEB07dtSvwGpjY6M/9uH06A+v0GpgYPDY65IkSZJUVskRhCXs0RaQvDVJVq5c\nydmzZwGoWDF/klSNRkNAQIB+7ZCOHTuWQE0lSZIkqXBkkFFMOnfuDMBXX33F0aNHSU1NZe7cufz1\n119UqFBB37rRrl07WrRoQUxMDPXq1cPe3p5hw4bpy/H19cXAwICuXbuSnp7O4MGD8fT0LJX3JEmS\nVJpu3LjBzp07CQoKKrIWXUVR8rVe5+TkYGdn99gCaf9VN27cYMOGDcVWvgwyiknv3r1p2rQpt2/f\nplmzZpibmzNp0iQAZs6cibm5OaBbXyQgIICRI0diampKTEwMFhYWTJo0iZkzZ+rHZzg6OvLll1+y\ncuXKUntPkiRJpSE1NZX+/fvj6upKz549ad68ObVq1eLYsWOFLtvMzIyzZ8/qF+Dct28fVapUKXS5\nL6I0loWXQca/lKGhIb/99hv+/v5UqlQJlUqFt7c3W7Zs0Q/wzFO+fHmWLVtGXFwcUVFR3Lt3jzlz\n5jBt2jQiIyPJzs4mKiqKKVOm6MdlSJIkvSxGjhzJxo0bMTQ0pEOHDjg5OXHlyhU6dOjAnTt3Cl1+\np06d9OPoNm7cSL9+/fSvpaamMnz4cF599VW8vLzYtUuXxPrGjRs0b96cBg0a0KBBA4KDgwG4c+cO\nLVq0wNPTE3d3d44cOQKg/8MSdKt5Dx06FHh8WfiCzrdmzRp69OhB165dqVatGosXL2bevHl4eXnh\n4+NDfLwu5+XTlp8fN24cr732Gq6urmzbtg2AKVOmcOTIETw9PZk/fz7nzp2jUaNGeHp6Ur9+fS5f\nvly4D/fR6SYl8SiNKazS08mpeWWPvCZlj7wmRetZprBGRUUJRVGEoaGhOHv2rBBClyKgTZs2AhCf\nffZZoaawmpmZibCwMPHmm2+K9PR04eHhIQ4ePCg6d+4shBBi6tSp4scffxRCCJGQkCBq1qwpUlJS\nRGpqqkhPTxdCCHHp0iXRsGFDIYQQc+fOFV988YUQQoicnByRnJysP0+erVu3iiFDhgghhBgyZIjo\n3LmzyMnJeer5Vq9eLapXry6Sk5NFTEyMqFChgvj222+FEEJMmDBBzJ8/XwghROvWrcWlS5eEEEKE\nhISIVq1a6c/z1ltvCY1GI86dOyeqV68uhBD53qsQQvj6+op169YJIYTIzMwUaWlpj31mL/0U1tu3\nb3PkyBGMjY1p27ZtvghSkiRJ+vcIDw9HCEHz5s2pW7cuoGspHj58OPv37yc0NLTQ56hfvz43btxg\n48aNvPHGG/le27t3L7t379avl5WRkUFUVBQODg74+vpy+vRp1Go1ly5dAuDVV19l+PDhZGdn06NH\nj2caQ9e7d2991uiCzge6iQLly5enfPnyWFhY0LVrV0C3UGh4eDgpKSkEBwfTu3dvfdkPLz/fo0cP\nVCoVderU4d69e0+sS5MmTZg5cybR0dH06tWLmjULXvTzWfynggyNRoOfnx+LFi1Co9EAuq6IBQsW\n5BtMWVwOHz7M+vXrSUhIoFGjRgwfPhxra+tiP68kSdJ/Vd5su/Pnz5ORkYGJiW7dp9OnT+d7vbC6\ndeuGn58fgYGB3L9/X79dCMH27dupVatWvv0/+eQT7O3tCQsLQ6vV6uvVokULDh8+zJ49exg0aBCT\nJk1i8ODB+WYWPpyaAPKvuVLQ+Y4dO4ax8d/LUqhUKv1zlUpFTk4OWq0WS0tL/WfzqIePFwWsW9a/\nf38aN27Mnj176NChA99//z2tW7d+4r7P4j81JuOrr77im2++AXTTPBs3bsyDBw8YPnw4Bw8eLLbz\nCiH44IMPeP3111mxYgVbt25l0qRJ1K1bl/PnzxfbeSVJkv7rvL29qVu3Lnfv3qVdu3asWbOGiRMn\n6pdiGDJkSJGcZ/jw4cyYMYN69erl296hQwcWLVqk/1LOazlJSkqicuXKqFQqfvzxR/0ftpGRkVSs\nWJF3332XESNGcOrUKQDs7e31613t2LGjwHoUdL5n8fDy86D7bgoLC3vqMQ8vXw9w7do1XF1dGTdu\nHN26dSM8PPyZz/8k/5kgIycnhwULFgCwY8cOfv31V0JCQpgyZQoA48aNo2vXrvTo0YNVq1aRlZVV\nZOfet28f8+bNw8jIiKlTp7JmzRp8fHy4e/duibSgSJIk/VcpisKPP/6IjY0NQUFBDBs2jPnz56PR\naPj4449p0qRJkZynatWqjB8//rHtH330EdnZ2dSvXx93d3c++ugjAEaPHs3atWvx8fHh0qVL+taI\nwMBAPD098fLyYvv27foyZ8+eTZcuXWjdujWVK1cusB4Fne9ZrV+/npUrV+Lh4UHdunX1A0cLUr9+\nfQwMDPDw8GD+/Pls3rwZd3d3PD09uXDhAoMHD36u8z/qhZd6L4yHl3o/fvw47dq1K3SZd+7cwcHB\nASsrK+7fv69vmgoODqZp06aP7d+0aVN+//33IlkaeMCAAWzYsIHPPvtM/x8iJSUFJycnEhISiIiI\noHbtglOalwVyCeuyR16Tskdek6L1PEu9x8XFsWrVKk6ePImdnR2DBw+mUaNGgFzqvaQ9z1Lvpd6S\n0atXL+Li4gpdjqWlJcbGxiQkJOSbcpOXDtzExIQffviBFStWUKVKFY4ePcqcOXMKfV7QfeBAvgE+\n5ubm1KihWzI+JiamSM4jSZL0srK1tWXy5Mls3ryZxYsX6wMMqWwr9SAjJSVFny67MExNTfVzm9u3\nb8/cuXOZOnUqhw8fBnTBxqBBg3j33Xf1y7UXxXkBvLy8APjuu+/0yVROnDjBX3/9hZGRkVzMTJIk\nSXoplXqQAbov50aNGtGtWzd27txZ4KjXf/L111/j5eVFZGQkkyZNYvbs2YCuT2/y5Mn6/V555RUA\nEhISCl95YNSoUZiZmfHzzz9To0YN2rRpw2uvvYYQguHDh2Nra1sk55EkSZKkf5MyEWScP3+eEydO\n8PPPP9OzZ08mTJjwQuVYW1sTEhLChg0beOedd/D19cXFxQUhBEuXLtUnB5k/fz6gm89cFFxcXPj1\n11+pVq0akZGRHDhwACEEI0aM0M92kSRJkvJTqVSPTeeUyraMjAxUqmcPHUp94KelpSX9+/fnvffe\n4/jx40ybNo2srCyCg4OLZNTwhg0bGDBgAAB16tQhMzOTq1evoigKf/zxR6Hm/z5Ko9Hw559/kpCQ\nQIMGDUot//2LkAPayh55TcoeeU2KlhCC+Pj4Qi92lpfXwsbGpiiqJT2FSqXC2to6X96Ppw38LPVk\nXNWrV2fdunUoikLz5s25e/cuc+fOZeLEidjb22Nra8vgwYNp0aLFC5Xfv39/kpKSmD59uj5nhYOD\nA/Pnzy/SAANArVbrV1eVJEmSnk5RlCIJDCIjIwHK/Cy+l1GpBxm1a9fOFxHlCQkJ0f+8cuVK/P39\n9WMsnteoUaMYOnQoJ0+eRK1W4+3tjaGh4QvXWZIkSZKkf1bqYzL27t2rX73u7t27LFy4ENAFHxs2\nbGDatGkYGhry1Vdf6VezexGmpqY0a9aMJk2ayABDkiRJkkpAqY/JkCRJkiTpv6HMJeOSJEmSJOm/\nSQYZkiRJkiQVi1LpLpEkSZIk6b9PtmRIkiRJklQsZJAhSZIkSVKxKPEgQ1GUjoqiXFQU5YqiKFNK\n+vwSKIriqCjKQUVRIhRFOacoyvjc7daKouxTFOVy7r9WpV3Xl42iKGpFUUIVRQnIfV5NUZRjuddk\ns6IoRqVdx5eNoiiWiqJsUxTlQu4900TeK6VLUZT3c393nVUUZaOiKCbyXimbSjTIUBRFDSwBOgF1\ngH6KosglSkteDvCBEOIVwAcYk3sdpgD7hRA1gf25z6WSNR6IeOj5V8D83GuSAIwolVq93BYAvwkh\nagMe6K6PvFdKiaIoVYBxgLcQwh1QA32R90qZVNItGY2AK0KIa0KILGAT0L2E6/DSE0LcEUKcyv35\nAbpfmlXQXYu1ubutBXqUTg1fToqiVAU6A9/nPleA1sC23F3kNSlhiqJUAFoAKwGEEFlCiETkvVLa\nDABTRVEMgHLAHeS9UiaVdJBRBbj50PPo3G1SKVEUxQXwAo4B9kKIO6ALRICKpVezl9I3wGQgb7Uo\nGyBRCJGT+1zeLyXPFYgFVud2Y32vKIoZ8l4pNUKIW8BcIApdcJEEnETeK2VSSQcZjy9SAnIObSlR\nFMUc2A5MEEIkl3Z9XmaKonQBYoQQJx/e/IRd5f1SsgyABsC3QggvIBXZNVKqcse/dAeqAQ6AGbou\n+EfJe6UMKOkgIxpwfOh5VeB2CddBAhRFMUQXYKwXQvyUu/meoiiVc1+vDMSUVv1eQk2Bboqi3EDX\njdgaXcuGZW6TMMj7pTREA9FCiGO5z7ehCzrkvVJ62gLXhRCxQohs4CfgNeS9UiaVdJBxAqiZOwrY\nCN1gnd0lXIeXXm5f/0ogQggx76GXdgNDcn8eAuwq6bq9rIQQU4UQVYUQLujuiwNCiAHAQeCt3N3k\nNSlhQoi7wE1FUWrlbmoDnEfeK6UpCvBRFKVc7u+yvGsi75UyqMQzfiqK8ga6v9DUwCohxMwSrYCE\noijNgCPAGf7u/5+GblzGFsAJ3Y3cWwgRXyqVfIkpitIS8BNCdFEUxRVdy4Y1EAoMFEJklmb9XjaK\noniiG4xrBFwDhqH7A03eK6VEUZRPgbfRzZQLBd5BNwZD3itljEwrLkmSJElSsZAZPyVJkiRJKhYy\nyJAkSZIkqVjIIEOSJEmSpGIhgwxJkiRJkoqFDDIkSZIkSSoWMsiQJEmSJKlYyCBDkiRJkqRi8f/c\ngJydGcuCcgAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"sensor_var = 5**2\n",
"process_var = 2\n",
"pos = (1000, 500)\n",
"process_model = (1, process_var)\n",
"N = 100\n",
"dog = DogSimulation(0, 1, sensor_var, process_var)\n",
"zs = [dog.move_and_sense() for _ in range(N)]\n",
"ps = []\n",
"\n",
"for z in zs:\n",
" prior = predict(pos, process_model) \n",
" pos = update(prior, (z, sensor_var))\n",
" ps.append(pos[0])\n",
"\n",
"book_plots.plot_measurements(zs, lw=1)\n",
"book_plots.plot_filter(ps)\n",
"plt.legend(loc=4);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Again the answer is yes! Because we are relatively sure about our belief in the sensor ($\\sigma^2=5^2$) after only the first step we have changed our position estimate from 1000 m to roughly 50 m. After another 5-10 measurements we have converged to the correct value. This is how we get around the chicken and egg problem of initial guesses. In practice we would likely assign the first measurement from the sensor as the initial value, but you can see it doesn't matter much if we wildly guess at the initial conditions - the Kalman filter still converges so long as the filter variances are chosen to match the actual process and measurement variances."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Example: Large Noise and Bad Initial Estimate\n",
"\n",
"What about the worst of both worlds, large noise and a bad initial estimate?"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAiIAAAC+CAYAAAAIj2Q7AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzsXWdYFFcbPbO7dCmCiAUVxC6xYDdq\nVOy9xG4sxK6xxxY/Y+9GE6Mxxtg1auyixt5b7Fiwi1hQBBuIgDDn+7HOdWd3QYwaSTLned4HuDtz\n587cZd5z33YlktCgQYMGDRo0aPgY0H3sAWjQoEGDBg0a/rvQiIgGDRo0aNCg4aNBIyIaNGjQoEGD\nho8GjYho0KBBgwYNGj4aDB97ANbw9OlTLYJWgwYNGjRo+JfB1dVVMm/TLCIaNGjQoEGDho8GjYho\n0KBBgwYNGj4a0qVrxhSurq4fewj/eZw4cQIAULJkyY88Eg0KtDlJX9DmI31Bmw9LNGvWDKtXr7Zo\nz58/P2bPno0WLVogKioKwcHBqFu3rtU+SpUqhRMnTmDTpk2oV68eACAuLg5eXl6IjY1FcHAwnJyc\nULx4cZXufvr0aapj0ywiGjRo0KBBw78U58+fx9ixY5EnTx7Ur18fer1efFa7dm3s2rULVatWxVdf\nfQUA2Lp1a4p9NWnSBADQv39/7NmzB6GhoQgKCkJsbCzs7OxQr149VKlSBdmyZcOIESMgy3Kaxpju\nLSIaNGjQoEHD34GkpCQ8e/YMbm5u0On+nnX6y5cvsWXLFly/fh2+vr6oW7cubG1t37lfkujfvz9m\nzJihavf398f58+dRsWJFbNmyRTUOACqiYo6ePXtixYoVCAkJQdWqVVWfJSQkwNvbG15eXjh58iTG\njBkDe3t7DBs27I1j1SwiGjRo0KDhP43Y2Fj07dsX7u7u8PDwQPbs2TFhwgQkJye/dV/Pnz/HzJkz\nUadOHdStWxc//fQTXrx4YfXYc+fOIW/evGjUqBEGDBiAJk2awM/PD6dPn37XW8KSJUswY8YM2NjY\noHPnzujfvz8yZsyI8+fPQ6/X48CBA/j+++8RHR2NTZs2YebMmQCABg0apNini4sL9u/fj+HDhyNf\nvnzInj07/Pz8AAAtW7bEzZs3ceLECaxduxYAMG3aNCQkJLx5sCTTnTx58oSKaPj4OH78OI8fP/6x\nh6HBBNqcpC9o85G+8DbzkZyczCpVqhAAAdDR0VH83r1797e6blRUFP39/cX5ipQoUcJCn8XHxzNn\nzpwEwHz58rFXr14sWLAgATBr1qyMi4t7q2ubo1y5cgTAn3/+WbQdPXqUAGhnZ2cxRgBs1KgRZVl+\nq+sUK1aMAHjo0CHRJsuyuLfQ0FCa6XQLnZ9mi4gkSfMlSYqUJOm8SdsUSZIuSZIUIknSOkmS3F61\n+0iS9EKSpDOvZI7JOSUkSTonSdI1SZJ+kCTJIqdYgwYNGjRo+Duwbds27NmzB56enjhx4gRiY2Ox\nadMm2NjYYM6cObh582aa+xoxYgTOnz+PfPnyYenSpVi4cCF8fX1x8uRJjBs3TnXspk2bEB4ejoIF\nCyIkJAQzZ87EmTNnUKRIEURERAirwl9FWFgYAKBGjRqirXTp0nB2dkZCQgLmzp2L0qVLw8nJCXnz\n5sWkSZOwatUqmKrkU6dOYdGiRdi2bRuSkpKsXsfd3R0AcOnSJdEWHR2N+/fvAwBsbGzeONa3cc0s\nBFDLrG0HAH+SRQBcATDU5LPrJIu9km4m7T8B6AIg7ysx71ODBg0aNGj4W7Bjxw4AQLdu3VCiRAlI\nkoR69eqhfv36IIndu3enqR+SWLp0KQBg9erVaNOmDdq3by/ali1bpjr+ypUrAIA6derAzs4OAGBr\naysyVq5evfpO95UvXz4AwLp160Tbnj17EBMTAwcHB0yfPh1RUVFo3bo1tmzZgkGDBgnSEBUVhapV\nq6JEiRLo0KEDatWqBT8/Pxw9etTiOm3btgVgDGD97rvvMHr0aOTMmROJiYkAgOLFi79xrGkOViW5\nX5IkH7O27SZ/HgXweWp9SJKUFYALySOv/l4MoBGAFMN0lTQsDR8f2lykP2hzkr6gzUf6QlrmIzo6\nGgBw/fp11fH37t0DANy9ezdN/SQnJ+PZs2cAjOmqyjlxcXHiOqb9KBklwcHB+Pzzz2EwGJCcnIyN\nGzeKz9/l+1S7dm3s27cPAwYMwMaNG+Hk5CRI14sXLxAaGgoAuHHjBn777TfMnTsXefPmBQD06NED\nx48fh7OzM8qWLYtLly4hPDwcNWrUwNq1a+Hm5iauU6hQIQQGBmLXrl0YMGCAaJckCTly5EB4ePgb\nx/o+g1WDoCYUvpIknZYkaZ8kSRVftWUHcMfkmDuv2jRo0KBBg4a/HZUrVwYArFmzBlu2bMH9+/ex\nePFiHD16FDY2NihXrlya+tHr9ShUqBAAYOnSpSL+YcmSJQCM2Srm13V3d8fly5fRqVMnzJ07F507\nd8aFCxfg6uqKatWqvdN9BQYGomvXrtDpdNi7dy82b94srBQ+Pj6YPXs2lixZgvLlyyM2NlZk11y9\nehXHjx+Hk5MTVq5cifHjx2PVqlUICAhATEwMNm3aJK6RlJSEly9fYvz48Zg0aRK8vb0BALlz58aW\nLVuwZs0aTJgw4c2DtRY4kpIA8AFw3kr7NwDWAZBe/W0HwOPV7yUA3AbgAqAUgJ0m51UEsMm8Py1Y\nNX1BC8RLf9DmJH1Bm4/0BWU+EhMT+ejRIyYnJ6d4rCzL7Nixo9XgzSlTprzVddetWyfOzZs3L3Pn\nzk0AlCSJ27Ztszj+8OHD9PDwUF0zY8aM3L9//1vfc0q4ffs2Z8+ezRkzZtDX15cAuHv3bvH5o0eP\naGNjQwB88uQJly9fTgBs3Lixqp85c+YQANu3b8+bN2+yefPm4rySJUsyODiYJUqUIADu27dPnCfL\n8vsLVk0JkiS1B1APQBvSyC5IJpCMfvX7SQDXAeSD0QLibXK6N4B77zoGDRo0aNCgQUFsbCwmTpyI\njBkzwt3dHTlz5sTUqVOtFtiSJAnz5s3DnDlzUKJECXh5eaFy5cpYv349qlSpggkTJmDq1KkipiM1\nNGrUCAsWLICXlxeuXr2KGzduIFu2bFi+fLkqaFRBuXLlcPPmTcybNw9Dhw7F3LlzERYWhooVK1rp\nPXXIsowLFy7g7NmzoiYIAHh7e6N79+7o06ePaDN1rTg6OsJgMEZpTJgwAVFRUQCAkydPqlJvDx8+\nDMCYwvvpp59i1apVePnyJQwGA06cOIH69euL6167dk2c96aqqgDezSICY6DpRQCeZsd5AtC/+j03\ngLsA3F/9fRxAWQASjK6cOubX0Swi6Qvaai/9QZuT9AVtPtIPXr58yU8++cRqOu6AAQPS1EdCQgKb\nN29uYSHp379/mtJbExISePToUR47doyJiYnvektvxNatW5k3b14xzixZsnDixIl89uyZ6rhOnToR\nAOvWrcvHjx8zPj5epPmaivLMypQpwx9++IFt2rQhAOp0Onbu3JkAWLZsWYaHhzMuLo6DBg0iAGbO\nnFlYdWbOnMl169axQoUKb7SIvA0J+Q1ABICXMFo2vgRwDUa3y5lXMufVsU0BXABwFsApAPVN+ikJ\n4DyMVpIf8cqdQ42IpFtoL9n0B21O0hf+CfNx/fp1rl27lgcOHEjVVfFPx+rVq4VSPHv2LGVZ5urV\nq6nT6WgwGHj37t039vG///2PAJghQwZ269aN7dq1o8FgIAAuXLgwxfPu3r3LRYsWccmSJXzw4MH7\nvK0UcfToUTG2zJkz08XFRRAKg8HA9u3b89GjRyTJK1eu0NXVlQBoa2urqidSuXJl9u7dm25ubgRA\nBwcHFTnR6/WcPHky8+TJQwDcuXMnZVnmjz/+SB8fH3Fc9uzZLYjNeyMif6doRCR94Z/wkv2vQZuT\n9IX0PB8xMTFs1qyZSjHkyZOHx44d+9hD+yDo1q0bAbBnz56q9lq1ahEAly9fnur5cXFxdHZ2JgDW\nrl2bmzZtYnJyMufOnUsALF26tMU5sixzyJAh1Ov14hnb2Nhw7Nixbxzv+fPnOWnSJE6cOJEhISGq\ncdy4cYOxsbF89uwZ586dy6+//pozZ85kdHS0OK5Ro0YEwM6dOwvLhbmUKVOGSUlJJMkzZ84wMDBQ\n9fmXX34p+jt+/DgB0MnJidOnT2fnzp05ePBgNmzYkDqdTpzj5+fHnj17Wr2ej48P69evz8DAQI4c\nOVIjIhreHen5JftfhTYn6QvpeT5atGghqmnWqlWLOXLkIAC6ubnx/v37H3t47x1fffUVATAoKEjV\nXqFCBQLg6tWrUzz30aNHolKoqTRo0IA3b94kAGbKlMnivNmzZwvXRd26dVmzZk1x7rJly6xeKzk5\nmV27drW4Vrt27di7d286OTkJy4W9vb3qGBsbGwYFBfHu3bvCHbJjxw4CoL29PXfv3i2sHVmzZiUA\nrl+/XnX9x48fi+qnly5dUn2WKVMmAuCdO3dIUripbGxsmCtXLosxf/rppwRAX19fenp6EgDnz58v\n+tOIiIZ3Rnp+yf5Xoc1J+kJK85GUlMS1a9eyXbt2bNWqFefPn88XL16kqc/w8HB27NiRLi4utLW1\nZc2aNVVltNOCmzdvUpIk2tnZMTQ0lCSZmJgoSpqnZcX+T8OuXbvEiv63337jzZs3OXr0aBH7kJpe\nUYiBsvIPCgpixowZCYDVqlUTBG7gwIG8cuWKOE+Jz1i8eLFomzlzpsgosYYffvhBEMSgoCB26tTJ\ngnAobhLFNaJkqShib28viEb//v0JgC1atGBYWJggDoqbqV+/fhZjUO7JNDvoyJEjBEAXFxfGx8fz\n2rVr4loXLlzgkydPWKBAAQsyYmotUZ7/kSNHSGpERMN7gKb00h+0OUlfsDYfCQkJrF27tsULu2jR\nooyKikq1v4iICHp7e1uca2Njwz179qR5XBs2bCAAVq9eXdW+ePFiAuDnn3+e5r7eFqdOneKsWbO4\ndOnSv/VdLssya9SoYdVlMGvWrBTPS0xMFFYIxb3j5OQklLU1cXR0VLlDFPcHSUZHR4tjrEFR5itW\nrBBtU6dOFX0p+86YS65cuejn5yf+VuJDFCvGJ598woCAAAJgq1at2KNHDwLgsGHDLMagpBtLksTP\nP/+cXbp0EW6p/v37kyRXrlxJAKxXr57q3kwtRwqBcnR0VI3b1dWVERERGhHR8O7QlF76gzYn6QvW\n5mPy5MkEQA8PD06ePJmzZs0SdSU6d+6can8DBgwgYIxHuHTpEiMjIxkUFEQALFWqVJrHpaxus2XL\nxvj4eNHet29fAmCPHj3e7kbTgJiYGNatW1elPDNkyPDG2Iz3iSNHjvDrr79m8eLFmSVLFlarVo2b\nN29O9ZwnT54IpRofH8+WLVtakIB8+fJZ3TBOkiQC6voZCgnMnTs3Dx8+zMmTJ3PKlCm8cOECSdLW\n1pYAGBMTQ9LoqhkzZkyKpMdUevfuTQAiSFRxsZhK1qxZOWrUKGFFOX36tNX7HjNmjIU1o3HjxsJy\nt3PnTgLGuCKFaCUlJYmgVVNxd3cXVpwiRYoQAMeMGaMREQ3vDk3ppT9oc5K+YG0+ChcuTADcsGGD\naLt48aJYOaaW1qmslg8cOCDa4uLiRFplWjMykpOTRV8VK1bk/Pnz2bt3b6F4/vzzz7e80zejXbt2\nwrTfvn17VqxYUbgWUlKG7xt79+7lwIED2bhxY7Zq1YqrV69WWSusQZZlEf+wZMkSkkarjmJ98PDw\nEBauJk2asHjx4gTAQoUKCUXs4eHBESNGcOjQoaq0YXPp3r27mJdly5Zx9OjR9PLysjhOSUM2d8lk\ny5aNANiwYUMCRrfLzJkzmT9/fqvXs+aWMcWtW7f4/fffc9KkSRbf45cvXwqiExgYyB9//FEE/qYk\n9erV44IFCwiAzZo104iIhneHpvTSH7Q5SV+wNh9K0N6tW7dEW1JSkjBjp/Z+e19EhDQqU/PqncCH\niQ95+PAhDQYD9Xo9L168KNq7dOlCAOzUqdN7v6Y57ty5IwJyTaV+/fpvrOmhxHUA4GeffcaSJUuK\nv9u0aUOdTkdJkhgVFSVqcgwZMoQAhIUjNTGN8/j8888JWMZWmErDhg2Fy8Wa9SFfvnwE1CnFu3fv\nZqNGjVigQAFWq1aNK1euTFPtE2u4fv06p06dykaNGlkdZ9GiRTllyhSL+xgwYIDI5vnqq680IqLh\n3aEpvfQHbU7SF6zNh5I5MXToUNGmrBJz586dqnJQXDNlypThpUuX+PDhQ3755ZcE3s41o+Dhw4ec\nPHkyW7Zsyd69e/PEiRNv3UdacOzYMQJgsWLFVO1KRkfFihU/yHVNoSh4Pz8/LliwgNOmTaO7uzsB\n8Mcff0z1XFmW+b///U/lflHqaeTJk4eSJFGSJIaEhAhyp5REz5QpE7du3co+ffoIC4ISb7F06VIR\nS6KUQc+fP79FWjUAq5YRc1FcQYAxRsQ0zuR9YfTo0arrpCQFChQQhMia7Nu3TyMiGt4dmtJLf9Dm\nJH3B2nwoyldZOZYvX178/dNPP6Xa3/sKVv27cefOHQLGTJB79+6J9m+++YYA2Lp16w96/WfPnlGv\n11On0zE4OFi0//bbbwSs1wCxhqioKK5bt47BwcF89OiRULRKYKhSL6R06dIiMLZ9+/Ykje4w03oi\nAJiQkMC7d+8SeF211MbGRgSnFihQgFWqVGGzZs3YpEkTi3k3Ly6miGKFkCTpjTEwbwMlvkWSJGbI\nkMHCqqNk6ihExVrKsyIdOnTQiIiGd4em9NIftDlJX0hpPhYtWiRW44oSGjt2bJpM5e8jffdjQAlU\n9fHx4ahRo9i+fXuhsD40ibp9+zYBY7aGafzLuXPnhCXqryAsLEzUIUnJTXL16lWSRquKQhyUKqNr\n164V8UEKmTEYDCxTpswbLQ6mogSClitXjsHBwYyPjxfl1c0tZXFxcdy+fbsgU2nBgwcPeODAARHX\nY1ql1VS++OKLFMfo6upqYbHRiIiGd4am9NIftDlJX0htPuLi4rht2zYGBwfz8ePHf9uYZFnmwYMH\n+eOPP3LVqlV8/vz533LdiIgI1V4vysp5woQJH/zaSUlJYrWuxMDIsizqgzRv3vyd+r948SJnzpzJ\nKlWq0MbGhnZ2dmzevLkoCPbo0SO2bNnSwqVha2urIqTWxNyKYipZsmThli1bhDvoxo0bvHr1Kjdv\n3szjx48LchMXF0eSXLJkiep6Dg4OHD16dIoE+Pnz5+zYsaPox1QUi4gSIJuaKARMkiRVTRSNiGh4\nZ2hKL/1Bm5P0hfQ2H5GRkaLapSIeHh5Wt6JPCUlJSTx06BC3bNmSanDsjRs3eOrUKRXRSUxM5O+/\n/87+/ftz1KhRvHz5MpOSkhgbG/uXAyfTiunTp4t7LlWqlEgzNRgM77WsvSzL4l4ePnzIU6dOsVSp\nUoJUpEYsmjZtytOnT6foclHEdCO7kydPiiBcaxvVGQwGvnz5krt27RJEqEiRIiqXYEp1VJRYFb1e\nz5IlS6rGrgTlphZUa3p8uXLlePfuXS5cuFAjIhreH9LbS1aDNifpDeltPqpXr07AGEAZFBQkClw5\nOjoyPDz8jefv3r1btZGZjY0Ne/Xqpco6OXfunErJubi48Ntvv7XYUO/hw4fs1KmTiI0oUKAAFy1a\n9MYxJCYm/qXN+WRZZpcuXVQr8mzZslmUOI+Pj+fatWs5YcIE9u7dm0OGDOGSJUuEVSE1hIeHc8yY\nMfziiy9YtGhRlSJ2cHBgSEgIw8PDRaaNqSLfsmWL6Mdapo0pOTENmh09ejT79eun+iwgIEBcO0OG\nDIyPjxcpxoMHDxbXWbRoEQFjMTRzInj58mUCxvopyl43K1asENfx8/OzmnVlSkyU6rMKETHf80Yj\nIhreGentJatBm5P0hvQ0H0osgpOTk9grRJZl1q9fnwA4YsSIVM+/cuWKUIa5cuVipUqVhNIZMGAA\nSaP7RUkrdXZ2VmVNDB8+XPQVGxsr6qmYr5wrVqzIy5cvW1x/y5YtInbC3t6eX3zxBW/fvv1Wz+D4\n8ePcs2cPd+zYwQMHDlik7R46dEi4cMzF29ub586dS7HvNWvWWCUQpvEUtWvXFscrVVoVt0dERIT4\nzFr1VMWqYl44bfTo0dy8eXOqFonffvuNWbJkIWB03yhITk4WRFDZMC8+Pp47d+7kwIEDCYD+/v7s\n2LEjhw0bxsuXL6usMX9VMmXKRDc3N42IaHh3pKeXrAYjtDlJX/iQ8/HkyROuWLGCCxcu5M2bN1M9\n9ty5c6r4DF9fX2F9UMq6vylOQqna2bRpU1EEbO/evcKi8vTpU3777bcEwEqVKvHZs2ckyY0bNwoC\n9PTpU5KvN4PLmzevqCthvvo3DWBds2aNcCuYxlnkzJmTkZGRaX5mpvPx8uVLfvfddyxUqBDd3NxY\nunRpEfegXEMhFooVxbSKqCkePHggjlHcI8q5ptkwAIQbqE6dOgReFydr2bIlHz9+zMePHwvSYXqe\nNdIGgKdOnRJuJ3d3d7q7uzNnzpwcMGCAIBMDBw4U11m7dq0Y96VLl8T9JSQkcOXKlaLOjTXR6XQp\nBucaDAa6uroSgMpVpJBVNzc30bdSHl8jIhreGZrSS3/Q5iR94UPNx9y5c8X+J4ri7Nq1K1++fGlx\nbFhYmCpA0VSRL1iwQJSIV6waKUFRQNu3b1e1+/v7EzBWY1UUzLp161THFC1alAB48OBBkq+3qO/T\np48gKT/88IModQ8YM1mSk5OZnJwsqpgOHjyYz58/5/Xr10Xdjf/9739pfm7KfMiybLVWBwChTGvW\nrMlHjx4JS4JiKdm2bRtlWebRo0f5+++/MyQkhDNmzCAA1qpVi8OGDRNjVaqsmj7zXr16CYJga2vL\nHTt2CEuTaQxJarEXirRv354vXrywCAJWnp/iiuvSpQuHDh0qyMqkSZM4a9Ys8Vy//PJLHjx4UFyz\nYMGCKuuOt7c3q1atquq/VatWzJIlizhHqT5ragEKCQkRBNZc7Ozs3i8RATAfQCSA8yZt7gB2ALj6\n6mfGV+0SgB8AXAMQAiDA5Jz2r46/CqC9+XU0IpK+oCm99AdtTtIX/up8REdHc/r06ezUqRNHjhyp\nMqcre3zgleWhUaNGYtVszb2iKPvAwEBBCJTiWIoC1Ol0qoqn1tCgQQMC4MiRI0XbkydPhBXhxo0b\notbF9OnTxTHx8fFiS/qzZ89y27Ztwn2jKN3hw4dTlmVh9lfuJzAwkL///jsBMHPmzCprxNatWwm8\nXSE3ZT6UnXhdXFy4Zs0anj9/3iLeoXLlykxISBApqYqlY9SoUWK/FEUUC8CoUaM4YcIEAsaKq4r7\nRXl25qLUjTl27BgDAwNFe2BgIA8dOiRIkLno9XpOnDiRSUlJHDdunIrspEZgrMV0FClShFFRUWzc\nuDEB434127ZtE1YMa/0oBehkWeY333xj9ZpTp05lYmKiqErr7+8vvne2trYcPHjweycilQAEmBGR\nyQCGvPp9CIBJr36vA2DrK0JSFsAxviYuN179zPjq94zUiEi6hab00h+0Oflr+PPPPzlq1CiOHj2a\np06dem/9/pX5OHr0qEVKp8FgEPucKDEdprumbt++Xax2ExISVP0pRaX27dvHK1euiJWrad+//vpr\niuNRNl0ztcD4+flxypQpLF26tEoxKaTBxcWFs2bN4o4dO8R4CxcuzJUrV1qtypkhQwZWqVLFqtJT\nlJz5vSnFtcqWLZvmZ6vMh7JK/+abb5iQkJBi4a1WrVoJK41CnhRS5eXlxQYNGggLCmB0s1y4cEFU\nWlUqqJqWbQ8ICGDr1q2FdcgUL168EJvKnTx5MsXy8IsXLxbnKOStdevWKRIQmJDObNmysW3btmzV\nqhV//fVXEYSrfC9CQ0OFu65Zs2biHipUqCBcRp06dWJkZKTKhWQuWbJkUc11p86deSc6hlVa9aBL\nmc/p9tmbC5pJNJKDNEOSJB8AwST9X/19GUBlkhGSJGUFsJdkfkmSfn71+2+mxylCsuurdtVxAPD0\n6VMxqKtXr77V+DRo0JD+8ezZM5w/fx62trYoWrQobGxsPuj1kpKSMHLkSGzbtk3V3qBBAwwbNgx6\nvf6DXt/aeBo2bIjIyEgUK1YM1atXx5kzZ7Bjxw7o9XqsW7cOPXr0wJ07d7By5Urkzp1bnFujRg08\nfvwYmzZtQpYsWUR7UFAQzp07h0mTJqFq1aqIj4/HH3/8gYkTJyI5ORlZsmSBLMsoVqwY2rVrh/z5\n86vGNHv2bCxYsAAA4ODggBcvXqg+9/T0xOzZs+Hj4wNZljF8+HDs2LFDdYyTkxMmTZqEb7/9FtHR\n0Wjbti3OnDmD8+fPWzwDvV6P5ORkGAwG1KpVC8HBwaKtUaNG6NSpEx4+fIhRo0YhLCwMhQoVwvPn\nz+Hg4IDAwEC0aNECDg4OqT7nyZMn4/fff0e3bt2QM2dODBs2DF5eXoiMjDQqQEmCNR2YIUMGxMbG\nws/PDwsWLICDgwMePXqEli1b4vHjxwCAzJkzw9XV1aqOGjp0KJo0aZLq2BQMHDgQ+/btQ40aNfDJ\nJ5/g6NGjuHz5MqKiopA5c2YMHDgQlSpVQvXq1RETE4NixYrhzJkzAABXV1c8ffpU1V/hwoXx7Nkz\n3L59G+PGjUONGjVUn7dr1w6hoaEYN24ccuXKhbZt28LR0RFxcXEwGAzYvn07+vbti5CQEPTv3x8H\nDhzA8ePHxT3b29sjPDzc4j70LpnhkLsEXMo0hY3b6+8l5GSc/eYz8aerq6tkfq4hTU8qdXiRjACA\nV2Qk86v27ABumxx351VbSu0aNGj4l4Mk5s6diyVLliAhIQEA4O7ujkGDBiEwMPCDXXfJkiXYtm0b\nHBwcUK9ePciyjODgYGzcuBF58uRBq1atPti1reHYsWOIjIxEzpw58dNPP8FgMKB58+aQZRm7du3C\nli1b4OnpiTt37uDs2bOCiISFheHx48ewtbWFq6urqs/AwECcO3cO06dPh16vR6ZMmbBnzx4kJycD\nAO7fvw8A2L59O/bt24cffvgBAQEBAICYmBgsX74cADB16lRUqlQJu3fvxoQJE/D06VNUqFABI0eO\nFNfU6XQYM2YMKlWqhD/++AP0RSliAAAgAElEQVTPnj1D4cKFodPpMGjQIMTFxQEAzpw5AxcXF6vP\nQBlXixYt0KdPH4SEhCA8PBw6nQ7r16/H+vXrxbGSJOHixYvi70uXLmHv3r2YM2cO7O3tU3zOZcqU\nwe+//45Vq1ahePHiAIAiRYpg586dAGCVhABAbGwsAKBq1aqC7Oj1ejg6OgoiEhkZicjISACAs7Mz\n3N3dodfr4enpiYcPH+L+/fsqopgSFCVvY2ODadOmqT6LjIzEoEGDEBAQgDx58uD06dMIDQ0Vn/v7\n++PQoUNwdHREQkICkpOTceHCBXTq1Anz5s3DhQsXLIhIvXr1EBoaiokTJ6J9+/bIlSsXbt26BQDw\n8PBA27Ztce/ePbi5uaFgwYL47rvvBGGbNGkSChYsiO7du+PMhctwzFMaDnlKw867MAzOHgCAhHtX\n8PLyHnzTpysKeNrB2daCd1jCmpkkNQHgA7Vr5onZ549f/dwMoIJJ+y4AJQB8DWC4Sfv/AAww7UNz\nzaQvaG6A9Id/6px89913woRbrlw5scusTqfj4cOHP9h1Fd++6X4cq1atImCsa/GueNv5mDdvHgGw\nbdu2qnbl+XTv3l3UfrC1tWX79u05btw4sf9Mx44dLfp8/vx5iiXDs2fPzh07dvDixYvCtF+0aFFR\nU2Lp0qUELOMwlPYGDRq88Z5Gjx6tuqapuV6v14sgSlPx9/cX8SDK2KdPn8569erR1dWV2bNnF8Gj\nDRs25J9//smNGzcK98LUqVOtjkWZj6SkJFauXNnqM+nVqxenTZsmsmAyZszIYcOGccGCBcINU6hQ\nIZLG4m6mz9Z0Y7pKlSrxt99+s8h6sbe3T9P+L6buOSWWxtRVo/Rr6jIzF9N9iXQ6HVu1akXAuPPt\nmjVreOzYMTHXiYmJVjOYTMXPz48nT54U9USUMc5ftpJLj4axxKClzPn1BuYaHMzsPRax1Q/buejw\nTXbsN1z0cfXqVYaEhPDw4cPvP2vGChG5DCDrq9+zArj86vefAbQyPw5AKwA/m7SrjqNGRNId/qlK\n79+Mf+KcJCYmCr+7sluoLMvs1asXAWO66IdAUlKSeDmaBkE+efJEKIx3xdvOx5EjR0Q8gpKWmpCQ\nIJTdhAkT2LRpU6tKImvWrMydOzcdHBzo4ODAOnXq8MiRIySNZGTSpEksUaIECxQoIBTmmjVrxLXj\n4+NFcGJwcLBKwep0Ok6aNEkorTFjxhAA69evn+r9xMbGiiyKlStXCuKnXD9jxoyCdNaqVUtcLyAg\ngLIsC4Xn4OCgKoMfHh5OwJh50b17d/bs2ZO//PILly1bRiDluBHT+YiJiRF7pyji4ODAcePGsV27\ndqLtwoUL4nwldgIw7qtimhGSMWNGxsXF8fTp0yKAV6n50bJlS86fP58NGzYkYMzMUdKbU4KSzaT0\nrRC01IiCqZin+fr6+lo9rmjRogwNDSVpjAdat24d27Vrx0aNGrFly5Zs1Lgx67bswO9+/Y3Hb0Tx\n6PUoLt+8h86lGjNzs5H07rWEuQYHM9fgYPr2nE/36t1p7xvAwp8U4eDBg+nr66vaIM+0DsnfQUSm\nQB2sOvnV73WhDlb9k6+DVW/CGKia8dXv7tSISLrFP1Hp/dvxT5uTZcuWCeUEgOXLlxdb0Z8/f168\nQD8UlJfz6tWrRZticfD393/n/t92PmRZFtkZ7u7ubNmypRij6WpYkiT6+vpaFLcyFxsbG+7evdvi\nOkqQoWkqbnJyssjSUMiDs7Ozap+R7t27i/oXiuTOnZu9e/fmzp07LapzHjt2jDCxIKQUrFqoUCHe\nvXtXKFxJkkRwKKDOBvrzzz8tAm4VUc4pWrToG+dj1qxZFueZi06nU1VUvXLlSorPeceOHeK4Dh06\niM9Mi5g9e/ZMBPiaBpxag0K2zMXanFeqVEkQnLSQlAwZMrBOnTqCEHp7e3P27NksVKwU7X2KMWu1\nIHp3m0fvr5apiIa5ZP1yNj3q9KVL6aa0yawmOtb2p1Ekc+bM9Pf3f+9ZM78BiADwEsbYji8BeMDo\ndrn66qf7q2MlALMAXAdwDkBJk36CYEzrvQago/l1TAf9ItGyqIyGvxf/NKX3X8A/aU6WL19u9SXl\n7OzMy5cvi8/TukX7X4Hi8rC1tRWZBMoLdM6cOe/c/1+Zj4iICIv9YKylR0qSZGH6z5Ejh4XFJCAg\ngHfu3OGsWbM4ZcoUHjt2jEOGDBHE7969e0xMTBRWDoWE1KhRg7Gxsdy2bZuFewGAqlS6IuXLlxcV\nOsnX1Vw9PDxENsjWrVtF/QrAWPCrQ4cOwjKi3BtgzLyYNm2aIDgPHjxQlQ03Pda0fkXv3r0tnmtc\nXBzHjx/P/v37c/v27YIAz58/n4mJiaoxmZKlMmXKUJZlJiUlsXPnzgTA6tWrc8iQISKN17wYnFK/\nAzCmJpvuXJvaGM2hVKZVvpPWNphzc3PjzZs3BSGaO3cu8+fPTycnJ7q4uLBAgQKsWLGiSCHOlNuf\ne05f5arj4Ry06hR9e/zK7N0XMFvXeWqS0XEms9Try8ARv7Fip5HMUKQ6nfKU4lfjf6KLfxXaevlZ\ndQuZz09q8o8vaLby+Jv3RdDwYfFPUnr/FfxT5kSWZbHp2Lhx49iiRQuxUlPIh/JC+/HHHz/YOJKT\nk0WtB1Ml1K9fv/eyCdvbzkdSUhLHjx8vVqp2dnZi9a+Y5Rs1aiQKYpkWAAPAnTt3kiS//PJLQbCs\nrU4DAwOF9UOn04nqn8Br07mptSQkJERlXjdNFVXmSVFKn3/+uThPlmVRu6Ru3brcuXMnf/75Z+EC\nUr4D1sTFxYU5c+Zk48aNuW/fPsbExHD8+PGCcKWm4NavX8/IyEiOGjWKVapUYZkyZVTjV8TV1ZXJ\nyclcvXo1gdepuZ6eniLtGDAW61JIgOkmecp+LDqdjmPHjuWRI0fE3CjkzdvbW8yDKaGzs7PjmTNn\nUv0+/Pjjj1bnz1wUEgmAiYmJPBP+mCuPh3Px4Zv8Zf919v7tFEsMX8fsPReryIbP4GAW7fMLPer0\noWfTEWwwbhVHLwymzslNkLEpU6ZQlmWxV42pODg4sFu3buzevbuIucmRI4eF1cvJyckqmf3HE5Ea\n3+374Ls1akgd/xSl91/CP2VOlJWym5sbX758yYiICObPn9/iRdWwYUOL/UA+BC5dusQZM2bw+++/\n57Vr195bv287H0pcjCkpU2TatGkEjPU44uLirK5GlbLoP/30EwF1nEDDhg3ZtWtXYTlo3bo1Gzdu\nLKwthQoV4qpVq1i2bFkCxpiTSpUqcd68eTx//rxQJL6+vmzfvj0BY2VUJY6jcuXKtLGxoU6n4717\n90gay6gPGzbM6o6zTZo0YWJiorCE5MmTh/PmzbNaJdT8mSjujc6dO6vImFLz4scff7RqPXB0dGTD\nhg1VhcJu3brFnj17CkKRmsLPmDEja9WqxWnTpvHhw4ckyZEjR1o9dvbs2SqilSNHDkHAlLlzdXVl\n48aNBYE0R3JyMrt3727Zv05Px9wlWLbzWGas1o1Zmg6n66et6d9hLCtN3m3hQvEZuJY+HabQo3Zv\nepRvxr7fLWHdVl9SZ/vaqmVvb8/r169buN4AY9Ez82ejuIjs7OwYHh7Oli1bWn0OxYoVs0pC/hVE\nJNfgYG49dy/N/+Aa3j/+KUrvv4T0Pif3799n8+bNVS+1gQMH8uXLl4yNjRUKIWPGjFy3bt1f2mU1\nrZBlmffu3eP9+/c/2DXeZj7CwsIoSRINBgM3btxIWZZ5+vRpocRHjRolLCX169e3ukouXbo0L1y4\nIBS1IqZl0E+fPi1WszExMXz+/Dmjo6MpyzI3bdqU6jb15gp/x44dnDhxIgFj8S+lpPmRI0eYlJRk\nNQtDp9NxyJAhTEpK4o0bNwgYrR8xMTFcs2aNSlGnlBGiKPRatWoxNjZWEAulaJcSM2FNAXbv3p3R\n0dHCSpEnTx7VBnxpFTc3N65bt47Dhw9nuXLlmCdPHubPn58tWrTgqlWrOGLECFGt1FRSim/55ptv\nGBQURC8vL3p5eTEoKEhU1L1w4QJtbO1on6soK/SbRe+vljHX4GDm/HoDc/RfzRz9fjeSjoHrmLXF\naLoG1KHBLQt1Tm7U2TkROutzak4uFIsQ8JrEmj9D02OUzKUmTZoIK0i9evVUgcepyT+eiNSasZ9l\nx+9kUrJmFflYSO9K77+I9DwnL168EO4FSZJUCq9JkybcsGGDCMwcN27cBx3LH3/8oSrTXapUKe7b\nt++9X+dt5mPBggUEjK4XUyixBR4eHpw6dWqKAarWgkAVUQKAFSjK0HSX28TERGbPnl0QA2tKy7z9\ns88+E1aKefPmqSwiK1euFKRywYIFPHz4sHDB5cmTh8nJyYIU5c2blyTFNvFdunQR18iWLZvVe1Pa\nFLeSolTN42vMN7BzcnIiSdarVy/F51WyZMkUPytQoAADAgJS/DwwMNAqAerduzc3b96sUv46nS5V\n4pcpUybuP3WBQ9aEMFe/lcw1OJh5h25iyx+2M6BhJ+ozeIh+dPbOlOzUxM1092NlLqxdx3wMpjsQ\nW/u+mZIRU7G1tWViYiKvXbuW6vfxX0NENofcY67Bwdx7Oe07L2p4v0jPSu+/ivQ8J4q74E1SokQJ\nxsTEfLBx7N69W7x4nZ2dxarb1taWf/7553u91tvMh1KbIzAwUNWuWImsEYMsWbIwW7ZsFiXhFWWq\nZOAoxC4pKYlTp04VCnr48OEiTXj//v1CUVu7nr29Pbdt26aKJ1GkYMGCwlqjpFsrQbPff/+9uJeX\nL18Kl8nJkycZFxcnrBu1a9cWbhpT94yPj4/qnqxdX5FSpUqp3C6mViOFZAFGi43yt2mabErKNbXP\n9Xq91ZiVZs2ace7cuWI8BoNBuN5MlbvOwYV23oVpmzUfMxUN5KQ1hzlm1SEWbz2YGat2os+gDcw/\nfAtrjlxBh7zlaO/kwq5du7JXr15iriRJok6n46xZs8R9WbOY6XQ6QfYUyZ8/f5o22Eur/PzzzyTJ\nUaNGvfGZ/uOJSPzLJBYdtY09lp5M0z+5hveP9Kz00jtCQ0O5cuVK7t271+q24n8V6XlOlNWZk5MT\nv/76a3bo0EH1AvTz8+PEiRM/KAkhKcz2PXv2ZHx8POPi4kTMw5vqYrwt3mY+oqKiRCbKuHHjePPm\nTS5evFgo3jZt2jBPnjz09va2WPUrUqlSJe7du1fswrt582ahgFq2bKnKDFEka9asvHz5Mv/44w8L\npWV+bOXKlXn16lWxeZr5qtc0a0Yxz69atUp1n8q+Lvv37+e9e/dSXF2nxUWUKVMmtm/fnlOmTLHq\nBipfvjznzp1r0a6QH71ez88++0wobVNLhnL/itI0t6woEhQURFmWOWnSJBUBcnBwoL29PYsUKfJ6\nR10HF7pWbEvPJv+jZ9MRLDR0A/MM25xiemyuwcH0ajiIYQ8e8+eff2bOnDkt7kXZhbhx48aMj49P\nlailVZycnDhq1Cirlh9rlo6hQ4eKZ+ju7s6XL1/y6tWrqrRoa8HC/3giQpJjgy8w99DNDIuKTdM/\nuob3i/Ss9NIrnjx5oorGVxTw+1qJp9c5iY2NFS/jzp07i3YlABMAN27c+MHHkZSUJF6kpgWlbt++\nTcBoIXmfMJ0PWZZ54MAB/vrrr9y+fbtVAqpsJ28uHTp0EMH5MTExIkbDmmzYsEHV55gxYyyUR548\nebh48WIRmFqtWjUeOHDAoi9ru78uWLCAOp2OBoOB58+f58yZMzlmzBiLOiLKrrBlypQRMSjKpngZ\nMmTgs2fPxP9CxowZ31gTBYBFQLO7uztz5coliIVyn6apxTlz5nxj1okiSh0Oa8rWWrqyIv7+/iJo\nVzLY0jFfebqUbkr3mj2ZrfNcerUcx2xdfhHkInvXefTrv4LNvwum/xff0j53CTr4laJdjk84ZPQk\nrtm4mfMXL6Vk60BbW1uLmB/AWBRu+/btIrOmVatWwvWlkKy3uQdzady4sco6ZjAY6OnpmeLxBQsW\nFL+buvBMd/w1/z79K4jIg2cvmO+bLRy4KvUUKA0fBulV6aVnKC9eR0dHNmjQQPjqM2bMKEzk74KP\nPSfHjh1jjx49+Pnnn3PMmDGMiIggSRGUqNz7nDlzeOrUKZEGqtPp+Pz5c5JkZGQkR44cyUqVKrF6\n9er86aefGB8f/17Gl5ycLBTezZs3RbsSq5A5c+b3ch1Zlnn8+HGOHTuW8+bNY1hYmMXq0s/Pz2r6\n5saNGxkYGEgvLy8WKVKEP/30kypod+3ataIPJycnDh8+nNOnTxfKOH/+/BZ9Xr9+XWSXDB48WBCG\n6OhooZze5IJQRDnuiy++sHrfW7ZsYevWrVmtWjVBmOzt7VXui5EjR/LevXuUJIl2dna8d+8enzx5\nwsmTJ6eaNaPIm+IPUtsVVhnP4sWLeevWLY4dOzZNfVpT8JLBljaevnQsWImejYcxW5dfRCBprsHB\nzNF7+SsSMpdebaewfJdx9A2olOb+gdfF1nLmzMl58+Zx4cKFIhunZ8+eosiaQrbs7e1TnMu03qO5\npETkihQpwiVLloh5NrWiKVsQREREcMiQIVbJ87+CiJDkyI3nmXvoZt58qFlF/m58bKX3T8OlS5eE\nIlai4RMSEoSrYPLkye98jY85J6a1DBRxc3PjsWPHUkw3VaRYsWIkjYTF1JevSIUKFVQVLt8FCvkp\nV64c9+/fz127dolsjx49erxz/7dv3xaxGaaKDzCuYtu0aSOCcrNkycLYWPW768SJE6riVwULFuS6\ndevE56aF4ObPny/alSJlOp3OqntLqedhunePLMuq523N9G+6olWkWrVqfPr0qap/WZZFwS9TMXV3\nZMqUiRMmTOD69esZGBgo2k6ePClcDKZiGh/ytqLMqTUxrXVCvg4I7tSpExs3bsxy5crR19fXqlXB\nJlNOZihWm5kaDWXOAWsF6fDutYSejYbRo94A2ucqSsnWwUL5S5LEOXPmqPqzFgRsTQ4cOCDGe+bM\nGQJGC44syxa1cN5GUrKuTZ06VVWYrWzZsqogVoWgTJw4URV3EhgYyIiICIv/1wsXLrBDhw7CRVOv\nXr1/DxF58PQF/Uf8wcazDjIx6cOl+mmwxH+ViNy+fZuzZs3i9OnTefbs2TSfp2ymZh6HoGx01qZN\nm3ce28eak+PHj4uXar9+/bh48WJWrVqVwOsMib59+xIwBuplzZpV5TP+448/SFLsxVG6dGlu2LCB\nixYtEopy0qRJ72WsYWFhVmtM+Pr6CgvOX0VycrKIgfDw8GDVqlWFktHr9aL/+Ph4oSh//fVXcf7F\nixfFc7G3txfnSpIkXC6KGwkAf/rpJ8qyzKtXr6rSQsPDLQs+KiShefPmojaL4k4AjMXRdu3alaLC\nUla7JUuW5MyZM/ngwQNV/xs2bCDwer+WVatW8bPPPiNgXDmHhoYyPj6enTp1suhbUfje3t4qE78i\nBQsWTNUtkBapXr266MPW1pbnz5/nd999x65du7JQoUIEwGXLlon7iYqJ5+Hjp5ghez46FqxEr5bj\nmbXjTOYctNGYOjtgLTNW60rHAhVo6+VH6K3XyjCXevXqpZqVo8inn37Kfv36ib+VuiWkMQNNaU9K\nSmJSUhKbNWumOt/W1lbclzIvSnqzqZh+bxTSlDVrVvE9TW0BYS52dnbcvHkzo6KiVN+N/fv3W+3n\nX0NESHLjmbvMNTiYS4+GWfzzafhw+C8SkbFjx1qsklq1asWEhIQ3nrtv3z4CxlWn6fFdu3YlAPbv\n3/+dx/ex5uSrr74iYCxwpSAxMVGY4w8cOMAXL15YlB83GAycNm0aSeM+HEo6oykh2LhxI4GU9w/5\nK7h79y4HDBjAwoUL09/fn8OGDXsvrrGdO3cSMKacRkdH8/jx4+zTp4+436VLl4pjlRiKAQMGUJZl\nHjlyRNSzKFu2LB8/fszExESxO22hQoX4zTffsGDBgipTeebMmVWr7kyZMlktAnfx4kWhiLJmzapK\nXwaMVqfo6GgOHz7cQmGkpHQWLVok+lcUoSlhjI2NFSmjFy9eFMGzjo6OnDJlCmvWrKnq09R9pdyT\ncq/mVoOU6lyYx5q4ubmlXMFV0tHgnp0u5ZrTpVxzdp+ymF//foaVJu+m75Bg5hq06XVcR4+FzNxs\nFF0/bU29S2Y6ODlbtd6ZStWqVS1cci4uLiKjRLk3BwcHi+DgFi1a8Pnz5+LvoUOHUpZlyrIsKswG\nBASIZ/3w4UPxLBwcHLhmzRphdXpbadGiheh38+bNVl09Tk5OFjE7yvdLp9OxUaNGvHPnDpOSkoQF\nsH79+hw2bNi/k4jIsszaM/az5nSt2urfif8aEVGKLUmSxCZNmrBjx44iQn3o0KFvPD85OVm8ECtU\nqMC5c+eq6iWEhIS88xjTMifPnz/nvHnz2KlTJw4cOJCnTp166+tcvHiRQUFBzJcvHwMCAoTZ39RV\nQL7OnFi7dq1oO3XqFKdPn845c+aoCEdERAQBo7nZNJDz3LlzBIxm+vSMiIgIsRtr9+7dSRrnwzSb\n4uuvvyZJVcnsKVOmsGPHjhYv+oCAAD579ozx8fEpVqY0VdqK4h4zZkyKY9y7d6+qtoSzszMHDx5s\n0b+Xl5fVuAAHBwf269dPjF2n04nvraL0Nm3apLqmYvlZuHChcLVky5aN06ZNY3R0NKtUqWKhqBVL\nCmC0DKUUo/Cm52IuOntn2ucuQY+6/Zmj/xrm6L/aIkulwDebGbTgT45cH0L3KkF0KdmAP64/QFtH\n5xSvmdZgWMBIApVFiSLh4eEWFh9HR0cePHhQ1ZY3b17VnjymmzWStLCK/FXZu3evql9TQmNK9KzF\nnOTKlUs8o3z58gly7uPjw5cvX1KWZVEG/19FREhy+bFbzDU4mEevR1l8puHD4L9GRJQX5tSpU0Xb\n3r17CRiDTZWUydRw4sQJqz736dOnv5cxvmlObt68abE/CaCuvPkmHDlyJEVz7aeffioCS0NDQ8VL\nS4mJSQ2yLIuxff/995RlmYmJiWzbti0BY0lyU1y4cIGtW7emp6cns2XLxh49eojS4n8VCQkJXL9+\nPadPn84NGzakqbz8kydP2LJlS9WK1s3Njffv3+fx48d56NAh8Rz8/Pw4ffp0sQGZvb09p0yZIl7w\n5tY2T09PYRF5k/IzGAzs27fvG9PBlYqtBw8eZExMDO/cuaMy2ZuvzM1X/V999RXHjx8vSLiTkxMH\nDx4s6nHUqlVLfAf27NkjlLe1rJgSJUqoLEb+/v48deoUnz17lmLxLavZNZKOOkc32mTKRQe/0nQO\nqEfPKu2ZMbALMzcbxew9FjFHnxWCbOT8egMztxjDjIGd6Vy0Jp28clGydaDB1Yu16jYQ86rMUUJC\nApcvX55qSrHy3FJyISnBxL1796Ysy6xWrZr4zNRVaLovjdJer149UacFMFq9fvnlF4u5VVxtyjNS\ngplNLRpKvFJqgavly5cXwePKdgzK8QcPHuSYMWMsvn86nU7sT3T37l1BmJTaKVWrVlWN9dtvv/33\nEZHnCS9ZcuwONp51ULOK/E34rxERb29vAuDVq1dV7coLJq2lwqOiojhlyhS2bduWAwYM4Llz597b\nGN80JwqZKly4MGfMmMFevXqJl2tK+12YQpZlYWpu2rQpT5w4wQ0bNqhepNmyZWP16tXFy898Z1IF\n9+/f59q1a7l161axM6tSXRQwxiwoNSbs7Ox4+vRpce7p06etBtnlyJHjL5ORM2fOWARr+vj4pDo/\nsiyLWBi9Xq/yybu4uHDIkCEqhWOuUNesWSNiSkwlJSUhSZLVgNIFCxZYve/79+/z559/5vTp01O0\nfA0aNIiAcSVr7v6wt7cX7pTUgj/Nx50lSxaWKVNG/K2QCsUd5OPjk2IRLb1er7La5MmTh3Xq1BF9\nGDy86ZyvDO1yfkLnkg3oXusrevdebrUGR45+vzPrl7OZqeEQetTsSeeSDWmfqyh1jq6q75kSvwW8\nzpySZVm4ysaOHcslS5akeN+maanbt29P8bh8+fIJF2BMTEyagnE//fRTxsTEMCEhgYcOHeLBgwfF\n/4s5nj9/riJwI0aMsCjYptPpVEGoKYmfnx9fvHghCu0pi4Rq1arx4cOHYudqRapVq6Yay6xZswgY\nqybr9XoaDAZRpiAmJoZly5b99xERklzxp9EqsvHMXaufa3i/+K8RkQoVKhAwbmal4M8//yRgNHGn\nJU7kQyO1Obl+/ToBYw0H063aR4wYQcAY62KKxMREXrp0iXfvvv5/UtJwXV1dVVHxykrMtJiSJEls\n0aKFRQZHcnIyBwwYoDJxe3h4cMWKFSTJ2bNnq4pcFShQgLt27VL1obxIGzZsyMuXL/PUqVMiZTMt\n26ub48WLF4JM5c+fnz169BBBfI6Ojhw0aBCvX79ucZ5iOnd2dlaREGvKde7cuZwxYwa7d+/O8ePH\n886dO5RlWbVa1ev1qVa5XL58OUlaBHyePGlZ2PH777+3cCM0btzYIptBqVGxfft23rt3j2fOnFFl\nsGzdulUQpzcpL3Oxs7MTFi0vLy/evn07bdvE6wy0y/EJi3/ek1tD7rJ422H0bPwNs3efb0k2+q5i\npgaDmKF4XWPgaNZ8RqKhtyEk9bO05lapWLEiDx8+rCImCkwJiqkFQFGs5n1JkmS1VodOp+Po0aP5\n6NEj1bM/e/ZsilYWT09PLl++/K03fVTmy5ooxDA8PNyiAJxer2fr1q1VcVz9+/cXhe5y584trLkG\ng8Hi/v39/VVGACXWqGvXrmI3aEmSWKpUKfEd+FcSkaRkY6xI+Qm7+CLx/VWr1GAd/zUioqwMDAYD\ng4KC2K9fP/EP1bdv3489PJKpz8mhQ4cIGM3hplBeXJUrVyZpXAnOmDFDRQYqVarE8+fPCzNt9uzZ\nVS+dHTt2EDBmVBw9epQbN25kWFiY1XEodRt0Oh0DAwPFKlmn04nU0vj4eJ48eZIXLlywsHDev39f\nHL9w4ULxoj527BgB41WjVNUAACAASURBVMr+bbFs2TICxtLi8fHxXL16tYXSsrGx4Zo1a1TnKeXS\nFfLg4uIiLGTmUqhQIV68eFF1vkJkFWnbti3Dw8NTTKmsXbs2Dxw4YFGl0sbGRhUIq/jllTkxXbGX\nL19eRZqVeAzFpeDg4KCq+XHjxo00raBNxcnJSWRPKBlV+fLlSzHV1NHNk44FP6NXm0kqF4qKcHT/\nlXk6TGKGojWZ69OGtM9dkjYZs7Jg4U+EIn3TuKxV9yxevLiKZH377beqOVqyZInKPVWoUCHu3r2b\n4eHhqudi7q5s2rSp+C44ODgwISGB58+fZ+/evRkYGMimTZtaBOuafpcAsF27dn9pgVO3bl0CRgth\nr169uHnzZqsZM6ZiWopfIVM6nY61a9cWBKRSpUoWFrypU6eK707nzp157Ngxzpo1SyxKdu/ezfj4\neHbv3l1FukuVKvXhiQiA/ADOmMgzAH0BjARw16S9jsk5QwFcA3AZQE3zPt9EREjy0LWHzDU4mDN3\nXXnrydPwdvivERFZljlgwACLf+BatWoJf+rHRkpzIssyIyIixKZkStqxLMts1aoVAaMvl1RXO/X2\n9hYvFA8PD1Xq63fffcekpCRGRUUJZTZo0KBUx5eYmCgKNCmVVGVZFlk35vUdzLFr1y4LRZ87d25e\nunSJISEhYszm2LFjB5s2bcpSpUqxdevWqloapNFfDRiDjqOjo8U9K1kBSpEtJycn1ar2l19+EePo\n2LEjX7x4wbt376qUYs6cOQURyJEjh8oiYV5TwsHBQRULYNpPSpYSpbaDwWAQsThKGrSikMylZs2a\nIpbEtNKveXaEJEns37+/1fog5seZtx06dIik0dqkKLI5c+awTp06NLh60b1sU7rX+oq5vxgngkaz\ndZ5Lv2ZD6FbxCzrm/5Q2mXIxi/+nlGzs6eDgIFbhO3fuFO4bvV5PvV7PwYMHvxVZsia+vr4W9VFI\no8tDIaamlrFt27al+DwUcqM8m969e6focsuePbtq3k2Pq1ChwluHG5w5c0aQCUdHR4sKqTqdjtWq\nVVNl9Fy7dk31v2Au1qxJEyZMIGkM5LdmIVLK3yt4+PAh9+3bJwj532oRAaAHcB9ALhiJyEArxxQC\ncBaAHQBfANcB6E2PSQsRIcmui0+wwPCtvPfk/RRA0mAd/zUiouDixYscO3YsR4wYwX370lem1t69\ne7l161YxpsjISHbt2lWsBBWFYG9vz8aNGwsFa2try9DQUL548UJsoLZgwQLKsswnT56I2JIhQ4ao\nlK+zs7NQXp6enrxz5w5JI7nYsGEDGzVqxHLlyrFbt268cOECw8LCCBjN9KbP7ezZswRe78JqDQ8f\nPhSWAuV+lJgGPz8/1qhRQ7z8TKGkOpqLabDf/PnzCRjLkc+ePZuAMbhOiYtYsmSJiAVRNvUijfE+\nSn/t2rXjypUrrQbyenl5CcW5ZMkScb6SiWWtlHpa5fTp02zevDmB16t5xU2kPKdRo0bx3r17qr0/\nNmzYwCdPnrxxpZxm0RlocM9Oe98AOub/lNV7jOWg389yzKYLbD5mMTM1GMSsHX6gd49Fr4uA9VnB\nHL2WMFO9gcyYt4RwpaSWhWKNkGXPnl3EcFkTUwuTjY0Nvb29LVxirVu3tkpCFChFu3LkyMECBQrQ\nw8NDKPuU6oLkzJmTjRs3thi3eWCyMr6UsoB8fHx469atNLwBXuPgwYNWq9S6u7tz9+7dJMnVq1eL\n9iJFivCLL75QHevk5MSJEyeKcQUFBbFhw4bs1q0bjx07prreiRMn2LZtW37yySesVq0aly1bpqoI\nbA1vIiIGvF8EArhO8pYkSSkd0xDACpIJAG5KknQNQGkAR6wdfOLEiRQv1iBnMnaHJuPrpYfRt4zr\nu41cwxuR2lz8W1GzZk3x+8mTJwEAz549w9KlS7F7924kJiaiRIkSaN++PXx8fD74eO7evYsZM2Zg\n//79kGUZ2bJlQ5s2bbB69WrcvHlTHBcdHQ0AiI+Px7p16wAAbm5u+PbbbxEbG4s1a9bg0aNHyJEj\nBwoXLizurVGjRtizZw+2bt2KIUOGIGvWrIiIiEBMTAwAIHPmzJgxYwYiIiIQERGBqVOnYuXKleK6\nR44cwfz58zF69Gjo9Xo8fPgQwcHBsLGxwfbt23H06FEAgIODg+r7lJSUhD179uDEiRO4ceMGYmJi\nULJkSQQFBeGrr77Cs2fPAADXr1/H9evX4eLignr16ok+bt++jW+++QaSJKFTp04oXbo09uzZg+XL\nl6NXr17w8fGBm5sbcufODRcXFxw7dgy3bt0CAISEhCAqKgoZM2aEj48PsmbNCgA4ffq0aowZMmRA\nbGwsFi9ejMWLF6vmRafTwdPTEw8ePICTkxMAYMeOHShQoAAA43fGYDDg/v37f2neg4KCkJSUJL5j\nZ86cwYkTJ+Dm5gYAiI2NRaFChVCnTh0cPHgQ0dHR0Ov1SE5Oxq+//oqwsDC8ePEixf7t7Ozg7++P\nxMREhIaGIikpSZyvz+ABuxyFYZetAOyy5YetV25Iehtx7hUAYaduQwaQJLvDs2BpxEbeRVzYKSTH\nPUNc6H7ont5FfHy8xXWTkpJSHJMsy2IMCu7evQvA+F1+8uSJ+Dx//vy4fPmyOE6n0+GTTz5B69at\nUbJkSYSGhsLW1haFChWCwWDAlStXUrxumzZtsH79ety+fdvisxMnTkCn00GWZeTLlw/lypXDokWL\ncOfOHTFOWZYBGP9XFi5ciLp164rzlf+jlO47LCwMlSpVwooVK2AwGCDLMm7duoWYmBg8fPgQkiQh\nICBAzDsAGAwGPH36FACQLVs2fPbZZzhz5gxCQ0NRp04dzJo1C0WKFEG1atWwc+dOhISEICQkRHXd\nGjVqIDAwEKdPn8bKlSuRkJCA4cOHq+7bFH369FH9ferUqRSfJwDkzZs31c/fNxFpCeA3k797SZLU\nDsAJAANIPgaQHcBRk2PuvGp7a2R20qNhfif8HvocNXI7oJCn7V8dt4b/IK5du4bVq1cjLCwMXl5e\naNSoEYoXL57qOTExMejUqZNK6QcHB2PPnj2YM2eOUDwfAk+ePEGXLl0QGRkJnU4HGxsb3Lt3D1Om\nTAFgfPH98MMPyJ49O5YuXYqff/4Zrq6u6NOnD9zc3FCmTBnY2hr/R+zt7QEYFWRiYiLs7OwAAFFR\nUQCML7eePXvi0aNHcHFxQdasWXHlyhVERkZi5cqVGD58uHhp2draolu3bihYsCDWr1+Pbdu2YerU\nqahSpQp27tyJoKAgPH78WKVQwsLCcPPmTfj6+iImJga9evXCxYsXVfcbGxuLgIAAzJo1CzNmzMCl\nS5cAAJIkQa/XY+7cuWjXrh3y5s2LnTt3giRq166NLl26AACKFSuG69ev49ixY9i/fz8aNGiA6Oho\ndOjQAb/++qsgBVFRUXB2dsaUKVOQkJCAXbt2AQDy5cunGk+dOnWwatUquLi44Pnz56r7kWUZDx48\nAADcuHEDAODh4QEAuHXrFnr16pWq0tXr9dDpdHj58iVGjhyJMWPGqPrfv38/ChQoIMamEJImTZr8\nn73rDovi6t5nd+kL0nsVEI2K2AWxEI0i9m7sHRV7iQ3UqLF3RTEYG8EuUQm22EswYjcaPw12UYMN\nEJS2+/7+WO91ZneWYjT5fvlynuc+4uzuzJ07d+557ynvoeTkZCIievr0Ka1YsYJ2795NALiSvnfv\nHt24cYOfq2nTpnT69Gl68+YNP5aXl8fBKBGR3MScjD0DyKRsdTL3/4JkcgWpC3Ip/8nvlHVuDxU8\nf0CFGU9JnZdDUBdSvYDy5OjoQEoLKwpr2pg8PAIpPd2bNmzYQAl/3Na5X5lMJuqjPmGfdezYkRIS\nEphVnTIzM8nY2Jjy8vKIiCgoKIhu3rzJFb1araaLFy/SxYsXKTAwkCIjI8nJyUnvdYTy8uVLysnJ\nIYVCQW5ubmRtbU1lypShkydPEhFRw4YN6eLFi3Tr1i2SyWTk6upKaWlplJaWJupTs2bNyN7enuzt\n7Sk9PV10DXYfREQeHh6Ul5fH58/9+/fp559/JoVCQYsXL9YBREZGRtSnTx8aMGAAyWQySklJoQcP\nHpCLiwtt27aNCgoKaMaMGXTjxg3Kzc2l/v37k7+/P02fPp1sbW1FGwcmiYmJVLVqVXJ0dCQizUZm\n69atfKNVqVKlEo3dB4uUmeRDGhEZEdFzInJ8939H0rhq5EQ0i4jWvTu+koh6CH63log6CM9VUtcM\nALzJK0TQ7MNotvQkClX/Pabzf5L8E10zO3fulDQLF0cvzjJPKlSogGPHjuHKlSvcT9+wYcNP2ucZ\nM2aASEOAJZXaSfSeulqtVvNS8FIVf9VqNQ9Ga9OmDU6dOoXvv/+em/SZCdnKyooTV6WkpHA/fVpa\nGoYMGQIijRuHiUql4vEW27dvl2S6ZJVPK1asCJVKxTND3NzcMG/ePFEaLCuaJxV8SO9M7Vu3buUc\nHJMnTxbdJ4vinz59One5sFaxYkXunrKyskLz5s15XErlypV1eDr++OMPvcydtra2ouA+xrXw+PFj\nnk3SsmVLXL58WRT7wtwMzZs35/Px6tWrRWauWFpaimjAGWlUUU0YhMkq8fJ+KAygrNwITr0Ww330\nDvh8lQCPcbs0gaNjEmDTZAgMHbx1MlP0NZlMhrlz5/J5dvjwYfTu3RstW7bUm3FkbW3N70MqG6U0\n1O/CjC7WlEold1O8efOmyMDQyMhIEGkKzbHnztwu7P5atGghcn9JNV9fX6jVaowZM0bvdxwcHBAT\nE6OzFvXt27fYoFzmOmTpswMGDADwPtOMnZO5pry9vfH69WvRXFAoFPx9UygUPM1YO8aldevWf6oG\n1F8WI0Ial8tPej7zIqJreB+oOknw2UEiChJ+vzRABACSrjyG54QkxJ7QTbv7V/68/NOAyOvXr3nM\nQZ8+fbB//35MnDiRs1bevHlT72+ZL5YR+gBAZmYmVxzCdFmh5Obm4tatW3o/L4mwQFHGF+Dl5YXL\nly+LfP+urq4oKCiASqXiaan6nt0vv/yiV8FrK5a4uDj8+OOPHADFxMRwX/rq1atF52UZAjt37uSL\nuoeHB8LDw3Hw4EFkZ2fzxfDw4cO8/yywLT09nSsjc3NzHQ6Gvn37iiinLSwsePqls7Mzvv76a1Su\nXBlKpZL76xmAYGXt2W+dnJx0wEVwcLBkDRdAEysydepUDqaISp7uOnfuXFEgtHCxZzE9X3zxBS8F\nQESiwEamXE6fPq3TL8b0qt28vLxEz9isXCCUlRuhTGAnOHSZCbs2E+D6LpbDpf8q2DSNQIt5SajU\nYyqMnP1AcgM4OTlJUnxr1/EZMmQI+vTpw//PFL9QVCoVz0AyNTXFsGHD+Jz68ssvdfofHBwsyuwh\nPUCDNWHNnq5du4r6bWtry0GYQqFA27Zt8Z///EenjwwQRUZGoqCggMcPaSvnsLAwREZG8jlmYGCA\ntm3bimKHrKysSlztWDinGGATvtva84zFWTH+F29vb54xZ2lpye91zpw5vK4PuzdfX18OkNl7pv3O\nd+zYEYMHD+ZjKizrUFr5K4HIViLqK/i/s+Dv0aSJCyEiqkTiYNU79IHBqkzUajUGbDyHcpP34Vpa\nyX7zr5Rc/mlAhHFhBAYGigIpe/fuDSJN6XJ9whY2YQBXfn4+tyBoF1MrLCzEtGnT+O5TLpejXbt2\nIs4OKSksLMSZM2fw008/8cJSLEiTkS/NmjVLdG22gzp06BBfcNzd3Ytkgv39998RERGBqlWrcoZE\nBwcHDiaYVUUqC6B58+Yg0mSazJs3DzVq1OD1UGQyGR4+fMhBU0xMjOi6HTt2BBHx3RyrLspkw4YN\nkot127ZtAbwvvscW+fj4eM6T8aFNLpdj4MCBJQpKvnDhAv+d1A5eXxs3bhzS09MlCa6MjIywe/du\nEfg4efIkTp8+jejoaK6UpAj11Gq1iLnU3NIaX46YimPXHqDh5DjYt4+CY9c5ojRZtyHr4To0Dvbt\np8DE6z2JGbM8lLaUfGhoKFq2bMn/b2pqiiVLluiM57Nnz7hlLTU1Fbt27ZK8lkwmQ1RUlCgN2N7e\nHvn5+YiNjS2yL4GBgTh37hy3DjDLl3YzNzfH3bt3Rf1jae4ODg6czMvBwaFYmnnGj/Po0SMdAMnu\nx83NTYfB1sjISIeXRzute/78+ToWPSJCbm4uCgoKOAkZy6xiz9DCwgLPnz/H3LlzQUTc+tGtWzfk\n5uZi5MiRomuzOcayZID3qefm5uZ6CdaKk78EiBCRGRG9ICJLwbHviehXIrpKRIkkBiaRpMmWuUlE\nYdrnKy0QAYAX2Xmo+c0hfL7wGDJySkcM898oWVlZiI6ORrdu3TBo0CAcP378b8va+KcBkZiYGBAR\nevbsKTrOeC+K4gph7oimTZvi+fPnuHnzJq8jU7FiRZ1nxCrREmlAAduNly9fXm8q8NGjR3nxKCLN\nTmjcuHGIjo4G0XvA0a9fPx79LrUrl8lk2L59e4nHhaX3Ll26lGd5SDULCwu+CxRykGi3jRs38gWw\nadOmPLL+xYsX3AJw5swZvmizqrMAMGXKFBAR38kxRTVjxgwA4Cm8bOFctWqVTkVZQ0NDBAcHS/ZN\nOyMjJCSEX0O7jo6UXLp0SXJnrr37lVJewiJlpqamop2wsLGdtaOjI8aMGQNTa0cYWLvg5cuXOHLm\nEiJjtuOrtQex8ugtLDt8C+ErEmHbfBTKD1qBcpH7OODwnZgIl4GxcBkQgzKBnWBg5QS5mRW/X2EW\nCgNVAQEBRRKuFTWm2qBi1qxZOuPXrVs3Pn/Gjh2LBg0aiH6jLzOGPX/gfW0bAwMD/h6wd8PU1BRT\np06FTCaDgYGBDpOssAUFBYn6plKpRDVwhK1Hjx4YPny4qIgd+0yYOfLixQs+FuXKlSvWjSNsXbp0\n0QEr+jKeDh48CEBTp0nbclSmTBnOosysHyw929bWlldVfvHiBef4YQDm2rVrojFh2V76OIOKk38k\noZk++eX2c/hO3ovua375fx0vcufOHVHJZtYiIiL+FjDyTwMily5d4gqVmWbT09P57p/tbKTkzp07\nehkjmU+ZyZMnT3gu//79+wFodkvM8hAbG6tz/v/85z980fHw8EBQUBBf2PX5yI2MjLgPW6FQQKlU\nonHjxiWichcKs1LExsbyGilSbfbs2byirHYpd0NDQ74rs7CwwO3bt7nZt1q1ahg0aBD/vE6dOlCr\n1ZgzZw7ve/PmzVG3bl1+vp9++kkEJry8vHD16lVuHWKK/uLFi/j6669BpHHdXL58GS9fvoRKpRL1\nz9raWtL3vnjxYp6uXKVKlSLH6dq1a3pdWtpKmP1fCihaWlpyWvkdO3bA29tbMm5JYWEL68/787gN\n7zHSRGCeE5LgFrEBLv1XocPCH7Hr4kOsP3IVfv4aDok+ffoU60aSun7NmjVLDUqEzcTERId199Wr\nVzogUS6XIyQkBEQaN01SUhI6deokArtXrlzBy5cvkZqaysFsx44dUVBQoBd0Ct1FSqUSCQkJePr0\nKd8kyGQynXL2WVlZiIiI4PPLyMgIU6ZM4aR6DDh99913vH/Hjh1DZmYm1qxZw1lLS8tS26RJE+Tl\n5UnyGElZjczMzDiV/Nu3b7Fhwwa+frRp0wY7d+7k3D1yuRy3bt3i42RjY4Mvv/ySW1NsbW15+v6C\nBQv4WFy8eJFf60PjRP6ngAjwnv594UFd39//F2Hms4CAAMTGxmLy5Ml8p7Jr166/vD//NCACgLsV\nDAwMULNmTb67rVChQrEMh3v27BEpM+HiLSyX/sMPP4CI0LhxY9HvGX9F9+7ddc4dEREBIkKnTp24\nS0VIpuTq6or69etLKobSWkCEkpubyxdPoc9bSAPNFt+WLVvil19+KdHCam5uLmkVqFq1Kh4+fAhA\nswMdOXKkaEyVSiUPxjtx4kSRfBPNmzcH8N6KIrRoJSUlib5bvnx5LFu2TOccixYtQnZ2Nr9vJk+e\nPMHGjRuxYcMGzp3SpUsXvtDri83QbkIqdQsLC/Tt2xe3bmnIGJ8/f45y5crp/MbQ1h1laneA27B4\neIxPhF3r8fDuPBm2YSNg/3lvNO4+FJ7lKkJmaKwJJJWLx8jJyYmPqZubG6ZMmYJp06ZBLpdDJpOh\nc+fOqFKlCry8vPQWN9RuwmckpRj1PafRo0frzDmVSoVDhw7h66+/xqJFi7Bv3z7+XhJpSMdGjBjB\nAbhcLketWrV0gCQrTpmVlSVy4zBrhHD+jRkzhl9fWBmXUeprC6sILZfLMXXqVBw/fpy/oyYmJnj5\n8iWnODc3N5d00zGLl7CuTmhoqI7VJT4+nm80X758Kaq+W1TT5tPZu3evJABavnw5CgsLce3aNR3Q\n5uXlhXPnzmHXrl38frt3744RI0bwjZf2Rqs08j8HRNRqNcZuvwzPCUlYf7r4SqD/bfLgwQMQadCn\nEKWzAK82bdr85X36JwKRrKws9OjRQ7SoNW3alCubooSVcm/Tpg0ePnwoCsDz9vbmJlpWu0G7NgPL\nvAkPD9c5d506dUCk2V0xuXXrFu/jpk2bMHbsWFSpUoUrD4VCgZCQEG6mLU6ePXuGOXPmoFWrVujR\nowcSExO5haGoxgrV1ahRQ7TLZMq1qN8KF8bOnTtLEiA9evQImzdvxnfffYdZs2Zh9OjRWLNmDV6/\nfo1Tp04hKChIR+n17NkTWVlZAN5T21tYWODQoUNQqVQlLpd+/fp17Nu3jy/KarUa06dP16k7MmnS\nJL4wHzp0CGPGjCkRSZlQaYeGhnJ2SwCYMGEiDB3KomLdL9B3ylJYBneFa8/57y0dA1bAv957inAL\nCws8ePAAarWaW7GINBYz5hpiYFIul+u4Jdicl8lkqF27No+fECpRYbAja0ZGRpKF+7SbXC7XoTSX\nyWSYNm2aXuKr48ePF2k9KGp+2djYcKtAcnKyDlCRyWTcSlCxYkXcunULKSkponsZPHgwtm3bhlev\nXun0jVn/pFrVqlVx8OBBSQp39szZJkcIPJydnXlMD+uH0AoBaILqmzVrJnldYYE7pVKpM66pqan4\n6quv0LJlS05KNnv2bO4GNTMzQ4cOHRATE4ODBw+K4simTZumAzJDQ0ORnZ1dovVFSv7ngAgAFBSq\n0G99CspF7sO95x8+eH+HsCC4zz77THT86NGjINIEYf3V8k8EIkyePn2K06dP6wSsFSVs9yosQFZY\nWMgDUhmYyc3N5bu58PBwnDt3DqtXr+YAQsp1wnaEK1as4MeYZYUtOtqLkpubW4lddr/99ptkIB1T\nZN9//70oVVEul3NLCNtZamdLlKRZWVlh8+bNkMlkMDQ0FAX1FhQUYNGiRfjss89gamqqswg6OTnx\nirx5eXm4ffs2kpOT8fDhQ6SnpyM1NRURERHw9vYWuUxK6k7w9/dHWFgYBx1t27bFd999x5VJWFiY\nKIaEKcWirDTFNWsnNxxMvoRj//kDZfsuFrlXPMYnwnf4BljX7QKFuS0yMjI4eCXSFLQ7efKkjhWl\nVq1aePr0KQ9mDgsL47EJZcqUQb169TgzqFwuF1kKqlevzmnAWbyAVGNAx9bWVm9sS7du3fTGZERG\nRurMSbVaza/Zo0cP3LhxAwkJCdz10r9/fx7XZWJiAjc3N7Rp04bHdLHjQjdhy5YtER8fj3379uHe\nvXs6FWT1NWNjY/j7+6NatWro1q0bzpw5A0BT06d+/fr8e5aWlvz+jYyMeHaYs7MzJkyYwIskCpsQ\nTBkZGXEAy+j5hQGiQhHWualQoQJmzpzJj7E5WVwQ6bBhwyT7Ua9ePZ00dUADZBYsWIAZM2bg5MmT\nfzok4H8SiADAk4y3qDztAOrNO4LU9NfF/+C/RDIzMzmCPnXqFACNCZMFdw0ePPgv79P/dyCSlpaG\nYcOGwd3dHS4uLujdu3eRKbrFCdvBMH4NQGNeZwu7sEZJQkKCZExC7969JV/uLVu2gEgDOGbNmoX4\n+HgEBASIftuyZUssW7ZMtPAmJSWVqO/MJBsUFITNmzdj1qxZvH99+/bl3xNmYNSpU0ev0mnbtq1e\nThPh4s76yCobu7i4oGrVqpgxY4ZOdVBhY2NatmxZvmvLzs7G8OHDi3QnMBBS0tRJ7cZ20EOHDhWZ\n1LXPGRYWhsWLF+vNyuC/cfKFVcM+CJmyBX4j1sNj7K734GPEJljW/RKLd57AvO+2wdBEKbr3rVu3\niuKSnJ2dRcGLwvm1cuVKTJw4sci+MCA6fPhwHDt2DNeuXYNareZWsdjYWCxZskRkLdHX3Nzc+FhL\nzXOZTCYCrmZmZjpWh9TUVBBp4ndyc3P58R07dnBlyYIto6OjoVarsW/fPnTq1EkH8JiammLUqFFI\nTk4WrVmFhYW8arNUMzAwkLxXmUyGDRs2AAD//YQJE1BQUIDc3Fyeacey6aKiovg1he447eBbBiAq\nVKjA57FUZWVAYymUshaxOVC5cmWoVCpkZmZKgop79+7xtPXExESo1WpcvnyZA6ERI0agRYsWqFq1\nKqpXr4527dph9erVf8oCoi3/s0AE0ASvVpyyH51WJ/+/qtLLCHAY2QxbCI2NjXH9+vW/vD9/JxDJ\nzc3FqVOncOrUKdEiVVJJS0vTiSYn0uxotCPDSyosuNLDwwPbtm3D4cOHudnVw8MDAwcORHx8PO/v\nuXPn0L17d1SqVAmNGjVCXFycXhO1SqVCr1699CpkuVyOwYMH850tW9C6du2qt783btxAeHg4XyxN\nTExEfCZsN1q1alV+LC8vj+9IWStTpgz69evHA9qINMF1d+7c0bEOsIwGovdBtgsXLtRL0qRUKvln\nDIize2P3/uOPPyIxMbHEvvPSNLlcjg4dOiA2NlYUKF6aFFZR3JCNGyq2jYBTW03dFWbpKDtsPXp8\nexo2jQfCvEoT7Ey5iwHhg/gYFHX+Fi1a8IBqImnLlLOzs6SrhTWhQuvUqZNonrBgXUdHR2zbtg1n\nz57lrh87OzuEPW52UQAAIABJREFUhobC19e3xJYmAwMDnonl5OTEFfPRo0d5YGV4eDh38zk7O4ve\nCxYbVbt2bZ6ZNnXqVEkCNwMDA0RHR/MaMlJrFntvi2rsedeqVYuDcaVSyStBKxQKUcDm3bt3Rc+u\nevXqPKB18+bN/Lyurq46Ac7CcezSpUuRa862bdtE80xIivfll1/yAHArKyuMGzdO1EeWCq/t1mcx\nVfpahQoVdOgIPlT+p4EIAGw79wCeE5IwMeHqnz7XXyX5+fkIDw8XLWzOzs7Yt2/f39KfvwuIrF+/\nXpQpYm9vL0qtVKlU+PXXX3H16lXJnQDwPvizdu3aOH/+PK5du4awsDAQaSwLHyI5OTk6/nOpVqVK\nFe67Lo2o1Wrs3bsXPXr0QJs2bTB//nxJXg0TExMeLMkCNrXl5MmTkmmmYWFh3MLAzmFqaopbt26h\nsLCQuybMzMzw3XffYc+ePXxxY9Y5pugqVKggchPI5XJRtU+ZTAaFQsEBoUKhwJEjR7Bv3z5uaRGm\nKy9cuJAHbAvBUHE8DkU1Q0NDhISEICgoSMfCJFzgT506hZMnT5bsvAoDGBoawqVibVTrPwsew76H\na8QGnt3iOSEJrhEb4dDpa1jV7wm5qWb33rNnT66EMjIykJqaWqRy9/DwwDfffIO8vDycO3euWMZN\nbaXKFJT259pp6nl5eTytWNjMzMy4dZZJcnIyhg4dim7duqFXr14oX758ka6quLg4bhVISkrSCyZn\nzpyJ/Px8PH78mMcETZ48GYcOHRLNOQMDA84bwyxUzs7OHARor1mFhYUcuAmtS+y37BhT6C4uLgDA\n3TFxcXF8/gmL0iUnJ4NIAzRY9oy/vz++/PJLyffOysoKdevW5S4ze3t7TJ06lfe7KNm6dSvvH5Em\nNoZZGIVjQ6SJd2MWVwaIGjVqJDofy1Bi92VmZsbHiIGmL7/8sth+lUT+54EIAMzdfwOeE5KQdOXx\nRznfXyWPHj3Crl27cPjw4RJN1E8lfwcQSUxM5C9VhQoVRObxkSNHYuvWrSLl5eHhIZl2y/LxhWbP\njRs38t/Vrl0ba9euLbJ6ZEZGBr7++mv4+/vDz88PQ4YMwfXr17F06VLUr1+f98PExAQTJ07EwoUL\n+bFu3bp9lPF48eIF380OHDgQUVFRIlfHwIED8dtvv4ncPWq1mjM0duzYEYcOHRLtiOPi4pCfn69T\nQl6o6Hr06MFLzufl5aGwsBDLly8HkSYLQLgwlrQtW7aM95GlCQsX0eDgYO7+Kin4EM4FYROe18LC\nglff1deMjY1RJUArIFMmh6GtO8w+a4AydTrCunE4XAZ9B4/xiXAbsQWeE5LgNT4R9m0nw671eFg1\n7APzKk1gaOdZbL8bN27MgbG+1qNHDwDA/fv3MXny5CI5MVjT3n1rW7eISHJjk5ubi2XLliEwMBCf\nffYZ+vfvzxlvtUWlUnGLh7754+fnh0WLFvGqwT4+Pny+KZVKuLu7w9/fXwTEhHFCzs7OePLkCdRq\ntaSlkFH8M2DDGI+11yxm0WDxERYWFiKgwCwawiq7wHtunW+//ZZnSwUGBuLw4cPYu3cvd4+OHTsW\nKSkpRb4PpqamfB1SqVTIysoqtmqttuTn5yM5ORmnTp3iGT2Ghobc5ZKcnMyfNYtBe/HiBb+vmTNn\n4vbt29i4cSMfY7ZBiI+PR1paGs+qYu4c7dTrD5F/gQiA/EIV2q48jUpTD/xPMq9mZWVh48aNmD9/\nPg4cOFDqyf9XAJG3b99i27ZtmDt3Lnbs2MEtDtOnT8eJEyckd3RsoRL6X7VjJdguhfGFLFiwQPI8\ngwYNkuxXRkYGKleurPN9a2trzgHB3DLCsvF37tzhL3JRJcdLI8KaFb6+vpKmfG9vb5w/fx6Ahu+C\nSEMaxVKSJ0yYIFK6TNEbGBgU6RoQmvs7d+7MF1ylUikCAaGhoahatSpXLEqlEi4uLqJofSGoXrp0\nabFKlTV7e3u9O2l9u3EpPh4igszIDM4urjByqQDzqmGwaRoBx+7z4D5qG3ejuA39Hu6jtsPjqz2i\nYFL3Udvh2HUOrBr0hk2z4fAM6QKFUjM/nZycis0gklLYrJUvX55bAVnsjZWVFY4ePSq5w1YoFAgN\nDS0y40SKf0ahUEhmiJRGGOmdhYUFoqOj8dNPP3FLllRfTUxMOBW/vucnZAlu164dbt9+X7ZDpVJx\njhknJyd8+eWXnOGYgTmWvq69Zr1584ZbP9hYCUGU9tyPiYnB+fPneRzG9evXce/ePR2iMSJNYgHL\ncHz79i13SwYHB+PJkydIT0/ncVAdO3b8U2MulNWrV4NIk4UmFBYjNH78eH6MbR6kGls/r127BpVK\nxddaZiViafZ/Rv4FIu/kScZbBM0+jFrfHELaK42JOTMzE0+fPv3bGEv/ChGav1kLCAgo1eT61EDk\n3LlzencS8+fP1+unNzU1RWZmJlQqFY9a184qYkFun3/+OaKjo0UKq2bNmli7di3fLZw5cwaPHj0S\n+VdZtoKfnx8OHjyIs2fP8lS9Jk2aAHhP+3758mXRtdk9lSYjRyiFhYU4deoU9u3bhz/++AMFBQUY\nP358kbU22CL+448/cneOMAOroKBAh8VS2Hx8fPRSlmvXRhGCQ4VCgf79+/O4mMzMTFy/fh23b99G\nQUEB1Go1H6evv/4aBQUFyMzM5LV7/pImk8PY3R8OnaZrwMa43e/BxcitcOw2F9ZfDIZl3S9hVb8H\nbJuPgnXjcFg16AVlpUYwdvSGlZ10xhFr58+fx9WrV0tNj87aL7/8gitXruiMd0nBTXHzgv1dXExC\ncZKRkcFdXMHBwTh58qSOO9nKygo1atRA9erVMWjQIPz2229cIcpkMkRHR+P48eOiGjM1a9bEy5cv\n9RJnsZIAAQEBPCj87NmzMDAwgEwm48yfUmsWCyxlY2lpaamXWl7oahQq+qdPn2LixImoVq0aatas\niW+++UYE6NRqNV9jhG7Ze/fu8Wt/LFm7di2IdF3MjMBMO0MpKSkJX3zxBVxcXFCrVi0efMvA+tCh\nQzm4Ya4jJyenIktElFT+BSIC+c+TLFSaegAtFh1GaLP35tDy5csXyab5/1UePHjAEX1QUBCGDx/O\n0W9QUFCJAdinBCI5OTl8t1y5cmWMHj1ah62TSLObkqp8ygjEcnJy+DFhvMjp06cld8uGhoY4ceIE\nAGDo0KEgeh+FbmpqioEDByIjI4O7Ng4dOsTP+eLFC25JyMjI4KRfQrIkFminnQkAaMyrCQkJiIqK\nwvLlyznVMpOsrCxs375dlI0ik8ng6OiIkSNH4urVqyJQJZPJ0L17d0yaNEmvK2PdunVQq9V48eIF\n3/25uLggOjoa8+fP1/m+i4sLr2hL9D6w7tSpU5LkW2xM2d+mpqZcKdnZ2aFdu3Yif7aVlZVoFx8U\nFPRxlK25DRQW9jDxqgbLet3g2mwQbJuPhGOnr+E+UsNI6j56B6wa9IJ143AoK32Oxq066p6nhHEY\nCoUC8fHxfM6y6s2sIrPw+QnHVt/YeXp6YsqUKXotPEXVtRECw6LiNaysrDj3yofIzZs3JS0DbDxE\nRfbMzJCamorCwkLcvXtXlCF19uxZqNVqJCYm8v56e3tLAvf8/HzuzmCK09TUVHQtX19fvsGSWrOe\nPXtWJPAtW7YsGjZsKKKJHzp0aKnqq6jVam55EXISMS4gKyurDxt0wfnz8vKgVqvx+PFjPm5LlizB\no0eP8P333/N1TKrqtlAuXLhQrOuTkcX9WfkXiGhJ7KEr8JyQhDJBnWFoaCha/FgJ9U8tubm5iI+P\nx7BhwxAZGfnJMmEY5XWrVq046Hjx4gU3uelLF9OWTwlE4uLiQKTJsmAm+9zcXJ1UutDQUMlCYaxA\n3W+//QYijW+c3atareYBb9qKxdnZmS8wQmIjoS+9bt26nP744sWLvM95eXl8Afzjjz9w6tQprmhq\n166NFi1a8OuNHz8ey5cvR//+/TF58mQcOXJEp5KpsbExNm/ejN9//x2tWrUSKS2p9FOlUilyUTRq\n1Ah5eXl4/PixaGFmfRcqOyF4YQv+vHnzJBchBhQMDQ15psyPP/7In4O9vT3S0tKKNPsWZ71h9/Po\n0SM8e/ZMhyhNuxlYOkLp/wWsvxgMmyaDYd9hKlwHfQeXAavhNixeh/Lc46s9cBsWD7fhm2DfcgzM\nygdDZmgsuQAbGxuXqoAd0fvKw0KXX4MGDXTI17QVnvaxolJLSwvQrK2tMXv2bL2f6Yv5KKkI3SNE\nYmDFsltMTU15AbxGjRpJAhcjIyOdOcre4ZMnTwLQFKBjbloTExP06NEDp06d0st14uHhgadPn+pd\ns96+fYv169eja9euaNCgARo3boyBAwdi//79fN149uwZfv311w92qbKNSbNmzfCf//wH169f5+9P\nr169PuicjDSRbU4cHR0xbdo0zJgxQ3Ic+vfvX6LzHjhwQPIZmJiYIDIy8qN5C/4FIloyctQo2LUa\nB8/xiYjaeQHbU+5h5sxv+AJR2viJ0sqDBw90eAmINEFEH1uYW+K7774THWe7tW3btpXoPJ8SiDDX\nx+TJk0XHWbaLdtNmdhw2bBgSEhJ4HEe/fv3w3XffoU2bNnzBVCqVmDZtGicGY4o+Pj4eu3fv5uea\nNWsW1Go1rl27xt0qzOfdqlUrZGZmIj8/n1M6V6pUCWq1GtnZ2ejSpYsI7MjlcnTu3FlvUTgfHx9M\nnjyZ+7YVCsUHVz1lix5zTxWl8Fjz8vICoHH/6CswxpqhoSG/jz179vDjrFaMMA6DmXSF7J3CMRky\nZAgHOCNGjCj2Xi3dykHp3wS2zUfCJXzNe1fK6J1wH7MTzv1Wwq7NBNi3nwK7sJHoO2cjLGu0gKlv\nHciMlZAZ6MZOSMVTyOVynhLNmpubmyRLJ1OiwkySlJQUhIWF/amaLFL1a+zt7XXclv3798fhw4f1\nnqd8+fKcDTQkJAStW7dGo0aN8PXXX0tW7i2N3Lx5U/NcLC1x69YtvfWPJk+ezJlqWWPuE31zXMjI\n6uPjg4SEBMnvu7m5cQtU+/btcefOHdy6dYuDuUmTJv2tlAM3btyQrEdlb28vinkpjbBim9pj0a5d\nO2zbtg3BwcGws7NDtWrVsHr16lLpMZVKhYsXL+L48ePYu3cvkpKSdGrv/Fn5F4hoSUBAAGTGSjSf\nv58vam1XnoaDj0aRfehEKYncu3ePL9pKpRJdu3bFgAED+OIlpPX+GMIUZufOnTmyzcrK4ouHsJR9\nUfIpX2qWxVCrVi3uUsnPzxfteJhVwMXFhUffSzVfX18dZaLdhG4FobXB3t5e9PIya1KvXr14loKJ\niYkoY+GHH35Adna2ZPl5CwsLvlOsWbMmoqOj0apVK/55cnIyv1b37t358bp16/LUV+3aK9rXYCZY\nNn+EfWOLlZ+fH7fAMF88+2zr1q2iWhrFKUo/Pz9OMkWkAW73798XfYdZlIQ1P7SVjfYxmaExFGUc\nYOpbBzZNI+DUeylch8aJYjjchm+CfbtIWNRso8lGUUi7HkJDQ/n9mZiYYMmSJbhw4QL3mxMRtmzZ\nUmScTEnb559/jt9//x0AMGDAAL33W5SVZcCAAVi6dKnOd2xtbTFq1Cg8fPhQJ6W2Ro0akgRzMpmM\nz2k2F1hF49evX2PmzJmoXLkyypYti549e+Lq1dJTGrDU5lq1amHHjh061j1Wk0WlUoloyLX7KfyX\ntbFjx6KgoIBncbB/v/rqK2RnZ+POnTsiy5GlpaWoLtT+/fv5PE1JSZFcs7KysnD37t0P4iQqjdy8\neRM9e/aEnZ0d7O3t0bdvX559Vlphbh0jIyMkJCRApVLh8OHD/BmfPn36I/f+48u/QERLmNLYs2cP\n3uYXYvu5B/CfdgDuwzfByKUC0tLSPvo1Ac2OSWrH07VrV0yePBlE0kXQ/ozcuXOHm6BDQ0MRFRXF\nFXG1atU+eYyIWq3GhQsXsGvXLr3up9evX3PlVbt2bURGRnJFzJSvg4ODzsJrZmaG0aNHIyQkBA0b\nNsTcuXM50ZG7uzuvB8NauXLl+GIv3MWx3XFISIioX4zMaMKECbh48aKoTsRnn32GhIQEAOBl7r28\nvLBr1y6cPn1axKHB7mPGjBkiqvaxY8fyazH3FBFh//793KQtbMePH9fZnetT9kTvI97Xrl3L7/fK\nlSs6ikOK7K2kbciQIdwlxhq7d6FrQqhwDGxc4VI7DGafNYRty7Fw7rMc7mN2vrd0jEmAQ6evNYGi\njQbAPKAZDG3d9VpOpNJStRWj0PSsUCiQmZnJ4ync3NyKtMqYmZnp3fUzhX/s2DFRXIH2dwwMDNC6\ndWs4Ozvz75UrVw43btxAfn6+KCWXZYsICeeE4K80rX79+igsLEROTo6k68fU1FSHH6Q4efbsGQwN\nDUVjJvxboVAgJiaGr2lEGkB48eJF/PDDD5JB6SYmJoiKiuIbEeG7ZmdnJwqWFBaALFOmDHJzc6FW\nq7F8+XLRGlG2bFlRFtuLFy/Qs2dPvh5aWVkhMjLyowRifmqJjo4GkS5p4ejRo0EkZnP9b5V/gYiW\nMMXh7e2NAwcO4PLlywj7sj9cB6+F5/hELDt8C9m5H3dyCmspEGl27suXL+e+X2ZS11aGH0O2b9+u\ns9vy8fERFd0qTj4EiKSmpupYJxo3bixpGj59+rSOQnFwcMDRo0clfe2+vr6SRGEsduHYsWP82uze\nFQqFKP1VoVDg8uXLePr0Kf/OtGnTcOPGDcTGxnKAIgz4ev78OdLS0kQAjinexMREAMCVK1dElhah\nf19Y2rt9+/YAoFO4bMuWLZKKRzuAV6lU4tSpUzqgR7ux4DxGA82UckREhCSltXZMijDo0dDQUFLR\nChWSlM/awMYNlvV7wK7lOBHZl8dXe+DQeQYcWo2FRY1WMHb9DJY2dpLXlmrF0bfXq1dPVMadKSiW\nbRAYGAiVSsUzBUrSPvvsM+zatUtkoWLuQjaPqlatKmLCJNIUPMvLy+OAgCnJ/v378+84OTlxpV6z\nZk0eM6VWq0VstlLNyckJjo6OOhanwMBAns7p5eWFffv24erVq5wTo2rVqlCr1bh58yaGDh2KOnXq\noHnz5ti6date876wzyWJAbKzs+MWCFY4kT0LIo2Lj3FVJCcnQy6Xc8BmZWUlsnqwasrsugMGDNAJ\ntmafGRsb49q1a8jPz+fviUwmE4GhgQMHAtBUu129ejWioqKwadOmUgWofmphdXY6dOggOs6C7KdO\nnfo39azk8pcBESK6R0S/EtFlIjr/7pgNER0iot/f/Wv97riMiJYTUSoRXSWi6viLgMjr168lF28L\nFx+0X/ITPCckoc6swx+1Pg3jc7CxsYGBgQEUCgWuX7+OJUuWgOg9X0BERMRHu6ZQ0tPTsXz5ckRG\nRmLbtm3Flrln8vr1axw7dgzz5s1DVFQUNm/eLKqjok9yc3O5wrOzs0NYWBhXyCyuQFuysrKwbt06\nTJkyBRs2bOB1DvLy8hAXF4cuXbqgc+fO2Lhxo16zKtsRPX78mP8ttDYIW0xMDP8d23Fot379+uHX\nX39Feno6MjMz8ezZM52+s6BR5uZiKYJCtsIVK1aASAOu2E68TJkyGD58OM8kYQuvh4cHfvzxR8ld\nuHDnGRgYiKSkJE4+RKShcJaqomtmZoa9e/dyBeLo6Ij8/Hy8evUK33zzjU45cn2NKVq5XC7K0JC0\nKMjkMLT3gm2LMe/dKyM2w7b5KBg5+8HAxo0zjQpjNvQV5NPXiuLPkMlkGD58OEaNGsXnQ1RUFHe7\nTZw4EQB01oOiAE5KSgoKCgqKDC5l85zFy7DGsr4cHByQlZWF27dvc3fK0aNHAWjM8MxKtXPnTj7P\n3r59K6pdUlzz9PTkz4jdz44dO0TnY59v2rRJEmDqq4d04sQJyTkmDEht1KiR6NqdOnVCSkoKxo8f\nz7+zZMkS/rxNTEzg6urK51J4eDiP++rfvz8ePnyIlJQUnsXWp08fyYBjLy8vpKWl8aJwffr04dwl\nHh4e3JV25MgRbtnZsGGDTkCwu7v7B5eA+Nhy7949TjAWGxuL58+fY+vWrfyZMd6g/2b5q4GIndax\n+UQ08d3fE4lo3ru/mxPRftIAkkAiOiv83acEIoBG6c2YMQOVK1eGt7c3+vTpwyPJU+6+QPUZGkAy\ne99veJVTMqVdlLDy5AEBAVxRKZVKkZ/a0NDwb5n4BQUF2L9/P9atW4eUlBSo1Wqo1WrMmzdP0pVk\namqK6OjoIs/JKIXLly/PI8+fPHnCAx5Z2mxx8uLFC+zcuRM7d+4Umar1CQssdXFx4YqdKQx7e3s+\n3jY2Nvw+T548iTFjxqB169aoUaMGvLy8ULduXTRp0kRyca5SpYqo2N2gQZo6IS1btkRWVhZfKNlY\nEWmsIkKFqb1rtbCwwLZt2/TSxuuLMRAe9/b2RkZGBlQqFV/s9aWgGhsbY8iQITpumpJcs0KFCrh/\n/z7UajV27dqlmbtGxli5YQvcglrCtvlIjXVRUEnWqn4PKCx0gRWzyIhqtOixgri7uxebPcKU2Jo1\na/QWazM2NuZKslKlSnj79m2pgoM7duxYbCE4BiKlAI2npyfPVmM8L+3atRPNYxZoOmzYMNHx3Nxc\nrFy5ElWqVIG9vX2RlYY7deqErKwskVVSmIKuUql4DBMLVu7YsSOOHj2K5cuXc4vP3r17dd6zc+fO\n8XMqFArExcXh0aNHolingQMHciAmBRjKli2Lp0+f6gSfE2l4SfLy8nDo0CHJ31aoUAGvXr3Czz//\nzEG0TCZDeHg4r43y/fffg0gTL8IC37Wr27KgffZuNmzYEFFRURwA+fr66i0d8VeLMJVe2ISFKv+b\npTggYkCfVtoQUci7vzcS0XEimvDueBwAENEvMpnMSiaTOQN4on2C8+fPf5KOhYWFUVhYGP9/Tk4O\nnT9/nmRENCnInDZdy6ZvT9yhH87do55VLMjfwYgsjOQfdK38/HwyNTWlK1euUNeuXalhw4Z04sQJ\nOnnyJBERGRkZ0cyZM+nt27ef7H6Fkp2dTYmJiXT8+HG6ceMG5ebm8s+qVatGwcHBFB0dLfnbt2/f\n0rBhw6iwsJCCg4Mlv7N//34iImrYsCHdunWLHw8ODqZdu3bRnj17yMzMrMg+bty4kdasWUN5eXlE\nRGRsbEzh4eHUq1cvvb8xMjIiIqLHjx/zY+fOnSMiIm9vbz627du3p5SUFJo+fTrvK5OqVavSmzdv\nKDk5mYiIZDIZA9Ukk8no6tWr1Lp1a1qwYAE1bNiQQkNDKT4+npKSksjBwYEKCgr4ucLDw2nv3r2U\nmprKj5mZmVHZsmVJqVSSq6sr+fv70+eff07m5uY0f/582rp1Kx06dIiys7Pp7du3lJGRIXo+RERy\nuZzUajU/LpPJyMvLixYtWkRNmzbl9//FF19Qbm4unTx5kgCQXC4nCwsLyszMpJiYGCIi8vDwoJYt\nW9KZM2fo0qVL/Bq5ubm8j8Jn2KxtZ7r/+CndvP+EnhvYk2/vuZRr6UHzb1iQosFgUubl0Jt7l8nw\n8VV6dvc3qmAtI3d1Dv38+hk/h4ODA6Wnp9PLly+JiEilUvHPCgsLRffq5OREO3bsIBMTE8rIyKD2\n7dvT69evJZ8/e07bt2+nmJgY6tKlC39+MpmMXF1dKS0tjY4ePUpGRkZ0/fp18vHx4b8jIjI0NCSZ\nTEb5+fmS19i5c6fkcaE8e6a51/z8fLK2tqZXr16Rj48P9erVix4/fkxRUVHk4OBANjY2RER07949\n0Xt/7do1IiLKzMzUWQ9q165NtWvXJiKiIUOG0Pnz58nS0pIyMzOJiMjOzo5evnxJP/zwA0VERFDT\npk35OcaPH09z586lMmXK0ObNm+nx48dkbW1Njx49IicnJxo7diwZGBhQUFAQ9e7dm1atWkXR0dHk\n4OAg6kNhYSFZWVlRRkYGWVpa0sWLF6lfv36iZ7dp0ybq06cPrVq1igoKCsjQ0JC/G0qlkpYvX069\ne/emy5cvk42NDdWrV4+ePHlC586do59//pnWrl1LtWrVom+//ZbWrVtHly5dIlNTU2rSpAn169eP\nUlNTycjIiKZMmUInTpwgAwMD6tSpEz169IgePXrE3wEDAwM+Nr/++qtoPO/du0dERHl5eRQYGEgL\nFiwgmUxGzZo1o86dO1NqairFxMRQYGBgsc/8U0u7du3I0NCQtm/fTg8ePCBHR0fq0KEDdezY8S/R\nGX9WypUrV+TnHxOIgIh+ere7+BZALBE5MnAB4IlMJmMz2pWIHgp+++jdMR0g8neIl5UhRdazplsv\nCmhZSiYt/iWTzAxk1K+aBdX3MCGFTFaq85mbm1PXrl1p3bp1NHHiRPL29iYzMzN68+YNmZmZUXx8\nPLm7u3+iuxHL06dPadCgQSJlTURkb29Pubm5dOnSJbp+/ToRaRaMnJwcWrRoESUnJ1NCQgKVLVuW\n7t69S1u3btULRKytrYmIRAoMAN28eZOIiC/A+mTfvn0cCFWvXp2IiC5evEgrVqwge3t7EYAU3teB\nAwdIJpORmZkZ5eTkiD4/e/YsEWmUc79+/WjLli20f/9+kslkZGlpSe7u7vTw4UO6fPmy6HcAyNTU\nlCwsLCg9PZ3q169Pp06dom+//ZYaNGhA7u7utHr1alq0aJHot4aGhrRy5UodxfrmzRs+vkRElpaW\nZG5uTkREpqam1LdvX+rbty8RaUDf+vXracOGDQSAbG1tKS8vj96+fUsmJiYciACgo0eP0tGjR2nW\nrFmkVquJiOjIkSOi6xsaGvJFmYmjoyNt3ryZMjIy+DGmvHNycuhW6h0yKVudrIO7ksLKiXbBmnbt\nfg8qyMqT3t76hWr5uVLBs3t0ZNsasjQ3ozmrV9PgwRvowq/i6xERpaen6xwTilwuJzs7O0pPT+cL\nbUpKChkYGJC/vz8HiS4uLqJ5bGBgQIWFhXTo0CEKCAjgY6NQKMjU1JSsrKyodevWFBcXR9nZ2WRv\nb6/zHgiylG7YAAAgAElEQVSBJJOQkBA6fvx4kX3WHjsmr169IqVSSV27dqV58+bRmzdvRPdpaGhI\nly5dohUrVlBYWBhduXKFEhISiIioUaNGRV7rxYsXREQUHR1Nz58/p9GjR1NBQQGZmJjQmzdv6NWr\nV3T//n0i0gD5S5cuUfPmzcnExIS/H82bN6dNmzaRvb09GRi8VwdOTk5ERKL+MjEwMKBBgwbRvHnz\n6OXLl7R06VL+GZuXb968oStXrtCkSZNo/fr19PTpU5LJZBQcHExjxowhExMTOnz4MCkUClq7di25\nubkREdHq1atp7dq1lJCQQLVq1SJ/f39asmSJ3jGwtLSkoKAgOnPmDI0ZM4b69OlDGRkZtGrVKiIi\nCg0NJX9/f9q0aRMlJCSQu7s7BQQE0P79++nKlSt8ztSpU4dk79Z1Y2Njql69Oj1+/FhnfvxdIpPJ\nqFWrVtSqVau/uyufRqTMJB/SiMjl3b8ORHSFiBoQUYbWd169+3cvEdUTHD9CRDXY/z+1a6Y0kl+o\nwpnbz9Fs6Ul4TkhCxKYLeJNXenOdSqXClClTRObUmjVr4tKlS5+g1/qlXbt2IHpfZdLb25v7iufO\nncuj91nAl6WlJVJSUrifVWjO1SePHj3iJtXevXsjLi6Om0Gtra15/Ic+YdTRQhcQi7OoVq2a5G9W\nrVoFIk0QaFZWlqQP387ODtevX8fLly8lXQ/CwLtKlSqJAmiZf/6LL77gZnBPT0/06NED3bp1Q4cO\nHTB79mxcunQJwcHBes323t7e+OGHH0TsmcJUXm1hfBElZdQsrtnZ2UmW/65Spcp795HCAH6NO6NC\n+DJ4vMto8R27HXatxsGqYW9Y1usO86phUJYLhMzITNKdMnz4cNy9excjR47kMVAeHh4YPXo06tev\nj44dO2LmzJkYMWIEhg0bhpEjR2Ls2LFYt24dsrOzOSGXdpwFa8JgUWE8DZu/RRWGY+6AefPmca6d\notqiRYtEAcXC95fVFRHeN6vYqlAo0K1bN1y+fJnHQjRt2hSrV6/mwaf63EJDhgwp5k0GT2UfOXIk\npk+frnMOT09P/h5u375dVNzQ2dkZ69evx/Pnz2FsbAyZTIaDBw8CAF69esWzC+fPn6/3+sJ3zMjI\nCJUqVRL9n4hw7949qFQqPHz4UESFfvnyZRBp3LdCOX36NB/bksqtW7c4uZr282FBp1IZZjKZjNeb\nadiwIQ/Off36NY/TOXLkSIn78a/ol78la4aIviaicUR0k4ic3x1zJqKb7/7+loi6Cr7Pv4f/MiDC\nJLegEDN/vA7PCUmoO+cI9l19/EGsc69fv8bZs2dx69atT9DLoiUjI4MXYmOcEqtWrcKmTZtApEm5\nFFIwsxiHLVu2cPZNplTq1KlT5LU2btyoE6NgYmIiWfFTW5iiF9abyM7OBpHGF37u3Dnk5+dDrVYj\nJiYGlSpV4teqWbMmz9ywsrLSUZIsPZL9f8OGDThx4gRXHqzVqlVLxF5aUspvX19fTlLm5+eHFi1a\n8DgSIg1pFbsvlm4cERGB/Px8HD16FImJiaLMojNnzvDfVqhQAZcuXcKrV694ei6rjilFoKSz8BoY\nw9TtM3z/UwoM7Txh5OQLZaVGcK3THLEnUlGp1wzYthzLC7+5Dl4HmyaDYVouCGZligY7lpaWmDx5\nsoiWfsSIEViwYAEHStqZUV5eXujXrx9WrVqlw2L58OFDPg+MjY3RrFkzEfGasD5JcS0wMBBpaWmI\niYkRKf7atWvzTCY7O7tSxYqYmpri8OHDPE6GNQaiid5nxrDv+Pv74+bNmzqEhsbGxqhXrx78/PwQ\nEhKC+Pj4YteWH374ocR1eiZMmIDnz5/rBCXb2triwIEDomyu8uXLi0oAFBWblZaWpsNvI5fLsWjR\nIg5koqKicPPmTZ3fvnz5EoaGhpDL5SKm16+++oo/39LI06dPMXXqVDRo0AChoaGYPHmyCOCr1WrE\nx8cjJCQEfn5+aNeuHX766SeMGjWKP3djY2OEhITwQPuKFSt+coLL/xX5S4AIESmJyELwdzIRNSOi\nBSQOVp3/7u8WJA5WTRGe778RiDA5e+cFQpecgOeEJJQPXwaltT3c3d0RGRlZ7E7/7xZWeMne3p6n\nDHfv3p3vTnx9fUUsmSwoT6lU8h0522GtWbOm2OvduHED48aNQ+fOnREVFYX79++XqJ/M6iIkeGPk\nbKw5OzujWbNmkgsv66MwuFFYaVOocGbPng0AePz4sc7nzAoipaBYBgT7bMyYMXxHyK7LaOGZImIW\nBxa5z9JIGzRoIKLJNjAwwIgRI1BQUIDCwkI+9vXq1UNycjLWrFkj6pPQWsKZTc1t4FO/DcyrNIF9\n+yi4DlkP9zEJOhTooqqyI7fCbfgm2LUYBRPvGiC5LviSqgPEWnJyMh48eFBkWrCvry/q1Kmj87mD\ng4PIOlhQUFBkqrBw7EeMGIGVK1eiXbt2fCyEAFQmk2H69Ok4fPhwsZYwBtT1XUsbkEoBVBMTE8yY\nMYODCZYe3KtXLz5HypYtK7KcWVpalpjNsihKfZlMhoCAAD7GhoaGyMzM5ODYxsYGvXv35pYcU1NT\n3L59G5GRkaL3JSQkRBJAaMvAgQNBpAFgs2bNwu3bt3mwurB17NhRZ31kXD9WVlYYPHgwmjdvzr9f\nWn4TbWGUA7m5uTh//jyuXbsmAncqlUrv+kGk4Xn5OzaL/1T5q4CIN2ncMVeI6DoRRb47bksat8vv\n7/61eXdcRkQrieg2aVJ+a0IPEGnfvj1atWqFZcuW/alCTR9T1m3YCIsareAxVsOJYN8uEgY2bjza\nuyhJTU3FN998g7Fjx5YqlfZjSEFBATdhLl26lC+ibAfAdqxeXl6SBeZY69ev30fZKWRnZyMuLg7T\np0/H5s2buRmVgQ57e3vMnj1bVH/EyspKRF2uUCgwadKkIk3xLVq0QH5+vl720M8//1xktvbz8yuS\nadTMzIyngzJ+mKFDh+Lhw4cixbR06VIAwP3797kiMzAwQEZGBrKzs7myEJJchYSE8Gsz2nupzALt\nJjcxh9K/CWyaRsBt2Pc6ZevtWo2DdaMBMC0XCGP3yrCp2gTW1cNg5FIBJmWrw8jJF9bW1lizZo3o\nvIGBgbx2RnGN7WJZeqeFhQW6du3KFU79+vVx69YtrugZYGTK2dvbG/v378eECRO4tcjU1BTTp0/n\nmS78fgXPx9HRET179pR8ZsIsJmELCAjA0qVLuYtSKiOnTJkyPNNq/Pjx3JIhlU3GSPV27dqlY0VI\nTk7m5yPSuDXT09O59YSdl82XoiQjI4NbIebOnYv09HQRKd369ev5d5l1ipGAmZmZ8aJwarWau0tZ\nldbs7GxcunSpxBsGALh06RIf92bNmoneVXNzc7Rt25YDyp49e4p+m5WVpZNubmRkhFWrVpX4+vrk\n3Llz+Oqrr0SuvfLly3NXCxsTGxsbnDhxApmZmYiIiOBpsqyK77/yceT/PaGZcJL6+fnx9KxPJXl5\nedi+fTsmTZqExYsX4/Hjx6LP3759yyf34Mi5GLXpLMpPToLH2AQoK4Zgw4aNes+9ZMkSncWyYsWK\nePToEdLS0rB06VJMnToViYmJnyxtbNGiRfzaUkXk7O3tcfHiRWRmZmLJkiVo2bIl/P39ERgYiNGj\nR+Pnn3/+KIWQfv75Zx3/v7OzMy5evIg3b97o0Fqz/ubk5ECtVvOaFLa2tvw8DRs21GEKlcvliIiI\n4LtI4TWrVaumN/bCz89PVCeGLab6OCZ69eoFtVotOr+hoSG6du2Kzz//XFRsLigoiFsN2Hnr1q2L\nFStW4MqVKzwuRKlU4vHjx5x8StxkMPGqijK128FrYDQnCvMYtxv2bSfDonpLGLtVgoGNK2RGpqJ5\n5+HhIbJ8EWnA2KxZs+Dj48OPdezYEWq1Gs+fPxf9XiaTYcuWLZzZkTV/f3+kp6dzDodatWohLy+P\nU32vXLmSc3h07tyZx12sW7dO5NLRbsHBwbxfbGcfEhKiw54r7AdzDchkMsyaNQvt2rUT3QNj+j12\n7BiIiANLfbWBFi5cyFMoJ0yYgDVr1mDcuHGYN28e0tPTiyT9U6vVvO4RkSYVmVnAXF1deTyMdrqu\nlDDrWnBwMD/WunVrfu7w8HAAGoDA5tfWrVtBpIlPEQpzyWoTZZVW1q9fr8PnYm1tzatKX79+nfMn\naa+narUaZ86cwYIFC7B69WqdStQfKsK6S76+vjxGx9jYGJcvX8aoUaNApMtKysowCAHdv/Ln5f89\nEFm5ciXi4uL4zkYbVX9MuXv3rk6JcyMjI8TFxfHvHD9+nAMIppCfZr5FrSiN2dtj6EZU6TcHAyMX\niF46tisiIvTo0QMzZszgi2vFihV18uWrVKmi89J+DFGr1Zg+fbrIt1umTBk0a9YM0dHRku6wj11r\n5vXr11xh16hRA+PHj+f+bldXV+Tm5qKwsBB79uzBwIEDuQJ59uwZP4d2xdjq1atDpVJJFhQUNgZU\nGKAwMzMTgYvw8HBRvIWxsTEiIyMRGxsrOo92vYzg4GDOpung4IARI0ZIXl/oUqlRo4ZkSXhhzIs2\ncFWUcUCZwE5w7hfNLR5OvZfCKqQvjBx9QFTyOAd3d3cMGTJEb2yEsFiiNumXlEvC3Nxcp78+Pj6c\nAbJHjx68JsuSJUs4ED5y5Ah/70xNTfVao4T93L17N27fvs2fEbufxMREqFQqFBYWioJ4he+XcA15\n9eoVnw/az1TospkyZQpCQkJA9L7ibmnekadPn+pUjK1YsSKuXbvGrS5t2rTBr7/+WuS7s3PnThBp\ngCMTIe25p6cnBg8ezIHVkCFDcPHiRRBpQLjQqswq5Y4cObLoF7YEkp6ejlWrVvHnyEogMGFA7K8I\n/lSpVNzStXLlSqjVauTn5/PA5O7du3OWZUZqx4S5a4Rr/r/y5+X/PRBhkpqayheMT1GwSK1Wc0Kp\ncuXKYcqUKXynoVAocOPGDQDA0aNHOVBgolKpULtOHSgrfQ6nnovhPnqHJtiv01Qc+0UTJ8B2b8Ia\nI+np6aIded26ddGnTx++O2zSpMlHv08mGRkZOHz4MH7++edi6y18LCBy+/ZtREVF8XEOCAjglp8/\n/viD70Y/++wzzJ8/nwcwsuNCunXtIMGIiAgRQyojJRI2Br6cnZ1x+PBhUZQ/a6ampti2bRv27duH\n3bt349mzZ/j5559LVVV14cKFvH9yuRyVKlVCx44d4eTsCpmRGRq2/hI7j53HnC1HUSawE0zKVke5\n8p+hZ8+eMDKzgMxYCUNbdxg6eKNMnY6wbT4aLr2XwGf8e3p05z7LoazUCAaWRTOR6uu3oaEhNm7U\nWO9u3ryJqVOnYujQoVi/fj0HR46Ojti5c6cooK8kTSaToVmzZhwUVqxYkQMXBmiYK8Tb21tUOI8p\nsn79+mHx4sU65zYyMsKiRYsAAD/99BOI3tfVmT59umi+MdDDnjuzSi1cuJB/h1kjgoKC9FpDhKDE\n3Nxckl24JO9IYWEhf7fLli2LyMhISatkt27dOL27tjx79owDr7Vr16KgoAApKSmSrqXmzZtzCyIj\nNqtUqRJmz57NrWwymeyDit/pE+aaESp4YW0fYWDqp5K0tDQ+x4Qu5CtXrvA5xzaUFhYW3J3GMvMM\nDQ0/yDLz7NkzXL58uUTs0/9r8o8BIoWFhXwx+BQPmgVs2tjYiNLMGBMqAxA5OTn8pVq4cCFyc3NF\ntQ46deqEbQm7UKXnVI3S+GoPwuPOIbDDIJBMjqSkJH7unLwCODg66SgMS0tLvmiywMYPlYyMDKxd\nuxazZ8/Gli1bsHLlSkybNg0JCQnIz8/H/fv3cfbs2SLH9GMAka1bt+pYfQwMDHDgwAH88ccfkgty\nxYoV8fz5c+4C8PHxwffff49NmzYVafnw9PTkrKHaAY8GBgaYP38+8vPzuVIICAjAnDlzuNnfxMSE\nuwALCgpE2TNFNRMTE0yKmob0rLd8ZzV3/kKsOXkbwzdfRIXIvXoDRT3G/gCf8Xukg0hHbYNTj4Vo\nNX0z1p5MhVO59zvroijOpUCJMM1RLpfzgFqhJCYmlvic2q1WrVq8DlBWVhZX7pGRkZKBns2bN+du\nKmGWTHZ2Nt98CLNtKlWqhB07dmDjxo3cutW+fXs+X1hA5PPnz/mu+NChQ3j9+jV3RRDppt7u2rWL\nz89WrVqhbNmykllfQlbdD3lHfv31V1H2D2t169ZF7969+XxlcRtSIkzVFa4btWrVwrJlyzBv3jwk\nJyfjwoULiI2NRadOneDt7a0zVxQKhaR158/IqVOneL8iIiKwYsUKHgsTGBhY6vPl5OToBWX6JDMz\nk9erEWagsc0BK/jZqVMnyTn8zTfflOp6L1++RNeuXfl8MTIyQr9+/Xj9nH/lHwBEmPuDFf7x8fH5\nUzEKarUa+/fvR9++fdGlSxesWrUKr1+/xu7du0GkCbgSSnx8PIg0/nImK1eulJzArq6uPDUzOzsb\ntn41YNM0ApWn7tNYSCI2ouKYeNSZdRjlJu9D2YlJcB+9A/YdpsI8IBRmNk6Qm4nTJBmF7w8//ICA\ngADY2dmhfPnyWLlyZbFxJHv27JEMrGNNqKSNjY0xePBgyWJPfxaIPH36lC+CXbp0EQW0WVhY6HAA\neHh4cJ9u+fLlERsbq2PWZkpp+vTpXIEIA0L1AQX2N+PS8PPzExUXY5H7CxYsAPDefK3dFAoF5GZW\nMA8IhU3oUDi1nYAqw2PhOfadi27MTriN2MzBRN05RxARfwFOId2hrPQ5TLxrwsjJFzIjU5j61IJ1\n43BYNxqAMnU6wDKoC5T+TTB57T607f6+wBgrlCdVWE67SVkwGjRogJycHJFit7W1xaBBg3R2qosX\nL5a0puizsLC5pJ1NxQIit23bhtTUVEydOhWtW7fW4T7RLq6XmZnJC1Sy3bzUcw0MDMSzZ894zIuT\nkxPatWvHwQ1z2TFZunSpyHpgaWnJ6w4xcMtqsjx58oSb862trfHo0SO9c7w078jbt28xf/58PgYD\nBgzgaxqzuNrY2Oi1VKrVasTGxvL+WltbY8yYMVzxHTt2TMfFLGx+fn6YOXMm7t69W6L+llak5qe7\nu3upslASExO59czQ0BBdunQpVQApc3fVrl0bu3fvxrp16zgwZe92fn4+FixYAD8/PyiVStSqVQub\nNm0q1b2qVCpemFOhUKBChQr83QsLC/so8XT/BPl/D0R8fHxEuflCv3VRsn37dgQGBkKpVMLHxwez\nZs1CTk6OqB4Ca76+vjhy5AhXjAxFCyujTpo0SXT+rVu38mwGhoS3b98u+g4z/f985hfEJP0C+7aT\nYN8+Cl5dpiBw8Hw4hg6B9ReD4T5yq3gXPDwe9u0iUaZOR1gGdUFAvS+KXFD279/PQcmFCxewZMkS\nzJkzhyv/2rVri3Z3jo6OfFGXy+WoUqUKf3m6d++uM5Z/FogsXboURBpTMSCOESlpCwoKwsKFCxEa\nGoqmTZti2bJlfOG9c+eOaI6wps2tMWbMGJ6Rw6whzC8/cuRIeHp68syGHj164O7du+8VutwAZcoH\nwSqoE2ybj4Zz/5XwGJ/I015dB62Fc79o2IQOhWVwV1g3GgDbsBEInRiLIzc080kfgBUqRSGQeP78\nOQ+mZH0ODAwUgYHSuIxWr14NlUolmV5rYmKi479/+PAhj91h742NjQ26d++uk87K+hEaGsoX3xcv\nXvBrsfoqTPLz85GUlITY2FgkJydzYMjOK4ydYdatQYMGYe7cuWjUqBFCQ0MRExPDgfPNmzd1wGpw\ncLAkeHj9+jUOHDiAgwcPilJKWRFKExMTDBgwAOHh4RxgMeWlT0r6jqjVahFvB2utWrXi98LmQUnc\nA7m5uSJld/36dVFxQuE1OnXqxEHY/v37iz33n5HLly9j3Lhx6NevH2JiYkqV8cjIE7XBp6urq2T1\nbinZvXu3pKutYcOGH7Wy7v79+0GkAcC3b98GoClyyp4hK4b5vy7/74GIcJGeOnUqUlNTi00dlfIt\nE71PtTQ3N8fMmTMRGxvLwULbtm15iqCTkxOGDBnCka6xsTGuXLmCs2fP8snGpKCggC8sYWFhPH6F\nTVBzc3Pcu3ePV1mVbHIDGLlUgFVwVwT2mwb7dpFwHbzuvdl+3G7Yt4uEY90O6D3sKzi7uuuco2LF\niqICV8J7njp1Kog0hdmESogpkV9++QUXLlzgwCU1NVV0j38WiLBsA2G56jNnzuhkoNjb20tmsbAF\nVRsMCkWtVuPEiRNFEnt5enrizZs3OiZ3mbESJmWrw9S7Jqwa9EaZwE6wqtEcvaathG3zUfAYsZnH\n/XhOSILbsO9h32EqrBr2gYlHFSgMNBaZ8PBwnDlzBsuWLRO5ob744gvJNFIpUMwUsbe3Ny5duoS4\nuLgiWVVL01JTUzFnzhzRsaZNm3KGTm9vb513ixUMGzVqFN+Bjxw5sshxrlWrFoYPH85dEEFBQZI7\nwz/++ANLly7FhAkTsG7dOvTs2VPvOV1dXZGWllbkPFOr1UhOTsaWLVt0gE9JpLCwkMeVCFufPn2K\ntT6uXr0ajRo1gr+/P1q0aIHExETJ77FibAYGBlxRsuf71VdfISUlBUSaDdGHpPYzXg8WWFuxYkVs\n2bKFv1/Tpk0DkSYG579RVCoVpxOIjIzE27dv8eDBA57qzlLai5Nz587hp/9j77rDorje7tldehNE\nRUUpRhRFhdh7LLF3MSr2gj3G2Hvv0diN+sMWu8bYsSvGFhU1lthbNLEjigJK2/P9sbnXmS2ASUzQ\nj/d57gM7Oztz596Zec99y3n37uW4ceNYpUoV1q5dm2FhYf94fKFY2AwePFi1XcyDiGf6/y4fPBA5\nfvw458+fr4raz5cvH9euXWv2gqOjo+Uq5ttvv2VUVBR37typUsBK8/H9+/dpZWVFjUbDbdu2mXA2\nODs7q3LhAQOx1NWrV+UxfvvtN7mSzp49u+oYw4cPlzwM2bNnZ2hoqAkjoiU/v3dACToVq8GstXsz\nT6+VakXYZDizVGzF3NXbM2tgdWps1VkwSvO7yNUPCwtTpfoJYCbGUnxnbJ5MC4j88ssv7NWrFxs1\nasRBgwbxxo0bPHLkCEeNGsWxY8dK5efv7y+tGFFRUSbxG5a4HMT/uXLlUp33woUL7NmzJ2vWrMmu\nXbvyzJkzciVSqVIlCTiGDx9OjUZD6xy+9K7Rns4lGtAxoCqzlGvBrDW606v/pregb6A6TsNr4Fbm\nazeFbtW70v6TUqpxVgKaoKAglbJNqwKuAFiW3EjGTVgFXF1dOXXqVLOuqrSaudTjw4cPMyEhQT4f\n/v7+7Nq169tq1H8qRq1Wy/r165t1+eTJk4f79u0zm4IbGBgouSuUsmnTJpP5z5MnD7dt28aQkBB6\neHjQxsaGrq6uDA0NNXuM9yXnz5/npEmTOHHixHSVYBDlBYzbyJEjTfYV2SMLFixQgRLxHhAA7+uv\nv/5LfReWwWnTphEwWAD0er0EhSK+JCQk5C8d/33LjRs3CBgyz5TgTwQmp5f6/Z/O9LMkwn3YqlUr\n1XYRb/a///3vvffhQ5APHohcuHBBVU5dWVdi48aNJhcs0tsqV66s2q70W4obNDk5mQkJCSZxFKVL\nl+aIESO4cuVKFT13kSJFpLLMlSuXirjo5MmTqkwNBwcHDh06VJJZ2djYqHycovaBWBWZe8Ebp3bm\nLFWHzqUaM1vDQczTdZF0DQj3gEerKczTYSazB49irnYzmLPtDLrX60e/qs1ok7sgy7bqxxyffk6b\n3P6Ezor2zq7U2jpy16Gf+fOtKAYEGSwqzZs357hx4/jrr7+SNDzUp06d4i+//MJt27Zz48aN3Lhx\nIy9fvizN2cYK1nibsBC4ubmxcePGqRKQiabRaGSpdPHCFrJ69WpTy4ZGI8ds9dr1bDNoCrOUb8mc\ndXoxR4uJFoNEszUcRDufT2nrWYhaW0dq7V1okzM/rbLmobWzuwokWcoeEW4nIbNnzyZgcP1otVpq\ntdp0UXJrNBrVOdzd3aU7AngLGnfs2GHCBaJsSiVvbj40Gg2nT59OvV5v1jJjZ2cny8ZPmDDB4nna\ntWsnLRXh4eEEDHwv33zzDXfv3m3Wevn7779L8F2rVi2OHTtWjo0yZVa0Pn36pMvX/vvvv7NPnz70\n9/dnQEAAhw4dqkr5fhfR6/Uy4yQ1UWaxtG/fnpGRkZwyZYq8N0W2nRARp3Dnzh3q9XoTLhYxJnFx\ncX+p38ISMmfOHJmSvGrVKglChVXrnw5S/afk9u3bBAyAW2m92Lp1K4G0S0sI+beAyO3bt+UzO2rU\nKB49elSS8dnY2MjA7f/v8sEDEfGSbN68OePj45mcnCxJkQICAkxeFMK/WK1aNdV2pUn6s88+k6BB\nuUr09fWVLxVfX1/evn1b1kM4dOiQHFBBlmTsN9br9bxw4QKPHDki2TNF7YScOXPy3Llzct+dO3dK\n0GPOl6kEXKL5+fmpGE81Vra0c3ajbd6idK/Thx6tpvLzidtYqO8K5mg+jjmaj2Oe3qstZ2oogIyS\nhTN31zB69vyeOZqPY5mB37PyuG306f3WIpO722LmbDeT2ZuOoGPRGoTGvKLr0qWLfPFaakJJKgmf\nRFu5ciUfPnxI6KxplcWDQZ83YdjhW5y/91c65SlIK/c8DO4+mH0WbGOlft8xe9ORzN1pPj1aTjSJ\nu8ndZRGzVGhFnaMbtfYutM7mRZ2jG3Pm9iTw1uKg1WotsnSmBh6srKz4008/kTRY2cQLX3Bo1KhR\nQ4JkS4DBUsufP78MvhPgOzIykseOHVNZ+sqUKcPmzZurOGICAwN55coVnjhxgmPGjJHuxsDAQD57\n9ozbt2+X+1pbWzM8PFzWcfH29par0tOnT7N3795s2bIlBw8eTMA0oHLfvn0ELBcmTElJ4YoVKyQz\nbq5cueSYxcfHS7Dn7OzMAQMGsGvXrvL5TIvX4datWzLA2fg5atiwIVu0aMHVq1enmYGRlJTE8ePH\ny/EYfgUAACAASURBVABqDw8PjhkzxuLvBE1/2bJlVYpPpOuPGzdOtb+oaTR79my5benSpfJeOHDg\nwN8KcBTMuG5ubiakgALgFihQIMOWo9Dr9dLa1759e96+fZtHjhyRz9PkyZPTdZx/C4iQb60ixi2j\ngr3/Qj54ICJS9MTqnDSwn4qVk3F9BuUKZfHixUxKSuLx48flS8rSijZHjhxMTEzk48ePJUgRSqRS\npUqqc6xYsYIA2KRJE4sDf+vWLbMpqblz52bPnj3Zrl07AgZypbCwMNatW9dsFVUPDw+VUlRaAcT/\nSsvJ9u3beezYMQJ/VmXVaGmfryTtPylNK9dctM0TYHBLlG9J10pt6VL2CzqXbEj7fCXpUrops9Xs\nwVzBw5m98RDmbPstPbsvoWfrKczeeBhdK7VhloqtmL3JcOZoMYGePb83cFp0nMs2U9ex4dhVdKve\nhVkqtqJTUB1WC25HjY09s7jnkGMslKSYh3nz5imuT0M770A6Fv2cTp/Wo39wP3q2nqxynVhqQWP3\n0LvbQuZoPo45235L97p9aZevpIFV1N6FVlZWLFWqlCzqJwCScKMJhVerVi0575Z4Jdzc3Ni3b1+Z\nEaJsPj4+0vpTsGBBaSXw8/Pj1q1b3zneQ9y3ItU0ICCAV69e5ZEjR6QfOnv27GZjNkJCQkyU2rNn\nz+T9Ym9vrwItIgYnOTlZWlvMVQbW6/USuPXv35+xsbG8ffu2rMZqLpZHr9fL/hq31q1bc8CAAfJ+\nVro0Fi1aRMAAVFMTkYpZqVIlHjt2jNu3bzcL8kTmkCVRxqko3WYtWrSQ+yQlJXHt2rVs1aqVnJc6\ndeqoFN+wYcMImMYOCNI7rVbLL774gp07d5bvstRSdtMrSUlJZu9L8b4IDg5OM9bmv5aDBw+adSMW\nKVLEpDiiJfk3gQhpqJLdrFkzlixZkiEhITx69Oi/du4PQT54ICI4HPbv3y8v6tGjR4b0Sa3WLLI3\nVxIbMETRm7vBhSIUWS/i5ff5559Lhb5o0SLJtSEsMh06dLA48GLlExAQYDb2QTTj7zw9PdOtpIQS\nVYIrR0fHNLklcufOzQ0bNjA8PJzNmzdn+fLl06wuK7739vZmaGioHDMH/0rM1XGuoVT84K3M+/UG\ns5aW3KELmafzPNaYtI0erab+WVK+A2ftPM9u3+3mJ6GzTWqkeA/ewVydv6Nb9a5sMHA2d//6kGNn\nL6ZjHn86FKxAh0KV6V6yLid+O1flpw8KCmJwcLAqYLRNmzbygVAq33r16pnwm4h7Qrld+NjFb1ML\nrNRqtWzUqBHv37/PxMREsyXKjcfVeG5EvIUl4KzcvnLlSv7xxx8cOXIka9asyRYtWnDbtm1mV9aJ\niYlcunSpiZuoadOmKjeKsJyI0vDGsnXrVhMmUsCQpmku20PwS9jb28tYJHNuGEBt/RDsqZ6enhaf\nteTkZDlXIpakd+/e8nhZsmTh3LlzJfhUBk0rRXAJ2dvbc9euXdTr9dy7d6+c89OnTzM+Pp5Vq1Y1\nOx9iBawsSx8eHq46h16v56hRo0wsbi1btvzH6k4lJydz3bp1bNKkCWvWrMkxY8YwMjJSxY+U0SUy\nMpJNmzZltmzZ6OPjw8GDB78Tf9S/DUQyJXX54IGISOvLnz8/t27dyoiICGmmbtCggdmL1uv1DAsL\nkyAmW7ZsHDhwoFyNVKhQgQcOHOD48eMJvF35CmAhzmm8yrSysmLLli3lSmvv3r1mz3/9+nUChkBL\nYbpNTdGXKFGCbdu2lYGWBQoUUIEJnU7HVq1aqUytxoDK1tbW4mq7SJEijIyMZHh4uDSLT5kyhUeO\nHGH16tVVL0UXFxeGh4czOjo6Tbp01djYKZSKVkcrt9yGImxVO7Lu2HXM3mQ4/UJnsc6Mg8zZZjo9\nuy2WRQO9Bmw2WDHq9aNjQFXqXHJQ55SVGht7FipUiJs3b2ZKSgo3bdpkMh9KBS7+FxkLSupre3t7\nuUqxZEpVNmWV2axZs8pKvJZWm0FBQVIhu7i4qMj4zKVrKude+blAgQK8evWqWeuYsbuuUKFC3LJl\nS5ovASEHDhwwAbpijkuWLCljnoTb0NbWNtWKsLt371ZllrVu3dpiwbQ+ffoQUKeQGt+/4v88efJI\nUCSCLpWU5saSkJBAwAAAX716Rb1er0qFdnNzI0lZw8fHx8fscQQxYWhoqGq7iOeaOHGiXIR4eHhw\n1qxZnD9/vgpQ+fj4yOepXLlyFjP87ty5wzlz5nD69Okql22m/DOSCUQylnzwQOTFixdmq4/myJEj\nXQQ5SUlJcmUoGCMFw19CQoJqtVq3bl3OnTs3Xebzrl27WvTliuqj/v7+Mp5EFLQD1HwRovn7+3Pa\ntGm0traWtMs//vijCQ25RqPh1KlT+fTpU86fP5+9e/c2ywuhbPb29jKPXwR9FShQwGzGhr29PR88\neGA2jVE0rVZrNkNCmakj+qr8u3LlShNrldbehRorW5M+iHESCjlbtmxSiU6cOFHGlBhfg7u7O3ft\n2sWUlBSmpKSYWBSUMSvu7u7ye5FZJOI9lL+pVKmStI5ZynKpWLGiVLYAOHfuXHk/iEDTEiVK0M/P\nz2LhPKGMU0uNFeC6dOnSDAoKYtGiRdm1a1eToEhjuXXrljy+g4MD/fz8VJ/FuCuL3g0cODDN54s0\nWFlSS6m/c+eOBFwCkKcVF1WjRg0V6Nu0aZPqmHq9nvHx8fIZFPdD7969+erVK9VxBRHckydPCBis\nWuZEFIQU1jMhgoBvypQpEsiLQF5SXUcKMMTatGvX7oOyQJCGMT127Bhnz57NVatWZZhq539FMoFI\nxpIPHoiQBqroKVOmyJdv//7936lUtZCYmBiZIfPNN98wOjo6XSyVgME0LF6iHh4eqQaUCcuLslWt\nWlXGJ6TWxItOkEslJyczPDycw4cP55QpU0x4TEhDKqxxUTJjMLV8+XKS5NGjR1Xfd+vWjdHR0SrA\nI/L402ppuXOULV++fNKSBRjAjDlAZq4Zu06eP3/OqKgosxV6RatTp44MDvX09OSAAQNULhnlWNet\nW5d6vZ6jR49+pyBVwGCZMgdO2rdvzz/++IOxsbFpjqdxv4xbWkATMIAJS35pvV5vlvDNyclJujiV\nPDeCs+evVoCOjY3l0aNHeebMGS5ZssRkfKytrWVKu7IdPHjQJK5Kp9Nx4sSJ8tivX7/m0KFDJSGe\nl5cXp0+fzj179si5c3Z2VrHsnj17Vs4vYGBn9vf3p52dHQMCArhgwQLq9XppybSysuLixYv56NEj\nLlu2TN5/V65cke8PZTZEQkKCPN+FCxfMFo7MSKLX63ngwAF27dqVISEhnDdvHu/cuaN6PgGDZe9d\nLG4ZSTKBSMaSjwKICNHr9Vy4cKEMlPPw8JCkN+kVUQ7euHl4eDB37twmyrVevXpy5ahMtRO1SIzl\n+vXrKhBgzsdvnNUglIJyn3ehQ46Pj1fxSuTNm5cbNmxQpXc2atSI0dHRskS76IcYO2O3R3qb8fW5\nu7tz3bp1kpG2UKFCJkDC2dmZly9fNhubYa5ZWVlx48aN8lwLFy7krVu3zGYWif2FEgMMK9krV67I\nlGGdTqc6d8WKFeVY/vbbb2nWltFoNFLpWYrhEH0QHDWpHS+1zCKlu0d5XAD86quv+PPPP0ulbi6L\njHybVgsYVvtbtmyRFiBxrypdQeXLl0+zCqxSEhMT+euvv/L27ducPHmy2dTsZs2aqVwYyjERQG3B\nggUyOPfrr7/mwoULVcyoSgp+5fyK469Zs8Ysv4qwHKU2B7179yZp2Y321VdfkXxLHT5mzBjZL/FO\nyZcvX7rH7L8SvV5vtmyBmBt3d3eGhoZKl5uNjc07vYsyimQCkYwl7x2IAMgLIALAFQCXAPT5c/sY\nAPcBnPuz1VX8ZiiAmwCuAahlfExLQGTIkCFmXxK1a9dOk21VKRs3bmSZMmVobW1NOzs72tvbW1zd\n79ixg8OHDycAVf0GSxUrRfn3Jk2ayGJcaSk14TMXyjEoKCjd15KUlCRN/8ZN6YvXarXSJSCUjqOj\no6yNk5ycbBKvoPxtp06dVGOk0Wg4cOBAmTXg7OzM/fv3MyEhgS9evJAxGwcOHOCjR4+4du1aNmnS\nhAA4aNAgrlu3zuy5lCDOxcVFBomOHz9eVblVZGik1Tp27Mjk5GQZXFq5cmXu2bOHz549U/FnrF27\nlsnJyTImQTQlSFDS4qcnzsRcU16Tsjk6OprEToh50mg0EnwrmyBRevPmjQRlly5dMrlHWrVqJX8z\ndOhQPn/+nPv27TNxAeXNm1elkAQIiImJ4ffff8/p06er0kv1ej3nz59vNm22aNGi8nq0Wi0vXLgg\nM0mMmxhXcQ3Fixc3C6hEGQY3NzcePnyY9+/fV92zIpaqf//+ZjNmBECys7PjunXrGBMTw5UrV8rn\n7tq1a9Tr9Vy6dClLlChBV1dXfvrppwwLC5P92bFjhzxeYGCgis3YuPpvRhRBb2Bvb8+RI0fyf//7\nnwTeWq2W9+7dI2mYW5HGrawY/qFIJhDJWPJvAJFcAIr/+b8zgOsACsMARAaY2b8wgPMAbAH4ArgF\nQEcLQOTx48dMSkri119/LR94a2trduzYkTt27JBxCbt375YX/eDBAx48eDBVv7mSKMu4KQP67O3t\nJUueaA4ODhYrK3722Weq/ly5coWTJ09WKVih0IODg82ulo394anJ//73P/lyTo8irFKlCkeMGCHN\n/Z9//jnv37/PX3/91cS9o2zmAgyNsx7y58/PDh06SOVdrFgxpqSk8PXr1xw8eLBUDnZ2dnKchKJN\nq986nU4VQGrcsmfPbpZGvXHjxvz6669NVuk6nc6kMJiyH0I5Xr9+XRZEVF5vamRif6UdOHCAKSkp\njIyMlHOTlutLackRQOXUqVMm94gSqJqLgQEMqcb9+vXj+fPnZVbI4MGDuXXrVpOxK1WqFB89eiQL\nUQKGAFMxfnZ2drxx44asXA0YAsHv37+vAghlypQxucYiRYpYLG4m2GqHDBnCpKQkaf0Q1iljt1rF\nihVVQCUkJIQA2KVLF9VxRWG7GTNmpOuZW7Jkiep5c3Z2Zt++fT8IxScsSkoeE6Ur+cGDB3K7cG3W\nr1//v+jq35JMIJKxJC0gYoW/KSQfAnj45/+vNBrNFQCeqfykEYB1JBMA3NFoNDcBlAbws7mdc+XK\nBQ8PDzx8+BAAYGVlhaSkJCxbtgyRkZFo1KgRli5dimXLlsHBwQGTJ0/G3r17kZKSAgAoWrQoxowZ\nAy8vL3nMN2/eoHfv3gCAunXrYufOnXBxcUFycjLi4+Px8OFDBAUF4dy5c3j9+jV27dql6lPTpk1x\n9epVsxdnbW0NANi2bRvc3d0BAGXKlIFWq5X7ODk5ISYmBocOHUL58uVx7Ngx6HQ6pKSkIFu2bMiV\nKxdOnz6dyhAC9+/fx5QpU3DixAkAQFxcHJydnfHq1SvVflZWVkhOToaDgwPCwsIwdOhQHDp0SH6/\nf/9+eHqaTpe9vT1ev34tP4vjuru7IzY2FgkJCYiPj4efnx+aN2+OpUuX4ubNm7h58yYAwM/PDxMm\nTMCZM2fQr18/HD16VB7rzZs3+Omnn+RnGgCqiWg0Guh0OiQnJyMlJQVXrlyxOB5Pnz7F06dPTbZv\n2bLF7P4pKSm4ceOG/Ozh4YHHjx/Lzw4ODnj58iXmzJmD4sWLAwDi4+Pl93fv3rXYl7TE0dER8fHx\nqus+efIknJ2dodFo0KNHD0ycOFHewwBgY2ODKlWqwNnZGT/++CMAw1xERkYiPDwc165dg4uLCxIS\nEuS9k5SUhOnTpyMiIkIehySSk5NN+nTt2jVcu3YNCxcuRNeuXREREYEtW7ZgxowZSEpKQmBgIPz8\n/BAREYHIyEjUr18f9+7dAwAMHjwYZcuWRZMmTWBtbY03b95gyJAhqvvq0KFDePDgAYYMGYLRo0fL\nawaArFmzolGjRihevDhKly5tcS6fPHkCwDD2M2bMwIULF5ArVy54eXnh5MmT6NatGxYuXAiS6NCh\nA3r16gUAWLp0KRYsWCDv++joaNXz9eLFC3nctJ47AChWrBi2bduG8+fPQ6/Xo1ixYnB0dASAdP3+\nv5Q7d+4AMDzfoq8ajUZ+v2PHDnz66acAgHXr1gEA7OzsMvx1WZIPtd8fm/j5+aX6vTbVb99RNBqN\nD4BPAZz8c9OXGo3mgkajWarRaNz+3OYJ4HfFz/5AKsBFo9FIEAIAJUuWxIYNG5A9e3b8+uuvUiFo\nNBqMGTNGgoaiRYvC2dkZFy9eRM+ePREXFyePcebMGbx69QoFCxZElSpVABhehuXLlwcA6PV6nDt3\nzqQvWq0WTZs2lS84c9KgQQMAQFhYGObMmYNNmzahe/fuiI+PR2BgIAoVKoSYmBgAwLNnz3Ds2DEA\nBsWo1WoxcOBAWFmljg9jY2PRo0cPnDhxQgKcxMREExACAMnJybC2tkZ8fDymT5+Oe/fuwdfXF8OG\nDUPVqlXl73U6HWxsbAAAvr6+WL58ucnNY2NjA41Gg4SEBAAG0PXgwQOcO3cO8+fPx6xZszB06FDM\nnDkTkydPhqurK86dO4ejR4/C2dkZixcvTnXslKLT6SwqTfG9sTg5Oak+Z82aFRMmTICHh4dqe6NG\njVCvXj3VtqSkJNXnly9fAgDmzZuH0NDQVPvq7OxsMmcBAQHYt2+f2bm0sbExAV/Dhg1DmzZtcPPm\nTQlya9WqBW9vbwBAtmzZkDdvXjx69Ej+ZufOnahXrx7Gjh0LAOjQoQPs7OwAGJR2586dsWnTJpBU\nKRtzUqlSJVSqVAnx8fFYsWIFAAP4TEpKwueff46wsDAMHjwYq1evhqOjI06fPo0nT57A3d0dwcHB\ncHJygkajgV6vBwCcP38eDRo0kP15+PAhRo4ciRkzZgAAvLy80LVrV0ydOhXh4eHo2bMnypYtqwLs\nxlK5cmUAwObNm7Fjxw4Ahnv11KlT0Ol0qF27thzXrFmzyt81btwYAPD8+XMAQHh4OI4cOYLk5GRE\nRERg7969ACCf//SInZ0dypQpg3LlykkQ8iFIgQIFABgAupirZ8+eye/Hjh0rFywbN26ERqOR45cp\nmfLexJyZ5K80AE4AzgBo+udnDwA6GMDORABL/9w+H0Abxe+WAAhWHktpxpk+fbqJuXzevHkybkPE\nPSxbtoyAwZUiCnbFxMTIYFAl3a5IYS1btqzZIDZPT0+Vmbdw4cKcPXt2qoW3fvvtN06bNo3Dhw+X\nsRDKljdvXt64cYMvXrzggAEDmDNnTup0Otrb2zNLliysW7eupJFPS4SvvWjRotI8rgzcFGy0Io5D\nZJdotVrqdDru3bvXJC3YuDk4OHD58uVmYxPMtZw5c/LChQts27at9Lk7OjrKWI5+/frJ/lsqkGbc\nhKlfq9XKeAlnZ2d5fWm19evXk6TMsEirlSlTRqZYW8qeEeMh+mBcD0i0mjVrSuru9DSlW0NsW7Zs\nGWvUqGHiStHpdKrskpw5c3LWrFkyjkFZ/C+9zc3NjQcOHFC5HIRbw7gIogh0Fc+biOVSBpIWKFCA\n8+bNMxu4WrFixXSVuDcWvV4vGYmN29ixY6nX66WrRxmvISphf/LJJ9INY9yMuUPeVT4UV8DFixfl\nO7NgwYKsVq2avNeNs7N0Ot0HS1P+oczH/xf5V7JmAFgD2AOgn4XvfQD8yreBqkMV3+0BUE65v7LT\na9askQ+GuXokgCEOYNKkSfJhatq0KcPDw6nX62VEe+fOneWgREVFqQiULDGROjs788SJE2kO8syZ\nM00Ul7+/Pzt16sTWrVtz7ty5vHfvHn///Xc+evSIkydPZuPGjdmhQwfu27cv3bUlLl26JMthC+WV\nJUsWiwyV06ZN46lTp1SZG+7u7jJDJ0uWLGkWnzOXTin+79mzJ2/cuCFTP1NLM+3WrZvqWkQg7/jx\n4zly5Ei2bduWo0aNkuRRLi4ukmq9V69eEog0aNBA1u8xji8Q6ajiswjEVdbncXNzo7e3twywVM7b\nqVOnmJycbLYInDiu+CvATceOHU1igFJrGo2GAQEB1Gg01Ol0qlgZ5T6dO3c2C4YKFizIu3fvMjIy\nkrt37+b169dVdVD0er0MIAYMKcrffvutyT0iwI2lzKUSJUrILDElg/Dz588lWBGBmtWrV+f+/fs5\nY8YMs32uU6cOt27dysWLF/PkyZN/q5ZKcnIy586dq4rvadiwIffs2aMqUJk7d27OmDGDU6dOlXM1\nfvx4JiUlcfLkyRII+/j4cPr06X85VVnIh6T4duzYYRKE3bNnT8bFxXH9+vUcOHAgp0yZ8pcoEjKK\nfEjz8f9B/o1gVQ2AFQBmGW3Ppfi/LwxxIQAQAHWw6m2kEqwaHR0tX/4VKlTglClTVKvpHj16cMOG\nDWZfgIMGDWKPHj0IgAMGDFANjPKlZS7C3s3NjSdPnkxzgAV1NWAozDdkyBCp5Bo2bMg7d+6wYcOG\nFgPqxDWk9XKOioqSx01P6XidTqcizmrVqlWqVPOiWQI1/v7+vHr1qur8fn5+JA0F0dI6ro2NDZct\nW8bff/+dc+bMkRUrFyxYwB9//JHHjh0zIUQTTaksK1euLIMvU7PW6HQ6GXgnghzF9tGjR8t6QkoA\ncfbsWZJvV9DG94NY8SutDY0aNbKYRmypiXtA/E6r1XL8+PHyumrVqiWJ9r766itev36dmzdvlgp1\n/fr1Fl+0ly5dIvA248bFxYUxMTEqyyLwlrJeeT8KXhWdTsf79+/z8uXL8tlr0KABR4wYIQnPypUr\nx4sXL5oFn76+vqxRowYbN27M1atXqwrj/ZMimFCVTaPRqICnaDVr1jRJ8/+74EMpH5riS0xM5IED\nB7hlyxZVgOrHIh/afHzs8m8AkYp/PuwXoEjVBbASwMU/t2+DGpgMhyFb5hqAOsbHVHZ6woQJFrMq\nunXrxvj4eKnABKAICAiQL1Dxol2/fr1K2YuIcKHkbG1t2aRJE6kMjMu6WxKxeh48eDAvXLjAChUq\nqPqo5H9QrtZbtWrFMWPGSEU4btw4fvbZZ7S2tmaWLFno7+/PmjVrctSoUbx//z6nTp1KwOA+EMpA\nq9VKha7MSDEHdgICAlTbs2bNapbhc8yYMSaslxqNhlu2bJGMlQKIeHt7kzS4AsS+RYoUYVRUFH//\n/XfJRpoaWDC3PWvWrCZzniVLFlV/dTqdClh5eHiY8HE4OjqyRo0aZunSlU0o/WrVqkmgJL4rV66c\n5I4QY2wJrKXWqlWrxrCwMBPLiZWVlSSbE4BJ1GIpUKCA6p6dOXMmAUMBNksvWlHwMDAwUFoQS5Uq\npWJ9Nae8lZ/79Okjj7dixQqT+6RAgQK8c+cOSfLevXscMGAAS5UqxSpVqvC7775TlW9/33L48GG2\nadOGlStXZpcuXXj27FkmJCRwzZo1bNeuHTt27MjNmzf/o6DDnGQqvowlmfORseSDJzQz9+LMnj07\nlyxZQr1eL+M9goKCuGfPnlTLqpcoUULGj4h6MspmbKZu165dmoWoBPBYt26dBEROTk6ql7enp6dU\nEEKJubq6Mi4uLl18FK6urhIgiZVtWmRgefPm5Zw5c/jDDz+omD0tWR1E27Jli0xXVsYLtGrViq9f\nv1a5x0JCQnjr1i0V+AoMDOSECRN48eJFXrx4UW7v0KEDS5YsSVdXV5UrLGvWrCr3j6DXjo2NTdNt\nZK7lyJGDs2bNYq1atVTby5Qpw7FjxzJfvnwSSNnZ2TE0NJQXLlywGEeydetWPn782MSF4uPjI9NB\n7ezsJHV99erVzcaNtGvXjqQhtVxp0frss8/4ww8/cMSIEXJOZ8+eLe9XpYiYkyZNmlh80b548ULe\nY4sXLzZLlpYjRw7WqlWLtWrVUlG629nZsX///iYWjAcPHnDGjBkcOnQof/jhB5UrKFMMkqn4MpZk\nzkfGko8CiGg0GgYHB7NDhw4SaIwYMYLk25dz2bJlGRUVxVu3bnHAgAFytazRaFi5cmWpgHPnzs3d\nu3erXszmVrgCSFSoUIFDhgzh9u3b5arq9evXvHz5Mh89eiTrUAh/eZUqVXj27FnVat/BwUEW3AoK\nCpJ8Fxs3bpSrXACylLmNjY3sr/CFi1W9cCnpdDq6urqmSkmePXt2Pnv2jJs3b5bbBM21RqNho0aN\npDneGIzZ29tLBlElXfa7gAIl70dUVBS3bNli1rqlPG6pUqXkzStiRLRaLYcNG8YWLVpYDA4FDHwH\nytX41atXuX37dp4/f171ULx584Z3795VlYO/fv06v/jiC3n9AgRlz56dbdu2lcXhHB0duWXLFiYn\nJ3P16tUEDHwwe/fuJWCwFohKwEogJ6wMer1eggNz1O6DBw9WlSJYunQpU1JSeOvWLUk8NW/evFRf\ntIMHD5bHK1KkiLy/lbFCwcHBHDlypJz/EiVKZHhq8owsmYovY0nmfGQs+SiAiJJoSLAruru7c/Xq\n1aqXvbW1NYcPHy6tDwA4adIkkoYVtsgCEMF8oaGhZuuALF68mF26dDHZXqpUKQ4dOlR1znLlyqmU\na/Xq1aX5Xbl99+7dUsmZAw82NjaS/XP06NGSebRKlSqplpFPq1WtWpWHDh2Sn2vUqCGLe6WnpeaG\n0Gg0dHBwSLN/+fLl45UrV0wUrznrla2tLUkyJSVFxoCI6qmPHz+W+7Vs2ZL79+/ngAEDVH1NK9ZG\nr9czISHB4n4pKSlMSkri/fv3ZcFC0fLmzauKGxLFDfPkycOXL19KIjwRf6FkHD127Bj1er2sxpwr\nVy7evn2bI0aMYN26ddmhQwdGRETIY4vga0BNJufv789Xr16l+qJNTk7mkCFDVHMXFBTE06dPc+HC\nhSaAsnDhwqlmhGVK2pKp+DKWZM5HxpKPAogIfzRpUCRK6mgAJjEAYruSwpykXKmK/U+fPs03b95I\nlkxx3MWLF6uO161bN5OVuLe3twQWdnZ2abKDpiddVSjqtWvXSirmatWqyayU1GqSGAMHpbukVqRP\nsgAAIABJREFUUqVKEuwAhrTfhg0bSiDg4eFhthqq8XgCBkvMsGHDJPgQNWXepQkgt23bNrMukQYN\nGqgAoqgCu3DhQrnt22+/ZWBgIB0cHFSK+sKFC9y0aZMsdCYkJSWFM2bMkGm3wqLUpUsX7t+/n1On\nTuWECRN44sQJnj17lp07d2aZMmVYpUoV9unThzt27DBxSaSkpEgrRVBQELt06WIx7sXd3V0VRDln\nzhyzD+wff/zB8PBwnjx5kvPnz5f3po2NDdu0acNHjx6RTN+L9sWLFzx69Ch//fVX1Vjcu3eP33zz\nDYcMGcKNGzdmulr+AclUfBlLMucjY8lHAUQWLVpE0lDcTVl4DjDQNcfHx7Nnz54mcRP58uVTBan1\n7NmTwNuU1BkzZvDNmzcyG0LQX9evX18qYJ1Ox6ioKJ49e1Yed9WqVZw0aZJF8OHg4MAvv/wy1eqw\nqTV3d3fpCujduze1Wi2trKzkSjZfvnz09fVNd9E4AZZ8fX1NVsPFixeXWSD+/v4msRBKECKCT0NC\nQrht2zYCb105VlZWPHfuHIODg9OkJhdgKWfOnGaLlCmbt7c3o6OjSVIG7FpqxuctXbo0b9++TfJt\nDaD0NHPzKlyBxnLx4kUTkKrRaOjp6akqsqec2xkzZkhg8PLlSz558oRxcXFs3769arzFvo8ePTLJ\n+Mh80WYsyZyPjCWZ85Gx5KMAIkLhmVO82bJl44ABA0wKb4nP9evX54YNGzhgwAD5kjdOZVQq5wIF\nCqhqzTRr1owkuWfPHrlNkCopy6dbitWws7OTx3dzc5NWjSFDhkgFZalMvL29vTyuiB8x7q+y+fr6\nmtRPsdRsbGzYoEEDadFwdXWlv7+/SYDojz/+KP8XRG3e3t6yZLqy7dy5k4cOHTI5hjnFbm5b1apV\nWadOHZPr8/Ly4qlTp0wqJzs6OppYw5ycnFi3bl1VjM3Vq1dldhFgCKidOXOmKmg2T548KndcYGAg\nIyIiOH78eDlPlgodvnr1imFhYfzqq684adIkyXNifJ3FihXjy5cvSRpiUurXr29SXdfcfRQUFMSo\nqCjVOTNftBlLMucjY0nmfGQs+WiAiLK5u7ubVbhKE33BggXNBgNOnDiREydOTJeyzpYtm2SA/P77\n783uY45HQaPRSDeIjY2NVGSFChVi2bJlCUAVULhz506LReusra3ZvXt3GRj5rk2pCLVarQpkpafN\nmjVLum3E+AYEBEh+FqXiNAcu0kv0NX/+fMbFxUnrgr+/P3v37i3jRFILylW2jh07MjIykk+fPpX3\niAAYwhIjSOqUlgytVqsiz3N1dZXWNEGyNmzYsDQfuGfPnslrDgsLY1JSEk+dOiXPtX79et6/f18C\nZZ1OZxKHo9FoGBISonLnNW/eXHWezBdtxpLM+chYkjkfGUs+CiCirH4rlLpy1QkYmFOFD1682L/7\n7jsOGzaMDRo0YJcuXXj8+HFGR0fL2IiRI0dyyJAhDAkJkSvo+vXrs3HjxvK4NWrUYIcOHcxaY1JT\nwpUqVWK5cuUsKkyxGtdoNPL6ChUqJMuMFy9enPv37+fjx4+p1+vTpGRPq4n+W3KbWFtbmz1HoUKF\nTNw1AjTpdDqVWyu181sKaNVqtdL1JoBA0aJFZdq04HsBDGnQ5sjDBDmZ8fkEH4cYXzHmV69eJUl5\nn4i+ixgiMUbPnj0jSZli3atXrzQfOJGhVLlyZdX2adOmSaAkQGjZsmXZq1cvk2saOXIkSXLVqlWy\nfzqdjk+ePJHHy3zRZizJnI+MJZnzkbHkgwci1atXJ0m5Ghepr4JEyVgBubu7S26E4OBgkwERvCPK\nEuokOWPGDAJv+R4WLlxolvDrrzZz1hllc3Jy4vbt22U6pUajYZkyZbhlyxbpBkkPM6pyHJRWHGVN\nHWOOjb/S8ubNyy1btvDx48fpCqK11EqWLMnJkyfz4cOHHDNmDAGD20qIkrdk/Pjx/PXXX1V9+OOP\nP9iiRQu5zcPDw8TVNXr0aBUAq1evnirbBjDEk1y+fFl+zpIlC5OTk/nw4UMJcI1rrpgTETtTtmxZ\n1XaRBRMaGirvW2P6fNGGDh1K8m0arnA/nTt3Th4v80WbsSRzPjKWZM5HxpIPHog0bdqUJOVqXWRZ\n9OnTR7KaajQaizTbjRo1UnFLCItD6dKlVQMlVr0dO3bkgwcPVPU6lK1IkSJmV+CiBQcHm3WzVKtW\nTWUh0Wq1KrdF7ty5LcZ+jBs3jgBkoTytVsvatWubpbIWzdnZmbVr1zb7nUhjfpdmZ2fHiRMnct26\ndVy+fDmfPHnC169fc+nSpdIF4unpySZNmnDp0qWyloy5Zu46HR0dJTgoVaqUdIsowWCbNm0YFRUl\nuVvMtSZNmvD777+XxQ41Gg0fPnwoi9lZai4uLmzfvr0KsBQpUkRaUQoXLpwuxtCYmBgJOqdMmcKn\nT59y586d0uK2detWVUZTgQIFePjwYRV4cnBw4KBBg+Q4CVefCNolM1+0GU3e93xcu3aNX3/9NatX\nr87WrVvzwIED7+1cH4NkPh8ZSz54ICIUgrFFIb0VVQGwf//+ckBevXolLQsTJkzg48ePuXPnTnm8\nLVu2SBbT3Llzq9w0ANi9e3eSZMeOHc2eS0niJZpQbl5eXpI1MzUXyeLFi/ny5UuOHz+egCEORXBT\nCBDk4eFhwsOh1Wpl39PTjH9vrmKrVqtllSpVuHr1atarV0+13Rx1ep06dXjx4kUOGDDAYjFBZbOx\nsZGAydXVVcbclC1b1mylVRcXF86dO1f2QShqwHLxwsTEROr1eq5YscIkTVkQhynbJ598IgGQRqNh\n/fr1ef/+/XQ9cL/88ovFCq+1a9dmcnKyisdl9OjRvHjxImvUqGH2N+KaOnXqpDrPf/WivX//Ps+d\nO8fY2Nh//dwZWd7nfOzatcvsvS1ceJliKplAJGPJRwFELDVLAZ4AVArHycmJe/fuZa9evdipUyeL\npcQLFSok04OdnZ35+PFjRkREmOwXEhJikpqbK1cui4pw1apVLF68OAGomEzr1KnDPXv28Ntvv5XA\npFOnTty0aRMHDBjAsWPHSjfTsGHD5O9Si8fw8fFJleZe2YwtE8rgTeNzpAacJk6cqPo+rXgR4+Pe\nvHlTkoeNGDHCbACws7OzTGkWAKRv375MTEyUIO2HH37g8OHD2bx5c3bq1ImAwdKSkpIiHwjholq+\nfDmfPn1Kkty+fTsBAygShGXR0dE8ffp0ugFIVFSUyT1ha2tLBwcHfvLJJ5wwYYK0qMTGxpp11dna\n2pqNRapbty5fvXqlOt+//aK9ffu2Ciw5OTlx8ODB762g3Ycm72s+3rx5IwObmzdvzh07dnDUqFHy\neROFGjNFLZlAJGPJRwVEtFotu3fvznXr1rFZs2Yy5VGZdWCcxmupeXl5sWzZsnR2dma2bNlMsjLc\n3d356tUrvnnzJs36LOZa1qxZ2b59e/lZKEvR3NzcVNwQgk/DUpbJoUOHuGHDBrNuoeDgYF67ds2i\nO+ld+m8MYipUqKACdXZ2dmzdurVqvGbOnMm1a9eagBU7OzuLbiDl7zt27MjevXsTAL/55hu+fPlS\nul98fHwkiFM2T09PPn/+nOTbWApfX1+uWLGC69atk7FEoaGhqgdCuPDu3bsnt6WkpMhx/6s050JJ\nZ8mShc2bN5duM1dXV1WQqRBR4M7e3p6enp5s2bIlu3btKu/NsLAwzpo1y+LL9N980cbExEhiNTs7\nOwkIAQPPTaa8v/kIDw8nYMhUU5LSffnllwTU1t5MeSuZQCRjyQcPRETwn2hLly5NteaJpdW4Tqdj\n+fLl2bhxYxkkKGjCxT6NGzdm8+bN5ee2bduSfJu9YKl5enpKhk3R8ubNy4SEBI4YMUJl/hduoSJF\niqgmSihiwBALMnToUFWZ+7x583Ls2LF8+fKlJFdzc3OT19u2bVuGhoaa9C0sLMyE1VUZuAq8DQA2\nbvny5ePTp08lfwgATps2jc+fP1eNdYECBUhSldI7depUmfETFBRk9vjC7eXm5iYZT3fu3EmS0i01\ncOBAvn79mkuWLGH58uVVMSOFCxdmeHg4Y2JizAIef39/mX4tpGrVqgQMga9CBJ1+1qxZGRAQQI1G\nw7x583LcuHFpFj0kyQsXLsi5/eOPP0iSSUlJMtvom2++MfnNkydP5DWL+1P8v379+jTP+W++aAV/\nS2BgoLQiHTx4UBLtPXz48F/pR0aW9zUfIm2/UaNGqu1iToxddplikEwgkrHkgwciiYmJZoHH38lo\nsbW1lSyqDRo0IKBmzlRaFnr16iVTVM21atWq8fLly3z69KmsgyMUdPv27Xnu3DkuX75cxl8sWbJE\nApMtW7aQNJjqBb9IWq106dIyc8Td3Z1z5syxyLHh4OAg91WOobHlonDhwpKYTQl8fvrpJ+r1elll\nVvRfr9erMj7c3Nyo1+uleyV//vyqm1C4SQCwX79+MrZEWK/EeAUEBMgg1R9++IGAgQ8mPj6eR44c\nUV2DcG3odDoePHiQcXFxnD9/PmvVqsXPP/+c3377LWNiYkweCBGsDBisPTVr1kzVldSwYcM069es\nXbtWAiulLFq0iMDbTCxjuXv3Llu1aiXv5RIlSnDbtm2pnkvIv/miFVlJixcvVm0XoC69ff6Y5X3N\nh8iYs7Ozk8Ubnz9/LhcTIvX9YxW9Xs+oqCg+efLkndqVK1d45cqVd/5dZvv7LSoqyuSdmWGBCIDa\nAK4BuAlgiPI7ZaeVloZ3iT0w14KCglScJMDb4NJTp06RJCMiIqQZWtm0Wi2bNm3KU6dO8dChQ3KV\nL9xDGo2GdevWlRkk5nz9tWvXZlJSkqyACxhW7cog0axZs6oCccV5ChcuLPs1e/ZsOS49evTgzz//\nzC5dusiYmUaNGpm9fmVwqfg/rYBSf39/Fa1+/fr1efDgQVXmh6Ojo4qq3dvbW8Y0PHr0SOXaadmy\nJTds2GDCvlq0aFH+9ttv8sZNSEiQYMfHx0dFxObl5cXY2FhpRapSpco7vdzmz5+vitGwsrKSVYaX\nLFnCly9fctWqVXJe0spQEEUFvby8VJk1wr2kTEc2J0lJSSYU7mnJvwlEOnfuTMAQWCskJSVF3uvK\nYn3/X+V9zocAglqtlqVKlZJWVR8fH5PYoY9NoqKi3vnZIA2Lu8yA6v9GXr9+bcIEnSGBCAAdgFsA\n8gGwAXAeQGHxfXqDVcXDmV4g4uTkxPj4eFkEzs7OTlpExo4dyytXrqQZ6KnVajlv3jyVn9zT01OV\nZQGAO3bsYOvWrenn58fSpUtzzpw50syfkpLCsWPHqpTxp59+Ksu0CxdH9uzZZdxAx44dJeFX1apV\nuXPnTrMBpAULFuTz589VVh3RJ3OkZhMnTuS8efPMxpek5gIz19zc3CSIypEjB+vXry+vMSAgINWx\n9fDwUAERkrx8+bIJg66vry8vXbokb24xJ2lZLYzlxYsX/PHHH7lu3TqZyVSnTh2OHDlSBsuK6+/R\no0eqx1Iq5TJlynDOnDmykrJWq5UEav+k/JtAZN++fQQMFrbZs2fzp59+kqnznp6emQGrfL/zERcX\nx06dOqmex8qVK/PWrVvv5XwZSczFV6VHMoHIfyvG85ZRgUg5AHsUn4cCGCo+GwMRnU7HadOmmcQa\n2NraqvzsymYpy6N8+fISvBQrVoy7d++WylpkqAhQoQzytLe3Z8uWLeVnodRtbW05duxYzp8/XwbN\n5suXj6Qh4j08PJxLly7l+PHj2alTJ/br149nzpwhaXjBnD59mjdu3OC2bdtM3E0CQGi1WkZGRkq3\nQoUKFUiSR44cYa1atejg4MAcOXKwd+/e0od/9erVNAN3bWxsOGrUKH799deqc3/55ZcmAa4ODg4m\nsSWAgdF22LBh7NGjB7dt28YrV66YzFPVqlX58OFDRkZGqtwx1atX56ZNm6RbyJy/Ozk5mbt375YW\njF9++UV+d+3aNQkw3xWIKGX58uUEoLqXlFapXLlypalsf/nlFxMuGyVr7D8t/yYQ0ev1ZuOPbGxs\nuGvXrn+lDxld/o35ePz4MY8cOcIbN2681/NkJMkEIh+mvCsQ0dAABP5V0Wg0zQDUJhn65+e2AMqQ\n/BIAYmJiZKdcXV1RokQJLFy4EE+fPkXdunXlcaysrJCSkoK/eg1dunRB165dsXz5cixYsAB6vV5+\nlytXLjx8+BBZsmSBvb09Hj16BG9vb9y9e1fuY2dnhzdv3pgct0SJEmjbti3GjRuH6Ohos+fu3Lkz\nunfvDgC4d+8eWrZsiaSkJDg5OSE2NlY5Vhg8eDBI4vvvv8ejR48QGhqKbt26pXl9UVFR2LhxI375\n5RdoNBpYWVnh8ePHSEhIQFxcHF6+fGnyGycnJ+zfvx9JSUk4dOgQrl69itWrVyNXrlzYunUrzp49\ni1OnTsHKygqenp6YO3cuoqKi5O99fX3x7bff4uXLl3j8+DG8vLyQP39+AIBer0eFChWQnJyM8PBw\n5MiRAwBw+/ZttGjRAlmyZMH+/fvNXsuUKVPw448/ws/PD71794ZWq8X8+fNx5coVNGzYECNHjkxz\nPFIbp3r16kGv10On02H69OnQarUYOnQo4uPjAQDTp0/HZ599lupxXr16hZ07d+LGjRtwd3dHvXr1\n4OXl9Zf79b7l5s2b2LVrF2JiYlCoUCHUrl0bjo6OZvcliQMHDiA8PBzR0dEoWLAgWrRogU8++eRf\n7nWm/H8SJycn5M2b97/uRqa8o/z+++8qPebn5yf/z5Ili8Z4//8KiHwBoJYREClNsjegBiI5cuRA\nYmIiQkNDUa1aNbRu3fovAw8bGxskJiYCAGxtbbFp0yapDC9duoQuXbogKSlJ9RsfHx/cv39fbndw\ncJDKCQDq1asHAIiLi0NycjKOHj2KChUqIDIyEomJiRKsaDQakES+fPlw9+5dpKSkYMGCBShZsiRm\nzpyJNWvWoEaNGpg4cSKuXbuGsLAwHD582Ox1FCtWDDNmzECWLFnSfe2JiYkYM2YM9u3bJ7fpdDoU\nK1YMRYsWRbly5dCrVy9oNBrs2LED2bJlAwD89NNPGDBgAPz8/LBmzRr529jYWDRu3BgxMTHIly8f\ngoKCcOzYMTx+/BiffPIJ1qxZA61Wq+pDSkoKypcvD71ejwMHDsDFxQUAcP/+fTRu3BhOTk6IiIgw\n2/9nz54hNDQUf/zxh2p7rly5sHjxYjmPf1X69euHI0eOmGz38fHBb7/9hhYtWmDAgAF/6xzmJC4u\nDrt378bVq1fh5uaGunXrwsfH5x8/j7EsX74c8+fPV23z8PDA/Pnz4e3t/d7PnymZkh7JCEDExcUF\nAQEB8vO6devw7NkzrFmzBtOnT8eqVatw9uxZzJgxA9u3b0f+/PlRqFCh/7DH/728KxDJ8K4Zc/Vk\n/onWqlUrlelIyUhqbW1tls+jbt26rF+/vnRV4E/z9N69e9mhQwfpwxXpsIKJ1MXFhYcPH6ZWq6W1\ntTX79+9PwEBZTlJm5WzatEnVJ2PuEY1GI/vVoEGDd7GUsV+/frLf7dq1UwXt7t27lyRlkGvp0qW5\ndetWLl++XJKcKfkibty4IevVeHl5yZTVly9fyj5bCvAUfBtt27blixcvGBUVJdODv/jii1SvISoq\niqNHj2aJEiVYvHhxjhgx4i+bbo1FpEk6OjpSp9PRy8uLEyZMkAGxgwYN+kfOo5RLly6pSOTEHM+a\nNSvN3/4dV8Dx48el66hbt26cM2eOdKcZlz7IlPRJZrro+5GM4JpxdHRM9ftly5bJgpjt27fnDz/8\n8E7H/xhjrD6UGBErALcB+OJtsGqA+N44RsTR0VGV3dGzZ09VSqhx8/Pzk0DBysqKO3fu5O7du/nl\nl1/KbI/WrVvLQRIprs7OzqxZs6bF44rsDxsbG1XWiKUmsg3y58/PZcuWyQwdUYlVFPQTAal9+vSR\nfbpz545KOSnjFwTguXnzZrpuitevX8tI+59//lluF/VXBKi5ffu2KjtFtE8//ZRHjhwhSX7//fcm\n8Te2trZcu3YtybepupMnT+bx48e5b98+3rlzR57zxIkTci51Op2Mg3FycuLFixfTdT3vQ4yrMl++\nfJmLFi2SwE8wrv5TotfrZT2c4sWLc/bs2aqyAcpYGHPydxSfiPcYMGCA3Pby5UuZdfVfzsOHKplA\n5P1IRgUiERERrFevHsm3QOTYsWN0c3Ojj48PAwMDefPmTd68eZO1atVi8eLFWbFiRV65coWkAbD0\n7duXVapUYb9+/f6RfmYk+SCACA1gpC6A6zBkzwxXfqfstDIN1tvbm6tWrSJpeJGLQnjOzs6sXLmy\nWQZRV1dXXr16VVXFVSi+Q4cOkXxbur1OnTocOnQoAUMarTIzRql0LQEPKysrVfEyS+nGAux8/fXX\nJA0vMfFd69atOXHiRFXgY1hYGMm3lV1FsK0g/0pLbt++TcBA4a6U8+fPEzBk2ihvoLFjx7Jy5cqs\nWbMmFy5cyGPHjjEyMpJ3796VIMgcvX7fvn1NVviiNWrUiM+ePSNJ/vzzz5KDQqPRsHbt2mkq3n9D\nvvvuO7N979at2z9+LjHnOXLkYFxcnNzes2dPEwuUpd//VcUnLHUbN25UbRfZZMJClinpl0wg8n7E\nWKE1X3g8Xa3Zd0fY7Lsjae6XHtFqtQwMDGRgYKDkCjIHREhTi0i1atV4/fp1koZFWNWqVeV+9erV\nk7xJH5u8KxCxwn8kJHcC2JnWfklJSXBzc8O+ffsQFBQEnU4HADhy5AguXbqE3Llz49q1a3BycgJJ\nVKtWDYcOHULv3r0RGRmJEydOoFixYkhMTISVlRWSk5Oh0WgQGxuLBg0a4Pr169Inf/LkSTx58gQA\nsGbNGqxZswbXr19HtmzZZEBmQkICrK2tkSdPHty5c0f2U6PR4NKlSyhQoAC++OILbNy40WIsy969\ne2FnZ4eePXsCAEqWLInZs2ejb9++WL16tcn+Z8+eBQA0aNAApUqVQmRkJACk23eaI0cO2Nra4sGD\nB7h8+TIKFy4MADhw4AAAqAIqs2fPjlGjRmHUqFFy2+nTpwEAq1atQnJyMvz9/XH16lX5vRjXmTNn\nWuzD1q1b0bRpU0RERKBs2bI4ePCgjJ2xtbVN13W8b+nRowfy58+POXPm4PLly/D09ERoaCjatm37\nj5/r4cOHAIDAwEA4ODjI7eXLl8d3332HBw8e/OPnFFKkSBGEh4dj5cqVaNKkCbRaLa5du4YTJ05A\nq9X+v/dvZ0qmKMXe3h7nzp1759/Fxsbi+PHj+OKLL+S2hIQE+f8XX3wh9dn/d/nPgEh6pXTp0jh1\n6hROnz6NEiVKyO0CBHz22WdwcnICYAADwcHBOHToEN68eYNFixahSpUqeP78OQAgOTkZLi4uWLdu\nHWbOnIl9+/Zh2bJlGDJkCMqUKYOTJ0/KQNThw4fjzJkzAKDKCgEM4OjOnTuwtbWVNxZJ2NnZAQBC\nQkKwcePGVK9r+fLlqgCer776CvXq1cOaNWsQHR2NU6dO4fjx49BoNFiwYAGio6MREBCAX375BYBB\nmRQpUiTVc/z666/4/vvv8fjxYwQGBuLUqVOoWrUqOnfujKdPn2L58uUAkK4MHAB49OgRAEOWDwBM\nmjQJEyZMUAXvCsmXLx8iIiIwaNAgrF+/HjY2Nvjpp59w4sQJlCtXDgDkeGUkqVGjBmrUqPHezyPA\n4JEjR3Dnzh34+voiJSVFAtG05vbvSPfu3TFnzhxs3boVRYsWhb+/P3bv3o2kpCSEhIQgT5487+3c\nmZIpf0fWdyuXrv3i4uIAwGIW2L8her0erq6uFkHMf9m3jCbatHf5byU4OBgAcOXKFdX2fPnyAQAO\nHTqEV69eATCAgfDwcABAzpw50bx5cwlChCQkJMDFxQXNmzeXx9VoNFi7di38/PxkOu6ZM2eg0RiC\ne7NmzQrAkHVjfCylnDt3Dnq9XmXV8Pb2RqdOnTBhwgQsXbpUgo88efLg8ePHGD9+POrVq4dWrVrh\nypUrGDFiBGbOnIkhQ4bIc2q1Wqxfvx6jRo1CcnIyrKyssHnz5lTHbdasWShatCimT5+OlStXypTb\nJ0+eYPLkyVi8eDGSk5MxePBgNG3aNNVjCSlatCgAID4+Ho6OjhgyZAhOnTpl9oFq3749vLy8MGHC\nBACQGTTCuvL/XT755BM0atQIb968QWBgIJo3b44iRYpg165dcHJyQpcuXd7buX18fLBt2zbkzJkT\nly9fxqZNmxAfH49GjRph0aJF7+28mZIpH7s4OztLfeTi4gJfX1/88MMPAAz66fz58/9l9zKsZHiL\nyE8//QTAACwWL16MzZs3IzExEb6+vnB2dsbDhw/h4eGBqlWrIiYmBseOHYODgwPi4uJw7do1+Pr6\n4s6dO8iePTtKly6N8PBw9O/fHwUKFAAA6ZqJi4tDxYoV0aZNGyxYsACPHj2SrpXo6GjY2tqidu3a\n2Lp1q+ybo6MjkpKSZEpwcHAwsmXLJi0HAFC1alUsWbIEgCEFtXfv3gAMnBNFihRRWVvWrl2Ljh07\nYsmSJahfvz5CQkKwdu1a1XhYWVlh06ZNkpvDnFy4cAF9+/YFAHTt2hUlS5bEihUrcPToUeTOnRtt\n27aFg4MDmjVrJlfm6ZGQkBCMHj0aDx8+RFxcHD777DNcuHABcXFxcpyFXL58WV4zAMnRIkBdphis\nYiEhIdi9e7d8WeXKlQtr1qyBp6fnez33559/jrt372L//v2Ijo5GiRIlMl0ymZIpf1NatmyJLl26\nYM6cOdi4cSNWr16NHj16YMKECUhKSkLLli0RGBj4X3cz44m5wJH/uhlnzdja2qa7KJyLiwt37dol\nMxKUjKfpaTY2NtyxYwdHjRolsyjKly/Ps2fP8urVq+9c70akSE6fPl3Wh6lWrZosEFepUiVu2LCB\nkydPlv0UabzJyclcsWIFq1evzmLFirFSpUosVaoUixQpwnbt2lkM8BSpusogy4SEBJntWEdmAAAb\nN0lEQVR5c/jw4fTGHJFUB+JdvHjRJCjYw8PDLB18o0aNVJV/XVxc+PLly3c699+RqKgozpgxg927\nd+ekSZNkmnFGkwsXLnD58uUMDw9nYmJiun6TGRyZsSRzPt6PZISsmUx5d/lgsmZSa8pOW1lZybTX\nnDlzct68eSqOj+rVq7Nr165SEe7fv58kZUaNoAY3BhDis7+/P48dO8bbt2+zffv2BAyF5vR6PadP\nn07AkH57+PBh3rhxw+Q4Op1OlUlTvnx5Dho0iJcuXeK4ceNMlHP+/PkZEREhM3qUxeEGDRpEAGzS\npIlqElNSUlT08qJZW1tzx44d1Ov1quhrUQfEuFqq4EB51zx345dsfHy8LHGvbKGhoaoCd8Z9/fHH\nH9/pvMai1+v5008/cenSpYyIiGBKSorFfQ8fPqwqJggYagtt3rz5b/Uho0im4stYkjkf70cygciH\nKR8dEDG2VghlXaJECWo0GlpZWTE+Pl5aAfr370+Sqoqx1apV461btySZlgAQgLqE+evXr6Xy+u23\n3/jq1StpWTFulSpV4q5du/jkyRMOHDhQgpunT59Sr9fzyZMnjIuL44ULFzh06FB2796dy5cvZ3x8\nPE+cOEHAUOvm5s2bqn4BhqqaSiW7fft2AoY05cWLF/PUqVOSc8LR0VGm0hYtWpQrVqzg1KlTCYCf\nffaZXGHfvn1bWlzetQibpZfsqVOnOHHiRE6bNk2mqN27d499+vShj48Ps2bNyvz587Nbt25/u/Db\nzZs3TWrdFC5c2OxxX79+LQFRlSpVOGvWLFnc0N7eno8fP/5bfckIkqn4MpZkzsf7kUwg8mHKRwdE\nPv30U9XKVlg+qlSpQicnJwLg06dPOXnyZAIGsjOS3LNnj6oyr6VKsr6+vjx//jxJA8OdKHYmKls+\nf/6cQ4YMoa+vr0np+lq1arFr165SwefJk4cLFy6U5eutrKzYokULE5dATEyM/I04n62trcrSM3Lk\nSMbGxvLhw4ds06YNAQNJmJDXr19b5DQZO3asBCfe3t5s2LChtAy9KyMrmfpL9vnz57x27ZqKC0Mp\ner2ejx49ksX4/ookJSVJTpfcuXOzdevWksHV19dXVjUWsmHDBgJgYGCgtBTp9XrJBjtz5sy/3JeM\nIpmKL2NJ5ny8H8kEIh+mfHRA5M2bN2zWrJlczRor3bx58/LGjRsyFmHx4sWsXr26WQVtDCREc3d3\n5/379yWZWf78+c2a/Z8/fy77oCRaE01QtQvrhXDjfPLJJ4yJiVEdS1h2hFVDVKUVYESn00nwJM65\nZMkS+fuVK1fK38+aNYsJCQmcO3cuAQNZ28GDB1XkagBYv359Pn/+/B1uJ4OYe8k+e/aMrVu3ln10\ndHRk3759+ebNG7mPMlYHMLitjh9PH4mQUrZu3UrAUNVYxJjExsayYMGCBMANGzao9p81axYBsHv3\n7qrt48ePJwAOHDjwnfuQ0SRT8WUsyZyP9yOZQOTDlI8OiJAGF4AyNsP4f/H5008/lTVjsmTJwiJF\nipi4Yiw1pfUktVgGQYsuwIb4nZeXl7Tc/O9//2NKSgrv3r0r3QkzZsxQHScpKckEKPj7+3Pfvn0q\nS4eyX1mzZuXDhw+p1+tZuXJlaXWJioqSxy1TpgwBA+tqcnIyIyIiuG7dOl6+fDmte8eiGL9kk5KS\nWLJkSdk/b29v2ceQkBCS5L59+2TfnZycJJiyt7d/ZxbVSZMmEYAJFfKQIUMIgKNHj1Zt37t3r7RQ\nCeD1+vVrCYqWL1/+F0YhY0mm4stYkjkf70cygciHKR8dEHnx4gV/+eWXNEFEmzZteOjQIWn5+OOP\nPxgbG/tORfNKlizJ7du3pzrAer2e06ZNkxYMrVbLxo0b84cffiBgiPtQyqpVqwhA0gErpXnz5gTA\nHj168MyZM9Tr9Zw5c2aqfdTpdKpieNWqVVMds3jx4gTAXbt2pXod7yLGL1lBiZ8nTx5Z7+bnn3+W\nYOPy5cuSUv+rr77imzdv+OrVK4aEhBAAmzVr9k7nX758OQGwbNmy0lKlBGOLFi1S7Z+SkiIBoIeH\nB1u3bi3BUu7cuS26kT4kyVR8GUsy5+P9SCYQ+TDlowMiefLkUWVomEuf1Wg0PHTokFT6wcHBcgBi\nY2NVmRw2Nja8evUqN27cqDpGx44d32mgExMTeefOHUZHR5OkDEA1DjSdP38+AdNMGJKyD66urlyy\nZAmPHz+uAhnZs2fnli1beOPGDZOUWREf4+Hhwf379zMqKooTJ06U1qB/8iE0fsmKQOD69etz+PDh\nXLVqFV+/fi0ze+bNmydBmrIfouaNu7v7O53/5cuXdHV1JQDWqFGDs2fPltWDnZ2dzbqbfvvtNwnK\nRPPz8/toCrplKr6MJZnz8X7kXYFIYmIiDxw4wPXr18s4v78rwNtK6eTbWEJzi8uPUe7cucPVq1e/\n028+OiBiDDgAsGLFirx9+7ZcYQNguXLleODAAQkGlAGMxjwiNWrU4OrVq2ljYyO3pWUJSUuSkpIk\nT0f37t159epVbt68WYKglStXmvwmJSWFwcHBFq0fs2fPJmlY/SsBSlhYGOPi4mThOOO28P/aO/Ow\nqq5rgf82F4KKCmIdcARRY6wK4qxo1NKq0YifQ15ftagxDi8SFU1N9KVYU2ycgjGSmsY4oHEgwSZB\n0ySSvDhVUmNNnLBxHnFEirlXQYb1/rjnnl4EFEXhivv3fee7dw/n7HXu/va566y99l7vvluqe7md\n2x+yRS0lbtCggWl9io+PN31onB11HYHe6tevf88yJCcnm8qX46hSpcodA//l5+fLjh07ZPny5ZKc\nnFyhAkzpPz7XQvfHw+FeFJG//e1vBYJuuru7S2RkpOTk5JRKBi8vLwkODpYbN26Y7QQFBZWLIlLa\ne7kfnAP8lZQKp4hs2bJFFi5cWMDR9E9/+pNMmjTJVEwcPhVXrlwx/S66du0q77zzjkRERBT48ypq\n9cwTTzxhWjH2798vr732mkRFRcnGjRvvqeOTkpKKvH5YWFixG1Xl5ubKihUrpFevXhIUFGT6uIB9\nBdDevXsL+ZJUqlRJVq9eLTabTWbNmiX+/v5SpUoV6datm3zyyScllrekOD9kL1++bDrUKqUkLCxM\nAgMDTdkqV64sGRkZpoNxjx49ZNeuXfLNN9+YPhqTJk26LzkuXbok8+fPl/Hjx8vcuXPlwoULD/I2\nHyn0H59rofvj4VBSReTAgQPmi2Xz5s3l6aefNn3UXnnllVLJ4OXlJTNmzDD3X/rtb38rc+fONf+c\nrVarjB49Wtq3by/BwcHmM/jkyZMSGhoqbdu2lbZt28rf//53ERFJS0uT7t27S1BQkPz85z83N5j0\n8vIy2/zoo49k5MiRImKP1BsVFSU9e/aUqVOnFtveypUrJTw8XAYMGCD+/v6yZMkSefPNNyU4OFg6\ndepkRj8/duyY9OnTR0JCQiQ0NFQOHz5stvPSSy9Jly5dJCAgwLzfTp06SfXq1SUoKEhiY2Pl4MGD\n0qFDBwkKCpLWrVubWzc4U+EUkfz8fBGxL8ctalpm7ty5piKSkZEhe/bsKTSNUdRUjnP65Zdflvz8\nfHPVjPMREhJyT0tPU1JSZMiQIdKwYUMJCgqSBQsWFFhJcjdyc3OlZcuWxcruGFxubm6ye/fuEl+3\nNDg/ZGNjYwUo4KDqfEyePFlERI4ePVrk5maBgYEVYh+P8kb/8bkWuj8eDiVVRMaOHWtOoeTl5YnV\napXPPvvMnMYuzVS1l5eX7Nu3T4YMGWI6vTtbCWbMmGFavDMyMqRZs2ZitVrFZrPJzZs3RUTkyJEj\n0q5dOxERWbhwocTExIiI/XnvWAl4J0Wkf//+pkW3uPZWrlwpgYGBcv36dbl8+bJUr15dli5dKiIi\nU6ZMMbct6N27t6k8fPvtt9KrVy+znaFDh0peXp4cOnRIAgMDRaSwRSQyMlI++OADEbHv2O2wFDlz\nr4qIy8eaCQ8P58MPP+RXv/oVo0aNYuXKlfj4+NC3b18iIiJYt24d2dnZhIaG4uPjQ7t27Thy5Air\nV6/mwIED+Pn5MXLkSKZPn84nn3wC2JUvByEhIcyfP5/Nmzfzxhtv4O7uzpgxY6hXrx7vv/8+e/fu\nZeLEiSQkJJRI3s6dO9818u6dsFgs7Ny5kxYtWnD58uVC5XPmzOH8+fPExcURFxdHfHz8fbd1Pzji\nybz44os0bdqUZcuWce7cOaxWK6dOnaJFixYANG3alD179rBw4UK+/PJLLBYL4eHhTJ06lZ/97Gdl\nKrNGo6nYOKKSjxs3zgyw+fTTT9OsWTOOHj3K8ePHadOmzX1fv02bNpw6dYr169fzzDPPFCjbsmUL\nSUlJLFy4EICsrCzOnDlDvXr1iIyM5IcffsBisXDkyBEAOnTowPPPP09OTg6DBg0iODj4ru0PGzYM\ni8Vyx/bAHtusWrVqVKtWDW9vb5599lnAHrB0//79WK1Wdu3axbBhw8xrOwdvHTRoEG5ubrRs2ZJL\nly4VKUuXLl2YM2cO586dY/DgwQWiyN83RWknJT2ABcC/gP3Ax4CPke8P3AR+MI53nc5pBxwAjgFv\nA+r2697uI+IwraWlpRXwlXAcnp6esnPnzkJa2e3Ex8dL8+bNxcvLSxo3biyxsbHm1Itj+/N58+aZ\n9U+ePCkWi0UsFkuBJbJlwcWLF6V///7mPQYEBMi7774r+fn5sn37dgGkY8eOZSKL89ve22+/bU65\nODR0q9Vq+sckJyeXiUyPO/oN3LXQ/fFwKKlFxLGHk8Ovzmq1yqlTp8xp5LS0tPuWwWGpmD17tvj6\n+sr+/fsLWAlCQkKK3OF51qxZMm3aNMnLy5OcnByxWCxm2fnz5+W9996TVq1aSXx8vIiIVK1a1Sxf\ns2ZNAYuIc1iO4tpbuXKlTJw40Uw3btzYtOY7yjIzM6Vu3bpF3uft7TjuuygfkWPHjsnixYslICBA\nvv7660LXuleLiFsp9ZhkoJWItAGOADOcyo6LSLBxTHDKXwqMA5oZR9+7NfLee++Rl5eHn58fKSkp\njBkzBh8fH6pUqcKzzz7Lzp076dat212FjYiI4McffzTf3qOiorBYLHz11VekpKQA9mixNpsNsIdL\n9/f3Jy8vr1jtEOyRdHfv3s3x48fvKkNJqVOnDitWrMDNzQ0PDw+2bdvG+PHjUUqZEYkbNGjwwNor\nKcOHD8fb25vt27fTsWNHpkyZQps2bTh79ixPPfUUvXv3LnOZNBrN482oUaMAePXVV4mOjmbVqlUM\nGDCArKws+vTpg5+fX6nbeP7554mOjqZ169YF8vv06cOSJUtMS7vDOpOZmYmfnx9ubm6sWbOGvLw8\nAE6fPk3t2rUZO3YsY8aMYe/evYD9mX/48GHy8/P5+OOPi5WjuPZKQvXq1QkICDCjfYsI+/btu+M5\n1apV46effjLTJ06coEmTJkyaNImBAweyf//+ErdfHKWamhGRLU7Jb4Ghd6qvlPIDqotIipFeDQwC\nPi/uHE9PTzIyMti+fTvVqlUDYMKECUyYMKFAvT179hR5fnZ2Nrm5uXh5eRUqy8/PJyYmhk2bNpl5\n8+fPZ/369SxdupT09HSOHz+Op6cnV65cKdRGbm4uS5cu5aOPPuLmzZuA3QT22muv0aRJkzv9FCWm\nR48ebN26lU6dOjFw4EAuXrzI5s2bAejZs2ex9/0wcLS1YMECpk+fzt69e81B1KhRI2JiYsy0pmwo\ny/7X3B3dHw+WqlWrUqVKlbvW69evH6NGjWLVqlX88Y9/NPMbNWpEbGys+XJ5v9hsNmrUqMELL7yA\nzWbj5s2b5OXlYbPZmDp1KtOnT6dVq1aICI0bNyYxMZFRo0YxfPhwEhIS6NGjB15eXthsNr788kve\neustPDw88PLyYtmyZdhsNv7whz/Qv39/6tevT8uWLbHZbNhsNnJzc8nKyjLvobj2srOzycnJMeuJ\nCDabjcqVKxcoW7ZsGVOmTOH1118nJyeHoUOH0rRp00LtOO47MDAQpRStW7dmxIgRZGVlsWHDBjw8\nPKhTpw7Tpk0r9Pump6dz+vRpM3236Rvl0KpKi1JqE5AgIh8opfyBQ9itJNeB10Rkh1KqPTBXRMKM\nc7oDr4jIAOdrZWZmmkL5+Pjg6+vL559/bs79lYTTp0+zZMkSduzYQX5+Pi1atGD8+PGEhoaadb74\n4gt+//vfU6lSJX75y18WUEhq1arF9evXyc7O5rnnnuN3v/tdoTYWLVrEunXrAAgMDOTixYvYbDZ8\nfX3ZsGEDNWrUKLG8xXHt2jUiIyM5evRogfyxY8cybty4Ul//fsnKymLr1q1cvnwZf39/unbtiru7\ny7scaTSaR4iqVavSsGHDEtUVEbZt20ZiYiJWq5XOnTszfPhw8wVWU3acPXsWq9Vqpp0VEW9vb1Xo\nhKLma6SgH8hXwMEijnCnOv+L3UfEodh4AjXlPz4hZ4HqQAfgK6fzugObbm/zdh+R2bNnFzmnVRxn\nzpyRWrVqmatLHMu6lFIFlreGhYUJIH/+859FxD6Pdns8m+eee870fHYmPT1dPD09RSll+kVcv35d\nunXrJoDMmTPnnmS+E7du3ZLExESJioqS6OhoOXTo0AO7dknQ89+uh+4T10L3x8NB76z6aPLAfURE\nJExEWhVxfAqglBoJDACGi9i1CxHJFpF04/s/geNAc+Ac4OzY0ABIu1P7ERERzJw5825iFuDNN9/k\nypUr9OzZk7S0NDIzM5k+fToiwsyZM825NceqlJCQEMA+z5iWlmau6ti0aRMJCQlUqlSpUBvff/89\n2dnZdOzYkbCwMMA+l/bSSy8BsGvXrnuS+U54eHgwZMgQYmNjmT17Ni1btnxg19ZoNBqNpjwplbOq\nUqov8AowUERuOOXXUkpZjO9NsDulnhCRC8BPSqnOSikFRACf3qmN+Pj4ezb5JycnAxATE0OdOnWo\nVKkSMTExeHt7k5qaSlqaXfdxLJtatmyZqZzs3r2bq1ev4u3tbSoYReHt7Q3AuXPnyMnJMfNPnDhR\noFyj0Wg0Gk3xlHZSPw77NEyyXa/gW7GvkOkBvK6UygXygAkics0453+AVUBl7E6qxTqq3i8eHh4A\n3Lhh6kbcunXLVBgc5ZMnT2bdunUsX76clJQU6taty9atWwGYNGlSAUtIeno6n376KVarlW7duhES\nEkLz5s05cuQIQ4cO5cUXXyQ1NZU5c+YA8Jvf/OZB35ZGo9E8Vri5uZGVlVWkVVrjmmRlZd2TPyeU\nftVM02LyNwIbiynbA7QqTbt3Y9CgQezbt48pU6bwl7/8hVq1ahEdHc2NGzfo0qULtWvXBuxTMomJ\niYwfP57U1FRSU1Nxd3cnMjKSWbNmmddbvnw5kZGRZGVlmXn9+/cnLi6OwYMHk5SURFJSklk2evTo\nQpveaDQajebe8PX15dq1awWWj5aE9PR0AGrWrPkwxNLcATc3N3x9fe/pnAq5zGHy5MkkJCSQmppK\n9+7dzfzKlSsTGxtboG54eDj9+vVj27Zt2Gw2OnfuTN26dc3ylJQUxo4di4gQFhZGo0aNSExM5LPP\nPqNu3brs27ePuLg49uzZg6+vLxEREYSGhvLGG2/w3XffUaNGDUaMGEGvXr0wrEYajUajKQFKqftS\nJhxLRx07PWtcmwe2fPdB4rx89359LdLT05k3bx4bN27k5s2b9OzZkxkzZhTajOZujBgxgrVr1xIV\nFWUqMQcPHqRNmzZ4eHhw8eLFAst0Dxw4QO/evbl69WqB60yePJlFixY9ksqIY2+E9u3bl7MkGge6\nT1wL3R+uhe4P1yIzM9P8XtTy3dLurOqy1KxZk/nz53P8+HHS0tJYt27dPSshgBkfYPDgwWZeq1at\nePLJJ7l165a5xz/Yl0KPHDmSq1evEhoaytq1a4mOjsbT05PFixebTrQajUaj0WjsuLxFRKPRaDQa\nTcXgsbKIaDQajUajcX20IqLRaDQajabccMmpGY1Go9FoNI8H2iKi0Wg0Go2m3NCKiEaj0Wg0mnLD\nJRURpVRfpdSPSqljSqlXy1uexwGlVEOl1DdKqcNKqUNKqclGvq9SKlkpddT4rGHkK6XU20Yf7VdK\nhZTvHVRMlFIWpdT3SqnNRjpAKfUPoz8SlFJPGPmeRvqYUe5fnnJXRJRSPkqpRKXUv4xx0kWPj/JF\nKRVlPK8OKqXWK6Uq6THy6OFyiogRLO8doB/QEvhvpZQON/vwyQWmichTQGdgovG7vwp8LSLNgK+N\nNNj7p5lxjAOWlr3IjwWTgcNO6XnAIqM/MoAxRv4YIMMIu7DIqKd5sCwGvhCRFkAQ9n7R46OcUErV\nByYB7UWkFWABfo0eI48cLqeIAB2BYyJyQkRuARuA8HKWqcIjIhdEZK/x/SfsD9n62H/7eKNaPDDI\n+B4OrBY73wI+Sim/Mha7QqOUagD0B9430groDSQaVW7vD0c/JQK/UI/iNr4uilKqOvZgnssBROSW\niPwbPT7KG3egslLKHagCXECPkUcOV1RE6gNnndLnjDxNGWGYLNsC/wDqiMgFsCsrQG2jmu6nh89b\nwHQg30jXBP4tIrlG2vk3N/vDKM806mseDE2AK8BKY6rsfaWUF3p8lBsich5YCJzBroBkAv9Ej5FH\nDldURIrSUPUa4zJCKVUVe+TkKSJy/U5Vi8jT/fSAUEoNAC6LyD+ds4uoKiUo05QedyAEWCoibQEb\n/5mGKQrdHw8Zwx8nHAgA6gFe2KfEbkePERfHFRWRc0BDp3QDIK2cZHmsUEp5YFdC1orIX43sSw6T\nsvF52cjX/fRw6QYMVEqdwj492Ru7hcTHMENDwd/c7A+j3Bu4VpYCV3DOAedE5B9GOhG7YqLHR/kR\nBpwUkSsikgP8FeiKHiOPHK6oiHwHNDM8n5/A7nyUVM4yVXiMudLlwGERiXUqSgJGGt9HAp865UcY\nqwM6A5kOE7Wm9IjIDBFpICL+2MfA/4nIcOAbYKhR7fb+cPTTUKO+ftt7QIjIReCsUupJI+sXQCp6\nfJQnZ4DOSqkqxvPL0Sd6jDxiuOTOqkqpZ7C//VmAFSIyp5xFqvAopUKBHcAB/uOTMBO7n8iHQCPs\nA3+YiFwzBn4c0Be4AYwWkT1lLvhjgFKqJ/CyiAxQSjXBbiHxBb4HRohItlKqErAGu2/PNeDXInKi\nvGSuiCilgrE7Dj8BnABGY3+Z0+OjnFBKzQb+C/uqv++BF7D7gugx8gjhkoqIRqPRaDSaxwNXnJrR\naDQajUbzmKAVEY1Go9FoNOWGVkQ0Go1Go9GUG1oR0Wg0Go1GU25oRUSj0Wg0Gk25oRURjUaj0Wg0\n5YZWRDQajUaj0ZQb/w9BStFfGeAqNgAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"sensor_var = 30000\n",
"process_var = 2\n",
"pos = (1000, 500)\n",
"process_model = (1, process_var)\n",
"\n",
"N = 1000\n",
"dog = DogSimulation(0, 1, sensor_var, process_var)\n",
"zs = [dog.move_and_sense() for _ in range(N)]\n",
"ps = []\n",
"\n",
"for z in zs:\n",
" prior = predict(pos, process_model) \n",
" pos = update(prior, (z, sensor_var))\n",
" ps.append(pos[0])\n",
"\n",
"book_plots.plot_measurements(zs, lw=1)\n",
"book_plots.plot_filter(ps)\n",
"plt.legend(loc=4);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This time the filter struggles. Notice that the previous example only computed 100 updates, whereas this example uses 1000. By my eye it takes the filter 400 or so iterations to become reasonable accurate, but maybe over 600 before the results are good. Kalman filters are good, but we cannot expect miracles. If we have extremely noisy data and extremely bad initial conditions, this is as good as it gets.\n",
"\n",
"Finally, let's implement the suggestion of using the first measurement as the initial position."
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAiAAAAC+CAYAAAAMerQGAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzsXWdYFFcXfmeXDoIUURQFsURBxBZ7\n70EEa6LGihoLlqAxdlGTGDWWGGKPvSbWqDF20agpGKOxJfZeUEEUlLb7fj/WudlhdwGJBb/M+zzn\ngb07c++dubNzzj1VIgkVKlSoUKFChYpXCc3rnoAKFSpUqFCh4r8HVQBRoUKFChUqVLxyqAKIChUq\nVKhQoeKVQxVAVKhQoUKFChWvHFavewLGSExMVD1iVahQoUKFiv8zuLi4SJnbVA2IChUqVKhQoeKV\nQxVAVKhQoUKFChWvHHnKBGMMFxeX1z2F/zyOHj0KAKhSpcprnokKGeqa5C2o65G3oK7Hv8fevXvR\ntGlT6PV6FClSBBqNBtevXwcA/PDDDwgODs5xX4mJiVl+r2pAVKhQoUKFChUAgEaNGmHdunXw8fHB\nzZs3cf36dRQtWhRr1qx5LuEjJ8izGhAVKlSoUKFCxatHmzZtEBYWhtOnT4MkAgICYGX14sWFN0IA\nIYn4+Hjo9frXPZX/FJycnAAA9+7de+5zNRoN3NzcIEkmjs8qVKhQoSKPQ6vVonz58i91jDdCAImP\nj4ejoyPs7Oxe91T+U3BwcAAAODo6Pve5KSkpiI+Ph7u7+4uelgoVKlSo+D/AG+EDotfrVeHjDYOd\nnZ2qsVKhQoUKFRbxRgggKlSoUKFChYr/L6gCiAoVKlSoUKHilUMVQHIIrVaLChUqCLpy5QqOHj2K\nQYMGAQCWLl2KAQMGAAA2b96MM2fOvM7pqlChQoUKFXkab4QTal6Avb09jh8/rmjz9fU1m/Bm8+bN\nCAkJgb+/f477z8jIeClhTipUqFChQkVehKoB+ReIiYlBSEiIou3IkSPYsmULhg0bhgoVKuDixYu4\nePEimjdvjsqVK6NOnTr466+/AADdu3fHkCFD0KBBAwwfPvx1XIIKFSpUqFDxWvBGbrnfm//zC+3v\n2z41sj3m6dOnqFChAgCgePHi2LRpk9njatasidDQUISEhKBdu3YADJnl5s2bh1KlSuHXX39F//79\nsW/fPgDAuXPnsGfPHmi12hd0NSpUqFChQkXeR7YCiCRJiwGEAIgjWe5Z23gAvQHIGapGkdz+7LuR\nAHoC0AEYRHLns/bmAGYB0AL4huTkF3spLxfmTDA5QVJSEo4cOYL27duLttTUVPF/+/btVeFDhQoV\nKlS8kbhz5w50Oh0KFy783Iknc6IBWQrgawDLM7XPJDnNuEGSJH8AHQAEACgMYI8kSaWffT0bQBMA\nNwDESpK0hWSuPDVzorHIK9Dr9cifP79F4SU3Sb5UqFChQoWK14lDhw5hyJAhiI2NBQAEBARgypQp\naNGiRY77yFYAIXlQkiTfHPYXBmAtyVQAlyVJugCg6rPvLpC8BACSJK19dqxFAUSuaggYUoLLWTlf\nJ5KTkxWfnz59Cp1Oh+TkZKSmpiI9PR3Jycmws7PD/fv3kZycDK1WCx8fH6xYsQJt2rQBSZw6dQqB\ngYHIyMhASkqKSb95Dbmd34MHD3D16tUXPBsVgPL3oeL1Q12PvIU3aT1OnTqF77//Hvfu3YOfnx/a\ntGkDb2/v1z2tLHH27Fn06tULaWlpcHBwgCRJOH36NEJDQ/HVV1+hWrVqAIBSpUpl2c+/cUIdIEnS\nn5IkLZYkyfVZWxEA142OufGszVL7/yXatWuHL7/8EjVr1sSlS5ewaNEiLF++HNWrV0eVKlWwbdu2\n1z1FFSpUqFDxmrFixQr06NEDmzdvxuHDh7FixQp06NABR44ced1TyxKLFy9GWloa3nnnHezcuRO7\nd+9Gx44dodfrsWDBghz3I5HM/iCDBmSbkQ9IQQD3ARDAJwC8SIZLkjQbwM8kVz47bhGA7TAIOs1I\n9nrW3gVAVZIDjcdJTEwUk3FxcRHt9+7dQ4ECBXJ8USpeDGTNR27NROq6vXjIOztz4d8qXj3+q+tB\nEj/99BNOnjwJLy8vBAcH54lyGW/Sepw9exb+/v6QJAmRkZGoXbs2Vq1ahQ0bNqBAgQK4du3aS72n\n6enp+OGHH3D58mX4+fkhODgY1tbWOTrX3d0d8fHxuHz5Mnx9fQEY+IWzszP0ej1SU1NhY2ODxMRE\ncY6Li4uJg0iuomBI3pX/lyRpIQB5S38DQFGjQ70B3Hr2v6V2FSpUqFDxhuDWrVsICwtTmDk8PT2x\nbt061K1b9zXO7M3CqlWrAADh4eGYPn06AKBVq1aoUKEC/vzzT+zcuRNhYWEvZewTJ04gNDQU165d\nE20+Pj7YunUrAgMDsz3f3t4eAHD//n0hgMgV621sbHIcWJErE4wkSV5GH1sDOPXs/y0AOkiSZCtJ\nUnEApQD8BiAWQClJkopLkmQDg6PqltyMrUKFChUqXg9Ion379jh69CgKFiyInj17onz58oiLi0PL\nli0RFxf3uqf4xuDBgwcAoEhYKUmS+BwfH/9Sxk1JSUGLFi1w7do1vPXWW4iIiEDp0qVx9epVtGjR\nQhGlaQlyionw8HDs2bMHP/30Ezp27AgAaN26dY4FkJyE4a4BUB+AhyRJNwBEAagvSVIFGEwwVwD0\nAQCSpyVJ+g4G59IMABEkdc/6GQBgJwxhuItJns7RDFWoUKFCRZ7A77//jiNHjsDd3R2nTp2Ch4cH\ndDodmjVrhr1792Lp0qX4+OOPX9r4R44cwZo1a5CYmIgaNWqgc+fOyJcv30sb72VCNhMtWbIEPXv2\nhIuLCy5cuCB8BF+WGWnTpk24efMmypUrh6NHj8LGxgZLly5FREQErl+/jvLly2Ps2LEoU6YM5s2b\nhwsXLqB48eLo06cPqlevDgAYPXo0tm/fjpMnT6JJkyaiby8vL3z++ec5nwzJPEMPHz6kTMaIi4uj\nilePpKQkJiUl5fp8dd1ePGJjYxkbG/u6p6HiGf5r67Fy5UoCYLt27RTtc+bMIQCGh4e/lHH1ej0j\nIyMJw6ZXkI+PDy9duiSOe5PWIzk5mb6+vgTA/Pnzs3bt2rSxsSEAtmjR4qWNO2HCBALg8OHDSZLD\nhw83ua+WaPbs2aKfBw8ecOzYsSxfvjwDAgI4ZMgQ3rx5UzFWJp5uwvPVVOwqVKhQoSJHkMNDf/nl\nFzx9+lS0x8TEAACKFi1q7rR/je3bt2PmzJmwsbHBsGHDMHfuXJQvXx5Xr15Fr169XsqYLxsODg7Y\ns2cPatSogYcPH+LQoUNIT0/Hu+++i9WrV7+0cYsVKwYA2LdvH/7++29MmTIFWq1WrF2HDh3EsZ07\nd8bOnTsRGRkJABg8eDBu3rwJAHBzc8PEiRNx4sQJnDp1CtOnT4eXlxcWL16MChUqCD+RLGFOKnld\npGpA8hZUDUjew5u0w/sv4L+2HjqdjmXKlCEABgUFcdKkSQwLCyMAWltbK7QRLxJt27YlAH7++eei\n7cGDB3R0dCQAXrlyheSbux6nT5/m7t27ef369Zc+1uPHj+nu7i40SADo4eEh/n711VdC4zFt2jRx\nXuvWrQmAM2fOtNj3qFGjFBqT/6QG5MaNG1i2bBlWrlyJe/fuZX9CDiBJErp06SI+Z2RkoECBAibF\n6P5fceXKlZcqlatQoSLvQ6PRYN26dShcuDBOnDiBUaNG4fvvv4eNjQ2WLVuG4sWL56rftLQ0JCUl\nWfz+7l1D4KWxX4SbmxtKlCih+P5Nhb+/Pxo3bvxKEpA5OTlh06ZNcHV1FYki79+/Dzc3N2zevFmh\n2UpLSxP/lyxZEgDw8OFDs/1ev34dkydPhkajwcKFCy0eZ4z/KwFEr9fjo48+gq+vL7p3744uXbrA\n29sbU6ZM+dd9Ozo64tSpU2Jxdu/ejSJFXk8utYyMjFc+piqAqFChAgDKlSuHc+fOYdGiRYiMjMTU\nqVNx6dIlEQXxPLh69So6dOgAJycn5MuXD0FBQdi4caPJcUFBQQAMCbD0ej0A4LfffsOff/4JOzs7\nlC5d2uQcFZZRp04dXLlyBSNHjgQA2NraYsWKFahZsyZsbW3FcQEBAQAMm3o5bFh2RM2MHTt2QK/X\nIzQ0FL169VLk8rIIc2qR10X/1gTz5ZdfEgC1Wi1DQ0PZtGlToQr67rvvctSHJTg6OnLkyJFct24d\nSbJLly6cPHmycBZKSkpijx49WKVKFVaoUIGbN28mSV6+fJm1a9dmxYoVWbFiRR4+fJgkeevWLdap\nU4dBQUEMCAjgwYMHxTgy1q1bx27dupEku3XrxsjISNavX59DhgyxON6SJUsYFhbGkJAQ+vr6Mjo6\nmtOnT2eFChVYrVo1PnjwgCR54cIFNmvWjJUqVWLt2rV59uxZMc7AgQNZo0YN+vr6csWKFSTJatWq\n0dnZmUFBQZwxYwZPnTrFt99+m0FBQQwMDOS5c+dM7plqgnnxeFNVzP+vUNcj97h79y69vb3FO1p2\nwATA1atXK449e/YsbW1tCYBlypRh8+bNaW1tTQAcOHCgOE5dj+dH+/btxX13cHBQmFC0Wi0rVqwo\n7n2VKlWo0+nM9jN//nwCYNu2bUVbdiaY1y50GNO/EUD0er3wKF67dq1onzFjBgGwRo0a2faRFRwd\nHXnixAm2bduWT58+ZVBQEPfv3y8EkJEjRwpmnZCQwFKlSjEpKYnJycl8+vQpSfLcuXOsXLkySXLa\ntGn89NNPSZIZGRl89OiRGEdGZgGkRYsWzMjIyHK8JUuWsESJEnz06BHj4uLo7OzMuXPnkiQ//PBD\nYb9r2LChEBp++eUXNmjQQIzTrl076nQ6xsbG0s/PjyQV10qSAwYM4MqVK0mSqampfPLkick9UwWQ\nFw/1BZu3oK5H7jF27FgCYNWqVXnt2jWmpKRw/PjxwjdBftfJ+PHHH1moUCHBHDUaDXv06MGUlBRx\njKX10Ol03LFjB6OiojhjxoxX4mvxMvD48WPu2bOHBw4cYGpq6gvpMzU1laNGjRJ+IZIkmUS/SJLE\nsLCwLN/ply9fpiRJ1Gq1XL16NdPT0/87AkhycjIB0MrKSiGh3blzhwDo4uKSbR9ZQRYMKleuzMWL\nF3PkyJEKply5cmUGBAQwKCiIQUFBLFq0KM+cOcOHDx+yc+fOLFeuHIOCgmhvb0+SPHDgAEuUKMGo\nqCj+8ccfJuOQpgLI0qVLxXeWxluyZAl79eoljitatChv3LhBkly0aBEHDx7Mx48f087OTpwbFBTE\nMmXKiHFkwSIpKYlOTk4kTQWQVatW0d/fn5MnTzar/SBVAeRlQGV4eQvqeuQe1apVIwD++OOPok2n\n09HLy4sAhFbWGGlpady1axfXrVvHq1evKr47cOAAW7VqxcaNG3PatGmMj48nSd6/f1+MJZOVlRW/\n/vrrl3uBzwm9Xs8DBw5w3Lhx/PTTT3n69GnFd9OmTWO+fPnENXh6enLNmjXZ9puRkcGHDx9a1FzI\nePz4MQsWLEgArFSpEkePHs3y5csTAF1dXUVAgl6v5/79+xkZGclBgwZx+/btou/ModL/GQFEp9PR\nzc2NAHjkyBHRvn79egKgv79/tn1kBVkwmDBhAt3c3Pjnn38qmHKlSpX4119/mZwXFRXFoUOHUqfT\nMT09nVqtVnx38+ZNLliwgOXKleOyZctIUjB8klyxYoVCAJHNP1mNt2TJEkZERIjPPj4+vHfvnuK7\nxMREFipUyOx1Go+TlJQkrjuzAEIazDizZs1i8eLFuXfvXpO+VAHkxUNleHkL6nrkHrVr1yYArl+/\nXrSlpqaK9/j58+dz1I9er+fgwYNNdu1eXl48c+YM27RpIz4PGzZMfM7MK14nnjx5wuDgYJNrGDJk\nCPV6PRctWiTaKlWqxBIlSojP+/btM9tnSkoKR4wYIe6np6cnx48fz7S0NLPHr169mgBYvnx5cUxG\nRgarVKlCAFy6dCnT0tIUJhuZmjRpwidPnlCn0zE6OpolS5b8b0XBaDQa9OzZEwAQGhqKqKgojBgx\nAt27dwcA9O7d+4WMEx4ejnHjxpnky2/WrBmio6MNUh2AP/74AwCQmJgILy8vaDQarFixAjqdDoDB\n+crT0xO9e/dGz549cezYMQBAwYIFcfbsWej1emzatMniPCyNlxM4OzujePHiWLduHQCDEHrixIks\nz8mXLx8eP34sPl+6dAl+fn4YNGgQQkND8eeff+Z4fBUqVKiQ65wMHz4cBw4cwMWLF9GnTx/Ex8cj\nICBARLhkh507d2LWrFmwsbFBjx49MG7cOFStWhW3b99G586dsWnTJtjY2OCXX37B1KlTsWHDBgwd\nOhQAMG/evJd2fc+DMWPGYPv27XB1dUVkZCR69uwJa2trzJgxAytXrsTkyZMBAFOnToWvry8uX74s\nzu3WrZsoHCqDJN577z1MnjwZ8fHxsLOzQ1xcHMaPH28xb8qVK1cAAE2aNBFF6bRarch0evnyZXz1\n1VdYt24d8uXLh5EjRyIqKgoeHh7YvXs3JkyYAI1GgwEDBuD8+fM5C5YwJ5W8Lvq3TqjJycls3Lix\niXTWoUMHpqen56gPSzA2jcgw1go8efKEH3zwAcuVK8eAgADRfu7cOQYGBrJatWocMWKE6Gfp0qUM\nCAhghQoVWLt2bRE/v27dOvr5+bFevXqMiIiwqAGxNF5ONCAkeenSJTZr1ozly5dn2bJlOWHCBJNx\njDUgaWlpbNiwIcuXL88ZM2Zw0qRJ9Pf3Z1BQEJs1ayacW42hakBePNQdd96Cuh65x+PHj1mhQgWT\n97WNjQ337NmT435CQ0MJgKVKlWKzZs04c+ZMJiYm0sXFRfRZsWJFxTm7d+8mANapU+dFX9ZzIy0t\njc7OzgTAX375RbTPnTuXAIT5yMbGhhUrVhQ5V2QtAwCGhYUp+jx8+DAB0NnZmQcPHqRer+fOnTtp\nZ2dHADx58iRJMiYmhu+++y7ffvtt1qhRgwAYEBAg/EvS0tLEGi1fvlzkgNm0aZMY69ChQwRAd3d3\n6vV6xTz+MyYYGTqdjtu3b+fgwYM5ZMgQHjhwwOSmqMgZ1ERkeQ8qw8tbUNfj3+Hhw4ccNWoU/fz8\n6OnpyTZt2jzX/fz9999pZWVlIsT06tWLlSpVEs6qVlZWvHjxojhv0KBBBMDu3buLtqSkJK5Zs4bR\n0dE8cuTIK+Mbd+/eFcKCMS5evEgALFy4MO3t7cW1FS1alNeuXeMPP/wgrg8Ajx8/Ls6NiooiAA4e\nPFjRZ7du3QiAM2bMEFGj5sjf35+RkZEMDAwkABYsWJDJycnCB0Xe1JIGM43suOrv708fHx+2atWK\nV65c+e8JICpeHFQBJO9BZXh5C+p6vD7o9XoGBQUJpvn222+zX79+YpcvSRJtbW1FBk8PDw9GRESw\nefPm4vvffvuNJLl161bmz59fwYSrVq3K+/fvv/TrSE9PF34axv4c06dPJwDWr1+f4eHhYl4tW7bk\nV199JRxGZa2IcZ2WTz/9VAhixpD9NyZOnEitVksAHDlyJA8dOsQRI0aYFUa8vLzEMy5rY7788kvR\n5zfffGP2PI1GowogKnIPVQDJe1AZXt6Cuh6vDydPnhQRGnL+isKFC7NIkSKCCUZERDAhIYF169ZV\nMEdbW1suXLiQpMGZXs5zIecWkcnJycmkwNrLwOjRowmA9vb27N69O9u0aSO0Chs2bGBcXBwLFChg\nwuQbNmzIOnXqCBNJ5ntjY2PDRYsW8fr164yOjqZGo6FGo+G4ceMIgG3atFHMo3r16or+CxYsyG+/\n/VZ8v3btWoXjaYsWLRTH+/j4sH379iJFviqAqMg1VAEk70FleHkL6nq8Phw8eJAAWLlyZcbExIg8\nUDIVKVJE+DLIIa6TJ0/m3LlzFe+mjz/+mACERiAzOTs78/Hjxy/1WlJTU9mxY0cTDcLEiRPFMX/8\n8Yf4LiAggOPGjWNERIQQXJYuXcqNGzfy4cOHvHv3rogyykxjxowRGhLZRPPo0SNOnjxZHOPg4EBP\nT0+hKdq1a5eYx+eff65IGieTp6en4N2yVuT/QgC5f/++SOal4tXh3wggT58+fSXqy/8aVIaXt6Cu\nx+tDfHy80FzExMQwIyODs2fPZunSpQmAo0ePzlE/cjE9Y/+Rq1evsmzZsqJt7NixL/lqDPjzzz85\nc+ZMzp49m9euXTP5fuLEiWaFCmM/GFtbWxNNDgB6e3tz1KhR3Lt3L3fu3CnMUmPGjFHkF5GpevXq\nfO+99wiAdevWVcwjLi6OK1euZL9+/RTnuLq6sl27duJzdgKIRBJ5BYmJiWIyxnnkSSI+Pl7UAFDx\navDgwQMAgLu7+3Ofq9Fo4ObmBkmSXvS0/tM4evQoAGVRLhWvD/8P66HT6fD9999j48aNSE9PR+PG\njdG5c+eclVN/zYiMjMSXX34JSZJQpUoVXLx4EfHx8cifPz9OnTqVo3pdAwcOxNdffw3AkKLgwYMH\nSEpKQvHixUVBtYCAAJw6dUqcc+bMGSxbtgxxcXGoUKECunbtCldX1xzN+ezZs1i6dClu376NgIAA\n9OjRA56ennjy5Am2bNmCGzduICAgAE2bNoVWqzU5f/fu3Zg/fz6uX78OwFATBwAaNWqEpKQk/Prr\nr9nOwc3NDR4eHjh37lyWx0mSBFlGiIyMxLBhw+Dl5QUA2Lt3L5o0aSK+12g0JjzauCCdi4uLKTMw\nJ5W8LrKkAVHxeqDu7vIe1DXJW3jT1yM1NdVsAqxy5cq9ESbU9evXC2dMmYoXL/5ca3L8+HGFJmHC\nhAlCiyKbZcqXLy+O//LLL03SlXt6eiqiUCxh7ty5Jue6uLhw9uzZ9PDwULTnz5+fM2bMYHJystm+\n9Hq9SEgm+3/Mnj1bnC9JEr/++mvhzCrTW2+9Jf43p/lo2LChWS0Lnplm5syZw/T0dJHyokOHDoox\njY//vzDBqHg9eNNfrv+PUNfk9SA5OZmrV6/m1KlTuW3bNlGn5E1fD5k5ubu7c9q0aZw/fz5LlSpF\nQBmi+iKQkpLyQn0pFi9ebJZJlixZ0iLTtoSPPvrIpB9jP4fx48eTJE+cOKEw1cyZM0c4bpYpU4Z/\n//23KH2RGX///bcImQ0PD+fChQvZoEEDBeOWnTeNydramkOGDDGp/fLkyRMhNBnXCDOeP0mTXCuz\nZ88WNXdkkk1ZOaU6deqIqKHFixezVatWJj40zs7OqgCiIvd401+u/49Q1+TV48CBAya70zJlyvDC\nhQtvxHrcv3+fo0ePZrly5fjWW29x4MCBwr9ArvWxceNGcfzff/8tmJJxobfc4uLFi2zXrp3wU6hY\nsSK///775+rj0aNHnDt3LsPDwzls2DDGxsaKqJCJEycyOTmZx44dY9GiRQmAc+bMee55yuG5mcnL\ny0v4s3344YcEwL59+4rznj59qkh6BhiKnx49elTR/5gxYwiAXbt2FW3p6eni2ZJDcc35b2Q+jzTk\nvJLHlcdatmyZwh8jIyPDpJ8ZM2bwwYMHijYnJycCECHM5si4EKAl7Ynx+c2aNVMFEBW5x5vwcv2v\nQV2TV4v79++Ll3ylSpU4cOBAEW1Rrlw5/vrrr3l6PeLi4oRGw5gKFCjAc+fOicJvxkm6dDqd2In/\nW0fy27dvizEkSVJoFYwzO2eFv//+m97e3maZoq+vryJhmJyAK3PdKnNITExkdHQ0O3bsyD59+jAm\nJoZTp04Vgo2VlRXbt2+vqJwrmxuWLFki2ozrtOTPn18wc61WS1tbW7q6urJ3794iB0flypXZo0cP\nbtu2TWFGMdYgeHt7s1WrVuKzrCEZOnQo/fz8aG1tzcDAQDZq1IiAIfx4ypQpIpxXPickJERoXWQ6\nceIEY2JiFEKEcaKz7CizmUWSJNaoUcPsGqkCiIpcQ2V2eQ/qmrxazJw5kwBYr149UfHz0aNHLFy4\nMAFw3rx5L2U9Dh06xPfff581atTg+++/z0OHDuWqH7k6aWBgIPfu3csjR46wXr16BAw5IOQ8DkOH\nDhWMfMmSJQQMOR2yywZ669Yt7tu3z2zlWpIcPnw4AbBmzZq8ceMGnz59KphkyZIls63QSpJVq1Yl\nAJYtW9ZEEwWAX3zxhTh27NixBMCQkJAs+7x48SJ9fHxM+oqIiKBer+eTJ08U5TuuX7/OP/74Q+TP\naNiwIdPT05mRkSGeBcBQwXfbtm1mS9qboxYtWijMH7L2IyoqSjG/rEwk5hh/ZqFDpsqVK3P27Nki\nV8qwYcNEHpHsSBYeZa1ZViQLX6oAoiLXUJld3oO6Jq8W/fv3JwBOnz5d0d61a1cC4KhRo174enz9\n9ddmX+q5KR9frFgxAsoaI7du3RI7/N27dwtmGRAQoEhEZZxZMzOSkpLYtWtXxa69Ro0aPHfunOI4\nOUuncbXsjIwMIUhcuHAhy/mfOnWKgMGcINcqKVu2rAnT7NatG2fNmiW0LfPnz8+yX1lzEBQUxAUL\nFnDUqFGCyW/evFkcd/HiRXGsrCmQr7lAgQKK70JCQqjX68U1A4b6NMbZWi0JCZkFFtkckznfhp2d\nHbdu3crHjx9z8eLFIrHY/Pnz2bNnT9aoUYNFihShlZUVnZychNnLXI6TmjVr8vHjx0xLS+PatWvZ\nsmVLkdBNkiSzQpRWq1WYWWrVqiXuuTlSBRAVuYbK7PIe1DV5tZg6dSoBsHnz5kIb8PTpU2GG+frr\nr1/oety8eVMwjWHDhjEmJobDhg0TAsOtW7eeqz85mZRxafvk5GQxxpMnT7h69WqFZsHe3p6ffPJJ\nltoPOdeDlZUVa9SoIRwSixYtqnA0lbUXW7ZsEW1Pnz4VxdeuXr2a5fzlonFyXRcXFxcmJCRww4YN\nFpleqVKl+OTJE4t9Xr16lYAhosO4iOYXX3xBAGzVqhVJQ50aWYCzt7cX99KSMHHlyhUh3FnSQPj4\n+Cg0JoDBDBIZGWm2pk1mcnBw4OHDhzlnzhwuWLCATZs2JQAuXLiQXbp0MXuOl5cXvby86OLiwkKF\nCrF27dpcvny5wqn1yJEjdHd3z3Jsa2trk4ijrIQPBwcHVQBRkXuozC7vQV2TV4s7d+6IXWGDBg04\nbtw4litXTjC6X3755YWux6x8l5yjAAAgAElEQVRZsxRMUIZc8TU6Ovq5+nv33XcJgO+99x4fP37M\n1NRUYZapVq0aSUM0Ra9evYT6X5IkhoaG8vbt22b7lJ1U7e3teerUKZIGfwp5pz9lyhT279+fHh4e\nos9ixYrx4MGDPH/+PDt37kwArFChQrZOrjdu3KBGoxE7+Nq1a1On05mkVjdm+tlVuD169CgBQ+E0\nY+zdu5eAQZND/lNPxcvLi5MnT1ZoBCRJYvHixcV9AMCmTZsqolDMUUBAAHU6nRDMMms/ciKEGJN8\nbs+ePU36yooGDx7MX375hbdv32ZycrLwe6latSpHjRolBGxL/VWuXFk4/AJQVOY1JlUAUZFrqMwu\n70Fdk1ePH374QTgWyuTt7c1Tp0698PX45JNPCIAffvihol2u3vrpp5+Ktjt37nD58uVcunSpxdDP\nEydOCAZpb28vnA41Gg137NhB8h9thiRJ9Pf3F2r/cuXKmYR+kuSqVavMCknR0dFiR58dA9RoNEI4\nKVy4MHv37m1Ru9OpUyfFebLTZmbSarXUarWUJCnL+i2JiYninuzZs4ebN2/mwoULRRRMv379uGbN\nGrNajM6dO7N+/foEDE60skZA1ugYk6enp3A8lUm+Z7Vq1VK016tXz6KppnTp0uzTp4+iLTQ0VGiF\n/g1JkiT6qVSpkgjnzcjIEAKGjY0Ne/bsyRYtWog1c3Z2ZkxMjHkzTT532hQqRZfanVQBREXuoTK7\nvAd1TSxDr9fz0KFDnDRpEmfNmqWIXsgOycnJXLNmDWfMmMGdO3eaOEc+ePCAs2fP5qhRo7hy5UpR\nGuJFr4e8Cy9QoICITLlw4YIwkezfv596vZ4TJ05UhGtqtVoOHz7crNnk559/Zs2aNcWxgYGB3LZt\nG0ny9OnTBAzq8j/++IOkwQzk5+dHAFy7dq1Jf9u3bydg8MUwvk+yv4ylXbq1tTXt7OwsmiesrKwU\nBdVkPH78mG3atLHIRLVarcIXAwCPHDmS5X3u27evRcHou+++U2giqlWrJoSyfPnyibWIiYnhO++8\nQ8Dgc9KrVy/Rh6VrBGBSs8a43svQoUNNBB69Xi+ca3NK5sbPnDY9M3300UdiHjqdTvihtHnvfV66\nl8Rzdx5x+YZt1Ng7U7KypUehInTzr0nnqm3p+d6n9B6wgkUj19Fn+Db6DN/GYsO+VwUQFbmHyuzy\nHtQ1MY/Hjx8Le7gxYzKOkLCEffv2mdi/AwMDeeXKlWzPfdHrodfrhYOllZUVy5UrJ5hhnTp1qNfr\nuWLFCjHPd955RxFqmVX+i7i4ON6+fVshpMhFwzp06MD4+HiuWbOGX375pdiN29jYsHXr1kI4IQ3Z\nU+WcEG3atOHChQvZpEkTxf0rVqwYJ06cKExHlsjZ2Vk4l8prZimiJjY21kRLYGtrK4QpYx8ISxqQ\ny5cvm1RwzUyy34cs1FgyQ3To0EGY5/7++2/h/+Hk5MTdu3ezUaNGCvORObK3t+eiRYu4atUqxsfH\n86+//lIIEG+//bZCA/RvKLOPiEajYZUqVcRnDw8Pfv75588EJIk2XqXp1rQ/iw/fKoQKS+TVI5qe\nLYfSvcUQ5qsSRvtS1Wnn5qUKICpyD5XZ5T2oa2IevXv3JmCIloiIiGDbtm3Fi3Xnzp0Wz7t7964w\nr1SqVIn9+/cXYY2VK1fONgz1ZaxHQkICO3bsKBiXVqtlx44dmZCQQJJCZW4sbCxfvpyAQV1vDklJ\nSZwxYwbr1avHWrVqcfz48bx37x6//fZbsSvPKheEvb09f/75Z5KG3fGcOXOyDA3dsGGDGNu4OJk5\nH4c9e/YoSs0PHTo0y/szY8YMxfkhISH88MMPRb4We3t7jh07VpGxVr6vsnCRlYZCprlz55rNTJqZ\njHOOyAy9a9euvHr1KmNjYxkYGEjAYJJxd3dn+fLlOXr0aJM52Nvbs0ePHgRMk369CAoICFB8liNq\ngipUoNbJjVYuBelcrR3dWwyh94AVQrh4q/tkrjt6nd/FXuOQOZuYr1IIfZr3ZuuxC+lXM5j2BYtb\nHPNfCyAAFgOIA3DKqM0NwG4A55/9dX3WLgH4CsAFAH8CqGR0Trdnx58H0M3cWKoAkregMru8B3VN\nTPHo0SPa2tpSkiQuXLhQOE/K6abDwsIsnjtlyhQCYOPGjYU5ISEhQUQ8ZKfKf5nrcffuXR49etSk\nJossKMgCCWnIqCm/9I2ZLmnweTAODZWpWLFiPHPmjELwMBYEALBHjx5CgPD29ma/fv1MTAiAIbqj\ncuXK4nPBggV5/vx57t271yRLqEwyA+7Zs6dQ9wNg27ZtFfPX6/U8efIkDx8+zLlz5z5X2vBKlSrx\nzp07JA1l5OW5yiYp2ZFUkiR+8sknIj/G81DhwoU5bNgwPnjwgAcOHDA7v8KFC/Pzzz/n3r17qdfr\nFanQHR0dTZLFDRo0yGQt/g1ZF/ClXfFKdPSvz3xVwuhSswPz1+tOj1YjWaT/MoU2w3vACnq0HEa3\nik1p7WEQ2Jo2bcpOnToJs1+zZs3MjuPm5sbw8HAhPL8IAaQugEqZBJCpAEY8+38EgCnP/g8G8OMz\nQaQ6gF/5j8By6dlf12f/u2YeSxVA8hZUZpf3oK6JKbZu3ap4CVpZWTE8PJw//fQTAYM5xRJku33m\nnBdyGfJly5ZlOfbzrkdaWhqPHTvGEydOmAgKOYUccWAc2rp//37B+DNj1KhRBEA/Pz9+99133Lp1\nqxAWOnXqJKJ6zJG7u7tJ2KjMaIwdc6dPn86VK1fmijnKTqWyI2fz5s3Zu3dvjhw5kmvWrDE7v8wJ\nyYxzU1StWpXDhw8XmqwWLVpwx44dJjk1MpPs95Jb8vf358OHDxkbG8tWrVoxf/789PDwEGYaY4FD\nnq9xJElOKCcaGcnGnrbeAXSu2poeYSNYpN8Ss2aTYkM3sUjfxfRsP4HOVdswX6UQ1m7eml988QU3\nbNjAlJQUs0nH5PwvkiTxq6++4tatW1mmTBnx/dy5c3n06FHWr18/WwFEokFAyBKSJPkC2Eay3LPP\nfwOoT/K2JEleAGJIviVJ0vxn/68xPk4mkn2etSuOk5GYmCgmc/78+WznpUKFiv82EhMT0b59eyQk\nJAAASpcujYsXL0Kn06FUqVI4f/486tWrh2nTppk9f9GiRZg3bx7q16+PqVOnQpIkpKSkoG3btoiL\ni8O8efNQuXJls+empqbip59+QlxcHHx8fFC9enWz5dNlbN++HV9//TXu3bsHAChcuDAiIyNRv359\nk363b9+Ow4cPAwBq1aqF4OBg2NraAgCWL1+O6OhoODo6om3btrCyssKGDRuQmJiI8PBw9OvXT9Ff\nq1atcPPmTcW13L59G6GhobC2toaLiwvu37+Phg0b4qeffkJ6ejoGDRqEuXPnIj093ey1WFtbw9PT\nEzdv3rR4vZkhSRKsra2RlpaW43NkuLq6QqfT4dGjRwCALl264MSJE/jzzz8Vx1WvXh3R0dEAgLi4\nOLRu3RppaWmwsbER45orG58T2NnZISUlRXyW+ylSpAju3r2LjIwMtG7dGqNGjQIAPH78GC1btkRy\ncjIAwz3LfD+1Wi0aNWoEADh06BCePHmS4/lYe/jAytULVvkLwcqlEGy9SsG6gA8kKxtIkgYAkP7w\nDtJun0PKleNIf3AduieJ0D9JhD49BSABKu9DpUqVMH/+fPH5008/xffff49atWrByckJCQkJSEhI\nwPnz5xEQEIA6depg/vz5yCxHODk5wdnZGWfOnBFtLi4uUuZrsMrx1SpRkORtAHgmhHg+ay8C4LrR\ncTeetVlqV6FChYpcY+vWrUhISICrqysSEhJw9+5dNGrUCLt37xabmLZt21o8v0WLFli8eDFiYmIw\naNAglC9fHnv27EFcXBx8fX1RsWJFs+edOHECH3/8MeLj40Wbr68vZs6cCW9vb5PjDxw4gKioKACA\nl5cXdDodbt26heHDh2POnDlCMEhKSkL//v1x9uxZxbmbNm3CnDlz4OTkhE6dOuH06dPYt28fli9f\nLo6rWLEi0tPTMXLkSBQqVAhhYWHw9fUVTK1QoULiWHd3d1hZWSE9PR0eHh64f/8+6tWrBzc3N6xf\nvx4LFiywKHxUrlwZv//+OzQajaLdx8cHt27dMjlPZtQkcyR8lC5dGiEhIfj+++9x8eJFAMAXX3yB\nr7/+GsePHwcAbNy4ET/++CPOnDmDMWPG4P79+wCADh06ADAIewsWLBDjGY8rCw05EZ4kSRLM1Vj4\nkPsBoOhn06ZNqFKlCpo2bYpt27YJ4WPAgAFISkrC0qVLFX3odDrs2rULnTt3Vggf4eHhSHz0CBu3\nbIek0cCmUElo83lAsrKBVb4CcHirFqzdCv8zl9RkpMVdRtKJXdA/fYTUOxeQEXcRGUkJJoJTVjh2\n7BjWr1+P5s2b48iRI/jxxx8BGIQ5WSCWcfr0aZw+fRoA0LRpU4UAlZSUhKSkpOwHNKcWyUwAfKE0\nwTzM9H3Cs78/AKht1L4XQGUAwwCMMWofC2Bo5nFUE0zegqruf3VITU3l9evXs8zgSD7/msTFxfHq\n1as5qrnxJuHChQvs37+/8C9o164dGzZsaKIu7tKlS7Z9bdy40cQBs2jRojx9+rTZ4xMSEujq6krA\nkIysXbt2om6Hv7+/2XstOyeOHz+eer2eOp2OgwcPJp7Z12XIScK8vb0ZGRnJSZMmCZ8LY+dMvV7P\n/fv3c8iQIYyMjOSECRNMfA+0Wi2XL1/OsLAwAoZ05SkpKdTpdJw4cSIBQyryefPmETCE4vbp08di\nNVaZwsPDCRiSghm39+vXz8Tfo1SpUuzWrRsBg79FZjOIra0t27dvL5wura2tRSZV41wZ/fr1EwnM\nZH+R33//ndevX1f02aZNG1F/5kWRpUJ4lkir1fLYsWMiCZy9vT2XLVsmzCcVKlQQx8o5U2xtbal1\ndKWVuzc9arRh/U++Z5kxP1qMOvF871M6VXiHNoVKUmPnlOO5Gadal9tatmwpHGXNkew/5O7ubvHZ\nMM79It8vFxeXFxMFY0YA+RuA17P/vQD8/ez/+QA6Zj4OQEcA843aFcdRFUDyJFQB5OUjLS2NI0eO\nFKms7e3t2bt3byYmJpo9Pqdr8scff4iiY4DBzr5q1aoXPf2Xgtu3b3Pr1q08cOCAoiCYjKNHj5pN\n/FS3bl3u3r2bEyZMEALCgQMHcjRmXFwcZ82axeHDh3PFihUiz4c5yLVaatWqJTKhPnr0SLx49+zZ\nozg+LS1NvPSNBUw5bDNfvnyizZzDZrVq1QgYoijM4dGjR+K8Nm3acOXKlYLpW1tbi/9lMo5EiY6O\nZkZGRpahqTY2Nly5cqUinwfMCCAyvfXWWyZt8piZQ1onTpzIhw8fcs2aNaJNdiI2nlNYWJjw6ZGp\nX79+wmm0fv36wqn1ebOJZiZJksw+X89LmX0/AFDr4EL3sjXoGNCQHk37Mn+9bnRrPpAF35+iDGsN\n/5rNR31D56pt6FytLe18gmiVvxC1+Two2eS8cm1myuzPY29vLwQlWZCTJIl2dnYsW7Yso6Ojn8tP\npXr16qLYYJ8+fV6aAPIFlE6oU5/93wJKJ9Tf+I8T6mUYHFBdn/3vlnkcVQDJW1AFkJcPuagZoIxA\nkFNOZ0ZO1uTChQuKkETjCIO8LISkpaUxIiJCwUCKFi3Kb775huHh4SxdurQiBXRISIjYvcvUq1cv\nBgcHEzCElubW0TMryJqLKVOmKNZD1gxkzsWh1+vF7vevv/4S7YcOHSJg2DGS5Pz587N8uWu1Wu7e\nvZvz5s3jzp07xbXJIbg1atRQhA23bNkyR0wjc40TWUg4duyYCPn19va2mM9Cq9UyODiYXbp04b59\n+xQ7/KxI1jpptVqR0AsAt2/fTpKKfCdNmjTh5s2bzWZBrVSpEn/++WdGRUVlmXMjO3JwcFD0by7/\nh4uLiyK3ida5AO1LVGW+KqHMX78H3YMj6RE2gh4hHzF/ve50Dx7MAu2iWKjzVBaJWK4QMvyGb6HP\nx1voHbGCXt1nMX+9boYolaJvmR3/xx9/NBs+LG9e/g1pNBrF787GxoYTJ06kXq83EaQCAgIs5kaZ\nPn26EMTXr1//QqJg1gC4DSAdBt+NngDcYTCvnH/21+3ZsRKA2QAuAjgJoIpRP+EwhOdeANDD3Fiq\nAJK3oAogLxdnz54lYPDgj4mJIWmo/imnd/7hhx9MzsnJmshZHoODg5mYmMiMjAxOmjSJgEETklfN\nMR999JF4GdavXz/LqAStVsv79++TpNn6G05OTvzpp59yNY8DBw4wJCSEBQsWpL29PQsVKsRBgwaJ\ncM7p06cLpvjbb78xNjaWKSkpIjrF3LrJtToCAgK4bt06rl69WjC7jz/+mLdv31Ywz7Zt25pk68xs\nvihVqhRPnz4t5tOvXz/FmAMGDBCMTNYIZcV8O3TooAixbd++Pc+dO2einndycmLNmjVZp04dE4Zv\nrIo3V+5eo9EoTBqenp4mfdjY2DA4OJhly5Y1O1dnZ2dWqVKFvr6+DAoKsliH5EWRxt6ZRWuFsetX\n29nlm19YNnIFiw3dyKIffpspqmQjvQeuYuFec+k9aA2LfbSJRfotYaFuX9Lzvc/oHjyY+aqE0c4n\niLYexWjn8I/pJLsaLo6Ojpw7d67Fe5KZYmJiLCYwkyRJbHZKliwpUtDLZLxhWbJkiSLCRZ5LduNX\nrFiRUVFRaiIyFbmHKoC8XMydO5cA2LFjR0X7mDFjCChTI8vIyZrIL6mZM2dy6tSpXL58OR8+fChe\nLNeuXXuh1/Ei8OjRI7HTiomJYWJiIi9duiQ0OSVKlODvv//Or776SrzkjMvTy8mpnJ2dOXLkyGyr\nrFqCXIvFHPn5+TEuLo53794Vc61SpQo/+OADsev39fXl1atX+dtvv/HevXui3zt37pjkegAMWgBf\nX1+zTLRs2bImu08XFxd26tRJCArFihXjjh07CBiSV8lC0sOHDwWTkU0issZB9pUxDqMtUKAAdTod\nU1JS6O/vr2BGxrkxBgwYIMxI5nxujOcJGFT+jRo1shgCW6JECbOhnsb3Z9CgQWzdujUbNWrEHj16\nmK01Y21tna3vSo6EDTsnOvrXp2e78fTqEc0ifb6hz8eGTKBvjdrGGlGbGDRwHl0b9aZbk77M93Yr\n2hR+ixr7zCYbZeG6nAgZ5o7JifBo7ny5zs93332n0Kz6+fkxIiKCHTp0EMcaC4BarZb79+8X2riA\ngIAs19kc2draClOPKoCoyDVUAcQ8Ll68yJEjR/K9997jiBEjeOHChVz1s2TJEgKGpD7GkGs2jBkz\nxuScnKyJubwJLi4ugglkTmyVFyBXKC1VqhTbtm1rsiuuWrUqSYOZRlY5ly5dmnq9ng8fPmTjxo0J\ngEOGDKFer+exY8e4Y8cOi0XaMjIyeP78eUW9mJMnTyrGrFWrFkNCQhQv6WHDhpE01EPJvBP09PRk\nnTp1xItdo9Hw/fff56NHj3j37l0OHTqURYoUoaOjY5Z+CiVKlDDJc2FMfn5+vHjxohAU1qxZw7ff\nfpuAQQPRvHlzxS5WzoAp554w56MB/ON7IZelN05P7+bmxg8++EDcz+PHj4vnat++fezbty9r1Kgh\nfCdkYSBz+XaZvL29zTp3Zi76J1/Ttm3bmJ6eLq65efPmotBbTivAymTt6kWHMnVYJDiC3SYtY77K\noXQPGUrvrtNYbNj39Bm+jUX6L2OBdlEM/GA6P1y4k4UDaxFS9tlTjUl+ZoxzlFgSkmTTStu2bRUm\nrJkzZyo0EAUKFODQoUPZrVs3enl50c3NjSVKlOA777zDpUuXigRnjo6O7NevH3v16iV+9926dTMx\n1xibdEqVKsWtW7eSJJ8+ffpc1yo/f8ZUtGhRVQBRkXuoAogpNmzYYLKbs7a25rp16567r7i4OBG5\nMH78eJ45c4azZ88W/RvX35CR3Zro9XrxYtdqtQwJCVHsaOVS43kNV65cUTATrVarcMg0TjE+cOBA\n0V6oUCGxs3d1deWuXbsUL3CNRsPOnTszKSlJnL906VKRkhsAy5Qpw2+++YYff/yxaLOxsWFiYiL1\ner2iP+N53L9/n8OGDWPXrl35zTffWHTWs7GxydJOX6ZMGROnx65du5rUPWnRooWYS82aNQVzL168\nOBcuXGhSkC1zfRtzpg7jz3KUTevWrQmAn332GSMjIxVMU6PRcNCgQcI/o02bNop1NNZQWRoHMDiK\npqamcvHixQSgiELy8PAQFWeNmbccKVOwYEGmpKSwQYMGgikrmKq9M22LBtKl4jvMX7crC7QaRY+w\nEfR8dyK9B60RJpPiI/6pcVKk/1K+NWgJa/WdzM6DRrHjM/NF1apVhVBUtmxZdujQIUcmCONnWaby\n5cs/l5bGwcFB9OHs7CzukYODA0+ePGn2d5SWlsYOHTqY9BUeHm6iTZOFYFkIMS5Z8OOPP4rjypYt\nazGbbeZnq3379jx79ixPnjzJ9PR0VQBRkXuoAogS8fHx4uXz7rvvcvny5SJjpoODg/BJeB7MmjXL\n7A968ODBZo/Pbk1+++03s8xGpv79+z/3HLPDnTt3uGvXLh49etSkdkpSUhKPHj0qKrtmBdkMYWdn\nx+nTp4sMnvLLMiEhgffu3RPF2ox3y3Xr1uXBgweFQ2WBAgVYr1498cLv0KEDyX8cNgFTW7YxE7S3\ntxemBuOS6n5+foo5y+thLLxYIk9PT5MQUa1Wy02bNvHXX3/N9vy3336bMTExFr8fNWoUT58+zW++\n+cbEsTQnZG9vL9KuW1tbZ3lNsv+Kj48PU1NTuWLFClaoUCFLbURmgahNmzZCYDF+XhcvXizMk5bm\n2a1bt3/CdDVWtC/xNj1aDqN3xAplyOqw7+nVcw6L9F1Er+6z6NZsAJ2CmtGmYAna2DkYQl/zK+uu\nuLq6Ci2QrIlq1qwZ4+Pj2bx5c4XW4Hm1Lzk5Txa0ZAHBwcGBdevW5erVq8X6dOrUKcvfUmxsLD/5\n5BNOmjSJJ0+eZEREhOi/dOnSZs2BgEHT1axZM/Hb8vDwYEpKCi9fvpxt/ZyCBQua/M5VAURFrqEK\nIEosWLCAANigQQPBaPV6vbCRNmzYkIMHD+aOHTuey9Fzx44dDA4Opp+fH+vVq8dVq1ZZLIKW3Zqs\nWrWKABgaGsrPP/+clStXpr+/vwjJ7datW47npdPpGBsby/379yvqjshISUlhnz59FOYEf39/xsbG\nUqfTcezYsQp7fY0aNUx2bidOnGCXLl1YqlQps7Z9Y8qXL58QKDw9PXnt2jWeP3+et27dok6nY8eO\nHQWDat++PX/77TeeOnVK1Im5cOGCcGw1rpybeXcn79gHDBjA2NhYhWDSt29fk/VYs2aNiTBjZ2en\nCIPOijQaDTds2GCRMa1bt06YVMyFdhrTkiVLhPNqVmacrMjKyoo9evTIluHIQkNOwjSNhUVLzFfW\nEu3atSvL3Bsau3x0qfEePd/7lIV7zWXRIesNwkbktyzQdhxdanWknV8Vap09CU3Oo2JCQ0NZt25d\nsSbG3zk6Omap+ZDvhZWVlcX7Jh9j/H1mjUiPHj1MnD6NadiwYQQMvjXPAy8vLwJgvXr1qNfrqdfr\nFQK+JRo4cKDoQ9ZKAQZtTqtWrYSg6+HhoTBnylAFEBW5hiqAKPHpp58SMPgZyEhNTTXrQPjOO+9k\nmUsit8huTQ4fPkzAsIuSEzrp9XpRHTYqKipH4+zfv19xXfb29hw5cqRCsJIZnUajYe3atcXOzcXF\nRWEmKVu2rDAxeHh4CF+Dffv2mS3c5eHhwbZt27Jnz57ctWuXCSNt1qyZIpxVr9eLJFXGJEkSGzdu\nLOzTcpisMX322WeMjY0lgGxzP7i7u/Py5cti3LS0NBHya47k/B2ZyRxzlZm4zOQmTpwodvgRERHc\nvXu3ReHDmKFrNBqFpsHR0ZEfffSRMKsYt1uat7HZI/P1V69eXdGW2bwiSRKHDRtmVgPj7e2tMBMV\nK1ZMIXja2tkTGis6uBWklbs37UvXoGNgY+arHEqXOp3pEfoxvcJns9hHm+kzfBsLdZ1Jj1Yj6dqw\nF+1LvE1oss//0bBhQ8bFxfHbb78V4wYGBloUiswJV7169TJ7/8qXL2+2/d+GyY4fP15EscnCfokS\nJXL8ztDpdKKvwMBApqamkiT37t0r2uvUqcPu3buzdu3aCgEpMDCQaWlpJJmlVmrNmjVmx1YFEBW5\nxn9dANHr9UxNTRXaiG3btokX54MHD0iSY8eOFT/C9u3bc+zYsWK3as6J9N8iJz4gsu9A6dKlOWbM\nGDZp0kQwiytXrmQ7xs8//yyYUJEiRUQWTwCcMGECSUOlVmtra2o0Gv7yyy8kDdqXzE6Eq1evJkk+\nfvxY7C6joqKo1+vFTq9Tp078448/RBguAPbu3Zt//vkne/fuTcCw47t8+TLj4+OZkZHBAwcOcP36\n9bxw4QLXrl2rGPN5ckE4OzsLj385eihzVlRJkhgSEqIQesh/CtllJxRkJkuVRGWSzRoHDhwQ12Jr\na6vQNMn3uXPnzhwyZIjFvtauXcuUlBRx7/8N1apVS6xHZvLw8OC4ceOEQ7ZcedYc2XgWp41XaQa/\n25VeVYPp1iyCXj3nGEJZnzmBmqPCHyxkwU6T6droA9oXLq3o09HRkRUrVsx27Z2dnYU/kPxcBwQE\n8Mcff2StWrUU6xYVFcUTJ06Y9CGvg6xVyI5yelxWz07FihUVFY2HDx+e43eGXq9XaPmKFi3KihUr\nWvRHkX+X8nW6uLiwQ4cOFqsQOzk5KXysjKEKICpyjf+qAJKWlsZPPvlEvDi8vb05efJkpqamigiT\n/PnzMzg4WOwWihYtKrJ27tu3T7x4XjRysibnz583yaFhb2/PDRs2ZHne6dOnFTtUBwcHLliwgCS5\nZcsWcd1Pnjzh7t27CRicIUnLSbQCAwPFy0k2MzRp0oSnTp0iYDClyDusjIwME8dL+UUoV379+eef\nTa7NksrbnPOjOW2VvJwMSiQAACAASURBVBOWnfeqVq3KCxcu8ODBg7x8+bLYMRrj4MGD/5qhmyNf\nX19hptq6dWu2TovXr183G4Eg09atW4XfQFaUXaXY7EhOPy5D3rG7FStNG6/SdPKvT48WQ1h0wApT\n4WLIehbuNpOujfvSpXYnOlVsQcfAxrT29KPW2ZP5PQubRKD4+PjkOuPpBx98wOTkZKEVdHV1ZUpK\nCkmazcgqm/Yyk3F4srl1cnFxybGPSIkSJUwE34YNG5qNCvLy8hIboJzCOCeMpfV7++23s30ONBoN\nt2/fzoMHD3L37t1CKFq8eLHZcVUBREWukRcEkHPnzrFXr1708/Nj2bJlOWbMGLP+CC8Sxi8c4x9s\neHg4r1+/bjYF9alTp8T5cuptAC886VdO1yQ1NZXffvstR48ezejoaEVOCnO4du2aUN1nfknJQojM\n+E+ePMljx44RMAgQCQkJ4lw5HFZ+qQH/lLqXE2aFhIQIZ8wiRYoospXKQkq+fPlYsmRJdujQgb/9\n9htJQ4p2eSfn4+OjEACBnCVI+uGHH0ycIQGDVkvWXEVHR5u9Rzdv3uTkyZM5YMAAFi9ePMsXenZk\nHKort3l7e3PJkiVcuXIlz507JwSj0NBQTpo0SWGDN8f4svMPsUQODg4i46lMOc1mWqCILx1KVaNz\ntbb07T6N7y84wnembGeR9mPp1X2WQtAo+uG39Gg1kk7lm9ChdE06VQymo28Q+w8YKNY0N/PPvDOX\nmWjTpk3Nmt3kZ8XY56hQoUKsW7euWA+NRsOzZ8/y/PnzJj4ZXl5ewtwoU40aNQgYnMdPnz6dpXCU\n+ZmxtbVVRGUZr+369etNMtra2toyKCiIixcvtugrlhn37t3LUT4R45wfvXr14pYtW0zSt4eGhopQ\n/qioKALgyJEjzY6rCiAqco3XLYAcP37cbPiXv7//SxNCZH8AR0dH4Uy6ZcsWYZKQBY3jx49z48aN\nQm1vnH5bzu9RpkyZlzK/l7EmQ4cOFS8gObxRrhFRuHBhxsXFiR3ajRs3qNfrRYZMmVl5eHgIhmjM\nTKpVq8bo6Gjxws+8W/T19eWdO3d49+5d4WMgm3qMIScJa9SoEdPS0nj79m0TxiCvnXG7scOpzGCc\nnZ3Nak5CQkKERsYY69evt6iClulF1A+RSRbe6tatK5hMZlNTZpKFInNMTqvVWtQUTZo0yUR4MTYb\naBzy07ZYIJ2rtWOB1qNZoM0Y5q/fgx6tRrL48C3/mEh6zWWhbl+yUOdpLNx7Ad+KWMiFBy/whz+u\nMqRrf0LS0NnZmZMnT1bkB5Gfi02bNimYpLlEWZbulbE2QmbYHh4eJoJCZpIkSfGsWllZmTDcnDBt\n2Tm0fv36TE9Pz7EAZ0zGQovx/1k9d6NHjxbP6JkzZ/jll18yOjqaly5dEu1nz57NcQZVY9Lr9cJ0\nl/l5qly5MtPS0sRmbN68eWbfK6oAoiLXeN0CiCyNt2jRgseOHePevXvFbmTs2LEvZUyZyWVOa929\ne3cC4LRp0xTtxmGdzZo1Y3BwsPixWvpR/hu8rDWR7eF79+4VOR6cnZ0FU5VNIw0aNBDn/P7774qE\nVzINHjyYR44cMevMKN+b4OBgxY7e2tpavHQLFiyoeIHKkFXmK1euJEn+9ddf2b5E3dzcTHw1Mr9M\ny5Yty3fffZffffed2doxN27cEEygZcuWwryQE5KTgGUmHx8fVqtWzSQpmJ2dHUuX/se/oXnz5tyx\nYwebNWummHeJEiWeu+6JRqNh3759s3CKlGhfshrz1+1Kt0Yf0KPVSHpnMpkU7j2fRfotZrGPt7BI\n/2X0bDuWI75aSccC/+SeKVKkCMeOHasovCczql69ellkqMuWLXsujZK1tTUrVapkIli5urpmKQDI\nx8sCdenSpRkbG8sdO3bw/PnzZrURgEHbl1l4LliwIMeNG6cwn9jZ2VkURnNqNjIWmjOTq6srW7Zs\nSY1GQ61Wy6tXr4pU/8bP+PDhw/n06VOLmqWszHvOzs7CzOjh4SHef8bnyc+2XPXWHFQBREWu8ToF\nkISEBAIGdaqxtkP2PQgICPhX/V+5coX9+vWjn58fS5UqxSFDhvDOnTuCufTu3Vtx/Pvvv0/AkJnQ\nGHq9np988onix2xlZcVRo0blWD0q48GDB/z999+F7dkccrMmN2/eZFRUFFu3bs2+ffsKk4Yx5Nwa\na9euZUZGhshvYkw2NjYcOHAg7969K867ffs2x44dK5hKx44deefOHcbExIhddMmSJdmoUSMhxHzw\nwQckDfdu8uTJijGMy4U3atSIv/76qxhLzhAbGRlJ0uDYarxzN/fSz04rIUkS//rrL27cuJHt27dn\n6dKlGRgYyPHjx4v3kOxQ2bJlS7Gmz5Oe2hxTtbGxMbH5G5MsaFsSMjp37sw7d+5kWS9HHseYWR4/\nfpwDBg6kVX4v2peoSufq7elcvT3zNwinV/evhCNo0Q+/ZZH+S+kR8hGdK7ekXfFKRmXfJUJrJbQO\n8vWVLVuWer2eOp3ORJAzdqAEYDb9enYapswk/w6M/XEsCVfGjF+OXKpfv754Rg8cOMDU1FRGR0eL\n98sXX3zBrl27imdMq9Xy+PHjnD17tojyMdaWlChRwqzmqVatWmZ9OcxRdmY04+dZFpTatGkj7l+X\nLl343nvviedGjlQrU6aMEGzN/SYyh8Db29sLrWinTp1EsrfM91fOhGsJqgCiItd4nQLI3bt3CRg8\nrI2dAOWU3c8ThpYZ586dM8meCBh2pXJomq2tLVeuXMn79+9zyZIl4gV2/vx5i/NdsWIFly9fzlu3\nbj3XfJKSktizZ08hxEiSxLCwMFHXwxjPuyaHDh0ym1/j888/VxwnJ0Tz9vbmmjVruHbtWou7SNlm\nXa1aNc6ePZtpaWlctWqVWUZbtWpVdu/eXcFIPT09RfE9kiahnZk1J7Vr1+bp06dFkjWNRsOIiAiT\nImmWyNy8ChUqJEwWlsJOAwIC+PDhQ5HEyVj7dfTo0X9VedUcyQzFXL8m2T41Gl6+fNkksVlm+qcv\niXa+FegeHMmiH35n4ghabOhGFuoyg47lGmabctxYUDCe67x589i5c2dxP+vUqcO9e/eSpGCSgCGc\n94svvhB+EzlluJnJxcWFmzdvVkTcmItgAqDIBiy3ffbZZwqnZGtraxF2u2jRIrHW69evz/JZAgym\nMp1Ox7i4OBOzT3BwsKjvJPdhHLIra2Rat27N+Ph4ixoYAOzevTt37dqlECxloUB21Cb/yVkkC1ij\nR4/mnDlzcvQcWjJB1axZk8ePHxfvhXbt2mXLq1UBREWu8bzM7saNGxwxYgRr167N5s2bc8mSJWbt\n6aRBfb5gwQKuXLmS8fHxJt/r9Xqh4hs5ciRTU1MZHx8vdi/yLjo3kFX5DRo0YGxsLA8fPixMEP36\n9TOpQiqTvPPOCXQ6HRMSEnJUDj4sLEy8mAICAsTLpXz58ib373nWJD09XbzMmjVrxtWrVzMyMlK8\n8I4fPy6Offr0KWvWrGn2uh0dHTlz5kyOGDHC7As4LCyMGRkZ3LlzJxs0aEAnJycWK1aMo0aNEmGb\nVlZWCju9o6MjL126xJs3byoYmnG+CmOtkoeHB2/evMnPPvvMZHxJkiwKA5kd7woUKCCOzUnkR9++\nfTl79mwCYPXq1cV6xMfHK8xPWq2WderUUVyjOUaYFU2ZMiXbeVlZWQlH3wkTJtDL63/sXXdYFFfX\nP9uX3ouADVSwIooF7F0UW+xYsHcFG7H3hua1xhJ7VCyoMdhLjN2oMVFjSDQqauzYQAUR2P19f2zu\ndWZ3Fhb0TXzzcZ7nPOLslDt3Zu7pv1MIMqUaKicvyJRqyLW20PiUhV2lcDg3GgD3DtPg1W/V+/LW\nEdtRvncsRiz7Bj/efo7XGVnYGLcFJJMjICAAQ4YMgbe3t1lQuJIlS+Lq1auifBMiQ4muFL6JXC7P\nsUyY6L0CyNBVP5Td3Nz4fJvzKHh4ePDKEKk5HzFiBK5fv46MjAzodDqL8kIGDRqExo0bW+ztIDJ8\nl0I0ZKFCJJfLTTrVurm5ISsrywRjRi6XizyuzIBjc1u3bl3odDrExMSYfRf9/Pxw/vx5vHr1Cj17\n9hR9f46OjqLvVCaT4ffff891DSpQQAoo35QXYXf16lXJ6oJmzZqJhOi7d+/QrVs30T7Cck8h7dq1\ni+9ja2vLFwkHBweznojcKDs7m39YDx484NsvXboEIoNlrNPpsHTpUpQvXx62trYIDAzEypUrLQqp\nZGVlYerUqdxF6+zsjDFjxvAyP2NiTb1sbW15+eX9+/d53HbHjh2i/fPyTJg3x8/Pj5cIA8CgQYP4\nIvv8+XOMHDkShQsXFi0wQpe1q6srXrx4wYUr+23RokVcwEuV+D579gxqtRoymQznz5/HpUuXRItf\n5cqVRcmOxYsX56Bjq1evRkJCAn/eRAZFdOfOnZILqKOjIxYsWMDnvWvXribJqAqFAuvWrRNZo8bM\nBBYTImq1Gi9evODjKlWqFCIjI/l1HBwccg3z1KpVC9u3bxcJBClmlqz4/mSQK5RQ2LvDqlQIrP1r\nwLHaZ7Cv3h5uYUPh3n4qCo/YKYmb4RO1FZ7d5sO1xWg41u4Om3INEFKjlghMDXhvLbOuzN9++22O\n93P+/HkRtLfwvtzc3NCiRQssXLiQh8yYwidl2Xft2pXnMuSmgFiixE2fPh0XLlwQeVw+++wzE4VJ\nCDCmVqsRHh6OHTt2mIzR3t4elStX5vfGtgcGBkqC3xmz8P1m44+Li8PWrVtFlXOLFy82WT+3bdvG\n0UrNKUBNmjThCb3fffcdP9+mTZtAZPD8sHe5WbNmWLRoEc/HUavVaNeuHXr37o1du3aZGEsvX77k\n4ItSLESENkcFCkgB5ZvyIuxYDkG9evWwf/9+rFq1ii/aQuWCZYtrtVp06NBBlIgodMsz2rVrlyiR\nr0GDBrhy5Uq+74mVyMpkMrx69YpvT0pKApHBYv4Q6t69Ox+r0B3csmVLyY+VuUW7desm2j516lQQ\nmXpd8vJMWNVEixYtRNtXrFgBIkLHjh1FrmnGSqUSR48eFcXthw8fDiKDMsPyDq5cucJLa5nwEtKp\nU6dAZFA0GK1du9YkEY9hqzBlxtfXF3q9nif4snGEhITwa0uF0LRarcjiFQoscwl3QoVAuL/Qk3H0\n6FFcuHAhV8jxQoUKoXnz5nwOx48fz38zDjcIr6tQKFCufHnItbZQuRaFtngl2FZoDJemQ1Fk5C6z\nwFw+w7bAq89yODXoC5vyDWEf0gF2VVpD61sZClvT5GDm1ShZsiRXiH/77Tf+7RIRKlWqxN9b5ikz\nFvyWYoYIcTCcnJw4VoxCoeDfNLsWKwMWXkvqGRvPnTGPHj0aP/74I/bt28e3+fn5IT4+PtfKFJlM\nZlaZlMvl3PtqZWXFv2Vh2bnwXRWeU5jvEhYWBsCAZ9OnTx80b94cMTExSEpKwtu3b3Hu3DkekgwP\nDzepfBK+3wqFAk+ePMGkSZP48x02bBj69+/PjYlly5Zh7969JqEpW1tbkcJijljImyX89ujRA3Fx\ncXxtZyE2c1SggBRQvslSYXfv3j0QGdzqqampfPv69etB9L5yIj09nS+Cp0+f5vuxOLZxZ01Ger0e\nT548+WjvBSstGzBgANLS0pCamspLTtu1a5fv87J27lZWVjh06BD0ej1OnjzJF7UzZ86YHMMslVq1\naom2M/wCY+j0vCgg169f5+NhKJ7p6encfcuEZUBAAG++xaypChUqiKxcZjUxFzEDJGPPuHXr1qJr\nP3nyhGMEGL8X7HmXL18ehw4dQnZ2tqhM0MHBATt27OBKAFPqWIhIGFaxt7c38agZKxBCVigUIiGn\nUCj48xEKPGH597p16/Do0SM8fPgQY8aM4dfXaDQm7earV6/O52jNmjWYOnWqibKxeMmX2HXkFBwq\nN4dTg35w7zhTMi+jWMxuBPadC4fQTrCtGAaNlz/UHn5Q2LlCpjafwColWHfu3ImkpCQeNvL29kb3\n7t1z7XLq4+MjClUYs5eXlygPxdra2qy1bmdnJ4mkWq1aNRQrVsyiezEODcnlcu5pYc/tzJkz0Ov1\nIsWKsbOzM0+uZN/G3Llz0b9/f9F+JUqUQJ06dbjSqVKpRHgcBw4cAGAwXKQ8M6VKlZJMMl63bh0P\ntQmZrRmAoT+SJSXd8+fPB2DwKrOwspD79+/PcYgePnyI2bNno3///pg3b54okTwn+uKLL0BkqF4S\nEpvDSZMm5Xh8gQJSQPkmS4VdYmIiiAwu1rS0NDx+/Bg6nQ4nTpwAkcG6AQwInWxRExILf5QuXfq/\nch/GdPz4cW6Fa7VabtFZW1uL8iLySgsWLACRIVFMSFFRUSCS7sOSkpLCQwUDBw7EsWPHMHnyZG59\nGsdZ85qXw1zRarUa9evX56EDDw8PnveyZ88ejt5aqlQpLpSOHTvG58bY6q1Tpw5GjBjB3buFCxfG\nsGHDcOvWLaxcudLE42Bra4vFixdj7Nix/FyDBg1C9erVUapUKTRo0EDSS+Hk5MSFDptH5tKXCvkR\nEccxsZSlSomFnFvppEKhEHlHDBavDBrv0ijfZRxK9JwLrz7L4T1gDapMTkC5SQffJ3+O+hae3b6A\nc5PBsAtuBWv/GtB4B0Bh74aWrT/DmzdvEBYWJrqecQKiuZwlIoPyMXjwYFy9etWk5JdxrVq18Pvv\nv3PIfuF9nTx5EjqdTrLnzaxZs5CZmSkp6M1xSEgI9u/fz8NNffv2FUH9s/uzJI+CKZnnzp0TdXed\nNGkSNmzYwJ9rjRo10KxZM0yZMgWPHj0ShWcYW1lZid6/RYsW8W+I9eQRCnmZTIa6deuKSqZ9fHz4\nOIYPH85LaSdMmMD3Y/1UZDIZRo4ciZ07d/K8J3d3d+6ZunbtGnr06AEfHx8UL14cTZo0QXBwMAoX\nLoxGjRph7969ou9cr9fj7NmzmDx5MqZNm/ZB65iQmIe2VatWou1M6TdOZjemAgWkgPJNeUHdZMKA\nCQcvLy/uZh0yZAgAIDU1FSqVCjKZTJTDsXDhQhAZILqvX7+OEydOSFaAfEw6evSoCMK6Tp06opLP\n/BAr4Wvfvr1oO8OhmDFjhuRxmzZtkgSJmjZtmsm+eVVAXr16hY4dO4qstAoVKuDq1at84Z82bRpq\n1qxpAvw0Y8aMHEtFpdjSUkopgCilUmniws6J7ezsUL9+fRMLlHklcnKpf0zWaDT48dIVqNyKw7Z8\nQzg1HAD/0du5guHVZzkKtZ+EZtO2ofPKHzB86yVsOncHI6YYLGH27K2trU2SaaVyA4Ts7u4OvV6P\njRs3WoR0ybwxnTp14gJXiO0SHx8v2t/BwQEtWrTgSpidnR0Pme3fvx8AzCo2uXHFihVF0P/Cd0+p\nVEqGTOzt7XmeBnvXkpKSeHm+MYeHh4vynwDw41kvI+NjXF1dkZaWBsCQTM48Whs2bODvmpTXIyAg\nAHv27OHjl8lkkMvlXOFxd3fnIWhhmb9Op+Nr5Z49eyz+tv8OevjwIX/2U6ZMweXLlzF37lw+b2wd\nZwrQ+vXrcfToUe55KVBACijfZKmwS0tLE7mihR+1Wq3mDaqA95qzt7c3pk6disGDB/OFULiQKZVK\n9OjRgy8E5kin0+HIkSP4/PPPMWHCBFE/CkvoxYsXH+19u3PnDuRyOeRyOZYsWYJ79+5hzZo13GI1\nbkUvpIsXL6Jnz54ICQlBhw4dcOTIEdHvWVlZOHfuHFauXImTJ0/ma2x79+7FxYsXefzaknbcRO/j\n9M2bNzfpqirk3PqWGLNSqcSqVatw6dIlDnTk4+NjgqliybnMVW1Isb+/v9lOtTmzDGqvAFiXrg27\nKq3hWDsSTnV7wjNyIYrG7BGVtDacEo8NJ69hw5Z4TJ8+HRs2bMDz58+h0+lw/PhxrF+/XhTyKVGi\nBF69esUTr80lXFaqVMnEG8W6Lg8bNixfigDRe4TfFy9emBWySqUSP/zwA09M9PPzw759+yQ9J+xv\ne3t7fp9sXdBqtejTpw9++OEHk/UiJ1YoFBg5cqQIdKtMmTJITEzk749Go4Gnpydq1KiBFStWmFSR\nPXv2jF/P19cXO3fuRKtWrUTvnK2tLVatWoXz58/z83p7eyMrKwvr1q0zec8LFy7Mk1xVKpWk0qtW\nq7F3717069cPRKZ4Qu3btweRAYztUyOW52XMzKP7559/mvQj8vf3x6+//lqggBRQ/slSBYRl0bu6\nuprElDUajajM9vnz56hatapZAWJvb4+qVavyRaxDhw5mr5uWlmaSBEZkyO342D1YjOnt27dYuXIl\nWrVqhZYtW2LFihVIT083W2ExdOjQXM95+PBhNG/eHH5+fqhTpw7i4uKg1+uRkJAgcvHb2tpi8uTJ\nmDFjBiIiIjBq1CgkJibmev7du3ejdu3acHBwQMmSJXNsYkZkyNEYO3asSKgYW+jW1tY59mBhuTXm\nuE2bNgAM1UnGFQgXLlxAdna2SQWDMbu4uOSpmdro0aN59RG7n3r16uHs2bOwdvOBlW8wtMUrwb5a\nO7iERcGj82x4D1xnggpaZNQuFBm5C56RC+FQozOsA2oioGo9EMkQFxeHxYsXmyRMmpurAQMGADB4\nCYXCX6iATZo0CXq9HosXLxYdW7p0aXTs2FEkyHOrGFGpVKL59vDwwJUrV3hJuKenp+h8FSpU4IbE\nq1evcvRUCUNao0aNEj2bwoULc4WJNTgUshRybF69cOydMA5TAO9bLQg9dcJwj1TZLlMeGN27dw+x\nsbEYOXIkNm7ciLdv3+LBgwdo1aqVCGXV398foaGhGDBgAFfw2FpZoUIFnhf1xx9/8PfCku/4n6CD\nBw8iPDwcAQEBaNq0KRISEgAYDEAGMOju7o5OnTrx98rb27tAASmg/JOlCgiLD3t4eCAoKAjDhg3D\n5cuXeeY/c9UyysrKwq5duxAdHY2xY8dyS7xChQr82V+9epUvXM2bN8eMGTNw7949HDx4EGvXrsW5\nc+d4ToCLiwvGjBmDwYMH84VFCCRkKbGk0XHjxmH8+PE4d+6cqHLlwYMHiI6Ohp+fn2SoISgoCC9e\nvMDmzZsREhICNzc3VKlSBWvWrMGrV68wf/581K1bFzVr1sT06dNFHS2//PJLyYW0ffv2ItwKcwJM\nJpNh+fLlZu8tJxAiY48V81J16NAh114awti7JWxrayuyIGUyGe7duwcAIpe7j48Pjh8/znNWjMcr\nFZawBBhMoVDgzJkzaNu9LzQ+ZeFUqSlcwqLQLHYvGn5x1CQR1HvwBnhExMKl+Qi4thoD24phULkW\ngUxj+hxYuaatrS3vByQ1NrVazQW9kKtXr55jp9+iRYti1apVouqanJ4l+7tt27YmVrlGozHbJl6j\n0aBx48YICwvDsGHDJL2Kr169wsyZMxEUFISAgAA0adJEUngbK0JCC1+q1b2xQmBvb49nz57h7t27\nvDS9QoUKmDlzJiZPnozAwED+TVhZWaFhw4Y830KtVvPka+E3LJPJoFar0bZtW77GsJyUdu3aYf36\n9ahXrx7KlSuHyMjIPOVTPH36FL///rsIhl5Ir1+/5gLayckJtWrV4mMwrlb7X6DvvvuOKxvM0Hz7\n9i2v/ClQQAoo32SJAnL27FnJhT80NJSXeOZW7sUqPoRdSKUEshTMMRGJxrhmzRoQGTLr80Lv3r2T\nDC907doVWVlZWLZsmaSV7ejoiLlz53IrPTo6GoAh4XbhwoXo3r07KlasKBlKKF68OB48eIBnz55x\nhWbSpElITEw0ez0ha7VarFmzhruk5XI5bty4Ab1ej9OnTyM6OhoDBgzA8uXL+aI+Y8YMXL58WSSo\nAgIC8PDhQ259MndwbspHfrhEiRImYGJz5szhpYfCLrFSrnn2uzEkNEsQZPPIz2PtCKuS1WFboRHs\nglvBpdlweA9cZ9KlteF/jqHVwqPwaNATGu/ScC9XEwqb3HMqpMY3YsQIDsplZ2eHmzdv8v46wnmw\n9HxElCvkukKhMBuu6tixY46KovC7kkrI9ff3z7E9AKPU1FSzpa5FihTBxo0bRfsbw/BLMbO0AUhW\nXD169Ijf+2+//YYff/wRFy5c4B2to6KiTMbJqlmKFSuGiRMnIiIigs+BJaWpH0p//PGHKAQok8nQ\nsWNHESzA/woxELX+/fuLtrOeWgUKSAHlm3JTQPR6vcgVa29vj1GjRonyQdzc3MyCcDFiJV0sWfXa\ntWuiRXHgwIHcalYqlejUqRNPuJPL5aJwy+3bt0FkwGTIC02ZMoXfw8iRIxEVFcUtOuMYt/DeiAxV\nL6xe3tnZOVfkx+bNm/OFunv37vj6669BZGhlLyRhyWJERAROnz5tUo3w9OlTPHjwgFscpUqVMgtx\nbWVlhV27dvE8A2FoY8WKFRzx09iSlbKq88sajQZ37tzJMbEyN85JMZPJZJBb2cM3rA9KDl1nip0x\nZKPBkxHUDNpiQVA6+4DkinwrW+bKfRmzd1oq36ZIkSJmm9VJsXHJb2hoaI6YGLmxnZ0dtmzZIlnC\nKXxniAhdunQx+WYyMjKwbNky1K9fHyEhIejYsaOJx0qr1SIkJARRUVEiT0JqamqOoTv2rr1584Yf\nw3IROnXqxLexSjtmcLA1iyWDGn9TgEFpkYLxnz59ep7WjA+lX3/9FYcPH8aff/75t173YxJLWg4M\nDOTrsF6v55VbBQpIAeWbclNAbt26BSJDpnx4eLjkIrJly5Zcr/Pzzz+DyGDFjR8/nlvgRAYrfP78\n+XwxIyIcPHgQjx494kqKsGRu7ty5IDJAD+eFmDv68OHDuHXrFsaPHy9ZXnjo0CETj4+9vT3evHkj\n2maMN0FkqLRhwpMBJWm1Wl6a17FjRwCGhT09PV0kGJYtW4ZWrVqZnDMnS9qccGLARcbCwhwQ18fm\nFi1amNyHTCaDi4tLvuL9MpkMjcLCofEOgGuL0SgyygDeVaj7fNhXawu1VwAUdq5Q2Yi9JkWLFhUJ\nwbzkkbA5yq3yj4tGLgAAIABJREFUxNnZGXq9nldICdnT01PSa1G6dOlcw0lDhw6FTqfjUN1s/4YN\nG5qF1Dfm2bNnc++Z8HpKpRJ16tQReZnUajXP3QAMeDJ5Kb9lzPrpHDhwAESGcAp75nZ2diaerX79\n+uHq1avYsmUL984I0YFZab+dnR1evHjB1yyWu9S9e3fJ7z0zMxPx8fGIjo7G5MmTLYIVLyBTevv2\nLTfE6tevjyVLlnBPslarLVBACsjQ7OzSpUu4c+dOno7LTQFh+B8+Pj549+4dFi1ahEqVKvEXMi+4\nHgy0SshKpRKHDh3iOAfMa8DiyMyKUSqV6Ny5MwfWIiJ88803Fl87KyuLH7d161bJag4mMJOTkzku\nAGOVSsVdjsx7wPIo2rRpw4Wcl5cXz4KfOHEiX/R/+eUXfp6QkBDuZRAKhby0KReyVK6Ku7u7aKEP\nCQkRKSOtW7eWzA/4UO9Hflmr1ZpeW6GC2rMkHOv0QJmRmwXhlHg4NegLlWtR0f6WluM6OTnlapnn\nlevXr8+RZC1h5s1iz0Sr1YpyRoQ5GcZooV26dMGDBw/4O2P83ki9D3K5XATOtW/fPgCGEkohUm5y\ncjK/LgOo8vLywpo1a0Res0qVKpkot6GhoXwsly9f5mWzFSpUwPHjx01CREWKFJFUzlq0aGECGV6n\nTh0QGSpioqKi0KZNG/6+nDhxwuJ1oIDyR8ePHzf5vtRqNXbs2FGggPx/pV9//RXjxo1D1apVRVZl\nrVq18Ntvv1l0jtwUkMzMTC6oFi5cCJ1Oh2fPnvEFISYmJk9jPnbsGLp3785bkVeoUAHp6emYNm0a\niN5XBFy5cgWZmZmScXGlUok5c+bk6boA+LmYFdyhQwdegscWcyJCz549Rd0xicSVDWyBnzVrFogM\nFpgwbMISZ5n1yEDacipv/VCuUKGCxdZ93759OYS6JcfkVCabm9IkZeXzHASZHNpiFeFUJxLOjQfD\npclguLWdBM9u8+E9eAOKjPrWoHTE7IZP1zlwCO0E61KhkGtt4erqipYtW3J0zbx4VYTNvxQKhWTb\neHNcp04dHD16NNeqHeP5EwpfuVzOFWAGd21lZSVSBISJnOzdYyEktVqNzZs3832ZYJgxYwb27duH\nly9f8tCeg4MD2rdvj/j4eBES7dChQ3nyNatisrOzg16vh16vx+rVq7l3zcHBAe3atZN85kKh1K1b\nN45YOnz4cLx9+5Y/63HjxuHu3btYuHAhr6Lbvn07Lly4gI4dO8LPzw9Vq1bFl19+Kdnc8vbt25J9\nZBjuzk8//YSlS5di06ZNIkTe7Oxss8miBZQ3Sk5Oxrx589C3b19Mnz6dh5UKFJD/h8T6iAhZWEHh\n4eEhsmbMkSVJqKysjAkPJrTc3Nxw//59yWPevXuHK1eu8IRJY0pJSeELaqFChUTIlh4eHli0aBF3\nMxctWpQnba5evdqiZDkpYmBo7BqtW7c2sbqZwJSyIl1dXbFmzRoe02ehIK1WK4J5NhbK3377LQAg\nMjJSJNA1Gg1XxPLCxkqDTCbj5Y7GgrhYsWIoW7Ysv2bdunWh1+t5eMgST8C2bdtMckbMKSVqtZrP\nqSivxMoemsLlYFsxDE4NB8C94wx4D1pvKHUdnQCfYZvhMzQOPkM2wSMiFtWjlsGpTndYlwqFws6Q\nS+Lr68uFolKpxM2bN3HmzBl+jSJFikiWbBuP2RiB0/h52djY8L4lxty2bVsAkKxwMWapEJ2lzDx+\nrJEb+/bM5bEY9yFKTk7ONQm2VKlSvKqH6H0PE5YrZY6Fz1WY3zJq1CisXr0aRIZ8JuB9UqkxN2rU\nyAQ8LDdKT0/HunXr0LZtW/To0QNXr17Fq1evTHKm7OzssHLlSvTr14+/32XKlDFJkC2gj0MFCsj/\nM2JlUcIW5WxhatSoERfc5lA5gfeodtHR0ZgwYQKePXuW4zXXrl3LS+SICI0bN8bvv/8OvV6PI0eO\nYNKkSYiNjcXNmzexZMkSkXs2KCgIP/zwg8k5f/nlF5NGacYLtouLCy5cuPDBcwYY6tmN8UnkcjnG\njBkjsmiFVrujoyOWLFmCU6dO8URbVr2j0WhyrDxwdHSEi4sLFAoFihUrxq3Fn3/+GX/++SfS0tLw\n5s0bSWGuUqk47LuxUMtJKAgVmqCgIH7vv//+Oy9NTE1N5d4bcyyTyfi4jJUPqdwRlWtRWBcug3nx\nx1Gq7Qi4toyBW5vx8IxcaIKtUTg6Hp6RC+HRJRbWATUhUxmUPSsrK7Rr1w53796FXq9H/fr1+fmL\nFStmkoPEkj+Fln1OLAX9nZOC4OnpKQLEYixElDV+Zl27dhVhbwwdOhSDBw9Gs2bNuHJoHDZhOUJS\nSZO5saOjI8aPHy+ZBP706VOMGTMG/v7+8PX1Re/evblHQip36Nq1a0hOTuYKLgtD1q1b1yQPRur+\nf/rpJ+716969O0JCQqDVauHm5obixYvD2dkZ/v7+mDVrlijXJK8kNJpYt1p7e3tERkaahE6Nv5nF\nixfn+7oFJE3/VQWEiO4Q0VUiukxEF//a5kxER4joxl//Ov21XUZEi4noJhH9QkSVjM9XoIB8OHXs\n2BFExC3q4OBgPHr0iFvtrBMqs2iMKSUlxQQeWavVYv369TleNzs7G7dv3+bYFqmpqTwUI8XFihXj\nC5eNjY1JvT7wXhHauXMnrl27hjt37mDq1Kno378/Fi9eLAI4+xjEmkSpVCqEhobi0KFDSE5O5mEm\ntvgqFArUq1cPKSkpePz4MUaNGoWAgAD4+/ujffv2OTbWcnBwkGxLzvjMmTNYt24dAgMDTbwZTEg5\nOztL9ubIS47G4MGD8euvvyIuLg5HjhzhY7p06ZJJPLdEiRImQqVSpUo8RGCyqNu5oGLrfnBuMhje\n/VeLK1FidsOr30p49f0KXl1j4dZ8OOyqtIG2eCUo7FxF88yE2Z9//imy4M1VGcnlcu5tYgoW29fZ\n2Rm+vr4mAFqhoaG55ofUq1fPxOvFQOIsVQyYp0volWEw6ocOHeJCP6dnyCqHrK2tERISIkJ/Na6Q\nkclkuHv3bp7e/wMHDkgqH6zp2bZt20Bk6EidmJjIlc/cPDkBAQEcSE8KK4TIoMjk1eshRUwBefLk\nCRQKBRQKhWhtYQaYg4MDEhMTkZmZyUtJHR0dc0VeLqC80d+hgLgabZtLRGP++nsMEcX+9XczIjpA\nBkWkOhGdNz5fgQIipuzsbOzbtw8zZ87E8uXLcfXqVbx+/TrHY5iWzyorvLy8kJmZyWPZDK6ZVVwY\nU0REBIgMyXifffYZr1eXyWSS4ZjU1FQMHz6cW0+BgYHYvHkzz59wc3PDqFGj0KlTJ77YDBkyBElJ\nSQgLC+Pxbk9PT+zevfujzNvdu3exbt06bNq0KVfvDSNLMAmMOSgoKNcW7TmxlNVtLnxhbuG2hOVy\nOWxsbESWqpSSpFar8e233/J7i46ONhFIQuAnIoJMpYW6UCl41O6MilGr4D1g7XtvRtRWuLWdhCL1\nOsOqZAhUrkVACsug1Rm7u7uLntPJkydB9B72XaVS8fwdHx8fXtJcu3ZtvH37ljcEs5Tt7OxEAtXR\n0ZErBS1btuTbV61aBQA4deqUaF6FFjVT6mQyGbKzs/Htt9+iadOmon2E89uqVSucO3cO58+f50qY\nt7c3ihQpgkGDBvFkZSl2dnbGzz//jNevX/PqKVZxkhe6desWYmJiEB4ejv79+4s8jKzkkvWOOX36\ntCjso1AoRPdjrEz5+fnx3+3s7FC2bFkMHDiQn2Pbtm15Hq8xMQXk7NmzIHqfY8WIKSD+/v6i7Wx9\nPHbs2AePoYDeU24KiJI+PrUiorp//f01ER0nos//2r4BAIjonEwmc5TJZIUAPJI6ycWLF/8LQ8sf\nAaB3796RRqMhmUz2t1zzyZMnFB0dTTdv3hRtl8vl1LBhQxo+fDi5urqaHOfm5kZERAcPHqQiRYrQ\nn3/+SaGhoXT16lWSy+W0evVqIiIKCgqib775hmxtbcnZ2ZmIiF68eEHbtm0jhUJBa9asocKFCxMR\n0dy5c2n79u00ffp0mjhxIr9WZmYm9evXjxITE/m2K1euUEREBCkUCpLJZLRs2TIqVqwYPXjwgLZu\n3UpERIcPH6alS5cyhZWIiB4/fkwtW7akmJgYat++fb7mTK/X0/z582n79u2k1+v5fDk4OJCzszPV\nqVOHIiIiyMHBQXTcr7/+SmPGjLHoGk5OTtS7d2/auHEjXbp0iYiIypQpQ71796bPP/+csrOziYio\nWrVq5OTkRAcPHjR7rjdv3pCNjQ1VqVKFjh8/TkTEj2ek0WhILpdTeno61atXj06cOMHvLTfSaDTk\n7e1NSUlJlJaWRmlpaWRnZ0evX7+mO3fukFwuJw8PD3r8+DFfENizfPv2LXXp0oVatmxJt2/fpjM/\nnKO4A6fonW9t8qv4Gb3WKUnh5E06axfSk+GbePr8Hr17fJ1e/7Sb3t69QllP75JapaSnmZkWjVdI\nMpmMAFCpUqVEa8GCBQuIiCg0NJTu3btHSUlJ5OjoSHZ2dnT//n0aNGgQ/71nz550+PBhfi5L6PXr\n11S5cmV6+PAhPXr0iFJSUkilUlGLFi0oOjqa9u3bRzqdjs6cOUMVK1YkrVZLrVq1ovXr1xMRkU6n\nI6VSSU2bNqXWrVtTnz59CAAFBQXR1atXTa6XkZFBtra2pFAoKCEhgRISEqho0aLk4eFB9+7do+Dg\nYIqJiSEioqlTp/LjgoKCqEyZMhQXF0fu7u6UnJxMo0ePpjlz5pCdnR0REf3222/5WkeNvz92Dicn\nJ9JoNHTs2DEaOXIkhYeHk1L5XoTMnTuXQkJC6O7duxQZGUmZmZm0bt06Sk5OJmdnZzp+/DjFxcXx\neU5MTKTExETy9fUlIqL169fzvz+Unj9/TkREiYmJdPDgQb5WPnjwgIiIFAoFvy8AlJqaSkREN27c\nIFtb248yhgIiKlmyZI6/f6gCAiI6/JfF8BWAlUTkwZQKAI9kMpn7X/t6E9E9wbH3/9omqYD8U5Se\nnk7Jycnk4uJCNjY2tGXLFtq6dSs9fvyYHBwcqFWrVtS3b1/SarX/1XFMnDiRbt68STY2NpSWlsa3\n6/V6Onz4MP3xxx+0ceNGev78Oe3YsYOuXbtGDg4O5O7uTnK5nBISEsjX19fkQ0tPTyd/f3+KjY2l\nly9fEhFR9erVKSYmhlJTU0mn05G/vz85OzvTwYMH6eXLl1SoUCEiIrp3755ojEeOHKHExETy9PSk\n2NhYKlGiBO3YsYMWLFhAOp2OChUqRMWKFSMiImtra37cH3/8QURESqWSypYtS1euXOG/ffnll9Ss\nWTOysbHhY75x4wY9e/aMihcvzsciRZs2beIKVJUqVejSpUuUnZ1NL1++pJcvX9KtW7do7dq1VKxY\nMercuTO1adOG0tLSaPr06UREZG9vT61ataL4+Hh69+6d5DVevnxJR44coaFDh9KECROIiGjy5Ml0\n+fJlys7OpsqVK9NPP/1EV65coeLFi/Pj+vTpQxEREdSwYUORAtG9e3eKjIykkJAQkZB0cnKiatWq\n0WeffUbLly+nS5cuUXJyMs2fP5/mzp1LDx8+5PvKZDLq2bMnJScn03fffUcZGRnk7OxMy5YtI19f\nX7py5QrduHGDXFxcqHDhwhQREcHfpUePDJ+fo6MjpaSk0J07d8jGxoaSUnT0xab9VKpSKJ2450R3\nHMLIs2srektE6bps0qWnUtbj26R4fZ5c5W/ot9MHSffqqWiugoOD+bxbSiVLliQ/Pz86duwYvXv3\njlq0aMF/y8rKovPnzxMR0YkTJ/j2n3/+mf+dlpZGzs7OVKNGDZo3bx4RkaTyUa1aNQoODqaVK1dS\nVlYWERGVK1eObt26RT/99BMFBgbSkydPSK/XU+PGjalSpUo0ceJE0ul0RES0ceNGSkpKovT0dP59\nTZo0iXx9fcnb25scHR2JiKh06dL0+++/SyofRMSVS71eT46OjvTu3Tu6e/cu/z0hIYEOHDhAKpVK\ntA58/vnn9Pr1a4qLi6M3b94QEdGxY8do//79XOktW7asRXNuKTk6OlK/fv1oyZIlNH/+fJo/fz7/\nLTAwkGrWrElyuZyKFy9OVlZWlJmZSa6urlSuXDnKyMigqKgoIiJydXWlVatW0R9//EGzZs2ipKQk\nIpJ+TvklT09PCg0NpbNnz1Lv3r2pRYsWdP/+fT63Dx8+pPPnz5Ovry9t3bqV7t69S87OzlSuXLkP\nui4A+vXXX+nnn38mjUZDdevWJU9Pz49xS/9OknKLWMpE5PXXv+5EdIWIahNRitE+L//6dx8R1RRs\nP0pElYX7/l0hmOzsbHzzzTfo0aMHunXrhri4OKSkpGDIkCE8zq5QKERVA0J3YtOmTSWrNz4WMVer\nvb09jz3Hx8fzkjgW7hg9erSkG1+KnZyc0KRJE1FzMG9vb35+Ly8vXL16lScYSlVAVKlSRTROFlZZ\nunSpaLsQjvnKlSt8u7Hbv2XLltz9KozD16pVC7169cJXX33FW8bTX67sdu3aiUrpGOl0Onh5eYGI\nsGvXLl7WmlNJpKurq8jdnls4xVwH1bVr13JcBBZ6UigUorDJpEmTAEAy/0MKc+PVq1c4ceKESZdX\nuVyOcePGYdu2bYiJieH3LGR7e3tcunRJND+PHz/GjJmzEFKnAdSeJVG5bhgWLVuJcbFfYmnCGfT7\nYgvcO0xDmeivETh+lyhvo1CvL+FUvw+sSobAxsUTc+bEYuvWrSLEVaVSCR8fHxQuXFgyj4G53seP\nH4/U1FRRhURgYKBkiKlXr15mcz8cHR0lE0xZCIu9NzKZDKtXr8bly5dF+wcEBHBwMBZC2bx5M3bs\n2CFqCS91H+XLlxe9NxqNBgsXLpT8lt++fSv5jHr37i3K4xk+fDh27twp2sc476RUqVKi8E2DBg1M\nmj8yLl++fK45FSdOnEC7du1QtmxZNG3aFDt37sxxXbt//z6mTJmCatWqwd3dHRqNhr+fTZs2RWpq\nKrKzs3kSs5+fH0fHPHjwoGgdXbRoETIyMjB48GA+5ri4uBzHawkJk1AfPnyIcuXKmcyN1Jogk8k+\n+PppaWkiLCJ2v7Nnz/7g+/pfpb+tCoaIphDRKCK6TkSF/tpWiIiu//X3V0TUWbA/3w9/owJiLi4s\njOMao/ExDg8P58LfuF36xyQWh2dlcDVr1gQAbNiwQbSdKR9SSXKMw8LC8NNPP2Hz5s2iZm2bN2+G\nXq/Hs2fPuGCdMWOGqLpAioULLeu3IEQiBcQKiL29vQjbQ4rr1atnFu6cPZuQkBA+9vDwcJM5e/ny\nJYgMuRJv377lZY75qR6oXbt2rvsYJ4iy/iZMMJUoUUKkVE2YMAHZ2dmSvTYYC+HJV69ebVJWyRZO\nhUKB27dv8/ueOHEiypQpA19fX/Tp0wfXr1/n83I+6TkGrToKr+5foPDw7SbQ5EL26rMcQVEr0Xv9\nj4haHA8H34pQuviIxqBUKjm408uXLyUTEJ2dnbmgEVbFFC9eHHq9Hk+ePBEpHE2aNMHTp08xZ84c\ntGzZEt26dcP+/ftFwvD169dcKTZXrdG7d29cv37d5FtgKJfC/kKBgYHo06cPiN7nk3z++eeS92Nt\nbY2wsDCTd0kmk6F+/fq5rgUMhj00NBRTp07lymHPnj35uVJTU/l3+Pnnn/P7Y6i1ZcqUMWtsSI2Z\nVQGZI1YSa8yjR4+W3P/EiROS158wYQJXgrRarej93rRpEz+eQaObMwhcXFzw7t27HMdsCRlDBzDE\n0xEjRmDatGn4448/kJaWhilTpsDPzw9OTk5o1KjRR1nPmTLl4OCAgQMHol27dvzZMHC3/2/0X1NA\niMiGiOwEf58loqZENI/ESahz//q7OYmTUC8Yn/PvUEBmzJgBIoP1O3fuXCxcuJCXhapUKhw4cMDE\n8hk5ciT3hjALd9SoUfj2229Rt25duLu7IygoCEuXLjVB6csPsS6R7IMvU6YM9Ho9F/hCAenj48Nf\n/M8++wwTJ04E0fv+JdbW1pLloAsWLODXY8BajRo1EmFWSC1y9vb2uHjxItasWcMTWgsVKoTvv/8e\nz58/54igjo6OFicA7ty5U2TZzZs3T5Twx7hixYr8OURERGDkyJE4c+YM9Ho9srKyuDW2d+9eyetI\nWYt5hd+2ZPH/b56LjXfatGkAgHdZOqS/y8bV+yk4nPgYcw/+joGbLqL/hovosuqcQbkYvRue3b6A\nS9gw2FVuCevSdWBTrj7sq34G69K1ofEO4I3XtFotvv/+e7Ru3Zp/E02aNBEpkBUqVIBerxfNc4MG\nDTBz5kwT4S+8J1tbW0ydOpUnjTLrtEmTJrl+E1evXgWRQbFLTExElSpVRNcR9hxq0qSJ6DcPDw+M\nHTuWo9Oy+xR6vKRKNInee0FYiba1tTV69uwpEi6zZs3KceyHDx/mY2QggD/++KPIy/jbb79xpY1V\nyri5uSElJUU0j/Xr15f0Tmo0GqxYsYInirq6upr1Zrx48YIrgKNHj8bFixfxn//8hytixt1fMzMz\nuRenadOm2LhxIwYNGsTH9c0334gq3vz8/ETKBwA8f/6cK4wDBgzgSZ/sno29qPklSzt4f2xKS0vj\ncypEqmXypnnz5n/7mD4F+m8qIL5kCLtcIaJEIhr/13YXMoRXbvz1r/Nf22VEtJSIbpGhdDfY+Jy5\nKSBJSUkYP348IiIiMGnSJNy5cweXLl3CN998Y3HLZIaYd+DAAb4tJiaGL7bMMhAiIMbExHBhyxYi\nc54Cf39/zJw5k7cYzy+xbG32gbLFUi6Xi9zyNWvW5K7w7777DnFxcSAyZNQLXc4lS5bkiwbjc+fO\nAXhvGbZu3Zo3ETJmc+WB5rAnVq5cKQmIlhuz7pXC+TUXEmLcs2dP6HQ6/oykSgnNCfeckDxzYnMt\n4a2trUXXMjdvUuORy+UYHjMGo/6zFi5VW8EuuCXsKoWjXq8xGPnVXgT0jIVnt//AIyIWxbvPgf/o\neBSN2S3yYviO2YeK43bCb8ha+A5chWr9ZnMsjaCgICQmJuLYsWOS12dCxhyOhfDfmzdvioR2WFgY\n6tata9G7QWSowmHWcGRkJJYuXYoLFy6YFZpPnjzhWCUMbI5VbBG994plZGSIvC6WNmtj3xS7dy8v\nL5FQZc/x6NGjfEws7FaxYsUcv2WdTsfPJZPJeKdcIuL4ORUrVuQeM7ZGDR48GD/88INoXJs2beLV\nNMLxMyyd7Oxsvk0KNRQANm3aBCLTfkkMqXT8+PGi7fv37weRYW0TGljMgzNu3DgABoCzP//8U9Qc\nUkhCEDPh9xwYGPhB2B9C+qcUkKSkJBAZPH5Cunz5MogMIb//j/SvASLbvn27SY8O44UyNDQ0186C\nbKF58uQJ3yZ0R7K4sLBhVlhYGIYOHSpagJklOmfOHOzfv18SC581Yrt58yYSEhLMLrA3btzA8OHD\nUb9+fXTu3BmHDx/GnTt3TIC4hNy8eXOoVCrI5XKurMTGxvK/J0+ezDVyGxsbPHv2DDqdDqVKleLn\naNmyJb7++msefgoMDBQt3mq1Go0aNTLJW9BoNOjQoYOohbqHhwe0Wi1CQ0ORkJCAjIyMXBt1GbON\njQ10Oh0yMjJE7l5fX1+8efNGlEPStWtXjBo1intEVq5cia+++ipfzczyWqopZCEAG5HByjcWepUq\nVRJtK1KkCAYNHgwvv9Kw8g2GfeVwONTsggqfb0PxMeZDJGXH74ZH13nw7D4fXn2Ww7XFaDjW62WA\nIQ+oBY13adi7uJsdq9DNLHymffv2NYvuWaZMGdSsWVMkhIlIFI4w1y03MjIS0dHRIDKfP2OsoDVs\n2BAvX76U/HZZG3V/f38sWLCAA00REZo1a4a1a9dysKuSJUvyPBOZTCYSeFFRUbzBmVRo0N7eHmfO\nnMH58+dNnq1er8ebN28QHR0tUlpmzZqVo/czNTUVvXv35h4iGxsbDB06FLdu3ZIMS3h4eGDBggX8\nnTde6xo2bMgNDKVSydcVFqYtWbKk2bF89dVXIBJ3lQXeIyhHR0eLtrPS5vbt24u2M/yMPn36mL2W\nkFhTPvbuWVlZoXfv3haXyltC/5QC8ubNG772CPPeZs+eDSLzuEv/dvpXKCBPnz7lD7dDhw5YtWqV\nyAvQpEkTLuzKlSuX40LAFighEiizZIiINwvLCSqZLcgNGjRAdnY2X0BYzJ7BHCuVShN3cPny5XH1\n6lV+7e+++05SaMbExCArKwsJCQno06cPgoKCUKxYMVSvXh3Lly9HVlaWKIHLeAEVwiiHhoby6x07\ndszisINCoZDc18/PD15eXlAqlXzsLVq0EM3ztWvX+EJrybWYAjd79myTRlYajQZffvmlCMabxYvX\nrVsHItPOrnlhS3I+2IIpFJoODg4ihU7I1apVg9rDDzblG8KqRFW41eoE19Zj4dFxOrwHrn3fy0SY\ng9FvFZzq9YaVbzDUjh6QWztAbmUPlVMhHiJhbCkuiFDAf/3119DpdNizZ49ImR8zZgy/H3PnyWuo\nSqFQ4NmzZ/jmm29AZMjjKVy4sOS7Xr16dfTo0YPnXjFI83v37mHevHn4/PPPER8fj9u3b8Pf3z/X\na7u4uODixYt4/PgxOnbsyL1cLi4umDp1KrKzs/H27VuufBh7aooWLYoHDx5wYc7eQSLC6dOnzXo/\nBwwYYHbdYfTq1SvcvHlTBHj17NkzTJkyBZUqVZJ8rsJtjo6OfA6F4a6GDRsiLCyMr1nLli0zO4bf\nfvuNv8/Mc3Lz5k3umdm1a5dof5YUb2tri6SkJACGkANbY3K6lhTp9Xo8f/78o+R8GNM/pYAA4E0z\nnZycMGzYMHTq1Il/f3v27PlHxvRP079CAVm6dCmIDDkKer0eCQkJog9w3bp1eP78Odes9+7da3ZC\nWF8MIkOmfG6tq4ULuK2tLRYtWoS1a9eCyBDmOHToEIgMVvqECRNAZAD7ErZSt7KyQuPGjTlaoaen\nJ1JSUpCH4Y3GAAAgAElEQVSZmck9Dm3btsW+ffswdepULhx++OEH6PV6HDhwAD169ED79u2xaNEi\nXgWSmZmJ6OhoswmoWq2Wu61v3rwJwPDxs0xtJycnUQjCXPKtpdygQQO8ffsWv/32G89XkRrTh1yD\nyOC+Z8Tacf+jLJND6VgI9pXD4dp6LDy7foEiQzaYKhh9V6JQr6VwaT4CjrW7w65SODQ+ZSG3cQQp\nTDvw5oWFCnmhQoUQExMj6UGTUgjzmsdSrFgxk+oCYwVlyJAhyMrKEoUbzPHSpUuxdetW1KtXj48l\nJibGRDFwcnLCoUOHMG/ePHTp0gVRUVE4e/YsfvrpJ77gx8bG4unTp6JvPjU1Fbdv3xYJPNaHpFSp\nUnj48CE3KszNLQtPMGVAq9Xy8XXu3BkqlQoymQy3bt0yu/ZYQunp6fjqq6/QsmVLtGrVinuQ3Nzc\nJEN+arVapEwqlUqMHTs21yo9YfiqaNGifJ2rUqWKZPUMC82ytYwp/F5eXpJVaf8U/ZMKyJs3b0yS\n6WUyGc/X+v9I/woFhGWCjx07FsB7VyHTwFn3U1aml1OfEwBYsWKFKGRibW2N2bNn49ixY2jXrh3K\nlSsHf39/ntHt6OiIUaNGcavl7t27kMvlUCqV3AvRtGlTrmDs2bOHZ7KrVCq+KKWnp/PywC+//JL3\nbSlZsqQobspaYw8ePBjdu3c3WXSKFi2KpKQkrsS8fPkSp0+fxsSJEyVbyRMZrNvIyEjuClepVDxn\ngsgQstHr9dw9a7wAS5WPSgkuBweHPKF2Ms9VTqETtjiy63Xp0oXP1eTJk032t7Q0OT8sU1tBU7gc\n7CqFw7PLXBTqsVjkzfDuvxruHWfApdlw2FUKR1DtxlB7luQw4+bmLcdr5rA/y8OQEk7/bVar1Vi/\nfr1JtY5CoUBkZKQo+Zn1ajGX+5Kf6zds2NDizs7GxDrCMpjxc+fOSb6Dtra2uHLlCt6+fWvSb4bI\nkAx94cIFbnAwhNSPRaykNSoqCklJSejVqxfc3d35NzZ06FA8ffoUmzdvxsaNG/Hw4UOLzpuRkYHh\nw4fzb0WlUqFLly68lYIxvXz50qTJXoUKFZCYmPgxb/eD6Z9UQACDgXfy5ElMnz4dX3zxBfcY/X+l\nf4UCwurj/fz8kJKSwmHGmeXPSvZYEtzKlStznZjXr19j37592L17t9mYs06nQ0pKiklIJyUlxWxM\nu3bt2sjIyOCLb2BgoOhY1m+kQ4cOvPqkadOmAAwfubDTK+tbwXIxxo4dy5Nj2WJpZWWFXr164dGj\nRzm60I0FR/v27UVW344dO/gYhcqZra0tunXrlmeh2aJFC2zdujXHfXx9faFWqyGTyUQWWUREBFav\nXm22R4dcLkfjxo1z7DXzsVimsYF16dpwCRsGj4g5KDLyPUaG96D18Og8G451ImFTviHUhaTDMRZf\ny4I5ViqVIq8VC/cZ92Ux5xXL6/WE7O/vj+TkZF4ho9VqodPp8O7dOxw6dMhsSLBPnz6i5GapxF+1\nWo3Y2FgTD5mVlRViY2N5ySx7/uz+XF1dzXZdzomGDx8OIgP+BqNLly5xL6CzszOGDBmCx48f89/1\nej26dOkCIoPil5iYyAUeC7V+/fXXktc7ceIEIiIiEBoaih49eljcRJEZBI0aNRJtZxgiS5YsyfO9\nCyktLQ3Xr183uwYKSafT4auvvkL9+vXRuHFjfPXVV59c75R/WgEpIDH9KxSQzMxMLtBdXV1FGeAO\nDg5Yu3Yt2rdvzxfFwYMHY8SIEfjuu+8+OmDYixcvRCBKxot+586dRXFqPz8/HnMeNGiQyK3MEv/k\ncjkmTpxoUR4DK2Fk98r+ZsfKZDIsXLgQ+/fvF7Ufb9CgAdzc3MyeV6PRYMGCBXj37p1kKEYmk5mN\nv0tZjjNnzgQAfPbZZ7kKvG7dunHgMKL3yXF37941SfI0J5TzIkilWBhCUNi7w65yC7h3nMG9Gz5D\n4+AREQu3xgNhVbI6bD2Lg2S5W+5S1n1O45UKUW3ZssVsAzZ2PqmKE+OuquxvSzvEGjPzNCYmJvJt\nZ8+e5d/GkCFDQERo06YNFi9ezMM0O3fu5MaBVquV9NJptVquTAm9Of369UNmZqaJl+XgwYP8nDEx\nMXn+jlmCqVqtxty5c3Hq1Cmu5Dg7OyM9PV20/927d3H27FkOqGVlZYUNGzZgz549PEFdrVYjOTnZ\n5FrCHDPhs1m7dm2u43z27Bn/vnr27ImdO3fycarVapGC9N+krKwsUVhZ+C6xqqRPgQoUkE+L/hUK\nCGAocxKiYkoJNCkB16JFC1E76tu3b+PIkSO4ceNGviaUgQr5+/vj4MGDOHXqlEkbdyJDORZTCpo0\naWKCM2BOCLF7EFqwlStXxqBBg0wUg5iYGOzYsYMv3EQGhYfRmzdvuKuWeUdKly6NKVOmmE0OFSoT\nwvh9YGCgpGLC9jfOAahRowYA4M6dO2Y9GTKZDH379kVaWpoJVknbtm0xb948keAcNGgQNm/ejHr1\n6omuOWLEiHwKVRms/YLh1HAAnJsMQUCvuSjUe9l7BNDey+BYJxJqrwA0/8v9np9wgVSL+txY+C4H\nBQVxxfNDmtIxlkJezY21Wi3PrcjOzuZzX7RoUUyfPl3UbPDixYsAgGnTpoGIEBISgqioKJP7EyrT\njP39/Xl4hMgQdmUKj3BODhw4gCNHjoDIUBqfH2JeECErlUqRN/DevXuiKimlUimJq0NEmDt3rsk1\nkpKSIJfLIZPJMHbsWHz//fdcYdFqtRZVgMTFxZkomHK5PNcO1R+Tli1bBiLDOjJr1iysWLGCGySd\nO3f+28aRGxUoIJ8W/WsUEMDgAr1w4QLi4+Px008/4caNGxg3bhw6derE3fEODg4YO3Ysxo0bxwXm\n1KlT8fTpU5MYboMGDSx23+p0Ojx79owvPsKuicnJyVwwLV68GHv27EFmZiZOnjxpAqVNZEBszGmx\nl8vlohBP6dKluftTan/jkkiGiZKZmSlSNOzs7PD8+XNeGpaTxyU0NBSLFi1C586dTdqjWyKwihQp\ngoyMDF6qa44LFy4sOUfGLATy0el0IoUjt0obuY0jrPyqwqFGBFyaj4BL+Eh4dJ6NwtHxhq6t0fHw\nGRoH36Eb4N5uCuyrtoHS6T18trlKl5yuLVQgLbk/cyxVfaLRaDB58mTJuTX3fD4UME2hUODKlSt4\n/fq1CDfHeJ8vv/xS9F0wZcdcbpKQq1atinfv3onK4m1tbdGuXTvRfkqlEk+ePOGYN3Xq1LHoG5Za\nT7799lu0aNECwcHB6NGjhwhEKiMjgwtZKysrBAUF8e+8YsWKqFy5MpydnVGpUiWTyhFG7FuLiIgQ\nbWfeyTVr1lg01sTERAwbNgzNmzfHkCFD8Msvv+TrnvNLbD0SwpXfvn0bMpkMKpUKb968+VvHY44K\nFJBPi/5VCkhOxOrlN27cyMMuDIHQy8uL51VotVrUrFmTJ1+VK1cux54J2dnZmDFjhkmMvX79+rze\nOyMjg3sCJk6ciMqVK6NcuXKIiorChQsX+AJavHhxXLp0icfDWRmg0MpngsLY0i1RogQHKCIyWNWd\nOnWStIhVKhUaN25sEnKpXr26KFObJbh6e3ujdu3akkLCwcEhVyXCnKAzzkNwcnISxfKNOadESiFy\nKwDRXPBrK9VQObhDW6wiHEI6wu2zifAe+L49fJHRCfAZvBHeA9fBs9t/4NRwAGzK1AXJc/ZG5cRC\nb0JOwFvmWC6Xm1SrqNVqEwwVlUrFYaO3bNmCp0+fYu3atejXrx+aN2+O1q1b8/nTarUmYbH8KiDb\ntm0zG97ZsmULtmzZgpEjR2LmzJkcHl5If/zxhyTMvlSJt1wuz1HZY6zVatGzZ0/uWRIqPR+TNm7c\nCCJDkjgLrVy9epV/c7/++muuAm/s2LEgeg/Wxcg4CfZTJwY1IEw61ev1PFE/P3k4/w0qUEA+Lfp/\noYCwahLGFStWxJEjR5CRkSHa7ubmhj///BP379/Hzz//zCs7zFkvwPvabim2trbGuXPneFhGKn7v\n4uKCFStWgMig7Oj1eq54sI/XuKTR2KqWCmGUKVPGRDCYw2ro0qVLruicNjY2OSYuKhSKDy6hjY2N\nBQDJBN7du3dDp9Nhw4YNPPTj7e2N0aNHG+63UUesOn4dC45cR5NZu+HeYRo8u36Bwj3mw7PbfBTq\nvRRFjFBBvfosh2v4KNhVaQOnUsEICpZOHDbmEiVK5EnpyisbKwP29vbYsWOHpKfEzc0NcXFxXKn+\n8ccfMWLECJNn1aBBgzwrQMHBwfzdlOJ+/fohPT2dj8vW1hYymQw1atTAwYMH8/SNPn78GKdPnzZ5\n90qXLm1SAmtnZ4cJEybg7NmzkmEaIdeqVeujoWgaE0uqZe8to44dO4LI0K8nN4HHeqB4e3tzkMRr\n165x7yxDI/7UieVyDR06lL+L27dvB5EBVuBjtKD4GFSggHxa9K9XQE6fPi3Kp2ALM6uHJ3ofamjV\nqhWvLCF6b3FXqVIFQ4YMwe7du5GdnY2srCz8+OOP2L59O2QyGV80q1WrZpJQZpzL4efnhz179uDU\nqVNo0KABiEhUN9+lS5dchZuxJyI8PBzt27fPNf/A1tZWBCFvbW2NKVOmiJpwSQlDqfyJGjVqSCaX\n+vj4YO/evaJ8kNy6yDL+z3/+AwCi+5dbO8K1bE38+iAFfz5Pw63k11i+5wc41o5E8U4T0WvtDygy\ncLURYNdKeEYuhHvH6fDoNNPwb9d5cKgRAdvAJtAWqwiZxjQ0klPyp4eHB5o3b45169ZxvIhffvnF\nRHGbOnUqB3ISzmFePAxqtdqkl4mQPT09Ua9ePZHgZ8mGCxcu5Ps1btwYHTp0EL0vTKk1VlBY2bhw\nm5WVlaiySsihoaE4deoUTw4ODg6GXq+HTqdDWloa1q5di0GDBmHixIm4du2a5Lep0+kQHx+PVq1a\noU6dOoiJieHCW6PRoEGDBrxxoVqtxpEjR3Dp0iWRO5/lHhQrVoyD8jHIeJVKZXHZaX6IGRb9+vXj\n2/R6Pc9F27FjR64CLzs7m8MFqFQqVKhQgSuKDNfof4HOnDnD15+yZcuKlMZ58+b908PjVKCAfFr0\nr1dAWIIYQ7OUyWQmAjEyMpL/RmSwOM2VrJYrV84EPIl5FljpXK9evUyEMnOZ9+zZk7sjnz59yhf9\n+Ph4sx4Kc4qFcV8RY7axsREloBIRpk+fjuvXr+PChQt48+YN0tPTuVASQpnnxFqtlntlpLwixh4Z\nlUpltoeMkO3s7PBZ27ZQuRaBQ80IeHSejSKjEyRhx4uMTkDx4VsROvsomv3nO5Ru1gsKOzfIlLmX\nl1rCKpVKMlRBZFC+Xr9+DQAi4dytWzcA4HD9UngjSqVSlCtgjtlzY+58Ns8eHh6S8OCFChXC06dP\nufImBDdiyZ7smu7u7khJSeFCgr2D3bp1439Ljd3R0VGy6sjGxoZb6jdu3DB5j2QymUkoQafTiUqr\nhe8OU8wZu7i4ICEhQfL7ZuHL1atXi7YzL1pePTF5IdYAj1WpHTp0iDejdHR0RFpamkUCLzk5GW3a\ntOHfslKpRLdu3T4pAC9LKD4+XhTW1Wg0GD9+/CelRBUoIJ8W/asVEL1ez4V6cnIyJk2aZGLljRs3\nDs+fP+dWR4kSJbBt2zaRFa7RaEwEfdGiRU1K/1gbbXMdYxmr1Wps27YNmZmZot4ziYmJGDhwIGrW\nrGm2MkSKbW1t0bRpU5MqIKFwYffTunVr0RydPn0aRJRjG3gmRKSEdH5yB9RqNXr06IF6jZtB6ewD\nbbEg2JRvCJdmw0U5GT7DNqNU25HQ+laGe+Um8KrZDk5VWsG6ZDWQTI7g4GB07doVgwYNMnkW7Dp5\nHRsT0uPGjePoln5+fli9ejVWrFjB8womTJgA4H0fDCLTBmUMkrtFixaIjo7GokWL8OzZM97NmMhQ\nAWX83NgY/Pz8eAUVqyLJqcqlcuXKPOfk+vXr/BkLx0hk8PQBwJw5cyyel/Lly+PNmzdIS0vDF198\ngeDgYAQEBKBv374iDwd7z8qWLYt58+ahR48e/B0RLvwM48bOzg6LFi3Cvn37OFZGYGAgfv/9d3z9\n9ddISEgwKXkVEsPdEFrZer2eJ4ceP37corUiv8SUO+NvbufOnQDyJvAePnyICxcuSJbq/q9QRkYG\njhw5gj179nzUHi4fiwoUkE+L/mcVEDc3N4SGhmLz5s0mGnZmZiamTp0qEkrDhg1DVlYWHj58yDPP\nbW1t+TG5NSkzjp8fO3YMjx8/Fm2vUaMGFi5cmKN1K7RyGHZDQECAyT0IMTUcHBxMBL21tTXat29v\nETy6k5MTh2wWNoZ69eoVpk+fbvYehcxwVNjY8yrYiQgylRYq16KoOPhLBM84YuLV8BkaB9dWY2Ab\n1Ax+ZStixYoVZsGrPgaz52RjY8M9OqwctESJElw5PHbsGMaNG4dKlSrx5+Lj4wPAIOyMuwgrlUoE\nBgZyrwUrO2X7M+Redn1ra2uTd8bDw4OHvnJ6n4x/YwoSA9u7ceMGD0kI38FVq1bxe2G/e3h4YMiQ\nIVizZg3q1asHZ2dnlC5dGrGxsRb15WAeAScnJ5H1zua0f//+fBvLGRAmD799+5Ync1uKoMnay2u1\nWrRv3x579+7leCMeHh7/lX4ixvT999+jc+fOqF27NgYMGCDq5VQg8D4tKngenxb9zyogwgV18uTJ\nopsSYg4IBXe1atXw3XffcYuzd+/e/BimrHTq1AlhYWEi61kul+Pp06eiKozatWsDsMyKZBUK5n6P\nj48XjV+v13MXvJOTE9LS0vD69Wue1MXGaRzqkRT6f90/ywM4efIkAGDbtm1myz+NwzYfwgobJ9Tp\nGgWXsCgUHr7dUNY6fDvK945F4ca9YV26DqxKVIXavTgeP0mGXq9HVlYWsrOzTdq3W3qvxspAbsc5\nODhAoVBALpfz9uZCj5BUDotMJhNZqi1btjT77E+dOgXAkAwtDNlYWVmJ5jqvGB5SCZgsdKjRaDBk\nyJBcweuY4q3VanPtFJ0bHThwgI9r/fr13FPJ3tvw8HC+LwuzGIdWAgMDQUQ4c+aMyfn1ej3279+P\niIgINGnSBFFRUWZB/xQKBbZv3/5B9/MxqEDgfVpU8Dw+LfqfVUDu37+PJUuW8CRQtnhevHgRRAar\n9tChQ1i6dKmkBVmkSBGcP38ex48fx+3bt7nVVL58eRw6dEhU+sg6ubJeLozfvXvHm53JZDJRPoRQ\n4ejYsSNPThUqNvb29tiyZYvogTx8+NDEJa9SqdC9e3dRfFWI9iolUKR49OjRyMjIwOXLl/MFmNWl\nSxfMmzfPRNCrXIvAtmIYbAObwr5aWzjW7Qn3DtPgM2TTe+9G1Fa4hI+EbYVGUNiZIq4atwdnXVLZ\n/UyaNAkLFizg+5sbv3EljrW1tUl4xvg5Mh4xYgTvs9OkSRORslClShUcPnyYJ0kSGbxqjJ4/fy6a\neysrK+6NcHFxwdGjR7kSKFT8ZDIZFixYgIEDB/J5HT58OGJiYiCTyaBUKrF582YcOnTILOYH81yx\n41lbeiFXr14dAwYMkMzZsbGxwe7du/m9pKWlISEhAVu2bLFYKUlOTuYJo4xtbW2xfft27u0QIpKO\nHz8eRIbqHAbXvX//fj4e4/wHvV5v1hvm4eGBpk2bikrhP5Xy1QKB92lRwfP4tOh/VgFhxBY31vJ5\n5syZICIMHDiQL2jMIjJWQIT/b9CgAa9lN+bAwECTJEqZTIaNGzdyCywyMhLAe8EpdHu7ubnxZDkh\n5oExdgUAE0TUvDKDbxeyXC5HvXr1uDdAKKQrV64smXxqzjuiUqkgl8sht7KHbcUwePVZbpogOvIb\neEYuhEvYMNhVbgGNd2mQTJ5jiMe4QzHDA2E5ELGxsbh37x7f3xh3JS9sZ2dn4hnx9vbmIHIymQzf\nf/89Nm3axH/39/c3Sf709PTk42V5FsHBwXjw4AG6desmSuRkSlCfPn2QkZHB31NzzKqx2rRpIwp/\nCdnBwcEkvKJWq3HmzBlcvHiRKyK1a9fmzQxTUlJ46XKlSpWwcuVKvHjxgt/Hli1bRMqzXC7HgAED\ncsTCAcAVYqbgGD9rrVYr6gR7//597mVycnISlZobY2IA7zF7tFotZsyYgXXr1vH9S5QowUOYrBFl\n27Ztcxzv30UFAu/TooLn8WnR/7wC0rVrVxARFi1aBOB9SKRnz55cmIeEhEgu4HK5HCEhIdxyrVCh\nAiZOnIiKFSvCy8vLxMoWNrkScqlSpXi/g4yMDJGFbbwQC5vECRd+AJgxY8YHKR9CFl7XHBqnQqEw\nqTjgLFdAYesMtYcfbMo1gENoJ3hExKLIyG9EyoZnt/mwrRgGpZMXlE5ehvJWiR4oOYUX5HI5qlSp\nInKZMyAmVilRqFAhnDt3TvRM1Gq1yfg9PDwkPRxVq1bFkiVLRJ6tGjVqYPjw4aI8Gk9PT2zduhWA\nob+F8Xnc3NywaNEirsgwYrk00dHROUKZC8tChc345HI5GjZsiGHDhomUPyaY7ezs0KtXL7NJv0zZ\nad68OV9gd+3axY9lPVn0ej1vVDZr1izR+yec38qVK6NZs2ZcURs/fry5NYR7AW1sbHDt2jUT75yV\nlRUOHDhgctylS5d4CSq7h/Hjx0tiRjBQvKlTp/Jjhe85y7M5efIkf96fAhUIvE+LCp7Hp0X/swqI\nXq/HgQMHuELA2m6zvhDMUpdSFoT/r1KlCiIiIrg1tm/fPp6waY6tra1Rp04dNG3aFPPnzzdxFx89\nejRHgSuTybB//37RMT/++KPJPh9DERGGBUqWLIlZs2ZJKiQa7wDYV/0Mbq3HwWfIRhPQrqKf70Wh\nnkvgVL8PHGpGwCmkPVr0GGpRV1VjDg8PN3t/ixcvBgAkJCSAyBC+MAZiY+zu7m62GR07P8PTiIiI\nQPny5eHo6Ijg4GARxHVaWhqOHz+O06dP4/z585g9ezbmzp2La9eucYTcDh064Pvvv0dqair3zgjh\n35kyIVRmunTpYoI2y5Qb4P/aO/O4qMr9j38eZlgGZFFUBAQBRb2SqamJS+6glmaACy6opKWphCua\n3jSzLNzqquntpt5cgDQR8bqhqZWpuCDX5ZdZCIaC4IKhyBVk5vv7Y+Y8zmEGUCE52PN+vZ4XnGXO\nec75zjnPd77PdyFKS0vj6zdv3szXl06cB4D+/e9/0/bt28tN9mZvb08eHh7Uvn17Cg0NNfn+N2/e\nnCvlGo2GsrKyZN9ByXdq8uTJJn1xdHQsM6GXZGns2bMnX5eamsqT9Bnfp9LodDr65ZdfKDk5me7e\nvVvmfpI1R7p/eXl5simpAwcOEBHxOipSSHR1IwY8ZSHkoSxqrAJi/CIODw8nIr31ISsryyQqQWoB\nAQHc16OsZvzZ+vXr09KlS2Vz2x4eHiaF6pKTk2n27Nk0btw46tGjB9nZ2ZGlpSV5enqa+GTY2tpS\nUFAQubm5kaWlJdnZ2VHTpk1NCli9/vrrFBcXV2kFRDpurVq1KD8/n+4XPaQPv9pGtXu9TXX6TKIG\nYcvJI/KbR0m83vqS6g6YQc49wsnBfzA17DiAhr09hZha72tQWnF47733aM2aNbRw4ULavHkz7d27\nlxITE+n333+npKQkmROko6Mjvf/++7JBurQyZG9vT3fv3qWSkhJZkS9zykVFbezYseU61H7yySdc\nhsXFxWbzUgQFBfGB3NnZmffd0tKSjh8/zj//4MEDWX4YT09PruwaKyENGjSgvXv30s6dO2XOrfPm\nzeOWPa1WW66PztChQ7k/SUhIiNnwa+PvfOmQbgcHBxMFmOhR5JWTkxPZ2dnRq6++SsePH+f9/PXX\nX82+RKTEaw4ODrLQS8mKFRERYfZzT4IU7tqtWzcelmvs+Dt48GAeAs0YoxMnTlT6nFWBGPCUhZCH\nsqixCgigN7cvXLiQ8vPzKTIykpuhHRwcKDAw0KR2yPr16836DkyYMIGbmo0tJD/99BMR6SteSgXd\nGGN08eJFHtIrJR56nKbRaCoM9zUeZGfOnPlU9UMAkNpaQ9YeL1CD3m9S7V5vkfe4FfRK9CFqNneP\nPhJlWjx5zkykBmFLqU7ABKrVqi+pHV344C79Las8utQvtVpttsaHTqejEydO0I4dO2TF8Ixb7969\nSafTcUVLOufu3buJSB+W+cEHH5CnpydZWVlR27ZtaePGjXTr1i0aPnw471fdunUpMjKS96l58+Y0\nbdo0WTZGOzs7iouLo+zsbFq+fDlXInJzc4noke+Ara0tjR8/nkaPHs2PP3nyZFlYdMuWLfkvbmOM\n83sYKyJSafeKmq+vL+Xk5HDrj7u7O/c7UavV1LRpU1q2bBnFxsYSoFeG79y5w5W4d955h4YMGSJT\n6k6ePEnFxcXc50Sj0ZjNM1HaiZZ/j9RqsrDQ+++UnjI0Rkr05+3tTXPnzqWBAwcSoJ9aqorCaDk5\nOfx5rlu3rtkK05L8nmUV2IoQA56yEPJQFjVWAfnjjz+ouLiYdDpdmT4eT5uvQmqZmZmUlJRktnCX\nsYNhVU2XVKap7GqTY5fh5BG2mJrMjJdlDPWYsoXcxq2hFmMXU53e40nTuD0xSxsTXw3GmMysXV6Z\n+OjoaP7/9OnTZV+qU6dOyRw2GWPUokULk1Bk40iFV155ha8v7ZBqzJUrVygyMpJatWpF7dq1ozlz\n5tCdO3eIiGjjxo0mMpdkM3ToUNlxpKRXGzZsIJ1Ox/1GkpKS+D7r168nQO+sqdPpKD09na5cuVJu\nZkfj3B1Tp06lmzdv8ky7gN7CJlmFateuLdsG6JOPSTKIjo7mtUIAfV2TPn368Gv67LPP+NTPiy++\naDZ7aceOHXnfpGlGc+nJpdwkgN6RdNKkSbKaPIMHDy7zmomIMjMzTVL2W1paPnY118chNTWVh+kC\neh+gyZMn06lTp2j16tW0adMm/l1QCmLAUxZCHsqixiogkqOfsZVD+qVm/BL08fF5qpBT6djSoGmc\nQAdjwCkAACAASURBVMz4fJVRGtRqtdn8IKX9BoybsYVGZV+PNL4dqV7QXPKM2kmeUTvJdcznVKdv\nBDl2CiWNrz/VcSlbiZCauVovISEh9OOPP5r4sjDGaOnSpfTBBx/wdcblzq9fv86vyc3Njbp3787v\n2ejRo2UDro2NDdnb25O7uzv/1a7RaMpMQX3hwgWzGVvbtWvHU6Onp6ebLWYHyNN1SzVM1q1bR/fv\n3+fyMFYucnJyCNBPSTwu5U2bST4S0lTNsWPHSKfT0ezZs02U2Lfeeos7Y65atUomB7VaTVFRUaTT\n6ejLL7/kSkNZ501ISKCUlBQC9FNxDx48MOm3FHUjOaiWbikpKRVee3FxMcXHx9OcOXNo+fLlJj4m\nVYFOp6Nz587R999/r8hMm6URA56yEPJQFjVWASnrZevn5yeLIliyZAkP4auqJikeT+OAadx27dr1\nWMnE9I2RdUM/cnplJNUf/IEsx4ZH5Dfk1HUUqWu7mXyuUaNGtGjRIrPHLGs66IsvvqCUlBSzUy+A\nPp27sSIWFBTEv1BSNMhLL73EC6SlpqaSWq0mlUolC58014xrmEjk5OTQ9u3b+SDZu3dv+vHHHykh\nIYGHEEsRHVIeGAsLC2rUqJFJRMzcuXPp22+/5VMLkkVDCpM1rh2ybt06fi1PwuLFi2X3jjFGAwcO\n5KGw0vdTipwiIrp48SLf3ziTpsQff/xB3377LcXGxlJ2djYVFRXRjBkzTHxomjRpQsOGDZOtc3Bw\n4IpbWf4Ykp/Td999R0eOHKGIiAgaM2YMV3x+//33J7oHAj1iwFMWQh7KosYqIOaiTMzlrli5cqXJ\nAPw4hdFKWzeMf6FW1ZRLaGio+XwWzIJqufuSlWtTqv9SINXpM4nc3/k3n1JxDV9Jzv0iqVab18jK\nrRkxtfmaJ9Lga5xRVApnfPnll7kyoNFo+EDm7+9POp2OD+xqtZrGjBlj1hdFWpeQkEBE+ggkY4uO\nRqOhadOmUXFxMXcQnDJlSrl+MB9//DH/cpaUlNDUqVNNplWMLRm7du0iANS6dWsiojKn48w140Ri\nkpOjra0tvfXWW7LCbE8zjXDnzh1KSEig7du3m0wLSM61kZGRVFJSQjqdjubPn0+A3przOISFhfHr\nMJ42K89nKCAgQFZJ1hipMnT79u0pLS2N7t69S++++y4BeqVeSQXFahJiwFMWQh7KosYqIA8ePDBJ\nM/3GG29QSEiIbF1mZqasRLmlpSVptVqzxcvK+sUvtYrSWj9NY1YasqznTQ7+g6lO3whyG7qAGk7a\nJAt/9ZiyleoFzSW7Ft31vhtlHMvZ2Zmb9z/44AOzSc38/f3JysqKGGNcGQkLC+NKyowZM2T+AMuW\nLSMiohMnTpj1qfH09KTCwkK6efOm7P4Y/z9+/Hiz4aNeXl7k4eFBAwYM4Epihw4d+JdTsqZYWFjI\nroUxxiNQJIuHr6+vzAlU8hWQlJ3SSuOcOXO4RYJIP30gFTYzbqNGjaIpU6ZQUFAQzZo1i9LS0ir9\n0B0+fJgruO7u7rJQ4h07dlT4+UuXLhGgt8D99NNPlJycLOuzSqWi0NBQWWTVjh07ylUicnNzzaac\nt7CwKNcnR1A+YsBTFkIeyqLGKiAlJSUVWiKsrKzon//8p0nWybZt21bovyFZAKRzWFlZybKYPs4v\nTlNlw5Zqte5HTt1GU4OwZdQwIkamaLhP2kiuY1ZQ3dejyK5lb/LuGkyRH60g57qPp/j4+vrSxo0b\nK1SmSltdpDBNOzs7k2mlZs2a0e3bt00qqhq3t99+mxf4k3J2qNVqGjFihInlyDi0ljHGXwZJSUkE\nPLIAFBUVcf+eXbt2kVarpcaNG/PPDho0iAoKCni0xbhx42j27Nl8u2QNGzRokCzsV6pQW5ZV48yZ\nM/Tpp5/SkiVLKDo62uR7YmVl9VhKQkUkJCTIMu+6u7vTpk2bHuuzX331FQH63CREer8I4+Rn9evX\nlynYbdq0eazjXr16lUaNGkUajYYYY9S1a1c6ePDgU1+jQAx4SkPIQ1nUWAVk/fr1lfbBeJxW2Uga\nlUM9cuo2hhqM+ow8Zybqp1GidpLLiGiqEziRHDqEkG3zLqR2ejRgSL/aK7q+1q1bc0VD6uf48eOp\nR48eT9zPpk2bcmWhd+/eMsWhR48eMkWLMSabRrG0tOTZL2NiYrg5v3T7+uuvSavVynJzDBs2jDIy\nMnhYpZRxMyMjgwB93oyioiLas2cPvf3224/uq0rFp41q1apFv/zyC8/hUl70jjQtVXqw12q1tH//\nfpoxYwbNmjWLdu7cyac2wsPDKS4ujoYMGcKVm7IcZZ8ErVZLZ8+epdTU1ApTnRsTExNDgNz5NyUl\nxaxSrVKpaP/+/U/UL51OZzYbqeDJEQOeshDyUBY1VgEp/aJ1d3eX1fgYOnSo2UqZzs7O5OLiYpKc\nqawmOe9JURMVNpUlWXu8QPbt36B6IfO434bv+C+o15TPyNqtmdlU5WW1zp0705o1a8pOmW5oHTp0\nKNcaY25w+uSTT+iHH36g8+fP09ixYwkATZo0iYiI3nnnnTKPFRUVRf/3f/8nO59k2ZCcSI8cOUJv\nvvkmH8Td3Nz4ly4+Pt6s9crDw4Pn5cjPzye1Wk2MsXJTm3fs2JFOnjxJRCSLzDHXjJU14wiKwsJC\nHpZbukmFCIn0A7M0FbRhw4anfeYqzZ07d7gPVFRUFJ05c4Y+//xzfn3Sve3cubOwYFQzYsBTFkIe\nyuK5UUCMm0ajofHjxxOgn25YuHAhLVy4kJv058+fTzdv3nxsJcC4mcu1AIBsvFpTncBJsmkV93fW\nk2OXEaR2cqXx48eXm7GyrLZmzRoiIlkkz8iRIykqKoomTZrEfV7eeustSk5OpsGDB5tUTbW2tqZb\nt26ZWFTCwsJIp9PR7t27uWVg1KhRlJubSw8fPuR1dkorOpIvgbGCJ4WDajQaio6Opj179siqslpa\nWtK1a9f4Fy88PFzWv+HDh5tEWkjTK4B+WsE4JXvjxo15mOfdu3dpzpw5jx0W3bBhQ9l5oqKiCNAr\nm3PmzKFp06ZxRbZv376yfSXFbOnSpY/7jP0prF271uy1DRs2jI4fP15m2nTBs0UMeMpCyENZKE4B\nAdAXwCUAaQBmG28z7mzpX9AqlYrs7e1NfgUOHTqUpk6dSkOGDOG1Ljw8PIiIuKOktbX1U+X0sKzn\nRc6vTiHXMSu4s2jdgbNI0+Rlcm/cvEqiZTw9PamkpIQePHjA/RoaN25MycnJtHr1av5L+LvvvuNC\nLZ0l0tHRkV878Gi6pnPnzjJFQGp16tShgIAAsxYVS0tLmjVrFq1evZrfMz8/P9JqtVzpK62wSVky\nfXx8KDo6miIiIricvv322zLN/e+//775+2747NmzZ+nAgQMyHw9JCSq97Orqyuu6GFtjtFott3Id\nPXqUr5fqAVlZWfEMoNevX+eK2qFDh57wUat6fvjhBwoJCaEWLVpQYGAgbd26lU6ePClesApCDHjK\nQshDWShKAQGgAnAZgA8AKwBnAbSQtht31vjXubOzM92+fZtyc3PJx8enwkHdwsKCiOS1JCpqKpWK\n1E6upGnakeoF/53c3vrSkNJ8G9Uf+hHV6zKUoKqcv4jxuYyXMzMzqbi42OyUEqD3UZCsEhkZGWUm\n4pJaacVIrVabVUQep6nVarpw4QIR6acodu7cSSEhIdStWzeaPn06paen0/Xr180WlJs2bRp98cUX\n1L59e2rUqBENHDiQfvzxR/7llJQmNzc38vDwoJ49e9K+ffv4dNiaNWtkeTBUKhWPKDH23WncuDER\nPcr2GRgYyM9RUFDAlRrjqJjMzEz+eScnJwoICODWr5dfflmxYaniBasshDyUhZCHsqhIAWGkVwye\nCYyxjgA+IKI+huX3AICIPgGA/Px83pkePXogNTUVANCmTRv861//wqJFi5CQkGD22CqVCt7e3khL\nSwNjDAcOHEBaWhomTJhQbp8avdAef9j7wLZpR1g1aAIA0D0oQHH2Lyi8fBqFvx6DtiBP9hm1Wg1X\nV1f4+flh3759ZfZHq9XK1kVERGDVqlUofc+7dOmC9PR0ZGdnw87ODp06dcKVK1dQp04d9O/fH4GB\ngbCwsMB///tfREZGorCwsMzrYYyZHB8AmjRpgoEDB2L58uWy7X/7298QEBCAFStWmHzGwcEBK1eu\nRIsWLco8n0RxcTEOHz6M1NRU2NraolevXti4cSMOHTpk0r958+ahpKQES5YsQXFxsWx7p06dcPny\nZeTm5iIoKAgJCQlo164dTp8+DSsrKyQmJiIsLAy3bt3in7G2tkazZs1w7tw5AMCKFSvQsWNHAHoF\nu3///rhx4waio6PRs2dPAEBcXByWL18OW1tb2f3s0KEDFixYAGdn5wqvWSAQCARl4+vry/93dHRk\npbc/awVkEIC+RDTOsBwGoAMRTQbkCoiTk5PssyEhIdi7d2+5g68xrq6ucHJywqVLl6DT6WTbLJ09\noGncHjbebaHxagUAKMq+BHX2Wdz85RQe3sqEruh+mcf29fVFVFQUbG1tMWvWLFy7dk22vVmzZrh7\n9y6uX78uW29OKTHGzc0NixYtgp+fn8k2nU6H4OBgZGVloUuXLujYsSNiYmKQnZ1t9lj9+/dHVlYW\nUlNTUbduXdy6dQuzZ89GUlISV+ymTZuGoUOHwsLCAkOGDEFGRgb69u0LGxsb+Pn5oU+fPtBoNPyY\nv/32G86fPw9bW1t06dIFtWrVKvNajh49iilTpqBWrVqYPXs2mjVrhoSEBMTGxppVknx9fXH16lU8\nePAAAODp6YmXXnoJO3bswMyZM7Fv3z6cP38er732Gu7fv4/vv/8etWrVQkFBAT+GRqPBlClTEBwc\nLDv2pk2bsGLFCqhUKnTt2hXFxcU4evQoAODjjz+Gj48Prl+/Dg8PD3h5eZV5TQKBQCB4fCpSQJ71\nFMxgAGuNlsMArJSWzTmhluVnIZngS09nmEuIBYCYpTVpmrxMdfpMIs8ZO3jFWKdXwkjlUM8k5TWg\nz39x8+ZNOnv2LO3bt49P75TVF6lt2LCh3HovUnNycqJdu3ZRbGwsHTx4sNzQyKNHjxKg9xkxDumU\nfBm8vLx4VdoWLVoQEdH06dMJeJS0a+DAgeTv70+A3vdBCjUtKSnhoa1nzpzhx5bMmQUFBfTGG2/I\n+l6rVi2KiYkps79SCvqPPvqIr7t+/brs/llYWJjNmmppaUmpqak0YcIEAvS1bLZs2WI2bNnFxYVW\nr15N8fHxZYbOarVaioiIkH2XLC0tZVlZawrCxKwshDyUhZCHslCaD0hHAElGy+8BeE9aNu5sy5Yt\n6dixY7Rp0yazg77kC1BW1AqztCa1c0N9bZUhH5Ln9Hju01Gnz2SysHMy+7nSCoIUbaDT6fgA+O67\n71KTJk3I09OT3nzzTTpx4kSFWVaNm7W1NYWGhspqhVTE7t27CdCnXTdGSkwWHBxMR44cIUCfXEyn\n01FGRobs/hinUbezs6Pt27fThQsXuH+Ij4+PzE9CepjHjRvH7/XIkSOpS5cuXIE4ffq02f5KWUdX\nrVrF15VOmV+/fn3Kysriyl/v3r25T4c5/51WrVrxfS0sLGj06NFPVMMkIyODvvrqK1q/fv0T3Xsl\nIV6wykLIQ1kIeSgLpSkgagDpALzxyAnVT9pu3FnjgfD48eOPPbhbaByoTsAEWVIwt3FrqHbvCeTU\nrAPZ2JlXWKQWGBgos14MHz6ciPSZLQF9PhJzDor79u2rMKmZnZ0dzZ8//6kcHLOzs0mlUpFKpaLk\n5GQiIrp37x6vjRIdHU1FRUU88mfWrFmUnZ1N//jHP2T9srKyMpuS29LSUlaojUj/MB88eJCndj93\n7hzfJoWrhoeHm+2vVOq+SZMmlJaWRjqdjisuKpWK93PTpk1c2XjllVe4xQPQZ3B99dVXTe6rt7c3\nXbp06Ynv4fOAeMEqCyEPZSHkoSwUpYCQXgl5FcCv0EfDzDXeZtzZ//znP/wivv76az74lJmMy0JF\ntV4MII/Ib8hzZiLV7fcu9Rn/dwoaZRo66ufnR0uWLKHvv/+ePv30U75eSt8dHx8vO19QUBAfBKOj\no8u82VlZWfT666/LBkzGGA0ePJi+++47unv3Lt/38uXLtGTJEvrwww/phx9+eCylRMoUyhijtm3b\n8vBUFxcXnngrJibG7LRV69atae/evXTz5k3asmULvfjii2Rvb0+Ojo70+uuvm7VknDp1iltY/Pz8\nZNsOHz5MgD5RmDkKCwt5ZAxjTGZ9admyJX322Wd8ubSCJFk5Tpw4QUREeXl5PB/KCy+8QEVFRRXe\nq+cV8YJVFkIeykLIQ1koTgEprxl31sbGhsLDw2nkyJEypWP37t2y4l4qe2dyfnUK+c5KoEazdpHL\nsE/I0tmDNmzYQA8fPqTIyEi+r6OjI2VlZckGe+mXOgDKycmhzMxMmj9/vmzAlAbRyZMnyywzZZGf\nn0/btm2jmJgYunr1qsn2Dz/80ERJCAgIoHv37pV73KKiIpo0aZIsEVn79u15mKzE/v37qVevXuTo\n6Eje3t40f/58KigoIK1WS6NHjzZRTmrXrk0pKSkm5zt16hTt3buXGGNkZWXFE4MRPcpKOnjw4DL7\ne+PGDQoLC+P9rVevnix/S79+/WTTaz4+PhQbG8v3NUYqZ+/t7V3uPXreES9YZSHkoSyEPJRFjVVA\nyprG8PT01E+12DqRXYvu1HDyZvKYto3e/PIw9R8/hwDGlQ0pM6pxK21puHnzJh8U27VrZ9bRMTw8\nnDIyMqpEIImJifr+W1jQ8OHDKTIykifKmjBhwmMd49atW/Tjjz/SxYsXn+jc27dv51NBS5cupR07\ndvAU8G3atDG5N9LDLE2ReHl50cKFC2ns2LFccThw4ECF571//z5lZ2dTSUkJrV271sSK5ezsTN98\n8w1ptVp68OAB91uRLCBERMuWLSMA1KtXrye65ucN8YJVFkIeykLIQ1nUWAVk27ZttGjRIurRowc5\nOjrywUrj25EavbOWp0N3HbuaLJ1NfRqkZvwL28vLy+xNCgsLK/Pzkn+EOUvG09CvXz8CQJMnT6Yj\nR47QvXv3eJl5jUZDBQUFVXIecwQHBxMAWrZsGV9XWFjIFaCff/5Ztr/0MOfk5PAIG+O2YMGCp+pH\neno6LViwgCZOnEhffvmlbGqK6FFkj6OjI02cOJFCQ0O5HOPj45/qnM8L4gWrLIQ8lIWQh7KoSAFR\nQ6GMHj0GLm16ICsjFyVaNawb+qF293BYuzeH9v4dWKRuR875n1CcexnQaXluih9++AFFRUX8ODqd\nDhYWFtDpdHjnnXfMnmvDhg1IS0vD8ePHZetHjBiBgoICJCYmIjY2FlFRUZW+rgsXLgAAVq1ahVWr\nVsHe3h5z5syBu7s7srKykJubCx8fn0qfxxx//PEHAHlstkajgYeHB/Ly8nDnzh2zn3NxcUFKSgp2\n7NiBY8eOwcHBAUOHDn2sBGXm8Pb2xrx588rcvmjRIly+fBn/+c9/sHr1agD6BGbz5883yfEhEAgE\ngpqJYhUQ5wmboFVbokHnR+tKCvJwe/9qFF48At2De7CxsQF0+sRe06ZNw8KFC3Hjxg34+Pjg/v1H\nicR0Oh1GjRqFadOmmT0XYwzDhg3D8ePH0aFDBwQHByMwMBCtW7fGRx99hMTERNy4caPS13T27Fme\ntMzBwQFeXl44d+4c3nvvPQCAra0tGjRoUOnz/O9//0NSUhLu3r0Lf39/NG3aFIA+y+ehQ4ewcuVK\nBAQEwMbGBgcOHMDZs2dha2trNgGa8TH9/f0RHBwMlUpV6T6Wh0ajQWJiIk6cOIFDhw7BxsYGQUFB\n8Pb2/lPPKxAIBIJnh2IVkOJbv6MgdTdaveAH37/54dst36Dw0lHQwwd8HylrJqBPKQ4A9evXx4QJ\nE7Bs2TJ06tQJKpUKlpaWqFevHi5fvoxmzZqZPV/r1q0BAOnp6Rg9ejRcXFxQUFCAuLg42fbKYJwG\n/d69e2jSpAnq1q3L05WPGTMGtra2lTpHQkICxo0bh7y8R+njQ0NDsX79ekycOBFr1qzBgQMH4OHh\nAQ8PD54VdfLkyXB0dDQ5Xm5uLkJCQpCYmAitVgtXV1dERUUhMjISjJkmtqsMd+7cwcmTJ2FjY4NO\nnTrB398f/v7+VXoOgUAgECgEc/My1dXMOaG6uLjw7KbGzosvvviizEfj/v37fN4pICDAbMiuSqWi\nmJgYunDhAk2ePJkCAwPp7bffplOnTpFOp+NZQu3t7em1117j+UC8vLyosLCw0vNhzZs3JwAUERFh\nNpy4tA/Gk3Lu3Dke0vrSSy9RcHAwv3eSg+vp06dl987W1pZmzZplNgvr4cOHeYZUlUolc+pduHBh\npfpqjE6no/fff1+WFdXV1ZV27NhRZed4XhBz3MpCyENZCHkoixrrhFp6cJYUDXPrAdCIESMoJiaG\nZ+CUWmhoKMXGxtKoUaMI0OecMDf4r169mnJycnhUiNTatGlDv/76a5UIQ0oaFhsbS1evXqUVK1bQ\n3//+d96f27dvV+r4Up6QMWPG8IiWM2fOEGOMrK2tedl5nU5H58+fpyNHjkhfDLNMnTqVK3vXrl0j\nnU5HmzdvJkCfFbWs1OdPyuLFi/n97tixI/n6+nJZnTx5skrO8bwgXrDKQshDWQh5KIvnSgGRWteu\nXWngwIHcQlI6U6YUMdGtWzdZaKmxchEeHk47d+6kiIgIPthlZmYSEdGFCxcoPj6eTp48WaVl2b/4\n4gsedrpy5UrasmULtW3blgBQ//79K338zp07EwA6ePCgbL0UwfKkg3nXrl0JAG3cuFG2Xupz6fM8\nDQ8fPiQXFxcCQFu3biUivYIkKVOhoaGVPsfzhHjBKgshD2Uh5KEsamwUTFmoVCq0bt0a69atAwDM\nnDkTAwYMwNq1a5Geng4fHx/odDosW7YMrVq1kvkpWFtbAwAaNWqE9evXAwAGDBiA7OxsxMfHY8uW\nLZgxYwb8/PzKdch8WsaNG4fdu3djz549iIiI4Os9PDywYsWKSh/f1dUVAHDs2DFedv7GjRv47bff\nZNsfFysrKwDA7du3+TqdTsf9S2xsbCrd5+zsbOTm5qJevXoYNGgQAL1T8MSJE/Gvf/0LKSkplT6H\nQCAQCJSHRXV3oDwWLlzIIx8k50ytVosVK1bg/v37GD58OCIjI9G0aVMsXrwY27Ztw+LFixEYGAgA\n2LZtG27evAkAyMvL42G2pR1Rmzdvzvf5M7GysuIhvUFBQejbty8+/fRT/Pe//62SCI+xY8cCABYs\nWICIiAgsX74cXbt2xYMHD9CnTx80bNjwiY7Xq1cvAHo5xMXF4fz58xg/fjwyMjLg4eGBl19+udJ9\ndnJygkqlQl5eHrKysvj68+fPAwDq1q1b6XMIBAKBQIGYM4tUVys9BePi4kLz5s2jnJwcXvzMx8eH\n5s6dS8nJyWVOj2i1WmrTpg0B+oJmgYGBvG4KAKpbty6vopqbm8tTuyckJFSB0al6mTNnjsmUVdOm\nTZ8qkVpycjIvIGfc1Gq1rFZPZZHqvPj5+dG6deto8eLFXF7//Oc/q+w8zwPCxKwshDyUhZCHsqho\nCoYR0bPXesogPz+fd8bJyYmvV6lU0Gq1UKlUOHz4MF555ZUKj3X9+nWMHDmSh7gCQOfOnfHw4UOc\nPHkS1tbWaNu2Lc6ePYv79++jZcuWOHPmDNTqGjcrZUJqairi4uKQn5+PTp06YciQIdBoNE98nNOn\nT6OkpAQpKSnYuHEj8vLy0K5dO0yfPh3t2rWrsv5mZWWhe/fuSEtLk60PDg7Gli1bnguZVBWnT58G\ngCq9/4KnR8hDWQh5KIv8/Hz+v6Ojo0neBsUqIMuXL8eXX36J3NxcAHqFZPPmzXjttdee6Jg///wz\nLl++DC8vL7Rs2RJ5eXkYO3YsEhMTIV17QEAAvv76a7i5uVXh1dR8nuXDfO/ePWzYsAHff/89NBoN\nBg0ahAEDBsDCQtGzhM8c8YJVFkIeykLIQ1nUWAXE0dERDx8+xPvvv4/o6GjY2tpi165d6N69e5Uk\nwMrMzMTly5fRqFGjPy31eU1HPMzKQ8hEWQh5KAshD2VRkQKiWNv2//73PwQFBSEpKQkAUFhYiJ49\neyIkJARxcXGwtLSs1PE9PT3h6elZFV0VCAQCgUDwhCjWvr1gwQIkJSXx0FlfX184ODggPj4en3/+\neTX3TiAQCAQCQWVQrAKyePFiAEBRURGsrKwQExODTZs2AQC++uqr6uyaQCAQCASCSqJYBUTyTWnT\npg3279+P9u3bo0uXLgAgyxchEAgEAoGg5qFYBURKzDV16lR069YNABAbGwsAaNGiRbX1SyAQCAQC\nQeVRrBOqZAEZM2YMtm7diocPH3KH1KlTp1Zn1wQCgUAgEFQSxSogV65cgUqlAgDs2rULgD6V+bx5\n8zB8+PDq7JpAIBAIBIJKolgFZPjw4YiNjUW/fv0QGhoKCwsLBAYGon79+tXdNYFAIBAIBJVEsQrI\nxx9/jNjYWJw4cQJ79uyp7u4IBAKBQCCoQhTrhHrr1i0AVVPyXSAQCAQCgbJQrAIyYsQIAIC1tTVm\nzJiB3377rZp7JBAIBAKBoKpQrALy66+/AgAyMjKwbNky+Pn5Yfv27dXcK4FAIBAIBFWBYhUQABg5\nciS2bt2KYcOG4eHDhxg9erSsuI1AIBAIBIKaiWKr4QoEAoFAIHg+MFcNV9EWEIFAIBAIBM8nQgER\nCAQCgUDwzFHUFIxAIBAIBIK/BsICIhAIBAKB4JkjFBCBQCAQCATPHMUoIIyxvoyxS4yxNMbY7Oru\nz18FxpgHY+wwY+wiY+z/GGORhvV1GGMHGGO/Gf7WNqxnjLEVBjmdY4y9VL1X8HzCGFMxxlIZY7sM\ny96MsRMGeWxhjFkZ1lsbltMM272qs9/PI4wxJ8bYNsbYL4bnpKN4PqoPxthUw7vqAmMsjjFmEozp\n0AAAA4RJREFUI56PmokiFBDGmArAFwD6AWgBYBhjrEX19uovQwmA6UT0NwD+ACYZ7v1sAAeJyBfA\nQcMyoJeRr6G9DWDNs+/yX4JIABeNlqMBfGaQxx0AYw3rxwK4Q0RNAHxm2E9QtfwDwD4iag6gFfRy\nEc9HNcAYcwfwLoB2RPQCABWAUIjno0aiCAUEwMsA0ogonYiKAXwDYGA19+kvARFdJ6Izhv/vQf9y\ndYf+/m8w7LYBwBuG/wcC2Eh6kgE4McZcn3G3n2sYYw0BvAZgrWGZAegJYJthl9LykOS0DUAvw/6C\nKoAx5gCgK4B1AEBExUT0B8TzUZ2oAWgYY2oAtgCuQzwfNRKlKCDuAK4aLV8zrBM8QwzmyTYATgBw\nIaLrgF5JAVDfsJuQ1Z/P5wCiAOgMy84A/iCiEsOy8T3n8jBszzfsL6gafADcBPBvw5TYWsaYHcTz\nUS0QURaApQAyoVc88gGkQDwfNRKlKCDmNFIRH/wMYYzVAhAPYAoR3S1vVzPrhKyqCMZYfwA3iCjF\neLWZXekxtgkqjxrASwDWEFEbAPfxaLrFHEIefyIGX5uBALwBuAGwg37aqzTi+agBKEUBuQbAw2i5\nIYDsaurLXw7GmCX0ykcMEUkV/3Il07Hh7w3DeiGrP5fOAF5njF2BfiqyJ/QWESeDyRmQ33MuD8N2\nRwB5z7LDzznXAFwjohOG5W3QKyTi+ageegPIIKKbRPQQwHYAnSCejxqJUhSQUwB8DZ7MVtA7Fe2s\n5j79JTDMh64DcJGIlhtt2glgtOH/0QASjdaPMnj7+wPIl0zRgspDRO8RUUMi8oL+OThERCMAHAYw\nyLBbaXlIchpk2F/8wqsiiCgHwFXGWDPDql4AfoZ4PqqLTAD+jDFbw7tLkod4PmogismEyhh7Ffpf\neioA64no42ru0l8CxlgXAEcAnMcjn4M50PuBbAXgCf1DP5iI8gwP/SoAfQEUAggnotPPvON/ARhj\n3QHMIKL+jDEf6C0idQCkAhhJREWMMRsAm6D33ckDEEpE6dXV5+cRxlhr6B2CrQCkAwiH/sebeD6q\nAcbYAgBDoY/gSwUwDnpfD/F81DAUo4AIBAKBQCD466CUKRiBQCAQCAR/IYQCIhAIBAKB4JkjFBCB\nQCAQCATPHKGACAQCgUAgeOYIBUQgEAgEAsEzRyggAoFAIBAInjlCAREIBAKBQPDM+X/V0mbNoYFl\nwgAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"sensor_var = 30000\n",
"process_var = 2\n",
"process_model = (1, process_var)\n",
"N = 1000\n",
"dog = DogSimulation(0, 1, sensor_var, process_var)\n",
"zs = [dog.move_and_sense() for _ in range(N)]\n",
"\n",
"pos = (zs[0], 500)\n",
"ps = []\n",
"for z in zs:\n",
" prior = predict(pos, process_model) \n",
" pos = update(prior, (z, sensor_var))\n",
" ps.append(pos[0])\n",
"\n",
"book_plots.plot_measurements(zs, lw=1)\n",
"book_plots.plot_filter(ps)\n",
"plt.legend(loc='best');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This simple change significantly improves the results. On some runs it takes 200 iterations or so to settle to a good solution, but other runs it converges very rapidly. This all depends on the amount of noise in the first measurement. A large amount of noise causes the initial estimate to be far from the dog's position.\n",
"\n",
"200 iterations may seem like a lot, but the amount of noise we are injecting is truly huge. In the real world we use sensors like thermometers, laser range finders, GPS satellites, computer vision, and so on. None have the enormous errors in these examples. A reasonable variance for a cheap thermometer might be 0.2 C$^{\\circ 2}$, and our code is using 30,000 C$^{\\circ 2}$."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Exercise: Interactive Plots\n",
"\n",
"Implement the Kalman filter using Jupyter Notebook's animation features to allow you to modify the various constants in real time using sliders. Refer to the section **Interactive Gaussians** in the **Gaussians** chapter to see how to do this. You will use the `interact()` function to call a calculation and plotting function. Each parameter passed into `interact()` automatically gets a slider created for it. I have written the boilerplate for this; you fill in the required code."
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "7cdc56e40a90494cbaca4f5fb4d145e7",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"A Jupyter Widget"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"from ipywidgets import interact, FloatSlider\n",
"\n",
"def plot_kalman_filter(start_pos, \n",
" sensor_noise, \n",
" velocity, \n",
" process_noise):\n",
" plt.figure()\n",
" # your code goes here\n",
" pass;\n",
"\n",
"interact(plot_kalman_filter,\n",
" start_pos=(-10, 10), \n",
" sensor_noise=FloatSlider(value=5, min=0, max=100), \n",
" velocity=FloatSlider(value=1, min=-2., max=2.), \n",
" process_noise=FloatSlider(value=5, min=0, max=100.));"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Solution\n",
"\n",
"One possible solution follows. We have sliders for the start position, the amount of noise in the sensor, the amount we move in each time step, and how much movement error there is. Process noise is perhaps the least clear - it models how much the dog wanders off course at each time step, so we add that into the dog's position at each step. I set the random number generator seed so that each redraw uses the same random numbers, allowing us to compare the graphs as we move the sliders."
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "c60f71af532746729d0fc85ce753d6c3",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"A Jupyter Widget"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"from numpy.random import seed \n",
"from ipywidgets import interact, FloatSlider\n",
"\n",
"def plot_kalman_filter(start_pos, \n",
" sensor_noise, \n",
" velocity,\n",
" process_noise):\n",
" N = 20\n",
" zs, ps = [], [] \n",
" seed(303)\n",
" dog = DogSimulation(start_pos, velocity, sensor_noise, process_noise)\n",
" zs = [dog.move_and_sense() for _ in range(N)]\n",
" pos = (0., 1000.) # mean and variance\n",
" process_model = (velocity, process_noise)\n",
" \n",
" for z in zs: \n",
" pos = predict(pos, process_model)\n",
" pos = update(pos, (z, sensor_noise))\n",
" ps.append(pos[0])\n",
"\n",
" plt.figure()\n",
" plt.plot(zs, c='k', marker='o', linestyle='', label='measurement')\n",
" plt.plot(ps, c='#004080', alpha=0.7, label='filter')\n",
" plt.legend(loc=4);\n",
"\n",
"interact(plot_kalman_filter,\n",
" start_pos=(-10, 10), \n",
" sensor_noise=FloatSlider(value=5, min=0., max=100, continuous_update=False), \n",
" velocity=FloatSlider(value=1, min=-2., max=2., continuous_update=False), \n",
" process_noise=FloatSlider(value=.1, min=0, max=40, continuous_update=False));"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Exercise - Nonlinear Systems\n",
"\n",
"Our equations for the Kalman filter are linear:\n",
"\n",
"$$\\begin{aligned}\n",
"\\mathcal{N}(\\bar\\mu,\\, \\bar\\sigma^2) &= \\mathcal{N}(\\mu,\\, \\sigma^2) + \\mathcal{N}(\\mu_\\mathtt{move},\\, \\sigma^2_\\mathtt{move})\\\\\n",
"\\mathcal{N}(\\mu,\\, \\sigma^2) &= \\mathcal{N}(\\bar\\mu,\\, \\bar\\sigma^2) \\times \\mathcal{N}(\\mu_\\mathtt{z},\\, \\sigma^2_\\mathtt{z})\n",
"\\end{aligned}$$\n",
"\n",
"Do you suppose that this filter works well or poorly with nonlinear systems?\n",
"\n",
"Implement a Kalman filter that uses the following equation to generate the measurement value\n",
"\n",
"```python\n",
"for i in range(100):\n",
" z = math.sin(i/3.) * 2\n",
"```\n",
" \n",
"Adjust the variance and initial positions to see the effect. What is, for example, the result of a very bad initial guess?"
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"#enter your code here."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Solution"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {
"scrolled": true
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAhUAAAC+CAYAAACCoP16AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzsnXVYFGsbxu+hU9pERQUbQQUVxVaw\nxe7uPuqnxzp2t8djtxhY2BjYrYACtoKKYICECCi1O98fjyML7MLusgn7uy6uhd2dmXeH2Xee94n7\nYViWhQYNGjRo0KBBQ0HRUvYANGjQoEGDBg2FA41RoUGDBg0aNGiQCRqjQoMGDRo0aNAgEzRGhQYN\nGjRo0KBBJujI+wCJiYmaTFANGjRo0KChEGJmZsYI/q3xVGjQoEGDBg0aZILGqNCgQYMGDRo0yAS5\nhz8EMTMzk+n+AgMDAQAuLi4y3a8G4WjOt2LRnG/FojnfikVzvhWLLM93YmKiyNc0ngoNGjRo0KBB\ng0zQGBUaNGjQoEGDBpmgMSo0aNCgQYMGDTJBY1RoUCt+pWUoewgaNGjQoEEEGqNCg1qQ8isdo9ac\nhWm7ZfC99VLZw9GgQYMGDULQGBUaVJ7Hb76g7qjt2HH+MUpZmWLIytMI+xSv7GFp0AAAiPj6Hefv\nv8GPlDRlD0WDBqWj0JJSDRpE8Tk2CZcDw1HK0gQVSlmgfAkz6OpoY83Re5i96xqKmxvj6pqBqFjK\nArVHbkP3eUdxf9MwGOrrKnvoGoowUd9+wH3iHkR9+wEdbS241bCFh0sleLpWgkuV0mAYJv+daNAg\nYzJ5fBy68hRe7lVRzFhfocfWGBUalM7t0Ah0n38MMQkpf55jGMDC1BDxP36ha+Nq2D61A6zMjAAA\nB2Z1RfuZhzDh3wvYOa2TsoatoQiw9MBtaGkxmNarIbS1szt2vyenou3fB5GYkoqDs7vi+YcYXAoI\nxz+7r+Of3dfR2qUi9s/sgpKWJkoavYaiyuWAcAxafgqnFvVCZ/eqCj22xqjQoDRYlsXWM4GYuPEi\nKpQyx6lFvZDJ4+Pd5wS8//odEdGJaOpUHoM8nbKt+No1cMDs/o2x5MBtuDuWw+A2zkr8FBoKK7dC\nIjB71zUAwNXH73FwdlcUtzAGAKSmZ8Jrjg9eR8bi4or+aFGnAgBgyfCW+PY9BYevPsOMHVfgNHwr\nvGd2gYdrJaV9Dg1FD2//UFgWM0Tb+g4KP7bGqNCgFNLSMzH+Xz/sPP8E7eo74OCcrjA3MQAANK5V\nPt/tFwxuhvvPozB2/XnUcSiFWpVKyHvIGooQmTw+xv/rh/IlzPB3n0aYsvkyao/chqNzu8OtRlkM\nXHoSN0MicPifbn8MCg4bc2NM7FYfLetUQK+Fx+E5/QCm926IxcNaQFdHW0mfSENR4UdKGk7deYUh\nbZyhp6v4601jVGhQOD9TM9D6f9649zwSs/s3xoLBzXK5lvNDW1sLh+Z0Re2R29B/qS+Cd4yGlpYm\nfq1BNmw+FYCn72Lgu7AnujSuBrcaZdF93lE0/WsvmjiVx/UnH7BmjAd6t6gpch81KhRHwNYRmLL5\nElb63MOdp5G4vm6QUiZ6dSbpZxoiohMR9e3Hn59SliYY0aGu5jsvBN/bL5GanokBHrWUcny1NipY\nlkVU3E/UZVlNQpQaMXPHFdx7HolDc7qiT0tHqfdTwtIEq0d7oN8SX5y59xpeCo4daiicRMcn4589\n1+HhUunPNeVsXxJB20Zi6Moz8L39EpO7N8CUnm757stQXxdbJndAbftSGLX2HM7ee41uTavL+yMU\nGgJefULzyfuQkppbn+Zy4Dvsn+kFY0M9JYxMdfG+HAr7MpZoUN1WKcdX65LSkw8j0XXFDUREi25u\nokG1uP7kPf71fYTxXVwLZFBw9GxeAxVLW2DpwdtgWVYGI9RQ1Jm54yp+pWXg3wltsi1WzEwMcHxB\nD4TuGo01Yz0k2uewdrVR2toUey4Gy3q4hRYej4/Ra8/DzMQAPv90w92NQxHh8xfS/edg7VgPnLzz\nEk0m7UXUtx/KHqrKEPXtB64Hv0f/1o5KW2irtVFRoyx1Pb3/PFLJI9EgDj9S0jBkxWnYl7HE8hGt\nZLJPHW0tzOjTCAGvPuNK0DuZ7FND0eVpRAL2XAzGlB5uqFLOOtfrDMPAsWIJiSdsbW0tDGhdCxcf\nheFLXJKshluo2XomEI/ffsHaMR7o1aImGtYsi3K/S80n93DD2SV98CYqDvXG7EDAq0/KHq5KcPBK\nKFgW6N9KOaEPQM2NikolTWGgq437z6Pkfqz0DB66zT2KLv8cwZFrz5DyK13uxyxsTN50EZHffsjc\nZTnQwwllrE2x5MBtme1TQ9GDx2ex6tRzlLY2xZwBTWS+/yFtnMHjszjgHyrzfRc2ouOTMXvXNbSq\nWxE9m9cQ+p72bpVxf9Mw6OvqoMmkvbgcEK7gUaoWLMvC+3IoGtYoi0plLJU2DrU2KnS0tVC9rBnu\nv5C/UTF3z3X43n6Ju88+oveiEyjRdTX6LDqBs/deg8fjy/346s7Ze6+x+0IwpvduCLcaZWW6b309\nHUzr1RA3QyJw9+lHme5bHUlLz0Ricqqyh6F2XHz8CS+jErFmjAdM5BCnr1LOGm41bLH3YogmVAcg\n/GsSZh98ghcfvuV6bfq2K/iZloH/JrbN0ytUs0JxPNw8HPZlLDF4xSl8L8LXfXDYVzz/8A39Wxc8\nrFwQ1NqoAADH8hYIDvsq10ZTV4PeYaXPXYzsUAdfjk/F9XWD0L91LfgHhqPTbB/UGrYVR68/B5+v\nmSiEEZv4EyNWn0WtiiUwf1AzuRxjePs6sDYzwtKDd+Syf3WBz2fRfuYhlOy2BhP+9cNHTb6R2By5\n+wEVS5igl4iVsSwY7OmMFxHfEPDqs9yOoS7sux6Oy8GfUXfUdmw5HfDH0LodGoH9l0Pwv54NhYag\nclLcwhj7ZnghJiEF07ZelvewVZYD/qHQ1dFCz2byu37FoVAYFZk8PgJfy+dLGpv4EwOWnUSVstZY\nO9YT2tpaaOZsh61TOuDLianw+acbWLDotfA4nIZvxYmbLzTGhQCvP8ai46zDiE/6hf0zvaCvJ5+C\nI2NDPUzu3gB+D9/iydsvcjmGOvDfyUe4+vg93B3LYdvZINj3/xfDV53R9ErJh8DXn/EyKhHd3MrL\nNcGtV/MaMNTXwZ6LT+R2DHXgR0oarj39gla1SqFJrfIYu94PXnOO4Gt8Msau90O5EmaY3b+x2Pur\nU7kU/terIXaef4KrRTC3KpPHx6Grz9C+QeU/ysPKohAYFeYAIJe8CpZlMWzlGcT9+IXD/3TLlQeg\nq6ONXi1q4umuMTg0pysyMnnoPv8Yag3bgt1+T5CaninzMakL6Rk8LPa+hVrDt+J1ZCy8Z3aBk31J\nuR5znJcrzIz1i6y34vXHWPy9/Qo6uFXG5VX9EXZgIkZ1rIsD/qGoMvA/7Dr/WNlDVFm2nQ2Ega42\n2tUpI9fjmJkYoGvjajh89VmRnh+O33yBtAw++japgAsr+mHtWA9cDAhDxb4b8Ox9DNaP85Q472re\noKZwsLXEyLXnilzO29Wgd/gan4wBrZWXoMmh9kaFpYk+KpW2wIOXsjcqtpwOxJl7r7FiZCs453FD\n1NbWQp+Wjni+Zyy8Z3WBtpYWhq06g/K912Phvpv49j1F5LaFkYcvolB31Hb8s/s6vBpVxYu949Ar\nD5EgWWFmYoDxXerhxK0XeBmRO05bmOHx+Bi84jQM9XWwfWoHMAyDciXMsHFiO7w/PAktalfAuA1+\nCA77quyhqhyJyak4dPUZPGuXhomh/BvUDW7jjMTfqodFlb2XglHexhg1y5lDS4vB5B5ueLh5OBzK\nWKFH0+pSac4Y6utix9SOePc5AXP3XJfDqFWXHecfw8LUAO0bKF6WOydqb1QAgFuNsrj/PEqmyU/P\n38dg6pbLaFvfHpO61RdrG21tLfRvXQvBO0fh6pqBcK1SGvP23kDZnuuw/viDQpmcdSXoHSZtvACv\nOT6oPWIbLDutQINxu5CQ9AunF/fGkXndFdpQaVK3+jDU18VKn3sKO6YiuRr0DleD3uW6llYfvYcH\nL6KwaVI7lLIyzfZaKStTHJrTFVZmRui54BiSfmpadAvi7R+Kn6kZ6OaWvzy8LGhRuwLKlTDD3iKq\nWRH+KR63Qz+ivYtttlCTs31JhOwajSPzuksdgmrqbIfRnepi/YmHeKiABH5VIPxTPE7eeYXRHV3k\nFl6WBJkZFQzDaDMM84RhmHOy2qe4uFW3xdf4ZJmKYC05cBsGejrYM72zxBc4wzBoUacCzi3ri5f7\nxsHT1R6TN13CoGWn5JpQqmhiElLQfuYh7PJ7gvDPCShjbYrezWti7VgPvNg7Dp0aVVH4mGzMjTGi\nfR0c8A8tdEmKQa8/o83fB9Hqf95wHr4N3pdDkJ7Bw9N30Zi75wa6N60uUjbaxtwYPv90Q/jnBIxa\nc65QGrjSwDW1c6lSGtVszRRyTC0tBoM8nHA5MLxICjftvxwChoHIUFNBc1pWjGyN0lamGLLyNJ6+\niy7QvtSB9SceQFuLwfgu9ZQ9FACy9VRMAvBShvsTG7caJEcqKxGsHylpOHnnFfq2rIkSBVxlVy1n\njZOLemHR0Obw9g9F44l7Cs3Nbvu5IKRn8BC4bSSe7h6Dc8v6YvPk9pjcww3FjPWVNq6pPd3AMMDq\nI4XHW5HyKx19l/iipKUJtk5uj0weHwOXnULFvhvQde5RmJsYYPNf7fKckBvXKo9FQ5rj8LVn2KnJ\nrwAA3H0WiecfvmFMJxeFHneQpxNYFth3qWh5K/h8FvsuhaB13UooYW4ol2MUM9bH7umdEBGdiFrD\ntqLdjIO4/uR9oTSk43/8wu4Lwejb0hGlrU3z30AByMRXwjCMLYD2AJYAmCLqfYGBgbI4XC7S4iNh\noKuN09cfw8Gs4K7dM48ikZqeCZeyejIbc5tqRjAa4oK5h4LhPGwzlg2og7qVrGSyb0UTGBiITB4f\nG47fQ4PKNkiO+YDAmA/KHlY22tQuje3nAtGxVjFYmCjPwJEFgYGBWHbiKd5GxWHLqAaoWxrYM9YV\n9998w4Gb7/A4PA4rB9ZFRNhLROSzr1aVDXC2sjUmbPCDCT8RDqWLKeQzqCqLDz2BiYEOHMzTwE2H\n8pqnctKgsjWWH7yN2qW0UNzMQCHHVDaBYbGIiE7E8JZZnV3lcb4tAJye0Qwn7kfg6N0PaDElDNVs\nzTC1U3U4VVCeMJSs2XMtDD9TM+BZvZjY51EW59vBQXTuhqw8FesBTAegFBUoTgQrNCJBJvvzexyF\nctaURCRLmlQvgb0TG8HUSBdjtj3A4mOhiEtSz/j21dAviP2Rht7udsoeilAGNquE9Ew+fO58UPZQ\nCszNZ1/h++AjBjSr9McQ1dJi0KhqcWwZ1QA3FnuiaU3xKmu0tBgs6OMMUyNdzDzwGOmZPHkOXaVJ\nSE7DtdCvaF/XFoZKiEVP86qJDB4fy048LZSraGGcC4yCsYEOmtWQbyUYAJgb62FYKwecntUCM7s5\nIi4pDfOPFB7hsYxMPo7e/YD6DtYqtTgo8DeJYZgOAGJYlg1iGKZZXu91cZGti5GzuFxcXODR4DtW\nH7mPGo5OMNSXPoM74ut3BIWfx6KhzeHq6iqrof7BBYBHUzcs3H8TG048xLVn0Zg7sCkmdq2v8i2R\nBc/3hD0hcLC1xIR+bVWy/bALgK4PY3DiwTusm9xdqeEYaQkMDETsj1QsP/USdRxKYcfMPjK7RvYZ\nFEf7mYfw7JsORnasK5N9qhurfO4ig8fH3OHtUN3OJtv1rQhcACxP0cfkTZfwKkEPAzycFHJcZZH8\nKx03nl9G35a14N6wvkLPt7sbUMU+GINXnEaGYUk0rClbVV9lsO9iMGJ/pOHA7O5wcbHP9/2yPN+J\niaJD+LLwVDQC0IlhmA8AfAC0YBjmgAz2KxFu1cvKRATrwBXS5e8vx3rfYsb6WD3GA892j0GTWuUx\nbas/ag7drDbZyo9efsKDF1GY0KWeShoUHDP7uiMxJQ1bzgQoeyhSweezWHAkBCmp6Tg4p6tMjc62\n9e1Rr2oZLDt0BxkivBVp6ZnYezEYkTGFIwdIED6fxbazQWhSqzyq29kobRwTutRDwxplMXHjxULf\naOz4zRdISc3AIE/lGE9dm1SDkYEu9l8OUcrxZQnLslhz7D5qVigOD9dKwt8UHg4owStTYKOCZdmZ\nLMvasixrB6A3gGssy/Yv8MgkhOsdXxARLJZlsf9yKJo6lYddSdmGPoRRpZw1zi3rC7/lfZGanol+\nS3yRpgaCOBtPPoKpkR4GeToreyh5UrdKabR2qYh1xx6oZdWNz90PePAmFmvHeqKqGHLFksAwDOYM\naIwPX7/j0JWnQt8zf98NDFlxGhX6bECvBcdx/3lkoXEd33n6EeGfEzCiQx2ljkNbWwu7p3dCanom\nRq89X2jOrzD2XgyGfRlLpXkJTI300cW9Ko5cf672wmP+ge/w9F3M76R0IQu7qCjA3h7YvFnhYysU\nOhUA6b8XVATr0ctPeBMZh4EKdkO2re+Anf/rhPDPCfjX96FCjy0psT9SceT6MwxtW1stQgqz+jVG\ndEKK2mkCBL3+jI3nX6JpjRIYJafwRAe3ynC2L4mlh+7kaor35O0XrPK5h57NamByjwa4FBCGhuN3\no/7YnfB78FYu41EkB/xDYWygiy5SiCzJmirlrLF4WHOcufcah68+U/Zw5MK7zwm4GRKBQZ5OcpVB\nz4+BHk74npyK8/ffKG0MsmDN0fsoaWmCPqJEBR/+vo/IIYSfHzI1KliWvcGybAdZ7lMSCiqCtf9y\nCAz0dNC9aXUZjyx/PFwroYNbZSzyvoXo+GSFH19cfB98RCaPrzI10fnR1Kk8GlS3xUqfeyLd/KpG\n0s809F50Alam+vinZy25TcIMw2BO/8Z4ExmHYzdf/Hk+k8fHsFVnYG1mhK1T2mPVaA9EHZuCTZPa\n4XtyKjrP8cEDNQnVCSM1PRNHbzxH18bVJJaClhd/dWuABtVtMWHjhUIZBtl94Qm0tBgMbqNc72bL\nOhVQysoE+y+rb/v5WyERuBwYjgld6okWu2JZoHZtwEnxoaZC46kAxBfBuhL0DrvOP852k0nP4MHn\n+nN4uVdV2gp8zRgP/ErLxJzd15Ry/PxIz+ThxP2PaFffAfZl1KMsi2EY/DOgCT58/a4W2gwsy2LM\nuvN49yUBi/rUhpmRfG96XRpXQ/XyNljsfetPI7w1R+/hyduv2DSpHSxMSUvAxFAPY71c8WjLCNja\nFEPvhccR/+OXXMcmL87df4PElDQM8FB+nwQObW0t7Pm7M36lZaDfEt9cniN1JpPHx56LwWjjag9b\nG+VWKWhra6F/q1rwe/hWLdsnfE9OxYBlJ2FfxhIT81J67t4dePwY0Ff8vaxwGRViiGCl/EpHn0Un\nMHz1WTgP34bLAeEAAL+HbxH/4xcGKnGiqVzWChO61MMuvycq2WnTP/gL4pPTMLGreLLlqkLb+vZo\nUqs8Fuy7iWQVbzS0/1IIDl55ivmDmqJ2RfkbblpaDGb3b4znH77h1J1XeBMZh/l7b6JL46roJsRj\nZ25igKPzuuNzXBKGrDitljkAB/xDUcrKBC1qV8j/zQqkajlrbJrUDteffMAi71vKHo7MuPQoDJ9j\nkzCsXW1lDwUAMMCjFjJ5fPhcU79Q09h15/Hp2w8cnN0VJqK8bHw+/SiJQmVUOFYsAWMDXZzPI+a7\n8/xjxCb+xOJhzZGWkQnP6QfQcdZhbDjxECUsjNHaRUQmrYKYO6gprIoZYfKmSyo1YfN4fOy5Fgb7\nkqZo7VJR2cORCIZhsGJUK0QnpGDdsfvKHo5IXn+MxdgNfmjmbIdZ/cRv+1xQejWvAQdbSyw+cAsj\nVp+Fvq42Nk1qJ/L9rlXLYNWo1jhz7zXWH3+gsHHKgrjEn/B7+BZ9WzpCW1v1pr8hbWtjkKcTFu6/\nWWhaeO+68AQ25kbo4FZZ2UMBQPcJZ/uS8PZXrxDIQf9QHL72DPMHN0O9anl0033yBLCyAm7eVNzg\nBFC9b1UB0NHWwpjOLjh09anQlX5aeiZWHbmHpk7lMbt/EzzfMxYrR7XCzZAPuBH8Af1aOUJHyRON\nuYkBFg1tjpshEfC9pRTVc6Ecuf4cEd9SMKK1g1ITraSlQXVbdGlcFauO3FOK2zM/d/a37ynoueA4\njPR1cXB2V4Xe8LS1tTCzrzuevP2KW6ERWDPGI1dTspxM7FYfXu5V8ff2K3j08pOCRlpwjlx/joxM\nvkq0iBbFpkntUK2cDfou8VX7/Iro+GScvfcGgzydVEqHZ6BHLQS8+qw23Yw/fP2OsRv84O5YDjP7\nuuf95gcPgO/fgQrK8cQVKqMCAGb3bwJLU0NM3XI510rf2z8Un2KT/qwC9fV0MK13I7zxnoClw1tg\neu9GyhhyLoa3rwPHisUxdctl7L0YjAcvovA9OVVp4+Hx+Fi4/ybsS5qimZjKjarI0uEtkZKagSUH\nbiv0uEGvP8O47VJM3nRRaGlraHg0XEfvwJuoOByY1UUpGv79W9dC1XLW8HSthKFiuKkZhsHu6Z1Q\n2soUPRccQ0KSeuRXePuHomaF4qhVqYSyhyISY0M9HJvfA8m/0tF3sXrnV+y/HEKJv+2UW7qbkz4t\nHaGlxcBbDRI2eTw+Biw9CQDwntUl/wXHgwdAqVJAWeWU7hY6o8LcxAALBjfD9ScfcObu6z/PZ/L4\nWH7oDlx+axcIUtLSBDP7NS5w8zBZoaOthU2T2iE+6ReGrDgNt3G7YNFxBUp1W4OF+xTv0vK59gyv\nI+MworWDSotd5UfVctYY2tYZm08H4P0X2Ui6i8PxWy+QnsnD+uMPUWfk9mwCbb63XqLh+F3I4PFx\na8NgeNbLXxlPHujqaCNo20j4Le8ntifKwtQQR+f1wKfYJIxYfValwnXCCPsUjwcvojCgtfwqamRF\ndTsbbJ7UDjeCP2CBEr7zsoBlWezye4KGNcrKXGeloJS0NIGnayUcuBL6J0FZVVl84BbuPP2IzZPa\niaef9OAB0KABoKRrvNAZFQAwqpMLqpW3xrRt/kjPoAqP4zdfIPxzAmb1c1f5CQWgjpLxZ/7GG+/x\nOLOkN1aMbIXKtlZYsP+mQruc8nh8LPS+hVoVS6i1l4Jj/qBm0NbSwtw9NxR2zEsB4WjsWB6XV/VH\n0s80NBi7E/P33sCCfTfQbd5R1KxQHIFbR8C1ah5xUgVgZKArsdFYr1oZLB7WHCduvVR5LZAD/qFg\nGKBvK0dlD0UsBrVxxtC2zljkfQtHrz9X9nAk5t6zSLyOjMPw9qqRoJmTgR5OiIz5gTP3Xuf/ZiWx\n6eQjzN97EwM9nNBPnJBdbCwQFkZGhZIolEaFjrYWVo/2wNuoeGw5HQA+n8XSg7dRrbw1OjdSvtiN\nuOhoa8HB1godG1bB9D6NsG+mF1iWxbaziumiCJCX4k1kHOYNaqrWXgqOMjbFMKlbfRy8EorgsK9y\nP150fDKevP0KT9dKaO1SCc/2jEXflo5YsO/mn8nixvrB+eYwqDLTejVC89p2mPDvBbyNilP2cITC\nsiwO+IeiuXMFpZc1SsLmv9rD3bEcBi0/pTYy/hy7/J7AxFAPPZrVEP6GzEzofvsGpCunIquLe1U4\nViyOkWvOqmTuyvazQRj/7wV0blQFO6d1FG8jHg+YORPw8JDv4PKgUBoVAJURtnapiAX7b8L7cgie\nvovBzL7u4t8Y4+KA+6pVKWBX0hwd3apgx/nHCpHzFvRSeKmA8qCs+LtPI1iYGqLRhN0YvfYcnr2P\nkdux/H9n8Hv+1uc3NzHA/lldcHZpH+z5uzP2zugMAyV0yJQlWloM9s3wgp6uNvot8VVJkbEHL6IQ\n/jlBpbQpxEFfTwcnF/VCaWtTdJrjg4iv35U9JLH4kZKGIzeeo3eLGiJLH83v3IFTu3bAU+Ey8fJG\nX08HPv90R/KvdAxYelKlclf2XQzG6HXn0K6+A47M7Q5dHTGTXEuUAJYuBZyVJzJWaI0KhmGwZowH\nElPSMGzVGdiVNEeflhK4PYcMARo2BKKj5TdIKRjfxRXfvv/MpoAoLwqbl4LDwtQQdzcORZ8WNbHv\nUggch25B88n7suXgyIpLAeGwMTdCbYdS2Z7v4FYZg9s4q0UoThzKFjfD9qkdEfDqs9JzACJjEuEy\najvseq9Hia6rYdZhOZpM2gtDfR10bVwt740zVa8nhLWZEc4v64u09Ex0mHUYP1LSlD2kfDl89Sl+\npmaITtCMiID9tGn0+zflVWBUt7PBxgltcfXxe6w4fFdp4xDk0JWnGLLyNFrVrYgTC3uKVs0UxtOn\nwM+f8hucGBRaowKgeuRhbWuDx2fxd59GkpWLfv6dTHfqlHwGJyUt61RElbJW+O/kI6GvZ/L4+Bxb\ncFdeZiH1UnBULWeNndM6IeroZKwY2QrvvySg8xwfmfa14PNZXAoIQ+u6lQqVUSaK7k2rY2hbZyw9\neBu3QiKUNo4NJx4iOOwrmjrZoYt7VQxt64z/9XLD4Tnd8lTLLeHtjdqtWgEXLihwtOJRtZw1Tizo\niVcfY9Fr4XFkqtCqOicfvn7HzJ1X4Vq1NOqL0lM4fjzrdyUaFQAwtF1t9GlRE3P3XMfdpx+VOpYj\n155h4LKTaOZsh1OLekvmxeTxgEaNgP/9T34DFINCbVQAwIpRrbB6TGsMbSthslDTpvR44oTsB1UA\ntLQYjPNyxcOXnxDwKrs+QCaPjw4zD6Fi3w149TG2QMc54B9aKL0UObEyM8L0PlRWXMrKBP+dEm6s\nSUNw2Fd8+/7zT+ijKLBhQltUKm2J/kt9lSLjnfIrHbv8nqB70+rYN9MLW6d0wLpxbbBsRCt0zss4\nfvQIZTZtApORAQweDKSonoRzy7oVsWVye1x8FIZ5e64rezhCSUvPRI/5x8Dnszg8p5toT9yxY0gt\n89vgULJRwTAMtk7pgPIlzdF3iXKuWwDwvhyCvkt80ahmOZxZ0gdGBrqS7eDVKyApSalJmkARMCos\nTA0xtWdDyYVX1qwBrlwB1q6Vz8AKwCBPZ5gY6mHTqYA/z7Esi/Eb/HDpt+z4+A1+Upf4paVnYv7e\nG6hbuRS6NC58Xgph6OlqY2SNATOnAAAgAElEQVSHurj4KAzhn+Jlss9LAWEAAI8fH6gN8WvVzTKX\nFSaGejg0pyu+xidj0PJTCi/XO+Afiu/JqZJJySclAX37IsPGBs+OHwcuXgSMjeU3yAIwvH0dDGnj\njBWH7yok0VhS/tp0EYGvP2PfDC9UEtUfKCICePgQsV5e4GtrU8WCkilmrI8jc7vjS5xyyqN3+z3B\noOWn0NzZDn7L+4qW4M6LB7/VbTVGhQrTsiVQU0RrWSVSzFgfAz1qwefaM8QmUvxs7bH72HY2CDP6\nNsLasZ64+vg9jkhZhrbj/GNERCdi6fCWhSbmLw4j2teBFsNg29kgmezvUkA4nO1LouTXj0B4OPBS\ndRRS5Ylr1TJYM8YD5+6/wZqj9xR2XJZl8a/vI9RxKPWnD5BYREcDBgZ4v3Ah0kuVou6OALBsGfDv\nv/IZbAFYM9YDNubGGLrytEqFQQ74h2LrmSBM790wb6/Q79BHfKtWiJo0CWjbVkEjzBuXKqWxeGgL\n+N5+qVA1461nAjFs1Rl4utrj7NI+0nfOffAAsLAAHBxkO0AJ0RgVwmBZwMUF2LEDuHYNWL1a2SPK\nxTivekjL4GGX32P43nqJaVv90aNpdSwZ1hKjOtZF3cqlMHnTJSRKqMSZ8isdi71voZmzndr1+Cgo\nZWyKwcu9KnZfeILUAlbXJP1Mw91nkRT6iPldXRISIoNRqgfju9RD96bVMXPHVdxRUJz62uP3eBHx\nDRO71pPMGLa3B0JCkFxbIETK5wOBgcCkScC2bbIfbAGwMDXEpknt8OTtV4UabRyxiT/x+mNstu/I\ns/cxGLnmLJo6lceS4S3z3kGlSsDo0Ui3tUVMnz5AY8X1ucmPKT3dUNuhJCZsvCDx3CkN/518hDHr\nzqNjw8o4tagXDPUlDHkIomTRKw6NUSGMHz+AoCB6vHSJ6n4TFKfAKA7V7WzQonYFrD32AP2X+qJ+\nNVvsm+kFLS0G2tpa2DK5PaITkjFXwtjrv74PEZ2QgiXDWhQpLwXHmE4uiPvxC8du5PbyRMcno+WU\n/djt9yTf/Vx/8gGZPH72fAoldg5UNAzDYOf/OqJCKQv0XnhcIf1WNp58BGszI/RqIaZ3MTKSjIaU\nFEA7R3hUSws4coQ8lceOyX6wBaRrk2ro1qQa5u25gTeRitEG4fH4WH/8Aex6r0fVQZtg1GYJyvZc\nh6aT9qLdjIMwMzaAz9zu+SfEe3kBW7YAAHRjYykXQEXQ0dbC9qkdEZ2Qgjm7r8n1WC8jvmHSfxfh\n5V4Vx+dLWOUhjB07gLlzZTO4AqAxKoTBlZEWL0596TMzgTNnlDsmIYzv4oqYhBSUtDTB6cW9s1m5\nrlXLYHRHF/x3KkDsNuoJSb+w0uceOrhVRsOaytGNVzYt6lRAlbJW2Hw6u8BYegYP3ecfw7Un7zFs\n1RksO3g7z7jrpYAwGBvoolHNcllJfz9+yHPoKoeZiQGOze+B2MSf6L/kpFzzK95/ScCZe68xqmNd\n8TLmWRYYNAjYvRv4KiI3QUcHqFYNiFJN0an/JrWDob4uhq8+I/fcleCwr2gwbhcmb7qEJk7lsW+G\nF+YPaoaWdSqABQtLU0Mcm98DJfNrdRAami0xs+zatUDnznIdu6S4VCmN8V6u2HQqQK6CY3P33ICx\ngS52/K+jbJqtNWig9HwKQGNUCIdzV5coQWGQcuWyl0CpCJ0aVsGq0a1xedUAFLfInVi2ZHgLWJsZ\nYcy682JNOquP3MP35FQsHtpc/EFcvQq8lV0ZprJhGAZjOrngwYsoPH6TZYxN3nQRd55+xL4ZXujf\nuhZm7byGKZsviTyvFwPC0bx2BZosqv6OL6uYt0sRONuXxMaJbXE5MBxzdl2TWwLc5tMB0GIYjO7k\nIt4GiYnA9evAtGnkjheFrS0ZFSrY16SkpQnWjvXA7dCP2H5ONnlAOUlLz8Tf2/zhMmo7PsYkwuef\nbji/rC8Gejph7qCm2DvDC7c2DEHwztFwdyyX/w6HDwfat//zZ6a5udKrP4SxaGgLlLYyxcg15+Qi\n5hb0+jOO33yBqT3dYG1mVPAdXrsGnDxZ8P3IAI1RIQxBo4JhyFtx+TJNRCqEtrYW/terIexFZFlb\nmBpi9ejWePjyE3b5Pc5zX1/jk7H+xEP0blETTvZi9vhITQVatQLmzZN06CrNoDbOMNTXwZYzVF2z\n2+8JNp8OxP96uWGgpxP2zfDCX93rY/3xhxi47GSuSSfsUzzefU7ICn2MHAnUqlUkjQqAKhZGtK+D\nZYfuYOaOqzI3LFJ+pWPn+Sfo1qS6+BLc3Hc8v/bQHTuSS5mneiqhADC4jTNa1a2IaVv95dKC/u/t\nV7DS5x4GeTrh5d5x6NWipvRh0Q8fgIAAoFu3P09lWFjQ9yIjd/deZVLMWB8bJ7ZF6LtobDjxUOb7\nn73rGqyKGWJydzfZ7PDff4EZM2SzrwKiMSqEYWICNGlC7WMBMipKlKBGLWpG/9a10KhmWczbewM/\nU0V/cRd730JaeiYWDmkm/s5v3KDHgQMLNEZVw9zEAP1aOeLglae49CgMY9afR6u6FbFsRCsApBWy\ndqwnlg5vgYNXnqLVVG/sOv8YYZ/iwbIsLj2i6yRbPsXly8DBg8r4OEqH0wEY08kFKw7fxaSNF4V6\neKLjkxEmRTnvwStP8T05FRO61hN/I251bGOT9/uaNwemT6dQiArCMAz2/N0ZxS2M0XLqfpmKjgW8\n+oR/fR9ibGcX7JreGZbFDAu2Qy43pUePP09lmv/uuhknIi/k6VMyQl7IX0E4J10aV0PnRlUwb69s\n81ZuBn/ApYBwzOznnqcYm0QEBpJXXQXQGBXC8PAAbt6knAqA4lQREUDdusodlxQwDIPlI1vhS1wy\nNp4UbnE/ex+DrWcCMaJDHTjYWom/8/PnAUNDwN1d8oGFhqrc6kSQMZ1c8SstE+1mHkIZa1P4/NMt\nWwIawzCY2a8xdk3rhJcfv2H46rNw6L8Rtj3XYdmhO6hQyjzLg9S0KancmeQTby7EaGkx2PRXO0zp\n0QAbTz7CqLVnwePxwbIsboVEoPfC47DtuQ4O/TfCfcJueF8OEVmBw+ezCHr9GSsO30GrqfsxceMF\n1HYoiUaS5AExDODkBJTJpzMsj0fffRX2MtnaFMPtDUNQtngxtPn7wB+jtiBk8vgYueYcSlmZYml+\n1RzicuwYzaEVs6rKMi0s6BdRIZDXrwFfX6XNFRsntoWOthYch23BiNVn8LqAooIsy2L2rmsobW2K\nsZ1dZTPI6Gjg0yeVMSpU0/yWN+fPA79+kQdCHDh3H49HGfy6BSj7UQLujuXQrr4DVhy+i1EdXWBu\nYvDnNZZlMWnjRRQz1seioS3E3ynLZp1Hc3NaaZiZibctn0/iYoaGwNatEn4axVCncik0qG6L0HfR\nOLWoN6xExD2HtquNIW2d8epjLG6GROBmSATuPvuIoW1rZ7mJP38GnjwBFi0C/vlHgZ9CtWAYBqvH\neMDIQBeLvW8j6lsSPsX+wNN3MTA3McCELvVQysoEO84/xsBlp/DXpksY0LoWrIoZ4ktcMr7EJ+NL\nXBLefor/o3roWLE4xnZ2xTgvV8nc8g0bAsFitGr//Bmws6Oy0pEjpfvgCqC0tSlurh8Mj2kH0HH2\nYRyZ2x1d8utzkgfrjz9AcNhXnFjQE2YC84XUJCdT6GP+/GxPp9SsCezbB5QuLXw7rl3Cxo3Azp0F\nH4eElC1uhifbR2H1kXvYczEYu/yeoHOjqpjRpxHqV5dAC+U3Fx6G4e6zSGyd3L5g5aOCBP3Op1GV\nRS/LsnL9+f79O8v9yJqAgAA2ICBA8g3Ll2dZNzfRrw8ZwrIdOmR/LiyMZYsXZ1kfH8mPpwI8efuF\nRbP57KwdV7I9f/zGcxbN5rP/+T7Mdx/ZzvfLlywLsGyrVvT4+LFkA5o5k7Y7dUqy7RTIl7gk9vXH\n2ILvyNqaPquxsUSbSX19qwFLD9xi0Ww+6zx8K7vjXBCb8iv9z2t8Pp+9GvSO7Tn/GKvbaiGLZvNZ\ny04r2BqDN7Gt/7efHb7qNHvgcgj7JS5JpmMSer7T01lWS4tl//lH9IahoSy7cCHL8ngyHY80JCT9\nYhuM3clqt1jA7rsYLNU+3n2OZw09F7OdZh1m+Xy+bAbG47FseDjLfvny5ymxru/p0+m7Y2DAspmZ\nshmLlETHJ7P/7LrGWnRczqLZfHbB3hsSnR8ej886D9/KVuy7gU3PkOFnWbqUZRmGZX/8yPNtspxP\nctzXs93zi6anIjUVqF5d9Otv3+aOodrZkafi0iWgVy+5Dk8eONuXRO8WNbH+xENM6FofJS1N8Cst\nA1O3XIZjxeIYJW7WPIe9PXD7NnkqrlwhxcjaYvZXCQkBxo6lxk0jRlB4qUQJyT+UnClpaZJ/iVx+\nsGxWgm9KCrlx1czTJQ9m9muM4e3rwNrMKJeHgWEYtKhTAS3qVEDKr3ToaGsVvIY/J0uWUMb81at5\nv09XFyhZMu+y0sBASubs2ROoUkW245QQcxMD+K8egM6zfTBo+Sm8+5KAeYOaiu3FYVkWY9f7QVtL\nC/9Nais7rRotrWxhjz/weMC9e5S/JixplvNUpKZSKCSveVvOFLcwxsKhzTG9TyOMW++HeXtv4Nn7\nGOyd4SVWn45jN54jOOwrvGd1Eb+VuTjMmAH07QuYmspunwWg6OVU/PxJMai7d0U3DYqJycqn4NDW\nBhwd1VpqeeGQZkhLz8Ri71sAgFU+9xARnYiNE9pK1sEVIKPL3T2rLjo8XPxtBw4Ehg0DDhwg7YYR\nI1SyZE8mpKaSIcG5d79/V+54VAgbc+N8b1rGhnqyNygASvx7/16893JlpaKYOJEeg+RT1ikpJoZ6\nuLCiHwZ5OmHBvpvov+Sk2AqxR64/x8VHYVg8tDnKFhcznCkOly5RH6Wc33OWpc6ae/cK387YOKvk\n93HeFWyKwsRQD3tndMaq0a1x/NYLuE/cjciYvCsDE5NTMWXLZThVKoE+4oqziQvDAOXLy3afBaDo\nGRUfPtDjq1eib4TR0cJXztWqkVGhpjdAB1srDGtXG9vPBeFG8AcsO3QHvZrXQFNnO8l29OMHMHky\nrRxMTSmD/t078bb9/p0yut3dgRo1gOXLKTdDRSYMmZOZSQZUy9/Jbiqc8Fek+PYt98JBFHkZFQkJ\nlC8AqIxRAVCDvD1/d8aSYS1w6OpTtJq6P19V09uhERi/wY/En7pIUEkjDkeOAKtW5ZaQ1tEBLC1F\nNxXbupXmagMDlZojGIbB/3o1xNklfRD2KR6uo3fgQR5CWTN2XMHX+GTs+F9HaEu6gMuLmBhg6FCV\nagFQ9IwKwdXJRyE9CdLSyF0tzKioXp1eE6XApwbMHdgU2lpa8Jx+AAwDrBrdWvKd+PsD69dn1fpP\nngy0EDPJ8/59Msq4ipGJEymJUZwko6dPKezySfb1+HLD1JQSzLiQmcZToRp8+5Z/OSnH2LGUZCsM\nwfkkMFD4e5QEwzCY1b8xjsztjqA3X9Bg3C74PXibSyeEZVmsPnIPzSfvg5WZEQ7N6SrbGx9AIWVR\nja5sbPIWwNLRIY9oqvx7cUhKe7fKeLBpOIwN9eAxzRtBrz/nes/t0AhsPROEv7rVh2vVfKqNJCUg\nANizR6XUeoueUVG1KpX3AcKNitRUik8Jyw9wdycFPjXuiVHGphjGd3FFegYPs/o1ls7Fef48dcNz\n+y3cMnOm+Hkmd+5QKKne75WQlhYJQwFZBocoZs4k79KlS5KPWVnw+fSZPDzIYK0n4xWgME6epPCe\nBtFIYlS0bJlNsCkbnIeuYUO6caqgF7Nn8xq4vm4QeDw+2s88hLqjtsP31kvw+SwSk1PRfd4xTNvq\nDy/3qgjYMkKysnJxkcaoSEqi74uvL+W/bN4s+3HJgOp2Nri5fjAsTQ3R5u+DeCVQdpqanokRq8/C\nrqQ5Fg6RQKlYXIKC6H4kbj6bAiiwUcEwTFmGYa4zDPOSYZjnDMNMksXA5EalSsCKFZSAFRmZ+3Uz\nMxIpatcu92vOzsDKlZS4pcbMG9QMu6d3wrReDSXfmM8H/PwAT8+sZFY+nww0cVQH79wB6tShWKkg\n/v40MT99KnpbblJJSpJ83MriyhU6T0FBgJ6ULY0lpWtXMoDjJReSKjLUqyd+CV5SEl23wrxMnFFx\n5AjNJyq64GhQ3RZvvCdg17RO+JGShm7zjqLWsC1wHbMDp+++wpoxHjg2v4fsxJgE+fGDQsqSGhWf\nP9NK/NcvlT2vHLY2xeC/egC0tBh4TPPGx2jKsVhy4BZeR8Zh25QO0rc0z4ugIEoOViENHFl4KjIB\nTGVZthqABgDGMQyjvBTd/AgNpfho2bLCPRX5rTRSUtTL/S4EE0M9DGlbW6oEOKNXr2iCEDS69u+n\nRCFx8ip27qSa85zU/J28dPas6G3LlgWMjEiMSF1ITCSji2GA8ePJyJAngobd69fyPZY64+sLjBsn\n3ntDQqg996NHuV+ztiYD29Y2d6dTFUNPVxtD29XGq/3jcXB2V7AskJKagevrBmFKTzf5dSWOiKDr\nX5RRMWuWcL0arvKjdGmas93cVLKxI4eDrRUureyPxJQ0tJ7mjWuP32P5obsY6OEED9c8+ssUhKAg\nlRG94ihwWjXLsl8AfPn9exLDMC8BlAGQS1c1UE4xR0n2W71fP6Tb2CBqyRJkmpsjM8e2VmfPotya\nNXjm44MMIR6JqkOGgG9ggDe/W/cWNfS+fkWGhQWelyz559yZZGSgKoA3Fy/ihzj9UbS1hcafq9ao\nAfj44JWnZ67XTB89gunjx7C0ssKPjx/xUcXi16KwDg6GHYCnnz7BcdMmRLEsvnLSxGIiyfWtGx0N\np9+/v/P3R7ymfFVicp5vvfh41ALw/s4dxFnm6LNTqxb9BAbCdt06pJcujRg1KDmvbA7sHecKHp+F\nTvo3BAbKt6kXc/s2wDBghVzLgQAlYuZ4zfLOHVQE8DQuDun6+qgdEIDokyfxSZRQloqwZlAdjN/x\nEC2n7oeFsR4GNCwul3uf1s+fqKajg28lSiBGgv3LYiwOogxEyDingmEYOwC1Aci+A4uM0Pv8Geml\nSyPV3h6Z1ta5XteNj4d2Sgp4ItQhU+3sYMBVkBRBvrdogZCLF7PkdQGk/ZY61s+nRXSxu3dhffq0\nSG9QYuPGMH7+HDpCMsGtLl5E8aNH8ezoUXxUkcY54qD9uzIgw8oKfD096BQwdKOdlAQmLU3k6/pf\nsjqrGggL72mA8fPnqNW+PUzEUdQEkPE790IvOjrP95mEhMD8+vUCj09RMAwjeSm5lLD6+mBFhP90\nv36Fhb8/tHIkYur9Dolk2NiA1dNDaqVK5ClVcZwrWGLFgLooZqiLGV1rwtxYPmFPvpERnh8/rnpG\nbE41LGl/AJgACALQVfB5lVLUjI8ndbZVq1j2yRNSIsup0jZlSt7KhytW0D7k8HlUnYAHD9iAR49y\nv8DjkeLdlCl576BTJ5Z1cBD9enAwndudO7M/z+ezbOnSLNujh+SDVjZz5pAiI5/PsiVLsuzw4WJv\nmuv6Tkig89O3r+iNvL3pPfm9ryhz+jSdnxxzR57zSYkSuf93GRmklrphA/09ZgzLFiumEsqaKsX6\n9aQ4moM/5/vgQfp/vHqV/Q07drBskyZZfw8dyrI2NvRdUgN4PNUap6IUNWVipjIMowvgBICDLMv6\nymKfcoEr/6pQgeKjs2YBAis7AJQvkFf9erXfevpqLIIlLVZ+fqjZpUtWrJODU8vLSwCLZakiIa/m\nY7VqAUePUqKhIM+f0zE9PUmF08NDtHCZqtGgATB1KsWULSwKVlLKxewPHxb9nq5dKdm1aVNNoqYo\nuFJocXUqAMrnyemJi4oifQWj331h6talpERJhOCKAkeP5q1cylXh5EzWHD6cGjty1KlD71GTnDYt\nLTknlw4dSuXOKoYsqj8YALsAvGRZdm3BhyRHuLBFhQo0SQC5kzVjYvKWjC7CRoX16dP0C9cSXpB/\n/gFGjRK98evX1HQsL6OCYagtskBoBQBw8SI9enrSTdnfX32SNdu3p4ohgCbPTPGUDYViakqTSLFi\nohOKjYwo6dXfnwwwDbkRt+25IGvWAIsXZ3+OS0zm5Ke5ahIVEsFSCfIqJwUo2RXIW6sCoETNzp1J\nFVkDldarkD4Fhyw8FY0ADADQgmGY4N8/QuoxVQA3N7Kaq1QBypWj53IaFe3b5625UKECsGEDlT8W\nJYKCYBoSgpiePYWXd/XuDbRtK3r7O3fosVGjvI+TnEwT+P37Wc9x9eq2tllytOqS1/LjB5CeTr/f\nuEEaEpKSlkY6CY8eAZUrU0WJqAl4xw46hiwSNFkWePhQJbUXCsS3b1TSbGgo/jZNmuQuQc1pVNSo\nQXML9//WkHWt5mVUiPJUNGiQvatvnTrAqVP0HSjqfPlC3ltV6UwqQIGNCpZl77Asy7AsW4tlWeff\nP36yGJzMKVWKVsLGxlmeipzJbJMmAX/9JXof2tqkAqnkxkEKZ8MG8IyMENepk/DXk5KoMZCosMSb\nNzR55Dch6OpSe+R9+7KeW7AAePCAfueMCnXxVHTsSOEaQPpa+6VLqQQyIYHOn46O8HJogLwiR45Q\nb4tu3Sh0JC2nTtHEvn+/9PtQRWrWBPr1k2ybyEgKOwkmE757R/8L298tsHV1SVJ64EDZjVXdefuW\nHiU1KliWlHaFGWi/fslufOoK5w1TsXJSoKgpavr7Z/0zihUjoSvByZllaWWZ38rs0yfg8mX5jVPV\n+PoV8PFBbMeO4IkSWbl9m7wQojToV66kSTi/G6u+Pt2Ez56l/wOfT89z25UqRZO3uhgViYl0nQF0\nU5LwhmMQHg4sW0Y3QU9PoFUrmlSFTSZ8Pp0XOzv63dc3bzGx/OBuoGpSvvuHpCTSoPD3F/760KHA\ntm2S7fPWLVLaFbzuHB0p5Jezo7GGLBISKHclL6NCX588mcOGZT0XF0cGRZkcstaTJmk8FYBKKmly\nFC2jYuJEannM8eoVsG5d1t9xcXQD2LQp7/3s2AG0aVN0LGYbG+DoUUT36SP6PVwnwbyS1MRVfevU\niVx7jx8DU6ZQqIkz9LS0yHjhkuNUne/fAU6X4uVL6szKGUr5wefDbulSMoC561RXV/RN7MsX6ohq\nZ5flkg8Lk37svXtTiEDdtC7OnSP1VS4XJyfShHM4b4SgZ7NPH+C//7K/z9+fQqsFOe+FidatKfm9\nZj6dORs1yq5ULCh8JUi5cpQgyyXbFlXKlQP691cpJU2OomNUsCzF4StUyHquZMnsEzRXh55fAle1\narS/N29kPkyVRFsb8PJCes5VgyB2dmQ5C1PV9PMjQ0HcRmzt2tG+zp6lG4OZWXYPx/XrwNy5En0E\npSHoqTA3z/KGiYHVhQswCQ2lltGC1+SSJcIbXHF5JnZ2ZHSVKVOwmxvDkLGobtUMT57Qo6jrrWLF\nrHbl4sKFSwUrQIRpjlhbk+GhSdaUjEuXyLPGwVV45DQq6tShR+5/XFQZMkRlw5KFz6iIj6fEtpxE\nR5M7V9CouHSJyv04OOs3r+oPIKsC5EUu0dDCx4kTdAPPQ3AJALkwbW2F34AuXyZ56pxqhKKwsSFZ\n5IcPqWpEiMKmWsDnkwHBGRVcVYuY7c8TmjXD29WrgQEDsr/w8CFw7FjuDbhQnp0dPdrbF8wgWL0a\nePYM8PKSfh/KgLshCUvmZVny6BgYSLZP7ubGGRWJieRB2rAh+/tq1KAeLxqjghg0iHKi8mPjxuyG\nspkZ0KVL1rXMwbn7i7JRkZysklUfHIXPqOjZM7uhwCGoUcHx+DGtArnkQnHr1ytXJjd8YS8rZVla\nFZ84IV4zLGGr2sxM4PhxoFkzyRpqXbuWdTNr0yb7awcP0uSdn6GjbHg8mihbtaK/JTQq+MbGSGza\nNHceioMDJcDlDKP06UP75uLXderQjU9aXrwgb8eQIdLvQxlwRoVgW3KOpCS6biQpJwXICLGxyTIq\nuH1zYREOPT3SW9EYFcT587l1bYSRs6lYw4bkucjpqTA3J0/T48eyHac6sWcPedlVVK+j8GUYmZpS\nTHXjxuyTsTCjgisrjYykluhc+CM/o8LAgPZT2I2KO3doRbB1q3iVC4sX5473nzlDF7+kbYu1tcmT\nVLZs7kqbzEy64UVG0mpcVdHVJYE1DhsbugllZOS/7bVrKOnri5jevXO/Vrkyed2iorKuYQ7BviJr\nCygbEx9PhlBkJLn1JSnBVCbcjV9Hh861YE4Id+OSRPiK4+LFLI2WnOWkgtStSxU4LKvy3TXlSkIC\n5anllaTJYWNDQmLcOcvr3P39d24tm6LEvn00J+YVjlYihctTweeTqzwiIneHxg4dSPtA8CaUs6zU\nxYVuAuK46ffvB5Yvl824VZUNG+jLm9P9LopGjYD69bM/t3kz3fjat5f8+Lq6VJKZc3JRF62K1FS6\nFjmPSqNGdK3lPEfC2LkTJQ4eBF9YkiQ3SXPlehxLlwrv9igtcXEU/ihXjkIu6kLJksDChRQOynn+\npBG+4qhTRzyjon17qtYpKoncohCnnJTDxoa+J7975aBLF6BFC+HvHTmSpAGKIs+fkxds0CBlj0Qk\nhcuoCAgAxoyh33OqCRYrRjX3gi74nAJYDRuSu19LjNPSsGFWxUNhJCqKRJRGjBC/0iIujlZoXIIc\ny5KRN2eOdG2hfXyEV+Koi1ZFYCDFhG/dkmy79HTAzw/fmzQRft4qVyaDmJuAOfbsIYEtjogIMmDO\nn5d05ERcXFZinDola965k100SRBLSyo3laYsMSAgK4fi3Tval7DGgx07UlWIulQoyQtJjQogy+iL\njBSd98KyVLlXFCtsvL1pTsirEk/JFC6jQjDbO2c52f795E4XpEwZWslwPRKiosSOd+PLF2DLFvEr\nGtSNX7+oj8TIkeJv8/49lSFyQlUMA0ybRoaJNIhyf9rakuGn6kYF1waeu/GkpdEq9tChvLe7eRNI\nTMT3pk2Fv25rS4Zw59ODd7MAACAASURBVM5Zz/H59BxncAHkZXr0SHoBLCcnymvR0VG/CTwpiSqO\ncia0Vq5MN3xpwmb+/iSM9/MnVSjNmSP6vTyeJq9CX5+8v8K8OTnx8iLDlVvoff4s2r3P45HC7po1\nshurOsDnU0l6mzb5FxMokcJlVHDNwfr3p0fBevScKo0AGRQ/f9KNDwC6d6ebojh8/Eh9GNTJLSwJ\nDg40IUvijeEmj/BwWkUfPCifZEpdXTJ4cibJqRpc8zAuz0FPjwzbZ8/y3u7UKcDICD/q1RP/WF+/\nkodDMFu+WDHKHZDWIDh8mFb8FSqoj6fixg3yzkRFUdVRTuGulBTpZbS56+3TJwqnTp4s+r3z51Nb\ngMK66BCH7t3JuyNOpQ2XgKmjQzlT0dG5kzQ5dHSoh5Bgs7GigJYWzR+CWksqSOEzKhiG3MCXLmWt\ndDMzyQgQTNLkyKlTIW4CV9Wq9FgYkzXfvMmdkyIOlpY0OYSH02q8f3/5rdaOHZPMi6IMcnoqxO1U\nmpICdOwINq/JeOXK7L1WBDUqBLG3L7iXQRb7UBRhYeSdMTIir03OCpC5c8Uvbc4JZ1RERFCisKBk\nd04GDqQk0S1bpDtWUSM5GVixgoyQ6GhaEIoyKgDqwvvyZdETwapRgzyIKkzhMypsbLIMBa4jZFQU\nucyEGRW7d2d114yJEd+oMDOji74wGhULF1L+iTQrOq6sdNMmwNmZVmtFlZxGBUBGV34htr17825v\nzu3b3z+rkiQ+ntT1choVlSpJZxB8/Ej7OnWKhKLycvWrElyZXalSNP6cRsW3b1ldMSWFMyoePqTJ\n3dtb9HsdHMibsWVL3sZHYcbBgQwFcWBZYMYMErbT1gYmTMjK5xFGs2b0KGm+kirB51PFizgkJVFy\nZkFk9xVE4TIqWrakixGgC5Sz6ISVk3K8fEn5FklJFAqRJFZVrVrhMyq+fyddir59JdOV4KhYkdzO\noaEUHpJXSd369bTqL0grcXnTqhWVdQp6HCws8jYqOEMuv/NWuTIZypyHokMHEsThPGgc7u6Aq6v4\n0uAcsbFZOStt2lC4SR349IkWBnp69H0XZlRIU/kBZBkV3I0sv1yBv/6i4/n4SHc8dSYujoxZcecQ\nExPKwfj2jap3/v2XrltR1KlDjSHVOQRy/z59VlE9agTx9aX7lAqLXnEULqOiV6+sFVWZMuSiDA/P\n26goV45WElwymyT169WqURZyYWoNfegQnQ/B5j6SsGwZVcaYmZFhIi+MjMgAEkdYR1m4uuaOuzs6\n5u3WdXWlpkn5wVUvCErFM0xuY2TkSDISxaloEiQujh6trChp99499XA1f/qUleDn5ETnSdDjJok3\nMidGRmTEdelCf+dnVLRoQT0vpGl3r+5wlR/iJsQyTJYAljh5L7q6lIw/f36BhqlUTpwgr0zx4vnn\n5u3fT9dbw4aKGVsBKFxGRXR01sqVizdfugQMHkwhEMHMeA5OqyIpiVz2kvzT5s6l/RYmgZtdu2gy\nlrb7nZ0dJWcOHkwrCXnBuflVuQIkLCx3L5RduyjkJur9oaHCjd+ccGV6nFExdWrecsiSGr5cRZSV\nFZ3jRo3UozNv5cpZrvExY8gYElwtF8RTAdAcEhVFNwNu7hAFw1DfG8GeFkUFScpJOTijYulS8lzk\n511zd6frUx1hWbouWremuXL4cNHf0Y8fKSw0cKBa3GsKj1HB55N7kms0ZW9P8eQLF2iVVqaM8Jp/\nroQpOZnc9ZLUr9vYUIZ9fLzk7mVVJDKSvDvDhkl/8WprU7LVsmWyHVtO1EEAa8IE8p6Jy+nT9ChY\nKioKKytqEc8lHZ47J7wXTVIS5ResXy/+OIAsT4WlJRk5DKMeyZrr1uWtJPrXX0C3btLv/8QJyr4v\nX168ludly9J3QpXDdPLg7Vuad8UpJ+XgjIrPnykMnZ93LTmZEpbv3y/YWJXB48dkrHfrRtfks2ei\njXZvbzI4xBUhVDKFx6iIi6MvLqd4B1As+No1SjwUpQ1QrhwZHB8+0CqRx5PsuJ8/k0t71Sqph64y\nlC1Ln6egvR4YRv6SzpwxqMqeCsEOpRw7d1LtvrBVyenT1DdCHE8Fw5AXbtAgMmgjInInaQIkW5+a\nKrlBYGtLOg+WlhTrLltWPYwKQZKTyeO2Y0fWc1OmkDiVtHAT/8qV4m9z5QqdT2EdfAsr1aoBQ4dK\nlpfl40P5Kp8+5R0i5NDTo/DH0aNSD1Np+PqSsdmpEwlZlS5NDfyEYWdHCwhJDDQlUniMCk6jQtCo\n6N+fXMJr1ohOhrG2JndmSgq5/SVdUZQqRW642bPVOxOZu8lZWJDrUdUxNKSqnRo1lD0S0Xz/nr0X\nB0BeraCgrCZ2HImJwN27NMlIAstS2C8tTXh4D5CuJLRTJzJyuJtCQTueKoL372lyPnOG/jY2phUz\nly+VmkqLB2l1KoCsZE1JZOerVaNFz8aN0h9X3ejTJ7sxJw4WFpTUnJfwlSB6elRdJqgiqy6MHEk6\nPlZW9DkmTiTjMzg493v79ZNeFVcJFG6jokEDYPx4ypjNb/UXHU03AH19yY7LMLT6rFSJhLO4pmTK\ngs+XTnDqyBESDeLOozqwdWtW0pwqIsxTkVen0vXrSTBIXLZvp/1zFUjCPBWAbHQmpC1NVSSRkXT9\ncl4yhqHvPRciCwmhv8XJthcFV44aGir+NmXKUPfkXbuKRj8QPj+3hLw43L1LScrv3onnqQBIryIk\nRHwlZFWhfPnsodFRo8grGBBAf/N41N+EqxwSJ9SmIhRuowKgLptA3kbF3Lkk3SttVripKbX3Tkig\nigdJQyiyZOpUsvYlHcOJE1mxTHUiKUnZIxCNMKOC81zkFMAyM6McDEmEbYoVo8//4gVQvbpo96i9\nPYVHxOmOytGtG7lcOSZMIJetKlc6cRoVgqtcwbLSgjQT4+AalHH5L+LSvj39r1Q5B0gYwcF0Lfz8\nKf424eE0J0paSvviBZWSDh9Ost3i0KQJXZN37kh2LGVy/HhuHRpzczKKuZYGM2Zk3VPUjMJjVNSu\nTa23cxoV//1Hj3kZDFyr5ILcUB0dqSOnvn5u17Yi+fdfeuQS7cTlyxdKUpW09FCZzJ5NNwhVTZLd\nuTN3Wa0oT8WzZ5LH3Lmk4tKlycWfU6OCo1kzaqIlySr5y5fsBoSjI9C4sWpnnwszKjgBLJbNKokt\niFExYAAtQmbOlGw7QYlvdWLbNjImjxwRfxvOcyZObpAgnBdo8GDSeBGH+vXJgFEnY23RIrpX5IRr\nQLd8OeVXjBuX1SBTjVCjO0g+ODnRTSZnguB//9E/sWVL0dtySX8549+SMmQIxb6KFaOmWl5elEyn\nyJvevHn0KKmmQFyc9PLFyqJ0aQr1qKp+Qu/elJQpSOnSdHPOGWabPFmyShEgd1mpKFq2pO6axYqJ\nv++c18OvX7TyFFZhoipERVE+kODnbNiQysvT0mTjqdDXpzwtSfOOqlQhY4Sba9SFzZvJMMvZNykv\nuGtElJErCu7/EhAgfm6boSEJtXGih6oOVzYuSkxuzhwyWFu0oEomNaTwGBXh4cLzASws6B+VV0yK\n+6L37FnwcXAruchIqpFv04ZWlIqSV+U6W0qa2xEfr35GhSq3QE9JodrynB6j6tUpobd+/ezPP38u\nedKpqSkp8s2cCYwenfd7JTW+4uKyawDweJR8J6nbX5E4Ouau5e/dm1bZBgZkVBgYyFc/RRQlSpAx\nIk3LdWXCMJRUePOm+Dk1L1+S8SysLXxecEbF6NH5G8qCSKP8qyw4zRJRRsXQoSRtcPx4VqhNzSg8\nRsXgwdL3mOeMClmuInr0IMPi0CFydc+YIbt958X793TBikraE0XLltROWJ1QtFYFy5LnYeHC/N/7\n5g2tNm7fzv+9CQlkEEtTycL1rckv3FWjBtXDiwOfT2MSNCpMTMiAUeUKkGHDSMBOGCxLSb3r1ysv\nhBMbmxVqVQfu3yfRM1dXCouK6614+ZKMZ0kR9CCJm6gJ0Jzn7q4e4mwnTgB164qu1KpYka5hLkyq\nhhQeo+LLl9z5FOJSvjzFs7gGULJCX58MncmTSVlPEXXq8+fTSkySluUAGT/SSnMrC0V7KmJjqRxU\nnNJhYc3EALq5Va+evSadK3mUxqiYO5eus/yMyLp1xU9my8ig1WmDBtmfV/UKEGEu858/KVa/ejXd\nIDkjTBl4eOTvUVIlbt0ib6uTE81ff/8t3najRknXQdjCgkorjYwk83KUKEGdaa9elfyYiuTnT/Jg\nFkR8TQ0oPEbF16/SGxUODpRUx4UOZM348VT2pAjxkrg4qsdXt4QwaShWjG6qiuqEylUSiTN5cdUd\nOfN0GIaqbD5+zHquIEZFTAyFNvKr62/cmDxngscVhb4+ddfMqcWgyi3Q+Xwyphcvzv68kRG99v49\nfQeV6SmwtVUvT8W9exSusbEBPD3FzyMZNow8tZLCMHQ9ly4tmTfJyIi8rNevS35MRWJkRAnZ06Yp\neyRypXAYFUlJZAFKa1QA5FGQJJFNEszNSSkRkG9JXloa1YcfOyZZq+rgYMqnUAf3YU4WLKAbpiKQ\npKJGlKcCyN2ptFMnirVKE37jlGKFSdAL4u5Oj+J4K3g84SXJ9vZkrKqi1kJMDIlaCXMbc2WlnTpR\nMreyKFNGfYwKliWjolGjrOd2786/6iUmBnj9Wvqyeh8f6QzX5s3Jiyhrb7M8UCPNCWkoHEaFKI0K\nVYJlyYKXZ5ay4E1PkkTN2Fi6yQm26FYX0tIkEyIqCFyTLe64eZGfUSGoU1GqFMX7pYn1jx1LJWj5\nuZsdHcloFseo8PeniS9n58QRI+jmLKlAnCLgPHNc6aYgnFFR0GZiBcXWlr6jqmiU5eTtW5oXBBss\nhoaSOnFsrOjtDh2iqg/B74ok+PpSxZykNG9OHqm8ru8+fYBZs6QblywYPlz9QsxSIBOjgmGYNgzD\nvGYYJoxhGAVlJApgYwPs3ZvdqlY1GIayeXfskJ9qpbRGhWBHSnVj5UrA2ZlUU+UNd367d89fDKhT\nJ2p5LaxM2dw8u6di586s2n5JMTCgWHd+N3ptbVIgHTo0/31ynzPn2EuUoNwNVdQyEaZRwVGhAq2e\nf/1SvlEBqEdoMi2NeqQIegGHDKF8G1F9lAC6jq2spD/PXbpkF10TFzc3oEMH0ZU9iYnkBZF3o8O8\nePxY+YrLCqDAswPDMNoANgFoC6A6gD4Mw0iR+lsALCyosZKkYiuKZto0SiaTV/1xpUqkj9Gxo+Tl\ng4D6lZQCFEtlWXJ9ypu4OFrtHzuWf3a2nR3plAgLSzRvnpUEGRdHHoALF2Q+3Fz06ZNbN0MYooxM\nHo8SHq9ckf3YCgoXVhBmVLRsmZUcJ61qrixwd6dFhTp8zxwdqYdKlSpZzzk5UcLvrl2iw7gvXlCv\nE0VjaAicPZvV9j4n3Pdr4ECFDSkXBcn7UyNkEdypByCMZdl3AMAwjA+AzgByqeQEBgbK4HC5eXry\nJHQSEpBSs6ZqrqIEqNCqFcw3bUJomzb/b+/M46Kq3j/+OTOgIJsIgizu+XPDBBVzyy1Nc8tKLUOT\nNK0My/rmki2a3699M82lTbM0s/KbpZZoZVlZVpqJqKlprqgooIKQIOtwfn88c52FO/sdZjvv14vX\nMDN37j1czpzznOc8z+eBxhkxHGo14sLDEZ2Xh8x9+6xyqcccPow4APvPngW3YhXlrP+jPaj9/JAE\nIHvzZuSGhDj1Wv4DB6JOUhJKMjJogjUTxxB09ChUpaW4LjeJ33UXPWZkIDgzE20AnPD3xz8m7qtS\n95tVViL0jz9QHhuLMjMGeOzhw4gFkHHqVI103cT581Fw550476hQnMIE+/khfMwYXDh/vqYnIDIS\n9YYPR7tNm3CysBBFFu6nU/t3YiJlgbl5xVL19evQyHyfGt5xB5q+9hr++uQT3DAWt+IciYcP41r/\n/jhnwz1U8n77FRZCExAAbrSV2/yDDxAaHo5DU6cCrhi/NBp0zstDTnU1Lrl4/FTifreShPdkUGIG\njgNwQe95tva1WiPyyy/R+rHH3FtCWEvuhAlQ37iBqM8/BwCE7t2LyM2bEbtiBQL//tuhcweeOIGI\n9HQU9e6Nc3PmWK3kWdqiBa6MGAHuSSIyWjRhYShr0gRBR444/VqVjRqhpE0bJA4YgNjVq80eG71u\nHZpYUR47UDu5lNaCl41pNGj57LOIsFDxUF1UhKqQENmAsvL4eNR1w2DD4k6dcGHGDJOGXmVEBLLm\nzEGJK1bREpyj3vHjqHvhguVjXYi6qAiJd9yBhtoxSp+CwYNR1K0bmEz6rt+1a/ArKkKprRo5ChF0\n9CgSBw5EqHEsEIDCPn2Qm5qKOjk5YLbUwFEIv8JCsOpqVHriFrOtcM4d+gEwGsD7es/HA3hTel5Y\nWMilH6XZt28f37dvH+fjx3PepIni53caq1Zxnp1Nvzdtyjk5EzkfM8ax8/7nP3SesjKHmyjHzfvt\nbqSkcB4X5/zrfPop5z/8wHlsLOepqeaPHTCA8+7d5d97803OQ0Pp/zR1Kv1eXV3jMKfc727dOO/V\ny/wxmzdzPn++/Htjx3IeH69sm5QgL4/z8nL590pLOWeM83//2+wpaqV/h4Vxnpbm3Gs4ytatNI78\n9JNtnysp4fyLLzg/dcqqwxW/32VlnAcEcD59uvz7GzbQ33X4sHLXtJYLFzgfMoTGDxeh5P02mtcN\nbAIlPBXZABrrPY8HcEmB81qPI8JXrmDyZN3e79atpB8wbBjlMDtCfj7lkms0FFthLkpbH2t19t2V\n6dOBjz5yfgXNF16goMqmTS0LbhUWmq4lo1JRYOm1a6RR0a5d7XnZevUioaCyMtPH3HMP8OKL8u91\n7UrxC+4WbNinT83ibRIBAdQ31q51fZVVT9Cq2L2bvFTJyaaPyc2tmfpZrx7FEdkqvKcUdetStoqx\nXsWuXTTGNmpEz3Nza79t8fFUF6p//9q/di2jhFGxD0ArxlhzxlgdAA8ASFfgvNaTm6vrMJ5Ghw7U\n4Tp2pJQ3Ryb4q1cpuO7MGYqG/vFH6z7Xpw8wZIj913U1XbpQ8KOzJ2apyJY1RoVc2XMJKcizsJCM\nSuMyyM7k9ttJz8HcvuqVK6aNjp49acJxt8JiFy/Kp5Pq4w4S455gVPz2G1V9lqpmGlNdTd85Y4XN\nXbusk6V3Jv36kciZFHzOOTBuHCl1utKo8CEcNio451UA0gB8C+AYgM8450cdPa9NeJqnQo4XX6R0\nI3PCKKNGAevWmX5fKgIllXC3Nn2poMD2qovuxvbtzs1K0GjICIiIIKPiwgXzMSvWGBXXrlFRsNrc\ng5Z0B3bvNn1M9+6m8+k7daK/beBA5dtmL//8QwJ45lRFpaBoV8ddubtRUVFBnixz6fkqFSlmbttm\nqEcxfz7w7LPOb6M5+vWjx59/pscDB+i7evfdujnCWSn95liyhMYNS/o2XoAi0l6c868BfK3Euezi\ns89cm3+uBJZ0BvLzqRjNpk1ASop8QFp+PtU5iIigL74tRoUnpLmZ44UXaLthwADnnL+wkFY9ERGU\nMsc5DRCBgfLHb9tmevtDen3XLvJU6K+inE1kJGkJmKuWaVz2XB+12vQK1lWY06iQOHnSUHDMVcTH\n0/eyosI9q2tqNMAbb5Dn1Bzjx1Nxts8+09Uz+esv+zQmlCQ5mfRYpJTtLVtoLBw2jBZO9eq5xlNx\n/jwtItxROE5h3Dv/0lr696dtBE9n8mTgrbfk35PqTgCmYyU2bwZWraIvUcOG1hkVnHuHUdG1K7Bv\nn9UZLzajr+UxcCCwcKFpgwKgwc1U2lV8POmqHD9OYjzOarMp2rQxnXpdVaXzyJjiu+9I+8FdlCGt\nMSqiotyj7PjYsaSZ4GqPiSkCA2kcslSxOCmJYoE++oieFxaSB8Ce6qRKUqcOFTSTqpxu2UJel8hI\nuufLl7umoJePaFQAXmBU+F29SmJE9srCuhN//GFaBEnfqLhkIg42NlZXuTM62jqj4vp1mki8waj4\n5x8qOe4MmjenwLThw+n59eumVTyLi6lOgiktgvh4ChoMCCCvRW0PNmfO0OpSLoVZWs2bMyrKyyle\nx130Slq0ICPPWDfBHWndmopz+fu7uiXy7NxpnYYGY+St2LOHxiNJEdaVKbsS+fnABx9QEPSff9LW\nh8QjjxhKj9cWOTmeG/dnIx5vVAQfPQqMGUPa/p5OQoLpDBBLRkVVFbBggW6gX7rUdAS/MTNn1ixz\n7WlIKyuZHHVF8PenqPawMDIaQkOpkqccFy9STMLvv5s+H+c04LVv75pV67vvygfyWqOuKlWFNReX\nYQ9nz5JhbSstWlAflmKJ3JnSUlo9nzzp6pbUhHPaWn3pJeuOnzyZApZjY3VGhas9FQDd24kTaTvm\n0iWSF5e4eJE8mrWNJycT2IjHGxX+0laAN/zDOnSgvTe5Snvh4bTCAeSNioICiiuQJtX+/c2nhEmE\nhtIqT6pi6am0bk1Bj86S687MpDoj16/T3myDBqYzQMwVE5OIjKRJ2Z5y547SvDl5R+Qi9cPD6e80\nJ+cdGUlbCUobFZ06AbfdRvEGtnDmjHUl3d2B8nJKu0yv3QQ5q7h4kVbUt91m3fEREUBjrZrA/ffT\nZO0i4SsDOnem7+jOnTQv6BvICxe6Jsh4yBDnxXu5Gd5hVDDmGasUS0hxIXLeirffpoGoceOa7wG6\nFabktj5zhoI6LeXll5XRJOjq/H1HUatp5e+suio//0wpdFLKr7m0UmkLwZyUtRSP4AqjgjFKLZWr\n6BgVRTVq9Gs+yNGjBxkVSvYb6b7Zqnj49NMUiOcJhIVR0St3zACRDPLOna3/zNmzwNChwOHDZIia\nka6vNfz9yeu7YkVNz2WjRjTe1XY80NKl5NnxAbzDqGjY0Dtq1HfoQO5D4wqY0sBdpw6tyOQ6p+Sx\nkYyKTZsoBbW42Pw1t2yhyc/eKpnuRLNmjg1q5gb6ggIKbpS8D+aMCms8FS1b0or18cfta6uj9OxJ\nqXbGktH5+aTnoNGY//yAATSJyHnV7OHKFXpctMh0pUk58vPJmDQXpOlOMEYxNe4mHgaQUaFSUX0S\na4mMJI9A9+6u16jQR/objA1UKX6pNjNAqqtrPxjbhXi+UZGf7x1bHwDQpAkFFxm751aupEwC/XLZ\nxkieishIerRWq0IKcPX0QE2ADK7HHqNVk6189hl5geRW7wDd3/BwXdaEZFTIrdStMSrCw+n/6aqA\nve7dyQgzntzWrQNuucVyKfmUFAoqVqqwmBQz1KoVsHGjdR6Qv/+mWKBLl4C0NGXaURu4q1ZFZiYF\nWtqSMhwSotuW3b7dOe2yh0WLaGFlrLfhCgGsPXtoQWitGKGH4/HL+/MzZqC+O+zjOZP9+2kCql8f\nmDePshA+/tjwGGNPhVTiOS+PJglTSEaFpVLenoBaTQGI7dvbnmIsBVWaCjSThMUk7r2XvA3V1TW9\nI6NHU+CoOWPX1au6Ll3kg5uNPTKWUEpvITycsgmyskh2fd8+83Ed167RhKFS0UrZFRH99hIf754T\nzKpV1mvb6PPAA8CXX7pOnluO4GD6jhrjCqMiN5c8f75QTAxe4KmoiInxDo0KiSVLdOJKEgcOUBAb\nY7TCkRuQUlNpQJDcwNZ6KvLzyd3sDaIscXEUiW5PBsHhw+QyNeWxKSgwHBR69wamTZPfbgkLA269\n1bwX4ttvgffes72dSmEq48TYI2OOxx83P/HbQnIyeUnGjaN7+uWX5o8PDwdef53+155kUAAUUO1O\nq3qJ2FjSn7CVMWPISE5NVbxJinPLLcCGDdYHoyqBpODpLR51C3i2UVFdjaj162lP1Vvw9ydRJMmS\nrqigCU/6ssfEkKFgvOft50feCWmSs2X7w5ss6K5dbTcqpAJsR46QwqUc6emG71VVURyK3P397jvA\nQml03Hkn5cy7ko8+okwQ/Tofxh4Zc8TFUd9UQqny4kWdYmnv3qaNirVrgR076PcJE9wj28BWbrnF\nPVIv9cnMBBYvti9GhjHKHrPGEHU1ISFkBEniWLVBbi7dG2lr2svxgF5gGr+iIjRZulSn8+4NSF4X\nKS7gr78o2EgyKmJjyeV++bLh5z7+mFZuElFRwE8/WVaPu+++moWBPJmuXUkAy1z8iTFHj1JAa1WV\nTiHQmMBAw8n22jWaGD79tOaxH38M/PvftrXbFYSE0HZDZqbuNVuMTMlDsGePY+0oLKQtAan/3n03\n/U+MtRyuX6e+umSJY9dzNbm5pJzrTmmwW7eS1oc7ZG84m99+s8+baS+5uYYLPi/Ho40Kr9KokEhI\noEfJqAgIoBWt5K6TLGxjrYrPPzcsNubnR9VHpdgKUwwfDkyd6ni73YWuXWn1bZzVYI7GjckQaNfO\ndADdzJnkgZCIjCRDQy4DxFwxMXdCErHSNwqefhqYPdu6z3ftSiswR/UqpCBNyaCWFBB/+MHwuNde\nI2N6/nzHrudqcnJo68xZmir2kJlJacSeXljQGtLSatfoHzDAswKJHcSjAzVvGhXepKkeGUlGkqRV\n0aaN4d578+YU8W6conT1ak332jffkGvfXA7/6dMUR+ANgZoAiX5ZIzOsT3g4ZTN89x0F/RlTUUHR\n5KGhuoJJjJlOKy0qUi4rwplER1N/0jcqhgyx/vPBwVR4ylGjQvKUSN64Zs0oGFk/8C87mzwZY8da\nJ+rmzkgl2o0N2Bs3dH+jueBqZ7B/P9C3b+1e01U0alS7gZoPPFB713IDvMNT4U1GBUABT1KedXa2\noQFx6600CRgPrHJ74YsWUcEqc/ToATz3nMNNdhukAMSyMssaHRLr1pFxFR9PHiDjeBVTabfmjApP\n8FQA5K3QF7H67TfbSkNPn04GmSNkZtK91/eqGWcSvPgi/V9eecWxa7kDkZGUMWNsVKxeTRLZSUk1\ns7ucSV4exbR06lR713QlMTG1W/48L08nmucDeIdR4U3bHwAZAk89RcZE27bAv/5l+TNynoro6Jqx\nF/p4S4VSY4qKVwu5+AAAGfxJREFUaLWrH2NiisuXKeBv0yaa2DSamvfMWK1UQs6o0GjoeE/pk/fc\nQyJpFRX006sX8P771n/+oYeozoIjZGbWnNCKiykTZP16et69OzB3rmcGZhrDGAW5GhsVERH0/0hK\novTa8eMNg2idxYkTtF1qi5KmJ9OoEU30tSFIVV1N/2tr66l4AR69/ZE3diyuDRyIDrYo8HkKZWUU\nqFZcXDNlduBA8mQsWkTPq6spiM140rNUqVSqUOpN2R8AeQmSkykYbuZM8yXKJX2KHj1oMB83jgIY\n9TFlVDzyCG0XcK7zkKjVFA9jSTzKXRg1in4AnUvY1v6Qk0MZWJIIkq28/HLN7begIPKaFBYCDz4I\nTJli37ndFTkBrAcfpB+pOOD+/bWT6n377TQW+EggIWJi6B4XFDg/IyM/nxYa3uZNN4NHeyp4QADK\npf1Jb+LPP2lQ/c9/6Llx7nh+vqGstkpFRoixNRwdTYOFKZ17aypSeirPPkveG1PZHBJ79uhWaUFB\nNQ0KQJdmZzzZJidTUKFkUFRUkIEXFma6Ros7UllJ7m9pm8dWo+LJJylNz16X8pgxNVVkGSMZ86++\nIuPZ29zH//ufYYryjh2676mfH3llvvyS7kNWFmlbOLNeRUCA+5ZjV5p776Utv9BQ51/LxzQqAA83\nKryWli1p9fvZZ/RFNy46FRtbM/uDsZqDgiWtCnsnEU+gd28yFF5/3bybc/duMtoCA6mC5IwZJEyl\nz/DhNPF27Gj4+o0bFNwpZZosX07HeIqXQmLYMBpo7TUy//tfunfPPGP7tQ8fpvQ+OVnukSPpceZM\n76udEBenm9SysoDBg6mCpj6S7kN6OnkuEhNNy8g7wgMP6LaZfIG4ONpOU0IJ1hKS98+HPBUu2/7g\nnKOgoADVDgwWwdr0pytSMSJv4t13aesjPLymIM2jj5LrVPq7i4pIz6J9e0Pre9AgCkAMDNQdq09U\nFLmYY2Nl31epVGjQoAGYKfVFd4Yx8laMHUsZHXfcUfMYjYZczJIIVZ06wBtv0GBu7MqXK1h39Sod\nt3Il7X8vXkxGRW2sgJSkUycyvqQ6ILYambfcQsG+8+ZRfIUtpaWXLKEsJTkvR8+e5MWYPLl2JoDa\n5NAh8lbMnk39BwAmTZI/9sknKbZqyhQylp94ggwQW2p0mOLqVVKYVEoZ1RMoLaX6MklJuhR+W7h8\nGfjwQ0q/tlTIUjIqfMhT4TKjoqCgAEFBQQgICLD7HPW0X6ogb4yp6NeP9pNbtqy539ypE1m+kZE6\nD0VsLHVcW++FGTd9WVkZCgoKEOGpnoxRo2hV0quX/PtqNRln5eX03FQA3fr1VEJ5+XLD12Nj6Rzn\nzlHdhMuXPTMgq3t38sT4+ZHeiT3pjLNmUcbCE0+Q98HaWID9+3US9Mb4+dGE542cPk2Gwd13U2Ds\nyJHmt8wGDqT7+vzzZPgGB1vO7LIGe8qdezoaDQUYv/qqfUbF3LlkCEZGAg8/bP7YxETyMnlKFV0F\ncNn2R3V1tUMGhdcjBRfKpSYGBZGhIXl5pP1mY6tZoyFL2VRqZUUFufBNVIQMCAhwyJPkcvz8KAjN\nnKelfn3dNhEgH0C3cydtRcmdPz6eqmUuXEh5/qYMGHemWzd6zMoiQ8weT0tAAPD22ySIZe3ef2kp\nedh8JZVRHykW7PXXadvJGnGk4GAybH/6iVJslcBYI8QXCA6mH3u1KpYupceFC2umnxtz663AnDnm\ng8W9DBFT4a7Ur08Dj9yEX78+eTCkaG1TRoVUgOz6dflrXL1Kg7o1ZaY9mRdekHctL1pEE6E+8fE1\ny4Gbk65u2hTYvJkGKE/0UgC0DdayJXlb5MS/rOXOO8lbYa3w1+HDNCj7slGxaRMpudoiPNWnjzJb\nHwB5Klq29AyxNiVxRKsiIIAWGX//Tf8/c5w5UzP+zcsRRoW7EhRE2xnm0rwkY6CqigwI44I+KhV9\nvrJS/vMaDR3jCYWAHKGqCvjgA/rR5513aNWnT1wcUFJiaGjl55sOXmzalAaoLVs8W5Fw0SLaRhs7\n1vFz/fknxQpYMlalVbIvGhXR0fTdfO45ql1ka9zSm29SKq6jhIXZFgPjLdirqpmeTp6HoUNJ7XjB\nAvP9fNIk4P777W+nB+Lls4mXUlkJHDxoGFxZp478wOTvb9qoqKpCVl4e1nt75PfcuTRwTpoErFlD\nr+XkkLvfuGz2q6/Se/r30lzlztmzgW3bgBEjbJ8Y3Il77qFgQCXSi3/+mVzDzzxjfsBNSSGjrmlT\nx6/paajVugBpe7QSMjNp68TRNNPVq4EVKxw7hydiylOxbBltYZra1li7ltLUAwMprmLtWvPf+9xc\nn8r8ADxc/MrbqKqqgp+laGKAtjmqqnTGQny8zp1q6lj5C5JRsXEjHnzwQfsa7QkEBlLO/z33kGFR\nXa2bPI2NCjnPkFptOnrb3UpY20tVFblylXCDp6VRIOKyZeSmX7BA/riQEHLl+yrHj9u/jTFuHE1o\nW7dShow96Iu2+RqLFsl7aJ9+mh6vXjWMtQIooHvHDjKGGbOu7+bk+JwnyKc9FVlZWWjTpg0eeeQR\nJCQkICUlBd9//z169uyJVq1a4Y8//kBJSQkmTpyI5ORkJCUlYcuWLTc/e/vtt6NTp07o1KkTdmuL\nKuXk5KB3795ITExEQkICfvnlFwC69FcA2LhxI1JTUwEAqampeOaZZ9CvXz/MmjXL5PXWrl2LkSNH\nYvjw4WjeogXe2rQJS1asQFJSErp164YCrebE6dOnMXjwYHTu3Bm33347jp8/D1RWIjU1FU8++SR6\n9OiBFi1aYOPGjYBGg9nLluGXX35BYmIilkoBSN6IZFgMH05Brrt3U4aCcYDahQu0BaBfJOvgQd9Z\nzRUWOn4OxiiYbcoUqtUhibjpU1FBHiSpcJ4v4khcRN++tAL+5BP7z/Haa2QU14YUuLvRpEnNhdjp\n0/S4bFlNgwIAfvmFgt6HDtW9lp9PmST6FYwlSksp3d+H0kkBd/JUyO1HjxlDZblv3JCtnug3diyq\nxo0jq1KSGpYw3is3walTp/D5559j1apVSE5Oxvr16/Hrr78iPT0dr7zyCtq1a4f+/ftjzZo1KCws\nRNeuXTFgwABERUVhx44dCAgIwMmTJzF27FhkZGRg/fr1GDRoEJ5//nloNBrcuHHDYhtOnDiB77//\nHmq1GnPmzJG9HgAcOXIEBw4cQFlZGW5p0QILZ8zAgQMH8PSkSVj39tuY/uKLmDJlClauXIlWrVph\n7969mDp7Nn7UlpDOycnBr7/+iuPHj2PEiBEYlZmJV195BYvfeQfbtm2z6n55NAEBFPvAGPWP3r1r\n6h+oVMCnn1J/NPZieDN+frRP37y5MudjjAyxsjISE5s5k7biTp2i1d7XX5NaZtu29qX1+TpqNUl6\nL18uvz137hwdI+fB5JwqH7/0EpUA8MUsvJMnSavikUeAhg3pNUnhdPhw8jCo1YZF7rZto3ulr3kT\nEkJjyZkz5JHQ9/xIooPCqPAtmjdvjg7a2hrt27fHHXfcAcYYOnTogKysLGRnZyM9PR2LFy8GQNoN\n58+fR2xsLNLS0nDw4EGo1WqcOHECAJCcnIyJEyeisrISI0eORKJUbdQMo0ePhlrrdv/uu+9krwcA\n/fr1Q0hICEJCQhAWEoLh2vTFDk2a4M+zZ1FcXIzdu3dj9OjRN89dXl5+0803cuRIqFQqtGvXDnl5\neZQ6qFQUuacgfenffFN+v18KjpXSSvPyaMX9r3+REeLNWJPWaAsqFe3ZV1SQ8ZaaSqJBAMVRPPqo\n4apPYBvjxlH2lnF20qFD1FdLS0k4bM4cnU7CjRu0UPvwQxJuq81qqO7E6dN0X/r00RkV27eTgGBE\nBHmB0tLIm6PPiBGGY2adOqTRkpYG7NpluCUSHk73uWdP5/89boRDRgVjbBGA4QAqAJwG8DDn3D7/\nqTnPQr16su9XlZTQL5GRVnsmjKmrJ9KjUqluPlepVKiqqoJarcamTZvQunVrg8/NmzcP0dHROHTo\nkIHmRu/evbFr1y589dVXGD9+PGbMmIGHHnrIQJWyzMjdqC/exTmXvd7evXsN2+rnh7pRUQDnUHGO\nqupqVFdXo379+jh48KDugzdukEu/utrg85xzcnVXVNh6y7wHuf1ktZoGFMmoyMmhiO8JE2q3bd6C\nn58u1XnUKOC222hF17Kl7+7nK0ViInl8jImOpmDDuDhKE169Gpg2jSbIuXOBdetI/fSFF3yniJgx\nkvdAP1jziy9orAwLI8/46tWUYSNpTCxbJn+uiRNpi+/ll4Eff9S9HhZGWyM+hqMxFTsAJHDObwVw\nAsBzjjfJvRg0aBDefPNNmoQBHDhwAABQVFSEmJgYqFQqfPTRR9Boo4XPnTuHqKgoTJ48GZMmTUKm\nNm0uOjoax44dQ3V1Nb744gubr1cDlYq+GBoNrbhVKoSGhqJ58+b4/PPPAZDhcGj/ftNlfk+dQgjn\nuG5Kx8JX0VfV9Ob6KLXNsGHA44+TYqcwKJQjO5u2gHNzKeC2USPaWlq1isqaP/AAcO0a3fMXXqDt\np7lzfdegAHQZGfpppYGBwP/9H/0+dSp997Vjqdm4k8BAygLbudPQqDh7lgoWWhLI8jIc8lRwzvWj\nU34HMMrUsQCQkZFx8/fg4OCbMtuOUiJ5LGzkxo0bqK6uvvn5qqoqlJWVoaSk5OZ7zzzzDGbOnImE\nhARwztG0adObgZYpKSnYsGEDevfujaCgIJSUlODbb7/FsmXL4O/vj6CgILz33nsoKSnBvHnzMHTo\nUMTFxaFdu3YoKSlBSUmJwTUBmLxeeXk5Kisrbx7HOUdJcTHqaQcGDecoKSnBe++9h+nTp2P+/Pmo\nrKzE6JEj0XHUKGgqKw2uI9G6deub2z3jxo1DmpELPD8/H+fOnTN4Tf//6I00i4qCuqgIpzMyEP7H\nH2gJ4GhODkpd9Hd7+/12Nzzpfvvl56PjkCG4PHo0wnbvRnHHjsiaO9fwoLQ0WnhIf1dYmO53N8Al\n91ujQWeVCjmZmbiUkYHYFSugCQtDnpQFFxKC9s2aQfPaazjerh3+b+pUVIWE4Ixx0TctrEsXxE6Y\ngMsVFajU/j2x776LmDVrsH/3brcy4JS4361atTL5HuMKqSkyxrYC2MA5N9ikKyoqunmBkydP3nw9\nODgYjT2pPLSboS4uRsCFCyiPiYF/fj4qGjWCRqbuB6uoQL3Tp1EeE4MqvXRBVVkZAs+eRVl8PDRy\n5b61XLhwAcWmZL59gIabNqHpq6/i0Ndfo1LaexUI3IjWU6Yg5MABaAIDceLtt1GijRETmOfWu+5C\nUY8eOP/cc+g4cCAK+/VDlp4qbtSGDWi8ZAn+WrcObSdMQF5KCi5Om2b1+ZsuWID6u3bhkHHVYy9A\n36gICwszcDta9FQwxr4HIBe++jznfIv2mOcBVAEwm9/URa8S3pUrVxwuBCatur2yoJgltO7juvXq\nAXFxMBm/rY31qKtSoa7+fdK65AKCgswWIYuIiECbNm0A6CzcLr5U0fDQIaBJE3Ts16/Wo+R98n67\nEI+937NmAZMnQ/3FF2grV43XTXH5/T52DA3r10fDXbuA4mJETpyISP22tG4NpKWhfUYGoNEgZtIk\nxFhq6969JLC3YgWNsY0bu01/UvJ+FxlXztbDYkwF53wA5zxB5kcyKCYAGAYghSvl9hBYxt+fHk2p\nZUqo1RR/YbyvZ6peiIDKwffqRWlnkyZRep4vpt0JPIP776f9fw8yKNyCyEga/7ZuJc0aY5GqkBDK\nUtq2jUThrEkxP3GCYlk2b6YgUB9LJwUcDNRkjA0GMAvACM65ZUEGgXJIxkBeHhW2MRcMlJRUM189\nJARo1aqmToOAglp/+40CrQQCT0AsDmxn2zYKsExPJ4NMzmNbWkrKpdHR1t3jBx8k7ZWXXqLChD4m\n0Q04nv3xFoAQADsYYwcZYysVaJPAGhgjb0V5OVUhNVcUTIq013ck+ftTwJYbBRC5DZIBlp0NPPss\n8MQTrm2PQCBQnt9/pxo17doBeto+BgQGkufBTMaeAWo1MH8+cOwYpaU+9ZRy7fUQHM3+uEWphgjs\nQKq0Z0nDn3MSewkM1IngFBfTFoivlTy2hthYeszOppQwsfUhEHgf0tbE++/Ly3JLTJ5s23nvvZc0\nRHbu9B15fz18uvaHxxMdDQQHW3bLMUaGRX6+zltx5QqgVeoUGFG3LsnzXrxovkKpQCDwXOS0KpRA\npSIPyKOPyusDeTk+b1S88cYbaNu2LcLDw/Hqq68CILVMSSZ77dq1uHTpkiubaBqNBigpsW6vr0ED\nUs+U0kOrqsQ+rDn69aOVjLEEskAg8A5CQ+nxv/9V/tx33kn1bvRUjH0Fn59V3nnnHXzzzTdobqKQ\n0tq1a5GQkIBYySVuBVaXMHeUvDwyFMLCLB9bvz5Z0Pn5FKQpjArzfPopeXUWLNCVSRcIBN5Dr15U\nUGzePFe3xKvwaU/FY489hjNnzmDEiBFYunRpDTXJjRs3IiMjAykpKUhMTERpaSn279+PPn36oHPn\nzhg0aBBytNrxffv2xZw5c9CnTx8sX768dv4AKa3UmrQltZoK3Fy7Ri45jUYEaVqitBRITqYsGYFA\n4F0EBlK1VinOTKAIbrNU7Tt9rc2fkeptqGUmx5+WpVr8/MqVK7F9+3bs3LlTtvT3qFGj8NZbb2Hx\n4sXo0qULKisrMW3aNGzZsgUNGzbEhg0b8Pzzz2PNmjUAgMLCQvz88882/x12I6WDVlZa52Zr2JCC\nDjkXngpLfPgh1Uc4dkxXUEggEAgEZhGzig38/fffOHLkCAZqRVI0Gg1i9PKQ77///tptkGRM5eZS\nkSZLBAfTD0BqcebSUH0dxkj06uJF6+6tQCAQCNzHqLDGs2BMbct0c87Rvn177NmzR/b9WpcLl1Id\nw8Ot/0x1NZU8Dw0VngpzSFoVrVoBhw8DCQmubY9AIBB4AGKpaoGQkJCbpcFbt26NK1eu3DQqKisr\ncfToUdc1zs8P6NLFtuyEsjLgzBng+HESzhLIo69AKsWuCAQCgcAswqiwQGpqKh577DEkJiZCo9Fg\n48aNmDVrFjp27IjExETs3r3b1U20DSk+oKyMAhEF8ugHb4nsD4FAILAKn/d/Z2VlASDjITU1FQDp\nVEjcd999uO+++24+T0xMxK5du2qc56effnJiKxWEMV0WiIipMI3+VpYt20sCgUDgw4hZxRdp1oxW\n4iEhrm6JezNtGul7iNgTgUAgsAoxWvoiarVPVs+zmZYtqSiQQCAQCKxCGBUCgSl8sMKgQCAQOILL\ntj9UKhXKyspcdXmBFZSVlUEl4i4EAoFAYCUu81Q0aNAABQUFN9M17SE/Px8AECEKPjkFlUqFBiLz\nQSAQCARW4jKjgjHmsDFw7tw5AECbNm2UaJJAIBAIBAIHEL5tgUAgEAgEiiCMCoFAIBAIBIrAOOdO\nvUBRUZFzLyAQCAQCgcAlhIWFMf3nwlMhEAgEAoFAEYRRIRAIBAKBQBGcvv0hEAgEAoHANxCeCoFA\nIBAIBIogjAqBQCAQCASK4NFGBWNsMGPsb8bYKcbYbFe3x9tgjDVmjO1kjB1jjB1ljD2lfb0BY2wH\nY+yk9lHUBlcIxpiaMXaAMbZN+7w5Y2yv9l5vYIzVcXUbvQnGWH3G2EbG2HFtP+8u+rfzYIw9rR1L\njjDG/scYCxB9XDkYY2sYY5cZY0f0XpPtz4x4Qzt//skY66REGzzWqGCMqQG8DeAuAO0AjGWMtXNt\nq7yOKgD/4py3BdANwBPaezwbwA+c81YAftA+FyjDUwCO6T1fCGCp9l5fAzDJJa3yXpYD2M45bwOg\nI+jei/7tBBhjcQCeBNCFc54AQA3gAYg+riRrAQw2es1Uf74LQCvtzxQAK5RogMcaFQC6AjjFOT/D\nOa8A8CmAu13cJq+Cc57DOc/U/n4dNODGge7zh9rDPgQw0jUt9C4YY/EAhgJ4X/ucAegPYKP2EHGv\nFYQxFgqgN4DVAMA5r+CcF0L0b2fiByCQMeYHoB6AHIg+rhic810ACoxeNtWf7wawjhO/A6jPGItx\ntA2ebFTEAbig9zxb+5rACTDGmgFIArAXQDTnPAcgwwNAlOta5lUsAzATQLX2eQSAQs55lfa56OPK\n0gLAFQAfaLec3meMBUH0b6fAOb8IYDGA8yBjogjAfog+7mxM9WenzKGebFQwmddEfqwTYIwFA9gE\nYDrn/B9Xt8cbYYwNA3CZc75f/2WZQ0UfVw4/AJ0ArOCcJwEogdjqcBravfy7ATQHEAsgCOSCN0b0\n8drBKeOLJxsV2QAa6z2PB3DJRW3xWhhj/iCD4hPO+Wbty3mSm0z7eNlV7fMiegIYwRjLAm3l9Qd5\nLuprXcWA6ONKkw0gm3O+V/t8I8jIEP3bOQwAcJZzfoVzXglgM4AeEH3c2Zjqz06ZQz3ZqNgHoJU2\ncrgOKOAn3cVt8iq0e/qrARzjnC/ReysdwATt7xMAbKnttnkbnPPnOOfxnPNmoL78I+c8BcBOAKO0\nh4l7rSCc81wAFxhjrbUv3QHgL4j+7SzOA+jGGKunHVuk+y36uHMx1Z/TATykzQLpBqBI2iZxBI9W\n1GSMDQGt5tQA1nDOF7i4SV4FY6wXgF8AHIZun38OKK7iMwBNQAPFaM65cXCQwE4YY30BPMs5H8YY\nawHyXDQAcADAOM55uSvb500wxhJBgbF1AJwB8DBosSX6txNgjL0M4H5QZtkBAI+A9vFFH1cAxtj/\nAPQFEAkgD8BcAF9Cpj9rDbu3QNkiNwA8zDnPcLgNnmxUCAQCgUAgcB88eftDIBAIBAKBGyGMCoFA\nIBAIBIogjAqBQCAQCASKIIwKgUAgEAgEiiCMCoFAIBAIBIogjAqBQCAQCASKIIwKgUAgEAgEivD/\nlfk/l5oLe+gAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"import math\n",
"\n",
"sensor_var = 30\n",
"process_var = 2\n",
"pos = (100,500)\n",
"process_model = (1, process_var)\n",
"\n",
"zs, ps = [], []\n",
"\n",
"for i in range(100):\n",
" pos = predict(pos, process_model)\n",
"\n",
" z = math.sin(i/3.)*2 + randn()*1.2\n",
" zs.append(z)\n",
" \n",
" pos = update(pos, (z, sensor_var))\n",
" ps.append(pos[0])\n",
"\n",
"plt.plot(zs, c='r', linestyle='dashed', label='measurement')\n",
"plt.plot(ps, c='#004080', label='filter')\n",
"plt.legend(loc='best');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Discussion\n",
"\n",
"This is terrible! The output is not at all like a sin wave, except in the grossest way. With linear systems we could add extreme amounts of noise to our signal and still extract a very accurate result, but here even modest noise creates a very bad result.\n",
"\n",
"If we recall the **g-h Filter** chapter we can understand what is happening here. The structure of the g-h filter requires that the filter output chooses a value part way between the prediction and measurement. A varying signal like this one is always accelerating, whereas our process model assumes constant velocity, so the filter is mathematically guaranteed to always lag the input signal. \n",
"\n",
"Very shortly after practitioners began implementing Kalman filters they recognized the poor performance of them for nonlinear systems and began devising ways of dealing with it. Later chapters are devoted to this problem."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Fixed Gain Filters\n",
"\n",
"Embedded computers usually have extremely limited processors. Many do not have floating point circuitry. These simple equations can impose a heavy burden on the chip. This is less true as technology advances, but do not underestimate the value of spending one dollar less on a processor when you will be buying millions of them.\n",
"\n",
"In the example above the variance of the filter converged to a fixed value. This will always happen if the variance of the measurement and process is a constant. You can take advantage of this fact by running simulations to determine what the variance converges to. Then you can hard code this value into your filter. So long as you initialize the filter to a good starting guess (I recommend using the first measurement as your initial value) the filter will perform very well. For example, the dog tracking filter can be reduced to this:\n",
"\n",
"```python\n",
"def update(x, z):\n",
" K = .13232 # experimentally derived Kalman gain\n",
" y = z - x # residual\n",
" x = x + K*y # posterior\n",
" return x\n",
" \n",
"def predict(x):\n",
" return x + vel*dt\n",
"```\n",
"\n",
"I used the Kalman gain form of the update function to emphasize that we do not need to consider the variances at all. If the variances converge to a single value so does the Kalman gain. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## FilterPy's Implementation\n",
"\n",
"FilterPy implements `predict()` and `update()`. They work not only for the univariate case developed in this chapter, but the more general multivariate case that we learn in subsequent chapters. Because of this their interface is slightly different. They do not take Gaussians as tuples, but as two separately named variables.\n",
"\n",
"`predict()` takes several arguments, but we will only need to use these four:\n",
"\n",
"```python\n",
"predict(x, P, u, Q)\n",
"```\n",
"\n",
"`x` is the state of the system. `P` is the variance of the system. `u` is the movement due to the process, and `Q` is the noise in the process. You will need to used named arguments when you call `predict()` because most of the arguments are optional. The third argument to `predict()` is **not** `u`.\n",
"\n",
"These may strike you as terrible names. They are! As I already mentioned they come from a long history of control theory, and every paper or book you read will use these names. So, we just have to get used to it. Refusing to memorize them means you will never be able to read the literature.\n",
"\n",
"Let's try it for the state $\\mathcal N(10, 3)$ and the movement $\\mathcal N(1, 4)$. We'd expect a final position of 11 (10+1) with a variance of 7 (3+4)."
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(11, 7.000)"
]
},
"execution_count": 31,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"import filterpy.kalman as kf\n",
"kf.predict(x=10, P=3., u=1, Q=4)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"`update` also takes several arguments, but for now you will be interested in these four:\n",
" \n",
"```python\n",
"update(x, P, z, R)\n",
"```\n",
" \n",
"As before, `x` and `P` are the state and variance of the system. `z` is the measurement, and `R` is the measurement variance. Let's perform the last predict statement to get our prior, and then perform an update:"
]
},
{
"cell_type": "code",
"execution_count": 32,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(11.364, 4.455)"
]
},
"execution_count": 32,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x, P = kf.predict(x=10, P=3., u=1, Q=2**2)\n",
"x, P = kf.update(x=x, P=P, z=12, R=3.5**2)\n",
"x, P"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"I gave it a noisy measurement with a big variance, so the estimate remained close to the prior of 11.\n",
"\n",
"One final point. I did not use the variable name `prior` for the output of the predict step. I will not use that variable name in the rest of the book. The Kalman filter equations just use $\\mathbf x$. Both the prior and the posterior are the estimated state of the system, the former is the estimate before the measurement is incorporated, and the latter is after the measurement has been incorporated."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Summary\n",
"\n",
"The Kalman filter that we describe in this chapter is a special, restricted case of the more general filter we will learn next. Most texts do not discuss this one dimensional form. However, I think it is a vital stepping stone. We started the book with the g-h filter, then implemented the discrete Bayes filter, and now implemented the one dimensional Kalman filter. I have tried to show you that each of these filters use the same algorithm and reasoning. The mathematics of the Kalman filter that we will learn shortly is fairly sophisticated, and it can be difficult to understand the underlying simplicity of the filter. That sophistication comes with significant benefits: the generalized filter will markedly outperform the filters in this chapter.\n",
"\n",
"This chapter takes time to assimilate. To truly understand it you will probably have to work through this chapter several times. I encourage you to change the various constants in the code and observe the results. Convince yourself that Gaussians are a good representation of a unimodal belief of the position of a dog in a hallway, the position of an aircraft in the sky, or the temperature of a chemical reaction chamber. Then convince yourself that multiplying Gaussians truly does compute a new belief from your prior belief and the new measurement. Finally, convince yourself that if you are measuring movement, that adding the Gaussians together updates your belief. \n",
"\n",
"Most of all, spend enough time with the **Full Description of the Algorithm** section to ensure you understand the algorithm and how it relates to the g-h filter and discrete Bayes filter. There is just one 'trick' here - selecting a value somewhere between a prediction and a measurement. Each algorithm performs that trick with different math, but all use the same logic."
]
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.3"
},
"widgets": {
"state": {
"58ed37dc23fe44cc9a0e20ffc9c47414": {
"views": [
{
"cell_index": 79
}
]
},
"8b8fb12fbc4048a0af7d29dfc57d5fb9": {
"views": [
{
"cell_index": 29
}
]
},
"ec6802d3ecf14e67bbcf34b40aa0e3c4": {
"views": [
{
"cell_index": 77
}
]
}
},
"version": "1.2.0"
}
},
"nbformat": 4,
"nbformat_minor": 1
}