The saga continues, and here's where things may begin to come as a surprise. The story so far is ultimately an old one: almost all the aforementioned was known even to the world of Antiquity. But even then, there was recognized to be an anomaly: the irrational numbers.
If we continue on our path, we ought now to iterate multiplication to get exponentiation, whose inverse is root-taking. If addition is repeated counting all-at-once, and multiplication is repeated addition all-at-once, then exponentiation is repeated multiplication all-at-once.
$2^{3} = 2 \times 2 \times 2 = 8$
Notice that the order matters:
$3^{2} = 3 \times 3 = 9$.
Root-taking is just the reverse:
$ \sqrt[3] 8 = 2 $
$ \sqrt 9 = 3$
But what about something like $\sqrt 2$?
Indeed, Pythagoras tells us that if we have a right triangle, then the relationship between the sides $a$ and $b$ and the hypoteneuse $c$ is:
$a^{2} + b^{2} = c^{2}$
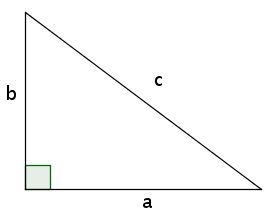
Suppose $a = 1$ and $b = 1$, then:
$ 1^{2} + 1^{2} = c^{2} \rightarrow c = \sqrt 2$
There is a famous proof that the square root of 2 can't be any rational number. It is, like the proof of the infinitude of primes, a proof by contradiction.
Suppose $\sqrt 2 = \frac{p}{q}$, where $\frac{p}{q}$ is a rational number in lowest terms, so that $p$ and $q$ share no prime factors in common. Then:
$\sqrt 2 = \frac{p}{q}$
We can square both sides: $ 2 = \frac{p^{2}}{q^{2}}$. We can also multiply both sides by $q^{2}$. This gives: $2q^{2} = p^{2} $. This says that $p^{2}$ has a factor of $2$, which actually means that $p$ has a factor of $2$ and $p^{2}$ has a factor of $4$. Let's factor out that $4$ by introducing a new symbol $r$.
$ 2q^{2} = 4r^{2}$, where $r^{2} = \frac{p^{2}}{4}$
We can then divide out by 2.
$ q^{2} = 2r^{2}$
This says that $q^{2}$ has a factor of $2$, really a factor of $4$, just as before with $p$. So we've shown that both $p$ and $q$ are even, but we assumed at the beginning that $p$ and $q$ had no factors in common! Therefore our initial assumption was wrong:
$ \sqrt 2 \neq \frac{p}{q} $
In other words, $\sqrt 2$ is not any of our rational numbers. It must be a new kind of number, an irrational number.
It's something to do with 2D. We can use a rational number to convert between a horizontal ruler and a vertical ruler; but we can't use a rational number to convert between either of those two rulers and a ruler at $45^{\circ}$. There is no way to come to a common "1" between them. Think about it like: the triangle is actually being displayed by tiny square pixels on a computer screen. This is no problem if we have horizontal and vertical lines, but a diagonal line would have to zig-zag.
![]()
The idea is that if we kept adding finer and finer zig-zags to the diagonal, we'd get ever closer to the hypoteneuse's "actual" length: $\sqrt 2$. If we assume that we can always refine our zig-zags, we're making an assumption about continuity, that between any two points, there always lies another point between them. If we allow the grid spacing to shrink to 0, then the diagonal's length will be exactly $\sqrt 2$.
Let us observe, however, that whether the length of something is irrational is somewhat in the eye of the beholder. For example, suppose we set $c = 1$ in $a^{2} + b^{2} = c^{2}$, and assume $a=b$.
$2a^{2} = 1$
$ a = b = \frac{1}{\sqrt 2} $
So if we imagine that the hypoteneuse is of length $1$, then the base and height must be $\frac{1}{\sqrt{2}}$!
Imagine instead we'd started with diagonal grid lines. Then the hypoteneuse would be "measurable," but the base and height would have to be approximated with zig-zags, unless we imagined shrinking the grid lines literally to an infinitesimally small size.
How can we work with the $\sqrt 2$ then? Well, we could treat it as a symbol to which we can apply algebra, obviously. But also, we could approximate it.
The following idea works for any $\sqrt n $. We make a starting guess at the $\sqrt n$. Call it $g_{0}$. Now if $g_{0}$ is an overestimate, then $\frac{n}{g_{0}}$ will be an underestimate. Therefore, the average of the two should provide a better approximation.
$g_{1} = \frac{1}{2}(g_{0} + \frac{n}{g_{0}})$
We then make the same argument about $g_{1}$, that if it's an overestimate, then $\frac{n}{g_{1}}$ will be an underestimate, and the average is our next guess $g_{2}$.
$g_{n} = \frac{1}{2}(g_{n-1} + \frac{n}{g_{n-1}})$
Clearly, the longer we do this, the closer our guess will be to the $\sqrt n$, and we say that the $\sqrt n$ is the unique limit of this procedure. And so, we can approximate $\sqrt n$ as closely as we like.
In the case of $\sqrt 2$, we could try:
$g_{0} = 1$
$g_{1} = \frac{1}{2}(1 + 2) = \frac{3}{2} = \textbf{1} .5$
$g_{2} = \frac{1}{2}(\frac{3}{2} + \frac{2}{\frac{3}{2}}) = \frac{17}{12} = \textbf{1.4}16\dots$
$g_{3} = \frac{577}{408}(\frac{17}{12} + \frac{2}{\frac{12}{12}}) = \frac{577}{408} = \textbf{1.41421}5\dots$
$g_{4} = \frac{665857}{470832} = \textbf{1.41421356237}46\dots$
And so, we get a series of fractions that get ever closer to the $\sqrt 2$.
Now, one thing that's nice about having exponents around is we can use a base-n system of representation for our numbers (as we just did).
For example, we write $123 = 1 \times 10^{2} + 2 \times 10^{1} + 3 \times 10^{0} = 100 + 20 + 3$.
This is called "base 10." We fix 10 numerals: $0, 1, 2, 3, 4, 5, 6, 7, 8, 9$, and we can then represent any number as an ordered sequence of these numerals, with the understanding that they weight powers of $10$ in the above sum. Every whole number will have a unique representation of this form.
$ \dots d_{2}d_{1}d_{0} = \dots d_{2} \times b^{2} + d_{1} \times b^{1} + d_{0} \times b^{0}$, for some base $b$.
We can use decimals to represent fractions too:
$ 1.23 = 1 \times 10^0 + 2 \times 10^{-1} \times 10^{-2}$
In other words, we continue with "negative powers," which are defined like:
$ a^{-b} = \frac{1}{a^b}$
So we have:
$ \dots d_{2}d_{1}d_{0}.d_{-1}d_{-2} \dots = \dots d_{2} \times b^{2} + d_{1} \times b^{1} + d_{0} \times b^{0} + d_{-1} \times b^{-1} + d_{-2} \times b^{-2} \dots$, for some base $b$.
Some rational numbers have infinite long decimal expansions which repeat. For example:
$ \frac{1}{3} = 0.\overline{333} $
Irrational numbers have infinitely long decimal expansions which don't repeat, e. g., $\sqrt{2}$.
Clearly, infinity is starting to play an important role at this stage of the game, but it's a different kind of infinity than we've met before. Before we dealt with the infinity of the counting numbers. But now we're dealing with a continuous infinity of rationals and irrationals, and this infinity is actually larger.
The famous proof is thanks to Cantor and very nicely it is known as the "diagonal argument."
Now it depends on the fact that you can prove that there are no more rational numbers than counting numbers: in other words, they are the same size of infinity, which means that can be placed in a 1-to-1 correspondence via some rule for enumerating them. I won't give the full proof, but the intuition is that there is the following more or less obvious enumeration of the rationals:
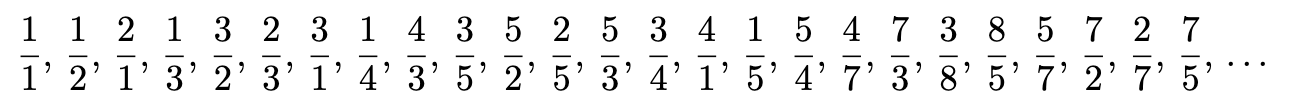
So in what follows, we'll prove the theorem for counting numbers, but it also applies to the rationals as a whole.
Suppose we're working in base-2, and we try to make a list of all the numbers.
$\begin{matrix} 0 & 1 & 0 & 0 & 1 & 1 & \dots \\ 1 & 1 & 1 & 1 & 0 & 0 & \dots \\ 0 & 0 & 1 & 0 & 0 & 1 & \dots \\ 1 & 0 & 0 & 0 & 0 & 1 & \dots \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ddots \\ \end{matrix}$
We think we can do this since it seems by enumeration which can obtain all possible sequences of 0's and 1's (imagine padding with 0's to the left as appropriate):
$ 0 \rightarrow 0 $
$ 1 \rightarrow 1 $
$ 2 \rightarrow 10 $
$ 3 \rightarrow 11 $
$ 4 \rightarrow 100 $
$ 5 \rightarrow 101 $
$ 6 \rightarrow 110 $
$ 7 \rightarrow 1111 $
But now go down the diagonal of our infinite list and flip every $0 \rightarrow 1$ and every $1 \rightarrow 0$.
$\begin{matrix} \textbf{1} & 1 & 0 & 0 & 1 & 1 & \dots \\ 1 & \textbf{0} & 1 & 1 & 0 & 0 & \dots \\ 0 & 0 & \textbf{0} & 0 & 0 & 1 & \dots \\ 1 & 0 & 0 & \textbf{1} & 0 & 1 & \dots \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ddots \\ \end{matrix}$
The sequence of 0's and 1's along the diagonal is different by construction from the first sequence in the list in the first place, the second sequence in the list in the second place, the third sequence in the list in the third place. Therefore this sequence of 0's and 1's is well defined, but it can't be found anywhere on our list which apparently enumerates all possible sequences of 0's and 1's. Such a sequence represents an irrational number, and you get a different one for each possible ordering of the counting numbers. This is a proof that the infinity of the "real numbers" is greater than the infinity of the counting numbers/rationals, in the sense that the real numbers can't be enumerated. (The argument can be iterated to show there is actually an infinite hierarchy of ever more infinite infinities.)
It's worth mentioning one nice definition of real numbers. It's based on an idea called the Dedekind cut. We imagine "cutting" the rational number line into two infinite sets $A$ and $B$ such that every element of $A$ is less than every element of $B$, and $A$ has no greatest element. We consider the least element of $B$. If this number is rational, then the cut defines that rational number. But there might be an irrational number which is greater than every element in $A$. Since $A$ has no greatest element, then the first number in $B$ ought to be that irrational number, but instead: there's a gap, since we're working with the rational number line. We fill in that gap: that is the irrational number defined by the "cut". $A$ then contains every rational number less than the cut, and $B$ contains every rational number greater than or equal to the cut.
Clearly, at this stage, infinity is taking center stage and also a kind of self-referential logic: approximations where we feed outputs reflexively back in as inputs, lists which we make and then negate to infinity, and so on...
The culmination of these ideas can be expressed in terms of computability: the general theory of following definite rules. After all, there are many ways to calculate things, feeding outputs back into inputs... and not all of them correspond to rationals, or even real numbers!
For example, let's build a computer out of fractions. This is an idea due to John Conway, and goes by the name "fractran."
A computer program in fractran is an ordered list of fractions. For example:
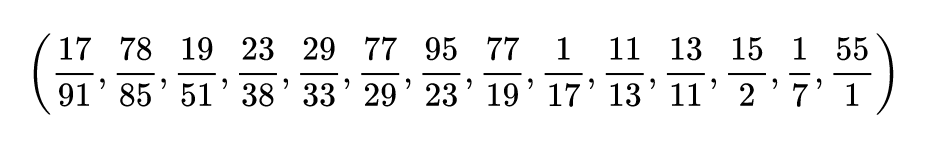
The input to the program is some integer $n_{0}$. The idea is: you start going through the list and you try multiplying $n$ by the first element in the list. If the denominator cancels out and you get an integer back, then that's the output: $n_{1}$. You stop, go back to the beginning, and start over with the input to the program being $n_{1}$. If you don't get an integer back, however, then you move on to the second fraction, and so on. If you get to the end of the list without getting an integer back, then the program halts. And that's fractran!
For example, the above program, if the input is $2$, generates a sequence of integers which contains the following powers of 2:
$ 2^{2} \dots 2^{3} \dots 2^{5} \dots 2^{7} \dots 2^{11} \dots $
In other words, it calculates the prime numbers!
A program which adds two integers is given simply by $ \frac{3}{2}$. Given an input $2^{a}3^{b}$, it eventually outputs: $3^{a+b}$: it adds the integers! More examples can be found on the wikipedia page.
This idea behind fractran is that just as we can write out an integer in a base-n representation as an ordered list of numerals, we can also write out an integer as a product of primes.
$60 = 2^{2}3^{1}5^{1}$
The primes are unorderd in the product, but the primes themselvs are ordered. In fact, we could really just denote 60 as $211$, where it is understood that the first digit is the exponent of the first prime ($2$), the second digit is the exponent of the second prime ($3$), and so on.
A computer needs a memory, a series of registers. Our computer uses an integer as its memory. Each prime within it acts as a register, and the value of the register is the exponent of that prime. Multiplying by fractions allows us to shift data between the registers, and these rules are complete for universal classical computation. In other words, this computer can compute anything any other computer can compute. For example, we could have a list of fractions which represents: a computer program that approximates the $\sqrt 2$.
Some computations can be shown to represent irrational numbers: if the more you run the computation, the more digits you get of some real number which the process is converging to. But of course, not all algorithms "converge" on a number. And in fact, not everything can be computed!
The famous proof of this is due to Godel/Turing. Godel actually used something quite akin to fractran in his proof, but Turing's argument is easier to understand. The whole thing rests on self-reference: the fact that the instructions of a computer program computing some numbers can also be regarded as numbers themselves, so that one can write computer programs whose input is another computer program. (We're used today to the idea that for a computer "everything is 0's and 1's" but it was quite radical at the time.) And it's yet another example of a "reductio ad absurdum" argument, and also a diagonal argument all in one!
So here we go. It would be great to have a computer program $H(A, I)$ that takes as input another computer program $A$ and an input $I$, and tells you whether $A$ will halt or run forever given input $I$. In some cases, it's clear, like if $A$ has an obvious infinite loop, or just returns a constant. But is there a program $H$ that can handle all cases?
Suppose there were. We have some $H(A, I)$ which returns true if $A$ halts, and false if $A$ doesn't, when run on $I$.
Now consider that Godel function: $G(A, I)$, which takes a program $A$ and an input $I$, and if $A$ halts, then $G$ loops forever; but if $A$ doesn't halt, then $G$ halts. This is akin to going along the diagonal in Cantor's proof and flipping the bits.
Now we consider: $H(G, G)$. This is supposed to return true if $G$ halts on $G$, but false if $G$ runs forever on $G$. If according to $G$, $G$ halts, then $G$ runs forever, but if $G$ runs forever, then $G$ halts! This is a contradiction, and so: there is no program $H$ that takes as input any computer program and a starting input, and can determine whether the program definitely halts or not on that starting input.
The moral is that if you want to know if a computer program halts or not, in general you have to run it potentially "forever" and just wait and see if it does actually halt. There may be no shortcut.
And so we see that there is an intrinsic limit to computation: there are questions which are in principle not computable.
Now Godel originally proved this theorem not in the context of computation per se, but in terms of mathematical logic. He assumed the axioms which give you the elementary operations of addition, multiplication, subtraction, and division, and the quantifiers like: There exists... and For all... He then set up a way of encoding states of mathematical logic into numbers, using an encoding based on the primes. Indeed, the primes in their interplay between addition and multiplication are necessary! In this way, statements of mathematical logic could talk about other statements. He then constructed a self-referential statement that led to a contradiction.
The full statement of Godel's "Incompleteness Theorems" is that:
A system of logic powerful enough to contain basic arithmetic is necessarily incomplete in the sense that there are statements that can neither be proved nor disproved by those rules of logic. One such statement is the consistency of that formal system, i. e. whether the rules of logic lead to a contradiction. So that: a system of logic powerful enough to contain arithemtic can't prove its own consistency. It may, in fact, be consistent; but that can only be proven in a different system of logic. Like: you could try to repair your incomplete system of axioms and rules of inference by adding yet more axioms and rules of inference, and then you might be able to resolve some previously unanswerable questions; but this will lead to yet more unanswerable questions, which can only be resolved by adding more axioms...
In other words, mathematics cannot be reduced down to a single set of axioms, from which all true statements can be derived via the mechanical procedure of following out all the rules of inference, like enumerating all the possible sequences of $0$'s and $1$'s.
This goes a long way towards answering our original question, whether in some sense all conceptual composites can be broken down into the same kinds of atoms, at least if by atom we mean: axioms, and by "breaking down," we mean applying mechanical rules of inference.
But the unpacking of our concept of atom is hardly complete, and many unanticipatable surprises are in store.
I have to mention at this point the Collatz sequence, which can be regarded as a special case of a fractran program. It relates to an interesting open conjecture. Maybe you can resolve it.
Here's the game. You start with a counting number N. The goal is to get to 1. If N is even, you divide out 2's until there are no more 2's, and you're left with an odd number. Well, you can add 1 to get an even number, then take out the 2's until you can't, add 1, divide out 2's...until you get to 1. That's trivial. But what happens if instead of just adding 1, you multiply by 3 and add 1? You'll get an even number. Take out the 2's until you're left with an odd number. Multiply by 3, add 1, etc. Will you always end up at 1?
Collatz conjectured yes. No one knows for sure.
Intuitively: imagine the number as a string of bits. Taking out 2's just pops off 0's from the left: it shrinks the string. Multiplying by three and adding 1 stretches the string. Will shrinking overcome stretching? The problem is also known as the hailstone problem, the metaphor being that the number is like a hailstone falling to the earth due to gravity but being buffeted back upwards by the wind. Will it stay up there forever, or fall down to earth?
And considering what we've learned about fractran, we can well imagine that the problem may very well be undecidable.
You can consider generalizations. For example, why not take out 2's and 3's, and then multiply by 5 and add 1? Why not take out 2's and 3's and 5's, and then multiply by 7 and add 1? Consider those four rules:
$N \rightarrow \frac{N}{2}$ if $N \mod 2 = 0$, else $N \rightarrow N + 1$
$N \rightarrow \frac{N}{2}$ if $N \mod 2 = 0$, else $N \rightarrow 3N + 1$
$N \rightarrow \frac{N}{2}$ if $N \mod 2 = 0$, else $N \rightarrow \frac{N}{3}$ if $N \mod 3 = 0$, else $N \rightarrow 5N + 1$
$N \rightarrow \frac{N}{2}$ if $N \mod 2 = 0$, else $N \rightarrow \frac{N}{3}$ if $N \mod 3 = 0$, else $N \rightarrow \frac{N}{5}$ if $N \mod 5 = 0$, else $N \rightarrow 7N + 1$
At least for low N, these rules seem to lead to 1. We can hear this!
Imagine starting with a number N and evaluating each of the four rules in parallel until they each hit 1, at which point they start repeating (consider the 3N+1 rule: if it hits 1, it goes to 4, then 2, then 1, then 4, then 2, then 1.) So imagine when a number hits 1, it just bounces like this waiting for the other three numbers to hit 1. And when they've all hit 1 at least once, we move on to the next number N+1. Think of this like a four lines of counterpoint.
Finally, interpret each number as a chord where the notes have frequencies corresponding to prime factors and amplitudes corresponding to the multiplicity of the given prime factors. Start counting 1, 2, 3, 4, and get the four part harmony for each number, and then play them one after the other. Next thing you know, you have music.
One reason I like the Collatz problem is Pythagoreanism-related. Pythagoras gets credit for the circle of fifths.
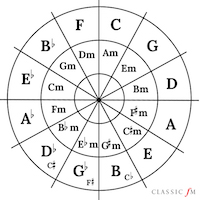
Going up a fifth from C you land on G; a fifth from G is D; a fifth from D is A; and if you keep going, you go all the way around through the 12 keys, ending up back at C.
Well, almost! Going up a fifth is multiplying by $\frac{3}{2}$. Indeed, it's going up by 3's. But going up an octave is multiplying by 2's. You'll never get a power of 2 by multiplying by 3's! And yet it seems by going around the 12 keys, we end up at C only some octaves higher.
Tha answer is that it happens that sometimes multiplying by 3's lands you close to a power of 2, perhaps so close the human ear cannot distinguish the difference. But there is a difference.
Modern instruments generally don't use this "Pythagorean tuning," or "just temperament." Instead they use "even temperament" so that the ratio between adjacent notes on the keyboard is $\sqrt[12] 2$, the twelfth root of two, so that going up 12 notes gives you: $(\sqrt[12] 2)^{12} = 2$, an octave as desired.
I feel, however, that the 3N+1 problem puts a new twist on this old conundrum.
What if instead of going up by 3's and futilely trying to take out 2's in order to return to 1, we go up by a 3, add 1, take out 2's, go up by 3, add 1, take out 2's, which is literally the next simplest thing you could imagine doing. If the conjecture were true, then would mean that a +1 solves Pythagoras's musical crisis, and the "next best circle of fifths" can close!
Before we go, let's listen to the hailstorm. We'll use the 3N+1 rule, start counting, and as we get to each number, that number is added to the storm, and tries to fall to 1. So the sky is quickly filled with number shooting down from heaven. Maybe you can hear whether the conjecture is true... Check it out here.
To return at last to our main subject, apparently: the real line.
The real line has a third point between any two points, contains rationals, irrationals, even uncomputable numbers!
If that's too much, you could imagine all the recursively defined algorithms that converge to a certain real number, for example, the $\sqrt 2$; or even just "the algebraic numbers," all the numbers you can get from repeated addition/subtraction/multiplication/division/exponentiating/root-taking. We'll take those numbers as our composites, each of which contain within themselves a whole completed infinity "all at once" of "rational atoms."
Recall that we're supposed to be working with exponentiation and root-taking.
But actually, there's something we've completely overlooked. What happens if we take $\sqrt{-1}$?
There is no rational (or even real number) such that when you square it, you get $-1$. So as usual, we have to add this number to our system. It's usually called $i = \sqrt{-1}$, because such numbers were originally thought of as "imaginary."
Once we have $i$, we can think of $\sqrt{-7}$ as $i\sqrt 7$.
Note that we have:
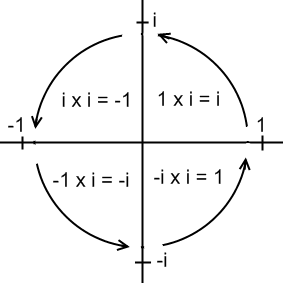
$ 1 \times i = i $
$ i \times i = -1 $
$ -1 \times i = -i $
$ -i \times i = 1 $
There's a four-fold repeating pattern. This suggest the interpretation of multiplying by $i$ to be a $90^{\circ}$ rotation.
So actually, we have more than just the real axis! There's a second axis, the imaginary axis, and actually our new kinds of numbers can live anywhere on the resulting plane, called the "complex plane."
So our "complex numbers" can have a real part and an imaginary part, and they can be written $z = a+bi$, which picks out a point on the plane.
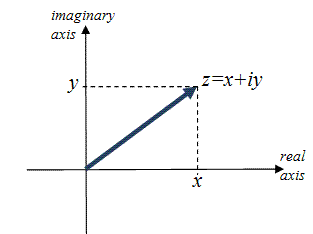
Alternatively, we could use polar coordinates: $z = r(cos(\theta) + i sin(\theta))$, where $r$ is the radius and $\theta$ the angle. If $r=1$:
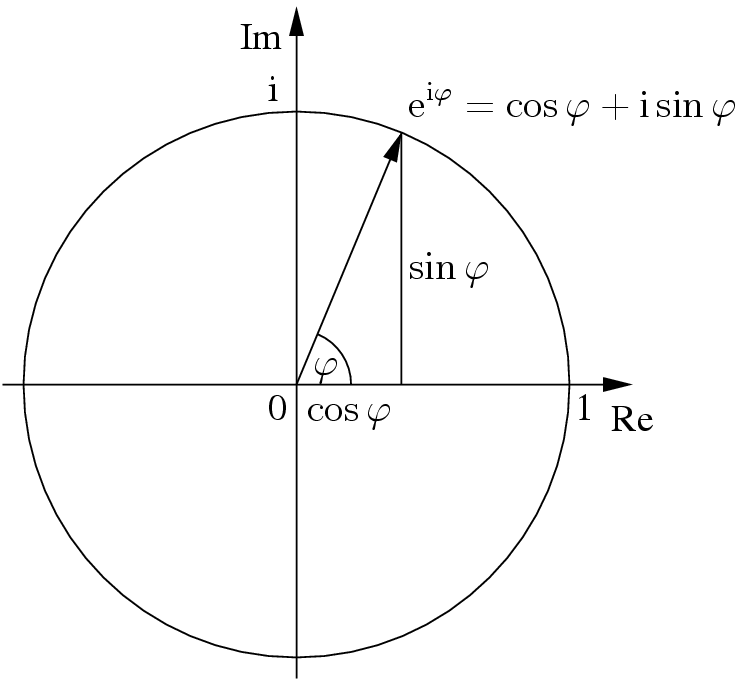
Later we'll come to understand why we can also write this $z = re^{i\theta}$, but for now take it as a useful notation.
Complex numbers follow the rules of algebra. You can add them:
$ a + bi + c + di = (a + c) + i(b + d)$
This just corresponds to laying the arrows represented by the two numbers end to end.
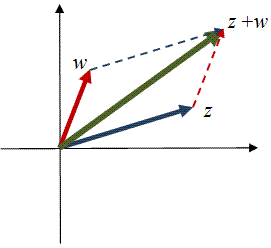
Multiplying complex numbers means to stretch the one by the other's length, and rotate by the other's angle.
$ re^{i\theta} \times se^{i\phi} = rs e^{i(\theta + \phi)}$
Finally, we have to mention complex conjugation. Given a complex number $z = a + bi = re^{i\theta} $, its conjugate $z^{*} = a - bi = re^{-i\theta}$.
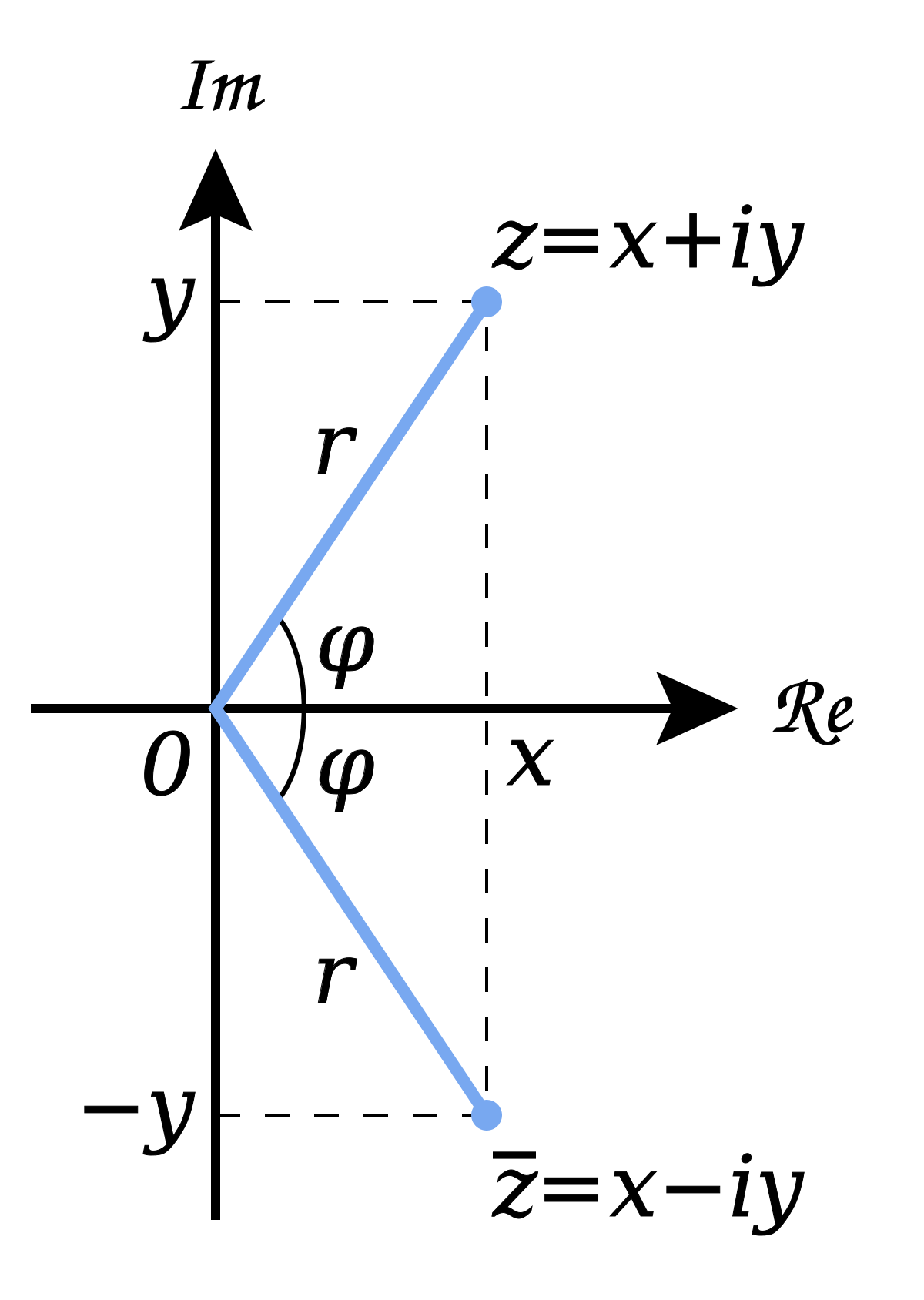
Look at what happens when we multiply a complex number by its conjugate:
$zz^{*} = (a + bi)(a - bi) = a^{2} - abi + abi - b^{2}i^{2} = a^{2} + b^{2}$
So if we consider a complex number $z$ to represent a right triangle with sides $a$ and $b$, the length of its hypoteneuse is given by $\sqrt{zz^{*}}$.
If it wasn't clear before, it is now undeniable: there is something actually two-dimensional going on at this stage of the game. In fact, our numbers now have two parts and live on the plane, where they can represent points/arrows, and rotations/stretches thereon.
And this is exactly what we need.
Think about it like, all this time, we've been providing more and more context to the interpretation of a single pebble. We've discovered: first, we have to decide whether the presence of the pebble or its absence is significant. Then, once we have multiple pebbles, we have to agree where we start counting from. Then, once we have integers, we have to agree on where $0$ is, and if we should consider the number to be positive or negative. Then, once we have the rational numbers, we have to agree on what is $1$, and we need a rational number to translate between our different units. But now at this stage, we need to agree on the angle between our axes. And that's just what a complex number can do. It can take a diagonal line, which has to be represented with an "unwritable" $\sqrt 2$, for example, and can translate it into "our reference frame" by multipling by $e^{-i\frac{\pi}{4}}$, which by a rotation aligns the diagonal line at $45^{\circ}$ with the real axis. So each stage in our journey represents another kind of context, another kind of number that we have to specify to align our reference frames, so that we can agree with certainty about the meaning of a pebble.
Before we transcend this plane, however, we have one final point to make. What about division by 0? Before, this wrapped up the line into a circle. Now that we have complex numbers, how can we interpret division by 0?
The answer is the Riemann sphere. Or the complex projective line.
In the case of the line, there were two infinities, positive and negative, which we joined as one. In the plane, the horizon is an infinite circle, and we have to imagine a point beyond the horizon, and you reach the same point no matter which direction you approach it in: that's the point at infinity. And if it's there, what it means is that our plane is really a sphere: and the point $\infty$ is just the point directly opposite you on the sphere.
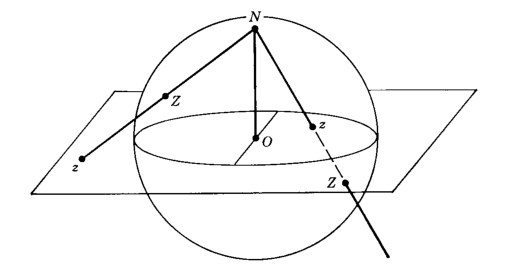
We imagine standing at the North Pole of the sphere, and drawing a straight line from that point to a chosen point on the complex plane. That line will intersect the sphere at one location. If the point on the plane is inside the unit circle, it gets mapped to the Southern Hemisphere and if the point on the plane is outside the unit circle, it gets mapped to the Northern Hemisphere. All points on the plane are mapped uniquely to a point on the sphere, but we have an extra point left over, and that's the one at the North Pole, the point of projection itself.
In what follows, however, we'll find it's most convenient to take our projection from the South Pole--although both are important: if we can't deal with the $\infty$, we can always switch over to the opposite projection pole and see what's going on at $0$!.
But anyway, for a South Pole stereographic projection, if we have a complex number $c = a+bi$ or $\infty$, then:
$ c \rightarrow (x, y, z) = (\frac{2a}{1 + a^{2} + b^{2}}, \frac{2b}{1+a^{2}+b^{2}}, \frac{1 - a^{2} - b^{2}}{1 + x^{2} + y^{2}})$ or $(0, 0, -1)$ if $c = \infty$.
And inversely, $(x, y, z) \rightarrow \frac{x}{1+z} + i\frac{y}{1+z}$ or $\infty$ if $(x, y, z) = (0, 0, -1)$.
And so, we discover that our numbers at this stage are actually: points on a sphere, picking out a direction in 3D space. At this level, such a number is a composite, a completed infinity defined by rational numbers. And we can count, add, subtract, multiply, divide, exponentiate, and take roots with wild abandon.
(By the way the stereographic projection was known to Ptolemy and is related to the Gnomonic projection: the ancient theory of sundials. And by the by, it happens that stereographic projection preserves angles (whereas a cylindrical projection (re: Archimedes) preserves areas), and we well know its intimate relationship to the Mobius transformations.)