Quantum Mechanical Puzzles of Supervenience, Pt. II¶
First, a brief word on the meaning of the word "supervenience." Wikipedia provides a nice definition:

In other words, to say that mental states "supervene" on physical states is to say that there can't be difference in mental states unless there is some corresponding different in physical states. Conversely, if physical states "supervened" on mental states, then there couldn't be a difference in physical states unless there was a difference in mental states. Philosophers, of course, differ on how they imagine mind/body interactions to work, whether it's a two way street or one way in one direction or another, or something altogether different. But the point of examining how "mental states supervene on physical states" is to ground an account of mentality on physics.
More on Bohmian Mechanics¶

In my mind, Bohmian mechanics is like steampunk physics. Having recourse to wikipedia again, we find steampunk defined as a: "retrofuturistic subgenre of science fiction that incorporates technology and aesthetic designs inspired by 19th-century industrial steam-powered machinery." Indeed, in Bohmian mechanics, we seem to have the revenge of the 19th century: a deterministic theory, in which randomness arises only through ignorance of the initial conditions, and not only that, but a theory which has a thoroughly materialistic ontology, consisting of point particles being buffetted by waves (albeit, satisfying the Schrodinger equation, which is first-order in time), with all higher level properties supervening on these basic elements. And yet, as soon as one looks more closely, the theory is really more like 19th century physics on an acid trip. To reproduce the predictions of quantum mechanics, the theory must be wildly nonlocal, the velocities of the particles depending on the entire rest of the world at a given moment, which in itself is unsettling, but for that matter conflicts with special relativity (although such violations would not necessarily be apparent, given that we're generally ignorant of the real locations of the particles). Depending on one's prejudices, however, this may be a feature: even as there was something comforting about the 19th century deterministic world, unfolding inevitably according to a grand plan imposed at the beginning by some God-given initial conditions, the old classical physics was depressingly insistent that, insofar as we're spatially separate configurations of atoms and fields, we are all metaphysically "alone." In contrast, in Bohmian mechanics, everything is connected to everything else so intimately that my thoughts could literally be determining your thoughts right now, with no intermediate step, and with cosmic inevitability.
But an even subtler feature is the contextuality of all observables other than position in Bohmian mechanics. As we've seen, if we send a particle surfing on a wavefunction in a superposition of spin $\uparrow$ and $\downarrow$ through a measuring device, the port at which the particle exits depends on whether the particle happened to be above or below the midpoint of the device: and consequently, if the device were flipped over, the particle would exit the opposite port, in other words, it would exit out the $\downarrow$ port instead of the $\uparrow$ port, even though nothing had changed with regard to the particle or its wavefunction. In other words, the measured value of the spin depends on the spatial context: exactly how the particle happens to be located relative to the device, exactly how the device is oriented, and so forth. Now there's nothing objectionable about a theory in which higher level properties bottom out at something more fundamental: observables in classical physics basically bottom out at the positions and momenta of the underlying particles. But here, the issue is that the measurable aspects of higher level properties seem to depend on something semantically irrelevant. In normal quantum mechanics, we can assign a sensible semantics to the spin part of a wavefunction, to its position part, and so forth. And even if the spin and the position can get entangled, they have a semantic identitity of their own. But in Bohmian mechanics, the outcome of spin measurements depends seemingly irrelevantly on how the apparatus is positioned relative to the point particle, so that the concept of spin itself can't be separated from the spatial configuration. And not just spin, but any observable property other than position in standard Bohmian mechanics is contextual in just this way, inevitably depending on contigencies which make it impossible to regard those properties as having any semantic meaning on their own.
Now you could bite the bullet and say, Well, that's just how it is! Get used to it! Contextuality sounds strange, but surely it's better than accepting that the outcome is literally random! At least, there is a reason, even if it's inherently, by definition, unsatisfying.
But consider than actually Bohmian mechanics isn't unique, and that actually there's an infinitude of equally good such theories, each of which reproduces the predictions of quantum mechanics, but which radically disagree about what are the particles and what are the trajectories. What do I mean?
Well, you might wonder, first of all, could we formulate Bohmian mechanics in the momentum representation? In other words, in the standard formulation, the position wavefunction is regarded as a "really existing" guiding wave, which tells point particles, specified by a list of positions, how to move. But what if instead you worked with the momentum wavefunction, regarded as a "really existing" guiding wave (in momentum space!), which tells point particles (specified by a list of momenta!), how to move? In fact, the physicist Epstein suggested this to Bohm even back in the 50's, and while there were originally some technical issues, recent work has shown that this is perfectly coherent. You'll end up with a deterministic, contextual theory, where everything supervenes on momenta, where momentum particles take definite momentum trajectories through momentum space, and all of it adds up to standard quantum mechanics, just as in the usual Bohmian theory. Moreover, there's a way of definining such momentum trajectories in the usual position-based theory, and a way of defining position trajectories in the momentum-based theory: and they disagree! And yet, they both add up to standard quantum mechanics.
For that matter, why not choose a basis in between position and momentum? Do a fractional Fourier transform, and repeat the construction. You'll get a new deterministic ontology, where everything supervenes contextually, and which reproduces quantum mechanics. And in fact, you could choose any continuous basis you like!
You could even use a coherent state basis, parameterized by position and momentum, in other words, where the state is decomposed into an infinitude of displaced Gaussians, and then you'd have Bohmian mechanics on phase space, where a guiding wave in phase space pushes phase space points around, and everything supervenes contextually atop that.
So how does this work? I'll mainly follow the account given in the very inspiring paper, "Experimental Comparison of Bohm-like Theories with Different Primary Ontologies."
So in the usual "$x$-Bohm" picture, we have a Hamiltonian:
$H(x,p) = \frac{p^2}{2m} + V(x)$
And the Schrodinger equation:
$i\hbar\frac{\partial}{\partial t}\psi(x, t) = H(x, -i\hbar\frac{\partial}{\partial x})\psi(x, t)$
And we write the wavefunction in "polar form":
$\psi(x, t) = r_{x}(x,t)e^{\frac{i}{\hbar}\theta_{x}(x,t)}$
We then have the "guidance equation", which gives us the velocities of our point particles (note that we could formulate things in terms of Bohm's "quantum potential" as well):
$v_{x}(x, t) = \frac{1}{2m}\frac{\partial \theta_{x}(x,t)}{\partial x} = \frac{j_{x}(x, t)}{|\psi(x, t)|^2}$
Here $j_{x}(x,t)$ is the probability current density:
$j_{x}(x, t) = \frac{\hbar}{2mi} \Big{(} \psi^{*}(x, t)\frac{\partial\psi(x,t)}{\partial x} - \psi(x, t)\frac{\partial \psi^{*}(x, t)}{\partial x} \Big{)}$
So we can define a trajectory for our points:
$\frac{dx(t)}{dt} = v_{x}(x(t), t)$
Now interestingly, it turns out that the guidance equation can be rewritten in the following suggestive form:
$v_{x}(x, t) = \frac{1}{m}\Re{\Big{[} \frac{\langle x \mid \hat{p} \mid \psi(t)\rangle}{\langle x \mid \psi(t) \rangle} \Big{]}}$
This looks like a "weak momentum measurement followed immedietly by a strong (projective) position measurement"!
On the other hand, we could adopt a "$p$-Bohm picture."
We'd have a Hamiltonian:
$H(x,p) = \frac{p^2}{2m} + V(x)$
And the Schrodinger equation:
$i\hbar\frac{\partial}{\partial t}\phi(p, t) = H(i\hbar\frac{\partial}{\partial p}, p)\phi(p, t)$
And we'd write the momentum wavefunction in polar form:
$\phi(p, t) = r_{p}(p,t)e^{\frac{i}{\hbar}\theta_{p}(p,t)}$
Now it turns out that there won't necessarily be as simple, general an expression for $v_{p}(p, t)$ in terms of which we can define trajectories:
$\frac{dp(t)}{dt} = v_{p}(p(t), t)$
Why? Well, all such Hamiltonians have the same dependence on $p$, but depending on the potential can have very different dependence on $x$. This is just to say, then, that the expression will depend on the particular potential. But we can still write:
$v_{p}(p, t) = \frac{j_{p}(p, t)}{\mid \phi(p, t)\mid^2}$
For one dimensional problems, we must have:
$\frac{\partial j_{p}(p,t)}{\partial p} = - \frac{\partial}{\partial t}\big{(} \mid \phi(p, t)\mid^2 \big{)}$
And so, if we assume that $j_{p}(p,t) \rightarrow 0$ as $\mid p \mid \rightarrow 0$, a unique current follows:
$j_{p}(p, t) = \frac{2}{\hbar}\int_{-\infty}^{p} \Im{\Big{[} \phi^*(p^{\prime},t)V(i\hbar\frac{\partial}{\partial p^\prime})\phi(p^\prime,t) \Big{]}dp^\prime}$
In higher dimensions, things are more complicated, but work by Struye, Valentini and others shows how you can define such currents for basically arbitrary Hamiltonians, although the answer might not always be unique.
More generally, following Holland, we can consider an arbitrary $\xi$-Bohm theory, where $\xi$ is an eigenvalue of some Hermitian operator $\hat{\xi}$ with a continuous spectrum. Then the value $\omega$ of a continous variable associated with another Hermitian operator $\hat{\omega}$ is:
$\omega_{\xi}(\xi, t) = \Re\Big{[} \frac{\langle \xi \mid \hat{\omega}\mid\psi(t)\rangle }{\langle \xi \mid \psi(t) \rangle} \Big{]}$
Which makes sense insofar as that implies that:
$\langle \psi(t) \mid \hat{\omega}\mid \psi(t) \rangle = \int \omega_{\xi}(\xi, t)\mid\langle\xi\mid\psi(t)\rangle\mid^2 d\xi$
Working this magic, in $x$-Bohm theory, we'd have:
$p_{x}(x, t) = \Re\Big{[}\frac{\langle x \mid \hat{p}\mid\psi(t)\rangle }{\langle x \mid \psi(t) \rangle}\Big{]}$
So that as expected $p_{x}(x, t) = mv_{x}(x,t)$
And then in $p$-Bohm theory, we'd have:
$x_{p}(p, t) = \Re\Big{[}\frac{\langle p \mid \hat{x}\mid\psi(t)\rangle }{\langle p \mid \psi(t) \rangle}\Big{]}$
And so, for example, we can follow $x_{p}(p,t)$ as $t$ advances and so obtain a trajectory in position space as well, in the $p$-Bohm theory.
Now, the authors very cleverly simulate experimentally the evolution of a massive particle under both $x$-Bohm and $p$-Bohm theories using the fact, which we appreciated ourselves not so many weeks ago, that light propagating the paraxial regime follows Schrodinger's equation! (Which is especially nice since it's not always a trivial matter to numerically calculate the trajectories.)
The analogy is that transverse position $x$ of the light beam corresponds to the $x$ position of the particle, the longitudinal position $z$ corresponds to the time coordinate $tc$ and the transverse angle $\theta=\frac{k_{x}}{\mid \textbf{k} \mid}$ corresponds to the momentum $\frac{p}{mc}$. They simulate the Bohmian trajectories of a massive particle by sending a 915 nm laser through a double slit and doing weak measurements to reconstruct the trajectories. (For how these are done, I refer you to the paper. The basic idea is to couple the desired observable, say momentum, to some pointer and then make a strong measurement, of say position, with reference to another pointer, and post-selecting.)
Here's what they get:
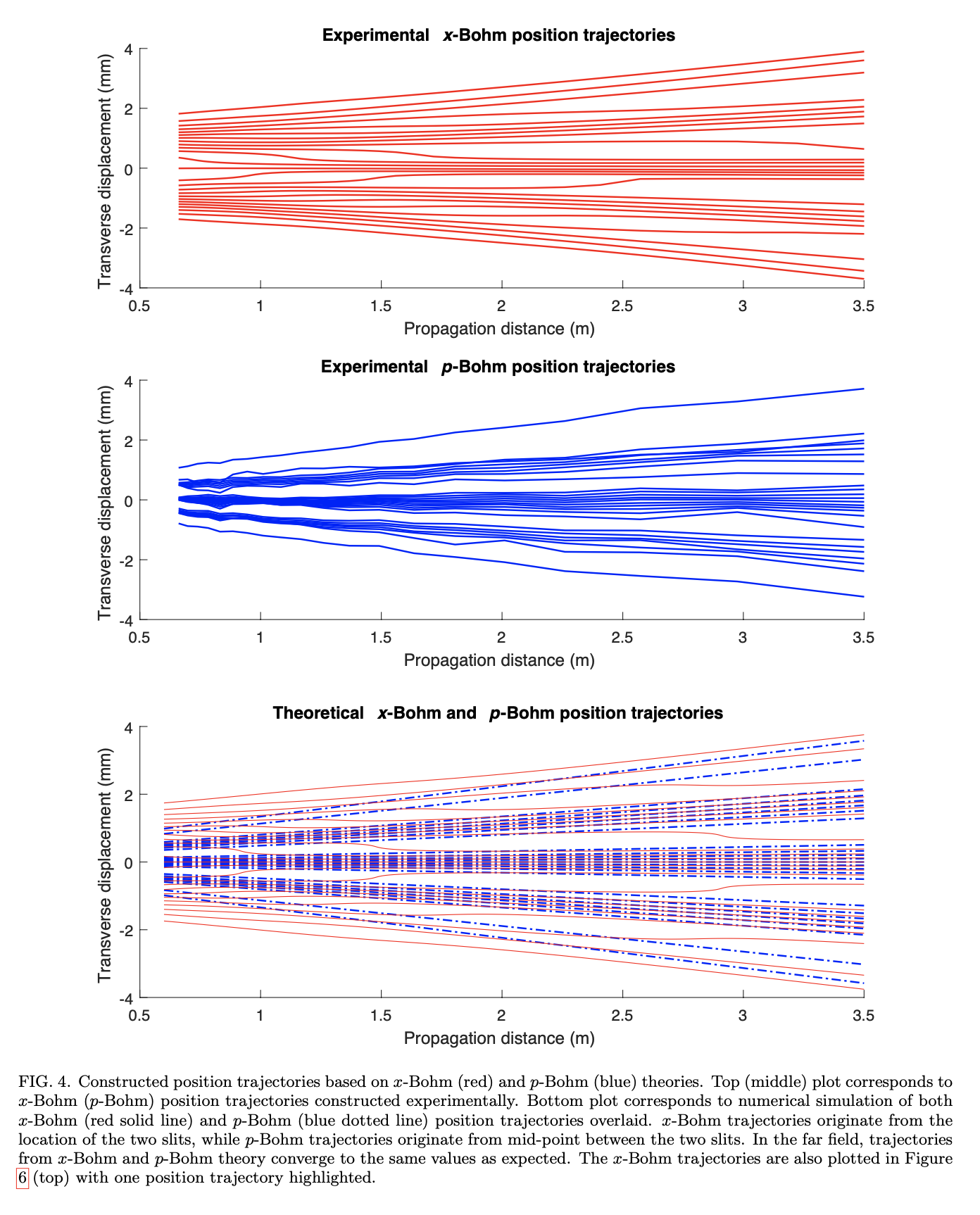
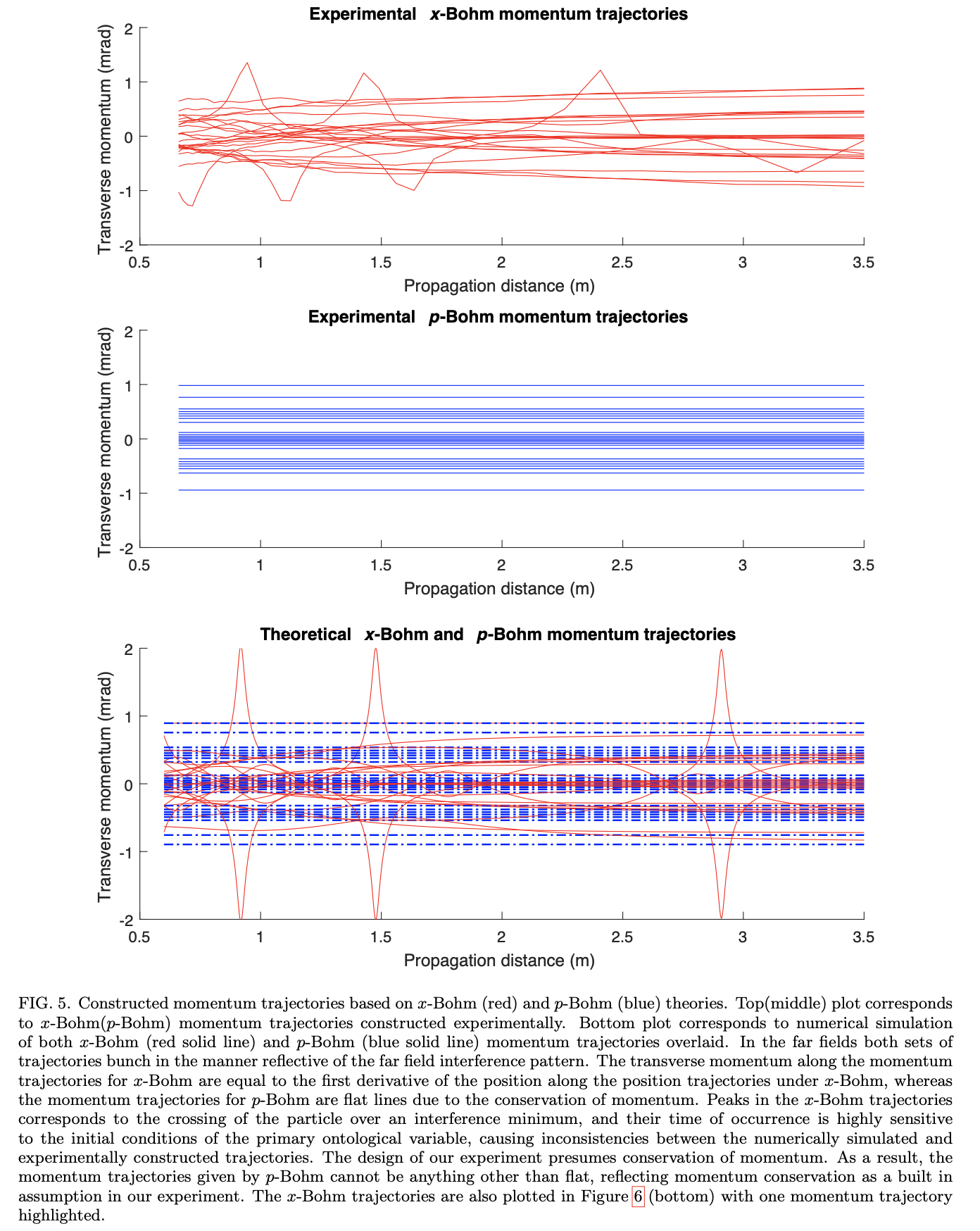
Their conclusion:
"When everyone is somebody, then no one’s anybody. -- W.S. Gilbert, The Gondoliers"
"...in contrast to classical physics, where both the initial position and momentum are necessary for predicting the dynamics that follows, in an x-Bohm theory the initial conditions are just the initial position of the particle, together with the initial wave function. It is therefore tempting to view the identification of the asymmetry as a profound discovery, suggesting that position is indeed more important than other variables. One could even hope that the realization that position plays a special role would lead to new experimental predictions. However, as emphasized in this work, the specific choice of position is not unique, leaving us with an infinite number of possible primary ontological variables – each allegedly more fundamental than all the others – or, as Gilbert’s line above implies, with none."
In $p$-Bohm theory, "the fundamental trajectories are paths through momentum-space, and the equations of motion take a form which is closer to that of Newton’s laws, with a first time-derivative for momentum. If the underlying phase-space dynamics of both theories were the same, one might say that the symmetry between position and momentum had been restored, removing a non-trivial assumption from Bohm’s theory. The pictures are, however, very different and so, the asymmetry in a Bohm-like theory is confirmed but ambiguous. One is left to wonder which of the two theories, or indeed of the infinite intermediate theories with other ontology, is correct, and possibly more importantly what is the primary ontological variable."
They then consider a harmonic oscillator related example.
We all know and love the oscillator Hamiltonian:
$\hat{H} = \hbar \omega(\hat{a}^{\dagger}\hat{a} + \frac{1}{2})$
But we could also write:
$\hat{H} = \frac{1}{2}\hat{p}_{\theta}^2 + \frac{1}{2}\omega^2\hat{x}_{\theta}^2$
For any real $\theta$, where:
$\hat{x}_{\theta} = \sqrt{\frac{\hbar}{2\omega}}(\hat{a}^{\dagger}e^{i\theta} + \hat{a}e^{-i\theta})$
$\hat{p}_{\theta} = i\sqrt{\frac{\hbar \omega}{2}}(\hat{a}^{\dagger}e^{i\theta} - \hat{a}e^{-i\theta})$
And indeed, $[\hat{x}_{\theta}, \hat{p}_{\theta}] = i\hbar$.
We could then construct a $\theta$-Bohm theory by taking $\hat{x}_{\theta}$ to be the position operator. For each $\theta$, there's a different physical picture, and weak $p_{\theta}$ measurements followed by strong $x_{\theta}$ measurements would allow one to experimentally simulate trajectories for each such theory.
If this Hamiltonian is taken to describe a mode of the radiation field associated with a standing wave, then $\hat{x}_{0}$ and $\hat{p}_{0}$ would be associated with the electric and magnetic fields respectively. In $0$-Bohm theory, any energy eigenstate would be associated with an ensemble of different values of the electric field, but the magnetic field would vanish for each member of the ensemble. But in the $\frac{\pi}{2}$-Bohm theory, $\hat{p}_{\frac{\pi}{2}}$ would correspond to the electric field and $\hat{x}_{\frac{\pi}{2}}$ would correspond to the magnetic field, and so any energy eigenstate would be associated with an ensemble of different values of the magnetic field, but with the electric field vanishing for each member of the ensemble. Would there be some physical motivation for supposing that one set of trajectories should be regarded as more real than another? They point out that people have made various arguments, but without any conclusive evidence.
Finally, I offer the following nice expressions taken from "Bohmian mechanics in momentum representation and beyond":
Continuity equation: $\frac{\hbar}{2}\frac{\partial}{\partial t}r_{a}(x, t) = \frac{1}{2i}\langle a \mid [\hat{H}, \hat{\rho}(t)] \mid a \rangle$
Modified Hamilton-Jacobi equation: $-r_{a}(x, t)\frac{\partial}{\partial t}\theta_{a}(x, t) = \frac{1}{2}\langle a \mid \{\hat{H}, \hat{\rho}(t)\} \mid a \rangle$
Okay, so back to the philosophy.
At first, Bohmian mechanics seems especially appealing since it promises a return to an ontology of particles taking definite, deterministic trajectories in space. The cost: nonlocality and contextuality. But actually you can pretty much choose whatever ontology you want and get the same effect: a set of definite particles taking definite trajectories that adds up to quantum mechanics. But which particles you get and which trajectories they take and what "space" they move around in, and exactly how they relate non-locally and how measurement results depend contextually on those particles, depends on your choice of ontology, and indeed, the stories that each theory tells are totally different from each other, even though they all add up to quantum mechanics.
For each choice of ontology, we get a particular brand of contextuality, a particular way that all non-fundamental physical concepts are "shattered" by being forced to supervene on positions or momenta or whatever, and a particular brand of non-locality that binds it all together. We may end up with a deterministic theory, but at the cost of imposing an arbitrary ontology.
The very fact that you can do this suggests something interesting about the quantum state itself, considered independent of its expression in any particular basis: that it is precisely independent of any ontology. In fact, you could regard standard quantum mechanics as just "ontology independent Bohmian mechanics." And the great benefit of the standard framework is that the resulting theory is local and its concepts are semantically stable (and maybe in some sense these are the same things!). In other words, precisely by refusing to commit to an ontology, the theory is able to tell a story in which all interactions are local, and in which different factors of the Hilbert space really refer to separate properties of physical systems, semantically solid in their own right. If we break the symmetry under ontology, we can tell a deterministic story, but one which is, as it were, a conspiracy whereby farflung systems and irrelevant concepts all collude to save the phenomena.
Perhaps we could even regard the indeterminism of standard theory as a consequence of nature's "symmetry under ontological shifts," nature's refusal to allow any one metaphor to conquer all its vast territories: after all, if there are an infinitude of equally good deterministic stories that could be told about why one outcome occurs over another, then maybe that's just another way of saying the outcome is indeterministic.
In other words, it's as if nature is saying that ontology is our construction, not hers. Indeed: the definition of an ontology is not just any old set of concepts that we might use the understand the world, but specifically the attempt to reduce all concepts to a unique set of irriducibly basic concepts. And the lesson of Bohmian mechanics is that such a reduction can be carried out, but a) the process isn't unique and b) the cost is that all the higher concepts will be semantically shattered by contextuality.
On the other hand, quantum mechanics itself shows us how an ontology independent description of the world can be constructed, which can encompass diverse concepts with equipoise.
And just to clarify, I'm emphasizing the fact that interactions are local in normal quantum mechanics. Of course, in normal quantum mechanics, one ends up with entangled states (which indeed correspond to nonlocality in the Bohmian picture), but just because the states are nonseparable, in the standard QM, this doesn't mean there's any nonlocal interaction or any nonlocal information transfer. Moreover, in many interpretations, a completely local gloss of nonseparable states can be given: in the Many Worlds interpretation, the correlations can be explained locally in terms of which branch you end up on; in Many Minds, the correlations can be explained by the local beliefs formed after experimenters compare results; and in the relational approach, the correlations are the result of the relationship between two systems depending on just the two systems alone, analogously to how a husband and wife are still married no matter where they roam on earth, so that the orientation of two spins might be well defined relative to each other, but not relative to anything else (in the maximally entangled, "monogamous" case).
By the way, I've heard it remarked that if Bohmian mechanics had been discovered first, the Copenhagen interpretation would have never arisen. I think we can question this, in light of what we've seen. We could imagine an alternate history where the pilot wave theory was discovered a decade or two earlier, and rapidly caught on. But then people found it useful for calculational purposes to work in different representations of the wavefunction, always switching back to the position ontology at the end. But after a while, it can't help but be noticed that the trajectories in each picture disagree with each other, and people argue about whether this is nominal or not. And after some struggle, people decide that actually none of these pictures can be better than any of other with regard to the experiments themselves, since the trajectories are never directly observed, and so decide that the wavefunction is the fundamentally invariant thing under all these pictures, and reinvent the Copenhagen interpretation all over again.
By the way, one can find comments very much in this spirit in Bohm's own texts (taken from "Wholeness and the Implicate Order"):
"Our theories are to be regarded primarily as ways of looking at the world as a whole (i.e. world views) rather than as ‘absolutely true knowledge of how things are’ (or as a steady approach toward the latter)."
"The whole object is not perceived in any one view but, rather, it is grasped only implicitly as that single reality which is shown in all these views."
While we're on the subject, I'd like to push back against the claim that Bohmian mechanics has been consistently sidelined from the physics mainstream. Undeniably, the theory has had a difficult history. But as I alluded to, probably as a result of Bell's sympathetic words in favor of the theory, Bohmian mechanics has had a revival starting in the 1990's, as the following graph, taken from Bohm’s approach to quantum mechanics: Alternative theory or practical picture? demonstrates:
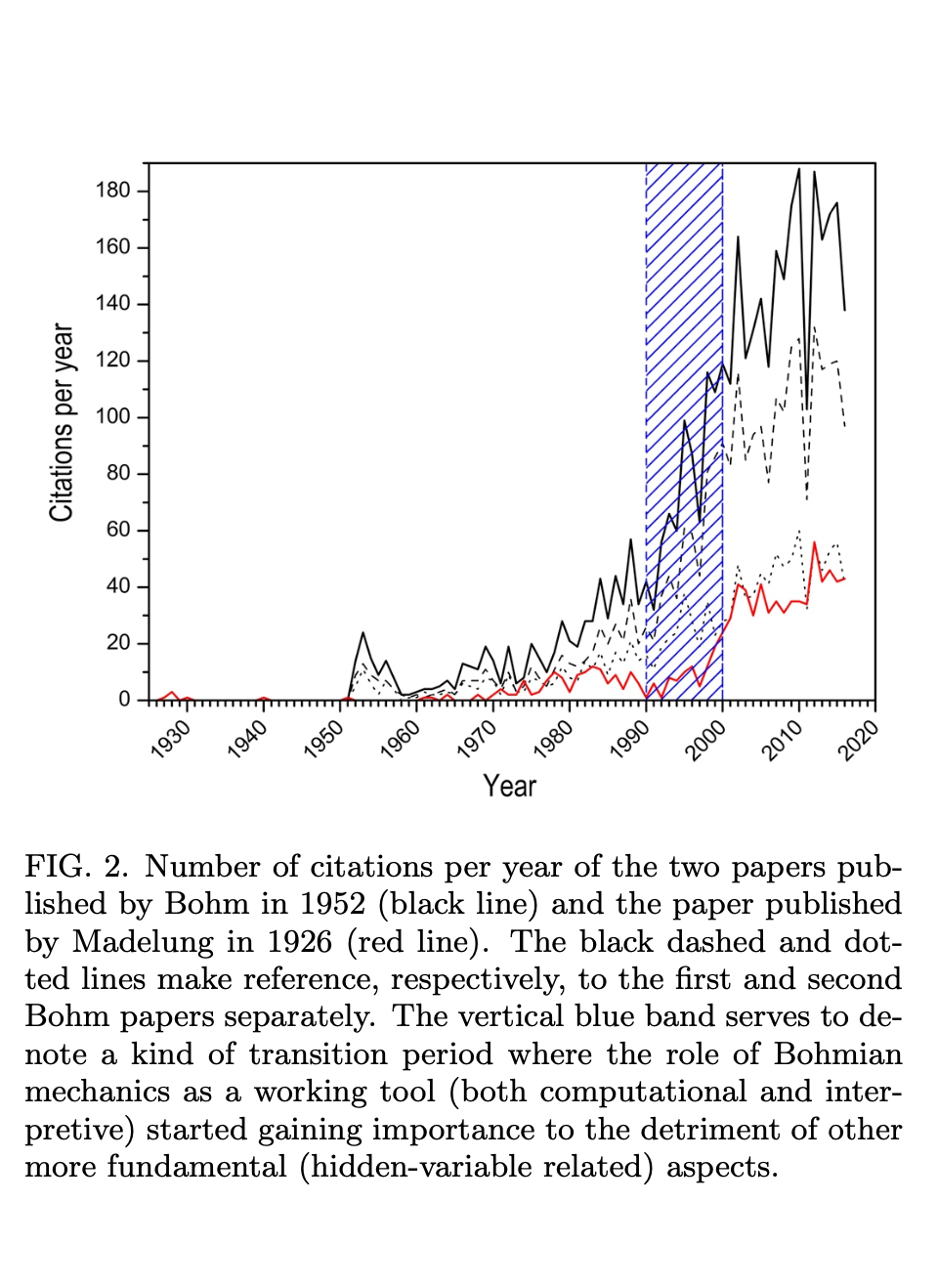
As I mentioned, discussions of Bohmian mechanics feature heavily in philosophy of physics discussions from the 90's onward. And the authors make the further point that much of the current revival comes out of work which doesn't commit to a metaphysical interpretation of the theory, but instead uses Bohmian mechanics as a useful tool, one among many. For a survey of this, I direct you to Applied Bohmian Mechanics. More theoretically, I've found papers exploiting the point particles of Bohmian mechanics to do everything from quantizing Julian Barbour's "shape space" to understanding Loop Quantum Cosmology.
In other words, Bohmian mechanics (in all its varieties) is a deeply important part of the story of quantum mechanics, and that has come to be appreciated more and more over time. It has important lessons for us, about the tradeoffs we must make in interpreting quantum mechanics in different ways, and provides a source of intuition and analysis in cases where our usual pictures may fail us. But like all "interpretations of quantum mechanics," it is just one part of a much grander story.
The central issue is that quantum mechanics is always "missing" something. The particles in Bohmian mechanics, among other things, select out which "branches" of the wavefunction are going to matter. In this way, Bohmian mechanics is analogous to the Single Mind theory: both posit that the whole wavefunction survives (without collapse), but one branch is picked out by something extra. This something extra is located internally in the Single Mind picture, and is located externally in the Bohmian picture: to precisely the same effect, experimentally. Similarly, the Many Minds picture is dual to the Many Worlds picture, both agreeing that the whole wavefunction survives, but locating the multiplicity of outcomes either internally or externally. That such alternative pictures are possible, is itself the deep fact that must be reckoned with. (And to be honest, makes something like Von Neumann's psychophysical parallelism ever more appealing.)
Finally, I also want to suggest why having an "ontology independent theory" would be a Good Thing to have anyway. If I wanted a theory of physics that would actually explain not just perspective shifts from a stationary frame to a rotating frame, but perspective shifts like: from what it's like to perceive the world through my body vs your body, we're going to need a framework which can precisely handle shifts of ontology, since our perceptual worlds, even if they supervene on similar stuff, are in themselves built out of different "mental furniture". (To take an example: for me, when I think of a triangle, with its three sided rigidity, I think of two stretched legs, and then somehow a third leg, as if for me the triangle is built perceptually/conceptually out of body parts. Your mileage may differ--and that's the point. I'd say the real goal isn't resolving what the "world is really made out of"; rather, we need a way of universally translating between all points of view.)
Which takes us to:
Supervenience and Quantum Reference Frames¶
We've seen how there are different ways of getting at the question of "what it would be like to be in an entangled superposition." We can approach the issue in terms of the "bare theory," and consider how such an entangled and superposed person would respond to questions, and show that (in ideal situations) they would respond as if they weren't in an entangled superposition at all! We can approach it from a Many Worlds angle, and suppose that the experimenter is actually in a different definite state in each of the different worlds described by the physics. We could approach it from a Many Minds point of view, and suppose that each one of the infinitude of the person's minds experiences at random a definite outcome.
It's worth considering the situation in the language of Quantum Reference Frames. QRF's can be understood in terms of two related conceptual frameworks. The first works purely operationally. We imagine our reference frames (rulers, clocks, gyroscopes) to be legitimate quantum systems in their own right, which can be in superposition and get entangled, and we analyze what information can be extracted from a given quantum system with reference to those quantum reference systems.
For example, in the absence of a shared 3D frame, we could only measure the spin of a particle with reference to, say, the spin of another particle. We could imagine the reference spin was in a nice spin coherent state with a j value much greater than the particle to be measured, and we could analyze things like how the reference system degrades the more it is used. Moreover, we could study the way that entanglement shared between parties can substitute for a shared classical reference frame, and so on.
The second approach tries to imagine what quantum state would be assigned to the rest of world supposing that a certain system is picked out to be the reference frame. In other words, a solution to Schrodinger's equation might assign a complex amplitude to each position in space, but the position coordinate itself is assumed to be defined with respect to some essentially classical set of rulers. But what if we allowed our ruler to be in superposition? What kind of quantum state would we have to assign to the rest of the world if we pick one quantum ruler over another? (And can we formulate something like Einstein's principle of covariance, so that all observers agree on the laws of physics no matter the reference frame?)
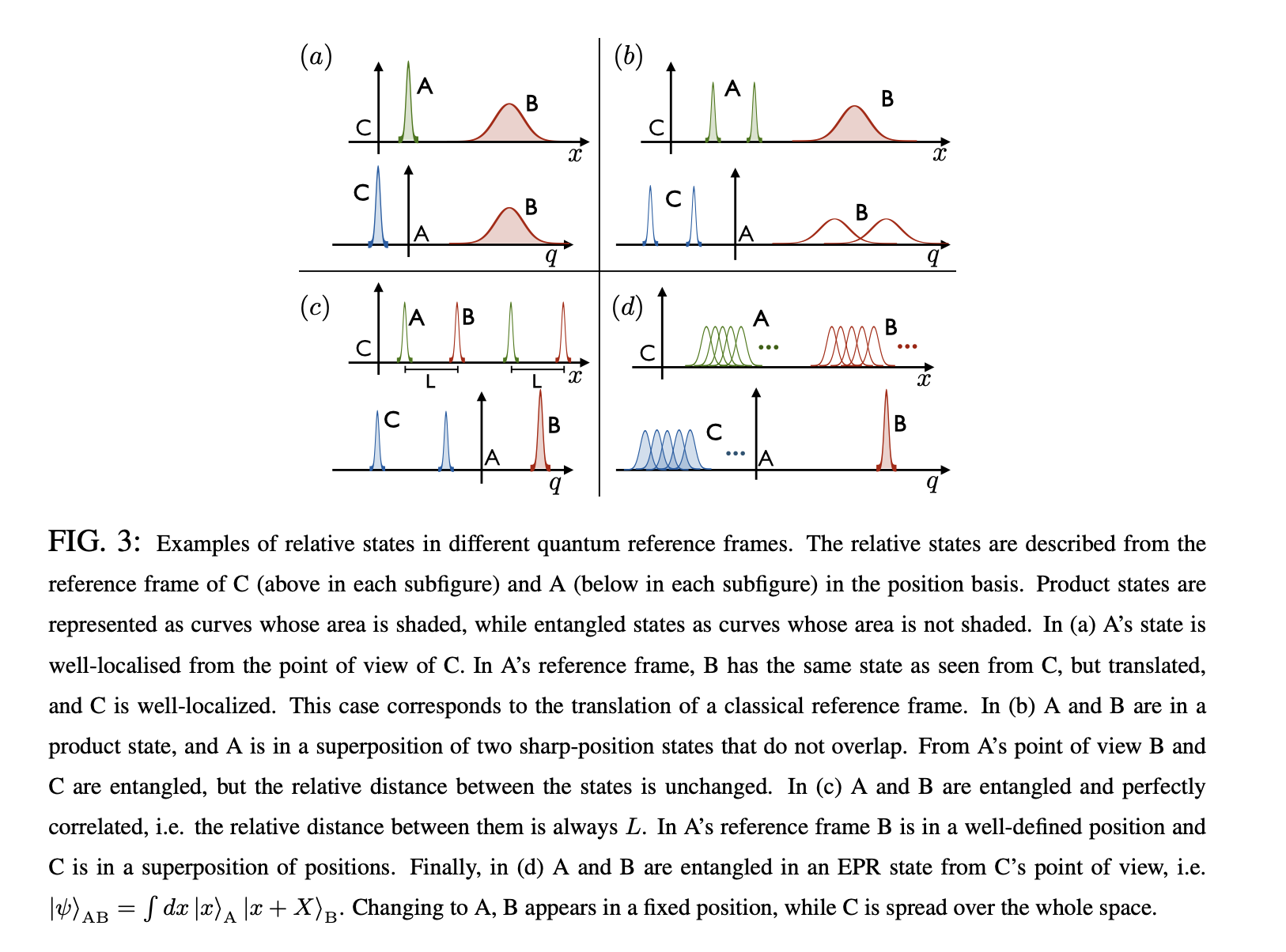
Following Giacomini, Castro-Ruiz and Brukner (as well as others including Galley and de la Hamette), the basic principle is that of a "coherent change of reference frame." Above, we see an example in terms of position, but the notion can be generalized for other observables related to other symmetry groups. We have three systems $A, B,$ and $C$. In (a), C is regarded as the reference, and so by definition it's at the origin and in a separable state which is a delta function at the origin, or better yet: it's simply the invisible background, the origin of the coordinate system with which we describe $A$ and $B$, or even more simply: it's the coordinate system itself. From $C$'s point of view, $A$ and $B$ are wavepackets located to the right. If instead we take $A$'s perspective, $A$ would be regarded as the origin, and $C$ would be to its left and $B$ would be to its right. This is no different from a classical change of reference frame.
The interesting case, however, is: what if $A$ is in a superposition of two wavepackets, and we want to jump from $C$'s perspective to $A$'s perspective? Since $C$ regards $A$ and $B$ as being in (basically) two locations each, $A$ conversely would regard $C$ and $B$ as being in two locations, and moreover in an entangled state, so that the two possible locations for $B$ and $C$ are correlated.
In other words, the supposition being made in this kind of work is that entanglement and superposition are entirely reference frame dependent. If a quantum system is chosen as a reference, what that means is that it's regarded as the "origin," as separable, in the "0" state, no entanglement, no superposition, nothing. If from another perspective, that system had been entangled and in superposition, that "quantumness" is precisely externalized to the systems coordinatized relative to the reference.
We could think in terms of spins: suppose $A$ is regarded as the reference, and therefore it's always just in the $\mid \uparrow \rangle$ state (or any other arbitrarily chosen state), and suppose $B$ and $C$ are in the $\mid \uparrow \uparrow \rangle + \mid \downarrow \downarrow \rangle$ state. If we switch to $B$'s reference frame, then now $B$ must be regarded as in the $\mid \uparrow \rangle$ state. Since $B$ and $C$ were in the entangled state $\mid \uparrow \uparrow \rangle + \mid \downarrow \downarrow \rangle$ relative to $A$, then $C$ must agree with $B$, and since $B$ is $\uparrow$, so $C$ must be be $\uparrow$. So $B$ and $C$ are in the $\mid \uparrow \uparrow \rangle$ state. But what about $A$'s state relative to $B$? From $A$'s perspective it was 50/50 whether $B$ (and $C$) were going to be $\uparrow$ or $\downarrow$, and so if now we regard $B$ (and $C$) to be $\uparrow$, then $A$ must be in the state $\mid \uparrow \rangle + \mid \downarrow \rangle$.
Lest this seem ad hoc, this procedure can be formalized as a certain unitary transformation. The argument of course depends on these systems all having essentially the same Hilbert space, with states being representations of the same symmetry group, and it's an interesting question how to fully generalize the idea when the reference system has many different kinds of systems associated with it. In the general case, it's possible the transformations won't necessarily by unitary.
Incidentally, this formulation of QRF's relates quantum states, each explitly from a "point of view," to each other, but the whole construction can be placed in a reference frame independent context. In other words, one can consider Dirac-type quantization, where one imagines, that for example, the overall momentum of all particles (say 3 particles) must be $0$ insofar as there is no external reference frame to distinguish anything other than that. Then one can posit that one of the particles is "standing still at the origin," and describe the quantum state of the other particles with reference to that particle.
With regard to supervenience, however, we have an interesting question. Insofar as we regard a quantum system as a reference frame, we precisely empty it of all content, regarding it as the invisible "0" by which we describe the rest of the world: all the properties and relations of the reference frame are externalized and attributed to the quantum states described in terms of that reference frame. In other words, we might be tempted to take our bodies to be our quantum reference frame for the world, and examine what the physical state of the world would be relative to that frame. But to do so would be as much to empty ourselves of all content whatsoever, leaving seemingly nothing that, for example, mental states could supervene on! (One is reminded of the Buddhist concept of "emptiness," referring to the way that all seemingly substantial structure dissolves into relativity upon analysis.)
There is clearly something deep still to be worked out with regard to our perception and the idea of a reference frame. We have no intrinsic knowledge of where we are located, what direction we're facing, and so forth, so that we really do have the experience of being the "0" of our world. In other words, on the one hand, we seem to be in the situation described by a quantum reference frame, whereby we always regard ourselves as being "at the center of the universe." But it seems we can't regard our whole body, as it were, as being our quantum reference frame, since in our very perceptions we are able to make comparisons, using one part as reference and another as object, so that we seem to deal with reference frames within reference frames. After all, precisely through comparison, we can gain information about location, orientation.
Indeed, this is a psychologically important fact. For example, we might be feeling uneasy, and not sure why. If, however, we can objectify that uneasiness, identify its origin, provide context for it, that's as much to switch to a reference frame where what before was perceived as distortion--as curvature, if you will--is now made concrete as an object against the backdrop provided by a new reference frame. Before the uneasy feeling was an invisible, yet consequential, part of our reference frame itself, but by switching to a new reference frame, so that that feeling is objectified against a new background, it can be dealt with, manipulated, overcome. One achieves a more spacious perspective, whereby the uneasy feeling can be confronted as object.
One wonders what, if any, is the material basis of such perspective switches? On the one hand, one ought to try to formalize in a very general way, what is involved in the act of comparison. The fundamental metaphor here, I think, is that of the "loop." For example, one can define the curvature of a space, which is a nonlocal quantity, in terms of the holonomy along a closed curve. For example, one could mark one's orientation, set off on a journey through a curve space (like the surface of the earth), and upon returning home, compare one's new orientation to the old: the difference is a measure of the curvature of the space. (Indeed, in loop quantum gravity, such loops are actually quantized!) Consider what's necessary to do this: one has to leave some kind of record at "home," go off on a journey, return, be able to recognize that indeed one has returned "home," which is to say, recognize that something has both changed and remained the same, enact a comparison, and finally relate semantically the results of the local comparison to a property of the outside space in which one journeyed. As such, there can be no real understanding of what is involved without an understanding of the nature of memory, of identity and difference.
As I say, one imagines a future more capacious physics able to account for reference frame switches that go beyond translations in positions and rotations and boosts, which would be able to relate the world as given to me in perception to the world as given to you in perception, from a comparison of our physical states. In principle, this is a matter for science, for such things are "measurable," and doesn't in themselves touch on thorny metaphysical issues like "what is consciousness."
On the other hand, there is an element of extra trickiness involved in any such endeavor, insofar as one would have to rely on internal comparisons made inwardly by individuals and reported externally. Indeed, I can quite easily imagine that no general rule could be given for what someone would necessarily perceive on the basis of their physical state (from the point of view of others).
Internally, after all, we only know what our reference frame was. It's always post-hoc. We can't identify a reference frame, as such, while we're using it. We can only identify it after we've somehow adopted a new reference frame: and indeed, what we can say about the the old reference frame is always with reference to the new reference frame. As such, any experiment that tries to confirm, on the basis of someone's physical state, that someone's perceptions are grounded in a certain reference frame, will be faced with the conundrum that the internal comparison can only be made from a new point of view.
A final point: one might confine oneself to the question of why only some aspects of our physical state are elevated to awareness. This is a question actually dealt with at some length by Bohm in his book about the implicate order. One thinks of the "scrambling" that happens in models of wormhole physics: a quantum system is scrambled across many degrees of freedom, but it can later be unscrambled and made to resurface elsewhere. One could easily imagine a kind of "quantum memory," whereby certain interactions act as triggers that cause certain quantum states to "resurface" in just this way. The metaphor here being that awareness would supervene on quantum state in terms of its tensor product structure, and that the "unconscious" would be encoded in the ever deeper layers of entanglement between the surface subsystems. (Then again, maybe it's the other way around, and one is more aware of what's deeper inside!)
Probability and Counterfactual Definiteness¶
One might desire a theory of physics that makes no necessary reference to statistical concepts. This is certainly possible, but the first point I'd make is the perhaps obvious one that nothing would prevent people from applying statistics to any such theory to great benefit. For example, I might be working in the context of Newtonian physics. Here everything proceeds deterministically and everything can be pictured in terms of particles moving under the influence of forces, and so forth. But statistics might still be useful. For example, suppose I was ignorant of the initial conditions of a situation, but wanted to know if I should expect a certain outcome to occur. Conceptually, I'd go over all the possible initial conditions, evolve each one in time, and see what proportion of those possible histories lead to the outcome I'm interested in. This would give me grounds for expecting that outcome with a certain probability, given my ignorance of the initial conditions. To the extent that I gained greater knowledge of those initial conditions, I'd update my probability accordingly, as certain cases were excluded.
At a deeper level, with regard to "counterfactual histories," we could have the interesting situation where a theory which tells a single deterministic story might have a dual description in terms of counterfactuals. This is the case for classical physics. Newtonian mechanics can be formulated in a "single story" way, in terms of particles and forces. But the very same theory can be reformulated, famously, in terms of the principle of least action. In other words, given the beginning and ending of a story, one could chart out all the possible histories that lead from beginning to end and assign a cost (the action, the difference between kinetic and potential energy integrated over the path the system takes) to each history. Classical physics can be reduced down to the statement that nature always follows the path of least action, in other words, nature takes the most efficient, or laziest path from A to B. The 19th century imagined nature as a kind of "economizer," which took stock of all the possible routes, and picked the "optimal" route. Insofar as one unique route is always actually taken, however, the alternate histories can be regarded as nominal, as conceptual devices which contextualize the path actually taken. This is worth thinking over since it gets at what we require when we want an answer to a question like "why?" Why does nature take the path it takes? The reason can be formulated by contrasting the path actually taken with all the paths it could have counterfactually taken. But of course, in classical physics, this could be regard as simply an alternative description of Newtonian physics, which in itself requires no appeal to counterfactuals.
Famously, however, quantum physics offers two twists to the story. First, it's found that actually nature doesn't always take the path of least action, but (seemingly randomly) can take any of those paths, and the theory allows probabilities to be assigned to each of those paths, so that the different paths can't be regarded as mere conceptual devices, but are in fact "live possibilities." By the same token, it can be shown that in certain limits, the highest probability must be almost always assigned to the classical path of least action, leading to the appearance of classical physics in the first place. The second twist is that, in some situations, it appears like nature takes multiple paths simultaneously. How can this be known? By studying interference: insofar as there is a "wave" which traverses each path (in the Hilbert space), when the paths converge, the waves are superposed, and the resulting interference is most definitely measurable.
In other words, physicists have gotten used to the idea that several incompatible histories must be appealed to explain the actual results obtained. Precisely insofar as a) we only measure a particle to be in a single location b) when we offer to the particle two slits to propagate through, the resulting position measurements accumulated over many runs of the experiment, show a characteristic interference pattern, which can be explained by supposing the wavefunction went through both slits, we assert that two possible histories of the particle have to be taken into account to explain the actual results we obtain.
But there is an additional overlay. We can consider a different kind of "counterfactual" situation: a different experiment, an experiment where instead we insert into the mix a detector sensitive to which slit the particle goes through. In this case, as we've discussed, the interference pattern disappears, and it seems like only one of the two histories is relevant. But of course, this is a different experiment.
In other words, the situation confronted in quantum mechanics is that in one experimental situation, it appears like two different histories have to be simultaneously appealed to explain the results, or at the very least, that the particle has to be regarded (before its measurement) as a wave, able to ripple through every path available to it (and in more general situations this wave wouldn't be regarded as simply propagating in 3D, but in the larger space of possibilities represented in Hilbert space). In another experimental situation, however, it appears like only one history has to be appealed to, and the particle can be regarded in the conventional way as "just a particle," taking a definite path.
In other words, whether "multiple histories" must be considered to explain the results is itself something which depends on the choice of experimental situation. The loophole is, of course, superdeterminism. In other words, if we have no real choice with regard to which experiments we perform, then whether an electron will reveal its wave-like or its particle-like aspects is something already determined. And if we take a Bohmian view, then in the interference situation, the particle really does take one path, whereas the wave takes both. But as we've seen, such particles and such paths are completely relative to one's choice of ontology.
Initial Conditions¶
Arguably, we should strive to formulate theories of physics without initial conditions. What could this mean? On the one hand, it could mean a theory so tightly constrained that it picks out both its laws and its initial conditions uniquely. On the other hand, one could consider the proposal of Rovelli, that initial conditions themselves are relative. The idea here is that insofar as time's arrow ranges from low entropy to high entropy, we have to assume that the initial state of the universe was in a low entropy state. But precisely to the extent that such a state is low entropy, you could say, it's special, and so demands an explanation. Why that particular low entropy state? On the other hand, there would be less of a question if the universe "began" in some high entropy state, since most states are high entropy. So Rovelli basically proposes that the universe as a whole is in a highly generic timeless/time-independent state, but that relative to subsystems within the universe, which interacts with the universe in very particular non-generic ways, subsystems such as ourselves, the universe will appear to have begun in a special low entropy state. In other words, it's not the initial conditions that are special: it's we who are special. The point is that entropy is always an observer-dependent quantity, in the sense that it's only defined in terms of the relationship between the macrostates (which are distinguishable by "someone"), and the many different microstates which appear indistinguishable insofar as they all give rise to the same macrostate. In this proposal, insofar as we interact with the world in highly non-generic and macroscopic ways, we effectively "coarse grain" the universe such that when we reconstruct "history," we recover a particular arrow of time that makes sense to us, leading from low to high entropy. But of course, there would be many such arrows of time. In a way, it's a sort of generalization of the many times of general relativity, but not for time in the sense of clock time, but for entropic time.
So we could have a theory so tightly constrained that laws and initial conditions all arise in one go. We could have a theory which essentially posits that the state/laws of the universe are highly generic, but a universe which manifests itself in highly non-generic ways relative to subsystems depending on how they interact with the rest of the world. Or we could take a page out of Wheeler, who supposes that every act of observation is an "elementary act of creation," bringing a new initial condition into being with each instance, so that it would be wrong to say there was one single initial condition at the creation of the world, but that the creation of the world is ongoing and ceaseless.
On "Measure"¶
As a setup up for the concluding, speculative section, I offer an interesting passage from Bohm's "Wholeness and the Implicate Order":
"Now, in the East the notion of measure has not played nearly so fundamental a role. Rather, in the prevailing philosophy in the Orient, the immeasurable (i.e. that which cannot be named, described, or understood through any form of reason) is regarded as the primary reality. Thus, in Sanskrit (which has an origin common to the Indo-European language group) there is a word ‘matra’ meaning ‘measure’, in the musical sense, which is evidently close to the Greek ‘metron’. But then there is another word ‘maya’ obtained from the same root, which means ‘illusion’. This is an extraordinarily significant point. Whereas to Western society, as it derives from the Greeks, measure, with all that this word implies, is the very essence of reality, or at least the key to this essence, in the East measure has now come to be regarded commonly as being in some way false and deceitful. In this view the entire structure and order of forms, proportions, and ‘ratios’ that present themselves to ordinary perception and reason are regarded as a sort of veil, covering the true reality, which cannot be perceived by the senses and of which nothing can be said or thought."
"One may speculate that perhaps in ancient times, the men who were wise enough to see that the immeasurable is the primary reality were also wise enough to see that measure is insight into a secondary and dependent but nonetheless necessary aspect of reality. Thus they may have agreed with the Greeks that insight into measure is capable of helping to bring about order and harmony in our lives, while at the same time, seeing perhaps more deeply, that it cannot be what is most fundamental in this regard."
"What they may further have said is that when measure is identified with the very essence of reality, this is illusion. But then, when men learned this by conforming to the teachings of tradition, the meaning became largely habitual and mechanical. In the way indicated earlier, the subtlety was lost and men began to say simply: ‘measure is illusion’. Thus, both in the East and in the West, true insight may have been turned into something false and misleading by the procedure of learning mechanically through conformity to existent teachings, rather than through a creative and original grasp of the insights implicit in such teachings."
Freedom and Law¶
The concept of freedom is a touchy subject, insofar as it has all sorts of social and cultural overlays. And even philosophically, "free will" is arguably an incoherent concept insofar as if it's really free, it's not your will. And along the same lines, one can rightly question whether the wiggle room supplied by supposed quantum indeterminism is enough to ground a concept of free will. We have intriguing proofs like Conway's Free Will Theorem, which demonstrates that precisely to the extent that we have the freedom to choose what experiments to perform, nature has the freedom to respond with whatever outcome it likes to these experiments. Of course, whether we do have such a freedom is exactly what's at issue in Bohmian mechanics and generally superdeterministic theories.
Moreover, it's clear in a practical sense that we are not free to simply "act differently" or even to "change our perspectives." If it were so easy, we wouldn't have such a vast literature of self-help books, aphorisms, religious teachings, philosophical tomes, which are constantly reminding us that we can act differently. Indeed, we need reminders, and in this sense, we have an obligation to share our thoughts with each other, about how things can be different, so that at the moments when we have to choose, the voices of others can return to us, and suggest in that moment, a different path. In other words, in a very important sense, our "freedom" must always be constructed.
On another level, the picture of freedom provided by something like the Free Will Theorem is supposed to have to do with the choices we make (to do an experiment) or the choices nature makes (to return an outcome)--but what about the laws themselves, which provide the context for such choices? Various thinkers have tried to imagine a physical picture where the laws themselves are subject to flux, whether evolving in accordance with metalaws, whether situated in a space of all possible laws which are quantum mechanically selected, or more exotic schemes, like Lee Smolin's proposal (which I've always found interesting) that imagines physical law to be analogous to "legal law": the idea being that when a new situation arises, what unfolds is random, insofar as there is no precedent to which one can appeal. But just as in the legal system, once one kind of case comes before a judge, future cases are judged on the basis of legal precedence, so that as time goes on, and precedents are accumulated, a stable "legal framework" emerges, giving the appearence of immutable physical law. The "simple" microworld has had lots of time to accumulate a rigid precendence structure, but when new physical situations are instigated, there is nevertheless room for freedom, which then constrains future judgements. On the other hand, this seems to assume a particular theory of time and space, and along those lines, one wonders if there is a need to posit one single "judge"--after all, following the analogy, in the human legal system, we have a whole hierarchy of judges, a whole overlapping patchwork system of laws.
Now at the end of this lengthy essay, at the risk of sounding crazy, I'd like to share with you some personal speculations. I'll offer merely a half-picture that I'm in no position to prove, only in the spirit of fun and speculation, and I ask pre-emptively for your forgiveness. What I'm about to say doesn't resolve by any means all of the questions we've raised, and it really only consists of two thoughts, as you'll see. Take them as you will. Indeed, I'm kind of afraid to even say them, since by putting metaphysical cards on the table, perhaps you'll doubt me when it comes to the physics. But I hope you can see that I always try to keep the two separate, physics and metaphysics, as much as possible: and moreover, insofar as I do offer a metaphysics, it's one which puts physics, and quantity, more generally at the forefront.
Here we go:
I've always imagined that we are completely free, that we move through the world seamlessly, and that the universe gets out of our way. That's the fundamental idea: the universe gets out of our way, and this is what drives the unfolding of events. As we move freely through it, the universe compensates for our movement by changing-- and so our free movement has consequences. These consequences aren't a restriction on our movement per se, but they condition what will be the future consequences of our movements. The consequences come from what the universe has to do, the pretzel in which it has to twist itself, in order to get out of our way. Indeed, we might not like the consequences: just because we are free doesn't mean we are free from consequences, and it might not be possible to achieve all the consequences we want at the same time. Moreover, each of us in our place has exactly this same amount of freedom, and the universe is getting out of the way of each of us, and the point is the answer to the question of "why" anything is the way it is, is always to be answered with reference to the free movement of somebody or something. Consequences can cancel out, however, and are often negotiable, and in these situations, the appearance of stable laws in certain domains emerges, which can be described using Hamiltonians or Lagrangians or whatever you like: the principle of inertia has its origin in collective habit. And I imagine that the way the consequences of our free movement manifest to each other supervenes in some way on entanglement, although as we've seen, figuring exactly how our points of view relate to each other will be an immensely subtle business--and along these lines, indeterminism would be the result of relation being established between the previously unrelated.
So that's the first thought. The second thought:
I've always imagined that the world has "qualities," a word which I'm not sure should be singular or plural, both or neither. Whatever we can formalize about the world, whatever we can successfully communicate about the world in a confirmable and reproducable way, whatever we can measure about the world, is inevitably about structure and relation, and structure and relation alone. In the realm of symbols and quantities, everything is always relational, and these are the things we can successfully come to agreement about through communication and experiment. We share structures with each other, and relate structures to other structures, which are "coordinated" with our experience insofar as experience can be made quantitative and those quantities coordinated into a structure. But this leaves open the question of what these structures refer to. Physics examines how structures relate to each other, evolve relative to each other, taking on new descriptions in different languages. But it seems to me that "qualities" are what fill these structures. And one of the most important qualities is the quality of quantity, which provides the ground for logical thought and communication, the qualitative recognition of quantitative structure itself supervening on qualities.
Insofar as the "logic" of these qualities can be formalized, their qualitative character is lost, and we're back in the realm of structure, measure, and the communicable. But that doesn't mean that the qualities are entirely private. I imagine the qualities like a supernal light, which is blocked and occluded precisely by quantity, and it is the pattern of blockage and darkness that is structure itself, so that what is ever communicated is the lattice work which is blocking out the light, giving it "form". But precisely by communicating structures, we can rearrange what is blocked and what is unblocked in each other, and allow different qualitative light to shine through, and so provide the occasion for an actually shared experience. This is a metaphor.
None of this is to priviledge quality over quantity: rather, they require each other, as each can only be understood as a kind of negation of the other. Their meeting point, the "navel of the world," to use an ancient turn of phrase, is the quality of quantity. So that one can't really understand the nature of the qualities without first having journied through the realm of quantity; just as without qualities, quantities are dead on the page.
The qualities are transcendent and self-revealing, and provide the ground for unformalizable intuitions, motivations, and meanings that populate our sphere of free movement. Insofar as we can explain ourselves and our experience and tell narratives about ourselves and others, we avail ourselves of the language of physics, measurement, and structure--and indeed, we do these things because they work, and explain how one structure depends upon another, why different structures survive or dissapear in different circumstances. But that doesn't exhaust the totality of what's going on. Even if immersed in a world of transcendental motivation and meaning, precisely insofar as I actually pursue such things, to greater or lesser success, in my relationship to others, in other words, to the extent that I put the transcendental into practice, I am able to be formalized and my behavior understood in a structural sense. But it seems to me that "true understanding," in the sense of sharing the same vision of the light, is something altogether different.
Bibliography¶
Quantum mechanics and the covariance of physical laws in quantum reference frames
Quantum reference frames for general symmetry groups
Bohmian mechanics in momentum representation and beyond
Experimental Comparison of Bohm-like Theories with Different Primary Ontologies
A causal quantum theory in phase space
Schrodinger revisited: an algebraic approach
On Epstein’s trajectory model of non-relativistic quantum mechanics
DeBroglie-Bohm Guidance Equations for Arbitrary Hamiltonians
Wholeness and the Implicate Order
Bohm’s approach to quantum mechanics: Alternative theory or practical picture?