{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# CS579: Lecture 06 \n",
"** Graph Partitioning **\n",
"\n",
"*[Dr. Aron Culotta](http://cs.iit.edu/~culotta)* \n",
"*[Illinois Institute of Technology](http://iit.edu)*\n",
"\n",
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Recall the network from last lecture:\n",
"\n",
"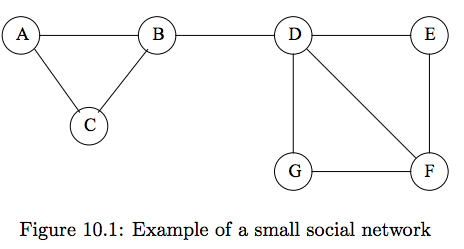\n",
"\n",
"We identified edge $(B,D)$ as a good candidate to remove to create two clusters based on *betweenness*."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Today we'll discuss an alternative clustering approach based on *graph cuts.*\n",
"\n",
"- A **cut** $C=(S,T)$ partitions the vertices $V$ of a graph into two subsets $S$ and $T$.\n",
"- The **cut-set** of $C$ is the set of edges that have one endpoint in $S$ and the other in $T$\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"**What makes a good cut?**\n",
"\n",
"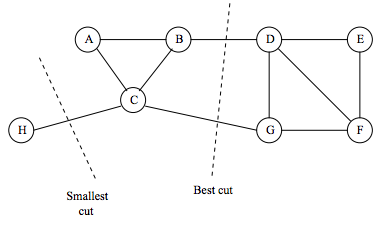\n",
"\n",
"The cut-set $\\{(H,C)\\}$ is smaller than the set $\\{(B,D), (C,G)\\}$. \n",
"\n",
"Why might we not like cut $\\{(H,C)\\}$?"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"A good cut is:\n",
"\n",
"- small\n",
"- balanced\n",
"\n",
"How to quantify these?\n",
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"$Vol(S)$: **volume** of a set of $S$ nodes is the number of edges with at least one end in $S$.\n",
"\n",
"\n",
"\n",
"$Vol(\\{A,B,C\\})=6$"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Let $Cut(S,T)$ be the number of edges in cut-set of cut $C=(S,T)$ (the cut **size**).\n",
"\n",
"The **normalized cut value** for $(S,T)$ is:\n",
"\n",
"$$NCV(S,T) = \\frac{Cut(S,T)}{Vol(S)} + \\frac{Cut(S,T)}{Vol(T)}$$\n",
"\n",
"\n",
"\n",
"Example:\n",
"\n",
"Consider the cut where $S=\\{H\\}$ and $T=\\{A,B,C,D,E,F,G\\}$.\n",
"\n",
"- $Cut(S,T) = 1$\n",
"- $Vol(S) = 1$\n",
"- $Vol(T) = 11$\n",
"- $NCV(S,T) = \\frac{1}{1} + \\frac{1}{11} = 1.09$\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"\n",
"\n",
"Example:\n",
"\n",
"Consider the cut where $S=\\{A,B,C,H\\}$ and $T=\\{D,E,F,G\\}$.\n",
"\n",
"- $Cut(S,T) = 2$\n",
"- $Vol(S) = 6$\n",
"- $Vol(T) = 7$\n",
"- $NCV(S,T) = \\frac{2}{6} + \\frac{2}{7} = 0.62$\n",
"\n",
"So, if one part of the cut has a small volume, the normalized cut value will be large."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Problem:** How do we identify the cut with the smallest normalized cut value?\n",
"\n",
"
\n",
"Like most good things, it is NP-hard."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Linear algebra to the rescue!**\n",
"\n",
"Below, we describe a way to approximate the optimal cuts using eigenvalue decomposition."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"** Representing Graphs with Matrices **\n",
"\n",
"- **Adjacency matrix** $A$: $A[i, j] = 1$ iff there is an edge from $i$ to $j$.\n",
"- **Degree matrix** $D$: $D[i, i] = deg(i)$, else 0\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAeIAAAFBCAYAAACrYazjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xd4lFXC/vHvhFAyEOkg0otR1AQXCEhTWNEQerEuSAgB\nhEVlVRYMuLrsK0R4owi+S15aCLEgRSOioIAr/JA6uITgSw0izRKQCEESJGR+f4SwBCaQDJk5U+7P\ndXGJU565FZ65c545c47FbrfbERERESMCTAcQERHxZypiERERg1TEIiIiBqmIRUREDFIRi4iIGKQi\nFhERMUhFLCIiYpCKWERExCAVsYiIiEEqYhEREYNUxCIiIgapiEVERAxSEYuIiBikIhYRETFIRSwi\nImKQilhERMQgFbGIiIhBKmIRERGDVMQiIiIGqYhFREQMUhGLiIgYpCIWERExSEUsIiJikIpYRETE\nIBWxiIiIQSpiERERg1TEIiIiBqmIRUREDFIRi4iIGKQiFhERMUhFLCIiYpCKWERExCAVsYiIiEEq\nYhEREYNUxCIiIgapiEVERAwKNB1AvENGRgbJSUnsT0vj7OnTVKpcmZCwMKKio6lZs6bpeCIiXsti\nt9vtpkOI57LZbMyIi+OzVavoD4Tn5BAMZAHbgoJIsdvpERnJmNhYwsPDDacVEfE+KmIp0pyEBF4d\nO5bx2dlE2e1UdfCYTCDJYmFaUBCT4uMZMWqUu2OKiHg1FbE4NCchgaljx/LFuXM0K8bj04EIq5Xx\nKmMRkRJREcs1bDYbvTt3ZsMVJdwIyCB/UoEdsABDgJlXPC8d6GS1smL9elq3bu3GxCIi3kuzpuUa\nM+LiGJ+dXWgkbAE+A86Q//nwGQqXMEAzYFx2NjPi4twTVETEB2hELIVkZGRwR8OGfJeTU+gz4cbA\nfOCPN3j+KaBphQrsP3JEs6lFRIpBI2IpJDkpiX7gcGJWcVQD+lksJCcllV4oEREfpiKWQvanpdEm\nJ8fhfX3JL9qql/45v4hjhGdns3/XLtcEFBHxMVrQQwo5e/o0wUXctxzoUoxjBANZmZmlF0pExIdp\nRCyFVKpcmawi7ivuZIIsILiqsxe3RUT8i4pYCgkJC2NbhQo3dQxbUBAhoaGllEhExLdp1rQUcr1Z\n0xlAmStuewj48Krna9a0iEjJaEQshdSqVYsekZEstFgK3X4I+I387w8X/Lq6hAEWWiz07N5dJSwi\nUkwaEcs1HK2sVRxaWUtEpOQ0IpZrhIeHMyk+ngirlfRiPqdgrelJ8fEqYRGRElARi0MjRo1ifHw8\nnaxW3rRYKOrLSKeANy0WOmnDBxERp+jStFzXtm3b6NmlC7/n5tK/TBnCs7P/sx9xhQoszsnhoa5d\n+VtcnEbCIiJO0IIecl1ZWVnUadaMNWvW8M7ChaTu2kVWZibBVatyT2godTIzOX78uEpYRMRJGhHL\ndT3xxBN07NiRZ555xuH9mZmZNG3alNTUVBo0aODmdCIi3k9FLEU6efIkzZo149ChQ1S9zkpZY8eO\nJTc3l7feesuN6UREfIOKWIr05ptvkpqaSnJy8nUfd/z4cUJDQzlw4ADVq1d3UzoREd+gWdPikN1u\nZ+7cuQwfPvyGj61bty79+vXjn//8pxuSiYj4Fo2IxaGvv/6a4cOHs3v3bixXrbLlyN69e7n//vs5\ndOgQFStWdENCERHfoBGxODRnzhyGDx9erBIGuPPOO+nYsSOJiYkuTiYi4ls0IpZrZGZm0rhxY9LT\n06lRo0axn7d161Yee+wx0tPTKVu2rAsTioj4Do2I5Rrvvfce3bp1K1EJA7Rt25YmTZqwePFiFyUT\nEfE9KmIppCSTtBwZP348U6dORRdaRESKR0UshdhsNs6ePUuXLl2cen5ERARlypRh5cqVpZxMRMQ3\nqYilkLlz5zJs2DACApz7q2GxWC6PikVE5MY0WUsuy8rKokGDBuzevZs6deo4fZzc3FxCQkJ49913\nad++fSkmFBHxPRoRy2UffPABnTt3vqkSBggMDGTs2LEaFYuIFIOKWC6bM2cOI0aMKJVjRUdHs3Xr\nVnbv3l0qxxMR8VUqYgEgNTWVjIwMHn744VI5XlBQEM8++yzTpk0rleOJiPgqfUYsAIwePZpatWrx\n6quvltoxC7ZI3LlzJ/Xr1y+144qI+BIVsXDu3Dnq169PampqqRfmiy++SF5eHtOnTy/V44qI+AoV\nsbBw4UKWLFnCZ599VurHPnbsGGFhYdoiUUSkCPqMWG5qJa0bqVevHn379tUWiSIiRdCI2M/t3r2b\nrl27cvjwYZdt1LBnzx46d+7MoUOHsFqtLnkNERFvpRGxn5s7dy5Dhgxx6W5JzZs3p3379toiUUTE\nAY2I/VhOTg7169dn69atNGnSxKWvtWXLFp544gkOHDigLRJFRK6gEbEfS0lJ4d5773V5CQPcd999\nNGrUiCVLlrj8tUREvImK2I+5cpKWI9oiUUTkWipiP5Wens63335Lnz593Paa3bp1w2KxsGrVKre9\npoiIp1MR+6l58+YxePBgypcv77bX1BaJIiLX0mQtP3ThwgXq16/PunXruPPOO9362rm5udx+++28\n//77tGvXzq2vLSLiiTQi9kMrVqwgJCTE7SUM2iJRRORqKmI/VJrbHTojOjqazZs3a4tEERF0adrv\nfP/997Ru3ZqjR48SFBRkLMdrr73GwYMHWbBggbEMIiKeQEXsZ1555RV+/fVXZs6caTTHqVOnaNas\nmbZIFPFiGRkZJCclsT8tjbOnT1OpcmVCwsKIio6mZs2apuN5DRWxH8nNzaVRo0asWrWK0NBQ03F4\n8cUXsdvtvPnmm6ajiEgJ2Gw2ZsTF8dmqVfQHwnNyCAaygG1BQaTY7fSIjGRMbCzh4eGG03o+FbEf\n+fTTT3nttdfYsmWL6SjAf7ZITE9Pp1q1aqbjiEgxzElI4NWxYxmfnU2U3U5VB4/JBJIsFqYFBTEp\nPp4Ro0a5O6ZX0WQtP+LulbRupF69evTp00dbJIp4iTkJCUwdO5YN587xlyJKGKAq8LzdzoZz55g6\ndixzEhLcGdPraETsJ3744Qfuuecejhw5QqVKlUzHuUxbJIp4B5vNRu/Ondlw7hzNrrrvfWA6sBe4\nBbgXmAB0ANKBTlYrK9avp3Xr1m7N7C00IvYTCxYs4NFHH/WoEob8LRLbtWun2dMiHm5GXBzjs7Ov\nKeE3gReAl4EM4AgwGlhx6f5mwLjsbGbExbktq7fRiNgP5OXl0bRpU5YtW0arVq1Mx7nGli1bePLJ\nJzlw4ACBgYGm44jIVTIyMrijYUO+y8kpdDn6DFAXWAj0v87zTwFNK1Rg/5Ejmk3tgEbEfmDt2rVU\nrVrVI0sY8rdIbNCggbZIFPFQyUlJ9INrPhPeDJwH+t7g+dWAfhYLyUlJLkjn/VTEfsDTJmk5oi0S\nRTzX/rQ02uTkXHP7L0ANilck4dnZ7N+1q7Sj+QQVsY/LyMhg7dq1/OlPfzId5boiIyOx2+18/vnn\npqOIyFXOnj5NsIPbqwMngbxiHCMYyMrMLNVcvkJF7OMWLlxI3759qVy5suko11WwReLrr79uOoqI\nXKVS5cpkObi9HVAe+LgYx8gCgqsW9YUn/6Yi9mF2u5158+Z5/GXpAo8//jhHjhzxmAVHRCRfSFgY\n2ypUuOb2W4BJ5M+SXg5kA7nA58BLVz3WFhREiAes6OeJNGvah61fv54///nPfPvtt1gsFtNxiuV/\n/ud/+PLLL0lJSTEdRUQuKWrWdIFF5H+NaS/5l6BbAROB+y7dr1nT16cRsQ8rmKTlLSUMMHToUDZt\n2sSePXtMRxGRS2rVqkWPyEiSingveRKwkX/5+Qfyv0N83xX3L7RY6Nm9u0q4CBoR+6hTp07RpEkT\nDh48SPXq1U3HKZH/+q//4tChQyQmJpqOIiKXpKSkMHTAAGx2+zWLelyPVta6MY2IfdQ777xDjx49\nvK6EAUaPHs3HH3/MsWPHTEcREeDLL79k5MiRdH/sMSKsVtKL+bx0IMJqZVJ8vEr4OlTEPshut3vF\nd4eLUq1aNYYMGcL06dNNRxHxa3a7nZkzZzJw4EA++OAD3vvgA8bHx9PJamW6xUJRX0Y6BbxpsdDJ\namW8dl+6IV2a9kGbN28mKiqKffv2edXnw1c6evQoLVq00BaJIoacP3+e0aNHs3XrVj755BMaN258\n+b7t27czIy6OT1eupJ/FQnh29uX9iG2X9iPu2b07Y2JjNRIuBhWxDxo6dCh33nkn48aNMx3lpkRH\nR9O0aVNefvll01FE/MrPP/9M//79qVWrFsnJyQQHO1rOA06cOEFyUhL7d+3i42XLeDAiglbt2zN4\nyBBNzCoBFbGPOXPmDA0bNmTv3r3Url3bdJyboi0SRdzv3//+N/369WPIkCG8+uqrBAQU7xPMkJAQ\nVqxYwR133OHihL5HnxH7mPfff58HH3zQ60sY8rdIvO+++7RFooibLF68mIiICN544w0mTZpU7BIG\nKFeuHBcuXHBhOt+lIvYx3jxJy5GXXnqJ+Ph4cnNzTUcR8Vl5eXlMnDiR8ePHs2bNGh555JESH6Ns\n2bL8/vvvLkjn+1TEPuSbb77hl19+4aGHHjIdpdS0a9eO+vXrs3TpUtNRRHzSmTNn6Nu3Lxs2bGDb\ntm3ce++9Th1HI2LnqYh9yNy5cxk2bFiJLid5g5deeklbJIq4QHp6Ou3ateO2225j7dq11KpVy+lj\naUTsPN96x/ZjZ8+eZcmSJURHR5uOUuoiIyPJy8vjiy++MB1FxGesXbuWDh068Mwzz/C///u/lCtX\n7qaOV7ZsWY2InaQi9hFLliyhY8eO1K1b13SUUqctEkVKT8EiHYMGDWLx4sWMKqXFNnRp2nkqYh/h\na5O0rvb444/z/fffa4tEkZtw/vx5hg0bxrx589i8eTOdO3cutWPr0rTzVMQ+4Ntvv+Xo0aNERkaa\njuIygYGBvPjii0ydOtV0FBGv9NNPP/HHP/6RzMxMNm3aVGilrNKgEbHzVMQ+YO7cuURHRxMYGGg6\nikvFxMSwadMm9u7dazqKiFf55ptvaNOmDQ899BDLli2jUqVKpf4aGhE7T0Xs5bKzs3nvvfeIiYkx\nHcXlrFYro0eP5r//+79NRxHxGh988AHdunVj+vTp/P3vf3fZtyo0Wct5KmIv9+GHH9K6dWsaNWpk\nOopbjB49mpSUFG2RKHIDeXl5TJgwgdjYWNauXcuAAQNc+nq6NO08FbGX8/VJWlerXr06UVFRvPXW\nW6ajiHisM2fO0KdPHzZu3Mi2bdto0aKFy19Tl6adpyL2Yvv27WPfvn306tXLdBS3euGFF0hMTCQz\ns6jdUEX8V3p6Ovfddx/16tVjzZo1btsFSSNi56mIvdi8efOIioq66S/ie5v69evTu3dvZs2aZTqK\niEcpWKTj2WefJSEhwa3vDRoRO09F7KV+//13kpOTGTZsmOkoRowbN463336b7Oxs01FEjLPb7cyY\nMYNBgwaxZMmSUlukoyQ0Wct5KmIvtXz5cu666y5uv/1201GMuOuuu2jbtq22SBS/d/78eWJiYpg/\nfz6bN2/mgQceMJKjXLlyGhE7SUXspfxtkpYj48eP1xaJ4td++uknunTpwunTp12ySEdJaETsPBWx\nF/ruu+/YsWMH/fv3Nx3FqPbt21O3bl1tkSh+qWCRjoiICJYuXeqSRTpKQpO1nKci9kLz589n0KBB\nVKhQwXQU47RFovijRYsWXV6k49VXX/WIrU81Wct55v/0pERyc3NZsGCB31+WLtC9e3cuXrzI6tWr\nTUcRcbmLFy8SGxvLhAkT3LJIR0no0rTzVMRe5rPPPqNx48bcddddpqN4BG2RKP6iYJGOzZs3u22R\njpLQZC3nqYi9jCZpXevxxx/n0KFDbN261XQUEZc4cOAA9913Hw0aNHDrIh0loRGx81TEXuTYsWNs\n2rSJRx991HQUj1K2bFltkSg+a82aNXTs2JHnnnuOWbNmUbZsWdORHNJkLeepiL1IYmIiTzzxBBUr\nVjQdxeMMHTqUr7/+mn379pmOIlIq7HY7b731FoMHD2bJkiWMHDnSdKTr0mQt56mIvcTFixeZP3++\nLksXoWLFitoiUXzG+fPnGTp0KAsWLDC6SEdJ6NK081TEXmL16tXUqlWLP/zhD6ajeKxnnnmGjz76\niOPHj5uOIuK0gkU6srKy2Lhxo9dscarJWs5TEXsJTdK6serVqzN48GBtkShea/v27YSHhxMREcGS\nJUuML9JREhoRO09F7AV++uknvvrqK5588knTUTzeCy+8wPz587VFonid999/n8jISGbMmOExi3SU\nhCZrOc+7/qT9VFJSEgMGDCA4ONh0FI/XoEEDevXqRUJCgukoIsVSsEjHxIkT+fLLL7126VpN1nKe\nitjD5eXlMW/ePF2WLoFx48Yxc+ZMbZEoHu/KRTpsNhthYWGmIzlNl6adpyL2cOvWrcNqtdKmTRvT\nUbzG3XffTZs2bUhKSjIdRaRIBYt0NGzYkDVr1lCjRg3TkW6KJms5T0Xs4QomaVksFtNRvIq2SBRP\nVrBIx5gxY/jnP//psYt0lIRGxM5TEXuwkydPsmrVKgYNGmQ6itfp0KEDt912G8uWLTMdReSyKxfp\nWLp0KU8//bTpSKVGk7WcpyL2YMnJyfTu3ZuqVauajuKVxo8fry0SxWNcvUjH/fffbzpSqdJkLeep\niD2U3W7Xd4dvUvfu3cnNzdUWiWLclYt0bNq0yWsW6SgJXZp2norYQ23cuBGAjh07Gk7ivQICAhg3\nbpw2gxCjtm/fTps2bejWrRtLlizx2bXiNVnLeSpiDzV37lyGDRumSVo36YknnuDgwYNs27bNdBTx\nQ1cu0vHKK6943SIdJaERsfMsdn2A5nF+/fVXGjVqxIEDBzxy31FvM3PmTNavX8+HH35oOor4iYsX\nLzJx4kSWLFnC8uXLCQ0NNR3J5c6ePcutt97K2bNnTUfxOr7745kXe++994iIiFAJl5KYmBg2bNig\nLRLFLU6fPk2fPn3YunUr27Zt84sSBk3WuhkqYg9jt9uZM2eOJmmVIm2RKO5y5SIdq1ev9vpFOkqi\n4NK0LrKWnIrYw9hsNs6ePcsf//hH01F8SsEWiT/88IPpKOKjVq9eTceOHXn++ed9ZpGOkggICKBM\nmTJaRMcJKmIPUzBJy5cndZhQvXp1nnrqKW2RKKXObrczffp0oqKiWLp0KSNGjDAdyRhN2HKOJmsZ\nkpGRQXJSEvvT0jh7+jSVKlem4R13MC0+nr1791KnTh3TEX3O4cOHadmyJQcPHqRKlSqm44iHcnRu\nhoSFERUdfc28jfPnzzNy5Eh27NjB8uXLadiwoaHUnqFy5cocOXKEypUrm47iVVTEbmaz2ZgRF8dn\nq1bRHwjPySEYyAI2lS3LRxcv0rdPH8bExhIeHm44re8ZPHgwzZs3JyYmpthvtuIfrndubgsKIsVu\np0dk5OVz88cff6R///7Uq1ePpKQkn/1+cEnUqFGDPXv26BwqKbu4zexZs+y3Wq326RaL/RTY7Q5+\nnQL7mxaL/Var1T571izTkX3OokWL7FXLl7dXKV/ePrRCBXsC2N8FewLYo4OC7FUqVLAP7NfPvm3b\nNtNRxY1Kem7Gjhtnr1evnv0f//iHPS8vz3R8j1GnTh378ePHTcfwOipiN5k9a5a9idVqP1DESX71\nrwNgb6IyLlUFb7ZvXHpT1Q9CYrc7d27eCvZRI0aYju5xGjRoYD906JDpGF5HRewG27Zts9/q4ERv\nCPYgsAeDvdKlf/549QlvtdptNpvp/wSvpx+ExBFH5+aV52U1sPcE+zFHZaxz8xpNmza179+/33QM\nr6OpuW4wIy6O8dnZNLvqdgvwGXCG/M+hzgC3XnF/M2BcdjYz4uLcE9RH2Ww2Xh07li/OnaMZ0Aiw\nApWBakBHYDZw5WSJZsAX587x6tixbN++3d2RxU0cnZtXnpc/ArWAZ696ns5Nx7QVonNUxC6WkZHB\nZ6tWEVXEnLgbzZSLstv5dOVKTpw4Ufrh/MTVb7YFb7SngcPAS8BUIOaq5+nN1rdd79wsuKUc8Aiw\n28HzdW5eS6trOUdF7GLJSUn0A5zdUbga0M9iITkpqfRC+ZGi3mwL/i0Y6AksBhZy7Ruu3mx9V3HO\nzXPk/91o5+A+nZvX0ojYOYGmA/i6/WlptMnJKfL+vvznD6Ez8JGDx4RnZ/P2rFmkpqVRpkwZAgMD\nKVOmzHV/X9zHmTiWO3eUKu4PQuFAPWADcNcVt1/5ZvviX//qopSuYc+fA0JeXt7lXxcvXiz07/58\n29avvmJ0EedmwXl5lvxL018U8f84PDub1F27XPMH6IU0InaOitjFzp4+TfB17l8OdLnBMYKBmlWr\n8tBDD3Hx4kUuXrxIbm7uDX9//vz5y78v7nOK8/ubeX5eXt7lpfDc8cNC2pYtPHudH4SudBtwysHt\n4dnZzJo9m2937/aYEinu7RaLhYCAgEK/ypQp45O3FfyZF/e5e222Is/NgvPSDnwM3A/sIb+Urz43\nszIzi/X3yx9oZS3nqIhdrFLlymRd5/7irKaSBdx5zz0MHjy4lFKZY7fbiyx0V/ywcHzv3uv+IHSl\n4+SPgK8WDFSuWJH777/f7WVzs8/XftZF27ZuHVlpaQ7vKzgvLUA/4Gnga6D/VY/LAoKrOvvBk+/R\npWnnqIhdLCQsjG0ffsjIYo7KHLEFBXG3j2ylZrFYCAwMJDDQPX/11q1cSVZq6g0fZwN+IH8G9dWy\ngLtbtCA6OrqU04lJxT03lwO/As0d3OdL52Zp0KVp52iylosNHjKEFMDRxavijFVOASl2O4OHDCnV\nXP4iJCyMbRUqFHl/FvAp8CTwFHC3g8fYgoII0Zutz7neudkLuIX8r7j9DUjm2iLWuXktjYidoyJ2\nsVq1atEjMpKFDi4RfgfcaLPDhRYLPbt319qtTirqzbYX+W+yDYA4YCyQ6OD5erP1XUWdm4eA38j/\nHvFpIA14wsHzFwAPd+2qc/MKGhE7R0XsBmNiY5kaFER6CZ+XDkwLCmJMbKwrYvkFR2+2BW+0p8kv\n6I3ASBxfodAPQr7tZs7NKYGB/GvLFj777DNXRPNKmqzlHBWxG4SHhzMpPp4Iq7XYJ3w6EGG1Mik+\nntatW7syns/TD0JSlJs5N+NmzmTp0qU888wzDBs2jDNnzrgyqlfQpWnnqIjdZMSoUYyPj6eT1cp0\ni8Xh51KQfyn0DYuFTlYr4+PjGTFqlDtj+iT9ICTXU5Jz882rzs3OnTuzc+dOAFq0aMG6devcFdsj\n6dK0c8r8/e9//7vpEP6iVXg4nSMi+PjkSUYfOsT+smX5ITeXfeRfHp0VFETMxYvwwAPMef99evXp\nYzqyz2gVHk5QtWoMXLsWy8WLNAeCHDzuFJBgsTDMauVl/SDkN250biYEBTEqMJBbevdmxvz5hc7N\n8uXL07t3b26//Xaio6M5duwYDzzwAGXLljX232PKF198QfXq1WnTpo3pKF7FYrcXsQiyuNSJEyfy\nN6bftYuszEyCq1YlJDSUU7/+ysmTJ5k9e7bpiD7HbrcTFhZGDauV1LQ0+lkshGdnX9783XZp8/ee\n3bszJjZWI2E/VdS5OXjIkBvOFfjll18YPXo0O3fuJDk5mfDwcDel9gx/+ctfaNiwIc8//7zpKF5F\nRexhjh8/TmhoKEePHqVixYqm4/iUr776ipEjR7J7925OnTrl9JutyI0sXryY5557jqeffpqXX36Z\ncuXKmY7kFn/961+pWbMm48aNMx3Fq6iIPVDPnj159NFHiYqKMh3Fp3Tt2pWBAwdqYQ5xix9//JFh\nw4bx448/kpyczD333GM6kstNnDgRq9XKxIkTTUfxKpqs5YFiYmJITHT0rVZx1tatWzlw4ACDBg0y\nHUX8RJ06dfj000/585//TJcuXZg2bRoXL140HculNFnLOSpiD9SjRw/27t3LgQMHTEfxGZMnT2bc\nuHF+OYFGzLFYLAwbNoxt27axcuVKHnjgAQ4ePGg6lsvo60vOURF7oHLlyvHUU09pVFxK0tLSsNls\nDB061HQU8VONGzfmX//6FwMGDKBt27YkJCTgi58KakTsHBWxh4qJiWHhwoXk5uaajuL14uLieP75\n5wkKcvSFJRH3CAgI4Pnnn2fDhg0kJibSrVs3jh07ZjpWqdLKWs5REXuo5s2b06hRI1atWmU6ilc7\ncOAAa9euZZS+Dyweonnz5mzatImOHTvSsmVL3n33XZ8ZHZcrV04jYieoiD1YTEwM8+fPNx3Dq73+\n+uuMHj2a4ODi7kos4nply5blb3/7G59//jmvv/46jzzyCCdOnDAd66ZpROwcFbEHe+yxx1i/fj0/\n/fST6She6ciRI6SkpPDcc8+ZjiLiUMuWLdm+fTtNmzYlLCyM5cuXm450UzRZyzkqYg8WHBxM//79\nSU5ONh3FK8XHxxMTE0O1atVMRxEpUoUKFZg2bRpLly7lhRdeICoqil9//dV0LKdospZzVMQeruDy\ntK98huQuP//8M++++y4vvPCC6SgixdKxY0d27tyJ1WolLCyMtWvXmo5UYro07RwVsYdr164dAQEB\nbNy40XQUrzJ9+nSefPJJ6tSpYzqKSLFVqlSJhIQE5s6dS3R0NM888wy//fab6VjFpslazlEReziL\nxaJJWyWUmZnJ3Llztd6teK2IiAjS0tI4ffo0f/jDH9i8ebPpSMWiEbFzVMRe4KmnniIlJYWsrCzT\nUbzC22+/Te/evWnYsKHpKCJOq1q1Ku+88w5xcXH069eP2NhYzp8/bzrWdWmylnNUxF6gdu3adOnS\nhcWLF5uO4vHOnj3L22+/zUsvvWQ6ikipGDBgADt37mTPnj20adOGnTt3mo5UJE3Wco6K2Evo8nTx\nzJ49my5dunDHHXeYjiJSamrXrk1KSgovvPACXbt2ZcqUKR656p4uTTtHRewlunXrxpEjR9i9e7fp\nKB4rJyeHN954gwkTJpiOIlLqLBYLUVFRfPPNN/zrX/+iY8eO7Nu3z3SsQjRZyzkqYi8RGBhIVFSU\nRsXXsWDf8p04AAAR90lEQVTBAlq2bMm9995rOoqIyzRo0IDVq1czaNAgOnTowMyZM8nLyzMdC9CI\n2FkWu76g6jXS09Pp0KEDR48epVy5cqbjeJQLFy4QEhLCe++9R/v27U3HEXGL/fv3ExUVhdVqJTEx\n0fgExT179tC/f3/27NljNIe30YjYizRr1ozmzZuzYsUK01E8zqJFi2jUqJFKWPxKSEgIGzZsoGvX\nrrRu3ZoFCxYYXfxHk7WcoyL2Mpq0da28vDzi4uKYOHGi6SgibhcYGEhsbCxffvklb731Fn369DG2\nPr0uTTtHRexlBgwYwJYtW3xuH9Ob8dFHH3HLLbfw4IMPmo4iYkxYWBg2m43Q0FDuvfdeli1b5vYM\nmqzlHBWxl7FarTz++OMkJSWZjuIR7HY7U6ZMYcKECVgsFtNxRIwqV64ckydP5uOPP2bChAkMHDiQ\nU6dOue31NSJ2jorYC8XExJCYmOgxMyVN+vzzz7lw4QK9evUyHUXEY9x3332kpqZSvXp1wsLC+Pzz\nz93yulpZyzkqYi/UqlUrKlWqxLp160xHMcputzN58mQmTJhAQID+KotcyWq1MnPmTBYuXMjTTz/N\nyJEjOXv2rEtfU5O1nKN3Ly9UsBFEYmKi6ShG/b//9//4+eefeeyxx0xHEfFYDz74IGlpaZw/f54W\nLVqwYcMGl72WLk07R98j9lK//PILTZs25fvvv6dKlSqm4xjx8MMP8/jjjxMTE2M6iohX+OSTTxg5\nciR/+tOfeO2116hQoUKpHt9ut1OmTBkuXLhAmTJlSvXYvkwjYi9VvXp1IiIieP/9901HMcJms7Fn\nzx6eeuop01FEvEbv3r3ZuXMn33//Pa1ateKbb74p1eNbLBaNip2gIvZi/vyd4ilTpvDXv/5VK4yJ\nlFDNmjVZunQpEyZMIDIykkmTJpVqcWrCVsmpiL1Y165dOXnyJKmpqaajuNW3337L5s2bGTZsmOko\nIl7JYrEwcOBAduzYwebNm2nXrl2pbSijCVslpyL2YgEBAURHR/vdqDguLo6//OUvWK1W01FEvFrd\nunVZtWoVw4cP5/777+eNN97g4sWLN3VMXZouOU3W8nKHDx+mVatWHDt2rNQnXniigwcP0rZtWw4e\nPEjlypVNxxHxGQcPHmTIkCEEBASwYMECmjRp4tRx6tevz8aNG2nQoEEpJ/RdGhF7uYYNG9KyZUtS\nUlJMR3GLqVOnMmrUKJWwSClr2rQp69ato1evXrRp04Y5c+Y4tYGERsQlpyL2Af4yaevYsWMsW7aM\nMWPGmI4i4pPKlCnD2LFjWb9+PbNnz6ZHjx788MMPJTqGJmuVnIrYB/Tt25fU1FQOHTpkOopLxcfH\nEx0dTY0aNUxHEfFpd999N1u2bCE8PJx7772XRYsW3XB0nJGRQfy0aZz56SfGPv00IwYNIn7aNE6c\nOOGm1N5LnxH7iOeee44qVarwj3/8w3QUl8jIyODOO+/k22+/5bbbbjMdR8Rv2Gw2Bg8eTGhoKLNm\nzbrmB2GbzcaMuDg+W7WK/kB4Tg7BQBawLSiIFLudHpGRjImNJTw83MR/gsfTiNhHxMTEkJSUdNMz\nHj3VjBkzeOyxx1TCIm4WHh7Ov//9b+rXr09YWBgrVqy4fN+chAR6d+5M648/5rucHObn5DASGAiM\nBBKzs/kuJ4dWH39M786dmZOQYOo/w6NpROxDWrduzeTJk4mIiDAdpVT9+uuvNGvWDJvNRuPGjU3H\nEfFb69evJzo6ms6dO9MiNJSZL7/MF+fO0awYz00HIqxWxsfHM2LUKFdH9SoqYh+SkJDAV199xZIl\nS0xHKVWTJ09m3759JCcnm44i4veysrIYPHgwXy1fzna7/ZoS7gykAT8DZa+6Lx3oZLWyYv16Wrdu\n7Ya03kGXpn3Ik08+yerVqzl58qTpKKXmt99+Y8aMGcTGxpqOIiJAcHAwFS0WXoVrSvgwsA2oBXzi\n4LnNgHHZ2cyIi3NxSu+iIvYhVapUoVevXrz77rumo5SauXPn0qlTJ5o3b246ioiQP3Hys1WrGOLg\nYmoy8BAwGEgq4vlRdjufrlyp2dRXUBH7mILvFPvCJw7nz58nPj6eCRMmmI4iIpckJyXRD6jq6D7g\nceBR4AvAUdVWA/pZLCQnJbkso7dREfuYBx54gOzsbGw2m+koN23hwoWEhobSqlUr01FE5JL9aWm0\nycm55vavgeNAb+B24G6gqE1aw7Oz2b9rl8syehsVsY+xWCwMHTrU61fays3NZerUqUycONF0FBG5\nwtnTpwl2cHsy8DBQ6dK/PwosLOIYwUBWZqYL0nknFbEPioqKYunSpfz222+mozht8eLF1K1bl44d\nO5qOIiJXqFS5MllX3ZYDLAH+BdS59OsNYCfgaNybBQRXdXRx2z+piH1Q3bp1ad++PcuWLTMdxSl5\neXlMmTJFo2ERDxQSFsa2q3Z6SwECgT3kl+/OS7/vhONRsS0oiJDQUBcn9R4qYh/lzZenly9fTlBQ\nEA8//LDpKCJylcFDhpACXHlhORkYCtQl/6tLBb9Gk/85cd4Vjz0FpNjtDB4yxC15vYGK2Ef17NmT\nffv2sX//ftNRSsRutzN58mQmTpyIxWIxHUdErlKrVi16REay8IrzcxUwzcFjHwV+oHDRLLRY6Nm9\nOzVr1nRtUC+iIvZR5cqV46mnnmLBggWmo5TI6tWryc7Opk+fPqajiEgRxsTGMjUoiPQSPi8dmBYU\nxBgt0FOIitiHxcTEsHDhQnJzc01HKbYpU6YQGxtLQID+aop4qvDwcCbFxxNhtRa7jAvWmp4UH6/l\nLa+idzsf1rx5cxo1asSqVatMRymWr7/+mmPHjvHEE0+YjiIiNzBi1CjGx8fTyWplusVCUV9GOgW8\nabHQSRs+FEmbPvi4+fPns2LFCj7++GPTUW4oMjKSfv36MWLECNNRRKSYtm/fzoy4OD5duZJ+Fgvh\n2dmX9yO2XdqPuGf37oyJjdVIuAgqYh+XlZVFgwYN2LNnD7feeqvpOEX65ptv6NOnDwcPHqR8+fKm\n44hICZ04cYLkpCT279pFVmYmwVWrEhIayuAhQzQx6wZUxH4gJiaGO+64g3HjxpmOUqRHHnmEDh06\n8Pzzz5uOIiLiVipiP7Bp0yaio6PZu3evR34laM+ePXTu3JnvvvuOihUrmo4jIuJWmqzlB9q1a0dA\nQAAbN240HcWhuLg4nnvuOZWwiPgljYj9RHx8PP/3f//ncd8r/u6772jTpg3p6elUqVLFdBwREbdT\nEfuJn3/+mTvuuIMjR45wyy23mI5z2ciRI6levTqTJ082HUVExAgVsR/p168f3bt3Z/jw4aajAPDD\nDz9wzz33sG/fPs2qFBG/pc+I/UhMTIxHbQTxxhtvMHjwYJWwiPg1jYj9SG5uLg0bNmT16tXcfffd\nRrOcPHmSkJAQ0tLSqFevntEsIiImaUTsRwIDA4mKiiIxMdF0FGbMmMEjjzyiEhYRv6cRsZ9JT0+n\nQ4cOHD16lHLlyhnJcObMGZo0acKWLVto1qyZkQwiIp5CI2I/06xZM5o3b86KFSuMZZg1axYREREq\nYRERNCL2S++88w6LFi1i5cqVbn/tc+fO0aRJE9auXcs999zj9tcXEfE0GhH7oQEDBrBlyxaOHTvm\n9teeN28e7dq1UwmLiFyiEbGfGjVqFHXr1uXll19222v+/vvvNG3alI8++ojw8HC3va6IiCfTiNhP\nxcTEkJiYSF5entte85133qF58+YqYRGRK6iI/VSrVq2oVKkS69atc8vr5ebm8vrrrzNx4kS3vJ6I\niLdQEfspi8Xi1pW2li5dSu3atbn//vvd8noiIt5CnxH7sV9++YWmTZty6NAhqlat6rLXycvLo0WL\nFkybNo3IyEiXvY6IiDfSiNiPVa9enYiICBYtWuTS1/n0008pW7Ys3bp1c+nriIh4IxWxn3P15Wm7\n3c7kyZOZMGECFovFZa8jIuKtVMR+rmvXrpw8eZLU1FSXHP/LL7/kzJkz9O/f3yXHFxHxdipiPxcQ\nEEB0dLTLRsWTJ08mNjaWgAD9VRMRcUSTtYTDhw/TqlUrjh07RoUKFUrtuJs2bWLgwIHs37+fsmXL\nltpxRUR8iYYpQsOGDWnZsiUpKSmletwpU6Ywbtw4lbCIyHWoiAUo/Ulbqamp7Nixg+jo6FI7poiI\nL9KlaQHg/Pnz1K1bF5vNRuPGjW/6eI899hht27blxRdfLIV0IiK+SyNiAaB8+fL86U9/YsGCBTd9\nrL1797Ju3TqefvrpUkgmIuLbNCKWy3bu3EnPnj35/vvvKVOmjNPHiY6OpnHjxrzyyiulmE5ExDcF\nmg4gnqNFixbUrl2bNWvWOL0K1uHDh/nkk09IT08v5XQiIr5Jl6alkJudtDVt2jSGDx/u0rWrRUR8\niS5NSyG//vorjRo1Ij09nRo1apTouT/++CN33303e/bsoXbt2i5KKCLiWzQilkKqVKlCr169ePfd\nd0v83OnTpzNw4ECVsIhICWhELNdYt24dzz77LGlpacXeqOHUqVPcfvvt7NixgwYNGrg4oYiI79CI\nWK7xwAMPkJ2djc1mK/ZzZs6cSd++fVXCIiIlpBGxODRlyhQOHz7M7Nmzb/jYrKwsmjRpwqZNm7j9\n9tvdkE5ExHeoiMWh48ePExoaytGjR6lYseJ1Hztt2jR27NjBokWL3JRORMR36NK0OFS3bl3at2/P\nsmXLrvu47Oxspk+fTmxsrJuSiYj4FhWxFGno0KE3/E5xYmIi4eHhhIWFuSmViIhv0aVpKdLvv/9O\n/fr12bBhAyEhIdfcf+HCBZo1a8aSJUto27atgYQiIt5PRSzXNXbsWM6fP0/D+vXZn5bG2dOnqVS5\nMiFhYZQtX54VK1awdu1a0zFFRLyW1pqWItlsNg6kprLmyy95okIF2uTkEAxkAVs/+ojFOTl06tAB\nm81GeHi46bgiIl5JI2JxaE5CAq+OHcv47Gyi7HYcrRydCSywWPjvoCAmxcczYtQod8cUEfF6KmK5\nxpyEBKaOHcsX587RrBiPTwcirFbGq4xFREpMRSyF2Gw2enfuzIarSvgD4C3gW6AS0BgYDBTUbjrQ\nyWplxfr1tG7d2q2ZRUS8mb6+JIXMiItjfHZ2oRJ+A3geGA/8DPwE/C+wCbhw6THNgHHZ2cyIi3Nn\nXBERr6cRsVyWkZHBHQ0b8l1OzuXPhM8AtwHvAn1v8PxTQNMKFdh/5Ag1a9Z0ZVQREZ+hEbFclpyU\nRD8oNDFrM/A70LsYz68G9LNYSE5KckE6ERHfpCKWy/anpdEmJ6fQbSeBGhT+i9KB/LK2Al9fdYzw\n7Gz279rlypgiIj5F3yOWy86ePk3wVbdVJ7+M8/hPGW+89M8Gl26/UjCQlZnpsowiIr5GI2K5rFLl\nymRddVs7oDyw3MHjHU0uyAKCqzr61rGIiDiiIpbLQsLC2FahQqHbKgOvAH8GPgTOkl/AqcA5B8ew\nBQUREhrq4qQiIr5Ds6blMkezpgssIv97xP8HVASaAMOAKP7z+YZmTYuIlJxGxHJZrVq16BEZyUKL\n5Zr7ngS2kj8i/pn82dQxFJ5ksNBioWf37iphEZES0IhYCilqZa0b0cpaIiLO0YhYCgkPD2dSfDwR\nVivpxXxOwVrTk+LjVcIiIiWkIpZrjBg1ivHx8XSyWplusVDUl5FOAW9aLHTShg8iIk7TpWkp0vbt\n25kRF8enK1fSz2IhPDv78n7EtqAgUux2enbvzpjYWI2ERUScpCKWGzpx4gTJSUns37WLrMxMgqtW\nJSQ0lMFDhmhilojITVIRi4iIGKTPiEVERAxSEYuIiBikIhYRETFIRSwiImKQilhERMQgFbGIiIhB\nKmIRERGDVMQiIiIGqYhFREQMUhGLiIgYpCIWERExSEUsIiJikIpYRETEIBWxiIiIQSpiERERg1TE\nIiIiBqmIRUREDFIRi4iIGKQiFhERMUhFLCIiYpCKWERExCAVsYiIiEEqYhEREYNUxCIiIgapiEVE\nRAxSEYuIiBikIhYRETFIRSwiImKQilhERMQgFbGIiIhBKmIRERGDVMQiIiIGqYhFREQMUhGLiIgY\npCIWERExSEUsIiJikIpYRETEIBWxiIiIQSpiERERg1TEIiIiBqmIRUREDFIRi4iIGPT/ATJtcsqQ\n1urWAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%matplotlib inline \n",
"import matplotlib.pyplot as plt\n",
"import networkx as nx\n",
"graph = nx.Graph()\n",
"graph.add_edges_from([('A', 'B'), ('A', 'C'), ('B', 'C'), ('B', 'D'), ('D', 'E'), ('D', 'F'), ('D', 'G'), ('E', 'F'), ('G', 'F')])\n",
"nx.draw(graph, with_labels=True)"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Adjacency matrix:\n",
" [[0 1 1 0 0 0 0]\n",
" [1 0 1 1 0 0 0]\n",
" [1 1 0 0 0 0 0]\n",
" [0 1 0 0 1 1 1]\n",
" [0 0 0 1 0 1 0]\n",
" [0 0 0 1 1 0 1]\n",
" [0 0 0 1 0 1 0]]\n"
]
}
],
"source": [
"# Print the adjacency matrix.\n",
"def adjacency_matrix(graph):\n",
" return nx.adjacency_matrix(graph, sorted(graph.nodes()))\n",
"\n",
"adjacency = adjacency_matrix(graph)\n",
"print('Adjacency matrix:\\n', adjacency.todense())"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"** What data structure should we use to store the adjacency matrix? **\n",
"\n",
"
\n",
"\n",
"- Naive 2d array: $O(V^2)$ space, for $V$ vertices.\n",
"- But, graphs are sparse ($E << V^2$), for $E$ edges.\n",
"- Instead, only store non-zeros\n",
"\n",
"E.g., list of tuples `[(0,1), (0,2), (1,2), ...]`\n",
" - Space = $O(E)$\n",
" - We'll look at these *sparse matrices* in more detail later."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Degree matrix:\n",
" [[2 0 0 0 0 0 0]\n",
" [0 3 0 0 0 0 0]\n",
" [0 0 2 0 0 0 0]\n",
" [0 0 0 4 0 0 0]\n",
" [0 0 0 0 2 0 0]\n",
" [0 0 0 0 0 3 0]\n",
" [0 0 0 0 0 0 2]]\n"
]
}
],
"source": [
"# Print the degree matrix.\n",
"import numpy as np\n",
"\n",
"def degree_matrix(graph):\n",
" degrees = graph.degree().items()\n",
" degrees = sorted(degrees, key=lambda x: x[0])\n",
" degrees = [d[1] for d in degrees]\n",
" return np.diag(degrees)\n",
"\n",
"degree = degree_matrix(graph)\n",
"print('Degree matrix:\\n', degree)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Laplacian matrix** $L = D - A$\n",
"\n",
"- **Adjacency matrix** $A$: $A[i, j] = 1$ iff there is an edge from $i$ to $j$.\n",
"- **Degree matrix** $D$: $D[i, i] = deg(i)$, else 0\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Laplacian matrix:\n",
" [[ 2 -1 -1 0 0 0 0]\n",
" [-1 3 -1 -1 0 0 0]\n",
" [-1 -1 2 0 0 0 0]\n",
" [ 0 -1 0 4 -1 -1 -1]\n",
" [ 0 0 0 -1 2 -1 0]\n",
" [ 0 0 0 -1 -1 3 -1]\n",
" [ 0 0 0 -1 0 -1 2]]\n"
]
}
],
"source": [
"def laplacian_matrix(graph):\n",
" return degree_matrix(graph) - adjacency_matrix(graph)\n",
"\n",
"laplacian = laplacian_matrix(graph)\n",
"print('Laplacian matrix:\\n', laplacian)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"**Properties of Laplacian matrix:**\n",
"- rows sum to 0; columns sum to 0\n",
"- symmetric\n",
"- positive-semidefinite ($z^TLz \\ge 0$ $\\forall $ nonzero $z$)\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"** Recall that a matrix is a type of linear transformation.**\n",
"\n",
"For an arbitrary vector $v$, what does $Lv$ mean?"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAeIAAAFBCAYAAACrYazjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAHyJJREFUeJzt3XtQ1XXi//HXB9cS1sta6patl0op4XBQBBUvrZRGaJk6\nWVlTqRDKJd0Wymy7jLOjqIsiiZC3fujWt81dt1LTNLuoTCaHEeQgXsZyan+7FbaiX1wPKHJ+f2j9\nVsPE5PA+l+djpj88F+ZlM82r15vPOR/L7Xa7BQAAjAgyHQAAgEBGEQMAYBBFDACAQRQxAAAGUcQA\nABhEEQMAYBBFDACAQRQxAAAGUcQAABhEEQMAYBBFDACAQRQxAAAGUcQAABhEEQMAYBBFDACAQRQx\nAAAGUcQAABhEEQMAYBBFDACAQRQxAAAGUcQAABhEEQMAYBBFDACAQRQxAAAGUcQAABhEEQMAYBBF\nDACAQRQxAAAGUcQAABhEEQMAYBBFDACAQRQxAAAGUcQAABhEEQMAYBBFDACAQRQxAAAGUcQAABhE\nEQMAYBBFDACAQRQxAAAGUcQAABhEEQMAYBBFDACAQb8wHcCfVVVVaU1hoQ6Vl+vkiRNq26GDQu12\nPTF5sjp37mw6HgDAC1hut9ttOoS/cTgcys3K0nubN2u8pJjaWrWTVCOpODhYb7vdGp2QoBmzZikm\nJsZwWgCASRRxM1teUKCXMzM10+XSE263OjbymmpJhZalBcHBmp2dreSUlJaOCQDwEhRxM1peUKD5\nmZnacuqUejXh9YclxYeEaCZlDAABiyJuJg6HQ2OGD9fOi0r4fyTlSDogqb2kvpKelzTk/POHJQ0L\nCdGG7dsVHR3dopkBAOZx1XQzyc3K0kyX64ISXiTp95JekFQl6StJaZI2/Ndrekl61uVSblZWi2UF\nAHgPFnEzqKqq0m09euiL2toffif8v5JukrRa0vjLvP+YpFvbtNGhr77iamoACDAs4mawprBQ46QL\nLszaJalO0tgmvP86SeMsS2sKCz2QDgDgzSjiZnCovFwDamsveOzfkjqp6f+CY1wuHXI6mzsaAMDL\nUcTN4OSJE2p30WPXS/pOUkMTf0Y7STXV1c2aCwDg/SjiZtC2QwfVXPRYrKRrJb3TxJ9RI6ldx8Y+\ndQwA8GcUcTMItdtV3KbNBY+1lzRb566SfleSS1K9pPclPdfIz3AEBys0IsLDSQEA3oarpptBY1dN\nf+9NnfsY0wGdO37uL+kPkgb912u4ahoAAheLuBl06dJFoxMStNqyfvTcREkOnTt6/pfOfYZ40EWv\n+T+SEuLjKWEACEAUcTOZMWuW5gcH6/AVvu+wpDmtWmnX3r3atWuXJ6IBALwYRdxMYmJiNDs7W/Eh\nIU0u4++/azpryRItWLBA48eP1+9+9zudPHnSk1EBAF6EIm5GySkpmpmdrWEhIcqxLF3qw0jHJC2y\nLA07f8OHqSkpmjBhgioqKlRdXa2IiAh98MEHLRkdAGAIF2t5QElJiXKzsrRx0yaNsyzFuFw/3I/Y\ncf5+xPeOGqUZs2Y1eqOH999/X1OnTtVdd92lhQsXqiMfawIAv0URe9DRo0e1prBQh5xO1VRXq13H\njgqNiNDjkyZd9sKsmpoazZo1S2+//bby8vI0bty4FkoNAGhJFLGX27lzp5KSkmS327VkyRLdcMMN\npiMBAJoRvyP2csOGDdPevXvVu3dv2e12rV69Wvy/EwD4DxaxD9mzZ48SExPVpUsXLVu2TD179jQd\nCQBwlVjEPiQqKkrFxcUaPny4oqOjtWTJEjU0NPW2EgAAb8Qi9lEHDhxQUlKSJGnlypW6/fbbDScC\nAPwcLGIfdfvtt2vHjh2aOHGihg4dqrlz5+rMmTOmYwEArhCL2A98+eWXmjp1qr799lutWrVKUVFR\npiMBAJqIRewHevTooc2bN+vpp59WQkKCZs2aJZfLZToWAKAJKGI/YVmWHn/8cZWXl+vzzz9X3759\ntXPnTtOxAACXwdG0n3r77beVnp6usWPHat68eWrXrp3pSACARrCI/dS4ceNUUVGhuro62Ww2bd68\n2XQkAEAjWMQBYNu2bUpOTtbQoUOVk5Oj66+/3nQkAMB5LOIAMGLECDmdTl1//fWy2Wxau3YtX5MJ\nAF6CRRxgdu3apaSkJPXu3Vv5+fnq2rWr6UgAENBYxAEmNjZWe/bskd1uV9++fbVq1SrWMQAYxCIO\nYOXl5UpMTFT79u21YsUK3XLLLaYjAUDAYREHMLvdrl27dikhIUEDBgxQTk6Ozp49azoWAAQUFjEk\nSYcPH1ZSUpJqa2u1cuVK2Ww205EAICCwiCFJ6tWrlz766CNNnjxZcXFxmj17tk6fPm06FgD4PYoY\nPwgKCtLUqVNVWloqh8Oh/v37y+FwmI4FAH6NIsaP/OY3v9GGDRv0/PPP67777lNmZqZOnTplOhYA\n+CWKGI2yLEsTJ06U0+nU119/Lbvdro8//th0LADwO1yshSbZsGGDUlNTNWrUKC1YsEAdOnQwHQkA\n/AKLGE1y3333qaKiQpZlyWazacOGDaYjAYBfYBHjin3yySdKSkpSTEyMXnnlFXXu3Nl0JADwWSxi\nXLHhw4ervLxc3bp1U0REhN544w2+JhMAfiYWMa5KSUmJpkyZou7du6ugoEDdunUzHQkAfAqLGFcl\nOjpaJSUlGjhwoKKiovTqq6+qoaHBdCwA8BksYjSbffv2KSkpSddcc41Wrlyp3r17m44EAF6PRYxm\nEx4erqKiIo0fP16xsbFasGCB6uvrTccCAK/GIoZHHDlyRMnJyaqurtaqVasUGRlpOhIAeCUWMTzi\n5ptv1tatW5WamqqRI0fqxRdfVF1dnelYAOB1KGJ4jGVZmjJlisrKylRRUaF+/frp008/NR0LALwK\nR9NoEW63W+vWrdP06dM1YcIEzZkzR23btjUdCwCMYxGjRViWpQceeEBOp1PHjx9XRESEPvjgA9Ox\nAMA4FjGMeP/99zV16lTdddddWrhwoTp27Gg6EgAYwSKGEffcc48qKir0y1/+UjabTX//+99NRwIA\nI1jEMK6oqEhJSUmy2WzKy8vTDTfcYDoSALQYFjGMGzp0qMrKyhQaGiq73a7CwkJuIgEgYLCI4VVK\nS0s1ZcoUdenSRcuWLVPPnj1NRwIAj2IRw6v069dPxcXFiouLU3R0tJYsWcJNJAD4NRYxvNbBgweV\nlJSkhoYGrVy5Un369DEdCQCaHYsYXuu2227T9u3b9cgjj2jYsGGaO3euzpw5YzoWADQrFjF8wpdf\nfqlp06bp66+/1muvvaaoqCjTkQCgWbCI4RN69OihTZs2KSMjQwkJCXruuefkcrlMxwKAq0YRw2dY\nlqXHHntM5eXlOnLkiPr27audO3eajgUAV4Wjafisd955R2lpaRo7dqyysrLUvn1705EA4IqxiOGz\nxo4dq4qKCtXV1SkiIkKbNm0yHQkArhiLGH5h27ZtSk5O1pAhQ5STk6NOnTqZjgQATcIihl8YMWKE\nnE6nOnXqpIiICK1du5avyQTgE1jE8DufffaZEhMT1bt3b+Xn56tr166mIwHAJbGI4XcGDRqkPXv2\nKDIyUpGRkVq5ciXrGIDXYhHDr5WXlysxMVHt27fX8uXLdeutt5qOBAAXYBHDr9ntdu3atUsJCQka\nOHCgFi1apLNnz5qOBQA/YBEjYBw+fFhJSUlyuVxatWqVbDab6UgAwCJG4OjVq5c++ugjJSYmKi4u\nTrNnz9bp06dNxwIQ4ChiBJSgoCAlJyertLRUJSUl6t+/v4qLi03HAhDAOJpGwHK73frLX/6ip59+\nWo8++qj++Mc/KiQkxHQsAAGGRYyAZVmWJk6cKKfTqW+++UYRERH6+OOPTccCEGBYxMB5GzduVEpK\nihISEvSnP/1JHTp0MB0JQABgEQPn3XvvvaqoqFBQUJDCw8O1fv1605EABAAWMdCITz75RE8++aT6\n9++vV155RV26dDEdCYCfYhEDjRg+fLj27t2r7t27KyIiQm+88QZfkwnAI1jEwGWUlJRoypQp6tat\nm1599VV169bNdCQAfoRFDFxGdHS0SkpKFBsbq6ioKBUUFKihocF0LAB+gkUMXIHKykolJibqmmuu\n0YoVKxQaGmo6EgAfxyIGrkBYWJiKioo0fvx4DR48WAsWLFB9fb3pWAB8GIsY+JmOHDmi5ORkHTt2\nTK+99poiIyNNRwLgg1jEwM908803a+vWrUpPT9fIkSP1wgsvqLa21nQsAD6GIgaugmVZmjx5svbu\n3avKykr169dPn376qelYAHwIR9NAM3G73Vq3bp2mT5+uCRMmaM6cOWrbtq3pWAC8HIsYaCaWZemB\nBx6Q0+nUiRMnFBERoa1bt5qOBcDLsYgBD9myZYumTp2quLg4LVy4UNddd53pSAC8EIsY8JD4+Hg5\nnU61bdtWNptN69atMx0JgBdiEQMtoKioSElJSbLZbMrLy9MNN9xgOhIAL8EiBlrA0KFDVVZWptDQ\nUNntdhUWFnITCQCSWMRAiystLVViYqI6deqk5cuXq2fPnqYjATCIRQy0sH79+mn37t268847FR0d\nrSVLlnATCSCAsYgBgw4ePKikpCQ1NDRo5cqV6tOnj+lIAFoYixgw6LbbbtP27dv16KOPatiwYZoz\nZ47OnDljOhaAFsQiBrzEl19+qWnTpunrr7/WqlWr1L9/f9ORALQAFjHgJXr06KFNmzYpIyNDo0aN\n0nPPPSeXy2U6FgAPo4gBL2JZlh577DGVl5fryJEjioyM1I4dO0zHAuBBHE0DXuydd95Renq6xowZ\no3nz5ql9+/amIwFoZixiwIuNHTtWFRUVOn36tGw2mzZt2mQ6EoBmxiIGfMSHH36oJ598UkOGDFFO\nTo46der0k6+vqqrSmsJCHSov18kTJ9S2QweF2u16YvJkde7cuYVSA7gcihjwIf/5z3/04osv6s03\n39TixYv14IMPyrKsC17jcDiUm5Wl9zZv1nhJMbW1aiepRlJxcLDedrs1OiFBM2bNUkxMjIm/BoD/\nQhEDPuizzz5TYmKievXqpYKCAnXt2lWStLygQC9nZmqmy6Un3G51bOS91ZIKLUsLgoM1OztbySkp\nLZodwIUoYsBH1dXVae7cuSooKNDcuXN19swZLcjM1JZTp9SrCe8/LCk+JEQzKWPAKIoY8HFOp1MP\nPfSQvjl4UMUNDT+UcE9JVZJ+Iam1pMGSXpV003+997CkYSEh2rB9u6Kjo1syNoDzuGoa8HERERHq\nGxqqF93uC5awJek9Sf8r6WtJXSQ9ddF7e0l61uVSblZWy4QF8CMsYsDHVVVV6bYePfRFbe0FvxO+\nWdIqSXee//NmSU9LOnDR+49JurVNGx366iuupgYMYBEDPm5NYaHGSY1emPW9U5LekhTbyHPXSRpn\nWVpTWOiBdAAu5xemAwC4OofKyzWgtrbR58bq3H/kJ3XuaHrLJX5GjMulMqfTMwEB/CQWMeDjTp44\noXaXeO5dnTt6rpO0RNIdOncB18XaSaqprvZMQAA/iSIGfFzbDh1Uc4nnvr8AxJI0TlIrSUWNvK5G\nUruOP3W4DcBTKGLAx4Xa7Spu0+ayr3tX0nFJfRp5zhEcrNCIiOaOBqAJuGoa8HE/ddV0lc6tYEtS\nD0nPS3r4ovdz1TRgFosY8HFdunTR6IQErb7oO6ePSPqPzn2O+ISkcv24hCXpNUkR4eGXvYkEAM+g\niAE/MGPWLM0PDtbhK3zfYUl/atNG3506pTvuuENOrpwGWhxFDPiBmJgYzc7OVnxISJPL+Pvvmv7j\nokVyOp169NFHdeeddyojI0M1NZe6/AtAc6OIAT+RnJKimdnZGhYSohzL0qU+jHRM0iLL0rD/uuFD\nq1atNG3aNO3bt0/Hjh1Tnz59tHbtWnEJCeB5XKwF+JmSkhLlZmVp46ZNGmdZinG5frgfseP8/Yjv\nHTVKM2bNuuSNHoqKipSamqpf//rXWrp0qUJDQ1v07wAEEooY8FNHjx7VmsJCHXI6VVNdrXYdOyo0\nIkKPT5rUpKujz5w5o7y8PM2ZM0fTpk3T888/r5CQkBZIDgQWihjAT/rnP/+pjIwM7d69W6+88oru\nu+8+05EAv0IRA2iSbdu2KS0tTbfffrtyc3PVs2dP05EAv8DFWgCaZMSIESovL9eAAQMUHR2tOXPm\nqK6uznQswOdRxACa7Nprr9Uf/vAHORwO7d69W3a7Xdu2bTMdC/BpHE0D+NnWr1+vGTNmaODAgVq4\ncKFuuukm05EAn8MiBvCzjRkzRvv27VOvXr0UGRmpnJwc1dfXm44F+BQWMYBmcfDgQaWnp+vbb79V\nfn6+hg4dajoS4BMoYgDNxu12a+3atcrIyNDIkSO1YMEC7ugEXAZH0wCajWVZeuihh7R//35dd911\nCg8P16uvvqqzZ8+ajgZ4LRYxAI8pLy9Xamqq6urqVFBQcMmv1AQCGYsYgMfY7Xbt2LFDaWlpuvfe\ne5Wamqrq6kvdjgIITBQxAI8KCgrSpEmTtH//fklSWFiYVq9ezZ2dgPM4mgbQohwOh1JSUhQSEqL8\n/HzZbDbTkQCjWMQAWlRMTIx2796tiRMnKi4uTpmZmaqpqTEdCzCGIgbQ4lq1aqWUlBTt27dP3333\nncLCwrR27VqOqxGQOJoGYNzOnTuVmpqqG2+8UXl5eQoNDTUdCWgxLGIAxg0bNkx79uxRfHy8Bg8e\nrBdffFGnTp0yHQtoERQxAK/QunVrZWRkaO/evTp06JDCw8O1ceNG07EAj+NoGoBX+uCDD5SWlqY+\nffooNzdXPXv2NB0J8AgWMQCvNHLkSDmdTsXExCg6Olpz585VXV2d6VhAs6OIAXita6+9Vi+88IIc\nDod27dqlyMhIffjhh6ZjAc2Ko2kAPmP9+vWaPn26Bg0apEWLFqlr166mIwFXjUUMwGeMGTNGlZWV\nuvXWW2W325WTk6P6+nrTsYCrwiIG4JMOHDig9PR0HT16VPn5+RoyZIjpSMDPQhED8Flut1tr167V\n73//e8XHx2v+/Pnq3Lmz6VjAFeFoGoDPsixLDz30kPbv369f/epXCg8P17Jly3T27FnT0YAmYxED\n8Bvl5eVKTU3V6dOnVVBQoP79+5uOBFwWixiA37Db7dqxY4dSU1M1evRopaWlqbq62nQs4CdRxAD8\nSlBQkCZNmqTKykqdPXtWYWFhWrNmDXd2gtfiaBqAX3M4HEpJSVFISIjy8/Nls9lMRwIuwCIG4Ndi\nYmK0e/duTZw4UXFxccrMzFRNTY3pWMAPKGIAfq9Vq1ZKSUlRRUWFjh49qrCwMP31r3/luBpegaNp\nAAHn+wu6brrpJuXl5al3796mIyGAsYgBBJw77rhDpaWluvvuuxUbG6uXXnpJLpfLdCwEKIoYQEBq\n3bq1MjIyVFZWpgMHDig8PFwbN240HQsBiKNpAJC0detWpaenKywsTLm5uerRo4fpSAgQLGIAkHT3\n3XfL6XQqOjpaUVFRysrK0unTp03HQgBgEQPARY4cOaKnnnpKhw8f1tKlS3XXXXeZjgQ/RhEDQCPc\nbrfWr1+vGTNmKDY2VgsXLlTXrl1Nx4If4mgaABphWZbuv/9+VVZW6pZbbpHdbtfixYtVX19vOhr8\nDIsYAJrgwIEDSktL03fffaf8/HwNGTLEdCT4CYoYAJrI7XbrrbfeUkZGhuLj4zV//nx17tzZdCz4\nOI6mAaCJLMvSww8/rP3796tDhw4KDw/XsmXL1NDQYDoafBiLGAB+pr179yo1NVX19fXKz89X//79\nTUeCD2IRA8DPFBkZqZ07d2ratGkaPXq00tPTdfz4cdOx4GMoYgC4CkFBQZo8ebIqKytVX1+vPn36\n6M9//jN3dkKTcTQNAM2ouLhYKSkpatu2rZYuXSqbzWY6ErwcixgAmtGAAQNUXFysBx98UHFxcXrm\nmWd08uRJ07HgxShiAGhmrVq1UlpamioqKlRVVaU+ffrob3/7G8fVaBRH0wDgYTt27FBqaqpuuukm\n5eXlqXfv3qYjwYuwiAHAw+644w6VlpZq5MiRio2N1UsvvSSXy2U6FrwERQwALaB169bKzMxUWVmZ\n9u/fL5vNpvfee890LHgBjqYBwIAtW7YoPT1dNptNixcvVo8ePUxHgiEsYgAwID4+Xk6nU1FRUYqK\nitK8efN0+vRp07FgAIsYAAz74osvNH36dH3++edaunSp7rzzTtOR0IIoYgDwAm63W+vXr9eMGTM0\nePBgLVy4UDfeeKPpWGgBHE0DgBewLEv333+/9u3bp549eyoiIkK5ubmqr683HQ0exiIGAC904MAB\npaWl6d///rfy8/M1ePBg05HgIRQxAHgpt9utt956SxkZGbrnnns0f/58derUyXQsNDOOpgHAS1mW\npYcffliVlZVq166dwsLCtHz5cjU0NJiOhmbEIgYAH1FWVqbU1FQ1NDQoPz9fUVFRpiOhGbCIAcBH\n9O3bV0VFRUpOTtaoUaOUnp6u48ePm46Fq0QRA4APCQoK0pQpU7Rv3z6dOXNGffr00euvv86dnXwY\nR9MA4MN2796tlJQUtW/fXkuXLlV4eLjpSLhCLGIA8GEDBw6Uw+HQhAkTNHz4cD377LM6efKk6Vi4\nAhQxAPi4Vq1aKS0tTRUVFfrmm28UFhamdevWcVztIziaBgA/s337dqWmpqpbt25asmSJevfubToS\nfgKLGAD8zG9/+1uVlZVpxIgRio2N1csvvyyXy2U6Fi6BIgYAP9S6dWtlZmaqtLRU+/btk81m06ZN\nm0zHQiM4mgaAALBlyxalp6fLZrMpNzdX3bt3Nx0J57GIASAAxMfHy+l0ql+/foqKitK8efN0+vRp\n07EgFjEABJzPP/9c06dP1xdffKH8/HzFxcWZjhTQKGIACEBut1vvvvuuZsyYoaFDhyo7O1s33nij\n6VgBiaNpAAhAlmVp7NixqqysVPfu3WW325Wbm6v6+nrT0QIOixgAoP379ystLU3Hjh1TQUGBYmNj\nTUcKGBQxAEDSuePqN998U88884wSEhI0b948derUyXQsv8fRNABA0rnj6kceeUSVlZVq27atwsLC\ntGLFCjU0NJiO5tdYxACARpWVlSk1NVUNDQ3Kz89XVFSU6Uh+iUUMAGhU3759VVRUpCeffFIJCQl6\n6qmndPz4cdOx/A5FDAC4pKCgICUmJqqyslJ1dXUKCwvT66+/zp2dmhFH0wCAJvvss8+Umpqq9u3b\na+nSpQoPDzcdyeexiAEATTZo0CA5HA498MADGj58uGbOnKmTJ0+ajuXTKGIAwBVp1aqV0tPT5XQ6\n9a9//UthYWFat24dx9U/E0fTAICr8sknnygtLU3du3fXkiVL1KtXr598fVVVldYUFupQeblOnjih\nth06KNRu1xOTJ6tz584tlNp7UMQAgKt25swZLV68WPPnz1d6erpmzpyp4ODgC17jcDiUm5Wl9zZv\n1nhJMbW1aiepRlJxcLDedrs1OiFBM2bNUkxMjIm/hhEUMQCg2fzjH//Q008/rdLSUuXl5SkhIUGS\ntLygQC9nZmqmy6Un3G51bOS91ZIKLUsLgoM1OztbySkpLZrdFIoYANDs3n//faWnp8tut2tA//5a\nMXeutpw6pZ8+tD7nsKT4kBDNDJAypogBAB5RW1ur6dOna+2KFSqRflTCwyWVS/pWUuuLnjssaVhI\niDZs367o6GjPhzWIq6YBAB7Rpk0bnfruO71sWT8q4S8lFUvqIml9I+/tJelZl0u5WVmejmkcixgA\n4BFVVVW6rUcPfVFb+6PfCf9RUomkgZJ2SdrQyPuPSbq1TRsd+uorv76amkUMAPCINYWFGic1emHW\nGkkPSZogaYuko4285jpJ4yxLawoLPZbRG1DEAACPOFRergG1tT96vEjSPyWNkdRbUrik/7nEz4hx\nuXTI6fRYRm9AEQMAPOLkiRNq18jjayTdLant+T9PkLT6Ej+jnaSa6moPpPMevzAdAADgn9p26KCa\nix6rlbRWUoOkG88/dlrScUlOSREXvb5GUruOjR1u+w8WMQDAI0LtdhW3aXPBY2/r3ALcL2nv+X/2\nSxqmxlexIzhYoREX17N/4appAIBHNHbVdILOrd4FF732r5JmSPq/+v8LkaumAQC4Cl26dNHohASt\ntqwfHtusH5ewdO73xP/ShaW02rJ076hRfl3CEosYAOBBDodDY4YP184mfr3l9/hmLQAAmkFMTIxm\nZ2crPiREh5v4nu+/a3p2drbfl7BEEQMAPCw5JUUzs7M1LCREOZalS30Y6ZikRZalYQF0wweJo2kA\nQAspKSlRblaWNm7apHGWpRiX64f7ETvO34/43lGjNGPWrIBYwt+jiAEALero0aNaU1ioQ06naqqr\n1a5jR4VGROjxSZP8/sKsxlDEAAAYxO+IAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgA\nAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIG\nAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKI\nAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMo\nYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAg\nihgAAIP+H/WC8adm/XSIAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# For a smaller graph.\n",
"graph2 = nx.Graph()\n",
"graph2.add_edges_from([('A', 'B'), ('B', 'C')])\n",
"nx.draw(graph2, with_labels=True)"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[[ 1 -1 0]\n",
" [-1 2 -1]\n",
" [ 0 -1 1]]\n"
]
}
],
"source": [
"laplacian2 = laplacian_matrix(graph2)\n",
"print(laplacian2)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let $v$ be a map from nodes to real values. \n",
"\n",
"E.g., $v = \\{f(A), f(B), f(C)\\}$\n",
"\n",
"Then, $Lv$ is:\n",
"\n",
"$$ \\begin{pmatrix}\n",
" 1 & -1 & 0 \\\\\n",
" -1 & 2 & -1 \\\\\n",
" 0 & -1 & 1\n",
" \\end{pmatrix}\n",
" \\begin{pmatrix}\n",
" f(A)\\\\\n",
" f(B)\\\\\n",
" f(C)\\\\\n",
" \\end{pmatrix}\n",
" =\n",
" \\begin{pmatrix}\n",
" f(A) - f(B)\\\\\n",
" -f(A) + 2f(B) - f(C)\\\\\n",
" -f(B) + f(C)\n",
" \\end{pmatrix}$$\n",
" \n",
"More generally:\n",
"\n",
"$Lv[i]= [deg(i) ∗ (f(i) − $average of $f$ on neighbors of $i)]$\n"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[[-1 0 1]]\n"
]
}
],
"source": [
"print(laplacian2.dot([1,2,3]))"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[[ 1 0 -1]]\n"
]
}
],
"source": [
"print(laplacian2.dot([3,2,1]))"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"** Review of Linear Algebra**\n",
"\n",
"A vector $\\mathbf{v}$ of dimension $n$ is an **eigenvector **of a square $(n×n)$ matrix $A$ if and only if \n",
"$$ A \\mathbf{v} = \\lambda \\mathbf{v} $$\n",
"\n",
"where $\\lambda$ is a scalar, called an **eigenvalue**.\n",
"\n",
"In otherwords, $\\mathbf{v}$ is just a linear scaling of $A$.\n",
"\n",
"
\n",
"Assume $A$ has $n$ linearly independent eigenvectors, $\\{\\mathbf{v}_1 \\ldots \\mathbf{v}_n\\}$. \n",
"\n",
"Let $V$ be a square matrix where column $i$ is $\\mathbf{v}_i$.\n",
"\n",
"Then A can be factorized as\n",
"$A=V \\Lambda V^{-1} $ where\n",
"\n",
"$\\Lambda$ is a diagonal matrix of eigenvalues: $\\Lambda[i, i]=\\lambda_i$."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"\n",
"\n",
"[source](http://en.wikipedia.org/wiki/Eigenvalues_and_eigenvectors)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"**What happens when we compute the eigenvalue decomposition of the Laplacian $L$**?\n",
"\n",
"- Smallest eigenvalue $\\lambda_0=0$\n",
" - Corresponding eigenvector $\\mathbf{v}_0 = \\mathbf{1}$"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[[0 0 0]]\n"
]
}
],
"source": [
"print(laplacian2.dot([1,1,1]))"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"**What about second eigenvector?**\n"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Help on function eigh in module numpy.linalg.linalg:\n",
"\n",
"eigh(a, UPLO='L')\n",
" Return the eigenvalues and eigenvectors of a Hermitian or symmetric matrix.\n",
" \n",
" Returns two objects, a 1-D array containing the eigenvalues of `a`, and\n",
" a 2-D square array or matrix (depending on the input type) of the\n",
" corresponding eigenvectors (in columns).\n",
" \n",
" Parameters\n",
" ----------\n",
" a : (..., M, M) array\n",
" Hermitian/Symmetric matrices whose eigenvalues and\n",
" eigenvectors are to be computed.\n",
" UPLO : {'L', 'U'}, optional\n",
" Specifies whether the calculation is done with the lower triangular\n",
" part of `a` ('L', default) or the upper triangular part ('U').\n",
" \n",
" Returns\n",
" -------\n",
" w : (..., M) ndarray\n",
" The eigenvalues in ascending order, each repeated according to\n",
" its multiplicity.\n",
" v : {(..., M, M) ndarray, (..., M, M) matrix}\n",
" The column ``v[:, i]`` is the normalized eigenvector corresponding\n",
" to the eigenvalue ``w[i]``. Will return a matrix object if `a` is\n",
" a matrix object.\n",
" \n",
" Raises\n",
" ------\n",
" LinAlgError\n",
" If the eigenvalue computation does not converge.\n",
" \n",
" See Also\n",
" --------\n",
" eigvalsh : eigenvalues of symmetric or Hermitian arrays.\n",
" eig : eigenvalues and right eigenvectors for non-symmetric arrays.\n",
" eigvals : eigenvalues of non-symmetric arrays.\n",
" \n",
" Notes\n",
" -----\n",
" \n",
" .. versionadded:: 1.8.0\n",
" \n",
" Broadcasting rules apply, see the `numpy.linalg` documentation for\n",
" details.\n",
" \n",
" The eigenvalues/eigenvectors are computed using LAPACK routines _syevd,\n",
" _heevd\n",
" \n",
" The eigenvalues of real symmetric or complex Hermitian matrices are\n",
" always real. [1]_ The array `v` of (column) eigenvectors is unitary\n",
" and `a`, `w`, and `v` satisfy the equations\n",
" ``dot(a, v[:, i]) = w[i] * v[:, i]``.\n",
" \n",
" References\n",
" ----------\n",
" .. [1] G. Strang, *Linear Algebra and Its Applications*, 2nd Ed., Orlando,\n",
" FL, Academic Press, Inc., 1980, pg. 222.\n",
" \n",
" Examples\n",
" --------\n",
" >>> from numpy import linalg as LA\n",
" >>> a = np.array([[1, -2j], [2j, 5]])\n",
" >>> a\n",
" array([[ 1.+0.j, 0.-2.j],\n",
" [ 0.+2.j, 5.+0.j]])\n",
" >>> w, v = LA.eigh(a)\n",
" >>> w; v\n",
" array([ 0.17157288, 5.82842712])\n",
" array([[-0.92387953+0.j , -0.38268343+0.j ],\n",
" [ 0.00000000+0.38268343j, 0.00000000-0.92387953j]])\n",
" \n",
" >>> np.dot(a, v[:, 0]) - w[0] * v[:, 0] # verify 1st e-val/vec pair\n",
" array([2.77555756e-17 + 0.j, 0. + 1.38777878e-16j])\n",
" >>> np.dot(a, v[:, 1]) - w[1] * v[:, 1] # verify 2nd e-val/vec pair\n",
" array([ 0.+0.j, 0.+0.j])\n",
" \n",
" >>> A = np.matrix(a) # what happens if input is a matrix object\n",
" >>> A\n",
" matrix([[ 1.+0.j, 0.-2.j],\n",
" [ 0.+2.j, 5.+0.j]])\n",
" >>> w, v = LA.eigh(A)\n",
" >>> w; v\n",
" array([ 0.17157288, 5.82842712])\n",
" matrix([[-0.92387953+0.j , -0.38268343+0.j ],\n",
" [ 0.00000000+0.38268343j, 0.00000000-0.92387953j]])\n",
"\n"
]
}
],
"source": [
"# Library to compute eigenvectors:\n",
"from numpy.linalg import eigh\n",
"help(eigh)"
]
},
{
"cell_type": "code",
"execution_count": 37,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"eigen values\n",
"[ -1.43917928e-15 3.98320868e-01 2.00000000e+00 3.00000000e+00\n",
" 3.33987689e+00 4.00000000e+00 5.26180225e+00]\n",
"eigen vectors\n",
"[[ -3.77964473e-01 4.92886500e-01 7.61771655e-17 -7.07106781e-01\n",
" -3.20722630e-01 -8.40213177e-17 -1.06502348e-01]\n",
" [ -3.77964473e-01 2.96559521e-01 1.92527950e-16 1.88737914e-15\n",
" 7.50451469e-01 6.04607112e-16 4.53891948e-01]\n",
" [ -3.77964473e-01 4.92886500e-01 -1.92527950e-16 7.07106781e-01\n",
" -3.20722630e-01 -4.36564477e-16 -1.06502348e-01]\n",
" [ -3.77964473e-01 -2.14220282e-01 4.01736195e-17 9.99200722e-16\n",
" 3.86384151e-01 2.68521841e-16 -8.13609130e-01]\n",
" [ -3.77964473e-01 -3.56037413e-01 7.07106781e-01 -3.88578059e-16\n",
" -1.65130120e-01 -4.08248290e-01 1.90907293e-01]\n",
" [ -3.77964473e-01 -3.56037413e-01 7.02923822e-17 -3.33066907e-16\n",
" -1.65130120e-01 8.16496581e-01 1.90907293e-01]\n",
" [ -3.77964473e-01 -3.56037413e-01 -7.07106781e-01 -8.04911693e-16\n",
" -1.65130120e-01 -4.08248290e-01 1.90907293e-01]]\n"
]
}
],
"source": [
"eig_vals, eig_vectors = eigh(laplacian)\n",
"print('eigen values\\n%s' % str(eig_vals))\n",
"print('eigen vectors\\n%s' % str(eig_vectors))"
]
},
{
"cell_type": "code",
"execution_count": 38,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"first eigen value=-1.43918e-15\n",
"first (normalized) eigen vector=\n",
"[[-0.37796447]\n",
" [-0.37796447]\n",
" [-0.37796447]\n",
" [-0.37796447]\n",
" [-0.37796447]\n",
" [-0.37796447]\n",
" [-0.37796447]]\n"
]
}
],
"source": [
"print('first eigen value=%g' % eig_vals[0])\n",
"print('first (normalized) eigen vector=\\n%s' % eig_vectors[:,0])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Eigen vectors have been normalized to unit length by $ v = \\frac{v'}{||v'||} $"
]
},
{
"cell_type": "code",
"execution_count": 39,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"array([ 0.37796447, 0.37796447, 0.37796447, 0.37796447, 0.37796447,\n",
" 0.37796447, 0.37796447])"
]
},
"execution_count": 39,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"v = np.array([1, 1, 1, 1, 1, 1, 1])\n",
"v / (np.sqrt(np.sum(v**2)))"
]
},
{
"cell_type": "code",
"execution_count": 40,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"second eigen value=0.40\n",
"second eigen vector=\n",
"[[ 0.4928865 ]\n",
" [ 0.29655952]\n",
" [ 0.4928865 ]\n",
" [-0.21422028]\n",
" [-0.35603741]\n",
" [-0.35603741]\n",
" [-0.35603741]]\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAeIAAAFBCAYAAACrYazjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xt8zvXj//HH5bwxs0JEjZwqLMyGnJXDltPiw5Q5dBDV\n51N9cqyPyqe0ZJS+MvqUZshKcqo5FEIik5hDWSKHoQ2zHK6N2fv3x+JXGobrul7Xde15v93cPrfP\ndl3v93OlPa/X6/16v942y7IsRERExIgipgOIiIgUZipiERERg1TEIiIiBqmIRUREDFIRi4iIGKQi\nFhERMUhFLCIiYpCKWERExCAVsYiIiEEqYhEREYNUxCIiIgapiEVERAxSEYuIiBikIhYRETFIRSwi\nImKQilhERMQgFbGIiIhBKmIRERGDVMQiIiIGqYhFREQMUhGLiIgYpCIWERExSEUsIiJikIpYRETE\nIBWxiIiIQSpiERERg1TEIiIiBqmIRUREDFIRi4iIGKQiFhERMUhFLCIiYpCKWERExCAVsYiIiEEq\nYhEREYNUxCIiIgapiEVERAxSEYuIiBikIhYRETFIRSwiImKQilhERMQgFbGIiIhBKmIRERGDVMQi\nIiIGqYhFREQMUhGLiIgYVMx0ABERcYy0tDTi4+JISU7mVGYmZfz9qR0URP+BA6lQoYLpeHIZNsuy\nLNMhRETk+iUlJTEpOpovlizhQSAkKws/4CSw0ceH+ZbFA2FhPDNqFCEhIYbTyqVUxCIiHuy92Fhe\nHjqUEXY7/S2LgHxekwHE2Wy86ePDmJgYBg0Z4uqYcgUqYhERD/VebCzjhg5l2Zkz1CzA63cDHX19\nGaEydisqYhERD5SUlETXNm1Ye0kJVwPSyFsAZAE2YADwzh/f3w209PVl8erVNG7c2IWJ5XK0alpE\nxANNio5mhN3+t5GwDfgC+J28a8S/8/9LGKAmMNxuZ1J0tGuCylVpRCwi4mHS0tKoExjInqysv10T\nrg58ALS7wvuPAzVKlSJl/36tpnYDGhGLiHiY+Lg4IiDfhVkFcRMQYbMRHxfnuFBy3VTEIiIeJiU5\nmdCsrMt+vzt5ZRvwx/9+kM9rQux2UrZtc05AuSba0ENExMOcyszE7wrfXwi0vcox/ICTGRmOCyXX\nTSNiEREPU8bfn5NX+H5BFv6cBPwCrndyWxxJRSwi4mFqBwWxsVSpGzpGko8PtevXd1AiuRFaNS0i\n4mGutmo6DSj6p6+1B+b96f9r1bR70YhYRMTDVKxYkQfCwphhs/3te3uB0+TdP3zhz7xLXjPDZqNz\neLhK2E1oRCwi4oEut7PW1WhnLfejEbGIiAcKCQlhTEwM7YoXZ3cB33Nhr+kxMTEqYTeiIhYR8VB+\n5cqR5edHCx8f3rLZuNzNSMeBiTYbLfXAB7ekqWkREQ+0ceNGHnjgAVasWMHZs2eZFB3N54mJRNhs\nhNjtF59HvAZYWqoUncPDeWbUKI2E3ZCKWETEwxw8eJCmTZsyZcoUunbtevHr6enpxMfFkbJtGycz\nMvALCGDJqlX83+TJdOvWzWBiuRIVsYiIBzl9+jStWrWiV69ejBgx4qqvf+GFFyhSpAivvfaaC9LJ\n9dA1YhERD5Gbm8uAAQOoV68ew4cPL9B72rdvz5dffunkZHIjNCIWEfEQL7/8Ml9++SUrV66kVAF3\n1srOzqZChQrs27ePAG1p6ZY0IhYR8QAff/wxM2bMYP78+QUuYYCSJUvSvHlzVq5c6cR0ciNUxCIi\nbi4pKYmnn36ahQsXcsstt1zz+zU97d5UxCIibiw1NZWIiAj+97//cc8991zXMTp06KAidmMqYhER\nN3XmzBm6devGk08+Sffu3a/7OHXr1sVut7Nnzx4HphNHURGLiLghy7IYOHAgd955J6NGjbqhY9ls\nNu6//36Nit2UilhExA3997//Zd++fbz//vvY8nnK0rXSdWL3pduXRETczNy5c3n++efZuHEjlSpV\ncsgxDx8+TN26dUlPT6do0aJXf4O4jEbEIiJu5Pvvv+fJJ59k4cKFDithgMqVK1OlShU2bdrksGOK\nY6iIRUTcxKFDh+jevTvTpk2jYcOGDj++pqfdk4pYRMQN2O12unfvzhNPPMGDDz7olHOoiN2TrhGL\niBhmWRYPPfQQNpuN2bNnO2RxVn5Onz5NpUqVOHz4MGXKlHHKOeTaaUQsImLY2LFj+eWXX/jggw+c\nVsIApUuXpnHjxqxevdpp55BrpyIWETFo3rx5vPfeeyxcuBAfHx+nn0/T0+5HRSwiYsgPP/zA4MGD\nWbBgAZUrV3bJOVXE7kdFLCJiwOHDh+nWrRuxsbE0atTIZedt1KgRR44cITU11WXnlCsrZjqAyAVp\naWnEx8WRkpzMqcxMyvj7UzsoiP4DB1KhQgXT8UQcJisri4iICB577DF69uzp0nMXLVqUdu3a8dVX\nX9G/f3+Xnlvyp1XTYlxSUhKToqP5YskSHgRCsrLwA04CG318mG9ZPBAWxjOjRhESEmI4rciNsSyL\nvn37cv78eebMmePUxVmX895777FmzRpmzZrl8nPL36mIxaj3YmN5eehQRtjt9LcsAvJ5TQYQZ7Px\npo8PY2JiGDRkiKtjijjM66+/zvz581mzZo1LFmflZ+/evTRr1ozDhw8b+SAgf6WpaTHmvdhYxg0d\nytozZ6gJVAPSyPtLWRy4F5gKVAGesyy6nDlDx6FDAVTG4pHmz59PbGws3333nbESBqhevTp+fn5s\n27aNoKAgYzkkjxZriRFJSUm8PHQoy/4oYQAb8AXwO3AYqAj880/vqQksO3OGl4cO1X654nG2bNnC\noEGDmD9/PrfeeqvpOFo97UZUxGLEpOhoRtjtF0v4ggvXSUoAPYGdl3y/JjDcbmdSdLSzI4o4zJEj\nR+jWrRvvvvsujRs3Nh0HUBG7E10jFpdLS0ujTmAge7Ky/nJNuDrwAdAOOAM8Sd4o+cNL3n8cqFGq\nFCn792s1tbi9rKws2rZtS8eOHXnllVdMx7noxIkT3H777aSlpVGqVCnTcQo1jYjF5eLj4oiAfBdm\ndQduAsoBXwFD83nNTUCEzUZ8XJzTMoo4gmVZPP7449x222289NJLpuP8Rbly5ahbty7ffvut6SiF\nnopYXC4lOZnQrKx8v7eQvBFvNvB/QCvyFnBdKsRuJ2XbNqdlFHGEcePGsXPnTuLi4ihSxP1+3bZv\n357ly5ebjlHoud/fDPF6pzIz8bvM9y5cJ7EBEUBR4Jt8XucHnMzIcEI6EcdYuHAhkydPZuHChfj6\n+pqOky9dJ3YPKmJxuTL+/pwswOsWAieAu/L53knALyC/yW0R87Zu3cpjjz3GZ599RtWqVU3Huaym\nTZuye/dujh49ajpKoaYiFperHRTExsssDukClAX8gdFAPPkX8Rpg++7drF27ltzcXGdFFblmv/32\nG926deOdd94hNDTUdJwrKl68OK1atWLFihWmoxRqKmJxuX4DBjDfsrh0YnkvcJq8+4gzgWQgMp/3\nHweWlCxJm7ZteeqppwgMDGToH/cW6yYAMSk7O5sHH3yQqKgo+vTpYzpOgWh62jwVsbjcqlWrsFkW\ncdf5/hk2G10eeICxY8eSnJzM0qVL8fHxoU+fPtSuXZvRo0ezY8cOR0YWuSrLshg0aBCVK1dmzJgx\npuMU2IUi1odYc3QfsbjM8ePHeeqpp9iyZQsjR45k5JNPXtzesqB2Ay19fVm8evXfNkawLIvNmzeT\nkJBAQkIC5cqVIzIyksjISGrUqOHQn0XkUm+++SYJCQmsXbuW0qVLm45TYJZlcdttt7Fy5Upq165t\nOk6hpBGxuMSSJUsICgqiUqVKbN68mf79+zMmJoaOvr7sLuAxdgMdfX0ZExOT7+5ENpuN4OBgxo8f\nz759+4iNjeXw4cPce++9hIaGMnHiRA4ePOjQn0sEYNGiRUyaNImFCxd6VAlD3n83mp42zBJxopMn\nT1qDBg2yAgMDrZUrV/7t+9OmTLEq+fpaMWAdB8vK588xsCbYbFYlX19r2pQp15zh3Llz1vLly61H\nHnnECggIsFq1amVNmTLFSktLc8SPKIVccnKyVb58eWvDhg2mo1y32bNnW926dTMdo9DS1LQ4zTff\nfEP//v1p3bo1b731Fv7+/vm+btmyZfTq3JkiRYsSUaQIIXb7xecRJ/3xPOLO4eE8M2rUDe/Tm52d\nzbJly0hISCAxMZGmTZsSGRlJ9+7dKVeu3A0dWwqf9PR0QkNDGTt2LA899JDpONctLS2N2rVrc/To\nUYoV00P5XE1FLA6XlZXFSy+9xKxZs5g6dSpdu3a94uvfeustfvjhByZMmEB8XBwp27ZxMiMDv4AA\natevT78BA5yyp/Tp06f5/PPPSUhIYOXKlbRt25Y+ffrQuXNnj5teFNfLzs7m/vvvp1WrVowdO9Z0\nnBvWoEEDpkyZwr333ms6SqGjIhaH+uGHH4iKiqJOnTpMnTq1QAXaoEEDJkyYwH333eeChPnLzMxk\nwYIFzJkzhw0bNhAWFkafPn3o2LEjJUuWNJZL3JNlWTz66KOcOHGCTz/91C23r7xWw4YNo0yZMrz8\n8sumoxQ6nv+3R9xCTk4Or732Gh07dmTkyJF8+umnBSrhrVu3cvz4cdq2beuClJfn7+9P//79Wbp0\nKT///DOtW7dmwoQJVK5cmUceeYTly5eTk5NjNKO4j4kTJ7J582bi4+O9ooQBOnTooAVbhmhELDds\n165d9O/fHz8/P6ZPn85tt91W4Pc+//zzlCpVym2n9g4ePMjcuXNJSEjg119/pWfPnkRGRtK8eXOv\n+QUs1+aLL77g8ccfZ8OGDdx+++2m4ziM3W6nYsWKpKamUrZsWdNxChX9JpHrlpuby+TJk2nRogVR\nUVEsW7bsmko4JyeH2bNn069fPyemvDFVq1blueee47vvvuPbb7+lSpUq2s2rENuxYwcDBw5k3rx5\nXlXCAD4+PjRt2pSvv/7adJRCR0Us1+XAgQN06NCB2bNns27dOp566qlrHiEuW7aMatWqUadOHSel\ndKwaNWrwwgsvaDevQuro0aN06dKFiRMn0qxZM9NxnEL3E5uhIpZrYlkW8fHxBAcH065dO9auXXvd\nu/HMmDGD/v37Oziha9StW5dXX32VlJQUEhISyMrKolOnTtSvX5+xY8fyyy+/mI4oDnT27Fl69OhB\n79696du3r+k4TqPnE5uha8RSYOnp6TzxxBP8/PPPzJw5kwYNGlz3sTIyMqhWrRp79+7lpptucmBK\nc3Jzc/n2229JSEhg7ty5BAYGEhkZSa9evdz6UXhyZZZl8fjjj3P06FE+++wzr14bkJubS6VKldi0\naZPXTb27M+/9GyUOtXDhQoKCgqhduzabNm26oRIG+Pjjj+nQoYPXlDBAkSJFaNGiBZMnTyY1NZWx\nY8eyY8cOgoKCaN26NbGxsaSnp5uOKdfo7bffJikpiVmzZnl1CUPe3+H77rtP09MuphGxXFFmZibP\nPvssa9asYcaMGbRo0cIhx23WrBkvvvginTt3dsjx3Nmlu3k1adKEPn36aDcvD7BkyRIeffRR1q9f\nT2BgoOk4LjF9+nSWL19OQkKC6SiFhopYLmvlypUMHDiQ8PBwxo8fT5kyZRxy3F27dtG6dWsOHDhA\n8eLFHXJMT6HdvDzHzp07adOmDQsWLChUu00dOHCARo0a8dtvv3n9DIC70D9l+ZszZ87wzDPP0K9f\nP6ZNm0ZsbKzDShggPj6ehx56qNCVMEDp0qXp3bs38+fPZ//+/URERPDhhx9SpUoV+vTpw8KFC8nO\nzjYds9C7sEJ6/PjxhaqEAW677TZuvvlmtmzZYjpKoaEilr/YuHEjjRo1Ij09neTkZDp16uTQ4+fm\n5jJz5kyPXS3tSPnt5jVx4kTt5mXY2bNn6dmzJz169Ci0f091G5NrqYgFgHPnzvHSSy/RpUsX/vvf\n//LRRx85ZSHVqlWruOmmm7jnnnscfmxPVqFCBQYPHszq1atJTk6mfv36jB49+uIGImvXriU3N9d0\nTK9nWRZPP/00fn5+REdHm45jjIrYtXSNWNixYwf9+vWjUqVKvP/++1SuXNlp5+rXrx8NGzbkueee\nc9o5vMkvv/zCxx9/TEJCAhkZGfTu3ZvIyEiCg4Ox2Wym43mdSZMm8f777/Ptt9/i5+dnOo4xv//+\nO1WqVCEtLQ0fHx/TcbyeirgQO3/+PG+//TZvvPEGr7/+Oo899phTf7mfOnWKqlWrsmvXLm655Ran\nncdb7dixg4SEBBISErAsi8jISPr06UPdunVNR/MKS5cuZeDAgaxfv55q1aqZjmNcixYteOmll+jQ\noYPpKF5PU9OF1N69e2nbti0LFy5k48aNPP74404fYc2bN4+WLVuqhK/Tn3fz+vjjj8nOztZuXg7y\n448/0q9fP+bOnasS/oOmp11HRVzIWJbF+++/T2hoKN26dWPVqlVUr17dJef25C0t3YnNZiM4OJjx\n48ezb98+YmNjOXz4MPfeey+hoaFMnDiRgwcPmo7pMY4dO0aXLl0YN26cw+6T9wYqYtfR1HQhcvjw\nYR5//HEOHTrEzJkzXTqluW/fPho1akRqaiqlSpVy2XkLk5ycHFatWkVCQgILFiygXr16REZG0rNn\nzwI9G7owOnfuHB06dCA4OJiYmBjTcdxKTk4O5cuX16UkF9CIuJCYO3cuDRo0oFGjRmzYsMHl1xVn\nzpxJr169VMJOVKxYMdq3b88HH3zAoUOHeP7551m7di21atWiY8eOxMXFceLECdMx3YZlWfzzn/+k\ndOnSjBs3znQct1OsWDHatm3LihUrTEfxehoRe7njx4/z9NNPs3nzZuLj4wkNDXV5BsuyqFOnDvHx\n8TRt2tTl5y/stJtX/iZPnszUqVP59ttvKVu2rOk4bmnKlCkkJSXx4Ycfmo7i1TQi9mLLli0jKCiI\nihUrsnnzZiMlDLB+/XpsNhtNmjQxcv7CTrt5/d2XX37Ja6+9xqJFi1TCV3DhOrHGa86lEbEXOnXq\nFMOGDSMxMZEPP/yQdu3aGc3zxBNPEBgYyAsvvGA0h/xVeno68+bNY86cOWzbto3u3bsTGRlJu3bt\nKFasmOl4TrNr1y5atWrF3LlzadWqlek4bs2yLKpXr86SJUu46667TMfxWhoRe5l169bRoEED7HY7\nycnJxkvYbrczd+5coqKijOaQvyuMu3kdP36cLl268Prrr6uEC8Bms9G+fXuWL19uOopXUxF7iezs\nbEaOHEnPnj2JiYkhLi4Of39/07FYtGgRjRo14rbbbjMdRa6gatWqPPfcc3z33XesX7/+YhkHBgYy\ndOhQNm3a5PHTk+fOnaNXr1507tyZRx991HQcj6HbmJxPU9NeYMuWLfTr14+aNWsydepUKlasaDrS\nReHh4fTp00cjYg/lTbt5PfXUU+zdu5fFixdTtGhR03E8xrFjx7jjjjtIT0+nRIkSpuN4JRWxB8vJ\nyWH8+PG89dZbxMTEEBUV5Vb7Dx8+fJi77rqL1NTUQr061xtYlsXmzZsvlnK5cuWIjIwkMjKSGjVq\nmI53VVOmTGHy5MmsX7/eLWaKPE3jxo2ZOHGipvOdREXsoX7++Wf69etH6dKlmT59OrfffrvpSH8T\nExPDjh07dOuDl8nNzeXbb78lISGBuXPnEhgYSGRkJL169aJq1aqm4/3NV199Rd++fVm3bp1HfGhw\nR6NGjaJYsWK8+uqrpqN4JV0j9jCWZTFlyhTuvfdeHnroIZYvX+6WJWxZlra09FJFihShRYsWTJ48\nmdTUVMaOHcuOHTsICgqiVatWxMbGkp6ebjomACkpKTz88MMkJCSohG+ArhM7l0bEhqSlpREfF0dK\ncjKnMjMp4+9P7aAg+g8ceNntCA8ePMgjjzzC77//Tnx8PLVr13Zx6oL74YcfiIiIYM+ePRQpos97\nhUF2djbLli0jISGBxMREmjRpQp8+fejevTvlypVzeZ6MjAyaNm3K0KFDefzxx11+fm+SnZ1N+fLl\n2b9/PwEBAabjeB0VsYslJSUxKTqaL5Ys4UEgJCsLP+AksNHHh/mWxQNhYTwzahQhISFA3uhy9uzZ\n/Pvf/+aZZ55hxIgRbn+f57PPPkvZsmX573//azqKGJDfbl6RkZF06dLFIesFrvZBNicnh7CwMOrW\nrcvbb7/tgJ9IOnXqxKBBg3jwwQdNR/E6KmIXei82lpeHDmWE3U5/yyK/z5UZQJzNxps+PoyJiSGi\nZ0+GDBnCTz/9xMyZM2nYsKGrY1+zc+fOUbVqVdatW0fNmjVNxxHDMjMzWbBgAXPmzGHDhg2EhYUR\nGRlJp06dKFmy5DUdq6AfZM8WK8bvv//O559/7vYfWj3FhAkT2L17N7GxsaajeB9LXGLalCnWHb6+\n1s9gWX/60xqsALDOXvL1n8EKLFnSKle2rDVs2DDLbreb/hEKbOHChVbz5s1NxxA3lJaWZsXGxlqt\nWrWyAgICrIEDB1rLli2zzp07d9X3Tpsyxark62u9ZbNZxy/57+XCn+NgTbDZrHI2m/XWhAku+IkK\nj61bt1o1atQwHcMrqYhdYOPGjValfEr4V7B8wKoD1qf5/FL5GayKJUtaSUlJpn+Ea/Lggw9a06ZN\nMx1D3NyBAwesiRMnWqGhoVbFihWtJ5980lqzZo11/vz5v732ch9kL/fnZ7Du8PW1pk2ZYuAn8065\nubnWLbfcYu3Zs8d0FK+jqWkX6PvggzResIBnL/lH/SqwCWgCrAcW5/Pet2w2NkdEMHPePOcHdYAL\nN//v27fPyAId8Ux79uy5eI9yRkYGvXv3JjIykuDgYDZt2kTXNm1Ye+YMFy50VAPSgOJAUeBuIAoY\nBFy4k3430NLXl8WrV9O4cWMX/0TeqW/fvrRq1YpBgwaZjuJVVMROlpaWRp3AQPZkZf3tmnAtYAwQ\nAtQFUoFL10sfB2qUKkXK/v0e8XD3d999l7Vr15KQkGA6inioS3fzKlusGFEpKTz3p19V1YHpQFvy\nrg+vBv4FtPnj6xd42gdZdxcfH8/ixYuZO3eu6SheRfeVOFl8XBwR8LcS/oa84u1KXiHXBT7K5/03\nARE2G/Fxcc6M6TC6d1huVN26dXn11VdJSUkhNjaWn3fvZkA+44ULX/EDOgMfAzOAnX96TX/L4vPE\nRLe5r9nT3X///axcuZLz58+bjuJVVMROlpKcTGhW1t++Hg90AMr88f//Qd4vkfyE2O2kbNvmnIAO\n9OOPP3Lw4EHat29vOop4AZvNxtYffuAfxYvne4fBpUKAqsDaP33N0z7Iurtbb72VypUrs3nzZtNR\nvIrW9TvZqcxM/C75WhbwCZALVP7ja2eBE8A2oP4lr/cDTmZkODOmQ8yYMYOHH35Yt4uIw1zug+zl\n3Ere5Zw/C7Hb2eIBH2Q9xYVdti7scyA3TiNiJyvj78/JS742n7xPQD8CW//48yPQkvxHxScBPzff\nzeb8+fPMmjVL09LiUPl9kL2SVPJGwX/mKR9kPYW2u3Q8FbGT1Q4KYmOpUn/5WjzwCFAFqPinP0+R\nd5340kexJ/n4ULv+peNk97JixQpuueUW6tWrZzqKeJH8PsheThJwCGhxyddPAudtNo9/nrK7aN26\nNZs2beLUqVOmo3gNFbGT9RswgPnk7Zh1wRLgzXxe+w/yfpH8+V/KcWC+ZdFvwACnZXSE+Ph4jYbF\n4fL7IHupk8DnQB/ybmG69EnJ64oW5cs1a6hevTpPPvkkn3/+OadPn3ZO4EKgdOnSBAcHs2bNGtNR\nvIaK2MkqVqzIA2FhzLjO5wTPsNnoHB7u1rcuXdhKsE+fPqajiJfJ74PsBV0Af+B2IBoYyl9vXYK8\nD7JfFC/OTykpfPHFF1SvXp0JEyZQqVIlOnXqxDvvvMPu3bud+jN4I01PO5buI3aBpKSkv21IUBCe\nsiHB9OnTWbRoEQsWLDAdRbzQ5TbEKYjL3UecmZnJV199RWJiIomJifj5+REeHk54eDitWrWi1FVG\n4YXdxo0beeSRR9i+fbvpKF5BRewi78XGMm7oUJYVsIx3Ax19fRkRE8OgIUOcHe+GtG7dmmeffZaI\niAjTUcQLOfuDbG5uLlu3br1Yytu2baNNmzYXi9kdn/dt2vnz56lQoQLbt2/n1ltvNR3H8xnaWrNQ\nurBp/cQrbFp/7I9N6yt5yD65e/bsscqXL29lZ2ebjiJezJV7TR89etT66KOPrL59+1rly5e36tWr\nZw0fPtz6+uuvrbNnzzrhp/NMPXr0sGbMmGE6hlfQiNjFNm3axKToaD5PTCTCZiPEbr/4GLd1RYvy\nRfHidA4P55lRo9x6OvqCMWPGcPToUf7v//7PdBTxchceIzrcbmfAZR4jepy8x4iO/+Mxojc6m3T+\n/Hk2bdp0cbS8e/du7r//fsLDw+nUqROVK1e++kG81LRp0/jmm2+YOXOm6SgeT0VsSHp6et6Dzbdt\n42RGBlk5OSQlJ7N5yxa3Xpj1Z5ZlUbNmTRISEnRzv7jElT7IfleyJJ+cPUuP7t155oUXnPJB9siR\nIyxdupTExES+/PJL7rjjjotT2KGhoRQtWtTh53RXe/bsoXnz5hw6dAjbdS5GlTwqYjdht9u5+eab\nycjIuOaHpZuydu1annjiCXbs2KH/EMWlLv0g6xcQQK369fnf++8zffp0mjdv7vQM586dY/369RdH\ny4cOHaJjx46Eh4fTsWNHypcv7/QMptWoUYMFCxZQ3833OXB3KmI3cs899/DBBx94xJQ0wGOPPUat\nWrUYMWKE6SgiAERHR7Nv3z6mTp3q8nMfOHCAJUuWkJiYyKpVq7j77rsvjpYbNmxIkSLed7fo4MGD\nqV27Nv/+979NR/FoKmI38sgjjxAaGsrgwYNNR7mqM2fOUKVKFbZv306VKlVMxxEBYP/+/TRs2JBD\nhw4ZnVnKzs5m7dq1F0fLmZmZhIWFER4eTvv27fH39zeWzZHmzZvH+++/z5IlS0xH8Wje9xHNgzVu\n3JhNmzaZjlEgCxYsIDQ0VCUsbuX2228nKCiIxMREozlKlizJ/fffz8SJE/npp5/45ptvaNSoEdOn\nT6dq1apYkjbeAAAbmUlEQVS0adOGN998k+3bt3v01pvt2rVj3bp1ZGdnm47i0VTEbiQ4OJjvv//e\ndIwC0XOHxV1FRUW53UreGjVq8PTTT5OYmMhvv/3G8OHD2b9/P126dCEwMJDBgwezaNEij9u/OSAg\ngLvvvptvv/3WdBSPpqlpN3Jhwdbx48fdemef1NRU6tWrR2pqKr6+vqbjiPxFZmYmgYGB7Nmzh5tu\nuvRZTO7Fsix++umni1PYGzdupFmzZhevLdeqVcvtF0KOHj2a8+fP8/rrr5uO4rE0InYjPj4+1KlT\nh+TkZNNRrmj27Nn06NFDJSxuyd/fn44dO/LJJ5+YjnJVNpuNu+66i+eff54VK1aQmprKkCFD2LFj\nB23btqVWrVr861//YunSpdjtdtNx86V9p2+citjNBAcHu/V1YsuyNC0tbi8qKopZs2aZjnHNypYt\nS0REBP/73/84ePAg8+bNo3LlyowdO5ZbbrmFzp07M2XKFH799VfTUS9q2rQpKSkpHDt2zHQUj6Ui\ndjPuvmDr+++/JysrixYtLn3qq4j76NixIykpKezZs8d0lOtms9m45557GDVqFGvXruXXX38lKiqK\n7777jtDQUOrWrcuwYcNYtWoVZ8+eNZazRIkStGzZkhUrVhjL4OlUxG7G3RdszZgxg379+rn9dSsp\n3IoXL07v3r09clR8OTfddBO9e/dmxowZHDlyhLi4OMqUKcPIkSOpWLEiPXr04IMPPuDQoUMuz6bp\n6RujxVpuJjs7m4CAAI4dO4aPj4/pOH9x9uxZqlSpwsaNG6levbrpOCJXtHHjRh5++GFSUlK8/oNj\nWlraxa03ly9fTmBg4MUFX02aNKFYsWJOPf/OnTsJDw9n7969Xv/P2hlUxG4oODiYd999l6ZNm5qO\n8hfz58/n7bffZvXq1aajiFyVZVnceeedxMfH06RJE9NxXCYnJ4cNGzZcXIl94MABOnTocPFBFc7Y\ny96yLCpXrsyAfv04fugQpzIzKePvT+2gIPoPHOgx++eboiJ2Q4MGDSIoKIinn37adJS/6N69O127\nduWRRx4xHUWkQF599VV+++03Jk+ebDqKMampqRe33lyxYgV33nnnxdFycHDwDW+9mZSUxKToaBYs\nXEiPokVpdu7cxQdxbPTxYb5l8UBYGM+MGqWHw1yGitgNvffee6xfv54PP/zQdJSL0tPTqVmzJgcO\nHKBs2bKm44gUyN69ewkNDSU1NZUSJUqYjmPc2bNn+eabby6Olo8dO/aXrTcDAvJ7uOTlXXg05Qi7\nnf6XeTRlBnmPpnzTQY+m9EZarOWG3PEWpjlz5tC5c2eVsHiU6tWrc+edd7Js2TLTUdxCiRIlaNeu\nHTExMezcuZMNGzYQGhpKfHw8gYGBtGrVijfeeIPk5OSrbr35Xmws44YOZe2ZMzx7mRIGCACesyzW\nnjnDuKFDeS821uE/l6fTiNgNXViwlZ6eTunSpU3HAfI+HERHR9OhQwfTUUSuybRp01ixYoVHbPBh\nkt1uZ/Xq1SQmJvLFF1+QnZ19cQr7vvvuw8/P7+Jrk5KS6NqmDWvPnKHmn45RDUgDigEWYANSgEp/\nfH830NLXl8WrV3vMU+ZcQUXspkJCQpg0aRL33nuv6Shs376dTp06sW/fvkL14HPxDhkZGVSrVo19\n+/ZRrlw503E8gmVZpKSkXJzC3rBhA02aNLlYzK+NGkXjhQt59pL6qA5MB9pe4dhv2Wxsjohg5rx5\nzvwRPIqK2E0NHjyYu+++m3/961+mozBs2DCKFi3KG2+8YTqKyHXp0aMHYWFhPPbYY6ajeKRTp06x\nYsUKEhMTWbx4MScOHyYV/jYdXR34AGh3hWMdB2qUKkXK/v1aTf0HXSN2U40bN3aLjT1ycnKYPXu2\ntrQUj+apW166izJlytCtWzemTZvGc88+S6+SJS97TfhqbgIibDbi4+IcmNCzqYjdlLss2Prqq6+o\nWrUqd911l+koItctLCyM7du3s2/fPtNRPN7Pyck0vcLzh7uTV7Y3AQ9e5jUhdjsp27Y5IZ1nUhG7\nqbp167J3717jzyfVAx7EG5QsWZJ//OMfzJ4923QUj3cqMxO/K3x/IXnTz8eBzy7zGj/gZEaGo6N5\nLBWxmypRogT169dny5YtxjJkZmayZMkSIiMjjWUQcZSoqChmzpx51dty5MrK+Ptz8grfL8g/3ZOA\n3zXes+zNVMRuzPT09CeffMJ9993HzTffbCyDiKM0a9aMs2fPsnnzZtNRPFrtoCA2lip1Q8dI8vGh\ndv36Dkrk+VTEbsz0gi1NS4s3sdls9O3bl5kzZ5qO4tH6DRjAfPJ2zLpUQR73cByYb1n0GzDAobk8\nmYrYjZkcEe/evZuff/6ZsLAwI+cXcYa+ffsyZ84ccnJyTEfxWBUrVuSBsDBm5POUpT1c+dYlgBk2\nG53Dw3Xr0p+oiN3Y3Xffzf79+zl58kpXZJwjPj6ePn36ULx4cZefW8RZatWqxR133KFn596gZ0aN\nYpyPD7uv8X27gTd9fHhm1ChnxPJYKmI3Vrx4cerXr88PP/zg0vPm5uYSHx+vaWnxSpqevnEhISGM\niYmho69vgct4N9DR15cxMTHa3vISKmI317hxY5dPT69ZswY/Pz8aNGjg0vOKuELv3r1JTEw0MtPk\nTQYNGcIzY8fSGJhos+V7zRjyrglPtNlo6evLCD19KV8qYjdnYsHWhUVatnyuAYl4uvLly9O6dWvm\naa/jG3bi999p0qEDP0REcEepUjzi40MsMAuIBR7x8aFGqVL8EBHB4tWrVcKXob2m3dy2bdvo2bMn\nu3btcsn5Tp8+TZUqVfjxxx+pXLmyS84p4mqffvopU6dO5auvvjIdxWMdOXKEunXrsmnTJqpXr056\nejrxcXGkbNvGyYwM/AICqF2/Pv0GDNDCrKtQEbu5nJwcypUrR2pqKv7+/k4/38yZM5kzZw6JiYlO\nP5eIKVlZWdx6660kJydTtWpV03E80pAhQ/Dx8WHixImmo3g8TU27uWLFihEUFOSyBVtapCWFQalS\npejRowcfffSR6Sge6aeffuLTTz/lxRdfNB3FK6iIPYCrFmwdOHCAzZs3061bN6efS8Q0bXl5/UaO\nHMnw4cO1656DqIg9gKsWbM2aNYuePXtS6ga3rxPxBC1atOD3338nOTnZdBSPsnbtWn744Qf++c9/\nmo7iNVTEHsAVO2xZlqUtLaVQKVKkiO4pvkaWZTFs2DDGjh2rD+wOpCL2AHfeeSdHjhzhxIkTTjvH\nxo0byc3NpVmzZk47h4i7iYqK4qOPPuL8+fOmo3iETz/9lLNnz/LQQw+ZjuJVVMQeoGjRotxzzz1O\nfWrMjBkz6Nevn+4dlkLlzjvvpEqVKqxcudJ0FLd39uxZRo0axfjx4ylSRNXhSPqn6SGcuWArOzub\nTz75hKioKKccX8SdaXq6YKZOnUqtWrW47777TEfxOipiD+HMBVuLFy8mKCiIwMBApxxfxJ316dOH\nRYsWcfr0adNR3NaJEycYO3Ys48aNMx3FK6mIPYQzF2xpkZYUZhUrVqR58+bMnz/fdBS3NW7cOB54\n4AGCgoJMR/FK2lnLQ5w/f56AgAD27dtHQECAw47722+/UadOHQ4ePEiZMmUcdlwRTzJnzhxmzJjB\n0qVLTUdxOwcOHKBBgwZs3bpVu5A5iUbEHqJo0aI0aNDA4dPTH330Ed26dVMJS6HWrVs3vvvuOw4f\nPmw6itsZPXo0gwcPVgk7kYrYgzhjwdaF1dIihZmvry/du3dnzpw5pqO4la1bt7J06VKGDx9uOopX\nUxF7kODgYIeOiLdu3crx48dp27atw44p4qmioqKYNWuW6RhuZfjw4fznP/9xyQNnCjMVsQdx9Ig4\nPj6eqKgo3RMoArRu3Zq0tDR27NhhOopbWL58OXv27GHQoEGmo3g9/Qb2ILVq1eL48eMcO3bsho+V\nk5PD7NmzNS0t8oeiRYvy8MMP655iIDc3l+HDhxMdHU2JEiVMx/F6KmIPUqRIERo2bOiQ6elly5ZR\nvXp16tSp44BkIt4hKiqK2bNnk5ubazqKUbNmzcLHx4cePXqYjlIoqIg9jKOmp3XvsMjf1atXj/Ll\ny7N69WrTUYyx2+385z//ISYmRlveuoiK2MM4YsFWRkYGy5cvp3fv3g5KJeI9CvuWl++88w6NGzem\nefPmpqMUGtrQw8P8/PPP3H///ezbt++6jzF16lRWrlzJJ5984sBkIt7h8OHD3H333aSmpuLr62s6\njksdPXqUO++8k3Xr1umylQtpROxhatSoQWZmJunp6dd9DE1Li1xe5cqVCQ0NZdGiRaajuNzYsWPp\n1auXStjFVMQepkiRIjRq1Oi6p6d37drF3r176dixo4OTiXiPvn37Frp7in/55Rfi4+N5+eWXTUcp\ndFTEHuhGnsQUHx/Pww8/TLFixRycSsR7RERE8M0335CWlmY6isu8+OKLPPvss9xyyy2moxQ6KmIP\ndL1PYsrNzWXmzJmalha5ijJlytClSxcSEhJMR3GJjRs3snbtWv7973+bjlIoqYg90PXewrRq1Spu\nvvlmPcpMpAAKy5aXlmUxbNgwxowZQ+nSpU3HKZRUxB7ojjvu4NSpU/z222/X9D4t0hIpuHbt2nHg\nwAF27dplOopTLV68mGPHjjFgwADTUQotFbEHstls13w/8cmTJ1m0aBF9+vRxYjIR71GsWDEeeugh\nr76nOCcnhxEjRjBu3DitGzFIReyhrnXB1meffUbLli21EEPkGlyYnvbWLS+nT59OpUqVCA8PNx2l\nUFMRe6hrXbClaWmRa3fPPfdQpkwZ1q1bZzqKw506dYpXXnmF8ePHaytLw1TEHupaFmzt27eP5ORk\nunTp4uRUIt7FZrMRFRXlldPTEyZMoE2bNjRu3Nh0lEJPW1x6KMuyKF++PNu3b6dy5cpXfO1rr73G\noUOHmDJliovSiXiPgwcPcs8995CamkqpUqVMx3GII0eOULduXTZt2kT16tVNxyn0NCL2UAVdsGVZ\nFvHx8ZqWFrlOVatWpUGDBnz++eemozjMK6+8woABA1TCbkJF7MEKsmBr/fr1FClShNDQUBelEvE+\n3rTl5Y8//si8efN48cUXTUeRP6iIPVhBFmxdWKSlxRgi169Hjx58/fXXHDt2zHSUGzZy5EhGjBjB\nTTfdZDqK/EFF7MGutmDLbrczd+5coqKiXJhKxPuULVuWsLAwPv74Y9NRbsiaNWvYunUrTz/9tOko\n8icqYg92++23c+7cOQ4dOpTv9xctWkRwcDBVq1Z1cTIR7+Pp09MXtrIcO3as1yw68xYqYg9ms9mu\nOCrWvcMijtOhQwd++eUXdu/ebTrKdZk7dy45OTnaXc8NqYg93OUWbB0+fJj169cTERFhIJWI9yle\nvDiRkZEeOSo+e/Yso0aNYvz48RQpol/77kb/Rjzc5RZszZ49m4iICD1NRcSBLmx56WnbL8TGxlKn\nTh3atWtnOorkQ0Xs4S5MTf/5F4NlWZqWFnGC4OBgihUrxoYNG0xHKbATJ07w+uuv8+abb5qOIpeh\nx214uBIlSnDm1CmievQg99w5yvj7U/rmmzlx4gQtW7Y0HU/Eq/x5y8tmzZqZjlMgb7zxBp07d6Ze\nvXqmo8hlaItLD5WUlMSk6Gi+WLKEB86epUVuLn7ASeCbokVZCHTr2pVnRo0iJCTEcFoR7/Hrr7/S\nuHFjDh06RIkSJUzHuaL9+/fTsGFDkpOTqVKliuk4chmamvZA78XG0rVNGxovWMCerCxm5eYyGHgY\nGAzMOn+e/efPE7xgAV3btOG92FjDiUW8R7Vq1ahbty6JiYmmo1zV6NGjGTJkiErYzWlE7GHei41l\n3NChLDtzhpoFeP1uoKOvLyNiYhg0ZIiz44kUCv/73/9YtmwZn376qekol7VlyxY6depESkoKZcuW\nNR1HrkBF7EGSkpLo2qYNa/Mp4Y+At4CfgLJAA+AFoDl5ZdzS15fFq1frkWciDnDixAkCAwP59ddf\nCQgIMB0nXx07dqRr16489dRTpqPIVWhq2oNMio5mhN3+txKeCPwb+A+QBuwHngIW//H9msBwu51J\n0dEuyyrizcqVK0eHDh2YO3eu6Sj5Wr58OXv37mXQoEGmo0gBaETsIdLS0qgTGMierCz+/Pn7d6AK\nMAN48ArvPw7UKFWKlP37qVChgjOjihQKCxcuZMKECaxZs8Z0lL84f/48wcHBvPTSSzz44JV+K4i7\n0IjYQ8THxREBXDoJth7IBrpf5f03ARE2G/FxcU5IJ1L4hIWF8eOPP/Lrr7+ajvIXs2bNwtfXV7vq\neRAVsYdISU4mNCvrb18/BpSnYP8iQ+x2UrZtc3Q0kUKpRIkS9OrVy622vLTb7YwePZqYmBg9+tSD\nqIg9xKnMTPzy+frNwFEgtwDH8ANOZmQ4NJdIYXZhcw93ucL3zjvvEBISwr333ms6ilwDFbGHKOPv\nz8l8vt4MKAksKMAxTgJ+brrCU8QTNWnShNzc3Cs+F9xVjh49yvjx44nWokyPoyL2ELWDgtiYzzNE\nywJjyFslvRCwAznAUmDkJa9N8vGhdv36Tk4qUnjYbDb69u3LzJkzTUfhtddeIzIyktq1a5uOItdI\nq6Y9xOVWTV8wh7zbmH4ibwo6GHgRaPrH97VqWsQ5fvnlF5o1a0ZqairFixc3lqFJkybs3LmTihUr\nGskg108jYg9RsWJFHggLY8ZlFmD0AZLIm34+RN49xE3/9P0ZNhudw8NVwiIOVqNGDWrWrMmyZcuM\nZXjhhRd47rnnVMIeSkXsQZ4ZNYpxPj7svsb37Qbe9PHhmVGjnBFLpNC78JxiE7777jvWrVvHc889\nZ+T8cuNUxB4kJCSEMTExdPT1LXAZX9hrekxMjLa3FHGSXr16sXTpUjIzM116XsuyGDZsGGPGjMHX\n19el5xbHURF7mEFDhjAiJoaWvr68ZbNxuZuRjgMTbTZa6oEPIk53880307ZtW+bNm+fS8y5evJjj\nx48zYMAAl55XHEuLtTzUpk2bmBQdzeeJiUTYbITY7RefR5zk48N8y6JzeDjPjBqlkbCIC8ybN493\n332XlStXuuR8OTk51K9fnwkTJhAeHu6Sc4pzqIg9XHp6OvFxcaRs28bJjAz8AgKoXb8+/QYM0MIs\nERfKzs7m1ltvZcuWLdx2221OP9+0adP45JNP+Oqrr7SLlodTEYuIOMgTTzxB9erVGTny0rv4Hevk\nyZPUqVOHxYsXExwc7NRzifPpGrGIiIO4asvLCRMm0K5dO5Wwl9CIWETEQXJzc6lRowafffYZDRs2\ndMo5Dh8+TL169fj++++pVq2aU84hrqURsYiIgxQpUsTpW16+8sorDBw4UCXsRTQiFhFxoF27dtGm\nTRsOHDhAsWLFHHrsH3/8kVatWpGSkkKAHuDiNTQiFhFxoDp16nDbbbexYsUKhx97xIgRjBw5UiXs\nZVTEIiIOdmHRliOtXr2abdu28fTTTzv0uGKepqZFRBwsPT2dWrVqcfDgQcqUKXPDx7MsiyZNmvDs\ns8/y0EMPOSChuBONiEVEHKxChQq0bNmSzz77zCHH++STT8jNzSUyMtIhxxP3oiIWEXGCvn37OuSJ\nTNnZ2bzwwguMHz+eIkX0K9sbaWpaRMQJ7HY7VapUYfv27dx6663XfZy3336bL7/8ki+++MKB6cSd\nqIhFRJzk0Ucf5a677mLo0KHX9f4TJ05Qu3ZtVq5cSb169RycTtyF5jlERJzkRjf3eOONN+jatatK\n2MtpRCwi4iS5ublUq1aNzz//nKCgoGt67/79+2nYsCHbtm27oaltcX8aEYuIOEmRIkV4+OGHr2vR\n1ujRo3nyySdVwoWARsQiIk60c+dO2rdvz/79+ylatGiB3rNlyxbCwsJISUnBz8/PyQnFNI2IRUSc\n6O677+aWW27h66+/LvB7hg8fzujRo1XChYSKWETEya5ly8tly5axb98+Hn/8cSenEnehqWkRESc7\ncuQId911F6mpqfj6+l72defPn6dRo0a88sorREREuDChmKQRsYiIk1WqVIkmTZqwYMGCK75u1qxZ\n+Pn50b17dxclE3egIhYRcYGoqKgrrp622+2MHj2a8ePHY7PZXJhMTNPUtIiIC5w+fZqqVauydu1a\nliYmkpKczKnMTMr4+1M7KIgTv//OTz/9xKeffmo6qrhYMdMBREQKg507d1LJz497GzbkH8WKEZKV\nhR9wEvhu3jw+zsqiQ/v2JCUlERISYjquuJBGxCIiTvZebCwvDx3KcLudAZZFQD6vyQDibDbe9PFh\nTEwMg4YMcXVMMURFLCLiRO/FxjJu6FCWnTlDzQK8fjfQ0deXESrjQkNFLCLiJElJSXRt04a1l5Rw\nAvA2sB0oA1QH+gEXanc30NLXl8WrV9O4cWOXZhbX06ppEREnmRQdzQi7/S8lPAF4DhgB/AYcAaYC\n3wLn/nhNTWC43c6k6GhXxhVDNCIWEXGCtLQ06gQGsicr6+I14d+BW4FZwNXuFD4O1ChVipT9+6lQ\noYIzo4phGhGLiDhBfFwcEfCXhVnrgbNA1wK8/yYgwmYjPi7OCenEnaiIRUScICU5mdCsrL987ShQ\nnr/+4m1OXln7At9ccowQu52UbducGVPcgO4jFhFxglOZmVz67KSbySvjXP5/Ga/7439v/+Prf+YH\nnMzIcFpGcQ8aEYuIOEEZf39OXvK1ZkBJYGE+r89vsc5JwC8gv7uOxZuoiEVEnKB2UBAbS5X6y9f8\ngZeAJ4F5wCnyCngLcCafYyT5+FC7fn0nJxXTtGpaRMQJ8ls1fcEc8u4j3gGUBu4AHgP68/+vF2rV\ndOGhEbGIiBNUrFiRB8LCmJHPk5T6AN+RNyL+jbzV1I/y10U7M2w2OoeHq4QLAY2IRUSc5HI7a12N\ndtYqXDQiFhFxkpCQEMbExNDR15fdBXzPhb2mx8TEqIQLCRWxiIgTDRoyhBExMbT09eUtm43L3Yx0\nHJhos9FSD3wodDQ1LSLiAps2bWJSdDSfJyYSYbMRYrdffB5xko8P8y2LzuHhPDNqlEbChYyKWETE\nhdLT04mPiyNl2zZOZmTgFxBA7fr16TdggBZmFVIqYhEREYN0jVhERMQgFbGIiIhBKmIRERGDVMQi\nIiIGqYhFREQMUhGLiIgYpCIWERExSEUsIiJikIpYRETEIBWxiIiIQSpiERERg1TEIiIiBqmIRURE\nDFIRi4iIGKQiFhERMUhFLCIiYpCKWERExCAVsYiIiEEqYhEREYNUxCIiIgapiEVERAxSEYuIiBik\nIhYRETFIRSwiImKQilhERMQgFbGIiIhBKmIRERGDVMQiIiIGqYhFREQMUhGLiIgYpCIWERExSEUs\nIiJikIpYRETEIBWxiIiIQSpiERERg1TEIiIiBqmIRUREDFIRi4iIGKQiFhERMUhFLCIiYpCKWERE\nxCAVsYiIiEH/D9YdeMijA46RAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"print('second eigen value=%.2f' % eig_vals[1])\n",
"print('second eigen vector=\\n%s' % eig_vectors[:,1])\n",
"nx.draw(graph, with_labels=True)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"What do you notice about the second eigenvector?\n",
"\n",
"(Note that first vector component corresponds to node 'A', the second to 'B', etc.)\n",
"
"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can think of eigenvectors as the cluster assignment to each node.\n",
"\n",
"E.g., nodes with negative values are in cluster 1, nodes with positive values are in cluster 2."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"**From eigenvalues to clustering**\n",
"\n",
"Method 1:\n",
"- Compute decomposition and examine second eigenvector\n",
"- Place nodes of positive values in cluster 1, negative values in cluster 2."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"**From eigenvalues to clustering**\n",
"\n",
"Method 2:\n",
"- Compute decomposition and examine second eigenvector\n",
"- Place nodes of values greather than $\\tau$ in cluster 1, and the remainder in cluster 2.\n",
" - The threshold $\\tau$ will determine balance of clustering\n",
" - E.g., for $\\tau=-.3$?"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"**Partitioning into more than 2 components?**\n",
"\n",
"- Just recursively repeat the above procedure."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"\n",
"- Or, consider multiple eigen vectors simultaneously."
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"third eigen value=2.00\n",
"third eigen vector=\n",
"[[ 7.61771655e-17]\n",
" [ 1.92527950e-16]\n",
" [ -1.92527950e-16]\n",
" [ 4.01736195e-17]\n",
" [ 7.07106781e-01]\n",
" [ 7.02923822e-17]\n",
" [ -7.07106781e-01]]\n"
]
}
],
"source": [
"print('third eigen value=%.2f' % eig_vals[2])\n",
"print('third eigen vector=\\n%s' % eig_vectors[:,2])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"$\\mathbf{v}_1: \\{A,B,C\\}, \\{D,E,F,G\\}$\n",
"\n",
"$\\mathbf{v}_2: \\{A,B,D,E,F\\}, \\{C,G\\}$"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"fourth eigen value=3.00\n",
"fourth eigen vector=\n",
"[[ -7.07106781e-01]\n",
" [ 1.88737914e-15]\n",
" [ 7.07106781e-01]\n",
" [ 9.99200722e-16]\n",
" [ -3.88578059e-16]\n",
" [ -3.33066907e-16]\n",
" [ -8.04911693e-16]]\n"
]
}
],
"source": [
"print('fourth eigen value=%.2f' % eig_vals[3])\n",
"print('fourth eigen vector=\\n%s' % eig_vectors[:,3])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"$\\mathbf{v}_1: \\{A,B,C\\}, \\{D,E,F,G\\}$\n",
"\n",
"$\\mathbf{v}_2: \\{A,B,C,D,E\\}, \\{C,G\\}$\n",
" \n",
"$\\mathbf{v}_3: \\{A,E,F,G\\}, \\{B,C,D\\}$"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"Method 3:\n",
"- Represent each node by all of its eigenvectors\n",
"- Cluster the result using a standard algorithm like $k$-means"
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"matrix([[ -3.77964473e-01, 4.92886500e-01, 7.61771655e-17,\n",
" -7.07106781e-01, -3.20722630e-01, -8.40213177e-17,\n",
" -1.06502348e-01]])"
]
},
"execution_count": 27,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# get first row of eigenvector matrix.\n",
"eig_vectors[0,:]"
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"matrix([[ -3.77964473e-01, 2.96559521e-01, 1.92527950e-16,\n",
" 1.88737914e-15, 7.50451469e-01, 6.04607112e-16,\n",
" 4.53891948e-01]])"
]
},
"execution_count": 28,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# get second row of eigenvector matrix.\n",
"eig_vectors[1,:]"
]
},
{
"cell_type": "code",
"execution_count": 41,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"A 0.492886499631 7.61771654839e-17\n",
"B 0.296559521215 1.92527950444e-16\n",
"C 0.492886499631 -1.92527950444e-16\n",
"D -0.214220281556 4.01736194763e-17\n",
"E -0.356037412973 0.707106781187\n",
"F -0.356037412973 7.02923822129e-17\n",
"G -0.356037412973 -0.707106781187\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAY0AAAEPCAYAAAC+35gCAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAH9xJREFUeJzt3XucXWV97/HPlwQKAYJyCxRIJICgCIGpQAq07EKp0dqC\nlWKQgnpOkYJQxB4FfNnDnGOL4rFeejheAshL1DbcVIJVCUK2Ly9cwjUEEi4FUi4SiJaLlGv4nj/W\nmmQzzJ5ZezL7MpPv+/Xar1lr7Wet9dsrk/nt53nWeh7ZJiIioooNuh1ARESMH0kaERFRWZJGRERU\nlqQRERGVJWlERERlSRoREVFZ15OGpDmSlku6V9IZQ7y/laQfSbpd0p2SPtiFMCMiAlA3n9OQtAFw\nL3AY8BiwGJhre3lDmbOBjW2fJWlr4B5gmu1XuhFzRMT6rNs1jf2B+2yvsP0yMB84YlCZx4HNy+XN\ngV8nYUREdMfkLp9/B+DhhvVHKBJJo/OBayU9BmwGvK9DsUVExCDdrmlUcRZwh+3fBfYF/p+kzboc\nU0TEeqnbNY1HgekN6zuW2xodBPwjgO1/l/QgsAdw8+CDScpAWhERLbKtqmW7XdNYDOwqaYakjYC5\nwIJBZZYBfwwgaRrwZuCBZge03dXX2Wef3fUYeuWVa5FrkWvR+9eiVV2tadheLekUYCFFArvQ9jJJ\nJxZvex7wGeAiSXcAAj5h+zfdizoiYv3V7eYpbP8Y2H3Qtq83LK8C/qzTcUVExOt1u3lqwqnVat0O\noWfkWqyVa7FWrsVa4/FadPXhvrEmyeP980yaNIlZs2ZhG0nMnTuXT3ziE90OKyImKEm4hY7wJI0e\nM3XqVJ555pluhxER64lWk0aap3rMeE96ETGxJWn0mOeff56+vj723Xdf+vr6uOyyy7odUkTEGmme\n6jFpnoqITkrzVEREtE2SRo8Z7zWliJjY0jzVYzbccEP22muvNbfczpkzh3POOafbYUXEBNVq81TX\nnwiP13r55Ze7HUJERFNpnoqIiMqSNCIiorIkjYiIqCxJIyIiKkvSiIiIypI0IiKisiSNiIioLEkj\nIiIqS9KIiIjKup40JM2RtFzSvZLOaFKmJuk2SUslLep0jBERUejq2FOSNgDuBQ4DHgMWA3NtL28o\nswXwS+BPbD8qaWvbq5ocb9yPPRUR0UnjbWj0/YH7bK+w/TIwHzhiUJn3A1fYfhSgWcKIiIj263bS\n2AF4uGH9kXJbozcDW0paJGmxpOM6Fl1ERLzGeBjldjLQBxwKbApcL+l62/cPVbi/v3/Ncq1Wo1ar\ndSDEiIjxoV6vU6/XR71/t/s0ZgP9tueU62cCtn1uQ5kzgI1t/69y/QLgR7avGOJ46dOIiGjBeOvT\nWAzsKmmGpI2AucCCQWWuBA6WNEnSFOAAYFmH44yICLrcPGV7taRTgIUUCexC28sknVi87Xm2l0u6\nGlgCrAbm2b67i2FHRKy3Mt1rRMR6bLw1T0VExDiSpBEREZUlaURERGVJGhERUVmSRkREVJakERER\nlSVpREREZUkaERFRWZJGRERUlqQRERGVJWlERERlSRoREVFZkkZERFSWpBEREZUlaURERGVJGhER\nUVmSRkREVJakERERlSVpREREZV1PGpLmSFou6V5JZwxTbj9JL0v6i07GFxERa3U1aUjaADgPeAew\nJ3CMpD2alPsscHVnI4yIiEbdrmnsD9xne4Xtl4H5wBFDlDsVuBx4opPBRUTEa1VOGpKmtOH8OwAP\nN6w/Um5rPO/vAkfa/iqgNsQQEREVTR6pgKQDgQuAzYDpkmYBJ9o+ud3Blb4ENPZ1DJs4+vv71yzX\najVqtVpbgoqIGI/q9Tr1en3U+8v28AWkG4GjgAW29y23LbX9tlGfde2xZwP9tueU62cCtn1uQ5kH\nBhaBrYHngA/bXjDE8TzS54mIiLUkYbtyK86INQ0A2w9Lrznm6lYDa2IxsKukGcCvgLnAMYPOPXNg\nWdJFwFVDJYyIiGi/Kknj4bKJypI2BE4Dlo3FyW2vlnQKsJCif+VC28sknVi87XmDdxmL80ZExOhU\naZ7aGvgy8McUTUQLgdNs/7r94bUmzVMREa1ptXlqxKQxniRpRES0Zsz7NMp+hNf9Jbb931qMLSIi\nxrkqfRo/aFjeGHgP8Fh7womIiF7WcvNUOaTHz20f2J6QRi/NUxERrWm1eWo0w4jsBmw7iv0iImKc\nq9Kn8SxFn4bKn4/z2ie0IyJiPTFi0rC9eScCiYiI3tc0aUjqG25H27eOfTgREdHLmnaES1o0zH62\nfWh7Qhq9dIRHRLQmD/dNoM8TEdFubRmwUNLbgLdSPKcBgO2LWw8vIiLGsyp3T50N1CiSxg+BdwI/\nB5I0IiLWM1We0zgKOAx43PaHgFnAFm2NKiIielKVpPG87VeBVyRNpZine6f2hhUREb2oSp/GzZLe\nAJwP3AL8Fri+rVFFRERPaunuKUlvAqbaXtKugNZF7p6KiGjNmI89JWmBpPdL2tT2Q72aMCIiov2q\n9Gn8E3AwcLekyyUdJWnjkXaKiIiJp3LzlKRJwKHACcAc21PbGdhopHkqIqI1bRkaXdImwHuBvwH2\nA745uvCGPPYcScsl3SvpdaPnlk1jd5Svn0vaa6zOHRERrRmxpiHpUmB/4MfAJcBPy1tw1/3kxYRO\n91I8B/IYsBiYa3t5Q5nZwDLbT0uaA/Tbnt3keKlpRES0oB3DiFwIHGN79ejDamp/4D7bKwAkzQeO\nANYkDds3NJS/AdihDXFEREQFIzZP2b66TQkDigTwcMP6IwyfFP4a+FGbYomIiBFUGrCwF0j6I+BD\nFHdyNdXf379muVarUavV2hpXRMR4Uq/Xqdfro95/2D4NSQJ2tP1w00LroOyv6Lc9p1w/k2KujnMH\nldsbuILirq1/H+Z46dOIiGjBmN49Vf4F/uE6R9XcYmBXSTMkbQTMBRY0FpA0nSJhHDdcwoiIiPar\n0jx1q6T9bC8e65PbXi3pFGAhRQK70PYySScWb3se8PfAlsBXyprPy7b3H+tYIiJiZFVuuV0O7Aqs\nAJ4DRPEHfe/2h9eaNE9FRLSmHbfcvmMd4omIiAmk0jAikmYBf1Cu/sz2HW2NapRS04iIaE07Rrk9\nDfgOsG35+rakU0cfYkREjFdV+jSWAL9v+7lyfVPg+vRpRESMf+0YsFBA4xPhq8ttERGxnqnSEX4R\ncKOk75XrRwLfaF9IERHRq6p2hPexdviOn9m+ra1RjVKapyIiWtNq81SVPo1v2T5upG29IEkjIqI1\n7ejT2HPQCSYBv9dqYBERMf41TRqSzpL0LLC3pGfK17PAE8CVHYswIiJ6RpXmqc/YPqtD8ayTNE9F\nRLSmHc1TN0naouEEb5B05Kiii4iIca1KTeN22/sM2nab7X3bGtkopKYREdGadtQ0hiozbmb8i4iI\nsVMladws6QuSdilfXwBuaXdgERHRe6okjVOBl4BLgPnAC8BH2hlURET0pkpPhEMxUOHAoIW9aiL0\naUyaNIlZs2ZhG0l8//vfZ/r06d0Oq5KB2F966SU23HBDjjvuOE4//XSKCRcjesfA7+qrr77K5MmT\nOe+885g9e3a3w+q4lStXst122w2s3gn8B/BR2/c326dKR/iBwAXAZranl3NrnGj75LEJe+xMhKQx\ndepUnnnmmW6HMSqNsa9atYpjjjmGgw46iP7+/u4GFjFI4+/qwoULOeecc6jX690NqgsOPPBArr/+\neoCrKLodvgtMtf2LZvtUaZ76IsXsfb8GKCdg+sN1jjaGNN6T3oCtt96aefPmcd5553U7lIjXafx/\n9vTTT7Plllt2MZruWLRoEZMmTRpY/Qgw1/adwyUMqHgXlO2HBzUxrG5WtlWS5gBfokhgF9o+d4gy\n/wy8k2KO8g/avn2szt9rnn/+efr6+rDNzJkzueKKK7od0qjtvPPOvPrqqzz55JNss8023Q4nYo2B\n/2fPP/88jz/+ONddd123Q+q4pUuXsvnmmwNr/sY/IWnfkQakrZI0Hi6bqCxpQ+A0YNk6RwxI2gA4\nDzgMeAxYLOlK28sbyrwT2MX2bpIOAL4GTNjGxylTpnDrrbd2O4wxM1FqTjGxNP4/u+GGGzjuuONY\nunRpl6PqvHvuuadx9TLg/cCwSaNK89TfUFRddgAeBfZh7O6e2h+4z/YK2y9T3J11xKAyRwAXA9i+\nEdhC0rQxOn+00QMPPMDkyZNTy4ieNnv2bFatWsWqVau6HUpHTZ8+nYceeggASQ8AHwf+cqT9Ks3c\nZ/tY29Nsb2v7r2z/ep2iXWsH4OGG9UfKbcOVeXSIMhPGeP5m3hj7k08+yUknncSpp2Y6+eg9jb+r\ny5cv59VXX2WrrbbqYkSdt3LlyjVf6GzPtD0DeELSScPtV6V56heSHqJ4TuMK20+ta7Dt1HinTq1W\no1ardS2W0RjPt6e+8MIL9PX1rbnl9vjjj+f000/vdlgRrzPwuzqQPC6++OJx/X+vFfV6nXq9zsUX\nX8zBBx/MFVdcgaT7gefLIgcCX222f9WZ+/YH5lJM9Xo3MN/2t9c1eEmzgX7bc8r1MwE3doZL+hqw\nyPYl5fpy4BDbK4c43ri/5TYiopPaMfYUtm+y/TGKPojfAN8cZXyDLQZ2lTRD0kYUiWnBoDILgONh\nTZJ5aqiEERER7Tdi85SkqcB7KP6g7wJ8jyJ5rDPbqyWdAixk7S23yySdWLztebZ/KOldZfXpOeBD\nY3HuiIhoXZUnwh8Evg9cavv6jkQ1SmmeiohoTavNU1WSxrj5SzyOQo2I6AmtJo0qd0/tJul/AG9q\nLG/70NbDi4iI8axKTeMOiqewb6Fh+BDbPTenRmoaERGtaUdN4xXbTe/ZjYiI9UeVW26vknSypO0l\nbTnwantkERHRc6rePTWYbc9sT0ijl+apiIjWjPndU+NJkkZERGvG/IlwSVMkfUrSvHJ9N0nvXpcg\nIyJifKrSp3ER8BLFIFZQjDL7D22LKCIielaVpLGL7c8BLwPY/i9g/RgOMiIiXqNK0nhJ0iaAASTt\nArzY1qgiIqInVXlO42zgx8BOkr4DHAR8sJ1BRUREb6o6n8ZWFPNyC7jBdk/Oi5i7pyIiWtOOAQv7\nhtj8NLDC9istxtdWSRoREa1pR9K4AegDllDUNN4G3AVsAZxke+Howx1bSRoREa1px8x9jwH72n67\n7d8D9gUeAA4HPje6MCMiYjyqkjTebPuugRXbdwN72H6gfWFFREQvqnL31F2SvgrML9ffB9wt6Xco\nn92IiIj1Q5U+jU2Ak4GDy02/AL4CvABMsf3btkbYgvRpRES0ZtwMWCjpjcAlwAzgIeBo208PKrMj\ncDEwDXgVON/2Pw9zzCSNiIgWjFnSkHSp7aMl3Un5NHgj23uPPkyQdC7wa9ufk3QG8EbbZw4qsx2w\nne3bJW1GMXvgEbaXNzlmkkZERAvGMmlsb/tXkmYM9b7tFaOMceD4y4FDbK8sk0Pd9h4j7PN94P/a\nvrbJ+0kaEREtGLNbbm3/qvw5kBx2K5efAH6zTlEWtrW9sjzH48C2wxWW9CZgH+DGMTh3RESMwoh3\nT0k6AfgwsCWwC7Aj8DXgsAr7XkPRH7FmE0VT16eGKN60ilA2TV0OnDZSx3t/f/+a5VqtRq1WGynM\niIj1Rr1ep16vj3r/KndP3Q7sD9xoe99y25229xr1WYtjLANqDc1Ti2y/ZYhyk4EfAD+y/eURjpnm\nqYiIFrTjifAXbb/UcILJDFMraMEC1o6W+wHgyiblvgHcPVLCiIiI9quSNH4q6ZPAJpIOBy4DrhqD\nc58LHC7pHoqmrs9C0QEv6Qfl8kHAscChkm6TdKukOWNw7oiIGIUqzVMbAP8d+BOKPomrgQt6sR0o\nzVMREa0ZNw/3tUOSRkREa9rRpxEREQEkaURERAuSNCIiorKmD/dJuophbq21/edtiSgiInrWcE+E\nf778+RfAdsC3y/VjgJXtDCoiInpTlVtub7b99pG29YLcPRUR0Zp23D21qaSZDSfYGdh0NMFFRMT4\nVmW619OBuqQHKB7um0ExgGFERKxnhk0a5dPgzwC7AQNzXSy3/WK7A4uIiN5TpU/jtoHRbXtd+jQi\nIlrTjj6NayW9V1Llg0ZExMRUpabxLEXH9yvAC5QTKdme2v7wWpOaRkREa1qtaYzYEW5783ULKSIi\nJorhngjfw/ZySX1DvW/71vaFFRERvahp85SkebY/LGnREG/b9qHtDa11aZ6KiGhN5tOYQJ8nIqLd\nxrxPozzogcCbGsvbvrjl6CIiYlwbMWlI+hawC3A7sLrcbCBJIyJiPVOlpvF24K1j3e4j6Y3AJRTD\nkjwEHG376SZlNwBuBh7JkOwREd1T5eG+pRRDo4+1M4Gf2N4duA44a5iypwF3tyGGiIhowXB3Tw1M\nwrQ5sA9wE7BmzKl1/cYvaTlwiO2VkrYD6rb3GKLcjsBFwD8CHxvuvOkIj4hozVh2hH9+mPfGwra2\nVwLYflzStk3KfRH4OLBFm+OJiIgRNE0atn8KIOlc22c0vifpXOCnIx1c0jXAtMZNFLWXTw11yiH2\n/1Ngpe3bJdXK/YfV39+/ZrlWq1Gr1UbaJSJivVGv16nX66Pev8rYU7fa7hu0bYntvUd91uIYy4Ba\nQ/PUIttvGVTmHOCvKMa92oSiqey7to9vcsw0T0VEtGDMRrmVdJKkO4HdJS1peD0ILBmDWBcAHyyX\nPwBcObiA7U/anm57JjAXuK5ZwoiIiPYbriN8C+CNwGco7nQa8Kzt36zziaUtgUuBnYAVFLfcPiVp\ne+B82+8eVP4Q4O/SER4RMXYyjMgE+jwREe3WjkmYIiIigCSNiIhoQZJGRERUlqQRERGVJWlERERl\nSRoREVFZkkZERFSWpBEREZUlaURERGVJGhERUVmSRkREVJakERERlSVpREREZUkaERFRWZJGRERU\nlqQRERGVJWlERERlSRoREVFZkkZERFTWtaQh6Y2SFkq6R9LVkrZoUm4LSZdJWibpLkkHdDrWiIgo\ndLOmcSbwE9u7A9cBZzUp92Xgh7bfAswClnUovoiIGES2u3NiaTlwiO2VkrYD6rb3GFRmKnCb7V0q\nHtPd+jwREeORJGyravlu1jS2tb0SwPbjwLZDlNkZWCXpIkm3SponaZOORhkREWtMbufBJV0DTGvc\nBBj41BDFh6oiTAb6gI/YvlnSlyiatc5uds7+/v41y7VajVqt1nLcERETVb1ep16vj3r/bjZPLQNq\nDc1Ti8p+i8Yy04Drbc8s1w8GzrD9Z02OmeapiIgWjKfmqQXAB8vlDwBXDi5QNl89LOnN5abDgLs7\nEl1ERLxON2saWwKXAjsBK4CjbT8laXvgfNvvLsvNAi4ANgQeAD5k++kmx0xNIyKiBa3WNLqWNNoh\nSSMiojXjqXkqIiLGmSSNiIioLEmjxzzxxBMce+yx7Lrrruy3334cdNBBXHnl6+4RiIjoiiSNHnPk\nkUdSq9W4//77Wbx4MfPnz+eRRx7pdlgREUA6wnvKddddx6c//WkWLVrU7VAiYj2RjvBx7K677qKv\nr6/bYURENJWk0cNOOeUU9tlnHw44IKPBR0RvSNLoIXvuuSe33HLLmvXzzjuPa6+9lieffLKLUUVE\nrJWk0UMOPfRQXnzxRb7+9a+v2fbcc891MaKIiNdKR3iPWblyJR/96Ee56aab2Gabbdh000056aST\nOOqoo7odWkRMQBlGZAJ9noiIdsvdUxER0TZJGhERUVmSRkREVJakERERlSVpREREZUkaERFRWZJG\nRERU1rWkIemNkhZKukfS1ZK2aFLuLEl3SVoi6TuSNup0rBERUehmTeNM4Ce2dweuA84aXEDSDOAE\nYF/bewOTgbkdjbJF9Xq92yH0jFyLtXIt1sq1WGs8XotuJo0jgG+Wy98EjhyizDPAS8CmkiYDU4DH\nOhPe6IzHX4J2ybVYK9dirVyLtcbjtehm0tjW9koA248D2w4uYPs/gX8C/gN4FHjK9k86GmVERKwx\nuZ0Hl3QNMK1xE2DgU0MUf92gUZJmAqcDM4Cngcslvd/2v7Qh3IiIGEHXBiyUtAyo2V4paTtgke23\nDCpzNHC47RPK9eOAA2yf0uSYGa0wIqJFrQxY2NaaxggWAB8EzgU+AFw5RJl7gL+XtDHwInAYsLjZ\nAVv54BER0bpu1jS2BC4FdgJWAEfbfkrS9sD5tt9dlvs4RXJZDdwG/LXtl7sSdETEem5CzacRERHt\nlSfC11HVhxTLshtIulXSgk7G2ClVroWkHSVdVz6weaekv+1GrO0iaY6k5ZLulXRGkzL/LOk+SbdL\n2qfTMXbKSNdC0vsl3VG+fi5pr27E2QlVfi/KcvtJelnSX3QyvlYkaay7ER9SbHAacHdHouqOKtfi\nFeBjtvcEfh/4iKQ9Ohhj20jaADgPeAewJ3DM4M8m6Z3ALrZ3A04EvtbxQDugyrUAHgD+0PYs4B+A\n8zsbZWdUvBYD5T4LXN3ZCFuTpLHuqjykiKQdgXcBF3Qorm4Y8VrYftz27eXyb4FlwA4di7C99gfu\ns72i7HebT3FNGh0BXAxg+0ZgC0nTmHhGvBa2b7D9dLl6AxPn92CwKr8XAKcClwNPdDK4ViVprLsR\nH1IsfRH4OEM8jzKBVL0WAEh6E7APcGPbI+uMHYCHG9Yf4fV/CAeXeXSIMhNBlWvR6K+BH7U1ou4Z\n8VpI+l3gSNtfpXierWd185bbcWMMHlL8U2Cl7dsl1ejxX4rhrOu1aDjOZhTfqk4raxyxnpL0R8CH\ngIO7HUsXfQlo7Ovo2b8RSRoV2D682XuSVkqa1vCQ4lBVy4OAP5f0LmATYHNJF9s+vk0ht80YXAvK\nccQuB75le6jnc8arR4HpDes7ltsGl9lphDITQZVrgaS9gXnAnHLYoImoyrV4OzBfkoCtgXdKetl2\nz900k+apdTfwkCI0eUjR9idtT7c9k2KU3uvGY8KoYMRrUfoGcLftL3ciqA5aDOwqaUY5hP9cimvS\naAFwPICk2RTjqa3sbJgdMeK1kDQduAI4zva/dyHGThnxWtieWb52pvhCdXIvJgxI0hgL5wKHS7qH\n4on1zwJI2l7SD7oaWeeNeC0kHQQcCxwq6bbyFuQ5XYt4DNleDZwCLATuAubbXibpREkfLsv8EHhQ\n0v3A14GTuxZwG1W5FsDfA1sCXyl/F27qUrhtVfFavGaXjgbYojzcFxERlaWmERERlSVpREREZUka\nERFRWZJGRERUlqQRERGVJWlERERlSRqx3pB0iKSrWii/vaRL2xnTupA03IjK7TrnIkl9nT5v9I4k\njVjfVH4wyfavbB/dzmDW0Sdb3aEcpiJi1JI0oiMkTZH0g/LJ3yWS/rLc3iepLmmxpB8NDBMuaRdJ\n15QTFd0saedy+/8pJ2+6Q9LR5bZDym/Al0laJulbDeedU267GRhyYhsVk2N9TtKN5flOKLfPkHRn\nubyJpEskLZX0XUk3DHzjlnS4pF+WcV4iaUq5/UFJ/ZJuKeN9swoPSpracP57JW0jaWtJl5dx3Cjp\nwPL9TSV9o7xut0t6j6TPAJuUT9R/qyz3sfLaLJF0WsNnWC7pm+Vn2bHhvO9orEmV13FBufwVSTeV\nxzu7yXV7tmH5vZIuKpeH/BwxQdjOK6+2vyj+YH+9YX1zigEzfwFsVW47GriwXL4B+PNyeSNg4/IY\nV5fbtqWYW34acAjwn8D2FKOD/hI4EPgd4D+AmeU+lwALhojtBOCTDedaDMwoX0vK7X8HfLVc3hN4\nCegDtgJ+CmxSvvcJ4FPl8oMUYwgBnATMK5e/CHygXN4fWFgufwc4sFzeiWJ8LiiGY/lCQ7xblD+f\nadjWB9xRXqdNgaXArPIzvALsN8TnngQ81BD7V4D3l8tvKH9uACwC3lauLwL6hjj/e4FvDPc58poY\nr4xyG51yJ/D58hvyv9n+uaQ9gbcB15TNJhsAj6kYNn0HlwO22X4JQNLBwL+W256QVAf2A54FbrL9\nq7Lc7cCbgOeAB2w/UMbwbYoEMdifAHsN1H6AqcBuwH0NZQ6mGL4a23dJWlJunw28FfhF+Rk2pEha\nA75X/rwFeE+5fCnwPykmqppLkcwA/hh4S0MT0maSNi23v2/ggF47cVGjg4Hv2X6hvAbfBf4AuApY\nYXvx4B1sr5b0Y+DPJF0B/CnFnC8Ac8sa12Rgu/IzLh10iGZNXUN9jim2/6tJ+RhHkjSiI2zfVzbn\nvAv4tKRrge8DS20f1Fi2TBpV+h4a/2i92LC8mrW/21Xa8AWcavuaQXHMqHBuUdQUjm1SbiCuNTHZ\nvr5sftuaYnbD/91wrANczO7WGEeza1G1f+K5Yd67hGIwvf8EFtt+TsXkWH8H/J7tZ8pmp42H2Lcx\nrsb3h/wcMTGkTyM6QtL2wPO2/wX4PEVzyj3ANiqGCEfSZElvdTEp0yOSjii3byRpE+BnwPvKPoht\nKL5JDzcy6nJgxkB/CHBMk3JXAyermOcDSbuV52v0C8pv+5LeSlFDgqIZ7SBJu5TvTZG0W4VL8j3g\nCxRNN0+V2xZSzCNPeaxZ5eI1wEcatr+hXHxJ0qRy+WfAkZI2Lmsn7ym3wfDJ5acU/xYnUExDCkVN\n67fAsyr6mN7ZZN/HJe2uYm7r9zRsb/Y5YgJI0ohO2Qu4SdJtFE0z/1B+Ez0KOLdsUroN+P2y/PHA\n30q6g+IP9jTb36No5roD+AnwcdtDTfRkANsvAicCP1TREd5s3ooLgLuBW8vO4q/x+lr4V4CtJS2l\nqBncBTxtexXFHCL/Wsb6S2D3xjiauJRiiPj5DdtOA95edpovLWMH+Edgy7JT+jagVm6fB9wp6Vu2\nb6No7loMXE/Rf3LHSHHYfhX4ATCn/IntJcDtFPO3fxv4eeMuDctnAf9Wvv9Yhc8RE0CGRo+ooPw2\nvaHtFyXNpPj2v7vtV7ocWkRHpU8jopopwCJJG5brJyVhxPooNY2IiKgsfRoREVFZkkZERFSWpBER\nEZUlaURERGVJGhERUVmSRkREVPb/AVcJNLpUoc9rAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# plot each point using 2nd and 3rd eigen vector\n",
"def plot_by_eigenvectors(eig_vectors):\n",
" plt.figure()\n",
" for i, name in enumerate(['A', 'B', 'C', 'D', 'E', 'F', 'G']):\n",
" v1 = eig_vectors[i, 1]\n",
" v2 = eig_vectors[i, 2]\n",
" plt.annotate(name, xy=(v1, v2))\n",
" print(name, v1, v2)\n",
" plt.xlim(-.5,.5)\n",
" plt.ylim(-.8,.8)\n",
" plt.xlabel('second eigenvector value')\n",
" plt.ylabel('third eigenvector value')\n",
" plt.show()\n",
" \n",
"plot_by_eigenvectors(eig_vectors)"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.0"
}
},
"nbformat": 4,
"nbformat_minor": 0
}