{
 "cells": [
  {
   "cell_type": "markdown",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "# CS579: Lecture 03  \n",
    "**Representing Graphs**\n",
    "\n",
    "*[Dr. Aron Culotta](http://cs.iit.edu/~culotta)*  \n",
    "*[Illinois Institute of Technology](http://iit.edu)*\n",
    "\n",
    "(Slides inspired in part by [Jure Leskovec](http://web.stanford.edu/class/cs224w/slides/02-gnp.pdf) and [Easley & Kleinberg](https://github.com/iit-cs579/main/blob/master/read/ek-02.pdf))\n",
    "\n",
    "<br><br><br><br><br><br><br><br><br><br><br><br>"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "# Terminology\n",
    "\n",
    "- **Graph:** A way to represent objects and their relations\n",
    "  - **Node:** represents an object\n",
    "  - **Edge:** represents a relation between two nodes. \n",
    "  - **Neighbor:** Two nodes are *neighbors* if they are connected by an edge.\n",
    "- **Directed Graph:** Represents asymmetric (one-way) relationships\n",
    "- **Undirected Graph:** Represents symmetric relationships\n",
    "\n",
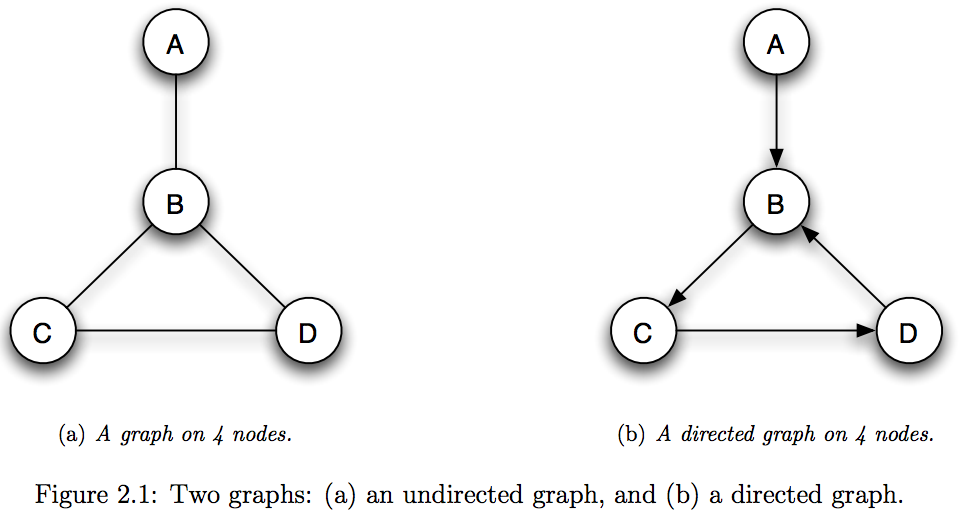    "![graph.pdf](graph.pdf)\n",
    "\n",
    "[Source](https://github.com/iit-cs579/main/blob/master/read/ek-02.pdf)\n",
    "\n",
    "Examples of **directed** and **undirected** graphs?\n",
    "\n",
    "<br><br><br><br><br>"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "**Path:** A sequence of nodes in which each consecutive pair are neighbors\n",
    "- E.g., $A,B,C$ in Figure 2.1(a)\n",
    "\n",
    "**Cycle:** A path of at least 3 edges, with first and last nodes the same.\n",
    "- E.g., $B,C,D$ in Figure 2.1(a)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "<br><br><br><br>\n",
    "\n",
    "**Connected:** A graph is *connected* if there exists a path between each pair of nodes.\n",
    "  - Example of a graph that is *not* connected?"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "<br><br><br><br>\n",
    "**Connected Component:** A maximal subset of nodes such that each pair of nodes is connected \n",
    "\n",
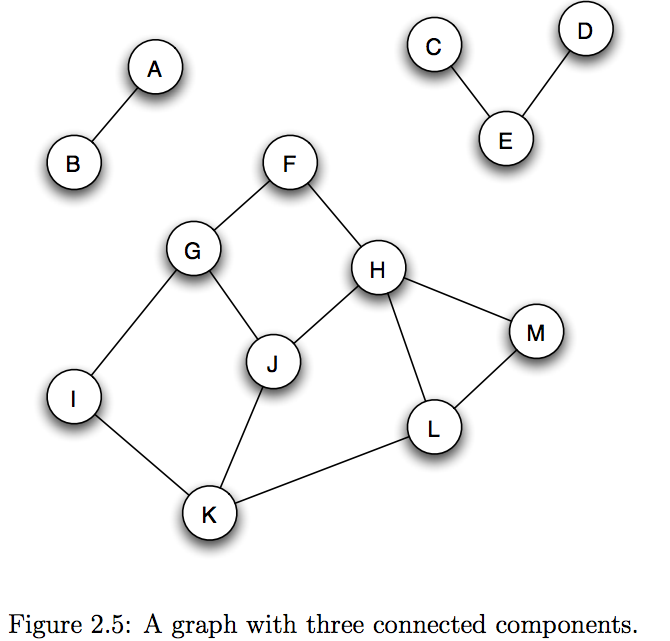    "![components](components.png)\n",
    "[Source](https://github.com/iit-cs579/main/blob/master/read/ek-02.pdf)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "- Is the global friendship network connected?\n",
    "\n",
    "<br><br><br><br>\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "# Giant Connected Components\n",
    "\n",
    "![giant](giant.png)"
   ]
  },
  {
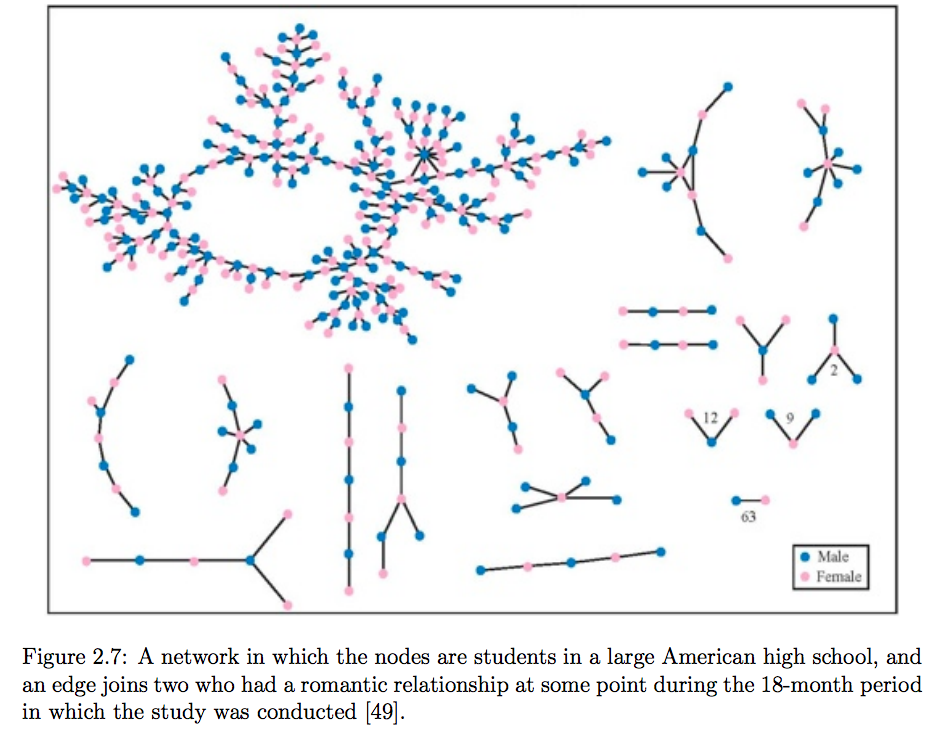   "cell_type": "markdown",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "**Node Degree:** Number of neighbors of a node.\n",
    "  - For directed graphs, distinguish between **in-degree** and **out-degree**\n",
    "  \n",
    "![graph.pdf](graph.pdf)\n",
    "\n",
    "[Source](https://github.com/iit-cs579/main/blob/master/read/ek-02.pdf)\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "# Number of edges\n",
    "\n",
    "If there are $N$ nodes, what is the maximum number of edges?\n",
    "\n",
    "<br><br><br><br><br><br><br><br><br><br><br><br>\n",
    "\n",
    "$$\\frac{N(N-1)}{2}$$"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 24,
   "metadata": {
    "collapsed": false,
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAZsAAAEKCAYAAADEovgeAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xd8V+X5//HXRdh7iuwhoAKiQBiuWhdusbXugYqiraOt\ntlZrf7XWtl+7XNXiAkXFgasidSGu4oIEEGSHJUE2GEYgIcn1++Pc0YiQfAicfJJP3s/H4zw+59xn\nXYeDXJ773Oe+zd0RERGJU41kByAiIqlPyUZERGKnZCMiIrFTshERkdgp2YiISOyUbEREJHZKNiIi\nEjslGxERiZ2SjYiIxK5msgOoLFq2bOmdO3dOdhgiIlVKZmbmOndvVdZ2SjZB586dycjISHYYIiJV\nipktS2Q7VaOJiEjslGxERCR2SjYiIhI7JRsREYldrMnGzJaa2Swzm2FmGaGsuZlNNLOF4bdZKDcz\nu9/Mssxsppn1K3GcYWH7hWY2rER5/3D8rLCvlXYOERFJjop4sjnW3Q9z9/SwfAswyd27A5PCMsAp\nQPcwjQBGQpQ4gNuBQcBA4PYSyWMkcFWJ/U4u4xwiIpIEyahGGwqMCfNjgLNKlD/pkU+BpmbWBjgJ\nmOjuG9x9IzARODmsa+zun3o03OiTOx1rV+cQEZEkiDvZOPC2mWWa2YhQ1trdV4b5VUDrMN8OWF5i\n3+xQVlp59i7KSzuHiIgE67fk8cfX5rAtvzD2c8WdbI5y935EVWTXmtkPSq4MTyQeZwClncPMRphZ\nhpllrF27Ns4wREQqlcIi54bnpjP2s2UsXb819vPFmmzcfUX4XQO8QvTOZXWoAiP8rgmbrwA6lNi9\nfSgrrbz9Lsop5Rw7x/eIu6e7e3qrVmX2tiAikjLumbiAj7LWc+dZvTm4TePYzxdbsjGzBmbWqHge\nGAJ8AYwHiluUDQNeDfPjgUtDq7TBQE6oCnsLGGJmzULDgCHAW2HdJjMbHFqhXbrTsXZ1DhGRam/S\n3NU88F4W5w/owLnpHcreYR+Is2+01sAroTVyTeAZd3/TzKYC48xsOLAMODds/zpwKpAF5AKXA7j7\nBjO7E5gatvuju28I8z8DngDqAW+ECeCu3ZxDRKRa+3J9Lr98fga92zXmD2f2qrDzWvRKQ9LT010d\ncYpIKtuWX8jZIz9mxdfbmHD9UXRoXn+vj2lmmSU+bdkt9fosIlINuDu3vTKLuas2MfqyAfsk0ewJ\ndVcjIlINPPnJMl6evoIbT+jBsQfuV+HnV7IREUlxU5du4M4Jczjh4NZce2y3pMSgZCMiksJWb9rO\nz8ZOo0Pz+tx93qHUqGFJiUPvbEREUlR+QRE/fTqTrXkFjL1yEI3r1kpaLEo2IiIp6s4Jc5j25dc8\neGE/erRulNRYVI0mIpKCXshYzlOfLuPqY7pyWp82yQ5HyUZEJNV8sSKH2/7zBUd2a8GvhxyY7HAA\nJRsRkZSyYWs+Vz+VSauGdbj//L7UTKsc/8zrnY2ISIooKCzi+mensXZLHi9eczgtGtZJdkjfqBwp\nT0RE9trf357PR1nr+dNZvenTvmmyw/kOJRsRkRTw6owVPPzBYi4a1LHCenLeE0o2IiJV3KzsHG5+\ncSYDOzfn9jMqrifnPaFkIyJSha3dnMeIpzJo2bAO/764H7VrVs5/1tVAQESkisorKOSnT2eyMTef\nl356BC0rUYOAnSnZiIhUQe7O7a/OJmPZRh64sC+92jZJdkilqpzPWyIiUqqnPl3Gc1OXc92x3Ti9\nT9tkh1MmJRsRkSrm40XruOO1OZxw8H7ceGKPZIeTECUbEZEqZPmGXK4dO42uLRtwz3mHJW3IgD2l\nZCMiUkVszSvgqiczKHJ49NJ0GiVxyIA9pWQjIlIFFBU5N437nAWrN/PAhX3p3LJBskPaI0o2IiJV\nwP3vLuTN2av47akHc3T3VskOZ48p2YiIVHITZn7Fve8s5Ox+7Rl+VJdkh1MuSjYiIpXY58u/5qZx\nn5PeqRl/+XFvzKpGg4CdKdmIiFRSX329jSufzGC/xnV4+JL+1KmZluyQyk09CIiIVEJb8wq4ckwG\n2/MLGXvloEo1Nk15KNmIiFQyRUXOL56fwbxVmxh92QB6tG6U7JD2WpnVaGZ2jpk1CvO/M7OXzaxf\n/KGJiFRPf31rHhPnrOb3p/fkhwful+xw9olE3tn8P3ffbGZHAScAo4CR8YYlIlI9jctYzsMfLObi\nwR0ZdkTnZIezzySSbArD72nAI+7+X6B2fCGJiFRPny5ez22vzOKobi25/YxeVbbl2a4kkmxWmNnD\nwHnA62ZWJ8H9REQkQUvXbeWapzPp2Lw+D17Uj1ppqfXPbCJXcy7wFnCSu38NNAd+negJzCzNzKab\n2YSw3MXMPjOzLDN73sxqh/I6YTkrrO9c4hi3hvL5ZnZSifKTQ1mWmd1SonyX5xARqYxytu1g+Jip\nAIwaNoAm9apOn2eJKjPZuHsusAY4KhQVAAv34Bw/B+aWWP4rcI+7dwM2AsND+XBgYyi/J2yHmfUE\nzgd6AScD/w4JLA14EDgF6AlcELYt7RwiIpXKjsIirh07jS835PLQxf2rXJ9niUqkNdrtwG+AW0NR\nLeDpRA5uZu2J3vU8FpYNOA54MWwyBjgrzA8Ny4T1x4fthwLPuXueuy8BsoCBYcpy98Xung88Bwwt\n4xwiIpWGu/Pbl2cxOWsdf/nRIQzu2iLZIcUmkWq0HwFnAlsB3P0rINFG3/cCNwNFYbkF8LW7F4Tl\nbKBdmG8HLA/nKABywvbflO+0z+7KSzvHd5jZCDPLMLOMtWvXJnhJIiL7xgPvZvFCZjY3HN+dc9I7\nJDucWCWSbPLd3QEHMLOEnvHM7HRgjbtn7kV8sXL3R9w93d3TW7Wqer2oikjV9cr0bP45cQE/7tuO\nX57QPdnhxC6RHgTGhdZoTc3sKuAK4NEE9jsSONPMTgXqAo2B+8JxaoYnj/bAirD9CqADkG1mNYEm\nwPoS5cVK7rOr8vWlnENEJOk+WbSem1+cyeFdW3DX2X1Sqonz7iTSQOAfRO8/XgIOBH7v7v9KYL9b\n3b29u3cmesH/rrtfBLwH/CRsNgx4NcyPD8uE9e+GJ6rxwPmhtVoXoDswBZgKdA8tz2qHc4wP++zu\nHCIiSZW1ZjNXP5VBpxYNeOji/tSumVpNnHcnob7R3H0iMHEfnfM3wHNm9idgOlGPBITfp8wsC9hA\nlDxw99lmNg6YQ9QS7lp3LwQws+uImmWnAaPdfXYZ5xARSZo1m7czbPRUatdM4/HLBtCkfuo1cd4d\nix4EStnAbDPhfU0JOUAGcJO7L44ptgqVnp7uGRkZyQ5DRFJUbn4B5z/yKQtXb+H5qwfTp33TZIe0\nT5hZprunl7VdIk829xK16HoGMKInjgOAacBo4IflD1NEJPUVFjk3PDuDL1bk8Mgl6SmTaPZEIpWF\nZ7r7w+6+2d03ufsjRL0JPA80izk+EZEqzd25c8Ic3pm7mj+c2YsTerZOdkhJkUiyyTWzc82sRpjO\nBbaHdaXXwYmIVHOjJi/hiY+XcuVRXbj08M7JDidpEkk2FwGXEHVZszrMX2xm9YDrYoxNRKRKG//5\nV/zpv3M5pff+/PbUg5MdTlKV+c4mNAA4YzerJ+/bcEREUsNHWeu4adwMBnZpzj3nHUaNGqn/LU1p\ndptszOxflFJN5u43xBKRiEgV98WKHK5+KpOuLRvy6KXp1K2VluyQkq60arQMIJPo6/9+RD09LwQO\nQ4OniYjs0vINuVz2+FQa163JmCsGpuRwAeWx2ycbdx8DYGY/BY4q7tjSzB4C/lcx4YmIVB3rt+Rx\n6egp7Cgs4rkRh7N/k7rJDqnSSKSBQDOifs2KNURNnkVEvmNrXgFXPDGVr77exujL0um2X6Kd41cP\niXzUeRcw3czeI/qo8wfAH+IMSkSkKtlRWMS1z0xj1oocHr4knf6dmic7pEonkdZoj5vZG8CgUPQb\nd18Vb1giIlWDu3PLS7N4f/5a/u/Hh3BiNf1osyyJjNRpwAnAoe7+KlDbzAbGHpmISBXwt7fm89K0\nbH55Qg8uGNgx2eFUWom8s/k3cDhwQVjeDDwYW0QiIlXE6MlLGPn+Ii4c1JEbju+W7HAqtUTe2Qxy\n935mNh3A3TeG8WNERKqtlzKz+eOEOZzUqzV3Du1dLQZA2xuJPNnsMLM0vh0WuhVQFGtUIiKV2Nuz\nV3HzSzM5slsL7ju/L2nVvHeARCSSbO4HXgH2M7M/E3VR85dYoxIRqaQ+XrSO656dTu92TXj4EvUO\nkKhEWqONNbNM4Hiips9nufvc2CMTEalkZmZ/zVVjMujUvD5PXDaAhnUSGuxYSHxY6HnAvJhjERGp\ntLLWbGbY6Ck0a1Cbp4YPolkDvbreE4lUo4mIVGvZG3O5+LEp1EyrwdgrB6kbmnLYbbIxszoVGYiI\nSGW0dnMel4yaQm5+AU9eMZBOLRokO6QqqbQnm08AzOypCopFRKRSydm2g2Gjp7AqZzuPXz6Ag9s0\nLnsn2aXS3tnUNrMLgSPM7Mc7r3T3l+MLS0QkubblF3LlmKksXLOZx4YNUH9ne6m0ZHMN0ZDQTfn+\nSJ0OKNmISEravqOQEU9lkLFsIw9c0I9jerRKdkhVXmnj2UwGJptZhruPqsCYRESSJr+giGvHTuN/\nC9fx95/04bQ+bZIdUkpIpOnzU2Z2A9HQAgAfAA+5+474whIRqXgFhUX84vnpTJq3hjvP6s056R2S\nHVLKSCTZ/BuoFX4BLgFGAlfGFZSISEUrLHJ+/eJMXp+1it+ddjCXDO6U7JBSSiLJZoC7H1pi+V0z\n+zyugEREKlpRkXPbK7N4ZfoKfn3SgVx5dNdkh5RyEvmos9DMDiheMLOuQGF8IYmIVBx3548T5vDc\n1OVcd2w3rj1WQwXEIZEnm18D75nZYqK+0ToBl8calYhIBXB37npzHk98vJQrj+rCTUN6JDuklJVI\nR5yTzKw7cGAomu/uefGGJSISv3vfWcjDHyzmksGduO20gzUmTYwS6hvN3fPcfWaYEko0ZlbXzKaY\n2edmNtvM7gjlXczsMzPLMrPniwdiM7M6YTkrrO9c4li3hvL5ZnZSifKTQ1mWmd1SonyX5xARKTby\n/UXcN2kh5/Rvzx1n9lKiiVmcHXHmAceFxgWHASeb2WDgr8A97t4N2AgMD9sPBzaG8nvCdphZT+B8\noBdwMvBvM0sLA7o9CJwC9AQuCNtSyjlERHj4g0X89c15nHloW+46uw81NPhZ7EpNNhYpV0Nzj2wJ\ni7XC5MBxwIuhfAxwVpgfGpYJ64+36H81hgLPhaerJUAWMDBMWe6+2N3zgeeAoWGf3Z1DRKq5Rz5c\nxP+9MY/T+7Th7nMP1SibFaTUZOPuDrxe3oOHJ5AZwBpgIrAI+NrdC8Im2UC7MN8OWB7OWwDkAC1K\nlu+0z+7KW5RyDhGpxh75cBF/eT1KNPeedxg10zTKSkVJ5E96mpkNKM/B3b3Q3Q8D2hM9iRxUnuPE\nxcxGmFmGmWWsXbs22eGISIwe/XAxf3l9Hqcp0SRFIn/ag4BPzGyRmc00s1lmNnNPTuLuXwPvAYcD\nTc2suBVce2BFmF8BdAAI65sA60uW77TP7srXl3KOneN6xN3T3T29VSt1tCeSqh79cDF/fn0up/Vp\nw31KNEmRyJ/4ScABRO9BzgBO5/u9QH+PmbUys6Zhvh5wIjCXKOn8JGw2DHg1zI8Py4T174ZqvPHA\n+aG1WhegOzAFmAp0Dy3PahM1Ihgf9tndOUSkmlGiqRzK/FN392VETxDHhfncRPYD2hB9DDqTKDFM\ndPcJwG+AG80si+j9SnGP0qOAFqH8RuCWcP7ZwDhgDvAmcG2onisArgPeIkpi48K2lHIOEalGHvtf\nSDSHKNEkm0UPAqVsYHY7kA4c6O49zKwt8IK7H1kRAVaU9PR0z8jISHYYIrKPPPa/xfzpvyHRnK9E\nExczy3T39LK2S+RP/0fAmcBWAHf/Cmi0d+GJiMTnkQ8XfZNo7lWiqRQS6Rst393dzBzAzBrEHJOI\nSLm4O/96N4u7Jy74ptVZLSWaSiGRuzDOzB4mauF1FfAO8Gi8YYmI7Bl35+9vzefuiQs4u1977j+/\nrxJNJZJIR5z/MLMTgU1AD+D37j4x9shERBJUPEzA4x8t5cJBHfnT0N7qgqaSSaQaDWAWUI+ou5lZ\n8YUjIrJnioqc3736Bc989iWXH9mZ35/eU51qVkJlPmOa2ZVE37X8mOjblU/N7Iq4AxMRKUvxUM7P\nfPYlP/3hAUo0lViig6f1dff1AGbWAvgYGB1nYCIipdlRWMQvn5/BhJkrufHEHlx/XDclmkoskWSz\nHthcYnlzKBMRSYq8gkKuf2Y6b89Zza2nHMTVxxxQ9k6SVLtNNmZ2Y5jNAj4zs1eJ3tkMBfaobzQR\nkX1lW34hPx2byfvz13LHmb0YdkTnZIckCSjtyab4w81FYSqmfsZEJClytu1g+BNTyfxyI3f9+BDO\nH9gx2SFJgnabbNz9jooMRESkNGs353Hp6ClkrdnMAxf047Q+bZIdkuyBMt/ZmFk6cBvQqeT27t4n\nxrhERL6xfEMul4z6jNWb8nhs2ACO6aEhQaqaRBoIjCVqkTYLKIo3HBGR71q4ejOXjJpCbn4BT185\niP6dmiU7JCmHRJLNWncfH3skIiI7+Xz51wx7fAq10mow7prDOWj/xskOScopkWRzu5k9BkwC8ooL\n3f3l2KISkWrv46x1XPVkBs0b1ubp4YPo1EJ9AFdliSSby4GDgFp8W43mgJKNiMTirdmruP6Z6XRp\n2YAnhw+kdeO6yQ5J9lIiyWaAux8YeyQiIsC4qcu55eWZHNqhKY9fNoCm9WsnOyTZBxLpf/tjM+sZ\neyQiUq25O/dPWsjNL83kyG4teXr4ICWaFJLIk81gYIaZLSF6Z2OAq+mziOwrBYVF/H78bJ757Et+\n3K8dfz27j8aiSTGJJJuTY49CRKqtbfmFXP/sdN6Zu5prjz2AXw05UB1qpqBEko3HHoWIVEsbt+Yz\nfMxUpi//mj8O7cWlh3dOdkgSk0SSzX+JEo4BdYEuwHygV4xxiUiKW74hl2GPTyF74zZGXtSPk3ur\n+5lUlsiw0IeUXDazfsDPYotIRFLe7K9yuOzxqeTtKGTslYMY0Ll5skOSmCU6LPQ33H2amQ2KIxgR\nSX2TF67jmqczaVy3Js/89Ai6t25U9k5S5SXSEeeNJRZrAP2Ar2KLSERS1vNTv+S2V77ggFYNGXPF\nQPZvoo81q4tEnmxK/m9HAdE7nJfiCUdEUlFRkfP3t+cz8v1FHN29JQ9e1I/GdWslOyypQIm8s9G4\nNiJSbtt3FHLTuM/576yVXDioI3ec2Uvf0FRDiVSj9QB+BXTmu+PZHBdfWCKSCtZtyeOqJzOYsfxr\nbjv1YK48uou+oammEqlGewF4CHgMKIw3HBFJFQtXb+byJ6aybkseIy/qz8m99092SJJEiSSbAncf\nGXskIpIyPsqKWpzVqZnG8yMO59AOTZMdkiRZIhWnr5nZz8ysjZk1L55ij0xEqqRxU5czbPQU2jSp\ny3+uPUKJRoDEks0womGhPwYyw5RR1k5m1sHM3jOzOWY228x+Hsqbm9lEM1sYfpuFcjOz+80sy8xm\nho9Hi481LGy/0MyGlSjvb2azwj73W6gM3t05RCQ+BYVF3DlhDje/NJPDD2jBiz89gvbN6ic7LKkk\nykw27t5lF1PXBI5dANzk7j2Jeo6+NgxVcAswyd27E43+eUvY/hSge5hGACMhShzA7cAgYCDRyKHF\nyWMkcFWJ/Yo7Dd3dOUQkBjnbdnDFmAxGTV7CZUd05vHLBqhps3xHbO0P3X2lu08L85uBuUA7YCgw\nJmw2BjgrzA8FnvTIp0BTM2sDnARMdPcN7r4RmAicHNY1dvdP3d2BJ3c61q7OISL72OK1W/jRvz/i\nk0Xr+L8fH8IfzuxFTTVtlp3scXc15WFmnYG+wGdAa3dfGVatAlqH+XbA8hK7ZYey0sqzd1FOKecQ\nkX3ogwVrue6ZadROq8HYKwczsIte58quxZ5szKwhUY8Dv3D3TSXb2Lu7m1msQxiUdg4zG0FUZUfH\njh3jDEMkpbg7oyYv4S+vz6VH60Y8Nixd72ekVAklGzPrw/c/6nw5gf1qESWasSW2X21mbdx9ZagK\nWxPKVwAdSuzePpStAH64U/n7obz9LrYv7Rzf4e6PAI8ApKena9wekQTkFRTyu1e+4IXMbE7q1Zq7\nzz2MBnUqpJJEqrAyK1bNbDQwGjgbOCNMpyewnwGjgLnufneJVeOJWrgRfl8tUX5paJU2GMgJVWFv\nAUPMrFloGDAEeCus22Rmg8O5Lt3pWLs6h4jshTWbtnPho5/xQmY2NxzfnZEX9VeikYQk8rdkcGhR\ntqeOBC4BZpnZjFD2W+AuYJyZDQeWAeeGda8DpwJZQC5wOYC7bzCzO4GpYbs/uvuGMP8z4AmgHvBG\nmCjlHCJSTpnLNvDTp6exeXsBD1zYl9P7tE12SFKFWNSQq5QNzEYB/3T3ORUTUnKkp6d7RkaZnw+J\nVDvuzpOfLOPOCXNo36weD13Sn4P2b5zssKSSMLNMd08va7tEnmyeBD4xs1VAHtHw0O7uffYyRhGp\n5LblF3LbK7N4efoKTjh4P/557mE0qafvZ2TPJZJsRhGqw4CieMMRkcriy/W5XP10JvNWbeLGE3tw\n3bHdqFFDPTZL+SSSbNa6+/jYIxGRSuP9+Wv4+XMzcHdGXzaAYw/cL9khSRWXSLKZbmbPAK8RVaMB\niTV9FpGqpajIefC9LO5+ZwEH7d+Yhy7uR6cWDZIdlqSARJJNPaIkM6REmQNKNiIpZOPWfG4cN4P3\n5q/lR33b8ZcfHUK92mnJDktSRCLDQl9eEYGISPJkLtvAdc9MZ/2WfO4c2ouLB3fSiJqyTyUyLPTj\nRE8y3+HuV8QSkYhUGHfn0f8t5m9vzqdt03q8/LMj6N2uSbLDkhSUSDXahBLzdYEfAV/FE46IVJSv\nc/P51Quf887cNZzSe3/++pM+GhZAYpNINdpLJZfN7FlgcmwRiUjspn25keufmc6azdv5wxk9GXZE\nZ1WbSazK06lRd0DtIEWqoOLemu96Yx77N6nLi9do2GapGIm8s9lM9M7Gwu8q4DcxxyUi+9i6LXnc\n/OJM3p23hiE9W/P3nxxKk/qqNpOKkUg1WqOKCERE4vPBgrXcNO5zNm3foWozSYpYx7MRkeTKKyjk\n72/O57HJS+jRuiFPXzlQnWhKUiRSjTYa6APM5tu+0fRRp0gll7VmCzc8O505KzdxyeBO3HbawdSt\npY80JTniHM9GRJLA3Xl+6nLueG0OdWvV4NFL0zmxZ+tkhyXVXCLJ5hMz65nq49mIpIKNW/P57Suz\neOOLVRzZrQV3n3sYrRvXTXZYIhrPRiRVvDtvNb95aRYbt+ZzyykHMeLorhoSQCoNjWcjUsVtySvg\nTxPm8NzU5RzYuhFPXD6AXm3V5YxULhrPRqQK+3Txen71wud89fU2rjnmAH55Ynfq1FQjAKl8NJ6N\nSBW0fUch/3hrPqM+WkLH5vUZd/XhpHdunuywRHZL49mIVDGzsnP45bgZZK3ZwsWDO3LrKQfToE55\nep4SqTgaz0akiti+o5B/vbuQhz5YTMuGtRlzxUCO6dEq2WGJJGS3ycbMbnb3v5nZv9j1eDY3xBqZ\niHwjc9kGbn5xJovWbuXsfu35/ek91a+ZVCmlPdnMDb8ZFRGIiHxfbn4Bf3tzPmM+WUrbJvX0NCNV\n1m6Tjbu/Fmafd/ftJdeZWctYoxIRJi9cxy0vzyR74zYuPbwTN598EA31bkaqqBoJbDPFzAYXL5jZ\n2cDH8YUkUr3lbNvBb16cycWjPqNWWg3GXX04fxzaW4lGqrRE/vZeBIw2s/eBtkAL4Lg4gxKpjtyd\n12et4o7XZrN+az7XHHMAvzihuzrPlJSQSGu0WWb2Z+ApYDPwA3fPjj0ykWpk2fqt/P7V2XywYC29\n2jbmsWHp9GmvETQldSQyxMAo4ACiYQZ6ABPM7F/u/mDcwYmkuryCQh79cDH/ejeLWmk1uP2Mnlwy\nuBM10xKp4RapOhKpRpsFXOnuDiwxs0HA3fGGJZL6Plm0nt/9ZxaL1m7ltEPa8P9O78n+TdRDs6Sm\nRKrR7t1pOQcYHltEIilu/ZY8/vz6XF6etoIOzevx+GUDOPag/ZIdlkisynxWN7PuZvaimc0xs8XF\nUwL7jTazNWb2RYmy5mY20cwWht9modzM7H4zyzKzmWbWr8Q+w8L2C81sWIny/mY2K+xzv4UB1Xd3\nDpFkKygsYszHSznunx/w2udfce2xB/D2L45RopFqIZGK4ceBkUABcCzR+DZPJ7DfE8DJO5XdAkxy\n9+7ApLAMcArQPUwjwvkws+bA7cAgYCBwe4nkMRK4qsR+J5dxDpGk+ThrHafdP5nbx8+md7vGvH7D\n0fz6pIOoV1stzaR6SCTZ1HP3SYC5+zJ3/wNwWlk7ufuHwIadiocCY8L8GOCsEuVPeuRToKmZtQFO\nAia6+wZ33whMBE4O6xq7+6fhXdKTOx1rV+cQqXDZG3P52dhMLnzsM7bmF/DQxf15evggurdulOzQ\nRCpUIg0E8sysBrDQzK4DVgANy3m+1u6+MsyvAooHRm8HLC+xXXYoK608exflpZ3je8xsBNGTFB07\ndtzTaxHZrW35hYz8YBEPf7AIM7jpxB5c9YOu+mZGqq1Eks3PgfrADcCdRB90Dit1jwS4u5vZ9zr4\n3JfKOoe7PwI8ApCenh5rLFI9uDuvzVzJXa/P5auc7ZxxaFtuPeUg2jatl+zQRJIqkdZoU8PsFmBv\nhxtYbWZt3H1lqApbE8pXAB1KbNc+lK0AfrhT+fuhvP0uti/tHCKx+mzxev7y+lw+z87h4DaNuee8\nwxjUtUWywxKpFBJpjZZuZq+Y2bTQUmymmc0s5/nG8+1T0TDg1RLll4ZWaYOBnFAV9hYwxMyahYYB\nQ4C3wrpNZjY4tEK7dKdj7eocIrFYtHYLVz2ZwXmPfMrqTXn845xDmXD9UUo0IiUkUo02Fvg10ced\nRYke2MxpRuAuAAAPTElEQVSeJXoqaWlm2UStyu4CxpnZcGAZcG7Y/HXgVCALyCU8Qbn7BjO7Eyh+\nuvqjuxc3OvgZUYu3esAbYaKUc4jsU+u25HHfOwt5ZsqX1KuVxq9POpArjuyiFmYiu2BRY65SNjCb\n7O5HVVA8SZOenu4ZGRq6R8qWm1/A6MlLeOiDxWzbUchFgzpyw/HdadmwTrJDE6lwZpbp7ullbZfI\nk83tZvYY0TcrecWF7v7yXsQnUuVs31HIM599yb/fz2LdlnyG9GzNb045iANalbdxpkj1kUiyuRw4\nCKjFt9VoDijZSLWwo7CIFzOz+dekhXyVs53Du7bg4Ut60L9T82SHJlJlJJJsBrj7gbFHIlLJFBY5\nr33+Ffe+s4Cl63Pp27Ep/zjnUI7opoFqRfZUIsnmYzPr6e5zYo9GpBIoKnLenrOKuycuYMHqLRzc\npjGjhqVz3EH7EbrgE5E9lEiyGQzMMLMlRO9sjOh7yT6xRiZSwQqLnAkzv+LB97JYsHoLXVs14IEL\n+3Jq7zbUqKEkI7I3Ekk2O3emKZJSdhQW8eqMr/j3e1ksXreV7vs15L7zD+P0Pm1JU5IR2ScS6UFg\nWUUEIlLR8goKeSlzBSM/yGL5hm30bNOYkRf146Re++tJRmQfS+TJRiSlbMkr4LkpXzJq8hJW5mzn\n0A5N+cMZvfRORiRGSjZSbazK2c7jHy/hmc++ZPP2AgZ1ac7fftKHo7q1VJIRiZmSjaS8eas28eiH\nSxj/+QoKi5xTDmnDiKO7cmiHpskOTaTaULKRlOTuTM5ax6P/W8KHC9ZSr1YaFw3qxPCjutChef1k\nhydS7SjZSErZklfAy9OyGfPxUhat3UrLhnX49UkHctGgjjStXzvZ4YlUW0o2khKy1mzhqU+W8tK0\nFWzJK6BP+yb885xDOa1PG42OKVIJKNlIlVVY5Lw7bw1PfrKU/y1cR+20Gpzepw2XHtGZw/Q+RqRS\nUbKRKmf5hlxeyFjOC5nZrMzZzv6N6/KrIT04f2BHdfMvUkkp2UiVkFdQyNuzVzMuYzmTs9YBcHT3\nVvz+9J6c2LM1NdPKHHRWRJJIyUYqtfmrNvP81OW8Mj2bjbk7aNe0Hj8/vjvnpHegXdN6yQ5PRBKk\nZCOVzqqc7Yz/fAWvTP+KuSs3USvNGNJzf84b0IEju7VUf2UiVZCSjVQKm7fv4M0vVvGfGSv4eNF6\n3AndyPTkjEPb0kLvYkSqNCUbSZpt+YV8sGANr81cyTtzVpNXUESnFvW54bjunNW3HV1aNkh2iCKy\njyjZSIXamlfAu/PW8MYXK3lv3lq27SikeYPanDegA2f1bUffDk3VT5lIClKykdjlbNvBe/PW8Pqs\nlXywYC15BUW0bFiHs/u349TebRjYpblak4mkOCUb2efcnUVrt/LuvNW8O28NU5dupLDI2b9xXS4Y\n2JFTD2lD/07N9KJfpBpRspF9Ir+giClLNjApJJhl63MBOGj/Rlz9g64cf3Br+nZoqkHJRKopJRsp\nl6IiZ/7qzXyUtY7JWeuYsmQDufmF1KlZgyO7teTKo7ty3EH76VsYEQGUbGQPLN+Qy8eL1jE5az0f\nZ61j/dZ8AA5o1YBz+rfn6O6tOLJbS+rVVseXIvJdSjayS4VFzvxVm8lYtoGpSzeSuXQDX+VsB6BV\nozr8oEeUWI7s1oI2TfT0IiKlU7IRAHJydzBrRQ7Tv9xIxrKNTFu2kc15BQC0blyH9M7NGdGpGUd0\na0n3/RqqebKI7BElm2po0/YdfLEih1nZOcwMv19uyP1m/YGtG3HmYW1J79yM9E7Nad+snpKLiOwV\nJZsUll9QxOJ1W1iwegsLVm1m/urNLFi9+ZuWYgDtm9WjT/smXDCwI4e0a8Ih7ZrQpH6tJEYtIqko\nZZONmZ0M3AekAY+5+11JDikW7s6azXksXbeVZRtyWbZ+K0vX5bJg9WaWrNtKQZEDkFbD6NKyAb3b\nNuGc/u05pH1TDmnXhOYNNFSyiMQvJZONmaUBDwInAtnAVDMb7+5zkhvZnssrKGTNpjxW5mxn1abt\nrMrZxsqc7azYuI0vN+SybH0u23YUfrN9Wg2jfbN6dN+vEUN6taZH60b0aN2Irq0aUKemWomJSHKk\nZLIBBgJZ7r4YwMyeA4YCSUk2RUXO9oJCtuYVkptf8M3vlrwCcrbtYMPWfDbm7mDj1nw25OZHv1vz\nWbclj3Vb8r93vAa102jbtB6dWtTnyG4t6dyiPh1bNKBzi/q0bVqPWur6RUQqmVRNNu2A5SWWs4FB\ncZzot6/M4tPF6ykscgoKnSJ3Coo8LBdRUORs21GIe+nHMYOm9WrRrEFtmtevTYfm9enbsSltmtRj\n/yZ12b9xXdo0qcv+TerSqK7eqYhI1ZKqySYhZjYCGAHQsWPHch2jXdN69GzTmJo1jBo1jJo1jLQa\nNUirATVr1KBmDaN+nZo0qJ1G/dpp1K9dkwZ1ot/6tdNoWr82zRvUpkm9WuorTERSVqommxVAhxLL\n7UPZd7j7I8AjAOnp6WU8e+zatcd2K89uIiLVSqpW7k8FuptZFzOrDZwPjE9yTCIi1VZKPtm4e4GZ\nXQe8RdT0ebS7z05yWCIi1VZKJhsAd38deD3ZcYiISOpWo4mISCWiZCMiIrFTshERkdgp2YiISOyU\nbEREJHbmZfWjUk2Y2VpgWTl3bwms24fhVAW65upB11w97M01d3L3VmVtpGSzD5hZhrunJzuOiqRr\nrh50zdVDRVyzqtFERCR2SjYiIhI7JZt945FkB5AEuubqQddcPcR+zXpnIyIisdOTjYiIxE7JZi+Z\n2clmNt/MsszslmTHsy+YWQcze8/M5pjZbDP7eShvbmYTzWxh+G0Wys3M7g9/BjPNrF9yr6D8zCzN\nzKab2YSw3MXMPgvX9nwYsgIzqxOWs8L6zsmMu7zMrKmZvWhm88xsrpkdnur32cx+Gf5ef2Fmz5pZ\n3VS7z2Y22szWmNkXJcr2+L6a2bCw/UIzG7Y3MSnZ7AUzSwMeBE4BegIXmFnP5Ea1TxQAN7l7T2Aw\ncG24rluASe7eHZgUliG6/u5hGgGMrPiQ95mfA3NLLP8VuMfduwEbgeGhfDiwMZTfE7ariu4D3nT3\ng4BDia49Ze+zmbUDbgDS3b030RAk55N69/kJ4OSdyvbovppZc+B2YBAwELi9OEGVi7trKucEHA68\nVWL5VuDWZMcVw3W+CpwIzAfahLI2wPww/zBwQYntv9muKk1EI7pOAo4DJgBG9KFbzZ3vN9FYSYeH\n+ZphO0v2Nezh9TYBluwcdyrfZ6AdsBxoHu7bBOCkVLzPQGfgi/LeV+AC4OES5d/Zbk8nPdnsneK/\nuMWyQ1nKCNUGfYHPgNbuvjKsWgW0DvOp8udwL3AzUBSWWwBfu3tBWC55Xd9cc1ifE7avSroAa4HH\nQ9XhY2bWgBS+z+6+AvgH8CWwkui+ZZLa97nYnt7XfXq/lWxkt8ysIfAS8At331RynUf/q5MyTRnN\n7HRgjbtnJjuWClQT6AeMdPe+wFa+rVoBUvI+NwOGEiXatkADvl/dlPKScV+VbPbOCqBDieX2oazK\nM7NaRIlmrLu/HIpXm1mbsL4NsCaUp8Kfw5HAmWa2FHiOqCrtPqCpmRWPaFvyur655rC+CbC+IgPe\nB7KBbHf/LCy/SJR8Uvk+nwAscfe17r4DeJno3qfyfS62p/d1n95vJZu9MxXoHlqy1CZ60Tg+yTHt\nNTMzYBQw193vLrFqPFDcImUY0buc4vJLQ6uWwUBOicf1KsHdb3X39u7emeg+vuvuFwHvAT8Jm+18\nzcV/Fj8J21epJwB3XwUsN7MDQ9HxwBxS+D4TVZ8NNrP64e958TWn7H0uYU/v61vAEDNrFp4Ih4Sy\n8kn2S6yqPgGnAguARcBtyY5nH13TUUSP2DOBGWE6laiuehKwEHgHaB62N6JWeYuAWUQtfZJ+HXtx\n/T8EJoT5rsAUIAt4AagTyuuG5aywvmuy4y7ntR4GZIR7/R+gWarfZ+AOYB7wBfAUUCfV7jPwLNE7\nqR1ET7DDy3NfgSvCtWcBl+9NTOpBQEREYqdqNBERiZ2SjYiIxE7JRkREYqdkIyIisVOyERGR2CnZ\niMTAzN43s9jHsTezG0JvzWP38XEvM7MH9uUxpXqrWfYmIlKRzKymf9tPV1l+Bpzg7tlxxiSyt/Rk\nI9WWmXUOTwWPhvFN3jazemHdN08mZtYydGNT/H/8/wnjgSw1s+vM7MbQkeWnoVv2YpeY2YwwbsrA\nsH+DMNbIlLDP0BLHHW9m7xJ9eLdzrDeG43xhZr8IZQ8RfYz4hpn9cqftLzOzl83szTAWyd9KrLvA\nzGaFY/21RPnlZrbAzKYQdeFSXN7KzF4ys6lhOjKUHxOub0a4lkZ7cz8kxSX7S1dNmpI1EXXBXgAc\nFpbHAReH+fcJX1IDLYGlYf4yoq+pGwGtiHoBviasu4eo09Li/R8N8z8gdPUO/KXEOZoS9T7RIBw3\nm/BV905x9if6srsB0BCYDfQN65YCLXexz2XAYqK+vOoCy4j6uWpL1GVLK6KajXeBs4i6lC8urw18\nBDwQjvUMcFSY70jUjRHAa8CRYb4hoYt+TZp2NakaTaq7Je4+I8xnEiWgsrzn7puBzWaWQ/SPLkQJ\noU+J7Z4FcPcPzayxmTUl6l/qTDP7VdimLtE/4AAT3X3DLs53FPCKu28FMLOXgaOB6WXEOcndc8I+\nc4BORF2WvO/ua0P5WKJkyE7lzwM9QvkJQM+oKzEAGocewT8C7g7HeNlVlSelULKR6i6vxHwhUC/M\nF/BtNXPdUvYpKrFcxHf/m9q5Lygn6ofqbHefX3KFmQ0i6uJ/X9r52sr733sNYLC7b9+p/C4z+y9R\nv3kfmdlJ7j6vnOeQFKd3NiK7tpSo+gq+7Q14T50HYGZHEfWkm0PUa+71ocdhzKxvAsf5H3BW6Km4\nAfCjUFYeU4BjwnuoNKLRGD8gGhzvGDNrEYaXOKfEPm8D1xcvmNlh4fcAd5/l7n8l6gH9oHLGJNWA\nnmxEdu0fwDgzGwH8t5zH2G5m04FaRL3nAtxJNCLoTDOrQTQs8+mlHcTdp5nZE0SJAuAxdy+rCm13\nx1ppZrcQdalvwH/d/VUAM/sD8AnwNVFP38VuAB40s5lE/2Z8CFwD/MLMjiV6opsNvFGemKR6UK/P\nIiISO1WjiYhI7JRsREQkdko2IiISOyUbERGJnZKNiIjETslGRERip2QjIiKxU7IREZHY/X+QRk1V\nT9zBbwAAAABJRU5ErkJggg==\n",
      "text/plain": [
       "<matplotlib.figure.Figure at 0x10b691a90>"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    }
   ],
   "source": [
    "import matplotlib.pyplot as plt\n",
    "%matplotlib inline\n",
    "\n",
    "sizes = range(1000)\n",
    "plt.plot(sizes, [s*(s-1)/2.0 for s in sizes])\n",
    "plt.xlabel('number of nodes')\n",
    "plt.ylabel('maximum number of edges')\n",
    "plt.show()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "Luckily, most real-world graphs are extremely sparse.\n",
    "\n",
    "- E.g., you are probably not friends with over 1,000 people."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "# Measuring Graphs\n",
    "\n",
    "- How can we summarize a graph?\n",
    "  - Besides number of edges and number of nodes.\n",
    "  \n",
    "<br><br>\n",
    "  \n",
    "- Allows us to determine if two graphs are \"similar\"\n",
    "\n",
    "<br><br><br><br>"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "# Degree distribution\n",
    "\n",
    "- Probability that a randomly chosen node has degree $k$\n",
    "\n",
    "<br><br>\n",
    "\n",
    "- $N_k$: number of nodes with degree $k$\n",
    "- $P(k) = $ ?\n",
    "\n",
    "<br><br><br><br><br><br><br><br><br><br>\n",
    "\n",
    "$$P(k) = \\frac{N_k}{N}$$\n"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 30,
   "metadata": {
    "collapsed": false,
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAdgAAAFCCAYAAABSJMy8AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXdYFFcXxt8FjaCgIh0pKnYFFVGjUdQosYAFgxpr7CVG\nY29YY8USFf0ssVfsXdHETqIiYI/YYu8Fg9LLvt8fsyDgAgvsspT7e555YGfu3Htmd2bOLafISBIC\ngUAgEAjUio62BRAIBAKBID8iFKxAIBAIBBpAKFiBQCAQCDSAULACgUAgEGgAoWAFAoFAINAAQsEK\nBAKBQKABhIIVCAQCgUADCAUrEAgEAoEGEApWIBAIBAINIBSsQCAQCAQaQChYgUAgEAg0gFCwAoFA\nIBBoAKFgBQKBQCDQAELBCgQCgUCgAYSCFQgEAoFAAwgFKxAIBAKBBhAKViAQCAQCDSAUrEAgEAgE\nGkAoWIFAIBAINIBQsAKBQCAQaAChYAUCgUAg0ABCwQoEAoFAoAGEghUIBAKBQAMIBSsQCAQCgQYQ\nClYgEAgEAg1QSNsCCLTImzfAhg3A9etAWBhQogTg6Aj07g2YmmpbOoFAIMjTyEhS20IIcpjAQGDO\nHMDPT/ocHf35mL4+QAKtWgETJgB16mhHRoFAIMjjCAVb0FixAhg9GoiKkhRpWshkkrJdsAAYPDjn\n5BMIBIJ8gpgiLkgkKtfIyIzLklK50aOlz0LJCgQCQaYQRk4FhcBALPvlFzhHRqIIgF6pDkcC+AmA\nCYASAFySDiiUbFBQjokqEAgE+QGhYAsKc+bAKi4OkwD0UXJ4AIBQACGKv4uSH4yKktZsBQKBQKAy\nYg22IPDmDWBnl2TMNAnAMwAbFIdvA6ir2Fc8rTr09IAnT4R1sUAgEKiIGMEWBDZsSPfwJQB2AKZC\nmiJ2ALAndSGZLMN6BAKBQPAZoWALAtevp3TFScUzADchrb2+ALAMwI+QpouTiIoCbtzQoJACgUCQ\nvxAKtiAQFpbuYX0AhSFNHX8FoDGApgD+SF3wwwcNCCcQCAT5E6FgCwIlSqR72FHJPpmygkZG6pBG\nIBAICgRCwRYEHB0BPT3EA4gGkKDYogHEQ3LJsQUwR/H5bwCnAbRIXoe+PuDgkJNSCwQCQZ5GWBEX\nBBRWxNOiozE91aGpAKYB+AdAPwDXIRk8zQLgkbygsCIWCASCTCEUbEGhQwdg//70wyOmhUwGeHgA\ne76wLRYIBAJBGggFW1AIDETcN9+gcFxc5s8tWhQ4exZwdla/XAKBQJBPEWuwBYQ1165hYpEiUCEK\ncUqKFpUC/gvlKhAIBJlCKNgCwM6dO+Hl5YW1hQvjzdixktKUKbUT/oxM9lm5ikD/AoFAkGmEgs3n\n+Pn54eeff0axYsXg7e2NMt7e0nSvh4dkuKSvn/IEfX1pv4eHVE4oV4FAIMgSYg02H+Pv74/vv/8e\n1atXR7ly5bBmzZqUBd6+lcIf3rghBZEwMpJccXr1EtbCAoFAkE2Egs2nBAcHo1WrVmjfvj2uXLkC\nf39/6OnpaVssgUAgKDCIhOv5kJCQELi7u+Pnn3/G8uXLcenSJaFcBQKBIIcRa7D5jEePHqFFixYY\nN24cVqxYga1bt8LW1lbbYgkEAkGBQyjYfMTLly/h6uqKUaNGwdfXF8OHD0ezZs20LZZAIBAUSMQa\nbD4hNDQUjRs3RpcuXfD48WO8e/cOu3fvhiwjdxyBQCAQaASxBpsP+PTpE1q1aoVWrVrB3Nwcmzdv\nRkBAgFCuAoFAoEWEgs3jREdHo3379qhRowY6duyI1q1b49y5cyhevLi2RRMIBIICjVCweZi4uDh0\n7twZpqammDFjBurWrYuVK1eiSpUq2hZNIBAICjxiDTaPIpfL0bNnT/z333/YvXs32rRpAycnJ3h7\ne2tbNIFAIBBAjGDzJCQxdOhQPH36FMeOHcP06dMhl8sxa9YsbYsmEAgEAgVCweZBvLy8EBAQgFOn\nTuHYsWPYtm0bgoKCUKiQ+DkFAoEgtyDeyHkMb29vHDhwAGfPnsWLFy8wcOBAHDlyBKYidrBAINA2\nb95I8c2vXwfCwoASJQBHR6B37wIZ31ysweYhVq1aBW9vb/j7+6N48eKoW7cuRo0ahX79+mlbNIFA\nUJAJDATmzAH8/KTP0dGfj+nrAyTQqhUwYQJQp452ZNQCQsHmEXx9fTFmzBicO3cOZcuWRceOHWFk\nZITVq1drWzSBQFCQWbECGD0aiIqSFGlayGSSsi1AOabFFHEe4NChQxgxYgROnjyJcuXKYf78+Xj8\n+DG2bNmibdEEAkFBJlG5RkZmXJaUyo0eLX0uAEpWjGBzOWfOnEGnTp1w5MgR1KlTB6dOnUK3bt0Q\nEBAggvgLBALtERgINGmCmMhI/ATgBIBQAPYA5gBoBeARgLIAiiU7bRyAyUWLAmfPAs7OOSx0ziJG\nsLmYwMBAdOrUCTt37kSdOnXw9OlTdOvWTWTIEQgE2mfOHCAqCvEAbACcBWAL4CiATgBuJCv6H1Ip\nm6go6fw9e3JKWq0gRrC5lJs3b6J58+ZYs2YN3N3dER0dDRcXF3h6emLs2LHaFk8gEBRk3rwB7OxS\nGjMlwxHAVAC1IY1g46BkNKenBzx5kq+ti0W6ulzIv//+i5YtW2LRokVwd3cHAAwbNgy2trYYM2aM\nlqUTCAQFng0b0jz0GsBdANWS7bMDYA2gN4B3iTtlsnTryQ8IBZvLeP78OVxdXTF58mR06dIFALB2\n7Vr4+/tj/fr1IkOOQCDQPtevKx29xgHoBuBHAJUBmAAIBPAYQDCAT4rjAKRp4hs3vqgjPyHWYHMR\n7969g6urKwYNGoSBAwcCAIKCgjBhwgScO3cOhoaGWpZQIBAIIAWRSIUcQA8AXwFYpthnACDRjMlc\nsd8SkqI1BIAPHzQsqHYRCjaX8PHjR7Rs2RLt27dPWmN99+4dPD09sXLlSlSuXFnLEgoEuRQRPSjn\nKVEixUcC6AtpevgogMJpnJY4/yZP3GFkpAHhcg9CweYCoqKi0KZNG9SrVy8pYH98fDx++OEH/PDD\nD+jQoYOWJRQIciHpRQ/auxeYOrVARg/KERwdJQtgxXc+GEAIJFcd/WTFAgCUBFABwAcAwwA0AVAC\nkIJOODjknMxaQFgRaxIVetaxsbHw8PBAqVKlsHHjRujoSMvi48ePR1BQEI4dOyaC+AsEqRHRg7TK\nlePHUa11a3wll+MxgDIAiiDliG0VJCOfiQDeACgOwBXAPAAWQIGwIhYKVhOoGJczYexYdFu8GFFR\nUdi9ezcKF5YmVvbu3YsRI0YgKChIBPEXCFKTmehBiRQtKpSsGvjnn38wefJkXLp0CedMTFD2+nXI\nsqJCZDLAwyPf+8GCAvWyfDlZtCgpk5GSKlW6yWUyRhcqxN8qVmRUVFTS6SEhITQ1NWVgYKAWL0Ig\nyKVcuiQ9X+k8W2luRYuS4rnKEvfv32f37t1pZmbGhQsXMjIyUvwWKiDcdNRJ8p51Br06GYki8fEY\n/vQp9NavBwB8+vQJHh4emDNnDpzzeQgxgSBLzJmDmMhI9IXkW2kIoCYAv2RFdgKoojhWFcD+xAOJ\n0YMEKvPs2TMMGjQI9erVQ8WKFXH//n2MHDkS+vr60rr2ggXS7EBmSJxNKADvODFFrC4UcTkzNW2V\nSNGi4Jkz6OjtjVKlSuH3339Xu3gCQZ5HET0oIjoa8wH0wufQfF0gheYrDCly0AEALRXHOkKKiWsG\nFIh1P3Xw9u1bzJkzBxs3bkT//v0xZswYGBsbKy+s4no4ZTLICth6uBjBqgtFXE5lbIfUoy4GKRC2\nf+oCUVG427s3njx5gqVLl2pUTADSi2rePKB7d6BNG+nvvHnA27eab1sgyCqKqD/FAEyDZFijA8Ad\nklINBvAMktVqK0guIW6K8v8m1lEAogdlh//++w+TJ09G5cqVERcXh5s3b2Lu3LlpK1dAUpZnz0pr\nqnp6kp1JMmJ0dBCrq4t71apJ5QqIcgUg1mDVwuvXpJ6e0rWGPwDaArwAMAHgM8WWulwUwGdXrmhW\nzkuXSA8PSdbU8urrS/s8PKRyAkFuo1s3pc/YK4BFAIYAjAfoAvCA4v99AEsDDE9+To8e2r6SXEd4\neDjnzJlDU1NT9u7dmw8fPsxaRW/ekPPmSd+xuzs/tm/PGcWL8+KhQ6xUqRLlcrla5c7tCAWrDry9\n01Sw9QGuUWHRP/6rr6QbU1OoaHxFmUwqt3y55mQRCLKCu/sX92sswGYAByTbtwZgMYC6APUBHk59\nj7u7a/tKcg3R0dH08fGhhYUFO3XqxJCQELXWL5fLWbJkSb569YpVqlTh2bNn1Vp/bkdMEauDNOJy\nJgAIAvAWQHlIwa5/BqBsIlk3NlZzcTkzYXyVIinyihWakUcgyAqpogcpC813AsBYAGcAxEJKodYP\nwNXkJ+bz6EGqEB8fj3Xr1qFixYo4fvw4jh49ih07dqg9YpxMJoOTkxMuX76MAQMGFDj7EqFg1YGS\nuJyAFDYsDsBuSOuuVwFcATAzrXo0EZczMBDLfvkFzpGRKALJMCSRrZBihSZuRSGtWwUDn5VsUJD6\nZRIIsoKjo7TGh5Sh+fbgc2i+qwBcIMW/1QFQB0A9SIoXQIGIHpQecrkcO3bsQLVq1bBp0yb4+vri\n8OHDqFWrlsbarF27NoKDg9GjRw8cPnwYoaGhGmsrtyEUrDpI1bNOJHGpfyikANcmAEZCsmxUiiZ6\n1nPmwCouDpMA9El1qBuA8GTbcgDlADglFhBuDYLcRK9eSf8mhuY7hJSh+ergc2cWkDq0/pDykwKQ\nZmiS1VNQIInDhw/DyckJCxcuxLJly3D69Gk0aNBA423Xrl0bly9fhrGxMVq3bo0tW7ZovM3cglCw\n6iBZzzo5RpCmhZMnmEsz2ZwmetZv3gB+fugAoD2AdOwAAQAbAfREMhlJ4OhRYV0syB2YmQGtWuEx\npDB8VyGF3EucgdkKoDEkC2NPSH6w30MK1fcdIFkQt25d4Fx0EhXphAkTMG3aNAQEBMDV1TXHUl86\nOTkhODgYANC/f3+sXr0aLCDeoULBqoN0esS9ASyFFIvzA4BFkNwKvkATPetMuCM8BnAOkoJNgXBr\nEOQmJkyAXdGiIIBopJyBScwz+jOA+5BSoj0AMCrxXH19KfB/ASEgIADNmzdH//79MXToUFy9ehXt\n27fP8ZzS9vb2CAsLw7t379CkSRNER0fj4sWLOSqDthAKVh0oetZQcuNOhjRtVRGSL2wtAF6pC2mq\nZ52G8ZUyNgFoBMmfMAUFICmyIA8hogdlyPXr19GuXTt4enqic+fOCAkJQdeuXaGrq6sVeXR0dFCr\nVi0EBwdDJpMljWILAkLBqosJE75wsAYk44vlAP4D8AqAD4AvJpM11bNOw/hKGZsA/JjWwXyeFFmQ\nxxg8GG/GjUMkpOhA6SKTFZhA//fu3UPXrl3x3XffoWnTprh37x769++flEREmySuwwLAjz/+iH37\n9uHjx49alkrzCAWrLrLYs2Zi6DBN9KzTML5Kzd8AXkBat1KKcGsQ5CLkcjl+OHMGe4YNgyyN6EFR\nMpm038Mj30cPevr0Kfr374/69eujWrVquH//PoYPHw49JXYh2iLRkhgAzM3N0axZM2zbtk3LUmke\noWDVyeDBwIIFiCtcGPIMilImQ4yuLlaUL4+EAQM0I4/C+Coe0npVgmKLBhCfrNhGSMYghsrqKOBu\nDYLcx+rVqxEREYGuv/0mpTt78gSYPh3o0QNwd8fTJk0wDQAfP5aO59Np4devX2P48OGoWbMmTE1N\ncffuXXh5ecHAwEDbon1BckMnAAVnmljbkS7yGx8/fqSrkREfOTszWiajPK2QhB06MPb8eTZt2pQj\nR47UjDCKEI5TJbfBFNvUZCEaSwA8kVZkJz09KfyZQJALePLkCU1MTHjz5s00y8TFxVEmk+XblI+h\noaGcOHEiS5UqxWHDhvHly5faFilDEhISaGhoyHfv3iV9trOzY1BQkJYl0yyF0le/gsyybNkymLRs\nieU2NijRsCGsT55Ehago1K9cWZpqdXCQrIVNTVEYwO7du1G/fn1UqlQJA9Q9klUYX03bvx/T0jCL\n14O0PqyUAurWIMidkMSgQYMwdOhQVKtWLc1yhQoVgpmZGbZs2ZKv0j6Gh4fDx8cHixYtQrt27XDl\nyhXY2tpqWyyVSDR0unz5MlxdXaGjo4N+/fph9erVqF27trbF0xza1vD5ibCwMJqamjIkJIRVqlTh\nzz//zLp16zI6Ojrd8+7evUtzc3P++eef6hdKJEWWRvLe3lKweHd36a+3txiZ5zE2bdpER0dHxsTE\nZFi2VatWdHR0zAGpNE9UVBQXL15Mc3Nz/vDDD7xz5462RcoSI0aM4Ny5c5M+P3v2jEZGRvz06ZMW\npdIsQsGqkV9//ZU9evTg3bt3WapUKVpYWPDJkycqnXvmzBmamZmpPdg2yc+B/jOrXPN6wH+RPSjf\n8OrVK5qZmak8pbhq1Srq6elpWCrNEhsby9WrV9PGxoZt2rTh1atXtS1Stti8eTM7duyYYl+bNm24\nddGifNsBFgpWTXz48IHGxsa8e/cuJ02aRH19fZ46dSpTdaxbt4729vZ8+/at+gVUMZtOQn7JpiOy\nB+UrPD09OW7cOJXLh4WFEQAfP36sQak0Q0JCArdt28by5cvz22+/5YULF7Qtklq4desWy5Ur93nH\npUt88fXXjJbJ8m0HWChYNTFlyhT27t2bUVFRNDQ0ZO/evbNUz7hx49ioUaMMp5WzRGAg2aGDdOPq\n66e4oaN1dRmrq0u/okUZe/68+tvOSQrqiD2fsnv3blasWJGRkZGZOq948eKcNWuWhqRSP3K5nAcO\nHKCDgwPr1avHEydOaFsktRIfH08DAwOGhoYmPaPyfN4BlpEFJCikOnjzRgobeP26FMShRAnA0REf\n2rdHhQYNcOnSJUydOhXbt29HWFgYimY22gwkHz9PT08YGhpiw4YNmglr9vatdB03bkhBJIyMcKdI\nEfwUEAA9Gxu0aNECw4YNU3+7OUFgINCkiZQNSEFqp4UoAD9BCmGZgqJFJZ/JfGQYk9cJDQ1F9erV\nsWvXLnzzzTeZOvebb76Bjo4O/P39NSSd+jh58iQmTpyIqKgozJo1C+7u7jkX0jCN9xp691a7gWOj\nRo2wunZtVF69OsUzmiF5NViItjV8niCDtbxYXV0G29lx78SJtLKyYuvWrbPVXHh4OJ2cnDh79mw1\nXUDGxMfH09ramrt376aZmRk/fPiQY22rFQ+PdKeFPymScZ9Nq7fcoYO2r0CQjJ49e3Lo0KFZOnf6\n9OksUaKEmiVSL+cVrnoVKlSgr68vExIScq5xLdgoLOjcmZ8KFWIfgLYADQDWAHhUyfM4XeFS+Gce\nNroUCjYjMrF2GQHQp2pVrl27NtvNPn/+nDY2Nty1a5caLkI1Jk6cyBEjRrBv374cP358jrWrNhR+\nv+n9ThsAlgUoF36/uZ6jR4+yTJkyWbYy/ffffwmAYWFhapYs+1y9epXu7u60sbHhmjVrGBcXl7MC\naMlG4ZGTEz9C8sN/CDAB4CGFon2YrN37AKsDtEyuYPNgB1go2PTIwlpeBMCwZKbo2eHy5cs0MTHh\npRxa5L979y7NzMz48OFDlipVSmUL6FyDt3eGCrYpPgfZULrp65Pz5mn7Sgo8YWFhtLW1zbbrWpEi\nRbhmzRo1SZV9bt++zc6dO9PCwoJLlixhVFRUzguhLRuF16+Z8NVXSut3ALg72ecWAI8AtEuuYPNg\nB1iESkyLwEBg9OjMrRMAKAqg+K+/AkFB2RahVq1aWLNmDdq3b4+nT59mu76MqFChAipWrIhr165h\n8ODBmDJlisbbVCsZZA96DOAs0klqAIjsQbmEcePGwdXVFc2bN89WPeXLl8f+/fvVJFXWefz4Mfr0\n6YOGDRuiRo0auHfvHoYNG5bz8YKz+F5DZKR0Xnbeaxs2QKbzpcp5DeAugMTQIbsAFAHQWlkdeSx9\nplCwaTFnjvSyTUUTSNGPEpM8V1J2blSUdL4aaNeuHUaMGIE2bdogPDxcLXWmR69evbB+/XqMHTsW\nfn5+uH79usbbVBsZZA/aDKAhlKTkS43IHqRVzpw5g0OHDmHBggXZrqtJkyYIUkNnN6u8evUKQ4cO\nhZOTE6ysrHDv3j1MmDBBe/GCFe+1ZQCcISmyXmkU/RWADMCJxB3Zfa9dvw5Zqg5wHKQ8vj8CqAwp\nh+9EAEvSqiOPdYCFglXGmzeAn580KaGEZfic5PmOsgIkcPSoZK2rBkaNGgVnZ2d06dIFCQkJaqkz\nLTp16oQzZ84gOjoakyZNwrhx4zTanlrJIHtQuin5kiOyB2mNyMhI9OvXD8uXL0fJkiWzXV+XLl3w\n+vVrxMbGqkE61QkNDcX48eNRrVo1FCpUCCEhIZg5c6ZarinLJHuvWQGYBKBPGkX/hTSStEy+MxPv\nNZJ4+fIlzp49i9WrV2PMmDG4dOJEijJyAD0AfAXpnQoA0xT7yqRXeR7qAAsFqwx1TEGocSpDJpNh\n+fLliIiIwNixY9VSZ1oYGhqibdu22Lp1KwYMGID79+/jRKoHI9eiyB6kjPMAngPomFEdInuQVpk8\neTLq1q2Ltm3bqqW++vXrQ0dHJ8fu4U+fPmHGjBmoWLEiQkNDcfXqVSxatAhmZmY50n66JHsfdQDQ\nHoBxGkWHAPCGpPxSkOq99vHjRwQFBWHbtm2YNm0aunbtCmdnZ5QoUQI1atSAl5cXLly4AGNjY1hU\n+jzfRwB9IU0P74GUNxsATkLKmW2h2J4C6KSQJYm81AHW9iJwrqRbtzQX+xsDNAFoDLABwNPpGQb0\n6KFWsUJDQ1mxYkWuWrVKrfWm5tSpU3RwcKBcLueuXbtYq1atnHUfyCrpWBEPANhdFWOOPGZEkZ+4\nePEizc3N+UbN37+dnR179uyp1jpTExkZyYULF9LMzIxdu3blvXv3NNpellDyXvMC+GOqfTsBtlX8\n/4WREcDz5cvTxcWF5ubmLFq0KGvWrMlOnTpx0qRJ3LRpEwMCAqRgEqlJZoQ4EGA9SG5zyet+B/Bl\nss1aIU9SuTxmhCgUrDLc3dN8AV8E+BFgNCSXDwNIJuVKy7u7q100jSYGUJCQkMAyZcowODiYcrmc\n9erV45YtWzTWnlrJwA82Q5eEPOYGkF+Ijo5m1apV6evrq/a6O3fuTHt7e7XXS0rxgleuXElra2u2\nb9+e169f10g7akHJey21gv0IsDw+u8woU7APHRx46tQpPnv2jHK5XOXm758/zxgdHT6SBrAsAskn\nPXHbouSZzOtWxELBKiOdEWzqrQVAnxwawSZy5syZpKw9mmLq1Kn8+eefSZL+/v60s7PTjktBZslG\n9qCYQoUYf/Gitq+gQDJ58mS2bds2Uy9sVdm9ezd1dXXVOgsTHx/PzZs3097enq6urgwICFBb3RpD\nhRHsSEgBHtJUcFl4r3348IEjR46kiYkJ71avnnF4xHzUARYKVhkq+FMmbi0BLlF2TMNTGRpNDEDy\nwYMHNDY2ToqJ3L59e86fP18jbambV9OmMSKTD69cX58LK1Sgu7s7P378qO1LKFBcvXqVpqamfP78\nuUbqj4iIoEwmU0tyb7lczr1797JatWps0KABT58+nX0B1UxERASvXbvGXbt2cdasWfzxxx9Zv359\nTtHXZ2QGCrYGpOUvc8WmA9AI4NwsvNfi4+O5atUqmpubs1+/fnz16lWBS58pFKwy0ljL+wDwGMAo\ngHGQpjSKAryj7GbIgamMcePGsWHDhppJDECySZMmSZGkQkJCaGJiwvfv32ukLXXx/v17VqhQgee6\ndmWUjo6UHSijXrHCiT4mJob9+/dn9erV+fDhQ21fSoEgLi6OTk5Oaol+lh6VS5XiwUaNspwSTS6X\n8/jx43R2dmbNmjV5+PBhjYy2VSUuLo7379/n0aNHuXjxYv70009s3rw5bWxsqKenx6pVq7J9+/Yc\nO3Ys165dS39/f765eZNyxXstTvEeGw/JNiHxnZbhGqiK77XTp0+zRo0abNSoES9fvpzy4PLljE0j\n4ES6yjUPBvwXCjYtlKzlvQHoDGndtQSkRfo/lI2GcmgqIyEhgR06dGDPnj018rBv3LgxRVzlQYMG\ncdSoUWpvR13ExMSwcePGHD16NHfs2MEuFSowQRFrNT71A50Ya7VDhxS9YrlczkWLFtHCwoJ//fWX\nFq+mYDBnzhy6urpqTlkp4u3G6OgwKnVnS8V4u/7+/nRxcWGlSpW4Y8eOHDP4k8vlfPnyJc+ePcvV\nq1dzzJgxbNeuHStXrswiRYrQzs6Orq6uHDJkCH18fHjs2DE+ePCA8fHxaVeqeK9NhbQOmnybquRd\nlmKKWIX32oMHD/j999/Tzs6OO3fuTPN3fTJxIiNlsnyfTlIo2LTIxlRGhEzG8z4+OSJmeHg4a9eu\nrZG0XOHh4SxZsiRfvHhBknz58iVLlSqVK0d3crmcvXr1Yvv27fnp0yfa2dnxzJkz0sE3b3i5Sxee\ntbOTRi89ekjTXOn0xI8ePUpTU1Nu3LgxZy6gABISEkJjY2PN3U/ZjLcbHBzMVq1a0c7OjuvWrdNY\nvOCwsDAGBQVx27ZtnDZtGrt06cLatWvT0NCQJiYmbNCgAXv16sU5c+Zwz549vHHjRqZT9yWhoSna\nT58+ceLEiTQ2NuaMGTMylC82NpbfFCnCuLZtlabPTKsDnNcQCjY9shizM+SXX2hjY8MhQ4YwIiJC\n42I+f/6c1tbW3Llzp9rr7tOnD729vZM+T5s2jd26dVN7O9llzpw5dHJyYnh4OGfMmMHvv/8+xfH5\n8+dz5MiRmarz5s2bLFeuHMePH5833JTyEPHx8WzQoAGXLl2qmQayEW/31q1b9PT0pKWlJZcuXaqW\nJZiYmBiGhITwwIEDnD9/Pvv160cXFxdaWFiwaNGirFGjBjt27Jjk6nLx4kXNLceoMRZxQkICN27c\nSCsrK3bv3p3Pnj1TWYw6derQ399f6ujOmyd1fFXsAOcVhILNiCz2gkNDQ9m1a1dWqlSJgTnQA9NU\nYgB/f3/8zDqcAAAgAElEQVRWqVIlaarn06dPtLS0ZHBwsFrbyQ67du2ijY0Nnz9/zmfPnrFUqVJ8\n8OBBijLDhw/nwoULM13327dv2ahRI7Zr1y7LWV0EX7JkyRI2bNhQMx0XxSitG0ALgIYAKwBcrXhW\nYwB+r5j+BFL6skfr6rJ5yZKcO3cuw8PDM9VsQkICnzx5whMnTnD58uUcPnw4W7VqRXt7exYpUoTl\ny5dn69atOWLECK5YsYInT57k06dPtdJ5C509mxGJy1lZnKI9f/4869aty7p16/LChQuZlmHQoEFc\nvHixOi4n1yIUrCoEBkpTFXp6TChSJMUNGCmTpTuV4evrS1NTU86YMUPjKan2799PKysrPn78WG11\nyuVyli9fnheTua+sXLmS3377rVaNPBIJCAigiYlJkiFFjx49OGHChC/KdezYMcs+ljExMezTpw9r\n1Kih1u+2oJJooX779m3NNKBYZ7wJyV+dAEMgWcUGKRTsIoD+CgWcXMEmAIxp0ybd6t+/f88LFy5w\n48aN9PLyoqenJx0dHVm0aFFaWlqySZMmHDBgABcsWMCDBw/y9u3bjImJ0cy1ZgG5XM62bdtyVf/+\nlHt4MEomY3yq91p6U7RPnz5lt27dWLp0aW7atCnLHYTVq1ezh4ZcGXMLQsFmhjdveKtPH/5paUm6\nuzO4WjX6NWuW4VTG06dP2axZM9avX1/jEV7mz59PR0dHtbqazJw5kwMHDkz6HBcXx0qVKvHo0aNq\nayMrPH78mFZWVjx48CBJKRKQlZWV0mv/5ptveO7cuSy3JZfLuXDhQlpaWvL8+fNZrqegI5fL2axZ\nsxTLDmolDQ+A2wpluiPV/tJQEo1NT4+Rjx/z+vXr3L17N2fPnp3k6mJsbMzixYvT2dmZ3bp14/Tp\n0+nr68vg4OA84961Y8cOVq1aldHR0bx16xYdLCwoV2GKNjIykr/++itLlSpFLy+vbM/oXL58mdWq\nVctWHbkdoWAzyfr165N6XVWqVFHZwTwhIYGLFy+msbExf//9d42N/uRyOfv160d3d/f0rQkzwZMn\nT2hkZJTCcGH//v2sXr262trILGFhYXRwcOBvv/1GUrrur7/+muvXr1davkyZMrx//3622z106BBN\nTEzyTmSrXMbq1atZu3Ztzc3mpPJhHwxQXzEVXAtfhuZTpmAjAY7T1WWVKlWSXF3WrFnDc+fO8dWr\nV7li5iarvHv3jhYWFkmdxFmzZnHIkCHpniOXy7l9+3ba2tqyY8eOajNKi4mJob6+fqan4vMSQsFm\nEm9vb44ePZp3796lhYVFpqdH/vnnH9asWZNt2rSRHK81QGxsLL/99luOGDFCbXW6urpy27ZtSZ/l\ncjkbNmzIdevWqa0NVYmLi2OrVq04aNCgpJfdli1b6OzsrPT3kMvlLFKkSNYtL1Nx/fp1lilThl5e\nXsL4KRM8e/aMJiYmvHbtmuYaURKtKF4xHTwDYKwqI1iACbnQkE8d9OzZk7/88kvS5zp16vDEiRNp\nlg8ODmbDhg1Zs2bNz1b5aqR27dr8+++/1V5vbkFk08kkr1+/hpmZGQ4dOoQ2bdpAR0kC4fSoWrUq\nAgICUL16ddSsWRMHDx5Uu4yFCxfG7t27ceTIEaxatUotdfbu3RsbkmXRkMlkmD9/PqZMmYLIzCZv\nziYjR45EfHw8fHx8IJPJEBERgfHjx2Px4sVKf4/379+jWLFi0NfXV0v7Dg4OCAgIwJkzZ9CxY0dE\nRESopd78DEkMGjQIQ4YMgaOjo+YaUpITWBdSHuBnAFaoWI1OBrmF8yLHjx/HuXPnMHPmTADAs2fP\ncP/+fbi4uHxR9vXr1+jXrx9at26Nnj17IigoCI0bN1a7TLVr10ZwcLDa680tCAWbSV6/fg1zc3Mc\nOnQoyym1vvrqK8yePRu7du3C8OHD0a9fP3z69EmtchoZGeHIkSOYOnWqWlJ1tW/fHoGBgXj69GnS\nvq+//hr169fHkiVppkdWO0uXLsXJkyexc+dOFC4sJbmaN28eGjZsiG+++UbpOc+fP4eVlZVa5TAz\nM8PJkydhaGiIRo0a4dmzZ2qtP7/h6+uLR48eYeLEiRqpnyRu3LiBkJcv0ywTDynPqUrkpZRoKhAe\nHo5BgwZh1apVScneDxw4ADc3t6TnCABiYmIwb948VKtWDSVLlsSdO3fQv39/6OrqakSu2rVr4/Ll\nyxqpO1eg7SF0XsPV1ZW7du1i8eLF1TLlGBYWxj59+tDe3l4jUyWJiQFu3bqV7boGDhzImTNnpth3\n7949Ghsbqz3FmDKOHDlCS0vLFC44jx8/ZqlSpdK17j169ChbtGihEZnkcjm9vb1ZunTpvBHwXQu8\nfv2a5ubmanUhk8vlvH//Pn///Xd27tyZZmZmLFeuHHfVrcu4woX5GqCvYs01HlKI06IADyS640AK\nD1ga4HHF//LkFrR5KCWaKvzyyy9fpOxr3rw59+zZQ1L6Pvfv3097e3u2adOGd+/ezRG5AgMD6eDg\nkCNtaQOhYDOJo6MjZ86cyXbt2qm13r1799Lc3JxeXl5qN+lfv349y5Url+3EABcvXmT58uW/MPIY\nOnQohw0blq26M+LatWs0NTX9woL3hx9+4JQpU9I9d/Xq1ezdu7cmxeOBAwdoYmKikXRreZ3OnTtz\n9OjR2a7n+fPn3LJlC3v37k07OztaWFiwW7duXLt27WfDG4UV8RuALpBCmhoCrA7w92RrrIk+sMm3\nh8msiPNDkINELly4QAsLC7579y5pX2hoKA0NDRkeHs4bN26wefPmrFq1Ko8fP56jskVHR1NfX19t\n9hG5DaFgM4mFhQXbtGmjkeDkL1++pJubG52cnNQy4kzO+PHjs50YQC6Xs3LlylL0lWS8efOGxsbG\nGnNBevnyJW1tbVMYWZHkX3/9RWtr6wytEKdNm8ZJkyZpRLbkXLt2jXZ2dpwyZYowflKwb98+VqhQ\nIUsv0Pfv33PPnj0cMmQIK1euTCMjI3p4eHDZsmW8detW2ta8IidwEol5dnfs2JFi/+bNm9myZUv+\n9NNPNDU1pY+PD2NjY7UiY61atbIUqCIvIBRsJkhISGChQoVYokQJjVkAy+Vyrly5ksbGxvTx8VHb\nizoxMUCPHj2y5Wbg7e3Nvn37frF/1qxZ7NSpU3ZEVEpERATr1KnD6dOnp9ifkJDA2rVrq+QuM2DA\nAK5YsULtsinj1atXrF+/Pjt27JgjYTJzM6GhobSysuLZs2dVKv/p0yf6+flxzJgxdHJyooGBAVu0\naMF58+YxKChIdZewApYSLT2mTp36RZ7d2NhY1qhRg4aGhvz5559TjGy1Qb9+/fi///1PqzJoCqFg\nM8Hbt29paGjI+vXra7ytu3fvsl69evzuu+8yFd8zPSIiIrKdGOD58+csWbLkF6PGiIgIli5dOkXE\np+ySkJBAT09Pdu/e/YtOwfr16/n111+r1Flwc3PjgQMH1CZXRkRFRbF79+6sXbu22n67vEjv3r35\n008/pXk8OjqaZ8+e5ZQpU9iwYUMWK1aMLi4unDZtGv39/bO3VKLGeLu5jtevJX/fDFLv3bx5kyYm\nJinuwWPHjrFy5crU1dXNVuAVdbJixQr26dNH22JoBKFgE1Hhpr158yaNjIw4Z86cHBEpLi6O06dP\np5mZmdoC+T9//pw2NjbZqq9169ZKs8ysXbuWjRo1Upsj/oQJE5ROa3/8+JFWVlYqGxXVqlVLLcm2\nM4NcLufs2bNpbW2dI7GocxvHjx+nnZ1diuhG8fHxvHTpEufOncvvvvuOBgYGdHZ25tixY3n8+HH1\nBxxQMY54PEB5XlCuitR71NP7MlpVqtR78fHxrFevHleuXEmSvHPnDt3c3Fi+fHl6eXnRxcVFyxfz\nmYCAANaoUUPbYmgEoWAzcdOePHmSRYoU4c2bN3NUxICAAFaoUIHdu3fnhw8fsl3flStXaGJikmWr\n1127drFp06Zf7I+Pj2e1atXUMlpct25dmoZZ48ePz1QMUzMzs6SUeznN3r17aWJiopFMR7mVjx8/\n0s7OjseOHePNmzfp4+PDdu3asWTJkqxatSqHDh3Kffv2MTQ0VPPCJIsjnjolWmyhQpTr6fGsqSl3\njh2reVmyQyaTjpzw9GTjxo35/v17jhw5ksbGxpw/fz6jo6PZp08fLlq0SNtXlERUVBT19fUZFRWl\nbVHUTsFWsJm8aY+1a8dixYppJVRaeHg4Bw8eTFtbW54+fTrb9R04cCDLiQGio6NpbGz8RcYaUnKl\nqVy5crZC4Z0+fZpmZmYMCQn54ti///7LUqVKqTz1GhMTw8KFC2stpCMpxVy1sbHh9OnT83SYPVV4\n8OABmzZtyrJly9Lc3JxlypRh3759uXXrVr58+VJ7gqVKiXbExITLypQh37zh9evXaWZmprn0cNkl\nC9PdEQAPu7vT3Nyc/fr1S7IZiYuLo4mJSa7L6VyjRo186eZWcBVsFm7aKB0dzihdWqtiHz16lFZW\nVhw1alS2e3wLFizIcmKAn3/+mdOmTftiv1wuZ9OmTblq1aovT1JhGv7OnTs0MzNLM3xbhw4dOGPG\nDJXlfPz4Ma2trVUurylevHjBevXq8YcffshXLgkvX77k1q1b2bdvX5YtW5ZGRkbU19fnkiVLlHbA\ncguTJ09miRIlkj4PHjxY465mWeLSJUbr67MPQFuABgBrADyqeCdtAVgs2ZYYdzlI8b4KSWUEePbs\nWdasWVNLF5M2ffr0yTFDxJykYCrYbFgZRuvqat3K8O3bt+zQoQMdHByyFdc1MTGAm5tbpkd4QUFB\nLFOmjFIr56CgIFpaWn7OtqHiNPyHP/5ghQoVuHr1aqVtnj59mnZ2dplSUIk5K3MDkZGR7NKlC+vU\nqaO1Kevs8uHDB+7bt49Dhw5l1apVWbJkSbZr144+Pj4MCgpihQoVuG/fPm2LmSE3b96kTCZLWnJ5\n+/YtTUxM+M8//2hZslR4eDAc4FSFn24CwEMKRftQyftpPcBykIJmyJW4HI0YMUJpx1jbLFu2jP36\n9dO2GGqnYCpYDw8uBVgb4FcAf0x2g6aXjJkAE3KJn5xcLueGDRtoYmLCefPmZXkKNKuJAeRyOR0c\nHHjq1Cmlx7t27Sq51qg4DS+XyRilo8M9rq5K64uPj2eNGjW+8OfLiN27d9PDwyNT52gSuVzOGTNm\n0MbGJimHbW4mPDycx48f59ixY+ns7EwDAwN+9913nDt3LgMDA1Pcd2PGjNGIq5YmkMvlLFy4MDdt\n2pS0b/Hixfzuu+9yzzR+Gqn3CNAB4G4l+5sAnJZ8X7KgGXK5nGXKlOHVq1e1fGFfcuHCBdaqVUvb\nYqidgqdgFTftHoD7AA5SomDTSsas7KbVNg8ePGCjRo3YuHFjPnr0KEt1hIaGsmLFikkWh6ry22+/\nfRF+Lblco4oWpTyVYUlGW1rWnKtWrcqShfKSJUsyTMelDXbt2kUTE5OkUHW5hZiYGPr7+3PatGl0\ncXFhsWLF2LBhQ06ZMoVnz55NM1DJpUuXaGZmxtevX+ewxFmnYsWKKTpfsbGxrFy5Mg8dOqRFqZKR\nKvVe4vYKYBFISeST738EUAfgg9QzRIqwj1evXmXZsmVzTwciGZGRkdTX189WIJzcSMFTsKluWq9U\nCjb5llYqq9wWqzQ+Pp7e3t40MTHhxo0bs/QA3bt3j+bm5vzjjz9UPuf169csUaKE8jXcS5cYU6hQ\nlqbhUzv7//fffzQ3N2dwcHCmr2vs2LGcPXt2ps/LCYKCgmhtbc2ZM2dq7aUXHx/PoKAgzps3jy1a\ntKChoSGdnJw4ZswY+vn5qZRUOyYmhg4ODty6dWsOSKw++vTp88X6vJ+fHytUqKD2cKVZQknqvViA\nzQAOUPLc/AqwsbLnSWFxP23aNLWmsMwS6dhhODg45Lg7naYpeAo21U2bJQWb7KbNTVy5coXVqlWj\np6dnlqKznD17NtOJAdq1a6c8bKSHh7QGlOp766aYGTAEWAHgamXfbapp+FGjRmXZEb179+5KfXZz\nC8+fP6ezszO7deuWI24Kcrmct27d4rJly+jh4UEjIyNWqVKFQ4YM4Z49e7JkSTtt2jS6u7vnypFR\nehw7dow6OjpfWLy7ublxwYIFWpIqGe7uKZenAHYG2Apf5rUlwPIA1yl7ntzdSUqWuqpG1VI7Kthh\nBNracu+ECdqRT0MUPAWb6qbNsoJV3LS5jaioKI4cOZKlS5fmsWPHMn1+ZhMD7Nu3jw0bNky5M521\no5uQMpkQ0hSXOSSLx7Sm4e/evUtjY+Msu3g0bdqUf/75Z5bOzSkiIiLYqVMnfv311xpxZXn06BHX\nrl3Lbt260dLSkra2tuzduze3bNnC58+fZ6vu69evfxEtKK8QHR1NmUz2RUSj27dv08TERCvT3W/f\nvuW+ffs4YsQIHilV6vPSCcBekNZYI5U8L39Byhb0MY3BwIMHD2hqaqoddzUV7TASZDJGFyqU+wN+\nZIKCp2Dz8Qg2OSdPnqSNjQ2HDBmS6Zi4mUkMEBsbSzMzs5TprdJYO0q93VaMZncoO66Yhm/Tpg29\nvb0ze/lJVKxYUe2JEzSBXC7ntGnTaGtrm20jlFevXtHX15f9+/dnuXLlaGpqys6dO/P333/n/fv3\n1TbSjIuLo7OzM3///Xe11KcNLCwslIZzHDlyJPv376/x9p8/f05fX18OHjyY1apVo6GhIVu0aMFZ\ns2bxweDBlCueo4EA60FKv6fsWeoPsIeS/XLFc7Ro0SLthCPMzyErVaDgKVg1rMHGFi7MD15e2r6S\nDAkNDWXXrl1ZqVKlTIXrS0hI4Pfff69yYoARI0bQK/n3oWTtKPk2GJ/99Wql89J43qwZ7e3ts2X4\nYGBgwP/++y/L5+c027dvp4mJCffv36/yOR8+fOCBAwc4bNgwVq9enSVKlGDbtm25ePFi3rhxQ2NT\nt/PmzWOzZs3y3NRwctzc3Fi9evUv9n/48IHm5uZqtfSWy+V88OABN2zYwD59+rB8+fIsVaoU27Vr\nx4ULFzIwMDDldLViJuiR4lkpgpQ+r1sUz0kUpLR8J5Q8Q1EAvUePZr169Xjw4EG1XYtKZODDS4XM\nlRTvgyaQDLWSlGw+CDFa8BSs4qaNU9x84wF2V/wfp/hx003GDDBGR4cVjYxYo0YNenl58fz581qN\nFJQRvr6+NDMz44wZM1SOsJSYGCB1gnVlXLt2jdbW1p+/g1TT8Mq2eEiW2jOgfD2JAE8ZGGTLpzIs\nLExrkbfSRIVgG5cuXWLp0qU5d+5cpbJHRETwzz//5Pjx41m3bl0aGBiwefPmnD17NgMCArIVRUtV\n7ty5k2Y0r7zEqlWrWKRIkTSPubi4ZPn+SVzvXrlyJbt27Upra2taWFiwc+fO/N///scbN25knC0r\nm6n3wpo3Z69evQiAnTt3VmsyjgzJwIf3LcDiAHcq3rGjIY3SE2XPDe6Q2aXgKViS9PDgVHyZcHmq\n4se1U3LsYaofPj4+nn/99RcnTJhABwcHmpqasmfPntyxY0euHDE9ffqUzZo1Y/369VXO25qYGEAV\n31MnJ6fPFsgZjGCTbwMBLknj2BYdHTZr1ox9+/blzJkzuWXLFv7999988eKFSmn8QkJCWLFiRZWu\nVeNkIuY1ST579oxOTk7s2bMnP336xL/++ou//vorGzduzGLFirFBgwacPHkyT58+neOuDQkJCWzY\nsCEXL16co+1qgnfv3lEmkyntKCT6XqsaRzo+Pp6XL1/m4sWL2aFDB5qamrJMmTLs2bMn16xZw3v3\n7mVeWash9d66devYpk0b/vbbbyxXrhzr1KnDzZs3a/a+UcGHdxXA+sn2hwPUQzL3o1zkDplVCqaC\n1UC+yEePHnH58uVs3bo1DQ0N2aRJEy5YsIC3b9/ONSOohIQELl68mMbGxvz9999VkkvVxAA+Pj7s\n0qWL9EHFNVgC7AtwmJL9EQDHFyrEmjVrslWrVvT09KSHhwfr1q1LMzMz6unpsVKlSmzRogUHDRpE\nb29v7tixg5cuXeKbN28ol8t54sQJNmnSRB1fXfbIZMzrhP/9j5cvX+asWbNoYWFBXV1dVq9enaNG\njeKRI0eyFNpSnSxbtowNGjTI1bM2mcHQ0DDNDFnpRQ+LjY3lhQsX6O3tTTc3N5YsWZKVK1fmgAED\nuGXLlizF+VbK8uWZ9idPvo7Zpk0bbt68maTUCTh06BBdXV1pbm7OKVOmZNvQTSkq+PAOgxSHIPnx\nakgWQCOXuUNmBRlJoiCyYgUwejQQGanyKbGFC+OrJUuAwYPTLRcZGYlTp07h8OHDOHLkCIoUKQJ3\nd3e4ubnBxcUFRYoUya702eLWrVvo3r07rK2tsXr1apibm6db/uDBgxg8eDAuXLgAW1tbpWXev38P\ne3t7PHr0CCVjYwE7OyA6OkWZNwBOAXAHoA/gBIAOAHwBtE1VX5yuLj798w8u3L+PCxcu4MKFCwgM\nDISVlRXq16+P2rVrw9raGrq6unj8+DEePXqEhw8f4uHDh3j06BFiY2NhZGQEkujQoQPKlCmDsmXL\nJv0tWbJklr67TJOF+ywSwDwzM7z5/ns0bdoUAQEB2LNnDw4ePAgHBwfNyaoCjx49Qp06deDv74/K\nlStrVRZ1Ua9ePejp6eHs2bNKj3t6eqJmzZoYNWoUAgICcO7cOZw7dw4BAQEoX748XFxc4OLigoYN\nG2b4LGWVHU2bov1ff6FIQoKkftJCJgP09YEFC4DBgxEeHg4rKys8fvwYRkZGKYqGhIRg2bJl2LZt\nG1q1aoWhQ4fi66+/hkwmy77A3bsDW7em2BUHoBUAewCrAPQFYApgbrIy3wDoD6BX4o4ePYBNm7Iv\nj7bQsoLXLpkYWUQXKsSTHTtmugm5XM6rV69y5syZrF+/PkuUKMEOHTpw7dq1Ws0uEhMTwwkTJtDC\nwkKl9HILFiygg4NDuqMnT0/Pz9GglKwdvQHoAskgwxBgdYC/K/m+4wFGu7l9UX98fDyvXr3K5cuX\ns0ePHixfvjxLlChBV1dXTpkyhX5+fkmxZf/77z8OGzaM7du356JFizhs2DC2adOGDg4ONDAwYMmS\nJVmzZk16eHhwxIgR9PHx4aFDh3jjxg2VgiuohGKmJK2wnP8o9pdUbM0U+5TNlGzdupWmpqY5b6iS\nDLlcTldX11wbuCOrTJo0iUZGRl/sDwsLo5+fHwcPHsxChQpRT0+P9erV49ixY3n48GG1pI5UhRs3\nbtDU1JQf/vyTH11dGQUwIa1lhg4dUtw3u3fvZvPmzdOt/8OHD1y0aBHt7e3p7OzMjRs3Zn/6WAUf\n3mGQDB6Tl6uOVCEgc6k7pKoU3BFsIkFBwJw5wNGjUu8vKirpULSODgrr6kK3TRuMDwtDrf790blz\n52w19/btW/j5+eHIkSP4448/UKFCBbi5ucHd3R21atWCjo5Odq8oU/z111/o2bMnvv32WyxatAiG\nhoZKy5HEwIED8eLFCxw4cAC6urpflDly5AhmzJiBixcvAoGBQJMmmRq5JRJXuDAKnz8PODtnWPbt\n27e4ePFi0ig3KCgItra2qF+/Ph4+fIi6deti1qxZKb5XkggNDU0x4k3918DAAGXLlk0x6k38a2dn\nBz09vYwvpEMHYP9+7CWhA+A4gCgAGxSH/1NsdgDkAP4HYA2A64B0L3p4AHv2JFUXEBCADh06YMSI\nERg1apR6RhqZYP369Vi6dCkCAgJQuHDhHG1bk9y6dQvVq1fHgwcPcO3ataQRakhICJydneHi4oJ/\n//0Xcrkcvr6+OSobSTRv3hweHh746aef0KRJE/Ro2RL9CxcGbtwAPnwAjIwABwegVy/A1DTF+T16\n9ED9+vXx008/ZdiWXC6Hn58ffHx8cO3aNfTv3x+DBg1C6dKlMy94shEsAfQB8AjAUUizVwDwO4CN\nAP5WfI6ANKK9DCBpbkSMYPMJqfJFRnfqRK8iRRipWEdxcXFJM7B9VomNjeXp06c5atQoVqpUiRYW\nFuzbty/37dunvlGUCoSFhbFPnz60t7fn33//na683377LYcPH670eFxcHC0sLJL8TqMXL2akjk6m\n1o4iZTLGLV2a5WuJi4tjcHAwly1bRhsbG5qbm7NkyZJs0aIFp0+fzj/++INhYWHp1iGXy/ny5Uue\nP3+e27Zt46xZs9i/f382b96c9vb2/Oqrr2hpackGDRqwa9eu9PLy4po1a3jixAn++++/jI2N5cf7\n9xlfuHCKa0vPJSwO4DJI7gpJ+5UYeTx58oQ1a9Zk7969czSc34sXL2hqasorV67kWJua5vnz59y+\nfTsHDx5MANTT00vyQfX3908xivv06RNLly7NCxcu5KiMu3fvZvXq1RkXF8cVK1bw66+/VnntOzY2\nlkZGRnz69Gmm2w0JCeGQIUNoZGTEzp078++//86cLUmyNdi0fHjfQLIi3g3JingsklkR55M1WKFg\n02Dr1q1s165d0ufKlStrPJXVvXv3uHjxYjZv3jwpa4mPjw///fdfjbabyL59+2hubk4vL680X96h\noaGsVKlSmrkbx4wZw7FjxzIhIYEdOnTgurp1pQD+KmTTiZTJeF2J039WqVevHv/++2++evWK+/bt\n49ixY9moUSMWK1aM1atXZ//+/blu3TqGhIRk6uURHx/PJ0+e8Ny5c9y4cSOnTZvG7t2709HRkSVK\nlKBMJuMYfBlxJy0FWwKgLkAZJLeljF4w4eHh9PDwYKNGjfgmB6ws5XI527Vrx0mTJmm8LU2hzAfV\nyMiIbdu25cKFC2lra8sOGbiFbNq0iXXr1lXJgl0dREZGskyZMjx16hSfPn1KExMT3rx5U+Xz//zz\nT9apUydbMvz3339cvHgxy5cvTycnJ27YsEGlkJ7/3b3LWF3dDH14/4TkB6sHKY7ywww6mHkNoWDT\noHPnzili7BoZGakcPlAdfPz4kXv27GHv3r1pbm7OKlWqcPTo0Txz5gxjY2M11u7Lly/p5uZGJyen\nNDOk8McAACAASURBVCMgpZcY4NatW7S0tOSYMWPYqFEjaRQQGCitDenpSfl0UymRaB0dBlhb8+ev\nv1arxbW1tbXSDEOxsbEMDAxMsny2s7NjqVKl2Lp1a86YMYMnTpzI0FI3NjaW58+f58yZM9m0aVMW\nK1aM9evXp5eXF48fP84PSnyB0xvBhgP8H8DDqY+lETEsISGBEydOZNmyZTP10s0K27dvZ9WqVfNU\nphO5XM6QkBCuWrWK3bp1o42NDS0sLNipUycuW7aM169fT6Eoe/fuTRsbm3TrTEhIYN26dVOkuNMk\nv/76Kz09PSmXy+nu7i6lf8wEQ4YMUdt6eUJCAo8cOcKWLVvSzMyMXl5eSsNjyuVybtu2jZaWlrxc\npozSeOSqbPGA8IPNr8TExLBkyZJ89epV0udChQrlWM81NQkJCbx06RKnTp3K2rVrJ03bbN68WSNK\nXy6Xc+XKlTQxMaGPj4/S604vMUDZsmVpaWn5pWxv3nCJjQ3ftGzJ+NatucfAgPcGDOCRDRuoq6vL\n69evq+0aEhISWLhwYZWnUV+8eME9e/Zw9OjR/Oabb1i0aFE6Ojpy4MCB3LhxI2/fvs0rV65w4cKF\ndHNzY/HixVmjRg2OGDGChw8f/mLaOcHNLVMKNtEQpBTA18n3Z2DksWnTJpqamvLIkSNZ/q7S4+3b\nt7SwsMjZAAVZID4+nleuXOGSJUv4/ffff+GDevfu3XQ7b35+ftTV1c3wGb9w4QKtrKw0voTz+PFj\nGhsb89GjR/T19WX16tUztSQgl8tZunRpjYQJvX37NocOHUojIyN26tSJ/v7+lMvlvHfvHl1dXeno\n6MgLFy7w3+3bGZEF5ZrY4YzL4el4TSAULPlFdJ0XzZpxqa1t0vTEs2fPaGFhoWUhP/PixQuuWbOG\n7du3Z/HixdmgQQPOnj2b165dU+sI8O7du6xXrx6/++47pb3VDRs2sFy5cimmKU+ePJkUT1UZpUqV\nSgqi7uvrS2dnZw4cOJAWFhYqO/SrwsuXL2lqaprl86Ojo7lz5056enrS2tqaOjo61NXVpZ2dHX/4\n4Qfu3bs36SUrl8t59+5dbt26lb/88gsbNGjAbalH6ioo2DjFVNllFUawyTl//jwtLS3522+/qd3n\numvXrhw5cqRa61QHynxQK1WqlGUf1NjYWMpksnRtEBLp3r07J06cmFXRVaJz586cMmVKljs4ly5d\nYsWKFTXqgx8WFkYfHx+WL1+elpaWLFasGGfPns3Y2FjeuHGDlpaWvNirV5ZiEU8xM1Nrh1tbFGwF\nm050ndhChZKi69zevJk1atTQtrRKiY6O5vHjxzl06FCWLVuWNjY2HDx4MA8fPqzUOT6zxMXFcfr0\n6TQzM1OqACdMmMBvvvmG0dHRvH37Ns3MzHjw4EEWL178i5R579+/p6GhYdJDn5CQkBTgfOvWraxV\nq5baXgjBwcGsWbNmps55+vQpN27cyJ49e9La2pqlS5dmz549uWHDBj558oTPnj3jrl27OGDAAFas\nWJGFCxemoaEhv/rqKxobG7Nly5acO3cuT506xajp05PuqbTCcv6hUKbxAMMADgVoqThOgNG6uvxP\nxXXPR48e0dHRkf369VOb8dPBgwdpb2+f6WQRmiAyMpJnzpzh9OnT2axZMxoYGLBGjRocOnQod+3a\nlTTblB3Mzc05dOjQDMs9e/ZMo2Eiz5w5Q1tbW0ZERLB79+5pGhWmx8SJEzlu3DgNSJeSM2fOsFKl\nSqxXrx6bNGlCU1NT9uvXj6ampty2bZtUKJOBVrh8OQd6eDCwY8d0Q4rmBQqugs3Ejx5XpAgXV66s\nbYkzJDH26bx589i4cWMaGhrSzc2NK1as4JMnT7JVd2KPuHv37in8/xITA3h6etLe3p7r1q0jSf7w\nww9cmsoa+NKlS6xVq1YKeZ2cnGhsbMzIyEg6ODjQz88vW3ImcvDgQbZu3TrdMm/fvuWuXbs4aNAg\nVqxYkcbGxvT09OSKFSt4584dyuVyhoaG8o8//uDMmTPZrl07WllZ0cTEhK1ateLEiRM5f/58Tp8+\nnZ6enrSysqKZmRnbtm1Ln0mTmPDVVySQZljOnZAMPIoBNAHYGuC1ZPdeFEBTgFWrVlUpXOWnT5/Y\ntm1bNm7cOEv5gJPz4cMHli5dmqdPn85WPVnl48ePPHbsGCdOnMiGDRuyWLFirFevHseMGcNDhw4x\nNDRU7W22bt2aDg4OKpWdMWMGv//+e7XLkBiecceOHfTz82PZsmUZHh6e6XqqVq2qUYvnt2/fslev\nXrS2tubevXuTOsYHDhxg0aJFWaxYMXbs2JHnzp2TjiWzw2DqqFTJfXg3bCA9PBhXqBBjlNhrpA4p\nmtspmAo2CymUonV181wKpdDQUPr6+rJ79+40Njamo6MjJ06cmOXkBBEREfzpp59oa2ub4sUbGhpK\nAwMDNmrUKGnf8ePHWbt27RTnb9u2jR2TBevYv38/q1atSjc3N/7222/cunVrijqyw4oVK75IN/bx\n40cePnyYI0eOZM2aNVm8eHG2bt2aCxcu5JUrV5Ji/i5atIhdu3Zl+fLlaWBgQBcXF44ePZo7duzg\ngwcP0hxly+VyPn78mNu3b+cvv/zCUyVLSsYaWdkUMa+Dg4P57bffUldXlwYGBuzfv3+6SdHj4+M5\nduxY2tvbZ2v9rV+/fhw0aFCWz88s79694/79+zly5Eg6OzuzWLFidHFx4eTJk/nnn3/miNvaypUr\nqaenp1LZyMhI2tnZqb0DsmLFCjZu3JhhYWG0s7PLUi7jO3fu0NLSUiM2I3K5nOvWraOZmRmHDx+e\nwhjwypUrNDc3586dO/nx40cuXbqUFStWZM2aNbl27VppRi2VOyR79JA+v3mTpZFubqfgKVgNxCHO\nC8THx/Pvv/9OSk5gYmLCHj16cPv27ZmOSHP06FFaWVlx1KhRjIyMZPfu3dm6dWtaW1snjbTi4+Np\nbf1/9q47rKnki15ApUtJQuhNUSmCFWzoIqKIhaJiYVEUXMCui9g7NnR1FRt2xd4VV7FiReyrWBC7\n2AC7dJJ3fn8E8qMkIUAorp7vex9k3ryZeXkvc6fce44h7sfGCve3HzVsiFvW1sDChchOTka9evVw\n4sQJ3Lt3DxwOB6mpqTA3N8fFixcrfL/Tpk3DlClTcPbsWUydOhWtW7eGqqoqnJycMGfOHJw/fx7X\nrl3D2rVrERAQADs7O6ioqKBFixYIDg7Gpk2bcO/evQrx7cbMmVNuJ4/i71p2djYmT54MNpsNOTk5\nNG/eHCdOnBBb9+bNm8HhcBATEyM6gwRVn1OnTsHY2LjUeOGK4O3bt9i9ezeGDRsGGxsbqKuro3Pn\nzggLC8OFCxekCgWRNT59+gQikjpudM+ePbCzs5MZJ/PHjx+ho6ODf//9FyNHjoSfn1+5ylm4cGGl\nDI4ePHiA9u3bo0WLFrh582aRczdv3gSXy8W+ffuKpPP5fMTExMDNzQ0cDgcTJ04UvT/+H9WN/fkM\nrAT5pyQSxGv5lDKr+C/g5cuXJcQJFi1aJHVMaFpaGry8vMDlcmFtbY2MjAyhMEB8fDxw7RruNWiA\nXAUFkeoxebVq4bKurnCpJyAgAKGhoYiMjCx1aVcc8vLyEB8fj7lz50JPTw+KiopwcHDAxIkTsXnz\nZmzcuFHohKSqqgpLS0sMGjQIK1aswNWrV2UWhsIwDMLCwmBsbIzkKVPK3HHwlZXBSOg4YmNj4eDg\nADk5OWhpaSEkJETkPunFixehq6uL5cuX//+ZlqLqwygq4riKCi7LUCmHYRg8f/4cW7Zsgb+/Pyws\nLIQxqIsXL8a1a9eqRGJPGqipqWHhwoVS5WUYBu3bt0dkZKRM6h4xYgSCg4Nx+fJl6OnpSVypkITW\nrVuLH1iVA5mZmZgyZQrYbDYiIiJKDChu3LgBHR0d7N+/X2I5SUlJGD16NLS1tdGrVy+cP39e8F7+\nhyc9P5eBlSChBCK4EKGdJANL9J8Ifi6OjIwMREdHIzAwEIaGhjA3N8eoUaNw8uRJiUZnx44dYLFY\n0NbWRnh4OHg8Ho4cOYIJGhoCIyEFuUTBKPTNmzfQ1tZGUlIS9PX1pWIM4vP5uHv3LpYuXYoePXpA\nQ0MDjRs3hr+/P8zNzeHu7o5OnTpBU1MTJiYm6N27NxYuXIjY2NhKm53l5OTAz88PzZs3x9u3bwWJ\nUi598eXkkKWggBA1Nejr66NXr15YvHgxLl++LHJG9/XrVwwfPhx169aFvLw8HB0dS3ibPn/+HDY2\nNggMDBQwZEnTjgrODkTFoHK5XLExqDUJ9vb2ZVJgKlgWrSgv8d27d8HhcPDmzRtYWlqW26P+7du3\n0NTUlJmj24kTJ1CvXj306dNHpOrO9evXoaOjUybd5m/fvmHFihVo2LAhbG1t8bxpU2QRiRVml8jZ\nXcMnPT+XgZUgo7aTCH1I4Hwi0cD+B+i7JKG4OEHdunXh6elZQpwgLi4OHA4Hd+7cwfPnz+Ho6Chw\nrgkLQ24xikBpl3qmTp2KgQMHYvHixfD29hbZtsePHyMyMhLe3t7gcDgwMzODm5sb+vbtC1dXV+jp\n6YHNZkNdXR2BgYE4evSoMCyosvHp0yc4OTnB3d29pGOKtE4e16+DYRg8ffoU27Ztw7Bhw9C0aVOo\nqKigVatWGDt2LPbs2VNiGfPgwYNo3Lgx5OTkoKurizlz5ggJSb5+/YoV1tbIKiNtpbRGtkCEoXAM\nqomJCXx9fbFu3Tqhw9iPgMmTJ0NbW7tM1wwdOrRCoUwMw8DJyQkrVqzAtGnT4OHhUe7va82aNf+X\njawA3r17h379+sHMzAzHjh0Tmefq1avQ0dGRSixEFPh8PmJ370aOvLxEYfbP+X8ZEnjcLyOBpuyP\nMOn5uQysGCHwr0SwIEKyNAaWSKrYxP8KUlNTsXXrVnh7e0NTUxMtWrTAqFGjwGKxEB0dLczH4/Gw\nZcQIkXuOH4ngQQSV/BHqdjGd+ffYWHC5XFy+fBlsNhuPHj3CmzdvEBUVBT8/PxgZGYHFYqF58+Zw\ncHCAiYmJWCckbW3tKqERLMDTp0/RqFEjjBkzRvKenCQnDwlIT09HbGws5s2bhx49eoDFYsHQ0BDe\n3t5YunQp4uPjkZOTg/fv32PgwIFQUVFBrVq14Orqiqe7dgnoKgt939kSZgylLcHl5uYiPj4e4eHh\n6N69uzAGdejQoYiKihLJnvWj4P79+5CTkytTiFtKSgrYbDYSExPLVee+ffvQuHFj3Lp1SziLLS+6\ndOkilce5OPD5fKxatQpsNhsTJ04UG6IVHx8PDodTpA8oFyRMegqE2QunieTsrsGTnp9LTadHD6Kj\nR0skjyYifSKaQEQziegJEW2TUEwci0UL2rQhFRUVUlVVJVVVVeH/ktKKn1NSUqpyRZSKIC8vj06c\nOEF+fn6koKBA8vLy5ObmRt27d6dOnTqR+qBBhEOHSK7YK9WfBGoxG4joXyLqRkRxRGRdOFO+eky4\ngwPt2LGDateuTYmJiQSAOBwO5ebm0sePH8nGxobs7e3J3t6eWrZsSY0aNSqh7JOdnU0aGhqUlZVV\nJepE8fHx5OnpSVOmTKERI0ZUen1ERADoSSGt3CtXrtDjx4+pSZMm1Lp1a2rVqhUlJyfT6tWracHj\nx+RORIW/pQwiWkQC3U1jEqic9CeiBCIyLVyRnBzxevSgy+PGCVVm4uPjydzcnDp06EDt27cnR0fH\nStNBrWoAIEVFRdq2bRt5e3tLfd1ff/1FsbGxdFRE/yIJWVlZZGlpSevXr6fJkyfT0KFDaejQoWVt\nNhERff36lQwNDenNmzdUt27dMl9/584dCgwMpFq1atGaNWvIxsZGZL4rV66Qu7s7bdq0ibp161au\ntgohQjeWiCiFBCpT/9L/lXU0iSidBH3JbCKaWviCGqq683MZWBEP818i8iGi20RUh6QzsO86daJr\nI0ZQZmYmZWRkUEZGhvB/SWnFz+Xm5lbYSEtKU1ZWlqmBycvLo27dulHDhg0pIiKCnjx5Qv/88w/9\n888/9PjyZXqUnU11GKbINRlEpEVE94ioQX6aLxEZUFGhZSKibCIyU1CgVIDk5OQIAHl6epKTkxO1\nbNmS7OzspBKrf/bsGXXs2JFevHhRwTsuHfv27aNhw4bJprOpIL5//07Xr1+nuLg4unLlCsXHx5Op\nigpdefu2xHMRBVsimkFEvYqlZxORe9OmZOvsTO3bt6e2bduStrZ2JdxBzUCDBg2oadOmtHv3bqmv\nyc3NJRsbG1q2bBl17dpV6utmz55NCQkJ1Lp1a4qOjqazZ8+We9C9a9cuioqKon/++adM16Wnp9PM\nmTNp69atNG/ePBoyZIjYfiMuLo48PDxoy5YtZbpPsRAx6SkuzF4YGSSQuDMhwUBdiO7diaKjK94e\nGaNWdTegSmFrK9DXzM4WJp0jgU6hcf7ndCLiE9EDEugSloCyMul17kzu7u4Vbg6Px6OsrKwyGemU\nlBSp82dnZ5OSklKZDLg4o66iokJLliyh3NxcmjhxIn3//p3MzMxo9OjRNHr0aMqeM4fkw8KIcnOL\n3GMSCV6yBoXS7IjovKgvRF6etrm40KVWrWj//v3k4uJCfD6fhg8fXqbv9c2bN6Svr1+2h1FGAKBF\nixZRREQEnTx5kpo0aVKp9UkDdXV16tixI3Xs2JGIBG1MCw0l+WXLiEoxsCkkeFbWIs4pKinRif79\nicaPl3mbayLatm1LsbGxZbqmTp06tGTJEho3bhx16tRJKr3cV69e0fLly+ngwYPk6elJ8fHxFVrR\nOnjwIHl4eJTpmiNHjtDIkSOpQ4cOdO/ePdLR0RGb99KlS+Tl5UVRUVHUpUuXcrezCDQ0inxkSDAA\nr0NEK0RkVyWiIBLoxj4kImFrtbRk0x4Z4+eawaamEpmYFDGwmUT0rVCWxSQwuKtJ8BBLQEmJ6NWr\nEsLGNREMw5TZgIubeT99+pRSU1OJy+VSVlYWZWZmUmZmJikqKpKKigqty84mLxHi6heJqA8RvS+U\nto6ItpNgcFMcVxs0oC3OznTgwAGqV68e3bx5k7y9vUlJSYkg8Bko9Xjx4gW9evWK2rZtK0xjGEbq\n60s7+Hw+JSUl0bdv38jGxobq1KlTrnJk2SZxx4qvX6lPTo7E90TSjEGIGroEVxk4fvw49ejRg/Ly\n8spk8ABQ165dqWvXrjR69OhS8/ft25caNWpEcXFx1LlzZxpfgQFMTk4OcblcevTokVTL9cnJyTRq\n1Ch68OABrV69WjgoE4eLFy+Sl5cXbd++nTp37lzudhZGZmYmJfr7k/WePaTIMGKF2YuDR0TqJNhm\nakpEpKxMNGtWjRwA/lwzWB0doq5diQ4dEmyPE5FK/lEANSJSIjHGVU6OyM3thzCuRETy8vLCWWlF\ncOTIEQoKCqJHjx6RiYmJMB2A0Niq9O1LdPZsiWvVqOgAhvI/q4upS6d2bbKysiIlJSXavHkzNWvW\njNLS0sjDw4Pk5OSkOmJiYkhNTY169OhBcnJyJC8vL/W1pR2ZmZk0Z84cMjY2pmnTppGqqmq5ypFl\nmyQdmgMHEp06JfbZljZjEOLzZ0ln/1NwcXEhhmHo+vXrZG9vL/V1cnJytGTJEurQoQP5+PgQm80W\nm/f8+fMUHx9PTk5O9PnzZxo7dmyF2nz27FmysbEp1bjyeDyKiIiguXPn0siRI2nXrl2lbrucP3+e\n+vTpQzt37qROnTpVqJ0A6OLFi7RlyxY6cOAAdWnalKLyBzHBJJiVnqaixvUUEbFJsIWRQYK9Vy0i\nsvx/oUR+fhVqV6WhrF5RPzz+w0HNlYFbt26BzWbj6tWrYvNkZWXhrbOzyO8snQi1SUDiUZDmS4QJ\nUnhoe3p6IjQ0FCwWq0xxq3/++afUZAFlwYsXL2BtbY1hw4bVGGIESfj48SOetmkj9n1miOBHhN+o\npDh8iby//17dt1Ol4HK55SLZB4BRo0YhODhY7Pm8vDzY2tpi7dq14HA4UsV8l4ahQ4di0aJFEvMU\ncIF37NgRjx49kqrcs2fPgs1m48yZMxVq39OnTzFjxgyYmZnB2toa4eHhOHPmDJydnXFKXR3PSLww\nu0TO7l9xsDUQ/1FaLlnj9evXMDQ0xN69e4ukF4gKLF26FF27doW6ujoijI0FCkQivru+ROiXb2wv\nEaEuEe6JyMdXUiribp+YmAg2m43evXtjwYIFUre7X79+2LZtm8y+B0AQUK+vr4+lS5fW6JjOx48f\n46+//hKKPWy2skKemLjkQCI4EOF7Ke9+BhHmaWtj6tSpMpdErKno2rVruRW0Pn36BB0dHdy5c0fk\n+VWrVqFDhw7w8vLCpEmTKtJMAIIQOS6Xi8ePH4s8/+XLFwwfPhy6urqIioqS+vmdOXMGbDa73HzL\nX758wfr16+Ho6AgOh4ORI0fixo0bSEtLw7Bhw8DhcBAREYG8uLj/7KTn5zSwgPTsOkTIqV37pzOu\n379/R9OmTTF//nwAgtnQ7t274e/vDyMjIxgbG2Po0KHYu3evQNlEAkvWRyK4kyAO1ojExMGSQD0m\nwN0dsbGxwk4gODgYvr6+4HK5UscmOjo64uzZszL7Lg4ePAg2m10mtpqqQgHH9IQJE2BpaQldXV0M\nHToU0dHRgu9LzHN5IWHGUDxvroICTFVVYWFhAR0dHVhYWGDKlCn4999//7PGdtWqVVBWVi739StX\nroSTk1OJ76eAb3jJkiVo0KCBTDiXL1++DBsbmxLpDMNg9+7d0NfXL1UkojhOnToFDoeDc+fOlakt\nPB4PMTEx6N+/PzQ0NODp6YlDhw4hJycHubm5WLZsGTgcDkaMGFFU8ek/Oun5eQ0sIBW7zg1TU+yT\nwSjzRwKPx0P37t3h5uaGqVOnwt7eHurq6nBzc8OyZcuQmJgoumP19AS/NCUMcYecHHK6d0dERASs\nra3RsGFDLFmyBA8fPoS2tjacnZ2xYsUKqdpfr149qZfAJIFhGCxZsgT6+vq4XoNGyd+/f8eBAwfg\n5+cHDocDW1tbTJ06FdeuXRNNQSiBf1ua5wIvL3z79g2rV6+Gra0tjIyM0KFDBxgaGsLCwgKTJ0/G\n7du3/1PGtoD4vzB7WVmQl5cHGxsbHDhwoEj68OHD4e/vD319fVy4cEEWTUVISAimFtMNfvr0KVxd\nXWFjY4NLly6VqbwTJ06AzWaXqX33799HaGgo9PX10aJFC0RERCAtLU14PiYmBpaWlnBxccG9e/dE\nF/JLTec/ikLsOtd1dfHM0VHIrtOzZ88SP5L/Kp4+fYrVq1ejfv36UFBQgK2tLSZMmIAzZ86USoTP\nMAy2jR5dbvUYptBSD8MwuHjxInx8fKChoQE7OzvY29vDxMRESP8nqR1KSkoVljfLy8sTKr3UBGai\nN2/eYM2aNUJxhk6dOmH58uV4/vx56RfL0O+AYRhcvnwZvr6+0NDQQNeuXTFgwACYmJigfv36mDRp\nEm7duvWfMLZqampYvHhxua8/ffo0zM3NhbPUAr7h33//XeIebVnAMAzq1asnVLfJycnBvHnzwGKx\nsGDBglJ/L8URExMDDocjlaJVWloali9fjubNm0NfXx+hoaG4f/9+kTyPHj1C9+7dUb9+fRw+fLj0\n96LQpIcvQoyiMKXoj4BfBrYYJkyYgLCwMOHnVq1a4fLly9XYosrDt2/fcPjwYQwfPhz169cHl8uF\ng4MDdHV18fDhQ6nLyc3NRWBgIBo3bowPYWFl7swz5eWx3dFRJMVgWloawsLCoKCgAGVlZQwcOFCi\nw9OnT59Qt27dcn0fBfj27Rvc3Nzg4uKCL1++VKis8qKAE3r27Nlo0aIFtLS0MGDAAOzatat8baqE\nJbi0tDQsWrQI9erVg52dHSZNmoTRo0fDzMwM9evXx8SJE3Hz5s0f1ti2bNkSHTt2rFAZHh4emD9/\nPhiGwW+//YZRo0bByMhIZmIT9+7dg5GRkXBQam1tDTc3Nzx79qzMZR07dgwcDkdif5eTk4ODBw/C\nw8MDGhoaGDBgAE6cOFHit/v582eMGzcOLBYL4eHhZVeqSk1F6vjxOKCmViZK0ZqGXwa2GNatW1dE\nh9HMzEys88CPBj6fj+vXr2Pu3Llo37491NTU4OzsjIULF+Lff//FiRMnwOVykZSUJHWZX758QefO\nndG1a9f/dxqrViFPUbFUsXEeEXiKishcsgQdOnRAv379xKqArF69Gubm5lBTU4OGhgb++OMP3Lp1\nq0S+hIQEWFpaluv7AYDk5GTY2dlh6NChZR79VxQ5OTk4ceIEhg8fDmNjY5ibm2Ps2LGIjY2VTVsq\naQmOz+fj5MmT8PT0hJaWFoKCgrBr1y5MmDAB5ubmqFevHiZMmIAbN278UMZ24sSJYLFYFSrjyZMn\nYLFYWLt2LaytrWFubl5x/t5CmDNnDgICAuDv7w8DAwPs3bu3XN/x0aNHweFwcOXKlRLnGIbB9evX\nMWLECLDZbDg6OmL9+vUiBwk8Hg+RkZHgcrkICAjA+/fvy3VfgOC3bG1tXe7rawJ+GdhiiI2NhaOj\no/Czqqoqvn37Vo0tqhhev36NTZs2oV+/fmCz2bC0tMTo0aNx7NixIoov9+/fB4fDwfnz56Uu+/nz\n57CyssLw4cOLhK0wDIOBVlZ47eAgcX/7tYMDepmYIDs7G5mZmejZsye6du0qkmA8Ly8PlpaWsLCw\nwPr164V6q/b29tiwYYPwmpiYGDg7O5fru7p16xYMDQ0RHh5eZYbg48ePiIqKQp8+faChoYHWrVtj\n/vz5uH//fuW0QYLfAVOgEVuBJbjXr19j5syZMDAwQJs2bbB161bExcVh4sSJqFevHszNzREaGvpD\nGNt79+6BiCos/TZu3DioqqrC29tbJko3BWAYBqamptDS0sLIkSPLPSs+cuQIOBxOCanDN2/eYOHC\nhbCysoK5uTlmzpyJp0+fii3n3LlzsLOzQ7t27UoIspcHN27cQNOmTStcTnXil4EthlevXkFPdsOG\ngQAAIABJREFUTw+AQMFESUmpxncEhZGZmYkTJ05g3LhxsLGxgZaWFvr06YN169bh5cuXIq9JSUmB\nmZkZtmzZInU9V65cgZ6eHpYvX17i3JkzZ9CwYUOBw40E9RiGYeDu7o7p06cDEBhRX19ftG3bVqS+\n5pEjR2BkZIRmzZqBYRjweDwcPXoUPXr0gLa2NkaOHIk5c+Zg4MCBUt9HAaKjo8Fms0uEJFUGiofS\nuLu7Y8OGDRUa7ZcZhZ5LWuvW2FGrFp4NGyazJbi8vDwcOHAALi4u4HA4GD9+PB4/foxbt25h0qRJ\nqF+/PszMzBAaGorr+RJ9NRG1a9eu8DsxadIk1KlTR6YKT4mJiWjTpg0UFBREzjqlxaFDh8DhcIRx\n7hkZGdixYwe6dOkCLS0t+Pv748KFCxKfz/Pnz9G7d28YGxtj9+7dMnuWcXFxcHBwkElZ1YVfBrYY\n+Hw+lJSUkJ6ejmfPnsHExKS6myQRDMMgISEBixcvRufOnaGmpoa2bdti1qxZiI+PlyydBgFJROvW\nrTFlyhSp69y1axc4HA6OHj0q8ryzszM2bdokVVmvX78Gm80Wehby+XyMHDkSdnZ2JQwOwzBo3749\n9PT0cPLkySLnXr58iWnTpkFNTQ1GRkbYvn271Ps+ERER0NXVrVBHJQk8Hg+XLl0SH0pTzXj27BlU\nVVURGRlZKeU/fvwYISEhYLPZ6Ny5Mw4ePIjc3Fzcvn0bkydPhoWFBUxNTTF+/Hhcu3atRhnb+vXr\no1+/fuW+/sWLF9DW1oauri7q169f4XvLysrC9OnTwWKx4OXlhd8rQABy4MAB6Ojo4Nq1a7hw4QL8\n/f2hpaWFLl26YPv27WKl6grw/ft3TJkyBdra2pg9e7bM3+Vz586hffv2Mi2zqvHLwIqAlZUV7ty5\ngytXrqBly5bV3ZwSSEtLw86dO+Hn5wd9fX2YmpoiMDAQBw4cEDnzEweGYdC/f394e3uLDu8QkT8s\nLAxGRkb4999/ReaJj4+HsbFxmfYMV61ahTZt2gjbwDAMZs6cCQsLixJeslevXoWWllaRZfzCCAwM\nhL+/v3DmFBISInZPmcfjYcyYMWjUqFG5nEIkocyhNNWInJwcyMvLY+TIkZVaT1ZWFqKiotCmTRsY\nGBhg5syZeP36tdCha8qUKWjQoAFMTU0REhKCq1evVruxHThwIMzMzMp9fZ8+fdCxY0e4urqiefPm\n2L59e7nLOn36NCwsLODl5YXk5GR07Nix3LHZ+/fvB4vFQmBgIMzNzWFlZYWFCxfi9evXpV7L5/Ox\ndetWGBgYwMfHB8nJyeVqQ2k4ceIEOnXqVCllVxV+GVgRKAjNOXz4MLp3717dzUFOTg7Onz+PyZMn\no0WLFqhbty569OiBFStWICkpqdyd0IwZM+Dg4CDVyDMnJweDBg1C8+bNJQpCu7u7IyIiokzt4PP5\naNu2LVauXFkkfdmyZTA0NCzh+t+7d29oamqK9HYsHFb1+PFjjB8/HhwOB506dcK+ffuEhj89PR09\ne/aEk5OTgChDBnj9+nX5Q2mqGdra2mjXrl2V1Xfnzh0EBQVBU1MTXl5eOHnyJPh8PhiGwZ07dzB1\n6lQ0bNgQJiYm+PPPPxEfH18txvbo0aOoVatWueqOjY2Fvr4+WCwWXrx4gUuXLsHQ0LCI74M0SElJ\ngY+PD0xMTIQOUh8+fIC6unqps8zi+Pr1K4KCglC7dm1oampixIgRZVqij4+Ph4ODA1q2bIm4uLgy\n1V1WREdHw83NrVLrqGz8MrAiMHbsWISHh2Pt2rXw9/ev8voZhsHjx4+xYsUK9OzZE3Xr1kXz5s0x\nefJknDt3rsJOFwCwbds2mJqaSrXv9+HDB3To0AEeHh4SO4d79+6ViXGpMO7fvw8Wi1ViNLx161Zw\nuVxcu3ZNmPbkyROoqqrCxcWlRDnNmzcv4ayRnZ2NHTt2CJeXR48eDRsbG/j5+VXou5R5KE01olmz\nZmCz2VVeb2ECi/r162Px4sVChh+GYXD37l1MmzYNjRo1grGxMcaNG4crV65UmbHNy8uDnJxcmZ12\nCviGGzVqVGTA2b9/f6HPQWng8/mIjIwU7mEX/u1t2bIF7u7uUpXD4/Fw4sQJDBgwACoqKlBUVMSS\nJUvK9O6/fv0avr6+0NfXx+bNm6tkFWb//v3w9PSs9HoqE78MbHGkpOCyhweu1K+PRw0b4pa1NbBw\nYaXHX3358gUHDhxAUFAQzMzMoKenBz8/P+zYsUNmjhEFuHjxIjgcDhISEkrNm5SUBAsLC4SEhJT6\no/r999+F1IrlwYwZM9CzZ88Snefhw4fB4XCK0B8OGzYMKioqAr7XlBTBM/LxwQlFRaR7eop9ZgcP\nHoS6ujqUlZXRrVs3REdHl7pPXRiVHkpTTfD29oaSklKZthhkieIEFr6+voiLixO+CwW+BtOnT4el\npSWMjIwwduxYxMXFVXpnr6Ojg3HjxpXpmpUrV8LCwgKtW7cu0r5Xr16BxWKJdTgswN27d9GmTRu0\natVKJKexp6cnNm/eLLGMBw8eYMKECTAwMEDz5s0xaNAgiRzJopCZmYmwsDCwWCxMnjy5wgQuZcGO\nHTvQt2/fKquvMvDLwBbg2jUBpZySEnh16ohmEPH0FOSTAXg8HuLj4zF79my0bdsWampqcHFxweLF\ni5GQkFBpI/QnT55AV1cXMTExpeY9f/48uFyuVM4vT58+BYvFqtDMLTs7G5aWliK9NmNjY8HhcHDo\n0CEAQGpqKtopKiJOV1fwbMSxvhR6ZgUsNTt27EBGRgY2btwIBwcHGBsbY86cOXj79q3IdlV5KE01\nYPz48TA0NKwRpCrFCSzWrFlTIlTu3r17mDFjBqysrGBoaIgxY8bg8uXLlWJsu3TpgiZNmkid/8OH\nD2CxWNDQ0MCDBw9KnJ85c6ZYw5Geno7Q0FBwOBysWbNG5P1kZGSgbt26Rbl8C9UdERGBli1bQk9P\nD+PHj8e9e/ewfft26Orq4u7du1LdA8Mw2Lt3L0xNTeHl5SUxPKeysHnzZvgWUtf6EfHLwAJVxoH5\n6tUrrF+/Ht7e3tDW1oa1tTXGjRuHmJiYKvEm/fTpExo1aoRVUrR/y5Yt4HA4OHXqlFRlBwUFlckT\nWRwuXrwIfX19kfui169fh66uriCcaNUq5NSuXSqZRcEzO9+/P7hcrkgKuFu3biEwMBCampro1asX\nTp06hcTERGEoTd26deHh4VH1oTRViBUrVqBhw4ZYt25ddTdFiOIEFsHBwSINRGFja2BggNGjR+PS\npUsyM7YrVqyAqqqq1PmDg4NhYmKC2bNnizyfkZEBIyOjEly/R48ehampKQYMGCDxPTt06BCcnJyE\nn3NycnDo0CF4enpCQ0MD/fv3R0xMjDA2PSoqCnp6elKtWAHA7du30b59e9ja2spUNKOsWLt2LQIC\nAqqtflngl4GtRBWHjIwMHDt2DKNHj4alpSVYLBb69euHjRs3SuWtJ0vk5uaiY8eOpWpc8vl8TJ06\nFWZmZiWci8Th7du30NLSktlSdlBQEIYOHSry3IMHDzBJUxO5YiTYxB0ZcnJImTVLbJ0F+1SdO3eG\noqIiFBQU4ODggO3bt9eIUJrKxpEjR9CoUaNya6BWNooTWERFRYlUorl//z5mzpwJa2trGBgYYNSo\nUbh48WKFjG0B8b807/edO3dQt25dWFpaStzj3LlzJ5o2bQoej4fXr1+jV69eqF+/fonwM1Hw8/PD\n33//jRs3bmDUqFHgcDho164d1q1bV2IFacuWLdDT05Pqt5ySkoI//vgDXC4Xa9asKdPWSWUgIiIC\nw4YNq9Y2VBQ/t4HNJ0GPIEJzItQhwqBiHfNpEoj9KpNAmPqFGBJ04P9OL+Hh4XB2doaamhrat2+P\nsLAwXL9+vdpeWIZh4O/vj+7du0tsQ1ZWFvr27YvWrVsjJSVF6vJDQkIwatQoWTQVgGA/2sDAQLRU\n1rVr4Bdnhioncb24UJqrV6/i8uXLGDRokJBvtbRg+x8d//77L4yNjdG5c+fqbopEFCawYLPZCAkJ\nwZMnT0TmffDgAWbNmgUbGxvo6+tj5MiRuHDhQrmMrZqaGpYuXSoxD8MwaNu2LdTV1Ys45YnL26ZN\nGyHD2rRp06SSrnv16hVUVFTQoEEDmJmZYcaMGWLvf9OmTdDX1xe5TF0YOTk5WLx4MdhsNsaOHVtt\n+/DF8ddff2Hs2LHV3YwK4ec2sPkyXvuJcJAIQcUMbBoJxMH3kECrNIQEAtXCpUcvL6SkpGDbtm3w\n9fUVBpMPGzYMhw8flhmhd0URHh4OOzs7iZSPKSkpaN26Nfr161cmjcqPHz9CS0sLr169kkVThTh4\n8KBovUwR0muSBkjFl4szunYtUyjNx48fsXTpUjRq1AhWVlZYvnx5jemAZInPnz9DRUUFBgYG1d0U\nqSGKwKIwZWdhPHz4ELNnz0bjxo2hp6eHESNG4Pz581IPeps3b15qTOaePXugqakp1SrAjRs30KhR\nI9SpU6dUKcTMzEzs3LkTrq6uUFNTA4vFwvnz5yUOFDZs2AADAwOJoh0MwyA6OhoWFhZwc3Mrk8BH\nVWD+/PmYMGFCdTejQvh5DawIIeopxTroSCK0LvQ5nQhKRHiY/zlbTg7m6urw8PDA6tWrq8URoDQc\nOHAABgYGEg3g/fv3YWZmhmnTppV5dD9z5kwMGTKkos0UCS8vr6I6l2LEw8UNkEQdWUQI6tWrzKE0\nDMPg3Llz6NevHzQ1NTF48OAaQYQgKzAMAzU1Naiqqv5wIUbiCCzEITExEXPmzIGtrS309PQwfPhw\nnDt3TqKxDQ0NlRjGlJGRAQ6HAz09PYmhbF+/fsWoUaPA5XKxefNm+Pn5Yfz48SXyFajjBAQEQEtL\nCy4uLti2bRuGDRsmdm+3AOvWrYOBgQESExPF5nnw4AG6dOmChg0b4tixYxLLqy7MnDkT06ZNq+5m\nVAg/r4FduLBUAzsqv9MunMeaCPvy/+fVqQNeBcJSKhs3btwAm83GjRs3xOY5efIkOBxOmXiIC/D9\n+3dwOByZiJuLwps3b8Bms//v2CLimUl6fqIORllZwMFbAaSkpGDBggUwMzND06ZNERkZWaXhC5UF\na2trWFlZVRplZFXgzp07CA4OhpaWVhECC3F49OgRwsLCYGdnB11dXQwbNgyxsbEljG1CQgLk5OTE\nhmJNnDgRKioqOH36tMjzDMNg3759MDQ0xJAhQ4QewO/evQOLxRKyjT1//hyzZs1CvXr1YGlpiQUL\nFggHCwzDwNjYWKIncGRkJAwNDcWyl338+BGjRo0Cm83G0qVLa3Ro2eTJk4tIh/6I+HkNrI9PqR30\nECJMKJanDRE2FU6roW7kr169goGBgUQqtQJZqbIo6BTGX3/9BW9v7/I2USqsWbMGDg4Ogg5PxDMr\nq4GV5TPj8/mIiYkp4uUqjkLyR4CbmxucnJywfv366m5KhSGJwEIckpKSMHfuXDRp0gRcLhfBwcE4\ne/as0Njq16qFu76+gvewe3fB34UL8ermTSgqKor9LTx//hzdunWDpaVlCc9hAJg1axaaNGmCDh06\ngM1mY/jw4SI5mW/duoV69eqJXTVZvXo1jIyMRMpr5uXlYeXKldDR0UFQUJDMY+srAyEhIQiv4GC4\nuvHzGtju3UvtoEcRIbhYHptCM1gQCcqpYfj27Rvs7OzEvpw8Hg9//vknLCwsyqT9WhjZ2dnQ19fH\n7du3K9LUUsHn8+Ho6ChQ7RHxzMplYCvhmb1+/RqzZs2CoaEhWrVqhc2bN/9w3sdBQUFwd3cvM6lC\nTUZpBBbi8PjxY8ybNw9NmzZFZy0t3DI1RRYRshUUir5LysrIlpfHYQUFfC02e83NzcXChQvBYrEw\nd+7cIl7FPB4PJ0+ehI+PD+rWrQtVVVVMnz5dokDF9OnT8eeff4o8t3LlShgbG4t0eDp9+jRsbGzg\n5ORUJpKJ6sbIkSPx999/V3czKoSf18BKMYONzJ+xFt6DVab/78HWxBksj8dDt27dEBAQILITSU9P\nh4eHBzp06ICPHz+Wu57IyMgq4wl9+PAhWCyWgKGpBs1gRSEvLw+HDx9G165dwWKxMGbMmBrnPCIO\n8+bNg5eXF7p06VLdTakUSENgUQKrVoGvpAR+KTHy/GIx8pcvX0bjxo3RpUuXIkbv4cOHmDhxIgwN\nDdGsWTMsW7YMqampOHToEKytrcU6aQFA48aNRcZxR0REwMTEpIQPyJMnT+Dh4QEzMzMcOHDgh/MX\nCAwMxOrVq6u7GRXCz2tgC+3n5ZHA+WUiEX7P/z+PCKkk8CLel58WSoW8iPNHrxXdz5M1xowZg44d\nO4rcW3nz5g2aNWuGQYMGVYiDNy8vD+bm5iJ/7JWFWbNmYWOjRgJR8IoY2Cp8Zs+fP8fkyZPB5XLx\n22+/YdeuXTLhka4sbN++Hd26dYORkVF1N6VSIS2BRXli5BllZWxr1w76+vrYtWsXGIbBhw8fsGLF\nCtjb2wvZlYqTPjAMA2dnZ6xYsUKQUIj+E92745u7O2aqqoL37l2R65YtWwZTU9MialBfv35FaGgo\nWCwW5s+fX6aogJqEwYMHY8OGDdXdjArh5zWwhTxSZxCBih0z8n8wp0gQB6tEhA5EeF74B6WkVOkc\nxWXBypUr0ahRI5EsSLdv34aRkRHmzp1b4ZHs9u3bxcrFVRZycnLQrkED8EQQTIgbIInsBKvhmeXk\n5GDPnj3o2LEjuFwuJk6cWCM9zi9evIhWrVpBVVW1xoSYVTbEEljkx8j7EEGXCOpEsCDCuvz36D4J\nQsM08w/n/DQQIbtWLXw6eRKHDx+Gl5cXNDQ00K9fPxw/flziDDUhIQEumprI6dZNJP1ntoJCEfrP\nJUuWwMzMTBhixufzsWHDBiGPuTjqzx8FAwYMQFRUVHU3o0L4eQ0sIDKmUuojPw62puD48ePgcrki\n92Cio6PBZrOxe/fuCtfD5/NhY2OD48ePV7issiIuLg7/KCqCKfbMJA2QCh88Itw2N69WB4/ExESM\nGzcObDYbXbp0kRi7WdV4+fIl9PX1RSoS/ddRQGDRuXNncDgc3K1fH4ycHO4RITv//XlIBC4RbhDh\nc/5gm8l/r5YRoXGh9+ygvDysra2xevVq6eOmV61Cdq1a4EvR9+TWro2phUQDLl26hObNm6N169al\nklzUeOTP3s8bG+NNs2ZCZ7KaNJmRFj+3gc0fpZbLwIpgcqouJCQkgMPhlFiyZRgGf//9N/T09GQW\nenH48GE0bdq02vZzFvTqhcxyDooYZWUs7NMHLBYLCxcurNals8zMTGzdulUYuzljxoxKE66WFnl5\neahduzZ8fHywcePGam1LdeJZfDxyizszESExfza7W8QKygoS+GcUpOUqKMClSROw2WwEBATgxIkT\nkkNiyrEczVdWxoewMPTr1w+GhobYvn37D7fPWgSFBFekEe/4EfBzG1igUrmIqwLv37+Hqakptm3b\nViQ9Ly8Pw4cPh5WVlcwEvxmGgYODg0i1m6oAwzAIDg7GMHl55CkqlvuZJSYmwt3dHaampti5c2e1\nd0p3797F8OHDoaWlBXd3dxw/frxK9DZFwdjYGKGhoWK9VX8KFIu3Ds43nkSEpkT4Xui90iCCAhHk\niDCnuEEID8fz58+xaNEi2Nvbg8Viwd/fHzExMUWNbSnL0VeI0IkIWkRgE6E3Ed7mn8sgwpqAgDKL\nuNc4VJHgSlXjl4EFftiHm5mZCQcHB8yYMaNI+tevX+Hq6orOnTvLlJXn7NmzaNiwYbVwKvP5fAQH\nBwsJ+KdxOALSiAo8s9jYWDRr1gz29va4dOlSld9TcXz//h3r1q1Ds2bNYGpqinnz5lW5ek+7du0w\nd+5cdO3atUrrrVEQEWHAI8LFfCOaW+xcOhFWEuFo8RWT338vUuyLFy+wePFiODg4gMViYciQIYLB\nlLs7IGE5+hgJ6Fq/5hvUwUToUlBHDduqKhd+8EmOJPwysAW4fl3woiopCUafopYnvLxqzLIwn89H\nnz590L9//yIzsBcvXsDGxgZBQUEy39vr1KkTNm3aJNMypQGfz0dAQADatGkjdL7p3bs3Vvj5iX1m\njJISsoiQ5eYm8Znx+XxERUXByMgIvXr1EhmkXx24fv06/P39oampCW9vb5w9e7ZKZto+Pj4IDw+H\nsbFxpddVE5Gbm4uvHTqI7dgDSbDfWmK5lgjaREgplHaECCoqKuByubC0tISjoyPc3d0xaNAgDBky\nBC4uLmhmaIgsEeWJW44GEW4SQa1wWg1ztiwT/iPbdOIgBwD0C/9HWhrR5s1ECQlEnz8TaWkRNW5M\n5OdHxOFUd+uEmDp1KsXGxtKZM2dISUmJiIiuX79OHh4eFBISQmPGjCE5OTmZ1Xft2jXq06cPPXny\nhGrXri2zcksDn8+nIUOG0MuXL+no0aOkpqZGRETv3r0jOzs7On36NNnq6Yl8ZuPv3ydlY2OaPXt2\nqfVkZWXR0qVLacmSJeTr60vTpk0jbW3tSr670vH161fatm0brV69mvLy8igoKIgGDRpUaW2bPHky\nKSoqUnh4OL1//57U1dUrpZ7qBgB6+/Yt3b17lxISEighIYHu3r1LSUlJtKt2bXL//l3kdQFEpEpE\ny4ql84hInYjiiKhpftpNKytaYGVFL1++pDdv3lBaWhopKyuTlpYWqaurk7KyMvmlpdGQly9JKb8b\nHkZEm4koK7+cC0SkVqyuv4loFxHF53/Oq12b7nt7U4qvL2loaJCmpiZpamqShoYGKSkpybQfkDm8\nvCjn4EEaRkSniegTEdUjovlE1DU/y3oiWkBE74moHRFtJCJ9IiI5OSJPT6L9+6u82dLil4H9AbFl\nyxaaNWsWXb16lTj5Rn///v0UFBREGzZsoJ49e8q8Tk9PT3J2dqYRI0bIvGxx4PF4NHDgQEpLS6PD\nhw+TiopKkfPr1q2jdevW0ZUrV0hBQaHE9UlJSdSuXTt68eJFiWvFISUlhWbOnEn79u2jSZMm0fDh\nw0lRUVEm91MRAKC4uDhas2YNRUdHU8+ePSkoKIhat24t0w50zZo1dPPmTbp58yatWbOG7O3tZVZ2\ndSE9PZ3u3bsnNKIFf2vVqkW2trbUuHFjsrW1pQYNGtCLFy8ob9486vvgAX0norNE1J2IlElgALyI\naGf+ZzYR2RJRBhFNJaJ9RPSMiJSIiF+nDsmHhZHc+PHCdvD5fEpJSaHk5GTh4bh2LbVITCzSXj4R\nXSGic0Q0gYgKD2fvEtFvRHSYiBwLpZ/R16c5Fhb0/ft3Sk9Pp69fv9KXL18IgNDYFja80v6vpqZG\n8vLysnkQxZGaSmRiQhnZ2bSIiPyIyJiIjhFRfyJKIKIXRORNRLFEZEFEo4noARGdLyhDSYno1asa\nNfkpjF8G9gfDhQsXqHfv3nTu3DmysrIiABQeHk4rVqygw4cPU7NmzWRe5/3798nZ2ZmePXsmtaGq\nKPLy8mjAgAGUnp5OBw4cIGVl5RJ5GIYhJycn8vLyotGjR4ssx9PTk1xcXGjYsGFlqv/Bgwc0fvx4\nSkxMpIULF1KvXr1qzEzgw4cPtGXLFoqMjCQlJSUKCgqi33//nerWrVvhso8fP05///036ejokLOz\nM/n5+VW8wVUEPp9PT548KTErfffuHVlaWhYxpo0bNyYul0sA6NKlSxQVFUX79+8nOzs7GuruTv0m\nTKAPOTnUm4juEBFDRCZENIqIhhLRXiKaRkSvSWBs7Ukw67LNb0uOnBy1NzUl94AA6t27N8nLy9P7\n9+/p3bt3RY6gf/6hVh8+iLyfICKyyq+TiOgJEXUgwWzOt1jeMyoqNFBTkzIzMykzM5N4PB6pqKiQ\nsrIyKSoqUp06dahOnTpUq1YtUlBQIDk5OZKTkyMAxDAM8fl8ysvLo7y8PMrJyaHs7GzKysqinJwc\nUlFRIXV1ddLQ0KC6deuSlpYWaWtrCw8tLS2hQS5upDU0NMSveIWHE82YQZSdXeKULRHNIMFAI4uI\nVuanvyUig/zvoh4RkbIy0axZRIUGMjUJvwzsD4THjx+To6Mjbdu2jTp16kS5ubk0bNgwunnzJkVH\nR5OhoWGl1Ovr60tWVlY0adKkSim/OHJycqhv377EMAzt3btX4gzy0aNH1LZtW7p58yaZmJiUOH/p\n0iUaPHgwJSYmipzllobTp09TSEgIqaqq0l9//UWtWrUqcxmVBYZhKDY2liIjI+nUqVPUp08fCgwM\npObNm5evwNRUer9wIV1bt44s9fXpm7w8NffzIxo8uMbNEFJTU4vMRhMSEujhw4ekq6tbxIg2btyY\n6tevT7Vq1SpyfVJSEkVFRdG2bdtIRUWFfH19ycfHh4yMjIiIiPHwIDp8mMozd2OI6CKLRb4qKvT+\n/XvKy8sjZWVlMjQ0JCsrKzI0NCQ9PT3S09OjLtu2kUFsrMhyCi9HvySBcZ1IAsNbAr6+RFu3Cj/y\neDzKysoSGtzMzMwSn0UdxfNkZGTQt2/fKD09ndLT0ykzM5Oys7MpOzubcnJyCIDQaMvLy5cw2jwe\njxQUFKhOnTqkpKREKioqpKKiQqqqqrTgzRvqnJpa4lZSSDCY+ZcEy8OZRLQq/9wbIjIkokNE5C7m\n3msUqn7b9xfKg48fP8LCwgKRkZEAgE+fPsHJyQk9evSoVKm0p0+fgsViVZlGaFZWFtzc3ODl5SU1\nrWBYWBjc3NxEOgEVhBYdOHCg3G3i8XjYuHEjDAwM0Ldv3yK0dDUF7969w9y5c2FiYoIWLVpg/fr1\n0oduFIo/LEFFWc3xh5mZmbhx4wY2btyIsWPHwtnZGTo6OtDS0kL79u0xYsQIREZG4sqVK6XyCqel\npQkpC7lcLsaMGYObN28WeW94PB6SkpIwpHHjcsdb59SqhWurVuH+/fv49OkT0tPTsW3bNnTs2BEs\nFgsjRozArVu3BBXmhwSlEGEnCUKAeESIIYIKEQ4T4TURzImwSFyd1UjZmpubi69fv+JwZfmoAAAg\nAElEQVTdu3d4+vQpEhIScPXqVZw7dw7Hjh3D3r17sXbtWsyfPx+hoaEYOnQovL294erqiktaWiXu\nJZcErFh/5H8+RQQWEe4QITM/XY4IOwpfVwMFVwrwy8D+AMjJyUGHDh2EsYlPnjxBw4YNMXbs2EoP\nmQkKCsLkyZMrtY4CZGRkwMXFBX379i2TTmVOTg5sbGywc+dOkef37t2LNm3aVLh96enpmDVrFrS1\ntRESEiI9Q08Vgsfj4Z9//kGPHj2gra2NESNGlOC9LYIaEqLG5/Px9OlTHDx4ELNnz0bv3r3RsGFD\nKCkpwdbWFj4+PliwYAGOHTuG5ORkqT2qs7KysHfvXnTv3h3q6upwcXHB1KlTsXz5ckydOhX+/v5w\nc3NDs2bNoKenBwUFBSgoKIDFYmFpw4bIKKNx5SkqIkRNDavEfE/Pnj3DjBkzYGJiAjs7O0wPCkK2\nnBxSidCeBHG16iRQ7VqbX+ZMEsTgqhY7hB7Mioo/phdxsXAoPhH6EqErFQ2FWkGE+kTQIcI8EvDD\nXyj8vdcwwZXC+GVgazgYhsHgwYPh7u4OHo+Hixcvgsvliv0ByxJv376FlpYWUlJSKr2u79+/47ff\nfsPvv/9ervCi+Ph46OrqilQI4vF4MDMzQ1xcnCyairdv3yIgIAA6OjpYvnx5jRWtfvXqFaZPnw59\nfX20a9cO27ZtK8peVU3xhx8/fsS5c+ewfPlyDB06FK1atYKamhqMjIzg5uaGiRMnYvv27UhISCh1\nFePbt2949OgRzp07h507d2LJkiUICQlB586dYWBgAAUFBdSqVQsKCgrQ19dHy5Yt0bNnTwQGBmLG\njBlYs2YNDh8+jGvXruHw4cPQ09PDsmXLwDAMpk6dimWNGoGRYgDCFBqAPHnyBJaWlggODhb7bjx4\n8ACOjo5QVlbGIXn50ukRxRx8IhypXRv+/v4yI5SpMhQi9GCI4EeE3/JnquLu91H+zP5TDZi9S4Nf\nBraGY/78+WjatKlwmYnD4VQZD/D48eMxatSoSq/n27dvaNeuHQYPHlyhGfnIkSMxePBgkeeWL1+O\nXr16lbtsUbhz5w46d+4MCwsLHDx4sNoZocQhNzdXyLPLZrPx559/4uW+fSKN6/P8GYQmCYgOhpMI\n4QQp4w9zcnJw584dREVFITQ0FK6urjAwMIC6ujratGmDwMBArFy5EhcuXCgiUMEwDNLS0nD37l2c\nOHECmzdvxoIFCzB69Gh4e3vD0dER9evXh6qqKpSVlWFubo62bduiS5cuaNmyJbS0tGBgYIAhQ4bg\nxIkTSE1NLZUZa9euXeBwODh69CgA4Ny5c9DV1cW7d+9KjZHPq10bZ7W1wRRaQv/69Su6desGJyen\nIkLvycnJCAgIAJvNxoIFC5CRkYFvZ84gt06dchlYqKjg65kzmDp1KrS1tREYGIhXr16V9RWpHhQS\nXAkkgVLZ92L3l0WEhHwD/JIEgiuTCuep4THAvwxsDcbevXthZGSE5ORk4bKSxOU+GeLjx4/Q1tau\n9B/rly9f0KpVKwQGBlaYHvDbt28wNjbG6WLC14Bghsxms0WKIVQUx48fh7W1NTp06IDrNTzw/cmT\nJwgNDcXROnVEzpq6kkDyL4sI70iwVFmCWKEYexDDMHj58iWOHj2KefPmoX///rC2toaSkhIsLS3h\n7e2NsLAwHDhwAFeuXMH169cRHR2NtWvXYtasWUKhd3t7exgZGaFOnTrQ1NSEpaUlOnbsCB8fH4SE\nhOCvv/7Cjh07EBsbi8TERHz9+hWpqamIiIgosq9669YtqQc7DMNgzpw5MDY2FoqRf/z4EUZGRjh2\n7FjRzKmpQHg4cvv3R7S8vICpKTwc/PfvYWtri4MHDxbJzuPxEBoaCnNzc1y+fBnjx4+HtrY2JkyY\nUFLxSgarCWlpaZgwYQK0tLQwYsQIvHnzpgxvRjXB0xMvSLAErkhFl8C3kUBUoXH+rJVLAsUsnpj3\nsCbil4GtLhTTeyyuGHH16lWw2WxcuXIFAwYMgL29vWA0XUWYNWsWhgwZUql1fPz4ES1atMDIkSNl\nNvuLjo5GvXr1kJmZWeLcpEmTMHz4cJnUUxx5eXlYu3Yt9PT04OPjI1Q5qZFISQEjhsu5ERH+KfQ5\nhP7vcFL4yKtVC6GDB6Ndu3bQ0NAAh8OBvb09evTogd9//x1DhgyBr68vXF1dYWdnBx0dHdSqVQtc\nLhdNmjRB165dMWTIEEyZMgUrVqzA/v37ERcXh+fPn4t8doWRlZWFPXv2oEePHqhbty769++PY8eO\nlXlrITs7G76+vmjZsqVQ2o1hGHh5eWHMmDESr1VTUyvi+Hfs2DFYWlqWaEN6ejr69OkDOTk5uLq6\n4vXr1+ILldF+eEpKCsaNGwctLS2MGTOmyuk2y4T/OJPTLwNb1ZBCMSK9Sxe4sljYunUr2rZtiz59\n+pTa6cgSBbO9xMTESqsjLS0NTZo0wZ9//inzpVVvb29MmDChRHrBnnLhJTtZ49u3b5g2bRq0tbUx\nadKkmqmrWozMvvCxhgi+JOC8fU0EayIcEJEvkwgzVFWhqqqK2rVrw9jYGA4ODvDw8EBwcDBmz56N\ndevW4ejRo7hx4wbevHlTIepOPp+P8+fPIyAgAFpaWujYsSM2bdpUquewOKSlpaFdu3bo1asXMjIy\nhOmRkZFo0qQJsrOzJV5fv359PHr0SPiZYRh06NAB69evByBYll+1ahX09PTg7e2NPXv2wMDAAAsW\nLJD8vucvR+fIyyOv2LJxppwcsuTk8NDKCu/zl7Il4e3btxg1ahS0tLQwfvz4apVplIhfXMS/IBNI\nOULlkcDVfyqLhUmTJlW5sspff/2FPn36VFr5KSkpsLGxwaRJkypl3/Ldu3fgcDi4fft2iXODBw9G\nWFiYzOssjuTkZAwaNEjokFZTNF8BiCSzLzgeEKEZCRRiKH+5mBGT91P37vjw4UOl7j0nJiZiypQp\nMDExgbW1NRYsWFBhWb+HDx+iXr16JX5b9+/fB5vNxsOHD0sto23btjh//nyRtCtXrsDAwABbtmxB\nvXr14OLiUmTLIDk5Gc2bN4ePj4/EATOfz4eFpia+Tp0K+Poi19UV22vVAm/BAtw4fhx//PEHtLS0\n4Orqij179pQ6GEhOTkZwcDC0tbUxefJkkY6A1Y5Vq5AjpRbuj2JcgV8GtupQjlFabp06Vf4iZWdn\nQ19f//9xejLG27dvYWlpiRkzZlRqx7x+/Xq0aNGihNPUvXv3oKurW2VasLdu3YKTkxMsLS1x9OjR\nmuEI1b27yPeNTwRjIoSRQNXlAxF6EmG8uHe0kuIPU1NTsXz5crRs2RK6uroYO3ZsmfZVJeH06dPQ\n0dEpoXeblZUFW1tbrFu3TqpyvLy8sGfPHuFnhmEQExMDDQ0NGBkZifQDAAShaP369UPLli3F7pE+\nfPgQZmZmRdJMTU2RlJRUpJyoqChhbO3IkSNL/c2+ePECQ4cOBYvFwvTp02tUmNm7d+/gpK6OjK5d\nfxjBFWnwy8BWBa5dQ0Tt2mhOhDr5s4KCF0eS1mN17DNERkZWmlRZcnIyLCwsqmQGyTAMnJycsGTJ\nkhLnXF1dsWHDhkpvQ+G2REdHo1GjRnB2dhY5s65SiJnBpuXPWr8USjuYv0ws0sDKMP4wKysLu3fv\nRvfu3aGhoYEBAwbg+PHjMp35r127Fjo6Ojh37lyJc6NGjUKvXr2kNuLBwcGIiIgAIAgR++2339Cw\nYUMsW7YMLBarpBNTITAMg7CwMBgaGuKaCPKODRs2wMfHp0iau7s79u3bJ7K8Z8+eYfr06TA2NkaT\nJk2wbNkyidsgT58+hZ+fH9hsNubMmVMjtjHGjh2L0aNHCz7kO5PB11cwiPP1FXyuqUvcEvDLwFYF\nPD2xP7+zCipmYCVpPQqXRKrIUy4vLw/16tXDxYsXZV72ixcvYG5ujkWLFsm8bHFISkoCi8UqER94\n+vRpWFpaVvnSe8G+HJfLhZ+fn2SHl8qEhD1YMyLMJ0FozmcieBChvyjjKoP4w+L7qs7Ozti8eXO5\n91XFgcfjISQkBBYWFkX2TQtw9OhRGBsbSzSKxVHg/ezp6QlDQ0OsW7dOOBgYOnSoSB+A4jh06BA4\nHA62b99eJN3f3x8rV64skjZt2jRMmzZNYnl8Ph+nTp3CgAEDoKGhgd69e+PYsWNiQ98ePXoEHx8f\ncDgczJ8/v1IZ4SThzZs30NbWrlInzqrCLwNb2SgU6wUiTClmYIsfJbQeiaos1mvHjh1wdHSUeblP\nnz6FiYkJli1bJvOyS8O8efPg6upaZGbCMAyaNGmCf/75p8rbAwhCkyZOnAhtbW1Mmzat6ju2Yu9k\n4eM2CWINNUlAUdeHCO9FvasVeCcL76va2Nhg4cKFFd5XFYf09HS4u7ujQ4cOIvce3759C11dXVy4\ncEHqMl+9eoU2bdpASUkJ4eHhJfZTX79+DW1tbanu6e7duzA1NS2yH2xpaVliuXfv3r1wd3eXuo2f\nP3/G6tWr0bJlS+jr62PSpElFlpgL48GDB+jbty+4XC4WL15cxOmrKjBy5EiMGzeuSuusKvwysJWN\nYrOF0gzsUhIEXMt6tlAa+Hw+bGxsZE5ikZSUBCMjoyphnhKF3Nxc2NralpglREVFwcnJqVraVIAX\nL17Ax8cHenp6WLduXaXTXhaBp2fp4SDijnKsqhTfVx03bhxu375dqXvSr1+/RrNmzeDn5yeSEYrP\n58PFxQXTp0+XqrwPHz7gzz//hLa2Nnr16gVXV1exeSdOnIiAgACpyk1NTUX79u3Rs2dPvHz5Eurq\n6iWWxpOSkmBqaipVecWRkJCAcePGQUdHB+3atcPGjRtFDuru3r0LLy8v6Onp4e+//64SP4Xk5GRo\na2vX7FCiCuCXga1sFNvvkmRg7+TvxV4Qdb6S+TaPHDmCpk2byrTDe/DgAQwMDIShC9WFq1evgsvl\nIi0tTZiWm5sLQ0ND3Lx5sxpbJsC1a9fg6OgIGxsbxMTEVFWllR5/mJmZWWRf1cfHBzExMVXiUX3r\n1i0YGhpi/vz5Yt/pRYsWoW3btqW25/v375gzZw5YLBaCg4Px9u1bxMXFwd7eXuw1nz9/BofDkcoj\nGRCwXv3xxx8wMTFB69atS5zn8XhQVVWtkOhGTk4ODh48iB49ekBDQwODBw/GhQsXSnw/t27dQs+e\nPWFgYICVK1eW6qVcEQQHByM0NLTSyq9u/DKwlY1iHpviDOxjIugTYau4Tq0SFSMKFGcKe0VWFAkJ\nCdDT08PWrVtlVmZFMHr0aAwcOLBI2qJFizBgwIBqalFRMAyDgwcPwsLCAl3+196dh8d4rn8A/8Ya\n25FtIiKbRCK22ItQPVWhQku0iuLU7sRSTlGlLaqLNvSopXKOcmptHMShLW05KNpoRZ3aqbV+paKW\nlkgmycx8f3+8k5FlJrNk3smI+3Nduci7zZM3zD3v89z383Tv7poZu1SoP9Tr9fz66685YsQIVcdV\nS7J161ZqNBqLSUEkeejQIWo0Gl66dMniMTk5OVyyZAkDAgI4YMAAnj171rTvwoULDA0NLbEdSUlJ\nTEhIsLndBoOB3bt3Z40aNbhnz55i+9u1a8dvvvnG5uuV5Ndff2VSUhIbNWrEBg0a8O233y6WE3Dw\n4EH26NGDISEhXLZsmdPn3P7555/p4+NT6INveSMBVm02PMFeAhgKMLmkNzYVn2B3797NqKgop3VR\n/u9//2NAQAA/+eQTp1zPGe7evcuQkBDu2LHDtO3333+nt7e3W826lJOTw4ULF1Kj0XDkyJHqJ37Y\nWJuttxJcT506xRkzZrhkXNUSg8HA+fPnMzAw0Gx2br67d+8yMjKS69evN7tfr9dz3bp1DA8PZ/fu\n3c2Wv9y7d49Vq1YtsccnKyuLwcHBPHDggM0/Q5cuXfjOO+/Q39+fycnJhfaNGjWqWPJTaRkMBh44\ncMBUW9ujR49itbVpaWmMi4tj/fr1+a9//ctpPRCjR4/m9OnTnXItdyUBVm3GMdg8KPO7vgJwsPHv\nebBhrUcXjMF27dq1WF2go9LT0+nv71/i00NZ2bZtG8PDwwslcbz00kumZQDdya1btzhlyhT6+Phw\nzpw56iaeWJnMPqdCBW6pWJFZRRKBMjIyuHDhQrZp08Zl46qW5ObmcvTo0YyJibH6gWno0KFmF4Uw\nGAzcvn07mzdvznbt2nH37t0lXqfodInmrFixgp07d7bpnuTl5bFWrVq8desWf/rpJ0ZHR3Ps2LGm\nJ8fFixdzzJgxVq/jqPza2scff5x+fn6cMGFCoZKyvXv38rHHHmODBg24Zs2aUn0gv3DhAn18fFSd\nVc0dSIBVmzFjcxaUGsOCX7Ngfa1HtbOIDx48yODgYJsXNy/JgQMHqNFouHXrVie0TB0DBw7k1KlT\nTd/nd1O5akF5e50/f57PPfcc69Wrx48//ljd0iIL9Yfzp01jVFQUFy9ezKysLK5fv549e/Z0+biq\nJbdv3+YTTzzBnj17Wu2KTklJYVRUVLEkn7S0NHbu3JnR0dHcvHmzTQExIiLCbNlPQXl5eWzcuLFN\nGeuHDx9mo0aNTN///vvvjI+PZ5cuXXjjxg3u27eP7du3t3odZzh//nyh2tpFixaZguHu3bvZsWNH\nRkdHMyUlxaF/k8OHD7dadlQeSIB1BRdnbNrXtAQuWrSo1NfZv38/NRpNmZW+2CojI4P+/v6Fuv2e\nf/55l9bnOiItLY0dOnRgixYtuGvXLpe+9oYNG9i0aVPWrFmT3t7e7Nq1K1etWlVmdZMFnTt3jtHR\n0Zw4caLVJ6qLFy9So9EUSmw7fvw4e/fuzeDgYK5YscKuDwqxsbE2lfds2bKFzZo1s9q+Dz/8kCNG\njCi0TafTcerUqYyIiOCBAwdYs2ZNl9Zv59fWDhw4kLVr12a/fv1MCyt89dVXbNeuHZs0acJNmzbZ\n3K6zZ8/S19eXt8+cKXHBk/JAAqwruOmKESdOnGCdOnVK3f24Z88e+vn5FRrfdGcff/wxW7VqZXoz\n/eGHHxgUFOS2C6fnMxgM3LBhA8PDw9mzZ0+ePHlS1dc7efIkp0+fzrp167JKlSqsX7++08cAS+Ob\nb75hQECATW3Ky8tjhw4dOH/+fJJKidTQoUOp0Wj4/vvvO1SSUnS6REsMBgNjY2OtJvwNGjTI4gxj\nq1atokajoUajKZRs5Uq3bt3i0qVL2bZtW9arV4/Tp0/nmTNnuG3bNrZu3ZrNmzfnli1brD79z+7Z\nkyejo0tc8IQJCcr75gNOAqyruOGKEUOGDOE777xTqmvs2LGDGo3G6niVOzEYDHziiSdMb7Yk+fjj\nj3Pt2rVl2CrbabVavv/++/Tz82NiYiIzMjKcdu2C46p169bl5MmTmZ6eTk9PT27atMnppVyOWrt2\nLTUajc1lTa+//jq7devGjIwMTpo0iT4+PnzttddKNTRQcLpEa/bt28fQ0NASS17q169fYlnPgQMH\n6OnpySFDhpT576Bobe2KFSuYkpLCmJgYtm7dmtu2bTPbxmuzZvEeQEMpl+R7UEiAdSUnrffoDBcu\nXKCvr2+p3mC2bdtGjUajytSKasvvprpw4QJJ5Wdp0aJFmb9x2ePGjRucOHEifX19+c477zi8pGHR\ncdXBgwfzq6++KtSl2bRpU/7www9s3Lgxd+7c6awfwW4Gg4EzZ85kWFgYjx8/btM5e/fupb+/P6dO\nnUpfX1+OGzfOKdnZs2fP5muvvWbz8b169eKCBQvM7rt69Sp9fHysdrNOmDCBdevW5ZAhQ1y2YEVJ\ncnJyuHnzZlNt7dChQzlnzhw2atSI7du3544dO+7/n1q6lNqKFd3qIUNtEmBdzUrGpqtWjEhMTOSM\nGTMcPj9/HlV7ShDczbvvvstu3brRYDBQr9ezUaNGFldBcWc//fQT+/bty5CQEK5du9amsTC9Xs89\ne/Zw+PDh9Pb2ZlxcHFevXm1xXPW5557junXr+PHHHzMuLs7ZP4JNsrOzOWDAALZv397mmX9+/fVX\nenl50cvLi88//zzPnTvntPYkJydz1KhRNh9/7Ngx+vv7m/1Qm5qayvj4eKvX2LBhA3v16sX+/fvz\nkUceMS0U7w6uXr3KpKQkRkdHMzIykv3792d4eDg7derE9KVLuahSJbMLnhDgvwFGQ5kmthGUedtd\nMUymNgmwZaUMV4zIX3jc0a7FTZs20d/fv9Balw+i3NxcNm/e3DQ2tnz5ctVWEnKFffv2sW3btmzT\npk2xtUrz5Y+rhoSEMCYmhvPmzbO4bFpBb7zxBmfMmMGcnBzWq1dPteUMLcnIyGCHDh3Yv39/m57U\ndTodV69ezerVqzM0NFSVFYzyZ0WyxwsvvGD2qXfy5Mk2rTJ1+vRphoeH02Aw8M0332RQUJDb/T80\nGAxMS0vjqFGj6OXlxZiYGG6rWpUbYX7Bk18AVoay8IkB4OcAqwHMcFGip5okwD6Epk6dygkTJjh0\nbkpKCgMCAsp+yTUnya/bvX79OrOzsxkQEOCaWZRUotfr+cknnzA0NJR9+vThmTNnmJGRwQ8++ICt\nW7c2jav++OOPdl1348aN7NOnD0llBqyBAweq0Xyzjh8/zvr16/P111+3+nRuMBj4+eefs1mzZgwP\nD2dERIRqU/1Zmy7RnEuXLpldOSY2NtamPAadTsfq1aublpjbvHkz/fz83GpSl4IyMzO5YckSagsM\nixWdbOc7gJoiT7R+ANNcVKqoJgmwD5mbN286PHvRqlWrWLdu3Qc6AJnzt7/9jYMHDyZJvvnmm2Yn\nIXjQ3Lp1iwMHDmTlypVZpUoV9uvXr9i4qj1OnDjByMhIkuQff/xBHx8f0/i1mr788ktqNBquWbPG\n6rHffPMNO3XqxMaNG3Px4sX09fVVNdM6f5Uoe7300kscO3as6XutVsvq1avbXPbUtm1bfvvtt6bv\njxw5wrCwMM6YMcPlSzDa5L33qK1QwWKA1QHsDHCr8e//AVgPYGbR4TOVFzxRgwTYh8wbb7zhUABZ\nvnw569Wrp3ppSFnIzMxkWFgYv/zyS964cYNeXl5uNbZlK71ez927d3PYsGH08vJiXFwclyxZwlGj\nRtHPz4/z5s1z+GkuNzeXnp6epsSaadOmOdwLYqulS5cyICDAahLd0aNH+dRTTzEkJIQrV65kZmYm\nmzdvzmXLlqnavszMTHp6etqdGHfjxg36+vqaym3S0tLYqlUrm88fMWJEsWkUr1+/zkcffZS9e/d2\n6bzPtrgZH1/o6dTcdLHLoUywU9HYPfy5uYQnlRc8UYME2IfI3bt3qdFoePr0abvOS05OZnBwsNVZ\nax5kX375JevXr8/MzEyOGzeuVAlgrnbixAm+8sorDA4Otjiuevr0aT799NOsX78+169f71C2dOPG\njU1dy1euXKG3t7cqU93pdDpOnDiR0dHRJSYlXbx4kX/5y1/o7+/PBQsWmIL/xIkT+cwzz7gkI9yW\n6RLNefvtt9m/f3+S5Pz58zlu3Dibz120aBH/+te/Ftuek5PDUaNGsWnTpi7pXbDVwTp1SgywOwH6\nAEyHMuf1QYABUNYmLhRgVVzwRC0SYB8if//739mvXz+7zlm4cCFDQ0N5/vx5lVrlPgYNGsTJkyeb\nSnjcYaYiS65du8YFCxawVatWDAwM5JQpU3jkyBGr5+3evZutWrVi+/btC3Uz2qJfv36FxvpGjBjB\nOXPm2N32kty5c4e9evXiE088wVu3bpk9JiMjgy+++CJ9fHw4c+ZM03gkqZRbhYSEWDzX2WyZLtGc\nzMxMBgYG8tChQ+zbt2+x9YpL8vXXXzM2NtbsPoPBwEWLFrFOnTr8+uuv7W6Xs/3www/cVKRaomiA\nnQewT5Fg2htm5meXJ1jhrrRard3Zn/PmzWN4eHiJS3qVJ9evX6e/v7/pTc8ZU0g607179/jJJ5+w\nR48erF27NocMGcIdO3bYPa6q1+u5atUqBgUF8dlnn7W5dGXWrFl89dVXTd+fOnWK/v7+DtffFnX5\n8mXGxMRw1KhRZmfV+uOPPzhr1iz6+PhwwoQJxbLgr169yoCAAIsZ1GqwdbpEc5KTk9m1a1cGBATw\n4sWLNp9369Yt1qpVq8Tx1p07d9Lf35///Oc/HWqbszz11FP85umnS1zw5GuAvgWeWA8bn2i/kjFY\n8aBYtmyZXSUob7/9NiMjI12+5FhZW7VqFVu2bMl9+/axfv36TlvCz1F6vZ67du3i0KFD6eXlxW7d\nunHNmjVOebq+d+8e33rrLfr6+vKll16y+tS3YcOGYuub9u7dm0udMBHAwYMHGRgYyPnz5xfr2tVq\ntfzggw9Yp04dDhkyxGz3p16vZ1xcnMsnkE9ISODGjRsdOjc3N5dhYWH08fGxuzs7ODjYaq9S/oo8\n48ePL5NpQA8ePMigoCBm//xziQueEOBigBHGOtj6AOcXfXqVLGLhrvLy8hgREWHTJ22DwcBZs2Yx\nOjr6gUz0KS2DwcC4uDgmJSUxNjbW4TfP0sofVw0KCmLz5s05f/58m+pVHXHt2jWOGTOGGo2GCxYs\nsLiy0vHjx9mwYcNC27799luGh4eX6oPIpk2b6Ofnxy1bthTartPpuGrVKoaGhrJnz54ldoHPnz+f\nsbGxLl/VJzExkUuWLHH4/BdffJFeXl52Z//27NmTmzdvtnrc77//zh49erBLly68efOmo810SI8e\nPe5/+HLjBU/UJAH2IfDJJ5+wU6dOVo8zGAycPn06mzZtavNMOeXR+fPn6evryw8//JCPPPKIy6ZP\nLDquOnXqVB49etQlr00qAbRHjx5s0KABU1NTi/3cOTk59PT0LJaJ3LFjR5smvS/KYDBw7ty5DAoK\nKrTCjcFg4NatW9mkSRN27NjR6gfDQ4cOUaPR2NXN6iz2TpdY1NixYxkcHGxx8XdLZsyYwdmzZ9t0\nrE6n45QpUxgREcETJ0440ky7paWlMSQk5P6/FTdd8ERtEmDLOb1ez6ZNm3L79pm4hbsAABigSURB\nVO0lHmcwGDh58mS2aNGCv/32m4ta576SkpLYpUsXRkRE8LtPP1VtWa2i46p/+ctfuHPnzjLtmt6x\nYwdjYmLYqVMnfv/994X2NWrUqFjQ37p1K1u3bk3DtWs236ecnBwOGzaMLVu25C+//GLavm/fPsbG\nxrJp06b89NNPrX64uXv3LqOiouwOUM5i73SJRbVs2ZKLFi1iRESEXWsyr1+/nn3tfKpbuXKly5aU\n7NatW/EyKTdc8ERtEmDLuU8//dTqJPYGg4ETJkxgmzZtXN6N5K7y8vI4KCqK6cHBzKlQwanLalka\nV83MzFTpp7GfTqfjihUrGBgYyAEDBpieDp955hmmpKQUOlb/3XfcUbMmdVWq2HSfbt68yccee4y9\ne/c2jSUfOXKEPXv2ZFhYGFevXm3zB4xhw4aV6cQgmzdv5tNPP+3QuXfv3mX16tWp1WrZrVs3u5YC\nPHXqFCMiIux+zbS0NAYGBjIpKUm1npn9+/czLCzM/LivGy144goSYMsxg8HA9u3bl9h9p9frOWbM\nGLZv375UK+uUO0uXUufpSZ0t40M2vhEcP36c06ZNKzSu6u7j3JmZmZw9ezZ9fHz48ssv8+WXXy6c\nSGR8w9Tb+IZ5bfZsRkZGcsqUKdTpdDx//jwHDx7MOnXqcOHChXZNhLF+/XpGRkaWaTlVWloa27Vr\n59C5u3fvNpXbHD58mHXr1rX5Z8nLy7Nr9qeCLl++zFatWqm2Ik+XLl0srmtL0m0WPHEFCbDl2J49\nexgVFWXxaUCn03HYsGHs1KlToVrCh54Tu7J+/fVX/v3vf2fLli3LZFzVWa5cucLhw4ezdu3abN68\nufJ04sB9ugdw3/PP89q1axw/fjx9fHw4e/Zsu2cfunjxIjUaDQ8dOqTST2wbR6dLJMm33nqLU6ZM\nMX0/cOBAu+qKW7duzbS0NIde+969e3zuuefYrl07p37I27NnDyMiImzLWi7DBU9cRQJsORYXF8d/\n/etfZvfl5eVx8ODBfPzxx916QgWXMyZjLAYsLq31kbGkoAbA7gCvFEnGuHfvHtetW8cnn3zSbcZV\nnWXTpk2sUaMGnwkJYV7VqhwEZdadWgAjjfcm/z79F2BDKFPf/RngJeP2nMqV2eVPf+KkSZN43YE3\n07y8PHbo0IHz5s1T4Se0j6PTJZJkfHx8oUzg/OQ6W+/J8OHD+Y9//MPu181nMBg4Z84cBgUFOeWD\nisFgYOfOnblq1apSX6u8kABbTh08eJDBwcFmEydyc3PZv39/xsXF8d69e2XQOjdmLCdIhfmltfZA\nWfnjOMAc4/7Oxn16Dw+mh4TQy8uL3bt359q1a91qXNUZtFotPT09eaVdO+qM90Fr/PlPAawD8BDA\n3wD+CeAGKBMKTAHYLv8+Aczs3t3hNsycOZPdunVzm4nta9SoYXcPkF6vp7e3d7FVdcaPH8+JEyfa\ndI0PPvig0KIBjkpNTaWfn1+pE8V27drFqKgol5dKuTMJsOVUQkICFy5cWGx7Tk4O+/bty/j4eFXG\nXx5oGRnFknSKTus2GeDYAt9fgVIwf874fV6lSrxWzlYbKiq2QQPqq1Qp1v172vg0+2+A/wTYocC+\nTICexiBcmokD9u3bx4CAgGKBqSxFRETwp59+suuckydPsn79+sW2Z2Rk0NfX16aSoz179rBjx452\nva4lP/74I8PCwvjqq6869MHFYDCwY8eOXLt2rVPaU15UgCh3Tp48iW+//RYjR44stD0nJwfPPvss\n9Ho9Nm/eDE9PzzJqoZtaudKmw2jm78eNf1aqXBl1vvjCiY1yP2M8PWHg/bswFkB1ANEA6gKIB3AC\nQPMC59QAEGHcDgDw8LD5fue7ffs2Bg8ejBUrViAgIMDR5jtdnTp1cO3aNbvOSUtLQ2xsbLHt/v7+\nGD9+PGbOnGn1Gs2aNcOxY8dA0uqx1jRv3hzff/899u7di2eeeQaZmZnmD7x+HUhKAgYPBp56Svkz\nKQlfb9yImzdvYsCAAaVuS3kiAbYcevfddzFx4kRUr17dtC07Oxt9+vRB1apVsXHjRlStWrUMW+im\njh4FtNoSD3kSwAYARwFkA5gDwANAVv4B2dnAsWMqNrLsxQColJdn+n4pgLsA9gPoC6AqgEwAtYuc\nV9t4HAC77xNJjBo1CgkJCYiPj3e47WqoU6cOMjIy7DrnwIEDZgMsAEyePBk7duzA0aNHS7yGr68v\natWqhUuXLtn12pb4+/tj165d8PX1RWxsbOHrpqcDffsCoaHArFnAunXA558D69aBs2cjdsAA7KxV\nCxUPH3ZKW8oLCbDlzMWLF7Ft2zaMHTvWtC0rKwtPP/00vL29kZKSgsqVK5dhC93YH39YPaQrgDcA\nPAMgzPhVC0BQwYNu33Z609yJxsy/n4oAOgH4BUAygJoA7hQ55g6Ue2Vix31avnw5zp07h/fee8/O\n1qrPkQBr6QkWAGrVqoVXX30V06dPt3qd5s2bWw3E9qhSpQo++ugjjBw5Eh06dMC+ffuA5GTgz38G\ntmxRPoAW+RDqkZ2NqiTqHTqkHJec7LT2POgkwJYz8+fPx5gxY+Dl5QUAyMzMRHx8PAIDA7FmzRpU\nqlSpjFvoxmoXfeYybxyAswAyoARaHYCmBQ/w9nZ2y9xK9cBAi/t0AM4DaALgSIHt9wpsN7HxPp06\ndQozZsxASkqKW/a8BAQE2BVgb926hV9++QVNmza1eMyYMWNw6tQp7N27t8RrxcTE4MiRIyUeYy8P\nDw+8+OKLWL16NT7r2RN5kyYBWVnK6HlJ55HKcVOmSJA1kgD7oDIzFnLn9dexY906TJo0CQBw584d\nPPnkk4iMjMTHH3+MihUrlnGj3VxMDGAcl9YB0ALQG7+0BbYdhzL2ehnAaAATAZhCRbVqQLNmLm22\nq9WKjUUWgOsA1kPpDtYD+ApACoAnACRAuU+pUO7ZHChdy9H5F7HxPmm1WgwcOBBvv/02GjVq5OSf\nxDnsHYP97rvv0LZt2xI/7FapUgVvvfUWpk2bVuIYq7OfYAuK8/LCnLw8/DU3F6FQeh9aACiYYZAF\nZQzeD8oQQGfgfpA9dEiVdj1QyjjJStjr4EGllMTTs1jGa06lSsytWJFMSOCdXbvYrl07JiYmuk05\ng9srkEU8C+aX1roNsBnA6saSlFeAwrM9PaDLatklI4NaDw9eN5Yo1TbWwTYFuKzAvdhprIP1BPgY\nwIsO3KdJkyaxb9++LltwwRH2Tpf46quv2rRAgF6vZ4sWLZiammrxmBMnTjAyMtLm17ZLQgIzjf/u\nLxrLqz6DsqRc/u9yEMD+AK8b/x8cyv/9PsAr4DiTBNgHiY3zeBo8PJjl4cF/P/64W78xuaWHdFkt\nex2oW9f69IilvE/bt29nSEiI28+P/e2339o1XWKXLl2sLr6R74svvmDDhg0t1pbm5eWxWrVqzq+3\nNlOylv/VDOAmY8lVLYB/WPo9PwwfNq2QLuIHRXKy0u1i41hINRL9vv8eHv/4h4saWE5Mn650Xzqi\nWjXl/IfA/558EjpHx/NtuE/Xrl3DiBEjsGbNGvj4+Dj2Oi5iT5KTTqdDeno62rdvb9Px3bt3R2Bg\nIFZaKGmqVKkSGjVqhOPHj5vd7zALr5cB4CcoY+kHAYQCmAWli7gZlCEBEwdKscobCbAPgvR05Eye\njBFZWWbHQnIBPAslo9UDwNfG7R4yFmK/tm2B+fOBAiVONqleXTmvTRt12uVmanftilVNm6pynwwG\nA1544QWMHDkSnTt3LmVL1Zc/Bksb6lGPHTuG4OBgeNuY4OXh4YF3330Xs2fPRlZWltlj1Eh0Mley\nlgdgEIAXoIyl/wJlnL02gKsAlhj3nco/4SEoWbNGAuyDYO5c6LKzEQxgL4A/ALwF4DkAl4yHdAKw\nFkCx8vvsbGDuXBc1tJxITLwfZD08Sj7Ww+N+0EhMdE373ECTJk2wMDdXlfu0YMEC3L1716bJFtxB\nzZo1UbFiRdy9e9fqsWlpaejQoYNd13/kkUfQoUMHLF682Ox+VRKdipSsGQAMAVAFSiAFgGoAKgN4\nzbj9MQCPA9hR8MRyXrJmVVn3UQsrbBgLKbitHpT5cmUsxAkeomW17JWdnU1PT09l1RQn3qdDhw5R\no9HYNFWgOwkPD7dpusTnn3++5KXcLDhz5gz9/PzMjkfv2rWLjz76qN3XLNGgQfdzOgAOhbJgQ1aB\n3+1/AVYGmFdg21MAPyj4+x8yxLntesBIUaS7s2EsxKr8sZCpU53WrIdCmzZAairw22/K/Tt2TPlE\n7u2tlJgMHQpoNGXdyjLh6emJ4OBgnDt3Do2cdJ8yMzMxcOBALFq0CGFhYWr/CE6VPw4bGRlZ4nFp\naWl4/fXX7b5+VFQU+vbti3fffRdJSUmF9sXExODo0aMgCQ9rPQm2iolRfqdaLRKhdPv+F8pTa77O\nAEIAzAUwHcD3APYAMLXuIShZs6qsI7ywosAnyfyvXIBPABxt5qnW7BOsfJIUKujduzc3bdrktOsN\nHz6cQ4cOddr1XCkhIYEbN24s8ZirV6/Sx8fH4bK5K1eu0MfHh5cvXy62LzAwkJcuXXLoumYZe84u\nQSlRqwplecb8r7XG95XjANtDKVtrBHCz9JwVImOw7s6GsRCbPOxjIcLpmjRpghMnTlg/0AYbNmzA\n/v37LY4zujtbMokPHDiADh06oEIFx952AwMDMWbMGMyePbvYPqcnOvn7Az16INTDA4QyWUhmga9B\nxsOaADgAZaauk1AmGAGg9JrFxz+0PTz5JMC6uwLT9xHACCjdw6lQEgxsVs6n7xOu17hxY5w8ebLU\n17l06RLGjx+PlJQU1KxZ0wktcz1bAqwjCU5Fvfzyy/jss8+K3XdVEp2kZK3UJMC6uwLT9+WPhXyG\nwmMhAJAD5VMmoJTtaIH7y6rJWIhQgTOeYHU6HQYNGoSXX34ZrVu3dlLLXM/WAGtpgn9beXl5Ydq0\naZgxY0ah7aqU6kjJWqlJgHV3Q4cCAH4G8E8AP0Ipxalp/FpnPKwhlKB7BUB3499/zr8GabqOEM7S\nsGFDnDt3DjqdzuFrvPnmm6hRowZeeuklJ7bM9QICAkqcjzgnJwdHjhxB27ZtS/1a48aNw+HDh5GW\nlmbalp/o5HRSslYqEmDdnY1jIZeAYpPnhgEyFiJUU61aNdSrVw/nzp1z6Pz9+/dj2bJlWLVqlcPj\nku7C2hPs4cOHER0d7ZQucE9PT8yZMwevvPKKaXKLhg0b4v/+7/8sTkZRKomJwN69QEKC0ptWtNu4\nWjVle0KCcpwEV5MH+1/1w0LGQoSbatKkiUPjsLdv38bgwYOxfPly1K1bV4WWuZa1AOuM7uGChgwZ\nglu3bmHbtm0AgMqVK6Nhw4bOnzIxX34p1uXLwBtvAEOGAL16KX++8YayPTVVuoWLkAD7IJCxEOGm\nGjdubPc4LEmMHj0affr0Qc+ePVVqmWvlB9j8J8qinB1gK1asiLlz52L69OnQ6/UA1F26zkSjUerp\nV68GPvtM+XPqVOkhs0AC7INCxkKEG3LkCXbFihU4e/Ys3nvvPZVa5Xo1a9ZEhQoVkJmZWWwfSadk\nEBfVq1cv1K5dG2vXrgWgUqKTKBUJsA8SGQsRbsbeUp3Tp09j+vTpSElJgacxO768sLTw+qVLl+Dh\n4YHQ0FCnvp6Hhwfee+89zJw5E1qtFq2Dg9F42zZg8GDgqaeUP5OSlBm2RJnwoKU+DeHeZPo+4Qay\nsrLg5+eHO3fuoJKV5etycnLQvn17JCYmYvTo0S5qoevExsYiKSkJnTp1KrR93bp1+M9//oNNmzap\n8rqTO3fGX2/fRoOzZ6HNySlcwletmlJF0KOHkovhhCxmYTuZi/hBlT8WIkQZql69OurWrYsLFy4g\nKiqqxGNfeeUVhIeHY9SoUS5qnWtZSnQ6cOCAU8dfC0lOxrz0dFCrhQeK18cjO1v5c8sW4KuvZNjI\nxaSLWAhRKrYkOn3xxRdITU3FRx995LwJ6d1MQECA2QDr7AQnk+RkYMoUVNBqUdHasSSQvz50crLz\n2yLMkgArhCgVa4lO165dw/Dhw7FmzRr4+Pi4sGWuZW4MNjMzE2fOnEHLli2d+2Lp6ciZPBkjsrIQ\nCqAWgBYAvjDu/g5AHAAfABoA/QD8CtwPsocOObc9wiwJsEKIUmkVFISwjRvNJtcYDAa88MILGDly\nJB577LGybqqqzHURHzx4EC1atEDVqlWd+2Jz50KXnY1gAHsB/AHgLQDPQZl05jaA0ca//wwlAA/L\nPzc7G5g717ntEWbJGKwQwjHp6cDcuXh22zbk5uUBBUtENm8GZs3C+QYNEOThgVmzZpVdO13EXIBV\npXv4+nXgiy9QA8DsApt7AagP4AcAzxQ5ZTwA08cbEti+XUmUlIRIVckTrBDCfsnJwJ//DGzZggq5\nufAsWoyQnQ1otQg/fhwfnT2LSh99VCbNdCVzY7CqBNiVK81uzgDwE5Ql5IraV3S7h4fF6wjnkQAr\nhLCPMbkGWVnK01AJKgKooNU+FMk1RcdgDQYDvvvuO6dPMIGjRwGtttCmPCjzkr8AILro4QDmAJhX\ncGN2tlLiJ1QlAVYIYbv09PvB1R4PQXJN0ekSz5w5Ay8vLwQEBDj3hf74o9C3BgBDAFQBsKTIoecA\n9ACwEMCjRa9z+7Zz2yWKkQArhLDd3Ln3aysLOAWgC4DaABoA+I+5c8t5ck3NmjXh4eFhmi5RtfKc\n2rVNfyWAEVC6h1MBVC5w2M8AugJ4HUoALsbb2/ltE4VIgBVC2MaYXFO0W1gHoDeUJJtbAJYBGAxl\nPLCQgsk15VTBcVjVAmxMjDIlKoBEKB9uPkPhSSauQPnAMx7AX81do1o1ZeY3oSoJsEII21hIijkN\n4CqAv0EZc+0CoCOANeYOLufJNQXHYVULsEOHAlCeUP8J4EcAAQBqGr/WAVgO4AKULOOaBb5MSNN1\nhHqkTEcIYRszyTWWEIDZlUnLc3LN9esYc+cOgmfMQG61aph17hyaffklUK+ec8th/P2BHj0QumWL\nxeXxAMBiYZSHBxAfLyU6LiBPsEII2xRJrsnXEIA/lCzVPAA7oEx+YDENqrwl16SnA337AqGhGHj6\nNEL370eVHTswQKdDxTlzgJAQZX96uvNec/r04qtp2apaNeV8oToJsEII2xRIrimoMoAtALZB6ap8\nH8qMQkGWrlOekmsK1ANDq0UV4+LnJsZ6YGzZohznrFKltm3vrw9tj/x1otu0cU47RIkkwAohbFMg\nuabYLihPrTcBfAVl/O8RcweWp+QaO+qBVZlsPzHxfpC1toCCh8f94Cqr6biMrAcrhLDN9etAaKjZ\ncdijAKKg1GQuBfAhlOSnYjPwenoCly8/+ON/6elY0rEjVubl4RiAgQBWGnddgjJlYY0Ch0+DUi4D\nQAl0e/c67yny0CGl/Gn7diWQFiyjyl8PNj5e6RaWJ1eXkiQnIYRtjMk12LKl2BPbGiiZq3lQJjTY\nCTPBtTwl18ydi8C8PLwG5Ym9eGUw8DssvMHm1wOnpjqnLW3aKNf67TclQ/vYMWWc29tb6S0YOrR8\n3PMHkDzBCiFsl56ujCXaO5MT4Pwnt7JS5En+NQC/oPgTbB5KeIIpL0/yokQyBiuEsJ0k19hcxxsK\nJdFrGIAbRXeW83pgoZAAK4Swz8OeXGOlHtgPQDqUiSB+AHAXykT8hZTnemBhIgFWCGG/xESluzch\nQenuLFqTWa2asj0hQTmuvARXwGI9cL6aANpA6R6uA2UC/h1QAm0h5a0eWBQjSU5CCMc8rMk1FuqB\nLcl/xjcU3VGe6oGFWRJghRClo9EAU6eWdStcJyYGSE2FTquFDoDe+KWF8ob6AwAvAJEAbgN4EcCf\noaw0ZFKe6oGFRZJFLIQQ9jBmEc/WavFGkV2zoEwdOQPAdQB/AhAHIAnKLFcmkkX8UJAAK4QQ9urb\n12w9sE08PJSxaWfVwQq3JQFWCCHsJfXAwgaSRSyEEPaSemBhA0lyEkIIR+SXHk2ZotS1ltQZ6OGh\nJDaVp3pgYZV0EQshRGnIZPvCAgmwQgjhDA9bPbCwSgKsEEIIoQJJchJCCCFUIAFWCCGEUIEEWCGE\nEEIFEmCFEEIIFUiAFUIIIVQgAVYIIYRQgQRYIYQQQgUSYIUQQggVSIAVQgghVCABVgghhFCBBFgh\nhBBCBRJghRBCCBVIgBVCCCFUIAFWCCGEUIEEWCGEEEIFEmCFEEIIFUiAFUIIIVQgAVYIIYRQgQRY\nIYQQQgUSYIUQQggVSIAVQgghVCABVgghhFCBBFghhBBCBRJghRBCCBVIgBVCCCFUIAFWCCGEUIEE\nWCGEEEIFEmCFEEIIFUiAFUIIIVQgAVYIIYRQgQRYIYQQQgUSYIUQQggVSIAVQgghVCABVgghhFCB\nBFghhBBCBRJghRBCCBVIgBVCCCFUIAFWCCGEUMH/A4mgXwgrlNdTAAAAAElFTkSuQmCC\n",
      "text/plain": [
       "<matplotlib.figure.Figure at 0x10b2284e0>"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    }
   ],
   "source": [
    "# See Karate Club network: http://vlado.fmf.uni-lj.si/pub/networks/data/Ucinet/UciData.htm#zachary\n",
    "# First, we print the degree for each of the 34 nodes.\n",
    "import warnings\n",
    "warnings.filterwarnings(\"ignore\")\n",
    "import networkx as nx\n",
    "G=nx.karate_club_graph()\n",
    "nx.draw(G, with_labels=True)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 31,
   "metadata": {
    "collapsed": false
   },
   "outputs": [
    {
     "data": {
      "text/plain": [
       "{0: 16,\n",
       " 1: 9,\n",
       " 2: 10,\n",
       " 3: 6,\n",
       " 4: 3,\n",
       " 5: 4,\n",
       " 6: 4,\n",
       " 7: 4,\n",
       " 8: 5,\n",
       " 9: 2,\n",
       " 10: 3,\n",
       " 11: 1,\n",
       " 12: 2,\n",
       " 13: 5,\n",
       " 14: 2,\n",
       " 15: 2,\n",
       " 16: 2,\n",
       " 17: 2,\n",
       " 18: 2,\n",
       " 19: 3,\n",
       " 20: 2,\n",
       " 21: 2,\n",
       " 22: 2,\n",
       " 23: 5,\n",
       " 24: 3,\n",
       " 25: 3,\n",
       " 26: 2,\n",
       " 27: 4,\n",
       " 28: 3,\n",
       " 29: 4,\n",
       " 30: 4,\n",
       " 31: 6,\n",
       " 32: 12,\n",
       " 33: 17}"
      ]
     },
     "execution_count": 31,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "# dict from node id to degree\n",
    "degrees = nx.degree(G)\n",
    "degrees"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 32,
   "metadata": {
    "collapsed": false
   },
   "outputs": [
    {
     "data": {
      "text/plain": [
       "Counter({1: 1,\n",
       "         2: 11,\n",
       "         3: 6,\n",
       "         4: 6,\n",
       "         5: 3,\n",
       "         6: 2,\n",
       "         9: 1,\n",
       "         10: 1,\n",
       "         12: 1,\n",
       "         16: 1,\n",
       "         17: 1})"
      ]
     },
     "execution_count": 32,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "# Count number of nodes with each degree value.\n",
    "from collections import Counter\n",
    "degree_counts = Counter(degrees.values())\n",
    "degree_counts\n",
    "# e.g., 11 nodes have degree of 2"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 34,
   "metadata": {
    "collapsed": false,
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "[(1, 0.029411764705882353), (2, 0.3235294117647059), (3, 0.17647058823529413), (4, 0.17647058823529413), (5, 0.08823529411764706)]\n"
     ]
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAY4AAAEYCAYAAABLOxEiAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAH+RJREFUeJzt3XmcHWWd7/HPl4SEHYkElywkQFSCQhhD4owKKBECIkEv\nDovMBEQRBxwdnRG4KHADKuKG9woKsgoDiOASZ4LIjg4CaSAsCUaaAFlkCYRNlkDgd/94nobKyenu\nU8mp6k7yfb9e59W1Ps9zquvUt7ZTRxGBmZlZq9bp6waYmdnqxcFhZmalODjMzKwUB4eZmZXi4DAz\ns1IcHGZmVoqDYw0m6UpJU9tU1gclzS30PyRpUjvKzuXNlrRru8orlPsWSTdJek7S99pdvrWPpBMl\nXVRi+j0k/brKNq0JJH1M0s/bWeZaGxx5w/di3qA8LelmSUdIWi2WiaSQ9Lykv0l6UtK1kvYvThMR\ne0bEBS2WtU1P00TEHyLinava7lzf+ZJObih/u4i4oR3lNzgceALYJCK+sqqFSTpE0h8L/ZtI+h9J\nV0gatKrlN6lvhWW1EvOHpAmFYdtIaukLXI3vt5/5BnBKXzdiVUkaImlxT8s5/x9ezZ/3rteuhfH/\nIOm2vD27W9IHusZFxG+B7SRt3642rxYbyQp9LCI2BrYkrYBHA+dUUZGkARUUu0NEbAS8Ezgf+JGk\nE9pdiaSB7S6zRlsCc2Ilvuna2/uWtBlwLfAwsH9EvNzO8ttoCbDS4VOHsstC0k7AphFxS0VNqtO3\ngftamO5PEbFR4XUDpOABfgt8B3gTcCrw27x+drmEtBPVHhGxVr6Ah4BJDcMmAK8B7879g4HvAvOB\nx4CfAOsXpv8q8AjwV+AzQADb5HHnAz8GZgDPA5NaKG9vYBbwNHAzsH0P7X+9rsKw/YCXgDfn/huA\nz+TubYAbgWdIe+A/z8NvymU9D/wN2B/YFVhICtJHgQu7hjUsv2OBOcBTwHnAenncIcAfm7WXtPK+\nAryc6/tt4/8jL6fT8nL9a+4enMd1te0rwON5+R/azTI6v6GuSS2W/fr7blLmIcAfgaH5f3UesE5h\n/EeBO4FngQXAiYVxo/JyOCyvAzfl4b/I9T2T/x/b5eHdLau3A1cAi4EHgX/tYT05H/h+Ln+XwroQ\nhWk2Je0wPQIsIoXMAGBb0vr0aq7/aWB0/rtOnvenwOOFsi4EvlRo53RScHUCny1MdyJwOXBRXlaf\nycMuyuPXJW3srgAGNXlfxwNnN1nH/gW4H3gOOAnYmvRZeha4rFgWPXzegGOAB3I5c4CPN1kHvkta\n9x8E9lzJ7dA/AH8CDqXhM9Nsvetm3N7A7IZhfwEOK/S/H3iwbdvPdhW0ur1oEhx5+Hzg87n7B3nF\nHwJsTEr1b+Vxk/OHcTtgg/wBaAyOZ/I/bB1gvV7K25G0IZyYP7RTcxsHd9P+ZsGxLrCsayVm+eC4\nBDiu0JYPdFcWaQO6jLQnNBhYn+bBcS8wIr+f/wFO7m4lb7JsTu7u/wFMA24BtiBtoG8GTmpo27T8\nfvcCXgA262Y5LVdXi2W//r6blHcIaUMym7RjoIbxuwLvyct5e9IOwr553Ki8HH4GbNhVPvDpvD50\nhdqsHtq/DnA7acM5CNgKmAfs0dP7B/6163/CisHxK+DM3KYtgNuAz/Xwv5wPvDd3z831b1sYt2Pu\nvgk4g7S+jSMF3YfzuBNJobhvfk/r52EX5e7/zm0f0M37+gXwH03Wsd8Am5A+l0tJR4RbkcJxDjC1\nlc8b8ElS8K1D2pl6HnhbYZm8Anw2z/t50k6I8vgzSGHU7HV3ob0DgDuA9zZbzk3Wu+dJO31/Ab4O\nDMzj9iYdVRenvx/4QaF/SF4+m7Rl+9mOQlbHF90Hxy2kDazyP2rrwri/J6c2cC55o1/8MLL8xvFn\nhfG9lfdj8gasMH4ueS+xSTtXCI48/FHgU7n7Bt4Ijp8BZwHDeyuLtPF7mXwEURjWGBxHFPr3Ah6I\nN1byVQmOB4C9CuP2AB4qtOPFrg9NHvY48L5ultNydbVQ9nLvu0l5h5D2Ql8BJrawnp3W9QHmjeDY\nqofp35Sn2bSb9k8E5jfMcyxwXk/vnxRK84E9KQQH8BbSBrZ45HsgcH0P/8sLgS8DbyWto6cCR1A4\nGiHtULwKbFyY71vA+bn7RPIRV2H8iaQdqxuB/0tDKDdMe3Vx/SusY+8v9N8OHF3o/x5w2kp+3mYB\nUwrLpLMwboNc91t7Wx8ayvw34MfdLeeGabfKy3cd0o7JHODYPO7NebkfSNqZmko6c3JmYf51cxtH\nlmljd6+1/RpHM8NIh9ZDSSvE7fni+dPA7/JwSHsjCwrzLWBFxWG9lbcl8JWucXn8iFxPSyStm8tb\n0mT0V0nhdVu+g+nTvRS3OCJe6mWa4vt7uExbe/H2XF53ZT8ZEcsK/S8AG7Wp7Fbe913AvwNXStqx\nOELSREnX54udz5A2qJs3zL+gMP0ASadIekDSs6QApck8XbYE3t6wnvxvUgB0KyKWkk7dnNSkvHWB\nRwrlnUk68ujOjaSQ3Zl0VHEDsEt+/SEiXiMt0yUR8VxhvodJn68uzT4z7yMdqZ3SlWzdeIp0lNbo\nsUL3i036u9aTHj9vkv5Z0qzCuHez/P/k0a6OiHghd7a6DiLp7aSjwONamT4i5kXEgxHxWkTcQzpy\n3i+PexKYQgrzx0hnQ64hnXbt0rWsnm61jT1ZnS96tl2+4DaMdP7yCdKKtl1ELGoy+SPA8EL/iCbT\nFFf83spbAHwjIr6xMm3PppBOtdy2QkMiHiUdWpPvuLhG0k0R0dlNWT19aLsU3/NI0uE6pCOrDbpG\nSHprybL/Svpgz25S9qrqrexW3jcR8UNJg4GrJe0aEffmURcDPyKdLnxJ0mmsGALFOg4i/d8mkUJj\nU9JGUd20ZwHpKHVMK+1scB7p+s0nGspbCmzeEMbN2trlRtKF2IW5+4+k63Uv5X5Iy3SIpI0L4TGS\ndA2lp7J/D9wNXJuX62NNpiFP845uxrWi28+bpC1J1252I12QflXSLN74n/RI0k+Ag7sZ/XBEbEe6\nnvo2YI4kSKfn1pf0KDAsIl7tpZooticibgR2yvUPJJ0+LN5+vi3pyPrZVt5Db3zEweu3VO4NXEq6\nOHdP3mv6KfADSVvk6YZJ2iPPdhlwqKRtJW1AOufYrRbK+ylwRN5jlaQNJX1UUrO9qsb2D5H0KeB0\n4Nt5D6Rxmk9K6gq6p0gr3mu5/zHSoXBZR0oanu/qOA7oulf8LtLtf+MkrUc6BVHUW32XAF+TNFTS\n5qTz+S3f39+LtpUdEacCPySFcNetyhuT9rRfyrfAHtRLMRuTNtxPksL2mw3jG5fVbcBzko6WtH4+\nYnl33unprb3LgBNI4dE17BHSxvp7+XOwjqStJe1SqH948VbjiLiftBN0MHBj3hg9BvwvcnBExALS\n9aNvSVov3wp6GC0s67xcLyaFR3dHXjNIRzgrq6fP24akz8diAEmHko44WhIRR8Tydz8VX9vlya4k\nnbocl1/Hk26qGNcsNCTtKektuftdpO3Nbwrjd5S0rqRNSBftF0TEVYUidsl1tsXaHhy/lfQcae/j\nONLdJ4cWxh9Nuhvklnwa4RrSra9ExJWk87DXd02T51naQ309lddBOiL4EWnD3kk679mTuyT9LU/7\nGeDfIuL4bqbdCbg1Tz8d+GJEzMvjTgQuyIfl/9hLnUUXkzY680jXDk7O7+UvpEPpa0gX6RrvTz8H\nGJvra/YFrpOBDtJe5T2kC4jtup20rWVHxEnA2aSN3Naku3qm5fXqeNIORk9+RjqFs4h03rrx9tLl\nllXeqOxN2tg8SDqSPZt0pNKKS0hHy0X/TLrQ3nWH3OWkvWGA60hHZ49KeqIwz42kU4YLCv0iLc8u\nB5I2jn8lXYA/ISKuaaWRebn+mhTKQ5qMvwN4RtLEVsprMn+3n7eImEPaW/8TKRDfQ7r5o20iYmlE\nPNr1It1I80ruRtJIpe9qjMyz7AbcLel5Umj+kuV3Mr5KWhcWkP53H2+o8kDSKci26LoLwFaRpG1J\ndxkN7uaQ38zaSNLuwL9ExL593Zb+TNLHgH+KiDI7hT2X6eBYeZI+Tkr/DYALgNe8EpvZmm5tP1W1\nqj5HuhX0AdKth5/v2+aYmVXPRxxmZlaKjzjMzKyUNfJ7HJtvvnmMGjWqr5thZrZauf3225+IiKG9\nTbdGBseoUaPo6Ojo62aYma1WJD3c+1Q+VWVmZiU5OMzMrBQHh5mZleLgMDOzUhwcZmZWioPDzMxK\ncXCYmVkpDg4zMyvFwWFmZqWskd8cX91cfOv8Sso9aOLI3icyMyvJRxxmZlaKg8PMzEpxcJiZWSkO\nDjMzK8XBYWZmpTg4zMysFAeHmZmV4uAwM7NSHBxmZlaKg8PMzEpxcJiZWSm1BYekyZLmSuqUdEyT\n8UdIukfSLEl/lDS2MO7YPN9cSXvU1WYzM1tRLcEhaQBwOrAnMBY4sBgM2cUR8Z6IGAecCnw/zzsW\nOADYDpgMnJHLMzOzPlDXEccEoDMi5kXEy8ClwJTiBBHxbKF3QyBy9xTg0ohYGhEPAp25PDMz6wN1\nPVZ9GLCg0L8QmNg4kaQjgS8Dg4APF+a9pWHeYU3mPRw4HGDkSD9O3MysKv3q4nhEnB4RWwNHA18r\nOe9ZETE+IsYPHTq0mgaamVltwbEIGFHoH56HdedSYN+VnNfMzCpUV3DMBMZIGi1pEOli9/TiBJLG\nFHo/Ctyfu6cDB0gaLGk0MAa4rYY2m5lZE7Vc44iIZZKOAq4CBgDnRsRsSdOAjoiYDhwlaRLwCvAU\nMDXPO1vSZcAcYBlwZES8Wke7zcxsRbX95nhEzABmNAw7vtD9xR7m/QbwjepaZ2ZmrepXF8fNzKz/\nc3CYmVkpDg4zMyvFwWFmZqU4OMzMrBQHh5mZleLgMDOzUhwcZmZWioPDzMxKcXCYmVkpDg4zMyvF\nwWFmZqU4OMzMrBQHh5mZleLgMDOzUhwcZmZWioPDzMxKcXCYmVkpDg4zMyvFwWFmZqU4OMzMrBQH\nh5mZleLgMDOzUmoLDkmTJc2V1CnpmCbjvyxpjqS7JV0racvCuFclzcqv6XW12czMVjSwjkokDQBO\nBz4CLARmSpoeEXMKk90JjI+IFyR9HjgV2D+PezEixtXRVjMz61ldRxwTgM6ImBcRLwOXAlOKE0TE\n9RHxQu69BRheU9vMzKyEuoJjGLCg0L8wD+vOYcCVhf71JHVIukXSvs1mkHR4nqZj8eLFq95iMzNr\nqpZTVWVIOhgYD+xSGLxlRCyStBVwnaR7IuKB4nwRcRZwFsD48eOjtgabma1l6jriWASMKPQPz8OW\nI2kScBywT0Qs7RoeEYvy33nADcCOVTbWzMy6V1dwzATGSBotaRBwALDc3VGSdgTOJIXG44Xhm0ka\nnLs3B94PFC+qm5lZjWo5VRURyyQdBVwFDADOjYjZkqYBHRExHfgOsBHwC0kA8yNiH2Bb4ExJr5GC\n7pSGu7HMzKxGtV3jiIgZwIyGYccXuid1M9/NwHuqbZ2ZmbXK3xw3M7NSHBxmZlaKg8PMzEpxcJiZ\nWSkODjMzK8XBYWZmpTg4zMysFAeHmZmV4uAwM7NSHBxmZlaKg8PMzEpxcJiZWSkODjMzK8XBYWZm\npTg4zMysFAeHmZmV4uAwM7NSHBxmZlaKg8PMzEpxcJiZWSkODjMzK8XBYWZmpTg4zMyslNqCQ9Jk\nSXMldUo6psn4L0uaI+luSddK2rIwbqqk+/Nral1tNjOzFdUSHJIGAKcDewJjgQMljW2Y7E5gfERs\nD1wOnJrnHQKcAEwEJgAnSNqsjnabmdmK6jrimAB0RsS8iHgZuBSYUpwgIq6PiBdy7y3A8Ny9B3B1\nRCyJiKeAq4HJNbXbzMwa1BUcw4AFhf6FeVh3DgOuLDOvpMMldUjqWLx48So218zMutPvLo5LOhgY\nD3ynzHwRcVZEjI+I8UOHDq2mcWZmVltwLAJGFPqH52HLkTQJOA7YJyKWlpnXzMzqUVdwzATGSBot\naRBwADC9OIGkHYEzSaHxeGHUVcDukjbLF8V3z8PMzKwPDKyjkohYJuko0gZ/AHBuRMyWNA3oiIjp\npFNTGwG/kAQwPyL2iYglkk4ihQ/AtIhYUke7zcxsRbUEB0BEzABmNAw7vtA9qYd5zwXOra51ZmbW\nqn53cdzMzPo3B4eZmZXi4DAzs1IcHGZmVoqDw8zMSikdHJI2zA8tNDOztVCvwSFpHUkHSfpvSY8D\nfwYeyY9A/46kbapvppmZ9RetHHFcD2wNHAu8NSJGRMQWwAdIT7H9dn6+lJmZrQVa+QLgpIh4pXFg\n/vb2FcAVktZte8vMzKxf6jU4ukJD0skR8bXiOEkDIuLVZsFi/dfFt86vrOyDJo7s8/rMrFplLo4P\nk3RgV4+kLYBr2t8kMzPrz8o8q+pzwFWSHgACOA84upJWmZlZv9VrcEj6GXAH6TfBjwQuBpYB+0ZE\nZ7XNMzOz/qaVU1XnAwIOBS4CRgFPAQdL2q+ylpmZWb/Uyqmq6yPiuq4eSQOBbYEdgAnA5ZIUEVFR\nG83MrB9p6Xsckr4gaSSkH2WKiHuAy0jXPC4AplbZSDMz6z9aOeKYDHwauETSVqTTVOuRfsnv98Bp\nEXFndU00M7P+pJXvcbwEnAGckb/otznwYkQ8XXXjzMys/2nlWVVTJT0haQlwNvA3h4aZ2dqrlWsc\nXwc+ArwLmA98s9IWmZlZv9bKNY5nC9cwvi7p1iobZGZm/VsrwfE2SYeTHqd+H+AHGpqZrcVaCY4T\ngPcAn8p/N5I0A7gLuDsiLqmwfWZm1s/0eo0jIs6KiC9ExC4RMQTYCvh/wNPAXq1WJGmypLmSOiUd\n02T8zpLukLSs8Rvpkl6VNCu/prdap5mZtV+ZhxwCEBELgYXAla3Ok39q9nTSRfaFwExJ0yNiTmGy\n+cAhwL83KeLFiBhXtq1mZtZ+pYNjJU0AOiNiHoCkS4EpwOvBEREP5XGv1dQmMzNbCWV+j2NVDAMW\nFPoX5mGtWk9Sh6RbJO3bbAJJh+dpOhYvXrwqbTUzsx7UFRyrasuIGA8cBJwmaevGCfK1mPERMX7o\n0KH1t9DMbC1RV3AsAkYU+ofnYS2JiEX57zzgBmDHdjbOzMxaV1dwzATGSBotaRBwANDS3VGSNpM0\nOHdvDryfwrURMzOrVy3BERHLgKOAq0hfIrwsImZLmiZpHwBJO0laCHwSOFPS7Dz7tkCHpLuA64FT\nGu7GMjOzGtV1VxURMQOY0TDs+EL3TNIprMb5biZ98dDMzPqB1eXiuJmZ9RMODjMzK8XBYWZmpTg4\nzMysFAeHmZmV4uAwM7NSHBxmZlaKg8PMzEpxcJiZWSkODjMzK8XBYWZmpTg4zMysFAeHmZmV4uAw\nM7NSHBxmZlaKg8PMzEpxcJiZWSkODjMzK8XBYWZmpTg4zMysFAeHmZmV4uAwM7NSHBxmZlZKbcEh\nabKkuZI6JR3TZPzOku6QtEzSfg3jpkq6P7+m1tVmMzNbUS3BIWkAcDqwJzAWOFDS2IbJ5gOHABc3\nzDsEOAGYCEwATpC0WdVtNjOz5uo64pgAdEbEvIh4GbgUmFKcICIeioi7gdca5t0DuDoilkTEU8DV\nwOQ6Gm1mZiuqKziGAQsK/QvzsLbNK+lwSR2SOhYvXrzSDTUzs56tMRfHI+KsiBgfEeOHDh3a180x\nM1tj1RUci4ARhf7heVjV85qZWZvVFRwzgTGSRksaBBwATG9x3quA3SVtli+K756HmZlZH6glOCJi\nGXAUaYN/H3BZRMyWNE3SPgCSdpK0EPgkcKak2XneJcBJpPCZCUzLw8zMrA8MrKuiiJgBzGgYdnyh\neybpNFSzec8Fzq20gWZm1pI15uK4mZnVo7YjDrO6XHzr/MrKPmjiyMrKNltd+IjDzMxKcXCYmVkp\nDg4zMyvFwWFmZqU4OMzMrBQHh5mZleLgMDOzUhwcZmZWioPDzMxKcXCYmVkpDg4zMyvFwWFmZqU4\nOMzMrBQHh5mZleLgMDOzUhwcZmZWioPDzMxKcXCYmVkp/ulYszao6udq/VO11h/5iMPMzEpxcJiZ\nWSm1BYekyZLmSuqUdEyT8YMl/TyPv1XSqDx8lKQXJc3Kr5/U1WYzM1tRLdc4JA0ATgc+AiwEZkqa\nHhFzCpMdBjwVEdtIOgD4NrB/HvdARIyro61mZtazuo44JgCdETEvIl4GLgWmNEwzBbggd18O7CZJ\nNbXPzMxaVFdwDAMWFPoX5mFNp4mIZcAzwJvzuNGS7pR0o6QPNqtA0uGSOiR1LF68uL2tNzOz160O\nF8cfAUZGxI7Al4GLJW3SOFFEnBUR4yNi/NChQ2tvpJnZ2qKu4FgEjCj0D8/Dmk4jaSCwKfBkRCyN\niCcBIuJ24AHgHZW32MzMmqorOGYCYySNljQIOACY3jDNdGBq7t4PuC4iQtLQfHEdSVsBY4B5NbXb\nzMwa1HJXVUQsk3QUcBUwADg3ImZLmgZ0RMR04BzgQkmdwBJSuADsDEyT9ArwGnBERCypo91mZrai\n2h45EhEzgBkNw44vdL8EfLLJfFcAV1TeQDMza8nqcHHczMz6EQeHmZmV4uAwM7NSHBxmZlaKg8PM\nzEpxcJiZWSkODjMzK8U/HduEfwbU+ru619E1pb7u6lzT62s3H3GYmVkpDg4zMyvFwWFmZqU4OMzM\nrBQHh5mZleLgMDOzUhwcZmZWioPDzMxKcXCYmVkpDg4zMyvFwWFmZqU4OMzMrBQHh5mZleLgMDOz\nUhwcZmZWSm3BIWmypLmSOiUd02T8YEk/z+NvlTSqMO7YPHyupD3qarOZma2oluCQNAA4HdgTGAsc\nKGlsw2SHAU9FxDbAD4Bv53nHAgcA2wGTgTNyeWZm1gfqOuKYAHRGxLyIeBm4FJjSMM0U4ILcfTmw\nmyTl4ZdGxNKIeBDozOWZmVkfUERUX4m0HzA5Ij6T+/8JmBgRRxWmuTdPszD3PwBMBE4EbomIi/Lw\nc4ArI+LyhjoOBw7Pve8E5lb6pt6wOfBETXW5vjWjTte3etfXF3XWVd+WETG0t4nWmN8cj4izgLPq\nrldSR0SMd32rZ319UafrW73r64s6++I99qSuU1WLgBGF/uF5WNNpJA0ENgWebHFeMzOrSV3BMRMY\nI2m0pEGki93TG6aZDkzN3fsB10U6jzYdOCDfdTUaGAPcVlO7zcysQS2nqiJimaSjgKuAAcC5ETFb\n0jSgIyKmA+cAF0rqBJaQwoU83WXAHGAZcGREvFpHu1tU9+kx17f61+n6Vu/6+qLOvniP3arl4riZ\nma05/M1xMzMrxcFhZmalODhWkqRzJT2ev39SR30jJF0vaY6k2ZK+WHF960m6TdJdub7/U2V9hXoH\nSLpT0n/VUNdDku6RNEtSRw31vUnS5ZL+LOk+SX9fcX1flHRv/v99qaI6VvgcSBoi6WpJ9+e/m1Vc\n33fyMr1b0q8kvanK+vLwL+Q6Z0s6tV31dVdnfhzTrPx6SNKsdtZZloNj5Z1PegRKXZYBX4mIscD7\ngCObPLalnZYCH46IHYBxwGRJ76uwvi5fBO6roZ4uH4qIcTXdI/9D4HcR8S5gByp8n5LeDXyW9JSF\nHYC9JW1TQVXns+Ln4Bjg2ogYA1yb+6us72rg3RGxPfAX4Ngq65P0IdITLXaIiO2A77axvqZ1RsT+\neT0dB1wB/LLNdZbi4FhJEXET6e6vuup7JCLuyN3PkTY6wyqsLyLib7l33fyq9E4KScOBjwJnV1lP\nX5C0KbAz6e5BIuLliHi6wiq3BW6NiBciYhlwI/CJdlfSzeeg+PigC4B9q6wvIn6f3yPALaTvelVW\nH/B54JSIWJqnebxd9fVQJwD5MUz/CFzSzjrLcnCshvKTg3cEbq24ngH5kPhx4OqIqLQ+4DTgq8Br\nFdfTJYDfS7o9P7KmSqOBxcB5+VTc2ZI2rLC+e4EPSnqzpA2AvVj+i7RVektEPJK7HwXeUlO9AJ8G\nrqy4jneQlu2tkm6UtFPF9RV9EHgsIu6vsc4VODhWM5I2Ih2qfikinq2yroh4NR8aDwcm5NMflZC0\nN/B4RNxeVR1NfCAi/o701OYjJe1cYV0Dgb8DfhwROwLP095TOMuJiPtIT5j+PfA7YBZQ+/ef8pd4\na7nnX9JxpFO6/1lxVQOBIaRTxv8BXJaPBOpwIH18tAEOjtWKpHVJofGfEVHbOc58SuV6qr2m835g\nH0kPkZ6e/GFJF1VYHxGxKP99HPgV1T51eSGwsHDUdjkpSCoTEedExHsjYmfgKdL5/zo8JultAPlv\nW0/lNCPpEGBv4FNR/ZfTFgK/zKdzbyMdIW9ecZ1dj2L6BPDzquvqjYNjNZH3aM4B7ouI79dQ39Cu\nu1MkrQ98BPhzVfVFxLERMTwiRpGeGnBdRBxcVX2SNpS0cVc3sDvp9E4lIuJRYIGkd+ZBu5GehlAZ\nSVvkvyNJG5yLq6yvoPj4oKnAb6qsTNJk0inOfSLihSrryn4NfCjX/Q5gEPU8uXYS8OeuJ4j3qYjw\nayVepMPFR4BXSHsgh1Vc3wdIh/x3k047zAL2qrC+7YE7c333AsfXuGx3Bf6r4jq2Au7Kr9nAcTW8\nr3FAR16mvwY2q7i+P5DC6S5gt4rqWOFzALyZdDfV/cA1wJCK6+sEFhQ+Fz+puL5BwEX5c3EH6e7D\nSpdpHn4+cETV62krLz9yxMzMSvGpKjMzK8XBYWZmpTg4zMysFAeHmZmV4uAwM7NSHBxmZlaKg8PM\nzEpxcJjVRNJuki7s63aYrSoHh1l9diB9G99stebgMKvPDsCdkgZLOl/SN2t8qqpZ2wzs6waYrUW2\nJz0p9irg7Iio9Om/ZlXxs6rMapAfif8E8DDwuYj4Ux83yWyl+VSVWT22BWaSfmio9h9UMmsnB4dZ\nPXYAbib91sh5kur8OVWztnJwmNVjB+DeiPgLcDTp50bX7eM2ma0UX+MwM7NSfMRhZmalODjMzKwU\nB4eZmZXi4DAzs1IcHGZmVoqDw8zMSnFwmJlZKf8fx2fVsnEvycUAAAAASUVORK5CYII=\n",
      "text/plain": [
       "<matplotlib.figure.Figure at 0x10b95bb38>"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    }
   ],
   "source": [
    "# Now, let's plot the bar graph for the distribution of P(k)\n",
    "# probability of a node having degree k\n",
    "p_k = [(degree, count / len(G.nodes()))\n",
    "       for degree, count in degree_counts.items()]\n",
    "p_k = sorted(p_k)\n",
    "print(p_k[:5])\n",
    "ks = [x[0] for x in p_k]  # Get the first element of each tuple (the degree)\n",
    "# Plot the bar chart.\n",
    "x_pos = range(len(ks))\n",
    "plt.xticks(x_pos, ks)\n",
    "plt.bar(x_pos, [x[1] for x in p_k], align='center', alpha=0.4)\n",
    "plt.xlabel('$k$')\n",
    "plt.ylabel('$P(k)$')\n",
    "mean = 1. * sum(degrees.values()) / len(G.nodes())\n",
    "plt.title(\"Degree Distribution for Karate Network (mean=%.2f)\" % mean)\n",
    "plt.show()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "A [Long Tail](http://en.wikipedia.org/wiki/Long_tail)\n",
    "- We'll see a lot of these.\n",
    "- The mean value of a long-tailed distribution is often misleading.\n",
    "\n",
    "<br><br><br><br>"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "**Diameter:** The maximum shortest-path between any pair of nodes.\n",
    "\n",
    "**Average path length:** The average shortest-path between any pair of nodes (in one component)."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "**Clustering coefficient:** The fraction of a node's neighbors that are neighbors  \n",
    "(number of neighbor-neighbor links divided by number of possible neighbor-neighbor links)\n",
    "\n",
    "$$C_i = \\frac{2e_i}{k_i(k_i - 1)}$$\n",
    "\n",
    "- $e_i$: number of edges between neighbors of node $i$\n",
    "- $k_i$: degree of node $i$\n",
    "\n",
    "**Average Clustering Coefficient:**\n",
    "\n",
    "$$C = \\frac{1}{N}\\sum_i C_i  $$\n",
    "\n",
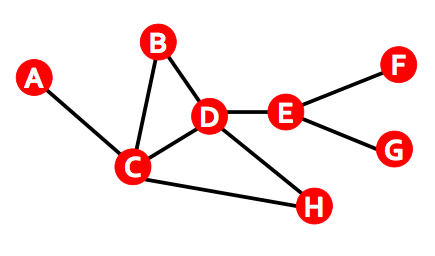    "![cluster](cluster.png)\n",
    "\n",
    "$$C_i = \\frac{2e_i}{k_i(k_i - 1)}$$\n",
    "\n",
    "[Source](http://web.stanford.edu/class/cs224w/slides/02-gnp.pdf)\n",
    "\n",
    "<br><br><br>\n",
    "What is clustering coefficient of node D?"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "$k_D=4, e_D=2, C_D=4/12 = 1/3$\n",
    "\n",
    "<br><br><br>\n",
    "\n",
    "...of node B?\n",
    "\n",
    "<br><br><br>\n",
    "\n",
    "$k_B=2, e_B=1, C_B=2/2 = 1$\n",
    "\n"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 43,
   "metadata": {
    "collapsed": false
   },
   "outputs": [
    {
     "data": {
      "text/plain": [
       "{0: 0.15,\n",
       " 1: 0.3333333333333333,\n",
       " 2: 0.24444444444444444,\n",
       " 3: 0.6666666666666666,\n",
       " 4: 0.6666666666666666,\n",
       " 5: 0.5,\n",
       " 6: 0.5,\n",
       " 7: 1.0,\n",
       " 8: 0.5,\n",
       " 9: 0.0,\n",
       " 10: 0.6666666666666666,\n",
       " 11: 0.0,\n",
       " 12: 1.0,\n",
       " 13: 0.6,\n",
       " 14: 1.0,\n",
       " 15: 1.0,\n",
       " 16: 1.0,\n",
       " 17: 1.0,\n",
       " 18: 1.0,\n",
       " 19: 0.3333333333333333,\n",
       " 20: 1.0,\n",
       " 21: 1.0,\n",
       " 22: 1.0,\n",
       " 23: 0.4,\n",
       " 24: 0.3333333333333333,\n",
       " 25: 0.3333333333333333,\n",
       " 26: 1.0,\n",
       " 27: 0.16666666666666666,\n",
       " 28: 0.3333333333333333,\n",
       " 29: 0.6666666666666666,\n",
       " 30: 0.5,\n",
       " 31: 0.2,\n",
       " 32: 0.19696969696969696,\n",
       " 33: 0.11029411764705882}"
      ]
     },
     "execution_count": 43,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "# dict from node id to clustering coefficient.\n",
    "import numpy as np\n",
    "# np.mean(list(nx.clustering(G).values()))\n",
    "nx.clustering(G)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 39,
   "metadata": {
    "collapsed": false
   },
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYIAAAEKCAYAAAAfGVI8AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAEa1JREFUeJzt3XuQJWV9xvHvAwsCggLuahQkoxQakRgwk4gYjQE0CgqW\ngoUlikpcSxOjRk2wtApiYgVELe/R9cLFeL+vQLgUCkQDxEVuC5SRwIoohlUUUcsg+Msf3SPLupfD\nzJzTzLzfT9Wp7e7Tp9/fO3N2ntOX83aqCklSu7YYugBJ0rAMAklqnEEgSY0zCCSpcQaBJDXOIJCk\nxhkEktQ4g0CSGmcQSFLjlgxdwCiWLl1aU1NTQ5chSQvKJZdc8qOqWra59RZEEExNTbFq1aqhy5Ck\nBSXJd0dZz0NDktQ4g0CSGmcQSFLjDAJJapxBIEmNMwgkqXEGgSQ1ziCQpMYZBJLUuAXxzWJJGtLU\nMacP0u6a4w+eSDvuEUhS4wwCSWqcQSBJjTMIJKlxBoEkNc4gkKTGGQSS1DiDQJIaZxBIUuMMAklq\nnEEgSY0zCCSpcQaBJDXOIJCkxo0tCJJ8NMnNSVavs2znJOck+U7/707jal+SNJpx7hGcDDxtvWXH\nAOdW1R7Auf28JGlAYwuCqroAuGW9xYcCp/TTpwDPGlf7kqTRTPocwYOq6qZ++ofAgybcviRpPYOd\nLK6qAmpjzydZnmRVklVr166dYGWS1JZJB8H/JnkwQP/vzRtbsapWVNV0VU0vW7ZsYgVKUmsmHQQr\ngaP66aOAL0+4fUnSesZ5+egngQuBRya5McnRwPHAU5J8Bziwn5ckDWjJuDZcVc/byFMHjKtNSdI9\n5zeLJalxBoEkNc4gkKTGGQSS1DiDQJIaZxBIUuMMAklqnEEgSY0zCCSpcQaBJDXOIJCkxhkEktQ4\ng0CSGmcQSFLjDAJJapxBIEmNMwgkqXEGgSQ1ziCQpMYZBJLUOINAkhpnEEhS4wwCSWqcQSBJjTMI\nJKlxBoEkNc4gkKTGGQSS1DiDQJIaN0gQJHlNkquSrE7yySTbDFGHJGmAIEiyC/C3wHRV7QVsCRwx\n6TokSZ2hDg0tAbZNsgTYDvjBQHVIUvMmHgRV9X3gbcANwE3ArVV19vrrJVmeZFWSVWvXrp10mZLU\njCEODe0EHAo8DHgIcN8kR66/XlWtqKrpqppetmzZpMuUpGYMcWjoQOD6qlpbVb8GvgDsN0AdkiSG\nCYIbgH2TbJckwAHANQPUIUlimHMEFwOfA74FXNnXsGLSdUiSOkuGaLSqjgWOHaJtSdLd+c1iSWqc\nQSBJjTMIJKlxBoEkNc4gkKTGGQSS1DiDQJIaZxBIUuMMAklqnEEgSY0zCCSpcQaBJDXOIJCkxhkE\nktQ4g0CSGmcQSFLjDAJJapxBIEmNMwgkqXEGgSQ1ziCQpMYZBJLUOINAkhpnEEhS40YKgiTnjrJM\nkrTwLNnUk0m2AbYDlibZCUj/1P2AXcZcmyRpAjYZBMDLgFcDDwEu4a4g+Bnw3jHWJUmakE0GQVW9\nC3hXkldW1XsmVJMkaYI2t0cAQFW9J8l+wNS6r6mqU2fTaJIdgQ8DewEFvKSqLpzNtiRJczNSECT5\nGLA7cBlwZ7+4gFkFAfAu4MyqOizJ1nTnISRJAxgpCIBpYM+qqrk2mOT+wJOAFwFU1e3A7XPdriRp\ndkb9HsFq4Pfmqc2HAWuBk5JcmuTDSe47T9uWJN1DowbBUuDqJGclWTnzmGWbS4DHAv9aVfsAvwCO\nWX+lJMuTrEqyau3atbNsSpK0OaMeGjpuHtu8Ebixqi7u5z/HBoKgqlYAKwCmp6fnfEhKkrRho141\ndP58NVhVP0zyvSSPrKpvAwcAV8/X9iVJ98yoVw3dRneVEMDWwFbAL6rqfrNs95XAx/srhq4DXjzL\n7UiS5mjUPYIdZqaTBDgU2He2jVbVZXRXIkmSBnaPRx+tzpeAvxxDPZKkCRv10NCz15ndgu7T/K/G\nUpEkaaJGvWrometM3wGsoTs8JEla4EY9R+DJXElapEa9Mc2uSb6Y5Ob+8fkku467OEnS+I16svgk\nYCXdfQkeAnylXyZJWuBGDYJlVXVSVd3RP04Glo2xLknShIwaBD9OcmSSLfvHkcCPx1mYJGkyRg2C\nlwDPBX4I3AQcRj+MtCRpYRv18tE3A0dV1U8AkuwMvI0uICRJC9ioewSPmQkBgKq6BdhnPCVJkiZp\n1CDYIslOMzP9HsGoexOSpHuxUf+Yvx24MMln+/nDgbeMpyRJ0iSN+s3iU5OsAvbvFz27qryHgCQt\nAiMf3un/8PvHXxs1dczpg7W95viDB2m3xT5r8bnHw1BLkhYXg0CSGmcQSFLjDAJJapxBIEmNMwgk\nqXEGgSQ1ziCQpMYZBJLUOINAkhpnEEhS4wwCSWqcQSBJjTMIJKlxgwVBki2TXJrktKFqkCQNu0fw\nKuCaAduXJDFQECTZFTgY+PAQ7UuS7jLUDejfCfw9sMPGVkiyHFgOsNtuu02orPnjnas0bkO9x3x/\nLT4T3yNI8gzg5qq6ZFPrVdWKqpquqully5ZNqDpJas8Qh4aeABySZA3wKWD/JP82QB2SJAYIgqp6\nQ1XtWlVTwBHAV6vqyEnXIUnq+D0CSWrcUCeLAaiq84DzhqxBklrnHoEkNc4gkKTGGQSS1DiDQJIa\nZxBIUuMMAklqnEEgSY0zCCSpcQaBJDXOIJCkxhkEktQ4g0CSGmcQSFLjDAJJapxBIEmNMwgkqXEG\ngSQ1ziCQpMYZBJLUOINAkhpnEEhS4wwCSWqcQSBJjTMIJKlxBoEkNc4gkKTGGQSS1DiDQJIaN/Eg\nSPLQJF9LcnWSq5K8atI1SJLusmSANu8AXltV30qyA3BJknOq6uoBapGk5k18j6Cqbqqqb/XTtwHX\nALtMug5JUmfQcwRJpoB9gIuHrEOSWjbEoSEAkmwPfB54dVX9bAPPLweWA+y2226zbmfqmNNn/dqF\nqsU+S5q9QfYIkmxFFwIfr6ovbGidqlpRVdNVNb1s2bLJFihJDRniqqEAHwGuqap3TLp9SdLdDbFH\n8ATgBcD+SS7rHwcNUIckiQHOEVTV14FMul1J0ob5zWJJapxBIEmNMwgkqXEGgSQ1ziCQpMYZBJLU\nOINAkhpnEEhS4wwCSWqcQSBJjTMIJKlxBoEkNc4gkKTGGQSS1LjBblUpzSdvzynNnnsEktQ4g0CS\nGmcQSFLjDAJJapxBIEmNMwgkqXEGgSQ1ziCQpMYZBJLUOINAkhpnEEhS4wwCSWqcQSBJjTMIJKlx\ngwRBkqcl+XaSa5McM0QNkqTOxIMgyZbA+4CnA3sCz0uy56TrkCR1htgj+FPg2qq6rqpuBz4FHDpA\nHZIkhgmCXYDvrTN/Y79MkjSAe+2tKpMsB5b3sz9P8u1Zbmop8KP5qWrBsM9tGKTPOWHSLd5NU7/n\nnDDn/v7+KCsNEQTfBx66zvyu/bK7qaoVwIq5NpZkVVVNz3U7C4l9boN9Xvwm1d8hDg19E9gjycOS\nbA0cAawcoA5JEgPsEVTVHUn+BjgL2BL4aFVdNek6JEmdQc4RVNUZwBkTam7Oh5cWIPvcBvu8+E2k\nv6mqSbQjSbqXcogJSWrcogmCzQ1bkeQ+ST7dP39xkqnJVzm/Rujz3yW5OskVSc5NMtKlZPdmow5P\nkuQ5SSrJgr7CZJT+Jnlu/3u+KsknJl3jfBvhfb1bkq8lubR/bx80RJ3zKclHk9ycZPVGnk+Sd/c/\nkyuSPHZeC6iqBf+gO+n8P8DDga2By4E911vnFcAH+ukjgE8PXfcE+vwXwHb99Mtb6HO/3g7ABcBF\nwPTQdY/5d7wHcCmwUz//wKHrnkCfVwAv76f3BNYMXfc89PtJwGOB1Rt5/iDg34EA+wIXz2f7i2WP\nYJRhKw4FTumnPwcckCQTrHG+bbbPVfW1qvplP3sR3Xc2FrJRhyf5J+AE4FeTLG4MRunvS4H3VdVP\nAKrq5gnXON9G6XMB9+un7w/8YIL1jUVVXQDcsolVDgVOrc5FwI5JHjxf7S+WIBhl2IrfrlNVdwC3\nAg+YSHXjcU+H6jia7hPFQrbZPve7zA+tqtMnWdiYjPI7fgTwiCTfSHJRkqdNrLrxGKXPxwFHJrmR\n7urDV06mtEGNdWiee+0QE5o/SY4EpoE/H7qWcUqyBfAO4EUDlzJJS+gODz2Zbo/vgiR/WFU/HbSq\n8XoecHJVvT3J44GPJdmrqn4zdGEL1WLZIxhl2IrfrpNkCd0u5Y8nUt14jDRUR5IDgTcCh1TV/02o\ntnHZXJ93APYCzkuyhu5Y6soFfMJ4lN/xjcDKqvp1VV0P/DddMCxUo/T5aOAzAFV1IbAN3RhEi9lI\n/99na7EEwSjDVqwEjuqnDwO+Wv1ZmAVqs31Osg/wQboQWOjHjmEzfa6qW6tqaVVNVdUU3XmRQ6pq\n1TDlztko7+sv0e0NkGQp3aGi6yZZ5Dwbpc83AAcAJHkUXRCsnWiVk7cSeGF/9dC+wK1VddN8bXxR\nHBqqjQxbkeTNwKqqWgl8hG4X8lq6kzJHDFfx3I3Y5xOB7YHP9ufFb6iqQwYreo5G7POiMWJ/zwKe\nmuRq4E7g9VW1YPd0R+zza4EPJXkN3YnjFy3wD3Uk+SRdoC/tz30cC2wFUFUfoDsXchBwLfBL4MXz\n2v4C//lJkuZosRwakiTNkkEgSY0zCCSpcQaBJDXOIJCkxhkEuldIclyS183idTsmecUs2zwjyY6z\nee04JFnWj4x7aZInJjk8yTX9SJvTSd69mdfPuj9JnpVkz9lVroVuUXyPQE3bkW5k2feP+oJ+sMFU\n1b1t+OIDgCur6q8AkpwJvLSqvt4/v8kvxs2xP88CTgOunsM2tEC5R6CJS/LCfkz1y5N8bAPPnzcz\nLESSpf1wESR5dJL/SnJZ//o9gOOB3ftlJ/brvT7JN/t1/rFfNtWPcX8qsBp4aJI1/fan+k/eH+rH\n9D87ybb96/6k385lSU7cxHjx/5Dkyr5Px/fL9u4HgrsiyReT7NQv3z3JmUkuSfIfSf4gyd7AW4FD\n+7aOBf4M+Ejf7pOTnNa/fvskJ/XtXZHkOf3yNf23i0ly5Do/qw8m2bJf/vMkb+nrvCjJg5LsBxwC\nnNivv/ucf8laWIYeh9tHWw/g0XTj4Szt53fu/z0OeF0/fR79fQToxpBZ00+/B3h+P701sC0wxTpj\nuANPpRuvPnQfdE6jG+t9CvgNsO86667ptz8F3AHs3S//DHBkP70aeHw/fTwbGC8eeDrwn9x174eZ\nPl0B/Hk//Wbgnf30ucAe/fTj6IY7gW6wvPeus911fw5PBk7rp0+Y2VY/v9N6/XkU8BVgq375+4EX\n9tMFPLOffivwpn76ZOCwod8fPoZ5eGhIk7Y/8Nmq+hFAVW1qDPb1XQi8McmuwBeq6jv53VtKPLV/\nXNrPb083CNsNwHerG8t9Q66vqsv66UuAqf54+w7VDWwG8AngGRt47YHASdXf+6Gqbklyf2DHqjq/\nX+cUuqE+tgf2465hPwDuM0Lf12/vt0OkVH8vgnUcAPwx8M2+jW2BmbGmbqcLx5l+PuUetq1FyCDQ\nvdEd3HXYcpuZhVX1iSQXAwcDZyR5Gb87wFqAf6mqD95tYXdr0l9sos11R2a9k+6P5zhsAfy0qvYe\n0/ah+xmcUlVv2MBzv66qmXFl7sS/AcJzBJq8rwKHJ3kAQJKdN7DOGrpPtNCNFEu/7sOB66rq3cCX\ngccAt9ENPz3jLOAl/SdvkuyS5IGzKbS6Mf1vS/K4ftHGBio8B3hxku1m+lRVtwI/SfLEfp0XAOdX\n1c+A65Mc3q+bJH90D0s7B/jrmZmZcw/rOBc4bKbfSXbO5u9Xvf7PUQ0xCDRRVXUV8Bbg/CSX091I\nZn1vA16e5FLuPs78c4HVSS6ju+/AqdWNtPmNJKuTnFhVZ9MdwrkwyZV0tyWdyx+4o+lGurwMuC/d\nne3W79OZdMMEr+rXm7kM9ii6E7BXAHvTnScAeD5wdN//q9jw7TY35Z+Bnfo+X053b+p167kaeBNw\ndt/2OcDmbmv4KeD16S5d9WRxYxx9VNqEJNtX1c/76WOAB1fVqwYuS5pXHh+UNu3gJG+g+7/yXdq6\nDaYa4R6BJDXOcwSS1DiDQJIaZxBIUuMMAklqnEEgSY0zCCSpcf8PQD8fMJmV+1wAAAAASUVORK5C\nYII=\n",
      "text/plain": [
       "<matplotlib.figure.Figure at 0x10b282048>"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    }
   ],
   "source": [
    "plt.hist(list(nx.clustering(G).values()), bins=10)\n",
    "plt.xlabel('clustering coefficient')\n",
    "plt.ylabel('count')\n",
    "plt.show()"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 45,
   "metadata": {
    "collapsed": false
   },
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYUAAAEKCAYAAAD9xUlFAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XmUXHWZ//H3J4FAmh0TFLN0B0UQEcekB/WnBxhBDYjB\nbRgwHETB6CioIypIUJSZKChuMMAYlM00IqBoUBkGFXV0ANNBZAminZCQBCTsWwJJyPP7497uVLqr\nqm931+1by+d1zj1V91tPV54UoZ6+97spIjAzMwMYU3QCZmZWP1wUzMysj4uCmZn1cVEwM7M+Lgpm\nZtbHRcHMzPq4KJiZWR8XBTMz6+OiYGZmfbYqOoGhmjBhQnR0dBSdhplZQ1m8ePEjETFxsLiGKwod\nHR10d3cXnYaZWUORtCJLnG8fmZlZHxcFMzPr46JgZmZ9XBTMzKyPi4KZmfXJrShIuljSGkl3VXhd\nks6V1CPpDknT88rFzGqnqws6OmDMmOSxq2v4caMZU4851TLvmomIXA7gAGA6cFeF1w8DrgcEvB64\nNcv7zpgxI8ysGAsWRLS1RcDmo60taR9q3GjG1GNOtcw7C6A7MnzHKnLcjlNSB/CziNi3zGvfAX4T\nET9Iz+8FDoqIB6u9Z2dnZ3ieglkxOjpgRZnR7jvtBB//+Obzc8+FJ5+sHjeaMfWY00jzbm+H5csH\ntlciaXFEdA4aV2BR+BlwVkT8Pj3/FXBKRAz4xpc0B5gDMHXq1Bkryv2rNLPcjRmT/K5ajrT5ebWv\nld640Yypx5xGmrcEmzZVfo+B8dmKQkN0NEfE/IjojIjOiRMHnaVtZjmZOrV8e3t78gXVe7S3Dx43\nmjH1mNNI867032KkiiwKq4EpJeeT0zYzq1Pz5kFb25ZtbW1J+1DjRjOmHnOqZd41laXjYbgH0EHl\njua3s2VH8x+zvKc7ms2KtWBBxLhxSYdne3vlDs8FC5LXpcpxoxlTjznVMu/BUHRHs6QfAAcBE4CH\ngDOArdNC9F+SBPwnMBNYC3wgyvQn9OeOZrPi7borHHUUXHBB0ZlYVln7FHJbJTUijh7k9QA+ltef\nb2b5eOwxePxxePnLi87E8tAQHc1mVj+WLk0eXRSak4uCmQ1JT0/y6KLQnFwUzGxIeovCtGnF5mH5\ncFEwsyHp6YHJk2H8+KIzsTy4KJjZkPT0+NZRM3NRMLMhcVFobi4KZpbZ00/DmjUuCs3MRcHMMvNw\n1ObnomBmmfWOPHrZy4rNw/LjomBmmbkoND8XBTPLrKcHXvxi2GGHojOxvLgomFlmHnnU/FwUzCwz\nF4Xm56JgZpmsWwerV7soNDsXBTPLZNmy5NGdzM3NRcHMMvHqqK3BRcHMMnFRaA0uCmaWSU9Psg3n\nLrsUnYnlyUXBzDLxyKPW4KJgZpksXeqi0ApcFMxsUOvXw4oVHnnUClwUzGxQy5fDpk2+UmgFLgpm\nNiiPPGodLgpmNigXhdbhomBmg+rpSVZGnTix6Ewsby4KZjao3pFHUtGZWN5cFMxsUD09HnnUKlwU\nzKyqjRvhvvvcn9AqXBTMrKqVK2HDBheFVuGiYGZVeeRRa8m1KEiaKeleST2STi3z+lRJN0n6k6Q7\nJB2WZz5mNnQuCq0lt6IgaSxwPnAosA9wtKR9+oWdDlwVEa8FjgIuyCsfMxuepUth/HjYffeiM7HR\nkOeVwv5AT0Qsi4j1wJXAEf1iAtgxfb4T8ECO+ZjZMPT0wB57wBjfbG4JW+X43pOAlSXnq4DX9Yv5\nIvA/kk4CtgMOyTEfMxsGL5ndWoqu/UcDl0bEZOAw4PuSBuQkaY6kbkndDz/88KgnadaqNm3yktmt\nJs+isBqYUnI+OW0rdTxwFUBE3AxsC0zo/0YRMT8iOiOic6Ln2ZuNmgcegOeec1FoJXkWhUXAnpKm\nSRpH0pG8sF/M/cDBAJJeSVIUfClgVic88qj15FYUImIjcCJwA3APySijuyWdKWlWGnYy8CFJfwZ+\nABwXEZFXTmY2NEuXJo8uCq0jz45mIuIXwC/6tX2h5PkS4I155mBmw9fTA1tvDVOmDB5rzaHojmYz\nq2M9PTBtGowdW3QmNlpcFMysIg9HbT2DFgVJ07K0mVlziXBRaEVZrhR+VKbtmlonYmb1Zc0aeOYZ\nF4VWU7GjWdLewKuAnSS9u+SlHUmGjppZE/PIo9ZUbfTRXsDhwM7AO0ranwY+lGdSZla83jkK3nGt\ntVQsChHxU+Cnkt6QzjY2sxbS05MsgtfRUXQmNpqyzFPokXQa0FEaHxEfzCspMyteTw+0t8O4cUVn\nYqMpS1H4KfC/wC+BF/JNx8zqhUcetaYsRaEtIk7JPRMzqys9PXDUUUVnYaMty5DUn3mbTLPW8thj\n8PjjvlJoRVmKwidICsNzkp6S9LSkp/JOzMyK0zsc1SOPWs+gt48iYofRSMTM6oeXzG5dWZa5kKRj\nJH0+PZ8iaf/8UzOzovQWhT32KDYPG31Zbh9dALwBeF96/gxwfm4ZmVnhenpg8mQYP77oTGy0ZRl9\n9LqImC7pTwAR8Xi6k5qZNSkPR21dWa4UNkgaCwSApInAplyzMrNCLV3qotCqshSFc4Frgd0kzQN+\nD3w516zMrDBPPw0PPeSRR61q0KIQEV3AZ4GvAA8C74yIq/NOzMwSXV3J+kO96xB1deUbs9deyfOv\nf718jDW5iCh7ADumj7uWOyr9XN7HjBkzwqxVLFgQ0dYWkWx5kxxtbUl7ETHWuIDuyPAdqyR2IEk/\ni4jDJd1H2p/Q+1JSS6KQwWqdnZ3R3d1dxB9tNuo6OmDFioHt220HRx6ZPL/qKnj22fxi2tth+fLh\nZG/1RNLiiOgcLK7a0tmHp4/eetOsIPffX7792Wfhl7/c/DzPmEo5WHPKMnntXZJ2KjnfWdI7803L\nzABe9KLy7e3tyZf1/fcnz/OMmTp16Hlb48oy+uiMiHiy9yQingDOyC8lMwNYuTL57X1Mv/9L29pg\n3rzN5/PmJW2jEWPNL0tRKBeTZdKbmQ3Tpk1w3HFJQTjnnOS3eCl5nD8fZs/eHDt7dtI2GjHW/Cp2\nNPcFSBcDT7B5aYuPkYw+Oi7f1MpzR7O1gm9+Ez71KbjoIjjhhKKzsWaQtaM5y5XCScB64Ifp8TxJ\nYTCzHNx5J3zuczBrFhx/fNHZWKvJsnT2s8Cpo5CLWct7/vnkds1OOyVXCVLRGVmrqVgUJH0rIj4p\n6Tq2nKcAQETMyjUzsxZ0+unJlcLPfga77VZ0NtaKql0pXJ4+njMaiZi1ut/8Jlla4iMfgbe/vehs\nrFVVKwpfAw4GDouIU0YpH7OW9MQTcOyxycqk5/jXMCtQtY7m3SX9P2CWpNdKml56ZHlzSTMl3Sup\nR1LZfglJR0paIuluSVcM5y9h1ohKF6ibNAlWrYIFC5KlJ8yKUu1K4QvA54HJwNdJ1jzqFcCbq71x\nugfD+cBbgFXAIkkLI2JJScyewOeAN0ayeY/volpL6OqCOXNg7drkfO1a2Hpr+NvfYH9vdmsFqnal\n8GBEHAp8LSLeHBH/VHJULQip/YGeiFgWEeuBK4Ej+sV8CDg/Ih4HiIg1w/lLmDWauXM3F4ReGzYk\n7WZFqlYUzk0fh7vO0SRgZcn5qrSt1CuAV0j6g6RbJM0s90aS5kjqltT98MMPDzMds/pRaZE5Lz5n\nRat2+2iDpPnAJEnn9n8xIj5eoz9/T+AgkttUv5P06nR9pdI/az4wH5IZzTX4c80KNXVq+SWxvfic\nFa3alcLhwK+B54DFZY7BrAamlJxPTttKrQIWRsSGiLgP+CtJkTBravPmwVb9fiXz4nNWD6rtp/AI\ncKWkeyLiz8N470XAnpKmkRSDo4D39Yv5CXA0cImkCSS3k5YN488yayiHHQZjx8K4cbBuXXKFMG+e\nF5+z4mVZ7XSdpF8BL46IfSXtB8yKiP+o9kMRsVHSicANwFjg4oi4W9KZJNvCLUxfe6ukJcALwGci\n4tER/Y3MGsCFFyZLWtx+O7zmNUVnY7ZZllVSfwt8BvhORLw2bbsrIvYdhfwG8Cqp1ujWrUvmJ0yf\nDtdfX3Q21ipquUpqW0T8sV/bxuGlZWaXXgpr1sApXifA6lCWovCIpJeRLoon6b3Ag7lmZdakNm5M\nlrF43evgwAOLzsZsoCx9Ch8jGQ66t6TVwH2Au8PMhuFHP4Jly5LC4GWxrR5l2U9hGXCIpO2AMRHx\ndP5pmTWfCDjrLNhrLzii/9x+szoxaFGQtBNwBnBAev5b4MyIeDLn3Myayo03JqONvve9ZBE8s3qU\n5Z/mxcDTwJHp8RRwSZ5JmTWjs85KVkP1XASrZ1n6FF4WEe8pOf+SpNvzSsisGf3xj3DTTUlfwjbb\nFJ2NWWVZrhTWSXpT74mkNwLr8kvJrPmcfTbsvHOyXLZZPctypfCvwGVp3wLA48BxuWVk1mTuvReu\nvRZOOw122KHobMyqyzL66HbgNZJ2TM+fyj0rsybyta8lt4w+Xot1hc1yNujtI0lflrRzRDwVEU9J\n2kVS1XWPzCzxwAPw/e/DBz8Iu3lfQWsAWfoUDi3d3yDdJe2w/FIyq73S/ZA7OpLz4cYNJWbSJFi/\nHl7+8hr9RczyFhFVD+AOYJuS8/HA3YP9XF7HjBkzwmwoFiyIaGuLSKaPJUdbW9I+1LhaxZiNNpLV\nqQf9js2ySuopwDvYPDfhAyQb43w1r0JVjVdJtaHq6Ci/y9n48cm+Br1+8YtkBdNqcSOJaW+H5cuH\nmr1ZbWRdJTVLR/PZkv4MHJI2/XtE3DDSBM1GS6V9j9etg7/8ZcvzweJGEuP9l60RZBmSSkT8N/Df\nOedilotK+yG3t8Ndd20+r3RFURo3khjvv2yNwCuwWNPLuh/yvHlJe7W4WsWY1SsXBWt6vfsht7Ul\ny1W3t8P8+QPXIJo9O2lvb68cV6sYs3o1aEdzvXFHsw3Vl78Mc+d6P2RrbTXraJZ0J+muayWeBLqB\n/4iIR4eXoln+1q2Db38bZs50QTDLIktH8/XAC8AV6flRQBvwd+BSkuGqZnWpdz/kU08tOhOzxpCl\nKBwSEdNLzu+UdFtETJd0TF6JmY1U6X7IBxxQdDZmjSFLR/NYSfv3nkj6R2Bseroxl6zMaqB3P+RT\nTvF+yGZZZblSOAG4WNL2gEh2Xjsh3bP5K3kmZzZc3g/ZbHiyzGheBLy6dz+F2HJv5qvySsxsJLwf\nstnwZBl9tA3wHqAD2ErpdXhEnJlrZmYj4P2QzYYny+2jn5IMQV0MPJ9vOmYjt2iR90M2G64sRWFy\nRMzMPROzGvF+yGbDl+Vu6/9JenXumZjVwL33wo9/DB/7mPdDNhuOLFcKbwKOk3Qfye0jARER++Wa\nmdkw9N4y8n7IZsOTpSgcOtw3lzQT+DbJvIbvRsRZFeLeA1wD/GNEeGEjG5YHHoDLL4cTTvB+yGbD\nVfH2kaQd06dPVziqkjQWOJ+kqOwDHC1pnzJxOwCfAG4davJm4P2QzWqpWp9C71pHi0kWv1tccmT5\nbX5/oCcilkXEeuBKoNw0on8Hzgaey5q0Wa+urqRDuXRTm9NPT9rNbOgqFoWIOFzJpIQDI2KPiJhW\ncuyR4b0nAStLzlelbX0kTQemRMTPh5O82dy5sHbtlm1r1ybtZjZ0VUcfRbLZQi5f2JLGAN8ATs4Q\nO0dSt6Tuhx9+OI90rEFV2vfY+yGbDU+WIam3pYvgDdVqYErJ+eS0rdcOwL7AbyQtB14PLJQ0YBOI\niJgfEZ0R0Tlx4sRhpGLNavLk8u3eD9lseLIUhdcBN0taKukOSXdKuiPDzy0C9pQ0TdI4kn0YFva+\nGBFPRsSEiOiIiA7gFmCWRx/ZUOy998A274dsNnxZhqS+bThvHBEbJZ0I3EAyJPXiiLhb0plAd0Qs\nrP4OZtVdf32y8N3MmXDPPckto6lTk4LgNY/MhifTHs2S3gTsGRGXSJoIbB8R9+WeXRneo9kAHnkE\nXv1qmDAhWeto222LzsisvtVyj+YzgE5gL+ASYGtgAfDGkSZpNhwRyTDUxx6DG25wQTCrpSx9Cu8C\nZgHPAkTEAySdxGaFuPRSuPba5DbRfl5sxaymshSF9enQ1ABId1wzK8SyZcm6RgcdBJ/6VNHZmDWf\nLEXhKknfAXaW9CHgl8B3803LbKAXXoBjj4WxY+Gyy7yjmlkesmzHeY6kt5DszbwX8IWIuDH3zMz6\nOfts+MMfYMECz0Mwy8ugv2tJOjsiboyIz0TEpyPiRklnj0ZyNrp6F5YbMyZ5LLd+UJaYWr5Xaczc\nufD618P73jesv56ZZRERVQ/gtjJtdwz2c3kdM2bMCKu9BQsi2toikrE9ydHWlrQPJaaW71UuZvz4\ngX+emQ2OZH7YoN+xFecpSPpX4KPAHsDSkpd2AP4QEcfkWq0q8DyFfHR0bLnSaK9tt4UDDkie/+53\n8FyZtWxLY7LGjSSmvR2WL6/2tzGz/moxT+EK4HrgK8CpJe1PR8RjI8zP6kylBeSeew6eemrz88Fi\nssaNJMaL3Znlp2JRiIgngSclnQ78PSKel3QQsJ+kyyPiidFK0vI3dWr5K4X2drj55uR5pauJ0pis\ncSOJcSezWX6yDOr7EfCCpJcD80lWPr2i+o9Yozm5zALm/ReWmzcvaasWkzWuVjFmVmODdTqQdjQD\nnwVOSp//KUuHRR6HO5rz8eEPR4wZEzFpUoQU0d5evkN3wYLktWoxWeNqFWNmg2OkHc29JN0KfAuY\nC7wjIu6TdFdE7JtnsarEHc2119MDr3wlfOQjcN55RWdjZnnI2tGc5fbRB4A3APPSgjAN+P5IE7T6\nccYZsPXW3sLSzLLNaF4CfLzk/D7Ak9eaxB13wA9+AKecAi95SdHZmFnRsiydfR/pYnilImKPXDKy\nUXX66bDjjvDZzxadiZnVgyw7r5Xeg9oW+Gdg13zSsdF0881w3XXJaJ5ddik6GzOrB4P2KUTEoyXH\n6oj4FvD2UcjNchQBp50Gu+2WLEVtZgbZbh9NLzkdQ3LlkOUKw+rYL38Jv/kNnHsubL990dmYWb3I\n8uX+9ZLnG4HlwJG5ZGOjovcqob092dbSzKxXltFH/zQaidjoufZa6O6GSy6BbbYpOhszqycVi4Kk\nqpsdRsQ3ap+O5e2FF5IRR3vvDccUss6tmdWzalcKO4xaFjZqurrgnnvg6qthK/cMmVk/1VZJ/dJo\nJmL56upK+hHuvx/GjYPnny86IzOrR1m247xM0s4l57tIujjftKyWurqSDuXefQjWr0/OK22laWat\nK8vaR/tFyd4JEfE48Nr8UrJamzsX1q7dsm3tWq91ZGYDZSkKYyT1zXeVtCuep9BQKu1U5h3MzKy/\nrPMUbpZ0dXr+z4C3OWkQN9xQ+TXvYGZm/WVZ5uJy4N3AQ+nx7ojw0tkN4Cc/gVmzYMoUGD9+y9e8\ng5mZlZPl9hERsSQi/jM9luSdlI3cFVfAe98L06fD7bfDRRclM5il5HH+fJg9u+gszazeuG+gCV10\nEXz4w3DggbBwIeywQ1IAXATMbDCZrhSGS9JMSfdK6pF0apnXPyVpiaQ7JP1KUnue+TSrri7o6IAx\nY2DXXZPhpjNnwi9+kRQEM7OscisKksYC5wOHAvsAR0vap1/Yn4DOiNgPuAb4al75NKLSL/uOjvLz\nCnrnIKxYkSx09/jjMHYs/Mu/DOxHMDMbTJ5XCvsDPRGxLCLWA1cCR5QGRMRNEdE7gv4WYHKO+TSU\n/l/2K1ZsnnC2di2sXg133w0nnzxwDsILLyT7LpuZDVWefQqTgJUl56uA11WJPx64vtwLkuYAcwCm\ntsg4ykoTzrIuYuc5CGY2HHXR0SzpGJLNew4s93pEzAfmA3R2dg7YL7oZVftSP+usZPvMnXeGk06C\nNWsGxrRI7TSzGsuzKKwGppScT07btiDpEGAucGBEtPwybRFw6aWVX29vh1NO2Xy+YUNyW6n0qsJz\nEMxsuPLsU1gE7ClpmqRxwFHAwtIASa8FvgPMiogyv++2lvvug7e9DT74QXjFK2Dbbbd8vdyX/ezZ\nyZwDz0Ews1rIrShExEbgROAG4B7gqoi4W9KZkmalYV8DtgeulnS7pIUV3q7plI4sam+HY4+FffeF\nm2+GCy6AJUvgu9/N9mU/ezYsXw6bNiWPLghmNlyKaKxb9J2dndHd3V10GiPSO7Kof0fyfvvBdde5\nP8DMak/S4ojoHCwu18lrVt5ppw0sCABPPOGCYGbFclHIQaVJZ3/5C3z+85VHFq1cWb7dzGy01MWQ\n1GbS/9bQihXwgQ8k8w5WrEgKxbbbwnPPDfxZXyWYWdF8pVBj5SadbdgADz4I3/wmrFqVdCC3tW0Z\n42GkZlYPXBRqrNKtoQ0b4JOfhN139zBSM6tfvn1UQ88/n/zG/+yzA1/rf2vIS1mbWT3ylUKNPPoo\nvPWtSUHYeustX/OtITNrFC4KNfDXv8LrXw+33JLseHbJJb41ZGaNybePRui3v4V3vSvZw+DXv4Y3\nvjFpdxEws0bkK4UhKp2DMGECvPnN8JKXwK23bi4IZmaNylcKQ9B/DsKjjybF4d/+DfbYo9jczMxq\nwVcKQ1BuDsKmTe5ENrPm4aIwBJXmIHiXMzNrFi4KQ1BpGQovT2FmzcJFYQhOPnlgm+cgmFkzcVEY\ngt69kF/6Us9BMLPm5NFHGT3/fFIA3vEOWNgy+8OZWavxlUJG11yTXCmceGLRmZiZ5cdFIaPzzoNX\nvAIOOaToTMzM8uOikMGiRcmM5RNPTCarmZk1K3/FZXD++bD99vD+9xediZlZvlwUBvHww3DllXDs\nsbDjjkVnY2aWLxeFQXz3u8nII3cwm1krcFGoYuNGuPBCOPhgeOUri87GzCx/LgpVXHcdrFzpqwQz\nax0uClWcd16yrtHhhxediZnZ6HBRqODuu+Gmm+CjH4WtPO/bzFqEi0IF558P22wDxx9fdCZmZqPH\nRaGMJ5+Eyy+Ho49Ottw0M2sVLgplXHopPPssnHRS0ZmYmY2uXIuCpJmS7pXUI+nUMq9vI+mH6eu3\nSurIM58sNm1Kbh294Q0wfXrR2ZiZja7cioKkscD5wKHAPsDRkvbpF3Y88HhEvBz4JnB2Hrl0dUFH\nR7JuUUdHcl4pbvfd4W9/S45KcWZmzSrPK4X9gZ6IWBYR64ErgSP6xRwBXJY+vwY4WJJqmURXF8yZ\nAytWQETyOGfOwC/83rjejXQeeaR8nJlZM8uzKEwCVpacr0rbysZExEbgSeBFtUxi7lxYu3bLtrVr\n4bjj4FWv2nwcd1z5uLlza5mNmVl9a4gR+JLmAHMApk6dOqSfvf/+8u0bN8I+JTezliwZ2s+bmTWj\nPIvCamBKyfnktK1czCpJWwE7AY/2f6OImA/MB+js7IyhJDF1anLLqL/2drj66s3nHR3l44ZYg8zM\nGlqet48WAXtKmiZpHHAU0H9344VA7y4F7wV+HRFD+tIfzLx50Na2ZVtbW9I+nDgzs2aWW1FI+whO\nBG4A7gGuioi7JZ0paVYa9j3gRZJ6gE8BA4atjtTs2TB/fnJlICWP8+cn7cOJMzNrZqrxL+a56+zs\njO7u7qLTMDNrKJIWR0TnYHGe0WxmZn1cFMzMrI+LgpmZ9XFRMDOzPi4KZmbWp+FGH0l6GCgzzSyT\nCcAjNUxntDRq3tC4uTvv0eW889ceERMHC2q4ojASkrqzDMmqN42aNzRu7s57dDnv+uHbR2Zm1sdF\nwczM+rRaUZhfdALD1Kh5Q+Pm7rxHl/OuEy3Vp2BmZtW12pWCmZlV0TJFQdJMSfdK6pFU89VY8yJp\nuaQ7Jd0uqW5XApR0saQ1ku4qadtV0o2S/pY+7lJkjuVUyPuLklann/ntkg4rMsdyJE2RdJOkJZLu\nlvSJtL2uP/Mqedf1Zy5pW0l/lPTnNO8vpe3TJN2afq/8MN0moKG1xO0jSWOBvwJvIdkWdBFwdERU\n2G+tfkhaDnRGRF2PhZZ0APAMcHlE7Ju2fRV4LCLOSgvxLhFxSpF59lch7y8Cz0TEOUXmVo2k3YHd\nI+I2STsAi4F3AsdRx595lbyPpI4/83Tv+O0i4hlJWwO/Bz5BsuT/jyPiSkn/Bfw5Ii4sMteRapUr\nhf2BnohYFhHrgSuBIwrOqalExO+Ax/o1HwFclj6/jOR//rpSIe+6FxEPRsRt6fOnSfYsmUSdf+ZV\n8q5rkXgmPd06PQJ4M3BN2l53n/dwtEpRmASsLDlfRQP8Q0wF8D+SFqd7VTeSF0fEg+nzvwMvLjKZ\nITpR0h3p7aW6ugXTn6QO4LXArTTQZ94vb6jzz1zSWEm3A2uAG4GlwBPphmLQWN8rFbVKUWhkb4qI\n6cChwMfS2x0NJ91mtVHuVV4IvAz4B+BB4OvFplOZpO2BHwGfjIinSl+r58+8TN51/5lHxAsR8Q8k\n+83vD+xdcEq5aJWisBqYUnI+OW2rexGxOn1cA1xL8o+xUTyU3kPuvZe8puB8MomIh9IvgE3ARdTp\nZ57e2/4R0BURP06b6/4zL5d3o3zmABHxBHAT8AZgZ0lbpS81zPdKNa1SFBYBe6YjBcYBRwELC85p\nUJK2SzvjkLQd8Fbgruo/VVcWAu9Pn78f+GmBuWTW+6Waehd1+JmnHZ/fA+6JiG+UvFTXn3mlvOv9\nM5c0UdLO6fPxJINW7iEpDu9Nw+ru8x6Olhh9BJAOcfsWMBa4OCLmFZzSoCTtQXJ1ALAVcEW95i3p\nB8BBJKtGPgScAfwEuAqYSrKy7ZERUVeduhXyPojkNkYAy4EPl9ynrwuS3gT8L3AnsCltPo3k/nzd\nfuZV8j6aOv7MJe1H0pE8luSX6asi4sz0/9ErgV2BPwHHRMTzxWU6ci1TFMzMbHCtcvvIzMwycFEw\nM7M+LgpmZtbHRcHMzPq4KJiZWR8XBbOcpSuAfrroPMyycFEwGwIl/P+NNS3/4zYbhKSOdC+Oy0lm\n2n5PUnfpuvpp3HJJX5J0W7oHxoC1cSR9SNL16axYs7qz1eAhZgbsCbw/Im6RtGtEPJbu0/ErSftF\nxB1p3CMRMV3SR4FPAyf0voGkE0mWR3hno896teblKwWzbFZExC3p8yMl3UayrMGrgH1K4noXplsM\ndJS0H0txqJBEAAAAp0lEQVSy0u17XRCsnrkomGXzLCTbL5JcARwcEfsBPwe2LYnr/cJ/gS2vxO8k\nKRKTc8/UbARcFMyGZkeSAvGkpBeT/PafxZ+ADwMLJb00r+TMRspFwWwIIuLPJF/wfwGuAP4whJ/9\nPclVxs8lTcgnQ7OR8SqpZmbWx1cKZmbWx0XBzMz6uCiYmVkfFwUzM+vjomBmZn1cFMzMrI+LgpmZ\n9XFRMDOzPv8fLydjW5W9LDwAAAAASUVORK5CYII=\n",
      "text/plain": [
       "<matplotlib.figure.Figure at 0x1068ba588>"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    }
   ],
   "source": [
    "plt.figure()\n",
    "plt.plot(sorted(list(nx.clustering(G).values())), 'bo-')\n",
    "plt.xlabel('rank')\n",
    "plt.ylabel('clustering coefficient')\n",
    "plt.show()"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 46,
   "metadata": {
    "collapsed": false
   },
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYUAAAEKCAYAAAD9xUlFAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAGkBJREFUeJzt3XuYXXV97/H3hwFxQGBMGXpkEpqAIZQaNWHk0tgWBZqA\nSFK8JcKpHBGeWi9YNBWUYkvRQKNUPGJrpBFULgcRQ45FY4qoLSdgJkQIhKJpwiUDNhEIoThKkn7P\nH2vtxc4ws2ftYa+99sz+vJ5nnpn122vWfIYJ8521fjdFBGZmZgB7lB3AzMxah4uCmZllXBTMzCzj\nomBmZhkXBTMzy7gomJlZxkXBzMwyLgpmZpZxUTAzs8yeZQeo14EHHhiTJ08uO4aZ2ZiyZs2aX0ZE\n90jnjbmiMHnyZPr6+sqOYWY2pkh6JM95fnxkZmYZFwUzM8u4KJiZWcZFwczMMi4KZmaWcVEwM7OM\ni4KZmWUKKwqSlkraIun+YV6XpC9I2iDpPkkzi8piZmb5FDl57Rrgi8DXhnn9ZGBq+nYM8A/p+5Y2\n+YJ/flHbw5e9pYQku1u2tp/FKx7i8W0DHNzVycLZ05g3o6fsWGY2xhR2pxARPwaeqnHKXOBrkbgL\n6JL0qqLyNMJQBaFWe7MsW9vPhbeso3/bAAH0bxvgwlvWsWxtf6m5zGzsKbNPoQd4rOp4c9pmdVq8\n4iEGduzarW1gxy4Wr3iopERmNlaNiY5mSedK6pPUt3Xr1rLjtJzHtw3U1W5mNpwyi0I/MKnqeGLa\n9iIRsSQieiOit7t7xEX+2s7BXZ11tZuZDafMorAc+NN0FNKxwDMR8USJecashbOn0blXx25tnXt1\nsHD2tJISmdlYVeSQ1BuAVcA0SZslnS3pzyT9WXrKbcBGYAPwFeDPi8rSKMONMip79NG8GT0sOn06\nPV2dCOjp6mTR6dM9+sjM6qaIKDtDXXp7e8P7KZiZ1UfSmojoHem8MdHRbGZmzeGiYGZmGRcFMzPL\nuCiYmVnGRcHMzDIuCmZmlnFRMDOzjIuCmZllXBTMzCzjomBmZhkXBTMzy7gomJlZxkXBzMwyLgpm\nZpZxUTAzs4yLgpmZZVwUzMws46JgZmYZFwUzM8u4KJiZWcZFwczMMi4KZmaWcVEwM7OMi4KZmWVc\nFMzMLOOiYGZmGRcFMzPLuCiYmVnGRcHMzDIuCmZmlim0KEiaI+khSRskXTDE64dIukPSWkn3STql\nyDxmZlZbYUVBUgdwFXAycCSwQNKRg067CLgpImYA84EvFZXHzMxGVuSdwtHAhojYGBHPAzcCcwed\nE8D+6ccHAI8XmMfMzEZQZFHoAR6rOt6ctlX7a+BMSZuB24APDXUhSedK6pPUt3Xr1iKympkZ5Xc0\nLwCuiYiJwCnA1yW9KFNELImI3ojo7e7ubnpIM7N2UWRR6AcmVR1PTNuqnQ3cBBARq4CXAwcWmMnM\nzGoosiisBqZKmiLpZSQdycsHnfMocAKApN8lKQp+PmRmVpLCikJE7AQ+CKwAHiQZZfSApEsknZae\n9lHgHEn3AjcAZ0VEFJXJzMxq27PIi0fEbSQdyNVtF1d9vB6YVWQGMzPLb8Q7BUlT8rSZmdnYl+fx\n0beGaLu50UHMzKx8wz4+knQE8HvAAZJOr3ppf5IOYTMzG2dq9SlMA04FuoC3VrU/C5xTZCgzMyvH\nsEUhIm4FbpV0XDqHwMzMxrk8o482SPoEMLn6/Ih4b1GhzMysHHmKwq3AvwL/AuwqNo6ZmZUpT1HY\nJyI+XngSMzMrXZ4hqd/x5jdmZu0hT1E4j6Qw/FrSdknPStpedDAzM2u+ER8fRcR+zQhiZmbly7PM\nhSSdKemv0uNJko4uPpqZmTVbnsdHXwKOA96dHv8Xyd7LZmY2zuQZfXRMRMyUtBYgIp5O90cwM7Nx\nJs+dwg5JHUAASOoG/rvQVGZmVoo8ReELwLeBgyR9Gvg34DOFpjIzs1LkGX10naQ1JNtmCpgXEQ8W\nnszMzJqu1tLZ+0fEdkkTgC0k22VWXpsQEU81I+B4dtGyddxw92PsiqBDYsExk7h03vRRXWvZ2n4W\nr3iIx7cNcHBXJwtnT2PejJ4GJx4/ucxsaLXuFK4nWTp7DWl/Qkrp8aEF5hr3Llq2jm/c9Wh2vCsi\nO663MCxb28+Ft6xjYEeyNFX/tgEuvGUdQKm/gFs1l5kNb9g+hYg4NX0/JSIOrXqbEhEuCC/RDXc/\nVld7LYtXPJT94q0Y2LGLxSseGlW2RmnVXGY2vDyT1/5E0gFVx12S5hUba/zbFVFXey2Pbxuoq71Z\nWjWXmQ0vz+ijT0XEM5WDiNgGfKq4SO2hQ6qrvZaDuzrram+WVs1lZsPLUxSGOifPpDerYcExk+pq\nr2Xh7Gl07tWxW1vnXh0snD1tVNkapVVzmdnw8vxy75N0BS8sbfEBks5newkqncmNGH1U6bRttVE+\nrZrLzIanGOEZtqR9gb8CTkybVgKXRsRzBWcbUm9vb/T19ZXxpc3MxixJayKid6Tz8kxeew64oCGp\nzMyspdWavPb5iPiIpP/L7vMUAIiI0wpNZmZmTVfrTuFr6fvPNiOImZmVr1ZRWEyy3tEpEfHxJuUx\nM7MS1RqS+ipJvw+cJmmGpJnVb3kuLmmOpIckbZA0ZL+EpHdKWi/pAUnXj+abMDOzxqh1p3Axyaij\nicDnSNY8qgjgzbUunO7BcBVwErAZWC1peUSsrzpnKnAhMCvdvOegUX0X1lBexM6sfdUqCk9ExMmS\nLo6IS0Zx7aOBDRGxEUDSjcBcYH3VOecAV0XE0wARsWUUX8cayIvYmbW3Wo+PvpC+H+06Rz1A9epu\nm9O2aocDh0u6U9JdkuaM8mtZg3gRO7P2VutOYYekJUCPpC8MfjEiPtygrz8VOJ7kMdWPJU1P11fK\nSDoXOBfgkEMOacCXteF4ETuz9lbrTuFU4AfAr0mWtRj8NpJ+oHohn4lpW7XNwPKI2BERm4CfkRSJ\n3UTEkojojYje7u7uHF/aRsuL2Jm1t2HvFCLil8CNkh6MiHtHce3VwFRJU0iKwXzg3YPOWQYsAL4q\n6UCSx0kbR/G1rEEWzp62W58CeBE7s3aSZ5XUAUm3S7ofQNJrJV000idFxE7gg8AK4EHgpoh4QNIl\nkiqzoVcAT0paD9wBLIyIJ0f1nVhDzJvRw6LTp9PT1YmAnq5OFp0+3Z3MZm0iz4J4PwIWAl+OiBlp\n2/0R8Zom5HsRL4hnZla/vAvi5blT2CcifjKobefoYpmZWSvLUxR+Kekw0kXxJL0deKLQVGZmVoo8\nm+x8AFgCHCGpH9gEnFFoKjMzK0We/RQ2Aiemm+3sERHPFh/LzMzKMOLjI0kHpNtx/gi4Q9LnJB1Q\nfDQzM2u2PH0KS4FngXemb9uBrxYZyszMypGnT+GwiHhb1fHfSPppUYHMzKw8eSevvbFyIGkW4IVw\nzMzGoTx3Cu8Hrq3qR3gaOKuwRGZmVpo8o49+CrxO0v7p8fbCU5mZWSnyjD76jKSuiNgeEdslvVLS\npc0IZ2ZmzZXn8dHJEfGJykG6beYpwIiL4lnznPGVVdz5H09lx7MOm8B15xw3qmt5O06z9pWno7lD\n0t6VA0mdwN41zrcmG1wQAO78j6c44yur6r5WZTvO/m0DBC9sx7ls7eCtMMxsPMpTFK4Dbpd0tqSz\ngZXAtcXGsnoMLggjtdfi7TjN2luejubLJd0LnJg2/W1ErCg2lpXF23Gatbc8fQpExPeA7xWcxVrA\nwV2d9A9RALwdp1l7yPP4yFrcrMMm1NVey8LZ0+jcq2O3Nm/HadY+XBTGgevOOe5FBWC0o4+8HadZ\nextxO85W4+04zczql3c7zhH7FCStI911rcozQB9waUQ8ObqIZmbWavJ0NH8X2AVcnx7PB/YBfgFc\nA7y1kGRmZtZ0eYrCiRExs+p4naR7ImKmpDOLCmZmZs2Xd0bz0ZUDSW8AKsNTdhaSyszMSpHnTuF9\nwFJJrwBEsvPa+9I9mxcVGc7MzJorz4zm1cD0yn4KEfFM1cs3FRXMzMyaL8/oo72BtwGTgT0lARAR\nlxSazMzMmi7P46NbSYagrgF+U2wcMzMrU56iMDEi5hSexMzMSpdn9NH/kzS98CRmZla6PHcKbwTO\nkrSJ5PGRgIiI1xaazMzMmi7XdpyjvbikOcCVJPMaro6Iy4Y5723AzcAbIsILG5XM23Gata9hi4Kk\n/SNiO/DsaC4sqQO4CjgJ2AyslrQ8ItYPOm8/4Dzg7tF8HWusynacld3XKttxAi4MZm2gVp9CZa2j\nNSSL362pesvz1/zRwIaI2BgRzwM3AnOHOO9vgcuBX+cNbcXxdpxm7W3YohARpyqZlPBHEXFoREyp\nejs0x7V7gMeqjjenbRlJM4FJEfHPtS4k6VxJfZL6tm7dmuNL22h5O06z9lZz9FEkmy3U/IU9WpL2\nAK4APjrSuRGxJCJ6I6K3u7u7iDiWGm7bTW/HadYe8gxJvSddBK9e/cCkquOJaVvFfsBrgB9Kehg4\nFlguacRNIKw43o7TrL3lGX10DHCGpEeA58g/JHU1MFXSFJJiMB94d+XFdA2lAyvHkn4IfMyjj8pV\n6Uz26COz9pSnKMwezYUjYqekDwIrSIakLo2IByRdAvRFxPLRXNeKN29Gj4uAWZvKs0rqI5LeCEyN\niK9K6gZekefiEXEbcNugtouHOff4PNc0M7PijNinIOlTwMeBC9OmvYBvFBnKzMzKkaej+U+A00j6\nE4iIx0k6ic3MbJzJUxSeT4emBkC645qZmY1DeYrCTZK+DHRJOgf4F+DqYmOZmVkZ8nQ0f1bSSSR7\nM08DLo6IlYUnawMnXfFDfr7luex46kH7svL848sLZKPiBQRtPMnT0Xx5RKyMiIUR8bGIWCnp8maE\nG88GFwSAn295jpOu+GE5gWxUKgsI9m8bIHhhAcFla/tH/FyzVpTn8dFJQ7SNejltSwwuCCO1W2vy\nAoI23tRaOvv9wJ8Dh0q6r+ql/YA7iw5mNhZ4AUEbb2r1KVwPfBdYBFxQ1f5sRDxVaCqzMeLgrk76\nhygAXkDQxqpaS2c/ExEPAxcBv4iIR4ApwJmSupqUb9yaetDQI3uHa7fW5AUEbbzJ06fwLWCXpFcD\nS0hWPr2+9qfYSFaef/yLCoBHH40982b0sOj06fR0dSKgp6uTRadP9+gjG7OUzEurcYJ0T0TMlPSX\nwEBE/G9JayNiRnMi7q63tzf6+ryQqplZPSStiYgRtybIc6ewQ9IC4E+B76Rte72UcGZm1pryFIX/\nBRwHfDoiNqX7I3y92FhmZlaGPDOa1wMfrjreBHjympnZODRiUZC0iXQxvGoRcWghiczMrDR5dl6r\n7ph4OfAOYEIxcczMrEwj9ilExJNVb/0R8XngLU3IZmZmTZbn8dHMqsM9SO4c8txhmJnZGJPnl/vn\nqj7eCTwMvLOQNGZmVqo8o4/e1IwgZmZWvlqrpJ5f6xMj4orGxzFrb96wx8pW605hv6alMLNsw57K\n/gyVDXsAFwZrmmGLQkT8TTODmLW7Whv2uChYs+TZjvPa6qWyJb1S0tJiY5m1H2/YY60gz9pHr42I\nbZWDiHgaKGWFVLPxbLiNebxhjzVTnqKwh6RXVg4kTcDzFMwazhv2WCvIO09hlaRvpsfvAD5dXCSz\n9lTpN/DoIyvTiJvsAEg6EnhzeviDdOXUUniTHTOz+uXdZCfXY6C0CNRdCCTNAa4EOoCrI+KyQa+f\nD7yPZKb0VuC96V7QZmZWgsL6BiR1AFcBJwGbgdWSlg+6y1gL9EbEryS9H/g74F1FZbLm82Ss8cE/\nx/aRp6N5tI4GNkTExoh4HrgRmFt9QkTcERG/Sg/vAiYWmMearDIZq3/bAMELk7GWre0vO5rVwT/H\n9lJkUegBHqs63py2Deds4LsF5rEmqzUZy8YO/xzbS0sMLZV0JsmS3H80zOvnAucCHHLIIU1MZi+F\nJ2OND/45tpci7xT6gUlVxxPTtt1IOhH4JHBaRPxmqAtFxJKI6I2I3u7u7kLCWuN5Mtb44J9jeymy\nKKwGpkqaIullwHxgefUJkmYAXyYpCFsKzGIl8GSs8cE/x/ZS2OOjiNgp6YPACpIhqUsj4gFJlwB9\nEbEcWAy8AvimJIBHI+K0ojKNZ604OsSTscYH/xzbS67Ja63Ek9debPCSy5D8Jbfo9On+H9fMgPyT\n14p8fGRN4tEhZtYoLTH6yF4ajw4xay2t+Dg3L98pjAMeHWLWOsb6ZD8XhXHAo0PMWsdYf5zrx0fj\ngEeHmLWOsf4410VhnJg3o8dFwKwFHNzVSf8QBWCsPM714yMzswYa649zfadgZtZAY/1xrouCmVmD\njeXHuS4KZmYtrNlzHlwUzMxa1OAlbCpzHoDCCoM7ms3MWlQZcx5cFMzMWlQZcx5cFMzMWlQZS9i4\nKJiZtagy5jy4o9nMrEWVMefBRcHMrIU1e86DHx+ZmVnGRcHMzDIuCmZmlnFRMDOzjIuCmZllXBTM\nzCzjomBmZhkXBTMzy7gomJlZxkXBzMwyLgpmZpZxUTAzs4yLgpmZZQpdJVXSHOBKoAO4OiIuG/T6\n3sDXgKOAJ4F3RcTDjc7RyI2vm72JtplZMxV2pyCpA7gKOBk4Elgg6chBp50NPB0Rrwb+Hri80Tkq\nG1/3bxsgeGHj62Vr+0u9lplZKyry8dHRwIaI2BgRzwM3AnMHnTMXuDb9+GbgBElqZIhGbnxdxiba\nZmbNVGRR6AEeqzrenLYNeU5E7ASeAX5r8IUknSupT1Lf1q1b6wrRyI2vy9hE28ysmcZER3NELImI\n3ojo7e7urutzG7nxdRmbaJuZNVORRaEfmFR1PDFtG/IcSXsCB5B0ODdMIze+LmMTbTOzZipy9NFq\nYKqkKSS//OcD7x50znLgPcAq4O3ADyIiGhmikRtfl7GJtplZM6nBv4N3v7h0CvB5kiGpSyPi05Iu\nAfoiYrmklwNfB2YATwHzI2JjrWv29vZGX19fYZnNzMYjSWsionek8wqdpxARtwG3DWq7uOrjXwPv\nKDKDmZnlNyY6ms3MrDlcFMzMLOOiYGZmGRcFMzPLuCiYmVnGRcHMzDIuCmZmlil08loRJG0FHik7\nB3Ag8MuyQwzBuerjXPVxrvq0Uq7fiYgRF48bc0WhVUjqyzM7sNmcqz7OVR/nqk+r5qrFj4/MzCzj\nomBmZhkXhdFbUnaAYThXfZyrPs5Vn1bNNSz3KZiZWcZ3CmZmlnFRqJOkSZLukLRe0gOSzis7UzVJ\nHZLWSvpO2VkqJHVJulnSv0t6UNJxZWcCkPQX6c/wfkk3pPt7lJFjqaQtku6vapsgaaWkn6fvX9ki\nuRanP8f7JH1bUlcr5Kp67aOSQtKBrZJL0ofS/2YPSPq7Zueql4tC/XYCH42II4FjgQ9IOrLkTNXO\nAx4sO8QgVwLfi4gjgNfRAvkk9QAfBnoj4jUkG0HNLynONcCcQW0XALdHxFTg9vS42a7hxblWAq+J\niNcCPwMubHYohs6FpEnAHwOPNjtQ6hoG5ZL0JmAu8LqI+D3gsyXkqouLQp0i4omIuCf9+FmSX3At\nsR+npInAW4Cry85SIekA4A+BfwKIiOcjYlu5qTJ7Ap3p/uD7AI+XESIifkyy82C1ucC16cfXAvOa\nGoqhc0XE9yNiZ3p4F8ne66XnSv098JdAKR2lw+R6P3BZRPwmPWdL04PVyUXhJZA0mWQr0bvLTZL5\nPMn/FP9ddpAqU4CtwFfTx1pXS9q37FAR0U/yV9ujwBPAMxHx/XJT7ea3I+KJ9ONfAL9dZphhvBf4\nbtkhACTNBfoj4t6yswxyOPAHku6W9CNJbyg70EhcFEZJ0iuAbwEfiYjtLZDnVGBLRKwpO8sgewIz\ngX+IiBnAc5TzKGQ36TP6uSRF62BgX0lnlptqaJEMEWypYYKSPknyKPW6FsiyD/AJ4OKRzi3BnsAE\nkkfNC4GbJKncSLW5KIyCpL1ICsJ1EXFL2XlSs4DTJD0M3Ai8WdI3yo0EwGZgc0RU7qZuJikSZTsR\n2BQRWyNiB3AL8PslZ6r2n5JeBZC+b5nHDpLOAk4FzojWGNN+GElxvzf99z8RuEfS/yg1VWIzcEsk\nfkJyF9/0TvB6uCjUKa3y/wQ8GBFXlJ2nIiIujIiJETGZpMP0BxFR+l++EfEL4DFJ09KmE4D1JUaq\neBQ4VtI+6c/0BFqgA7zKcuA96cfvAW4tMUtG0hySR5SnRcSvys4DEBHrIuKgiJic/vvfDMxM/+2V\nbRnwJgBJhwMvo3UWyBuSi0L9ZgH/k+Qv8Z+mb6eUHarFfQi4TtJ9wOuBz5Sch/TO5WbgHmAdyf8L\npcw+lXQDsAqYJmmzpLOBy4CTJP2c5K7mshbJ9UVgP2Bl+m//H1skV+mGybUUODQdpnoj8J4Wubsa\nlmc0m5lZxncKZmaWcVEwM7OMi4KZmWVcFMzMLOOiYGZmGRcFsyFI+mtJHys7h1mzuSiYFSRdaM9s\nTHFRMEtJ+qSkn0n6N2Ba2naYpO9JWiPpXyUdUdV+l6R1ki6V9F9p+/HpectJZ25LOlPST9LJXl+W\n1JG2/7GkVZLukfTNdD0ts1K5KJgBko4iWR7k9cApQGU1yyXAhyLiKOBjwJfS9iuBKyNiOsmyCtVm\nAudFxOGSfhd4FzArIl4P7ALOSDeBuQg4MSJmAn3A+YV9g2Y5+fbWLPEHwLcr6/mkf+m/nGSRvG9W\nLWy5d/r+OF7Y4+B6dt885ScRsSn9+ATgKGB1eo1OksXtjgWOBO5M219GskSCWalcFMyGtwewLf0L\nvx7PVX0s4NqI2G2HMklvBVZGxIKXmNGsofz4yCzxY2CepE5J+wFvBX4FbJL0DkhWyJX0uvT8u4C3\npR/X2sbzduDtkg5KrzFB0u+knz9L0qvT9n3TVTTNSuWiYAakW6z+H+Bekt3EVqcvnQGcLele4AGS\njXkAPgKcn678+mrgmWGuu56k7+D76bkrgVdFxFbgLOCGtH0VcEQB35pZXbxKqtkopLt9DURESJoP\nLIiIuSN9nlmrc5+C2egcBXwx3aBnG8l+xWZjnu8UzMws4z4FMzPLuCiYmVnGRcHMzDIuCmZmlnFR\nMDOzjIuCmZll/j+f/KqUE2YPjgAAAABJRU5ErkJggg==\n",
      "text/plain": [
       "<matplotlib.figure.Figure at 0x10c0ad710>"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    }
   ],
   "source": [
    "plt.figure()\n",
    "plt.scatter(list(nx.degree(G).values()), list(nx.clustering(G).values()))\n",
    "plt.xlabel('degree')\n",
    "plt.ylabel('clustering coefficient')\n",
    "plt.show()"
   ]
  }
 ],
 "metadata": {
  "kernelspec": {
   "display_name": "Python 3",
   "language": "python",
   "name": "python3"
  },
  "language_info": {
   "codemirror_mode": {
    "name": "ipython",
    "version": 3
   },
   "file_extension": ".py",
   "mimetype": "text/x-python",
   "name": "python",
   "nbconvert_exporter": "python",
   "pygments_lexer": "ipython3",
   "version": "3.6.0"
  }
 },
 "nbformat": 4,
 "nbformat_minor": 0
}