

| k-Wave Toolbox |
 
|
| On this page… |
|---|
This example demonstrates how to record the particle velocity using a Cartesian or binary sensor mask. It builds on the Homogeneous Propagation Medium and Heterogeneous Propagation Medium examples.
By default, the first-order simulation functions in k-Wave return the pressure field recorded at each time step at the positions specified by sensor.mask. This data is assigned directly to the output argument sensor_data. It is also possible to control the acoustic variables that are recorded by the sensor mask by setting the value of sensor.record. The desired field parameters are listed as strings within a cell array. For example, to record both the acoustic pressure and the particle velocity, sensor.record should be set to {'p', 'u'}. If a value for sensor.record is set, the output sensor_data returned from the simulation is defined as a structure, with the recorded acoustic variables appended as structure fields. For example, if sensor.record = {'p', 'p_max', 'u'}, then the individual output variables are accessed as sensor_data.p, sensor_data.p_max, sensor_data.ux, sensor_data.uy (similarly for other dimensions). A full list of other sensor.record options is given in kspaceFirstOrder2D.
In the previous examples, makeGrid is used to define the spatial discretisation. After the kWaveGrid object is created, the only parameter that can be modified by the user is kgrid.t_array. This describes the array of time values over which the simulation is run (including the time step), and is set to ‘auto’ by default. In this case, the time array is automatically calculated within kspaceFirstOrder2D using the function makeTime. This sets the total time to the time it would take for an acoustic wave to travel across the longest grid diagonal at the minimum sound speed. The time step is based on a Courant-Friedrichs-Lewy (CFL) number of 0.3 and the maximum sound speed in the medium, where kgrid.dt = CFL*dx_min/c0_max (see the k-Wave manual for a detailed discussion on the relationship between the CFL number and accuracy and stability).
Instead of leaving kgrid.t_array set to 'auto', it is also possible to set the time array manually, either by calling makeTime within the simulation script, or by setting the time array explicitly. Here the time array is defined using makeTime using the default CFL and a simulation time of 6 us.
% create time array t_end = 6e-6; kgrid.t_array = makeTime(kgrid, medium.sound_speed, [], t_end);
After creation, the number of time points and the size of the time step can be queried using kgrid.Nt and kgrid.dt. Note, the time array must be evenly spaced and monotonically increasing.
The simulation is run in the same way as in previous examples. In this example, four sensor points are defined centered about the position of a small circular source, and the sensor is set to record both the acoustic pressure and the particle velocity. A plot of the initial pressure distribution and the sensor mask is given below.
% define four sensor points centered about source.p0
sensor_radius = 40; % [grid points]
sensor.mask = zeros(Nx, Ny);
sensor.mask(Nx/2 + sensor_radius, Ny/2) = 1;
sensor.mask(Nx/2 - sensor_radius, Ny/2) = 1;
sensor.mask(Nx/2, Ny/2 + sensor_radius) = 1;
sensor.mask(Nx/2, Ny/2 - sensor_radius) = 1;
% set the acoustic variables that are recorded
sensor.record = {'p', 'u'};
% run the simulation
sensor_data = kspaceFirstOrder2D(kgrid, medium, source, sensor);
The pressure and velocity signals recorded at the four sensor positions are shown below (these are indexed top to bottom, left to right). The recorded pressure signals are shown in the left column. As the sensor points are all equidistance from the center of the source, the signals appear the same. The recorded particle velocity signals in the x-direction are shown in the central column. The signals from the second and third sensor points are mirrored as the wave at these points is travelling in opposite directions. The signals at the first and fourth sensor points are almost zero because the wave at these positions is travelling largely in the y-direction. The recorded particle velocity signals in the y-direction are shown in the right column. The signals from the first and fourth sensor points are mirrored as the wave at these points is travelling in opposite directions. The signals at the second and third sensor points are almost zero because the wave at these positions is travelling largely in the x-direction.
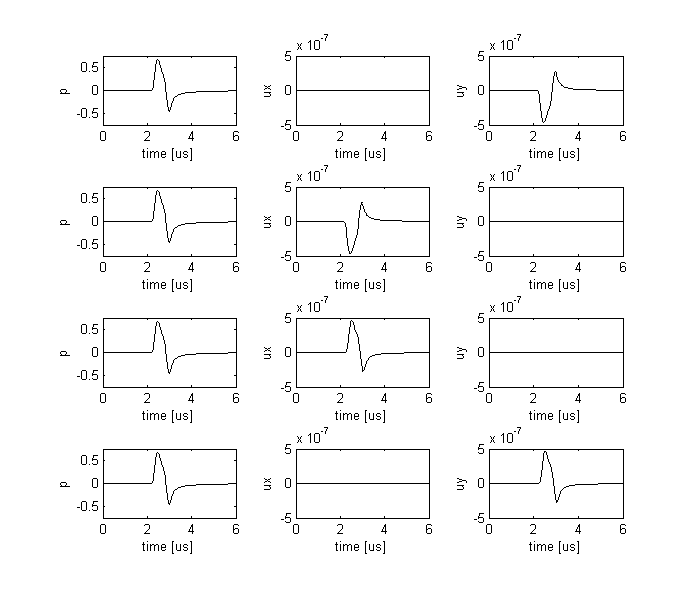
Note, the first-order simulation functions use both spatially and temporally staggered grids. This means the output pressure and velocity values are offset from each other. For example, sensor_data.ux is obtained at grid points staggered in the x-direction by +kgrid.dx/2 and in the temporal direction by -kgrid.dt/2. More information is given in the k-Wave Manual.
 |
Saving Movie Files | Defining A Gaussian Sensor Frequency Response |  |
© 2009-2014 Bradley Treeby and Ben Cox.