k-Wave Toolbox

Steering A Linear Array Example

Overview

This example demonstrates how to use k-Wave to steer a tone burst from a linear array transducer in 2D. It builds on the Simulating Transducer Field Patterns Example.

• open the file in the MATLAB Editor
• run the file in MATLAB

 Back to Top

Defining the linear array and input signal

The source mask is defined by creating a binary mask with the desired source points set to 1.

% define source mask for a linear transducer with an odd number of elements   
num_elements = 21;      % [grid points]
x_offset = 25;          % [grid points]
source.p_mask = zeros(Nx, Ny);
start_index = Ny/2 - round(num_elements/2) + 1;
source.p_mask(x_offset, start_index:start_index + num_elements - 1) = 1;

The input signal to each element is then created using the function toneBurst with a geometrically steered temporal offset that varies across the source.

% define the properties of the tone burst used to drive the transducer
sampling_freq = 1/dt;   % [Hz]
steering_angle = 30;    % [deg]
element_spacing = dx;   % [m]
tone_burst_freq = 1e6;  % [Hz]
tone_burst_cycles = 8;

% create an element index relative to the centre element of the transducer
element_index = -(num_elements - 1)/2:(num_elements - 1)/2;

% use geometric beam forming to calculate the tone burst offsets for each
% transducer element based on the element index
tone_burst_offset = 40 + element_spacing*element_index*sin(steering_angle*pi/180)/(medium.sound_speed*dt);

% create the tone burst signals
source.p = toneBurst(sampling_freq, tone_burst_freq, tone_burst_cycles, 'SignalOffset', tone_burst_offset);

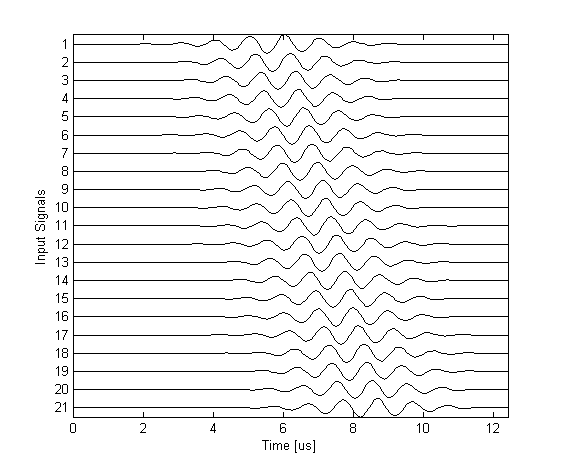
A plot of the input signals for each transducer element is shown below.

 Back to Top

Running the simulation

Visualisations of the pressure field at two different times for steering angles of +30 and -20 degrees are shown below.

 Back to Top

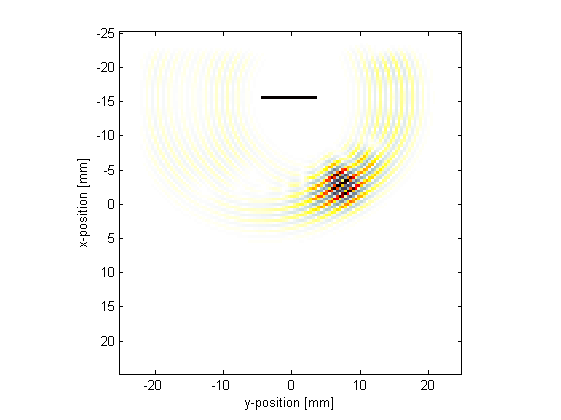
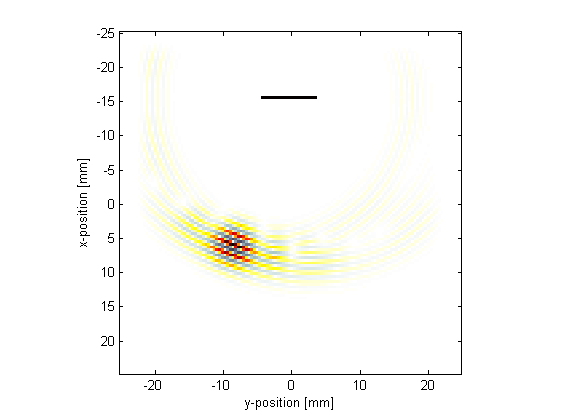
Simulating Transducer Field Patterns

Snell's Law And Critical Angle Reflection

© 2009-2014 Bradley Treeby and Ben Cox.