{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"\n",
"# Cellular automata I: Heat diffusion\n",
"\n",
"---\n",
"\n",
"\n",
"\n",
"This notebook is licensed under a [Creative Commons Attribution-ShareAlike 4.0 International License](http://creativecommons.org/licenses/by-sa/4.0/)."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Load packages"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"%matplotlib inline\n",
"\n",
"from pathlib import Path\n",
"\n",
"import matplotlib.pyplot as plt\n",
"from matplotlib import animation, rc\n",
"import numpy as np\n",
"import pandas as pd\n",
"import seaborn as sns\n",
"from IPython.display import HTML\n",
"\n",
"rc(\"animation\", html=\"html5\")\n",
"\n",
"np.random.seed(1189773503)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Background: Heat Diffusion"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
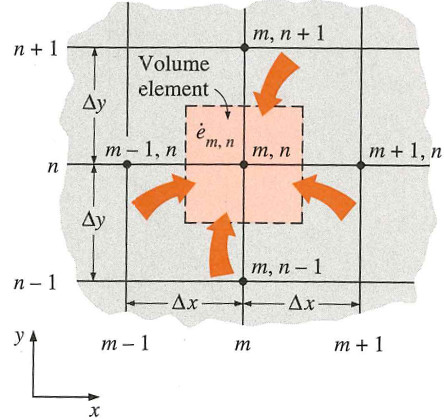
"We will be building a cellular automata simulation of the diffusion of heat within a bar. Unlike a system dynamics model, this simulation will allow us to observe the heat flow at different positions within the bar. In effect, we will be able to simulate what the temperature of the bar will be not only at a given time, but at a given position in the bar.\n",
"\n",
"The general idea of what we want to do is to to scale down **Newton's law of heating and cooling**. This states that the rate of change of the temperature with respect to time of an object is proportional to the difference between the temperature of the object and temperature of its surroundings. In the context of cellular automata, a cell's *surroundings* is defined by its surrounding neighbors in a grid."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"There's different ways to define a cell's surroundings, or neighborhood. For our purposes, we will use the so-called **Moore neighborhood**, which consists of a cell's NW, N, NE, W, E, SW, S, and SE neighbors:"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"
\n",
"\n",
"
\n",
"
NW
\n",
"
N
\n",
"
NE
\n",
"
\n",
"
\n",
"
W
\n",
"
site
\n",
"
E
\n",
"
\n",
"
\n",
"
SW
\n",
"
S
\n",
"
SE
\n",
"
\n",
"\n",
"
"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Having decided upon this, the simulation will require us to apply the diffusion formula to every site for each time step will be as follows:\n",
"\n",
"$$\n",
"\\dfrac{T_{m,n}^{i+1}-T_{m,n}^{i}}{\\tau}=\\sum_{m',n'}^{\\text{neighborhood}}\\left(T_{m',n'}^{i}-T_{m,n}^{i}\\right)+\\dfrac{\\dot{e}_{m,n}^{i}l^{2}}{k}\n",
"$$\n",
"\n",
"where $\\tau=\\dfrac{\\alpha}{l^2}\\Delta{}t$ is the so-called dimensionless mesh Fourier number, $\\alpha=\\dfrac{k}{\\rho c}$ is the thermal diffusivity, $k$ is the material's thermal conductivity, $\\rho$ is the material's density, and $c$ is the material's specific heat. $\\dot{e}_{node}^i$ is the *rate of heat generation* within the cell and $l$ is the cell's length, $l=\\Delta{}x=\\Delta{}y$. Note that the term *rate of heat generation* corresponds to the rate at which other forms of energy are converted into thermal energy. This may include things like chemical reactions, heat energy from biological processes, and electrical current.\n",
"\n",
"By rewriting the formula slightly, the connection of this expression with the finite difference equation becomes clear:\n",
"\n",
"$$\n",
"T_{m,n}^{i+1}=T_{m,n}^{i}+\\tau\\left[\\sum_{m',n'}^{\\text{neighborhood}}\\left(T_{m',n'}^{i}-T_{m,n}^{i}\\right)+\\dfrac{\\dot{e}_{m,n}^{i}l^{2}}{k}\\right]\n",
"$$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Applying the Moore neighborhood to our finite difference equation and assuming that $\\dot{e}_{m,n}^{i}=0$ for all cells and for the entire simulation, the expression reduces to:\n",
"\n",
"$$\n",
"T_{m,n}^{i+1}=\\left(1-8\\tau\\right)T_{m,n}^{i}+\\tau\\sum_{m',n'}^{\\text{Moore}}T_{m',n'}^{i}\n",
"$$\n",
"\n",
"If we explicitly write out all the terms for the summation over the Moore neighborhood, we get:\n",
"\n",
"$$\n",
"T_{m,n}^{i+1}=\\left(1-8\\tau\\right)T_{m,n}^{i}+\\tau\\left(T_{m+1,n}+T_{m,n+1}+T_{m-1,n}+T_{m,n-1}+T_{m+1,n+1}+T_{m-1,n+1}+T_{m+1,n-1}+T_{m-1,n-1}\\right)\n",
"$$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Stability criterion\n",
"\n",
"For the simulation to be stable, the following inequality must be satisfied: \n",
"\n",
"$$\n",
"\\tau=\\dfrac{\\alpha\\Delta{}t}{l^2}\\leq\\frac{1}{\\text{number of neighbors}}\n",
"$$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Building up our cellular automata simulation"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [],
"source": [
"def apply_hot_cold(bar, hot_sites, cold_sites, hot, cold):\n",
" \"\"\"Apply hot and cold temperatures to listed sites.\n",
" \n",
" Parameters\n",
" ----------\n",
" bar : np.array\n",
" A grid of temperatures\n",
" \n",
" hot_sites : list\n",
" A list of coordinates inside the `bar` grid that have temperature\n",
" `hot`\n",
" \n",
" cold_sites : list\n",
" A list of coordinates inside the `bar` grid that have temperature\n",
" `cold`\n",
" \n",
" hot : float\n",
" The initial temperature of each coordinate in `hot_sites`\n",
" \n",
" cold : float\n",
" The initial temperature of each coordinate in `cold_sites`\n",
" \n",
" Returns\n",
" -------\n",
" new_bar : np.array\n",
" `bar` grid of temperatures updated with hot and cold sites\n",
" \"\"\"\n",
" # grid dimensions\n",
" m, n = bar.shape\n",
"\n",
" # without copying, changing new_bar will also change bar\n",
" new_bar = bar.copy()\n",
"\n",
" # site numbers count from left to right, going row by row\n",
" #\n",
" # find site index by using dimension n in combination with integer\n",
" # division and the modulus operator\n",
" new_bar[hot_sites // n, hot_sites % n] = hot\n",
" new_bar[cold_sites // n, cold_sites % n] = cold\n",
"\n",
" # Output the updated temperature grid\n",
" return new_bar"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [],
"source": [
"def init_bar(m, n, hot_sites, cold_sites, hot, cold, ambient):\n",
" \"\"\"Initialize an m ⨉ n grid of temperatures.\n",
" \n",
" Cells with coordinates in `hot_sites` have the value `hot`; cells with\n",
" coordinates in cold_sites have the value `cold`; and all other cells have\n",
" the value `ambient`.\n",
" \n",
" Parameters\n",
" ----------\n",
" m : int\n",
" Number of rows in the grid\n",
" \n",
" n : int\n",
" Number of columns in the grid\n",
"\n",
" hot_sites : list\n",
" List of sites inside the `bar` grid that have temperature `hot`\n",
"\n",
" cold_sites : list\n",
" List of sites inside the `bar` grid that have temperature `cold`\n",
"\n",
" hot : float\n",
" The initial temperature of the `hot_sites`\n",
"\n",
" cold : float\n",
" The initial temperature of the `cold_sites`\n",
" \n",
" ambient : float\n",
" The initial temperature for all other sites\n",
" \n",
" Returns\n",
" -------\n",
" bar : np.array\n",
" Grid of temperatures containing the specified hot, cold, and ambient\n",
" sites\n",
" \"\"\"\n",
" # create numpy array with dimensions (m, n) and fill with ambient\n",
" # temperature\n",
" ambient_bar = np.full((m, n), ambient, dtype=np.float64)\n",
" \n",
" # update specified hot and cold sites with appropriate temperatures and\n",
" # output the temperature grid\n",
" return apply_hot_cold(ambient_bar, hot_sites, cold_sites, hot, cold)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let's test that the above functions are working as desired. Let's assume a $10\\times{}30$ grid, and set the ambient temperature to $25^{\\circ}\\text{C}$, the hot temperature to $50^{\\circ}\\text{C}$, and the cold temperature to $0^{\\circ}\\text{C}$. All sites will be ambient except for the following:\n",
"\n",
"* **Hot sites**: 278, 279, 280, 281, 282\n",
"* **Cold sites**: 22, 90, 120, 150"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [],
"source": [
"bar = init_bar(\n",
" m=10, n=30, hot_sites=np.array([278, 279, 280, 281, 282]),\n",
" cold_sites=np.array([22, 90, 120, 150]), hot=50, cold=0, ambient=25)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Since the bar's grid is relatively small, a reasonable approach would be to print the contents of the `bar` array to check if `init_bar()` worked as desired. However, it's even better to inspect using a visualization, as this can be easily scaled to any size bar. A good visualization choice is to plot a heatmap of the grid (with no interpolation), which we can do using the matplotlib code snippet contained in the function below."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [],
"source": [
"def visualize_bar(bar, cmap=\"afmhot\", fig_width=18, fig_height=6):\n",
" \"\"\"Visualize a rectangular 2D numpy array using a heatmap.\n",
"\n",
" Parameters\n",
" ----------\n",
" bar : np.array\n",
" A grid of temperatures\n",
" \n",
" cmap : str\n",
" Color scheme for the heatmap scale, see colormaps_ reference.\n",
" \n",
" fig_width : float\n",
" Figure width in inches\n",
" \n",
" fig_height : float\n",
" Figure height in inches\n",
" \n",
" Returns\n",
" -------\n",
" fig, ax : tuple of plt.figure and plt.subplot\n",
" Matplotlib figure and subplot axis objects\n",
" \n",
" .. _colormaps: https://matplotlib.org/examples/color/colormaps_reference.html \n",
" \"\"\"\n",
" # grid dimensions\n",
" m, n = bar.shape\n",
"\n",
" # create matplotlib figure and subplot objects\n",
" fig, ax = plt.subplots(figsize=(fig_width, fig_height))\n",
"\n",
" # imshow visualizes array as a two-dimensionl uniform grid\n",
" im = ax.imshow(bar, cmap=cmap, interpolation=\"nearest\")\n",
"\n",
" # show reference colorbar\n",
" cbar = fig.colorbar(mappable=im, orientation=\"vertical\")\n",
"\n",
" # find the starting and ending coordinates for heatmap for creating\n",
" # grid lines\n",
" xticks_start, xticks_end = ax.get_xlim();\n",
" yticks_start, yticks_end = ax.get_ylim();\n",
"\n",
" # separate grid cells by white lines\n",
" ax.xaxis.set_ticks(np.linspace(xticks_start, xticks_end, n + 1),\n",
" minor=False);\n",
" ax.yaxis.set_ticks(np.linspace(yticks_start, yticks_end, m + 1),\n",
" minor=False);\n",
" ax.axes.grid(True, linestyle=\"-\", linewidth=1, color=\"white\",\n",
" which=\"major\");\n",
" \n",
" # we don't need ticks and tick labels because we have grid lines\n",
" ax.tick_params(labelbottom = False, labelleft=False, bottom=False,\n",
" left=False);\n",
" \n",
" # Return matplotlib figure and subplot objects\n",
" return fig, ax"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"So, for our example, we get the following heatmap:"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA4oAAAFeCAYAAADDveHoAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4wLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvqOYd8AAAE2tJREFUeJzt3V2o5Vl6F+Df2zNBOx/dTXVnMCWJnQ8Ru1tC0pu+E2Ji4nSYDga8SBxQEJ3JIEK88EIQaipfFzrJjQixAmMkjBeTgQSH6Ua8EaMkKXdJYmbKizh+IJZCSprGNrSOVa8XtWvn/OtUn1Nn9jnr7LV5Htj0/lzv+vc+dfHjXWvt6u4AAADAQ09d9gQAAADYL4IiAAAAC4IiAAAAC4IiAAAAC4IiAAAAC4IiAAAAC4IiAADAgamqX6yq362qL25uz1bV56vqdlV9oaqeO+nzgiIAAMDh+VCSP9fdr3T3K0k+luRmd7+UZJ3kEyd9WFAEAAA4PB9KcvfI49eSvLW5/2aSV0/68AcvaFIAAABcnm9M8qtV9XySTyV5Psm7m9feSXLlpA8LigAAAIN8+MMf7rt3757+xhPcunXrS0neO/LUje6+8cjb/lKS30zybJLfSPKfHnm9T6ohKAIAAAxy9+7drNc3dxqj6gPvdffq/V+vDyb57e5+L8l7VXUzD5aiPrt5yzNZLks9xh5FAACAw/J1SX69qp6uqq9N8p1J/kWSNzavv57kxLSqowgAADBMJ7l/sRW636mqv5fkVh40B/9hkk8n+UxV3U7y5SQfPWkMQREAAGCoiw2KSdLdn86DcHjUR57084IiAADAUBcfFHdljyIAAAALOooAAADDXPwexfMgKAIAAAwlKAIAALClowgAAMAx+x8UHWYDAADAgo4iAADAMJaeAgAAcIygCAAAwIKgCAAAwNYcS08dZgMAAMCCjiIAAMBQ+99RFBQBAACGmWPpqaAIAAAw1P4HRXsUAQAAWNBRBAAAGGr/O4qCIgAAwDD2KAIAAHCMoAgAAMDWHB1Fh9kAAACwoKMIAAAw1P53FAVFAACAoQRFAAAAtubYo3imoPjCCy/0iy++eEFTAQAAeLz/fPtW7v5+12XP43wcWFB88cUXs37j1kXN5Q9c6+T6oL8BteapdYjXpNY8ddSap45ac9U6xGva1KoaU6v7AP8fHvDfxcHVGnhNqztDyrBh6SkAAMAwB7j0FAAAgF0JigAAACzsf1B86rInAAAAwH7RUQQAABjGHkUAAACOERQBAADY0lEEAADgmP0Pig6zAQAAYEFHEQAAYKj97ygKigAAAMPYowgAAMAxgiIAAABbc3QUHWYDAADAgo4iAADAUPvfURQUAQAAhhIUAQAA2LJHEQAAgAnpKAIAAAy1/x1FQREAAGCYOZaeCooAAABDCYoAAAAs7H9QdJgNAAAACzqKAAAAw9ijCAAAwDH7HxSru5/4zavVqtfr9QVOBwAA4LjV1cr6Ttdlz2NXq9W39Xr9MzuNUfWjt7p7dU5TeqyzdxSvD/hurvWYOmrNVesQr0mteeqoNU8dteaqdYjXpNY8ddSap87B2f+OosNsAAAAWLBHEQAAYKj97ygKigAAAMPMceqppacAAABD3d/xdrqq+mBVfbGqfqyqnqmqz1fV7ar6QlU9d9rnBUUAAIDD8+NJvn5z/+NJbnb3S0nWST5x2ocFRQAAgGEeLj29uI5iVf3RJD+U5Jc2T72W5K3N/TeTvHraGIIiAADAUBe+9PRTSf52knubx88neXdz/50kV04bQFAEAAAY5lw6ii9U1frI7WMPR6+q703yf7v7X58yiRM59RQAAGConU89vdvdq/d57a8m+a6q+q0kfyTJV5JcTfLs5vVnktw9rYCgCAAAcCC6+y8+vF9Vn0zyP/IgJL6R5DeTvJ7k5mnjCIoAAABDDf8dxZ9P8pmqup3ky0k+etoHBEUAAIBhHu5RHFCp+5NHHn7kLJ8VFAEAAIYa3lE8M0ERAABgmHEdxV34eQwAAAAWdBQBAACG2v+OoqAIAAAwlKAIAADAlj2KAAAATEhHEQAAYKj97ygKigAAAMPMsfRUUAQAABhKUAQAAGBh/4Oiw2wAAABYqO5+4jevVqter9cXOB0AAIDjVlcr6ztdlz2PXa1WV3u9/thOY1Rdv9Xdq3Oa0mOdfenp9QHfzbUeU0etuWod4jWpNU8dteapo9ZctQ7xmtSap45a89Q5NPf3f+mpPYoAAACjdE8RFO1RBAAAYEFHEQAAYKQJOoqCIgAAwCid5J6gCAAAwNYcexQFRQAAgJF6/4Oiw2wAAABY0FEEAAAYZZKfxxAUAQAARhIUAQAA2OoIigAAABw1x9JTh9kAAACwoKMIAAAwSie5t/8dRUERAABgmDmWngqKAAAAI00QFO1RBAAAYEFHEQAAYJRO0vvfURQUAQAAhrFHEQAAgEcJigAAAGz1HB1Fh9kAAACwoKMIAAAw0gQdRUERAABglI6gCAAAwFGd3BMUAQAAeGiSjmJ19xO/ebVa9Xq9vsDpAAAAHLe6Wlnf6brseexq9fKVXn/2z+40Rr3yy7e6e3VOU3qsM3cUqy7+u+nu5Pqgv4Frak1T6xCvSa156qg1Tx215qp1iNek1jx11JqnzkHppPe/o2jpKQAAwEgTLD0VFAEAAEbpniIoPnXZEwAAAGC/6CgCAACMNEFHUVAEAAAYSVAEAABgqzu5JygCAABw1AQdRYfZAAAAsKCjCAAAMMokP48hKAIAAIzUgiIAAABH6SgCAACwNcnSU4fZAAAAsKCjCAAAMNIEHUVBEQAAYJRJlp4KigAAACNNEBTtUQQAADgQVfWBqvp0VX2pqv5dVX1/VT1TVZ+vqttV9YWqeu60cQRFAACAUTrJvfu73U72Q0nudffLSX44yaeSfDzJze5+Kck6ySdOG0RQBAAAGGazR3GX20mjd/9Kd/+1zcMPJbmb5LUkb22eezPJq6fN0h5FAACAkXrnPYovVNX6yOMb3X3j4YOq+oYkv5HkxTwIiX8/ybubl99JcuW0AoIiAADAKOdz6und7l69f4n+X0lerqo/neQXkrz36FtOK2DpKQAAwIGoqj9VVX8ySbr715J8a5K3kzy7ecszebAc9USCIgAAwEgXuEcxyR9P8sl64OUk/zXJzSRvbF5/ffP4RJaeAgAAjHSxv6P4q0l+IMntJP87yY8l+d0kn6mq20m+nOSjpw0iKAIAAIxyPnsUTxi+7+dBOHzUR84yTnWfuo9xa7Va9Xq9Pv2NAAAA52h1tbK+03XZ89jV6tuf7vXPfOtOY9SP/PtbJx1mcx7O3FGsuvjvpruT64P+Bq6pNU2tQ7wmteapo9Y8ddSaq9YhXpNa89RRa546DGfpKQAAwCgXvPT0vAiKAAAAIwmKAAAALPT+B0W/owgAAMCCjiIAAMAo9igCAABwjKAIAADAlo4iAAAAx0wQFB1mAwAAwIKOIgAAwCidKTqKgiIAAMAwndwTFAEAAHhIRxEAAIClTnr/g6LDbAAAAFjQUQQAABjJ0lMAAAC27FEEAABgqacIivYoAgAAsKCjCAAAMNIEHUVBEQAAYJTu5J6gCAAAwFE6igAAAGxNcuqpw2wAAABY0FEEAAAYppPe/46ioAgAADDSBEtPq7uf+M2r1arX6/UFTgcAAOC41dXK+k7XZc9jV6ur1f/mY7uN8dT13Oru1fnM6PHO3FGsuvjvpruT64P+Bq6pNU2tQ7wmteapo9Y8ddSaq9YhXpNa89RRa546B2aChqLDbAAAAFiyRxEAAGCQ7uT+vcuexekERQAAgIHuP/kxMZdGUAQAABikY48iAAAAE9JRBAAAGMUeRQAAAB41w9JTQREAAGCQbofZAAAA8IgZOooOswEAAGBBRxEAAGCQWX4eQ1AEAAAYxamnAAAAHNWZ4zAbexQBAABY0FEEAAAYpe1RBAAA4BH2KAIAALDVOooAAAA8ymE2AAAATEdHEQAAYJCOpacAAAAcZY8iAAAAj3LqKQAAAFsdh9kAAAAwIR1FAACAUSbZo1jdT973XK1WvV6vL3A6AAAAx62uVtZ3ui57Hrt6+Ur1Z79vtzFe+VxudffqfGb0eGfvKF4f8N1c6zF11Jqr1iFek1rz1FFrnjpqzVXrEK9JrXnqqDVPnUMySUfRHkUAAIADUlU/V1VfqqrbVfWDVfU1VfWPN8/9WlV982ljCIoAAAAD3e/dbiepqjeSfEuSV5L8+ST/YPPf/9fdLyf5dJK/c9ocHWYDAAAwSF/80tP/nuSnurur6j8m+UNJXkvy1ub1N5P89dMGERQBAAAGOoeg+EJVHT1l9EZ330iS7j76/I8k+ZUkzyd5d/PcO0munFZAUAQAABikO7l/b+dh7p526mlV/YkkfyvJ9yT52UencVoBexQBAAAOSFU9l+SfJPnL3f12kreTPLt5+Zkkd08bQ1AEAAAY6IIPs/lAHoTEn+ju39o8fTPJG5v7r28en8jSUwAAgIEu+DCbH07yZ5J8S1X99Oa5v5nkflXdTvJ7SX70tEEERQAAgEHOaY/iCeP355J87jEv/fOzjCMoAgAADHTBHcVzYY8iAAAACzqKAAAAg3ROP5BmHwiKAAAAo/QcS08FRQAAgIFmCIr2KAIAALCgowgAADDIRf88xnkRFAEAAAZymA0AAABbnTn2KAqKAAAAo0yy9NRhNgAAACzoKAIAAAxk6SkAAABb3Q6zAQAA4BE6igAAAGzNcuppdT9533O1WvV6vb7A6QAAABy3ulpZ3+m67Hns6tu/tvrvfsduY/yF38mt7l6dz4we7+wdxesDvptrPaaOWnPVOsRrUmueOmrNU0etuWod4jWpNU8dteapc0gm+XkMS08BAAAGcpgNAAAAW91z7FF86rInAAAAwH7RUQQAABjIHkUAAAC2Zll6KigCAAAM5DAbAAAAtjpzdBQdZgMAAMCCjiIAAMAo9igCAADwKKeeAgAAsOXUUwAAAI6Z4dRTh9kAAACwoKMIAAAwSMceRQAAAI6yRxEAAIBHzRAU7VEEAABgQUcRAABgkM4cp54KigAAAKPYowgAAMBRTj0FAABgaZKOosNsAAAAWNBRBAAAGMhhNgAAAGx126MIAADAI2bYo1jdT973XK1WvV6vL3A6AAAAx62uVtZ3ui57Hru6WtUf33GMTya3unt1HvN5P2fvKF4f8N1c6zF11Jqr1iFek1rz1FFrnjpqzVXrEK9JrXnqqDVPHYaz9BQAAGCgCVaeCooAAAAjCYoAAABsdeYIik9d9gQAAADYLzqKAAAAA83QURQUAQAABpll6amgCAAAMJCgCAAAwMIMQdFhNgAAACzoKAIAAAxijyIAAADHCIoAAABszdJRtEcRAABgoPs73p5EVb1aVf+oqq5tHj9TVZ+vqttV9YWqeu6kzwuKAAAAB6SqvjPJTya5l+TpzdMfT3Kzu19Ksk7yiZPGEBQBAAAGuuiOYnf/dnf/YJJ/deTp15K8tbn/ZpJXTxrDHkUAAIBBLnGP4vNJ3t3cfyfJlZPeLCgCAAAMdA5B8YWqWh95fKO7b5xxjD7pRUERAABgLne7e3XGz7yd5NnN/WeS3D3pzfYoAgAADPJw6elFn3r6GDeTvLG5//rm8fvSUQQAABjokvYo/nySz1TV7SRfTvLRk94sKAIAAAw0Kih29y8euf9Oko886WcFRQAAgEEu8dTTM7FHEQAAgAUdRQAAgIFm6CgKigAAAIPMsvS0uk/8ncWF1WrV6/X69DcCAACco9XVyvpO12XPY1dXqvr7dxzjs8mtr+J3FM/k7B3F6wO+m2s9po5ac9U6xGt6WAse59D+3g/537Ba+19HrblqHeI1HWqtkdfEUJaeAgAADDTD0lNBEQAAYJBZ9igKigAAAAMJigAAAGzN0lF86rInAAAAwH7RUQQAABhoho6ioAgAADDILEtPBUUAAICBBEUAAAAWZgiKDrMBAABgQUcRAABgEHsUAQAAOEZQBAAAYGuWjqI9igAAACzoKAIAAAw0Q0dRUAQAABhIUAQAAGBrlj2KgiIAAMBAMwRFh9kAAACwoKMIAAAwiKWnAAAAHCMoAgAAsCAoAgAAsDXL0lOH2QAAALCgowgAADDQDB3F6u4nf3PV7yX5Lxc3HQAAgMf6Y939jZc9iV09XdXfseMYX0xudffqXCb0Ps7UUTyELwYAAOAyzdBRtEcRAACABXsUAQAABpqhoygoAgAADDLLz2MIigAAAAMJigAAAGzN0lF0mA0AAAALOooAAAADzdBRFBQBAAAGEhQBAADYmmWPoqAIAAAw0AxB0WE2AAAALOgoAgAADGLpKQAAAMcIigAAACzMEBTtUQQAAGBBRxEAAGAQexQBAAA4RlAEAABgS0cRAACAY2YIig6zAQAAYEFHEQAAYKAZOoqCIgAAwCD2KAIAAHDMDEHRHkUAAIBBHnYUd7mdpqp+vKpuV9XvVNX3fjXz1FEEAAA4EFX1TUn+SpLvSvLNSf5pkpfOOo6gCAAAMNAFLz397iT/srv/T5L/UA98fXe/e5ZBBEUAAICBLjgoPp/kaCh8J8mVR547laAIAAAwzj9L8sKOY/zhqlofeXyju2+c8P4+awFBEQAAYJDu/vAFl3g7ybNHHn9Dkv951kGcegoAAHA4/m2S76mqp6vq25J8pbt//6yD6CgCAAAciO7+b1V1Iw8C41eS/I2vZpzqPvNyVQAAAA6YpacAAAAsCIoAAAAsCIoAAAAsCIoAAAAsCIoAAAAsCIoAAAAsCIoAAAAsCIoAAAAs/H9YC2a39gKZsQAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"visualize_bar(bar);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This is exactly what we expected to see."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Boundary conditions"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"There are a few different kinds of boundary conditions we could choose, which include\n",
"\n",
"1. Absorbing boundary conditions\n",
"2. Reflecting boundary conditions\n",
"3. Periodic boundary conditions\n",
"\n",
"In this ongoing example, we will implement the **reflecting boundary conditions**.\n",
"\n",
"In practice, implementing the absorbing or reflecting boundary conditions will require the use of **ghost cells**. You can also use ghost cells for periodic boundary conditions, but it isn't required. The following function sets up the ghost cells in `numpy`:"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [],
"source": [
"def boundary_condition(bar, condition=\"reflecting\"):\n",
" \"\"\"Setup ghost cells for boundary condition.\n",
" \n",
" Parameters\n",
" ----------\n",
" bar : np.array\n",
" A grid of temperatures\n",
" \n",
" condition : str, optional\n",
" The boundary condition to use when creating ghost cells.\n",
" \"\"\"\n",
" if condition == \"reflecting\":\n",
" extended_bar = np.pad(array=bar, pad_width=(1, 1), mode='edge')\n",
"\n",
" else:\n",
" raise ValueError(\n",
" \"{0} is not a valid boundary condition\".format(condition))\n",
"\n",
" return extended_bar"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"After adding the ghost cells, we now have an extended bar. With this set up, we can now go through each site and look up the neighboring temperatures in the Moore neighborhood. We can do this efficiently using `numpy`:"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [],
"source": [
"def get_neighbor_temperatures(extended_bar,\n",
" ghost_width=(1, 1),\n",
" neighborhood=\"moore\"):\n",
" \"\"\"Get the temperature of each site's neighbors in a single sweep.\n",
" \n",
" Paramters\n",
" ---------\n",
" extended_bar : np.array\n",
" A grid of temperatures with ghost cells\n",
" \n",
" ghost_width : array-like\n",
" A number pair that specifies how many rows and columns make up the\n",
" ghost cell region\n",
" \n",
" neighborhood : str, optional\n",
" Determines which cells will be counted as neighbors\n",
" \n",
" Returns\n",
" -------\n",
" bar_with_neighbors : np.array\n",
" An array of temperatures for each site and its neighbors\n",
" \"\"\"\n",
" m_extended, n_extended = extended_bar.shape\n",
" m, n = (m_extended - ghost_width[0], n_extended - ghost_width[1])\n",
" \n",
" if neighborhood == \"moore\":\n",
" bar_with_neighbors = np.array([\n",
" np.roll(\n",
" extended_bar, shift=(1, 1),\n",
" axis=(1, 0))[ghost_width[0]:m, ghost_width[1]:n],\n",
" np.roll(\n",
" extended_bar, shift=(0, 1),\n",
" axis=(1, 0))[ghost_width[0]:m, ghost_width[1]:n],\n",
" np.roll(\n",
" extended_bar, shift=(-1, 1),\n",
" axis=(1, 0))[ghost_width[0]:m, ghost_width[1]:n],\n",
" np.roll(\n",
" extended_bar, shift=(1, 0),\n",
" axis=(1, 0))[ghost_width[0]:m, ghost_width[1]:n],\n",
" np.roll(\n",
" extended_bar, shift=(-1, 0),\n",
" axis=(1, 0))[ghost_width[0]:m, ghost_width[1]:n],\n",
" np.roll(\n",
" extended_bar, shift=(1, -1),\n",
" axis=(1, 0))[ghost_width[0]:m, ghost_width[1]:n],\n",
" np.roll(\n",
" extended_bar, shift=(0, -1),\n",
" axis=(1, 0))[ghost_width[0]:m, ghost_width[1]:n],\n",
" np.roll(\n",
" extended_bar, shift=(-1, -1),\n",
" axis=(1, 0))[ghost_width[0]:m, ghost_width[1]:n]])\n",
"\n",
" else:\n",
" raise ValueError(\n",
" \"{0} is not a valid type of neighborhood\".format(condition))\n",
"\n",
" return bar_with_neighbors"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now that we've collected all the temperatures of each cell's neighbors, we apply our diffusion formula,\n",
"\n",
"$$\n",
"\\begin{aligned}\n",
"T_{m,n}^{i+1}&=\\left(1-8\\tau\\right)T_{m,n}^{i}+\\tau\\sum_{m',n'}^{\\text{Moore}}T_{m',n'}^{i} \\\\\n",
"&=\\left(1-8\\tau\\right)T_{m,n}^{i}+\\tau\\left(T_{m+1,n}+T_{m,n+1}+T_{m-1,n}+T_{m,n-1}+T_{m+1,n+1}+T_{m-1,n+1}+T_{m+1,n-1}+T_{m-1,n-1}\\right)\n",
"\\end{aligned}\n",
"$$\n",
"\n",
"to each site in the grid. As usual, we can do this efficiently with `numpy` and vectorization. Note that we do not have any `for` loops below."
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [],
"source": [
"def diffusion(bar, bar_neighbors, diffusion_rate):\n",
" \"\"\"Update site temperatures using Newton's law of heating and cooling.\n",
" \n",
" Parameters\n",
" ----------\n",
" bar : np.array\n",
" A grid of temperatures\n",
"\n",
" bar_neighbors : np.array\n",
" An array of temperatures for each site and its neighbors\n",
"\n",
" diffusion_rate : float\n",
" Paramter measuring ease of temperature flow from hot to cold sites.\n",
" \n",
" Returns\n",
" -------\n",
" bar_update : np.array\n",
" A grid of temperatures after applying Newton's law of heating and\n",
" cooling to all grid sites.\n",
" \"\"\"\n",
" num_neighbors, m, n = bar_neighbors.shape\n",
" \n",
" bar_update = (\n",
" (1 - num_neighbors * diffusion_rate) * bar +\n",
" diffusion_rate * np.sum(a=bar_neighbors, axis=0))\n",
"\n",
" return bar_update"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now we sweep over all lattice points. In addition to the diffusion routine defined above, we reset the hot and cold points so that they stayed fixed at their respective temperatures. We also append the updated grid to the `simulation_history` list so that we can animate the diffusion simulation."
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [],
"source": [
"def sweep(bar, diffusion_rate, hot_sites, cold_sites, hot, cold, nstep,\n",
" simulation_history):\n",
" \"\"\"Sweep over grid and update temperatures.\n",
" \n",
" Parameters\n",
" ----------\n",
" bar : np.array\n",
" A grid of temperatures\n",
"\n",
" diffusion_rate : float\n",
" Paramter measuring ease of temperature flow from hot to cold sites.\n",
"\n",
" hot_sites : list\n",
" A list of coordinates inside the `bar` grid that have temperature\n",
" `hot`\n",
"\n",
" cold_sites : list\n",
" A list of coordinates inside the `bar` grid that have temperature\n",
" `cold`\n",
"\n",
" hot : float\n",
" The initial temperature of each coordinate in `hot_sites`\n",
"\n",
" cold : float\n",
" The initial temperature of each coordinate in `cold_sites`\n",
"\n",
" simulation_history : list\n",
" Time-step history for the simulation's run.\n",
" \"\"\"\n",
" extended_bar = boundary_condition(bar) \n",
" bar_neighbors = get_neighbor_temperatures(extended_bar)\n",
" bar_diffused = diffusion(bar, bar_neighbors, diffusion_rate)\n",
" bar_full_update = apply_hot_cold(\n",
" bar_diffused, hot_sites, cold_sites, hot, cold)\n",
" bar[:, :] = bar_full_update\n",
" simulation_history.append([nstep, bar_full_update])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Simulation Program"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Finally, we bring it all together into a function that runs the full simulation from start to finish. This is where we put our `for` loop over time."
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [],
"source": [
"def diffusion_simulation(number_time_steps, m, n, hot_sites, cold_sites, hot,\n",
" cold, ambient, diffusion_rate):\n",
" \"\"\"Run temperature diffusion simulation.\n",
" \n",
" Parameters\n",
" ----------\n",
" number_time_steps : int\n",
" Sets the number of time steps over which to run a simulation.\n",
"\n",
" m : int\n",
" Number of rows in the grid\n",
" \n",
" n : int\n",
" Number of columns in the grid\n",
"\n",
" hot_sites : list\n",
" List of sites inside the `bar` grid that have temperature `hot`\n",
"\n",
" cold_sites : list\n",
" List of sites inside the `bar` grid that have temperature `cold`\n",
"\n",
" hot : float\n",
" The initial temperature of the `hot_sites`\n",
"\n",
" cold : float\n",
" The initial temperature of the `cold_sites`\n",
" \n",
" ambient : float\n",
" The initial temperature for all other sites\n",
"\n",
" diffusion_rate : float\n",
" Paramter measuring ease of temperature flow from hot to cold sites\n",
" \n",
" Returns\n",
" -------\n",
" simulation_history : list\n",
" The temperature grid as a function of time during the temperature\n",
" diffusion simulation\n",
" \"\"\"\n",
" # Initialize bar according to parameters\n",
" bar = init_bar(\n",
" m=m, n=n, hot_sites=hot_sites, cold_sites=cold_sites, hot=hot,\n",
" cold=cold, ambient=ambient)\n",
"\n",
" # Initialize record keeper for the simulation history\n",
" simulation_history = [[0, bar.copy()]]\n",
"\n",
" # Run simulation for specified number of time steps\n",
" for nstep in np.arange(number_time_steps):\n",
" sweep(bar=bar, diffusion_rate=diffusion_rate, hot_sites=hot_sites,\n",
" cold_sites=cold_sites, hot=hot, cold=cold, nstep=nstep,\n",
" simulation_history=simulation_history)\n",
"\n",
" return simulation_history"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Display Simulation"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Having successfully run our simulation, now we would like to see it in action! The code below is similar to the animation we created for the Random Walk in module 9.5. We advance each frame of the animation by incrementing the index on `simulation_history` by 1."
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [],
"source": [
"def diffusion_animation(simulation_history, cmap=\"afmhot\", fig_width=12,\n",
" fig_height=4):\n",
" \"\"\"Animate the temperature diffusion simulation using Matplotlib.\n",
"\n",
" Parameters\n",
" ----------\n",
" simulation_history : list\n",
" Time-step history for the simulation's run.\n",
" \n",
" cmap : str, optional\n",
" Color scheme for the heatmap scale, see colormaps_ reference.\n",
" \n",
" fig_width : float, optional\n",
" Figure width in inches\n",
" \n",
" fig_height : float, optional\n",
" Figure height in inches\n",
" \n",
" Returns\n",
" -------\n",
" anim : matplotlib.animation.FuncAnimation\n",
" Animated object for the simulation run.\n",
" \n",
" .. _colormaps: https://matplotlib.org/examples/color/colormaps_reference.html \n",
" \"\"\"\n",
" # grid dimensions\n",
" m, n = simulation_history[0][1].shape\n",
"\n",
" # create matplotlib figure and subplot objects\n",
" fig, ax = plt.subplots(figsize=(fig_width, fig_height))\n",
"\n",
" # imshow visualizes array as a two-dimensionl uniform grid\n",
" im = ax.imshow(bar, cmap=cmap, interpolation=\"nearest\")\n",
"\n",
" # show reference colorbar\n",
" cbar = fig.colorbar(mappable=im, orientation=\"vertical\")\n",
"\n",
" # find the starting and ending coordinates for heatmap for creating\n",
" # grid lines\n",
" xticks_start, xticks_end = ax.get_xlim();\n",
" yticks_start, yticks_end = ax.get_ylim();\n",
"\n",
" # separate grid cells by white lines\n",
" ax.xaxis.set_ticks(np.linspace(xticks_start, xticks_end, n + 1),\n",
" minor=False);\n",
" ax.yaxis.set_ticks(np.linspace(yticks_start, yticks_end, m + 1),\n",
" minor=False);\n",
" ax.axes.grid(True, linestyle=\"-\", linewidth=1, color=\"white\",\n",
" which=\"major\");\n",
" \n",
" # we don't need ticks and tick labels because we have grid lines\n",
" ax.tick_params(labelbottom = False, labelleft=False, bottom=False,\n",
" left=False);\n",
" \n",
" # Initialization function, clears out the data on the im object\n",
" def init():\n",
" im.set_array(np.array([[]]))\n",
" return (im, )\n",
"\n",
"\n",
" # Animation function. Input i is the frame number of the animation, and is\n",
" # to be used for referencing how the data changes over time\n",
" def animate(i):\n",
" # Get the simulation history at time step i and set as the underlying\n",
" # data for the im object\n",
" bar_i = simulation_history[i][1]\n",
" im.set_array(bar_i)\n",
"\n",
" return (im, )\n",
"\n",
" # Suppress static matplotlib window\n",
" plt.close()\n",
" \n",
" # Use animation.FuncAnimation to put the animation together.\n",
" # frames controls the number of frames in the movie.\n",
" # interval controls the delay in milliseconds inbetween each frame\n",
" # blit optimizes the animation size by only storing the changes between\n",
" # frames instead of as a series of full plots\n",
" anim = animation.FuncAnimation(fig=fig, func=animate,\n",
" frames=len(simulation_history),\n",
" init_func=init, interval=100, blit=True);\n",
"\n",
" return anim"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Example Run"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now that all the pieces are in place, let's run the simulation with the following initial parameters, which match the parameters suggested on page 429 of the textbook."
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [],
"source": [
"m, n = (10, 30)\n",
"hot, cold, ambient = (50, 0, 25)\n",
"hot_sites = np.array([278, 279, 280, 281, 282])\n",
"cold_sites = np.array([22, 90, 120, 150])\n",
"diffusion_rate = 0.1\n",
"number_time_steps = 50\n",
"simulation_history = diffusion_simulation(\n",
" number_time_steps=number_time_steps, m=m, n=n, hot_sites=hot_sites,\n",
" cold_sites=cold_sites, hot=hot, cold=cold, ambient=ambient,\n",
" diffusion_rate=diffusion_rate)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We then build our animation:"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [],
"source": [
"anim = diffusion_animation(simulation_history)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"And view it:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"HTML(anim.to_html5_video())"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Basic analysis of simulation outputs"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [],
"source": [
"middle_column_over_time = []\n",
"middle_row_over_time = []\n",
"check_correlation = []\n",
"for time_step in simulation_history:\n",
" middle_column_over_time.append([time_step[0], time_step[1][:, 14]])\n",
" middle_row_over_time.append([time_step[0], time_step[1][4, :]])\n",
" check_correlation.append([time_step[1][7, 5], time_step[1][5, 9]])"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([25., 25., 25., 25., 25., 25., 25., 25., 25., 25.])"
]
},
"execution_count": 17,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"middle_column_over_time[0][1]"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAmgAAAGjCAYAAACYKOmjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAASdAAAEnQB3mYfeAAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4wLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvqOYd8AAAIABJREFUeJzs3Xt8VPd95//Xd0ajOwghITAIMOYibrJBGBtsJGETJ+l2m6SbpsZ2c1kMcZx663jb/B7bbNN0u03TbpvaMXYSx5e2ycMOSbvbertp6zhgS8KOHBtxERjExYARNyEhCTS6zGjm+/vjjKQZzeg2GsGMeD8fj3mMZubMOecLNrz5Xj5fY61FRERERJKH63rfgIiIiIhEUkATERERSTIKaCIiIiJJRgFNREREJMkooImIiIgkGQU0ERERkSSjgCYiIiKSZBTQRERERJKMApqIiIhIklFAExEREUkyCmgiIiIiSSZhAc0Y81NjjDXGbAx7b4Ux5jVjTEfo8box5tZEXVNERERkMkpIQDPG/DrwmUHv5QE7gdnAFmBr6OedxpjpibiuiIiIyGQ07oBmjMkFvgu8Neijh4Ai4FPW2p9aa3cAvw4UAL8z3uuKiIiITFaJ6EH7JuAPPYdbB5yw1p7oe8Naewo4BtyRgOuKiIiITEpp4/myMWYt8LvAr+GEtHCzgKYYX2vC6VkTERERkRjiDmjGmDTgeeDH1trXwxcHhKQTHdoAAqHPhjt3ETBj0Nu5wBLgIOCL555FRERErpF0YC5QZa1tH+uXx9OD9gehC98Xx3ftCJ9/GfhGHOcVERERSSafBP7vWL8UV0AzxiwE/hh4HGgN9aa5Qx+7jTFunF6uvBhfTweujHCJ7wL/MOi9pcA//vM//zOLFi2K57ZFREREronjx4/zqU99CuBMPN+PtwftD4As4AehR7hfAKdxVnWWxPjuTKBhuJNba5sYNH/NGAPAokWLWLFiRVw3LSIiInKNxTUtK95VnH8JrB30+FLosy8BvwH8EpgXXpjWGLMYuAWojfO6IiIiIpNeXD1ooXIZp8LfC9VDA2iw1tYbY84AfwT8b2PMHwO9OMOiF4Afx3vDIiIiIpPdhO3Faa1tAzYBHwAvAH8LnAM2WWtHmoMmIiIicsMaVx20cNbaNwEz6L1DwMcSdQ0RERGRG8GE9aCJiIiISHwU0ERERESSjAKaiIiISJJRQBMRERFJMgpoIiIiIklGAU1EREQkySigiYiIiCQZBTQRERGRJKOAJiIiIpJkFNBEREREkowCmoiIiEiSUUATERERSTIKaCIiIiJJRgFNREREJMkooImIiIgkGQU0ERERkSSjgCYiIiKSZBTQRERERJKMApqIiIhIkkm73jcgIiIici1Yv5/Our0E2ttw500ju2w1xuO53rcVkwKaiIiITGrW76f5+edpffkVAi0t/e+7CwvJf/ABCrdtS7qgpoAmIiIik5b1+znz2GN4q6rBmIjPAi0tND+9ne79Byh+ZntShTTNQRMREZFJq/n5551wBmBt5Ieh1x1VVbS88MI1vrPhKaCJiIjIpGT9flpffiWq5yyKMVx++RWs339tbmwUFNBERERk0rHBIFf+9d+cOWeDe86iDrYEmpvprNt7bW5uFDQHTURERFJa4MoVehoa6G446jwfbaDn6DFsV9fYztPeNkF3OHYKaCIiIpISbCCA7/TpUBhroOeIE8Z6z51PyPndedMScp5EUEATERGRpBNoaxvoEWs4Qk/DUXqOHcP29Az7PdeUKWSULCFzSQnpixZx6TvfIXjlyvDDnMbgLiggu2x1glsRPwU0ERERuW5sby++U6foPtIwMDx5pIHeixeH/6LLRfr8+WSUlJC5tISMJSVkliwhbfZsTNiigEBbK81Pbx/hJizTH3owqcpsKKCJiIgIMPGV9nsvXx4Ynmw4SnfDEXzHT2B9vmG/58rLI3PJEjKWLiWzZAkZJSVkLFqEKytrxGsWbttG9/4DdFRVOas5w3vSQq9zKysp2Lp1vM1LKAU0ERGRG1yiK+1bn4+ek6foOdpA95HQ8GRDA72XLg3/RZeL9AULyCwpcUJYyRIyly4lbebMiF6xsTAeD8XPbKflhRe4/PIrBJqbB9pXUMD0hx6kYOvWpOo9AwU0ERGRG9p4K+33Njf3T9jvORpaSXniBIxQU8w9bVpYj9hSMkqWOL1iGRkJbR84Ia3w0Ucp2Lp18u/FaYxJA34P2AbMB84DPwX+zFrrDR3z28BPYnz9HWvtunivLSIiIokx2kr7zc89x5RNm/qHJ/uGKsN73GJKSyNjwYLI4cklJaQVzYi7VyxexuMh5847ruk14zWeHrTvAw8CfwLsBZYC/xOYA3wudMwcwAt8fNB3r4zjuiIiIpIAEZX2Ryjm2vzMszQ/8+ywx7gLCqKGJ9NvuQVXenoib/uGEFdAM8ZMAb4AfMta+79Cb79ujCkAvmaM2Wqt9QHFwBlr7e6E3K2IiIgkTGfd3pF7wGLxeMhYuNDpEVtSQsbSEjJLSkgrLEz8Td6g4u1B8+KEr/ZB73eEzpkF+HB60M7EfXciIiKScDYYpPvQIVp37BjT9/I/91mmffq3yFhwM0a9YhMqroBmrQ0CFwCMMW4gE7gL+APgJWttX3CbA8w2xjQAC0Pf2W6t/cvx3riIiIiMXm9rK9633sZbU01HzW4Cly+P+RxTNn2EzJIlE3B3MlgiVnHuB1aEfv534NGwz9qAbOBbwGXgIeAvjDFt1trnhjqhMaYImDHo7YUJuFcREZEbQl8vWUd1Nd7qGrrq6yEYjD7Q7YZAYPiTJWGl/ckuEQHtfiAfpwftj4Fv46zuxFr7G4OO3WWMmQt8DRgyoAFfBr4R64Pa2louXLhAcXExCxYsoKampv+zTZs2UV9fT1NTEwAlJSXk5ORQV1cHQE5ODuvWraO2thav1wtAWVkZXq+XhoYGAIqKiigtLWXnzp395y0vL+fkyZM0NjYCsGDBAoqKinjnnXcASE9Pp7y8nLq6OlpbWwFYuXIlAAcPHgQgPz+fsrIyampq8IUK8t155500NTVx8uRJALVJbVKb1Ca1SW0aV5tuLigg9/gJGl99lYzDh3F3dBAlKwvPmjVcmltMz/LlTN9/AM8//mP0ceGsJW/z/eyqrtbv0yjbVFtbO/yv6QiMHWHVxphOZsx/A74JzLXWnhvimK8ATwJTrbVXhzhmqB60Vw8ePMiKFStifEtEROTGMtpesozFi8gpryC3osKp/RU2f8z6/TQ+9l9GrLQ/VB00ie3QoUN9wXGltfbQWL8f7yrOWcCngJ9Za8MXARwAXMB8Y4wFPgb8U9icNAD3SOe31jYBTYOuGc+tioiITCq9ra14d79FR0013t1vxZxL5srOJvuu9eSWV5BbvgHP7NlDni9VK+1PdvEOcWYA3wP+EPiLsPdvCz2fDj3/LU4gezHsmI8Ap4fqPRMREZEB/b1kVdV01FTTfaA+Zs2yjMWLyakoJ7c8updsJKlYaX+yi3cV52ljzE+Br4d6tvbghLOvAT/qG940xvwQ+GtjTA5wFPgkTtHabQm4dxERkUlpzL1kFeV4brpp3NdNpUr7k914Fgl8Fvh94D/jLA74EGf+2bfDjvlS6P3HceqmnQZ+z1r7wjiuKyIiMqnYYJDugwfpqK6ZsF4yAX/Qz76mfbT3tJOXkceqolV4XMnZQxh3QAvtFPCt0GOoY7qAr4ceIiIiEhLRS1azm0BoRWI4V04OOXetJ6e8nNzyxPSS3Yj8QT8v1r/IjiM7aOke2DmhMKuQ+0vu5+HSh5MuqCWizIaIiMikZ/3+cc3PGnMvWUUl2atXqZdsnPxBP4/vepyaszUYIhcctnS18Oy+Z6lvruepe55KqpCmgCYiIjIM6/fT/PzztL78SsS+le7CQvIffIDCbduGDGpOL9luOqpr8O5WL9n18GL9i9ScdWqdWSIDcd/r6sZqXqp/iUdue+Sa399QFNBERESGYP1+zjz2GN6qaqcmWJhASwvNT2+ne/+B/hpho+4lW7KE3Ipycsor1Es2gfxBPzuO7MBgosJZOINhR8MOtpRuSZpeNAU0ERGRITQ//7wTziA6aIVed1RVcfYPvopJTx9dL1lFBZ5Zsyb61m9o/oCf423H+dkHP4uYczYUi6W5q5l9TftYO2vtNbjDkSmgiYiIxGD9flpffiW6un4MV197Leo99ZJdG/6An2Ntx3i/5f3+x9HWo/iD/jGfq72nfeSDrhEFNBERkRg66/ZGzDkbicnMJLe8PFQGo1y9ZBPAF/BFhbFjrcfiCmOx5GXkJeQ8iaCAJiIiEoPvww/HdPzsP/8mU//Df5igu7nx+AI+jrYejQxjbcfoDfYO+Z3stGyWTl/K8oLlLC9YTkl+Cdte30Zrd+uIc9AKsgpYVbRqIpoSFwU0ERERwFpLz9GjdOzaxdVdb9BdXz+m77sLCifozia/nkAPRy+HwthlJ4wdbz1Orx06jOV4ciLC2PKC5dw89WZcxhVx3ANLH+DZfc8Oe32LZXPJ5qRZIAAKaCIicgOzfj+de/ZwdecuOnbtwn/27NhPYgzuggKyy1Yn/gYnoe7e7qiesRNtJ4YNY7meXJYVLGP5dCeILStYxvyp86PCWCwPlz5MfXM91Y3VUas5+15XFFewpXRLQtqXKApoIiJyQwlcvYq3poaru96go7qa4JUrUcdkLF5E7r2bCLRepu2n/zD8Ca1l+kMPTopNxRO9FVJXb1fMMBawgSG/M8UzxQljYT1jc6fMHVUYi8Xj8vDUPU/xUv1L7GjYQXNXc/9nBVkFbC7ZnFTlNfoooImIyKTnP3eOq2+8QcfOXXjffRf8gyaVu91kr1lD7r33MOXee0mfNw9weth6LzbRUVUVvZoz9Dq3spKCrVuvYWsSLxFbIXX1dtFwuYFDLYf6w9jJ9pPDh7H0Kf29Yn2P4inFcYexoXhcHh657RG2lG6Z/HtxioiIJCtrLd3vv0/Hrje4+sYuet4/HHWMKzubnIoKptx7D7kVFbinTYs6xng8FD+znZYXXuDyy68QaB7ofXEXFDD9oQcp2Lo1pXvP4tkKqdPfSUNrQ0TP2AftHxC0wSGvMzV9akTP2IrpKyieUowZVAB4InlcnqSpczYSBTQREZkUrM+H91fv0rFrJ1d3vUHvhQtRx6TNnBnqJdtE9p134BpFbTLj8VD46KMUbN06rr04k9Vot0J6fNfjTMuY5vSMXTk5bBjLy8iL6hmbkzvnmoaxVKeAJiIiKSvQ3k5HdTVXd+3CW11D0OuNOiZj6VKm3HsvuffeS+aK5XGHBOPxkHPnHeO95aQy2q2QgP4QN9i0jGkRQWx5wXJm58xWGBsnBTQREUkpvsZGOnY6vWSd770HgUFznNLSyLljLbn3bmLKPRvxzJlzfW40Bexr2jeqrZD65HpyuW3GbRFh7KacmxTGJoACmoiIJLW+Dciv7tpFx85d9Bw7FnWMa8oUcisqyO2bTzZlynW409Tx4ZUPqWqs4p+O/dOYvvend/0p99183wTdlYRTQBMRkaQT7OnB+8tf0rHrDTreeIPeS5eijvHMnk3upk1Mufcestes0V6Xw+gN9rL/0n6qzlTxZuObnGw/Gdd5pmVGL6SQiaGAJiIiSaG3tZWON6vo2LWTjrfexnZ2Rh2TuXKlM8l/0yYylizR0Nowrvqu8ta5t6g6U0XN2ZqYG4HflH0TrT2tdAe6hz1XMm6FNNkpoImISEJYv3/Mqxx7Tp50SmHs2kXX3r0QjFwZaDwestetY8qme8nduFEbkI/gzJUzvNn4JlWNVey5sCeqOr/BUDqjlI3FG6mcW8niaYt57sBzKbkV0mSngCYiIuNi/X6an3+e1pdfIdAyMOHcXVhI/oMPULhtW39Qs4EAXfsP9JfC8H3wQdT53Hl55G6sJPeee8nZsAF3bs41a0uqCQQD7L+03wllZ6r4oD361zM7LZu7Zt9F5dxKyueUU5BVEPF5qm6FNNkpoImISNys38+Zxx7DW1XtVNYPE2hpofnp7XTt3cu0z3yGjqoqOt6sighxfTzz5oVKYdxDdlkZJk1/PQ2lw9cRMXTZ1tMWdcxNOTdRWVzJxrkbWTtrLenuoefnpepWSHEJ+OHDWuhqhax8mLcO3MnZLv0fICIicWt+/nknnEHkNkhhr701u/HW7I78zBiybr2V3HvvZcqme0lfuFDzyYZx5uqZ/gn+ey7uoTcYe+iysriSyuJKluSPbX5eKm6FNCYBP+x+En71A/CGLTjJLYK122DDE0kX1BTQREQkLtbvp/XlV6L3qBxKejq5d9/tTPLfuJG0GTMm/iZTVCAY4EDzAd484wxdnmg/EXVMVlqWM3RZXEl5cTmFWYXjvm4qbYU0agE/7HgQjv0cBm1lRccleOOb0PgebH45qUKaApqIiMTl6htvxByuHMrcZ7aTW1ExgXeU2vqGLqsbq6lprKG1pzXqmFk5syKGLjPcGdfhTlPM7idD4QyI2i0h9PrYa7D7Kaj86rW8s2EpoImIyKgEfT666urw7t5Nx+636DlyZGzf7x6+lMONqPFqI1WNVbx55k3eu/he7KHLwlIq58Y3dHnDC/idYU0M0eEsnIF3fwAbvpI0vWgKaCIiEpO1Ft+pU3h3v4V39268774bszbZaLnzVOQ0EAxQ31zvDF02VnG87XjUMVlpWay/aT0b525M2NDlDevIzyLnnA3JQkeTs4BgQfmE39ZoKKCJiEi/QEcHnbW1dOx2Jvb7z56NPsgYMleuJHv9Otp+8hOCV64OPwfNGNwFBWSXrZ64G78G/EF/XBPoO3wdvH3ubaoaq4YcupyZPZONczdSWVzJHTfdoaHLeHRcgvP74NzegcfV82M7R1f07831ooAmInIDs8Eg3Yfex/vWbjp276Zr337o7Y06Lm3GDHI2bCBnw93k3HUXafn5ALgyM2l+evsIF7FMf+jBEYvWJit/0M+L9S+y48iOiI3FC7MKub/kfh4ufTgqqJ3tONs/wf/di+9GDV0CztBlcSWVcyspyS/R0OVYdF4eFMb2QfuZ8Z83K3/850gQBTQRkRuMv6kJ71tvO8OWb79NoDW618Ckp5N9+xpy7t5AzoYNZCxZHDNAFG7bRvf+A3RUVUWv5gy9zq2spGDr1ols0oTxB/08vutxas7WYAatAGzpauHZfc9S31zPtyu/zZHLR/rnkw01dLnupnVsnLuRiuIKDV2OVnc7nN8f2TPWemr47+QvgNmrYdat8NZTzjlGmoOWO8Opi5YkFNBERCa5oM9H1549zrDl7rfoaWiIeVz6LbeQs+FucjdsIHvtWlxZWSOe23g8FD+znZYXXuDyy68QaB4ocuouKGD6Qw9SsHVryvaevVj/IjVnawAiKuyHv65urKbiJxV09XZFfX9m9sz+XrI7Zt1BZlrmxN90KuvpgAsHIsNYS3TYjZA3D2avcgLZ7NVw022QPX3g86DfKaUxLAtrv5g0CwRAAU1EZNKx1uI7ecpZbfnWbjp/9S62Kzo8uKZMIWf9eieU3X03njlz4rqe8XgofPRRCrZuHfNenMnMH/Sz48iOqO2PYgkPZysLVlIxt4KNxRtZOn2phi6H4u+CC/WRYexSA8P2dE2ZPRDEZq92glnOCD2RG55w6pwde43o1Zyh14s/5qzgTCIKaCIik0Dg6lW8tbVO1f7du/GfOxd9kDFk3lpKbmjYMuvW0oRuqWQ8HnLuvCNh57ve9jXti5hzNpLPL/88n1/xeWZkp3AB3onaCqm3By4ejJwz1nQYbGDo7+TMgNllkWFsyqyxX9vtcYrQ7n7KKaXR0TTwWe4Mp+csicpr9FFAExFJQc7k/kP9Ncm69u2DQPRfdmlFReRs2EDuhrvJXr++f3K/DK29p523zr7FTxp+MqbvrSpalbrhLJFbIQX8TvgK7xm7eMgZahxKVv6gMLYaps6O2t81bm6PU4R2w1cm/16cxpg04PeAbcB84DzwU+DPrLXe0DFzgSeBjwAZwD7gv1lrq8Z53yIiKcf6/eMaAvRfbML71lsDk/vbojfJdib3396/4jJjcezJ/TLAWssH7R9Q1VhF1Zkq9l/aT2C4np0h5GXkTcDdXQPj2Qop0AvNRyPD2IV6CPQMfb2MvMg5Y7NXw7R5iQtjw3F7kqbO2UjG04P2feBB4E+AvcBS4H8Cc4DPhQLcvwF5OEGuA3gCeM0Yc6u19ug4ri0ikjKs30/z88/T+vIrEVsjuQsLyX/wAQq3bYsZ1II9PaHJ/U4o6zka+4/N9IULyd1wNzkbNpB9++2jmtx/o+sJ9PDehfeoaqyiurGasx3R9d6y07LpDfbiC/qGPZfBUJBVwKqiVRN1uxNrtFsh1TwJKz41KIwdAP8wxYvTc51J++FhLH8BuFwT0ZJJJa6AZoyZAnwB+Ja19n+F3n7dGFMAfM0YsxWn12wFsMlauyv0vdeBRuBLwH8d572LiCQ96/dz5rHH8FZVR/UQBFpaaH56O937D1D8zHZIS8N38mRo2DI0uT/G9kiuqVMjJ/fPnn2tmpPSLnVeouZsDVVnqvjl+V/GXHU5b8o8KoorqJxbyZqiNbx48EWe3ffssOe1WDaXbB5V0dqkM+qtkIA3/xzeHGY1ZFoW3HRrZBgrWAQudyLv+IYRbw+aFygG2ge93xE6ZxawDvABb/R9aK29aoypBSbPLFIRkWE0P/+8E84gutp+6HVHVRWnNj9AoLU19uR+l4us0tL+Ycus0sRO7p+sgjbI4ZbDztBlYxXvt7wfdUyaSaNsZpkTyooruTnv5ojPHy59mPrmeqobq6NWc/a9riiuYEvploluzsT4sHaUWyFBRIBzp8Os0sgwVlgCbv13mShx/Upaa4PABQBjjBvIBO4C/gB4yVrbboyZBTRbG7X/RxNwZ/y3LCKSGqzfT+vLr0QXcI2h+9ChiNdps2b11yTLWbcO9zTtYzkaXr+X2nO1/UOXsVZh5mfkU15cTkVxBXfNvosp6VOGPJ/H5eGpe57ipfqX2NGwg+augTpvBVkFbC7ZzJbSLanZe+bzwoldY/vO7VtgzRdgxjJIS5+Q2xJHIqLufpyhTIB/Bx4N/ZwOxFqyEQh9NiRjTBEweCnMwnHco4jINddZtzdiztlIMleuZOqv/zq55RtIX7hQk/tH6czVM1Q3VlN1por3Lr6HP8ZqwZL8EiqKK6gorqC0sBT3GIbdPC4Pj9z2CFtKt8S1F2fSsBaaj8Hx1+HY63D6LQgMP78uyor/5MwpkwmXiIB2P5CP04P2x8C3cRYFDGeEgW6+DHwj1ge1tbVcuHCB4uJiFixYQE1NTf9nmzZtor6+nqYmp8ZJSUkJOTk51NXVAZCTk8O6deuora3F6/UCUFZWhtfrpSFUWbuoqIjS0lJ27tzZf97y8nJOnjxJY2MjAAsWLKCoqIh33nkHgPT0dMrLy6mrq6M1tGXKypUrATh48CAA+fn5lJWVUVNTg8/n/A9x55130tTUxMmTJwHUJrVJbZoEbTLd3czr6iLr1ClafvavjOWv74IvbmN/Vha+06fh9OmkaVOy/T5lZGeQsSCDHb/awf6r+7nYezHq19JjPKyfs56ZHTNZnrmc/LR8ylc6bXqz/s1xtekjZR+hpqaG6kPVCWvTRP0+ZbqD3D07yKW3Xyb3Qi1Z3dG/VpaotZsxjjGQM4M3jndiP9h5XduUKn9G1NbWjvCrOjwTPQI5jpMZ89+AbwJzcVZ3ftJaO3PQMa8AZdbapcOcZ6getFcPHjzIihUrYnxLROTa621upnNPHZ173qNrTx3dhw9DMBjXueb9/d9PqkKvidTW3cbuc7upPlPN7nO7ueq7GnVM+LZKa2etJSvtBlzNai20nAj1kv0cTr0Vu+RF3jxY/BFY/FGnhEbNX4987nv+yKklJqNy6NChvuC40lp7aKTjB4t3Fecs4FPAz6y14dvHHwBcOHXRLgEFxhiPtTa8v3kmTs20IVlrm3DmqoVfM55bFRFJGGst/g8/pPO9PXTW7aHrvT1Ob9cQ0hctwn/mDLZnmJpQAMbgLiggu2x1gu84dVlrOd52vH8u2f5L+wnayOBrMNw641YqiyupKK5gSf6SG/PvCl8nnNo9MHTZejL6GJcH5t8Fi++DRffBjJKBVcWLPuLULkuxrZAmu3iHODOA7wF/CPxF2Pt9A9OngV8CbuDXgP8LYIyZCqwHvhPndUVErhkbCNB95Ahde+ro3OOEssCl5tgHezxkrVhB9u1ryCpbQ3bZatzTpnHpu9+l+entI1zIMv2hB1N638pE6An08Kvzv+oPZee90f+Wz/Xkcvecu6ksruTuOXczPXN6jDPdAFpOOGHs+OtOOOuNLsfC1OKBXrIFFZAxxGKIFN0KabKLdxXnaWPMT4Gvh/61sgcnnH0N+JG19pwxpgk4BLxgjPlDoAWnUK0FnkvEzYuIJFKwu5uuAwfo2rOHzj11dO3dSzA0z2QwV04OWatXk72mjKw1a8i69VZcmZlRxxVu20b3/gN0VFVFr+YMvc6trKRg69aJatY14w/6xzyJ/qL3ItVnq6lurOad8+/ErE1289Sb+3vJVs9cnVoT8xPF3+UMVx77uRPKLn8QfYwrDeatd3rJFn8UZiwdfXX+FNwKabIbzyKBzwK/D/xnnMUBH+LMP/s2gLW21xjzcZytnv4GZ+VmHfBRa+2pcVxXRCQhAm1tdNbtpatuD53v7aHr0CHwx94v0F1YSPaaNWSvWUPWmjIyS0pGVYvMeDwUP7Odlhde4PLLrxBoHuiBcxcUMP2hBynYujWle8/8QT8v1r/IjiM7IspaFGYVcn/J/Txc+nB/qAraIIeaD/X3kh2+fDjqfGmuNNbMXNMfyuZPnX/N2pJULn8Ax37hBLKTNRAjvDJ1jjNEufg+WFAJmVPHd80U2gppskvoIoGJZIxZARzUIgERiZf/3LmwCf176Dl2fMhj0+fPJ+v2NWSXrSH79jV45s0b9/ym8e7FmYz8QT+P73qcmrM1QxZyvWv2Xfzmot9k99nd1Jyt4XL35ajzTM+cTvmccirnVrL+pvXkpudey2YkB383nN49EMpaYvz36UqDuetCvWT3QdFdzozWAAAgAElEQVTya7OHpYzZdVkkICKS7GwwiO/ECWfuWCiU9Z4bYn2Sy0XmsmVkrSkje83tZJetJm3G4IXk42c8nkm3SvPF+hepOeuUKbCDKij1vX773Nu8fe7tqO8um76sv4L/isIVuMwNuD9j6ylnLtmx1+Fkdexesik3hXrJPgq3VEJmim7KLmOigCYiSWG8vUvW56Pr0CG66uqc4cq6OgLtg3ejc5iMDLJuu61/Qn/WqlW4c3MS1ZQbhj/oZ8eRHVE9Z0PJcGWwfs56KosrKZ9TzsycmSN+Z9Lp7XEKxB77hTOfrOVY9DHG7cz96hu6nLlSvWQ3IAU0EbmurN9P8/PP0/ryKxFV992FheQ/+ACF27bFDGqBDi9d+/b11x/rOnAg5sbiAO68PLLWrCF7TRnZa9aQuXw5Jl3b1MQraIOcbD/J/zn2f2JupTSU79z7He6ec/cE3tkEC/jjm0DfejpUAuMXcLIK/J3Rx+TOclZcLroPbtkIWdra60angCYi1431+znz2GPOZuKDeggCLS00P72d7v0HKH5mO4H29oj6Y91HjgxZEDZt9k3OUGUolKUvXIhx3YDDZwniC/g41HKIvU172XtxL3sv7aW9J3bv5HBirdBMCQE/7H4SfvWDyI3Fc4tg7TbY8ERkUOvtgdNvw/FfOEOXzQ3R5zRumHvHwNDlrFL1kkkEBTQRuW6an3/eCWcQvZl46HVHVRXHNpQPOVwJkLF48cCE/jVleGbPnqhbviG097Sz/9J+6i7WsbdpLwebD+ILjnHPxhjyMlJw7lTADzsedIYjB2+I1HEJ3vimU4n/438BJ990AtkHVeCPUZ4lpyhUKPYjsPAepxdOZAgKaCJyXVi/n9aXX4muDRZDRDjzeMhaubK//lj2aqcgrMTHWss577n+MLa3aS/H24Ze3Tondw6ri1azumg1pYWlPPqLR7ncfXnYOWgGQ0FWAauKVk1EEybW7idD4Qyit5EOvT72WqgK/yDGBcVrB6r3z7oV1JMro6SAJiLXjLWW3nPn6D58mCuv/yJiztlI8j79afI++YkhC8LK6ASCAY62HqWuqY59Tfuoa6qjqbMp5rEu42JJ/hJWF62mrKiMVUWrmJUzK+KYzUs38+y+Z4e9psWyuWRz6hWYDfidYc2o7Y+GkTNjYHL/LfdA9g2604GMmwKaiEwIGwjgO3mS7sOH6X7/MN2HD9Nz+PCwQ5XDya2sIOeOyVWi4lro9HdysPkgdU1OD9n+S/vxxhp+AzLdmdw649b+QHbrjFtHrEf2cOnD1DfXU91YPWQdtIriCraUbklouyZcMAj7XomcczaS//gklH1BvWSSEApoIjJuwZ4eeo4eDQWx950w1nB0yFWV8XDnaRhzNJq7mvt7xvZe3MuRy0fotb0xj52eOb2/Z6ysqIylBUvH3MvlcXl46p6neKn+JXY07KC5a2CnhIKsAjaXbGZL6Zbk7z0LBuDiQWdfy1NvOaUwutvGdo7sQoUzSRgFNBEZk8CVK3QfPkL34ffpCfWO9XzwAQQCQ38pLY2MRYvIXLbMeSxfRvqiRXzw6/+RwOXLw89BMwZ3QQHZZasT35gUZ63l1JVT/XPH9jbt5fSV00Mef/PUm/vnj5XNLGPelPHvjgBOSHvktkfYUrplzHtxXjeBXrhwwAlip3bD6V9CHCtTI2jSvySQApqIxGStpbfpUkQQ6z58GH9j47DfM9nZZJaU9AexjGXLyFi8GFeMumP5Dz1I89PbR7oRpj/0YMpviQTxbSYe8f2An8OXD7O3aS91F+vYd2lfzG2TANJMGssLljuBbOZqVs1YRUFWQaKaEpPH5WHtrLUTeo24BXrh/H44VeOEsg9roedK7GOnzIab73Y2Ht/1Z07ds2HnoBnIneHURRNJEAU0kRQxkfs42mAQ/4cfRswX6z58eMRJ/O78/IgglrlsOenz52Hc7lFdt3DbNrr3H6Cjqip6NWfodW5lJQVbt46nedfdWDYTD3fVdzWi3EV9cz09gZ6Y18j15HJb0W2UFZWxumg1KwtXkpWWNWFtSnoBP5zbG+odCwUyX0fsY6cWw80bnFB28wbIXzBQk6yzxSmlMSwLa784uqK1IqOkgCaS5OKttD/k+Xw+ek6ciAhiPUeOEPTGnjjexzN7NhnLQ0OUy5aTuXwZaTNnjmuIzHg8FD+znZYXXuDyy68QaB6Yv+QuKGD6Qw9SsHVrSveeDd5MPFxLVwvP7nuW+uZ6nrrnKVq6Wqi7WNe/wvJo69Ehy1fMzJ7phLGZzoT+RdMW4XaNLhhPSr0+OFcXmkO2G878KnYtMoBp82D+hoFQNm3+0EViNzzh1Dk79hrRqzlDrxd/DDZ8JbHtkRuesSPUH0oWxpgVwMGDBw+yYsWK6307ItdEVKX9IXqYip/ZHjPEBL1euhsaIibv+44dx/r9Q1/U5SL9lgVOCAv1jmUuXTrhtcYmsofwevr+/u+PWIYCnB6wDn/sHh6DYVH+ov7esbKiMm7KvSnRt5paenvg7J7IQDbUTgX5NzthbH5fIJs3tmsF/LD7KXj3B9ARVpIkt8jpOdvwFfWeSZRDhw6xcuVKgJXW2kNj/b560ESS2Ggr7be88ALT7r+/P4j1zRnznT497AR8k5FBRt98sWVLyVy2jIwlS3BlXfuhMePxkHPn5CqjMZbNxMPDWborndIZpf2B7Lai25iaPnWibze5+buh8d2BSf2N70LvEKuEpy8MDVeWw/y7IW/O+K7t9kDlV50gFs9enCJxUEATSVJjqbR/afszXPrO08Me45o6lcylS8lc7gxPZi5bRvqCBZg0/TGQKEEb5OzVs5xoP8HxtuO8c/6dMW0m/pkln+ETCz/B8oLlpLtv8M3cfZ1OCOubQ9b4Hgwx/46CxaHhyg1OIJs6Qb2Lbg8sKJ+Yc4sMoj+ZRZKUt7Z29JX2B20anjZz5qDJ+8vwzJmTkJIK4gSxcx3nONHmBLG+55PtJ+kOxF/77a7Zd6Xmdkh9Av74e5h8XmeYMjyQBYcYip+x1AlifYFsyszEtUEkSSigiVxHwZ4e/B9+iO/0aedx6nT/z70XL47pXFM/8RvkfeKTZC5bSlrBxJZTuFFYaznvPR8Rwk60neCD9g/oGmq+U5ip6VO54huilEMMKbmZOITmaD3pbIsUXnk/twjWbnMm2g8Oaj0dcKbWKQp7arczwT8Yu6AuRcsHwtj8u52SFiKTnAKayASzPh++xsaw8HVqIISdvzDi8OVoTfv0b026OVzXirWWC94L/QHsRPsJ57ntBJ29nSN+vyCzgEXTFrFw2sL+x6Jpi8j2ZHPfP9w3uTcTD/hhx4OhDcUH9dB2XHJKVDS+B5/6XmiVZY0Tys7tBRuruLGBmSudOWR9gSxH/+CQG48CmkgCWL/fCWGnT+MP7w378EP8585FDUEOxZ2Xh+fm+aTPn49nTjGtP/oRwY4hajf1mSSV9sdbxHU0rLVc7LwY0RvWF8iG2p8y3PTM6U4Ay1vYH8gWTVvEtMyhV7hO6s3Ewek5O/bz0IvBITT0+thr8FcLY3wOYGBWqTOhv684rDYYF1FAk8ljoss02N5e/OfORQ1F+k6fxn/27PBbHYVxTZlC+vz5A4+bB34eXMrCeNImfaX9eIu4Dsday6WuSxEh7HjbcT5o+4Cr/qsjfn9axrT+8BX+PD1z7MFh0m4mDk7v2a9+QHR9sFhCnxsX3HTbwByyeeshS/usigymgCYpL5GFXG0ggP/8+VDvV6g3rC+MnT0Lw9UPC+PKyXF6webPC4Wvm/vDmDs/f9ST9Sd7pf2xFHGNFdKstTR3NUfMEfug/QOOtx3nqm/kIJaXkRfVG9YXxBK1oGLSbCbu74KW49B8FJpDz2frIuecjWTTn8DaLZCZonPtRK4hFaqVlBZPIVcbDNJ74ULMifn+M2eGL+IaxmRlRfaEhfWGuQsKEvYXvPX7Y1faLyxM+Ur7oy3i+tiqx/j0kk9HDU0ebzs+qkn4U9KnRIWwRdMWUZCZuN+n0bgWw7jjYq1TiLX5aOhxDFqOOT+3nWHkXrIR/PaPYPknEnKrIsluvIVqFdAkpV367ndHHgIEssrKcE/Pd3rEPjyD7RmintIgJiOD9Hnz+oOXpz+M3Uxa0Yxr+pf7ZKu07w/6RzWBHhhVoVeAKZ4pEZP0b5l2C4umLWJG1rX9vUp6vT5oPRkZxPoePe2jO0feXMgugPP7Rn/dz/8/1RGTG4Z2EpAbjg0ECFy+jP/8eS7/3d+P6jtddXVDfmbS0/HMmzswDNn/mOfsNelyJerWxyXVK+1ba7niu8IF7wUudl4cUxHXweEsx5Mz0BsWNkRZlF2U3EFsPHXC4tF5ORS8woPYUWg9NcQKykHSMp0isIV9jyXOc8EiSM9x2vM3y8DbzPC9a8YpjTFvXYIaJjL5KaDdIFKh9yXY3U1vczO9TZfobb5E76XQo7l54OdLlwi0XB71qshwabNmkbl0adTE/LRZszDu5N9kOpmHxwaHr8HPF70Xudh5cVS1w4byiYWf4NcW/BqLpi1iZvb4Nmm/5uKpEzbqc/dC2+mw+WFhQaxzlIWOc2eGha+wIJY3F4b7B4rbA3d80SmlMSzr7FmpbZFERk0BbZJL5AT6uK5vLcErVyLDVlPs4BW8OvKk7vGY+bU/ZOpHPzqh15gIE7HKcSxiha/BwWu84Ws0PrXoU6ydtXZCrzEhRlsnbPPLwweY7iuh+WDHwnrFjsHlExDwjXwfLg9MvyWsJyysN2w8qyg3POHc/7HXiF7NGXq9+GPOPpYiMmoKaJNY1AT6MIGWFpqf3k73/gMRE+hHfe7eXnpbLofCVVNE2AoMCmHWN4q/PIbicuEumE7ajBkDj8JC0mbMINDWRvP2Z0Z9Knde6i3lH+8qx5FYa2nvaR+y1+tC5wUuei/GtX2Ry7gozCpkVvYsZubMZGb2TGblzOp/Lsgs4Hf+7Xdo7W6dvEVcYfR1wnY/BeW/D1fORvaC9YWyq+dHd72s/IHw1RfEChZD/vyJ6cFye5xwufspePcHziKDPrkznJ6zDV9R75nIGCmghaTCEOBYNT//vBPOILpafeh1R1UVLS+8QOGjjwIQ7OqK6NXqvdQcc6gxcPnyuCrgm4yMyNA1YwZpMwqjQph7+vQhhx+t30/rKz8e+V5SuJDri/UvUnO2Boieh9X3urqxmpfqX+KR2x6J/DwUvvpCVn/wGhTCxhW+QoGrP3zlzGRW9iwngGUVjBgaH1j6wOQu4jqWOmFVfwE134bR9EQaF0ybHx3ECpdcn6r7bg9UftUJYtdyjp3IJHbDB7TrPQQ4UazfT+vLr0SXnojh0ne/R9s/v0qguZmgd+Rq6sNx5+XhjghasUOYKzd33HOIjMdD/kMPTtpCrv6gnx1HdoxqBePfHvpbunq7aOpsighgPYHRrVYN5zIuZmTN6A9bsXq/CrMKSXON/4+PSVPENRh0Vj96W6Cz2Zk039kCZ98bfZ2wYG/0XpTpU8Im6IcFsem3QFpG4tsxXm6PVmmKJMgNXWYjnhpaE8Vai+3sJNj38Hqjf/Z2Euz0Os+xPg/7OXD16qiLqo7I7XZ6tAoLY/d2hXq83DNm4EpPT8w1R8n6/Xz42GN0VlVjiZzh0/c6u7KCec88k7QBzR/0c6XnCld8V2jvaeeKz/n5wKUD/PjIjxN6LbdxMyN7RmSvV/ZMJ4yFfk5U+Botv7+Tl/71i+xo2Ueze+B3sDBg2Vywii3/4Qd4PNnX7H4AZ+J9Z0voERa4+p5jvTeaVZEjWXQfLPnYQBCbMitqeoKIpAaV2RiHeIYAnY8s1ucbCEThwanTOyhURYcn6+0k0OnFesPe7+pK2KbZ8chctYqs0tKYIcydn580pSYG63XDX/0nQ4F18bE9QfLDOgDbcuC1NS4uf9rF37hhIuNZIBigw9/BlZ4rtPvaYwaumD/3XBnVZtyj4cJFUU5RzF6vvt6wgqyCaxq+RhTw4/np53nk2M/ZgmFfZjrtLhd5wSCrun14PjwDHV8YeQL9SPxdoSDVHOrlCg9ZMd7rbktYE8fk7sfVAyUiwDgCmjHGBfw+sA2YD5wHXgW+Ya1tCx3z28BPYnz9HWvtdS2IM6YhwGe/S9u//L+IHi56e4f9zkQyHg+u7GxMTjbunBxMdjau7GxcOTnOc3Y2gStXuPqv/zbqcxY98URK1th6sf5Fqi68BXe7eHWdoaTRktsNHZnQUGwIuA2c3x1zjtZg1lq8fu+wYWqo8NXh6xhVIdWJ9Nx9z7FudorVmQqbQO/BsrY7xpBs3wT6yq86r62F7vaBHq7+kNUc473Q61FshD5qmdOcAq05hZBd6Mz5yi6M/V7GVHhmzQ1TJ8wfCPLeqVbau3zkZaVz+835eNzJ+Y+7eEz29sHkb2MqtW88/5R+CngE+F/AbmA58KfAUuBjoWPmAF7g44O+O/LeLBOss25vxJyzYfX24v/gg/gu5HJFhaeYP+eE/zz8sWYUw4jW7+fYO7+it6Vl8ML+yOOAtMLClJxAP3iOVsBteH9+7Nb+3aG/w+Py4O31RgSrvrDV9xxIxDBVDJnuTKamT2VqxtSI57yMPOd1+M8ZU8lLzyPbk81n/uUztHZfHumvdgoyC1gza82E3HtCBYPQ2+08uq9A7fewod/BoVjAVP8lHPqngQAWTNDwvXGHBauCQSErxnvZ08fek3cD1AnzB4J8780T/PCXp2juGFi1PSM3g8+un8+jGxcm7V+CozHZ2weTv42p2L64ApoxZgbwu8C3rLVfD739mjHGDfyVMWa+tfY0UAycsdbuTsztJk6gfWxDGJmrVpFxyy3DBKwcJ2QN+txkZl6XgprG4+HYPYu45R+HD6EGOH7PQpZM8PysoA3SE+ihp7eH7kA3Xb1d9AR66O7tpjvQHfnc201PoCf2MWE/t3S1jLoSfYe/gyfrnhxXG9JcaUOGqZECV4Y7vgndmzOK+W735WGPscD9GcXxrXIM+J3hv97ucTx3OysPR/McY9HCSP93mL77bBrFFI60zMgerPBgFRG8Qu9lThu+EGsC+Nc/zqHaX7Cq6x2CFlxhDe57vT/rTpav/70JHYafKP5AkC/+8D3eaLgU9XvZ3NHD37x+lH1n2njus2uS7i/A0Zjs7YPJ38ZUbV+8PWh5wI+B/z3o/fdDz9OB0zg9aGfivMaEGmtNrFQbAvQH/fzlggN8cSGsOcGQE+j3LITnbj7AbVfPErCBUQen7kB3f9jqO6ant4euQFfMEBbPasKJYDADvVgj9GANDl1ZaVlDh21rwQYhGHBW4tmA87MNQteVQe8FnJ6kkd4L9PDZ+ioOFmRSnZOFsRYbdv2+1xXeLj57+hfg+SoEfSMEpUEBa4J6DCfETath1opBIasgMoyl51zvu4zyvZoPebr1d/mSex6fS/s5RQzsddlMHj/0f5Tvd/8Gj9d8yH/ZtPg63ml8vvfmCd5ocFaqDlHljV1Hmvj+myfUviQ12duYqu1L6CpOY8xfAZ8F5llrfcaYGmA20AssBC4A2621fxnHuRO6itN7tZ36ynVM7Rz+X/AWuJIDtzz1ZTyZGQSCAXqxBGyQgA3Sa4P0Eoh4HflZ2Gsij+k/NvS+P+zn3v6fLb02EHasjX3uiOODtPV28YG/FXfA8slaGzWBvjU0gf7VdaF5WkkqDUOmcZOJiwzjIsu4ycBFpnHREwxwMNgx6nM9zSwqTQ6uviAVEY4CMd7rdULTaN6zY996arT8wEvTprJjyhSa0wZqwhX2Bth89Spb2q5cn56XtCzwZIaeQ4+0zLDnzEHHRD4H2j7EXTt8DbRwvZ/9F9IWVkxggxLPHwiy/ls7aenwOdMJ6OV211Hy6KCdXN4LLqGXNAxQmJvB2394b1L9C34kg9s3FLUveU32Nl7P9o13FWfCApoxZg3wNvCEtfa7off+BSegfQu4DDwEbAG+ZK19bphzFQEzBr29EHg1UQHtp68/zfs/fY77a0b+i3VHhYv/c3fq/AcZiztgY0+gj4PLWjL7HkHnOcNasmyQzKDz8+DPnWOCZFpL1pDHBJ33g5as0DmH6+L1A/fNncNltyuiZ2kwYy0FgSA/P3M2JYeQ+viBfZkZYasceyLa00M6Xa5sfCYdPxn4TDo+M8wz6UN+5jfp+IY5hx/PuMs/eDu7+Nu2L1BAe8Sw32BB6/Q0bZn2d+RkZ43rmtfalS4/hy+MfguzZbOmMDUrdf4rVfsipVr7YPK3cazt+/G2daxfmJhiz0lRZsMYMxdnBee/A9/re99a+xuDDt0VOvZrwJABDfgy8I1YH9TW1nLhwgWKi4tZsGABNTU1/Z9t2rSJ+vp6mpqcrUZKSkrIycmhrq4OgJycHNatW0dtbS3HTh3in9cbFp0zrDlhhxkCNLy67tr3MLmtxW0hjchnN5a0GK/7n0OhpsMYDmUOzHsabgI9wOfb2ynp8fcHo8HhKjMUvjJD5x/uVyRonSnfFhN6OD9D9Pv0v3Zhcfcf48fgi3m86f9OOj42X73Ks/nDD1dbY9h89SpngzNpZQq9uAjiImBdBEI/9+J23sNFABP5XsRxrrDjXARw93/Wd1zfI/ZxJuw4d8Rx4ecO4qKED/mT9B/1t8MDsVc59v0e+v4/aoPLh/21GD9/6JEYP3Tfx+97/nHYY1wGfuj/KAcvdgETu9/n9TaWv0hSkdqX+iZ7G9u7fKPOEd5QYfeysjK8Xi8NDQ0AFBUVUVpaSm1t7bjuZdw9aMaY6TirODuAe6y1w65nN8Z8BXgSmGqtjfk7fa160P7nuedHPQS4uHMhQfdSjHVhjBuDC2NdgAuDCxeh93CDdYV+DntYd+hYd9T7g9+zuKL2XbRRkSg6IoUfM6djH28W/GjUvUt3X/4Cjbll/WGo7xrWRIcrBgUmi7kuxTTnX6njm96v8ZWZM6jOHmaOVmcXT128xH/P+XNOTy275vcZr8new3Sly8+xC60853mSTe69Q06g3xlYzSP+J1g8Kz+l/uUO6p0YTO1LPpO9jancgzaugGaMyQZ2AlOBCmttS9hnN+GU2/gna2172Pu/D/w1wwS0Ia6V0Dlond1ePv7yHbS5DdaYIYcAjbXkByz/9tCvyM5MvgnIQ/H7enjmuyt5KT9zxGO3tHbz2JcP4klPwq1jhuH39XDlzxeTa9v5u/yh52h9ofUKV8008r52NKXa6A8EeeGbX+LRYKxSgpG+53qArf/9uyk5N6S9o5NH3P/iTKA3AxPom2weP+z9KM8FfoNpuTkpN/cFNL+nj9qXvCZ7G1N5Dlrcd2GMSQP+AZgF3BcezsL8LfBbg977CHB6LOFsImRn5lDuKunvcXGGAF38qsTF+/Nd/fOzrDGUu5amVDgD8KRncHvep6jodIaEzKAg3ve6orOL2/M+lVLBpY8nPYOj8x8gw8AjbVf4+ZmzvHT+Ik9evMRL5y/y8zNneaTtChkGjs3fnHJt9LhdBNY/wc6AU6MuOOhPl77XOwOrCa5/PKX+0ASnfZ9bfzN+0ngm8Jvc1bOdzb4/4hHfV9js+yPu6tnOM4HfxE8an1s/P+XaBwNtHOmfwRZSso1qnyNV2weTv42p3L7x3MkLwH3AnwC3GGM2hD1KrbXngR8Cf22M+T1jzMeNMd/DKVr7Z+O+8wT47w/8iFXdzl/aQwWYVd0ZfO2BH17ze0uEdQ/9GVuuLOCx1jamByIXQ0wPBHmstY0tVxaw7qGk+O2Iy+0P/Sn7s+4EwG2dOVof6exibXcP7tBv6f6sO7n9oT+9jncZv0fuLWHHLd/ir/2foZm8iM+ayeOv/Z9hxy3f4ov3llynOxyfRzcu5N6lRQAESKM2uJzXgndQG1xOIDRF9t6lRXxp48LreZvjEt7GoSYqpHIb1b7Ubh9M/jamavviHuI0xgz3xSpr7UZjTBbOgoAHcYrWnsYps7E9juslfLN0cIY6//zHn6MmeITLaQN5dXpvkHLXUr72wA9TrvcsnN/Xw3sv/zELTu/gTGZX/wrAud1ZnJy/mdsf+tOU61karK+Ni0/voJCBAsTNTOPYJGijPxDk+2+e4OW3T3BzV31/iYZTWaU8dNdCvpSEFbDHoq99P/zlaS51DCyCmJGbwefWz0/59sHkb6Pal9rtg8nfxuvRvqQpszHRJiqg9ens9vL/al6krfMi07Jn8h/LH07pYDaY39fD0Xd/ga+jmfTcQpas/UhKh5ZYJnsbU2kPuXhM9vbB5G+j2pf6Jnsbr2X7FNBEREREksx1WyQgIiIiIhNDAU1EREQkySigiYiIiCQZBTQRERGRJKOAJiIiIpJkFNBEREREkowCmoiIiEiSUUATERERSTIKaCIiIiJJRgFNREREJMkooImIiIgkGQU0ERERkSSjgCYiIiKSZBTQRERERJKMApqIiIhIklFAExEREUkyCmgiIiIiSUYBTURERCTJKKCJiIiIJBkFNBEREZEko4AmIiIikmQU0ERERESSjAKaiIiISJJRQBMRERFJMgpoIiIiIklGAU1EREQkySigiYiIiCQZBTQRERGRJKOAJiIiIpJkFNBEREREkowCmoiIiEiSiTugGWNcxpivGmOOGmN6jDGnjDHfMcZMCztmrjHmH40xbcaYLmPML40xlYm5dREREZHJaTw9aE8Bfwb8BPgE8B1gS+g1xpg04N+AO4HfAx4CeoHXjDFLxnFdERERkUktLZ4vGWNmAL8LfMta+/XQ268ZY9zAXxlj5gMrQo9N1tpdoe+9DjQCXwL+63hvXkRERGQyircHLQ/4MfC/B73/fuh5OrAO8AFv9H1orb0K1AJ3xHldERERkUkvroBmrT1urf0da+3eQR/dA1wEDgGzgGZrrR10TBNQFM91RURERG4EcQ1xxmKMWYMz1+wJa63PGJMO+GMcGgDSRzhXETBj0NsLE3KjIiIiIkkuIQHNGDMXeBX4d+B7o/jK4OhopmkAABJhSURBVF61wb4MfCPWB7W1tVy4cIHi4mIWLFhATU1N/2ebNm2ivr6epqYmAEpKSsjJyaGurg6AnJwc1q1bR21tLV6vF4CysjK8Xi8NDQ0AFBUVUVpays6dO/vPW15ezsmTJ2lsbARgwYIFFBUV8c477wCQnp5OeXk5dXV1tLa2ArBy5UoADh48CEB+fj5lZWXU1NTg8/kAuPPOO2lqauLkyZMAapPapDapTWqT2qQ2TZI21dbWMh4megRyjCcwZjqwG+gA7rHWekPv/wD4pLV25qDjXwHKrLVLhznnUD1orx48eJAVK1aM655FREREJtKhQ4f6guNKa+2hsX5/XD1oxphs4Gc4PWK/1hfOQi4BBcYYj7U2fKhzJnB+uPNaa5tw5qqFX2s8tyoiIiKSMsZTqDYN+AecxQD3WWtbBh3yS8AN/FrYd6YC63FWcoqIiIhIDOPpQXsBuA/YBtxijLkl7LN2nPloh4AXjDF/CLQAT+D0tj03juuKiIiITGrjCWifDz3/XYzPqqy1G40xHweeBP4GZ+VmHfBRa+2pcVxXREREZFKLO6BZa0ecFGatbQQ+E+81RERERG5E49mLU0REREQmgAKaiIiISJJRQBMRERFJMgpoIiIiIklGAU1EREQkySigiYiIiCQZBTQRERGRJKOAJiIiIpJkFNBEREREkowCmoiIiEiSUUATERERSTIKaCIiIiJJRgFNREREJMkooImIiIgkGQU0ERERkSSjgCYiIiKSZBTQRERERJKMApqIiIhIklFAExEREUkyCmgiIiIiSUYBTURERCTJKKCJiIiIJBkFNBEREZEko4AmIiIikmQU0ERERESSjAKaiIiISJJRQBMRERFJMgpoIiIiIklGAU1EREQkySigiYiIiCQZBTQRERGRJKOAJiIiIpJkFNBEREREksy4A5oxZokx5s+NMWdifPbbxhgb41E73uuKiIiITFZp8X7RGHMf8D+A9UDvEOeaA3iBjw96/0q81xURERGZ7OIOaEAFcAz4eujnP45xTDFwxlq7exzXEREREbmhxB3QrLVf7/vZGFM+xGFzgKihTxEREREZ2nh60EZjDjDbGNMALAQuANuttX853JeMMUXAjEFvL5yYWxQRERFJLhMd0NqAbOBbwGXgIeAvjDFt1trnhvnel4FvxPqgtraWCxcuUFxczIIFC6ipqen/bNOmTdTX19PU1ARASUkJOTk51NXVAZCTk8O6deuora3F6/UCUFZWhtfrpaGhAYCioiJKS0vZuXNn/3nLy8s5efIkjY2NACxYsICioiLeeecdANLT0ykvL6euro7W1lYAVq5cCcDBgwcByM/Pp6ysjJqaGnw+HwB33nknTU1NnDx5EkBtUpvUJrVJbVKb1KZJ0qba2vGthzTW2nGdAMAY8yfAN6y1ZhTH/hwosdbOH+aYoXrQXj148CArVqwYz+2KiIiITKhDhw71BceV1tpDY/3+RPegxfL/t3f3QX5ddR3H3x/ShoeFloLdgqRi6EBgkgCzDm0QlocJUJCRFrWDUx1lnAEiMCAKfziIbX2odsQHxhEFGSw4AkJxrCMPtWSgE7AbRkMlGyG1GKAZGratgakLbUL5+sf9JbNuN2l2N3d/57f7fs1kbvbcvb/zvXPz8Nlzzz33k8CLkzyqqu5Z6BuqagaYmduWPGj2kyRJWhV6W6g2yeOTvDrJ2fN2reurT0mSpNWg7zcJ/A3wc/PaXgR840SjZ5IkSWtdb7c4q+qOJB8E3plkDLgVuIRu0drX9NWvJEnSqOt7DtoO4JvAm+kWrf0G8Kaqel/P/UqSJI2s03KLs6quXOgJzqr6flW9o6ouqKqHVtVTqurPT0efkiRJq1Xfc9AkSZK0SAY0SZKkxhjQJEmSGmNAkyRJaowBTZIkqTEGNEmSpMYY0CRJkhpjQJMkSWqMAU2SJKkxBjRJkqTGGNAkSZIaY0CTJElqjAFNkiSpMQY0SZKkxhjQJEmSGmNAkyRJaowBTZIkqTEGNEmSpMYY0CRJkhpjQJMkSWqMAU2SJKkxBjRJkqTGGNAkSZIaY0CTJElqjAFNkiSpMQY0SZKkxhjQJEmSGmNAkyRJaowBTZIkqTEGNEmSpMYY0CRJkhpjQJMkSWrMsgJakqckuTrJ7QvsOz/JdUm+k+T7SW5O8vzl9CdJkrQWnLGUg5K8GLgKeDbwg/mfk+QM4FPA2cCbgP8F3gLckOTpVXXrcoqWJElazZY6gvY84L+AFwFXL7D/JcBm4Jer6oNV9Q/ATwH3ATuW2KckSdKasKQRtKp6x7HfJ5lc4Fu2AUeAz8455p4kU8CFS+lTkiRprejrIYHHAXdVVc1rnwHGe+pTkiRpVVjSCNopWA8cXaD9/sG+k0oyDpw7r/mC01CXJElS8/oKaCczf1RtIa8Hrlhox9TUFIcOHWLDhg1s3LiRXbt2Hd+3fft29u7dy8zMDACbNm1ibGyMPXv2ADA2Nsa2bduYmppidnYWgImJCWZnZ9m/fz8A4+PjbN26lZ07dx7/3MnJSQ4cOMDBgwcB2LhxI+Pj4+zevRuA9evXMzk5yZ49ezh8+DAAW7ZsAWB6ehqAc845h4mJCXbt2sWRI0cAuOiii5iZmeHAgQMAnpPn5Dl5Tp6T5+Q5rZJzmpqaYjnywLuQi/yA5ErgiqrKnLb3ApdU1XnzvvdDwERVPfVBPvNEI2jXT09Ps3nz5mXVLEmS1Kd9+/YdC45bqmrfYo/vawTtTuCxSc6sqrm3Os8D7niwg6tqhm6+2nFJTvDdkiRJq0tfDwncDKwDXnasIclZdOumLW/MT5IkaZXrawTt08A+4H1JfhO4m26h2gLe01OfkiRJq0IvI2hV9QPgpcBNwJ8AH6YLgy+pqq/30ackSdJqsewRtKq6ErhygfaDwGXL/XxJkqS1pq85aJIkSVoiA5okSVJjDGiSJEmNMaBJkiQ1xoAmSZLUGAOaJElSYwxokiRJjTGgSZIkNcaAJkmS1BgDmiRJUmMMaJIkSY0xoEmSJDXGgCZJktQYA5okSVJjDGiSJEmNMaBJkiQ1xoAmSZLUGAOaJElSYwxokiRJjTGgSZIkNcaAJkmS1BgDmiRJUmMMaJIkSY0xoEmSJDXGgCZJktQYA5okSVJjDGiSJEmNMaBJkiQ1xoAmSZLUGAOaJElSYwxokiRJjTGgSZIkNab3gJbkk0lqgV87+u5bkiRpFJ2xAn08AbgOeNe89ttWoG9JkqSRsxIBbQPwoar6/Ar0JUmSNPJ6vcWZ5GHAY4Db++xHkiRpNel7DtoTBts3Jrk7ydEkU0m29dyvJEnSyOr7FufDgIPAXuDtwGOB3wFuSPLkqppZ6KAk48C585ov6LNQSZKkVvQa0KpqH3D+3LYk/w58FXgDcMUJDn39ifZNTU1x6NAhNmzYwMaNG9m1a9fxfdu3b2fv3r3MzHS5b9OmTYyNjbFnzx4AxsbG2LZtG1NTU8zOzgIwMTHB7Ows+/fvB2B8fJytW7eyc+fO4587OTnJgQMHOHjwIAAbN25kfHyc3bt3A7B+/XomJyfZs2cPhw8fBmDLli0ATE9PA3DOOecwMTHBrl27OHLkCAAXXXQRMzMzHDhwAMBz8pw8J8/Jc/KcPKdVck5TU1MsR6pqWR+wpE6TW4CvVdXPnmD/iUbQrp+enmbz5s19lyhJkrRk+/btOxYctwwGrBal1xG0JJPAWVX1iXm71gEnTIaDW5//7/ZnktNfoCRJUoP6fkjgucBHkjz6WEOS84FNwHTPfUuSJI2kvgPa+4HvAZ9IcmmSy4B/BmaBv+i5b0mSpJHUa0Crqm8DzwfuAt4HXAvcCWyvqjv77FuSJGlU9f4mgar6KnBJ3/1IkiStFr2/LF2SJEmLY0CTJElqjAFNkiSpMQY0SZKkxhjQJEmSGmNAkyRJaowBTZIkqTEGNEmSpMYY0CRJkhpjQJMkSWqMAU2SJKkxBjRJkqTGGNAkSZIaY0CTJElqjAFNkiSpMQY0SZKkxhjQJEmSGmNAkyRJaowBTZIkqTEGNEmSpMYY0CRJkhpjQJMkSWqMAU2SJKkxBjRJkqTGGNAkSZIaY0CTJElqjAFNkiSpMQY0SZKkxhjQJEmSGmNAkyRJaowBTZIkqTEGNEmSpMb0GtCSXJrkliT3JrkrybVJHtNnn5IkSaOut4CW5DnAx4GvAZcBVwCvBK7rq09JkqTV4IweP/vNwO3AZVX1Q4Ak9wAfSPL0qvpyj31LkiSNrD5vcW4DbjwWzgZuHGwv7LFfSZKkkdZnQHscMDOv7djX4z32K0mSNNL6vMV5JnB0bkNV3Z8EYP3JDkwyDpw7r/mpALfddttpLFGSJOn0m5NXTpp5TqTPgHYy9SD7X0/3UMEDXHrppae/GkmSpH6cD3xpsQf1GdCOAg+f25DkWIq870GOfTfwsXltjwSeAkwDR05HgQu4ALgeuITu6VONHq/haPP6jT6v4ejzGp4e6+nC2U1LObjPgHYn3Ty0uc4bbO842YFVNcMD568B7D4NdZ3Q4PYrwNeqal+ffakfXsPR5vUbfV7D0ec1PK0WPXJ2TJ8PCdwMXJzkzDltFw+2Uz32K0mSNNL6DGh/RjfR/5+SvCLJDuCdwCeran+P/UqSJI203gJaVX0e+Bng8XTzyX6P7i0Cl/fVpyRJ0mrQ61OcVXU93UTDUXEncNVgq9HkNRxtXr/R5zUcfV7DBqTqwVa8kCRJ0krqcw6aJEmSlsCAJkmS1BgDmiRJUmMMaJIkSY0xoAFJLk1yS5J7k9yV5Nokjxl2XTp1SR6S5G1Jbk1yX5KvJ3lXkkcPuzYtXpKPJqkkLxh2LVqcJJsG/4Z+M8lCb4RRw5K8NsneJLNJDiS5JsnYsOtai9Z8QEvyHODjdO8bu4zuJe2vpFuzTaPjz+jW2vt74BXAu4BfGXytEZLk5XR/FzVikmyne7XNBHAN8KrhVqTFSPI64D3ATrp1TN8NvGnQphW25pfZSPJR4ELgSVX1w0HbLwEfAJ5RVV8eZn16cEnOBQ4Bf1BVvzWn/a3AHwE/XlXfGFZ9OnVJHgnsA24HngO8sKo+N9SidEqSPAq4le5VfpdV1Q+GXJIWKckXgPur6nlz2q4G3gY8qqruHVpxa9CaH0EDtgE3HgtnAzcOthcOoR4t3tnAh+lGQuf6z8HW29Wj4/eBo4OtRsurgB8BXms4G1mPAL47r+1uukXtH7ry5axtBjR4HDB/nsSxr8dXuBYtQVXdVlW/WFVfmrfrhcC36UZk1LgkzwLeAPwq8P0hl6PFexHwFeB3k/xPkqNJPpfkacMuTKfsPcBLk1ye5KwkzwbeDHykquYHN/Ws11c9jYgz6X5iP66q7k8CsH4oFWnZkvwE3dyJt1TVkWHXo5NLcgbw18CHq+pGHw4YSU8GtgJ3Ab8AjNFNMfhUkqd6e6x9VfVXSTYDfzen+V+BVw+norXNEbSTW9sT9EZUkvPp3gH7aeAvh1yOTs1bgfOBXx92IVqys4Fp4OKq+lRVXUd32/OJwOVDrUynJMnPAzuAq+nuQLwR2Az84TDrWqscQetGzx4+tyHJsZGz+1a+HC3HYHmUG4BvAZfXWn8KZgQkuQD4bbpbKYcHo2nrBrvXJVlXVfcPrUAtxn9U1fE7ElX1xSTfpRtZU8OSPITuafi/raq3D5o/l+R7wPuTvLeqvjK8CtceR9DgTrp5aHOdN9jescK1aBmSPAL4BN3I58uqanbIJenUvJXuh6T30v3AdBT4zGDfZ+iWwFH7vgX82ALtYd40EjVpnO7/vn+b1/7FwfbpK1uODGhwM3BxkjPntF082E4NoR4twWDU5WN0YfvFVXX3kEvSqbsGeNa8XzsG+3YAPz2kurQ4NwA/meRJxxqSbAPOAm4ZWlU6VYeBe4FnzGt/5mB7aGXLkeugJc8FbgL+hW6+0o/S3W//QlW9fJi16dQluZZunstreOCIy3erau+KF6UlGzwk8FlcB21kJDmbLogdpbtlfQbdcin3AM906Y32JfljuqkG19D9v/hk4Crgv4Ft85ajUs/WfEADSHIJ3R/Cp9H9Y/KPwG/4WPHoSHKyP8g3VdULVqoWLZ8BbTQleSLwp8BLgB/S/eD7a1V1cKiF6ZQkWUe3zM3rgCfRLVN0PXBVVX1nmLWtRQY0SZKkxjgHTZIkqTEGNEmSpMYY0CRJkhpjQJMkSWqMAU2SJKkxBjRJkqTGGNAkSZIaY0CTJElqjAFNkiSpMQY0SZKkxhjQJEmSGmNAkyRJaowBTZIkqTEGNEmSpMb8H2G28sE2CCo/AAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"fig, ax = plt.subplots(figsize=(6,4), dpi=120)\n",
"\n",
"ax.plot(np.arange(10), middle_column_over_time[0][1], '-o');\n",
"ax.plot(np.arange(10), middle_column_over_time[10][1], '-o');\n",
"ax.plot(np.arange(10), middle_column_over_time[20][1], '-o');\n",
"ax.plot(np.arange(10), middle_column_over_time[50][1], '-o');\n",
"\n",
"ax.set_ylim([0, 40]);"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAmgAAAGjCAYAAACYKOmjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAASdAAAEnQB3mYfeAAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4wLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvqOYd8AAAIABJREFUeJzs3XeYVNX5wPHvmdnZNtsbVTqiUgUpShEUUGNN1IBYYhDEgiJqkp8mmkRjjMZCNNJBxahYY4lRQVRY1AWkl4CAsHSW2crOttmZ+/vj7uzO7k65U5BheT/PMw/MLeeemZ3yzinvUZqmIYQQQgghoofpZFdACCGEEEI0JgGaEEIIIUSUkQBNCCGEECLKSIAmhBBCCBFlJEATQgghhIgyEqAJIYQQQkQZCdCEEEIIIaKMBGhCCCGEEFFGAjQhhBBCiCgjAZoQQgghRJSRAE0IIYQQIspELEBTSr2tlNKUUiM9tvVUSn2ulCqvuy1VSvWJ1DWFEEIIIVqiiARoSqnLgeubbEsFlgFtgYnApLr/L1NKZUTiukIIIYQQLVHYAZpSKgmYCXzTZNeNQA5wjaZpb2uathi4HMgEbgr3ukIIIYQQLVUkWtCeABx1/3oaAuzWNG23e4OmaXuBncCgCFxXCCGEEKJFignnZKXUQOBu4DL0IM1Ta6DAy2kF6C1rQgghhBDCi5ADNKVUDDAPeFPTtKWekwPqxNI8aANw1u3zV3YOkN1kcxJwJrAFqAmlzkIIIYQQP5FY4AxguaZppcGeHE4L2oN1Fx4TwrlagP13AX8MoVwhhBBCiGhyNfBRsCeFFKAppboCjwLTgOK61jRz3W6zUsqM3sqV6uX0WKAswCVmAu802XYW8O4HH3xAt27dQqm2EEIIIcRPYteuXVxzzTUA+0M5P9QWtAeBBGBu3c3TF0A++qzOHl7ObQXs8Fe4pmkFNBm/ppQCoFu3bvTs2TOkSgshhBBC/MRCGpYV6izOp4CBTW531O27A7gS+A7o4JmYVinVHegC5IV4XSGEEEKIFi+kFrS6dBl7PbfV5UMD2KFp2mal1H7gD8B7SqlHgVr0btEjwJuhVlgIIYQQoqU7YWtxappWAlwM/AjMB14GDgEXa5oWaAyaEEIIIcRpK6w8aJ40TfsaUE22bQUuidQ1hBBCCCFOByesBU0IIYQQQoRGAjQhhBBCiCgjAZoQQgghRJSRAE0IIYQQIspIgCaEEEIIEWUkQBNCCCGEiDISoAkhhBBCRBkJ0IQQQgghoowEaEIIIYQQUUYCNCGEEEKIKCMBmhBCCCFElJEATQghhBAiykiAJoQQQggRZSRAE0IIIYSIMhKgCSGEEEJEGQnQhBBCCCGijARoQgghhBBRRgI0IYQQQogoIwGaEEIIIUSUkQBNCCGEECLKSIAmhBBCCBFlJEATQgghhIgyEqAJIYQQQkQZCdCEEEIIIaKMBGhCCCGEEFFGAjQhhBBCiCgjAZoQQgghRJSRAE0IIYQQIspIgCaEEEIIEWUkQBNCCCGEiDISoAkhhBBCRBkJ0IQQQgghokzIAZpSKkYpdb9S6n9KqQql1G6l1JNKKavHMb9USmlebnmRqb4QQgghRMsTE8a5s4EJwJ+A9cBZwONAO+CWumPaAXbg0ibnloVxXSGEEEKIFi2kAE0plQzcCjypadrTdZuXKqUygYeVUpM0TasB2gP7NU1bGZHaCiGEEEKcBkJtQbOjB1+lTbaX15WZANSgt6DtD7l2QgghhBCnoZDGoGma5tI07YimaZVKKbNSyqqUGgM8CCzUNM0duLUDuiqldiilapVSB5RSv4tU5YUQQgghWqJwxqC5bQR61v3/M+BOj30lQCLwJFAE3Aj8TSlVomnaHF8FKqVygOwmm7tGoK5CCCGEEFEvEgHaOCAduAB4FHgWuBdA07Qrmxz7pVLqDOBhwGeABtwF/NHbjry8PI4cOUL79u3p3Lkzubm59fsuvvhiNm/eTEFBAQA9evTAarWybt06AKxWK0OGDCEvLw+73Q5A//79sdvt7NixA4CcnBx69+7NsmXL6ssdPnw4e/bs4cCBAwB07tyZnJwcVq1aBUBsbCzDhw9n3bp1FBcXA9CrVy8AtmzZAkB6ejr9+/cnNzeXmpoaAAYPHkxBQQF79uwBkMckj0kekzwmeUzymOQxtZDHlJcXXsIKpWlaWAU0Kkyp/wOeAM7QNO2Qj2PuA54HUjRNO+7jGF8taB9u2bKFnj17ejlLCCGEECI6bN261R049tI0bWuw54c6i7M1cA3wiaZpnpMANqGPa+uolNKAS4B/e4xJAzAHKl/TtAKgoMk1Q6mqEEIIIcQpJ9REtXHALPQxZZ761v2bX/fvy8B1TY4ZDeT7aj0TQgghhDjdhdSCpmlavlLqbeCRupattejB2cPAa+7uTaXUIuCZutUFfgCuRk9aOzkCdRdCCCGEaJHCmSRwM/AA8Gv0yQH70MefPetxzB1126eh503LB+7VNG1+GNcVQgghhGjRQg7Q6lYKeLLu5uuYSuCRupsQQgghhDAg5MXShRBCCCHEiSEBmhBCCCFElJEATQghhBAiykiAJoQQQggRZSRAE0IIIYSIMhKgCSGEEEJEGQnQhBBCCCGijARoQgghhBBRRgI0IYQQQogoIwGaEEIIIUSUkQBNCCGEECLKSIAmhBBCCBFlJEATQgghhIgyEqAJIYQQQkQZCdCEEEIIIaKMBGhCCCGEEFFGAjQhhBBCiCgjAZoQQgghRJSRAE0IIYQQIspIgCaEEEIIEWUkQBNCCCGEiDISoAkhhBBCRBkJ0IQQQgghoowEaEIIIYQQUUYCNCGEEEKIKCMBmhBCCCFElJEATQghhBAiykiAJoQQQggRZSRAE0IIIYSIMhKgCSGEEEJEmZiTXQEhxMmnORxUrFuPs7QEc2oaif3PRVksJ7taQghx2pIATYhTXDjBleZwYJs3j+LX38BZWFi/3ZyVRfqEG8iaPFkCNSGEOAkkQBPiFBVucKU5HOyfOhX78hWgVKN9zsJCbC+8SNXGTbT/54sSpAkhxE8s5DFoSqkYpdT9Sqn/KaUqlFK7lVJPKqWsHsecoZR6VylVopSqVEp9p5S6MDJVF+L05Q6ubC+8iLOoqNE+d3B1YOo9aA6HzzJs8+bpwRmApjW5gH6/fPlyCufPD6pe9lWrKVuyBPuq1X6vL4QQwrdwWtBmAxOAPwHrgbOAx4F2wC1KqRjgUyAVuBcoB6YDnyul+mia9kMY1xbitBZMcJV1550Nu5xOXBUVOMvKKF70WuALKUXR62+QOWlSwNY46SoVQojIUVrTD3cjJymVDBQDT2qa9ojH9j8BDwNJwGjgE+BiTdO+9DjvALBA07T7g7xmT2DLli1b6NmzZ9B1FqKl0BwOdo4cpbecBXr/ms3EtG6NVlmJq6ICraoqpGtmTJxI8pjRxHXtijklpVl9GnWVetap7n7ShRdKV6kQ4rSydetWevXqBdBL07StwZ4faguaHWgPlDbZXl5XZgIwBKgBvnLv1DTtuFIqDxgU4nWFaDFCHdx//KuvG7VS+eV0UnvwYJg1haKFCylauBCAmJwc4rp1JbZrN+K6dqVy8+aQWvOEEEL4FlKApmmaCzgCoJQyA/HABcCDwEJN00qVUq0Bm9a8ia4AGBx6lYU4tQXbHajV1lK5cSPlubnYV+RStW1bUNdLOO884rp3w5SYWHez4jh6lOJXXgmp/rUFBdQWFGD/9jvjJxnsKhVCCKGLxCzOjYC7z/EzwP0TORbwNkLYWbfPJ6VUDpDdZHPXMOooRFQwOnOy1R8fpeK7PD0o+/ZbXGVlIV8z+557sA5u3GitORyUffxx4G5SpTBnZtLh5YU48vOp3rWb6t27qd69i5rdP6JVVxurhKbhtNmoWLe+WV2EEEI0F4kAbRyQjt6C9ijwLPqkAH8CDXy7C/ijtx15eXkcOXKE9u3b07lzZ3Jzc+v3XXzxxWzevJmCggIAevTogdVqZd26dQBYrVaGDBlCXl4edrsdgP79+2O329mxYwcAOTk59O7dm2XLltWXO3z4cPbs2cOBAwcA6Ny5Mzk5OaxatQqA2NhYhg8fzrp16yguLgZw9zuzZcsWANLT0+nfvz+5ubnU1NQAMHjwYAoKCtizZw+APKbT4DFtePSPxBvoDiy/6GK8Ud26kjRsOKVvv42qqEB5PaquOMCVksIOBf2h2WPissvgX//yU4Jep+IhQ9i/bx89zjoL64ABbF+3DrgEa0ICZ+7N5+hjj/kvw8PWV1+hT48zyT961PffyWSif6KVnevXc1xzUdO1K7369gXktSePSR6TPKZT5zHl5eURjpAmCfgsTKn/A54AzkCf3Xm1pmmtmhzzBtBf07Sz/JTjqwXtQ5kkIE5VQQ3ur2NKTSVp6AVYh48gadhQYrL1t8WxmTOxvfBiwPOzp93rc9yX5nBwYOo9lC9fHvLgfvuq1ez71a8MPZb6ouPjSbrwQlIuu5SkESMwJSbW10dmggohWoqTMkmgbnzZNcAnmqbt99i1CT23WkfgGJCplLJomubZ1dkKOOyvfE3TCtDHqnleM5SqChE1KtatNz64H2j1yB9IHz8eZTY325c1eTJVGzcFDK4yJ03yWb6yWGj/zxcpnD+fotffwGmz1e8zZ2aSceOEgGPGEvufizkz01jQWVcvraqK459/zvHPP0clJJB04YUkjxlD6b//jX3lSkmaK4QQhN7FGQfMAh4C/uaxvW/dv/nAd4AZuAz4CEAplQKcD/wjxOsKccpylpYEdXxMdrbX4AwiE1y5y8m6804yJ00KaUapslhIv3GCoda8rLvvIr5nT45/9hnHl32Jq7wcrbJSv//ZZw0HykxQIYQIeRZnvlLqbeCRupattejB2cPAa5qmHVJKFQBbgflKqYeAQvREtRowJxKVF+JUUbN/P8VvLg7qHHNqmt/94QZXTcsKdfC+0da8rClTUBYLyaNG4aqpwb7yG8o++5TjXyxDq6gwUEmZCSqEOH2EPAZNKRULPADcij7mbB/wCvCsu0tTKdUeeB4Yiz5zcx3wW03TvgnhepKoVpxyao8dwzZrNsXvvANGlz2qmznZ/asvT5lARHM4vLfmZWUFbM0rX7mS/ZMmG75Wh1dflZmgQoiod7IS1aJpWg3wZN3N1zEHgOtDvYYQ0SpQklnn8eMULlhA0auL0Cor67fHdu9Gzc5dAQrXyLhxwikTnEF4rXkuI61nHmoLbYEPEkKIU1wk0mwIcdoINNMw4+abKXn7HQrnzsVZ2rDQhnXoULKnTye+x5mGZk76G9wfzULpKg3UldvUkT8/Ru2hQ6SNG4c5OTmoc4UQ4lQR0TQbJ5J0cYqTzciakyo2Fq0u5w5AfJ8+5Nw/HeuQIY3KCbU7sCUKJf0IgMlqJW3cODJuuRlL69Zeyw13bJ4QQoQq3C5OCdCEMMho7jGA2C5dyJ5+H8mjR/tMESMBRAOjz23SmDE49u6h2rOb2GIh9YoryJz4a+K6d5d8akKIqCABmhA/gWBaeUxJSXTPXYEpIeEnqt2pL5ikucTEYF+xgsL5C6hYs6ZROdbhw3GVlVG5cWPIyXeFECISwg3QTJGvkhAtT32SWQM/aFzl5VRu2vwT1KrlcOd1y552L+bMzEb7zJmZZE+7tz6oUkqRdOGFdHxtEZ3efovkSy6pT25rz83VgzMImE9NCCGimUwSEMKAYJPMBnu8CG0maEKfPrT/xwxq8vOxLVhA6dvvGLiQ5FMTQkQ/aUETwoBgZxoGe7xo4J4JmjJ2LNbBgwwFUbEdO5J6+RXGLqBpOG02KtatD7OmQghx4kgLmhABaC4XFWtWGzu4LslsYv9zT2ylRDPSyimEaEkkQBPCD2dJCQd/9zs9tYYRJyHJrMPlYEPBBkqrS0mNS6VfTj8spuCuH4kyTrZgWy1d5fYTVBMhhAifBGhC+FC5ZSsH770Xx6FDAFg6dCAmJ4fK77+PSJLZcIMih8vBgs0LWLx9MYVVDekkshKyGNdjHLf1vi1geZEoI1ok9j8Xc2am4Xxqh3//eyrWfk/2Pfd4zaMmhBAnk6TZEKIJTdMoeecdjj7+F7S69TOTx4ymzV//iik+Puwks5EKrKZ9OY3cg7koFBoN72P3/RHtRzBj1AyfZUWijGhjOFedR4Ct4uLIuOVmMidNwpya2ugwyVUnhAiV5EETIoJclZUc+fNjlH7wgb7BbCbngQfI+PWtjRLOhvrFHamgaPbG2by04aWA15vabypT+k45YWU0dbK7So3mU8uefh/HXvwn5cuW1e82paaSdfvtpN90I8pkkmS3QoiwSIAmRBD8BVY1+fkcuHca1Tt2AGDOzqL9c8+ROHBgxK4falBU66qlpLqEoqoiCioK+M3y31DuKA9YTmJMInf2vZOk2CTiY+JJiEkgISYBi8nC9K+nU1pd6vd8hSIzIZMl1y3xG2hFU1dpMEtpVaxdS8Ezz1K5vmFGp7l1a2JSU/XXgSS7FUKESAI0IQwItPxPXLduHH7497jK9aAn4bwBtHvuOSw5OV7LC6WlyOFyMOadMRRVFTVqOfMm1hRLr6xelFaXUlRVREl1ScBzTqTnRz7PxR0u9rpsVbR2lRpt5dQ0jfIvv6Tg2eeo+fFHw+VnT7uXrDvvjGSVhRAtiARoQgRgZJFzTxkTJ5Iz/T6vX+bhtBTlHcpj8tLJkXlQJ4HVYqVDcgc6pXSiY2rH+v9/ue9L5m8JnJk/mK7Sk0GrraX43Xc5+ufHAk8yqEun0v2rL6UVTQjhVbgBmsziFC2ebd68hjQZPpb/AT1BattnnyFl7Fiv5TRtKfJUWFnISxteYrNtc31LUWl1KRuPbWTTsU1sPLaR9QXBJUbtnNKZrmldyYjPICMhQ/83PoOCigKeXvO04XJeGPUCZ2eeTVVtFZW1lVTWVrKxYCPPrXsuqPrYHXb+V/Q//lf0v6DOA70lbfGOxUzsPdFQS+PJGMemYmKI69zF0AxQz2S31sGDTnjdhBCnHwnQRIumORwUv/6G15aypkxJSSSPGuVz/4LNC8g9mKuX26S70X1/xYEVTPhkAlW1Vewt2xtW3R85/xEGtm4+/s3diheoq9Q9fmxY+2HNApze2b15ddurhrpbU2JTmNx7MgfKD5Bflk9+WT5H7EeC6nLV0LBV2lh7ZC1D2g7xekw0jGOTZLdCiGghAZpo0eoXOTfAWVzss0XE4XKwePviZmOsvNletL3Ztq6pXemd3Zul+UuxO/wnSHUHVv1y+nndbzFZGH/W+ICTDTQ0xvcY7zWoMVoGwC3n3MKtvW5ttK2qtor9x/fz8e6PeXnrywHLcLt72d30ye5D3+y+9f9mJmQG3Tp5ogSb7NbUJC2HEEJEigRookWLVIvIhoINjVp1AumV2Yvh7YfTN7svvbN7kxKbAkC7pHZhBVZut/W+jc22zaw4sMLvwPyJvSeekDLiY+Lpnt6d4e2HBxWg1bhq+P7o93x/9Pv6be2T2pMQk8DOkp31j9+TZ+vkws0LT+g4tmCT3dpemklMejrxZ555wuokhDg9yWLpokWLxCLnBRUF/Hvnv4Mq57bet3FXv7sY2m5ofXDm3j6i/QiAZi1F7vuBAivQW8BmjJrB1H5TyUzIbLQvMyGTqf2mBmxtikQZ/XL6kRmf2eyxeJNkSeLa7tfSI70HJtXw0XOg/EB9cOaPexybw+UIeCzorZ5rjqzhi/wvWHNkjaHzlMVC+o0TjI1DAypXr2bPz3/Bkcf/grNEujuFEJEjszhFi6Y5HOwcOSpwN2eTWXkVjgqW7VvGx7s/ZtWRVbg0V1DXXXjJQq/jx0APHBZuXsjiHYuxVTbk6cpKyGJ8j/GGBtI3Le9krsUZSm43u8POVttWNh7byPL9y9lo22i4rrNHz2Zou6E+94c7ls1Islvr0AuwdOhIydtvg9MJgDktjexp95L2y1+izOZmZcqKBEKcXiTNhhAB5E+eTEXuyoDHpd1zF/m/GMjHuz9maf5SKmsrG+03KzNOzem3DKOJXeHkZ92PFIfLwX1f3Rewq9RXa9wX+V8w/evphq8Xo2IY0GoAg9oMYlDrQfTM6llfbqRyshlNdlv1ww8c/euTVOTl1R8T16MHrX7/MNZBgwLm35MVCYRouSRAE8KPokWLOPrXJ+vva9CoM859f21XxazxyZS5Khqdnx6XzmWdL+OqrleRezA34ksjtRThtAquObKGiZ/779L1JzEmkQGtBjC4zWD2le3j7R/eDniO0b+RkZYvTdM4vnQpBU89jePgwfrtSWPH4iotoWLValmRQIjTkARoQvjgGZwdj4NveioG79BI95hEWWyFzweY+HCIwmnWQzeLycLIM0ZyZZcrGdZuGBZzQ+tMOC1Fp4MTucKCQpFkSeLSzpey5siakNOYBNPKGQxXVRVFL7+Mbe48tMrKwCfUkRUJhGiZJEATwouiRa9x9K9/BeB4PDw2wUx+K4XZqdHjgEZSFZTHw472DYEZwM1n38yUvlNIjfOePiHS48ciwumAfXlQWQwJ6dBhCJhPrQAxlHFsR+1HWX1kNasOr2L1kdUcth8O6pr+xgm6hRRwHj7M0af/zvFPPw1cCVmRQIgWS1YSEKIJz+DMlZzIY9dXk99KD8KcZsW2jr5nHPZv1d9ncAZ669qUvlOY2Hti+OPHwg2snA5Y+Tysngv2Yw3bk3Jg4GQYNt14eSc5yAsl5Ucrayuu7HolV3a9Ek3TeGv7Wzyx+gnD11x5cCVnZZxFcmxys33hTDSwtGlD+vjxxgI0WZFACOGDBGiiRfEMzsypqRT+7W7y9xlfFslfcObJosHAyiqorABXHEGtYx6JwMrpgMUTYOcSaJriovwYfPUEHPgexr/uv6xIBnnu8kII9NwpP7y1TmYmZAZsnVRK0TW9q/F6Agu3LOTVra/SM6snQ9oMYUibIfTN7otSKuykubIigRAiXBKgiRaj6LV/1QdnptRU1v3+al44PMvQuYGy99cLN6CJVGC18vm6MqB5dFh3f+fnsHIGXPibE1sXd1lhBnr1rZPn3MyGLW9Sai8g1ZpDv143YLEk+r8+DTnZjCxfVV9tzcmmY5vYdGwTczfNJSEmgeyEbPYd3weEnjQ3Evn3hBCnN0lUK1qEotf+xdEn9O6t2uQEnphg4YniNzjuOG7ofCPZ++sDmq+eALut8T53QLP4Rv04X4IJrPzVY/VcmgVVzShYM9d3fSJRF3d9wn1e3OUsfxrLjD4M/PB+Rn/xNwZ+eD+Wf/SF5U8HPN+9fJWR4GxKnynMGj2LX53zK3qk96jfXllbWR+c+RMoaa57RQJU4AS+xMRgSrIGPk4IcVqRFjRxyvA1YNszOKtIMPGn62rYm6Z/cXZL68Zdfe/ig53vs+LQSpSmoXl8abrvj2g3LGD2/rBarVxOPXjJM9aiR+6zULwHXLXgrNGDE2eNfrPbGrdS+aRBeQHMHw1JrfQWLHOsfjOZYcv7xuqyahacexNYs7y3gkVRa57RsWxT+k7BYrIwrN0wQO+6XH1kNf/Z/R9WHFzh+7mof1T64u8bCjZ4nWjgXpHA9sKLAcuitpa9vxxH+oQJZN8zFXNKSuBzhBAtnsziFFHPPWD77a1vkr3LVj8D09Y9m2n7zqb7y18D+rbHbjCzt7WirbUtd597N5d3vhyz5sLx5g0stK1icXIytpiGLO9ZtU7GHz/OxKwhWG54w/eXv9MBz51d10IU4D1jjoMzBkJVKVSWQlUJVJdF5sk42SyJEJ8G8al1txTYsxxqqwOcqCApG6Zv8/4cL39aD8ICGfUH30FeHYejgoX/vZ3FhRuweczQzXJqjM/sx8SfzfXZZRps0tycxBxGnTGKwW0GM7DVQNLiG7oqa6or+GLCWDpvLfSZf680M57U4hpw6StVmDMzyXnwQVKvvgplkg4OIU5lkmZDtGgOl4PpS+8h691cLlnrIs0jj2xFLCTW6P93B2dlnTK5vc/tXH/m9cSaY/WdHl/+DmBDfBylJhOpLhf9qqqpDxdGPgz9b4Hjh6DsMBw/DGWH9H+PboMjxpcjioj4dD0Acrd6mS0QEwc1FXB0s/Fyss4CS3zjVriqMqgqPnF19yWzO2R0AWu23iJnzdYnE3z+kF4nv8FvgCAPGrXEOVBsiI/1+FvXYEGD7pf4bIkLJ2muQtEjoweDWg9icJvBbCjYwMINc7k6T+OStS6f+fceyL6BEW/voGLNmvr9CeeeS+tHHyH+7LPrt8lyUUKcWk5agKaUMgEPAJOBjsBh4EPgj5qmldQd80vgLS+nr9I0bUiQ14v6AM3hdPH93mJKK2tITYjlvE7pWMzB/wqORDktpS5z1r5E0qMv0X+31qwVwq3WBH/6VSxjLr2Tm8+5GavFYzxPMC1fkeQORBLS9BanhHSoKIQ184yX8av/QOfhzbcbfkx+Apo9ufDqFcbrMugOPaCqKqm7leq34nwoyTdeTiSM+j10vlB/bNYciLU2jPUKsyVOT5o7um6igX+JMYmck3kOm45tosZV4/dYX/n33JNTPr/2cyo/XUrBU09Re6yu+9pkIn38eLLuvovit96i+PXXcRYWNZSZmUn6jROCXi7qZL+npS6nYV1qqvlhzRfUlNuITcrizIGjscTGBV+XCJQTqboYcTLzoM0ApgBPAyuBc4DHgLOAS+qOaQfYgUubnNtC+nt0DqeLWV/vZtF3e7GVN3xQZyfFcfP5HblzZFdDL+hIlNOS6uJwOSiZ/zIjdutflb6GW8e4YOBeS0NuqqpSsO2EYztg9zKD47V8UGZIbq0HAbYfjJ93xfPNgyunA7Z9gGa3ofx8/WsoVFK2nqLCG7MFBt1uIBDRYODt3lubOgwBa7bxulzyF+/lBBvote2vj6uzH9Nvrlrj57p99UTjxx6ToAdriVlwdIvPQN5NQ6HWzIVh9zV7TBaThfHxZ/BSVZGPsxtMTDqTKZe+TFVtFRuPbaxPmLvFtqXZmq2+8u+5x7JtPLaRgVdcTtLIkdhmzqRo0SKoraX4jTcofvttqK2l6UJlzkIbthdepGLDBjq89FLAIM39fnz92110rtxCKuWUksTehN5MuKDraff5InUxVpewXi811Xz/+qOTqaj/AAAgAElEQVScmf8mPSmt325bmsbOjuM578bHDAVHkSgnUnX5KYXUgqaUygaOAE9qmvYHj+0PAn8HOmmalq+Uehb4maZpZ/soKphrRmULmsPp4vZF3/PVjmMoGrdnuO9fdFYOc24e4D8YiUA5La0uaw58R+1VE0mtCPSFCyVWsNzdloFFB6D8iJ+jA+j/KzjzEkhuAylt9S44kxmcDrTnzgb7sYB1wZqDut97N5zzq6cwL/9rwGo4R/4e88jf+tzvqKlm6/NX0q9yFS4NTB6Vct/fmDCYc6Z/7PNDJyJ1Ced50TS9NW7HZ/DBHQHrEXHpnSD1DEjMgIQM/d+4VGpy/870tHhWJCb4nlRSUcnz5YpYL39nu8POgs0LmLfZeGvpvefey629bq2fRVy9axdHHv8LFatWGTo/Y+rdtJo61ed+h9PFna/mcfbuBdwSs5Rs1fAFVaCl8lrtGLZ3m8TMWwafNp8vUhf/dQn79VJTzbbnr6Bv5eqQP6MiVY5nGdUabEpoGObSp7KaOIN1CVa4LWihjkJNBd4E3muyfVvdvxl1/7YD9od4jVPCrK9389UOvYXGx/w1vtxewOyvd5/wclpaXSrXriUtQHAG+v50O1Ru3tE8OFNBvsR7Xw9nXQ7t+ustZ6a6CQVmC3lZ1xqqS17WL3yOkZpVexXLnOcC+oeLJ/f9Zc5zme240u91ZuXu47riu3nGcT02GifXtZHKM47rubb4bmbn+k4ZEZG6hPO8KKV3/fa+Drslo1kdmnJpUGFJh0lfwI3vwtUzYfSf4fyp0GcctOoVoBZNFO+Fvbmw7UNY+7I+c/aLR4mtPs6Mo8eYWlxCptPV6JRMp4upxSXMOHqMWHsBvPYL+Pg+WPoorPg7rJqLddvHnF/j8n5NH15Y/wJD3xzKHUvvYP7m+exIraDNnJm44mICpg3R0LC9PB/N4TsNyZwvdzBhz0M8YHmXTI/WA4AsSnnA8i7jf3yIuV/u8FmG53vaTC1DTNu4xLSaIaZtmNFbQk+lz5eWXpdw/kaReL18//qj9K1cDTQOqjzv961cxfevP+q3Lp7lOBWsiY/ji8QE1sTH4TRYzvevP8o5lauZnZbCJR3aMbFNK6a3ymZim1Zc2qEds9NSOMdAXX5qIXVxapq2C7jJy65RwFHAHSm2A9oqpXYAXdFb3V7UNO2pUK4bbRxOF4u+29vsl4o3c1b8SFJ8DOamr1TA6dKYs8L/GyZQOZEo40TVJYZazjP9UN9E/r3rTGrrXno+66JpxH6fS7ahmtRdpzaV3W1GUJrUhVJrZ0qtXSiNbcXlX15KBqXNPiQ8uTQoJI1PDrTCdGRvs/1Ol8aMvcN5zrWKi83rff6SW+Y8lwf2jmDaN3u8Pi+zVuZT7ZjOHa6PuSVmCTmeTe2kssgxltnOK4lfuY/ExHi/f6NaYvin8+fMdl4Z9PMbybpE4nkprxnNPert5n8YDyYF82vGkpyfhdmUDXQHM5Ci37Itq7ns6GS/ZXg6mqqvGhDrKCW+poRYRykm9MDKAkwpKWNiSZnvSSUAe1fotyb6AZlntKPIbGrUAteMptWPn6usreSbQ9/wzaFv9DLyTTxcXUugnygKhbJX8/6rH2HvOaDZfqdLQ1v5HBeZNwC+vywvNq9n68rneTnxIZ/v6RhqudP8kc9WlVnOq07rz7poqEsk/kbhvl5ctTVcsfdNXHXH+5qc5dKg297FvJJ7G6aYukldmobSajG7HOCo4NK9b1ANvJyewuLkZAqbzMIfd/w4E4vLOHvvv/j8oz6YTGbQXCjNhcIFTgfn7l3EtNbZ5Na1insqNJt4KT2NTbFxPJq/GEdN9HR1RmwWp1JqAPAtMF3TtJl12z4G2gJPAkXAjcBE4A5N0+b4KSsHmn03dwU+jKYuzu92F3LDvLyTXY2oZeSDotbjN0IyFQw1bWGUaQOp1i28VxXL/d6mmPjw9vARvJx5VbPt95jf5wHLuwHPf8ZxPf90/jzgY7rDXBfQNHlMi2r1gKbW4O8ef4HrTy3cuoT7vMRQyxzL8wGDvCmO6T7LiaGW7+LuIdNAMG4jlQuqX2xUlsLFKNN6FsY+a/hxH3alY1FOkqkgTjUeTzc7LYWX0gOvEHBrSRk9ampYkxDPmvg49teNJRu0w8WD7xtviSs/P4697c6gFCulmpWyun/LiecZyxxSsAf8svT2vLjFUMtci/7FHerfyFuZ0fIeiCahPi+R+BsF8z4qJpnbah4kQdWQRCVWqkhSlZyj9jIh5iscwII034HVbSVlWIAyLR6FIhZHs/eRA5jWqiG48jXkYMbRY/gahWn0vTi1uIRhA2fTc+jlAY81IirSbCilzgC+A9YC12h+ClVKLQF6aJrW0c8xfwL+6G3f/Pnz6dSpE+3bt6dz587k5ubW77v44ovZvHkzBQUFAPTo0QOr1cq6desAsFqtDBkyhLy8POx2fc57//79sdvt7NihN9Xm5OTQu3dvli1bVl/u8OHD2bNnDwcOHACgc+fO5OTkMPOjb5m5KUB29NOUsQ+Kfjxfex3DTVsYad5Af7UTk3IyJy2V2WkpmFww659OQ2PQHAkunrpkIt/SvJsrEl/+3sqUL5bmwnleIhH8hhuMhxPkxeIgmQqSVQXnq608FruQ+1plBxzLNuPoMWyudGKUkySqKIlxsiYhno3FVq57z/hrqnJkGf1bl/vcb/TLcobjF3zn6omNFI5paZSRCKiI/9AJ5sdboLKi5b0YiR864Twvwf+NNBKpJlOVkkUZWaqUgabt3B7zX8N19iUSgRUEF1zdVlKG3aSoUCbsJhN2k6JMmfhdThbHTcrvyh5K08h0uni63YPEtxsYkThiwYIFTJo0CU5WgKaUykCfxVkOjNI0zR7g+PuA54EUTdO8rsPTUlvQ5tzUn/M6ZTTb/v3eIqb8a11Y5USijEjWZcubfzD0QeGpwGzm/7IzWZMQD0CsZmLO3CqsRYHHkcX1qmHXo18xoEurZnWZ8q91hr/8T6e/UbTWJdCXnL+63P2v1YaD8ZduGhTWa/cZx/X0vuFxr3VZ++NRzn1vGCmU8kpd14y3BMm3FpdRSiobrl3Z8Np11aJqynn/6+fo+dePAv5AcauwwNYLFCndKxhSWUZrZ8NM0nC+LDVzLFWxmcRUFBCD0+/qVe7AtdHj8eD+Gxlt5fH1N3K/p40EM0Zfu6G87iJZl3CfF/drLtCPC02DWsw4EluR4ChG1Vb6PpgAuSP9CCawuiZxICltuoE5Fs2k53usUSa2HdjGb5yrKTOZ/C+b5o5jjCytFsAjbSfzyzH3hl0OnNw0GyilEoFP0BsxLvMMzpRSbdDTbfxb0zTPUYZmAtA0rQAoaHKtcKp6QpzXKZ2spFgKy2sCZaMiKymOi85u5XXGy0Vntwq7nEiUEbG6nJnBeZalzT5k/FmZ04WHk0wUa/q08K6pXXny4FAoWlh/jK9s7Iltq/i01xhu69nez/OC3/FaCn0a+mnzN4riutQSQ57rnJDqkpaUyB3l05niZ1zdHOeVpCdZfdbl0fjr6FezO2CQ9278dUzzUZdRPdsz/4NLudP1lv+xbAreM/2MSY1eu3GAlZ6Dr+LzAf9hXK6xbs5EBwxcrrF/awLTx1gp630GgzN6cl6tiR3b3iI3MQGg2Zg49/0ViQksTEthSknjLEjKWUNC5WFDUaJJQQ6ljP7+DkyH+uozoVPaQko7SGnLRWe24oHET7jIFXh80wOWT7no7Cu9/o1aWU08WdMQzHhyD2LvZ9rN72P/L+Brt7S8gjv8BFeznVeR5uf1Eqm6GH1eHor5kIsyu2E5sk1PpF12CMoOMvrIZkyqlECUAgtOLJWH/B5ntMXVOfL3mDueD3FJEJcCsUlUYOKNt0c2+zHQjKbxckoqNX1HUlRTTEFFgX4rLaDInerGHDBkiEhg5pbSpXvEygpXyAGaUioGeAdoDQzVNK3Qy2EvowdkCzy2jQbyfbWenUosZhO3nN+J55b6z4+lAbec39HndORIlBNVdTm4Wp/5Y+A94wD+OXg8Cwu+rZ9p8fNuP2eaYwQFD08DoDZe0apzGSV7EnFWNbxZY+KdZHS3s/HMbjiHTjf0vPj68j/t/kYtvC6BJk/4q8uNF3RjytLAkyem+ckDZTGbcJ4/nWUrfuBi83rMGgysalgOy1X362KZ81xcQ6d5Lee8doP43ZA4uh2qZMBu3z9Q1naF5f3MTFwRS9qxSs6wwaNvuvjurH0suugA76QqSEutn5DgM2mupvFmSgoTr/sAS3WZvo6rvUD/9+BayP/G79/Hk2nfN7Cv+fEWYArKc26EVy4NbjEvwYKTpskGLGYTM9p/zfn5gYOZxPZfYTE3TcPZUM6tg9tzzoo7AgZX2wfP8vl6iUhdcPIr8xJcTv8/ajUNbuM9mNM0gUIIKRk6DoW25zas6OG+xadRNvsi/i8jJuCg+ieLXaQOn95s1vrWI2sojjFQI6Wwm2HuliASePtxSadL6JPVB6vFitViJdGSyL6yfTy1xvi8xExrVkTqEgnhtKDNB8agryTQRSnVxWNfqaZpm5VSi4BnlFJW4AfgavSktcanWkW5O0d2ZcP+Er7cXtBsn2femTtGdjVcjr/8Nf7KiUQZESmnsvESQr6ayA+bzfwmJ4uNBd8CkBCTwCNDHmGsqRd7x40HlwsVH8+b439HxvEvuLnXEpJslThrTJhjXZRnJfCK6zJ2dLuNmRf1iP7nReryk9bF2SQYd3/vGa3LP7f/nDnOKxngEeStdZ2JgxhDdZlyUQ/uOvAk63ct8Bno+XvtWkwWxp97G8+oWV6XiyrxWC5qSr87GfzHydheeRnbrFmoymrO367Rf5eT9y8w8Z/BCpeCa75zNVsyrdgKS/qb+OB8RaHZxIYYFwPbj2pcmSYJiQN2e6W00z8HHBU0ZUIL+OPNpMDqKISXBkNmN0jKgaRW+i0xgyFHFxtISAxDbO+D00eSZeDOmI8wG5itONLyMeAlnafTwRDbe8bqcnQxrD0HKmx60Ft+tOHfskMkOgL3ZfsMahOzIC4Zivf4L8DTyIe8r1QCvN5zKLmlm/S6+2hxzbUm8GbbvvzScZzdx3bzY8mP7C7V/91WtK1ZmYGkxaXRKrEVOYk55CTm0CqxFXaHnVe3vWq4jHE9xjGw9cBG2xwuB/M2z6OosijgHykzIZN+Of2CrvuJEs5ST/5OXK5p2kilVALwMDABaA/ko6fZeDGE60VlolrQ023M/no381b+SFllwwyU7KQ4bjm/I3cEkbl59te7WfRdPsfKG35tB1NOJMoIqxxHFXz6W1j3qt8m8kFVVeQmxHO8rvm6R3oPnrnwGc4wZbL3l+Oo2aN/0LR7/jkSxl7C7K938/q3u+lUublRRusbL+h6ajwvUpfTui6hvnYdLgf3LruXlYdWYq510eMgDS1f7cAZY2JY22G8cPEL9UluHUePUvD03yn75JP6co6kQnkCdDviryVO8cy1JqYP/g03n3MzJs8cgnXLi9XYbSxMS/ad7qDkOLHu5cVMMXoiYo9uOHZ/Bds+CPi8RdQ510BWd4iJB0siWBL0m9kC/5mOVlUaMLhScSkw5nF9HdvaSnBU6sFn4Y+w/eOf6pE0GHwnnH2l3n2c3KZhrd3nzq5fHcRXEF2/OoiPNW2DWe5MoQLm6TNi9ujZDG031EddxtTVxfd13EumLbluSf37oFH5G2fz0oaXAtZjar+pTOk7JbjK+xEVszh/CtEcoLm9tWY/v3tP/9Xxj3H9+FmfNqfPOmyaBts/gSW/h+K9fgclN+3fGHfm9fxm0O+IJYb9d92FfbmeVyrzzjvImTYtoo8pqtank7pIXYyc63KwcPNC3tz+JoVVDSNJMuMzueGsG5jYe6LXLyX76tUc/csTVP9gfImyxSNMvD/UREZ8BoNbD2ZI2yEMaTOEtkltcXz9N6b9b37giQZnT8Yy8nfeLxD00mADwOVo6G7VgksAHLVikz1aBXPA5Qwu0PO1Tu/yp3F89UTgsWM+1qIFWHNkDRM/nxjsIwL0XpAuqV3olNKJr/Z/RUVt8xZUT4ECK4hMcOVwObjvq/tYcWBFs6DSfX9E+xHMGDXDZz1CIQFaFJm34kee+O//ANj0p7GkxEfuDx3Vjm6Dz/4P9iyv3zQ7uzUvJcUGPPXSxE78/Xr9g6ngmWconK8PV0y6+GLav/gCyhTqYhdCtCwOl4MNBRsorS4lNS6Vfjn9An6ZaLW1HHttEban/h5wSKiG3m16191mnObGR3dI7kCyJYmtBrqupva9iyn97vS+s66VB7sN/+m9lb6+qmcrj8sJFUWw41P4+J6A9ahnjgdXTeSDO3Oc3kro8Ju4oLFfzNNXKom1Nt4ezvPiweGoYNqbF5Gr2X0H0SqJGTcsw2JJBKC0upSthVvZatvKZttm1h5dS1mN8eWyr+p6FZd2upSuaV1pbW1d3/IaqVarSAVX7h86i3csxlZpq9+elZDF+B7jff7QCcdJncUpGiuq0GcgxpgUyXEt5Kl1OmBfnj6eJCFdX2Tb/cFQUQRfPwlrFoB7cej4NBwj/4/F+YtRBprIv3cdx+FyUPGfT+uDs7ju3Wj71FMSnAnhwWKyNBtfE4iKicF6Ti+8zeBqdiz6kmlPpNzMsqyjrDq8qv6Let9x30uGNS5DsfiHt5nYZ5L3LzuzBQbdXr/Yve+xbBoMvL1xEGIy68FJvxvgy8eCC2ZMMXr3pKNCH4bhqID8b+Ej3+uXNnPtQuhyod49GhNfv0ZvUIFVz597Hw/X5Hnxzcvz4mHBtkXk1iVT8DlbVytn2vIHSYlLYattK3vL9ga4pn/XdLvG6+vytt63sdm2OWBgNbG3/9Y6i8nCjFEzvAZXmQmZhoMri8nClL5TmNh7YtA/dE6WFhJFRIdiux6gpVtjozItSFCcDlj5PKyeC/ZjDduTcmDAbZCQBsv/1jAhQJngvNtg1MNsKNtN4Y6Zhi5jqypk04r3sf5BX7TbnJpK+5kzMSdZA5wphDDCWVoS1PHDU87l8pFjcbqcbC/azneHv2PJ3iX8r+h/Ac/V0LBV2thQsMF3MDlsOo79a1hgy/PdDZc1BMuw+7yfH2owExOn3xLqdqd1gGV/Nh5cnXNV88AoQoEVAMOmw4HvYefnOFBsiI/1CFxrsKBB90vAx/PicDlYvH2xoXFhuQdzvW5vl9SOczLP4ZuD3xjunvQ1qD5SgZW7rEgFV6H80DlZJECLoOK6FrSMxMBde1HN6YDFE2DnEppNeykvgOVPNt7WeQRc+jdopXc9lx4znrg0rVwj7vfPo9XUgNlMu3/MIPaMM8J8AEIIN3Nq4GSh3o43m8z0zOpJz6yedErpxPSvpxsu4/HvHmdsp7EMbD2Qvtl9iY+Jr9/nUDCtVRa5zjSfKRw2t85ihsJ3QlSPYKZhnq9b3X0/wYz+ACMUXEWiLnX1cfzyFRb8dwqLi9ZT6DGtNMupMS7zXG772RwsPuqReyC30RjFQJItyfTL6UfvrN70zOpJr6xeZMTryW+NdE9qaIzvMd5vgBTpVqtIBFeaw0HFuvU4S0swp6aR2P9clEVa0Fq8Yru+7FNaYnT+sQ1b+XxdcAZ+f1nGp8LVM/UxFR4thqlxqYYuY6nVePA9J+ZCPf1Aq4cewjpkSKi1FkJ4kdj/XMyZmTiLihoyrvtR9ul/ievejZiMhkz1Rt/TbnvK9jBn0xzmbJqDxWShT3YfBrYeyMBWA1l9ZDW5h1YCfrrhDq5k4eaFvscmmS0w/nVYOQPWzNV/OLolZesB1bD7/LdYQeQCvQjUxeFyMG35g+SWbKgb3tFQl0KziZdKNrB5xW+YMWoGADuLd7Lp2CY2HdvExmMbDXdDu/35gj8zptMYr/si1T3pFqlWq3CCK83hwDZvHsWvv4GzsCGQNWdlkT7hBrImT466QE0mCUTQ6OeWs6ugnMt6tWbWTQNOdnVCY3hMBWDNgfubD1Z1uByMemsUpTV+slprGnf/x8WFW/RrpF1/Pa0f+/Op3zUsRBQ6NnMmtheMZzcyJSWROeV2Mm65BVNcnOF0BwDx5njaJ7dnV8mukOtrZHafm8NRwYYtb1JqLyDVmkO/XjfUD4A3xOnwEVzlGA/0IlAXo4Pq21jbUFxVTJWzylC5viy8ZKHfoOlkDKr3JdzgSnM42D91qp4hQKnGP1Tq7iddeCHt//liRIM0mSQQRTzHoJ2y9uU1HnPmj71AP77JdO8fS36k0tmwvpu3zOWXrtXqg7OEAQNo/cgfJDgT4gTJmjyZqo2bKF++3OcXVMJ556FiYqjIy8NVXs6xZ5+j5M3FZN9/PymX/4zxZ42vDyB8rUYAMKn3JKb0nUJRVRFrj65lzZE1rDmyJqiAzchYNofLwYLNC1i8fXGjrr2snf9iXI9x3Nb7NmMBhNkCF/4GxwV3hxxchVuXYMaPHbYfbnQ/NS6VPll96JnVkzf+9wbHa44byhkWKCFrtAyqbxZceXAWFmJ74UWqNm7yG1zZ5s2rT9/UrBW57n758uUUzp9P1p0+ZiCfBBKgRYjLpbWMMWhNVgEI9vgfS37k9qW3U+OswezUuOY7rVnm8vJ4SKz78RfTpg3tX/gHKvYUfs6EiHLKYqH9P1+kcP58il5/A6etoUXEnJlJxo0TyJw0CWJisOfmcvTpp6nZtRvHoUMcevBBihYtYsJvH2Brm2FkvrPC52oEhdc3dHtlxGcwpuMYxnTUu9GKqop4ecvLvLL1FcP1nrFuBiPajaBHRg/OyjiLVomtUErp3YFfTiP3YC6qyTjZwspCXtrwEpttmw3ltYpEcBVKXYqqithdspudxTv57tB3QY0fG3XGKEZ3HE2frD50TOlY/+PWrMwRGTvm6WSP+wonuNI0DWdhIcWLXgt8IaUoev0NMidNipquTgnQIuR4VW39Wm6n9Bi0hPSQj99ftp/JSyZTVFWE2akx64tOpK3b3ey3nLWqbuqByUT7F/5BTGZmuLUWQgSgLBay7ryTzEmT/H5ZJo0YgfWCCyh59z2OvfACzqIiqjZt4uBNv+KerCycNlez93SaHcblukg0uYgZhdeFITPiMxjRfkRQAZp7jJVbalwqPdJ7UO2sZuOxjQDNWovc91ccWOF/HBuhB1eeFmxeUD8r0l9d7v/qftomtWVXyS52lexqWAw8BFd1vYrRHUc32x7psWPhikTXZPHrbzRv9fXCNnce1Xv24iwuprbQhtNWSG1REdTW+j2v4WIaTpuNinXrsQ4eZOycE0wCtAhx50ADyDiVuzg7DIH4NH2JFr/qpp530Af1H7EfYdKSSRRU6mM4/rZ3MGnrvnUf2fRMncuFfeVKEnr3jlj1hRD+KYsl4BeQiokhffw4Uq64nMK58yh65RW0mpr6ljdf7+mK5Sv8dhP1y+lHZnymobFssaZYMuMzOVzR0KVXWl3K6iOr/Z7nadG2RQxpM4SMhAzS4tJIsiQ1GkphNLhqGug5XU7KHeUUVxXzr23/MlSXrw987XNfnCmOale1z/1N+Zq0EcnUFuEKt2tSc7ko++yzRoGd3+tVVlL20Udh1zvYtDQnkgRoEVJkbwjQTukxaEV7oNbI4NOGqee2ShuTlkzikP0QALefPZEuc9/DGehXTxQ2KQshGpiTksi5fzpp113Lj1dehVYdIIgI8J62mCyNxrL5c3uf25nSdwql1aX8UPwDO4p2sL1oO+sL1huesVhWU8ZNn97U8HiUmdS4VFJiU0iNTTW8qPfsTbP5fO/nlDvKOV5znHJHuaHzmrKYLHRP7063tG50S+tG17SudEvrRlZCFmPfHWt4zUl/48eiZeyY0a5J27z5pF37C6p/2En1To/b7t1olZUEw5SWRmy7dpgzM4jJzCImKxNnuZ2SN980XEawaWlOJAnQIqTYI0A7ZceglRfA69c2CdD8Tz0vqSph8pLJ5JflA3DT2Tfxa+0C9hfODXy9KGxSFkI05zh8JHBwBobe08F2w6XGpeopOurGQX2R/0VQOdk8OTUnRVVFQXcv1rpq2VmyM6Rrevrb8L8xttNYr/uMBK7BjB87maktguqafPFFbC+8EHY9Adr/4x/NXneaw8HxJUsCp5lRCnNmJon9z41IXSJBArQIKT7VuzhrKuDN8VBS98t0xO/02U1+8vocd1Yx5Ysp9bOzru1+Lb8d+FuOL10a1KWjqUlZCNFcsO9Rf8eH2w0XbE62e/rdQ441h9LqUkqrSympLqG0upQ9pXuCCrp6ZfaiS1oXUmJTSI5NJjk2GVuljYVbFhouIz3e9xjfljR+rGLdesNdk02DJnN6OnFnnklc9+7EdunCsX/8A1dZWcjBlbJYSL9xQuA0M5pGxo0Toqo3RwK0CPEM0E65SQIuJ7w/GQ6u1e/3uxFGPaT/+hl2n9e1OCscFdz1xV1sK9S7CC7vcjmPDHkEpVTImcuFENEp2Pfo8S+/wjp4MOZU32OlQu2GMzqOzd0d+Ovev/Za5poja5j4ufFg5/7z7m/WIuVwOfhw14cR65o8lcePaU4nVdu3U7l2LaWf/Deo66X+4hekXnkFcWee2WzSmLOkOOzgykiamaQLL9RnMkcRCdAipKhuFQGLWZF0qi2UvuQPsP0/+v87XwhXzGh4U5otzfKcVdVWce+X97Lh2AYARncYzV+G/gWzSV9Tz3Dm8ihsUhZCNBf0agQffED50qWkT5hAxq9vbbQqgacYJ5yTr+EsdWFO1YjJxOsMUE9Gx7EF6g4MNtDzFlxFqi6e5Z1K48cO//kxYtu3p2LtWirXr8dVHtrYvNSrr/bZJR6J4Mpomploaj0DCdAipj5JbeIptlB63mzIq1vYPPts+OUiiGnoonW4HI0+KHpm9uTB5Q+y6sgqAIa1G8bTI54mxtTwUjqVm5SFEM0Zfk8DMTk51BYU4LLbKZw3j6LXXiN93DgyJk7E0ioHCD/9QiS6AyMVXDLKcXwAACAASURBVJ2IrsmTuaB3MOPHSt991+t2c1YWrrIyfY1lfwz8SI9UcGU0zUw0kaWeIuT2Rd+zZNtRzmqdzGf3jTjZ1TFm+yew+EZAg6RWMGkZpOkLlftK3hhriqXGpb/pBrUexEsXv9RoIWQ3x9Gj7Bo9BhyO5tc9gUtrCCFODM3h4MDUewK2ZLR78QUqVq3CNnMWlevXNxxisZB63bVk3norR/7617CX3YnEUkQOl4P7vrovYHAVKOFtNC2L5BZqclj7qtXs+9WvgrqWpWMHEgecR+KAASSeNwBLhw7YZs0yFNBnT7vXcPb+U2mhcwh/qScJ0CLk+tnfsmZvMUO6ZLD49vNPdnUCO7AWXrkcaivBYoVf/xfa6k34TZM3emv+T45N5rNffEZKXEqzfZqm6R/ky5YBYEpOxnX8eP1+c1ZW1DYpCyF80xwO7y0ZXt7TmqZRsWo1ttmzqcjLayjEZAKXK+C1jH5xN23lD7Y7MJLBVbh1iYRQWyc1TaNmzx4K5y+g9P33DV+v9eOPk379dV7rYSSgb8k/0iVAixIXP/s1u4/Z+Vnv1sy8McoXSi/eC/NH62tuKhPcsBjOvKR+t9FFe6f2m+o1S3fJ+//m8MMPA5B82aW0feopKtdvOGV+9Qgh/Au2JaNi3Xpsc2Y3jGsKpK7rq/tXX/5knxXREFyFK9hFwZ0lJdjz8ihfuRL7N99Se/iw78J96PDqqz7HjwUT0LdEEqBFif6PL6XIXsONgzvwxM+jODN+ZTEsGAu2H/T7lz8LAxsGVzpcDsa8M8bwwNkl1y1p9CHmOHiQH6+6GpfdTkx2Np0/+pCY9CCXjxJCtEhFb73F0T/+yfDx/r78RXPHZs401K2YMGggWlU1VZs3ex9nZqSVM4gg+lTrmoyUcAM0mSQQAS6XRol7ofRozoFWWw2Lb2oIzi64t1FwBrChYIOhRXs1NGyVNjYUbKgfzKq5XBx66GFcdjsAbZ74iwRnQoh6wX4eSI5E44IZ3F+5ek2j+yo+nsRBA0kaNgzr0KGUffY5thcjN8nLyPJiojkJ0CKgrMrhsVB6lARoTkfj/GVnDIYPp0L+Sn3/OdfA6D83O620ujSoy3geX7RoERWr9XXy0saNI2nEKTJZQgjxkwg2n1rpRx9jyckhvm9fn7PjW2LrTCiPKajksOgD+1PGjsU6dCgJ/ftjim347sq6fTJVm069vGEtjQRoEeC5DmeG9SR/MDgdsPJ5WD1XH2PmZrGCQ2/Z4ozB8PPZejN2E8Fm6XYfX71rF8eee16/1Bln0Oq3vwmt/kKIFivYfGrlX3xB+RdfYOnQgdQrLifliiuJ69IZCD9VRzQK5THV2mzYV62i5D3jA/sBch54gJSx3pedOlXzhrU0EqBFgOcqAuknswXN6YDFE2DnEvQ1Mz24gzNLIly/CCwJXotwJ28M1M3pmbxRq6nh0G9/p+e8MZlo+9TfMFmtEXhAQoiWJJh8apYOHXAcOAAuF459+7DNnIVt5izie/Yk5fKfUb4iV58dajDTfbQzmr2/9V8ep3LdeipWrcK+ehU1u3aHdL1ArZmnYt6wlkYCtAhwryIAJ3kM2srn64IzwNcAf0cFrH8NLvTewmUxWbi8y+Us2rbI76U8kzcem/0CVdv0JZ8yb7uNxP79Q30EQogWzmhm+Pb/fBFnSQll//0vpR//h6otWwCo2rqVqq0e4639ZLovnD//J82xFU4ZRrP37xruY+hIXJw+sN9b7klPQa7gIuPHTh4J0CIgKlrQnA69WxOFz+AM9P1r5uprbJq958LZXrTdz9mNM2NXbtyIbc5cgP9v787jo6zP/f+/rkwmKxCSkICyaEAFBRRjKyAEsNSt55zWbxfr0lZrte3psdrankd7emrX0+V0tafndFW7aj21Pb9aa11ppUENtQYQqOJCRKJACFnISiYzn98f98xkkkyWycxkkvB+Ph55ZLjve+77um9v9eKzXeQuXsysD9+Q3H2IyJSWSPdZdlkZJVdfTcnVV3Nsbx1H//AHWu67j979+0dxIaPpzrtG7IpLRVdpsudIZIB/9Pb8fvJXrKBg1UoKV64k78wzOXLbbargMoUoQUuB5pgxaMWZakF7pab/mLMhOWhv8I4fUGMT4J7n7+GvB72B/meUnkFDZ8OQRXt9x3p55ROfhGAQ8/s58Wv/2W+gqYhIPGPpPstdWEHZjR8mf+W57L/6mpEv4hzBxkbqP/Yxpq9fT+5pi8k99RSy8voqn4ylKPigy4zhHMH2dnpeeoljL77EsZdeovNvTyU0wL/8E5+g+IrL+90LTN6i4BKfErQUaAq3oOX4sijM8WUmiK7mpI9/tf1Vvvm3bwIwp3AOt194O7nZuUMu3njwG/9Jz8svA96q33mLFyd1CyJyfBlL91moNbGZ5u0PP0L7w494f8jKIufkk8ldfBp5ixdz7MWXRtWtOFxX6Wi7Jve9+z1kFRZy7KWX6D14MKF7GMg/98RByRlocP9UowQtBaKF0gv9mSuUnp/gemMDjg+5EJ99/LN09nYC8PnzPs+0nGkAcYv2tj/+OM133umdqrKSkve+dwxBi4gkJtGlOvD7+8ZlhUL07N1Lz969tD3w4KhP0fjDHxE41OCNIAk5CIVwoSCuN0jbg6M7T9f27UPG5y8vJ/Dqq6OOZ7hnoMH9U4cStBSITBLI6AzOBaugsAw6GhlxDNq0Mu/4GPfsuYetB7cC8PbT3s55J5435BmCra0c+NS/e2crKODEr34F82Wo5VBEjiujXqojPBj+lEceJnDgAMf27KH7uT3e7+f30Pva6Msaue5uWu6+O+nY/fPnk3/mmeSesoicRYvIPeUUcubPB+CFDeeP+p5GM8Bfg/snPyVoKRCpIpDRBM3nh3PfD3/+0ggHOnj9+/tNEKhvq+ebT3tdmycUnsDHzvnYsGc4+B9fovfQIQBmf+IT5CxYkFToIiKjNeqlOsKD4bPy88lduJDchQuZcckl0d0t997LgU98ctTXzSoowPLyICvL6ynJyiLUc4xQ8+irHZT/68eHXHsskXtSS9jxQQlaCjRNlDJPaz8KLz4K+7fG2Rme3XnqRd4MzrCQC/GZJz5DV28X0L9rM56jDz7I0fvuA6Bw/TpmXvaOVN6BiMiIUjEY3j/nhISuOe/73x/UItWx9a+8cvXVoz7HcF2TGuAvAw1eSn6UzCzLzP7VzJ43s2Nm9rKZfcfMZsYcM9/MfmNmLWbWZWZPmtn61IQ+ccSOQcsonx/yS+Lvm1YG538aLr+zX+vZ/+75X5466NVlu+y0y1h94up+X3OBAB1b/8rRhx+m9aGHOBAudOwrKuKEL34xc2PuROS4FRkMX3bTjfhKS/vt85WWUnbTjSMuUhvpKh0483LwxQzfrFlxuxVTcY5U3pNMLcm0oN0KfAD4GrAFOAP4ArAEuMjMsoEHgCLgRqAd+CjwkJmd6Zx7PpnAJ4pgyNHS5Y1BK8l0Hc6GZ+H5B7zPZ78Lzry8rxbnglWD1j3b37afbz/tlWc6sfBEbn7dzdF9Q63rEzH7M7fgLy9P372IiAwj2cHwiXaVxjtnKs4x8Hwa4C8RY0rQzKwM+BfgK865W8KbHzIzH/B1MzsJWBr+2eic+1P4e48A9cAHgZsHn3nyOdoViLZEZ2wNtIgtt3q/LQvW3gyli4Y8NORC3PL4LdGuzS+s+QKFfq8803Dr+kQc/f19zLjwQv1HQ0QyKpnB8KnoVkxH16QG+AuMvYuzCPgV8NsB2/8e/l0CrAJ6gD9Hdjrn2oAaYMq8eU0ToYoAQPM+2HmP9/mMtwybnAH86rlf8fShpwF45+J3svKEldF9w67rExZZG0hEZLJKRbeiuiYlXcbUguacexF4V5xd5wOHgN3APwONzg36P3wDsHLgFyerCVFFAOCJ/wIX9D6vHb5xcv/R/Xyn9jsAzJ02l5vP6d+1OaqSI6MsoyIiMpGloltRXZOSDimbxWlm5+CNNfuoc67HzHKAeFVbg8CwmYyZlQNlAzYP3ySUIU0xCVrGxqC1N8C2X3qfT7kATjhzyENDLsSnH/90tGvzi2u+SIG/ILq/s3bb6EqOhMuodNZuU1O8iEx6qehWVNekpFJKEjQzmw/cCzwIfH8UXxmpGuyHgM/G21FTU8PBgweZN28eFRUVVFdXR/dt3LiRnTt30tDQAMDixYspLCyktrYWgMLCQlatWkVNTQ0dHR0AVFZW0tHRwZ49ewAoLy9n+fLlbNq0KXreqqoq6urqqK+vB6CiooLy8nK2bt3KE6/2Ro97tW4PDXvaAFi2bBkAu3btAqC4uJjKykqqq6vp6fGSupUrV9LQ0EBdXR3A2O+p/UHo7Qbg6YL1LGxuHvKeNrdtprbV++7Fsy/m6O6jbNq9KXpPO7ZUM8Q80LiCrS3puacU/3MCyMnJoaqqitraWpqbm8f/n5PuSfeke9I96Z6Om3uqqakhGTa4BzLBE5iV4M3ibAfOd851hLf/CHiLc272gOPvAiqdc0uGOedQLWj37tq1i6VLlyYVcyr9YPNLfPWB5wDY/fmLKMwd56Xlulrg28ugpw3mr4L3PTTkofuO7uPtv3873cFu5k6by/+9+f/6tZ5B4uv6LPjZz/Q3RhERkQF2794dSRyXOed2J/r9pLIJMysA7sdrEbskkpyFHQZKzczvnIvt6pwNDFtjwznXgDdWLfZayYSaNpExaDnZWRRkolD6U7d5yRlA1dAVAIKhILc8fgvdQa+lbWDXZkS0jMpI3ZwJlBwRERGRxCSzUG02cA8wB7jAOTfw/+hPAj7gkpjvzABW483knBIiY9BKCnLGP4ns6YSacI/y7OVw6gXRXYFQgKcOPsWj+x7lqYNP8fPdP2dbwzYArlxyZdwC6BBe1+fKK0e+tkqOiIiIpE0yLWi3ARcA1wMLzWxhzL5WvPFou4HbzOzfgCN4C9U64IdJXHdCaY7U4czEDM5tv4TORu/z2o+AGYFQgNt33s7dz93Nke7BrWDzps3jpsqbhj1t7mmnDb1TJUdERETSLpkELTJQ6adx9m12zm0ws4uBbwPfwpu5WQtc6Jx7OYnrTijNnV7vbXHBOLckBQPe0hoAxRVwxqUEQgFu+tNNVL9ajRG/Na80vxS/b+hYQz09NHzj6wBYbi5ZhYUEm5qi+32lpZRcdaWW1xAREUmjMSdozrkR+/Occ/XAlK6m3VeHc5xb0HbeA637vc9rPwK+bG7f8QOqX/Vmo7ghJsruOLyDO3bewQfO+kDc/c2/+CWBfa8AUP6xmym+4gqt6yMiIjLOxnnK4dQTqSQwrmughUJ9ZZ2mnwBnXUEgFODu5+7GsCGTMwDDuHvP3Vy7/Fr8Wf0Trd7GRhq/9z0AchYupPiKK7Suj4iISAaMeZKAeIXSW8OF0se1BW3P/dDorbfC6n+B7Fy2N2znSPeRYZMz8FrWGrsa2d6wfdC+hltvJRRe12X2v31SLWUiIiIZogQtCa0xhdJLxmsMmnNQ/U3vc95MOOcaL5ZjrQmdZuDxXbt30/rb/wNg2vr1TKuqSjpUERERGRslaEloykQdzr2PwWvechms/CDkTgegKLcoodPEHu+c49CXv+Ilf9nZlH/yE6mKVkRERMZACVoSIktsABSP1xi0Ld/yfvsLYWXfQP8V5SsozSsdcvZmhGHMyp/FivIV0W1tDzxA19NPA1DyrneRW1GR+rhFRERk1JSgJaFfofTxaEGr/xvU/cX7fM41UNBXNdOf5efyJZePagza5Ysvj04QCHV1cejr3wDAV1LCrA/9c1pCFxERkdFTgpaE5vHu4qwOt55l+b3JAQO8b/n7WHnCyrhfjbSsrZu3jmuXXxvdfuSOO+g94FXeKvvITfhmzEhx0CIiIpIoJWhJiCxSC+OwUG3Ds97sTYAVV0DR3EGH+LP8LCmJX4O+NL+UG1bcwK3n3xptPQscOMCRH98GQO7ppzPzbW9LT+wiIiKSEK2DloTIGLTc7Czy/WkulB5Z98yyYM1H4h7S1tPGb5//LQBnl53Nhys/TOuxVopyi1hRvmLQumcN3/gmrtsrnj7nU/+G+TJQ7F1EREQGUYKWhGih9MI0F0pvftmrHABwxlugdFHcw37z/G9oD7QDXnfnUAXRATprazl6v9ciN/3iiyl4/dDHioiIyPhSF2cSomWe0j2D84nvggt6n9d+NO4hPcEefvn3XwKwqGgRVfOGXsfMhUIc+tKXAa/eZvnHP57aeEVERCQpStCSEOniLC5M4/iz9gbY5iVenHIBnHBW3MPu33s/DV0NAFyz7BqybOh/tK3/3+/o3r0bgNL3XUvOvMHj2URERCRzlKAlITJJIK0taDXfg15vnBhVN8c9JORC/GT3TwAozy/nHyr+YcjTBdvbafj2twHInj2b0uuuS228IiIikjSNQUtC7Bi0lAoG4JUaaK2Hmh942+avgpPOi3v45v2bqWutA+DdZ7wbv2/oFr0jP/whwcZGAMo//jGyCgpSG7uIiIgkTQnaGPUGQ32F0lPVghYMwJZvw19/BB2H+++bucDbHyf5irSeTfdP5+2nvX3I0/fs20fTT38GQP6KFcz4x39MTdwiIiKSUkrQxqilq28NtJS0oAUDcPeV8MLDEK9c085fQ3crXH5nvyRtW8M2tjV4tTkvW3wZ03KmDXmJQ1/7Oi7gxT373z+V3pmnIiIiMmYagzZGLTF1OGemYpHaLd8OJ2fAUOWaXniobz20sDt23QF4i9RedfpVQ56+44knaN+0CYCiSy8lf/nypEMWERGR9FAL2hg1daSwBS0Y8Lo1MYZMzsDb/9SPYO1HwOdnb8teHtv/GABvXvRmygrKoke6QIDO2m0EW1vImjadQ1/2ltXIKiig7Ob4S3WIiIjIxKAEbYxiC6UnPQbtlZrBY87ict6yG6/UQEUVP939U8Crs3n10qu9IwIBGn/8Y5rvvIvgkSODzlBy/fX4y8uTi1dERETSSgnaGDXHdHEm3YLW1Zzw8Q2dDdy39z4A3rDgDVQUVeACAfbfcAMdm/8CQ4wv66qtxQUCmD/NtUNFRERkzDQGbYxiE7SkW9DyixM+/pfP/pLeUC8A7132XgAaf/xjLzkDcPG7Sjuqqzly221jDlVERETSTwnaGEXKPOX5s8jPSbLI+IJVUFhG3Nmb/RhMK6dtzlLu2ePV5qwsr+SssrNwgQDNd941ZMtZ3ymMpjvvis7mFBERkYlHCdoYRSYJlKRiDTSfH859P8NPEMDb//r3c89Lv4sWRb922bUA3oSAI0eGbDnrO4Uj2NhIZ+225OMWERGRtFCCNkZ9dThTtEjt2o/CqRcNsTPcKnbqRfSs/lC0KPopM0+JFkUPtrYkdLlEjxcREZHxowRtjCIJWsrKPPn8cNkvIDtv8L5pZXD+p+HyO7l/38Mc7vJmfF6ztK8ouq9oZmKXS/B4ERERGT+axTlGkTFoM1NZKP3ws32F0VffAPNXehMIFqwCn79/UfSCct5U8aboVwsqz8ZXWkqwqWn4bk4zfKWlFFSenbq4RUREJKXUgjZG0ULpqagiEFG3ue/z66+DM94MFVXR0k6P7X8sWhT9PWe8p19RdPP7Kb7qylGNQSu56kotsyEiIjKBKUEbg0AwxNFub4mLlI1BA9j7mPd75klQUjFo90929RVFf9upbxu0f9b111OwenX8c4dnd05bv57S665LSbgiIiKSHkrQxqClM8WF0gEC3bDvSe/zwg2Ddm9r2Mb2w9sBeOeSd8Ytim5+P3mnL4l7el9pKWU33ci8//6uWs9EREQmOI1BG4P+hdJTlKDV/xV6u7zPCzcM2j2aoujBo0dp+d9fA5BXWUn5TTcRbG3BVzSTgsqzlZiJiIhMEkrQxiC2DmdK1kGDvu5NgIr1/XcNKIo+K39W3FM0/+puQh0dAJR94P0Urjw3NbGJiIjIuFIX5xj0K/NUmKJWqUiCNudMKCzttysyc9Mwrll6Tdyvh7q7afrFLwDIPe00CtetS01cIiIiMu6UoI1BpIoApGgMWlcLvBZe2X/hhn67DnUc4g97/wDAxgUbObno5LinaP3d7wg2NgJQev312Egln0RERGTCSjpBM7PTzOzLZrY/zr7LzMzF+alJ9rqZlNJC6QAvbwEX8j4v3NBv153P3jmoKPpArreXI7eHx6jNncuMSy5OPiYRERHJmDGPQTOzC4DPA6uB3iHONRfoAAZmDEfHet2JILJIbb7fR54/yULp0Ne96cuBBasJhAJsb9jOwY6D/Oq5XwFwzuxzOLPszLhfP/rQQwT2e/lxybXvxbI1tFBERGQyS+b/5OuAF4Bbwp8/E+eYecB+59yWJK4z4TSlusxTOEELzD+X25/9OXc/dzdHuo/0O+SEwhMIhAL4s/qPeXPOceTHtwHgKylh5lvfmpqYREREJGPGnKA5526JfDazqiEOmwsM6vqc7CItaCmZINBaD0deIADcVBCkevv/YAweP/aHvX/gaM9Rbj3/1n5JWseWLRx77jkASt7zbrLy85OPSURERDIq3ZME5gKLzGyPmfWaWb2ZfWKkL5lZuZktjf0BFqU51lFrCi9Um5LxZ3u98k63z5xBdderADjil2v6S/1fuGPnHf22HfnRjwHIKiig+Iorko9HREREMi7dg5VagALgK0ATcBXwVTNrcc79cJjvfQj4bLwdNTU1HDx4kHnz5lFRUUF1dXV038aNG9m5cycNDQ0ALF68mMLCQmprawEoLCxk1apV1NTU0BFeL6yyspKOjg727NkDQHl5OcuXL2fTpk3R81ZVVVFXV0d9fT0Ah1uDAPS0NbFp0yZycnKoqqqitraW5uZmAJYtWwbArl27ACguLqayspLq6mp6erwWuJUrV+Ke+QN5wK9mzBjN8+TOv9/JW+e9lWe2P4O/ro6yp54CoGvdOh7729/GfE8VFRWUl5ezdetWgKTuqaGhgbo6r2ZoJv856Z50T7on3ZPuSfeUqXuqqUluPqS5kYprj+YkZp8DPuucG3FtBzN7GFjsnDtpmGPKgbIBmxcB9+7atYulS5cmE27Sln/uIdq6e7nmvJP53JuTiMU5+OZinupt4doTZo/6a3dcdAevn/N69t9wA+2PbsL8fhY9+ij+2eVjj0VERERSZvfu3ZHEcZlzbnei38/EdL8/AheY2XTnXFu8A5xzDUBD7LaJsq5XIBiiLVIoPdkuzsPPQfshWgsSGzfWeqyVYy+9RPuj3t84ZrzlzUrOREREppC0jUEzsxPM7BozKxqwKwXrUmRO7BpoJclOEgjP3iwKhRL6WlFuEUduu937gxml174vuThERERkQkn3JIGfAG8fsO2NwL6hWs8mupbOvioCSRdKDydoK/yllOaVxp29GcswZuXPYmlwDq333QfA9AsuIHdhRXJxiIiIyISStgTNOXcA+DnwDTO70cwuNrPv4y1a+x/pum669SuUnsw6aMGAV0EA8C/cwOVLLh9y9maEw3H54stp+/kvodfrZi29/rqxxyAiIiITUrrHoH0QeAW4CW/R2n3Ajc6529J83bRp7khRmadXn4aedu/zwg28b/lb2dm4k7/U/2XQoYbhcKybt46r57+Vl399EQAFq1eRv3z52GMQERGRCSklLWjOuc/Fm8HpnOtyzt3inFvknMt1zp3mnPtuKq6ZKU2dKWpBi5R3Ali4Hn+Wn0+v/HTcQ0vzS7lhxQ3cev6ttN31a1xXFwCzrr9+7NcXERGRCUtFGxPUfwxaEpMEIgla2ekwfQ4ATx54Mrr7U+d+irKCMopyi1hRvgJ/lp9QZyfNv/gFAHlLl1KwevXYry8iIiITlhK0BEXGoBXkJFEo/Vg71HsLzLJwQ3TzY/sfA6A4t5jLFl+GL6v/+Vt+81uCra0AlF5//YRZekRERERSK92zOKecaB3OZMaf7XsCQt4g/0iCdix4jJoD3qrDVfOqBiVnLhDgyE9+AkDOSScx/YI3jv36IiIiMqEpQUtQZAxaSsafmQ9OXgPAUwefoqvXG1u2ft76QV9pvf9+eg8c8K79vmsx36ReTk5ERESGoQQtQdEWtFQkaPNeB7nTgb7uzeysbM478bx+h7tQiCO3eRNfs8vKKLr00rFfW0RERCY8JWgJag5PEige6wSBtkPQEC7JtXADAM656PIar5v9OqblTOv3lfbHHqPnxZcAKLnmarJyklwgV0RERCY0JWgJSnoMWl3MOmcLNwDwQssLHOjwui8Hdm865zjywx8BkDV9OjPf+c6xXVdEREQmDSVoCejpDdF2zBvcP+YxaJHuTX8hzH0dAJv3b47uHpigdf3tb3Tt2AFA8ZVX4pvWv3VNREREph4ts5GAlphFasc0Bs25vgTt5DWQ7Z1jc72XoC0sWsj8GfNxgQCdtdsItrZEx55Zbi4l735XUvGLiIjI5KAELQHNMYvUjmkMWtNeOFrvfV64wdvU3cQzh58BYMOcKg5/73s033kXwSNH+n0197RT8RUVjSVsERERmWTUxZmAfoXSxzIGbe+f+z4v3ABAdX01Docv6HjjD/5G4399l2BT06Cvdu/cRf0NH8YFAoP2iYiIyNSiBC0Bzcl2cUa6NwvLoPwMoK97851/zSG7xhtrhnNxv96+eXO0y1NERESmLiVoCejXgpZoghYK9s3grFgPZgSCAZ547Ql8QcdFtSEYqXSTGU133qVWNBERkSlOCVoCmmMStIQLpR/YDt1eHc1I9+bfDv2NjkAHi+sd+UePDdlyFuUcwcZGOmu3JXZtERERmVSUoCUgMkmgMMdHbnaCpZYi3ZsQTdAii9PO6E7sH0OwtSWxa4uIiMikogQtAZExaGMbfxZe66xkEcycj3MuWt7phBNOTehUvqKZiV9fREREJg0laAmIjEFLePxZoAteqfE+L9wAQN3ROurbvSU3FlX9A77S0lGNQfPNmkVB5dmJXV9EREQmFSVoCYi2oCW6ZPomoAAAHIRJREFUxMYrNRA85n1euAHoXz1gXcUbKL7qylGNQSu56krMP8Y6oCIiIjIpKEFLQF+ClmCCFB1/ZlBRBfQtr7Fg+gJOnnEys66/nmnr18f/frhlbdr69ZRed12iYYuIiMgkowQtAc0d3iSBhMegRRK0E8+G/GJaj7WyvWE7AOvmrcPMML+fso/cFPfrvtJSym66kXn//V21nomIiBwHVOpplI71BmmPFEpPpIuzswkOhBegXei1kG15dQtBFwRgw/wN0UPbHnkk+vnEr/0nlpeHr2gmBZVnKzETERE5jihBG6WW2DqcibSg1f0FCI8tW7gB6OvenOafRmV5JQDOOY7+8QEA8pYupejNb042ZBEREZmk1MU5SrFVBBKaJFAXngyQnQfzV9Eb6mXLq1sAOO/E8/D7vJaxY88+S8/LLwMw401vSknMIiIiMjkpQRul/nU4E+hujIw/W7AK/Hlsa9hGW08bAOvn900KOPrAA9HPMy65OKlYRUREZHJTgjZKkQkCkMA6aM37oGmv93nhBqCveoBhVM31ZnQ65zh6/x8ByD/7bPwnnpiSmEVERGRyUoI2Sk0xLWijniRQ17fW2cDxZ2eVnUVxXjEA3Tt2EHjtNQBmXHJJ0rGKiIjI5KYEbZT6F0ofZYIW6d7ML4Y5Z/LK0Veoa60DhujeNGP6xRelIlwRERGZxJSgjVJkDNq03Gxyskfx2EKhvvqbFesgyxdtPQNYP89L0FwoxNEHHgSg4Nxz8ZeXpzZwERERmXSUoI1SpAVt1BMEGnZDZ6P3ucJLxiIJ2omFJ3LKzFMA6Hr6aXobGgB1b4qIiIhHCdooNYXXQRv1+LO9/ceftfW08fTBp4G+6gEArX/0Jgfg8zH9ogtTFa6IiIhMYkrQRqmvBS3B8WdFC6BkIU+89gS9zqtEEKke4Hp7aXvoYQAKV68mu7g4lSGLiIjIJKUEbZT6CqWPIkHr7YF9j3ufF64Hs+jyGvnZ+bxuzusA6Ni6lWBTE6DFaUVERKRPUgmamZ1mZl82s/1x9s03s9+YWYuZdZnZk2a2Pt55JoNoC9poErT6pyDQ6X1euIFgKEh1fTUAq09YTa4vF4Cj4e5N8/uZ/saNKY9ZREREJqcx1eI0swuAzwOrgd6B5zGzbOABoAi4EWgHPgo8ZGZnOueeTybo8dYdCNLR4xU3LxlukkAwAK/UwFO39W2rWM/Oxp00H2sGYro3e3poe+RRAAqrqvDNmJGW2EVERGTyGWux9HXAC8At4c+fGbD/QmApsNE59ycAM3sEqAc+CNw8xutmxIiF0oMB2PJt+OuPoONw3/asbHj6J2wu7HvMVfO86gHtjz9O6OhRQN2bIiIi0t+YEjTn3C2Rz2ZWFeeQVUAP8OeY77SZWQ1w7liumUmxhdIHzeIMBuDuK+GFhwHrvy/UC3/+EpsrTgVgWekyZuXPAvoWp7W8PKafvyFdoYuIiMgklK5JAnOARuecG7C9AZh0K7G2dA5TRWDLt8PJGcDA24XXsn28wDGgr3pAqLub9kc3ATBtwwayCgtTH7SIiIhMWmPt4hxJDhCIsz0Y3jcsMysHygZsXpSCuMakXx3O2C7OYMDr1sSIl5wBbM7Pj35ef+IaANo3/4VQpzeJYMabtDitiIiI9JeuBG048TOZ/j4EfDbejpqaGg4ePMi8efOoqKiguro6um/jxo3s3LmThvDK/IsXL6awsJDa2loACgsLWbVqFTU1NXR0dABQWVlJR0cHe/bsAaC8vJzly5ezadOm6HkP554c/by7div+JQspLy9nz0O3c07smLM4Nhd4CVp5by9L2pqpfq6awp/+lHzACgo4PH8+T4WvNZ73VFVVRV1dHfX19QBUVFRQXl7O1q1bAcjJyaGqqora2lqam70JDsuWLQNg165dABQXF1NZWUl1dTU9PV4Su3LlShoaGqirq9M96Z50T7on3ZPu6bi9p5qaGpJhg3shEzyB2eeAzzrnLGbbj4C3OOdmDzj2LqDSObdkhHMO1YJ2765du1i6dGlSMSfqO4++wLcf9SaevvClS/D7wj3Df/89/PrdQ36v04y1J80jYMY7jrbxmY3/ReikjTy/Zi2uu5sZb/4n5n7ta+NxCyIiIjKOdu/eHUkclznndif6/XS1oB0GSs3M75yL7eqcDRwY6cvOuQa88WpRkdJImRBZpHZ6bnZfcgaQP/zK/0/m5xEIx72+swvyi2n782O47m5AtTdFREQkvnRNEngS8AHRDMTMZuCtm5Zcm18GRKsIDFxiY8EqKCxj0OzNsL+EuzdzQyHO9c2ABauii9NmzZjBtDVr0haziIiITF7pStAeBHYDt5nZ+8zsUuA+vPFnP0zTNdOmaag6nD4/nPt+4g2rC9E3QWBV9zHyX/9+gh1dtIf7uqdf8EYsZ5R1PUVEROS4kpYEzTnXC1wMbAa+BfwKrzv1Qufcy+m4ZjpFWtBKCuJUEVj7UTj1okGb/56Tw5FsHwDrplXA2o/Q9ugmCHg9vlqcVkRERIaSdILmnPtc7ASBmO31zrl3OOeKnHP5zrk1zrnHk71eJjR3eElV3DqcPj9cfies/2S/zZHZmwDr3vIT8Pmj3Zu+khIKV65MX8AiIiIyqaWri3NKGXIMWoTPD4tjBvyv/Gc2z/em/J5ecjpzZsyjt7mZjiefBGD6RRdi2ZlY4UREREQmAyVoI+gOBOmMFkofZszYgR3Rj4eWvYVn2/cDsG7eOgDaHnoYgt55itS9KSIiIsNQM84ImmOqCMTt4ow4sIMAsH1aEQ/sfzi6ef08r7xTpPZmdnk5+eeck5ZYRUREZGpQgjaCfoXSC+NMEgACoQC3H3qCu+fP9SYGvPAbAAxjy2tbOCVUSudf/wrAjEsuxrLUcCkiIiJDU4I2gpbOvnV2BxVKx0vObtp0I9XZHZjrn3g5HN/b/j2yXniAdeGKDZq9KSIiIiNRU84I+regDU7Qbt95O9WvbQHADVHtoPzJFwDwz51L3plnpiFKERERmUqUoI1guDFogVCAu5+7e4g6Ap7SVseSV73PhZdclNGSVSIiIjI5KEEbQWwL2swBC9Vub9jOke4jceoI9Dnvub69r608OcXRiYiIyFSkMWgjiIxBm543oFA60HqsdcTvn/f3EACvlYCbPzP1AYqIiMiUoxa0EURa0OKNPyvKLRr2u7ObHIsOep8fP90oylOCJiIiIiNTgjaCaBWBODM4V5SvoDSnCHPxOznPe7Zv+7Nnl7KifEV6ghQREZEpRQnaCIZrQfNn+bm89OwhZ2+uedbr3txXBhuq3oU/K/46aiIiIiKxlKCNoDmcoA2cIBDxPjeDdZ1dg7bPO+xYcNj7/NqqhVy7/Nq0xSgiIiJTixK0ETSHJwmUDFHmyX9wJ7ceOsylgf4J3Hnh1jOAd37ov9R6JiIiIqOmBG0YXT1BugJegfPieIXSnYMDO/ADc6edGN38xfO+wFv3lQOQt3QphRWLxiNcERERmSKUoA0jdpHaeGPQaHkFulsA2Jbt8AUdb2gsp6q6maz6Q4BKO4mIiEjitA7aMGIXqY03i5MDOwDoDcGCR+q55qkgMztfo4GvRw/pbTyMCwQwv7o4RUREZHTUgjaM2ELpxfEmCRzYgQvBC4/P4q2beyjqHHxI009+Sv0NH8YFAoN3ioiIiMShBG0YTSN1cR7YQePfp8Gr3r6hqmy2b97MkdtuS0OEIiIiMhUpQRtGc2wX58AEzTncq9tpfqFw2FqcAJjRdOddakUTERGRUVGCNox+hdLzB3Rxth2k8+VWgsd8Q7acRTlHsLGRztptKY9RREREph4laMOIzOKckZdN9oBC6RzYQbAnsccXbG1JVWgiIiIyhSlBG0Z0kdohxp/5ckKDtw/DV6Ri6SIiIjIyJWjDiIxBi7tI7YEdFJT10F3AqMag+WbNoqDy7JTHKCIiIlOPErRhRAulD7EGmmXBE6/LHdUYtJKrrtRaaCIiIjIqStCGERmDNqgFraMRjtbTacYdq4I8vWiIFM287dPWr6f0uuvSGaqIiIhMIUrQhhFN0AYuUhuuIPBMbg49PvjG27I4dkbFoO/7Skspu+lG5v33d9V6JiIiIqOmUk9D6OoJ0h3wJgEMakELJ2jb8nIBCPqMgm5HEMg59VTKPnwDvqKZFFSercRMREREEqYEbQj9qggMHIMWTtC2FxYBcFZoLsG9LwNQ9KZLmHHhheMSo4iIiExN6uIcwrBVBA7sIAjsyPEB8MaDs6K7CteuHY/wREREZApTgjaE2CoCxbEtaF0t0FzHizl+OvC6QE9/oRsA38yZ5J1xxrjGKSIiIlOPErQhNPcrlB4zjuzgTgC25Xrjz7JCjhnPvAxA4Zo1mM83bjGKiIjI1JT2BM3M/mhmLs7PB9N97WQ0D9WCNmCCQOXh6dDeAah7U0RERFJjPCYJzAV+A3xnwPYXx+HaY9YULvNkBkWxhdIjEwTyCwA4/0Ax4NXYLFxz3rjGKCIiIlPTeCRo84C7nHNbxuFaKRNpQZuR5+9fKP3ADg76fLzm8xahXRIef5a7ZAn+8vJxj1NERESmnrR2cZpZHlAC7E/nddIhMgatX6H0ng5ofJ7t4e7N6Z2OaS8dBGDa2jXjHqOIiIhMTekegzY3/PsGMztiZgEzqzGzVWm+btLiVhE4uAtw0QkCK/ZlYc4rlV64tmq8QxQREZEpKt1dnHlAPbAT+HegFPgC8JCZneqca4j3JTMrB8oGbF6UzkAHaurwxqD1a0EbMEFg3aszgCNYQQEFlWePZ3giIiIyhaU1QXPO7Qbmx24zs6eB54B/AT47xFc/NNS+mpoaDh48yLx586ioqKC6ujq6b+PGjezcuZOGBi/vW7x4MYWFhdTW1gJQWFjIqlWrqKmpoaPDm3lZWVlJR0cHe/bsAaC8vJzly5dzsOkoAF2tR+jp6aGuro7ptQ8w04znc/zgHKc81w7AsVNOwXJyqK2tpbm5GYBly5YBsGvXLgCKi4uprKykurqanh6vdW7lypU0NDRQV1cHkPZ72rRpU/S8VVVV1NXVUV9fD0BFRQXl5eVs3boVgJycHKqqqnRPuifdk+5J96R70j2N4Z5qampIhrlwF914MrPtwEvOubcNsX+oFrR7d+3axdKlS9Man3OOJbc8yLHeEO9ft5BPvel0b8f311LT+jzXnzCbBQ2Ob9weBGD2LZ+m5Kqr0hqTiIiITB67d++OJI7Lwg1WCUlrC5qZVQEznHP3D9jlA4bMDMNdn/26P80s9QEOoSsQ5FhvuFB6ZA20QDccfpZtM7zlNc7a2xf+NK1/JiIiIimU7kkCa4G7zWxmZIOZzQcWA7vSfO0xiy3zFK0i0PB3CPWyPTxBYNUr3m///PnknHTSuMcoIiIiU1e6E7Q7gE7gfjO71MzeAfwB6AD+J83XHrPm8AQBiGlBixRIz8slt8excN8xAKZVqfVMREREUiutCZpz7hCwHmgEbgN+ChwGNjrnDqfz2sloiqnDWVzYl6C9mOOnIyuLM15x+MJdoCrvJCIiIqmW9koCzrnngLek+zqp1NIZpw7ngR3URtY/i4w/y86m4NyV4x2eiIiITHFpL5Y+GfUfg5YDwQAc2t1XIL3Oe2wFlZX4phVmJEYRERGZupSgxRGpwxktlH54DwSPsT0vl/Jmx+wmb3kNdW+KiIhIOihBiyMyBq0o348vy6IF0g9kZ3NWXezyGqq/KSIiIqmnBC2O5s5wmaeY8WeRAumR8We+WbPIXbIkI/GJiIjI1KYELY5IF2fsDM5tubn4go5l+7wEbdqa87AsPT4RERFJPWUYcUQmCRQX5EAoCAd3si0vl9Nehfzw/AGNPxMREZF0UYIWR3N4DFpJoR+OvERnbyfP5/hZsddb+wwzCtdo/JmIiIikhxK0AZxz0UoCxQU5cGAHz+TmEDSL1t/MO+MMsktKMhmmiIiITGFK0Abo7AnSEwwXSi/MgQPb2ZaXS1GHY+Eh7xh1b4qIiEg6KUEboN8iteEWtG15uZwZu7yG6m+KiIhIGilBG6C5X5knP8EDz/BMbm50eY2swkLyzzorU+GJiIjIcUAJ2gCxLWizQwd5wXXSaRZtQStYvQrz+zMVnoiIiBwHlKAN0BJepBagvP05tuXmcvIhKOr0tk1bW5WhyEREROR4oQRtgNgWtKKWv7Mtr697EzRBQERERNJPCdoAkTFoWQZ5jbvYnpfLWeH1z3IqKsiZNzeT4YmIiMhxQAnaAJEWtJn5fg4deoaWoI/TXvX2qfVMRERExoMStAEiY9BOyT/KdtfBsn2O7HABgWlrVT1ARERE0i870wFMNJEWtMrsV9jmy41WD7CcHApe//pMhiYiIiLHCbWgDRAZg3aG1bEtZv2zgtedQ1ZBQSZDExERkeOEErQBIi1oc0MvcLQjm/JWb3vhGo0/ExERkfGhBC2Gcy7agtYS2svyur59hSrvJCIiIuNECVqMjp4ggaBjFq08n93VV96pvIzcU0/NcHQiIiJyvFCCFqM53L25NOtlnsnO5YxXvARt+toqzCyToYmIiMhxRAlajMj4s9NtL92Hc8gLV32apu5NERERGUdaZiNGU3j82ay8F7EXvW0uyyhcvTqDUYmIiMjxRi1oMVrCCVpP/oHo+mdZp5+Gb+bMTIYlIiIixxklaDGaOgLMoJ1DwQAnHfa2lWzYmNmgRERE5LijBC1Gc0cPS7P2ETqQG902TfU3RUREZJwpQYvR1NlDhf85TtrnzdjsLcghf/nyDEclIiIixxslaDGaO3rIz3uRM+vC9TdXno1lax6FiIiIjC8laDGaO3vIaz/M9G7vz3POvzizAYmIiMhxSQlajO72VgpeC0X/XLRuQ+aCERERkeNWWhM0M7vUzLabWbeZNZrZT82sJJ3XHKuOtlZWvvJ9Fu/xHsnR2fn458zJcFQiIiJyPEpbgmZma4DfAi8B7wA+C/w/4DfpuuZYdLS1cvd1Vexcv4pLH3yeuU3e9twjXdx9XRUdba2ZDVBERESOO+kcAX8TsB94h3MuBGBmbcDPzOxM59wzabz2qHS0tfKny9ZwVl0QN2BfTi+ctaWRTZetYeOvH6dwelFGYhQREZHjTzq7OFcBj0SSs7BHwr/PTeN1R+2+j/4jp9QFARhYCj3y51Prgtx38z+Na1wiIiJyfEtngjYHaBiwLfLn8jRed1Q62lo5ubZxUMvZQA44ufawujpFRERk3KSzi9MPBGI3OOeCZgaQM9wXzawcKBuweQnAiy++mJLgNv/qW8xrPjYog4zrGPzsP29m/RU3p+TaIiIiMrXF5CvD5jxDydQqrCM1XH0Ib1LBIJdeemnqoxmNL9XBl+7IzLVFRERkspoPbEv0S+lM0AJAfuwGM4tkkcdG+O73gHsGbJsGnAbsAnpSEWAci4B7gbfgzT6V1NGzTS893/TRs00vPd/00bNNr5Gebw5ecrZ5LCdPZ4J2GG8cWqzZ4d8Hhvuic66BwePXALamIK4hhbtfAV5yzu1O57WON3q26aXnmz56tuml55s+erbpNcrnm3DLWUQ6Jwk8CVxkZv6YbReFf9ek8boiIiIik1o6E7Rb8Qb6/97M3mxmHwS+AfzRObcnjdcVERERmdTSlqA557YAbwVOwBtP9h94VQSuTNc1RURERKaCtM7idM7dizeAbrI4DHw+/FtSS882vfR800fPNr30fNNHzza90vp8zbmRVrwQERERkfGUzjFoIiIiIjIGStBEREREJhglaCIiIiITjBI0ERERkQlGCRpgZpea2XYz6zazRjP7qZmVZDquqcLM/mhmLs7PBzMd22RkZqeZ2ZfNbH+cffPN7Ddm1mJmXWb2pJmtz0Sck9EIz/ayId5jLbw9AjPLMrN/NbPnzeyYmb1sZt8xs5kxx+jdHaNRPl+9v2NgZtlmdrOZPWtmnWb2kpl9xcwKY45Jy7ubqWLpE4aZrQF+C/wOuAVYAHw5/PsNGQxtKpmLtwbedwZsfzEDsUxaZnYB3pTu1UAvA/79NbNs4AGgCLgRaAc+CjxkZmc6554f34gnj5GebdhcoAO4eMD2o+mNbkq4FfgA8DVgC3AG8AVgCV7FGb27yRn2+YaP0fs7Nj/AW7/1c3hlm5YAX8R7nu9J67vrnDuuf4BfAy8DWTHb3gM44MxMxzcVfoAjwCcyHcdk/wn/R+FnwEa8ZMIN2P+m8Hv7hpht04FW4FuZjn8i/4z0bMPHfBN4NtOxTrYfvIoyQeA/Bmz/ePh9PUnvbnqfb/jPen8Tf7bT8f7C9sUB2z8H9OAVQ0/bu3vct6ABq4CHnHOhmG2PhH+fCzwz/iFNHWaWB5QAg7qMJDHOuVsin82sKs4hq/D+o/HnmO+0hbswzk1/hJPXKJ4teH9j1nucuCLgV3g9FbH+Hv5dgt7dZIzm+e5D7+9YdADz8JKtWO14rez5pPHd1Rg0mAM0DNgW+XP5OMcyFc0N/77BzI6YWcDMasxsVUajmprmAI0u/Fe4GA3oXU6FucAiM9tjZr1mVm9mn8h0UBOdc+5F59y7nHPbBuw6HzgE7Ebv7piN8vmC3t+EOedCzrmDzrkuM/OZWWF4OMTHgTucc62k8d1VggZ+IBC7wTkXDH/MGf9wppw8oB7YCbwduAKYgdc/r//wplYOA97lsCB6l1OhJfzz78CFwEPAV83sAxmNahIys3Pwxut8wTkX6SrSu5sicZ4v6P1N1g68lrOH8cai/XN4e9reXXVxDk91sJLknNsNzI/dZmZPA88B/wJ8NhNxHYf0LifJOfdPAzb9yczmA58CfpiBkCal8DO7F3gQ+P4ovqJ3NwFDPV+9v0l7J1AMnAd8Bm9M340jfCepd1cJmpf55sduMLNI1nts/MOZ+pxzdWb2LLAs07FMMT0MeJfDctC7nC5/BC4ws+nOubZMBzPRhZcvegh4DbgypltI724KDPN8h6L3d5TCjQ0AW8wsC/iSmX2VNL676uL0qtDPGbBtdvj3gXGOZcoxsyoz+4c4u3zob8apdhgoNTP/gO2z0bucFDM7wcyuMbOiAbt8GQloEjKzAuB+vH/vL3HOdcTs1rubpOGer97fsTGzOWb2wXBLY6xn8PKnk0jju6sEDZ7EW4cn9uFG1o3RAn7JWwvcPXBBSmAxsCtjUU1NT+L9B/eSyAYzm4G3tpfe5eT9BG8cZaw3AvvU+jC88FpR9+D9ZfgC59yRAYfo3U3CKJ4v6P0di1y8buKrBmw/K/x7H2l8d9XF6S3w9/+A35vZ94ETga8Cf3TO7cloZFPDHcBHgPvN7Ot4kzI+jTd9+X8yGdgU9CDejK3bzOzf8Naf+yje36g1xiQJzrkDZvZz4BvhFcSfB96Ct+jn9RkNbnK4DbgA71ktNLOFMfta0bubrGGfr3Nup97fxDnn9pnZr4FbzAzgabzk7FPAL5xzr5lZA+l6dzO9ENxE+MF7Ubfj9Rc34r3sRZmOa6r84K28fG/42XYAjwKVmY5rMv/gLZTo4myfh/c36VagC3gcWJPpeCfTzzDPNh9vQduXwv+teB74cKbjnQw/4f9ZDfXzWPgYvbvpfb56f8f2bHOAfwP2AJ14E9w+CfhjjknLu2vhk4uIiIjIBKExaCIiIiITjBI0ERERkQlGCZqIiIjIBKMETURERGSCUYImIiIiMsEoQRMRERGZYJSgiYiIiEwwStBEREREJhglaCIiIiITjBI0ERERkQlGCZqIiIjIBKMETURERGSCUYImIiIiMsEoQRMRERGZYP5/93PHp3d+eNUAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"fig, ax = plt.subplots(figsize=(6,4), dpi=120)\n",
"\n",
"ax.plot(np.arange(30), middle_row_over_time[0][1], '-o');\n",
"ax.plot(np.arange(30), middle_row_over_time[10][1], '-o');\n",
"ax.plot(np.arange(30), middle_row_over_time[20][1], '-o');\n",
"ax.plot(np.arange(30), middle_row_over_time[50][1], '-o');\n",
"\n",
"ax.set_ylim([0, 40]);"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAmwAAAGgCAYAAAAXVzt3AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAASdAAAEnQB3mYfeAAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4wLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvqOYd8AAAIABJREFUeJzs3X18VOWd///XlckNkCAEyIAQCCHcKSAaqBA1NRKtdaur263bGwu9VbFd7dq73fbb1v22tXbbrrXt97vo1m39xrb+WtfdWm2riwE02CQaopAgBAlJIEKYBEIwAZJh5vr9MZOQ+0xmJsncvJ+Ph48455w55zqC+uY65/p8jLUWEREREYlcCRM9ABEREREZngKbiIiISIRTYBMRERGJcApsIiIiIhFOgU1EREQkwimwiYiIiEQ4BTYRERGRCKfAJiIiIhLhFNhEREREIpwCm4iIiEiEU2ATERERiXAKbCIiIiIRToFNREREJMIlTvQAAmWMmQZcCxwBuiZ4OCIiIiLDSQbmAy9ba9tCPVnUBDZ8Ye3ZiR6EiIiIyCjcCvwh1JNEU2A7AvD73/+exYsXT/RYRERERIZ08OBBbrvtNvDnl1BFU2DrAli8eDErVqyY6LGIiIiIBCIsr3Fp0YGIiIhIhFNgExEREYlwQQc2Y0yiMeaLxph9xpgzxphaY8xDxpjUXsdcbYwpNsa0G2NOGGO2GmPeE56hi4iIiMSHUGbYHgW+C/wS3wqIR4B7gC0Axpj1wDbgPLAR+CwwHdhujFkawnVFRERE4kpQiw6MMVOBTwIPWWt/4N+81RgzE/i6MeazwNeBd4BbrLVd/u/9xb/to8D/DnHsIiIiInEh2FWiHUAm0L8QXLv/nJOBGuCl7rAGYK09bow5CcwI8roiIiIicSeowGat9QJNAMYYBzAJuAr4MvALf0Xfr/T/njFmJZCB71HpkIwxTv9xveUEM1YRERGRaBeOOmy7ge7CaC/ge49tAGNMMvDvQDnw3Ajn/BzwwGA7ysrKaGpqIjMzk+zsbEpKSnr2FRYWUlVVhcvlAmDZsmWkpqZSWVkJQGpqKuvXr6esrIyOjg4AcnNz6ejooKamBgCn08mqVasoLi7uOW9+fj51dXU0NjYCkJ2djdPppLy8HIDk5GTy8/OprKyktbUVgJUrVwJQXV0NQHp6Orm5uZSUlNDV5Zt0XLduHS6Xi7q6OgDdk+5J96R70j3pnsbtnt7cU8XBU15MSipXrFjOuca9eM+7o/qeIunXqaysjHAy1trQTmDMCiAd3wzbt/DNsN03yHFPALcA6621b49wzqFm2J6trq5W4VwREZEguT1etuyopai0npb2CzVdM9JS2JiXxT0FOSQ5VPUrVHv37u0OkiuttXtDPV/IM2y9BrHTGJMAPGiM+b619mj3McaYfwE+DNw4Uljzn9MFuHpvM8aEOlQREZG45vZ4uauogu01zfT/v2pLeycPbz3A1rea+Or7l7N+0UwFtwgS7CrROcBtwB+ttb17ZO3BVyokCzjqP/Z+4IvA31hrXwltuCIiIhKsLTtq2V7TDED/52vdn6veOc3G/3iNjLQUPrZuAWsXptPReZ5pk5NZuzBdIW6CBDvDloKv3trXgO/32r7a/7MBwBjzMeCHwCestc8HO0gREREJjdvjpai0HsPAsDaY5vZOflLc96GYHptOnGBXiTYYY34HfNP/qHIXvrD2deBJa+1RY8z7gCeAp4AGY8w1/U7zurW2M+iRi4iISMAq6lv7vLMWDD02nTihvMO2EfgS8Cl8iw0OAw8C/+rf/zEgCfi4/6/+soH6EK4vIiIiAWo7G1pYg4GPTWelJXPdMicFyzKYkZqiR6ZjKOjA5i+I+5D/r8H2fxJfNwQRERGZYNMmJ4f9nC3tXTy9q5Gnd/lKcOiR6djRP00REZE4sHZhOrPSkgesDg2n7kemH/y3Vyl5uxm3xzuGV4svCmwiIiJxIMmRwKa8hQEtOAhW/0emVz20jZ8Wv63gFgYKbCIiInHinoIcNix3AozpTFu3Zv+M2989WsqZrvPjcMXYpcAmIiISJ5IcCTy2cQ1fumEps9JSxu26bxw5xdrvvqTZthAosImIiMSRJEcC9xYu4S9f28CvPnMlK+ddNC7XPdPl0fttIVBgExERiUNJjgSuWZLBf3/uar50w1IyxmnGTe+3BSfk5u/jxd9kvlrN30VERMLP7fFSUd9K29ku0lISqahv5dflh2luH9sa96vmXRSTRXjD3fxdgU1EREQG5fZ4KT90gu+/sJ/qd06P6bVirYZbuANb9P8TERERkTExno9Nm1XDbViaYRMREZGAdD82PdHRySs1zWzb76KlI/SWV4OJ9hm3cM+whdJLVEREROJIkiOBvJyZANx82dwxfWTaPeP25pFTPLZxTVSGtnCK77sXERGRoPV/ZDol2RH2a2zb7+L/bj8Y9vNGGwU2ERERCUl3bbeKb1zPFfOnh/38Pyl+mx9vPRDX77UpsImIiEhYTElO5Heb88K+QMFaX2iL5xZXCmwiIiISNmPZSSGeW1wpsImIiEjYjVVJkO4WV3c/uSuuQpsCm4iIiIyZsZpx27bfxdf/qypuQpsCm4iIiIy5sZhxe3pXI3nfK46LR6QKbCIiIjJuwj3j1tLRFRePSBXYREREZNz1nnH7h+uXYExo54v1em3qdCAiIiITJsmRwD9cv7SndEcoflL8NtbC329YHHOdEWLrbkRERCQq/f2GxWxY7gzpHN2hLxYfjyqwiYiIyIRLciTw2MY1YWlxtW2/i0d31IZpZJFBgU1EREQiQjhbXG15uTamuiIosImIiEhE6d3ialZaclDnONPl4Y6fl8fMo1EFNhEREYk43bNtpV8r5PY1mUGd440jp2Jm5agCm4iIiESsJEcC3/vgqqAXJPyk+G1+vPVA1M+0KbCJiIhIROtekBBMvbZYWTmqwCYiIiIRr7te230blgT1/WhfOarAJiIiIlHj7zcsDmoFqQGKShuidpZNgU1ERESiRpIjgV/fuW7Utdos0NzeSfmhE2MzsDGmwCYiIiJRZUpyIpuvzQnqu99/YX9UzrIpsImIiEjUuacgJ6iVo9XvnI7Kd9kU2ERERCTqhLJyNBq7ICiwiYiISFQKduVoNHZBCDqwGWMSjTFfNMbsM8acMcbUGmMeMsak9jtuqjHm08aYV4wxnwh9yCIiIiIX/P2Gxayad9GovvPGkVNR9Wg0lBm2R4HvAr8EbgUeAe4BtgAYY2YaY4qAJuAxIB/fqloRERGRsElyJPDV9y8f9feiqcxHUIHNGDMV+CTwr9baH1hrt1prf4YvtH3EGJMMZAKLgPuBtWEar4iIiMgA6xfNHHWj+Ob2TirqW8doROEV7AxbB75A9r1+29uBRGCytXa3tfYaa+2/A20hjFFERERkWEmOBDblLRz19050dIZ/MGMgqMBmrfVaa5ustWeNMQ5jTKox5gbgy8AvrLUhBTRjjNMYs6L3X0BwBVdEREQkLtxTkDPqLgiv1DSP0WjCKzEM59gNrPD//Qv43mML1eeABwbbUVZWRlNTE5mZmWRnZ1NSUtKzr7CwkKqqKlwuFwDLli0jNTWVyspKAFJTU1m/fj1lZWV0dHQAkJubS0dHBzU1NQA4nU5WrVpFcXFxz3nz8/Opq6ujsbERgOzsbJxOJ+Xl5QAkJyeTn59PZWUlra2+qdWVK1cCUF1dDUB6ejq5ubmUlJTQ1dUFwLp163C5XNTV1QHonnRPuifdk+5J96R7CvGe7lzs5f6jhk6PJRB/3tNI4fRmEhNMWO+prKwsoOsHylgb2A0NeQLf7Fc6cBXwLXwzbPf1O2YhUAd8ylr7RADndAIZ/TbnAM9WV1ezYsWKQb4lIiIiAl95ejdP72oM+Pin7lxPXs7MsI5h79693UFypbV2b6jnC3mGrdcgdhpjEoAHjTHft9YeDeGcLsDVe5sZbVU8ERERiUsFyzJGFdii4T22YFeJzjHGbDbGzO+3a4//nFkhj0xEREQkCDNSU0Z1fDS8xxbsKtEUfPXW7ui3fbX/Z0PQIxIREREJwdqF6aMq8bFtvyvi67EFu0q0Afgd8E1jzD8ZY24wxnwZ+DrwZCiPQ0VERERCkeRI4LplgTeGb+noivh6bKF0OtiIr9PBp4Bngc8CDwKfCcO4RERERIJWsKz/2sXhtZ3tGqORhEfQiw6stV3AQ/6/Rjq2HrWlEhERkXEy2vfY0lLCUels7IQywyYiIiISkUb7HlssPxIVERERiUhJjgTuWBd40Ypflx+O6IUHCmwiIiISk9YuTA/42EhvBK/AJiIiIjGpo/P8qI6P5IUHCmwiIiISk6ZNDvwdtmCOH08KbCIiIhKTVs+fRqCdLY3xHR+pFNhEREQkJu0+0oa1gR1rre/4SKXAJiIiIjFptO+k6R02ERERkXGmd9hEREREItzahelMSXYEdOyUZMeoyoCMNwU2ERERkQinwCYiIiIxqaK+lTNdnoCOPdPlUeFcERERkfGmRQciIiIiES4tJXFUx2vRgYiIiMg4e30Ujzgz0lK06EBERERkPLk9Xn5d3hDw8XesX0CSI3JjUeSOTERERCRIFfWttLQH/k7amqzInV0DBTYRERGJQaNdQNDReX6MRhIeCmwiIiISc2JpwQHA6O5GREREJMK5PV5+XnIooGMNMCvCFxyAZthEREQkxmzZUcvLB1oCOtYCm/KyInrBASiwiYiISAxxe7wUldZjAjy+YFkGmwtyxnJIYaFHoiIiIhIzRrs69DPXZEf87Bpohk1ERERiSKytDu2mwCYiIiIxwe3xUrzPNarvRPrq0G56JCoiIiJRz+3xcldRBdtrmgM6PlpWh3bTDJuIiIhEvS07agMOaxA9q0O7RccoRURERIYw2pWhABuWO6NidWg3BTYRERGJat0rQ22Ax9++JpPHNq6Jmtk1UGATERGRKDfalaGFlzijKqyBApuIiIhEsVheGdqbVomKiIhIVIr1laG9aYZNREREolKsrwztLfpGLCIiInEvHlaG9qbAJiIiIlEnHlaG9hb0qI0xicaYLxpj9hljzhhjao0xDxljUnsdM98Y85/GmFPGmLPGmFJjzLXhGbqIiIjEq3hYGdpbKIsOHgU+Bvwz8AawHPgOMA/YZIxJBP4MTAPuA9qB+4EXjTGXWWsPhHBtERERiWNpKaOLMNG4MrS3oAKbMWYq8EngIWvtD/ybtxpjZgJfN8Z8FrgeWAEUWmu3+b+3FWgENgNfDHHsIiIiEmfcHi9bdtTy//5SF9Dx0bwytLdgZ9g6gEygrd/2dv85JwPrgS5ge/dOa+27xpgy4MogrysiIiJxqncZj0AXG0TzytDeggps1lov0ARgjHEAk4CrgC8Dv7DWthlj5gAt1tr+7wO6gHXDnd8Y4wQy+m2OzmUdIiIiEha9y3iMtNjA+I+J5pWhvYWjcO5ufI8+AV4A7vH/fTLgHuR4j3/fcD4HPDDYjrKyMpqamsjMzCQ7O5uSkpKefYWFhVRVVeFy+SoeL1u2jNTUVCorKwFITU1l/fr1lJWV0dHRAUBubi4dHR3U1NQA4HQ6WbVqFcXFxT3nzc/Pp66ujsbGRgCys7NxOp2Ul5f7bjQ5mfz8fCorK2ltbQVg5cqVAFRXVwOQnp5Obm4uJSUldHX5XpRct24dLpeLujrftK7uSfeke9I96Z50T7qnwe/p1dIyHi/pJFAz05K5dq7hffPaeGXH9nG/p7KysoDHGggzcAJslCcwZgWQjm+G7Vv4ZtjuM8Y8ARRYaxf2O/4J4FprbfYw5xxqhu3Z6upqVqxYMci3REREJFaV1p7goz8PPAQ9+ZkryV/SP0qMn71793aH45XW2r2hni/kGbZeg9hpjEkAHjTGfB/f+2uTB/lKMjBsRLbWuvA9Ou1hzGhK44mIiEgsGW0Zj47O82M0kokR1Bt4xpg5xpjNxpj5/Xbt8Z8zC2gGZhpjkvodMxs4Fsx1RUREJL64PV5Ka09Q0/TuqL4X7WU8+gt2hi0F2AJ8Dfh+r+2r/T8bgFLAAdwE/AHAGHMRkAf8JMjrioiISBzoLt9RVFpPS3vgs2uxUsajv2BXiTYYY34HfNP/qHIXvrD2deBJa+1RY4wL2As8boz5GnACX+FcCzwWjsGLiIhI7AmmfEe3WCnj0V8od7MR+C7wKeBZ4LPAg8BnAKy154H3Ay8DDwNP4QuI77PW1odwXREREYlhoynf0a072MVKGY/+gl50YK3tAh7y/zXUMY3A7cFeQ0REROKL2+OlqLS+p45aoGalpbApL4vNBTkxN7sG4anDJiIiIhIWFfWto3pn7f7rl3Jl9gzWLkyPyaDWTYFNREREIsZoy3csm5NGXs7MMRpN5IjdKCoiIiJRZ7TlOGKtfMdQFNhERERkwnXXWzvZ0cm0yf1LuA5kgIwYLN8xFD0SFRERkQkTbL21WC3fMRQFNhEREZkQwdRb6149GqvlO4aiwCYiIiITIph6a7FevmMoCmwiIiIy7kZTb23apCQe/OBKZqamxHz5jqEosImIiMi4G029tbZzbmampsRF+Y6hxF9EFRERkQk32nproz0+1iiwiYiIyLhTvbXR0SNRERERGXNuj5eK+lbaznYxbXIyq+dPIzXFQUenZ9jvGXwLDeKl3tpQFNhERERkzAxVZ23qpMQRwxrEX721oSiwiYiIyJgYrs7au+fO9/ncf7VovNZbG4oCm4iIiIyJQOusXZ0zkwPH22lu7+zZFq/11oaiwCYiIiJhF2idNQMcON7Oy18tYPeRtp533OK13tpQFNhEREQk7AKts2aB5vZOdh9pi+s6ayNRdBUREZGwU5218FJgExERkbBTnbXwUmATERGRsFu7MJ20lJHfvDJAhuqsjUjvsImIiEhI+hfFXbswnV+VNdDeeX7E76rOWmAU2ERERCQoQxXFTU120NHlK4rrSDB4vFZ11kKkwCYiIiKjNlxR3O6wluQwPPXZdZQeOklRaYPqrIVAgU1ERERGLZCiuG6PpfTQSe4tXMLmgpwBj00V1AKnwCYiIiKjMpqiuEWlDT2zaKqzFjxFWxERERmV7qK4w4U1uFAUt6K+dTyGFdMU2ERERGRUVBR3/CmwiYiIyKioKO740ztsIiIiMirtXe6AjjP4VoOqKG7oFNhERERkgMGK4SY5EvhVWQMP/GFvQOdQUdzwUWATERGRHkMVw81ISyZrZioVDb4FBMkOw7I5U6l657SK4o4DBTYREREBhi+G29zeRbM/wM1MTeLxT7yHlfOm8eiOWhXFHQcKbCIiIgIEVgwX4G+uyOSKBb730lQUd3wosImIiMioiuE+++ZR/vGm5T2hTEVxx57ir4iIiKgYboQLOrAZYxKMMV8xxhwwxnQaY+qNMT8xxkzvdcwSY8xzxpg2Y0yrMeZXxpiM8AxdREREwkXFcCNbKI9EHwHuBn4A7AQuBb4NLAduNMakA68AbcCdQJr/2EuMMeustedDGbiIiIiEj4rhRragApt/luzzwEPW2m/6N79ojHEAPzTGZAEfATKAfGvtQf/3jgF/Am4Hngp18CIiIhIeM1OTcBiDxw7/UFTFcCdGsI9Ep+ELXM/02/6W/+cMYD2wvzusAVhr/ww0AdcHeV0REREJs5feOs7fbikdMayBiuFOlKBm2Pwh7OOD7LoOOA7sBSYB5wY5ph7IHO78xhgnvtm53lR5T0REJEiDdS5wGMNPit/mJ8Vv9xyXNXMKDSfOqBhuhAlbWQ9jzBrgPuB+a22XMeYA8F5jzHRr7Sn/MYnAbODMCKf7HPDAYDvKyspoamoiMzOT7OxsSkpKevYVFhZSVVWFy+UCYNmyZaSmplJZWQlAamoq69evp6ysjI6ODgByc3Pp6OigpqYGAKfTyapVqyguLu45b35+PnV1dTQ2NgKQnZ2N0+mkvLwcgOTkZPLz86msrKS11bdqZuXKlQBUV1cDkJ6eTm5uLiUlJXR1+V7UXLduHS6Xi7q6OgDdk+5J96R70j3pnsJ+T+uvuppv/qaEP73dzule6wSmJkNqoqHpjC+WTXLAZ1YmcdksD9XnF/Lr145w8qyn5/iZaclcM9vLTfPaeGXHdv06jXBPZWVlhJOxAUx/jngSY+YDpcAu4DZrrTXGXAFUAL8HvgAkAT8CPgg8a629bZjzDTXD9mx1dTUrVqwIecwiIiKxrn/ngqH+j589awo/37SWxc6pfb6rYrjB27t3b3eQXGmtDaz56jBCnmEzxswAXgSOAh+z/gRorX3DGHMn8GPgCOABfgjU4nssOiRrrQtw9btOqEMVERGJK4F2LvjAqrl9whqoGG6kCSkqG2OmAH/E9/vgJmttR+/91tpfABcDKwEn8D1gAfCXUK4rIiIiw+vduWA4Bvjt60dwe7zjMCoJViiFcxOBp4E5wA3W2hODHWetPWOt3WutPQn8M9AC/CHY64qIiMjI1LkgtoTySPRx4AZ8RXEXGWMW9drXZq2t8tdl2wBkA5uAXOBWa+1gq0dFREQkTNS5ILaEEtg+4f/5xCD7XgYKgKn4Hpk2AduAO621+0K4poiIiAQgNXl0/4tX54LIFnRgs9aOuArAX85DvwNERETG0eETZ/jh/9QEdKw6F0SHsNVhExERkYn3/J6jfO2ZKt7tDKxltzoXRAcFNhERkRhwtsvDt5/fy1OvHenZ9sm8hdSf7GDHIHXY1LkguiiwiYiIRImhitkeOP4uf/+bSg4cbwdg+pQkfvSh1Vx/6WzcHi+P7qilqLSB5vbOnnPNSkthU14WmwtyNLsWBRTYREREIpzb42XLjlqKSutpab+wmjMjLZnV86fzyoFmujy++bMrF87gJx+9nIunTQZ8BXDvLVzC5oIcdS6IYgpsIiIiEax/e6nemtu7eGnfhcZAXyhcwr0bFpM4SBBT54LopsAmIiISwQJtL3X7mkzuv2Hp+AxKxp3mQkVERCLUaNpL7ahpVnupGKbAJiIiEqHUXkq6KbCJiIhEKLWXkm4KbCIiIhFqtE841V4qdmnRgYiISISx1vKH3Uf5xn9XBXS82kvFPgU2ERGRCHKyo4tv/L6KP1U1BfwdtZeKffqVFRERiRDF+47zvh+/0hPWZqYm82935LJhuRNgwGrR7s9qLxX7NMMmIiIyToZqLfXuOTffef4tflfR2HPsjStm8+DfrGJWWgo3XDpb7aXinAKbiIjIGBu6tVQKBcsyePVgC0fbzgEwNSWRf/7rFXwwdx7G+ObQ1F5KFNhERETG0PCtpTp5eteFWbVrFs/iBx+6jLnTJw96LrWXil8KbCIiImMo0NZSG5Y7eXzTWhISRuprIPFI86giIiJjJNDWUgBVjW147Eg9DSReKbCJiIiMkUBbS4FaS8nwFNhERETGiFpLSbgosImIiIyR2ub2UR2v1lIyFC06EBERCbPmdzv55+f28sc9xwI6Xq2lZCQKbCIiImFireXpXY08+Md9tJ11A5CcmEDX+eG7uKu1lIxEvzNERETCoL6lgzseL+er/7mnJ6zdtHIOO750rVpLScg0wyYiIhKC8x4vj++s48dbD9Dpn0mbfVEK3751JTeumAPAYxvXqLWUhESBTUREZBhD9f8EX+20f3xmD28dO91z/B3rFvCPNy3noklJPdvUWkpCpcAmIiIyiOH6f37kyvmc6TzPL/9Sj9dfZC0nI5WHPngZV2bPGPKcai0lwVJgExER6Wek/p8/23aw53OSw3BPwWI+f10OKYmO8R2oxA0FNhERkX4C7f958bRJPPGpK1k2Z+r4DEzilh6ci4iI9DKa/p/nPV4WZaSO9ZBEFNhERER6G13/zy71/5RxocAmIiLSi/p/SiRSYBMREfGz1lL1TtuovqP+nzIetOhAREQE2N90mm/9fi+v1Z8M6Hj1/5TxpMAmIiJx7fQ5N49sfZv/V1qPx19UbUqygzNdnmG/p/6fMp6C/l1mjEkwxnzFGHPAGNNpjKk3xvzEGDO91zGrjTF/Msa0GGNO+P/+svAMXUREJHjWWv6rspENP3qZX7xah8drcSQYPn11NiX/eJ36f0pECWWG7RHgbuAHwE7gUuDbwHLgRmPMXGAbcAi4C9/v8W8BxcaYy6y1x0IZuIiISLD2HTvNt56t5vVeKzyvzJ7Bt29dwfI5FwHq/ymRJajAZozJAD4PPGSt/aZ/84vGGAfwQ2NMFvA+YAbwHmvtIf/3qoAa4K+A/wh18CIiIr0N1/cTfI8/H/6fAzxZ1tDz+DNjagr/668u4dbL52LMhfk09f+USBLsDNs04CngmX7b3/L/nAFM8f997+U2J/w/04K8roiIyADD9f3cmJfF5msX8dzuYzz05/20+GfLHAmGT121kC9cv4SpvRq196f+nxIJggps1tqDwMcH2XUdcBzY6//5APAzY8yX8D0S/RFwEvjdcOc3xjiBjH6b9aKAiIgMMFzfz5b2Th7eeoD/2FlH21l3z/Z12TP49q0r1VJKokbYVokaY9YA9wH3W2u7gKPGmJuB7cBH/YedA94bwPtrn8MX9gYoKyujqamJzMxMsrOzKSkp6dlXWFhIVVUVLpcLgGXLlpGamkplZSUAqamprF+/nrKyMjo6OgDIzc2lo6ODmpoaAJxOJ6tWraK4uLjnvPn5+dTV1dHY2AhAdnY2TqeT8vJyAJKTk8nPz6eyspLWVt/7ECtXrgSguroagPT0dHJzcykpKaGry/env3Xr1uFyuairqwPQPemedE+6J91TEPf03KHzbK89Dwzs+9n9uTuszZjs4G9zElg3p4OkM820t5uIvKdY/HWKt3sqKysjnIy1gTTfGOEkxswHSoFdwG3WWuufJSsHDgP/gm9F6teBWcBV1tqWYc431Azbs9XV1axYsSLkMYuISPRze7zkPVTMiQBaSU1OcvDqP13HjNSUcRmbxLe9e/d2B8mV1tq9oZ4v5Bk2Y8wM4EXgKPAxeyEBfhmYDqy21p72H7sTaPDv+6ehzmmtdQGuftcJdagiIhJjuvt+BuKs20NNUzt5OQpsEn1CWuZijJkC/BHfrPNN1tqOXrsvA97uDmsA1tpTwAFgdSjXFRERAfX9lPgRSuHcROBpYA5wg7X2RL9DjgGgcJN5AAAgAElEQVQ5xpjUXt9Jw/dosynY64qIiHRLTnSM6nj1/ZRoFcoj0ceBG4A7gUXGmEW99rUB/wf4GPCcMean/u3/AKT694mIiATlvMfL7yoa+df/2R/Q8er7KdEulMD2Cf/PJwbZ97K1tsAYczXwIL5wZ4AK4Bpr7a4QrisiInHslQPNPPjHfdQcfzfg76jvp0S7oAObtXbEVQDW2grgxmCvISIi0u3t4+/y4J/2saOmuWfbvOmT+fKNy3juzXfY5q/D1nu1aPdn9f2UaBe2OmwiIiJj4UR7Jz9+6QBPvXakp51UWkoin7suh09fnc2kJAc3X3ax+n5KTFNgExGRiHTO7eGJv9Tzf7cd5N1OX2HcBAMfuXIB91+/lIypF8pzqO+nxDoFNhERiSjWWv5YdYzv/3k/ja1ne7bnL5nFNz5w6bDtpNT3U2KVApuIiIwbt8c77AzYG4db+c7zb1F5+FTPtiXONP7XBy6hYJlzIoYsEhEU2EREZMy5PV627KilqLS+T2eCjLQUNuZl8derL+bhrW/zh91He/bNTE3m/huW8pH3zCdRjzUlzimwiYjImHJ7vNxVVMF2/yrO3lraO3l46wF+/NIBuhsbJjsS+PQ12XzuuhwumpQ07uMViUQKbCIiMqa27Khlu78UR/8G7d2fu8PazZddzD++fznzZ0wZt/GJRAMFNhERGTNuj5ei0voB9dEGM31KEj/+8OVa1SkyCP1bISIiY6aivpWW9q4RwxrAqTNuKupbx3xMItFIgU1ERMZM29mukQ8K4XiReKHAJiIiY+LwiTP8quzwqL4zbXLyGI1GJLrpHTYREQkr17vn+D/bDvLUa4dxewJ5GOrr+TkrLYW1C9PHdnAiUUqBTUREwqLtrJvHXq7ll6/Wc9bt6dm+1JnGAVf7sN+1wKa8LC04EBmCApuIiITkbJev5+ejL9fSdtbds/29SzP4yvuWsfziqdz95C627XcNWC3a/XnDciebC3LGeeQi0UOBTUREguL2ePnt60f4afHbuN7t7Nl+xYLpfPXG5X16ej62cQ2P7qilqLSB5vYLx85KS2FTXhabC3I0uyYyDAU2EREZFa/X8tyeozy89QANJ870bF86O40vv28ZN1w6G2P69jRIciRwb+ESNhfkDNtLVEQGp8AmIiIBsdayo6aZH7xYw75jp3u2Z6ZP5os3LOXWy+fhSOjffKqvJEdCn5k3EQmMApuIiOD2eIed+Xq9/iQ/eGE/r/cqbDsrLZl7NyzhI1fOJyXRMRHDFokbCmwiInHM7fGyZUctRaX1tLRfKFqbkZbCxrwsCpZm8Ejx22zb7+rZNzUlkbuvXcSnrs4mNUX/GxEZD/o3TUQkTrk9Xu4qqmB7TTP9H2S2tHfy8NYDPLz1QM+2lMQEPnnVQjZfm0N6qgrciownBTYRkTi1ZUct22uagYGN2fuU3jDwkfcs4AuFS5gzbdK4jU9ELlBgExGJQ26Pl6LS+gF10QaTPiWZb9+6Qqs5RSaQ/u0TEYlDFfWttLR3jRjWAE52dFHRa7GBiIw/BTYRkTjU2Hpm5IN6aTvbNfJBIjJm9EhURCSOnGjv5Ocldfzy1bpRfW/aZC0yEJlICmwiInGgpb2Tn79yiCfLGjjT5Rn5C34GX/uotQvTx25wIjIiBTYRkRjW0t7Jv79yiCdLGzjrvhDU3rMwnQUzUnmmsnHY71tgU16WFhyITDAFNhGRGNT8bif//kotT5Y1cM7t7dl+5cIZ/MP1S8jLmcl5r6X1TBfb9rsGrBbt/rxhuZPNBTnjPHoR6U+BTUQkhrjePcdjLx/i1+X9glq2P6gtmtnTmD3JYXhs4xoe3VFLUWkDze2dPcfPSkthU14WmwtyNLsmEgEU2EREYoDr9Dke9Qe1zvMXgtr6RTP4QuHSIRuuJzkSuLdwCZsLcobtJSoiE0uBTUQkih0/fY4tO2p56rXDfYJa3qKZfOH6JaxfNHhQ6y/JkTBkqBORiafAJiIShZrazvHoy7X85rXDdPUKalflzOQLhUtYF2BQE5HooMAmIhJB3B7vsI8mm9rOsWXHQZ56/UifoHbN4ll84folvGfhjIkYtoiMMQU2EZEI4PZ42bKjlqLSelraL3QVyEhLYWNeFrddPpefl9Tx29eP0OW5ENTyl8ziC4VLWKugJhLTFNhERCaY2+PlrqIKttc0Y/rta2nv5OGtB/jx1gN9ym7kL5nFP1y/hDVZCmoi8SDowGaMSQC+BNwJZAHHgGeBB6y1p4wxw/UUttZaLT8SEQG27Khle00zwIBm7Lbfz2uXZnBf4RLWZKnzgEg8CWWG7RHgbuAHwE7gUuDbwHLgRiB/iO/9G3AkhOuKiMQMt8dLUWn9gMK1g5k+JYnHP7FW5TZE4lBQgc0YkwF8HnjIWvtN/+YXjTEO4IfGmCxr7c5BvrcSWIVvZk5EJO5V1Lf2eWdtOKfOuKmob1X5DZE4FOwf06YBTwHP9Nv+lv/nUC9VfBnYa63dGuR1RURihrWW1+pOjuo7bWcDC3ciEluCmmGz1h4EPj7IruuA48De/juMMXOBj+KbmRuWMcYJZPTbrGZ2IhITvF7L/7x1nC0v17L7yKlRfXfa5OQxGpWIRLKwrRI1xqwB7gPut9YO9kfA+4DTwK8CON3ngAcG21FWVkZTUxOZmZlkZ2dTUlLSs6+wsJCqqipcLhcAy5YtIzU1lcrKSgBSU1NZv349ZWVldHR0AJCbm0tHRwc1NTUAOJ1OVq1aRXFxcc958/Pzqauro7GxEYDs7GycTifl5eUAJCcnk5+fT2VlJa2trQCsXLkSgOrqagDS09PJzc2lpKSEri7fP55169bhcrmoq6sD0D3pnnRPMX5P5a/v4s/7Wnih3kPTmZHeWBsofbKDy+am9rn2RN9TLP466Z50T+G4p7KyMsLJWDv6/2gMOIkx84FSYBdwm+13UmNMGr6FBj+z1n4rgPMNNcP2bHV1NStWrAh5zCIi46W98zxPlR/mP3bW0XT6XM/2aZOT+EReFl0eL4++fGjE83zphqXcW7hkLIcqImGyd+/e7iC50lo74MnjaIU8w2aMmQG8CBwFPtY/rPndCUzBt0J0RNZaF+Dqd50QRyoiMr5a2jt54tV6ikrrOX3ufM/2ORdN4rP52Xz0ygWkpiTi9ng5cLydbftdA1aLdn/esNzJ5gK9GSISr0IKbMaYKcAf8f335CZrbccgxyQCXwD+P2ttUyjXExGJBkdOnuHnJYf47etH+jRkz8lIZfO1Odx6+TySEy+s+UpyJPDYxjU8uqOWotIGmts7e/bNSkthU14WmwtyVM5DJI6FUjg3EXgamANcba09McShf4evsO4jwV5LRCQa7Dt2mkdfruX5PcfweC/Mk10+fzr3FORwwyWzSUgY/GlBkiOBewuXsLkgZ9heoiISn0KZYXscuAHf485FxphFvfa1WWur/H//JeBla+0bIVxLRCQidZfm2PJyLTv83Qq6Xbs0g3sKcliXPSPg1zqSHAmqsyYiA4QS2D7h//nEIPteBgqMMRuAXOBvQriOiEjE8XotL+3zleZ44/CF0hwJBm6+bC53X7uIFXOnTeAIRSSWBB3YrLUj/nHRWrsNBvQyFhGJSG6Pd8THkV3nvTz75js89sohDrrae7anJCZw+9pM7srPYcHMKeM9dBGJcWGrwyYiEq3cHi9bdtRSVFrfp01URloKG/OyuKcgh67zXp56zVea41jbhdIcUyclsikvi09elU3G1JQJGL2IxAMFNhGJa26Pl7uKKthe0zzgcUBLeycPbz3Af1U2crKjq09pDufUlJ7SHFMnJY3voEUk7iiwiUhc27Kjlu3+xQL9i0h2f64/caZn26JZqdx97SJuu2IeKYmO8RmkiMQ9BTYRiVtuj5ei0voBxWoHk5hgeOTDl3PTqotxDFGaQ0RkrCiwiUjcqqhv7fPO2nDOey0z01IU1kRkQqgao4jELde750Y+qJe2s4GFOxGRcNMMm4jEnaOnzlJU2sCTpfWj+t60ycljMh4RkZEosIlI3Kg83Movdtbx5+qmPq2jRmLw9fRcuzB97AYnIjIMBTYRiWluj5c/Vzfxi511vHnkVJ9971mYzpyLJvHcnmPDnsMCm/Ky1NNTRCaMApuIxKRTZ7r4zWuHKfpLA02nL7yrlphguGX1XD519UIuy5yO2+Olo8vDtv2uAatFuz9vWO5kc0HOON+BiMgFCmwiElMOut7ll6/W80xlI+fc3p7tM1KTuWPdAj6+PovZF03q2Z7kSOCxjWt4dEctRaUNNLd39uyblZbCprwsNhfkaHZNRCaUApuIRD1rLa+83cIvdtbx8oHmPvuWzZ7Kp69ZyK2Xz2NS0uCFbpMcCdxbuITNBTkj9hIVEZkICmwiErXOdnn4rzca+eWr9X0asQMULnfy6WuyuSpnJsYEVjstyZFAXs7MsRiqiEhIFNhEJOocazvLk6UN/Oa1w5w64+7ZPjnJwe1rM/nkVQtZlJE2gSMUEQkvBTYRiRpvHjnFL3bW8aeqY5zvVZZj3vTJfOKqLD68dgHTpqgRu4jEHgU2EZkQbo83oPfFznu8vLDXV5aj8nDfshxrs9L59DXZvO/S2STqXTMRiWEKbCIyrtweL1t21FJUWt+nj2dGWgob87K4x78is+2Mm6deP0zRX+o52ta3LMfNl13Mp67OZvX86RNwByIi40+BTUTGjdvj5a6iCrbXNNN/GUBLeycPbz3Aq7Ut5MxK5b/fOMpZt6dnf/qUJO5Yl8XGvL5lOURE4oECm4iMmy07atle4yu70b8xVPfn8kMnKT90smf7Emcan74mm9sun8fk5MHLcoiIxDoFNhEZF26Pl6LS+gHdBIZy7dJZfDZ/EdcsnhVwWQ4RkVilwCYi46KivrXPO2sj2XztYtVEExHx07IqERkXLb1aPgWi7Wzg4U5EJNZphk1ExlRj6xmeeu0wT5YeHtX3pk1OHqMRiYhEHwU2EQk7j9fy8gEXvyo7zPYaFzaQl9b8DL6m62sXpo/Z+EREoo0Cm4iEjevdczxd0chvyg/zzqmzffblLpiOc+okXtjbNOw5LLApL0tN10VEelFgE5GQWGspO3SSX5U38GJ1U5+WUanJDm67Yh53rMvi0rkX4fZ4ufvJXWzb7xqwWrT784blTjYX5IzzXYiIRDYFNhEJStsZN89UNvLr8gZqmzv67Fs+ZyofX5/FbVfMIy3lwn9mkhwJPLZxDY/uqKWotIHmXgsRZqWlsCkvi83+TgciInKBApuIBMxay+7GNn5d1sBze45yzu3t2ZecmMDNqy7mjvULyF2QPmTttCRHAvcWLmFzQU5AvURFRESBTUQCcKbrPM++eZRflzdQ/c7pPvsWzpzCHeuy+Ns1mcxIDXxlZ5IjQXXWREQCpMAmIkOqaXqXX5c38N+V7/Bu5/me7Y4Eww2XzObj67O4KmcmCQnqRCAiMpYU2ESkj87zHl6obuJXZQ28Xt/aZ9+ciybx0SsX8JEr56sBu4jIOFJgE4lhbo834PfEGk508JvXDvN0RSMnOy50GTAG3rskgzvWLWDDcieJes9MRGTcKbCJxCC3x8uWHbUUldb36d+ZkZbCxrws7vGvxDzv8VK838Wvyw/zyoHmPueYkZrM7WszuePKLBbMnDLOdyAiIr0psInEGLfHy11FFWyvaab/m2Ut7Z08vPUA5YdOkJuVztMVjTSdPtfnmCsXzuCO9Qt4/8o5pCQ6xm/gIiIyJAU2kRizZUct22t8s2X9O0J1f3619gSv1p7o2T41JZEP5s7jY+uyWDZn6vgMVEREAhZ0YDPGJABfAu4EsoBjwLPAA9baU72Omwx8AfgwsBj4uLX22VAGLSKDc3u8FJXWD+giMJQVc6eycf1Cblk9l9QU/flNRCRShfJf6EeAu4EfADuBS4FvA8uBGwGMMRcBxcAlwE+BCqAkhGuKyDAq6lv7vLM2km984FLycmaN4YhERCQcggpsxpgM4PPAQ9bab/o3v2iMcQA/NMZkWWsbgO8BS4DV1trasIxYRIa0v+n0yAf10nbWPUYjERGRcAp2hm0a8BTwTL/tb/l/zjDGtAKfBr6usCYydk6fc/P87mM8vesIbxw+NfIXepk2OfDOBCIiMnGCCmzW2oPAxwfZdR1wHNgLbAAm4wtvNfjeX2sEvmOtfXy48xtjnEBGv805wYxVJBZ5vZa/1J7g6V1HeKG6ic7z3pG/1IvB12x97cL0sRmgiIiEVdjeMjbGrAHuA+631nYZY5b4d20GvgkcBD4D/NwY84619s/DnO5zwAOD7SgrK6OpqYnMzEyys7MpKbnwSlxhYSFVVVW4XC4Ali1bRmpqKpWVlQCkpqayfv16ysrK6OjoACA3N5eOjg5qamoAcDqdrFq1iuLi4p7z5ufnU1dXR2NjIwDZ2dk4nU7Ky8sBSE5OJj8/n8rKSlpbfZXhV65cCUB1dTUA6enp5ObmUlJSQleX7x2jdevW4XK5qKurA9A96Z5GvKfkmfPY2ejm6YrDnOxbjYP0FMi72MHU9Jn89g0Xw7HAzcsv4pUd2yf8nmLx10n3pHvSPemeysrKCCdjbSBryUY4iTHzgVJgF3CbtdYaY74BfAfIs9aW+Y8zQBVw0lr73mHON9QM27PV1dWsWLEi5DGLRIuOzvP8seoY/1nRyGv1J/vsS05M4MYVc/jQmkyuWTwLR4LB7fFy95O72LbfNWC1aPfnDcudPLZxzZBdD0REJDR79+7tDpIrrbV7Qz1fyDNsxpgZwIvAUeBjdmACrOj+G3+QKwY2DndOa60L6DNF4Mt6IvHB67W8Vn+Spysa+XP1Mc50efrsXz1/Oh9ak8lfXzaXaVOS+uxLciTw2MY1PLqjlqLSBprbO3v2zUpLYVNeFpv9nQ5ERCQ6hBTYjDFTgD/i+0P7Tdbajl67j/p/LgAO9f4acD6U64rEqsbWMzyz6x2eqWzk8MkzffbNSkvhg7nz+NCaTJbOHr64bZIjgXsLl7C5ICfgXqIiIhK5Qimcmwg8DcwBrrbWnuh3yEuAF9/ihG/7v5MAFAJvBntdkVhztsvDC3uP8XRFI3+p7fuvUZLDULh8NrevzeTapRmjbrye5EggL2dmOIcrIiITIJQZtseBG/B1OlhkjFnUa1+btbbKGPNT4JvGGAtUAp/CV0T3zhCuKxL1rLVUHm7l6YpGnt9zjPbOvpPOl158EbevzeTWy+cxI1WlN0RE4l0oge0T/p9PDLLvZaAAX+uqk8BdgBPYB/yNtfYvIVxXJGo1tZ3jmcpGntnVyKGWjj77ZqQmc+vlc/nQmkxWzJ02QSMUEZFIFHRgs9aOuArAWuvFt1L0O8FeRyQSuT3egN8NO+f2sPWt4zy9q5Gdbzfj7bUsx5FguG5ZBh9aM58Ny50kJ+r9MhERGUjdnkVGwe3xsmVHLUWl9X16dmakpbAxL4t7/KsvrbXsaWzj6V1H+MObRzl9ru8jz6Wz07h9zXxuu2IeGVNTxvkuREQk2iiwiQTI7fFyV1EF22ua6T+93NLeycNbD1Bed4JrFs/iv994hwPH2/scc9GkRG69fB63r81k1bxpKlUjIiIBU2ATCdCWHbVsr2kG+haj7f351YMnePXghZWeCQbyl2Rw+9pMrr9kNpOSHOMzWBERiSkKbCIBcHu8FJXWD+gcMJTsmVO4/T3z+eAVmcyZNmmMRyciIrFOgU0kABX1rX3eWRvJ9z64irycWWM4IhERiSdakiYygiMnz/Db1w+P6jttZ91jNBoREYlHmmETGURT2zme33OU5/YcY/eRU6P+/rTJKnYrIiLho8Am4tfS3smfq47x3O5jvN5wEtvvZTWHMXj6b+zH4Ov5uXZh+tgNVERE4o4Cm8S1tjNuXtzbxHN7jvLqwZY+RW0BFsyYwi2rL+aW1XN5sbqJH7/09rDns8CmvCw1WBcRkbBSYJO40955npfeOs5zu4/yytvNuD19U9rF0yZx82W+kNa7XlpORhq7G9vYtt81YLVo9+cNy51sLsgZr1sREZE4ocAmceGc28O2/S6e33OU4n0uOs97++yflZbMB1ZdzM2r57JmQToJCQOL2iY5Enhs4xoe3VFLUWkDze2dvb6fwqa8LDb7Ox2IiIiEkwKbxKyu815K3m7mud1H2frWcTq6PH32T5ucxE0r53DL6rmsy55BYgBBK8mRwL2FS9hckBNwL1EREZFQKbBJTDnv8VJ66ATP7T7KC9VNA3p4pqUk8r5LZ3PL6rlcvXhW0M3WkxwJ5OXMDMeQRURERqTAJlHP67W8Xn+S5/cc409VxzjR0bfA7aSkBAovmc0tl82lYFmG2kOJiEjUUWCTiOH2eAN+zGitZXdjG8/tPsof9xyj6fS5PvuTHQlcuyyDW1bPpXC5k9QU/VYXEZHopf+LyYRze7xs2VFLUWl9n/ZPGWkpbMzL4h7/i/zWWvYde5fn9hzl+T1HOXLybJ/zOBIM1yyexc2XXcz7Vsxh2uSkcb4TERGRsaHAJhPK7fFyV1EF22ua6b8us6W9k4e3HuDVgy1cmT2DP1Udo7a5o88xxsC67BncsnouN628mBmp6jAgIiKxR4FNJtSWHbVsr2kG+tY16/25vO4k5XUn++zLXTCdW1bP5a9WXczsiyaN/UBFREQmkAKbTBi3x0tRaf2AIrRDWTF3KresnscHVl3M/BlTxnh0IiIikUOBTSZM+aETfd5ZG8k3PrBCpTRERCQuKbDJuDp1pouXDzRTvM/F1reaRvXdtrOBhzsREZFYosAmY8paS21zOy/tc7Ftn4uKhpMDGqwHatpkLSgQEZH4pMAmYdd53sNrdScp3udi234Xh0+eGXDM1JRErlk6i5IDLXR0nh/2HTaDr1fn2oXpYzZmERGRSKbAJmHR0t7J9v2+gPbKgeYBfTsBFs6cQuElsym8xMl7Fs4gyZHAT4vf5uGtB4Y9twU25WWpV6eIiMQtBTYJSncR2237j/PSPhe7G09h+02TORIMVy6cQeElTjYsd7IoI23Aee4pyOHNI6fYtt81YLVo9+cNy51sLsgZw7sRERGJbApsErBzbg+ltSd4ad9xtu13cazt3IBjpk9J4rplvoD23qUZI3YbSHIk8NjGNTy6o5ai0gaa2zt79s1KS2FTXhab/Z0ORERE4pUCW5wYTZ/O3prazrFtv4tt+4+z82AL59zeAccsnZ3GhuW+R51XzJ9O4ijDVZIjgXsLl7C5ICeoMYqIiMQ6BbYYF2ifzm5er6XqnTaK/SGt+p3TA86Z7Ehg3aIZFC53UnjJ7LAVsU1yJKjOmoiIyCAU2GJYIH063zxyiof/bjXldScp3necbfubaen1WLLbrLQUNizPYMPy2VyzZBZpKfqtIyIiMl70f90YFkifzm37Xaz5zkt4+q8YAFbMvYjC5U42XDKby+ZNIyGhf+wTERGR8aDAFqNG06ezO6ylJCZwzeJZbPCv6rx42uSxHqaIiIgEQIEtRhXvOz6qPp1fuXEpn756EZOTHWM4KhEREQmGAlsM8HgtNU3vsutwK280tLLrcCsNJwZ2FxhOTkaawpqIiEiEUmCLQm1n3FQeaaWyoZXKw628efjUoJ0FRkN9OkVERCJX0IHNGJMAfAm4E8gCjgHPAg9Ya0/5j/k74LeDfL3cWrs+2GuPhbazXfzoxRqaTp9jzkWT+PKNy0IOMcHWPuvN67UcamlnV0MrlQ2n2HW4lYOu9iGPnzY5idwF07l8/nR+8Wodp8+qT6eIiEi0C2WG7RHgbuAHwE7gUuDbwHLgRv8x84AO4P39vjuwuNcEaTvbxc0/3cmR1rN9tj9Zdpj56ZN5/r5rRh3cRlv7rLf2zvPsPnKKSv+jzcqGVk6fOz/ktZY401iTlU7ugnRys9JZNCu1ZzWnMUZ9OkVERGJAUIHNGJMBfB54yFr7Tf/mF40xDuCHxpgsa20DkAkcsdbuDM9ww6vtbBdrv/sSbs/gc1BHWs+y9rsvUfGN6wMObYHWPnts4xoSEwyHT56h8nAruxpa2dVwipqm03iHmBJLTXZwxYJ0chdMJzcrnSvmpzNtytCtn9SnU0REJDYEO8M2DXgKeKbf9rf8P2cADfhm2I4EeY0xd/NPdw4Z1rq5PZZbfraTV766IaBzBlr77P2PvELbWfewKzkXzpxCrn/2bE1WOktnT8Uxilpo6tMpIiISG4IKbNbag8DHB9l1HXAc2Ov/PA+Ya4ypAXKAJuBn1tp/Cea64dR2tmvAY9ChHD55ll/urBtxFaXHa/n3Vw4FdM7a5o4+n1MSE1g9f3pPOLtiwXRmpaUEdK7hqE+niIhI9AvbKlFjzBrgPuB+a233tNEpYArwEHASuAP4vjHmlLX2sWHO5QQy+m0O63O7H71YM6rj//fzb4180CitXzSDG1fMIXdBOpdcfBHJiWMXoNSnU0REJHqFJbAZY+bjWyH6ArCle7u19pZ+h27zH/t1YMjABnwOeGCwHWVlZTQ1NZGZmUl2djYlJSU9+woLC6mqqsLlcgGwbNkyUlNTqaysBCA1NZX169dTVlZGVW3rqO8z3D6cO4fVMyx1B3ZRcoCQ76mjwzdrl5ubS0dHBzU1vlDqdDpZtWoVxcXFPefNz8+nrq6OxsZGALKzs3E6nZSXlwOQnJxMfn4+lZWVtLb6/lmtXLkSgOrqagDS09PJzc2l5P9v715j5SjLAI7/n5Yecgr0aIMGaCiGakQPkqCJVFMVsAWJoSVIMCIRNTaQaAsfatQIXkANISLegh8k4WaEpPFSERNQEpEijQFq0lMJTZvSQkSLCKWAUCmvH2aOLNuzt+47PbN7/r9ksmfn8s68+/TZPJ3Zeee++9i7t6jRTznlFHbt2sX27dsB+2Sf7JN9sk/2aWb2acOGDeQUaYpnSPbUQMR8irtEnwdOSym90GH9y4DrgHkppT0t1ml1hm3dxMQE45OKhvcAAAgdSURBVOPjfR0zwBW/3sStG3Z2vf7H3n0Ma848oe06D+94hs//fGPXbd62crFnvSRJGkKbN2+eLCRPTClt7rR+J32dYYuIucCdFL+nP6uxWIuIoymG9/hVSml3w2Ydh9NPKe0CdjXtq59D3c+aM9/eU8H2tbPHO94pesb4oRx5+AhPP7/Xsc8kSVI2B/yjqYg4BFgLHAUsSyk9PcVqNwLnNc1bCuxodXbtYBkbHeHYN3b3cPOF80e7GtZjzuxZfOp9b+n4sHXHPpMkSb3o5wzbDcAyiicdHB8Rxzcs251S2hQRtwDfjYjDgC3ACopBdFf2sd9sfrt6Sdtx2ADmzA7uWLWk6zYd+0ySJOXWT8F2Ufl60xTL7gVOBS4BdgKXUgyiuwNYnVK6oY/9ZjM2OsKDly/l7B+tZ+e/9x/iY+H8Ue5Y1duTDhz7TJIk5db3TQcHS0SMAxO5bjpoVtdniUqSpMFTq5sOhsnY6AhXnfOurG069pkkScrB0z2SJEk1Z8EmSZJUcxZskiRJNWfBJkmSVHMWbJIkSTVnwSZJklRzFmySJEk1N0jjsI0AbN26dbqPQ5Ikqa2GeqW/UfhLg/Skg+XAuuk+DkmSpB6sSCn9pt9GBqlgGwM+BDwO7K1oN4soisIVwLaK9qH+GKP6M0b1Z4zqzxjVWzfxGQGOBe5NKe3ud4cDc0m07GzfFWo7ETH557Ycz/1Sfsao/oxR/Rmj+jNG9dZDfDbm2qc3HUiSJNWcBZskSVLNWbBJkiTVnAXb6z0FfLN8VT0Zo/ozRvVnjOrPGNXbQY/PwNwlKkmSNFN5hk2SJKnmLNgkSZJqzoJNkiSp5izYJEmSas6CTZIkqeaGsmCLiFkR8cWI2BIRL0fEYxHxg4h4Q8M650dEmmLa0KHtJRFxf0S8GBHPRsQvI+K46ns1XCqO0fUttru6+p4Nj25iVK43GhFfjoiNEbEnIlZ00bZ5lEHFMTKPMugUoxaf8eT0aoe2zaMMKo5RtjwamGeJ9uj7wMXANcB64J3AlcAJwJnlOguAF4CPNG37XKtGI+J44G7gL8AngTHg28BdEXFSSqmqh9IPo0pi1LDdeuArTfMf7+N4Z6KOMYqIecA9wDuAHwIPAve1a9Q8yqqSGJXMozw6xegDLba7njaftXmUVSUxKuXLo5TSUE3Am4B9wLea5q8BEnBc+f5a4JEe274GeB44omHeB8t2l0933wdlqjJG5XYPAT+Z7n4O8tRDjH4MPAss6qFt86jmMSq3M48OUoym2O7EcvmyNm2bRzWPUbletjwaxkuiY8BtwC+a5v+tfJ1fvi6g9wp3MfBASmlPw7z1wEvAe3tsayarMkb9bKfXdIxReebms8A3UkrbemjbPMqjyhiBeZRDt991zdYAm1NKv2/TtnmUR5Uxgox5NHQFW0ppa0rpwpTSxqZFpwH/BDaX7xcAiyLi0Yh4JSKeiIgvdWj+KGBX0/5eBf4FvDnD4c8IVcYoIuZQxOLciHiy3G4iIj6avSNDrMsYvR8YpSgMHo2IfRGxIyI+16F58yiDKmNkHuXRw3fd/0XEMcAnKC7TtWMeZVBljHLn0dAVbFOJiPcAq4Er02vX9Z8tp68CZwB3AVdHxMVtmhoB/jvF/H3lMh2gjDGaB2wHHgMuAs4BdgPrImK8mqOfGaaI0dvKRZcA36OI0f3ATyPirDZNmUcVyRgj86giLb7rGq2m+J3uzzo0ZR5VJGOM8ubRdF8/PgjXp48FngDWUT47tc26dwM72ix/DLipxfwbp7uvgzrljFGLbeZRPKD35unu66BOU8UIuJziNxyLG9YLYAL4U5u2zKOax6hF++ZRBTFqWn448AxFodCpLfOo5jFq0f4B59FQn2GLiPkUZ2X+DlyQyk+rjd8BCyPiiBbL91JcXmg2Arx8wAc6g1UQo/2klJ6jOKtw4gEf6AzWRYwenPyjXHYP7T9r8yizCmK0H/OoP11+160E5lLcfdiJeZRZBTHaTz95NLQFW0TMBe6k+N/lWSmlFxqWHR0Rn46IsabNZndo9imK3w007mcWcCTwZP9HPbNUEaOIODkiPj7FotnlftSDdjGi+FIDWNi8GfBKm2bNo4yqiJF5lFeHGE2ucwhwKXB7SukfXTRrHmVURYxy59FQFmzlh7qW4h/zspTS01OsdiNwXtO8pRSX2/ZMsT7AA8DiiDiyYd7pwByg7WCuer0KY3QCcHtEvLVhX4dR3FE10feBzyBdxOgPwKvAhQ3bzAI+DPy1TdPmUSYVxsg8yqTL7zqA84Hj6HyzwSTzKJMKY5Q1j6LzFajBExE3ARdQnLpsvpV9d0ppU0TcDCwHvg5sAVZQ/DB3ZUrphrKdRcBT5SnMyfebyukaitOi36G4nn1ySmlfxV0bGhXGaC7FuDcJuAp4EbgMWAKclFJ6pOKuDY0uY3Qd8AWKQSYfBj4DnAssSSn9uWzHPKpIhTEyjzLpJkbleg8Be1JKp7ZoxzyqSIUxyptH0/0Dvyqm8sNpNf2xXGe0/AC3UVzv3wKsamjjUIrLCdc2tb2E4vrzSxR3e6wFFkx3nwdtqjhGC4BbKS4L/Ifif6JLp7vPgzZ1GaNZwBUU4wy9THHWZkUXMTKP6h8j8+jgxej08v05LdowjwY3RtnyaCjPsEmSJA2TofwNmyRJ0jCxYJMkSao5CzZJkqSas2CTJEmqOQs2SZKkmrNgkyRJqjkLNkmSpJqzYJMkSao5CzZJkqSas2CTJEmqOQs2SZKkmrNgkyRJqjkLNkmSpJr7H1tOVQ4mVeDdAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"check_correlation = np.array(check_correlation)\n",
"fig, ax = plt.subplots(figsize=(6,4), dpi=120)\n",
"\n",
"ax.plot(check_correlation[:, 0], check_correlation[:, 1], '-o');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Credits"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"* Dr. Will Holmes, [\"Heat Diffusion Example using Cellular Automaton\" Jupyter notebook](https://github.com/Learning-Computational-Science/Cellular_Automaton/blob/master/CA_Heat_Diffusion.ipynb)"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.5"
}
},
"nbformat": 4,
"nbformat_minor": 2
}