Restore the index vector to index matrix in layer_fun

Restore the index vector to index matrix in layer_fun

restore_matrix(j, i, x, y)

Arguments

j	Column indices directly from layer_fun.
i	Row indices directly from layer_fun.
x	Position on x-direction directly from layer_fun.
y	Position on y-direction directly from layer_fun.

Details

The values that are sent to layer_fun are all vectors (for the vectorization of the grid graphic functions), however, the heatmap slice where layer_fun is applied to, is still represented by a matrix, thus, it would be very convinient if all the arguments in layer_fun can be converted to the sub-matrix for the current slice. Here, as shown in above example, restore_matrix does the job. restore_matrix directly accepts the first four argument in layer_fun and returns an index matrix, where rows and columns correspond to the rows and columns in the current slice, from top to bottom and from left to right. The values in the matrix are the natural order of e.g. vector j in current slice.

For following code:

    Heatmap(small_mat, name = "mat", col = col_fun,
        row_km = 2, column_km = 2,
        layer_fun = function(j, i, x, y, w, h, fill) {
            ind_mat = restore_matrix(j, i, x, y)
            print(ind_mat)
        }
    )  

The first output which is for the top-left slice:

         [,1] [,2] [,3] [,4] [,5]
    [1,]    1    4    7   10   13
    [2,]    2    5    8   11   14
    [3,]    3    6    9   12   15  

As you see, this is a three-row and five-column index matrix where the first row corresponds to the top row in the slice. The values in the matrix correspond to the natural index (i.e. 1, 2, ...) in j, i, x, y, ... in layer_fun. Now, if we want to add values on the second column in the top-left slice, the code which is put inside layer_fun would look like:

    for(ind in ind_mat[, 2]) {
        grid.text(small_mat[i[ind], j[ind]], x[ind], y[ind], ...)
    }  

Examples

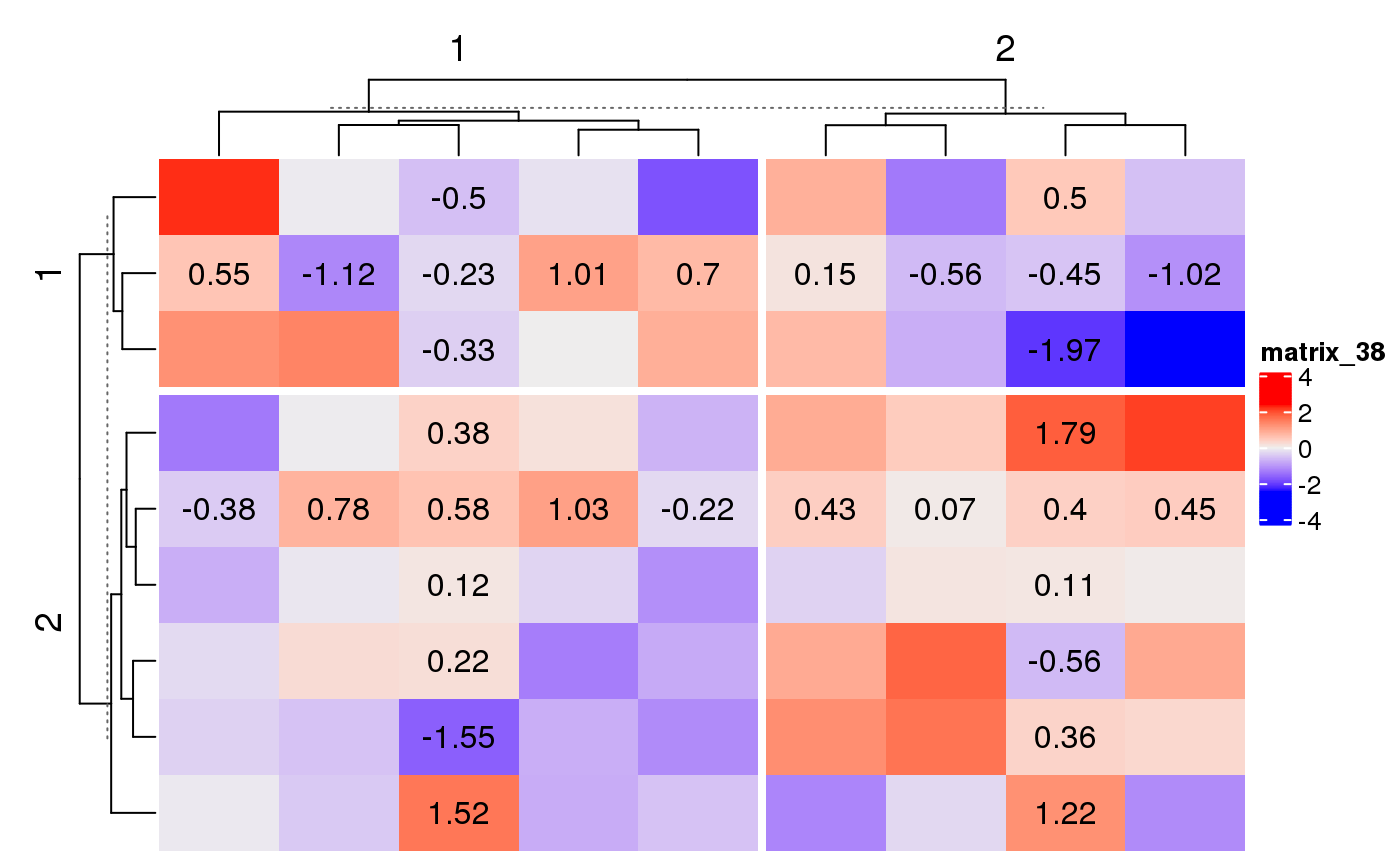
set.seed(123)
mat = matrix(rnorm(81), nr = 9)
Heatmap(mat, row_km = 2, column_km = 2,
    layer_fun = function(j, i, x, y, width, height, fill) {
       ind_mat = restore_matrix(j, i, x, y)
       print(ind_mat)
})
#>      [,1] [,2] [,3] [,4] [,5]
#> [1,]    1    4    7   10   13
#> [2,]    2    5    8   11   14
#> [3,]    3    6    9   12   15
#>      [,1] [,2] [,3] [,4]
#> [1,]    1    4    7   10
#> [2,]    2    5    8   11
#> [3,]    3    6    9   12
#>      [,1] [,2] [,3] [,4] [,5]
#> [1,]    1    7   13   19   25
#> [2,]    2    8   14   20   26
#> [3,]    3    9   15   21   27
#> [4,]    4   10   16   22   28
#> [5,]    5   11   17   23   29
#> [6,]    6   12   18   24   30
#>      [,1] [,2] [,3] [,4]
#> [1,]    1    7   13   19
#> [2,]    2    8   14   20
#> [3,]    3    9   15   21
#> [4,]    4   10   16   22
#> [5,]    5   11   17   23
#> [6,]    6   12   18   24

set.seed(123)
mat = matrix(round(rnorm(81), 2), nr = 9)
Heatmap(mat, row_km = 2, column_km = 2,
    layer_fun = function(j, i, x, y, width, height, fill) {
       ind_mat = restore_matrix(j, i, x, y)
       ind = unique(c(ind_mat[2, ], ind_mat[, 3]))
       grid.text(pindex(mat, i[ind], j[ind]), x[ind], y[ind])
})