# 动态规划之四键键盘




**通知:算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
| LeetCode | 力扣 | 难度 |
| :----: | :----: | :----: |
| [651. 4 Keys Keyboard](https://leetcode.com/problems/4-keys-keyboard/)🔒 | [651. 4键键盘](https://leetcode.cn/problems/4-keys-keyboard/)🔒 | 🟠
**-----------**
力扣第 651 题「四键键盘」很有意思,而且可以明显感受到:对 `dp` 数组的不同定义需要完全不同的逻辑,从而产生完全不同的解法。
首先看一下题目:
假设你有一个特殊的键盘,上面只有四个键,它们分别是:
1、`A` 键:在屏幕上打印一个 `A`。
2、`Ctrl-A` 键:选中整个屏幕。
3、`Ctrl-C` 键:复制选中的区域到缓冲区。
4、`Ctrl-V` 键:将缓冲区的内容输入到光标所在的屏幕上。
这就和我们平时使用的全选复制粘贴功能完全相同嘛,只不过题目把 `Ctrl` 的组合键视为了一个键。现在要求你只能进行 `N` 次操作,请你计算屏幕上最多能显示多少个 `A`?
函数签名如下:
```java
int maxA(int N);
```
比如说输入 `N = 3`,算法返回 3,因为连按 3 次 `A` 键是最优的方案。
如果输入是 `N = 7`,则算法返回 9,最优的操作序列如下:
`A`, `A`, `A`, `Ctrl-A`, `Ctrl-C`, `Ctrl-V`, `Ctrl-V`
可以得到 9 个 `A`。
如何在 `N` 次敲击按钮后得到最多的 `A`?我们穷举呗,每次有对于每次按键,我们可以穷举四种可能,很明显就是一个动态规划问题。
### 第一种思路
这种思路会很容易理解,但是效率并不高,我们直接走流程:**对于动态规划问题,首先要明白有哪些「状态」,有哪些「选择」**。
具体到这个问题,对于每次敲击按键,有哪些「选择」是很明显的:4 种,就是题目中提到的四个按键,分别是 `A`、`C-A`、`C-C`、`C-V`(`Ctrl` 简写为 `C`)。
接下来,思考一下对于这个问题有哪些「状态」?**或者换句话说,我们需要知道什么信息,才能将原问题分解为规模更小的子问题**?
你看我这样定义三个状态行不行:第一个状态是剩余的按键次数,用 `n` 表示;第二个状态是当前屏幕上字符 A 的数量,用 `a_num` 表示;第三个状态是剪切板中字符 A 的数量,用 `copy` 表示。
如此定义「状态」,就可以知道 base case:当剩余次数 `n` 为 0 时,`a_num` 就是我们想要的答案。
结合刚才说的 4 种「选择」,我们可以把这几种选择通过状态转移表示出来:
```python
dp(n - 1, a_num + 1, copy), # A
解释:按下 A 键,屏幕上加一个字符
同时消耗 1 个操作数
dp(n - 1, a_num + copy, copy), # C-V
解释:按下 C-V 粘贴,剪切板中的字符加入屏幕
同时消耗 1 个操作数
dp(n - 2, a_num, a_num) # C-A C-C
解释:全选和复制必然是联合使用的,
剪切板中 A 的数量变为屏幕上 A 的数量
同时消耗 2 个操作数
```
这样可以看到问题的规模 `n` 在不断减小,肯定可以到达 `n = 0` 的 base case,所以这个思路是正确的:
```python
def maxA(N: int) -> int:
# 对于 (n, a_num, copy) 这个状态,
# 屏幕上能最终最多能有 dp(n, a_num, copy) 个 A
def dp(n, a_num, copy):
# base case
if n <= 0: return a_num;
# 几种选择全试一遍,选择最大的结果
return max(
dp(n - 1, a_num + 1, copy), # A
dp(n - 1, a_num + copy, copy), # C-V
dp(n - 2, a_num, a_num) # C-A C-C
)
# 可以按 N 次按键,屏幕和剪切板里都还没有 A
return dp(N, 0, 0)
```
这个解法应该很好理解,因为语义明确。下面就继续走流程,用备忘录消除一下重叠子问题:
```python
def maxA(N: int) -> int:
# 备忘录
memo = dict()
def dp(n, a_num, copy):
if n <= 0: return a_num;
# 避免计算重叠子问题
if (n, a_num, copy) in memo:
return memo[(n, a_num, copy)]
memo[(n, a_num, copy)] = max(
# 几种选择还是一样的
)
return memo[(n, a_num, copy)]
return dp(N, 0, 0)
```
这样优化代码之后,子问题虽然没有重复了,但数目仍然很多,在 LeetCode 提交会超时的。
我们尝试分析一下这个算法的时间复杂度,就会发现不容易分析。我们可以把这个 dp 函数写成 dp 数组:
```python
dp[n][a_num][copy]
# 状态的总数(时空复杂度)就是这个三维数组的体积
```
我们知道变量 `n` 最多为 `N`,但是 `a_num` 和 `copy` 最多为多少我们很难计算,复杂度起码也有 O(N^3) 吧。所以这个算法并不好,复杂度太高,且已经无法优化了。
这也就说明,我们这样定义「状态」是不太优秀的,下面我们换一种定义 dp 的思路。
### 第二种思路
这种思路稍微有点复杂,但是效率高。继续走流程,「选择」还是那 4 个,但是这次我们只定义一个「状态」,也就是剩余的敲击次数 `n`。
这个算法基于这样一个事实,**最优按键序列一定只有两种情况**:
要么一直按 `A`:A,A,...A(当 N 比较小时)。
要么是这么一个形式:A,A,...C-A,C-C,C-V,C-V,...C-V(当 N 比较大时)。
因为字符数量少(N 比较小)时,`C-A C-C C-V` 这一套操作的代价相对比较高,可能不如一个个按 `A`;而当 N 比较大时,后期 `C-V` 的收获肯定很大。这种情况下整个操作序列大致是:**开头连按几个 `A`,然后 `C-A C-C` 组合再接若干 `C-V`,然后再 `C-A C-C` 接着若干 `C-V`,循环下去**。
换句话说,最后一次按键要么是 `A` 要么是 `C-V`。明确了这一点,可以通过这两种情况来设计算法:
```java
int[] dp = new int[N + 1];
// 定义:dp[i] 表示 i 次操作后最多能显示多少个 A
for (int i = 0; i <= N; i++)
dp[i] = max(
这次按 A 键,
这次按 C-V
)
```
对于「按 `A` 键」这种情况,就是状态 `i - 1` 的屏幕上新增了一个 A 而已,很容易得到结果:
```java
// 按 A 键,就比上次多一个 A 而已
dp[i] = dp[i - 1] + 1;
```
但是,如果要按 `C-V`,还要考虑之前是在哪里 `C-A C-C` 的。
**刚才说了,最优的操作序列一定是 `C-A C-C` 接着若干 `C-V`,所以我们用一个变量 `j` 作为若干 `C-V` 的起点**。那么 `j` 之前的 2 个操作就应该是 `C-A C-C` 了:
```java
public int maxA(int N) {
int[] dp = new int[N + 1];
dp[0] = 0;
for (int i = 1; i <= N; i++) {
// 按 A 键
dp[i] = dp[i - 1] + 1;
for (int j = 2; j < i; j++) {
// 全选 & 复制 dp[j-2],连续粘贴 i - j 次
// 屏幕上共 dp[j - 2] * (i - j + 1) 个 A
dp[i] = Math.max(dp[i], dp[j - 2] * (i - j + 1));
}
}
// N 次按键之后最多有几个 A?
return dp[N];
}
```
其中 `j` 变量减 2 是给 `C-A C-C` 留下操作数,看个图就明白了:
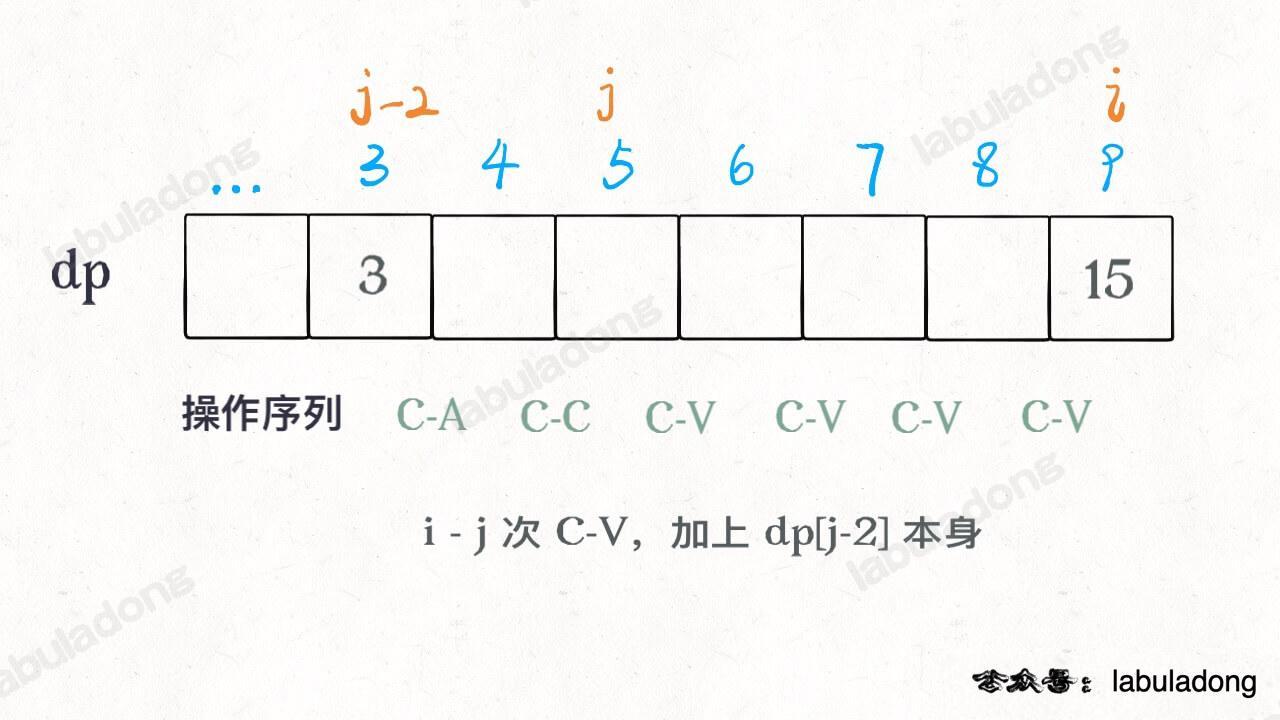
这样,此算法就完成了,时间复杂度 O(N^2),空间复杂度 O(N),这种解法应该是比较高效的了。
### 最后总结
动态规划难就难在寻找状态转移,不同的定义可以产生不同的状态转移逻辑,虽然最后都能得到正确的结果,但是效率可能有巨大的差异。
回顾第一种解法,重叠子问题已经消除了,但是效率还是低,到底低在哪里呢?抽象出递归框架:
```python
def dp(n, a_num, copy):
dp(n - 1, a_num + 1, copy), # A
dp(n - 1, a_num + copy, copy), # C-V
dp(n - 2, a_num, a_num) # C-A C-C
```
看这个穷举逻辑,是有可能出现这样的操作序列 `C-A C-C,C-A C-C...` 或者 `C-V,C-V,...`。然这种操作序列的结果不是最优的,但是我们并没有想办法规避这些情况的发生,从而增加了很多没必要的子问题计算。
回顾第二种解法,我们稍加思考就能想到,最优的序列应该是这种形式:`A,A..C-A,C-C,C-V,C-V..C-A,C-C,C-V..`。
根据这个事实,我们重新定义了状态,重新寻找了状态转移,从逻辑上减少了无效的子问题个数,从而提高了算法的效率。
引用本文的文章
- [一个方法团灭 LeetCode 打家劫舍问题](https://labuladong.online/algo/fname.html?fname=抢房子)
- [最优子结构原理和 dp 数组遍历方向](https://labuladong.online/algo/fname.html?fname=最优子结构)
**_____________**
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:

======其他语言代码======
### javascript
[651.四键键盘](https://leetcode-cn.com/problems/4-keys-keyboard)
**1、第一种思路**
```js
let maxA = function (N) {
// 备忘录
let memo = {}
let dp = function (n, a_num, copy) {
if (n <= 0) {
return a_num;
}
let key = n + ',' + a_num + ',' + copy
// 避免计算重叠子问题
if (memo[key] !== undefined) {
return memo[key]
}
memo[key] = Math.max(
dp(n - 1, a_num + 1, copy), // A
dp(n - 1, a_num + copy, copy), // C-V
dp(n - 2, a_num, a_num) // C-A C-C
)
return memo[key]
}
return dp(N, 0, 0)
}
```
**2、第二种思路**
```js
var maxA = function (N) {
let dp = new Array(N + 1);
dp[0] = 0;
for (let i = 1; i <= N; i++) {
// 按A键盘
dp[i] = dp[i - 1] + 1;
for (let j = 2; j < i; j++) {
// 全选 & 复制 dp[j-2],连续粘贴 i - j 次
// 屏幕上共 dp[j - 2] * (i - j + 1) 个 A
dp[i] = Math.max(dp[i], dp[j - 2] * (i - (j - 2) - 1));
}
}
// N 次按键之后最多有几个 A?
return dp[N];
}
```



