# 动态规划设计:最长递增子序列




**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
| LeetCode | 力扣 | 难度 |
| :----: | :----: | :----: |
| [300. Longest Increasing Subsequence](https://leetcode.com/problems/longest-increasing-subsequence/) | [300. 最长递增子序列](https://leetcode.cn/problems/longest-increasing-subsequence/) | 🟠
| [354. Russian Doll Envelopes](https://leetcode.com/problems/russian-doll-envelopes/) | [354. 俄罗斯套娃信封问题](https://leetcode.cn/problems/russian-doll-envelopes/) | 🔴
**-----------**
也许有读者看了前文 [动态规划详解](https://labuladong.online/algo/fname.html?fname=动态规划详解进阶),学会了动态规划的套路:找到了问题的「状态」,明确了 `dp` 数组/函数的含义,定义了 base case;但是不知道如何确定「选择」,也就是找不到状态转移的关系,依然写不出动态规划解法,怎么办?
不要担心,动态规划的难点本来就在于寻找正确的状态转移方程,本文就借助经典的「最长递增子序列问题」来讲一讲设计动态规划的通用技巧:**数学归纳思想**。
最长递增子序列(Longest Increasing Subsequence,简写 LIS)是非常经典的一个算法问题,比较容易想到的是动态规划解法,时间复杂度 O(N^2),我们借这个问题来由浅入深讲解如何找状态转移方程,如何写出动态规划解法。比较难想到的是利用二分查找,时间复杂度是 O(NlogN),我们通过一种简单的纸牌游戏来辅助理解这种巧妙的解法。
力扣第 300 题「最长递增子序列」就是这个问题:
输入一个无序的整数数组,请你找到其中最长的严格递增子序列的长度,函数签名如下:
```java
int lengthOfLIS(int[] nums);
```
比如说输入 `nums=[10,9,2,5,3,7,101,18]`,其中最长的递增子序列是 `[2,3,7,101]`,所以算法的输出应该是 4。
注意「子序列」和「子串」这两个名词的区别,子串一定是连续的,而子序列不一定是连续的。下面先来设计动态规划算法解决这个问题。
### 一、动态规划解法
动态规划的核心设计思想是数学归纳法。
相信大家对数学归纳法都不陌生,高中就学过,而且思路很简单。比如我们想证明一个数学结论,那么**我们先假设这个结论在 `k < n` 时成立,然后根据这个假设,想办法推导证明出 `k = n` 的时候此结论也成立**。如果能够证明出来,那么就说明这个结论对于 `k` 等于任何数都成立。
类似的,我们设计动态规划算法,不是需要一个 dp 数组吗?我们可以假设 `dp[0...i-1]` 都已经被算出来了,然后问自己:怎么通过这些结果算出 `dp[i]`?
直接拿最长递增子序列这个问题举例你就明白了。不过,首先要定义清楚 dp 数组的含义,即 `dp[i]` 的值到底代表着什么?
**我们的定义是这样的:`dp[i]` 表示以 `nums[i]` 这个数结尾的最长递增子序列的长度**。
::: info
为什么这样定义呢?这是解决子序列问题的一个套路,后文 [动态规划之子序列问题解题模板](https://labuladong.online/algo/fname.html?fname=子序列问题模板) 总结了几种常见套路。你读完本章所有的动态规划问题,就会发现 `dp` 数组的定义方法也就那几种。
:::
根据这个定义,我们就可以推出 base case:`dp[i]` 初始值为 1,因为以 `nums[i]` 结尾的最长递增子序列起码要包含它自己。
举两个例子:
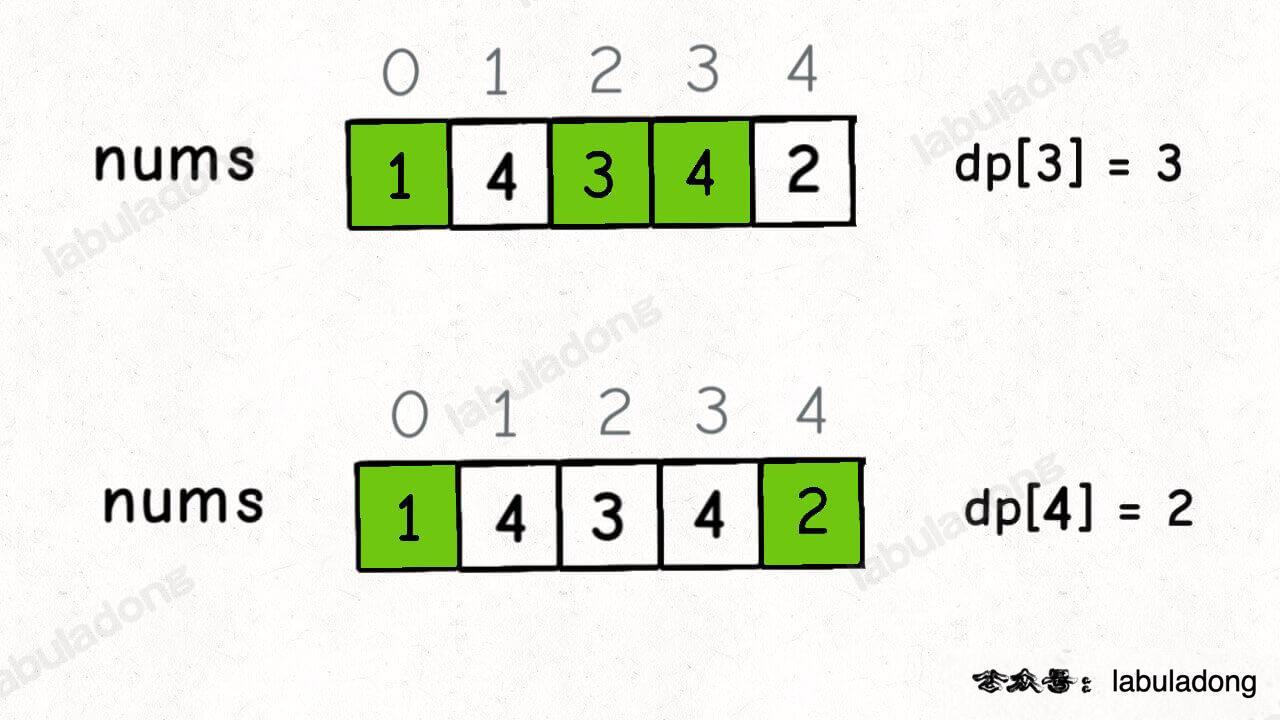
这个 GIF 展示了算法演进的过程:
根据这个定义,我们的最终结果(子序列的最大长度)应该是 dp 数组中的最大值。
```java
int res = 0;
for (int i = 0; i < dp.length; i++) {
res = Math.max(res, dp[i]);
}
return res;
```
读者也许会问,刚才的算法演进过程中每个 `dp[i]` 的结果是我们肉眼看出来的,我们应该怎么设计算法逻辑来正确计算每个 `dp[i]` 呢?
这就是动态规划的重头戏,如何设计算法逻辑进行状态转移,才能正确运行呢?这里需要使用数学归纳的思想:
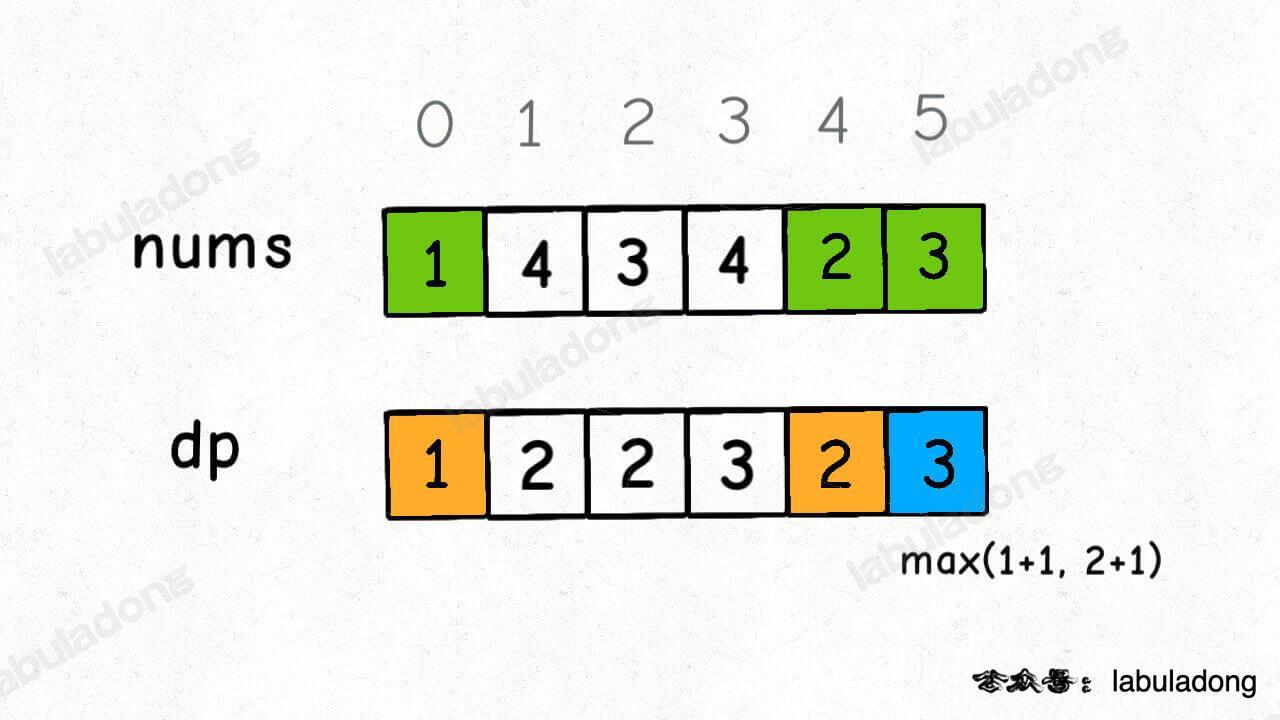
**假设我们已经知道了 `dp[0..4]` 的所有结果,我们如何通过这些已知结果推出 `dp[5]` 呢**?

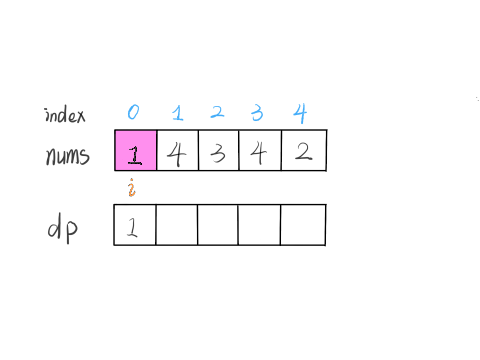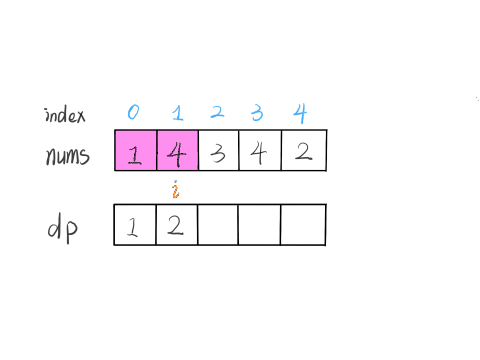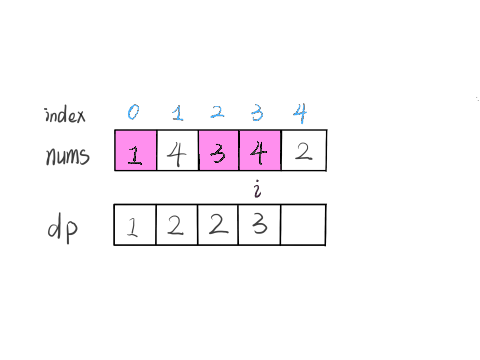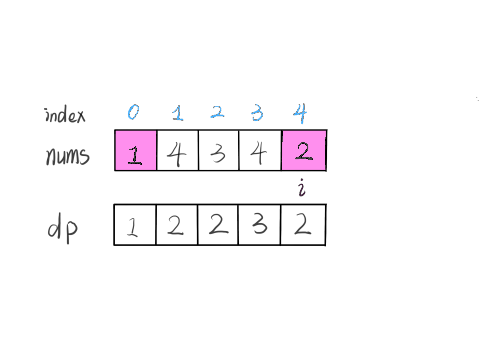
根据刚才我们对 `dp` 数组的定义,现在想求 `dp[5]` 的值,也就是想求以 `nums[5]` 为结尾的最长递增子序列。
**`nums[5] = 3`,既然是递增子序列,我们只要找到前面那些结尾比 3 小的子序列,然后把 3 接到这些子序列末尾,就可以形成一个新的递增子序列,而且这个新的子序列长度加一**。
`nums[5]` 前面有哪些元素小于 `nums[5]`?这个好算,用 for 循环比较一波就能把这些元素找出来。
以这些元素为结尾的最长递增子序列的长度是多少?回顾一下我们对 `dp` 数组的定义,它记录的正是以每个元素为末尾的最长递增子序列的长度。
以我们举的例子来说,`nums[0]` 和 `nums[4]` 都是小于 `nums[5]` 的,然后对比 `dp[0]` 和 `dp[4]` 的值,我们让 `nums[5]` 和更长的递增子序列结合,得出 `dp[5] = 3`:
```java
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
```
当 `i = 5` 时,这段代码的逻辑就可以算出 `dp[5]`。其实到这里,这道算法题我们就基本做完了。
读者也许会问,我们刚才只是算了 `dp[5]` 呀,`dp[4]`, `dp[3]` 这些怎么算呢?类似数学归纳法,你已经可以算出 `dp[5]` 了,其他的就都可以算出来:
```java
for (int i = 0; i < nums.length; i++) {
for (int j = 0; j < i; j++) {
// 寻找 nums[0..j-1] 中比 nums[i] 小的元素
if (nums[i] > nums[j]) {
// 把 nums[i] 接在后面,即可形成长度为 dp[j] + 1,
// 且以 nums[i] 为结尾的递增子序列
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
}
```
结合我们刚才说的 base case,下面我们看一下完整代码:
```java
int lengthOfLIS(int[] nums) {
// 定义:dp[i] 表示以 nums[i] 这个数结尾的最长递增子序列的长度
int[] dp = new int[nums.length];
// base case:dp 数组全都初始化为 1
Arrays.fill(dp, 1);
for (int i = 0; i < nums.length; i++) {
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j])
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
int res = 0;
for (int i = 0; i < dp.length; i++) {
res = Math.max(res, dp[i]);
}
return res;
}
```
至此,这道题就解决了,时间复杂度 `O(N^2)`。总结一下如何找到动态规划的状态转移关系:
1、明确 `dp` 数组的定义。这一步对于任何动态规划问题都很重要,如果不得当或者不够清晰,会阻碍之后的步骤。
2、根据 `dp` 数组的定义,运用数学归纳法的思想,假设 `dp[0...i-1]` 都已知,想办法求出 `dp[i]`,一旦这一步完成,整个题目基本就解决了。
但如果无法完成这一步,很可能就是 `dp` 数组的定义不够恰当,需要重新定义 `dp` 数组的含义;或者可能是 `dp` 数组存储的信息还不够,不足以推出下一步的答案,需要把 `dp` 数组扩大成二维数组甚至三维数组。
目前的解法是标准的动态规划,但对最长递增子序列问题来说,这个解法不是最优的,可能无法通过所有测试用例了,下面讲讲更高效的解法。
### 二、二分查找解法
这个解法的时间复杂度为 `O(NlogN)`,但是说实话,正常人基本想不到这种解法(也许玩过某些纸牌游戏的人可以想出来)。所以大家了解一下就好,正常情况下能够给出动态规划解法就已经很不错了。
根据题目的意思,我都很难想象这个问题竟然能和二分查找扯上关系。其实最长递增子序列和一种叫做 patience game 的纸牌游戏有关,甚至有一种排序方法就叫做 patience sorting(耐心排序)。
为了简单起见,后文跳过所有数学证明,通过一个简化的例子来理解一下算法思路。
首先,给你一排扑克牌,我们像遍历数组那样从左到右一张一张处理这些扑克牌,最终要把这些牌分成若干堆。
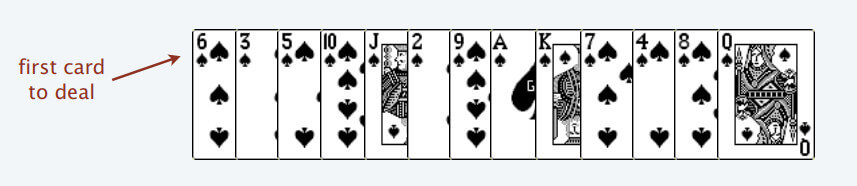
**处理这些扑克牌要遵循以下规则**:
只能把点数小的牌压到点数比它大的牌上;如果当前牌点数较大没有可以放置的堆,则新建一个堆,把这张牌放进去;如果当前牌有多个堆可供选择,则选择最左边的那一堆放置。
比如说上述的扑克牌最终会被分成这样 5 堆(我们认为纸牌 A 的牌面是最大的,纸牌 2 的牌面是最小的)。
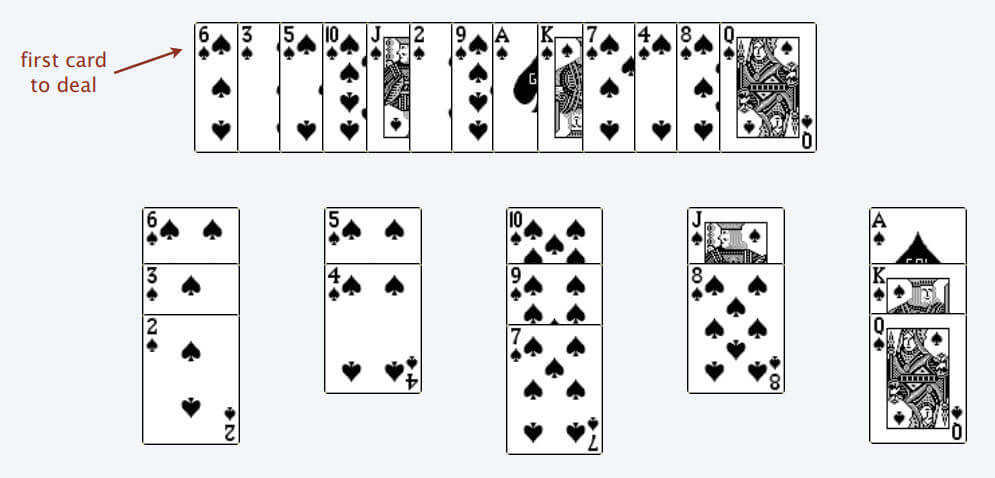
为什么遇到多个可选择堆的时候要放到最左边的堆上呢?因为这样可以保证牌堆顶的牌有序(2, 4, 7, 8, Q),证明略。
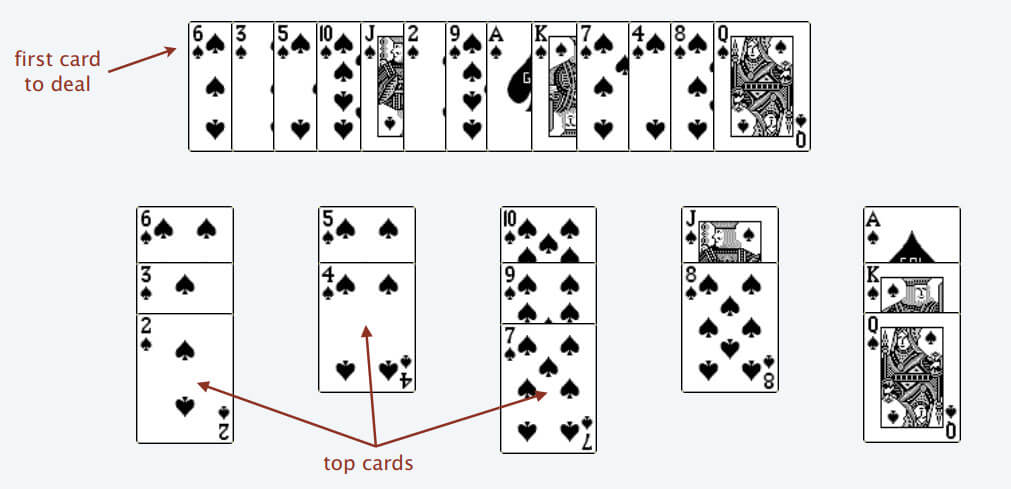
按照上述规则执行,可以算出最长递增子序列,牌的堆数就是最长递增子序列的长度,证明略。
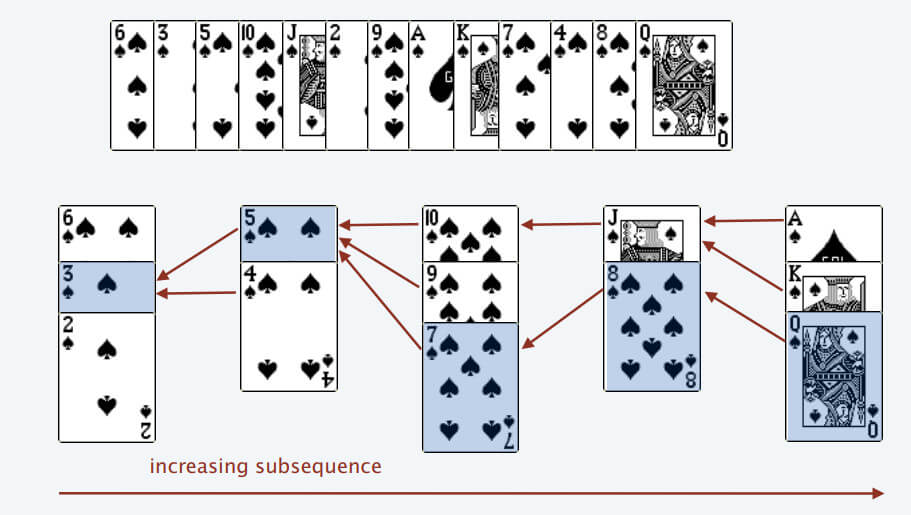
我们只要把处理扑克牌的过程编程写出来即可。每次处理一张扑克牌不是要找一个合适的牌堆顶来放吗,牌堆顶的牌不是**有序**吗,这就能用到二分查找了:用二分查找来搜索当前牌应放置的位置。
::: tip
前文 [二分查找算法详解](https://labuladong.online/algo/fname.html?fname=二分查找详解) 详细介绍了二分查找的细节及变体,这里就完美应用上了,如果没读过强烈建议阅读。
:::
```java
int lengthOfLIS(int[] nums) {
int[] top = new int[nums.length];
// 牌堆数初始化为 0
int piles = 0;
for (int i = 0; i < nums.length; i++) {
// 要处理的扑克牌
int poker = nums[i];
/***** 搜索左侧边界的二分查找 *****/
int left = 0, right = piles;
while (left < right) {
int mid = (left + right) / 2;
if (top[mid] > poker) {
right = mid;
} else if (top[mid] < poker) {
left = mid + 1;
} else {
right = mid;
}
}
/*********************************/
// 没找到合适的牌堆,新建一堆
if (left == piles) piles++;
// 把这张牌放到牌堆顶
top[left] = poker;
}
// 牌堆数就是 LIS 长度
return piles;
}
```
至此,二分查找的解法也讲解完毕。
这个解法确实很难想到。首先涉及数学证明,谁能想到按照这些规则执行,就能得到最长递增子序列呢?其次还有二分查找的运用,要是对二分查找的细节不清楚,给了思路也很难写对。
所以,这个方法作为思维拓展好了。但动态规划的设计方法应该完全理解:假设之前的答案已知,利用数学归纳的思想正确进行状态的推演转移,最终得到答案。
### 三、拓展到二维
我们看一个经常出现在生活中的有趣问题,力扣第 354 题「俄罗斯套娃信封问题」,先看下题目:
**这道题目其实是最长递增子序列的一个变种,因为每次合法的嵌套是大的套小的,相当于在二维平面中找一个最长递增的子序列,其长度就是最多能嵌套的信封个数**。
前面说的标准 LIS 算法只能在一维数组中寻找最长子序列,而我们的信封是由 `(w, h)` 这样的二维数对形式表示的,如何把 LIS 算法运用过来呢?
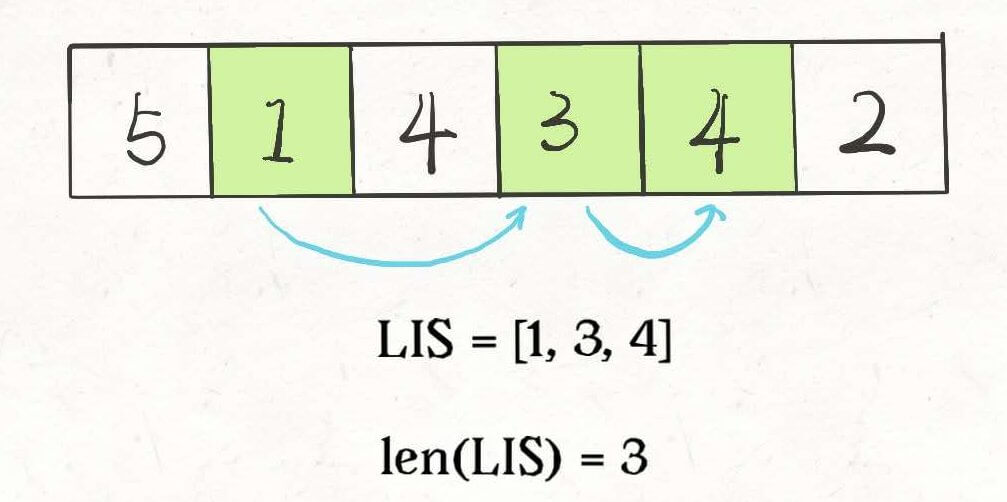
读者也许会想,通过 `w × h` 计算面积,然后对面积进行标准的 LIS 算法。但是稍加思考就会发现这样不行,比如 `1 × 10` 大于 `3 × 3`,但是显然这样的两个信封是无法互相嵌套的。
这道题的解法比较巧妙:
**先对宽度 `w` 进行升序排序,如果遇到 `w` 相同的情况,则按照高度 `h` 降序排序;之后把所有的 `h` 作为一个数组,在这个数组上计算 LIS 的长度就是答案**。
画个图理解一下,先对这些数对进行排序:

然后在 `h` 上寻找最长递增子序列,这个子序列就是最优的嵌套方案:

**那么为什么这样就可以找到可以互相嵌套的信封序列呢**?稍微思考一下就明白了:
首先,对宽度 `w` 从小到大排序,确保了 `w` 这个维度可以互相嵌套,所以我们只需要专注高度 `h` 这个维度能够互相嵌套即可。
其次,两个 `w` 相同的信封不能相互包含,所以对于宽度 `w` 相同的信封,对高度 `h` 进行降序排序,保证二维 LIS 中不存在多个 `w` 相同的信封(因为题目说了长宽相同也无法嵌套)。
下面看解法代码:
```java
// envelopes = [[w, h], [w, h]...]
public int maxEnvelopes(int[][] envelopes) {
int n = envelopes.length;
// 按宽度升序排列,如果宽度一样,则按高度降序排列
Arrays.sort(envelopes, (int[] a, int[] b) -> {
return a[0] == b[0] ?
b[1] - a[1] : a[0] - b[0];
});
// 对高度数组寻找 LIS
int[] height = new int[n];
for (int i = 0; i < n; i++)
height[i] = envelopes[i][1];
return lengthOfLIS(height);
}
int lengthOfLIS(int[] nums) {
// 见前文
}
```
为了清晰,我将代码分为了两个函数, 你也可以合并,这样可以节省下 `height` 数组的空间。
由于增加了测试用例,这里必须使用二分搜索版的 `lengthOfLIS` 函数才能通过所有测试用例。这样的话算法的时间复杂度为 `O(NlogN)`,因为排序和计算 LIS 各需要 `O(NlogN)` 的时间,加到一起还是 `O(NlogN)`;空间复杂度为 `O(N)`,因为计算 LIS 的函数中需要一个 `top` 数组。
接下来可阅读:
* [动态规划之最大子数组](https://labuladong.online/algo/fname.html?fname=最大子数组)
引用本文的文章
- [二分查找高效判定子序列](https://labuladong.online/algo/fname.html?fname=二分查找判定子序列)
- [动态规划之子序列问题解题模板](https://labuladong.online/algo/fname.html?fname=子序列问题模板)
- [动态规划穷举的两种视角](https://labuladong.online/algo/fname.html?fname=动归两种视角)
- [动态规划解题套路框架](https://labuladong.online/algo/fname.html?fname=动态规划详解进阶)
- [动态规划设计:最大子数组](https://labuladong.online/algo/fname.html?fname=最大子数组)
- [我的刷题心得:算法的本质](https://labuladong.online/algo/fname.html?fname=算法心得)
- [最优子结构原理和 dp 数组遍历方向](https://labuladong.online/algo/fname.html?fname=最优子结构)
引用本文的题目
安装 [我的 Chrome 刷题插件](https://labuladong.online/algo/intro/chrome/) 点开下列题目可直接查看解题思路:
| LeetCode | 力扣 |
| :----: | :----: |
| [1425. Constrained Subsequence Sum](https://leetcode.com/problems/constrained-subsequence-sum/?show=1) | [1425. 带限制的子序列和](https://leetcode.cn/problems/constrained-subsequence-sum/?show=1) |
| [256. Paint House](https://leetcode.com/problems/paint-house/?show=1)🔒 | [256. 粉刷房子](https://leetcode.cn/problems/paint-house/?show=1)🔒 |
| [368. Largest Divisible Subset](https://leetcode.com/problems/largest-divisible-subset/?show=1) | [368. 最大整除子集](https://leetcode.cn/problems/largest-divisible-subset/?show=1) |
| - | [剑指 Offer II 091. 粉刷房子](https://leetcode.cn/problems/JEj789/?show=1) |
**_____________**
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:

======其他语言代码======
### javascript
[scuhzs](https://github.com/brucecat)提供[300.最长上升子序列](https://leetcode-cn.com/problems/longest-increasing-subsequence)
动态规划做法如下:
```javascript
let lengthOfLIS = function (nums) {
// 用1填满dp数组
let dp = [];
dp.fill(1, 0, nums.length);
for (let i = 1; i < nums.length; i++)
for (let j = 0; j < i; j++)
nums[i] > nums[j] && (dp[i] = Math.max(dp[i], dp[j] + 1))
return nums.length < 2 ? nums.length : Math.max(...dp)
};
```
二分法做法如下:
```javascript
let lengthOfLIS01 = function (nums) {
let top = new Array(nums.length);
for (let i = 0; i < nums.length; i++) {
top[i] = 0;
}
// 牌堆数初始化为 0
let piles = 0;
for (let i = 0; i < nums.length; i++) {
// 要处理的扑克牌
let poker = nums[i];
/***** 搜索左侧边界的二分查找 *****/
let left = 0, right = piles;
while (left < right) {
// 记住这里要向下取整
let mid = Math.floor((left + right) / 2);
if (top[mid] > poker) {
right = mid;
} else if (top[mid] < poker) {
left = mid + 1;
} else {
right = mid;
}
}
/*********************************/
// 没找到合适的牌堆,新建一堆
left === piles && piles++;
// 把这张牌放到牌堆顶
top[left] = poker;
}
// 牌堆数就是 LIS 长度
return piles;
}
```
### python
```python 动态规划
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
n = len(nums)
f = [1] * (n)
for i in range(n):
for j in range(i):
if nums[j] < nums[i]:
f[i] = max(f[i], f[j] + 1)
res = 0
for i in range(n):
res = max(res, f[i])
return res
```
```python 二分查找
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
stack = []
def find_index(num):
l, r = 0, len(stack)
while l < r:
mid = l + r >> 1
if stack[mid] >= num:
r = mid
else:
l = mid + 1
return r
for num in nums:
if not stack or num > stack[-1]:
stack.append(num)
else:
position = find_index(num)
stack[position] = num
return len(stack)
```
### c++
[Kian](https://github.com/KianKw/) 提供 C++ 代码
```c++
class Solution {
public:
int lengthOfLIS(vector& nums) {
/* len 为牌的数量 */
int len = nums.size();
vector top(len, 0);
/* 牌堆数初始化为0 */
int piles = 0;
for (int i = 0; i < len; i++) {
/* nums[i] 为要处理的扑克牌 */
int poker = nums[i];
/***** 搜索左侧边界的二分查找 *****/
int left = 0, right = piles;
while (left < right) {
int mid = left + (right - left) / 2;
if (top[mid] > poker) {
right = mid;
} else if (top[mid] < poker) {
left = mid + 1;
} else if (top[mid] == poker) {
right = mid;
}
}
/*********************************/
/* 没找到合适的牌堆,新建一堆 */
if (left == piles)
piles++;
/* 把这张牌放到牌堆顶 */
top[left] = poker;
}
/* 牌堆数就是 LIS 长度 */
return piles;
}
};
```



