# 如何高效寻找素数




**通知:算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
| LeetCode | 力扣 | 难度 |
| :----: | :----: | :----: |
| [204. Count Primes](https://leetcode.com/problems/count-primes/) | [204. 计数质数](https://leetcode.cn/problems/count-primes/) | 🟠
**-----------**
素数的定义看起来很简单,如果一个数如果只能被 1 和它本身整除,那么这个数就是素数。
虽然素数的定义并不复杂,恐怕没多少人真的能把素数相关的算法写得高效。
比如力扣第 204 题「计数质数」,让你写这样一个函数:
```java
// 返回区间 [2, n) 中有几个素数
int countPrimes(int n)
// 比如 countPrimes(10) 返回 4
// 因为 2,3,5,7 是素数
```
你会如何写这个函数?我想大家应该会这样写:
```java
int countPrimes(int n) {
int count = 0;
for (int i = 2; i < n; i++)
if (isPrime(i)) count++;
return count;
}
// 判断整数 n 是否是素数
boolean isPrime(int n) {
for (int i = 2; i < n; i++)
if (n % i == 0)
// 有其他整除因子
return false;
return true;
}
```
这样写的话时间复杂度 O(n^2),问题很大。**首先你用 isPrime 函数来辅助的思路就不够高效;而且就算你要用 isPrime 函数,这样写算法也是存在计算冗余的**。
先来简单说下**如果你要判断一个数是不是素数,应该如何写算法**。只需稍微修改一下上面的 isPrime 代码中的 for 循环条件:
```java
boolean isPrime(int n) {
for (int i = 2; i * i <= n; i++)
...
}
```
换句话说,`i` 不需要遍历到 `n`,而只需要到 `sqrt(n)` 即可。为什么呢,我们举个例子,假设 `n = 12`。
```java
12 = 2 × 6
12 = 3 × 4
12 = sqrt(12) × sqrt(12)
12 = 4 × 3
12 = 6 × 2
```
可以看到,后两个乘积就是前面两个反过来,反转临界点就在 `sqrt(n)`。
换句话说,如果在 `[2,sqrt(n)]` 这个区间之内没有发现可整除因子,就可以直接断定 `n` 是素数了,因为在区间 `[sqrt(n),n]` 也一定不会发现可整除因子。
现在,`isPrime` 函数的时间复杂度降为 O(sqrt(N)),**但是我们实现 `countPrimes` 函数其实并不需要这个函数**,以上只是希望读者明白 `sqrt(n)` 的含义,因为等会还会用到。
### 高效实现 `countPrimes`
接下来介绍的方法叫做「素数筛选法」,这个方法是古希腊一位名叫埃拉托色尼的大佬发明的,我们在中学的教课书上见过他的大名,因为他就是第一个通过物体的影子正确计算地球周长的人,被推崇为「地理学之父」。
回到正题,素数筛选法的核心思路是和上面的常规思路反着来:
首先从 2 开始,我们知道 2 是一个素数,那么 2 × 2 = 4, 3 × 2 = 6, 4 × 2 = 8... 都不可能是素数了。
然后我们发现 3 也是素数,那么 3 × 2 = 6, 3 × 3 = 9, 3 × 4 = 12... 也都不可能是素数了。
Wikipedia 的这个 GIF 很形象:
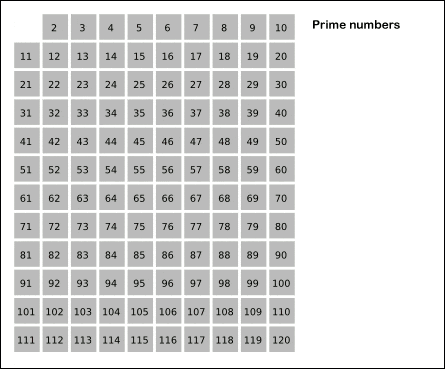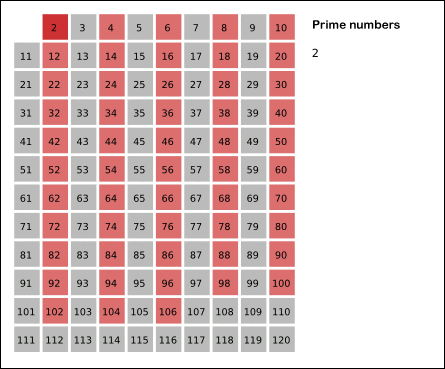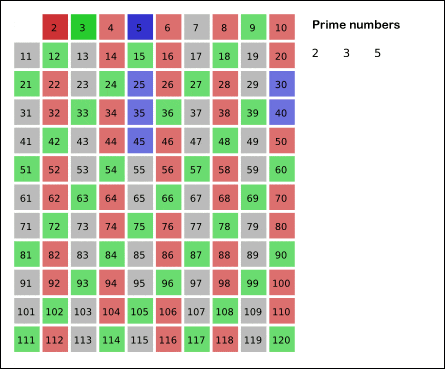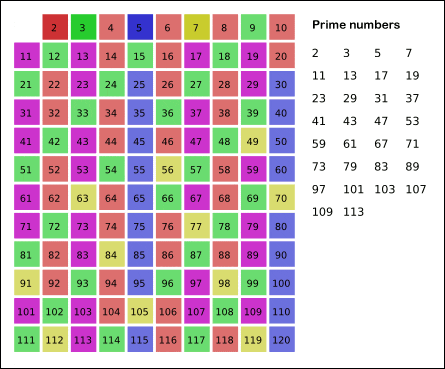
看到这里,你是否有点明白这个排除法的逻辑了呢?先看我们的第一版代码:
```java
int countPrimes(int n) {
boolean[] isPrime = new boolean[n];
// 将数组都初始化为 true
Arrays.fill(isPrime, true);
for (int i = 2; i < n; i++)
if (isPrime[i])
// i 的倍数不可能是素数了
for (int j = 2 * i; j < n; j += i)
isPrime[j] = false;
int count = 0;
for (int i = 2; i < n; i++)
if (isPrime[i]) count++;
return count;
}
```
如果上面这段代码你能够理解,那么你已经掌握了整体思路,但是还有两个细微的地方可以优化。
首先,回想刚才判断一个数是否是素数的 `isPrime` 函数,由于因子的对称性,其中的 for 循环只需要遍历 `[2,sqrt(n)]` 就够了。这里也是类似的,我们外层的 for 循环也只需要遍历到 `sqrt(n)`:
```java
for (int i = 2; i * i < n; i++)
if (isPrime[i])
...
```
除此之外,很难注意到内层的 for 循环也可以优化。我们之前的做法是:
```java
for (int j = 2 * i; j < n; j += i)
isPrime[j] = false;
```
这样可以把 `i` 的整数倍都标记为 `false`,但是仍然存在计算冗余。
比如 `n = 25`,`i = 5` 时算法会标记 5 × 2 = 10,5 × 3 = 15 等等数字,但是这两个数字已经被 `i = 2` 和 `i = 3` 的 2 × 5 和 3 × 5 标记了。
我们可以稍微优化一下,让 `j` 从 `i` 的平方开始遍历,而不是从 `2 * i` 开始:
```java
for (int j = i * i; j < n; j += i)
isPrime[j] = false;
```
这样,素数计数的算法就高效实现了,其实这个算法有一个名字,叫做 Sieve of Eratosthenes。看下完整的最终代码:
```java
class Solution {
public int countPrimes(int n) {
boolean[] isPrime = new boolean[n];
Arrays.fill(isPrime, true);
for (int i = 2; i * i < n; i++)
if (isPrime[i])
for (int j = i * i; j < n; j += i)
isPrime[j] = false;
int count = 0;
for (int i = 2; i < n; i++)
if (isPrime[i]) count++;
return count;
}
}
```
**该算法的时间复杂度比较难算**,显然时间跟这两个嵌套的 for 循环有关,其操作数应该是:
n/2 + n/3 + n/5 + n/7 + ...
= n × (1/2 + 1/3 + 1/5 + 1/7...)
括号中是素数的倒数。其最终结果是 O(N * loglogN),有兴趣的读者可以查一下该算法的时间复杂度证明。
以上就是素数算法相关的全部内容。怎么样,是不是看似简单的问题却有不少细节可以打磨呀?
引用本文的文章
- [一文秒杀所有丑数系列问题](https://labuladong.online/algo/fname.html?fname=丑数)
- [配套 Chrome 刷题插件](https://labuladong.online/algo/fname.html?fname=chrome插件简介)
引用本文的题目
安装 [我的 Chrome 刷题插件](https://labuladong.online/algo/intro/chrome/) 点开下列题目可直接查看解题思路:
| LeetCode | 力扣 |
| :----: | :----: |
| [264. Ugly Number II](https://leetcode.com/problems/ugly-number-ii/?show=1) | [264. 丑数 II](https://leetcode.cn/problems/ugly-number-ii/?show=1) |
| - | [剑指 Offer 49. 丑数](https://leetcode.cn/problems/chou-shu-lcof/?show=1) |
**_____________**
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:

======其他语言代码======
[204.计数质数](https://leetcode-cn.com/problems/count-primes)
### C++
采用的算法是埃拉托斯特尼筛法
埃拉托斯特尼筛法的具体内容就是:**要得到自然数n以内的全部素数,必须把不大于根号n的所有素数的倍数剔除,剩下的就是素数。**
同时考虑到大于2的偶数都不是素数,所以可以进一步优化成:**要得到自然数n以内的全部素数,必须把不大于根号n的所有素数的奇数倍剔除,剩下的奇数就是素数。**
此算法其实就是上面的Java解法所采用的。
这里提供C++的代码:
```C++
class Solution {
public:
int countPrimes(int n) {
int res = 0;
bool prime[n+1];
for(int i = 0; i < n; ++i)
prime[i] = true;
for(int i = 2; i <= sqrt(n); ++i) //计数过程
{ //外循环优化,因为判断一个数是否为质数只需要整除到sqrt(n),反推亦然
if(prime[i])
{
for(int j = i * i; j < n; j += i) //内循环优化,i*i之前的比如i*2,i*3等,在之前的循环中已经验证了
{
prime[j] = false;
}
}
}
for (int i = 2; i < n; ++i)
if (prime[i]) res++; //最后遍历统计一遍,存入res
return res;
}
};
```
### javascript
```js
var countPrimes = function (n) {
let isPrime = new Array(n);
isPrime.fill(true, 0, n)
// 计数过程
// 外循环优化,因为判断一个数是否为质数只需要整除到sqrt(n),反推亦然
for (let i = 2; i * i < n; i++) {
if (isPrime[i]) {
// 内循环优化,i*i之前的比如i*2,i*3等,在之前的循环中已经验证了
for (let j = i * i; j < n; j += i) {
isPrime[j] = false;
}
}
}
let res = 0;
for (let i = 2; i < n; i++) {
//最后遍历统计一遍,存入res
if (isPrime[i]) res++;
}
return res;
};
```



