{
 "cells": [
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "# Lesson 5 - Random forest deep dive\n",
    "\n",
    "> A deep dive into how Random Forests work and some tricks for making them more accurate."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "[![Binder](https://mybinder.org/badge_logo.svg)](https://mybinder.org/v2/gh/lewtun/dslectures/master?urlpath=lab/tree/notebooks%2Flesson05_random-forest-deep-dive.ipynb) \n",
    "[![slides](https://img.shields.io/static/v1?label=slides&message=lesson05_random-forest-deep-dive.pdf&color=blue&logo=Google-drive)](https://drive.google.com/open?id=1xRpRXFY_wMzHn2QgW3nDzULh8Y7G5IVt)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Learning objectives"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "* Understand how to go from simple to complex models\n",
    "* Understand the concepts of bagging and out-of-bag score\n",
    "* Gain an introduction to hyperparameter tuning"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## References"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "This lesson is adapted from Jeremy Howard's fantastic online course [_Introduction to Machine Learning for Coders_](https://course18.fast.ai/ml), in particular:\n",
    "\n",
    "* [2 - Random Forest Deep Dive](https://course18.fast.ai/lessonsml1/lesson2.html)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Homework\n",
    "\n",
    "* Solve the exercises included in this notebook\n",
    "* Read chapter 7 of _Hands-On Machine Learning with Scikit-Learn and TensorFlow_ by Aurèlien Geron"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## The data"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "In this lesson we will analyse the preprocessed table of clean housing data and their addresses that we prepared in lesson 3:\n",
    "\n",
    "* `housing_processed.csv`"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## How does a random forest work for regression tasks?"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "<div style=\"text-align: center\">\n",
    "<img src='images/rf-regression.png' width='700'>\n",
    "</div>"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "When we use a Random Forest to solve a regression task, the basic idea is that the _leaf nodes_ of each Decision Tree predict a numerical value that is the average of the training instances associated with that node. These predictions are then _averaged_ to obtain the final prediction from the forest of trees. In this lesson we will look at how we can build predictions from a single tree and get better predictions by adding progressively more trees to the forest."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Import libraries"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "# reload modules before executing user code\n",
    "%load_ext autoreload\n",
    "# reload all modules every time before executing Python code\n",
    "%autoreload 2\n",
    "# render plots in notebook\n",
    "%matplotlib inline"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "# uncomment to update the library if working locally\n",
    "# !pip install dslectures --upgrade"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "# data wrangling\n",
    "import pandas as pd\n",
    "import numpy as np\n",
    "from numpy.testing import assert_array_equal\n",
    "from dslectures.core import *\n",
    "from dslectures.structured import *\n",
    "from pathlib import Path\n",
    "import pickle\n",
    "\n",
    "# data viz\n",
    "import matplotlib.pyplot as plt\n",
    "import seaborn as sns\n",
    "from sklearn.tree import plot_tree\n",
    "\n",
    "sns.set(color_codes=True)\n",
    "sns.set_palette(sns.color_palette(\"muted\"))\n",
    "\n",
    "# ml magic\n",
    "from sklearn.model_selection import train_test_split\n",
    "from sklearn.metrics import r2_score\n",
    "from sklearn.ensemble import RandomForestRegressor"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Load the data"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "Dataset already exists at '../data/housing_processed.csv' and is not downloaded again.\n"
     ]
    }
   ],
   "source": [
    "get_dataset('housing_processed.csv')"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "We also make use of the `pathlib` library to handle our filepaths:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "housing.csv                  keep_cols.npy\n",
      "housing_addresses.csv        submission.csv\n",
      "housing_columns_to_keep.npy  submission_mean.csv\n",
      "housing_gmaps_data_raw.csv   test.csv\n",
      "housing_merged.csv           train.csv\n",
      "housing_model.pkl            uc\n",
      "housing_processed.csv        word2vec-google-news-300.pkl\n",
      "imdb.csv\n"
     ]
    }
   ],
   "source": [
    "DATA = Path('../data/')\n",
    "!ls {DATA}"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/html": [
       "<div>\n",
       "<style scoped>\n",
       "    .dataframe tbody tr th:only-of-type {\n",
       "        vertical-align: middle;\n",
       "    }\n",
       "\n",
       "    .dataframe tbody tr th {\n",
       "        vertical-align: top;\n",
       "    }\n",
       "\n",
       "    .dataframe thead th {\n",
       "        text-align: right;\n",
       "    }\n",
       "</style>\n",
       "<table border=\"1\" class=\"dataframe\">\n",
       "  <thead>\n",
       "    <tr style=\"text-align: right;\">\n",
       "      <th></th>\n",
       "      <th>longitude</th>\n",
       "      <th>latitude</th>\n",
       "      <th>housing_median_age</th>\n",
       "      <th>total_rooms</th>\n",
       "      <th>total_bedrooms</th>\n",
       "      <th>population</th>\n",
       "      <th>households</th>\n",
       "      <th>median_income</th>\n",
       "      <th>median_house_value</th>\n",
       "      <th>city</th>\n",
       "      <th>postal_code</th>\n",
       "      <th>rooms_per_household</th>\n",
       "      <th>bedrooms_per_household</th>\n",
       "      <th>bedrooms_per_room</th>\n",
       "      <th>population_per_household</th>\n",
       "      <th>ocean_proximity_INLAND</th>\n",
       "      <th>ocean_proximity_&lt;1H OCEAN</th>\n",
       "      <th>ocean_proximity_NEAR BAY</th>\n",
       "      <th>ocean_proximity_NEAR OCEAN</th>\n",
       "      <th>ocean_proximity_ISLAND</th>\n",
       "    </tr>\n",
       "  </thead>\n",
       "  <tbody>\n",
       "    <tr>\n",
       "      <th>0</th>\n",
       "      <td>-122.23</td>\n",
       "      <td>37.88</td>\n",
       "      <td>41.0</td>\n",
       "      <td>880.0</td>\n",
       "      <td>129.0</td>\n",
       "      <td>322.0</td>\n",
       "      <td>126.0</td>\n",
       "      <td>8.3252</td>\n",
       "      <td>452600.0</td>\n",
       "      <td>69</td>\n",
       "      <td>94705</td>\n",
       "      <td>6.984127</td>\n",
       "      <td>1.023810</td>\n",
       "      <td>0.146591</td>\n",
       "      <td>2.555556</td>\n",
       "      <td>0</td>\n",
       "      <td>0</td>\n",
       "      <td>1</td>\n",
       "      <td>0</td>\n",
       "      <td>0</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>1</th>\n",
       "      <td>-122.22</td>\n",
       "      <td>37.86</td>\n",
       "      <td>21.0</td>\n",
       "      <td>7099.0</td>\n",
       "      <td>1106.0</td>\n",
       "      <td>2401.0</td>\n",
       "      <td>1138.0</td>\n",
       "      <td>8.3014</td>\n",
       "      <td>358500.0</td>\n",
       "      <td>620</td>\n",
       "      <td>94611</td>\n",
       "      <td>6.238137</td>\n",
       "      <td>0.971880</td>\n",
       "      <td>0.155797</td>\n",
       "      <td>2.109842</td>\n",
       "      <td>0</td>\n",
       "      <td>0</td>\n",
       "      <td>1</td>\n",
       "      <td>0</td>\n",
       "      <td>0</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>2</th>\n",
       "      <td>-122.24</td>\n",
       "      <td>37.85</td>\n",
       "      <td>52.0</td>\n",
       "      <td>1467.0</td>\n",
       "      <td>190.0</td>\n",
       "      <td>496.0</td>\n",
       "      <td>177.0</td>\n",
       "      <td>7.2574</td>\n",
       "      <td>352100.0</td>\n",
       "      <td>620</td>\n",
       "      <td>94618</td>\n",
       "      <td>8.288136</td>\n",
       "      <td>1.073446</td>\n",
       "      <td>0.129516</td>\n",
       "      <td>2.802260</td>\n",
       "      <td>0</td>\n",
       "      <td>0</td>\n",
       "      <td>1</td>\n",
       "      <td>0</td>\n",
       "      <td>0</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>3</th>\n",
       "      <td>-122.25</td>\n",
       "      <td>37.85</td>\n",
       "      <td>52.0</td>\n",
       "      <td>1274.0</td>\n",
       "      <td>235.0</td>\n",
       "      <td>558.0</td>\n",
       "      <td>219.0</td>\n",
       "      <td>5.6431</td>\n",
       "      <td>341300.0</td>\n",
       "      <td>620</td>\n",
       "      <td>94618</td>\n",
       "      <td>5.817352</td>\n",
       "      <td>1.073059</td>\n",
       "      <td>0.184458</td>\n",
       "      <td>2.547945</td>\n",
       "      <td>0</td>\n",
       "      <td>0</td>\n",
       "      <td>1</td>\n",
       "      <td>0</td>\n",
       "      <td>0</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>4</th>\n",
       "      <td>-122.25</td>\n",
       "      <td>37.85</td>\n",
       "      <td>52.0</td>\n",
       "      <td>1627.0</td>\n",
       "      <td>280.0</td>\n",
       "      <td>565.0</td>\n",
       "      <td>259.0</td>\n",
       "      <td>3.8462</td>\n",
       "      <td>342200.0</td>\n",
       "      <td>620</td>\n",
       "      <td>94618</td>\n",
       "      <td>6.281853</td>\n",
       "      <td>1.081081</td>\n",
       "      <td>0.172096</td>\n",
       "      <td>2.181467</td>\n",
       "      <td>0</td>\n",
       "      <td>0</td>\n",
       "      <td>1</td>\n",
       "      <td>0</td>\n",
       "      <td>0</td>\n",
       "    </tr>\n",
       "  </tbody>\n",
       "</table>\n",
       "</div>"
      ],
      "text/plain": [
       "   longitude  latitude  housing_median_age  total_rooms  total_bedrooms  \\\n",
       "0    -122.23     37.88                41.0        880.0           129.0   \n",
       "1    -122.22     37.86                21.0       7099.0          1106.0   \n",
       "2    -122.24     37.85                52.0       1467.0           190.0   \n",
       "3    -122.25     37.85                52.0       1274.0           235.0   \n",
       "4    -122.25     37.85                52.0       1627.0           280.0   \n",
       "\n",
       "   population  households  median_income  median_house_value  city  \\\n",
       "0       322.0       126.0         8.3252            452600.0    69   \n",
       "1      2401.0      1138.0         8.3014            358500.0   620   \n",
       "2       496.0       177.0         7.2574            352100.0   620   \n",
       "3       558.0       219.0         5.6431            341300.0   620   \n",
       "4       565.0       259.0         3.8462            342200.0   620   \n",
       "\n",
       "   postal_code  rooms_per_household  bedrooms_per_household  \\\n",
       "0        94705             6.984127                1.023810   \n",
       "1        94611             6.238137                0.971880   \n",
       "2        94618             8.288136                1.073446   \n",
       "3        94618             5.817352                1.073059   \n",
       "4        94618             6.281853                1.081081   \n",
       "\n",
       "   bedrooms_per_room  population_per_household  ocean_proximity_INLAND  \\\n",
       "0           0.146591                  2.555556                       0   \n",
       "1           0.155797                  2.109842                       0   \n",
       "2           0.129516                  2.802260                       0   \n",
       "3           0.184458                  2.547945                       0   \n",
       "4           0.172096                  2.181467                       0   \n",
       "\n",
       "   ocean_proximity_<1H OCEAN  ocean_proximity_NEAR BAY  \\\n",
       "0                          0                         1   \n",
       "1                          0                         1   \n",
       "2                          0                         1   \n",
       "3                          0                         1   \n",
       "4                          0                         1   \n",
       "\n",
       "   ocean_proximity_NEAR OCEAN  ocean_proximity_ISLAND  \n",
       "0                           0                       0  \n",
       "1                           0                       0  \n",
       "2                           0                       0  \n",
       "3                           0                       0  \n",
       "4                           0                       0  "
      ]
     },
     "execution_count": null,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "housing_data = pd.read_csv(DATA/'housing_processed.csv'); housing_data.head()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "With the data loaded, we can recreate our feature matrix $X$ and target vector $y$ and train/validation splits as before."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "---\n",
    "\n",
    "#### Exercise #1\n",
    "\n",
    "* Create the feature matrix $X$ and target vector $y$ from `housing_data`\n",
    "* Create training and validation sets with a split of 80:20\n",
    "\n",
    "---"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Baseline model"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "As a sanity check, let's see how our baseline model performs on the validation set:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "model = RandomForestRegressor(n_estimators=10, n_jobs=-1, random_state=42)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "RandomForestRegressor(bootstrap=True, ccp_alpha=0.0, criterion='mse',\n",
       "                      max_depth=None, max_features='auto', max_leaf_nodes=None,\n",
       "                      max_samples=None, min_impurity_decrease=0.0,\n",
       "                      min_impurity_split=None, min_samples_leaf=1,\n",
       "                      min_samples_split=2, min_weight_fraction_leaf=0.0,\n",
       "                      n_estimators=10, n_jobs=-1, oob_score=False,\n",
       "                      random_state=42, verbose=0, warm_start=False)"
      ]
     },
     "execution_count": null,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "model.fit(X_train, y_train)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "To simplify the evaluation of our models, let's write a simple function to keep track of the scores:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "def print_rf_scores(fitted_model):\n",
    "    \"\"\"Generates RMSE and R^2 scores from fitted Random Forest model.\"\"\"\n",
    "\n",
    "    yhat_train = fitted_model.predict(X_train)\n",
    "    R2_train = fitted_model.score(X_train, y_train)\n",
    "    yhat_valid = fitted_model.predict(X_valid)\n",
    "    R2_valid = fitted_model.score(X_valid, y_valid)\n",
    "\n",
    "    scores = {\n",
    "        \"RMSE on train:\": rmse(y_train, yhat_train),\n",
    "        \"R^2 on train:\": R2_train,\n",
    "        \"RMSE on valid:\": rmse(y_valid, yhat_valid),\n",
    "        \"R^2 on valid:\": R2_valid,\n",
    "    }\n",
    "    if hasattr(fitted_model, \"oob_score_\"):\n",
    "        scores[\"OOB R^2:\"] = fitted_model.oob_score_\n",
    "\n",
    "    for score_name, score_value in scores.items():\n",
    "        print(score_name, round(score_value, 3))"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "RMSE on train: 19173.912\n",
      "R^2 on train: 0.96\n",
      "RMSE on valid: 46106.026\n",
      "R^2 on valid: 0.779\n"
     ]
    }
   ],
   "source": [
    "print_rf_scores(model)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## The simplest model: a single tree"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Let's build a model that is so simple that we can actually take a look at it. As we saw in lesson 4, a Random Forest is a simply forest of decision trees, so let's begin by looking at a single tree (called _estimators_ in scikit-learn): "
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "RandomForestRegressor(bootstrap=False, ccp_alpha=0.0, criterion='mse',\n",
       "                      max_depth=3, max_features='auto', max_leaf_nodes=None,\n",
       "                      max_samples=None, min_impurity_decrease=0.0,\n",
       "                      min_impurity_split=None, min_samples_leaf=1,\n",
       "                      min_samples_split=2, min_weight_fraction_leaf=0.0,\n",
       "                      n_estimators=1, n_jobs=-1, oob_score=False,\n",
       "                      random_state=42, verbose=0, warm_start=False)"
      ]
     },
     "execution_count": null,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "model = RandomForestRegressor(n_estimators=1, max_depth=3, bootstrap=False, n_jobs=-1, random_state=42)\n",
    "model.fit(X_train, y_train)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "In the above we have fixed the following hyperparameters:\n",
    "\n",
    "* `n_estimators = 1`: create a forest with one tree, i.e. a _decision tree_\n",
    "* `max_depth = 3`: how deep or the number of \"levels\" in the tree\n",
    "* `bootstrap=False`: this setting ensures we use the whole dataset to build the tree\n",
    "\n",
    "Let's see how this simple model performs:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "RMSE on train: 65040.247\n",
      "R^2 on train: 0.545\n",
      "RMSE on valid: 67579.11\n",
      "R^2 on valid: 0.525\n"
     ]
    }
   ],
   "source": [
    "print_rf_scores(model)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Unsurprisingly, this single tree yields worse predictions ($R^2 = 0.53$) than our baseline with 10 trees ($R^2 = 0.78$). Nevertheless, we can visualise the tree by accessing the `estimators_` attribute and making use of scikit-learn's plotting API ([link](https://scikit-learn.org/stable/modules/generated/sklearn.tree.plot_tree.html)):"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAABpgAAAIuCAYAAACrewsjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8li6FKAAAgAElEQVR4nOzdd3QUZcPG4Xs3PYQeSAi9995LKAmEZJbPgoq9IxZeFVEE7GCjCTZeUQFBwAKCjZ2EElqQDgYUpDdJICEhgYTUzeb7A13NS0SCwAr8rnM8h8zMM3PP5shh997nGUtISEihAAAAAAAAAAAAgPNkdXcAAAAAAAAAAAAAXFkomAAAAAAAAAAAAFAiFEwAAAAAAAAAAAAoEQomAAAAAAAAAAAAlAgFEwAAAAAAAAAAAEqEggkAAAAAAAAAAAAlQsEEAAAAAAAAAACAEqFgAgAAAAAAAAAAQIlQMAEAAAAAAAAAAKBEKJgAAAAAAAAAAABQIhRMAAAAAAAAAAAAKBEKJgAAAAAAAAAAAJQIBRMAAAAAAAAAAABKhIIJAAAAAAAAAAAAJULBBAAAAAAAAAAAgBKhYAIAAAAAAAAAAECJUDABAAAAAAAAAACgRCiYAAAAAAAAAAAAUCIUTAAAAAAAAAAAACgRCiYAAAAAAAAAAACUCAUTAAAAAAAAAAAASoSCCQAAAAAAAAAAACVCwQQAAAAAAAAAAIASoWACAAAAAAAAAABAiVAwAQAAAAAAAAAAoEQomAAAAAAAAAAAAFAiFEwAAAAAAAAAAAAoEQomAAAAAAAAAAAAlAgFEwAAAAAAAAAAAEqEggkAAAAAAAAAAAAlQsEEAAAAAAAAAACAEqFgAgAAAAAAAAAAQIlQMAEAAAAAAAAAAKBEKJgAAAAAAAAAAABQIhRMAAAAAAAAAAAAKBEKJgAAAAAAAAAAAJQIBRMAAAAAAAAAAABKhIIJAAAAAAAAAAAAJULBBAAAAAAAAAAAgBKhYAIAAAAAAAAAAECJUDABAAAAAAAAAACgRCiYAAAAAAAAAAAAUCIUTAAAAAAAAAAAACgRT3cHAAAAAHB5/bhlsyoHBbs7Bq4yyUnH1LpNW3fHAAAAAHCZUDABAAAA15jKQcHK2hrt7hi4ylRuGeXuCAAAAAAuI5bIAwAAAAAAAAAAQIlQMAEAAAAAAAAAAKBEKJgAAAAAAAAAAABQIhRMAAAAAC6JlybP0ZS5Z571NPiNKTLjNl2ya900dIy2/LLvkp3/SvDCe7P10uQ5f7n/pz0Hdduz49X57mf1wEvv6tdjKa59vx5L0cOjJ6vL3c/qhidf1+ofd7j2bdqxVwOeGatu9w7XnSPf0s97D13S+wAAAABwZaBgAgAAAHDJTX7uERmh7S7Z+edPHKE2jetesvNfatt2H9SoKV9c8PjlG7YpevXmv9yfm5evoROm697rwrTqkzfUsUUDDX97piTJ6XRq6Phpat+svlbPHKNn7++v4ZNmKjsnVwVOp4a99YmG3nOD4maM0fU9O2r4pJkXnBMAAADA1cPT3QEAAAAAuFdicqruf+ld9e/dWZ/ZV8nXx0svDLpVyzds0+K1Pyo4sLzGPnWf6lYLVr6jQFPmRsset0kFTqdsoe00+DabvDw9lJqeoZf+O0c//rJfjetUl5+vt0IqVZAkDXzlPV3Xs4Ou69lRP+89pEmzvtP+I8fkcBQorGMLvfTIbfKwWmUMHqVb+nTVvCU/KCs7VxFdWuu5gbf87T0Yg0dp9GN3qF3T+mo9YIiG3XejPvkmVoWFhbo1MlQP3RQhSdp54IjemDpPew8fVbWgihrx4M1q07iukk+c1LhPFmjT9j0K8PfTgL7ddHe/nrJYLBr4ynvq1KKhFq7cqOQTJ3V9r45q06SuJn76rbKyc/XwLX11h9FDkrRu2y5NmvWtEo+fUJO6NfTCQwNUPTiw2MwFTqeWbdim2QtX6OjxNN0WFSpJeu2jucXO9nr/uYeLLdHSTmXqnTnf67peHVVQUFDstTZu36OyAf6K6tb2zO+jf4Tm2Fdq35FjysjMUm5evh68sY8sFou6tGqs6aOfkNVq1anMLKVnnFa+o0CFhYWyWi3y8eZtJAAAAAAKJgAAAACSkk+cVH5+gZZNe00ffbVIT42bqhcGDdDIgTdr1AdfaMY3sXr1P3fq0++WadOOvZrz5tOyWi16+q3pmr1wue6/obde/ehLVShTWsunva5tuw/qsdenqFndGmdda/ikmXr01ij1695eCcmpumvkRK3ftktdWjWWdKak+XLcMCWlntS9L7wtI7SdWjWsXaL7+XnvYX3//gv6afchPfraB7quZweVLxOgJ8d+rHuvC9OA0d20bP02PT1huhZ/OEpPT5imhrWqKWbKK0pKSdd/3vxQ5UqX0nU9O0iSFq+N1/RXn1RGZpZuGjpGicknNH/iCP24c7+eGjdVN/fpquNpJzXsrU804ZkH1KZxXX0Rs0pDx0/Tl+OHyWotunjE7IUr9Hn0KlUsV1q3R3VX706t5OXpIUl6YdAAvTBowHnf65tTv9K914crKSVNicdPFHvMwYRk1QoJcv3sYbWqWlCgDiYkKSXtlGpXDdJrH83Vsg3bFBxYXs/e318+3l7y8fbSjWGd9MSYj+RhtcrH20sfvvRYiX4XAAAAAK5OLJEHAAAAQJJ0V7+e8rBa1aZxXfn7+eiGsE7y8vRUu6b1lJSaLkn6fuUGPTogShXLlVb5MgF6qH+Evl+5Qbl5+frhxx16ZECkfLy91L5ZfXVv27TY60x58TH1695eGVnZSk3PUNkAf6WkZ7j239ynq0qX8le9GlXUoGaIfj12vMT3cqfRQ77e3mrfrL4qliutI0mpit+1X1arVXcYPeTp4aGILq31zvCHlHg8TTsPHNHT994gX29v1QyprHuvC5P9T7OI+nVvrwplAlQzpLICy5fRDeGd5O/ro84tGirfUaDUkxmK+WGLQts2VcfmDeTl6aG7+/XSycwsbd93+Kx878z5XlUrV9SYJ+9RVLe2rnKppBat2aLTOTm6MazTOY/Lzs2Tr49XkW2+Pl7Kyc3XqdPZ+iH+FzWuU02LPxyle/6vl54aN1UnM0+rwOlUKX9f/ff5R7Rm1jgNvs3QsIkzlJ2bd0F5AQAAAFw9mMEEAAAAQJJUNsBfkuRhtSjA39e13Wq1yFnolCQlpabrmbemy2KxnNlZKMkinczMkqPAqcoVyrrGVQksX+x14nft12OvfyBHgVNN6lRXnsPx24nOKF+mlOvPHh5WFRYWFnOWczv7HE6lpmeoUvkyRY5r0aCWtu4+oHKlA+Tn4/1H9koVlPxbqSb98dpIZ16P0r+9Pr/PTCp0OpWUmq7Y9VsVet9217EOR4GOpaSref2i+Ra+/6I+j16lO0a8pbZN6umufj3VulEdSdIbU+cV+zyld0cMch0jSanpGXr/c7s+fvk/f/t6+Pp4KTcvv8i2nNx8+ft6y8vTQ1UqldfNfbpKkqK6tdUn3yxV/M4Dys3L18GEZD19zw2SpDuMHpq7aLXW/7RbPds1+9vrAgAAALh6UTABAAAAkKQ/SqNzqFiujMYMuUfN6tWUJJ3OzlF6xmmVDfCXp4eHjqakqUZwJUnS8fRTRYoq6UxB9fpH8zT7zaGqV6OKJOnWYeMu8p0Ur3KFcjqedqrItv9+aap/eGelZ2QqOydXfr4+kqSE5FSVLxvgOu48XhpVLFda1/fqWOSZUYcSkxVcTNEWVLGchtx1nR66KUILYtfquXdnqUpgeU0f/YSeG3jLeT13at22XUpJz9Atz4yVJOXlO+R0FmrngSOaO2F4kWNrhQTp+5UbXT8XOJ369dhx1QypLEnKzMopcnyBs1CFkpJOpCvf4Siyz9PTQ54eLIYBAAAAXOt4VwAAAADgvEV1a6sp82KUnnFa2bl5evXDLzVm2nz5eHsprGMLvf+ZXdm5eYrfdUArN/581vjM7BxZLJKPt5cKnE4tiF2rPYePyuFwXvLszevXlNVi0dzFq1XgdGrJunh9vWydKpYrrRYNamvirG+Vk5enQ4nJmvX9ckV2aVOi80d0bq0la+O1bfdBFRYWKnb9Vt06bLzSM07/5ZhSfr66u18vff/eC7q7X88SXc/WvZ3WzhqnuBljFDdjjO6/PlxR3dqcVS5JUvtm9XQiPUPfr9ygfIdDUxcsVvWgQNWpFqxOLRrKw2rVHPsKOZ1O2VdtUmr6KbVvWk8dmjVQ/M4DWrZhm5xOp75dvl4nM7LUqmGdYhIBAAAAuJYwgwkAAADAeXvopgi9/7ldtw4bp6ycXLVrUk+jHrtdkvT8wFv0ygefK3zgC6pdLajYZzDVrRasO209ddfIibJaLWpRv5b6dGqp/QnHLnl2by9PvT18oN6c+pXem7NQ1YMD9fawgfLy9NSbT96jMdO+UuQjr8jby0sD+nbVLRFdS3T+2lWDNHrwHXrt47lKTE5VlcAKGv/0/QqqWO5vx3p6eKhXhxYXemvFMuM2adrXSzV/4gj5envr3ZGD9PrHczVm2nw1rFVVY5+6T5Lk5+ujj14erDemztOUuTEKDiyvicMeVCk/XzWsVVWvPX6XJn9h6uXJn6lO9WC9N3LQWTPTAAAAAFx7LCEhISVf0BwAAADAFSshIUFZW6PdHQNXGf+WUapataq7YwAAAAC4TFgiDwAAAAAAAAAAACXCEnkAAAAA/vX6PvKyMk5nF7tv9OA71btTy8ucCAAAAACubRRMAAAAAP71Fk0Z5e4IAAAAAIA/oWACAAAAcEX5ee8hjZk2XwcTk9SgZlU9N/AW1atRRZK0dN1WTf7CrqTUdNWuFqRn7++vlg1qS5J+2nNQr388T4eOHlfj2tU06rE7VD048G/HLd/4k97/3K6k1DTVqFJZz953o1o1qlMk0/qfduvR1z7Qli8nSZKmLViiaV8vce0vLCxUTl6+Pnn1SbVqWFtxW7brrZnfKOnESXVoWl8vP3a7KpQJkCQ989YnWr1lh6xWiySpVkhlfTb2mSLX+3rZOn08f5HMyS8X+xrt+/Woxkyfr50HjqhsQCk9cENv9e/dWZK0acdeTZjxtX49lqKgiuX05J3/px7tmkmS9hxO1KsffqkDR5JUuWI5DbnrOoW2aXKBvykAAAAAVzOewQQAAADgipGRla0nxnwsI7Stlk97Q/17d9bgN6YoOydXicmpemnyHI0efIfWzBqnARHdNHzSTElSbl6+hk6YrnuvC9OqT95QxxYNNPztM/vONS4hOVUvvT9HIwferFWfvKm7bD00ZNxUnc7OcWXKzMrR6ClfqLCw0LXtwf59tGbWONd/N/Xpoj6dWqlVw9pKST+l596dpRcGDdCKaa+rYrnSev2jua6xuw8laMZrT7rG/m+5dDQlTZNmfXvO1+npCdMV2rqJVkx/Q28984De+3yh4nfuV3ZOrp4aN1WPDIjSD5+O1YgHb9KIt2e67ufF9+fohrBOips5RkPu+j89O/ET5eTl/YPfGAAAAICrFTOYAAAAAJwlMTlV97/0rvr37qzP7Kvk6+OlFwbdquUbtmnx2h8VHFheY5+6T3WrBWvzjn0aO/0rHU1JU7WgQD1xRz91btlIkhS9erM++mqRTpzMVLum9fT8Q7eoQtnSZ12vy93PnrWtSqUKmj9xRJFt8TsPKMDfV3cYPSRJ/bq31yffxGrdT7vVq31zLf34Vfn7+ijf4dDJjNMqG+AvSdq4fY/KBvgrqltbSdLA/hGaY1+pfUeOqW614L8cdzQlTTeGd1a7JvUkSUZoO437ZIEOHT2uJnWqS5ImzPxaYR1baPbCFcW+llt3H1DM6i1aMGmkJGnZhm1q3aiO2jWtL0l64s7/U59BLyozK0dWq0XHUtJUp1pwsecqLCzUqA8+1/W9Oip2/dZij0nPOK3qwZV0V7+eslqtalirqto0rqttew6pVaM6WjRllPx9fVTgdCrtVKZK+fnK08NDknT46HE5CgrkdDplsVjk7eVV7DUAAAAAgIIJAAAAQLGST5xUfn6Blk17TR99tUhPjZuqFwYN0MiBN2vUB19oxjexevU/d+qNqfP0n9tt6tW+uRau2qg3p32l7959QfE792v8jK/13+cfUe2qQXrvs4V6cfIcTX7ukbOutWbWuPPK5HQ65evjXWSbh9WiI0kpkiR/Xx/tOZyo24aNl4eHVe+OGCRJOpiQrFohQX8aY1W1oEAdTEhS3WrBfzmuXZN6rnJJkrbtPqic3HzVCK4kSYrbskO/HkvR6MF3/GXBNPHTb/XwLZEq81tp9b9ZypUupQB/P/167LjyHA75+fjo8Tc/1O5DiWpQq6pGPHCTalc9c/y8xT8osFwZ9Wjb9C8LpnKlS+m9kYNcP2dkZSt+137d3KeL6zXKzMpRzweek7OwUK88ert8vM8USfddH66x0+Zr3PQFslikcUPvl6+3d7HXAQAAAHBtY4k8AAAAAH/prn495WG1qk3juvL389ENYZ3k5empdk3rKSk1XZIU4O+rmNWbtXnHPkV2baNv33lekrRw1Ub1D++sRrWrycfbS4Nvt2n9tt1KTc+44DwtG9ZWUkq6vluxQfmOAkWv3qwDCUnKy3O4jqkVEqR1cybo+YcG6Jm3puvEqUxl5+bJ16fobBxfHy/l5Oafc9yfHT52XM+89YkeuzVKAf6+OpWZpQkzv9Yrj94uy1/kjd91QInJJ3R9r46ubcVm8fZSTl6+snPy1LxBTT37wE2K+eAVtWpYW0PGTVW+o0BHklI0275Cz97f/7xfr+zcPD09frqa1a2pTi0aurb7+Xpr7exxem/kIL05dZ72Hj4qSbJaLXrt8bu0dvY4vfHkPRr1wedKPpF+3tcDAAAAcO1gBhMAAACAv/T7UnEeVosC/H1d261Wi5yFTknS2CH36r3PFurpCdNUWCjdf0O47rs+XMdS02VftUlfLopzjfP08NDRlBOqWK7oMnmh9xVdCk+SqgSW19wJw4tsK1e6lCYOe1ATZn6tSbO+Vd8urdWpRaMi2bw8zyz3dn2vjpq9cIW27NgnXx8v5eblFzlXTm6+/H29zzmud6eWkqSf9x7SE2M+1oCIrrrnurAz9z19vm7t203VgwOVmJxa7OtnX7VRRmhbeXv98dbL17uYLHlnsrRuVKdIEfTILZH6zL5SBxKSNHb6fA295wbXTKi/c+Jkhp4Y87HKlSmlsUPvlcXyRw3mYbXKw2pV11aN1aFZA63ZulM5eXmKXr3FtSxhn06t9HXsWi1dt9W1JCEAAAAA/I6CCQAAAMBf+nMpURxHQYEOJibrtcfvUmFhoTb8vEdDxk5V19aNFVi2tB6+JVL3XR/uOv5AQpKqBweedZ64GWPOK09uXr4C/H30+dhnJJ1ZMs8YPFoP3Nhb67bt0oxvYzXlxcdcx+c7HCpdyk8+3kH6fuVG1/YCp1O/HjuumiGVzzlOktbE/6Lhk2bqqXuuV//wzq5jYtdv06ot2/XB3GgVFhZKOlOUvTtikFo3qiNJWv3jLxoz5J4i91C7apDWbN3p+jntVKYys7JVPbiSVm3erqycXEV2bePK6XA6lXE6W9v3HtaL788+s73AqZy8fIXeN0JzJwxXlcDyRa6RePyEBo2arA7N6uu5h25xPWNp/5FjGj5ppr4cP0xW65kFLfJ+u9ek1HTlOxxFzuPp4SHP34o3AAAAAPgzlsgDAAAAcME8rFa98sHn+jp2nSwWiyqWKy2L1aLS/n6KCm2neYt/0P4jx+R0OvWZuVIPvPSu8h0FF3w9R0GBHnjpPW3dfUD5Doemfb1Upf391LJBLTWsVVW/7D+imB+2yFFQoC9i4lTgdKplw1pq36yeTqRn6PuVG5TvcGjqgsWqHhSoOtWCzznu0NHjGjZxhl5+9PYi5ZIkrZszXnEzxihuxhjNHf+spDNF2e/lUmp6hlLSTqlJnepFxvVs30ybd+zVum27lJuXr/c/t6t722by9/VRvsOh8TMWaP+RY8rLd+i9zxaqfo0qatukbpHrvTviIQUHllPcjDFnlUv5jgI9MeYjdW/bVC89cpurXJKk6sGVlJOXp0+/X64Cp1PLNmzTzgNH1L1NU7VsWFsnTmboi5g4OZ1O/RD/i37cuV/dWje54N8XAAAAgKsXM5gAAAAAXDCLxaIxQ+7V2Onz9dan36hsaX+NfPBmBQeWV3BgeQ26ua+Gjp+mlPRTql01SO+OeEh+Pt5/f+K/UMrPV68/cbdefH+OTpzMUIsGtfTO8IGyWq0qXyZAbw8fqLHT5+v1j+eqce3qem/kIPl6n7neuyMH6fWP52rMtPlqWKuqxj51nySdc9z8JWuUnZunlybP0UuT57hyvP/cw2rTuO45sx5NOaGyAf7y8iz6tqtyhXIaO+RejftkgZJPpKt1o7oaPfgOSVJ4x5Y6kpSqx16folOZWWrduI7G/Zbz3NdK001Pvan5k0Zqz6FE7fv1mBKST+ibZetcxzx4Yx892L+P3n52oF7/eJ6mLViimiGV9e6Ih1xLFr49/CFN/PRbTf7criqVK2j80PsVUqnC314fAAAAwLXHEhISUujuEAAAAAAun4SEBGVtjXZ3DFxl/FtGqWrVqu6OAQAAAOAyYYk8AAAAAAAAAAAAlAgFEwAAAAAAAAAAAEqEggkAAAAAAAAAAAAlQsEEAAAAAAAAAACAEvF0dwAAAAAAuBSmzI1W4vETGj34TrdliF2/VV/ExOnjl//j2jbx02/15aI4eVjPfN/Px9tLy6e9Lkl65q1PtHrLDlmtFklSrZDK+mzsM5KkO0a8pQMJSbL8dp5OLRpq4rAHi1xv8hemfty5T1NfefwS3xkAAACAax0FEwAAAABcAt8uX683p36lZvVrFNm++1CC3nzyHoV1aHHWmN2HEjTjtSfVqHa1ItsLnE7t//WYFn84SmUC/Iu93vZ9hzXzu1i1aFDrot0DAAAAAPwVCiYAAAAAl0yB06k3Pp6nZRu2ydvLU51bNNRzDw2Qt5enft57SJNmfaf9R47J4ShQWMcWeumR2+RhtcoYPEp3RPXQHHOlMk9n64Ebe8vf10cfzV8kq8WqZx/orz6dWum7Feu1dN1WOQsLtXnHPjWqVVWjBt+hGsGViuTIdxRoytxo2eM2qcDplC20nQbfZpOXp4c279insdO/0tGUNFULCtQTd/RT55aNzrqXLnc/e9a2KpUqaP7EEWdtf/9zuzbt2Ks7bT20dfeBIvt2H0pUg5ohZ43JysnVsZQ01akWfNa+g4nJKl+m1F+WS3n5Do2e8oVu7tNVuw8lFHsMAAAAAFxMFEwAAAAALpll67dp/5FjMv/7shwFBXp41GQtXvuj+nVvr+GTZurRW6PUr3t7JSSn6q6RE7V+2y51adVYkvRD/C+aP3GEft57SI+++oGu69VRMR+8om+WrdfET79Vn06tJElxW3bopUdu06RhD2ryF6ZGTJrpWlbud59+t0ybduzVnDefltVq0dNvTdfshct1/w299cbUefrP7Tb1at9cC1dt1JvTvtJ3775w1r2smTXuvO/71shu+s/tNn23Yn2Rgul42kmdzDitCTO/0dZdB1Q9OFDP3HujWjSopT2HE+Xn46PH3/zwTAlVq6pGPHCTalcN0u6DCbJarbrn+Uk6kpSq1o3qaPgDN6lyhbKSpP9+aap722aqHlyRggkAAADAZWF1dwAAAAAAV68Af18dTEyWGbdJ2Tl5mv3mUPXr3l6SNOXFx9Sve3tlZGUrNT1DZQP8lZKe4Rp7U+8u8vf1Udsm9eQsLNRtkaHy8vRU55YNlZSa7jqufs0Q3RjWSV6ennp0QJT2HD6qI0kpRXJ8v3KDHh0QpYrlSqt8mQA91D9C36/c4MoYs3qzNu/Yp8iubfTtO8//4/uuVL5ssdvTM06rXdN6uv+GcC3+cJRuCOukJ8d+rPSM08rOyVPzBjX17AM3KeaDV9SqYW0NGTdV+Y4CFRYWqmndGhr71H1a+P6LKhPgr+fe/VSSFL/rgNZt26VBN0f849wAAAAAcL6YwQQAAADgkuncspEev6Of5i9dozenfqUWDWtp9GN3qFpQoOJ37ddjr38gR4FTTepUV57DIanQNbbsb8vBeVjPfC+utL+vJMlqsaiw8I/jqlWu6Pqzj7eXypUupdSTfxRVkpSUmq5n3poui8VyZkOhpN/+OHbIvXrvs4V6esI0FRZK998QrvuuDz/rXkLvO3spvCqB5TV3wvDzfj3q1wjRhy8Ndv3cP7yzPjdXKX7XAfVs10ydWjR07Xvklkh9Zl+pAwlJMkLbyQht59r35J3/p14PPq/MrBy9+uGXeu0/d8rLk7d3AAAAAC4f3oEAAAAAuGSOJKWoVcPa6h/eWanpGRo3Y4EmzfpOz97fX69/NE+z3xyqejWqSJJuHVZ0Cbrfu6C/k5J+yvXnnLw8pWdkqnKFckWOqViujMYMuUfN6tWUJJ3OzlF6xmk5Cgp0MDFZrz1+lwoLC7Xh5z0aMnaqurZurPo1ij4nKW7GmJLe/lnid+7X7sOJGhDRzbUtz+GQj5enVm3erqycXEV2bSPpzPOrHE6nfLw8tXDVRlUsW9r1bKi8fIesFot2H0pQYnKqBo2eLElyOAqU7yhQ6H0jLkpeAAAAAPgrLJEHAAAA4JLZ8NMejXznU504maEyAf7y8fJU2QB/ZWbnyGI5M+OowOnUgti12nP4qBwOZ4mv8dOeQ1q2YZvyHQ7994toNa9fS1UCyxc5JqpbW02ZF3NmKbrcPL364ZcaM22+PKxWvfLB5/o6dp0sFosqlisti9Wi0v5+F+slKMLLy1Nvz/pOP+7cL0dBgT4zVyov36E2jesq3+HQ+BkLtP/IMeXlO/TeZwtVv0YV1QyprLRTmRo/Y4GSUtOVlZOrt2d/p96dWqpN47paO3u84maMUdyMMRo58Ga1alSbcgkAAADAJccMJgAAAACXzPVhHbX7cKJuGjpG+Q6H2japp5cfvV0VygToTltP3TVyoqxWi1rUr6U+nVpqf8KxEl+jQc0QfbNsnV6e/JmaN6ipMUPuOeuYh26K0Puf23XrsHHKyslVuyb1NOqx22WxWDRmyL0aO32+3vr0G5Ut7a+RD96s4P8pqE2z03QAACAASURBVC6WpnVraOTAm/Xy5M90PP2UGtaqqndHPCQfby+Fd2ypI0mpeuz1KTqVmaXWjeto3FP3SZLuMHooJe2U7hzxlnLy8tS1dRO9MGjAJckIAAAAAOfDEhISUvj3hwEAAAC4WiQkJChra7S7Y1wU361Yr+9WbNDUVx53d5Rrnn/LKFWtWtXdMQAAAABcJiyRBwAAAAAAAAAAgBKhYAIAAAAAAAAAAECJ8AwmAAAAAFes63p21HU9O7o7BgAAAABcc5jBBAAAAAAAAAAAgBJhBhMAAAAAt2g9YIjs77+okMoV3Zbh572H9Ny7s/Tduy8U2TZm2nwdTExSg5pV9dzAW1SvRpUi42YtXK49hxI1evCdrm1zF6/WJ9/E6lRmlprUra7nH7pFtUKCzrlv2oIlmvb1Etc5CgsLlZOXr09efVKtGtYuNnNCcqpue3a84maMcW3LycvTmKlfadnGn+Tt6ak7bT10/w29dTQlTTc99WaR8bl5+bohrJNefPjWC3/hAAAAAFzzKJgAAAAAXJPitmzXi+/Pkb+fj2tbRla2nhjzsQb276NbIrpp0ZotGvzGFH3z9nPy8/VRgdOpmd8t0+TP7bJ1b+cat+WXffpo3iJNG/W4qgcH6qOvFmn0lC81ffQT59z3YP8+erB/H9d5Jsz8WsmpJ/+yXNq2+6CGvz1TmVk5RbZP/PRbpWWcVswHryj9VKbuffEdNa9fU+2a1teaWeNcx23fd1hPjZumgTdFXKyXEQAAAMA1iiXyAAAAAPwjwyZ+omkL/piFs2P/rwob+IIcBQX6ee8hPfjye+r14PMKvXeEXv7vZypwOouM37R9j4zBo1w/JyanqvWAIa6f123bpVuHjVPofSP08Kv/1a/HUorNcdPQMepy97Nn/VecBUvX6u3Z3+u+68OLbI/feUAB/r66w+ghL08P9eveXgH+flr3025J0kvvz1H8zv26MbxzkXFtGtfVd++9oJohlZWbl6/MrByVDfD/231/tnX3AcWs3qIXBg0oNvParTs14p2Zuv9/Muc7HFq4cqNGPHiz/H19FFK5oqaNelz1aoQUOc5RUKCX//uZhtz1f6oSWL7YawAAAADA+WIGEwAAAIB/JKpbW304L8Y1E2fxmh/Vp1MreXp4aPikmXr01ij1695eCcmpumvkRK3ftktdWjU+r3MnJKdq2FufaMIzD6hN47r6ImaVho6fpi/HD5PVWvT7cvMnjjjvzD3aNdMNYR215Zd9mrv4j+1Op1O+Pt5FjvWwWnQk6UypNeTu61SpfFlNmRutxOMnihzn7+ujVZu366lxU1XK31dTX3n8vPb9buKn3+rhWyJVppjySZIa16mub995XsdPnCyy/fDR4/Lx9tLyDds0a+EKWS0W3Xt9mAZEdCty3LfL18vf10dGaDsBAAAAwD/FDCYAAAAA/0i31k10NCVNhxKTJUlL1sYrqlsbSdKUFx9Tv+7tlZGVrdT0DJUN8FdKesZ5nzvmhy0KbdtUHZs3kJenh+7u10snM7O0fd/hf5S5YrnSZxVUktSyYW0lpaTruxUblO8oUPTqzTqQkKS8PIckqVL5suc8b6cWDbVuznjdaeuhJ8d+rHyH47z2xe86oMTkE7q+V8e/PHe50qXk5Xn2dwRPnc5Wxuls7TqYoAUTR2jisAf1wZfR2rR9j+uYwsJCzfp+uR64sc9Z4wEAAADgQjCDCQAAAMA/4u3lqfCOLbV4bbw6t2yoQhWq5W/PEIrftV+Pvf6BHAVONalTXXkOh6TC8z53Umq6YtdvVeh9213bHI4CHUtJV/P6RY8d8MxYHU1JO+sccTPGnPf1ypUupYnDHtSEmV9r0qxv1bdLa3Vq0UgB/r7nNd7b68xbrIf6R2j29yu05/BRNalT/W/32VdtlBHa1nVMSXh5eqjA6dSjA6Lk5+ujhrWqKrJrG63cvF3tmp55kX7ee0iZWTkKbdOkxOcHAAAAgOJQMAEAAAD4x6K6tdGkWd/pdHaO+nZpI4vFoqTUdL3+0TzNfnOo6tWoIkm6ddi4s8ZaLFYVFPzxXKb0zCzXnyuWK63re3XUcwNvcW07lJis4GKeITR3wvB/fB+5efkK8PfR52OfkXRmyTxj8Gg9cGPvc477bsUGbdq+R6MH33lmXGGhHE6nSvv7nXPf71b/+IvGDLnngjJXDw6UxWJRZlaOa5vTWajCwj+KvNU//qKe7ZvJo5hZWwAAAABwIXh3AQAAAOAfa9eknk6czJAZt1lR3dpKkjKzc2SxSD7eXipwOrUgdq32HD4qh8NZZGy1oIpKTc/Qjzv3KzcvX5+ZK137Ijq31pK18dq2+6AKCwsVu36rbh02XukZpy/JfTgKCvTAS+9p6+4Dync4NO3rpSrt76eWDWqdc1zz+jUVu36bNu/Yp3yHQ5M/t6thraqqFlTxnPskKTU9Qylpp1yzmUqqbEAphbZuoqkLFis7N0+7DyUq5octCu/Y0nXMz3sPqXn9c98DAAAAAJQEM5gAAAAA/GNWq1URXVpr7dadalAzRJJUt1qw7rT11F0jJ8pqtahF/Vrq06ml9iccKzI2qGI5PXprlJ6dNEOSNOimvrKv2iRJql01SKMH36HXPp6rxORUVQmsoPFP36+giuUuyX2U8vPV60/crRffn6MTJzPUokEtvTN8YLHPa/qz2lWD9Np/7tSrH36htFOn1aZxHY0fep8sFss590nS0ZQTKhvgX+zzlbrc/azef+5htWlc95zXf+3xOzV2+gLZBo+Wp4eHBt9uqHWjOq79R4+nKbB8mQt4RQAAAACgeJaQkJDzXwAdAAAAwBWpTp06MgxDhmGoZcuWytoa7e5IuMr4t4zS7NmzZZqmfvjhBzkcDndHAgAAAHAJsUQeAAAAcJVq2LChhg4dqqVLl2revHkKDg7Wa6+95u5YuIrt379fTz/9tOLj4/X222+rT58+8vHxcXcsAAAAAJcAM5gAAACAq0jz5s1ls9lkGIZ8fHxkmqbsdrs2b96swsIz//RPSEhgBhMuOv+WUapataokqUqVKoqMjJTNZlOTJk20fPlymaapZcuWKTs7281JAQAAAFwMFEwAAADAFcxisaht27YyDENRUVFyOByy2+0yTVPbtm0rdgwFEy6FPxdMfxYYGKjIyEgZhqHWrVtr9erVMk1TS5cuVUZGhhuSAgAAALgYKJgAAACAK4zValXHjh1dpdLJkyddM5V27tz5t+MpmHAp/FXB9GflypVTRESEDMNQp06dtGHDBi1cuFBLlixRWlraZUoKAAAA4GKgYAIAAACuAJ6enuratasMw1Dfvn119OhRmaYp0zS1b9++Ep2LggmXwvkUTH8WEBCg3r17yzAMhYaGKj4+XqZpKiYmRsePH7+ESQEAAABcDBRMAAAAwL+Uj4+PunfvLpvNpt69e2v//v2u5e9+/fXXCz4vBRMuhZIWTH/m5+enXr16yTAMhYWF6ZdffpFpmoqOjlZiYuJFTgoAAADgYqBgAgAAAP5F/Pz8FBYWJsMw1KtXL23fvt01q+Po0aMX5Ro/btmsykHBF+VcwO+Sk46pdZu2//g8Pj4+Cg0NlWEYioiI0IEDB1zF6uHDhy9CUgAAAAAXAwUTAAAA4GalS5d2LRXWrVs3bdmyxVUqpaamujse4Daenp7q0qWLbDab+vbtq6SkJNfzxvbu3evueAAAAMA1jYIJAAAAcIPy5curT58+6tevnzp06KB169bJNE0tXrxY6enp7o4H/OtYrVZ16NBBhmHIMAxlZGS4yqYdO3a4Ox4AAABwzaFgAgAAAC6TwMBARUVFyTAMtWrVSnFxcbLb7YqNjVVmZqa74wFXDIvFojZt2rjKpoKCApmmKdM0FR8f7+54AAAAwDWBggkAAAC4hEJCQlylUqNGjbR8+XLZ7XYtX75cOTk57o4HXBWaNWsmm80mwzDk5+en6Oho2e12bdq0SU6n093xAAAAgKsSBRMAAABwkdWoUUOGYchms6l27dpavHixTNNUXFyccnNz3R0PuKo1aNDAVTZVrFhRMTExMk1Ta9euVUFBgbvjAQAAAFcNCiYAAADgIqhXr57rQ+2goCDFxMTIbrdr7dq1cjgc7o4HXJNq167tWkavevXqrrJ39erVysvLc3c8AAAA4IpGwQQAAABcoCZNmrg+vC5TpozrGTAbNmxgWS7gX6Zq1aqu/18bNGig2NhYmaapFStWsFwlAAAAcAEomAAAAIASaNWqletDaqvV6iqVfvzxRxUW8k9r4EoQFBSkyMhI2Ww2NW/eXCtXrpRpmoqNjdXp06fdHQ8AAAC4IlAwAQAAAOdgsVjUrl079evXT1FRUcrOzpbdbpfdbtf27dvdHQ/AP1ShQgX17dtXhmGoffv2WrNmjUzT1JIlS3Ty5El3xwMAAAD+tSiYAAAAgP/h4eGhzp07yzAMRUZGKjU1VXa7XaZpavfu3e6OB+ASKVOmjPr06SObzaYuXbpo48aNMk1TixYt0okTJ9wdDwAAAPhXoWACAAAAJHl5eSk0NFSGYSgiIkKHDx+WaZqKjo7WgQMH3B0PwGVWqlQphYeHyzAM9ejRQz/99JPsdrtiYmKUlJTk7ngAAACA21EwAQAA4Jrl6+urHj16yGazKSwsTHv27HE9UykhIcHd8QD8S/z574rw8HDX3xV2u52/KwAAAHDNomACAADANeXPsxK6d++un376yTVTKTk52d3xAPzLeXt7q1u3bjIMQ3379nXNdjRNk9mOAAAAuKZQMAEAAOCqV6ZMGUVERMgwDJ6rAuCi+fPz2qKiopSSkuIqm3bt2uXueAAAAMAlRcEEAACAq1KFChXUt29fGYahdu3aac2aNTJNU0uWLNGpU6fcHQ/AVcZqtapdu3ay2WyKiopSTk6O7Ha77Ha7fv75Z3fHAwAAAC46CiYAAABcNYKCghQZGSmbzabmzZtr5cqVstvtio2NVVZWlrvjAbiGtGrVSoZhyDAMeXh4uGY2bdmyRYWFvA0HAADAlY+CCQAAAFe0qlWruj7ErV+/vpYtWya73a6VK1cqJyfH3fEAQE2aNJHNZpNhGCpdurSio6NlmqbWr18vp9Pp7ngAAADABaFgAgAAwBWndu3arlKpevXqWrRokUzT1OrVq5Wfn+/ueADwl+rVq+cqm4KCgrRo0SLZ7XatWbNGDofD3fEAAACA80bBBAAAgCtCgwYNXB/KVqxYUTExMTJNU2vXrlVBQYG74wFAidWsWVNRUVGy2WyqXbu2lixZItM0tWrVKuXm5ro7HgAAAHBOFEwAAAD412rWrJmrVPLz85NpmrLb7dq8eTPLSgG4qoSEhCgqKkqGYahx48Zavny57Ha7li9fruzsbHfHAwAAAM5CwQQAAIB/DYvFotatW8tmsykqKkpOp1N2u12maWrr1q3ujgcAl0WlSpUUGRkpwzDUqlUrxcXFyTRNLV26VJmZme6OBwAAAEiiYAIAAICbWa1WdejQwfVMpVOnTsk0TZmmqR07drg7HgC4Vfny5RURESGbzaYOHTpo/fr1stvtWrx4sdLT090dDwAAANcwCiYAAABcdp6enurSpYtsNpv69u2rY8eOuZa/27dvn7vjAcC/UunSpdW7d28ZhqHQ0FBt2bJFpmkqJiZGKSkp7o4HAACAawwFEwAAAC4Lb29vde/eXYZhKCIiQgcOHHAtf3f48GF3xwOAK4qfn5/CwsJks9nUs2dP7dixQ6ZpKjo6WkePHnV3PAAAAFwDKJgAAABwyfj5+alXr14yDEO9evXSL7/84vq2fWJiorvjAcBVwcfHR927d5fNZlPv3r114MABLVy4UKZp6tdff3V3PAAAAFylKJgAAABwUQUEBBRZwik+Pl52u50lnADgMvDy8lKXLl1kGIYiIyN19OhRliAFAADAJUHBBAAAgH+sXLlyioiIkGEY6tixozZs2CC73a4lS5YoLS3N3fEA4Jrk4eGhjh07yjAMRUVF6eTJk66y6ZdffnF3PAAAAFzhKJgAAABwQQIDAxUZGSnDMNS6dWvFxcXJNE3FxsYqIyPD3fEAAH9isVjUtm1bGYYhwzDkcDhcz8HbunWru+MBAADgCkTBBAAAgPMWHBysqKgo2Ww2NWnSRMuXL5fdbtfy5cuVnZ3t7ngAgPPUvHlz2Ww22Ww2eXt7Kzo6Wna7XZs2bVJhIR8TAAAA4O9RMAEAAOCcqlevLsMwZLPZVKdOHS1ZskSmaWrVqlXKzc11dzwAwD/UqFEj18ymChUqKDo6WqZpat26dSooKHB3PAAAAPxLUTABAADgLHXr1pXNZpNhGKpSpYpiYmJkt9u1Zs0aORwOd8cDAFwiderUcZVN1apV06JFi2SaplavXq38/Hx3xwMAAMC/CAUTAAAAJEmNGzd2fahYtmxZ1zfY169fL6fT6e54AIDL7PcZrIZhqG7dulq2bJkWLlyoVatWKScnx93xAAAA4GYUTAAAANewli1bupa/8/DwkGmaMk1TW7Zs4RkcAACX4OBgRUZGymazqWnTplq5cqVM01RsbKyysrLcHQ8AAABuQMEEAABwDbFYLGrbtq369eunqKgo5ebmyjRN2e12/fTTT+6OBwC4AlSsWFGRkZEyDENt27bVDz/8INM0tWTJEp06dcrd8QAAAHCZUDABAABc5Tw8PNSpUycZhqHIyEidOHHCNVNp165d7o4HALiClS1bVhERETIMQ507d9aGDRtkmqYWLVqktLQ0d8cDAADAJUTBBAAAcBXy8vJSt27dZBiG+vbtqyNHjshutys6Olr79+93dzwAwFWoVKlSCg8Pl81mU/fu3bVt2zaZpqno6GglJye7Ox4AAAAuMgomAACAq4Svr6+6d+8um82m8PBw7d271zVT6ciRI+6OBwC4hvj6+qpXr14yDENhYWHavXu37Ha7TNNUYmKiu+MBAADgIqBgAgAAuIL5+/srPDxchmGoR48e+vnnn2W32xUTE6OkpCR3xwMAQN7e3goNDZVhGIqIiNChQ4dcX4A4ePCgu+MBAADgAlEwAQAAXGHKlCmj3r17y2azqUuXLtq8ebNM01RMTIxOnDjh7ngAAPwlT09Pde7c2fVcwJSUFNntdtntdu3Zs8fd8QAAAFACFEwAAABXgPLly6tv374yDEPt27fX2rVrZZqmlixZopMnT7o7HgAAJWa1WtW+fXsZhiHDMHT69GmZpim73a7t27e7Ox4AAAD+BgUTAADAv1TlypUVFRUlwzDUokULrVy5UqZpKjY2VqdPn3Z3PAAALhqLxaJWrVq5yiZJio6Olt1uV3x8vAoL+egCAADg34aCCQAA4F8kJCTE9eFaw4YNFRsbK9M0tWLFCuXk5Lg7HgAAl0XTpk1ls9lkGIZKlSrlembTxo0b5XQ63R0PAAAAomACAABwu1q1arlKpZo1a2rRokUyTVOrV69WXl6eu+MBAOBW9evXd5VNlSpV0qJFi2S327V27Vo5HA53xwMAALhmUTABAAC4we8fltlsNgUGBiomJsb1YVlBQYG74wEA8K9Uq1YtRUVFyWazqWbNmlq8eLFM01RcXBxfygAAALjMKJgAAAAuk+KW+7Hb7dq0aRPL/QAAUEL/u6zssmXLZJqmli9fzrKyAAAAlwEFEwAAwCXy+wPLbTaboqKiJMlVKsXHx7s5HQAAV4/KlSsrMjJShmGoZcuWiouLk91uV2xsrDIzM90dDwAA4KpEwQQAAHARWa1WtW/f3vWN6szMTNeDybdv3+7ueAAAXPXKly+vvn37yjAMdejQQWvXrpVpmlq8eLFOnjzp7ngAAABXDQomAACAf8jT01OdO3eWzWZT3759dfz4cdntdtntdu3du9fd8QAAuGaVKVNGvXv3lmEY6tatmzZv3izTNBUTE6PU1FR3xwMAALiiUTABAABcAG9vb4WGhsowDEVEROjgwYOumUqHDh1ydzwAAPA//P39FRYWJpvNph49emj79u2y2+2KiYnRsWPH3B0PAADgikPBBAAAcJ58fX3Vq1cvGYahsLAw7dy5U6ZpKjo6WomJie6OBwAAzpOvr6+6d+8um82m8PBw7du3z/WcxCNHjrg7HgAAwBWBggkAAOAcAgICFB4eLpvNptDQUG3dutVVKh0/ftzd8QAAwD/k5eWlrl27yjAMRUZGKiEhQXa7XaZpav/+/e6OBwAA8K9FwQQAAPA/ypYtq4iICBmGoU6dOmnjxo2y2+1avHix0tLS3B0PAABcIh4eHurUqZOrbEpLS3Mtgbtz5053xwMAAPhXoWACAACQVLFiRUVGRsowDLVp00arV6+WaZpaunSpMjL+n737jorq+AI4/t2ld0SkiiDYC4qKvaOIYDf2EntvscUSjd3YozExamJsv1hijYIde+9YYwFBQZr0Drv8/kDXbDBRU8SY+zmHc9iZ9+bdt+s57nDf3Eku6PCEEEII8Y4pFAqqVq2Kn58fvr6+ZGVlaVY2BQUFFXR4QgghhBAFThJMQgghhPjPsrOzw8fHBz8/P8qXL8+xY8cICAggMDCQtLS0gg5PCCGEEO8Rd3d3fH19adGiBbq6upqVTZcvXyY3V/60IoQQQoj/HkkwCSGEEOI/pWjRoponkd3c3Dh8+DD+/v6cOHGCzMzMgg5PCCGEEP8CZcuWxdfXF19fXywsLNi/fz8BAQGcP38elUpV0OEJIYQQQrwTkmASQgghxAfP1dUVX19f/Pz8cHBw4MCBA/j7+3PmzBmys7MLOjwhhBBC/Iu5ublpkk0ODg6aZJN8zxBCCCHEh04STEIIIYT4IJUpU0bzx55ChQqxb98+ebJYCCGEEP8oJycnzUMtrq6uslJaCCGEEB80STAJIYQQ4oPxYm8EPz8/9PT0ZG8EIYQQQhQYe3t7fHx88PX11ez16O/vT2BgIOnp6QUdnhBCCCHEXyYJJiGEEEL8aykUCqpWrapZqZSdnY2/vz8BAQEEBQUVdHhCCCGEEABYW1vTrFkz/Pz88PDw4NSpUwQEBHD48GGSk5MLOjwhhBBCiD9FEkxCCCGE+FfR0dGhRo0a+Pr64uPjQ0JCgmal0t27dws6PCGEEEKIP2RpaYm3tze+vr7UrFmTCxcu4O/vz8GDB4mPjy/o8IQQQggh3pgkmIQQQgjx3tPT06N27dr4+fnRrFkzIiIiNEmlhw8fFnR4QgghhBB/iqmpKV5eXvj5+VGvXj2uXbtGQEAA+/fvJyYmpqDDE0IIIYT4Q5JgEkIIIcR7ycDAgPr16+Pn50eTJk14+PChJqn0+PHjgg5PCCGEEOJvZWhoSKNGjfDz86NRo0bcvXuXgIAA9u3bR0REREGHJ4QQQgiRjySYhBBCCPHeMDIywsvLC19fXxo2bMitW7fw9/dn//79REZGFnR4QgghhBDvhIGBAfXq1cPX1xdvb29CQkI0+0yGhYUVdHhCCCGEEIAkmIQQQghRwMzMzGjSpAm+vr7UrVuXK1euaErDPHv2rKDDE0IIIYQoULq6utSqVQs/Pz98fHyIiooiICAAf39/Hjx4UNDhCSGEEOI/TBJMQgghhHjnChUqhLe3N35+fnh6enLu3DkCAgI4dOgQCQkJBR2eEEIIIcR7SalUUr16dXx9ffH19SU5OVmTbLp9+3ZBhyeEEEKI/xhJMAkhhBDinShSpAg+Pj74+flRqVIlTp48ib+/P0eOHCElJaWgwxNCCCGE+FdRKBR4eHhokk1qtVqzX+W1a9cKOjwhhBBC/AdIgkkIIYQQ/xgHBweaN2+Or68vZcqUITAwkICAAI4ePUpGRkZBhyeEEEII8cGoUKECfn5++Pr6YmRkxL59+/D39+fSpUuo1eqCDk8IIYQQHyBJMAkhhBDirbVo0YKHDx9y586dfH3Ozs6aJ2ldXFw4ePAgAQEBnDx5kqysrAKIVgghhBDiv6VUqVL4+vri5+dH4cKF2b9/PwEBAZw9exaVSlXQ4QkhhBDiAyEJJiGEEEK8lZ49ezJ06FDatm1LREQEACVKlNA8MWtjY8OBAwfw9/fn7Nmz5OTkFHDEQgghhBD/XcWLF6d58+b4+fnh5OSk9fBPdnZ2QYcnhBBCiH8xSTAJIYQQ4o317t2bAQMG0LFjR8zNzTUrlUxNTTU1/y9evChlWIQQQggh3kOOjo6a728lS5YkMDAQf39/jh8/LuWLhRBCCPHWJMEkhBBCiDfSv39/Bg0axMGDB6lXrx5KpZKAgAD8/f25du0aubnylUIIIYQQ4t/CxsZGs1dmxYoVOXHiBAEBARw5coTU1NSCDk8IIYQQ/wKSYBJCCCHEa02ePJkhQ4YQHx/PyZMn2bFjB0ePHpXyd0IIIYQQHwArKyuaNWuGr68vnp6enDlzhoCAAA4ePEhSUlJBhyeEEEKI95QkmIQQQgjxWu7u7nh7e2NmZoabmxuurq7Y2tpy6dIlOnXqVNDhCSGEEEKIv4m5uTlNmzbF19eX2rVrc+nSJQICAjhw4ABxcXEFHZ4QQggh3iOSYBJCiNe4euUKNra2BR2GEO9cdFQUHlWq/G6/gYEBpqamPHv27B1GJYQQQggh3hVjY2O8vLzw8/OjQYMG3LhxA39/f/bv309UVNRfGvvq5YvY2Dn8TZEKkSc6MgKPqp4FHYYQQvxnSIJJCCFeIzw8nKyw6wUdhhDvnH6xSjg6OhZ0GEIIIYQQ4j1gaGhIgwYN8PPzo3Hjxty/f5+AgAACAgIIDw/XOrZChQoMHz6ckSNHkpGR8crxwsPDSfh59rsIXfyHWLaaLHMYIYR4h5QFHYAQQgghhBBCCCGEeL9lZGRw4MABRowYgYeHB8uWLaNUqVLs27cPf39/hg4dSvHixQG4c+cOmZmZrFu3DiMjowKOXAghhBD/FEkwCSGEEEIIIYQQQog3lp2dzdGjRxk3bhweHh7MnTsXR0dHtm/fzqFDhxgxYgTffPMNT58+Zf369RgbGxd0BHS4RgAAIABJREFUyEIIIYT4B0iCSQghRIEJj4wu6BCEEEIIIYQQf4FKpeLUqVNMmjSJatWqMWnSJCwsLFi/fj0eHh5YWFiwc+dOTExMCjpUIYQQQvzNdAs6ACGEEP9Oq3/cwdPoWKaOGvDG5zyNjqV130+4sGcDsfEJtO0/hgt7NvzpGC5ev8VnC77hwMavAajYtCN9OrXmk37dNMeER0bj02MYNw5t1fr996jVanx6DMOuSGHWfzlTq6/3mGnk5KhYt2Q6SuXLZzSadR/KrHFD8KxUnt5jphF05z46Onn9hgb61KvuwZgBPbGyNP/T9/omTpy/woJv1xEVG0f1yuWZMWbIK695PySMjwaNw0BfX9M2e/xQmtar+Y/GJ4QQQgghPmxqtZqHDx9y+PBhQkJCqF69Oh4eHjg7O7N27Vo6dOjwzmOasfk09lYm9PeuzKjvDuNTxRWfKq7/yLU6L9zNp+1q4uFq+4+M/75KzcimydTNGOjpaNoGeFema4NyWsetPXKDtYE3NK/VublkZqtYPdSHKw+jfrfP3cWGO0+eMW/7OR5FJ1KsiDkT2teknJP1P39zQggh/pAkmIQQQvwp/bu2e+tz7G2sNQmlzMws0jMy/+6wWL9tL971alK+tNufOv/s5SCKOdrz6EkE90PCKFm8mFb/tdu/sHFnAD3bt/jdMaaM7E+bZg0BiI1LYNay7xg8aQ6bls/RSky9SlxCElv2HKCae3k8K5X7w2N/LTYugQlzl7F0+jjcy5Zk7vI1zFy6iiWfj8137C/BodSvUZWvZox/4/GFEEIIIYR4EzNnzsTGxobg4GCCgoLYuXMnwcHBhIaGFnRofNmvyT86/uaxrf/R8f9pN0Jj+PnCfSZ3qP1W5z14Go+rnSX/G93yD4/r5VWRXl4VNa+//Pki0YlpuLvY4O5i87t9qRnZjFkTyDDfKjSv6squ8/eZtOEEuya9/ZxUCCHE30sSTEII8SecOH+FpWs2EREZTQmXYkwY0kuT0Dh7JYiFKzfw5GkUJVycmD56ECVcnHgWn8ic5d9z4dotzE1NGNT9I1o2rQ/AjbsPWLRqA8FhT8jOzsGrbg2mjx6Ejo6SZt2H0rFFU7buPURqWjo+DWvz2Yh+r42xWfehtPVpxJY9B1GpVHz8UUv6dm4D5K306diiKfuOnWHKiH5UrViWL775gQvXbmFqYkyXVs3o+VELYuMSaN1vNDNGD6JJvRqcvHCVSfOWs3P1IrbuPUh4ZAyzxw9l8vyvsbay5OzlIB49iaCupwedW3kzc9l3xD6Lp0OLpozu311rBVGv0Z8DUL1lDz7/ZCDzV6wlcPMqzcqfPmOn08GvCc0b1Xmrz6ZFk3p8tvAbtn4zDz29t/9vbueBozSqXY3YZ/Fs3XuIycP7avW3atqA5Wu30LBmNYo52r12PGsrS+Z8OgyvzgM5cf4KDWtVe+VxDx49ZuMOf/YfP0v9GlVo26wRl2/cYfCkOfnv0atevpVjR05fwKNCGTwrlQdgVL9uNOo4gJTUNExNtGve3wsOpbSr82tjF0IIIYQQ4m0NHTr0T50XEZfCgG/206ZGSbacvIOBvi4T29fk+M0wDl0Pxc7ShNk96uNqa0mOSs2qg9fYdzkYdW4uPh6uDG7uga6OkmfJ6czccpprIdGUKVoYQ31d7K3yyvMNXnEAv2putPAswa2wWL7yv0xIVALZKjUNKxRjcoda6CiVtJmznXa1SrPj7C+kZmbTtJIL49u9frV/mznbmdKpDlXd7Kgxbj2ftPJk/dGb5Obm0qFOGfo0cQfgl/BnzN9xnoeRCThamTK2bQ08XG2JSUxj0e4LXH4YiamhPh/VLk3X+uVQKBQMXnGA6qXsCbgcTExiGi09S1DZ1ZZley6RlplNP+9KdKpbFoDz9yL4au9lnsanULZoYSa0r0VRa7NXxqxSqzl28zGbTtwmMj6FDnXKAPDF9nPsvxKc7/glfb3yrdC6/zSOkvaF3vzDBm48iuHA1RC2jMuflPtt38nbj3GxscC3Wt6cu3X1kpQpWhi1OhelUvFW1xVCCPH3kgSTEEK8pV+CQxk7awlLpo6hRpWK7Dl0gsGT57BnzVKyc3L4ZPoiZo0dQuM6nqzbtpdP5y5j+8oFTPziK4o52nFk07eEPA5n0KQ5OBe1x71sScbNXsLQnp1o2bQ+T55G03X4RM5dCaKOZ2Ugb1XNT9/OJyrmGd1HfkYLr3pULl/6tbEGnrnIT9/OJzkljT5jp+HmXFST4NDX1+PYllWo1Gr6jptOGTcXDm/6lsiYWAZPmoulhRmtvRsybmAPvlixFveyJZm2ZCWTh/fF2soy37X2Hj7B2iUzMDU2omXvUURExbB+yQxi4hLoNORTOrbwRvGr7/5rF0/Hp8cwLuzZgFqtZtHKDVy5eQfPSuWJjU/g9v1gGtSs+tafT7/ObRkzczErNm5jRO/Ob3VuYlIKpy5eY/LwviQlp9Jl2EQ+6dcNYyNDzTGelcpjZGjAlEUrWLtoGgrF6yc0xkaGVC5fhis37+ZLMF27fY9vN/zEnQeP+MjPiz1rvqRI4bzJmd2vVny9TkhYOMWdHDSvLc3NMDUxJiwiknIltUuA/PIwlOycHLy7DUGhUNDBrwn9urR9o+sIIYQQQgjxT4lJTCM7R83+aR35/lAQ49YeZUL7moxrW4NZP51lw9GbfN65LhuP3corqTbSDx2lgk/XHePHE7fp2agCc7edpZCpIQemdeJGaAwjvztMeafC+a41eeMJBjSrhG9VNyLikum9LICL959Ss7QjkJek2fBJS6ITU+m3fB8+VVxxd7F5q/u5/TiWHRPbcjM0lhGrD+FXzY1CpoaM+eEoPRqWp32t0hy7GcaE9cfY+9lHfLruGKUcrdjz2UdEJ6Qx6rvDWJoY4vc8sXL4eiirhviQnJ5F54W7iYhLYdPYVlwPiWbc2qO0rVmK2KQ0Jm44zryeDfFwtWXrqbuMX3eUjZ+0zJeM2XTiNltO3cXKzJBOdcvg5e6C7vMH/ia0r8mE9m9WQvt+RDxhsUl0mL+L9MxsmlYuzpDmHujp6vzuOUv3XqK/dyXMjQ1e23cvIg4HK1MmbjjOpQdPKW5ryYR2NSW5JIQQ74E/rtMjhBAinwPHz9KwVjXqeFZGV0eHtj6NcHKw48SFK5y8cIXSbi40qVcDpVJJ97a+TPtkIDHP4rl4/RZjBvRAX1+P0m4utPFuyO6DxwBYPW8KLZvWJzk1jWfxCViYmRIbn6C5ZocWTTE3NaFk8WKUdnUmLCLyjWId2LU91oUsKe7kQLvmjTl44pymr1mD2ujr6xHzLJ4790MYN+hjDA30cSnqQO+Ordhz+CQAbX0a4+rkSJdhE6lcrhQ+DV9dLsGrbg2c7G0pZGGOm3NRWnjVo5CFOaWKF8O6kCWRMbG/G6dSqcS7fk0OnTwPwOGT56lX3UMrsfOmdHV1mDluCBu27+XOg5C3Otc/8BR1qlWikIU5zkXtKVm8GAFHT+U7bnT/7kRGx/Lj7v1vPLaFuQkpqWn52ncdOErQ3Qd8/skAhn3cSZNcelvpGZkYGmhPzgwN9MnIzHpFLKY0qFGFXd8t5pvZE9kWcIRdB479qesKIYQQQgjxd+pavyw6SiUerrYYG+jRqnpJ9HR1qOpmS1RC3vdp/8sP6e9dicJmRliaGNLbyx3/Sw/JzFZx5m44/b0rYaCnQ7USdtQtW/SV11k+oCm+Vd1ISc/iWXIG5sYGPEvO0PS3q1kKMyN93OwKUcK+EE9ik9/6XjrXK4uhni7VSthhZWZERFwKQY+i0VEo6FS3LLo6SppUcmFh78Y8jU/lbvgzRrWshqGeLsWKmNO9YQX2XX6oGc+3qiuFTA0pVsScwmZGtKpeAmMDPWqUciBbpSYuOZ2D1x5Rt2xRPEvao6ujpGuDciSlZXL7Sf752PKAKzhYmTKrW32aebhqkktvy9hAj6putvww3JfvhjXnarD2fkq/FfQomoi4FFp4lnijvuT0LA5cDca3qisBUzpQr2xRxq07So5K/afiFUII8feRFUxCCPGW4hOTcLAtotXmYFuEqNg4yM3F9lcJAj09XSqWKcGNuw9QqdV4dR6o6VOp1VR/Xs7s6q1fGDBhNiqVinIlXcnKziE39+X4Vpbmmt91dHRQq3/V+QeK2r98ws7WujA3776cnFgXyluFFJeYhKWFGUaGL5MTeffzTPO6TbOGfDp3Gb6N6/7utSzMTDW/K5VKrbJsSqWS3Nw/jtmnYW3GzFrCxKG9OXD8LN3b+r7BHb5a2RLF6flRCz5b8A2Lp4x+4/N2HThKWEQkDTv2ByAtPYP0zEw+8tWu1W5sZMi00QMZNW0h9WtUeaOxE5JSKO7kmK998vC+eJQvzdfrtrL0+x/p3s6Plk3qY2igz5Wbdxn22Rf5zvFtXDdfmURDQ30ys7STSRmZWRgb5k/SzZ80UvO7m3NRurRqxrGzlzT7RgkhhBBCCFFQXqxaUSoVmBrqadqVCoVmThGVkMqE9cd5sYAlF1AASWmZqNS5FDF/ORexK2TyyusEPYpmxOpDqNS5lClamOwcldacxdL05fdoXaUS9WvmM69iafLrMRSoc3N5lpyBtbmR1nEVnYtw41EMliaGGOq//FOdfSETohNfPqT269U+OkoFpkb6AJqVPOpciE5I5eiNULymPNEcm61SExWfSoVi2vPYHRPasvXUXT5eupcqrnZ0qV+WysXzyt/N33GOA1fzP7C3qE9jzTEvjGz5skqDqZE+PRtVYG3gDfp7V37l+7LvcjA+VYqj/4oVTq/q09NR4u5iQ71yTgB0b1ieHwJv8Cg6kRJvWZpPCCHE30sSTEII8ZZsra0IDgvXaguPjKZ2VXd0dHQ4dfGapj07J4cvv/uR7u18MTI04NSONSiVeU+FxcYloFQqiYx5xowvV7Fp+VxKFi8GwEcDx/0tscbEJfB8aygio2OxsX755ftFZTc7aysSEpNJS8/QrBgKj4zGytICyEuyLPthM35edVm0agO1q1bSSkb9drw/q1K5UugolZy+dJ17IaHUq+7xl8Yb1O0jAk9fZNWPO97o+F8ePiI8Kprd3y9B5/lnlJmVRdv+Y7hx9wEVy2g/XVerijvNG9Vh2uJvX5s8S0vPIOj2Pbq29snXp6erS2vvhrT2bsjpi9dYu20Py9Zs4pvZE6lSoQxndq19o/iLOzly+tJ1zev4xCRSUtPy7ROVkZnF1+u2MKBbe8yeJwGzsrPR19dDCCGEEEKIgvYmJagLmxkxq1t9yhezBiA1I5vEtLxVSLo6SiITUnGyzntILzYpXStRBXkJqi+2n+OHkb642eXNkbov3vM338mr2VgYE5uUrtW28sA12tQoSUJqBulZ2Rg9/24eEZdCoV8lut5kymVlZkRLzxJae0aFxSRha5k/0WZracLwFlXp08Sd3efv8/mPp7AtZMKqIT6Mb1fzjfadAlh14Bp+1dxwLJy3z1O2SvXK5NELZ+6GM6tb/Tfucypizq3HLx+AzM2F3Nxc/kTOTwghxN9MSuQJIcRbatagNsfOXuL0xWvkqFTs3H+U4LBw6lWvQl1PD+6FhHHs7CXUajU/7tzHxaBb2NtYU6ZEcb5ev5Xs7ByiYuPoO246uw8eIzUtHYVCgaGBPiqVmu0BR7gXEkaOKucvx/r95l0kpaQSHPqEHfsD8WtcL98xdjbWVCpXikWrNpCRmcWjJxGs/WkPzZ+Xwvvqh824FLXniwkjcLSz4au1m/9yXAD6enmTphdl4xQKBc0a1GLx6o00qFH1Lyc89PR0mTl2MP5HTubri4x5pvWTlp7Bjv2BeNWpjq21FdZWllhbWeJoZ0PDmlXZsufgK68xdkAPQsMjeRr9++X/omLjmDjvK1ydi1LX89VP8L1Qx7Myq+dN4bsFUzEzNf7DY3+rUW1PLgfd5szlIDKzsli6ZhMNalbNV2bQ0ECf05eu8+2GbWTn5HA/JIzNPx+gZZNXT/CEEEIIIYR43zTzKM7qQ9dJTM0gIyuHudvPsmDnBQz0dGhYoRgr9l0lIyuHoEfRnLz1ON/5qZnZoAADXV1UajW7z9/nQWQ8Oep/vuRa+WLWKBQKtp/5BZVazZGgUH6+cB8rU0PcXWxYtucyGdk5hMUk8b/jt2ha2eWtxm9SyYUjQaHcCI0hNzeXozdC6b54DwmpGb97jomhHl0blGP7hLZ0q1/ure/pXkQc3zx/z5/Gp7A+8CbNq7i+8thnyenEJqdTpqjVG/c1ruhMaHQigUGhqNRq1h+9ibW5MSXs8+8NLIQQ4t2SFUxCCPGWijs5sGDyKBat3siTp1G4FivKitkTsbbK+3K7dNo4Fny7jolffEWZEsVZOPkTABZMGsncr9fQuPNAlEoFLbzq07N9C3R0lPRo50fnYRNRKpRUKlcS7/o1862S+jNcnBxoP2AsKpWawT06ULNKxVceN3/SSGYv/54mXQZhoK9Hp5bN6NTSm+u377F93xG2r1wAwGfD+9Fh8Hh8Grx6H6a3YW1lSR3PyjTuPJAfv5pDCRcnfBrWYe1PexjVt+tfHh+gQukSfNyhJWu27NZqb9p1sNbrCUN6ERB4mi8mDM83Rosm9RkzczHjBvXM12dqYsy0TwYyeNIcrfaZS1czZ/n3KBQKzExNaFCjCjPHDtGsXnud0q7Ob3Tcr9laW7Fg8ijmffMDUbFxVKlQhtnjh2r6q7fswYo5k6hasSxLpo5h1lffUa99X0xNjOnXpe1fXjEmhBBCCCHEu9KniTsr9l2l25K9pGdmU8XNjimd8uYon7arwaytZ/CZvhUXGwvqlsu/B5OrrSVd6pWj9zJ/FAoFFZ2L4OXuzKOoxH88dn1dHRb2bsT8nef5et8VihY2Y0GvRujp6jCzaz0W7DxPy1nbMNDVoX3t0rSvVfqtxnexsWBKpzp8sf0cEXEp2BcyYW7PBq9cwfRbujpKGlQo9tb3NPGjWszfkRe3jlJJ21qlaFerFABrj9zgWkgUX/bLKzseGZ+KuZE+eq9Y4fR7fbaWJizt14QlP19k5tbTuNpaMu/jhm+02k0IIcQ/S+Hg4CALSoUQ4g+Eh4eTFXb99Qe+Z5p1H8qscUPwfL7P079BbHwCbfuNIXDLSvR05RmIgqZfrBKOjvn3jRJCCCGEEOKvCg8PJ+Hn2QUdhvjAWLaaLHMYIYR4h+Svd0IIId4LD0OfsGn3fpo3qiPJJSGEEEIIIYQQQggh3nPyFzwhhPiX8uoyiOSU1Ff2/bo02r/F6BmLUCqVrJ43RdO2ePVGNv984JXH16rqztJp495VeEIIIYQQQoj/uBaztpGSnvXKvqmd6tDY/e1LXQshhBD/ZlIiTwghXuPfWiJPiL9KSuQJIYQQQoh/ipTIE/8EKZEnhBDvlqxgEkII8dbiE5OYtmQl56/exMzEmGG9OtHauyEAoU+eMnXRCu48CKGYgx3TRw+ifGm3P+y7fOMOgyfN0bpGekYmI3p3pn/Xdly5eZf5K9bx6EkEttZWjOzblca1Pdl75CQzvlyV77wvJo7Ar3FdAs9cZNmaTUTGPMPZ0Z4JQ3rhUaGM1vHnrtxgwIRZBB3comnbsucg32/eRWJyCuVLuTFlZH+KOzkAsPvgMb7duJ3EpGTqVvdgysj+mJkY53uP4hKSmDz/a67cvIN1IUsmDutDXc/KWsdkZGbRYdA4+nZuS5tmee/foycRzFy6mlv3gnGyt+XTIb2o5l7u7T8kIYQQQgghxD/mwdN45m47S0h0IjYWxgz3q0qdskW1jvnx+G0ePI1nauc6+c5ftOsC5sb69Pd+OUfYe/EBqw5eIzk9iwblizHho5oY6uX96e7jpf48ikpEocg7tnpJe+b3aqQ15rf7r3I9JJoVg5tp2tYF3mDTyTvkqNS0qObGiBbVUCrzBtl3OZiVB66RmJZJ5eI2TO1Uh0KmhuSo1HwdcIV9V4JRKhS0q1mKvk3dUSgUqNW5fLnnEvuuPERHoaRrg3L0bFThle/R8ZthrNh/laiENIoVMWd0K08qFbcBwP/SQ74/dJ3EtExql3Hk03Y1MTXSB+DcLxEs+fki0YmplHKw4rOOtXGyNn+bj0cIIcQ7oizoAIQQQvz7TJr3NdaFLDm57XuWzRjPnOVreBwRCcC42V9Sv0YVTu/8gW5tfRkxbQFZWdl/2Fe1Ylku7Nmg+Zk3cSTOjvZ0bu1DWnoGIz9fQK8OLTmz8wcmDu3DpHnLefI0mhZe9bTOG9mnC5XLlca7fk2ePI1m8rzlTB7ejzM7f6BHez+GT51Palq65j5SUtOYtuRbcnNfLua9fOMOKzb8xKp5n3F211qquZdl2uJvAbh68y5zlq9h1rghHP/pO0yNjZg8f/kr36PpX66kqL0Np7avYeKwPoyfs5TY+AStY5Z+/yNhz983AJVKzcjPF1C2RHFObvueMQN6MOLzBUTFxv09H5wQQgghhBDibzF98ylaVS9J4MwuDPOrysQNx8nIzgFApVazLvAGX/lfzndeZraKxbsvsvX0Xa32e+FxfOV/mcV9vNj7WQcS0zJZuf+aZryQyAT2fNaeY7O7cmx213zJpTuPY9l47JZW2/GbYfx84QFrR/iyZVxrroZEs+1M3nVvhsXw5Z6LzPu4AQendaSQiSFf7c2Ld+OxW5z7JYK1I3z53+iWnLkbzuZTdwDYevouN8Ni2PZpW1YP82HH2XucvP04331GxCUzfctpxretwZEZnelSryxj1waSmpHN9ZBoFu46z5ROddj/eUdMDPWZvuU0AE/jU/jsfycY3dqTIzO64OFqy5yfzr715yOEEOLdkBVMQgjxngqPjKbnJ1P5yLcJG3f6Y2hgwOejBhB4+gL7j5/F3saahZ99gptzUS4F3WbO8jVERsdS1N6WUX27UrtaJQD8A0/x7cZtxCUk4ulenikj+1O4kEW+61Vv2SNfm4NtEXZ9t1irLTLmGVdu3mHJ59+hp6dL2RLF+fGrOVhZWhAc+oTHEZH06tAKHR0lbX0asX77Xs5dvUFRO5vf7atfo4pm/JTUNKZ/uZLFU8dgZmJMcFg49ap74NOwNgA1q1SkmKMddx4EU9TeRuv9+nr9T2z5ei56uro8jY6lva8XnpXyVv+08KrHF1//wKMnTylfyhWA+d+uw6tODdZv36sZp2rFsgSs+wpjI0PS0jNITk3DwtwUgKNnL9G8YW2qViwLwLBenWnUqT+JySlYmJlqxkhLz+D42csEblmFnp4udT0rU6VCaQ6fPE/nVnlPE168fpugO/epXK605rxHTyKIiIphVL9u6OroULNKRSqXK8WhE+fo3s73tf9mhBBCCCGE+JBExKUw4Jv9tKlRki0n72Cgr8vE9jU5fjOMQ9dDsbM0YXaP+rjaWnI1OIqFO88TmZCKY2EzhjSvQs3SeVUIDlwN5vtDQcSnZFDFzY5P29fAytQo3/UaTv4xX5tdIRM2j22dr/1xbDI5KjVqdS5KhQIDXR1N34zNp0nOyKJ1jZJkZau0zhux+hCOVmY0rFBMq/3gtRCaVHKhhH0hAAY0q8wn3x1hZMtqhMYkYWlqgLmxwSvfp6wcFbN/OkvbWqV4EBGvNWbbmqWwK5Q3V/m4UQU2HLtJx7pl+fn8fTrUKUNpx8IAfNLak7jkvIfxjt8K4+PGFTTndWtQjrWBN+hSrxwHr4bQrWF5LIwNsDA2oEOd0uy7HEy9ck5aMUXGp9K6ekmquNkB4FPFlUW7LxAWm8SJW49pWskFD1dbAAY2q4zvjJ9ISstk/5VgGlRwokapvM+ul1dFHsckv/K+hRBCFDxZwSSEEO+x6Ng4srOzOfHT97TzacyIqfOpVK4UJ7d9Txk3F9Zs2QXArGXfMaxXJ87sWkuPdn7M/up7IG/FzfwVa5k/aSSBm1dib2vN5AVfv/Jav14J9OLnt8klgHvBoTgXtWflxm006jSAln1G8ehxBCbGRoQ8jqCYoz06Oi//eynu5EDI44g/7Pu17zfvwrNSeao8L2XnWsyROZ8O0/SHR0YTHPqEEi7aE7KlazbRwa8JTg55ExjPSuUYO7Cnpv/67XtkZGbi7JjXf+L8FcLCI+nS2iffPRobGXL83GVqtfmY3QePM/TjTkDeCiNDg5eTOh2lErU6l/DIaK3zQ8OfYmZqgpXlyzIOLkUdCHkcDuQloGYtW82MsYNRKl++Hyq1Gj1dXXR+1aajVPL46ctVTkIIIYQQQvyXxCSmkZ2jZv+0jrTyLMG4tUep4FyEg9M6UsrRig1HbwIwb8c5BjSrzJGZXehcrywLdp0H4HpINEt2X2Jmt3rsndIBu0ImzNh8+pXXerE66Nc/r0ouAfRoWIGFuy5Qd+JGxv4QyGcda2vK2Q1vUZXFfbwobGaY77zZ3esztXMdTAz0tNofRSfiYvPyQUDnIubEp2aQmJbJ/Yh4lAolfb4KwGfaVj5dd4yYxDTNsSv3X6NuuaKUdrD6zZhJ2mPamPMoOgmAexHx6Crzxmw2bQvzd5zDyiwv6aZS52ruBUCpVPDkWUremDGJuNi8nOc4F7EgNDox331WcbNjZMtqmtc3QmPIzFLhZG2GOjcXA33t8dW5uUTEpXAvIh5LY0OGrzqE9+dbmLD+OObG+vnGF0II8X6QBJMQQrznen7UAh0dJVUrlsXY2Ii2Po3R09OleuXyRMY8A8DUxJiAwFNcCrpN88Z12Lt2KQA/Hz5B++ZelC1RHAN9fUb07sK5y0H5SrW9jcTkFO49DEWhVHJgw9dMHdmfSfOX8+hJBGkZGRgaaj9VZ2hgQEZm5h/2vZCWnsFW/0P069L2ldeOS0hi2JR5tPVprNkTCeBpdCzHz12mZ/sWrzwvLDyS0TMWMaxXJ0xNjElMTmH+inXMHDtYU8P8t2pVcefS3v/Ro50fw6fMIzs7h/o1qrD3yElu/fKQzKwsvtmwFR2lUlMC8IX0jEwMDbT26gpQAAAgAElEQVQnQYYGBmRkZAGwaNUGWjZtgJuzdo324k4OWFqYserHHWRn53Dh2k3OX7tJ5m/GF0IIIYQQ4r+ka/2y6CiVeLjaYmygR6vqJdHT1aGqmy1RCXmJFlNDfQ5eC+FqcBTelYuzbXwbAAIuP6R1jZKUdiyMgZ4Og308uHD/Kc+S0//okq+lVMK0LnU4PrsrM7vVZ9ZPZ4h+nvSxNs+/R+sLv9eXkZWDgd7LVVAvEjwZWTnk5uZSzqkwc7rXZ8fEtpgb6zP1x5MABD2K5sL9CPo2cX/lmIb62mNmPi/jl5yexe4L95nSsTY7JrQjK0fNkt0XAahbtijrj90kNimNuJR0tpy6S1aO6uWYv0o+GerrkPGbVVq/9Tg2iYnrjzGgWWVMDfWpU9aR/VeCufM4lsxsFd8dvI6OUkFWjorktEx+vnCfAc0qs+ezjyha2JRpm0794fhCCCEKjpTIE0KI99yL0ms6OkrMTF5ORhSKvNUzAAsnj+LLNT8yatpCcsmlb6c29OnUmsjoZ+w9fILNPx/QnKerq8PTqFisC1lqXad2m175rm1nY82OVQu12vT0dFHqKBnSswO6Ojp4VipP9UrlOX3pOraFrcjMzNI6PiMzE2MjQ4wMDH6374UT56/gZG9HaVfnfLGEhUcyaNJsqrmXY+LQ3lp9AYGnqFOt8itL/924+4BhU76gU0tvenVoBcDcr9fQpXUznBzs8q0+ekFfP++JwoHd2rF+2x7uhYRRw6MCw3p1YsysxahUagZ2b4+xkSGmJtqTREMDfTKzXn2vZy4HcedBCJOG9c13TT1dXZZOG8esZd+xYbs/taq607xhHa3PXQghhBBCiP+aF6XhlEoFpoYvV/4oFQrNfqqzu9fnm4ArjF93FHKhZ6MK9GhUgajENPZdCdbsPQSgq1QSGZ9KYTPtMnleUzblu7adpQn/G9NKq+1WWCwHroZoVjd5uTuz+/w9jt4IpVPdsn/qHg31dcn8VaLmxX5OxgZ6+FRxxaeKq6ZvmG8VvKdtJSUjiznbzjKtc130flWiTzOmnnbyJyM7B6PnK4d0dZR4Vy5Ocdu8eWFvr4oMX30IgI8bVyQhNZMeS/ZSyNSQ9rVKExKV95Cigd5v4sxSacZ8lVthsYxZE0j72qXo3rA8ANVK2DOwWWUmbjiBOldNnybuGOnrYmqoj66uDg0qFKOicxEA+ntXxvvzLaRmZGNiqPe71xFCCFEwJMEkhBDvOcXvLbF5LkelIuRJBHM/HU5ubi7nrt5kxNR51K3ugbWVBYN7dKBPp5dlHYLDwin2vEzcr53ZtfaN4nFxdEClUpGRkalJrKjUasjNpXgxRx4/jUStVmtKv4U8jqCtT2McbIv8bt8LJy9coUnd6vmueft+MIMmzqZLax8G9+iQr//khat0bNE0X/vpi9cYO2sJYwf2pL2vl6b98MnznDh3ha/XbUX9fEJau00vls+awOOISC5cu8Xs8UMBUOfmolKrMTc1Jj4xidpVK2n2UXr0JILsnByci9prXbeYgx3JKWkkJqVo9m969CSCetWrcPDEWR6GPqFe+z5A3qqtm7884OYvD5g0rA9ZWdmsWzJDM1b3kZ/RqaX3H34mQgghhBBCfMhePydSExqdyLQudcnNhYsPnjLuh6PUKuNIYTND+jetRI9GFTTHP4pOpGhhs3zjHJnZ5Y3iiU5MJVul1mrT1VGiq/zzhYKci1gQFpukeR0ak4SVqSFmRvoEXH6IlamRZk+prBw1SoWC+xHxRMSlMHTlQQCyVWpyVGq8pmziyMwuONtY8DgmCZ7nvEKjk3AukvdQXrEi5qRkvHwoTp2bC3lTI54lp9G3qTvj29UAYOe5e5R8vjeUi405YTFJuNpZPo8zEedflcz7tXO/hDNp4wlGtqhG6xolNe0JqRnUKOXAR7XzyqKHxSSRrVJTrIg5xazNiU5MfRmXOheFAk0iUQghxPtFSuQJIcS/nI5SyZSFK9i+7wgKhQJrK0uUSiXmJsb4Na7H1r0HCQ59glqtZuOOAHqNnkr286fh/ozSbs64OTvx7cZtZOfkcP7qTS4F3aZ+zaq4ORfFrog1323aRXZ2DrsOHCMxKYXqlcv/Yd8LN+4+xL1sSa3rJSQlM/SzL+jXpe0rk0tqtZrb94NxL1tKqz30yVNGz1zMjLGDtZJLAJf8/8eZXWs5s2st21cuAPISbFUqlKFimZIcPnWeS0G3yc7OYdmaTZR2daGovS2/PAxlwISZxMYnkJSSyqKVG2jt3RA9Xe3nNUxNjKnrWZllP2wiMyuL0xevceXGXbzqVGfaJwM5//N6zfU9KpRh8vB+fDaiHwqFglHTF7L/2BlUKjW7Dx7jcUQUjWt7/unPSwghhBBCiA+djlLBzK1n2H3hPgoFFDYzQqFQYGakj4+HK9vP3iMkKgG1OpfNJ+8w8Jv95PwmQfQ23J1tiEvO4KfTd1Grczl7N5zrIdHULuv4p8dsUtmFg1dDuPvkGakZ2aw6cI1mHsUBSEjJZMnPF4lKSCUtM5uv/C/T2L0YHq62nJjTjSMzu3BkZhfGt61BJRcbTaKsaWUXfjp9l/BnycSlpLPu6E2aVckbs3kVV/ZfCSYkKoH0rGzWHA6iUcW8fW5/vvCAedvPkZWjIiwmiQ1Hb9KmZt58q2ml4qw/epO4lHSexCbz0+lfaObhmu9+wmKSmLjhOJ91qK2VXAK4HxHP8FWHeZacTnJ6Fsv2XqJFNTd0dZT4VCnOuV8iuB4STXaOilUHruFZwh5TI9mHSQgh3keygkkIIf7lFAoFCyePYs7yNSz4dj2W5mZMHt4XOxtr7GysGdjtI0ZOW0BMXAKuxRxZPnMCRr/ZC+ltr7diziRmLV1Nw479MTc1Zc74YTjZ2wLw5edj+HzxStZs3Y2TvS3LZozDQF//tX0AT6NjsLYqpHW9gMDTxMYlsHztFpav3aJpnzpqAC286hGfmEx6RiZFCmuX/PvJ/xDpGZlMnv81k+d/rWlfMWcSVSv+ftkK12KOzPl0GNOXrCQuMYmqFcuyeOpoFAoFNatUpLV3I9oPGIdKpaJp/ZqMG9TzeeyxtO77Cbu/X4K9jTXTRg9i+pcradRxAIULWTB/8iisrSx/97ov3tsFk0cxY+lqPl/8LSWLF2Pl3MmYGBv94XlCCCGEEEL8lykUCmZ3r8/CXRdYuucSFsYGjG9XA1tLE2wtTfJW46w7RmxSOsVtLFjUpzGGf1DW7XUKmxuxqHcjlu69zIr9V7EvZMrcHg2wL2T6p8csW7QwI1tWY9KG4ySkZVKvnBODmnsA0KleGWKT0+i11J+MbBW1yzgyoX2t147ZqKIzT2KTGbTiABnZOfhVdaPD81VDjd2dSUzLZOzao8QlZ1C7jCMjWlYD4OPGFZi19QzNp2/F2ECP7g3L06SSCwAd65YhJimNbov2kAt0q1+O+uWdANh/JZi1gTfYPLY1O8/dIz0rhxlbTjNjy2lNTEv6euFZ0p4Wnm50W7wHlVpN44rOjGyZ91BdOSdrpnepyxfbzxGZkEJF5yJM6VTnT7+vQggh/lkKBwcHWWMqhBB/IDw8nKyw6wUdhhDvnH6xSjg6/vmnMIUQQgghhPg94eHhJPw8u6DDEB8Yy1aTZQ4jhBDvkJTIE0IIIYQQQgghhBBCCCGEEG9FEkxCCCGEEEIIIYQQQgghhBDirUiCSQghhBBCCCGEEEIIIYQQQrwVSTAJIYQQQgghhBBCCCGEEEKIt6Jb0AEIIYT4cH2zfivhkTHMHj+0wGI4fPI8P+7ez5qFn2vagu7cZ+bS1YSGP6VsieLMGjcEJwc7rfPWbdvLveBQTeyrf9zB6k07Nf25ublkZGax4cuZVC5fmm0Bh/l+824SEpMo7ebClJH9cXMu+m5uUgghhBBCCPHeW33wGk/jUpnauc47v/ZPp+/y5Z5L6Om8fNZ8x8S2WJkaERgUyrf7rxKdmIaLjQVjWlenoksRAK48jGTRrgtExKfiXMSccW1rUL6YNQC7zt9jfeBNEtIyKeVgxfh2NXC1tXzn9yaEEKLgyAomIYQQH6yd+48y4Ytl5Obmatoys7IYNW0hvTu24vSOH6hZxZ2xs77U9KtUar7bvIvFqzdojdW/azsu7Nmg+enQoine9WtSuXxprt36ha9+2Myy6eM4teMH6npWZuTnC97ZfQohhBBCCCHEH7kfEccw3yocm91V82NlakREXAoztpxmauc6HJvdlfa1SzNp43EAVGo1E9YfZ0TLagTO7EwLTzcmbzwBQNCjaL7dd40FvRtxaHonapZ2YPzaowV5i0IIIQqArGASQogPnEqlZuay1Rw5dQF9fT1qV3Vnyoj+6OvrcePuAxat2kBw2BOys3PwqluD6aMHoaOjpFn3oXRr25yNOwJITkmlX5e2GBsZ8u3G7SiVCiYO7YN3/ZrsOnCMQyfPoVbncvnGbcq4uTBr3FCKOWqvCMrOyeGbdVvZc+QkapWaFk3qMbx3Z/R0dbkUdJs5y9cQGR1LUXtbRvXtSu1qlfLdS/WWPfK1OdgWYdd3i/O1L1uziYvXb9OjnR/Xbt/TtF+4dgsLc1N8G9cFYEDXdmzY4c/D0Ce4ORdl8oLlJKek0b65F5lZ2a98T6/dvkdA4Cl2f78EgKjYOHp1aEXJ4sUA6NLah6VrNpGQlIyludkbflJCCCGEEEKIf5pKrWbejvMcuxGGvp4ONUrZ82m7mujr6nArLJav/C8TEpVAtkpNwwrFmNyhFjpKJW3mbKdT3bJsPnmH5IwsejWuiJG+Lt8fDkKpUDCmTXW83J3Ze/EBgTdCUefC1YdRlHIsxNROdXCyNteKI0elZtXBa+y7HIw6NxcfD1cGN/dAV0fJ1eAoFu48T2RCKo6FzRjSvAo1Szvku5eGk3/M12ZXyITNY1vna7//NB5vj+L52h2sTAmY2gFjAz2yc1QkpmZiYWwAQHJ6FolpmeSo1OTmglKhxEBPB4CYxDS6NSyHm10hADrULsOKfVdJTM3AwsTw7T8YIYQQ/0qSYBJCiA/c4VPnCQ59wsH/fUOOSkXfcdM5cPwsLZvWZ9zsJQzt2YmWTevz5Gk0XYdP5NyVIOp4Vgbg1IVr7PpuMTfuPmDAhJm08W7E4R9XsHN/IAtXrse7fk0ATpy/wvTRg1g2fRxfrd3M2NlL2PrNPK041m79mYtBt9n89Vx0lEpGTV/E+m176du5DbOWfceIPl1oXNuTPYdOMPur7/FftyzfvVzYsyFf2+/p0tqHEX26sOvAMa0EU8jjcIo7vZyc6egocbK3JSQsHDfnoozp34MihQtpyvu9ysKV6xnSowMWZqYANGtQS6v/xPkrFLEqJMklIYQQQggh3jPHboQREpXAz5Pbk6NSM2TlQQ5ff4Rv1bzVOQOaVcK3qhsRccn0XhbAxftPqVnaEYAzd8PZNLYVtx/HMnzVYVp4urFncnv2XHzAsj2X8HJ3BuD0nXAmd6jFgo8b8u3+a0zeeIL1o1poxbHx2C2uPIxi7Ug/dJQKPl13jB9P3KZnowrM23GOwT4eNKhQjIDLD1mw6zzbP22b/15md32je1ap1TyMTODHE7f57H8nKWxmxODmHtQtm1fS29hAjwdP4+mxZC86SgWL+jQGwNLEkNbVSzB6TSA6SgUGejosH+ANgFclF61rnL77BGtzI0kuCSHEf4yUyBNCiA+cmYkxj55EsPfISdLTM9i8fC4tm9YHYPW8KbRsWp/k1DSexSdgYWZKbHyC5twOLZpgbGRINfdyqNW5dG3jg56eLrWqVSIy5pnmuFKuzrRr3hg9PV2GftyR+yFhPH4apRXHz4eOM6RnR6wLWVLIwpyBXdux+2Be6QVTE2MCAk9xKeg2zRvXYe/apX/5vosULvTK9vSMTAwNDLTaDA0NSM/M/MPzXrh26xfCI6Np06zRK/uD7txnxper+HRIr7cPWgghhBBCCPGPMjHUJywmiX1XgknPymHtCD98q7oBsHxAU3yrupGSnsWz5AzMjQ14lpyhObdtzVIYG+jh4WqLOjeXDnXKoKerQ41SDkQlpmqOK2FfiFbVS6Knq8OAZpV5GJlA+LNkrTj8Lz+kv3clCpsZYWliSG8vd/wvPQTA1FCfg9dCuBochXfl4mwb3+Yv3XNiWiblnaxpX6s0eya3Z7CPB1P+d4LQ6ETNMS42Fpyc241P29dkwvrjxKdkoFKrMTHUZ2m/Jhyb3ZWBzTyYtOE4GVk5WuPfDIvhi+3nGN3K8y/FKYQQ4t9HVjAJIcQHrna1Sozs05Wf/A8ze9l3VCpfmlnjhuBkb8vVW78wYMJsVCoV5Uq6kpWdw6+2K9Ks0NF5vhGsqYkxAEqFQmtfo6L2NprfDfT1sTQ341n8y8kKQGTMM0bPWIRSoQAgNzcXxfPfF04exZdrfmTUtIXkkkvfTm3o0yl/WYfabXrla7OzsWbHqoVv/H4YGhiQkZml1ZaRkYmx0Zs9abfn8AlaeNVDX18vX9/xc5eZMHcZYwf2zLeqSQghhBBCCFHwapZ2YEjzKuw8d48FO89T0bkIUzvVwbGwGUGPohmx+hAqdS5lihYmO0elNe8xf146Tkf5fH5kqA+AQqHQmkc5WplqfjfQ08HC2IC4XyWqAKISUpmw/jjKvCkRucDzX5ndvT7fBFxh/LqjkAs9G1WgR6MK+e7Fa8qmfG12lib8b0wrrTYrUyNWDG6meV23XFGquNpx7l4EzjYWAOg+n/O19CzBphO3uRochTo3l0fRiYxsWQ2AzvXKsv3sL1y4/5T65Z0AOHX7CVM3nWRki2r5VjUJIYT48EmCSQghPnCPn0bhUb407X29iI1PYN43a1m8agOfDunNjC9XsWn5XM3eQR8NHKd17osE0OvEPnu56ikjM4uExGRsra20jilcyJIFk0dRsUwJAFLT0olPTCZHpSLkSQRzPx1Obm4u567eZMTUedSt7kGp53G9cGbX2re9/XyKOznw86HjmtcqlZrHEZEUL5q/pvmrnLxwlfmTR+Vr37n/KAu+Xce8SSOpX6PKX45TCCGEEEII8fcLf5aMu0sRWtcoybPkdBbvvsiyvZcZ3dqTL7af44eRvpp9hbov3qN17htOj4hNTtf8npGdQ0JqBkUsjLSOKWxmxKxu9SlfzBqA1IxsEtMyyFGpCY1OZFqXuuTmwsUHTxn3w1FqlXGkhL12tYUjM7u8UTzBUQmcuPmYXl4VNW1ZOSr0dXW4cC+CDcdu8dWAppq+bJUaMyN97kfEk6NSa42lq1RqklF7Lj7gy58vMqNrPU25PSGEEP8tUiJPCCE+cOev3mD8nKU8i0/EwswUfT09LMxMSU1LR6FQYGigj0qlZnvAEe6FhJGjynn9oL8RdPc+R05dIDs7h+X/Z+++o6qsHziOvy8bEURUZLj3yK25tXCmpuVKzVLSHKVZilhuTc2Bq8xKc1vmyMw9ya1obk1NxQkCgoCIzHv5/eEvinDmuICf1zmc473P+jxXj/Dh+3yfZ/5PlC9dHHfX3GnWad6gDjMXLifqVgxx8QmMmvod42bMwdLCgmF+3/Dzhm0YDAZyuzhjYWGB0/9nSz1tL1d8iYjIKFZv2UFSUjKzflxJPo+8FCn48EIUHhnFjZuRlC1eJM37h06c5ouv5zJz3GANLomIiIiIZGAHz19n2A+7uHk7jhzZbLG1siRHNhtiE5LAALZWVhhNJn4NOMf5kEiSTaaH7/RfTl0JZ/uJKyQlG/lu41FeKpgHt5zZ06zTpFJhZm85RnRsPPGJyXzx8z4m/XIASwsDny/by68HzmEw3B2IMhgMONrb/OdzdrC1Zt62E/gfv4zJlMJvJy7zx9Vw6r+UnxKeLpy5FsHmoxdJNppYvucMRqOJcoXyULW4G8cuhrH9xBVMphTWHDxP9J0EyhfKw5HAUPx+OcC0bg01uCQi8gLTDCYRkSzuzSZe/Bl4hTff709iUjLVypdh1IDeuDg78U7r5nTo8xkWBgsqlClO43o1CLwS9NjHKFmkICs3+jN00teUL13injN8enZqw5fzltCm50Di4uKpWqEMn/t8gMFgwG/Ix4ybMZdJ3y7E2cmRIX274favAaqnxc7Whq/HfMbn02cz9qs5lCpaiMlDP3mkba+HhpPDMTvW1mm/ff7wy3oSEhPpMejzNO//OmdquoE2ERERERExn9erFeP89Ug6+q0mMdlElaJ5GdKuFjmz29Gxbhm8v1yHwWCgXME8NChfkEuh0Q/f6b8Ud8/J6oPnGL1sDy8VyM2Yt+ulW+e9huX5ZsMR3p66lriEJCoXdWPYW7UwGAyM7VwPv1UHmL7md3Jks8W3dXXyOjv853PO6+zAF+/WZ8a6Q4z6aQ/5cjsyqeuruGS/O6tqkverTF51gAk/76ekZy6mdmuAnbUVJTxcGNmxDt9uOsLoZXsokteZqd28yG5nw9Ldp0lMNtJ39pY0x/rJp2W6wTQREcm6DB4eHikPX01E5MUVFBRE4pVj5o6RYa3atJ1fN29n3uSR5o4iT5lNgQp4enqaO4aIiIiIZEFBQUFErR5r7hhP3dqD51n3+4U0zzyS58e55RB1GBGR50i3yBMREREREREREREREZHHogEmEREREREREREREREReSx6BpOIiDyRN5q8whtNXjF3DBEREREREbNrUa0YLaoVM3cMERGR50IzmEREREREREREREREROSxaAaTiMgLrFyj9mxcNANPN1ezZThx5jyffvEl6xZ8mfrej6s2Mum7BVhb/f1tasPCGeTKmSP19YXL12jfexCr505Nl//fy9Zu28XoabPSrBMXn8D4zz6iuVedR9onQFJyMmO/moP/ngMYDAaaN6iLT493sLCwID4hkRFTvmVXwGGyZbOnb9e3aNX4FQBCbkQwauosjv1xFns7Wzq0bML7nVo/0ecmIiIiIiJPrvrAhfzyWWs8XLI/92MHhkQxaVUAfwbdxCmbLV28XuKN6iUAiIqNZ9zyfRw8H4KjvTU9m1SiedWiabb/7cRllu05wze9mqS+d/LKDSb8vJ8rN2Iomc+F4e1rky+34wOXbTwcyPif96fZd1xiMqM71aFJpSL3zB59J4Eu09Yxs1fj1M/ulSE/plknMdlIlaJufNWjEaFRsUz6JYBjF8OwtbHizeol6Nao/JN9gCIiYnYaYBIREbPZGXCYwRNm4JDNPs37fwZe4pPub/Numxb33C7ZaGSY30wSk5IeaVmLBnVp0aBu6usfflnPxu37aFyvxiPt8y9LV2/memg4Gxd9TXxCIu/5jGRNkYK0avwK0+f+SFx8PNt++o7Ay9foNXgcpYoWomTRQgydNJMyxQvz1ee+hN+M4u2+gylXqjg1Kpd75M9KRERERESylkELt9Pq5eLM6NGICyFR9PluC4VdnalQ2JWRP+3B3dmBzSPbExgaRa9vNlGhkGvqYNGag+eZtDKAsgVyp+4vIcnIoAXb+ahFVbzKFWDBbycZ8sNOFvRr/sBlTSsXoWnlvweSlu4+zdajl2hQvtA9c18Ki2bI4p1cj7yd5v3tYzul/vl65G26z9jAB80qAzBm2V4K5c3BF+/U58atOPrO2kK+3NnvO4AlIiKZg26RJyKSBfQfPYXZP65MfX3qz0Dqt+tOstHIiTPn6dp/BPXadqNmqy4MnTQTo9GUZvuDx07RpPOHqa+DQsIo16h96uu9h47TtudAar3Rle6+n3M1OOSeOd7o3p+XX38n3de9rFi/lSmzF/PeW63SLTsbeJmSRQrd93y/X/ILlcqWeuxlf53b1wuXM27Qh2lmSD1sO4DLQdcxmkyYTHc/P4PBgK2NDQDr/ffQs1Mb7O1sKVuyKK+9Wpt1/rsBmDnmUz56ryNWlpZE34rBaDLh6JDtgccSEREREZFH99miHczfdiL19elrETQduYxko4lTV8Lp9c0mmoxcitewJYxeugejKW0nOnQhhDfG/Zz6OvjmbaoPXJj6OuDPYDpPWUODYUvo891mroXH3DNHB79feWXIj+m+/i06Np58uRzpVK8MlhYWlPBwoVKRvJy8coPQqFiOXQylX8uqWFtZUtIzF3P6NiNndjsAvtlwhNUB5+hQr3S6c3Cyt6VJpcJYW1ni3aAcQRExBIZGPXDZPwXfvM3szccY0aEOVpbpf214MTSKD77dTKd6Ze73VwHA+BX7aVurJKXz5cJkSsHW2pKuXuWwtrLEwyU79crm58TlGw/ch4iIZHwaYBIRyQKae9Vh0459qa837dhLo7o1sLK0ZODYqbR5rQE7V8xh+beT2BlwiP2Hjz/yvq9dD2PA6Mn49HyXHSu+p+7LlfhoxKTUQZZ/WvX9FA6sWZTu615eqVmVlbP8KFcq7QNwjUYT5y9dZeHPa6nf7n3a9BzIzoDDqcvPXrjEph376OvdId0+H7TsL9PnLqFd84bk93B7rO0A2rzWgHMXL1O7tTf123WnSAFPmr5Si+iY29yMiqZwAc/UdQvl8+DilSAAbGyssbK0pGOfz2jby5d61StTtmTR+x1GREREREQeU5OKhdl67FLq661HL+FVviBWlhYMWbyTli8XY9PIt1j8SQv2nL7GwXPXH3nfwTdj+GzRDvq9XpVNI9+iVql8+C74DZMpJd26P/m0YvvYTum+/i2Hgx1TuzXAwsIAwO24RI5dCqOoW07OXY8kf24n5m49TrPRy2k/cRVXwm7hYGcNQLvaJZnd5zUK5HZKs8/LYdEUdP37PUsLCzxzOXI5LPqBy/7pmw2HebNG8dSZUv/mmsOBFYPeSHe7vn/afzaYS2HRdK5fFgALCwN+3l7kcrx754pko4mAP4Mp6pbzvvsQEZHMQQNMIiJZQN2XKxEcFs6la8EAbN65L/XZQrMnDOP1RvWIib1DRGQUORyzEx4Z9aDdpbFx+x7q1ahCjcrlsLayokvbFtyKuc3JsxeeKHPunM5YWKT/NhR1K/+0wJ8AACAASURBVIaXShbjrdcbs/XHb/jIuwMDx07j4tVgkpKSGeb3DcP7vY+drU2a7R607C/Xw8LZsf9QmlvvPcp2f0lMSqKZVx12rpjDxkUzCLwSxJJfNxIXnwCQZnt7OxviEhLTbD9/yijWzpvOgaOnWLZ2y4M/IBEREREReWS1SnsSEhXLlRu3ANh2/DJNKhUGYEaPRjSrUpTbcYlExMTjlM2WiJj4R9735qOXqFM6H9WKu2NlaUGn+mW4dSeBP66FP5Xs8YnJ+C7YTtn8ualewp2YO4mcvx6JhcHAqsGtGdSmBqOW7k49t9xO974bQlxiMnbWaZ+GYWdtSXyi8YHL/hISeZvdp6/R8QGzkxzsrMlma/3A8/lhxyk61S+DtZVlumVGk4nRS/dgbWX5wEEqERHJHPQMJhGRLMDGxppGdaqzacc+alWpQEoKVCxbEoAjp87S49OxGI1GyhQvQmJSMinpL7S7r5AbEWzdFUCtgK6p7yUlJ3M9LJzypYunWbd1Dx9CwtKXrL2r5j/y8XLlzMG8ySNTX9evUYVqFcqw9/ejRETdomqFMlR6Kf2t7L5ZvOK+y/6y3n83tatWJFfOHI+13V+G+c1krO+H5HDMTg7H7Lzf8U3mL19Ds1fvDubFJySSzf7ubSvi4hPJZm+bZntbGxsK5nOnY8sm7Aw4RPsWjR56TBEREREReTgbK0teLVeArccuUb2EB5BC+UJ5ADh+KYyPZm/BaEqhVL5cJCUbSXmMUhQWFctvJy7TYNi11PeSjCZCI2N5qUCeNOu+PXk1IVGx6fax7fOO99z3zdtxDJjrTw4HO8a+Uw+DwYC1lQUWBgPdG1XAytKCKkXdqFLUjf1ngyiQx+me+wGws7YiIdmY5r34JCPZbK0euOwvm49eokZJT1yyp31G7uMIv3WHoxdDGdu5XrplcYlJDF60k5u345nevQE29xiAEhGRzEUDTCIiWUQzrzpMnrWI2DtxNH2lFgaDgZAbEYyeNoslM76geOECALTtOTDdtgaDgWTj32Uj6tbfD2vNldOZN5u+ytCPuqe+d+laMO6uufm3lbP8nvg8Lly+hv+eA7zfqXXqe4mJydjY2LBl137CIyJZtfG31GVteg5kWL/3H7jsr9lcuw4cSTeo8yjb/SU0/CZJScmpr62srLCysiSHU3ZcnJ24HHSd0sXuXiV56VowhfJ5kJKSQrtevowd1IeSRQrePZ+kJBwdHJ70oxIRERERkX9oUqkwX649RGx8Eo0qFsJgMBAaFcv4n/czr1+z1FuydZ6yJt22FgYDyf+45V30nYTUP7s42vN6tWL4tq6R+t6VG7fI65z+Z/ofBrR85LzXI2/zwbebqVbMDd/WNVKfeVQgtxNGUwrxSclkt7x7lwSjKYWHDYkVdHVi3aG/7zRhNJm4Fn6LAnmcsLK0uO+yv+w9E8SbNUo8cv572Xc2mEpF8uKULe3FdrfuJNB39lZyO9rzbe/G2Ns8eBaUiIhkDrpFnohIFlGtQhkioqJZt20Xzf4/MBJ7Jw6DwYCdrQ1Go4mf12/jz4tXSDYmp9k2n3teIm5GcfjkGRISE/nhl/Wpy5rUr8nmnfs49sefpKSksHVXAG17DiQy+t4PtX1SDtnsmb3kF7bs2o/JZGLrrgBOnj2PV61qrJk7jX2/LmDvqvmps6J+/m4Szb3qPHAZgMlk4o9zgZQvnbYwPWy7f6pdtQIzFiwlJvYO4TejmLv0VxrVvVsym75Si5kLlhF7J45Tfway3n83zV6tg8FgoESRgnyzcDnxCYlcuHyNn9ZspkWDus/k8xMREREReVFVLuLGzdvxbDoSSOOKRQCITUgCA9haWWE0mfg14BznQyJJ/tczZT1csnMzJo6jF0NJSDKydNfp1GUNKxRi2/HLnLh8g5SUFH47cZnOU9YQFfvot9n7t2Sjif5z/KlTJh+D29VKHVwCKO6RkyJ5czBny3GSjSZ+P3+dI4Gh1Cmd74H7rFLMjZsxcaz//QJJyUbmbTuBZy5HCud1fuAyAJMphTPXIihXMP2FhI/jjyvh6WZ1AQxZvBM3Zwcmdn1Fg0siIlmIZjCJiGQRFhYWNK1fi72HjqXOlClaMB/vtG5Ohz6fYWGwoEKZ4jSuV4PAK0FptnXLk4s+Xd/C5/OpAPTq3IY1W3cCUKSAJ2MGfsjo6bMJCgnD3TU3U4YPwC1PrmdyHm55cjF5WH+mzF7MkIlfk9/DjemjfNPc1u6/iIyOIS4+gTy5nB9ruze696d7xzdp0aAuw/v14IuZc2nepS9Wlla0bFyfd9o0B6Dfe50YN2MuTd/pg52tDb69u1CqWCEAPv3Qm7FfzaFhx144OTrQp8tb1K5W8YnOR0RERERE0rKwMNCoQiH2nw2muMfd2UpF8jrTsW4ZvL9ch8FgoFzBPDQoX5BLodFpts3r7ECPJhUZsvhuD+rWsDwbDgcCUMg1B8Peqs34n/cTfPM27jkd+OLd+vecwfSo9p8NJjA0iuCbt1lz4Hzq+129ytG1QTmmdm/IxJX7eW3UMhztbRjRoTaeuRwfuE87ayumdGvAhJ/3M2lVAMU9XBjXuf5DlwFE3YknLjGZXI7pn+/Uwe9XunqVo2nlIg89r+tRsamf/V8uhERy4Nx1bK0saTDsp9T3m1Yuwqdtavx7FyIikokYPDw8HuNJHCIiL56goCASrxwzdwyR586mQAU8PT3NHUNEREREsqCgoCCiVo81dwzJYpxbDlGHERF5jnSLPBEREREREREREREREXksGmASERERERERERERERGRx6IBJhEREREREREREREREXksGmASERERERERERERERGRx6IBJhEREREREREREREREXksGmASERERERERERERERGRx2Jl7gAiIhldWGgorgUqmDuGyHMXFhpq7ggiIiIikkWFhQTj2nKIuWNIFhMWEmzuCCIiLxSDh4dHirlDiIjI09OwYUO++OIL/P39GTNmDDExMeaO9EJr2bIlI0eO5Ndff2XixInExcWZO5KIiIiISJamTpSxqBOJiGRdGmASEckiXFxcGD16NBUrVsTX15e9e/eaO5L8X86cORk1ahRVq1bF19eX3bt3mzuSiIiIiEiWo06UcakTiYhkTZaOjo4jzR1CRESeTKtWrZg3bx4HDx6kV69eXLx40dyR5B/i4+PZsGEDly5dYtKkSRQvXpyAgAASEhLMHU1EREREJEtQJ8rY1IlERLImC3MHEBGR/87d3Z358+fTt29fvL29GTNmDPHx8eaOJfexbds2vLy8SE5Oxt/fn8aNG5s7koiIiIhIpqZOlLmoE4mIZC2awSQikgkZDAbefvttvv32WzZs2EC/fv0IDtbDTDODxMREtm3bxvHjxxk7dizVqlUjICCAO3fumDuaiIiIiEimoU6UeakTiYhkHZrBJCKSyRQqVIhly5bRoUMH2rVrx7Rp00hKSjJ3LHlM+/fvp2HDhly9epWtW7fSunVrc0cSEREREckU1ImyBnUiEZHMz+Dh4ZFi7hAiIvJwlpaWdO/enT59+vDll18yZ84cTCaTuWPJU1C+fHkmT57M9evX+fTTT3XlpYiIiIjIPagTZV3qRCIimZNukScikgmUKlWKefPmkS9fPry9vfH39yclRdcHZBWhoaEsWbKEfPnyMWXKFGJjYzl+/Li5Y4mIiIiIZBjqRFmbOpGISOakGUwiIhmYjY0Nffv2pUuXLnzxxRcsWbLE3JHkGStevDiTJ08mKSmJgQMHEhgYaO5IIiIiIiJmo0704lEnEhHJPDSDSUQkg6pUqRILFy7ExsaGrl27sn//fnNHkufg5s2bLF26lOzZszN9+nQMBgOHDx/W1ZkiIiIi8sJRJ3oxqROJiGQemsEkIpLB2Nvb4+vrS6tWrRg5ciSrV682dyQxk/z58zNx4kScnZ0ZMGAAf/zxh7kjiYiIiIg8c+pE8hd1IhGRjE0zmEREMpDatWuzaNEioqKi8Pb25tixY+aOJGZ069Ytfv75Z5KSkpg+fTpOTk78/vvvGI1Gc0cTEREREXkm1Inkn9SJREQyNs1gEhHJAJycnBg6dCivvPIKn376Kf7+/uaOJBmMq6srY8eOpXjx4vj4+PD777+bO5KIiIiIyFOjTiQPo04kIpLxaAaTiIiZNWrUiEWLFnHu3Dm6d+/O2bNnzR1JMqDY2FjWrFnDjRs3mDJlCp6enhw4cICkpCRzRxMREREReSLqRPIo1IlERDIezWASETGTXLly8fnnn1OuXDl8fHwICAgwdyTJJHLmzMmIESOoXr06gwYNYufOneaOJCIiIiLy2NSJ5L9SJxIRyRg0g0lExAxat27N3Llz2bdvHx988AGXL182dyTJROLj49m4cSMXLlxg4sSJlClThv3795OQkGDuaCIiIiIij0SdSJ6EOpGISMZgYe4AIiIvEg8PDxYuXEjv3r159913GTduHPHx8eaOJZnU9u3b8fLyIjY2lm3btvHaa6+ZO5KIiIiIyAOpE8nTpE4kImJeukWeiMhzYDAYeOedd/Dx8eH7779n5syZJCcnmzuWZCHVqlXDz8+Ps2fPMmTIEG7cuGHuSCIiIiIiqdSJ5FlTJxIRef40g0lE5BkrXLgwy5cvp02bNrRu3Zovv/xSRUqeuoMHD9K4cWMCAwPZunUr7dq1M3ckERERERFAnUieD3UiEZHnTzOYRESeEUtLS3r06EHv3r2ZNm0a8+fPx2QymTuWvABeeuklJk+eTHh4OL6+vgQFBZk7koiIiIi8gNSJxFzUiUREng9LR0fHkeYOISKS1ZQpU4b58+fj5uaGt7c3O3bsICVF4/nyfISFhfHTTz/h5ubGtGnTiI+P59ixY+aOJSIiIiIvEHUiMSd1IhGR50MzmEREniIbGxv69etH586dGTt2LMuWLTN3JHnBFS1aFD8/PwB8fHy4cOGCmROJiIiISFamTiQZjTqRiMizoxlMIiJPSZUqVVi0aBEGg4GuXbty4MABc0cSITIykmXLlmFnZ8eXX36JlZUVhw8f1q1JREREROSpUyeSjEidSETk2dEMJhGRJ5QtWzYGDRpEixYtGD58OOvWrTN3JJF78vT0ZMKECeTJk4f+/ftz6tQpc0cSERERkSxAnUgyC3UiEZGnSzOYRESeQN26dVm8eDE3btzgvffe48SJE+aOJHJfMTExrFy5koSEBKZPn46zszMHDx7EaDSaO5qIiIiIZFLqRJKZqBOJiDxdmsEkIvIf5MiRg2HDhlGnTh0GDRrEjh07zB1J5LHkyZOHMWPGULp0aQYMGMDBgwfNHUlEREREMhF1Isns1IlERJ6cZjCJiDympk2bsmDBAk6fPk2PHj04d+6cuSOJPLY7d+6wdu1aQkJCmDx5MgUKFCAgIICkpCRzRxMRERGRDE6dSLICdSIRkSenGUwiIo/or6ubSpUqhY+Pj65ukiwjR44cDB8+PPXq0+3bt5s7koiIiIhkQOpEklWpE4mI/DeawSQi8gjatm3L999/z+7du/nwww+5cuWKuSOJPDUJCQls3ryZs2fPMmHCBMqVK0dAQADx8fHmjiYiIiIiGYQ6kWRl6kQiIv+NhbkDiIhkZJ6enixevJj333+ft99+m/Hjx5OQkGDuWCLPxK5du2jQoAHR0dFs3bqV5s2bmzuSiIiIiJiZOpG8SNSJREQej26RJyJyDwaDgXfffZcBAwYwa9Ysvv32W5KTk80dS+S5qVq1Kn5+fpw7d44hQ4YQFhZm7kgiIiIi8hypE8mLTp1IROThdIs8EZF/KVq0KHPmzKFUqVJ069aNTZs2YTKZzB1L5LkKDg5myZIlFC9enEmTJhEZGcmpU6fMHUtEREREngN1IhF1IhGRR6EZTCIi/2dlZUWvXr3o2bMnkydPZsGCBaSk6L9IkbJly+Ln50dUVBS+vr5cvXrV3JFERERE5BlQJxK5N3UiEZF70wwmERHu/rC4YMECXFxc6Nq1K7t27TJ3JJEM48aNG/z000/kzp2badOmkZiYyLFjx/TLBhEREZEsRJ1I5P7UiURE7k0zmETkhWZra8snn3xCx44dGTNmDMuXLzd3JJEMrUiRIkyaNAkrKyt8fHw4d+6cuSOJiIiIyBNQJxJ5POpEIiJ/0wwmEXlhVatWjUWLFmE0GunatSsHDx40dySRDC8yMpLly5djbW3N9OnTsbGx4dChQ7onv4iIiEgmpE4k8vjUiURE/qYZTCLywnFwcOCzzz6jadOmDBs2jA0bNpg7kkim5OHhwfjx43F3d6d///6cOHHC3JFERERE5BGoE4k8HepEIvKi0wwmEXmh1K9fn0WLFnH9+nW6devGyZMnzR1JJNOKiYnhl19+ITY2lunTp+Pi4sLBgwdJTk42dzQRERERuQ91IpGnR51IRF50msEkIi8EZ2dnRo4cSfXq1fH19dUDa0Wesly5cjFmzBjKlSuHj48P+/fvN3ckEREREfkHdSKRZ0udSEReRJrBJCJZXvPmzZk/fz4nTpygR48eXLhwwdyRRLKcuLg41q1bR1BQEJMnT6Zw4cIEBASQmJho7mgiIiIiLzx1IpFnT51IRF5EFuYOICLyrLi6ujJr1iwGDhxIz549GTFiBHfu3DF3LJEsbdOmTXh5eWFpaYm/vz9eXl7mjiQiIiLywlInEnn+1IlE5EWiGUwikiW1b9+e2bNns2PHDvr06cPVq1fNHUnkhZGQkMCWLVs4ffo048aNo2LFiuzfv5/4+HhzRxMRERF5YagTiZiPOpGIvCg0g0lEspT8+fOzZMkSvL296dSpExMnTiQhIcHcsUReSLt376Zhw4ZERESwbds2WrZsae5IIiIiIlmeOpFIxqFOJCJZncHDwyPF3CFERJ6UhYUFXbt25ZNPPmHmzJnMmjULo9Fo7lgi8n+VK1fGz8+PS5cuMXjwYEJCQswdSURERCRLUScSydjUiUQkK9It8kQk0ytWrBhz586lWLFivPfee2zZsoWUFI2di2Qk169fZ8mSJRQuXJjJkycTHR3NiRMnzB1LREREJEtQJxLJ+NSJRCQr0gwmEcm0rKys+OCDD+jevTt+fn4sWrRIJUokEyhdujR+fn7ExsYycOBALl++bO5IIiIiIpmSOpFI5qROJCJZhWYwiUimVK5cORYtWoSTkxNdu3Zl9+7d5o4kIo8oPDycpUuXkjNnTqZNm4bRaOTIkSP6ZYiIiIjIY1AnEsm81IlEJKvQDCYRyVTs7Ozo378/7du3Z/To0axcudLckUTkCRQqVIhJkyZhZ2eHj48PZ8+eNXckERERkQxNnUgka1EnEpHMTDOYRCTTqF69OosXLyY+Pp6uXbty+PBhc0cSkScUFRXFihUrMBgMTJ8+HTs7Ow4dOoTJZDJ3NBEREZEMR51IJOtRJxKRzEwzmEQkw8uePTuDBw+mcePGDB48mM2bN5s7kog8A+7u7owfPx5PT098fHw4evSouSOJiIiIZAjqRCIvBnUiEclsNINJRDI0Ly8vFi5cyNWrV+nWrRt//PGHuSOJyDNy+/ZtVq1aRXR0NNOmTcPV1ZUDBw6QnJxs7mgiIiIiZqNOJPLiUCcSkcxGM5hEJEPKmTMno0aNokqVKgwaNEgPrBV5wbi4uDB69GgqVqyIr68ve/fuNXckERERkedKnUjkxaZOJCKZgWYwiUiG07JlS+bNm8eRI0fo2bMngYGB5o4kIs9ZXFwc69ev5+rVq/j5+VGsWDECAgJITEw0dzQRERGRZ06dSETUiUQkM7AwdwARkb/kzZuXuXPn8vHHH9O9e3dGjRpFXFycuWOJiBlt2bIFLy8vUlJS8Pf3p1GjRuaOJCIiIvLMqBOJyL+pE4lIRqYZTCKSIXTs2JHvvvuOrVu38tFHH3Ht2jVzRxKRDCIxMZGtW7dy6tQpxo4dS+XKldm/f79+2SIiIiJZijqRiNyPOpGIZFSawSQiZlWgQAGWLl1K586deeutt5g8ebKme4vIPe3du5eGDRsSEhLCtm3beOONN8wdSUREROSJqROJyKNSJxKRjMbg4eGRYu4QIvLisbCwoFu3bnz00UfMmDGD77//HqPRaO5YIpJJVKxYET8/P4KCgvjss88IDg42dyQRERGRx6JOJCJPQp1IRDIC3SJPRJ67kiVLMm/ePAoWLIi3tzfbtm0jJUVj3SLy6EJCQliyZAn58+dn8uTJxMTEcOLECXPHEhEREXkk6kQi8qTUiUQkI9AMJhF5bqytrenTpw/e3t5MmDCBH3/8USVKRJ5YyZIl8fPzIz4+Hl9fXy5evGjuSCIiIiL3pE4kIs+COpGImItmMInIc1GhQgUWLlyIg4MDXbt2Ze/eveaOJCJZREREBEuXLiVHjhxMmzYNk8nE0aNH9csaERERyVDUiUTkWVEnEhFz0QwmEXmm7OzsGDhwIK1bt2bkyJH8+uuv5o4kIllYgQIFmDRpEtmzZ8fHx4fTp0+bO5KIiIi84NSJROR5UicSkedJM5hE5JmpWbMmixcvJiYmBm9vb44ePWruSCKSxUVHR7NixQpSUlKYPn06Dg4O/P7773pgtoiIiJiFOpGIPG/qRCLyPGkGk4g8dY6OjgwdOhQvLy8GDx7Mli1bzB1JRF5Abm5ujBs3jkKFCuHj48Phw4fNHUlEREReEOpEIpIRqBOJyLOmGUwi8lQ1atSIhQsXEhgYSPfu3TUVW0TM5vbt2/z6669ERkYydepU3N3dCQgIIDk52dzRREREJAtTJxKRjEKdSESeNc1gEpGnwsXFhdGjR1OxYkV8fX31wFoRyVBy5szJqFGjqFq1Kr6+vuzevdvckURERCSLUScSkYxMnUhEngULcwcQkczF1taWnj17pnnvjTfeYNu2bYSEhNCwYUMVKRHJcCIjI/noo48YNmwYU6ZMYdKkSTg5OaUud3BwoGrVqmZMKCIiIpmFOpGIZEbqRCLyLGiASUQeS8+ePVN/4HB3d2f+/Pl8+OGHdO3alTFjxhAfH2/mhCIi97dt2za8vLxISkrC39+fJk2aAJA9e3bmz5+Pu7u7mROKiIhIRqdOJCKZmTqRiDxNukWeiDwyDw8PNm/eTLNmzahXrx6+vr7MnTuXr7/+mqSkJHPHExF5LNWrV8fPz49Tp04xdOhQvL29KViwIH369DF3NBEREcmg1IlEJCtRJxKRJ6UBJhF5ZDNnzuTmzZuULFkSOzs7BgwYwJ9//mnuWCIi/5mdnR39+/enffv2jB8/nv79+9O3b18CAgLMHU1EREQyIHUiEclq1IlE5ElogElEHknt2rWZNWsWJpOJBQsWsHPnTtzc3Lhy5QpHjx41dzwRkf+kcOHCJCQk4OrqyqRJkzAajdja2tKwYUOMRqO544mIiEgGok4kIlmROpGIPAlLR0fHkeYOISIZ39q1a3F2dsba2poiRYpQqVIl3NzcuH79OufOnTN3PBGR/2Tq1Kl8/PHHeHt7YzKZsLe3p1ChQjg4OLBjxw5zxxMREZEMRJ1IRLIidSIReRKawSQij6Rs2bJERkYSGhqqK1hEJMuxsrIib968eHh4UKlSJc6cOcPOnTvNHUtEREQyEHUiEcnK1IlE5L/QAJOIiIiIiIiIiIiIiIg8FitzB5Anc+TwIVzzupk7hkimFRYaQqXKVcwdQ0Qe05EjR3B1dTV3DMliwsLCqFSpkrljiMgzcOTQ77i6uZs7hshzFxZynUpVqpo7hog8A4d/P0Bed09zx5AsJvR6EJWrvmzuGJKJaIApk3PN60bciU3mjiGSabmWa2LuCCLyH7i6upKScMfcMSSL0aClSNbl6ubOLf9vzR1D5Llz9epl7ggi8ozkdfckbEZ7c8eQLCZvn2XmjiCZjIW5A4iIiIiIiIiIiIiIiEjmogEmeW6CwiLMHUFERERERESeouCIaHNHEBEREREz0QCTPJFffwug2/AvH7re9oMnGPH1D6mva3b24fqNm88y2jNXse1HGWLQ7LXeIzl48txjb3e//EFhEVRs+9HTiHZfMbFxDPlyIa++9xkNug9hwpwVJCUl33NdH785VO80gJqdfajZ2YeOvhNTl+09eprWH4+lVueBvDdsOleu3wBgzHdLU9ev2dmH6p0GULHtR4RGRD3T8xIRERERyUzmbTjAFz9ufaxtQm7eot7HMwCIuBXLW6MXPlGGQ39epeWQOamvq/Weyle/7EqzTnBENNV6T0335/sxmVJ4fcj3dPdbmm5ZzynL6TbpJ0ymlDTvtxwyh0N/Xk1dp3bfL6n38Qzq9vuKRgO/ZeT8jUTGPPvb8+4+EUibEfOp2+8rPpm56r7HPB8UTvUPplHv4xmpX/6HH78XioiIiDwJPYNJnovo23dI+cfP7/sW+5kvjDw1x/+8yC/b9jGid6fH2m7qol9JSExm3dcjiU9M5OMJs1mw2p/ubRqnW/fspWAWjPmYUkXyp3k/+MZNBk2dz8T+3lQvV4KZS9cz6pslzBn9EUN7vsXQnm+lrjtg0hzyueUmby7n/3aiIvLC+nTocDw9POj7QS/e7/0hLVs05/XmzZ7JsVq82YaRQ4dQtUrlZ7L/jComJobPv5jArj17sLSwpGmTRvgO6I+NtXW6dTdu3sKU6V9xMzKSMqVLMXr4UAoVLAhAmw6dCAy8iMFgAKBWzRrMmDaFxKQkxk/0Y/2mzZiMRl59pT7Dh3yGQ7Zsz/U8RUQyIu/XHv8h3m4uTuyc1geAhKRk4hPvfaHYk/hh62EaVC5OmYJu/2n7gDOXyZ/HmcthkZwPCqeYZ+40y48HXuen347QqcH9v+d+2qkBr9csC0B4dCwTfvKn34xfmD+oExYWhgcePzLmDit2HKNyifxUKZHvkXOHR8cybN5G/Hq9zkuF3Zm09De++HEbE3u+nm7dc0E3qFOuMJN7t3rk/YuI/Bdjt1zB3cmG96q74fNrII1L5aRxyZzP5Fjv/HAGn1fyUcEz13XRbgAAIABJREFU+zPZf0a25HAYS4/eICE5hZoFHRnUID+2VunnhhwJus20HUGE3EqkQE5bPqmfjzJud7vN2bA7+P12jcuRCeRztmXgq/konffust/OR/Hd3utExSVTIo89A73yk9/Z9rmeo2RNGmDKYoLCInh38BRer/8yyzfvxiWHE77vtaZu5bs/GO86fIqvflhD8I2bFM3vjq93G8oWK/DA7Q6ePMfwr39gwzcjU4/R/INRHF2RduZSXHwCE+b+zIGTfxIRFUPRfG6M+vBtLC0tGDtrKclGI+0HjGfZ5E+p2PYj1s0cgadrrgdm8h46jZavVmf5pt3Y29nSs11T3mxQ84k+g9OBVxk/ZwUXroZQyMOVwe+3o0zRAhw8eY5J81eS3d6OwGsh/DDBB0/XXA881i/b9rFh1yFuxd6ha6sGdGt9d4Dk+J8X8Zv/C4HXQvBwzcXHnVtSq2Lpe352f30WbrlyMnb2MvwDjmFjbUXNCqUY0qM9NtbW3IyO4Yvvl3Pw5DkcHbLRs10TWtT/uwzuOnSKcbOXERoRRctXq/Npt7YAXAwKZcKcFZw8f4Xczo6837YJzetVu+d5fLN0PYlJybRuWOuB52w0mvA/cIxFa37jengkHV+rB9ydNbRu18F06389uDeVyxRN815KSgrvt21CNntbstnb8lqdKuw7dibdtnfiEggJv0mR/OmL5bqdB/F6uTw1K5QCoHvrxqkzmP5p4+5DXAwKZfwnXR94XiIiDzP7m6+f6f7X/vLzM93/s3b02HFWrPyFMaNGPNZ2E6dMIyEhga0b1pEQH0/vjz5m7vyF9Hq/W5r1IiJuMmzUaBbPm0OxokWZ9tUMho8ew8I5szEajZy/EMjObZvJ4eSUZrs58+ZzPjCQLetWY2lpRb8BPnw/dx79+nz4xOcsIpnbnpMX+XrVboIjblHUIxcD2r+SOqARcPoy03/eSVB4NEU9cjOkc0OKeuTm5q07TFrqz8GzV3HKZkf35tVpVr0MAKcuhTB95U4uXr9JUrKRVysVY2jnRlhaWNByyBza1CvPzzuPcychkYZVSvBpxwYPzdhyyBxa1i7Lih3HMJpS6NywCl2a3P15vlrvqbSpW57Nv5/l044NqFTcE79lv3Hoz2s42NnQ7pWKvN2gMhG3Ymk/aiFD32mEV6Xi7Dl5kRHzN/LTsHdZues4wRG3GNmlCSMXbCKXUzYCTl/hcuhNar9UmLb1KjB+yTbCo2NpU688fd+sS3BENK2GzuXgN5/QY/JyAOp9PIPBnRoyZfl2NkzogaXF3V+I9Zq6nNZ1ytO4WsnH+rtpVr00oxZsZvHgt7G2snysbQFW7z1F/QpFCY+OZeWu4/h28EqzvHmNMny7Zi91yxUhv+vDL0LLncOB0V2b8tqns9h9MpB65Yvec70LweEs8T/C1kN/Uuelwrxe6yWOnLtGv69XpVv3tZdL8Vmnhmne2370PBWLelClxN2L6/q8UYemg2ZxOy6B7PZpfwl47toNiufL89DsIiJPk1+rIs90/4veLvVM9/+snQqJZc2pm3zaIP/DV/4H/3NRrDoRwcw2xXC2t2Lo+kv8cCiM96qn/X2Y0ZTCsPWXGNGkIFXzZ2fViQhGbrrMsi6luZNoxHfNRXrXcqdJqZysOXWTERvvLou8k8TEbVf5qk0xCrvYMXvfdSb5X+XL1sWe5unLC0oDTFlQRFQMUTGx+M8Zx96jp/GdMo81Xw3nZnQMvlPmMdmnGy+XK8HaHQfpM+4bVk0f+sDtHtX8X7dxMzqGn6cOxsJgYOTMH5mzcjPjP+nKkB5vsfq3AOaMTnvrtT8vBT0wU9jNaJKSjWz9fiwbdx9i/JzlNKtbFVub9Fc1P8pnYGtjzQdjvsGn65s0qV2ZbQHH6PvFd6z+alhqnikD72bJns3+oed8KSiUldMGc/bSNboOnUaL+tWwsrSk9+czGdStLc3qViXg+Fl8/OayZNJArCzvX462BRwj8FoIG74dRXKykR6jvmLz3iO0qP8yg6cvpIB7HjbPGs3FoDA+HPMNBd1dKVeiEADH/rzIwnH9iYq5zVs+E2lSuzJli+an9+czadOoFl991pMzl4LoM/Yb8uZypmrZ4qnHPR14Fb/5K/luRB+K5nPjs+n3v8XFojW/sWTDDnLlcKRjs/o0qlkptfD9e9bQg4zo3THN692H/6Bk4fRX9p27Eoy9nS19xn7HuStBlCjoyafd21HYMy9nLwbhmTcXvUZ/zZmL1yhbrCDDe6U9frLRyPTFqxna863/VExFJPO4FhTM2128ad+2NQsX/4idnR2jRwxl67bfWL9pMx5ubkz1m0CxokVJSkriq5nfsnrtOowmIy2bN+fjvh9ibW1NeEQEnw0dzqHDRyhTpjTZ7O3x9PAA4J33uvNmq5a0btWS4ydOMnHKVC4EBpKUlEyjBl6MGTkcS0tLvJo2o2P7dixZtpzY2Ds0a9KYEUMHP/QcvJo244vPR1O9WlVKla/EYN+BzJ47j5SUFN7u+Ba9e7wPwB+nzzBq7DjOnTtPvnz5GD74U6pWqUxoWBhjx08k4ODvOGbPTqcO7fF+9x0MBgPvvNed2jVqsGrNWsLCwmj9ZiuqVq7MxMlTiI29w4e9e/Lu23dno+7Zt59JU6YSFBzMS2XKMGr4UArkv3dBMhqNbNnmz/xFiwm+fp3OHTsAMOLzMaxZuz7d+rNmzkg/Qyslhd49uuOQLRsO2bLRotlr7Nm7P922wSHXSUhIJDnZCICFhSW2NjYAXLx0CZecOdMNLgH06PYe3u++g52dHTfCw4mLi8M5h2a0irzozl27wWffr2NCjxZUK1mA9QGn6TdjFStGdiUp2cigWWsZ/m5jXqlQjB+2HmLY3A38OPQdhs/fQP48OVn/xftcCo3ko69WUsA1Jy8Vdmfw9+vo+XpNmlUvQ1B4NF0nLOHAmSvULFMIgP2nL/PDkLcJjbxNt0k/8drLpalQ1OOhWXccvcAPQzoTcyeBXlOXU9jdJXWAw8bako0TemBKSaHX1BWUzJ+HtePeJzQyhn4zfsHZwY4WNcvycdt6TF6+nXKF3Rn3w1Z8O3iRO4dDumNtCDjNrAHtyW5vS9uR8wmOuMX3Pm8RHh3LO1/8QOu65TH8Y/LOrAHtaDV0Ljun9cFkSmH6yp0cPR9ElRL5ibgVy5krYdQt//i/jOzatBqfzl7H9+v207tV7cfaNjo2nn2nLjGogxe37sTTZfwS+r5ZF3vbvztklRL5sLex5vNFm/muf7vU2a8PYm9rTYWiHhy7EJxugOl4YDCz1+3nz6s3eKNOOVaM7ELuHHevvndzcUyd8fUwl0JvUtDNJfW1c3Z7stvbcO1GFKUK5E2z7rlr4SQZjbw+5HsMGHizbjm8mz7+jDQRyTqu30rkwxXnef0lF5YfDcfOyoKBXvnYeSEa/3NR5HW0YdRrBSnsYkeyMYU5ASFsPhuJMSWFxiVz0qOGO1aWBm7eSWLclqscvx5LiTz22Ftb4O509+fuvivP81ppF5qVduGPkDvM3BPMpZvxJJtSqFc0B4O88mNpYaDd/D94o1xuVp0I506SCa/izgx45eEzOtvN/4PBDQtQKV926n51jI/qerD4UBgArcvnpku1u/8X/nnjDlO2BxEYEY+7kw3963tSwTM74beTmLYziCNBt3GwsaR1uVy8VSkPBoOBvivPUy2/IxvPRBIem0Sz0i5U8HTg693B3Ek08V71vLStcHfg/uCVGGbuCSbkViIlXbMx0CsfnjnuPdvHaEphZ2A0y47cICQmkTbl786a9fvtGpvPRqZbf9LrhdPN0FpzKgLvl/Pi8f9jDG1cgITklHTbxiQYiY43kmxKIQWwsDBgY3n3e9jui7co5GJH09J3v4+0KOtCSVd7TCkphMYkkWhMwfj/28Pe3U5PzpGnQ/+SsqhP3mmFrY01r75cnlKF8rH78Ck27ztC/arlqFWxNFaWlrzhVYP8bnnYfeSPB273qDo2q8+Yvu9gZWlJSHgkjg72hEfdeuA2j5KpS0svrK0sea1uFWLjErgZHfOfP4PdR/6ggHsemte7OxDUpFZlPF1zsfvw3eP9tf6jDC4BdG/TBFsba8qXKEwuZyeCw26y4/eTFM3vTstXqmNlaUntSmWoV6Usm/cceeC+smez43JwKOt2HiQuIZEfxvvQov7L3IiM5vdT5/jk3TewsbamZCFPWr5andXbA/7+jFo1wNHBnvxueShe0IPgsAgOnw7EZDLRvXVjrK2tKFe8IG0a1WLdzrSzjPwDjvPqyxV4qVhB7O1s+eCt+9/6afoPq/F0zcX4T7rSrG7VpzJoM23RrwQGhfJuS690y+ISEilXvBCDurVh47ejqVCqCP3GzyIp2UhM7B1+2baPDzo0Y9N3o8nvlpvB0xel2X7z3iPkcHSgdqUyT5xTRDK+0LAwEhOT2LvDnzZvvsEHH31CxQrl2bfzN0qXLsXsufMBmDN/IQd+/50VP/3A6hXLOHb8OPMXLQZg+KjPcXFxYd/O3+jTuxf79gfc81ifDBxEu9Zvsm/Hb6xa9hPbd+5k7z/W3bN3P6uWLWXR3O/5de06Dh89+tjnc/zkSbasX4PfhC+Y8c13hISEkpiYSO++/Wj+WlMO7NlJ7x7d6dt/AIlJSfT9eAA5czqzY8tGZn/zNUuWLmfV6jWp+9uweTM/LpjLz0uX/H/ZWtb88jN+48cxaco0EhMTuXYtiH4DBjJoQH/2bvenXt06fNivPyaTKV2++YsW07h5S+YtWMTbHTqwbcM6enR7D4BRw4ZyOGBvuq973f7v85HDKVXy7yvbd+7aTYni6a+kK1u6NC9XrUqbDp0oX7U6P/+yiuFDPgPgzNk/sbCw4K2336VWfS/6fjKA0LC7RdTS0hI7OzsmTp5KvQaNuR0bS5vWbzz234eIZC1bD/1JvXJFqFmmEFaWFrSsVZb8eZzZc/Iie09dpES+PHhVKo6FhYEOXpUY0rkR4dG3+f3sNfq1qYuNtRUl8uXh9ZplWbvvbpf4ul8bmlUvw+24BG7euoNTNjsiomNTj9mmbnkcs9lRzDM3xfPl4dqNR3s+6HvNqpPLyYFCbi60ql2Obf94zk7DKiWwsbbiRtTdwZxP2tbHzsaKgnlz8m7jqqwPOA1Ay1ovUdjNhS7jf6R8EXcaV733jKJXKxUnXx5nnLPbU9jNhddeLoVzdnuKeeYml5MDoZH372IWFgYaVC6O/5HzAPgfOU+tsoXSDOw8KitLC0a825gfth3m7NWwx9p208Ez1CxTEOfs9hRwzUkxj1xsPJj+bgl936xDyM0Ylm1/9O/RTg523I5LSPf+mn2nOHUxhMFvN6TX6zVTB5ceV3xCMnY2aa8DtrOxvudtCHM42FGnXBGWDe/CtD5vsGr3Cdbse/T+LiJZ043YJJKMKazpXpbmZVz4bO1FXnLPxtr3y1I8jz0//n+w5sfDYRwNus3st4ozv2NJ/gi5w9Kjd+8KM8n/GjmzWbGme1neq+7G71dv3/NYIzddpkVZF9a+/xJzO5Rg78Vb/H717+8TB67EMLdjSb5qXZRNZyI5cT32nvt5kNOhd1jWpTQjmhRkXkAIYbcTSTSa+HTNJRqWcGZ9j5foUi0vQ9ZfIsloYvD6SzjbW7HSuwx+LYvwy4kINp75e5DH/1wUX7ctxvdvlWDViXA2no5kYaeSjGhSgJm7r5NoNBEcncCwDZf4sI4Ha7q/RI1CTgxedwlTSvoBn6VHbtBx0Rl+OnyD1uVzs7xLGTpXvTsI5vNqPjb3Kpfu6163/zt3I47biUa6/HiWVnNOseBAKLkc0s8Lcba3okUZF3zXXMTr6+N8vTuYwQ0LpO7D3cmGYRsu0Xz2Sfr+fAEbSwssDAZKuNpT0TM73Zeeo8HM46z74yb9X/F87L8PkXvRDKYsyNHBnhyOf1+NljeXMxHRMUTeuo1HnrT3SHXP7UJoRNQDt/PMm/Z+1fdz6/Ydxs5aypmL1yiczw07G2vu8X9vGg/LBOCSwxEgdfbPvf5D/7f7nYuFhQWnLlyhzruDUpclG42EhEfiksMRF6fsj3T12j+P8xcrS0uSjab/n5NLmvXc86Q9p3upVbE0fTu9zoote/li9nIqlCzM6D5vE3krFqMphUbvD0td12QyUe2lv2chOWa7dw633DnTnI97bhfOXLyW5rgR0TG4uuRIk/V+1n09nB/X76ST7ySqli1O5xavUKn03av3xs5exoZdh9Jt89VnPVLX+adko5Gxs5Zy8OQ5Zo34EGfH9FdQ1ihfkhrl/y6/vdu/xo/rtnPxWghWVlZ4vVye8iUKpy6r7/0ZsXHxONjb3c274yBveNW47/mISNbT9d3OWFpaUq1KZRb/uIQ2b94dSKherSqr/z+jZtXqNQwb/Cm5c929DWqvHu8zbsIk3n27Ezt372Hj6lXY2tpS4+VqvFK/3j2PM2/2txTIn5+YmBjCIyLI4ZSD8PDw1OUd2rfFyckRJydHSpUswZUrV6lcseJjnUuXzm9jZ2dHjZerkTtXLq5eu8aly5extLRInW30WpPGuLu5ERwczB9nzrBgzizs7OwoXKgg3by7sHrtOt5s1RKAVq+3wMXFBRcXF/Lkzk27Nm/gkC0btWvVJCkpifCICNZt3Mgr9epSs0Z1ALzffYd5Cxdx4uQpKpQvlybf5KnTqVypEmNHjySf58OvwH8UflOnc+HiRSZ+MTbdsvj4BPLn8/wfe3cZ3cbRNmD4lmRbZmZ2OHEcZmqYuU3DzNhgw8zMzMxMDjMzc2InZmbJFn0/lMhxHSy+7TfXOTqn2t2ZHa1TrXaemWfYvmkD+fLmYd7CxQz8dRg7Nm9Ep9MRUNCfXwcNwMbGhqnTZzJ42Ag2rlllKP9Ln1707NaFwcNHMmb8RObMmPantFkQhH+n+BQFrg5ZZz262lsRlZCMTgdOtpmdP8ZGMvx9XXkUFIFWp6XOsJWGfVqt1pDO7N6rMPos2INGqyWftwsqtYaPn1zsrDJ/s8uk0m96rgHwcMz8re5iZ8njoAjDewdri/efJw1bS1NMP8r04GpvTVRCZqdgg7L+jFpzlFolP59+yNo8c3S2VCrNkpZNKpGg+0qbaxTPy4hVhxn8c2VO3npOi6pFv+ETflpeL2daVy/O+PXHmNat/jeXO3D5ESHRCdQauhyANGUGygw1TSpkvY+Zm5owsk11fl1+kPIF/b6p7sQUJb4u2Z+XhraoSuEc7iw/eJnF+y7SompR6pYugKmJEXdfhjJgyf5sZWqVzJstTaKpiRHpvwkmKTNUnwzSTeqcOTAwh5sDzSoX4fz914Z1owRB+P+reREnZFIJhT0s2HVfRr0C+ueeYp4WHH+m75sKfBrPgB88sDfXf7+0K+nCgvOh/FTYkSvBSWxpkw+5kZRinpaU882eJQBgbuMceNjISUnXEK9QY21qRFxa5ndY44IOWMllWMnNyOVoSmhCOgFu2ft+vqRZESdDO+zNjQlLzOBdfDpSKYbZRlVz2+JiZUxEsorn0WksaJITuZEUbzs5rYo7c+xpPHXez+qpnc8OOzMj7MyMcLAwpr6/PeYmMkp6W6HS6ohPU3PqRQLlfK0p4aXvj2xR1Intd6J4EpmGv2vW9i+7HE4hdwuGVfMyzPL6PVLSNRx7Gs/Mhn4Yy6SMOPyGTTc/nSLPwkTG7EY5KOJhwf4HsYwJDGJT63wkp2s48SyeCXV8GFPTmx13Yxhx+A0bW+dDpdXibmPCsma5yOVoxqqrEYwLDGb5z7m/qx9UED5FBJj+g1IVShTpGZjJ9V9s4THxlC9aAI1Gy+vQyCzHhkbFUrZw3i+Wk0olaDQaQ5nE5E+POJiycgeF8vixdHQvpFIpmw6d4cz1B19sq4u97Rfb9Ht97rMAlA7Iy+KRPQzHhkTGYG9txaNXb+FP+FJ1cbDl3M2HWbaFRsXi6+6M9H39ao0GI5mMhI+uZUhkDEXy5aBp9XLEJiQxY80e5m7Yz+AOTTCTm3B+3VSk73OZx8QnfXVhWRd7W8Jj4tHpdIabRWhULPbWVlmOc7S1IiQy1vD+S7POXBzsGNC2Ed1+qsWek5cZMX8Dro52rJ3Un5Fdf2Zk15+/4QpBhkrFgBmrSUxOZcOUgYYg4m+dv/mQNGU6tSsUB0Cj1aLWaJGbGOPj7kTUR0E7jVaLRCJB+366b3qGiusPnzOud6tvapMgCP8Ntjb6TjipTIalVWbnoEQqRavTz8KJiIyk38DBhu9RnU7/9Z+QmIharcbZxdlQzt3N7ZPnuX3nLp2790KjUeNfoAAZqoysnYh2mYMnZDLZN3cifixLHUb6OmJiY3FyyrreQpHChbhz7x52traYmWV2Xnq4uRERmTnq28Yms4NSKpNiaan/7v1wb9FqdURERHL85ClKlq9oOFalUhMeEZEtwHTiyCE2btnKjy1aUapEcTq0bUPxYvqOxPGTpnDo6NFsn2nZwgWGYz6mVqsZN3Ey127cZN3K5djZZk9ht2XbdiQSiaEdg/r3o2S5ijx/8YIG9erSoF5mR9ugAb9QtlIVUlJSsLTU/zuQy+XI5XL69upBu05ds9UvCML/L852lgSFx2XZFhabRJkCPsikUq48DjJsV2s0LNx7kZZVi2JmYsypWT0N95CYxFRkUgmR8clM3XKSdUNbkctDP0Cv1eRNf0pbYxJTyfN+rZ2IuOQswa8Pjy/OtlYkpChRpGcGI8JiErG30i/srUhXsWT/JWqXysf8PecpU8AnSzAqs74/9jxUKIcbUqmEK4+DeRkaTXl/3z9UX5e6pTl79yVrjl7/puOfh0QTHpvIjrHtDc9eGWo1zSds4FFQBP6+WTvqSuf3oWbJvEzedBIdX75XK9JVPHgTzs+VC2fbZySTUb+sP/XL+nPlcRCbTtxiyf5LzO/ThCK5PDgzp9c3td/H1Z6rH/3bS0hRkKLIwMsp631RmaFm+cHLdK5b2hAEVKk0yEVacEEQAGtT/XeBTCLB0iQzeZVEIjE8l0SlZDDqSBAfupZ0gARIVmrQaMHJMvMe4WL96ZmoD8JSGbjvNRqdjrxO5qg02izfpLZmmd3OMqmE7DkRvi5rHfpnt3iFGkeLrG3yd7XgYXgqNqZGmBpnfmZXK2OiU1SG91ammfVJJWBpInv/3/oLodVBVIqKc68SqbM8s09TpdURlazC/zdLhG9vn49d92Losv05RT0s+bmII4Xc9ffp2WdDOPmJFHnTG/gZjvnASCbhx8KOOFvq+zFbFHFiwycCTOdeJRIcr6RPRf0Av2ZFnNj7IJab75Ixlkko6GZBeT/9c1+rYk5svBlJcLySq8HJSN5fJ4Du5dyos/whr2KV5HL8tixOgvA5IkXef5BWq2PptiOo1BpOv1/Xp2Jxf2qWK8q5mw+4fPcJao2Gfaev8iY0ggrF/L9YztPFgdiEZO48eUV6hooth8998rzJaQpM5cZIpVJevQtne+AF1O8DUybGRqQqlNnKfK1Nf/Y1qFjcn8ev3nL+5kN0Oh13nr6m2aBpvAqJ+Hql36hCMX+CwqI4ePY6ao2GS3cec/7mQ6qVKYK9jRUWZnKOX76DWqNh/f5Thoe4a/efM2zeeuISk7G2tMDExAhrS3PcnOzJ5+fJ0u1HUanURMYm0G38Qg6c/fJDVkBuH0xNTFi15zgqtYYHL4LZc+oKNctnTU9Us1xRzt54wJ0nr1CmZ7Bse/YOwd+yMDOlbYOqHFw8hrafSG33NdNW7yY5NY2V4/t+NrgEoFJrmLF2D69DIshQqViw+SC5vd3wcXembsUSXLr7hDtP9eufLN1+hFIBeQyzyp4HheJoa42Tnc1n6xcE4b/nWzrGHB0cWLtiGTcuXeDGpQucPRHI3u3bsLWxwdjIiPDwcMOx0THR2cpHREQyduJkFs+fy+ljR1k4dzbWVp//LvszuTg7Ex2dtU0LFi/B1cWF+IQE0tIUhu0hoaE42GcGqb7p2jg68GPjRoZrc+PSBfbu2EaVT8zkcnV1YcjA/pwKPEyxokUYMnwErdvrU+SNHTUiSx0fXp8KLmVkZNCrX3+ev3jJto3rP7veU0RUJCpV5sOhVCpFKpNhZGTE/oOHuHj5SpY6pVIpxsbGjJs4mW07dmbZ93f9vQRB+N9VvVgezj94zZXHQag1Wg5cfkRQRBzl/P0o5+/Ly5AYzt9/hVarY9uZu9x+HoKrvTV5vZxZfugKKrWGqIQUes3bxaErj0lVZgASTE2M0Gi17Lv4gJeh0ag1v6c7Lav1x26QnKbkTXgs+y8/pHap7DOQXO2tKJTTjfm7z6PMUBMcGc+mk7eo8T4V3pL9l/B2sWNixzq4O9iw9MDlP9wuAJP3AY0PaeMkEgnVi+Vh4d4LVAjIgYnxHxvTamwkY0y7mgRef5JtX2R8cpaXIl3FgUsPqVwkF862ljjaWOBoY4G7gw2VCuVk1/l7nzzHL00r8TY6noi4z6f/i0pIYczao/i52VPO/8uzncoW8GXxLz+ytP9PWWaAfYsfCufk9otQrj0JJl2lZvH+i1QslANz06yj4k1NjLj6JJiVh6+i1mh4GRrDznN3qVM6/3edTxCE/6Zv+d1vb27M3MY5Odo9gKPdA9jTsQCrW+TBylSGkVRCZHLm7+7Y1OxpOqNSMph5JoSp9X3Z1aEAk+v5Yin/e4LcjhbGxKSqsmxbdTUCJ0tjEpVqFKrMQfJhSRnYmWfei75lHIW9uRF1C9gbrs3R7gGsaZGXcn7ZZ3I5W5rQq7w7O9vnp6CbBROOv6X3Ln2q2EGVPbPU8eH12+ASgJetnNT0zN8MWh2fHPYQlaJCrc26x0gqwUgq0deRkfnZdR/VE52iT534gVSifxl9ZfC6IHwLEWD6j9Kho3qXkSzZfoR5Q7tia2WBr4cL0/t3YO6G/VRsP5Qdxy6yaGRPHO2sv1jOxcGOXi3q8uuctdTvPZ7CeT/9g3qnocwGAAAgAElEQVRQuyYcPHudcm2GMGT2Wur/UJK34dGoNRqKF8hFqkJJnR5js5T5ljb9mdfA1sqC+cO6smrPcSq2H8rohRsZ1rkZAbl9/vD5PrC1smDh8O7sOHaBSu2HMXv9Pqb2b09eXw/kJsb82uknFm09RPUuozA2NsLVUd/517hqGYrlz8mPA6ZQueMwklLS6NtKnwpi2oAOvA6JoEa30bQYMoPyRQvQtn6VL7bD2NiIBcO7cePBC6p0Gs6wuev4pXVDKhXPGrzL5e3OmB4tGDF/AzW6jcbH3ekzNWZnJJNRtVSh77o+yakK9p2+wtM3IVTtPIKybQZTts1gek9aCsCq3ccN/12tTGHaNaxKz4lL+KHjcF69DWfmIH3nZcFcPkzp145Jy7fzQ8fhhETGMqF3a8N5wmLi/pR/R4Ig/Pc0qFeHRUuXEZ+QgEKhYMz4iUycOg25XE6N6lWZu2ARCoWC23fvcupM9kEVKakpSCQSTE3laDQadu7ew7PnL1Crsj94/dkKFwpAIpGydfsONBoNgcdPsHPPXhwcHChSuBAzZs9BqVTyJiiYNes3Urd27e+qv06tmgSeOMHde/fR6XQcP3mKxs2aEx//+TSvlhYWdGzXluOHD9Kxfdvv/kwTp04nMSmJ9atX4ODw+TStFcqV43DgMW7fvYtarWbJ8pV4uLvj6+NDXHw8U6bPJCIiktS0NGbOmUetGtWRy+UEFPRnzfqNREREkpCYyIJFS2lYv953t1MQhP8WX1d7Jneuy4I9F6g6aAm7zt9jfp/GONpYYGdlzsweDVlx6CpVBy3hwv3XTOmi/96Y3Lkub8JjqTNsBW0mb6Ksvy+tqhcjh5sDraoVo/20LdT6dTnn7r+iWrE8BEXEfaUlX+fjYkfLSZvoNX83XeuWoVQ+708eN7lTXWKTUqk/YiU95+6kYTl/fqpUiAevw9l/+SFDW+gHhg1tWZU9F+7z8E34J+v5Hg7WFpQt4Evd4St5FaZPFVuzRF5ehsZ8dp2n7+Xv60rr6sWzba8/YlWW1/5LDwm88ZTqxfNkO7Zu6fycuPmcpNTsgx4tzeSMbF0j2/ZpW05Rqf8ifui/iI4ztuJgbcH83o2/mknig9yeTvi42H39wI8421oypUtdZu84S61flxOdkMrI1tUN+yv1X8SdF/qU59O71edlaAzVBy/jl8V76VC71Den+hMEQaiZ15a11yNIVKhRqrTMOB3C3HOhyI2kVMppw4or4ShVWh6Ep3LxdWK28qkZWiQSkBtJ0Wh1HHwUy6sYJWrN92du+F4FXM2RSiTsfRCDRqvjzMsEDj2Oxd7ciIKuFiy+GE66Wsvb+HS23Y6mWu7s2RG+pGouW868SOBRRCo6nY5zLxPouPUZicrPP++Zm8hoUdSJbe3y07zot/erfVArrx17H8QQnaIiQaFm651oKufMPmC6hKcl98NSOf8qEa1Ox+HHcSQq1QS4W/BDThvexqdz9mUCGq2OTTejcLQwJqeDKaW8rTj1IoEH4amotTrWX4/E1doEL9vvGwghCJ8icXd3/+v/zxf+MqGhoSgeHMt8HxVLvV7jubtrwffV8zvL/S/6L30W4a9nFlALDw+xsKEg/NuEhoaiS08zvA8JDaN6nXo8vX8HgGs3bjJ89BhOB+rXXdqz/wB79x9g45pVZGRkMHfBIo4EHiNNkUapEiWYMGY0Dg72JCYlMXLMOC5fuUqOHH54eniQM0cO+vbqQdtOXWjSqCFNGzVk7oJFbNuxE4lUSpFChTAzM8XZ2YnhQwZTtXZdpk6cQOmSJQCylPuSj8vlK1SUk0cPG9Y2+njfs+cvmDB5Ks9evMDby4vxo0cSUNCfyKgoJk6Zxo1bt5HLTWj1889079oZiUSSrQ2/bePH5zt7/gJzFywkJDQMdzc3Bg/oxw8VK3623X9EcnIypStWxsjIyLDWIkDxYkVZuXQxy1au5tbt26xcuhiArdt3sGb9RhITEwkIKMi4USPw8vREo9Ewe94CDhw6jEKp5IeK5Rk3ahTW79PCLlq6nO07dwFQr25tBv7SDxPjT6SGkpuLe4Ig/EeFhoaSdHrZP92M79Zw5GrGtq9pWOfp3yA2KZXmEzYQOL1blu924Z9hXbWHuLcJwn9UaGgoUYsylyoIT8rg5/VPuNBXn8rzTkgKU06+ZWcH/ZIRR57EcfRJHAub5iJDo2XllQhOPU9AodJQxMOSX6t6YmduTLJSzdRT77j5LgUfOzlu1ib42pvSqbQrffe8pE5+e+rmt2fFlXD2PYhFKtGnXjM1kuBoaUzfih40W/eYEdW9Keqpn63zcbkv+bhcxYX32NE+v2Fto4/3vYpRMOdsKK9iFXjYyBlcxZP8LubEpKiYcy6Ee2GpmMgkNAlwpG0JZyQSSbY2/LaNH5/v8pskVlwJJzwpA1drE3qUc6PsZ9ai+jNodTo23ozi4KNYUjO01MhjS9+K7hjLpBx/Fs/Gm5FsbK2fwXz2ZQKrr0UQnaLCz96UAZU9yOOkT4l7PyyVhRdCCY5PJ4eDKUOreeFnr1+nfO+DGLbdjiYpXUN+FzMGV/bE3SZ7gMm5zw5x3xC+iwgw/cuJAFN2/6XPIvz1RIBJEP6dfhtgEoQ/gwgwCcJ/lwgw/T1eh8ey8+w9pFIJQ5p/OeOC8PcQASZB+O/6bYBJEP4MIsAkfK8/lhBZEP4BL4LDaDdyzmf3rxjb9w+fIzlVQc3uoz+7f+W4vhTM9eel1RMEQRAEQRAE4f+fesNXkvx+/aLfGteu1t/cmj9u2IpDSKUSFvX70bBt4d4L7Dz36fWPSufzZmaPL8/wFQRBEARBEP53iRlM/3K/ncEkCML3ETOYBOHf6d84g+mH6rVITv70AuJTJ02gVo3qn9wn/H3EDCZB+O/6t85gEoQ/SsxgEoT/rn/jDKamax6TkqH55L4R1b2onOv71ksS/nxiBpPwvcQMJkEQBEEQhL/BuZNiQIggCIIgCIIgCP9/7elU4J9ugiAIfzIRYBL+X9p29Dyz1u/F2Chz0dnDi8dib2PFzUcvmL56N2HRsfi4uzC8SzMCcvuwavdxVu89bjhep9WhzFCxblJ/iuTLwY5jF1i79ySJKWkUyOnFqG7N8fVwAfjd+z64dv8ZPSYu4c7O+YZtJ67cYcHmg8QnpZDPz5PRPVrg4+YMwJq9J9geeAFlegZ1KpZgULvGGBsbGfZtOnQWlVpNoyqlGdiuMVKpNNs1uvnoBTPX7uFdRAyujrb80qYhP5QIAPRpCicu38brkAic7W0Z0K4RFYv5A3Dm+n0WbjlEZGw8Pm7ODOn0I0Xz5fjDfzNBEIT/ouMnT7Fp6zY2rF5p2Hb95k0mTZ1BaFgYfr4+jBkxnEIBBQF4+Pgx4yZO5vXrN/j6+DB+zCgCCuq/f/fuP8CS5StJSEygUoUKjBs1AisrKwAuXr7C1BkzCY+IpEC+vEyeMA4fb28AlixfwY5de0hLS6NY0aKMGzUCV1f9fejAocPMX7SEhMREShQrytSJ47G31y+Ku2L1GtZv3IxKpaJJ44YMHTQQqVSKSqVi+uw5BB47gVqjoVKF8owePhQrKyu0Wi3TZs5m/6HDyKRSOrZvS9dOHT95be7df8C4SZMJCgqmQP78TJ00Hm8v/Rokp86cYe6CRYRHROLr483Iob9SrGgRlq1czYpVqw11aHU6lEolWzaspViRIn/mn04QBOFfLyFFweRNJ7jx7B2WZnJ6NChL/bL6e8qt5yHM2XmWkOgEXOys6NOkApUK5eTOixB+WbwvSz2KdBW9GpanY51SvI2KZ+KG4zwLicbTyZZRbapTwMcVgJehMUzZfJLX4bE421nyS9NKlC/ol6Wu1+GxtJ2ymZ3j2uPuYGNoy6wdZwiPTcLbxY6hLari76uv89Tt5yzad5H4ZAX5vJ0Z0bo63s52AOw4e5f1x2+gUKoomtuDka1rYG9tbjhXhkpN19k76Ne04mfXuDp9+wVLDlwiKiEFX1d7Bv9cmUI53L/arkNXHrHqyDUSU5WU9/dlWKtqWJplX0hdEATh/7MEhZoZp99x610KlnIZXcq4Uie//lnjTmgKC8+HEpKYgbOlMT3Lu1Hez+ar5d4lpDPt5DtexCjwsDFhaFUv8rnov/t334th0cUwjGUSQxu2t8uHnbkxZ18msPJKBNGpKnzs5PxSyYOCbhYcfxbPrDMhWdqtUGkZU9ObGnntuBKUxJJLYUQlqyjkbsGQqp44W5oAMOpIEFeCkpBJ9efzspWzukUeQz06nY4Rh4OomNOGuu/b/1uvYhTMPBNCUJwSJ0tjepV3p6yvNQCPIlKZfSaEdwkZ5HEyY0QNLzxs9Pea0MR0ZpwO4UlkGo4WxvSr6E6Z9+UE4c+WvVdZEP4feBYUyi+tG3Jl0yzDy97GCo1Gy+BZaxjYvjEXN8ygUZXSDJ27FoAuP9bMcvxPNctTo2wRiuTLwe3Hr1i+M5BlY3pzccN0ihfIxfilWwF+974PUtIUjF+2FZ0uM5tlXGIy45duY/bgzpxbO42A3L5MXLYNgCMXbrL1yDkWj+zB0aXjCY+OY+6m/YA++LP31BU2TxvEvvkjuf34FdsDL2S7PgplOv2nr6Jn87pc3jSTYZ2bMXTOOlIVSgBGLdxI46pluLhhBv3bNmLIrDUo0zMIjYxl9KJNjOjajAvrp9O6fmX6T1thKCcIgiBk2r1vP0OGj8zy/a7RaOg3cAhDBw/k5uULNG3UiAFDhgKQkppKzz6/0KZlC25dvUTzn3+i/+BfAbh95y4Tp05n6sTxXDp7GktLC4aNGgNAaFgYA4cMZcTQX7l5+QIlihdn1LgJABw8fJSDh4+yef0aLp45ibubKyPGjgP0AZ6pM2excO5srpw/g52dHTPmzAP0AZ5de/axc+smjhzYy81bt9m8bTsAq9dt4MmTZxzcs5OTRw+RlpZmKLdpyzbu3X/AsUP72bpxHdt27OL02XPZrk16ejp9Bgykc4f2XLt0nnJlSxuuQ0hIKENHjmHMyOHcuHSeDm3b0LNff1JSU+nRtTO3r102vJo3+5HaNWuI4JIgCMInjF0XiIO1BSdm9mB2z4bM3H6GkOgEFOkqBi87QLf6ZTk3rw9DmldhxKojpCozKJrbk/Pz+hheEzvWwdvZlmaVCwMwYtURKgTk4PTsnrSoUpQhyw6SoVIbztewnD9n5/amX5OKDF1xCGWG2tAetUbLhA3HyVBnpk7SaLUMXXGQ/j9W4sycXjQo68+IVYcBiEtKY9Kmk8zo1oBTs3vi7+vKlM0nAXj2Loq1gddZPbg5gdO7YW5qwsJ9mc890Qkp/LJoH4+DIz97fcJiExm34Rjj2tfi/Lw+/FSpMMPfn/tL7br3KpSZ288wtl1Njs/ojoWZCePWi1nMgiAIvzX5xFvszY051NWfqfV9mXsulNDEdBQqDSMOvaFTaVeO9whgwA8ejA0MJu19ar3PlQMYGxhMOT9rjnQtyE+FnRhxOIgMjRaAlzEKepRz43iPAMPLztyY8KQMppx8x4gaXhzvEUDjAEfGBgYDUDOvXZbju5V1paCbOVVy2RKWmM6Yo8F0Lu3K4a4FCXCzYNihIMPz3asYBUub5TKU/Ti4lJyuYVxgMBffJH31GtUrYE9g9wB6lnNn9NEg0tVa0tVaRh4JolVxZ45086eEt6Whzdr3gavinpYEdi/IL5XcGRMYjEL16dSEgvBHiRlMwl8mNCqWjqPm8WONcmw+fA5TE2NG92jB6Wv3OX75Nq6O9swY2IGcXm7cevySaat2ER4Tj6eLA/1aN6BckfyAPmCyYmcgcUkplCiQi1Hdm2NvY5XtfGXbDM62zc3Rnj3zRmTb/jw4lDoVimfbnpSaRkJyKmqNBp1Oh0wqRW5snO24e8/ecPTiLfbOGwlAsQI5ObhwDOZmchTKdFLSlNhYWfyhfR/MWreXaqULs/HgGcO28Oh4MlQqNFr9TVL6UTvPXL/Pz7UrkstbP7Ku60+16D1pKUM6NOXoxVv8VKM8bk76kRGdmtZg7b6TtKz7Q5ZzmpnKOb58AuZmcjQaLfFJKViYm2Ik08/4ehsRjVqjQavVIpVIMDHRnzs8Jo6m1cpRwj83APUqlWTGmt0Eh0VRIKd3tusoCILwVwoJDaN1+478/FNTNmzagqmpKRPGjuLkqTMcOXYcd1dX5s6aTq6cOblx8xYTp04nPCIcLw9PBvbvR4VyZQF9EGbJ8hXExcVRqmQJxo0aiYND9hFmxUqXy7bN3d2NQ3t3Z9s+d8Eirt+8Sfs2rblzL3Ph86SkJBISElCrVeh0OqQyKXK5fhTambPnyOHnR+OGDQBo1rQJ/gXyo9VqOXXmLPVq16JE8WIA/NK7FxWq1iAxKYmDh45QvVpVypctA0CPrp0JfvsWgMSkRLp17oiHu/6e0bzZT7Rs1wGAXXv20qZlCwrkzwfAiF+HEBMbC8ChI4E0b/YT7m5uAHTr3IlVa9fRtlVLlEolPbp1wc5OP4K8aeNGzF2w6H25o3Tq0A5bGxtsbWxo3bI5Bw4dpmrlrPeha9dvYGttQ/26dd63uQvrN27m5atXxMXH06xpE0qVKAFAg3p1mTRtBkHBwRQskJly4869exw+Esjh/XuyXX9BEIS/S1hsIl1n7aBxhQC2nb6NqYkxI1pX58zdl5y89RwXOyumdq1HDjcHbr8IYeb2M0TEJePhaEOfxhUoU8AHgMDrT1l15CrxyWkUy+PF8JbVsszG+aBS/0XZtrnaW7FjTPss2yLjk7n7MpTpMxpgbCQjr5cza4e2xM7KHDO5MYendMHc1ASNVkt8igILMxOMZFnHp6Yo0pmy5STTu9bH0kzOm/BYQqITaFOjODKplIbl/Nly6hY3nr2jfEE/3kUnoNZo0Wp1SCQS5MayLPWtO3adwjndeRQUYdiWnJZOYqoStUaLTgcyqQST95kZIuKTyFCpDc9EMqkUEyP9vpDoBLQ6Her3nYoyiQT5+30pinTaTNlM6+rFCIlJ+Ozfzt3BhsBp+uCUSq0hMVWBjYXZV9t17t4rapTIS9HcngD0aFCO2kNXkJSqxNrC9LPnEwRB+CuEJ2XQe9dLGhS0Z+fdGEyNpAyp6sn5V4mcfpGAi5UJ4+v44Gdvyt3QFOaeCyUqOQM3Gzk9yrlRylvf/3biWTzrrkcSr1BT1MOSwVU8sDPP3l9Wc9mDbNtcrIzZ2Dpflm1RKRncC0vlYBdfjGVS8jiZs/zn3NiZGWFmLGN3xwKYm8jQaHUkKNRYmMiQSSVfLBcUpyQsMZ0WRZ2QSSXUK2DPjrvR3HqXQllfa17FKKieJ/saT27WJuzrpD+fSqMlSanG2lSW7bjwpAxWX4tkVfPcGMkkXAtOpqCbuWHdqDYlnNl0K4pXMUrcbUyITFbha//p7/3O257zQ04bCrplv5d/LCQxA7VWh1anQyoBk/f34jshKVjLjaieR//M1a6ECzvuxvAmTkmyUkO6WkvbEs5IJBJK+1iz5MdcSCWSL51KEH43EWAS/lJRcYlkqDScWT2F5bsC6T9tJaO7N2dEl2aMW7qFtftOMalvGyav2EHfVvWpUqoQh85dZ+qqXRxcNJo7T18zc+0elo7qiZ+nKws2H2T0wk0sHtUz27mubJr1TW3SaLS8ehvOxoNnGDZvPY62VvRp1YBKxf2xs7akSbWy9J2yXB9cMjFm+dg+2eqYvX4vPZrVwdoy80Zgbibn/M2H9J+xEgszU1aP7/eH9124/Yh3EdFM6N0mS4Apfw5PSvjnouWvM5FJpdhaW7B+8gAAtFodpiYmhmNlUimJKWkkpaQRFBpJ/UolDft83Z0JCv30qD1zMzkpaQp+6DAcrU7H+N6tkL8PJHVsVJ1pq3cxffVuJBKYOagTpnITSvjnNgSXAO4/f4MyQ4W3m9PX/zCCIAh/gcioKDIyVFw+d5rFy1bQq98AJowZxeiRwxk1djwr16xj+uSJjJ88hQH9+lCtShX2HzzExClTOXboALfv3GXqjJmsWraEnDn8mDN/IcNGjWbl0sXZznX72uVvblfrls0Z0K8Pe/YfyBJgsrOzo1nTJnTv3Q+ZTIZcLmfdyuUAPHn6DE9Pd34ZNISr12+QK0cOxo0eiVQqRaPVYGqa+fAilcnQarWEhITy5NkzPD086NS9J4+fPKVQQX8mjBkNQJuWLbK069yFC+TJnUt/vmfP8PDwoHnrdrwNeUe5MmUYO1I/aOP1mzc0rF/PUM7P15fXb4IA6N+392frfB0URA4/vyzl9h04lO36vA4Kws/P1/BeJpPh5eXJ6zdB1KxezRBcArh77z5KpRJf76wDGabPmkOfnt2xsRapIARB+GdFJaSgUms4PrMHqw5fZdDS/YxoXZ2hLaoyceNxNhy7wbgOtZm29RS9G1Xgh8I5OXLtMTO2nWbPhI7cexXKnJ1nWdivKb6u9ized5Fx64+xoG+TbOc6Py/7s8unvAiJxtvZjtVHrnLwyiMszeT0blyBHG4OAJibmpCiSKf64KVodTrGtK2J3Dhr98H6YzcontuTIrn0C4EHRcbj7WyL7KP02z4udgRFxFG+oB/tapZg5vYzzNpxBpAwvVt9TE30dT4PiebEzeesH9aKLaduG8rbWprRqHxB+i/eh0wqQW5sxJL+PwGQz8uFYnk8aTt1CzKpBBtLM1YPbg5AmQK+ONtY0mTMWmRSCZ5Otqweor/nmZoYsX1MO2wtzdh17v4Xr5O5qQkvQ2NoPXkTMpmUub0afbVdGq3O8LlAPxhQq9MRFpsoAkyCIPwjolNVqDQ6DnbxZ931SIYfesOQqp4MrOzBtFMhbLkVxcga3sw+G0K3sm5UzGFD4NM45p4NYWu7/NwPS2XBhTBmN/LDx86U5VfCmXziHbMaZV8O4XiPgG9q08toJV62ctZdj+TIkzgsTWR0L+eG3/uAjLmJjNQMDfVWPESrg+HVvZAbSb9Y7m18Cp62ckNKOtCnpQuOT6eUt47XcUq2341m/LG32Jsb0a2sG+X8rA3nexWjoNO258gkEqY38MvW5hVXwmnkb29IQ6fR6TA1yrznSQCpRJ+eTqnWYmosZciBN7yKUZDL0YwBP3jg8/7zLfkpF44WxvTd8/KL16lVMWfmnQtl/rlQkMDEOr7IjaQEx6fjbZeZelUmleBhY8LbOCWxaWp87EyZeSaE868ScbYyoX8ld+RGIpGZ8NcQ/7KEv1zbBlWQyaQUz58TczM5jauVxdjYiJL+uYmMjQfA0tyUoxdvcevxS2pXKM6BhaMAOHTuOk2rlyNfDi/kJsb0aVWfq/efEZvw5SmkX5KYkop/Lh9+rl2BY8vG06dlfYbNXUdQaCQajRZLc1OWjOrJlc0z6d2yHr/OXoMiPcNQ/u7T14RFxdGoaulsdZcpnJdrm2fTpn5lfpm2ApVK/bv3JaWkMXPtHsb1aqW/S30kPUOFh4sjG6cM5PKmmdSrWJKhc9eh0+moWNyfHccuEBweRapCydp9+jQR6So1ivQMTOWZwSdTuQnKdNVnr5WZXM7VzbNYNKI7U1bs4OXbMAAkUgmT+rbl6uZZTO3fnnFLthAZm3X039vwaAbNWkOv5nWxNDf7hr+MIAjCX6NDuzbIZDJKFi+Ghbk5PzZpjImxMaVLliAiQh9kt7S05NCRQG7cvEW9OrUJPKhPLbrv4CGa/diUAvnzIZfL6d+3N5evXjPM5Pm9nJ0+HXjXaDRYWFqwatkS7ly7TP8+vek/eAgKhYKkpCQOHj5Kowb1uXD6BFV+qESf/gNQqVRUrliRA4eP8ODRI9LT01m0dBkymYz0jHSSkpLYtWcv/Xr15NyJQLy8PBkyYmS2c58+c5ZlK1bx60D9gIWkpGR27dnLlInjOHHkEBkZGUyZMRMAhUKJ2UcBLTMzU5TK7OlQt2zbQeCxE/Tr3fN9OQVmZh+VM/10OYVCkaX+zx0b/PYt/QYNpl/vXlhaWhq23757l9DQMJo2bvTJ6ywIgvB3a1WtGDKplKK5PTGXm9CwXEGMjWSUyOtFZHwKAJZmcgJvPOX2ixBqlsjH7vEdADh89QmNKwSQ18sZubERvRqV5/rTYGKTUn93e5LS0nkRGo1UIuHApM4Mb1WNcesCCY6MNxxjJjfmwvy+zOvdhGlbT/MyNMawT5GuYs+F+3SsXSrLNlOTrKPZTU2MDWnwpBIJ4zvU5sL8vkzuXIeJG48bgm8TNhxnROtqWQIzoE9FZ2FqwsK+TTk/rw89GpZj2MpDKDNUpKvUeDjasPbXFpyb14c6pfIzcvURdDod6Rlq8vk4s2NMO07N7kVeL2embtE/FxnJZNhafvvzia+rHZcW9mVYy2oMXXGI+OS0L7arQkE/Aq8/5XFwBOkqNSsPXUEmlZAuUhMJgvAPal5EP6unsIcFZiYy6hVwwFgmpZinBVEp+n4hSxMZJ5/Fczc0hep57NjSVj/r6NjTOBr425PHyRy5kZRuZdy4+S6ZuLTP9yd9TXK6hlcxCqQS2NkhP4OreDLpxFvexqcbjjE1knKiZwAzG/ox+2wIr2MVXyynUGmzBHw+1JGu1s9Kyu9iTpMAR3Z3zE/Xsm6MOxbM2/jM5wsfO1NO9SzEoCqejDoSRLwis98uMjmDS2+SaF408zmulLcVt0JSuBachFqjY8vtaJRqLRkaHUqVFn9Xc/r/4MHujgX06fMOv0Gt0afPc7TIPvvrU6QSGFXDmxM9Axhby4dpp94RnaLSB7A+8VmVah3J6RquBSeR19mcvZ0K0KqYE8MPB5GkVH/mLILwx4gZTMJfzub9LB+pVJol0CCRStFq9V+sMwZ2ZMHmgwycsQod0LFxdTo2rk5ETAKHz93Isk6QkZGMsOh4HGyzjkiu0G5otnO7Odqxc86wLNvsbaxYPSFzllClEgUp4Z+Ly3ef4mAXypvQSAa1148GbF2vMjuOXeTa/WdULqkfhXH4/A3qViqByYuUl9MAACAASURBVCdS533Y1vXHWmw8eIYXb8MMqeG+d9+mQ2dpUbsSXq5OhEZl7cjcFngBCRCQxxeAfm0aUKHdUF4Eh9GoSmnComLpOnYhchMTuv5Uk+OX72BlboqpiQnKjMwfAMr0DMxMP7/YrEwmRSaTUr5oAUoF5OHy3aco0lUcvXDLkHqwRtmi7Dl5hVNX79Gqnj7F0YMXwfSbupyfa1WgfaNqn61fEATh72Bro18MViqTYWmVGYSQSKVodfrUOXNnTmfO/IX0GTAIdDq6dupIl04diIiI4MChw2zZvt1QzsjIiLCwcBwdHLKcp2T5itnO7ebqxoHdO765rcdPnuLNmyCGDR4EQLs2rdiyfQdXrl7D2NiYYkWKGNLJde7YnmWrVvP6TRBlSpfil9696D/oV7RaLT27dcXc3AwrSyuMjY2pXq0KRQoXAqBvr56UqViZlNRULC30aVl37NrDjDlzmTtrOsWK6tcrMjY2ol6d2uTMoR+Z2KNrFzp11weKTE1NUaZnPvwpFErMfzOYYOGSZWzdvoNVy5bg8352kampKUrlR+WU2ct9qv7MYzNnDt9/8JAeffrRsvnPdO7QLsuxBw4epkG9uph8NKNXEAThn2TzfuaKTCrB0izz97dEIkH7fq2GKZ3rsXj/RX5dfhCdTkf7WiVpV7MkkfHJHLn2hJ3nMme8GsmkRMQl42CdNb12lYFLsp3b1d6KraPaZtlmbCRFKpXStX5ZjGRSiufxongeL64+DsLHxe59W6XIpFDO35eS+by4+iSYXB6OAFx48BoPJ1tye2Z2tJmaGKFUZe28UmaoMJMb8ygogsAbTw2p+qoVy8O+iw85ffsF8clpFM/jSeGcHtnafvrOC4Ij4xnwk/7e17JqMXadu8+1J28JjoxDgoSCfvp0rX0aV6DKwMW8DI1h94X7eDvZ4fd+RtaAnypRZ9hKUhTpWa7/t/iQJvxDyr87L0LR6LSfbdcPhXPSvUE5hq88jEaro3Pd0pjJTbA0E/ckQRD+OR9SvskkEixNPpp189F9aFxtH5ZfCWfkkSB0Omhd3JnWxZ2JSlFx7Fk8e+9nDjSQSSVEJKmw/02avDrLs6fIc7YyYX2rvFm2GcskSCUSOpZ2xUgqoainJcU8Lbn+NglvOyfDOWToU7wV97TienAyzlYmny3nZGFMulqb5TxKtRYzYyl25sYsbJrLsL28nzVFPSy5/jYZbzv9PdpIph/d/SG13r3QFEP6u5PPEyjtY5UlLaC3nSkjqnux8EIYyekamgQ44mtnioWJjBLeVpTwzlzeo1NpF3beiyYoXkkux28b5PA4Io0Tz+MN6QWr5LLl4KNYzr1KQG4kJV3z6c9qJJXgYmVCo4L6e2D1PHZsvBnFg/BUyvvZfNO5BeF7iACT8JeTfCXHp1qjISgsisn92qLT6bj24Dn9p6+kQtECONpa0f3nOnRsXN1w/JvQSLxcHbPVc3HD9G9qz6t34Zy5/oAuP9Y0bMtQqTExMSIqNgGVOuvIMiOZzPBQAXDx9mOmDeiQ5ZgDZ69x4+ELJvZpA2DI921lYfa79526do/ztx6xZPsRdO87QCu0G8rC4d2ytVMqkSCTSjAykhEdn0TT6uXo1UKfuujy3Sd4uTpiZirH18OZ4LAoKO4PQFBYFL7uztmu0euQCH6ds5Yds4YifZ/iIkOlxsrC7PPX6P3Iict3n/DrnLUMbNeYptWzr0ciCILwd/vqfUit5k1QEDOmTEKn03Hl2nV69etPxQrlcXR0pE+P7nTp1MFw/Os3b/D28spWz41LF7Jt+14RkZGoVFlHAhobGWFkZISvjw/3Hz40bNfpdGi1WkBHfHw85cuVoVWLnwF4ExSMSqXG18cbXx8fIiIz06FqNRokEgm692tWLF62nC3bdrBm+VIKBRQ0HOfr40NyckpmOa0W3j985vDzJSg4GKj4/nxB+Pn4Gto1etwEbty+zdaN6wzBpY/L5c6VM7Ocr2+265DDz5d9Bw4a3ms0Gt6+e4efr34tkguXLjNgyFCGDhpAsx+bZit//uJFZs+Y9okrLAiC8M/4+jORluDIOCZ0qI1OBzeevWXQ0v2U8/fDwdqCbvXL0K5mZqrroIg4PJ2yryNxZk6vb2qPt7MdGo0WZYbKEHDR6nTodPAmPJbhqw6zZWRbpO/TDKnUGqw+CsxcfviGKkVyZanT19We0OgEtFqdoVxwZDwNyxUkMj4Z9W86/YxkUoxkUk7deUFMYioHLj8y7Gs1aRPDWlYjNin1E88e+nJR8SmoNL99Jsrc52xr+VEZGRIJWdL3fc21J8FsOH6Txb/8aNimUmuxNJfzIiT6s+1KSFFQJr8PzX4obLgGKrXGELgTBEH4J3z1PqTV8S4+ndE1vNEBt96lMOzQG8r4WGFvbkTHUq60Lp7ZfxQcp8TDNnvA/mj3b0uR52UrR6PTka7WYmSi73PTvB+EHhSnZGxgMGtb5jGsG6TSaLGUy75YztvelNDEjPfrFenLvUtIp34Be97EKbnwKpF2JV0MbVBptJjIpNx8m8zm21HMbZzzo306LOWZfYFXgpJoHJB1gGFqhgYfe1M2tclneL/xZiS5nEy59CYJhUpjWCNJowONNnMNpW8RnZJhmPH0gZFUYkiHF/gkzrBdo9URmpCZNi81I+s96sM9XhD+CiJFnvCPk0mljF28mT0nryCRSHC0tUYikWBlYUbdiiXYefwir0Mi0Gq1bD58lk6j52X7Mf89LM1NWbXnOCev3tUvjH71Hg9fvqVqqUKUCsjL3aevOX3tHlqtln2nr5KYnEqRfPrcq7EJSUQnJFEgR9aOxYDcvpy6eo9bj1+iUqlZtOUQeX098HRx/N37rm2ZzcUN07m4YTo7ZutnYV3cMJ2i+XNStkh+jl26zd2nr1FrNKzYdQx3Jwd83Jy5dOcxg2etIVWhJDo+kSXbjhgCPbXLF2d74HlCImOIS0xmzZ4T1K1Ygt/ycnVCmZ7B+gOn0Wi0nL52j6dvQqhU3J/Cef2IS0xi29HzaLVaLt15zJ2nr6lQzJ/g8CgGz1rDuF6tRHBJEIR/DZlMxojR49i5e6/+PuTggFQiwdraigZ167B1x05evX6NVqtlw6YttO7QKVsQ6M9StnQpbt25y4lTp9Fqtezet5+ExESKFS1CzRrVePMmiGMnTqLRaFixei3OTk7kyZ2bp8+e06lbT2JiY0lKSmbG7Dk0adgAY2NjGtSry8VLl7l95y4ZKhULFi+lbOlSWFlZcfDwUTZu2cbm9WuyBJcAGtavx8HDR3j1+jVpaQqWLF9Bzer6Wal1a9di89btvAsJITY2jhWr11C/Xh0Alq9aw/Wbt9i6fm2W4NKHcitXryU2No63796xeet2GtStk+06lC5ZktjYOPYdOEiGSsWylavw8vQiZ44cBAUH88ugIUweP/aTwaWY2Fiio2PwL1Dgz/qzCIIg/OVkUgkTNh5n36WHSCTgYG2BRKKf7VS7VD52n7/Pm/BYtFodW0/fpuvsHag1v/+ZKI+nEzncHVh15BpqjYYbT99y+0UIFQL88HK2RZmhZtPJm2i0Ws7cfcnTt1FUCMhcj+JRcCQB72cOfZDDzQEXOyvWHbuOSq3h4JVHJKYqKZHXi0I53IlLTmPH2btotTouPwri7qswyhf0Y9e4Dpyd25szc3oZAmRbRrWhdql8lMznzb1XoZy5+xKtVseBy49ITFVQOKc7ZQr4cOLmM+69CkOt0bL6yFXcHKzxdrGjrL8vO8/dIygijnSVmkX7LlLO3w8z+belJALI6+XM07eRHL/xDLVGy46zd9FotRTK4f7Fdj0PiabPgt3EJqWSnKZk/u7z1C9bIMugRUEQhP81MglMPfWOg4/ikAD25kZIJRIs5TJq5LVj/8NYguKUaHU6dt6Npvful9mCH98jl6MpvvamrLseiVqj49a7ZO6FpVLO1xpPGzlKlZatt6PRaHWcf5XI82gF5fysv1jOz94UZ0tjNt2MQqXRcuRJHIlKNUU9LbEwkbLxZhRnXyag1ek49zKBJ5FpVMxhTS4nM55FKTj5PB61VsfuezFotDoC3PSzhLU6Hc+jFRRwMc/yGeLS1PTa9ZJ3CekoVBqWXgqnmKclzpYmqDVaFpwPIyhOSYZGy/LL4eRwMM2ybtLXFHSzIC5Nze57MWh1Oq4FJ/EgLJWyPtYU87QkXqEm8EkcKo2WDTcjcbeR42tvSklvS2RSCTvuRqPV6Tj2NJ64NDXFPC2/flJB+B3EDCbhHyeRSJg+oAPTVu9i9vq92FhZMKJrM1wd7XB1tKPbT7UZMGMVMfGJ+Hm4smBYd8zkvz+9gIuDHbMGdWLepv2MWrgJb1dH5g3tgr2NFfY2Vkzu15ZFWw8zZvFmcni6smhEd0Nqv7DoeGwszTH+zQK3fh4uTOrXlgnLthGflEKx/DmZNbgTEonkd+/7kkrF/enftiGjFm4kMSWNgrl8mDu0CzKZlIaVS/P49Tvq9hyHTCajSbWytG9YFYBqZQrzNiKazmMWoEzPoEHlUrSoox99fvvxK3pPWcqVTbMwNpIxb1g3Ji/fzuo9x/Fxd2bh8O6GtITzh3Vjzvp9LNp6CHcne2YN7oS7kz1z1u9DkZ7B6EWbGL1ok6G9i0f0pFiBnNk/iCAIwv8AiUTCnJnTmDRlOtNmzcbW1oYxI4fj5uqKm6srvXp0o/cvA4mOiSGnnx/LFi7AzOyvWVsuX968zJgyifmLFjN89Fhy5czB8sULsbS0xNLSklXLljBlxkyGjx5L7lw5WTRvNhKJhLJlStO0cUMa/fgzao2GWjWqM2yIPs1eQEF/Zk6bzNgJkwgND6dokcJMnTgBgHUbN5KSkkLTn1tmacfta5epVaM6CYmJ9OrXn5jYOH6oWJ6hgwcCULN6Nd6+fUfbjl1QKJU0blifNi1bvK9zE6kpKVSvU99Qn7u7G4f27qZtq5ZERUXT6Kef0el0dGzXlqpVKgNw8PARlq9azaG9uzE1NWXZ4gWMmziZCVOmkT9vXubN0s9U3r5zNwqFguGjxjB81BjDOVYsWUSJ4sUICwvHxsbmk6lsBUEQ/ldJJBKmdK7HzO1nmLfrHDYWZgxtURVXeytc7a3oXLcMg5cdJDYpFV9Xe+b2apRtvaPvPd/8Pk2YtuUUtX5djpW5KePa1zLMiprdsyHTtpxizdHr+LjYMa934yzp+MJjk3C0schW74zuDZi06QQbjt/Ew9GGWT0aIjc2Qm5jxOyejZi/+xxL9l/C3cGaaV3r4eZgna2Oj+XxdGJChzosPXCJ8euPkcPdgfl9mmBpJqdCQA76NqnI2HWBJKUq8fd1ZWb3BsikUn6qVIj45DR6L9hNeoaaknm9GNuu5hfPBXD0+hPWBl5nx5j22FqaMbtnI2ZuP8PUrafI5+XMvN6NMTUx+mK7SuXzpn5Zf1pN2oRGq6Vq0dyGVHqCIAj/qyQSCeNq+zD3XCiLLoZhYypjYGUPXKxMcLEyoX1JF0YcDiI2VYWPvSnTG/hhavz75y1IJBJmNczB7LMhNFz9CCu5jJHVvXC30QdgptX3Y9aZEDbejMTbVs70Bn6GdHxfKje5ni/TT71j860oPGxMmFrPD7mRFGdLEybW8WHp5XAmn3iHh40JU+r7GVLeTavvy7xzocw+E0IeZ3NmNtSXA0hUqFGotDj8Zt0kL1s5Pcu50X/vK9IyNJTwtmJ0Tf0Aux9y2RKalMGg/a9JTtdQyM2CCXV8vnpd7oWmMOTgG473CMDBwphpDfxYfDGMlVfDcbUyYWIdX1yt9X2iMxror9Gcc6HkdjQz1G9mLGN+k5zMPhvCmmsRuFiZMKWuL+YmYqCD8NeQuLu7iwly/2KhoaEoHhz7p5shCP9aZgG18PDInu9dEIT/baGhoejS0/7pZgj/MRK5ubgnCMJ/VGhoKEmnl/3TzRCEv5111R7i3iYI/1GhoaFELfr5n26G8B/j3GeHuG8I30WkyBMEQRAEQRAEQRAEQRAEQRAEQRC+iwgwCYIgCIIgCIIgCIIgCIIgCIIgCN9FBJgEQRAEQRAEQRAEQRAEQRAEQRCE7yICTIIgCIIgCIIgCIIgCIIgCIIgCMJ3EQEmQfhGS7cfYfSiTf/IueOTUhgwYxXl2w6hdo+x/8feXUdHdbQBHP7tbrJRkpCEeCBYkDS4FAkUD+7Q4u4NXrS4uxctWiju7k6wAMFDDKIQ103Wvj+WbroNtPBVUug85+Sc7Nw79753OSfD3Jl5h0MX/HOdc/bGffpMXmZQtmjzAap8M4JqXUZRrcsovuo5Llc9/wfPKN9+6N8WuyAIgvDXWb5qNWMnTsrTGOLi46lWuw7+t27ry8LCw+ncvRcVqlanVfuOBD56lKveqTNn6da7r0HZzdu3adG2AxWr1aTdN515EPjwb49fEARB+P+tPXKdKZtP5sm97zyPoPPMbdQetoIOUzdz6UGw/tiLyDh6zfuZr4avpMO0zVx9GKo/du5uEO2mbKLWsBV0m7OdByFR+mNXH4bSYdpmvhq+kqEr9hObmPqPPpMgCILw8X70j2Hm6Zd5GsPFF0n47XthULbyShT1Vj2g4epAGq4OpNm63H2b269SqbX8vkHZ/sA42m16TMPVgfjte8HLRMXfGrsg/NXEAJMgfAImLt+GvU0+Lvw4myXf9WHO+j28inmjP37g3A3GL9uCVmtY71l4JHOGdef6tgVc37aACxtnGxxPy8hk6uodaH9bURAEQRDeY/K0GSQnpxiUjRg9lq9q++B/5SJdO3diyNARZGdn64/vPXCQ0eMmGLQ3arUavxGjGTNqBLevXaZNy5YMHz3mH3sOQRAE4dORmaVk1OpD9GtWjYtLhjC6Yx3Grz9GukLX1kzedIIW1b24sHgwfq19GLP2CIpsFVHxyUzZcpIp3RtxackQ2tUqy7j1RwGIeJPE2HVHGNCsOmcWDKBsURdG/nBI9I0EQRCE33X0cQLTTr3kt63Fi7hMJjcqxKkB3pwa4M2Rvl8YHE/PVjPvXIRBvfuRaWy6GcuilkU50f8LyrlaMvdsxN/+DILwVzLK6wAE4WOo1RpmrtvFOf/7yI2NqFa2JBP6dUBubExgUDhLth4gJCIGpUpN3aplmTzgG2QyKY0HTqFTk9psP3qB1IxMerdugJmpCWv3nEQqkTCmd1saVCvPwfP+nLl+D41Wy53HLyhZ2I1pgztT0LmAQRxKlZofdh7j6KVbaDQamtSqzJBvmmFsJOPO4xfMWb+H6LhE3Bzt8OvcnOrlSuV6lmpdRuUqc7a3Zd+S8QZlsfGJBDwJZuGomRgbG1GyiDtbZ4/A1jofAMu3H+H2oyA6N/2K+89CDeo+D4vE08P1vd/ngk37qVe1LFsPn//gfwNBEIT/OrVazZQZszh99hwmcjk1qldjysTxyOVyHgQ+ZN6ixQSHhKBUqmhQry4zpkxCJpNR17cJ3Tp3Ysu2n0hJTaN/n16Ym5uzavVapFIpE8Z+h2/DBuw7eIiTp8+g1Wi4dfsOpUqVZPb0qRQqWNAgDqVSyfJVqzl05ChqjZoWTZsy7NvBGBsbc+v2HabPnkt0TDTurm6MGOZHzerVcj1LharVc5W5uDhzZP/edz77wcNHkEqlODk56suCQ0J4GRFBr+7dkMlktG3Vkk1btnHd35/aPj4sXraCm7dv071LZwLu58zWS0lJISkpCZVKiVarRSqTYmJi8v/+swiCIPxnqDUa5uw4y/mAF5gYG1G1VCHGflMXubERj8JiWLrvEqHRCShVauqUL8bELg2QSaW0mLCBr+uWZ8e5u6RmZNHTtwpmJsZsOOaPRAKjO9ahXgVPDl9/xLm7QWi0Wu4GRVDC3YHJ3Rrh7mBjEIdKrWbN4escu/kEjUZL4yolGdSyBkYyGXeDIpi/8zwxCam42lszpFVNvixdKNez1Bq2IleZk20+dk3qblBmZmLM0Vl9MDeVo9ZoSEzLxMJMjpFMN2f21ZskVGoNGo0WiUSCibEMABc7a07M6Ye5qRylSk1yeibWFmYAXH8cTpkiLtStUByAHo2qsPnkLYIi4/B0M+z/CYIgCIbUGi0LL0RwKTgZuUxK5YKWjKzjhlwm5XFMBquuRhGWoECl0VKrqDVj6rojk0pov+kx7coWYPf9N6RlqelayREzYymbbsYikcCw2q7UKWbDsScJXHiRhFYL9yLTKV7AlPH1C+JmY9hfUKm1bPCP4dSzRNRaLQ1L5Kffl84YySTci0xj8cVIXqdm42xtwoDqzlQpmC/XszRcHZirzDGfMVs7l8xVvvZ6NAGRaXQoV4CHMekGx17EKShmb/re72z55ShqFbFm572cCeNlXS3Z0bUk5nIZmUo1adlqrExlf/j9C8K/iRhgEj4pZ/3vExIRw/HVU1Gp1PSbupxT1wJoVrsKYxZvZFDHJjSrXYXI2Hi6jFuAf+Az/eDO1YDH7F08nocvwhkwfSUt61Tl5OqpHDh3g0WbD9CgWnkALt99xOSB37Dkuz6s+PkoYxZvZMe87wzi2HzwLLcfBbF97iikUikj529g2+Fz9GzdgJlrd/Ftp2bUqVKGIxdvMnv9Hg6v+D7Xs1zftuCDnvlZWBSFXAqwds9JDp33x9LcFL/OzSnq7gzA1419+LZTMw6e9zcYYHqTmExyWjoLNu7j/vNQ3BztGd2zDWU8C+uf81XMG6YN7iIGmARBED7C6bPnCA4J4fzJY6hUKrr36c/xk6do2bwZw0ePwW/wQFo2b0ZERCTtO3fh2g1/fGroBnIuXbnK4f17CQx8SK/+A2nTsgXnT59g3/4DzFu4CN+GDQC4eOkyM6ZMYsXSxSxdvpLho8eyb+d2gzg2bNrCzdu32fPzT8ikUr4dPpJNW7fRt1dPps6cxXC/IdSrU4eDh48wfdZsTh45lOtZ7vpf++Dnjo19zao1a9m+eRPtO3fRl4eEhlGooDsyWU5HqLBHIUJCw6jt40Pnbzoy3G8I+w4eMhhgyp8/P+3btKb/YD9kMhkmJiZsWrfmg+MRBEH4rzof8ILQ6ASOzOqDSq1h4OI9nLn7nCZVSzN+/VH6N69Gk6qliYxLpsfcHdx8+pJqpT0AuPYolJ3fd+NRWAxDlu2jeTUvjszqw6FrD1my9xL1KngCcOVhKBO7NGDBgBb8cOgq49cfZev4zgZxbD11hztBEWwZ2wmZVMp3aw7z05m7dG9UmTk7zjK4ZU1qly3KMf/HzPv5HPum9cz1LJeWDPng5zY3lZOWmUX9UT+g0WqZ1LUhJsa6VxrdGlZi/s7zLNh1HpAwt18zTOVG+novIuPoPHMbMpmUxYNaAqDRaPTnAEgkIJFIiHiTJAaYBEEQ/sCl4GTCEhTs6VEalUbL0P3BnAtKwrekLVNOhtOrqiO+JW2JSs6i364gbr9KpWohKwD8w1PY0qkET2IzGHEwhMalbNnbsxRHHyew8koUdYrpJjRcD0tlTF03ZjX1YN2NGCafCGfD154GcWy/+5p7kWms61gcqUTCxGNh7Lz3hs4VHVh4IYJ+1ZzxKWLNiacJLL4QwY5uuSeAnxrg/cHP3aaMPf2qOXPsSYLBAFNcupIUhYrll6MIjE7H1doEv1oueDlZvH2WFCKSshhf391ggAnAXC7jamgK44+GYi6XsbxN0Q+ORxD+DUSKPOGTYmluSnhULEcv3SIzK5uf5oyiWe0qAKyZNJhmtauQmp5JfHIKVpYWxCXlpPBp17AG5mYmVCxdDI1Gy9eNa2NsbES1ciWJiU/Sn+dZyIXW9aphbGzEoI5NCHoZTURsnEEchy/eZGDHJtjZWJHfypI+bRty6MJNfYzHr9zhzuMX+NasyKHlE//UM6emZ/A8LAqpVMKxHyYzoV9HJi7fRnjUawAK5Ld+Z72klHQqlS5Oz9YNOLVmOq3rVcNv9lqSUtNJSctg/sZ9TBnUCSR/KjxBEIT/HEtLS0LDwjh09BgZmZns2bGNls2bAbBx3WpaNm9GamoqcfHxWFtZExeX04Z0bNcWC3NzKleqiEajoUunr5EbG1OjejWiY2L155XwLE67Nq2RGxvjN3ggQUFBvIowTJVw4NBhvh00EHs7O/Lnz8+Afn3Zf/CwPsYjx05w6/Ydmjb25cThg3/6ub+fOg2/wYOws7M1KM/MzMTM1HCmnpmpKQqFLne4Q4F3v6RTq9VYWFqwfvUqAvyvMWzIYIaNGk1mZuafjlUQBOFzZmlmQnhsIsf8n5CZpWTz2E40qVoagJVD29KkamnSMrNISMnAytyU+OScF2BtapbB3FROBU83NFotHeqUw9hIRtVShQz2Hyruak/LGl9gbCSjf/PqvIiKI+JNkkEcR248pn+zathZWWBjaUavxlU5cuOxPsYTt55yNyiChpVKsndqj7/k2c1MjLm89FuWDG7NnB3neBGpa2OlEglTe/hyeem3zOzdmOlbT/E6KU1fz8MpP1eXf8vYb+oxZu0RElMzqFqqELeeveL64zBUajVbT99Gka0iW6n+S2IVBEH4nFmYyHiZmMWpZ4kolBrWdSyOb0ldP2FxqyL4lrQlLUtNYqYKK1MjEjJU+rotvrDDXC6jnKslGi20K2OPsUxKlYL5eJ2q1J9X1M6UZl52GMuk9K7qREi8gqjkLIM4TjxNpFdVJ2zNjbExM6JbZUeOP0kAwFIu48yzRO5FplHfMz/bu+ZekfSx7C2M31menKminKslnSs6sL9XaZp52TLmcCjJmSpSFSqWXY5kXH13JJJ3v4SrXNCSMwO96VDOnrFHQlGqNX86VkH4p4gVTMInpXq5UnzbqTl7Tl9j9rrdlC1RmGlDOuPmaM+9p6EMnL4KtVpDqSLuZCtVBnsSWVuaAyB7m0bB0lz3MkwikRjk2XZ1tNf/biI3xsbSgvgkw81eY+MSGbVgAxLJL2O0Wn4ZqZk3oifLfjrMiHnr0QI9W9WnZ6v6uZ6lZrfc+0w42+dnYOAWSwAAIABJREFU96KxBmVGRjKkUgkDOjTGSCaj8hfFqfxFca7de0IhF4f3flfFC7mwdkrOjMA29auz/dhF7j0N4dS1AL72rYW7UwEiX8e/9xqCIAhCbjWrV2OE37fs3LOXaTNnU75sGWbPmIa7mxt3A+7Ru/8g1GoVXqVLk63MNsixbW2tmxTwy2ofS0tdigaJRGrQFrm7uel/NzExwcbGhrh4w7/XMbGx+I0YhVSqa3+0Wt3sa4DF8+eyaOlyhgwfCVotfXv1pE+vHrmepXINn1xlzk7OHNq7y6Bs9959mJiY0LSxb67zTU1NUWQZdvQyFQrMzcxznftrp86cJTQ0jLGjRgLQrUsntu/cxfUb/tSt89Xv1hUEQfgv+7J0IQa3rMG+K4HM+/kcZYq4MKlbQ9wK2HA/OIohy/ah1mgoWdARpUpt0A5ZWej6QDLp2z6RmRwAqVRi0Hdytc+ZxGZibIS1hSkJqRkGccQmpjJm7RH9yzKtVqv/fVbvpqw8eIXv1hxGq9XSvVFlujWsnOtZ6oxYlavMyTYfOyZ2feezy6RSZFKo7uVB5ZLu3HgSTpZSxYlbT/Vp9epV8OTAlYecuxvE13V1WSqM3ra7Lap7sf3sHQKCIqlboThTujVi0e6LpGQoaF+7LEWcbfXfiSAIgvB+VQrmo391Zw49jGfRhQi+cLZgfH13XKxNCIxKZ8SBENRaLSUKmKNUawzbIlPd62jZ236MhYnub7REIjE4z8U65++xiZEUK1OZwUAVwOu0bCYeC+PtpX71dg6m+BZizfVoJhwLQ6uFzhUd6Fwx93u0xmtyp8hzyCdnc6cSH/x9FLU3Y2nrnJVHzb3s2HM/jsDodM69SKJtGXtcrU2ITsl+Z33523eV3Ss7sjPgDSHxCko4/H5/ShD+LcQAk/BJiYiNo1zJIrSpX534pBTm/biPxVsO8l2vNsxYu5Of5oykWEEXADqMmvub2h+2VCcuMVn/uyIrm6TUNBxsDVcJ2dlYMWd4D7yL6/KIp2cqSEpJR6VWExb1mpl+XdFqtfgHPmfY3HXULF+a4oVcDK5xZctv43u3Qs4OqDUaFFnZWJrr8oWrNRr+aO/ZgKchBIVH0qFRzsvDbKUKubERZ/3vc+nOI1btPIZWq5sVUbPbGJaP60f5UmIpriAIwu95FRFBhfLlaN+2DXHx8cyaO495CxczYcx3TJ4+k93bt+FZvBgArdp3NKj7vhlrv/XmTc6qJ4VCQWJSEo4Ohp0hezs7Fs2bQxlv3eaxaenpJCUmoVKpCA0LY96sGWi1Wq7732SQ3zB8ataghGdxg2vcunr5g+I5cfoM9+4/0A9IpaWlM3CIHwP69aHuV7V59SoCjUaD9O0Ly9CwcNq1bvW714yJjUWpVBqUGRsZYWQk/nsqCILweyLeJFG2qAutanoTn5LOwl0XWLbvMiM7fMXs7WfYNKYTxVx1k+Y6zdxmUPcDmyHifrXqSZGtIilNgYONpcE5dlbmzOrTFC8PJwDSFdkkpWWiUmsIj01gWg9ftFq49ewlI384SHWvwvq4fnF+0aAPiic0Op5x64+yfUJX/cQKpUpNPjMTYhNTUakMZ3obyaQYyaT4Pwlny6nbrBzaVn9MqdJgaW5CWmYWHs627J6sG5hKy8xi04mbFBfp8QRBEP5QVHIW3s4WNPeyIyFDydJLUay6Go1fLRfmn49gXcfiFLHTvcPqueOZQd0PTaQTn54zmJSl0pCsUFHA0nAFka25MVMaFaK0k24wJiNbTVKmCpVGy6vELL5vUBAtcOdVGmOPhPJloXwUtTczuMbx/h+eIu99HkSlExyfSWvvnHYuW61BbiTl4otkroemsOFGDJq37/IarwlkbvPCRCZnczcijQkNdPvtarSg1oClidiHSfh0iBR5wifF/8Fzxi7ZTEJyKlaWFsjlRlhZmpOWoUCCbsWRWq1h35lrBIVHoVJ9fHqDwKBwzvnfR6lUsernY3gX98C5gGE6oCY+lVi96zhJqelkZmUzffXPzN6wG5lUyuSVP7HvzHUkEgn2NlZIJBLyWZi9525/rISHK0XdnFm7+yRKlZqbgc+58/gFtSp5/W49uZERi7ceJOBJMCq1mu1HL6JUqqhYuhj+2xdyZctcrmyZy66FuhVTV7bMFYNLgiAIH+D6jZuMHDOO+PgErK2skMtNsLG2Ji09DYlEgqmpCWq1mt179/HseRAqpeqPL/ob9wMDOX32HNlKJUtXrKKstzcuzs4G5zRv2pgVP6wmMSmJzMxMJk2dzvTZc5DJZIz/fgq79+7XtUV2dkglEqyscm9o+6E2rF7FnetXuHX1MreuXsbZ2YkfViyjX+9eFCtaFCcnR9au/5FspZJ9Bw+RlJxE1Sq5Z6r/WrWqVbgTcI/TZ8+h0WjYe+AgScnJVChf7v+OUxAE4b/g1rNXTPjxOAkpGVhbmCI3NsLKwpR0RTYgwVRuhFqj4cCVQF5EvkH1f6TZeRgWw/l7L1Cq1Kw+fA3vwk442VoZnONbpRRrj1wnKS0TRbaSWT+dYf7O88ikEqZtPcWBqw+RSMDOygKJRIKlmcl77vbH3B1sUGSr2HbmNmqNhvP3XvD05WtqehemTBEXElIz2HXhHhqNlmuPwrgXHEWNLwpTwt2Bpy9jOXXrGSq1hl0X7qHWaPR1+szfycvXiWRmKVm+/zIVPd1xzP//t5eCIAj/FbdfpTH1ZDiJGUqsTIyQyyTkM5GRnq1BItGtOFJrtBx+FE9wnAKV+g9mSb/D49gMLgUno1RrWH8jBi9HCxzzGa4ybVjCho03Y0jOVKFQaph3LoLFFyORSWD22VccfpSABLA1N0IqkfxtAzdymYQfrkbzICoNlUbLnvtvUKq1lHWx4OygMhzv783x/t5sersq6nh/b8q4WFLa0ZyLwcnci0xDqdaw7no0xQqY4mIlVtMKnw4xRVT4pLSq+yVBL6NoO3wW2UoVlbyKM3ngN9ha56Nzszp0HrsQqURCGU8PGlQrR2hkzEffw9PDlf1nbzBp5U94F/dgzvAeuc7p264hK7YfpcPIOWQosqnkVYxpgzsjkUiYO7wHczbsYeHm/Vjns2B83/Y42ef/v59ZIpGwYsIAZq3bRb0+E7CyMGPGkK64Odr/bj2vYgUZ36cDk1b+xJvEFEp4uLJsXH9M5O/OFysIgiB8mLatW/Is6DnN2rQlO1tJlUoVmTl1Mra2tnTv0pn233RBIpVSrkwZfBs2IDg05KPvUbKEJ3v2H2Dc95MpW8abRfPm5DpnYL++LF62glbtOpKRmUGVSpWYNW0qEomERfPnMGPWXOYsWIiNjTWTJozD2cnpr3j8d1q+eCETp0xj3cZNFHR3Y9XSJZiY/P6LxJIlSjBv1gyWrljJuO8nU6xoEdasXI6lpeXv1hMEQfiva1HdixeRcXScvgWlSk2F4m5837UB+fOZ06leBbrP2Y5EIsG7iDP1KngSFpPw0fco7laAQ1cfMnXzSbwLOzOzT9Nc5/RuXIVVh67ReeY2MrKUVPR0Y1LXhkgkEmb1bsr8nedZsuci1hZmjPm6Lk62///AjZFMxsKBLZiz/Sw/Hr9JIcf8LBncCjsr3ebpCwe2ZOnei6w6eBUXOyvm9G2Ks52V/tj8neeZveMsJd0dWDK4FaZyIwo65OfbNj4MXLKHDIWSqqUKMq1n4/87RkEQhP+SpqVtCY7PpOtPz1CqtZR3s2RMPXfymxnRoVwB+u4MQioBLycL6hSzJjxR8dH3KGZvypHH8cw685LSTuZM8S2U65xulR1Zdz2Gnjuek6lUU87VkvFv9zqa4luIxRcjWXElCmtTGSO+cs01QPVXKelozojarsw684r4dBXFCpgyt1lhTIx+f21HIVtTJjYoyLxzESRlqijrYsH0xh4fnPlCEP4NJC4uLh8/hCz8a0RGRpIZeDKvw/hsHDzvz6Hz/myY5pfXoQj/EDPvRri6uuZ1GIIgfKTIyEi0WRl/fOInaN/BQ+w/eIitP67P61D+cyQm5qJNEITPVGRkJCnnVud1GJ+Ew9cfceT6Y9aMaJ/XoQh/Aau6A0TbJgifqcjISF6v6JDXYfwtjj1J4PiTBJa3KZbXofznOAzZJdoN4aOIFHmCIAiCIAiCIAiCIAiCIAiCIAjCRxEDTIIgCIIgCIIgCIIgCIIgCIIgCMJHEXswCcKvtKxTlZZ1quZ1GIIgCMJ/WJuWLWjTskVehyEIgiD8RzWv5kXzal55HYYgCILwH9aklC1NStnmdRiCIHwAsYJJEARBEARBEARBEARBEARBEARB+ChiBZPwySrXzo+jqybj6mCXZzEEBoUzfukWDq/4Xl8WFB7F9DU/ExIRg4OtDcO7tcSnghdHL91ixtqdBvUzFdnMGtqNJj6VuHz3EYu3HCQ2PpFyJYsyaUBHHO3yG5zv/+AZA6avImD30lyxzN2wBytLcwZ2bPK7MSuysuk4eh69WjfQr9a6dPshI+avx9g450/Cuinf8kWxQtx+FMT8jft4FROHk70NQ7u0oHYl74/+rgRBED5HJcuU58zxo7i5uuRZDA8CHzJ63HhOHjmkLwsLD2fCpKk8efqUggXdmT5lEt5eutnoN2/fZva8BYS/fIWzkyMjhw2l7le1AbhzN4DZ8xcQGhaOk6MDI4Z+S706dQzut3HLVp49D2LOjGkArF63gbXrN+iPa7RaFAoF27dspEK5cgZ1FQoFE6dM4+Lly1iYWzB0yCBav12tFRMTy9SZs7gbcA9TU1M6tm/LoP79AHj2PIhpM2fz9PlzbKytGdivD+3atP6Lv0lBEIRPT+WBizk4oxcudtb/+L2Do+KYv/M8z169wcrchB6+VWhdU9dPuPM8gkW7LxDxJgnH/PkY0romtcoUNagfn5LO19O3MqdvUyp6ugOw68I9Fu+5iLGRTH/egWm9sLUy138OiY6n66yf2D2le67n/unMHYIi45jSvdE7Y641bIXB52ylikol3Fnh15YXkXF0nrkNE3lOn2hKt0bUrVCcy4EhjF59GLlxTlw/DGuHl4fTx3xlgiAInyWf5ffZ1b0Uzlbyf/zewXGZLLoQyYu4TKzNjOhWyYFmXrr3hKHxChZfjCDoTSb5TI3oUtGBFl/ojiVlqph37hV3XqVhaSKjz5dONH67Yio4LpP55yMIS1BQwNKYQTVcqOZhBcDKK1HsexCHTCoBQC6TcKTvFwDsD4zjpzuvSVGoKelgxqg6bhTMb/re2LVaLX77gynvakmvqrr2JEulYe7ZV1wPS8FcbhjX67RsFl2I5EFUOqZGUlp8YUePKo5/w7cqCB9HDDAJwv/p0p1HfL98K+Zmho3FxOVb6ejrQ5v61bl05xGjF/zIhY2zaVqrMk1rVdaft/3oRU5eu0uDauWJiI1j9MKNzPi2C7UrebPp4BmGzlnHjnmjkUh0jVZaRiZTV+9Aq9Ua3C8rW8nSnw6x4/gl+rf3/cO4l20/zKuYNwZlz8Ijad/IhzG92hqUZyqyGDZ3PTO+7cJXlb25Gfgcv9lrOLthJhZm728kBUEQhH/GhUuXGTPheywszA3KR4weS2Pfhmxav4ZDR48xZOgITh87jEqlZvDQ4cydMZ26db7ihv9NBnw7lCvnzyCRSBg8bASTxo/Ft2ED/G/eYsjwkRzcvRM3N1fUajUbNm1myfKVtGjWVH+vAX17M6Bvb/3n2fMXEBv7OtfgEsDiZSvIzMzk0plTvAgJoe/AIZQqWYKSJUowfvIUihYuzNJFC3j9+g29+g3A3c2dZk188Rsxki6dvmHbpg28CA6hQ6cuVKpYAY9Chf6+L1cQBEH4Xd+tOUKrml+wcmhbgqPiGbRkD0WcbfF0c2DU6kNM6d6I2mWLcuvpS4avOsjJef2xMM15+Th7+1lS0hUG13we8YZvW/vQqV6Fd95TpdYwbcspslVqg3K1RsPW07f54eA1Glct9d6YLy0Zov89Oj6FXvN/ZnDLmgAERb6hpndhFg5smateUMQb2tUuw6gOdXIdEwRBEPKGVqtl4rEw2pa1Z0XbooQlZNFvVxBlXS1xtzFhwrEwmnvZsrhVUULjFQw7EIyHrSllXCyYefoljvnkHOnrRWiCgiF7gynjYoGrtQkzT7+kdRl7mnvZcS00he+Ph3G07xeYGEl5EZfJ5EaFqFXUcILD/cg0Nt2MZXmbYrjZyNl0M5a5ZyNY2a7Ye+PffT+OB1HplHe11JetuR5NplLD/l5ehCUoGHUohOL2ZhQrYMacM68oZGvK9MaFiEtXMfxAMK7WchqUyP/eewjCP0GkyBPy3KgFP7J+7yn958fBL6nTazwqtZrAoHB6T1pKnV7jqNntOyat/Am1WmNQ/9bDIBoPnKL/HPk6nnLt/PSfr99/SodRc6nZbQz9p67INbjyizbDZlGty6hcP++y9/Q1lmw9SI9W9XMdexnzBpVajUajQSqRIJcb5zon8nU8P+w6xoxvu2BsJONqwBPKlihM/S/LYWwko3frBryMfsPz8Ch9nQWb9lOvatlc1xo4fRWp6ZnvPPZbtx8FEfg8jLKehQ3Kn4dFUqJQ7tn3ZqYmnFozja8qe6NWa0hMScPC3BQjmSzXuYIgCJ+yoSNHs3pdziqch48fU712XVQqFQ8CH9KlZ2+q1a5Dpeo+jPt+Mmq14Yst/1u3qeubs4I0IjKKkmXK6z9fvX6DVu07UrmGDz379uflq1fvjKNZ67ZUqFo918+77NqzjwWLl9C3Zw+D8uCQEF5GRNCrezeMjY1p26olVlZWXPf3x9zcjAunT1K3zleo1WoSEhOxtLDA2MiI2NhYatesQRPfRkilUqp9WZVCBQvy6MkTAMZOnMSdgHu0b/v+lUMB9+9z9NgJpk6a+M7jR44dZ0C/PpiZmeHt5UXTxo04fPQ4Go0GE7mc/n17Izc2xs3Vhbp1anPvwX0kEgn7d+2kyzdfA5CUlISRsRFmZmbvjUMQBOFTM3bdETYev6n//CQ8loajV6NSa3gUFkO/RbtoMHo1Xw1fydQtJ1FrDPtEd56/osWEnHYsKj6ZygMX6z/7Pwmn08xt1BmxikFL9hDxJumdcXSYtplaw1bk+vmtpLRM3B1s6FyvIjKpFE+3AlQo7kZgaAxmJsYcndWH2mWLotZoSEzLxMJMjpEs5/XDMf/HSCUSHPPnM7huUMQbirvav/d72nTyJmWL5u63TNl8kvsvomhV84v31v2tWdvP0L52WUoVcsy5t1uBd54bFPEGz/ccEwRB+Fx8fzyMLbdi9Z+fvc6g+fpHqDRaHsdkMGTvC5qte4jvmkBmnXmJWmM4ATogIo32mx7rP0enZOOz/L7+862XqfTc8YzGawIZtj+YyOSsd8bR9aenNFwdmOvntyQSCT9+40nbMrp2I1mhwkgKZkZSkjNVuFrL6Vi+ADKphGIFzCjnasnjmHRep2VzPyqdb31cMJZJ8SxgzpoOxclvpluHEZGcjUqjRaPVIpWA/Fft14s4BcXsc0+4LutqyY6uJSmY34QslYa0bDVWpu9/d/YyMYtDD+PxKWI4UHXmWRLdKztiaiylpKM59TxtOPU8EY1Wi9xIStdKDhjLpDhbyalZ2JqHMenvvYcg/FPECiYhzzXxqcjq3Sfo07YhACevBdCgWjmMZDLGLN7IoI5NaFa7CpGx8XQZtwD/wGdUL/f+WWm/Fhkbz+iFP7JwVG8qlC7Gz8cvMnzeenYtGINUaji+um/J+A+O+avKX9C63pfceRzMrpNXDI71bFmfORv2MHfDXiQSmD+yF6YmhsuEl28/QrsGNXB30nVSNBoNZr8aiJJIJEilEiJi4ijh4crlu494FfOGaYO7sPXweYNrzR3RgwL5rfl+xbbfjTkjM4tZ63Yxf2QvZq3bbXDseXgUaRkKVv58FHMzU3q2qk+rul8CYG5mQlpGJrV7jEOj1TJ1cCdM3jFoJgiC8Clr1qQxK1ev0a/EOX7iFL4NG2BkZMTw0WPwGzyQls2bERERSfvOXbh2wx+fGu8e+PmtiIhIho4czfJFC6hUsQLbdvzM4KEjOLhnZ6626Mj+vR8cc906tWnXphW37tyFXbv05SGhYRQq6I7sV5MBCnsUIiQ0jNo+PliYm5OWlkZVn6/QaDTMmjYFExMTihQuzNxZM3LijowiOCSE4sV0s+5GjxiGQ4ECLF+1msionAkQvzZ3wSKGDOyPtZVVrmPJKSnEJyRQpHDOJIfCHh5cvXYdqVTKD8tz0r8qlUquXrtBl066QSVzc91gUvXadUlITOTbQQNwdHD44O9KEATh365R5ZKsO3qDno2rAHD6zjPqVfDESCZl/Pqj9G9ejSZVSxMZl0yPuTu4+fQl1Up7fNC1I+OSGbP2CPP6N6dCcVd2nr/HqNWH2D6hK9K3KX5+sWtS9w+6po2lGUsGt9J/TsvM4n5wFG18ygBgbionLTOL+qN+QKPVMqlrQ0zepuN+nZTG+qP+rB/VkR5zd+ivodZoCI6KZ/vZu0z88Th2VuYMalmDmt5FAN3qptO3n7N5bCe2n71rEM/QNj7YW1uy9sh1ouJT/jD+G4/DCYtJYNGvVisFRcShVKtpPmE9EiS09vGmp2+Vt/eOIy0zmx8OXcPcRE73RpVpUd3rg74rQRCET0UDz/xsvBlDt8q6gfezQUnUKWaNkVTClJPh9KrqiG9JW6KSdSuFbr9KpWqh3P/vf5eo5Cy+Px7GjCYelHOxZM+DOMYfDWPjN55IJYZt0dbOJT84ZrO3qUubr39EUqaKXlUdsbfUvbOa36KI/ry0LDUPotJp8YUdL94ocLcxYdPNWI49ScBSLqN/dWcK2+oGjjpVcGDJxUiWXowECUxv7IGJkZS4dCUpChXLL0cRGJ2Oq7UJfrVc8HKyAMBcLuNqaArjj4ZiLpexvE1R3kWt0TL7zEuG1Xbl5NNEfXmqQkVipoqC+U30ZQVtTLn1KhWpRMKcZjn9KJVay61XqfrBNUHIS2IFk5DnalYoTfSbBMKjXgNw+noAjX0qAbBm0mCa1a5Canom8ckpWFlaEJf0xx2GX5y4egefCl5ULVMCYyMZXZvXJTktg0cvXv6pmO1srHK9FPyFRCphxrddufHTAmYP686UVduJjc+ZIRj9JoFLtx/StXlOeoVqZUvi//A51+49QalSs+ngWRRZ2WQplaSkZTB/4z6mDOoEktz3K5D/w/KtL956gGa1q1DU3dmgXKPR4GhrQxOfShxdNZlpgzuzaMsBbj0M0p9jZmLCjZ8WsGJ8f2at3cWLl+9+sSgIgvCpqu1Tk6ioaELDwgE4ceo0zZo0BmDjutW0bN6M1NRU4uLjsbayJi4u7oOvffTECb6q5UO1L6tibGxMz25dSU5JJvDhoz8Vs72d3TvboszMTMxMDWfVmZmaolDkpCEyMzMj4OZ11q5cztSZs3ke9MLg/ISEBAYO8aNt61YUKewBgEOB35+5fffePSIjo2jTKndqIYDMjEx9LO+LC0CtVjPu+8nI5ca0btHc4Nj5U8fZvWMbW7Zt5/LVa78bjyAIwqekhpcHMfEphMfqXjSdvRuEb5USAKwc2pYmVUuTlplFQkoGVuamxCd/+IzlU7efUdO7CFVKFsRIJqNz/YqkpCt4HB7zl8SuyFYyevVhSns4UrVUQX25mYkxl5d+y5LBrZmz4xwvInVt58xtpxnQvLrBvkoAyWkKvDycaFe7LEdm9WFgyxpM2HCMsJgElCo107acYnznepjKc8+Ttbe2zFX2e7aduU3nehUN9nqytjClpncRdk3qzpIhrThwJZDD1x+h0WhxyG+Jb5WSHJzei8ndG7J070XuPH/3amRBEIRP1Zce+YhJVfIyUbey6MKLZOp76tKvLW5VBN+StqRlqUnMVGFlakRChuqDr302KInqHlZUcs+HkUzC1+ULkKJQ8SQ24y+JfU+PUqzrUJzd9+LwDzd8b6hQaphwLIxSjuZUdrckNUtNcFwmUgns7lGKUXXcmHH6pf65pRKY2KAgpwd6M7lRIeacfcWbNCXJmSrKuVrSuaID+3uVppmXLWMOh5KcmfM9VC5oyZmB3nQoZ8/YI6Eof5OFCeDngDcUtTejkrvhKt5Mle5cU+OcPp6psQSF0vAaao2WWWdeYiyT4FtKpMcT8p5YwSTkObmxMfW/LMupawF8WbYkWi2UK6Eblb/3NJSB01ehVmsoVcSdbKWK32xB9Lti4pM463+fmt3G6MtUKhXRcYl4e3oYnNt+xByi4xL5rStb5n7w/QKDwjl++Y5+NVSDauXZd+Y6Z2/cp1NT3QbqJ67coXq5Utha5zQkHq6OTB/Shfkb95GSnkHHRj4UcXPC0tyMORv28LVvLdydChD5Ov7DH/5Xrt9/ypOQCMb2bp/rmFQqZe2UnFzkZUsUpolPJS7eDqTyF8UBkMmkyGRSapQvTRVvT67de0qxgnm3ob0gCMJfTS6X07B+PU6cOkWNatXQoqV8OV3q0bsB9+jdfxBqtQqv0qXJVmbzEU0RMTGxnDpzlso1fPRlSqWK6JgYypbxNji3RdsORMdE57rGrauXP/h+pqamKLIM001kKhSYm+W8yJPJZMhkMnxq1uDLKlW4cu0ansV1K5XCX76k78AhVK5UgYljv/vg+x46fJTmTZsgl797c1/Tt3v3KRRZ+hVJmQoF5uY5cWVkZDJ89HfExcez/oeVua5lYmKCt5cXzZo25sKlSx+8ikwQBOHfTm5sRN3yxTlz5zlfli6EVgtliuj+v30/OIohy/ah1mgoWdARpUr9Ue1QbGIq5wOCqDMiVF+mVKmJSUjli8KGk8++mbGVmITUXNc4v2jQO6+dkJLB8FUHsLE0Y3afZvr9YwFkUikyKVT38qBySXduPAnnYWg0cmMjGlYuketatlbmrBmR01/x8S5CBU83bjwOJzE1g4qebpQt6voRT/5ucclpBARFMqt3U4PyGb1zUt0Wcbaj/Vd0jJthAAAgAElEQVTluPQghObVvPhhWDv9sTJFXPCtUopLD0Ko6On+p+MRBEH4t5DLpNQuas35F0lUds+HVqvF21n3f/XAqHRGHAhBrdVSooA5SrXmo9qi12lKLgYn03hNTqo7pUbL61QlXk6G53bf/ozXqdm5rnG8v3eusl+YGOlSyjUoYcO1sBT9yqrEDCVjDodibWbEtMaFkEgkGMskSCUSelZ1wkgqobybJRXcLLn5MoW0LAtOP0/Ur6KqU8yGw4/iuRicRLuyBVjaOmdVUnMvO/bcjyMwOp2ab1Pd/ZJOr3tlR3YGvCEkXkEJh5z+Tmi8gqOPE1jfsXiuZzA10tXNUmn0K7MUSi1mvxpwylSqmXQ8nMRMFQtaFDFI3ycIeUUMMAn/Co1rVmLRlgOkZSrwrVEBiURCbHwiM9bu5Kc5I/WDGR1G5R7skUolBnthJKfmzOazt8lHy7pfMqFvB31ZeNRrnOxzj/DvXjT2Tz/H6/gklL/ZcNZIJsPIKOcP/pWAx7RrWNPgnLSMTAq7OrJ/6QT95w37T1PCw4XRC3/k0p1HrNp5DK1WN2uhZrcxLB/Xj/Kl3r3c9rdOX79HSEQMtXuOAyBTkcWjF+E8fBFOv3aN2H70In6dm+s7hNlKFeamFoRExPDdoo0GKQWzlSryWYh9LwRB+Pw0a9KYeQsXk5aWTlPfRkgkEmJiYpk8fSa7t2/TD8C0at8xV12pRIL6V3//k5JzVq7a29vRtlVLJk/MScUaGhaOi/NvelLAob27cpV9rCKFPXj1KkK3F+Dbv92hYeG0a92K4JAQho0aY5CeL1uZjVU+3aSHR4+f0GfgIDp//TVDBvb/qPteunKFhfPmvPe4jbU1tvnzExYeTulSJd/GFUZhDw9Al0KvV78BFLAvwNYfN+gHoVJTU2nd4Rv2/PwTNta6jlt2thJ7O9uPik8QBOHfrlHlEizdd5l0RRYNKnnq+kSJqczefoZNYzpR7O3eRJ1m5k6NLZFIDPZlSk7LWR1qZ2VB8+pejP2mnr4sPDYRJ1vDmdMAOyZ2/eB4o+NTGLB4N5VLFmTsN/X0eyyFRsczbv1RgxR8SpWafGYmnLnznMDQaOqMWAVAuiKL4asO0qtxFWqVKcrFe8H6NIG/1JMbyzgbEERccjqHruWs/u00Yxtjv6mHb5UPT6UEcO1ROBWKu2FlkbOiVpGtYs3ha/RuUhVLM11qIqVSjYmRjLjkNHacC2BIq5o5/SWVCnMT0ScSBOHz08DThpVXo0nPVlOvuA0SiYTXadnMPx/Buo7FKWKn+9vXc8ezXHUlEvj1gp0URc7KHltzI5qUtmXkV276speJWTjmy70Fw+ZOuSchvEtalppePz9nfcfiWJnqXnEr1VpszXW/x6Rk47c/mIpuloys44bR2zbJ3cYEtVZLlkqDkVw3kPPLflJv0rJRqQ2HzoykEmRSCQ+i0gmOz6S1d05aumy1BrmRlONPErgbkcaEBrqVvBqt7ruwNDHch+lySDJx6UrabtTtVaVQ6fZ5evo6g3nNi2BjZsSrpCw8C+gGpV4mKfQp81IVKoYfDMHO3JjlbYrqB6EEIa+JYU7hX6GSVzESklM5dvk2jWtWBCAtQ4EEMJEbo1Zr2HfmGkHhUah+M4Dj5mhHfFIqAU+CycpWsv3oRf2xhtUrcOZ6AA+eh6LVajl74z4dRs0lKTXtb3mOsiUKk5Ccws/HL6HRaLga8JiApyHUrKDLz63RaHgc8ooyxT0M6sUnp9Jj4hLCo1+TqchiydZDVPIqjqNdfvy3L+TKlrlc2TKXXQt1g2BXtsz94MElgEkDvubatvn665QrWYRxfTswoW8HrCzMOXjen5+OXkCj0XD3cTCnrt2liU9F3J0KoMjKZvOhc6jVGs753+dpaAS1Kop844IgfH6qVK5EfEICh48d06fHS0tPQyKRYGpqglqtZvfefTx7HoRKaZgOwt3Njbj4eO7cDSArK4ut27brjzVu1JATp09z7/4DtFotp86cpVX7jiQmvnuD9T+rWNGiODk5snb9j2Qrlew7eIik5CSqVqlMQXd3FAoFP27aglqt5vTZczx+8pSvatciMSmJAUP86N+n90cPLsXFx/PmTRxepUv/7nlNGjdi+aofSEtP5+Hjxxw5doKmjX0BGD56DC7Ozqxcukg/uASQL18+nBwdWL7qB5RKJXcD7nHq9BkaN2r08V+OIAjCv1hFT3cSUzM4cfMpvpV1gybpimxAgqncCLVGw4ErgbyIfIPqNyl3XO2tiU9J596LSLKUKn4+H6A/1qCiJ2fvBhEYEo1Wq+VcQBCdZ24lKS3z/45VpVYzbOUBfMoUYWKXBvrBJQB3BxsU2Sq2nbmNWqPh/L0XPH35mprehVnu14YLiwdzftEgzi8ahFN+KxYPakmPRlWwMJXz4wl/zt0NQqPRxfkoLJavyhZjz5QeBvUAtk/s8tGDSwCPw2L4orDhJA9TuRE3noSz7ugNVGo1LyLj2H3xHo2rliKfuSlHrj9mx7kANBotAUERnL79nEaVP/7egiAI/3bl3SxJylBx+lki9UvoJmenZ2uQSHSrhNQaLYcfxRMcp8g1EONiLSchQ8mDqDSyVBp238tJK163mA3ng5J4FJOOVqvl4oskeu54RrLiw9Ps/ZaliQwHS2M2+MegUmt5EJXOhRfJ1C1ug0qt5bvDodQobMWYeu76wSWAYvameNiasulmLCq1ljuvUrkflU51Dyu+cLYgIUPF3vtxaLRa/MNTCIxKp1ohK+QyCT9cjeZBVBoqjZY999+gVGsp62JBaUdzLgYncy8yDaVaw7rr0RQrYIqLlWFGhm6VHTk1wJvj/XU/9T1t6FzRgXnNdftF1Stuw4/+sWRkq3n2OoMzz5P0aQonnwjH0VLOrKYeYnBJ+FcRK5iEfwWpVEqjGhW4du8pnh66tAdF3Z3p3KwOnccuRCqRUMbTgwbVyhEaaZgr3NEuP4O+bsJ3izYC0K+dL0cu3QKgsKsjUwd3YcaanUS+jse5gC0LRvXC0e7vyVFqn9+KpWP7sWjzAVbsOILL2/u5FNDNsk5KTSdTkY19fsNNEAs5OzCsS0v6TVlBemYWX5YpwSy/D589+C7RbxJoM3wW+xaPx7nA+2d5m8iNWTq2H/N+3MPKn49ib2PN5IHf6FeNLRnbj5lrdrJh3ykKuTiwfFx/7Gw+bBNHQRCET4lUKqWxb0OuXr1OCU9PQDdY071LZ9p/0wWJVEq5MmXwbdiA4NAQg7pOTo74DR7IsNG6lHKD+/fj4JGjABQpXJjZ06cxefoMIiKjcHF2Ztmi+Tg5Of5tz7J88UImTpnGuo2bKOjuxqqlSzAx0c18W7VsCVOmz2T1+g0U9ijEmhXLsLezY9uOn3kTF8eyFatYtmKV/lpTJ02kedMm77sVAFFR0VhbWyM3zj0DsULV6qxdtYJKFSswws+P6bPnUL9xM8xMTRk3eiSlSpbgedALrl2/gYmJCZWr56QSbN6sCVO/n8iCObOZPH0G1b+qi5ODI3NnzdCvKBMEQfhcSKUS6lf05MbjcIq76fa9K+JsR6d6Feg+ZzsSiQTvIs7Uq+BJWEyCQV3H/Pno37w649br2p4+TapyzP8JAB5Otkzu1pDZ288QFZ+Ck20+5vZrjmP+3CuYPtT1x+GERMcTFZ9ssKqoZ6Mq9GxchYUDWzBn+1l+PH6TQo75WTK4FXZWFr97Tcf8+ZjTtxnL919m8uYTuBewYcGAFrn2avpYtYatYOngVpQvrps1H52QQnG33Juiz+3XjLk7zlF/1GoszOT08K1CjS90qdsXDWrJgp3nWX34GvZWFnzftYF+RZkgCMLnRCqRULe4DTdfplLMXjfpq7CtKR3KFaDvziCkEvBysqBOMWvCEw33UnWwlNP7SycmndDta9ujsiMnn+m2oihka8r4+gWZfy6C6JRsnKzkzGjigYPlu9Nrf6hJjXTXbL7+IQUs5UxsUJAidmZcDU0hNEFBdEo2Rx/ntJldKjrQrbIjC1oUYeGFCFpseEQ+ExkT6rvjYq3rL81pXpiVV6JYdyMap3xypjf2wMlKjpOVnBG1XZl15hXx6SqKFTBlbrPCmBhJKWRrysQGBZl3LoKkTBVlXSyY3thDv/K14epA5jcvTFnX398zsH91JxZfjKTD5ieYGEn5tqYLxQuYERKfya1XachlEhqvfag/v2GJ/Iyq4/Y7VxSEv5/ExcXlY1JmCv8ykZGRZAaezOswBOGTZebdCFfXP5/LXRCEf1ZkZCTarL9mQ1hB+IXExFy0CYLwmYqMjCTl3Oq8DkMQ/nFWdQeItk0QPlORkZG8XtHhj08UhI/gMGSXaDeEjyJS5AmCIAiCIAiCIAiCIAiCIAiCIAgfRQwwCYIgCIIgCIIgCIIgCIIgCIIgCB9FDDAJgiAIgiAIgiAIgiAIgiAIgiAIH0UMMAmCIAiCIAiCIAiCIAiCIAiCIAgfRQwwCYIgCIIgCIIgCIIgCIIgCIIgCB9FDDAJgiAIgiAIgiAIgiAIgiAIgiAIH8UorwMQ/pzXsTE4eDfK6zAE4ZP1OjYmr0MQBOH/8Pr1axwcHPI6DOEz8/r167wOQRCEv8nrmGgc6g7I6zAE4R/3OiY6r0MQBOFvEhsdieOQXXkdhvCZiY2OzOsQhE+MxMXFRZvXQQjCP61mzZosW7aMJk2aEBPz6Q4weHp6smfPHjp27MiTJ0/yOhxBEAThA0mlUrZv305AQABz587N63D+lMWLFyOTyfDz88vrUARBEISPIPpEgiAIQl4SfSJB+DzI8uXLNyWvgxCEf5KTkxPbtm3Dz8+Px48f53U4f0p8fDwxMTHMnj2b3bt3k52dndchCYIgCB9g9OjRuLi4MGLECLTaT3uuz8WLF/Hz80MikXD//v28DkcQBEH4AKJPJAiCIOQ10ScShM+DWMEk/KcYGRmxe/duzp8/z7Jly/I6nL/MrFmzsLe3p1+/fnkdiiAIgvAH6tWrx5w5c/D19SU+Pj6vw/lLFC5cmAMHDtCtWzfRoRIEQfiXE30iQRAEIa+JPpEgfD7ECibhP+X777/H3Nyc8ePH53Uof6nLly/Tp08f8uXLx507d/I6HEEQBOE93Nzc2Lx5M/379yc4ODivw/nLJCUlER4ezoIFC9i7dy8KhSKvQxIEQRDeQ/SJBEEQhLwk+kSC8HmR5nUAgvBPadq0Kb6+vgwdOvSTX3r7W9nZ2fTv358BAwZQpUqVvA5HEARBeAcTExPWrl3LypUruX37dl6H85c7fvw4R44cYenSpUgkkrwORxAEQXgH0ScSBEEQ8pLoEwnC50esYBL+E4oUKcL69evp1asX4eHheR3O3yI1NZVnz56xdOlS9u/fT0ZGRl6HJAiCIPzKzJkzyc7OZurUqXkdyt/m6tWrdO7cGWdnZ27cuJHX4QiCIAi/IvpEgiAIQl4TfSJB+PyIFUzCZ8/MzIy1a9cyb948Hjx4kNfh/K0uXLjAjh07WLVqFTKZLK/DEQRBEN5q27Yt1atXZ+TIkXkdyt9KrVYzcOBAunTpgo+PT16HIwiCILwl+kSCIAhCXhN9IkH4PElcXFw+r3XxgvAb/2PvPsOiOPs2jJ+7SAdBIaDYa+yxENtjTWIvscfYe1dE7L13FFRUsFcsYC+xBXtX7LGhIoiAKEXpsLwfSDC8aKKxzC78f8fBl1l25pql7Fxzzz3r6uoKgIODg8JJvg61Ws2GDRu4efMms2fPVjqOEEJkeSVKlGDbtm20a9eOu3fvKh3nq6hWrRpubm40bdqUoKAgpeMIIUSWJ51ICCGEkqQTSScSmZfcIk9kap06daJ+/fr06NGDpKQkpeN8FSkpKfj4+DBjxgz8/f159OiR0pGEECLLMjMzY8uWLcyZM4dTp04pHeerCQwMRE9Pj6FDh+Ll5YVGo1E6khBCZFnSiaQTCSGEkqQTSScSmZvMYBKZVrly5di4cSMtWrTIkoWiYsWKrF69mubNm/P06VOl4wghRJbk4eHBq1evGD16tNJRFLF69WoCAgKYNGmS0lGEECJLkk4knUgIIZQmnUg6kcjc5DOYRKZkaWmJu7s7Y8aMyZJFCuDq1au4urri4eGBoaGh0nGEECLL6d27N3nz5s3SRWLo0KH89NNPNG/eXOkoQgiR5Ugnkk4khBBKk04knUhkfjKDSWQ6KpWKdevW4efnx5QpU5SOozg3Nzeio6MZOXKk0lGEECLL+P7771mxYgVNmzYlMDBQ6TiKKl26NJ6enrRq1YqHDx8qHUcIIbIE6UTpSScSQoivTzrRW9KJRGYmM5hEpjNkyBDMzc2ZMWOG0lG0wogRI6hcuTLt2rVTOooQQmQJ1tbWLFu2jGHDhmX5IgVw+/ZtZs6cyYoVKzAxMVE6jhBCZAnSidKTTiSEEF+XdKL0pBOJzExmMIlMpWbNmri4uNC4cWNCQkKUjqM1ihUrhre3N7/++iu3b99WOo4QQmRaenp6eHp6cunSJebNm6d0HK3i7OyMoaEhgwYNUjqKEEJkatKJ3k06kRBCfB3Sid5POpHIjPTMzc0nKx1CiM8hd+7cbNiwgcGDB3P37l2l42iVV69eERQUxKxZs/Dy8iI+Pl7pSEIIkSmNGjUKGxsbhg8fTkqKXMPzdydPnmTQoEGo1WquX7+udBwhhMiUpBO9n3QiIYT4OqQTvZ90IpEZyS3yRKagr6/P8uXLWb16NWfPnlU6jlbavXs3Pj4+LFiwQOkoQgiRKdWrV49WrVoxcOBANBqN0nG0TlxcHL1792bYsGFUqFBB6ThCCJHpSCf6d9KJhBDiy5JO9M+kE4nMSGYwiUxh0qRJGBoaMm7cOKWjaLXTp0/Ts2dPLCwsuHz5stJxhBAi08ifPz9r1qyhT58+PHr0SOk4WisyMpJHjx6xYMECvL29iYuLUzqSEEJkGtKJPox0IiGE+DKkE30Y6UQis5EZTELnNWvWjHr16uHg4CBTb/9FYmIiffv2pW/fvlSpUkXpOEIIkSkYGhri7u7O4sWLuXLlitJxtN7hw4fZvXs3ixcvRq2WQ1EhhPgcpBN9OOlEQgjx+Ukn+jjSiURmIjOYhE4rUqQIHh4edOvWjYCAAKXj6ITXr1/zxx9/sGjRInbt2kV0dLTSkYQQQqfNnDmT2NhYpk2bpnQUnXH27Fnat29Pnjx5OH/+vNJxhBBCp0kn+njSiYQQ4vOSTvTxpBOJzEIGmITOMjY2xtPTk8WLF3Ps2DGl4+gUf39/TE1N6d+/P97e3nKVoxBC/Edt27alVatWdO3alcTERKXj6IyUlBSOHz/OnDlzuHfvHv7+/kpHEkIInSSd6L+TTiSEEJ+HdKL/RjqRyCxUdnZ2chQldNKiRYtITk7G0dFR6Sg6SaVSsWHDBu7cucPMmTOVjiOEEDqnZMmSbN26lTZt2nD//n2l4+ikKlWqsHz5cpo0aUJQUJDScYQQQudIJ/o00omEEOLTSCf6dNKJhK6TGUxCJ3Xp0oUff/yRnj17kpSUpHQcneXj48P06dN5+vQpfn5+SscRQgidYW5uztatW5k5cyZnzpxROo7OevbsGSqVimHDhuHl5YVGo1E6khBC6AzpRJ+HdCIhhPhvpBN9HtKJhK6TGUxC53z33XesX7+eFi1a8PjxY6Xj6Lzy5cuzbt06mjdvLtNxhRDiA3l4eBAWFsbYsWOVjpIprFy5kufPnzNhwgSlowghhE6QTvR5SScSQoiPJ53o85JOJHSVWukAQnyMHDly4O7uzujRo6VIfSbXrl1jwYIFrFixAiMjI6XjCCGE1uvbty92dnZMnjxZ6SiZhqOjI3Xr1uXnn39WOooQQmg96USfn3QiIYT4ONKJPj/pREJXyQwmoTNUKhXr16/n3r17TJ8+Xek4mc7ixYtJSEjAyclJ6ShCCKG1/ro/dtOmTXn27JnScTKVUqVKsWXLFlq3bs2DBw+UjiOEEFpJOtGXJZ1ICCH+nXSiL0c6kdBFMoNJ6AwHBwdMTEyYNWuW0lEypZEjR1KhQgXat2+vdBQhhNBK33zzDW5ubjg6OkqR+gLu3LnD9OnTWbFiBaampkrHEUIIrSSd6MuSTiSEEP9MOtGXJZ1I6CKZwSR0Qq1atViwYAGNGzcmNDRU6TiZVpEiRdi5cye//vort2/fVjqOEEJoDT09PbZs2cL58+dxdnZWOk6mNnfuXMzMzBgwYIDSUYQQQqtIJ/o6pBMJIcS7SSf6eqQTCV2iZ25uPlnpEEL8Ezs7OzZs2MCgQYO4d++e0nEytfDwcAIDA5kzZw5eXl7Ex8crHUkIIbTC6NGjsbKyYuTIkaSkyLU5X9LJkycZMGAA+vr6XLt2Tek4QgihFaQTfT3SiYQQ4t2kE3090omELpFb5Amtpq+vj7u7OytWrODcuXNKx8kS9u7dy9GjR3FxcUGlUikdRwghFFevXj1atmzJoEGD0Gg0SsfJ9OLj4+nTpw8ODg5UrFhR6ThCCKE46URfn3QiIYRITzrR1yWdSOgSmcEktNrkyZPJli0b48ePVzpKlnLmzBm6detGjhw5uHTpktJxhBBCMQUKFGDNmjX07t2bx48fKx0ny4iMjMTPz4+FCxfi7e1NbGys0pGEEEIx0omUIZ1ICCFSSSdShnQioStkgElorebNm9O5c2c6d+4styX4yjQaDSdOnMDZ2ZkbN24QGBiodCQhhPjqjIyM2Lx5MytXruTgwYNKx8lyHj16hJWVFd27d2fnzp1yGw4hRJYknUg50omEEEI6kdKkEwldoLKzs5PfTKF1ihYtyo4dO+SDVRVWs2ZNFi5cKB8kLITIkubNm4eJiQkDBw5UOkqWpaenh6enJxcuXJAPEhZCZDnSibSDdCIhRFYmnUh50omEtpMZTELrmJiYsGXLFlxcXPDx8VE6Tpb29OlTTExMGDBgADt27JD77Aohsox27drRokULunXrRmJiotJxsqyUlBR8fHyYM2cO9+/f58mTJ0pHEkKIr0I6kfaQTiSEyKqkE2kH6URC28kMJqF1lixZQnx8PE5OTkpHEYBKpWLdunXcv3+f6dOnKx1HCCG+uNKlS+Pp6Unr1q158OCB0nEEULlyZdzd3WnatCnPnj1TOo4QQnxx0om0i3QiIURWI51I+0gnEtpKZjAJrdK1a1fq1q1L7969SUpKUjqO+NPx48eZOnUqgYGBPHz4UOk4QgjxxWTPnp0tW7Ywffp0zp49q3Qc8ae/CpSTkxNeXl4kJycrnEgIIb4c6UTaSTqRECKrkE6knaQTCW0lM5iE1qhQoQJr167l559/lumeWui7775j/fr1tGjRgsePHysdRwghvohVq1bx/Plzxo8fr3QU8Q4eHh68ePGCcePGKR1FCCG+COlE2k06kRAiK5BOpN2kEwlto1Y6gBAAOXLkYPny5YwYMUKKlJa6fv06zs7OeHh4YGRkpHQcIYT47Pr374+NjQ1Tp05VOop4DycnJ2rVqkXLli2VjiKEEJ+ddCLtJ51ICJHZSSfSftKJhLaRGUxCcWq1mg0bNnD79m1mzpypdBzxLxYtWkRycjKOjo5KRxFCiM+matWqLFu2jCZNmhAUFKR0HPEPSpYsydatW2nTpg33799XOo4QQnwW0ol0i3QiIURmJJ1Id0gnEtpEPoNJKM7R0ZGCBQvi6OhISoqMd2q748eP4+joSFJSEjdv3lQ6jhBCfDIbGxs2bdqEo6Mjt27dUjqO+BdhYWGEhYUxffp0tm/fTmJiotKRhBDik0kn0i3SiYQQmY10It0inUhoE5nBJBRVp04d5s+fT6NGjXjx4oXSccQHKlKkCDt37qRDhw5y4CGE0Gl6enps3bqVM2fOsHDhQqXjiI8wZ84cLCws6Nevn9JRhBDik0gn0k3SiYQQmYV0It0lnUhoA5nBJBRjZ2fH+vXrGTBggEzn1DHh4eEEBAQwd+5cvLy8iI+PVzqSEEL8J2PHjiVHjhyMGjVK6SjiI506dYp+/fphZGSEr6+v0nGEEOI/kU6ku6QTCSEyC+lEuks6kdAGaqUDiKzJwMAAd3d33N3duXDhgtJxxH+wb98+Dh8+jKurKyqVSuk4Qgjx0Ro0aEDz5s0ZPHiw3I5IB8XHx9OnTx8GDx6Mvb290nGEEOKjSSfSfdKJhBC6TjqRbpNOJLSBzGASipgyZQoqlYqJEycqHUV8gtOnT9OlSxesra25ePGi0nGEEOKDFSxYkNWrV9OzZ0+ePHmidBzxH0VFRfHgwQNcXFzYsWMHsbGxSkcSQogPJp0oc5BOJITQVdKJMgfpREJpMoNJfHUtWrSgTp06DBs2TOko4hMlJSXRr18/unfvTvXq1ZWOI4QQH8TIyAgPDw8WLFjAtWvXlI4jPtGxY8fw8vLCzc0NtVoObYUQukE6UeYhnUgIoYukE2Uu0omEklR2dnYy/1F8NcWKFcPb25v27dtz584dpeOIz6RGjRq4urrSpEkTgoODlY4jhBD/yNnZGUNDQwYNGqR0FPGZqNVqPD09uXz5MvPmzVM6jhBC/CPpRJmTdCIhhC6RTpT5SCcSSpEhTfHVmJqasmLFCqZPny5FKpM5ffo069atY9myZWTLlk3pOEII8V7t27enYsWKjBw5Uuko4jPSaDQMGDCAdu3a8cMPPygdRwgh3ks6UeYlnUgIoSukE2VO0omEUmQGk/hqli5dSnR0NCNGjFA6ivgCVCoVa9euxc/Pj6lTpyodRwghMihdujSenp60atWKhw8fKh1HfAH29vasXLmSpk2bEhgYqHQcIYTIQDpR5iadSAih7aQTZX7SicTXJjOYxFfRvXt3ihQpwoQJE5SOIr6QlJQUHBwcaNSoEU2aNFE6jhBCpGNhYYGHhwfjx4+XIpWJXb58GTc3Nzw8PDA0NFQ6jhBCpCOdKPOTTiSE0GbSibIG6UTia5MZTOKLq1SpEqtXr6ZZs2Y8ffpU6TjiC1c1vjUAACAASURBVCtXrhwbN26kRYsWPHr0SOk4QgiBSqVi9erVBAQEMHHiRKXjiK/A3d2d8PBwRo8erXQUIYQApBNlNdKJhBDaRjpR1iOdSHwtMoNJfFE5c+Zk2bJlDB8+XIpUFnHjxg3mzp2Lh4cHxsbGSscRQggGDBiAlZUV06ZNUzqK+EqcnJyoXr06rVu3VjqKEEJIJ8qCpBMJIbSNdKKsRzqR+FpkBpP4YtRqNZs2beL69evMnj1b6TjiK3N1dQXAwcFB4SRCiKysevXqLFmyhCZNmvD8+XOl44ivqESJEmzbto127dpx9+5dpeMIIbIo6URZm3QiIYQ2kE6UdUknEl+Dnrm5+WSlQ4jMycnJiXz58jFs2DBSUmQcM6s5fvw4Q4cORaPRcOPGDaXjCCGyIFtbWzZt2sTQoUO5ffu20nHEVxYWFkZoaCgzZsxg+/btJCQkKB1JCJEFSSfK2qQTCSGUJp0oa5NOJL4GmcEkvoi6desyb948GjZsSFhYmNJxhEIKFy7Mrl276NSpkxQqIcRXlS1bNrZt28bJkydxcXFROo5Q0OzZs8mZMyd9+vRROooQIouRTiRAOpEQQjnSicRfpBOJL0lmMInPLk+ePKxfv55+/frx4MEDpeMIBYWHh/P06VPmzZuHt7c3cXFxSkcSQmQR48aNw9zcXD7QVHDq1Cn69OmDiYkJV69eVTqOECKLkE4k/iKdSAihFOlE4i/SicSXpFY6gMhcDAwM8PDwYNmyZVy8eFHpOEIL7N+/n99++41FixahUqmUjiOEyAIaNWpEkyZNcHBwkNsRCeLj4+nTpw8DBw7E3t5e6ThCiCxAOpH4/6QTCSG+NulE4u+kE4kvSWYwic9q2rRpJCcnM3nyZKWjCC1y5swZOnXqhI2NDRcuXFA6jhAiEytUqBArV66kZ8+ePHnyROk4QktERUXx4MEDXFxc2LFjB7GxsUpHEkJkYtKJxLtIJxJCfC3SicS7SCcSX4rMYBKfTcuWLalZsyZOTk5KRxFaJikpif79+9O1a1dq1KihdBwhRCZlZGSEh4cHzs7OXL9+Xek4QsscO3aMbdu2sXTpUtRqOQQWQnwZ0onE+0gnEkJ8DdKJxD+RTiS+BJWdnZ3MkxSfrHjx4nh5efHLL7/wxx9/KB1HaKnq1auzZMkSGjduTHBwsNJxhBCZzMKFC9HT02PIkCFKRxFaSq1Ws2nTJq5du8acOXOUjiOEyGSkE4kPIZ1ICPElSScS/0Y6kfjc5BZ54pOZmpqydetW5s+fz4kTJ5SOI7RYQEAA+vr6DBkyBC8vLzQajdKRhBCZRIcOHWjUqBE9evQgKSlJ6ThCS6WkpODj48PMmTN5/Pgxjx49UjqSECKTkE4kPpR0IiHElyKdSHwI6UTic5MZTOKTLV++nMjISEaNGqV0FKEDVCoVa9as4cmTJ3JfeiHEZ1GmTBk2b95My5Yt8fPzUzqO0AGVKlVi1apVNGvWjICAAKXjCCEyAelE4mNIJxJCfG7SicTHkk4kPhe52aL4JD179qRAgQJMnDhR6ShCR6SkpODg4ED9+vVp2rSp0nGEEDrO0tISDw8Pxo4dK0VKfLArV66wePFiPDw8MDQ0VDqOEELHSScSH0s6kRDic5JOJP4L6UTic5EZTOI/s7e3Z+XKlTLSLf4TubpGCPGpVCoVa9eu5fHjx3L1r/hPli1bRlRUlMw4EEL8Z9KJxKeQTiSE+FTSicSnkk4kPpXMYBL/iZWVFcuWLcPJyUmKlPhPbt26xezZs/Hw8MDY2FjpOEIIHTRo0CAsLCyYPn260lGEjho+fDhVq1albdu2SkcRQugg6UTiU0knEkJ8KulE4lNJJxKfSmYwiY+mVqvZvHkzvr6+zJkzR+k4QsctXLgQPT09hgwZonQUIYQOqVGjBosWLaJx48YEBwcrHUfosOLFi+Pl5cUvv/zCH3/8oXQcIYSOkE4kPifpREKI/0I6kfhcpBOJT6Fnbm4+WekQQreMGDECOzs7hg0bRkqKjE+KT3PixAmGDBmCSqXi+vXrSscRQuiAXLlysXHjRoYMGcKdO3eUjiN03MuXLwkODmbWrFls376dhIQEpSMJIXSAdCLxOUknEkJ8LOlE4nOSTiQ+hcxgEh/lxx9/ZPbs2TRs2JCXL18qHUdkEoUKFWLXrl106dJFCpUQ4h9ly5aN7du34+Pjw6JFi5SOIzKRmTNnYm1tTZ8+fZSOIoTQctKJxJcgnUgI8aGkE4kvRTqR+C9kBpP4YHnz5mXdunX07dtXPoBUfFYRERH4+/szf/58vL29iYuLUzqSEEJLTZgwARMTE8aOHat0FJHJnDp1il69emFubs6VK1eUjiOE0FLSicSXIp1ICPGhpBOJL0U6kfgv1EoHELrB0NAQDw8P3NzcuHz5stJxRCZ08OBB9u/fj6urKyqVSuk4Qggt1KRJExo2bIiDg4Pcjkh8dgkJCfTt25f+/ftTuXJlpeMIIbSQdCLxpUknEkL8G+lE4kuSTiT+C5nBJD7IjBkzSEhIYMqUKUpHEZnY2bNn6dixI7lz5+b8+fNKxxFCaJHChQuzcuVKevTogb+/v9JxRCb1+vVr7t27h6urKzt37iQmJkbpSEIILSKdSHwN0omEEO8jnUh8DdKJxMeSGUziX7Vu3Zrq1avj5OSkdBSRySUlJdG/f386d+5MzZo1lY4jhNASxsbGeHh4MHfuXG7cuKF0HJHJ+fj4sGXLFpYuXYqenp7ScYQQWkI6kfhapBMJId5FOpH4mqQTiY+hsrOzk/mUIh2VSpU2zbZEiRJs27aNdu3acffuXYWTiayiWrVquLm50bRpU4KCgoD0v5dCiMzv73/zrq6uADg4OCgZSWQharWajRs3cuPGDWbPng3I+5AQWY10IqE06URCCOlEQknSicSHkhlMIoNTp05hamqKmZkZHh4eTJkyRYqU+KrOnTvHqlWrWL58Ofr6+hQqVIgdO3YoHUsI8ZW0bds27QNrO3XqROnSpRk1apTCqURWotFoGDRoEK1ataJevXpAaqmXK8mFyDqkEwmlSScSImuTTiSUJp1IfCgZYBLp2Nrakj17dqKjo1mwYAFnz57F29tb6VgiC1q6dClhYWGMHz+e58+fU7ZsWfT19ZWOJYT4Cuzt7QkMDKRcuXKMHDmSPn36EBcXp3QskcW8evWKfv36MW/ePPLnz09QUBD29vZKxxJCfAXSiYS2kE4kRNYlnUhoA+lE4kPIAJNIp2zZsty8eZM+ffqQJ08eJk2apHQkkUWlpKQwdOhQfvrpJ+rXr4+/vz/FixdXOpYQ4isoW7Ys/v7+eHh4MHr0aB49eqR0JJFFXb16FVdXV1asWMHdu3cpW7as0pGEEF+BdCKhLaQTCZF1SScS2kI6kfg3MsAk0ilTpgxhYWEMGDCAMWPG4OTkxOnTp8mWLZvS0UQWYmlpycWLF+nevTuOjo5Mnz4df39/eRMTIgvQ19enePHi9OrViwMHDpCQkMDu3bvp2bOn0tFEFjN69Gg2b97MnTt3ePjwIfXr15f3ISGyCOlEQhtIJxIi65JOJLSFdCLxIWSASaRTqVIl6tevj6+vL5s3b8bY2Jh27dqRlJSkdDSRhURERPDrr79SsGBBVq9eja+vL/b29lSoUEHpaEKIL6x48eLExMSQN29eatSowahRo1ixYgVr1qxROprIYpydndm9ezfOzs7kyZMHe3t7cuTIgZWVldLRhBBfmHQioQ2kEwmRdUknEtpCOpH4EDLAJNKpVq0aRkZG+Pn58cMPPzBhwgSCgoKUjiWyID8/PxwdHWnUqBHPnz/H0tKSBg0aKB1LCPGFNW7cGCsrK+Li4pg3bx716tVj3759aDQapaOJLCYxMZGtW7dSu3Zt1q5dS0JCAsbGxvz4449KRxNCfGHSiYS2kE4kRNYknUhoC+lE4kOo7OzsUpQOIbSHg4MDGzdu5OXLl0pHESKdggULUr9+fTw8PJSOIoT4gipUqECxYsXYtm2b0lGESEelUtGjRw9+//13Hj9+rHQcIcQXJJ1IaCvpREJkDdKJhLaSTiTeRQaYhBBCCCGEEEIIIYQQQgghxEeRW+QJIYQQQgghhBBCCCGEEEKIj5JN6QD/he+Vy9jkyq10DKFFQoOfU6GSvdIxtJrv1SvY2OZSOobQEaEhwVSoWEnpGFrF19cXGxsbpWMIHREaGiofwv0Ovr5XsbGxVTqG0AGhoSFUqFBR6Rhax/fKJWxy2SkdQ+iI0OAgKlT6XukYWkv6kXgX6UEf5+rli9jmzqN0DKFFQp4/o6J9ZaVjaLWrly5ga5dX6RhCR4QEBVLx+ypKx/hHOjnAZJMrN69PrFY6htAiNrV7KB1B69nY5iLe74LSMYSOsCmi3W9eSpDBJfEx5Pfl3WxsbEmOCFI6htABNjYyiPIuNrnsiNw/V+kYQkfYNBmpdAStZmObi7h7p5SOIbSMzbc1lY6gU2xz5yFsdW+lYwgtYttjhdIRtJ6tXV6CplZXOobQEXYTzyod4V/JLfKEEEIIIYQQQgghhBBCCCHER5EBJiGEEEIIIYQQQgghhBBCCPFRdPIWebrkYeALZmz8jUdBYdjmMGdIm7rUKFsEgFuPgpi56RBPQ8Ipkd+Wyd0ak9cmBwcv3GbmxkPp1hMbn8j0ns1oWKVU2rJHQWF0mr4Wr6m9sbO2AODYlXss3XWS0IjXFMplxfD2P1GuSPr74W48cpGHgS+Y3L1J2rKdp66x9uAFIt7E8G0+W0Z3rE9hO2tSUlLw2HuGHSevEZeQSKVv8zO2UwOsLcwAOH/7Mc7bjhHy6jXf5rdhYtfG5LPJAcDKfWfYeeo6MfEJlC+al9Ed62ObI3uG1+jKvac4bztGYGgEtjnNGdyqDrW+K5rue36/eo+tv1/Fffiv//VHIXTI5Zt3meu+kafPQ8llnZOhPX6hTpXUzzK5evse8zw28yTwObbWOXHo1pa61VLvkX3q0nUWrNpC8IuXVChdnIlDepDLOicAh09fxHXNNsIjX1OyaEEmDu5OgTyp91zffeQUbhu9iXoTww/VKjFxcHeMDA0AWLVtL1v2HSMuPp7GdaoxvFcH9PVT/3XWbj+QuISEtNytGtRmVN9OaDQa5q3YzL7fz6BWq+naqhE92jYF4HV0DLOWrufMlZuo9dQ0qFkZp56/oq+fjeCwV8xwW4fv7fsYGRrQtlFd+nZokeH1mbZ4Dft83k6R1Wg0xCckcmS9C7bWOdmy9yirtu8jJi6OSmW+ZdKQnlhZZicxMYm5Hps4dOoCyRoNdapUYNyArpgYG33uH6HQEocPH2bDhg1s2LAhbdmhQ4dYuHAhISEhFC5cmPHjx6d9VtDTp0+ZMGECN27cwMbGhrFjx1K7du1/fewvDx8+pGXLlhw8eJC8eVPvKT1nzhw2btxItmypfzcGBgZcuJB6u86dO3fi5uZGREQEtWvXZvLkyZibmwPg5ubGtm3biImJoVKlSkyePJlcuXKRmJjIggUL2L17N2q1mvbt2zNw4EBUKlW6LCNGjEBPT4/Zs2e/87W5fv06kyZN4smTJ5QqVYrZs2eTP39+AC5evMi0adN49uwZhQoVYtKkSZQrVw6AIUOGcPz4cfT09AAoVKgQO3bs+I8/IaELjvicZNO2naxdtjBt2aWr15jhvJhnQcEUKpCP8SMcKFe6JABbvHezYr0nkVFRlCnxLZNGO1KoQP5065zhvAiL7NkZ1LsbAJNnL2Dvb0fSHtdoNMTHJ+Czdxu2Nt+wYt1mPL12ERsXT5MGPzLSoT8G+voA/K9BC+Li49Oe26Z5E8YMG0R0dAwznBfjc+osJibG9O7yK+1b/5wuR2DQc1p37s2FY/sy7PeN238wcuIMfvPe+N7XxnX5Krx27ycpKZna/6vCpNHDMDYyIjEpielzXTh64jQqlYpmDX9ixJD+qNVqHvg9pmWnXhj++T4LMGviaOr/UPu92xG6adupO7jsuYC+3ttrGneOa0dOc2MCw6KYuf00t/1f8I2FKcNaVKF6yXzpnr/p+E0ePg9n0q+10pZ5nfmD9b9fJyomgZJ5rRndtjoFbCzTPe/i/SAGux/kgnPPtGWn7zzFZfdFQiOjsS+amwnta5LDzDjd8+bvOEd2E0P6NEz97K9Z28/w25WHaY9rNCnEJyWzb2J7bCxNAUhJSWHEmqPUKVOAppWLA5CYlMzC3Rc4cu0RGk0KNUvnZ2Tr6pgY6md4jSLexDFj22kuPwjCzNiAvo0q0fT7YgA8fRHJtC2nuP/sJXmtszPulxqUyvcNALf9XzBvx1n8QyMpapeT0W2qUyR3zg/8yQhddfnWPeau2EJAcGpHcujamjqVywNw8/4jZrlv5klgMMUL5WNc/04UK5CH/cfPM23phnTriY2LZ5ZTbxrXroLPeV8WbdhJSNgrCuSxZWSv9lQolfo7ePLSDeav3kpIWDiVy5VgypDu5LRIPU47cuYyruu8CY96Q4ki+Zk4sAsF7FI/Y/HXYdN4FPA87disavlSuIwdmC7Dko278L1zn1Uz397GcZ/POdw27Sby9Rsqli7GVIce5LQwJzEpCefV2zh8+jLJyRr+V6kMY/p2wNzU5L2vld/TINo7TmXX0unksbUG+Md9FVmD15VnLP79Efp6b3vD9r6VyWH69pjkcVg0PdZeZXPv78ltkdqTfZ9GsPCoH88j48if0xinekUpZZf+3NbCow/JbpSNnjUKpi278PgVi449IuR1PMVtTBnb+Fvy5jAmJSWF1Wf82X0tmNjEZCrmt2Rkg2JYmaXm2H8zmFWn/ImKT6J2MStGNiiGob5euu3tvf6ctWef4t0/463t3/XYmjP+7Ln+nNgEDeXyZmd4/WLYZDfM8NyAV7HMPHiPByFvyJPDmNENi1Myd+rf/Z2gKBYc9cP/ZQxFbUwZUb8Yhb8x/dCXX+ionfdiWXo1hmx/m6Ky+ecc5DBSs+xqNDvvxfHXoZ6BnordbVKPR+69TGLhxTf4RyWTz1yPYVXMKGGVek5g38M4PG/HEhmfQpEcejhWNqWgRfohiv0P49hwK5YtLXL8LUscnndiiU1KoZxNNoZXMSOHUfq5M6uvx3AjNBGXeqnnyZM0Kay4FsORx/GogObFjOhS1hiVSkWSJgWXS9GcDkhABfxUyJD+FU1Q/+3cQkpKCo5Hoyhvq0+3cu9+3/m3/UlJSWHCydfUyGtAwyIZz7/9/8y6SGYwfWET1+zj5/+V48QiR4a0rsuo5buIS0gkPjGJ4ct20qVBFXxcHKhSqiBjVuwBoFGV0pxaPCzta2CLWpQrkoefKn2btt6kZA1T1h4gISk5bVlQWCST1+5nSvcmnFo8jDZ1KjDGY3fa48kaDWsPnmeR1/F0Ga/7BbJ01ymcB7bidxcHqpUpxPClqSfLDl64w9Erd9k0oRvHFgwhh7kJrn8+//nLSMas2I3TLz9y3HUoFYrlY9r6gwD8duEOBy/cYeXIjhyaN4hcObMzde3BDK9PbHwCTkt30LdZDU4udmTkr/UY47Gb6Li3J0r2nLnBhFX7SCHl034YQifExMXjMNWF/p1acd7bgzH9uzBythvRMbHExMYxdJorXVs14sz25Yzu35mx890JDH5B4PNQnGYuZkCnVpzcupTypYozZMpCUlJSeBkRxRTX1SwcP4RTW5dR9tvCTF28BoC7fv4sWLWFJZOdOLbBlcjXb1iy3guA/T5n2bznCEunDufQ2oUEhb5kweotAISEvSIpOZkLO1akfY3q2wmAzXuOcOOuH/tWzmOD80S2Hfid4xd8AViwagvxiYkcXOOM99IZ3Lr/iLU7DgAwaeFK8th+g8+mxaybP549x06z3yfjvVYnDO6ebrs17L+jW+vG2Frn5K6fPyu27mH9/PH4bFqMqbExLqu3ArDGaz+PAoLYv2o+R9a78iriNau3ZzypKDIHb29vhg8fnm5ZYGAgo0ePZs6cOfj6+tKhQweGDh0KpJ7QHjhwIFWrVuXKlSuMHz+eoUOHEhMT84+P/SUpKYkxY8aQ8LdBV4C7d++yYMECfH198fX1TRtcunLlClOnTmX27NmcPXsWU1NTRo0aBcDevXvZu3cvmzdv5syZM+TOnZuxY8cCsGrVKk6dOoWXlxd79uzhxIkTrFu3Lt02jx49yr597//djo+PZ+DAgfTq1YuLFy9SvXr1tNchOTmZwYMHM3r0aK5cuUKrVq3SHvtrf7Zs2ZK2PzK4lLnt2HuQkZNmpDsGSU5OxmH0JEYO6c/F3/fRsmlDnMZNBeCy7w3cVq5j1eJ5XDy2D/uK3zFhxvy058bHJzBrwRI2bduZbjuTRw/jyvGDaV+1qlWhR6dfsLX5hn2HjrJx2w7cXeZwdPcWngeH4LzYHYCQ0BckJSWle+6YYYMAmOu6lKDnwRz02sC6ZQtZs2kbR0+cTtvm9Zt36NrfkddvojPs94nT5+g7dDRJyUnvfW2OnTiNz6mz7N2yhqO7PAkJDWP1xtT3my1euwgKDuHILk/2eK7h9PlL7Dl4GIC7Dx5S+39V02WWwaXM6UHQSwY1/Z4Ts7umfeU0N0ajSWHE6qPYF7XDZ2YXnFpWZex6H2LjE4HUzrLu2HUW772Ubn2+j4JZediXxX0b8fuMzlQokovpW0+n+543cQnM2HaKlL/VhrCoGCZuPMGYtv/jyLSOWJkbM3v72+Or+MQkFuw8z7bTd9Kta0zb/6XLXr1kPjrVLZs2uPQ6Np5xG3w4eetpuuet97nB4+AIdo5tx76J7Ql/E8f632+88zWavPkEVtmNOTytI/N7/MT8HecIDIsCYNx6H2qUysexGZ1pX6s0I1cfJSEpmTexCQxbdZiGlYpwZHonWlb7FgePQ2mvn8icYuLiGTpjCQM6/My5rW6M7tOBUXM9iI6J43V0DIOnLaZJ7aqc2ORC6wa1GDDZhZi4eJrUqcr5bW5pX4M7t6R8iSLU+18lAoNfMN5lNeP6d+S05yI6Na+Hw4wlRMfEERYeydgFK5gwoDMnN7lincOC6X8OVL2MiGLKknUsGDOAk5tcKVu8EFPd1gOQnKzB72kQR9bMS9vm/x9cuv3gCWt3/JZu2Y17j5i/aisLxgzgxEYXcmQ3Z+Ga7QCs23GIu48C8F4yhQMrZhMTF8/CNV7vfa2SkpOZuGgNCYlv38P+aV9F1vEwNJr+dQpxdFiNtK+/Dy4laVKYeeA+Ccl/O+7TpDBu1x0G1S3M4aHVaVI2FxP3/JH2eHySBpejfnhdSf8Zo8GRcUzafReHH4tweGh1yuezYPbB+wAcvhPK73fDWNOtIgeHVMPSRB+3448AuB/yhqU+j5nXtgy7B1QhMjYJj1NP0q87Kg43n8fv3Md3PXb4TiiH74SyrGN59gyqim12Q2YevPfO50/c8wf/K2LFbw7VaVcpD2N23CYhScOb+CRGeN+mfikbDg6pxs/f5WbYtpvEJiS/cz0i8/ALT6ZPeRMO/mKV9vXXoI5feDITapilLf9rcCkmMYWxx6No+a0xB9rlpFkxI6aceg3ArReJrLoWw/Ta5uxuk4PKuQ2YcOJ1um2GRCez3Dcm3bKHr5LYdDuGxfWz490qBybZVHj8v++59zKJLXdi0y3bcieWi0GJLGtowaomlpwPSsT7Xur//l334wiJ1uDZIgdrmlpy6Xkihx/Hp3u+9704br54fyf6t/15k6Bh6uk3nAl893HauzLrokwxgykoLJJeczfSslZ5PI9exsggG2M7N+S4732OXL6Lbc7szO7zM4XtrLl6P4C5nkcIfhVFHmtLBreqTdXShYDUQZEV+84Q/jqGSt/mZ0zH+uTMnnE0vubgBRmW5c6ZnW1TemVYHhAaTlKyBo0mBZUKDP+c+XD5rj/ZTY1oWDl1RlKPxtXYfPQSj4LCKGxnnW7f3PeeZsPYrmTL9vaKhbUHz1G+WF5uP3metszO2oJD8wZhYmRAYlIykdGxWJi+vTJv8pr9vI6Jp0XN79IdbL0If0Pn+pUpmif1irh2dSvitvMkEW9iaVSlFHUrFMPY0IDXMXFEx8bzjWXq7KUD529Tp3xxqpYqlLYPAaHhAERGx9K9UVVyW6WOvrauVYEeczJeAWtsaMCBOQMwMTIgWaMh/HUMZsaGZPvzynC3nSe5cv8pHX6y57rfswzPF//ds5AXdB0+nTaN6rJx1yGMDA2YNKQHx85e5tDJC+SysWL+mEEUyZ+HyzfvMmvZBoJfvCRPrm8Y2r0d1SuWBVIHYdw9d/MqIorvy5Vg/KDuWFlmnKlWpVXGD/60s7Fm5/JZ6ZaZGBlyZL0LJsZGJCdrCI+MwtTEmGzZ9AgKCaOG/Xc0rF0VgKrlS5M/Ty7+ePiElxGRlC9ZjHo1vgegV7umrN6+j/uPA0hKSiI+IZGkZA0AarU67crvgyfO06BWFYoXSr1qdmCnVvSfOJ/hvTvgc+4qvzT9iWIFU2di9P31Z/pPmMfIPh25/ziAYgXTX2n7lwPHz9GtTWMszM2wMDfj12b12HfsDHWqVCAlJYU+7X/GxNgIE2MjGtepxtmrt9BoNBgY6NP7l2bo62cjj+031K1akRt3H9Kk7vs//PHgifM8CXzO3NEDAHj6PARNSgrJafuqwsAgdV97tmtGl1aNMDI0IOxVBLFx8VhkN3vvusU/CwwMpEOHDrRr147169djZGTEtGnTOHLkCAcOHMDOzg4XFxeKFi3KpUuXmDp1Ks+fPydfvnw4OTlRo0YNIHUwxc3NjVevXlG5cmWmTJmClZVVhu39Ncvo7+zs7Ni/f3+G5QsXLuTChQt069YNX1/ftOV58+bl9OnTmJqakpCQQEREBJaWqVd++/r6EhcXR79+/VCpVNSsWRNPT0/09PT+8bG/uLu7U6lSJW7cSH8S7e7du5QoUSJDxmPHjtGkSRPs7e0BGDp0KP/73/+IjIwkMjKSvn37kidP6gzc9u3bHCFXZgAAIABJREFU0759eyB18KhPnz7Y2dkB0KNHD9zd3enWrRsAr169Yt68ebRq1Yrk5HcXnvPnz2NpaUnTpqkzC/v378+6det4+PAhOXPmJCIigqSkJFJSUtDT08PQMPXqvujoaIKCgihatOg71ys+3rOgYDr1GUzbFk1Zv9UbY0NDJo9x4tiJ0xw84kPuXDYsmDGJooULctn3OtPnL+J5cAh589gxbEBv/lc19X/+vkNHWbZqPS/DI6hcsTyTRjlilTNHhu1VqtMowzK7XLbs3bI2w3KXZSu5dPUaXdq34drN22nLo16/ISIyisQ/f0fUanXabBz7CuX4zXsTpibGxMTG8uZNNJYWb98Tew0ZQb48ualX5/0fIH7g8O888n/K/BkTgdSBnF/btKBYkdTjrX49OtPHYRSjHQdy94EfxYsWeed6jp08w6I5U7G0yI6lRXbatWzG7v2H+Kl2Dc6cv8Sk2c706tyeafNc0z1v+659rN/iRa8u7fH03v3OdQP4BzxDo9GQnKxBPxuo9dQYGhikPZas0aD52/vuX4/de+BHiWLvziw+XtCr1/RZvI8WVUuw5eQtjAyyMaZtDY7ffMLRa4+xzWHKzC4/UDhXDq76PWf+jnMEh0eTx8qcgU3tqfpt6jHOb1f8WHXEl/DXsVQsmpvRbf5HTnPjDNurPXpdhmW5cpixdVTrDMsfBL2ifsWMP+ub/qHEJybR/afvUKlUVCuRF49BTVCrU68WnbL5JK/jEvi56rfpLqarUDgXO8a2xcRQn9j4RN7EJWBhmv7q64W7LlC3bEE2n7iVtuz4TX++K2xLpaK5ARjY9HsaTdrMm7gEzIwMGOz+G3msslO3bMH3vs6Hff14EhrBjC5105Z1ct7FD+UKUq6gTbrv7fbjd3SsXRYjg2yERcUQm5CIhUnGq8RDIqK59jiE37r9iH42Pb7Na81qh2bkMDPicUgEgS+j6FS3LHpqNc0qF2fz8Vtcup96AtPMyID2tcoA0Ni+GOuO3eDigyBqlynw3n0QH+ZZSBjdRs+hdYNabNpzBCNDQyYO7Mzv5305dOoSub7JybyR/SiS344rt+4zy30TwWGvyGP7DQ5dW1O9QmkADpy4gPuWvbyKjMK+zLeMH9D5nR2paruBGZbl/saKnW5T0y0zMTLk8Op5bztS1GtMTYzIlk2PizfuY25iTMfmPwHQrG41Vnsd5MK1O9St+vb48VlIGMs278FzwXj0s6XePaFV/ZrYl0m9kLVJnarMWeGJf1Awt+4/pnzJYnxfNvUYzqFLa37s6sSbmFiCX7wiPiGRZE3q/3g9tRrDP7vVk2fB5MhuTnazd89qSEhMZMqSdbRtVJv7jwPSlu88cor2TX+kZJHUGb8jerXnVUTqYGtcQgK92zUhR/bUWRQtfvofizfszLjyP63afoAKJYty6/7bk+z/tK+lihZ877rEx3seGUf/jddoXj432y4/wyibmpENi3PyfhjH7r7ANrsh034uSSFrU64FRLDgiB8hUXHYWRrTr3ZBqhT68w4kd0JZc8af8JhEKuS3YGT9YukGg/7y04LTGZbZZjdiUy/7DMsfvoimXqlv3pt9w7mnlMubnTvP354cfh2XRGRsEkma1MuN1Gow+NvMXMetN7CzNKZ2cet06zp0O5Raxa2oXCj1eLRrtfwEhKeeRK5fyoZaxawxNtDjdVwSMfFJWJmlvk8c/SOUH0p+Q5E/Zwb1qlkAp+23GPxD6vtpSkoKsw7cp0k5W47fC0u3zfc9FhWbSOeq+cj154ysFhXs6LvxWob9fxIWw7PwWH6tnBc9tYom5XKx5VIgl/0jADAz1KOdfWo/a1jGlg3nA7jsH07NYtYZ1iU+TvCbZAYfjqJpMUO878ZhqKfCqYoppwMS8PFPwMZUzaSaZhS0yMb1kEQWXY4mJFqDnZma3hVM+D536t/G0cfxrL8VQ0RcCuVt9XGsbJphhg9Ao60vMyyzNdVjbVPLDMv9IpL4oWDG4xgAv/Akilhm/H9/JjCBAhZ6NCic+rwmRQ0pnjMbmpQUwmI0/FLKmEKWqefHW35rxMrrMUTGa7AwVJOSksK889E0KmzIyYC3F68+e5OMJgX+rBeoVSoM/jaxLyE5hXkX3tCsmBF+4UnpsnQobYytaeo3/1LSiE23Y2lTwphnr1PXqfnzyiQ1YKB+O3spICqZfQ/iqZE34/+ev/zb/vQ+EEmt/AaUts44BPO+zLooUwwwAYRGvCEhMZkjCwazct8ZnNy8GdupIaM61GfquoOsO3SBKd2bMHvTIQa0rE2d8sXYf+4WczyPsHN6H649DMR52zEWO7SjUG4rluw4weQ1+1nk0C7Dtk4tHvbBubo2qMJczyPM23IEUDGnXwuMDPR5EvyKgrne3sZAT60m7zc5eBL8Mt0Ak9uuE7SqVZ68Nm9PktwPCOXw5busH9uFTUfSX9lnYmTAw8AXdJi2Bj09NQsHvS17Dq3rYm1phvue0zx/GZm2/Cf79Cf+Tt/ww9rCDMs/bxthbGjA1t+vMH/rUWwszVkzunNaDjtrCwYu3MrdpyGULpSbcZ0bAPDLD5XSr/OmH0XzvPtNx8TIgDex8fzo6IomJYVJXRunDcT9UrciA1vWYu/ZmzLA9AWEvgwnITGRE55uLPfcxZApC5k4pDvjBnRlkstKVm/fxwynvsxwW8eQrm2oW60Se4+dYebS9exbOQ/f2/eZ67GJ5dNHUDifHa5rtzPe2YNl04Zn2NaFHSs+OJeJsRFvYmKp2a4/mpQUpjr2wtDAgEL57Jg5vG/a9z0LecGjp88oWjAvL66GY2T09p++SqVCrVIR8DyEH6pVwr5cCdoPmYieWo2lhTkb5k8A4HFgENUqlEl7XsG8uQmPfE3k6zckazQY/+0WPmq1msjX0US9iebeo6dEvYmmzcBxvIyIokalcozq1wkzE2OeBD6nUF67t+vMk4s9R1MPfCc7vL1dC8CpSzcoUaQAarWaxZMc05YnJiVx9uotOjSv997XKSk5GZfVW5kwuDv6f95+7H8Vy2JjlYPGPYejp1aTz86WDc6p+6qnp0ZPzwDnVZ6s3/EbxQvlo1V9uWr8U4SEhJCYmMi5c+dwc3Ojf//+TJ06lYkTJzJu3DhWrFjBnDlzmDx5Mo6Ojvz000/s2rWLqVOncvjwYa5cucLMmTNZtWoVRYoUwdnZmVGjRrFy5coM2/r7QNG/6dixI46OjuzYsSPD80xNTbl37x4tWrRAT08Pd/fUmRB3796lSJEiTJw4kSNHjpA7d27GjRuHoaHhPz7213MPHjyIl5cXa9asSdtWaGgoERERzJw5E19fX/Lnz8/YsWMpX748Go0GI6O308PVajUajYbAwEA6deqULvOJEyf49tvUEwIajQZj47cnPfX09Hj69O3V41OmTKFXr14EBwfz7Nm73zceP35M4cKF060jX758PHr0iKJFi9K2bVv69OmTNrj01wyp+/fvY2JiQu/evbl37x4lSpRgwoQJFCkiJ8s/RciLMBISEznz206WrlrPoBHjmDzaifEjHJgwfR6rNngya9IYpsxZyND+vfixdg32HDjMtHmu/Oa9kavXbzJ7oRsernMpUrAAC5euYMzU2Xi4zMmwrSvHM86mfp+ObVsytH8vdu77Ld0AUw5LC9r83IT+w8agp6fG0NCQ1Uuc0x43NTHm+OlzDBoxHjNTE9Ytc0l7bMGMiXxjbcXYqe++dWNSUjLObh5MHj0s7f+6JlmDsdHbUqenVhMZFUVk1GvuPfAj6vVrWnbsSdircGpWq8LYYYMwMzMlOTn935ienpqAZ6knp0uXLM6B7Rt48eIlkH6AqW7N6rRu3pjLvjf+cYCpUb26bPHeTc1GrVCr1ZQvU4ouv7YBoPXPTeg9ZARV6zVHo9HQ4MfaNKr3A5A6wJSYmMSPP7dHpYJ2LZrRp1vHf/xZiH8WGhlDQnIyh6Z1ZNXhawxffYQxbWswsnV1pm89xfrfbzC5Q23meJ1lQBN7apcpwIHLD5jnfQ7vsW25/jiEhbvPs6hPAwraWuK2/zJTPE/i2qdBhm2dmN31gzIlazT4BYez+cQtJmzwIae5CQOaVKJGqfzcf/aSgraWzNp+huM3/bG1NMWpZdW04/8hzStjnd0Ej9+u8jz8Tbr1mhjqc+r2U0asPoqpkT7LB7695feZOwEEhkUx8dda6QaY/EMjKGjz9pYjlqZGmBkbEBgWRYm81szs8gPW2U2Y4nnynfuSlKxhyb5LjGlTg2x/O6m4akgzrLOb0M8t/YUeemo1egZqFu25yKYTNymaOyfNqxTPsN4HQS/J/012Vh+5xt6L9zEzNmBAY3sK58rBk/tB5LO2QE/9dnsFbCx4EhpB/m8s0l6rt9tUpc18Ep8u9GU4iYmJHN/ggvvWvThMX8KEgV0Y27cjkxavZY33QaY79mT6so0M6dySulUrsNfnHLOWb2Kv+0x87zxg7sotLJvsSOF8uVm03psJLqtZOnlohm2d3+b2wbn+6ki1OjikdqQh3TA00CdZo0m7vfdf9NQqAoJfpFu2eMMO2jSsRb7cqYOi9mW+TRtwAbhx14+4+ATy29my1+cchfLmSnvMMrsZZibGBDwPpWSR/NiX+Zb2jtNSu1V2M9bPHQPA/ccBqNVqOg2fSWDICyqULMqYvh2xsUo9aem2cRe1vv+OfLm/STfAdO9RAHlsrFOfFxxK1fKlGNsv9XhwUKeW6fbj1OWbFCuQ/mMA0tbzOIBDpy+x2Xk8G3a/vfXsP+2r+PxevEkgMVnD/sHVWHPGn9HetxjZsDhO9Ysy6+B9Nl4IYEKTEsw79JB+tQtSs5g1v90KYcGRh2ztU5kbgZG4HvNjYbuyFLAyYfmJx0zffw/ndmUzbOvosBoflClZk8KjF9FsufSMSXvuYmVqQN/aBaleJPXCvgehbzh29wWrulRgy6W3HcLSRJ9m5XIxwusWeiow0Ndj0S9vc0z9uSTWZoZM359+RtCD0DfktjBi6NYb3A95Q8nc5oxqkPpeoFKpMDbQw+vKM1yO+mFjboh759Q+4f8ylu8Lvj3Jnz+nCRExiUTFJpLdWJ+dvs+xMjPgf0WtMgwwve+xNpXS/72c9XtJEeuMgwL+r2LIm9MYvb+dYM+f04SnL1OXG2VLf5s+PbWKZ+EyC/BzCYvVkJgMO1vnYP2tWMadeI1TFVMcvjdl3vk3eN6OY0x1MxZeiqbXdybUyGfA4UfxuF6KZmNzA26GJuJ2JZq5P2SngIUeK67FMPvsG+b8kPHihoO/ZLyg9V2SNSk8jkhm+x+xTD/zmhxGanqVN6FaHgNexmqISkjB7Wo0t18kYWemxyB7E0pZ6+MXnkQuMz0mn3qNb3AiBSxSbxunVqmoUyD9YNX5ZwlYGauwMEw95tn9IJ6cRiqq5zVIN8D0fW4DrE1i6bgnArUK8pirWVL/7fHd6usxVM9jgJ2ZOt1gTXIKGP3tsEmtgqDXqaNUTYoYMeL3KJpvD0eTArXzG6QNpiVrUphz7g2DvzflyP+b1fR3/7Y/SxpYYGWsZuiRyAzPfV9mXZSpbpHXsd736KnVVCiWDxMjA36uUQ79bHrYf5ufkFepB9xmxoYcuniHq/cDaFC5FDumpc6q2H/uFi1qfEeJ/LYY6mdjYItaXPjjCS+jMt425GOoVCqm9mjK6SVOzOjdjGnrDhAa/prYhESMDNLfh9vIIBtxCW9/oYJfRnHquh8df/o+bVliUjJT1h5gbKcGGZ7/l4K5cnLWzYkxHeszavkuwl+nThm0tvz3mQq3HgUxc+Mhhv/yY7rlLWp+x6nFw6hepjCj3HcB8Domjt2nb9Dv5xocmDuAvN9YMmFVxlsSnbj2gFUHzjKkTd0Mj/3F2FCf00uccB3cllmbDvPw2YsPziw+TZeWDdHTU1OpzLeYmBjRsn5t9PWz8f13JQl+8QoAM1NjDhw/x+Wbd2lUpyp7V8wFYO/vZ2jdsA4lixTE0MCAwV3acN73Fi/DM/7j/FjGhv/H3lmHVZl1ffg+AYduAbEQuwMVQRQdGbu7O8au0bG70FGxu7vFwO5WxMBWBEFKujn9/XH04BFHnXhnvved574ur0v2E3stDvs8z9prr9+WcefwBlbOGMOclVt5Ff7O4HhSahpDpy+mdQMfihbMj2fVCtx+8JTr9x6hVKnYfCCQHLkCuUJJjkJJQed87Fg8jVuH1tG0nhfj/Fah1WrJzpEbBGQf/58tV+BTozJ7jp/jbVQsmVnZbP4gJydXKJFKJVQqU5x1c3/h0Kq5JKWmMX+NTjYiO0dukJgykckM9sf4yJJNewmLjKZnm0YG7Wq1himL12NsJKWF72+/MJ++chtrKwu8q1XUt+UolJQt7sqRNfO4tm81pYsV0csBfmRo97Zc27caJ3tbZnx2TOD306tXLyQSCdWrV8fc3Jx27dphbGyMh4cHMTG6KlNLS0uOHz/O3bt3adasGadP6/bZCwgIoEOHDpQtWxaZTMaoUaO4ceMGCQkJX+vymzg6On71uJubG48ePWLGjBkMGzaMpKQkUlNTuXLlCuXKlePKlSv07duXIUOGkJKS8tVjCoWCCRMmMGPGDIPJbIDk5GRq1KjBgAEDuHLlCu3bt2fgwIEkJyfj4+PDsWPHCAkJQS6Xs2LFCiQSCfLPxsr58+dZvXo1Y8eOBaBu3bqsX7+e9+/fk5iYyLZt2/SyfIGBgWRmZtK+ffuv+p+VlZXHVlNTU7Kzs1Gr1VhYWLBx40YePHjAyJEjGTFiBNnZ2WRnZ1OpUiWmTJnC5cuXqVq1KoMHD0apFGSJ/iy9urRHIpFQrUpFzM3MaNuiCcZGRtRwr0xsnO6dwNLCghNnzhN0/yFNGtTn5AHdd25A4BnatWxK2VIlkMmMGTGoLzfvBJGQmPSnbMrn8OXAS61WY25uxvqlC7h36SQjBvZh1MQZZOfkBtheNdwJvnKKHp3aMfjnSSg+/I381j0/cur8RWysrajtWUPf5uPtya4DRwiPeEdmZhYbtu8GQKFQIJVKqVy+LBtXLOLo7s0kJSczd/FyAOp612Tl+i2kpWfwLjqGg0cDkct1Y8XG2lpfyfs5DvZ2iMXfDhHkcgVeHtW4eGwfVwIPIpVKWbp6o962Zg19uX76CGcP7yY07C279h/+0LcVPt6eHNuzmTWL53Mg4ASHj5/6WlcC30EXn/JIxGIquzljJjOihUdJjKQS3Iu7EJeii2csTI05HRxKcGgMDaoU48AEXUIw8O4rWtYsRamCDsiMpAxuUo07L6NITP/jch2pmXLKFc5HO68yHJvaiUFN3Jm8/RJv36eQli3n5vN3lC7owIlpnehWrwI/bzpHaqbu+9/B6rf3VQHwKFWAq3496VynPGM2nkGpUpOWJWdxwC2mdKrNZ1vyka1QYfJZQsbEKDfu+lZ/5x6EYW1mgmeZggbt37puYOOqnJ/dHUcbc+btv57neHqWglfRSYhEEDClI+Pb1WLG7iu8fZ9KjkKFibHhRJ7MWEqOUkUFV0fep2Rw/O4rVGoNp4NDCYtLMaj2EvjzdG/ZQBcjlSuJmakJrX/01sVIFUoTm6BT7bA0NyXwym3uPX5J4zo1OLpmDgDHLt6kbYPalClWGJmxEUO7t+bWg6d/WYx0e/8qVk4dwZzVO3n1NorKpYsTm5DE0fPXUapUnLx8m7B3sSgUue8nMfGJXL77kO4tG3zxvhHRcYyev5ohXVthYWaaJ0YCXZyULVfoY6vtCydyc99KmtatybiFa9FqtWi0WsqXcGXhLwMJXDcPa0tzJixaB8CDZ6+5+eApAzs2y9N/WkYmh85eZeaIXpxYNx+FUsXCDXvynLc38CJnrt1lcJeWeY4plSqmLt3MlMHd89j+NV8F/jN0qq6rgqlcyBozYynNKjpjJBFTtbAN79N03/cWMilnnsbzIDIF37KO7Omvm/s69TiOFpWcKelkgUwqZmAdV+6GJ5OUqfhal18lLVtJ2fyWtK7iwuHBHgyo48rUo895m5iFUq1hbuDLL+51pNZoMZdJWNyhPOdGezOgtiuTA56Ro9R95zpYfLmyIz1HxbFHsfTzduXw4JoUsDFl5vHnBuc0r5Sf86Nr4eFmy6QjOpnWHKUak09sMDESf2jXEJWSzd6gd4z0zbu47WvHPuXqq0S23ohgSL2ieY7lKNWYSA3fAU2MxOSo1FQoYEVcupzAkFhUag1nn74nPDEL+cdyEoG/hPZlTJCIRVR0NMLMSESTYiYYSURUdjYiPkv3N2dhJOJ8uJyHcUrquxqzvbkuIXkmTE7T4iaUsJNiLBHRt5IZQbFKkrL/+GeUptBS2l5Ky5Im7G1lS79KZsy6lk5EmprUHA2VHKV0KWvK/ta2NC0uY8KldFLlGtIVWs6FyWlQVMaBNrZ4FjBmypV0VBrDrU+eJihZfCeToe66hGd0upoDz7MZVi1vAlSu1lLSTsqWZtYca29HCVspi+/o3nEfxyu5F6uke/m83+meBYzZ/SSHxGwNyTkaDr7IQfHBDoVGi29RGUfa2rK7pQ1vU9Uc/iCft+9ZDm42EtydvxwzfYnP/QGwN/1yXPU1m/8b+Z+pYAKwNtdNFonFYixMc7/kxWKRvtxt7oCWrDx8mbGrD6HVQs9GNenZyIO45HQCbz1h/6Vg/XVSiYSYxFTsP5PJqzvCn89xtrNiz7Q+Bm2Pw6I5feepXjrP1700R64+5ELwC0yMpcgVhtnJHIXKYPPXU3ef4lmuqIFM3/rj13EvVYjKxQ0DnE/5KKXXolZFdp69S/DLSOp/sn/Tb3H10WsmbzjGqPY/5Klq+rhKbkhrH3xHLyMlIxupVELdKiWo4KZbDTGwhTf1Ry0jM0eO+YeVtoevPsB//0XmDWj5VZslYjESMXiVd6NGmSLcehKml+wT+M9ibalL4knEYizNcgNlsUhXmgqwcPwQlm7Zz6jZS9FqoU/7ZvRp35TY+ESOX7jO3uPn9ddJpRKi3ydgb2u4OV2t9j/l6ds5nz0HV835ol26ahsx3tUqUqNSWW4Eh+il6iKi4xg0ZSHVKpRm/IeVbUUL5mf26AEsWLeTtIwsOjWtj1thFyzNzdhz7BwiRFQsrXvZGtm7A17tBvIqPBITmQz5J5r1OR8m38xMZLT8sTZRcfH0HT8PE5kx/Tu14PTVO1iYm9GrbRMDe4d0a8OASbrEm4nMmJxP9qHJkcsxM82dzFap1cxavoW7j56xft4v2HyQewCdvvrYeStITE5l9ayxvzkBCHD8wo08FUirdx6isIsTboV143Js/y7U7zac9Mws/Ua4MmNjZMbGDO7Whj7j5+W5r8Dv46PEnFgsxtIy97MUi3PH0JIlS1i0aBFDhw5Fq9XSv39/+vfvT0xMDAEBAezcuVN/nVQqJTo6GgcHw6rPj1Jyn5I/f36OHTv2u202+vB31bZtW7Zs2cLdu3cxMjLCxcVFL0XXrFkz1q5dS3Bw8FePPXz4kBo1auDu7p6nn1KlShnsj9S+fXu2bdtGcHAw9evXZ/jw4YwYMQKNRsPgwYMxMzMz+B3u27cPPz8//P399ff/mKBq3bo1dnZ2dO7cmdevX5OQkMDixYvZvn17Hjs+x9TUlJwcw9V22dnZmJubc/r0ad68ecP48eMB6NmzJ7t27eLGjRvUr18fL69cycphw4axdetWQkNDvygDKPD9WFvpVtZJxBIsPpHVEYvFaLS6oGjRnKksWbWeYeOmokVL/x6d6du9M7Fx8Rw7eZbdB47or5NKpUTHxuFgb7jpvUf9vJNa+Z2dOLJz43fbeubiFcLCI/hlhE6atHunduw+eJSbd+7xQ51aABh/kIP7qU93tuzaz6vXbyhX5tvvYkdPnqVtc0MZv9bNGhEVHUPvwaOQyWT81Kcbp85dwsLCnD7dOhqcO2xAb/oO1yVjx48ayqwF/jRu141CBVxo1bQhp89f/m4/v8W8xSto3bwRTo6697WRg/vx0+gJjB3+E5NmLWDetPFYW1libWXJwF7d2LRzL13at2bhrCn6exR3c6Vzu1ZcvHqD1s0a/VZXAt/BRwk2iViExScV3WIR+mfR3O71WHkiiHGbz4NWS4/6lejxQ0XiUjIJvPeaA9dy95SQisXEJmVg/5lM3g8T837HOtuas2tsG4M2O0tTg+qi2uUKU7WYM7eeR2EkkeBsa0EbL933ZsOqxdh6/iGPwuOoXa7wN301/hDr9PmxMjsvh/A6Jpndlx/ToVZZCjpYEZ1kqONvYiRFrjRMvuQoDeOur3Hy3usvViB9C5mRFJkRDGhYlUGrAvMcl0rFiEUi+jesilQixr14ftyL5+fWi3c4WpvnsVmuUGFmbISNuQkL+viy5Mhtlh69TYPKbtQsVcDgcxf481hb6p5FYrEIy09k58ViEdoPz6UFYweydNtBRs1biVarpU/bxvRu25i4hCROXLzF3sCL+uukUgnR8Yl5YiTvzsPy9O3sYMeB5TO+aNfHGKmWe3lqVCrNjeDH9GzdEP+JQ1mwYQ+LNu2nYe3qeFYpi8Undp+8codaVcp/UaYv5OUbhs1aTsfGdenZWle5aCIzRq4wXECTI1dgZiJj74kLiEQiKpbSVYOP6NmWWp2G8Sr8HU3r1qRp3Zr6a0b2bIdPt5FkZGUzY8U25o7ui5FR3mkoIyMpjWrXwK2QTgWif4emDJxquDXB6l0B7D15idUzRn2x8mjt3mNUq1CKKmVLfPF391u+CvxnsPpQMiAWizCX5SZMRCL0++TNbFmaNZfDmXDoKVqge81CdPUoRFy6nFNP3nMoOHdfI4lETGxqDnafyeQ19M+bwHeyMmFbH8PYxNbcmBVdKul/rlXcnqqFrLkTlkxyloIqhaypWND681tx6UUCbxOz9RJ1HaoV4ND9aO6Gp1C7xG8vHJJKRPiUsKd8Ad2Y6+ddhMbLbpIpV2Eu0/1uZB+SOT/5FKXJspsxL1S5AAAgAElEQVSkZiuRGYmRq3ITAjlK3f9NjMTMOPycofWKYWVi+PzSaHV7R33p2KccfRDDiotvmNmy7Bd9lUklBn1/7N/USIK1qRHz25Rl6fk3rLj4hvplHKnhaouF7H9qWvkfx8pYt0pGIgJzo9wVM2LgY25mqrcF6x9kMfVKOlqgc1lTOpczJT5Lw9kwOUde5sa5UrFuPyO7z5IczfblXYjnZC5mY1NDiTxbEzH+P+b+rXgWNKaykxF3oxW0LW3KYt/cY02Lm3DweQ6P41VIxVA+nxSvD9JyncrqZOkiUtW42er+Zm6+UzDnRgaDqppRt4gMjVaL360MBlU1x1ImBgzfg7Y8yqKgpYQi1rrrB7ub0+5QMhkKDb/ezmSilwVGks9WGQFdy5mSmqOhf2AKNjIxLUua8DZVd+8FNzMZ72WBpUyMpQy6lTdl79NsKjtJORmaw5rGeSUDf4vP/fkaOSrtV23+b+R/6ptA9Plytc9QqTW8jU1iZp9maLVw53k4Y1YeolZ5N+ytzBnQ3JuejTz054fHJBpI033k0tK8pe1f4n1yOsrPsvlSiQSpREJBR1tO3MyVblBrNES+T6bIJ7J5N0Le0ManssH15++9ICE1g6PXQ/RtnWduYkLXhthamrH19C1WjeqkP6ZUa7D8gub35xy9/ojF+y4wp18LvCvmrnjYeOIGcqWKwa3q6O6nUiERizGTGVHEyZa45NwA7uM+Ux/et1l//Dr7LwazclRHyhd14UuExSQwfm0Au6f20euuK5RqLL7DZoG/hm+PGzXh72KY+/NAtFottx88ZfjMJXhXq4iDrTU/dWlNn/a5EwhhkdEU+sIL//X9a77LnjcRUfw8byUHVs7Wr6BWKlX65MjT1+EMmryQTs19GdQ1Vy4hIysbt8IuBKz10/+8Yd8xSroV5kZwCEpVbkJXLBIhEYuRSiQULZif8KhY/bHwdzHY21pjZWHO+8Rk2jaqy5DuOqnJG8EhFMrviJmJjB1HTlOlbAnKldQFVgqlCtmHqsKihVx4GxVL8SK6hFh4VCyuBZw/nKdk5KylpKRlsH3xVIMgLy09kwGT/HCws2HTgkmYmfz2OJArFNx5+JSZowz3fotLSMbxkwlVqUSCSCRCIpEwa8UWShUtTIemP+ht/vh7FfjjfHMMqVSEhYWxcOFCtFotN2/eZNCgQdSpUwcHBweGDh1K//65e5SFhoZSpEjePRSCgoL+tK03btxg/fr1BjJ2CoUCKysrihYtSkaGoRSRRqNBq9V+9djp06eJj4/n4MGD+mMtWrRgxowZuLi48OLFC7p06WLQn0wmIykpCW9vb7p21UljhYWFoVQqcXV1BWDFihXs2rWLzZs3U7FibpXe+/fvGTJkCNOmTQNg7969lC5dmuvXr5OQkEDz5s0BkMvlaLVanjx5kicJ5+bmxuHDudr9arWaiIgIihYtypUrV/JUJBkZGSGVSrl48SJZWVk0bdpUf51ardZLBQr8cb49jtSEvY3Eb/pEtFott+4GM2TsJGp7euBgb8uQ/j3p272z/vw34REULphXPuf2+byV1r+XuPfxBs8U0E0cSqVSjpw4xZ17D5g7VZeg1Gi0qNVqLC2/XZEtlyu4HXSfOZPHGbTHJyTSrlUzhg3ULWS6fusuhQq6YGZqyvY9B6hSqQLlPySvFEqlfq+jxKRkpo0fhaWFru8lq9ZT6i/c+yguPt5grEilUowkutAi7n3eY1KphJwcOcvXbeanPt30dimUCv3zU+CP811xUHwqM7r6oNXC3VfR/LzxLF6lC2JvZUr/hlXp8UPud214XAoFHfJORF+Y2/277HkTm8zlx2/p7ZsbyyhVaoyNJDjZmpOZY/g9q9Zo9Ymw3+L43Vfcex3DtM66uESj1aLWaLE0Nebio3CuPY1k7alg/X1+mLidxf1+xNXJmlvPc+WOUjJyyMhWfNG/z5ErVQS9imZKp9/eN+1z5h+4TgkXO9p6ldH7bWGaN/lTJJ81ao2WHKUKC4nuuEajAa1ODi8qIQ2NRquPkd6+T6WFR0nkShUWJsZsH9PqwzVaWszeS8/6lfL0IfDH+a4YKSqWuaP76WKkh88YMWcF3u4VsLex5qfOzendNnfBQNi7GL003adc2738u+x5ExnN2AVr2b90mj5G+vguL1coMTczYa+/bu8+jUZDo36/0Kdd7oK4a0EhtG+UVxr7evBjxi1Yy5g+7WnToI6+vWjB/NwIzpWHTU5LJyMrm8L5HTly7tqXYyuphGMXb2JvY6Xfi0qhVCEWi3gZFkl0XAL9J/8KgFKpRqlS4d15GNd2L6eIixMZWblVk+oP75mgS5LPWLGVe09esc1v/G/K2p29fo+E5FQCzuXuydN++HQmD+5OEx+P3/RV4D/DN8eQRktEUjZTm5VCCwSFp/DLoSfUdLPD3tyYvt5F6OqRu+fx28QsCtjmXel/emSt77InLCGTK68S6emZu5BBodZgLBVz8UUCiRkKToTkzgv02HSPsQ1LkPRB7u9TpGIRUvHX/Stka0Z8eq4yg1qrRQRoga03IpCr1Ayoo6siUqg0SMQiTI0kFLEzIzIpS39dRFIWduZGZCnVPI1JZ/YJXRWU7vmhoaH/dbb2cf/qMWcrEzZdf8uh4Gj8O1agrMuXn39F7E2JSslBo9Ui/vD5RSRl0ayiM3KVBjNjKZt7VQV0z+C2q2/T3fPL+1IL/DG+NW7UGi2RaWomelmgBYJjlUy6nI6HixG2JmJ6VjCjc7nccRKRqqaAZd4KmuMd7PK0fYnwVBXXIhV0K587b6RUg7FERMh7JW9S1LQsmbuYWqnRYiyBQlYSnifmPie06P5mPr7pnQzNYeW9LCbVssCzgO4dKD5Lw/NEFfNu6OYd1FotcpUuGbaxqTUJWRrymeX6IhWBCHidrCY2Q83oczrlMpVGi1Kju+54BzsSszX0qGDGyBq62OPYqxyKfUhyxWdpUKpz3z+lYt1irevvFMRna+hwWFexLFfrxu+LRBXz6n1BcvAL/nyNl0mqr9r838j/lETet5CIRczcGsiRaw8RicDBygKRSISFmYzGHmU5ePk+YTEJaDRadp8Pot/Cnaj+hNRAxWIFSErLZO+Fe2g0Wm48fsOD1++oVcGNaqUKk5SWxfGbj1Gq1GwKvEnBfDYUza9bsa7RaHkWEUsFN8PEzMFZ/bm8bBSXlo7UJ7p2T+1DI4+ylCrkyPO3cZy+8xSVWsPeC/dQqzVULPZlfeKP3H8VyYLd51g2vL1BcgmggpsLBy/f5010AjlyJUsPXMK3WimMjaQ08ijHzSdhPHj9DqVKzZqjV6leuggWZjJO3X7KnvP32DCu628mlwAK5bMlR6Fi+5k7qDUaLt5/yfOIOGpXFDZQ//+CRCxmypINHDx9CZFIhL2tNSKRCCsLM5rU82Jf4HneROg2+t5x5DS9xs5Bqfzj2qGFXJzIkSvYcvAkarWG8zeCeBYajk+NyqSkpTN02iL6dWxukFwCSExOpcfPs3gbFUtWjpwlG/dQvWIZnB3s8KpagVNXbvPg6StUajVrdwfg4pSPIgXy06iOBycv3eTp63Ays7JZueMQTXx0q+6uBT1i9JzlZGZlE5+UwoptB2nbSCf1+C72Pb9u2E1qegbJqems2H6QZj/oXm4b1fFg477jJKakERkTx+5jZ2lST1f1MG/1dtIyMtk4f0KeFYRj568kv6M9S6eM/GpyCXQ65Q621uSzM1xRUcu9AnuPnyPsXQxyhYKlW/bhXa0iZiYyypcsytZDgcQmJJGanmFgs8B/DolEwoQJE9i/fz8ikQgHBwfEYjFWVla0aNGC3bt3ExoaikajYevWrXTt2vU/JrlWunRpnjx5wokTJ1CpVOzYsQO1Wk2VKlXw8vJCIpGwZcsWNBoNAQEBJCQk4OHh8dVjp06d4t69ewQFBemTYEePHqV58+YYGxuzcOFCgoKCUKlUejm76tWr8+LFC3r37k1CQgJpaWn4+fnRunVrjIyMOHbsGNu3b2fXrl0GySWAgwcPMm3aNBQKBeHh4axfv54OHTrQsmVLHjx4oLdjwIABNGvW7IsVXh4eHiQmJnLkyBEUCgWrV6+mcOHCFCtWDE9PT+7du8fZs2fRaDQcPHiQlJQU3N3dUSqVzJkzh9DQUBQKBYsWLaJkyZIULZpXYkLgr0UiETN5lh8HAk7oxpG9HWKRGEtLC5o18mXPwaOEhr1Fo9Gwfc8Bug8cjlL1nxlHNatVJfhhCOcuXUWj0XDo2ElSUtOoWrE8FcuV5czFKwTdf4hCqWTpmg2ULlmMQgV++13oI89fvcbB3i6PjN7Vm7cZOWEamZlZxCcksmzdJjq00lViRURFs2DpKlJS00hOSWXZ2k20aKzbu2/t5h0sXb0RtVpNyNPnHAg4QbsWTfP0+0fxrlmd9Vt3EZ+YREZGJivWbabBD7oJO2/P6ixfu5n0jAziE5PYuH03Der5YGIi4/rtu6zauA2lSsWr0DB2HwigeeMvSzYJ/HVIxCJm7rlKwK0XiERgb2mKSCzC0tSYhlWLc/DGM8LiUtBotOy58pgBK06g+hOyN+Ymxmw+95ALD8PQaLRcfBTOk4gEfMoXwaNkAcRiEbsvP0aj0XIy6DWJ6dm4F8//1XuWL5yPi4/CCQ6NQalSszowiJIudhSwt+Tqgl5cmNudC3O7s3Os7h3xwtzuVHZzpk65IgSHxnL7RRRypYpVgUHULlf4uyqYXkUnYW9l+k05vE8pWygfOy+GEJeSSWqmnDWn7tHEPW9sU8LFDjdnGzaeuY9KreHuq2iCQ2PxLlcIN2dbHG0s2HL+IUqVmuN3XpKaJce9eH5Uag0DVpzgUXgcSpWazecfYGliTEVXYS+ZvxOJWMzUZZs5dOaq7rn0IUayNDejad2a7Dt5mTeR0Wg0GnYePUfv8X55Fif8HgrldyRHrmDr4dO6GOlmMM9DI/CpXhGVSk3vCX48fK7b427D/kAszc2o/EG9QaPR8DT0LRVKuRnc8210HD/7rWbG8F55Ei51PSpz78kLbt5/glyhZPm2w9SpXhEzUxO8qpTn1NU7PHj2GpVazbq9x3FxtKeIizPJqeksWL+buIQksrJzWLJlP75e7lQtV5LbB1Zxbfdyru1ezsRBXalStrg+wdasnicnLt3iTWQ0WTly1u09jq+XrgJl4/5AgkJesPUrySWAgNWzub5nub4PgP3LptPEx+Orvgr8M0hEMDfwBccexiIC7C2MEYvAQiahQVlHDt+PJjwhC41Wy76gKAbvfPjnnkvGUrbdjODii3g0Wi2XXiTwLCadOiXs2d2/OmdG1eL0yFr6hNW2Pu40KOuIu6sNj6LSuPwyAY1Wy4lHsaRlq6hY8OuLFBqWc+R2WBKP3qWiVGvYcPUt7kVssJBJKediyeH7MYQlZJKjVLPy0ht+KOWAsVRM/TL5OPs0nhex6WTKVWy4+pYfyzjibGXCxTHeehsXtCuPk5WM0yNrffPYmafvOXAvitVdK/9mcgmgqIM5TpYytt+M1O2hFRJLao6KqkVsUKk1DN71kMdRaSjVGrbdjMBCJqVCgW8v1hD46xCLwO9WJidC5YgAOxMxYsDCWIRvURlHX+XwNlWFRqvlwPNshp9NRfknVAzNjUTsfJzN5Qg5Gq2WKxFyniWq8C5kjLFExJr7mYS8V6LWaDn4PBulGio5GlGnkDERaWouR8hRa7TsepKNg6kYNxsJj94rWXY3E796lgbJGCdzCac72XO8gx3HO9gxr64VjuZijneww8lcQnUXY468zCEiTY1CrWX9gyxquBhR2cmIU59cN7K6ORXySfWJmpOhcpbcyUCh1vIuTc2ep9k0K66bb6vuYsTmR1lkKDQkZWvY/SQbn8LGdCtvxsmOufes7yqjSznTLyaXfsufr1HR8es2/zfyP1XB9C1EIhFzB7Rgwa5zLNl3EWsLE8Z3+RFnOyuc7azo18yLMasOk5iagauzPf5D22HyndIJX8LB2oLFQ9rif+Aiq45cwcXBGr+Brchvrysh9B/Wjnk7TrNg11lKFnJk/oBcHeGUjCyy5UocrL9/DyIbSzMWD2nLgj1nmbfzDKULO7F0eLvf3KvpI7vPB6FQqhjiv9egff/0ftQo48rgVj4MX7afHIWS2hWLMaajLwDlXPMzq29z5u44TWxiGhWLuTC9l27iYue5u2Rky+k6e4vBPa8uH839V5EMX7afq8tHI5VKWDy0DfN2nGFT4A2KONuzdFi7PLKEAv8cIpGIheOHMHf1Nn5dvxsbSwsmDemJcz57nPPZ81PnVoyYtZSEpBSKFnJh+fTRBpuR/16MpFKWTRvJrBVb2LD3KK4F87Ni+hjsba3ZfewsCcmprNh+kBXbc6slpg7rTdN6Xozq05F+E+aTlZ1DzSrlmDdWJ8tXp0ZlRvXpyMRf15KakUGFkm4snTICiURM2RJF+bl/F36eu4KUtHTqelRhWE/d/i0tfWvz9HUYjXqPRiKR0KahD70+rEQc3qsD81dvo3n/cWg0Whr5eDCku04epkvLBrxPSqHdkElotVp6tG5MvZpVSc/M4vCZy0glUup2Gaq3v2q5Uozu24mb9x8jMzbCq/1A/bFm9byYMqw3sz7slTRlWG8AYt4n4GCXt1y3Y9P6JKWkMWCiHzlyOR6VyjFrtK46pnUDH2Ljk+gyQlf50aSuJ4M/S9QJ/PWIRCKWLFnCrFmzmDdvHra2tkybNo38+fOTP39+hgwZwuDBg4mPj6dYsWKsXbsWU9P/jA6vnZ0dq1atYvbs2UybNo2yZcuybt06/X5E27ZtY/r06SxfvhwXFxdWrlyJxYcqg68d+y0qVKjAtGnTmDBhAvHx8ZQuXZo1a9Ygk8nw9PSkTZs2tGjRArVaTcOGDZkwQbdB9ObNm8nIyKB1a8O/z/v37zNgwAAmTpyIl5cX5ubm9O3blyZNmnypewOOHj3K2rVrOXHiBCYmJqxdu5Zp06YxY8YMypQpg7+/Tv62dOnSLFy4EH9/f8aPH0+JEiVYt24dFhYWNGjQgIiICPr06UNaWhru7u4sXbr0d38OAr8fkUjEojlTmf3rMvyWrsLG2oop40aQ38mR/E6ODOrbg2HjphCfkIhb0cKsWjQX08/22fqrKF2yOH7TJ7J0zUYmzvSjuJsra5bMx8LCHAsLc+ZPn8jUuYtISkmhWuWK+M+b8c3ViADRsXHks88bVLRq2ognz1/i26ozUomEti2b0LurThpv1OD+zPl1GU3ad0ej1dLkx3oMG6B7Tvw8/CcmzphHTd8W2NvZMmnMcCpVKPunfB8w8hfcK1dgYK9uDBvQhxy5gjbd+oEWfvCpxZhhuufXtF9GM3fxchq17YZUKqVlk4b07Kx7tvrPm8Gshf54/dgSSwtzBvTsQh0vj691K/AXIBKJmNu9HgsP3cT/6B2szWSMa+uFk60FTrYW9GtQhbGbzpGYloWrkw2L+/2IifEfDxWdbMyZ3/MHlh+7y/TdVyhob8WvfXyx+yC5t3pwE/wOXGfd6WCcbSxY2McX829IvLk62TC9Sx3m7rtOSkY2lYs5M79X/W+OL0cbc+b0qMfiI7d4n5JJZTcnpnXOW8nxJWKSM3Cw/H3V3i08ShKXkkGvJQGATgKwf8MqANx/E8vIdae5PL8nIpEI//4N8Tt4g0ZTd2JpJmN6Fx8K2OsmLxb0rs+cvdfYfuERBRws+bWPr152b2ZXH2bsukJSejblXR1Z1O9HfaWTwN+DSCRiwdiBzFu7i1837dXFSD91xTmfHc757BjYqRkj564kISmVooXys2zKcEz/RMWzkVTK0slDmb1qBxv2B1KkgBPLpw7XS+7NG92fyUs2kpiSRsXSxVg2eZi+0ik5LYPsHHmehWkHTl0mO0fBZP9NTPbfpG9fNW0EVcuVxG/sQBZs2ENcQjJVy5Vg1khdJW2d6hUZ1bMdk5ZsJDU9k/Ili+I/aSgSiZiuzX1JSE6l8+jZ5MgVeFerwJTBPb7pn6+XOylpGYyYvYLElDS8q1VgTJ8OAGwPOEtGdjZN+o/Xn58/nz2HV87kxKVbbNgfyOGVM796/2/5KvD3IxKJmNmiDIvPhbLs4husTaSM+bE4TlYmOFmZ0NurCOMPPyExQ4GrvRkL2pUz2Jvo9+JoJWN2y7KsuvSG2SdeUNDGlPltymFr/vVnTwlHC6Y2K8W6K+HMOfGCog7m/Nq+vF7m7rcok9+Sac1Ls+D0K2LT5FRwsWJyU13FeTVXWwb6uDJm/2PkSg1exez0eyeVdrZk2A9uTA54RmqWEu8S9gys4/qH/QbYc/cdGXI1vbfcM2g/N9qbB5Gp/Lw/hHOjdXs/z2ldlvmnXrLjdiQFbEzwa1MOmVSMTCpmWrPSzDrxnKRMJeVdrFjQrry+0kng70EkEjHV24JldzNZdS8TK5mYETXMcTSX4GguoUcFU6ZcTicxW0thawlz61piIv3jn1E+MwnTa1uy9n4W829k4GIpYbaPJbYmYmxNxIysbsH8mxkkZWsoZitlbl1LjCUiHM0lLKhnxcp7mfjdzKCojZSZPpaIRCIOPs9BoYGfL6QZ9LWlmQ1O5r89xluWkJGSo+Hn82nIVVqqOBsx3vPbc+ady5my4GYGbQ4mY2YkomMZE+p9kLAbXcOc5UGZdDuaglQMDYvKaF/62zHkjsdZhLxX4feD1R/2538NkYuLy9e1CP4fEhUVRfrlTd8+UeBfg6VPHwoU+Hql1r+dqKgo5KG3/2kzBP5LkBXzEMbUZ0RFRX37JAGBTxDGUF6ioqJQp0R/+0SBfz0SGxdhDH2BqKgoUk8s+KfNEPgvwbrpOGEcfYWoqChyXlz9p80Q+H+GSanawrj5HURFRZGwqf+3TxT41+DQZ70whr5BVFQU0TO9vn2igADgMvXG//sx9a+SyBMQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBD48wgJJgEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAYHfhZBgEhAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEPhdCAkmAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBgd+F9J82QEDH2qPXiElMZXrvpn973w9evWPxvvO8jUvC0daSIa19qFu5BACXHrxi1eHLxCWnU9jJjjEd61O5eEGD6+88C2eI/17urv0lz70X7jmHlZkJA1t4/y2+CPy7WbXjENHvE5g9esDf3ndQyHMWrN1BRMx7nB3sGNmnI3U9qgAQ8iKUeau3ExYZTUm3wkwe0osSrobjaNuhk7wMjzSwfe+J82zad5zUjEzKlSjK5KG9KFow/9/ql8C/i+XLlxMVFcX8+fP/9r6DgoKYN28eYWFhODs7M3r0aHx9fQE4ffo0S5YsIS4uDjc3NyZPnkyVKrrxdfnyZRYsWEBMTAzu7u7MmjULZ2dnAE6dOsWiRYtISkqibNmyzJo1C1dX17/dN4F/DyvWbyE6Jpa5U8f/YzacvXiFnfsOs2X1En1bxLsops1bxKMnz3DKl4/xo4ZQx8sDgPOXr+G/egOxcfG4Fi7IhNFDqVqpAgCXr93Eb+lq4t7H41GtCrMnj8PO1uYf8Uvg38O6U8HEJGcwrXOdv73vB29iWRJwm4j3qTjamDO4aTV8yhcB4PrTSJYdu8P7lEwqFXViQgdvnGzMAThy8zlbLzwiJTOHki72/NLOCzdnWwB6LA4g/H0Kog991ChZgIV9fP923wT+nazeFUD0+0Rmjezzt/cd8vIN89buIvxdLCWLFmLSoG6UKGK4Sfm2I2d4Ff7ui/bdfviMgVMX8yBg/d9lsoBAHjZeCycmVc7kpqX+9r6fRqex+FwobxOzKO5oztgGJXDLp3vu3I9IYcm5UGJScyhsZ8qYH4tT1sWKrTcj2H4zQn8PjRbkKg1rulaiQkHrv90HAQGALY+yiM3UMN7T4m/v+/CLbFYFZyH9pMRmV0tbbE3ErA7O5PCLHCQfjhlLRAS0swPgRaKKJXcyeJumppClhNEeFpS2F9Iov4VQwfQvJytHwZhVh+jWoAYX/UcytpMv0zYdJyohhaiEFKZtOs4vXRpw0X8kXXyrMWblQTJz5PrrM7LlzN52Cq3W8L5ypYpFe8+x98K9v9kjAYG/n6wcOSNm+jOoWxtuHVzHhEE9GDd/JZlZ2aRnZjF0+mKa1PXkyt5VtGtUj0FTFpL1YRyp1Ro27jvG4k17DO557/EL1uw6wto547ixfw3u5UsxfenGf8I9AYH/OJmZmQwZMoS+ffsSFBTElClTGDduHJGRkbx7947x48fj5+fH/fv36dKlCyNHjgQgMjKSESNGMHz4cG7fvk3VqlUZNGgQWq2WxMREJk+ezPLly7lz5w6VKlViypQp/7CnAgL/WQ4dO8m4aXPQkvtiptFoGDZuCh7VqnL3wgkmjhnK6EkzyMrO5l10DBNmzGfquJHcPn+MHp3bMeTnyWRmZhGfmMS4aXOYPn40N84E4GBvx4z5i/9B7wQE/rNkyZWM3XyObnUrcH5Od8a09mT6zstEJaYTlZjGhG0XGNioKmdnd6NiUSd+3ngWrVbLo7A4Vp+8x699fDk3uxuepQsydvM5ANQaDWGxyRyf2onL83tyeX5PIbkk8K8gPTOLYbOW09SnJpd3+tO2YR0GT/c3jIEOBLJky/4vXp+Rlc305VvRfj7RICDwLyFDrmLswSc0KOvIyeGetKyUn9H7QshWqFFrtEw68pSh9dw4M9KLphWcmXr0GQA9PQtzbrS3/l+ryvn5oZSDkFwS+NcSmqxmQGUzTna01/+zNRHrj03xttC3f0wuZSm1TLyURutSpgR2sKN5CRNmXE3/J934f4+QevsEtUbD/J1nuBD8EpmRBI+yRZnQtQHGRlIeh0Wz7MAl3sQkoFSp+aFqSSb3aIxELKb5hNV0+qEau88HkZ6VQ+8mnpjJjNlw/DoikYixnWi6eb4AACAASURBVH3xdS/NsRshnL/3Ao1WS/DLSEoVcmR676YUcrQ1sEOlUrP22DUCbz1BrdHS2KMsQ1rVQSqVEPwykgW7zxKblEYBBxuGtfGhZrmieXypPSzvBEB+Oyv2zehn0PY+OZ1aFdxoUL0MADXKuFLI0Zbnb+OwsTClde1KuJcqDEBjj3L8uuccEXHJlCmiWx2+eN956lUtyc6zdw3uO9R/LwUcbKhXpeQf/0AE/itRqzXMXrmF8zeCMDYywqtqeSYP7YWxkREhL0JZvHEPbyKiUapU1PeqxvQRfZFIxDTqNZquLRuw48hp0jOz6NexOWYmJqzZfQSxSMT4Qd1p4F2DgLNXOXvtDhqtlqCQ55QpVoRZowdQ2MXJwA6lSsWqHYc5fuE6Go2GpvW8GNazHUZSKUEhz5m3ejux8YkUcM7HyN4d8KpaIY8vHm3652lzcXTg8Jp5Bm1mJjLObvPHzNQEtVpDcmoa5mamSKUS7jx8hqW5Gd1aNQSgef1abNp/nNv3H1PP053Ji9eRnpFJ24Z1kSuV+nu6ly/FiQ0LMTM1IStHTkZWNjaWf/9qD4G/H7VazfTp0zlz5gwymYxatWoxY8YMjI2NefToEQsWLOD169colUoaNGjA7NmzkUgk/PDDD/To0YOtW7eSlpbGwIEDMTc3Z+XKlYjFYiZPnkyjRo04dOgQp0+fRqPRcPfuXcqUKcP8+fMpUqSIgR1KpZLly5cTEBCAWq2mRYsWjBo1CiMjI+7evcvMmTOJiYmhUKFCjBkzBm/vvJWqH6uMPsXFxYUTJ04YtMXGxuLj40OTJk0A8PT0xNXVladPn9KwYUOuXbuGubk5CoWClJQUbGx0FRRXrlyhSpUqNGyoG18DBw5k3bp1vHjxAqVSiVwuR61WAyCRSJDJZH/+AxL4f49arWam3xLOXrqKzNgYL49qTPtllG4MPXnGr8vXEBr2FqVShW/d2sya9DMSiQTfVp3o3rEt2/YcJD09gwG9umJmasLqjdsRiUVMGjOchvV9OHz8FGcuXEaj0RJ0/yFlShZnztTxFClkuCpbqVKxYt1mjp08i1qjoXkjX0YM6qd7Dt1/yOxflxETG0fBAi6MHtyfWjWr5/HFvW7jPG0uzk4c27MlT7v/6g3cDX5Aj07teBDyRN/+IOQJOXI5A3t1RSQS4V2zBjvWLkMilhATG0e7lk2pXrUyAM0b/cjcRSsIj4gk5OlzqlaqQA133bHRQ/pTp3FbMjIysbAw/zMfkcB/AWqNBr8DN7gYEo5MKsGjVAF+aVcLY6mEJ2/jWXbsDmFxKSjVaupVcGVSR28kYjEtZ+2lY51y7LnymPRsBb3qV8JMZsTGM/cRiUT83MaT+pWKcvzOS84/Cker0RL8JpZSBeyZ2qkOhfJZGdihUmtYdyqYwHuv0Wi0NHIvxuAm1ZBKxASHxvDroZvEJmdSwN6SIc2qUbNUwTy++IzfmqfN2daCvb+0NWh7n5KJV5lC/FjFDYAaJV0olM+KF+8SSMrIpqKrIz9U0sVdvepXYtuFR7yKTuJ9ahbd6lagWH7dpER77zKsCgwiJTOHpPRsbCxMsDITnj//ZtRqDXNW7+D8zWCMjY3wrFyWyYO76eKjl29YsvkAbyKjdfMMnlWYPrQXEomYxv1+oUvz+uw8eo70zGz6tm+CmYmMtXuOIRaLGT+gMz/WqkbA+eucvX4PrVZD0OOXlHYrzKwRvb8YH63edZTjl27q4iOfmgzt3hojqZR7j18yb+1OYhOSKOCUjxE92+JVpVweX2p2GJKnLX8+ew6vnGnQ9uDZayzNTOnaQpdQbV7Pk00HTnL7wVPq1azCZP+NpGdm06ZBHRQKZZ57Ltywl/qeVdgecPbP/OoF/kdQa7T8euYVl18mYCwRU6OoLT83KIGxVMzT6DRWXgojPCELpVqDT0kHxjcuiUQsou3q27SvVoB9QVFk5Kjo4VkYU2MJm6+/RSwSMcq3GPVK5+NESCyXXiSg0Wp5EJlKSUcLJjUtRUFbUwM7VGoNG6695fSTONRaaFjWkYF1XJFKxDyITGHx2VDi0nJwsTHlJx9XPIra5fHFd/G1PG1OVibs7FfNoO3RuzQsZBI6VNO9XzYq78T2W5EEvU2mQgFrUrNVqDS6JUViMRhL8tYPPI5K4+yz93nuLfDvRK3RsuRuJlcjFRiLRVTLb8SoGuYYS0Q8S1Cy5n4Wb1PVqDRQu5AxP3uYIxGL6HQkmbalTDj4PIcMpZau5UwxkYrY/jgLETC8ujk+hWWcCs3hcoQCLfAwTklxOynjPS0oYCkxsEOl0bL5UTZnw+RotFp8XWX0q2yGVCziYZySZUGZxGVqcLEQ07+KGdXzG+fxpfHexDxtTuYStjTLq7QQmqLiB9cvv4eFJqsoZpM3rrn+TkERawkN3XTXNS0uo6SdFI1Wi1gkynO+gJBgMuBi8EveRCdwYv4gVGoNPy3ezdmg5zT1LM/EdUcZ2MKbpp7liUpIoefcbdx5Fo5nOV0AcuPxG/ZN78uT8BiGLNlL81oVOOE3mIDrj/DffxFf99IAXAsJZXKPRiwa3IZVR64wYV0AOyb3MrBj25k73HsRwbZJPZGIRIxdc5gd5+7Sq1FN5u88zeAPEnYnbj7Gb/dZDs/OKwd2dfno7/LZNb89M/s00/8cnZBKWEwixQo44Opsr08uAYS8iSJHodInxK6FhPLufQrTejfJk2Ca178lDjYWTN9sOIko8L/P+RtBvImI4vSWJajUavpNmM/pK3doXr8WY+evZEi3tjSvX4t3sfF0HTmdWw8eU8u9IgDXgh5xeM08Ql68YeBkP1r61uHsVn8On7nCovW7aeBdA4Ardx8yfURflk4ZyfJtBxg7fyV7lxkGNVsOBhIU8ow9S2cgFosZNXsZ2w+fok/7ZsxZuZXhPdtRz9OdY+evM3fVNo5vWJjHl9uHvl+OwczUhIysbGp3GIRGq2XmqH7IjI1RazSYyAwfiGKxmMiY9wCM7tuJfHY2enm/z+95+fZ9Rszyx9zMlM1+E7/bHoH/Xs6cOcPr16+5dOkSKpWKnj17EhgYSKtWrRg5ciTDhw+nVatWREZG0r59e27cuEHt2rUBXcLl+PHjPHr0iD59+tCmTRsuXbrEwYMH8fPzo1GjRgBcunSJ2bNns3LlSvz9/Rk1ahSHDh0ysGPjxo3cuXOHgwcPIhaLGTZsGJs3b2bAgAFMnz6dUaNG4evry5EjR5g5cyZnzpzJ48v9+/e/y+dixYqxYMEC/c/v3r3j9evXlCihk2s1NzfnxYsXtGrVColEwtq1awFdZYaJiYn+OpFIhFgsJiIiAl9fX2rUqEGbNm2QSCTY2tqyZ49hpaDA/yZnL10lNOwt54/uRaVS0XvwaE6du0SLJg0YM2kmwwb0pkWTBryLjqFj70HcvHsP75q658vVG3c4unszIU+f0W/YWFo3a8T5Y3s5dOwkC5atpmF9HwAuX7/FrEk/s3zhLJat2ciYSTM4sG2dgR2bduzhbvBD9m1Zg0QiYfgvU9m6az/9enRmht8SRg7qR30fb44GnmHWwqWcOrgjjy/3Lp38br+7tm/NyEH9OHz8lEGC6fnL1xRzLcL0eYs4d/kazk6OTBw9DJnMmOpVK+uTSwAPQ56SI8+hSKGCBASeoWiR3PdAG2trLCzMiXgXRdnSwgKi/3UuPnpLWFwKx6Z0QqXWMHh1IOcevKFJtRJM3K6r5GlSrQRRien09j/KnZfReJbWJXduPotkz7i2PImIZ9iaUzSrUYJjUztx9M5Llh69Tf0PSZrrTyOZ1MGbhX18WX3yHpO2X2Db6FYGdmy/+Ih7oTFsHdUSiUjEuC3n2HkphJ71K+F34IZewi4w6BULD97k4MT2eXy5PL/nd/ns6mTDjC4++p+jk9IJi02hWH5b4l9kYWKUGzqLRLp/UYnp+FY2XOx3/VkkDlZm2JibcPtFFGKxiD7+R4lKSqdSUSfGtvEkn7WQpP03cf5mMKGR0Zza5IdKpab/5F85fS2I5vU8GbdgHYO7tqR5PU/excbT7ec53Hr4lFpVywNw7d5jDq2YScjLMH6atpiW9WtxZtNCDp+7xqJN+/ixlm7i+GrQI6YN7Yn/xKGs2HGYcQvXsmfJVAM7th46TdDjF+xeNBmxRMzouavYHnCWPm0bM3v1DoZ3b029mlU4dvEm89bs5NjauXl8ubVv5Xf5/KUYSCIWERkbD8Do3u3JZ2ejl/D7lKtBj4iMec/MEb2FBJMAAJdfJhCekMWhQR6oNFqG737EhefxNCrvxNSjz+jn7Uqj8k5Ep2TTf9sDgsKT8XDTJXduvUliR99qPItJY+TeEJpUcObwYA+OP4pl+cU31CudD4AboUmMb1SC+W3Kse5KOFMDnrGpV1UDO3beecf9iFQ29qyKWCRi4uEn7LkbRbeahVh4+jU/+bhSu4QDpx7Hsfjsa/YOqJHHl3Ojv2/7CI1Wi4nUcGJeIhYRlZxD7RIONK/ozNgDj5GIwNhIwrKOeRfMLr/whj61imBlYvRdfQr8b3M1UsHbVDV7W9mi0mgZfT6NS28VNHCTMfNaBr0rmtHATUZMhppBp1K5F2tMDRfd9/idaCWbm9nwLFHF2AtpNHKTsbeVLSdD5ay+l4VPYV0i5la0kp89zJlVx5KND7OYcS2ddY0Nkz57nmbzME7JmkbWSEQw9Uo6+5/l0LmcKUvuZtKvkhnehYw580bO0ruZ7GiRN8F0sqP9d/ms1mgJS1Gz/1k2s6+nY2sipl9lMzwLGJOYrSFNoWVlcCZP4lW4WEgYWs2Msg5GhCarcLaQMP1qOvdjlRSxljCqhrmQXPoKgkTeJ1iYyngbl0Tg7SdkKxRsm9iTpp66F7tVozrS1LM8GVlyktIysTI3JTE1U39tmzqVMTMxpmrJQmi0WjrWc8dIKqFm2aLEJafpzytRMB+tvCthJJXwU8vavI6K5118ioEdx28+ZkALb+ytzLGxNKNvEy+O3wjR23j6zlOCX0bSsEZZDs3KW2HxR0lOz2LkigO0qFURV2fDwRr5Pplxa47wU0tvLExlpGXmsHjveab2bIyIvAPMwUaotPi3YmFuSvi7WE5cvEF2jpzd/tNpXr8WAOvn/kLz+rVIz8wiMSUVK0tzEpJT9de2a1wPM1MTqlUojUajpUuLHzEykuJVtTyxCUn680oWLUSbhj4YGUkZ0r0Nr8IjefchYfORo+euMbhrG+xtrbG1tmRA5xYEnLuqtzHw0k2CQp7TuG5Njq1fwF+BqUzGncMbWDljDHNWbuVV+DsqlylObHwSAeeuolSpCLx0k7DIaH21Uj67r+9l4Vm1PHcPb+T/2DvrsKqS94F/btEtImIhqCAimGBgrcXa3a6x5tq6tmIXJnatuXZ3d3e3YtDScC9cbv7+uO7FK+zqxvfnxvk8z3m8Z87MnHeOZ5jzzjvvO52bBTNg4nzUas1fIqvA3xdbW1tev37N/v37ycjIYOfOnTRrZphwW7duHc2aNSM9PZ3ExETs7e1JSMg2TLZt2xZra2sCAgLQ6XR07twZMzMzgoKCiImJMebz8vKidevWmJmZMWjQIJ4/f05ERISJHHv27GHAgAE4Ozvj5ORE37592bNnj1HGgwcPcuPGDRo1asSxY8f+svYnJSXRp08fWrVqhYeHhzHdw8OD+/fvM2nSJAYMGEBSUhJVq1bl6tWrXLhwAbVazerVq1EqlWRlZaFUKilUqBDbt2/nzp07Rg8sIdTKvx9ba2tev4vgwJETZGYq2b5uOU0a1APgp8VzaNKgHulyOYmJydjb2ZGQmD2+tGneCGsrSyqW9Uen09GxdXPMZDKqBlYgNi57nPEq5kHLJg0xk8kY0Ks7z1+9JiIq2kSOfYeO079nV5zzOOHoYE+fbp3Ye+ioQUYbGw4dP8XNO/doUK82R3Zu/NPtzuucu6KVli7nwpVr+HiX4MzBHXTv2Jb+w8eRkppmku9tRBSDRk9gQK/u2NhYk6lUYmlhutrPwsKCzI9CJQv8e7GxlPH2fSpHbr0kU6Vm3eCmNKhgMPov6fMtDSoUR56pIik9EzsrcxLTM41lm1f2xspcRjlPV3R6PW2CfAx6kVcB4lKy9adi+Z1oWskLmVRC7+ByvIxJJirR9L08dOMlveqXI4+tJQ42FnSvW4ZDN158kNGMY7dfcftVDPXKerJzdKu/rP3J8kyGrj5Ok8ASFHFxoJJXAW68iObK00g0Wh0bzzxAqdKQpdaalHv49j0zdlxiaLNKAOj1enwK5WV6l2/YM7YNdlbmjP/57F8mp8A/AxtrS95GxXLozFUylSo2zx1H41qVAVg5ZSiNa1UmXZFBUkoadrbWJH6kH7UOrmHQj3y90On0tG9U26AflS1FbEKyMV8J94K0qFcNmUzKDx2b8eJtFJEfjDm/sP/MZfq2b2LQj+xs6dm2EftPXQLA1tqSw+evcevhc76tHsD+5dP+VJvLeBcjNiGJ/acuodZoOHLuGq8jY43eSr+mA6XJFYSu3sakgV0RCRN5Ah+wNpfwLimTY4/ek6nSsrpLWYJ9DR56C9r6EeybD3mWhiSFGltLKYkKlbFs0zL5sTKTUKaQAzo9tCrvhuyDF9T7tOxvmmJ5rWnsnx+ZREyPau68ilcQlZJpIseRh3F8H1QEJ2szHKxkdKlSmMMPYgGwMZdy/HE8dyNSqOPjwtaeOT3Tfw+lC9gRl57F4QexaLQ6Tjx+z5vEDLK0OrQ6PdbmEua18eXk0CB6VXNn3L4nKD8akx5EphKTqqRhadc/JYfAvwdrMxERaVpOvM5CqYHlwfbU++ChM6e2HfU8zJGrdCQrddiZiUhS6oxlGxU3x1Imwt9Fik4Pzb0skEkMXlDvM7LzeThIaFjMcK27vxWvU7REp5t+Kx0Pz6KrnyVOlmLsLcR0Km3J0XBDX7SRiTj1Jot7cWpqu5uxsfGf2/s1TaXHO4+UpiUs2NbMkR7+Vky5mM67NC2pSh3+LlI6+Fiyo7kjDYuZM/psOqlZOtJVek6+zqJeUXN2tnCkcgEzxp9PR6MT5hJ+DcGD6SMqlSpK/+Y12H3+LrM2H8fPswATujakYF4H7r6Kot+C7Wh1OkoWcUWt0fDxa2VvbVhBLREbbHY2loZOKhaJTPYnKuCc3TnMZVLsrS1JSstWtADiktIYuXyv8YNKr9cbf0/v1ZQle84xfNlu9HroElyJLsGBOdpSc9CCHGmuTnZsnZD75p4R75MZELadciUKMbydaVzwh6+jGbJ4F61qlKVzPcO9Zm89QZta5Sjo4kh0QmpuVQr8R6lSrjQDu7Zm55EzTFuyHv+SxZk6tCcF87tw5/ELeo+djVarxae4u8FY8lH/sLc1rOaUfHDvtrE2uKSLxCKTSeGCri7G3+ZmZjjY2pCYYvoexiUkMXTaQsQf+uTH/Wj2qH6ErdvBkKlh6PXQvXUjurdumKMtVVv3yZHmmjcPu5bmrnBJJGIkEjFBFfwI8Pfh8u0HdGnxLQvGDyJ05Sbmrt5CcPVKVC7ni62V1WefJYCZzLDaqFe7JmzYfYQXbyLwKZ4zLKbAv4egoCCGDRvG1q1bmTRpEmXLlmXmzJkUKlSI27dv0717d7RaLaVKlUKtVpv0DXt7Q2xticSw2s3GxmDsF4lM+1ChQoWMv83NzXFwcDAxVIEhbN2AAQNy7UPz589n7ty59O/fH71eT8+ePenZM+eChwoVcoZjyJ8/PwcOHMi17W/fvqVHjx5UrFiRcePGmVyTfegLLVu2ZN26ddy4cYP69eszc+ZMpk+fTlpaGh06dMDT0xNbW1s2bdqESCTC398fgGHDhlGhQgWePXuGt7d3rvcX+HdQtVJFhvzQk+17DjBl9gLKlPZleshIChVw4879h/QcOAKNVksp7xKo1CqT7zR7O0N4rl/6kO2HPiQWiU3HoQJuxt/m5mY42NuRmJQ90QcQG/eeQaMmIBb/8j1n8HgAmDsthPlLVzFgRAh69PT8rj3fd26foy2BtRvlSMvvmo+9m758Tz6ZTIqbqyttWzQBoGH92qzasJk79x9Sq1oVAO4/esIPw8bQrmVTundqC4CFhTnKLJVJXUqlEisr03AxAv9OKnkV5IeGFdhz5Smhuy5T2t2FCe2rUyCPHfdexzFgxVG0Oh3eBZ1Ra7R83JF+CQeXrRcZVp6KPtWL8tgaf5vLpNh/YqgCiEuRM2rdqWy9CL1xcdv0zrVYcugmI9aeAr2e72r78903fjna8s2YnAZcV0drNg9vkWvbI+LTGLTyKGU98zOsucEIUMTFgQntqzN/71XSMlW0rlqSovkcsbHMXhV+4dE7QjadZVCTQKNXU3D5YgSXL2bM079RReqN34RcqcLGIueKXIF/J1XKlmLgdy3YefQ805dvwt/bkymDu1PQNS93n7ykz4T5aLVaSnoWQa02nWews/lEP/rwN/jTb7sCrnmNv83NZB/0I1ODbVx8MsNmLst1XAod3puwDbsYMmMJer2e7i2/pVvLnGFag9oPyJHm6uzEzkWTTNIc7GxYMKY/oau3MnfNDupXq0jlsj5G/e7XmLFiM+0a1qJQfhei4hJ+M6/Af4fAok70ruHOvrsxzD3+At8Cdoxt6EUBB0seRKUxZPsDtDo9Xq42qDU60z70wXtH8uG9tzE3TIOKRSKTfG4O2VERzKVi7C1lJCtMwze+T8ti7N7HfKjKpA9NburN8nNvGL37MXqgc6VCdAwsxKfUX3ApR1o+Ows2dC9vkmZvKWNmCx/CToWz+Ew4tUu6EODuiI25lLPPEnibmMmAbzwBaFOhALvvRHPjTQrVihsWHB199J56pVwwkwp+BQIGKuY3o2cZKw68ULLghgJfZykjK9vgZivhYbyGEafT0OqgRB4pKh0mc3V2Zob3yNiPZIZ/xSJM+5FN9vtmJhFhZyYi+SNDFcD7DB0TzsvJbQ1BSJANq+5mEHI+HT3Q3seS9qVyjhuNtiflSMtnLeanhqYGKUcLMQvqZu8/VrmgGWXyybgRraKltyXz6mRfa1jMEAbwYbwGqRh880qpUtDwrdbOx4JNjzJ5l6rFw1EwpeSG8FQ+IjI+Bf9iBWhWzZ/ENAVztp4kbOcZfmxXmxk/H2P9mO8oVsDw4dZh8lrTwl+4uiYhVW78rVSpSZFn4uJga5LH2d6aaT2b4FvUMHmhUGaRIs9Eo9XxNjaJyd0bodfD9advGLZkN1V9PShWMK9JHWfDBn9xu5++jaV/2Hba1CpHr8am7rpXHoUzasU+hrT+hmbV/I3pp28/58L9Vyzff9H4YVtz0AIW9G9FmeI5Y58L/HeIjHlPWZ/itAyuSWJyKrNW/Mzcn7Yysk8npixay+YFkyjubnhHWvc3nUD+0lVq8UnZXn/KLBUpaXJc8pjuZZbH0Z7QkT9Q2svw0aXIyCQ5TY5Gq+VNZAzTf+yNXq/n2t3HDJw8n6AKfpQoavoBeGnH8i+SJ/xdFD/OWMLOJVONk/FqtQZbayuyVCpsrCzZvmgKYAjpVb/rUL5vk3PS8GP2nbzAjftPmDrUEAJTp9ej0Wqxtfkyw5TAP5eIiAjKlStH69atSUhIYNq0aYSGhjJ27FhCQkLYuXMnJUoYwlM1bdrUpOwX96H47BWtSqWS5ORk8uUzjdPv7OzM/Pnz8fMzTNbJ5XKSk5PRaDS8fv2a2bNno9fruXLlCn379qV69ep4eXmZ1HHz5s0vbvejR4/4/vvv6dSpE/379zemX758mVWrVrF2bfa4q1KpsLOzQy6X4+npyZEjR4wyrlixAm9vby5evIj6o33NxGIxYrHYaKgS+PcSERVNWT9fWjVtSEJiEjPmLWbOwuWMHjqAiTPnsX3tcop7GiZ/m3cy3Zvyi/tQQnY4H6Uyi5SUVFzyOpvkcc7jxJyp4/ErZdjnUqHIIDk1FY1Gy+u3EcyaOAa9Xs/VG7fpN3ws1SoHUqKYh0kd104d/N3t/5QihQshV5guZtJqtcbvt4tXrzN0zGRGDOpLq6bZiy08ihTm4tXsEMjJKanI5QoKFzTda0rg30lUYhr+RfPRrJIXiemZzNtzhYX7bzC0eSVm7rjEuiFNjHsOdZyzx6Tsl/ajxLQM42+lSkOKQonLJ6Hj8thaMa1zLUoVMeg6CqWKFEWWQS+KT2VSxxro9XDjRTQ//nSCKt4FKeZmuufF6emdv7jdTyMTGLjiGK2DStKzfnZoJLlShXs+B7aPamU8X3fyHsXdDBN5B64/Z/7ea0zpVJMgn+zQkodvvsDJ1tK4N5Rao0UsEiHLZa8MgX8vkbHxlClZjBb1qhv0o9Vbmbd2ByN7tmPK0o1smjuO4kUMf1vbDDI11HypE09CUvZiu2z9yHSiLY+jHbOG96J0CcNYo8hQkpyWbtCPomKZPrSHQT+694RB0xYTVL60UW/7hYtbFn2RPFkqNdZWFmxbYAjTp9PpCO4xku6tGvxmuVNXbnPh5n2Wbd6H7sNK8aD2A1g4fiDlfIp/0b0F/n1EpWTiV8CeJv75SVKoWHDyFUvOvGZwbU9Cj73gp+/K4pHXMH50WXvLpOwX9yF59qKaLLWWlEw1zramCwHyWJsxqYk3Pm6GBUmKLA2pmWo0Oj3vkjIJaeSFHrj5JoWRux9RycMJz7ym49qxwVW/SJ4sjQ4rMylrP4Tp0+n1tFx2jc6VC/EkOh211nTSXioWIRVnN/ZKeBKTm5T8ssYL/CeITtfim1dKw2IOJGXqWHxLwfI7GQyoYMW863KWB9tT1MFgJuhx2DTS1pf2o8TMbHNTlkZPapYeZyvTbx4nSzHjq9pQ0tmgl2eo9aRmGTzzItK0jKligx64Hatm7Ll0At1kOYw6B9vk3N8sN96kargYoaKTb/Y8mlprMH49eK8mPEVL0xLZxmW1To+ZBArZSXiamB09SI+hDwr+S7+O8GX7ETeevmHsqgMkpSmwt7L44GFkFStnigAAIABJREFUgSLTMNBYyKRodTr2XrjHi6j3aLTaz9SYk4evYzhz5zlqjZbl+y5Q2sMN1zymm9kGB/qw8sAlUuSZKLPUTNt4jNDNJ5CIRUxef5i9F+8hEoGznQ0ikQibP7FpbIo8k0GLdtLt28o5jEvv4pIYuXwfIV0amBiXAC4tGcbZsMGcDRvMlhCDV9TZsMGCcUmAq/ceMTJ0GYkfQjyYmcmwt7VGkZGJSCTCwlyGVqtj19GzPH8dgVr7+0O+PXj2ilOXb6JWa1i8cRelvT3J72I6sdewZmWWbdpDSlo6mcosJi1ay4xlG5CIxYyfv5pdx84iEonI42iPSCTC7k8Ybgq55UOZpWLdriNotTpOXb7Jk1dvqBFQBo1GS9cR07j35AVqtYbV2w5ga21FmZK/rSD5eXly8tJNbj54ilqtYdH6nXh7FDHx3hL4d3LlyhWGDh1qDIFnbm6Ovb09crnc0IcsLNBqtezYsYNnz56h0fz+PnTv3j1OnDiBSqUiLCwMf39/3NzcTPI0btyYRYsWkZycTGZmJiEhIUyZMgWJRMLo0aPZsWMHIpEIZ2dnxGIxdnZ2v3K3z5OcnEzv3r3p06ePiXEJwNvbm0ePHnHo0CE0Gg0///wzWq2WsmXLkpCQQPv27Xnz5g0ZGRmEhoYSGBiIq6srQUFBHDp0iNu3b6PRaFi6dCkFChTA3d39D8sp8M/g6o3b/Dh+ColJydjb22Fuboa9vR1yhQIRIszNzdBqtezcd4jnL8P/UB+6/+gJJ89eQKVWs3DFGvx8fXBzNTXSNqpfhyWr1pOSmkqmUsmEGXOZOjsMiUTMuCmz2LnvkKEP5XFCLBJja/u/CS9cJaA8YrGYDVt2otPp2H/kBAmJyQSWL8ubd5EMHj2RqeOGmxiXAL6pXpWbd+5x+dpNsrJULFi6iprVqmAteDD9J7jxPJpxG8+QlJ6JvZU5ZjIpdlZmKJQqEBk8jrQ6HXuvPuNlTBKaTya6voSH7+I5c/8Nao2WFUdv4VvEBVdH034QXN6TVcduk6JQolRpmLHjEnN2XzboRVsvsO/qM0QiyGNriUgswtbyj3sFpSiUDFl1nK51/E2MSwBJ6Zn0XHSQd/GpZGapWXTgBuWL5SefgzV3wmOZvfsKC3rVMzEuASTLlczbc5W4FAUZWWoWHrjBN/7umMuEdZ7/Ja7de8KoOauM+pG5zKAfyTOUiBBhYWbQj3YfP8/zN5FoNL9/nuHB83BOXbmNWq1hyaa9lPbyIH9e09CpDWpUYvmW/aSkycnMymLykg3MXLkZiVhMyMK17D5+wTAufdCPbK3/uH6k0WjpNnoW956+MuhAOw4bdCBvz98sd33nMi5uWcTFLYvYsXAiYDBqCcal/za33qQw4cATkhUq7CykmEnF2FlIUag0iAAzqRitTs/+ezG8eq9Aq/3908CPY9I59zwBtVbHqgtvKeVmi6udhUmeuj4u/HTpLamZapRqLaHHXjDvxCskIph++BkH7sUiAvLYmCEWgY25JPebfQEarY4fNt/jYVQaaq2ODVfeYWMupXQBO8q7O3A/Ko1zzxPQ6fUcuh9LWqYGv4IGfSxJoSJRrsLLVdi6QiCb23FqplySG0LgmYuMHkYKtd7QjyQitDo9h14qCU/WovkD1pQniRouRGSh1upZcz8DH2cp+axN+0Edd3PWP8gkNUuHUqNn7jU5YTcUiEUw66qCQ6+yEAFOFmLEgI3ZHw+Xai0TselhJufeZaHT6zn/LosniRqCCplhJhGx/I6CB+/VaHV6dj3NRK0FfxcZ1QuZ8S5Ny7l3WWh1ejY/ysTZUoyHwx/v0/92hC/bj2hS1Y8XkfG0mfgTao2WciUKE9LlWxxtrehQpyLfTd+ASCTCz9ONOuW9eR2T+PlKP6FEQRf2XbzPxLWHKO3hxvSeTXLk+b5BFZbuPU+HyWvIyFJTvkRhJnRtgEgkYnqvJoRuPsn87Wewt7FgVIe6uDr98Um9Y9cfk5imYPn+Cyzff8GYPqZTfZ69iyNTpWLiukNMXHfIeG3hwNaULZ7T1VdAAKB53Rq8eB1Biz6jUanVVPAryaTB3+Nkb0enZvVpP2giYrEIP+9i1AuqyOt30Z+v9BO8PAqz59g5xs9bhZ+3J6Ejf8iRp1f7pixcv5NW/caRqcyiQmlvJg/piUgkYvaofkxftoE5q7bgYGvD2H5dcM37ZZsE5oZMKmXhhMFMWbyO1dv2414wP4snDiOPo8HddsbwPoydu5LE5FT8SxZj0cQhRk+nX6NoITemD+vNpIVrSE5Np7yvF3PHDhBikf8HaNmyJc+ePaNhw4aoVCoCAgKYPn06Tk5OdO3alVatWiESiShbtizBwcG8evXqd9/D29ubnTt3MmrUKMqUKcP8+fNz5Pnhhx+YP38+TZs2JSMjg4CAAGbMmIFIJGL+/PlMmTKFGTNm4OjoyIQJE8ifP/8fbvOhQ4eIj48nLCyMsLAwY/qkSZNo0qQJS5cuZerUqUyYMAEfHx9WrlyJhYUF7u7uDB8+nC5duqBQKKhSpQqzZ88GoGbNmgwfPpwRI0aQmpqKn58fS5cuNYY+E/j30qLxtzx7GU6T9t1QqdQElC/DlLHDcXJ04Lv2rWjTrS9ikYgypUtRv3YNwt+8/d338Cruya79hxkzeRb+viWZO3V8jjx9undiwbKfaN6xBxmZmVQsV4Zp40ciEomYOy2EqXMWMitsKQ72dowfMYj8+f43CwisLC1Zt3Q+k0Pns3jVOvK7urAodArW1lYsWb2ezEwloyfPZPTkmcYyK+bPokJZP+ZOC2H6vMXEvY+nfJnSzJgw+n8io8Dfj8aBJXgRk0y70N0GvahYfsa1DcLRxpL2NXzpOn8fIrGI0kVcqO1flNfvUz5f6ScUd3Ni//XnTN56Ht8iLkzrXCtHnu51y7Ds8E06zdlDRpaGcsVcGd+uukEv6lzLYNjZfx17K3NGtKxCPsc/Ppl2/HY4iemZrDhyixVHslfAj25dleDyxRjQqCI/LDtChlJNgJcbkzrWBGDb+Ueo1FoGLD9qUt+2kS1pV70UiWmZdJm/jyyVhiolCzK69ZetXhf499CsThDP30TSsn8IKrWGCqW9mDigK072tnRqWocOw6YiFonx8/agbtXyhEfGfL7ST/AqWog9Jy4SEraW0l4ezBreK0eeXm0bsmjjHloPmkSmUkkFXy8mDeyGSCQidHhvZqzYzJw12wz6UZ+OuOb9shXiuWFtZcGMoT0ZN/8nElPS8PP2ZOG4AZ/VgQQEcqOhnysv4xV0+ukWKq2OsoXtGf1tCRytzGhbsQA9NtxBLAJfNztqeeflTWLG5yv9hGIu1hy8H8u0Q88o5WaXq/dP1yqFWXn+DV3W3CJTraVsYQfGNiiBSCRicpOSzDv5ioVnwrG3kDKsbjHyfWKg+j1Ym0uZ0MibKYeekqRQ4+tmR2grX8QiEcVdbAhp5MXK82+YdugZRZ2tmdPaF+sP4f9iU5XYWUoFb1kBE771MCc8WUu3gymotVAmn5ThlWxwsBDTytuSvkdTEYmglLOUGoXNeJv6+xc7eDpKOPwyi1lXFJR0ljI+KOd3WSdfS366l0GPQ6lkavSUyWcI1ScSiQgJsmHhDQVLbymwMxczKMAaF+s/rr/ntZIwsZotK+5kMPOyHDdbCVNr2OJoIcbRQszgijbMvCInKVOHp6OU6TVtMZOIcLGWEFrLjiW3FMy6Iqeog5TJNWyF+bjfQOTm5vaP8/CKiooi/dyary3G7+bA5QccuPyAlT92+Nqi/OuwrdGdAgWEkC2/RVRUFFmvrn1tMf40+05cYN/JC6yZNeZri/KvxtwzUOhTnxAVFfW1RfhL2L17N3v27GHjxpx7Ugj8tQh9KCdRUVFoU37/woK/E3sOHmXvoaOsX5Zzv0uBvw6Jg5vQh3IhKiqK1EOhX1uMP83B6885eOMFy/vl3ANT4K/DvuEIoR/9BlFRUSifXfh8xr85+05dYv+pS/w0fcTXFuVfgYVXNaHf/A6ioqJIWJNzL9Z/EocexHLkQRyLO/h/PrPAZ3HuvkroQ58hKiqK6MlVvrYYfylHXyk5Gp5lsueRwF+DW8jlv32fEszZAgICAgICAgICAgICAgICAgICAgICAgICAr8LwcAkICAgICAgICAgICAgICAgICAgICAgICAg8LsQ9mD6f6RxldI0rlL6a4shIPCPpmndajStW+1riyEg8I+lRYsWtGjR4muLISDwj6V5o2CaNwr+2mIICPyjaRRQgkYBJb62GAIC/wqa1q5K09rC3l4CAn+UhqVdaVja9WuLISDwjybY04Jgzz++75jAPxvBg0lAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEDgdyF4MP0GFXrNYv/0Prg5//9vUPYqOp7QzSd5FhGHvbUFXb+tRPNqZQC4+yKSedtP8TYuCRdHW/o1r0HNMsUBiHyfzLSfj/HwdTR5HWwZ1uYbqpb2NKn75xPXeRkZz8RuOTfVvf7kDf0WbOPGipEArDl8hbVHrhiv63R6stQafhrZEX/PgrnKHpWQQscp6zgbNvhPt0fgn41fg+84snYuBfLl/WoyPHj2itGzl3Nw9WxjWnJqOpMWruHa3UfY2ljRr3NLmtap9tlrb6NiCVmwmqev3lLYLR8TB3anVAmPP1XuUxat38nu4+fQaDRUq1iG8f27YmlhTroigxlLN3Dp1gPEEjH1qwUw7Pv2yGRSYhOSmLxwDfeevMTSwpy2jWrTs22T/+VjFfhKeHl5cerUKQoWzP3v7/+SmJgYxo0bx71797C3t6d///40b94cgGfPnhESEsLLly9xdXVlxIgR1KhRA4B3794xfvx47t+/j4uLC2PGjDFe+4W1a9fy7NkzZs6caUx7+PAhEyZMIDw8HHd3dyZNmoSfn18OuZ4/f07Tpk2xsMheLTVz5kzq16/PmTNn6N+/P2ZmZsZr69evx8/Pj59//pmZM2cik8mM106ePEmePHn+mgcm8LfBJ7AWJ/ZsoYDb11uZev/RE0aETOPorp+NabfuPmDWgiW8fhtBPpe8DPmhB7VrBJmUexn+hlZdenFo2waj/Ddu32Xa3EVERcdStEghxg0fhF+pkgDs2HuQ1Ru2kJySincJT0JGDKGYhzsAq9ZvZsvOvWQqs2hYvzYjBvXF7KP3/xdu3L7LjPlLeBcZhauLC8P696JWtSpfLPO6zdt5/jKc6SGj/rLnJ/D3IWDoT+wd1wY3J9v/93u/ik1mzq4rPItKxM7KnK61/WhW2RuA7Rces2D/NWSS7PWTe8a2wcnWktP3XrPsyC3epyhwz+fAsOaV8HPPZ1J3eGwy383bx/ZRLY1tu/0yhjl7rhCTJKewiz0jWlShVBHDN+3OS0/YcPoeaRkqShZ0ZlTrKhRxccgpc0wSHefsxVwmMaZNaF+db/yL8vZ9KjN3XuJpRAIFnG0Z2qwS5Tzz/+XPTeDr49+kB4dXzaRAPuevJsOD5+GMmbuaAyumA3D70XN+mBRmkidTmcWATs3p0aYhNx8+I3TVViJi3+Pq7MSgLi2pGVDGWNeMFZt5ExlLiaKFGNu3E8WLGDYfP3P1Dgs37iEuIYkiBfIxokc7yvoYdPvth8+wZtcRUuUKfIq5M75vZ9wL5hybK7XpZ3KuUqmp6OfNislDjWl6vZ4eY2dTwdeLvh2amuSPjI2n3ZDJXNyy6E8+NYG/C1VnnWdnnwDy2///e0e8ilcw5/gLXr5XYG8ppUvlwjT2N/ytTs5QMfXQM+5FppHHWsaQOsWo5OFkUj5LraXLutt0rlTI6CX1LimD2cde8DRWTgEHCwbX8aRMIQfuRqTy444HJuUz1Tp6VXenS+XCxrQkhYrOP91iSrOSlCucc+zRaHUsOhPO6afxaHV6Knk4MbRuMWzMDVPAm69FsPVmFCq1jkqejowOLoG5TIIiS0Nw2GXMpdljaY8gd9oF/P/rngJ/LbU2JbKlqQOuNpLPZ/6LCU/WsOCGglfJWuzMRXTytaRhMUNfztLoWXBDwcVIFTIxtPa2pH0pSwCuRKoYfz6djz6hmF/HHu88UlKVOuZck3M7VoONmYhu/pYEexjqfJKgZuFNBe9SdXg6ShgSYE1RB8O7fzFCxep7GcQrdBS0E9O/vDWlXXLqQ3KVjjnXFNyOVWMugRZe2XKlKHXMvCLn/ns1TpZiBlawJsDN7LPt+bcjeDD9TRm+bC9Bfh6cmj+Q2X1bsHj3ee6+jCRDqWLY0t10qhfAmQWDGd6uDhPWHCQqIQWdTs+wpbup4FWYc2FDGN6uNqNX7iczSwWAVqdj3ZGrLNx5Ntd7yjOzmLrhKHp9dlr3BpW5sGio8WhZowx1ynv9qnHpQXgUvedsQZ6Z9afbIyDwZzl//S4/hMxBo9GapI+du4I8jvac37qUsJDBzFi2kYiYuM9eGz5zCTUCynBx+zI6NqnHoClhqNTqP1XuY85cucXZa3fYs2w6R9fOIy4hiXW7DgMw76etZKnVHFk7l11Lp/HweTjrdhuujZ+3kmJFCnJu6xJ+nj+BbQdPcfXuo//NQxX4zzJ16lRKly7N9evXWbhwIRMmTCAiIgKAkSNH0qpVK27dusXw4cMZOHAgSqUSnU5Hv379qFSpErdu3WLcuHEMHjyYjIwMALRaLStXriQ0NNTkXnK5nD59+tC5c2du375Nu3btGDx4cA6ZAJ4+fUrNmjW5c+eO8ahfv77xWvv27U2u/WKkevr0KT/++KPJNcG4JPC/4NzFK/QePAqNVmNMU2RkMmDEOLp1bMO1UwcY++MARk2cQWR0jDGPRqNl7NRZqFTZ44VWq2XQqAmMGNiX66cP0rxRMMPGTgbgzv2HhC3/icWzp3LlxD6CKgUwYMR4AA4eO8nP23ezYsEsTu7bSkxsHHMXrcgha0ZmJv2Hj6N/z67cPHOYccMHMmzsZBSKjM/KrNVqWbV+M3NyqVdA4K9g5NpTVPUpxImpHQntVpslh29y77XhW+tFdCL9G1Xk3MwuxsPJ1pLopHQmbTnPhPbVOTezC62qlmTMhjMm9Wq0OqZsvYDqo+9FrU7HyPWnGNQkkNPTO9M4oDhjNp4G4E54LKuP32FR7285Pa0zZT1dmbrtYq4yv4hOIsinkIlc3/gXRavTMWLtSbwL5uH4lI4MbBzI8DUneZ+i+B89PYH/Mudv3KffpDA02ux3vFypElzdvsR4zBzWk8Ju+WjbsBYZyiwGT1vMDx2acmXbEkb16sDI0JUoMpSkKzIYMGURDWtU4tymBbSsX50fJi4gQ5lFZGw84xasYWzfjlzcspBOTeoyaNpiFBlKbj96zvKtB1g+eSiXtiyiQqkSTFy8Pld5P5Zr9+LJODnYMug70/DOm/af5PbjFznK3n/6ih5jZ5OuyPxrH6LAfxK9Xs+YPY/4xjsvxwdXIbSlLwtOvSIiyfB+hR59gZuDJUcGVmZInWJM3P+UJIXKpI5l594QlZz9Pmp1ekbvfoxXPlsOD6xM/1oejNr1mPj0LMoUsufk0CDjMaFxSQo5WtKynJtJnaHHXpCmzDmf8AubrkfyPE7Oxu4V2NE7gEyVliVnwgE49SSePXdjWN7Rn90/BJKSoebnawad7lW8Ag9naxMZBOOSwJ9Br9cTciGdmkXMONjGkek1bVl8U0FkmmE8WnpbQVqWju3NHFla355dzzK5G2d4t1+laGhawoIjbfMYD+88BkPRjCtynCzF7G3lyNQatiy8oSAqXYtcpWPM2XRqu5uzr7UjjYpZMOJ0OpkaPTFyLTOvyBlc0ZoDbRxp5W3JuHPpZKj1OeRe/yATS6mIXS0cCatrz46n2XLNvSYnv42Yfa2cGFjBmimX5CRl6j7bnn87/wkD08jle1lzONsL58nbWOoOW4RGq+Ph62h6zd5MnaELqTFwPpPWHUKr05mUv/nsHY1HLzOeRyekUqHXLOP51cev6TB5LTUHLeCHeVuJfJ+cqxxtJqym2oB5OY5PSZFnUiivAx3rBCARiylRyIVyJQrxMDya98npVC3tQb2KJRGLRQSUdKeQiyNP38ZxPzyKLLWG7g0qIxaLqFzKg9UjOiIWG/6bJ649xN2XkTSr5p+rfPO2n6JWuV+PhX7/VRTHrj9hTKfc9x24+ug1Y1btp0tw4F/SHoG/D8OmL2LVtv3G88cvXlOjfT80Wi0Pnr2i24hp1GjXjyqtejN+3iq0WtM+dOP+E4K7Zq84i4qLx6/Bd8bzK7cf0rr/OKq27kPPMTONhplPad5nNIEteuY4cmPn0TPMX7ONbq0amaTHJiRx+9FzhvfsgEwmpaSnO5vmT8DJ3u43r4W/iyIy5j1dWjRAJpXSrF517GysuXb38R8u9ylvo+PQ6XVodYYBTiIWY25mWE2h1+vp1a4pVpYWONnb0aBmZe49eQnAkknDGNi1NVKJhNQ0OVqdDlur/8YqiX8qAwcOZPny5cbzhw8fUrlyZTQaDffv36dTp05UqlSJ8uXLM3r0aLRaUyPptWvX+Oabb4znkZGReHl5Gc8vXbpE06ZNqVChAl27duXdu3e5ytGwYUPKli2b48iNt2/fotVq0el0iEQiZDIZEonEeE2tVhuvmZubA3Dnzh2USiV9+vRBLBZTrVo1tmzZYiw3cuRIbt26RevWrU3udfr0aTw8PGjWrBkikYjWrVuzcOFCdJ+Mz2AwFHl7e+cq8+euffzMBP7+DB49kRXrsj2AHj15RlBwczQaLfcfPeG7PoOoWr8ZAd80YszkWTn6zfVbd6nTrJ3xPCo6Fp/AWsbzy9du0rxTDwJrN6J7/2G8i4zKVY7G7bpSvua3OY7c2LH3IHMWr6DHd+1M0uPex1O9SiDf1v0GsVhM5YrlKVKoAI+fPjfmWbV+E+X8TffuTEuXk5KahlqjQa/XIxaLMTc3rJiLi0+gW8e2FPcsikQioWPr5ryNiCQlNZVT5y7SvlUzinsWxdrKkj7dO7P/yAn0elOFysrSktMHdvBN9apotVqSk1OwtrZCKpV+VubRk2dy+94DWjXN6SEv8Pdj1PpTrD1513j+JCKB+iGb0Gh1PHobT+/Fh6g3fhO1xmxg8pbzOfSjWy9jaDplm/E8OimdgKE/Gc+vPYui45w9fDNmI/2WHSEyIS1XOdrO2kWNUetzHJ+SolBSyNmWDjV8DfpEgTyU88jPw7fvAYMhp7ibU45ybk62HJnUAd8iLqg1WlIVWdhbmZvkWX/qHv5FTT2a0jNUpCqy0Gh16PUgFokxlxrGrrIeruwe05oiLvZkqTXIlSrsrU3r/IXnvyLX2/epRCel069hRWRSCQEl3PBzd+H0/de51iPw9+DHmctYvf2Q8fzxyzfU7DzEoBM9D6f76FBqdhpM1XYDGB+2JqdO9OAp3/YYaTyPikvAv0kP4/mVO49oM2gSQe0H0Gv8XCJi3ucqR/N+IVRq0y/HkRu7jp1n/rqddGvx63sHyjMymbxkA5MGdsXW2gorC3OOr5lNzcAyaLU6ktPSsbayQCqVcPfJS2ytLOnYpA4yqZTGtSpjY2Vp1Ila1KtGBV8vxGIxDWtWAuBtdCzlSpXg4IrpuBdwRalSI8/IxMHW+rPPfMqSDbRtUAufYu7GtDdRsew6fp5vKpUzyXv5ziNGzllJt5a5j8kCX59xex+z/kq2XvI0Np2Gi66g0el5HJ1Gv833aLjwCvXmX2LaoWdGvfgXbr9LoeWya8bzmFQlVWedN55ff51Ml7W3qL/gEoO23icyOXdDY8fVN6kz72KO41NEIhHrupan1QcDT5pSjVQswkImJkOl5dLLRLpXLYxMIqaShxN+Be04+yzBWP7OuxQeRafhW8DOmPYuKYOYVCV9ahZFJhFTwd0R3wJ2nPmoHIAiS0PoseeMblDC6HkEcPRhHGKRCBfb3McdMHhNda1cGAcrGdbmUhr6ufIwyjAO778XQ/eqRXBzsMTKTEJII28afPCsevleQTGXz/dLga/HxAvp/Pwww3j+LFFD851JaHV6niSoGXQilWY7k2i0PYlZV+Q5+tDdODXt9mbPWcfKtdTalGg8vxmjosfhFBptT2LYqTSi0k31qV/oejCFb7cl5jg+RSQSsaqBA81LGLyL0rL0SMQiLKQi1Fo9x19nMbCiNZYyEa42EsLq2lPUwfC99TJZi6djTo+r+Awt99+r+aGcNTKJiOJOUpYG2+NoIeZhvAZrMxGtvC2RikXU8zDH2kzErRg1cQodDYuZUyafDLFIRN2ihj4UkZazjZFpWrR6PXpAJAKxCMwkkKnWczlKTZfSVsgkIgLczCidV8r5CNVn2/Nv5z8RIi840IdVBy7RvUFlAI7feEKd8l5IJWLGrNxP7yZBNKzsS1RCCl2mb+D6kzdULpV7+KpPiUpIYeTyvczu25xyxQux9cwthi3dzZaQ7ojFIpO82yf1+JVaTHGwsSRsYPZkmzwji3svI2lZvQzu+fMwuXv2hHl0QiqvYxLxLODM9SdvKZo/D9N/PsaZO8/J52jH8HZ1MJcZ/psHtayFs4MNK/ZfJCYx1eSeFx+8IvJ9ChO6NWDTiRu5yrVgx2l6Nq6KnXXubsneRVzZPaUX8Sly4MSfbo/A34cGNSuzfPNeY9i1o+evUS8oAKlEwvCZS+jXqSWNa1clMjaejoMncvXuQ6qWzxnKKjciY+MZNn0R88YNpLyvF1v2n2DQ5DB2LplqNI7+wp7lM75Y5lqB5WhRrwa3Hj5j+6FTxvTn4e8oUsCVFVv2se/EeWysrRjUtTWehQtw6+GzX732OjKGwm75kHwUesW9YH5eR0Sj1+v/ULlqFU2NvcHVA9l26BS1OvRHLBbh712Mzs0MyuDEQd+b5L1w4z7enkUAjCGOOgyeyMPn4TSvV/1XQ/AJ/D1o3Lgxixcvpk+fPgAcPnyY4OBgpFIpgwcPZuDAgTRr1oyIiAhat27N5cuXqVaVuGMyAAAgAElEQVSt2hfVHRERwcCBA1m8eDEVKlTg559/pl+/fuzbty9Hnzp06NCv1JKTbt26MWHCBH766Se0Wi0hISG4uRmUrR49ejBlyhSmTp2KSCQiLCwMCwsLnj59iqenJyEhIZw4cYL8+fMzduxYowFqxIgRuLi4sGjRIqKisifznzx5QsGCBRk4cCDXrl3D09OTSZMm5ZAfDOH5VCoVtWrVQiQS0bZtW3r37g0YjEhyuZwFCxZgbW1Nr169aNmyJVqtlhcvXrBu3TqGDRuGs7MzQ4cOpWbNml/8PAT+/2lUvzZLVq+nd9dOABw5eYb639RAKpUwbOxkBvTqRpMG9YiMjqFtt75cuXGLoEoBX1R3ZHQMg0dPJGzWJCqU9WfT9t0MGDGePT+vzvHeHdi67otlrlWtCi2bNODmnfts2bXPmO7hXpiZE8cYz6OiY3n15i3FPYsC8PT5S46cPMP2tctZv3mHMZ+jgz2tmjak79DRSCRizM3NWbN4LgDBtWua3Pvcpavkdc6Dg709Oq0OS4vsiQiJWExqWhqpaek42NuZlLO2skQuV1C5XhN0Oj3Txo/A3NzsszIPH9CHvM55WLxqHdExsV/8jAS+DvXLerL6+B261TGEvDpxN5za/kUN+tHG0/QOLkeDCsWJSkyn24L9XH8eTWXvL1vFHJWYzqj1p5jVtQ7lPF3ZduERw9ecZNOPzXPoR9tGtvyiOh2sLZjfs77xXJ6p4t7rWJpX8UKr0/EqNpnN5x4yfuMZnGyt+KFheYJ8DOGErMxlvIxOotPcvUjEIub1qGes53lUIifuhrNucFM2n3uYfT8bC5oGlmDI6uNIxCLMZVKW9MmetLYyl3Hh0TuGrzmJtYWM5f1yN6y+iE5Co9HRZMpWRIhoXtmbrnX80en0yCQSJB89D7FYTGRC+hc9D4Gvw7c1Almx9QA92hj+v49duEG9qhWQSiSMCF3JDx2b0rhWZSJj4+n04zSu3ntM1XK+X1R3ZGw8P85azrzRP1CuVHG2HDzN4OlL2BE2IadOtGTyF8tcM8Cf5nWDuPXoOduPnM01z5qdR6hQ2otyPtlh6q0sLZBnZFK9wyB0ej2TB3bF3EyGVqfDwtzMpLxELCIiNp7vmtWjgm/24p37T1+hzFJR2C2fsc5zN+4xeNpirC0tWTN9+G/KfvnOI15HxrBw3ABjmlarIyRsLaN6deDgmSsm+X08i7B/2TTeJwnRUP6u1PVxYc2lt8Zwb6eexPONlzNSsYiQ/U/oEeROsG8+olMy6bnhLjffJBPokdNInxvRKZmM2/uY6c19KFPInp23ohm9+xHru5dHLDIdezb1qPDFMluaGSaHGy66QkqGmu+DipDX1pzncXJsLKQ4WmX3h8JOVrxNMkz+Z6i0zDn+kqnNSjL3+EtjHp0eZBIRko9EEoshKsXUGLbxagRlCzngXzB7y4749CzWXn7L8o5l6LHhzq/K3Kt6UZPzy6+S8MxrMBy9fK9AnqXhuzW3SM5QUdMrLwNqeXy4JuddUibtVt0gU6WlTsm89KlR1CT8rMDXpba7GesfZNLJ1wqAM2+zqFHYDIlYxOSLcrr5WVHPw5wYuZa+R1O5FWtmDN/2OWLkWiZekDOpui3+LlJ2P1My/lw6qxva5+hD6xrlDM34a1hKDWWb70wiJUtPVz9LnK3EvE7RYC4RcTFCxY4nSkQiaOdjSdMPxqjwZA0KtZ419zKwkopoX8qSbz0teJmspaCdhA0PMzn6Som1mYieZaxwt5ei04O5xFRWiQii5VralLSkTL7scHiPE9QotXoK2uV8v5t7WTDxQjqn3iSh00Pbkhb4OMt4kWQIyedgkV2mkJ2Ed2laItO1v9mefzv/ib8SVX09iElK5W1cEgCnbj2jfoAPAEuHtKVhZV/kGVkkpSmws7YkMfXLQxMcv/GEan7FCCjpjlQqoVPdANIylDx+E/P5wl+AMkvNj8t2U6pofgJ93E2uJadnMHjxTppU9cPdNQ9pGUouPwzHu7ArR0L70bl+AMOW7iL1g3u4s4NNrvdIUyiZt+0UIV2+RYQo1zz3XkUSlZBKkyqlc70OBkOSTPrbltnf0x6Bvw/VKvoT/T6BN5GG9/r4xes0qGkw2K6aPpLGtauSrsggMSUVO1trEpJTf6s6E46eu0r1gDJUKlMKmVTKdy2+JU2u4OHzP7eCM4+jfa6T0WlyBc/D3yEWiTi6bh7j+3dl7NyVvImM+c1rmcosLMxNVwlZmJuhzFL94XKfkqVSU6WsLyc2LOD0pkVIpVIWbtiRI9/8Ndt4HRFNl09WIq4NHcOBVaFcv/+EHYdP/5HHJvD/RI0aNYiOjub1a8N7fvToURo1Mhjb161bR7NmzUhPTycxMRF7e3sSEhJ+qzoTDh8+TM2aNalcuTIymYxu3bqRkpLCgwcPPl/4N9DpdAwfPpy7d++yceNGwsLCePTIEIpRLBYTGhrK3bt3mTt3LmPHjiUuLo7U1FTOnz9PqVKlOH/+PN9//z39+vUjJcWg+Lu4uOR6r7S0NA4cOECzZs24cOECtWrVol+/fqhzCS3p4OBArVq1OHToECtXrmT79u3s3r0bnU6Hq6srjRs35vTp08ycOZNZs2Zx7do1UlJS8PPzo0OHDpw9e5YhQ4YwZMgQwsPD/9QzEvjfUr1KIDGxcbx5ZwjjcezUORrWrw3AT4vn0KRBPdLlchITk7G3syMhMemL6z58/DQ1gipRuWJ5ZFIpXTu0ITUtnQePn/4pmZ3zOOU6Fn1MUnIKfYeNpmXjBhQtUhiVWs3YqaFMHDUUCwvT8UOr1WJtbcWqsFBunT3CoN7dGTJmEplKpUm+ew8fM3HmPEYP7Q9AjaDKbN65lzfvIlEoMli9cQsAKlXOsQjA0tKCW+eOsnz+TCbPWsCLV6Zj8qcyA+R1Fr7d/klU9SlEbLKct+8N32yn7r2mfjnDvq1L+nxLgwrFkWeqSErPxM7KnMT0Lw83deJOOEE+hQko4YZUIqZjzdKkZWTxOCL+L5FdqdIwfO1JfArnJbBEAVIVWZQqnJdWVUpyIKQdfRuUZ9zGs7x9nz3J7J7PgYuhXRnVuiqj1p0iWZ6JWqNlytYLjG4dhIWZ6bpLrU6HtYUZC3vX59zMLvT5thyjN5xCqcoOdRnoVYALs7rQvrovw346jlqTcwWsvZU5QaUKsW1ES+b3rMfeq884eP057vkccLA2Z83Ju6g1Wm6+iObmi2iTMH0Cfz+qVShN9PtE3kQZjOjHL93i2+qGhQwrpwylca3KpCsySEpJw87WmsTfoRMdu3CD6hX9CPQvadCJmtUjNV3Bwxdv/pTMv6YT/UKGMosdR8/So1WDHNcszc25tmMpS0IGMW3ZJl68jaKMdzFiE5LYf+oSao2GI+eu8Toy1iScK8C76DiGzlxGv47NsPkoskLlMj5c37GMTk3rMnDqItRqzae3NbJ+zzE6N6uHTJbdP9fvPUZx94IE+pfMkd/BzsYkr8Dfj8oeTsSlZvHugxHmzLN46voY9IEFbf0I9s2HPEtDkkKNraWUREXu3ym5cfJJPFWKOVHB3RGpREy7gIKkKTU8iflrDPe7+way+ruybL8ZxbXwJDLVWiw+mf8yl4lRqg2ei0vOhBPs60JRZ1OPoCJOlthbylh/5R1qrY5bb1O4/TYFlSbb4zFTpWXv3Ri+q1zIpOzMo8/pGeSOo/WXGQwAdt+O5vTTeHpUcwcgXanm6MM45rTyZUP38ryIk7PxqsGrzNJMQrnCDqz+riwrOpfhbkQqG67kHglD4OsQ6GZGnEJn9Lo5905FbXeDvjCnth31PMyRq3QkK3XYmYlIUuaMAPJrnH6jolIBGeVdZUjFItqUtCRdpeNp4q//nf49bGvuyPJge3Y9VXI9WoVcpSddpedlspa1jR2YUsOWtfczuBunRqfX42wlpo67OZubOjKysg3LbhuuyVV6XiVrEQNbmjkyNMCGGZflRKRpKZVXSnyGjqPhSjQ6PafeZPE2VYtKa+rJFZWuZcL5dLr7WWEtyzlGanXQuqQlh9o4saqBPafeqLgSqUKp0WPxiQHLXCIiS6P/zfb8F/hPjL5mMinflPPixM2nVPJxR48ef0/DJpR3X0XRb8F2tDodJYu4GkKO/I6645LSOX37GTUHvTKmqTVaYpPS8PUwjZPabtIaYpNyhoc4G5b7vhJJaQoGL96Fg40lM3o1RfSRxTjifTIDwrZTrkQhhrerA4BMIsHVyZ6WNQwrEYMDfFh35Cr3XkZR3b/Yr7Zh9tYTtKlVjoIujkQn5P4RfPjqIxpUKoXZn/hg+73tEfj7YCaTUadKRY5fuE7lcr6ghzIfVrjdefyC3mNno9Vq8SnublASfkcnik1I5OSlm1Rt3ceYptZoiI1PxM/b0yRvyx/GEhuf0+320o7lOdJ+DZlUilgspm+n5kglEir6laSiX0ku335AHgf7X73mkseRrE8m4pRZKiwtzX+zzt8q9ymzVvxMs7rVyedsWKU1sEsr+k2Yx7Dv2wOg0WqZsmgdN+4/YdWMkTjYmW6wbW5mRpECrrRrVIdz1+/SusE3Oe4h8PfAzMyMevXqceTIEYKCggAoV84Q5uP27dt0794drVZLqVKlUKvVOcJY/RYxMTEcP36cChWyV+ap1Wqio6Px9zf1mmvcuDExMTkXRNy8edPkPC4ujtDQUK5du4ZYLCYgIIDg4GD279+PVqvl4MGDRm+o4OBgduzYwbFjx5DJZLi5udGunSE8WKNGjVixYgW3b982CfH3KTKZjHLlyhnz9OjRg+XLlxMeHp4jrN3cuXONv4sVK0bHjh05ffo0LVq0YP367DBLZcuWNRqbAgMD2bhxo/FarVq1CAwM5OLFi3h4CN5/f1fMzMyoW6s6R0+epUpgBfToKetnWBl+5/5Deg4cgUarpZR3CVRqFb+j2xD7/j0nzpwnsHa2V7VarSEm7j3+vj4meZt1/P7/2rvv6KiqvY3jz0yGFJLQQjqEQCB0pEiTJkoHFRWxoSLYFUFRQEUEFYyIUnJBUBBFuFwFRQURItJ7lSq9DwkhnQQy/f1jcMIQVMarF3j9ftZyLT1nzsw+cc7M7P3s/TtKTSteynXDTwt8PqdjJ8x6YsAgNW5wg14d6J6h/eG0GWrS8IZi5fEkKWXZSh05elyD+z8jSXrovh6a/dV3Wrdxi25p3UKStHz1Og0aNlKD+j/tWdV0Z7dOMp9K1aPPvKCAgAA91aeXFi1ZrpCQy5dB8fPzk5+fn1o1b6JmjRtq9fpNnpVKl2szrj/+Jj+1rRevJdsPq1liBckl1Yt3D/JtP3Ja/aYsksPpVI0K5d3BiQ8X1OmcfC3bcVS3vFr0OWtzOJSWXaA6lbwf+8B7Xystu/jkvqWjHrrsc2edPa8Xp6aoTHCgRj18iwwGg8qFBnmtIGpVO04NE6K0fq9ZlSLcM2xNF2Zf39YkUf9evkvbDqVpnzlTDatGFSuPJ0lLdxzVsfQcDbjDXfr7vtZ1NHfNXm3cb1brCyfhf2FgsU/7+pq1YqcOpmarZkXvKgxvP1RUhrNKVFnd07KmVu4+rm5NEvVen3ZKmrtWs1fsVtPEGLVvUEUhgVc+aIj/PXefqKFSVm9W8wa1JLlUv6a7n/3zLwf11Btj5XA4VDOhkmw238YV0jKytGTtFq3avMOzzWZzKO1MlupV9/5t0qPfG0rLKD6JYvXsZJ/PaeWm7aoYFaHEyhWL7fPzM8rPz6gWjeqoyQ01tHbrLj1yZ0eNe/U5jZ76H73/yRx1bNVYzRvUUkhwUYi0c/9h9XsrWfd2vlmP3NnR6zl/rbzwRM+u+vybFB04dtKr/N2vzmTlaOvu/Xpv0JOebQePm/XNktWa/f7rPp8nrg3+JqPaVC+vpXvPqEl8WblcUt0L5eN2mvP0wpc75XC6VD0qRDa706drKP2sRSv2ZajjoTWebTaHS6fzLKrtPTSnhz/ZotN5hbrU4gEtfvP5A0xG1YwOVYdaEVpzKEtd60bKYvcevLfYnAoq4aeNR7K1/3S+XmxffBzO5GdU0l219V7KAX2xyazG8WV1a80IBV9UBm/NoUzFlglU1YiiSeLfbU+Vv8modrUuP0HvcqatPqqvt6VqbM+6qlA2yPP69zSKVUQp93jEfY0raMa64+rbMl79bikafwkJMKlXs4qase6E+raMv+LXxN/L38+g1hX9tfyYRTdGl5BLUp1w93tn1xm7Bi3Nk8MpJYaZZHXKp7G59HMOrTxuVTdz0feL3elSeoFTtS4pMtX3+xydLigeXi3o+dsrDv39DKoeZlK7+ACtN9vUvrK/nC7p0XpBCjIZVLWsSbfEB2jtSavqR5bQB+2KVu/VDi+hdvEBWnPSqlrlTfIzSL3rBcnPaFD9yBJqEFlCm1Ktuqt6kN5qHaqJWwr04dZzuqWSv26MLuEVIv2SYdOry8/qjsRA3Vur+K0lbA6XRq7N18zbyyjwQru6Jwbqh8MW9aoTJMslYZXF4VKQySCTUb97Pv/f/SMCJskdtoybs0wF5y3q0LimDAaDTmfn6Z2Zi/XZqw+ramy4JOmBN6cXO9ZoMHjVT8696IaRYaWDdXuLehryYFGphWOnsxRVzrvciCT9540+V9ze1MxcPfX+bDWuUUlDHuzo6RRJ0t5jaXpu/Jfq2bahnritpWd7pciyKii0eD2P0+n8w4HJpVv3a9WOQ5r83WrPY2/uP07jnuuh+tXcpTDW7DysUY/ffsXt/yvOB9eWLjc31/vTZiv/3Hl1atNUBoNBaRlZeit5uv49boSqxbvfK/c8N7TYsQaDweumsrl5+Z5/L1+2jLp3aKWhz/b2bDt6MlXREcVnQn81aeR/fR6VYqPkcDpUaLF6ZtO5r5Pf31e5YoxOpKbL6XR6ZgEePZmqOzu0Vni5Mn/quEudzsiWzV40O8Tk5yfThcELq82mAW+NV05evj7/YJjCyrg/Y1wul3r2e10jBz6hxMpxnseWCi75X/+t8Pfq1q2bRo8erfz8fHXp0sV9TaWladiwYZo7d64SE933xLvjjjuKHWs0GmW/6L3y64ogSSpfvrzuvvtuDR8+3LPtyJEjnnJ2F5s/f/4VtTUjI0NWq9XrfWwymWQymZSWllZsZdGv+2JiYpSfn++170q+l+Lj47VjR9EAi8vluuxxhYWFGj9+vJ555hmFhroDV6vVqoCAAKWnp2vGjBkaOHCgZ0KD1WpVcHCwDh48qCVLlnhKFF58HK5tXTveqvcmTFZ+QYG6tHcPLqedPqPhSR/oy+mTPSHInb2KlyU2Gg1yXLQ6ICe3aFJN+XLldNdtnTVs0AuebUePn1B0ZPGB529mTSu27c/Ys3e/Hu8/SA/cc6eefewRz/aUpSt0JiNLX8//wbOt+4N99caQF5SRmeX1PSFJJpOfTCb3T/qv5/+gd8dN1HtvvqY2LZt7HnMmI1M9undTvyfdv0XXrN+kihViVDLIu1N16MgxvfjaCK/SgFarTaUu3Cfjt9qM61PHhgma8N1GFRTa1L5BFXf/KKdASXPW6NMXbldCtHuQ4MEx84odazDI675MuQVFfZCw0JK6rUk1De5RNFB3LD1XUWWLB5r/fvmuK25vatZZPT3pBzWuFq3BPVp4+hOH07K1YtcxT7k/yT3hz7+EnzbuN2vG0h3610Xl7WwOp0KCArR0x1Fl5J3T/A0HPPsefG+eBvdoocyz52S75P45Jj+DTH5GLdh0QFsOpuqN+92/5ZwulxxOl0KDvMOhQqtdHy3aqj7t6yvkwj6r3SF/k5+cTpcsdoc+7lcUavedMF89biq+KgPXls6tm+qD6XNUcO68OrZq7L5uMrL01qTPNev9oapWyT2RtWf/EcWONRqMsl88rnC26DdSWNnS6t6upV57updn21FzmqLDi/eJ5iYXf+4/a/Xmnbq1ufe9jA6fOKWXR0/xKs9ntdkVGlxSFqtNwSUD9cW4YZLcv+s6PTZYfS6sgFqzdZcGjZ6igX3u0V0X9Xe++2mNNu3cp7cGuL+HnC6X7A6HQn+jz7Jm6y41qlNdpS6aCLFs/TalZ+aoY193ab3zFquMBoN2Hzymfw17/i/6i+Dv1qFWuP617IgKLA61qxkhg8Gg9DyLRi8+oGkPN1CVC6XcHpm+pdixRoO87imTe76oD1Iu2F9d60XppQ5FpR6PZ51TZKni5alm9Gl0RW3Nt9j16PStmvZIA5UKcg8Q2xxOlS3prwplg3TWYlfeeZtn3/Gsc2qeUE7L9p3Rkcxz6jJhrST3iqQ9qWf1S+pZvdi+qix2pz58sOg768nPf9ZdDaM9/73ucJbaJHqP6C/bm6Fdp/LUcZw7QCuwODRo7i49clOcHmoW5/VYl8ulpEUHtP1Erqb0qu8JlySpYrkg5VuKfks6L9xnRpKmrjqqznUjFVsm6MK5uuRPebxrzq3xAZq8tUAFNpduqeQvg8GgM+cc+mBjviZ3Kq3KZdz9gscWFi8XapB7dc6vci1F11O5IKM6JwTohSZFweaJPIcig4u/B6Z1vbISeflWp574IVeTO5VWqYAL3ydOl8oFGhUb6ieDpAJbURucTpdcfgZlnnfqq73n9Xj9kkV9eadLpUsYVTHUTw6XVOhwKfhCqWGHyz0XyupwKbiEQR91cbfP6XLpvm9y9GBt97jaxlNWvbk6X083LKmuVS9fuu683aUCm0u2iz5rTEZ3qb3YUKPyrS7lWZye8zmR51DTGP/fPZ9/gn/MJ0WjxDhlny3Qoo171OlCebyC8+5VBYElTHI4nfpm1XYdMKd7DYRLUmx4aWXmFejnAydlsdk1+6eimd3tG9XQki17tfOwWS6XS0u37tMDb05XTv45/Vl2u0P9k+eqVb2qGvpwZ68wJif/vPonz9WjnZsXC2Oa1oqXn9Gofy/ZJKfTpYXrdyszr0A31oi79CW8rJk4UMvHD9Dy8QM0e5j7B9/y8QM84VJmXoEycvNVs1LU//R8cG1pXK+GsnLytHD5Ok95vIJz52UwGBQYUEIOh1NfLVqu/UdOyObwHvyqEB2hzOxcbd29TxarVTO/TfHs69iqiX5ctUnb9x6Uy+XSkjWbdM9zQ5Wd5z0o/VepXiVOCXEVNPnf38hmt2vDz3u0eedetWlS/3f3JcTFKiq8nKZ+uUA2m13f/rhKuWfz1eSGmn/6uEu1aFRXU7+cr4ysHOWfO69Js+apfYvGkqR3PvxcefkFmpb0iidcktzhXbX4ivpw1jwVWqw6dNysLxb8pK633PS3/P3w12natKkyMzM1f/58T3m8/Px89zUVGCiHw6E5c+Zo3759XmGSJFWsWFEZGRnavHmzLBaLZsyY4dnXuXNnLVq0SD///LNcLpdSUlJ0xx13KDs7W39W1apVVaZMGY0dO1Z2u107d+7U999/rw4dOqhBgwbKyMjQzJkz5XQ6tXLlSm3ZskVt2rTRTTfdJD8/P3366adyOp369ttvlZGRoaZNm/7u63Xs2FFHjhzR4sWL5XA49NFHHykiIqLY6qXAwECtXr1aEydOlM1m0/79+zVr1izdfvvtKl26tL7++mt99tlncjqd2rx5sxYuXKhu3bopJCREkydP1uLFi+V0OpWSkqIdO3aoXTtW0F7rmjSsr6ysbC1Y/JO6dnCXx8svKJBBBgUE+MvhcGjut99r/8HDxa6bCjExysjK0pafd8piserzL77y7OvUrq0W/7RC23fukcvl0o/LVurOXo8pO+fKyxv5Iic3V0+9+Iqe6P1gsaDm+y9naOPSBdrw0wLPqqhvZk1Tt47t1OzGhtq6faeWLF8lp9Opr+f/oJzcPDWsV0ebt+3QyDETNGXcu17hkiStWrdBA155QwUF53QmI1MTPvpEPbt306XiKsaqsNCi6bO+kMPh0JLlq7Rn3361adH8d9uM61OjhGhl55/X4i2HPOXxCgqtkkEK+LV/tH6fDqZmeQ2KS1JsWCllnj2vnw+nyWKz6z+rdnv2tatfWT9tP6qdR9Plcrm0bMdR9RozTzkF3hPhfGF3OPXC1BS1ql1Rr93byqs/ERzor+lLtmvp9iNyOt2vt/t4htrUqaTEmDDtPZGhlG2HZHc49eWqPXI4naoXH6E5Q3po2aiHtXTUQ54VU7NevlOdGiWocbUYbT98Wst2HJXT6dL8jfuVW2BRvcqRqhMXrmU7jmrroVTZ7A59uHCzEmPKKTbMe2V5oL9J6/ed1NSUbbI7nDqUmqW5q39RlxurymCQBk//ST9uOyyH06kFmw7InJGn1nV+v9+Gq69x3erKyj2r71dsUJfW7t8z+ecKZZBBgf7uPtHXKSu1/+hJ2S8peVghqry7T7TngCxWm2bNL7pPbMeWN+rHNZu1Y+8hd59o7Rb17D9COXl/7325dh04orqXrJCqGB2hQotVn81bLIfDqZ/WbdXeQ8fVpnE92e0OPfrKu9q+95BsNrumzlmo0OCSql8jQcdOndZL736oEc/39gqXJKlu9Spasm6LtuzaL5vNruTP56lG5YqqEBV++XbtP1Js5dbjPbtp/ZcTtXp2slbPTlaX1k3V5+7OhEvXmQZxZZRdYFXKnnS1r+X+/19gtcsg9wonh9Ol77an6lB6gRyXrBSIKR2krAKrtp/MlcXu1JzNRfdwvbVGuDuEMefJ5XJp+b4MPTJ9q3LP/fnyVCEBJoWH+mvq6mOyO5zacTJXy/ZlqF3NcAUHmNSsSllNWXlUFrtTGw5nafvJXLWuVl6DOyVqyQsttHiA+596FUprYIeqeqlDNRkkvTZvj5b8ki6H06WFO9NkzjmvllWLwuRfTp1V7RjvSetj762rHy96zshSARrdo06xcEmSZqw/oW3Hc/Rhrxu8wiVJ6lQ7UvO2perMWYtyztk0e+NJ3XwhzNqfnq8pK46q0OZQWm6hZq4/oU51rnzFFP436kealF3oLv/2a3m8ApvLfQ35GeRwupimhPwAAAyESURBVPT9wUIdznbIfsm8zphQo7IKndqZbpPV4dJX+4oWULSNC9CK41btyXBXUFl53KLHFuYo13LlZfYuFeJvVHiQUZ/uOC+706Wd6TatPG5V20r+KhVgVLPYEpq567wK7S4dyrZr6TGrWlf0V6i/QYsOW/TVvkI5XS7tSLdp+TGr2sX7K6Gsn+JL+2nGTvdzbk2zaXu6Tc1j/WV3Ss//mKvdZ2yyOVyateu8QkoYVDvcpJN5Dg1fdVYvNwv+zXBJkkoFGFUjzE8fbTsnq8Ml81mHvtlfqDZx/gouYVTTmBKatt29b+Mpq3ak29Wq4u+fzz/BP2YFk9FoUPvGNbVu9xFVq+D+gKwSU14PtGush0fNkMFgUL2EGLVrVENHUr1LcEWWLaWn7milIR+5b878WLebtHC9uxMVHx2m4b27atTMxTqVkauocqX07lPdFVm2+AqmK7VuzxEdPpWhUxm5+nZN0QzuRzs3V3CgvzLzCjT5u1Wa/N0qz75Xe3VU56a1NXngfXpnVoqmfLdaUeVKacwzdyk48L+bkZ2amavSwZe/v1Krfh9owvP3qEG14kvq/4rzwbXDaDSqU+umWrN1p2elTEJcrHp176j7+w+X0WhQvRpV1aFlYx05fsrr2Kjy5fTsQ3fr5XcmSpKevL+7Fix1z7ypXDFGb734uN5Kni5z2hlFR5TXB689r6jyV3YzT18ZDAZNenOg3p74mdo+0E+lQoI1cuATqhDt/lz4vX1jhz6v4eM/0fQ5C1QxOkLjhw1QgL//f3Xc06+PUcM6iXr83tv17EN3yWK16p5+r8vlcumW5o30Qt/7dLbgnOalrJDJz6SbH3jOcy4Na1fXh2+9pCFP9dKoSTPU/uH+KhUSrOceulstGtX7W/5++OsYjUZ16dJFq1evVo0aNSS5g5zevXurR48eMhgMatCggTp16qRDhw55HRsVFaX+/ftrwAB3idVnn31W337r/o5KSEhQUlKShg0bppMnTyo2NlbJycmKivpzkwQkKSAgQFOmTNHIkSPVrFkzhYWF6fXXX/eU3Js8ebKSkpI0duxYxcbGasKECYqNdc/gnTFjhoYPH67k5GTFxMRo4sSJCgm5/D0BfxUdHa2pU6dq1KhRGjJkiBITEzVx4kTP7KUGDRro448/1o033qjk5GSNGDFCTZs2VWhoqJ566im1adPG0663335b48ePV3h4uEaOHOlZGTZ+/HiNGTNGgwcPVlxcnCZNmqSwMO4hc60zGo3q1L6t1qzfpOrV3APiVavE6+H7e6jno0/LaDCoft3a6nhrGx0+eszr2KjIcPV7oo9efM098/vpvg/rux9+lCRViY/TqNcHa3jS+zp5Kk0x0ZEa984IRUVefuDrv/V9ylJlZGZpwpRPNGHKJ57tw4e8qNs6tf/N42okVtW7w1/V+MnT9Oqb76pqlXhNHpukkJBgzfziK1msVvXt95LXMfP/86m6d+2k3Xv3q133+2Xy89Pdd3TRow/eK0navG2HnnxhsLYs/0ElTCb9a8zbGpE0VlOmz1LlShX14QfvqHxYOc2aM+9PtRnXLqPRoHb1q2j9vpOqFuP+3VUlqqzub1NHvcd+K4PRoLqVInTrDZV1JN17FmxkmWA92amRXp2xTJLUt0N9/bDZfRPz+MgyGnZ/K70zZ41Ss84qqmyIknrfqsgyly/JeCXW7T2pw2k5OpWVr+827Pds793uBj3arr6SHrlFyfM3afjslaoQVkpj+rRTuVD3oNqYvu01Zt46Jc1Zq+oVwjTu8Q7F7rl0qcTYMI14sI0m/7BFb/5npapEldW4xzsoJNBfIYH+Gv5Aa436co1y8s+rfkKUknrf6vmOajPkM417oqMaVHFvH/3VWrUfOlPBQf7q3e4G3VTT3W8a+VBbJc1do5FfrlZCdFlNeLKTgimRd80zGo3q2PJGrd2221NWLiEuRr3uaKcHBr4to8GoejWqqH2LRjp80rsMcWT5cnr2we4aNNpd3vuJe2/TgmXrJEmVK0Trzf599Nakz2U+naHoiDC9P+RpT+nsv0tqepbCy5X22lbCZNL4oc/p7UkzNXXOQlWKjVTysOcVVtb9uHdefFxDx05TZk6e6tVI0ISh/WQ0GjV30QqdL7Rq6LhPNHRc0ffEpDf6q2HtRI184TGNmPiZsnPPqlHtRI0Z8rTnumnW81nP4yQp9UzmZcv24fpnNBh0a81wbTiS7SkBV7l8sO5tHKvHZmyT0SDViSmltjXCdTTTe+J2RKkAPdYqXq9/+4sk6dGb4rRod7okqVJYSb3WNVHvLT6gU7mFiioVoJHda3lKwf1Zw2+rqdGLD6hr8jqFhwZoWLfqnlVWr3RK1LuLD+j2f61T2WB/jbi9psJCfv9z3GAwaMTtNfReykElLTqghPLB+qBnXa8SeWl5FpX/g+e51MAvd6pexdJ6pHmcvth0UgUWh+6ZvNGzP7JUoGY9dqPubRwri92hJ2f+rHMWh9rXCtcDTd2Ty4d0StSYlIPqPmmD/IwGda8fre71o3/rJXGVGA0Gta3kr02pNiWUdb9v4kub1KNGkJ5elCuDQapd3qQ2cf46lus90SG8pJ/61CupEavdkxcerlNSPx5xL76IK+2nwc1D9P6GAqXlOxUZbNSIVqEKL1l8LNgXQ1u6n7P73GyFlzTqlZtCPKusXr0pRBM2Fej+b7JlMkp9byipuhHuFYEj24QqefM5Tdt+TmFBRr3cLNhzXFLbUI3bWKC7vspWqL9BrzQPUUyou52vtQjVO+vylX3epVrhJo26OVRGg0HzDxaq0C4lrctX0rqiCe3vti2lehEl1PmLTM+/v9EyVBM2F6jH19kqWcKgu6sH6uZK7s+Sl5qF6P0N+brrq2yVCzRoWMsQlQsy/uH5/H9niImJ8aWs6TXBbDbr7IpP/viB+McIbdPHM5iJyzObzbIc2nC1m4HrREBCU66pS5jN5j9+EHARrqHizGazHDmn/viB+MfzKxPDNXQZZrNZud+PvtrNwHWidNdBXEe/w2w2q3Dfqj9+IP5RAqu34rrxgdlsVsYnj1/tZuAaUr7Px1xDf8BsNuvUm1SdwZWJGbb2mr+m/jEl8gAAAAAAAAAAAPDXIGACAAAAAAAAAACATwiYAAAAAAAAAAAA4BMCJgAAAAAAAAAAAPiEgAkAAAAAAAAAAAA+IWACAAAAAAAAAACAT0xXuwF/RnpaqiLa9LnazcA1JD0t9Wo34ZqXfjpNEQlNr3YzcJ1IP512tZtwzUlPT1dERMTVbgauE+np6Ve7Cdek9PTTioiIudrNwHUgPf301W7CNSk97ZQiug662s3AdSI97dTVbsI1Lf10miKqt7razcA1hn6Qb06nmhXZ5+Or3QxcQ06nmq92E655p0+dVMywtVe7GbhOnD518mo34Q8ZYmJiXFe7EQAAAAAAAAAAALh+UCIPAAAAAAAAAAAAPiFgAgAAAAAAAAAAgE8ImAAAAAAAAAAAAOATAiYAAAAAAAAAAAD4hIAJAAAAAAAAAAAAPiFgAgAAAAAAAAAAgE8ImAAAAAAAAAAAAOATAiYAAAAAAAAAAAD4hIAJAAAAAAAAAAAAPiFgAgAAAAAAAAAAgE8ImAAAAAAAAAAAAOATAiYAAAAAAAAAAAD4hIAJAAAAAAAAAAAAPiFgAgAAAAAAAAAAgE8ImAAAAAAAAAAAAOATAiYAAAAAAAAAAAD4hIAJAAAAAAAAAAAAPiFgAgAAAAAAAAAAgE8ImAAAAAAAAAAAAOATAiYAAAAAAAAAAAD4hIAJAAAAAAAAAAAAPiFgAgAAAAAAAAAAgE8ImAAAAAAAAAAAAOATAiYAAAAAAAAAAAD4hIAJAAAAAAAAAAAAPiFgAgAAAAAAAAAAgE8ImAAAAAAAAAAAAOATAiYAAAAAAAAAAAD4hIAJAAAAAAAAAAAAPiFgAgAAAAAAAAAAgE8ImAAAAAAAAAAAAOATAiYAAAAAAAAAAAD4hIAJAAAAAAAAAAAAPiFgAgAAAAAAAAAAgE8ImAAAAAAAAAAAAOATAiYAAAAAAAAAAAD4hIAJAAAAAAAAAAAAPiFgAgAAAAAAAAAAgE8ImAAAAAAAAAAAAOATAiYAAAAAAAAAAAD4hIAJAAAAAAAAAAAAPiFgAgAAAAAAAAAAgE8ImAAAAAAAAAAAAOATAiYAAAAAAAAAAAD4hIAJAAAAAAAAAAAAPiFgAgAAAAAAAAAAgE8ImAAAAAAAAAAAAOATAiYAAAAAAAAAAAD4hIAJAAAAAAAAAAAAPvk/ovM9JzNGZ4EAAAAASUVORK5CYII=\n",
      "text/plain": [
       "<Figure size 2160x720 with 1 Axes>"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    }
   ],
   "source": [
    "# get column names\n",
    "feature_names = X_train.columns\n",
    "# we need to specify the background color because of a bug in sklearn\n",
    "fig, ax = plt.subplots(figsize=(30,10), facecolor='k')\n",
    "# generate tree plot\n",
    "plot_tree(model.estimators_[0], filled=True, feature_names=feature_names, ax=ax)\n",
    "plt.show()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "From the figure we observe that a tree consists of a sequence of binary decisions, where each box includes information about:\n",
    "\n",
    "* The binary split criterion (mean squared error (mse) in this case)\n",
    "* The number of `samples` in each node. Note we start with the full dataset in the root node and get successively smaller values at each split.\n",
    "* Darker colours indicate a higher `value`, where `value` refers to the _average_ of of the prices. \n",
    "* The best single binary split is for `median_income <= 4.068` which improves the mean squared error from 9.3 billion to 6.0 billion."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## A slightly better model"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Right now our simple tree model has $R^2 = 0.53$ on the validation set - let's make it better by removing the `max_depth=3` restriction:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "RandomForestRegressor(bootstrap=False, ccp_alpha=0.0, criterion='mse',\n",
       "                      max_depth=None, max_features='auto', max_leaf_nodes=None,\n",
       "                      max_samples=None, min_impurity_decrease=0.0,\n",
       "                      min_impurity_split=None, min_samples_leaf=1,\n",
       "                      min_samples_split=2, min_weight_fraction_leaf=0.0,\n",
       "                      n_estimators=10, n_jobs=-1, oob_score=False,\n",
       "                      random_state=42, verbose=0, warm_start=False)"
      ]
     },
     "execution_count": null,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "model = RandomForestRegressor(n_estimators=10, bootstrap=False, n_jobs=-1, random_state=42)\n",
    "model.fit(X_train, y_train)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "RMSE on train: 0.0\n",
      "R^2 on train: 1.0\n",
      "RMSE on valid: 58570.323\n",
      "R^2 on valid: 0.643\n"
     ]
    }
   ],
   "source": [
    "print_rf_scores(model)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Note that removing the `max_depth` constraint has yielded a _perfect_ $R^2=1$ on the training set! That is because in this case each leaf node has exactly one element, so we can perfectly segment the data. We also have $R^2 = 0.64$ on the validation set which is better than our shallow tree, but we can do better."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Introduction to bagging"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Bagging is a technique that can be used to improve the ability of models to generalise to new data.\n",
    "\n",
    "The basic idea between bagging is to consider training _several_ models, each of which is only partially predictive, but crucially, uncorrelated. Since these models are effectively gaining different insights into the data, by averaging their predictions we can create an _ensemble_ that is more predictive!\n",
    "\n",
    "As shown in the figure, bagging is a two-step process:\n",
    "\n",
    "1. Bootstrapping, i.e. sampling the training set\n",
    "2. Aggregation, i.e. averaging predictions from multiple models\n",
    "\n",
    "This gives us the acronym Bootstrap AGGregatING, or bagging for short 🤓.\n",
    "\n",
    "The key for this to work is to ensure the errors of each mode are uncorrelated, so the way we do that with trees is to _**sample with replacement**_ from the data: this produces a set of independent samples upon which we can train our models for the ensemble.\n",
    "<div style=\"text-align: center\">\n",
    "<img src='images/bagging.png' width='700'>\n",
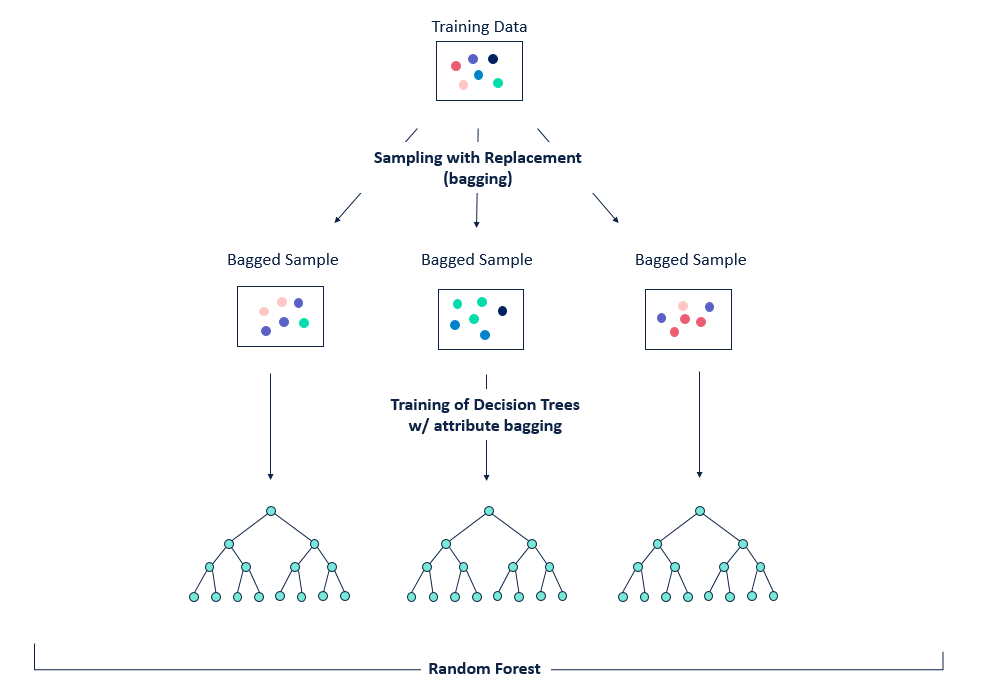
    "<p style=\"text-align: center;\"> <b>Figure reference:</b> https://bit.ly/33tGPVT </p>\n",
    "</div>"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Hyperparameter tuning"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "If we revisit our very first model, we saw that the number of trees (`n_estimators`) is one of the parameters we can tune when building our Random Forest. Let's look at this more closely and see how the performance of the forest improves as we add trees."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "RandomForestRegressor(bootstrap=True, ccp_alpha=0.0, criterion='mse',\n",
       "                      max_depth=None, max_features='auto', max_leaf_nodes=None,\n",
       "                      max_samples=None, min_impurity_decrease=0.0,\n",
       "                      min_impurity_split=None, min_samples_leaf=1,\n",
       "                      min_samples_split=2, min_weight_fraction_leaf=0.0,\n",
       "                      n_estimators=10, n_jobs=-1, oob_score=False,\n",
       "                      random_state=42, verbose=0, warm_start=False)"
      ]
     },
     "execution_count": null,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "model = RandomForestRegressor(n_estimators=10, bootstrap=True, n_jobs=-1, random_state=42)\n",
    "model.fit(X_train, y_train)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "After training, each tree is stored in an attribute called `estimators_`. For each tree, we can call `predict()` on the validation set and use the `numpy.stack()` function to concatenate the predictions together:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "preds = np.stack([tree.predict(X_valid) for tree in model.estimators_])"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Since we have 10 trees and 3889 samples in our validation set, we expect that `preds` will have shape $(n_\\mathrm{trees}, n_\\mathrm{samples})$:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "(10, 3889)"
      ]
     },
     "execution_count": null,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "preds.shape"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "**Note:** To calculate `preds` we made use of Python's list comprehension. An alternative way to do this would be to use a for-loop as follows:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "preds_list = []\n",
    "\n",
    "for tree in model.estimators_:\n",
    "    preds_list.append(tree.predict(X_valid))\n",
    "\n",
    "# concatenate list of predictions into single array \n",
    "preds_v2 = np.stack(preds_list)\n",
    "\n",
    "# test that arrays are equal\n",
    "assert_array_equal(preds, preds_v2)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Let's now look at a plot of the $R^2$ values as we increase the number of trees."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "def plot_r2_vs_trees(preds, y_valid):\n",
    "    \"\"\"Generate a plot of R^2 score on validation set vs number of trees in Random Forest\"\"\"\n",
    "    fig, ax = plt.subplots()\n",
    "    plt.plot(\n",
    "        [\n",
    "            r2_score(y_valid, np.mean(preds[: i + 1], axis=0))\n",
    "            for i in range(len(preds) + 1)\n",
    "        ]\n",
    "    )\n",
    "    ax.set_ylabel(\"$R^2$ on validation set\")\n",
    "    ax.set_xlabel(\"Number of trees\")"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAZAAAAEJCAYAAAC61nFHAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8li6FKAAAgAElEQVR4nO3deVxU9f4/8NdsrAMMwgyY4pK7CEWpLJpLV0MTM5Vy6xqVVLZY5PVqZhfTe8uF1JsZbfa9fW+L13K7WJn29Xp/V7DUurmAW1mCG4MMOwOzfX5/oKPkBodZYOb1fDx84DkzZ+b9UZgX5/M55/ORCSEEiIiImknu7gKIiKhtYoAQEZEkDBAiIpKEAUJERJIwQIiISBIGCBERScIAISIiSZTuLsDVyspqYLM1/9aXsDA1SkurnVBR68U2ewe22fO1pL1yuQyhoYHXfMzrAsRmE5IC5NKx3oZt9g5ss+dzRnvZhUVERJIwQIiISBIGCBERScIAISIiSRggREQkidddhUVE5A5CCLjrui9nrdrBACEicpB6sw0lFRaUVJihv/j1ym2TxT0R0i5IiaxHo6BUyBz6ugwQIqImstkEDNUW6MstKKm8FA4W6C8GRWWttdHz/VQyaENU0GlUiO7sj0BfhVvq7nRLIBROGLBggBARXSSEQHXd5bMI+9dKC/TlZpRWWWC1XX6+XAaEBSuhDVEh7tYA6DRKaINV0IY07Avyl0Mmc+xv/VJotUEoKaly+OsyQIjIq5gsNpwuqcPRX2rtIaG/IiyMpsbdTEH+cmhDVLg10hfxvdT2cNCFKNEuSAmF3P0B4S4MECLyOCazDfoKC4rLzThfZoa+3Nzw93IzyqqsjQazVQoZdBolwoNV6NXBzx4Ql776+/Bi1ethgBBRm1RvtkFf3hAS9j9lDV8N1Y3HIoL85YjQqNCnoz8iNCp0iwqCn9wCbbASIYGKVtHN1BYxQIio1ao3264IhsZhUXaNkIgMVaFPp4aQiNQ0DF5HaJQI9Gs8eO2sMQFvwwAhIreqM9mgr2joaiout9jPIvTlZpTVNA6J4AAFIjRKRHfyR2TopYBo+BPgy64mV2OAEJFDCSFQZxaoNlpRZbShus6KavtXK6rrbKg2WlFWbcX5cjMqfhMSIQEKRISq0K+Lvz0cIkJViAhRwZ8h0aowQIjoumw2gZp623XCoOFrlfGKfRfD4cpLXX8rwFeOIH85QgKViO3ScCZxKSh0Gg5atyUMECIvc+lmuOLyhnsbrPJaFF8wXj5DuCIgautt151+QyEH1H4KqP3lUPspEBmqarQd5H/575e+BvrJvfqyV0/DACHyQBarQGllw6CzvuLSwHPDdkmFGZbGvUbwVckufujLofZXQBuibPTBr/a/Mhgavvr5yHj1kpdjgBC1USaLzX4TXHG5Bfqyy1coXai04MoVTH2UMkRoVOjQToU7bg2wDz7rNEp066xBRVmN+xpCbRYDhKgV++29Dvryy2cThipLo+4lfx8ZIkJV6Brpi4TeavuYQkTIje918FFyzIGkYYAQuZnZInCm1NToHgf9xfGJ317GGuQvh06jQq+Ofg0BEaK0X6Wk9msd8y6R92CAELmYTQicvmBC/ikjDp8y4tiZukbTfGsCFYjQXL6M1d7dFHL1DXFE7sQAIXKB0irLxcCoRUFRnX3a71vaqTC0XxB6dfRruDEuRAU/XsZKbQQDhMgJauttOFJkRP4pI/ILjThXZgbQcJNcv07+iO7sj+hO/mgXxB9Barv43UvkABarwM/n6nD4YmCcPF8Pm2i4+ql3Rz8Mjw1CdKcAdAxXcZyCPAYDhEgCIQTOlJpxuLDhLOPoaSPqzQIyGXBrhC9SBmrQr5M/ut/i5/BlRIlaCwYIUROVVVuQX3i5W6r84hVSkaEqDO4bhOhO/ugT5ceBbvIabgmQnJwcZGdnw2w2Iy0tDdOmTbM/duTIEcybN8++bTAYEBISgq1bt2Lz5s3IyspCWFgYAGDYsGHIyMhwef3kHYwmG46evhwYZ0obxjGC/OWIvmIcIzxY5eZKidzD5QFSXFyMlStXYuPGjfDx8cHkyZMRHx+P7t27AwD69OmDLVu2AACMRiMeeOABLFy4EABw6NAhzJs3DykpKa4um7yAxSpQcKoGuQfKcLjQiJ/P1cFqa1ixrldHP9wV3XCWEaX1gZzjGESuD5C8vDwkJCRAo9EAAJKTk7Ft2zY888wzVz33nXfewYABA9C/f38ADQFy6tQpvPvuu+jZsydefvllhISEuLR+8ixmi8DhwlrsO16DH36uRW29DTIAXSJ8cW9/DaI7+aP7Lb68W5voGlweIHq9Hlqt1r6t0+lw8ODBq55XWVmJ9evXIycnx75Pq9Xi8ccfR2xsLFasWIFFixbh9ddfd0nd5DlMZhsOnTJi3/Ea/PdkDYwmgQBfOeK6BWDo7WHoGAKo/TmOQXQzLg8QIa6eHPpalzXm5ORgxIgR9vEOAFizZo397zNmzMCIESOa/f5hYepmH3OJVhsk+di2ylPaXGeyYf/xSuw+VIG9RythNNkQ5K/AkNhQDO4Xgtu6qaHy4rMMT/l/bg5va7Mz2uvyAImIiMD+/fvt23q9Hjqd7qrnffPNN3jiiSfs21VVVdiwYQPS0tIANASRUtn88ktLq2GzXW+Fg+vzxjWU23qb60w2HPilFvtO1ODHk7UwWQSC/OVI6BWIAT0D0bujv/0S2/KLs9G29TZLwTZ7vpa0Vy6XXfcXb5cHSFJSElavXg2DwQB/f39s374dixcvbvQcIQTy8/MRFxdn3xcQEID3338fcXFxuO222/DRRx9h5MiRri6fWjljvQ0//lKLvcercfAXI8xWgZAABQZHB2Fgj0D06ujHBY2IHMQtZyAZGRmYPn06zGYzUlNTERsbi/T0dMyaNQsxMTEwGAxQqVTw9fW1H6dQKLBq1SosXLgQdXV16NKlC5YtW+bq8qkVqqmz4seTtdh7ogaHf20IjdBABYbFBGFAz0D0vMUPcoYGkcPJxLUGJTwYu7CarjW3udpoxX9P1mLv8RocPlULqw1op1ZgQM9ADOihRvdbfCVdatua2+wsbLPn85guLCKpqoxW/PBTDfYer0FBkRFWGxAerMQ9cSEY2DMQXSOlhQYRScMAoVatstaK/T/VYN/xGhwpMsImAF2IEqPuDMGAHmp0jfDh5IREbsIAoVanvNrSEBonanD0dB2EACI0KowZoMGAnoHorGVoELUGDBBqNU5fMGHzt2XYd7wGAkD7dircN1CDgT3VnAadqBVigJDbnSk1Ycu3ZfjuWA18VTLcOyAEg/sGoUOYj7tLI6IbYICQ25wrM2HLnnLsOVoNH5UMYwZoMLp/CII4jQhRm8AAIZcrLjNj83dlyDtSDZVChnv7h2B0fw2CAxgcRG0JA4RcRl9uxpbvypBbUA2FXIZRd4RgzAAGB1FbxQAhpyupMOOf35Vjd0EV5DIZRsYFY8wADTSB/PYjasv4E0xOc6HSgpzvyvD/8qsgkwF3xwYjZaAGoWp+2xF5Av4kk8MZqizI2VuOXYcqAQDDYoIxdqAG7YL47UbkSfgTTQ5TVn05OIQAhvQLwtiBoQgP5rcZkSfiTza1WHmNBVv3luNfB6tgtQncFR2E++I10Iao3F0aETkRA4Qkq6ix4Iv9Fdh5oBIWq8CgvmqMiw+FTsPgIPIGDBBqtspaK77cX45vfqyE2SqQ1EeN++NDERHK4CDyJgwQarIqoxVf7a/Ajh8rYDILJPZWY1yiBu1DOeUIkTdigNBNVRut2PZDBbb/UIF6s0B8r0CMSwjlXFVEXo4BQtdVbbRiY54BX/9QAaNJYGDPQNyfEIqO4QwOIpIYIMXFxYiIiGi076effkL37t0dUhS539c/VGDzt7+ips6GAT0agiNKy+AgosuaFSDl5eUAgPT0dPz973/HpeXULRYLnnrqKWzfvt3xFZLLffV9OT79twH9ewZh3MBgdNb5urskImqFmhUgs2fPRm5uLgAgPj7+8osolRgxYoRjKyO3yC2owqf/NmBAj0BkPtwVhtJqd5dERK1UswJk7dq1AIAXX3wRr732mlMKIvc58Est3t9egr5RfnhytA4KOVcAJKLrk0s56LXXXkNdXR2OHTsGIQTq6uocXRe52ImzdVidU4yocB88d18kVEqGBxHdmKQAOXDgAEaMGIEnnngCxcXFGDJkCH744QdH10YucqbUhBWbzkMTqMDs8ZHw95X0bUFEXkbSJ8XSpUvxt7/9DRqNBpGRkVi+fDn+8pe/OLo2coHSKguWbzgHpVKGP05sjxCu0UFETSQpQOrq6hpdsjt06FBYrVaHFUWuUWW0YtmGczCabJgzIZJzWBFRs0gKEKVSiYqKCshkDf3kJ0+edGhR5Hz1ZhtWbDqPCxUWZIyLRCctL9UlouaR1F8xc+ZMPPTQQ7hw4QJeeOEF5ObmYtGiRY6ujZzEYhVYnVOMk8X1mDU2Ar2j/N1dEhG1QZICZPjw4bj11luRm5sLm82Gp556inehtxE2IfD+1yU4+KsRj44Mx53dA91dEhG1UZIvt5HL5Zg6dSq0Wi22bduGqqoqR9ZFTiCEwKf/NiDvaDVSB4ViWEywu0siojZMUoD86U9/wnvvvYeff/4ZixcvxpkzZ/DSSy85ujZysC/2VeDrHypwT1zDGuVERC0hKUAOHz6MhQsXYseOHRg/fjxee+01nDlzxtG1kQP9+3Al1u82IKFXIKYOC7NfAEFEJJWkABFCQC6XIzc3FwkJCQAAo9Ho0MLIcX74uQYf7LiAfp398fgoHeQMDyJyAEmD6J06dUJ6ejpOnz6NgQMHYvbs2ejdu3eTj8/JyUF2djbMZjPS0tIwbdo0+2NHjhzBvHnz7NsGgwEhISHYunUrzp49izlz5qC0tBRdu3ZFVlYWAgM5CHwjx04bsWarHl11vpg1NgJKBcODiBxDUoC89tpr2LFjB+68806oVCr0798f999/f5OOLS4uxsqVK7Fx40b4+Phg8uTJiI+Pt1/F1adPH2zZsgVAw1nNAw88gIULFwIAXnnlFUydOhVjxozBmjVr8NZbb2HOnDlSmuAVikpMWLmlGOHBSrwwPhJ+PpyihIgcR9InSkBAAMaNG4eOHTsCAKZMmQJ//6bdS5CXl4eEhARoNBoEBAQgOTkZ27Ztu+Zz33nnHQwYMAD9+/eH2WzGvn37kJycDACYMGHCdY8joKTCjOUbz8FXJcOciZEIDlC4uyQi8jAun/hIr9dDq9Xat3U6HQ4ePHjV8yorK7F+/Xrk5OQAAMrKyqBWq6FUNpSs1WpRXFzsmqLbmMpaK5ZtOA+TRWDBpFsQHswpSojI8VweIJdWMbzSta4IysnJwYgRIxAWFtas424mLEzd7GMu0WqDJB/rKrX1Viz+x88oq7bg1ce6IbpLy8aI2kKbHY1t9g7e1mZntNflARIREYH9+/fbt/V6PXQ63VXP++abb/DEE0/Yt9u1a4fq6mpYrVYoFAqUlJRc87ibKS2ths12dRjdjFYbhJKS1n2zpNkisGLzefx81ojnxkVAF2hrUc1toc2OxjZ7B29rc0vaK5fLrvuLt6QA2bt3L1avXo2KiopGZwaXuptuJCkpCatXr4bBYIC/vz+2b9+OxYsXN3qOEAL5+fmIi4uz77s0WP/ll19i7Nix2Lx5M4YMGSKlfI9kswm8+7Ue+YVGpCdrEXcrr04jIueSFCCLFi3CxIkT0bdv32Z3I0VERCAjIwPTp0+H2WxGamoqYmNjkZ6ejlmzZiEmJgYGgwEqlQq+vo1niM3MzMS8efOQnZ2N9u3bY8WKFVLK9zhCCHz0r1J8d6wGk+5qh7uivevUnIjcQyauNbhwE+PHj8emTZucUY/TeWIX1uZvy7Axrwyj7wzBlKFhDnvd1txmZ2GbvYO3tdlZXViSLuPt0aMHjh07JqkYcqydByuxMa8Mg/qqMWlIO3eXQ0ReRFIXVlFRESZMmIAOHTo06mZqyhgIOc6+49X48P8u4LauAXhspJZTlBCRS0kKkIyMDAghcObMGVitVkRFRUEu513OrlRQaET2V3p0i/TFMyk6TlFCRC4nKUB0Oh2efvppFBcXQwiB0NBQvPPOO46uja7jV309Vv3zPCI0KrxwfyR8VQxvInI9SZ88ixcvxowZM7B//358//33mDlzJl555RVH10bXUFxuxusbzyPAV445E9pD7c8pSojIPSQFSGlpKcaPH2/fnjhxIsrKyhxWFF1beY0Fyzecg9Um8MeJ7dEuyOX3gRIR2UkKEKvVivLycvu2wWBwWEF0bbX1NmRtPI/yGitmj4/ELe183F0SEXk5Sb/CPvTQQ5g0aRJGjx4NAPjqq6/w8MMPO7QwusxksWHVlvM4U2pCxv2R6Nbez90lERFJC5BJkyahU6dO2L17N2w2GzIzM5GUlOTo2ggNU5S8/aUeR0/X4cnRWsR2CXB3SUREAFowmWJiYiISExMdWQv9hhACH/7fBez/qRbThoUhqQ+nKCGi1qNZAfLcc8/hr3/9K8aOHXvNx3kjoWMd/MWIfx2qQsoADZLvCHF3OUREjTQrQNLT0wEAM2bMQPv27Rs9duLECcdVRQCAg7/Wwkcpw/jEUHeXQkR0lWZdhdWxY0eUl5dj7dq16NWrF3r27ImePXvi1ltvxYcffuisGr1WQZERvTr4QaXkXeZE1Po06wxk9uzZyM3NBQDEx8dDJpNBCAGlUokRI0Y4pUBvVV5twZlSMwb35bgHEbVOzQqQtWvXAgBefPFFvPbaa04piBrkFxoBANGd/N1cCRHRtUm6kZDh4XwFRUYE+snRSccbBomodZJ0Ge9///tfvPvuu6itrYUQAjabDadPn8auXbscXJ53EkIgv9CIvlH+nKKdiFotSWcgCxYsQFxcHKqrqzF27Fio1Wrcc889jq7NaxWXW2CosrL7iohaNUlnIDKZDI8//jjKyspw66234r777sOUKVMcXZvXujT+0ZcBQkStmKQzkMDAQABAp06dcOLECfj6+sJqtTq0MG9WUGhEWJASERrOtktErZekT6jY2Fg8//zzeO655/DEE0/g119/hULBdSkcwSYECoqMuKNbAGQc/yCiVkzSGcj8+fORlpaGrl27Yv78+bDZbMjKynJ0bV6pUG9CTZ2N4x9E1OpJHgO5/fbbAQDDhg3DsGHDHFmTV7OPf0QxQIiodWtWgPz+97+/YbfK//7v/7a4IG+XX2hEhzAVNGqOfxBR69asT6mHHnoIALBjxw5UV1dj4sSJUCgU2LJlC4KDg51SoDcxWwSOn6nDsBhOX0JErV+zAiQ5ORlAw5Qm69atg1zeMIQybNgwTJo0yfHVeZmfz9XBZBG8fJeI2gRJg+hlZWWor6+3b9fU1KCiosJhRXmrw4VGyGRA744MECJq/SR1tKekpODBBx/EyJEjIYTAtm3b8MADDzi6Nq9TUGjErZG+CPCVlOtERC4lKUCee+459OvXD3v27IFMJsOLL76IIUOGOLo2r2Kst+Hk+XqkDNS4uxQioiZxyJK23377LZYvX84lbVvg6BkjbIKX7xJR2yFpSduXX37ZKcV4s/xTRqgUMnS/xdfdpRARNUmzAqRfv34AgIEDBzqlGG9WUGhEr45+8FFy/IOI2oZmBchvu65+i11Y0lTUWHC61IykPrz/g4jajmYFCLuunKOgqA4Ap28noralWQHiqK6rnJwcZGdnw2w2Iy0tDdOmTWv0+MmTJ5GZmYmKigpotVqsWLECISEh2Lx5M7KyshAWFgag4QbGjIwMh9TkTvmnjAjwlaMLl68lojbE5UvaFhcXY+XKldi4cSN8fHwwefJkxMfHo3v37gAalnOdOXMmXnrpJQwZMgRZWVl49913MWfOHBw6dAjz5s1DSkqKlLJbJXFx+va+UX6Qyzl9OxG1HS5f0jYvLw8JCQnQaDQICAhAcnIytm3bZn88Pz8fAQEB9vtKnnzySfsZyqFDh7B582bcd999+MMf/uARd7/rKyy4UGlh9xURtTkuX9JWr9dDq9Xat3U6HQ4ePGjfLiwsRHh4OObOnYuCggL07NnTPvai1Wrx+OOPIzY2FitWrMCiRYvw+uuvN6v2sDB1s55/Ja3W8YPc+34pBQDcdXs4tFo/h79+Szmjza0d2+wdvK3NzmivpAD57ZK2d955Z5OXtBVCXLXvyiniLRYL9u7di48++ggxMTFYtWoVlixZgiVLlmDNmjX2582YMQMjRoxodu2lpdWw2a6u4Wa02iCUlFQ1+7ib+S6/DKFqBXyECSUlZoe/fks4q82tGdvsHbytzS1pr1wuu+4v3pK6sGJiYvD8888jISEBH3zwAZYsWdLkJW0jIiJw4cIF+7Zer4dOp7Nva7VadO7cGTExMQAa5t06ePAgqqqq8Le//c3+PCEElMq2vWaGTQgUFBoR3cmfy9cSUZsjKUBeeuklyUvaJiUlYc+ePTAYDDAajdi+fXujebTi4uJgMBhw9OhRAMDOnTsRHR2NgIAAvP/++zhw4AAA4KOPPsLIkSOllN9qFJWYUM3la4mojZL0K/zs2bPx4IMPAmj+krYRERHIyMjA9OnTYTabkZqaitjYWKSnp2PWrFmIiYnBmjVrsGDBAhiNRkRGRmLZsmVQKBRYtWoVFi5ciLq6OnTp0gXLli2TUn6rUXBp+VoGCBG1QTJxrUGJm/j000+xadMmlJWVITU1FRMmTGg0MN6ataYxkKyN51BSacHStCiHvq6jeFs/McA2ewtva3OrGgOZMmUK1q9fj7fffhsVFRWYPHkynn76aUnFeSuLVeDo6Tp2XxFRm9Wimfvq6upgMpkghGjyIDo1uLR8LQOEiNoqSWMgH3zwATZt2gSTyYTU1FSsX78e4eHhjq7No+Xbl69tffd+EBE1haQAyc/Px4IFCxAfH+/oerxGfqERXXW+CPTjmRsRtU2SAqS5d39TY3WmhuVr7+3P5WuJqO3i6kVucOx0Haw2Xr5LRG0bA8QNDhc2LF/boz2XryWitosB4gYFhUb06OAHHxX/+Ymo7ZI0BrJ3716sXr0aFRUVjSZH5JK2N1dZa0XRBRMeGBzq7lKIiFpEUoAsWrQIEydORN++fTkJYDMVFF2cviSK4x9E1LZJChCVSoVHHnnE0bV4hUvL13aN4PgHEbVtkjrhe/TogWPHjjm6Fq9QUGREn45cvpaI2j5JZyBFRUWYMGECOnToAF/fy79JcwzkxkoqzCipsGDUHSHuLoWIqMUkBUhGRgaEEDhz5gysViuioqIgl/OKopvJ5/TtRORBJAWITqfD008/jeLiYgghEBoainfeecfRtXmc/EIjNIEK3NJO5e5SiIhaTNJpw+LFizFjxgzs378f33//PWbOnIlXXnnF0bV5FC5fS0SeRlKAlJaWYvz48fbtiRMnoqyszGFFeaLTF0yoMtrYfUVEHkNSgFitVpSXl9u3DQaDwwryVJeWr+X6H0TkKSSNgTz00EOYNGkSRo8eDQD46quv8PDDDzu0ME+TX2hEZKgK7YIk/ZMTEbU6kj7NJk2ahE6dOmH37t2w2WzIzMxEUlKSo2vzGBarwLHTdRjUN8jdpRAROYzkX4cTExORmJjoyFo81snz9agzC45/EJFH4c0bLlBQaIQMQB8uX0tEHoQB4gL5hUZ0jvCB2p/L1xKR52CAOFm92YafztXx6isi8jg3DBCr1Yrt27fjm2++gdVqte//6quvnF6Yp7i0fC0DhIg8zQ0D5I9//CMOHz6MI0eOYNq0aTh16hQA4NNPP3VJcZ4gv9AIpQLocQvHP4jIs9zwKiy9Xo/XX38dADBhwgTMnTsXzzzzjEsK8xT5hUb0aO8HXy5fS0Qe5oafamazGSaTCQDQoUMHvP322/jggw9w/PhxlxTX1lUZrSgsMSG6M7uviMjz3PAMZP78+aisrER4eDgAQK1WIzs7G1u3bnVJcW3dES5fS0Qe7IYBEhsbe9U+hUKBcePGOa0gT5JfaIS/jwxdI7l8LRF5nmZ1zJeXl6OwsPCaj13q6qLL8k8Z0bujPxRcvpaIPFCTA+Tzzz/HoEGDkJycjAceeADl5eWorq7Gxo0b8fTTTyM+Pt6ZdbY5FyrN0FdYePkuEXmsJs+F9dZbb2Hp0qUYMGAAVqxYgTlz5uDAgQOIjIzE0KFDORvvb3D5WiLydE0OEIPBgJSUFADASy+9hIEDB+KNN97APffc0+w3zcnJQXZ2NsxmM9LS0jBt2rRGj588eRKZmZmoqKiAVqvFihUrEBISgrNnz2LOnDkoLS1F165dkZWVhcDAwGa/vysUFNYhJFCBDmFcvpaIPFOTu7Dk8stPDQ4ORmBgoKTwKC4uxsqVK/HJJ59gy5Yt+Mc//oGffvrJ/rgQAjNnzkR6ejr++c9/ok+fPnj33XcBAK+88gqmTp2Kbdu2oV+/fnjrrbea/f6uIC4uX9s3isvXEpHnanKA1NbWIikpCTNmzMDKlSths9lw+vTpZr9hXl4eEhISoNFoEBAQgOTkZGzbts3+eH5+PgICAjBkyBAAwJNPPolp06bBbDZj3759SE5OBtBwY+OVx7UmZ0rNqKi1cvyDiDxak7uw9u7diyNHjtj/REVFYdSoUfD19UWPHj3Qs2dPLFq06Kavo9frodVq7ds6nQ4HDx60bxcWFiI8PBxz585FQUEBevbsiZdffhllZWVQq9VQKhtK1mq1KC4ubk5bAQBhYepmH3OJVtu0BaFyj5cAAO6KC4dW4yP5/VqDprbZk7DN3sHb2uyM9jY5QIKDgxEfH9/oaiuTyYQTJ06goKAAR48ebdLrCCGu2ndlN4/FYsHevXvx0UcfISYmBqtWrcKSJUuQkZFxw+OaqrS0Gjbb1TXcjFYbhJKSqiY9d29BOSI0SsjM9SgpqW/2e7UWzWmzp2CbvYO3tbkl7ZXLZdf9xbtFC3T7+PggOjoa0dHRTT4mIiIC+/fvt2/r9XrodDr7tlarRefOnRETEwMASElJwaxZs9CuXTtUV1fDarVCoVCgpKSk0XGthdUmcOS0EYm9pZ/pEBG1BS6f4S8pKQl79uyBwWCA0WjE9u3b7eMdABAXFweDwWA/o9m5c8TfLccAAA8oSURBVCeio6OhUqnQv39/fPnllwCAzZs3NzqutTh5vh51JsHxDyLyeC06A5EiIiICGRkZmD59OsxmM1JTUxEbG4v09HTMmjULMTExWLNmDRYsWACj0YjIyEgsW7YMAJCZmYl58+YhOzsb7du3x4oVK1xd/k3Zl6/l/FdE5OFk4lqDEh7M2WMgr64/C6PJhsUPdZRSXqvibf3EANvsLbytzc4aA+EiFQ7E5WuJyJswQBzo+Jk6WKycvoSIvAMDxIEKCo1QyIFeHbh8LRF5PgaIA+UXGtGdy9cSkZfgJ52DVButOKXn8rVE5D0YIA5ypMgIAXAAnYi8BgPEQfKL6uCnkqFrBJevJSLvwABxkPxTRvTq6A+lgtO3E5F3YIA4QGmVBcXlZo5/EJFXYYA4QMHF5WujOX0JEXkRBogD5BcaERygQMdwLl9LRN6DAdJCQgjkFxrRN8qPy9cSkVdhgLTQWYMZFTVcvpaIvA8DpIXyL45/cP4rIvI2DJAWKig0QheihDaE4x9E5F0YIC1gtQkcKTLy7IOIvBIDpAV+La6HkcvXEpGXYoC0wKXxDy5fS0TeiAHSAgWFRnTS+iA4QOHuUoiIXI4BIpHJbMOJs/Uc/yAir8UAkej42TqYrRz/ICLvxQCRqKCwjsvXEpFXY4BIVFBoRLf2fvDz4T8hEXknfvpJUFNnxS/F9egbxbMPIvJeDBAJjhTVNSxf2znA3aUQEbkNA0SCgkIjfFUydIvk8rVE5L0YIBLkFxnRq4Mfl68lIq/GAGkmQ5UF5wxmXr5LRF6PAdJMBUUXl6/l+udE5OUYIM2UX2hEkL8cHcN93F0KEZFbMUCaQQiBgkIj+kT5Q87la4nIyzFAmuFcmRll1Vy+logIYIA0S8HF6dsZIEREgNJdb5yTk4Ps7GyYzWakpaVh2rRpjR5/8803sWHDBgQHBwMAHnzwQUybNu26+10hv9CI8GAldBouX0tE5JYAKS4uxsqVK7Fx40b4+Phg8uTJiI+PR/fu3e3POXz4MFasWIG4uLhGx15vv7M1LF9bhwE9Al36vkRErZVburDy8vKQkJAAjUaDgIAAJCcnY9u2bY2ec/jwYbz33nsYO3YsFi1ahPr6+hvud7afzhhRW2/j+h9ERBe5JUD0ej20Wq19W6fTobi42L5dU1ODPn36YO7cudi0aRMqKyvx1ltvXXe/Kxz4uQoAOIEiEdFFbunCEkJctU92xWWxgYGBeO+99+zbjz76KObPn4+MjIzr7m+qsDC1pJp//FmPLpF+6N4lVNLxbZVWG+TuElyObfYO3tZmZ7TXLQESERGB/fv327f1ej10Op19++zZs8jLy0NqaiqAhsBRKpXX3d8cpaXVsNmuDrAbMVlsyP+1BsNjg1BSUtWsY9syrda72guwzd7C29rckvbK5bLr/uLtli6spKQk7NmzBwaDAUajEdu3b8eQIUPsj/v5+WH58uUoKiqCEAIff/wxRo4ced39zvbT2XqYLALRnTh9OxHRJW47A8nIyMD06dNhNpuRmpqK2NhYpKenY9asWYiJicGiRYswc+ZMmM1m3HHHHXjkkUfg4+Nzzf3Oll9obFi+tiPHP4iILpGJaw1IeDApXVjvfa2H0SzDrBTtzZ/sQbztNB9gm72Ft7XZWV1YbruRsC15dKQWoe3UqCyvcXcpREStBqcyaQKFXAZfFf+piIiuxE9FIiKShAFCRESSMECIiEgSBggREUnCACEiIkkYIEREJInX3Qcil0tfy7wlx7ZVbLN3YJs9n9T23ug4r7sTnYiIHINdWEREJAkDhIiIJGGAEBGRJAwQIiKShAFCRESSMECIiEgSBggREUnCACEiIkkYIEREJAkD5CZycnJw7733YuTIkfj444/dXY5LvPnmmxgzZgzGjBmDZcuWubscl1q6dCnmzZvn7jJcYufOnZgwYQJGjRqFP//5z+4uxyW2bNli/95eunSpu8txmurqaqSkpOD06dMAgLy8PIwdOxb33HMPVq5c6bg3EnRd58+fF8OHDxdlZWWipqZGjB07Vpw4ccLdZTlVbm6umDRpkqivrxcmk0lMnz5dbN++3d1luUReXp6Ij48Xc+fOdXcpTldYWCgGDx4szp07J0wmk5gyZYrYtWuXu8tyqtraWjFgwABRWloqzGazSE1NFbm5ue4uy+F+/PFHkZKSIqKjo0VRUZEwGo1i6NChorCwUJjNZvHoo4867P+aZyA3kJeXh4SEBGg0GgQEBCA5ORnbtm1zd1lOpdVqMW/ePPj4+EClUqFbt244e/asu8tyuvLycqxcuRJPPvmku0txiR07duDee+9FZGQkVCoVVq5cidtuu83dZTmV1WqFzWaD0WiExWKBxWKBr6+vu8tyuPXr1yMzMxM6nQ4AcPDgQXTu3BlRUVFQKpUYO3aswz7HvG423ubQ6/XQarX2bZ1Oh4MHD7qxIufr0aOH/e+//vorvvzyS6xbt86NFbnGn/70J2RkZODcuXPuLsUlTp06BZVKhcceewwlJSUYPnw4nn/+eXeX5VRqtRrPPfccRo8eDT8/PwwcOBB33HGHu8tyuL/85S+Ntq/1OVZcXOyQ9+IZyA2Ia0xULJN5xxTQJ06cwKOPPoq5c+eiS5cu7i7HqT777DO0b98eiYmJ7i7FZaxWK/bs2YPly5dj/fr1OHToEDZt2uTuspzq6NGj2LBhA/71r39h9+7dkMvlWLt2rbvLcjpnfo4xQG4gIiICFy5csG/r9Xr7aaEn+/7775GWlobZs2dj/Pjx7i7H6b788kvk5uZi3LhxeOONN7Bz5068+uqr7i7LqcLDw5GYmIh27drBz88Pv/vd7zz+7Hr37t1ITExEWFgYfHx8MGHCBOzdu9fdZTmdMz/HGCA3kJSUhD179sBgMMBoNGL79u0YMmSIu8tyqnPnzuHpp59GVlYWxowZ4+5yXOJ//ud/sHXrVmzZsgWzZs3C3Xffjfnz57u7LKcaPnw4du/ejcrKSlitVvznP/9BdHS0u8tyqt69eyMvLw+1tbUQQmDnzp2IiYlxd1lOd9ttt+GXX37BqVOnYLVasXXrVod9jnEM5AYiIiKQkZGB6dOnw2w2IzU1FbGxse4uy6nWrl2L+vp6LFmyxL5v8uTJmDJlihurIke77bbbMGPGDEydOhVmsxmDBg3CxIkT3V2WUw0ePBgFBQWYMGECVCoVYmJi8Pjjj7u7LKfz9fXFkiVL8Oyzz6K+vh5Dhw7FqFGjHPLaXJGQiIgkYRcWERFJwgAhIiJJGCBERCQJA4SIiCRhgBARkSQMEPJYp0+fRq9evfDZZ5812r927VqHzrh7991349ChQw57vRuprq7G5MmTMWbMGHz99deNHtu1axf++te/uqQOIoD3gZCHk8vlWLp0Kfr374+uXbu6u5wWO3LkCEpLS7Fjx46rHjt06BAqKircUBV5KwYIeTQ/Pz888sgjmD17NtatWwcfH59Gj8+bNw89evTAY489dtX23XffjZSUFOzatQvl5eV49tln8cMPPyA/Px9KpRLZ2dmIiIgAAHzyySc4evQoTCYTHnnkEaSmpgJoWHMjOzsbZrMZfn5+mDt3LuLi4rB69Wr8+OOP0Ov16NWrF7KyshrV9c033+DNN9+E1WqFWq3Giy++CLVajfnz56O4uBjjxo3DP/7xD/j5+QEADhw4gHXr1sFqtSIoKAidO3fG559/DqPRCLVajb///e/47LPP8Omnn8Jms0Gj0eDll19Gt27dYDKZkJWVhX379sFqtaJv375YsGAB1Go1PvnkE6xbtw4qlQq+vr5YtGgRunfv7uz/NmorHDIpPFErVFRUJG6//XZhtVrF1KlTxZIlS4QQQrz//vv2NT/mzp0r3n//ffsxV24PHz5cvPrqq0IIIb744gvRu3dvceTIESGEEE899ZTIzs62Py8zM1MI0bCGTEJCgjh+/Lj45ZdfREpKijAYDEIIIY4fPy4GDRokampqxBtvvCGSk5OF2Wy+qu6ffvpJJCUlicLCQiFEwzolgwYNElVVVeLbb78VY8aMuWZ733jjDfHKK68IIYTYsGGDGDBggKiqqhJCCPHdd9+JqVOnitraWiGEEP/5z3/E6NGjhRBCrF69WixZskTYbDYhhBCvv/66yMzMFBaLRURHR4vi4mIhhBCbNm0S69ata8b/AHk6noGQx5PL5Vi+fDnGjx+PwYMHN+vYe+65BwAQFRWF8PBw9O7dGwDQqVOnRt1FkydPBtAw/c3gwYOxZ88eKBQK6PV6pKWl2Z8nk8lQWFgIALj99tuhVF79I/jtt98iISEBUVFRAGCf9PDw4cPNmkW1V69eUKvVABrGR06dOmWvEwAqKipQXl6OXbt2oaqqCnl5eQAAs9mMsLAwKBQKjBo1CpMnT8awYcMwaNAgjB07tsnvT56PAUJe4ZZbbsHChQsxd+5c3H///fb9Mpms0XTXZrO50XFXdnmpVKrrvr5cfvl6FCEElEolrFYrEhMTsWrVKvtj586dg06nw44dOxAQEHDN1xLXmF1ICAGLxXLDGn7ryte32WwYN24c5syZY9/W6/UICQmBzWbD/PnzMXToUABATU0N6uvrAQBZWVk4fvw48vLy8N577+Hzzz9HdnZ2k2sgz8arsMhrjB49GkOGDMGHH35o3xcaGorDhw8DAAwGA/bv3y/ptS+tpXH27Fnk5eUhMTERCQkJyM3Nxc8//wwA+Pe//4377rvP/uF8PZeOKyoqAgDs2bMH586du+mKgQqFAhaL5ZqPDRo0CF988QX0ej0A4NNPP8XDDz8MoGGSwY8//hgmkwk2mw0vv/wyVqxYAYPBgKFDh0Kj0SAtLQ3PP/88jh071vR/FPJ4PAMhr7JgwQJ8//339u3f//73+MMf/oDk5GR07NgRAwcOlPS69fX1GD9+PMxmMxYsWGC/4mvRokV44YUX7Gcl2dnZ1z3zuKR79+7IzMzEM888A6vVCj8/P7z99tsICgq64XGJiYl49tlnoVKprpqa/a677kJ6ejoeffRRyGQyqNVqvPnmm5DJZHjqqaewdOlSjB8/HlarFX369MG8efOgVqsxc+ZMpKWlwc/PDwqFAn/+858l/fuQZ+JsvEREJAm7sIiISBIGCBERScIAISIiSRggREQkCQOEiIgkYYAQEZEkDBAiIpKEAUJERJL8f0EaulLtcbYIAAAAAElFTkSuQmCC\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    }
   ],
   "source": [
    "plot_r2_vs_trees(preds, y_valid)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "As we add more trees, $R^2$ improves but appears to flatten out. Let's test this numerically."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "---\n",
    "\n",
    "#### Exercise #2\n",
    "\n",
    "* Increase the number of trees in the forest by changing `n_estimators` from 10 to 20, 40, and 80 and print their metrics.\n",
    "* For the forest with 80 tree, generate the array of predictions for each tree and plot the $R^2$ value against the number of trees.\n",
    "\n",
    "---"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Out-Of-Bag (OOB) score"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "So far, we've been using a validation set to examine the effect of tuning hyperparameters like the number of trees - what happens if the dataset is small and it may not be feasible to create a validation set because you would not have enough data to build a good model? Random Forests have a nice feature called _**Out-Of-Bag (OOB) error**_ which is designed for just this case!\n",
    "\n",
    "The key idea is to observe that the first tree of our ensemble was trained on a bagged sample of the full dataset, so if we evaluate this model on the _remaining_ samples we have effectively created a _validation set per tree._ To generate OOB predictions, we can then average all the trees and calculate RMSE, $R^2$, or whatever metric we are interested in.\n",
    "\n",
    "To toggle this behaviour in scikit-learn, one makes use of the `oob_score` flag, which adds an `oob_score_` attribute to our model that we can print out:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "RMSE on train: 16755.861\n",
      "R^2 on train: 0.97\n",
      "RMSE on valid: 44145.602\n",
      "R^2 on valid: 0.797\n",
      "OOB R^2: 0.786\n"
     ]
    }
   ],
   "source": [
    "model = RandomForestRegressor(n_estimators=40, bootstrap=True, n_jobs=-1, oob_score=True, random_state=42)\n",
    "model.fit(X_train, y_train)\n",
    "print_rf_scores(model)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "OOB score is handy when you want to find the best set of hyperparameters in some automated way. For example, scikit-learn has a function called [grid search](https://scikit-learn.org/stable/modules/grid_search.html) that allows you pass a list of hyperparameters and a range of values to scan through. Using the OOB score to evaluate which combination of parameters is best is a good strategy in practice."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## More hyperparameter tuning"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Let's look at a few more hyperparameters that can be tuned in a Random Forest. From our earlier analysis, we saw that 40 trees gave good performance, so let's pick that as a baseline to compare against."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "RMSE on train: 16755.861\n",
      "R^2 on train: 0.97\n",
      "RMSE on valid: 44145.602\n",
      "R^2 on valid: 0.797\n",
      "OOB R^2: 0.786\n"
     ]
    }
   ],
   "source": [
    "model = RandomForestRegressor(n_estimators=40, bootstrap=True, n_jobs=-1, oob_score=True, random_state=42)\n",
    "model.fit(X_train, y_train)\n",
    "print_rf_scores(model)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### Minimum number of samples per leaf"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "The hyperparameter `min_samples_leaf` controls whether or not the tree should continue splitting a given node based on the number of samples in that node. By default, `min_samples_leaf = 1`, so each tree will split all the way down to a single sample, but in practice it can be useful to work with values 3, 5, 10, 25 and see if the performance improves."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "---\n",
    "\n",
    "#### Exercise #3\n",
    "Train several Random Forest models with `min_samples_leaf` values of 3, 5, 10, and 25. By comparing the scores, do you see an improvement in performance compared to our baseline?\n",
    "\n",
    "---"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### Maximum number of features per split"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Another good hyperparameter to tune is `max_features`, which controls what _**random**_ number or fraction of _**columns**_ we consider when making a single split at a tree node. Here, the motivation is that we might have situations where a few columns in our data are highly predictive, so each tree will be biased towards picking the same splits and thus reduce the generalisation power of our ensemble. To counteract that, we can tune `max_features`, where good values to try are `1.0`, `0.5`, `log2`, or `sqrt`."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "---\n",
    "\n",
    "#### Exercise #4\n",
    "\n",
    "Train a Random Forest model with `max_features` values of 0.5, 1.0, 'log2', and 'sqrt'. By comparing the scores, do you see an improvement in performance compared to our baseline? Hint: you may find it useful to create a for-loop over the list `[0.5, 1.0, 'log2', 'sqrt']`.\n",
    "\n",
    "---"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": []
  }
 ],
 "metadata": {
  "kernelspec": {
   "display_name": "Python 3",
   "language": "python",
   "name": "python3"
  }
 },
 "nbformat": 4,
 "nbformat_minor": 4
}