{
 "cells": [
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "# Lesson 9 - Overfitting\n",
    "\n",
    "> What is overfitting and how can it be avoided?"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "[![Binder](https://mybinder.org/badge_logo.svg)](https://mybinder.org/v2/gh/lewtun/dslectures/master?urlpath=lab/tree/notebooks%2Flesson09_overfitting.ipynb) [![slides](https://img.shields.io/static/v1?label=slides&message=lesson09_overfitting.pdf&color=blue&logo=Google-drive)](https://drive.google.com/open?id=1xH2FnIzrrub1ZJmyJAhYrUOyhJ5ov13x)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Learning Objectives\n",
    "Overfitting is a phenomena that can always occur when a model is fitted to data. Therefore, it is important to understand what it entails and how it can be avoided. In this notebook we will address these three questions related to overfitting:\n",
    "1. What is overfitting?\n",
    "2. How can we measure overfitting?\n",
    "3. How can overfitting be avoided?\n",
    "\n",
    "## References\n",
    "* Chapter 5: Overfitting and its avoidance of _Data Science for Business_ by F. Provost and P. Fawcett\n",
    "\n",
    "\n",
    "## Homework\n",
    "* Work through part 2 of the notebook concerning the housing dataset.\n",
    "* Solve exercises in the notebook. In particular, tune a random forest for the churn dataset in part 3."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## What is overfitting?\n",
    "\n",
    "Already John von Neumann, one of the founding fathers of computing, knew that fitting complex models to data is a tricky business:\n",
    ">With four parameters I can fit an elephant, and with five I can make him wiggle his trunk.\n",
    ">\n",
    "> \\- John von Neumann\n",
    "\n",
    "<div style=\"text-align: center\">\n",
    "<img src='images/elephant.jpg' width='300'>\n",
    "    <p style=\"text-align: center;\"> <b>Figure reference:</b>Irrelevant image. </p>\n",
    "</div>\n",
    "\n",
    "\n",
    "When we fit a model to data we always have to be careful not to overfit. If we overfit the model this means that the model learned specific aspects of the training data and does not *generalise* to new, unseen data. Instead of learning useful relations between the input feature and the target the model has memorised the training samples. If this happens the model we perform very poorly on new data and therefore we want to make sure this does not happen.\n",
    "\n",
    "Fortunately, there are tools that can help detect and avoid overfitting. One tool we already used: splitting the data into two sets. Measuring the performance difference between the training and validation set already helps identifying when we are overfitting. In this lecture we will see an even more systematic way of splitting the data namely *cross-validation*."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Load libraries"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "# reload modules before executing user code\n",
    "%load_ext autoreload\n",
    "# reload all modules every time before executing Python code\n",
    "%autoreload 2\n",
    "# render plots in notebook\n",
    "%matplotlib inline"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "import numpy as np\n",
    "import seaborn as sns\n",
    "import pandas as pd\n",
    "import matplotlib.pyplot as plt\n",
    "from pathlib import Path\n",
    "from tqdm import tqdm\n",
    "import time\n",
    "\n",
    "from sklearn.model_selection import train_test_split, cross_validate\n",
    "from sklearn.ensemble import RandomForestRegressor, RandomForestClassifier\n",
    "\n",
    "from dslectures.core import rmse, make_polynomial_data, PolynomialRegressor, get_dataset\n",
    "from dslectures.structured import proc_df\n",
    "\n",
    "np.warnings.filterwarnings('ignore')"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Part 0: tqdm\n",
    "Before starting with overfitting we introduce the tqdm library. In this notebook we will make extensive use of for-loops and tqdm is a very handy addition to them. With just one expression you can add a progress bar to your for loop. Let say you have a for-loop that does some computation:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "for i in range(1000):\n",
    "    #do something\n",
    "    a = i**2\n",
    "    time.sleep(0.01)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "100%|██████████| 1000/1000 [00:10<00:00, 92.63it/s]\n"
     ]
    }
   ],
   "source": [
    "for i in tqdm(range(1000)):\n",
    "    #do something\n",
    "    a = i**2\n",
    "    time.sleep(0.01)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "100%|██████████| 5/5 [00:05<00:00,  1.00s/it]"
     ]
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "sum: 15\n"
     ]
    },
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "\n"
     ]
    }
   ],
   "source": [
    "sum_i = 0\n",
    "for i in tqdm([1,2,3,4,5]):\n",
    "    sum_i += i\n",
    "    time.sleep(1)\n",
    "print('sum:', sum_i)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### Installation\n",
    "If you run tqdm in Jupyter notebooks locally you might need to run the following in the terminal:\n",
    "\n",
    "```\n",
    "jupyter nbextension enable --py --sys-prefix widgetsnbextension\n",
    "```\n",
    "\n",
    "For Jupyterlab run additionally this command:\n",
    "\n",
    "```\n",
    "jupyter labextension install @jupyter-widgets/jupyterlab-manager\n",
    "```"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Part 1: Overfitting Polynomials\n",
    "\n",
    "### Polynomials\n",
    "To study the nature of overfitting we start looking at a the toy example of a polynomials. Later we will see our findings are not specific to polynomials and can be extended to other *supervised* machine learning methods such as linear regressors, tree classifiers or random forests. \n",
    "\n",
    "A polynomial of degree $n$ has the form:\n",
    "$$f(x) = w_0 + w_1\\cdot x + w_2\\cdot x^2 +\\ldots+w_n\\cdot x^n$$"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### Generate data\n",
    "\n",
    "In this block we generate a random polynomial of degree 3 With the helper function `get_polynomial_data`. The polynomial has the form:\n",
    "$$f(x) = 10 \\cdot x^3 -5 \\cdot x $$\n",
    "If you are interested in creating or fitting polynomial data check out the functions `numpy.polyval` and `numpy.polyfit`. In this lesson we will use wrapper functions around them. The function `get_polynomial_data(w, n_samples=100)` evaluates the polymial defined by `w` on `n_samples` random points and adds some noise to it."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "weights = np.array([10, 0, -5, 0])\n",
    "X, y = make_polynomial_data(weights, n_samples=100)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "We can plot the polynomial data in a scatter plot:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "def scatter_plot_polynomial(X, y, label='', title='Polynomial data'):\n",
    "    plt.title(title)\n",
    "    plt.scatter(X, y, label=label)\n",
    "    plt.xlabel('x')\n",
    "    plt.ylabel('y')\n",
    "    plt.grid(True)\n",
    "    plt.legend(loc='best')"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYAAAAEWCAYAAABv+EDhAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8li6FKAAAgAElEQVR4nO3df5QcdZnv8feTYUIGJmYCeAcYIgmuBtEYQwZhCVcTZA3+ghhZjSsqrntzxZXj2avRcMNZsyome+Pq9R7d48Ufiy7I8EOdjSKLYDKronghhhh+GAFZJSNgRCZmzESG5Ll/dE3o6anq7uru6qru+rzOyclMdXX309U19XzrqW99v+buiIhI/kxLOwAREUmHEoCISE4pAYiI5JQSgIhITikBiIjklBKAiEhOKQFIyzOz9WZ2TdpxFDOzt5nZd6tcN1b8ZuZm9me1RydSoAQgmWFm/2lmY2Y2amZPmNnVZtaddly1cPdr3f3VacZgZnODZHFEmnFIdikBSNa8wd27gdOBfuCKlOMRaVtKAJJJ7j4M3AK8BMDMTjSzzWb2ezN7yMz+W9jzzOxmM7usZNnPzOyNwc9uZu8xswfNbMTMPmdmFjw2zcyuMLNfmdlvzeyrZjYreGyiNf0uM3vUzJ4KXueM4PVHzOyzRe95iZn9sOj3zwTP+4OZbTOz/1rttjCzNWb2mJn9xsz+uuSx15nZ9uB1HzWz9UUPfz/4fyQ4q/pzM3u+mW0xsyfN7Hdmdq2Z9VQbi7QXJQDJJDObA7wW2B4sGgB2AycCFwGfMLNzQ576FeDiotdZCPQBNxet83rgDOClwJuB5cHyS4J/y4BTgG7gs0x2JvAC4C3A/wbWAecBLwbebGavjPhIdwEvA44BvgbcaGYzItY9zMzOBz4I/EXwvueVrPJH4B1AD/A64FIzWxE89org/x5373b3HwMGbKCwHV8EzAHWV4pD2pMSgGTNoJmNAD8E/oPCgX4OsAT4sLsfcPd7gC9SOPCV2gy80MxeEPz+duB6d3+6aJ2N7j7i7r8GtlI4MAO8DfiUu//S3UeBy4FVJTX0jwUxfJfCwfc6d/9tcMbyA2BR2Idy92vc/Ul3f8bd/wk4EphfxfZ4M/Av7n6vu/+RkoO1uw+5+053P+TuPwOuA6KSEO7+kLvf5u5/cvc9wKfKrS/tTQlAsmaFu/e4+8nu/l53H6PQWv29u+8rWu9XFFr2k7j7AeB64GIzmwa8FfjXktUeL/p5P4WWPsH7/KrkPY4AeouWPVH081jI76EXrc3sg2b2gJntDRLcLOC4sHVLnAg8WhJT8eueaWZbzWyPme0F3lPudc2s18wGzGzYzP4AXFNlHNKGlACkFfwGOMbMZhYtex4wHLH+Vyi05l8F7A9KH9W+z8kl7/EMkw/ysQX1/g9RaM3PdvceYC+Fckwlj1Eo0xTHVOxrFM565rj7LODzRa8bNtTvJ4LlC9z9ORTKZdXEIW1ICUAyz90fBX4EbDCzGWb2UuDdFFqvYev/GDgE/BNTW//lXAf8nZnNC7qffoJC+eiZuj4AzKSQSPYAR5jZ3wPPqfK5NwCXmNlpZnYU8JGQ1/69ux8ws5cDf1X02B4K2+GUkvVHgb1m1gesif1ppG0oAUireCswl0Ir/ZvAR9z99jLrfxVYQESSiPBlCgnj+8AjwAHgsrLPqM6twL8Dv6BQwjnA5LJOJHe/hcLF5i3AQ8H/xd4LfNTM9gF/TyFhTDx3P3AlcEfQS+ks4B8odLHdS+HC+Ddq/1jS6kwTwkg7MrN3AKvd/Zy0YxHJKp0BSNsJSiXvBa5KOxaRLFMCkLZiZssp1L6foHCBVEQiqAQkIpJTqZ4BmFmPmd1kZj8P+kj/eZrxiIjkSdqjBH4G+Hd3v8jMpgNHlVv5uOOO87lz58Z6gz/+8Y8cffTRtUeYEMUVX1Zjy2pckN3YFFd89cS2bdu237n7c6c84O6p/KNwJ+QjBGWoav4tXrzY49q6dWvs5zSD4oovq7FlNS737MamuOKrJzbgbg85pqZ2DcDMXkahl8b9wEJgG/B+L4x3UrzeamA1QG9v7+KBgYFY7zM6Okp3d/aGlFdc8WU1tqzGBdmNTXHFV09sy5Yt2+bu/VMeCMsKzfhHYaz3Z4Azg98/Q2GgLZ0BpCircblnN7asxuWe3dgUV3xJnAGkeRF4N7Db3X8S/H4ThTsURUSkCVK7COzujwcTWMx3910UBu66P+7rjI+Ps3v3bg4cOBD6+KxZs3jggQfqjLbx4sQ1Y8YMTjrpJDo7OxOOSkTyJO1eQJcB1wY9gH4JvCvuC+zevZuZM2cyd+5cgomdJtm3bx8zZ84MeWa6qo3L3XnyySfZvXs38+bNa0JkIpIXqSYAL0zsMfXCRAwHDhyIPPi3AzPj2GOPZc+ePWmHIiJNNLh9mE237uI3I2Oc2NPFmoUHG/4ebTEURLse/Ce0++cTkckGtw9z+Td2MjwyhgPDI2MMPzXG4PaoKTBq0xYJQESknWy6dRdj45Nb/Ifc2XTrroa+jxJAg61fv55PfvKTkY8PDg5y//2xr3WLSI78ZmQs1vJaKQE0mRKAiFRyYk9XrOW1yl0CGNw+zJKNW5i39maWbNzSkJralVdeyQtf+ELOOeccdu0qnKJ94Qtf4IwzzmDhwoW86U1vYv/+/fzoRz9i8+bNrFmzhiVLlvDwww+Hrici+bZm+Xy6OjsmLZtmxprl8xv6PrlKAGEXVi7/xs66ksC2bdsYGBjgnnvu4Tvf+Q533XUXACtXruSuu+5ix44dvOhFL+JLX/oSZ599NhdccAGbNm3ijjvu4PnPf37oeiKSbysW9bFh5QL6erowoK+ni77ZXaxY1NfQ90n7PoCmCruwMjZ+kE237qp5w/7gBz/gjW98I0cdVRjI9IILLgDg3nvv5YorrmBkZITR0VGWL18e+vxq1xORfFmxqG/ScWloaKjh75GrBNCsCysAl1xyCYODgyxcuJCrr7468surdj0RkUbLVQkoiQsrr3jFKxgcHGRsbIx9+/bxrW99Cyjc6XvCCScwPj7Otddee3j9mTNnsm/fvsO/R60nIpK0XCWAsAsrXZ0ddV1YOf3003nLW97CwoULec1rXsMZZ5wBwMc+9jHOPPNMlixZwqmnnnp4/VWrVrFp0ybOOeccHn744cj1RESSlqsS0EQ9bdLt1cvn131hZd26daxbt27K8ksvvXTKsiVLlnD//fcfHgvo0ksvDV1PRCRpuUoAMPXCiohIXuWqBCQiIs9qiwTgKU1r2Szt/vlEJB0tnwBmzJjBk08+2bYHyYn5AGbMmJF2KCLSZlr+GsBJJ53E7t27I8fLP3DgQCYPnnHimpgRTESkkVo+AXR2dpadKWtoaIhFixY1MaLqZDUuEcmPli8BiYhIbZQARERySglARCSnlABERHJKCUBEJKdavheQiEg7GNw+3PBxyipRAhARSdnEbIUTE1ZNzFYIJJoEVAISEUlZudkKk6QzABGRBopbyhncPsxwE2crLKYEICLSIHFLORPrR6lntsJqpF4CMrMOM9tuZt9OOxYRkXrELeWErT+h3tkKq5F6AgDeDzyQdhAiIvWKKtnEXQ6wYeWCxHsBpZoAzOwk4HXAF9OMQ0SkEaJKNnGX9/V0NWXmQktzHH0zuwnYAMwEPujurw9ZZzWwGqC3t3fxwMBArPcYHR2lu7u7AdE2luKKL6uxZTUuyG5s7RrXyNg4w0+NcajouDrNjL7ZXfR0dda1fj2xLVu2bJu79095wN1T+Qe8Hvjn4OelwLcrPWfx4sUe19atW2M/pxkUV3xZjS2rcblnN7Z2juubP93tZ2/4ns/98Lf97A3f82/+dHdD1q8nNuBuDzmmptkLaAlwgZm9FpgBPMfMrnH3i1OMSUSkLisW9cUq38Rdv5FSuwbg7pe7+0nuPhdYBWzRwV9EpHmy0AtIRERSkIkbwdx9CBhKOQwRkVzRGYCISE4pAYiI5JQSgIhITmXiGoBIPdKYSEOkHlnZZ5UApKWlNZGGSK2ytM+qBCSJGdw+zJKNW5i39maWbNzC4Pbhhr9HWhNpiNQqS/uszgAkEc1q5dQyyqJImrK0z+oMQBLRrFZO3FEWRdKWpX1WCUAS0axWzprl8+nq7Ji0rBkTaYjUKkv7rEpAkogTe7pC5zltdCtnopyUhR4VItXI0j6rBCCJWLN8/qRrAJBcKyfN0RRFapGVfVYJQBKRpVaOiIRTApDEZKWVIyLhdBFYRCSndAYgIlKnrAztEJcSgIhIHbI0tENcKgGJiNQhS0M7xKUEICJShywN7RCXEoCISB2yNLRDXEoAIiJ1yNLQDnHpIrCISEylvX7etLiPrT/fo15AIiLtLKzXz9e3DbNh5YKWOOgXUwlIRCSGqF4/H7hhR6KTHyVBZwAiIjFE9e456A7oPgARkbZVTe8e3QcgItKGwnr9hCk9U2jGHNlxqQQkIhKh3Bg/E8unmR0u/xQrPlPI6nARqSUAM5sDfBXoBRy4yt0/k1Y8IiLFKh20Jw7cpesBWLD+ko1bWLN8ftnhItJMAGmWgJ4BPuDupwFnAX9rZqelGI+IyGHVjvGzYlEfG1YuoC9o8RuFFi08mzTCpkedeDxNqSUAd3/M3X8a/LwPeADI9iVzkZiyWPeV6sQZ42fFoj7uWHsufT1dlBaDSpNIsQ6zekKsm3lI7arpQZjNBb4PvMTd/1Dy2GpgNUBvb+/igYGBWK89OjpKd3d3YwJtIMUVX1Zji4prZGyc4afGOFT0NzbNjL7ZXfR0daYaW9paIa5dj+/j6YOHpqwzvWMa84+fGfr8ncN7Y7/ngr5ZsWOLa9myZdvcvb90eeoJwMy6gf8ArnT3b5Rbt7+/3+++++5Yrz80NMTSpUtrDzAhiiu+rMYWFdeSjVtCT/H7erq4Y+25TYis9bZZ2orjCqvtd3V2lL3jN+o774i4UBxnX6hnm5lZaAJItRuomXUCXweurXTwl2xSiSNaKw8TLJNr+0bhYF1puIeoLqJHHmF0dkwu92RhwLg0ewEZ8CXgAXf/VFpxSO2y2rUtK07s6QptDbbCMMHtpJ7pGot7+1S7PsD6zfcxMjZ+ePn+8UN0TjNmH9XJyP7xzAwYl+YZwBLg7cC5ZnZP8O+1KcbTUrLQ8m7lmZCaoZWHCW4XE42U4ZExnGcbKUn+vaxY1MfRR05tW48fco6afgSPbHwdd6w9N/WDP6R4BuDuP6TQY0piykrLu51KHElM6l16w1BWWn15klb/+1b529CdwC0oKzeVtEuJo9qEWkuSiFtCkMZK60DcKn8bGguoBWWldVFriSML5ati1ZSy0iglSP1qma6xEftnq5T/dAbQguppXTSy1FFLiaOa1nYS5Zhyqkmo5ZLElWepHZVVa5bPD+3KGXUgHhkb5/Lv1V9ebZXynxJAC4q7U08Y3D7Mmht3MH7o2XHL19y4A6j92kHcEkel8lW5BNFTU4SVVZNQyyeJoxOKTOoV90D8xN4DjI1PTui1lldbofynBNCCam1drN983+GD/4TxQ876zfc1bUet1NpOo6VdTUJtlZquTBXnQFy483fqfpa1i7eNogTQomppXRT3S65meRIqHUjTaGlXk1DLJom9DyYSlzTf9I7wRka7JnolAKlZLbX6Sq3ttK5vVEqo5ZLE0JASQDsY3D4cOlxDFi/eNooSQI7MPqqTp/ZPbe3PPir+wGS13otQqbVda0u7GfdGtEJNV2ozsf+899TJCWD2UZ185A0vbtvvXQkgR1730hO45s5fhy6Pq557EcodSGttaWfl3ghpTWH7D8BR049o6/1HCSBHtv58T6zl5SR5L0Jpgpjol71qzj7WBTMslf5RJhXPFYM7ue4nj3LQnQ4z3nrmHD6+YkFdrynZk5V7a5pNCSBHonbm4qnrwrpahtXWm9UrZlJpZ86zpZ27f/V7tv58D8MjY3SYTZmEoxHxXDG4c9IZ00H3w78rCbSXvPby0h0sLaBRd86W25knDqylPYIGtw+z5qYdk+6AXXPTDpad+tym3OkYVdq59s5fH/6DDbtw14h4rvvJo7GWS+tqlTt3G00JIOMaOQRB1FjlE8bGD/LE3gOTlv3Dt+5j/GDJvQMHnZt/9ljssdJrEXXWUmkao0bEE5VYopZL65oY+396x7RE9+esUQko4xp5cbP4AmvUZNSlU+CF9RqaWN6MXjFRp+blGDRkxq2oWZzSnsdVkrFiUR9Dex/kkY1L0w6laXQGkHGNvjhVPHl1mKgbYdISdtZS6fDbqLrtW8+cE2u5SKvJ1l+7TFHLaIbViKp59s6aMWlZ1OTlzZrUvHhaPiicmr/trOdFlrIMWHbqcxvy3h9fsYCLz3re4RZ/hxkXn/U8XQCWtqESUMbVOvBbJVH97XtKbrZaf8GLJw0gB9A5zVh/wYvrev+4sRbuAxjisrctBaD/5GNCS1kOfH3bMP0nH9OQ8tTHVyzQAV/alhJAxtU7rGy54RHCavilN1tFvT/Ako1bUhvqdiL2JRu3TEkC5a6RNHuoackm7QcFSgAtoPQgPDFRSaUdtlHDI4TdmJWFKSkh3jWSpOIeGRtPNRlKPGkMOZ5VugbQAqrpChp2r0BSk7ZnaTL4ONdIkoh7cPsww0+NaaawFpKl/TdtSgAtoNIOG5UgorpP1nt7e5Zum49zA08ScW+6dReHSrqK5vVg0iqytP+mTSWgFlDrJCpR/djr7UGUpdvm41wjSSLu34yMQUiv0DweTFpFrftBO1430BlAC6hU5og62Bx0T+T29qzdNj9xb8MjG1/HHWvPjfyjTCLupLrpSnJq2Q8aeUd+ligBtIBKO2zUwWbidvZGD9dQ3De/lW6bTyLuNcvnM63kzuBWHUOmUWNOZV0t+0G7XjdQCagF1DOJSlLDNbTq5CiNjnvFoj4GH7+fvp6Oli4NZKlnVzPE3Q/a9bqBEkDCGlU3rHUSFUleT1cnd6xdmnYYddGEOuVl6bpXIykBJKhSf+NGXlRq1Ra5ZEO7tnAbJak78tOW6jUAMzvfzHaZ2UNmtjbNWJJQrlU1MjbekItKeanbSrJ0Mbu8Vr3uVUnFMwAzuwy4xt2fauQbm1kH8DngL4DdwF1mttnd72/k+6SpXKvqib2HGBufnH/jnnLnrW4ryammhduO3SDjaMez7GrOAHopHJxvCFrsjRoM/eXAQ+7+S3d/GhgALmzQa2dCuVZV6bj7E+KccjejZ4LOMPKhUgu3XbtB5p15FbMbBQf9VwPvAvqBG4AvufvDNb+x2UXA+e7+N8HvbwfOdPf3lay3GlgN0Nvbu3hgYCDW+4yOjtLd3V1rmHUZGRtn+KmxSXeKTjOjb3YXzxzYz2P7pz5nesc05h8/s6rX3zm8N/KxBX2zYscLk7dXufibNRx0VGxZktW4oHGx7Xp8X2ijJc7+mkRcpUbGxnli7wGePniI6R3T6J01I9a+2q7f5bJly7a5e3/p8qouAru7m9njwOPAM8Bs4CYzu83dP1RTRFVy96uAqwD6+/t96dKlsZ4/NDRE3Oc0UtRp8+Att/HPPz045ZR7w8oFLK3yNHNdyEiYUGi9TQybHFfx9iqMtDl13P2+no5Uer2k/V1GyWpc0LjY3rX2ZjykYGBQ0wxaSWyzwe3DXP69nUFptRBrV+dBNqw8rerSTR6+y2LVXAN4P/AO4HfAF4E17j5uZtOAB4FaE8Awk2+iPylY1lai6oY9XZ1sWHlaXTXVpHsmqGeITGiFbpDqyhpfNWcAxwAr3f1XxQvd/ZCZvb6O974LeIGZzaNw4F8F/FUdr9dy6r2olHT//1b4o5fmyEI3yLCzaXh2/48qZqvBEq1iAnD3j5R57IFa39jdnzGz9wG3Ah3Al939vlpfL6/iJJG4vTiy8Ecv2ZD2zYZhPd7W3LgDDMYPlr+OGafBkre5HVK9EczdvwN8J80Y8qKWLqNp/9FLtqTZDTKsvFM8TWmUOA2WZ+d2KFz3ykO3at0JnBO11kfbse+ztJ5ayjh9MRssm27dxao54XM7tOvfgBJATuiCbmvI4s1WcWNK4jNEXY+KYsAda8+N9R55nNtBw0HnhG71z74s3mwVN6akPsOa5fPpnFb9Pai17Nd5/BtRAsiJrE3iIlNlccz5uDEl9RlWLOqje0Z1BYta9+t2mtuhWioB5YQu6EarVLJoVlkm6TJdLZ8jbkxJfoaR/eNlHzeoe8j1dpjbIQ4lgJQ1s+arC7pTVeod1cwB95K876LWzxE3piQ/Q7nrAH09XbFr/mHaYW6HOFQCSlEWa755U6lk0cyyTJJlulo/R9yYkvwMUdcBOjusrcs0SVICSFEWa755U6lk0czeU0mOOV/r54gbU5KfYcWiPjb95cJJg7vNPqqTTRct1JltjVQCqiDJEo26Ztamkd9JpZJFs4fDSKpMV8/niBtTkqXGWl47i11rs0JnAGUkXaLJY7ezejX6O6lUsmiX3lPt8jniUpm1PCWAMpIu0eT1j7Iejf5OKpUsWnUqwImJfHYO72XJxi0ALfk56hW1v6zffJ8mOkIloLKSLtGoa2Z8SXwnlcoKrdZ7alKPnznPtno3rFzQkJ4y5d43a/ty1H4xMjbOyFihW2lxj6iepkWWDUoAZTSj/ttqB5e0tesQ1Y08eCY1Ln65GLM6P3W1Q0hMbJ8rz8pXUSRfnzYmlWiypx2/k7A69d9dfw9zayxPJHGWFBbjmht3sOij32Xe2pv5wA07MtmjLWx/iZLHzhc6AyhDJZrsacfvJKzFPjEmZS0t6STOkqKGY34quDv3YMTc4mkfVMP2l/1PP3M47mKtfhZZCyWAClSiyZ52+04qHSTjlm+SmMin1gN50gfVakpnpftLabkKirbP3gcTjTdrVAISSVk1B8k4B+DinkvQmB4/tRzIky7N1drFs1V7diVBZwAidYo7jWBpq3XZqc/l69uGp5RYisU9AE+0eoeGhrjsbUtjPTdM2FlFmA4zDrk3pTRXz8XudjuLrJUSQEKy2CVOGi/uNIJhvWW+vm2YNy3uY+vP9zA8MobBpAnOs3CRu7SWPqurkz8+/cyk+Xi7Ojua2pLWnfT1UwJIQFa7xEnjxZ1GMKrVuvXnew730c9q4yGslp5mnO3aJbiZlAASkFQ/bMmeuNMIVrO8VcoTaceZxMXuvFECSIBOTfOj0NrcF7E8fP2st1rTbtlXqx27BDebEkACWuGPXBpjzfL5DD+wbdKySuPlZ7nV2mrly7TPQlqduoEmoB3vVpVwKxb10Te7KxPj5TeC5qjIF50BJECnpvkSdxrBLLdaVb7MFyWAhGT5j1wkisqX+aISkIgcpvJlvqRyBmBmm4A3AE8DDwPvcveRNGIRkWepfJkvaZWAbgMud/dnzOwfgcuBD6cUi4gUUfkyP1JJAO7+3aJf7wQuSiMOkTyptn9/q9wHIPUzjxjHu2kBmH0LuN7dr4l4fDWwGqC3t3fxwMBArNcfHR2lu7u77jgbTXHFl9XYshoXPBvbyNg4w0+Ncajo732aGX2zu+jp6jy8rNr1GhVX1mQ1LqgvtmXLlm1z9/7S5YklADO7HTg+5KF17v5vwTrrgH5gpVcRSH9/v999992x4hgaGmLp0qWxnhNXLS2mZsRVi6zGBdmNLatxAQzechubdnRETovY19M1aZ7gJRu3hK5bul69srrNshoX1BebmYUmgMRKQO5+XoWALgFeD7yqmoN/VrXanZOSH6UjlYYp7d+v+wDyJa1eQOcDHwJe6e7704ihXhOt/rDWkgZ+kywIG6m0VGn//qzdB6DrEclK6z6AzwIzgdvM7B4z+3xKcYQa3D7Mko1bmBcxKXfxTERR1GKStFXaB8P692fpPoBaZ/yS6qXVC+jP0njfalRT0gkbL6WU7pyUtEWNVAqFmn7U/LmQjfsANKx68jQURIlqdrpaWlYizRY1Ummlweeych+ArkckTwmgRDU7XVSdFKJbViJJiaqTr1jUx+Dj99PX05Fqaz4svp4qnpe16xHtSAmgRDU7XdSY7lka1lfyoVLJMu5IpVHvUWtJKCq+DWdH90yakPW5E9qBBoMrUc1FsKyP6S75kfT4/fVeiI2K74m9Byo+V39nydMZQIlqL4JlpU4q+ZZ0nbzeC7FRcTx98FBV76+/s2QpAYTQTietIuk6eb0JJiq+6R0qPmSBvgWRFpZ0v/1yk9tXIyq+3lkz6o5N6qcEINLCkq6T15tgouJr5MByUjuVgERaXJIly0bcGBYW39DQgw2NU2qjBCAiZUUlGI3T0/qUAEJoxxYpT6PgtgddAyihAahEKkv6/gNpDiWAEtqxRSrTOD3tQQmghHZskcrq7R4q2aAEUEI7tkhlWZo3QGqnBFBCO7ZIZRqnpz2oF1CJLE2IIZJlGjKl9SkBhNCOLSJ5kOsEoP7+IpJnuU0AupFFRPIutxeB1d9fRPIutwlA/f1FJO9ymwDU319E8i63CUD9/UUk73J7EVj9/UUk73KbAED9/UUk33KdAHQfgIjkWarXAMzsA2bmZnZcs99b4/6LSN6llgDMbA7wauDXaby/7gMQkbxL8wzg08CHAE/jzXUfgIjknbk3//hrZhcC57r7+83sP4F+d/9dxLqrgdUAvb29iwcGBmK91+joKN3d3VOW73p8H08fPDRl+fSOacw/fmas96hFVFxpy2pckN3YshoXZDc2xRVfPbEtW7Zsm7v3ly5P7CKwmd0OHB/y0Drgf1Io/1Tk7lcBVwH09/f70qVLY8UxNDRE2HNGSsYCgsJ9ABtWLmBpEy4ER8WVtqzGBdmNLatxQXZjU1zxJRFbYgnA3c8LW25mC4B5wA4zAzgJ+KmZvdzdH08qnrAePxtWLlAvIBHJraZ3A3X3ncB/mfi9UgmoEaJG/tywcgF3rD03qbcVEcm0XAwFoR4/IiJTpX4jmLvPTfo91ONHRGSqXJwBaORPEZGpcpEANPKniMhUqZeAmkEjf4qITJWLBAAa+VNEpFQuSkAiIjKVEoCISE4pAYiI5JQSgIhITikBiIjklBKAiEhOKQGIiOSUEoCISE4pAYiI5JQSgIhITikBiIjklBKAiEhOKQGIiORUbkYDjRI2WbxGDRWRPMh1AoiaLB5QEgZLrVYAAAcRSURBVBCRtpfrEpAmixeRPMt1AtBk8SKSZ7lOAJosXkTyLNcJQJPFi0ie5foisCaLF5E8y3UCAE0WLyL5lesSkIhInikBiIjklBKAiEhOKQGIiOSUEoCISE6Zu6cdQ9XMbA/wq5hPOw74XQLh1EtxxZfV2LIaF2Q3NsUVXz2xnezuzy1d2FIJoBZmdre796cdRynFFV9WY8tqXJDd2BRXfEnEphKQiEhOKQGIiORUHhLAVWkHEEFxxZfV2LIaF2Q3NsUVX8Nja/trACIiEi4PZwAiIhJCCUBEJKdaPgGY2V+a2X1mdsjMIrtImdn5ZrbLzB4ys7VFy+eZ2U+C5deb2fQGxnaMmd1mZg8G/88OWWeZmd1T9O+Ama0IHrvazB4peuxlzYorWO9g0XtvLlqe9jZ7mZn9OPjef2Zmbyl6rKHbLGq/KXr8yGAbPBRsk7lFj10eLN9lZsvriaOGuP6Hmd0fbJ/vmdnJRY+Ffq9NjO0SM9tTFMPfFD32zuC7f9DM3tnkuD5dFNMvzGyk6LHEtpmZfdnMfmtm90Y8bmb2f4K4f2Zmpxc9Vt/2cveW/ge8CJgPDAH9Eet0AA8DpwDTgR3AacFjNwCrgp8/D1zawNj+F7A2+Hkt8I8V1j8G+D1wVPD71cBFCWyzquICRiOWp7rNgBcCLwh+PhF4DOhp9DYrt98UrfNe4PPBz6uA64OfTwvWPxKYF7xORxPjWla0H106EVe577WJsV0CfDbkuccAvwz+nx38PLtZcZWsfxnw5SZts1cApwP3Rjz+WuAWwICzgJ80anu1/BmAuz/g7pVmcX858JC7/9LdnwYGgAvNzIBzgZuC9b4CrGhgeBcGr1nta18E3OLu+xsYQ5i4cR2WhW3m7r9w9weDn38D/BaYcpdjA4TuN2XivQl4VbCNLgQG3P1P7v4I8FDwek2Jy923Fu1HdwInNei9646tjOXAbe7+e3d/CrgNOD+luN4KXNeg9y7L3b9PoeEX5ULgq15wJ9BjZifQgO3V8gmgSn3Ao0W/7w6WHQuMuPszJcsbpdfdHwt+fhzorbD+KqbudFcGp32fNrMjmxzXDDO728zunChLkbFtZmYvp9Cie7hocaO2WdR+E7pOsE32UthG1Tw3ybiKvZtCC3JC2PfaKNXG9qbgO7rJzObEfG6ScRGUy+YBW4oWJ7nNKomKve7t1RIzgpnZ7cDxIQ+tc/d/a3Y8xcrFVvyLu7uZRfa5DTL6AuDWosWXUzgITqfQB/jDwEebGNfJ7j5sZqcAW8xsJ4UDXF0avM3+FXinux8KFte8zdqRmV0M9AOvLFo85Xt194fDXyER3wKuc/c/mdl/p3AGdW4T37+SVcBN7n6waFna2ywRLZEA3P28Ol9iGJhT9PtJwbInKZxOHRG03iaWNyQ2M3vCzE5w98eCg9Vvy7zUm4Fvuvt40WtPtIT/ZGb/AnywmXG5+3Dw/y/NbAhYBHydDGwzM3sOcDOFRsCdRa9d8zYLEbXfhK2z28yOAGZR2K+qeW6ScWFm51FIqq909z9NLI/4Xht1MKsYm7s/WfTrFylc95l47tKS5w41K64iq4C/LV6Q8DarJCr2urdXXkpAdwEvsELvlekUvuDNXriSspVC7R3gnUAjzyg2B69ZzWtPqTkGB8CJuvsKILSXQBJxmdnsifKJmR0HLAHuz8I2C77Db1Koi95U8lgjt1noflMm3ouALcE22gysskIvoXnAC4D/V0csseIys0XA/wUucPffFi0P/V4bFFe1sZ1Q9OsFwAPBz7cCrw5inA28mslnxInGFcR2KoULqj8uWpb0NqtkM/COoDfQWcDeoKFT//ZK6sp2s/4Bb6RQ+/oT8ARwa7D8ROA7Reu9FvgFhay9rmj5KRT+MB8CbgSObGBsxwLfAx4EbgeOCZb3A18sWm8uhWw+reT5W4CdFA5i1wDdzYoLODt47x3B/+/OyjYDLgbGgXuK/r0siW0Wtt9QKCldEPw8I9gGDwXb5JSi564LnrcLeE2D9/tKcd0e/D1MbJ/Nlb7XJsa2AbgviGErcGrRc/862JYPAe9qZlzB7+uBjSXPS3SbUWj4PRbs07spXLN5D/Ce4HEDPhfEvZOi3o71bi8NBSEiklN5KQGJiEgJJQARkZxSAhARySklABGRnFICEBHJKSUAEZGcUgIQEckpJQCROpjZGcGgZjPM7GgrzFHwkrTjEqmGbgQTqZOZfZzCHcFdwG5335BySCJVUQIQqVMwtsxdwAHgbJ88iqRIZqkEJFK/Y4FuYCaFMwGRlqAzAJE6WWGO2AEKk4ic4O7vSzkkkaq0xHwAIlllZu8Axt39a2bWAfzIzM519y2VniuSNp0BiIjklK4BiIjklBKAiEhOKQGIiOSUEoCISE4pAYiI5JQSgIhITikBiIjk1P8HwRoicm/gSg0AAAAASUVORK5CYII=\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "scatter_plot_polynomial(X, y, label='data')\n",
    "plt.show()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### Train and validation sets\n",
    "We have already discussed in previous lessons that a validation set helps us investigate overfitting. The model is trained with the training set and its performance is measured using the validation set. We will do the same here."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "X_train, X_valid, y_train, y_valid = train_test_split(X, y, test_size=0.2,)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYAAAAEWCAYAAABv+EDhAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8li6FKAAAgAElEQVR4nO3deZxU1Znw8d9D20izSKMYlIYRzDiINEtLu0xwaUSFcSGIimR0EpwY3piJkzeZdAIxH0RjAgkmmkziGJdMJtGIiIpkjOICnbi/ssjigoig0LgA0i1IIw39vH/cqqa6urZbVbfurbrP9/PpT3ffusvTt6rvc+45554jqooxxpjw6eJ3AMYYY/xhCcAYY0LKEoAxxoSUJQBjjAkpSwDGGBNSlgCMMSakLAGYoicis0XkXr/jiCUiV4rIkxmu6yp+EVER+fvsozPGYQnABIaIbBaRFhHZIyIfisjvRaSn33FlQ1XvU9Xz/YxBRAZFksVhfsZhgssSgAmai1W1J3AyUAv80Od4jClZlgBMIKlqI/A4UA0gIv1FZLGIfCwib4vI1xJtJyKPich1ccvWiMglkZ9VRL4uIhtEpElEfiMiEnmti4j8UETeFZGPROQPItI78lq0NH21iGwRkV2R/ZwS2X+TiPw65pjTROS5mN9/GdnuExFZISJnZnouRKReRN4XkW0i8q9xr10oIqsi+90iIrNjXv5b5HtT5K7qH0Xk8yKyVER2isgOEblPRCozjcWUFksAJpBEZCBwAbAqsmg+sBXoD1wG/EREzkmw6f8AV8XsZyRQBTwWs85FwCnACGAKMD6yfFrkayxwPNAT+DUdnQacAFwB3AZcD5wLDAOmiMjZSf6kV4BRwJHAn4AHRaRbknXbicgE4LvAeZHjnhu3yqfAl4FK4ELgWhGZFHntrMj3SlXtqaovAgLMwTmPQ4GBwOx0cZjSZAnABM0iEWkCngP+inOhHwiMAb6vqvtU9VXgbpwLX7zFwD+IyAmR3/8FeEBV98esM1dVm1T1PWAZzoUZ4ErgF6r6jqruAWYCU+Pq0H8UieFJnIvv/ar6UeSO5VmgJtEfpar3qupOVT2gqj8HDgeGZHA+pgD/rarrVPVT4i7WqtqgqmtVtU1V1wD3A8mSEKr6tqo+paqfqep24Bep1jelzRKACZpJqlqpqsep6jdUtQWntPqxqu6OWe9dnJJ9B6q6D3gAuEpEugBfAv4Yt9oHMT/vxSnpEznOu3HHOAzoF7Psw5ifWxL8nrDRWkS+KyJviEhzJMH1BvomWjdOf2BLXEyx+z1NRJaJyHYRaQa+nmq/ItJPROaLSKOIfALcm2EcpgRZAjDFYBtwpIj0iln2d0BjkvX/B6c0Pw7YG6n6yPQ4x8Ud4wAdL/KuRer7v4dTmu+jqpVAM051TDrv41TTxMYU6084dz0DVbU3cEfMfhMN9fuTyPLhqnoETnVZJnGYEmQJwASeqm4BXgDmiEg3ERkBfBWn9Jpo/ReBNuDndC79p3I/8G0RGRzpfvoTnOqjAzn9AdALJ5FsBw4TkVnAERluuwCYJiIniUh34IYE+/5YVfeJyKnAP8e8th3nPBwft/4eoFlEqoB613+NKRmWAEyx+BIwCKeU/ghwg6o+nWL9PwDDSZIkkvgdTsL4G7AJ2Adcl3KLzCwBngDewqnC2UfHap2kVPVxnMbmpcDbke+xvgHcJCK7gVk4CSO67V7gx8DzkV5KpwM34nSxbcZpGH84+z/LFDuxCWFMKRKRLwPTVfUMv2MxJqjsDsCUnEhVyTeAO/2OxZggswRgSoqIjMep+/4Qp4HUGJOEVQEZY0xI+XoHICKVIrJQRN6M9JH+Rz/jMcaYMPF7lMBfAk+o6mUi0hXonmrlvn376qBBg1wd4NNPP6VHjx7ZR+gRi8u9oMYW1LgguLFZXO7lEtuKFSt2qOrRnV5QVV++cJ6E3ESkGiqTr9GjR6tby5Ytc71NIVhc7gU1tqDGpRrc2Cwu93KJDViuCa6pvrUBiMgonF4arwMjgRXAt9QZ7yR2venAdIB+/fqNnj9/vqvj7Nmzh549gzekvMXlXlBjC2pcENzYLC73colt7NixK1S1ttMLibJCIb5wxno/AJwW+f2XOANt2R2Aj4Ial2pwYwtqXKrBjc3ics+LOwA/G4G3AltV9eXI7wtxnlA0xhhTAL41AqvqB5EJLIao6nqcgbted7uf1tZWtm7dyr59+xK+3rt3b954440co82/MMTVrVs3BgwYQHl5eV72Z4zJL797AV0H3BfpAfQOcLXbHWzdupVevXoxaNAgIhM7dbB792569eqVYEt/lXpcqsrOnTvZunUrgwcPzkNkxph88zUBqDOxR+eGCRf27duX9OJv/CMiHHXUUWzfvt3vUIwpSotWNTJvyXq2NbXQv7KC+pEH836MkhgKwi7+wWTvizHZWbSqkZkPr6WxqQUFGptaaNzVwqJVyabAyE5JJABjjCkl85asp6W1Y4m/TZV5S9bn9TiWAHLU1NTE7bffntW2F1xwAU1NTSnXmTVrFk8/nWrYe28sWrSI11933SZvjMmDbU0trpZnyxJAjlIlgAMHUk8k9Ze//IXKysqU69x0002ce+65WceXLUsAxvinf2WFq+XZCl0CWLSqkTFzlzJ4xmOMmbs05zq1GTNmsHHjRkaNGkV9fT0NDQ2ceeaZTJw4kZNOOgmASZMmMXr0aIYNG8addx4aon7QoEHs2LGDzZs3M3ToUL72ta8xbNgwzj//fFpanEw/bdo0Fi5c2L7+DTfcwMknn8zw4cN58803Adi+fTvnnXcew4YN45prruG4445jx44dHeI8ePAg06ZNo7q6muHDh3PrrbcCsHHjRiZMmMDo0aM588wzeeutt3jhhRdYvHgx9fX1jBo1io0bN+Z0jowx7tSPH0JFeVmHZV1EqB8/JK/H8bsbaEFFG1aidWuNTS3MfHgtAJNqqrLa59y5c1m3bh2vvvoqAA0NDaxcuZJ169a1d3/83e9+x5FHHklLSwunnHIKl156KV27du2wnw0bNnD//fdz1113MWXKFB566CGuuuqqTsfr27cvK1eu5Pbbb+eWW27h7rvv5sYbb+Scc85h5syZPPHEE9xzzz2dtnv11VdpbGxk3bp1AO1VT9OnT+eOO+7ghBNO4OWXX+Y73/kOf/3rX5k4cSIXXXQRl112WVbnxRiTvej1KLYXUFWfg1lfp5IJVQJI1LDS0nqQeUvW5/XEnnrqqR36vv/qV7/ikUceAWDLli1s2LCBYcOGddhm8ODBjBo1CoDRo0ezefPmhPuePHly+zoPP+xM5/rcc8+173/ChAn06dOn03bHH38877zzDtdddx0XXngh559/Pnv27OGFF17g8ssvb18veudhjPHXpJqqDtelhoaGvB8jVAmgUA0rsUO2NjQ08PTTT/Piiy/SvXt36urqEj61fPjhh7f/XFZWlvRCHF2vrKwsbRtDrD59+rB69WqWLFnCHXfcwYIFC7jtttuorKxsv3sB50EwY0w4hKoNwIuGlV69eqW8aDY3N9OnTx+6d+/Om2++yUsvvZT1sZIZM2YMCxYsAODJJ59k165dndbZsWMHbW1tXHrppdx8882sXLmSI444gsGDB/Pggw8CztO7a9euzejvMsYUv1AlgEQNKxXlZTk1rBx11FGMGTOG6upq6uvrO70+YcIEDhw4wNChQ5kxYwann3561sdK5oYbbuDJJ5+kurqaBx98kGOOOabTcA6NjY3U1dUxatQorrrqKubMmQPAfffdxz333MPIkSMZNmwYjz32GABTp05l3rx51NTUWCOwMSUqVFVAiRpW6scPybn+/09/6jj3eF1dXfvPhx9+OI8//ninbXbv3t1ez9+3b9/2xlmA7373u+0///73v2//ObZdoLa2tr1OsHfv3ixZsoTDDjuMF198kVdeeaVDlRLAyJEjWblyZac4Bg8ezBNPPNEhLnDuKqwbqDGlLVQJADo3rJSC9957jylTptDW1kbXrl256667/A7JGFMEQpcAStEJJ5zAqlWr/A7DGFNkQtUGYIwx5hBLAMYYE1KWAIwxJqQsARhjTEhZAvBBz549Adi2bVvSsXbq6upYvnx5yv3cdttt7N27t/33TIaXzrfNmzd36gZrjCkOlgB81L9///aRPrMRnwAyGV463ywBGFO8wpcA1iyAW6thdqXzfc2CnHY3Y8YMfvOb37T/Pnv2bG655Rb27NnDuHHj2odufvTRRzttu3nzZqqrqwFnELapU6cydOhQLrnkkg5jAV177bXU1tYybNgwbrjhBsAZYG7btm2MHTuWsWPHAoeGlwb4xS9+QXV1NdXV1dx2223tx0s27HSsBx98kOrqakaOHMlZZ50FOMNJ19fXc8oppzBixAh++9vftv/9zz77LKNGjWofYtoYUyRUtWi+Ro8erfFef/31TstiffLJJ4d+Wf2A6s39VG844tDXzf2c5VlauXKlnnXWWe2/Dx06VN977z1tbW3V5uZmVVXdvn27fv7zn9e2tjZVVe3Ro4d+8sknumnTJh02bJiqqv785z/Xq6++2glz9WotKyvTV155RVVVd+7cqaqqBw4c0LPPPltXr16tqqrHHXecbt++vf3Y0d+XL1+u1dXVumfPHt29e7eedNJJunLlSt20aZOWlZXpqlWrVFX18ssv1z/+8Y+dzld1dbVu3bpVVVV37dqlqqq//e1v9Uc/+pGqqu7bt09Hjx6t77zzji5btkwvvPDCpOcn3fvjxrJly/K2r3wKalyqwY3N4nIvl9iA5ZrgmhquO4BnboLWuBJva4uzPEs1NTV89NFHbNu2jdWrV9OnTx8GDhyIqvKDH/yAESNGcO6559LY2MiHH36YdD9/+9vf2sf/HzFiBCNGjGh/bcGCBZx88snU1NTw2muvpR2i4bnnnuOSSy6hR48e9OzZk8mTJ/Pss88CmQ07PWbMGKZNm8Zdd93FwYPO8NlPPvkkf/jDHxg1ahSnnXYaO3fuZMOGDa7OlTEmWML1JHDzVnfLM3T55ZezcOFCPvjgA6644grAGWRt+/btrFixgvLycgYNGpRwGOh0Nm3axC233MIrr7xCnz59mDZtWlb7icpk2Ok77riDl19+mccee4zRo0ezYsUKVJX//M//ZPz48R3W9WKMcmNCac0CpzDavBV6D4Bxs2DEFE8PGa47gN4D3C3P0BVXXMH8+fNZuHBh++Qqzc3NfO5zn6O8vJxly5bx7rvvptzHWWed1d6Yum7dOtasWQPAJ598Qo8ePejduzcffvhhh4Hlkg3ZfOaZZ7Jo0SL27t3Lp59+yiOPPMKZZ56Z8d+zceNGTjvtNG666SaOPvpotmzZwvjx4/mv//ovWltbAXjrrbf49NNPbdhoY/JhzQL4879D8xZAne9//vec2yjTCdcdwLhZzkmNrQYqr3CW52DYsGHs3r2bqqoqjj32WACuvPJKLr74YoYPH05tbS0nnnhiyn1ce+21XH311QwdOpShQ4cyevRowBnFs6amhhNPPJGBAwcyZsyY9m2mT5/OhAkT6N+/P8uWLWtffvLJJzNt2jROPfVUAK655hpqamqSzjIWr76+ng0bNqCqjBs3jpEjRzJixAg2b97MySefjKpy9NFHs2jRIkaMGEFZWRkjR45k2rRpfPvb33Zz6owxkLp62sO7AHHaB4pDbW2txveNf+ONNxg6dGjSbXbv3t1xbHwfbrMyiisg8h1XuvfHjYaGhg5DbQdFUOOC4MZWynEtWtXoasj5RasamfjoMLqQ6FosMLsp59hEZIWq1sYvD9cdADgXex8u+MaY0rdoVSMzH17bPvd4Y1MLMx92ZtlLlASi69fKUQzosqPzDnOsnk7H9zYAESkTkVUi8r9+x2KMMbmYt2R9+8U/qqX1IPOWrE+5/s8OTGGvdu34Yh6qp9PxPQEA3wLeyGUHxVSNFSb2vpiw2dbUuVddJssXt53BjNZr2NrWlzYVtrb1hYt/Vdq9gERkAHAhcHe2++jWrRs7d+60i03AqCo7d+6kW7dufodiTMH0r6zIevnitjM4Y/+vOP6z+7ii+10Fqar2tRFYRBYCc4BewHdV9aIE60wHpgP069dv9Pz58+Nfp0ePHpSVlcVvCjgXIhHJd+g5C0NcBw8e5NNPP81bct6zZ0/7QHpBEtS4ILixlWpcTS2tNO5qoS3mM99FhKo+FVRWlOe0fi6xjR07NmEjsG/DOgAXAbdHfq4D/jfdNomGgkgnqI92W1zuBTW2oMalGtzYSjmuR1Zu1S/MeUYHff9/9QtzntFHVm7Ny/peDAXhZy+gMcBEEbkA6AYcISL3qupVPsZkjDE5mVRTlbLbZ67r55NvbQCqOlNVB6jqIGAqsNQu/sYYUzhB6AVkjDHGB4F4EExVG4AGn8MwxphQsTsAY4wJKUsAxhgTUpYAjDEmpALRBmBMTgIywqsxmXI7YqhXLAGY4hadSCM6lnp0Ig2wJGACye2IoV6yKiDjmUWrGhkzdymDZzzGmLlLWbSqMf8H8WCeZ2O85HbEUC/ZHYDxRMFKOR7N82yMV9yOGOoluwMwnihYKcejeZ6N8YrbEUO9ZAnAeKJgpZxxs5yJM2IVYCINY7JVP34IFeUdRy+uKC+jfvyQgsdiCcB4omClnBFTnIkzeg8ExPlegIk0jMnWpJoq5kweTlVlBQJUVVYwZ/Jw6wVkSkf9+CEd2gDAw1KOzfNsioyfI4DGsgRgPBH9cAehr7MxJjFLAMYzQSnlGGMSszYAY4wJKbsDMMaYHAVlaAe3LAEYY0wOgjS0g1tWBWSMMTkI0tAOblkCMMaYHARpaAe3LAEYY0wOgjS0g1uWAIwxJgdBGtrBLWsENsYYl+J7/Vw6uoplb263XkDGGFPKEvX6eWhFo2/j+eTCqoCMMcaFRL1+zjv4V05/9GyYXQm3Vjsz1RUBuwMwxhgX4nv3TOzyHHPL76Y7+50FRTQtqd0BGGOMC/G9e7532AK6y/6OKxXJtKSWAIwxxoX4Xj/9ZUfiFeOmJS3IHNkuWRWQMcYks2aBU5Jv3upMMzpuFpNqnGqdaC+gj+RojmF7521jpiUN6nARviUAERkI/AHoByhwp6r+0q94jDGmgzULnLr81kidf0zd/qSaKYcu3Gs+7bge0MLhzNh+McvnLqV+/JCUw0X4mQD8rAI6APyHqp4EnA78m4ic5GM8xhhzyDM3dbioA4nr9mOmJVWERu3L9/d/lUfbzmgv6TcmGRYi2fJC8e0OQFXfB96P/LxbRN4AqoDX/YrJmLxLUIUQ9J4hJiKuDj/l8si0pGfMXdrpoh5f8o9VJpJLhDkTVfU1AAARGQT8DahW1U/iXpsOTAfo16/f6Pnz57va9549e+jZs2d+As0ji8u9oMaWNK6WXU61gbYdWiZdnInrK/r4G5vPiiKuj16Hg/s7r1TWFT6XuLJibWOz62MOr+rtPjaXxo4du0JVa+OX+54ARKQn8Ffgx6r6cKp1a2trdfny5a7239DQQF1dXfYBesTici+osSWN69ZqJwHE6z0Qvr3O87igCM+ZzzrEFd8GAFBe4VT3JLmLG5PgDgCckv7BBNfaqsoKnp9xjvvYXBKRhAnA126gIlIOPATcl+7ib4IpiF3bAsNNFYIJnpi6fRDne4qLPyQeGA6g62FCeVnH6p4gDBjnZy8gAe4B3lDVX/gVh8leULu2BUbvAUnuAAZ0Xma8k0s7TKRuP1PRz/2Nf36NXXtb25e3tLZR3kXo072cpr2tgRkwzs87gDHAvwDniMirka8LfIynqASh5F3MMyEVxLhZTpVBrPIKZ7kpjGg1TvMWQA915fRwrJ5JNVV079q5bN3apnTvehib5l7I8zPO8f3iD/72AnoO8LcJvEgFpeRdzDMhxfNkUu9oydF6AfknVVdOD9+HYvnfsCeBi1BQHirpX1mRsMGrGGZCipVpQs0qSbisQjB55lM7TLH8b9hYQEUoKKWLbGdCCkL1VaxMqrKiSaKxqQXlUJLwO3aTRrL2lhTtMPn4fBbLLGF2B1CEcild5LOqI7qdm/1lUtr2pDomhUwSaqok8ePTrRwVWONmJe7KmaQdpqmllZnP5F69ms3/hh8sARSh+vFDOlxEIfOSd/3C1bQedPojNza1UL9wNZB928GkmipX26arvkqVICqzijC9TBJq6iTRw6PITM5ctsN82LyPltaOCT3b6lW3/xt+sKJLEZpUU8WcycOpqqxAcB4myWQ6uhv//Fr7xT+q9aBy459f8zDajtKVtv3oWZTJ7Xqyu6ug1emaBEZMcR68m93kfE/RJrP/YFvC5UFrvM0XuwMoUtmULmL7JWey3AvpStt+lLQzuV1PedfVvMGTuEzhdS1LXCYu1URvCcBkLZu6+nTVV361b6RLqKmSREODJYCSsGYBJ7Cddw6/nm16FD87MIXFbWcEsvE2XywBhEhlRTlNLZ1L+5UV5a73le2zCOlK29mWtAvxbEQx1OmaLEUeGOty/Ay6iDJAdjC3/G6OLO/KqAunl+z7bgkgRC4aeSz3vvRewuVu5fIsQqoLabYl7aA8G2GKVIIHxrrLfmb3eAhqbvQpKO9ZAgiRZW8mmLYuxfJUvHwWIT5BRPtlTx24m+sjMyzFX9S9iueHi9Zy/8tbOKhKmQhfOm0gN08antM+TQCFdOA+SwAhkuxi2NjUwpjIhTVRV8tEdeuFetKxQ9XOwENVO8vf/Zhlb26nsamFMhGSDWqeSzw/XLS2wx3TQdX23y0JlJiQDtxn3UCLQL6enE11MYxeWOPbCKLPDsQ+AVu/cDVjTzy6IE86Jqvaue+l99oTUKJx1vMRz/0vJ7ggpFhuilhIB+6zBBBw+RyCINlY5VEtrQf5sHlfh2XJnh14bM37WT2L4Fayu5Z00xjlI55kiSXZclPEomP/l3Ul07H/S4FVAQVcPhs3YxtYk01GHf8gTKpnBwrRKyZZVVMqAhnPspRKslmc/J7H1XhkxBT4uAGmNPkdScHYHUDA5btxc1JNFc/POIeqJNVByR6E8Uuiu5Z0l998tUN86bSBrpYbU2yC9d9uOvFqCIJkwx/0692tw7Jkzwhk8+xANmKHvQCnaufK0/8uaVWWAGNPPDovx7550nCuOv3v2kv8ZSJcdfrfWQOwKRlWBRRw2Q78lk6y/vaVcQ9bzZ44jPoHV9PadqgqpLyLMHvisJyO7zZW5zmABq67sg6A2uOOTFiVpcBDKxqpPe7IvFRP3TxpuF3wTcmyBBBwuQ4rm2p4hER1+PEPWyU7PsCYuUt9G+o2GvuYuUs7JYGUbSS5zA9rSod9DgBLAEUh/iIcHRkz3QU3X8MjJHowKwhTUoLLNpLo/LDRJz6j88NCTv/8TS2tviZD41KqzwGf8y0sP1gbQBHIpCtoomcFvBpaOUiTwbtqI0k1P2yWFq1qpHFXi80UVkw8+BwUK0sARSDdBTdZgkjWfTLX4RGCMiUluJx6z4PH/ectWU9bXFdRv5KhyVBIh31IxKqAikC2k6gk68eeaw+iIE147aqNxIPH/bc1tUCCXqGlOoFIScjyc1DoqUoLwRJAEch2EpWDqlSUl+W9B5FXPZOylfEDaS7nh82E8x7sTrLcBFKqz8HHiTcJUrtXPlkVUBFIV82R7GITHQ4h38M1ZDslpe+ij/v3Hki+HvevHz+ELnFPBhfrBCL5GnMq8LL4HASp3Suf7A6gCOQyiYpXwzUU7eQoI6bktbvfpJoqFn3wOlWVZUVdNVCqJdykXH4OgtTulU+WALyWp/7G2U6iYrxXWVHO8zPq/A4jJzahTmpBavfKJ0sAXkrT3zifjUpFWyI3gVCqJdx8CVq7V7742gYgIhNEZL2IvC0iM/yMxRMp+hs3tbTmZZjn0NTbGk95NeZUqSjadq800t4BiMh1wL2quiufBxaRMuA3wHnAVuAVEVmsqq/n8zi+StHf+MPmfbS0dsy/bm+5Q1dvazyTSQm3FLtBulGKd9mZ3AH0w7k4L4iU2PM1GPqpwNuq+o6q7gfmA1/M076DIVm/4t4DOo27H+XmlrsQPRPsDiMc0pVw8zkxkQkO0QxmN4pc9M8HrgZqgQXAPaq6MesDi1wGTFDVayK//wtwmqp+M2696cB0gH79+o2eP3++q+Ps2bOHnj17Zhtmblp2OfX+GnOxly7QeyA79nXh/b2dN+la1oUhx/TKaPdrG5uTvja8qrfbaIGO56uppZXGXS0dnnTtIkJVn4qCDQedLLYgCWpckL/Y1n+wO2Ghxc3n1Yu44jW1tPJh8z72H2yja1kX+vXu5uqzWqrv5dixY1eoam388owagVVVReQD4APgANAHWCgiT6nq97KKKEOqeidwJ0Btba3W1dW52r6hoQG32+RVwl5Al7Do8ae4feXBTrfccyYPpy7D28zrE4yECU7pLTpsslux58sZabPzuPtVlWW+9Hrx/b1MIqhxQf5iu3rGY2iCCgMBNs11v38vztmiVY3MfGZtpGrVibWi/CBzJp+UcdVNGN7LWGmrgETkWyKyAvgZ8DwwXFWvBUYDl+Zw7EY6PkQ/ILKstIyYAt9eB7ObnO+RLqCVFeU5Nyq5GgcnC9YzxEQVQyNxqT6s5aVM7gCOBCar6ruxC1W1TUQuyuHYrwAniMhgnAv/VOCfc9hf0cm1Ucnr/v+l2vfZuBeEbpCJGqHh0Oc/WWW2FViSS5sAVPWGFK+9ke2BVfWAiHwTWAKUAb9T1dey3V9YuUkibntxBOGf3gSD3w8bJurxVr9wNSj8E8/yQNcF9JcdbNO+/OzAFBa3ndG+rasCS8suuLU6NBPF+PogmKr+BfiLnzGERTZdRv3+pzfB4mc3yETVO60HlYldnmNu+d10l/0ADJAdzC2/G1phcdsZ7gosaxZA8weHRgrN04RBQWZPAodEto/6l2LfZ1N8klXjfO+wBe0X/6jusp/vHbaAFd3Pc1dgeeYmOOaajsuiE8VYAjDFzBp0i0MQH7ZyHZMH8+0mbY+SHQnXH9BlJ8/POMfdQZq3wjFJlpcoGw46JIqhF0fYBfFhK9cxRce/at4C6KFqlDULcoqjfvwQyss6P4O6Tfsm3iCbSX5SPLhZqg4Y8QsAABFCSURBVCwBhITXXUZN7oLYjdF1TB7NtzuppooeXTtXWPzswBT2ateOC7Od5GfcLOdBzXzsq0hYFVBIWINucumqOApVLeN1NV02f4frmDycb7e5pbXTssVtZ0Cr0xYwoMvO3KqcRkyBxkecCWKsF5AphELW+VqDbmfpekcVcsA9L5+7yPbvcB2TB/Mup4tlcdsZrOh+nvs6/0Qq+jgPbIaEVQH5KIh1vmGTroqjkNUyXlbTZft3uI5p3Cyn2iRWnqpR6scPobxL53aA8jKxqswsWQLwURDrfMMmXRVHIXtPeTnmfLZ/h+uYPJh3OTaWeZeP7DC4W5/u5cy7bKTd2WbJqoDS8LKKxrpmZief70m6Ko5CD4fhVTVdLn+H65jyPO9yTrEQzK61QWF3ACl4XUVjXTPdy/d7kq6Ko1R6T5XK3+GWVbOmZgkgBa+raML6T5mLfL8n6ao4inUqwOhEPmsbmxkzdylAUf4duUr2eZm9+DWb6AirAkrJ6yoa65rpnhfvSbpqhWLrPdWhx8/AQ6XeOZOH56enTIrjBu2znOxz0dTSSlOkW2lsj6jKgkUWDJYAUihE/W+xXVz8VrJDVOdx+IRsx31KJ9UFPqjzUyf7vMSLnp8fnx6uSpFw/bUuWRVN8JTke5Jg+ISWh7/Jt34wM6vqCS/ukhLVpT/3yO3s/emJMLuS0x89m/MO/rXDNkHo0Zbo85JMGDtfWAJIoVjrf0tZSb4nCYZPqOAz6g9bkFWjpRedC+LvKiZ2eY6b5E66t7wPKMewnbnldzOxy3MdtvP7opro89Kne+I5gov+LjILVgWUhlXRBE/JvSdJhknoLzsB99U3XkzkE38hTzUM8+L9WU7Gko0Mqs7iPy/x1VUQc36aN3gbb8DYHYAxfksyTMI2PerQzy5K0rGlXsjPXVL8hTzZMMzRpAUFqJrLcuTRkryLzJLdARiTo6aWVsbMXZr9ePknnA+r/9ShGmivduVnBw6VZN2WpKOl3oaGBq67ss7tn9RJ/F3FNu3LgARJ4CPpi0Ti9bwXUKqRR9M0oJfcXWSWLAF4JIhd4kz+LVrVSOOuFhqbnIbGtL1foqXW6IWreYtz8R/5z7DhSbR5K9v0KH7aemhe2yA0csd3Wb6761X8UO/gsIP7Dq1UXsExF/+ETSMuLExQHo48GhaWADwQ1C5xJv/mLVnP1IHaYVnKOvtkpdYNT8K31yHAK6saWbFkPRKwwkPHUvOFsGZY3mf+csXDkUfDwhKAB7zqh22CZ1tTCwxMsjyRDEqtRVM94eGYPxkZN6vj3RSU/AQu+WYJwAM2yFt4OHXzu5MsT6AISq1FU30ZTT5+3oUUOUsAHijZp1VNJ/Xjh9D4xooOy9KOlx/gUmvRVV/6fRdS5KwbqAdK8mlVk9Ckmiqq+lQEYrz8fLA5KsLF7gA8YIO8hUtlRTnPz6jLfIMAl1qt+jJcLAF4pGga8oyJYdWX4WJVQMaYdlZ9GS6+3AGIyDzgYmA/sBG4WlWb/IjFGHOIVV+Gi19VQE8BM1X1gIj8FJgJfN+nWIwxMaz6Mjx8SQCq+mTMry8Bl/kRhzFhkmn//qJ5DsDkTFQ1/VpeBiDyZ+ABVb03yevTgekA/fr1Gz1//nxX+9+zZw89e/bMOc58s7jcC2psQY0LDsXW1NJK464W2mL+37uIUNWngsqKQ+PjZ7pevuIKmqDGBbnFNnbs2BWqWhu/3LMEICJPA8ckeOl6VX00ss71QC0wWTMIpLa2VpcvX+4qjoaGBurq6lxt41Y2JaZCxJWNoMYFwY0tqHEBLHr8KeatLks6LWJVZUWHeYLHzF2acN349XIV1HMW1Lggt9hEJGEC8KwKSFXPTRPQNOAiYFwmF/+gKronJ01oxI9Umkh8/357DiBcfOkGKiITgO8BE1V1rx8x5GrRqkbGzF3K/33gVXty0gTSvCXrO1TlJNJpohcPppPMyZoFcGs1zK50vqeZ7MW449dzAL8GegFPicirInKHT3EkFL24D57xWMJJuWMnyE7GSkzGb+k+g4n69wfqOYAsZ/wymfOrF9Df+3HcTGRSpZNovJR49uSk8VuykUrBqdNP1FYVqOcAcpjxy2TGhoKIk8lY/tmUrIwptGQjlaab/zYwzwHYjF+eswQQJ5NGsGTjpUDykpUxXknWC21STRWLPnidqsoyX0vzieKrzGTDIpg7odhZAoiTyWBY8RNkQ2YlK2PyLV2VpeuRSpMcI9sqoWTxzflC8p5J7QI+d0IpsMHg4mTSCDappoo5k4dnPga8MR7xevz+2A4PyqELeHzHCLfxfdi8L8kWMQI+d0IpsDuAOJk2ggWmntSEmtf99nOd3zpZHPsPtmUWQIDnTigFlgASsIu7KRZej9+fa4JJFl/XMqt8CAJ7F4wpYl7328/1wbBk8fXr3S3n2EzuLAEYU8S8bo/KNcEkiy+fA8uZ7FkVkDFFzssqy3w8GJYovoaGDXmN02THEoAxJqVkCcbmDSh+lgASWbPAedy8eavz0Mm4WdYTwZgYNgpuabA2gHg2AJUxaXn9/IEpDEsA8VINQGWMAWzegFJhCSCeDUBlTFqBmzfAZMUSQLxkA03ZAFTGtAvUvAEma5YA4o2b5Qw4FcsGoDKmAxsPqzRYL6B40d4+1gvImJRsyJTiZwkgERuAyhgTAuGuArIJp40xIRbeO4Bof/9ol89of3+w0r8xJhTCewdg/f2NMSEX3gRg/f2NMSEX3gRg/f2NMSEX3gRg/f2NMSEX3gRgE04bY0IuvL2AwPr7G2NCLdQJwCa0MMaEma9VQCLyHyKiItK30MeOTmjR2NSCcmhCi0WrGgsdijHG+MK3BCAiA4Hzgff8OL5NaGGMCTs/7wBuBb4HqB8HtwktjDFhJ6qFv/6KyBeBc1T1WyKyGahV1R1J1p0OTAfo16/f6Pnz57s61p49e+jZs2en5es/2M3+g22dlnct68KQY3q5OkY2ksXlt6DGBcGNLahxQXBjs7jcyyW2sWPHrlDV2vjlnjUCi8jTwDEJXroe+AFO9U9aqnoncCdAbW2t1tXVuYqjoaGBRNs0xU1qDc6EFnMmD6euAA3ByeLyW1DjguDGFtS4ILixWVzueRGbZwlAVc9NtFxEhgODgdUiAjAAWCkip6rqB17Fk6jHz5zJw60XkDEmtAreDVRV1wKfi/6ergooHxbFlfajPX7mTB7O8zPO8eqwxhgTaKF4Eth6/BhjTGe+PwimqoO8Pob1+DHGmM5CcQfQv7LC1XJjjAmDUCSA+vFDqCgv67CsoryM+vFDfIrIGGP853sVUCFEe/ZYjx9jjDkkFAkAnCRgF3xjjDkkFFVAxhhjOrMEYIwxIWUJwBhjQsoSgDHGhJQlAGOMCSlLAMYYE1KWAIwxJqQsARhjTEhZAjDGmJCyBGCMMSFlCcAYY0LKEoAxxoSUJQBjjAmp0IwGmkyiyeJt1FBjTBiEOgEkmywesCRgjCl5oa4CssnijTFhFuoEYJPFG2PCLNQJwCaLN8aEWagTgE0Wb4wJs1A3Attk8caYMAt1AgCbLN4YE16hrgIyxpgwswRgjDEhZQnAGGNCyhKAMcaElCUAY4wJKVFVv2PImIhsB951uVlfYIcH4eTK4nIvqLEFNS4IbmwWl3u5xHacqh4dv7CoEkA2RGS5qtb6HUc8i8u9oMYW1LgguLFZXO55EZtVARljTEhZAjDGmJAKQwK40+8AkrC43AtqbEGNC4Ibm8XlXt5jK/k2AGOMMYmF4Q7AGGNMApYAjDEmpIo+AYjI5SLymoi0iUjSLlIiMkFE1ovI2yIyI2b5YBF5ObL8ARHpmsfYjhSRp0RkQ+R7nwTrjBWRV2O+9onIpMhrvxeRTTGvjSpUXJH1DsYce3HMcr/P2SgReTHyvq8RkStiXsvrOUv2uYl5/fDIOXg7ck4Gxbw2M7J8vYiMzyWOLOL6joi8Hjk/z4jIcTGvJXxfCxjbNBHZHhPDNTGvfSXy3m8Qka8UOK5bY2J6S0SaYl7z7JyJyO9E5CMRWZfkdRGRX0XiXiMiJ8e8ltv5UtWi/gKGAkOABqA2yTplwEbgeKArsBo4KfLaAmBq5Oc7gGvzGNvPgBmRn2cAP02z/pHAx0D3yO+/By7z4JxlFBewJ8lyX88Z8A/ACZGf+wPvA5X5PmepPjcx63wDuCPy81TggcjPJ0XWPxwYHNlPWQHjGhvzObo2Gleq97WAsU0Dfp1g2yOBdyLf+0R+7lOouOLWvw74XYHO2VnAycC6JK9fADwOCHA68HK+zlfR3wGo6huqmm4W91OBt1X1HVXdD8wHvigiApwDLIys9z/ApDyG98XIPjPd92XA46q6N48xJOI2rnZBOGeq+paqboj8vA34COj0lGMeJPzcpIh3ITAuco6+CMxX1c9UdRPwdmR/BYlLVZfFfI5eAgbk6dg5x5bCeOApVf1YVXcBTwETfIrrS8D9eTp2Sqr6N5yCXzJfBP6gjpeAShE5ljycr6JPABmqArbE/L41suwooElVD8Qtz5d+qvp+5OcPgH5p1p9K5w/djyO3fbeKyOEFjqubiCwXkZei1VIE7JyJyKk4JbqNMYvzdc6SfW4SrhM5J8045yiTbb2MK9ZXcUqQUYne13zJNLZLI+/RQhEZ6HJbL+MiUl02GFgas9jLc5ZOsthzPl9FMSOYiDwNHJPgpetV9dFCxxMrVWyxv6iqikjSPreRjD4cWBKzeCbORbArTh/g7wM3FTCu41S1UUSOB5aKyFqcC1xO8nzO/gh8RVXbIouzPmelSESuAmqBs2MWd3pfVXVj4j144s/A/ar6mYj8H5w7qHMKePx0pgILVfVgzDK/z5kniiIBqOq5Oe6iERgY8/uAyLKdOLdTh0VKb9HleYlNRD4UkWNV9f3IxeqjFLuaAjyiqq0x+46WhD8Tkf8GvlvIuFS1MfL9HRFpAGqAhwjAORORI4DHcAoBL8XsO+tzlkCyz02idbaKyGFAb5zPVSbbehkXInIuTlI9W1U/iy5P8r7m62KWNjZV3Rnz69047T7Rbevitm0oVFwxpgL/FrvA43OWTrLYcz5fYakCegU4QZzeK11x3uDF6rSkLMOpewf4CpDPO4rFkX1msu9OdY6RC2C03n0SkLCXgBdxiUifaPWJiPQFxgCvB+GcRd7DR3DqRRfGvZbPc5bwc5Mi3suApZFztBiYKk4vocHACcD/yyEWV3GJSA3wW2Ciqn4Uszzh+5qnuDKN7diYXycCb0R+XgKcH4mxD3A+He+IPY0rEtuJOA2qL8Ys8/qcpbMY+HKkN9DpQHOkoJP7+fKqZbtQX8AlOHVfnwEfAksiy/sDf4lZ7wLgLZysfX3M8uNx/jHfBh4EDs9jbEcBzwAbgKeBIyPLa4G7Y9YbhJPNu8RtvxRYi3MRuxfoWai4gC9Ejr068v2rQTlnwFVAK/BqzNcoL85Zos8NTpXSxMjP3SLn4O3IOTk+ZtvrI9utB/4pz5/7dHE9Hfl/iJ6fxene1wLGNgd4LRLDMuDEmG3/NXIu3wauLmRckd9nA3PjtvP0nOEU/N6PfKa34rTZfB34euR1AX4TiXstMb0dcz1fNhSEMcaEVFiqgIwxxsSxBGCMMSFlCcAYY0LKEoAxxoSUJQBjjAkpSwDGGBNSlgCMMSakLAEYkwMROSUyqFk3EekhzhwF1X7HZUwm7EEwY3IkIjfjPBFcAWxV1Tk+h2RMRiwBGJOjyNgyrwD7gC9ox1EkjQksqwIyJndHAT2BXjh3AsYUBbsDMCZH4swROx9nEpFjVfWbPodkTEaKYj4AY4JKRL4MtKrqn0SkDHhBRM5R1aXptjXGb3YHYIwxIWVtAMYYE1KWAIwxJqQsARhjTEhZAjDGmJCyBGCMMSFlCcAYY0LKEoAxxoTU/wf7NgXKWPQssAAAAABJRU5ErkJggg==\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "scatter_plot_polynomial(X_train, y_train, label='training set')\n",
    "scatter_plot_polynomial(X_valid, y_valid, label='validation set')"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Now lets fit a polynomial to the generated data. We can use `PolyFit` class to fit a polynomial to the data. We can pass the the degree as an argument and then use the same functions `fit`, `predict` and `evaluate` functions known from `scikit-learn`. "
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "<dslectures.core.PolynomialRegressor at 0x11cf2a518>"
      ]
     },
     "execution_count": null,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "pr = PolynomialRegressor(degree=3)\n",
    "pr.fit(X_train, y_train)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Now we want to see how that polynomial looks like on a range from [-1, 1]:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "X_lin = np.linspace(-1, 1, 1000)\n",
    "y_fit = pr.predict(X_lin)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYAAAAEWCAYAAABv+EDhAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8li6FKAAAgAElEQVR4nO3de3yO9f/A8ddns7EZm0M5jHLIKXOYQymSUayopEzn6EAokq8i/eggFEU6oQNCMcd8ky8q+4bwdRqSMxVzGtlsbO30+f1x31v3tvve7uOue7vfz8djD7uv+zq8d923631dn6PSWiOEEML3+BkdgBBCCGNIAhBCCB8lCUAIIXyUJAAhhPBRkgCEEMJHSQIQQggfJQlAlHpKqdeVUguMjsOSUupRpdQ6O9d1KH6llFZK3eB8dEKYSAIQXkMp9btSKk0plaqUOqeUmquUCjE6LmdorRdqrbsbGYNSqp45WZQzMg7hvSQBCG9zj9Y6BGgDtANeMzgeIcosSQDCK2mtE4A1QASAUqq2UmqVUuovpdRRpdSz1rZTSq1WSr1QYNlepdT95t+1Uuo5pdQRpVSSUupjpZQyv+enlHpNKfWHUuq8UuorpVSo+b3cu+kBSqmTSqlL5v20N+8/SSn1kcUx+yulNlm8/sC83WWl1E6l1G32ngul1Cil1Bml1Gml1FMF3uuplNpt3u9JpdTrFm//bP43yfxUdYtSqqFS6iel1EWl1AWl1EKlVJi9sYiyRRKA8EpKqbrA3cBu86JFwCmgNvAgMFEp1dXKpvOAxyz20woIB1ZbrNMLaA+0BGKAHubl/c0/UUADIAT4iPxuBhoB/YDpwFjgDqA5EKOUut3Gn7QdaA1UBb4GliilKthYN49SKhr4F3Cn+bh3FFjlCvAEEAb0BAYrpXqb3+ts/jdMax2itd4CKGASpvPYDKgLvF5cHKJskgQgvM1KpVQSsAn4L6YLfV2gI/CK1jpdax0PfI7pwlfQKqCxUqqR+fXjwGKtdYbFOpO11kla6z+BDZguzACPAu9rrY9rrVOBMcBDBcrQ3zLHsA7TxfcbrfV58xPLRiDS2h+ltV6gtb6otc7SWr8HlAea2HE+YoA5WutftdZXKHCx1lrHaa33aa1ztNZ7gW8AW0kIrfVRrfV6rfXfWutE4P2i1hdlmyQA4W16a63DtNbXa62HaK3TMN2t/qW1TrFY7w9Md/b5aK3TgcXAY0opP+BhYH6B1c5a/H4V050+5uP8UeAY5YAaFsvOWfyeZuW11UprpdS/lFIHlFLJ5gQXClS3tm4BtYGTBWKy3O/NSqkNSqlEpVQy8FxR+1VK1VBKLVJKJSilLgML7IxDlEGSAERpcBqoqpSqZLHsOiDBxvrzMN3NdwOumos+7D3O9QWOkUX+i7zDzOX9L2O6m6+itQ4DkjEVxxTnDKZiGsuYLH2N6amnrtY6FJhpsV9rQ/1ONC9vobWujKm4zJ44RBkkCUB4Pa31SeAXYJJSqoJSqiXwNKa7V2vrbwFygPcofPdflG+AEUqp+ubmpxMxFR9lufQHQCVMiSQRKKeUGgdUtnPbWKC/UupGpVQwMN7Kvv/SWqcrpW4CHrF4LxHTeWhQYP1UIFkpFQ6McvivEWWGJABRWjwM1MN0l74CGK+1/qGI9b8CWmAjSdjwJaaE8TNwAkgHXihyC/usBf4DHMZUhJNO/mIdm7TWazBVNv8EHDX/a2kI8KZSKgUYhylh5G57FXgb2GxupdQBeANTE9tkTBXjy53/s0Rpp2RCGFEWKaWeAAZqrTsZHYsQ3kqeAESZYy4qGQLMNjoWIbyZJABRpiilemAq+z6HqYJUCGGDFAEJIYSPMvQJQCkVppRaqpQ6aG4jfYuR8QghhC8xepTAD4D/aK0fVEoFAsFFrVy9enVdr149pw505coVKlas6NS2niRxOUbicozE5RhvjQtci23nzp0XtNbXFHpDa23ID6aekCcwF0PZ89O2bVvtrA0bNji9rSdJXI6RuBwjcTnGW+PS2rXYgB3ayjXVsDoApVRrTK00fgNaATuB4do03onlegOBgQA1atRou2jRIqeOl5qaSkiI9w0tL3E5RuJyjMTlGG+NC1yLLSoqaqfWul2hN6xlhZL4wTTWexZws/n1B5gG2pInAC8gcTlG4nKMxOU4TzwBGFkJfAo4pbXeZn69FFMPRSGEECXAsEpgrfVZ8wQWTbTWhzAN3PWbo/vJzMzk1KlTpKenF7leaGgoBw4ccDJazynLcVWoUIE6deoQEBDgpqiEEO5kdCugF4CF5hZAx4EBju7g1KlTVKpUiXr16mGe2MmqlJQUKlWqZPN9o5TVuLTWXLx4kVOnTlG/fn03RiaEcBdDE4A2TexRuGLCAenp6cVe/EXJU0pRrVo1EhMTjQ5FiFJp5e4Epqw9xOmkNGqHBTGqVbbbj1EmhoKQi793ks9FCOes3J3AmOX7SEhKQwMJSWkkXEpj5W5bU2A4p0wkACGEKEumrD1EWmb+O/4crZmy9pBbjyMJwEVJSUl88sknTm179913k5SUVOQ648aN44cfihr23jO+++47fvvN4Tp5IYQbnE5Kc2i5syQBuKioBJCVVfREUt9//z1hYWFFrvPmm29yxx13OB2fsyQBCGGc2mFBDi13ls8lgJW7E+g4+Sfqj15Nx8k/uVymNnr0aI4dO0br1q0ZNWoUcXFx3Hbbbdx7773ceOONAPTu3Zu2bdvSvHlzZs/+Z4j6evXqcfHiRX7//XeaNWvGs88+S/PmzenevTtpaaZM379/f5YuXZq3/vjx42nTpg0tWrTg4MGDACQmJnLnnXfSvHlznnnmGa6//nouXLiQL87s7Gz69+9PREQELVq0YNq0aQAcO3aM6Oho2rZty2233cbBgwf55Zdf+P777xk1ahStW7fm2LFjLp0jIYRjRvVoQlCAf75lfkoxqkcTtx7HpxKAtYqVMcv3uZQEJk+eTMOGDYmPj2fKlCkA7Nq1iw8++IDDhw8D8OWXX7Jz50527NjBjBkzuHjxYqH9HDlyhKFDh7J//37CwsJYtmyZ1eNVr16dXbt2MXjwYKZOnQrAG2+8QdeuXdm/fz8PPvggf/75Z6Ht4uPjSUhI4Ndff2Xfvn0MGGBqcTtw4EA+/PBDdu7cydSpUxkyZAi33nord999N1OmTCE+Pp6GDRs6fX6EEI7rHRnOpD4tCA8LQgHhYUGEVwmid2S4W49jdD+AEmWtYiUtM5spaw+59cTedNNN+dq+z5gxgxUrVgBw8uRJjhw5QrVq1fJtU79+fVq3bg1A27Zt+f33363uu0+fPnnrLF9ums5106ZNefuPjo6mSpUqhbZr0KABx48f54UXXqBnz550796d1NRUfvnlF/r27Zu33t9//+3kXy2EcKfekeH5rktxcXFuP4ZPJYCSqlixHLI1Li6OH374gS1bthAcHEyXLl2s9louX7583u/+/v55RUC21vP39y+2jsFSlSpV2LNnD2vXrmXmzJnExsYyffp0wsLCiI+Pt3s/QoiSdfXqVWbMmOGRJ3GfKgLyRMVKpUqVSElJsfl+cnIyVapUITg4mIMHD7J161anj2VLx44diY2NBWDdunVcunSp0DoXLlwgJyeHBx54gAkTJrBr1y4qV65M/fr1WbJkCWDqvbtnzx4AQkJCivy7hBAlY+3atYwZM8Zq0a6rfCoBWKtYCQrwd6lipVq1anTs2JGIiAhGjRpV6P3o6GiysrJo1qwZo0ePpkOHDk4fy5bx48ezbt06IiIiWLJkCTVr1iw0jENCQgJdunShdevWPPbYY0yaNAmAhQsX8sUXX9CqVSuaN2/Ot99+C8CDDz7IlClTiIyMlEpgIQy0dOlSqlatSqtWrdy/c2tDhHrrj7XhoH/77Te7hkO9fPmy1lrrFbtO6Vsn/ajrvfKdvnXSj3rFrlN2be8puXG5Ij09XWdmZmqttf7ll190q1atXN6nO+LS2v7Px17eOlyvxOUYics+aWlpulKlSvrpp5/2yHDQPlUHAIUrVsqCP//8k5iYGHJycggMDOSzzz4zOiQhhBusXbuWlJQUYmJiPLJ/n0sAZVGjRo3YvXu30WEIIdwsNjaWqlWrEhUVxebNm92+f5+qAxBCiNIiLS2NVatW0adPH4/NqSEJQAghvNDatWtJTU3N10/H3SQBCCGEF1qyZAnVqlUjKirKY8eQBCCEEF4mt/jn/vvv9+iUqpIADBASEgLA6dOnefzxx62u06VLF3bs2FHkfqZPn87Vq1fzXtszvLS7/f7773z99dclekwhyrrc4h9Ptf7JJQnAQLVr12b+/PlOb18wAdgzvLS7SQIQwv1KovgHfDEB7I2FaRHwepjp372xLu1u9OjRfPzxx3mvX3/9daZOnUpqairdunXLG7o5t4etpd9//52bb74ZMD3yPfTQQzRr1oz7778/31hAgwcPpl27djRv3pzx48cDpgHmTp8+TVRUVN6XpF69ennDQL///vtEREQQERHB9OnT845na9hpS0uWLOHmm2+mVatWdO7cGTANJz1q1Cjat29Py5YtmTVrVt7fv3HjRlq3bp03xLQQwnnp6el5rX/KlfNwS31rvcO89cflnsB7Fms9oYbW4yv/8zOhhmm5k3bt2qU7d+6c97pZs2b6zz//1JmZmTo5OVlrrXViYqJu2LChzsnJ0VprXbFiRa211idOnNDNmjXTWmv93nvv6QEDBmittd6zZ4/29/fX27dv11prffHiRa211llZWfr222/Xe/bs0Vprff311+vExMS8Y+e+3rFjh46IiNCpqak6JSVF33jjjXrXrl36xIkT2t/fX+/evVtrrXXfvn31/PnzC/1NERER+uDBg1prrS9duqS11nrWrFn6rbfe0lqbeh63bdtWHz9+XG/YsEH37NnT5vmRnsDGkrgc4w1xLV26VAN6/fr1+ZZ7oiewbz0B/PgmZBa4481MMy13UmRkJOfPn+f06dPs2bOHKlWqULduXbTWvPrqq7Rs2ZI77riDhIQEzp07Z3M/P//8M4899hgALVu2pGXLlnnvxcbG0qZNGyIjI9m/f3+xM3Vt2rSJ+++/n4oVKxISEkKfPn3YuHEjYN+w0x07dmTw4MF89tlnZGebhs9et24dX331Fa1bt+bmm2/m4sWLHDlyxKFzJYQo3sKFC6lZs6bHi3/A13oCJ59ybLmd+vbty9KlSzl79iz9+vUDTB9iYmIiO3fuJCAggHr16lkdBro4J06cYOrUqWzfvp0qVarQv39/p/aTy55hp2fOnMlPP/1EXFwcbdu2ZefOnWit+fDDD+nRo0e+dT0xRrkQPmdvLPz4JknnTrJ6VQpDHr4Lf3//4rdzkW89AYTWcWy5nfr168eiRYtYunRpXqeN5ORkrr32WgICAtiwYQN//PFHkfvo3LlzXmXqr7/+yt69ewG4fPkyFStWJDQ0lHPnzrFmzZq8bWwNRX3bbbexcuVKrl69ypUrV1ixYgW33Xab3X/PsWPHaN++PW+++SbXXHMNJ0+epEePHnz66adkZmYCcPjwYa5cuVLscNhCiGLsjYV/D4Pkkyz7LYOMbM0jIVtdrp+0h289AXQbZzrRlsVAAUGm5S5o3rw5KSkphIeHU6tWLQAeffRR7rnnHlq0aEG7du1o2rRpkfsYPHgwAwYMoFmzZjRr1oy2bdsC0KpVKyIjI2natCl169alY8eOedsMHDiQ6OhoateuzYYNG/KWt2nThv79+3PTTTcB8MwzzxAZGWlzlrGCRo0axaFDh1BK0a1bN1q1akXLli35/fffadOmDVprrrnmGlauXEnLli3x9/enVatW9O/fnxEjRjhy6oQQFkXTC/dl0qiqH+2uzTQtb+nZZqCGV+w68uOO4aD1nsVav99c6/Ghpn9dqAB2B3cNu+xuMhy0YyQux5TluBwdcj5nfKjW4yvrUyNCtAL9+u3lzY1UQt0WGzIctFnLGM9nVSGET1q5O4Exy/flzT2ekJTGmOX7AKwOQ79ydwLtdTXC1QUW/ZqJBh5pYb4su1g0bQ/D6wCUUv5Kqd1Kqe+MjkUIIVwxZe2hvIt/rrTMbKasPWRz/XcyY7iqA1m4L5P2tf1oVM2fNMq7XDRtD8MTADAcOODKDkxPOMLbyOcifM3ppMKt6opbviqnEwPP9Gb32RweaRHIqZzqjM54ukRKKgxNAEqpOkBP4HNn91GhQgUuXrwoFxsvo7Xm4sWLVKhQwehQhCgxtcOCnFr+719TQPnx3g2f0SljBjsq3+mxGC0pIy+cSqmlwCSgEvAvrXUvK+sMBAYC1KhRo+2iRYsKvk/FihWLbTOrtUYp5a7Q3aYsx5Wdnc2VK1fcmpxTU1PzBtPzJhKXY8pqXElpmSRcSiPH4jvvpxThVYIICyo8qmdSWiYnL17hjZeeo3qNmgwd/YbN9V2JLSoqaqfWul2hN6zVDJfED9AL+MT8exfgu+K2sdYKyF5ludWBJ0hcjpG4HFOW43K0FdBbs2M1oKv3Glnk+mWtFVBH4F6l1N1ABaCyUmqB1voxA2MSQgiX9I4Mt9rix5ajm1dTuXJl/lj8JsHBwR6MrDDD6gC01mO01nW01vWAh4Cf5OIvhPAlKSkpLFmyhH79+pX4xR+8oxWQEEL4pKVLl3L16lX69+9vyPG9oiOY1joOiDM4DCGEKFFz5syhcePG3HLLLYYcX54AhBDCAEePHmXjxo3079/fsJaAkgCEEMIA8+bNw8/PjyeeeMKwGCQBCCFECcvJyWHevHnceeedhIfb32LI3SQBiLLBzXM9C+FJb82O5eTJk+wq34qOk39i5e4EQ+LwikpgIVySO6FG7jwPySdNr0FGfhVeZ+XuBN778FP8ylckqFGHYkcM9SR5AhAetXJ3Ah0n/0T90as9d6fjgbmehfCUt5dtJeXgL1SM6IYqFwgUPWKoJ8kTgPAYR8dGd5qH5noWwhOObV4NOVmEtI7Ot9zWiKGeJE8AwmMcHRvdaR6a61kId8vJySFt3zrK17mRwOrX5XvP1oihniQJQHiMo2OjO63bONPczpbcMNezEO62YcMG0i8mULVtz3zLgwL8GdWjSYnHIwlAeIyjY6M7rWUM3DMDQusCyvTvPTOkAlh4nVmzZlG1alWmjx5EeFgQCggPC2JSnxYlXgEMUgcgPGhUjyb56gDAg3c6Mtez8HLnzp1jxYoVvPDCC8R0aEhMh4ZGhyQJQHhO7h3NlLWHOJ2URu2wIEb1aGLInY4QRps7dy5ZWVkMHDjQ6FDySAIQHuXo2OhClEU5OTnMnj2bzp0707RpU6PDySN1AEII4WHr1q3j+PHjDBo0yOhQ8pEnACGEcNHK3QlFFnXOmDGDmjVr8uCDDxoYZWHyBCCEEC7I7fCYkJSG5p8Oj7m93o8cOcKaNWt47rnnCAwMNDbYAiQBCCGEC4rr8PjRRx8REBDgdcU/IAlACCFcUlSHx8uXLzNnzhz69etHzZo1Sziy4kkCEEIIFxTV4XHevHmkpKQwbNiwEo7KPpIAhBDCBaN6NCEowD/fsqAAf0be2YgPP/yQDh060L59e4OiK5q0AhJCCAcVbPXzQNtwNhxMzNcKqPzZvRw5coQ33njD6HBtkgQghBAOsDbM+bKdCYXG84mOfppatWrxwAMPGBVqsSQBCCGEA6y1+rkz+790+PZ5+PYChNZhb90nWbt2LRMmTPC6pp+WJAEIIYQDCrb6uddvE5MDPieYDNOC5JNM/WocFYPKM3jwYAMitJ9UAgshhAMKtvp5uVwswSoj7/WfyTl8szedZ9tXpGrVqiUdnkMkAQghhAMKtvqprS7ke3/61gy0hhcjM/MtL5H5sR0kRUBCCGHL3lj48U3T/NKhdaDbOHpHmuadyG0FdF5dQ00SAbiUpvlsVwYPRQRw/fX/TPlYYvNjO8iwBKCUqgt8BdQANDBba/2BUfEIIUQ+e2Ph38Mg01zmn3zS9BroHRnzz4V775W89WbuyCA1A164NYThifewY/JPjOrRhNdX7bc5XISRCcDIIqAsYKTW+kagAzBUKXWjgfEIIcQ/fnzzn4t/rsw003JL5ilJ04PD+WBbBrc3DGJh1UF8m9OJhKQ0Ri3ZQ1Ja/uKgXG6fH9tBhj0BaK3PAGfMv6copQ4A4cBvRsUkhEdYKUaQ6StLgeRT9i9vGcNXW5M4d2UQut1Yfs9pnfdWZo62eQi3z4/tIKW17eBKLAil6gE/AxFa68sF3hsIDASoUaNG20WLFjl1jNTUVEJCQlwL1AMkLseUurjSLpmKDnTOP8uUn2ni+qAqxsVlsFIR1/nfIDuj8Er+gXBt/sKKrKwsHn/8cQKDKzHyjXdRStl1vLpVgwkLCnA8NgdFRUXt1Fq3K7jc8EpgpVQIsAx4seDFH0BrPRuYDdCuXTvdpUsXp44TFxeHs9t6ksTlmFIX17QIUwIoKLQujPjVuLgMViri2ns+fx0AQEAQ3DMDWnbJt92cOXM4e/YsTZ94nvd/te+CXiU4gN2P3ulcbG5iaDNQpVQApov/Qq31ciNjEc7zxuZtXsORYgThXcxl+4TWBZTp33tmFCq+y8rK4u2336ZNmzZMHP5koYHhrAkK8Gf8Pc09FLj9jGwFpIAvgANa6/eNikO4xlubt3mN0Do2ngDqlHwsvsqVOpiWMcWu+80333Ds2DFWrlzJfW3qoJTijX/v59LV/BW/ClNzx3ArU0YaxcgngI7A40BXpVS8+eduA+MplYy++y5uNiSf122cqdjAUkCQabnwvNymnMknAf1PU869sW7ZfXZ2NhMmTKBVq1bce++9gOnGJziw8L117sV/8+iuXnHxB2NbAW3ClBSFk7zh7ruo2ZBKm+Im9nZK7t2jtAIyRlFNOd3wGSxevJjDhw+zdOnSfBW/peX/heGVwMJ5Rd19l1QCqB0WRIKVL7XRzdscZW8ydSpJ2FGMIDzEg3UwWVlZvPXWW0RERHD//ffne6+0/L+QsYBKMW+4y7A1G9KoHk2K3dbo4itL9hRl5SaJhKQ0NP8kCan09mK26lqKqIOx93s5f/58Dh48yJtvvomfX/5LqSv/L0qSPAGUYs7eZbizqCN3O0f3V9wdt0eKY4pgTzItKkm83UHupbxSt3HWm3LaqINJSstkzI/FPwmmp6czfvx4brrpJnr37l1oP87+vyhpkgBKsVE9muS7iELxdxnWLrwjFsez44+/mNC7hVNx9I4Md/iLXdwdt63kEOZUhMWzJ5kWnSQqeigy4RIH62DOJaeTlpk/mVsrVp05cyYnT55kzpw5Njt9OfP/oqTJbUsp1jsynEl9WhAeFoTC1MKg4LR0BVm78Gpg4dY/S7Qoo6iLqREti+x5ZLf1ZOVt5bqigJYxpk53ryeZ/i2iPiYjO8fqcsvva0pKCm+//TZ33HEH3bp1c3u4JUmeAEo5R+8ybF14NXhN5bERd9r2PLIX+cSVfMQjcYmSFehv/Z7YMsm///77XLhwgYkTJ5ZUWB4jCcDH2LrwguOVx6mpqSQkJPDt/47w1c+HSExKoWpQOfreVI+o5uFUqFCBa665hmuvvZZKlSrle1Qu6mI6Ze0hp1tQuFJ3UFwyLSpJxMVJAij19sbSiESOlx/LaV2Nd7NiWJXTKd+TYGJiIlOnTqVPnz60b9/e4IBdJwnAx4zq0YQRi+OxNgSgrQvshQsX2LJlC3v37mXPnj0cOHCAkydPkpycXGjd88Bb8+GtAssrVKhA/fr1ady4MY0bN6ZJkyYMjLiOJUf9OZOSUehi7cyddkn0iygN5brCCeYOY34NRuOnNHXUBSYHfE7VgEBa9xyY95mPGzeOtLQ03n77bYMDdg9JAD6md2Q4S3b8yeZjfxV6L6rpNQBkZGTwv//9j+XLlxMXF8e+ffvy1mnQoAHNmzenS5cu1K1bl893JpGUE4hfQHlUufLg5w/ZmVQL8mfK/U1JTEzk3LlznD17lhMnTnD48GHWrFlDRoZplMWgoCDatGnDrbfeSnBiFlevVnH6Ttsb+kWIUspKh7FglcHrFZdB5BsA7Nu3j9mzZzN06FCaNm1qRJRuJwnAB/1+sXDxitY5LF/1PX8un8KqVatITk4mODiYjh078vDDD3PbbbfRqlUrKlWqlG+7T0evJtjKMa4Ad911l9XjZ2dnc/z4cbZv38727dvZtm0b06dPZ8qUKZQvX56OHTty1113MT+mDw0aNMjbbuXuBM6dTWHA6NVWi3c81S/itZX7+GbbSbK1xl8pHr65rtMtpoSXKqbDmNaakSNHEhoayvjx40swMM+SBOCDLC+I2Vcukbp3PSl71pKdfI4jQZXofMdd3HFLa0aMGEGFChXy1jWVr2/Pd1fuTF8Ef39/GjVqRKNGjXjkkUcAuHLlChs3buSHH35g/fr1jBo1ilGjRhEZGckDDzxAWPPOfLTzCkOa5qDxyyve2fHHX2w4mGizXqO4WIrz2sp9LNj6Z97rbK3zXksSKEOKGbTv+++/Z/369UyfPp1q1aqVcHCeIwmgFHFX56jaYUH88ecfXN62nNS969BZGVS4viVVbn+S4Ea3cDqoAs1a++e7+L+2ch8Lt/6ZV3eQewF+oG04y3YmONQXwZqKFSsSHR1NdHQ0ACdOnGD58uUsW7aM1157DYDA2k3YHN2VnMpd8CtfkbTM7HwxWeNq78tvtlm5KJiXSwIoQ3I7jFkydxjLzMxk5MiRNG7cmCFDhhgTn4dIAigl3FXBee7cOUJ2zCFhxTcAVGzeldCbHyCg2j9d49MyszmX/M9Qtit3J1i90KZlZrPhYCKT+rRwe4/H+vXrM3LkSEaOHElCQgItHh9H6r4fWPzlp6hyXxLc+BZCIntSPrypzY44/koV2y+iONk2ZsyztVyUUrl9Aw5ewDT2/z8dxj6ePp1Dhw6xatUqAgLsm+yltJAEUEq4WsGZlpbGtGnTmDRpEunp6dz14GOcr9+DC1S2ur5lh5gpaw/ZvMs+nZTm8ZYx4eHhNOv+KKfa30/figeZtXIDV377L1d+iyOw5g1UansPFZt2RpXL/58zR2uX4/JXyurF3t/OKf9EKdIyBv6Kg5ikvEWnT59m3Lhx9OjRg169ehkXm4dIT+BSwpUKzn+SPngAACAASURBVB9//JGIiAjGjh3LHXfcwf79+/l+8Vx2TH6YcBvl45YdYoo6Rkn1gh3VownBgeW4vmEjqnUfQp0hc6nafQg6828urp7GqU/7k7RxIdlX/2ma6o7YHr65rkPLRdny0ksvkZGRwUcffWT3PL+liSSAUsKZYQguXbrEU089xR133IG/vz8//vgjK1asoHHjxnnr2BoCoUboP+X/to6hzNuXhNxhLwL9/VBA3WurMnjwczR4bhbX9ptA+dpNSP7lGxJmPsVfP35GdsqFvGatrpjQuwWPdbgu747fXyke63CdlP/7gPXr17N48WLGjBnDDTfcYHQ4HiFFQKWEowO//fe//+XRRx/l7NmzjB49mnHjxhEUVPhCbqvNfZhFhytrx1bAox2uK9H29b0jw4lLPsKJyV3ylrW7vipT1pYnoV5rMi78yeVtS0nZ+W9Sdq3moy13EK7GMvi+Ti4dd0LvFnLB9zHp6ekMGTKEG264gVdeecXocDxGEkApYe/wsrmTVEyYMIGGDRuybds22rZtW2QLImtl+JYdrmwdG6Dj5J8MHe42N/aOk38igeuo3vMlwjo9SvK25STvXceQPuvYOWAA48aN47rrrvtnQ1fmiRWlXzGf/7vvvsvRo0dZt25dvtZwZY0kgFKk4IU4d3TM3OUXLlygb9++xMXF8cQTT/DRRx9RqVIlt7QgKpgkvGE6SkuW9RTlQmtQrftgwm59iMvbljJ//nzmz5/PoEGDePXVV6l5/uf8Y8TnzhMLTieBpLRMw5OhsFPuPMHWPn+u5bfffuPtt9+mX79+3HnnnYaFWRKkDqAUKWpGqr1799K+fXs2/7KFGx58mZ9rxRD98fa8O393D6/sbZPBW6un8A+pQsQDwzh69ChPPvkkn3zyCQ0bNmTMiKH8dflq/pVz54l1wsrdCSRcSpOZwkqLIuYJzs7OZsCAAVSqVIkZM2YYE18JkgRQiti66I6Z9iW33noryalp1H70HTIbds53IXLX6J/2bGvUpNdFjedft25dZs+ezYEDB+jduzfv/HSBhjNSmLblbzKyLZp4OjlP7JS1h8gp0FTUyGQoilHEsA+xsbH873//4+OPP+baa68t2bgMIAmgFLF2cU2J/w8HF7zOjTfeSMNnZ8C1+VsrpGVm22yz7kozSW+bHMWeyXEaNWrEwoULif9XQ24O9+eldX/T/JMrLD+Qida6yHlii+JtyVAUw8bnfCD9GubMmUOfPn2IiSlcFOhNc1i7iySAUsTy4qq1JvmXxfy19iPCGrcnLi6OCznWJ0vJ1trtE1R746TXvSPD2Ty6Kycm92Tz6K42y+BbPj6R/wyozppHgynvDw/EpnH7vHR21HzUqeN6WzIUxeg2zjTMg4Vs/wo8tUYRFBTEJ598UqjNf1HFr6WZJIBSJPeiq7Xm0k+fk7RxPpUjuvLZV4sIDg62ecHJvRt2ZOrI4jgzHaXXaBkD98wgum194p8LYVbfWhxKCab9I6/y2GOPcfKk9fF/bBnVowl+BS4YRidDZ5XFu9xCzJ8/oXUxDftQl0nnurB17xFeeOEFatSoUWgTb6vzchdpBVSK9I4MR2vN0BeGkbLjW2rd2oePZkynT1tTr9Si+gp4YriGUj05SssYaBlDOWAg8NDly7zzzju89957rFixgrFjxzJy5EjKly9f7K56R4az8uxvhIf5l+pWQN7WssujzJ8/wJYtW3h91G08/PDDNuf4LavFfPIEUFL2xsK0CHg9zPTv3liHd6G1ZuOC9znzywpGjBhBwqaleRd/KOV35QarXLkyb7/9NgcPHiQ6OpqxY8cSERHB6tWr7do+LCjAruInb1ZW73KLkpyczCOPPELdunX59NNPbQ73UFaL+eQJoCQU0+7YnmGetda88sorTJs2jeHDh/Pee+9Z/bKW6rtyL1CvXj2WLVvG+vXrGTZsGL169aJXr15MmzatzA4HkKus3uXaorXmueee4+TJk2zatInQ0FCb6zraE7+0MPQJQCkVrZQ6pJQ6qpQabWQsHlVEu+OktEy7KpemTp3KlClTGDJkCNOmTbNaSVXmy25L0J133smePXuYOnUqcXFxNG/enLFjx3LlyhWjQ/OYsnqXa8vcuXNZtGgRb7zxBh06dChy3bL6dF1sAlBKvaCUquLuAyul/IGPgbuAG4GHlVI3uvs4XqGIdsfnktOLfexesGABL7/8Mv369ePDDz/0mRYKRgsMDGTkyJEcPnyYfv36MXHiRJo2bUpsbKyp2WgZY0/LrrJyo7F7926GDBlCVFQUo0fbd+9pbyuz0sSeJ4AawHalVKz5jt1dY6LeBBzVWh/XWmcAi4D73LRv72KrfXlonXzj7lvKfexet24dAwYMICoqinnz5uHnV/gjK4my27LyH98ZtWrV4quvvmLTpk1Ur16dfv360a1bN/bv3290aG5V3F1uWbnR+Ouvv3jggQeoXr06ixYtwt/fv/iNyihlz52M+aLfHRgAtANigS+01secPrBSDwLRWutnzK8fB27WWj9fYL2BmBpqUKNGjbaLFi1y6nipqamEhIQ4G65r0i6Zyv21xcVe+UFoXS6k+3HmauFNAv398E89x7Bhw6hduzbTp0+3Gf++hGSrywFahNsu1yyK5flKSssk4VJavt6ufkoRXiWIsKCSnSHJ0M8R04T23333HV988QVXr16lT58+PPnkk2itDY3LFneer0NnU6zesAT6+9GkZiXD4iooKS2Tc8npZGTnEOjvR43QCnnf0+zsbF599VV2797N9OnTufHG/IUORn+/iuJKbFFRUTu11u0KLrcrAQAopVphSgDRwAagA7Bea/2yMwHZmwAstWvXTu/YscOZwxEXF0eXLl2c2tYtbIw+uHLNesb8kl2ocml0VG3GP3Uv2dnZbNu2jdq1a9vcdcfJP1kd7iE8LIjNo7s6Fa7l+fLE/p1l+OdoduHCBV599VU+//xzatSowVNPPcWECRO8btIQd56v+qNXW50ZTgEnJvd0aF+e+hwLNmUF0/+n3CeZsWPHMnHiRGbOnMmgQYNKLC53cCU2pZTVBGBPHcBwpdRO4F1gM9BCaz0YaAs84FQ0JgmA5bRKdczLyqaWMTDiV3g9yfSvuQ1yWFBAocfut+5pypdvvMC5c+dYsWJFkRd/8HyvXF9rHWKP6tWrM3v2bLZt28Z1113HxIkT6dy5M3v27DE6NI8pDZXERRWHzps3j4kTJ/LMM88wcOBAgyL0LvY0A60K9NFa/2G5UGudo5RyZZLM7UAjpVR9TBf+h4BHXNhfqVWw6ebQoUP5+eefWbBgAe3aFUraVreH4ucKcFbtsCCrTwDe9B/fKO3bt2fLli288sorzJ07lzZt2jBkyBDeeustwsLCjA7PrbyhKWTBJtNRTa9hw8HEvNe2Bj48vvd/PDtuHN26dbM61IOvKvYJQGs9vuDF3+K9A84eWGudBTwPrAUOALFa67JVq+aEzz//nE8++YRRo0bx6KP2j03jSAsFRyt0vXHcH2/i5+dHz549OXToEIMHD+aTTz6hcePGfPnll+TkWK/kL42MbgpprRJ6wdY/aXt5PRsDh7Ex7X42BQ7jXr9N+bbL/CuBCysncsMNN7B06VICAoqot0q75HKHzdLE0I5gWuvvge+NjMGb7Nmzh+eff57u3bszadIkjxzDme7+nn7CKCuqVq3KRx99xNNPP83zzz/P008/zWeffcZHH31E27ZtjQ7PLYzsaGiteOdev01MDvicYJUBQB11gckBn0MmrMrpRFbKBRJjxxFcPoDvvvuu6KeyvbGQfNbUYAPcMlGQt5OhILxEamoqMTExVK1alfnz53usaZqzTUbLYhtoT4mMjGTTpk3MmzePEydO0L59e5577jkuXrxodGilmrU6p5fLxeZd/HMFqwxeDVxCztVk/lo6jnJZV/hx/VoaNGhQ9AF+fDN/Sz1waaKg0kASgBfQWjN48GCOHj3K119/7dGJKKRCt2QopXjiiSc4dOgQw4cP5/PPP6dx48bMmjWL7OzsIrf1xj4XDsfkhrGvCrJW51RbXbC6bvDfidTYMg19+TxrVn9nV11aUR02yypJAF5g3rx5LFiwgPHjx3u8CVppaMlRloSGhjJt2jTi4+Np0aIFzz33HDfffDNbt261ur43drZyOKbcsa+STwL6n6IUF5NAVNNrCi07rasXWnb5b03PxVnEx8ezdOlSbr/9dvsOUESHzbJKEoDBEhISGDp0KFFRUYwdO9bjx5MKXWNERESwYcMGvvnmG86cOcMtt9zC008/zfnz5/Ot540jcjocUxFjX7liw8HEQsvezYrhqg7Me52Urum+IJ0tf6bz9ddf07OnA/0Tuo0zddC0FBBkWl5GSQIwUHZ2NpMmTSIwMNCj5f6WjG7J4a2KK+JwR7GMUoqHHnqIgwcP8vLLL/PVV1/RuHFjZsyYQUaGqRzbk0V0zv4NDsfkoaIUa8dbldOJ0ZnPcCqnOhevarotzGTX2RyWLl1G3759HTtAyxjTJDEWE8Vwz4wyWwEMMhy0oaZOncr+/ftZsGAB289DzPyfSqSVjQwZnV9xLaPcPVFKpUqVeOeddxgwYADDhg1j+PDhfPjhh0yePJlaoWGcTk4vtI2rRXSu/A0O9wMJrfNPS5qCy11gK45VOZ34JaMV6d9P4GjiUVZ+u4q7777buYMEVTF11PQR8gRgkH379jFu3Dg6d+5McLPbva7c15cUV8ThqWKZpk2bsnbtWlavXk358uV58MEHubR4NPps/v26o4jOlb/B4WJDK3PuuqMoZVSPJgT4Fe7AlXPhOCe+fJGTJ0+yZs0a5y/+PkgSgAEyMjJ44oknCAsLY8SIEUxdd9jryn19SXFFHJ4sllFKcffddxMfH89nn31G0rlT/DlvJCmr3yHrrwS3FdG58jc4XGxoZc5ddxSl9I4MZ0rfVvkGIPRPiCfxmzEElw9g8+bNREVFuXQMXyNFQA6wZ+Yue7zzzjvEx8ezcuVKQkNDOZ1kfZIRaZppm7s+Cyi+iKMkhsIoV64czzzzDA899BDvvfceU6ZM4fLBLdz77LO0u+ZVl/fv6t/gcLGhxZy77pQbh9aayZMn89qUcbRo0YLVq1cTHm49Pnd+V8oaeQKwk7ua5x0+fJi3336bfv36cd99pukPpGmmY9zdVLK4Io6SbDkVEhLC+PHjOXr0KM888wyff/45N9xwA8OHD+fMmTNO77cstf5KTk6mT58+vPrqq8TExLB58+YiL/5SvGqbJAA7uaMcWGvNoEGDCAoKYvr06XnLy9J/zpLg7jL54oo4jGg5VbNmTT799FMOHz7M448/zscff0yDBg0YOXIk586ds2sfK3cncOhsCvVHr2bK2kM80Da81Lf+2rp1K23btuXf//4306dP5+uvv6ZixYo217f1XXl91X6v62xnBCkCspM7yoHnzp1LXFwcs2bNombNmnnLZawdx3iiTL64Ig6jWk7Vq1ePzz77jNGjRzNhwgSmT5/OzJkzefbZZxkxYgTXX3+91e1y73yHNM1B40dCUhrLdiZ49KLvyaKWzMxM3nzzTSZOnEjdunWJi4ujU6dOxW5n6zuRlJZJUlomkL9FVNkav7V48gRgJ1eLaRITE/nXv/5Fx44deeaZZwq9L2Pt2K/MFpkVMXxCw4YNmTNnDgcOHKBv3758/PHHNGzYkEcffZT4+PhCu/JUyyVbfQk8WdSybds2brrpJiZMmMATTzzB3r177br4g/3fCV9tdCEJwE6uFtP861//IiUlhdmzZ1ud11fYr0wWmVkZPiFt+fMMf3VMvgtt48aNmTt3LsePH+fFF19k1apVREZG0r17d77//vu8cYY88ZRk7SK/acUnXH2nKfd+25z1ami+oZhdvaj+9ddfDBo0iFtuuYXz58+zfPly5syZQ+XKle3eh7Xvii2+2OhCrkR2cqUceMuWLXz11VeMHDmy0BykwnFlsjezleETgvibUeVird5N161bl6lTp3Ly5EkmTZrEvn376NmzJzfccAOTJ0+mernCncnAtaekgk8V9/pt4k01m+C0M/ihqeNnGorZMgk4c1G9evUqU6ZMoVGjRnzxxRe8+OKLHDhwgPvvv9/hfVn7rlQJtj4fQKl/gnSC1AE4wJly4JycnLyJ3UtirB9fUeZ6M9sYJqG2Mg0hnXs3XfBvDgsLY/To0bz00kusWLGCTz/9lDFjxlCuXABBjW/lt5zOaNqh/PxdfkoqeDG3NRTzy+ViWZVhKqJx5KJ69epV5s6dy4QJEzhz5gzR0dG88847tGzZsugNbcy3navgd8XWvMGjejSB5CN2x1sWyBOAh82dO5cdO3bwzjvvEBISYnQ4wlvZGCbhtK72z+9F3E0HBgbSr18/4uLi+O233xgyZDA5J+OZOeUtTn38JH///AUDGmVyX+ui55cuSsGLua2hmHOTlr0J5+zZs/zf//0f1113HUOHDqVBgwb897//Zc2aNfZd/B0cebRMPkE6SZ4APCg5OZkxY8Zwyy23ODS9oyh9ktIy6TjZgbGcCt61NuoOe77OVwx0VQfybtY/d7L23k03a9aMDz74gHfffZcpU6YQHx/Pd999xytPruDDsXXo1asX99xzD127dqVChQp2/40F5wQ+ratTx0oSOK2rEV7MOcjIyGDp0qV89dVXrFmzhuzsbO677z5eeuklOnXqZP+cvUWNPFpER7Qy9wTpJEkAHvTWW2+RmJhIzb6v02DM99K8s4xauTuBhEtpJCSZKhuLHWgt964198KVfNJ08W/1CBxZh04+xWldjXcyY1iVYypKcab4pnz58nTq1InXXnuNpKQkVq5cyapVq5g/fz4zZ84kODiY22+/nc6dO3PbbbfRrl07ypcvb3N/BZsrfx74GK/pmZTLtqhvCAiizj2T2Nyya6Htz58/z5o1a1i9ejXff/89V65coXbt2owYMYJnn32WRo0aOfT3AT45iYs7SQLwkKNHjzL9gw+o3Ko7ySHXAa6PIim805S1h3iors63zFaZPWD7rvXIOhjxKwrYvjuBnWsPodzUpj4sLIz+/fvTv39/0tPTiYuL47vvvmPDhg2MGTMGgAoVKtC6dWtatmyZ91O/fn1q1aqVN1R5/jvnnrC3eaHyd92iL2dOn+bQoUMcOHCAbdu2sWXLFo4cMZWv16pVi9tvv53hw4fTrVs314ZB99DIo75CEoCHjB07Fq3KEdIxf9FPkRcGUSqdTkqDujaWW2PHXasniygqVKhAdHQ00dHRAFy4cIFNmzbx888/s3v3bpYsWcLs2bPz1i9Xrhzh4eHUqlWL0NBQKleunFeflZOTQ3Z2JJcvN+TChQtcmPl/nD79NKmpqXnbX3vttdxyyy089dRTdO/endatW/Pzzz+7Z/a7buPyP01BmZ/ExZ0kAXjA9u3biY2NJfTWhygXUrXQ+77Y3rgsM5XNp9hYboWX3bVWr16d3r1707t3b8A0ZMkXa3fw/uIfOX/mFBX+vkS94HTK/Z3MpUuX+OOPP0hNTUUphZ+fH35+flSqVInq1avTunVroqOjady4MU2aNKFx48bUrVvX/jJ9R+WW8xfRCkjYJgnAzbTWvPLKK1SvXp0Gdz7COSvNsX2xvXFZNqpHExIO7My3rNjx8r34rvXb+NO8t/kiaTVaEFKjBQDnAvy9t6WMh0Ye9QXSDNTN/vOf/7BhwwbGjRvHmPvalL0eq6KQ3pHhhFcJMny8fHfxxnmJhWfIE4AbZWdn88orr9CgQQMGDRpEYKBpsmoZ5K3sCwsKYPPoLvZv4MV3rZ6cAEd4F0kAbvTNN9+wb98+vvnmm7yLv7Q3FqVNSUyAI7yDFAG5SVZWFm+88QYtW7YkJsY77+yEsEeZHGxPWGXIE4BSagpwD5ABHAMGaK2TjIjFXb7++muOHj3K8uXLZbRPUarJ/BS+w6gioPXAGK11llLqHWAM8IpBsbgsKyuLt956i9atW+c1pROiNJOiS99gSALQWq+zeLkVeNCIONxlwYIFHD16lJUrV3quvbMQbmDvrF0ykbpvUFrr4tfyZABK/RtYrLVeYOP9gcBAgBo1arRdtGiRU8dJTU31yGicWVlZPPnkk1SsWJFZs2Y5nAA8FZerJC7HlIa4ktIySbiURo7F/3k/pQivEkRY0D9j5Nu7nrvi8ibeGhe4FltUVNROrXW7gss99gSglPoBqGnlrbFa62/N64wFsoCFtvajtZ4NzAZo166ddrb7eFxcnHu6nhfw5Zdfcvr0aVatWkVUVJTDd06eistVEpdjvDmupNBGTFl7iISkDKDwuDvhYf75mrB2nPxT3sB2Ra3nalzeer68MS7wTGweSwBa6zuKel8p1R/oBXTTRj+GOCkrK4sJEybQrl07evXqVWiiCRn8TRgtKS2TMT/uK9Sxy1LB9v3SD8B3GNUKKBp4Gbhda33ViBjcYfHixZw4cYLytz1FgzHf46cU2dqBUSGF8LBzyemkZRbdKq3QRC/e1A+gmNm+hGuMaq/4EVAJWK+UildKzTQojmKt3J1Ax8k/UX/06nyTc2utefX1twi85nqu1myFhkIX/1xy5ySMkpGdU+T71tr3e00/ACdm+xKOMaoV0A1GHNdRRRXpBJyO58+jh6jW8yWUcuwOS4iSEuhv+7tpa9Yur+kH4ORsX8J+MhREEYoaFMv/+3fwr3wNFZt1LnIf0oNSGKlGaAWCArILTYBe3MieXtEPQGb78jhJAEWwVXRz/NednN24kfq9hpLjX/gU+itFjtbSflqUGFutz8KCApjU50bD7+YLxdfKdqV0Hi+bN6EskgRQBFuVYX/vWkG1atWYOGY4b6w55vDdlRDuVFRRZRjuuZt3pWOYtfgSLmWzcndC0fvw8nkTygIZtKYI1irD/C6d5NKBLQwbNoyHbm3EpD4t7B8HXggP8PT4/bkX8ISkNDT/JJjcBhHOxJejdfHxefm8CWWBPAEUwVplWOD+HzkXHMzQoUPz1pELvjBS0e32K7q8/6ISjD3ffZf6FXjxvAllgSSAYlhe4M+ePct1475l0KBBVKtWzeDIhDDxdLt9VzuGeVW/ApGPFAE54NNPPyUrK4thw4YZHYoQeTzdbt/WhdreC7jVolSlpHWcF5AEYKf09HQ+/fRTevbsSaNGjYwOR4g8vSPDPVoX5WqCsRZfeJUgKTr1AlIEZKdFixaRmJjIiy++aHQoQhTiybood3QMKxhfXFycu8MUTpAEYAetNdOnTyciIoKuXbsaHY4QJc5WgpF5A0o3KQIqyt5YmBbBfwdUYs+ePQx/4FaZ8EUIM1ebhwrjSQKwxWIgqulb/6ZakOJRVspAVEKYebr/gfA8SQC2mAeiOn4ph1WHsniuXQBBpJuWCyFk3oAyQBKALeYBpz7dnoGfgsHtAvMtF8LXudo8VBhPEoAtoXVIz9LMic+kd9NyhFf2y1suhPCieQOE0yQB2NJtHEsPKS6maZ7LvfuXgaiEyOPp/gfC86QZqC0tY5h5dByNrkmna/1ypoGoZDo6IfKRsbBKN0kANuzbt4/N8YeYOnUqfiNHGh2OEEK4nSQAsDrx9MxZ/6V8+fL079/f6OiEEMIjJAHktvfPnXQi+SSpS59n/rxUYmJiZNRPIUSZJQnAysTTX+9OIeVKOoMHDzYoKCGE8DxpBVSgXb/Wmpk7MmhZw48OHToYFJQQQnieJIAC7fp3n81h99kcBnWqIeP+CCHKNEkA3caZ2vebfbk7gwrl4JEX3zYwKCGE8DxJABYTT6dnwcJfs+nTvSNhnQYYHZkQQniUJAAwJYERv7IyYhZJaTk89dIbRkckhBAeJ62A+GdSi12z3qV8WA2SwxobHZIQQnicoU8ASqmRSimtlKpuVAy5k1r88ccfpP8eT4Xm3Ri7cr9MaiGEKPMMSwBKqbpAd+BPo2KAfya1SP31R0AT0qKbTGohhPAJRj4BTANeBrSBMXA6KQ2tc0jd9wMVrm9FudAaecuFEKIsU1qX/PVXKXUf0FVrPVwp9TvQTmt9wca6A4GBADVq1Gi7aNEip46ZmppKSEhIoeWHzqbw6749fDTx/3hiyAja3Xo7AIH+fjSpWcmpY7kjLqNJXI6RuBwjcTnOldiioqJ2aq3bFXpDa+2RH+AH4FcrP/cB24BQ83q/A9Xt2Wfbtm21szZs2GB1+Ypdp3TliK5ala+o6760TF//yne66Wtr9Ipdp5w+ljviMprE5RiJyzESl+NciQ3Yoa1cUz3WCkhrfYe15UqpFkB9YI+5p20dYJdS6iat9VlPxZMrt8XP6aQ0aocF8ULnumQc28q1raLwDyhP7bAgRvVoImOcCyHKvBJvBqq13gdcm/u6uCIgd8pt8ZOWmQ1AQlIaL035nPS0q6yd8jKdO3f2dAhCCOE1fKojWG6LH0uX9v5IYNi1dOrUyaCohBDCGIYnAK11vZK4+4fCLXuyr1wi/cRugprejp+f4adCCCFKlE9d9WqHBeV7feXARtA51O8QbVBEQghhHJ9KAKN6NCEowD/v9ZXf4ihfsyHjn+hhYFRCCGEMn0oAvSPDmdSnBeFhQWT9lUDGmcM8/PAj0uJHCOGTfCoBgCkJbB7dladrJaCU4u1/PWd0SEIIYQifSwBg6vy2cOFCunXrRu3atY0ORwghDOGTCWDbtm0cO3aMxx57zOhQhBDCMD6ZABYuXEiFChW4//77jQ5FCCEM43MJIDs7myVLltCrVy8qV65sdDhCCGEYn0sAGzdu5Ny5c8TExBgdihBCGMrnEkBsbCzBwcHcfffdRocihBCG8qkEkJWVxbJly+jVqxcVK1Y0OhwhhDCUTyWAn3/+mfPnz0vxjxBC4GMJIDY2looVK3LXXXcZHYoQQhjOZxJAdnY2y5Yt45577iE4ONjocIQQwnA+kwDi4+O5cOGCFP8IIYSZzySADRs2EBISQnS0DP0shBDgD/D+IgAAB7pJREFUIwkgMzOTjRs3cu+99xIUFFT8BkII4QNKfE5gI2zYsIHLly8XW/xTcMJ4mRxeCFGW+UQCyO381aOH7YlfrE0YP2b5PgBJAkKIMsknEsC4ceO44YYbqFChgs11rE0Yn5aZzZS1hyQBCCHKJJ+oA7juuuvo0KFDkesUnDC+uOVCCFHa+UQCsEfBCeOLWy6EEKWdJACzghPGAwQF+DOqRxODIhJCCM/yiToAe+SW80srICGEr5AEYKF3ZLhc8IUQPkOKgIQQwkdJAhBCCB8lCUAIIXyUJAAhhPBRkgCEEMJHKa210THYTSmVCPzh5ObVgQtuDMddJC7HSFyOkbgc461xgWuxXa+1vqbgwlKVAFyhlNqhtW5ndBwFSVyOkbgcI3E5xlvjAs/EJkVAQgjhoyQBCCGEj/KlBDDb6ABskLgcI3E5RuJyjLfGBR6IzWfqAIQQQuTnS08AQgghLEgCEEIIH1WmEoBSqq9Sar9SKkcpZbO5lFIqWil1SCl1VCk12mJ5faXUNvPyxUqpQDfFVVUptV4pdcT8bxUr60QppeItftKVUr3N781VSp2weK91ScVlXi/b4tirLJYbeb5aK6W2mD/vvUqpfhbvufV82fq+WLxf3vz3HzWfj3oW740xLz+klLI9KbVn4npJKfWb+fz8qJS63uI9q59pCcXVXymVaHH8Zyzee9L8uR9RSj1ZwnFNs4jpsFIqyeI9T56vL5VS55VSv9p4XymlZpjj3quUamPxnmvnS2tdZn6AZkATIA5oZ2Mdf+AY0AAIBPYAN5rfiwUeMv8+ExjsprjeBUabfx8NvFPM+lWBv4Bg8+u5wIMeOF92xQWk2lhu2PkCGgONzL/XBs4AYe4+X0V9XyzWGQLMNP/+ELDY/PuN5vXLA/XN+/EvwbiiLL5Dg3PjKuozLaG4+gMfWdm2KnDc/G8V8+9VSiquAuu/AHzp6fNl3ndnoA3wq4337wbWAAroAGxz1/kqU08AWusDWutDxax2E3BUa31ca50BLALuU0opoCuw1LzePKC3m0K7z7w/e/f7ILBGa33VTce3xdG48hh9vrTWh7XWR8y/nwbOA4V6OrqB1e9LEfEuBbqZz899wCKt9d9a6xPAUfP+SiQurfUGi+/QVqCOm47tUlxF6AGs11r/pbW+BKwHog2K62HgGzcdu0ha658x3fDZch/wlTbZCoQppWrhhvNVphKAncKBkxavT5mXVQOStNZZBZa7Qw2t9Rnz72eBGsWs/xCFv3xvmx//pimlypdwXBWUUjuUUltzi6XwovOllLoJ013dMYvF7jpftr4vVtcxn49kTOfHnm09GZelpzHdReay9pmWZFwPmD+fpUqpug5u68m4MBeV1Qd+sljsqfNlD1uxu3y+St2MYEqpH4CaVt4aq7X+tqTjyVVUXJYvtNZaKWWz7a05s7cA1losHoPpQhiIqS3wK8CbJRjX9VrrBKVUA+AnpdQ+TBc5p7n5fM0HntRa55gXO32+yiKl1GNAO+B2i8WFPlOt9THre3C7fwPfaK3/VkoNwvT01LWEjm2Ph4ClWutsi2VGni+PKXUJQGt9h4u7SADqWryuY152EdOjVTnzXVzucpfjUkqdU0rV0lqfMV+wzhexqxhghdY602LfuXfDfyul5gD/Ksm4tNYJ5n+PK6XigEhgGQafL6VUZWA1puS/1WLfTp8vK2x9X6ytc0opVQ4IxfR9smdbT8aFUuoOTEn1dq3137nLbXym7rigFRuX1vqixcvPMdX55G7bpcC2cW6Iya64LDwEDLVc4MHzZQ9bsbt8vnyxCGg70EiZWrAEYvqwV2lTrcoGTOXvAE8C7nqiWGXenz37LVT2aL4I5pa79wasthbwRFxKqSq5RShKqepAR+A3o8+X+bNbgalsdGmB99x5vqx+X4qI90HgJ/P5WQU8pEythOoDjYD/uRCLQ3EppSKBWcC9WuvzFsutfqYlGFcti5f3AgfMv68FupvjqwJ0J/+TsEfjMsfWFFOF6haLZZ48X/ZYBTxhbg3UAUg23+S4fr48VbNtxA9wP6ZysL+Bc8Ba8/LawPcW690NHMaUwcdaLG+A6T/oUWAJUN5NcVUDfgSOAD8AVc3L2wGfW6xXD1NW9yuw/U/APkwXsgVASEnFBdxqPvYe879Pe8P5Ah4DMoF4i5/Wnjhf1r4vmIqU7jX/XsH89x81n48GFtuONW93CLjLzd/34uL6wfz/IPf8rCruMy2huCYB+83H3wA0tdj2KfN5PAoMKMm4zK9fByYX2M7T5+sbTK3YMjFdv54GngOeM7+vgI/Nce/DooWjq+dLhoIQQggf5YtFQEIIIZAEIIQQPksSgBBC+ChJAEII4aMkAQghhI+SBCCEED5KEoAQQvgoSQBCuEAp1d48qFkFpVRFZZqfIMLouISwh3QEE8JFSqkJmHoDBwGntNaTDA5JCLtIAhDCReaxZbYD6cCtOv8okkJ4LSkCEsJ11YAQoBKmJwEhSgV5AhDCRco0R+wiTJOI1NJaP29wSELYpdTNByCEN1FKPQFkaq2/Vkr5A78opbpqrX8qblshjCZPAEII4aOkDkAIIXyUJAAhhPBRkgCEEMJHSQIQQggfJQlACCF8lCQAIYTwUZIAhBDCR/0/ZFpdNpgE5mkAAAAASUVORK5CYII=\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "scatter_plot_polynomial(X_train, y_train, label='training set')\n",
    "scatter_plot_polynomial(X_valid, y_valid, label='validation set')\n",
    "plt.plot(X_lin, y_fit, label='fit', c='black')\n",
    "plt.show()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### From underfitting to overfitting"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "We can investigate the shape of the fitted curve for different values of `degree`:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYAAAAEWCAYAAABv+EDhAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8li6FKAAAgAElEQVR4nO3de3xU9Zn48c+TECAaJIgWJVDBrkKEBAKh+BNUECttrYq0oq7WYttlxW5363ax2Pqz9LagtLXa2tZLrdVqkWJNseqPqpD1VruAXAQR8YKQUBGQRCJBQnh+f5wzYTKZ25nbmcl53q9XXsmc6zNnJuc553u+F1FVjDHGBE+R3wEYY4zxhyUAY4wJKEsAxhgTUJYAjDEmoCwBGGNMQFkCMMaYgLIEYLJKROaJyO/9jiOciFwhIn9Nctm48YvIbBHZKSItItLf/X1yGrHVi8hXU13fGC8sAZikiMhWEWl1T3A7ReQ+ESnzO65UqOqDqnpeutsRkRLgp8B5qlqmqnvc32+58+8TkR+mu59CIo6bRWSP+3OziIjfcZnoLAEYLy5Q1TJgDFAL3OhzPH4bAPQGNvodSCIi0iNHu5oFTANGAdXABcC/5mjfxiNLAMYzVW0EngRGAojIQBFZKiLvi8gbIvIv0dYTkcdF5OsR09aLyMXu3yoi14jIFhFpEpE7QlePIlIkIjeKyDsi8p6I3C8ifd15Q9x1rxaR7SKy193OOHf7TSLyi7B9zhSR58Ne3+au94GIrBaRMxMdAxE5FdjsvmwSkeVh7+GfRGQWcAVwvXvX9FiM7XxKRF4TkWY3RomY/2UR2eS+p2UiclLYvPNEZLO77i9F5H9CxUfue3xBRG4VkT3AvCS2N1xEnnI/x80iMiPRcYjiS8BPVLXB/Z78BJiZwnZMDlgCMJ6JyGDgs8Aad9IioAEYCHwB+G8ROSfKqr8DrgzbziigAng8bJnPAeNwrh5nAFPd6TPdn8nAyUAZ8As6Gw+cAlwK/Az4DnAuMAKYISJnx3hLK4HRwLHAQ8AfRaR3jGUBUNXX3e0ClKvqORHz7wIeBG5xi4UuiNyGiBwH/AnnTuo44E1gQtj8i4BvA9OB44HngD+ErbsEuAHoj5OMzohyPN7CuVP5UYLtHQ085b7/jwGXAb8UkdPc+XPdRBr1J2yfI4B1Ya/XhR0nk29U1X7sJ+EPsBVoAZqAd4BfAqXAYKAd6BO27HzgPvfvecDv3b97A3uBU9zXPwZ+GbaeAhPDXi8G5rp/PwNcGzZvGNAG9ACGuOtWhM3fA1wa9voR4Bvu3zOB5+O8173AqMj4oywX2m+PiPfwT+7f9wE/jLOfq4CXwl4LTiL9qvv6SeArYfOLgP3ASe66f4tYd3vYujOBbRH7i7e9S4HnIpa/E/iux+9JOzA87PUp7jERv7/D9tP1x+4AjBfTVLVcVU9S1WtVtRXnqv99Vd0Xttw7OFf2najqAeBh4EoRKQIuBx6IWOzdsL/341zp4+7nnYh99MC5ug3ZGfZ3a5TXUR9ai8h/ucUize7VbF+cK/JsG4hz0gZAnTPm9rD5JwG3hV1lv49zoq+IsW5DxPa3R7yOt72TgPERV/VXACd4fE8twDFhr48BWtz4TJ6xBGDStQM4VkT6hE37ONAYY/nf4ZxYpgD7VfVvHvZzUtjrjwOH6HyS98wt778ep7ipn6qWA81ElMWnKNFJ7x84d1ChWCT8Nc4J/F/dpBv6KVXVF911B0WsO4jOIvcfb3vbgf+JmFemqrPd7X/bfZYR9SdsHxtxHgCHjKIAHpIHlSUAkxZV3Q68CMwXkd4iUg18BYhad9494R/GeTgYefUfzx+A60RkqDjVT/8beFhVD6X1BqAPTiLZBfQQkZvofAWbjp04zytieRwYISLTxaml8+90vuL+NXCDiIwAEJG+InJJ2LpVIjLNXfdrJL5aj7e9vwCnisgXRaTE/RknIpUAqvrfbkKI+hO2j/uB/xSRChEZCHwTpyjM5CFLACYTLscpD98BPIpTbvx0nOXvB6qIkSRiuBcnYTwLvA0cAL4ed43kLAP+H/A6TrHSAboWnaTqN8BpbpFKXeRMVd0NXAIswHlmcQrwQtj8R4GbgUUi8gGwAfhMxLq3uOueBqwCPooVTILt7QPOw3n4uwOnKO5moJfH93wn8Bjwirv9x91pJg+JFc2ZXBORq4BZqjrR71i6C/eZSgNwhaqu8DseUxjsDsDklIgcBVwL3OV3LIVORKaKSLmI9MKp3inASz6HZQqIrwnA/fIucRvCbBKR/+NnPCa7RGQqTln7Tpz65iY9/wen7cBunBa309yaWcYkxdciIBH5HU7d43tEpCdwlKo2JVrPGGNM+nxLAOI0418LnGx1hI0xJvdy1UFUNENxigN+63YJsBr4D1X9MHwht0+VWQClpaVjBw8e3GVDyTh8+DBFRfn3yMPi8sbi8sbi8iZf44L0Ynv99dd3q+rxXWb41QQZpzfJQ8B49/VtwA/irTN27FhN1YoVK1JeN5ssLm8sLm8sLm/yNS7V9GIDVmmedQXRADSo6t/d10twuhk2xhiTA74lAFV9F9guIsPcSVOAV/2KxxhjgsbPZwDgtOR80K0B9BZwtc/xGGNMYPiaAFR1Lc6zgJS1tbXR0NDAgQMH4i7Xt29fNm3alM6ussLiOqJ3794MGjSIkpKSnO7XmHxUt6aRhcs2s6OplYHlpcwZ1Z7xffh9B5C2hoYG+vTpw5AhQ5A4Q4/u27ePPn36xJzvF4vLoars2bOHhoYGhg4dmrP9GpOP6tY0csOfXqG1zTnpNza10ri3nbo1jUyr6dLTesrys76TBwcOHKB///5xT/4m/4kI/fv3T3gnZ0wQLFy2uePkH3JYlYXLNsdYIzUFnwAAO/l3E/Y5GuPY0RS9R49Y01PVLRKAMcZ0JwPLSz1NT5UlAB9MmjSJVatW+bLvM86IHDe8q7KyqCMndjJv3jx+/OMfx12mrq6OV1+1mr3GeDVn6jBKS4o7TSsSYc7UYTHWSI0lgIB58cUXc7YvSwDGpGZaTQXzp1dRUV7qDNpcXkpFv9KMPgCGACaAujWNTFiwnKFzH2fCguXUrYk1dG1ytm7dyvDhw7niiiuorKzkC1/4Avv37wfgmWeeoaamhqqqKr785S/z0UedB2u69957+da3vtXx+u677+a6665j69atVFZW8i//8i+MGDGC8847j9ZWp+xv7dq1nH766VRXV3PxxRezd+9ewLmruO6666itraWyspKVK1cyffp0TjnlFG688caOfYSu7ltaWpgyZQpjxoyhqqqKP//5zwnf649+9CNOPfVUJk6cyObNRx5G3X333YwbN45Ro0bx+c9/nv379/Piiy+ydOlS5syZw+jRo3nzzTejLmeMiW5aTQUvzD2Htxeczwtzz6G8NPPVowOVAEJVqxqbWlGcqlU3/OmVtJPA5s2bufbaa9m0aRPHHHMMv/zlLzlw4AAzZ87k4Ycf5pVXXuHQoUP86le/6rTejBkzePLJJ2lrawPgt7/9LV/+8pcB2LJlC1/72tfYuHEj5eXlPPLIIwBcddVV3Hzzzaxfv56qqiq+973vdWyvZ8+erFq1imuuuYaLLrqIO+64gw0bNnDfffexZ8+eTvvu3bs3jz76KC+//DIrVqzgm9/8ZqiPpqhWr17NokWLWLt2LU888QQrV67smDd9+nRWrlzJunXrqKys5De/+Q1nnHEGF154IQsXLmTt2rV84hOfiLqcMcY/gUoA0apWtba1p121avDgwUyYMAGAK6+8kueff57NmzczdOhQTj31VAC+9KUv8eyzz3Zar6ysjLPPPpu//OUvvPbaa7S1tVFVVQXA0KFDGT16NABjx45l69atNDc309TUxNlnnx11mxdeeCEAVVVVjBgxghNPPJFevXpx8skns31752FuVZVvf/vbVFdXc+6559LY2MjOnTtjvsfnnnuOiy++mKOOOopjjjmmY18AGzZs4Mwzz6SqqooHH3yQjRs3Rt1GsssZY3Kj4BuCeZGtqlWR1Re9VGe86qqruO222xg+fDhXX32kJ4xevY6MxV1cXNxRBBRPaJ2ioqJO6xcVFXHo0KFOyz744IPs2rWL1atXU1JSwpAhQ1Kugz9z5kzq6uoYNWoU9913H/X19WktZ4zJjUDdAWSratW2bdv429/+BsBDDz3ExIkTGTZsGFu3buWNN94A4IEHHui4cg83btw4tm/fzkMPPcTll18edz99+/alX79+PPfcc3G3mYzm5mY+9rGPUVJSwooVK3jnnXfiLn/WWWdRV1dHa2sr+/bt47HHHuuYt2/fPk488UTa2tp48MEHO6b36dOHffv2JVzOGOOPQCWAaFWrSkuK065aNWzYMO644w4qKyvZu3cvs2fPpnfv3vz2t7/lkksuoaqqiqKiIq655pqo68+YMYMJEybQr1+/hPv63e9+x5w5c6iurmbt2rXcdNNNKcV8xRVXsGrVKqqqqrj//vsZPnx43OXHjBnDpZdeyqhRo/jMZz7DuHHjOub94Ac/YPz48UyYMKHTdi677DIWLlxITU0Nb775ZszljDE+iTZIQL7+RBsQ5tVXX01qQIQPPvhAVVUffblBz5j/jA751l/0jPnP6KMvNyS1fixvv/22jhgxIuX1P/jgAz3//PP16aefTiuOTAsdr1xL9Hnm64AdFpc3Fpd32RgQJlDPAMCpWpXpurSpampqora2lpqaGqZMmeJ3OMaYgAlcAsi0IUOGsGHDhpTWLS8vZ82aNXnZG6gxpvsL1DMAY4wxR1gCMMaYgLIEYIwxAWUJwBhjAsoSgA9CHbLt2LGDL37xi1GXSabL6J/97GedOlT77Gc/S1NTU+YCTcLWrVt56KGHcrpPY0xmWALw0cCBA3nggQdSXj8yATzxxBOUl5dnIrSkWQIwpnAFLwGsXwy3joR55c7v9YvT2tzcuXO54447Ol6HBkpJprvlrVu3Mn78eABaW1u57LLLqKys5OKLL+7U98/s2bOpra1lxIgRfPe73wXg9ttvZ8eOHUyePJnJkycDTpXU3bt3A/DTn/6UkSNHMnLkSH72s5917C9WN9Ph/vjHPzJ+/HhGjRrFWWedBUB7eztz5sxh3LhxVFdXc+edd3a8/+eee47Ro0dz6623pnUsjTE5Fq11WL7+pN0SeN3Dqj8coPrdY478/HCAMz1FL7/8sp511lkdrysrK3Xbtm3a1tamzc3Nqqq6a9cu/cQnPqGHDx9WVdWjjz5aVZ1WxJWVlaqq+pOf/ESvvvpqVVVdt26dFhcX68qVK1VVdc+ePaqqeujQIT377LN13bp1qqp60kkn6a5duzr2HXq9atUqHTlypLa0tOi+ffv0tNNO05dfflnffvttLS4u1jVr1qiq6iWXXKIPPPBAl/c0cuRIfe2111RVde/evaqqeuedd+oPfvADVVU9cOCAjh07Vt966y1dsWKFnn/++Skfv0jWEjizLC5vfItr3cOqPx2h+t2+zu8o56RstAQO1h3AM9+Htogr3rZWZ3qKampqeO+999ixYwfr1q2jX79+DB482HN3y88++yxXXnklANXV1VRXV3fMW7x4MWPGjKGmpoaNGzcmHGXr+eef5+KLL+boo4+mrKyM6dOnd3QgF62b6UgTJkxg9uzZ3H333bS3O91n//Wvf+X+++9n9OjRjB8/nj179rBlyxZPx8oYE8X6xfDYv0PzdkCd34/9e9qlE8kIVkvg5gZv05N0ySWXsGTJEt59910uvfRSIHPdLb/99tv8+Mc/ZuXKlfTr14+ZM2em3G0zJNfN9K9//WuWL19OfX09Y8eOZfXq1agqP//5z5k6dWqnZa1LZ2PSFO/CtHpGVncdrDuAvoO8TU/SpZdeyqJFi1iyZAmXXHIJkFp3y6GHqRs2bGD9+vUAfPDBBxx99NH07duXnTt38uSTT3asE9ndcsiZZ55JXV0d+/fv58MPP+TRRx/lzDPPTPr9vPnmm4wbN47vf//7HH/88Wzfvp2pU6fyq1/9qmP0stdff50PP/wwZgzGBJXXYWc1SxemyQjWHcCUm5xbq/BsW1LqTE/DiBEj2LdvHxUVFZx44omA093yBRdcQFVVFbW1tQm7P549ezZXX301lZWVVFZWMnbsWABGjRpFTU0Nw4cP7zTyGMCsWbP49Kc/zcCBA1mxYkXH9DFjxjBz5kw++clPAvDVr36VmpqaqMU90cyZM4fNmzcjIkyZMoVRo0ZRXV3N1q1bGTNmDKrK8ccfT11dHdXV1RQXFzNq1ChmzpzJdddd5+XQGdOthIadDY08GBp2FojaCWXdmkbGaX8qZHfXjaV5YZoM0TjjwOaCiBQDq4BGVf1cvGVra2s1sm78pk2bqKysTLifffv2OZ2urV/s3Fo1NzgHeMpNWb/NSiquPONXXIk+z/r6eiZNmpS7gJJkcXnTXeOasGA5jVFGGKwoL+WFuedEXX7sB0+xoOQejpKDHdNb6UXp9F90OjelE5uIrFbV2sjp+XAH8B/AJuCYnOyteoavJ3xjTPflddjZHU2tNDIR2uD6HosZKHvYof1ZeGgGt+XgPOVrAhCRQcD5wI+A//QzFmOMSdfA8tKodwDxhqNtbGpl6eGJLD04sWN6RZrD1CbL74fAPwOuBw6nsxG/i7FMZtjnaAqd12FnszVMbbJ8ewYgIp8DPquq14rIJOC/oj0DEJFZwCyAAQMGjF20aFGn+WVlZQwYMIC+ffsiIjH3197eTnFxccz5frG4HKpKc3MzO3fupKWlJeZyLS0tHX0p5ROLy5vuHFdTaxs7mw9wsP0wPYuLGNC3N+WlJWkvn05skydPjvoMwM8EMB/4InAI6I3zDOBPqnplrHWiPQRua2ujoaEhYd34AwcO0Lt377TjzjSL64jevXszaNAgSkpi/7N014eH2WJxeZOvcUE3ewisqjcANwCE3QHEPPnHUlJSwtChQxMuV19fT01NjdfNZ53FZYzxi9/PAIwxxvgkH6qBoqr1QL3PYRhjTKDYHYAxxgSUJQBjjAkoSwDGGBNQlgBM95Dhkd6MCYK8eAhsTFpCA2qEenkNDagB1u+TyUt1axpZuGwzO5paGVheypypw6L2FpptdgdgCl8WRnozJltCXUY3NrWiHOkyOtG4AdlgdwAmq3JypePjgBrGeLVw2eaO8QJCWtvaWbhsc87vAuwOwGRNzq50sjTSmzHZ4LXL6GyyBGCyJt6VTkZNuckZ2S1cBkZ6MyYb4nUNnWuWAEzW5OxKp3oGXHA79B0MiPP7gtvtAbDJS353AR3OngGYrPE6OEZabKQ3UyBC5fz5UAvIEoDJmjlTh3UaIBv8u9IxJp9Mq6nw5YQfyRKAyZp8utIxxnRlCcBkVb5c6RhjurIEYIwxacqXlr1eWQIwxpg0hNq7hJ51hdq7AHmfBKwaqDHGpCFn7V2ywBKAMcakIZ9a9nplCcAYY9KQTy17vbIEYIwxacinlr1e2UNgY4zxKLLWz+fHVrDitV1WC8gYY7qzaLV+HlndyPzpVQVx0g9nRUDGGONBtFo/n2r/H07/89kFNySp3QEYY4wHkbV7Lix6ngUl93AUB50JBTQkqd0BGGOMB5G1e67vsZij5GDnhQpkSFJLAMYY40FkrZ+Bsjv6ghFDktataWTCguUMnfs4ExYs92UM4EhWBGSMMR5E9nL7nhzPCezqumDYkKT52l2EJQBjjIll/WKnKKe5wTmhT7kJqmd07uV2/YdOmX/bkWcDrfRi7q4LWLVgOXOmDmPe0o15MxB8ON8SgIgMBu4HBgAK3KWqt/kVjzHGdLJ+cecTe6yHu6G/n/k+2tzADu3PzW0zWHp4IjS1MueP62g7rFF34Xd3EX7eARwCvqmqL4tIH2C1iDylqq/6GJMxmRfjKtLkuWe+3+mqHjjycDfy83OHJJ24YHmXYVBjnfzB/+4ifEsAqvoP4B/u3/tEZBNQAVgCMN1HsleRJv9EPMRNOB3vV/R+dxchqrGzU86CEBkCPAuMVNUPIubNAmYBDBgwYOyiRYtS2kdLSwtlZWXpBZoFFpc3BRfXe69C+8Gu04t7wsdO8y8unxVEXCl8dpvf3cfB9sNJ7atHkVB54jGpxebR5MmTV6tqbZcYUtpaBolIGfAI8I3Ikz+Aqt4F3AVQW1urkyZNSmk/9fX1pLpuNnWHuHI5GlLBHa9503AecUUSmNGU5agK8Hj5rFNc69/r8nCXklK44HaonhR1/aaI2j4AJUUCAm3tR74HpSXFzJ9exSQP/yfZOGa+JgARKcE5+T+oqn/yMxaTmnyt3pY3+g5yin2iTTf5LezhbrLPb8KriDY2tVIsQtthpby0BBFo2t+WV53F+VkLSIDfAJtU9ad+xWHSE280pHz4gvtuyk3RryKn3ORfTEGTzkN49+GuF6HvffiFUVNrG6Ulxdx66ei8+r/wsyXwBOCLwDkistb9+ayP8RQkv1sXFvJoSDlRPcMpMug7GBDn9wW32wPgXAk9hG/eDuiRh/BZ7qytUIaJ9LMW0POA+LX/7iAfil8Glpd2qfYWml5oknmWkdLzjhSuIk2GeKnKmUGFcmFkfQEVsHy4yijk0ZDChZJpY1MrypFkGn5HlcwyJs+kUJUzE3fVhTJMpCWAApYPVxnTaiqYP72KivJSBKgoL016YIx4/2i5LtpKJpnmQ8I1HsV62B5jelNrW0aSfKFcGPleDdSkLtXil7o1jXzvsY3s3d8GQHlpCfMuHJFysVGnflGSFK/4Cog5rzylCBNLJpnGX+bobIRl0uXxIfzO5gO0tnW+Lk6lUkNkh3H5VPMnnCWAAjZn6rAudY4TXWXUrWlkzpJ1neokN7W2MeeP64DcPTtIdDUda96PTs/OTWsyybQ7Pe8IDI9VOZ1GXF2/Y6ncVadyYZRrVgRUwFIpflm4bHOnk39I22HNaVFGvKtpP4q2krllL5TbehOhegZctwHmNTm/4zz87Vkc/ZTYXZO83QEUOK9XGfFOoqmeYFOpGZPoajrXV9rJ3LLHW6a+fkvWYjM5sn4xp7CLt3p9hx3an1sOOT16duckbwkgYGKdeEPzvEq1Kmqi4quY85rjn2jT6ZYimWRaCLf1JgVue4Gik+dSJMog2c2Ckns4tqQno8+f1W0/cysCCpg5U4dRUty1+UWRpNYzYao1Y+IVX6Vas8iqaZqURWkvcJQcZN7Rj3Tbkz/YHUDgTKupYNU77/P7l7Z1ml4sqbXJS6e8Pt7VdCpX2tYthUlZCu0FugNLAAG04rWu45eGHgLHO1FGK17JZc2YujWN7Hx3H1fPfbxL8U7dmsaYRVvpPjy+se4V/vD37bSrUizC5eMH88NpVWlt0+SZgHbaZ0VAARTrhNjY1Bqz0VWs4pXJw4/PSc2Y0P4Pth/utP8b615h9Pf+yjceXhtz3XSS0Y11r/D7l7bR7o6b0a7K71/axo11ryRY0xSUKTc57QPCBaDTPksABSRTrWPjnRBDJ9am1rZO07/3WPRBrVe8tivllsBexCreefClbV1iDZduMvrD36NcFcaZbgpUqNO+4p4EqdM+KwIqEJns+C1aDZxwrW3t7Gw+clKtW9PY0Wo40o6m1pzUjIl115JoPLt0k1F7jBHzYk03Bax6Brxfn5OBevKF3QEUiEz2QxNeyyaW8GHt4u0jVw1kUtlPRXlp2okp1sPxVB+aG5NPLAEUiEy3jp1WU8ELc8+JmQTCW0TG20euGshEa4Ub7xQswOThx6e938vHD/Y03ZhCYgmgQGSre9lY3RsM6Ns74T7KS0tyVr0ydNfSs7io41nDFad/vEvsIQo8srox7TYAP5xWxZWnf7zjir9YhCtP/7jVAjLdgj0DKBCpdPwWLlYL2VjdG5SHtbiNte95F47I0LtLzrSaCuqbt/D2gkkd02pPOrZj/NVImWoD8MNpVXbC727SGSayG7EEUCBCJ7Hwbpx79UjuBi7RA+RoD3HD+7aJlSQAJixY7mt3t6HYh859POoD4ZjFV3YCCK7QMJGhlr+hYSIB+JhvYfnBEkCBOdB25OFsaPAKoFODqMgTdSZayEYmiXwYjjKcpwZp8U4AKSaBptY235OhSVK8YSJrfuFPTD6xZwAFJFFNoFiNtbLRQjbfRsfy1FVzvBNACurWNNK4t9X6ICoUAe32IRpLAAUkUU2gWCflWFUW03mAnA/DUYbz1IFchk8AC5dt5nBEuwAbKjKPeRwmMiTXw5TmghUBFZBExRyxTr7tqpSWFKf8ADmVWPyQdIO0DPf7sqOpFaLUCvUrGZoE4g0T+X70VfKtyDNT7A6ggCQq5oh18g1dDWeyu4aCHh0rw/2+ZKuKrsmSULcPfQeTbLcP+VbkmSl2B1BAEo1aFa+qaKa7ayiUQa+j8jhObCJzpg6jcdPqTtMKJhlGSGdAnYJSPcPT551vRZ6ZYgkgVzJU7TBRH/qQu5NyQY+O5fEEEM+0mgrq3n2VivLigj5xdtdijkzIxyLPTLAEkAs5rHdc0CflAlZeWsILcyf5HUZabECd2NJtiJmvLAHkQoJ6x5m47Q7MrbvJmu5azJEJBV3kGYevCUBEPg3cBhQD96jqAj/jyZo41Q6bWtu44Zn0brvt1t1kQnct5siU7nh3LepTv+YiUgy8DnwKaABWAper6qux1qmtrdVVq1Z53tc3vvEN6uvrKS8vTzXc9DSshEMfdZ3eoxc7ep7Mtpaus3r1KKbm48nFu2ZbEx8d6tq3v5dtRGpqavLveMVhcXnjJa7dLR/x1q4PO7VpKBLh5OOP5riyXh3LbH+/lY8OtdOrRzGDjy3tmJetuHIpX+MCOO6441iyZElK64rIalWtjZyesBqoiHxdRPqltNf4Pgm8oapvqepBYBFwURb2479+Q0AiDrUUQb8hxErA0U7oscRa1ss2Etnd8hFrtjXx0lt7WLOtid0tURKaKWjHlfXi5OOPplcPp3pvrx7FXU7+b+36sON79dGhdt7a9aF9FwpYMkVAA4CVIvIycC+wTDNz21ABhLfGaQDGRy4kIrOAWQADBgygvr7e846mTZvGueeeS1lZWWqRZkLrXtj3D2g/6Aw71+dEKO3H7r3N/GN/18V7Fhcx7IQ+SWomBPwAABRcSURBVG1687v7Og3gkso2IrW0tHQcr6bWNhr3tna5MqzoV0p5aUlK209VeFz5JAhxZfJ7ls3j1dTaxs7mAxxsP0zP4iIG9O2d9Pc0Xz9HcGJL5fwXT8IEoKo3isj/Bc4DrgZ+ISKLgd+o6psZjSb6/u8C7gKnCGjSpEkpbae+vp5U182muief4pcvt3epXTB/ehWTkixvbIp4BpDKNiKFH68JC5bT2NS13/2K8uKc13zJ188xCHFdPfdxNEqhgUCnLrpzHVe4ujWN7jO1IkIFHKUl7cyfflpS5ff5+jlCdmJLqiWwe8X/rvtzCOgHLBGRW9LYdyOdG9APcqcFSnlpSdqtdD31g5MCqx1ioDBaPHfXFrvZkvAOQET+A7gK2A3cA8xR1TYRKQK2ANenuO+VwCkiMhTnxH8Z8M8pbqugZaJ2QTZrKFjtEAP5URc+srrz5OHHs+K1XR2vs9HzbXeWzDOAY4HpqvpO+ERVPSwin0t1x6p6SET+DViGUw30XlXdmOr2TPK8thnIh3984z+/68JHq+78+5e2cWHR8zzcczEDW3ezo+dx3HJoBksPT+y0btIXK6174daRgRkoKJlnAN+NM29TOjtX1SeAJ9LZhvEmlTYDfv/jm/zhZ134aMU7FxY9z4KSezhKDgIwSHazoOQeaKMjCSR9sbJ+MTS/e6Sn2AwMFJTvrCVwwKTa3L87NoIxhSVaMc71PRZ3nPxDjpKDfLvnH3nswERvFyvPfB9O+GrnaaEW+5YATHdgD3TzXz526+E5piyMuRytjH+g7I667Ans5u0F53vbQXMDnBBjejdl4wEETCHU5AiyWMN6+jn6lOeYQp0fNm8H9EhRyvrFacUxefjxXabt0OOiL5zK4D4pjhRWyCwBBExBD+QSAPlYjdFzTBkeczlkxWu7uky75dAM9mvPzhNTHdxnyk1dW+ynMVBQIbAioDyRq9t+e6AbXaLjn6vPJ5tFdKm+B88xZWnQ9Wj7W3p4IrQ5zwIGFe1Jr7ipegY0PuqMEGa1gEyu5Lo3T3ug21mi45/LzydbbS7SeQ+eY8rwmMuJ4lh6eCKrj/oUL8w9J63tA1DaD67bkP52CoQVAeWBfLztD5JExz+Xn0+2iujSeQ+eY8rwmMvhcZQUSZfpJcViRZgpsjuAPGA1c/yV6Pjn8vPJVhFdOu/Bc0wZHnM5Mo55SzfS1NoGQL+jSvjuBSPiHp98rFWVLywBeJCtL5J1teBdJj+LRMc/159PNoro0n0PnmPK4JjL6cRhgyXFZ0VAScpm9TyrmeNNpj+LRMe/O3w+3eE9pMKKV+OzBJCkbH6Rst2bZ3eT6c8i0fEv1M+nbk0jm9/dx9C5j7Nw2WY+P7ai4N5DumIVcTU2tTJhwXKGzn2cCQuW+9rOwk9WBJSkbJcDW82c5GXjs0h0/Avt8wndJV07/DBKEY1NrTyyujGrJ/18LGuPVfQl0DE9vFgoPweDzB67A0iStaDNH932s1i/2OmJcl658zuNlrPZumOtW9PY6cp55dI74daR6LxyxtWdxdgPnsqbFswQvehLgMghDYNaLGQJIElBLUPNR93ys4jSfULrn/6N//j2DSkVUWTjLiny2cvYD55i5OoboXk7glLh9sR5YdHzQH6cVKMV38UazzaIte6sCChJ1oI2f3TLzyJK9wmlfMScHouZ2DTRc82VbNRciryruL7HYkqj9MR5fY/FLD3odMWcDyfVyOI7Z4hTq3UHlgA8KbRy4O6s230WMbpJGCh7gOS67A4XGsTHGcHVke5dUuTJPFZPnKGYIUcnVY89j8Yd4Kh5S/bjzSNWBGRMPojRTcIO7X/kbw9X06Gij57FRRmr9RN5Mo/VE2co5pwUy6XQ82ih1urKBrsDMCYDmlrbmLBgeer95Z9yHqx7qFMx0H7tyS2HjlzJer2anlZTQX3zFt5eMMnr24kq8sr5lkMzuLnknk7FQK30YuGhGVTkqlguXs+jce4Cut0dZIosAWRZPlaNM5lVt6aRxr2tNDY5D6YTtjYNXbWGTlzN252T/6h/hi1/RZsb2KH9ublthvdhDbMo8tnL6mM+xYbThjDuzZ93JLLSKTdxWy57z8xSz6NBYQkgi6wZejAsXLaZywZ3rlsSt8w+1lXrlr/CdRsQYOWaRlYv24zk2YVD1yvnc4B/9SucrPU8GhSWALIo1fF3TWHZ0dQKg2NMjyaJq1YrokjSlJs6301Btx/EJZMsAWSR9fIZDE7Z/L4Y06MogKvWgim6zFLPo0FhCSCLrJfPYJgzdRiNm1Z3mpawv/w8vmotuKLLLPU8GgRWDTSLumWLVdPFtJoKKvqVJl+tsHoGXHC7M/Qg4vy+4Pa8OYlZD5rBYXcAWdQtW6yaqMpLS3hh7qTkV8jjq1YrugwOSwBZZg/zTKGxosvgsCIgY0wnVnQZHL7cAYjIQuAC4CDwJnC1qjb5EYsxpjMrugwOv4qAngJuUNVDInIzcAPwLZ9iMcZEsKLLYPAlAajqX8NevgR8wY84jAmaZOv3F0w7AJMWUY01PEKOAhB5DHhYVX8fY/4sYBbAgAEDxi5atCil/bS0tFBWVpZynNlicXljcXkTHldTaxuNe1s5HPY/XyRCRb9SyktLOqYlu1ym4son+RoXpBfb5MmTV6tqbeT0rCUAEXkaOCHKrO+o6p/dZb4D1ALTNYlAamtrddWqVSnFU19fz6RJk1Ja1wuvV065issri8ubfI6rqe8pLFy2OWrNHnDaLbww95yO17EGTIlcLt248vV45WNckF5sIhI1AWStCEhVz00Q0Ezgc8CUZE7+haDgWlCabq+ptY0bnnmlS8OucJH1+60dQHD4VQvo08D1wNmqut+PGDIl/Iq/SIR29dArpDFZtrP5AK1t8Wt7R9bvz6t2AB5H+zLe+NUO4BdAH+ApEVkrIr/2KY6E6tY0MmHBcobOfbzL4NyRg2RHnvxD7MrJ+OVg++G486PV78+bdgApjPZlvPGrFtA/+bFfrxIV6UTrMyUaa0Fp/NKzOPY1XqxRu/KmHUCKo32Z5FlXEHEk6s8/mSt7a0Fp/DSgb29KS9q7DICeaAzcvGgHYKN9ZZ0lgDgSPQyLVVZaLMJhVas/bXImVu2z8tIS5k8/zfer+S7xjUp851wI4yYUOksAcSR6GBY5SDYkd3VlTCbFK6osJzNX8+k0DIsWX+PedurWNMbfRp6Pm9AdWGdwcSR6GDatpoL506uS7wfemCzIdv/9kZUdQgkmvEKE1/gOqyaOL8/HTegO7A4gjmQehuVFWakJtPhFlUenvf10x7ZOq11BHo+b0B1YAkjATvAm32W73n66DcPyql2B6cSKgIwpcNmutx/rRJ3sCTxafEUiVjsuD1gCMKbAZftZVLoJJlp8Ff1K7c46D1gRkDHdQDaLKjPRMCwyvvr6+kyHaVJgCcAYk1CsBGPjBhQ2SwDxWEdUxsRkvd8WPnsGEIt1RGVMXNluf2CyzxJALPE6ojLG2LgB3YAlgFisIypj4kq3eqjxnyWAWGJ1OGUdURkD5NG4ASZllgBimXKT0/FUOOuIypgO1hdW4bNaQLGEavtYLSBjYrKuUgqbJYB4rCMqY0w3ZkVA4FTtvHUkzCt3fltVT2NMANgdQKi+f6jKZ6i+P9jVvzGmW7M7AKvvb4wJKEsAVt/fGBNQlgCsvr8xJqAsAVh9f2NMQFkCsIGnjTEBZbWAwOr7G2MCyRIANqiFMSaYfC0CEpFvioiKyHF+xRAa1KKxqRXlyKAWdWsa/QrJGGNywrcEICKDgfOAbX7FADaohTEmuPy8A7gVuB5QH2OwQS2MMYHlSwIQkYuARlVd58f+w9mgFsaYoBLV7FyAi8jTwAlRZn0H+DZwnqo2i8hWoFZVd8fYzixgFsCAAQPGLlq0KKV4WlpaKCsr6zK9qbWNxr2tHA47DkUiVPQrpby0JKV9ZSIuv1lc3lhc3lhc3qUT2+TJk1eram2XGaqa0x+gCngP2Or+HMJ5DnBConXHjh2rqVqxYkXMeY++3KBnzH9Gh3zrL3rG/Gf00ZcbUt5PJuPyk8XljcXljcXlXTqxAas0yjk159VAVfUV4GOh14nuADItVpVPq/ZpjAmaQLUDCFX5DNX6CVX5BCwBGGMCx/euIFR1SK6u/q3KpzHGHOF7Asglq/JpjDFHBCoBWJVPY4w5IlAJYM7UYZSWFHeaVlpSzJypw3yKyBhj/BOoh8ChB73W8ZsxxgQsAQBW5dMYY1yBKgIyxhhzhCUAY4wJKEsAxhgTUJYAjDEmoCwBGGNMQFkCMMaYgLIEYIwxAWUJwBhjAsoSgDHGBJQlAGOMCShLAMYYE1CWAIwxJqAC1xlcPLHGCzbGmO7IEoDLxgs2xgSNFQG5bLxgY0zQWAJw2XjBxpigsQTgsvGCjTFBYwnAZeMFG2OCxh4Cu2y8YGNM0FgCCGPjBRtjgsSKgIwxJqAsARhjTEBZAjDGmIDyLQGIyNdF5DUR2Sgit/gVhzHGBJUvD4FFZDJwETBKVT8SkY/5EYcxxgSZX3cAs4EFqvoRgKq+51McxhgTWH5VAz0VOFNEfgQcAP5LVVdGW1BEZgGz3JctIpJq5zzHAbtTXDebLC5vLC5vLC5v8jUuSC+2k6JNzFoCEJGngROizPqOu99jgdOBccBiETlZVTVyYVW9C7grA/GsUtXadLeTaRaXNxaXNxaXN/kaF2QntqwlAFU9N9Y8EZkN/Mk94f+viBzGyW67shWPMcaYzvx6BlAHTAYQkVOBnuTvbZcxxnRLfj0DuBe4V0Q2AAeBL0Ur/smwtIuRssTi8sbi8sbi8iZf44IsxCbZP+8aY4zJR9YS2BhjAsoSgDHGBFS3SgAiconbtcRhEYlZXUpEPi0im0XkDRGZGzZ9qIj83Z3+sIj0zFBcx4rIUyKyxf3dL8oyk0VkbdjPARGZ5s67T0TeDps3Oldxucu1h+17adh0P4/XaBH5m/t5rxeRS8PmZfR4xfq+hM3v5b7/N9zjMSRs3g3u9M0iMjWdOFKI6z9F5FX3+DwjIieFzYv6meYorpkisits/18Nm/cl93PfIiJfynFct4bF9LqINIXNy+bxuldE3nOfiUabLyJyuxv3ehEZEzYvveOlqt3mB6gEhgH1QG2MZYqBN4GTcWofrQNOc+ctBi5z//41MDtDcd0CzHX/ngvcnGD5Y4H3gaPc1/cBX8jC8UoqLqAlxnTfjhdOY8JT3L8HAv8AyjN9vOJ9X8KWuRb4tfv3ZcDD7t+nucv3Aoa62ynOYVyTw75Ds0NxxftMcxTXTOAXUdY9FnjL/d3P/btfruKKWP7rwL3ZPl7uts8CxgAbYsz/LPAkIDhtp/6eqePVre4AVHWTqiZqKfxJ4A1VfUtVDwKLgItERIBzgCXucr8DpmUotIvc7SW73S8AT6rq/gztPxavcXXw+3ip6uuqusX9ewfwHnB8hvYfLur3JU68S4Ap7vG5CFikqh+p6tvAG+72chKXqq4I+w69BAzK0L7TiiuOqcBTqvq+qu4FngI+7VNclwN/yNC+41LVZ3Eu+GK5CLhfHS8B5SJyIhk4Xt0qASSpAtge9rrBndYfaFLVQxHTM2GAqv7D/ftdYECC5S+j65fvR+7t360i0ivHcfUWkVUi8lKoWIo8Ol4i8kmcq7o3wyZn6njF+r5EXcY9Hs04xyeZdbMZV7iv4FxFhkT7THMZ1+fdz2eJiAz2uG4248ItKhsKLA+bnK3jlYxYsad9vApuSEiJ08WEqv451/GExIsr/IWqqojErHvrZvYqYFnY5BtwToQ9ceoCfwv4fg7jOklVG0XkZGC5iLyCc5JLWYaP1wM4bUkOu5NTPl7dkYhcCdQCZ4dN7vKZquqb0beQcY8Bf1CnJ+B/xbl7OidH+07GZcASVW0Pm+bn8cqagksAGqeLiSQ1AoPDXg9yp+3BubXq4V7FhaanHZeI7BSRE1X1H+4JK17vpzOAR1W1LWzboavhj0Tkt8B/5TIuVW10f78lIvVADfAIPh8vETkGeBwn+b8Utu2Uj1cUsb4v0ZZpEJEeQF+c71My62YzLkTkXJykera6ve9CzM80Eye0hHGp6p6wl/fgPPMJrTspYt36DMSUVFxhLgO+Fj4hi8crGbFiT/t4BbEIaCVwijg1WHrifNhL1XmqsgKn/B3gS0Cm7iiWuttLZrtdyh7dk2Co3H0aELW2QDbiEpF+oSIUETkOmAC86vfxcj+7R3HKRpdEzMvk8Yr6fYkT7xeA5e7xWQpcJk4toaHAKcD/phGLp7hEpAa4E7hQw7pcj/WZ5jCuE8NeXghscv9eBpznxtcPOI/Od8JZjcuNbTjOA9W/hU3L5vFKxlLgKrc20OlAs3uRk/7xytaTbT9+gItxysE+AnYCy9zpA4Enwpb7LPA6Tgb/Ttj0k3H+Qd8A/gj0ylBc/YFngC3A08Cx7vRa4J6w5YbgZPWiiPWXA6/gnMh+D5TlKi7gDHff69zfX8mH4wVcCbQBa8N+RmfjeEX7vuAUKV3o/t3bff9vuMfj5LB1v+Outxn4TIa/74nietr9Pwgdn6WJPtMcxTUf2OjufwUwPGzdL7vH8Q3g6lzG5b6ehzNWSfh62T5ef8CpxdaGc/76CnANcI07X4A73LhfIayGY7rHy7qCMMaYgApiEZAxxhgsARhjTGBZAjDGmICyBGCMMQFlCcAYYwLKEoAxxgSUJQBjjAkoSwDGpEFExrmdmvUWkaPFGZ9gpN9xGZMMawhmTJpE5Ic4rYFLgQZVne9zSMYkxRKAMWly+5ZZCRwAztDOvUgak7esCMiY9PUHyoA+OHcCxhQEuwMwJk3ijBG7CGcQkRNV9d98DsmYpBTceADG5BMRuQpoU9WHRKQYeFFEzlHV5YnWNcZvdgdgjDEBZc8AjDEmoCwBGGNMQFkCMMaYgLIEYIwxAWUJwBhjAsoSgDHGBJQlAGOMCaj/D8vBiKVy0505AAAAAElFTkSuQmCC\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYAAAAEWCAYAAABv+EDhAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8li6FKAAAgAElEQVR4nO2de3hV1bXofyMhQABJEJFHoCS2ChESCAT1CApIK9YnoqA9WottD7fa03OutweLtdfahweUtj5aW1+1VqtFxJpi1UtVSH33APIQREQkQnYAeSUE2ZFNMu8fa+2w985+v9Z+jN/37S97PedYc+3MMeeYY44hxhgURVGU/KPAaQEURVEUZ1AFoCiKkqeoAlAURclTVAEoiqLkKaoAFEVR8hRVAIqiKHmKKgAlpYjI7SLyJ6fl8EVErhGRv0d5blj5ReQGEdkjIodFpL/995QEZKsXkW/He72ixIIqACUqRKRBRNx2A7dHRB4TkT5OyxUPxpgnjTHnJ3ofESkCfgWcb4zpY4zZb//92D7+mIj8PNFysgkRmSoiK0WkRUQanJZHCY8qACUWLjHG9AHGAbXAjxyWx2kGAj2BTU4LEgkR6Zamoj4DHgXmpak8JQFUASgxY4xxAS8BowFEZIiILBORAyLykYj8W7DrROQFEflewL4NInK5/d2IyHdEZKuINIvI/SIi9rECEfmRiHwiIp+KyOMiUmIfK7evvV5EdorIQfs+E+z7N4vIb3zKnCMib/hs32tfd0hE1ojIOZHqQEROA7bYm80issLnGb4kInOBa4Cb7VHT8yHu8xUR+cDuMf8GkIDj3xSRzfYzLReR4T7HzheRLfa1vxWRf3jNR/Yzvikid4vIfuD2KO43UkRett/jFhGZHakeAjHG/I8x5gng41ivVdKPKgAlZkRkGHAhsNbetRhoBIYAVwL/LSLnBbn0j8C1PvcZA5QBL/icczEwAagGZgPT7f1z7M9U4BSgD/Ab/DkTOBW4CrgHuBX4MjAKmC0ik0M80ipgLHAi8BTwjIj0DHEuAMaYD+37ApQaY84LOP4Q8CRwl20WuiTwHiJyEvAXrJHUScA2YKLP8cuAHwIzgQHA68Cffa5dCtwC9MdSRmcHqY+PsUYqd0S4X2/gZfv5TwauBn4rIqfbx+fbijToJ1xdKRmMMUY/+on4ARqAw0Az8AnwW6AYGAa0Ayf4nLsAeMz+fjvwJ/t7T+AgcKq9/Qvgtz7XGWCSz/YSYL79/VXgRp9jIwAP0A0ot68t8zm+H7jKZ/tZ4H/b3+cAb4R51oPAmED5g5znLbdbwDN8yf7+GPDzMOVcB7zjsy1YivTb9vZLwLd8jhcAR4Dh9rVvB1y70+faOcCOgPLC3e8q4PWA8x8Efhzn7+XLQIPTv1v9hP/oCECJhRnGmFJjzHBjzI3GGDdWr/+AMabV57xPsHr2fhhj2oCngWtFpAD4GvBEwGm7fb4fwerpY5fzSUAZ3bB6t172+Hx3B9kOOmktIv9lm0Va7N5sCVaPPNUMwWq0ATBWy7nT5/hw4F6fXvYBrIa+LMS1jQH33xmwHe5+w4EzA3r11wCDEn9MJVNJ18SQkrs0ASeKyAk+SuALgCvE+X/EavTfAI4YY96OoZzhPttfAI5hNfJDY5baxrb33wxMAzYZYzpE5CABtvg4iRRqdxfWCMori/huYzXgdxhjngy8UEROxee57WsD6yGw/HD3Gw78wxjzlWCCisgPscxHQTGWc4CSZegIQEkIY8xO4C1ggYj0FJFq4FtAUN95u8HvAH5J195/OP4M3CQiFWK5n/438LQx5lhCDwAnYCmSvUA3EbkN6JvgPb3swZqvCMULwCgRmWl76fwH/j3uB4BbRGQUgIiUiMgsn2urRGSGfe13idxbD3e/vwGnicjXRaTI/kwQkUoAY8x/G2suI+jHW4A9Wd8TKLI2paeIdI9YU4ojqAJQksHXsOzhTcBzWHbjV8Kc/zhQRQglEYJHsRTGa8B2oA34XtgromM58P+AD7HMSm10NZ3Ey++B022TSl3gQWPMPmAWsBBrzuJU4E2f488BdwKLReQQsBH4asC1d9nXng6sBj4PJUyE+7UC52NN/jZhmeLuBHrE+MznYpnbXsQapbmBqBbdKelHLNOhoqQPEbkOmGuMmeS0LLmCPafSCFxjjFnptDxKdqAjACWtiEgv4EbgIadlyXZEZLqIlIpIDyz7vADvOCyWkkU4qgDsH+9SeyHMZhH5FyflUVKLiEzHsrXvwfI3VxLjX7DWDuwDLsHy0nI7K5KSTThqAhKRP2L5Hj9iTxT1MsboohJFUZQ04JgCEGsZ/zrgFKMTEYqiKGnHyXUAFVjmgD/YIQHWAP9pjPnM9yQ7pspcgOLi4vHDhg3rcqNo6OjooKAg86Y8VK7YULliQ+WKjUyVCxKT7cMPP9xnjBnQ5YBTS5CxokkeA860t+8FfhbumvHjx5t4WblyZdzXphKVKzZUrthQuWIjU+UyJjHZgNUmw0JBNAKNxph/2ttLscIMK4qiKGnAMQVgjNkN7BSREfauacD7TsmjKIqSbzgdC+h7wJO2B9DHwPUOy6MoipI3OKoAjDHrsOYC4sbj8dDY2EhbW1vY80pKSti8eXMiRaUEles4PXv2ZOjQoRQVFaW1XEXJROrWuli0fAtNzW6GlBYzb0x70stwegSQMI2NjZxwwgmUl5djBUQMTmtrKyeccEIaJYsOlcvCGMP+/ftpbGykoqIibeUqSiZSt9bFLX95D7fHavRdzW5cB9upW+tiRk2XSOtxk5n+TjHQ1tZG//79wzb+SuYjIvTv3z/iSE5R8oFFy7d0Nv5eOoxh0fItIa6Ij6xXAIA2/jmCvkdFsWhqDh7RI9T+eMkJBaAoipJLDCktjml/vKgCcIApU6awevVqR8o+++zAvOFd6dMncnKn22+/nV/84hdhz6mrq+P999WzV1FiZd70ERQXFfrtKxBh3vQRIa6ID1UAecZbb72VtrJUAShKfMyoKWPBzCrKSoutpM2lxZT1K07qBDDkoQKoW+ti4sIVVMx/gYkLV1C3NlTq2uhoaGhg5MiRXHPNNVRWVnLllVdy5MgRAF599VVqamqoqqrim9/8Jp9/7p+s6dFHH+UHP/hB5/bDDz/MTTfdRENDA5WVlfzbv/0bo0aN4vzzz8fttmx/69at46yzzqK6uprLL7+cgwcPAtao4qabbqK2tpbKykpWrVrFzJkzOfXUU/nRj37UWYa3d3/48GGmTZvGuHHjqKqq4q9//WvEZ73jjjs47bTTmDRpElu2HJ+Mevjhh5kwYQJjxozhiiuu4MiRI7z11lssW7aMefPmMXbsWLZt2xb0PEVRgjOjpow355/H9oUX8eb88ygtTr57dF4pAK9rlavZjcFyrbrlL+8lrAS2bNnCjTfeyObNm+nbty+//e1vaWtrY86cOTz99NO89957HDt2jN/97nd+182ePZuXXnoJj8cDwB/+8Ae++c1vArB161a++93vsmnTJkpLS3n22WcBuO6667jzzjvZsGEDVVVV/OQnP+m8X/fu3Vm9ejXf+c53uOyyy7j//vvZuHEjjz32GPv37/cru2fPnjz33HO8++67rFy5ku9///veGE1BWbNmDYsXL2bdunW8+OKLrFq1qvPYzJkzWbVqFevXr6eyspLf//73nH322Vx66aUsWrSIdevW8cUvfjHoeYqiOEdeKYBgrlVuT3vCrlXDhg1j4sSJAFx77bW88cYbbNmyhYqKCk477TQAvvGNb/Daa6/5XdenTx8mT57M3/72Nz744AM8Hg9VVVUAVFRUMHbsWADGjx9PQ0MDLS0tNDc3M3ny5KD3vPTSSwGoqqpi1KhRDB48mB49enDKKaewc6d/mltjDD/84Q+prq7my1/+Mi6Xiz179oR8xtdff53LL7+cXr160bdv386yADZu3Mg555xDVVUVTz75JJs2bQp6j2jPUxQlPWT9QrBYSJVrVaD7YizujNdddx333nsvI0eO5Prrj0fC6NHjeC7uwsLCThNQOLzXFBQU+F1fUFDAsWPH/M598skn2bt3L2vWrKGoqIjy8vK4ffDnzJlDXV0dY8aM4bHHHqO+vj6h8xRFSQ95NQJIlWvVjh07ePvttwF46qmnmDRpEiNGjKChoYGPPvoIgCeeeKKz5+7LhAkT2LlzJ0899RRf+9rXwpZTUlJCv379eP3118PeMxpaWlo4+eSTKSoqYuXKlXzyySdhzz/33HOpq6vD7XbT2trK888/33mstbWVwYMH4/F4ePLJJzv3n3DCCbS2tkY8T1EUZ8grBRDMtaq4qDBh16oRI0Zw//33U1lZycGDB7nhhhvo2bMnf/jDH5g1axZVVVUUFBTwne98J+j1s2fPZuLEifTr1y9iWX/84x+ZN28e1dXVrFu3jttuuy0uma+55hpWr15NVVUVjz/+OCNHjgx7/rhx47jqqqsYM2YMX/3qV5kwYULnsZ/97GeceeaZTJw40e8+V199NYsWLaKmpoZt27aFPE9RFIcIliQgUz/BEsK8//77USVEOHTokDHGmOfebTRnL3jVlP/gb+bsBa+a595tjOr6UGzfvt2MGjUq7usPHTpkLrroIvPKK68kJEey8dZXuon0PjM1YYfKFRsqV+ykIiFMXs0BgOValWxf2nhpbm6mtraWmpoapk2b5rQ4iqLkGXmnAJJNeXk5GzdujOva0tJS1q5dm5HRQBVFyX3yag5AURRFOY4qAEVRlDxFFYCiKEqeogpAURQlT1EF4ADegGxNTU18/etfD3pONCGj77nnHr+AahdeeCHNzc3JEzQKGhoaeOqpp9JapqIoyUEVgIMMGTKEJ554Iu7rAxXAiy++SGlpaTJEixpVAIqSveSfAtiwBO4eDbeXWn83LEnodvPnz+f+++/v3PYmSokm3HJDQwNnnnkmAG63m6uvvprKykouv/xyv9g/N9xwA7W1tYwaNYof//jHANx33300NTUxdepUpk6dClguqfv27QPgV7/6FaNHj2b06NHcc889neWFCjPtyzPPPMOZZ57JmDFjOPfccwFob29n3rx5TJgwgerqah588MHO53/99dcZO3Ysd999d0J1qShKmgm2OixTPwmvBF7/tDE/H2jMj/se//x8oLU/Tt59911z7rnndm5XVlaaHTt2GI/HY1paWowxxuzdu9d88YtfNB0dHcYYY3r37m2MsVYRV1ZWGmOM+eUvf2muv/56Y4wx69evN4WFhWbVqlXGGGP2799vjDHm2LFjZvLkyWb9+vXGGGOGDx9u9u7d21m2d3v16tVm9OjR5vDhw6a1tdWcfvrp5t133zXbt283hYWFZu3atcYYY2bNmmWeeOKJLs80evRo88EHHxhjjDl48KAxxpgHH3zQ/OxnPzPGGNPW1mbGjx9vPv74Y7Ny5Upz0UUXxV1/gehK4OSicsWGY3Ktf9qYX40y5scl1t8gbVIqVgLn1wjg1Z+CJ6DH63Fb++OkpqaGTz/9lKamJtavX0+/fv0YNmxYzOGWX3vtNa699loAqqurqa6u7jy2ZMkSxo0bR01NDZs2bYqYZeuNN97g8ssvp3fv3vTp04eZM2d2BpALFmY6kIkTJ3LDDTfw8MMP095uhc/++9//zuOPP87YsWM588wz2b9/P1u3bo2prhRFCcKGJfD8f0DLTsBYf5//j4StE9GQXyuBWxpj2x8ls2bNYunSpezevZurrroKSF645e3bt/OLX/yCVatW0a9fP+bMmRN32GaILsz0Aw88wIoVK6ivr2f8+PGsWbMGYwy//vWvmT59ut+5GtJZURIkXMe0enZKi86vEUDJ0Nj2R8lVV13F4sWLWbp0KbNmzQLiC7fsnUzduHEjGzZsAODQoUP07t2bkpIS9uzZw0svvdR5TWC4ZS/nnHMOdXV1HDlyhM8++4znnnuOc845J+rn2bZtGxMmTOCnP/0pAwYMYOfOnUyfPp3f/e53ndnLPvzwQz777LOQMihKvhJr2lmToo5pNOTXCGDabdbQylfbFhVb+xNg1KhRtLa2UlZWxuDBgwEr3PIll1xCVVUVtbW1EcMf33DDDVx//fVUVlZSWVnJ+PHjARgzZgw1NTWMHDnSL/MYwNy5c7ngggsYMmQIK1eu7Nw/btw45syZwxlnnAHAt7/9bWpqaoKae4Ixb948tmzZgogwbdo0xowZQ3V1NQ0NDYwbNw5jDAMGDKCuro7q6moKCwsZM2YMc+bM4aabboql6hQlp/CmnfVmHvSmnQWCBqGsW+tigulPmezrerMEO6bRICZMHth0ICKFwGrAZYy5ONy5tbW1JtA3fvPmzVRWVkYsp7W11Qq6tmGJNbRqabQqeNptKR9mRSVXhuGUXJHeZ319PVOmTEmfQFGicsVGrso1ceEKXEEyDJaVFvPm/POCnj/+0MssLHqEXnK0c7+bHhTP/I1f25SIbCKyxhhTG7g/E0YA/wlsBvqmpbTq2Y42+Iqi5C6xpp1tanbjYhJ44OZuSxgi+2ky/Vl0bDb3pqGdclQBiMhQ4CLgDuD/OCmLoihKogwpLQ46AgiXjtbV7GZZxySWHZ3Uub8swTS10eL0JPA9wM1ARyI3cdqMpSQHfY9KthNr2tlUpamNFsfmAETkYuBCY8yNIjIF+K9gcwAiMheYCzBw4MDxixcv9jvep08fBg4cSElJCSISsrz29nYKCwtDHncKlcvCGENLSwt79uzh8OHDIc87fPhwZyylTELlio1clqvZ7WFPSxtH2zvoXljAwJKelBYXJXx+IrJNnTo16ByAkwpgAfB14BjQE2sO4C/GmGtDXRNsEtjj8dDY2BjRN76trY2ePXsmLHeyUbmO07NnT4YOHUpRUeh/llydPEwVKldsZKpckGOTwMaYW4BbAHxGACEb/1AUFRVRUVER8bz6+npqampivX3KUbkURXEKp+cAFEVRFIfIBDdQjDH1QL3DYiiKouQVOgJQFEXJU1QBKIqi5CmqABRFUfIUVQBKbpDkTG+Kkg9kxCSwoiSEN6GGN8qrN6EGaNwnJSOpW+ti0fItNDW7GVJazLzpI4JGC001OgJQsp8UZHpTlFThDRntanZjOB4yOlLegFSgIwAlpaSlp+NgQg1FiZVFy7d05gvw4va0s2j5lrSPAnQEoKSMtPV0UpTpTVFSQawho1OJKgAlZYTr6SSVabdZmd18SUKmN0VJBeFCQ6cbVQBKykhbT6d6NlxyH5QMA8T6e8l9OgGsZCROh4D2RecAlJQRa3KMhNBMb0qW4LXzZ4IXkCoAJWXMmz7CL0E2ONfTUZRMYkZNmSMNfiCqAJSUkUk9HUVRuqIKQEkpmdLTURSlK6oAFEVREiRTVvbGiioARVGUBPCud/HOdXnXuwAZrwTUDVRRFCUB0rbeJQWoAlAURUmATFrZGyuqABRFURIgk1b2xooqAEVRlATIpJW9saKTwIqiKDES6PVzxfgyVn6wV72AFEVRcplgXj/PrnGxYGZVVjT6vqgJSFEUJQaCef18pf0fnPXXyVmXklRHAIqiKDEQ6N1zacEbLCx6hF4ctXZkUUpSHQEoiqLEQKB3z83dltBLjvqflCUpSVUBKIqixECg188Q2Rf8xICUpHVrXUxcuIKK+S8wceEKR3IAB6ImIEVRlBgIjHL7qQxgEHu7nuiTkjRTw0WoAlAURQnFhiWWKael0WrQp90G1bP9o9xu+Myy+XuOzw246cH8vZeweuEK5k0fwe3LNmVMInhfHFMAIjIMeBwYCBjgIWPMvU7JoyiK4seGJf4Ne6jJXe/3V3+KaWmkyfTnTs9slnVMgmY3855Zj6fDBC3C6XARTo4AjgHfN8a8KyInAGtE5GVjzPsOyqQoySdEL1LJcF79qV+vHjg+uRv4/uyUpJMWruiSBjVU4w/Oh4twTAEYY3YBu+zvrSKyGSgDVAEouUO0vUgl8wiYxI24n9h79E6HixBjQmuntAkhUg68Bow2xhwKODYXmAswcODA8YsXL46rjMOHD9OnT5/EBE0BKldsZJ1cn74P7Ue77i/sDief7pxcDpMVcsXx7rbsbuVoe0dUZXUrECoH941PthiZOnXqGmNMbRcZ4rpbEhGRPsCzwP8ObPwBjDEPAQ8B1NbWmilTpsRVTn19PfFem0pyQa50ZkPKuvq6fQbWFFcgArObUyxVFtaXw/jJteHTLpO7FBXDJfdB9ZSg1zcHePsAFBUICHjaj/8OiosKWTCziikx/J+kos4cVQAiUoTV+D9pjPmLk7Io8ZGp7m0ZQ8lQy+wTbL+S2fhM7kY7f+PrIupqdlMogqfDUFpchAg0H/FkVLA4J72ABPg9sNkY8yun5FASI1w2pEz4gTvOtNuC9yKn3eacTPlGIpPw9uRuLHh/974do2a3h+KiQu6+amxG/V84uRJ4IvB14DwRWWd/LnRQnqzE6dWF2ZwNKS1Uz7ZMBiXDALH+XnKfTgCnC+8kfMtOwByfhE9xsLZsSRPppBfQG4A4VX4ukAnmlyGlxV3c3rz7s41o5jLimu+IoxepJIlYXDmTSLZ0jDQWUBaTCb2MbM6G5ItXmbqa3RiOK1PfEVU05ygZRhyunMkYVWdLmkhVAFlMJvQyZtSUsWBmFWWlxQhQVlocdWKMcP9o6TZtRaNMM0HhKjESarI9xP5mtycpSj5bOkaOu4Eq8ROv+aVurYufPL+Jg0c8AJQWF3H7paPiNhv5xUWJknDmKyDksdK4JIxMNMo0/Dm9UyGWkigxTsLvaWnD7fHvF8fj1BAYMC6TPH98UQWQxcybPqKLz3GkXkbdWhfzlq7380ludnuY98x6IH1zB5F606GO3XFWagat0SjTXJrvyBtidOW0FnF1/Y3FM6qOp2OUbtQElMXEY35ZtHyLX+PvxdNh0mrKCNebdsK0Fc2QPVuG9UoA1bPhpo1we7P1N8zkb/fC4E1irip5HQFkObH2MsI1ovE2sPF4xkTqTae7px3NkD3cOfX1W1Mmm5ImNizhVPbycY9baTL9ueuYFdEzl5W8KoA8I1TD6z0WK/G6okYyX4U81hK+oU0kLEU0yjQbhvVKHNjrBQpOmU+BGIbKPhYWPcKJRd0Ze9HcnH3nagLKM+ZNH0FRYdflFwUSX2TCeD1jwpmv4vUsUjdNJW6CrBfoJUe5vfezOdv4g44A8o4ZNWWs/uQAf3pnh9/+QolvTV4i9vpwvel4etoalkKJmzjWC6SSQ4cOsX37dhoaGti+fTvbt29nwoQJSS9HFUAesvKDrvlLvZPA4RrKYOaVdHrG1K11sWd3K9fPf6GLeadurSukaSvRyeMf1b3Hn/+5k3ZjKBTha2cO4+czqhK6p5JhpDlon9vt7mzcfRt57/aBAwf8zu/duzdlZcnvxKgCyENCNYiuZjcT7Rymgf72oWz9V4wv49k1rphcUePBW/6NIzswFHSWv/qTA/xt/S6a3Z6Q1yaijH5U957faKndmM5tVQI5hHe9gC8JBO07evQoO3bs8Gvcfb/v2bPH7/wePXpQXl5ORUUFZ5xxBhUVFVRUVHTu69+/P//4xz/ifbqQqALIIpIVdz/cRLC3YV1wtr+740+eD57UeuUHe1kwsyrlC15CmXeefGdH0Gj7XhJVRn/+Z5Beob1fFUAO4XUN/WAfVtC+8OsF2tvbcblcIXvwLpeLjo7jiWEKCwv5whe+QEVFBRdffHFnw+5t5AcNGkRBQfqnZFUBZAnJDPwWzAPHF7ennT0tx3vUdWtdnauGA2lqdqfFMybUqCVSPrtow1KEoj1ExrxQ+5Uspno2HKiH2c0YY9i9ezcNb78dtAe/Y8cOjh071nmpiFBWVkZFRQVTpkzp0oMvKyujW7fMa24zTyIlKMmc4AxMWhEM37R24Tx60rVAJtyoJRRlpcUJK6ZCkaCNfbyT5kpmYIzhwIEDXRr2NWvWcOjQIRoaGmhra/O75uSTT+400cyePbuzka+oqGDYsGH06NHDoaeJH1UAWUKyV8d6e+0TF64I2rD6rogMV0a6Fsh4Ry3g0+si9AhAgKkjByRc7tfOHNbFY8q7X8lsWltbu5hmfL+3trb6nd+vXz9OOukkqqqquOiii/x68OXl5fTq1cuhJ0kdqgCyhFR524RakDWwpHvEskuLi9LmXuktZ8+WdxFbpqkjB3SZgPZigGfXuKgdfmJCMnrt/OoFlHl4PWlCTbQG86Tx9th9zTTeBr6kpCRjcxWnClUAWUI8gd98CTWBHCq8QanPittQZd9+6agkPV10zKgpo75lK9sXTuncVzv8xJCmrGStAfj5jCpt8B3g6NGj7Ny5M2QPfvfu3X7n9+jRg+HDh1NRUcGECRP8evBeTxrxmu68aSLXNcL2GNNE5hCqALIEbyPmG8a5R7fovAYiTSAHm8T1jW0TSkkATFy4wtFwt17ZK+a/ENQcFNJ8lUieWCUpeD1pQvXgw3nSXHjhhV0mWqP2pPGmifSu/PWmiQTg5OQ/aAajCiDLaPMc/4fwJq8A/BZEBTbUyZhADlQSmZCO0peYTGThGoA4lUCz2+O4Msw0jDHs2bMnaOO+efNm9u7di8dz3LvM60lTXl7eaaLx7cEnzZMmXJrImt8kfv8sQhVAFhGpIQ/VKIdy90xkhWymhV2IyUSW5DyxdWtduA66cTVbayecVobpwutJE6oHH86TZsSIEVx33XV+jfwXvvCF9HjSZFjYBydRBZBFRPIECtUoh3JlTGQCORPSUfoSUwamJDcAi5Zv4eph/vWbKzGIfD1pgjX0wTxpysvLOf3007nooov8evDDhw+nd28rc5qjk61xhn1I1kLMTEIVQBYRycwRqvFtN4biosKkhmvIxOxYUS9IS3Lcl6ZmNwTxCnVKGcaC2+3mk08+CdnI79+/3+98rydNeXk5kydP7uIqWVqaqqSdSSRcmsgDwS/JNJNnslAFkEVEMnOEapTLfOYCktV7SdQryVFizBMbCUvptYbY7yzHjh1j27ZtQcMVbN++vYsnTffu3Tsb9AkTJnQJWXDSSScd96TJVsKliayvD3pJppk8k4UqgCwikpkjXKOc7HAN2ZL0Oigx5omNxLzpI3BtXuO3L13KsL29naamppA9+MbGxtgikhoAABnQSURBVKCeNOXl5Z2eNL6N/Du72vnly1vZ0uymtbSY6ednyTuNlerZMb3vTDN5JgtVAOkiSW6HkWLoQ/oa5azOjhVjAxCOGTVl1O1+n7LSwqTXu68nTTAb/I4dO7p40gwZMoSKigrOPfdcRISpU6d2NvRDhw4N6UlTt9bFrXWbcs7MkQwy0eSZDFQBpIM0+h1ndaOcxZQWF/Hm/CkxX2eM4eDBgyF78A0NDbjd/g3PySefTHl5ObW1tcyaNcuvBx/oSRPLZGuumjmSQVabPMOgCiAdRPA7ToZ3QS56KOQKra2tIW3wwTxpSktLqaiooLKykq9+9at+Nvjy8vJOT5pkk6tmjmSQ1SbPMDiqAETkAuBeoBB4xBiz0El5UkYYt8Nmt4dbXk3MuyBXPRSyhba2Nnbs2MFLL70U1EwT6EnTq1evzkZ98uTJXSZanfKkyVUzR7LIxdG1YwpARAqB+4GvAI3AKhFZZox53ymZUkYYt8M9LW24Pf7L12MdduvQPbV4PJ6QMWnCedKUl5czfvz4LiELMtWTJhozh440c4uICkBEvgf8yRhzMMllnwF8ZIz52C5nMXAZkHsKIIzb4dH3OoCu8UtiGXanY+iey//4vp40wXrwwTxphg0b1hmTpry8nLa2ts7vgwcPdiS7U6JEMnPoSDP3EBMhs5GI/By4GngXeBRYbiJdFE3BIlcCFxhjvm1vfx040xjz7wHnzQXmAgwcOHD84sWL4yrv8OHD9OnTJzGhE8F9EFp3QftRKOwOJwyG4n7sO9jCriNdT+9eWMCIQSdEdestu1v9ErjEc49AfOur2e3BddBNh89rLxChrF8xpcVFcd0/XuJ5j96J1t27d7Nr1y527drF7t27O7c//fTTLtmd+vfvz6BBgxg8eDCDBg3q/D548GAGDBhAYaF/ykzHf18hSKZcyfydpbK+mt0e9rS0cbS9g+6FBQws6Rn17zRT3yMkJtvUqVPXGGNqA/dHHAEYY34kIv8XOB+4HviNiCwBfm+M2RaXNDFgjHkIeAigtrbWxLt8PFPjfNe99DK/fbe9y7B7wcwqpkTZq2oO6JnFc49AfOvLShpT2OWcstLCuDxfEiHYe/T1pAnWgw/mSTNgwAAqKio455xzutjghw8fHnNMmkz9fSVTruvnv4AJMloV8AvRnW65fKlb67Ln1ArwjqyLi9pZMPP0qEYpmfoeITWyRTUHYIwxIrIb2I2VkqkfsFREXjbG3Bxn2S78F9APtfflFaXFRSyYeXpC5pVUeyhkgnfI4cOH2b59O2+++SYbNmzo4lFz6NAhv/NLS0spLy9n5MiRnZ40viELUuVJk8tkwySxzofFRjRzAP8JXAfsAx4B5hljPCJSAGwF4lUAq4BTRaQCq+G/GvjXOO+V1STDuyCVHgrp+Mdva2sLm90pnCfNueee22WiNSti0mQZmeALHzgXNXXkAFZ+sLdzO1TeaHVlDU40I4ATgZnGmE98dxpjOkTk4ngLNsYcE5F/B5ZjuYE+aozZFO/9lOiJdUI3Gf/4vp40wRr5Xbt2+Z3fvXv3zuxO48eP72zYDxw4wJVXXpmxnjS5jNO+8MEmof/0zg4uLXiDp7svYYh7H03dT+KuY7NZ1jHJ79qoOyvug3D36LxJFBTNHMCPwxzbnEjhxpgXgRcTuYcSG/F4ckTzj+/1pAnVgw/nSXPBBRd06cGH8qSpr69nwIDEk70r8eGkL3ww886lBW+wsOgReslRAIbKPhYWPQIeOpVA1J2VDUugZfdxl+0kJArKdHQlcJ4Rr430srFD+Jch3Tob9s3/75+8+Lvjjfwnn3ziF5MG8ItJEzjROmzYsORkd1LyhmBmnJu7Lels/L30kqP8sPszPN82KbZRyqs/hUHf9t+XQKKgbED/A/OMULZQ18EjftmdXnnlFZYuXerXmw/lSTNu3DiuuOKKLtmdevbsmY5Hyjkycc1FzDKlIOdyMBv/ENkX9NxB7GP7wotiK6ClEQaF2J+jqALIIw4fPkxJ2y6aGndwrHkPx1qOfzpaPqX/XZ/5nV9SUkJFRQUjR47sYqYpLy/PWH/pbCYTF1vFLFMKci4DTB05gD+9s8NvX5M5iaHBlEA8yX1CXRNnoqBsQBVADtHW1hY2u9O+ff7/KFLUg259B9K93yAmT53MtDOqOnvwLpeLiy+Oe45fiZNMdGOMWaYk51z2svKDvV323XVstt8cABB/cp9pt8H7/mE9EkkUlA2oAsgQohliez1pQk20hvOkGTduXGcP/pPPe/HMh0fZ6+lBWb9eQctqaWlJ+TNnEpHqP11mmVSuuYj3GWKWKUVJ14OVt6xjEnisuYChBfsTMzdVzwbXc1AyTL2AlPThHWIfOeqhvfUA23bu5sa3X+TpIdCzbX9nQ79z504/T5qCgoIunjS+k63hYtLEu3gjF4lk4kinWSZVay4SeYaYZUpyzuVIcizrmMSaXl/hzfnnJXR/AIr7wU0bE79PlqAKII0YY/j000/9eu1vvfUWr3+wi8/2N3GsZS90HI9Js5jjnjSTJk3q4io5dOhQiorSG4snF4lk4kinWSZVi60SeYaYZUpyzmVfOeY9sx5Ph38osqJCyfrELE6hCiDJRMrudOSIf+S3kpIS3L1OpvvAL9HrtIl0KzmZbiUD6VY6iG59B/DJLy536Enyh0gmjnSGwkjVYqtEniFmmZKcczlQjtuXbaLZbbkc9+tVxI8vGRW2fjLRqypTUAUQA3VrXSxcto6dOxroe+wgEwd20PdYs18jH2g793rSnHbaaUyfPr1LTJrVq1dz6zsdQYe2ZRkUYyXTSOY/dSQTR7pj4KRisVWizxCzTEnMuZyIHJnoVZVJqAIIwOtJE5j0Y+37H7J9+3baj1hBx5qAD4DuPXvypVNO6WKm8Tbw/fr1i1hmJsRYySaS/U8dqf5z4f3kwjPEQyZ6VWUSeacAPB4PjY2NIc00TU1Nfud7PWn2mr4Un3o23UoH0q3vyZaJpmQgw4YM4q1bpiUkk9MxVrKNZP9TR6r/bH0/dWtd7NndyvXzX2BIaTFXjC/zC5yWDc+QKCEXPja7mbhwRV7VRTDyQgE88MADPPjggxw8eJDGxkba2483Hr6eNOeff36XHvyQIUMoKCigYv4LBMuCs6ulLSky5mK+0VSRCpt8pPrPtvfjHSXdOLIDQwGuZjfPrnGxYGZVyp4jE23toUxfAp37fUeQ+RZDNi8UQHNzMx6Pp9NE4+sqGa0nTTbEQs8XcvZdJDF8QqpMH4GN/D2nb2XCtl9jWhqZYPoz3jMbF5MyxtYezPQl0KUz562bO87KvlSeiZAXCmD+/PmcddZZCWXTyVcbaiaSk+8iSPgE91/+nfmL17K671di7k2nYpQUOPcy/tDLjF7zCMhRBCgLiMSZCbb2YOa78DkD8itRUF4ogGSQrXbgXCQn30WQ8AnFfM68bkuY1Dwp5t50KkZJgaOKm7stoThIJM6buy1h2VErFHMmJGIJNN9ZKU5zcAQZB6oAYiDb7MC5TM69ixBhEoaIlQkt1t60d5RkZXC1SHSUFNiYh4rE6ZUZ0tSoxmg6CzuCbNmaenkziPwyeClKphIiTEKT6X/8ewy96Rk1ZSyYWUX3wgLLPFNanPAEcGBj3mROCnqeV+a0mOW8prOWnYA5Hnl0w5KQl3jrpqy0OGl1k63oCEBRkkCz2xObW2Fgr/XU82H9U35moCOmO3cdO96TjbU3PaOmjPqWrWxfOCXWxwlKYM/5rmOzubPoET8zkJseLDo2m7J0meXijDyacyPIOFEFkGIy0TVOSS51a124DrpxNRcCccbLX/8UjPlX2Pp3TEsjTaY/d3pmx57WMIUEzr2s6fsVNp5ezoRtv+5UZMXTbuPedEbPTFHk0XxBFUAK0WXo+cGi5Vu4epi/Y2Fc8fK3/h1u2ogAq9a6WLN8C5JhHYeuPefzgP/llDgpizyaL6gCSCG6DD0/aGp2w7AQ+4MRRa9VTRRRkqLIo/mCKoAUks4okopzWLb51hD7g5AFvdasMV2mKPJovqAKIIXk7IpVxY9500fg2rzGb58T8fKTRdaZLlMUeTQfUDfQFDJv+giKiwr99mXCZJ6SXGbUlFHWrzh6t8Lq2XDJfVbqQcT6e8l9GdOIhTNdKrmFjgBSSE6uWFWCUlpcxJvzp0R/QQb3WtV0mT+oAkgxOpmnZBtquswf1ASkKIofarrMHxwZAYjIIuAS4CiwDbjeGNPshCyKovijpsv8wSkT0MvALcaYYyJyJ3AL8AOHZFEUJQA1XeYHjigAY8zffTbfAa50Qg5FyTei9e/PmnUASkKIMcESHaZRAJHngaeNMX8KcXwuMBdg4MCB4xcvXhxXOYcPH6ZPnz5xy5kqVK7YULliw1euZrcH10E3HT7/8wUilPUrprT4eFa8aM9LllyZRKbKBYnJNnXq1DXGmNrA/SlTACLyCjAoyKFbjTF/tc+5FagFZpooBKmtrTWrV6+OS576+vqEMoJFS6w9p3TJFSsqV2xkslzNJaeyaPmWkJmwykqLeXP+eZ3boRKmBJ6XqFyZWl+ZKBckJpuIBFUAKTMBGWO+HEGgOcDFwLRoGv9sIOtWUCo5T7Pbwy2vvtdlYZcvgf79ug4gf3DKC+gC4GZgsjHmiBMyJAvfHn+BCO0mhqiQipJi9rS04faE9/YO9O/PqHUAMWb7UmLDqXUAvwFOAF4WkXUi8oBDckSkbq2LiQtXUDH/BSYuXEHdWpffsVv+8h6uZjcGujT+XrTnpDjF0faOsMeD+fdnzDqAOLJ9KbHhlBfQl5woN1YimXSCxUwJhq6gVJyie2HoPl6orF0Zsw4gzmxfSvRoKIgwRIrnH03PXldQKk4ysKQnxUXtXRKgR8qBmxHrADTbV8pRBRCGSJNhoWylhSJ0GKP+00raCOV9VlpcxIKZpzvem+8i35jII+dsyJuQ7agCCEOkybDAJNkQXe9KUZJJOFNlKcnpzSeyMCyYfK6D7dStdYW/R4bnTcgFNBhcGCJNhs2oKWPBzKro48ArSgpIdfz+QGcHr4LxdYiIVb4OYyLLl+F5E3IBHQGEIZrJsIywlSp5TXhTZe+E759obuuE1hVkcN6EXEAVQAS0gVcynVT77Se6MCyj1hUofqgJSFGynFT77YdqqKNtwIPJVyCi3nEZgCoARclyUj0XlaiCCSZfWb9iHVlnAGoCUpQcIJWmymQsDAuUr76+PtliKnGgCkBRlIiEUjCaNyC7UQUQDg1EpSgh0ei32Y/OAYRCA1EpSlhSvf5AST2qAEIRLhCVoiiaNyAHUAUQCg1EpShhSdQ9VHEeVQChCBVwSgNRKQqQQXkDlLhRBRCKabdZgad80UBUitKJxsLKftQLKBRebx/1AlKUkGiolOxGFUA4NBCVoig5jJqAwHLtvHs03F5q/VVXT0VR8gAdAXj9/b0un15/f9Dev6IoOY2OANTfX1GUPEUVgPr7K4qSp6gCUH9/RVHyFFUA6u+vKEqeogpAE08ripKnqBcQqL+/oih5iSoANKmFoij5iaMmIBH5vogYETnJKRm8SS1czW4Mx5Na1K11OSWSoihKWnBMAYjIMOB8YIdTMoAmtVAUJX9xcgRwN3AzYByUQZNaKIqStziiAETkMsBljFnvRPm+aFILRVHyFTEmNR1wEXkFGBTk0K3AD4HzjTEtItIA1Bpj9oW4z1xgLsDAgQPHL168OC55Dh8+TJ8+fbrsb3Z7cB100+FTDwUilPUrprS4KK6ykiGX06hcsaFyxYbKFTuJyDZ16tQ1xpjaLgeMMWn9AFXAp0CD/TmGNQ8wKNK148ePN/GycuXKkMeee7fRnL3gVVP+g7+Zsxe8ap57tzHucpIpl5OoXLGhcsWGyhU7icgGrDZB2tS0u4EaY94DTvZuRxoBJJtQLp/q9qkoSr6RV+sAvC6fXq8fr8snoApAUZS8w/FQEMaY8nT1/tXlU1EU5TiOK4B0oi6fiqIox8krBaAun4qiKMfJKwUwb/oIiosK/fYVFxUyb/oIhyRSFEVxjryaBPZO9GrgN0VRlDxTAIC6fCqKotjklQlIURRFOY4qAEVRlDxFFYCiKEqeogpAURQlT1EFoCiKkqeoAlAURclTVAEoiqLkKaoAFEVR8hRVAIqiKHmKKgBFUZQ8RRWAoihKnqIKQFEUJU/Ju2Bw4QiVL1hRFCUXUQVgo/mCFUXJN9QEZKP5ghVFyTdUAdhovmBFUfINVQA2mi9YUZR8QxWAjeYLVhQl39BJYBvNF6woSr6hCsAHzResKEo+oSYgRVGUPEUVgKIoSp6iCkBRFCVPcUwBiMj3ROQDEdkkInc5JYeiKEq+4sgksIhMBS4DxhhjPheRk52QQ1EUJZ9xagRwA7DQGPM5gDHmU4fkUBRFyVuccgM9DThHRO4A2oD/MsasCnaiiMwF5tqbh0Uk3uA8JwH74rw2lahcsaFyxYbKFRuZKhckJtvwYDtTpgBE5BVgUJBDt9rlngicBUwAlojIKcYYE3iyMeYh4KEkyLPaGFOb6H2SjcoVGypXbKhcsZGpckFqZEuZAjDGfDnUMRG5AfiL3eD/j4h0YGm3vamSR1EURfHHqTmAOmAqgIicBnQnc4ddiqIoOYlTcwCPAo+KyEbgKPCNYOafJJOwGSlFqFyxoXLFhsoVG5kqF6RANkl9u6soiqJkIroSWFEUJU9RBaAoipKn5JQCEJFZdmiJDhEJ6S4lIheIyBYR+UhE5vvsrxCRf9r7nxaR7kmS60QReVlEttp/+wU5Z6qIrPP5tInIDPvYYyKy3efY2HTJZZ/X7lP2Mp/9TtbXWBF5237fG0TkKp9jSa2vUL8Xn+M97Of/yK6Pcp9jt9j7t4jI9ETkiEOu/yMi79v186qIDPc5FvSdpkmuOSKy16f8b/sc+4b93reKyDfSLNfdPjJ9KCLNPsdSWV+Pisin9pxosOMiIvfZcm8QkXE+xxKrL2NMznyASmAEUA/UhjinENgGnILlfbQeON0+tgS42v7+AHBDkuS6C5hvf58P3Bnh/BOBA0Ave/sx4MoU1FdUcgGHQ+x3rL6wFhOean8fAuwCSpNdX+F+Lz7n3Ag8YH+/Gnja/n66fX4PoMK+T2Ea5Zrq8xu6wStXuHeaJrnmAL8Jcu2JwMf23372937pkivg/O8Bj6a6vux7nwuMAzaGOH4h8BIgWGun/pms+sqpEYAxZrMxJtJK4TOAj4wxHxtjjgKLgctERIDzgKX2eX8EZiRJtMvs+0V73yuBl4wxR5JUfihilasTp+vLGPOhMWar/b0J+BQYkKTyfQn6ewkj71Jgml0/lwGLjTGfG2O2Ax/Z90uLXMaYlT6/oXeAoUkqOyG5wjAdeNkYc8AYcxB4GbjAIbm+Bvw5SWWHxRjzGlaHLxSXAY8bi3eAUhEZTBLqK6cUQJSUATt9thvtff2BZmPMsYD9yWCgMWaX/X03MDDC+VfT9cd3hz38u1tEeqRZrp4islpE3vGapcig+hKRM7B6ddt8diervkL9XoKeY9dHC1b9RHNtKuXy5VtYvUgvwd5pOuW6wn4/S0VkWIzXplIubFNZBbDCZ3eq6isaQsmecH1lXUpICRNiwhjz13TL4yWcXL4bxhgjIiF9b23NXgUs99l9C1ZD2B3LF/gHwE/TKNdwY4xLRE4BVojIe1iNXNwkub6ewFpL0mHvjru+chERuRaoBSb77O7yTo0x24LfIek8D/zZWJGA/xfW6Om8NJUdDVcDS40x7T77nKyvlJF1CsCECTERJS5gmM/2UHvffqyhVTe7F+fdn7BcIrJHRAYbY3bZDVa46KezgeeMMR6fe3t7w5+LyB+A/0qnXMYYl/33YxGpB2qAZ3G4vkSkL/AClvJ/x+fecddXEEL9XoKd0ygi3YASrN9TNNemUi5E5MtYSnWysaPvQsh3mowGLaJcxpj9PpuPYM35eK+dEnBtfRJkikouH64Gvuu7I4X1FQ2hZE+4vvLRBLQKOFUsD5buWC97mbFmVVZi2d8BvgEka0SxzL5fNPftYnu0G0Gv3X0GENRbIBVyiUg/rwlFRE4CJgLvO11f9rt7Dss2ujTgWDLrK+jvJYy8VwIr7PpZBlwtlpdQBXAq8D8JyBKTXCJSAzwIXGp8Qq6HeqdplGuwz+alwGb7+3LgfFu+fsD5+I+EUyqXLdtIrAnVt332pbK+omEZcJ3tDXQW0GJ3chKvr1TNbDvxAS7HsoN9DuwBltv7hwAv+px3IfAhlga/1Wf/KVj/oB8BzwA9kiRXf+BVYCvwCnCivb8WeMTnvHIsrV4QcP0K4D2shuxPQJ90yQWcbZe93v77rUyoL+BawAOs8/mMTUV9Bfu9YJmULrW/97Sf/yO7Pk7xufZW+7otwFeT/HuPJNcr9v+Bt36WRXqnaZJrAbDJLn8lMNLn2m/a9fgRcH065bK3b8fKVeJ7Xarr689YXmwerPbrW8B3gO/YxwW435b7PXw8HBOtLw0FoSiKkqfkowlIURRFQRWAoihK3qIKQFEUJU9RBaAoipKnqAJQFEXJU1QBKIqi5CmqABRFUfIUVQCKkgAiMsEOatZTRHqLlZ9gtNNyKUo06EIwRUkQEfk51mrgYqDRGLPAYZEUJSpUAShKgtixZVYBbcDZxj+KpKJkLGoCUpTE6Q/0AU7AGgkoSlagIwBFSRCxcsQuxkoiMtgY8+8Oi6QoUZF1+QAUJZMQkesAjzHmKREpBN4SkfOMMSsiXasoTqMjAEVRlDxF5wAURVHyFFUAiqIoeYoqAEVRlDxFFYCiKEqeogpAURQlT1EFoCiKkqeoAlAURclT/j8p1D/47iORIwAAAABJRU5ErkJggg==\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYAAAAEWCAYAAABv+EDhAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8li6FKAAAgAElEQVR4nO3deXxU5b348c83IQmBAAFEloAsFiFAgJAgyiIgFmzdkCpStRbbXqq2vfdne7Fo+7N2u6B4a/XWrtZatyLVmmKtP6tCbkWlQtgEARFBSCJhkYQEBsjy/P44M8PMZPbtzGS+79drXpk5c5bvnJk833Oe85znEWMMSimlMk+W3QEopZSyhyYApZTKUJoAlFIqQ2kCUEqpDKUJQCmlMpQmAKWUylCaAFRCich9IvK03XF4EpGbROQfYc4bNH4RuV1E6kSkSUR6O/8OiyG2ShH5WrTLKxUJTQAqLCKyT0QczgKuTkSeEJECu+OKhjHmGWPM7FjXIyI5wM+A2caYAmPMUeffj5zvPyEiP4l1O+lERBaLyDYRaRSRvSKy2O6YVGCaAFQkrjLGFAATgHLg+zbHY7e+QGdgu92BhCIinZK1KeAWoCdwOfBNEVmQpG2rCGkCUBEzxtQArwBjAERkgIisEpFPReRDEfk3f8uJyMsi8i2faVtF5FrncyMit4nIbhGpF5FHRUSc72WJyPdF5GMROSQiT4pID+d7Q5zL3ioiB0TkmHM9E53rrxeRX3hsc6GIrPV4/bBzueMiUiUi00LtAxG5ANjlfFkvIqs9PsNnRGQRcBNwl/Os6aUA6/msiOwUkQZnjOLz/ldEZIfzM70qIoM93pstIrucy/5SRP7XVX3k/IxvichDInIUuC+M9Y0Ukdec3+MuEZkfaj/4MsY8YIzZaIxpMcbsAv4KTIl0PSo5NAGoiInIIODzwCbnpBVANTAAuA74LxG51M+ifwRu9ljPOKAIeNljniuBicBYYD4wxzl9ofMxExgGFAC/wNskYDhwA/Bz4HvAZcBoYL6ITA/wkdYD44FewLPAn0Wkc4B5ATDGfOBcL0ChMeZSn/d/CzwDPOCsFrrKdx0icg7wF6wzqXOAPXgUliJyDXAPMA/oA7wJ/Mlj2eeBu4HeWMlosp/98RHWmcpPQ6yvK/Ca8/OfCywAfikio5zvL3EmUr8Pf/vImbynkQZnSBnLGKMPfYR8APuAJqAe+Bj4JZAPDAJagW4e8y4FnnA+vw942vm8M3AMGO58/SDwS4/lDDDV4/VKYInz+RvAHR7vjQCagU7AEOeyRR7vHwVu8Hj9AvB/nM8XAmuDfNZjwDjf+P3M59puJ5/P8Bnn8yeAnwTZzi3AOo/XgpVIv+Z8/QrwVY/3s4CTwGDnsu/4LHvAY9mFwH6f7QVb3w3Amz7z/wb4QQy/mR8CW4A8u3+/+vD/0DMAFYm5xphCY8xgY8wdxhgH1lH/p8aYRo/5PsY6svdijDkFPAfcLCJZwBeBp3xmO+jx/CTWkT7O7Xzss41OWEe3LnUezx1+Xvu9aC0i/+msFmlwHs32wDoiT7QBWIU2AMYqNQ94vD8YeNjjKPtTrIK+KMCy1T7rP+DzOtj6BgOTfI7qbwL6RfPBROSbWEnqCmPM6WjWoRIvWReGVMdVC/QSkW4eSeA8oCbA/H/EKvTXAieNMe9EsJ3BHq/PA1qwCvmBEUft5KzvvwuYBWw3xrSJyDF86uKjFKqr3U+wzqBcsYjna6wC/KfGmGd8FxSR4Xh8bueyvvvBd/vB1jcY+F9jzGf9BSoi92BVH/llrMYBrnm/AiwBLjHG+CYllUL0DEDFxBhzAHgbWCoinUVkLPBVwG/beWeB3wb8N+2P/oP5E3CniAwVq/npfwHPGWNaYvoA0A0rkRwGOonIvUD3GNfpUod1vSKQl4HRIjJPrFY6/473EfevgbtFZDSAiPQQkes9li0RkbnOZb9B6KP1YOv7G3CBiHxJRHKcj4kiUgxgjPkvY13L8PtwbUBEbsL6bj5rnM1hVerSBKDi4YtY9eG1wItY9cavB5n/SaCEAEkigMexEsY/gb3AKeBbQZcIz6vA/wM+wKpWOkX7qpNo/R4Y5axSqfB90xhzBLgeWIZ1zWI48JbH+y8C9wMrROQ4sA34nM+yDziXHQVsAAJWt4RYXyMwG+viby1WVdz9QF6En/knWBel1ztbPzWJyK8jXIdKErGqDpVKHhG5BVhkjJlqdywdhfOaSjVwkzFmjd3xqPSgZwAqqUSkC3AH8Fu7Y0l3IjJHRApFJA+rfl6AdTaHpdKIrQnA+eN93nkjzA4RudjOeFRiicgcrLr2Oqz25io2F2PdO3AEuAqrlZbD3pBUOrG1CkhE/ojV9vgxEckFuhhj/N5UopRSKr5sSwBi3ca/GRhm9EKEUkolnZ33AQzFqg74g7NLgCrgP4wxJzxncvapsgggPz+/bNCgQe1WFI62tjayslLvkofGFRmNKzIaV2RSNS6ILbYPPvjgiDGmT7s37LoFGas3yRZgkvP1w8CPgy1TVlZmorVmzZqol00kjSsyGldkNK7IpGpcxsQWG7DBpFhXENVAtTHmX87Xz2N1M6yUUioJbEsAxpiDwAERGeGcNAt43654lFIq09jdF9C3gGecLYA+Am61OR6llMoYtiYAY8xmrGsBUWtubqa6uppTp04Fna9Hjx7s2LEjlk0lhMZ1VufOnRk4cCA5OTlJ3a5SqahiUw3LX91Fbb2DAYX5LB7XGvdt2H0GELPq6mq6devGkCFDsDpE9K+xsZFu3bolMbLwaFwWYwxHjx6lurqaoUOHJm27SqWiik013P2X93A0W4V+Tb2DmmOtVGyqYW5pu57Wo5aa7Z0icOrUKXr37h208FepT0To3bt3yDM5pTLB8ld3uQt/lzZjWP7qrgBLRCftEwCghX8Hod+jUpbaev89egSaHq0OkQCUUqojGVCYH9H0aGkCsMGMGTPYsGGDLduePNl33PD2Cgr8jpzo5b777uPBBx8MOk9FRQXvv68te5WK1OI5I8jPyfaaliXC4jkjAiwRHU0AGebtt99O2rY0ASgVnbmlRSydV0JRYb41aHNhPkU98+N6ARgyMAFUbKphyrLVDF3yMlOWraZiU6Cha8Ozb98+Ro4cyU033URxcTHXXXcdJ0+eBOCNN96gtLSUkpISvvKVr3D6tPdgTY8//jjf/e533a9/97vfceedd7Jv3z6Ki4v5t3/7N0aPHs3s2bNxOKy6v82bN3PRRRcxduxYrr32Wo4dOwZYZxV33nkn5eXlFBcXs379eubNm8fw4cP5/ve/796G6+i+qamJWbNmMWHCBEpKSvjrX/8a8rP+9Kc/5YILLmDq1Kns2nX2YtTvfvc7Jk6cyLhx4/jCF77AyZMnefvtt1m1ahWLFy9m/Pjx7Nmzx+98Sin/5pYW8daSS9m77AreWnIphfnxbx6dUQnA1bSqpt6BwWpadfdf3os5CezatYs77riDHTt20L17d375y19y6tQpFi5cyHPPPcd7771HS0sLv/rVr7yWmz9/Pq+88grNzc0A/OEPf+ArX/kKALt37+Yb3/gG27dvp7CwkBdeeAGAW265hfvvv5+tW7dSUlLCD3/4Q/f6cnNz2bBhA7fddhvXXHMNjz76KNu2beOJJ57g6NGjXtvu3LkzL774Ihs3bmTNmjV85zvfcfXR5FdVVRUrVqxg8+bN/P3vf2f9+vXu9+bNm8f69evZsmULxcXF/P73v2fy5MlcffXVLF++nM2bN3P++ef7nU8pZZ+MSgD+mlY5mltjblo1aNAgpkyZAsDNN9/M2rVr2bVrF0OHDuWCCy4A4Mtf/jL//Oc/vZYrKChg+vTp/O1vf2Pnzp00NzdTUlICwNChQxk/fjwAZWVl7Nu3j4aGBurr65k+fbrfdV599dUAlJSUMHr0aPr3709eXh7Dhg3jwAHvYW6NMdxzzz2MHTuWyy67jJqaGurq6gJ+xjfffJNrr72WLl260L17d/e2ALZt28a0adMoKSnhmWeeYfv27X7XEe58SqnkSPsbwSKRqKZVvs0XI2nOeMstt/Dwww8zcuRIbr31bE8YeXlnx+LOzs52VwEF41omKyvLa/msrCxaWlq85n3mmWc4fPgwVVVV5OTkMGTIkKjb4C9cuJCKigrGjRvHE088QWVlZUzzKaWSI6POABLVtGr//v288847ADz77LNMnTqVESNGsG/fPj788EMAnnrqKfeRu6eJEydy4MABnn32Wb74xS8G3U6PHj3o2bMnb775ZtB1hqOhoYFzzz2XnJwc1qxZw8cffxx0/ksuuYSKigocDgeNjY289NJL7vcaGxvp378/zc3NPPPMM+7p3bp1o7GxMeR8Sil7ZFQC8Ne0Kj8nO+amVSNGjODRRx+luLiYY8eOcfvtt9O5c2f+8Ic/cP3111NSUkJWVha33Xab3+Xnz5/PlClT6NmzZ8ht/fGPf2Tx4sWMHTuWzZs3c++990YV80033cSGDRsoKSnhySefZOTIkUHnnzBhAjfccAPjxo3jc5/7HBMnTnS/9+Mf/5hJkyYxZcoUr/UsWLCA5cuXU1payp49ewLOp5Syib9BAlL14W9AmPfffz+sARGOHz9ujDHmxY3VZvLSN8yQ7/7NTF76hnlxY3VYyweyd+9eM3r06KiXP378uLniiivM66+/HlMc8ebaX8kW6vtM1QE7NK7IaFyRS8SAMBl1DQCsplXxbksbrfr6esrLyyktLWXWrFl2h6OUyjAZlwDibciQIWzbti2qZQsLC9m0aVNK9gaqlOr4MuoagFJKqbM0ASilVIbSBKCUUhlKE4BSSmUoTQA2cHXIVltby5e+9CW/84TTZfTPf/5zrw7VPv/5z1NfXx+/QMOwb98+nn322aRuUykVH5oAbDRgwACeeuqpqJf3TQB///vfKSwsjEdoYdMEoFT6yrwEsHUlPDQG7iu0/m5dGdPqlixZwqOPPup+7RooJZzulvft28ekSZMAcDgcLFiwgOLiYq699lqvvn9uv/12ysvLGT16ND/4wQ8AeOSRR6itrWXmzJnMnDkTsJqkHjlyBICf/exnjBkzhjFjxvDzn//cvb1A3Ux7+vOf/8ykSZMYN24cl1xyCQCtra0sXryYiRMnMnbsWH7zm9+4P/+bb77J+PHjeeihh2Lal0qpJPN3d1iqPmK+E3jLc8b8pK8xP+h+9vGTvtb0KG3cuNFccskl7tfFxcVm//79prm52TQ0NBhjjDl8+LA5//zzTVtbmzHGmK5duxpjrLuIi4uLjTHG/Pd//7e59dZbjTHGbNmyxWRnZ5v169cbY4w5evSoMcaYlpYWM336dLNlyxZjjDGDBw82hw8fdm/b9XrDhg1mzJgxpqmpyTQ2NppRo0aZjRs3mr1795rs7GyzadMmY4wx119/vXnqqafafaYxY8aYnTt3GmOMOXbsmDHGmN/85jfmxz/+sTHGmFOnTpmysjLz0UcfmTVr1pgrrrgi6v3nS+8Eji+NKzK2xbXlOWN+NtqYH/Sw/vopkxJxJ3BmnQG88SNo9jnibXZY06NUWlrKoUOHqK2tZcuWLfTs2ZNBgwZF3N3yP//5T26++WYAxo4dy9ixY93vrVy5kgkTJlBaWsr27dtDjrK1du1arr32Wrp27UpBQQHz5s1zdyDnr5tpX1OmTOH222/nd7/7Ha2tVvfZ//jHP3jyyScZP348kyZN4ujRo+zevTuifaWU8mPrSnjp36HhAGCsvy/9e8y1E+HIrDuBG6ojmx6m66+/nueff56DBw9yww03APHrbnnv3r08+OCDrF+/np49e7Jw4cKou22G8LqZ/vWvf83q1auprKykrKyMqqoqjDH8z//8D3PmzPGaV7t0VipGwQ5Mx85P6KYz6wygx8DIpofphhtuYMWKFTz//PNcf/31QHTdLbsupm7bto2tW7cCcPz4cbp27UqPHj2oq6vjlVdecS/j292yy7Rp06ioqODkyZOcOHGCF198kWnTpoX9efbs2cPEiRP50Y9+RJ8+fThw4ABz5szhV7/6lXv0sg8++IATJ04EjEGpTBXpsLMmQQem4cisM4BZ91qnVp7ZNiffmh6D0aNH09jYSFFREf379wes7pavuuoqSkpKKC8vD9n98e23386tt95KcXExxcXFlJWVATBu3DhKS0sZOXKk18hjAIsWLeLyyy9nwIABrFmzxj19woQJLFy4kAsvvBCAr33ta5SWlvqt7vFn8eLF7Nq1CxFh1qxZjBs3jrFjx7Jv3z4mTJiAMYY+ffpQUVHB2LFjyc7OZty4cSxcuJA777wzkl2nVIfiGnbWNfKga9hZwG8nlBWbaphoelMkR9qvLMYD03CICTIObDKISDawAagxxlwZbN7y8nLj2zZ+x44dFBcXh9xOY2Oj1ena1pXWqVVDtbWDZ92b8NOssOJKMXbFFer7rKysZMaMGckLKEwaV2Q6alxTlq2mxs8Ig0WF+by15FK/85cdf41lOY/RRc64pzvII3/eL7zKplhiE5EqY0y57/RUOAP4D2AH0D0pWxs739YCXynVcUU67GxtvYMapkIz3NVpJQPkKLWmN8tb5vNwEsopWxOAiAwErgB+CnzbzliUUipWAwrz/Z4BBBuOtqbewaq2qaw6M9U9vSjGYWrDZfdF4J8DdwFtsazE7mosFR/6Pap0F+mws4kapjZctl0DEJErgc8bY+4QkRnAf/q7BiAii4BFAH379i1bsWKF1/sFBQX07duXHj16ICIBt9fa2kp2dnbA9+2icVmMMTQ0NFBXV0dTU1PA+Zqamtx9KaUSjSsyHTmuekczdQ2nONPaRm52Fn17dKYwPyfm+WOJbebMmX6vAdiZAJYCXwJagM5Y1wD+Yoy5OdAy/i4CNzc3U11dHbJt/KlTp+jcuXPMccebxnVW586dGThwIDk5gf9ZOurFw0TRuCKTqnFBB7sIbIy5G7gbwOMMIGDhH0hOTg5Dhw4NOV9lZSWlpaWRrj7hNC6llF3svgaglFLKJqnQDBRjTCVQaXMYSimVUfQMQCmlMpQmAKWUylCaAJRSKkNpAlAdQ5xHelMqE6TERWClYuIaUMPVy6trQA3Qfp9USqrYVMPyV3dRW+9gQGE+i+eM8NtbaKLpGYBKfwkY6U2pRHF1GV1T78BwtsvoUOMGJIKeAaiESsqRjo0DaigVqeWv7nKPF+DiaG5l+au7kn4WoGcAKmGSdqSToJHelEqESLuMTiRNACphgh3pxNWse62R3TzFYaQ3pRIhWNfQyaYJQCVM0o50xs6Hqx6BHoMAsf5e9YheAFYpye4uoD3pNQCVMJEOjhETHelNpQlXPX8qtALSBKASZvGcEV4DZIN9RzpKpZK5pUW2FPi+NAGohEmlIx2lVHuaAFRCpcqRjlKqPU0ASikVo1S5szdSmgCUUioGrvtdXNe6XPe7ACmfBLQZqFJKxSBp97skgCYApZSKQSrd2RspTQBKKRWDVLqzN1KaAJRSKgapdGdvpPQisFJKRci31c8XyopYs/OwtgJSSqmOzF+rnxeqalg6ryQtCn1PWgWklFIR8Nfq57Ot/8tFf52edkOS6hmAUkpFwLd1z9VZa1mW8xhdOGNNSKMhSfUMQCmlIuDbuueuTivpIme8Z0qTIUk1ASilVAR8W/0MkCP+Z/QZkrRiUw1Tlq1m6JKXmbJstS1jAPvSKiCllIqAby+3h6QP/TjcfkaPIUlTtbsITQBKKRXI1pVWVU5DtVWgz7oXxs737uV26wmrzr/57LUBB3ksOXwVG5atZvGcEdy3anvKDATvybYEICKDgCeBvoABfmuMediueJRSysvWld4Fe6CLu67nb/wI01BNrenN/c3zWdU2FeodLP7zFprbjN9N2N1dhJ1nAC3Ad4wxG0WkG1AlIq8ZY963MSal4i/AUaRKcW/8yOuoHjh7cdf3+3MOSTp12ep2w6AGKvzB/u4ibEsAxphPgE+czxtFZAdQBGgCUB1HuEeRKvX4XMQNOZ3Ij+jt7i5CjAmcnZIWhMgQ4J/AGGPMcZ/3FgGLAPr27Vu2YsWKqLbR1NREQUFBbIEmgMYVmbSL69D70Hqm/fTsXDh3lH1x2Swt4oriu9t1sJEzrW1hbatTllDcv3t0sUVo5syZVcaY8nYxRLW2OBKRAuAF4P/4Fv4AxpjfAr8FKC8vNzNmzIhqO5WVlUS7bCJ1hLiSORpS2u2v++ZiXeLyJTC/PsFRpeH+splXXFsPtbu4S04+XPUIjJ3hd/l6n9Y+ADlZAgLNrWd/B/k52SydV8KMCP5PErHPbE0AIpKDVfg/Y4z5i52xqOikavO2lNFjoFXt42+6Sm0eF3fDvX7j2US0pt5BtgjNbYbC/BxEoP5kc0p1FmdnKyABfg/sMMb8zK44VGyCjYaUCj9w28261/9R5Kx77Ysp08RyEd55cTcSrt+954FRvaOZ/JxsHrphfEr9X9h5J/AU4EvApSKy2fn4vI3xpCW77y5M59GQkmLsfKvKoMcgQKy/Vz2iF4CTxXURvuEAYM5ehE9wZ23pMkykna2A1gJi1/Y7glSofhlQmN+u2ZtreroJ51pGVNc7ojiKVHESSVPOOEqXAyPtCyiNpcJRRjqPhuTJlUxr6h0YziZTzzOqcOZRKSaKppzxOKtOl2EiNQGksVQ4yphbWsTSeSUUFeYjQFFhftgDYwT7R0t21VY4yTQVEq6KUKCL7QGm1zua45Lk0+XAyPZmoCp60Va/VGyq4YcvbefYyWYACvNzuO/q0VFXG3n1ixKmYNVXQMD3CqOKMLRwkmnwebomIiwVqwgvwtc1nMLR7H1cHE2jBt8O42Jt+XPixAlaWlqiWjYYTQBpbPGcEe3aHIc6yqjYVMPi57d4tUmudzSz+M9bgORdOwh1NB3ovZ9elJiT1nCSaUe63pExImzKad3E1f43Fs1ZdTQHRi6HDx/mrbfe4s033+TNN99k48aNPPjgg1x22WVRrS8QTQBpLJqjjOWv7vIq/F2a20xSm25GU32VyCPtcJJp0HkadickLhUHEVyEz832f4CRyCRvjGHfvn3uwn7t2rXs3LkTgLy8PCZNmsSSJUvo06dP3LetCSDNRXqUEbqAjVw0LWNCHU0n+0g7nGQabJ7KSk0AaW/rSoZzmI/yvket6c0DLVaPnvGuu29tbWXbtm2sXbvWXejX1tYCUFhYyJQpU1i4cCHTpk2jrKyMvLw8wLoTON40AWSYQAWv671IRdsUNdQRd7RH2rF0SxFOMo3ltF6lMOf9AlnDlpAlhoFyhGU5j9ErJ5fxVyyK6Ttvampi/fr1vP3227z11lu8/fbbNDQ0ADBw4ECmT5/O1KlTmTZtGqNHjyYrK3ltczQBZJjFc0a0uwYAkCXR9UwY7Z3A4RxxR3qknQr3Rag05ed+gS5yhvu6vgClPwx7NcYY9u7dyzvvvMPbb7/NO++8w5YtW2hrszqIKy4u5oYbbmDatGlMnTqVwYMHY3WKYA9NABlmbmkRGz7+lKfX7feanh3ljzCWpqjBjqajOdLWbilU1KK4XwDA4XBQVVXlVeDX1dUBUFBQwKRJk7jnnnuYPHkykyZNolevXvGOPCaaADLQmp3txy8N5yKwv+qVZLaMqdhUQ93BRm5d8nK7M4aKTTUBq7ZivS/i+xXv8ad/HaDVGLJF+OKkQfxkbklM61QpJsxO+w4cOMA777zjLvA3bdpEc7PVnPr8889n9uzZXHzxxUyePJkxY8aQnZ3dfp0pRBNABgpUINbUO5jiHMPUt719oOqVL5QV8UJVTURNUaPh2v4dI9swZLm3v+HjT/nblk+odzQHXDaWZPT9ive8zpZajXG/1iTQgbjuF/DQ1JZHVY/reHf5ct59913WrVtHdbV1RtC5c2cmTpzIt7/9bS6++GIuvvhizj33XDsij4kmgDQSr373g10IdhWsSyd7H7n88CX/g1qv2XmYpfNKEj4eQKDqnWfW7ffb275LrMnoT//yc1TonK4JoONoGTWPbTv38dLr7/L0BgfvHsxie10jbW1W/f/QoUOZMmUKkydP5uKLL2bcuHHk5ubaHHXsNAGkiXhe4PTXAseTo7mVuoazR9QVm2rcdw37qq13JKVlTKCzllDj2YXbLUUgrQFGzAs0XaU+V7v7d9991/2oqqrC4bB+Y7169eLCCy/k2gsv5ELnIxFt8FOBJoA0Ec8LnL6DVvjjOaxdsL5uknUXbLCzlkCKCvNjTkzZIn4L+2gvmqvkO3LkCBs2bODdd9/lX//6F++++y5HjhwBrKqcCRMm8PWvf50LL7yQtrY2brzxRltb5iSTJoA0Ee+O31xH7VOWrfZbsHreERlsG8nq3Mp11gJn+0MRAp8BCDBzZOxHbV+cNKhdiynXdJV6Dh06RFVVFVVVVWzcuJGqqir277e+PxFh1KhRXHXVVe4j+5KSEnJyctzLV1ZWZkzhD5oA0kaiWtsEuiGrb4+z9ZuBtl2Yn5O05pWu7dTt2og4Y5o5sk+7C9AuBnihqobywb1iitFVz6+tgFLPwYMH3YW9q8B3XaQFGD58OJMnT+Zb3/oWZWVllJeX061bNxsjTj2aANJENB2/eQp0ATnQDVmFHnfcBtr2fVePjtOnC8/c0iIqG3azd9kM97Tywb0CVmXF6x6An8wt0QLfRsYYamtrvY7qq6qq+OSTTwDryH7EiBFccskllJWVUVZWRmlpKd27dw+80liGiexANAGkCVch5tmNc16n8G4ZD3UB2d9FXM87bgMlCYApy1YntPVPKK7Yhy552W91UMDqKy0AUlJrayu7d+9m8+bNbNmyhc2bN7Np0yb3zVVZWVmMHDmSyy67jAkTJlBWVsb48eMjO7J3DRPpuvPXNUwkAOnXlDMWmgDSzKnmsxdnXYNXAF43RPkW1PG4gOybJFKt24WIqsiCFQBRJoF6R7PtyTDdNDY2snXrVq/Cftu2be7WODk5OYwaNYrLL7+csrIyJkyYwPjx4+naNcYeYYMNE1n6i9jWnWY0AaSRUAV5oEI5UHPPWO6QTbVuFyKqIovzOLEVm2qoOeagpt66d8LuZJhqjDHs37/fXdBv2bKFdevWuXvABKvp5fjx487LHF0AABw4SURBVLntttsYN24c48ePp7i4ODFt7aPs9qEj0gSQRkK1BApUKAdqyhjLBeRUGI7SU0RjI8S5AFj+6i4WDPLev5naB1FDQwPbt29n27ZtbNu2ja1bt7Jlyxbq6+sBq77+M5/5DMOHD+eOO+5wF/ZFRUXJa30TZrcPvuJ1I2Yq0QSQRkJVcwQqfFuNIT8nO67dNaTi6Fhh35AWZQEQSG29A/y0CrUrGSaDw+Fgx44d7oLe9Thw4Ox+LSgoYMyYMSxYsMBd0I8ZM4aCggIqKyuZMWOGPcEHGybyU/+LpFqVZ7xoAkgjoao5AhXKRR7XAuJ19BJrqyRbRThObChW0msMMD29NTc3s3v37nYF/Z49e9xdHOfm5lJcXMwll1zCmDFj3I/zzjsvqX3bhy3YMJEBBl1JtSrPeNEEkEZCVXMEK5Tj3V1DvAe9TqoIx4kNZfGcEdTsqPKaljbJ0OnUqVN88MEHPPXK2zz32jo+rd2LOXaAM0eqaWmxWp1lZWUxfPhwxo4dy4033ugu6D/zmc/QqVOaFSURDBMJqVflGS9p9q2lsTg1OwzVhz4kr1BO69GxIiwAgplbWkTFwfcpKsxO+WT46aefsnPnTnbs2OH1d+/eve4jehA69TiXnN6D6H5hOV/63FQWXnkJI0eOpHPnzrbGb5dUrPKMB00AyZDEdsdpXSinscL8HN5aMsPuMABoa2ujurqaHTt28NJLL7FixQp3YX/o0CH3fHl5eVxwwQWUlZVx0003seKDVhrz+9Kp5wCycs4W9Os75fPz8ePt+CgpI62rPIPQBJAMIdodx6N1QUdsoaACM8Zw6NAhdu/eze7du/nggw/czz/88ENOnjzpnrdnz54UFxdz5ZVXUlxcTHFxMSNHjmTIkCFeA5Y8ueRl/DW6TPdqjnhI6yrPIGxNACJyOfAwkA08ZoxZZmc8CROk2WG9o5m734itdUFHbaGgrCob3wLe9Th+/Lh7vk6dOjFs2DCGDx/OpZdeyogRIyguLubo0aNce+21YTWx7KjVHPHSEc+ubUsAIpINPAp8FqgG1ovIKmPM+3bFlDBBmh3WNZzC0ezdUiLS1gUdtYVCJjDGUFdXx0cffeR+fPjhh+4C/9NPz7ZLzMrKYvDgwVxwwQVcfPHFDB8+3P0YMmSI3wuxkfRuGU41h55pdiwhE4CIfAt42hhzLM7bvhD40BjzkXM7K4BrgI6XAII0OzzzXhvQvqlcJKfdyWihoP/40Tt58iR79+71KuQ/+ugj9zRX1wcugwYNYvjw4Vx//fVccMEF7kJ+6NCh5OXlJSzOUNUceqbZ8YgJMbKRiPwEWABsBB4HXjWhFgpnwyLXAZcbY77mfP0lYJIx5ps+8y0CFgH07du3bMWKFVFtr6mpiYKCgtiCjoXjGDR+Aq1nIDsXuvWH/J4cOdbAJyfbz56bncWIfuF1cLXrYKPXAC7RrMOX5/6qdzRTc8xBm8fXniVCUc98CvNzAq0iIWz/Hv1oaWnh448/prGxkYMHD1JbW8snn3zifngexQPk5+fTv39/BgwYQP/+/b2e9+vXL67dH8Rzf8Xzd5bI77He0UxdwynOtLaRm51F3x6dw/6dpuLvyyWW2GbOnFlljCn3nR7yDMAY830R+b/AbOBW4BcishL4vTFmT1TRRMAY81vgtwDl5eUm2rsHbb3zMIiKV17jlxtb2512L51Xwowwj6rqfY7MolmHL8/9ZQ0ak91unqLC7KS3fLHje2xoaGD//v3s37+fjz/+uN3f2tpaPI+JsrKyGDRoEMOGDeOiiy5i2LBhXo/evXsnrduDeO6vW5e8jPFztirg1UV3suPyVLGpxnlNLQvXmXV+TitL540K6ywlVcsJSExsYV0DMMYYETkIHMQakqkn8LyIvGaMuSvKbdfgfQP9QOe0jFKYn8PSeaNiql5JdAuFjnoTDMCZM2f45JNPqKmpCVjINzQ0eC2Tk5PDoEGDGDx4MJdddhmDBw/m5MmTzJ49m2HDhjFo0KAOMWC4r3S4SKzXwyITzjWA/wBuAY4AjwGLjTHNIpIF7AaiTQDrgeEiMhSr4F8A3BjlutJaPFoXJLKFQjr84/syxtDQ0EBNTU27R3V1tfu5Z7t4l8LCQgYPHsyQIUOYPn065513HoMHD+a8887jvPPOo1+/fu26OEjlI8d4SYW28L7XomaO7MOanYfdrwONG90RDlYSIZwzgF7APGPMx54TjTFtInJltBs2xrSIyDeBV7GagT5ujNke7fpU+CK9oJsK//guxhiOHz/OwYMHOXjwIHV1dRw8eLBdwV5TU+PVFt6ld+/eFBUVUVRURFlZmft5UVGRu4APOpJUBrO7Lby/i9BPr9vP1VlreS53JQMcR6jNPYcHWuazqm2q17JhH6w4jsFDYzJmoKBwrgH8IMh7O2LZuDHm78DfY1mHikw0LTmS8Y9/8uRJd2HuWbD7vq6treXMmTPtls/NzWXAgAEUFRVRWlrKlVde6VW4FxUVMWDAgIztyiBe7GwL76965+qstSzLeYwuYv0mBsoRluU8Bs24k0DYBytbV0LDwbNNtuMwUFCq0zuBM0y0daSR/OO7jtKPHDnCkSNHOHz4cLvnnn/r6upobGzfm6aIcM4559C3b1/69evH1KlTaW5upry8nH79+rkfffv2pXfv3qnZ86SKG3/VOHd1Wuku/F26yBnuyf0zL52aGtnByhs/gn5f854Ww0BB6UATQIaJ5IKuMQaHw8GxY8fcj/r6eq/X/gr3I0eO0Nzc7Hc7ubm5nHPOOfTp04dzzjmHsrIydyHuW6j36dOHnBzv5nuZUNeeivdcRBxTAsZc9lfHP0CO+J23H0fYu+yKyDbQUA39AkzvoDQBdGBtbW00NTVx/PhxGhsbOX78OF2OvM/ho/W0nTlJ26km9yOvzcEV7/3SXbDX1dVx4sQJv9Utnnr16uUu0IcNG8aFF17oLtw9C3rX84KCguSN/JSGUvFmq4hjSsCYywAzR/bh6XX7vabVmnMY6C8JRDO4T6BlohwoKB1oAkgBxhhOnz7NyZMnOXHiBCdPnvR6+E47ceKEV6Hu+9f1vKmpKYytC1mdu9Kldy8OZp1Dz549KSoq4vzzz2f06NH07Nkz4KNHjx5enYmp2KViM8aIY4rzmMsua3YebjftgZb5XtcAgOgH95l1L7x/0HtaDAMFpYOMSAANDQ0cPnyYjz/+mNbWVlpaWvz+DTWtubmZ06dPc+bMGU6fPu31CHeaq6B3FeSNjY2cPn2aSG+u7tSpE927d6d79+5069aN7t2707t3b4YOHeo1zfXX8/n6GgdPVx3i8JlODDy3N3d9rrjdP3ImVLV4ClXFkaxqmUTecxHtZ4g4pgQNuu5ve6vapkKzdS1gYNbR2Kqbxs6HmhehxyBtBdSR3H333fzqV79K6DY6depEXl6e1yM3N7fdtO7du9OlSxe6du1Kly5dOHr0KPQYQOWeBlqycpGcPLJy8sjrnM/XZozks+MG06VLF69H165dycvLi7oqZSpw5w3x/fzpLFQVRzKrZRJ1z0UsnyHimOI85nKoOFa1TaWqy2d5a8mlMa0fgPyecOe22NeTJjIiAdx444106dKFUaNG0alTJ7Kzs91/PZ+Hes9VyPsW7Lm5uVG3QKmsrOR769ro0rv9D/u14/ncN2VKrB9fhRCqiiOZ1TKJuucils8QcUxxHnPZM47Ff95Cc5v32XJOtqT9wCx2yYgEMHXqVFpaWlK2SqMjd7WQDkLt/2R+P4m65yKWzxBxTHEec9k3jvtWbafeYbUy69klhx9cNTro/knFVlWpIiMSQLwk6oeUjl0t2C2e30Wo/Z/s7ycRN1vF+hkijimOYy7HEkcqtqpKJXrnTJhcP6SaegeGsz+kik2x91+3eM4I8nO8W9N0hPFGEyXe30Wo/d8Rvp+O8BmiEazqS2kCCFsif0hzS4tYOq+EosJ8BCgqzGfpvBI9Qgkg3t9FqP2frt9PxaYadh1sZOiSl1n+6i6+UFaUdp8hVoGquGrqHUxZtpqhS15myrLVcTmQS0daBRSmRNcDd8TxRhMlEd9FqP2fbt+P6yzpjpFtGLKoqXfwQlVNQgv9VKxrD1T1JeCe7lktVJjM4FKAngGEKVBdqdbTJ1+H/S62rrR6oryv0Pq7dWXUq0rUGWvFphqvI+f1q34DD43B3FfIxIpLKDv+WtyrSGPhr+pLAN+7bjK1WkgTQJgytQ41FXXI78LVfULDAcBAwwEcf/km/3HP3VFVUSTiLMn32kvZ8dcYU/V9aDiAYChy9sR5ddZaIDUKVX/Vd4FuuczEVndaBRQmu/tCV2d1yO/CT/cJ+ZxmcaeVTK2fGnHLlUS0XPI9q7ir00ry/fTEeVenlaw6Y3XFnAqFqm/1nTXEqba6A00AEUm3euCOrMN9FwG6SRggR4HIbzxz3bxljeBqifUsybcwD9QTpytmSFKhGmHPo0FvbGvYnfh4U4hWASmVCgJ0k1Brep99HsHRtKvqIzc7K26tfnwL81pzjt/5XDEnpVrOT9UZL/170Osn6dqqKxH0DECpOKh3NDNl2ero+8sfPhu2POtVDXTS5PJAy9kj2UiPpueWFlHZsJu9y2ZE+nH88j1yfqBlPvfnPOZVDeQgj+Ut8ylKVrVclD2PdrgzyChpAkiwVGwap+KrYlMNNccc1NRbF6aj6i9/y7Mw7kbY/Q9MQzW1pjf3N8+PfFjDBPK99lLV/bNsGzWEiXv+x53I8mfdy8PJ7D0zQT2PZgpNAAmkt6FnhuWv7mLBIO+2JVH1l7/7H3DnNgRYv6mGqld3ISl24ND+yPlS4Ot2hZOwnkczhSaABErFwT1U/NXWO2BQgOn+hHHUqlUUYUpQz6OZQhNAAmkvn5nBqptvP6h9svvLj6e0qbpMUM+jmUITQAJpL5+ZYfGcEdTsqPKaZkd/+fGSdlWXCep5NBNoM9AE6pB3rKp25pYWUdQzP/xmhWPnw1WPWEMPItbfqx5JmUJMe9DMHHoGkEAd8o5V5Vdhfg5vLZkR/gIpfNSqVZeZQxNAgunFPJVutOoyc2gVkFLKi1ZdZg5bzgBEZDlwFXAG2APcaoyptyMWpZQ3rbrMHHZVAb0G3G2MaRGR+4G7ge/aFItSyodWXWYGWxKAMeYfHi/XAdfZEYdSmSbc9v1pcx+AiokYE2h4hCQFIPIS8Jwx5ukA7y8CFgH07du3bMWKFVFtp6mpiYKCgqjjTBSNKzIaV2Q846p3NFNzzEGbx/98lghFPfMpzM9xTwt3vnjFlUpSNS6ILbaZM2dWGWPKfacnLAGIyOtAPz9vfc8Y81fnPN8DyoF5JoxAysvLzYYNG6KKp7KykhkzZkS1bCQiPXJKVlyR0rgik8px1fcYzvJXd/lt2QPWfQtvLbnU/TrQgCm+88UaV6rur1SMC2KLTUT8JoCEVQEZYy4LEdBC4EpgVjiFfzpIuzsoVYdX72jm7jfea3djlyff9v16H0DmsKsV0OXAXcB0Y8xJO2KIF88j/iwRWk0EvUIqlWB1DadwNAdv7e3bvj+l7gOIcLQvFRm77gP4BdANeE1ENovIr22KI6SKTTVMWbaaoUtebjc4t+8g2b6Fv4seOSm7nGltC/q+v/b9KXMfQBSjfanI2NUK6DN2bDdSoap0/PWZ4o/eQanskpsd+Bgv0KhdKXMfQJSjfanwaVcQQYTqzz+cI3u9g1LZqW+PzuTntLYbAD3UGLgpcR+AjvaVcJoAggh1MSxQXWm2CG3GaPtplTSBWp8V5uewdN4o24/m28U3LvSZczqMm5DuNAEEEepimO8g2RDe0ZVS8RSsqrKQ+BzNx3JjmL/4ao61UrGpJvg6UnzchI5AO4MLItTFsLmlRSydVxJ+P/BKJUCi++/3bezgSjCeDSIija/NmNDxpfi4CR2BngEEEc7FsJSoK1UZLXhVZdeY1x/r2NYx3VeQwuMmdASaAELQAl6lukS324/1xrCUuq9AedEqIKXSXKLb7QcqqMMtwP3FlyWireNSgCYApdJcoq9FxZpg/MVX1DNfz6xTgFYBKdUBJLKqMh43hvnGV1lZGe8wVRQ0ASilQgqUYHTcgPSmCSAY7YhKqYC099v0p9cAAtGOqJQKKtH3H6jE0wQQSLCOqJRSOm5AB6AJIBDtiEqpoGJtHqrspwkgkEAdTmlHVEoBKTRugIqaJoBAZt1rdTzlSTuiUspN+8JKf9oKKBBXax9tBaRUQNpVSnrTBBCMdkSllOrAtAoIrKadD42B+wqtv9rUUymVAfQMwNXe39Xk09XeH/ToXynVoekZgLb3V0plKE0A2t5fKZWhNAFoe3+lVIbSBKDt/ZVSGUoTgA48rZTKUNoKCLS9v1IqI2kCQAe1UEplJlurgETkOyJiROQcu2JwDWpRU+/AcHZQi4pNNXaFpJRSSWFbAhCRQcBsYL9dMYAOaqGUylx2ngE8BNwFGBtj0EEtlFIZy5YEICLXADXGmC12bN+TDmqhlMpUYkxiDsBF5HWgn5+3vgfcA8w2xjSIyD6g3BhzJMB6FgGLAPr27Vu2YsWKqOJpamqioKCg3fR6RzM1xxy0eeyHLBGKeuZTmJ8T1bbiEZfdNK7IaFyR0bgiF0tsM2fOrDLGlLd7wxiT1AdQAhwC9jkfLVjXAfqFWrasrMxEa82aNQHfe3FjtZm89A0z5Lt/M5OXvmFe3Fgd9XbiGZedNK7IaFyR0bgiF0tswAbjp0xNejNQY8x7wLmu16HOAOItUJNPbfaplMo0GXUfgKvJp6vVj6vJJ6AJQCmVcWzvCsIYMyRZR//a5FMppc6yPQEkkzb5VEqpszIqAWiTT6WUOiujEsDiOSPIz8n2mpafk83iOSNsikgppeyTUReBXRd6teM3pZTKsAQAaJNPpZRyyqgqIKWUUmdpAlBKqQylCUAppTKUJgCllMpQmgCUUipDaQJQSqkMpQlAKaUylCYApZTKUJoAlFIqQ2kCUEqpDKUJQCmlMpQmAKWUylAZ1xlcMIHGC1ZKqY5IE4CTjheslMo0WgXkpOMFK6UyjSYAJx0vWCmVaTQBOOl4wUqpTKMJwEnHC1ZKZRq9COyk4wUrpTKNJgAPOl6wUiqTaBWQUkplKE0ASimVoTQBKKVUhrItAYjIt0Rkp4hsF5EH7IpDKaUylS0XgUVkJnANMM4Yc1pEzrUjDqWUymR2nQHcDiwzxpwGMMYcsikOpZTKWHY1A70AmCYiPwVOAf9pjFnvb0YRWQQscr5sEpFoO+c5BzgS5bKJpHFFRuOKjMYVmVSNC2KLbbC/iQlLACLyOtDPz1vfc263F3ARMBFYKSLDjDHGd2ZjzG+B38Yhng3GmPJY1xNvGldkNK7IaFyRSdW4IDGxJSwBGGMuC/SeiNwO/MVZ4L8rIm1Y2e1wouJRSinlza5rABXATAARuQDIJXVPu5RSqkOy6xrA48DjIrINOAN82V/1T5zFXI2UIBpXZDSuyGhckUnVuCABsUniy12llFKpSO8EVkqpDKUJQCmlMlSHSgAicr2za4k2EQnYXEpELheRXSLyoYgs8Zg+VET+5Zz+nIjkximuXiLymojsdv7t6WeemSKy2eNxSkTmOt97QkT2erw3PllxOedr9dj2Ko/pdu6v8SLyjvP73ioiN3i8F9f9Fej34vF+nvPzf+jcH0M83rvbOX2XiMyJJY4o4vq2iLzv3D9viMhgj/f8fqdJimuhiBz22P7XPN77svN73y0iX05yXA95xPSBiNR7vJfI/fW4iBxyXhP1976IyCPOuLeKyASP92LbX8aYDvMAioERQCVQHmCebGAPMAyr9dEWYJTzvZXAAufzXwO3xymuB4AlzudLgPtDzN8L+BTo4nz9BHBdAvZXWHEBTQGm27a/sG4mHO58PgD4BCiM9/4K9nvxmOcO4NfO5wuA55zPRznnzwOGOteTncS4Znr8hm53xRXsO01SXAuBX/hZthfwkfNvT+fznsmKy2f+bwGPJ3p/Odd9CTAB2Bbg/c8DrwCCde/Uv+K1vzrUGYAxZocxJtSdwhcCHxpjPjLGnAFWANeIiACXAs875/sjMDdOoV3jXF+4670OeMUYczJO2w8k0rjc7N5fxpgPjDG7nc9rgUNAnzht35Pf30uQeJ8HZjn3zzXACmPMaWPMXuBD5/qSEpcxZo3Hb2gdMDBO244priDmAK8ZYz41xhwDXgMutymuLwJ/itO2gzLG/BPrgC+Qa4AnjWUdUCgi/YnD/upQCSBMRcABj9fVzmm9gXpjTIvP9Hjoa4z5xPn8INA3xPwLaP/j+6nz9O8hEclLclydRWSDiKxzVUuRQvtLRC7EOqrb4zE5Xvsr0O/F7zzO/dGAtX/CWTaRcXn6KtZRpIu/7zSZcX3B+f08LyKDIlw2kXHhrCobCqz2mJyo/RWOQLHHvL/SbkhICdLFhDHmr8mOxyVYXJ4vjDFGRAK2vXVm9hLgVY/Jd2MVhLlYbYG/C/woiXENNsbUiMgwYLWIvIdVyEUtzvvrKax7Sdqck6PeXx2RiNwMlAPTPSa3+06NMXv8ryHuXgL+ZKyegL+OdfZ0aZK2HY4FwPPGmFaPaXbur4RJuwRggnQxEaYaYJDH64HOaUexTq06OY/iXNNjjktE6kSkvzHmE2eBFaz30/nAi8aYZo91u46GT4vIH4D/TGZcxpga59+PRKQSKAVewOb9JSLdgZexkv86j3VHvb/8CPR78TdPtYh0Anpg/Z7CWTaRcSEil2El1enG2fsuBPxO41GghYzLGHPU4+VjWNd8XMvO8Fm2Mg4xhRWXhwXANzwnJHB/hSNQ7DHvr0ysAloPDBerBUsu1pe9ylhXVdZg1b8DfBmI1xnFKuf6wllvu7pHZyHoqnefC/htLZCIuESkp6sKRUTOAaYA79u9v5zf3YtYdaPP+7wXz/3l9/cSJN7rgNXO/bMKWCBWK6GhwHDg3RhiiSguESkFfgNcbTy6XA/0nSYxrv4eL68GdjifvwrMdsbXE5iN95lwQuNyxjYS64LqOx7TErm/wrEKuMXZGugioMF5kBP7/krUlW07HsC1WPVgp4E64FXn9AHA3z3m+zzwAVYG/57H9GFY/6AfAn8G8uIUV2/gDWA38DrQyzm9HHjMY74hWFk9y2f51cB7WAXZ00BBsuICJju3vcX596upsL+Am4FmYLPHY3wi9pe/3wtWldLVzuednZ//Q+f+GOax7Pecy+0CPhfn33uouF53/h+49s+qUN9pkuJaCmx3bn8NMNJj2a849+OHwK3JjMv5+j6ssUo8l0v0/voTViu2Zqzy66vAbcBtzvcFeNQZ93t4tHCMdX9pVxBKKZWhMrEKSCmlFJoAlFIqY2kCUEqpDKUJQCmlMpQmAKWUylCaAJRSKkNpAlBKqQylCUCpGIjIRGenZp1FpKtY4xOMsTsupcKhN4IpFSMR+QnW3cD5QLUxZqnNISkVFk0ASsXI2bfMeuAUMNl49yKpVMrSKiClYtcbKAC6YZ0JKJUW9AxAqRiJNUbsCqxBRPobY75pc0hKhSXtxgNQKpWIyC1AszHmWRHJBt4WkUuNMatDLauU3fQMQCmlMpReA1BKqQylCUAppTKUJgCllMpQmgCUUipDaQJQSqkMpQlAKaUylCYApZTKUP8fuBcz/slLl7sAAAAASUVORK5CYII=\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYAAAAEWCAYAAABv+EDhAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8li6FKAAAgAElEQVR4nOydd3hUxdeA30lIQpASQEAICEGQmmAgWKgiTbEBShNRVOQnKiCfgiCoKAgqKqhYQKSIIlIEkSKCEMROD00ITSBIlYSWwCaZ74/dDZtkd7M1d5Oc93n2yd65c++cvbuZM3PmzDlKa40gCIJQ9AgyWgBBEATBGEQBCIIgFFFEAQiCIBRRRAEIgiAUUUQBCIIgFFFEAQiCIBRRRAEIfkUpNVop9aXRctiilOqtlPrRxbpO5VdKDVBKnVBKXVBKlbf8remFbPFKqX6eXi8I7iAKQHAJpdQhpVSqpYM7oZSaqZQqabRcnqC1/kpr3cHb+yilQoD3gA5a65Ja6zOWvwcs52cqpcZ6205BQik1RCl1QCl1Til1TCk1USlVzGi5BPuIAhDc4V6tdUmgMRAHjDJYHqOpBBQHdhotSF7kYye8BGistS4NNAQaAYPyqW3BTUQBCG6jtU4CVmD+B0cpVUUptUQp9Z9Sap9S6kl71ymllimlBuYoS1BKdbG810qpp5RSiUqpZKXUR0opZTkXpJQapZT6Ryl1Uin1hVKqjOVcDcu1jymljiilzlru09Ry/2Sl1GSbNvsqpX6xOX7fct05pdQmpVTLvJ6BUupGYI/lMFkptcbmM9RSSvUHegPDLLOm7x3cp71S6m+lVIpFRpXj/ONKqd2Wz7RSKVXd5lwHpdQey7UfK6XWWc1Hls/4q2UEfgYY7cL96iqlVlm+xz1Kqe55PYecaK33a62TrbcEMoFa7t5HyB9EAQhuo5SqBnQCtliK5gJHgSrAg8A4pdQddi6dBTxsc59GQCSwzKbOPUBTIAboDnS0lPe1vNoANYGSwGSycwtQG+gBTAJGAu2ABkB3pVRrBx9pA3ATUA6YA8xXShV3UBcArfVey30BIrTWd+Q4PxX4CnjbYha6N+c9lFLXAt9inkldC+wHmtucvx94CegKVADWA1/bXLsAGAGUx6yMmtl5Hgcwz1TeyON+1wCrLJ+/ItAT+FgpVd9yfrhFkdp95fhcDymlzgGnMc8Apjh7loKBaK3lJa88X8Ah4AKQDPwDfAyEA9WADKCUTd3xwEzL+9HAl5b3xYGzQG3L8TvAxzbXaaCFzfE8YLjl/U/A0zbn6gAmoBhQw3JtpM35M0APm+OFwHOW932BX5x81rNAo5zy26lnbbdYjs9Qy/J+JjDWSTuPAH/YHCvMirSf5XgF8ITN+SDgElDdcu3vOa49YnNtX+Bwjvac3a8HsD5H/SnAq178ZmoDY4DrjP79ysv+S2YAgjt01lpHaK2ra62f1lqnYh71/6e1Pm9T7x/MI/tsaK3TgG+Ah5VSQUAvYHaOasdt3l/CPNLH0s4/Odoohnl0a+WEzftUO8d2F62VUi9YzCIpltFsGcwjcn9TBXOnDYA295pHbM5XB963GWX/h7mjj3Rw7dEc9z+S49jZ/aoDt+QY1fcGrvP0w2mtEzGvj3zs6T0E/yKr84K3HAPKKaVK2SiB64EkB/VnYe70fwEuaa1/d6Od6jbH1wPpmDv5qm5LbcFi7x8GtAV2aq0zlVJnyWGL95C8Qu3+i3kGZZVF2R5j7sDf0Fp/lfNCpVRtbD635dqczyFn+87uVx1Yp7Vub09QpdRLmM1HdtFm5wB7FANucHSdYCwyAxC8Qmt9BPgNGK+UKq6UigGeAOz6zls6/EzgXXKP/p3xNTBEKRWlzO6n44BvtNbpXn0AKIVZkZwCiimlXgFKe3lPKycwr1c4YhnQQCnVVZm9dAaRfcT9KTBCKdUAQClVRinVzebaaKVUZ8u1z5D3aN3Z/ZYCNyql+iilQiyvpkqpegBa63HavJZh92VtQCnVTylV0fK+PuY1ip/ykEswCFEAgi/ohdkefgxYhNluvNpJ/S+AaBwoCQdMx6wwfgYOAmnAQKdXuMZK4AdgL2azUhq5TSee8jlQ32JSWZzzpNb6NNANeBPzmkVt4Feb84uAt4C5lkXVHcBdOa5923JtfWAjcNmRMHnc7zzQAfPi7zHMpri3gDA3P3NzYLtS6iKw3PJyOHMQjEWZTYeCkH8opR4B+mutWxgtS2HBsqZyFOittV5rtDxCwUBmAEK+opQqATwNTDValoKOUqqjUipCKRWGeZStgD8MFksoQBiqACw/3gWWjTC7lVK3GSmP4F+UUh0x29pPYPY3F7zjNsx7B04D92L20ko1ViShIGGoCUgpNQuz7/E0pVQoUEJf3UUoCIIg+BHDFIAyb+PfCtTUshAhCIKQ7xi5DyAKszlghiUkwCZgsNb6om0lS0yV/gDh4eFNqlWrlutGrpCZmUlQUOAteYhc7iFyuYfI5R6BKhd4J9vevXtPa60r5Dph1BZkzNEk04FbLMfvA2OcXdOkSRPtKWvXrvX4Wn8icrmHyOUeIpd7BKpcWnsnG7BRB1goiKPAUa31n5bjBZjDDAuCIAj5gGEKQGt9HDiilKpjKWoL7DJKHkEQhKKG0bGABgJfWTyADgCPGSyPIAhCkcFQBaC13op5LcBjTCYTR48eJS0tzWm9MmXKsHv3bm+a8gsi11WKFy9O1apVCQkJydd2BSEQWbwliQkr93AsOZUqEeEMbZTh8zaMngF4zdGjRylVqhQ1atTAHBDRPufPn6dUqVL5KJlriFxmtNacOXOGo0ePEhUVlW/tCkIgsnhLEiO+3U6qydzpJyWnknQ2g8VbkugcmyvSuscEpr+TG6SlpVG+fHmnnb8Q+CilKF++fJ4zOUEoCkxYuSer87eSqTUTVu5xcIVnFHgFAEjnX0iQ71EQzBxLth/Rw1G5pxQKBSAIglCYqBIR7la5p4gCMIDbb7+djRs3GtJ2s2Y584bnpmRJR8mdrjJ69Gjeeecdp3UWL17Mrl3i2SsI7jK0Yx3CQ4KzlQUpxdCOdRxc4RmiAIoYv/32W761JQpAEDyjc2wk47tGExkRbk7aHBFOZNlwny4AQxFUAIu3JNH8zTVEDV9G8zfXsHiLo9S1rnHo0CHq1q1L7969qVevHg8++CCXLl0C4KeffiI2Npbo6Ggef/xxLl/Onqxp+vTpvPjii1nHn332GUOGDOHQoUPUq1ePJ598kgYNGtChQwdSU822v61bt3LrrbcSExNDly5dOHv2LGCeVQwZMoS4uDjq1avHhg0b6Nq1K7Vr12bUqFFZbVhH9xcuXKBt27Y0btyY6Ohovvvuuzw/6xtvvMGNN95IixYt2LPn6mLUZ599RtOmTWnUqBEPPPAAly5d4rfffmPJkiUMHTqUm266if3799utJwiCfTrHRvLr8Ds4+Obd/Dr8DiLCfe8eXaQUgNW1Kik5FY3ZtWrEt9u9VgJ79uzh6aefZvfu3ZQuXZqPP/6YtLQ0+vbtyzfffMP27dtJT0/nk08+yXZd9+7dWbFiBSaTCYAZM2bw+OOPA5CYmMgzzzzDzp07iYiIYOHChQA88sgjvPXWWyQkJBAdHc1rr72Wdb/Q0FA2btzIU089xf33389HH33Ejh07mDlzJmfOnMnWdvHixVm0aBGbN29m7dq1PP/889YYTXbZtGkTc+fOZevWrSxfvpwNGzZknevatSsbNmxg27Zt1KtXj88//5xmzZpx3333MWHCBLZu3coNN9xgt54gCM65ePEiY8aM4cSJEz6/d5FSAPZcq1JNGV67VlWrVo3mzZsD8PDDD/PLL7+wZ88eoqKiuPHGGwF49NFH+fnnn7NdV7JkSVq3bs3SpUv5+++/MZlMREdHAxAVFcVNN90EQJMmTTh06BApKSkkJyfTunVru/e87777AIiOjqZBgwZUrlyZsLAwatasyZEj2dPcaq156aWXiImJoV27diQlJTn9ga1fv54uXbpQokQJSpcundUWwI4dO2jZsiXR0dF89dVX7Ny50+49XK0nCMJVVq5cySuvvEJSkncDVXsU+I1g7uAv16qc7ovuuDM+8sgjvP/++9StW5fHHrsaCSMs7Gou7uDg4CwTkDOs1wQFBWW7PigoiPT09Gx1v/rqK06dOsWmTZsICQmhRo0aHvvg9+3bl8WLF9OoUSNmzpxJfHy8V/UEQbjKwoULKV++PI0aNfL5vYvUDMBfrlWHDx/m999/B2DOnDm0aNGCOnXqcOjQIfbt2wfA7Nmzs0butjRt2pQjR44wZ84cevXq5bSdMmXKULZsWdavX+/0nq6QkpJCxYoVCQkJYe3atfzzzz9O67dq1YrFixeTmprK+fPn+f7777POnT9/nsqVK2Mymfjqq6+yykuVKsX58+fzrCcIgn3S0tL4/vvv6dKlC8HBwXlf4CZFSgHYc60KDwn22rWqTp06fPTRR9SrV4+zZ88yYMAAihcvzowZM+jWrRvR0dEEBQXx1FNP2b2+e/fuNG/enLJly+bZ1qxZsxg6dCgxMTFs3bqVV155xSOZe/fuzcaNG4mOjuaLL76gbt26Tus3btyYHj160KhRI+666y6aNm2adW7MmDHccsstNG/ePNt9evbsyYQJE4iNjWX//v0O6wmCYJ+VK1dy/vx5unXr5p8G7CUJCNSXvYQwu3btcikhwrlz57TWWi/afFQ3G/+TrvHiUt1s/E960eajLl3viIMHD+oGDRp4fP25c+f03XffrVevXu2VHL7G+rzym7y+z0BN2CFyuYfI5Rq9e/fW5cqV01euXPFLQpgitQYAZtcqX/vSekpycjJxcXHExsbStm1bo8URBCGASEtLY8mSJXTr1s1vEXKLnALwNTVq1GDHjh0eXRsREcGWLVsCMhqoIAjGsmrVKv+afyhiawCCIAgFhfnz51O2bFm/WgdEAQiCIAQYly9f5rvvvqNz585+TZAkCkAQBCHAWLVqFefOnfOr+QdEAQiCIAQc8+fPJyIiwu/OIaIADMAakO3YsWP06dPHbh1XQkZPmjQpW0C1Tp06kZyc7DtBXeDQoUPMmTMnX9sUhMKMrfknNDTUr22JAjCQKlWqMHv2bI+vz6kAli9fTkREhC9EcxlRAILgW1atWkVKSorfzT9QFBVAwjyY2BBGR5j/Jszz6nbDhw/no48+yjq2JkpxJdzyoUOHuOWWWwBITU2lZ8+e1KtXjy5dumSL/TNgwADi4uJo0KABr776KgAffPABx44do02bNrRp0wYwu6SePn0agPfee4+GDRvSsGFDJk2alNWeozDTtsyfP59bbrmFRo0a0apVKwAyMjIYOnQoTZs2JSYmhilTpmR9/vXr13PTTTcxceJEr56lIAjmcDLly5enffv2/m/M3u6wQH15vRN42zdaj62k9aulr77GVjKXe8jmzZt1q1atso7r1aunDx8+rE0mk05JSdFaa33q1Cl9ww036MzMTK211tdcc43W2ryLuF69elprrd9991392GOPaa213rZtmw4ODtYbNmzQWmt95swZrbXW6enpunXr1nrbtm1aa62rV6+uT506ldW29Xjjxo26YcOG+sKFC/r8+fO6fv36evPmzfrgwYM6ODhYb9myRWutdbdu3fTs2bNzfaaGDRvqv//+W2ut9dmzZ7XWWk+ZMkWPGTNGa611WlqabtKkiT5w4IBeu3atvvvuuz1+fjmRncC+ReRyD8Pk2vaN1u810OdHlNYlQpUe0L19rir+2AlctGYAP70OphwjXlOqudxDYmNjOXnyJMeOHWPbtm2ULVuWatWquR1u+eeff+bhhx8GICYmhpiYmKxz8+bNo3HjxsTGxrJz5848s2z98ssvdOnShWuuuYaSJUvStWvXrABy9sJM56R58+YMGDCAzz77jIwMc/jsH3/8kS+++IKbbrqJW265hTNnzpCYmOjWsxIEwQ4J8+D7QZByhCV7TFy6onmo9EavrROuULR2Aqccda/cRbp168aCBQs4fvw4PXr0AHwXbvngwYO88847bNiwgbJly9K3b1+PwzaDa2GmP/30U9asWUN8fDxNmjRh06ZNaK358MMP6dixY7a6EtJZELzEZmA6Z7uJ68somlVJN5fHdPdr00VrBlCmqnvlLtKjRw/mzp3LggULshZuPAm3bF1M3bFjBwkJCQCcO3eOa665hjJlynDixAlWrFiRdU3OcMtWWrZsyeLFi7l06RIXL15k0aJFtGzZ0uXPs3//fpo2bcrrr79OhQoVOHLkCB07duSTTz7Jyl62d+9eLl686FAGQSiquJt2VlsGoKcvZbJyfzq9GoYQpJTXA1NXKFozgLavmKdatmagkHBzuRc0aNCA8+fPExkZSeXKlQFzuOV7772X6Oho4uLi8gx/PGDAAB577DHq1atHvXr1aNKkCQCNGjUiNjaWunXrZss8BtC/f3/uvPNOqlSpwtq1a7PKGzduTN++fbn55psB6NevH7GxsXbNPfYYOnQoe/bsQSlF27ZtadSoETExMRw6dIjGjRujtaZChQosXryYmJgYgoODadSoEX379mXIkCHuPDpBKFRY085aMw9a084CdoNQLt6SRFNdnkh1mgW70knPhIeiLTt/vRyYuoLSTvLA5gdKqWBgI5Cktb7HWd24uDid0zd+9+7d1KtXL892zp8/bw66ljDPPLVKOWp+wG1f8fs0yyW5Agyj5Mrr+4yPj+f222/PP4FcRORyj8IqV/M315BkJ8NgZEQ4vw6/w279JudW8WbINO6ceZYzqZodA64hTRUnvOvkbH2TN7IppTZpreNylgfCDGAwsBsonS+txXQ3tMMXBKHw4m7a2WPJqSTRgvOnU1h/+BPGtAkjSVdggqk77+dDP2XoGoBSqipwNzDNSDkEQRB8gbtpZ63li3eZFcQnN35EiysfsLF0PuwBwPhF4EnAMCDTm5sYbcYSfIN8j0JBx920s0M71qF4sSAu7owntHIdQiKu80maWlcxbA1AKXUP0Elr/bRS6nbgBXtrAEqp/kB/gEqVKjWZO3dutvMlS5akUqVKlClTBqWUw/YyMjL8klTZW0QuM1prUlJSOHHiBBcuXHBY78KFC1mxlAIJkcs9CrNcyakmTqSkcSUjk9DgICqVKU5EuOOQzpt37Ob5gU/Tre//aNvxbof1vZGtTZs2dtcAjFQA44E+QDpQHPMawLda64cdXWNvEdhkMnH06NE8fePT0tIoXry413L7GpHrKsWLF6dq1apO458X1sVDfyFyuYcRcg0ePJhPP/2Uf//9l3LlyjmsV6gWgbXWI4ARADYzAIedvyNCQkKIiorKs158fDyxsbHu3t7viFyCUHS5cuUKc+bM4f7773fa+fsLo9cABEEQiizLly/n9OnT9O3b15D2A8ENFK11PBBvsBiCIAj5ysyZM7nuuuvo0KGDIe3LDEAQBMEATp06xbJly+jTpw/FihkzFhcFIAiCYABz5swhPT2dRx991DAZRAEIgiAYwMyZM7MSPRmFKAChcODjTG+C4E+2bt3K1q1bDVv8tSIKQCj42CTUAG3++/0gUQJCwDLq7Q9RwSG8tbecSyGj/YUoAKHg44dMb4LgL775fR8rFs0j/MZmBIWXzgoZbYQSCAg3UKHwsnhLEhNW7uFYcipVIsIZ2rGO3bjoXuGnTG+C4A9GTfyczLQLlLrpana9VFMGE1bu8f3/Rh7IDEDwG9bkGEnJqWjw30jHT5neBMEfHPl9CcXKViGsWnS2ckcho/2JKADBb0xYuScrM5IV60jHp7R9xZzZzRYfZHoTBF+za9cuLh/dRclGd+YKXukoZLQ/EQUg+A13k2N4TEx3uPcDKFMNUOa/934giX+EgOOzzz6jWLEQro3NHu8/P0NA2yJrAILfqBIRbjc9nl9GOpLpTQhw0tLSmDVrFg880JWefVr6f23MBUQBCH5jaMc62RJkg3EjHUEwmoULF3L27Fn69+/PHbGRhnT4OREFIPgN6w88EEY6gmA0U6dOpVatWgGVB0EUgOBXOgfISEcQjGTXrl38/PPPvPnmmwQFBc7SqygAQRAEL8lrv8vkyZMJCwvj8ccfN1DK3IgCEARB8ALrfhfrWpd1vwuYZ8ApKSl88cUX9OrViwoVKhgpai4CZy4iCIJQAMlrv8uMGTO4ePEiAwcONEI8p4gCEARB8AJn+10yMzP56KOPaNasGY0bN85nyfJGFIAgCIIXONrXUiUinB9++IF9+/YF5OgfRAEIgiB4xdCOdQgPCc5WZt3v8uGHH1K5cmUeeOABg6RzjiwCC4IguElOr58HmkSy9u9T2byA6l9zkR9++IHXXnuNkJAQo0W2iygAQRAEN7Dn9bNwUxLju0Znc/0cPHgwISEh9O/f3yhR80QUgCAIghvY8/ppn7GOW797Fr47DWWqktz0eaZPn06PHj247rrrDJI0b0QBCIIguEFOr5/7gn7hzZBplOCKuSDlCJ++PogLFy7wwgsvGCCh68gisCAIghvk9PoZVmweJdSVrOPL6Zr3f79I+xuvoVGjRvktnluIAhAEQXCDnF4/VdTpbOe/2m7i+AXN0Jt1tvLFW5Jo/uYaooYvMzQRvC1iAhIEQXCDnFFuT6oKXMcpADK15p3frnDTdUG0i62RdU1e4SKMQhSAIAiCIxLmwU+vQ8pRc47ptq9ATPfsUW4TLsL3g8CUyvLEdHafzmR6l1I8d/o+Nr65hqEd6zB6yU6H4SKKpAJQSlUDvgAqARqYqrV+3yh5BEEQspEwL6tjByDliPkYsmefs77/6XXe+e1vqpQOZmPtp1iW2QKSUxk6fxumzOzmICtGJIK3xcg1gHTgea11feBW4BmlVH0D5REE/5AwDyY2hNER5r8J84yWSHCFn16/2vlbMaWay3MS050NLWaw7p8MUuMeY5lqffUSB50/GJMI3hbDZgBa63+Bfy3vzyuldgORwC6jZBIEn+PqKFIIPFKOulU+btw4gsKuoWRMB5ebMDo9qtLasXbKNyGUqgH8DDTUWp/Lca4/0B+gUqVKTebOnetRGxcuXKBkyZLeCeoHRC73KHByndwFGVdylweHQkX/T3gL3PMymGxyufHd7d+/n379+nH3Az3p2KWnS20VC1LUq1zaM9ncpE2bNpu01nG5ZPDobj5EKVUSWAg8l7PzB9BaTwWmAsTFxWlP82nGx8cHVC5OK4VBrryyIRklV37iUK7RnTEvceVEQfdkP0tVAJ+XwWSTK+Fk9tkbQEg43PsBxNye7bqPP/6YUqVK0XPgKN5YfSTbgm9IkAIFpoyrv4PwkGDGd43mdjf+T/zxzAzdB6CUCsHc+X+ltf7WSFkEz7C6tyUlp6K56t4WCD7OAUGZqu6VC4FDTHdzZ1+mGqDMf+/9IJfpbteuXSxYsICBAwfycOsGjO8aTaTFth+sFKZMzTWhxShbIgQFREaE54obZBRGegEp4HNgt9b6PaPkELzDWTakQPiBG07bV+yPItu+YpxMRQ0HrpwuEdM9z7pvvPEGJUqUYMiQIcBVv35bv//kVBPhIcFM7HFTQP1fGDkDaA70Ae5QSm21vDoZKE+BxOjdhc6yIQm4PIoU/IR1ET7lCKCvLsL7yBMrMTGRuXPnMmDAAK699tqs8rzSRAYKRnoB/QIoo9ovDATC7sIqEeEk2ensjXZv8wRX1jI8Wu9wYRQp+Alnrpw++E7GjRtHaGhorqBvBWVgJLGACjCBMMpwlg2pIOHKWoasdxRA3HTlBNdn1Xv27OGLL77gqaeeolKlStnOOUsTGUiIAijABMIoo3NsZNail7sLXM7+0fLbtOWKMg0EhSu4iZuL8MmpJpeV/Msvv0x4eDgjRozIda6gDIwMdwMVPMdT88viLUm89v1Ozl4yARARHsLo+xp4bDbKFhfFRZyZrwCH5yI8kjBvXFGmzutc4w+xBG9xcxH+REoaqabs42J7Tg2bN29m/vz5vPzyy1SsWDHXfXIGjPO3e7SniAIowAztWCdbRwl5jzIWb0li6IJt2XySk1NNDJ2/Dci/tYO8RtOOzr1xq38mra4o08K03lFksInT44oX0JWMTOwZRnIq/1GjRlG2bFmef/55h017MjDKb8QEVIDxxPwyYeWebJ2/FVOmzldThrPRtBGmLVem7AVlWi/kIKY7DNkBo5PNf50s/oYG2+8SbZX8+vXrWbFiBcOHD6dMmTI+Fzc/kRlAAcfdUYazTtTTDtYTz5i8RtP5PdJ2ZcrurE58fKLfZBPyiYR51OYUB8JGckyX5+307izJbJFNyWuteemll6hcuTLPPvuswQJ7jyiAIoajjtd6zhkZGRkkJiayd+9e/vnnHw4fPsyfOxLZvP9f0i+noq+kcQx46KNiRFUsTfVK5ahQoQIVKlSgUqVK3HDDDdSuXZtatWrlab5yeC7FeUfrTVgKV5RpQZjWCx5g2S8QVHM4QUpTVZ3mzZBplAsJ5aa7+2d950uXLuWXX37h448/pkSJEgYL7T2iAIoYQzvWybUGABCkckcmTE5OZt26daxZs4a//vqLhIQELl26lHW+ePHi6BJl0SElUCHFCQo3B7bSmRkcPZtGuDrJzp07OXXqFKmp2ZVOVFQUlWs1IKlYFdIialCjbiOG35vdfOXuSDsQ9kUIBRQ7+wVKqCuMvmYhxL4GgMlk4oUXXqBu3br069fPCCl9jiiAIkbn2Eg2/vMfX/5xOFt5sDLvyUtKSmLBggVMmzaNXbt2kZmZSXh4OE2bNuXJJ58kNjaWevXqUb16dSpWrEjNEcsdhTpj45t3Zx2fO3eOffv2Zc0gtm/fzoYNG/jn0FIAzoaG8v7aZuxs14527dpxb1yc2522hKUQPMaF/QKffPIJe/fuZenSpYSEhOSTYP5FFEARZO3fp7Id63QTyXt/49G5L3HuoNkbqGbNmowcOZK2bdty6623EhYWdtW8svsUVSIuMLRjusueMaVLl6Zx48Y0btw4W/mpU6fYsGEDa9euZfXq1YwaNYpRo0ZRsWJFOnfuTNeuXWnTpg2hoaEs3pLEiePneWz4slzmncVbkhyatrxdPB61eDtf/3mEDK0JVopet1RjbOdor+4pBB37iZsAACAASURBVBhlqlrCRdgpB/777z9Gjx5Nu3bt6NSp8ESsEQVQBLF2iBmXUji3cQkXtv1A5qUUikVcR7V2fXnx6cdoUDYzW+hZR+aVB5pEsnBTkluuqLZUqFCBTp06Zf1TnTp1itWrV/Pdd98xZ84cpk6dSpkyZWh6Ryf2lm7C8+1uQBOU1f7Gf/5j6bZ/SU41OWzDm8XjUYu3Z5stZWiddSxKoBBh3S9gi81+gbFjx5KSksJ7772HUoUngo0ogAKEr+LuXxucyt7VX3N+yzK06QrhtW6mVGwnikfFolQQkzdfYnyz7O6Or31vP6n12r9PMb5rtM82vFSoUIFevXrRq1cv0tLSWL16NfPnz+fLufPIvPI1Y3+ojOnGdlzTsC2ppa/lqz8O2zVBWfHWTfPrP+2MCi3logAKEVbX0L9PYw7ad3W/QGJiIpMnT+aJJ54gOrpwfeeiAAoIvljgTE1N5Z133mH7e+O5fPky19RrRZnbehBybbXs9UwZnEi5OqJevCUpa9dwTo4lp/rNM6Z48eLcc8893HPPPcSXv5eLe36jzMFV7Fs/m+RfvqLEjbdRqsm9hFVt4HBU5m3c9QwHGfMclQsFmJju8F98tkQ9Wmuee+45wsLCeP11O7mACziiAAoI3ixwaq2ZP38+Q4cO5fDhwzzwwAPc0WcwX+02ObSbm3dEXm3bEfm1C7ZqxXIkhbZl0EOteXP9aS5sWc6FhB+5tOdXQirUoFTjeyjZ8A5UsdCsayIjwr1WTMFK2e3sgwuRGUBwzHfffcfy5ct57733uO6664wWx+fITuACgqe7Y5OSkrj//vvp0aMH5cqVIz4+ngULFvD0/S35dfgdWZmLcmK7I9JZG/m1C9Z2F25IxHWUbfM4VZ+eSbmO5s04/62cTNKnT5Dy50IyL19CAW3qVvC63V63VHOrXCg8XLx4kUGDBhEdHc3AgQONFscvyAyggOBuHBqtNTNnzmTIkCFcuXKFiRMnMnDgQIKDs9v2HW3IqlTm6kjaUdsR4SH55l5pbefEns0oi0xt6l7PwhLXULJRR9L+2ca5PxaQHD+Dc7/Po1STe/nG1Jm46uW8ktFq5xcvoKLHmDFjOHLkCHPmzKFYscLZVRbOT1UIcSfw27lz5+jfvz/ffPMNrVu3Ztq0aew4H06rCetyLdQ6Cm8QYbPj1lHbo+9r4MdPnJvOsZHEpyRy8M3bs8riqpdjwso9JKmbCK9xE5f/3UvKH/NJ+W0u5zYs4pmN99Py248pX768x+2O7RwtHX5hI480kbt27eLdd9+lb9++tGjRwkBB/YsogAKCtaO2DeMcViy3BW/z5s10796dQ4cOMX78eIYNG8aSbf86XUC2t4hru+PWkZIAaP7mGkPD3Vpljxq+DA2EVb6Ril1GcuX0Yc79Po9jP88nKmoFzz//PEOGDKF0afNuZa/yxAoFG2uaSOvOX2uaSAAqkpmZydNPP02pUqV4++23DRMzPxAFUMBIM11dnLUmrwBzR/jll1/y+BP9UOGlqdBzHN8TR91t//pkh2xOJRFoYRdymqlCr72ea+99gdod+lDz8DJGjx7Nhx9+yIsvvsgzra6jxOqh9jsAD5VAcqrJcGUouIizNJGxk5k6dSrr1q1j6tSpVKjg/TpSICOLwAUIRx352yt2M3LkSPr06UNI5TpUfGQSYVUbZHXK/tghG2jZsRyFan71kY4sXLiQDRs2EBcXx7Bhw6jV4XE+/zOFjEwb7x5rB+ABi7ckkXQ2VVJFFhSchH04fvw4Q4cOpW3btoUm3o8zRAEUIOx12Jmmy2yb9Srjxo2jUtO7ubbb6wSXuBqjPNWU4dBl0RsXzkBIR2lLXrkR4uLi+OGHH/j555+pUVrT7/s0Gk+9yOoD6Vdv4iRPrDMmrNxDZg5XUUkVGcA4SAepS0fy7rvvorVm2rRpufaW5Hea0vxATEAFiJxmjszLlzi58HUuH93Je++9x/vHa4Odzj5Da8JDgj0O1+CKLLblRuHKhrSWLVvy65A6zP/9IC+uTqP97EvcXbsYE9qHUa9WDY/aPZacCna8Qo1ShkIeOEgTOeN8KzZu/JTJkydTo0aNbJcEmsnTV8gMoABha+bIuJTCia9HcDlpN/83bjJDhgwhsqz9+OTW0bAnidtdkcVKQcmOpdq9SvebSrP7mZK83S6M9YfTif70Is/+WZVTp07lfYMcOFJ6kioyQInpDvd+AGWqYQ77UI2jN7/K/038mpiYGAYMGJDrkkAzefoKmQEUIKwd9hvzf2XbVy+Sce4koyZNZ8zARwDnrqK+DtdQUJJe28Wy0Fv8p9cZ2vwofVvVYPTO6ny6YDVf/lCbMWPGMGDAAJd9v4d2rEPS7k3ZygqKMsyJr+JNBTwx3bN+BxkZGfRp14709HSGDRtGUFDeOYHzKi8oiALIL3zkdnhblWJcWPQqYVeSWb5mNS1btsw6l9+dcoHOjmXTAVQAPgKe2bWLwYMHM2jQID777DMmT55Mq1at8rxV59hIFh/fRWREcIHuOAurmSMvJkyYQHx8PNOnTycy0v7nDESTpy8QBZAf5OF37CqnT5+mXbt2HD58mBUrVmTr/K0U6E7ZYOrXr8+PP/7IokWLGDJkCK1bt+ahhx5iwoQJVKlSxem1EeEh/Dr89vwR1E8UxYQ6GzZs4OWXX6Zbt2707duXdevW2a3nzkbMgoSsAeQHzvyOcc27IDk5mfbt27Nv3z6WLFmSa2RaGD0UjEApRdeuXdm9ezcvv/wyCxcupE6dOkyYMIErV64YLZ5fKaxmDkdcuHCB3r17U7lyZaZMmeI0zn9eXmYFFUMVgFLqTqXUHqXUPqXUcCNl8StO/I6tm7mc+ZBfvnyZLl26sHPnThYtWkTbtm2z3cY6dRc/dN9RokQJXn/9dXbu3EmbNm0YNmwYMTExrFq1ymjR/EZRWszWWvP000+zb98+Zs+eTdmyZfO8pnNsJL8Ov4ODb97Nr8PvKPCdPxioAJRSwZhNr3cB9YFeSqn6RsnjVxz4HVOmKidS0px6F2RmZvLYY48RHx/PjBkzuPPOO3PdprB6KAQCN9xwA0uWLGHp0qWkp6fToUMHHnjgAQ4fPpz3xQUMVzy7CstM89NPP2X27Nm8+uqrtG7d2mhxDCNPBaCUGqiUyls9us/NwD6t9QGt9RVgLnC/H9oxnravmNPL2WJJN2cbd98W67T7pZde4uuvv2b8+PH07t3baV1Xyz2hsPzje8rdd9/Njh07GDt2LCtWrKBu3bqMGzeOy5cvGy2az8jLzFFYZpp//vkngwcPplOnTrz88stGi2MoSueR2UgpNRboCWwGpgMrdV4XudKwUg8Cd2qt+1mO+wC3aK2fzVGvP9AfoFKlSk3mzp3rUXsXLlygZMmS3gntDaln4fy/kHEFgkOhVGUIL8vpsyn8eyl39dDgIPb8tZaJEydy33338dxzzzm0Ue45ft6uIgkNDqLOdaU8Etf2eSWnmkg6m5ptt2uQUkSWDSciPMSj+3uK4d8jcPz4cT7++GPWr19P1apVGThwIPXr1zdcLnv48nn58nfmz+8xOdXEiZQ0rmRkEhocRKUyxbN+p8nJyfTv35/g4GCmTJlyNThgPsjlLd7I1qZNm01a67ic5XkqAABl7nk6AI8BccA84HOt9X6PpMF1BWBLXFyc3rhxo0ftxcfHZ0tyHigsXrGKEb9l5PIu6FPjEq8+1YMOHTrw3XffOfVJz+m+Z72HN4tUts+r+Ztr7LrARUaE8+vwOzy6v6cE0ve4cuVKBg4cSGJiIi1btuTLL7/k+uuvN1qsbPjyeVkjruZEAQffvNute/nre3T2v9CpQQU6dOjAn3/+yW+//UZsbGy+yeULvJFNKWVXAbi0BmAZ8R+3vNKBssACpZQ3sVKTyL6BvqqlrEgRER6Sa9r9fPPyvP/SAKKiovjqq6/y3JDkbw+FouYd4iodO3Zk+/btjBs3jr/++qtQmoVsKQiLxA4DJv7wN/3792fdunV8/vnndjv/okie+wCUUoOBR4DTwDRgqNbapJQKAhKBYR62vQGorZSKwtzx9wQe8vBeBRpb3/20tDRatWrFpUuXWLt2LREREW7fw9cU1k0wviAsLIwRI0ZQs2ZN5s+fz8iRI5k5cyYffPCB3QX7gkwg+MLn3Kncpm4F1v59KuvYUeTb3T98we8/f8Grr77KQw8VyW7GLq7MAMoBXbXWHbXW87XWJgCtdSZwj6cNa63TgWeBlcBuYJ7Weqen9yssPPPMM2zYsIHZs2dTv75/nKLcXdAtyHF/8otKlSqxYMECVq5ciVKKu+66i65du/LPP/8YLZrPMNoX3t4i9Jd/HKbJuVWsDx3E+tQu/BI6iPuCfsl23cW/fyH55y/o1asXr776qvNGUs/CxIYwOsL8N2Ge/z5QAJDnDEBr7fCJaa13e9O41no5sNybexQmZs+ezfTp0xk5ciSdO3f2SxuebPcv0HF/8pkOHTqQkJDAe++9x9ixY6lXrx4jR47khRdeICwszGjxvMbIneb2zDv3Bf3CmyHTKKHMm/SqqtO8GTINTLAkswWph7ZyZuk71G0Ux/Tp051u9iJhHqQcN+/UB58kCgp0ZCdwgLB3714GDBhAy5YtGT16tN/a8XTPQGHcBOMvrGah3bt306lTJ0aNGkXDhg354YcfjBatQGNvzWlYsXlZnb+VEuoKL4XO58qxPZxeNJbro2rx29ofKV68uPMGfnoddA4vJy8SBRUERAEEAJcvX6Znz56EhYW5tOjrDbKgm39cf/31WWahoKAg7rrrLrp06cKhQ4ecXheIey7clilhns9NKfbWnKqo03brnjl5gsvL3qBG1Sr8/vMal3b6OtuxX1gRBRAAvPjii2zZsoXp06dTrZqdzCI+pCB4chQ2rGah8ePH8+OPP1K/fn3Gjh1LWlparrqBuNnKbZmswQ9TjgD6qinFSyXQpm7u/LzH9LW5ynaczOCO2amEhoayatUqKleu7FoDTnbsF1ZEARjMX3/9xfvvv8/AgQO5/37/b4SWBV1jCAsLY/jw4ezevZu7776bl19+mejoaFasWJGtXiCG9XBbpjyCH3rK2r9zJ+t5O707l3Ro1vG24xm0mXWJ4PDSrF27lpo1a7reQNtXQOXoEi079gsrogAM5OzZs0yYMIH69evT4qHB+TLtN9qTI1DJy8ThK7PM9ddfz/z58/nxxx8JCgqiU6dOdOnShQMHDgD+NdF5+hnclslPphR77S3JbMFwUz+OZl7L5n8zuWN2GsVLlWPdr39St25d9xqI6W7OEmaTKYx7Pyi0C8Ag+QAMZciQIfz333+8OGkWry5LzLdEHJIzIDt5eUb5I1FK+/btSUhIYOLEiYwZM4a6devy7LPPUqFkK05eyR1ew1sTnTefwe19IGWqXvWkyVnuBY7kWJLZgp+OlePIvDGUvTbS/ZG/LeFlYcgOr+QsSMgMwCC+//57Zs2aRe/evVl0pHjATfuLEnmZOPxllrGahfbu3UufPn2YNGkSuyb15dKmxej0q54tvjDRefMZ3DYbOgl+6A1DO9YhJCi3G2fqrrXsmfUS1atX59dff/W88y+CiAIwgP/++4/+/fsTExNDnz59xDPHYPJ6/v7+fiIjI/n888/Ztm0bLZvfxqnV0zgx/Wku7oqnSukwn5jovPkMbpsN7SRd94UppXNsJBO6NcoK7Ka15vJf8zj5/bu0btWKX375hapVc88yAtGrKlAQE5Ab+Cph9pAhQzh9+jTLly8nJSWFKhHBEmrBTXyZvDwvE0d+hcKwLgqvXr2aoUOHsvX7d6jxbzzhTcaidRXnm5jywNvP4LbZ0Cbnsi+xynHu3Dn69u3LorWL6NOnD9OmTSM0NDRX/aKa59hVZAbgIr5yz1uzZg1ffPEFw4YNywpIJZ457uFrV8m8nn9+fz/t2rVj06ZNzJo1i5MnT3LnnXfSokULVq9ejaeR2AvTb2z37t3cfPPNLFmyhIkTJzJr1iy7nT8EpldVICEKwEV88UO6fPkyAwYM4IYbbmDUqFFZ5eKZ4x6+/qfO6/kb8f0EBQXxyCOPkJiYyCeffMLhw4dp3749rVu3Jj4+3qV7LN6SxJ7j54kavowJK/fwQJPIAv0b01ozZcoU4uLiOHv2LD/99JPTPBng2MSVlJwqZiHEBOQyvrADv/XWW+zdu5eVK1cSHp596i2eOa7jD5t8Xs/fqO8nNDSUp556ir59+zJt2jTGjx9PmzZtaN26NS+++CJ33nmn3Q7QOkt6um4mmiCSklNZuCnJr52+L81yOTlx4gT9+vVj6dKltG/fnhkzZhAZmfe9HZm+FGSV25qFXIu9W3iQGYCLeLuDNjExkXHjxtGzZ086dOjgS9GKHIV2N7OT8AnFixfn2WefZd++fUyaNIl9+/bRqVMnYmJimDVrFleuZI+H4y/TR84F1Q1LpsDEhujRETRd3Iom51b5dAdzZmYmn3/+OQ0aNGD16tW8//77/PDDDy51/mDf9KUgV2KbomoWEgXgIt7YULXWPP300xQvXpyJEyf6S8QiQ2GyZ2dhJ3xC6rfPMvilEdlMFOHh4QwePJgDBw4wa9YsAPr27UvNmjWZMGECZ86cAfwzS8q59tLk3CoabhoFKUdQaCItkTit4Zi97VQTEhJo2bIl/fr1o379+mzatIlBgwYRFOR6t2XPfOdoFaUoet2JAnARb+zAixYtYvXq1bzxxhtcd911/he2kFMo10zshE8I5zJDi82zO5oODQ3lkUceISEhgeXLl3PjjTcybNgwIiMjeeSRRyiZcsDugrE3s6Scs4phxeYRbicS57BiV2cunnSqhw4dom/fvsTGxrJ3715mzpzJunXrPM6PkTOSbWRhnUF6gKwBuIEnduC0tDReeOEFGjZsyP/+9z8/SVb0KHRrJg7CJFRR5hG9dTSd8zNbk8/cddddJCQkMGXKFGbPns3587MJq1CD+I5tyShzO8Ely3o9S8rZmTuKxGmVGdzrVA8ePMi7777L1KlTCQ4O5v/+7/8YMWIE5cqVc35hwjyzAk05at5t3PYVpy6oTjObpSS6LG9hQGYAfmbSpEkcPHiQSZMm+TXMs1DAcRAm4Zguf/V9HqPpmJgYPvroI44dO8bUqVOJLF+Kb7/8nKMfP0rywldpH/I3d9xQymMRc3bm9iJx2srsisLRWvPbb7/RrVs3atWqxZQpU3j00UdJTExkwoQJrnX+bkYeLZQzSA8RBeBH/v33X9544w3uv/9+2rZta7Q4gh9JTjV5Fy+/dodc4RMu6VDeTr86knV1NF2yZEmefPJJ9u9OMGeYe2kE5TL+48NXh1ChQgU6dOjABx98wP79+936jDnXXt5O706qzu5/n0oYE9K759mpnjx5kvHjx1O/fn2aN2+etfnt4MGDfPbZZ3Z39NrFw8ijkuDIjAxJ/cjIkSNJS7vM4VoPEDV8maRSLKQs3pJE0tlUkpLNnWOeu02to1Zrx5VyBLbNgUYPQeKP6JSjHNPlecvUnSWZLQDPF7mjoqJ47LHHGDNmDH/++ScLFixg2bJlDB48mMGDB1O7dm1atWpFy5YtadmyJVFRUQ796nOmBt1Uuj076teg6f4Ps8wv4W1f4X075heTycTmzZtZvnw5S5cuZfPmzQC0bNmSF154gR49elCyZEm3P19RTOLiS0QB+InNmzczc+ZMyt76AP8VM09jZRt64WTCyj30rJZ9wdWRzR5wPGpN/BGG7EABG7YksWnlHpSPfOqVUtx6663ceuutvPPOO+zbt49ly5axatUqFi5cyOeffw6Yk9vHxMQQHR1NTEwMtWrVolq1alSpUoVixYrZWXu5A7i6tqW15szp0yQmJvL333+za9cu/vjjDzZu3EhaWhpBQUHcdttt9OvXj+HDh3PDDTd4/JkAv0UeLSqIAvATL774IsHhpbjmlm7Zyp12DEKB5FhyKthJ5OZNvHx/L3LXqlUraxaQmZnJzp07Wb9+PRs2bGD79u18/PHH2TKWBQUFUalSJcqUKUOpUqUoWbIkQUFBmEwm0tPTuXjxIqdOneLUqVOYTKas60JDQ4mNjeWpp57itttuo23btpQvX574+HjvO38wL/jazqag0Cdx8SWiAPzA6tWrWb16NWXveJKgsGtynS+K/saFGbNt/ryDcjsE2Kg1KCiI6OhooqOjs8oWbjzMG1+vJenIP5RKT6HxtRmUzrzAuXPnuHDhAufPn0drTbFixShRogTly5enSZMmVKxYkUqVKlGrVi3q1KlDVFSUf50frOYmN7yAhKuIAvAxmZmZDB8+nOuvv54qt3fl34sZueoURX/jwszQjnVI2r0pW1me8fIDeNS6eEsSo77bRWrItYTXvJZ0YHtIcOB6yvgp8mhRQLyAfMzChQvZtGkTr7/+Oi/eE134dqwKuegcG0lk2XDD4+X7ComgWXSQGYAPMZlMjBw5koYNG/Lwww8THGzu/P0VIEsIHCLCQ/h1+O2uXxDAo1ZJUFR0EAXgQ6ZPn05iYiJLlizJ6vwL3Y5VodCTXwlwBOMRE5CPuHz5MmPHjqVZs2bcc889RosjCB5TKIPtCXYxZAaglJoA3AtcAfYDj2mtk42QxVdMnz6do0ePMmPGDK9S9wmC0eTc8CWmy8KLUSagVcAIrXW6UuotYATwokGyeM3ly5cZP348zZo1k5APQqFATJdFA0MUgNb6R5vDP4AHjZDDV8ycOZMjR44wbdo0Gf0LAY2rWbv8md1LCByUp0mmfSaAUt8D32itv3Rwvj/QH6BSpUpN5s6d61E7Fy5c8CzWSB6YTCb69OlD+fLlmTx5stsKwF9yeYvI5R4FQa7kVBNJZ1PJtPmfD1KKyLLhRISHZJW5Ws9XcgUSgSoXeCdbmzZtNmmt43KW+20GoJRaDdjLfjJSa/2dpc5IIB34ytF9tNZTgakAcXFx+vbbb/dInvj4eDy91hmfffYZJ06cYObMmbRp08btkZO/5PIWkcs9Almu5DK1mbByD0nJV4DgXHUiI4KzubA2f3NNVmA7Z/W8lStQn1cgygX+kc1vCkBr3c7ZeaVUX+AeoK02ehriISaTiXHjxnHzzTfTsWPHrJR51k00EvxNMJrkVBMjftqea2OXLTn9+2UfQNHBKC+gO4FhQGut9SUjZPAFX375JYcOHSK8dX9qjlhOkFJkaDeiQgqCnzmRkkaqybm3d07//oDaB+Bmti/BPYzaBzAZKAWsUkptVUp9apAcebJ4S5LdRB+ZmZm8MmY8YZVqcrFSNBpydf5WZOQkGMWVjEyn5+359wfMPgAPsn0J7mGUF1AtI9p1F2cmnaAjmzh6MJFr7x2a58Kv7KAUjCI02PEYL9LBGlXA7ANwlu1LZgE+QUJBOMFZUCy19G2CS1ekRN0WTu8hOygFI6lUpjjhIRm5EqDnFdkzIPYBSLYvvyMKwAmOTDcHdmzi+K+/EnXvs2QG5faWCFaKTK3Ff1rINxx5n0WEhzC+a33DR/O55GvkeFE6iwDLm1AYEQXgBEeLYZc3L6Z8+fKMGz6I11bsd3t0JQi+xJmpMgLfjOa92RhmT76ksxks3pLk/B4BnjehMCDB4JxgbzEsKCWJs7t/49lnn6Vns9qM7xrtehx4QfAD/o7fb+3Ak5JT0VxVMFaHCE/ky9Q6b/kCPG9CYUBmAE6wtxgW/vcajoeH88wzz2TVkQ5fMBLnfvu5U5K6izMF48pv36t9BQGcN6EwIAogD2w7+OPHj3P9K9/y5JNPUqFCBYMlEwQz/vbb93ZjWEDtKxCyISYgN5gyZQomk4nnnnvOaFEEIQt/++076qhd7cDtmlKVEu+4AEAUgItcuXKFTz75hE6dOlG7dm2jxRGELDrHRvp1LcpbBWNPvsiy4WI6DQDEBOQi8+bN48SJEwwaNMhoUQQhF/5ci/LFxrCc8sXHx/taTMEDRAG4gNaa999/nzp16tC+fXujxRGEfMeRgpG8AQUbUQDOsASi+nPnITZuvMhHLz1OUJBYzQQBnO8/ECVQMJDezBE2gag++PMypcPgkeDvJRCVIFjw9/4Dwf+IAnCEJRDVsfOZzN+VzhOxoZQMumwuFwRB8gYUAkQBOMIScOrTjVfIyIRnmoZmKxeEoo637qGC8YgCcESZqpgyNJ9tNtGpdjFuKBeUVS4IQgDlDRA8RhSAI9q+wvf7gzh+QfNUnCURtgSiEoQs/L3/QPA/4gXkiJjuTDn0BtUidnNXrRBzICpJRycI2ZBYWAUbUQAOOHDgAD/+nsBrr71G8Csy6hcEofAhCgDsJp6eOmczwcHBPPHEE0ZLJwiC4BdEAVj9/a1JJ1KOcGXRQGZ8dpl77rmHyEiZ3gqCUDgRBWAn8fTiHec5+V8q//vf/wwSShAEwf+IF5Adv/4pm65QvYyiQ4cOBggkCIKQP4gCyOHXn3gmgzUHM3iyWQWCg3MnfBcEQSgsiAJo+4rZv9/CjK0mgoPg8ecl5IMgCIUbUQA2iaczMuGL7Znc2bwxlduK/V8QhMKNKAAwK4EhO1jV7BuSUtJ5bPBLRkskCILgd8QLiKtJLbbOGkex8FJkVo01WiRBEAS/Y+gMQCn1vFJKK6WuNUoGa1KLw8dPcSnxD8Lr384rS/eyeEuSUSIJgiDkC4YpAKVUNaADcNgoGeBqUotLu9ZBhomS0e0kqYUgCEUCI2cAE4FhgDZQhqzkFRd2rCakYhShlW7IVi4IglBYMUQBKKXuB5K01tuMaN+WKhHhXDn1D1f+TaRkw3bZygVBEAozSmv/DMCVUquB6+ycGgm8BHTQWqcopQ4BcVrr0w7u0x/oD1CpUqUmc+fO9UieCxcuULJkyVzlyakmPpz8MfErv2fMh9MpVboMQUoRWTaciPAQj9ryhVxGI3K5h8jlHiKX+3gjW5s2bTZpreNyndBa5+sLiAZOAocsr3TM6wDX5XVtkyZNtKes4wcQNgAAClRJREFUXbvWbrnJZNIR5Svocg1a6BovLtXNxv+kF20+6nE7vpLLaEQu9xC53EPkch9vZAM2ajt9ar67gWqttwMVrcd5zQB8jdXl81hyKlUiwmlX6l+Sz5zi28+m0KXL3fkhgiAIQkBQpPYBWF0+U00ZACQlpzJpzgyuKVWGTp06GSydIAhC/mL4TmCtdY38Gv1bXT6tZJrSOL/nN66p25ywsLD8EEEQBCFgMFwB5Cc5XTtTE/9EX0lF1WphkESCIAjGUaQUQE7Xzou74gkuWZ6aDZsaJJEgCIJxFCkFMLRjHcJDzDH+My6lkHpwM2Ua3s6wu+oZLJkgCEL+U6QWgTvHmvP7Tli5h7+3LIfMDEYN7p9VLgiCUJQoUjMAMCuBX4ffQb2L26hfvz7P9WhvtEiCIAiGUOQUAMChQ4f49ddf6d27N0opo8URBEEwhCKpAL7++msAevXqZbAkgiAIxlEkFcDcuXO59dZbiYqKMloUQRAEwyhyCmDv3r0kJCTQo0cPo0URBEEwlCKnAObPnw/Agw8+aLAkgiAIxlLkFMC8efNo1qwZVatWNVoUQRAEQylSCsBq/unWrZvRogiCIBhOkVIAYv4RBEG4SpFSAGL+EQRBuEqRUQBHjhwhISGB7t27Gy2KIAhCQFBkFMC6desAeOCBBwyWRBAEITAoMgpg7dq1Yv4RBEGwoUhEA927dy8HDhxg0KBBTuvlzBc8tGMdiRQqCEKhpUgoAKv3jzPzj718wSO+3Q4gSkAQhEJJkTABVaxYkY4dOzo1/+TMFwyQaspgwso9/hZPEATBEIrEDODJJ5+kdu3aTuvkzBecV7kgCEJBp0jMAFwhZ77gvMoFQRAKOqIALNjmC7YSHhLM0I51DJJIEATBvxQJE5Ar2OYLFi8gQRCKAqIAbOgcGykdviAIRQYxAQmCIBRRRAEIgiAUUUQBCIIgFFEMUwBKqYFKqb+VUjuVUm8bJYcgCEJRxZBFYKVUG+B+oJHW+rJSqqIRcgiCIBRljJoBDADe1FpfBtBanzRIDkEQhCKLUW6gNwItlVJvAGnAC1rrDfYqKqX6A/0thxeUUp4G57kWOO3htf5E5HIPkcs9RC73CFS5wDvZqtsr9JsCUEqtBq6zc2qkpd1ywK1AU2CeUqqm1lrnrKy1ngpM9YE8G7XWcd7ex9eIXO4hcrmHyOUegSoX+Ec2vykArXU7R+eUUgOAby0d/l9KqUzM2u2Uv+QRBEEQsmPUGsBioA2AUupGIJTAnXYJgiAUSoxaA5gOTFdK7QCuAI/aM//4GK/NSH5C5HIPkcs9RC73CFS5wA+yKf/3u4IgCEIgIjuBBUEQiiiiAARBEIoohUoBKKW6WUJLZCqlHLpLKaXuVErtUUrtU0oNtymPUkr9aSn/RikV6iO5yimlVimlEi1/y9qp00YptdXmlaaU6mw5N1MpddDm3E35JZelXoZN20tsyo18XjcppX63fN8JSqkeNud8+rwc/V5szodZPv8+y/OoYXNuhKV8j1KqozdyeCDX/ymldlmez09Kqeo25+x+p/kkV1+l1Cmb9vvZnHvU8r0nKqUezWe5JtrItFcplWxzzp/Pa7pS6qRlTdTeeaWU+sAid4JSqrHNOe+el9a60LyAekAdIB6Ic1AnGNgP1MTsfbQNqG85Nw/oaXn/KTDAR3K9DQy3vB8OvJVH/XLAf0AJy/FM4EE/PC+X5AIuOCg37Hlh3kxY2/K+CvAvEOHr5+Xs92JT52ngU8v7nsA3lvf1LfXDgCjLfYLzUa42Nr+hAVa5nH2n+SRXX2CynWvLAQcsf8ta3pfNL7ly1B8ITPf387LcuxXQGNjh4HwnYAWgMO+d+tNXz6tQzQC01ru11nntFL4Z2Ke1PqC1vgLMBe5XSingDmCBpd4soLOPRLvfcj9X7/sgsEJrfclH7TvCXbmyMPp5aa33aq0TLe+PASeBCj5q3xa7vxcn8i4A2lqez/3AXK31Za31QWCf5X75IpfWeq3Nb+gPoKqP2vZKLid0BFZprf/TWp8FVgF3GiRXL+BrH7XtFK31z5gHfI64H/hCm/kDiFBKVcYHz6tQKQAXiQSO2BwftZSVB5K11uk5yn1BJa31v5b3x4FKedTvSe4f3xuW6d9EpVRYPstVXCm1USn1h9UsRQA9L6XUzZhHdfttin31vBz9XuzWsTyPFMzPx5Vr/SmXLU9gHkVasfed5qdcD1i+nwVKqWpuXutPubCYyqKANTbF/nperuBIdq+fV4FLCamchJjQWn+X3/JYcSaX7YHWWiulHPreWjR7NLDSpngE5o4wFLMv8IvA6/koV3WtdZJSqiawRim1HXMn5zE+fl6zMe8lybQUe/y8CiNKqYeBOKC1TXGu71Rrvd/+HXzO98DX2hwJ+H+YZ0935FPbrtATWKC1zrApM/J5+Y0CpwC0kxATLpIEVLM5rmopO4N5alXMMoqzlnstl1LqhFKqstb6X0uH5Sz6aXdgkdbaZHNv62j4slJqBvBCfsqltU6y/D2glIoHYoGFGPy8lFKlgWWYlf8fNvf2+HnZwdHvxV6do0qpYkAZzL8nV671p1wopdphVqqttSX6Ljj8Tn3RoeUpl9b6jM3hNMxrPtZrb89xbbwPZHJJLht6As/YFvjxebmCI9m9fl5F0QS0AaitzB4soZi/7CXavKqyFrP9HeBRwFcziiWW+7ly31y2R0snaLW7dwbsegv4Qy6lVFmrCUUpdS3QHNhl9POyfHeLMNtGF+Q458vnZff34kTeB4E1luezBOipzF5CUUBt4C8vZHFLLqVULDAFuE/bhFx39J3mo1yVbQ7vA3Zb3q8EOljkKwt0IPtM2K9yWWSri3lB9XebMn8+L1dYAjxi8Qa6FUixDHK8f17+Wtk24gV0wWwH+//27pilrSiMw/jz1qEWddGpnYqTg4ODLo5udvATlELr4uA3cHEQ/ARujqJCtw4FQe3m4mKRDm0zduk3UDIch3MK1yIkcDWJnOcHIclNDnlzcm/+3Jvcc26Bv8BJWf4G+Np43jvgFznBtxrLZ8kbaAf4DLx8pLpmgDPgN3AKTJfli8B+43lvyan+4r/258A1+YvsAJgcVF3Acnnt7+V6fRT6C3gPdIGrxmXhKfrrofWFfEhprdweL++/U/pjttF2q7T7Caw+8vreq67Tsh38658vvT7TAdW1C/wor/8NmGu0/VT6sQN8HGRd5f42ea6SZrun7q8j8r/YuuTvr3VgA9gojwewV+q+pvEPx7b95VAQklSpGg8BSZIwACSpWgaAJFXKAJCkShkAklQpA0CSKmUASFKlDACphYhYKoOajUfEROT5CeaHXZfUD08Ek1qKiB3y2cCvgD8ppd0hlyT1xQCQWipjy1wCN8Byuj+KpDSyPAQktTcDTAJT5D0B6VlwD0BqKfIcscfkSURep5Q2h1yS1JdnNx+ANEoi4gPQTSkdRsQYcBERKyml815tpWFzD0CSKuVvAJJUKQNAkiplAEhSpQwASaqUASBJlTIAJKlSBoAkVeoORkVb2cpwg0AAAAAASUVORK5CYII=\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYAAAAEWCAYAAABv+EDhAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8li6FKAAAgAElEQVR4nOydfXzN5fvA3/dmswnbCDG+ocKwMSYVyYhVUspzj0hKUpEVQlJ9KaUH9FyknwjVUMmzPJSv58eQRJjI02azjT3cvz/O2Zxt55ydx33Otuv9ep3Xzuf+3J/PfZ3PObuv+77u674upbVGEARBKHv4GS2AIAiCYAyiAARBEMooogAEQRDKKKIABEEQyiiiAARBEMooogAEQRDKKKIABK+ilBqvlPo/o+WwRCn1oFJqmYN17cqvlBqslDqllEpVSlU1/63vhmxrlFIDXb1eEJxBFIDgEEqpI0qpdHMHd0opNVMpVdFouVxBaz1ba93Z3fsopQKAKUBnrXVFrfVZ89+/zOdnKqVec7edkoRZYWaafyep7ipEwbuIAhCcoavWuiLQAogBxhgsj9HUAIKAvUYLUhRKqXLF2Nw3ZkVY0VIhCr6HKADBabTWicASoCmAUqqWUmqRUuqcUupPpdTj1q5TSv2olBpaoGyXUuo+83utlHpSKXVQKZWklJqulFLmc35KqTFKqb+VUv8qpWYppULM5+qar+2vlDqmlDpvvk8r8/2TlFLTLNrsp5Rab3H8nvm6C0qprUqpW4t6BkqpBsAB82GSUmqVxWe4Xik1CHgQeME8Cl5s4z6dlFL7lVLJZhlVgfMDlFL7zJ9pqVLqWotznZVSB8zXfqCU+iXXfGT+jBuUUu8opc4C4x24XyOl1HLz93hAKdWrqOcglGxEAQhOo5SqA9wFbDcXzQWOA7WAHsB/lVIdrFz6JfCQxX2aAeHAjxZ17gZaAVFALyDOXN7P/IoF6gMVgWnkpzVwA9AbeBd4CbgdaAL0UkrdZuMjbQaaA1WAr4H5SqkgG3UB0Fr/Yb4vQKjWukOB858As4E3zaPgrgXvoZS6GvgO00zqauAQ0Mbi/L3AaOB+oBqwDphjce0CYBRQFZMyusXK8/gL00zl9SLudxWw3Pz5qwN9gA+UUo3N50eaFanVV4F2u5qVyF6l1GB7z1EwGK21vORV5As4AqQCScDfwAdAMFAHyAYqWdSdCMw0vx8P/J/5fRBwHrjBfPwW8IHFdRpoa3E8Dxhpfr8SeMriXEMgEygH1DVfG25x/izQ2+L4W+A58/t+wHo7n/U80Kyg/Fbq5bZbrsBnuN78fibwmp12HgE2WhwrTIp0oPl4CfCYxXk/IA241nztbwWuPWZxbT/gaIH27N2vN7CuQP2PgZed/J00xjQQ8MekkP4B+hr9+5WX9ZfMAARn6Ka1DtVaX6u1fkprnY7pn/2c1jrFot7fmEb2+dBaZwDfAA8ppfyAvsBXBaqdtHifhmmkj7mdvwu0UQ7T6DaXUxbv060cW120VkqNMJtFks2j2RBMI3JvUwtTpw2ANvWgxyzOXwu8ZzHKPoepow+3ce3xAvc/VuDY3v2uBVoXGNU/CFzjzAfSWv+utT6htc7WWv8KvIdpVij4IMW5MCSUTk4AVZRSlSyUwH+ARBv1v8TU6a8H0rTWvznRzrUWx/8BsjB18rWdltqM2d7/AtAR2Ku1zlFKnaeALd5Figq1+w+mGVSuLMryGFMH/rrWenbBC5VSN2Dxuc3XFnwOBdu3d79rgV+01p2sCaqUGo3JfGQVbXIOsHoKzzxLwQvIDEBwC631MeBXYKJSKkgpFQU8Blj1nTd3+DnA2xQe/dtjDjBMKVVPmdxP/4vJ2yTLrQ8AlTApktNAOaXUOKCym/fM5RSm9Qpb/Ag0UUrdr0xeOs+Qf8T9ETBKKdUEQCkVopTqaXFtpFKqm/naIRQ9Wrd3vx+ABkqph5VSAeZXK6VUBIDW+r86v2dPvlduA0qpe5VSYcrEjebPtLDIJyUYgigAwRP0xWQPPwF8j8luvMJO/VlAJDaUhA2+wKQw1gKHgQxgqN0rHGMp8DPwByazUgaFTSeu8jnQ2GxSSSh4Umt9BugJTMK0ZnEDsMHi/PfAG8BcpdQFYA9wZ4Fr3zRf2xjYAlyyJUwR90sBOmNa/D2ByRT3BlDeyc/cB/gTSMH0Pb+htf7SyXsIxYQymQ4FofhQSj0CDNJatzValtKCeU3lOPCg1nq10fIIJQOZAQjFilKqAvAU8InRspR0lFJxSqlQpVR5TPZ5BWw0WCyhBGGoAjD/eBeYN8LsU0rdbKQ8gndRSsVhsrWfwuRvLrjHzZj2DpwBumLy0ko3ViShJGGoCUgp9SUm3+PPlFKBQAWtdcFNJYIgCIIXMEwBKNM2/h1AfS0LEYIgCMWOkfsA6mEyB8wwhwTYCjyrtb5oWckcU2UQQHBwcMs6deoUupEj5OTk4Ofne0seIpdziFzOIXI5h6/KBe7J9scff5zRWlcrdMKoLciYoklmAa3Nx+8Br9q7pmXLltpVVq9e7fK13kTkcg6RyzlELufwVbm0dk82YIv2sVAQx4HjWuv/mY8XYAozLAiCIBQDhikArfVJ4JhSqqG5qCPwu1HyCIIglDWMjgU0FJht9gD6C+hvsDyCIAhlBkMVgNZ6B6a1AJfJzMzk+PHjZGRk2K0XEhLCvn373GnKK4hcVwgKCqJ27doEBAQUa7uC4IskbE9k8tIDnEhKp1ZoMPHNsj3ehtEzALc5fvw4lSpVom7dupgCIlonJSWFSpUqFaNkjiFymdBac/bsWY4fP069evWKrV1B8EUSticy6rvdpGeaOv3EpHQSz2eTsD2RbtGFIq27jG/6OzlBRkYGVatWtdv5C76PUoqqVasWOZMThLLA5KUH8jr/XHK0ZvLSAzaucI0SrwAA6fxLCfI9CoKJE0nWI3rYKneVUqEABEEQShO1QoOdKncVUQAG0L59e7Zs2WJI27fcUjBveGEqVrSV3OkK48eP56233rJbJyEhgd9/F89eQXCW+LiGBAf45yvzU4r4uIY2rnANUQBljF9//bXY2hIFIAiu0S06nIn3RxIeGmxK2hwaTHhYsEcXgKEMKoCE7Ym0mbSKeiN/pM2kVSRst5W61jGOHDlCo0aNePDBB4mIiKBHjx6kpaUBsHLlSqKjo4mMjGTAgAFcupQ/WdMXX3zBiy++mHf86aefMmzYMI4cOUJERASPP/44TZo0oXPnzqSnm2x/O3bs4KabbiIqKor77ruP8+fPA6ZZxbBhw4iJiSEiIoLNmzdz//33c8MNNzBmzJi8NnJH96mpqXTs2JEWLVoQGRnJwoVFZ+17/fXXadCgAW3btuXAgSuLUZ9++imtWrWiWbNmdO/enbS0NH799VcWLVpEfHw8zZs359ChQ1brCYJgnW7R4WwY2YHDk7qwYWQHQoM97x5dphRArmtVYlI6GpNr1ajvdrutBA4cOMBTTz3Fvn37qFy5Mh988AEZGRn069ePb775ht27d5OVlcWHH36Y77pevXqxZMkSMjMzAZgxYwYDBgwA4ODBgwwZMoS9e/cSGhrKt99+C8AjjzzCG2+8wa5du4iMjOSVV17Ju19gYCBbtmzhySef5N5772X69Ons2bOHmTNncvbs2XxtBwUF8f3337Nt2zZWr17N888/nxujySpbt25l7ty57Nixg59++onNmzfnnbv//vvZvHkzO3fuJCIigs8//5xbbrmFe+65h8mTJ7Njxw6uu+46q/UEQbDP5cuXmTFjBikpKR6/d5lSANZcq9Izs912rapTpw5t2rQB4KGHHmL9+vUcOHCAevXq0aBBAwAeffRR1q5dm++6ihUrctttt/HDDz+wf/9+MjMziYyMBKBevXo0b94cgJYtW3LkyBGSk5NJSkritttus3rPe+65B4DIyEiaNGlCzZo1KV++PPXr1+fYsfxpbrXWjB49mqioKG6//XYSExM5deqUzc+4bt067rvvPipUqEDlypXz2gLYs2cPt956K5GRkcyePZu9e/davYej9QRBuMLKlSsZMGAAe/bs8fi9S/xGMGfwlmtVQfdFZ9wZH3nkEd577z0aNWpE//5XImGUL38lF7e/v3+eCcgeudf4+fnlu97Pz4+srKx8dWfPns3p06fZunUrAQEB1K1b12Uf/H79+pGQkECzZs2YOXMma9ascaueIAhXWLBgAZUrV6Zly5Yev3eZmgF4y7Xq6NGj/PbbbwB8/fXXtG3bloYNG3LkyBH+/PNPAL766qu8kbslrVq14tixY3z99df07dvXbjshISGEhYWxbt06u/d0hOTkZKpXr05AQACrV6/m77//tlu/Xbt2JCQkkJ6eTkpKCosXL847l5KSQs2aNcnMzGT27Nl55ZUqVco3bbVVTxAE62RmZpKQkEDXrl0JDAz0+P3LlAKw5loVHODvtmtVw4YNmT59OhEREZw/f57BgwcTFBTEjBkz6NmzJ5GRkfj5+fHkk09avb5Xr160adOGsLCwItv68ssviY+PJyoqih07djBu3DiXZH7wwQfZsmULkZGRzJo1i0aNGtmt36JFC3r37k2zZs248847adWqVd65V199ldatW9OmTZt89+nTpw+TJ08mOjqaQ4cO2awnCIJ1Vq1axblz5+jVq5d3GrCWJMBXX9YSwvz+++8OJUS4cOGC1lrr77cd17dMXKnrvviDvmXiSv39tuMOXW+Lw4cP6yZNmrh8/YULF3SXLl30ihUr3JLD0+Q+r+KmqO/TVxN2iFzOIXI5xoABA3TlypV1enq6VxLClKk1ADC5Vnnal9ZVkpKSiImJITo6mo4dOxotjiAIPsTly5f57rvvuPfeewkKCvJKG2VOAXiaunXrurw6Hxoayvbt230yGqggCMayYsUKkpKS6N27t9faKFNrAIIgCCWFefPmERISQqdOnbzWhigAQRAEH+PSpUskJCRw3333ecX7JxdRAIIgCD7G8uXLSU5O9p73jxlRAIIgCD7GvHnzCAsL87pziCgAA8gNyHbixAkefvhhq3UcCRn97rvv5guodtddd5GUlOQ5QR3gyJEjfP3118XapiCUZjIyMorF/AOiAAylVq1afPXVVy5fX1AB/PTTT4SGhnpCNIcRBSAInmXp0qWkpKR43fwDZVEB7JoH7zSF8aGmv7vmuXW7kSNHMn369Lzj3EQpjoRbPnLkCK1btwYgPT2dPn36EBERwX333Zcv9s/gwYOJiYmhSZMmvPzyywC8//77nDhxgtjYWGJjYwGTS+qZM2cAmDJlCk2bNqVp06a8++67ee3ZCjNtyfz582ndujXNmjWjXbt2AGRnZxMfH0+rVq2Iiori448/zvv869ato3nz5rzzzjtuPUtBEEzmn6pVq9KhQwfvN2Ztd5ivvtzeCbzzG61fq6H1y5WvvF6rYSp3kW3btul27drlHUdEROijR4/qzMxMnZycrLXW+vTp0/q6667TOTk5Wmutr7rqKq21aRdxRESE1lrrt99+W/fv319rrfXOnTu1v7+/3rx5s9Za67Nnz2qttc7KytK33Xab3rlzp9Za62uvvVafPn06r+3c4y1btuimTZvq1NRUnZKSohs3bqy3bdumDx8+rP39/fX27du11lr37NlTf/XVV4U+U9OmTfX+/fu11lqfP39ea631xx9/rF999VWttdYZGRm6ZcuW+q+//tKrV6/WXbp0cfn5FUR2AnsWkcs5DJNr5zdaT2miU0ZV1hUClX68e8dCVbyxE7hszQBWToDMAiPezHRTuYtER0fz77//cuLECXbu3ElYWBh16tRxOtzy2rVreeihhwCIiooiKioq79y8efNo0aIF0dHR7N27t8gsW+vXr+e+++7jqquuomLFitx///15AeSshZkuSJs2bRg8eDCffvop2dmm8NnLli1j1qxZNG/enNatW3P27FkOHjzo1LMSBMEKu+bB4mcg+RgL92eSdlnzUOg2t60TjlC2dgInH3eu3EF69uzJggULOHnyZN6uPU+FWz58+DBvvfUWmzdvJiwsjH79+rkcthkcCzP90UcfsWrVKtasWUPLli3ZunUrWmumTp1KXFxcvroS0lkQ3MRiYDp7dyb/CVG0Dc8ylUeJG6jnCKntXLmD9O7dm7lz57JgwQJ69uwJuBZuOXcxdc+ePezatQuACxcucNVVVxESEsKpU6dYsmRJ3jUFwy3ncuutt5KQkEBaWhoXL17k+++/59Zbb3X48xw6dIhWrVoxYcIEqlWrxrFjx4iLi+PDDz/My172xx9/cPHiRZsyCEJZxdm0s9o8AP33Yg7LDmXxYGQAfkq5PTB1hLI1A+g4zjTVsjQDBQSbyt2gSZMmpKSkEB4eTs2aNQFTuOWuXbsSGRlJTExMkeGPBw8eTP/+/YmIiCAiIiIv+UOzZs2Ijo6mUaNG+TKPAQwaNIg77riDWrVqsXr16rzyFi1a0K9fP2688UYABg4cSHR0tFVzjzXi4+M5cOAASik6duxIs2bNiIqK4siRI7Ro0QKtNdWqVSMhIYGoqCj8/f1p1qwZ/fr1Y9iwYc48OkEoVeSmnc3NPJibdhawGoQyYXsirXRVwtUZvtmTRbaGByPNuX/dHJg6gtJ28sAWB0opf2ALkKi1vtte3ZiYGF3QN37fvn1EREQU2U5KSoop6NqueaapVfJx0wPuOM7r0yyH5PIxjJKrqO9zzZo1tG/fvvgEchCRyzlKq1xtJq0i0UqGwfDQYDaMLOzV02bSKlpeWM6kgM+I/fwcl7Nh+xMVSac8wfdPy9c3uSObUmqr1jqmYLkvzACeBfYBlYultahehnb4giCUXpxNO3siKZ1E2pJ06hybEj/hzduDOJ5zNZOzevFeMfRThq4BKKVqA12Az4yUQxAEwRM4m3Y2t3zRnhRA8V6Dj2h7+X22VPZeBFBLjF4Efhd4Achx5yZGm7EEzyDfo1DScTbtbHxcQ4LK+XFx7xqCro2iXKWrPZKm1lEMWwNQSt0N3KW1fkop1R4YYW0NQCk1CBgEUKNGjZZz587Nd75ixYrUqFGDkJAQlFI228vOzsbf39/meaMQuUxorUlOTubUqVOkpqbarJeampoXS8mXELmcozTLlZSeyankDC5n5xDo70eNkCBCgwNs1t+0fRcvDn+WBx4fSrsOnWzWd0e22NhYq2sARiqAicDDQBYQhGkN4Dut9UO2rrG2CJyZmcnx48eL9I3PyMjwWlo1dxC5rhAUFETt2rUJCLD9z1JaFw+9hcjlHEbI9dRTTzFjxgxOnjxJSEiIzXqlahFYaz0KGAVgMQOw2fnbIiAggHr16hVZb82aNURHRzt7e68jcglC2SUjI4M5c+bQvXt3u52/tzB6DUAQBKHMkpCQQFJSEv379zekfV9wA0VrvQZYY7AYgiAIxcqMGTO49tpr8yL6FjcyAxAEQTCAo0ePsnz5ch599FH8/IzpikUBCIIgGMCsWbPQWtOvXz/DZBAFIAiCUMxorZk5cyaxsbEOObF4C1EAQunAw5neBMGbrFu3jkOHDhm2+JuLKACh5GORUAO06e/iZ0QJCD7LK29Nx798BcbsqOBQyGhvIQpAKPl4IdObIHiLOesPsPrnRQQ3bIsKCMoLGW2EEvAJN1Ch9JKwPZHJSw9wIimdWqHBxMc1tBoX3S28lOlNELzBmLc/QmdmUDGqc15ZemY2k5ce8Pz/RhHIDEDwGrnJMRKT0tHgvZGOlzK9CYKn0Vpz/LfFBFSvR2Ct/AHfbIWM9iaiAASvMXnpgbzMSLnkjnQ8Ssdxpsxulngg05sgeJrNmzdz+dQhKjW/s1DwSlsho72JKADBazibHMNlonpB1/chpA6gTH+7vi+JfwSf46OPPiIouAJVm+XPDlacIaAtkTUAwWvUCg22mh7PKyMdyfQm+DhJSUnMnTuXhx96iLv63uT9tTEHEAUgeI34uIb5EmSDcSMdQTCar776ivT0dJ544glaRocb0uEXRBSA4DVyf+C+MNIRBCPRWvPxxx8TExNDy5YtjRYnD1EAglfp5iMjHUEwkg0bNrB3714+/fRTo0XJhygAQRAENylqv8tHH31E5cqV6dOnj4FSFkYUgCAIghvk7nfJXevK3e8CphnwyZMnmTdvHk888YTP5UEWN1BBEAQ3KGq/y8cff0xmZiZDhw41Qjy7iAIQBEFwA3v7XS5fvsyHH37InXfeSYMGDYpZsqIRBSAIguAGtva11AoNZt68eZw6dYpnn322mKVyDFEAgiAIbhAf15DgAP98ZcEB/ozo3ID33nuPhg0b0qlTJ4Oks48sAguCIDhJQa+f7i3DWb3/dD4voBoZR9myZQvTp083LOdvUYgCEARBcAJrXj/fbk1k4v2R+Vw/+/YdQUhICI888ohRohaJKABBEAQnsOb10yn7F25a+DQsPAMhtUls+jQLFizgmWee8TnXT0tEAQiCIDhBQa+fe/zWMyngMypw2VSQfIxprz1PTk42Q4YMMUBCx/FNw5QgCIKPUtDr54Vy86igLucdX7ik+fB/aXSPrET9+vWLWzynEAUgCILgBAW9fmqpM/nOf7r1MsmXIL5VfjNRwvZE2kxaRb2RPxqaCN4SMQEJgiA4QcEot/+qalzDaQAuZ2ve2XiZ2Lr+tGpcN++aosJFGIUoAEEQBFvsmgcrJ0DycVOO6Y7jIKpX/ii3uy7C4mcgM52vd2eSmKL54J6KPHu6K1smrSI+riHjF+21GS6iTCoApVQdYBZQA9DAJ1rr94ySRxAEIR+75uV17AAkHzMdQ/7sc+b3OctfYfKv+4moEcjyOk+yOKctJKUTP38nmTnaahNGJIK3xMg1gCzgea11Y+AmYIhSqrGB8giCd9g1D95pCuNDTX93zTNaIsERVk640vnnkpluKi9IVC9+avgGv5/O4d9WQ1msb71yiY3OH4xJBG+JYTMArfU/wD/m9ylKqX1AOPC7UTIJgsdxdBQp+B7Jx50qf+ONN/CvXI2rGt1q9bw1jE6PqrS2rZ2KTQil6gJrgaZa6wsFzg0CBgHUqFGj5dy5c11qIzU11Sc3ZIhczlHi5Pr3d8i+XLjcPxCqe3/CW+Kel8Hkk8uJ727Xrl08++yz9HxkILd2vtuhtsr5KSJqVnZNNieJjY3dqrWOKVhuuAJQSlUEfgFe11p/Z69uTEyM3rJli0vtrFmzhvbt27t0rTcpDXIVlQ3JKLmKE5tyjQ/FtMRVEAXjk7wsVQl8XgaTT66CszeAgGDo+n6h2dvtt9/Onj17eO+79Yxf8me+Bd8APwUKMrOv/A6CA/wLhY5wSjYnUUpZVQCG7gNQSgUA3wKzi+r8Bd8k170tMSkdzRX3Nl/wcfYJQmo7Vy74DlG9TJ19SB1Amf5a6fw3bNjAypUriY+Pp/ct1zPx/kjCzbZ9f6XIzNFcFViOsAoBKCA8NNjpzt9bGOkFpIDPgX1a6ylGySG4h71sSL7wAzecjuOsjyI7jjNOprKGDVdOh4jqVWTdCRMmUK1aNZ588kngil+/pd9/UnomwQH+vNO7uU/9Xxg5A2gDPAx0UErtML/uMlCeEonRuwvtZUMScHgUKXiJXDNO8jFAX1mE95An1saNG1m2bBnx8fFcddVVeeVFpYn0FYz0AloPKKPaLw34wu7CWqHBJFrp7I12b3MFR9YyXFrvcGAUKXgJe66cHvhOJkyYwNVXX83gwYPzlZeUgZHEAirB+MIow1Y2JKPd25zFkbUMWe8ogTjpygmOz6o3b97MkiVLeP755wt559hLE+lLiAIowfjCKKNbdHjeopezC1z2/tGK27TliDL1BYUrOImTi/BJ6ZkOK/kxY8ZQtWpVqyGfS8rASGIBlWBcNb8kbE/klcV7OZ+WCUBocADj72nistkoX1wUB7FnvgJsngt1ScKicUSZ2q9zldVzgsE4uQh/KjmD9Mz842JrTg2rVq1i2bJlTJkyhUqVKhW6T8GAcd52j3YVUQAlmPi4hvk6Sih6lJGwPZH4BTvz+SQnpWcSP38nUHxrB0WNpm2de/0m70xaHVGmpWm9o8yQa+d30AvocnYO1gwjlspfa82oUaOoU6dOIdu/Ja4MjIobMQGVYFwxv0xeeiBf559LZo4uVlOGvdG0EaYtR6bsJWVaLxQgqhcM22PaeDdsj93F30B/612ipZJfuHAhmzZtYvz48QQFBXlc3OJEZgAlHGdHGfY6UVc7WFc8Y4oaTRf3SNuRKbu9OmvWHPSabEIxsWseN3Cav8q/xAldlTezerEop20+JZ+dnc3o0aNp1KiRTyd7dxRRAGUMWx1v7jl7aK05evQoe/fuZe/evRw9epQtvx9ix4HDZKVdQGdlcjQ7k+6vZFGpQhChla6iQoUKVKlShZo1a1KzZk3q1KlDo0aNeCgijPc2pZNhYemx/EezadpKtt/RuhOWwhFlWhKm9YILmPcL+NUfiZ/S1FZnmBTwGVUCAmneZVDed/7VV1+xb98+5s+fT7lyJb/7LPmfQHCK+LiGhdYAAPxU4ciEOTk5bNmyhdWrV7Nu3To2bNhAUtKV+DWhoaFcCgyB4DACr6mOKheI8g9A+ZcjyF9zW6MqpKWlcfbsWfbs2cOyZcu4cOFKrL+AwPKUr14XVaMB11wfxbCHu+brXJ0dafvCvgihhGJlv0AFdZnxV30L0a8AkJaWxrhx42jZsiXdu3c3QkqPIwqgjNEtOpwtf5/j/zYezVfur0x78rKzs1mxYgXTpk2jb9++nDx5EoCGDRvSo0cPYmJiaNKkCU2aNCEsLIx6I3+0FeqMLyd1KVSelJTEvn372LdvH7///jtbt25l06aVHNy6mCe+eZ03r7uOO+64gzvuuIOlT7d3KvqhhKUQXMaB/QJvv/02x44d4//+7/9QqnTsYRUFUAZZvf90obK0syd4evhsnj74C4mJiQQHB9OlSxfuvfdeOnXqRI0aNa6YV35Iptb67cTHNXTaMyY0NJSbb76Zm2++Oa8sKyuL3bt3s379epYtW8aMGTOYPn06gYGBxMXF0bt3b7p27cqqQymcOplC/5E/FjLvJGxPtGnacnfxeEzCbub87xjZWuOvFH1b1+G1bpFu3VPwMUJqm8NFWCkHEj4C6YcAACAASURBVBMTmTRpEt27d6ddu3bFLJz3EAVQBrHsEC+dOEDy/xaQ/sdGUIrQBq14YfI4OkbVpXPnznn1bJlXurcM59utiU65ohakXLlyREdHEx0dzdChQ7l06RIbNmzghx9+YP78+SxevNhkLqrXkt53tCMn4Ka89rf8fY4fdv5DUnqmzfu7s3g8JmF3vtlSttZ5x6IEShG5+wUssdgv8NJLL5GVlcWbb75pgHDeQxRACcJTcfdrhQZzaM9WktbO4tKxPfgFVaTyzb2o1PxOylW+mkXJ/tycnX+K+8pi60mtV+8/zcT7Iz264aV8+fJ06NCBDh068NZbb/Hbb7/RI/5tTu9aw+fv/YrfVaFUbHo7mc06M3tjtlUTVC7uumnO+Z+VUaG5XBRAKSLXNXT/GUxB+67sF9iyZQtffvklL7zwAvXr1zdUTE8jCqCE4KkFzn379pG19E1OrVmKf8UqhHV4nIrNOuMXeGWUnJ6ZzankKyPqhO2JebuGC3IiKd2rnjF+fn60adOGoHZJhLftR1z2//i/RSu5sOk7LvxvAUHXNqdyq3sJqt8SpQr7cLsbdz3bRsIkW+VCCSaqF5xbA72uODporRk2bBjVq1fnpZdeMk42LyEKoITg7gLnxYsXGT9+PO+88w4VKlTggade4FCNdpxMs17ftCPyStu2KK5dsLlrDZHNbqR6wC1kpZzl4u4VpGz/iX8XvEK5KrWp3KobVzWJxS+gPGDaGOeuYvJXympn719KFgEF+3z99desX7+ejz/+mMqVHU/fWFKQncAlBHd2x/744480btyYt956i/79+3Po0CFmT3+DjeO65GUuKojljkh7bRTXLtiCu3DLVapK6C29CX/yc67uOgK/wCDOLZ1G4of9Sdowh5yMVGIbVXO73b6t6zhVLpQekpKSGD58ODfeeCMDBw40WhyvIDOAEoIrcWhSUlJ49tlnmTFjBo0bN2bdunW0bds2Xx1b8YRqhAQW2XZocECxuVfmtnPqwDaUWabYRtX4dmsiqnF7KkTcxqXje7nwv29JXj+bC5sT+GjbvTQKG81DtzVxud1cO794AZU9XnrpJc6cOcOSJUvw8yudY2VRACUEZwO/bdq0iQceeIC//vqLUaNGEd3tcV5cdZgTP+R3obQV3iDUYsetrbbH3+N6x+oK3aLDWZN8kMOT2ueVxVxbhclLD5CYlE5QnaYE1WnK5VOHSPp1LmfXfU2/uAT2Pf8cw4cPp2rVqi61+1q3SOnwSxtFpIncvHkzH374IU8//TQtWrQwUFDvIgqghJDbUVuGcS5frvCoRGvN+++/z4gRI6hVqxZr1qzhXKXr7C4gW1vEtdxxa0tJALSZtMrQcLe5sltuSAuscR3V73uJy/8eJvnXb5g4cSLTpk1j5MiRPPvss1SoUMG9PLFCySY3TWTuzt/cNJEAVCc7O5vBgwdTo0YNXn31VcPELA5K57ymFJOReWVxNjd5RW6yirS0NGLv7sFzzz1HQL0Yruk3lXOVrvNIIpNu0eFsGNmBw5O6sGFkBwCfyo5lzRQWWL0ezfu9wq5du7jtttsYPXo0119/PZ++/ARZCUM9mic2KT3T0NzMghPYSxMJfPDBB2zdupV33nmHkJAQAwQsPkQBlCDsdeTHjx8nsmVrfvnpe0LaPki1+0Zz6pJ/XidtDXd2yPpadix7oZqbNm3KokWLWLduHfXq1WPQhE9o+v4ZvtuXic718LHoAJwlYXsiiefTfUYZCkVgJ+zDiRMnGDlyJHfccQe9e/cuXrkMQBRACcJWh33k4D5uuukm/j78F9W6jyW0Td88n/j0zGybLovuuHD6QjpKSxzJjdC2bVvWr19PQu8K+CnoPi+ddjPT2PaPWZHZyRNrj8lLD5BTwFVUUkX6MDbSQeZUCmfy5MmUK1eOTz75pFC8n+JOU1ocyBpACcKaN07G0V2c+f51alQJocYDbxBQvV6h67K1JjjA361wDY7IkltuFI5sSFNKcW/renRpcJQZ2zN5adUlYj65yIDoAF7vVp8aLrR7IikdrHiFGqUMhSKwkSbyo3M3sWPHF3z22WfUqZP/Cy2tkWZlBlCCKGjmSPvjN/6dN45atcL57bffqNugsdXrckfDriRud1QWKEHZsTqOo1z5CjzeMpCDQysy/OZAZu3K5IY3j/LWW29x+fJlp25nS+lJqkgfJaoXdH0fQupgCvtQh8PRY3jhvW+IiYlhwIABhS7xNZOnp5AZQAnC0hvn4MblnFk8mRuaNGPjLysICwsjPs7fpquop8M1lJSk11axyBMbwnHe6nkDg0YO5PlPVxIfH8/HH3/MlClT6Nq1q0O3i49rSOK+rfnKSowyLICn4k35PFG98n4H2dnZPNapE35+fowYMcJqqGdfM3l6ClEAxYWH3A67RYdz6Y/1PDhmMrfcfBM//fRT3hb14u6US3R2LIsOAKABsPie5/j5558ZNmwY99xzD3fffTfvv/8+9eoVNqtZ0i06nISTvxMe6l+iO87SauYoismTJ7N69Wo+//xzatSwbgT0RZOnJxAFUBwU4XfsDHPnzuXBBx+kTZs2/Pjjj1SqVCnf+RLdKfsAd9xxBx07duT999/n5ZdfpnHjxowZM4YRI0ZQvnx5m9eFBgewYWT74hPUC5TFhDqbNm1i7Nix9OzZk/79+/PLL79YrefsRsySgqwBFAdF+B076l2wZMkSHn74Ydq2bctPP/2Ur/MvjR4KRhEQEMDzzz/P/v37ufvuuxkzZgxRUVEsX77caNG8Smk1c9giJSWFvn37UqtWLateP5Y44mVWEjF0BqCUugN4D/AHPtNaTzJSHq9hx+84KT2TUSuLnnb/9ttvdO/enaioKBYvXpwvVWJZnbp7m9q1azN//nyWLl3K008/TefOnenduzdvv/024eGl77mWVjOHLYYMGcKRI0f45ZdfCA0NLbJ+aZxdGzYDUEr5A9OBO4HGQF+llHU3lpKODb9jQmpzKjmjSO+CvXv30qVLF2rXrs2SJUsKhaUtrR4KvkJcXBy7d+/mlVdeISEhgUaNGvHOO++QlZVltGgexRHPrtIy0/ziiy/46quvGDt2bKEAiWWJIhWAUmqoUirMC23fCPyptf5La30ZmAvc64V2jKfjOFN6OUvM6eYs4+5bkjvtTkxMJC4ujqCgIJYtW0b16oXXDIpj6l5a/vFdJSgoiHHjxrF3717atWvH8OHDadGiBRs2bDBaNI9RlJkjd6ZZ0nc8b9myhaeeeorbb7+dsWPHGi2OoShdRGYjpdRrQB9gG/AFsFQXdZEjDSvVA7hDaz3QfPww0Fpr/XSBeoOAQQA1atRoOXfuXJfaS01NzWc2KXbSz0PKP5B9GfwDoVJNCA7jzPlk/rGSlCXQ349rQwN49tlnOXbsGFOnTuW6666zeusDJ1OsKpJAfz8aXlPJyhVFY/m8ktIzSTyfnm+3q59ShIcFExoc4NL9XcXw7xFTwL3169czbdo0/v33X+68804efPBBnzQLefJ5efJ35s3vMSk9k1PJGVzOziHQ348aIUF5v9Pk5GSeeOIJAD7++ONCsX584fdlC3dki42N3aq1jilYXqQCAFCm1ZHOQH8gBpgHfK61PuSSNDiuACyJiYnRW7Zscam9NWvW0L59e5eu9SYJS5Yz6tfsQt4Fr3drwpxJw/n2229ZtGgRd999t+17FFgDyL2HO4tUls+rzaRVVm3D4aHBeYHhigtf+h5TU1N59dVXmTJlChUqVODtt99mwIABPhU73pPPyzLiqiUKODypi1P38tb3aO9/oWvUNdx5552sXbuW9evXExNTqD/0qd9XQdyRTSllVQE49Es1j/hPml9ZQBiwQCn1pkvSmEgk/wb62uayMkVocIDVaffORZ+xYMECJk+ebLfzB+97KJQ17xBHqVixIm+88Qbbt2+nbt26PP7447Rt25adO3caLZpXKAk7nu2thw0fPpzly5czffp0q51/WaRILyCl1LPAI8AZ4DMgXmudqUzRxg4CL7jY9mbgBqVUPUwdfx/gARfvVaIp6F2wYMECJkyYQP/+/Rk+fLhL9/AkZc07xFmaNm3Ku+++y7FjxxgxYgQtWrTgmWee4ZVXXilVeWR9wRe+4E7l2EbVWL3/dN6xrci3+1fO49cVH/Pcc8/x2GOPFZu8vo4jM4AqwP1a6zit9XytdSaA1joHsD80tYPWOgt4GlgK7APmaa33unq/0sKBAwfo378/N910Ex9++KFd32RXcXZBt0TH/SkmlFI88sgj7N+/n0GDBvHee+8RERHBvHnz8MCSmU9gtC+8tUXo/9t4lJYXlrMu8BnWpd/H+sBnuMdvfb7r0g9t5tzKT7nnnnt466237DeSfh7eaQrjQ01/3cgRURIocgagtX7Zzrl97jSutf4J+Mmde5Qm0tLS6NGjB+XLl2fevHl2d566iit7Bkp03J9ipkqVKnz44Yf069ePwYMH07t3bz7//HOmTZvGDTfcYLR4bmOkL7w18849fuuZFPAZFZQpgF9tdYZJAZ9BJizKacvlU4c4s+hN6jdszOzZs/H397d2axO75kHySXOiIPLv2C+l2eJ8Z7VKYMiQIezdu5fZs2cXCkfrKVzdM1AwI5h0/vZp3bo1mzdvZurUqWzcuJGmTZvy8ssvk55ettdN3MHamtML5ebldf65VFCXGR04n8yzxzg9fxxVq1Rh7Yqfi/agWTkBdAEvJzcSBZUERAH4CF988QUzZ85k7NixxMXFea0dWdAtPvz9/Xn66afZv38/PXr0YMKECURGRvLzzz/bvc4X91w4LdOueR43pVhbc6qlzliteynpX/x+fp2qFYPYsHa1Yy66dnbsl1ZEAfgAf/zxB0OHDqVjx46MGzfOq22VBE+O0kbNmjWZPXs2K1asoFy5ctx555306NGD48cLdyy+uNnKaZlygx96MOcyQGyjaoXKTuirC5WdTM2h09eXSE1NZenSpY6b3uzs2C+tiAIwmKysLB566CGCgoKYNWuWfRulB5AFXePo2LEjO3fu5LXXXuPHH3+kUaNGvP3222RmZubV8cWwHk7LVETwQ1dZvf90obI3s3qRpgPzjo9fyOG2L9M5kar48ccfadasmeMNdBwHqkCXaN6xX1oRBWAws2bNYvPmzTw28r/0nLXf69N+oz05fJWiTByeMsuUL1+el156id9//5327dszYsQIoqOj8yKNetNE5+pncFomL5lSrLW3KKctIzMHcjznao4kadp9eYmTGYEsW7GKW265xbkGonqZsoRZZAqj6/uldgEYJB+Aofz666/Mnj2b2K49WXzhWtLNoyZvR/MsjVEN3aEozyhvRFutV68eixcvZuHChQwfPpzOnTvTpUsXQhv04HxgYVOHuyY6dz6D0/tAQmpf8aQpWO4GtuRYlNOW9WkRnP1+LBdyLrBi1TJatWrlWiPBYTBsj1tyliRkBmAQqampPPzww1SvXp2LLR72uWl/WaIoE4e3zDJKKbp168a+fft48803Wbt2LbunPs6FVZ+SnZ6SV88TJjp3PoPTZkM7wQ/dIT6uIQF+hffFZP2zjz8/f460tDRWr17teudfBhEFYBAvvfQShw8fZtSoUfybYf1rEM+c4qEoE4e3PafKly9PfHw8f/75JwMfe4zkrYs5+ekgUrYsomalAI+Y6Nz5DE6bDa0kXfeEKaVbdDiTezbLF4BQHf6Nf+eO4ZpqV7Nx40aaN29e6Dpf9KryFcQE5ASeSpj966+/MnXqVIYMGUJUVBS10nIk1IKTeDJ5eVEmjuIKhVG9enU++ugjhgwZwvDhw1mx4hPO/L2K9PoTyGnW260gc+5+BqfNhgVyLnuKXDlycnKYOHEiY+a9Tps2bVi4cCFVq1YtVF+SJdlHZgAO4in3vIyMDB577DHq1KnDf//7X0A8c5zF066SRT3/4v5+IiMjWbZsGT/88AMVKlTggQceIDo6mh9++MHlsBKl6TeWlJREt27dGDNmDA8++CArVqyw2vmDb3pV+RKiABzEUz+k119/nf379/PJJ5/k5fQVzxzn8PQ/dVHP34jvRylFly5d2L59O19//TVpaWl07dqVNm3asGbNGofukbA9kQMnU6g38kcmLz1A95bhJf43tn37dmJiYliyZAlTp07lq6++IigoyGZ9WyauxKR0MQshJiCH8YQdeOfOnUyaNIlHH3200G5f8cxxHG/Y5It6/kZ9P35+fvTt25cePXowc+ZMXnnlFWJjY7ntttsYPXo0nTp1showMHeW9FSjHDR+JCal8+3WRK92+p40yxUkKyuLN954g/Hjx1O9enV++eUXh9w8bZm+FOSVW5qFis4MXLqQGYCDuLuDNicnh8GDBxMWFsaUKVM8KVqZo9TuZrYTPiEgIIDHH3+cgwcP8u677/Lnn38SFxdHq1at+O6778jJyR/Dxlumj4ILqpsXfQzvNEWPD6VVQjtaXlju8R3MBw4c4NZbb2XMmDH06NGD3bt3O+zjb830paBQYpuyahYSBeAg7tpQZ82axW+//cbkyZOpUqWKN0QsM5Qme3YeVsInpH/3NM+OHpXPRBEcHMyzzz7LoUOH+PTTT0lOTqZ79+40bdqUzz77jLQ0U35Rb8ySCq69tLywnKZbx0DyMRSacHMkztxwzO52qhcvXmT06NFERkZy4MAB5syZw5w5c5z6/7FmvrO1ilIWve5EATiIO3bg8+fP88ILL9CmTRsefvhh7wtbyimVayZWwicEc4n4cvOsjqbLly/PwIED2b9/P3PnziUwMJDHH3+c2rVr88ILL1AlJ8lqM+7MkgrOKl4oN49gK5E4Xyh3ZebiSqeak5PDnDlziIiIYOLEiTzwwAPs37+fPn36uCR3wUi24aV1BukCsgbgBK7agceOHcvZs2eZPn26T+WLLcmUujUTG2ESaqmzwJXRdMHP7O/vT+/evenVqxfr1q1j6tSpTJkyhZycHK66/kZ2XYpFl2uN8g9we5ZUsDO3FYkzV2ZwrlPVWrNo0SLGjh3L7t27adasGV9//TVt27a1f+GueSYFmnzctNu44zi7Lqh2M5slH3RY3tKA9EZeZtu2bXz44YcMGTLEucBUQtnCRpiEE/qKe6O90bRSinbt2jF//nyOHDnC6NGjKXfuLz57dxLHpz/KpbWf81ijHO5tXstlEQt25tYicVrK7KjCycjIYMaMGURHR9OtWzcyMjKYM2cO27Ztc6zzdzLyaKmcQbqIKAAvkpOTw5AhQ7j66quZMKH0JpUQICk90714+Td0LhQ+IU0H8mbWlZGso6Pp2rVr89prr3H65AkmTpxIj653cH7bT8Q/1IXrr7+e559/nvXr15OdnV30zSwouPbyZlYv0i0icQKkU57JWb0c6lT37NnDyJEj+c9//sOAAQPIzs7miy++4Pfff6dPnz6OzZZdjDwqCY5MiAnIi8yZM4eNGzdyfY94oidtkFSKpZSE7Ykknk8nMcnUORa52zR31JrbcSUfg51fQ7MH4OAydPJxTuiqvJHZi0U5phGwK+abcuXKcdNNNzFy5EjOnz/Pt99+y3fffce0adOYMmUK1apV4/bbb6dDhw7ExsZSv359uzmoC6YG3Vq5E3sa16XVoal55pfgjuN4z4b5JScnhx07drBkyRJmzJjBoUOH8Pf356677uK5554jNjbW+RzYZTCJiycRBeAl0tPTGTbiRcpfcx2X69+a53cs29BLH5OXHqBPnfy+JbZs9oDtUevBZTBsDwrYvD2RrUsPoDzkUx8WFsbAgQMZOHAgFy5cYMmSJSxcuJBVq1YxZ84cAP7zn//QqlUrWrRoQYsWLYiKiqJmzZr5OuXCay8dgCestpmamsrOnTvZtGkTmzZtYvXq1Zw6dQqAiIgIpk6dSq9evahevbrLn8tbkUfLCqIAvMT777/P6ZOJ1OjzX5RFkgm7HYNQIjmRlA5WUji7Ey/fm4vclStXpnfv3vTu3RutNfv372fVqlX88ssvbNu2jW+//TavblBQEHXr1qV+/fpcc801hIaGEhYWRsWKFfMUQ3Z2NsnJyZw7d46zZ89y7Ngx/vzzT06ePJl3nzp16hAbG8udd95JXFwc+/bto3379u5/mI7j8s+moNQncfEkogC8wOnTp/nvf/9L8PU3EnRtVKHzZdHfuDRjss2n2Ci3gg+NWpVSREREEBERwZAhQwBITk5m6vzlfLF4LWf/Oc6/aWe4dOhvdu7cyfnz5/P2GhS8T2hoKFWqVCE8PJy77rqL66+/nsaNG3PjjTdSs2bNfPX37dvnmQ+Qa25ywgtIuIIoAC/wyiuvcPHiRSK7Psl5K+fLor9xaSY+riGJ+7bmKysyXr4Pj1pX/5XK7L8rkhMRR1iEqax8gD9TzIu6ly9f5uLFi3n1lVJUqlTJ6+lMbeKlyKNlAfEC8jAHDhzgo48+YtCgQbz8cOfSt2NVKES36HDCw4INj5fvKYoKIxEYGEhYWFjeKzQ01LjOX3ALmQF4mBdffJEKFSrkBa0CvBYgS/AdQoMD2DCyveMX+PCo1dsJcATfQRSAB9m0aRMLFy5kwoQJeZ1/qduxKpR6iisBjmA8YgLyIGPHjqVq1ao899xzRosiCC5TKoPtCVYxZAaglJoMdAUuA4eA/lpr69GrSghr165l2bJlTJ48OS/RiyCURApu+BLTZenFKBPQcmCU1jpLKfUGMAp40SBZ3EZrzZgxY6hZsyZPPfWU0eIIgtuI6bJsYIgC0FovszjcCPQwQg5PsWLFCtatW8e0adOoUKGC0eIIgk0czdrlzexegu+gXE0y7TEBlFoMfKO1/j8b5wcBgwBq1KjRcu7cuS61k5qaSsWKFV2W0xZaa5566inOnz/PrFmzCAwMLPqiYpDLXUQu5ygJciWlZ5J4Pp0ci/95P6UIDwsmNDggr8zRep6Sy5fwVbnAPdliY2O3aq1jCpZ7bQaglFoBXGPl1Eta64XmOi8BWcBsW/fRWn8CfAIQExOjXd0+vmbNGs9sPS/A4sWL2b9/P59//jmdO3d2euTkLbncReRyDl+WKynkBiYvPUBi0mWgsL9+eKh/PhfWNpNW5QW2s1fPXbl89Xn5olzgHdm8pgC01rfbO6+U6gfcDXTURk9DXERrzauvvkr9+vV55JFH8lLm5W6ikeBvgtEkpWcyauXuQhu7LCno3y/7AMoOhriBKqXuAF4A7tFaFw4sUkJYsWIFmzdvRjXrxg1jlvL8vJ1eScQtCK5yKjnDbucPhf37bfn7G7IPoGDeBDuJXgTnMWofwDSgErBcKbVDKfWRQXIUScL2RJuJPp4bOZZylaqSWf9WNJBtYyIjIyfBKC5n59g9b82/32f2AbiQ7UtwDqO8gK43ol1nsWfSufriYX7f9j/COg5ClbO/MCY7KAWjCPS3PcYLt7FG5TP7AOxl+/LRMBolDQkFYQd7QbEq/zIZvwohVGzW2e49ZAelYCQ1QoIIDsgulAC9qHSNPrEPQLJ9eR1RAHawZbo5vG8X//z8M/+JG4gKCCp03l8pcrQW/2mh2LDlfRYaHMDE+xsbPpovJF8zB/IR+1DehNKKKAA72AqKdWnrt4SGhjLxped5ddkRp0dXguBJ7JkqQ/HMaN6djWHW5Es8n03C9kT79/DxvAmlAQkGZwdri2F+ySc4t3c9Q4cO5YFbGzHx/kjH48ALghcoKn6/u+R24IlJ6WiuKBhLhwhn5cvRumj5fDxvQmlAZgB2sLYYdtUfa/gnKIihQ4fm1ZEOXzAS+377V7l9f3sKxpHfvlv7Cnw4b0JpQBRAEVh28KdOneLa8d/Sr18/qlWrZrBkgmDC2/H73d0YJvkFfBcxATnBBx98wOXLlxk2bJjRoghCHt7223d3Y5hVU6pS4h3nA4gCcJC0tDSmT59O165dadhQfriC79AtOtyra1HuKhhr8oWHBYvp1AcQE5CDzJo1i7NnzzJixAijRRGEQnhzLcoTG8MKyrdmzRpPiym4gCgAB8jJyWHKlCm0atWKtm3bGi2OIBQ7thSM5A0o2YgJyB7mQFSLH6jEwYMHGdGzDUopo6USBJ/AXfdQwXhEAdjCIhDVlI2XuDZEcX/61xKIShDMeHv/geB9RAHYwhyIatepbNb+nc3TNwZSLifDVC4IguQNKAWIArCFOeDU9E2XCSoHA6ID85ULQlnHp/IGCC4hCsAWIbU5n675v92ZPBgZQJVglVcuCIIP5Q0QXEYUgC06jmPmbk1aJgxpZR79SyAqQcjD2/sPBO8jbqA2yGnag+l7nqFNvRyia5Yzjfw7jpO4JIJggcTCKtmIArDBzz//zKFjp3htzhzo08docQRBEDyOKAAwuXaunGBa4DWP9KdNm8k111zD/fffb7R0giAIXkEUQK6/f27SieRj/DnzKZYsOcvLL79MYGCgsfIJgiB4CVkEtpJ4+oPfUijnB4MGDTJIKEEQBO8jCqCAX39GlubLnZnc1yiAWrVqGSSUIAiC9xEFUMCv/7t9WZxL1wxqJ52/IAilG1EAHceZ/PvNfLrtMvXC/OnwxCQDhRIEQfA+ogAsEk8fPJvDmiPZDHyoJ37NxfVTEITSjSgAMCmBYXv4rMJT+Pv703/UFKMlEgRB8DqiADDFNb/5taW8Ne0TQhrexP9O5hgtkiAIgtcxVAEopZ5XSmml1NVGyZCb1OLPLWvISUuiXOPbJamFIAhlAsMUgFKqDtAZOGqUDHAlqUXqzqX4V6pGUL0WktRCEIQygZEzgHeAFwBtoAycSEonK/kUGUd2UDGqE8rPP69cEAShNGOIAlBK3Qskaq13GtG+JbVCg0nduQyUomJUp3zlgiAIpRmltXcG4EqpFcA1Vk69BIwGOmutk5VSR4AYrfUZG/cZBAwCqFGjRsu5c+e6JE9qaioVK1YsVH7u4iUGPvoQ14T/h8EvmGL9+ylFeFgwocEBLrXlCbmMRuRyO8aP8QAACpBJREFUDpHLOUQu53FHttjY2K1a65hCJ7TWxfoCIoF/gSPmVxamdYBrirq2ZcuW2lVWr15ttXzFihUa0A36jtF1X/xB3zJxpf5+23GX2/GUXEYjcjmHyOUcIpfzuCMbsEVb6VOLPRqo1no3UD33uKgZgKdJ2J7I5KUHOJGUTq3QYALXf0hISAg7Ph9NcLCYfQRBKDuUqXDQuS6f6ZnZABw7dZbjy37g9ru7S+cvCEKZw3AFoLWuW1xt5bp85pL2x6/ozEv8U711cYkgCILgM5SpncAFXTtT96ykXFhNUkLqGySRIAiCcZQpBWDp2pmVfIpLR3dzVZMOhIdVMFAqQRAEYyhTCiA+riHBAaaNXql7VgFQtXkn4uMaGimWIAiCIRi+BlCcdIsOB+DNn/eTuHcVles34+0Bt+eVC4IglCXK1AwATEpgcrsgss7/w3tjn5POXxCEMkuZUwAAs2bNokKFCnTv3t1oUQRBEAyjzCmAy5cvM3/+fLp160alSpWMFkcQBMEwypwCWLp0KefPn+eBBx4wWhRBEARDKXMKYM6cOVSpUoVOnToVXVkQBKEUU6YUwMWLF1m4cCE9e/YkMDDQaHEEQRAMpUwpgEWLFpGWlkbfvn2NFkUQBMFwypQCmDNnDuHh4dx6661GiyIIgmA4ZUYBXLhwgZ9//pk+ffrg51dmPrYgCIJNykxPuHbtWjIzM8X8IwiCYKbMKICVK1fSoEEDWrRoYbQogiAIPkGZUACJiYns3LmTvn37opQyWhxBEASfoEwogG+++QattZh/BEEQLCgT0UCzs7OJiYmhYUP7YZ8L5guOj2soweIEQSi1lAkFEB8fT6tWrezWKZgvODEpnVHf7QYQJSAIQqmkTJiAHKFgvmCA9MxsJi89YJBEgiAI3kUUgJmC+YKLKhcEQSjpiAIwY5kv2JFyQRCEko4oADOW+YJzCQ7wl3zBgiCUWsrEIrAj5C70iheQIAhlBVEAFnSLDpcOXxCEMoOYgARBEMooogAEQRDKKKIABEEQyiiGKQCl1FCl1H6l1F6l1JtGySEIglBWMWQRWCkVC9wLNNNaX1JKVTdCDkEQhLKMUTOAwcAkrfUlAK31vwbJIQiCUGYxyg20AXCrUup1IAMYobXebK2iUmoQMMh8mKqUcjU4z9XAGRev9SYil3OIXM4hcjmHr8oF7sl2rbVCrykApdQK4Borp14yt1sFuAloBcxTStXXWuuClbXWnwCfeECeLVrrGHfv42lELucQuZxD5HIOX5ULvCOb1xSA1vp2W+eUUoOB78wd/ialVA4m7XbaW/IIgiAI+TFqDSABiAVQSjUAAvHdaZcgCEKpxKg1gC+AL5RSe4DLwKPWzD8exm0zkpcQuZxD5HIOkcs5fFUu8IJsyvv9riAIguCLyE5gQRCEMoooAEEQhDJKqVIASqme5tASOUopm+5SSqk7lFIHlFJ/KqVGWpTXU0r9z1z+jVIq0ENyVVFKLVdKHTT/DbNSJ1YptcPilaGU6mY+N1MpddjiXPPikstcL9ui7UUW5UY+r+ZKqd/M3/cupVRvi3MefV62fi8W58ubP/+f5udR1+LcKHP5AaVUnDtyuCDXcKXU7+bns1Ipda3FOavfaTHJ1U8pddqi/YEW5x41f+8HlVKPFrNc71jI9IdSKsninDef1xdKqX/Na6LWziul1PtmuXcppVpYnHPveWmtS80LiAAaAmuAGBt1/IFDQH1M3kc7gcbmc/OAPub3HwGDPSTXm8BI8/uRwBtF1K8CnAMqmI9nAj288LwckgtItVFu2PPCtJnwBvP7WsA/QKinn5e934tFnaeAj8zv+wDfmN83NtcvD9Qz38e/GOWKtfgNDc6Vy953Wkxy9QOmWbm2CvCX+W+Y+X1YcclVoP5Q4AtvPy/zvdsBLYA9Ns7fBSwBFKa9U//z1PMqVTMArfU+rXVRO4VvBP7UWv+ltb4MzAXuVUopoAOwwFzvS6Cbh0S713w/R+/bA1iitU7zUPu2cFauPIx+XlrrP7TWB83vTwD/AtU81L4lVn8vduRdAHQ0P597gbla60ta68PAn+b7FYtcWuvVFr+hjUBtD7Xtllx2iAOWa63Paa3PA8uBOwySqy8wx0Nt20VrvRbTgM8W9wKztImNQKhSqiYeeF6lSgE4SDhwzOL4uLmsKpCktc4qUO4Jamit/zG/PwnUKKJ+Hwr/+F43T//eUUqVL2a5gpRSW5RSG3PNUvjQ81JK3YhpVHfIothTz8vW78VqHfPzSMb0fBy51ptyWfIYplFkLta+0+KUq7v5+1mglKrj5LXelAuzqawesMqi2FvPyxFsye728ypxKSGVnRATWuuFxS1PLvbksjzQWmullE3fW7NmjwSWWhSPwtQRBmLyBX4RmFCMcl2rtU5UStUHVimldmPq5FzGw8/rK0x7SXLMxS4/r9KIUuohIAa4zaK40HeqtT5k/Q4eZzEwR5siAT+BafbUoZjadoQ+wAKtdbZFmZHPy2uUOAWg7YSYcJBEoI7FcW1z2VlMU6ty5lFcbrnbcimlTimlamqt/zF3WPain/YCvtdaZ1rcO3c0fEkpNQMYUZxyaa0TzX//UkqtAaKBbzH4eSmlKgM/YlL+Gy3u7fLzsoKt34u1OseVUuWAEEy/J0eu9aZcKKVux6RUb9Pm6Ltg8zv1RIdWpFxa67MWh59hWvPJvbZ9gWvXeEAmh+SyoA8wxLLAi8/LEWzJ7vbzKosmoM3ADcrkwRKI6ctepE2rKqsx2d8BHgU8NaNYZL6fI/ctZHs0d4K5dvdugFVvAW/IpZQKyzWhKKWuBtoAvxv9vMzf3feYbKMLCpzz5POy+nuxI28PYJX5+SwC+iiTl1A94AZgkxuyOCWXUv/f3t2zNhWFARz/PzpYsQ7aqU7SqYODgoJ0dCjoEHCXgnbp4Dfo4iD0EzgIjqKCWwehUOumg4tSiqgZXRzdlAzH4RzhVJQEbvNSzv8HITc395Anz73Jk/uSc+IK8BjoparL9f+t0wnGtVg97AGfyvQOsFriOwescnhPeKxxldiWySdU31XzxpmvUWwDa+VqoOvAj/Ijp3u+xnVmexo34Db5ONgv4DuwU+ZfAF5Vy90CvpAr+GY1f4n8Ae0DL4FTRxTXAvAa+ArsAufL/KvAk2q5i+SqfuKv9nvAPvmL7CkwP6m4gJXy2h/L/fos5Au4AwyAD9Xt8jjy9a/thXxIqVem58r775d8LFVtN0u7z8DNI97eh8W1Wz4Hf/KzPWydTiiuLeCgvP4bYLlqe6/ksQ/cnWRc5fED8lgldbtx5+s5+Sq2Afn7ax3YADbK8wE8KnHvU13h2DVfdgUhSY1q8RCQJAkLgCQ1ywIgSY2yAEhSoywAktQoC4AkNcoCIEmNsgBIHUTEtdKp2VxEnIk8PsGlaccljcI/gkkdRcRD8r+BTwPfUkpbUw5JGokFQOqo9C3zHvgJrKTDvUhKM8tDQFJ3C8A8cJa8JyAdC+4BSB1FHiP2BXkQkcWU0v0phySN5NiNByDNkohYAwYppWcRcRJ4GxE3Ukp7w9pK0+YegCQ1ynMAktQoC4AkNcoCIEmNsgBIUqMsAJLUKAuAJDXKAiBJjfoN3Ic2ERVA1AkAAAAASUVORK5CYII=\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYAAAAEWCAYAAABv+EDhAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8li6FKAAAgAElEQVR4nOydd3hURdfAf5NGAoEEkBqRJk0IIRRRAaX4CqgIgjRFiiKKXV+D4OsLFgQUEeRDkSqKICIlIsiLCIQqSu+iIjX0kpBAQtp8f+wmbJLdZGvuJjm/59kn2bn3zpy9d3fOzJkz5yitNYIgCELxw8doAQRBEARjEAUgCIJQTBEFIAiCUEwRBSAIglBMEQUgCIJQTBEFIAiCUEwRBSC4HaXUO0qpb4yWwxKl1BNKqZ/tPDdP+ZVSQ5VS55RSiUqp8ua/tVyQLUYpNdjZ6wXBWUQBCDZRSh1TSiWZO7hzSqk5Sqlgo+VyBq31PK31A67Wo5TyBz4BHtBaB2utL5n//mM+PkcpNdrVdgoTSql2Sql1Sql4pdQxK8drmI9fV0r9oZS63wAxBSuIAhDyo4vWOhhoCjQH3jZYHqOpBAQCB4wWJD+UUn4F1NQ1YDYQZeP4t8AuoDzwH2CRUqpCAckm5IEoAMEutNaxwEqgEYBSqqpSaplS6rJS6m+l1DPWrlNKrVBKvZSjbK9S6lHz/1op9ZxS6i+lVJxS6jOllDIf81FKva2UOq6UOq+U+lopFWI+VsN87SCl1Eml1BVzPS3M9ccppaZYtDlQKbXJ4v2n5uuuKqV2KKXa5HcPlFJ1gcPmt3FKqbUWn+F2pdQQ4AlgmHnW9KONev5lHgnHm2VUOY4/pZQ6ZP5Mq5RS1S2OPaCUOmy+9nOl1PpM85H5M25WSk1USl0C3rGjvvpKqdXm53hYKdUrv/uQE63171rrucA/Nu5ZU2CU1jpJa70Y2Af0cLQdwf2IAhDsQilVDXgQ00gOYAFwCqgKPAaMUUq1t3LpV0A/i3oigDBghcU5DwMtgMZAL6CjuXyg+dUOqAUEA1PITkugDtAbmIRphHk/0BDopZS6z8ZH2gY0AcoB84HvlVKBNs4FQGv9p7legFCtdfscx6cD84CPzGahLjnrUErdAizBNJO6BTgCtLI43hV4C+gOVAA2YhpBZ167CBiBaTR9GLjHyv34B9NM5YN86isFrDZ//opAH+BzpdQd5uPDzYrU6iuve2VBQ+AfrXWCRdkebt5HwUBEAQj5EW3+sW8C1mPq6Kth6rTe1Fona613AzOB/lauXwbUVUrVMb9/EvhOa51icc44rXWc1voEsA5Txwym0fQnWut/tNaJmDq+PjlMG++bZfgZkyniW631efOMZSMQae1Daa2/Mdvv07TWE4ASQD0H740zPAgc0Fov0lqnYlJaZy2OPweM1Vof0lqnAWOAJuZRe+a1S8zHJue4FuC01vr/zJ8rKZ/6HgaOaa2/NJ+/C1gM9ATQWo/TWofaetn5eYOB+Bxl8UBpO68XPIgoACE/upl/8NW11s+bO5WqwOUco7rjmEb22dBaJwPfAf2UUj5AX2BujtMsO7HrmDoNzO0cz9GGH6bRbSbnLP5PsvLe6qK1UuoNs1kk3qzgQjCNyD1NVeBk5httisZ40uJ4deBTi1H2ZUwmojAb157KUf/JHO/zqq860DLHqP4JoLLrHzOLRKBMjrIyQIKVc4UCRhSA4AyngXJKKctR3G1ArI3zv8LUsXQArmutf3WgneoW728D0sjeyTuM2d4/DJO5qax5NBtPDlu8k+QXXvcMUM1CFmX5HlMH/myO0XaQ1nqL+dpbc1x7K9nJ2X5e9Z0E1uc4Fqy1Hmqu/y3zWobVl5334wBQK8d3JYJCsIheHBAFIDiM1voksAUYq5QKVEo1Bp4GrPrOmzv8DGACuUf/efEt8JpSqqYyuZ+OwWQ+SnPpA5jMD2nABcBPKTWS3KNUZzmHab3CFiuAhkqp7mZT1stkH3F/AYxQSjUEUEqFKKV6WlwbrpTqZr72BfIfredV33JM5rknlVL+5lcLpVQDAK31GLNCsPrKbECZFusDAX/TWxWolAow1/EnsBsYZS5/FNNaz+J85BYKAFEAgrP0BWpgGqUvxeTl8Use538NhGNDSdhgNiaFsQE4CiQDL+V5hX2sAv4H/InJrJRMbtOJs8wC7jCbVKJzHtRaX8RkYx8HXMK0gL3Z4vhS4ENggVLqKrAf6Jzj2o/M194BbAdu2BImn/oSgAcwLf6exmSK+xDTeogj3IvJ3PYTpllaEmC56a4PJhfiK+bP/ZjW+oKDbQgeQElCGKEgUEr1B4ZorVsbLUtRwbymcgp4Qmu9zmh5hMKHzAAEj6OUKgk8D0w3WpbCjlKqo1IqVClVApN7pwK2GiyWUEgxVAGYv8iLzJtiDiml7jZSHsH9KKU6YrK1n8Pkby64xt2Y9g5cBLpg8tJKMlYkobBiqAlIKfUVsFFrPdO8aFRSa23vBhNBEATBBQxTAMq0pX83UEvLQoQgCEKBU1DBoqxRE5Np4EtzeIAdwCta62uWJylTfJUhAEFBQc2qVauWqyJ7yMjIwMfH+5Y8RC7HELkcQ+RyDG+US2tNWloavr6+Tsv2559/XtRa5w7Ap7U25IXJLSwNaGl+/ymmbf02r2nWrJl2lnXr1jl9rScRuRxD5HIMkcsxvFGu33//XQP6vffec7oOYLu20qcaqepOAae01r+Z3y/CFDVQEARBMHPo0CEAqlevns+ZjmOYAtBanwVOKqUyA3B1AA4aJY8gCII3cvDgQQICAggLyxVqy2WMXAMA067OeWYPoH+AQQbLIwiC4FUcPHiQevXq4evr6/a6DVUA2hRGuLkrdaSmpnLq1CmSk5PzPC8kJCRrKuVNiFw3CQwM5NZbb8Xf379A2xUEbyR6VyzjVx3m9w2/E3JbA+KSUt3ehtEzAJc5deoUpUuXpkaNGpiCI1onISGB0qW9LwS5yGVCa82lS5c4deoUNWvWLLB2BcEbid4Vy4gl+7iWmEBa/DnSQx8g9koS0bti6RbpPlOQd/k7OUFycjLly5fPs/MXvB+lFOXLl893JicIxYHxqw6TlJpO6sUTAPhXqEGG1oxfdTifKx2j0CsAQDr/IoI8R0EwcTrOFN0j5cIxAAIq1shW7i6KhAIQBEEoSlQNDQIg9cIxVEAQvmUqZit3F6IADKBt27Zs377dkLbvuSdnDvHcBAdbzaKYjXfeeYePP/44z3Oio6M5eFA8ewXBUaI61iPI35eUC8cIqGBa3/RRiqiO7k1bLQqgmLFly5YCa0sUgCA4R7fIMMY82oj0i8fxr1CdsNAgwsoGuXUBGIqhAojeFUurcWupOXwFrcatJXqXrTS29nHs2DHq16/PE088QYMGDXjssce4fv06AGvWrCEyMpLw8HCeeuopbtzInrhp9uzZvPnmm1nvZ8yYwWuvvcaxY8do0KABzzzzDA0bNuSBBx4gKclk+9u9ezd33XUXjRs35tFHH+XKlSuAaVbx2muv0bx5cxo0aMC2bdvo3r07derU4e23385qI3N0n5iYSIcOHWjatCnh4eH88MMP+X7WDz74gLp169K6dWsOH765GDVjxgxatGhBREQEPXr04Pr162zZsoVly5YRFRVFkyZNOHLkiNXzBEGwTouKkJaUwIfPdGHz8PaEBrnfPbpYKYBM16rYuCQ0EBuXxIgl+1xWAocPH+b555/n0KFDlClThs8//5zk5GQGDhzId999x759+0hLS2Pq1KnZruvVqxcrV64kNdXk3/vll1/y1FNPAfDXX3/xwgsvcODAAUJDQ1m82JRCtX///nz44Yfs3buX8PBw3n333az6AgIC2L59O8899xxdu3bls88+Y//+/cyZM4dLly5lazswMJClS5eyc+dO1q1bx7///e/MGE1W2bFjBwsWLGD37t389NNPbNu2LetY9+7d2bZtG3v27KFBgwbMmjWLe+65h0ceeYTx48eze/duateubfU8QRCss2/fPgDCw8M91kaxUgCZrlWWJKWmu+xaVa1aNVq1agVAv3792LRpE4cPH6ZmzZrUrVsXgAEDBrBhw4Zs1wUHB3PfffexfPly/vjjD1JTU7Meds2aNWnSpAkAzZo149ixY8THxxMXF8d9991ntc5HHnkEMH1hGjZsSJUqVShRogS1atXi5MnsKW+11rz11ls0btyY+++/n9jYWM6dO2fzM27cuJFHH32UkiVLUqZMmay2APbv30+bNm0IDw9n3rx5HDhwwGod9p4nCALs3LkTgMaNG3usjUK/EcwRbLlQuepaldN90RF3xv79+/Ppp59Sv359Bg26GQmjRImbebl9fX2zTEB5kXmNj49Ptut9fHxIS0vLdu68efO4cOECO3bswN/fnxo1ajjtgz9w4ECio6OJiIhgzpw5xMTEuHSeIAiwfft26tatS0hIiMfaKFYzAFsuVK66Vp04cYJff/0VgPnz59O6dWvq1avHsWPH+PvvvwGYO3du1sjdkhYtWnDy5Enmz59P375982wnJCSEsmXLsnHjxjzrtIf4+HgqVqyIv78/69at4/jx43mef++99xIdHU1SUhIJCQn8+OOPWccSEhKoUqUKqampzJs3L6u8dOnSJCQk5HueIAi52b59O82buxQpJ1+KlQLIdK2yJMjf12XXqnr16vHZZ5/RoEEDrly5wtChQwkMDOTLL7+kZ8+ehIeH4+Pjw3PPPWf1+l69etGqVSvKli2bb1tfffUVUVFRNG7cmN27dzNy5EinZH7iiSfYvn074eHhfP3119SvXz/P85s2bUrv3r2JiIigc+fOtGjRIuvY+++/T8uWLWnVqlW2evr06cP48eOJjIzkyJEjNs8TBCE7586d49SpUx5XAIYlhHHmZS0hzMGDB+1KiHD16lWttdZLd57S94xdo2u8uVzfM3aNXrrzlF3X2+Lo0aO6YcOGTl9/9epV/dBDD+lffvnFJTncTeb9Kmjye57emLBDa5HLUUSuvFmxYoUG9Pr167PKXJENGwlhitUaAJj8a93tS+sscXFxNG/enMjISDp06GC0OIIgeAnbt29HKUVkZKRH2yl2CsDd1KhRg/379zt1bWhoKLt27fLKaKCCIBjH9u3bqV+/vsf7hmK1BiAIglAY2LFjh+ft/4gCEARB8CrOnDnD6dOnRQEIgiAUNzJdyu+8806PtyUKQBAEwYvYtGkTgYGBNG3a1ONtiQIwgMyAbKdPn+bJJ5+0eo49IaMnTZqULaDagw8+SFxcnPsEtYNjx44xf/78Am1TEIoymzdv5s477yQgIMDjbYkCMJCqVasyd+5cp6/PqQB++uknQkND3SGa3YgCEAT3cf36dXbu3JkVW8zTFD8FsHchTGwE74Sa/u5d6FJ1w4cP57PPPst6n5koxZ5wy8eOHaNly5YAJCUl0adPHxo0aMCjjz6aLfbP0KFDad68OQ0bNmTUqFEATJ48mdOnT9OuXTvatWsHmFxSL168CMAnn3xCo0aNaNSoEZMmTcpqz1aYaUu+//57WrZsSUREBPfeey8A6enpREVF0aJFCxo3bsy0adOyPv/GjRtp0qQJEydOdOleCkJx5/fffyctLa3AFIDhu3sdebm8E3jPd1qPrqT1qDI3X6MrmcqdZOfOnfree+/Net+gQQN94sQJnZqaquPj47XWWl+4cEHXrl1bZ2RkaK21LlWqlNbatIu4QYMGWmutJ0yYoAcNGqS11nrPnj3a19dXb9u2TWut9aVLl7TWWqelpen77rtP79mzR2utdfXq1fWFCxey2s58v337dt2oUSOdmJioExIS9B133KF37typjx49qn19ffWuXbu01lr37NlTz507N9dnatSokf7jjz+01lpfuXJFa631tGnT9Pvvv6+11jo5OVk3a9ZM//PPP3rdunX6oYcecvr+5UR2ArsXkcsxDJNrz3daf9JQj25XQgP68sZZuU7xxE7g4jUDWPMepOYY8aYmmcqdJDIykvPnz3P69Gn27NlD2bJlqVatmsPhljds2EC/fv0AU/hXyxCwCxcupGnTpkRGRnLgwIF8s2xt2rSJRx99lFKlShEcHEz37t2zAshZCzOdk1atWjF06FBmzJhBeropfPbPP//M119/TZMmTWjZsiWXLl3ir7/+cuheCYJghb0L4ceXIf4km06m0bCCD2XXv+WydcIeitdO4PhTjpXbSc+ePVm0aBFnz56ld+/egPvCLR89epSPP/6Ybdu2UbZsWQYOHOh02GawL8z0F198wdq1a4mJiaFZs2bs2LEDrTX/93//R8eOHbOdKyGdBcFFzAPT9AzNryfT6d3Q/+bAtHEvjzZdvGYAIbc6Vm4nvXv3ZsGCBSxatIiePXsCzoVbzlxM3b9/P3v37gXg6tWrlCpVipCQEM6dO8fKlSuzrskZbjmTNm3aEB0dzfXr17l27RpLly6lTZs2dn+eI0eO0KJFC9577z0qVKjAyZMn6dixI1OnTs3KXvbnn39y7do1mzIIQnHF0bSz2jwA3XU2g/gbcF8N87jcxYGpPRSvGUCHkaaplqUZyD/IVO4CDRs2JCEhgbCwMKpUqQKYwi136dKF8PBwmjdvnm/446FDhzJo0CAaNGhAgwYNaNasGQARERFERkZSv379bJnHAIYMGUKnTp2oWrUq69atyypv2rQpAwcOzNpIMnjwYCIjI62ae6wRFRXF4cOHUUrRoUMHIiIiaNy4MceOHaNp06ZoralQoQLR0dE0btwYX19fIiIiGDhwIK+99pojt04QihSZaWczMw9mpp0FrAahjN4VSwtdnjB1kV/+MSVt6lDTHLLexYGpPSidRx7YgkAp5QtsB2K11g/ndW7z5s11Tt/4Q4cO0aBBg3zbSUhIMAVW2rvQNLWKP2W6wR1GenyaZZdcXoZRcuX3PGNiYmjbtm3BCWQnIpdjFFW5Wo1bS6yVDINhoUFsHt7e6vnNrq5mnP9MHpl7hfPXNHuHBpNECYK6T8nWN7kim1Jqh9Y6V2wJb5gBvAIcAsoUSGuNexna4QuCUHRxNO3s6bgkYmlN2vVUNp34hKHN/TmVcQvj03rxaQH0U4auASilbgUeAmYaKYcgCII7cDTtbGb54pNluZGumV9tBK1TJrO9zL88JqMlRi8CTwKGARmuVGK0GUtwD/IchcKOo2lnM89PPr4bfHwpUa2RW9LU2othawBKqYeBB7XWzyul2gJvWFsDUEoNAYYAVKpUqdmCBQuyHQ8ODqZSpUqEhISglLLZXnp6Or6+vjaPG4XIZUJrTXx8POfOnSMxMdHmeYmJiVmxlLwJkcsxirJccUmpnItPJiU9gwBfHyqFBBIa5J/n+a+88Dx+/v4Me/dDm+e7Ilu7du2srgEYqQDGAk8CaUAgpjWAJVrrfrausbYInJqayqlTp/L1jU9OTiYwMNBlud2NyHWTwMBAbr31Vvz9bf9YiurioacQuRzDCLnOnDlD1apVGT16NP/5z39snlekFoG11iOAEQAWMwCbnb8t/P39qVmzZr7nxcTEeDy/pjOIXIJQvFmxYgUAXbp0KfC2jV4DEARBKNYsX76c2267jfDw8AJv2ysUgNY6Jr89AIIgCEWN5ORkVq9ezcMPP5znGqan8AoFIAiCUBxZu3Yt169fN8T8A6IABEEQDOPHH3+kVKlShi2IiwIQBEEwgPT0dJYuXUrnzp0N8wQUBSAUDdyc6U0QPM2GDRs4d+4cvXoZF5pGFIBQ+LFIqAHa9PfHl0UJCF5L9K5Y+o6YiPIvwYRDpfINGe0pRAEIhR8PZHoTBE8RvSuW4Yt2c2HfBoJq38nZ65oRS/YZogS8IRqoUISJ3hXL+FWHOR2XRNXQIKI61rMaF90lPJTpTRA8wfhVh7lyZDcZ1+MpVd+UqCkpNZ3xqw67/7eRDzIDEDxGZnKM2LgkNDeTY7h9pOOhTG+C4AlOxyVx7WAMKiCIwFrNspUXNKIABI8xftXhrMxImWSOdNxKh5GmzG6WuCHTmyB4gkpBcP2PTZSs1xof/5s5um2FjPYkogAEj+FocgynadwLukyGkGqAMv3tMlkS/wheyZ3qL3RqMsGN788qK8gQ0JbIGoDgMaqGBllNj+eRkY5kehMKCXvXRlOlWg1qNGzGmfhkz62N2YEoAMFjRHWsly1BNhg30hEEb+Cff/5h/fr1ptDPIzoYLY4oAMFzZI5oPO4FJAiFhK+++gqlFP379zdaFEAUgOBhukWGSYcvCEBKSgrTp0+nY8eOVKtWzWhxAFEAgiAILmPPfpelS5dy9uxZXnzxRYOkzI0oAEEQBBfI3O+SudaVud8FyKYEpkyZQq1atejcubMhclpD3EAFQRBcwJ79Lrt372bTpk288MIL+Ph4T7frPZIIgiAUQuzZ7zJlyhSCgoIYNGhQQYllF6IABEEQXMDWvpbM8jNnzjB37lz69+9P2bJlC1K0fBEFIAiC4AJRHesR5O+brcxyv8unn35KWloab7zxhhHi5YksAguCIDhITq+fHs3CWPfHhVxeQPHx8UydOpWePXty++23Gy12LkQBCIIgOIA1r5/FO2IZ2z08l+vn1KlTuXr1Km+++aYRouaLmIAEQRAcwJrXz7/S13PXD/dlS0malJTEpEmTeOCBB4iMjDRI2ryRGYAgCIID5PT6ecRnE+P8Z1KSFFOBOSXptPgVnDt3jhEjRhggpX3IDEAQBMEBcnr9DPNbSEmVkq0s8dp1xk6dR/v27Wnbtm0BSucYogAEQRAcIKfXT1V1Mdc5U35P4XxiOqNHj84qi94VS6txa6k5fAWtxq01LBG8JWICEgRBcICcUW7PqwpU5kLW8bhkzUebb/DQHcHcfffdgP3hIgoaUQCCIAi22LsQ1rwH8adMOaY7jITGvbJHud17DX58GVJNawMTf73BlWQo3fIxWo1bS1THeryz7IDNcBHFUgEopaoBXwOVAA1M11p/apQ8giAI2di7MFvHnrm4C2TPPpf5/5r3OBt7gglbU6ldrx6/VnwM4pKI+n4PqRnaahNGJIK3xMg1gDTg31rrO4C7gBeUUncYKI8geIa9C02ugRYugkIhYM17Nzv/TFKTTOU5adwLXttPk433ci3Nh6R7X795iY3OH4xJBG+JYTMArfUZ4Iz5/wSl1CEgDDholEyC4HbsHUUK3kf8KYfK9+3bx7ltKynd9GH8y9ln1jE6ParS2rZ2KjAhlKoBbAAaaa2v5jg2BBgCUKlSpWYLFixwqo3ExESCg4NdE9QDiFyOUejkOn8Q0lNyl/sGQEXPT3gL3f0ymGxyOfDstNYMGzaMg4f+4L8TplIquHS+bfn5KBpUKeOcbA7Srl27HVrr5rlkcKo2N6KUCgYWA6/m7PwBtNbTgekAzZs318761MbExHilP25RkMuebEhGyFWQ2JTrnW6YlrhyoqBXnIelKoT3y2CyybX3fPbZG4B/EHSZDI3bZrtu5cqVbN++nafeeIevTt2SbcHX30eBgtT0m9+DIH9fxnYPp60DvxNP3DND9wEopfwxdf7ztNZLjJRFcI5M97bYuCQ0N93bvMHH2SsIudWxcsF7aNzL1NmHVAOU6W+XyblMd6mpqbzxxhvUqVOHqR+MYGz3cMLMtn1fpUjN0JQK8KNsSX8UEBYaZDVukBEY6QWkgFnAIa31J0bJIbhGXtmQvOELbjgdRlofRXYYaZxMxQ0brpx20bhXvudOnjyZgwcPsmzZMgICArK+95Z+/3FJqQT5+zKxdxOv+l0YOQNoBTwJtFdK7Ta/HjRQnkKJ0bsL7cmGVKyxcxQpeIjMRfj4k4C+uQjvJk+sU6dOMWrUKLp06UKXLl2yyu1JE+kNGOkFtAlQRrVfFPCG3YVVQ4OItdLZG+3e5gz2rGU4td5hxyhS8BB5uXK64Zm8/vrrpKen8+mn2bcwFZaBkcQCKsR4wygjv2xIhQV71jJkvaMQ4qArJ9g/q/7555/5/vvvefvtt6lZs2a2Y/mlifQWRAEUYrxhlNEtMixr0cvRBa68fmgFbdqyR5l6g8IVHMTBRfi4pFS7lPyNGzd48cUXqVu3rtVUj4VlYGS4G6jgPM6aX6J3xfLujwe4cj0VgNAgf955pKHTZqNscVHsJC/zFWDzWKhTEuaPPco073NKeUIswVUcXIQ/F59MUmr2cbE1p4aPPvqIv/76i59//pkSJUrkqidnwDhPu0c7iyiAQkxUx3rZOkrIf5QRvSuWqEV7svkkxyWlEvX9HqDg1g7yG03bOvbBXZ6ZtNqjTIvSekexwSJOjz1eQCnpGVgzjFgq/0OHDjF69Gh69+7Nv/71L5tNOzMwKmjEBFSIccb8Mn7V4WydfyapGbpATRl5jaaNMG3ZM2UvLNN6IQfmOD28E2f6m8fib4Cv9S4xU8mnp6fz9NNPExwczOTJkz0ibkEiM4BCjqOjjLw6UWc7WGc8Y/IbTRf0SNueKXte58TE/OUx2YQCYu9C6nCBf0r8h9O6PB+l9WJZRutsSv7zzz/n119/Ze7cuVSsWNFggV1HFEAxw1bHm3nMUfKy5XdtUpWEhAQuXrzIpUuXuHTpEjdu3CAjI4NWvueZ/89pUn1L4BNQEp/AUgSXq5T1Q7Np2orPu6N1JSyFPcq0MEzrBScw7xfwqTUcH6W5VV1knP9MyvkH0OShIXSLDOPYsWOMGDGCzp0788QTTxgtsVsQBVDMiOpYL9caAICPci4y4fhVh7l+I4XUy7GknDtC6vmjnI87wxMzz+GTeJ7ExESH6nvuy0pUr16dqpVrcjTjFpLKVKN63UYMfyQ835G2N+yLEAopVvYLlFQpvFNqMUS+i9aaZ599FqUUX3zxBaZABoUfUQDFjG6RYWw/fplvtp7IVu7rwBc6ISGBTZs2ERMTw455P5Jy/h906g1zRX74hVTGv2wVnur1MNWqVeOWW27hlltuoVy5cpQoUQJfX198fX1JTU0lISGBq1evcvnyZU6cOMHx48c5evQo+35dy4ULpjR7F/38GP/znexo357y5cvTunVr/Pxyf3UlLIXgNPnsF/j666/5+eef+eyzz7jtttsKUDDPIgqgGLLujwu5yjIXga11lBkZGezYsYPx0yFb9oMAACAASURBVOex8n+rSIz9E3QGfn7+BIXVJaBxRwIq1yag0u34l78V5eNLWGgQnw5v77SMWmvOnDnDrl272LJlC2vWrGHMmDFkZGTw77dGcUuj1jw34HHeHtILf39/onfF2jRtubp4/Hb0Pr797STpWuOrFH1bVmN0t3CX6hS8jJBbzeEicpefPXuW1157jdatW/Pcc88VvGweRBRAMcRWhxgbl5SVw7RkSgrLly9n2bJl/Pjjj5w9exaUDyWq1KXMXT0JvC2c0BoN6XlXbRbviHXIFdUelFJUrVqVqlWr8tBDD9HisecZNn8r96Zu49vVW7mwZx3vvfgTE/77KqUadsDvjvvxL1vFal2uLB6/Hb0v22wpXeus96IEihCZ+wUs8Q9Ct/8vgwcPJikpiZkzZ+LjU7QcJ0UBFCLcFXff1kKwzkjnyJ7fGPjdeNL+3sS1xERKly5Np06d+C29Bhm3RuIbdDOBxQ1Ms4mx3cM9vuFl/KrDpPgGEtHkbn4JbINOSyHp6E4S967m/ObvYdN3BFaPoHSLbgTVap5lo3VVGX37m5VRoblcFEARItM19I+LmIL2mfYLzN6WwIoVK/j000+pV6/oufuKAigkuHOBM+cGstSLJ0nc+zPXDq0nPfEyKiCIO1vexagRUXTo0IGfDlzg9+9242ulrtNxSQXiGZNz1qL8AihZ5y5K1rmLtISLXNu3hoTd/+PConfxv6U6ZVp2p1SDexnrYvjddBsZ82yVC4WYxr3gckxWop6jR4/y6quNadeuHS+++KKxsnkIUQCFBHcucHaLDCPlRjJvT5zFiV9/5MbJ/eDjR1Dt5pRqcB9Bt7fgiaZ+dO7cOattWxTULti83Ff9St9CyD29KdOyB9cObeDqb4u5tGIiCZvnceWOcaSFP2l10dgefJWy2tk7smguFD7S09MZMGAAPj4+zJkzp8iZfjIpmp+qCOKu3bEnT54kKiqK5x9uyV8Lx6KuXSa07UBufX4OFbu/TakGbfDxD8y2IzKvNgpqF6y1Xbg5u2Dl60dwo/ZUeWoKFR8bRflbKvDUU08RHh7O4sWLcSb/dd+W1RwqF4oGkyZNYuPGjUyePLlIef3kRBRAIcHV8LK7du2iX79+1KpVi4kTJ9KuXTtWr17NvJ+3Url1b3xL3QyzFuTvS6WQwHzbCA3yLzD3ysywFwG+PllhL56467ZcSgFMC8hBtVtQpvd4ho2fjlKKxx57jJYtW7J161aH2h3dLZx+d92WNeL3VYp+d90m9v8izIEDB3jrrbfo2rUr/fv3N1ocjyImoEKCM4HfADZu3Mi7777LmjVr8AkIIjjyYeq078UTve/lfnPn7ePjk2sRN9Rix62ttt95pKGbP2XedIsMIyb+L46Oa5tV1rx6OcavOmzVPJSclsGmtNrs27ePuXPn8tZbb3H33XczYMAAxo4dS5Uq1r2GcjK6W7h0+EUNG2kiU1NT6d+/PyEhIUyfPr3IbPiyhSiAQkLmSNsyjHMJP9sTuK1bt/Lf//6XX375hbK3VKRC+6cIDH8An8BgLkK2BWRri7iWO25txcABaDVuraHhbjNlrzl8BdYMPKfjkvD19WXgwIH06NGDMWPG8Mknn7D4++8Y2T6EV5sk4V+ummN5YoXCTWaayMydv5lpIoFZs5awc+dOli5dWiRi/eSHKIBCRnJqRtb/mckr4GYn/X+L1zHqPyO4cvg3/EqFMPC1/3Io9C7OXs/ePTq6gJxTSXhb2AV7QjWXLl2asWPH8nSrKrweFcWw5eeYt82HGV2O0eK62QfcSSUQl5RquDIU7MRGmsifPx/Gd98d57nnnqNbt27GyFbAyBpAISIvT6ArV67w8ONP83LP+4k7tp/Qe/tTZchMtpa6J1fnn4krO2S9LTuWI6Gab/9rOst6BxLdO4gL1zV3zbrG68uvcO2nd5xqO3pXLLFXkiRVZGHBStiH89cy6P/NCapXr86ECRMMEMoYZAZQiLDWYWutObzhB+p83ItLl68QHNGR0Db98C0ZApg6ZVuujK64cHpDOkpLHMrAZO4Autb3p20NP0asSWbi1hSWHPqDaZGr6Nixo0Ntj191mD7VXJthCQVIjrAPGVozIDqJuBvw+ciRlCxZ0upl7tqI6U2IAihE5DRzpMWf49L/ppB8bBdt2rThyO098a9YK9d16VoT5O/r1nAN3pgdy+4NaRYdQEig4vOHgng83J9nVqTRqVMnnnnmGSZMmEDp0qXtavd0XBJY8Qo1ShkK+ZAjTeSnW1P439/pfPbWU9Sqlfv3A95n8nQXYgIqRGSaObTWJOz+H6dnvUDK6T94dsQYYmJiqFHXuldOZqYwZxK35yeLJYUmO1aHkaa8sBa0rl2a3StmM2zYMGbOnElERAQbN260qzpXXXSFAqZxL+gyGUKqsfNMBm+uSaFru+YMHT3T5iXeZvJ0FzIDKER0iwzjemICL784lMt7Ywi5vSnjP53KMw/eCeTtKurucA2FJem1VWzkiS3RuBcfNn+CLl26MGDAAO677z5ef/11Ro8eTWBgoM3qojrWI/bQjmxlhUYZ5qAomjms0rgX8dU70qtZMypWTmbW9//L0+XT20ye7kIUQEFhw+/YEXbt2sXIQT2JO3aMsWPHMmzYsGxb1Au6Uy7U2bEa97J5/1u3bs2ePXuIiopiwoQJrFy5kq+//ppmzZpZPb9bZBjRZw8SFupbqDvOomrmsIbWmoEDB3L8+HFiYmIoX758nud7o8nTHYgCKAjy8DsG+3yNlyxZQr9+/Shfvjzr16+nVatWVs8r1J2yFxEcHMzUqVPp2rUrTz/9NHfddRfvv/8+UVFR+Prm3n0cGuTP5uFtC15QN1KcEupMmDCB6OhoPvnkE5u/JUuc3Yjp7cgaQEFgw++YNe8BppFXq3FrqTl8Ba3Grc3mPqi1Zty4cfTo0YOIiAi2b99u9QubVx2C83Tq1In9+/fTvXt3RowYwf3338+pUzayRxVyiqqZIycbNmxg+PDhPPbYY7z66qt2XZMZisSd62jegKEzAKVUJ+BTwBeYqbUeZ6Q8HiOPdHNxSamMWGN92v1IRBVeeuklPv/8c/r27cvs2bOt2qKL09TdCMqWLcuCBQvo1KkTL730Eo0bN2bGjBn06NHDaNHcSlE1c1hy9uxZevfuTe3atZk1a5ZDoR6K4uzasBmAUsoX+AzoDNwB9FVK3WGUPB4l5Fab5efik61Ouz9aeZCnn36azz//nDfeeIN58+bZXIgsqh4K3oRSikGDBrFr1y5uv/12HnvsMQYPHuxw0ntvxh7PrsI800xNTaVPnz7Ex8ezaNEiypQpk/9FRZx8FYBS6iWlVFkPtH0n8LfW+h+tdQqwAOjqgXaMx4rbIf5B0GEkKekZuU7XGensmfs+c+bM4d133+Wjjz4y3EOhMP/w3UmdOnXYvHkzI0aMYPbs2TRt2pTt27cbLZZbyM/MkTnTLKw7nl999VXWr1/PjBkzCA+X4H4AKr8Y6Uqp0UAfYCcwG1ilnQmsnrvex4BOWuvB5vdPAi211i/mOG8IMASgUqVKzRYsWOBUe4mJiQQHB7smtCskXYGEM5CeAr4BULoKBJXl4pV4zly/eVpGRgbzZ/wfv29cx7PPPkufPn3yrfrw2QSriiTA14d6le3bzJQTy/sVl5RK7JUkMiweu49ShJUNIjTI36n6ncXw52jB7t27GTNmDJcvX6Zfv37079/f6xKHuPN+ufN75snnGJeUyrn4ZFLSMwjw9aFSSCAbVq9k4sSJ9OnTh2effdYQuVzFFdnatWu3Q2vdPGd5vgoAQJmGnw8Ag4DmwEJgltb6iFPSYL8CsKR58+ba2dFWTEwMbdu2depaTxK9cjUjtqSTlJqO1pora2eSsP0H+jz3b76d+rF9deRYAwDT1N2VRSrL+9Vq3FqrtuGw0CA2D2/vVP3O4m3P8fLlyzz77LMsWrSIdu3a8fXXX3PrrTZMfgbgzvtlK+KqAo6Oe8ihujz1HK39FjJiD3B6wX/o1LEjP/zwg1UvLk/L5Q5ckU0pZVUB2DVcMY/4z5pfaUBZYJFS6iOnpDERS/YN9Leay4oVoUH+WdPuhN+XkLD9Bx7q+xTzPx9vdx2e9lAoLt4hzlCuXDkWLlxIVFQUv//+O40bN2bJkiVGi+URCsOO55zrYalxZ4ldNJqAclWZP39+np1/cSRfLyCl1CtAf+AiMBOI0lqnKqV8gL+AYU62vQ2oo5Sqianj7wM87mRdhZpukWH4ntpJ17fm0KtXL779ZobDiSg86aFQHLxDXEEpxYMPPsgzzzzD448/To8ePRg8eDATJ070WnOCM3iDL3zOncrt6ldg3R8Xst5bfk8zkhO5sOg9QFOu29uy6GsFe2YA5YDuWuuOWuvvtdapAFrrDOBhZxvWWqcBLwKrgEPAQq31AWfrK8zs37+fxx9/nKZNm/Lll1963I7s6IJuoY77U4BkLhAPHz6cWbNmERERwZYtW4wWy20Y7QtvbRH6m60naHZ1NRsDXmZj0qNsCniZR3w2odNSOL9kNKlXTnNLtxFUr1nbvkaSrsDERvBOqOnv3oUe/UxGk+8MQGs9Ko9jh1xpXGv9E/CTK3UUdhITE3n66acJDg7mhx9+sBmK1l04s2egUMf9KWACAgIYO3YsDz74IP3796dNmzaMGDGCkSNHEhAQYLR4LmOkL7w1d+dHfDYxzn8mJVUKALeqi4zxm8HK6GhunPyDW7pEUe72pvYNVvYuhPizN0NFW+7YL6LZ4iQUhIForfn44485fvw4GzZsICzM8z8sZ7f7F8VNMJ6kTZs27Nmzh1dffZUPPviAlStX8s0339CgQQOjRSu0WFtzGua3MKvzz2Tk6gT+PnSJsm2fou49newfrKx5DyoPzl6WuWO/iCoA7/JZK2ZMnz6d9evX88EHH3DPPfcUSJuyoFtwlClThtmzZ7NkyRJOnDhB06ZNmTx5MhkZuV0pLfHGPRcOy7R3odtNKdbWnKqqi9nej998g4lbU3j5zgAurZ3J5uHt7R+45LFjv6giCsAg9u/fz6uvvkqLFi2IiooqsHYLgydHUePRRx9l3759tG/fnldeeYWOHTvajCfkjZutHJYpM/hh/ElA3zSluKgE2tWvkKvstL4l6/8pv6cw7Jcb9G7oxye9bnfYkSKvHftFFVEABpCamsqAAQMoXbo0w4cPL9DNQ7KgawyVK1dm+fLlfPHFF2zZsoVGjRoxa9Yscu7D8cawHg7LlE/wQ2dZ98eFXGUfpfXiug5g5s4UXlqZTNd6fsztVQ7ff9lcurRNh5GgcvwWzTv2iyqyBmAA48ePZ+fOnSxatIhy5coBBZeIQxZ0rZPf/XfH81FK8eyzz9K+fXsGDx7M4MGDWbBgAdOnT6dmzZqAZ010zn4Gh2XykCnFWnvLMlrzx879/LJ8OZ1u9+O7p+vg3/Ed52z2jXtB7FIIqeZS3o7ChCiAAubAgQO8++679OzZkx49ehATE1Pg0TxlQTc7+d1/dz+fOnXqsG7dOqZNm8awYcMIDw9n7NixvPDCCx7bc+HKZ3BYphxJ17OVu4A1ORJ2/4/Vq1YQUjuSJXs3UyLIRVNmUFl4bb9rdRQixARUgGRkZDB48GDKlCnDlClTssq9cdpfnMjv/nvi+fj4+DB06FAOHDhAmzZtePnll7n33nvpU8fHIyY6Vz6Dw2bDPIIfukJUx3r4+9y061/9fSmXV02hZO1mTPt6IUGudv7FEFEABcicOXPYunUrEyZMoGLFm5nAxDPHWPK7/558Prfddhs//fQTX331FQcPHuTffR/gjtjlVC6JWzdbufIZHN4AZpF0HZTpb5fJLptSukWGMb5nBCGBfsRtnMeVdbMIbdiGOfMX0vue221e541eVd6CmIAcwBU78JUrVxg+fDitWrXiySefzHZMQi04jjvXTPK7/55+Pkop+vfvT6dOnXjzzTeZ8+VnVKu2jEmTJvHoow867s1iBVc/g8NmwzxyLrvCgw0rsPyz79m75Vueeuoppk+fnmd8H0mWlDcyA7ATV93zRo0axaVLl5gyZUquH7R45jiGu10l87v/BfV8KlasyJdffsnGjRspW7YsPXr0oHPnzvz5558u110UvmNXrlyhU6dOzJo1i7fffpsZM2bkG9xNzKt5IwrATlz5Iu3fv5/PPvuM5557jiZNmuQ6bnSMlcKGu3/U+d3/gn4+rVu3ZseOHUyaNIktW7bQsGFDXn75ZS5evJj/xRZE74rl8NkEag5fwfhVh+nRLKzQfscOHz7M3XffzebNm/n66695//337XKftmXiio1LErMQYgKyG1dsqMOHD6d06dK8955tP2jxzLEfT9jk87v/Bf18/Pz8eOWVV+jduzejRo3is88+46uvvmLEiBG88sor+S54Zs6Snq+fgcaH2LgkFu+I9Win7ylX5m+//ZYhQ4YQGBjIL7/8Qps2bey+1pbpS0FWuaVZKNRlaQsXMgOwE2d30G7YsIEVK1YwYsQIypcv7wnRih1FdjezlfAJlStXZtq0aezfv5/77ruPESNGUK9ePWbPnk1qaqrNqjxl+si5oLpt2TSY2Aj9Tigtou+l2dXVbtvBnJyczPPPP8/jjz9OREQEu3fvdqjzB+umLwW5EtsUV7OQKAA7ccaGqrXmzTffJCwsjJdfftnTIhYbioI9OxdWwickLXmRV94aQatxazmcXIZly5axbt06KleuzNNPP03dunWZMWMGKSkpuarzxCwp59pLs6urabTjbYg/iUITpi4yzn8mj/hsAlzrVLdu3UpkZCRTp04lKiqKdevWORUs0Zr5zlYOxOLodScKwE6csQNHR0ezdetW3n33XfFRdiNFcs3ESviEIG4Q5bcw22i6bdu2/PbbbyxfvpwKFSowZMgQ6tSpw9SpU0lKunm9J2ZJOWcVw/wWEpQjEmdJlcIwv5sxfxztVK9fv86wYcNo1aoV165dY9WqVXz00Uf4+zufe7pbZBibh7fn6LiH2Dy8PWFFdQbpBKIAHCDnFymvDicjI4ORI0dSv359BgwYUIBSFg8ceRaFAhthEqqqS0D20bRSioceeojffvuNlStXUrVqVZ5//nmqVavG22+/zenTpz0yS8rZmeeMxJlTZrC/U9Vas2DBAurXr8/48eMZPHgw+/fv54EHHsj/YgcjjxbJGaSTiALwENHR0ezfv5+RI0fi5ydr7UI+2AiTcFrfXDfK2QErpejUqRNbtmxh3bp1tG7dmjFjxlC9enW+/3gYT9ZMwt9HuW2WlLMzt4zEaU1mezvVTZs20aZNG/r27Uv58uVZv34906ZNsy+FoxORR4vkDNJJpGfyAFprRo8eTZ06dejVq+gGkhJuEpeUSqtxa+33gNm70GT2yQw6VucB2DM/mxnoug7go7Sb3x9bo2mlFG3btqVt27YcOXKEKVOmMGvWLObPn09YWBhDhw6l/xP9qVbNtQ4uZ07gj9J68aH/zGxmoCRKMD6tF2H53AOtNWvWrOH9999n/fr1VKxYkRkzZjBo0CDHErfnFXk0j41o4nVnQmYAHmDFihXs2rWLt956ix/3nhV/4yJO9K5YYq8kuRYvf898iHgcQqqhUcTqWxieOphlGa0B+0fTtWvXZuLEiZw+fZo5c+ZQoUIF3n77bapXr869997LpEmTOH78uFOfM+fIeUeZf7G/2ehsIR+Cuk/h0zFjbZrl4uLimDJlCoMHD+b+++/nzz//ZOLEifzzzz8MHjzYsc4fimUSF3ciMwA3kzn6r1GjBsF3tJVt6MWA8asO06dadt+SPNNs2hq1/vUzvLYfBWzbFcuOVYdRTvrUBwcHM2DAAKpXr85tt93G3LlzWbx4Ma+99hqvvfYaTZs2pVOnTrRr14577rnH7lzUuUfO7YFn87wmPj6eFStWEB0dzfLly0lKSqJOnTpMmzaN/v37ExgYaPfnyoWHIo8WF0QBuJlffvmF3377jWnTpjFx7T9O5d8VChen45Kgmo1ya9gxanWniaJWrVqMGjWKUaNG8ffff7N06VJ++OEHPvzwQ8aMGUNAQAB33nknzZo1o2nTpkRGRlK/fn2nPG+01pw5c4adO3eyefNmNm3axG+//UZqaiqVKlViwIABDB48mISEBNq2bev6h+sw0jSbslSoRTyJizsRBeBmxo8fT5UqVRgwYABjR/1i9Zzi6G9clDHZ5hNslFvBwFHr7bffTlRUFFFRUSQkJLBp0ybWrl3Lpk2bmD59epYrqY+PD35lbkGVrkiZ8pW5s341mta5lZCQEHx8fEhPTycjI4PExEQuXLjAhQsXOHHiBH/88QcJCaZ74e/vT7NmzXj99dfp2rUrLVu2zArfEBMT454PlGnnt1xPKeJJXNyJKAA3sm/fPlavXs2YMWMoUaKERPksJkR1rEfsoR3ZyvKNl+8Fo9bSpUvTuXNnOnfuDEB6ejqHDx9mxtI1zF21leTLZ0iLP8flo/tY+cdWfrpxLVcKS6UU5cuXp0KFCoSFhTFgwADq169Po0aNaNGihd2mJZfwUOTR4oAoADcyceJESpYsybPPmmyiOb0moPj6GxdlukWGEX32IGGhvvZ5AXnpqNXX15c77riD35edJfieWgTnOF61TAlWvtACrTW+vr74+vpSokQJxxduBa9BFICbOHfuHPPmzWPw4MFZeX4l/27xITTIn83D29p/gRePWm2ZKM9cvUFISEgBSyN4ElEAbuLzzz8nNTWVV155JVu5+BsLhQ0xXRYfZB+AG0hKSuLzzz+nS5cu1K1b12hxBMElJFRC8cGQGYBSajzQBUgBjgCDtNZxRsjiDr777jsuXrzIq6++arQoguAyYrosPhhlAloNjNBapymlPgRGAG8aJIvLTJ06lQYNGrjHr1kQvAAxXRYPDFEAWuufLd5uBR4zQg53sHPnTn7//Xc+/fRTtyTvFgRPYm/WLk9l9xK8C5XTr7fABVDqR+A7rfU3No4PAYYAVKpUqdmCBQucaicxMZHg4JyOba7z8ccfs2bNGr7//nun6veUXK4icjlGYZArLimV2CtJZFj85n2UIqxsEKFBN3f92nueu+TyJrxVLnBNtnbt2u3QWjfPWe4xBaCU+gWobOXQf7TWP5jP+Q/QHOiu7RCkefPmevv27U7JExMT43YTTXx8PFWrVqVv377MnDkTcHzk5Am53IHI5RjeLFdcSB3Grzps1bMHTOGQNw9vn/W+1bi1Vs/NeZ6rcnnr/fJGucA12ZRSVhWAx0xAWuv78xFoIPAw0MGezt8b+eabb7h+/TrPPfcccDNlngR/E7yFuKRURqzZlysmlSU5/f49kU5S8E6M8gLqBAwD7tNaXzdCBlfRWjN16lRuvyOCV365yulFK/BRinTtQFRIQfAw5+KTSUrN29s7p3+/V+0DyJk3wQt2TBcljNoHMAUoDaxWSu1WSn1hkBz5Er0r1mo8/02bNnHgwAESa7XLigOfs/PPREZOglGkpGfkedyaf7/X7ANwItuX4BhGeQHdbkS7jpKXSWfx9On4BpbCv07rfOuRHZSCUQT42h7j2cra5TX7AJzM9iXYj4SCyIPxqw5bjec/9oed7Fu8mJL12+ITkHcyC9lBKRhJpZBAgvzTcwUkzC8HrlfsA5BsXx5HFEAe2DLdHPltNUlJSYTf/RBXrRz3VYoMrcV/WigwbHmfhQb5M7b7HYaP5nPJF2F7UToLyfblcUQB5IGtxbCUQ2tp0KAB7w7uyltL9zs8uhIEd5KXqTIU94zmXdkYZk2+2CvpRO+KzbsOL8mbUJSRYHB5YG0xzOfqGRKOH2DQoEE82vTWbEmyw0KDpPMXChxbpsrxqw67pf7MDtzupPd2yJehdf7yNe4FXSZnSzpPl8li/3cjMgPIA2uLYZXP7+aEry/9+vXLOkc6fMFI8vbbL+Vy/XkpGHu++y7tK/DivAlFAVEA+WDZwaenp3PbbU/SqVMnqlSpYrBkgmDC0377rm4M86p9BUI2xATkAKtXr+b06dMMGjTIaFEEIQtP++3b6qjt7cCtmlKVEu84L0AUgAN8+eWXlC9fni5duhgtiiBk0S0yzKNrUa4qGGvyhZUNEtOpFyAmIDu5fPky0dHRPPvsswQEBBgtjiBkw5NrUe7YGJZTvpiYGHeLKTiBKAA7WbBgASkpKWL+EYolthSM5A0o3IgCyAuLQFRfzr5BRL3qREZGGi2VIHgFEv228CNrALawCES1/3wa208mM7D2JQlEJQhmPL3/QPA8ogBsYRGI6stdqfj5wBN3mMsFQZC8AUUAUQC2MAecSk3XfLMvlYfr+lGhlI8EohIEM666hwrGIwrAFuaAU6uOpHH+mmZQE/9s5YJQ3PGavAGC04gCsEWHkeAfxJzdqVQoqeh8u58EohIECzy9/0DwPOIFZIvGvbgUl8CPo57h+eb++Je7TdLRCUIOJBZW4UYUQB4s2JdMSrpmwBe/QZMmRosjCILgVsQEBCbXzomN4J1Q01+zq+dXX31FREQETaTzFwShCCIzgEx//8ykE+bE0wf+Psm2bduYOHGisfIJgiB4CJkB2Eg8/dWUsfj5+fH4448bI5cgCIKHEQVgxa8/LUPzzbbLPPjgg1SsWNEAoQRBEDyPKAArfv2rj6RxJlEzcODAgpdHEAShgBAFYPb3t+SrfRmUDy3NQw89ZJBQgiAInkcUQI7E05f9qhB9OIO+/QZI3H9BEIo0ogDApARe2w/vxDG39FBupKQyePBgo6USBEHwKOIGys2kFrFXrnN+zkTqNookIiLCaLEEQRA8iqEzAKXUv5VSWil1i1EyZCa1iI1LIjn2EEnnj3O1xn1E74o1SiRBEIQCwTAFoJSqBjwAnDBKBsie1CJxz/9QAUH412ktSS0EQSjyGDkDmAgMA7SBMmQlr0hPTuT6H5so1bAdPgGBktRCEIQijyEKQCnVFYjVWu8xLlGwzAAACqdJREFUon1LMpNXXNu/Bp2WQumIjtnKBUEQiipKa88MwJVSvwCVrRz6D/AW8IDWOl4pdQxorrW+aKOeIcAQgEqVKjVbsGCBU/IkJiYSHBycqzwuKZWTlxJ5999DCQktx6sjx+KjFGFlgwgN8neqLXfIZTQil2OIXI4hcjmOK7K1a9duh9a6ea4DWusCfQHhwHngmPmVhmkdoHJ+1zZr1kw7y7p162weGz5hpgZ0ha7D9T1j1+ilO0853Y475TISkcsxRC7HELkcxxXZgO3aSp9a4G6gWut9QFaAnfxmAO4m0+XzdFwSVUODiOpYjy0/fE316tX5e9H7+PmJZ6wgCMWDYtXbZbp8Znr9xMYl8eqUxRzfsIGPP/5YOn9BEIoVhvd4WusaBdWWpctnJuc3zMc3MFh2/gqCUOwoVqEgcrp23jj7N0l//0bp5l0JCQkxSCpBEARjKFYKIKdrZ/ymefiUKEXdDpLoXRCE4kexUgBRHesR5O8LQNLRXSQd2Ub5e3oxomszgyUTBEEoeAxfAyhIukWGAfDhin3sWDOdEuWqMGXMf7LKBUEQihPFagYAJiXQKu4XUi+dZMncmfS6q7bRIgmCIBhCsVMAS5YsYcKECQwdOpQHH3zQaHEEQRAMo9gogPT0dGbMmEHfvn25++67+fjjj40WSRAEwVCKxRrAO++8w6RJk4iPj6dDhw4sXLiQkiVLGi2WIAiCoRSLGUD16tW55557+P7771m1ahXlypUzWiRBEATDKRYzgEGDBlGzZk3atm1rtCiCIAheQ7GYAQiCIAi5EQUgCIJQTBEFIAiCUEwRBSAIglBMEQUgCIJQTBEFIAiCUEwRBSAIglBMKRb7AOzFWr5giRQqCEJRRRSAGWv5gkcs2QcgSkAQhCKJmIDMWMsXnJSazvhVhw2SSBAEwbOIAjCTM19wfuWCIAiFHVEAZnLmC86vXBAEobAjCsCMZb7gTIL8fYnqWM8giQRBEDyLLAKbyVzoFS8gQRCKC6IALOgWGSYdviAIxQYxAQmCIBRTRAEIgiAUU0QBCIIgFFMMUwBKqZeUUn8opQ4opT4ySg5BEITiiiGLwEqpdkBXIEJrfUMpVdEIOQRBEIozRs0AhgLjtNY3ALTW5w2SQxAEodhilBtoXaCNUuoDIBl4Q2u9zdqJSqkhwBDz20SllLPBeW4BLjp5rScRuRxD5HIMkcsxvFUucE226tYKPaYAlFK/AJWtHPqPud1ywF1AC2ChUqqW1lrnPFlrPR2Y7gZ5tmutm7taj7sRuRxD5HIMkcsxvFUu8IxsHlMAWuv7bR1TSg0Flpg7/N+VUhmYtNsFT8kjCIIgZMeoNYBooB2AUqouEID3TrsEQRCKJEatAcwGZiul9gMpwABr5h8347IZyUOIXI4hcjmGyOUY3ioXeEA25fl+VxAEQfBGZCewIAhCMUUUgCAIQjGlSCkApVRPc2iJDKWUTXcppVQnpdRhpdTfSqnhFuU1lVK/mcu/U0oFuEmuckqp1Uqpv8x/y1o5p51SarfFK1kp1c18bI5S6qjFsSYFJZf5vHSLtpdZlBt5v5oopX41P++9SqneFsfcer9sfV8sjpcwf/6/zfejhsWxEebyw0qpjq7I4YRcryulDprvzxqlVHWLY1afaQHJNVApdcGi/cEWxwaYn/tfSqkBBSzXRAuZ/lRKxVkc8+T9mq2UOm9eE7V2XCmlJpvl3quUampxzLX7pbUuMi+gAVAPiAGa2zjHFzgC1MLkfbQHuMN8bCHQx/z/F8BQN8n1ETDc/P9w4MN8zi8HXAZKmt/PAR7zwP2ySy4g0Ua5YfcL02bCOub/qwJngFB336+8vi8W5zwPfGH+vw/wnfn/O8znlwBqmuvxLUC52ll8h4ZmypXXMy0guQYCU6xcWw74x/y3rPn/sgUlV47zXwJme/p+meu+F2gK7Ldx/EFgJaAw7Z36zV33q0jNALTWh7TW+e0UvhP4W2v9j9Y6BVgAdFVKKaA9sMh83ldANzeJ1tVcn731Pgas1Fpfd1P7tnBUriyMvl9a6z+11n+Z/z8NnAcquKl9S6x+X/KQdxHQwXx/ugILtNY3tNZHgb/N9RWIXFrrdRbfoa3ArW5q2yW58qAjsFprfVlrfQVYDXQySK6+wLduajtPtNYbMA34bNEV+Fqb2AqEKqWq4Ib7VaQUgJ2EASct3p8yl5UH4rTWaTnK3UElrfUZ8/9ngUr5nN+H3F++D8zTv4lKqRIFLFegUmq7UmprplkKL7pfSqk7MY3qjlgUu+t+2fq+WD3HfD/iMd0fe671pFyWPI1pFJmJtWdakHL1MD+fRUqpag5e60m5MJvKagJrLYo9db/swZbsLt+vQpcSUuURYkJr/UNBy5NJXnJZvtFaa6WUTd9bs2YPB1ZZFI/A1BEGYPIFfhN4rwDlqq61jlVK1QLWKqX2YerknMbN92supr0kGeZip+9XUUQp1Q9oDtxnUZzrmWqtj1ivwe38CHyrTZGAn8U0e2pfQG3bQx9gkdY63aLMyPvlMQqdAtB5hJiwk1igmsX7W81llzBNrfzMo7jMcpflUkqdU0pV0VqfMXdYeUU/7QUs1VqnWtSdORq+oZT6EnijIOXSWsea//6jlIoBIoHFGHy/lFJlgBWYlP9Wi7qdvl9WsPV9sXbOKaWUHxCC6ftkz7WelAul1P2YlOp92hx9F2w+U3d0aPnKpbW+ZPF2JqY1n8xr2+a4NsYNMtkllwV9gBcsCzx4v+zBluwu36/iaALaBtRRJg+WAEwPe5k2raqsw2R/BxgAuGtGscxcnz315rI9/n97988aRRAGYPx5tTBiLGJsYqUBIYWFgoLEziKgRVCwsJCApknhN0hjIeQTWAiWooKCkEIIxNgpaKMEFTWljaWdkmIsZgKbEM3J3p+EeX5w5G7vhnvz7t6+t7Nzs2UnuNHvfgXYdrRAL+KKiJGNLpSIOApcAD4NOl9l3T0n940+2/JcN/O17fbyj3ivASslP4vA9cijhE4AJ4G3LWL5r7gi4gxwH5hOjSnX/7ZO+xjXWOPhNPC53F8Cpkp8I8AUm4+EexpXiW2CfEL1TWNZL/PViUVgpowGOg/8LF9y2uerV2e2B3EDrpL7wX4DP4ClsvwY8KLxusvAV3IFn28sHyd/QNeAp8CBLsU1CrwEvgHLwJGy/CzwoPG64+Sqvm9L+xVglbwjewgM9ysuYLK894fyd3Y35Au4AawD7xu3073I13bbC7lLabrcHyr//1rJx3ij7Xxp9wW41OXtfae4lsvnYCM/izut0z7FtQB8LO//CphotL1V8rgG3OxnXOXxHfK1Sprtep2vx+RRbOvk/dcsMAfMlecDuFfiXqUxwrFtvpwKQpIqVWMXkCQJC4AkVcsCIEmVsgBIUqUsAJJUKQuAJFXKAiBJlbIASC1ExLkyqdlQRByKfH2CU4OOS+qEPwSTWoqIu+RfAx8EvqeUFgYcktQRC4DUUplb5h3wC5hMm2eRlHYtu4Ck9kaBYeAw+UhA2hM8ApBainyN2Cfki4iMpZRuDzgkqSN77noA0m4SETPAekrpUUTsB15HxMWU0spObaVB8whAkirlOQBJqpQFQJIqZQGQpEpZACSpUhYASaqUBUCSKmUBkKRK/QE7HRPoeUw2LAAAAABJRU5ErkJggg==\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYAAAAEWCAYAAABv+EDhAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8li6FKAAAgAElEQVR4nOydd3jT1frAPyfpChRaNlJG2bMMAWU4WFIVRxUF9cf1KgoOFEUviDJEwQuKA8d14kLxAl4UUVBAoKIMBSmzUFqG0rSU2UJpOpKc3x8ZJGnSJm3SdJzP8+Rpcr7nnO+bNDnvOe95z/sKKSUKhUKhqHlogi2AQqFQKIKDUgAKhUJRQ1EKQKFQKGooSgEoFApFDUUpAIVCoaihKAWgUCgUNRSlABR+RwgxSwjxZbDlcEQI8X9CiLVe1i1RfiHEI0KILCFErhCigfVvm3LIliiEeLCs7RWKsqIUgMIjQohjQgiDdYDLEkJ8JoSIDLZcZUFKuVhKOby8/QghQoHXgeFSykgp5Rnr3yPW658JIeaU9z5VCavCLLJ+T3JdFaIQoqcQ4k8hRJ71b89gyqu4hFIAitK4WUoZCVwO9AGmB1meYNMEiAD2B1uQ0hBChFTg7ZZaFWGki0IMA74DvgTqAZ8D31nLFUFGKQCFV0gp9cCPQDcAIUQzIcRKIcRZIUSaEGKcu3ZCiFVCiMddyvYIIW6zPpdCiIeFEKlCiGwhxH+EEMJ6TSOEmC6E+EsIcVIIsUgIEWW9Fmtte78Q4rgQ4py1n77W/rOFEO843PM+IcRvDq/ftLY7b52VXl3aZyCE6ACkWF9mCyE2OLyHdkKI8cD/AVOss+DvPfRznRDioBAixyqjcLk+VghxwPqe1gghWjlcGy6ESLG2fVcI8YvNfGR9j5uFEG8IIc4As7zor5MQYp31/5gihBhV2ufgI4OAEGCBlLJASvmW9f0O8fN9FGVAKQCFVwghWgA3AknWoiVAOtAMuAP4txDC3Y/6c2CMQz89gBhglUOdm4C+QHdgFBBvLb/P+hgMtAEigXdw5kqgPTAaWABMA4YBXYFRQohrPbyl7UBPoD7wFfC1ECLCQ10ApJSHrP0CREsph7hc/xBYDLxinQXf7NqHEKIh8A2WlVRD4DAw0OH6rcBzwO1AI+BX4L8Obf8HPAs0wKKMBrj5PI5gWam8VEp/tYF11vffGLgLeFcI0cV6fapVkbp9uNz3ZqsS2S+EeMShvCuwRzrHnNnj8DkqgomUUj3Uw+0DOAbkAtnAX8C7gA5oAZiAOg515wKfWZ/PAr60Po8AzgHtra9fBd51aCeBqxxeLwOmWp+vBx51uNYRKMIyo4y1to1xuH4GGO3wejnwpPX5fcBvJbzXc0APV/nd1LPdN8TlPbSzPv8MmFPCfe4Ftjm8FlgU6YPW1z8CDzhc1wB5QCtr260ubY87tL0P+NvlfiX1Nxr41aX+B8DzPn5PumCZCGixKKRM4G7rtRnAEpf6i4FZwf5+q4dUKwBFqSRIKaOllK2klI9KKQ1YfuxnpZQXHOr9hWVm74SUMh9YCowRQmiAu4EvXKqdcHieh2Wmj/U+f7ncIwTL7NZGlsNzg5vXbjethRD/sppFcqyz2SgsM/JA0wzLoA2AtIyIxx2utwLedJhln8Uy0Md4aJvu0v9xl9cl9dcKuNJlVv9/QFNf3pCUMllKmSGlNEkptwBvYlkVgmUCUdelSV3gAoqgoxSAoixkAPWFEHUcyloCeg/1P8cysAwF8qSUW324TyuH1y0BI86DvM9Y7f1TsJib6kkpo4EcXGzxZaS08LqZWFZQNlmE42ssA/hDVqVre+isA2sm0NylbXOccb1/Sf0dB35xuRYppXzE2v9zwtmzx+lRymdg+yz3A91t+zpWulMFNtFrAkoBKHxGSnkc2ALMFUJECCG6Aw9g8fRwV38rYAZeo/jsvyT+C0wSQrQWFvfTf2PxNjGW6w1AHSyK5BQQIoSYSfFZalnJwrJf4YlVQFchxO3C4qUzEecZ9/vAs0KIrgBCiCghxJ0ObeOEEAnWthMofbZeUn8/AB2EEP8QQoRaH32FEJ0BpJT/ls6ePU4P2w2EELcKIeoJC1dY39N31suJWMyFE4UQ4UKIx6zlG0qRW1EBKAWgKCt3Y7GHZwDfYrEb/1xC/UVAHB6UhAc+waIwNgFHgXzg8RJbeMca4CfgEBazUj7FTSdl5WOgi9WkssL1opTyNHAnMA/LnkV7YLPD9W+Bl4ElQojzwD7gBpe2r1jbdgF2AAWehCmlvwvAcCybvxlYTHEvA+E+vue7gDQsZp1FwMtSys+t9ygEErDsX2QDY7GYFQt9vIciAAiLGVGhCCxCiHuB8VLKq4ItS3XBuqeSDvyflHJjsOVRVD3UCkARcIQQtYBHgQ+DLUtVRwgRL4SIFkKEY3HvFMC2IIulqKIEVQFYv8j/sx6KOSCE6B9MeRT+RwgRj8XWnoXF31xRPvpjOTtwGrgZiznFEFyRFFWVoJqAhBCfY/FDXigsR8NrSSldD5goFAqFIgAETQEIy5H+XUAbqTYiFAqFosKpyGBRrrTGYhr41Boe4E/gCSnlRcdKwhJfZTyATqfr3aJFi2IdeYPZbEajsVi8srKyuHjxIm3alDmCr99wlKsyoeTyDSWXbyi5vCMtLY06derQpEmTcsl26NCh01LKRsUuBOsIMpbIkkbgSuvrN4HZJbXp3bu3LCsbN260P3/wwQdls2bNytyXP3GUqzKh5PINJZdvKLm8o0GDBnLChAlSyvLJBuyQlSwURDqQLqX83fr6f1hCDisUCoWiAgiaApBSngCOCyE6WouGAsnBkkehUChqGsHcAwDLqc7FVg+gI8D9QZZHoVAoagxBVQBSyl1Y9gIUCoVC4cCKJD05hiIWbT1G0rwNTO5h8vs9Ks92t0KhUCgAy+D/7Dd7MVsd5PXZBvTnDKxI8hRwt2woBaBQKBSVjPlrUjAUOc/4zVIyf02KhxZlQykAhUKhqGRkZLuP7uGpvKwoBaBQKBSVjGbROp/Ky4pSAAqFQlHJmBzfEV2o1qlMIwST4zt6aFE2gu0GqlAoFAoXEnpZ0mvf+brldUy0jph6Jnu5v1ArAIVCoaiEJPSKIUoXyr39Y9k8dQjRulC/30MpAIVCoaihKAWgUCgUNRSlABQKhaKGohSAQqFQ1FCUAlAoFIoailIACoVCUUNRCkChUChqKEoBKBQKRQ1FKQCFQqGooSgFoFAoFDUUpQAUCoWihqIUgEKhUFRSpJQB7V8pAIVCoajECCEC1rdSAAqFQlFDUQpAoVAoaihKASgUCkWw2bMM3ugGs6Itf/csq5DbqoxgCoVCEUz2LIPvJ0KRNeF7znHL6wpArQAUCoUimKx/8dLgb6PIYCkPMDV2BRBo9yqFQlEzWZGkZ/6aFDKyDTSL1jE5vmOJuXzzTh/n93QjV7XUEqp18PjJSQe0Htv5gxq5AgikW5VCoai5rEjS8+w3e9FnG5CAPtvAs9/sZUWS3mP9F7ZqGbIoj/8lG50vRjUPuLxBVwBCCK0QIkkI8UOwZVEoFIryMH9NCoYik1OZocjE/DUpHuuvPG1ZHaSfN19qQzgMnRk4Qa0EXQEATwAHgi2EQqFQlJeMbIPP5X/l6QBIzY3ALAXp5oZMLXwAuo8KmJw2gqoAhBDNgRHAwmDKoVAoFP6gWbTO53JjzkkAFp/vSZuCxVxV+BY76l4XMBkdCfYKYAEwBTCXVlGhUCgqO5PjO6ILdd641YVqmRzf0W39fw3vgOm8RQHIwvxS6/uboHkBCSFuAk5KKf8UQgwqod54YDxAkyZNSExMLNP9cnNz7W0zMjIoLCwsc1/+xFGuyoSSyzeUXL5RXeWKBuYO0JKVU0ShyUyYVkOTqDCic1JJTEwtVj/kwgXMhRbzUMuIfCb1NDvVNxqN6PV6EhMTA/OZSSmD8gDmAunAMeAEkAd8WVKb3r17y7KyceNG+/Nx48bJyy67rMx9+RNHuSoTSi7fUHL5hpLLQlJSkgQkIK+66qpi1+vXry8fe+yxcssG7JBuxtSgmYCklM9KKZtLKWOBu4ANUsoxwZJHoVAoKppjx44BFuuGweB+oziQBHsPQKFQKGosf/31FwCdOnWquQpASpkopbwp2HIoFApFRfLXX3+h0+lo0aJFzVUACoVCURM5evQosbGx6HQ6pQAUCoWiJpGamkr79u2VAlAoFIqahMlkIi0tjY4dOxIREaEUgEJRZoKUUEOhsHHu3Dmee+459u/f71X9v//+m4KCAjp06EBoaChGo7H0Rn5GKQBF1ceWUCPnOCAvJdRQSkBRgUybNo25c+dy1113lRpufkWSnhtf+C8Ab+64yOHTBsxmM2ZzxQZFUApAUfUJYkINhQIsB2q/+eYbAPbt28fBgwc91rWFjM5ISQJNCDm1m/NzyhkAioqKKkReG0oBKALKiiQ9A+dtoPXUVQyct8FjXPRykZPuW7lC4WcOHjxIVlYWkydPBmDbtm0e69pCRhccTyasaVs0oREYrUOxqwIobSVRXpQCUAQMX5NjlBlPiTMqIKGGQgGwefNmAMaOHUvt2rVJSkryWDcj24C5qICCzENENO8KgNBYAsi52wcIZAIrpQAUAcPX5BhlZuhMCHUJtxuqq5CEGgoFwP79+9HpdHTo0IEePXqwa9cuj3WbResozDwEZiPhLSwKAKsCUCYgRbXB1+QYZab7KLj5LYhqAQjL35vfqpCEGgoFQHJyMp07d0aj0RAXF1eiJ9Dk+I6YMi05sMJjugAQFhoGVLwCqLFJ4RWBp1m0Dr2bwd5Tcoxy0X2UGvAVQSM5OZlBgwYB0LZtW86ePUtOTg5RUVHF6ib0iuHf8gQXG7UgRFeHZtE6evVtxX9+dG8CCiRqBaAIGL4mx1AoqiJ5eXmkp6fTsaPle92mTRvAEubBE+mH9jIy/lqOzhvB5qlDuKJtI0CZgBTViIReMcy9PY6YaB0CiInWMff2OBJ6xQRbNIXCb/z9998AxMbGApcUwOHDh93Wz8zMJDMzkz59+tjLQkNDAWUCUlQzEnrFqAFfUa2xxfR3VQBHjhxxW992RqBr1672MqUAFNUWKSX79++nfv36NGvWLNjiKBR+xaYAnlyl58wPq2gWraNWZB3S092fQ0lJsXjB2UxGcEkBqD0ARbXCbDbzj3/8g7i4OFq1asXnn38ebJEUCr+y7o99oAnhlElnP+9ijIjmj33FcwCDRQHodDpiYi6tjENCLHNxtQegqFa89957LF68mEmTJnH11Vfz4IMPcuDAgWCLpVD4jU1/JhNSt6H9MBeAJrIh+1KPua1vCwGt0VwafoNlAlIKQBEwDAYDs2fPZvDgwbz22mssXbqUyMhInnvuuWCLplD4jQunMwmJauxUpo1sgCH7lNv6f/31F61bt3YqUwpAUe1YsWIFWVlZTJs2DSEEjRo14pFHHuG7774r0UVOoahKmC+cQlu3iVOZtk4DTBfPYjKZitU/fvw4LVq0cCpTJiBFtWPRokW0atWKwYMH28seffRRNBoNH3zwQRAlUyj8Q35+PkUXzqCr56wAdNGNwGwmKyvLqTwnJ4ecnBxatmzpVG5TAO4URiCpsQog0FH2ajqnT59m7dq1jBkzxsnW2bx5c4YPH87SpUvV/0BRZbFFuW03cREA/Xt2cjrv8sDw3gDFPIGOHz8OUGwFoNVa9g+UAqgAAhldT2Fh3bp1mM1mbrnllmLXRo0axbFjx9i+fXsQJFMoyodjlNui8xY7/66zoUyO72g/2XvHtT0A0OudI9/aFIDrCsCmAFRCGEW1YO3atdSvX5/evXsXu5aQkEBISIg9gYZCUZVwjHJrsiqAwXWO0u+7a+0pSWOydwDFFYDt1LCrArCtktUKQFHlkVKydu1ahg0bZp/ZOBIdHc3AgQP56aefgiCdQlE+HKPZGq0K4M36X9OUU9hSkjb8bTqhIVq3JiCtVstll13mVK5MQIpqw759+8jIyCA+Pt5jnRtuuIHdu3eTkZFRgZIpFOXHMZqt8fwpGkdqiQ5x9t7RmPKJqatxuwKIiYkpNjFSCkBRbfj1118BnLx/XLn++usBWLNmTYXIpFD4C8cot6bzp2hdPOIzADG1zU4rgBVJer7bvIcsc2Sx9KhKASiqDVu3bqVp06b24Fju6N69O5dddhk//vhjxQmmUPgBxyi3xgunaRwV4bZe8wa17SsA28Zx3tkstHUaFUuPqhSAotqwZcsWBgwYUKK3lRCC6667jg0bNlS454NC4TV7lsEb3eybu+xZBliUwG/PDCbUcIb2vQcVS0lqIJxDYR05fOxvvt2ZzqyV+8krLMJ44TQhdS2x/x3To9Y4LyAhRAshxEYhRLIQYr8Q4olgyaLwHydPnuTIkSP079+/1LrDhg3jzJkzJeZPVSiCxp5l8P1EyDmObXOX7yfalcCZM2cwGAy07H2dPSWpRKCXDXmm8AGORfbEXFTA04t+I9tQhCn3HJiMTmEjbBvKNdELyAg8LaXsAvQDJgghugRRHoUf2Lp1K4DXCgDg559/DqhMQcfDLFJRyVn/IhS5pDQtMljKcXHp7D4KJu3jqohvGFjwFivNV9kHekO25TSw6fxJAPsKAC5tKNc4E5CUMlNKudP6/AJwAFCZQ6o4W7duJTQ01K3/vyuXXXYZXbt2rd4KoJRZpKISk+M+nr+t3N2hLkcXUZsCMOVYBn6j9a/WQQHY0qN6UgCBPi1fKRLCCCFigV7A726ujQfGAzRp0oTExMQy3SM3N9feNiMjg8LCwjL35U8c5apMlFWuH3/8kXbt2rFt2zav6nfq1Invv/+etWvXEhYWFjC5Ao1HuU6ehjZTi5cfPA1n3dT3M1Xu8woyTnJ1+TeYCotX0oZBYiLr168HLCuBCxcuADC1p5lCk8WOf7F1fZ79DK6qfYLBcUZ+/iuLlcCk/g2I0BkJ0Qiic1JJTEzl7NmzABw4cMDpczEajej1ehITEwPymQVdAQghIoHlwJNSyvOu16WUHwIfAvTp00cOGjSoTPdJTEzE1va///0vYWFhlLUvf+IoV2XCF7lWJOmZvyYF/dlcjh88xA0j7/G6bW5uLsuXLyckJMSrNlXu85qVALibxQkYlR1gqarg5xVknOTac9KyWnM0A4XqLPb+7oNYtWoV4eHhJCQk2B0esq3ePoYiE1JGI8J0bEg5w95WoZxIOYMmIpL/pNVBF6pl7u1xDLKmSz19+jQAbdu2dfpcQkJCaN68OYMGDQrIZxZULyAhRCiWwX+xlFLFBaiCOMZFKTyTjrkwn50X6zv5OJfEtddei1arrb5moKjmvpUrKg/dR9k3d0FY/t78lqUcy8y/ZcuWTt5uji6iQghCohpTmJNF7bAQNBdPEVK3MTHROubeHueUK7smegEJ4GPggJTy9WDJoSgfjnFRCk9YUuCJxm3t7m2lUadOHfr161d9FcDQmcVcBAnVWcoVFUN5NuGtm7vMyrb8tQ7+AEePHqVVq1bFmiT0irEfFgup2xhjzkmyDUXkn8uiR+d2bJ46xGnwh5rpBTQQ+AcwRAixy/q4MYjyVElsYWlbT11V7HRhReC46VWQmYoI0xFSP8apvDSGDRvGjh07OHfuXCBEDC6lzCIVASaAm/BpaWm0b9/e7TXbxCgkqgnG7EykyUjhWT16Wc9t/WB5AQVtD0BK+Rug4jKXgxUO9kbAfroQKDbDCBTNonXorYN94YlUwpq2QwiNU7yU0hg2bBgvvPACGzdu5Pbbbw+UqKVi28vIyDbQLFrH5PiOxT5Hb+oUo/soNeAHi5JcOcvxPzlz5gznzp2jXbt2bq/bJkChjWKRhQbyj+0Ck5HCOs3c1q9xbqCK8uNofrHheLqwIrAtdaWpiMKTRwhv2h5dqNbu3uYNV155JZGRkUE1AznuZUgodlTf2zqKSkYprpzu8GZVnZaWBuBxBWCbAIU1tuT+vZicaClv3cFtfaUAFD7jyczii/mlvNg2vaLzT4DJSNO2XYttcHnC9kPrMGMtoc27seKHH4tdqyjTljfKtDIoXIWP+LgJn20o8krJp6Za9rs8rQBsE6PQRq1AaCwKQBPCc/cMc1u/xpmAFOXH0fziWl4SK5L0vPD9fs7lWULYRutCmXVL1zKbjRJ6xZDVTfAw8NNL99O6tXeDv6P5ipg4Mtdv48NV22jcrIVH01Z0mSQsHW+Uacl1agdCLEV5GTrTvSunh034rJx8DEXO82Kbknf8faSlpSGEoE2bNm77sdWdvyaFk827UHB8H3G9r2R0f/cKw7YJXGO8gBTlxzEsrY3SzC8rkvRM/t9u++APllnP5K93l2uWvX37dho0aFBiBFBHXGfTEa16AvDKJ/8Lykzbk9J0LPemjqKS4eMmvO0Qlyuuyv/QoUO0bNmS8PBwj7dO6BXD5qlDWLf4Xa688koWvuPZ2VEIgRBCmYAU3uPkcwxu/Ytdmb8mhSJT8YNJRWZZrgF2+/bt9OnTx+t8y64/qNCGLdHWrseJA9uDYtryRpmWReEqKgEluHK6EqZ1PyS6Kvndu3fTo0cPr25/9dVXs23bNq644ooS62m1WmUCUvhGQq8Yn0w3ngbR/PQD7PlpPe9HH2LcuHE+ybB0Sxp79u3jr9qdGThvg1eeMa7mKyEEEbE9KTiWxGV1w8k4X+C2TaBwXLJ78vApqU5iYmrAZFNUEHuW0Z5THAmfRoZswCvGUaw0X1VMyRsMBg4ePMjIkSP9enulABQBx92+Qf7fe8haMh2h0fDIIz+xe/duRo8e7VV/K5L0TPlwJZjNhF3WwWtX1MnxHZ33AIC6bXqRuX8jd7aVfLhP63TN/iPMKXmgLZObphVvlKmvCldRRbCeF9C0mYpGSJqL00yXH5H19xFGjJvh9D/fs2cPZrPZ6xWAtwRDASgTUA1jcnxHQrWXzDTSZOTMT28TWu8yvtiwm6effpr333+f338vFpfPLfPXpHAh/SAAYU0tG1ze2Ovdma9mT7gbAHP6Hp9NW6DcNBXlwOW8wMVCybULz7Hsv8v41+ghpKRc+j5v2rQJgAEDBvhVBKUAFD6xe/duBg8ezIQJEygqKiq9AZaBd3TfFvbXufs2YDyXScMhY6ldJ4p///vftGvXjo8//tirULQZ2QYKMlLQRjYgpE4Dp3JvZNk8dQhH541g89QhPBDfh86dO7Nu3bpi17yZdSs3TUWZcTkX8OqWQg6eNvPacEu6x9tuu428vDwA1q9fT5cuXbjsssv8KoJWq1VeQArvyMvL48Ybb2THjh28++67zJgxw+u2Gw+esj+/sPMHQhu3JrTNFcxfk0JYWBjTpk0jNTW1WL5ed775zaJ1FKQnE97cOZdPWe31N9xwAxs2bLCHx3W9f8qJC27PBqxI0rt1iYXybx5PX7GXts+uJnbqKto+u5rpK/aWqz9FJcThXIDJLPlwZyE3tAvhqevb8tVXX3Hw4EGeeuopMjMzWb9+PTfccIPfRdBoNGoFoPCOjz/+mIyMDFavXs0///lPFixYQEZGhldtbQNiYdYRik4eIbL7cIQQ6LMNDJy3gcgug2jQoAHvvfeevY0n88rlDYyYLpx2UgDl8YwZM2YMRUVFLFvmHKvFdv9Ck9np/tNX7KXnC2t5cqnntJLl2TyevmIvX277G5N1NWSSki+3/a2UQHXDIWjfluMmMi5I7utdG4bOZNiwYUyZMoUPPviA+Ph4jEYj48eP97sIGo1GrQAUnnGcgT/78ju069KDq6++mhkzZlBQUMBnn33mVT+2AdF2OrF2l2vt1/TZBmZ8f5BBw4azevVq0tMtS+MXvt/v1ryyZv0vALTo3Msne70nevbsSdeuXVm0aJFTuSfzzuJtf5Nt8Gz+Kq+b5n9/P+5TuaKKYjsvoA1j/VETGgHXPfa63WV09uzZjBw5kv379zNr1iw6dHAf0qE8KAWg8IjjDLwo5yQX9YfIuawPK5L0tG3blquvvppFixZ5Zbe3+bPnpf1BRMs4tLq6TtcNRSZ6DRiM2Wzmk08+YUWS3ungmCMnDu2mTp06/Pn6Az7Z6z0hhOCf//wnW7duZe/eS7NsT2ac0t5teZQRYJ/5e1uuqMJ0HwWNu7De1JfeffpS76qx9kuhoaH873//o7CwkOeffz4gt9doNAFPAVnsnhV6N0WZcZwB5/9lMXeEtLrcvsH5j3/8g5SUFHbt8mwKsZHQK4aJfSIxnk1H17av2zp1GzTmuuuuY+HChbzyY7LHvoz6ffTv35+QEP95FD/wwAPUqlWLV1991V5WFjNOTLSu3C6bWg8H2zyVK6o2BoOBbdu2MXToULfXbTF7AoFaAVQgFa1py4vjDDj/+D40urqENmxpL7/11lsRQvDDDz941V/hsT8BaN3rarfXw7Qaxo8fz/HjxzmctNltHeP5UxhO/kV8fLwvb6VU6tevz/jx41m8eDH79u0D3J/CLWkIFsDgTo1KqOEdd1/ZwqdyRdUmLS0No9HIwIEDK/zeSgFUEN6GK6hMOM6A8//eR0SLbggh7OWNGzemb9++rF692qv+fvjhBzp37syMewa7DW/QJCqCW265hUaNGmFMdh+mWaTvBvC7AgCYNm0aUVFRPPTQQxQVFdnPDYRpNfa9hv/r15KIEA1SFv/RSGD5n/pynwGYkxDHmH4t7TN+rRCM6deSOQlx5epXUTmx+fv37t27wu+tFIDCI7YZsPHCaUznTxLeoluxDc4bb7yR33//nVOnThVr77iBfOWs70lM/IWbbrrJYzyhaF0oYWFh3H///WSnbCM0P8epP12olmYXDtC8eXO6dOlS7H7lpWHDhrz99tts2bKF++67D4PBQEKvGDo2rcPaBzowMmwXm9+cyOFXEjj+6m1kfvYEF3auQpqM9j7KcwagsLCQd999l2HDhpH46iP8U7eDvdOu4fDcG9XgXx3wkCby0KFDNG3a1O8+/t6gFIDCI/YZcM7fAIQ1bUt4iPO/b8SIEUgpWbNmjVO5qwvnkd1bMRqLiO7Yz963p0NXDz74IGaTiSuNe5yUxHNDm7Pztw2YYvvR5tnVAYnZf8899/DSSy/x1Vdf0bJlS4YOHcpdd91Fhw4dePrppzlz5gyPPzaByZXvKEgAACAASURBVP96GjQazq57jxNf/gvj+UsK0OMZgBLyxGZkZHD11VczYcIETp48iZSS559/niuvvJLjx5X3T5WnhDSRhw4dCsrsHyyWCVcFEGhTtYoFVMXIzTgCQFijWHvyCrAM4pdffjnRDRoxaf4nzNhXzx4Lx9WF0pD2B5qISH44UYfnSrlf+/btGTp0KBu//YLDh2cREWE5GfnwtHkYjUXQ7monv3ybLP7iueeeY+DAgXzwwQccO3aMLl26MH36dG666San0NO/Rg8n9fefOfPjm5z44mma3D2X0Pox7jePbQOA7ei/bQAATjYdxDXXXMOJEydYtmwZd9xxB0IINmzYwG233cZNN93Eli1bqF3bOf5/tqGIgfM2lCkGkaKC8ZAmMv+nWRw/fpx77703KGJ58gIKpMlarQCqEPPXpHDxxBG0dRujCbcMQI5mjpW7M5HNe3I25Q/MZpN9UHY8ISvNJgxHdhDRujeZFwq9uu+0adPIyMjg/fffByxJKxZ99J7lBHHjSwkxAhV24dprr+Wrr75iy5YtzJw5k8cee6xY3oEp13eiYdy1NB0zH2k2kbVkGtrcU+7PAHgYAPJ+nMXNN9+MXq9n3bp13HnnnfYf35AhQ1i6dCl79+5l6tSpTk1XJOnRnzOoGERVBQ/pIFOOHMdsNtOtW7cKFsiCMgEpSiQj20DRyaP2PKOO5WBREGGt+2IuuEiB/gBgGZQdXRYLMg5hzsuhVrsrvHatHDx4MNdddx0zZsxg//79vP766xhO/U1U/9HFZicVmY7SEZuJrHX7zjQdPRthLMCw8gX6N3OzyHUzAJjMkns+TWX79u189dVX9O/fv1id66+/ngkTJvDuu+/y559/2svnr0nB7DJzUzGIKjEe0kEmX7Tkm/O0pxXoNKVKAShKpGltLUVn9YQ1inUqtw3kGdkGImJ7giYEQ9of9usmKe2ePoa030GjpV7HK3w6IfvRRx8RGRlJt27dmDx5MvW7XkWtjsVd5YKZHcu2l6H/5HE2rV9D9uksbrjhBs6fP+9c0WUAkFIyaU0B36UYWbBgAbfddpvHe8yePZtGjRrx1FNP2csqQ25mhQ84hH2wE6ojWXcFGo3GbaL3iog0qxSAokTuaAtIM6EOKwBHT6Bm0To04bWIaNENw+Ed9jo2z56YaB2GtN+Jat2DV+7p75ONulWrVmzbto2pU6fy+uuv8/4ni6gV5jy7rkzZsfr378/y5cvZu3cvCQkJ5OfnX7roMgD8+9dC3v6jkEljRjBx4sQS+42Ojua5555j06ZN/PKLJQyGShVZxfCQJjL5DMTExLhN81gRkWaVAlCUSP2CTABatO3kNu6OzVVU164vRWf+puhcpn1QTugVwye3xVB05jgvTvxnmTYoW7Vqxdy5c5k0aRJ3XtG6TDH7K5IbbriBTz/9lI0bNzJ69GguXrxouWAdAGTd5szfXMj0jQWMGXE1r36+0qt+x40bR9OmTXnxxRcBy+eucTGFVSZl6AuBNnNUGtykidy/f7/HnNYVscpz5wUUaJQXUEWxZ5ll8zEn3WKCGDqzxNykbrvYswedTsf2V8a4PZJuG3xnF57j3PqP0B7dwtyHZ9vLFy1ahEaj4c477yz/+6FqZMcaM2YMOTk5PP744/Tr14/XX3+dwYMHczi8B8//EcfSn5O58847+WTxYjQa7+ZDOp2OKVOm8NRTT7Ft2zYS+vVjxYlkYqK1VdoLyGbmsM10A+XZVRkpKCggLS2Nvn3dh0Zxl0nPVu4vVCyg6ooHv+PcbYswGLyfQezZs4du3bqVGI8koVcMf758N4MHDybsyCZu7dkMAJPJxBdffEF8fHxQDrkEkwkTJvDjjz9y7tw5hg8fTmhoKJ06dWLFihXMmTOHJUuWEBoa6lOf48aNo27durz11lsAROtCfU5gU9moyQl1UlNTMZlMtGrVyu11d6FI/L3KC4YJSK0AKgI3bocpmblcOfh+zKG1eenTlSxJNZc4e5RSsnv3bo8blK65cPsOvpWNM59k9erVjBgxguXLl3P8+HHeeOONgL3Nykx8fDypqan88MMPHDhwgEaNGnHLLbcQE1O2gToyMpIHHniAt99+2yloXVWmJm9mJydbAh56MgHZfo9lzTftDTVOAQghrgfeBLTAQinlvGDKEzDcuB1OWlOA0WSmyFzAs1On0HCkJcSsp2V3ZmYmZ86coXv37sX6crd0P6NpS5OYlkyePJm4uDieeeYZOnfuTEJCQiDeYZVAp9P5zfwFlpXFggULeP/99xkyZIjf+g0WFWHmqKwkJyej0Who0cJzkL9Amzxr1CawEEIL/Ae4AegC3C2E8H9QmcqAi9thVq6ZNYeNPHFtQ+JvvYOLadsx5py0X3e37N6zZw+AWwXgbumebxY0iJ/AwYMHadWqFXq9noULFwY0nG1No23bttx00028//77FBZ6d6iuMuONmaO6bhInJyfTpk0btx5AFUWlVABCiMeFEPUCcO8rgDQp5REpZSGwBLg1APcJPi5uh6tTjZgljBo/mcsHWLJxXTywyamJ67J7925L5E13CsDTEj2vUVc2bdrE1KlT2bx5MwMGDCjzW6iuP/zyMnHiRE6dOsWGDRuCLUq58RQY0DbrrQhf+GCRnJxM586dgypDZfUCagJsF0LsBD4B1kj/bFXHAI6RtdKBK10rCSHGA+MBmjRpQmJiYplulpuba2+bkZFBYWFhmfvyncZw+XtwIRNMhSxLXErduvs527Av3ULOE9OqNbqs7UyMu2SeCdNqnORbt24djRs3tisCR6b2NFNoKv7FCdNqMBqNxMfHc/HiRZ/er+PnlW0oQn/OwF0tJLQAuID+wJ+sOJFMtM63zdPy4ihXZUCr1dKqVSu+/vpr4uPjK12ocV8/r2jgpX4awBrrKCeVxMRUALJOXODRTq7fMyNZKTtJzEkNqFwlodfr+eijjzh9+jQ333wzV14zhKycfApNZsK0GppERZT4PTUajaSkpNCjR4+gfr9yc3MxmUxO9zcajaSnp5OYmBgQ2UpVAFLK6UKIGcBw4H7gHSHEMuBjKeVhv0rj/v4fAh8C9OnTRw4aNKhM/SQmJmJru2TJEsLCwihrX+XlwRnvMHjwEAYPHsyKH9dhaNYb/e8rmP9nEZowHbpQLXNvj2OQg73xscceo2/fvm5lznbZAwDc9uELjp/XwHkb0GcXNx3FRGvZPLW4PIHEUa7KwrRp0xg/fjwajYZrr7229AYViD8/r/unrkK6MRoI4Og83+7hL7n+/vtvRo8eTUFBAc2bN2fevHk02X2BiO43YDNw6EJNzL29i0f7/YEDBzAajVx//fVERkYG7fsVHR1NRESE0/1DQkJo3rw5gwYNCsh336s9AOuM/4T1YQTqAf8TQrxSjnvrsc4nrTS3llVrcnJyOHz4MFdccQVgcR+ceO9IMBspOL7P7YEqg8HAwYMH6dmzp9s+S1u6l5ea7B3iDWPGjCEqKqrae1hVthPPUkoeeughDAYDW7duZffu3UR3uIKT6z6iKPuEvV5prqw2D6BA5LXwhUrpBSSEeAK4FzgNLAQmSymLhBAaIBWYUsZ7bwfaCyFaYxn47wLuKWNfVQZbikNHW/4z9yUw98lwxrS8wGtTi3uT7N+/H5PJRK9evTz2G0gPhZrsHeINOp2OW265hS+//JK0tDTatWsXbJECwuT4jm5XmhV54tnR3TnixG4O/vQTsSMe4cbPj9AsOpPaQx8l+/A4zm/7mgbXP25vV9JkJTk5GSEEnTt35o8//vBYL9BUyk1goD5wu5QyXkr5tZSyCEBa8vDdVNYbSymNwGPAGuAAsExKub+s/VUV3HnzRERE0L9/f4/2PVuid08rAF/xdUO3Ig7BVHUSEhIIDQ1lwYIFwRYlYAR6pVkarpvQR39ejDaqCTd2jeTXsIn8ariNbQ1fJK57N3L3rsd44Yy9bUmTleTkZGJjY6lVqxYYznlMFBRoKuUKQEr5fAnXDpTn5lLK1YB3SWyrCXv37iUqKqqYv/HgwYOZNWsW586do149Z6erXbt2UadOHVq3dg4DXRbKcty/Ig7BVHXq16/PmDFjWLhwIc8880yJ/uRVmWCG/3B0dy7ISKFAn8w1w4YxP+JTagmLG25zcZovB5yjR5KRi/s3ENXvzlInK/v377eYf/Ysg5wT1hP7OCUK8jVsS1kIhheQCgVRwezdu5e4uLhi3iKDBg1CSsmmTZuKtUlKSqJnz55ex6opibIe9y8pbaTCwsyZM5FS2oPEKfyLoxknd886RGg4H1yeZh/8bXRvaOKKlhFc3LueZlERJa5SbB5AXbp0sZzYly4DcJHBUl4BVFYTkMKPHDx40O1m05VXXklEREQxM5DZbGb37t1+M/+oDd3A0apVKx5++GE+/fRTDhwo++K4Mp658FmmEnIulxWbGUcaC8k7+Cu1OgygQ8RZt3XH9RAUnU3n9cG1S5ysHDlyhMLCQrp27eoxU5jHcj+jgsFVc7Kzszl9+rTbhBPh4eEMGDCAjRs3OpXv37+fixcv0qdPH7/IUNk8Oaob06ZNo27duowdOxaTyVR6Axcq42Ern2UqIel6eRjcqREAeWl/YC64SO2ug8mQDd3WHdW/FREREXz11Vcl9rl/v2XbsXPnzh4zhXks9zNqBVDNSUtLA/DoJTJ48GB2797NmTOXNq9sJqFrrrnGLzKoDd3A0rhxY9555x22bdvGrFmzPNY7cuQITzzxBG3atEEIQcuWLZk1axYv/7C30kXk9Nls6CHncnlNKRsPngLg4v6NaCPrE9GqB68YR5Enw5wrhuqoO+IFRowYwbJlyzAajR77TEpKQqPRWPIAD50JwmVIDNVZyisApQCqOSUpgBVJepam1wFg4JP/sc+uNm3aRIsWLTyGqfWVYHtyVFZKM3H4YgK5++67uf/++5kzZw5z5sxx+lEfOnSIe++9lw4dOvDee+/RvXt3pk+fTvfu3XnhhRdIev9JzAUXi/XpDxNdWU1LPpsNA2RKycg2YC7Iw3D0T2p1uhqh0bLSfBVTix4k3dwQx+xedB/FXXfdRVZWlj1zmzt27txJ586dLR5A3UdZ2rtkCquIDWCopF5ACv9hUwBt2rRxKrctsfPqtEKEhqPft41nv7kCs9nML7/8wrBhw/waYqAqJHKpSErzjPLVc0oIwQcffEBBQQEzZszg888/p2/fvhw5coTff/8dnU7HE088wVNPPeUUjnr58uXcOfouTn33Mo3vnIVwmI2W10RXnmQvPp8DiWp+yZPGtbwcNIvWcWjbb2AyUqt9P3v5SvNV/FnrOja7nKG58cYbiYyMZMmSJQwdOtRtnzt37uS66667VKCrZ8kQFgTUCqCSYzQay/UPSktLIyYmxjLbcMC2xBbaUHRt+pJ3aCt5BYU8/9G3ZGVlcf3115dXdEUJlGbiKIvnVGhoKF9++SXLli0jNjaWrVu3otFomDNnDkePHuW1114rlotg5MiRjH9mNvlHd3Lhzx/s5f4w0ZUn2YvPZkMPSdfLa0qZHN+RgrTf0UTUIbz5JUeKUK1wK0utWrW49dZbWb58udtorZmZmWRmZnL55ZeXSy5/4c4NNNCbwmoF4CXp6el069aNcePGMX/+/DL1kZqa6tb847iUrt3lWvJSfiPv0FbOHt1JeHg4t9xyS5nlVpROaSaOsnpOCSG48847fcpB8N6cZ/h9w0/s3fwVkV2upUWzpn45c1Ee7y+fz4HYTCblTIHqyohujZHHdxLV8UqExqKQ6tUK5fmbu3qU5e6772bx4sX0GP8q+U17OMluO/Xbu3fvcsnlLzx5AQUywKBSAF7y448/kpOTw6uvvsrXmmuJqVfL5x9mWloaN998c7FyxyW2rt0VhNRvztk1/8FckMuERx+lbt26fnsf1QXXDGjlGSRLM3FUZCgMIQSLP36X7t27k8A23pr6ll/6Le978Nls2H2U323nv/32G7nnc1g+8xFuv32EV23yGnVBExHJ8R0/0/CmHk6mr02//EJERITfPOzKizIBVSC+Lq2+27DV/tyUl+2ze9758+c5efKk2xWA4xJbaLQ0vPlfaELDad+1R4meJDUVf7tKlmbiqGjPqS5dunDffffx0UcfcfLkydIbeEF18P767rvvCA8PZ/jw4V63WbDhKLU6DCAvdRvmonzgkukrMTGR/v37ExERESiRfUIpgAqiLEuqrXsO2Z8Xnv4b8M097/BhS+Rsd2cAXD1z2nSK4+tfdnFobxING7r3c67J+Dt5eWmeUcHwnJo8eTIFBQW8/fbbZe5jRZKelBMXaD11FfPXpDCyd0yV9f6SUrJy5UqGDRtGZGSk1+0ysg3U6nwNstCA4fAOe/nxE6dI2rWLpKJmleawnfICqsTknjlBaOM2FJ08QtGpv9C16gF4755X2hkA5ZnjPYE4zVza51/R/5+OHTty66238u677zJt2jSfZ6m2VdKjncxINOizDSz/Ux/QQd+fZjlXkpOTOXr0KM8884xP7ZpF60hvGYemdjR5BzZRu9NVABgObwcpiYjt6WQWivaLtGVDrQAqMaIgl7BGrRBhtTBmZ9rLvbWhpqZaMia1bds2IPLVJKrtaWaX8AkTbujK2bNn+fbbb33uytdVUkZGBhs3bmTnzp0lHpxyPUuwfeUH8EY35Kxo+q64ht7n1wXkBPOqVasAGDHCO9u/jcnxHakVHkbtTleTd3g7prwcBJC7PxFtnUaENbOYwIJ92A5UMLhKjdZoIKxWXUKiGmO0JpvwxYaalpZG06ZNfVq+KtxTHezZxXATPqG//gPqRkfx8PSXfR5IvV0lpaamcv311xMTE8OQIUPo3bs3DRs2ZNKkSWRkZDjVdd176X1+Hd3+nA45xxFIYsRp5oUu5BbNb4B/B9VVq1bRvXt3mjf37SyBzXzX7tqRYDZRtO0r8jNTyT/6J5E9hjudtQh2PCwVC6iSYjabMVy8wLCesdRp1AxjzkmfbaieXEAVvlMtTzO7CZ9QWxTySC8N54/s5umPfvRJCXizStq0aRO9e/dm27ZtvPjii6xbt44lS5YwYsQI3n77bdq3b8+CBQvsMY1cVxVTQpahc4nEWUsUMiXkUswffwyq586dY/PmzT7P/m0k9Iph52v/5F9PP0XW9lVkLZ6CNrI+dXs7e+QFewWp9gAqKefPn0dKSb9OLWlWCz7+eA+/PTPYp83k1NRUbrzxxgBKWbOodnsmHsIkPN7TyMuJGk7vXMP8NW28fs+27F2WDK4WHFdJycnJjBgxghYtWvDTTz/RsmVLe73Ro0cze/ZsJk6cyKRJk1iyZAlffPFFscG8mTjt9t7NhHeJWLxl7dq1mEwmzwpgzzKvzhzMnTuXevXq8cOGzWS2vQkZcWk1bv9sfExu7080Gk2ZAgiW654VercqSk5ODmBJ2hwbG0tubq5TwLbSOH/+PFlZWXTo0CFQIiqqOh7CJMjIRuja9uHi/g3oz+Z63Z1tlRSm1RRbJV28eJHbbruNWrVqsXbtWqfB30abNm34/vvvWbx4MYcOHaJXr16EHN7kZKLwFIkzQzYA/GeWW7VqFfXr16dfv37FL/oQeTQkJITnnnuOLT+v4o2Hb6l0K0ghRIWbgNQKwAuys7MBiwKoX78+AMeOHfPaRdPmAeTOBVRRPcg2FDFw3gbvPWBcZ63th8Pur5zMQHkyjFeMo4iM03Aq7Q90J/cB3p8KT+gVQ2JOKkfnDXIqnzlzJocOHWLjxo0l2tSFENxzzz1cffXV/OMf/+CX/71C3a5/EHXdI2jCa/OKcRQvhy50MgMZCGe+cRQxfvICMplM/Pjjj1x//fVotdriFUqKPFrCQbTKuIIMhgJQKwAvcFQAtrSMx44d86rtiiQ9d79q8eKYvelspfA3VviXFUl69OcM5YuXv/sr6HEPRLVAItDLhkwtepCV5qvQte2LtlZd6qVvLresu3btYsGCBTz00EMMGjTIqzYtWrRg/fr1zJkzh9yDv3Ly8ycp0B/kz7rXsa/3HKfombrb3+HNf8/1W9a4HTt2cPr0ac/mnyAncfEnSgFUUhwVgC0sszcKwOY1kZVuqXs2pH7Qk3so/M/8NSmYXX64ZYqXn7oWJu1DzMpme8Im/qx7HQJo3qAuN942mh2b1nH6tHu7u7dMnz6dqKgo5s2b51M7rVbLtGnT+O3XX7ksKpzTS6ZyX4PD9L3lIUv0zFnZlr9+Dv+watUqNBqN54CIQU7i4k+UAqikOCoA2+Po0aOltrN5TRjP6tHWaYgmNKJS+Bsr/Esg4uW75mB+6ZnHKSoqKjXDVUn8/vvvrFq1in/9619ER5ftyFP//v1JSkpi2LBhjB8/nieeeCKgniurVq2if//+dtNrMQIUeTQYKAVQSbFtAtuCsrVu3dqrFYBtACg6l0FIvWbFyhXVA58PppVh1hoXF0fv3r359NNPfRXPzsyZM2nYsCETJ04stW5JyWOio6P5/vvvefLJJ3nrrbcYN25cQJRAZmYmO3fuLNn9s/soS9KWICVx8SdKAVRSLl60ZGiyHeKKjY31SgE0i9YhpcR4Vk9o/WZO5Yrqw+T4jmhcXIIDES9/7Nix7Nq1i6SkJJ9l/O2331i7di3PPPNMqYcRvQm2FxISwhtvvMHMmTP55JNPePjhh/0+eP3wgyUnQqn+/91HBdQMVVEoBVBJMRgMCCEIDw8HLimA0v5Zk+M7EpqfjTk/l7BGsUA1OLGqKEZCrxhi6um8dyss46z17rvvJjw8vEyrgBkzZtC0aVMeffTRUuv6EkZi1qxZPPvss3z00Ue89tprPstVEsuXL6dt27bExcX5td/KinIDraTk5eWh0+nsB79iY2PJy8vj1KlTNG7c2GO7hF4x/LlZMgcIaxTrN9c4ReUjWhfK5qmDvG9Qhnj59erVIyEhgcWLFzN//nz7hKQ0NmzYQGJiIm+++WaxbHTu8GVPQwjBSy+9RFpaGlOmTCEuLo74+Hiv5CqJc+fOsX79eiZNmhTQhCiVCRUKopJiMBjQ6S4t2X1xBY28aImnkvzOeL+5xilqLvfffz9nz57l+++/96q+lJIZM2bQvHlzxo8f71UbX/c0hBB8+umn9jwG5fVUAov5x2g0MnLkyHL3VVVQweAqKXl5eU4zp9jYWMA7BbBnzx5atGhBvXr1AiSdoiYxbNgwmjdvzieffOJV/T/++IMtW7b4FFK6LMH2ateuzeLFizl79iwPPfRQuWeyy5cvJyYmhr59+5arn6pEjdkDEELMF0IcFELsEUJ8K4QIZhjuUnFdAdgUgDeuoElJSXTv3j1QoilqGFqtln/+85+sWbMGvb7k8yRms5mFCxfSunVrxo4d6/U9yhpsr0ePHsyZM4dvvvmGJUuWeH0/V3Jzc1mzZg233347Gk3NmaPWGAUArAO6SSm7A4eAZ4Mkh1e4rgDq1KlDgwYNSl0BnD17lgMHDjBgwIAAS6ioSdgG8zfeeKPEel9//TVpaWm8+OKLhIWF+XQP13MI3poun3rqKfr27cukSZPs52d85dtvvyU/P58777yzTO2rKjVGAUgp10opbWEKtwGV+tie6woAvHMF3bJlCwADBw4MlGiKGkibNm0YM2YM7777LllZWW7r5OXl8eyzz9KmTRvuvvtue3lJ/v2OeFvPFa1Wy/vvv8+pU6eYPn26728O+Oyzz2jTpg1XXXVVmdpXVWqqF9BYYKmni0KI8cB4gCZNmpCYmFimm+Tm5trbZmRkUFRU5HVfmZmZhIeHO9WvXbs2+/fvL7GPhQsXEh4eTn5+vsd6jnJVJpRcvlHRcl133XV8+eWXjBs3jqeeeqrY9Q8//JCjR48yd+5cfv31V8ASsE5/zsBdLSS0ALiA/sCfrDiRTLQu1N7W23olYUtn2a1bNzp16lTsuqfP68SJE2zYsIH777+fX375xat7+ZNgfr/0ej1Go9Hp/kajkfT0dBITEwMiW8AUgBDiZ6Cpm0vTpJTfWetMwxKwfLGnfqSUHwIfAvTp00d6G8DKlcTERHvwq6VLlxIaGup1MKywsDCaNWvmVH/AgAFs3bqVfv36OW2u2fKi6s/mkrlxM70GDCrRLc5RrsqEkss3giHXzp07eeONN3jyyScZMmSIvXzDhg0sW7aMsWPH0q9fP7Kj2lu+k9mFQPGImjHRWicX1oHzNqDPLr1eSfTq1Ytt27bx4Ycf8scffxAS4jzUePq8Zs+eDcDzzz9vj7tVkQTz+7Vy5Uo0Go3T/bVaLS1atGDQoEEBkS1gJiAp5TApZTc3D9vgfx9wE/B/sqLXPT7iugcA0K9fP4qKitixY4e9zPEE5cXUbRSeP83xer1V8DdFQJg9ezadOnXijjvuYOvWrQBs3LiR22+/nY4dO7JgwQKyDUX276QnXP37fY5t5IaoqCjefPNNkpKSeOedd7xqU1hYyAcffMCwYcOCMvgHmxpjAhJCXA9MAa6VUuYFQwZfcLcHYNvY/WDpKp75rZCMbANFJ49QcCYdc0EeOb8tJqR+c0LaXsn8NSnK/1/hd2rXrs3q1asZMmQIAwcOJDY2lqNHj9KpUydWr15NnTp1yMrJx1BU8jzP1b+/WbTOrcLwNYTJHXfcwY033sj06dMZOXIkLVq0KLH+0qVL0ev1LFy48FKhl9m+qgM1ZhMYeAeoA6wTQuwSQrwfJDlKZUWSnowzOXyz55TTZlijRo3o0K0Xy5Ys5viJU5z6/lX0n07k9MpXOLvmHdCG0ChhKkKjVcHfFAGjdevW7Nq1i+eff54+ffowb948/vjjD/sMutBU8sEid/79ZTkH4A4hBP/5z38wm808/vjjJdY1mUzMnz+fbt26XTKZ+pDtqzpQY1YAUsoqkR3dZtIxFRZASJg9KBZY3OTMneMp3DeP9P/cizQZiRpwF7U6XY0IDSekTkOE1vLxquBvikASFRXF888/7/ZamNbzg5XhZwAAGjZJREFUHM9TaBLb6/lrUrzPcOaB2NhYXnjhBaZMmcJnn33Gfffd57beF198wd69e/nvf/97KfRDGbN9VVWCEQqiMngBVVrmr0khr9CILCpAE2KJu2ILipXQK4ai1gOIuur/KDpznLp9biW8WfEZkgr+pggmTaIi0IWanIK76UK1pR7s8mfKxEmTJrF69WoeffRR+vTpQ7du3Zyunzx5kmeeeYYrrriC0aNHX7pQjbJ9eYMKBVHJyMg2gMkISERouHM5EFOvNtED76bRLVOcBn+tEJUq2bSi+uPJbz9aF1qmU73+JCQkhH88+xpGbQQ9Bwzm8n8tIttQBEB+fj733HMPOTk5LFy40DnwWzXK9uUNNcYEVFVoFq3jeJYlF4DNnGMrB4ut9Nlv9vo8u1Io/InNVGn7HjqaKqPxz2ze5t5cFpPQiiQ98389ScM7XyBryXR2/+cxFmXewdb9R/nlf5/w+++/8+mnnxYP+zx0psXm72gGqqLZvryhJm0CVwkmx3ckXFiXZFrLARhHk05ZY6YoFP7El/j9ZcGbBDHeyBfWuA1Nx8wntFErvv3qU16Z/BBHjhxh6dKl7vcGqlG2L29QK4AKxJsPOqFXDGdOtuPBN0CjDXW7aeZPW6lCURZK9tuvXe7+S1Iw3nz3HeULrR9D03vmcV8TPR/uusiRDx4pOUppGfImVFWUAqggfEkwMaRDAwBevas39903pJTaCkXF4y+/fU+U92CYO/kaNG5C6851vA5RXRNQJqBKSFGRZbPK12iKCkVF4S+/fU/4nPTeBXfyaYRQ3nEuKAVQCSksLASUAlBUXgK9F1VeBeNOvph6OmU6dSEYqS9rpAnIF5QCUFQFArkX5Y+DYa7yVcaIrsHGpgCklBWmDJQCKAWlABQKzwqmPO6hCmeCoQCUCagk9iyj8EtLMo2wlQ9X2xgkCkVZKK97qMIZW/rLitwHUArAE9ZAVIXnTwIQln+qWgeiUih8JdDnD2oatll/RYaDUArAE9ZAVIUmizYO04pLgagUCoVf8gYoLuFoAqoolALwhDXgVKF1ghOmdS5XKGo65XUPVTijFEBlwhpwqpgCqKaBqBQKXwn0+YOahlIAQWbp0qXk5VkTlA2dCaE6ZxNQNQ5EpVD4ioqF5V+CoQCUG6iVXbt2cddddzFmzBi++OILe/yRwr2TgAzCoi+Dm+fUmLgkCoU3qFhY/kOtAIKIzQVr27Ztlwq7j6Jw0AwAQh/5RQ3+CoUiYCgFECz2LMO86DYAMv8+4uTqqQ6CKRSKisCdAgi0MlAmIJu/f04uAIVGs8XfHywrAKUAFApFBeBpBRDIU8FqBWD19y+ybvZKcPL3VwpAoVBUBMoEFAxc/P1dy23hoENDQytSKoVCUcNQCiAYuPj72z97W3lhISEhIfZNYoVCoQgEKhZQMLD6+xeZHT50B3//wsJCZf5RKBQBJxixgNQmsM3fP+1fwHHLHoBD4mmlABQKRUWgTEDBovsoCuNfsTwXGid/f6UAFApFRaAUQJBYkaRnxje7ATBL6RTPXCkAhUJREdQ4BSCEeFoIIYUQDYMlgy2pxdkL1hhAUjoltVAKQKFQVAQ1SgEIIVoAw4G/gyUDOCS1MBvtZY5JLZQCUCgUFUFNCwb3BjAF+C6IMtiTV0iT0W25UgDlo6ioiPT0dPLz8/3SX1RUFAcOHPBLX/6kpsgVERFB8+bN1bmYAFBjFIAQ4lZAL6XcXVHJjz3RLFqHPtsAZlOxclAKoLykp6dTp04dYmNj/XKk/cKFC9SpU8cPkvmXmiCXlJIzZ86Qnp5O69at/dKn4hLVSgEIIX4Gmrq5NA14Dov5x5t+xgPjAZo0aUJiYmKZ5MnNzbW31ev1FBUVkZiYyOQeJvTnTKz722RfikzubiKmnonExESysrLIz88v8319kasy4S+5oqKiaNCgAbm5ueUXCjCZTFy4cMEvffmTmiJXWFgY2dnZ5f5uVPfvfVk4dOgQAJs3b6ZhQ8u2qMlk4vjx4yQmJgZGNillhT6AOOAkcMz6MGLZB2haWtvevXvLsrJx40b780ceeUQ2atTI/vrbnemy1fXjJJZQQPLbnen2a9dcc40cNGhQme/ri1yVCX/JlZyc7Jd+bJw/f96v/fmLmiSXP/6n1f17XxY++OADCcj09EvjT2RkpHzqqaeklOWTDdgh3YypFb4JLKXcK6VsLKWMlVLGAunA5VLKExVx/xVJer7ZqefMxUIGztvAiiQ9Cb1ieOiaS0vaW3pcZn+uTEAKhaIiUKEgAozN5fNioWXDV59tsLt8Oh6/NhovbQgXFhaqDa8axqBBg9ixY0dQ7j1gwIBS60RGRpZaZ9asWbz66qsl1lmxYgXJycley6YILMEIBRF0BWBdCZyuiHvZXT4tNwYuuXw6fui2CKCgVgAVzYokPQPnbaD11FX2FVpNYsuWLRV2L6UAKhc16hxAMLC5doIoVl7SCkApgIrBtkLTZxuQOK/QysqxY8fo1KkT//d//0fnzp254447yMuzHPpbv349vXr1Ii4ujrFjx1JQUODU9pNPPuHJJ5+0v/7oo4+YNGkSx44do3PnzowbN46uXbsyfPhwDAbLd2vXrl3069eP7t27c9ttt3Hu3DnAsqqYNGkSffr0oXPnzmzfvp3bb7+d9u3bM336dPs9bLP73Nxchg4dyuWXX05cXBzffVe6t/RLL71Ehw4duOqqq0hJSXGSu2/fvvTo0YORI0eSl5fHli1bWLlyJZMnT6Znz54cPnzYbT1FxaEUQICxuXa6K/e0AigqKlIKoIJwWqFZcTyUV1ZSUlJ49NFHOXDgAHXr1uXdd98lPz+f++67j6VLl7J3716MRiPvvfeeU7tRo0bx/fff278Pn376KWPHjgUgNTWVCRMmsH//fqKjo+0D9L333svLL7/Mnj17iIuL44UXXvj/9s48uKoqz+OfH0kgIUAIAm1YhGAJxOwBjCUGBrDA0TIsLSSWVBPchuhgKUINrVVjiyPd01pA4SDYNIILSGOUtAsWisQCepSOWBCCikHZUZb0BCO7yZk/7n2vX8J74SVvuSHv96l69e492/3md2/O751z7/ldd3vt27fniy++YMaMGYwfP54lS5ZQWVnJqlWrqK6ubnDs2NhY1q9fz5dffklZWRlPPPFEkx3Djh07WLt2LTt37mTDhg2Ul5e78yZNmkR5eTm7du0iJSWFFStWcMstt5Cfn8/zzz/Pzp07uf76672WU8KHOoAQM2fcIOJiohqkxcVEMWfcIB0BtAL+OULzL91f+vbty/DhwwGYOnUq27ZtY+/evSQnJzNw4EAApk2bxpYtWxrU69SpE6NHj+b999/nm2++4dKlS6SnpwOQnJxMVlYWAEOGDOHQoUOcPn2ampoaRo4c6bXN/Px8ANLT00lNTSUpKYkOHTowYMAADh8+3ODYxhiefPJJMjIyuO222zh69CjHjx/3+Tdu3bqViRMn0rFjR7p06eI+FkBlZSV5eXmkp6ezevVq9uzZ47UNf8spoaFNrQNojUzI7g1A8aYozgK9u8YxZ9wgJmT3prxEHYDTuBfleUkPhMYL0JqzIO2BBx5g/vz5DB48mOnTp7vTO3To4N6OiopqcM34wlWnXbt2Deq3a9fusvqrV6/m5MmT7Nixg5iYGPr379/i1dRFRUWUlpaSmZnJqlWrfD5L7m85JTToCCAMTMjuzaScPnSLb8/f5o52OwW9Cew8TY3QAuHQoUN89tlnAKxZs4Zbb72VQYMGceDAAfbt2wfA66+/7v7l7klubi6HDx9mzZo13HPPPU0eJyEhgcTERLZu3dpkm/5w+vRpevbsSUxMDGVlZRw8eLDJ8iNGjKC0tJRz585RW1vLe++9586rra0lKSmJS5cusXr1and6586dGywS81VOCQ86AnAQnQJyHpczfn7jXo7VnKOXxwgtEAYNGsSSJUu47777uPHGGykuLiY2NpaVK1cyefJkfvnlF4YNG8aMGTO81p8yZQo7d+4kMTHxisd69dVXmTFjBmfPnmXAgAGsXLmyRZrvvfde7rrrLtLT0xk6dCiDBw9usnxOTg4FBQVkZmbSs2dPhg0b5s579tlnyc3NpUePHuTm5ro7/cLCQh588EEWL15MSUmJz3JKeHDCAYR9JXAgn2CtBH744YdN9+7dG+TPnj3bvRJ4z5497vSoqCjz1FNPtfi4zdHVmmgrK4H3799vUlNTAzrmnXfeaTZt2tRkGV0J3Dza+nXfEt544w0DmL1797rT4uPj29ZK4NaKtxFAXV0ddXV1OgKIUGpqahg4cCBxcXGMGTPGaTlKG8fXCCCUATN1Csimru6fjx+6HIDrXoA6gKuX/v37U1lZ2aK6Xbt2dQfoUpRQo6EgHMTbTeCLFy8C6gAURQk9ERkKorXgbQpIHYCiKOFCHwN1EB0BKIriJOoAHERHAIqiOIk6AAfREYDiwhWQ7dixY9x9991ey/gTMnrRokUNAqrdcccd1NTUBE+oHxw8eJA1a9aE9ZhKy1AH4CBNjQD0fQBhpGIdLEyD33W1vivWOSalV69elJSUtLh+YwewYcMGunbtGgxpfnPo0CF1AFcJ6gAcRKeAWgEV6+C9R+H0YcBY3+89GpATmDt3LkuWLHHvu16U4k+45QMHDpCWlgbAuXPnKCwsJCUlhYkTJ7rDPwMUFxczcuRIUlNTefrppwFYvHgxx44dY9SoUYwaNQqwHkk9dcp69cWCBQtIS0sjLS2NRYsWuY/nK8y0J2+99RZpaWlkZmYyYsQIwHqMec6cOQwbNoyMjAxefvllAJ5++mm2bt1KVlYWCxcubLEdldCjoSAcxNsUkK4DCDOfzINLjTq8S+es9IwpLWqyoKCAxx57jEceeQSAdevWsXHjRne45S5dunDq1Cluvvlm8vPzfS66Wbp0KR07duTrr7+moqKCnJwcd95zzz1HTEwMHTt2ZMyYMVRUVPDoo4+yYMECysrK3C/4drFjxw5WrlzJ9u3bMcaQm5vLyJEjSUxMpKqqijfffJPly5czZcoU3n77baZOndqg/rx589i4cSO9e/d2TymtWLGChIQEysvLuXDhAsOHD2fs2LE888wzvPTSS7z//vstsp8SPnQE4CCeDuCRN8oZ/ofNfFJpvYhEHUCYOH2keel+kJ2dzYkTJzh27Bi7du0iMTGRvn37Njvc8pYtW9wdcUZGBhkZGe68devWkZeXR3Z2Nnv27LniW7a2bdvGxIkTiY+Pp1OnTkyaNMkdQK5xmOkDBw5cVn/48OEUFRWxfPly9wLGjz76iNdee42srCxyc3Oprq6mqqqqWbZSnEVHAA5y8NTPWG8KM5i6Oo7WnGNZpfUiEnUAYSKhjz394yU9ACZPnkxJSQk//vgjBQUFQPDCLe/fv58XXniBzZs3c91111FUVNTisM1weZhpb1NAy5YtY/v27XzwwQcMGTKEHTt2YIzhxRdfZNy4cQ3KbtiwocValPCiIwAH+epoDRJt3ew19davqgsX9B5AWBnznxDTKPZ/TJyVHgAFBQWsXbuWkpISJk+eDLQs3LLrZmplZSUVFRUA/PTTT8THx5OQkMDx48f58MMP3XUah1t2kZeXR2lpKWfPnuXMmTOsX7+evLw8v/+e7777jtzcXObNm0ePHj04fPgw48aNY+nSpe5py2+//ZYzZ87QqVMnjep5leBEKAgdAdicvfgLtIsGLoKxHICpt24GqwMIE655/k/mWdM+CX2szr+F8/8uUlNTqa2tpXfv3iQlJQHND7dcXFzM9OnTSUlJISUlhSFDhgCQmZlJdnY2Q4YMoV+/fu43jwE89NBD3H777fTq1YuysjJ3ek5ODkVFRdx0002A9dKZ7Oxsr9M93pgzZw5VVVUYYxgzZgyZmZlkZGRw4MABcnJyMMbQo0cPSktLSUtLIyoqiszMTIqKinj88cebYzoljDgRCkIdgE1ctHA+OgZzEUyd1fG7vtUBhJGMKQF3+N7YvXt3g/3u3bu7XxLTmJ9//hloGEguLi6OtWvXei2/atUqamtr6dy5c4P0mTNnMnPmTPe+Zwc/a9YsZs2a1aB848B1s2fP9nq8d95557I0EWH+/PnMnz+/QXptbS2bN2/22o7SutApIAe5oWc87aLs5/1tDxyDNRJQB6AoSqhRB+Ag13bpwDUJ8dZO/S/07hrHr7OuBdQBKIoSetQBOEh9fT3dOncEYM7YG/jb3NGkJVkOQR1AYITzglZCi57L0KEOwEHq6+vdHb2uBA4esbGxVFdXa8fRBjDGUF1dTWxsrNNS2iS6DsBB6uvriY62zKHB4IJHnz59OHLkCCdPngxKe+fPn2+VHVCk6IqNjaVPn8DWZSjeUQfgIPX19URFRRETE6MjgCASExNDcnJy0Nr79NNPyc7ODlp7wUJ1KYESUVNAIjJTRL4RkT0i8kendLior6+nXbt2REdHXzYC0GigiqKEmogZAYjIKGA8kGmMuSAiPZ3Q4YnLATQeAURHR7tX6CmKooSKSBoBFAN/MMZcADDGnAi3gMZG9jUC0F//iqKEAydCQYgTT2eIyE7gr8DtwHlgtjGm3EfZh4CH7N1BwN4WHrY7cKqFdUOJ6moeqqt5qK7m0Vp1QWDa+hljejRODNkUkIhsAq71kvWUfdxuwM3AMGCdiAwwXryRMeZPwJ+CoOcLY8zQQNsJNqqreaiu5qG6mkdr1QWh0RYyB2CMuc1XnogUA+/YHf7fRaQey7sF51lBRVEU5Yo4dQ+gFBgFICIDgfa03mGXoihKm8SpdQCvAK+ISCVwEZjmbfonyAQ8jRQiVFfzUF3NQ3U1j9aqC0KgzZGbwIqiKIrz6APuiqIoEYo6AEVRlAilTTkAEZlsh5aoFxGfj0uJyO0isldE9onIXI/0ZBHZbqf/RUSCEgRIRLqJyMciUmV/J3opM0pEdnp8zovIBDtvlYjs98jLCpcuu1ydx7Hf9Uh30l5ZIvKZfb4rRKTAIy+o9vJ1vXjkd7D//n22Pfp75P3WTt8rIuMa1w2xrlki8pVtn09EpJ9HntdzGiZdRSJy0uP4D3jkTbPPe5WITAuzroUemr4VkRqPvFDa6xUROWHfE/WWLyKy2NZdISI5HnmB2csY02Y+QArWYrFPgaE+ykQB3wEDsJ4+2gXcaOetAwrt7WVAcZB0/RGYa2/PBf77CuW7Af8AOtr7q4C7Q2Avv3QBP/tId8xewEDgBnu7F/AD0DXY9mrqevEo8zCwzN4uBP5ib99ol+8AJNvtRIVR1yiPa6jYpaupcxomXUXA/3ip2w343v5OtLcTw6WrUfmZwCuhtpfd9gggB6j0kX8H8CEgWGuntgfLXm1qBGCM+doYc6WVwjcB+4wx3xtjLgJrgfEiIsBooMQu9yowIUjSxtvt+dvu3cCHxpizQTq+L5qry43T9jLGfGuMqbK3jwEngMtWOgYBr9dLE3pLgDG2fcYDa40xF4wx+4F9dnth0WWMKfO4hj4HwhHH2R97+WIc8LEx5h/GmP8DPsaKFuCErnuAN4N07CYxxmzB+sHni/HAa8bic6CriCQRBHu1KQfgJ72Bwx77R+y0a4AaY8wvjdKDwa+MMT/Y2z8Cv7pC+UIuv/ies4d/C0WkQ5h1xYrIFyLyuWtailZkLxG5CetX3XceycGyl6/rxWsZ2x6nsezjT91Q6vLkfqxfkS68ndNw6vq1fX5KRKRvM+uGUhf2VFkysNkjOVT28gdf2gO211X3PgBpIsSEMeav4dbjoildnjvGGCMiPp+9tT17OrDRI/m3WB1he6xngf8DmBdGXf2MMUdFZACwWUR2Y3VyLSbI9noday1JvZ3cYnu1RURkKjAUGOmRfNk5NcZ8572FoPMe8KaxIgH/G9boaXSYju0PhUCJMabOI81Je4WMq84BmCZCTPjJUaCvx34fO60aa2gVbf+Kc6UHrEtEjotIkjHmB7vDair66RRgvTHmkkfbrl/DF0RkJTA7nLqMMUft7+9F5FMgG3gbh+0lIl2AD7Cc/+cebbfYXl7wdb14K3NERKKBBKzryZ+6odSFiNyG5VRHGjv6Lvg8p8Ho0K6oyxhT7bH7Z6x7Pq66/9Ko7qdB0OSXLg8KgUc8E0JoL3/wpT1ge0XiFFA5cINYT7C0xzrZ7xrrrkoZ1vw7wDSsiKXB4F27PX/avWzu0e4EXfPuEwCvTwuEQpeIJLqmUESkOzAc+Mppe9nnbj3W3GhJo7xg2svr9dKE3ruBzbZ93gUKxXpKKBm4Afh7AFqapUtEsoGXgXzjEXLd1zkNo64kj9184Gt7eyMw1taXCIyl4Ug4pLpsbYOxbqh+5pEWSnv5w7vAb+yngW4GTts/cgK3V6jubDvxASZizYNdAI4DG+30XsAGj3J3AN9iefCnPNIHYP2D7gPeAjoESdc1wCdAFbAJ6GanDwX+7FGuP5ZXb9eo/mZgN1ZH9gbQKVy6gFvsY++yv+9vDfYCpgKXgJ0en6xQ2Mvb9YI1pZRvb8faf/8+2x4DPOo+ZdfbC/xrkK/3K+naZP8fuOzz7pXOaZh0/R7YYx+/DBjsUfc+2477gOnh1GXv/w7rXSWe9UJtrzexnmK7hNV/3Q/MAGbY+QIssXXvxuMJx0DtpaEgFEVRIpRInAJSFEVRUAegKIoSsagDUBRFiVDUASiKokQo6gAURVEiFHUAiqIoEYo6AEVRlAhFHYCiBICIDLODmsWKSLxY7ydIc1qXoviDLgRTlAARkf/CWg0cBxwxxvzeYUmK4hfqABQlQOzYMuXAeeAW0zCKpKK0WnQKSFEC5xqgE9AZaySgKFcFOgJQlAAR6x2xa7FeIpJkjPl3hyUpil9cde8DUJTWhIj8BrhkjFkjIlHA/4rIaGPM5ivVVRSn0RGAoihKhKL3ABRFUSIUdQCKoigRijoARVGUCEUdgKIoSoSiDkBRFCVCUQegKIoSoagDUBRFiVD+HxBPK5vi8gcyAAAAAElFTkSuQmCC\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "for degree in [0, 1, 2, 3, 5, 10, 50]:\n",
    "    pr = PolynomialRegressor(degree=degree)\n",
    "    pr.fit(X_train, y_train)\n",
    "    y_fit = pr.predict(X_lin)\n",
    "    \n",
    "    title = f'Polynomial fit degree={degree}'\n",
    "    scatter_plot_polynomial(X_train, y_train, label='polynomial data', title=title)\n",
    "    scatter_plot_polynomial(X_valid, y_valid, label='validation set', title=title)\n",
    "    plt.plot(X_lin, y_fit, label='fit', c='black')\n",
    "    \n",
    "    plt.ylim([-6, 6])\n",
    "    plt.show()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "By just looking at the curves we can observe **3 regimes**:\n",
    "\n",
    "**Underfitting (degree<3):**\n",
    "The model is not able to fit the complexity data properly. The fit is bad for both the training and the validation set.\n",
    "\n",
    "**Fit is just right (degree=3):**\n",
    "The model is able to caputre the underlying data distribution. The fit is good for both the training and the validation set.\n",
    "\n",
    "**Overfitting (degree>3:**\n",
    "The model starts fitting the noise in the dataset. While the fit for the training data gets even better the fit for the validation set gets worse.\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### Fitting graph\n",
    "In the next step we want to quantify the previous observation. To do this we calculate the training and and validation error for each degree and plot them in a single graph. The resulting graph is called the **fitting graph**."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "100%|██████████| 30/30 [00:00<00:00, 1358.22it/s]\n"
     ]
    }
   ],
   "source": [
    "rmse_train = []\n",
    "rmse_valid = []\n",
    "degrees = list(range(0, 30))\n",
    "\n",
    "for degree in tqdm(degrees):\n",
    "    pr = PolynomialRegressor(degree=int(degree))\n",
    "    pr.fit(X_train, y_train)\n",
    "    rmse_train.append(pr.evaluate(X_train, y_train))\n",
    "    rmse_valid.append(pr.evaluate(X_valid, y_valid))"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "def plot_fitting_graph(x, metric_train, metric_valid, metric_name='metric', xlabel='x', yscale='linear'):\n",
    "    plt.plot(x, metric_train, label='train')\n",
    "    plt.plot(x, metric_valid, label='valid')\n",
    "    plt.yscale(yscale)\n",
    "    plt.title('Fitting graph')\n",
    "    plt.ylabel(metric_name)\n",
    "    plt.xlabel(xlabel)\n",
    "    plt.legend(loc='best')\n",
    "    plt.grid(True)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYMAAAEWCAYAAACEz/viAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8li6FKAAAgAElEQVR4nO3de3xU5bXw8d+ayUySyXWSQIAABkEuclXwXm1Qa62tij3eqPW0PbW0PXpa31NPa+1Fe+rpay/2c/St1Xpaa+1R0WpVtFrFFkStqGC5IwiCQiBACIRM7pf1/rF3Qkgzuc6eyUzW9/OZz96zr+txZK/s53n2s0VVMcYYM7z5Eh2AMcaYxLNkYIwxxpKBMcYYSwbGGGOwZGCMMQZLBsYYY7BkYFKMiIwXkYiI+Puxz9kissXLuOJFRFREJiU6DpN8LBmYpCQiO0Wk3r3wt3/GqOqHqpqtqq3udstF5Lou+x5zwVTVV1V1SrzLYMxQYsnAJLOL3Qt/+2dPogMaDBFJS3QMZviyZGBSioiUun/5p4nIfwFnA79w7xx+ISIr3E3XusuuEpEyEdnd6Rg7ReQmEVknItUi8piIZHRa/00R2Ssie0Tkup6qZkRkgoisEJEaEXlZRO4Rkf/tEusXReRD4K/u8j+ISIV77hUiMr3T8R4UkftEZKl7zFdE5Lgupz1fRN4TkcPu+SQm/3FNSrNkYFKWqn4HeBW4wb1zuEFVz3FXz3aXPRZl9yuBC4EJwCzg8wAiciHw78D5wCSgrJcwHgHeAgqB24Bru9nmo8A04OPu9xeAE4CRwDvAw122vwb4IVAErOlm/aeAU9y4r+x0XGOismRgktnT7l+/h0Xk6Rgf+25V3aOqVcCzwBx3+ZXAb1V1o6rW4VzguyUi43Euyt9X1SZVfQ1Y0s2mt6lqrarWA6jqA6pao6qN7vFni0hep+3/pKor3PXfAc4QkXGd1t+hqodV9UNgWafYjYnKkoFJZgtUNd/9LIjxsSs6zdcB2e78GGBXp3Wd57saA1S5SaOn7TuWiYhfRO4Qke0icgTY6a4q6m57VY0AVe65eovdmKgsGZhUF+thefcCYzt9HxdtQ3fbAhEJ9bJ95xg/A1yKUw2VB5S6yzvX+3ccQ0SygQIgqRvPTeJZMjCpbh9wfB+W9dXjwBdEZJp7kf9etA1V9QNgFXCbiARF5Azg4l6OnwM0AgeBEPCjbra5SEQ+IiJBnLaDlara0x2KMb2yZGBS3V3A5SJySETudpfdBvzObWu4sj8HU9UXgLtx6uK3ASvdVY1RdrkGOAPn4n478FgP2wI8BHwAlAObOh2/s0eAW3Gqh+YCn+1PGYzpjtjLbYwZOBGZBmwA0lW1pQ/bPwa8q6q3DvB8DwK7VfW7A9nfmGjszsCYfhKRy0QkXUTCwI+BZ6MlAhE5RUQmiojP7ZZ6KRDrnk/GDJolA2P678vAfmA70Ap8tYdtRwHLgQhO9dJXVfXvXgdoTH9ZNZExxhi7MzDGGANJNzBWUVGRlpaWDmjf2tpasrKyYhtQgqVamVKtPJB6ZUq18kDqlam78qxevbpSVUdE2yfpkkFpaSmrVq0a0L7Lly+nrKwstgElWKqVKdXKA6lXplQrD6Remborj4h80NM+Vk1kjDHGkoExxhhLBsYYY0jCNgNjjOmv5uZmdu/eTUNDQ7fr8/Ly2Lx5c5yj8kZGRgYDeZ+RJQNjTMrbvXs3OTk5lJaWdnuhrKmpIScnJwGRxZaqcvDgwQH1jLJqImNMymtoaKCwsHBAfzEnExGhsLAQv9/f730tGRhjhoVUTwTtBlrO4ZMMDmxh4rZfQ0tToiMxxpghx7NkICLjRGSZiGwSkY0i8vVuthERuVtEtonIOhE52at4OLSTcbufhfde8uwUxhjTncOHD/PLX/6y3/tddNFFHD582IOI/pGXdwYtwDdU9UTgdOB6ETmxyzafAE5wP4uAez2LZuJ5NAXyYO2jnp3CGGO6Ey0ZtLT0/AqM559/nvz8fK/COoZnyUBV96rqO+58DbAZKOmy2aXAQ+pYCeSLyGhPAvKnsa/4o7D1Rair8uQUxhjTnZtvvpnt27czZ84cTjnlFM4++2wuueQSTjzR+ft4wYIFzJ07l+nTp3P//fd37FdaWkplZSU7d+5k2rRpfOlLX2L69OlccMEF1NfXxzTGuAxhLSKlwApghqoe6bT8OeAOVX3N/f4X4FuquqrL/otw7hwoLi6eu3jx4gHF4du/gXM2fYetJyxiT8knB3SMoSYSiZCdnZ3oMGIm1coDqVemZCxPXl4ekyZNAuDHL23n3X2RY9ar6qAamKcWZ/OtCyZGXf/BBx9w5ZVX8uabb/Lqq69yxRVXsHLlStoH3ayqqqKgoID6+nrKysp4/vnnKSwsZMaMGbzyyitEIhHmzJnDK6+8wqxZs/jc5z7HJz7xCa6++upuz/fee+9x5MiRY5bNnz9/tarOixaj588ZiEg28CRwY+dE0B+qej9wP8C8efN0oANKLV8OHJzB5LrVTC776YCOMdQMhwG2kl2qlSkZy7N58+aO5wgCwcA/dL1sbW0dUHfMdoFgoMfnFLKzs/H5fOTk5BAKhTj11FOZOXNmx/o777yTp556CoDy8nIqKio6noloT7wTJkzgrLPOAuC0005j3759Uc8pIv3+jTxNBiISwEkED6vqH7vZpBwY1+n7WHeZd2ZfDS99Fw5shRGTPT2VMWboufXi6f+wLN4PnXV+KGz58uW8/PLLvPHGG4RCIcrKyrp9Ujo9Pb1j3u/3x7yayMveRAL8Btisqj+PstkS4J/dXkWnA9WqutermACYeSWIzxqSjTFxk5OTQ01NTbfrqqurCYfDhEIh3n33XVauXBnn6Bxe3hmcBVwLrBeRNe6yW4DxAKp6H/A8cBGwDagDvuBhPI6cYph4Hqx7DM79HviGz6MWxpjEKCws5KyzzmLGjBlkZmZSXFzcse7CCy/kvvvuY9q0aUyZMoXTTz89ITF6lgzcRuEeW2TUab2+3qsYopp9NTz5Rdi5Ao4vi/vpjTHDzyOPPNLt8vT0dF544YVu1+3cuROAoqIiNmzY0LH8pptuinl8w/PP4qmfhPRcWDuwXknGGJNqhmcyCGTC9AWwaQk0Rnrf3hhjUtzwTAYAsz8DzbWw+dlER2KMMQk3fJPB+NMh/zjrVWSMMQznZCACsxfCjhVQvTvR0RhjTEIN32QATq8i1Olmaowxw9iwSgYVtW3HLiiYAOPPcHoVxWGMJmOM6Yv2ISj27NnD5Zdf3u02ZWVlrFq1qtt1AzFsksGTq3dzy2v1vPPhoWNXzF4IlVthzzuJCcwYY6IYM2YMTzzxRFzONWySwcemF5OfLtz0h7U0NLceXTF9AfjTYY01JBtjvHHzzTdzzz33dHy/7bbbuP322znvvPM4+eSTmTlzJs8888w/7Ldz505mzJgBQH19PVdffTXTpk3jsssui/nYRJ6PWjpU5GYE+OKMdH66qpafvriF733Kfc9ORp7zENqGJ+DjP4K0YGIDNcZ464WboWL9MYsyW1vAP4jL4aiZ8Ik7oq6+6qqruPHGG7n+emfAhccff5wXX3yRr33ta+Tm5lJZWcnpp5/OJZdcEnUo7XvvvZdQKMTmzZtZt24dJ58c2xdDDps7A4DpRX4+e/p4Hnh9B2/t6PSCmzmfgfpD9kpMY4wnTjrpJPbv38+ePXtYu3Yt4XCYUaNGccsttzBr1izOP/98ysvL2bdvX9RjrFixgs9+9rMAzJo1i1mzZsU0xmFzZ9Du25+Yxoqtldz0h7W88PWzyUpPg+PnQ3ax88zBtE8lOkRjjJe6+Qu+Pg5DWF9xxRU88cQTVFRUcNVVV/Hwww9z4MABVq9eTSAQoLS0tNuhq+NlWN0ZAGSlp/HTy2ex61Add7zwrrPQnwYzr3BeiVl7MLEBGmNS0lVXXcXixYt54oknuOKKK6iurmbkyJEEAgGWLVvGBx980OP+55xzTsdgdxs2bGDdunUxjW/YJQOA044v5AtnTuD3Kz/g9W2VzsLZC6GtGTY8mdjgjDEpafr06dTU1FBSUsLo0aO55pprWLVqFTNnzuShhx5i6tSpPe7/1a9+lUgkwrRp0/j+97/P3LlzYxrfsKsmavfNC6ewfMt+vvnEOv5849nkjJoBxTOdqqLTFiU6PGNMClq//mjDdVFREW+88Ua320UizgCapaWlHUNXZ2ZmMtD3v/fFsLwzAMgI+PnZlbPZW13Pf/1ps7NwzkLneYMDWxIbnDHGxNmwTQYAJ48Ps+iciSx+exfLtux32g3Eb4PXGWOGnWGdDAD+z8dOYHJxNjc/uY5qXxgmnQ/rHoe21n/cuLXZuWvY+BQs+7/w2LXw+0/bOxGMSQI6TIacGWg5h22bQbv0ND93XjGHBb98nR88u5Gfz74anviCkxDSc2D/Zjiw2ZlWvuc0MgOID0JFULsfDrwLY+cltiDGmKgyMjI4ePAghYWFUR/qSgWqysGDB2lt7eaP2V4M+2QAMHNsHtfPn8Tdf3mPi6bN5fz0PHj6K0c3yB8PI0+EEy5wpiOnQtFkJwncXwaR6A+KGGMSb+zYsezevZsDBw50u76hoYGMjIw4R+WNjIwMamtr+72fZ8lARB4APgXsV9UZ3azPA/4XGO/G8TNV/a1X8fTmhvmTeHnTPm5espW/Xv47cuvLYeQ0KJoC6dnd75Rd7ExrKuIXqDGm3wKBABMmTIi6fvny5Zx00klxjMhbvT2z0B0v2wweBC7sYf31wCZVnQ2UAXeKSMIGBgqm+fj5VbOprm/m2+/kwUmfhZK50RMBQNYIQCCyP25xGmOMFzy7M1DVFSJS2tMmQI44FXjZQBXQ4lU8fTF1VC43nj+Zn764hRHZG5k4MpvCrCAFWcGOaX4oiN/n1jn6AxAqtGoiY0zSEy9b2N1k8FyUaqIcYAkwFcgBrlLVP0U5ziJgEUBxcfHcgT54EYlEOl4aEU1rm3LXO42sq+y+AUaA7ADkBIWcoPA/Td8kI38Um2Z+Z0AxDVZfypRMUq08kHplSrXyQOqVqbvyzJ8/f7WqRu3pksgG5I8Da4BzgYnAUhF5VVWPdN1QVe8H7geYN2+elpWVDeiEy5cvpy/7nncuNLe2cai2iYO1TVS1TyONR+drm9hRWcvOSB7zfE19Oq4X+lqmZJFq5YHUK1OqlQdSr0wDKU8ik8EXgDvUuTXZJiI7cO4S3kpgTB0Cfh8jczMYmRu9h8FbO6rY9UA+vtrtcYzMGGNiL5EPnX0InAcgIsXAFOD9BMbTbwVZAQ5oPoGGA/YOZWNMUvOya+mjOL2EikRkN3ArEABQ1fuAHwIPish6nKr4b6lqpVfxeCE/FOSA5uFva3ZejhMqSHRIxhgzIF72JlrYy/o9wAVenT8e8jMD7Nd850tkvyUDY0zSGvZjEw1Gmt9HJFjofLHupcaYJGbJYJBaMkc4M5YMjDFJzJLBILWE3CEpLBkYY5KYJYNBSs/Ko5GgJQNjTFKzZDBIBVnpHJR8G5/IGJPULBkMUn4oyP62PBu51BiT1CwZDFI4FKCiLZ82qyYyxiQxSwaDFM5yHjyjxqqJjDHJy5LBIIVDQQ5oPr6GKmhpSnQ4xhgzIJYMBikcCrAf9ynkWrs7MMYkJ0sGg9RRTQTWvdQYk7QsGQxSezURYN1LjTFJy5LBIOWHOg1WZ91LjTFJypLBIGUE/NQH3dFK7c7AGJOkLBnEQHYoRK0/z9oMjDFJy5JBDOSHAhzyhS0ZGGOSliWDGCjIClJJviUDY0zSsmQQA/mhoNOIbMnAGJOkLBnEQDgUYE9LDtTsA9VEh2OMMf1mySAGwqEgu1tyobURGqoTHY4xxvSbJYMYCIcC7G+zB8+MMcnLs2QgIg+IyH4R2dDDNmUiskZENorIK17F4rVwVpAD7eMTWbuBMSYJeXln8CBwYbSVIpIP/BK4RFWnA1d4GIunnCEpbHwiY0zy8iwZqOoKoKqHTT4D/FFVP3S3T9r6lXB7byKwZGCMSUqiHvZ+EZFS4DlVndHNuv8GAsB0IAe4S1UfinKcRcAigOLi4rmLFy8eUDyRSITs7OwB7duTA3Vt/MeKOrZlfI494y7h/Ymfi/k5ovGqTImSauWB1CtTqpUHUq9M3ZVn/vz5q1V1XtSdVNWzD1AKbIiy7hfASiALKALeAyb3dsy5c+fqQC1btmzA+/akpqFZj/vWc3rkR5NVn1zkyTmi8apMiZJq5VFNvTKlWnlUU69M3ZUHWKU9XFvTvMhKfbQbOKiqtUCtiKwAZgNbExjTgGQF/QT9Po6kFZJj1UTGmCSUyK6lzwAfEZE0EQkBpwGbExjPgIkI+aEAh31h61pqjElKnt0ZiMijQBlQJCK7gVtx2ghQ1ftUdbOI/BlYB7QBv1bVqN1Qh7pwKEhlWz5E3k10KMYY02+eJQNVXdiHbX4K/NSrGOIpnBVg35F8qKuE1mbwBxIdkjHG9Jk9gRwj4VCQ8pZc50vtgcQGY4wx/WTJIEbyQ0F2N7lduawR2RiTZCwZxEhBVoAdjTnOlxpLBsaY5GLJIEbCoSAVrTYkhTEmOVkyiJH8UJBK2pOBdS81xiQXSwYxUpAVoIkALcE8iFQkOhxjjOkXSwYxkh8KAtCYMcKqiYwxSceSQYyE3WRQGyy0aiJjTNKxZBAjBW4yOJJWYHcGxpikY8kgRnIy0vAJHJaw07XUw6HBjTEm1iwZxIjPJ+SH3NdfttRDY02iQzLGmD6zZBBD4VCAfW3tbzyzdgNjTPKwZBBDzvhE7lPI1r3UGJNELBnEUH4oyIdN7cnAGpGNMcnDkkEMFWQF2NHQngysmsgYEyOq8PjnYP0Tnp3CkkEMhUNBdtYHUV/A7gyMMbGz9c+w6WloPOLZKSwZxFB+KEhTi6LZI23kUmNMbLS1wss/gIKJcNK1np3GszedDUcFWc7bzVoyRxC0OwNjTCysewwObIYrHvT0DYp2ZxBD7eMTNaQXWZuBMWbwmhtg2Y9gzElw4gJPT2XJIIaOHZ/IupYaYwbp7V9D9S44/zYQ8fRUPSYDETm30/yELus+3cu+D4jIfhHZ0Mt2p4hIi4hc3peAh7JwyLmFO5JWCLWV0NqS4IiMMUmroRpe/RkcPx+OL/P8dL3dGfys0/yTXdZ9t5d9HwQu7GkDEfEDPwZe6uVYSSGc5dwZHJIwoFBXmdiAjDHJ6/W7of6Qc1cQB70lA4ky3933Y6jqCqCql+P/G06SSYkK9vxM587ggLpvPKuxqiJjzADUVMDKX8L0T8OYOXE5ZW/JQKPMd/e9X0SkBLgMuHcwxxlK0vw+cjLS2Kc2PpExZhBe+Qm0NsG5vVXAxE5vXUuPF5ElOHcB7fO43ydE361P/hv4lqq2SS8NIyKyCFgEUFxczPLlywd0wkgkMuB9+yrT18ravY0AvLt6BRV7gp6eLx5liqdUKw+kXplSrTwwtMqUWbeXU1Y/yN7RF/De+l3Arn4fYyDl6S0ZXNpp/mdd1nX93l/zgMVuIigCLhKRFlV9uuuGqno/cD/AvHnztKysbEAnXL58OQPdt69Gb3yd2mA2HIGpJflMPcfb88WjTPGUauWB1CtTqpUHhliZ/vAFSEunZOFdlOQUD+gQAylPj8lAVV/p/F1EAsAMoFxVB1UHoqoddxYi8iDwXHeJINmEQwEORBTS82xICmNM/+z5O2z8I5zzHzDARDBQvXUtvU9EprvzecBa4CHg7yKysJd9HwXeAKaIyG4R+aKIfEVEvhKj2IekglCQQ3VNzg9pycAY0x8v/wAyC+DMr8X91L1VE52tqu0X7y8AW1V1gYiMAl4AHo22o6r2mCy6bPv5vm471OWHghyqbYLiYmtANsb03fZl8P4y+PiPICM37qfvrTdRU6f5jwFPA6iq9ZmMIhwKUNvUSmtohHUtNSaR2loTHUHftbXBy7dB3jiY98WEhNBbMjgsIp8SkZOAs4A/A4hIGpDpdXDJqP3Bs8aMEXZnYEwi1FU5Y///5HjYuy7R0fTNpqdh7xqYfwsEMhISQm/J4MvADcBvgRs73RGcB/zJy8CSVfv4RJFAITTXQmMkwREZM4xsXwb3ngnvPgc+PzxyFVSXJzqqnrU2w19/CCNPhFlXJSyMHpOBqm5V1QtVdY6qPthp+Yuq+g3Po0tC7eMTVfsLnAXWiGyM95ob4MXvwO8XQDAbrvsL/PMSaKxxEkJjTZzjqe/7H4LvPARV78N533cSWIL02IAsInf3tF5V49/kPcR1jE/kCzsLIvugcGICIzImxe3bBE9eB/s3winXwcd+CMGQs+7KB+HhK52++wsXgz8Or3DZ9Aw8c4PzVrJgNmQXQ86o7qehQnjlxzDudJjc41Bunuvtv8xXgA3A48AeehmPyBytJjqAOz6R3RkY4422NnjrV7D0Vqf3zWceh8kfP3abSefDJ++E526EF77pzHs1FHRLE7x8qzOmUMlcmHax88bDSIUz3bsGtu5zqo+7uvIhz4eo7k1vyWA0cAVwFdACPAY8oaqHvQ4sWeW71UQVrTY+kTGeObIXnvlX2P5XOOHjcOk9kD2i+23nfQEO7YDX74KC4+HMG2IfT/Vu+MPnYffbcOqX4YLbIS3KUDSNNZ2SRAUEs2D86bGPqZ96ewL5IHAfcJ+IjAWuBjaJyLdU9ffxCDDZZAT8hIJ+9jZlgi/NupcaE2ubn4UlX3Pq5T/5c5j3L73/VX3ebXBoJ7z0XQgf5/zVHivvLYU/LnIagq94EKZf1vP26TnOp2hS7GKIgT5VoInIycBCnGcNXgBWexlUsguHglTVt0DWSLszMENLW6tTdXlkj/PX7JFyp7fNkXJoaex0UZWj8yLHfJ96sBpalkPeWMgb707Hxv5BqZZGJ8bqXXD4Qzi8C/ZtgC3Pw+jZ8Olfw4jJfTuWzweX/cop95Nfgs//CcbOHVx8ba3OKylf/RkUz4ArfjfkLvD90VsD8n8CnwQ2A4uBb6uqvb6rF/mhAIfrmiF7pLUZmMQ5uN3pqVK96+gFv2YvtHX5J5yWCXklEAgB6g5Or6B67BRAlbzIIfjb69DWfOxx0vOOJob2TzA7SlLpMu3uwh/Zx7Ej5QvkjIazb4KPfit6NUw0gUy4+lH49Xnw6FVw3csQLu3fMdrV7IMnvwg7X4WTPgsX/cw5fhLr7c7gu8AOYLb7+ZE7yqgAqqqzvA0vORVkueMT5RU7//iMiSdVWPUbeOl7TtVF+4X5uLMgd4xz4c8d605LIDPcr8bLN5cvp+ycc5yLdfsFvHp3p88up+68vrd3W3XhCzgx5Y93Gn7zxzlP5LZPc0v6nwC6yh4B1zwBv/mY08voiy9BZn7/jrHzNXjiX6DhCFz6SzjpmsHFNET0lgwG+86CYSk/FGRXVR2MLXZ6EBgTL0f2wpIbYNvLMPFcp2E1d0zsz+PzQe5o5zPulO63aap1+v93d5ehbccu8wcga0R8+tmPmAxX/S/8/jJ4/Fq4pusbfaNoroeV9zoPiBUcD9c+BcXTvY01jnprQP6gu+Ui4sNpQ+h2/XAXDgU4VNfs9COuPeDULSbwYRIzTGz4I/zp350L8EU/c/rcJ7K7YjDL+QxFE86GS/4fPP0Vp9tp3j85nT2OudMpP/aup/2d5tM/DZfc7TQCp5De2gxygeuBEmAJsBRneIpv4Axn/bDXASajcCjIkYZmWkMj8Gsb1B102g+M8UL9IXj+P2D9H5z+7Zf9CopOSHRUQ9+chU4Po1fu4BxZDK90GdgumH20im3MHGdaPMN5OCzBzwR4obdqot8Dh3DeS3AdcAtOe8ECVbX6jyjCoQCqUBcsJAecvzgsGRgvbF8GT/+rU39fdguc/Y34PGWbKspuhswwuze+yfiZZzptEx29o/JS8qIfTa/vQFbVmQAi8mtgLzBeVRs8jyyJtQ9JUe13k4F1LzWx1lTnDHn81q+gaDJc/TCUnJzoqJKPCJz+Fd5vmMr4U8sSHU1C9ZYMOvqOqWqriOy2RNC7fHdIiipfmLFg3UtNbO35u/OQU+VWOO0rcP5tSd+t0SReb8lgtogccecFyHS/t3ctjf/reJJAgZsM9re1j09kTyGbGKmthN9dCunZcO3TMHF+oiMyKaK33kTWBWYA2scnqmpKg/RcqyYysfPKT6ApAtcthRFTEh2NSSG9vdzGDEDHMNZ1TfYUsomdg9udh8lO/mdLBCbmLBl4ICvoJ+j3UVXX5DxrYHcGJhZevg386VD27URHYlKQZ8lARB4Qkf0isiHK+mtEZJ2IrBeRv4nIbK9iiTcRccYnqnXHJ7KRS81gffgmbF4CZ30dcooTHY1JQV7eGTwI9PTqnh3AR92uqz8E7vcwlrgLh9zxibJH2Z2BGRxVWPo95y7zjOsTHY1JUZ4lA1VdAUQdqUpV/6aqh9yvK8HphZkqwlmBo20GTTXOOC3GDMTmZ2HXmzD/FqcXkTEeEFXtfauBHlykFHhOVWf0st1NwFRVvS7K+kXAIoDi4uK5ixcvHlA8kUiE7Oz4/GP6xd8b2BNp44FJbzB1y92sPO0+GjJHx/w88SxTPKRaeWBwZZK2Fk55+99Q8bNq3l3oEBjjyn6joa+78syfP3+1qs6LupOqevYBSoENvWwzH+d9CYV9OebcuXN1oJYtWzbgffvr5ifX6dwfvqT63lLVW3NVP3jDk/PEs0zxkGrlUR1kmVb+yvn/Z8ufYxbPYNlvNPR1Vx5glfZwbU1obyIRmQX8GrhUnVdspoyCLGfkUs1yxySy7qWmvxqq4ZU7oPRsOOGCREdjUlzCkoGIjAf+CFyrqlsTFYdXwqEgrW1KTaDQWWCNyKa/Xr/LGfH2gh8OqwHTTGJ4NryhiDwKlAFFIrIbuBUIAKjqfcD3gULgl+7b01q0p/qsJNM+PtEhzSFX/Na91PRPdTm8cQ/MvALGnJToaMww4FkyUNWFvay/DmdY7JRUkOUOSVHfynFZI6yayPTPsv9y3gZ27vcSHYkZJuwJZI+03xkcrnMfPLNqItNXFethzSNw2pchfFyiozHDhCUDj4RDnccnKraRS03fLf2+82KVs7+R6EjMMGLJwCPtw1hX1TY5wwfYnYHpi21/ge1/hXP+AzLDiRnPbcMAABXASURBVI7GDCOWDDySk5GGT9qridxk0NaW6LDMUNbWCktvhfzj4NQvJToaM8xYMvCIzyfkd4xPVAza6nQTNCaadY/BvvVw3vchLT3R0ZhhxpKBh8KhwNFkANajyETXVAd/vR3GnAzTP53oaMww5FnXUuOOXFrb3CUZ9DhMkxlOairgvaWwbSlsXwaNR+DT94PP/kYz8WfJwEP5oSC7D9VBdomzwBqRh7fWFihfBe+95CSBinXO8pzRMH0BTL8MSj+S2BjNsGXJwEMFWQHWl3euJrLupcPOkb0UV/wVnnjI6SnUcBjED+NOg/NuhRM+BsUzbLgJk3CWDDzkvOCmGQ1mIcFs52GiD990/+HL0SntE3eZ+CEQgkCm+wk5DYp2wRi62trg0A7Yu9b5nSvWwd51ULufaQBZI2HqJ52L//HzITM/0REbcwxLBh7KDwVpammjvrmVUP5xsOFJ5zMQ4uuSILIgkMms+jY4OBmyRkBWkfsZcfR7qAiCWZZIYqm1GfZvci727Rf9fRugKeKs96XBiKkw6XwYNZNVlUHmffJfrC3ADGmWDDwUDrnjE9U2EfrMY1C5FVBQ3Kl2mnZapq3Q3ADNtdBcD811zrSp7uh8cy001ZFW86HzFqzaSmdZd9IynSExCidC4QlQOAmKJjnzuSV2keqJKhzaCeWrnc/uVc5f/62NzvpgtlPNM+czMGomjJoFI6cd0zU0sny5/Tc2Q54lAw+Fs46OTzS2ZBzkj4v5Od5ZvpyysjLnS1Md1FVC7QEnOdS683WVcGQvHNwGux4++hcsOImiIzm4CSJnFGTkQnquMyxCei6kBWMe+5BUVwXl77gX/1XOtP35kLRMGDPHeSCs5GQYPQfCE+xCb1KCJQMPHTM+UTwEQxAcD/njo2+j6nRxrXwPDr4Hlduc6Z41sOkZZ6TM7qRluMkh9+g0mO1UX/VFzigong7FM2HkVKfqKl7qDx1NjnXt04POp/Oy2kqo2ePuJE5Vz5RPQMlcKJnn/MXvD8QvbmPiyJKBhzpXEw0ZIs6FOWcUTDj72HUtTU4jaGS/0+e94UinaXWX70ec7fr0Dm11xtvpuCMRKDjeSQ6jZrpJYrozDMNgNTc41Ti73z76OVLe/bbBbAgVOm0rOaOd6p6iE2DsPOev/ozcwcdjTJKwZOChztVESSEtCCOmOJ9Ya2uDwx/Avo1OY2v7Z/OzuI0oEMzhpIwxsG+Kk6yyi93pKGewv+xRzsW7vVpG1Tnm7lXORX/XW05Pnjb3v3f+eBh/Boye7Ryn/cIfKnLmAxmxL6cxScqSgYfyM507g7hVEw1lPh8UTHA+0z51dHljBPZvdpPDRtreexMOvAvvv+LcjfzDcdKcbprZI52/+GsPOMsDIWcohzNvgLGnONU6OcXxKZsxKcCSgYfS/D5yMtKS584gEdKzYdwpzgdY27VBPLLP+dRUHJ22z4+Y6uw39lQYeSL47X9nYwbK/vV4rCArOLTaDJJJMHT0bsIY4ynrE+exjmGsjTFmCLNk4LFwKGDVRMaYIc+zZCAiD4jIfhHZEGW9iMjdIrJNRNaJyMlexZJIBSGrJjLGDH1e3hk8CFzYw/pPACe4n0XAvR7GkjD5oSCHrZrIGDPEeZYMVHUFUNXDJpcCD6ljJZAvIqO9iidRwqEAtU2tNLa0JjoUY4yJKpG9iUqAXZ2+73aX7e26oYgswrl7oLi4mOXLlw/ohJFIZMD7DtSBcqe94PmXXyGcEfvcm4gyeSnVygOpV6ZUKw+kXpkGUp6k6FqqqvcD9wPMmzdPO/qh99Pyzn3Y46R23V4e2vQO0+bMY+qo2A9vkIgyeSnVygOpV6ZUKw+kXpkGUp5E9iYqBzoP4znWXZZS2scnOlRrPYqMMUNXIpPBEuCf3V5FpwPVqvoPVUTJrn18InvWwBgzlHlWTSQijwJlQJGI7AZuBQIAqnof8DxwEbANqAO+4FUsiRT3YayNMWYAPEsGqrqwl/UKXO/V+YeKfLeayB48M8YMZfYEsscyAn5CQb89eGaMGdIsGcRB2MYnMsYMcZYM4iDfxicyxgxxlgziwIaxNsYMdZYM4sDGJzLGDHWWDOIgHApwyKqJjDFDmCWDOMgPBamub6altS3RoRhjTLcsGcRBgfusQXW93R0YY4YmSwZxcHRICksGxpihyZJBHOTbkBTGmCHOkkEcFLQnA+teaowZoiwZxIGNT2SMGeosGcRBe5tBlVUTGWOGKEsGcZAV9BP0+6zNwBgzZCXFay+TnYiQHwqwdOM+DtQ0OssQd527Tce2HLP+mGVHF3XssXdvI0sPrccngoizVDrmBZ84+/l9PrLT/WSnp5GdESA7PY2cjDT3exo57jQz4EeOPZExZhiwZBAnH58+imVb9vPWjipUj12n7gLt+N5pnbv02GVHt2tqamF9VQUKtKmi6hxP1dlOVWlTaG1Tmvrw0JtPIDPgJ5jmIz2tferrMvWTnuYjkObrSD7QnojoNH90ud8nBNN8BPzOcQJ+X8f3YJqPoF8I+H1sL2+mbv1eMgI+MtL8pAec82UE/M6ygDPffgxjTGxYMoiTHy6Y4clx+/Pi66aWNmobW4g0tlDT4Ewjjc3UNHT63tBCfXMrTS1tNLa0T9uOmR6ua3LmW9s6MlN74jk6377cSUytbUpzq3OM5tY2mluV1jbtNk7Wv9On8oSCfgqyghRmBZ1pdnq38/mhAD43Mfl80pG0hH+8m/KL4PMJaT7B737SfGJ3SyblWTIYRoJpPoJpwY4G7URrTxBNrU6SaW5tY8VrbzBn7ik0NLc6n5a2jvnGljYam1tpaHaWVdc3c7C2iYO1TRyINPJuRQ0Ha5toaon9sB8iHE0QIqQH/IzOy6AkP5OScCYl+ZmMDWdSkh+iJJxJOBSwBGKSiiUDkzDOX95OtU+74iwfU0blDPiYqkptUysHI40crG2iKtJEdX2zU4VG1yq0o3cuHVVqbUpLm9KmzrS1VWlV5y6m/dPSptQ1tbK3up4dlbW8tq2SuqbWY+IIBf2McRNEVlMTOno/c48Lk5sRGHDZjPGSJQOTUkTEaRRPT+O4wqy4nFNVOVzXTPnhenYfqqf8cD3lh+opP1zHrqp6tlQ086ffvo1PYNroXE6dUMBpEwqYV1pAUXZ6XGI0pjeeJgMRuRC4C/ADv1bVO7qsHw/8Dsh3t7lZVZ/3MiZjYk1ECGc51W8zSvL+Yf2LLy8jp3Qmb+6o4u2dVTz61of89vWdAEwckcWpEwo5dUKY048vZHReZpyjN8bhWTIQET9wD/AxYDfwtogsUdVNnTb7LvC4qt4rIicCzwOlXsVkTCKkpwlnTirizElFgNOQv768mrfc5PDcuj08+taH+AQunVPC1887gdKi+NzVGNPOyzuDU4Ftqvo+gIgsBi4FOicDBXLd+Txgj4fxGDMkBNN8zD0uzNzjwnyVibS2Ke9WHOGZNXt46I2dLFm7h386uYR/O/cExhWEEh2uGSZEu3Z6j9WBRS4HLlTV69zv1wKnqeoNnbYZDbwEhIEs4HxVXd3NsRYBiwCKi4vnLl68eEAxRSIRsrOzB7TvUJVqZUq18kD/ynS4sY0/vd/Msl0tqMLZY9O4+PgAhZlD55mK4f4bJYPuyjN//vzVqjov2j6JbkBeCDyoqneKyBnA70Vkhqoe0zdQVe8H7geYN2+e9rVffVf96ZOfLFKtTKlWHuh/mRYAe6vruWfZNh57exd/29PGwlPHcf38SYzMzfAszr6y32joG0h5vPxzoxwY1+n7WHdZZ18EHgdQ1TeADKDIw5iMSQqj8zK5fcFMlt1UxqdPLuF/3/yQs3+yjNuf20RlpDHR4ZkU5GUyeBs4QUQmiEgQuBpY0mWbD4HzAERkGk4yOOBhTMYklbHhEHf80yz++o2P8qlZY3jg9R2c/eNl3PLUela+f5C2aE9xG9NPnlUTqWqLiNwAvIjTbfQBVd0oIv8JrFLVJcA3gP8Rkf+D05j8efWqEcOYJHZcYRZ3Xjmbf50/kXuWbeOpd8p55M0PKc5N51OzxnDx7DHMHptnTz2bAfO0zcB9ZuD5Lsu+32l+E3CWlzEYk0omjsjm51fO4fYFLfxl836WrN3D79/4gN+8toPxBSEunj2aS2aXDOopbjM8JboB2RgzAKFgGhfPdu4IquubeXFjBc+u3cN9r7zPPcu2M7k4m4tnjeH8E4spyAqSGfQTCvhJs5FeTRSWDIxJcnmZAa6cN44r542jMtLIC+v38uzavdy5dCt3Lt16zLZBv4/MoJ+soN9JEME0d+onzde3RFF1sIEn9/6djDQf6Z2GGs9whxrvvMzv61u1VUaan8nFOYwNZ+Lr4z4mtiwZGJNCirLTufaMUq49o5Q9h+t5e2cVtY2t1DW1UNfUSl1TK/Wd5tuXV9U20dLat+a6I3VtHCqv7hhJtn1U2Vi0ZWcF/UwZlcPU0blMc6dTRuXYAH9xYMnAmBQ1Jj+TS+eUxPy40fqwt7+vomP48eY2+tofpKaxha0VNbxbUcPmvUd4bu0eHnmzpWN9SX4m00bnMHVULmdNKuK0CQV2BxFjlgyMMTER8Dtvn8tOH9hl5eTx4Y55VaXiSAPv7q1hc8UR3t1bw7sVR1i25QC/WLaN0XkZXDJ7DAtOKmHa6Nwejmr6ypKBMWbIERFG52UyOi+T+VNHdiyva2rh5c37efrv5fzmtR38asX7TCnO4dKTxnDpnBJK8m3U14GyZGCMSRqhYBqXzB7DJbPHUFXbxJ/W7eHpNXv4yZ+38JM/b+HU0gIuPWkMn5w5mvzQ0HijX7KwZGCMSUoFWcGOxvJdVXU8s6acp9fs4TtPbeC2JRs5bUIho/MyOt6HXZjtvBO7KDudAvf92J3fsjfcWTIwxiS9cQUhbjj3BK6fP4mNe47wzJpy/rb9INv2R6iqbaKptfv3Ymenp1GYHaStqYGCja+TnuYjPc1H0O90mw36fQTTfKSn+Qmm+QgF/YRDRxNLYVY6hdlBwqEgwbTkfobDkoExJmWICDNK8o5545yqUtPYQlWkiYO1jRyMNDnvx65tojLSSFVtEx/u2UdOZoCmllYijS00tbTR1OL0jnKmrTS1tFHfQxfanIy0Y+460t3k0HmIkPa59kUCZAb9TByRzZRROUwpzmFETnpChhWxZGCMSWkiQm5GgNyMQNQ3yDndZU/t9VhtbUp1fXNHUqmqdRKLM9/YkWR2VdU5dyNu4uicP9q727Yvq2looap2V8f6/FCAycVOYpjsJogpxTnkhbx91sKSgTHG9JHPd/R915NG9r59X1VGGtm6r4atFTVs2Rdh674anl5TTk3D0WctinPTue4jx/Olc46P3Yk7sWRgjDEJVpSdTlF2OmdOPPo6l/ZnLbZU1LB1Xw1bKiKMzE33LAZLBsYYMwR1ftaibEoMb0OiSO7mb2OMMTFhycAYY4wlA2OMMZYMjDHGYMnAGGMMlgyMMcZgycAYYwyWDIwxxgDS19fSDRUicgD4YIC7FwGVMQxnKEi1MqVaeSD1ypRq5YHUK1N35TlOVUdE2yHpksFgiMgqVZ2X6DhiKdXKlGrlgdQrU6qVB1KvTAMpj1UTGWOMsWRgjDFm+CWD+xMdgAdSrUypVh5IvTKlWnkg9crU7/IMqzYDY4wx3RtudwbGGGO6YcnAGGPM8EkGInKhiGwRkW0icnOi44kFEdkpIutFZI2IrEp0PP0lIg+IyH4R2dBpWYGILBWR99xpOJEx9leUMt0mIuXu77RGRC5KZIz9ISLjRGSZiGwSkY0i8nV3eVL+Tj2UJ5l/owwReUtE1rpl+oG7fIKIvOle8x4TkWCPxxkObQYi4ge2Ah8DdgNvAwtVdVNCAxskEdkJzFPVpHxYRkTOASLAQ6o6w132E6BKVe9wk3ZYVb+VyDj7I0qZbgMiqvqzRMY2ECIyGhitqu+ISA6wGlgAfJ4k/J16KM+VJO9vJECWqkZEJAC8Bnwd+Hfgj6q6WETuA9aq6r3RjjNc7gxOBbap6vuq2gQsBi5NcEzDnqquAKq6LL4U+J07/zucf6hJI0qZkpaq7lXVd9z5GmAzUEKS/k49lCdpqSPifg24HwXOBZ5wl/f6Gw2XZFAC7Or0fTdJ/j+AS4GXRGS1iCxKdDAxUqyqe935CqA4kcHE0A0iss6tRkqKKpWuRKQUOAl4kxT4nbqUB5L4NxIRv4isAfYDS4HtwGFVbXE36fWaN1ySQar6iKqeDHwCuN6tokgZ6tRhpkI95r3ARGAOsBe4M7Hh9J+IZANPAjeq6pHO65Lxd+qmPEn9G6lqq6rOAcbi1IRM7e8xhksyKAfGdfo+1l2W1FS13J3uB57C+Z8g2e1z63Xb63f3JzieQVPVfe4/1jbgf0iy38mth34SeFhV/+guTtrfqbvyJPtv1E5VDwPLgDOAfBFJc1f1es0bLsngbeAEt3U9CFwNLElwTIMiIlluAxgikgVcAGzoea+ksAT4nDv/OeCZBMYSE+0XTddlJNHv5DZO/gbYrKo/77QqKX+naOVJ8t9ohIjku/OZOB1lNuMkhcvdzXr9jYZFbyIAt6vYfwN+4AFV/a8EhzQoInI8zt0AQBrwSLKVSUQeBcpwhtvdB9wKPA08DozHGar8SlVNmgbZKGUqw6l+UGAn8OVO9e1Dmoh8BHgVWA+0uYtvwalnT7rfqYfyLCR5f6NZOA3Efpw/8B9X1f90rxGLgQLg78BnVbUx6nGGSzIwxhgT3XCpJjLGGNMDSwbGGGMsGRhjjLFkYIwxBksGxhhjsGRgTLfcUSxvSnQcxsSLJQNjPNLp6U9jhjxLBsa4ROQ7IrJVRF4DprjLJorIn93BAF8Vkamdlq903ydxu4hE3OVl7nZLgE3uss+6482vEZFfuUOqIyIXiMgbIvKOiPzBHS/HmISwZGAMICJzcYYpmQNcBJzirrof+DdVnQvcBPzSXX4XcJeqzsQZEbKzk4Gvq+pkEZkGXAWc5Q4k1gpcIyJFwHeB893BBlfhjD9vTELYbawxjrOBp1S1DsD9yz4DOBP4gzOkDQDp7vQMjo4P/wjQ+aUob6nqDnf+PGAu8LZ7jEycQd1OB04EXneXB4E3Yl4qY/rIkoEx0flwxoSf08/9ajvNC/A7Vf125w1E5GJgqaouHGSMxsSEVRMZ41gBLBCRTHc02IuBOmCHiFwBzoiXIjLb3X4l8E/u/NU9HPcvwOUiMtI9RoGIHOfuf5aITHKXZ4nI5JiXypg+smRgDOC+CvExYC3wAs6w5wDXAF8UkbXARo6+LvVG4N9FZB0wCaiOctxNOG0DL7nbLsV5B+8BnPcIP+ouf4MBvJDEmFixUUuNGQARCQH1qqoicjWwUFXtvdomaVmbgTEDMxf4hfuylMPAvyQ4HmMGxe4MjDHGWJuBMcYYSwbGGGOwZGCMMQZLBsYYY7BkYIwxBvj/jd43TGUaXEwAAAAASUVORK5CYII=\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "plot_fitting_graph(degrees, rmse_train, rmse_valid, metric_name='RMSE', xlabel='degree')"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "We can make a few observations:\n",
    "1. The training error always decreases when adding more degrees.\n",
    "2. There is a region between 3-15 where the validation error is stable and low. \n",
    "\n",
    "Ideally, we would choose the the model parameters such that we have the best model performance. However, we want to make sure that we really have the best validation performance. When we do `train_test_split` we randomly split the data into to parts. What could happen is that we got lucky and split the data such that it favours the validation error. This is especially dangerous if we are dealing with small datasets. One way to check if that's the case is to run the experiment several times for different, random splits. However, there is an even more systematic way of doing this: **cross-validation**.\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### Cross-validation\n",
    "\n",
    "The idea behind cross validation is to split the data into k equally sized parts, called folds. Each fold gets to be the validation set once while the other folds play the training set part. That means we run k experiments and aggregate the training and validation metrics by averaging them. This is a more robust approach to monitoring overfitting and thanks to `scikit-learn` we only have to adjust one line by adding the `cross_validate` function!\n",
    "\n",
    "<div style=\"text-align: center\">\n",
    "<img src='images/cross-val.png' width='400'>\n",
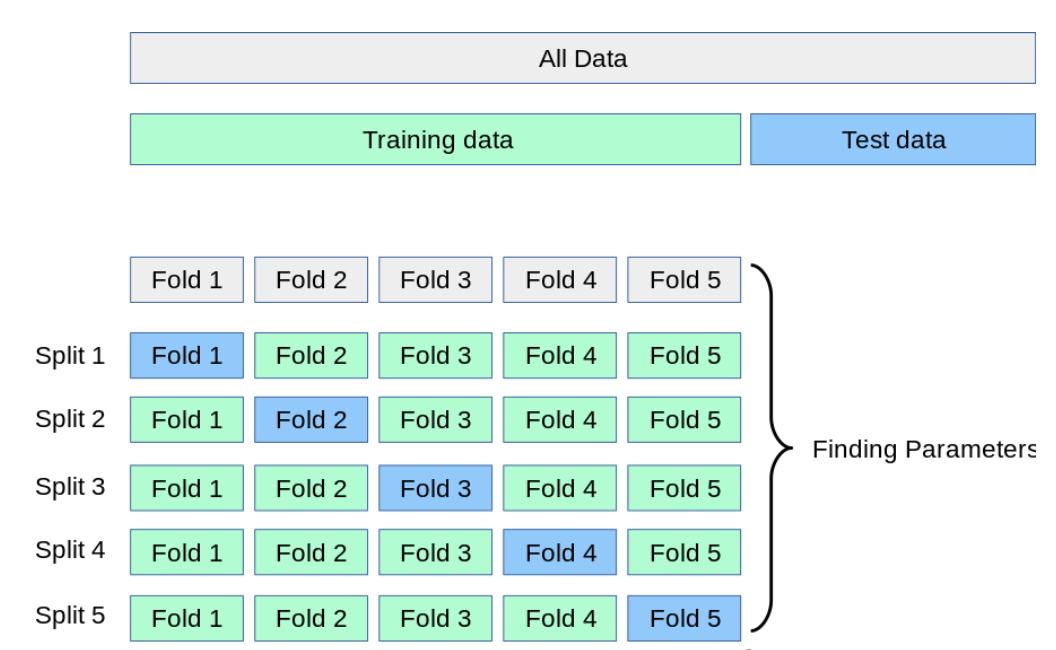
    "    <p style=\"text-align: center;\"> <b>Figure reference:</b> https://scikit-learn.org/stable/modules/cross_validation.html </p>\n",
    "</div>\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Cross-valida takes care of all the steps, we just have to pass an initialized model, the full dataset and the number of folds with the keyword `cv`. Furthermore, we need to specify the metric to be evaluated and also that we want it to return the scores on the training sets."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "100%|██████████| 16/16 [00:00<00:00, 235.88it/s]\n"
     ]
    }
   ],
   "source": [
    "rmse_train = []\n",
    "rmse_valid = []\n",
    "degrees = list(range(0, 16))\n",
    "for degree in tqdm(degrees):\n",
    "    pr = PolynomialRegressor(degree=degree)\n",
    "    results = cross_validate(pr, X, y,\n",
    "                             cv=5,\n",
    "                             return_train_score=True,\n",
    "                             scoring='neg_root_mean_squared_error')\n",
    "    \n",
    "    # we average the scores and append them to the list\n",
    "    rmse_train.append(-np.mean(results['train_score']))\n",
    "    rmse_valid.append(-np.mean(results['test_score']))"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYUAAAEWCAYAAACJ0YulAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8li6FKAAAgAElEQVR4nO3dd3xV9f3H8dcnA8IIM+wAQcMeIgmIigriABVFRYajalFb66i2tmK1lbba2v782Z8W1FpFxYUWqwIyXCAOUIbI3jPsTQKBkOTz++OchJtws3Nzzs39PB+PmHv2O4nczz3f7znfI6qKMcYYAxDldQBjjDH+YUXBGGNMPisKxhhj8llRMMYYk8+KgjHGmHxWFIwxxuSzomCqLRFpIyIZIhJdhm0uEJE1ocxVVURERSTZ6xwmvFhRMGFPRDaLSKZbAPK+WqrqVlWtq6o57npzROSOQtsWeONU1a9UtWNV/wzG+IUVBVNdDHELQN7XDq8DVYSIxHidwUQmKwqm2hKRJPdMIEZEngQuAMa5ZxLjRGSuu+qP7rwRItJfRNIC9rFZRB4SkaUiclhE3hWRuIDlvxWRnSKyQ0TuKK7JRkTaichcEUkXkc9EZLyIvFko62gR2Qp84c7/j4jsco89V0S6BuzvNRF5UUQ+dff5pYi0LXTYS0RknYgcco8nlfLLNdWWFQUTEVT1UeAr4F73TOJeVb3QXXyWO+/dIjYfDgwC2gE9gNsARGQQ8CvgEiAZ6F9CjLeB74HGwFjgliDrXAR0Bi53p2cA7YGmwGLgrULr3wT8GUgAlgRZfhXQ2809PGC/xgRlRcFUFx+6n4YPiciHlbzv51R1h6oeAKYCPd35w4FXVXWFqh7DeaMPSkTa4Lw5/0FVs1T1a2BKkFXHqupRVc0EUNUJqpquqifc/Z8lIvUD1v9YVee6yx8FzhWR1gHLn1LVQ6q6FZgdkN2YoKwomOpiqKo2cL+GVvK+dwW8PgbUdV+3BLYFLAt8XVhL4IBbPIpbP3+eiESLyFMiskFEjgCb3UUJwdZX1QzggHuskrIbE5QVBRNJKntI4J1AYsB066JWdNdtJCK1S1g/MOONwDU4zVP1gSR3fmC/QP4+RKQu0AgI60524y0rCiaS7AbOKMW80noPuF1EOrtv9r8vakVV3QIsBMaKSA0RORcYUsL+44ETwH6gNvCXIOtcISL9RKQGTt/CfFUt7ozFmGJZUTCR5FlgmIgcFJHn3HljgdfdvojhZdmZqs4AnsNpq18PzHcXnShik5uAc3He5J8A3i1mXYCJwBZgO7AyYP+B3gYex2k2SgFuLsvPYExhYg/ZMaZyiEhnYDlQU1WzS7H+u8BqVX28nMd7DUhT1cfKs70xwdiZgjEVICLXikhNEWkI/A2YWlRBEJHeInKmiES5l7NeA1T2lVLGVIgVBWMq5mfAHmADkAPcXcy6zYE5QAZOs9PdqvpDqAMaUxbWfGSMMSafnSkYY4zJF9aDbiUkJGhSUlK5tj169Ch16tSp3ECVzO8Z/Z4PLGNl8Hs+8H9Gv+VbtGjRPlVtEnShqobtV0pKipbX7Nmzy71tVfF7Rr/nU7WMlcHv+VT9n9Fv+YCFWsT7qq+aj0SkjogsFJGrvM5ijDGRKKRFQUQmiMgeEVleaP4gEVkjIutFZEzAoodx7hI1xhjjgVCfKbyGM+RwPvfRiOOBwUAXYJSIdBGRS3Hu2twT4kzGGGOKEPJLUkUkCZimqt3c6XNxhge+3J1+xF21LlAHp1BkAteqam6Q/d0F3AXQrFmzlEmTJhVeTp06dYiOLv6xvKqK3583UlLGnJwcjh49Sqj/hkXJyMigbl1/D7ppGSvO7/nA/xn9lm/AgAGLVDU12DIvrj5qRcEhg9OAc1T1XgARuQ3YF6wgAKjqS8BLAKmpqdq/f/8Cyzdt2kR8fDyNGzcu9g01PT2d+Pj4CvwYoVdcRlVl//79pKen065duypO5pgzZw6Ff/9+Yxkrzu/5wP8Z/Z4vkK86mgFU9TVVnVbcOiIyREReOnz48GnLjh8/XmJBqA5EhMaNG3P8+HGvoxhjqhEvisJ2Co4jn+jOKzVVnaqqd9WvXz/o8upeEPJEys9pjKk6XhSFBUB79yHmNYCRBH8soTHGhL/D22m5fQZkHfU6SamE+pLUd4B5QEcRSROR0eqMIHkvMAtYBbynqivKuN8im4+8dujQIZ5//vkyb3fFFVdw6NChECQyxnjmcBq8OpgO616E8efAmhleJypRSIuCqo5S1RaqGquqiar6ijt/uqp2UNUzVfXJcuy32OYjLxVVFLKzix9ef/r06TRo0CBUsYwxVe3wdnjtKsg8yJoO90CNuvDOSJh0k1MsfMp3Hc3hbsyYMWzYsIGePXvSu3dvLrjgAq6++mq6dOkCwNChQ0lJSaFr16689NJL+dslJSWxb98+Nm/eTOfOnbnzzjvp06cPl112GZmZmV79OMaY8jiyE14fAkf3wS0fsLPlZfDzr+CSP8L6z2FcH/h2HOSU+CymKheWA+KJyBBgSHJycrHr/XHqClbuOBJ0WU5OTon3MgTTpWU9Hh/StcjlTz31FMuXL2fJkiXMmTOHK6+8kuXLl+dfNjphwgQaNWpEZmYmvXv35vrrr6dx48YF9rFu3TreeecdnnnmGUaPHs3777/PzTfbUxaNCQvpu+D1qyBjN9zyASSmwvo5EB0L/R6ArtfC9N/AJ4/Cj5Pgqn9A695ep84XlmcKfm4+KqxPnz4F7iN47rnnOOuss+jbty/btm1j3bp1p23Trl07evbsCUBKSgqbN2+uqrjGmIpI3+2cIRzZCTe/D637nL5Ow7Zw47sw4k04th9euRSmPgCZB6s+bxBheaZQWsV9oq+qm9cCh8udM2cOn332GfPmzaN27dr0798/6H0GNWvWzH8dHR1tzUfGhIOMvTDxaqcv4ebJ0KZv0euKQOchcEZ/mP1X+O4FWD0NLv8LdL/BWe6RsDxT8PPVR/Hx8aSnpwdddvjwYRo2bEjt2rVZvXo18+fPr+J0xpiQOLrPOUM4tBVueg/anle67WrGw6C/wF1zoEEb+O+dMPEa2Lc+lGmLFZZFwc/NR40bN+b888+nW7du/OY3vymwbNCgQWRnZ9O5c2fGjBlD377FfJIwxoSHo/vh9avh4GanWSipX9n30eIsGP0pXPm/sGMJvHCucwZxsupHLKjWzUdeefvtt4POr1mzJjNmBL9OOa/fICEhgeXLT400/tBDD1V6PmNMJTl2wGkyOrDBKQjtLiz/vqKiofcd0GkIzPodfPkULPuPUyjOHFB5mUuKUWVHMsaY6iSvIOxbByPfdvoHKkN8Mxj2inPlEgpvDIX373A6satAWBYFP/cpGGMiQOZB581671oY9TYkD6z8Y5x5Mdw9Dy56GFZ+BON6w4KXITfoANKVJiyLgp/7FIwx1VzmIXjjWtizCka+BcmXhO5YsXEw4Hdw97fQ8iz4+NfOJaw7l4bskGFZFIwxxhPHD8Ob18Gu5TD8DWh/adUcN6E9/GQKXPuS06H90kWwJHjfZUVZR7MxxpTG8SPw5vXOp/ThE6HjoJK3qUwicNYI6HAZfPEkJF0QksNYUTDGmJKcSIe3hsGOH+CG16HTFd5lqdUQrnw6ZLsPy+aj6tTRnPfc1h07djBs2LCg6/Tv35+FCxdWZSxjTJ4TGfDWDZC2EIZNgM5XeZ0opMKyKFTHjuaWLVsyefJkr2MYYwJlHYW3h8O2753LRLtc43WikAvLouBnY8aMYfz48fnTY8eO5YknnmDgwIH06tWL7t2789FHH5223ebNm+nWrRsAmZmZjBw5ktTUVK699lob+8gYL2Qdg7dHwNZ5cP2/ndFNI0D17lOYMQZ2LQu6qFZONkSX48dv3h0GP1Xk4hEjRvDAAw9wzz33APDee+8xa9Ys7r//furVq8e+ffvo27cvV199dZHPWH7hhReoXbs2CxcuZNOmTfTq1avsOY0x5Zd1DN4ZAVu+gev+Dd2u9zpRlaneRcEDZ599Nnv27GHHjh3s3buXhg0b0rx5cx588EHmzp1LVFQU27dvZ/fu3TRv3jzoPubOncv9998PQI8ePejRo0dV/gjGRLaTmTBpFGz6Cq79F3QP3tdXXVXvolDMJ/rMEA6dfcMNNzB58mR27drFiBEjeOutt9i7dy+LFi0iNjaWpKSkoENmG2N84OOHYOOXMPQF5xLQCBOWfQp+v/poxIgRTJo0icmTJ3PDDTdw+PBhmjZtSmxsLLNnz2bLli3Fbn/hhRfmD6q3fPlyli4N3d2LxpgAGXth6btwzs+g5yiv03giLIuC368+6tq1K+np6bRq1YoWLVpw0003sXDhQrp3787EiRPp1KlTsdvffffdZGRkkJqayh/+8AdSUlKqKLkxEW7Jm5B7ElJHe53EM9W7+chDy5ad6uBOSEhg3rx5QdfLyMgAICkpKX/I7Fq1ajFp0qQqezqcMQZnoLlFr0HbftCkg9dpPBOWZwrGGFPpNs52xhVKvd3rJJ6yomCMMQCLXoXajZ1nJ0ewalkUVNXrCFUiUn5OY0IufResng49b4KYml6n8VS1KwpxcXHs37+/2r9hqir79+8nLi7O6yjGhL8f3gDNgZTbvE7iuWrX0ZyYmEhaWhp79+4tdr3jx4/7/g21pIxxcXEkJiZWYSJjqqHcHFj0uvM4zcZnep3Gc9WuKMTGxtKuXbsS15szZw5nn312FSQqv3DIaEzYW/85HN4Glz3hdRJfCMvmI7/fvGaMCSOLXoU6TaHTlV4n8YWwLAp+v3nNGBMmDm+HtTPh7JshOtbrNL4QlkXBGGMqxeKJoAopt3qdxDesKBhjIlNOtlMUkgdCwySv0/iGFQVjTGRa9wmk74CUyL6DuTArCsaYyLRwAsS3gA6DvE7iK1YUjDGR5+AWWP8Z9PpJ+Z7AWI1ZUTDGRJ7FE0HEKQqmACsKxpjIknPSGdai/WVQ30YEKMyKgjEmsqyZDhm7rYO5CFYUjDGRZeGrUC8R2l/qdRJf8k1REJHOIvKiiEwWkbu9zmOMqYYObHQeppNyK0RFe53Gl0JaFERkgojsEZHlheYPEpE1IrJeRMYAqOoqVf05MBw4P5S5jDERatHrINFw9i1eJ/GtUJ8pvAYUuAhYRKKB8cBgoAswSkS6uMuuBj4Gpoc4lzEm0mRnwQ9vQsfBUK+F12l8K6RFQVXnAgcKze4DrFfVjaqaBUwCrnHXn6Kqg4GbQpnLGBOBVk+FY/si/hnMJZFQP6FMRJKAaarazZ0eBgxS1Tvc6VuAc4DJwHVATWCpqo4vYn93AXcBNGvWLGXSpEnlypWRkUHdunXLtW1V8XtGv+cDy1gZ/J4PSpfxrCWPEXd8D9+d8yJI1Xan+u13OGDAgEWqmhp0oaqG9AtIApYHTA8DXg6YvgUYV559p6SkaHnNnj273NtWFb9n9Hs+VctYGfyeT7UUGfeuVX28nurcp6skT2F++x0CC7WI91Uvrj7aDrQOmE5055WaPWTHGFMmi16DqBjoebPXSXzPi6KwAGgvIu1EpAYwEphSlh2oPWTHGFNaJ4/Dkreg01UQ38zrNL4X6ktS3wHmAR1FJE1ERqtqNnAvMAtYBbynqitCmcMYE8FWTYHMg9bBXEohHR5QVUcVMX86FbjsVESGAEOSk5PLuwtjjBdWToEF/4bLnoQWParmmAsnQKMzIOnCqjlemPPNHc1lYc1HxoSZExnw0T3w3i2w+WuYeDXs/DH0x92zCrbOg5TbICos3+6qXFj+lqyj2Zgwsm0BvNgPlrwNFzwE9yyAGnXh9athx5LQHnvRaxBdA3rarU+lFZZFwc4UjAkDOdkw5ymYcDnk5sBtH8PA30NCMtw2DWrWg4nXwI4fQnP8rGPw4zvQ+WqokxCaY1RDYVkUjDE+d2AjvDoY5vwVug+Du7+GtuedWt4wqWBh2L648jOs+ACOH7YO5jKyomCMqTyq8MNb8OIFsHcNXP8KXPcSxAU5q2/YFm7/2Fk2cShsX1S5WRa9CgkdoK2Nr1kWYVkUrE/BGB86dgD+cyt89Ato0RPu/sY5SyhOgzZw23So1QAmXgtplVQYdi2DtAXOg3REKmefESIsi4L1KRjjMxtmwwvnwerpcMkf4dYp0KB1yduBs95tH0PthvDGUEhbWPE8C1+F6Jpw1siK7yvChGVRMMb4RPYJmPWo82ZeMx7u+Az6PVD2B9jkF4bGTlPStu/Ln+lEBix9D7peC7UblX8/EcqKgjGmfPasgn9fDPPGQe874K4voWXP8u+vfqJTGOo2gTeug63flW8/y9+HrHTrYC6nsCwK1qdgjIdyc2H+i/CviyBjN9z4Hlz5v1CjdsX3Xb+VWxiawpvXwdb5Zd/HolehaRdofU7F80SgsCwK1qdgjEfSd8Fbw2Dmw3BGf7h7HnS4vHKPUa+lc7lqfHN483rYMq/02+74wfmyDuZyC8uiYIzxwKpp8Py5sOVb58zgxnedpp5QqNcSbp0G8S3cwvBt6bZb+CrE1IIew0OTKwJYUTDGFCs6OxOm3Afv3uR0CP9srtOHEOpP4vVaOGcM9VvBm8Ng8zfFr3/8CCybDN2udy5xNeViRcEYU7Q9q0lZ9CAsfgP6PQijP4MmHaru+PHNnTOG+q2cZqvNXxe97rL/wMmjkPrTqstXDYVlUbCOZmOqyOd/IvZkhvOJ/ZKxEFOj6jPEN3M6nxu0gbdugE1zT19H1Wk6at4dWvWq+ozVSFgWBetoNqYKnMyEDV+wp2k/SOrnbZa6TeHWqdCgLbw1HDZ+WWBxfPpa2L3MOpgrQVgWBWNMFdg0F7Iz2ZfQx+skjrzC0KgdvD0cNs7JX9RyxyyIrQPdb/AuXzVhRcEYE9yaGVCjLocadPc6ySl1m7iF4Ux4e4QzvEbmIZru+Qp63ABx9bxOGPasKBhjTqcKa2fCmQPQqFiv0xRUJ8EZW6lxMrwzEj7+NdG5WU7TkakwKwrGmNPtXALpO6HDYK+TBFcnAX4yBRq3h+WTORKfXLEhNky+sCwKdvWRMSG2ZiYglX+3cmWq09g5Y+gylE3tbvE6TbURlkXBrj4yJsTWzoDWffz/GMvajWD46xxsZGcJlSUsi4IxJoQOb4edP0KHQV4nMR6womCMKWjtTOd7R5/2J5iQsqJgjClo7UxomARNOnmdxHjAioIx5pSso87dwh0G253BEcqKgjHmlI1zIOcEdLT+hEhlRcEYc8qa6VCzHrQ5z+skxiNWFIwxjtxcWPsJJF/izWioxhfCsijYzWvGhMCOxXB0j111FOHCsijYzWvGhMCaGSDRzpmCiVhhWRSMMSGwZga06evcJWwilhUFYwwc2gp7VljTkbGiYIzBHQAP/46KaqqMFQVjjDMAXuNkSEj2OonxmBUFYyLd8SOw6SsbAM8AVhSMMRu+gNyT1p9ggBKKgohcHPC6XaFl14UqlDGmCq2dCXENoHVfr5MYHyjpTOHpgNfvF1r2WCVnMcZUtdwcWDsL2l8G0TFepzE+UFJRkCJeB5s2xoSbbd9D5gEbAM/kK+mjgRbxOth0hYnIUOBKoB7wiqp+UtnHMMYEWDsDomLsLmaTr6SicIaITME5K8h7jTvdrujNThGRCcBVwB5V7RYwfxDwLBANvKyqT6nqh8CHItIQp+nKioIxobRmJrQ9H+JsyBjjKKkoXBPw+ulCywpPF+U1YBwwMW+GiEQD44FLgTRggYhMUdWV7iqPucuNMaGyfwPsWwOpt3udxPhIsUVBVb8MnBaRWKAbsF1V95TmAKo6V0SSCs3uA6xX1Y3uficB14jIKuApYIaqLi7VT2CMKZ+8ZzHb/QkmgKgW3TUgIi8C/1TVFSJSH5gH5ACNgIdU9Z1SHcQpCtPymo9EZBgwSFXvcKdvAc4B1gK3AguAJar6YpB93QXcBdCsWbOUSZMmle4nLSQjI4O6deuWa9uq4veMfs8HlrE4Zy15jBpZh1jQZ1yx69nvsOL8lm/AgAGLVDU16EJVLfILWBHw+gHgQ/d1c+CH4rYttJ8kYHnA9DCcfoS86VuAcaXdX95XSkqKltfs2bPLvW1V8XtGv+dTtYxFOnZQ9Y+NVD99vMRV7XdYcX7LByzUIt5XS7okNSvg9aXAh24h2VWO4hRoO9A6YDrRnVcq9pAdYypo/WeQm20D4JnTlFQUDonIVSJyNnA+MBNARGKAWhU47gKgvYi0E5EawEhgSgnb5FN7yI4xFbNmBtRuDInBWxBM5CqpKPwMuBd4FXgg4AxhIPBxaQ4gIu/g9EV0FJE0ERmtqtnufmcBq4D3VHVFaUPbmYIxFZBzEtZ/Cu0vh6hor9MYnynp6qO1wGmXJqjqLJw39BKp6qgi5k8HppdmH0G2nQpMTU1NvbM82xsT0bbOh+OHbQA8E1SxRUFEnituuareX7lxjDEht3YmRNeAMy8ueV0TcUq6ee3nwHLgPWAHPhnvSESGAEOSk+2BIMaUiSqsmQ5JF0BN/1wiafyjpD6FFsBLwOU4l43GAh+p6uuq+nqowxXFOpqNKad96+DARms6MkUqtiio6n5VfVFVBwC3Aw2Ale7NZsaYcLN2hvPd7mI2RSjVAOoi0gsYhXOvwgxgUShDGWNCZM1MaNYdGrQueV0TkUp68tqfRGQR8CvgSyBVVUfrqYHrPGGXpBpTDscOwLb59uwEU6yS+hQew2kyOgv4K7BYRJaKyDIRWRrydEWwPgVjymHdJ6C5dhezKVZJzUelemaCMSYMrJkBdZtBy7O9TmJ8rKSb17YEmy8iUTh9DEGXh5pdkmpMGWVnwfrPodu1EFVSA4GJZCX1KdQTkUdEZJyIXCaO+4CNwPCqiXg6az4ypoy2fANZ6dZ0ZEpUUvPRG8BBnLGL7gB+h3MD21BVXRLibMaYyrJmBsTEwRn9vU5ifK7EZzSrancAEXkZ2Am0UdXjIU9mjKkcqs79Ce0ughq1vU5jfK6kxsWTeS9UNQdIs4JgTJjZswoObbW7mE2plHSmcJaIHHFfC1DLnRZAVbVeSNMVwTqajSkDu4vZlEFJw1xEq2o99yteVWMCXntSENxc1tFsTGmtmQEtekK9Fl4nMWHArk0zpjrL2AtpC63pyJSaFQVjqrN1swC1omBKzYqCMdXZmhlQrxU07+F1EhMmrCgYU12dPA4bvoAOl4P44vlYJgxYUTCmutr8FZw8ZncxmzIJy6JgQ2cbUwprZkBsbWh3oddJTBgJy6Jgl6SaaiE7C+a/QN30jZW/b1VYOxPOvBhi4yp//6baKtWT14wxIfDV0/Dl30gFOPgRnHe/8yZeGe3/u5bCke3Q/5GK78tElLA8UzAm7O1YAnOfhq7XseGMW2HvGnjzOnjxAvjxXcg5WfI+irNmJiBOJ7MxZWBFwZiqln0CPrwb6jSBq55hW5vr4JdL4ZrnITcbPrgLnu0J346DE+nlO8baGZCYCnWbVm52U+1ZUTCmqn35N9izEq5+Dmo1dObF1ICzb4K7v4Ub34OGSfDJo/BMV/j0cUjfVfr9H9kJO36wsY5MuVhRMKYqbV8EX/8Det4cvGknKsqZf/vHcOcXcOYA+PY5+L/u8NE9TjNTSdbOdL7bXcymHKwoGFNVTh6HD+6G+BZw+ZMlr98qBYa/Dvctgl63wrL3YXwfeHsEbP7GucIomLUzoX4baNqlcvObiBCWRcHuUzBhafaTsG+N22zUoPTbNToDrnwaHlwB/X8HaQvgtSvg5YGw4kPIzTm1btYx2DjHOUuwu5hNOYRlUbD7FEzY2fodfPtP5xN/8iXl20edxtD/Yac4XPkMHDsA/7kV/pkCC16Gk5mw6UvIPg4drT/BlI/dp2BMqGUdc642qp8Ilz1R8f3F1oLeoyHlNlg9Db55Dj7+Ncz+i9M0VSMe2var+HFMRArLMwVjwsoXT8CBDXDNOIirxGdTRUVDl2vgjs/g9hmQ2Ad2L3fOEmJqVN5xTESxMwVjQmnLtzD/eeh9B5zRPzTHEIG25zlfh7ZBnDWrmvKzomBMqGQdhQ9/AQ3awCV/rJpjNmhdNccx1ZYVBWNC5bM/wsFNcNvHULOu12mMKRXrUzAmFDZ9Bd//C875OSRZp68JH1YUjKlsJ9Lho1849xcM/IPXaYwpE2s+MqayffoHp8P3pzOhRh2v0xhTJnamYExl2vAFLJwA594Dbfp6ncaYMrOiYExlOX4EProPGreHix/zOo0x5eKboiAiZ4jIKyIy2essxpTLJ49C+g4Y+oJz17ExYSikRUFEJojIHhFZXmj+IBFZIyLrRWQMgKpuVNXRocxjTMis+wwWT3Qeqdm6t9dpjCm3UJ8pvAYUGJlLRKKB8cBgoAswSkRsjF8TvjIPwZT7oEkneyayCXuiRY3JXlkHEEkCpqlqN3f6XGCsql7uTj8CoKp/dacnq+qwYvZ3F3AXQLNmzVImTZpUrlwZGRnUrevvG4r8ntHv+aBqMnZc/SzNd81hca+/k16vfZm39/vv0e/5wP8Z/ZZvwIABi1Q1NehCVQ3pF5AELA+YHga8HDB9CzAOaAy8CGwAHinNvlNSUrS8Zs+eXe5tq4rfM/o9n2oVZFw9Q/Xxeqqf/ancu/D779Hv+VT9n9Fv+YCFWsT7qm/uU1DV/cDPvc5hTKkdOwBT74emXeGi33qdxphK4cXVR9uBwFG7Et15pWZPXjO+MONhOLYfrn0BYmp6ncaYSuFFUVgAtBeRdiJSAxgJTCnLDtSevGa8tmoqLHsPLvwNtDjL6zTGVJpQX5L6DjAP6CgiaSIyWlWzgXuBWcAq4D1VXVHG/dqZgvHO0f0w7UFo3h0u+LXXaYypVCHtU1DVUUXMnw5Mr8B+pwJTU1NT7yzvPowpt+kPOZeh3vIhRMd6ncaYSuWbO5qNCQsrPoAV/4X+D0Pzbl6nMabShWVRsOYjU+VysmH7Ivj419CiJ5z/oNeJjAkJ31ySWhbWfGRCLmMvpH0PaQtg2wLYsRhOHoOYWnDtixAdlv90jCmR/Z9tTM5J2L3cefPPKwQHNzvLomKgeQ/o9RNI7O08RS2+uadxjQmlsCwKIjIEGJKcnOx1FBOO0nc7b/7bvoe0hbDjB8jOdJbFt3De/FNHQ+s+zrNDRX4AABShSURBVOWmNuKpiSBhWRSs+ciUluSehLRFzqf/tO+ds4HDW52FUbHOm37q7U4hSOwN9RNBxNvQxngoLIuCMaXy2Vj6fTse5mY50/VaOW/85/zMOQto3gNi47zNaIzPWFEw1dOWefD1PziQcA5NBvzCPQto5XUqY3zPLkk11U9uDkz/DdRrxarOv4KuQ60gGFNKYVkUbOwjU6yFE2D3Mrj8SXKjrXnImLIIy6JgTJGO7oMv/gztLoIuQ71OY0zYsaLgRwc3w4e/oMmer7xOEn4+/yNkHYXBf7eriIwpB+to9pOTmfDNs/D1PyD7OB2j4+Dw7c5lkqZkaYtg8Rtw7j3QtJPXaYwJS2F5plDtOppVYfV0GH8OzPkrdLwCbp+BaK7TYRri52hXC7m5zuildZvCRQ97ncaYsBWWRaFadTTv3wBvD4dJo5w7Z38yBW54Fdqex+akUbBmuvNAF1O8JW864xNd+meIq+d1GmPCljUfeSXrKHz1DHz7HETXhMuedG6qChifPy3xas48uhhm/BbOuAjiqkERDIXMg/DZWGhzLvQY7nUaY8JaWJ4phDVVWPkRjOsDXz0NXa+F+xbCefee9sAWjYqBIc9C+i74/M8eBQ4Ds//iFIYr/sc6l42pIDtTqEp71zqf+jfOhmbd4Pp/Q9vzit8mMcU5g/juX86n4NZ9qiZruNi1DBa8DL3vcB6PaYypEDtTqAon0uGT38ML58L2xc7lknd9WXJByHPxY1CvJUz9pTPMs3GoOh3xtRrCgN95ncaYaiEsi0LYXH2kCssmw7jeTt/BWSPhvkVu30EZTtJqxjtNI3tWwrf/DF3ecLP0Pdg6Dy4Z6xQGY0yFhWVRCIurj3avhNeHwPujncskR38G14yHuk3Kt79OV0LnIfDl3+DAxsrNGo6OH4FPfw8te0HPm71OY0y1EZZFwdeOH4aZj8CL/ZyneV31D7hzNrTuXfF9D/678wyAaQ/avQtf/g0y9sCVT0OU/W9sTGWxf02VRRWWvAP/TIX5LziPb7xvMaT+FKKiK+cY9VrCJY/DxjlO00mk2rMavnsRet0CrVK8TmNMtWJXH5XXsQOwfz3sWwf718GmubB9EbRKhRvfhVa9QnPc1J/C0ndh1iOQfAnUaRya4/iVqnMFV406MPBxr9MYU+1YUShOdhYc3HTqjX/fevf7Osg8cGq9qBhonAxXj4OeN4W2OSMq2rl34V8XOm3qQ58P3bH8aOVHsOlLuOJpqJPgdRpjqh0rCqqQsfv0N/796+HgFtCcU+vWaQoJ7Z0O34T20Li9871B27JdTVRRzbrCefc5A+f1GOHc7RwJso7CrEed+xFSf+p1GmOqpcgsCms/ofPKcbB2rFMEstJPLYuJcz71N+8B3a533/iTnXl+GmbioodhxYdOp/Pd30bGs4a/+l84kgbDXqm8fhpjTAGRWRT2r6P+4ZXQqhv0HOW84TdOdj7110sMj6tZYms5Vza9MdQZLuPix7xOFFr7Nzj3aPQYCW36ep3GmGorLIuCiAwBhiQnJ5dr+yWtbuS/rTpwfkp3msTXpEndmjSJr0lcbJh9+jxzgNN89PX/OWc1TTt7nSg0VGHGw87AgZf+0es0xlRrYVkUVHUqMDU1NfXO8mz/xeo9TFyZxcSViwrMj4+LKVAk8r8KTTeuU5PoKJ8MvHb5X2DdJ84QGLfPDI+znLJaOxPWf+qMJBvf3Os0xlRrYVkUKur+ge05I3c7yd1T2Jtxgr3pAV/u9ModR9iTfoKME9mnbR8l0KjO6UWjVYM4WjWsRcsGtWjVoBbxcbFBjl7J6iQ4b5Yf/QIWv1b9OmBPHnfOEhI6OsODGGNCKiKLQkx0FA3ioujWquSO42NZ2exLz2JvxvGgxWNv+gnW705nb8YJTuYUvMu4XlwMrRrWplWDWvkFo1WD2u73WiTUrYFUxlDPPW+EH9+BT8c6T22rTp+mv30ODm1xHj4UXQVF1pgIF5FFoSxq14ihTeMY2jSuXex6ubnK3owTbD+UyfaDmQW+px08xncb95Ne6KyjRkyUWzCcr5YNauUXjMSGtcgt7VAWInDV/8EL5zmfqoe/Xt4f118ObnGuOOp6beRcdmuMx6woVJKoKKFZvTia1YujV5vgI3YezjyZXyh2HDpVONIOZfL56j3syzhRYP028VHUabufc84oxV3LCclw4W9g9hOwZiZ0HFQZP5a3Zv0OJAoue8LrJMZEDCsKVah+rVjq14qlS8vgzxA+fjKHnYePs/1gJuv3pPPcp6sY8dJ8ruzRgkcGdyKxYfFnK5z/S1g+2XmAfVI/qFk3BD9FFVn/GayeBgP/APUTvU5jTMSohpeqhK+42GjaJdShX/sEbju/HX+9oBYPXNKez1ftZuD/fskzn6zhWNbpHd/5Ymo4Q2Ac3uY8ojJcZWc5zWCNzoBz7/U6jTERxYqCj9WMFh64pANf/Lo/l3dtznNfrOfip7/kwx+2o0X1N7TpCym3w3cvwI4fqjZwZZn/vDPMyOC/Q0xNr9MYE1GsKISBlg1q8dyos5n883NpEl+TB95dwvUvfMuP2w4F3+CSsVCnCUy5H3KKObMor8PbYeEEOq7+J8z+qzOMd9oiyDxY8X0f2QFf/t25iqr9pRXfnzGmTKxPIYykJjXio3vOZ/LiNP4+cw3XjP+GYSmJ/PbyjjStFzD2Ua0GMPhv8J/bnOcOnFfBJpjcXNj5g9OBvXYm7FoKQEJMPOz6HAg4a6nVCBqfCY3OdL+fcWo6LnhfSgGf/B5ys52b8owxVc6KQpiJihKGp7ZmcLfmjJ+9gQlfb2LGsp3cc3EyPz2/3amhOroMhfaXw+wnnVFdG7Yt24GyjjoP81kzw7ljOmO3cyVQ63OcM5EOg/lmxU769zsXDm6GAxucx4Tu3+C83vw1LJ1UcJ91mhQsFoEFo2Zd2PSV01F+0Rho1K7ivyxjTJn5piiISB3geSALmKOqb3kcydfi42IZM7gTI3u35snpq/j7zDVM+n4bj17Zmcu6NHNuirvyaRh/jnM10o3vOfczFOdwmnMmsGam89CgnBNQsx4kD4QOgyD50oIP9Vm5yxmdtWkn56uwk5lwYJNTJPKKxf6NsOELWFLoz1u3GeSchAZtoN8DFf8FGWPKJaRFQUQmAFcBe1S1W8D8QcCzQDTwsqo+BVwHTFbVqSLyLmBFoRSSEurw75+k8vW6ffxp2gp+9sYizjuzMX8Y0oVOzds4o6fO+h2s+AC6XVdw49xcpzN67QynEOxe5sxv2A56j4YOl0Ob85yrmsojthY06+J8FZZ1tOCZxf6NcHgr9PuVs50xxhOhPlN4DRgHTMybISLRwHjgUiANWCAiU4BEwH1XIgdTJv3aJzD9/gt4+/utPPPpWq549ituOqctvxp4Ow2Xvutc4nnmAIiKhY2znTOCtZ/A0T1us1BfuPRPzhlBQoeSzyoqqkYd52E5zbuH9jjGmDKRIi9trKwDiCQB0/LOFETkXGCsql7uTj/irpoGHFTVaSIySVVHFrG/u4C7AJo1a5YyadKkYKuVKCMjg7p1/X1zV3kzZmQpH67P4ott2dSKgV8kpvGLnWM4HteUmif2EaXZZEfX4UCjs9mX0JsDjVLIjo2vsnxVyTJWnN/zgf8z+i3fgAEDFqlqarBlXvQptAK2BUynAecAzwHjRORKYGpRG6vqS8BLAKmpqdq/f/9yhZgzZw7l3baqVCTjVZfB2t3p/HnaSv5nHdSpP5Jro+eT1u5Gdjbrz75GvU4bYC7w5ECQoPMDrdqxii6tOwRsU1Bp9xc4KQIiztpRIu706fOi3GkCXkdFOd8lbztg4w+LaZPcEyFgXwhRUeTPi3J3FLjfvNcEvC7yuPk5C65TID9ClLtO3vc8fv9/0e/5wP8Z/Z4vkG86mlX1KHB7adat6EN2IkWHZvFM/GkfPlu1hyc/rs3Y/VfBfmAlef+puKVhcIPcvG+8ThBUXuECkE+mn1YcIaCYFvwWdJ286cACFh11qghFBxSkvPlRIkQFvhanYDr7EKIF0o9k8vzqefn7DFwe5f4MgdN560je/oIU1cBCS0Bxzi/eBBb3U/PyCj8FCi1s3ZLF4qw1EHg8d/2Cv5OA/QXmL/SBIsr9fYlAdJTz+wr8HTq/MyE66tTvzVkHZ52oUz97dJSw5UgOq3cdISYqipgoISZaiI2OIjpKiI2KIjpanPkBx/KKF0VhO9A6YDrRnVdqFX3ITiQRES7t0owBHZuw8/Dx/Pl5rYYacI9BYEtiYKNiYBNj4PzvvvuePn36BFlS3L4K5it8fFVnXt7rXHXWUFVy1dkiN3BZEevnOgv4celSunXrfto+nHVPbZs3Im3B/Z7aj7rHDVyG5mVxv7vHKJxDNXD+qX3lbb9lyxbatG0T5G9T9N+K09Y5lT/vuLm5pzI7087rnICMObkFX5/6eZQc93VmlPPGlrfOyRx3fwV+9lP714BjnnpdcJkG/B60wN8k7+/t/s6CvM5bp8DfJVdh0/rT/v/ylW+/KvWqeYUjJirK/e68jo4SYqOdwvGbyzsxqFvlD5PvRVFYALQXkXY4xWAkcKMHOSJKTHQUrRuVMKBeGW2rG0VyU/+0kwYju2Lo36WZ1zGKNWfOTvr3D3JJr084TR/+fi52YPOMBilCUKgoAZobWJhOFbfCBdMplqcKYf50LuTkF9xTy9QtvIHb/7hsGZ27dOVkTi45uUp2jpKdq2Tn5rqvc53pvPnueidzlJzcXE7mKjk5ysncU9vXrxWa54uE+pLUd4D+QIKIpAGPq+orInIvMAvnktQJqrqijPu15iNjTFB5zV7Rp/VyeSdmzyr6d2/hdYxSCWlRUNVRRcyfDkyvwH6t+cgYY0LABsQzxhiTLyyLgogMEZGXDh8+7HUUY4ypVsKyKKjqVFW9q379+l5HMcaYaiUsi4IxxpjQCMuiYM1HxhgTGmFZFKz5yBhjQiMsi4IxxpjQCPkoqaEkInuBLeXcPAHYV4lxQsHvGf2eDyxjZfB7PvB/Rr/la6uqTYItCOuiUBEisrCooWP9wu8Z/Z4PLGNl8Hs+8H9Gv+cLZM1Hxhhj8llRMMYYky+Si8JLXgcoBb9n9Hs+sIyVwe/5wP8Z/Z4vX8T2KRhjjDldJJ8pGGOMKcSKgjHGmHwRWRREZJCIrBGR9SIyxus8gUSktYjMFpGVIrJCRH7pdaaiiEi0iPwgItO8zhKMiDQQkckislpEVonIuV5nCiQiD7p/4+Ui8o6IxPkg0wQR2SMiywPmNRKRT0Vknfu9oQ8z/o/7d14qIh+ISAM/5QtY9msRURFJ8CJbaURcURCRaGA8MBjoAowSkS7epiogG/i1qnYB+gL3+CxfoF8Cq7wOUYxngZmq2gk4Cx9lFZFWwP1Aqqp2w3kK4UhvUwHwGjCo0LwxwOeq2h743J320mucnvFToJuq9gDWAo9UdagAr3F6PkSkNXAZsLWqA5VFxBUFoA+wXlU3qmoWMAm4xuNM+VR1p6oudl+n47yRtfI21elEJBG4EnjZ6yzBiEh94ELgFQBVzVLVQ96mOk0MUEtEYoDawA6P86Cqc4EDhWZfA7zuvn4dGFqloQoJllFVP1HVbHdyPpBY5cFOZQn2OwT4B/BbwNdX90RiUWgFbAuYTsOHb7oAIpIEnA18522SoP4P53/wXK+DFKEdsBd41W3iellE6ngdKo+qbgeexvnUuBM4rKqfeJuqSM1Udaf7ehfQzMswpfBTYIbXIQKJyDXAdlX90essJYnEohAWRKQu8D7wgKoe8TpPIBG5Ctijqou8zlKMGKAX8IKqng0cxftmj3xuu/w1OMWrJVBHRG72NlXJ1LmG3befdEXkUZwm2Le8zpJHRGoDvwP+4HWW0ojEorAdaB0wnejO8w0RicUpCG+p6n+9zhPE+cDVIrIZp/ntYhF509tIp0kD0lQ17yxrMk6R8ItLgE2quldVTwL/Bc7zOFNRdotICwD3+x6P8wQlIrcBVwE3qb9uwDoTp/j/6P6bSQQWi0hzT1MVIRKLwgKgvYi0E5EaOJ17UzzOlE9EBKcdfJWqPuN1nmBU9RFVTVTVJJzf3xeq6qtPuaq6C9gmIh3dWQOBlR5GKmwr0FdEart/84H4qCO8kCnAre7rW4GPPMwSlIgMwmnOvFpVj3mdJ5CqLlPVpqqa5P6bSQN6uf+P+k7EFQW3M+peYBbOP8L3VHWFt6kKOB+4BefT9xL36wqvQ4Wp+4C3RGQp0BP4i8d58rlnMJOBxcAynH+Lng+FICLvAPOAjiKSJiKjgaeAS0VkHc4ZzlM+zDgOiAc+df/NvOizfGHDhrkwxhiTL+LOFIwxxhTNioIxxph8VhSMMcbks6JgjDEmnxUFY4wx+awoGFMCERkrIg95ncOYqmBFwZgq4A56Z4zvWVEwJggReVRE1orI10BHd96ZIjJTRBaJyFci0ilg/nwRWSYiT4hIhju/v7veFNy7qUXkZhH53r3B6l/uUO6IyGUiMk9EFovIf9yxr4ypclYUjClERFJwhu/oCVwB9HYXvQTcp6opwEPA8+78Z4FnVbU7zhAGgXoBv1TVDiLSGRgBnK+qPYEc4Cb3gSuPAZeoai9gIfCrkP2AxhTDTmmNOd0FwAd5Y+i4n/TjcAas+48zVBEANd3v53LqGQNv4wyJned7Vd3kvh4IpAAL3H3Uwhlcri/OA5++cefXwBkmwZgqZ0XBmNKJAg65n/DL4mjAawFeV9UCTwUTkSHAp6o6qoIZjakwaz4y5nRzgaEiUktE4oEhwDFgk4jcAM5otiJylrv+fOB693Vxj9T8HBgmIk3dfTQSkbbu9ueLSLI7v46IdKj0n8qYUrCiYEwh7uNQ3wV+xHmC1wJ30U3AaBH5EVjBqce4PgD8yh2NNRk4XMR+V+L0HXzirvsp0EJV9wK3Ae+48+cBnULwoxlTIhsl1ZgKcp+slamqKiIjgVGq6pvnfhtTFtanYEzFpQDj3IflHMJ5RrAxYcnOFIwxxuSzPgVjjDH5rCgYY4zJZ0XBGGNMPisKxhhj8llRMMYYk+//Aa1QJjAoBIiwAAAAAElFTkSuQmCC\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "plot_fitting_graph(degrees, rmse_train, rmse_valid, metric_name='RMSE', xlabel='degree', yscale='log')"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "We can use `np.argmin` to find the element with the minimum validation error. The function returns the index in the array with the minimum value."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "3"
      ]
     },
     "execution_count": null,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "np.argmin(rmse_valid)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Since we start counting from 0 in programming this means we are looking for the fourth element in the degrees list:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]"
      ]
     },
     "execution_count": null,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "degrees"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "3"
      ]
     },
     "execution_count": null,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "degrees[np.argmin(rmse_valid)]"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### Findings"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "In these experiments we made some key observations:\n",
    "\n",
    "1. We can fit polynomials (hurray)\n",
    "2. There are three regimes when fitting polynomials: **underfitting**, **good fit** and **overfitting**\n",
    "3. These regimes depend on the degree of the polynomials we are fitting.\n",
    "4. Increasing the degree of the polynomials always decreases the training error.\n",
    "5. The validation error decreases in the from the underfitting to good fit regime and then increases in the overfitting region.\n",
    "\n",
    "These observations are not special about polynomials - they hold for fitting machine learning models in general. Let's translate these observations to general machine learning models:\n",
    "\n",
    "The challenge in fitting models in machine learning is to find the **good fit**. A model that is **too simple** will not be able to capture the complexity of the data and lead to **underfitting**. A model that is **too complex** has the capacity to \"memorize\" aspects of the data and cause **overfitting**. If we are overfitting our model will not predict well unseen data - we say it does not **generalise**. The goal is to find a model that has just the right complexity to fit the data. The **fitting graph** is a tool to identify the sweetspot of model complexity.\n",
    "\n",
    "**Complexity**\n",
    "\n",
    "The model complexity comes in different form and shapes. In our polynomial example the complexity is controlled by the `degree` parameter. For a Random Forest the complexity is given by several parameters such as `tree_depth` of and `n_estimators`. \n",
    "\n",
    "**Classification**\n",
    "\n",
    "We can also create fitting graphs for classification tasks. Instead of looking at RMSE we can look at the accuracy. The difference is that the graph will look inverted in the y-axis; instead of looking for the lowest validation error we will look for the highest validation accuracy.\n",
    "\n",
    "**More data**\n",
    "\n",
    "There is another way to reduce overfitting: get more data! In the following exercise you explore how more data influences the fitting graph.\n",
    "\n",
    "### Exercise #1\n",
    "Use the `get_polynomial_data` and generate `100_000` samples. Create another fitting graph with cross-validation and compare it to the one with `100` samples.\n",
    "\n",
    "In the following section we will investigate overfitting in Random Forests.\n",
    "\n",
    "\n",
    "\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### Train/validation/test set\n",
    "Before we move to RandomForests we want to clarify some ambiguity about the terms train, validation and test set. So far we have concentrated on the train and validation set: We train a model on the train set and we evaluate the metrics on the validation set. However, sometimes we also come across the term test set. For example the function we used to split the dataset in to sets: `train_test_split`.\n",
    "\n",
    "In machine learning each of these sets has a distinct function:\n",
    "\n",
    "- The **train set** is used to train a model.\n",
    "- With the **validation set** the model is evaluated. With this information we tune the parameters.\n",
    "- We only evaluate the final, tuned model on the **test set**. We do not use it to tune the model parameters.\n",
    "\n",
    "The reason we make the distinction between validation and test set is that by tuning the parameters on the validation performance we might start to overfit the validation data. The test set gives a final sanity check that we actually have a performant model.\n",
    "\n",
    "In **cross-validation** the concept of train and validation is melted and all training data is also validation data at some point."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Part 2: Housing dataset\n",
    "In this section we want to use cross-validation to sytematically tune the parameters of the Random Forest without overfitting. We do it in a linear fashion and tune one parameter after another. This does not guarantee that we find the best global parameters, but runs much faster than a global grid search. We will tune the following parameters:\n",
    "\n",
    "* n_estimators\n",
    "* max_depth\n",
    "* min_samples_leaf\n",
    "* max_features\n",
    "\n",
    "First we load the processed housing data:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "Dataset already exists at '../data/housing_processed.csv' and is not downloaded again.\n"
     ]
    }
   ],
   "source": [
    "get_dataset('housing_processed.csv')"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "autos.csv                    median_submission.csv\n",
      "churn.csv                    sample_submission.csv\n",
      "housing.csv                  solution.csv\n",
      "housing_addresses.csv        test.csv\n",
      "housing_gmaps_data_raw.csv   train.csv\n",
      "housing_processed.csv        word2vec-google-news-300.pkl\n",
      "imdb.csv                     zero_submission.csv\n"
     ]
    }
   ],
   "source": [
    "DATA = Path('../data/')\n",
    "!ls {DATA}"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/html": [
       "<div>\n",
       "<style scoped>\n",
       "    .dataframe tbody tr th:only-of-type {\n",
       "        vertical-align: middle;\n",
       "    }\n",
       "\n",
       "    .dataframe tbody tr th {\n",
       "        vertical-align: top;\n",
       "    }\n",
       "\n",
       "    .dataframe thead th {\n",
       "        text-align: right;\n",
       "    }\n",
       "</style>\n",
       "<table border=\"1\" class=\"dataframe\">\n",
       "  <thead>\n",
       "    <tr style=\"text-align: right;\">\n",
       "      <th></th>\n",
       "      <th>longitude</th>\n",
       "      <th>latitude</th>\n",
       "      <th>housing_median_age</th>\n",
       "      <th>total_rooms</th>\n",
       "      <th>total_bedrooms</th>\n",
       "      <th>population</th>\n",
       "      <th>households</th>\n",
       "      <th>median_income</th>\n",
       "      <th>median_house_value</th>\n",
       "      <th>city</th>\n",
       "      <th>postal_code</th>\n",
       "      <th>rooms_per_household</th>\n",
       "      <th>bedrooms_per_household</th>\n",
       "      <th>bedrooms_per_room</th>\n",
       "      <th>population_per_household</th>\n",
       "      <th>ocean_proximity_INLAND</th>\n",
       "      <th>ocean_proximity_&lt;1H OCEAN</th>\n",
       "      <th>ocean_proximity_NEAR BAY</th>\n",
       "      <th>ocean_proximity_NEAR OCEAN</th>\n",
       "      <th>ocean_proximity_ISLAND</th>\n",
       "    </tr>\n",
       "  </thead>\n",
       "  <tbody>\n",
       "    <tr>\n",
       "      <th>0</th>\n",
       "      <td>-122.23</td>\n",
       "      <td>37.88</td>\n",
       "      <td>41.0</td>\n",
       "      <td>880.0</td>\n",
       "      <td>129.0</td>\n",
       "      <td>322.0</td>\n",
       "      <td>126.0</td>\n",
       "      <td>8.3252</td>\n",
       "      <td>452600.0</td>\n",
       "      <td>69</td>\n",
       "      <td>94705</td>\n",
       "      <td>6.984127</td>\n",
       "      <td>1.023810</td>\n",
       "      <td>0.146591</td>\n",
       "      <td>2.555556</td>\n",
       "      <td>0</td>\n",
       "      <td>0</td>\n",
       "      <td>1</td>\n",
       "      <td>0</td>\n",
       "      <td>0</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>1</th>\n",
       "      <td>-122.22</td>\n",
       "      <td>37.86</td>\n",
       "      <td>21.0</td>\n",
       "      <td>7099.0</td>\n",
       "      <td>1106.0</td>\n",
       "      <td>2401.0</td>\n",
       "      <td>1138.0</td>\n",
       "      <td>8.3014</td>\n",
       "      <td>358500.0</td>\n",
       "      <td>620</td>\n",
       "      <td>94611</td>\n",
       "      <td>6.238137</td>\n",
       "      <td>0.971880</td>\n",
       "      <td>0.155797</td>\n",
       "      <td>2.109842</td>\n",
       "      <td>0</td>\n",
       "      <td>0</td>\n",
       "      <td>1</td>\n",
       "      <td>0</td>\n",
       "      <td>0</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>2</th>\n",
       "      <td>-122.24</td>\n",
       "      <td>37.85</td>\n",
       "      <td>52.0</td>\n",
       "      <td>1467.0</td>\n",
       "      <td>190.0</td>\n",
       "      <td>496.0</td>\n",
       "      <td>177.0</td>\n",
       "      <td>7.2574</td>\n",
       "      <td>352100.0</td>\n",
       "      <td>620</td>\n",
       "      <td>94618</td>\n",
       "      <td>8.288136</td>\n",
       "      <td>1.073446</td>\n",
       "      <td>0.129516</td>\n",
       "      <td>2.802260</td>\n",
       "      <td>0</td>\n",
       "      <td>0</td>\n",
       "      <td>1</td>\n",
       "      <td>0</td>\n",
       "      <td>0</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>3</th>\n",
       "      <td>-122.25</td>\n",
       "      <td>37.85</td>\n",
       "      <td>52.0</td>\n",
       "      <td>1274.0</td>\n",
       "      <td>235.0</td>\n",
       "      <td>558.0</td>\n",
       "      <td>219.0</td>\n",
       "      <td>5.6431</td>\n",
       "      <td>341300.0</td>\n",
       "      <td>620</td>\n",
       "      <td>94618</td>\n",
       "      <td>5.817352</td>\n",
       "      <td>1.073059</td>\n",
       "      <td>0.184458</td>\n",
       "      <td>2.547945</td>\n",
       "      <td>0</td>\n",
       "      <td>0</td>\n",
       "      <td>1</td>\n",
       "      <td>0</td>\n",
       "      <td>0</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>4</th>\n",
       "      <td>-122.25</td>\n",
       "      <td>37.85</td>\n",
       "      <td>52.0</td>\n",
       "      <td>1627.0</td>\n",
       "      <td>280.0</td>\n",
       "      <td>565.0</td>\n",
       "      <td>259.0</td>\n",
       "      <td>3.8462</td>\n",
       "      <td>342200.0</td>\n",
       "      <td>620</td>\n",
       "      <td>94618</td>\n",
       "      <td>6.281853</td>\n",
       "      <td>1.081081</td>\n",
       "      <td>0.172096</td>\n",
       "      <td>2.181467</td>\n",
       "      <td>0</td>\n",
       "      <td>0</td>\n",
       "      <td>1</td>\n",
       "      <td>0</td>\n",
       "      <td>0</td>\n",
       "    </tr>\n",
       "  </tbody>\n",
       "</table>\n",
       "</div>"
      ],
      "text/plain": [
       "   longitude  latitude  housing_median_age  total_rooms  total_bedrooms  \\\n",
       "0    -122.23     37.88                41.0        880.0           129.0   \n",
       "1    -122.22     37.86                21.0       7099.0          1106.0   \n",
       "2    -122.24     37.85                52.0       1467.0           190.0   \n",
       "3    -122.25     37.85                52.0       1274.0           235.0   \n",
       "4    -122.25     37.85                52.0       1627.0           280.0   \n",
       "\n",
       "   population  households  median_income  median_house_value  city  \\\n",
       "0       322.0       126.0         8.3252            452600.0    69   \n",
       "1      2401.0      1138.0         8.3014            358500.0   620   \n",
       "2       496.0       177.0         7.2574            352100.0   620   \n",
       "3       558.0       219.0         5.6431            341300.0   620   \n",
       "4       565.0       259.0         3.8462            342200.0   620   \n",
       "\n",
       "   postal_code  rooms_per_household  bedrooms_per_household  \\\n",
       "0        94705             6.984127                1.023810   \n",
       "1        94611             6.238137                0.971880   \n",
       "2        94618             8.288136                1.073446   \n",
       "3        94618             5.817352                1.073059   \n",
       "4        94618             6.281853                1.081081   \n",
       "\n",
       "   bedrooms_per_room  population_per_household  ocean_proximity_INLAND  \\\n",
       "0           0.146591                  2.555556                       0   \n",
       "1           0.155797                  2.109842                       0   \n",
       "2           0.129516                  2.802260                       0   \n",
       "3           0.184458                  2.547945                       0   \n",
       "4           0.172096                  2.181467                       0   \n",
       "\n",
       "   ocean_proximity_<1H OCEAN  ocean_proximity_NEAR BAY  \\\n",
       "0                          0                         1   \n",
       "1                          0                         1   \n",
       "2                          0                         1   \n",
       "3                          0                         1   \n",
       "4                          0                         1   \n",
       "\n",
       "   ocean_proximity_NEAR OCEAN  ocean_proximity_ISLAND  \n",
       "0                           0                       0  \n",
       "1                           0                       0  \n",
       "2                           0                       0  \n",
       "3                           0                       0  \n",
       "4                           0                       0  "
      ]
     },
     "execution_count": null,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "housing_data = pd.read_csv(DATA/'housing_processed.csv')\n",
    "housing_data.head()"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "X = housing_data.drop('median_house_value', axis=1)\n",
    "y = housing_data['median_house_value']"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### Untuned model\n",
    "We want to first evaluate the untuned model to get a baseline:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "Train score: 15834.9\n",
      "Validation score: 60426.9\n"
     ]
    }
   ],
   "source": [
    "rf = RandomForestRegressor(n_jobs=-1)\n",
    "results = cross_validate(rf, X, y,\n",
    "                         cv=5,\n",
    "                         return_train_score=True,\n",
    "                         scoring='neg_root_mean_squared_error')\n",
    "print('Train score: %.1f' % -np.mean(results['train_score']))\n",
    "print('Validation score: %.1f' % -np.mean(results['test_score']))"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Now we tune one parameter after another and always choose the best one of the round based on the fitting curve."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### n_estimators"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "100%|██████████| 4/4 [03:18<00:00, 49.67s/it]\n"
     ]
    }
   ],
   "source": [
    "rmse_train = []\n",
    "rmse_valid = []\n",
    "\n",
    "n_estimators = [25, 50, 100, 200]\n",
    "for n in tqdm(n_estimators):\n",
    "    rf = RandomForestRegressor(n_estimators=n, n_jobs=-1)\n",
    "    results = cross_validate(rf, X, y,\n",
    "                             cv=5,\n",
    "                             return_train_score=True,\n",
    "                             scoring='neg_root_mean_squared_error')\n",
    "    \n",
    "    # we average the scores and append them to the list\n",
    "    rmse_train.append(-np.mean(results['train_score']))\n",
    "    rmse_valid.append(-np.mean(results['test_score']))"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAZEAAAEXCAYAAABsyHmSAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8li6FKAAAgAElEQVR4nO3de5RU5Znv8e/TF7oBG1AwrYIJJGEM4I2LiKMmPTpj0ETRiYIZE03G0blojHFcGTLJGU1i5pgzlxw9MWYYJWKOjhIzGckZDTFKaeISFRQRRQMqSnO/yKXtBvrynD/2W927q6uquzdd1V3w+6xVq3a9+313PbW7u369L1Xb3B0REZEkyvq7ABERKV0KERERSUwhIiIiiSlEREQkMYWIiIgkphAREZHEFCIigZl92MwazKy8F2PONrM3C1lXsZiZm9nH+7sOKS0KETnsmNk6M2sKgZG+Hefu77n7Ee7eGvqlzOwvMsZ2eqN199+6+wnFfg0iA4VCRA5XF4bASN829ndBB8PMKvq7Bjk8KUREAjMbG7Y0Kszse8DZwA/DlsoPzeyZ0PWV0DbHzOrMrD62jHVmdrOZrTSz3Wb2sJlVx+Z/3cw2mdlGM/uLfLuQzGycmT1jZnvN7DdmdpeZ/d+MWq82s/eAp0L7z8xsc3juZ8xsUmx595nZj83sibDMp83sIxlP+8dmtsbMdoXnsz5ZuXLIUoiIZOHu3wR+C1wftlSud/dPhtmnhLaHcwyfDcwExgEnA18CMLOZwE3AHwMfB+q6KeNB4AVgJHAr8MUsfT4FTAA+HR4/DowHPgS8BDyQ0f8K4LvAKGBFlvmfBU4Ldc+OLVckK4WIHK7+K/y3vcvM/quPl32nu290953AL4FTQ/ts4Cfu/pq7NxIFQ1Zm9mGiN/N/cPcD7v47YFGWrre6+wfu3gTg7vPdfa+77w/LP8XMhsf6/7e7PxPmfxM4w8yOj82/3d13uft7wJJY7SJZKUTkcHWxu48It4v7eNmbY9ONwBFh+jhgfWxefDrTccDOEDb5+re3mVm5md1uZm+Z2R5gXZg1Klt/d28Adobn6q52kawUIiK59fVXXG8CxsQeH5+rY+h7lJkN6aZ/vMY/A2YR7S4bDowN7fHjGu3LMLMjgKOAkj6pQPqXQkQkty3AR3vQ1lMLgS+b2YQQDv8jV0d3fxdYBtxqZoPM7Azgwm6WXwPsB3YAQ4B/zNLnAjM7y8wGER0bWeru+baIRPJSiIjkdgdwqZm9b2Z3hrZbgQXhWMrs3izM3R8H7iQ61rAWWBpm7c8x5ArgDKJQuA14OE9fgPuBd4ENwOux5cc9CNxCtBtrKvCF3rwGkUymi1KJ9A8zmwCsAqrcvaUH/R8G3nD3WxI+331Avbt/K8l4kWy0JSJSRGZ2iZlVmdmRwPeBX+YKEDM7zcw+ZmZl4fTgWUBfn0kmclAUIiLF9ZfAVuAtoBX46zx9jwFSQAPRbrC/dveXC12gSG9od5aIiCSmLREREUnssPvStlGjRvnYsWMTjf3ggw8YOnRo3xZUIKVUK5RWvaVUK5RWvaVUK5RWvQdT6/Lly7e7+9FZZ7r7YXWbOnWqJ7VkyZLEY4utlGp1L616S6lW99Kqt5RqdS+teg+mVmCZ53hP1e4sERFJTCEiIiKJKURERCQxhYiIiCSmEBERkcQUIiIikphCREREEjvsPmyY2LKfULv5HXijEQaPgOrhUD0imq4cAmbdL0NE5BCjEOkJd3j860xoPQBv3NF1flllCJYRHffVw7u2ZZtXVaMAEpGSpRDpqZt/z9LUYmaccgI07YJ9u7re79sdTTduhx1rO9q8LfdyrTxL4AzPHj6ZIVQ1HMq0R1JE+o9CpCfMYPCR7Bt8DBw3uXdj29rgwN6uQZMthNL3u97rmG7Ld60ig+phWYJmOB/dtgfanoXKaqgYDJXhVlEdux8Smx/rV1GtcBKRHlGIFFpZWdiyGA58pHdj3eHAB1mCZnfuENq7CZp2MbppF6w/iOsXlVflDqAuYZRuG9w5lCqH5OhX3fVeREqSQmQgM4OqI6Lb8DG9GvrbVIq6T30KWvZBc1PHfXy6U1sTNO/LuM/Rv3FnRltjNKY13+W/8zu7bBA8PzRPAOULpczw6ibQygfpONShzD3ahZy+J/aYbPM8z7xc46LnGfJBPWx7M8cy48sgz7xc47I9zjcu3+tr40Nb3gHq+nx1FzREzGwEcA9wItFq/HPgTeBhYCywDpjt7u+bmQF3ABcAjcCX3P2lsJyrgPR1oW9z9wWhfSpwHzAYeAz4avjGSYHojTL9RlsMbW1RqMSDpdtQivpteOf3fPiYo2P9YmMbt2eMDfNaDyQs1JIHUEU1o+vfhaWre/jGk+OPP+EbQed5nmdex7hJW7fAlnv6/E0pSS3dLf8PD+yHFyoy5tHD9Zfn2GOBTAd4sehPm8jHK0cAt/b5cgu9JXIH8Ct3v9TMBgFDgL8HnnT3281sLjAX+DvgfGB8uJ0O3A2cbmZHAbcA04h+nZab2SJ3fz/0uQZ4nihEZgKPF/g1SS5lZTBoSHTjqF4NfTuV4sN1db17vrbWnKHUoy2qXG37dndeRnpLLRyfGg+wtneldrAo3K0sTJdlPM6czjUvcxxd54XpIY2NsGN3bB45ltF5XPu89luWeV3G5agz52vtPG/bps2MPm50ntdKL9ZfWcZ66ck4erDMjppfX72aiZMm9eC1Jl1HCX5e8dcQm7ds6Qv8YdJf2zwKFiJmNhz4JPAlAHc/ABwws1l0bFMtILqG9N8Bs4D7w5bEUjMbYWbHhr5PuPvOsNwngJlmlgKGufvS0H4/cDEKkcNHWXnH7r5iaG2BliZ+98wSzjrzrF6+maXfMIvvxVSKut4GdD9Zk0oxukRqBdi6M8XEE+v6u4weOVCV+D+fvAq5JTIO2Ab8xMxOAZYDXwVq3X1T6LMZqA3To4H1sfH1oS1fe32W9i7M7FrgWoDa2lpSqVSiF9TQ0JB4bLGVUq1QWvU27C8j9cLK/i6jx0pq3ZZQrVBa9Raq1kKGSAUwBfiKuz9vZncQ7bpq5+5uZgU/huHu84B5ANOmTfOk/5WlSug/ulKqFUqr3lKqFUqr3lKqFUqr3kLVWsgPA9QD9e7+fHj8CFGobAm7qQj3W8P8DcDxsfFjQlu+9jFZ2kVEpEgKFiLuvhlYb2YnhKZzgdeBRcBVoe0q4NEwvQi40iIzgN1ht9di4DwzO9LMjgTOAxaHeXvMbEY4s+vK2LJERKQICn121leAB8KZWW8DXyYKroVmdjXwLjA79H2M6PTetUSn+H4ZwN13mtl36TiR7jvpg+zA39Bxiu/j6KC6iEhRFTRE3H0F0am5mc7N0teB63IsZz4wP0v7MqLPoIiISD/QFySJiEhiChEREUlMISIiIokpREREJDGFiIiIJKYQERGRxBQiIiKSmEJEREQSU4iIiEhiChEREUlMISIiIokpREREJDGFiIiIJKYQERGRxBQiIiKSmEJEREQSU4iIiEhiChEREUlMISIiIokpREREJDGFiIiIJKYQERGRxBQiIiKSmEJEREQSU4iIiEhiChEREUlMISIiIokpREREJDGFiIiIJKYQERGRxBQiIiKSmEJEREQSU4iIiEhiBQ0RM1tnZq+a2QozWxbajjKzJ8xsTbg/MrSbmd1pZmvNbKWZTYkt56rQf42ZXRVrnxqWvzaMtUK+HhER6awYWyJ/5O6nuvu08Hgu8KS7jweeDI8BzgfGh9u1wN0QhQ5wC3A6MB24JR08oc81sXEzC/9yREQkrT92Z80CFoTpBcDFsfb7PbIUGGFmxwKfBp5w953u/j7wBDAzzBvm7kvd3YH7Y8sSEZEiKHSIOPBrM1tuZteGtlp33xSmNwO1YXo0sD42tj605Wuvz9IuIiJFUlHg5Z/l7hvM7EPAE2b2Rnymu7uZeYFrIATYtQC1tbWkUqlEy2loaEg8tthKqVYorXpLqVYorXpLqVYorXoLVWtBQ8TdN4T7rWb2C6JjGlvM7Fh33xR2SW0N3TcAx8eGjwltG4C6jPZUaB+TpX+2OuYB8wCmTZvmdXV12bp1K5VKkXRssZVSrVBa9ZZSrVBa9ZZSrVBa9Raq1oLtzjKzoWZWk54GzgNWAYuA9BlWVwGPhulFwJXhLK0ZwO6w22sxcJ6ZHRkOqJ8HLA7z9pjZjHBW1pWxZYmISBEUckukFvhFOOu2AnjQ3X9lZi8CC83sauBdYHbo/xhwAbAWaAS+DODuO83su8CLod933H1nmP4b4D5gMPB4uImISJEULETc/W3glCztO4Bzs7Q7cF2OZc0H5mdpXwaceNDFiohIIvrEuoiIJKYQERGRxBQiIiKSmEJEREQSU4iIiEhiChEREUlMISIiIokpREREJDGFiIiIJKYQERGRxBQiIiKSmEJEREQSU4iIiEhiChEREUlMISIiIokpREREJDGFiIiIJKYQERGRxBQiIiKSmEJEREQSU4iIiEhiChEREUlMISIiIokpREREJDGFiIiIJKYQERGRxBQiIiKSWEV/FyAiMpA1NzdTX1/Pvn37uswbPnw4q1ev7oeqeq8ntVZXVzNmzBgqKyt7vFyFiIhIHvX19dTU1DB27FjMrNO8vXv3UlNT00+V9U53tbo7O3bsoL6+nnHjxvV4udqdJSKSx759+xg5cmSXADnUmBkjR47MusWVj0JERKQbh3qApCV5nQoREZEBbNeuXfzoRz/q9bgLLriAXbt2FaCizvKGiJmdE5selzHvTwtVlIiIRHKFSEtLS95xjz32GCNGjChUWe262xL559j0zzPmfauPaxERkQxz587lrbfe4tRTT+W0007j7LPP5qKLLmLixIkAXHzxxUydOpVJkyYxb9689nFjx45l+/btrFu3jgkTJvCVr3yFSZMmcd5559HU1NRn9XV3dpblmM72OPsCzMqBZcAGd/9s2KJ5CBgJLAe+6O4HzKwKuB+YCuwA5rj7urCMbwBXA63ADe6+OLTPBO4AyoF73P32ntQkIpLEt3/5Gq9v3NP+uLW1lfLy8oNa5sTjhnHLhZNyzr/99ttZtWoVK1asIJVK8ZnPfIZVq1a1n0E1f/58jjrqKJqamjjttNP43Oc+x8iRIzstY82aNdxzzz3cd999zJ49m5///Od84QtfOKi607rbEvEc09ke5/JVIH5y8veBH7j7x4H3icKBcP9+aP9B6IeZTQQuByYBM4EfmVl5CKe7gPOBicDnQ18RkUPW9OnTO52Ce+edd3LKKacwY8YM1q9fz5o1a7qMGTduHCeffDIAU6dOZd26dX1WT3dbIh81s0VEWx3pacLjbk8kNrMxwGeA7wE3WXTo/xzgz0KXBcCtwN3ArDAN8Ajww9B/FvCQu+8H3jGztcD00G+tu78dnuuh0Pf17uoSEUkic4uhPz4nMnTo0PbpVCrFb37zG5577jmGDBlCXV1d1lN0q6qq2qfLy8uLujtrVmz6nzPmZT7O5n8DXwfSa3kksMvd00eE6oHRYXo0sB7A3VvMbHfoPxpYGltmfMz6jPbTsxVhZtcC1wLU1taSSqV6UHpXDQ0NiccWWynVCqVVbynVCqVV70Csdfjw4ezduzfrvNbW1pzz+tKePXvYu3cvjY2NtLS0tD/n5s2bqampobW1leXLl7N06VIaGxvZu3cv7k5DQwMNDQ20tbW117p//37279+fs+59+/b16meQN0Tc/en4YzOrBE4kOr6xNd9YM/sssNXdl5tZXY8rKgB3nwfMA5g2bZrX1SUrJ5VKkXRssZVSrVBa9ZZSrVBa9Q7EWlevXp1za6MYWyI1NTWcddZZnHHGGQwePJja2tr257zkkktYsGAB06dP54QTTmDGjBkMGTKEmpoazIwjjjgCgLKyMsrLy6mpqaGqqorm5uacdVdXVzN58uQe15c3RMzsx8D/cffXzGw48BzRwe2jzOxmd/+PPMPPBC4yswuAamAY0UHwEWZWEbZGxgAbQv8NwPFAvZlVAMOJDrCn29PiY3K1i4gcMh588MGs7VVVVTz++ONZ56WPe4waNYpVq1a1b3ncfPPNfVpbdwfWz3b318L0l4Hfu/tJRGdQfT3fQHf/hruPcfexRAfGn3L3K4AlwKWh21XAo2F6UXhMmP+Uu3tov9zMqsKZXeOBF4AXgfFmNs7MBoXnSB+zERGRIujumMiB2PSfAD8DcPfNB/E1AH8HPGRmtwEvA/eG9nuBn4YD5zuJQoGwFbSQ6IB5C3Cdu7cCmNn1wGKiU3znxwJPRESKoLsQ2RWObWwg2j11NUDY3TS4p0/i7ikgFabfpuPsqniffcBlOcZ/j+gMr8z2x4DHelqHiIj0re5C5C+BO4FjgBvdfXNoPxf470IWJiIiA193Z2f9nugDfpnti4l2I4mIyGGsu7Oz7sw3391v6NtyRESklHR3dtZfAWcBG4m+/2p5xk1ERAaY9OdDNm7cyKWXXpq1T11dHcuWLTvo5+rumMixRAe75xCdGfUw8Ii7F/5L6kVE5KAcd9xxPPLIIwV9jrxbIu6+w91/7O5/RPQ5kRHA62b2xYJWJSIi7ebOnctdd93V/vjWW2/ltttu49xzz2XKlCmcdNJJPProo13GrVu3jhNPPBGApqYmLr/8ciZMmMAll1zSZ9+f1d2WCABmNgX4PNFnRR5Hu7JE5HD0+FzY/Gr7w8GtLVDeo7fR3I45Cc7PfxWLOXPmcOONN3LdddcBsHDhQhYvXswNN9zAsGHD2L59OzNmzOCiiy7KeYnbe++9lyFDhrB69WpWrlzJlClTDq7uoLsD698h+hbe1UTXAPlG7MsTRUSkCCZPnszWrVvZuHEj27Zt48gjj+SYY47ha1/7Gs888wxlZWVs2LCBLVu2cMwxx2RdxrPPPstNN90EwMknn9z+1fAHq7sI/RbwDnBKuP1jSDkD3N37pgoRkVKQscXQVMSvgr/ssst45JFH2Lx5M3PmzOGBBx5g27ZtLF++nMrKSsaOHZv1a+ALrbsQ6faaISIiUnhz5szhmmuuYfv27Tz99NMsXLiQD33oQ1RWVrJkyRLefffdvOPPPPNMHnzwQc455xxWrVrFypUr+6Su7j5smLUqMysjOkaSv2oREekTkyZNYu/evYwePZpjjz2WK664ggsvvJCTTjqJadOm8YlPfCLv+KuvvpobbriBCRMmMGHCBKZOndondXV3TGQYcB3RRaAWAU8A1wN/C7wCPNAnVYiISLdefbXjoP6oUaN47rnnsvZraGgAYOzYsaxatQqAwYMH89BDD/V5Td3tzvop0XXQnwP+Avh7ouMhF7v7ij6vRkRESkq311gP1w/BzO4BNgEfDt+4KyIih7nuvvakOT0RruFRrwAREZG07rZETjGzPWHagMHhcfoU32EFrU5EZABw95wf4juURBeT7Z3uzs4qT1yNiMghoLq6mh07djBy5MhDOkjcnR07dlBdXd2rcQf5eX0RkUPbmDFjqK+vZ9u2bV3m7du3r9dvuv2lJ7VWV1czZsyYXi1XISIikkdlZSXjxmX/3HUqlWLy5MlFriiZQtXa3YF1ERGRnBQiIiKSmEJEREQSU4iIiEhiChEREUlMISIiIokpREREJDGFiIiIJKYQERGRxBQiIiKSmEJEREQSU4iIiEhiChEREUlMISIiIokpREREJLGChYiZVZvZC2b2ipm9ZmbfDu3jzOx5M1trZg+b2aDQXhUerw3zx8aW9Y3Q/qaZfTrWPjO0rTWzuYV6LSIikl0ht0T2A+e4+ynAqcBMM5sBfB/4gbt/HHgfuDr0vxp4P7T/IPTDzCYClwOTgJnAj8ys3MzKgbuA84GJwOdDXxERKZKChYhHGsLDynBz4BzgkdC+ALg4TM8Kjwnzz7XogsazgIfcfb+7vwOsBaaH21p3f9vdDwAPhb4iIlIkBb08bthaWA58nGir4S1gl7u3hC71wOgwPRpYD+DuLWa2GxgZ2pfGFhsfsz6j/fQcdVwLXAtQW1tLKpVK9HoaGhoSjy22UqoVSqveUqoVSqveUqoVSqveQtVa0BBx91bgVDMbAfwC+EQhny9PHfOAeQDTpk3zurq6RMtJpVIkHVtspVQrlFa9pVQrlFa9pVQrlFa9haq1KGdnufsuYAlwBjDCzNLhNQbYEKY3AMcDhPnDgR3x9owxudpFRKRICnl21tFhCwQzGwz8CbCaKEwuDd2uAh4N04vCY8L8p9zdQ/vl4eytccB44AXgRWB8ONtrENHB90WFej0iItJVIXdnHQssCMdFyoCF7v7/zOx14CEzuw14Gbg39L8X+KmZrQV2EoUC7v6amS0EXgdagOvCbjLM7HpgMVAOzHf31wr4ekREJEPBQsTdVwKTs7S/TXRmVWb7PuCyHMv6HvC9LO2PAY8ddLEiIpKIPrEuIiKJKURERCQxhYiIiCSmEBERkcQUIiIikphCREREElOIiIhIYgoRERFJTCEiIiKJKURERCQxhYiIiCSmEBERkcQUIiIikphCREREElOIiIhIYgoRERFJTCEiIiKJKURERCQxhYiIiCSmEBERkcQUIiIikphCREREElOIiIhIYgoRERFJTCEiIiKJKURERCQxhYiIiCSmEBERkcQUIiIikphCREREElOIiIhIYgoRERFJTCEiIiKJKURERCSxgoWImR1vZkvM7HUze83MvhrajzKzJ8xsTbg/MrSbmd1pZmvNbKWZTYkt66rQf42ZXRVrn2pmr4Yxd5qZFer1iIhIV4XcEmkB/tbdJwIzgOvMbCIwF3jS3ccDT4bHAOcD48PtWuBuiEIHuAU4HZgO3JIOntDnmti4mQV8PSIikqFgIeLum9z9pTC9F1gNjAZmAQtCtwXAxWF6FnC/R5YCI8zsWODTwBPuvtPd3weeAGaGecPcfam7O3B/bFkiIlIEFcV4EjMbC0wGngdq3X1TmLUZqA3To4H1sWH1oS1fe32W9mzPfy3R1g21tbWkUqlEr6OhoSHx2GIrpVqhtOotpVqhtOotpVqhtOotVK0FDxEzOwL4OXCju++JH7ZwdzczL3QN7j4PmAcwbdo0r6urS7ScVCpF0rHFVkq1QmnVW0q1QmnVW0q1QmnVW6haC3p2lplVEgXIA+7+n6F5S9gVRbjfGto3AMfHho8Jbfnax2RpFxGRIink2VkG3Ausdvd/jc1aBKTPsLoKeDTWfmU4S2sGsDvs9loMnGdmR4YD6ucBi8O8PWY2IzzXlbFliYhIERRyd9aZwBeBV81sRWj7e+B2YKGZXQ28C8wO8x4DLgDWAo3AlwHcfaeZfRd4MfT7jrvvDNN/A9wHDAYeDzcRESmSgoWIu/8OyPW5jXOz9HfguhzLmg/Mz9K+DDjxIMoUEZGDoE+si4hIYgoRERFJTCEiIiKJKURERCQxhYiIiCSmEBERkcQUIj308nvvU7+3jc2799F0oJXojGQRkcNbUb6A8VDwZ//+PE3NrXzr2ScBqCw3hg+uZFh1JcMGR7focUV03/44uo/aonk11ZWUl+nSJyJS+hQiPeDu/NsXp/Lc8lcY89Hx7G5qZk9TS3S/r5k9Tc3sbjzAezs+YM++qL21Lf+WSk1VRXv4ZA+eivbHmfOqK8vQ9bdEZCBQiPSAmfHJPziato0V1J3+kW77uzuNB1rbQ2Z3Y3N7uOxpamZ3uKUDaE9TC+/uaIz6NjXTeKA17/IHlZcxLIRMeksnCpmK9scb32tm67L1VJYbFWVlVJaXRdPhPnpcRkWZtc+rLC+jIj2vrIzKivRYU2iJSFYKkQIwM4ZWVTC0qoLjGNzr8c2tbVG4ZARPOmQyt4J2NR7g3WxbQa+v7LPXVFFmUcCUlVFZ0Tl8KspjIVXWEVCZoZUOpE5hFUKu/r0DvGlvUVFexqAwrqLMGFSRf1zWAExPh3HlZQpBkUJRiAxAleVljDyiipFHVPV6rLvzwYFWnljyDNOmz6ClzWlpbeNAaxstrU5LWxsHWqL75tY2mludllYP0220tHmsvaNP53ltYUy6vWOZLa3OgdY2Gg+00NLmHGhpa6+huTVjfFvU1h56a97o4zXZYVAIlngwVZRbrD0Kx8qyLGFVHm8vY8vm/SzZvao9mMygzAwL02YW3ZO+D/PDNKFvvC3buLLYNF36W8eY9HgsGhOmCXW9uaGZnS/Vt9cJHeMya6B9GR3LLQsd0s8br6tTLbHpsrCsrq8/XXfn6fT629jQxtqtDV3XaXxcltrp1L9jPu3P1bX2bOs0/dql5xQihxgz44iqCo6sLuP4o4b0dzk90tbmPJVKccaZZ7eHUDyQehJyLW1tNLdEwdTRP4RcaxvNbU5zS5YgbG9v40BYZkur09TcmqMGZ9/+Fl7avpG2NscBHBxoc8cdnHAfn47N7xevvtJPT5zA757u7wqALP8ctAdzRxC1tbZSuWRx15DN/Kcitox4UGWGaK5xXcK/rHOQ0x6QWUI0LKPlg30U4vpZChHpd2Vl0RbC0KrS+HXsiyvEeQiUNo+CKFf4xOfT6bG3B1M6xNLj2rxj+QDPLV3K9Omnt49rC8mXGW49C8B0XR01eOZ0Ru2k62qjU+3pGtPj2tx57fXXmTBhAnSpK94/S+3RSu1SV1tYCZ3r6pgG2v8ZiK8/MpbR9WcU3a9fv57RY46PPY93qSveP7OGjp9dqD3b+un0c43/DOJ1ZVk/8T5t0Fqgf2BK469W5BDTvtsn59US+s5bQ8oYO2powZ+nL9S8/3vqTh3d32X0WCq1lbq6if1dRo8U6lrw+rChiIgkphAREZHEFCIiIpKYQkRERBJTiIiISGIKERERSUwhIiIiiSlEREQkMTvcLq5kZtuAdxMOHwVs78NyCqmUaoXSqreUaoXSqreUaoXSqvdgav2Iux+dbcZhFyIHw8yWufu0/q6jJ0qpViitekupViitekupViitegtVq3ZniYhIYgoRERFJTCHSO/P6u4BeKKVaobTqLaVaobTqLaVaobTqLUitOiYiIiKJaUtEREQSU4iIiEhiCpEszOx4M1tiZq+b2Wtm9tXQfquZbTCzFeF2QX/XmmZm68zs1VDXstB2lJk9YWZrwv2RA6DOE2Lrb4WZ7TGzGwfSujWz+Wa21U+2BjEAAAaoSURBVMxWxdqyrkuL3Glma81spZlNGQC1/pOZvRHq+YWZjQjtY82sKbaOf1zMWvPUm/Nnb2bfCOv2TTP79ACo9eFYnevMbEVo79d1m+c9q/C/t9ElFXWL34BjgSlhugb4PTARuBW4ub/ry1HzOmBURtv/AuaG6bnA9/u7zoz6yoHNwEcG0roFPglMAVZ1ty6BC4DHiS5lPQN4fgDUeh5QEaa/H6t1bLzfAFq3WX/24W/uFaAKGAe8BZT3Z60Z8/8F+IeBsG7zvGcV/PdWWyJZuPsmd38pTO8FVgOlc83ODrOABWF6AXBxP9aSzbnAW+6e9BsECsLdnwF2ZjTnWpezgPs9shQYYWbHFqfS7LW6+6/dvSU8XAqMKVY93cmxbnOZBTzk7vvd/R1gLTC9YMVlyFermRkwG/iPYtWTT573rIL/3ipEumFmY4HJwPOh6fqw+Td/IOweinHg12a23MyuDW217r4pTG8GavuntJwup/Mf4UBdt5B7XY4G1sf61TOw/uH4c6L/ONPGmdnLZva0mZ3dX0Vlke1nP5DX7dnAFndfE2sbEOs24z2r4L+3CpE8zOwI4OfAje6+B7gb+BhwKrCJaHN2oDjL3acA5wPXmdkn4zM92oYdMOdzm9kg4CLgZ6FpIK/bTgbauszFzL4JtAAPhKZNwIfdfTJwE/CgmQ3rr/piSuZnH/N5Ov8DNCDWbZb3rHaF+r1ViORgZpVEP4wH3P0/Adx9i7u3unsb8O8UcdO6O+6+IdxvBX5BVNuW9CZquN/afxV2cT7wkrtvgYG9boNc63IDcHys35jQ1q/M7EvAZ4ErwpsHYbfQjjC9nOgYwx/0W5FBnp/9QF23FcCfAg+n2wbCus32nkURfm8VIlmE/Z33Aqvd/V9j7fF9hpcAqzLH9gczG2pmNelpogOrq4BFwFWh21XAo/1TYVad/pMbqOs2Jte6XARcGc52mQHsju0+6BdmNhP4OnCRuzfG2o82s/Iw/VFgPPB2/1TZIc/PfhFwuZlVmdk4onpfKHZ9Wfwx8Ia716cb+nvd5nrPohi/t/11NsFAvgFnEW32rQRWhNsFwE+BV0P7IuDY/q411PtRorNYXgFeA74Z2kcCTwJrgN8AR/V3raGuocAOYHisbcCsW6Jw2wQ0E+0rvjrXuiQ6u+Uuov88XwWmDYBa1xLt707/7v449P1c+P1YAbwEXDhA1m3Onz3wzbBu3wTO7+9aQ/t9wF9l9O3XdZvnPavgv7f62hMREUlMu7NERCQxhYiIiCSmEBERkcQUIiIikphCREREElOIiIhIYgoRkSIws1MzvuL8IjOb20fLvtHMhvTFskR6S58TESmC8DUk09z9+gIse11Y9vZejCl399a+rkUOP9oSEYkJFxdabWb/Hi7u82szG5yj78fM7Ffhm5N/a2afCO2XmdkqM3vFzJ4JXzb5HWBOuGDRHDP7kpn9MPS/z8zuNrOlZva2mdWFb7NdbWb3xZ7vbjNbFur6dmi7ATgOWGJmS0Lb5y26QNkqM/t+bHyDmf2Lmb0CnGFmt1t0EaOVZvbPhVmjcsgr9tce6KbbQL4RXVyoBTg1PF4IfCFH3yeB8WH6dOCpMP0qMDpMjwj3XwJ+GBvb/pjoazQeIvoqilnAHuAkon/ylsdqSX9lRTmQAk4Oj9cRLkhGFCjvAUcDFcBTwMVhngOzw/RIoq8SsXiduunW25u2RES6esfdV4Tp5UTB0kn4yu0/BH5m0SVS/43o6nIAzwL3mdk1RG/4PfFLd3eiANri7q969K22r8Wef7aZvQS8DEwiunJdptOAlLtv8+jCVA8QXaEPoJXoW14BdgP7gHvN7E+Bxi5LEumBiv4uQGQA2h+bbgWy7c4qA3a5+6mZM9z9r8zsdOAzwHIzm9qL52zLeP42oCJ8i+3NwGnu/n7YzVXdg+XG7fNwHMTdW8xsOtHVJS8FrgfO6eXyRLQlIpKERxf8ecfMLoPoq7jN7JQw/TF3f97d/wHYRnTdhr1E175OahjwAbDbzGqJrseSFl/2C8CnzGxU+GryzwNPZy4sbEkNd/fHgK8BpxxEbXIY05aISHJXAHeb2beASqLjGq8A/2Rm44mOcTwZ2t4D5oZdX/+zt0/k7q+Y2cvAG0Rf8/5sbPY84FdmttHd/yicOrwkPP9/u3u268jUAI+aWXXod1NvaxIBneIrIiIHQbuzREQkMe3OEumGmd0FnJnRfIe7/6Q/6hEZSLQ7S0REEtPuLBERSUwhIiIiiSlEREQkMYWIiIgk9v8B5NtLdBat9iUAAAAASUVORK5CYII=\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "plot_fitting_graph(n_estimators, rmse_train, rmse_valid, metric_name='RMSE', xlabel='n_estimators')"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "We can zoom in a little bit further to get a better picture of how the validation error behaves:"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "We see that adding more estimaters further decreases the validation error. We do not overfit by adding more estimators. However, it takes longer to train and evaluate the model as we add more estimators. This is usually not a major concern when experimenting with models but it can be a major constraint when putting it in production. See [this](https://www.wired.com/2012/04/netflix-prize-costs/) example from Netflix.\n",
    "\n",
    "We choose `n_estimators=100` for the sake of speed but we keep in mind that we could probably further improve the model by adding more estimators. We continue tuning the other parameters:"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### tree_depth"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "100%|██████████| 7/7 [03:29<00:00, 29.99s/it]\n"
     ]
    }
   ],
   "source": [
    "rmse_train = []\n",
    "rmse_valid = []\n",
    "\n",
    "max_depths = [1, 2, 4, 8, 16, 32, 64]\n",
    "for d in tqdm(max_depths):\n",
    "    rf = RandomForestRegressor(n_estimators=100, max_depth=d, n_jobs=-1)\n",
    "    results = cross_validate(rf, X, y,\n",
    "                             cv=5,\n",
    "                             return_train_score=True,\n",
    "                             scoring='neg_root_mean_squared_error')\n",
    "    \n",
    "    # we average the scores and append them to the list\n",
    "    rmse_train.append(-np.mean(results['train_score']))\n",
    "    rmse_valid.append(-np.mean(results['test_score']))"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAZEAAAEXCAYAAABsyHmSAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8li6FKAAAgAElEQVR4nO3deXxU9bn48c+TjaxkgwRIAkFEFlFAEEHRxh20Fm1dayv6s6XX2lbtir1tsVp79d7eWrnVWqxWaLVqcUOLUlTGFVBQlLBJQJaAELZAAmFJ8vz+ON/AJCSZZDKTySTP+/Wa15zznO/5nufAMA/nfM+cI6qKMcYYE4yYSCdgjDEmelkRMcYYEzQrIsYYY4JmRcQYY0zQrIgYY4wJmhURY4wxQbMiYowjIn1FpFJEYluxztkisiacebUXEVEROTHSeZjoYkXEdDkiskFEqlzBqHv1UdVNqpqqqjWunU9EvtVg3XpftKr6jqoOau99MKajsCJiuqrLXMGoe22NdEJtISJxkc7BdE1WRIxxRKTQHWnEici9wNnAH92Ryh9F5G3X9BMXu0ZEikSk1K+PDSLyYxH5VET2isgzIpLot/ynIvKFiGwVkW81dwpJRPqLyNsiUiEir4vIQyLy9wa53iwim4A3XfyfIrLNbfttETnZr78nROQREZnv+nxLRPo12OwFIrJWRMrd9iQkf7im07IiYkwjVPU/gXeA77kjle+p6jlu8XAXe6aJ1a8GJgD9gVOBGwFEZALwQ+AC4ESgKEAaTwEfANnAXcA3G2nzJWAIcLGbfxUYCOQAHwFPNmh/PXAP0ANY1sjyLwOnu7yv9uvXmEZZETFd1Yvuf9vlIvJiiPuerqpbVXU38DIwwsWvBv6qqitU9QBeYWiUiPTF+zL/laoeVtV3gTmNNL1LVferahWAqj6uqhWqesj1P1xE0v3a/0tV33bL/xMYJyIFfsvvU9VyVd0ELPDL3ZhGWRExXdXlqprhXpeHuO9tftMHgFQ33QfY7LfMf7qhPsBuV2yaa380JiKxInKfiKwTkX3ABreoR2PtVbUS2O22FSh3YxplRcSYpoX6FtdfAPl+8wVNNXRts0QkOUB7/xy/DkzCO12WDhS6uP+4xtE+RCQVyAKi+qICE1lWRIxp2nbghBbEWupZ4CYRGeKKwy+baqiqG4ElwF0ikiAi44DLAvSfBhwCdgHJwG8baXOJiIwXkQS8sZFFqtrcEZExzbIiYkzTHgSuFJE9IjLdxe4CZrqxlKtb05mqvgpMxxtrKAEWuUWHmljlemAcXlH4DfBMM20BZgEbgS3ASr/+/T0FTMM7jTUK+EZr9sGYhsQeSmVMZIjIEKAY6Kaq1S1o/wywWlWnBbm9J4BSVf1FMOsb0xg7EjGmHYnIFSLSTUQygfuBl5sqICJyuogMEJEYd3nwJCDUV5IZ0yZWRIxpX98ByoB1QA1wSzNtewE+oBLvNNgtqvpxuBM0pjXsdJYxxpig2ZGIMcaYoHW5m7b16NFDCwsLA7bbv38/KSkp4U8oTKI9f4j+fbD8Iy/a96Gj5L906dKdqtqzsWVdrogUFhayZMmSgO18Ph9FRUXhTyhMoj1/iP59sPwjL9r3oaPkLyIbm1pmp7OMMcYEzYqIMcaYoFkRMcYYE7QuNyZijDGtceTIEUpLSzl48GC7bzs9PZ1Vq1a12/YSExPJz88nPj6+xetYETHGmGaUlpaSlpZGYWEh7f2gx4qKCtLS0tplW6rKrl27KC0tpX///i1ez05nGWNMMw4ePEh2dna7F5D2JiJkZ2e3+ojLiogxxgTQ2QtInWD204pIS9TWwkezYNPiSGdijDEdihWRlhCB134OK56PdCbGmC6mvLychx9+uNXrXXLJJZSXl4cho/qsiLSECGT0hfJNkc7EGNPFNFVEqqubfwTN3LlzycjICFdaR9nVWS2VUWBFxBjT7qZOncq6desYMWIE8fHxJCYmkpmZyerVq/nss8+4/PLL2bx5MwcPHuS2225jypQpwLFbPFVWVjJx4kTGjx/P+++/T15eHi+99BJJSUkhyc+KSEtl9IWNCyOdhTEmgn798gpWbt0X0j6H9unOtMtObnL5fffdR3FxMcuWLcPn83HppZdSXFx89DLcxx9/nKysLKqqqjj99NP52te+RnZ2dr0+1q5dyz/+8Q8effRRrr76ap577jm+8Y3QPBnZTme1VEZfOLQXqsJ/jtEYY5oyZsyYer/jmD59OsOHD2fs2LFs3ryZtWvXHrdO//79GTFiBACjRo1iw4YNIcvHjkRaKr3Aey/fBEnhP89ojOl4mjtiaC/+t4b3+Xy8/vrrLFy4kOTkZIqKihr9nUe3bt2OTsfGxlJVVRWyfOxIpKUy+nrvezdHNg9jTJeSlpZGRUVFo8v27t1LZmYmycnJrF69mkWLFrVzdnYk0nIZ/bx3G1w3xrSj7OxszjrrLIYNG0ZSUhK5ublHl02YMIFHHnmEIUOGMGjQIMaOHdvu+VkRaankLIhPtiJijGl3Tz31VKPxbt268eqrrza6rG7co0ePHhQXFx+N//jHPw5pbnY6q6XstyLGGHMcKyKtYUXEGGPqsSLSGun2g0NjjPFnRaQ1MvrCwXI4GNofGxljTLSyItICNbXKnE+2sqGmhxewy3yNMQYIcxERkTtEZIWIFIvIP0QkUUT6i8hiESkRkWdEJMG17ebmS9zyQr9+7nTxNSJysV98gouViMjUcO1HjMCdz33K/K0JXsBOaRljDBDGIiIiecAPgNGqOgyIBa4F7gceUNUTgT3AzW6Vm4E9Lv6Aa4eIDHXrnQxMAB4WkVgRiQUeAiYCQ4HrXNtw7AsDclJZVtHdC5TbkYgxpuNKTU0FYOvWrVx55ZWNtikqKmLJkiVt3la4T2fFAUkiEgckA18A5wGz3fKZwOVuepKbxy0/X7zHbE0CnlbVQ6r6OVACjHGvElVdr6qHgadd27AY0DOVj3fGQVwilG8M12aMMSZk+vTpw+zZswM3bIOw/dhQVbeIyO+ATUAV8G9gKVCuqnU3wi8F8tx0HrDZrVstInuBbBf3/y2//zqbG8TPaCwXEZkCTAHIzc3F5/MFzL+ysrJeO6k8zNZ9R6jMzKZq7VJWdAvcRyQ1zD8aRfs+WP6RF4p9SE9Pb/K2I+FWU1NDRUUF06ZNIy8v7+ht3n/7298SFxfHO++8Q3l5OUeOHOGXv/wll1566dF1Kyoq2LhxI1dffTWLFy+mqqqKW265heLiYk466SQqKyvZv3//cft28ODBVv2Zha2IiEgm3pFBf6Ac+Cfe6ah2p6ozgBkAo0eP1qKiooDr+Hw+/NtVZX/B82s/QrNPpGftPlrSRyQ1zD8aRfs+WP6RF4p9WLVqFWlpad7Mq1Nh2/K2J+av1ykw8b5GF1VUVJCWlsY3v/lNbr/9dn70ox8B8NJLLzFv3jx+8pOf0L17d3bu3MnYsWO55pprjj4nPS0tjdTUVGJiYkhLS+PRRx8lPT2dNWvW8Omnn3LaaaeRkpJybN+cxMRERo4c2eL0w3nbkwuAz1V1B4CIPA+cBWSISJw7GskHtrj2W4ACoNSd/koHdvnF6/iv01Q85AbkeOcYd8XlkFZWHKC1McaEzsiRIykrK2Pr1q3s2LGDzMxMevXqxR133MHbb79NTEwMW7ZsYfv27fTq1avRPt5++21+8IMfAHDqqady6qmnhiS3cBaRTcBYEUnGO511PrAEWABciTeGMRl4ybWf4+YXuuVvqqqKyBzgKRH5PdAHGAh8AAgwUET64xWPa4Gvh2tn+mUnEyOwWXtSeGAXHN4PCSmBVzTGdB5NHDG0h6uuuorZs2ezbds2rrnmGp588kl27NjB0qVLiY+Pp7CwsNHbwIdb2AbWVXUx3gD5R8Byt60ZwM+AH4pICd6Yx2NulceAbBf/ITDV9bMCeBZYCbwG3KqqNe5I5nvAPGAV8KxrGxbd4mIpyEpm7aEsL2BXaBlj2tE111zD008/zezZs7nqqqvYu3cvOTk5xMfHs2DBAjZubP6Cn3POOefojRyLi4v59NNPQ5JXWO/iq6rTgGkNwuvxrqxq2PYgcFUT/dwL3NtIfC4wt+2ZtsyAnqks31l3me8myBncXps2xnRxJ598MhUVFeTl5dG7d2+uv/56LrvsMk455RRGjx7N4MHNfx/dcsst3HTTTQwZMoQhQ4YwatSokORlt4JvhQE9U3itJNX7U7PLfI0x7Wz58mOD+j169GDhwoWNtqusrASgsLDw6G3gk5KSePrpp0Oek932pBUG9EyltLo7GpNgtz4xxhisiLTKgJxUlBiqknvbrU+MMQYrIq0yoKd3me+ehF5WRIzpQlQ10im0i2D204pIK2SlJJCRHM9WetrVWcZ0EYmJiezatavTFxJVZdeuXSQmJrZqPRtYb6UBPVNZvz+L0/eXwZEqiE+KdErGmDDKz8+ntLSUHTt2tPu2Dx482Oov9bZITEwkPz+/VetYEWmlAT1TKN6RwTXgHY30PCnSKRljwig+Pp7+/ftHZNs+n69VtyCJBDud1UoDeqayuirDm9lr4yLGmK7NikgrDeiZSqn29GZscN0Y08VZEWmlATmpbCeTWomzImKM6fKsiLRSQWYSsbGx7EvIsSu0jDFdnhWRVoqLjaFfdgrbJMeORIwxXZ4VkSAM6JnC59XZVkSMMV2eFZEgDOiZymcHM6ByG1QfinQ6xhgTMVZEgjCgZyqbat0VWntLI5uMMcZEkBWRIAzI8b/M124Jb4zpuqyIBOGEnil8ru45xpsWRTYZY4yJICsiQeieGI+m9WJF2pnwwaPe89aNMaYLsiISpAE9U3gy9gqo2g0f/S3S6RhjTESErYiIyCARWeb32icit4tIlojMF5G17j3TtRcRmS4iJSLyqYic5tfXZNd+rYhM9ouPEpHlbp3pIiLh2p+GBvRM5V97C9G+42DhH6HmSHtt2hhjOoywFRFVXaOqI1R1BDAKOAC8AEwF3lDVgcAbbh5gIjDQvaYAfwIQkSxgGnAGMAaYVld4XJtv+603IVz709CAnqnsrTrCvlG3eo/KLX6uvTZtjDEdRnudzjofWKeqG4FJwEwXnwlc7qYnAbPUswjIEJHewMXAfFXdrap7gPnABLesu6ouUu9pMbP8+gq7ATneUw5Xp46FnKHw7h+gtra9Nm+MMR1Cez1P5FrgH246V1W/cNPbgFw3nQf434yq1MWai5c2Ej+OiEzBO7ohNzcXn88XMOHKyspm2+0+6BWMF99ZRvesixiy+g8sf/5/2dXj9IB9t4dA+UeDaN8Hyz/yon0foiH/sBcREUkAvgLc2XCZqqqIhP2Zk6o6A5gBMHr0aC0qKgq4js/nI1C7h1b4KK1JYshVv4Dpz3HKvjfgyp+EIOO2a0n+HV2074PlH3nRvg/RkH97nM6aCHykqtvd/HZ3Kgr3XubiW4ACv/XyXay5eH4j8XZz3uAcFq/fzf5qgXHfg00L7XcjxpgupT2KyHUcO5UFMAeou8JqMvCSX/wGd5XWWGCvO+01D7hIRDLdgPpFwDy3bJ+IjHVXZd3g11e7OHdwDodranm3ZCec9k1IyvLGRowxposIaxERkRTgQuB5v/B9wIUisha4wM0DzAXWAyXAo8B3AVR1N3AP8KF73e1iuDZ/ceusA14N5/40dHphFmnd4nhzVRkkpMAZ34HPXoXtK9szDWOMiZiwjomo6n4gu0FsF97VWg3bKnBrE/08DjzeSHwJMCwkyQYhPjaGc07qyYI1ZagqMmYKvPcgvD8drngkUmkZY0y7sV+st9G5g3MoqzjEiq37IDkLTpsMy/9pTz00xnQJVkTaqGhQT0TgzdXu+oBx7mBq4UORS8oYY9qJFZE26pHajVPzM44VkYwCOOUq+GgmHNjd/MrGGBPlrIiEwHmDcviktJxdle4ph2fdBkcOwAczIpuYMcaEmRWREDhvcA6q4FuzwwvkDIGTJsLiR+w28caYTs2KSAic3Kc7PdO68eaasmPB8XdA1R74aFbkEjPGmDCzIhICMTHCuYN68vaaHRypcTdh7HsG9B0H79tt4o0xnZcVkRA5b3AOFYeqWbJhz7Hg+DtgXyksnx25xIwxJoysiITI+IE9iY8VFvif0hp4kXeb+Hd+B2WrIpecMcaEiRWREEntFscZ/bOPXeoLIAIX/Br2bYWHx8JT19oNGo0xnYoVkRA6d3AOJWWVbN594FjwpIvg9mIouhM2L4LHL4bHLoY1r9pDrIwxUc+KSAidNzgHoP7RCEBKNhRNhTtWwIT7Yd8W+Me18KczYdk/bODdGBO1rIiEUP8eKfTvkXJ8EamTkAJj/wN+8DFcMcM73fXif8CDI2Dhw3Cosn0TNsaYNrIiEmLnDsph4fpdHDhc3XSj2HgYfg3c8j58/Z+Q0Rfm3Ql/GAYLfgv7d7VfwsYY0wZWRELsvME5HK6u5b2SFhQCEW/M5P+9CjfPh75nwlv3wwMnw9yfwJ6N4U/YGGPawIpIiI3pn0VKQmzTp7SaUjAGrnsKbv0Ahn0NlvwVpo+E574F24rDk6wxxrSRFZEQS4iLYfzAHvjcg6parecguPwhuO0TGHuLdxXXI2fB36+EDe9CMH0aY0yYhPXJhl3VeYNzmLdiO6u+qGBon+7BdZKeBxffC+f8GD58zLuZ4xOXQp/ToM9ISOkBydnHXv7zcd1Cu0PGGNMEKyJhcO4g71LfBWvKgi8idZIyvUIy7lZY9iQsfQJWvODd3JEmjkoS0jgjJhnW5rvC0sN76mK9YuPeU7KhWzrE2EGpMVFB1Z2RUNBaN1/rvRrGUL9p8f69h1hYi4iIZAB/wXsOugL/D1gDPAMUAhuAq1V1j4gI8CBwCXAAuFFVP3L9TAZ+4br9jarOdPFRwBNAEjAXuE2DOocUWjndEzklL503V5dx67knhqbT+CQ4/VveC6C2xiskB3bB/p3e+wH3vn8X+z5fSVJiHFRu9265sn8nVFc13rfEuiLjV1j8C01jsfjE0OxXtPL/h9vEK+5IhXelXXPt/P+R1/uHX9tEjABfGLX1+2uyTWNfNPW/jHp9sRI+2hzavpvdt8baNbVey7Z/8o4dsO3RFnzRhmD7zX6JB7f9c2pq4G3qbz9YKTnwk7XBr9+EcB+JPAi8pqpXikgCkAz8HHhDVe8TkanAVOBnwERgoHudAfwJOENEsoBpwGi8f0JLRWSOqu5xbb4NLMYrIhOAV8O8Ty1y7uAc/vjmWnbvP0xWSkLoNxAT6x1VpPTwxlEaWOXzkVtUVD94+MBxxabefF2sbLWL7YYmj3ZSjx3d1BWWxO71/7E0+uXT2KvxNqfu2gmbMhr8Y2zui7sFbVrUD4H7aIHxAO+18O+zAxoM3n/5Qk1iAPHeRRrM18Xk+DZNridNtkmqqoLd++r3G2j7MbGt2D4N8m6u72a231g7hNLNpfTt168F+9/M9utiCclh+MsMYxERkXTgHOBGAFU9DBwWkUlAkWs2E/DhFZFJwCx3JLFIRDJEpLdrO19Vd7t+5wMTRMQHdFfVRS4+C7icDlJEzhucw/Q31vLWZ2VcMTI/0ul4EpK9V0ZBy9rX1sDBvY0c6bgCczS2E3asgUP7jn1oG36IG51v+OVRv01c9X44HH/8ejGxAfppZDvHxZtoE8J+1q5bx8CBg5rvB/H2J8CX4fG50YI2LfuibeqLbtGixYwdd2aAvmn8C6u5vtvREp+PoqKidt1mKK33+ejbwfMP55FIf2AH8FcRGQ4sBW4DclX1C9dmG5DrpvOAzX7rl7pYc/HSRuLHEZEpwBSA3NxcfD5fwOQrKytb1K4ptap0T4Cn3yomc29J0P0Eq635Ny7NvQohEe+VFeJN+KmsrCQ1NTV8G2grd0ajKZUZfdlS1R751yXShlMdjaisScG3bF1I+2xv4fl30H6iIf9wFpE44DTg+6q6WEQexDt1dZSqqoiEfQxDVWcAMwBGjx6tLfmfiS8E/4O5cMcnzF+5jfFnn0NcbEyb+mqtUOQfadG+D5Z/5EX7PkRD/uH8ZisFSlV1sZufjVdUtrvTVLj3ul/lbQH8z7Pku1hz8fxG4h3GeYNz2Hewmo82lUc6FWOMCYuwFRFV3QZsFpG6Ud/zgZXAHGCyi00GXnLTc4AbxDMW2OtOe80DLhKRTBHJBC4C5rll+0RkrLuy6wa/vjqEs0/qQVyMtP7X68YYEyXCfXXW94En3ZVZ64Gb8ArXsyJyM7ARuNq1nYt3eW8J3iW+NwGo6m4RuQf40LW7u26QHfguxy7xfZUOMqhep3tiPKMLM1mwuoypEwdHOh1jjAm5sBYRVV2Gd2luQ+c30laBW5vo53Hg8UbiS/B+g9JhXTi0F/e8spLV2/YxuFcbf3hojDEdTPuO9nZBXx2ZR7e4GGa+b3fkNcZ0PlZEwiwzJYFJI/rw4sdb2HvAnmBojOlcrIi0gxvGFVJ1pIZ/Lt0cuLExxkQRKyLtYFheOqP7ZTJr4UZqayN+ay9jjAkZKyLtZPKZhWzafYC3PtsR6VSMMSZkrIi0kwnDepGT1o0n3t8Q6VSMMSZkrIi0k/jYGK4/ox9vfbaDz3fuj3Q6xhgTElZE2tF1ZxQQHyvMWrgh0qkYY0xIWBFpRzlpiVxySm9mLyll/6HqSKdjjDFt1mwREZHz/Kb7N1j21XAl1ZndMK6QikPVPP9xh7pXpDHGBCXQkcjv/Kafa7DsF5hWO61vBqfkpTPr/Q10gCf5GmNMmwQqItLEdGPzpgVEhBvG9WNtWSUL1+2KdDrGGNMmgYqINjHd2LxpocuG9yEzOZ6ZCzdEOhVjjGmTQHfxPUFE5uAdddRN4+b7N72aaU5ifCzXjunLn99aR+meA+RnJkc6JWOMCUqgIjLJb/p3DZY1nDet8I2x/fjzW+t4cvEmfjbBnjVijIlOzRYRVX3Lf15E4vGe37FFVe1xfW2Ql5HEhUNzefqDTdx2/kAS42MjnZIxxrRaoEt8HxGRk910OvAJMAv4WESua4f8OrXJZxay58ARXv5ka6RTMcaYoAQaWD9bVVe46ZuAz1T1FGAU8NOwZtYFjDshm5NyU5m50C73NcZEp0BF5LDf9IXAiwCqui1sGXUh3uW+hRRv2cdHm8ojnY4xxrRaoCJSLiJfFpGRwFnAawAiEgckBepcRDaIyHIRWSYiS1wsS0Tmi8ha957p4iIi00WkREQ+FZHT/PqZ7NqvFZHJfvFRrv8St27U/XblipF5pCXGMdPu7muMiUKBish3gO8BfwVu9zsCOR/4Vwu3ca6qjlDV0W5+KvCGqg4E3nDzABOBge41BfgTeEUHmAacAYwBptUVHtfm237rTWhhTh1GSrc4rhpVwNzlX1C272Ck0zHGmFZptoio6meqOsEVgSf84vNU9UdBbnMSMNNNzwQu94vPUs8iIENEegMXA/NVdbeq7gHmAxPcsu6quki9AYVZfn1FlW+O60d1rfLUB5sinYoxxrRKs5f4isj05par6g8C9K/Av0VEgT+r6gwgV1W/cMu3AbluOg/wfwh5qYs1Fy9tJB51+vdIoWhQT55cvInvFp1IQpzdXNkYEx0C/djwP4Bi4FlgK62/X9Z4Vd0iIjnAfBFZ7b9QVdUVmLASkSl4p8jIzc3F5/MFXKeysrJF7UJlZGo1vopD/P6fbzK2d6C/lsDaO/9wiPZ9sPwjL9r3IRryD/Rt1Ru4CrgGqAaeAWaraosuJVLVLe69TERewBvT2C4ivVX1C3dKqu5Hi1uAAr/V811sC1DUIO5z8fxG2jeWxwxgBsDo0aO1qKiosWb1+Hw+WtIuVM6pVZ7f4GNJeTemXndmm/tr7/zDIdr3wfKPvGjfh2jIP9CYyC5VfURVz8X7nUgGsFJEvhmoYxFJEZG0umngIryjmjlA3RVWk4GX3PQc4AZ3ldZYYK877TUPuEhEMt2A+kXAPLdsn4iMdVdl3eDXV9SJiRG+ObYfSzbuoXjL3kinY4wxLdKik+/uctvbgG8ArwJLW7BaLvCuiHwCfAD8S1VfA+4DLhSRtcAFbh5gLrAeKAEeBb4LoKq7gXuAD93rbhfDtfmLW2edyy1qXTW6gKT4WHt8rjEmagQaWL8buBRYBTwN3KmqLXquq6quB4Y3Et+Fd4lww7gCtzbR1+PA443El+Ddy6tTSE+K54rT8nhuaSl3ThxCZkpCpFMyxphmBToS+QXeKazhwH8BH7kfAi4XkU/Dnl0XNHlcIYeqa3lmyebAjY0xJsICDazbM0Pa2aBeaYw9IYu/LdzIt88+gdiYqPsRvjGmCwk0sL6xsRfe7zbGt0+KXc+NZxaypbyKN1Ztj3QqxhjTrEC3gu8uIneKyB9F5CJ35dT38QbAr26fFLueC4bk0ic9kVkLN0Y6FWOMaVagMZG/AYOA5cC3gAXAlcDlqjqpuRVN8OJiY7h+bD/eLdlJSVlFpNMxxpgmBSoiJ6jqjar6Z+A6YChwsaouC39qXdu1pxeQEBdjRyPGmA4tUBE5UjehqjVAqararWbbQXZqNy47tQ/PLS2l4uCRwCsYY0wEBCoiw0Vkn3tVAKfWTYvIvvZIsCubfGY/9h+u4bmlpYEbG2NMBAS6OitWVbu7V5qqxvlNd2+vJLuqU/MzGFGQwayFG6mttcfnGmM6HrvneAd345mFrN+5n3dLdkY6FWOMOY4VkQ5u4im96JGaYI/PNcZ0SFZEOrhucbF8fUxf3lxTxqZdByKdjjHG1GNFJAp8/Yx+xIrwt0UbIp2KMcbUY0UkCvRKT+TiYb145sPNVB2uiXQ6xhhzlBWRKDF5XCH7Dlbz4rJGH95ojDERYUUkSpxemMmQ3t2Z+f4GvEevGGNM5FkRiRIiwuRx/Vi9rYKF63ZFOh1jjAGsiESVy0fm0Sc9kbtfWUl1TW2k0zHGGCsi0SQxPpZffnkoq7dV8LdFdmNGY0zkhb2IiEisiHwsIq+4+f4islhESkTkGRFJcPFubr7ELS/06+NOF18jIhf7xSe4WImITA33vnQEE4b14pyTevL7f39GWYXdC9MYE1ntcSRyG7DKb/5+4AFVPRHYA9zs4jcDe1z8AdcOERkKXAucDEwAHnaFKRZ4CJiId4v661zbTk1E+LBCZo8AABTbSURBVPVXTuZQdS3/NXd1pNMxxnRxYS0iIpIPXAr8xc0LcB4w2zWZCVzupie5edzy8137ScDTqnpIVT8HSoAx7lWiqutV9TDwtGvb6fXvkcJ3vnQCL3y8hcXrbZDdGBM54T4S+QPwU6BuFDgbKFfVajdfCuS56Ty8Z7fjlu917Y/GG6zTVLxL+G7RieRlJPHLl4o5YoPsxpgIiQtXxyLyZaBMVZeKSFG4ttPCXKYAUwByc3Px+XwB16msrGxRu0j6Wv9apn9cxS9nvcGE/vH1lkVD/oFE+z5Y/pEX7fsQDfmHrYgAZwFfEZFLgESgO/AgkCEice5oIx+o+wn2FqAAKBWROCAd2OUXr+O/TlPxelR1BjADYPTo0VpUVBQweZ/PR0vaRdKXVCmuWsLL63dxx9fOJrd74tFl0ZB/ING+D5Z/5EX7PkRD/mE7naWqd6pqvqoW4g2Mv6mq1wMLgCtds8nAS256jpvHLX9TvZ9mzwGudVdv9QcGAh8AHwID3dVeCW4bc8K1Px2RiDDtsqEcqVV+869VgVcwxpgQi8TvRH4G/FBESvDGPB5z8ceAbBf/ITAVQFVXAM8CK4HXgFtVtcYdyXwPmId39dezrm2X0i87hVu+NICXP9nK+/bgKmNMOwvn6ayjVNUH+Nz0erwrqxq2OQhc1cT69wL3NhKfC8wNYapR6ZaiAbzw8RZ+NWcFc39wNglx9htSY0z7sG+bTiAxPpa7vjKUkrJKHn/v80inY4zpQqyIdBLnDc7lwqG5TH9jLVvLqyKdjjGmi7Ai0on86stDqalVfvOvlZFOxRjTRVgR6UQKspL53rknMnf5Nop3VgdewRhj2siKSCcz5UsnUJidzN9XHuZQtT1K1xgTXlZEOplucbHc9ZWT2XZA+cs7NshujAkvKyKdUNGgHEblxvJ/b66ldM+BSKdjjOnErIh0Ul8fnIAg3P2yDbIbY8LHikgnlZ0Uw/fPP5F/r9zOgtVlkU7HGNNJWRHpxL41/gRO6JnCXS+v4OARG2Q3xoSeFZFOLCEuhru/MoyNuw7w57fWRzodY0wnZEWkkxs/sAeXntqbh30lbNplg+zGmNCyItIF/PLSocTGCHe/0uVucmyMCTMrIl1Ar/REbr9gIK+vKuP1ldsjnY4xphOxItJF3HRWfwbmpNoguzEmpKyIdBHxsTHcPWkYpXuqeHhBSaTTMcZ0ElZEupBxA7KZNKIPj7y1ng0790c6HWNMJ2BFpIv5z0uGkBAXw10vr8B7hL0xxgTPikgXk9M9kTsuPAnfmh3MW2GD7MaYtrEi0gVNHtePwb3SuOeVlRw4bM8dMcYEL2xFREQSReQDEflERFaIyK9dvL+ILBaREhF5RkQSXLybmy9xywv9+rrTxdeIyMV+8QkuViIiU8O1L51NnBtk31JexR/ftEF2Y0zwwnkkcgg4T1WHAyOACSIyFrgfeEBVTwT2ADe79jcDe1z8AdcOERkKXAucDEwAHhaRWBGJBR4CJgJDgetcW9MCY/pn8dXT8nj0nfWs21EZ6XSMMVEqbEVEPXXfTvHupcB5wGwXnwlc7qYnuXnc8vNFRFz8aVU9pKqfAyXAGPcqUdX1qnoYeNq1NS1058QhJMbHctccG2Q3xgQnLpydu6OFpcCJeEcN64ByVa07EV8K5LnpPGAzgKpWi8heINvFF/l167/O5gbxM5rIYwowBSA3Nxefzxcw98rKyha166hamv+k/jH8fdVO/ueZNxjTK6wfh1brKn8HHVW05w/Rvw/RkH9YvzVUtQYYISIZwAvA4HBur5k8ZgAzAEaPHq1FRUUB1/H5fLSkXUfV0vzH19Ty0R/f4/n1h7n1ivGkdOs4haSr/B10VNGeP0T/PkRD/u1ydZaqlgMLgHFAhojUfVPlA1vc9BagAMAtTwd2+ccbrNNU3LRCXGwM91w+jG37DjL9zbWRTscYE2XCeXVWT3cEgogkARcCq/CKyZWu2WTgJTc9x83jlr+p3on6OcC17uqt/sBA4APgQ2Cgu9orAW/wfU649qczG9Uvk6tH5/PYO5+zdntFpNMxxkSRcB6J9AYWiMineF/481X1FeBnwA9FpARvzOMx1/4xINvFfwhMBVDVFcCzwErgNeBWVa1x4yrfA+bhFadnXVsThJ9NGExKtzh+9ZINshtjWi5sJ8BV9VNgZCPx9XhXVjWMHwSuaqKve4F7G4nPBea2OVlDdmo3fnLxIH7xYjFzPtnKpBF5gVcyxnR59ot1c9R1Y/pyan469/5rFRUHj0Q6HWNMFLAiYo6KjRHumTSMHZWHePB1G2Q3xgRmRcTUM7wgg2tP78tf39/A6m37Ip2OMaaDsyJijvPTiwfRPTGOX71og+zGmOZZETHHyUxJ4GcTBvPBht288LH99MYY0zQrIqZRV48uYHhBBr+du4q9VTbIboxpnBUR06iYGOE3k4axa/9hHpj/WaTTMcZ0UFZETJNOyU/nG2f0Y9bCDazYujfS6RhjOiArIqZZP75oEJnJCfzqpRXU1toguzGmPisiplnpyfFMnTiYpRv38NxHpZFOxxjTwVgRMQF97bR8RvXL5L5XV7P3gA2yG2OOsSJiAoqJEe6edDJ7Dhzmd/9eE+l0jDEdiBUR0yIn90nnhnGF/H3xRpaX2iC7McZjRcS02B0XnkR2Sjd+8VKxDbIbYwArIqYV0pPi+fklg/lkcznPLtkceAVjTKdnRcS0yhUj8xhTmMX9r61mz/7DkU7HGBNhVkRMq4gId19+MvsOVvPf82yQ3ZiuzoqIabXBvbpz05mFPP3hJpZtLo90OsaYCLIiYoJy2wUD6ZnajV++WEyNDbIb02WFrYiISIGILBCRlSKyQkRuc/EsEZkvImvde6aLi4hMF5ESEflURE7z62uya79WRCb7xUeJyHK3znQRkXDtj6kvLTGe/7x0CMu37OUfH2yKdDrGmAgJ55FINfAjVR0KjAVuFZGhwFTgDVUdCLzh5gEmAgPdawrwJ/CKDjANOAMYA0yrKzyuzbf91psQxv0xDXxleB/GnZDN/8xbw67KQ5FOxxgTAWErIqr6hap+5KYrgFVAHjAJmOmazQQud9OTgFnqWQRkiEhv4GJgvqruVtU9wHxgglvWXVUXqff4vVl+fZl2IOL9kn3/oWruf211pNMxxkRAXHtsREQKgZHAYiBXVb9wi7YBuW46D/D/8UGpizUXL20k3tj2p+Ad3ZCbm4vP5wuYc2VlZYvadVTtmf+F/eJ4dkkpJ8Xu5MTM2JD1a38HkRXt+UP070M05B/2IiIiqcBzwO2qus9/2EJVVUTCPiqrqjOAGQCjR4/WoqKigOv4fD5a0q6jas/8Tx9Xzcf/+xZPfCacN7gHBZnJFGQlkZ+ZTEFWMulJ8UH1a38HkRXt+UP070M05B/WIiIi8XgF5ElVfd6Ft4tIb1X9wp2SKnPxLUCB3+r5LrYFKGoQ97l4fiPtTTtL6RbH768ezm9fXcULH2+h4mB1veXpSfEUZCW54pJMQWYS+VnJFGQmk5+ZRGJ86I5ejDHtK2xFxF0p9RiwSlV/77doDjAZuM+9v+QX/56IPI03iL7XFZp5wG/9BtMvAu5U1d0isk9ExuKdJrsB+L9w7Y9p3pkn9uCV758NwN4DR9i85wCbdx9g0+4DbrqKNdsreGN1GYera+utm5PW7WhxKciqKzTJ7KyqpaZWiY2xi+6M6ajCeSRyFvBNYLmILHOxn+MVj2dF5GZgI3C1WzYXuAQoAQ4ANwG4YnEP8KFrd7eq7nbT3wWeAJKAV93LRFh6cjzpyekMy0s/blltrbKj8hCb/YpL3fSHG/Yw55Ot+P/sZOo7r9InI6nekUx+XbHJTKZHagJ2ZbcxkRO2IqKq7wJN/es+v5H2CtzaRF+PA483El8CDGtDmqadxcQIud0Tye2eyOjCrOOWH6mpZWt5FZt3V/H6oo9J7lnA5j1eoXl91XZ2Vta/X1dSfCz5mUn0zTq+wBRkJZGWGNx4jDGmZdrl6ixjWio+NoZ+2Sn0y06heks8RUWD6y0/cLiaUldUvCOYqqOnzRZ/vpvKQ/XHYzKS448WlILMZDcW4xWdvMwkusXZeIwxbWFFxESV5IQ4TspN46TctOOWqSrlR8djqo6Oy2zeU8XqLyp4fWUZh2uOjceIQG5a4nEFpm5cplf3RBuPMSYAKyKm0xARMlMSyExJ4NT8jOOW19YqZRWH2LznAJt2HahXbBat38UXy7agfuMx8bFCXkaSO02WfNwVZlkpNh5jjBUR02XExAi90hPplZ7I6Y2MxxyuduMxjRzJzFuxjd0Nnp+SnBB73G9ivLEZr9gY0xVYETHGSYiLobBHCoU9Uhpdvv9Q9XFXlG3eXUXpngMsXLeL/Ydr6rVPi4cTit89+psY/yOZvIwkEuLsJtom+lkRMaaFUrrFMbhXdwb36n7cMlVlz4Ej9YrL4hUl1CTGs2LLXv69YhtHao6dKxOBXt0TyctIIj62bcVECc1NH7RBN+XlVfxpzcJW5hKKRELRhdfJ3r1VPLT6/eD7CUkuwdu7t4r/W/U+GoJEMpITePzG09vcT0NWRIwJAREhKyWBrJQEhhd44zFD2ExR0RkA1NQq2/cdrHdF2eY9B9haXhWa57GEaGimrd0IXoFsaycSgkxEIFZoc5EOxbBXsPtzMNa7jD0UeSQlhOdKRCsixrSD2BihT0YSfTKSOCPSybSQd9+mcZFOo028fRgb6TSC5uXfsT8xdlLWGGNM0KyIGGOMCZoVEWOMMUGzImKMMSZoVkSMMcYEzYqIMcaYoFkRMcYYEzQrIsYYY4Imofg5fTQRkR14T1QMpAewM8zphFO05w/Rvw+Wf+RF+z50lPz7qWrPxhZ0uSLSUiKyRFVHRzqPYEV7/hD9+2D5R16070M05G+ns4wxxgTNiogxxpigWRFp2oxIJ9BG0Z4/RP8+WP6RF+370OHztzERY4wxQbMjEWOMMUGzImKMMSZoVkQaEJEJIrJGREpEZGqk82kJEXlcRMpEpNgvliUi80VkrXvPjGSOzRGRAhFZICIrRWSFiNzm4lGxDyKSKCIfiMgnLv9fu3h/EVnsPkvPiEhCpHNtjojEisjHIvKKm4+2/DeIyHIRWSYiS1wsKj5DACKSISKzRWS1iKwSkXHRkL8VET8iEgs8BEwEhgLXicjQyGbVIk8AExrEpgJvqOpA4A0331FVAz9S1aHAWOBW9+ceLftwCDhPVYcDI4AJIjIWuB94QFVPBPYAN0cwx5a4DVjlNx9t+QOcq6oj/H5bES2fIYAHgddUdTAwHO/vouPnr6r2ci9gHDDPb/5O4M5I59XC3AuBYr/5NUBvN90bWBPpHFuxLy8BF0bjPgDJwEfAGXi/NI5z8XqfrY72AvLxvqTOA17Be1x61OTvctwA9GgQi4rPEJAOfI672Cma8rcjkfrygM1+86UuFo1yVfULN70NyI1kMi0lIoXASGAxUbQP7lTQMqAMmA+sA8pVtdo16eifpT8APwVq3Xw20ZU/gAL/FpGlIjLFxaLlM9Qf2AH81Z1S/IuIpBAF+VsR6QLU+29Mh7+WW0RSgeeA21V1n/+yjr4PqlqjqiPw/kc/Bhgc4ZRaTES+DJSp6tJI59JG41X1NLzT0beKyDn+Czv4ZygOOA34k6qOBPbT4NRVR83fikh9W4ACv/l8F4tG20WkN4B7L4twPs0SkXi8AvKkqj7vwlG1DwCqWg4swDv9kyEicW5RR/4snQV8RUQ2AE/jndJ6kOjJHwBV3eLey4AX8Ip5tHyGSoFSVV3s5mfjFZUOn78Vkfo+BAa6q1ISgGuBORHOKVhzgMluejLeOEOHJCICPAasUtXf+y2Kin0QkZ4ikuGmk/DGc1bhFZMrXbMOm7+q3qmq+apaiPeZf1NVrydK8gcQkRQRSaubBi4CiomSz5CqbgM2i8ggFzofWEkU5G+/WG9ARC7BOz8cCzyuqvdGOKWAROQfQBHebaO3A9OAF4Fngb54t76/WlV3RyrH5ojIeOAdYDnHzsn/HG9cpMPvg4icCszE+8zEAM+q6t0icgLe/+yzgI+Bb6jqochlGpiIFAE/VtUvR1P+LtcX3Gwc8JSq3isi2UTBZwhAREYAfwESgPXATbjPEx04fysixhhjgmans4wxxgTNiogxxpigWRExxhgTNCsixhhjgmZFxBhjTNCsiBhjjAmaFRFjOgh3K/MeQa57o4j0CUVfxrSGFRFjOocbgT6BGhkTalZEjGlARArdg4GeEJHPRORJEblARN5zDwca414L3R1X36+7XYWI3CEij7vpU0SkWESSm9hOtoj82z3I6i94t1+vW/YN96CrZSLyZ/esG0SkUkQecOu84W65ciUwGnjStU9y3XxfRD5yD2oa7Nb/kmuzzOWeFr4/SdMVWBExpnEnAv+LdzfewcDXgfHAj/FuybIaONvdcfVXwG/deg8CJ4rIFcBfge+o6oEmtjENeFdVT8a7ZUdfABEZAlwDnOXuDFwDXO/WSQGWuHXeAqap6mxgCXC9eg9kqnJtd7q72v7J5Y17v9X1ezZQ19aYoMQFbmJMl/S5qi4HEJEVeE+XUxFZjvcAsHRgpogMxLs9dzyAqtaKyI3Ap8CfVfW9ZrZxDvBVt96/RGSPi58PjAI+9O5NSRLH7t5aCzzjpv8OPE/T6pYtrdsO8B7wexF5EnheVUub+0MwJhA7EjGmcf43Gqz1m6/F+8/XPcACVR0GXAYk+rUfCFQS/BiFADPdUcUIVR2kqnc10ba5m9/V5VzjckZV7wO+hVeY3qs7zWVMsKyIGBOcdI49X+PGuqCIpAPT8Y4yst14RVPexjtNhohMBDJd/A3gShHJccuyRKSfWxbDsduzfx14101XAAHHN0RkgKouV9X78R59YEXEtIkVEWOC89/Af4nIx9Q/LfwA8JCqfgbcDNxXVwwa8WvgHHe67KvAJgBVXQn8Au9Rr5/iPW63t1tnPzBGRIrxHh51t4s/ATzSYGC9Mbe7wf5PgSPAq63ZaWMaslvBGxNFRKRSVVMjnYcxdexIxBhjTNDsSMSYMBORm4DbGoTfU9VbI5GPMaFkRcQYY0zQ7HSWMcaYoFkRMcYYEzQrIsYYY4JmRcQYY0zQ/j+MNF2j9bRN7AAAAABJRU5ErkJggg==\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "plot_fitting_graph(max_depths, rmse_train, rmse_valid, metric_name='RMSE', xlabel='max_depths')"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "16"
      ]
     },
     "execution_count": null,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "max_depths[np.argmin(rmse_valid)]"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### min_samples_leaf"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "100%|██████████| 5/5 [02:39<00:00, 31.93s/it]\n"
     ]
    }
   ],
   "source": [
    "rmse_train = []\n",
    "rmse_valid = []\n",
    "\n",
    "min_samples_leaf = [1, 3, 5, 10, 25]\n",
    "for s in tqdm(min_samples_leaf):\n",
    "    rf = RandomForestRegressor(n_estimators=100, max_depth=16, min_samples_leaf=s, n_jobs=-1)\n",
    "    results = cross_validate(rf, X, y,\n",
    "                             cv=5,\n",
    "                             return_train_score=True,\n",
    "                             scoring='neg_root_mean_squared_error')\n",
    "    \n",
    "    # we average the scores and append them to the list\n",
    "    rmse_train.append(-np.mean(results['train_score']))\n",
    "    rmse_valid.append(-np.mean(results['test_score']))"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAZEAAAEXCAYAAABsyHmSAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8li6FKAAAgAElEQVR4nO3de3yU5Z3//9cnB3Ig4QwBEiQoAVFQFASstE1ra9HaYlurXW1FS8Vu7a49+Nvabre1re7P7vbbXVl36/oVCp4WWa1Kt1rXWqNiPXAQBUQBIUDCIZzJQEJOn+8f950whBxgyGSSzPv5eMxj7rnua+65Lkfmnfu+7vu6zd0RERGJRUqiGyAiIt2XQkRERGKmEBERkZgpREREJGYKERERiZlCREREYqYQEQmZ2RlmFjGz1FN4z0fN7IN4tquzmJmb2ehEt0O6F4WIJB0zKzWzqjAwGh/D3X2ru+e4e31Yr8TMvtHsvcf90Lr7q+4+trP7INJVKEQkWX0uDIzGx/ZEN+h0mFlaotsgyUkhIhIys8JwTyPNzO4GPgrcF+6p3Gdmr4RV3wnLrjWzYjMri9pGqZndbmbvmtlBM3vczDKj1v+dme0ws+1m9o22DiGZ2Sgze8XMKs3sT2b272b2SLO2zjazrcCfw/L/NrOd4We/YmbnRm1vgZndb2YvhNt82cxGNvvYT5nZBjM7EH6edch/XOmxFCIiLXD3vwdeBb4d7ql8290/Fq4+Pyx7vJW3XwPMAEYB5wE3ApjZDOB7wKeA0UBxO814DHgLGAjcCXythTofB8YBnwlfPwcUAUOAlcCjzepfD/wCGASsamH9lcBFYbuvidquSIsUIpKsng7/2j5gZk938Lbnuvt2d98H/B6YGJZfA/zW3de6+xGCYGiRmZ1B8GP+E3evcfelwJIWqt7p7ofdvQrA3ee7e6W7Hw23f76Z9Y2q/wd3fyVc//fAxWY2Imr9Pe5+wN23Ai9FtV2kRQoRSVZXuXu/8HFVB297Z9TyESAnXB4ObItaF73c3HBgXxg2bdVvKjOzVDO7x8w+NLNDQGm4alBL9d09AuwLP6u9tou0SCEi0rqOnuJ6B1AQ9XpEaxXDugPMLLud+tFtvA6YSXC4rC9QGJZHj2s0bcPMcoABQLc+qUASSyEi0rpdwJknUXayFgM3mdm4MBz+obWK7r4FWA7caWa9zOxi4HPtbD8XOArsBbKBf2yhzhVmNt3MehGMjbzh7m3tEYm0SSEi0rp7gavNbL+ZzQ3L7gQWhmMp15zKxtz9OWAuwVjDRuCNcNXRVt5yPXAxQSjcBTzeRl2Ah4AtQDnwXtT2oz0G/JTgMNYk4Kun0geR5kw3pRJJDDMbB6wBMty97iTqPw687+4/jfHzFgBl7v7jWN4v0hLtiYh0IjP7gpllmFl/4JfA71sLEDO7yMzOMrOU8PTgmUBHn0kmcloUIiKd6xagAvgQqAf+uo26Q4ESIEJwGOyv3f3teDdQ5FTocJaIiMRMeyIiIhKzpJu0bdCgQV5YWMjhw4fp3bt3opuTMMncf/U9OfsOyd3/0+n7ihUr9rj74JbWJV2IFBYWsnz5ckpKSiguLk50cxImmfuvvhcnuhkJk8z9P52+m9mW1tbpcJaIiMRMISIiIjFTiIiISMwUIiIiEjOFiIiIxEwhIiIiMVOIiIhIzJLuOhERkbhzB2+Ahnrw+mbP3kJZPTQ0tFDe0MZ2Wij3hla2U8/QHaVAcYd3VSEikoxa/JFraOPHrHl5Q9s/Zs3Lj6vTzvZbaldr229xXes/xhN2V0DZv51kW5qvO4W63pDob/gEZ6b3I7gtTcdSiEjP1dAAtUeg5jDURMLnw/Tb/w5sPNUfofAvyA74i/CE8qb3n9oPYix1P1ZfBy83dMkfufYZpKSCpR57thRISTm+LKWxvFndlBR61RyBIw3Hr0tJg7SMFrZhLZSltv55rXzmyddtpd2t9rGF7Te9/8TtLHv9TS6Jw7cS1xAxs37Ag8B4gntBfx34gOAObYVAKXCNu+83MyO4k9wVwBHgRndfGW5nFtB4I5273H1hWD4JWABkAc8Ct3m8piW+54zgH2JaJqRnhc+ZkJbVQc/hdnv1how+wf/AyaS+DmoPN/3QN/3oH40cFwDNA6HNdbWHW/yoiQDvxKMT1sI/5jZ+SE62bvSPXLvbbV5+/PK2snJGjhx1UnXb/pFr/tnttOWE7bWx/VbXnf6/iRVJPO1Jba8+cdluvPdE7gX+6O5Xh/d0zgZ+BLzo7veY2R3AHcAPgMuBovAxFfgNMNXMBhDcznMyQRCtMLMl7r4/rHMz8CZBiMwAnotLT6bcEvww1VVBbfWJz9UHm5VXQ20VNNSe+mdZKmT1g6wBkNX/+Ed2dFm/8Dksy+gT/KONJ3eor2nnx/wkf+Sjl+uqT74Nqb2CsO2VEz6Hj+wBUa+brWt8nZ7N22ve54ILJ0X9EJ7MX7In8wPb9YN/c0kJI5P0R1TiI24hYmZ9gY8BNwK4ew1QY2YzOTa6s5Dgpjs/ILhr20PhnsQbZtbPzIaFdV9w933hdl8AZphZCdDH3d8Iyx8CriJeIfLJv4/tffV1wQ9kY6i091wTgar9xz8qd0DFumC5prL1z7IUyOzXSuD0PxY4GbkM2r0SVm2P7Ue/od07uR6Tnn3iD3lGLuQObfZD39pys9fpvSGtV2zfRehgWSqcMe20tiEigXjuiYwCdgO/NbPzgRXAbUCeu+8I6+wE8sLlfGBb1PvLwrK2ystaKO9aUtMgNQcycjpme/W1UHUgDJh9JwbOkaiySAXs/iCof/TgcZsZD7A2qsBSWv7x7j0Y+he280PfynJ6dvAXuoj0WPEMkTTgQuBv3P1NM7uX4NBVE3d3M4v7rRXNbA4wByAvL4+SkhIikQglJSXx/uhOkBU+hgdX/eSEj2asoY60usOk1VWSVneESHUdGbkDqU/NpD41k4aUXid/OKYeqAofTWrCx/7T6Uyn6Dnf/alL5r5Dcvc/Xn2PZ4iUAWXu/mb4+gmCENllZsPcfUd4uKoiXF8OjIh6f0FYVs7xJzcXEBwCKw+Xm9c/gbs/ADwAMHnyZC8uLk7q+wpAcG+BaUna/2T+7pO575Dc/Y9X3+M2CuvuO4FtZjY2LLoUeA9YAswKy2YBz4TLS4AbLDANOBge9noeuMzM+ptZf+Ay4Plw3SEzmxae2XVD1LZERKQTxPvsrL8BHg3PzNoE3EQQXIvNbDawBbgmrPsswem9GwlO8b0JwN33mdkvgGVhvZ83DrID3+LYKb7PEa9BdRERaVFcQ8TdVxGcmtvcpS3UdeDWVrYzH5jfQvlywjFiERHpfJqAUUREYqYQERGRmClEREQkZgoRERGJmUJERERiphAREZGYKURERCRmChEREYmZQkRERGKmEBERkZgpREREJGYKERERiZlCREREYqYQERGRmClEREQkZgoRERGJmUJERERiphAREZGYKURERCRmChEREYmZQkRERGKmEBERkZgpREREJGYKERERiZlCREREYqYQERGRmClEREQkZgoRERGJmUJERERiphAREZGYKURERCRmChEREYmZQkRERGKmEBERkZgpREREJGYKERERiZlCREREYqYQERGRmClEREQkZnENETMrNbPVZrbKzJaHZQPM7AUz2xA+9w/LzczmmtlGM3vXzC6M2s6ssP4GM5sVVT4p3P7G8L0Wz/6IiMjxOmNP5BPuPtHdJ4ev7wBedPci4MXwNcDlQFH4mAP8BoLQAX4KTAWmAD9tDJ6wzs1R75sR/+6IiEijRBzOmgksDJcXAldFlT/kgTeAfmY2DPgM8IK773P3/cALwIxwXR93f8PdHXgoalsiItIJ0uK8fQf+18wc+E93fwDIc/cd4fqdQF64nA9si3pvWVjWVnlZC+UnMLM5BHs35OXlUVJSQiQSoaSk5DS61r0lc//V95JENyNhkrn/8ep7vENkuruXm9kQ4AUzez96pbt7GDBxFYbXAwCTJ0/24uJiSkpKKC4ujvdHd1nJ3H/1vTjRzUiYZO5/vPoe18NZ7l4ePlcATxGMaewKD0URPleE1cuBEVFvLwjL2iovaKFcREQ6SdxCxMx6m1lu4zJwGbAGWAI0nmE1C3gmXF4C3BCepTUNOBge9noeuMzM+ocD6pcBz4frDpnZtPCsrBuitiUiIp0gnoez8oCnwrNu04DH3P2PZrYMWGxms4EtwDVh/WeBK4CNwBHgJgB332dmvwCWhfV+7u77wuVvAQuALOC58CEiIp0kbiHi7puA81so3wtc2kK5A7e2sq35wPwWypcD40+7sSIiEhNdsS4iIjFTiIiISMwUIiIiEjOFiIiIxEwhIiIiMVOIiIhIzBQiIiISM4WIiIjETCEiIiIxU4iIiEjMFCIiIhIzhYiIiMRMISIiIjFTiIiISMwUIiIiEjOFiIiIxEwhIiIiMVOIiIhIzBQiIiISM4WIiIjETCEiIiIxU4iIiEjMFCIiIhIzhYiIiMRMISIiIjFTiIiISMwUIiIiEjOFiIiIxEwhIiIiMWszRMzsk1HLo5qt+2K8GiUiIt1De3siv4pafrLZuh93cFtERKSbaS9ErJXlll6LiEiSaS9EvJXlll6LiEiSSWtn/ZlmtoRgr6NxmfD1qNbfJiIiyaC9EJkZtfyrZuuavxYRkS6itr6BLXsPs35XhPW7KvngwxqKizv+c9oMEXd/Ofq1maUD44Fyd6/o+OaIiMipqG/wprDYsKuS9RXB84e7I9TWB6MOZpDf23B3zDp2OLvNEDGz+4F/c/e1ZtYXeB2oBwaY2e3u/l8d2hoREWlRQ4Ozbf+Rpj2LDbsq+WBXhA93R6ipa2iqV9A/izF5uXx87GDGDMllTF4uo4fk8OZfXu3wAIH2D2d91N2/GS7fBKx396vMbCjwHKAQERHpQA0NTvmBKjZUVDYFxvpdlWysiFBdeywshvfNpCgvl+mjB1KUF4RF0ZAceme097Pesdr7tJqo5U8D/w3g7jtPNtHMLBVYTnAI7MrwosVFwEBgBfA1d68xswzgIWASsBe41t1Lw238EJhNsBf0t+7+fFg+A7gXSAUedPd7TqpRIiIJ5u7sOFgd7lUcC4sNFRGO1NQ31cvrk8GYvFyumzKSMXk5FOXlUpSXQ5/M9AS2/pj2QuSAmV0JlAOXEPyQY2ZpQNZJfsZtwDqgT/j6l8C/uPui8HDZbOA34fN+dx9tZl8J611rZucAXwHOBYYDfzKzMeG2/p0g3MqAZWa2xN3fO8l2iYjEnbtTUXk0DIlIeBiqko27IlQerWuqNygngzF5OVwzeQRFeTmMzculaEgufbO7Rli0pr0QuQWYCwwFvuPuO8PyS4E/tLdxMysAPgvcDXzPgt2XTwLXhVUWAncShMjMcBngCeC+sP5MYJG7HwU2m9lGYEpYb6O7bwo/a1FYVyEiIp3O3dkTqQkGt8PxisblQ9XHwmJA714UDcnhqgvyGZOXw5jwUFT/3r0S2PrYtXd21npgRgvlzwPPn8T2/xX4OyA3fD0QOODujf9Fy4D8cDkf2BZuv87MDob184E3orYZ/Z5tzcqnttQIM5sDzAHIy8ujpKSESCRCSUnJSXShZ0rm/qvvJYluRsJ0VP8ra5zySMOxR2XwHKk9Vqd3OuTnpHDh4BTyc3pRkJNCfk4KfTIMOBo8ju6haiu8s/W0m9SueH337Z2dNbet9e7+t22890qgwt1XmFlxbM3rGO7+APAAwOTJk724uJiSkhKK43HSdDeRzP1X34sT3YyEOdX+HzxSy/qKYG9i/c7wcFRFJXsix4aLczPSKMrrw5Wjc5v2Ksbk5TA4NyMuZ0PFKl7ffXuHs74JrAEWA9s5tfmyLgE+b2ZXAJkEYyL3Av3MLC3cGykgGG8hfB4BlIVjLn0JBtgbyxtFv6e1chGRk3aoupYNUeMVjQPdFZVHm+r07pXK6LxcPjF2CGOH5oZnROUwtE9mlwqLztZeiAwDvgxcC9QBjwNPuPuB9jbs7j8EfggQ7onc7u7Xm9l/A1cTnKE1C3gmfMuS8PXr4fo/u7uHU608Zma/JhhYLwLeIgi0ovBsr3KCwffGsRYRkRNU1zmrth04tmcRXpi342B1U52s9FRGD8lhetEgxjaeOpuXw/C+WaSkJG9YtKa9MZG9wP3A/eEg+VeA98zsB+7+cIyf+QNgkZndBbwNzAvL5wEPhwPn+8LPIrzQcTHBgHkdcKu71wOY2bcJxmZSgfnuvjbGNolID1JVU8/Giki4V1HZdGZU+YEq+NNrAPRKS2H04BymnTmQorycpgvzCvorLE7FSV2VYmYXAn9FcDrtcwTXd5w0dy8BSsLlTRw7uyq6TjXBXk9L77+b4Ayv5uXPAs+eSltEpOeorq3nw92R406fXb8rwrb9R/BwnvFeqSmcObg3F47sz9TBdXxm2nmMycvljAHZpCosTlt7A+s/JzhFdx3B4acfRp1ZJSLSKY7W1bN5z2E+2HlsvGJDRYQtew/TEIZFWooxalBvJhT05UsXFjRdmFc4MJu01OCuFyUlJRSfOzSBPel52tsT+TGwGTg/fPxjOIBkgLv7efFtnogkk9r6BjbvOdxsz6KS0r1HqA/TIjXFGDkwm7OH5vK584c3XWtROLA3vdLau0WSdLT2QkT3DBGRDldX30Dp3iNNh5/WVwRjF5v3HD5u5tmRA7IZk5fL5eOHBeMWebmcObg3GWmpCe6BNGpvYH1LS+VmlkIwRtLiehERCKYp37rvSNOss40TCm7afZia+mOTCY4YkMXYvFwuHZcXHIYaEsw8m5musOjq2hsT6QPcSnCF+BLgBeDbwPeBd4BH491AEen6Ghqcsv1VwWGoimPjFhsrIhyNmqY8v18WY/Jy+PiYwU3XWYwekkN2r86deVY6Tnvf3MPAfoJrN74B/IhgPOQqd18V57aJSBfjHk5TvivqjKgwNKpqj808OyycpvziMwc2XWdRlJdLTidPUy7x1+491t19AoCZPQjsAM4IT8cVkR7K3dl5qPq4we3G5cNR05QPyQ2mKf/KlBFN032MHpJL36yuPfOsdJz2QqRpOjF3rzezMgWISM/h7uyuPHrsbnlRN0KqrI6eprwXRUNyuXpSQdMNkMbk5dAvu3vOPCsdp70QOd/MDoXLBmSFrxtP8e3T+ltFpCvZEznKur31bPlLadMNkNbvinCw6tjUs/2z0ynKy2XmxOHhnfKCsBiYk5HAlktX1t7ZWTo1QqSb2X+4JhzgDicU3BlcmLfvcOPMs2vpk5nGmLxcrpgwrOk6i6K8HAbndK2ZZ6Xr0yiXSDd1sKr2uNNmG/cs9kSOzTybk5FGUV4Onx6XR1FeDtW7NvHly6YzpItNUy7dl0JEpIurrK5lQ0XkhMDYdehYWGT3SqVoSA7FYwc3TfcxNi+XYX2Pn6a8pGQreX0yE9EN6aEUIiJdxOGjdWysOH6vYsOuSrZHTVOemZ7C6CE5XHLWoCAohgYX5uX308yzkhgKEZFOVlVzbObZ6Bsgle2vaqrTKy2FswbncNGoAcfdLa+gv2aela5FISISJ9W19WzafZgNFcHgduOFeVv3HZumPD3VOHNQDhNH9OOayceutThjwLGZZ0W6MoWIyGmqqQtmno2+AdKGXRFKo6YpTw2nKT93eB+umpjP2KFBWIwc2Jt0hYV0YwoRkZNUW9/Alr2H+WDn8Rfmle45TF2YFikGhQN7U5SXw2fPG9Z0KGrUIE1TLj2TQkSkmbr6BrbsO3Lc2VAbdkXYtCdy3DTlZwzIpmhILp85N6/pwrwzB/fWzLOSVBQikrQaGpxt+480XYzXeEbUh7sj1ETNPFvQP4sxebl84uwhTRfmnTU4h6xeCgsRhYgkjaqaep5ZVc6Sd4/yq9WvsrEiQnXtsbAYHs48+9GiQRQNCcJi9JAcemvmWZFW6V+H9Hi7DlXz0OulPPrmVg4cqaVfhjHhjF5cP3Vk04V5RUNyyM3UzLMip0ohIj3WmvKDzFu6mf95dzt1Dc5l5+Qxe/qZHC59h098YmqimyfSIyhEpEepb3BeXLeLeUs38+bmffTulcr1U0dy0yWFjBzYG4CSLbpYT6SjKESkRzh8tI4nVpTx29c2U7r3CPn9svjRFWdz7UVn6AZJInGkEJFubfuBKhb+pZT/emsrh6rrmDiiH/d9Ziwzzh2qK75FOoFCRLqlVdsOMG/pZp5dvQN35/Lxw/j69FFMGtk/0U0TSSoKEek26huc/127k3lLN7N8y35yM9K46SOFzPpIISMGZCe6eSJJSSEiXV5ldS2LlwfjHWX7qxgxIIufXHkOX55coNNyRRJMISJd1rZ9R1jwl1IeX7aNyNE6Jo/sz48/O45PnzNU06GLdBEKEelyVmzZz7ylm/jjmp2YGZ+dMIzZ00dx/oh+iW6aiDSjEJEuoa6+gefWBOMdq7YdoE9mGjd/7ExmXVzI8H5ZiW6eiLRCISIJdbCqlseXbWXBa6VsP1hN4cBsfj7zXL50YYHmrBLpBvSvVBJiy97D/Pa1UhYv38aRmnqmnTmAn80czyfPHqLxDpFuRCEincbdeWvzPuYt3cwL63aRlmJ87rzhfH36KMbn901080QkBgoRibuaugaeXb2DB5duYk35Ifplp/Ot4rO44eJC8vpkJrp5InIaFCISNweO1PDYW1tZ+JdSdh06ypmDe3P3F8bzxQsKdEMnkR5CISIdbtPuCPNf28yTK8qpqq1n+uhB3PPF8/j4mMGkaLxDpEdRiEiHcHde/3Av85Zu5sX3K+iVmsLMicF4x7hhfRLdPBGJk7iFiJllAq8AGeHnPOHuPzWzUcAiYCCwAviau9eYWQbwEDAJ2Atc6+6l4bZ+CMwG6oG/dffnw/IZwL1AKvCgu98Tr/5Iy47W1fP7d3Ywb+lm1u04xMDevfjbS4v42rSRDM7NSHTzRCTO4rknchT4pLtHzCwdWGpmzwHfA/7F3ReZ2f0E4fCb8Hm/u482s68AvwSuNbNzgK8A5wLDgT+Z2ZjwM/4d+DRQBiwzsyXu/l4c+yShvZGjPPrmVh5+Ywu7K48yJi+HX35pAjMn5pOZrvEOkWQRtxBxdwci4cv08OHAJ4HrwvKFwJ0EITIzXAZ4ArjPzCwsX+TuR4HNZrYRmBLW2+jumwDMbFFYVyESRxt2VTL/tc38bmU5R+sa+PiYwcz+8ig+WjSI4OsSkWQS1zERM0slOGQ1mmCv4UPggLvXhVXKgPxwOR/YBuDudWZ2kOCQVz7wRtRmo9+zrVl5izfONrM5wByAvLw8SkpKiEQilJSUnFb/urNT6b+7s3ZvPc+X1rF6Tz3pKfCR4WlcVphBfs4RGrav5eXt8W1vR0rm7z6Z+w7J3f949T2uIeLu9cBEM+sHPAWcHc/Pa6MdDwAPAEyePNmLi4spKSmhuLg4Ec3pEk6m/9W19Tz9djnzX9vM+l1HGJSTwfc/fRbXTT2DgTndd7wjmb/7ZO47JHf/49X3Tjk7y90PmNlLwMVAPzNLC/dGCoDysFo5MAIoM7M0oC/BAHtjeaPo97RWLqdhd+VRHn5jC4++sYW9h2sYN6wPv/ry+Xzu/GFkpGm8Q0SOiefZWYOB2jBAsggGwH8JvARcTXCG1izgmfAtS8LXr4fr/+zubmZLgMfM7NcEA+tFwFuAAUXh2V7lBIPvjWMtEoP3dx5i3qubeWbVdmrqG7j07CHMnj6Ki88aqPEOEWlRPPdEhgELw3GRFGCxu/+Pmb0HLDKzu4C3gXlh/XnAw+HA+T6CUMDd15rZYoIB8zrg1vAwGWb2beB5glN857v72jj2p0dqaHBeXr+beUs3s3TjHjLTU7jmogJuumQUZw3OSXTzRKSLi+fZWe8CF7RQvoljZ1dFl1cDX25lW3cDd7dQ/izw7Gk3NgkdrXceeWML81/bzKbdh8nrk8HfzRjLdVPOoF92r0Q3T0S6CV2xnmSO1NTxm5IPmf/qEQ7XrmFCfl/+9dqJXDFhGL3SUhLdPBHpZhQiSaR0z2G++cgKPthVyQWDU7njC1O4qLC/xjtEJGYKkSTx5/d3cduiVaSmGAtumoJvX8uUUQMS3SwR6eZ0/KKHa2hw/uWF9Xx9wXLOGJDN7789nY+PGZzoZolID6E9kR7s4JFavvP427z0wW6+dGEBd39hvOa1EpEOpRDpodbtOMQtD69gx8EqfnHVeL469QyNfYhIh1OI9EBPv13OHb97l75Z6SyaczGTRvZPdJNEpIdSiPQgtfUN3P2HdSz4SylTRg3gvusuYEiu7mEuIvGjEOkhKg5Vc+tjK1lWup/Z00dxx+Vnk56q8yZEJL4UIj3A8tJ9/PWjK4lU1zH3ry7g8+cPT3STRCRJKES6MXdn4V9KuesP6yjon8XDs6dw9lDdz1xEOo9CpJuqqqnnR0+t5qm3y/nUuCH8n2sm0jcrPdHNEpEkoxDphrbsPcwtDwfTl3z/02O49ROjSUnR6bsi0vkUIt3MS+9XcNuitzEz5t94EZ8YOyTRTRKRJKYQ6SYaGpy5f97AvS9uYNzQPtz/1UmcMTA70c0SkSSnEOkGDlbV8r3HV/Hi+xV88YJ87v7CBLJ6afoSEUk8hUgXt27HIb75yArK91fx85nn8rVpIzV9iYh0GQqRLuyZVeX84Ml36ZOZzuO3TGPSSE3dLtLZamtrKSsro7q6OtFNOS19+/Zl3bp1bdbJzMykoKCA9PSTP9NTIdIF1dY38I/PruO3r5UypXAA912v6UtEEqWsrIzc3FwKCwu79VGAyspKcnNzW13v7uzdu5eysjJGjRp10ttViHQxFZXVfPvRt3mrdB83XVLIj64Yp+lLRBKourq62wfIyTAzBg4cyO7du0/pfQqRLuTtrfu55eEVHKqu5d6vTGTmxPxEN0lEoMcHSKNY+qkQ6SJe3bCbOQ+tYHBuBgu/PoVxwzR9iYh0fTpO0gX8cc1OZi9YzsiB2Tz51x9RgIhIkwMHDvAf//Efp/y+K664ggMHDsShRcdTiCTYfy/fxrceXcH4/D48PudiBudmJLpJItKFtBYidXV1bb7v2WefpV+/fvFqVhMdzkqg+Us38/P/eY/powfxn1+bRO8MfR0iXdwCZc8AAA68SURBVNnPfr+W97Yf6tBtnjO8Dz/93Lmtrr/jjjv48MMPmThxIunp6WRmZtK/f3/ef/991q9fz1VXXcW2bduorq7mtttuY86cOQAUFhayfPlyIpEIl19+OVOnTmXZsmXk5+fzzDPPkJWV1SHt155IArg79/5pAz//n/f4zLl5zLtxsgJERFp0zz33cNZZZ7Fq1Sr++Z//mZUrV3Lvvfeyfv16AObPn8+KFStYvnw5c+fOZe/evSdsY8OGDdx8882sXbuWfv368eSTT3ZY+/TL1cncnbv+sI55SzfzpQsL+OWXJpCmU3hFuoW29hg6y5QpU467jmPu3Lk89dRTAGzbto0NGzYwcODA494zatQozjvvPAAmTZpEaWlph7VHIdKJ6hucH/7uXRYvL+PGjxTykyvP0RTuInJKevfu3bRcUlLCn/70J15//XWys7MpLi5u8cr6jIxjY62pqalUVVV1WHsUIp3kaF093318Fc+u3sltlxbxnU8VJc255yISu9zcXCorK1tcd/DgQfr37092djbvv/8+b7zxRie3TiHSKY7U1PHNR1byyvrd/Piz4/jGR89MdJNEpJsYOHAgl1xyCePHjycrK4u8vLymdTNmzOD+++9n3LhxjB07lmnTpnV6+xQicXawqpbZC5axcut+/ulL53HNRSMS3SQR6WYee+yxFsszMjJ47rnnWlzXOO4xaNAg1qxZ07Q3c/vtt3do2xQicbQncpQb5r3FhopK7rvuQq6YMCzRTRIR6VAKkTgpP1DF1x58k+0Hq3hw1kV8fMzgRDdJRKTDKUTiYNPuCF998E0qj9bx8OypXFSo+4CISM+kEOlga7cfZNb8t3CHRXOmce7wvolukohI3ChEOtCKLfu48bfLyM1I4+FvTOWswTmJbpKISFwpRDpI41TuQ/tm8sg3ppLfr2PmpRER6co030YH+OOaHcxesJzCQb1ZfMvFChARSaicnOAoyPbt27n66qtbrFNcXMzy5ctP+7PiFiJmNsLMXjKz98xsrZndFpYPMLMXzGxD+Nw/LDczm2tmG83sXTO7MGpbs8L6G8xsVlT5JDNbHb5nriXgEvBgKveVjM/vw6Kbp2kqdxHpMoYPH84TTzwR18+I5+GsOuD77r7SzHKBFWb2AnAj8KK732NmdwB3AD8ALgeKwsdU4DfAVDMbAPwUmAx4uJ0l7r4/rHMz8CbwLDADaPnKmzhonMr9o0XBVO7ZvXR0UKRHe+4O2Lm6Y7c5dAJcfk+bVe644w5GjBjBrbfeCsCdd95JWloaL730Evv376e2tpa77rqLmTNnHve+0tJSrrzyStasWUNVVRU333wz77zzDmeffXaHzZ8Vtz0Rd9/h7ivD5UpgHZAPzAQWhtUWAleFyzOBhzzwBtDPzIYBnwFecPd9YXC8AMwI1/Vx9zfc3YGHorYVV9FTuc84dygPzpqsABGRuLn22mtZvHhx0+vFixcza9YsnnrqKVauXMlLL73E97//fYKfwpbNmzeP7Oxs1q1bx89+9jNWrFjRIW3rlF8+MysELiDYY8hz9x3hqp1A40Qw+cC2qLeVhWVtlZe1UB5XDQ3BVO7zX9vM1ZMKuOeLmspdJGm0s8cQLxdccAEVFRVs376d3bt3079/f4YOHcp3v/tdXnnlFVJSUigvL2fXrl0MHTq0xW289tprfO973wPgvPPOa5oa/nTFPUTMLAd4EviOux+KHrZwdzez1qOz49owB5gDkJeXR0lJCZFIhJKSklPaTn2Ds2BtDa+W1/HpkWlcMWgfS199JQ4tjr9Y+t9TqO8liW5GwsTS/759+7Y6i25n+vznP88jjzxCRUUFM2fOZN68eezYsYOSkhLS09MZP348e/bsaZoqvrKykkgkQkNDA5WVlbg7R44caepLQ0MDhw8fPqFv1dXVp/TfKK4hYmbpBAHyqLv/LizeZWbD3H1HeEiqIiwvB6JnJywIy8qB4mblJWF5QQv1T+DuDwAPAEyePNmLi4spKSmhuLi4peotOlpXz3cWreLV8p1851NF3HZp957K/VT735Oo78WJbkbCxNL/devWkZubG58GnYIbbriBm2++mT179vDyyy+zePFihg8fzoABA3jppZfYunUrOTk5TW3Nzc0lJyeHlJQUcnNzmT59Ok8//XTTGMmaNWvo3bv3CX3LzMzkggsuOOl2xfPsLAPmAevc/ddRq5YAjWdYzQKeiSq/ITxLaxpwMDzs9TxwmZn1D8/kugx4Plx3yMymhZ91Q9S2OtSRmjq+sXA5z63ZyT9ceQ7f+dSYbh0gItL9nHvuuVRWVpKfn8+wYcO4/vrrWb58ORMmTOChhx7i7LPPbvP9s2fPJhKJMG7cOH7yk58wadKkDmlXPPdELgG+Bqw2s1Vh2Y+Ae4DFZjYb2AJcE657FrgC2AgcAW4CcPd9ZvYLYFlY7+fuvi9c/hawAMgiOCsrLmdmpZjR4M4/XX0e10zWVO4ikhirVx87M2zQoEG8/vrrLdaLRCIAFBYWsmbNGgCysrJYtGhRh7cpbiHi7kuB1v5cv7SF+g7c2sq25gPzWyhfDow/jWaelMz0VB7++lTdylZEpBmdVnSSFCAiIidSiIiItKOt6y96klj6qRAREWlDZmYme/fu7fFB4u7s3buXzMzMU3qfLrMWEWlDQUEBZWVl7N69O9FNOS3V1dXtBkRmZiYFBQVt1mlOISIi0ob09HRGjRqV6GactpKSklO6/uNk6XCWiIjETCEiIiIxU4iIiEjMrKefcdCcme0muFJ+ELAnwc1JpGTuv/qevJK5/6fT95HuPrilFUkXIo3MbLm7T050OxIlmfuvvidn3yG5+x+vvutwloiIxEwhIiIiMUvmEHkg0Q1IsGTuv/qevJK5/3Hpe9KOiYiIyOlL5j0RERE5TQoRERGJWVKGiJnNMLMPzGyjmd2R6PZ0JjMrNbPVZrbKzJYnuj3xZmbzzazCzNZElQ0wsxfMbEP43D+RbYyXVvp+p5mVh9//KjO7IpFtjBczG2FmL5nZe2a21sxuC8uT5btvrf8d/v0n3ZiImaUC64FPA2UEt939K3d/L6EN6yRmVgpMdvekuODKzD4GRICH3H18WPZPwD53vyf8I6K/u/8gke2Mh1b6ficQcfdfJbJt8WZmw4Bh7r7SzHKBFcBVwI0kx3ffWv+voYO//2TcE5kCbHT3Te5eAywCZia4TRIn7v4KsK9Z8UxgYbi8kOAfV4/TSt+TgrvvcPeV4XIlsA7IJ3m++9b63+GSMUTygW1Rr8uI03/cLsqB/zWzFWY2J9GNSZA8d98RLu8E8hLZmAT4tpm9Gx7u6pGHc6KZWSFwAfAmSfjdN+s/dPD3n4whkuymu/uFwOXAreEhj6TlwfHcZDqm+xvgLGAisAP4P4ltTnyZWQ7wJPAddz8UvS4ZvvsW+t/h338yhkg5MCLqdUFYlhTcvTx8rgCeIji8l2x2hceMG48dVyS4PZ3G3Xe5e727NwD/lx78/ZtZOsEP6KPu/ruwOGm++5b6H4/vPxlDZBlQZGajzKwX8BVgSYLb1CnMrHc4yIaZ9QYuA9a0/a4eaQkwK1yeBTyTwLZ0qsYf0NAX6KHfv5kZMA9Y5+6/jlqVFN99a/2Px/efdGdnAYSntf0rkArMd/e7E9ykTmFmZxLsfUBwa+THenrfzey/gGKCabB3AT8FngYWA2cQ3BbgGnfvcQPQrfS9mOBQhgOlwC1RYwQ9hplNB14FVgMNYfGPCMYFkuG7b63/f0UHf/9JGSIiItIxkvFwloiIdBCFiIiIxEwhIiIiMVOIiIhIzBQiIiISM4WIiIjETCEiSc3MPt8dbgcQTuE/qIO2tcDMro7xvYPN7E0ze9vMPtoR7ZHuLS3RDRBJJHdfQpLMWNBBLgVWu/s3Et0Q6Rq0JyI9lpkVmtn74V/e683sUTP7lJm9Ft6UaIqZ3Whm94X1F5jZXDP7i5ltauuvdTMbZmavhDf2WdP4V7mZ/cbMloc3AvpZVP1SM/v/G28GZmYXmtnzZvahmX0zrFMcbvMPFtw07X4zO+HfqJl91czeCrf1n2aWGj4WhG1ZbWbfPcn/RpPM7OVwVufno+aVutnMlpnZO2b2pJllm9lE4J+AmeFnZ53K9yE9k0JEerrRBDOVnh0+rgOmA7cTTAPR3LBw/ZXAPW1s9zrgeXefCJwPrArL/97dJwPnAR83s/Oi3rM1rP8qsAC4GpgG/CyqzhTgb4BzCGZb/WL0h5rZOOBa4JJwW/XA9QRTWeS7+3h3nwD8to22N24rHfg34Gp3nwTMBxqnwfmdu1/k7ucT3ItitruvAn4CPO7uE929qr3PkJ5Ph7Okp9vs7qsBzGwt8KK7u5mtBgpbqP90OMPpe2bW1r0mlgHzwx/ip8MfWIBrwvu0pBEE0jnAu+G6xsNmq4Gc8GZBlWZ21Mz6hevecvdNYXv/iyDQnoj63EuBScCyYI49sghmov09cKaZ/RvwB+B/2/sPA4wFxgMvhNtKJZgeHGC8md0F9ANygOdPYnuShBQi0tMdjVpuiHrdQMv//0fXt9Y26u6vhPdi+SywwMx+TbCHcTtwkbvvN7MFQGYL245uR/O2NJ/MrvlrAxa6+w+bt8nMzgc+A3yT4DaoX2+t/VHbWuvuF7ewbgFwlbu/Y2Y3EkzcKHICHc4SiYGZjQR2ufv/BR4ELgT6AIeBg+FezOUxbHpKeJuCFILDVkubrX8RuNrMhoTtGGBmI8Mzt1Lc/Ungx2F72vMBMNjMLg63lW5m54brcoEd4Z7W9TH0Q5KE9kREYlMM/H9mVgtEgBvcfbOZvQ28T3AL5tdi2O4y4D6CsZyXODZ1PwDu/p6Z/ZjgFscpQC1wK1AF/DZqIP6EPZXm3L0mPHlgrpn1Jfg9+FdgLfAPBNOm7w6fc2PoiyQBTQUv0kWYWTFwu7tfmei2iJwsHc4SEZGYaU9EpA1mNgF4uFnxUXefmoj2nAoz+3fgkmbF97p7u6f/ipwshYiIiMRMh7NERCRmChEREYmZQkRERGKmEBERkZj9PwH083G9/3VgAAAAAElFTkSuQmCC\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "plot_fitting_graph(min_samples_leaf, rmse_train, rmse_valid, metric_name='RMSE', xlabel='min_samples_leaf')"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "5"
      ]
     },
     "execution_count": null,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "min_samples_leaf[np.argmin(rmse_valid)]"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### max_features"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "100%|██████████| 5/5 [01:22<00:00, 16.48s/it]\n"
     ]
    }
   ],
   "source": [
    "rmse_train = []\n",
    "rmse_valid = []\n",
    "\n",
    "max_features = [.1, .25, .5, .75, 1.]\n",
    "for mf in tqdm(max_features):\n",
    "    rf = RandomForestRegressor(n_estimators=100, max_depth=32, min_samples_leaf=5, max_features=mf, n_jobs=-1)\n",
    "    results = cross_validate(rf, X, y,\n",
    "                             cv=5,\n",
    "                             return_train_score=True,\n",
    "                             scoring='neg_root_mean_squared_error')\n",
    "    \n",
    "    # we average the scores and append them to the list\n",
    "    rmse_train.append(-np.mean(results['train_score']))\n",
    "    rmse_valid.append(-np.mean(results['test_score']))"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAZEAAAEXCAYAAABsyHmSAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8li6FKAAAgAElEQVR4nO3deXxV1bn/8c+TmTBPRiaBCiqgMkXF6xSHItpewDqgtdX2Wm2ttLbe2qK9v2odemsnW1urxUrVVosWr5ValDqlWisqCDKriAxhljCFIZDk+f2xV8hJyMRJTk6G7/v1Oq+zz1pr7/3sRTjP2eMyd0dERCQeKckOQEREWi4lERERiZuSiIiIxE1JRERE4qYkIiIicVMSERGRuCmJiARmdpSZFZlZ6mHMc4aZvZ/IuJqKmbmZDUp2HNKyKIlIm2Nmq8xsb0gY5a/e7r7G3Tu4e2lol29mX6kyb6UvWnd/3d2PbeptEGkulESkrfrPkDDKX+uTHVBDmFlasmOQtklJRCQwswFhTyPNzO4GzgB+E/ZUfmNmr4Wm74WySWaWZ2YFMctYZWbfMbOFZrbDzJ40s6yY+u+a2QYzW29mX6ntEJKZDTSz18xsl5m9ZGb3m9mfqsR6jZmtAV4J5X8xs41h3a+Z2bCY5T1iZg+a2Ythmf80s/5VVnuemX1oZtvD+qxROldaLSURkWq4+/eB14HJYU9lsrufGaqHh7Ina5j9MmAcMBA4EfgSgJmNA24CzgMGAXl1hPEE8DbQHbgd+GI1bc4ChgDnh8/PA4OBI4B3gcertL8SuBPoASyopv6zwEkh7stilitSLSURaav+Gn5tbzezvzbysu9z9/XuXgj8DRgRyi8D/uDuS9x9D1FiqJaZHUX0Zf4Dd9/v7v8CZlbT9HZ33+3uewHcfZq773L34rD84WbWOab93939tVD/feBUM+sXU/9jd9/u7muAV2NiF6mWkoi0VRPdvUt4TWzkZW+Mmd4DdAjTvYG1MXWx01X1BgpDsqmt/cEyM0s1sx+b2UdmthNYFap6VNfe3YuAwrCuumIXqZaSiEjNGvsR1xuAvjGf+9XUMLTtZmbZdbSPjfHzwASiw2WdgQGhPPa8xsFlmFkHoBvQoi8qkORSEhGp2SbgU/Uoq6+ngC+b2ZCQHP5fTQ3dfTUwF7jdzDLM7FTgP+tYfkegGNgKZAM/qqbNhWZ2upllEJ0bmePute0RidRKSUSkZr8CLjGzbWZ2Xyi7HXg0nEu57HAW5u7PA/cRnWtYAcwJVcU1zHIlcCpRUrgLeLKWtgCPAauBdcDSmOXHegK4jegw1mjgC4ezDSJVmQalEkkOMxsCLAYy3b2kHu2fBJa7+21xru8RoMDd/yee+UWqoz0RkSZkZheZWaaZdQXuAf5WUwIxs5PM7GgzSwmXB08AGvtKMpEGURIRaVpfBTYDHwGlwPW1tD0SyAeKiA6DXe/u8xMdoMjh0OEsERGJm/ZEREQkbm3uoW09evTwAQMGJDuMBtm9ezft27dPdhjNgvqiMvVHZeqPCg3ti3nz5n3i7j2rlre5JDJgwADmzp2b7DAaJD8/n7y8vGSH0SyoLypTf1Sm/qjQ0L4ws9XVletwloiIxE1JRERE4qYkIiIicWtz50RERA7HgQMHKCgoYN++fckOpUE6d+7MsmXL6myXlZVF3759SU9Pr9dylURERGpRUFBAx44dGTBgAC15oMddu3bRsWPHWtu4O1u3bqWgoICBAwfWa7k6nCUiUot9+/bRvXv3Fp1A6svM6N69+2HtdSmJiIjUoS0kkHKHu61KIvW1+P9g/YJkRyEi0qwoidRH6QF45S54+NPw1u9AzxsTkSa0fft2fvvb3x72fBdeeCHbt29PQEQVlETqIzUdvvISHH0OPP9dePILsHdbsqMSkTaipiRSUlL7MDSzZs2iS5cuiQoLUBKpv+xucMV0OP9/4YPZ8OAZsPbtZEclIm3AlClT+OijjxgxYgQnnXQSZ5xxBuPHj2fo0KEATJw4kdGjRzNs2DCmTp16cL4BAwbwySefsGrVKnJzc7n22msZNmwYY8eOZe/evY0Smy7xPRxmcOrX4agxMOPLMG0cnPv/4D9uhBTlY5HW7od/W8LS9TsbdZlDe3fitv8cVmubH//4xyxevJgFCxaQn5/PZz7zGRYvXnzwMtxp06bRrVs39u7dy0knncTFF19M9+7dKy3jo48+4sknn+Shhx7isssu4+mnn+YLX2j46Mj65otHn1Hw1ddg6Hh46XZ4/BIo2pLsqESkjTj55JMr3cdx3333MXz4cMaMGcPatWv58MMPD5mnf//+jBgxAoDRo0ezatWqRolFeyLxyuoMl/wBBp4FL0yBB0+Dzz0Enzor2ZGJSILUtcfQVGIf6Z6fn89LL73Em2++SXZ2Nnl5edXe55GZmXlwOjU1tdEOZ2lPpCHMIPfLcO0rUVJ5bAK8cjeU1n6yS0TkcHTs2JFdu3ZVW7djxw66du1KdnY2y5cvZ86cOU0aW0KTiJl1MbMZZrbczJaZ2almdruZrTOzBeF1YUz7W8xshZm9b2bnx5SPC2UrzGxKTPlAM3srlD9pZhmJ3J4a5QyD6/JhxOfhtZ/AY+Nh5/qkhCIirU/37t057bTTOP7447n55psr1Y0bN46SkhKGDBnClClTGDNmTJPGlujDWb8CXnD3S8IXfDZwPnCvu/8stqGZDQUuB4YBvYGXzOyYUH0/8GmgAHjHzGa6+1LgnrCs6Wb2IHAN8ECCt6l6Ge1h4m9h4Jnw3E3wwGlw0e/gmLFJCUdEWpcnnnii2vLMzEyef/75auvKz3v06NGDt95662D5d77znUaLK2F7ImbWGTgTeBjA3fe7e213vUwAprt7sbt/DKwATg6vFe6+0t33A9OBCRbdm38OMCPM/ygwMTFbcxiGXw5f/Sd06gNPXAr/+B8o2Z/sqEREEiKReyIDgS3AH8xsODAPuDHUTTazq4C5wH+7+zagDxB7MK8glAGsrVJ+CtAd2O7uJdW0r8TMrgOuA8jJySE/P79hW1YPKcf8gKNTp9Hn379m56IXWDr0Zva1y2mUZRcVFTXJNrQE6ovK1B+VNUZ/dO7cucbzES1JaWlpvbdj37599e63RCaRNGAU8A13f8vMfgVMAX4D3Al4eP858F8JjAN3nwpMBcjNzfUmG3P53LGw9Fk6PfsNxiy4GSb8GoZOaPBiNW50BfVFZeqPyhqjP5YtW1bnI9Rbgvo8Cr5cVlYWI0eOrFfbRJ5YLwAK3L38QNwMYJS7b3L3UncvAx4iOlwFsA7oFzN/31BWU/lWoIuZpVUpb16GToCvvQY9BsFTV0XnSw607MFtRETKJSyJuPtGYK2ZHRuKzgWWmlmvmGYXAYvD9EzgcjPLNLOBwGDgbeAdYHC4EiuD6OT7THd34FXgkjD/1cCzidqeBuk6AL78AvzHN2Duw/D78+CTQ28GEhFpaRJ9n8g3gMfNbCEwAvgR8BMzWxTKzga+DeDuS4CngKXAC8ANYY+lBJgMzAaWAU+FtgDfA24ysxVE50geTvD2xC8tA8beBZ//C+xcB787C96bnuyoREQaJKFJxN0XuHuuu5/o7hPdfZu7f9HdTwhl4919Q0z7u939aHc/1t2fjymf5e7HhLq7Y8pXuvvJ7j7I3S919+JEbk+jOGYsXP8G9B4Bz3wVnrkeiouSHZWItCIdOnQAYP369VxyySXVtsnLy2Pu3LkNXpfuWE+GTr3hqplw1vfgvT/DQ2fDxsV1zycichh69+7NjBkz6m7YAEoiyZKaBmffClfPhH074aFz4J2HNeCViBxiypQp3H///Qc/33777dx1112ce+65jBo1ihNOOIFnnz30lPCqVas4/vjjAdi7dy+XX345Q4YM4aKLLtKj4FuNgWfC1/4VHdr6+03w8Wsw/r7oWVwi0rw8PwU2LmrcZR55Alzw41qbTJo0iW9961vccMMNADz11FPMnj2bb37zm3Tq1IlPPvmEMWPGMH78+BrHSH/44YfJzs5m2bJlLFy4kFGjRjVK+NoTaQ469IQrZ8B5P4Rlf4PfnQnr5iU7KhFpJkaOHMnmzZtZv3497733Hl27duXII4/k1ltv5cQTT+S8885j3bp1bNq0qcZlvPHGGwfHDznxxBM58cQTGyU27Yk0FykpcPq34KhT4elr4OHz4dM/hDFfj54WLCLJV8ceQyJdeumlzJgxg40bNzJp0iQef/xxtmzZwrx580hPT2fAgAHVPgI+0bQn0twcdUo04NUx58PsW+HPl8OewmRHJSJJNmnSJKZPn86MGTO49NJL2bFjB0cccQTp6em8+uqrrF69utb5TzvttIMPcVy8eDELFy5slLiURJqj7G4w6U9wwU/go1fgwdNh9b+THZWIJNGwYcPYtWsXffr0oVevXlx55ZXMnTuXE044gccee4zjjjuu1vmvueYaioqKGDJkCD/4wQ8YPXp0o8Slw1nNlRmc8lXod0o0nvsjn4G8W+GMm5IdmYgkyaJFFSf1e/TowZtvvlltu6Ki6N6zAQMGsHhxdPtAu3btmD698W9w1p5Ic9d7RHR46/iL4dW74I8XkVG8LdlRiYgA2hNpGTI7RuO3DzwLZt1MbsECGNQZjj4n2ZGJSBunPZGWwgxGfRGue5UD6Z3hj5+Dl36o8dxFmoC3oZuAD3dblURamiOGMG/0z6KE8q9fROdKdhQkOyqRVisrK4utW7e2iUTi7mzdupWsrKx6z6PDWS1QWWomjP91dHjrbzdGV29N+C0cd2GyQxNpdfr27UtBQQFbtmxJdigNsm/fvnolh6ysLPr27Vvv5SqJtGQnXAK9R0ZXb02/Ak65PrpBMS0z2ZGJtBrp6ekMHDgw2WE0WH5+fr1HKzwcOpzV0nU/Gq55EU75Grz1ADw8FgpXJjsqEWkjlERag7RMuOAemPQ4bFsFD54JixL7+GcREUhwEjGzLmY2w8yWm9kyMzvVzLqZ2Ytm9mF47xrampndZ2YrzGyhmY2KWc7Vof2HZnZ1TPnoMEriijBv237I1JDPRk8EzhkaPX9r5jdh/55kRyUirVii90R+Bbzg7scBw4mGt50CvOzug4GXw2eAC4jGVR8MXAc8AGBm3YDbgFOAk4HbyhNPaHNtzHzjErw9zV+XfvClv8PpN8G7j0bjlGxenuyoRKSVSlgSMbPOwJmEcc/dfb+7bwcmAI+GZo8CE8P0BOAxj8wBuphZL+B84EV3L3T3bcCLwLhQ18nd53h07d1jMctq21LT4bzb4AtPw+4tMDUP3v2jBrwSaSvc4cBe2L0Vtq+BzcvpuPPDhHwHJPLqrIHAFuAPZjYcmAfcCOTEjKu+EcgJ032AtTHzF4Sy2soLqik/hJldR7R3Q05ODvn5+XFvVHNQVFRUz21II2P4Txmy7F66zpzMpjl/4YNjvkZpWnaiQ2wy9e+LtkH9UVmz7Q93zEtILd1HamkxKWXRe2rpPlLKig9OV/0cTZfPU9Gm8udo2qicMEYDr7XvT1lqRqNuSiKTSBowCviGu79lZr+i4tAVAO7uZpbwn8fuPhWYCpCbm+t5eXmJXmVC5efnc1jb8OkJ8PrPycn/X3JKCuDSP0Cv4QmLrykddl+0cuqPyhrUH6UlcGB3dF7xQHjt3xNTtjdmurqy2Hn2wP7doT5Me+nhxZOaAentIL09ZGRDeja07wDpPaPpjPbRe3p2Rf3BsnYsen8lZ+adHR2paESJTCIFQIG7vxU+zyBKIpvMrJe7bwiHpDaH+nVAv5j5+4aydUBelfL8UN63mvZSVUoqnPVd6H9adML9oXOh+6DoDyyjPWR0iJkOnzM7VFNXdboDpDXurxqReisri/mi3l35CzuUHblhPrz1fpX68GVe7Twx9aX7Dy8eS630pX1wOiMb2vcMZdkxSSA2IbSvpr5KQmjgl//WrfmNnkAggUnE3Tea2VozO9bd3wfOBZaG19XAj8N7+ejyM4HJZjad6CT6jpBoZgM/ijmZPha4xd0LzWynmY0B3gKuAn6dqO1pFQacBl97A177KexaD8VF0X+kPYWwP0zv3x39J6qvlPRDE0xmh1qST3vI6FhLYmofXbLcxi+0a5HKyqBkX+XXgfLpYijZG95jy2PqD+yt3O6QX/F7Kn/5l9Q9it9xAO+Xf7JqfqW3i6bb9a5cV+VXfKWEULX+4Jd8Rpv8u030HevfAB43swxgJfBlopP5T5nZNcBq4LLQdhZwIbAC2BPaEpLFncA7od0d7l4+1N/XgUeAdsDz4SW1ad+97iE+y3/hHUwsMQmmfLq4qEp5lXY71h5aV18pafXbC8poT7+CTfD2h1WSWDVJKi2rbfwHd4eS/XV/QVf7RV7Xl3vVdlXKDveXe1WpGdG/U/kr9pd5+561/IqPTQiVf8W/+e5CTj3j3KisrfwNNLGEJhF3XwDkVlN1bjVtHbihhuVMA6ZVUz4XOL6BYUpVKSnR3kRmh8ZbZllZ9AVWnlCKq0lMB6erS167YdeGmAQW1R+NRz9P6mIpMYmmukN1MZ8P2ZOq2rZjxZdWTV9Ktf4qr88XdJVf7/Vsd9aBffDPsgb8Q1m0XQe/yMu/1DMhrV3UD+17hs8xX/hpmWG+0K68Pj2rlnZV6lIa/2LR4qyN0Q8nSRg9O0uaRkpKxZcwRzTOMt157ZV/cOYpo6oknF017yEVV6kr2lSl7S7w+n4JW0VySU2P+UJvjF/lmTFfutV8EVf3RZ6exep1mxhw9DFVvsgP48s9JU2/1uWwKIlIy2UWPdG4Q0+gZ+Ms0z1KAod7GK/0QM2/sqv+mq/x13goT82M+1f5qvx8BpyZ1zh9IVIPSiIisSwczklvB+17JDsakWZPD2AUEZG4KYmIiEjclERERCRuSiIiIhI3JREREYmbkoiIiMRNSUREROKmJCIiInFTEhERkbgpiYiISNyUREREJG5KIiIiEjclERERiVtCk4iZrTKzRWa2wMzmhrLbzWxdKFtgZhfGtL/FzFaY2ftmdn5M+bhQtsLMpsSUDzSzt0L5k2EERRERaSJNsSdytruPcPfYEQ7vDWUj3H0WgJkNBS4HhgHjgN+aWaqZpQL3AxcAQ4ErQluAe8KyBgHbgGuaYHtERCRoToezJgDT3b3Y3T8mGmv95PBa4e4r3X0/MB2YYGYGnAPMCPM/CkxMQtwiIm1WopOIA/8ws3lmdl1M+WQzW2hm08ysayjrA6yNaVMQymoq7w5sd/eSKuUiItJEEj2y4enuvs7MjgBeNLPlwAPAnUQJ5k7g58B/JTKIkMCuA8jJySE/Pz+Rq0u4oqKiFr8NjUV9UZn6ozL1R4VE9UVCk4i7rwvvm83sGeBkd3+tvN7MHgKeCx/XAf1iZu8byqihfCvQxczSwt5IbPuqcUwFpgLk5uZ6Xl5eA7csufLz82np29BY1BeVqT8qU39USFRfJOxwlpm1N7OO5dPAWGCxmfWKaXYRsDhMzwQuN7NMMxsIDAbeBt4BBocrsTKITr7PdHcHXgUuCfNfDTybqO0REZFDJXJPJAd4Jjr/TRrwhLu/YGZ/NLMRRIezVgFfBXD3JWb2FLAUKAFucPdSADObDMwGUoFp7r4krON7wHQzuwuYDzycwO0REZEqEpZE3H0lMLya8i/WMs/dwN3VlM8CZtWwjpMbFqmIiMSrOV3iKyIiLYySiIiIxE1JRERE4qYkIiIicVMSERGRuCmJiIhI3JREREQkbkoiIiISNyURERGJm5KIiIjETUlERETipiQiIiJxUxIREZG4KYmIiEjclERERCRuSiIiIhI3JREREYlbQpOIma0ys0VmtsDM5oaybmb2opl9GN67hnIzs/vMbIWZLTSzUTHLuTq0/9DMro4pHx2WvyLMa4ncHhERqawp9kTOdvcR7p4bPk8BXnb3wcDL4TPABcDg8LoOeACipAPcBpxCNBTubeWJJ7S5Nma+cYnfHBERKZeMw1kTgEfD9KPAxJjyxzwyB+hiZr2A84EX3b3Q3bcBLwLjQl0nd5/j7g48FrMsERFpAmkJXr4D/zAzB37n7lOBHHffEOo3Ajlhug+wNmbeglBWW3lBNeWHMLPriPZuyMnJIT8/vwGblHxFRUUtfhsai/qiMvVHZeqPConqi0QnkdPdfZ2ZHQG8aGbLYyvd3UOCSaiQvKYC5Obmel5eXqJXmVD5+fm09G1oLOqLytQflak/KiSqL2o9nGVm58RMD6xS97m6Fu7u68L7ZuAZonMam8KhKML75tB8HdAvZva+oay28r7VlIuISBOp65zIz2Kmn65S9z+1zWhm7c2sY/k0MBZYDMwEyq+wuhp4NkzPBK4KV2mNAXaEw16zgbFm1jWcUB8LzA51O81sTLgq66qYZYmISBOo63CW1TBd3eeqcoBnwlW3acAT7v6Cmb0DPGVm1wCrgctC+1nAhcAKYA/wZQB3LzSzO4F3Qrs73L0wTH8deARoBzwfXiIi0kTqSiJew3R1nytXuq8EhldTvhU4t5pyB26oYVnTgGnVlM8Fjq8tDhERSZy6ksinzGwm0V5H+TTh88CaZxMRkbagriQyIWb6Z1Xqqn4WEZE2ptYk4u7/jP1sZulEh4/WhSuuRESkDavrEt8HzWxYmO4MvEd0Z/h8M7uiCeITEZFmrK5LfM9w9yVh+svAB+5+AjAa+G5CIxMRkWavriSyP2b608BfAdx9Y8IiEhGRFqOuJLLdzD5rZiOB04AXAMwsjejeDBERacPqujrrq8B9wJHAt2L2QM4F/p7IwEREpPmr6+qsD6hmjA53n030OBIREWnDak0iZnZfbfXu/s3GDUdERFqSug5nfY3ooYlPAeup+3lZIiLShtSVRHoBlwKTgBLgSWCGu29PdGAiItL81Xp1lrtvdfcH3f1sovtEugBLzeyLTRKdiIg0a/Ua2dDMRgFXEN0r8jwwL5FBiYhIy1DXifU7gM8Ay4DpwC3uXtIUgYmISPNX157I/wAfE40LMhz4URhkyoiGADkxseGJiEhzVlcSafCYIWaWCswlevLvZ83sEeAsYEdo8iV3XxCGuP0V0eiGe0L5u2EZV1MxHO9d7v5oKB9NxciGs4Abw+BWIiLSBOq62XB1deVmlkJ0jqTa+ipuJDoc1imm7GZ3n1Gl3QXA4PA6BXgAOMXMugG3AblEoynOM7OZ7r4ttLkWeIsoiYxDQ+SKiDSZuh4F38nMbjGz35jZWIt8A1hJxdjotc3fl+icyu/rEcsE4DGPzAG6mFkv4HzgRXcvDInjRWBcqOvk7nPC3sdjwMR6rEdERBpJXYez/ghsA94EvgLcSnQ+ZKK7L6jH8n9J9Mj4jlXK7zazHwAvA1PcvRjoA6yNaVMQymorL6im/BBmdh1wHUBOTg75+fn1CL35KioqavHb0FjUF5WpPypTf1RIVF/UOcZ6GD8EM/s9sAE4yt331bVgM/sssNnd55lZXkzVLcBGIAOYCnwPuCOO2OvN3aeGdZGbm+t5eXm1z9DM5efn09K3obGoLypTf1Sm/qiQqL6o61HwB8on3L0UKKhPAglOA8ab2Sqiy4PPMbM/ufuGcMiqGPgDcHJovw7oFzN/31BWW3nfasoTYt7qbSxZv6PuhiIibUhdSWS4me0Mr13AieXTZrazthnd/RZ37+vuA4DLgVfc/QvhXAbhaqyJRM/mApgJXBXOu4wBdrj7BqKnBY81s65m1hUYC8wOdTvNbExY1lXAs3H1Qh0OlJZx4/T53PD4uxQV6zYZEZFydT32JNXdO4VXR3dPi5nuVNu8tXjczBYBi4AewF2hfBbRCfsVwEPA10MMhcCdwDvhdUcoI7T5fZjnIxJ0ZVZ6agq/uGwEawr3cOv/LUJXEYuIROr12JOGcvd8ID9Mn1NDGwduqKFuGjCtmvK5wPGNFWdtTh7YjZs+fQw/+8cHnDaoO5NOOqopVisi0qzVdThLYlyfN4jTB/XgtplLeH/jrmSHIyKSdEoihyE1xfjFpOF0yExn8hPvsme/zo+ISNumJHKYjuiYxS8njWDFliJun7kk2eGIiCSVkkgcTh/cg8lnD+KpuQU8M7+g7hlERFopJZE43XjuYE4e0I3vP7OYlVuKkh2OiEhSKInEKS01hV9dMYLMtBRueGI++w6UJjskEZEmpyTSAL06t+Pnlw1n2Yad3P33ZckOR0SkySmJNNA5x+Vw7RkD+eOc1Ty/aEOywxERaVJKIo3g5vOPY3i/Lnz36YWsLdyT7HBERJqMkkgjyEhL4TdXjARg8p/ns7+kLMkRiYg0DSWRRtKvWzY/ufhE3lu7nZ/OXp7scEREmoSSSCO64IReXHVqfx56/WNeXrYp2eGIiCSckkgju/XCIQzt1Yn//st7bNixN9nhiIgklJJII8tKT+U3nx/JgZIyvvnn+ZSU6vyIiLReSiIJ8KmeHfjR507gnVXb+OVLHyY7HBGRhFESSZAJI/owKbcf9+ev4PUPtyQ7HBGRhEh4EjGzVDObb2bPhc8DzewtM1thZk+aWUYozwyfV4T6ATHLuCWUv29m58eUjwtlK8xsSqK35XDdPn4Yg3p24NtPLmDzrvoOTS8i0nI0xZ7IjUDsM0HuAe5190HANuCaUH4NsC2U3xvaYWZDicZoHwaMA34bElMqcD9wATAUuCK0bTbaZaRy/5WjKCou4VvTF1BapmF1RaR1SWgSMbO+wGeIxkHHzAw4B5gRmjwKTAzTE8JnQv25of0EYLq7F7v7x0TjqZ8cXivcfaW77wemh7bNyjE5Hfnh+GH8+6Ot/PbVFckOR0SkUSV6T+SXwHeB8kuUugPb3b18SMACoE+Y7gOsBQj1O0L7g+VV5qmpvNm5LLcfE0b05t6XPuCtlVuTHY6ISKNJS9SCzeyzwGZ3n2dmeYlaTz1juQ64DiAnJ4f8/Pwmj2FcD2dOO+Nrj77FHae1o2OGxb2soqKipGxDc6S+qEz9UZn6o0Ki+iJhSQQ4DRhvZhcCWUAn4FdAFzNLC3sbfYF1of06oB9QYGZpQGdga0x5udh5aiqvxN2nAlMBcnNzPS8vr8EbF49+Q3bwud/+m2fWd+D3V+WSkhJfIsnPzydZ29DcqC8qU39Upv6okKi+SNjhLHe/xd37ulf2WdcAABRwSURBVPsAohPjr7j7lcCrwCWh2dXAs2F6ZvhMqH/F3T2UXx6u3hoIDAbeBt4BBoervTLCOmYmansaw/F9OvM/nx3CK8s38/C/Pk52OCIiDZaM+0S+B9xkZiuIznk8HMofBrqH8puAKQDuvgR4ClgKvADc4O6lYU9mMjCb6Oqvp0LbZu2LY/ozbtiR3PPCcuav2ZbscEREGiSRh7MOcvd8ID9MryS6sqpqm33ApTXMfzdwdzXls4BZjRhqwpkZ91xyIp+573UmPzGfWd88g87Z6ckOS0QkLrpjPQk6t0vn11eMZNPOfXzv6YVER+1ERFoeJZEkGXlUV7437jheWLKRP85ZnexwRETioiSSRNecPpBzjjuCu55bxuJ1O5IdjojIYVMSSaKUFONnlw6nW/sMJj/xLkXFJXXPJCLSjCiJJFm39hncd8VI1hTu4db/W6TzIyLSoiiJNAMnD+zGt887hpnvreepuWvrnkFEpJlQEmkmvn72IE4b1J3bZi7hg027kh2OiEi9KIk0E6kpxr2TRtAhM40bHn+XvftLkx2SiEidlESakSM6ZvHLSSNZsaWI22c2+5vvRUSURJqb0wf34Ia8QTw5dy1/nV/t8yRFRJoNJZFm6FvnDeakAV35/jOLWLmlKNnhiIjUSEmkGUpLTeG+K0aSkZbC5Cfms++Azo+ISPOkJNJM9ercjp9fNpylG3byo1nL6p5BRCQJlESasXOOy+HaMwby2JureX7RhmSHIyJyCCWRZu7m849jeL8ufPfphawt3JPscEREKlESaeYy0lL4zRUjAZj85/nsLylLckQiIhWURFqAft2yuefiE3lv7XZ+Ont5ssMRETkoYUnEzLLM7G0ze8/MlpjZD0P5I2b2sZktCK8RodzM7D4zW2FmC81sVMyyrjazD8Pr6pjy0Wa2KMxzn5lZorYn2S48oRdfHNOfh17/mAWb9bRfEWkeErknUgyc4+7DgRHAODMbE+pudvcR4bUglF0ADA6v64AHAMysG3AbcArRsLq3mVnXMM8DwLUx841L4PYk3fc/M4QhvTrx+0XFbNixN9nhiIgkLol4pPxOufTwqu055xOAx8J8c4AuZtYLOB940d0L3X0b8CJRQuoFdHL3OR49P/0xYGKitqc5yEpP5f7Pj+RAGdz45wWUlOr8iIgkV1oiF25mqcA8YBBwv7u/ZWbXA3eb2Q+Al4Ep7l4M9AFin4NeEMpqKy+opry6OK4j2rshJyeH/Pz8hm9cEl1+tPPoB4V8e9pLXDw4I9nhJFVRUVGL//dsTOqPytQfFRLVFwlNIu5eCowwsy7AM2Z2PHALsBHIAKYC3wPuSHAcU8O6yM3N9by8vESurgnks7dTV/4yr4BJeaM4fXCPZAeUNPn5+bT8f8/Go/6oTP1RIVF90SRXZ7n7duBVYJy7bwiHrIqBPxCd5wBYB/SLma1vKKutvG815W3C7eOHMahnB7715AI279qX7HBEpI1K5NVZPcMeCGbWDvg0sDycyyBcSTURWBxmmQlcFa7SGgPscPcNwGxgrJl1DSfUxwKzQ91OMxsTlnUV8Gyitqe5yc5I4/4rR1FUfIBvP7mA0jINqysiTS+ReyK9gFfNbCHwDtHJ8eeAx81sEbAI6AHcFdrPAlYCK4CHgK8DuHshcGdYxjvAHaGM0Ob3YZ6PgOcTuD3NzjE5Hfnh+GG8sWIrD+SvSHY4ItIGJeyciLsvBEZWU35ODe0duKGGumnAtGrK5wLHNyzSlu2y3H78+6Ot/OLFDzh5YHdOHtgt2SGJSBuiO9ZbODPj7otO4Khu2Xzzz/Mp3L0/2SGJSBuiJNIKdMhM4zefH0Xh7v185y/vUabzIyLSRJREWonj+3Tm+58ZwivLN/Pwvz5Odjgi0kYoibQiV53an/OH5XDPC8tZsHZ7ssMRkTZASaQVMTN+cvFwcjplMfmJd9mx90CyQxKRVk5JpJXpnJ3Orz8/ko079jHl6YVEF72JiCSGkkgrNOqornx33LE8v3gjf5qzOtnhiEgrpiTSSn3l9E9x9rE9ufO5ZSxZvyPZ4YhIK6Uk0kqlpBg/v2wEXdunM/mJ+RQVayArEWl8SiKtWLf2Gdx3+UhWb93N959ZpPMjItLolERauVM+1Z1vn3cMzy5Yz1/mFtQ9g4jIYVASaQO+fvYgThvUnR/MXMwHm3YlOxwRaUWURNqA1BTj3kkj6JCZxg2Pv8ve/aXJDklEWgklkTbiiI5Z3DtpBCu2FHH7zCXJDkdEWomEDo8rzcsZg3vy9byjuf/Vj5i7upD+3dtzVLds+nfPPvjet2s2WempyQ5VRFoIJZE25tvnHUN2RhoLC7azeuse5qzcyp4qh7eO7JTFUd2z6R8SS79u2fTv3p7+3bLpkp1ONJCkiEgCk4iZZQGvAZlhPTPc/TYzGwhMB7oD84Avuvt+M8sEHgNGA1uBSe6+KizrFuAaoBT4prvPDuXjgF8BqcDv3f3Hidqe1iItNYUbzh508LO7s3X3flZv3cOawt2s2bqX1YW7WbN1D//8YAubdxVXmr9jZlqUYMqTS7f2B/dkenXOIi1VR0hF2pJE7okUA+e4e5GZpQP/MrPngZuAe919upk9SJQcHgjv29x9kJldDtwDTDKzocDlwDCgN/CSmR0T1nE/0djtBcA7ZjbT3ZcmcJtaHTOjR4dMenTIZHT/rofU791fyprCPawp3MPqrbvD+x6Wb9jFi0s3caC04t6TtBSjb9d2HNW9PUd1a0f/bu05KiSYo7pl0z5TO74irU0ih8d1oCh8TA8vB84BPh/KHwVuJ0oiE8I0wAzgNxYdN5kATHf3YuBjM1sBnBzarXD3lQBmNj20VRJpRO0yUjn2yI4ce2THQ+pKy5wNO/ZGSWbrHlaHZLNm6x4WrNnGzn2V75Lv0SEzSi7hXMzB8zHds+nZIVOHyURaoIT+NDSzVKJDVoOI9ho+Ara7e/m3SwHQJ0z3AdYCuHuJme0gOuTVB5gTs9jYedZWKT+lhjiuA64DyMnJIT8/v0HblWxFRUXNbhuOBI7MglN6E+0vksnuAxls3lPG5j3Olj1lbN5byuainby2eQeF+5zY++czUuGIdkbP7BSOyDZ6tovej8hOoUc7Iy2l+gTTHPsimdQflak/KiSqLxKaRNy9FBhhZl2AZ4DjErm+WuKYCkwFyM3N9by8vGSE0Wjy8/Np6dtQXFJKwba9rNm65+AhsjWF0eGyf67bw74DFXsxKQa9Orc7eO4lOukfnYvZvfTdFt8Xjak1/G00JvVHhUT1RZMcpHb37Wb2KnAq0MXM0sLeSF9gXWi2DugHFJhZGtCZ6AR7eXm52HlqKpdmLjMtlaN7duDonh0OqXN3Nu8qrkguW3cfPFT24tJNbN29v1L777/5D/p3K7+KLEow5dNHdsoipYa9GBFpuERendUTOBASSDuiE+D3AK8ClxBdoXU18GyYZWb4/Gaof8Xd3cxmAk+Y2S+IDpQMBt4GDBgcrvZaR3Tyvfxci7RgZkZOpyxyOmVx0oBuh9Tv2neAtYV7WVO4m1feWUR6l16sKdzDwoIdPL94I6VlFQfKMlJT6NutXbhcufK5mH7ddE+MSEMlck+kF/BoOC+SAjzl7s+Z2VJgupndBcwHHg7tHwb+GE6cFxIlBdx9iZk9RXTCvAS4IRwmw8wmA7OJLvGd5u66FbsN6JiVztDe6Qzt3YmsT94nL++Eg3UlpWWs376P1YW7Wb11D2vD3szqwj28/XEhu6vcE5PTKbPSVWQVN162p6vuiRGpUyKvzloIjKymfCUVV1fFlu8DLq1hWXcDd1dTPguY1eBgpdVIS02JEkL3bM4YXLnO3SncvZ/VhTHJJSSa1z/cwqadle+J6ZCZVimxlJ+LOapbNr276J4YEdAd69KGmBndO2TSvUMmo46q/p6YtdtiLlcO98W8v2kXLy/bzP7SsoNt01KMPl3bHTw81qtzFlnpqWSmpZAZ3rPq+a5kJC2ZkohI0C4jlWNyOnJMTvX3xGzaua/SVWSrw5Vlf1+0ge17DsS93tQUIyskn6yYJBT7ufJ7CllpqZXfwzwfrS9h3+INZIbyzLRUsmp4T081Ha6TBlMSEamH1BSjd5d29O7SjlOP7n5IfXFJKcUlZRQfKGPfgWi6/L24yue63quW7dh7gM3VtN13oJSy6garXPhuvbYpxag1yWTGvB+StA6+h+RW0zJi9rgOJse0FCWvVkRJRKQRRF+YqZDVtOs9UFo56bz+xpucODKX4pJS9h0oq/ReXOXzIfVVklRRcQmfFO2vdt7Yx93Eoz6H+VJTjNQUIyXFSLUwbUaKUW15agqklE9bVL929X4Wl31Yqa2ZkVplGZXro7qq5dGyqSg/uN7ythz8XLW8fNqqKY9ta0aLS7BKIiItWHpqCumpKXQIzyU7sn0KQ3t3Svh6S8u8xkRV555WHXtgew+Usm3PfkrLPHq5U3bwHco8Ki9/j6Y52Na9ogyAFR8kvD8a08EkWSnhlCenahJVilWaJyUm6aXGlO/csZdTTy+Nfuw0IiURETlsqSlGdkYa2RnJjqRm7s6r+fmcfsZZlRJPWRmUVpuIKpJR1fJD6kPCqqiPyt0PLY9tW57gSr1y+cEkGVNeViWJljnVlpcv65DkWr6s8vU4GI2/l6MkIiKtkoVf5RlpuvoNoseeJKIv1LsiIhI3JREREYmbkoiIiMRNSUREROKmJCIiInFTEhERkbgpiYiISNyUREREJG7m3rBn4LQ0ZrYFWJ3sOBqoB/BJsoNoJtQXlak/KlN/VGhoX/R3955VC9tcEmkNzGyuu+cmO47mQH1RmfqjMvVHhUT1hQ5niYhI3JREREQkbkoiLdPUZAfQjKgvKlN/VKb+qJCQvtA5ERERiZv2REREJG5KIiIiEjclkWbKzMaZ2ftmtsLMplRTf5OZLTWzhWb2spn1T0acTaWu/ohpd7GZuZm16ss669MfZnZZ+BtZYmZPNHWMTaUe/1eOMrNXzWx++P9yYTLibApmNs3MNpvZ4hrqzczuC3210MxGNXilHsYk1qv5vIBU4CPgU0AG8B4wtEqbs4HsMH098GSy405mf4R2HYHXgDlAbrLjTvLfx2BgPtA1fD4i2XEnsS+mAteH6aHAqmTHncD+OBMYBSyuof5C4HnAgDHAWw1dp/ZEmqeTgRXuvtLd9wPTgQmxDdz9VXffEz7OAfo2cYxNqc7+CO4E7gH2NWVwSVCf/rgWuN/dtwG4++YmjrGp1KcvHOgUpjsD65swvibl7q8BhbU0mQA85pE5QBcz69WQdSqJNE99gLUxnwtCWU2uIfp10VrV2R9ht7yfu/+9KQNLkvr8fRwDHGNmb5jZHDMb12TRNa369MXtwBfMrACYBXyjaUJrlg73u6VOaQ0KR5LOzL4A5AJnJTuWZDGzFOAXwJeSHEpzkkZ0SCuPaC/1NTM7wd23JzWq5LgCeMTdf25mpwJ/NLPj3b0s2YG1BtoTaZ7WAf1iPvcNZZWY2XnA94Hx7l7cRLElQ1390RE4Hsg3s1VEx3pntuKT6/X5+ygAZrr7AXf/GPiAKKm0NvXpi2uApwDc/U0gi+hhhG1Rvb5bDoeSSPP0DjDYzAaaWQZwOTAztoGZjQR+R5RAWuvx7nK19oe773D3Hu4+wN0HEJ0jGu/uc5MTbsLV+fcB/JVoLwQz60F0eGtlUwbZROrTF2uAcwHMbAhREtnSpFE2HzOBq8JVWmOAHe6+oSEL1OGsZsjdS8xsMjCb6OqTae6+xMzuAOa6+0zgp0AH4C9mBrDG3ccnLegEqmd/tBn17I/ZwFgzWwqUAje7+9bkRZ0Y9eyL/wYeMrNvE51k/5KHS5VaGzP7M9GPhx7hHNBtQDqAuz9IdE7oQmAFsAf4coPX2Ur7UkREmoAOZ4mISNyUREREJG5KIiIiEjclERERiZuSiIiIxE1JRERE4qYkItKEzCzTzF4yswVmNimO+Sea2dBExCYSD91sKNK0RgK4+4g4558IPAcsre8MZpbm7iVxrk+kVtoTEQHMbICZLTezR8zsAzN73MzOC0/B/dDMTg6vN8PgRv82s2PDvN82s2lh+gQzW2xm2dWs4wjgT8BJYU/kaDMbbWb/NLN5Zja7/LHcZnatmb1jZu+Z2dNmlm1m/wGMB34aM39++TPCzKxHeHYYZvYlM5tpZq8AL4eym8MyF5rZD0NZezP7e1jP4nj2jqSNS/YgKnrp1RxewACgBDiB6MfVPGAa0eA9E4ieRdUJSAvtzwOeDtMpRINhXQTMBU6rZT15wHNhOh34N9AzfJ5E9NgOgO4x89wFfCNMPwJcElOXTxiAi+ihgqvC9JeIHsLYLXweSzQ4k4V4nyMawOhi4KGY5XVO9r+FXi3rpcNZIhU+dvdFAGa2BHjZ3d3MFhElmc7Ao2Y2mOgZTOXPJCozsy8BC4Hfufsb9VzfsURPH34xPP8sFSh/GN7xZnYX0IXoGWmz49ieF929fICiseE1P3zuQPRU39eBn5vZPUTJ7fU41iNtmJKISIXYx+mXxXwuI/q/cifwqrtfZGYDiPYCyg0GioDeh7E+A5a4+6nV1D0CTHT390KCyqthGSVUHJbOqlK3u8q6/tfdf3dIENGAXhcCd5nZy+5+R723QNo8nRMRqb/OVIy98KXyQjPrDNxHdHiou5ldUs/lvQ/0DAMlYWbpZjYs1HUENphZOnBlzDy7Ql25VcDoMF3bemcD/2VmHcK6+pjZEWbWG9jj7n8iejL0qHrGLgIoiYgcjp8A/2tm86m8F38v0XjmHxANgPTjcBK9Vh6NCX4JcI+ZvQcsAP4jVP8/4C3gDWB5zGzTgZvDyf2jgZ8B14eYahxoyd3/ATwBvBkOz80gSkYnAG+b2QKix4bfVVfcIrH0KHgREYmb9kRERCRuOrEukgBm9mXgxirFb7j7DcmIRyRRdDhLRETipsNZIiISNyURERGJm5KIiIjETUlERETi9v8BOZsuzLJlkQ0AAAAASUVORK5CYII=\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "plot_fitting_graph(max_features, rmse_train, rmse_valid, metric_name='RMSE', xlabel='max_features')"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "0.5"
      ]
     },
     "execution_count": null,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "max_features[np.argmin(rmse_valid)]"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "rf = RandomForestRegressor(n_estimators=100, max_depth=32, min_samples_leaf=5, max_features=0.5, n_jobs=-1)\n",
    "results = cross_validate(rf, X, y,\n",
    "                         cv=5,\n",
    "                         return_train_score=True,\n",
    "                         scoring='neg_root_mean_squared_error')"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "Train score: 28674.0\n",
      "Validation score: 58935.2\n"
     ]
    }
   ],
   "source": [
    "print('Train score: %.1f' % -np.mean(results['train_score']))\n",
    "print('Validation score: %.1f' % -np.mean(results['test_score']))"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "We see that we improved the RMSE on the validation set by more than $2000 which corresponds to 3-4% improvement!"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Part 3: Churn\n",
    "Now we want to follow the same procedure to optimise the parameters of the Random Forest classifier on the churn dataset. Since this is a classification task there are two things we need to change in our code:\n",
    "\n",
    "1. We replace the `RandomForestRegressor` with the `RandomForestClassifier``\n",
    "2. During cross-validation we want to measure the accuracy instead of the RMSE."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "Dataset already exists at '../data/churn.csv' and is not downloaded again.\n"
     ]
    }
   ],
   "source": [
    "get_dataset('churn.csv')"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "churn_data = pd.read_csv(DATA/'churn.csv')"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "X, y, nas = proc_df(churn_data, \"Churn\")"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "Train score: 1.000\n",
      "Validation score: 0.794\n"
     ]
    }
   ],
   "source": [
    "rf = RandomForestClassifier(n_jobs=-1)\n",
    "results = cross_validate(rf, X, y,\n",
    "                         cv=5,\n",
    "                         return_train_score=True,\n",
    "                         scoring='accuracy')\n",
    "print('Train score: %.3f' % np.mean(results['train_score']))\n",
    "print('Validation score: %.3f' % np.mean(results['test_score']))"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "We see that we have about 79% accuracy on the validation set. Let's see if we can improve on that."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### n_estimators"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "100%|██████████| 4/4 [00:15<00:00,  3.83s/it]\n"
     ]
    }
   ],
   "source": [
    "acc_train = []\n",
    "acc_valid = []\n",
    "\n",
    "n_estimators = [25, 50, 100, 200]\n",
    "for n in tqdm(n_estimators):\n",
    "    rf = RandomForestClassifier(n_estimators=n, n_jobs=-1)\n",
    "    results = cross_validate(rf, X, y,\n",
    "                             cv=5,\n",
    "                             return_train_score=True,\n",
    "                             scoring='accuracy')\n",
    "    \n",
    "    # we average the scores and append them to the list\n",
    "    acc_train.append(np.mean(results['train_score']))\n",
    "    acc_valid.append(np.mean(results['test_score']))"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYgAAAEXCAYAAAC3c9OwAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8li6FKAAAgAElEQVR4nO3de5QV5Z3u8e/TTUODIFfFC2hjQhRQRwXv0TQTx6BRMYmKOerETDyeZGkSzWTm6MpFx5jEzGTOWePS0TEZBjPRoMGTHDJjDtEMPThREyEqIqigQW0QRYyGNiBN9+/8UdWwu3m72X3ZvXvD81lrr656662qZxdN/bqq9q5SRGBmZtZRVbkDmJnZwOQCYWZmSS4QZmaW5AJhZmZJLhBmZpbkAmFmZkkuELZXkHSIpCZJ1d2Y5zRJz5cyV3+RFJLeX+4cVllcIGyPImmtpC15MWh7HRQRr0TE8Ihoyfs1SLqiw7ztdqIR8UhEHN7f78FsoHCBsD3RuXkxaHutL3eg3pA0qNwZbO/kAmF7BUl1+RHCIEnfBE4DbsuPMG6TtCTv+nTeNkdSvaTGgmWslfRlScslvSPpPkm1BdP/WtJrktZLuqKr0zqSJklaImmzpIcl3S7phx2yfkbSK8B/5O0/lrQhX/cSSdMKljdP0p2SHsqX+Z+SDu2w2jMkrZb0dr4+9cnGtT2WC4TtdSLiK8AjwNX5EcbVEXF6PvlP8rb7Opn9ImAWMAk4GrgcQNIs4EvAGcD7gfrdxLgX+A0wFrgRuCzR50PAFOAj+fjPgcnA/sBvgXs69L8E+AYwDngqMf0c4Pg890UFyzVLcoGwPdFP87+S35b00z5e9q0RsT4i3gJ+BhyTt18E/EtEPBsRfyTb6SdJOoRsR/31iNgWEf8FLEx0vTEi3o2ILQARMTciNkfEe/ny/0TSyIL+/x4RS/LpXwFOljSxYPotEfF2RLwCLC7IbpbkAmF7ovMjYlT+Or+Pl72hYPiPwPB8+CDg1YJphcMdHQS8lReSrvrvaJNULekWSS9K+gOwNp80LtU/IpqAt/J17S67WZILhO2t+vo2xq8BEwrGJ3bWMe87RtKw3fQvzPjfgNlkp7BGAnV5e+F1hB3LkDQcGANU9AV6Ky8XCNtbvQ4cVkRbse4HPi1pSr7j/1pnHSPiZWApcKOkwZJOBs7dzfJHAO8Bm4BhwLcSfc6W9EFJg8muRTweEV0dyZh1yQXC9lb/AFwg6feSbs3bbgTuzq9dXNSdhUXEz4Fbyc7trwEezye918kslwAnk+3wbwbu66IvwA+Al4F1wMqC5Re6F7iB7NTSdODS7rwHs47kBwaZ9T1JU4AVwJCI2F5E//uA5yLihh6ubx7QGBFf7cn8Zik+gjDrI5I+JmmIpNHAd4CfdVYcJB0v6X2SqvKPyM4G+voTV2a94gJh1nf+B/AG8CLQAnyui74HAA1AE9mpqc9FxJOlDmjWHT7FZGZmST6CMDOzpD3mJmDjxo2Lurq6Hs//7rvvss8++/RdoBKqpKxQWXkrKStUVt5KygqVlbc3WZctW/ZmROyXnBgRe8Rr+vTp0RuLFy/u1fz9qZKyRlRW3krKGlFZeSspa0Rl5e1NVmBpdLJf9SkmMzNLcoEwM7MkFwgzM0tygTAzsyQXCDMzSypZgZA0V9IbklZ0Ml2SbpW0Jn+E43EF0z6VPxpxtaRPlSqjmZl1rpRHEPPIHs3YmbPIHp84GbgSuANA0hiyO1KeCJwA3JDf28bMzPpRyb4oFxFLJNV10WU28IP8c7iPSxol6UCyZ/k+FNkjHZH0EFmh+VGpsu7Jss8zZ0+eiQhaA4K8rXAYaM37Evlw2/z5NDr0i8Ll58tqjZ3zRD68bnMrz2/YXDDfrutvLZiHHctpnzm1/p252pZTuP7CnB3eU4ccbdOea2zmjSf65hEK0YfPJOrsjjjPv9rMht+80v3l9TJPu2UVubAXXm1m/a93n7U/tlsxXnilmcbHX965rD7I004f3uZow4btu30Iek+U85vUB9P+MYuNeVtn7buQdCXZ0Qfjx4+noaGhx2Gampp6NT9kO57mVtjWAs2twXst0NwK77UEzS35z1bY1hJsa4Ft7Ybzn+3m3dm2rSV29N/eGsRD/06+L925M85ztOYDA+ouW79aUu4ExVuxvNwJuufZZ8qdoHiVlBVgZfIM+YBTNyI4vpf7r5SKvtVGRNwF3AUwY8aMqK+v7/Yytja38MtVb/D0uhXU7TeJLdtaeG97K1u2tbC1uYUtzS1sbW5la3PheAtbmlt5r914Nl9P/iioEtTWVDO0pprammpqa6qoralmWE01Yzq0Da2p5vXX1nHIxIlIICn7SfazqmBYtJ9eJXbMk613Z7+2YfJ5qgrmr8oG2vXLm7LlF85TuP582qqVKznyyGk75mFHlnyZVdk8dMjSlpl27y/13gozt627/XDVjpztM3d877/+9eOcfPLJ3f9H7IR236X4ZSUW9thjj/U4r/owXSpbR48++iinnHJKccvrZZ6+WFgqb19uMyhuuxXj8UcfpSf7v90pZ4FYR/vn8E7I29ZBu6OlCWS3RS6Jd9/bzlX3/jYbeWbnXwud7bSH1lQzbPAgxuyTtbVNHzq4mtpBVdQOrqZ2UFtbVTactw0d3H6etuUOrq7asdMuRkPDm9TXT+3rTVEyI37/AvVHHVjuGEV5cWgVB48aWu4YRRtTW8WBIysj7+jaKsbvW1vuGEUbNaSK/UdURt7hg/u2cLUpZ4FYCFwtaT7ZBel3IuI1SYuAbxVcmD4TuL5UIUYNG8z/u+Y0lv92KR/64Ck93mmbme1pSlYgJP2I7EhgnKRGsk8m1QBExJ3Ag8DZZM/v/SPw6XzaW5K+ATyRL+qmtgvWpVBdJY44YF82DKusv27MzEqtlJ9i+uRupgdwVSfT5gJzS5HLzMyK429Sm5lZkguEmZkluUCYmVmSC4SZmSW5QJiZWZILhJmZJblAmJlZkguEmZkluUCYmVmSC4SZmSW5QJiZWZILhJmZJblAmJlZkguEmZkluUCYmVmSC4SZmSW5QJiZWZILhJmZJblAmJlZkguEmZkluUCYmVmSC4SZmSW5QJiZWZILhJmZJblAmJlZkguEmZkluUCYmVmSC4SZmSW5QJiZWZILhJmZJblAmJlZkguEmZkluUCYmVmSC4SZmSW5QJiZWZILhJmZJblAmJlZkguEmZkllbRASJol6XlJayRdl5h+qKRfSlouqUHShIJpLZKeyl8LS5nTzMx2NahUC5ZUDdwO/BnQCDwhaWFErCzo9l3gBxFxt6Q/Bb4NXJZP2xIRx5Qqn5mZda2URxAnAGsi4qWI2AbMB2Z36DMV+I98eHFiupmZlUkpC8TBwKsF4415W6GngY/nwx8DRkgam4/XSloq6XFJ55cwp5mZJSgiSrNg6QJgVkRckY9fBpwYEVcX9DkIuA2YBCwBPgEcGRFvSzo4ItZJOozsKOPDEfFih3VcCVwJMH78+Onz58/vcd6mpiaGDx/e4/n7UyVlhcrKW0lZobLyVlJWqKy8vck6c+bMZRExIzkxIkryAk4GFhWMXw9c30X/4UBjJ9PmARd0tb7p06dHbyxevLhX8/enSsoaUVl5KylrRGXlraSsEZWVtzdZgaXRyX61lKeYngAmS5okaTBwMdDu00iSxklqy3A9MDdvHy1pSFsf4FSg8OK2mZmVWMkKRERsB64GFgGrgPsj4llJN0k6L+9WDzwv6QVgPPDNvH0KsFTS02QXr2+J9p9+MjOzEivZx1wBIuJB4MEObV8vGF4ALEjM9yhwVCmzmZlZ1/xNajMzS3KBMDOzJBcIMzNLcoEwM7MkFwgzM0tygTAzsyQXCDMzS3KBMDOzJBcIMzNLcoEwM7MkFwgzM0tygTAzsyQXCDMzS3KBMDOzJBcIMzNLcoEwM7MkFwgzM0tygTAzsyQXCDMzS3KBMDOzJBcIMzNLcoEwM7MkFwgzM0tygTAzsyQXCDMzS3KBMDOzpN0WCEmflzS6P8KYmdnAUcwRxHjgCUn3S5olSaUOZWZm5bfbAhERXwUmA/8MXA6slvQtSe8rcTYzMyujoq5BREQAG/LXdmA0sEDS35Ywm5mZldGg3XWQ9EXgz4E3ge8DfxURzZKqgNXAX5c2oplZaTQ3N9PY2MjWrVt3mTZy5EhWrVpVhlTdV0zW2tpaJkyYQE1NTdHL3W2BAMYAH4+IlwsbI6JV0jlFr8nMbIBpbGxkxIgR1NXV0fHy6ubNmxkxYkSZknXP7rJGBJs2baKxsZFJkyYVvdxiTjH9HHirbUTSvpJOzFdaGeXVzCxh69atjB07dpfisKeRxNixY5NHSl0ppkDcATQVjDflbWZmFW9PLw5tevI+iykQyi9SA9mpJYo7NWVmZl14++23+cd//Mduz3f22Wfz9ttvlyBRe8UUiJckfUFSTf76IvBSqYOZme3pOisQ27dv73K+Bx98kFGjRpUq1g7FFIjPAqcA64BG4ETgylKGMjPbG1x33XW8+OKLHHPMMRx//PGcdtppnHfeeUydOhWA888/n+nTpzNt2jTuuuuuHfPV1dXx5ptvsnbtWqZMmcLnP/95pk2bxplnnsmWLVv6LN9uTxVFxBvAxX22RjOzAehvfvYsK9f/Ycd4S0sL1dXVvVrm1IP25YZzp3U6/ZZbbmHFihU89dRTNDQ08NGPfpQVK1bs+KTR3LlzGTNmDFu2bOH444/nE5/4BGPHjm23jNWrV/P973+fefPmcdFFF/HAAw9w6aWX9ip3m2K+B1ELfAaYBtS2tUfEX/RJAjMzA+CEE05o9zHUW2+9lZ/85CcAvPrqq6xevXqXAjFp0iSOPvpoAKZPn87atWv7LE8xF5v/FXgO+AhwE3AJUNTHWyXNAv4BqAa+HxG3dJh+KDAX2I/so7SXRkRjPu1TwFfzrjdHxN3FrNPMrCc6/qVfju9B7LPPPjuGGxoaePjhh3nssccYNmwY9fX1yY+pDhkyZMdwdXV1n55iKuYaxPsj4mvAu/lO+qNk1yG6JKkauB04C5gKfFLS1A7dvgv8ICKOJis+387nHQPckK/nBOAG31HWzPY0I0aMYPPmzclp77zzDqNHj2bYsGE899xzPP744/2crrgjiOb859uSjiS7H9P+Rcx3ArAmIl4CkDQfmA2sLOgzFfhSPrwY+Gk+/BHgoYh4K5/3IWAW8KMi1mtmVhHGjh3LqaeeypFHHsnQoUMZP378jmmzZs3izjvvZMqUKRx++OGcdNJJ/Z5PBV9xSHeQrgAeAI4C5gHDga9FxD/tZr4LgFkRcUU+fhlwYkRcXdDnXuDXEfEPkj6er2cc8GmgNiJuzvt9DdgSEd/tsI4ryT9RNX78+Onz588v9n3voqmpieHDh/d4/v5USVmhsvJWUlaorLwDMevIkSN5//vfn5zWFxep+0uxWdesWcM777zTrm3mzJnLImJGqn+XRxD5Dfn+EBG/B5YAhxWduDhfBm6TdHm+/HVAS7EzR8RdwF0AM2bMiPr6+h4HaWhooDfz96dKygqVlbeSskJl5R2IWVetWtXpdYY96V5MbWprazn22GOLXm6X1yDyb0339G6t64CJBeMT8rbC5a+PiI9HxLHAV/K2t4uZ18zMSquYi9QPS/qypImSxrS9ipjvCWCypEmSBpN9l2JhYQdJ4/KjFIDryT7RBLAIOFPS6Pzi9Jl5m5mZ9ZNiLlLPyX9eVdAW7OZ0U0Rsl3Q12Y69GpgbEc9KuglYGhELgXrg25KC7BTTVfm8b0n6BlmRAbip7YK1mZn1j2K+SV38zcN3nfdB4MEObV8vGF4ALOhk3rnsPKIwM7N+Vsw3qf881R4RP+j7OGZmNlAUcw3i+ILXacCNwHklzGRmZgltHxNev349F1xwQbJPfX09S5cu7ZP1FXOK6fOF45JGAT3/woGZmfXKQQcdxIIFybPzfaonD/55F+jxdQkzM8tcd911TJw4kauuyj4DdOONNzJo0CAWL17M73//e5qbm7n55puZPXt2u/nWrl3LOeecw4oVK9iyZQuXX345K1eu5Igjjujf231L+hnZp5YgOyU1Fbi/zxKYmQ0EP78ONjyzY3Roy3ao7uXDMw84Cs66pdPJc+bM4ZprrtlRIO6//34WLVrEF77wBfbdd1/efPNNTjrpJM4777xOHxl6xx13MGzYMFatWsXy5cs57rjjepe5QDHvvvD2FtuBl9vuuGpmZj137LHH8sYbb7B+/Xo2btzI6NGjOeCAA7j22mtZsmQJVVVVrFu3jtdff50DDjgguYwlS5ZwxRVXAHD00UfvuPV3XyimQLwCvBYRWwEkDZVUFxFr+yyFmVm5dfhLf0s/3WrjwgsvZMGCBWzYsIE5c+Zwzz33sHHjRpYtW0ZNTQ11dXXJ23z3h2I+xfRjoLVgvCVvMzOzXpozZw7z589nwYIFXHjhhbzzzjvsv//+1NTUsHjxYl5++eUu5z/99NP58Y+zXfKKFStYvnx5n2Ur5ghiUERsaxuJiG35rTPMzKyXpk2bxubNmzn44IM58MADueSSSzj33HM56qijmDFjBkcccUSX83/uc5/j0ksvZcqUKUyZMoXp06f3WbZiCsRGSeflt8ZA0mzgzT5LYGa2l3vmmZ0Xx8eNG8djjz2W7NfU1ARAXV0dK1asAGDo0KHMmzevJKfDiikQnwXukXRbPt4IJL9dbWZme45ivij3InCSpOH5eFPJU5mZWdnt9iK1pG9JGhURTRHRlN+C++b+CGdmZuVTzKeYzsof4gNA/nS5s0sXycys/+zusct7ip68z2IKRLWkIW0jkoYCQ7rob2ZWEWpra9m0adMeXyQigk2bNlFbW9ut+Yq5SH0P8EtJ/wIIuBy4u9sJzcwGmAkTJtDY2MjGjRt3mbZ169Zu71DLpZistbW1TJgwoVvLLeYi9XckPQ2cQXZPpkXAod1ai5nZAFRTU8OkSel7jzY0NHDsscf2c6KeKVXWYk4xAbxOVhwuBP4UWNXnSczMbEDp9AhC0geAT+avN4H7AEXEzH7KZmZmZdTVKabngEeAcyJiDYCka/sllZmZlV1Xp5g+DrwGLJb0PUkfJrtIbWZme4FOC0RE/DQiLgaOABYD1wD7S7pD0pn9FdDMzMpjtxepI+LdiLg3Is4FJgBPAv+z5MnMzKysiv0UE5B9izoi7oqID5cqkJmZDQzdKhBmZrb3cIEwM7MkFwgzM0tygTAzsyQXCDMzS3KBMDOzJBcIMzNLcoEwM7MkFwgzM0tygTAzsyQXCDMzS3KBMDOzJBcIMzNLcoEwM7OkkhYISbMkPS9pjaTrEtMPkbRY0pOSlks6O2+vk7RF0lP5685S5jQzs1119UzqXpFUDdwO/BnQCDwhaWFErCzo9lXg/oi4Q9JU4EGgLp/2YkQcU6p8ZmbWtVIeQZwArImIlyJiGzAfmN2hTwD75sMjgfUlzGNmZt2giCjNgqULgFkRcUU+fhlwYkRcXdDnQOAXwGhgH+CMiFgmqQ54FngB+APw1Yh4JLGOK4ErAcaPHz99/vz5Pc7b1NTE8OHDezx/f6qkrFBZeSspK1RW3krKCpWVtzdZZ86cuSwiZiQnRkRJXsAFwPcLxi8DbuvQ50vAX+bDJwMryY5qhgBj8/bpwKvAvl2tb/r06dEbixcv7tX8/amSskZUVt5KyhpRWXkrKWtEZeXtTVZgaXSyXy3lKaZ1wMSC8Ql5W6HPAPcDRMRjQC0wLiLei4hNefsy4EXgAyXMamZmHZSyQDwBTJY0SdJg4GJgYYc+rwAfBpA0haxAbJS0X36RG0mHAZOBl0qY1czMOijZp5giYrukq4FFQDUwNyKelXQT2SHNQuAvge9JupbsgvXlERGSTgduktQMtAKfjYi3SpXVzMx2VbICARARD5J9dLWw7esFwyuBUxPzPQA8UMpsZmbWNX+T2szMklwgzMwsyQXCzMySXCDMzCzJBcLMzJJcIMzMLMkFwszMklwgzMwsyQXCzMySXCDMzCzJBcLMzJJcIMzMLMkFwszMklwgzMwsyQXCzMySXCDMzCzJBcLMzJJcIMzMLMkFwszMklwgzMwsyQXCzMySXCDMzCzJBcLMzJJcIMzMLMkFwszMklwgzMwsyQXCzMySXCDMzCzJBcLMzJJcIMzMLMkFwszMklwgzMwsyQXCzMySXCDMzCzJBcLMzJJcIMzMLMkFwszMklwgzMwsqaQFQtIsSc9LWiPpusT0QyQtlvSkpOWSzi6Ydn0+3/OSPlLKnGZmtqtBpVqwpGrgduDPgEbgCUkLI2JlQbevAvdHxB2SpgIPAnX58MXANOAg4GFJH4iIllLlNTOz9kp5BHECsCYiXoqIbcB8YHaHPgHsmw+PBNbnw7OB+RHxXkT8DliTL8/MzPqJIqI0C5YuAGZFxBX5+GXAiRFxdUGfA4FfAKOBfYAzImKZpNuAxyPih3m/fwZ+HhELOqzjSuBKgPHjx0+fP39+j/M2NTUxfPjwHs/fnyopK1RW3krKCpWVt5KyQmXl7U3WmTNnLouIGalpJTvFVKRPAvMi4u8lnQz8q6Qji505Iu4C7gKYMWNG1NfX9zhIQ0MDvZm/P1VSVqisvJWUFSorbyVlhcrKW6qspSwQ64CJBeMT8rZCnwFmAUTEY5JqgXFFzmtmZiVUymsQTwCTJU2SNJjsovPCDn1eAT4MIGkKUAtszPtdLGmIpEnAZOA3JcxqZmYdlOwIIiK2S7oaWARUA3Mj4llJNwFLI2Ih8JfA9yRdS3bB+vLILoo8K+l+YCWwHbjKn2AyM+tfJb0GEREPkn10tbDt6wXDK4FTO5n3m8A3S5nPzMqotRWiBVpbOvwssj1a8+HWRN/etx/y8hr4zydKuM7uvM+u+x4zbBLUP9rn/0TlvkhtNrBF9G5n0K5Pd3aIxa1z4iurYcnSfl1n93fWWd/Ttm+DR9jZPsAdBvC7ggZVg6qgqjobrkqNV0NVVYfxLtqrBsGgIYn+Bcttt47UsqvYuHEbo0qwDVwgeiICWrdDSzO0bMuHt+XjzdCat7fk7cnx5iLmaU6uY9obG2DD97IcxM5MRBdttJ++SxtF9utOW9Yyo2kzrNynG1m7aqMH83aVtf02OG17M/wX7Xd8A9j7AF7q0Fjszqk7O7dBg3u5E6tm3bp1HHJIXS+ydX+dvWlf8sivOL1+5s72AWxdQwOTS7BcF4g/vgU//hTHvPUmrB5W/A6/lFQF1YOhqgaq216Ds782qgczdMtWeGszSIBAO2YsaNOubdBhemdt2vkfotvzdmyDrds3MXzMfgXTishadFvfvvf1jY1MPOTQPtrR9HDH1432Jf/1KKd/qL6gfccGGXBeamjgkAr52ChAa/Xg7P/eXswFQlWwfRuhaqjdt92OuP3OuePOOr3z3tFWlbdXDyqif4fxquouIy+toM9nA6yooLwvNjQwsUKyArRWD8lOUZiVgAvE0FHwmUU8XUE7MTOz/jCwT6yZmVnZuECYmVmSC4SZmSW5QJiZWZILhJmZJblAmJlZkguEmZkluUCYmVlSyR452t8kbQRe7sUixgFv9lGcUqukrFBZeSspK1RW3krKCpWVtzdZD42I/VIT9pgC0VuSlnb2XNaBppKyQmXlraSsUFl5KykrVFbeUmX1KSYzM0tygTAzsyQXiJ3uKneAbqikrFBZeSspK1RW3krKCpWVtyRZfQ3CzMySfARhZmZJLhBmZpa01xUISRMlLZa0UtKzkr6Yt98oaZ2kp/LX2eXO2kbSWknP5LmW5m1jJD0kaXX+c/QAyHl4wfZ7StIfJF0zkLatpLmS3pC0oqAtuS2VuVXSGknLJR03ALL+naTn8jw/kTQqb6+TtKVgG9/Zn1m7yNvpv72k6/Nt+7ykjwyArPcV5Fwr6am8vazbtot9Vul/byNir3oBBwLH5cMjgBeAqcCNwJfLna+TzGuBcR3a/ha4Lh++DvhOuXN2yFcNbAAOHUjbFjgdOA5YsbttCZwN/JzsAdYnAb8eAFnPBAblw98pyFpX2G8Abdvkv33+f+5pYAgwCXgRqC5n1g7T/x74+kDYtl3ss0r+e7vXHUFExGsR8dt8eDOwCji4vKl6ZDZwdz58N3B+GbOkfBh4MSJ68+32PhcRS4C3OjR3ti1nAz+IzOPAKEkH9k/SdNaI+EVEbM9HHwcm9Fee3elk23ZmNjA/It6LiN8Ba4ATShaug66yShJwEfCj/srTlS72WSX/vd3rCkQhSXXAscCv86ar80OyuQPhlE2BAH4haZmkK/O28RHxWj68ARhfnmidupj2/8EG6raFzrflwcCrBf0aGVh/TPwF2V+KbSZJelLSf0o6rVyhElL/9gN5254GvB4RqwvaBsS27bDPKvnv7V5bICQNBx4AromIPwB3AO8DjgFeIzvEHCg+GBHHAWcBV0k6vXBiZMeVA+bzypIGA+cBP86bBvK2bWegbcvOSPoKsB24J296DTgkIo4FvgTcK2nfcuUrUDH/9gU+Sfs/bgbEtk3ss3Yo1e/tXlkgJNWQbeh7IuL/AETE6xHREhGtwPfox8Pd3YmIdfnPN4CfkGV7ve2wMf/5RvkS7uIs4LcR8ToM7G2b62xbrgMmFvSbkLeVlaTLgXOAS/IdA/mpmk358DKyc/ofKFvIXBf/9gN12w4CPg7c19Y2ELZtap9FP/ze7nUFIj+/+M/Aqoj4XwXthefoPgas6DhvOUjaR9KItmGyi5QrgIXAp/JunwL+b3kSJrX7C2ygbtsCnW3LhcCf558KOQl4p+CQviwkzQL+GjgvIv5Y0L6fpOp8+DBgMvBSeVLu1MW//ULgYklDJE0iy/ub/s6XcAbwXEQ0tjWUe9t2ts+iP35vy3Vlvlwv4INkh2LLgafy19nAvwLP5O0LgQPLnTXPexjZpz2eBp4FvpK3jwV+CawGHgbGlDtrnmsfYBMwsqBtwGxbssL1GtBMdm72M51tS7JPgdxO9hfjM8CMAZB1Ddn55bbf3Tvzvp/Ifz+eAn4LnDtAtm2n//bAV/Jt+zxwVrmz5u3zgM926FvWbdvFPqvkv7e+1YaZmSXtdaeYzMysOC4QZmaW5AJhZmZJLhBmZpbkArUqVJcAAAMBSURBVGFmZkkuEGZmluQCYdZH8i99PZzfEnpOD+Y/X9LUUmQz64lB5Q5gtgc5FiAijunh/OcD/wasLHYGSYNi591dzfqUjyBsj5c/8OU5SfMkvSDpHklnSPpV/rCVE/LXY/kdOx+VdHg+77WS5ubDR0laIWlYYh37Az8Ejs+PIN4naXp+989lkhYV3Dfnv0t6QtLTkh6QNEzSKWQ3OPy7gvkbJM3I5xknaW0+fLmkhZL+g+ybtEj6q3yZyyX9Td62j6R/z9ezoidHNbaX6++v4/vlV3+/yB74sh04iuyPomXAXLJbEswGfgrsy84H8ZwBPJAPVwFLyO4jtBQ4tYv11AP/lg/XAI8C++Xjc4C5+fDYgnluBj6fD88DLiiY1kB+mwRgHLA2H76c7PYQbbdWOBO4K38/VWRHIaeT3SLiewXLG9md7eaXXz7FZHuL30XEMwCSngV+GREh6RmyAjISuFvSZLL73tQARERrfvfU5cA/RcSvilzf4cCRwEPZvdaoJrv3D8CRkm4GRgHDgUU9eD8PRUTbA2/OzF9P5uPDyW4o9wjw95K+Q1a4HunBemwv5gJhe4v3CoZbC8Zbyf4ffANYHBEfyx/K0lDQfzLQBBzUjfUJeDYiTk5MmwecHxFP58WnvpNlbGfnaeDaDtPe7bCub0fEP+0SInse8dnAzZJ+GRE3Ff0ObK/naxBmmZHsvGf+5W2NkkYCt5Kdshkr6YIil/c8sJ+kk/Pl1Eialk8bAbyW3+P/koJ5NufT2qwFpufDXa13EfAX+QNlkHSwpP0lHQT8MSJ+CPwd2TOYzYrmAmGW+Vvg25KepP2R9f8Gbo+IF8huX31LfkG6SxGxjWyn/h1JT5PdovmUfPLXyB4Z+SvguYLZ5gN/lV8ofx/wXeBzeaZxXazrF8C9wGP5KbMFZIXmKOA3kp4CbiC73mFWNN/u28zMknwEYWZmSb5IbdZNkj4NfLFD868i4qpy5DErFZ9iMjOzJJ9iMjOzJBcIMzNLcoEwM7MkFwgzM0v6/1NU86OkvYPcAAAAAElFTkSuQmCC\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "plot_fitting_graph(n_estimators, acc_train, acc_valid, metric_name='Accuracy', xlabel='max_features')"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Note: since we want to maximise the accuracy we need to change `np.argmin` to `np.argmax`:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "200"
      ]
     },
     "execution_count": null,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "n_estimators[np.argmax(acc_valid)]"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Following the same argument as with the housing dataset we will stick to `n_estimators=100` for now but you can experiment with more estimators if you want."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### Exercise 2\n",
    "Run the same optimisation steps as we did with housing dataset to tune the Random Forest for churn classification.\n",
    "\n",
    "Optimise the following parameters:\n",
    "* max_depth\n",
    "* min_samples_leaf\n",
    "* max_features\n",
    "\n",
    "Note: You will probably see a ~1% improvement. While this not might seem like very much keep in mind that Netflix paid \\\\$50'000 for a 1% improvement in predictions and $1'000'000 for a 10% improvement (see [link](https://en.wikipedia.org/wiki/Netflix_Prize)). In Kaggle challenges this can make the difference between being top-10 and top-100."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": []
  }
 ],
 "metadata": {
  "kernelspec": {
   "display_name": "Python 3",
   "language": "python",
   "name": "python3"
  }
 },
 "nbformat": 4,
 "nbformat_minor": 4
}