\n",
"
\n",
"
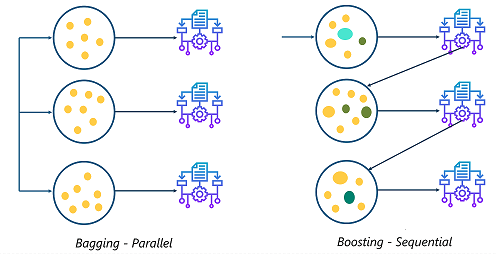
Figure reference: https://www.quora.com/Whats-the-difference-between-boosting-and-bagging
\n",
"
 \n",
"
\n",
"  \n",
"
\n",
"