{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Introducción a la Programación en MATLAB (C10)\n",
"\n",
"Mauricio Tejada\n",
"\n",
"ILADES - Universidad Alberto Hurtado\n",
"\n",
"Agosto 2017"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Contenidos\n",
"\n",
"- [Ecuaciones No Lineales](#10.-Ecuaciones-No-Lineales)\n",
" - [Métodos Numéricos y Ecuaciones No Lineales: Ideas Básicas](#10.1-Métodos-Numéricos-y-Ecuaciones-No-Lineales:-Ideas-Básicas)\n",
" - [Las Funciones fzero y fsolve](#10.2-Las-Funciones-fzero-y-fsolve)\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 10. Ecuaciones No Lineales\n",
"\n",
"*La exposición en esta sección sigue de cerca el capítulo 3 del libro de Miranda y Fackler.*\n",
"\n",
"Los problemas que envuelven sistemas de ecuaciones no lineales son muy comunes en economía. Éstos se presentan en dos formatos:\n",
"\n",
"- Búsqueda de raíces: $$f(x) = 0$$ con $f:R^n \\rightarrow R^n$ y $x\\in R^n$\n",
"- Punto fijo: $$x = g(x)$$ con $g:R^n \\rightarrow R^n$ y $x\\in R^n$ \n",
"\n",
"Ambas formas son equivalentes: \n",
"\n",
"- Problema de raíces expresado como un problema de punto fijo: $$g(x) = x - f(x)$$\n",
"- Problema de punto fijo expresado como un problema de raíces: $$f(x) = x-g(x)$$\n",
"\n",
"En muchas aplicaciones económicas, no es posible encontrar una solución analítica a un problema no lineal y por tanto la solución tiene que hallarse de manera numérica.\n",
"\n",
"Problemas:\n",
"- Los métodos numéricos con iterativos y son sensibles a la condición inicial.\n",
"- Los sistemas no lineales pueden tener más de una solución.\n",
"\n",
"Vamos a analizar métodos que no usan derivadas (método de bisección y método de iteración de la función) y métodos de usan derivadas (Método de Newton y Método de quasi-Newton). \n",
"\n",
"Existen métodos más sofisticados basados en los métodos mencionados y sólo realizaremos una descripción escueta."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 10.1 Métodos Numéricos y Ecuaciones No Lineales: Ideas Básicas"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Método de Bisección\n",
"\n",
"Es el método más simple y robusto para hallar la raíz de una función no lineal definida en $R$ en el intervalo $[a,b]$.\n",
"\n",
"Buscamos resolver: $$f(x)=0$$ con $f:R \\rightarrow R$.\n",
"\n",
"Es un método iterativo que evalúa el signo en los puntos extremos y en el punto medio del intervalo y en función de ello reduce el intervalo de búsqueda. Repite este proceso hasta que el intervalos resultante sea menor que un nivel de tolerancia.\n",
"\n",
"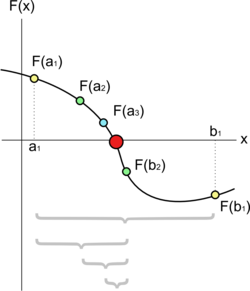\n",
"Fuente: Wikipedia.\n",
"\n",
"Requerimientos: La solución debe estar contenida en $[a,b]$ y la función debe ser continua en el intervalo. \n",
"\n",
"La siguiente función implementa el método de Bisección:\n",
"\n",
"```\n",
"function root = bisect(f,a,b)\n",
"\n",
"% bisection implementa el Método de Bisección\n",
"% Uso: root = bisect(f,a,b)\n",
"\n",
"if f(a)*f(b)>0 \n",
" error('La función debe ser de signo distinto en los extremos');\n",
"else\n",
" tol = 1.5e-8;\n",
" \n",
" s = sign(f(a));\n",
" x = (a+b)/2;\n",
" d = (b-a)/2;\n",
"\n",
" while d>tol\n",
" d = d/2;\n",
" if s == sign(f(x))\n",
" x = x+d;\n",
" else\n",
" x = x-d;\n",
" end\n",
" end\n",
" root = x;\n",
"end\n",
"\n",
"end\n",
"```\n",
"Para probar el método creamos un m-file con la siguiente función:\n",
"\n",
"```\n",
"function fval = ff(x)\n",
"\n",
"fval = x^3-2;\n",
"\n",
"end\n",
"```\n",
"Buscamos la raíz en el intervalos $[1,2]$."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"1.2599\n"
]
}
],
"source": [
"x = bisect(@ff,1,2);\n",
"disp(x);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Iteración de la Función\n",
"\n",
"El método de iteración de la función es un técnica iterativa usada para encontrar un punto fijo $x=g(x)$ con $g:R^n \\rightarrow R^n$. Este método también puede ser aplicado al problema de búsqueda de raíces usando la transformación apropiada (ver más arriba).\n",
"\n",
"La iteración se inicia con una conjetura inicia $x^(0)$ para el punto fijo y se la actualiza usando la siguiente regla: \n",
"\n",
"$$x^{(k+1)} \\leftarrow g(x^{(k)})$$ \n",
"\n",
"Este proceso continúa iterando hasta que $g(x^{(k)})$ se \"suficientemente\" cercano a $x^{(k+1)}$.\n",
"\n",
"La convergencia está garantizada si:\n",
"\n",
"- $g$ es diferenciable.\n",
"- la conjetura inicial $x^{(0)}$ está suficientemente cerca del punto fijo $x^*$.\n",
"- $||g'(x^*)||<1$.\n",
"\n",
"La siguiente figura ilustra la iteración de una función en $R$:\n",
"\n",
"\n",
"Fuente: Miranda y Fackler (2002)\n",
"\n",
"La siguiente función implementa el método de iteración de la función:\n",
"\n",
"```\n",
"function [x, gval] = fixpoint(g,x0)\n",
"\n",
"% fixpoint implementa el Método de Iteración de la Función\n",
"% Uso: [x, gval] = fixpoint(f,x0)\n",
"\n",
"tol = 1.5e-8;\n",
"maxiter = 1000; \n",
"\n",
"x = x0;\n",
"\n",
"for i=1:maxiter \n",
" gval = g(x);\n",
" if norm(gval-x)Fuente: Miranda y Fackler (2002)\n",
"\n",
"La siguiente función implementa el método de Newton:\n",
"\n",
"```\n",
"function x = newton(f,x0)\n",
"\n",
"% newton implementa el Método de Newton\n",
"% Uso: x = newton(f,x0)\n",
"\n",
"tol = 1.5e-8;\n",
"maxiter = 1000; \n",
"\n",
"x = x0;\n",
"\n",
"for i=1:maxiter\n",
" [fval,fjac] = f(x);\n",
" x = x - fjac\\fval;\n",
" if norm(fval) < tol\n",
" break;\n",
" end\n",
"end\n",
"\n",
"if i == maxiter;\n",
" disp('No se obtuvo convergencia');\n",
"end\n",
"\n",
"end\n",
"```\n",
"\n",
"Para probar el método usemos la función ya creada $f(x) = x^3 - 2$. Buscamos la raíz partiendo de la conjetura $x=1$.\n",
"\n",
"```\n",
"function [fval, fjac] = ff2(x)\n",
"\n",
"fval = x^3-2;\n",
"fjac = 3*x^2;\n",
"\n",
"end\n",
"```"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"1.2599\n"
]
}
],
"source": [
"x = newton(@ff2,1);\n",
"disp(x);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### El Método de Quasi-Newton\n",
"\n",
"El problema del método de Newton es que requiere la matriz Jacobiana para realizar la linealización. En muchos problemas es difícil encontrar dicha matriz.\n",
"\n",
"El Método de Quasi-Newton sigue la misma lógica que el método de Newton pero reemplaza la matriz Jacobiana por una aproximación fácil de computar. \n",
"\n",
"El costo viene asociado a que es más lento en converger y requiere de una aproximación inicial a la matriz Jacobiana. \n",
"\n",
"*Método de la Secante*\n",
"\n",
"El *Método de la Secante* es el método de Quasi-Newton univariado más usado. La idea es reemplazar la derivada con una aproximación construida con los valores de la iteración anterior. La regla de actualización sería entonces:\n",
"\n",
"$$ x^{(k+1)} \\leftarrow x^{(k)} - \\frac{x^{(k)}-x^{(k-1)}}{f(x^{(k)})-f(x^{(k-1)})} f(x^{(k)})$$\n",
"\n",
"La siguiente función implementa el método de la secante:\n",
"\n",
"```\n",
"function x = secante(f,x0)\n",
"\n",
"% secante implementa el Método de la Secante\n",
"% Uso: x = secante(f,x0)\n",
"\n",
"tol = 1.5e-8;\n",
"maxiter = 1000; \n",
"\n",
"x1 = 0.5*x0;\n",
"\n",
"for i=1:maxiter\n",
" fval0 = f(x0);\n",
" fval1 = f(x1);\n",
" x = x1 - ((x1-x0)/(fval1-fval0))*fval1;\n",
" if abs(fval1) < tol\n",
" break;\n",
" end\n",
" x0 = x1;\n",
" x1 = x;\n",
"end\n",
"\n",
"if i == maxiter;\n",
" disp('No se obtuvo convergencia');\n",
"end\n",
"\n",
"end\n",
"```\n",
"\n",
"Para probar el método usemos la función:\n",
"\n",
"```\n",
"function fval = ff(x)\n",
"\n",
"fval = x^3-2;\n",
"\n",
"end\n",
"```\n",
"Buscamos la raíz conjeturando $x=1$."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"1.2599\n"
]
}
],
"source": [
"x = secante(@ff,1);\n",
"disp(x);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"*Método de Broyden*\n",
"\n",
"El *Método de Broyden* es el método de Quasi-Newton multivariado más usado. El método parte con una conjetura inicial para la raíz $x^{(0)}$ y para la matriz Jacobiana $A^{(0)}$. Las ecuaciones de actualización son para la raíz:\n",
"\n",
"$$f(x) \\approx f(x^{(k)}) + A^{(k)}(x-x^{(k)}) = 0$$\n",
"\n",
"$$ x^{(k+1)} \\leftarrow x^{(k)} - [A^{(k)}]^{-1} f(x^{(k)})$$\n",
"\n",
"y para la matriz jacobiana:\n",
" \n",
"$$f(x^{(k+1)}) - f(x^{(k)}) = A^{(k)}(x^{(k+1)} - x^{(k)})$$\n",
"\n",
"$$A^{(k+1)} \\leftarrow A^{(k)} + \\left[f(x^{(k+1)}) - f(x^{(k)}) - A^{(k)}d^{(k)}\\right] \\frac{d^{(k)}`}{d^{(k)}` d^{(k)}}$$\n",
"\n",
"con $d^{(k)} = x^{(k+1)}-x^{(k)}$.\n",
"\n",
"El toolbox CompEcon de Miranda y Fackler (2002) tiene implementado éste y los otros métodos descritos antes."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"### 10.2 Las Funciones fzero y fsolve"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Matlab cuenta dos funciones diseñadas para lidiar con problemas no lineales: (1) fzero y (2) fsolve.\n",
"\n",
"**fzero**\n",
"\n",
"`fzero` es un función para buscar la raíz de una función definida en los reales. Usa una combinación de métodos entre los cuales se encuentra los de bisección y el de la secante.\n",
"\n",
"La sintaxis de esta función es:\n",
"\n",
"`[x,fval,exitflag] = fzero(fun,x0,opt)`\n",
"\n",
"donde `fun` es una función definida en $R$, `x0` es la conjetura inicial (el intervalo de búsqueda si se provee un vector $2 \\times 1$) y `opt` define las opciones del método.\n",
"\n",
"Entre los resultados tenemos: `x` la raíz, `fval` el valor de la función evaluada en la raíz, y `exitflag`un indicador con el resultado de método ($x>0$ indica que se encontró la solución).\n",
"\n",
"Las opciones se manejan usando la función `optimset` de Matlab. Sólo para tomar un ejemplo:\n",
"\n",
"`opt = optimset('Display','iter','TolX',num,'MaxIter',num)`\n",
"\n",
"No usar `opt` sólo hace que la función use las opciones por defecto."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"x =\n",
"\n",
" 1.2599\n",
"\n",
"\n",
"fval =\n",
"\n",
" 0\n",
"\n",
"\n",
"exitflag =\n",
"\n",
" 1\n"
]
}
],
"source": [
"[x,fval,exitflag] = fzero(@ff,1)"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"Ahora usemos las opciones de la función."
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [],
"source": [
"%opts = optimset('Display','iter');\n",
"%x = fzero(@ff,1,opts);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**fsolve**\n",
"\n",
"`fsolve` es un función para resolver numéricamente sistemas de ecuaciones no lineales. Esta función usa variaciones (más robustas y eficientes) del método de Newton.\n",
"\n",
"La sintaxis de esta función es:\n",
"\n",
"`[x, fval, exitflag] = fsolve(fun,x0,options)`\n",
"\n",
"donde `fun` es un vector de `n` función definidas en $R^n$, $x0 \\in R^n$ es la conjetura inicial y `opt` define las opciones del método (al igual que en el caso anterior).\n",
"\n",
"Resolvamos el siguiente sistema de ecuaciones no lineales usando `fsolve`.\n",
"\n",
"$$e^{-e^{-(x+y)}} = y(1+x^2)$$\n",
"$$x \\cos y + y \\sin x = \\frac{1}{2}$$\n",
"\n",
"Primero requerimos generar un `m-file` con las ecuaciones:\n",
"\n",
"```\n",
"function f = sistemanl(x)\n",
"\n",
"f = zeros(length(x),1);\n",
"\n",
"f(1) = exp(-exp(-x(1)+x(2))) - x(2)*(1+x(1)^2);\n",
"f(2) = x(1)*cos(x(2)) + x(2)*sin(x(1)) - 0.5;\n",
"\n",
"end\n",
"```\n",
"\n",
"La conjetura inicial será $x=y=0$."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Equation solved.\n",
"\n",
"fsolve completed because the vector of function values is near zero\n",
"as measured by the default value of the function tolerance, and\n",
"the problem appears regular as measured by the gradient.\n",
"\n",
"\n",
"\n",
"\n",
"x =\n",
"\n",
" 0.3931 0.3366\n",
"\n",
"\n",
"f =\n",
"\n",
" 1.0e-10 *\n",
"\n",
" -0.2027\n",
" -0.0095\n",
"\n",
"\n",
"ef =\n",
"\n",
" 1\n"
]
}
],
"source": [
"x0 = [0,0];\n",
"[x, f, ef] = fsolve(@sistemanl,x0)"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"ans =\n",
"\n",
" 1.0e-10 *\n",
"\n",
" -0.2027\n",
" -0.0095\n"
]
}
],
"source": [
"sistemanl(x)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Ahora usemos las opciones de la función."
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [],
"source": [
"% opts = optimset('Display','iter');\n",
"% x0 = [0,0];\n",
"% [x, f, flag]= fsolve(@sistemanl,x0,opts)"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Matlab",
"language": "matlab",
"name": "matlab"
},
"language_info": {
"file_extension": ".m",
"help_links": [
{
"text": "MetaKernel Magics",
"url": "https://github.com/calysto/metakernel/blob/master/metakernel/magics/README.md"
}
],
"mimetype": "text/x-octave",
"name": "matlab",
"version": "0.9.4"
}
},
"nbformat": 4,
"nbformat_minor": 1
}