# Introduction to Neural Networks
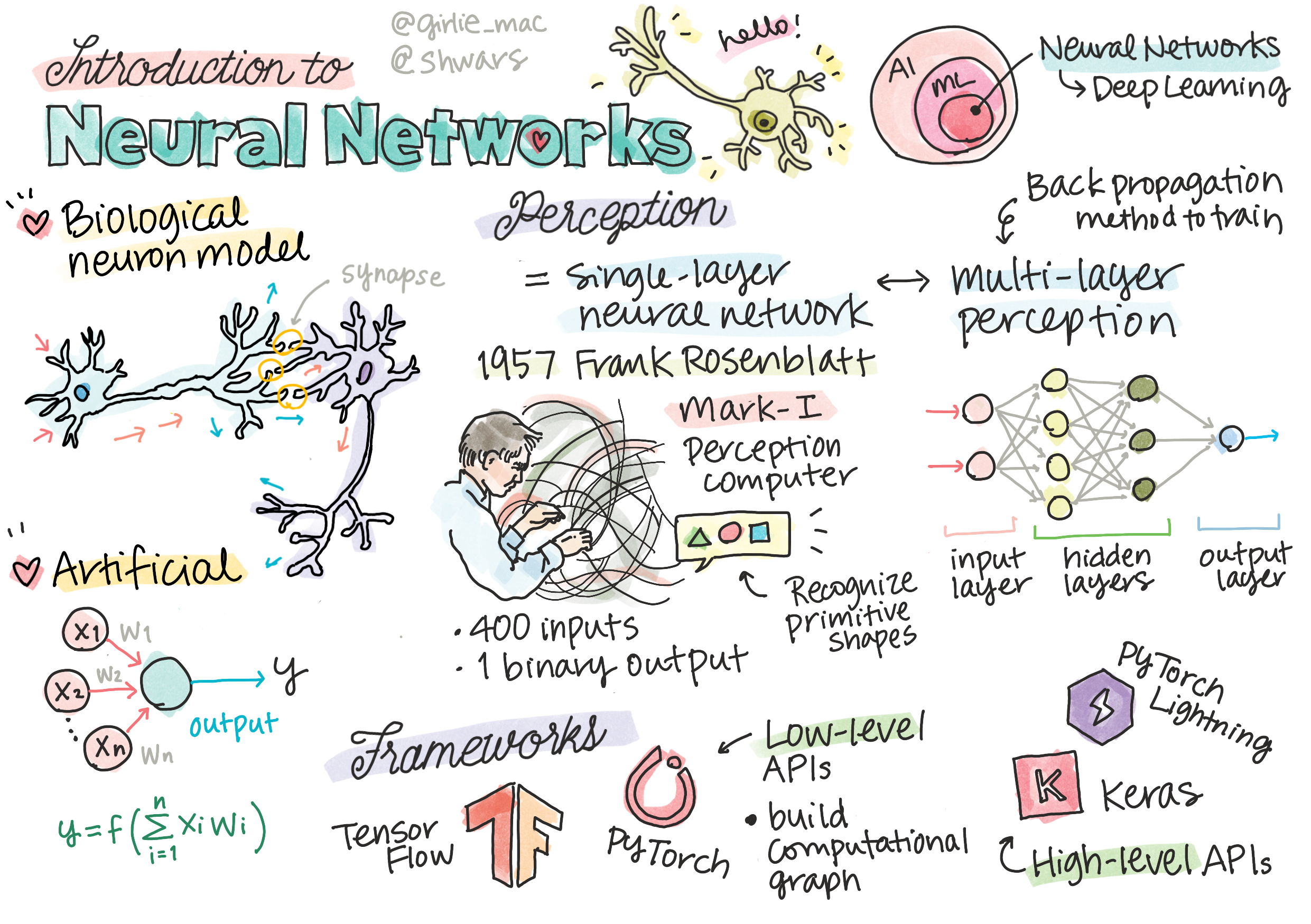
As we discussed in the introduction, one of the ways to achieve intelligence is to train a **computer model** or an **artificial brain**. Since the middle of 20th century, researchers tried different mathematical models, until in recent years this direction proved to be hugely successful. Such mathematical models of the brain are called **neural networks**.
> Sometimes neural networks are called *Artificial Neural Networks*, ANNs, in order to indicate that we are talking about models, not real networks of neurons.
## Machine Learning
Neural Networks are a part of a larger discipline called **Machine Learning**, whose goal is to use data to train computer models that are able to solve problems. Machine Learning constitutes a large part of Artificial Intelligence, however, we do not cover classical ML in this curricula.
> Visit our separate **[Machine Learning for Beginners](http://github.com/microsoft/ml-for-beginners)** curriculum to learn more about classic Machine Learning.
In Machine Learning, we assume that we have some dataset of examples **X**, and corresponding output values **Y**. Examples are often N-dimensional vectors that consist of **features**, and outputs are called **labels**.
We will consider the two most common machine learning problems:
* **Classification**, where we need to classify an input object into two or more classes.
* **Regression**, where we need to predict a numerical number for each of the input samples.
> When representing inputs and outputs as tensors, the input dataset is a matrix of size M×N, where M is number of samples and N is the number of features. Output labels Y is the vector of size M.
In this curriculum, we will only focus on neural network models.
## A Model of a Neuron
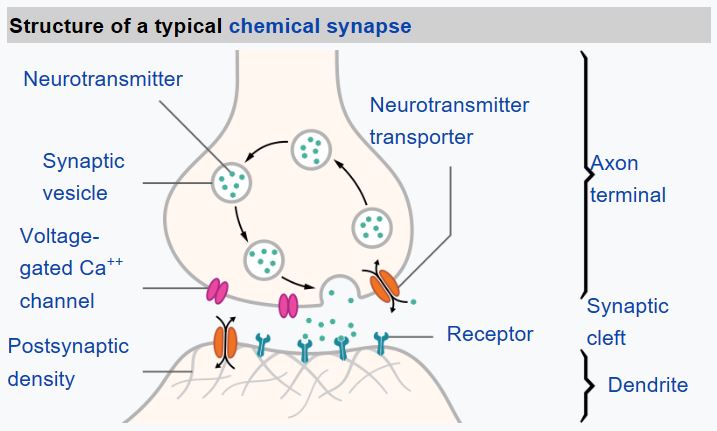
From biology, we know that our brain consists of neural cells (neurons), each of them having multiple "inputs" (dendrites) and a single "output" (axon). Both dendrites and axons can conduct electrical signals, and the connections between them — known as synapses — can exhibit varying degrees of conductivity, which are regulated by neurotransmitters.
 | 
----|----
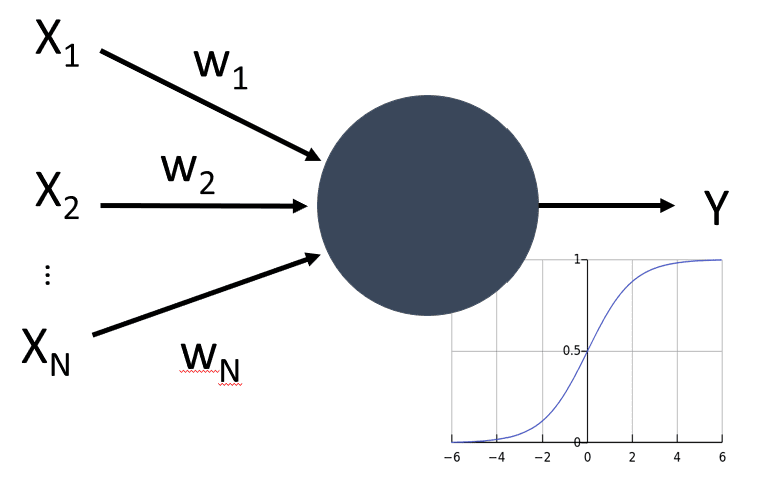
Real Neuron *([Image](https://en.wikipedia.org/wiki/Synapse#/media/File:SynapseSchematic_lines.svg) from Wikipedia)* | Artificial Neuron *(Image by Author)*
Thus, the simplest mathematical model of a neuron contains several inputs X1, ..., XN and an output Y, and a series of weights W1, ..., WN. An output is calculated as:
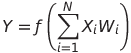 where f is some non-linear **activation function**.
> Early models of neuron were described in the classical paper [A logical calculus of the ideas immanent in nervous activity](https://www.cs.cmu.edu/~./epxing/Class/10715/reading/McCulloch.and.Pitts.pdf) by Warren McCullock and Walter Pitts in 1943. Donald Hebb in his book "[The Organization of Behavior: A Neuropsychological Theory](https://books.google.com/books?id=VNetYrB8EBoC)" proposed the way those networks can be trained.
## In this Section
In this section we will learn about:
* [Perceptron](03-Perceptron/README.md), one of the earliest neural network models for two-class classification
* [Multi-layered networks](04-OwnFramework/README.md) with a paired notebook [how to build our own framework](04-OwnFramework/OwnFramework.ipynb)
* [Neural Network Frameworks](05-Frameworks/README.md), with these notebooks: [PyTorch](05-Frameworks/IntroPyTorch.ipynb) and [Keras/Tensorflow](05-Frameworks/IntroKerasTF.ipynb)
* [Overfitting](05-Frameworks#overfitting)
where f is some non-linear **activation function**.
> Early models of neuron were described in the classical paper [A logical calculus of the ideas immanent in nervous activity](https://www.cs.cmu.edu/~./epxing/Class/10715/reading/McCulloch.and.Pitts.pdf) by Warren McCullock and Walter Pitts in 1943. Donald Hebb in his book "[The Organization of Behavior: A Neuropsychological Theory](https://books.google.com/books?id=VNetYrB8EBoC)" proposed the way those networks can be trained.
## In this Section
In this section we will learn about:
* [Perceptron](03-Perceptron/README.md), one of the earliest neural network models for two-class classification
* [Multi-layered networks](04-OwnFramework/README.md) with a paired notebook [how to build our own framework](04-OwnFramework/OwnFramework.ipynb)
* [Neural Network Frameworks](05-Frameworks/README.md), with these notebooks: [PyTorch](05-Frameworks/IntroPyTorch.ipynb) and [Keras/Tensorflow](05-Frameworks/IntroKerasTF.ipynb)
* [Overfitting](05-Frameworks#overfitting)
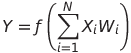 where f is some non-linear **activation function**.
> Early models of neuron were described in the classical paper [A logical calculus of the ideas immanent in nervous activity](https://www.cs.cmu.edu/~./epxing/Class/10715/reading/McCulloch.and.Pitts.pdf) by Warren McCullock and Walter Pitts in 1943. Donald Hebb in his book "[The Organization of Behavior: A Neuropsychological Theory](https://books.google.com/books?id=VNetYrB8EBoC)" proposed the way those networks can be trained.
## In this Section
In this section we will learn about:
* [Perceptron](03-Perceptron/README.md), one of the earliest neural network models for two-class classification
* [Multi-layered networks](04-OwnFramework/README.md) with a paired notebook [how to build our own framework](04-OwnFramework/OwnFramework.ipynb)
* [Neural Network Frameworks](05-Frameworks/README.md), with these notebooks: [PyTorch](05-Frameworks/IntroPyTorch.ipynb) and [Keras/Tensorflow](05-Frameworks/IntroKerasTF.ipynb)
* [Overfitting](05-Frameworks#overfitting)
where f is some non-linear **activation function**.
> Early models of neuron were described in the classical paper [A logical calculus of the ideas immanent in nervous activity](https://www.cs.cmu.edu/~./epxing/Class/10715/reading/McCulloch.and.Pitts.pdf) by Warren McCullock and Walter Pitts in 1943. Donald Hebb in his book "[The Organization of Behavior: A Neuropsychological Theory](https://books.google.com/books?id=VNetYrB8EBoC)" proposed the way those networks can be trained.
## In this Section
In this section we will learn about:
* [Perceptron](03-Perceptron/README.md), one of the earliest neural network models for two-class classification
* [Multi-layered networks](04-OwnFramework/README.md) with a paired notebook [how to build our own framework](04-OwnFramework/OwnFramework.ipynb)
* [Neural Network Frameworks](05-Frameworks/README.md), with these notebooks: [PyTorch](05-Frameworks/IntroPyTorch.ipynb) and [Keras/Tensorflow](05-Frameworks/IntroKerasTF.ipynb)
* [Overfitting](05-Frameworks#overfitting)