{
 "cells": [
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "###### Content under Creative Commons Attribution license CC-BY 4.0, code under MIT license (c)2014 M.Z. Jorisch"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "<h1 align=\"center\">Orbital</h1>\n",
    "<h1 align=\"center\">Perturbations</h1>"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "In this lesson, we will discuss the orbits of bodies in space, and how those bodies can be affected by others as they fly by.  We will look at Encke's method, which was created by Johann Franz Encke in 1851, and uses a second order ODE to describe the true orbit of a body when affected by the pull of an additional body flying by.\n",
    "\n",
    "In traditional orbital dynamics, the standard two-body problem is used to describe two bodies in motion with one orbiting the other.  This fails to take into account the affect of outside bodies on the orbital trajectory and can produce an orbit very different than the \"true\" orbit.\n",
    "\n",
    "These orbits play a large role in our daily lives.  There are numerous satellites currently orbiting Earth, which are used for communications, GPS, as well as other data grabbers.  These satellites can have slight changes to their orbits around Earth caused by other satellites, planets, moons, or comets that need to be taken into consideration when designing orbital parameters for them."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "We will compare the traditional two-body motion and Encke's method to see how much the orbits vary over time.\n",
    "\n",
    "For our example, we will use Mars and Jupiter orbiting the Sun, with Jupiter being the disturbing body.  These two planets were chosen for their proximity to one another and for Jupiter's large mass (Over 300 times greater than Earth!)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "<h2 align=\"center\">Encke's Method</h2> "
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
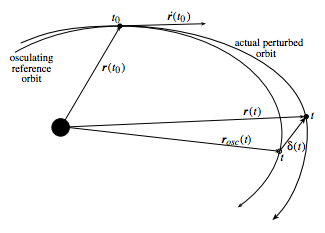    "![Screen Shot 2015-12-01 at 10.42.54 AM](./Figures/Screen Shot 2015-12-01 at 10.42.54 AM.png)\n",
    "<h4 align=\"center\">Figure 1. Visualization of Encke's Method ([Analytical Mechanics of Aerospace Systems Pg 342](http://www.control.aau.dk/~jan/undervisning/MechanicsI/mechsys/chapter10.pdf))</h4>"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Encke's method uses the difference between the standard Keplerian orbit and the true orbit affected by a third body, and can be represented by the following equations.\n",
    "\n",
    "The Keplerian orbit or the osculating orbit is represented by the equation:\n",
    "\n",
    "$$\\frac{d^2 \\vec{r}_{osc}}{dt^2} = - \\frac{\\mu}{r^3 _{osc}} \\vec{r}_{osc}$$\n",
    "\n",
    "The perturbed orbit is represented by a similar equation:\n",
    "\n",
    "$$\\frac{d^2 \\vec{r}}{dt^2} = - \\frac{\\mu}{r^3} \\vec{r} + \\vec{a}_d$$\n",
    "\n",
    "When looking at the two equations, the only difference between the osculating orbit and the perturbed orbit is the term $\\vec{a}_d$, which is the acceleration vector caused by the third body flyby."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "The acceleration vector can be found using the following:\n",
    "\n",
    "$$\\vec{a}_d = \\frac{1}{m_2} \\vec{f}_{d_2} - \\frac{1}{m_1} \\vec{f}_{d_1}$$\n",
    "\n",
    "The two accelerations cancel out many times. (Schaub pg 257)\n",
    "\n",
    "This leads to: \n",
    "\n",
    "$$\\vec{a}_d = \\frac{1}{m_2} \\frac{G m_2 m_3}{|\\vec{r}_23|^3} \\vec{r}_23 - \\frac{1}{m_1} \\frac{G m_1 m_3}{|\\vec{r}_13|^3} \\vec{r}_13$$\n",
    "\n",
    "Where $m_1$ is the mass of the central body, $m_2$ is the mass of the body orbiting around $m_1$, and $m_3$ is the mass of the disturbing body."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Initially, at time $t_0 = 0$, the osculating and perturbed orbits are equal.  The change occurs at a time $t = t_0 + \\Delta t$.\n",
    "\n",
    "Let's define the difference between the radius of the osculating and perturbed orbits as $\\delta$ and the difference between the velocities of the two orbits as $\\gamma$\n",
    "\n",
    "Therefore at time $t$, which we just defined, the radial and velocity components are:\n",
    "\n",
    "$$\\vec{\\delta}(t) = \\vec{r}(t) - \\vec{r}_{osc} (t)$$\n",
    "$$\\vec{\\gamma}(t) = \\vec{v}(t) - \\vec{v}_{osc} (t)$$"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "We have some initial conditions as well.  As mentioned before the obrbits are equal at $t_0$ which gives us $\\vec{\\delta} (t_0) = 0$.  The velocity difference at $t_0$ is also zero. $\\frac{d \\vec{\\delta} (t_0)}{dt} = \\vec{\\gamma} (t_0) = 0$"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "If we subtract our two initial equations we get:\n",
    "\n",
    "$$\\frac{d^2 \\vec{\\delta}}{dt^2} = \\vec{a}_d + \\mu \\left( \\frac{\\vec{r}_{osc}}{r_{osc} ^3} + \\frac{\\vec{r}}{r^3} \\right)$$\n",
    "\n",
    "This can be simiplied to:\n",
    "\n",
    "$$\\frac{d^2 \\vec{\\delta}}{dt^2} + \\frac{\\mu}{r_{osc} ^3} \\vec{\\delta} = \\frac{\\mu}{r_{osc} ^3} \\left( 1 - \\frac{r_{osc} ^3}{r^3} \\right) \\vec{r} + \\vec{a}_d$$"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Our term $1 - \\frac{r_{osc} ^3}{r^3}$ can be an issue because at the beginning of flight $r_{osc}$ and $r$ are approximately equal. That can't be too good, can it?  We'll take a look at that a little later on."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "We can find the radial and velocity components using the initial values of the radius and velocity along with the Legrangian coefficients in terms of the eccentric anomaly $E$, where the eccentric anomaly is the angle between the major axis and any point on the orbit. \n",
    "\n",
    "$$\\vec{r} = F \\vec{r}_0 + G \\vec{v}_0$$\n",
    "$$\\vec{v} = \\dot{F} \\vec{r}_0 + \\dot{G} \\vec{v}_0$$\n",
    "\n",
    "Where\n",
    "\n",
    "$$F = 1 + \\frac{a}{r_0} \\left[ cos(E - E_0) - 1 \\right]$$\n",
    "$$G = \\frac{a \\alpha _0}{\\mu} \\left[ 1 - cos(E - E_0) \\right] + r_0 \\sqrt{\\frac{a}{\\mu}} sin(E - E_0)$$\n",
    "$$\\dot{F} = - \\frac{\\sqrt{\\mu a}}{r r_0} sin(E - E_0)$$\n",
    "$$\\dot{G} = 1 + \\frac{a}{r} \\left[ cos(E - E_0) - 1 \\right]$$\n",
    "\n",
    "(Tewari pg 104)\n",
    "\n",
    "The eccentric anomaly, $E$, is equal to $M + e  sin(E)$.  $M$ is the mean anomaly and $e$ is the eccentricity."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
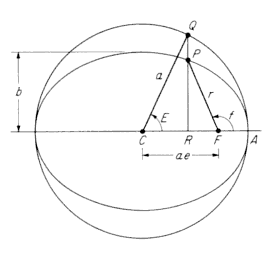    "![Kepler1](./Figures/Kepler1.png)\n",
    "<h4 align=\"center\">Figure 2. Orbital anomalies for elliptic motion ([AIAA pg158])"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "As you can see from the equation, the eccentric anomaly is a function of itself.  In order to calculate it we will have to start with a guess and then iterate until the difference between our new value of E and the guess is within a certain tolerance.  This is based on Newton's approximation using a Taylor series expansion of $f(E) = E -e sin E - M$"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "The expansion is: $f(E + \\Delta E) = \\sum_{k = 0} ^{\\infty} f^{(k)} (E) \\frac{(\\Delta E) ^k}{k!}$, in which $f(k) \\approx \\frac{d^k f(E)}{dE^k}$  The first two terms of the Taylor series can be used for Newton's approximation:\n",
    "\n",
    "$$f(E + \\Delta E) \\approx f(E) + f^{(1)} (E) (\\Delta E)$$"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "The following method and code for the eccentric anomaly approximation, are based upon those from Ashish Tewari's book,  _Atmospheric and Space Flight Dynamics_.  The initial guess we will start with uses the mean anomaly $M$ to give $E$:\n",
    "\n",
    "$$E + M + e sin M$$\n",
    "\n",
    "$\\Delta E$ will be calculated using $-\\frac{f(E)}{f^{(1)} (E)} = \\frac{-E + e sin E + M}{1 - e cos E}$ so $f(E + \\Delta E)$ is equal to $0$.  After that, the value of E is updated, where $E = E + \\Delta E$.  This operation is repeated until a small enough difference is found, and our $E$ value is found.\n",
    "\n",
    "Let's get to the coding!"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 1,
   "metadata": {
    "collapsed": true
   },
   "outputs": [],
   "source": [
    "from matplotlib import pyplot\n",
    "import numpy\n",
    "from numpy import linalg\n",
    "%matplotlib inline\n",
    "from matplotlib import rcParams\n",
    "rcParams['font.family'] = 'serif'\n",
    "rcParams['font.size'] = 16"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 19,
   "metadata": {
    "collapsed": true
   },
   "outputs": [],
   "source": [
    "def Kepler_eqn(e, M):\n",
    "    \"\"\"Takes the eccentricity and mean anomaly of an orbit to solve Kepler's equation\n",
    "    \n",
    "    Parameters:\n",
    "    ----------\n",
    "        e : float\n",
    "            eccentricity of orbit\n",
    "        M : float\n",
    "            Mean anomaly of orbit\n",
    "        \n",
    "    Returns:\n",
    "    -------\n",
    "        E : float\n",
    "            Eccentric anomaly\n",
    "    \"\"\"\n",
    "    \n",
    "    E = M + e * numpy.sin(M) # eccentric anomoaly\n",
    "    fofE = E - e * numpy.sin(E) - M #eccentric anomaly as a function of E\n",
    "    fdotE = 1 - e * numpy.cos(E) #derivative with respect to E of fofE\n",
    "    dE = - fofE / fdotE # change in E\n",
    "    Enew = E + dE\n",
    "    tolerance = 1e-2\n",
    "    \n",
    "    while abs(fofE) > tolerance:\n",
    "        E = M + e * numpy.sin(Enew)\n",
    "        fofE = E - numpy.sin(E) - M\n",
    "        fdotE = 1 - e * numpy.cos(E)\n",
    "        dE = - fofE / fdotE\n",
    "        Enew = E + dE\n",
    "    \n",
    "    return E\n",
    "    \n",
    "    #Based on code from Ashish Tewari"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "The Kepler_eqn function uses the eccentricity, $e$, and mean anomaly, $M$, and then uses the iterative method to spit out our value of $E$."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "The eccentric anomaly $E$ is the basis for the elliptical trajectory and is the value that changes at each time step, in turn changing the radial and velocity vectors.\n",
    "\n",
    "Now let's define a function, that given our orbital parameters, will give us our trajectory at a time $t$.\n",
    "\n",
    "The orbital elements that we will need to input into the function are:\n",
    "\n",
    "* $a$, the semi-major axis, the distance from the center of the orbit to either of the foci \n",
    "* $P$, the period, the time to complete one orbit\n",
    "* $\\mu$, the gravitational parameter, the gravitational constant $G$ times the mass of the body,\n",
    "* $e$, the eccentricity \n",
    "* $t_0$, an initial time \n",
    "* $r_0$, an initial radial vector\n",
    "* $v_0$, an initial velocity vector\n",
    "* $t$, a time, where the new radial and velocity vectors will be found."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Using these initial values, we have equations that are set up within the function to give us our radial and velocity vectors.  We also have to calculate our Legrangian coefficients, described earlier, $F$, $G$, $\\dot{F}$, and $\\dot{G}$"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "We will use the following equations:\n",
    "\n",
    "* $\\alpha _0 = r_0 \\circ v_0$ : a constant that is used in the coefficient equations\n",
    "\n",
    "* $\\theta _0 = \\pi$: our initial true anomaly (We are starting at the semi-major axis where it is equal to $\\pi$)\n",
    "\n",
    "* $n = \\frac{2 \\pi}{P}$: the mean motion, which is $2 \\pi$ over the period\n",
    "\n",
    "* $E_0 = 2 \\tan ^{-1} (\\sqrt{\\frac{1 - e}{1 + e}} \\tan (0.5 \\theta _0))$: initial eccentric anomaly\n",
    "\n",
    "* $\\tau = t_0 + \\frac{- E_0 + e \\sin (E_0)}{n}$: where $t - \\tau$ is the time since the closest point of orbit\n",
    "\n",
    "* $M = n (t - \\tau)$ : the mean anomaly which is used for the eccentric anomaly iteration in Kepler's equation"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 3,
   "metadata": {
    "collapsed": true
   },
   "outputs": [],
   "source": [
    "def ellip_orb(a, Period, mu, e, t0, r0, v0, t):\n",
    "    \n",
    "    \"\"\"Calculates the orbital position for an elliptical orbit\n",
    "    \n",
    "    Parameters:\n",
    "    ----------\n",
    "    \n",
    "    a  : float\n",
    "        Semi-major axis\n",
    "    Period : float\n",
    "        Period of planetary orbit\n",
    "    mu : float\n",
    "        Gravitational parameter\n",
    "    t0 : float\n",
    "        Initial time t = 0\n",
    "    r0 : array of float\n",
    "        Initial positional array\n",
    "    v0 : array of float\n",
    "        Initial velocity array\n",
    "    t : float\n",
    "        time\n",
    "    \n",
    "    Returns:\n",
    "    -------\n",
    "    \n",
    "    r : array of float\n",
    "        Array of radius at each time t\n",
    "    v : array of float\n",
    "        Array of velocity at each time t\n",
    "    \"\"\"\n",
    "    \n",
    "    r0_norm = numpy.linalg.norm(r0) # Normalized initial radius\n",
    "    \n",
    "    v0_norm = numpy.linalg.norm(v0) # Normalized initial velocity\n",
    "    \n",
    "    alpha = r0 * v0 # Constant used for Legrangian coefficients\n",
    "    \n",
    "    theta0 = numpy.pi # Initial true anomaly\n",
    "            \n",
    "    n = 2 * numpy.pi / (Period) # Mean motion, given the period\n",
    "\n",
    "    E0 = 2 * numpy.arctan(numpy.sqrt((1 - e) / (1 + e)) * numpy.tan(0.5 * theta0)) # Initial eccentric anomaly\n",
    "    \n",
    "    tau = t0 + (- E0 + e * numpy.sin(E0)) / n # t - tau is time since Perigee\n",
    "\n",
    "    M = n * (t - tau) # Mean anomaly\n",
    "\n",
    "    E = Kepler_eqn(e, M) # Eccentric anomaly found through Kepler's equation\n",
    "    \n",
    "    r_leg = a * (1 - e * numpy.cos(E)) # Radius used for legrangian coefficients\n",
    "    \n",
    "    #Legrangian Coefficients\n",
    "    \n",
    "    F = 1 + a * (numpy.cos(E - E0) - 1) * r0_norm\n",
    "    \n",
    "    G = a * alpha * (1 - numpy.cos(E - E0)) / mu + r0_norm * numpy.sqrt(a / mu) * numpy.sin(E - E0)\n",
    "    \n",
    "    F_dot = - numpy.sqrt(mu * a) * (numpy.sin(E - E0)) / (r_leg * r0_norm)\n",
    "    \n",
    "    G_dot = 1 + a * (numpy.cos(E - E0) - 1) / r_leg\n",
    "    \n",
    "    r = numpy.zeros_like(r0)\n",
    "    \n",
    "    v = numpy.zeros_like(v0)\n",
    "    \n",
    "    r = F * r0 + G * v0 # Radial value of orbit for specified time\n",
    "    \n",
    "    v = F_dot * r0 + G_dot * v0 # Velocity value of orbit for specified time\n",
    "    \n",
    "    return r, v"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Now that we have a function to solve for the orbital trajectory of an elliptical orbit (which Mars and Jupiter both have) we have to create a function for the disturbing acceleration caused by the third body, Jupiter.\n",
    "\n",
    "The equation for $a_d$ as mentioned earlier, is:\n",
    "\n",
    "$$\\vec{a}_d = \\frac{1}{m_2} \\frac{G m_2 m_3}{|\\vec{r}_23|^3} \\vec{r}_23 - \\frac{1}{m_1} \\frac{G m_1 m_3}{|\\vec{r}_13|^3} \\vec{r}_13$$\n",
    "\n",
    "Our inputs for this function will be the mass of the Sun ($m_1$), the mass of Mars ($m_2$), the mass of Jupiter ($m_3$), and the radial vectors of Mars and Jupiter with respect to the Sun. "
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 4,
   "metadata": {
    "collapsed": false
   },
   "outputs": [],
   "source": [
    "def acceleration_d(m1, m2, m3, r, r3):\n",
    "    \n",
    "    \"\"\"Calculates the acceleration due to the disturbing orbit\n",
    "    \n",
    "    Parameters:\n",
    "    ----------\n",
    "    m1 : float\n",
    "        Mass of central body\n",
    "    m2 : float\n",
    "        Mass of second body\n",
    "    m3 : float\n",
    "        Mass of third (disturbing) body\n",
    "    r : array of float\n",
    "        Radial distance between body two and one\n",
    "    r3: array of float\n",
    "        Radial distance between body three and one\n",
    "        \n",
    "    Returns:\n",
    "    -------\n",
    "    a_d : array of float\n",
    "        Acceleration due to the disturbing orbit\n",
    "    \"\"\"\n",
    "    a_d = numpy.zeros((2, 1))\n",
    "    \n",
    "    G = 6.674e-11 # Gravitational constant\n",
    "    \n",
    "    r13 = r3 # Radial distance between Jupiter and the Sun\n",
    "    \n",
    "    r23 = r - r3 # Radial distance between Jupiter and Mars\n",
    "    \n",
    "    r23_norm = numpy.linalg.norm(r23) # Normalized radius between Jupiter and Mars\n",
    "    \n",
    "    r13_norm = numpy.linalg.norm(r13) # Normalized radius between Jupiter and the Sun\n",
    "    \n",
    "    a_d = (((1 / m2) * ((G* m2 * m3)/ (r23_norm ** 3))) * r23) - (((1 / m1) * ((G * m1 * m3) / (r13_norm ** 3))) * r13)\n",
    "    \n",
    "    return a_d"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Now that we have our Kepler function, our elliptical orbit function, and our acceleration function, we can set up our initial conditions.  After that we will be able to get our final radial and velocity vectors for the osculating and perturbed orbits in addition to Jupiter's orbit."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "<h3 align=\"center\">Initial Conditions</h3>"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 5,
   "metadata": {
    "collapsed": false
   },
   "outputs": [],
   "source": [
    "mu3 = 1.2669e17                  # Standard gravitational parameter of Jupiter in m^3 / s^2\n",
    "m3 = 1.8983e27                   # Mass of Jupiter in kg\n",
    "e3 = .0489                       # Eccentricity of Jupiter\n",
    "a3 = 778000000.                  # Semi-major Axis of Jupiter in km\n",
    "Period3 = 4332.589 * 3600 * 24   # Period of Jupiter Orbit in seconds\n",
    "\n",
    "mu = 4.2828e13                   # Standard gravitational parameter of Mars in m^3 / s^2\n",
    "m2 = 6.4174e23                   # Mass of Mars in kg\n",
    "e = .0934                        # Eccentricity of Mars\n",
    "a = 228000000.                   # Semi-major Axis of Mars in km\n",
    "Period = 686.980 * 3600 * 24     # Period of Mars Orbit in seconds\n",
    "\n",
    "mu1 = 1.3271e20                  # Standard gravitational parameters of the Sun in m^3 / s^2\n",
    "m1 = 1.989e30                    # Mass of the Sun in kg\n",
    "\n",
    "dt = 24 * 3600                   # Time step\n",
    "tfinal = 4000 * dt               # Final time\n",
    "N = int(tfinal / dt) + 1         # Number of time steps\n",
    "\n",
    "t = numpy.linspace(0,tfinal,N)       # Time array\n",
    "r0 = numpy.array([228000000., 0.])   # Initial radius of Mars\n",
    "v0 = numpy.array([-21.84, -10.27])   # Initial velocity\n",
    "r3_0 = numpy.array([778000000., 0.]) # Initial radius of Jupiter\n",
    "v3_0 = numpy.array([-13.04, -.713])  # Initial velocity of Jupiter\n",
    "\n",
    "# Set arrays for radial and velocity components\n",
    "\n",
    "r = numpy.empty((N, 2))\n",
    "v = numpy.empty((N, 2))\n",
    "gamma =  numpy.empty((N, 2))\n",
    "delta = numpy.empty((N, 2))\n",
    "r_n = numpy.empty((N, 2))\n",
    "v_n = numpy.empty((N, 2))\n",
    "a_d = numpy.empty((N, 2))\n",
    "r_osc = numpy.empty((N, 2))\n",
    "r_osc_n = numpy.empty((N, 2))\n",
    "v_osc = numpy.empty((N, 2))\n",
    "v_osc_n = numpy.empty((N, 2))\n",
    "r3_n = numpy.empty((N, 2))"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Next we will have a for-loop that will give us our solution at every time step for each of our orbits. In this case, we will use a final time of 4000 days.  Each time step will be one day (in seconds), and we will be able to see the trajectories over that time period.\n",
    "\n",
    "The loop uses a crude method of integration (Tewari pg 166) to solve for $\\gamma$ and $\\delta$, the difference between the osculating and perturbed radial and velocity vectors respectively.\n",
    "\n",
    "The osculating orbit is used here as our base orbit.  The orbit for Jupiter is calculated as well and used with the osculating orbit to get our disturbing acceleration.  The acceleration is then used to find $\\gamma$, which in turn is used to calculate $\\delta$.\n",
    "\n",
    "$\\delta$ is added to the radial vector of the osculating orbit at every time step to give us our perturbed orbit.  The same is done with $\\gamma$ for the velocity vector for the perturbed orbit.  The solutions are then entered into arrays so that we can plot them!"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {
    "collapsed": true
   },
   "outputs": [],
   "source": [
    "for i,ts in enumerate(t):\n",
    "    delta = numpy.zeros_like(r0)\n",
    "    gamma = numpy.zeros_like(r0)\n",
    "    r_osc, v_osc = ellip_orb(a, Period, mu1, e, t[0], r0, v0, ts) # Trajectory of the osculating orbit of Mars\n",
    "    r_osc_norm = numpy.linalg.norm(r_osc) # Normalized osculating orbit of Mars\n",
    "    r0_norm = numpy.linalg.norm(r0) # Normalized initial orbit of Mars\n",
    "    r3, v3 = ellip_orb(a3, Period3, mu3, e3, t[0], r3_0, v3_0, ts) # Trajectory of Jupiter\n",
    "    a_d = acceleration_d(m1, m2, m3, r_osc, r3) # Acceleration due to Jupiter\n",
    "    gamma = mu3 * (dt) * ((1 - (r_osc_norm / r0_norm) ** 3) / r_osc_norm ** 3) + a_d * (dt) # Difference in velocity between osculating orbit and perturbed\n",
    "    delta = gamma * (dt) # Difference between osculating orbit and perturbed orbit radius\n",
    "    r = r_osc + delta # Perturbed orbital radius\n",
    "    v = v_osc + gamma # Perturbed orbital velocity\n",
    "    r_osc_n[i,:] = r_osc # Value of osculating orbital radius for every time step\n",
    "    v_osc_n[i,:] = v_osc # Value of osculating orbital velocity for every time step\n",
    "    r3_n[i,:] = r3 # Value of Jupiter's radius for every time step\n",
    "    r_n[i,:] = r # Value of the perturbed orbital radius for every time step\n",
    "    v_n[i,:] = v # Value of the perturbed orbital velocity for every time step\n",
    "    "
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "We mentioned earlier that sometimes the term $1 - \\frac{r_osc ^3}{r^3}$ can cause issues because towards the beginning of orbit the two terms are approximately equal and can cause the solution to blow up, but this can be solved as follows:\n",
    "\n",
    "$$1 - \\frac{r_{osc} ^3}{r^3} = -B \\frac{3 + 3B + B^2}{1 + (1 + B) ^{\\frac{3}{2}}}$$\n",
    "Where $$B = \\frac{\\vec{\\delta} (\\vec{\\delta} - 2 \\vec{r})}{r^2}$$"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Now that we have our solutions arrays, we can plot our answers.  Each array contains an x and y component for each time step.  We will look at a plot of the osculating orbit and the perturbed orbit of Mars, and in a separate plot, we will look at those two orbits along with Jupiter's orbit."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 10,
   "metadata": {
    "collapsed": false,
    "scrolled": false
   },
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAApkAAAJ4CAYAAAAut/h1AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnWeYVEXWgN/TMzgwpCFPDyhBSSLJHNYVBHQxrAqmXXcR\nUDEgq6ICKkEwoogJwy4GMLtijqsogwL6YQIBEQUJEgSUJHEC5/tRt3tu93RPYlIz532efmaq6ty6\n5966XX1unVNVoqoYhmEYhmEYRmkSqGgFDMMwDMMwjP0PMzINwzAMwzCMUseMTMMwDMMwDKPUMSPT\nMAzDMAzDKHXMyDQMwzAMwzBKHTMyDcMwDMMwjFLHjEwjHyKyQkQ+8T4zRGSviCz2pdeJyJ/38Rwp\nIrJKRI4oRb1PEpGLS6u+skJEkkVkqojMFZEvROQ/BcgeLSJviMhn3r2fIyLXiEhSeepcUkTk2BjP\n0P+JyPciMrwUzzNGRA4qxfruFJHlIvJJadXp1TvZ+/48VQTZDBF5XEQ+9+7bFyJyn4jUK+K5inQN\nInK/iEz0pet697NOUc7jO66F19a7QueN6kfWicifY+nlXeuvIhIsxvn+5T1TPxcid5aInFWITJH6\nvJLoWRkRkS4ikiUio2OUHef1M5neM3dqDJm/ev1Xptc35evHReRSEflKRD4Vkf+JSKsi6JXu9Xdz\nvGOvjyHTTkQ+9ur9UkT+Ucxr7ysi34rI3uIcZ5QQVbWPfSI+wM9R6b3AP33pp4A/7+M5AsBHQOtS\n1HsM8ElF378i6NkPWOpLXxtH7hxgPXCsLy/Nu29vVPR1FPOao5+h44Fs4PpSrH+fnskYdZbJ8wQ8\nDTxViMwhwFrgCl+eAOOBH4FGpXUNwFBgqC/d3LufB5Xw+pYDo2Pkh/uNaL2A+kAmkFbMc10c3V+V\n8H4Xqc8rqZ6V6eM9R7OAbdHtBBwIbAa6e+kuwB9AB5/MEV5eWy99OvAb0Ngncxbwa+g5BQYDS4ED\nCtHrS+BWL13HO+ZSn0xNYCXQ30s3BX4HehXzHpwE5FZ0W1SFj41kGrF4IEae+P5/A1ixLydQ1b2q\n2ktVf9qXehKUFsCqUEJV891vEamP+3G8VVW/8MluAf4BnCIiV5W9qqVK+BlS1TnAQuC8ilOnUjMF\n+ExVHw9lqGM47gf+kdI6kapOVNWJviwBymKXjvuA7+LosElVu3nPd0VQpD6vEuhZGgwGZuKMs2iu\nwb0AzwBQ1XnAp8Awn8wI4ANVXeLJvIt7GR7skxkJPKOqG730v4GGwEUF6HU60BmY6NW7zTtupE9m\nAFBdVad4MmuAl6JkjEqEGZlGPlT1oULK3wK2+Fxj13vu3889N9NBnus65H6aIyJPiUjdUB2+Y/v5\n8hqJyEs+N8yzItLAf24RGSoi80Vkpoh87bneqovIDUB/oIvvvM29Yw4RkXc918p8zwVZwyv7s0/v\nvp6r5gcR2S4i33j5s0Wkgyf/tlf2WLz7IyL/8Nwxn3t1XOQruxPXUYb0nBSnmouB2sArMe7/etxo\nypW+eq/1rm+6iMwSkWt8ZUneffrOu69fishNcXS/VUS2iQtlGOO7np8892EnEenq1fOJd2+eFJHG\n8e5HAVQDsnznPtVzz33qXcNgX1nIxTrDewbe9/ScJCIzPLEHPJ3GiMhAiXKlish7/meugLb3u19F\nRG4SkY/EuVQfEpGArzDVe56+8c79hoi0iLqno7xjZ4jIfUCBoQ4i0gU30puv7T1eBs7xvi/7dA0i\ncoP/PonIYcCL3nEvedd0eUH6FgURWa6qi2IZZyLSUGL3B0287+0P4tytF3nX+Y2InBdVx8Ve+/4o\nvjAMEZkA/AX4i3eOT0QkJVqHIvZ5O6P1lDyX/XJPhw9EZKmI9BeRZiLynIgsFJEXRKRalM5DxfUT\nM7zvU/ci3s4SIyJNgUuAcXFEegBfReV9CfTypXsWJCMiabjRzq9DhaqaA8yLqifWuZd5xqW/3gNF\npI1P5psY5z5eRKrHq1hcCMA8r+97HWgTVR4QkYfF/faEwpLO9JV/5j17X4tIDy9vsohsEZG3vHTc\nPrhKU9FDqfap/B+c66hfnLLlwLdAXS/9OtAMuAsY7JP7D/BkjGP7+dKfAuN96fuBmb70INwIYMgF\ncxCwCc+tRwzXIHAAsAy4xUsnAf8DnvPJhNyDT3npFGA2UAPnUrrAJ9sKeK2Ae3UKsB1o46Xbeeme\nPpmiuDBfBjYWUD4RyPV0PNrTs6ZX1hr40Sd7J65jruGlDweyCqj7QeCLqLz/+q5pEXnuKgGmU4ir\nOvoZAi7w9O8XdZ86e+k04OfQeXz3bStwhpfuC4zw1X9i1DnzuVJjPHMx2953vj+APl66Ic5VN8x3\n/LPAS770tcBPQJKXvhDnfmzupUNtFdd9i3t5yMXnoowq/6tX/pdSuoaI++TVlwscWJx+IuoeR7th\no9sh1nc1um0+AF73pR/w9DoxSvedeK5toIMn09InU6i7vLDntRA9LwZ2AH/z0j2B3d41itcey4l0\nv18CLAHqeOkjgF3AIQXodDEwA/jE+zsjKv0J0KmQ65oGnFJAO22NkXeFd0+rA/Vi3RvgbuBX7/+u\nxAhfwY04flGAbm/GeCbaeXWFnvX50W2Je4nIBdrFqbcmsBEvLMm7jkx87nKvjX4GUr10a9z3tpVP\nZikw3JeuBcyK+l7H7IOr8sdGMo3S4HVV3Qqgqueo6mqcETTZJzMN1xnERES6ASfgXGohngBO9EZX\nAG7G54JR1VW4jnx7AbpdhIvbud87JtfT7W/ijXT6eNqT2aOqJ6jqLtxo0iU+mQE4V2Y8bgbeVNUf\nvbp+AN728otDPdwPVzxC15wGZADJuHgq1IUgXATgvd1fCzzqXQ+q+g3uJSAeU4GjRaStV0ca0CR0\nTbj72dyrS4HLieMGjWKEN5L0Be6eXqiqz3hlw4FPVXW+V+8W3DNzdVQdv6vqO57Mq6p6t69MKDkR\nbe/L36Sqr3llvwHPAf8CEJGWwN/x3HseTwAHA7299BDgLVVd6dUxFzeiUxChiT3x2n877lqjJwAV\n+xoKYV/uZ3/xTaQp7sHeyNUpuBeeEA95OsXS63kAVV0EbAE6FV/lfUJwL4bgXlAPAH5Sxx7caFtX\nn/xI3Ev3NgBV/RpYgDPoYqKqU1W1u6qe7P3tHpU+WVXjfg9F5K9Ajqp+WMB11AT2ROWF0qleOXFk\nUn11aCEyJTl3UWWiuQhnED4OoKq7gWf8Al4bnaiqO730T8Bi3MhpiKnAQF/6AtzLNxTQB1d1kita\nAWO/4JcYedWBO0XkUFwnUA9IL6COkCH5koiEYsKScW/b6SKyAjdyucx/kKo+XIhuHYD1oc7DYynu\nR+Ew3KgO3vlWxzj+KWCmiBzolffGGbYFXcfMqLyluNGN4rCZvA49FrVwOm8B3gc+A+aLyP9w7s6Q\nq/UQXFtE37e416Cq34jIItwEpVtwnenLPpERwP0icr53rqe0aDFqd6nqs3HKOuLa2T8Tui75Q3pi\nPWv7Sry2h7znI8QyICgitXHPlgATRSTk9hfcMxsK82iPm6jlZxUFs9n7G6/9a3l/N/nySnQNqvpH\nIbqUlCmqGnbJSiEzwGPQDndNK3x58e7bRlX1zxTehps0Up6EdVDVXa4LY52vfAfueUZEauFe0vqJ\nSOjFW3DtXdB3vsSISE3gdgp2V4f0jA4nCKV3kherG0sm1MfuIG8EN55MvHPXLuDcRdEvFu1wvwG7\nfXmxnqWeXhhEMm70tB2Rv1lTgDEi8idVnYWLje/rlRXUB1dpzMg0SoPcGHkf4GbBdlPVbBE5CefO\nKQjFzRLMV5/XMZc1+c6rqrNFZBluBHMuzp1THktffAGcKyINVDVWgH47YEFodBI4VUSOwsWl/hu4\nWkRO3IfzPwsMFpGRwN9wM90BUNXHReRVXCd7GXCjiPRU1S8LqbOwkbEZqvrPQmRiPWvx0Bh58eIh\ni1Nv9Dn6qWpxjKhYevn5Anev2uFCE6JpD+TgRsf8lPQayhxVLXT5mqJUEyc/1nXvyyhsSYilQ3Re\ntE4TVbXQpazCB7vl2foT+z6EXsyvjTOaeRzuhe1FzwAWnAHV3/MiPaaqr+BcxtGDAek4V/huYLeI\nbIkjE3qRXe7LiycTi5+B6OWS0r3rWuaTiVXvXoo3GTXiHnoxvk/gXPyfe3kziJys+IuIfAwMFJHf\ngA2quskr20OcPricfi8qLfuFu9wXlFtq6+QZJUfczOj2uGV2sr3sfMH2USzAfaHbRtX1oIikq+p2\n3NvnIVHl/5C8iRZ7ffnVROQA3AzmJiLid6Uc4skuLOIlPY0zMi/BjWwWxMJoHXHu0wVFPFeIqbgR\nmXyzr8VNsumGNyNWRNqKSAdV/VJVBwPH4n5UOuNGUXdH6yQiV3tu8Hg8h3MBXQ78pqqh0TVEpK+q\nblTV+3Ejt4twBue+sID8bd9aRO4o4vHhHw3fC8kf+EZGRCQZKO4Epeg+5RBgnTcCuNA7b7sovW8R\nkZC7djEujregOiNQ1W9xLtd4M+/PA54P/cAVgYKuIRZ78f24ltMLXjQ/eDr47110eEtR8fcLKd5z\nUGF4fdlK8j83Z4vI3wo4zu8uj/4U6C5X1emqephfHrfE0NNeOjTq9hFwZNThR+LirkNML0jG82p8\n5Zfx7nln8o/q+/kIOEQi12c9CvhF81Yh+QgXU06UzJyokUo/i3G/Af6JQdHP0onA6pCB6XFAjLqe\nxn3/rvX+Bwrtg6s0CW9kikhfXCxfvrc7EakpbvbpD94Mvw889220XLKI3CZuluB33sywE6LlPNlr\nRWSRN1PtKylkkd+qiPfjtx442Zd9diHHzMS5G26R0Ku2m913pKr+6ondAfxTRJp45W1xrutQ+Qbc\nOnYA1+OMwhdwbsRrvWOSvf9fCMXJET/OK8RU3GSmDC/GsiDuAM4Ukdbe+doBZ3j5Rca7hxcDo0Xk\nmFC+Zxg+A0xT1ale9rFExnwegDMsV3kd7/3AlZ7LDG+E85KCXNyquhY38jyRqPglYLLkzSYP4Dwi\nP7Jv3A10CrkPvXYaR35XbzzWA/XFzeANxTzOB+qF2gJnCEePKhTU9oJzK5/t6dQIF2f1IICqrsDF\nAt4Y+gETkSM9mcVeHQ/hnoeWXvlRwDEUzsXACSIyKKyMmwF7F+6F7drSuAafjJ/fcKNw9UUkHc8D\nISK9vJf5upQxXvzvB8CQUH+AGzWP7ueLMmLp7xceoHCXcXEpyajpbbi+rDmEX8xvo/gvo/tKtO4P\n4Qy9bp5enXEG2HifzN24UbtQzPZpuNFE/7Jat+Our5GXHoR7rl4In1jkmajwmPdx393rvPI6uDa/\nzSczFTeaerEn0xQXzuOXieYF3AvnVd4xNYiMrQT4Hsjw+utQvHUsA/F13Pq+p+EmkIaI2wcXoFfV\nQCvB7KOSfnBLoPyIm1iRS9TiwbiH9lMgxUuPw3U4wSi5x3FvzvW99CW42I9OUXIjvONbeOmeuCVY\nTq3oe1FG9/dY3KzFXNyXcJyvLOCV7fTKpkQdezxuCYt5wGvkzQz9BG/RXvLP0myA+9FehHsrfhlI\nj6r3Wtwkk0xPpkvU8bNxxup0oJ6XfzDwHs69+J3X3qFZhIcDn3u6zSH+wujv4wyzoty3i3Az7j/H\nzer+u6/sTpzLZ5N3L04ppK7DcWv0febd71nA5VEyrXEd6SyvzjlAb195Es7IXeDV8Q6+2bcFnPvv\n3vOeHJU/zru2j4H/A+4FpIjP0LsFnK8HLiTh/3Df2xt9ZTdH3bd2Ucde4dU/B7jMl38Tro94Hzca\n/bMnd1VBbe9rpxm4H8yPce64B4CAT6467sd1sSfzNt4s/CjdV3h1PYp7xtcStdpCjPuR7j2rc7xr\n/hz3A1876vko8TUAN3i67/TOEfpehAyez8mbzT+EAmbM4tZ/DfUJP3v1BWPI+b8Db+FmvPv7kqs8\nuSbAu7hZ2O/hZtXvBY7zygf6dP/Ay3vPV09o5YLWuO9jJm4Gc3IB11BQn5dPz2gdcLHnoeO/wXkc\nxnvtvRZ40Fffv3B93afeMX8pTv9c0g95s9RjtpN3D+Z49+v/iLHQOe7Fea4n8xlweAyZgbjfgE+B\nD/HN1PbK/4sbgYx+5t/0zv81vk0CfDJtPJ0/xY2YXlSEaz7Gewa+wvV/15D3e9Qa10c+jPt+vIf7\n3n3r3Z9hUXU9BtwWlVdgH1yVP+LdoIRERK7DLf3wEzAa98O5yivrhXvT6K5ulAxvlONX3CjWEC+v\nDa6TGKh5I0OIyEJguaqe6aXrAmuAe1V1rE/uHdzyJB3L+nr3B8Q32UBEfsEZEi9VsFqFIiJzcJ1t\nQTO+DWO/RNxWll/ilnB5tZzO2VDdbPhQOojzSjRT1XXxjzSMskNE3sAZv8WdzFYlSVh3uedeuAE3\nUhGLvrhRxtmhDHXxgbPJmxEG0Mf7mxl1/Ce4XVVCsXy9cWsSxpI7VPIWizUK5gNxi4M3ARrhXJqV\nEhG5Stw+zicAi8zANKowBwI3l5eB6fGYiPhDbq4GMs3ANMobETnPixFvgdsa0wzMIpLIs8tH49ZM\n/CUvZCeCjsBadTsN+FkOnO57S+6Ic8FEx04sx92fQ3FD7B19+dFy4NZl29e4tKrAItz9zAVuUNXF\nhchXJAfhdN2Ai/sxjCqJugklRVkLtTR5E7hLRELL1qzArXRgGOVNY9yko/W4+FKjiCSkkekF8p+L\nm8Ecj4a4YN9oQltWNcAFIjcEdmr+uAG/XKg+YtS5DRc83QCjUFQ1Yb6gqjoCF4drGEY5o6rP4VY5\nMIwKRVUfIXJik1FEEtVdfjduYeeyWkjYMAzDMAzD2AcSbiTTW37lMOB8f3YM0d+AYIz80Bpcv/vk\nUkVEokYzY8mBW3dvcwFy0fom7swqwzAMwzCqHKpaKhsaJJyRiVs2KAB8KZE7FwC8J257t5tx8UNH\niEhyVFxmS9wWUyGj8TvgQlxg+6oouRzcUhUhOXDLdETLKQXEKyXyDP6qTv/+/ZkyZUpFq2GUAGu7\nxMbaL3Gxtkts4sxzKREJ5y5X1TGq2lpVD/c+XfE2vsetS3W4qn6AW5uxGm69RiC8hNEJwDRfla97\nf7tFnao78D/N2/P6A2BXDLmTge/VLR5sGIZhGIZhkIBGZhxCZnf4elT1I9w6mbd5K/wDjMSNTt7l\nk/sR+A9wk4g0ABCRAbjtzG7xyW3FLVA82Ld7R0/c7hHXl81lGRVNixYtKloFo4RY2yU21n6Ji7Wd\nESIR3eVhRKQ3bveIJl7WuyKSpaqhvU3Pxe22ME9EcnAL+XaLsc7a1bjtCWd77vY/cAtvR2zxparj\nRWQX8I6IZOOW4TlXVT8si+szKp5u3bpVtApGCbG2S2ys/RIXazsjREIbmar6Pm67uHjlO3FboRVW\nTy5u3c3RRZB9CLe/q2EYhmEYhhGH/cVdbhiGYRiGYVQiEnrv8kQg/8pIhmEYhmEYlRMRKbUljGwk\n0zAMwzAMwyh1Ejom0zDKmszMTAtiT1Cs7cqfFi1asHLlyopWwzCMGDRv3pwVK1aU6znNyDQMwzBK\nhZUrV9rmE4ZRSSnNRdaLfE7rEMoWi8k0DKOq4MVyVbQahmHEoKjfT4vJNAzDMAzDMCo1ZmQaRgFk\nZmZWtApGCbG2MwzDqFjMyDQMwzAMwzBKHYvJLGMsJtMwjKqCxWQaRuXFYjINwzAMwzCM/QIzMg2j\nACyuL3GxtjPKi86dO9O4cWMCgQApKSlkZGQQDAapW7cu9evX59RTT2X69OkVrWaps2zZMoLBILVr\n1yYQCPDpp5+Wy3k///xzgsEgqampBAIBVq1aVazjs7OzmTx5Mr169SIjI4OMjAyaNWvGGWecwfPP\nP1/i0fgzzjgj/BwMHDiwSMdkZWXRoUMHevXqVaJzVnbMyDQMwzCMfWD+/Pl8+eWXAJxwwgmsXbuW\ndevWsXXrVmbNmsXGjRs55ZRTmDJlSpnqMXPmTAKBAOPGjSvT84Q4+OCDWbduHTfccEO5rsF43HHH\nsW7dOi644IJin3fFihUcddRRPPTQQwwbNoxffvmFtWvXsmzZMvr168eIESM48cQT2bhxY7H1eued\nd8LPQVHJzc1l69atbNq0KV9Z//79S2REVybMyDSMArAdYxIXazujMnDooYfyzDPPADB06FCys7Mr\nWKOqy7Zt2/jLX/7Cjh07mD17Nr169SIpKQmAlJQUzj//fGbNmsWiRYs4/fTTycrKKnOdatSowcqV\nK/nqq6/ylYlIhSygXpqYkWkYhmEYZchhhx1GnTp12Lp1KwsWLCiz89ikq4K59dZb+emnn7j99tup\nU6dOTJnmzZtz/fXX89VXX/Hwww+Xi15JSUkxjcn9oT3NyDSMArC4vsTF2s6oTIQMBr8xkZWVxe23\n30779u1p2LAhjRo14tRTT+WTTz6JOLZz5840aNCAQCDA2LFjefnllznyyCNp2LAhgUCAAQMGcPbZ\nZ9O3b19EhAkTJoRjDc8880wA2rVrR1paGoFAIDyyCnDttdfGjCPMzMyMiHtctGgR1113Ha1btyYl\nJSVmDGZWVhYjR46kTZs2pKWl0bZt27iG2o8//shFF11EkyZNaNiwIS1btuSqq65i/fr1+WQ3bNhA\n//79adiwIRkZGRx77LG88847xbr/2dnZPPHEEyQlJXHWWWcVKHveeecB8Nhjj4XzCmuDWDGY7733\nHsceeywZGRk0bNiQAQMGsGHDhnD5xx9/HDO2dOXKlQSDQV555RUAjjrqKILBIBkZGTz33HPFuu4K\nR1XtU4Yfd4uNRGXGjBkVrYJRQqztyp+q3N+tWLFCRUS7d++er+ybb75REdFGjRppdna2qqpmZ2dr\nt27dtFGjRuFndfv27Tpo0CANBAL60ksvRdSRmZmpIqKHH364DhkyRHfu3Kl79+7VCy+8UAcMGBAh\nM27cuJg6TpkyRQOBgE6dOjWm7qF6/PTv318DgYB269ZN3333XVVVXb16tdavX19nzpypqqq33nqr\nioh27dpVn3zySc3JydHs7GwdN26ciojefPPNEXV+9dVXWrduXe3du7du3LhRVVUXLlyobdu21ebN\nm+tvv/0Wlv3jjz+0TZs22qhRI/3iiy9UVfX333/Xvn37art27TQQCOjKlStjXq+f2bNnq4ho+/bt\nC5Xdu3ev1qhRQwOBgK5ZsyacX5Q2CN3Ldu3a6bnnnqu///67qqp+8cUX2rBhQ23Xrp1u37495j2O\nvo5Q/qpVqwrVuSgU9fvpyZWKDWQjmYZRABbXl7hY2xkVTW5uLnPnzuXiiy8mKSmJhx9+mOTkZAAe\neOABZs6cydixY8PPas2aNXnkkUdo2rQp1157bcz4zT/++IMHH3yQGjVqICKMHj2af/7znxEyWgZu\n1h49enDaaacB0LRpUyZPnkzr1q0jZDp37szAgQNJSkoiOTmZUaNGceSRRzJ+/HiWLl0aluvfvz85\nOTk8++yzNGzYEIAOHTrwwAMPsGrVKm6//faw7D333MPSpUsZN24cxxxzDAD169fnySefZM2aNUXW\nf+3ateFjC0NESEtLizjOT1HaYN26dTz11FPh8x1zzDGMHTuWJUuWMH78+CLrDYntNjcj0zAMw6gw\nRMr3U9bMmTMn7Kpu0qQJ5557Lm3atOGzzz7jggsuCMs999xziEjYcAuRnJxM165d2bBhA3Pnzs1X\n/8knnxzhcm/fvj3du3cvuwvy6NmzZ0S6T58+BIPBcFpEYi7Dc9ppp6GqvP7664Cbib9o0SKOOuoo\nGjRoECF79NFHA0S4wkPHnXrqqRGydevWDcuXJbFiJYvSBkcffTS1a9eOyAu19auvvloGmlZOkita\nAcOozGRmZtqIWIJibZcYJPAgTUyOP/74fDGVsfjxxx8BtxxPNHv27KFmzZoxR9HS09P3XckSUJTz\n+o3OEM2aNUNVwyOZS5YsAWDu3LlkZGTkk69VqxabN28Op0PHxZKNlRePkGyspYKiUVW2bNkCuFHb\naPblXoBbX7SqYEamYRiGYZQzoZGwJUuW5BvxKohAoPQdkHv37i2z8+7evTsiHbruU089lddee63I\n9ezZs4eUlJQS6QBu8kytWrVYtmwZu3fvpnr16nFlf/rpJ3bv3k27du1iGpSldS+qAuYuN4wCsJGw\nxMXazqjMtG3bFiDmQts7duzg448/ZseOHaV6zmrVqqGq+WI9Y83oLgnr1q3LlxcajT3kkEOAvOv+\n5ZdfYtaxdOnSiDCB0HGxRnVj5cWjWrVqDBo0iJycHN56660CZV955RVEhCFDhhS5/mgKuhcHH3xw\nietNNMzINAzDMIxy5h//+AeqGl6mxs8TTzzBP/7xj2KP3NWsWRMgbETm5uYyZMgQVq9eDeS5a6MN\n29JY7ktV+eijj/Llv/HGGyQlJXHOOecA0KlTJzp27Mi8efP4+eef88lfcMEFvPTSS+F0nz59UFXe\nfvvtCLmtW7cWe3ed0aNH07ZtW0aNGsW2bdtiyqxYsYL77ruP7t27M2jQoGLV72fu3Lls3749Ii8U\nX3ruuecWqY7o9pw9ezZ33nlniXWqCMzINIwCsLUWExdrO6M8Ke4M4H/9619069aN+++/P2xAqSpv\nvvkmo0ePZuLEieGZ6EWtv3Xr1lSvXp3vvvsOgBkzZvDEE0+EjZXjjjuOYDDI888/z4oVKwA3Uenj\njz8u9LoKOn+oLDMzk6lTp5KTk0N2djbjxo1jyZIlDB8+PDwiCfD0009Tq1YtBgwYwMqVKwFnNF55\n5ZVs2rSJYcOGhWVvvPFG2rRpw4QJE/jiiy8A+P333xk4cGD4uop67+vUqcOHH35IrVq1OPHEE/nw\nww/Jzc0FnDv+lVde4aSTTuLoo4/mtddeC+8GFH2dBRGSqVmzJgMGDAjHgH7xxRfcd999tGvXLuL6\n/MdE19+pUyfATZYC+Pe//823335bpGutNJTWWkj2sXUy90dsrcXExdqu/Kmq/V2nTp20cePGGggE\nNCUlRdPT07Vdu3aFHpeVlaV33XWXHnbYYdqwYUNt3ry59uzZUz/88MMIuZ49e2qDBg00EAho7dq1\nNRgM6j0N/WggAAAgAElEQVT33BOzzueff15bt26tjRs31jZt2ujzzz8fUf79999rr169tF69etqy\nZUsdPHiwLlq0SAOBgKampmowGNRZs2bpokWLND09XVNTUzUQCGjjxo01GAxGrOW4dOlSTU9P19q1\na2tSUpK+/fbbOmTIEG3VqpWmpaVp27ZtddKkSTH1XLp0qfbr108zMjI0GAzqIYccoldeeaWuXr06\nn+yGDRt0wIAB2rBhQw0Gg9q1a1d99tlndcCAAWHdzjjjjELvd4icnBx96qmntGfPnhoMBjUYDGrT\npk319NNP11deeSXmMUVpg9NPP10bNWqkgUBABw4cqM8//7x26dJF09PTtWHDhjpgwADdsGFDWH76\n9On57vHZZ58dLt+9e7cOGDBA09PTNSMjQ3v06KE///xzka8zmqJ+PynFdTJF97epfZUMEVG7x4Zh\nVAVEpNgjeoZhlA9F/X56cqWy4Je5yw3DMAzDMIxSx4xMwygAi+tLXKztDMMwKhYzMg3DMAzDMIxS\nx2IyyxiLyTQMo6pgMZmGUXmxmEzDMAzDMAxjv8CMTMMoAIvrS1ys7QzDMCoWMzINwzAMwzCMUsdi\nMssYi8k0DKOqYDGZhlF5sZhMwzAMwzAMY7/AjEzDKACL60tcrO0MwzAqFjMyDcMwDMMwjFLHYjLL\nGIvJNAyjqmAxmYZRebGYTMMwDMMwDGO/wIxMwygAi+tLXKztjIpg8eLFXHXVVbRt25aMjAwyMjLo\n2LEj1113HStXrqxo9WKSmZlJMBgkNTWVQCDAqlWryuxcGzZsoFmzZlx22WVldo59YfXq1dx44410\n7Ngx3H5t27Zl0KBBLFy4sER1Llu2jGAwSO3atQkEAnz66adFOu6jjz4iLS2NqVOnlui8lQEzMg3D\nMAyjFJgwYQJdunShXr16zJgxg7Vr17J27VreeOMNtm3bRtu2bXn66acrWs18dOvWjXXr1nHBBRcg\nsu9e0hYtWtCqVauYZXv27GH79u1s2rRpn89T2rzwwgu0bduWrVu38sYbb4Tb75NPPqF+/fp07dqV\n22+/vdj1Hnzwwaxbt44bbrihWPd3+/btbN++na1bt+YrCwQCnHzyycXWpbxJrmgFDKMy061bt4pW\nwSgh1nZGefL4448zbNgwHn74YQYPHhxRdvDBB/Pkk09Ss2ZNLrnkEurWrUufPn0qSNOypyBD6sAD\nD2Tjxo1Uq1atHDUqnHfffZd+/fpx3XXXce+990aUNW3alLvvvpv09HSGDh1KamoqQ4cOLXOdzjnn\nHHbu3MkBBxxQ5ucqK2wk0zAMwzD2gfXr13PDDTfQvn37fAamn7vvvps6depw1VVXsXv37nLUsHJR\n2QzM3bt3c/nll1O3bl1uu+22uHLXXHMNrVu3ZuTIkaxbt65cdEtkAxPMyDSMArG4vsTF2s4oL558\n8kl27drFOeecU6BcamoqvXv3ZuPGjUybNi2cn5WVxbhx4zj00ENp2rQpBx10ECeddBITJkxg27Zt\nEXVs2LCBq6++mpYtWxIMBmnRogXdunVj/PjxbN68GYBevXrRoEEDAoEA48aNCx973333EQwGi+1q\nfeWVV+jbty+tWrUiPT2dJk2acPbZZ/Ptt99GyL344osEg0FWr17NL7/8QkZGBsFgkIyMDH7++Wem\nTJlCMBgkJSWFpKSk8HHRMYvTp09n1KhRtG3blrp163L88cfz+eefx9Rt+vTpHH/88dSuXZvmzZtz\nzjnn8OOPPxIIBEhJSSEjI4PnnnuuwOt77bXXWLt2Lb1796Z69epx5USEPn36sGfPHp588kkgfzzr\nokWLuO6662jdujUpKSkxYzCzsrIYOXIkbdq0IS0tjbZt2/Lwww9HyAwaNChmW91zzz0Eg0FEhDlz\n5kTc4+zs7AKvs0JQVfuU4cfdYiNRmTFjRkWrYJQQa7vyp6r2d7169dJAIKAvv/xyobJ33nmniohe\ndtll4bxLL71UmzZtqosXL1ZV1dzcXH344YdVRHTmzJlhuV9++UWbNm2qnTt31qVLl6qq6o4dO/Rf\n//qXiohOnTo1LJuZmakiomPHjs2ng4ho9+7d8+X3799fA4GArly5MiK/RYsW2rdvX920aZOqqq5f\nv17PPvtsTU1N1fnz5+erp0WLFtqyZcu496Bbt24aCATy5d96660qInrCCSfoW2+9paqqGzZs0K5d\nu2rt2rV148aNEfLvvPOOJicn61lnnaVbtmxRVdXZs2dr165dNRAIxLzGWFx22WUaCAR0/Pjxhcq+\n8MILKiLaq1eviPzQvevWrZu+++67qqq6evVqrV+/frgNQ9fXtWtXffLJJzUnJ0ezs7N13LhxKiJ6\n88035ztfvLaKl18QRf1+enKlYgPZSKZhFIDF9SUu1nZGebF27VoA6tevX6hsgwYNIo4BN5J27LHH\n0q5dO8BN6rj66qs544wzSE1NDctdeeWVrFu3jilTpnDwwQcDbnT0gQce4JBDDim164mmQ4cOPPLI\nI9SrVw+Axo0bM3XqVPbs2cP48eNL/XxHHHEEZ555JgCNGjXiyiuvZMeOHXzwwQdhGVXl6quvplq1\nakyZMoW6desCcPzxx3P11VcXa73WfW0/Pz169OC0004DXCzn5MmTad26dYRM586dGThwIElJSSQn\nJzNq1CiOPPJIxo8fz9KlS4usdyJgE38MwzCMCkPGlsqaz0VGx1SOxeL9k2PS09N59913mTRpEv36\n9aNOnToAvPXWW2GZLVu28P777xMMBunSpUu+uqZNm0ajRo3KRNd33nknX16dOnVo2rQp8+fPL9Vz\niQgnnHBCRF7z5s1RVVavXh3O++abb1i5ciUnnngiaWlpEfKnnHJKqeoUT89Y9OzZMyIdPcFLROjV\nq1e+40477TS+/vprXn/9dW688cbSU7SCMSPTMAogMzPTRsQSFGu7xKCyGH37QkZGBosXLy7Ssjwh\nmaZNm4bznn32WS666CKuueYabrjhBrp168b555/PhRdeGB7J/Omnn9i7dy8HHnhgzHo7depUClcS\nmx9++IEHHniAOXPmsGHDBgKBAKrKxo0bOeigg0r9fI0bN45Ip6SkAC6WMURoxC8jIyPf8bHyCiIk\nX9L285Oenl5oHcFgMF9es2bNUNX9biTT3OWGYRiGsQ90794dVWXBggWFyn733XeICN27dw/nHX74\n4SxevJjp06dz6aWX8s0333DppZfSoUOHfEbHnj179knX4riRARYuXMiRRx7J7NmzefbZZ/n1119Z\nu3Yt69ati2vw7iuBQNFNk329H1D89gPiTpwqju5+9tfVBszINIwCsJGwxMXazigvBg4cSGpqKq+9\n9lqBcrt27eL999/nwAMPjJiJnpubCzhjZ9KkSaxdu5aRI0eycuVK7rjjDgBat25NIBBgzZo1Meve\ntGlTxEhcaJmg6BnH69evL9a1Pf300+zatYvRo0fTuXPnYh1bloRiUGPFRsaLl4zHOeecQ9OmTXnv\nvfcKNFpVlVdffZVatWoxYMCA4insI9byRyGdyzK2tiIwI9MwDMMw9oEmTZowceJEfvjhBx599NG4\ncjfffDM7duxg8uTJEesfVqtWjY0bN4bTycnJDBs2DCC8LFFaWhpnnHEGv/32G3PmzImoNycnh44d\nO/LUU0+F85o1awaQb4vI4i7tFXJVR7N7925+/fXXmGU1a9aMMG6nTJnCK6+8UqzzFsbhhx9OixYt\n+Oabb/Lp8dFHHxWrrurVq/Of//yHbdu2MWrUqLhyDz30EEuXLuXBBx8scfyrqsbU74033iApKanQ\nZbBCpKamRtzjiRMnMmPGjBLpVJaYkWkYBWBrLSYu1nZGeTJo0CAmTJjA9ddfz8iRIyNG05YtW8al\nl17KE088wYsvvhhz4sd1110XHonMyspiwoQJiAj9+vULy0yaNImmTZsyZMgQli1bBsDWrVu57LLL\nqFOnTsR+4AcddBBHHHEE77zzDvPmzQPcvur+9TmjCbnS/S71888/n2rVqjFu3DiWLFkSPuegQYPi\njvp16tSJDRs2sH79enbs2MHdd9/Nhg0b8p0n3vmLki8iTJo0CYDLL788bIx//vnnvPjii3GvMR69\ne/fmueee47HHHuOKK64I319wo4w33XQTI0aM4MEHH4w5ihnr3sWTyczMZOrUqeTk5JCdnR2+t8OH\nDy/ySGanTp1YunQpO3fuZOPGjdx+++3s3LmzOJdcPpTWWkj2sXUy90dsrcXExdqu/LH+TnXJkiU6\nePBgbdu2rQaDQU1PT9fDDjtMr7/+el29enXMY1544QXt06ePtmrVSjMyMrRZs2baq1cv/eCDD/LJ\nrl+/XocMGaLNmzfXYDCoLVu21EGDBunatWvzya5evVr79OmjjRo10mbNmunf//533bhxowYCAU1J\nSdFgMKgvvviizpgxQ9PT0zU1NVUDgYA2btxYzz777HA9M2fO1JNPPlkbNGigTZo00a5du+qjjz6q\nLVq00OTkZA0GgzplypSw/M8//6w9evTQRo0a6YEHHqgDBgzQrKwsffrppzU9PV1TUlI0EAhoMBjU\nIUOG6LZt2zQ9PV1r166tgUBAGzRooH379lVV1T59+miDBg00EAho7dq1NRgM6q5du8Ln+vjjj/X4\n44/X2rVra4sWLfRvf/ubrlmzRkVEe/ToUez2W7NmjQ4fPlw7duyowWBQg8GgtmnTRq+44gpdsmRJ\nPvlFixblu3fBYDBirdGlS5eGry8pKUnffvttHTJkiLZq1UrT0tK0bdu2OmnSpIh6L7vsMk1PT8/X\nViG+/vprPeaYY7RRo0Z60EEH6Y033ljotRX1+0kprpMpWswgYKN4iIjaPTYMoyogIsWeWGIYpc2v\nv/5KRkYGF1xwQYlGNfdXivr99ORKZW0xc5cbhmEYhpFwvPrqq4wZMyZf/meffQa4hdGNisWMTMMo\nAIvrS1ys7Qxj/+a3335j4sSJvP/++4AL/5szZw7Dhw/nqKOOiohnNSqGhDQyRaSViEwQka9E5EsR\nWSIin4rIaVFyNUVkkoj8ICILReQDETk0Rn3JInKbiCwWke9EZJaInBAt58leKyKLRGSed/6zyuo6\nDcMwDMOITY8ePRgwYADDhg0jIyOD+vXr079/fy688EJmzJgRMYPfqBgSMiZTRAYDw4GTVHW5l3cn\nMAzorqqfeXnvAzWBXqq6R0TGAVcAnVV1na++x4FuwPGquklELgEeAo5T1e98ciOAocDRqrpCRHoC\n7wFnqur/4uhqMZmGYVQJLCbTMCovFRGTmahG5tlAfVV9ypdXF9gMTFTVG0SkF/A/nNE505OpBvwK\nvKCqQ7y8NsBiYKCqTvXVtxBYrqpn+upfA9yrqmN9cu8AzVW1Yxxdzcg0DKPYbN61mZcXvczzC55n\n1qpZFa1OXI5uejQXdbyICw+7kCa1mpiRaRiVlIowMhNy73JVfSNGdl3vb2gxrr5AFjDbd1y2iMz2\nyoZ42aHd6zOj6vsEuFxEUlV1J9AbqBFH7l4RaaOqPxb/aozKjO1/nbhUtrbbkbWDWz65hQf/78GK\nVqVUmbtmLnPXzOWaD66paFUMw6hkJKSRGY2INAUmAV8Boe0WOgJrVTUnSnw5cLqINFTV3zy5vcCq\nGHLJwKFevR19+dFyAJ0AMzINo4ry8c8f0/PZnvtcT+9DetOvcz/ObHMmNQ+oWQqalQ9ZuVmk3Bp7\ndxjDMKomCW1kikgrnEu8FfA+cI6qbveKGwJ/xDhsm/e3AfCbJ7czhk/bLxeqjxh1bgPEJ2fsR1Sm\nkTCjeJRF2/130X+5YNoFxT7uyIwjmXLWFDo07lDqOlUWDkiySRaGYUSS0Eamqv4MtBaRWsBtwHci\ncqaqzinkUMMwjLiMmD6C8bPHF1n+ssMv4+HeD5OSbCN5hmEYIRLayAzhjV5eJyKn4tzlXXCjlMEY\n4nW8v797f38DUiX/DJ1YcgC1cROM4skZ+xGVLa7PKDpFabvvN35Ph0eLNrp4druzeanvS5XSkMzK\ngp9+gsWL3eeHH9znxx9h+/bCj69RA1q0gNat4dBDoUMH6NQJ2reHatXKXH3DMPZTEtLIFJHqqro7\nRtECoK83i/w74AgRSY6Ky2wJrPfiMfHkLgQOJDIusyWQA3zvkwNoEUNOfeX56N+/Py1atAAgLS2N\nLl26hH/8QgtGW7pypufNm1ep9LF0ydPLNy+n1XWtANy3FvIiqn3pXgf34oORHxCQQLnot3s3fPdd\nN8aOhZ07Mz1Funl/yye9a1c3z0DN5K23Sl5fSkoQkVKZlGoYRikTDAYjXr5D/VHo/xUrVpT6ORN1\nCaMZwAhV/b+o/LnAIapa31vC6APcEkafeuWhJYyeV9V/eXmhJYwGqOozvroW4JYw+quXDi1hdI+q\njvPJ2RJGhlHJ2Kt76fx4ZxZuWFig3Pwr5tOpSacy0WHXLrjlFrj//tKvu3FjOOUUOOYYOPpoN/pY\nq1bpn2fbNliwAL7+2n1mzIBffin984wYAWPHwgFlFNa5YP0COj1ecDu3TGvJD1f/YLGlRpXH1sl0\nRuYe4O+qusnL+xdwPzAutI6liLyHW4z9L6q6S0TG4hZj7xK1GPtjuFfxP6nq7yIyADdb/VhVXeCT\nG45bjP1YVV3uLcb+Lm4x9g/j6GpGpmGUMUt+W0K7R9oVKPNJv0/o3rJ7qZ1TFe65xxlIJeWSS2DU\nKGjevNTUqnT89BOMHg0vvVTyOm6/HW6+GUpzkPR/S//HX57/S4Eyy69ZTou0FqV3UsNIAMzIFDkO\nuBQ4CufSroGLmXxEVV/yyaUC44FTPLnVwLWqujiqviRgDHA+bm3NP4AbY00g8ozZy4FsIBe4VVXf\nLkBXMzITGL9rwag8FDYydXrr07k+eD3du++7Ufntt3D44cU7pnlzmDYNjjxyn09fZcjMhDPOgB07\nwjnkueXj89VXcMQRpaPDDR/ewH2f3xe3/ItLvuCYZseUzsn2Y6zfTGyqvJGZSJiRmdhYZ1k5WL55\nOa0eahW3/N2/v8tprU+LyCtu261dC02bFl2nhx+GwYNLd3TNyMPffqpw770wfHjRj1+7FoKxpn4W\ng2fmP8PFb1wct3zVtas4sO6B+3aS/RDrNxMbMzITCDMyDaNkdHqsEws2LIhZNu28afQ9tG+J6373\nXTdqVhiNGsG8eZCRUeJTGWXMxo0uLrUocxZefBEuvLDk58pckUn3qbFHx9s2aMviwYtt4pOR8JiR\nmUCYkWkYRePDZR9y6nOnxiy775T7GHrc0BLV+/XXRXNbz5wJf/5ziU5hVEIyM6Eo0RILFsBhh5Xs\nHONmjmNM5piYZfv6ImQYFYUZmQmEGZmJjbl9ypZ/vPYPnl/wfMyyrJFZVEsq3iKNqvDXv8I770BB\nMX2l4Uo1ypay+O799psbnS6ILl3gm2+KHwaRszeHarfFfl77tu/LtPOnFa/CBMb6zcSmNI3MhFwn\n0zCMxCR3by7Jt8Xudl49/1X6tO9TrPp27Ch86Z5vvoGuXYtVrbGf0rChexHxM2cOnHBCXnrePAgE\nImV27IDU1ILrTg4ko2PyKn//p/c57QUXJ/zq4leRsXm/2TmjckgKJJXoGgwjkbCRzDLGRjKNqs6e\nnD1Uv6N6zLJ1168jvVZ6kevavdvtThOPDh1g/nxIst9vo4Sowp/+5IzPeGzZAnXrFr3OjTs20nhC\n45hlW0dspU5KnZhlhlERmLs8gTAj06iKFGRY7h29t1iTI/70J5g9O3bZ5ZfD44+XREPDKDqDBsHk\nybHLjj3WGaRFfaRVlaRxSSj5fxd237K7Um5balQtzMhMIMzITGwstqjoqCqBcYGYZcUxLD/5BHr0\niF3Wt69bf7IoWNslNpW5/QoyOt9/H/5S8BrvEQTvC/Lr9l/z5SeyS70yt51ROBaTaRhGpeGkKSfx\n6cpP8+X749MKo1UrWL48dtnu3ZBigztGJeI//3EfgKysyOezd++8/+vUca71gt6v1l0f3nwuIm4z\nFLtcv0Z9fh/2e6nobRjljY1kljE2kmnsjzz25WNc9d5V+fKzR2WTHCj83XXzZqhfP3bZ228XbQ1L\nw6iMTJ8OvXrFLvvtN2jQoPA69upeksblH8WcctYULu4Sf3F4wygNzF2eQJiRaewv7MjaQa278k/l\nLur+zt98E3/7PxutNPZHsrPhgANil82aFTmrPR4bdmygyYQm+fI3DdtEvRr19lFDw8hPaRqZsQOo\nDMMAXGxRVefsl85GxkqEgTn5zMnoGEXHaIEGZmhChEikgdmrl5vFG/qUhYFpbZfY7A/tV61a5HPu\nd6X/6U95340PP4xfR+OajcPftUdOeyScX/+e+shYodWD8bdbrSj2h7YzSgeLyTQMIx9r/1hL04n5\nN/IuSpzl3LlwzDH580eNgnHjSkM7w0hM3nsv7/9HH4XBg93/p/o2uvryy/g7VF111FVcdZQLUwmM\nDaAoy7csD8dyrh26lmBt22XAqDyYu7yMMXe5kUgMfncwj371aETe3EvnclTTowo8buNGaBxjGcA7\n74SbbipNDQ1j/+Ohh+Caa/Ln//wztGxZ8LE//PYD7R9pH5F3UceLeK7Pc6WooVGVsJjMBMKMTKOy\nE2+SQWGjlqr5d0YBuOEGuPfe0tLOMKoWN94IEybkz8/Njf198+OfnR5i1y27qJ4ce81aw4iFxWQa\nRjmxP8cWfbnmS2SsRBiYL/Z9MRz/FY9LL3VxZP4fvIMOyos7qywG5v7cdlWBqtp+996b913yrxeb\nlOS+d/37xz829N197+95fvkad9RAxgqfrfys7JSOoqq2nZEfi8k0jCrGiOkjGD97fERe1sgsqiVV\ni3vMypXQokX+/KwsN7nBMIzSZ/p09zcnJ+97NnWq+wAsXOi2Uo2md+vezuD0bZDw5yl/BuDKI6/k\n0dMfzX+QYZQB5i4vY8xdblQWol1pjVIbseHGDQUe06QJbIgSycyEk04qZeUMwygSc+bEXvqosJ+Z\ndpPaseT3JZHHFGPDBKPqYDGZCYQZmUZFEmurx/E9xzPshGFxj1m2DA45JDKveXNYsaIMFDQMo8Sc\nfDLMmBGZ9/330L59bHmAR798lMHvDY7IK+omCkbVwIzMBMKMzMQmUffgzcrNIuX2yMUnF121iEMb\nHRr3mL594bXXIvNWrnTxlolIorad4bD2Kzpr10LTqBXHevTIc7fHYtmmZRzycOTb5PabtlPzgJr7\nrI+1XWJje5cbhhGTzbs2U/+eyP0atwzfQt3qdWPK+2O9QtSpA1u3lpWGhmGUNhkZee7yAw+E1avh\n44/z9kyPtaPWwfUPRscoe3L2UP0ON/s8tOHChhs20Khmo/JS39iPsZHMMsZGMo3yYN0f68iYmBGR\nV9BknnnzoGvXyLwPPohcFNowjMRl1iw48cTIvDlz4LjjYsvHWspszdA1ZNTOiH2Asd9i7vIEwoxM\noyzZtGsTDe5pEJG3d/ReRGL3D2PG5N91Jzsbks2nYRj7JXv3uuWP/AwdCvfdF1s+Vhz3ymtXclDd\nBI2bMYqNGZkJhBmZiU1ljS3anrWd2nfVjsgraKZogwawaVNeulYt+OOPstKuclBZ284oGtZ+pU/L\nlpET+JKSXMhMPKJXpCgo9MaPtV1iY4uxG0YVZU/OHmSsRBiYe0fvjWtgirhPyMC89VYXu7W/G5iG\nYeRn+fLIDRNyc/P6iFhjIdEbM6SNT0PGCtm52eWksZHo2EhmGWMjmUZpET2qkDs6l4Dkf0+Mtd3j\n7Nlw/PFlqZ1hGInGd99B586ReTk5+d3rENuNXlBojpG4mLs8gTAj09hXoo3L3bfsJiU5JZ9cdjYc\ncEBkXiIvQWQYRvnw++/QsGFkXrzdvGItj2aLuu9fmLvcMMqJityD96yXzoowMJcOWYqO0XwGZna2\nc3f5DcytW92IZlU2MG3/5MTG2q/8aNDA9Rc7d+blHXCA61d27YqUPSDpAHSMsmlYXpC3jBX6v9E/\nnLa2M0KYkWkYlYw3f3gTGSu8teQtAKadNw0doxxc/+AIuVA8ld+43LPH/VjUqVOeGhuGsT9Qo4br\nP7J9IZepqa6fycqKlK1Xox46Rvl60NcATJ0/FRkrfLTso3LU2KjsmLu8jDF3uVFUdmbvpOadebtt\nXNr1Uib/dXI+uVgxl7EWWzYMw9gXYi1/lJubv/8BGD1jNLd9els4vXn4ZtKqp5WxhkZZYDGZCYQZ\nmUZRiI67LGi2uJ/t26Hmvu8CZxiGEZdY8d7xftaq316dPbl78uQsXjPhsJhMwygnyjq26KLXLoow\nMHffsjtmp5ySEmlgbtzoOnkzMONjcWGJjbVf5aFaNdffbNuWlyeSf7IQwO6Ru/n4zx/nyY0Vrnr3\nqnLQ0qiMmJFpGBXAmm1rkLHCCwteAGD6P6fHnNQzcGBkPNT8+a6zj9W5G4ZhlCW1a7v+Z/lyl/79\nd9c/XXJJpFxAAugY5cerfwTgsa8eQ8YKq7etLmeNjYrG3OVljLnLjWj8I5ftG7bn+8Hf55N56y04\n66y89FNPwYAB5aGdYRhG0Zg9G/70p7z0e+9B79755c575TymfT8tnDYXeuXGYjITCDMyjRATP5/I\n9R9eH07HWsh42zao69u17a9/hTffLC8NDcMwis/YsW43sRCbNkG9epEy0Yu539XjLkb8aUT5KGgU\nCzMyEwgzMhOb0tiDNzs3mwNuz4uan3beNPoe2jefXPSkHnts9g3bPzmxsfZLPNLS3Bq9kAl0i9mH\nzV0zl2OeOCac3nnzTmpUq1FOGhpFwSb+GEaCcOwTx0YYmDpG8xmYZ50VaWBmZ5uBaRhG4rFli1vi\nKISI88b4Obrp0egYpUt6FwBS70ylxzM9ylFLozyxkcwyxkYyqybb9myj7t15fu+NN26kYWrkbJ0F\nC6BTp7y07S9uGMb+wrJlcMgheelvv4UuXSJldmTtoNZdtcLp34f9Tv0a9ctJQyMe5i5PIMzIrHrU\nuo9/APYAACAASURBVLMWO7J3ANAirQXLr1meT8Y/ctmzJ3xkm2QYhrEfMmIEjB+fl967N39o0N9f\n/TsvLnwRgIPqHsTKa1eWo4ZGNOYuN4xyojhr9W3YsQEZK2EDc+fNO/MZmKEliUKomoFZVtg6i4mN\ntV/i4m+7u++ODP8JBOCKKyLlX+j7Atmj3F6Wq7auQsYKq7auKgdNjbLGjEzDKAVaPNCCJhOaAHBa\n69PQMRoRzL5pkzMun37apefOtbhLwzCqDqrOhQ7w73+7/nDdurzy5EAyOka56U83AdD8geY0f6B5\nBWhqlCbmLi9jzF2+fxM9c3z3LbvzLajuH7msV88ZnIZhGFWVPn3g9dfz0tE/kdHLHe26ZRfVk6uX\nk3aGucsNoxJwxTtXhA3MhqkN8+3YM39+pIGZlWUGpmEYxmuv5Z+F/tVX/rSgY5QLD7sQgBp31GDo\n/4aWs5ZGaWBGpmEUQLy4MBkr/PvrfwOwZugaNt64MbJc8mZSXnede1OvVq0sNTWisZi+xMbaL3Ep\nStsFAq5ffPJJlz7qqPwTgl7s+yJbhm8B4P4v7o/YLc1IDMzINIxiMHvV7IiOTscoGbUzwukZM/JP\n7Jk4sTw1NAzDSBwGDox0l4uA30atW71uxDaUMlZ48wfbBi1RsJjMMsZiMvcf/MblO397h9PbnB5Z\n7jMuH3oIhgwpL80MwzASn7fecptThIj+6Zz36zy6/rtrXrntgV4m2DqZCYQZmYnPXt1L0rikvHTU\nnuOLFsFhh+XJW3MbhmGUHP8L+1dfwRFHRJX7XvizR2WTHEguJ82qBjbxxzDKiZueuClsYDau2Rgd\noxEGpkiegXn77WZgViYspi+xsfZLXPa17VTd5CCAI4/MH6upY5S/HfY3AKrdVo3XF7+OUTkx898w\n4iBjBZYDLeG7K76jY5OO4bJt26Bu3q6RMXexMAzDMErGOec4YzPUr4rA5s2QlubSL/R9gTt73EnL\nB1vS5799AHOfV0bMXV7GmLs8MYme3OPn/PPhlVfc/7YlpGEYRtkyfDjcc4/7v18/mDo1stzfX+eM\nyiEpkIRRciwmM4EwIzOx+H7j93R4tAMAAQmQOzo3otw/Wrl1K9SpU57aGYZhVE127YLU1Lx09M/q\nhdMu5OVFLwMw99K5HNX0qHLUbv/CYjINowz464t/DRuYr53/Grmjc8OxRd99l39pIjMwKzcW05fY\nWPslLmXRdjVquH63Xj2XFnHb84Z46dyXWDx4MQBHP3E0/3z9n6Wug1F8zMg0DJy75e0f3wYga2QW\n57Q/J1yWkQGdO7v/n3nGJvcYhmFUFJs2weefu/+POQbats0ra9ewHXtH7wXgue+es8XbKwHmLi9j\nzF1e+Sko/tI/epmb63apMAzDMCoW1cj+OPpn1t+v547OJSDWeRcVc5cbRimwZtuacEfUoVGHCANz\nyZL87nEzMA3DMCoHIq5fbtcuLz1/fl65jlEu7XopAEnjkli4YWEFaGnYz6ZRJXn4/x6m2f3NAHj5\n3JdZeFVeB3T22Xkd16hRmeYeT1Aspi+xsfZLXMqz7RYvhlmz3P9dusApp+SVTf7rZL69/FsAOj7W\nkTs/u7Pc9DIctk6mUeVIvSOVXTm7ANg8fDNp1dPCZf7Ry6wsmD27vLUzDMMwisMJJ7i1igMBt6Rc\naJQToEt6F3JG5ZB8WzK3fHILU+ZN4cchP1aswlUIi8ksYywms3IRL/4yOxsOOCBPzprMMAwj8fAP\nFOzaBdWr+8oKiL838qjyMZki0llE/iMi34vIfBFZKCIPikjDKLmaIjJJRH7wZD4QkUNj1JcsIreJ\nyGIR+U5EZonICXHOfa2ILBKReSLylYicVVbXaZQu8TqYzz7LMzDPO88MTMMwjERFFe66y/1fowb4\nPff+ft9mnpcPCWlkAi8D9YDDVbUz0As4BZglIik+uWlAJ6Czqh4GzAUyRSQYVd8k4DzgBFXtBDwN\nfCginfxCIjICuBk4XVW7ACOAV0Tk1FK/QqPUUNW4BuY558Cf/+z+nzcP/vvfyGMtLixxsbZLbKz9\nEpeKbrsRI2DlSvd/9+6unw+hY5QeLXsAztDck7OnAjSsOiSqkbkXGKaquwFUdR1wL9AaOA1ARHoB\npwKjVDX0FN0GJOEMRTy5NsBlwF2qusmr70ncrtV3+OTqAiOBR1R1hSc3HfgQmFBWF2rsG+u3rycw\nzj3mgw4fFPkmK/DGG+7/3Ny8tTANwzCMxOagg1ycJrh+3u9Gn95vOk+c+QQA1e+ozs+bf64ADasG\niWpkdlLV5VF5awHBjXAC9AWygPDUDVXN9tJ9fcf18f5mRtX3CXCKiIQ2suoN1Igjd6hnrBqViFmr\nZpF+XzoAb//tbf595r/DZUVdnqhbt25lqKFRlljbJTbWfolLZWk7/wSg6PQlh1/CkquXAHDwQwfz\n2crPKkDD/Z+ENDJVNSdGdlvcCOdML90RWBtDdjnQxBe/2dE7blUMuWTgUJ9cKD9aDpxb3qgkTJ03\nlROfPhGANUPXcEabMwDYvTvPwAwELP7SMAxjf0c1z2UeCMD27e7/Ng3asHXEVgD+POXPPP3t0xWk\n4f5LQhqZ0YhIABgIPKGqy7zshsAfMcS3eX8b+OR2xpgCHkuOGHVuw42gNsCoFNz44Y30f7M/ALtu\n2UVG7QwAFixwgeDgAsNzcwuvq6Jji4ySY22X2Fj7JS6Vse1eew2mTXP/164NX3/t/q+TUoecUW4s\nauBbAxn6v6EVpOH+yX5hZAKjca7x6ypaEaNi6T61OxM+dyGye0fvpXqyW79i0iTo5I01f/utCww3\nDMMwqg59+8Ivv7j/jzwSJk50/ycFksLx+vd/cX/YC2bsOwm/GLuIDADOBU5S1V2+ot+A6FnkAHW8\nv7/75FIl/4KWseQAagObC5DLR//+/WnRogUAaWlpdOnSJRyzEnrjs/S+p6vdVo2cZe6NVKdouHzI\nEFi40Mm//34mW7YAFK3+UF5luD5LFy/drVu3SqWPpa39LF050jk53UhOhuuvz2TyZFi8+P/Zu+/4\nqMrsj+Ofk9CLIKAgiIINdRWxdwXbFuvasC+6iLvurmvvghTFLrrqrhW7C/ayP7tgwS5WRLEhKqgU\nkRJayPn9cWcyk0ommZk7T/J9v155zb13nswcPCZzcp9znxs9P2H3CQy4cwCv8Ro23Jiw+4SCiDfX\n+8nt6dOnk21BL8ZuZscCZwF7uvvsSs/9GzgeaJfel2lmTwDbuHv3xP45wKVAb3efkTbueuAkYHV3\nLzGzgcD9wAB3fyVt3OlEV7Zv4u5VbiOgxdjzo6Yliipf4CMiIgI1fz409UXbm/xi7ABmdgyVCkwz\n29fMTkwMeQRoDuyU9j3NgZ2J1s9MejTx2L/SWwwAnnX3ksT+M8CSasbtAXxaXYEp+ZHLAjP9Lz0J\ni3IXNuUvXKHkrvKV5+XHtWh71gRZZJrZ0cAtwJ1EywwdnTi2P4kpcnd/HngWGGlmics9uBAoBUYn\nXytRHN4CnGdmnROvfzywHnBB2rhfidbZ/JuZ9U6M24toIfgzcvaPlVrpDKaIiNSXCs3cCnK63Mzm\nAh1reHq4u49IjGsDXE50N6BS4HvgVHefWun1ioFhwOFEFxAtBM5y99eree9TiKbRVwArgYvd/cla\nYtV0eY6owBQRkWzYdlt4991ou6lPnWdzujzIIjMkKjJzY1UF5vrrw5df5jsqEREJ1UknwS23RNtl\nZanPk6ZWaKonU5q06n7g038hHHVU9grMUHqLpCrlLmzKX7hCzd3NN6eWNSoqguXLo21NndefikwJ\nSnUFZmkpFBdHx0aNgvvuiyMyEREJ3WmnweOPR9stW8KSxMKIKjTrR9PlOabp8uxZbfRqLFwe3XAp\n+QO/fHn0iwCiv0KHDIkrOhERaSxefhmSyyUvXAjt2kXbyQJztZarld+SsrHRdLk0Odvcsk2VAnPp\n0lSBef/9KjBFRCQ7dt8d3nor2m7fPio0IfX5s2DZAna+Y+eYoguHikwpeAMfGsh7s6IbzaYXmMn7\nkD/8MBx5ZG7eO9TeIlHuQqf8haux5G677WDy5Gh7tdWqFpqvf/c6f378zzFFFwYVmVLQrnnjGsZP\nGQ+kfrCXLUsVmE88AQcfHFd0IiLSmG25ZcVCc8GCaDv5eXTHB3dw6auXxhRd4VNPZo6pJ7P+Js2Y\nxC5jdwFSP9ArV0KzZtHzTz4J++0XV3QiItJUfPBBVHAClJSkTnQkezQfPvxhDt6kcZzx0DqZAVGR\nWT+zF89mzavWBGDZhctoUdwC92hZCYh6MHM1RS4iIlLZ5Mmw9dbR9ooV0QkPd6doRPTB9PUpX9N7\n9d4xRpgduvBHGrWVZSvLC8xvT/2WFsUtgFSBed11+SswG0tvUVOk3IVN+QtXY83dVlvBiy9G282b\nR3cGMjMWnbcIgPWuX49lpctijLDwqMiUgtNsZDQf/vTRT7NOh3WA1ELrZ54Jp5wSV2QiItKU7bFH\nNJMGqRMfbVu0ZcrJUwBodUmrmCIrTJouzzFNl2cm2d9y/i7nc8mel0THEgXmH/8IjzwSV2QiIiKR\nyy6D886LtpMf8Xd9cBeDHh8UHQv49pPqyQyIisy6SxaYa6+2Nt+d9l10LPG/+XrrwVdfxRWZiIhI\nRccdB/fcE20nP+YPf/BwHvz0wehYoIWmejKl0el9XapZunKBCfEVmI21t6gpUO7CpvyFq6nk7u67\noW/faDv5eTX+sPHlzxcNV4ml/wISu1veu4Xp86cDqb/80gtMnQgWEZFC9OGHqe3k51byc8xxrpx0\nZQxRFQ5Nl+eYpstr992v37HOmOjinuQP5hFHwLhx0fP6TyciIoUuWWAefHB0FzpItYCFtrSRpsul\n0UgWmL+c8wsA996rAlNERMKS/Lx65JFUn+bSC5YC0dJGTfVkk4pMiU3yr7zHj3icjq068v33cOyx\n0XNlZTEGlqap9BY1Rspd2JS/cDXV3CXryOOOgy++gJbNWjLphEkA5Qu2NzVN818tsUsWmN3adeOA\nPgfgDj17Rs/NnVuxJ1NERCQES5ZEjxttBMuWwU49d+LYvtHZk+TnXlOinswcU09mVUMnDGXkKyOB\nqhf6PPUU7LtvXJGJiIg0zNSpsOmm0Xby4z9ZYB61+VHcd/B9MUVWN1onMyAqMiv6cdGPrHX1WkDV\nAnO//eDJJ+OKTEREJDuuvx7++c9ou3Kh+dUpX7He6uvFFNmq6cIfCVaywJx/znyg4rR4IRaYTbW3\nqDFQ7sKm/IVLuYtuf9ytW7SdvP1k6UWlAKx//foxRZV/KjIlb5J/xd3w+xvo0KoD11+fek4ne0VE\npDGZNSt6dIdrr4XiomKeOvIpoOn0Z2q6PMc0XR75w31/4OkvnwaiafJ586Bz5+g5/ecREZHGKjlj\n9913sPba0OaSNiwpXcKAXgN46U8vxRtcNdSTGRAVmTBz4Ux6XNMDqNqHOXs2dOkSV2QiIiK5tXQp\ntG4dbZeVRZ9/yTOZH/7lQ/p27RtjdFWpJ1OCkiwwl1wQre2QLDAvu6zwC0z1FoVLuQub8hcu5a6i\nVq3gueei7WR/ZtnQaDHoLf6zRUxR5YeKTMmp5F9rw/sPp1WzVnTqlHrunHNiCkpERCSP9t4bttkm\n2l5ttehs4avHvwo07v5MTZfnWFOeLr/opYsY9eooIJomf/FF2Guv6Lkm+p9ERESasMprQicLzGG7\nD+Pi/hfHF1ga9WQGpKkWmWVeRvGIYiAqMN3TpgnKdEcfERFpmpKff6WlUFycKjSXXbiMFsUtYows\nop5MKXjJAnPa36cBqQLz5ZfDKjDVWxQu5S5syl+4lLvaffll9NisWfQ4+6zZALQc1TKmiHJHRaZk\n3YC7BpRvb9h5Q9q3Tz23224xBCQiIlIg1l8fDjww2jaDLm268IcN/wBA338X1pXmDaXp8hxratPl\ni5Yvov3oqKr0Yc7778NWW0XPNaH/DCIiIrVKzuq98ALsuWdq2vzbU79lnQ7rxBiXejKD0dSKzOQP\nya/n/spqLVcr/yFSH6aIiEhF6Z+RTsVrGeKLST2ZUoDWuTb6y2u7HttVKDDvvTfcAlO9ReFS7sKm\n/IVLuau7t96KHouKoMiKuGDXCwDofV3vGKPKHhWZkhXLSpfx3YLvAHhr8FuMGJF67uijYwpKRESk\ngG23XWr7nHNg1B7Rsn/T50/n16W/xhRV9mi6PMeaynR5cpr8l3N+oUPLjuVXkzeBf7qIiEiDJGf7\nli0DK15Bi1HRUkZxTJtrulwKyuAnBpdvd2yVKjA/+yymgERERAIyd2702LIlNC9uzgF9DgDg0PGH\nxhhVw6nIlAZxd25///Zoe5iz//6p5/r0iSmoLFJvUbiUu7Apf+FS7jLXqRP89rfR9k47weNHPA7A\nw1MfZsXKFTFG1jAqMqVBikZE/wtNOXkKK1ZEt8oCTZOLiIhk4plnosc33oCFC2He2fMAyqfOQ6Se\nzBxrzD2ZE76ZwB537wFEZzGTPSU//wxrrBFjYCIiIgFauhRat4623aFoeBGO88jhj/DHTf6YlxjU\nkykFIb3AHJxqy1SBKSIiUg+tWsHvfx9tDxwIZcPKADh4/MExRlV/KjKlXpJrYg7ZagjucHvUltno\npsnVWxQu5S5syl+4lLuG+b//ix7Hj4eVK+Gug+4CYM0r14wxqvpRkSkZc/fyNTFv3v/m8qvJp0yJ\nMSgREZFGYs6c6LFZMzhui+MAmF0yO7iLgNSTmWONsScz/f6qrzy5DsceGx1vZP9MERGR2LRqFa2b\nOWYM/Pmvi2g/uj2Q+7Uz1ZMpsfn4p4/Lt9fpoAJTREQkF5YujR5PPRXatWhXfvz5r56PKaLMqciU\njPT9T1+g4tXk//53jAHlmHqLwqXchU35C5dylz2TJkWPZqkzmPvcu0+MEWVGRabU2XVvXgdAlzZd\nKClJHf/LX2IKSEREpBHbaafU9uzZcOr2pwJw/ovnxxRRZtSTmWONqScz2YuZfhazpCS1ppeIiIhk\nlzvlF9i6V/wszgX1ZErebXnzlgCcv8v5jB2bOq4CU0REJHfMYOuto+3rr4fHBj4GwCY3bhJjVHWj\nIlPq5IMfPwDgkj0v4YQTomON5ARtrdRbFC7lLmzKX7iUu+x7993o8Z//hAM3PhCAz+Z8FmNEdaMi\nU1YpeWr+teNfo0OH6Njo0TEGJCIi0sQ8/XT0aAZfn/J1tD08K7PaOaOezBxrDD2Z1fViBv5PEhER\nCU7yM3jlSigeGe2sHLqSIsveOUP1ZEreJAvMz//+efn/3FOnxhiQiIhIEzV/fvRYXAwl50fLvBSP\nKI4xotqpyJQ66dlmo/LtjTeOMZA8U29RuJS7sCl/4VLucifZsgZQsiB15W2Zl8UQzaqpyJQaJc9i\nTv/ndNq0iY4tWxZjQCIiIk1cWaKe7NIFFp+/GCjcs5nqycyxkHsyy6fKj3T69ImOBfpPERERaTSS\n7WuTJ8NWT0Q7ZUPLMGt4K2U2ezJVZOZYqEVmssCcefpMuq+2FqACU0REpFAk68mFyxbRfnR7IDsL\ntOvCnwQzW8vMnjGzwmxGaAS+m7pW3CHESr1F4VLuwqb8hUu5y48994weX3y6XfmxQjupFWyRaWYH\nA68D6wE1/lc1s7ZmdoOZfWZmnySK0k2rGdfMzEaa2VQz+8jMXjOznWt4zVPNbIqZfWBm75rZgVn7\nhxWA5FnMyUMms/320bEC+/9WRESkSXvhhejxoIPg13N/BaBoRGGVdYUVTWbOAvYCJq1i3ENAX2AL\nd98MeBuYaGaVT9HdABwG7OzufYGxwHNm1jd9kJmdC5wP7Ovu/YBzgQfN7LcN/QcVmgXTtow7hNj1\n798/7hCknpS7sCl/4VLu8ufww6PHF/63WryB1CDkInNnd/+qtgFmtjfwW+Aid09eFz0SKCYqFJPj\nNgJOBEa7+zwAd78d+Aa4JG1cB+BC4EZ3n54Y9wLwHHBVdv5Z8dr/gf0BGHvgWJK/J3QWU0REpPCM\nGxc9HnIIfPiXDwHY/c7dY4yoomCLTPc6LQp1CLCctLOd7r4isX9I2riDE48TK33/S8A+ZpZYwIff\nA61rGLdpolgN2lPTngJgvQWD4g2kQKi3KFzKXdiUv3Apd/l1wAHR48z3o4nXV759JcZoKgq2yKyj\nzYGZ7l5a6fg3QFcz65I2rgyYUc24ZsCmaeOSxyuPg2haPlj3fXQfAH/a4k/snvhDSGcxRURECtfj\nj0ePv/89XLPPNQDc+t6tMUaU0tiLzC7AwmqOL0g8dk4bV1LNWkPVjaOa11wAWNq4IB3z6DEAXNzv\nzngDKSDqLQqXchc25S9cyl3+7bRT9Lhd2WkADHlqSIzRpDT2IlPqqGRFSfl2797Ro85iioiIFL5J\niabAXXaBLbpuAcDncz6PMaJIs7oMMrMNgCOBXYGNiM7otQBKgB+AT4gufhnv7tWdOYzLHKC6hR6T\nl2HNTRvXxqqunF7dOID2wC+1jKtg0KBB9OrVC4COHTvSr1+/8r/0kr0rce8PeHkAAM/s8BK/YyJQ\nWPHFtT9mzJiCzJf2V72f3hdWCPFoX/lrKvvJY4UST1PZh2j/uYM/oOu/jY3P3JgJgybUKV8TJ05k\n+vTpZFutd/wxs87AdcARRGc9ZwOzgMVAKVGhuTrQA2hLNI18sbtfm/VIa45xLHCcu1e5caeZ/Rs4\nHmiX3pdpZk8A27h798T+OcClQG93n5E27nrgJGB1dy8xs4HA/cAAd38lbdzpwJXAJu4+rVIMQdzx\nJ7k2JhdHsa5cCUVFMQZUICZOnJj2AywhUe7CpvyFS7mLT/ldJS+ONupzB6C83PHHzLoTrSnZBzgK\n6OLuXd29n7vv7O67u/uO7r6xu7cnOsN5GXCemd2djeCy4BGgObBT8oCZNQd2Jlo/M+nRxGP/St8/\nAHjW3ZNzyc8AS6oZtwfwaeUCMxS/uek3ALx74rvlx1RgRvSLMlzKXdiUv3Apd/H78YyfgNTne1xq\nKyXGAf9x923dfXxy/ciauPuX7j4aWB/oYWanZjPQWtRYbbv788CzwEgza504fCHRWdjRaeOmAbcQ\nFcidAczseKK7CV2QNu5XonU2/2ZmvRPj9gL2Bs7I4r8prz6d/SkA2/TYGoBZs+KMRkREROpj8eLo\nsVv7NYHU53tcqi0yzawtcIG7X5npCyZ6MvcDPmxgbLUysyvM7P3Ee2FmkxNflftMDwU+Aj4wsynA\nDkB/d69cSv0deBCYZGYfAYOBvd394/RB7n450QLtT5nZB8DlwKHu/lyW/4l58f2C7wHo0b5H+bFu\n3eKKpvCk96xIWJS7sCl/4VLu4tOmTWp7yFZDAPjgxw9iiqaGC3/cfTHwSnXP1YW7LwEm1Pf76/ge\nZ9dxXAnwjzqMWwkMTXytauz1wPV1ef9C1/PangD8peR7LgKuvjreeERERKT+3ngDdtwRFo+7GTa8\nhS1v3rJevZnZUOuFPxm/mNlL7r5H1l6wESj0C38qX/BTwKGKiIhIHTTkAqC8XPhTwxsXmdkOZnao\nmR1X+QvYMhtBSX6c8WzURjpu/6djjkRERESy5Xe/ix7fOzxaWfF39/4uljjqfCbTzLYiulq7JzVf\nbOPVLSXUlBXymUydxVw1LcURLuUubMpfuJS7wlDfs5nZPJNZp8XYE/4NzASGA98DyyvHBTycjaAk\n9wq18BUREZHsW1m2kuKi/J4HzORM5i/A2omLgmoa8y93X+VFNk1JoZ7JTJ7FHDhtGePub8Grr0a3\noxIREZHwff899OwJA/YoY8JuUXFZl7OZcfVkfgKsWMWYjJc8kniNu78FoAJTRESkMVl77ehxwkvx\n3V0lk3f+JzDazFavZcybDYxH8mBl2cq4QwiG1nsLl3IXNuUvXMpd4dh77+hx3/UOAWD24tl5ff86\n92S6+2Qz2w74zsymA3OAskrDOmUxNsmRZiMTaR8eFZtllbMoIiIiwXvuuegCoP8d9xBcbKx51Zp5\nXTMzk57Mc4huxbgcmEvVC38g6tlsnr3wwleIPZm6qlxERKRpyPQq87h6Mk8BTgfau3sPd+9d+Yvo\n7KYUsBUrK7bV/u1vMQUiIiIiOffAA9Hjbp0OB2Dx8hqv3866TIrMYncf4+61XfxzWEMDktxqMSq6\n0IeLoznyG26IMZgAqLcoXMpd2JS/cCl3heWII6LHV04ZB0C70e3y9t6ZFJkvmdlGqxizY0OCkXzK\nyplwERERkWpl0pPZD7gEeAp4h+ov/HnH3btmNcLAFVpPZno/5s03w5Ah8cYjIiIiufXhh9CvHzS/\nuC0rKKFsaBlm1Z9symZPZiZFZrKgrPUbdFvJigqpyDz6kaO5/+P74cqfYPGauuBHRESkiTADbCUM\na8YGnTbgi398UcO4eG4ruRi4qpbnjejCIClQ9398f7SxeM14AwmI7sEbLuUubMpfuJS7ApY4D/jl\nvC/z8naZFJmL3H14bQPM7JgGxiN5ct99cUcgIiIi+fLxx7D55vl9z0ymy1u7+5JVjNnf3Z/MSmSN\nRKFMl3825zM2uXETeOwO+OB4TZWLiIg0MWZA93dhyLa8evyr7LJO1XtKx9WT+ZK777GKMTPdvXs2\nAmssCqXI1ALsIiIiTVtdFmaPazH2zWp6wszamdktgK4sD8Chh8YdQTi03lu4lLuwKX/hUu4K1z33\n5Pf9Mikyu5jZbZUPmtnewCfAYFZx5bkUhgcfjDsCERERybdj8nzlTCZF5myghZmNBTCz9omi8xmg\nJXBwYowUmP9+8t9o498fxhtIgHSFZLiUu7Apf+FS7gJwySIAzn3h3Jy+TSY9mccC9wJjgc7AFsDa\nwAPAP9x9npnt4u6v5SrYEBVCT6b6MUVERARgs81gyhRq7MuMpSfT3e9JVEvHE52x7A4c6u5Hu/u8\nxLDfZCMoyZ1ffok7grCotyhcyl3YlL9wKXeF7aOP8vdemUyXA+CRE4A7gEOt4n2JhmUtMsmJsFgg\nfAAAIABJREFUjh3jjkBERETiUpRx5Vd/NU6Xm9nKunw/lS720W0lK4p7uvyDHz9gy5u3hDtegRm7\naqpcRESkiTMD2v4MZ3Xl0YGPctDGB6U9l4d1Ms2sBBiXyWsBh7l722wE1ljEXWSm92Nutlm04r+I\niIg0XVdeCWefTbV9mfkqMme5+1oZvVg9vqexK6Qis6wsbSFWqRPdgzdcyl3YlL9wKXdhMCPnRWZt\nM/O71+P1Nq1vIJJ7KjBFREQkX+q8hJHUT0GcyfxqL7jnefVjioiICJA48fSbcXDYESw6bxFtW7RN\nHM/xmczEQuvvmNlG9XlRMxtiZrc2LDRpqDOfOzPauPdZ1l473lhERESkcIwaBUwZCMCB/z0wJ+9R\nbZHp7guBy4CJZnaimTWry4uZWTcz+xdwIXBR9sKU+rj6jaujDS/im2/ijSVUWu8tXMpd2JS/cCl3\nYbjggtT2i9+8mJP3qLF4dPeHzawYuAW41MxeBT4DfgQWA6VAc2B1ojv/bAHsAHwO9Hf3H3MSsdRL\nszr9mSAiIiKSHavsyTSzrsDpwEBgnRqGlQHvArcDY929NJtBhizOnsz0K8vVjykiIiLpqrvCPJs9\nmas8v+XuPwHnAOeYWU9gI6J7l7cASoCZwFR3/zUbAYmIiIhInnx8JGz+QE5eOqObC7n7d+7+oruP\nd/d73f0Rd39TBWbhmTRjUrRxzQyefDLeWEKm3qJwKXdhU/7CpdyFY9Ys4NG7ALjrg7uy/vp5vIOl\n5NMuY3eJNhb0ZL/94o1FRERECk+3bkBZcwAGPT4o66+vdTJzLK6eTPVjioiIyKpU7svM1x1/RERE\nRETqRUWmSC3UWxQu5S5syl+4lDtJUpHZyJ18ctwRiIiISKF6+mlgQY+cvLZ6MnMsjp5Md6doRBE8\ncw1lr58W9VuIiIiIVMO6vwcnbcPi8xfTtkXb/K2TWSUQs37A74A13f30xNqZXdz9/WwEJA035s0x\n0cabKjBFRERkFWZtDcDpz56e1Zet83S5mRWZ2VjgPeBSYHDiqR7A22Z2j5k1z2p0Ui+nP5fd/0ma\nMvUWhUu5C5vyFy7lLlw3v3dzVl8vk57MM4BDgKuIbjG5BMDd3wTWJbrl5GlZjU5EREREglTnnkwz\n+wQ4092fSezPdPfuac+vA/yfu2+Wk0gDFUdPptbIFBERkbpKXyuTi4llncxuyQKzOu4+A+jY8JAk\nW9q2jTsCERERKXSnnpqb182kyHQzW62mJ82sG1Dc8JAkW95+O+4IwqfeonApd2FT/sKl3IXn0ktz\n87qZFJkvAXdUV2gmrjC/C3gxW4FJw226adwRiIiISKFr3To3r5tJT+aGwFtEZyvfBXYAniW6unwr\nYD6wnbt/k5tQwxRnT6YPU0OmiIiIrJodfBxscU88PZnu/gWwM/AO0B9oDRwEbEN0lnMnFZgF5L3B\nqx4jIiIiAjBxWNZfMqPbSrr7VHffC1iT6EzmDsAa7v7bRBEqMVtZtjLaeENrZWaDeovCpdyFTfkL\nl3IXqF/Wz/pLZnzHHwB3nwvMzXIskgVPTnsy2pizSbyBiIiISJOWSU/mFkDyXOpwd/8wcbw7MA64\n2N114U8l+e7J3HXsrrw24zWtkSkiIiJ1Vr5W5sXxrJN5MlEv5tvAd2nH5wGvAA+Z2T7ZCErq77UZ\nr8UdgoiIiASmYw5WOs+kyNwZ2N/dL3P3ecmD7r7U3S8ADgeGZjtAqZ9eveKOoHFQb1G4lLuwKX/h\nUu7CdP752X/NTIrMTu4+qaYn3f15oHfDQ5JsuOCCuCMQERGRUJx0UvZfM5OezJ+Addx9WQ3PtwK+\ndfeuWYwvePnuyUyukbnkHKdVq7y9rYiIiATOhsfXk/kWcK2ZVbl1pJk1A65MjGnUzGwNM7vXzD4z\ns6lm9qCZ9Yg7rspUYIqIiEicMikyhwODgG/N7C4zG21mV5vZ/cBM4M/AxdkPsXCYWXPgBaA5sAmw\nKbAYmGBmbeKMTXJDvUXhUu7CpvyFS7mTpDqvk+nu75nZH4BbgGMrPf0FcKi7T85mcAVoELAZcEBy\nDtzMzgF+AP4KXB1faCIiIiKFo849meXfYGbAlsAGiUNfAB/k/QbdMTCzp4GN3b13peMfAYvcfadq\nvieWnkzdt1xEREQyke2ezIzv+JOomCYnviows03cfWo2AitQfYHPqzn+DbBHnmMRERERKVgZ3bu8\nDhr7HX+6AAurOb4AaGNmLfMcj+SYeovCpdyFTfkLl3InSRmdyTSzA4GDgO5EF79U1ikbQYmIiIhI\n2OpcZJrZqcA1QCkwG1hezbAqyxs1MnOA9tUcXw0oqWkN0UGDBtErcQuejh070q9fP/r37w+k/uLL\n1j7fVHzvbL9+U9tPHiuUeLRf9/3+/fsXVDzaV/60r/1C3E9uT58+HT4gqzJZjP1L4DbgGnevrsDE\nzGa5+1pZjK+gJC786ePu61U6rgt/REREJGhxLsbeIXHf8moLzIQjGxpQgXsEWNfM1kkeMLOuRGtm\nPhRbVJIz6X/pSViUu7Apf+FS7iQpkyLzEzPrnMXXC9GdwMfA5WZWbGZFwGXA18B/4gxMREREpJBk\nMl2+GXARMMrdP65hzEx3757F+AqOma0BXAtsC5QBnwCnuvsPNYzXdLmIiIgUvDjXyXwCaAccamZL\niC6CKas0Zo1sBFXI3H02cEzccYiIiIgUskymt3sAU4BXgHeIrmP+Nu1rBrAy2wGKxEm9ReFS7sKm\n/IVLuZOkTM5kznP3AbUNMLNZDYxHRERERBqBTHoy93T3Wu/oY2Z93f2jrETWSKgnU0REREIQ2xJG\nqyowE7ZtQCwiIiIi0khke8mhkVl+PZFYqbcoXMpd2JS/cCl3kpRRkWlmh5rZ22a22MxWVv4CuuYo\nTqmrt/4RdwQiIiIiGfVkHgqMB94CpgGHAeMST68L9AcedfdDsh9muPLek9n5SzhlQ1ZctIJmRZlc\n1yUiIiJNWZy3lTwLOMPdd3T3PwHz3f34xNcewGBAV5fHbd4GADwy9ZGYAxEREZFQlHnlpc8bLpMi\ncyPgurT9ylXuWGCXBkckWTHmzTFxh9AoqLcoXMpd2JS/cCl3Ybrnw3uy/pqZFJmL3SuUuUvNrF3a\nfjHRtLkUgDe+fyPuEERERCQQxz9+fNZfM5Mi8wczG5i2/wVwYdr+cOCnrEQl9bb55nFH0Lj0798/\n7hCknpS7sCl/4VLuwuRk//qRTIrMx4H7zOw/if1/A2eb2QIz+xU4F7gt2wFKZk4+Oe4IRERERDIr\nMq8DtgCuAHD3R4FTgK+AqcDZwNXZDlAyc+yxcUfQuKi3KFzKXdiUv3Apd5JU5zVu3H0xMKXSsRuA\nG8ysbeJ5iVnbtnFHICIiIpLBmUwzu6mWpy8zs9lm9ocsxCRSMNRbFC7lLmzKX7iUO0nKZLr8oFqe\nGwGcjqbLC8N8XeQvIiIi8crKvcvdfTZwL9ApG68nDfTA4wDMXjw75kDCp96icCl3YVP+wqXchad8\nIfYnbsnq69bak2lmd6TtdjCz26m6CHvydfoAM7MYm9TXT1sAsMfde/DxXz+OORgREREpZGc/f3a0\nMflEYEjWXrfWe5ebWfri6071BSZACdEV5qe4u1YBT5Pve5dH7wlcHKXKh+X3vUVERCQsNjxR3l0c\nlXrZund5rWcy3b18Ot3MZrn7Wtl4UxERERFp3DLpyTwvZ1GIFCj1FoVLuQub8hcu5U6S6lxkuvud\n1R03sxZmtnrWIpIGO/vsuCMQERGR0GyySXZfr9aezAoDzQYAFwEz3H1Q4tipwGVAc+B54FB3X5Td\nEMMWR09maSk0/8uO0PNN9WSKiIhIrZI9mdMHOb16Za8nM5Pp8hOAtsB9AGa2OdG6mDOAa4D1iO5f\nLjFr1gy4awIAN71T2xr6IiIi0pRNnjU52rh+GutmeZntTIrMHYCD3f35xP4QoAz4vbufBfwOOCy7\n4Um9lbYC4G//97eYAwmbeovCpdyFTfkLl3IXlq1v2TramLdh1l87kyKzjbv/AGBmBvwReNbdvwJw\n96+BdlmPUERERESCk0mRuczMVkts7wV0Bx5IPmlmLYCVWYxNJHa6B2+4lLuwKX/hUu4kqdZ1Mit5\nBhhnZk8BpwFzgYfTnr8Q+CKLsYmIiIhIoDI5k3kR0Br4F7AGMNjdl5pZkZktBC4AHsxBjFIPjz4K\n3PI2ANPmTos3mICptyhcyl3YlL9wKXfhWFa6LNp4+jr+8pfsv36dz2S6+1ygv5l1AErcfUXieJmZ\nbZYY9kP2Q5T6OOgg4I/bAtDnhj5aykhEREQqWP/69aONt07hphzcFLzO62TW6cXMjnH3e7P2go1A\nHOtkpt4b3cNcREREqpV+z/JkqWIWzzqZdXFFll9PRERERAJUY5FpZsPM7Lq0/a9X9UXUqymFZE6f\nuCMImnqLwqXchU35C5dyJ0m1nck8CTjBzFol9nsA39byNQMtYVRQ9tgDuHEKAEc8dES8wYiIiEjB\nKL8j4BWzc/YeNfZkmllXoKW7z0jsz3L3tWp9sTqMaWri7MksLYXmzVFfpoiIiFSQ3o/544/QtWvi\neBZ7Mmu8utzdf6p06KQ6vF5dxkieNMtkFVQRERFpkpIFZrbV+cIfd38iG2NEQqLeonApd2FT/sKl\n3ElSnYpMM9vZzO40sy/MbJGZLTSzaWZ2h5ntkOsgpYEuXQDAnx//c8yBiIiISNzGTxkfbdz8bk7f\np9Z1Ms2sOXATcAJQ0/y8A7cDJ7t7adYjDFycPZkA//0vHHkk6ssUERERoGI/5uDBcOutac/lcZ3M\nG4A/A88BhwHrAq2ANsB6wFHAK8DgxFgpMEfoonIRERGpwS235O61a1snczui4nGIu//e3R929+/c\nfbm7L3X36e7+X3cfAJwKnGhm2+YuVGmQ+esCEOdZ1RCptyhcyl3YlL9wKXdhsaycs6xebWcyTwRu\ndffbVvUi7n49MBYYkq3AJMvGfANAm0vbxByIiIiIxGXAXQOijZFLc/5eta2T+SlwmLtPqdMLmW0O\njHf3TbIYX/Di7skEOO88uOwy1JcpIiLSxKX3Y663Hnz1VaXn89ST2bmuBSaAu38MdGl4SJJto0fH\nHYGIiIgUmi+/zO3r11ZkltXj9XR1eSG76SMArpx0ZcyBhEO9ReFS7sKm/IVLuStcr3z7SrTx1L+B\n3PZjQu1FZn3mVDUPW8h+3hyAs184O+ZAREREJN92v3P3aOPdv+Tl/WorMruZ2cpMvoAc3ZhIGurJ\nJ+OOIEz9+/ePOwSpJ+UubMpfuJS7MIwalfv3qO3u1iuA1zN4LQN0958Ctd9+iY2XL4TdR/HJz5+w\n2ZqbxRqTiIiI5MfMhTOjjY+jBbQvuCD371nb1eWz3H2tjF6sHt/T2BXC1eVJ5b0Xusq8ziZOnKi/\nygOl3IVN+QuXcleY0q8qB6ipNMnX1eXn1eP16vM9kicdO8YdgYiIiDQVtd67XBqukM5kukNREbDb\nSNhjKK8d/xo7r7Nz3GGJiIhIDs0tmUuXK7vQbGk3Si+bxaJF0LZt9WOzeSZTRWaOFVKRCZoyFxER\naWrqOlUO+ZsuF2nytN5buJS7sCl/4VLuJElFZhPz88/R4wZTbwbgkamPxBiNiIiI5NLE6RMB2H7F\nuQBMqfO9HBuutqvL27n7ovyF0jgV2nQ5aMpcRESkqchkqhzyN10+LRtvkCsWOdvMlprZcXHHIyIi\nIiIptRWZXczsPDNrkbdo6sjMegIvAQOB5qsYe7SZfZD4+sjMBtcwbh8ze8vMPjSzT83sXLOqd/U0\ns63NbGLitaaa2ZVm1jIr/7A8mT07etz4qVkAdLmiS4zRFDb1FoVLuQub8hcu5a5wXPBitOL6wCUv\nAfDGG/l9/9qKzEXAhsCnZnZInuKpqzOA24DTie40VC0zOwK4Hfizu/cDjgbGmNmJlcbtAjwJjHL3\nLYB9gH8AoyqN25CouH3I3fsC2wO/Be7I0r8rL7okasrP3u0GwNwlc2OMRkRERHLh0tcuBWDc5QMA\n2CHP92WsrSfzYXc/xMy2Aq4mKkhPcfcPa3wxs4vd/eKcRFrxfYrcvczMdgcmAIPc/e5KYwz4FnjR\n3Y9PO34D0RnQ7u6+InFsErDC3funjTuTqMjs5e4/Jo7dB+zo7uuljTsUGA9s6+7vVRNrwfVkQqov\ns92l7Vm0fBE/nfkTa7ZdM96gREREJCuWrFhCm0vbRDt17MeEPPVkuvshicfJ7j4AuB540MxuM7Oa\nqpEh2QhqVdy9rA7DtgPWBiZWOv4S0AkYAGBm3YAdiYrVyuNaAAckxhUntl+uZhxAoZ3trVVJSfS4\n6PyFAHS9qmuM0YiIiEg2JQvM3ndHJdOsWfmPoc5LGLn7w8DmwAbA12ZW5QtYI1eB1kNfwIFvKh3/\nhmiKvW9if/O045XHkTZuPaBt5XHuPg9YmDYuCK1bxx1BGNRbFC7lLmzKX7iUu8LyzdfRSclu3fL/\n3nUuMs1sB6KzeLsCLYkKtcpfhSR5NcvCSscXJB47p43zOo6r7vWSYztXc7ygbbRR9Pjk/u8A0Pff\nQdXJIiIiUo2//e9vAIw/+LFY46ixyDSzexOPPc3sfmAS0RT0C8AW7t678hcwJ9MAzGxPMyurw9dL\nq341ycTnn0eP+2+9DQAf//xxjNEUpv79+8cdgtSTchc25S9cyl38bnr3JgAO73sgAGV1aTLMgWa1\nPPc7MxsFnAa0Jlo38wx3/18t33NTPWKYBGxch3ElGb5usuBtX+n4aonHuWnjrI7jqnu95NigL9Hu\n36s/E6dP5NVvX2XXdXeNOxwRERGph9mLZ1c5VnVBxvyorcjsBJwH/ApcANzg7qW1vZi7j8w0AHdf\nSm4Wfv+IqHjsBbySdrw30fT4R4n95Om7XpW+v3fa6wB8DSyuPM7MOhEVnjVedT9o0CB69Yq+rWPH\njvTr16/8L71k70pc+1ddNZEzz4SN35zAxG7GbsN2Y8KgCQUTX9z7Y8aMKah8ab/u++l9YYUQj/aV\nv6aynzxWKPE0tf0BL0fLFZ0ybwLXM5Frrql9fHJ7+vTpZFttSxiVAv8BhiYubik4dVzC6AV3PyHt\neHIJox7uvjxxbBKwzN33SBuXXMKot7vPShy7D9jB3ddPG3coMI5oCaPJ1cRYkEsYpat8m8nSi0op\nLiqOL6ACMnHixPIfSAmLchc25S9cyl183J2iEUXRTgbLFqXL5hJGtRWZs9x9rWy8Sa6YWX+iJYSq\nFJmJ5wcCY4Fd3H2ymW0OvA6c5u63pY3bGXgRONTdnzKztYE3gTvd/cK0cRsA7wIXuPuNZtaB6GKo\nT9z9mBpiDKbInPnzMrrf1ArQ/cxFRERCk7xP+dwzFtC5fdTdV6hF5vru/lU23iTbEnfo+RfRkkLr\nA98B84ju2PNIpbFHAucSTZEXAde5++3VvObewCVEa2O2AO5y98urGbcVcA3R1ebNgCeAC5NnRasZ\nX/BFJlQ9m6kiU0REJCzJIjN5FrO0FIoznJjMS5Ep2RFakfn1vG9Y7/r1ABWaoGmfkCl3YVP+wqXc\nxaPXmF58++u3vHb8a+yy7s5A5mcxIU93/JGm5bPPoscte/eufaCIiIgUnG9//RaA68+KCsxHHqlt\ndH7oTGaOhXImE1JnM5/6/H/s98B+9OvWj/dPej/eoERERKRW5zx/Dle8fgVn7HgGV//2KqB+ZzFB\nZzIlRwYPjh5/fHVfAD748YMYoxEREZG6uOL1KwD4XVFUYG6zTZzRpKjIlHK33ho9Dh4MQ3cbCsDA\nhwbGGFH80tcRk7Aod2FT/sKl3OXX+S+eD8CftvgTe+8dHXvnnRgDSqMiU6o1sOtwAMZPGR9zJCIi\nIlKT0a+NBuDqXe+MN5BqqMiUCpI9HL/5DYzeM/ofd9/7940xonjpCslwKXdhU/7Cpdzlz9AJ0azj\nUZsfRZcu0bG47lNeHV34k2MhXfiTlLwA6NdfocO1WjdTRESkECXXxVx5kZevh9nQkkMX/khOJf8K\n6tABrvvddQDsNna3GCOKj3qLwqXchU35C5dylx8jXh4BwOG/Oby8wFy8OMaAqqEiU6qwtL9f/rrV\nKQC8OuPVmKIRERGRyoZNHAbAfw8ZV36sTZu4oqmepstzLMTpcoBly6BVdBtz7nz/LgY9PgjQtLmI\niEjc+v2nHx/+9CFDdxvKiD2iC3XnzIHOnRv+2rqtZEBCLTIhdUZz+XJocal6M0VERApBshezbKhT\nlJiTzlapoZ5MyYulS6PHFi3g879/DqT+x24q1FsULuUubMpfuJS73Ep+Dr886OXyAvOnn2IMqBYq\nMqVGLVumttdpu1H59pIVS2KIRkREpGlLnxnddZ3UBblrrhlHNKum6fIcC3m6HGDFiuhMJsCy0uW0\nHBVVnpo2FxERya/kWcw5Z82hS9uoAXPuXOjUKYvvoelyyZfmzVPb8+e2KN9++4e3Y4hGRESkafp+\nwffl222LUlf4ZLPAzDYVmbJKyXUzu3ZNncHc/rbtY4wof9RbFC7lLmzKX7iUu9zoeW1PAMqGltG6\ndXRs2bIYA6oDFZmySunrZk6cCAdtfBAAO92+UzwBiYiINCEn/+9kANZebW2++ir1odyiRU3fURjU\nk5ljofdkpksWm+6pvhD1ZoqIiORW+mdu8rO4rKziSaCsvZd6MiUO220XPZ5xBkw5eQrQ9JY0EhER\nyafk5+yLx73I7benHQ/g41dFptTZW29Fj9dcA5uusWn58c/mfBZTRLmn3qJwKXdhU/7Cpdxlz0+L\nUgtg7tF7DwYPjrZDmSBVkSkZufXW6NEsNVW+yY2bxBiRiIhI49Tt6m4ArBy6kvXXj46ddlqMAWVI\nPZk51ph6MpOSp+hXrIDDHz6YRz97lA4tOzD/3PnxBiYiItJI/HHcH3nss8do16IdC85dmPXbR9ZE\nPZkSq19+iR6bN4dHBj4CwK/LfqVkRUmMUYmIiDQOZV7GY589BsDC81IF5hdfxBhUPajIlIx17Jja\n/t//YMG5CwBoe2nbmCLKHfUWhUu5C5vyFy7lruGKRxQDMP2f0/nww9TxDTaIKaB6UpEp9ZI8Xb/f\nftC+Zfvy48c9elxMEYmIiITvopcuKt9et+O69OsXbSdvjBIS9WTmWGPsyUw691y4/PJoO33tzLKh\nZVgIayuIiIgUmPQ1MbfaCt5/H/bdF556Kk/vn8WeTBWZOdaYi0xIXQRUUgIzFn/OxjduDGiRdhER\nkUwlC8y3B7/N1mttS3E0a57XJYt04Y8UjIULo8c2baBPlz7lxw978LCYIsou9RaFS7kLm/IXLuWu\nfsa8OaZ8e9seqQJz+vR44skGFZnSIO3apbYHD06dwXzo04dYVrospqhERETC4e6c9my0AKYPc665\nJvXcuuvGFFQWaLo8xxr7dHlS+r1U55TMZs2r1gQ0bS4iIrIqyWnyj//6MZutuVn5Z2oc5YOmy6Xg\nTIluZU5REazRdg3W6bAOAN2v7h5jVCIiIoVtu1u3K99OLzCffz6mgLJIRaZkxaapW5lz1VXw7anf\nAjBr0Sy+nf9tTFE1nHqLwqXchU35C5dyV3dzSubwzsx3gGjmb/z41HN77RVTUFmkIlOyJnla/6yz\nou1lF0Y9mb2u6xVfUCIiIgVqjSvXAKDk/OiOeQMHRscbS5edikzJqnffjR6LiqBFcQuu2OsKINVv\nEpr+/fvHHYLUk3IXNuUvXMpd3SQ/F4/e/GhaN29dPk3+4IMxBpVlKjIlq7beOrU9eDCctfNZ5fsn\nPXlSDBGJiIgUlhvevqF8+96D761wNfmhh8YQUI6oyJSsS57mv/12WL48dYX5LZNv4delv8YYWebU\nWxQu5S5syl+4lLvaLS1dyj+e/gcQfT66wxlnRM81lmnyJBWZkhM//BA9tmwZPc47ex4AHS/vGFNE\nIiIi8Wt9SWsAZpw6A4jaywA++iiuiHJH62TmWFNZJ7M6PXrAzJnRtjsMfmIwt79/e7Sv9TNFRKSJ\nSfZhHrbpYYw/bDxbbJEqLgulVNA6mRKE5NlMgHfegdsOuK18f6+7G8HaDCIiInV03gvnlW+PP2w8\nP/xQeAVmtqnIlJwqK4set0usNZs8g/niNy8yedbkmKKqO/UWhUu5C5vyFy7lrqo5JXO4bNJlQOpz\ncO21o+eWNeI7MKvIlJwyg4ceSm0DlF5UCsDWt2xNU20lEBGRpiO5Hubcs+cCqc/DkSOhRYu4oso9\n9WTmWFPuyUyX/IHaait47z148esX2eueaMpc/ZkiItJYJfswb97vZoZsPYQjjoBx46LnCrE8yGZP\nporMHFORmZIsND/6CDbfHDb610Z8Me8LQIWmiIg0PskCs03zNiw+fzHffQfrrBM9V6ilgS78kSCt\nWBE99u0bPU77x7Ty57a9ddsYIlo19RaFS7kLm/IXLuUucvQjR5dvLz5/MZAqMEtK4ogo/1RkSt40\nawZPPBFtJ89qJs9gvjvzXf77yX9jikxERCR73vnhHe7/+H4g9TmX/Ny74QZo3TquyPJL0+U5puny\nqlZbDRYujLaT/2mSUwo/n/kza7RdI6bIREREGmbFyhW0GBVdzVN6USnFRcW0aQNLlkTPF3pJoOly\nCdqCBantkSOjxx/P+BGANa9aM4aIREREsiNZYL41+C2Ki4q5555wCsxsU5EpsUj+oA0dGt0VqGu7\nrtzzx3uA1FnNQqDeonApd2FT/sLVlHOX/PwaOWAk2/XYjvnz4bjjoueaWoEJKjIlRvPnR489ekQ/\nfMf0PYadeu4EFFahKSIisirJz60+nftw4W4XArD66tFz6XfAa0rUk5lj6sms3fjxMHBgtF25PxO0\ntJGIiBS+6j63khf6XH01nH56HFHVj9bJDIiKzFXbait4//1oW4WmiIiEZOc7dub1714HqhaYEN40\nuS78kUZlctotzDt0iB7TC8ujHj4qzxGlNOXeotApd2FT/sLVlHJ3+WuXVykwBwxIPR8nEy4ZAAAg\nAElEQVRagZltKjKlICR/EBcsgEsvTRxL/MA+8MkD3PTOTTFFJiIiUtW4T8Zx7ovnAqnPq7FjIVlj\nN/UCEzRdnnOaLs9McorhzTdh++3B3SkaEf0t9NjAxzhw4wNjjE5ERARe/fZVdrtzNwBWDl1JkRUx\nbRr06RM9X1ZWcco8JOrJDIiKzMwsXw4tW0bb8+ZFV+aVlpXSfGRzAF4/4XV27LljjBGKiEhT9vmc\nz9n4xo0BKDm/hNbNW7N0aeouPr/+Gt10JFTqyZRGq0UL+PLLaLtTp+ivwWZFzVh4XnSLoJ3u2Ilp\nc6fV8grZ1ZR6ixob5S5syl+4GnPufl78c3mB+fOZP9O6eVRZJgvMt98Ou8DMNhWZUnDWXx8eeija\nLi6OHtu1aFd+V6A+N/Thp0U/xRSdiIg0RSUrSuh6VVcAPv/75+W3QE5Oi19zDWy7bVzRFabgpsvN\nrCMwGBgItCIqlL8HRrj7pGrGHw2cldgtAq5399uqGbcPMDLxms2Bu4HLK891m9nWwNVAp8S4p4AL\n3X1ZDfFqurye/vEPuOGGaDv5n/CLuV+w0Q0bATDv7Hms3nr1mKITEZGmYmnpUlpfEp2ufO3419h5\nnZ2BVIG5557wwgtxRZddTX26/C/A2cBx7r45sBnwKfCyme2VPtDMjgBuB/7s7v2Ao4ExZnZipXG7\nAE8Co9x9C2Af4B/AqErjNgReAh5y977A9sBvgTuy/q8U/vUv6NUr2k7+IG/YeUPe+PMbAHS6ohNz\nS+bGE5yIiDQJS1YsKS8wHz784SoFJjSeAjPbQiwyHfiPu08FSJwmPBdYSVQYAmBmBlwBPODu7yXG\nfgzcCVxqZs3TXvNy4A13fzIx7nvgWuAMM+uWNu5iYK6735AYtwAYARyZOMMpWfbNN6nt5A/0Dmvv\nwFuD3wKgy5Vd+Hnxzzl7/8bcW9TYKXdhU/7C1Zhyt2j5Itpc2gaAp458ioM3ORgIe7H1fAqxyLwC\nGJZ+IDFV/QuQPne6HbA2MLHS979ENNU9ACBRRO4ITKhmXAvggMS44sT2y9WMAzgk43+J1En6D3Dy\nB3u7Htvx3pD3AOh6VVdmLZwVQ2QiItJYLVi2gPaj2wPw3DHPse9G+wIqMDMRXJHpCenHEn2aXahY\nKPYlOuv5DRV9A1jieYDN045XHkfauPWAtpXHufs8YGHaOMmB6grNrdbaig//8iEA3a/pzvcLvs/6\n+/bv3z/rryn5odyFTfkLV2PI3S9LfqHDZdEt6Cb8aQJ7r783oAIzU8EVmTU4EfgJGJN2rEvicWGl\nsQsSj53Txnkdx1X3esmxnas5LllUXaHZt2tfppw8BYCe1/Zk6uypMUQmIiKNxZySOXS6ohMAk06Y\nRP9e/QHo2jU1RgVm3cReZJrZnmZWVoevl2r4/t8QXQh0hLv/kt/oJd+qKzQ3XWNTpv09Wjtz05s2\n5fmvns/a+zWm3qKmRrkLm/IXrpBz9/FPH7PGldHSRG8Pfpudeu4EQO/e8HOi/V8FZt01izsAYBKw\ncR3GlVQ+YGbrAE8Ag9391UpPz0k8tq90PLlM6ty0cVbHcdW9XnJsjZc5Dxo0iF6Jy6Q7duxIv379\nyqcTkj+M2q/7/oQJMGBAtG8W7ffv35+5Z8+l8187s8/Ifbjpbzfx123/2uD3++CDD2L/92pf+9rX\nfkj7SYUST133R941kqEThkJvmPb3afzw8Q9M/GIixx/fn+nTAaLPGyiMeLOZr4kTJzI9+kdmVXDr\nZCaZWU/geeA8d3+0mue3B94ABrn73WnHDwYeBH7v7s8lLvyZCVzs7iPSxm0FvAv8xd1vSVz4Mx94\n0N1PSBvXiagAHe3uF1QTh9bJzJHqemOWr1xOy1HRfSlP3uZkbtz3xhgiExGRkAyfOJyLX74YgPnn\nzKdDq6gfs3t3mJW4rrSpfJQ39XUykwXmc1QqMM3s8bRhbxMt0t6/0rfvAcwDJgK4+49ExWh145YT\nrZ+Ju68kOmu6ezXjHHi4nv8cqafqps5bFLegbGgZADe9exM73LZDDJGJiEgofn/f78sLzNKLSssL\nzDZtml6BmW3BFZlmtjbRVeQfA23M7OjE1zGkrhRPrp95FnBE4qwkZrY58Cei4nR52sueDexkZvul\nvcepwFXunr42zjCgs5n9LTGuA3Ah0Vqck3PzL5baVFdomhk+LHrirR/ewobX/w+yytM/Eg7lLmzK\nX7hCyl2LkS145stnAPBhTnFRdC9jM1iyJBqjArP+CqEnM1OnAb0TX5XXppyevuPu48ysCBhrZk5U\nVJ/q7rdXGjfJzPYHLjGzUUTrY/7L3S+vNO5LM9sDuMbM/kr03+8JokJTYuKeXmCmfiH4MC8vMG14\nqvAUERFJPwGR/vmgZYqyJ9iezFCoJzN/avrFUNMvEhERaZpUYNasyfdkilSnuqlziH6BdG/fPTo+\n3CgtK81zZCIiUgjKvEwFZh6pyJRGpaZC84fTf+CCXaOL/5uPbM7Xv3xdp9cLqbdIKlLuwqb8hatQ\nczfj1xkUj4h6Lk/od4IKzDxQkSmNjjtsskm0nd6jOWqPUbw8KLr1/PrXr89lr10WU4QiIpJP9350\nL+uOWReAZ495ltsPTF2akSwwmzdXgZlt6snMMfVkxmfIELj11mh7/nzoEK1KwaLli2g/OrWmvvo0\nRUQar93v3J1Xvn0FgLlnz6VT6+iWkcuXQ8toWWX23x+eeCKuCAtLNnsyVWTmmIrMeI0fDwMHRttv\nvgnbb596ThcEiYg0bjX9nv/yS9hww2j7mmvgtNPyHVnh0oU/InV0+OHwxRfR9g47wOjRqecq9OMM\nN1aWrazy/YXaWySrptyFTfkLVyHkrrYLfMaOTRWYr7+uAjOXVGRKo7fBBrBsWbR9/vmw3nqp53yY\nc9TmRwHQbGSz8ikVEREJ0zs/vFN+gc+evfesUGDuvjuckLgx9Pz5sOOOcUTYdGi6PMc0XV5YarqC\n8M3v32TH26PfNn069+Gzv3+W58hERKShDnjgAJ6c9iQAk06YxE49dyp/Lv33f1lZxX1JUU9mQFRk\nFp6aCk13p2hE6uS++jRFRMKRPj1eelFp+S0iQUsUZUI9mSIN4A6doosLMYNffkluW5U+zaeeeyqG\nCCUbCqEvTOpP+QtXvnO3ZMWSKv2XyQJz2TIVmHFSkSlN0ty5cOON0XanTnD//annfJgzdLehAOx/\n//4Mnzg8hghFRGRVLnvtMtpc2gaAQzY5pMKJgueeg1atou1TT1WBGQdNl+eYpssL28yZ0KNHtN2z\nJ8yYkXpuTskc1rhyjfJ9TZ+LiBSO9LOXP5z+Q/ntgwG22Qbeey/a/vTT1A06ZNXUkxkQFZlhqG06\nJf0X2c9n/swabddARETiUbKihLaXti3fr3wCQBf4NIx6MkWyrPI9zxcsiLYnTpyID3NO3+F0ANa8\nak0Of/DwGCKUTKmnL2zKX7hymbtLX720vMA8/DeHVygwly+vesJABWa8VGSKJLjDuedG2x06wLXX\npp67+rdXs+i8RQA8+OmDFc5uiohI7tlw44KXLgBg5ukzGXfouPLnHnwwdYvII49U/2Wh0HR5jmm6\nPDw//QTduqX2a5s+f+6Y59h7/b3zFJmISNPz+nevs/MdO5fv1zY9PnUqbLxxviJrnNSTGRAVmeFK\n/8VVWgrFqSXXeOjThzjswcPK93VRkIhI9qX/UX/ngXfyp35/Kt93h6K0+Vh91GaHejJF8sAd1lln\nIgDNmkX3u006dNNDq6ypOX3+9PwGKLVST1/YlL9wZSN3c0vmVln7Mr3AfPLJVIG5+uoqMAuVikyR\nWtx1V7T8BUT3u63cRJ5+UVDv63rTYmSLPEcoItK4bHnzlnS5sgsAA38zsNrp8QMOiLbffBPmzct3\nhFJXmi7PMU2XNx7pBebChdCuXWp/ZdlKmo1sVr4/8/SZrNV+rTxGJyIStvlL57P65auX75ecX0Lr\n5q3L95cvT13cA1qeKFc0XS4SA3c4+OBou317OPbY1HPFRcX4MGef9fcBoPs13XUFuohIHTUb0ay8\nwOzTuQ8+zCsUmGeemSowN9tMyxOFQmcyc0xnMsM2ceJE+vfvX+HY3LnQpUtqv3J6S8tKaT6yefn+\n1L9NZeMuutwx36rLnYRD+QtXJrmb8esM1h2zbvn+kguW0KpZqwpj0ovJ779P3aVNckNnMkVi1Llz\n1cXb7747td+sqBk+zDlp65MA2OTGTXRWU0SkEhtu5QVm8r7j6QXm//1f1cXVVWCGRWcyc0xnMhu3\n116DXXdN7VdOtbtTNCL1t9zYA8cyqN+g/AQnIlKAXvj6Bfa+J7W+8MqhKymyiue80ovLxx9PXegj\nuad1MgOiIrNpSP+F+MILsOeeFZ+/bfJtnPjkieX7pReVUlxUjIhIU1H5j+5zdz6X0XuNrjDmvfdg\nm23Svydf0UmSpstF8qSu6725w803R9t77VW1IX3wVoMrLMPRbGQzul/dPUtRSnW0zmLYlL9wVZe7\nTW/ctEKB6cO8SoFpliowR45UgdkYqMgUyZIhQ6r2aj70UMUxPsz56cyfAJi1aBY23Jg0Y1IeoxQR\nyZ/JsyZjw42pc6YC8O2p31ZZ9/LFFyv+YV5WBhdemM8oJVc0XZ5jmi5vmh54AI46KrVf3f8Cxz56\nLPd+dG/5/oqLVtCsqFnVgSIiAUq/4PHw3xzOuEPHVR2TVlxedx2ccko+IpPaqCczICoym7b0X6Bn\nnw2XX17NmEpXnus+6CISsqLhRTip32PV/U4bMwZOOy21r4/JwqGeTJE8aWhfmDu8+mq0fcUVUdG5\neHGlMcOc+efML9+34cawCcMa9L6inr7QKX/hGT5xODbc8G+iivGbf35TpcBcsSL6PZgsMJ95RgVm\nY6YiUyTHdtml4i/Rdu2qXhjUoVUHfJhz90HRgpsjXhmBDTfenfluHiMVEcnclJ+nYMONi1++GIBT\ntj8FH+b06tirwrhmzaBFi9S+O/z2t/mLU/JP0+U5pulySbdkCbRpk9p/7DE48MCq43pe25PvF3xf\nvj//nPl0aNUhDxGKiNRN5bubrb3a2nx32ndVxj33XMVict48WH31KsOkQKgnMyAqMqU6l1xS8erJ\nZcsq/oWfVLlfs2xoGaYb9opIzOrSS/7/7d15mBTV1cfx72FHBDcCRsVAVMQIcUvigoniFsElvojg\nFoMa0MQYRcWAG4G4ocQVExXFqFHUuLxR44o4RnFLALfoq0YhUUEUEEF2nPP+catnanqbnpnu6S74\nfZ6nn6Zu36q+PZeaOX3r1L3V1dAyNh3wiBFw1VWlbpk0lYLMBFGQmWylXj85PV7M9l+l2qtpOa7u\nxO26Oah+Wvs62dR/lSk9uFwyagkd23asU1ZVVUW/fvvWKdOfweTQjT8i6wh3WLq0dtsMRo6sW6eF\ntcDHOJ+e/WltvbGm9dBFpNmk/875aMRH+BjPCDAvuwz69avdnj9fAeb6TCOZJaaRTCnUvffC0UfX\nbr/5JvTunVnvjflvsNONO9Up08imiJRC7z/05l+f/6tme+bwmezyzV0y6r37LvTqVbt93XVw+unN\n0UIpNl0uTxAFmdJQ220H//537fby5dC+fWa96f+dzt637V2z3aVDl5rVhEREmmK767fj34tqfxE9\ncswjHNrz0Ix6a9dC69p7f9h4Y/jii+ZooZSKLpeLNJNyzNX3/vt1Ly9tsEFm7iZA36374mOcx497\nHIDPln2my+gxmmcx2dR/5ZH6HZIKMG8YcAM+xrMGmGZ1A0z3EGCq7yRFa9iJVCh3WL0a2rYN26lA\nM31g/OBtD8bHOI++9yiHTTks1I0CTV1GF5FCpH85fWjIQxzR64jsddO+xy5dGub/FUmny+Ulpsvl\nUgxz5kCPHrXb3bvD7NnZ686cN5Pdbt6tTpmmPhKRbNKDy+knTWevbntlrbvbbjBzZu32G29Anz6l\nbJ2Ug3IyE0RBphTT44/DgAG12/vuC88+m73uR19+xNbXbF2nbP458+nSoUvpGigiFW/xysVsMr7u\nbOjvnPYOvTr3ylr/2GNhypTa7VyLSMi6QTmZIs2k0nKL+vcPl8snTw7bVVXh0tWgQZl1u23UDR/j\nLBm1pKas64Su2FjjoXceap4Gl1Gl9Z00jPqv+J749xPYWKsTYH52zmf4GM8aYJ5xRvj9kgowr7oq\n/P6pL8BU30mKgkyRBDrxxPDL/sorw/YDD4Q/BkdkSaHq2LYjPsbr5GcOvG8gNtY44p7sOVcisu4Y\ncv8QbKzR/67+NWWp3wnf6PCNjPonnhh+n1x3Xdg+++zw+2bEiOZqsawrdLm8xHS5XJrDmDEwblzt\n9o47wltv5a7/4z//mKc+eKpO2doL19KyRcsce4hIkrg7LcbVHUfq260vL5z0Qs59+vULV0dSfv1r\nuPbaEjVQKpZyMhNEQaY0p2uvhTPPrFuW77/fQ+88xMD7BtYpe/SYRzmk5yElaJ2IlNq02dPY/479\n65TdNfAuju1zbM59NtoIltRm1TB2LFx0UalaKJVOQWaCKMhMtqSun/zgg3DkkXXLqquzz7cJsObr\nNbS5uE2dsnat2rHi/BUlamHpJbXvJFD/NUy2+XG/Gv0VHdp0yL1P2i6TJ4dL5U2lvks23fgjInkN\nHBhGMGfMqC1r0SL8UVm8OLN+65ata3K0jul9DAAr166smZj5uTnPNVPLRaRQ7y18L2MBhiN3OLLm\nXM4WYC5bFn4PxAPMqqrw+6IYAaZInEYyS0wjmVIJvvgCNt20btmTT8JBB+Xe55Mln7DV1VtllGvO\nTZHyyZZrCfDRiI/YqlPm+Zrywgvwwx/WLZs3DzbfvNgtlKTT5fIEUZAplcQ9jGjGHXxwmH8zn6H/\nO5TbX7+9TtmFP7qQcf3G5dhDRIpp9NTRXD798jplO2++M7NOmZV3v+OOg7vvrluWL3VGREFmgijI\nTLZ1Obdor73gpZfqlq1eXXct4nQr166k/SXtM8rzrRJSLuty360P1H/w/sL36TmxZ0b58vOW0751\n5nmYUl0NLdMmiujVC955p9gtzE59l2zKyRSRJnvxxTCy+fTTtWVt2oQRjnvuyb5Pu1btavK9nv5p\n7Y59J/etyQ37cuWXJW65yLpr8crFNedSPMB84rgnas69XAHmww+H8zceYN5zTzjPmyvAFInTSGaJ\naSRTkuLrr6FVq8zyQi6tnfnEmVz7SuaEektHL2XDNhsWqYUi66YVa1awwaUbZJTv8619qBpaVe/+\n2c7PVavCl0aRhtLl8gRRkClJdMYZtat9pNx2GwwdWv++m0/YnPnL5meUK+AUqZVt2jCA7ht3Z/YZ\ns+vd/5FH4PDD65YNHw433VSsFsr6SkFmgijITLb1Pbdo2TLYMEtcuGIFtGtX//5dJ3Tls2WfZZTP\nPmM23Tfu3vQG5rG+913SrYv99/GSj+l2dbeM8tYtWrP6wtX17r9qVfbz7osvYOONi9HC4lgX+259\nopxMEWkWHTqEfC53uOKK2vL27cMluu23z7///HPm1+SRdenQpaa8x7U9avLO7nz9zhK1XqT8prw5\npeb/enqAWX1RNT7G6w0wd989nG/xAHP06Npzs5ICTJE4jWSWmEYyZV2TbRokgPHj4dxzCzvGrx//\nNde/en1G+dYbbc2cM+ZoHk5JtAPvPJCpH07NKB++63BuOqyw69mTJ8PJJ2eWa/ohKTVdLk8QBZmy\nLps3D7bYIrP8iSfgxz8u7BjPzn6W/e7YL+trfzv2bwzYbkATWihSeo+//zgD7s7+//Tpnz7NAd8+\noKDjPPMMHJCl6ocfQo8eTWmhSOHW6yDTzFoApwOHApsCbYBWwH3Ape6+Kq3+ccDIaLMFcJ2735Ll\nuAcBvwPaAa2BO4Dx6RGime0G/D5679bAo8AF6e8bq68gM8GUW1S4xx6DQw7JLJ82Dfr1K+wYa6vX\n0vp3uSfqXHjuQjZtv2nO1+PUd8lWyf23dNVSOl3eKefr9c1jGffKK7DHHpnl994Lgwc3toXlVcl9\nJ/UrZpCZZcKSitceuBo4xd0nQU3g9xzwTWB4qqKZHQ3cCvR19xlm1gd4yULkNylWb2/gEWCQuz9i\nZlsBrwAdgfNj9bYDpgHnu/tEM+sEvABsARxXyg8tUukGDAiX0gEmToTTTw//3i82SPnYY9C/f+5j\ntGrRCh9T+6XsmQ+f4YA7a4d2Nrtiszr1vxr9Vdb1mUWKafma5XS4NPf/s6qfVbFP930KPl6uEcuG\npJyIJEESRzLbAXe4++C08oeAH7p752jbgP8Az7j7ibF6E4EhwBbuviYqmw6scfd9Y/XOAS4Gurv7\np1HZXcCe7v7tWL1BhFHU77v7jCzt1UimrNeuuQZGjMgsP/tsmDChYce6YNoFXPL8JTlf/8+Z/2Hr\njbZuYAtF6pq7dC5bXrVlztcH7ziYewfd26BjjhkD47KswjpuHFx4YUNbKFI66/Xl8lzM7BlC4LhD\ntL078BJworvfHqs3EPgL0N/dnzKzzYG5wFh3HxurtyvwT+BUd7/ZzFoCi4H704LWTYEFwOXufl6W\ndinIFIlMmQLHHpv9tcbc0HDyX09m8muTc75+06E3MXy34TlfFwG44dUb+NXjv8r5+mnfP42JAyY2\n6JjuYXGD6urM1yZPhhNPzCwXqQQKMmPMrDUwDLgUOMrdn47KhwE3Av3c/e+x+rsAM4Bz3X2CmR0I\nPAkMdfc7YvU2ARYCf3D3X0WXyt8Ffuvudb6PmtmXwPPufmiW9inITDDlFpXOBx/Atttmf23qVNh/\n/4Yf89637uXoB44OG7OBLDdLVOI665KpVOfeq5+8yu637J63zh8P+SOnfu/UBh/7xRehb9/sr739\nNuywQ4MPmUj6vZls63tOZg0zmwL8hDCS+NNUgBnpHD0vTdttSfS8WayeF1gv2/FSdTfLUi4iOWyz\nTW0OZ/qSlun5aqtXQ+vc9wPVGNJ7CEN6DwHCH7odv78jXSZ0qVOn7+TMKOC+Qfdx1I5HNaj9Uvnu\n+9d9DLl/SN46La0li36ziE5tc9/Ik8vq1dC2be7X166tu464yPqm7EGmme0PPF1vRahy9zrznLj7\nMVHuZX/gLjOb5O5Km5ai0bfx5tGyZW3ACZl3qsfXYO7bF55/vv5L66m+i99IBPDugnfpdUOvOmWD\n7x8M99fdf8uOWzLzlJl1JpGX5tOQc2/h8oVsc902fLnqy3rrvnHqG/Tp2qfR7TrqKLj//uyv/eUv\nMGhQow+9ztDvTUkpe5AJTAd61VsLlmcrjK5FP2Zm44FLzGyKu88ijG5CuEM8LvV1dWH0vACwAutl\nO16q7sIs5QAMHTqU7t27A7Dxxhuz884715yEVVVVANrWtrZj2wMG7It72HaHUaP25dVXAaqYPh1a\ntAj1oYo99oAXX9wXs8KPnwo8U9u77rkrO924E3NmzQmH7QGfLP2Erqd1rdkGwiV44NHzHuWQnodU\nzM9rfdkeceMIrnn5moz+yLa9zSbbcF2v69igzQZ1jrfwnYUQdWt97/fss1WMHAkzZuwbHbgqeg7b\nO+5YxfXXQ79+tftXVVXOz0vb2i5kO/XvOXPmUGyJy8mMbsBpkbozPFbeH/gbMMzdb43d+JOea5nr\nxp86uZZ5bvz5i7ufFKuXuvHnMnevme4o9rpyMhOsqkq5RZVm7VrYaCNYnvVrZ7B4Mcya1fS+mzF3\nBt+b9L0G7XPSzidxwyE30K5VAYu7Sx2ffvUpQ/93KE9+8GTOnNpsijVp//LlYSnVfFasyL5+uNTS\n781kW99zMo8H9gTSs7J7EHIrUyOKrwIfE75y3hGrtx+wiOgrqbt/amYvRfXGpdVbTZg/E3f/2swe\nBtInQ9svet8HGv+RRKRQrVrBsmW122vXhtVQPv64tix9Lecrr4Rzzmn4e+22xW4Zl9sBVqxZwS/+\n9gtuf/32jNcmvzY57x3vAP237c+l+1/Kzpvv3PBGJdRzc55j1DOjePnjlxu1/1l7nMWVB11JC2tR\ntDZNmAAjR+Z+fcstYc6cuvnCIlK4JI5k/gy4DjjY3V+KynYEHge+AnZJrb5jZkOA24C93X1mNBn7\ni8CI+Ko/ZtYXeIYwGfuj0WTsLwN/cvcLYvW2JYxunu/uN5jZRoRJ4N9y9+NztFcjmSLN7PLLYfTo\n/HXuuQeG5L8npNFmzZvF8Q8dz9ufv120Y27YZkNO+O4JnLDTCfxgyx+UZX33aq9m+n+nc/ebd3P3\nW3ezZNWS+ncq0D7f2oc7/+dOum3UrWjHjHvoIRg4MH+dkSPhiitK8vYiibFeT2FkZl0IUxYdTu2S\nkhCWd5zg7gvT6h8DjCKMNrYArnX3W7Mc90DgkuiYbYDb3X18lnq7AlcR7jZvBTxMWFZydY72KsgU\nKbNly2CrrcJl9HwOOCDcdFTInexNtbZ6LXe9cRejnxnNvK/mlf4Ny2SHzjtw+QGXc1jPw5olMF6z\nBg49FJ56Kn+9DTeEefPCs4jUWq+DzKRRkJlsyi1Krvr6bsEC2GKLEJTU5/jj4bbbKuey6bsL3mXG\nvBm89ulrNY/Pl39e9Pfp1LYTfbr0oXeX3vTu0psB2w3g25t8u+jvk019/ff113DKKXBrxpBBppYt\nYe5c6KKJApqFfm8m2/qekyki0mSdO4d5DtNdeWXm+tF//nN4ZDNxIvzylw1fragptu+8Pdt33p5j\n++RYPmkd4Q6TJoVgslC//z2cdVbp2iQihdNIZolpJFNk3TBpEgwf3vD9Lrss3HRUKaOglWTt2hDU\nn5exIG/9broJhg1r3uBeZH1QzJHM4t2mJyKyDhs2LIyspT+qq8PoWS6jR4ccT7P8j8MPh5kz605K\nn0Tu8NxzIb+1vs/cunX+APOii0Igmu3nPny4AkyRSqeRzBLTSGayKbcouSqp7559Fk44oe40S6XU\nvn1YF37rraFjx3BzS/v2YQnEFi1CYFxdHeZ8XL4cPvsMZs8O0/WsXNk8bezaFdiWWA0AABXpSURB\nVKZMgX79sr9eSf0nDaO+SzblZIqIJEi/fvDRR/XXq66GF16Am2+Gu+5q/PutWAFvvhkezWnw4DDC\n2K9fCGZFZP2mkcwS00imiIiIJIVyMkVERESkoinIFMmjqqqq3E2QRlLfJZv6L7nUd5KiIFNERERE\nik45mSWmnEwRERFJCuVkioiIiEhFU5Apkodyi5JLfZds6r/kUt9JioJMERERESk65WSWmHIyRURE\nJCmUkykiIiIiFU1Bpkgeyi1KLvVdsqn/kkt9JykKMkVERESk6JSTWWLKyRQREZGkUE6miIiIiFQ0\nBZkieSi3KLnUd8mm/ksu9Z2kKMgUERERkaJTTmaJKSdTREREkkI5mSIiIiJS0RRkiuSh3KLkUt8l\nm/ovudR3kqIgU0RERESKTjmZJaacTBEREUkK5WSKiIiISEVTkCmSh3KLkkt9l2zqv+RS30mKgkwR\nERERKTrlZJaYcjJFREQkKZSTKSIiIiIVTUGmSB7KLUou9V2yqf+SS30nKQoyRURERKTolJNZYsrJ\nFBERkaRQTqaIiIiIVDQFmSJ5KLcoudR3yab+Sy71naQoyBQRERGRolNOZokpJ1NERESSQjmZIiIi\nIlLRFGSK5KHcouRS3yWb+i+51HeSoiBTRERERIpOOZklppxMERERSQrlZIqIiIhIRVOQKZKHcouS\nS32XbOq/5FLfSYqCTBEREREpOuVklphyMkVERCQplJMpIiIiIhVNQaZIHsotSi71XbKp/5JLfScp\nCjJFREREpOiUk1liyskUERGRpFBOpoiIiIhUNAWZInkotyi51HfJpv5LLvWdpCjIFBEREZGiU05m\niSknU0RERJJCOZkiIiIiUtEUZIrkodyi5FLfJZv6L7nUd5KS+CDTzH5uZtVmdlG52yIiIiIiQaJz\nMs2sA/A+0BUY6+7jstQ5DhgZbbYArnP3W7LUOwj4HdAOaA3cAYxPT6g0s92A3wObRvUeBS5w91U5\n2qicTBEREUmEYuZktirGQcroXOCfwCHZXjSzo4Fbgb7uPsPM+gAvWYj8JsXq7Q08Agxy90fMbCvg\nFaAjcH6s3nbANOB8d59oZp2AF4AtgONK8glFREREEiixl8vNbEvgZOC3QEbEbWYGXAFMcfcZAO7+\nJvAn4FIzax2rPh54yd0fiep9DFwNnG1mm8fq/RZY6O4To3pLgHHAMdEIp6xjlFuUXOq7ZFP/JZf6\nTlISG2QClwDXAgtzvP4DYCugKq18GuFSdz+AKIjcE3g2S702wOFRvZbRv5/LUg/gyIZ+AKl8r732\nWrmbII2kvks29V9yqe8kJZFBppntCvyQEGTm8l3Agdlp5bMJI5/fjbb7xMrT6xGr922gQ3o9d18E\nLI3Vk3XI4sWLy90EaST1XbKp/5JLfScpiQwygQmEm21W56nTOXpemla+JHreLFbPC6yX7Xipuptl\nKRcRERFZL5U9yDSz/aMpiOp7TIvqHw5s6O5Tytx0WQ/MmTOn3E2QRlLfJZv6L7nUd5JSCXeXTwd6\nFVBveZQXOR44JVae6zb7BdFzx7TyTtHzwlg9K7BetuOl6ubKDSXcgyRJdfvtt5e7CdJI6rtkU/8l\nl/pOoAKCTHdfCbxXSF0z+w4hyLsmFri1jZ5PNbMjgJfd/ZfAG4TgsTvw99hhehAuj78Rbb8ZPXdP\ne7se0XOq3ofAsvR6ZrZp1KbXs7W5WHNNiYiIiCRJ2S+XN4S7v+3uW7n7rqkHMCB6+Y9R2S+j7VeB\nj4F90w6zH7CI6K5zd/8UeClHvdWE+TNx96+Bh4F9stRz4IEmfTgRERGRdUiigswcLO0ZgGiZnZHA\n0dHd6ESTsf8MGJ1209C5wF5mdmhUbyvgTGCCu8+L1RsDbGZmp0X1NgIuIMzFObPon0xEREQkoZK+\nrOQ/gPbADsB84FPgInd/NFbnGGAUYbSxBXCtu9+a5VgHEubebBM9bnf38Vnq7QpcRbjbvBVhdLO+\nO91FpBlEizCMJCySMNzd7yhzk6RA6juRdU+ig8xKYmYbAz8HhhDWP29BuFw/zt2nF7D/GOAkMm8g\n+ru7n1nk5kqapvZfdIyDgN9F+7cG7gDGa/H65mFm3Qg/807AzsCJhQYqOv/Kqyl9F+2vc6/MzOxM\nYBiwBlgL/M7d/1rAfjr3moGZfYOwkuH3CINubwFnuvsnBezbinAldxChf5cAvynkb2PZb/xZh5wK\nnAXs4+7vRN/KrwKeM7OD3X1qAce4UN/ey6ZJ/WdmexPydwe5+yNRysUrhJvCzi9x2yU4G7iF8OUg\nfQWvQuj8K59G953OvfIzs1GE358/cPc5ZnYA8JiZHebuTxZwCJ17JRQtoz0V+D/ClV+A24BnzWxn\nd19ezyEmEu5b2cvdF5nZycBTZranu7+Rb8d1ISezUjhwo7u/AzU5oaOAr4HTy9kwKUhT+2888JK7\np24U+5jwrfHsaOlSKb2z3P2ucjdCGqUpfadzr4xi9ybc4O5zAKIv5U8RFk6R8hsK9AbO9QjwG8JK\nhr/It6OZ9SSMUF8WrXBIlHI4m5BimJeCzOK5gjCcXMPdVwFfAJuUpUXSEI3uv+gP2Z5kjsBMI+T3\nHl68Zkou7l5d7jZI4zS273TuVYT+hHsjqtLKpwHfiYIUKa+BwH/d/T+pAnefD7wNHFnAvpC9fw8y\nsw3y7awgs0hi3w5qRHl+nSn88k9/M5tqZm+Y2T/NbKyZtS96YyVDE/uvT/Q8O608ta117ZNB51/y\n6Nwrv2L0gc690voumf1DVNYnS3lcH6Aa+G+WfVsB38m3s4LM0hpGuOv9mgLqLge+Aga6+3eBk4Hj\nganRSkfS/Artv86Ey+3p69oviZ61rn3l0/mXTDr3yq9z9JytD4z6+0DnXul1JrN/IPTRBmbWNstr\n8X2XZ7mJrqBzTEFmDg1dUz3L/jsS5t882t2/qO/93P1Kdx/m7kui7dcJORN7AoOL+NHWC83df1Jc\nTe2/htL5VzzN3XdSXDr3pJh0d3luBa+pnl5gZlsT5s/8ubs/34Q2vBI97wFMacJx1kfN2X8LCN/Y\n09e17xQ951zXXnJqdP8Vkc6/xmnOvtO5V3wN7b8F0XNHQg57SlP6QOdecS0g8xyB0EfLo/sP8u27\ngZlZ2mhmQf2rIDOHhqypHhfN9/YUcE4hc4TF9uvs7gvSir+OnnXJoIGauf/ejJ67p5X3iJ7zTvEg\nmRrbf42l8694mrnvdO4VWSP6L/Uz7k7dvL0ehFSGvH2gc69ZvAFsn6W8B7XnUL59jwa6kdm/awk3\nD+Wky+VFFAtQRrv7Q7Hyv6bVa29mndJ2/080N2Pc96LnGUVvrGRobP+5+6fAS4R5xOL2A1YT5vCT\nCqHzL7l07lWkJ4AVZO+Dt929JmDVuVc2DwLfiq7SAWBmXQlzZt4fr2hmXdL6I/W3cN+0Y/YDnqxv\njk0FmUViYQLgZwnfCjYws+Oix/Fk3r31GvB+2t1z7YCxZtYiOt63gMuAd9DlgpIrQv+dC+xlZofG\njncmMMHd55X+E0hM+h+sdDr/Kldj+k7nXhm5+5eE1ZZOM7MeABYmYz+QMMl+nM698vgT4W/beDNr\nGf2sLwc+BG5MVTKzvYC5hMnXAYi+JNwMjDazzaJ6JxLm2Kx3sQNdLi+eEYTh4x5kzjs1J217LrCK\nMNScchxwLDDLwhJO7YHHCWuxryxFg6WOJvWfu083s8OAS8zsYsIcfde7+/iStVjqsLDyy/VAB8Jl\nunEWlrq72N0fjFXV+VdhmtJ3OvfKz93Hm9kK4FEzW0O43D3I3Z9Kq6pzrwzcfY2ZHUhYpOBtwpRE\nbwH7pY1EfgUsJvRT3K8I80hPN7PVhDvVD3T3+i61a+1yERERESk+XS4XERERkaJTkCkiIiIiRacg\nU0RERESKTkGmiIiIiBSdgkwRERERKToFmSIiIiJSdAoyRURERMrAzL5pZk+YWXW521IKCjJFRKTJ\nzKxjGd+7Q7neW6SxzGwg8CJh9ZxGT1puZq3M7Bgzm2pm/zKzN83sH2b2syx1f2Zm88xsZuwxy8zu\na8JHyUlBpohUHDP7u5ktNrNqM1tjZnPN7H+i13pGvySXmtny6LUt8xxraFR/VXS8udH2fDN728wm\nmdkPcuzbNao/plSfdV1gZkcC06J/p/pnuZl93UxN2M3MnjezLZrp/USKYSRwADC9icfZDfgzcLO7\n7+jufQjLRt5mZmOz1P+ju+8ae+zi7oOb2IasFGSKSMVx9x8BvYFlhG/4B7v7Q9Fr7wFbE5b7PNzd\nt3D3T/Ic60/u/k3CiIFH9b/p7l2BowhL4L1kZjeZWeu03dsCHYFNG/M5oqB2cmP2TQozG0xYEvI4\nCP0T/bzvba42uPvfgYeB51PrK4skQF93/6BIx5ru7jWjke7+APACcEaRjt8oCjJFpCK5+8fAWKAV\ncGPay6OB19x9ahPf41/ufipwCjAM+EPa6/8FvuHuZf1FXanMrCtwMzAmCv7Lxt2vBBYB15azHSKF\ncveC8jDN7EfRSP17ZvaBmf3ZzDaPHecVoF+WXecCHaI14ctCQaaIVLKrgbeA3c1sGICZbU8ICIsW\n+Ln7LcCTwElm1jfttZXFep910FnAGuC2cjckciVwtJltW+6GiBRD9PvoaeB/3b0n0BNoDzwTv/Li\n7tlSU3oCL7r72rTy3c3sb1Eu5utmdlWprgAoyBSRihX94jw12rzMzL5BGNU8z90XFfntbgGMEMBi\nZofHcjk/jFc0s83M7A9m9qGZfWJm75vZnWbWL3p9qJnNI1zqHxLldc41sz9Er3cws/PM7BUz+9jM\nvoj+PSjtffaPt8HMepvZs2b2uZn928zOzPZBzGw3M3s4yjuda2ZvRekAO6XV287M7o2OtyCqN9LM\nCv3bMAR4PssfsWxt+mnUnmoz+8zMpplZ+1h+bbWZ7Wxmd5vZp9HP9TfRvrtGIzmpn9OuOd5mKuHv\n2jEFtl+k0o0H5rr776Hmd+J5wA7k+X8e5Zn3ierGrSR8MTzJ3XcBjgB+REgZ6lT01ru7HnrooUdF\nP4BJQDXwLvBUI4/xLPB1nte7Re/xfpb9PkwrqwIeBzpF21sCrwDT0upVA7dmea8dgbXAkGi7BTAi\nqj8oR9s/I+Q5bhaVjYrq/ySt7r7AcsKl/7ZRWV/CpeQHY/V2iMruj32Og4ElwG0F/DxTP69Lc7x+\nW/znTQjg7wBuyVJ3THSsvwE9o7Izo7JTgd8DbYAOhNzaOUCLHO87v7H/R/TQoxyP9HMlVt4++j0x\nJa3cgFXA5BzH2xB4Azi3wPf/XnSujS72Z9NIpogkwW+ABcC2wK0leo/50fM381Uys40I3/wfdfcl\nAB5uPLoA+G+2XbKUrSAEW/dG+1e7+9WEQPXcHG+9GXCxuy+Mtq8i/AE6ItY2I+RILgJOd/dV0fGn\nA1ekHe96oCVhRCP1OZ4A/gicYGY75/whBD2j50/rqZdqV+oP6c9zVHPCzzSV23kDsBqYQPjcq919\nGeELRzcg64wAwLxY20SSbFPCF9D9LDblEDAT+JzwxasOM2tD+OL4hLunn/O5zCSMbu5RnGbXKlsy\nqIhIAywhjOR1Bn5rZg+6+5oiv0fqS3d989UtB5YCI8zsPWCqB08Tcqfq5e4fUpsGEPceMChLOcAK\nd38zdozVZvY5EJ+2ZxdCIH6nZ+Zo3UwYfSXKv+oHVKUCzJh/EgLjg4HX8nyMVA7Xsjx1Um4ljMAe\nVk+9f6T+4e5rzGwh8IW7fxGr83HUvq1yHGMZ4WcgknSLCCOMj+T5clYjytF8AHjL3bN+WTWzzu6+\nIK3Yo0fLJrY3g0YyRSQJziV8c/8XYZRqVAneI3W35rx8laLg9gRgI8LNQh+Z2fVm1qchb2Zm/2Nm\nT5nZ7CgvcS5hSqV2OXZJ/8MAYaQvPu1SKriam6Xdi9z99WhzG0KgtkcsX3Ru1IaJwFdAl3o+QmoU\nJW8+ppndTPh57WT1T9ie/hlX5ygD2CDHMdaSZYRHJGncfQUhPWSn9NfM7GwzOyq2nQow33P3c2Ll\nN0azQKT8I20bQu5mG2BGMdsPCjJFpMJFdwqPAE4i3JTjwCgz+3aR3yp1qeiF+iq6+18Jl2x/Shjt\nOxV4LdeNOOnM7FeEPwgzgT4e5u3cgvxzSzZk2blCg6wnPcwbGn90dfdO7n5WPfsuj57T5xaNM0J+\n2GDCyOPV9Rwz22ds6HJ7bWJtE0mCbCk1KecCvc1seE1ls30JMzv8I9puDTwI9ABmmtlx0eN4QmpP\n27RjXmpmbaN9NyN8sfyUtCncikFBpohUuj8ScvJmu/vLhF+E7Qk5e8V0CiGAvbm+imbWwt1Xuvtd\n7n4o0Av4ALg8yomqz8nAV+4+yt2/alKr63o/es7IKzWzdla7Is6/CZ8160pJZraHmXWr571So6Wb\n5KnjwHHu/iAwBTjRzA6s57hNtQmQc3J+kUphZleY2Szg0Gg7lXdZk8oY/c7rBxwTXfX4B2GloAHu\nPieqdjAwAPgO4ea61ON2MvOTTyXcQPeqmb1J+KI7B9jT3edTZMrJFJGKZWHt3Q7uHp9gezRwOHCQ\nmQ322CoXTXifXwP7EG7Gebmeut8izN1Zc+nX3T8ws78SRhc6UHtJdznR71kL0y9dRLjUv4rsuZ/f\naton4TVCoHmAmbXyulMLXUgY1fihuy8ys6mEGwq6uftHsc+3BfA84caaj8jtHcIoY67cSCAssRT9\n83RgP2CSmfUucnAdtyXwWImOLVI0ufIms9RLBZq5Xn+EAvMp3f1JQppPs9BIpohUJDPrDFxMuExe\nI7rD+BeES0xXFZDnV3PILO/Rx8xuIVzGvRn4ZSH7ARuY2bjUqGV06f4nwNNpN6m8A2wf3V19MHB0\n1P6/ABua2SVm1sqCkwjTDxXU9myigG4Y4RL11WbWLmrfgdFn+22s+q+AxcAtFq0eYmZbE0Yc73H3\nWfW815eEm4Qy8sWytdnDvKa/ICwJelW+uvXIWTdKregAPNWA44lIqRR7TiQ99NBDj6Y+CAnoiwgT\nB88FTom9dhrh5py1hHXHFxKColzHGhrVXxnVnxttf04IAicB38+y3+Gx/dZE+x1PGJk8FXiGMGXR\nJ4T5Oy8GNkw7xp7ALML0SO8QLnFBCJTOAf4P+IIwAjmRkKeZauPJwHeztGE/QjA6LypL/Yx2iL3v\nroS1vOdH7XsBOCjLZ+wB/Dk61seEEdpzgdYF9tOw6P03j5VtEh1vWeyznALsndZvc4HDCJful0Rl\n8wmXAlN1459va8K0Swujul+QOS/paOBLoGO5/w/roYcejrnXN1uHiIhIpih3bAbwd3c/vcxt6UjI\ni73Mw5yjIlJmCjJFRKTRolSBKsLNWfXeNFWiNrQHHgU+cfcTytEGEcmknEwREWk0DxPL/wD4fhmb\nsQdhwmoFmCIVRCOZIiIiIlJ0GskUERERkaJTkCkiIiIiRacgU0RERESKTkGmiIiIiBSdgkwRERER\nKToFmSIiIiJSdAoyRURERKTo/h9WwVPlsVo4qAAAAABJRU5ErkJggg==\n",
      "text/plain": [
       "<matplotlib.figure.Figure at 0x1083bf9b0>"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAqQAAAJ4CAYAAACzuvH9AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXl4FUX2sN9zAwbCFiFgbsIqQkDZB1zwp7K6+6mgooMi\nQcURxX0bFwQGUVxRdEZFtlERB1xGQR1BCQ4gIi6oiCgwhCXsKMiaEM73R/UNNzc3GyS5ucl5n6ef\npKtPVZ2u6u57uurUaVFVDMMwDMMwDCNS+CKtgGEYhmEYhlG5MYPUMAzDMAzDiChmkBqGYRiGYRgR\nxQxSwzAMwzAMI6KYQWoYhmEYhmFEFDNIDcMwDMMwjIhiBmkUIiJrROQzb5srIodEZHnQ/kYROfMo\n64gVkbUi8qcS1PssEbm2pMorLUSkiohMEZHFIrJIRF4pQPZkEXlPRP7rtf1CEblNRGLKUN9Tw1wH\nX4rITyJyXwnW84iINC7B8kaLyP9E5LOSKtMrd7x3D0wsyXKLWPcHIvKbiAwrQOa+oP76SUQeKWEd\nkkRkk4j4g9IuFpGLS7KefOoWEblFRBZ41+ECr01OK2L+M0XkC69t8r3WRKSz93w6JijtWhE56wh0\nfsm7DvcFPUMDf78VkUn56SUi74rIbcWoq2VQ3+f7jBaRJoVdF979GPrc/y1E94lHomd5xLu2vhSR\n1WGO1fL6abGILBGRx0XEFyKT6D2rF3oyd4Upp5WIfCoin4vIVyJydRF1e0BEvvbKni4i9UOOVxGR\nZ7x6F4vIKyISV4xzr+H16T4RGVDUfFGHqtoWZRuwOmT/EHBN0P5E4MyjrMMHzAZalKDejwCfRbr9\niqDnAGBl0P7t+chdCmwGTg1Ki/fa7b0I6B16HXQFsoC7SrD8o7quyuqaACYBEyN0/cwFhhW3v0qw\n/rpAGhBf1u0BTAc+AmoHpZ0ObAMuL2IZTYBsoHEBMinAJ4AUt93zKe+R0Oeql35moN3C6QU8DfQ7\ngvoKvJeAs4BDRdB5QEgffxZSxsSj0bM8bcBQYEc+/fQOMMX7vyqwAHg06LgAXwHDvf3awErg+iCZ\nGkA6MNDbTwa2A70L0etWYBlQ3dt/EpgfIvMM8GngegX+BbxxBG3wv+A+r2ibjZBGJ2PDpEnQ/+8B\na46mAlU9pKq9VfXXoyknSmkKrA3sqGqe9haRurgfgOGquihI9nfgauBsERlS+qrmIec6UNWFwI/A\n5RHQwygaUrhI8VDVHarazbsWywwRuR44D+ivqruC9FkAjAQmho4cHSmqukJVz1bvV7oU+QFnzOWn\nx12q+lYp1CtAYec2F/iugONrcL8FpalnmSAiScAg4OUwx9oAlwBjAFQ1C/cbeVvQKOQFQHucYYh3\nfb4MPBRUVCpQTVUnezIbgGkhMqF1C/AA8KKq7vOSnwS6ikh3TyYeuBl4Ouh6fRK4SkSOL3orVHzM\nII1CVPX5Qo6/D/weNMR/l7gp6JwpJ3HT54Fp/4UiMlFE6gTKCDc9ICL1RWSaN+WQJiKviUi94LpF\n5E4RWSoi87wpjNEiUk1E7gYGAh2C6m3i5TlBRGZ5UyRLvSm06t6x4Kmyvt6Uy88isltEvvHSF4jI\nSZ78B96xf+TXPiJytTed9YVXRv+gY6NxD6aAni/kU8y1QC3ciFBo+2/GjVDdFFTu7d75zRGR+cHT\nZyIS47XT9167fiUif81P/2JSFcgMqusccW4In3t63Bx0LDCFPtfrx49EZJeIvCAicz2xsV67PCIi\ng8RNGa4OKuPD4OumgP4LnnYTEfmriMwW547yvARNt4lInHdNfOPV/Z6INCV3AQ97eeeKyNNAoS4T\nIjLMu5bnipsKvC7oWLDeV4jIO+Km16eKSNUguRgRGefVPVtEHii8S8Lq0klCpoS9/shxPZDc0713\neG29RES+E5FTPZkECbl3ReQp4FzgXDk8HR3rHevsXXPzxbmdDA+0vYjc6vXv/0TkGhGZKSJbJH9X\niFuANFXdEebYNNwIVECnD8VNLz8uIi96OmTL4WlsAU4T91z43tOvpZe3jYRMe4vI60AHYKB3fu8e\nST8EIyKTgLaquiyf409JGJeToGsxzbtu3/T6cUJIES1E5F/inkUfiTNcEJFewLPe/4FnZR53C1X9\nXFW/z09/VU1X1fdD9Qy5jq4Xkbe8a/stcc/qYeKe30tFpH3IueV7vZQyzwP3AfvDHOsJ7FPVn4LS\nvgLigP8LklkV/KLkyTQKXFeezDchZX+FMy6r5aNXO6AB8HUgQVW34AY0entJ3YAqwTLAt7jR9l75\nlBuYpp8qIqu96+O6MDJ9xP3+feo9P54JPJ9E5G4R2SEiGSLypJfWV9zzd4WInCIiHb3+DLjXTBCR\nBvnpVOpEeojWtqPfcNM/YYfxcUP83wJ1vP13gYbAY8DNQXKvABPC5A2eEvocGBO0/ywwL2h/MO5G\nrO/tN8ZNsTT29vNMzwLHAKuAB739GOA/wOtBMk28cwxMP8XipmSqA7sImooCjgfeKaCtzgZ2Ay29\n/Vbefq8gmUKnkYG3gK0FHH8G98CpDpzs6VnDO9YC+CVIdjTuQRiY8ukEZB7tdQD083QYEHKu7b39\neGA13hRV0LnvBC709vsC9weVf0ZIndeS14Uk9LoJ239B9f0B9PH2E3DTZvcG5X8NmBa0fzvwKxDj\n7V8J/AY08fYD7V3gFDXwM5Do/V8P2AD8Xxi9X/D2qwHrgGuDZO732jDe27/Ma+OiTtmHtlPolHCe\nqXYv3wIg1tu/F9gCxBXQB+HKqYe7P88P6peFeNOaQf27Bxji7XcB/h7mXOI8vZ4s4Hx3hPTjXK+v\nG3r7Y3HT+4F2f4PDU5x/B34M0w5nhpRXYlP2XpsFlx+uf3I9K/K5Fg/k04fv4QxvARYBjwQdPwvI\nLuY55JqyD3N+oc/eQ8DbXv2B5/BHwPHe8cdCzq3Q6yVMvcd5/fKZ93duyP5nBN3r+ZRxEfBmAf30\nXJi0at75/cXb/3eY82/lyZzr7S8N00/nen3eKh/dLg29Jrz0RYFrHbgDOBgm7ybg8QLO+yWvnGO8\n/TuBveS+r98ELvD+j/H676Gg48OAn0LKncLh34BlHHZREGAOJeyWVZzNRkgrB++q6k4AVb1UVdfj\nDKbxQTIzcDdfWESkG+7HInj66lXgDHFTJuCmLv6pqlu9utbiHiC7C9CtP85X51kvT7an21XijaAG\nMcmTOaCqp6ubIpkOBL85pgKTC6jvAeDfqvqLV9bPwAdeenE4FvdDnR+Bc44HknBvyI28On/FnTfe\nm/ftuB/5fd7xb3A/BkfC/d7b7iJcu1ypqv/0jt0HfK6qS716fsf1+y0hZWxX1ZmezNuq+njQsaOZ\nYs7Vf0HpO1T1He/YNuB1nF8WItIM+DPeVJvHq0Bz3PQwON+y91U13StjMQVPZQbopaqbvDzbgXlB\nZQYz1ZPZDyzGjcQFGIq75n/3ZGbgfrRLm/GqesD7/wWgDq6disNQYJOqfgiuX3BtPzRELgb3woqq\nfqWq4VxR4r2/hd0Tx4akfeo9j1DV29VN7wcYr94vJe75cKI3elha+INGJOcC5xxBGeGuxS/zkf2X\neuBeMDrkI1eazPBUyASW4F7yArMX/yXvtR7uegl9fuSgqptVtbuq9vD+dg/Z76GqT+SXX0RqAKOA\nghZk1cAZ/cEE9uNKWCZc3cFywfmCy80KkzdYJhfeeQ8EXvL6BuBF3O9IMHep6izI+e18l9zPsMlA\niniLCkWkFu6FY6l3PBn3ooV3Hd4I5DvqXtqEnpxRMVkXJq0aMFpETsTdGMcCiQWUETA6p4lIwL+p\nCm4kJlFE1uBGRFcFZ1LVcYXodhKwWVX3BqWtxBk+bXAjKHj1rQ+TfyIwT0QaecfPwxnBBZ3HvJC0\nlRQwdZIPv3H4YRSOmjidf8e9tf4XWCoi/8G91Qam+k/A9UVouxV0DgXxmKq+ls+xtri+Cp5irENe\n151w18vRkl//weE+DrAKZxzUwl0fAjwjIoEHs+Cuu4C7SGvcQrJg1lI4HUTkVdyPQjZuxGRfiIwC\nG4P2/8AtiEBEagN+8vprF6XuoyXYx3mviGzGtUNxaAM0CLkeauDcfWqqauClarOqHiykrIC/amH3\nRKixnt+1puRux9VeWmvcKE5psFFVewR2CnBNKIjiXIvB19UuvOuqjNkU9P9eck+J78E9HwLkd73s\nDLleSpK/4YyyLd5+uBfiPbjR2mAC+3uDZGoVQaawcsLVHSwXnC+43KrkJVgmlOa4Ues1gQRVPSAi\nW0Lk4sW55DTGuWb5vXyBPGu9/roO+AK4Cje7F+B+4FkRuQL3uzRRy9j3PBgzSCsH2WHSPgZ+Abqp\napa4cCmFhd9R3IrDPOWJSM2jV7NQ8tSrqgtEZBVuZHQxblrmUBnosgi4TETqeaNrobQCftDDju7n\niEgX3Fvvy8AtInJGKehV2AjmXFW9phCZcNdLfmiYtPz8N4tTbmgdA4JGboqaJ19E5BTclOlVqjrd\nS5tE+PYL1lvzkSly3cXMFwMUZgweDcuDjbB8KLTfPKP4B9x1nwfPLy0e96NYrLIjhaoOKqmi8kkP\nPfcSX+BWBEJ1KKw/inK95CAix+H8h8O1QWBg4+MCRkl7AJ1E5HJPvilwnGdk/U9Vr8O9rIT6PQYG\nV1Z6f1eTd8Q70at/VZBM6KBMIm5af00++q329Eok94tHIm5VfY6MiDQIGNbiwgLWI2QgogjktKO4\nBVuf4QY3+quqigurGDqYMRF4Sdy6hf64BWCuMNWXRORt3ELcG4B7RKSXqn5VTL1KBJuyr4SIWyHe\nGheaKDCVEPqGF8oPuBsvJaSs50Qk0Xs7Xosb8Qs+frUcXoByKCi9qrgYgj/iHjDBUxcneLI/FvGU\nJuEM0utwN19B/BiqI+5t9Ici1hVgCm5UI88Kdu/HtxteNAQRSRGRk7zpzpuBU4HTcKs+V+JGJULb\n7ZbAIocS5Afy9l8LEXm0iPmDH4aBF5A/CBp5EJEq5P1xKIzQeJMn4Ear/sD1lxJi6IjIgyLSzttd\njvMdLqjMUAIuAzOC0o4JJ5gf6hZIbDyCuvPjD9w9FjySk5yPbHAszDicr95P+chC7nsv1uunH4Dm\n3oxH4Fi8FBB3txDGAd2850so/XCjqP8McywcQu52bO6lLS8gT/A5Vi+jxTahHMm1GI7gcxEpRszK\nUqTY10vIlH3oVuiUvap2UBcxooeqdsdNQW/y9gOuWrOB6t5sX4AuuNHHhUEyJ3izGsEy6/RwJJnZ\nOP99QmQWeu464fgeF/qvcyDBe/435vBI+Tzc6GXnoHydcPZXfqP9q3DT/DnXkvd7eVyQTCvcs3ZG\nkGtLuGfYu7jraSSQoaq/BZXZV1W3quqzuBHwZTjjNCKYQVoJUbcKdjPu7TPAJfmIB/LMw007Pxh4\nIInIRUDngB8e8ChwjfdWjIik4N7WAse34GIkAtyFMyCn4qZyb/fyVPH+nxrww+Kw439+TMEt1EpS\n5xNaEI8CF4lIC6++VsCFXnqR8drwWmCYN9qGV1487kd3hqpO8ZJPJbeP6jE4I3St96B7FrjJ8xvC\nGzm9LjB1IiI3iEhJTKM8DrQTkXO9cqvgHlKhU+b5sRmoK24VZ8BHcylwbKA9cQ+z0BHqgvpPcNPz\nl3g61ce9xT8HoKprcItb7vH8bRGRzp5MwDh5HtenzbzjXYBTKJifvLp7eHnq4mJOFlXvAM8DVweM\nMBHpi5s2KzbeD0U6Ln5s4NrMz6/wajm88ncozth7s4Dig++9sbgVwC/grsUbg+QexMUMDVDkUTtV\nfRXnj/2a5I7Y0RV3/V9dxOnAQJ03BRmVd+AWZxQ0XR98ju/gvXyJyHopPCh8Uc6zqNdD6LXYsQhl\nhxIYSYvHXcuTjqCMoyX0XItyvZQ2edpf3er6d4F7wA124HzQnw1yBfsI98y6w5OpjRsR/FtQUVOA\n/d4oIyKSjHuRypERkfPErVpv69WtuEWpQ4JeGu7GLdpM82R+x/l/3iEuKofgfv+mqur/wp2kqu7B\nDa4MDrnPg89/Dc7o7unpFoNbABZa1n7cs+F28g7YjJfDq+p9uFnzX8LpVCZohFZT2Xb0G87QmYub\nZvkJGBl0zOcd2+sdmxyStysuDMV3uIf3WK+cz4AGnkzoSt16OONgGe7N7i28VcpBMrfj3hrTPJkO\nIfkX4AzbOcCxXnpz4ENciI3vcasL47xjnXDTfNm4t938gtR/hDPiitJu/XGRB77ArW7/c9Cx0bgp\nlh1eW5xdSFmdcFO///Xaez5wY4hMC5zhPd8rcyFwXtDxGJxB/INXxkygWdDxp4BPinEdzCpAtifO\nteFLXNSEe4KOPRBy7q1C8v7FK38hcENQ+l9xD7GPcCPVqz25IQX1X1Bbz8UtXPgU95AdC/iC5Krh\nHujLPZkP8KIkhOi+xivr77jrNIOQyBEheR728szGvUTM9vI8E0bvVp6+GQGZoL4b65Uzx+vHud55\nPZpf3V7eQ7iptuC0c722m4uLqzjFq++VkHzX436El+Du4VO8Ywnkvu8Dq+Nb4K75NNyK4ypeekcv\n7WvcSM6YQNvj4j4u98r6DOfeU5T76y+4+/wz3DX/LtAxROZfeEHOcVO2gfQzvXY/6NX/H9x9MZ/D\nkTHacPh6/4bDERpOw42opwX6HecmkAmcVoC+L3l6BM4zNYxMQK/A9dAVd18G7pf3w1yLn3kyrwEv\ne8eSQnTvhjOeAuVMDSpnktdnCwP9W8A5vOddJ4F7NzjiQi4989FhDIev7ceB7hwOTfQZ4C/seinN\njcOr9cP2E84/eRLu2bYEtyjUF1JGIu7aX+jpf2eYelp6ZX/ulRN6f17stWPo9fxXry0X4mZdEkKO\nV8UtCF7i6fgKXlSVAs65Bm7R2CrcfXA7h5+tQ4P0+QnnQvY2bsHnXvJGFDgFWBOmjpG46/pT3G/C\nk3D4YxNlvQVCahgG4FbhqZsqRUTW4QyWaRFWq1BEZCHOv7WgVb5Rh7hIA18Cl2hQAH4j+vBGf/eo\n87esgZui762qnxaSNbScQzjj8PPS0LMiISLPACeo6v8ro/qq4Vaq7wlK+w8uPuuRRs4wjKNCRC7F\nDQ4d6WLZMsGm7I1QPvamFY4D6uOmZMslIjJEROqIyOnAsopmjHqcgFt4Y8Zo9DOEw6GZzsQZpF/n\nL24cDd4U5hbgijKstiduhD6gQxvcDMa/ylAHwwh8JOMGb/cGCl9fEXFslb0RyjLctEI2cLeqFrSI\nINI0xum6BefrU+Eo7uiZUa75GvibiFyNm47rr8UIsSLuizIv4xZ5jRWRUerFbzXyoi4ayOOFCpYs\nP+NC8XyBC6fnw7kUFHc1tWEcLVWAESJyI+5jMUVdKxAxbMreMAzDMAzDiCg2ZW8YhmEYhmFEFJuy\nLyeIiA1VG4ZhGIYRNahqiX3QwQzScoS5T0QvAwcOZPLkyZFWwzgCrO+iG+u/6Mb6L3oJ+kZCiWBT\n9oZhGIZhGEZEMYPUMEqApk2bRloF4wixvoturP+iG+s/I4AZpIZRAnTr1i3SKhhHiPVddGP9F91Y\n/xkBzCA1DMMwDMMwIooZpIZhGIZhGEZEscD45QQRUesLwzAMwzCiAREp0bBPNkJqGIZhGIZhRBSL\nQ2oYJUBaWpo550cp1ndlT9OmTUlPL/ef1jaMSkuTJk1Ys2ZNmdZpBqlhGIZRpqSnp9uHQAyjHFPS\nQe+LVKc9FMoH5kNqGEZlwfM9i7QahmHkQ1HuUfMhNQzDMAzDMCoUZpAaRgmQlpYWaRWMI8T6zjAM\nI/KYQWoYhmEYhmFEFPMhLSeYD6lhGJUF8yE1jPKN+ZAahmEYhmEYlQ4zSA2jBDA/xOjF+s4oK9q3\nb0+DBg3w+XzExsaSlJSE3++nTp061K1bl3POOYc5c+ZEWs0SZ9WqVfj9fmrVqoXP5+Pzzz8vk3q/\n+OIL/H4/cXFx+Hw+1q5dW6z8WVlZjB8/nt69e5OUlERSUhINGzbkwgsv5I033jjiUf4LL7ww5zoY\nNGhQkfJkZmZy0kkn0bt37yOqMxowg9QwDMMwyoClS5fy1VdfAXD66aeTkZHBxo0b2blzJ/Pnz2fr\n1q2cffbZTJ48uVT1mDdvHj6fj5EjR5ZqPQGaN2/Oxo0bufvuu8s0vuVpp53Gxo0b6devX7HrXbNm\nDV26dOH555/n3nvvZd26dWRkZLBq1SoGDBjA/fffzxlnnMHWrVuLrdfMmTNzroOikp2dzc6dO9mx\nY0eeYwMHDjwig7u8YQapYZQA9qWf6MX6zigPnHjiifzzn/8E4M477yQrKyvCGlVedu3axbnnnsue\nPXtYsGABvXv3JiYmBoDY2FiuuOIK5s+fz7Jly7jgggvIzMwsdZ2qV69Oeno6S5YsyXNMRCISyL6k\nMYPUMAzDMMoBbdq0oXbt2uzcuZMffvih1OqxBWUFM3z4cH799VdGjRpF7dq1w8o0adKEu+66iyVL\nljBu3Lgy0SsmJias4VlR+tMMUsMoAcwPMXqxvjPKEwHjItjwyMzMZNSoUbRu3ZqEhATq16/POeec\nw2effZYrb/v27alXrx4+n48RI0bw1ltv0blzZxISEvD5fKSmpnLJJZfQt29fRISnnnoqxzfyoosu\nAqBVq1bEx8fj8/lyRmwBbr/99rB+j2lpabn8NJctW8Ydd9xBixYtiI2NDeszmpmZyUMPPUTLli2J\nj48nJSUlX6Pul19+oX///hx33HEkJCTQrFkzhgwZwubNm/PIbtmyhYEDB5KQkEBSUhKnnnoqM2fO\nLFb7Z2Vl8eqrrxITE8PFF19coOzll18OwD/+8Y+ctML6IJzP6Icffsipp55KUlISCQkJpKamsmXL\nlpzjn376aVhf2PT0dPx+P9OnTwegS5cu+P1+kpKSeP3114t13uUCVbWtHGyuK4xoZe7cuZFWwThC\nrO/Knsr8vFuzZo2KiHbv3j3PsW+++UZFROvXr69ZWVmqqpqVlaXdunXT+vXr51yru3fv1sGDB6vP\n59Np06blKiMtLU1FRDt16qRDhw7VvXv36qFDh/TKK6/U1NTUXDIjR44Mq+PkyZPV5/PplClTwuoe\nKCeYgQMHqs/n027duumsWbNUVXX9+vVat25dnTdvnqqqDh8+XEVEO3bsqBMmTNCDBw9qVlaWjhw5\nUkVEH3jggVxlLlmyROvUqaPnnXeebt26VVVVf/zxR01JSdEmTZrotm3bcmT/+OMPbdmypdavX18X\nLVqkqqrbt2/Xvn37aqtWrdTn82l6enrY8w1mwYIFKiLaunXrQmUPHTqk1atXV5/Ppxs2bMhJL0of\nBNqyVatWetlll+n27dtVVXXRokWakJCgrVq10t27d4dt49DzCKSvXbu2UJ2LSlHuUU+mxOwgGyE1\njBLA/BCjF+s7I9JkZ2ezePFirr32WmJiYhg3bhxVqlQBYOzYscybN48RI0bkXKs1atTgxRdfJDk5\nmdtvvz2sv+kff/zBc889R/Xq1RERhg0bxjXXXJNLRkthqrdnz56cf/75ACQnJzN+/HhatGiRS6Z9\n+/YMGjSImJgYqlSpwsMPP0znzp0ZM2YMK1euzJEbOHAgBw8e5LXXXiMhIQGAk046ibFjx7J27VpG\njRqVI/vEE0+wcuVKRo4cySmnnAJA3bp1mTBhAhs2bCiy/hkZGTl5C0NEiI+Pz5UvmKL0wcaNG5k4\ncWJOfaeccgojRoxgxYoVjBkzpsh6Q/RP3ZtBahiGYZR7RMp2K20WLlyYM11+3HHHcdlll9GyZUv+\n+9//0q9fvxy5119/HRHJMfICVKlShY4dO7JlyxYWL16cp/wePXrkmvZv3bo13bt3L70T8ujVq1eu\n/T59+uD3+3P2RSRs6KLzzz8fVeXdd98FXESCZcuW0aVLF+rVq5dL9uSTTwbINR0fyHfOOefkkq1T\np06OfGkSzrezKH1w8sknU6tWrVxpgb5+++23S0HT8kuVSCtgGBWBtLQ0G2mLUqzvooMoH/zJQ9eu\nXfP4gIbjl19+AVwIo1AOHDhAjRo1wo7OJSYmHr2SR0BR6g02UAM0bNgQVc0ZIV2xYgUAixcvJikp\nKY98zZo1+e2333L2A/nCyYZLy4+AbLjwSqGoKr///jvgRoNDOZq2ABe/tTJhBqlhGIZhlFMCI2wr\nVqzIM5JWED5fyU+AHjp0qNTq3b9/f679wHmfc845vPPOO0Uu58CBA8TGxh6RDuAWBtWsWZNVq1ax\nf/9+qlWrlq/sr7/+yv79+2nVqlVY47Ok2qKyYFP2hlEC2Ahb9GJ9Z5RnUlJSAMIGPd+zZw+ffvop\ne/bsKdE6q1atiqrm8U0Nt7L9SNi4cWOetMAo7wknnAAcPu9169aFLWPlypW5XBUC+cKNFodLy4+q\nVasyePBgDh48yPvvv1+g7PTp0xERhg4dWuTyQymoLZo3b37E5UYjZpAahmEYRjnl6quvRlVzQvsE\n8+qrr3L11VcXe0SwRo0aADkGZ3Z2NkOHDmX9+vXA4SnjUCO4JEKkqSqzZ8/Ok/7ee+8RExPDpZde\nCkC7du1o27Yt3333HatXr84j369fP6ZNm5az36dPH1SVDz74IJfczp07i/1VpGHDhpGSksLDDz/M\nrl27wsqsWbOGp59+mu7duzN48OBilR/M4sWL2b17d660gD/sZZddVqQyQvtzwYIFjB49+oh1ihRm\nkBpGCWCxLKMX6zujLCnuSuhbb72Vbt268eyzz+YYW6rKv//9b4YNG8YzzzyTsyK/qOW3aNGCatWq\n8f333wMwd+5cXn311RzD5rTTTsPv9/PGG2+wZs0awC3C+vTTTws9r4LqDxxLS0tjypQpHDx4kKys\nLEaOHMmKFSu47777ckY6ASZNmkTNmjVJTU0lPT0dcAbmTTfdxI4dO7j33ntzZO+55x5atmzJU089\nxaJFiwDYvn07gwYNyjmvorZ97dq1+eSTT6hZsyZnnHEGn3zyCdnZ2YBzCZg+fTpnnXUWJ598Mu+8\n807OV5xCz7MgAjI1atQgNTU1x2d10aJFPP3007Rq1SrX+QXnCS2/Xbt2gFsIBvDyyy/z7bffFulc\nyxUlGUMSvRTOAAAgAElEQVTKNotDWlmxWJbRi/Vd2VNZn3ft2rXTBg0aqM/n09jYWE1MTNRWrVoV\nmi8zM1Mfe+wxbdOmjSYkJGiTJk20V69e+sknn+SS69Wrl9arV099Pp/WqlVL/X6/PvHEE2HLfOON\nN7RFixbaoEEDbdmypb7xxhu5jv/000/au3dvPfbYY7VZs2Z6880367Jly9Tn82lcXJz6/X6dP3++\nLlu2TBMTEzUuLk59Pp82aNBA/X5/rliZK1eu1MTERK1Vq5bGxMToBx98oEOHDtXjjz9e4+PjNSUl\nRV944YWweq5cuVIHDBigSUlJ6vf79YQTTtCbbrpJ169fn0d2y5YtmpqaqgkJCer3+7Vjx4762muv\naWpqao5uF154YaHtHeDgwYM6ceJE7dWrl/r9fvX7/ZqcnKwXXHCBTp8+PWyeovTBBRdcoPXr11ef\nz6eDBg3SN954Qzt06KCJiYmakJCgqampumXLlhz5OXPm5GnjSy65JOf4/v37NTU1VRMTEzUpKUl7\n9uypq1evLvJ5hqMo9yglHIdUtIhvDEbpIiJqfWEYRmVARIo8WmUYRtlTlHvUkymxIGk2ZW8YhmEY\nhmFEFDNIDaMEMD/E6MX6zjAMI/KYQWoYhmEYhmFEFPMhLSeYD6lhGGWCKuzbB7t3u78HD0JWVvgN\nwOdzW0xM3v+POQaqV4e4uMN/q1YtVAXzITWM8k0kfEjtS02GYRjRhips3w5btsC2be7/7dsP/x/4\nu3OnMzwD2x9/wJ49zpCsWdMZkVWqOCMy3CYChw65LTv78P+B/cxMZ9Tu3ev+BgK0BwzUWrXg2GMh\nPt79DWyGYRghmEFqGCWAfQ89eil3facKmzbB6tWwdi1kZMCGDbm3jRud0XfccVCvntsSEg7/bdXK\n/R8f7wzPmjWdcVizJtSo4YzQ0iIr67Bxuns3/Pbb4e33391fwzCMEMwgNQzDKGuysmDVKli50v1d\nvfrw9r//OeOxWTNo0gSSkiA5Gbp0cX+TktwWFxfpswhPYHS1du38ZR54oOz0MQwjKjAf0nKC+ZAa\nRgVk/35YsQKWL4effjr8d/VqZ1y2bAnHH++25s3d32bN3EhmBcZ8SA2jfBMJH1IzSMsJZpAaRpSz\ndSt8+23uLT3dGZonngitWx/+27Kl87GspJhBahjlGzNIKzFmkEY35c4P0SgyR9R3W7fCokWwZMlh\n4/OPP6BDB+jY8fDWqlWRVp1XNswgNYzyja2yNwzDKG8cPAjff+8M0C++cNu2bXDKKc6v89prYexY\nN9UuJfZsNgzDqFTYCGk5wUZIDaOcsG8fLFwIaWnw3//C119D48Zw2mlw6qnub+vWLg6ncUTYCKlh\nlG9syr4SYwapYUSI/fvd6Ofcuc4I/fpraNcOuneHM890I6Hx8ZHWskJhBqlhlG8iYZDaK75hlAD2\nPfQo4tAh5/P52GPQvTtpxx4L99/vgrw/8ICLAbpwITz6KJxzjhmjRqmwfPlyhgwZQkpKCklJSSQl\nJdG2bVvuuOMO0tPTI61eWNLS0vD7/cTFxeHz+Vi7dm2p1bVlyxYaNmzIDTfcUGp1HA3r16/nnnvu\noW3btjn9l5KSwuDBg/nxxx+PqMxVq1bh9/upVasWPp+Pzz//vEj5Zs+eTXx8PFOmTDmiessLZpAa\nhlHx2b4dpk1z/p5JSXDllc7wvOcemDHDjZA+9pgzQCt4yCUj8jz11FN06NCBY489lrlz55KRkUFG\nRgbvvfceu3btIiUlhUmTJkVazTx069aNjRs30q9fP6QE/KWbNm3K8ccfH/bYgQMH2L17Nzt27Djq\nekqaqVOnkpKSws6dO3nvvfdy+u+zzz6jbt26dOzYkVGjRhW73ObNm7Nx40buvvvuYrXv7t272b17\nNzt37sxzzOfz0aNHj2LrEgkqxKImEfkvcDrQVFVL75XNMPLBVtiXM1Thhx/gvffgww9d7M9u3eDc\nc+GRR1y8T49uEVPSqIy89NJL3HvvvYwbN46bb74517HmzZszYcIEatSowXXXXUedOnXo06dPhDQt\nfQoyuho1asTWrVupWs6iVMyaNYsBAwZwxx138OSTT+Y6lpyczOOPP05iYiJ33nkncXFx3HnnnaWu\n06WXXsrevXs55phjSr2u0iTqR0hFpC/OGM3j7CAiNUTkBRH5WUR+FJGPReTEMHJVRORvIrJcRL4X\nkfkicno+9d0uIstE5DsRWSIiF+cj19+T+c4r8/qjPVfDMAogOxs+/xzuvNPF/rz4YveZykcfdWGa\n3n8fhgzJZYwaRlmyefNm7r77blq3bp3HGA3m8ccfp3bt2gwZMoT9+/eXoYbli/JmjO7fv58bb7yR\nOnXq8Le//S1fudtuu40WLVrw0EMPsXHjxjLRLdqNUYhyg1REqgKPAbPyEZkBtAPaq2obYDGQJiL+\nELkXgMuB01W1HTAJ+ERE2oXUdz/wAHCBqnYA7gemi8g5IXJXAhOA6zy5/sBYESmfzjDGUWM+pBHi\nwAFnaA4aBImJcNttUKcOvPuu+xrSs89Cz54QG5tvEdZ3RlkxYcIE9u3bx6WXXlqgXFxcHOeddx5b\nt25lxowZOemZmZmMHDmSE088keTkZBo3bsxZZ53FU089xa5du3KVsWXLFm655RaaNWuG3++nadOm\ndOvWjTFjxvDbb78B0Lt3b+rVq4fP52PkyJE5eZ9++mn8fn+xp3unT59O3759Of7440lMTOS4447j\nkksu4dtvv80l9+abb+L3+1m/fj3r1q0jKSkJv99PUlISq1evZvLkyfj9fmJjY4mJicnJF+pjOWfO\nHB5++GFSUlKoU6cOXbt25Ysvvgir25w5c+jatSu1atWiSZMmXHrppfzyyy/4fD5iY2NJSkri9ddf\nL/D83nnnHTIyMjjvvPOoVq1avnIiQp8+fThw4AATJkwA8vrfLlu2jDvuuIMWLVoQGxsb1mc0MzOT\nhx56iJYtWxIfH09KSgrjxo3LJTN48OCwffXEE0/g9/sRERYuXJirjbOysgo8z4ihqlG7AXcArwOP\nANlA46BjvYFDwFlBaVWB7cC4oLSWXt5rQ8r+EfggaL8OsBt4JERuJvBD0L4Aa4FJIXIvAFuBqvmc\nixrRy9y5cyOtQuUhM1P1449VBw5UPfZY1TPPVH3uOdX//e+IirO+K3sq6/Oud+/e6vP59K233ipU\ndvTo0SoiesMNN+SkXX/99ZqcnKzLly9XVdXs7GwdN26ciojOmzcvR27dunWanJys7du315UrV6qq\n6p49e/TWW29VEdEpU6bkyKalpamI6IgRI/LoICLavXv3POkDBw5Un8+n6enpudKbNm2qffv21R07\ndqiq6ubNm/WSSy7RuLg4Xbp0aZ5ymjZtqs2aNcu3Dbp166Y+ny9P+vDhw1VE9PTTT9f3339fVVW3\nbNmiHTt21Fq1aunWrVtzyc+cOVOrVKmiF198sf7++++qqrpgwQLt2LGj+ny+sOcYjhtuuEF9Pp+O\nGTOmUNmpU6eqiGjv3r1zpQfarlu3bjpr1ixVVV2/fr3WrVs3pw8D59exY0edMGGCHjx4ULOysnTk\nyJEqIvrAAw/kqS+/vsovvTCKco96MiVm00XtCKmI1AXuBv6aj0hfIBNYEEhQ1Sxvv2+QXMBBJy0k\n/2fA2SIS5+2fB1TPR+5EEWnp7Z8MNMxHri7QPR99jSjGfEhLmexsF5LpL39x34AfPtx9FenHH2He\nPLj1Vmja9IiKtr4zyoqMjAwA6tatW6hsvXr1cuUBN0J36qmn0qpVK8AtWLnlllu48MILiYuLy5G7\n6aab2LhxI5MnT6Z58+aAG3UdO3YsJ5xwQomdTygnnXQSL774IsceeywADRo0YMqUKRw4cIAxY8aU\neH1/+tOfuOiiiwCoX78+N910E3v27OHjjz/OkVFVbrnlFqpWrcrkyZOpU6cOAF27duWWW24pVvix\no+2/YHr27Mn5558PON/T8ePH06JFi1wy7du3Z9CgQcTExFClShUefvhhOnfuzJgxY1i5cmWR9Y4W\nonlR0zDgn6q6Lh/H6LZAhqoeDEn/H3CBiCSo6jZP7hBuVDNUrgpwIrDEkwukh8qBcw34xfur+ciJ\nd/yTQs/OMAxncE6ZAlOnQoMGbnX8l1+6ryIZlQoZUbZfwdJHykec1ODft8TERGbNmsULL7zAgAED\nqF27NgDvv/9+jszvv//ORx99hN/vp0OHDnnKmjFjBvXr1y8VXWfOnJknrXbt2iQnJ7N06dISrUtE\nOP303Es9mjRpgqqyfv36nLRvvvmG9PR0zjjjDOJDQridffbZJapTfnqGo1evXrn2QxeviQi9e/fO\nk+/888/n66+/5t133+Wee+4pOUXLAVFpkIpIC+AyoHUBYgnAH2HSA4429YBtntxezfuaFCwXKI8w\nZe7CGZpFkQsuz6hA2LfsS5Dt2+HNN2HyZBea6ZprYM4c93WkUsD6LjooLwbi0ZCUlMTy5cuLFMoo\nIJOcnJyT9tprr9G/f39uu+027r77brp168YVV1zBlVdemTNC+uuvv3Lo0CEaNWoUttx27dqFTS8J\nfv75Z8aOHcvChQvZsmULPp8PVWXr1q00bty4xOtr0KBBrv1Yz1c8MzMzJy0wkpiUlJQnf7i0ggjI\nH2n/BZOYmFhoGX5/6HIXaNiwIapaIUdIo3XK/nHgMVUNZ3AahhFtHDwIM2fCZZe5FfILF8Lo0ZCe\n7uKDlpIxahhlSffu3VFVfvjhh0Jlv//+e0SE7t0Pe3l16tSJ5cuXM2fOHK6//nq++eYbrr/+ek46\n6aQ8BsqBAweOStfiTGUD/Pjjj3Tu3JkFCxbw2muvsWnTJjIyMti4cWO+xvHR4ivG53uPtj2g+P0H\n5LsorDi6B1ORoy5EnUEqImcAbYCXgpPDiG4DaoVJr+393R4kFyd5x9XDyRGmzCOVMyoQNsJ2hKxb\n5+KCNmniDNBzznFG6NSpcPbZELTCtrSwvjPKikGDBhEXF8c777xToNy+ffv46KOPaNSoUa4V+dnZ\n2YAzjF544QUyMjJ46KGHSE9P59FHHwWgRYsW+Hw+NmzYELbsHTt25BrhC4RWCl15vXnz5mKd26RJ\nk9i3bx/Dhg2jffv2xcpbmgR8ZsP5cubn35kfl156KcnJyXz44YcFGriqyttvv03NmjVJTU0tnsJB\nhAsZFdC5NH2BI0XUGaRAL5zeX4nINyLyLXCjd+xDL+1c4HsgSURC3RKaAZs9/1E8OR8Q+grXDDgI\n/BQkB9A0jJwGHf8eZyAXJpeHgQMHMnz4cIYPH87YsWNzhaNJS0uzfduvGPvZ2aSNGUPa6adD+/aw\nYwdpo0aRNno03HAD1KlTvvS1/RLfr6wcd9xxPPPMM/z888/8/e9/z1fugQceYM+ePYwfPz5XfMmq\nVauydevWnP0qVapw7733AuSEcoqPj+fCCy9k27ZtLFy4MFe5Bw8epG3btkycODEnrWHDhgB5PgNa\n3P6KzSe02v79+9m0aVPYYzVq1MhlCE+ePJnp06cXq97C6NSpE02bNuWbb77Jo8fs2bOLVVa1atV4\n5ZVX2LVrFw8//HC+cs8//zwrV67kueeeO2J/XVUNq997771HTExMoaHDAsTFxeVq42eeeYa5c+cW\nS5fA/ZuWlsbw4cMZOHAgAwcOLFYZRaIkl+xHauNw2KdGQWm9vbQzg9ICYZ+eD0pr6ckNCCnzB+D9\noP1A2KdhIXL5hX2aGCIXCPt0TD7nECaoghEtWOigIrB5s+ro0apNm6p26qQ6frzqH39EWivruwhQ\n2Z93zzzzjFarVk0ffPBB3bBhQ076ypUr9brrrtOaNWvqjBkz8uQTEe3fv79u375dVVUPHDigjzzy\niPp8Pn377bdz5NatW6eNGjXSTp065YR9+v3333XgwIHaqlWrnNBHATp37qx169bVb7/9VlVVf/rp\nJ+3bt2++IYOuvfZa9fl8umbNmpy0b7/9VmNjY7VNmzb6888/59R5zTXXqIiEDe901VVX6THHHKOb\nNm3S3bt3a0pKir7wwgs5x88666ywYZ8C5xwc6krV3cvhQljNmjVLq1atqv/v//2/nJBUCxcu1N69\nex9RWKRp06ZpzZo19cYbb8xpX1XVDRs26P3336/VqlXTcePGhc0bru3CnZ+IaNOmTXXy5MmalZWl\nmZmZOmLECPX5fPrggw/myZPfeZx22mmamJioe/bs0S1btuixxx6rM2fOLPQci3KPUsJhnyJuTJbI\nScBwz6hsEpL+ITAPqO7tjwA2A/4QuX8Ay4F63n4qsAdoGyJ3n5e/mbffCzgAnB0i1w/YC3Ty9tvi\nFjldX8A5FNr5RvnFjJoCWLpUNTVVNT5eddAg1a++irRGubC+K3vseae6YsUKvfnmmzUlJUX9fr8m\nJiZqmzZt9K677tL169eHzTN16lTt06ePHn/88ZqUlKQNGzbU3r1768cff5xHdvPmzTp06FBt0qSJ\n+v1+bdasmQ4ePFgzMjLyyK5fv1779Omj9evX14YNG+qf//xn3bp1q/p8Po2NjVW/369vvvmmzp07\nVxMTEzUuLk59Pp82aNBAL7nkkpxy5s2bpz169NB69erpcccdpx07dtS///3v2rRpU61SpYr6/X6d\nPHlyjvzq1au1Z8+eWr9+fW3UqJGmpqZqZmamTpo0SRMTEzU2NlZ9Pp/6/X4dOnSo7tq1SxMTE7VW\nrVrq8/m0Xr162rdvX1VV7dOnj9arV099Pp/WqlVL/X6/7tu3L6euTz/9VLt27aq1atXSpk2b6lVX\nXaUbNmxQEdGePXsWu/82bNig9913n7Zt21b9fr/6/X5t2bKl/uUvf9EVK1bkkV+2bFmetvP7/bli\nua5cuTLn/GJiYvSDDz7QoUOH6vHHH6/x8fF5DHZVFxs1MTExT18F+Prrr/WUU07R+vXra+PGjfWe\ne+4p0vlFwiAVV2Z0IiLnAaOB47xtOZCpqp2843HAGOBs3PT7euB2VV0eUk4MbpT1Clzs0j+Ae1Q1\n93yHk70V5yKQhTOCh6vqB2HkrsJ9yUlxLgHPqeqEAs5Fo7kvDCMXhw65b8g/+yz8/DPcfDMMHgwJ\nCYXnNSo8IoI974xIs2nTJpKSkujXrx9vvvlmpNUpVxTlHvVkSiweW1QbpBUJM0iNCsHu3S5u6HPP\nQa1acMcdcMUVEOQHZxhmkBplydtvv83333/PiBEjcqVPnz6dfv368corr3D99ddHSLvySSQM0mhc\n1GQY5Y5Kv2Bj+3b39aRmzeDTT2HCBFiyBK6+utwbo5W+7wyjgrNt2zaeeeYZPvroI8C5Ki5cuJD7\n7ruPLl26MGDAgAhraIAZpIZhHA0bNsBdd0GLFi6E0/z58M47cMYZkM8XSgzDMMqSnj17kpqayr33\n3ktSUhJ169Zl4MCBXHnllcydOzdXJAMjctiUfTnBpuyNqOLXX+GJJ+Dtt+Haa51R6oWPMYzCsCl7\nwyjf2JS9YRjlmxUroH9/6NoV/H745Re3cMmMUcMwDOMoMIPUMEqACu+HuHKlGwn9v/+Dk06C1ath\n5MgKsWq+wvedYRhGFGAGqWEY+bNmDVx/PZx6Khx/vDNMH3jAraA3DMMwjBLCfEjLCeZDapQrNmyA\nUaPgX/+CIUPgzjvh2GMjrZVRQTAfUsMo35gPqWEYkWXnTjcC2q4d1K7tfEb/9jczRg3DMIxSxQxS\nwygBot4PMTMTnn8eWraETZtg6VIYM6ZC+IgWRtT3nWEYRgWgSqQVMAwjgqi6afkHHoCUFJgzB9q2\njbRWhmEYRiXDfEjLCeZDapQ5Cxa4T3tmZ8OTT0KPHpHWyKgkmA+pYZRvIuFDaiOkhlHZ2LAB7rsP\n0tLg8cfhz38Gn3nvGIZhGJHDfoUMowSICj/E/fth9Gho3x6aNIGff3bfmq/kxmhU9J1RIcjMzMTv\n95OUlESVKlXw+XwkJSVx0UUXlZkOkyZNIj4+njlz5pRZnfnRtGlTBg0aVCplZ2VlMX78eHr37k1S\nUhJJSUk0bNiQCy+8kDfeeOOIR+gvvPBCGjRogM/nK7LumZmZnHTSSfTu3fuI6qwsVO5fIsOoDKjC\ne++5gPaLF8OXX8Kjj0LNmpHWzDAqFccccwwbN24kIyODRo0aISJkZGTwwQcflJkOu3btYvfu3eze\nvTtXenp6erGMrJJApMRme3OxZs0aunTpwvPPP8+9997LunXryMjIYNWqVQwYMID777+fM844g61b\ntxa77JkzZ/LVV18VK092djY7d+5kx44deY4NHDgQn8/H2rVri61LRcOm7A2jBOjWrVukVQjPypVw\nyy2wdi384x9w9tmR1qjcUW77zjBKgdtuu42bbrqJY445JtKqlAq7du3i3HPPJTs7m6+//pratWvn\nHIuNjeWKK67glFNOoUOHDlxwwQXMnz+/1NuievXqOQZ/KCJSaoZ5tGEjpIZREcnMdKOgp54KPXu6\nME5mjBqGAWENsIqyyGz48OH8+uuvjBo1KpcxGkyTJk246667WLJkCePGjSsTvWJiYsIanhWl3UsC\nM0gNowQoV36I//0vdOgAX3wBX38N99wDVatGWqtyS7nqO6PS0rt3b+rVq4fP52PkyJE56U8//TR+\nvx+fz0ePoEgYaWlp+P1+4uLi8Pl8LFq0iGuvvZamTZtSp04dOnTowLRp03LVcd5554X1fxw6dCgn\nn3wyIsJbb71FUlISfr+fDh065Mr/yy+/0L9/f4477jgSEhJo1qwZQ4YMYfPmzfnqtWzZMu644w5a\ntGhBbGwsPp+Pzz//HAg/Ovjzzz9z1VVX0bRpU5KTk2nZsiVXXnkl//73vwttw6ysLF599VViYmK4\n+OKLC5S9/PLLAfjHP/6Rk9a+ffucPhgxYgRvvfUWnTt3JiEhIV93hg8//JBTTz2VpKQkEhISSE1N\nZcuWLTnHP/3001ztEZiaT09Px+/3M336dAC6dOmS41/8+uuvF3quFRJVta0cbK4rjGhl7ty5kVZB\ndds21euuU01OVp0xQ/XQoUhrFBWUi76rZNjzTrVp06bq8/lypaWlpamI6IgRI/LIi4h27949T/rA\ngQNVRDQlJUXff/99PXTokO7bt08HDx6sIqKvvPJKLvk1a9aoiGhqamqR0gMsWbJE69Spo+edd55u\n3bpVVVV//PFHTUlJ0SZNmui2bdvy6OXz+bRbt246a9YsVVVdv3691q1bV+fNmxe2jh07dmhiYqIO\nGDBA9+zZo6qqmzdv1nPPPVebNWsWNk8wCxYsUBHR1q1bFyp76NAhrV69uvp8Pt2wYUNOeqAPOnXq\npEOHDtW9e/fqoUOH9Morr8xpm0BbtWrVSi+77DLdvn27qqouWrRIExIStFWrVrp79+6w7ZGenh42\nfe3atYXqXJYU5R71ZErMDrIRUsMoASLqh6gK06a5RUtxcfDTT9C3L5hfUpEwH1Ij2hERrrrqKi66\n6CJEhGrVqvHiiy+SlJTEXXfdxa5du466joEDB3Lw4EFee+01ErwvuJ100kmMHTuWtWvXMmrUqLD5\nevbsyfnnnw9AcnIy48ePp0WLFmFl58+fz+bNm7n88suJi4sDoEGDBjz55JM0b968UB0zMjIAqFu3\nbqGyIkJ8fHyufMH88ccfPPfcc1SvXh0RYdiwYVxzzTW5ZDZu3MjEiRNz6jvllFMYMWIEK1asYMyY\nMYXqEIza1L0ZpIYR1Wza5IzPv/0N3n/fff4zH78pw4hqRMp2izJCQwpVqVKFXr16sWfPHv7zn/8c\nVdlLly5l2bJldOnShXr16uU6dvLJJwNu9Xk4evXqlWu/T58++P3+sLKJiYkAPPjgg6SlpeUYaW3a\ntGH27NlHdQ4FEc63s0ePHrnSW7duTffu3XPJnHzyydSqVStXWsD4fvvtt0tB04qNGaSGUQKUuR+i\nKrzxhosp2ro1fPMNeD8MRvEwH9IoQbVstygjnJHXsGFDAFauXHlUZa9YsQKAxYsX58T0DGxt2rSh\nZs2a/Pbbb2HzBozMotClSxeeeOIJVq1aRY8ePUhOTmbw4MHMnz+/SPmTkpIAwoZXCkVV+f333wE3\ncnskehfU5qtWrSo0v5EbM0gNI9rYuBEuucR9ZenDD91q+tjYSGtlGEYpcaTTufv37y+R+gMjheec\ncw4ZGRl5tl27drFt27awecOFOiqIu+++m4yMDCZMmEDHjh2ZPHkyZ555Zp7p8nB06dKFmjVrsmrV\nqkLP/ddff2X//v2kpKSENT6Lq3eAkmrzyogZpIZRApSJH2LwqGi7drBkCfzpT6VfbwXHfEiN8kJV\nLxpGVlZWrvTgVez5sXHjxjxpAd/IE0444aj0SklJAWDdunVhj69cuZLFixcfVR0BVJXatWuTmprK\nrFmzWLVqFZ07d2bq1KnMmzevwLxVq1Zl8ODBHDx4kPfff79A2enTpyMiDB069Ih1LajNi+LzauTG\nDFLDiAZ++w2uusqNhn78sfMZtVFRw6hQBKZ7Q7/aUxS3klAfywMHDvDxxx9Ts2ZNzjnnnELz16hR\nA8htDD/44IMsXbqUdu3a0bZtW7777jtWr16dJ2+/fv3yhJg6EqZMmcIFF1yQK61Ro0YMGDAAIF+3\ngGCGDRtGSkoKDz/8cL6LudasWcPTTz9N9+7dGTx48BHru3jx4jxfvHr33XcBuOyyy4pURmi7L1iw\ngNGjRx+xTtGMGaSGUQKUqh9iWpqLK9qggYsr2qlT6dVVCTEfUqO80LhxY/70pz8xc+ZMvvvuOwCW\nL1/OjBkzCsynqsyePZtZs2ahquzdu5dbb72VnTt38vTTT+cKEJ/f9H9CQgKJiYksW7aM7OxsVqxY\nwZNPPkmVKu6DjpMmTaJmzZqkpqaSnp4OwM6dO7npppvYsWMH9957bx6dCqovP+bMmcO0adM4dOgQ\n4EZlX3vtNZKTk+nZs2eh+WvXrs0nn3xCzZo1OeOMM/jkk0/Izs4GnJE+ffp0zjrrLE4++WTeeecd\nYmKV9V4AACAASURBVGJiwupdEAGZGjVqkJqamuOzumjRIp5++mlatWpV5PZo164d4BaOAbz88st8\n++23hepQISnJGFK2WRzSykqpxLI8cED13ntVk5JUP/yw5Ms3VNXikEYCe965OKQxMTF50tevX699\n+vTR+vXra8OGDfXPf/6zbt26VX0+n8bGxqrf79c333wzRz4Qx/KHH37QIUOG6PHHH6+1a9fW9u3b\n61tvvZWr7HPPPVcbNGigPp9P4+Li1O/36/z583OOz549W9u2bav169fXZs2a6TPPPJMr/8qVK3XA\ngAGalJSkfr9fTzjhBL3pppt0/fr1OTLLli3TxMREjYuLU5/Ppw0aNFC/358n/mY4Nm3apKNHj9au\nXbtqw4YN1e/3a/PmzXXIkCG6bt26IretqurBgwd14sSJ2qtXL/X7/er3+zU5OVkvuOACnT59etg8\nvXr10nr16qnP59NatWqp3+/XJ554IpfMBRdcoPXr11efz6eDBg3SN954Qzt06KCJiYmakJCgqamp\numXLlhz5OXPm5GmPSy65JOf4/v37NTU1VRMTEzUpKUl79uypq1evLta5lgZFuUcp4TikosV8ezFK\nBxFR6wsjh+XLoX9/aNQIXn0V6tePtEaGUWKISLFHzioafr+f/fv3F2kauiBSU1P55z//yf/+9z8a\nN25cQtoZlZ2i3KOeTInFSLMpe8Mob0yeDGeeCTfeCO+9Z8aoYUQ5jz32GH//+99z9vft28fWrVtp\n27ZtBLUyjPKFGaSGUQKUiB/inj0wcCA88YTzG73xxqgM0B1tmA+pUdr88ssvvPTSS/z+++9kZ2fz\n5JNPoqpHtaAmQGAUq7KPOBvRjxmkhlEeWLYMunRxoZ2++sp9BtQwjArBRRddRO3atWnZsiX169dn\nxowZvPzyy1x99dVHXGZaWhp+v5/p06cD7qtBl156aUmpbBhljvmQlhPMh7QSM3ky3HMPPPmkGyE1\njAqO+ZAaRvkmEj6kVUqqIMMwisnevTBkCHz5JcydC23aRFojwzAMw4gINmVvGCVAsf0Q09Ph//4P\nMjPdFL0ZoxHDfEgNwzAijxmkhlHWfPYZnHIKXH21+xRozZqR1sgwDMMwIor5kJYTzIe0EqAKzz7r\nVtFPnQo9ekRaI8OICOZDahjlG/MhNYyKyt69MHgw/PST8xlt0iTSGhmGYRhGucGm7A2jBCjQD3H9\neucvCjB/vhmj5QzzITUMw4g8NkJqGKXJkiVwySVw221w990W6N4wgCZNmiB2LxhGuaVJBAZOzIe0\nnGA+pBWQd95xX1saP94ZpYZhGEbZoQovvACjR8O0aXDWWZHWqEJR0j6kZpCWE8wgrUCouoVLL7wA\n//43dOoUaY0MwzAqL3PmQP/+8NRTcM01kdamwlDSBqn5kBpGCZDjh5iZCddfD2+9BYsWmTEaBZgP\naXRj/RfdlEn/9erlPj7y8MMwapQbNDDKHWaQGkZJsXMnnHsubNsGn38OycmR1sgwDMMAOPFE+OIL\nePddF/EkKyvSGhkh2JR9OcGm7KOcjRvhvPPcavrnnoOYmEhrZBiGYYSyezf06wfZ2TB9OtSqFWmN\nohabsjeM8saKFdC1K1xxBYwbZ8aoYRhGeaVmTefb36QJnHkmZGREWiPDwwxSwzgavvwSunUj7Yor\n4IEHLKxTFGI+iNGN9V90E5H+q1IFXnrJDSKcfjr8+mvZ62DkweKQGsaR8tFHcO21MHGifY/eMAwj\nmhCBv/4V6td34aA+/BA6dIi0VpUa8yEtJ5gPaZTx+usu0P2778Jpp0VaG8MwDONImTEDhgxxsaMD\nX9UzCsV8SA0j0rzyCtx/P3z2mRmjhmEY0c5ll7lBhj593MyXERHMIDWM4vDss+6rH2lpLoyIh/mx\nRS/Wd9GN9V90U2767+yz3WKngQPhzTcjrU2lxHxIDaOoPPooTJ7sYow2bhxpbQzDMIyS5LTT3Fed\nzj0X9u+H1NRIa1SpMB/ScoL5kJZjVOHBB+H992H2bPD7I62RYRiGUVqsWOG+7vTII+7Le0ZYStqH\n1EZIDaMgVOH222H+fDdNn5AQaY0MwzCM0iQlxa0R6NnTBdC/8cZIa1QpMB9Sw8gPVbjjDvdN+k8/\nLdAYLTd+UEaxsb6Lbqz/opty238tWsDcuW7NwIsvRlqbSoGNkBpGOFRdWKf5851PUXx8pDUyDMMw\nypLmzd3MWI8ecPAg3HZbpDWq0JgPaTnBfEjLEaourNPs2c4YrVs30hoZhmEYkSI93Rmlt98OQ4dG\nWptyg/mQGkZpogoPPQQff+x8iMwYNQzDqNw0aeJ+D848E+Li4LrrIq1RhcR8SA0jmBEj3Gr6OXOg\nXr0iZyu3flBGoVjfRTfWf9FN1PRfkyZu1mzYMJg6NdLaVEhshNQwAjzxBPzrX85nqH79SGtjGIZh\nlCdatoT//MeFhKpeHS69NNIaVSjMh7ScYD6kEebVV13g+/nzITk50toYhmEY5ZWvv4bzzoN//tMF\n0a+klLQPqRmk5QQzSCPI2287R/V581yoD8MwDMMoiIUL4eKL3e/HmWdGWpuIUNIGqfmQGpWbOXPg\npptg1qyjMkajxg/KyIP1XXRj/RfdRG3/de0K06bBZZfBDz9EWpsKgRmkRuXlyy/hz392b7gdO0Za\nG8MwDCOa6NkTnn8ezj/fhYYyjgqbsi8n2JR9GfPTTy6u3KuvwoUXRlobwzAMI1p57jn4xz/cGoRK\n9Hlpm7I3jKNl0yb3RjtmjBmjhmEYxtHx/9m77zCpiqyP499DUjCAKOYACIqBYAIVUTBgWnNOgCDm\nhK5iDihmjJhF3F0TAgYwIQaCigFYEUTEAAoirsKr5FzvH9Wt4zgzTOjuutX9+zzPPEN319w+cBRO\n3zpVddFFcOSR/t+ThQtDRxMtFaRSWBYs8H9pdO0KnTtn7LLR9kGJchc55S9ueZO/W2+FZs3g+ONh\n+fLQ0URJBakUjhUr4KSToHlzuPba0NGIiEi+MIPHH/en/Z1/vv8uFaIe0oRQD2mWpf+SmDoVXn8d\natYMHZGIiOSb+fNhr738DNwll4SOJqt0lr1IZfTpA6NH+y8VoyIikg3rrANDh8Iee8DWW/u9SqVc\nNGUv+e/FF/0qyNdeg7p1s/IWedMHVYCUu7gpf3HLy/xtuSW8/DKccQaMHx86mmioIJX8NmECnHWW\n/8thiy1CRyMiIoVgt938VlBHHAE//hg6miiohzQh1EOaBb/8Aq1b+9WPJ54YOhoRESk0t94KAwf6\ndrG11godTUbpLPs8pYI0w5YtgwMOgLZt4ZZbQkcjIiKFyDm/wGn5cnj2Wb8aP09oY3yR8rjoIt8v\nevPNOXm7vOyDKhDKXdyUv7jlff7M4NFH/Q4vffqEjibRtMpe8s/DD8OoUTBmDFTTZy4REQmodm14\n6SVo0wZatYL99w8dUSJpyj4hNGWfIR98AEcf7b83aRI6GhEREe+99/zhLGPGQKNGoaOpMk3Zi5Tm\nf//zi5eefFLFqIiIJEuHDnDFFXDUUbBoUehoEkcFqeSHlSv9J8/OneHQQ3P+9nnfB5XHlLu4KX9x\nK7j8XXSRP776zDN1vGgxKkglP1x3nW8ev/HG0JGIiIiULL3IacIEeOKJ0NEkinpIE0I9pFXw6qtw\nzjkwbhxsuGHoaERERMo2ZQq0awdvvw0tW4aOplLUQypS1LRp0K0bPP+8ilEREYlDs2Zwzz1w/PEw\nf37oaBJBBanEa9kyOOEE6NnTb4AfUMH1QeUR5S5uyl/cCjp/p57q75KedZb6SVFBKjG7/npo0AB6\n9AgdiYiISMU98ABMmqR+UtRDmhjqIa2gd9+F006D//5XU/UiIhKvdD/piBGwww6hoyk39ZCK/Por\ndOoE/furGBURkbg1awa33QYnnwxLl4aOJhgVpBIX5+CMM/wG+B07ho7mDwXdBxU55S5uyl/clL+U\nrl2hcWO45prQkQSjs+wlLo88AjNmwAsvhI5EREQkM8zg8cf9WfcHHwz77hs6opxTD2lCqIe0HKZM\ngb328ufUb7tt6GhEREQya9gwPws4YQLUrx86mjJluodUBWlCqCBdjRUr/NZOnTrBeeeFjkZERCQ7\nLroIfvoJBgzwd04TSouapDDddResvbY/kSmB1AcVL+Uubspf3JS/Etx2G0yeDM89FzqSnFIPqSTf\npEnQpw+MHQvV9BlKRETyWO3a8NRTcOihsN9+sNFGoSPKCU3ZJ4Sm7EuxfDm0aQPnnuv7akRERArB\nlVfC1KkwaFAip+41ZS+F5ZZb/KfDbt1CRyIiIpI7118PX34JAweGjiQnVJBKcn3+OfTt67fCSOCn\nw6LUBxUv5S5uyl/clL8yrLkmPPkkXHgh/PJL6GiyTgWpJNPKlXDmmdC7N2y+eehoREREcm/33eHU\nU+GCC0JHknXqIU0I9ZAW07ev3/Ji5EgtZBIRkcK1eDG0bAl33glHHBE6mj9oH9I8pYK0iBkzYKed\nYPRo2G670NGIiIiE9e67cPrp8MUXfgvEBNCiJslvzsH55/uviIpR9UHFS7mLm/IXN+WvnPbdF/be\nG268MXQkWaOCVJLlpZf8NhdXXhk6EhERkeTo0wf+9S+/4DcPaco+ITRlD8yf7++KPvcctGsXOhoR\nEZFkeewxv2n+++8HX1+hKXvAzFqa2WNmNtnMJpjZJDO7z8w2KDZuLTPra2ZTUmPeNLPtS7heDTO7\nycy+NLPPzex9M2tbyntfbGZfmNlnZjbWzErsMDazU1JjPktdU7u6r87NN/tpCRWjIiIif5c+IOaJ\nJ8LGkQVRFqTAAGA9YGfnXEvgAKAj8L6ZrVFk3CCgBdDSObcj8Akwwsw2KXa9vsBxQFvnXAugP/CW\nmbUoOsjMrgCuAg51zrUCrgAGmtmBxcadCPQDuqXGnQLca2bdM/B7z09ffQX9+sHtt4eOpFLUBxUv\n5S5uyl/clL8KqlYNHnkErrkm7/YmjbUgXQVc7pxbAuCc+wm4E2gKHAJgZgcABwLXOueWpn7uJqA6\nvqgkNW4boDtwq3Nubup6/YBpQO8i4+oC1wAPOuemp8a9DbwF3FVknAF3AM8558alxk0EngJuMbOa\nGfxzyA/OwUUX+b7RTYp/VhAREZE/tGgBJ50E110XOpKMirUgbeGcm1bsuVmA4e+cAhwDLAM+SA9w\nzi1PPT6myM8dnfo+otj13gU6mlmd1OODgdqljNs+VdgCtAY2L2VcfaBD6b+tAjVkCPzwgz+NIlLt\n27cPHYJUknIXN+UvbspfJV1/Pbz4Yl4tcIqyIHXOrSjh6W3xd05Hph43B2aVMHYasFGRftPmqZ/7\noYRxNYDti4xLP198HPjWgPR3V8o4KzJOwG/4e/HFcP/9UFM3j0VERFarfn1flF58sZ9lzANRFqTF\nmVk1oCvwhHPu29TTGwDzSxg+L/V9/SLjFpWwxL2kcZRwzXn4QrM844peT8BvY7HzzrD//qEjqRL1\nQcVLuYub8hc35a8KzjzT95G+9FLoSDKiRugAMuQ6/PR8j9CBSAX8/DPccw98+mnoSEREROJSowbc\ne69feX/IIbDmmqEjqpLoC1IzOx04FtjHObe4yEu/AiWtkFk39X1OkXF17O8bgZY0DmAd4P/KOa6s\n9/2bLl260LBhQwDq1atHq1at/uivSX+KzKvHd99N+86doXHjZMRThcfp55ISjx6X/3H79u0TFY8e\nK3+F9Fj5q+Lj/fZjxGabwfnn0z61FVS23i/96+nTp5MNUW+Mb2anAZcB+znnfin22sPA6cDaRftI\nzWwIsKtzbtPU457ALUAj59wPRcbdD5wFrOecW2RmJwDPAh2cc6OKjLsEv8J/O+fcVDNrA4wBujjn\n/l1k3NHAQOBg59xbJfxeCmtj/C+/9MegffWV74URERGRivvmG9h9d//vaoMGOXtbbYyfYmanUqwY\nNbNDi+z1+SJQE9izyM/UBNri9ydNSzdftC/2Fh2AYc65RanHbwKLSxi3LzDZOTc19fgTYGYp4+YC\nI8rz+8t7PXv6rzwpRot+gpS4KHdxU/7ipvxlQJMmcPLJcNNNoSOpkigLUjM7BXgMv7dnx9SpSKcA\nh5GapnfODQeGATeZWe3Uj14DrABuTV8rVUg+BlxpZuunrn860Bi4usi43/H7mJ5nZo1S4/bHb8p/\naZFxDl8on2hmO6fGNQc6A1c655Zl9A8jRiNHwsSJcP75oSMRERGJ37XXwrPP+rulkYpyyt7M5gD1\nSnn5Rudcr9S4OsDt+FOcVuDvXF7snPuy2PWqA9cDx+MXR80HLnPOfVjCe1+In8pfDqwEbnDODS1h\n3En4k5wcvvC/L7Xhfmm/p8KYsncO2rSBHj38xr4iIiJSdQ88AI0awT/+kZO3y/SUfZQFaT4qmIL0\n5Zfhxhth3Dh/BJqIiIhERz2kEq9Vq/y0Qq9eeVeMqg8qXspd3JS/uCl/kpZfVYEk28CBUKdOzqYT\nREREJA6ask+IvJ+yX7ECdtzRHxHasWPoaERERKQKNGUvcXr2Wb8/2gEHhI5EREREEkYFqWTf8uV+\nIdPNN4Nl7MNUoqgPKl7KXdyUv7gpf5KmglSy77nnYKutYJ99QkciIiIiCaQe0oTI2x7SVatghx2g\nb1/Yb7/Q0YiIiEgGqIdU4vLyy7DOOrDvvqEjERERkYRSQSrZ4xzceitcdVXe9o6mqQ8qXspd3JS/\nuCl/kqaCVLLn7bdh0SI4/PDQkYiIiEiCqYc0IfKyh7RDB+jWDU49NXQkIiIikkHqIZU4fPwxTJ8O\nJ54YOhIRERFJOBWkkh333gsXXQQ1aoSOJCfUBxUv5S5uyl/clD9JU0EqmTdzJgwbBl27ho5ERERE\nIqAe0oTIqx7SK66AJUv8XVIRERHJO5nuIVVBmhB5U5AuXAgNG/oe0saNQ0cjIiIiWaBFTZJs//kP\n7LVXwRWj6oOKl3IXN+UvbsqfpBXGihPJjVWr4L774JFHQkciIiIiEdGUfULkxZT9O+9Ajx4wYULe\nn8wkIiJSyDRlL8n16KNw1lkqRkVERKRCVJBKZvz8MwwfXrCnMqkPKl7KXdyUv7gpf5KmglQy48kn\n4ZhjoG7d0JGIiIhIZNRDmhBR95CuWgVNmsCAAbDbbqGjERERkSxTD6kkz/DhUK8e7Lpr6EhEREQk\nQipIpeoef7zgFzOpDypeyl3clL+4KX+SpoJUqmbuXH+H9MQTQ0ciIiIikVIPaUJE20P68MMwciQ8\n/3zoSERERCRH1EMqyfLvf0OnTqGjEBERkYipIJXKmzoVpk2Djh1DRxKc+qDipdzFTfmLm/InaSpI\npfL+8x84+WSoUSN0JCIiIhIx9ZAmRHQ9pKtWQePG8PLL0KpV6GhEREQkh9RDKskwZgystRa0bBk6\nEhEREYmcClKpnIED4fjjC3rv0aLUBxUv5S5uyl/clD9JU/OfVNyqVTBoELz1VuhIREREJA+ohzQh\nouoh/eADfzLTpEmhIxEREZEA1EMq4Q0cCMcdFzoKERERyRPlKkjNrImZXWtmb5nZdDNbYGbLzOw3\nM/vCzAaYWTczWyfbAUtg6el6FaR/oT6oeCl3cVP+4qb8SVqZBamZrW9mTwNTgBuBlsBvwARgDPAl\nUB04BHgcmGlmPbIasYQ1ZgzUqwfbbx86EhEREckTpfaQmtmmwGhgLnAn8LZzbm6pFzJrAhwH9ADe\ndM7pPMkKiKaHtGdPqFkTbr45dCQiIiISSKZ7SMsqSEcDQ5xzd1bogn7a/mVgqHPu3qqHWBiiKUi3\n3x7694c2bUJHIiIiIoHkZFGTma0FXF3RYhTAOTcf+Ad+Wl/yybffwty5sNtuoSNJHPVBxUu5i5vy\nFzflT9JK3IfUObcQGFXZizrnFgPvVfbnJaFefRUOPRSqaXMGERERyZyM7kNqZu865/bN2AULSBRT\n9gccAOeeC0cdFToSERERCShnPaSlvHk1oDWwOVCnhCH3OefWy1BsBSXxBem8ebD55jBrFqy9duho\nREREJKBgG+Ob2c7Ad8AHwAvAUyV8rZupwCRhhg+HPfdUMVoK9UHFS7mLm/IXN+VP0ipylv3DwCz8\nfqQzgWXFXjdgcIbikqQZPhwOPDB0FCIiIpKHyj1lb2b/B2yeWvBU2pgHnHMXZCq4QpL4KfsmTeCl\nl6B589CRiIiISGAhz7KfBCxfzZgKbxMlEZg2DRYsgB13DB2JiIiI5KGKFKQXAbeaWVmLlj6qYjyS\nRO+8A/vvD5axD0J5R31Q8VLu4qb8xU35k7Ry95A658abWWtghplNB34FVhUbVj+DsUlSvP02HHRQ\n6ChEREQkT1Wkh7QncCt+MdMc/r6oCXyPac3MhVc4EttDumoVbLQRjB8PW2wROhoRERFJgEz3kFZk\nlf2FwCXAg865EntJzeynjEQlyTFpEqy3nopRERERyZqK9JBWd87dW1oxmnJcVQOShHn/fdh779BR\nJJ76oOKl3MVN+Yub8idpFSlI3zWzbVYzZo+qBCMJ9P770LZt6ChEREQkj1Wkh7QV0Bt4FfiUkhc1\nfeqc2yijERaIxPaQbrmlX2XftGnoSERERCQhgp1lb2bp4rPMH3DOVa9qUIUokQXpDz/ArrvCzz9r\nyycRERH5Q8hFTQuBu8p43fCLniRffPAB7LWXitFyGDFiBO3btw8dhlSCchc35S9uyp+kVaQgXeCc\nu7GsAWZ2ahXjkST54AP1j4qIiEjWVWTKvrZzbvFqxhzmnBuakcgKTCKn7HfZBfr2hT20Vk1ERET+\nFLKH9F3n3L6rGTPLObdpRiIrMIkrSJcu9fuPzpkDtWuHjkZEREQSJNMFaUW2fdqxtBfMbG0zewzQ\nCvt8MXEiNGmiYrSctJdevJS7uCl/cVP+JK0iBekGZvZE8SfN7ABgEnAGq1mBLxEZN85P2YuIiIhk\nWUWm7H8GhgErnXOnm9k6wD3A6cD/gHOAh51zm2Qr2HyWuCn7M8+EFi3g/PNDRyIiIiIJE3LK/p9A\nZx+DDQW+ALoCzwM7OOdeRkeH5o+xY/0epCIiIiJZVu6C1Dn3n9QtvNOBX4BNgWOdc6c45+amhu2Q\nhRgl15YuhSlToGXL0JFEQ31Q8VLu4qb8xU35k7SK3CEFwHldgSeBY83+smv69RmLTMKZPBkaNdKC\nJhEREcmJUntIzWxleX6eYguZdHRo5SSqh/Tpp2HoUBgwIHQkIiIikkC5PDp0KVCRisRQD2l++OIL\n2EHdFyIiIpIbZRWkvzvnTq/IxczswCrGI0nwxRfQuXPoKKKi85jjpdzFTfmLm/InaWX1kO5Tiett\nX9lAJEEmT9YdUhEREcmZcu9DKtmVmB7SRYtg/fVh/nyoUdYNdBERESlUOdmH1MzWMbNPzWybylzU\nzM40s8erFpoEMWUKNG2qYlRERERypsSC1Dk3H7gNGGFm3c2sXNWJmW1sZg8A1wDXZi5MyZmvvoJm\nzUJHER3tpRcv5S5uyl/clD9JK7XQdM4NNrPqwGPALWY2GpgCzAYWAiuAmsB6wOZAS2B34CugvXNu\ndpZjl2z49lvYeuvQUYiIiEgBWW0PqZltBFwCnABsWcqwVcBYoB/Q3zm3IpNBFoLE9JCefjq0bQtn\nnBE6EhEREUmoXO5DCoBz7megJ9DTzLYAtgHWB2oBi4BZwJfOud8zFZQE9O230KlT6ChERESkgFTo\n6FDn3Azn3DvOuRecc0875150zn2kYjSPaMq+UtQHFS/lLm7KX9yUP0mr8Fn2kscWL4Y5c2CzzUJH\nIiIiIgVE+5AmRCJ6SCdPhqOO8ivtRUREREqRk31IpUB9/z00bBg6ChERESkwKkjlTz/+qOn6SlIf\nVLyUu7gpf3FT/iRNBan8adYsFaQiIiKSc+ohTYhE9JCedRa0agXnnBM2DhEREUm04D2kZtbKzK4w\ns7tTj7cws50yFZAEpCl7ERERCaDcBamZVTOz/sA44BYgfZTPZsAnZvYfM6uZhRglV1SQVpr6oOKl\n3MVN+Yub8idpFblDeilwDHAX/hjRxQDOuY+ArfDHivbIdICSQ7Nmwaabho5CRERECky5e0jNbBLw\nT+fcm6nHs5xzmxZ5fUvgdefcjlmJNM8F7yFduRLWWAOWLIEaqz1RVkRERApYyB7SjdPFaEmccz8A\n9aoekgTx22+wzjoqRkVERCTnKlKQOjNbt7QXzWxjoHrVQ5Ig5s6F9dcPHUW01AcVL+Uubspf3JS/\nZDro6YOwG+0vX9lWkYL0XeDJkopSM9sC+BfwTqYCkxybM0cFqYiISIGzG41h3w4r8fmsvm8Fekib\nAh/j74KOBXYHhuFX2e8M/Aa0ds5Ny06o+S14D+lrr8GDD8Lrr4eLQURERIK5/f07uOKdngC8ubvj\nwAP9/aoN+v5ZjLrrfa0SrIfUOfc10Bb4FGgP1AaOBHbF3z3dU8VoxObOhfr1Q0chIiIigaSL0Y8P\n9sUo+MnTZVf9ecNs5aqVWXnvCm2M75z70jm3P7Ah/g7p7kAD59yBqYJVYqUp+ypRH1S8lLu4KX9x\nU/6So/XDe/tfvNKP1q3/+lrNmnDu3EUA1LgpO4ufK3WWvXNujnPuk9TX3EwHJQHMmwd164aOQkRE\nRAL49H+jAXDju5b4+oP31c7q+1fkpKaWZvZi6qtlkec3NbPRZrZfdkKUnFi4ENZaK3QU0Wrfvn3o\nEKSSlLu4KX9xU/6SYcmKJeUat8OHHwPQ98MnMh5DRe6QnovvHf0EmFHk+bnAKGCQmXXMXGiSUwsX\nQp06oaMQERGRHKvd29/9HH/4qjLHTRrm5/IvGN494zFUpCBtCxzmnLut6DS9c26Jc+5q4HjgukwH\nKDmiO6RVoj6oeCl3cVP+4qb8JctOO2V/v9HSVKQgre+c+6C0F51zw4FGVQ9Jgli0SAWpiIiIlG12\ni6xctiIFaXUzW6O0F81sTUDnTsZKU/ZVoj6oeCl3cVP+4qb8JciPu5Zr2NAjx2Tl7StSkH4MYcHd\niQAAIABJREFU3GNmfzse1MxqAHemxghgZg3M7Gkzm2JmX5rZQDPbLHRcpdKUvYiISMF56uPBALx5\nwqhyjf/Hgdm5eVWRgvRGoAvwvZn9y8xuNbM+ZvYsMAvoBtyQ+RDjY2Y1gbeBmsB2wPbAQuA9M0vm\nbchly6BWrdBRREt9UPFS7uKm/MVN+Qvv9DePBeDA/bK7rdPqlHuK3Tk3zswOAR4DTiv28tfAsc65\n8ZkMLmJdgB2Bw9PngZpZT+BH4BygT7jQSrFyJVT/281vERERkawr91n2f/yAmQE7AU1ST30NfBb2\nIPZkMbM3gGbOuUbFnv8cWOCc27OEnwn7R9i6NfTty9+OZxAREZG8ZTf6lfXpM+rL/TM3kNGz7Cu8\nCClVNY1Pff2FmW3nnPsyE4FFrgXwVQnPTwP2zXEs5bNyJVSr1MFdIiIiIlWS6QrknQxfL1YbAPNL\neH4eUKes3QqCWbVKU/ZVoD6oeCl3cVP+4qb8SVqF7pCa2RHAkcCm+AU7xdXPRFASgO6QioiISDns\nNhM+zfA1y12QmtnFwN3ACuAXYFkJw3SLzfsVWKeE59cFFjnnlpb0Q126dKFhw4YA1KtXj1atWv2x\nR1v6U2TWHs+fD+PH075ly9y8X549Tj+XlHj0uPyP27dvn6h49Fj5K6THyl/4x0zjL0obn/719OnT\nmT2SjCv3oiYz+wZ4ArjbOVdSMYqZ/eSc2ySD8UUptahpW+dc42LPJ3dRU/Pm8Mwz0CI7JzCIiIhI\n8lRmUdOxxxuDB2Z2UVO1CoytmzrHvsRiNOWkqgaUJ14EtjKzLdNPmNlG+D1JBwWLqiw1a8Ly5aGj\niFbRT5ASF+Uubspf3JS/ONVYlflrVqQgnWRm62fwevnsKWAicLuZVTezasBtwHfAIyEDK1WtWipI\nRUREZLVCF6QXAA+ZWfMyxjxdxXjygnNuOXAAsBKYDHwBrA3s65xbFDK2UukOaZX80Ysj0VHu4qb8\nxU35i1M2CtKKrLIfgi+qjjWzxfiFO8VDapCpwGLnnPsFODV0HOVWs6Y/PlREREQKx+wWsPHnFfqR\n0HdIN8Pf6RuFX+0/Dfi+yNcP+DuCEiNN2VeJ+qDipdzFTfmLm/IX3gNthgHwwfRPyv0zNQPfIZ3r\nnOtQ1gAz+6mK8UgomrIXEREpOOd32ZgLboS9/tWmXCvtX5z0OrWzUC5U5A5peaafD6xsIBJY7dqw\nKJntrTFQH1S8lLu4KX9xU/7ic8zgQ1k7Cx1+5S5InXPlORZ0tyrEIiGtuy7ML+m0UxEREZE/BS1I\ny+mmDF9PcmWddVSQVoH6oOKl3MVN+Yub8pcQH1wGwNQ5U8s1PHhBambHmtknZrbQzFYW/wI2ynyI\nkhPrrgvz5oWOQkRERHJs/ot3ALBt323LHLfJ7Q0B2G3JcRmPodwFqZkdC7yAX0k/CFgK/Dv1NRIw\n4OWMRyi5oTukVaI+qHgpd3FT/uKm/CXD2muXb9zsJd8DsFvTFRmPoSJ3SC8DLnXO7eGc6wz85pw7\nPfW1L3AGoFX2sVpnHd0hFRERKVBbvjoJ+PNs++IuG3aF/8WUI2DBgoy/f0UK0m2A+4o8Lh5xf2Cv\nKkckYWjKvkrUBxUv5S5uyl/clL/k+P7THf74dfFeUuccd310OwBLnnoZ/u//Mv7+FSlIFzrnim6F\nusTMit7krQ5slZmwJOfWWy8r/4GJiIhIHC763W8wum3fbZkwewIAi5cvplqvVLn4+MessQbwyy8Z\nf29zbvWboAKY2cfA3c65AanHbwHjnXNXpB73Bo5xzjXLeJQFwMxceXORFePGQffuMH58uBhEREQk\nKNt0HJy1699fGH0l7u1b/K/XXhtbuBDnXMnz+5VQkZOaXgGeMbMOzrmzgYeBwWZ2LuDw59z3zFRg\nkmMNGsD//hc6ChEREQnIzdqFzTd3/Ni9SK158yLc8tr+14sXZ+Vkx4pM2d8HtATuAHDOvQRcCHwL\nfAlcDvTJdICSIw0a+FvwIe/SRkx9UPFS7uKm/MVN+UummTPBXe/+/EoXowBz5sAGG2T8Pct9h9Q5\ntxD4othzfYG+ZrZW6nWJVe3aUKuWX9hUt27oaERERCSJfv3VF6SzZmX0shXZh/ShMl6+zcx+MbND\nMhCThLLhhllpVC4E2ksvXspd3JS/uCl/Efrll6zcIa3IlP2RZbzWC7gETdnHTX2kIiIiUpaffoJN\nNsn4ZTNylr1z7hfgaaB+Jq4ngWyyScZvwRcK9UHFS7mLm/IXN+UvQjNnwhZbZPyyZfaQmtmTRR7W\nNbN+/H1D/PR1tgVUzcRsyy1hxozQUYiIiEhSzZgBO+6Y8cuWuQ+pmRXdCN9RcjEKsAi/0v5C59yY\nzIVXOILvQwrQp4//5HPPPWHjEBERkWQ67DA44wzsyCNztw+pc+6PKX0z+8k5l/mmAUmOLbaAMfo8\nISIiIqWYORM23zzjl61ID+mVGX93SRZN2Vea+qDipdzFTfmLm/IXoSz1kJa7IHXOPVXS82ZWy8zW\ny1hEEs4WW8APP4SOQkRERJJo8WK/X3kWtn2qyFn2HYBrgR+cc11Sz10M3AbUBIYDxzrnFmQ8ygKQ\niB7SlSuhTh3/H9saa4SNRURERJJl8mQ46ij46ivMLKM9pBWZsu8KrAU8A2BmzfH7jv4A3A00Bq7I\nVGASQPXq/i7p9OmhIxEREZGk+eYbaNIkK5euSEG6O3C0c2546vGZwCrgYOfcZcBBwHEZjk9ybZtt\n4OuvQ0cRHfVBxUu5i5vyFzflLzJffw1Nm2bl0hUpSOs4534EMDMDjgKGOee+BXDOfQesnfkQJae2\n2QamTg0dhYiIiCRNQu6QLjWzdVO/3h/YFHgu/aKZ1QJWZjA2CaFpUxWklaDzmOOl3MVN+Yub8heZ\nhBSkbwIDzOw84GFgDjC4yOvXAJrrjZ2m7EVERKQkCZmyvxaoDTwANADOcM4tMbNqZjYfuBoYmIUY\nJZc0ZV8p6oOKl3IXN+UvbspfRJYuhZ9+8nuWZ0GZJzUV5ZybA7Q3s7rAIufc8tTzq8wsfajpj1mI\nUXJpiy3g119h4UJYa63Q0YiIiEgSTJkCW28NNWtm5fLl3oe0XBczO9U593TGLlhAErEPaVqrVvDE\nE7DrrqEjERERkSR45hkYMgQGDAAIug9pedyR4etJCC1awMSJoaMQERGRpJg4EXbccfXjKqnUgtTM\nrjez+4o8/m51X/jeUoldixbw+eeho4iK+qDipdzFTfmLm/IXkUmToHnzrF2+rB7Ss4B1zKync24J\nsBnwYRnjDb8VlMSuRQt4443QUYiIiEhSTJyY1YK01B5SM9sIWMM590Pq8U/OuU3KvFg5xkjJEtVD\nOnu2vy3/yy9gGWsPERERkRjNmwebbuq/V/OT6znrIXXO/ZwuRlPOKsf1yjNGkm6jjfx/cLNnh45E\nREREQps0Cbbf/o9iNBvKfWXn3JBMjJEImPlp+wkTQkcSDfVBxUu5i5vyFzflLxLjxsHOO2f1LcpV\nkJpZWzN7ysy+NrMFZjbfzKaa2ZNmtntWI5Qwdt4Zxo4NHYWIiIiE9umnWd8Kssx9SM2sJvAQ0BW/\naKkkDugHnOucW5HxCAtEonpIAQYNgn//2+85JiIiIoVru+3g+eehZcs/nsr1PqR9gW7AW8BxwFbA\nmkAdoDFwMjAKOCM1VvJF69bwySeQpCJZREREcmvePJgxA3bYIatvU9Y+pK3xheaZzrmDnXODnXMz\nnHPLnHNLnHPTnXPPO+c6ABcD3c1st6xGK7mzxRb++4wZYeOIhPqg4qXcxU35i5vyF4Fx4/yd0Rrl\nPm2+Usq6Q9odeNw598TqLuKcux/oD5yZqcAkMDNo08bfJRUREZHC9OmnsFv27zeWtQ/pZOA459wX\n5bqQWXPgBefcdhmMr2AkrocUoHdv+P13uEMnwoqIiBSkY4+Fo46CU075y9O57CFdv7zFKIBzbiKw\nQdVDksRo3Ro+/jh0FCIiIhKCc/D++9C2bdbfqqyCdFUlrqdV9vmkTRsYPx6WLg0dSeKpDypeyl3c\nlL+4KX8J9803ULMmbLVV1t+qrIK0MvPHCZtzlipZd11o1sz3j4iIiEhhGT0a2rXLyTHiZfWQrqIS\nBaZzrnpVgypEiewhBbj0UqhfH66+OnQkIiIikktdusDuu8PZZ//tpUz3kJZVkC4FPqzItYDdnXNr\nZiKwQpPYgnTIEHjwQRg2LHQkIiIikktbb+3rgBL2IM1lQfqTc26TCl2sEj8jXmIL0rlzoWFDmDPH\n95FIiUaMGEH79u1DhyGVoNzFTfmLm/KXYLNmQfPm8MsvUO3vHZ65XGV/ZSWuV5mfkSSrXx8aNYL/\n/jd0JCIiIpIrI0f6/tESitFsKPMse8mdxN4hBbjwQthsM+jZM3QkIiIikgtdu8LOO8P555f4cq7P\nsheBAw6At94KHYWIiIjkgnMwfDh07Jizt1RBKqvXoYM/QnThwtCRJJb20ouXchc35S9uyl9CTZkC\n1atD06Y5e0sVpLJ6a68Nu+4K+otDREQk/w0f7mdHc7D/aFpZq+zXds4tyFkkBS7RPaQAt93mV9zd\nf3/oSERERCSb/vEP6NwZjjuu1CG53PZplnNu00y9kZQt8QXp+PFw0knw1VehIxEREZFsWbYMGjSA\nadP8TjulyOWipg3M7Eozq5WpN5OItWoFv/0G06eHjiSR1AcVL+Uubspf3JS/BHr/fX9seBnFaDaU\nVZAuAJoCk83smBzFI0lVrRoceCC8/nroSERERCRbhgyBww/P+duWNWU/2Dl3jJntDPTBF68XOucm\nlHoxsxucczdkJdI8l/gpe4BBg+Dxx3WMqIiISD5yDho39kVp8+ZlDs1ZD2kJb3wMcCswCrjKOfe/\nEsao77SSoihI58/3G+TPmAF164aORkRERDJp4kQ44gj49tvVrrAPtjG+c24w0BxoAnxnZn/7Ahpk\nKjBJoHXWgb33hjfeCB1J4qgPKl7KXdyUv7gpfwmTnq7P4XZPaeUuSM1sd2Ak0A5YA7ASviTfHXEE\nvPxy6ChEREQk0155JUj/KJTdQ/q0c+5UM9sCuB04AV90Dgd6OOcml/AzPznnNslmwPkqiil7gNmz\nYbvt/Pc11ggdjYiIiGTCrFmw447w889Qs+Zqh+dyyv4gM7sZmAKcCHwNHOacO7CkYjTloUwFJgm1\n8caw/fbw3nuhIxEREZFMeeklOOSQchWj2VBWQVofuBJYClwC7Oice62siznnbspgbJJURx/tV9zL\nH9QHFS/lLm7KX9yUvwQZMABOOCHY25dVkK4CHgaaOOfudc6tyFFMknTHH+8/SS1bFjoSERERqaqZ\nM2HSJOjYMVgIZfWQqh80h6LpIU3be2+4/HJ/3q2IiIjE65574PPPoX//cv9ILntI98rUm0geOvFE\neP750FGIiIhIVQWerocyClLn3Le5DEQic+yx8NprsGhR6EgSQX1Q8VLu4qb8xU35S4Dp0/1G+Pvt\nFzSMcu9DKvIXG24IrVv7olRERETi9MILcNRRwVbXp5X76FDJruh6SMH3mgwZ4hc4iYiISFyc82fW\nP/gg7LNPhX402Fn2kl1RFqTz5sGWW8I338AGG4SORkRERCpi7FjfO/r111CtYpPmwc6yF/mbddeF\nww6DZ54JHUlw6oOKl3IXN+UvbspfYE89BZ07V7gYzYbwEUjcTj8dnnzS3/YXERGROCxd6nfL6dQp\ndCSApuwTI8ope4BVq2DrrWHwYNh559DRiIiISHkMGgQPPwzvvFOpH9eUvSRLtWrQpUuFNtMVERGR\nwPr39/9+J4QKUqm6zp3huef87f8CpT6oeCl3cVP+4qb8BfLjj/Dhh3D00aEj+YMKUqm6hg2hVSt4\n8cXQkYiIiMjqPP44nHQSrLVW6Ej+oB7ShIi2hzRt8GC4914YPTp0JCIiIlKa5cv9jaQ33/R7kFaS\nekglmY44AqZNg88/Dx2JiIiIlGboUGjUqErFaDaoIJXMqFEDzjwTHnoodCRBqA8qXspd3JS/uCl/\nATz8MJxzTugo/kYFqWRO9+4wYAD8/nvoSERERKS4qVNhwgQ49tjQkfyNekgTIvoe0rQTToB27eD8\n80NHIiIiIkVdcgnUrAm3317lS+ks+zyVNwXpyJFw9tkweTJYxv47FRERkaqYP98vZho71veQVpEW\nNUmy7b03rLGGX71XQNQHFS/lLm7KX9yUvxx68knYd9+MFKPZoIJUMssMLr0U+vQJHYmIiIgArFzp\nt2a89NLQkZRKU/YJkTdT9gDLlkHjxvDqq37DfBEREQln0CC4+25/OlOGaMpekq9WLbjwQt0lFRER\nSYK770703VFQQSrZcuaZ8NprMHNm6EhyQn1Q8VLu4qb8xU35y4ExY2D2bDjyyNCRlEkFqWRHvXrQ\nqRPcf3/oSERERArXXXfBxRdD9eqhIymTekgTIq96SNOmT4dddoFvvoH11gsdjYiISGH54gu/sv67\n72CttTJ6afWQSjwaNoTDD9ddUhERkRBuvdXfHc1wMZoNKkglu666Cvr2hXnzQkeSVeqDipdyFzfl\nL27KXxZ98w0MGwbnnRc6knJRQSrZ1bQpdOwIDz4YOhIREZHCcdttvhhdd93QkZSLekgTIi97SNMm\nT4YOHbLSwyIiIiLF/PAD7LQTfP011K+flbdQD6nEZ/vt/ZGijzwSOhIREZH8d/vt0L171orRbFBB\nKrlxzTV+64lFi0JHkhXqg4qXchc35S9uyl8WfP89PP88XHJJ6EgqRAWp5EbLlrDXXvDAA6EjERER\nyV+9esE558CGG4aOpEKi6yE1s3rAGcAJwJr4onom0Ms590EJ408BLks9rAbc75x7ooRxHYGbUtes\nCfwbuL14Y6eZ7QL0Aeqnxr0KXOOcW1psXGPgPmDr1Pu+D/zTOfdbKb+v/O0hTZsyBdq18z0t9eqF\njkZERCS/fPWVv/mTg39n1UMKZwOXA52cc82BHYHJwEgz27/oQDM7EegHdHPOtQJOAe41s+7Fxu0F\nDAVuds61BDoCFwA3FxvXFHgXGOScawG0AQ4Eniw2rj4wEpjinNseaA5slXqPwtWsmd+X9M47Q0ci\nIiKSf667zp9ZH+FNnxgLUgc84pz7EiB1W/EKYCW+iATAzAy4A3jOOTcuNXYi8BRwi5nVLHLN24Ex\nzrmhqXEzgXuAS81s4yLjbgDmOOf6psbNA3oBJ6XunKZdCtQDrk+NWw5cCbQ1s2My8GcQr+uv94ub\nZs8OHUlGqQ8qXspd3JS/uCl/GfTf/8Lo0XDBBasfm0AxFqR3kCr00lLT5f8HFD2fsjWwOTCi2M+/\ni59u7wCQKjj3AN4rYVwt4PDUuOqpX48sYRxA0ULzaGCsc+6PFTzOubHAvGLjCs+WW8Jpp0Hv3qEj\nERERyR/XXgtXXhnt9orRFaQupehzqb7SDfhrUdkCfzd1WrFLTAMs9Tr46XRKGUeRcY2BtYqPc87N\nBeanx5nZGkDTEq4H8H2R6xWuq66CZ5+FaSX9EcWpffv2oUOQSlLu4qb8xU35y5BRo2DSJDjzzNCR\nVFp0BWkpugM/A/cWeW6D1Pf5xcamz7Bcv8g4V85xJV0vPTY9rj7+z3V14wrXhhvChRf6T3IiIiJS\neatW+S2ebrsN1lgjdDSVFrwgNbP9zGxVOb7eLeXnd8AvcjrROfd/uY1eKu2f/4QPPoAPPwwdSUao\nDypeyl3clL+4KX8Z8PTTULMmnHBC6EiqpEboAIAPgGblGPe3HdXNbEtgCHCGc250sZd/TX1fp9jz\n6UNd5xQZZ+UcV9L10mPT4+bi77iubtzfdOnShYYNGwJQr149WrVq9cd0Rvp/2rx5/OmncOqptO/R\nA8aMYcSoUcmKr4KPP/vss0TFo8d6rMd6rMcF8HjhQkZceilcfz3tzbL6fulfT58+nWyIbh/SNDPb\nAhgOXOmce6mE19sAY4Auzrl/F3n+aGAgcLBz7q3UoqZZwA3OuV5Fxu0MjAXOds49llrU9Bsw0DnX\ntci4+vhi9Tbn3FWp574EfnLO7Vsspt+A151zJ5cQb/7vQ1rcqlXQpg306AEn/+2PRERERMrSqxd8\n8QUMGJDzt9Y+pPxRjL5FsWLUzF4pMuwT/Ib57Yv9+L74u5gjAJxzs/GFa0njlpHaO9Q5txJ/N3af\nEsY5YHCR514EdjOz2kVi2xV/h3RQuX6ThaBaNbj7brjiirw9UlRERCQrZs2C++7zvaN5ILqC1Mw2\nx6+mnwjUMbNTUl+n8ueK+fT+pJcBJ6budmJmzYHO+EJ2WZHLXg7saWb/KPIeFwN3Oed+KjLuemB9\nMzsvNa4ucA1F9jpN6YO/m3pjatwaQG/gfefcixn6o8gP7dr5u6R33x06kiopOqUhcVHu4qb8xU35\nq4Krr4Zu3aBRo9CRZEQSekgrqgfQKPVVfE/P6UUfOOcGmFk1oL+ZOXwBfrFzrl+xcR+Y2WFAbzO7\nGb//6APOuduLjfvGzPYF7jazc/B/fkPwRWnRcXPNbB/8qVCTU+87ij+PMJWi7rgDdtsNOnXy+5SK\niIhI6T74AN56C778MnQkGRNtD2m+Kcge0qJ69YLPPoMXdQNZRESkVCtWwK67Qs+ecNJJwcJQD6nk\np8svh4kT4Y03QkciIiKSXA8/DPXrw4knho4ko1SQSjKsuSY88IA/g3fJktDRVJj6oOKl3MVN+Yub\n8ldBs2f7GcW+fcEydnMyEVSQSnIcdBC0bAm33776sSIiIoXm8svh9NNh++1DR5Jx6iFNiILvIU2b\nMQN22gk+/hi23jp0NCIiIskwahSccopfyLT22qGjUQ+p5LkttvCN2mefDSrQRUREfCtb9+5w//2J\nKEazQQWpJE+PHjB3Ljz1VOhIyk19UPFS7uKm/MVN+SunXr2geXM46qjQkWRNjPuQSr6rUQP69YOO\nHeHgg2HjjUNHJCIiEsZnn8ETT8Dnn4eOJKvUQ5oQ6iEtwdVXw1dfwSCdtioiIgVoxQp/muF550HX\nrqGj+Qv1kErhuPZamDRJm+WLiEhhuuceWG89v7I+z6kgleRac00/TXHBBfB//xc6mjKpDypeyl3c\nlL+4KX9l+OYbvw3iY4/l3Z6jJVFBKsm2115w9NG+KBURESkEK1dCp05+prBx49DR5IR6SBNCPaRl\nWLTI7016881w3HGhoxEREcmuW2+Ft9+G4cOhWjLvHWa6h1QFaUKoIF2NTz6Bww7zqw032SR0NCIi\nItnx2WdwwAEwbhxsuWXoaEqlRU1SmFq39pvld+uWyA3z1QcVL+Uubspf3JS/YpYsgdNOgz59El2M\nZoMKUonHNdfAL7/Ao4+GjkRERCTzrrsOttnGF6UFRlP2CaEp+3KaMgXatYMPP4SmTUNHIyIikhmj\nRsGJJ8KECdCgQehoVktT9lLYmjXznyBPOQWWLQsdjYiISNXNmQOnnuq3OoygGM0GFaQSn/PP98eJ\nXnVV6Ej+oD6oeCl3cVP+4qb84ddFdO3qd5E55JDQ0QSjs+wlPmbQv7/fCqpDBzj00NARiYiIVE7f\nvvDjjzBwYOhIglIPaUKoh7QSRo/2nyjHjYPNNgsdjYiISMX897/QsSOMGQNNmoSOpkLUQyqS1q6d\nn74/5RR/qoWIiEgs5s+HE06A+++PrhjNBhWkErcrr4Tq1eGmm4KGoT6oeCl3cVP+4law+XMOzj3X\n31g56aTQ0SSCekglbtWrw9NPwy67wJ57+qkPERGRJHvkEb+905gxoSNJDPWQJoR6SKto5Eg/9fHR\nR9CwYehoRERESvbRR3D44X4/7Yin6tVDKlKSffaBnj3hmGNg8eLQ0YiIiPzd//7nF+M+8UTUxWg2\nqCCV/HHxxf70pnPPzfl59wXbB5UHlLu4KX9xK6j8rVjhT2Lq3NnfIZW/UEEq+cMM+vWDsWN13r2I\niCTL1VdDjRpw442hI0kk9ZAmhHpIM+jrr6FtW3jlFdhjj9DRiIhIoRs4EC67zN8w2WCD0NFkhHpI\nRVanaVN/p/S442DmzNDRiIhIIRs3zreSvfxy3hSj2aCCVPLTYYfBBRf4Pp2FC7P+dgXVB5VnlLu4\nKX9xy/v8zZoFRx7p28hatQodTaKpIJX8dfnl0KIFdOoEq1aFjkZERArJ4sW+GD3rLDj66NDRJJ56\nSBNCPaRZsnQp7L8/7L039O4dOhoRESkEzsHJJ/vFts8847/nmUz3kOqkJslva6wBL74IbdpAs2Zw\n2mmhIxIRkXzXuzd8+60/tCUPi9Fs0JS95L8GDWDoULj0Uvjgg6y8Rd73QeUx5S5uyl/c8jJ/zz4L\njz3mFzHVrh06mmioIJXCsMMO8O9/+5OcvvoqdDQiIpKP3nvPH9Ly+uuw6aaho4mKekgTQj2kOdK/\nP9x0k79TuskmoaMREZF8MXEi7LcfDBgAHTqEjibr1EMqUhWnnw4//giHHOJ7e9ZdN3REIiISu5kz\n4dBD4d57C6IYzQZN2Uvhufpqv8jpmGNg2bKMXDIv+6AKhHIXN+UvbnmRv99/9zc5zj/fr6yXSlFB\nKoXHDPr2hTp1oGtX7VEqIiKVs2SJ32N077390aBSaeohTQj1kAawaJHfo3TPPeHOO7U1h4iIlN+K\nFf6I6po14bnnoHr10BHllM6yF8mUOnX8dlDDhmnTfBERKb9Vq6BbN3+H9OmnC64YzQYVpFLY1l8f\n3noL/vUv34xeSXnRB1WglLu4KX9xizJ/zvmtnb77DgYPhlq1QkeUF7TKXmSTTeDtt30P0Drr+E+9\nIiIiJbn+enj/fb/naJ06oaPJG+ohTQj1kCbA1Kl+u46774YTTggdjYiIJM3dd8Ojj8Lo0bDhhqGj\nCUr7kIpkyzbbwJtvwgEH+E+9hx0WOiIREUmKBx7wXyNHFnwxmg3qIRUpqnlzGDLET9u//nq5fyzK\nPigBlLvYKX9xiyZ/Dz7o746+9x5suWXoaPKSClKR4lq39kVply7w6quhoxERkZAeesg1YpsKAAAg\nAElEQVRvDfjee9CwYeho8pZ6SBNCPaQJ9Mknftr+iSc0fS8iUogefhhuuw1GjIBGjUJHkyjah1Qk\nV1q39ndIu3Xzd0xFRKRwPPqoL0bfe0/FaA6oIBUpy267+V7S7t3h5ZdLHRZNH5T8jXIXN+UvbonN\n3wMPwC23wLvvQuPGoaMpCFplL7I6u+7qi9JDDoFly+D440NHJCIi2XLLLfDkk341vXpGc0Y9pAmh\nHtIITJgABx8MN97o75iKiEj+cA6uusofKT18uD80RUqlfUhFQmnZ0n9iPuAA+P13+Oc/Q0ckIiKZ\nsGoVXHghfPSRX8C0wQahIyo46iEVqYimTf2Rcf36wdVX+0/UJLgPSlZLuYub8he3RORvxQro2tXP\ngr3zjorRQFSQilTU5pvDqFH+VKfzz/efrEVEJD6LF8Nxx8GsWf7v9Lp1Q0dUsNRDmhDqIY3Q77/D\n4YfDZpvBU09BrVqhIxIRkfKaO9f/Hb7VVtC/v/4OryDtQyqSFHXr+k/UixfDQQfBb7+FjkhERMrj\nhx9gr71g993hP/9RMZoAKkhFqqJ2bRg0iBF160K7djBjRuiIpIIS0cMmlab8xS1I/j7/HNq29bul\n3HUXVFMplATKgkhVVa/uV2d27gx77un/shMRkeQZMQL2398Xoj16hI5GilAPaUKohzRPDBgAF1wA\nzz0H++0XOhoREUn7z3/g0kv939MdOoSOJnqZ7iFVQZoQKkjzyKhRftXm7bdDly6hoxERKWyrVsF1\n18Gzz/pN73fYIXREeUGLmkQS6C99UHvv7aeFbr4ZLrsMVq4MFZaUg3oQ46b8xS3r+Vu0CE44wf+d\n/PHHKkYTTAWpSDZst53/y2/8eL+tyLx5oSMSESksP/0E++zjF5++8w40aBA6IimDpuwTQlP2eWr5\ncrjoIn/k6NCh0Lhx6IhERPLff/8LRxwBZ58NV14JlrGZZUnRlL1ITGrWhIcegvPO8yvwNb0oIpJd\nzz4LHTtCnz5w1VUqRiOhglQkA1bbB3XuufDMM76X6cEHQXfDE0M9iHFT/uKW0fytWOFX0V97rZ+i\nP+64zF1bsq5G6ABECsZ++8GHH8Ixx8BHH8Gjj0KdOqGjEhGJ3y+/+A/8tWrBp59C/fqhI5IKUg9p\nQqiHtIAsWuT7miZMgMGDoUmT0BGJiMRr7Fj/Qf/UU6FXL39YiWSdekhFYlenDvzrX3DWWb6vdMiQ\n0BGJiMTHOXjySTj4YLjnHujdW8VoxFSQimRAhfugzHxf6ZAhfsHT1Vdrv9JA1IMYN+UvbpXO34IF\n/rjmPn38LiZHH53RuCT3VJCKhLT77jBuHIwZ489XnjUrdEQiIsk2aRLsthvUqAGffALbbx86IskA\n9ZAmhHpIC9zKlXDLLX4Ffr9+cOihoSMSEUmW9BT9FVfAXXf5O6QSjM6yz1MqSAWA0aPhlFP8diW3\n3upXjIqIFLoFC+Ccc/yG9y+8oLuiCaBFTSIJlLE+tnbt/F+4334LbdvCN99k5rpSKvUgxk35i1u5\n8vfpp7Dzzv4Duqbo85YKUpGkWX99eOklPx21xx7w9NPaSF9ECs+KFXDzzfCPf/jv/fpp7+Y8pin7\nhNCUvZTos8/83nrbbQcPPwwbbBA6IhGR7PvuOzjtNKhdG556CjbfPHREUoym7EUKSatWftPnrbaC\nFi3gtddCRyQikj3O+X2a27SBY4+Ft95SMVogVJCKZEBW+9jWXNOvKH3uOb9n6Zln+gZ/yQj1IMZN\n+YvbX/L3v//5BZ133eXPou/RA6qpTCkUyrRILPbZBz7/3PdVtWwJ778fOiIRkapzDp5/3s8CNW7s\nFzG1aBE6Kskx9ZAmhHpIpUJeecVvgXLssX7/0rXXDh2RiEjFzZ7tT62bMgX69/dT9RIF9ZCKCBxx\nhD+tZN482HFHGDYsdEQiIuXnHDzzjJ/tadYMxo9XMVrgVJCKZECQPrb69f3q00cfhbPPhi5dYO7c\n3McROfUgxk35i9DMmf5D9W23MaJXLz/Ls+aaoaOSwFSQisTuwANh4kSoW9ffLR00SPuWikjyrFgB\n997rdw/ZaScYNw623TZ0VJIQ6iFNCPWQSkaMGQPduvmFAfff77+LiIQ2diycdRasuy488ogK0Tyg\nHlIRKd0ee/jN9Nu1g9at4aabYMmS0FGJSKGaNw8uvNCftnTRRfDuuypGpUQqSEUyIFF9bLVqQc+e\nfjps/Hho3txvLi0lSlTupMKUv4RyDl54wZ87v3AhfPEFdOoE9tcbasqfpNUIHYCIZMlWW8FLL/nT\nnc4+G3bZBe65R6eeiEh2ff65vys6d64/0KNdu9ARSQTUQ5oQ6iGVrFq8GG69FR580E+b/fOfUKdO\n6KhEJJ/8+itcdx0MHgw33ADdu0MN3ffKV+ohFZGKq10bevXyCwsmTfL7/j37rFbji0jVrVgBDzzg\np+erV4cvv/QHd6gYlQpQQSqSAdH0QTVq5Pu6nnkG7r4b9twTPvoodFRBRZM7KZHyF5Bz8Oabfhun\nl1/2C5YeeMDvkVxOyp+kqSAVKUTt2sEnn/je0mOPhVNOge+/Dx2ViMRi/Hg44ADfAnTTTfD2234f\nZJFKUg9pQqiHVIJZsADuuMP3l3bqBFddBQ0ahI5KRJJo2jS45hp47z3fL9qtG9SsGToqCUA9pCKS\nWWuv7ftLv/gCli+H7bbzj+fPDx2ZiCTFnDlwySWw666wzTYwdaqfYVExKhmiglQkA/KiD2rjjaFv\nXz+VP3UqNG3qT3taujR0ZFmVF7krYMpflv3+O9x4o9/MfskS/8H1+uv9B9kMUP4kTQWpiPxV48bw\n9NMwbJj/atYM+vXzd09FpDDMnw+9e0OTJvDdd37x40MP+Q+uIlmgHtKEUA+pJNb77/s7JN984/tL\nO3f2p0GJSP5ZsMD3k/fp4xctXXedjvqUEqmHVERya6+9YPhwf9d04EA/lf/II3k/lS9SUBYsgLvu\n8ndEx4+HESP89nAqRiVHVJCKZEBB9EG1bQtvvQXPPw+vvOIL04ce8qdARawgcpfHlL8qmjPH94Q2\nauT7x4cPhwED/Cb3OaD8SVr0BamZnWFmq8zsutCxiBSEPfaAN97wd0vfeMP/Q9a7tz+3WkTiMHMm\n9OjhP1jOmgUffugPzWjePHRkUqCiLkjNbC2gF1Bq86WZnWJmn6W+PjezM0oZ19HMPjazCWY22cyu\nMLO/9UaY2S5mNiJ1rS/N7E4zW6OEcY3NbGjqWlPM7Akzq1eV368kV/v27UOHkHtt2sDQofDOO76/\ntEkT/w/cDz+EjqxCCjJ3eUT5q6CpU+GMM6BFC6hWDSZOhMcf94VpAMqfpEVdkAKXA2NLe9HMTgT6\nAd2cc62AU4B7zax7sXF7AUOBm51zLYGOwAXAzcXGNQXeBQY551oAbYADgSeLjasPjASmOOe2B5oD\nW6XeQyS/7LAD9O8Pn3/uz67eaSc47TT/WETCc85/cDzsMN8Tvvnm8PXXfuHSZpuFjk4EiLggNbPN\ngG7ADUBJdzINuAN4zjk3DsA5NxF4CrjFzIru5ns7MMY5NzQ1biZwD3CpmRXd4+IGYI5zrm9q3Dz8\nHdqTzGyXIuMuBeoB16fGLQeuBNqa2TFV+o1LIqkPCv+P3J13wrff+iMEDzoI9t3Xn3G9cmXo6Eql\n3MVN+SvDkiXw5JPQsiVceCEcfjhMnw433ADrrx86OkD5kz9FW5ACvYH7gDmlvN4a2BwYUez5d4H6\nQAeAVMG5B/BeCeNqAYenxlVP/XpkCeMAihaaRwNjnXOL0k8458YC84qNE8k/9epBz57+H77u3eH2\n22HrrX2xqj5Tkez76Se/XdNWW8Hgwf5O6KRJ/v/HOnVCRydSoigLUjPbGWiHL0hL0wLfWzqt2PPT\n8HdUW6QeNy/yfPFxFBnXGFir+Djn3Fxgfnpcqp+0aQnXA/i+yPUkj6gPqgS1asFJJ8GYMTBokP8H\nceut/T+KCZrOV+7ipvylOAfvvgsnnOBXyP/6K4waBa+95vcT/fuSiERQ/iQtyoIUuAu4xjm3rIwx\nG6S+Fz+Qe17q+/pFxrn/b+/e4+2azv2Pfx5JRG6IxCXuKSckFSQu1VISrbgVPVr0HLcc+anU5ZSq\nuPwo7eGntKW/lxZF67SqjqP0FHUI0n1EiFtst0RCCWVHSCTkglz2c/54xkpWVta+ZO+191xz7e/7\n9RqvteZcY8455hp7r/WsMccYs5X5yu2vkLeQbxPifW0pn0jXseee8NvfwsyZ0Wpz2GHwpS9F39Ml\nS7IunUh+zZ8P11wTd1T77ndh//3j6sT112sOUcmVzANSM/tKmrappTQp5T8S6Ovud2RcdJFV1A+q\nlTbbDC6+OL4wL7gA7rkHttkGvvMdeO65TIqkusu3Lll/7nEHtRNPjKsO9fXRV/TFF+GMM2CjjbIu\nYat1yfqTsrpnXQBgCrBzK/ItTf04rwJOK1rf1HWIeemxX8n6DdPj/KJ81sp85fZXyFvI9yHR4tpS\nvrWMHTuW7bffHoCNN96Y3XfffdXljMI/rZarc7m+vr6qylP1y48/DhtuyKj77oN33qHuBz+Aww9n\n1JZbwqmnUrfNNtC3b/WUV8taroblHXaA226j7oYbYvmcc+DnP6fupZdg+XJGpcvyVVNeLdfUcuH5\n7Nmz6Qi5upe9mQ0DJgLvF63uCQwF3ktpqrufbmZfAJ4Exrr774r2cTRwF3Cou09Mg5oagMvc/UdF\n+UYSU0qNd/ebUjC8ELjL3U8pyrcJEaz+2N0vSutmAHPc/cCS8i8EHnD3fy5zbrqXvXRtK1fCI4/E\nnIgPPwxjxsAJJ8Chh0Z/VJGuaMkS+NOfosvLc8/BscfC2LExD3CV9guVrqFL38ve3ae7+9buPrKQ\ngMPSyzekdaen5aeBd4BRJbs5kGjFrEv7fI8IXMvlW0aaO9TdVwL3AgeUyefA3UXr7gH2MrNehRVm\ntifRQvrHdThlka6jWzc4+OAYADV7dgzE+OlPY57EM86AqVPjUqVIrVu5MgYojRsX06n94Q8xmf27\n78KNN8I++ygYlZqTq4C0CVbyCEBqbjwP+FZq7cTMhgMnAxeWDIiaAHzJzL6W8m0NnA381N3nFOW7\nFBhgZmekfBsBF1M012nyM6I19YcpX09imqrH3f2e9p+yVJviSxpSAf37w7e/DZMnx/21Bw2Ck0+G\nIUNiOpuXXqpYcKq6y7eaqb/GxugXetZZEYSee24MVHrlFXjggRg936tXy/vJmZqpP2m3XAekZvYM\ncD/RQjnezKYVgkoAd7+TmDz/VjOrB24Hznb3W4r34+5TgCOAH6R8E4Hr3P3iknyvEy2ix5jZy8BT\nKe8pJfk+JFpSdzaz6cALxJRPR1Ts5EW6isGDYyDUq6/C7bfHJcyvfQ2GDoVLLomBHGo5lTxyjx9c\n554bs0+MHx8D//7nf+D55+G882DLLbMupUinyFUf0lqmPqQi66DwRX7XXXGJv2dPOOYY+MY3YPfd\ndTlTqteKFdHy/+c/R1p//Wj9PO64uA2vSE5Uug+pAtIqoYBUpI3c4dlnIzi9+25YvjxaUI84AkaP\nhg02yLqE0tUtXgwPPRQB6F/+Eq3+Rx0Vafhw/YCSXOrSg5pEqpX6QWXIDPbaC66+Gl5/HR58MC5/\nXnEFbL45HH10TMD//vtlN1fd5VvV1t8bb8Tk9IcfHpfdf/WrGBlfXx8/oC65BHbdtcsHo1Vbf9Lp\nqmEeUhGRyjCL2yYOGwbnnx+3T3zgAbjvPjjnHNhxxxi9P2ZM3CmqZ8+sSyy1YvFiqKuLltAHH4RF\ni2LWiBNPjFHyOZqsXiQLumRfJXTJXqSDLVsGTz0FEyfGPKfTp8N++0WAetBB0X+vi7dWyTpYsQKm\nTVsdhD79dLTUH3wwHHKIWj+l5qkPaY1SQCrSyRYsiLkeJ06M9Mkn8OUvx73A998fdtkl5kYVgeib\nXAhA6+rgiSeia8gBB0SL++jR0Ldv1qUU6TQKSGuUAtJ8q6urW3WbNcmXVXX31lvw2GORJk+GuXNh\n331XB6l77KE7RlWhDvvf+/hjeOaZuCHD5Mnw5JMxGOmAA2DUqPi7GDiw8sftYvTZmV+VDkjVh1RE\nBKK168QTI0EEpJMnRzr9dJg1K0ZE77336rTjjrCexobmXmNjzHP75JMRgE6dCm++CSNGxF2RTjst\n5sAdMCDrkorULLWQVgm1kIpUucWL45Lt00+vTgsXRr/BvfeGkSNht93gc59TkFrNli+HGTNitPvz\nz0eqr4/Wzn32ifTFL0Yf0B49si6tSNXSJfsapYBUJIfmzo3Luk8/HYHNiy/C/PnR/3S33SKo2W23\naFnVKOvO5R71M2NGDGArBJ7Tp8O220br54gRcSOFESNg002zLrFIriggrVEKSPNN/aDyq+J1t3Bh\nBKaF9MIL8PLL0L8/7LQTDBkSj4W03XYaPNUOdY8+yqjBg+OS+4wZqwPQGTPifR06NFIh8Nx1V+jT\nJ+tiS6LPzvxSH1IRkWq28carR+oXNDbC22/DzJnRF3XmzLhjz8yZ8MEHsMMOcal/++0jQC1+HDCg\na08f5B6tzrNnx2TzhfTmm/H49tswaFAE98OGwZ57Rj/gYcPU6imSI2ohrRJqIRXpopYsgddei4Br\n9uwY7V94fOst+PTTCE632gq22KLp1L9/vvqufvZZBJrz5sXje+/Bu+9GamhY/XzOHOjdO4LzwYMj\ncC9O226rGxyIZECX7GuUAlIRKWvRoghMGxoiaCukOXPWfL5oEWy4YQSm/ftHS23hef/+MUdm797Q\nq1f5xx49IqDt1i0eS583NsaAoKbSJ5/EwK/Fi6MsheeFtGDBmgHosmXR+ltIW2wRQfdWW8WtNgvP\nBw2K8olIVVFAWqMUkOab+kHlV83U3YoV8NFHEfgtWBB9WQvPFyyIltilSyNwLPe4YgWsXBmBZ2Pj\n2s/XWy+C1qZSr17Qr18EvqWpT58IigcOXB2A9utXka4INVN/XZTqL7/Uh1RERNbWvfvqYE9EJGfU\nQlol1EIqIiIieVHpFtIc9YAXERERkVqkgFSkAurq6rIugrSR6i7fVH/5pvqTAgWkIiIiIpIp9SGt\nEupDKiIiInmhPqQiIiIiUlMUkIpUgPpB5ZfqLt9Uf/mm+pMCBaQiIiIikin1Ia0S6kMqIiIieaE+\npCIiIiJSUxSQilSA+kHll+ou31R/+ab6kwIFpCIiIiKSKfUhrRLqQyoiIiJ5oT6kIiIiIlJTFJCK\nVID6QeWX6i7fVH/5pvqTAgWkIiIiIpIp9SGtEupDKiIiInmhPqQiIiIiUlMUkIpUgPpB5ZfqLt9U\nf/mm+pMCBaQiIiIikin1Ia0S6kMqIiIieaE+pCIiIiJSUxSQilSA+kHll+ou31R/+ab6kwIFpCIi\nIiKSKfUhrRLqQyoiIiJ5oT6kIiIiIlJTFJCKVID6QeWX6i7fVH/5pvqTAgWkIiIiIpIp9SGtEupD\nKiIiInmhPqQiIiIiUlMUkIpUgPpB5ZfqLt9Uf/mm+pMCBaQiFVBfX591EaSNVHf5pvrLN9WfFCgg\nFamAhQsXZl0EaSPVXb6p/vJN9ScFCkhFREREJFMKSEUqYPbs2VkXQdpIdZdvqr98U/1JgaZ9qhJm\npooQERGR3KjktE8KSEVEREQkU7pkLyIiIiKZUkAqIiIiIplSQJohCxPM7FMzOynr8oiIdAVmtrOZ\nLTezSVmXRUSCAtKMmNk2wCTgOKBHG7YfY2ZPmdkLZjbdzC4ws4p1LpbmmdnZZvaKmdWb2bNmdtQ6\nbHtmqrcX0j7+w8x26MjyypraWX99zOxKM3subf+Wmd1rZtt3XImloD11V+Qn6PsvE22pPzPrbmb/\nZGaPpG1fMrNnzOzkzihzV2Nmm5rZ783sVTObYWZ3mdlWrdy2u5n9W9ruRTN73Mz2bdWB3V0pgwT8\nHDgeOABoBE5ah233Az4DjkjLWwPvAldkfV5dIQEXAO8D26flrwLLgINbse05wEpgTFreAHgE+BvQ\nJ+tz6wqpnfXXE5gKXA6sl9ZtB7wH7J/1udV6ak/dFe3jQKAemA1MyvqculJqa/0BX0ifm8cWrftG\n+u78YdbnVUuJaCB7AbgTsJT+HZgF9G7F9jcCrwKbpOVxwBJg1xa3zfrku2oq+jJrS0A6BagrWfd9\n4FNgi6zPrZYTsBGwGLi0ZP39wEut2P4p4PmSdV9PH7YHZX1+tZ4qUH8XAi+WWb8PMCDr86vl1N66\nS3kNmJYCoTcVkOaj/lJA+liZ9Y8BC7M+t1pKwKnp+2i7onWbAyuAc1vYdkja9uSS9S8D97V0bF2y\nyIi7N7ZlOzPbAvgi8NeSlyYB6wNHtrNo0rxDgV5AXcn6ScAwMxvSwvYrgO4l6wpdNrq1u3TSkvbW\n3zjgL6Ur3X2qu8+vSAmlKe2tO4CxwHvu/khliyat0Ob6c/engNFlXmoA+phZ6WeqtN3RwNvu/lZh\nhbvPBaYTrdItbQvl63iMmfVubmMFpPkzPD2+WbK+sLxrJ5alK2rv+38lsIOZHQ9gZgOB7wGvAI9W\nqpDSpDbXn5ltBnwO+MDMfmxm08xslpn9p5l9vgPKKmtq1/+emfUCLiOuJknna1f9ufvKMquHAE+4\n+4p2lk1W25W164i0bniZ9cWGE1d83y6zbXdgWHMbKyDNn4GAA4tK1n+cHgd0bnG6nIHpsdz7b7Tw\n/rv7/cRAtqvNbA7R9/fvwH7uvrzCZZW1taf+tkmPlwEfAXsBuxOt3k+2soVO2q5d/3vABOAhd59e\n6YJJq7S3/tZgZnsTAdBF7S+aFBnI2nUEUU+9zaxnC9su9XSdvmRbaKGOFZBWgJl9xcwaW5E0xUiV\n6ey6M7N/Be4ATnH3QcQ/aCPw32a2cSWO0ZV0cv1tkB7nuPuV7r7S3ZcCZxHdZc6vwDG6jM6sOzMb\nBIwHLm5/yQWy/d4zs77ALcD/dfcpld6/ZEP9LipjCrBzK/ItrcCx5hG/JvuVrN8wPaof27pZ17qb\nlx77AQuKXm/x/U8B51XAbe7+EIC7Lzaz8Wm/lwDntr7oQifWH6tbDV4oXunu883s70SLqbReZ9bd\nvwE3uPv761RCaU5n1t8qZrY+8EfgQXe/ujXbyDqZx9rxBUQ9LXX3z1rYtreZWUkraavqWAFpBbj7\np8SUCJ3hpfS4fcn6wenxxU4qR01oQ90V3t/tWbOfzGCiK0Vz7/8QYtqg10vKsNDM5gF7r0M5hE6v\nv9eJEaTlriw1tV6a0Ml1tx+wzMy+npYN2BIYYGbPA8vdXf9/66CT6w8AM+sB3A287O4T1uHY0nov\nAjuVWT+Y1fFHc9t+i+jeVFrHK4iBUU3SB2iVM7NeZlb4dYG7vwc8CYwqyXogMZ/bfZ1Xui7pQeAT\nyr//09191Qd0ad0R8+8BbFu8YRp5OIDVLQjScdpcf+ny/CRKOvabWT+iTp/uoDJLaE/d7ezuu7r7\nyJRGECO0n3X3EQpGO0V7PjuLg9FZ7v79ovU3mtnmHVbqruceYDszW/U9ld7foUTLNEXrNzNb44Y8\nf0qPo0r2OZrov938VeKs57zq6ilVXJPzkAIzgblAr6J1+xJzjn4tLW8NvANcnvX5dIVE9BWcCwxO\ny18lblQwphV1dy8xIGaPtNwNuIH49ah5SKu//vYkLkGekZYN+GWq0yFZn1utp/bUXZl9aR7SnNQf\nMTXefUQL3fFF6QSi1W3brM+tVlJ6r+uJsQ7diIbLW1Od9C7K96X0vfXLku1vAGaQ5mUG/oWYGH94\nS8fWJfuMmNl+wHVAH+JyxY/M7GwiqLynKGsD8Q+7aloLd59iZkcAV5jZ5cSAiuvc/apOO4EuzN2v\nMrNPgPvNbDlxufab7j6xJOtadQccS9yt6Tfph2UPYpT9ge7+WIcXXtpVf+7+rJmNAa5M/6/diEmf\n9/WiFh7pGO383wPAzG4gbmQwiLhkPw24190v69DCS3vq7xDgsPT8d6W77ajydkXuvtzMDgKuJYL9\nRuIz7kBfs4VzMbCQqKtiZwKXAlPMbBnR9/4gd2/pcj+WIlgRERERkUyoD6mIiIiIZEoBqYiIiIhk\nSgGpiIiIiGRKAamIiIiIZEoBqYiIiIhkSgGpiIiIiGRKAamIiIhIFTOzQWb2oJk1Zl2WjqKJ8UVE\npNOYWT93X5TRsfu4+5Isji3SVmZ2NPAzYDntuBGAmXUHjgHGETeGaCTu+vgLd/9tSd7ZwIeluyDu\nU/+Kux/Q1nI0RS2kIpJbZvaYmS00s0YzW25mDWb2j+m1IWY2x8wWmdnS9NpWzexrbMr/WdpfQ1qe\na2bTzexmMyt7z3Mz2zzlv7SjzrUWmNk3gEnpeaF+lprZyk4qwh5mNtnMtuyk44lUwnnEbVantHM/\newC/B25y98+7+3Dgx8CtZvbDkryN7j6yJI0APgBub2c5ylJAKiK55e77A7sQ90p24BB3/1N6bRaw\nLTAbONLdt3T3d5vZ17+7+yDgiVj0Ld19kLtvTrQqrASeNLNfmVmPks17Av2ATdpyHikA/k1bts0L\nMzuWuF3y8RD1k97vOzurDOn2vPcCk81sQGcdV6Sd9nX3v1VoX1Pc/T8LC+5+N/A48N2SfGeXbmhm\nXwa2Av5QobKsQQGpiOSau78D/JDognRjycsXAvXu/kg7j/GKu48HTgNOBa4vef1tYFN3L/1QF6IF\nGbgJuDT9UMiMu/+EuBT5/7Msh0hruXur+o2a2f7pCsAsM/ubmf3ezLYo2s9TwOgymzYAfdIl/ULe\ne8vkGwfc6e6L1/EUWkUBqYjUgmuBl4EvmNmpAGa2ExE8VixIdPdbgIeAU8xs35LXPq3UcWrQ94j+\nb7dmXZDkJ8C3zGzHrAsiUgnp8+hh4L/cfQgwBOgFPFp8Rcfdy3WPGQI84e4rmtn/hsSVotIf/RWj\ngFREci99yI5Pi1ea2abEB+dF7l7aMb+9biE69xcC3yOL+p6+UZzRzAaY2fVm9rAXnnwAAAfpSURB\nVIaZvWtmr5nZbWY2Or0+1szmEN0Njkv9UBvM7Pr0eh8zu8jMnjKzd8xsQXr+zZLjfKW4DGa2i5n9\n1cw+MLPXzWyty29puz3M7N7UT7bBzF5OXRJ2K8n3D2Z2Z9rfvJTvPDNr7XfIccDk5r7wio51YipP\no5m9b2aTzKxXUX/gRjPb3cz+YGbvpff1/LTtyNRCVHifRjZxmEeI779/amX5RardVUCDu/8MVn0m\nXgQMpZm/89QvfnjK25wTgJnu/lxliluGuyspKSnVRAJuJkaOzgQmtnEffwVWNvP6NukYr5XZ7o2S\ndXXAfwMbpuWtgKeASSX5GoFflznW54EVwHFpeT3gnJT/m02U/X2iX+aAtO6ClP+okryjgKVE94Oe\nad2+xOXse4ryDU3r/lh0HocAHwO3tuL9LLxf/6+J128tfr+JYP93wC1l8l6a9vUXYEhad3ZaN54Y\nibw+0IfoCzwbWK+J485t69+IklIWqfR/pWh9r/Q5cUfJegM+A37TxP76Ai8CE1px7OeA0zry/NRC\nKiK15HxgHrAj8OsOOsbc9DiouUxmthGwP3C/u38M4DGo6mLg7XKblFn3CRGY3Zm2b3T3a4mgdkIT\nhx4AXO7u89PyNcSX1deLymZEn84PgbPc/bO0/ynA1SX7uw7oBpxSdB4PAjcAJ5nZ7k2+CWFIenyv\nhXyFchW+dP9PE9mceE8LfVF/CSwDfkqc9zKPqZ1uJoLhsjMjAHOKyiaSZ5sQP1YPNLNphQRMI0bF\nr1+6gZmtT/zIfNDdS//nS/OOJP5XOmR0fYHmIRWRWvIx0UI4ELjMzO5x9+UVPkbhh3xL8wEuBRYB\n55jZLOARDw8Tfb1a5O5vsLorQrFZwDfLrAf4xN1fKtrHMjP7ACie6mgEEbTf5mv3KbuJaNUljUQf\nDdQVgtEizxJB9CFAfTOnURjN3pr5P39NtOwe0UK+ZwpP3H25mc0HFrj7gqI876Tybd3EPpYQ74FI\n3n1IXCW4r5kfcqukPqV3Ay+7e1M/bIuNA/7DO2gwU4FaSEWklkwgWgReIX7RX9ABxyiMWp3TXKYU\nCJ8EbEQMhPq7mV1nZsPX5WBm9o9mNtHM3kz9KBuIwQUbNLHJvDLrlgHFU1UVArGGMuX+0N1fSIs7\nEEHdPkX9WxtSGX4BLAY2a+EUCq0zzfYfNbObiPdrNzPr18I+S89xWRPrAHo3sY8VlGk5Eskbd/+E\n6KKyW+lrZnaumR1TtFwIRme5+/eL1t+YZsMo3X4D4J+BX3VE2YspIBWRmpBGTJ8DnEIMOHLgAjP7\nXIUPtU96fLyljO7+Z+Ky8YlEK+J4oL6pQUalzOxM4stjGjDcY17ULWl+7s51ubVgawOyhzzmZS1O\nm7v7hu7+vRa2XZoeS+duLWZEf7ZjiRbNa1vYZ7lzXNdbKq5fVDaRPCjXradgArCLmX17VWazUcQM\nF8+k5R7APcBgYJqZHZ/SCUT3op5l9nssMNvdn63MKTRNl+xFpFbcQPQhfBN4M41UP5PoY3hoBY9z\nGhHs3tRSRjNbz2M6qNuB281sB+Jy+I/N7Hp3X9b8HhgHLHb3Srf0vpYe1+oHm1pENnH3BuB14lzL\n3uHKzPYB3nX3vzdzrEIrbP9m8jhwvLu7md0B/IuZ3Zm6N3SU/kCTN0oQqRZmdjVwEPHjltQ/FGBv\nTzNXuPvUNHvHlWZ2IXHF4H3gMHefnfIfAhyWnv+u5DBNdUEaRye0joJaSEWkBpjZyUAfdy+e7PxC\nYvDQGIu7BFXiOP8KHECMiJ/aQt7tgI+K13ncbeXPRGthn6KXlpIaCMxs03Rpvw8xQrbcF8V2bT6J\nUE8EpV+1osmwk0tILbAeU2Y9Aow0s22KM1ncfnMy0V+3OTOI1sum+nKSjlU4z7OIL9Kbzaxvy6fS\nZlsRc9eKVDV3n+DuI9x9oLt389W38lxRkm+qu49298Huvpe7H17U/QZ3vy9tXy5197jBR+mxD3D3\nDpt7tJgCUhHJNTMbCFxOXKpfJY20/g5xmeuaVvRLXLXLMscYbma3EJeSbwJOb812QG8z+1Ea0Urq\nPnAU8HDJAJwZwE5plPkhwLdS+e8C+prZFWbW3cIpxJRNrSp7OSn4O5W4TH5tahXFzA5K53ZZUfYz\ngYXALZbu+mJm2wJ3EAMdnm/hWB8RA6DW6t9WrswpCP4OcdvXa5rL24Im86buHX2AieuwPxHpSB05\np5SSkpJSRyZibrwPgU+JS8OnFb12BjHwaAVxH/r5RADV1L7GpvyfpvwNafkDImC8GdirzHZHFm23\nPG13AtHiOR54lGipfZeYH/VyoG/JPr4IPE9MKTWDuMwGEVR9H3gVWEC0bP6C6FdaKOM4YNcyZTiQ\nCFznpHWF92ho0XFHEvd2n5vK9zgwpsw5DgZ+n/b1DtGyOAHo0cp6OjUdf4uidf3T/pYUnctpwH4l\n9dYAHEF0H/g4rZsLnFeUt/j8tiWmqpqf8i5g7XlfLyRar/tl/TespKQUydxbmrlERESk7VK3gOeA\nx9z9rIzL0g/4G3Clx5yuIlIFFJCKiEiHS90V6oiBZy0OCOugMvQC7icGYp2URRlEpDz1IRURkQ7n\nMcn/3sBeGRZjH2LycAWjIlVGLaQiIiIikim1kIqIiIhIphSQioiIiEimFJCKiIiISKYUkIqIiIhI\nphSQioiIiEimFJCKiIiISKYUkIqIiIhIpv4XBsKFMjht20kAAAAASUVORK5CYII=\n",
      "text/plain": [
       "<matplotlib.figure.Figure at 0x1090a9ac8>"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    }
   ],
   "source": [
    "x = numpy.linspace(t[0], t[-1], N)\n",
    "pyplot.figure(figsize = (10,10))\n",
    "pyplot.grid(True)\n",
    "pyplot.xlabel(r'X Distance (km)', fontsize = 18)\n",
    "pyplot.ylabel(r'Y Distance (km)', fontsize = 18)\n",
    "pyplot.title('Trajectory of Osc vs Perturbed Orbit, Flight Time = %.2f days' %(tfinal / dt), fontsize=14)\n",
    "pyplot.plot(r_n[:,0], r_n[:,1])\n",
    "pyplot.plot(r_osc_n[:,0], r_osc_n[:,1])\n",
    "pyplot.legend(['Perturbed Orbit', 'Osculating Orbit']);\n",
    "\n",
    "pyplot.figure(figsize = (10,10))\n",
    "pyplot.grid(True)\n",
    "pyplot.xlabel(r'X Distance (km)', fontsize = 18)\n",
    "pyplot.ylabel(r'Y Distance (km)', fontsize = 18)\n",
    "pyplot.title('Trajectory of Osc, Perturbed and Jupiter Orbit, Flight Time = %.2f days' %(tfinal / dt), fontsize=14)\n",
    "pyplot.plot(r_n[:,0], r_n[:,1])\n",
    "pyplot.plot(r_osc_n[:,0], r_osc_n[:,1])\n",
    "pyplot.plot(r3_n[:,0], r3_n[:,1])\n",
    "pyplot.legend(['Perturbed Orbit', 'Osculating Orbit', 'Jupiter\\'s Orbit']);"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Looking at our first plot we can see that there is a change in Mars' orbit due to the gravitational pull from Jupiter as it flies by!"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "<h3 align=\"center\">Dig Deeper</h3> "
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "See what happens when you change the orbital parameters! What happens with different planets or with a satellite orbiting earth?  What about when both planets don't start at the zero point of the y axis?"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "<h2 align=\"center\">References</h2> "
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "* [NASA Mars Fact Sheet](http://nssdc.gsfc.nasa.gov/planetary/factsheet/marsfact.html)\n",
    "\n",
    "* [NASA Jupiter Fact Sheet](http://nssdc.gsfc.nasa.gov/planetary/factsheet/jupiterfact.html)\n",
    "\n",
    "* [Standard Gravitational Parameter Wikipedia](https://en.wikipedia.org/wiki/Standard_gravitational_parameter)\n",
    "\n",
    "* [Perturbation (Astronomy)](http://tinyurl.com/gwz68sp)\n",
    "\n",
    "* Battin, Richard H., AIAA Education Series, _An Introduction to the Mathematics and Methods of Astrodynamics_, AIAA, 1999\n",
    "\n",
    "* Schaub, Hanspeter & John. L Junkins, AIAA Education Series, _Analytical Mechanics of Aerospace Systems_, AIAA, 2000\n",
    "\n",
    "* Tewari, Ashish, _Atmospheric and Space Flight Dynamics: Modeling and Simulation with MATLAB and Simulink_, Birkhauser, 2007"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 7,
   "metadata": {
    "collapsed": false
   },
   "outputs": [
    {
     "data": {
      "text/html": [
       "<link href='http://fonts.googleapis.com/css?family=Alegreya+Sans:100,300,400,500,700,800,900,100italic,300italic,400italic,500italic,700italic,800italic,900italic' rel='stylesheet' type='text/css'>\n",
       "<link href='http://fonts.googleapis.com/css?family=Arvo:400,700,400italic' rel='stylesheet' type='text/css'>\n",
       "<link href='http://fonts.googleapis.com/css?family=PT+Mono' rel='stylesheet' type='text/css'>\n",
       "<link href='http://fonts.googleapis.com/css?family=Shadows+Into+Light' rel='stylesheet' type='text/css'>\n",
       "<link href='http://fonts.googleapis.com/css?family=Nixie+One' rel='stylesheet' type='text/css'>\n",
       "<style>\n",
       "\n",
       "@font-face {\n",
       "    font-family: \"Computer Modern\";\n",
       "    src: url('http://mirrors.ctan.org/fonts/cm-unicode/fonts/otf/cmunss.otf');\n",
       "}\n",
       "\n",
       "#notebook_panel { /* main background */\n",
       "    background: rgb(245,245,245);\n",
       "}\n",
       "\n",
       "div.cell { /* set cell width */\n",
       "    width: 750px;\n",
       "}\n",
       "\n",
       "div #notebook { /* centre the content */\n",
       "    background: #fff; /* white background for content */\n",
       "    width: 1000px;\n",
       "    margin: auto;\n",
       "    padding-left: 0em;\n",
       "}\n",
       "\n",
       "#notebook li { /* More space between bullet points */\n",
       "    margin-top:0.8em;\n",
       "}\n",
       "\n",
       "/* draw border around running cells */\n",
       "div.cell.border-box-sizing.code_cell.running { \n",
       "    border: 1px solid #111;\n",
       "}\n",
       "\n",
       "/* Put a solid color box around each cell and its output, visually linking them*/\n",
       "div.cell.code_cell {\n",
       "    background-color: rgb(256,256,256); \n",
       "    border-radius: 0px; \n",
       "    padding: 0.5em;\n",
       "    margin-left:1em;\n",
       "    margin-top: 1em;\n",
       "}\n",
       "\n",
       "div.text_cell_render{\n",
       "    font-family: 'Alegreya Sans' sans-serif;\n",
       "    line-height: 140%;\n",
       "    font-size: 125%;\n",
       "    font-weight: 400;\n",
       "    width:600px;\n",
       "    margin-left:auto;\n",
       "    margin-right:auto;\n",
       "}\n",
       "\n",
       "\n",
       "/* Formatting for header cells */\n",
       ".text_cell_render h1 {\n",
       "    font-family: 'Nixie One', serif;\n",
       "    font-style:regular;\n",
       "    font-weight: 400;    \n",
       "    font-size: 45pt;\n",
       "    line-height: 100%;\n",
       "    color: rgb(0,51,102);\n",
       "    margin-bottom: 0.5em;\n",
       "    margin-top: 0.5em;\n",
       "    display: block;\n",
       "}\n",
       "\n",
       ".text_cell_render h2 {\n",
       "    font-family: 'Nixie One', serif;\n",
       "    font-weight: 400;\n",
       "    font-size: 30pt;\n",
       "    line-height: 100%;\n",
       "    color: rgb(0,51,102);\n",
       "    margin-bottom: 0.1em;\n",
       "    margin-top: 0.3em;\n",
       "    display: block;\n",
       "}\t\n",
       "\n",
       ".text_cell_render h3 {\n",
       "    font-family: 'Nixie One', serif;\n",
       "    margin-top:16px;\n",
       "    font-size: 22pt;\n",
       "    font-weight: 600;\n",
       "    margin-bottom: 3px;\n",
       "    font-style: regular;\n",
       "    color: rgb(102,102,0);\n",
       "}\n",
       "\n",
       ".text_cell_render h4 {    /*Use this for captions*/\n",
       "    font-family: 'Nixie One', serif;\n",
       "    font-size: 14pt;\n",
       "    text-align: center;\n",
       "    margin-top: 0em;\n",
       "    margin-bottom: 2em;\n",
       "    font-style: regular;\n",
       "}\n",
       "\n",
       ".text_cell_render h5 {  /*Use this for small titles*/\n",
       "    font-family: 'Nixie One', sans-serif;\n",
       "    font-weight: 400;\n",
       "    font-size: 16pt;\n",
       "    color: rgb(163,0,0);\n",
       "    font-style: italic;\n",
       "    margin-bottom: .1em;\n",
       "    margin-top: 0.8em;\n",
       "    display: block;\n",
       "}\n",
       "\n",
       ".text_cell_render h6 { /*use this for copyright note*/\n",
       "    font-family: 'PT Mono', sans-serif;\n",
       "    font-weight: 300;\n",
       "    font-size: 9pt;\n",
       "    line-height: 100%;\n",
       "    color: grey;\n",
       "    margin-bottom: 1px;\n",
       "    margin-top: 1px;\n",
       "}\n",
       "\n",
       ".CodeMirror{\n",
       "    font-family: \"PT Mono\";\n",
       "    font-size: 90%;\n",
       "}\n",
       "\n",
       "</style>\n",
       "<script>\n",
       "    MathJax.Hub.Config({\n",
       "                        TeX: {\n",
       "                           extensions: [\"AMSmath.js\"],\n",
       "                           equationNumbers: { autoNumber: \"AMS\", useLabelIds: true}\n",
       "                           },\n",
       "                tex2jax: {\n",
       "                    inlineMath: [ ['$','$'], [\"\\\\(\",\"\\\\)\"] ],\n",
       "                    displayMath: [ ['$$','$$'], [\"\\\\[\",\"\\\\]\"] ]\n",
       "                },\n",
       "                displayAlign: 'center', // Change this to 'center' to center equations.\n",
       "                \"HTML-CSS\": {\n",
       "                    styles: {'.MathJax_Display': {\"margin\": 4}}\n",
       "                }\n",
       "        });\n",
       "</script>\n"
      ],
      "text/plain": [
       "<IPython.core.display.HTML object>"
      ]
     },
     "execution_count": 7,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "from IPython.core.display import HTML\n",
    "css_file = '../numericalmoocstyle.css'\n",
    "HTML(open(css_file, \"r\").read())"
   ]
  }
 ],
 "metadata": {
  "kernelspec": {
   "display_name": "Python 3",
   "language": "python",
   "name": "python3"
  },
  "language_info": {
   "codemirror_mode": {
    "name": "ipython",
    "version": 3
   },
   "file_extension": ".py",
   "mimetype": "text/x-python",
   "name": "python",
   "nbconvert_exporter": "python",
   "pygments_lexer": "ipython3",
   "version": "3.4.3"
  }
 },
 "nbformat": 4,
 "nbformat_minor": 0
}