{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Three state Model"
]
},
{
"cell_type": "code",
"execution_count": 135,
"metadata": {},
"outputs": [],
"source": [
"import numpy as np\n",
"import pandas as pd\n",
"import matplotlib.pyplot as plt\n",
"import seaborn as sns\n",
"sns.set()\n",
"%matplotlib inline"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Master Equation of Three State Model"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"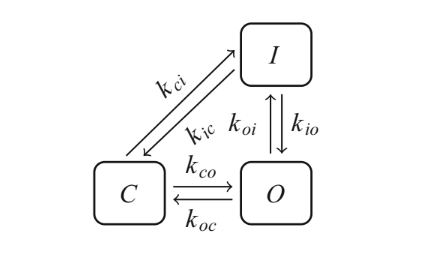"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For equilibrium condition, we get\n",
"\n",
"$k_{co} c = k_{oc} o => c = \\frac{k_{oc}}{k_{co}}o$\n",
"\n",
"$k_{oi} o = k_{io} i => i = \\frac{k_{oi}}{k_{io}}o$\n",
"\n",
"$k_{ic} i = k_{ci} c$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"$ o + c + i = 1$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Model Parameter"
]
},
{
"cell_type": "code",
"execution_count": 136,
"metadata": {},
"outputs": [],
"source": [
"k_oi,k_oc = 0.5,0.9\n",
"k_io,k_ic = 0.3,0.72\n",
"k_co,k_ci = 0.6,0.8\n",
"dt = 0.01"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 1. Monte Carlo Simulation"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"$P(O) = [1-(k_oc + k_oi)d\\tau, k_oc d\\tau, k_oi d\\tau]$,\n",
"\n",
"$P(C) = [k_co d\\tau, 1-(k_co + k_ci) d\\tau, k_ci d\\tau]$,\n",
"\n",
"$P(I) = [k_io d\\tau, k_ic d\\tau, 1 - (k_io + k_ic) d\\tau]$"
]
},
{
"cell_type": "code",
"execution_count": 137,
"metadata": {},
"outputs": [],
"source": [
"M = {\"O\": [1-(k_oc + k_oi)*dt, k_oc*dt, k_oi*dt],\n",
" \"C\": [k_co*dt, 1-(k_co + k_ci)*dt, k_ci*dt],\n",
" \"I\": [k_io*dt, k_ic*dt, 1 - (k_io + k_ic)*dt]}\n",
"\n",
"states = [\"O\",\"C\",\"I\"]"
]
},
{
"cell_type": "code",
"execution_count": 138,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"([0.986, 0.009000000000000001, 0.005],\n",
" [0.006, 0.986, 0.008],\n",
" [0.003, 0.0072, 0.9898])"
]
},
"execution_count": 138,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"M[\"O\"],M[\"C\"],M[\"I\"]"
]
},
{
"cell_type": "code",
"execution_count": 139,
"metadata": {},
"outputs": [],
"source": [
"current_state = \"O\"\n",
"T =1000\n",
"N =10000\n",
"\n",
"SS = [[\"O\" for n in range (T)] for t in range(N)]\n",
"\n",
"for n in range(N):\n",
" no,nc,ni =0,0,0\n",
" for t in range(T):\n",
" new_state = np.random.choice(states, p = M[current_state])\n",
" #print(new_state)\n",
" SS[n][t] = new_state\n",
" current_state = new_state "
]
},
{
"cell_type": "code",
"execution_count": 140,
"metadata": {},
"outputs": [],
"source": [
"ss = np.array(SS)"
]
},
{
"cell_type": "code",
"execution_count": 141,
"metadata": {},
"outputs": [],
"source": [
"Data = []\n",
"X = []\n",
"for t in range(T):\n",
" X.append(t)\n",
" o = list(ss[:,t]).count(\"O\")/float(N)\n",
" c = list(ss[:,t]).count(\"C\")/float(N)\n",
" i = list(ss[:,t]).count(\"I\")/float(N)\n",
" Data.append({\"O\":o,\"C\":c,\"I\":i})"
]
},
{
"cell_type": "code",
"execution_count": 142,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
"
\n",
" \n",
" \n",
" | \n",
" C | \n",
" I | \n",
" O | \n",
"
\n",
" \n",
" \n",
" \n",
" | 0 | \n",
" 0.3640 | \n",
" 0.3967 | \n",
" 0.2393 | \n",
"
\n",
" \n",
" | 1 | \n",
" 0.3650 | \n",
" 0.3958 | \n",
" 0.2392 | \n",
"
\n",
" \n",
" | 2 | \n",
" 0.3638 | \n",
" 0.3960 | \n",
" 0.2402 | \n",
"
\n",
" \n",
" | 3 | \n",
" 0.3635 | \n",
" 0.3962 | \n",
" 0.2403 | \n",
"
\n",
" \n",
" | 4 | \n",
" 0.3623 | \n",
" 0.3965 | \n",
" 0.2412 | \n",
"
\n",
" \n",
"
\n",
"