{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"[Sebastian Raschka](http://sebastianraschka.com), 2015\n",
"\n",
"https://github.com/rasbt/python-machine-learning-book"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Python Machine Learning Essentials - Code Examples"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
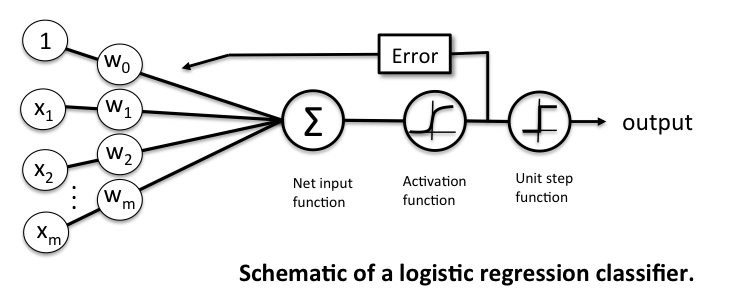
"# Bonus Material - A Simple Logistic Regression Implementation"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Note that the optional watermark extension is a small IPython notebook plugin that I developed to make the code reproducible. You can just skip the following line(s)."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Sebastian Raschka \n",
"Last updated: 12/22/2015 \n",
"\n",
"CPython 3.5.1\n",
"IPython 4.0.1\n",
"\n",
"numpy 1.10.2\n",
"pandas 0.17.1\n",
"matplotlib 1.5.0\n"
]
}
],
"source": [
"%load_ext watermark\n",
"%watermark -a 'Sebastian Raschka' -u -d -v -p numpy,pandas,matplotlib"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# to install watermark just uncomment the following line:\n",
"#%install_ext https://raw.githubusercontent.com/rasbt/watermark/master/watermark.py"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Overview"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Please see Chapter 3 for more details on logistic regression.\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Implementing logistic regression in Python"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The following implementation is similar to the Adaline implementation in [Chapter 2](../ch02/ch02.ipynb) except that we replace the sum of squared errors cost function with the logistic cost function\n",
"\n",
"$$J(\\mathbf{w}) = \\sum_{i=1}^{m} - y^{(i)} log \\bigg( \\phi\\big(z^{(i)}\\big) \\bigg) - \\big(1 - y^{(i)}\\big) log\\bigg(1-\\phi\\big(z^{(i)}\\big)\\bigg).$$"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"class LogisticRegression(object):\n",
" \"\"\"LogisticRegression classifier.\n",
"\n",
" Parameters\n",
" ------------\n",
" eta : float\n",
" Learning rate (between 0.0 and 1.0)\n",
" n_iter : int\n",
" Passes over the training dataset.\n",
"\n",
" Attributes\n",
" -----------\n",
" w_ : 1d-array\n",
" Weights after fitting.\n",
" cost_ : list\n",
" Cost in every epoch.\n",
"\n",
" \"\"\"\n",
" def __init__(self, eta=0.01, n_iter=50):\n",
" self.eta = eta\n",
" self.n_iter = n_iter\n",
"\n",
" def fit(self, X, y):\n",
" \"\"\" Fit training data.\n",
"\n",
" Parameters\n",
" ----------\n",
" X : {array-like}, shape = [n_samples, n_features]\n",
" Training vectors, where n_samples is the number of samples and\n",
" n_features is the number of features.\n",
" y : array-like, shape = [n_samples]\n",
" Target values.\n",
"\n",
" Returns\n",
" -------\n",
" self : object\n",
"\n",
" \"\"\"\n",
" self.w_ = np.zeros(1 + X.shape[1])\n",
" self.cost_ = [] \n",
" for i in range(self.n_iter):\n",
" y_val = self.activation(X)\n",
" errors = (y - y_val)\n",
" neg_grad = X.T.dot(errors)\n",
" self.w_[1:] += self.eta * neg_grad\n",
" self.w_[0] += self.eta * errors.sum()\n",
" self.cost_.append(self._logit_cost(y, self.activation(X)))\n",
" return self\n",
"\n",
" def _logit_cost(self, y, y_val):\n",
" logit = -y.dot(np.log(y_val)) - ((1 - y).dot(np.log(1 - y_val)))\n",
" return logit\n",
" \n",
" def _sigmoid(self, z):\n",
" return 1.0 / (1.0 + np.exp(-z))\n",
" \n",
" def net_input(self, X):\n",
" \"\"\"Calculate net input\"\"\"\n",
" return np.dot(X, self.w_[1:]) + self.w_[0]\n",
"\n",
" def activation(self, X):\n",
" \"\"\" Activate the logistic neuron\"\"\"\n",
" z = self.net_input(X)\n",
" return self._sigmoid(z)\n",
" \n",
" def predict_proba(self, X):\n",
" \"\"\"\n",
" Predict class probabilities for X.\n",
" \n",
" Parameters\n",
" ----------\n",
" X : {array-like, sparse matrix}, shape = [n_samples, n_features]\n",
" Training vectors, where n_samples is the number of samples and\n",
" n_features is the number of features.\n",
" \n",
" Returns\n",
" ----------\n",
" Class 1 probability : float\n",
" \n",
" \"\"\"\n",
" return activation(X)\n",
"\n",
" def predict(self, X):\n",
" \"\"\"\n",
" Predict class labels for X.\n",
" \n",
" Parameters\n",
" ----------\n",
" X : {array-like, sparse matrix}, shape = [n_samples, n_features]\n",
" Training vectors, where n_samples is the number of samples and\n",
" n_features is the number of features.\n",
" \n",
" Returns\n",
" ----------\n",
" class : int\n",
" Predicted class label.\n",
" \n",
" \"\"\"\n",
" # equivalent to np.where(self.activation(X) >= 0.5, 1, 0)\n",
" return np.where(self.net_input(X) >= 0.0, 1, 0)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Reading-in the Iris data"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"
\n",
" \n",
" \n",
" | \n",
" 0 | \n",
" 1 | \n",
" 2 | \n",
" 3 | \n",
" 4 | \n",
"
\n",
" \n",
" \n",
" \n",
" | 145 | \n",
" 6.7 | \n",
" 3.0 | \n",
" 5.2 | \n",
" 2.3 | \n",
" Iris-virginica | \n",
"
\n",
" \n",
" | 146 | \n",
" 6.3 | \n",
" 2.5 | \n",
" 5.0 | \n",
" 1.9 | \n",
" Iris-virginica | \n",
"
\n",
" \n",
" | 147 | \n",
" 6.5 | \n",
" 3.0 | \n",
" 5.2 | \n",
" 2.0 | \n",
" Iris-virginica | \n",
"
\n",
" \n",
" | 148 | \n",
" 6.2 | \n",
" 3.4 | \n",
" 5.4 | \n",
" 2.3 | \n",
" Iris-virginica | \n",
"
\n",
" \n",
" | 149 | \n",
" 5.9 | \n",
" 3.0 | \n",
" 5.1 | \n",
" 1.8 | \n",
" Iris-virginica | \n",
"
\n",
" \n",
"
\n",
"