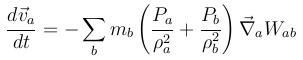
LIGGGHTS(R)-PUBLIC WWW Site - LIGGGHTS(R)-PUBLIC Documentation - LIGGGHTS(R)-PUBLIC Commands

pair_style sph/artVisc/tensCorr command

Syntax:

pair_style sph/artVisc/tensCorr kernelstyle args keyword values ...

sph/artVisc/tensCorr = name of this pair_style command
kernelstyle = cubicspline or wendland
args = list of arguments for a particular style

  cubicspline or wendland args = h
    h = smoothing length

zero or more keyword/value pairs may be appended to args
keyword = artVisc or tensCorr

  artVisc values = alpha beta eta
    alpha = free parameter to control shear viscosity
    beta = free parameter to control bulk viscosity
    eta = coefficient to avoid singularities
  tensCorr values = epsilon deltap
    epsilon = free parameter
    deltap = initial particle distribution

Examples:

pair_style sph/artVisc/tensCorr wendland 0.001 artVisc 1e-4 0 1e-8
pair_style sph/artVisc/tensCorr cubicspline 0.001 artVisc 1e-4 0 1e-8 tensCorr 0.2 1e-2

Description:

The sph/artVisc/tensCorr style uses the smoothed particle hydrodynamics (SPH) method according to Monaghan (1992). The acting force is calculated from the acceleration as stated in the equation:

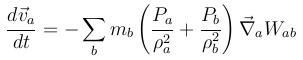
Whereas the indices a and b stand for particles, P_j stands for pressure and ρ_j for the density. W_ab represents the kernel, which is defined by the kernelstyle.

For kernelstyle cubicspline a piecewise defined, 3-order kernel is used:

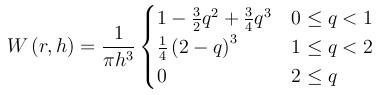
The wendland kernel (Wendland,1995) is defined as

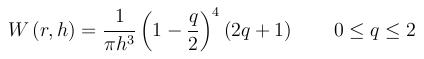
The smoothing length h is the most important parameter for SPH-calculations. It depends on initial particle spacing, initial density ρ₀ and mass per particle m_j. In case that the smoothing length is about 1.2 times the initial particle spacing and it is a 3-dimensional cubic lattice (therefore the summation is over 57 particles), you can use the following equation (Liu and Liu, 2003, p. 211-213):

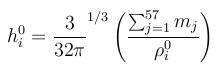
The atom style sph/var uses the input argument h as initial smoothing length for all particles. In case the atom style sph (per-type smoothing length) is used an additional per-type property sl must be defined, e.g.,

fix           m2 all property/global sl peratomtype 0.0012

For further details on the basics of the SPH-method we recommend the papers from Monaghan (1992), (1994), etc.

Optionally, this pairstyle can take into account the artificial viscosity proposed my Monaghan (1985), if the artVisc keyword is appended. In this case, Π_ab is added to the bracket term in the above acceleration equation, where Π_ab is given by

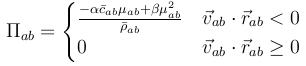
and

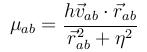
This expression produces a shear and bulk viscosity. The quadratic term enables simulation of high Mach number shocks. The parameter η² prevents singularities. A good choice is normally η²=0.01h².

The choice of α and β should not be critical, although there are some aspects which you should take into account:

"In the present case, with negligible changes in the density [weakly compressible SPH], the viscosity is almost entirely shear viscosity with a viscosity coefficient approximately αhc." (Monaghan, 1994)

Bar-parameters like c_ab and ρ_ab are mean values of particle a and b. NOTE: ρ_ab is calculated, and for the calculation of c_ab the per-type property speedOfSound has to be defined, e.g.,

fix 		      m1 all property/global speedOfSound peratomtype 20.

By appending the keyword tensCorr you enable the tensile correction algorithm (Monaghan, 2000) which improves results in combination with negative pressures (e.g. EOS like Tait's equation). This method adds R*(f_ab)ⁿ to the bracket term, where the factor R is related to the pressure and can be calculated by R=R_a + R_b. In case of negative pressures (P_a < 0) we use the rule

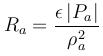
otherwise R_a is zero. Typical values of epsilon are about 0.2. fab is calculated by

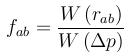
where Δp denotes the initial particle spacing. NOTE: In a next version this calculation should be improved too.

Mixing, shift, table, tail correction, restart, rRESPA info:

The pair_modify mix, shift, table, and tail options are not relevant for sph pair styles.

These pair styles write their information to binary restart files, so a pair_style command does not need to be specified in an input script that reads a restart file.

These pair styles can only be used via the pair keyword of the run_style respa command. They do not support the inner, middle, outer keywords.

Restrictions:

...

Related commands:

pair_coeff

Default: none

(Liu and Liu, 2003) "Smoothed Particle Hydrodynamics: A Meshfree Particle Method", G. R. Liu and M. B. Liu, World Scientific, p. 449 (2003).

(Monaghan, 1992) "Smoothed Particle Hydrodynamics", J. J. Monaghan, Annu. Rev. Astron. Astrophys., 30, p. 543-574 (1992).

(Monaghan, 1994) J. J. Monaghan, Journal of Computational Physics, 110, p. 399-406 (1994).

(Monaghan, 2000) J. J. Monaghan, Journal of Computational Physics, 159, p. 290-311 (2000).