In mathematics, it is often the case that the result of one function is evaluated by applying a second function. For example, consider the functions defined by and First, g is evaluated where and then the result is squared using the second function, f.
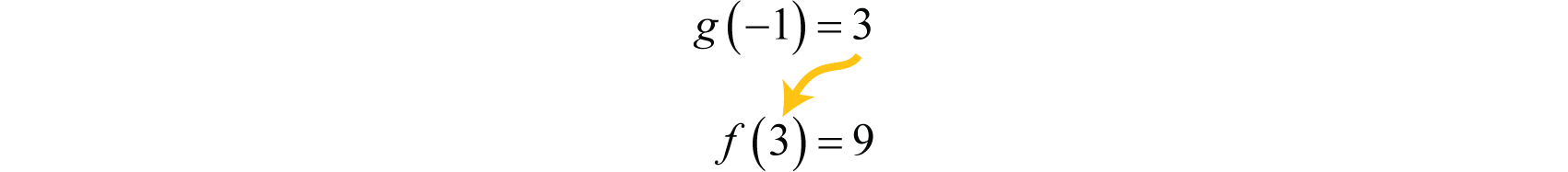
This sequential calculation results in 9. We can streamline this process by creating a new function defined by , which is explicitly obtained by substituting into
Therefore, and we can verify that when the result is 9.
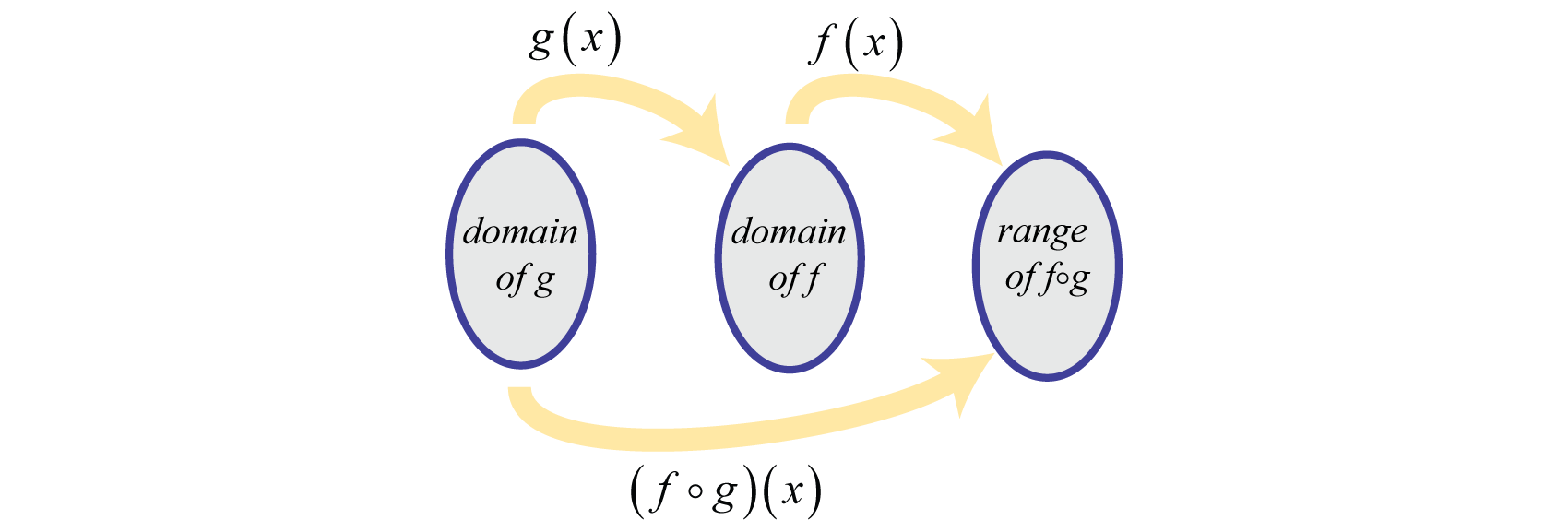
The calculation above describes composition of functionsApplying a function to the results of another function., which is indicated using the composition operatorThe open dot used to indicate the function composition (). If given functions f and g,
The notation is read, “f composed with g.” This operation is only defined for values, x, in the domain of g such that is in the domain of f.
Given and calculate:
Solution:
Substitute g into f.
Substitute f into g.
Answer:
The previous example shows that composition of functions is not necessarily commutative.
Given and find
Solution:
Begin by finding
Next, substitute 4 in for x.
Answer:
Functions can be composed with themselves.
Given find
Solution:
Answer:
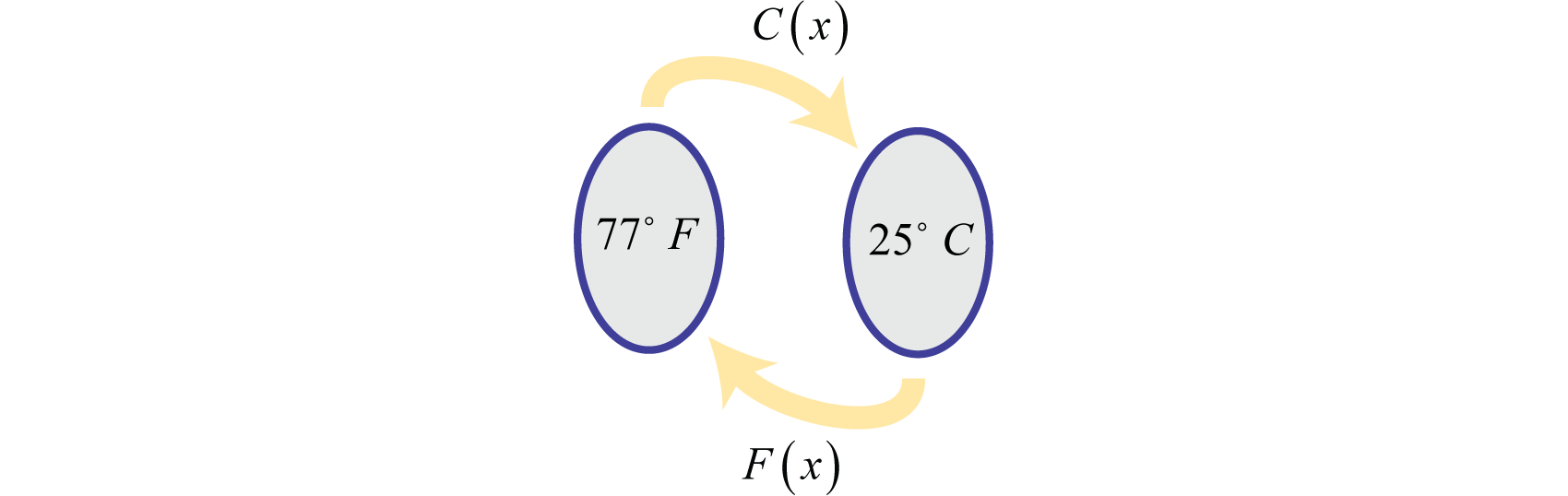
Consider the function that converts degrees Fahrenheit to degrees Celsius: We can use this function to convert 77°F to degrees Celsius as follows.
Therefore, 77°F is equivalent to 25°C. If we wish to convert 25°C back to degrees Fahrenheit we would use the formula:
Notice that the two functions and each reverse the effect of the other.
This describes an inverse relationship. In general, f and g are inverse functions if,
In this example,
Verify algebraically that the functions defined by and are inverses.
Solution:
Compose the functions both ways and verify that the result is x.
Answer: Both ; therefore, they are inverses.
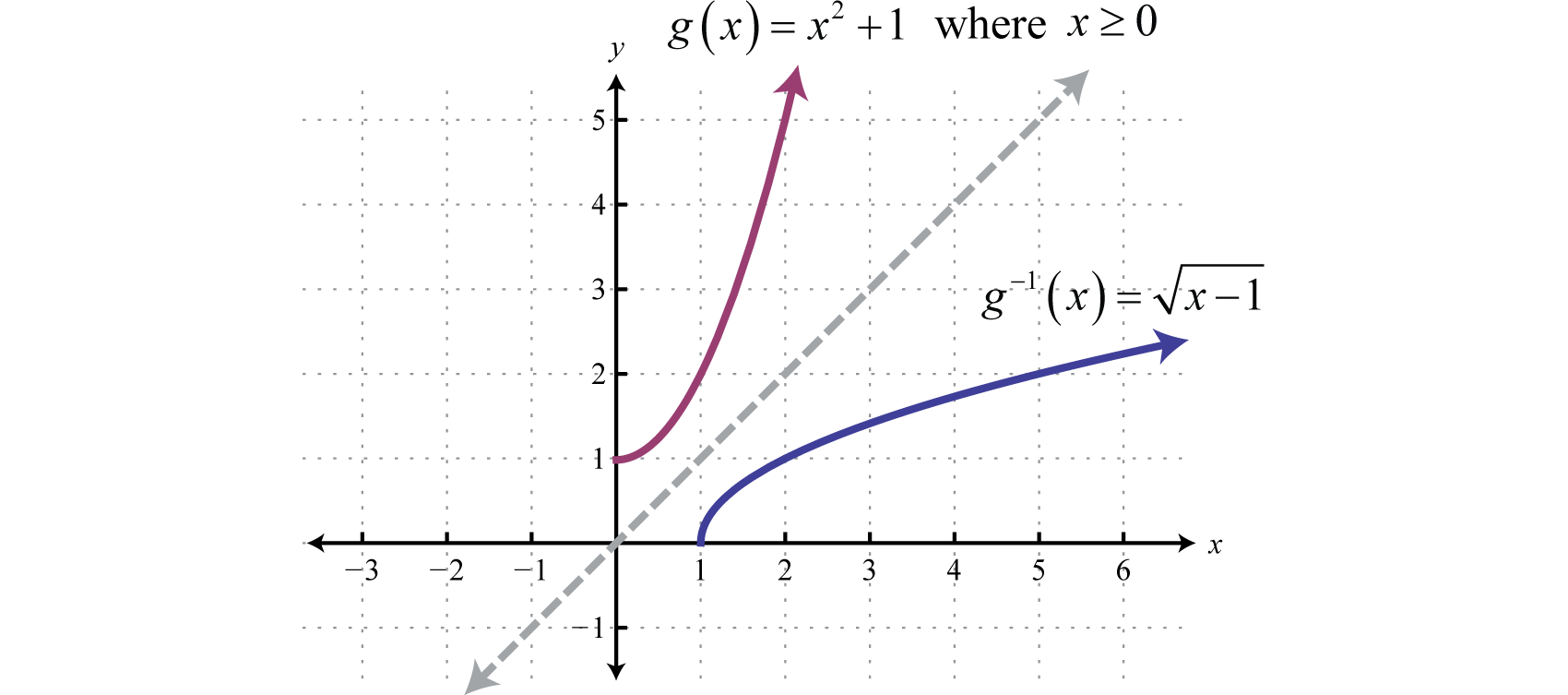
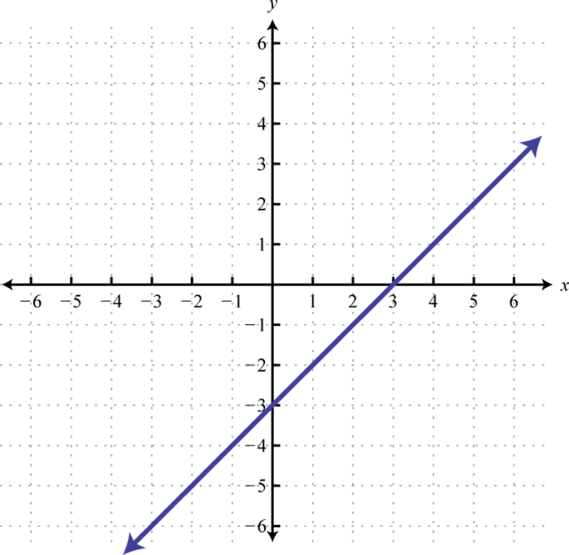
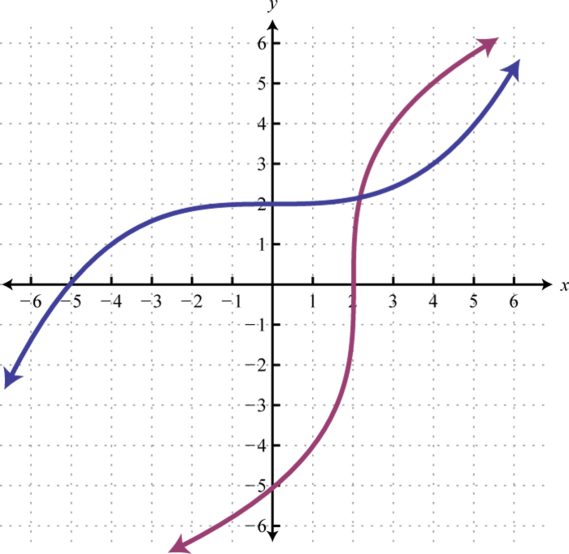
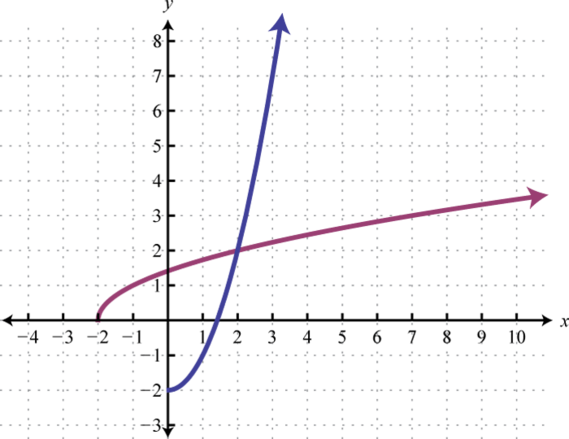
Next we explore the geometry associated with inverse functions. The graphs of both functions in the previous example are provided on the same set of axes below.
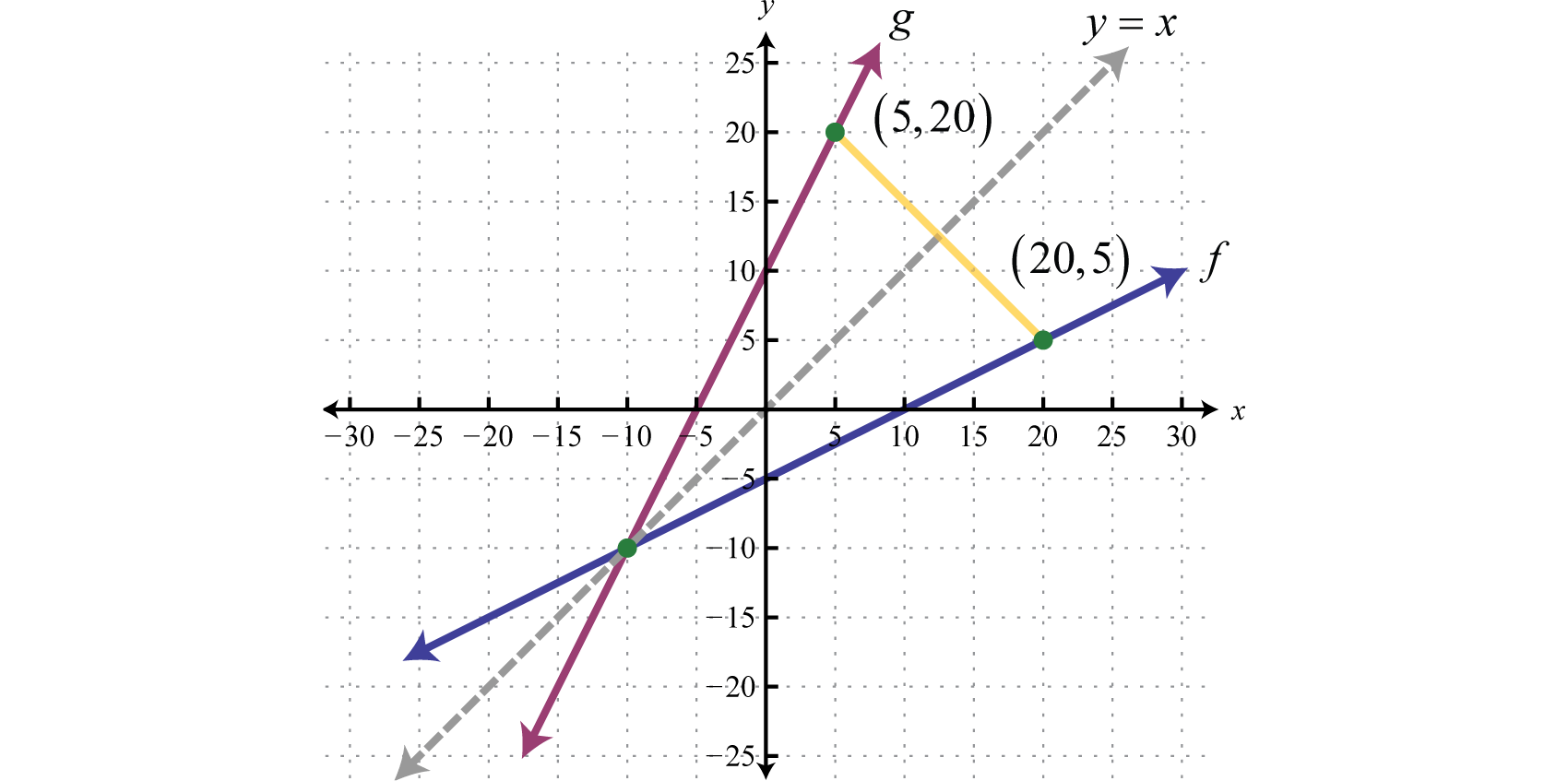
Note that there is symmetry about the line ; the graphs of f and g are mirror images about this line. Also notice that the point (20, 5) is on the graph of f and that (5, 20) is on the graph of g. Both of these observations are true in general and we have the following properties of inverse functions:
Furthermore, if g is the inverse of f we use the notation Here is read, “f inverse,” and should not be confused with negative exponents. In other words, and we have,
Verify algebraically that the functions defined by and are inverses.
Solution:
Compose the functions both ways to verify that the result is x.
Answer: Since they are inverses.
Recall that a function is a relation where each element in the domain corresponds to exactly one element in the range. We use the vertical line test to determine if a graph represents a function or not. Functions can be further classified using an inverse relationship. One-to-one functionsFunctions where each value in the range corresponds to exactly one value in the domain. are functions where each value in the range corresponds to exactly one element in the domain. The horizontal line testIf a horizontal line intersects the graph of a function more than once, then it is not one-to-one. is used to determine whether or not a graph represents a one-to-one function. If a horizontal line intersects a graph more than once, then it does not represent a one-to-one function.
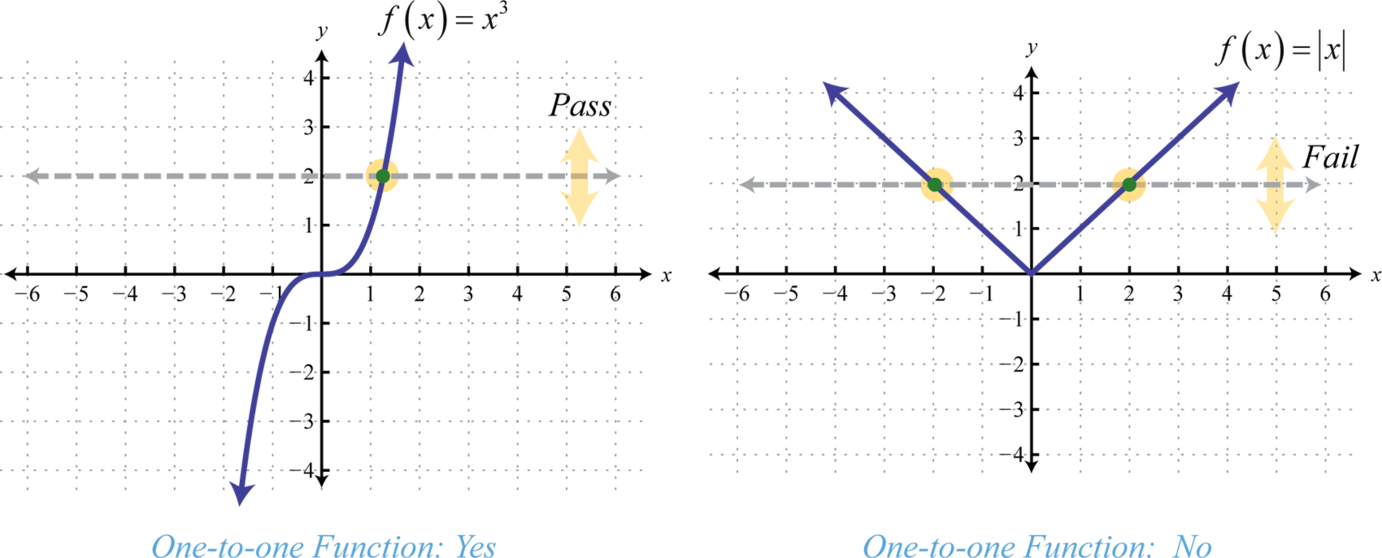
The horizontal line represents a value in the range and the number of intersections with the graph represents the number of values it corresponds to in the domain. The function defined by is one-to-one and the function defined by is not. Determining whether or not a function is one-to-one is important because a function has an inverse if and only if it is one-to-one. In other words, a function has an inverse if it passes the horizontal line test.
Note: In this text, when we say “a function has an inverse,” we mean that there is another function, , such that
Determine whether or not the given function is one-to-one.
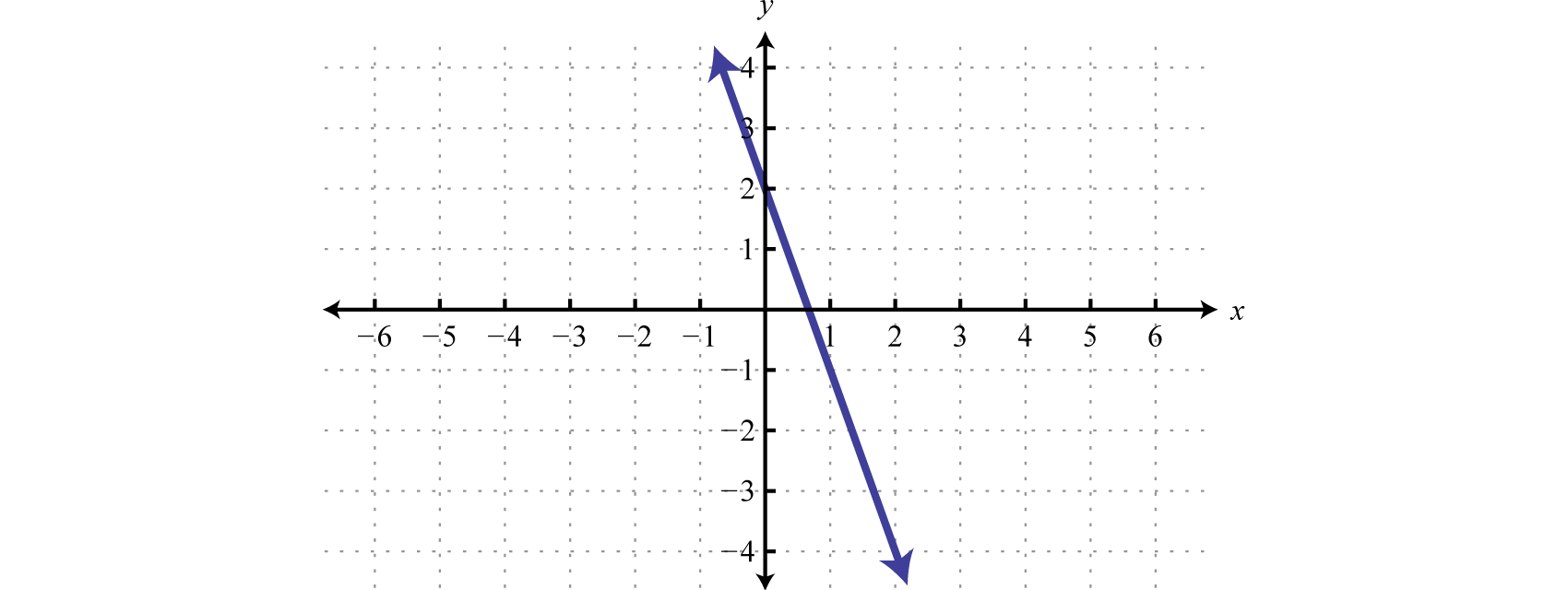
Solution:
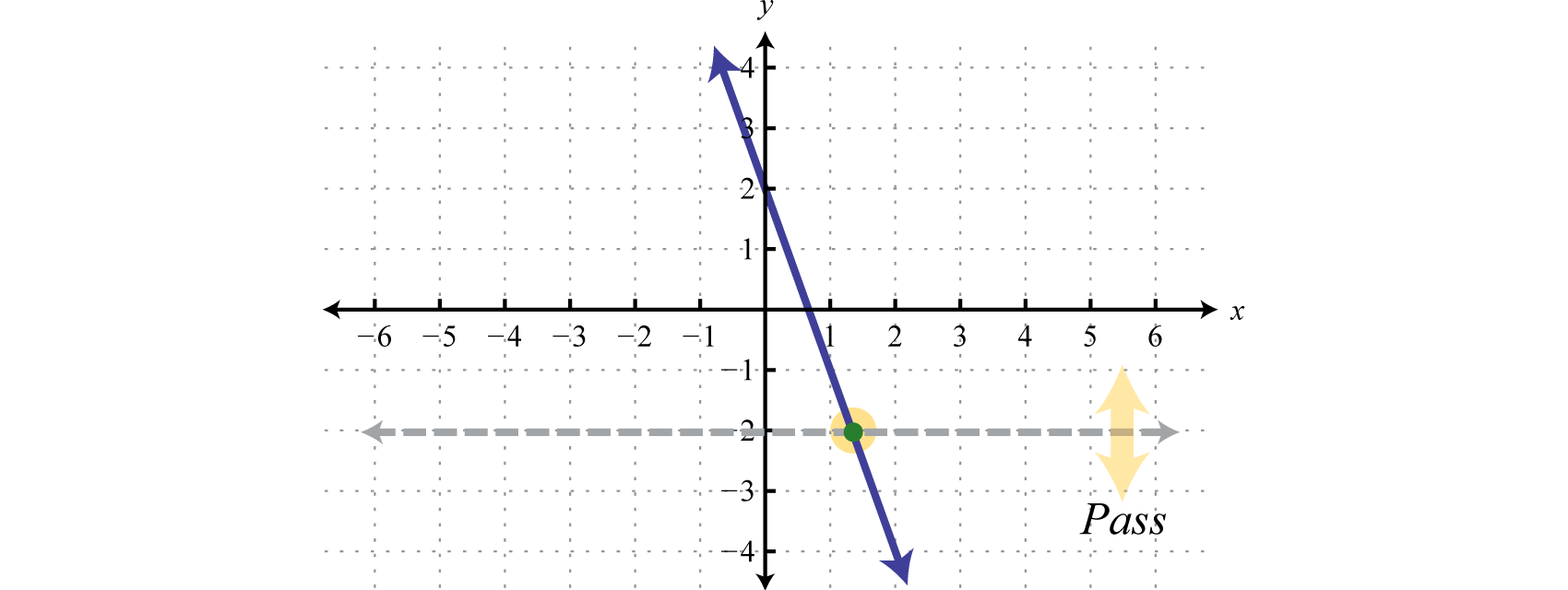
Answer: The given function passes the horizontal line test and thus is one-to-one.
In fact, any linear function of the form where , is one-to-one and thus has an inverse. The steps for finding the inverse of a one-to-one function are outlined in the following example.
Find the inverse of the function defined by
Solution:
Before beginning this process, you should verify that the function is one-to-one. In this case, we have a linear function where and thus it is one-to-one.
Step 1: Replace the function notation with y.
Step 2: Interchange x and y. We use the fact that if is a point on the graph of a function, then is a point on the graph of its inverse.
Step 3: Solve for y.
Step 4: The resulting function is the inverse of f. Replace y with
Step 5: Check.
|
Answer:
If a function is not one-to-one, it is often the case that we can restrict the domain in such a way that the resulting graph is one-to-one. For example, consider the squaring function shifted up one unit, Note that it does not pass the horizontal line test and thus is not one-to-one. However, if we restrict the domain to nonnegative values, , then the graph does pass the horizontal line test.
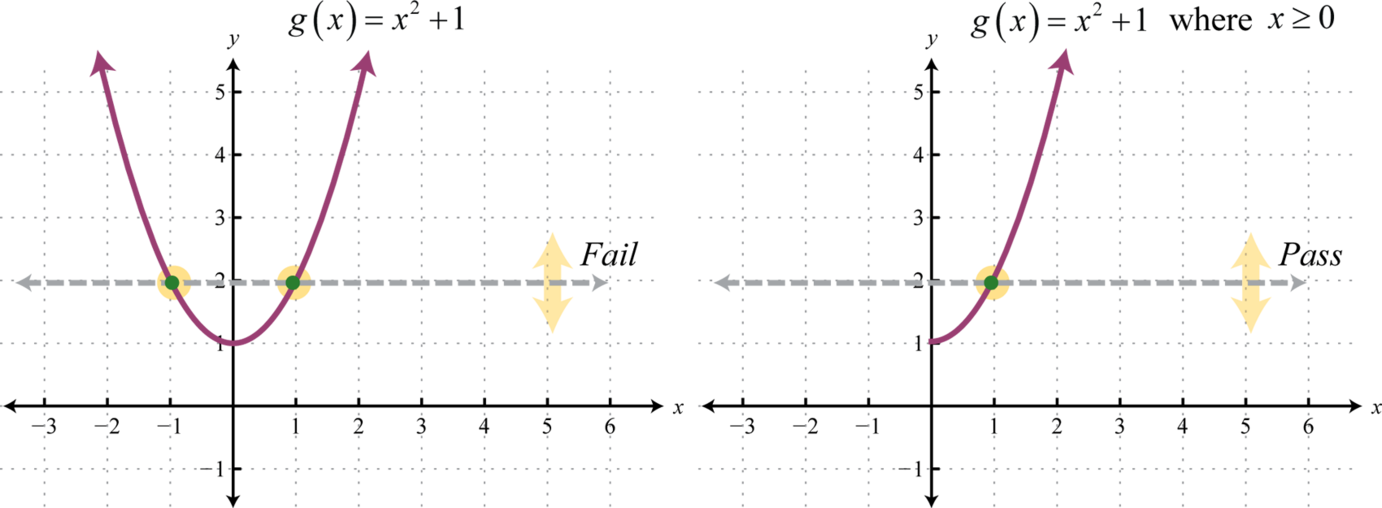
On the restricted domain, g is one-to-one and we can find its inverse.
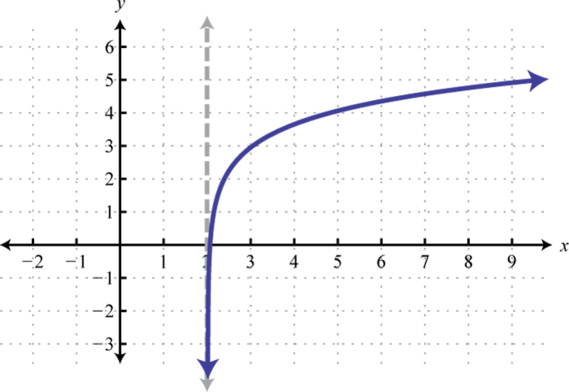
Find the inverse of the function defined by where
Solution:
Begin by replacing the function notation with y.
Interchange x and y.
Solve for y.
Since we only consider the positive result.
Answer: The check is left to the reader.
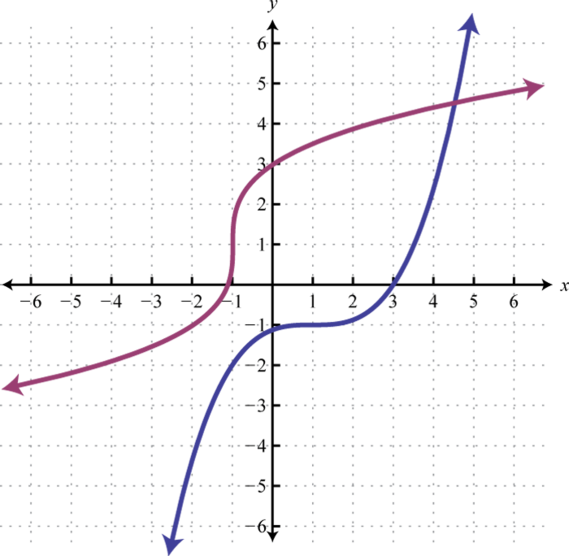
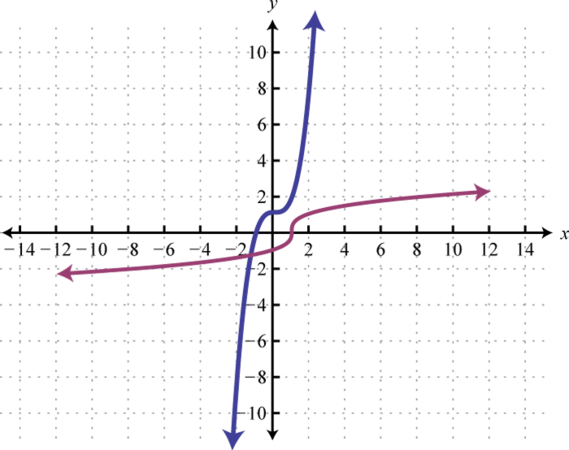
The graphs in the previous example are shown on the same set of axes below. Take note of the symmetry about the line
Find the inverse of the function defined by
Solution:
Use a graphing utility to verify that this function is one-to-one. Begin by replacing the function notation with y.
Interchange x and y.
Solve for y.
Obtain all terms with the variable y on one side of the equation and everything else on the other. This will enable us to treat y as a GCF.
Answer: The check is left to the reader.
Given the functions defined by f and g find and
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
Given the functions defined by , , and , calculate the following.
Given the functions defined by , , and , calculate the following.
Given the function, determine
Are the given functions one-to-one? Explain.
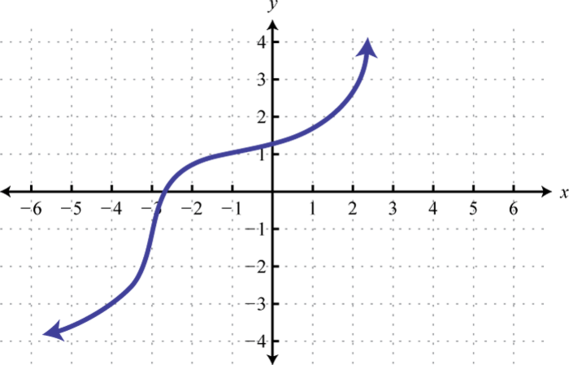
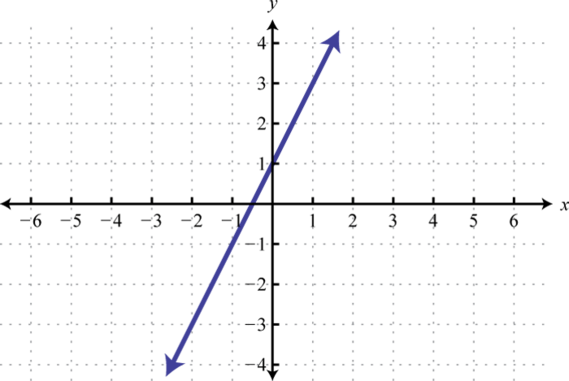
Given the graph of a one-to-one function, graph its inverse.
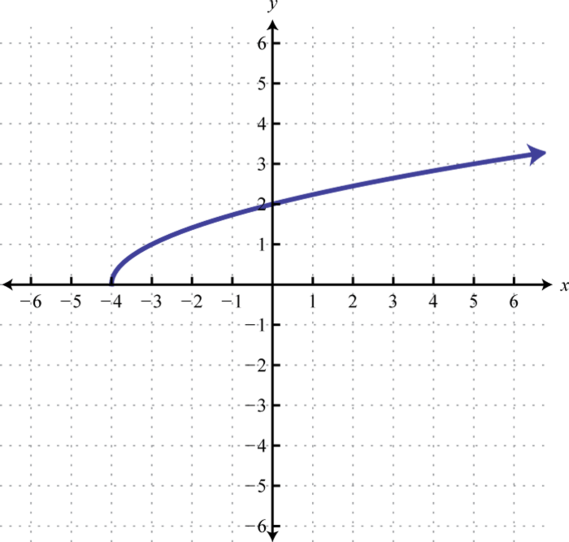
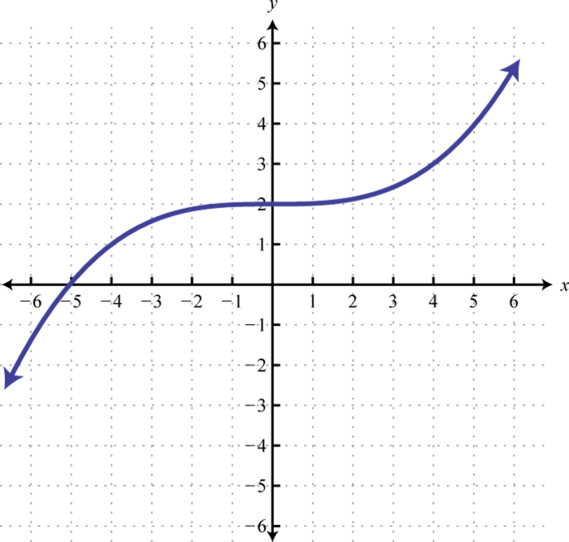
Verify algebraically that the two given functions are inverses. In other words, show that and
,
,
,
,
, ,
,
,
,
,
,
Find the inverses of the following functions.
,
,
,
,
,
,
,
Graph the function and its inverse on the same set of axes.
,
,
Is composition of functions associative? Explain.
Explain why and define inverse functions. Prove it algebraically.
Do the graphs of all straight lines represent one-to-one functions? Explain.
If the graphs of inverse functions intersect, then how can we find the point of intersection? Explain.
;
;
;
;
;
;
;
;
361
−9
7
2
2
21
0
5
No, fails the HLT
Yes, passes the HLT
Yes, its graph passes the HLT.
No, its graph fails the HLT.
Yes, its graph passes the HLT.
Proof
Proof
Proof
Proof
Proof
Answer may vary
Answer may vary
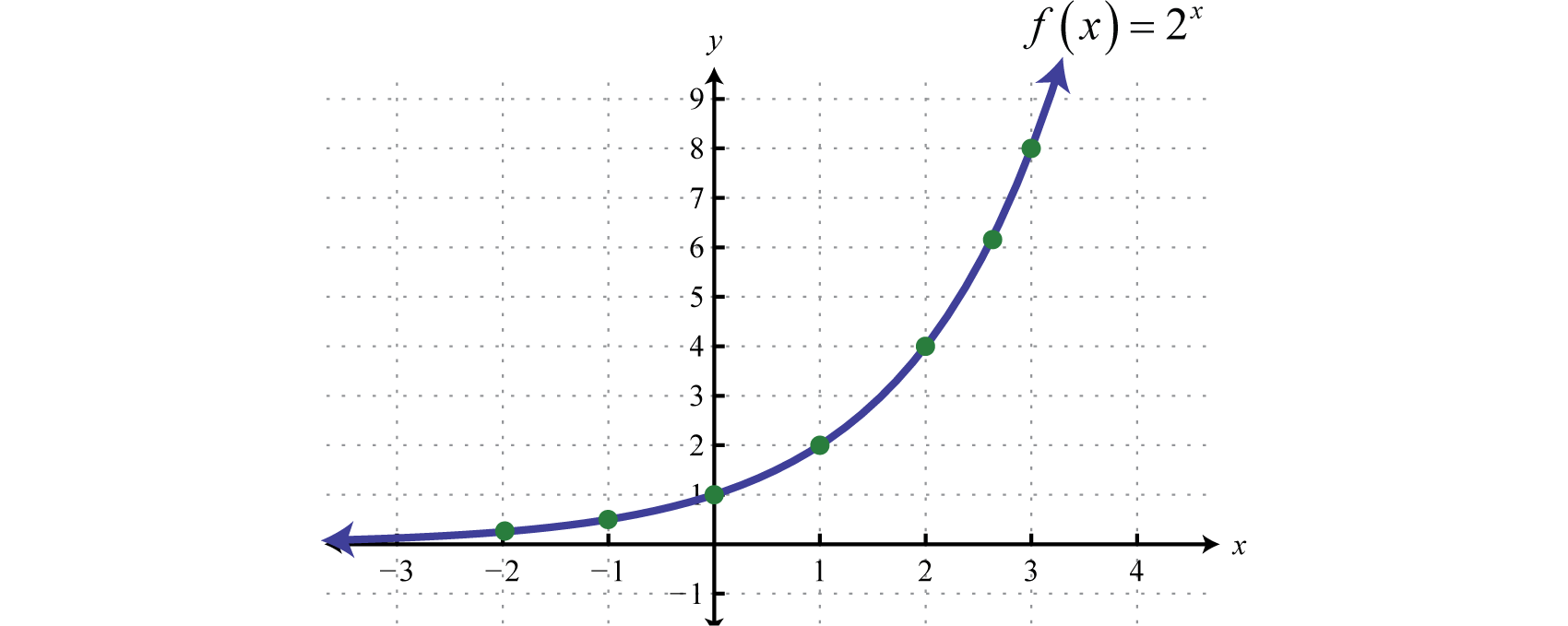
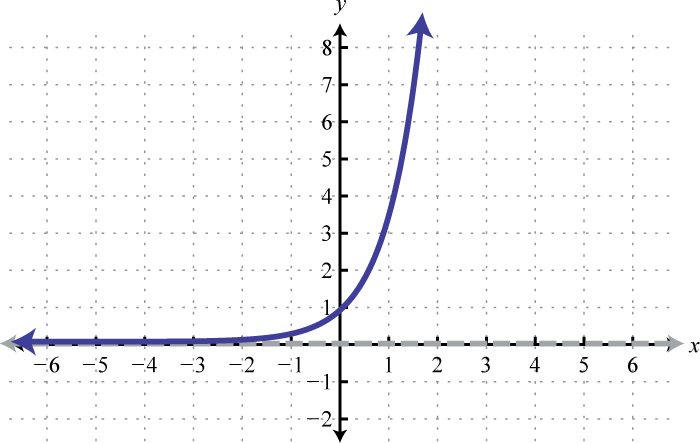
At this point in our study of algebra we begin to look at transcendental functions or functions that seem to “transcend” algebra. We have studied functions with variable bases and constant exponents such as or In this section we explore functions with a constant base and variable exponents. Given a real number where an exponential functionAny function with a definition of the form where and has the form,
For example, if the base b is equal to 2, then we have the exponential function defined by Here we can see the exponent is the variable. Up to this point, rational exponents have been defined but irrational exponents have not. Consider , where the exponent is an irrational number in the range,
We can use these bounds to estimate ,
Using rational exponents in this manner, an approximation of can be obtained to any level of accuracy. On a calculator,
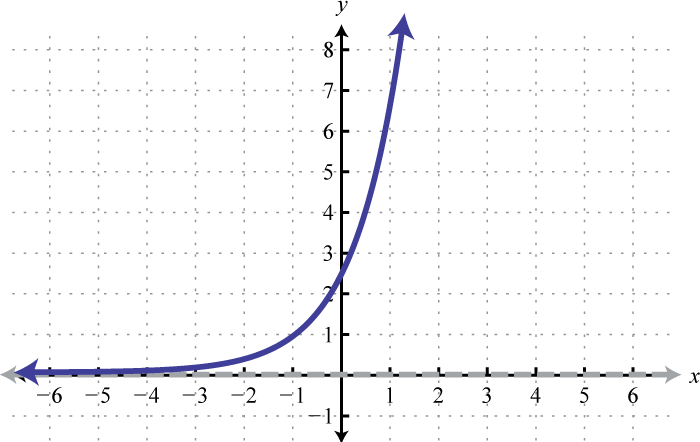
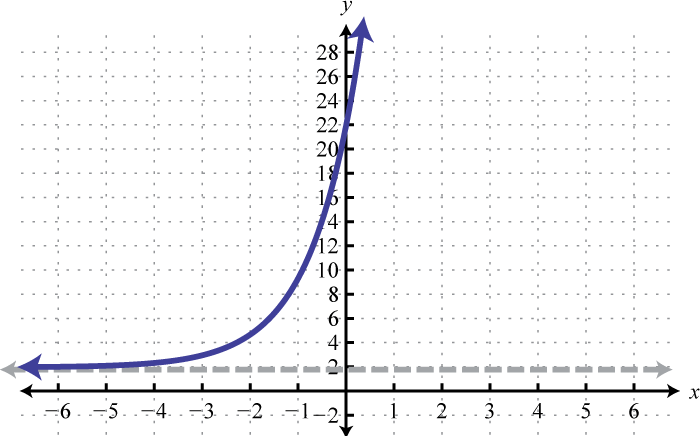
Therefore the domain of any exponential function consists of all real numbers Choose some values for x and then determine the corresponding y-values.
Because exponents are defined for any real number we can sketch the graph using a continuous curve through these given points:
It is important to point out that as x approaches negative infinity, the results become very small but never actually attain zero. For example,
This describes a horizontal asymptote at , the x-axis, and defines a lower bound for the range of the function:
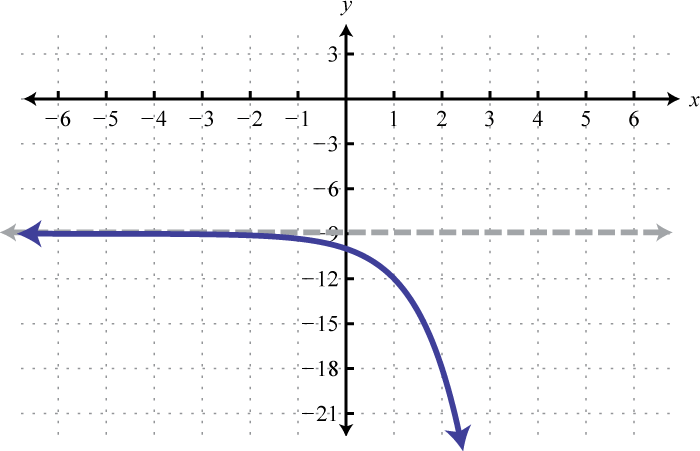
The base b of an exponential function affects the rate at which it grows. Below we have graphed , , and on the same set of axes.
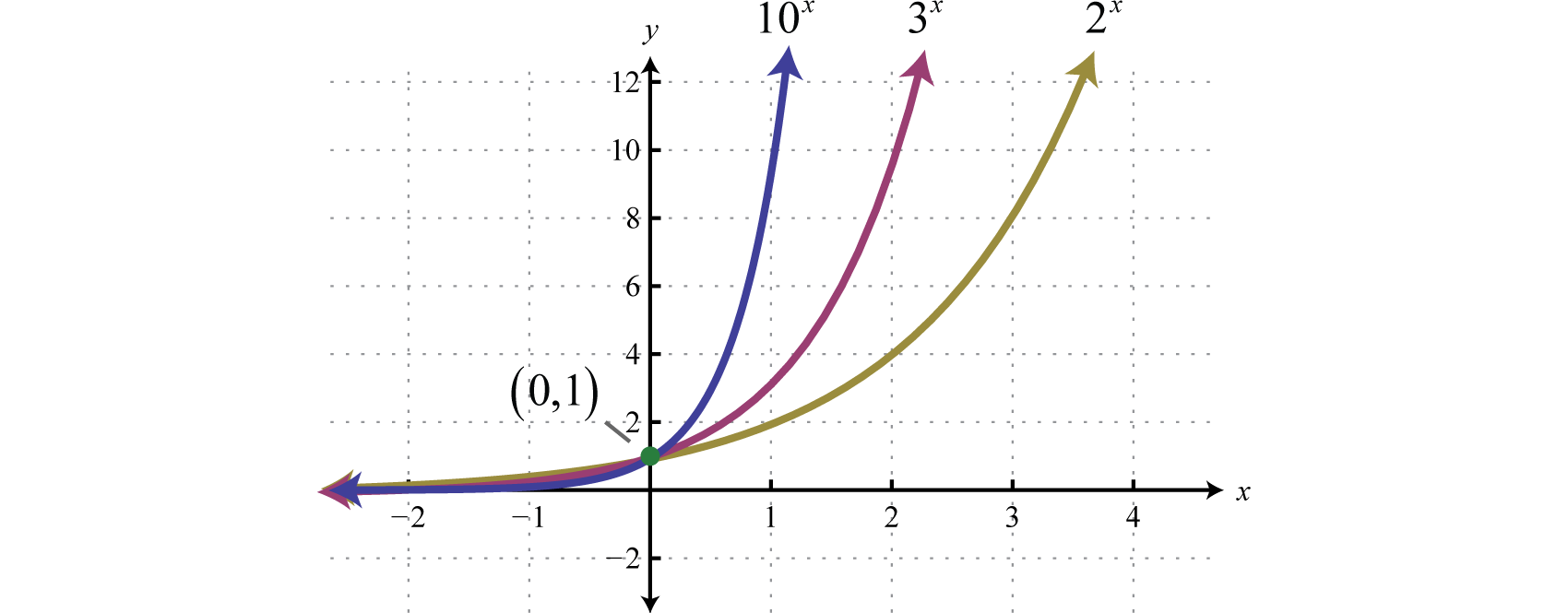
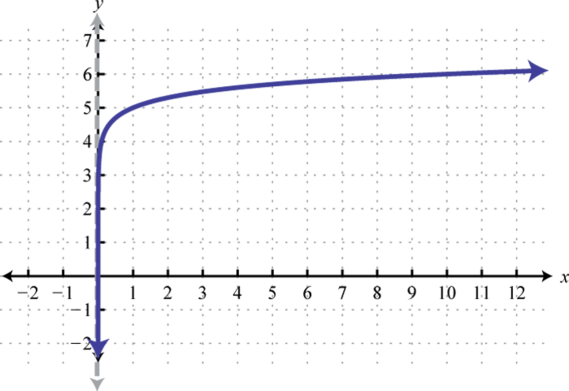
Note that all of these exponential functions have the same y-intercept, namely This is because for any function defined using the form As the functions are read from left to right, they are interpreted as increasing or growing exponentially. Furthermore, any exponential function of this form will have a domain that consists of all real numbers and a range that consists of positive values bounded by a horizontal asymptote at
Sketch the graph and determine the domain and range:
Solution:
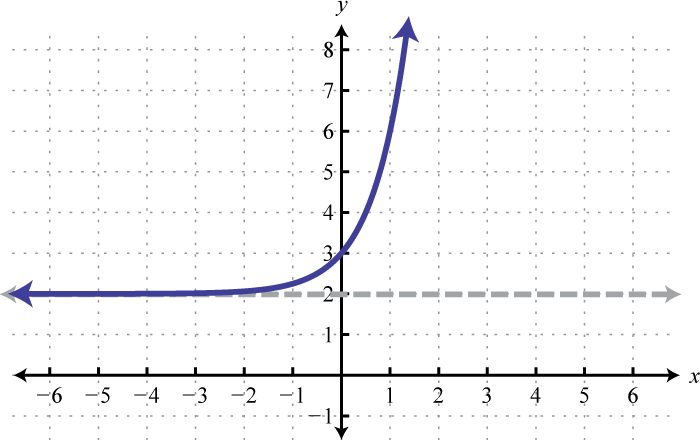
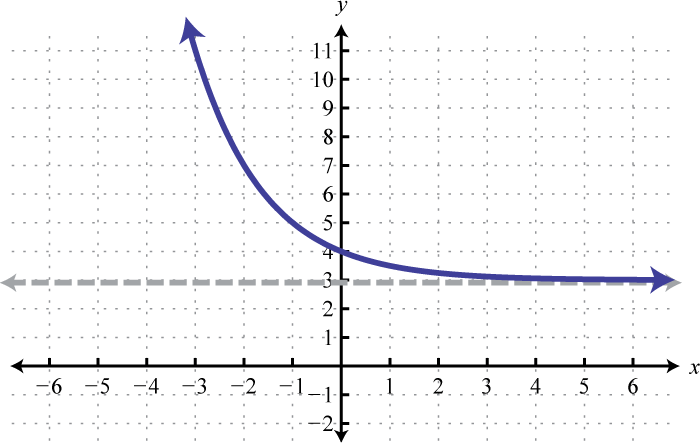
The base 10 is used often, most notably with scientific notation. Hence, 10 is called the common base. In fact, the exponential function is so important that you will find a button dedicated to it on most modern scientific calculators. In this example, we will sketch the basic graph and then shift it up 5 units.
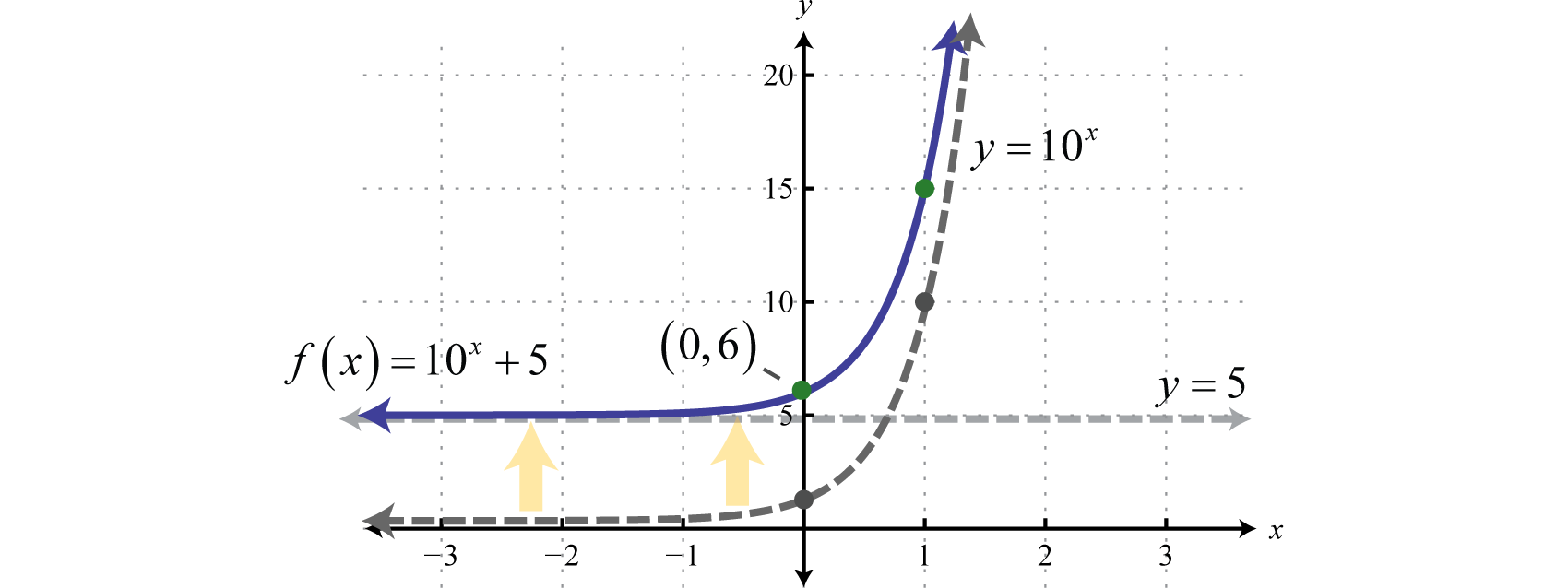
Note that the horizontal asymptote of the basic graph was shifted up 5 units to (shown dashed). Take a minute to evaluate a few values of x with your calculator and convince yourself that the result will never be less than 5.
Answer:
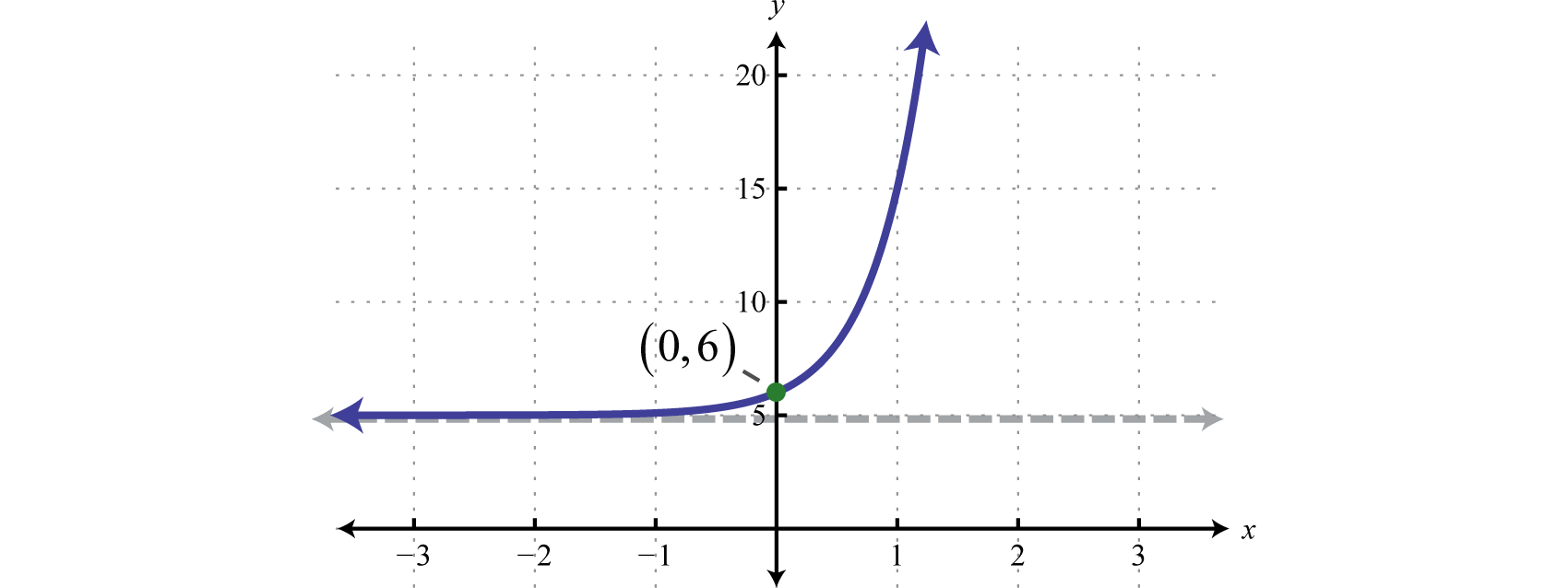
Domain: ; Range:
Next consider exponential functions with fractional bases For example, is an exponential function with base
Plotting points we have,
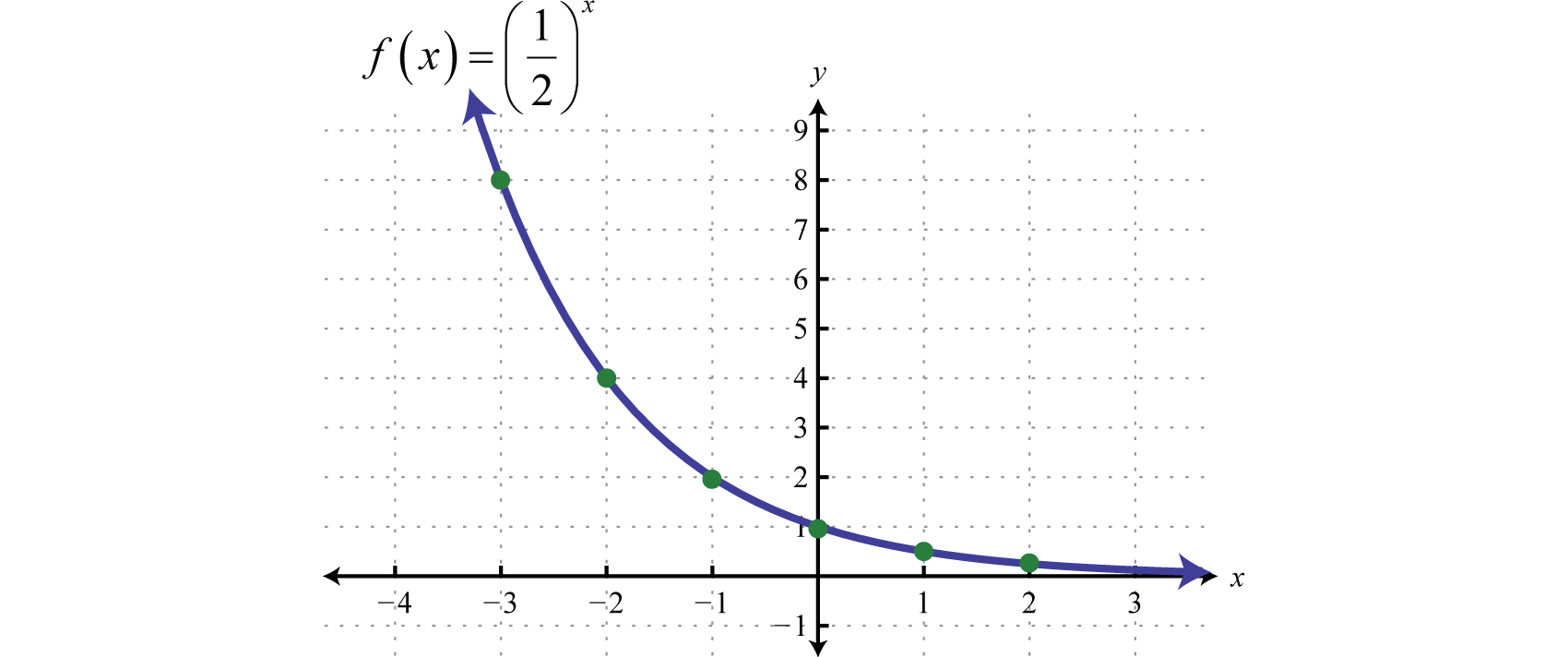
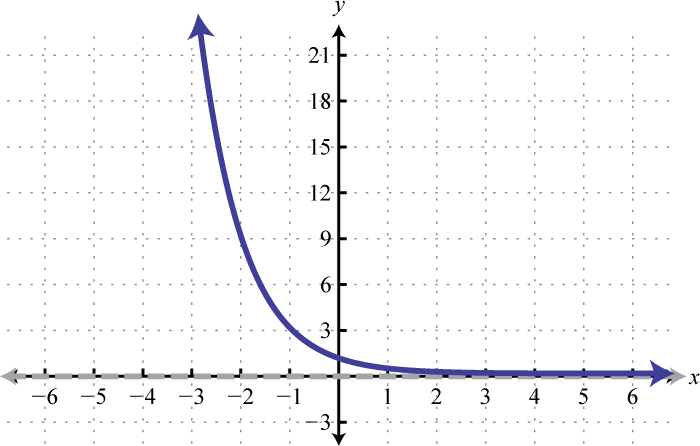
Reading the graph from left to right, it is interpreted as decreasing exponentially. The base affects the rate at which the exponential function decreases or decays. Below we have graphed , , and on the same set of axes.
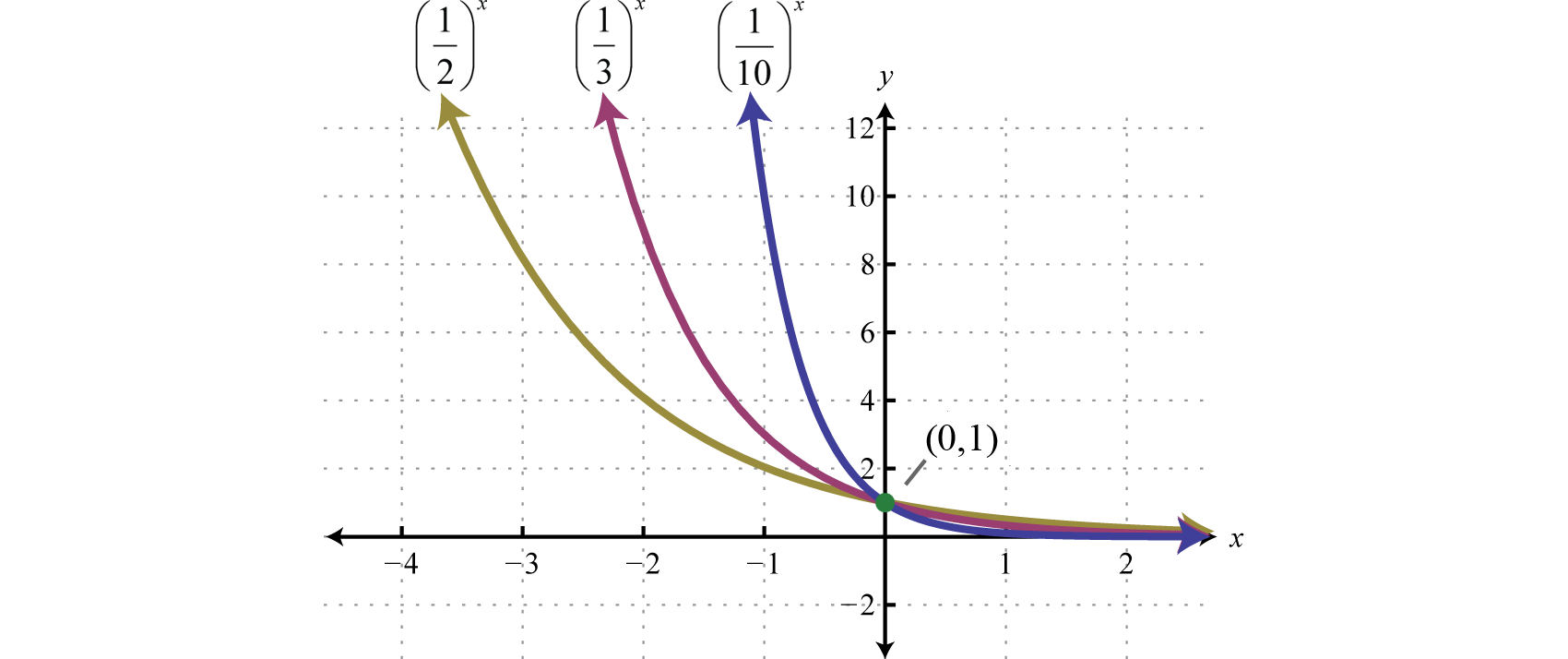
Recall that and so we can express exponential functions with fractional bases using negative exponents. For example,
Furthermore, given that we can see and can consider g to be a reflection of f about the y-axis.
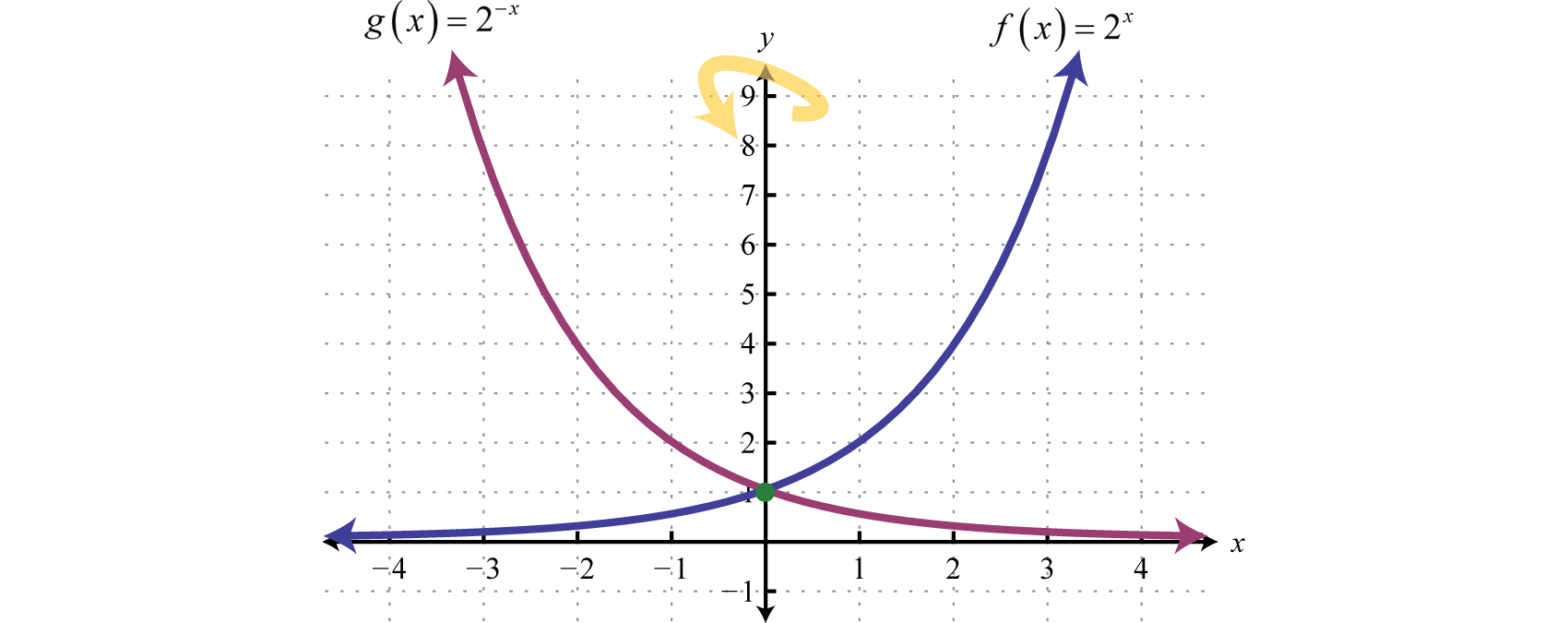
In summary, given
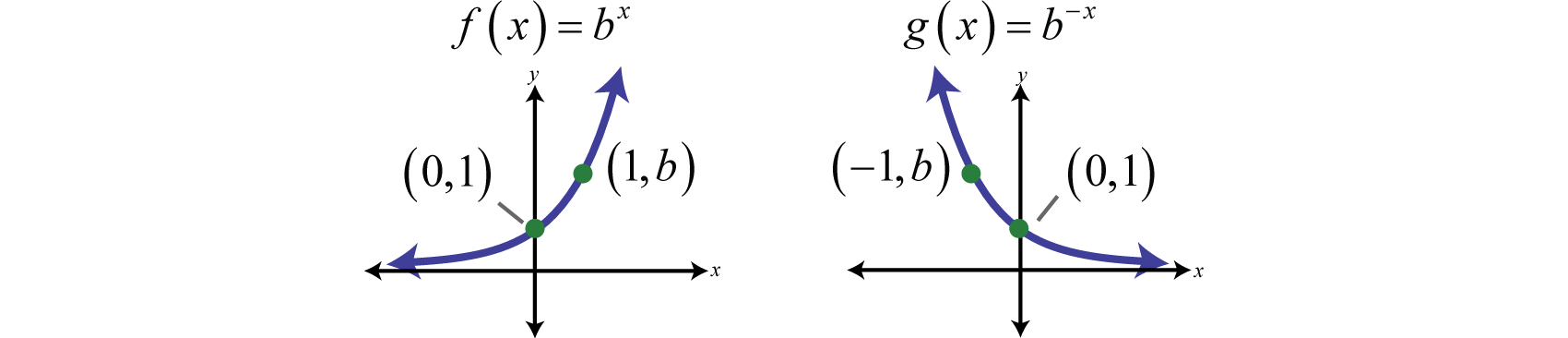
And for both cases,
Furthermore, note that the graphs pass the horizontal line test and thus exponential functions are one-to-one. We use these basic graphs, along with the transformations, to sketch the graphs of exponential functions.
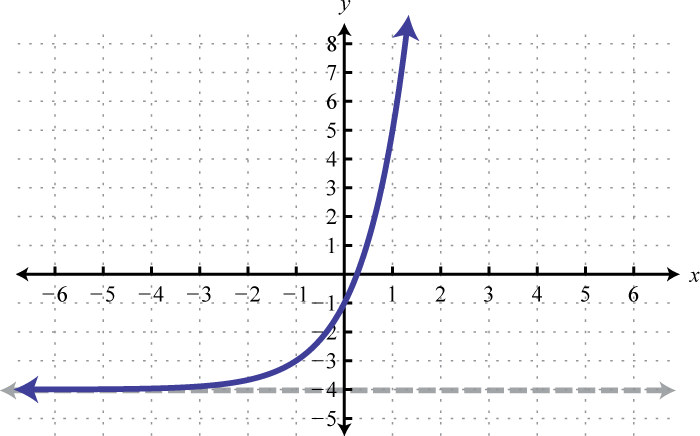
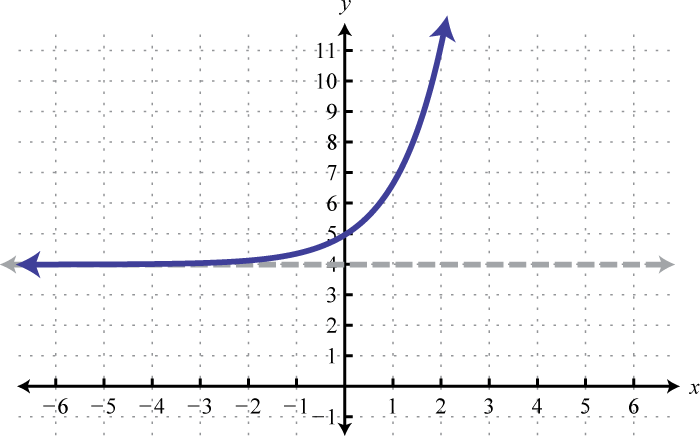
Sketch the graph and determine the domain and range:
Solution:
Begin with the basic graph and shift it down 10 units.
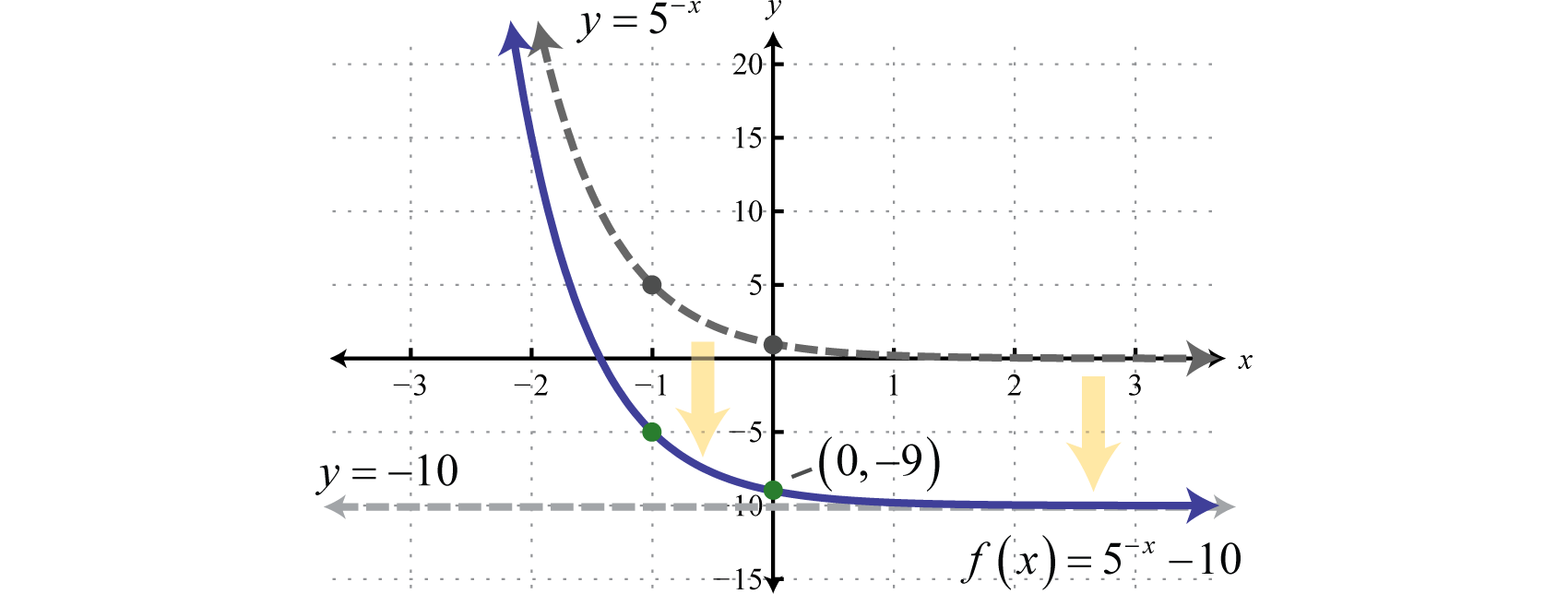
The y-intercept is and the horizontal asymptote is
Answer:
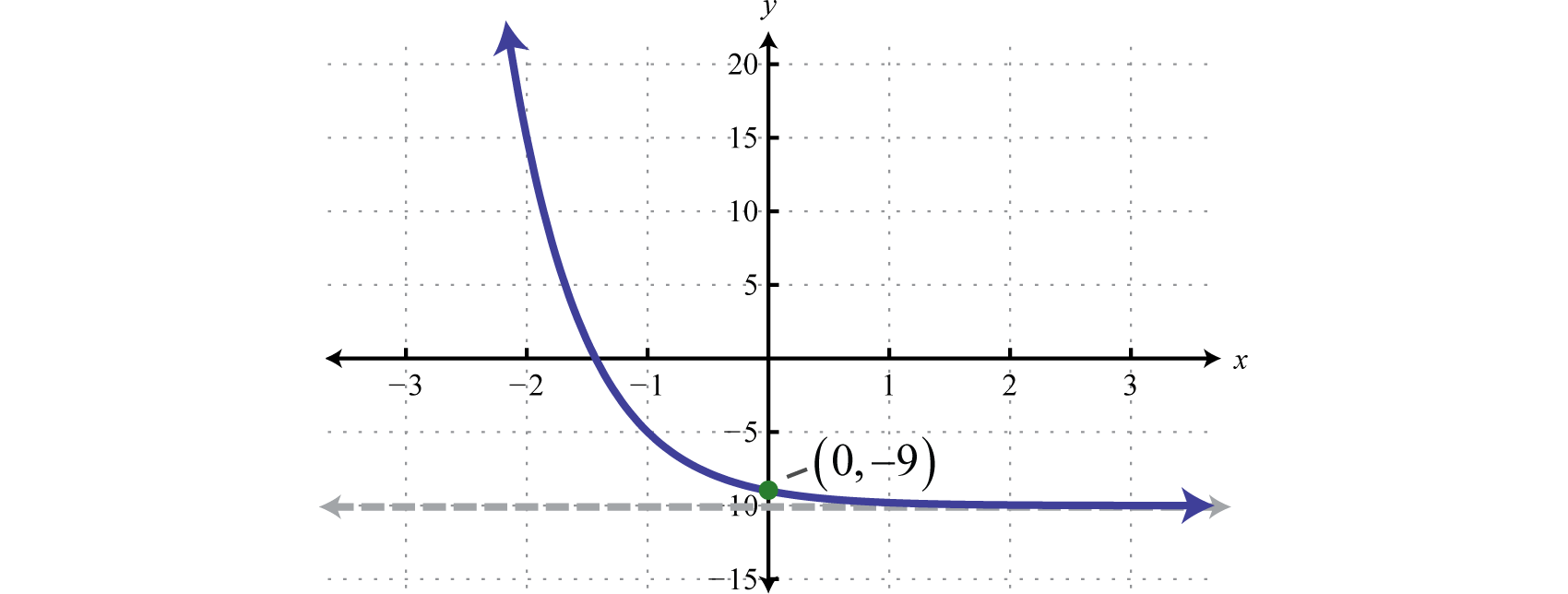
Domain: ; Range:
Note: Finding the x-intercept of the graph in the previous example is left for a later section in this chapter. For now, we are more concerned with the general shape of exponential functions.
Sketch the graph and determine the domain and range:
Solution:
Begin with the basic graph and identify the transformations.
Note that the horizontal asymptote remains the same for all of the transformations. To finish we usually want to include the y-intercept. Remember that to find the y-intercept we set
Therefore the y-intercept is .
Answer:
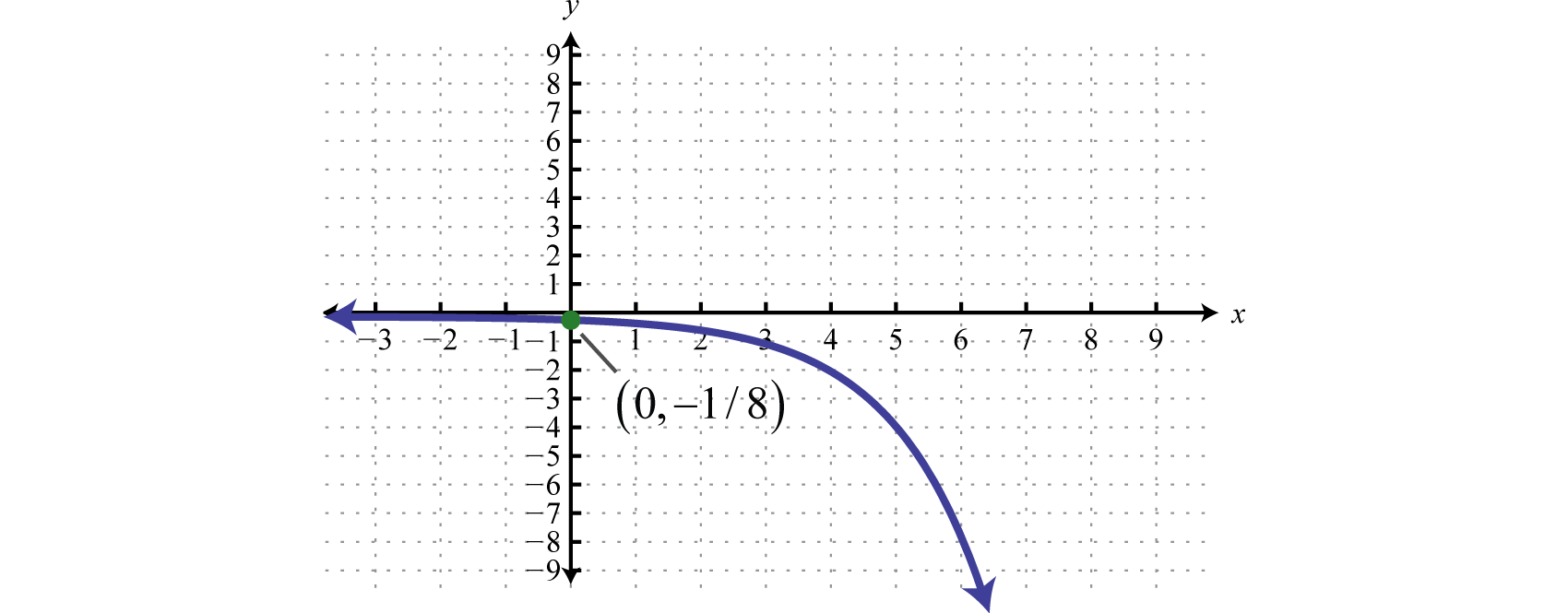
Domain: ; Range:
Try this! Sketch the graph and determine the domain and range:
Answer:
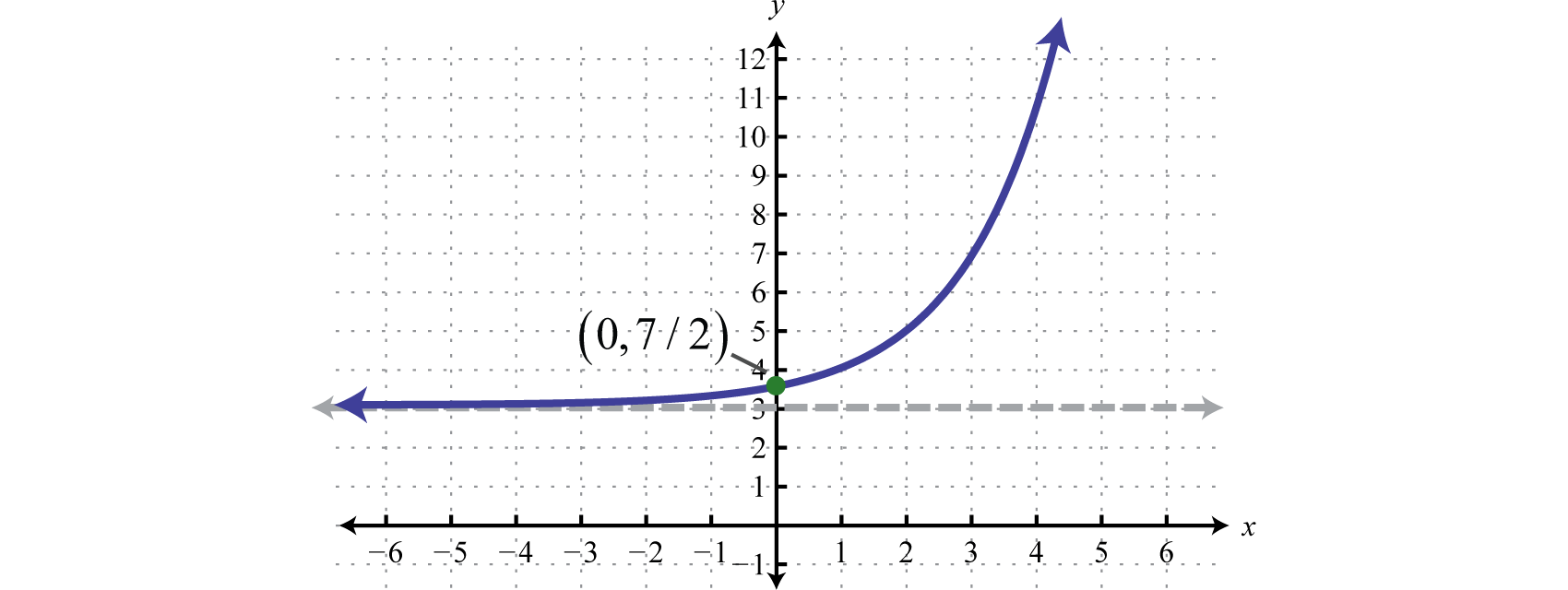
Domain: ; Range:
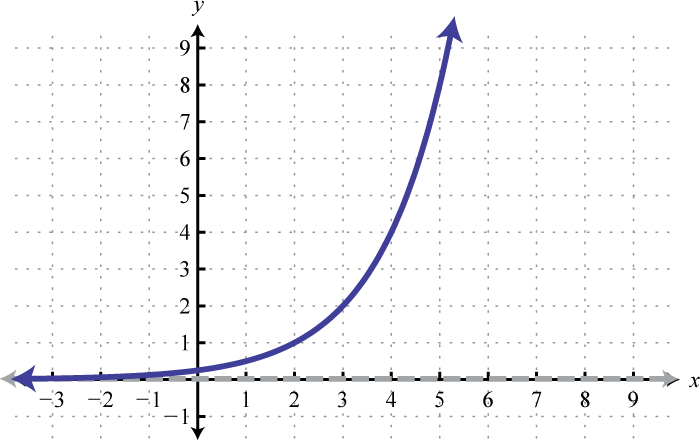
Some numbers occur often in common applications. One such familiar number is pi (π), which we know occurs when working with circles. This irrational number has a dedicated button on most calculators and approximated to five decimal places, Another important number e occurs when working with exponential growth and decay models. It is an irrational number and approximated to five decimal places, This constant occurs naturally in many real-world applications and thus is called the natural base. Sometimes e is called Euler’s constant in honor of Leonhard Euler (pronounced “Oiler”).
Figure 7.1

Leonhard Euler (1707–1783)
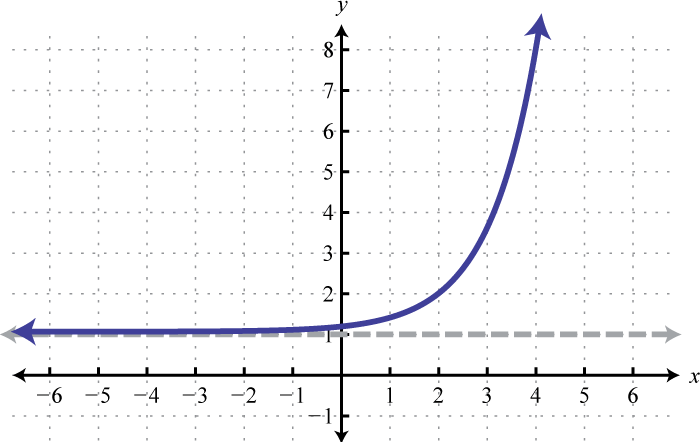
In fact, the natural exponential function, is so important that you will find a button dedicated to it on any modern scientific calculator. In this section, we are interested in evaluating the natural exponential function for given real numbers and sketching its graph. To evaluate the natural exponential function, defined by where using a calculator, you may need to apply the shift button. On many scientific calculators the caret will display as follows,
After learning how to use your particular calculator, you can now sketch the graph by plotting points. (Round off to the nearest hundredth.)
Plot the points and sketch the graph.
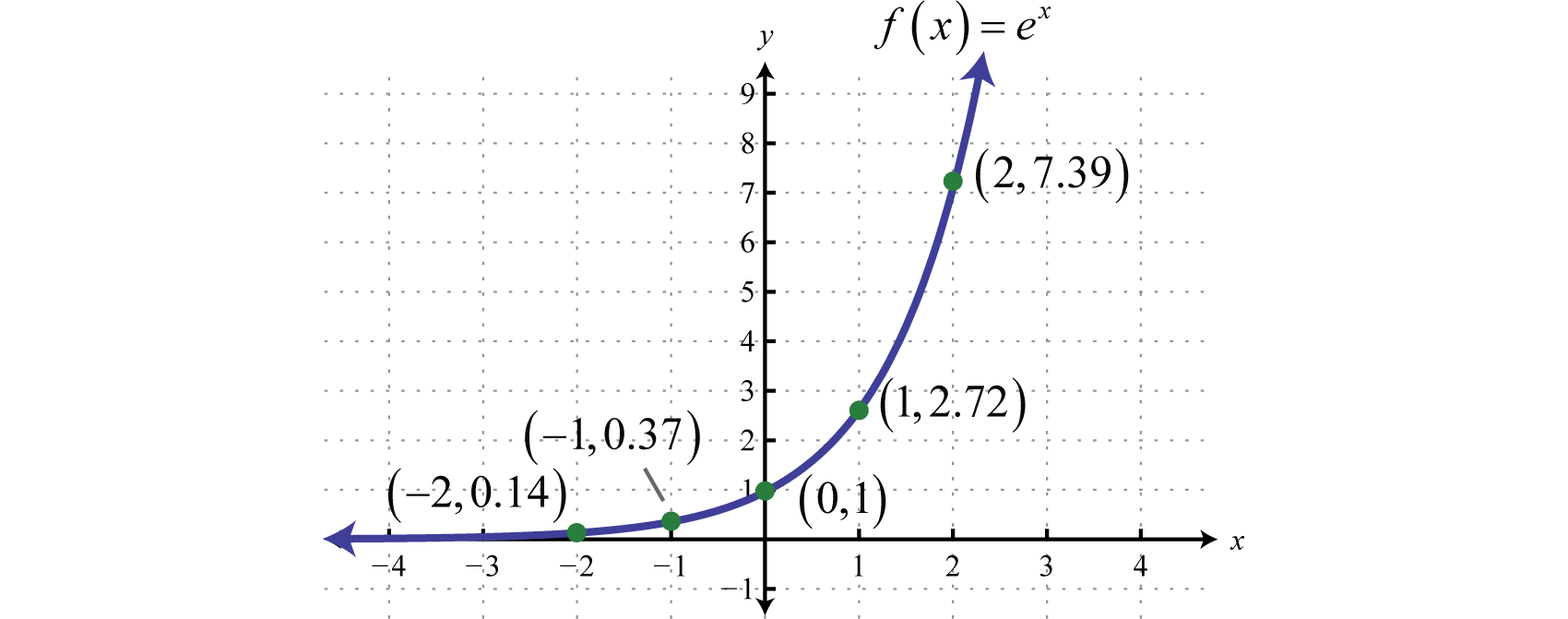
Note that the function is similar to the graph of The domain consists of all real numbers and the range consists of all positive real numbers. There is an asymptote at and a y-intercept at We can use the transformations to sketch the graph of more complicated exponential functions.
Sketch the graph and determine the domain and range:
Solution:
Identify the basic transformations.
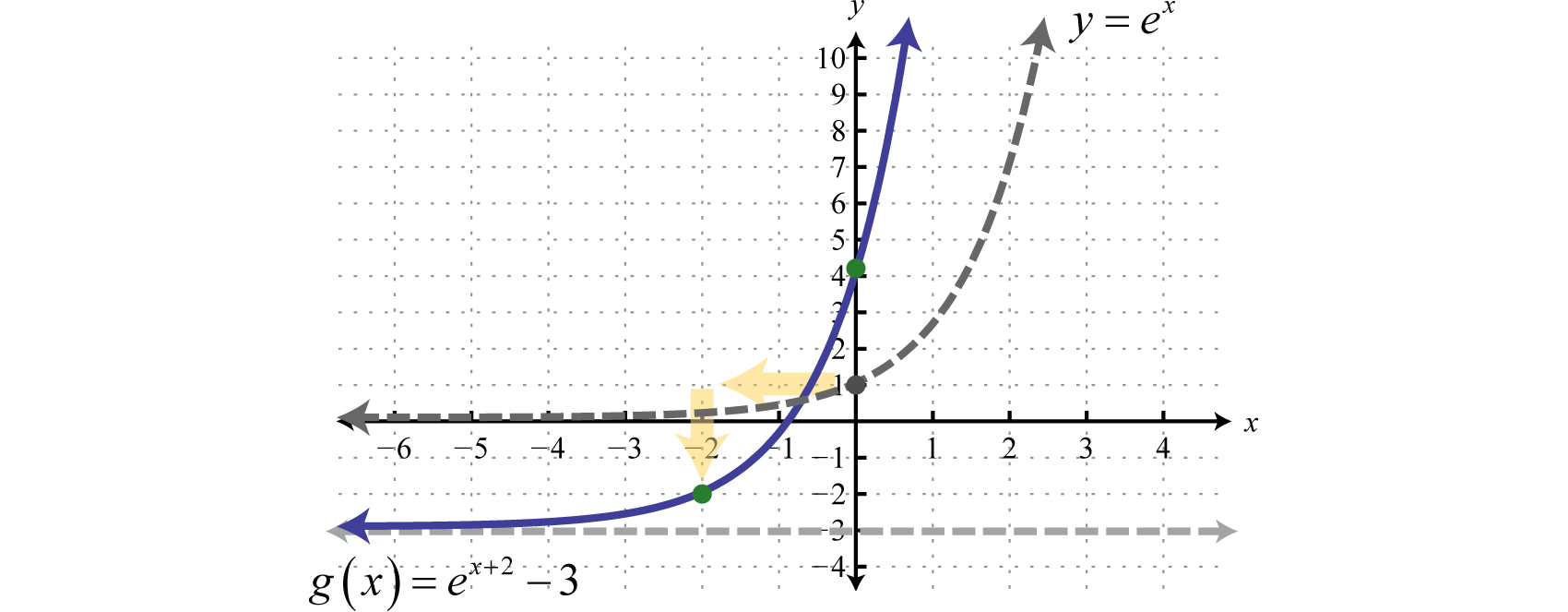
To determine the y-intercept set
Therefore the y-intercept is
Answer:
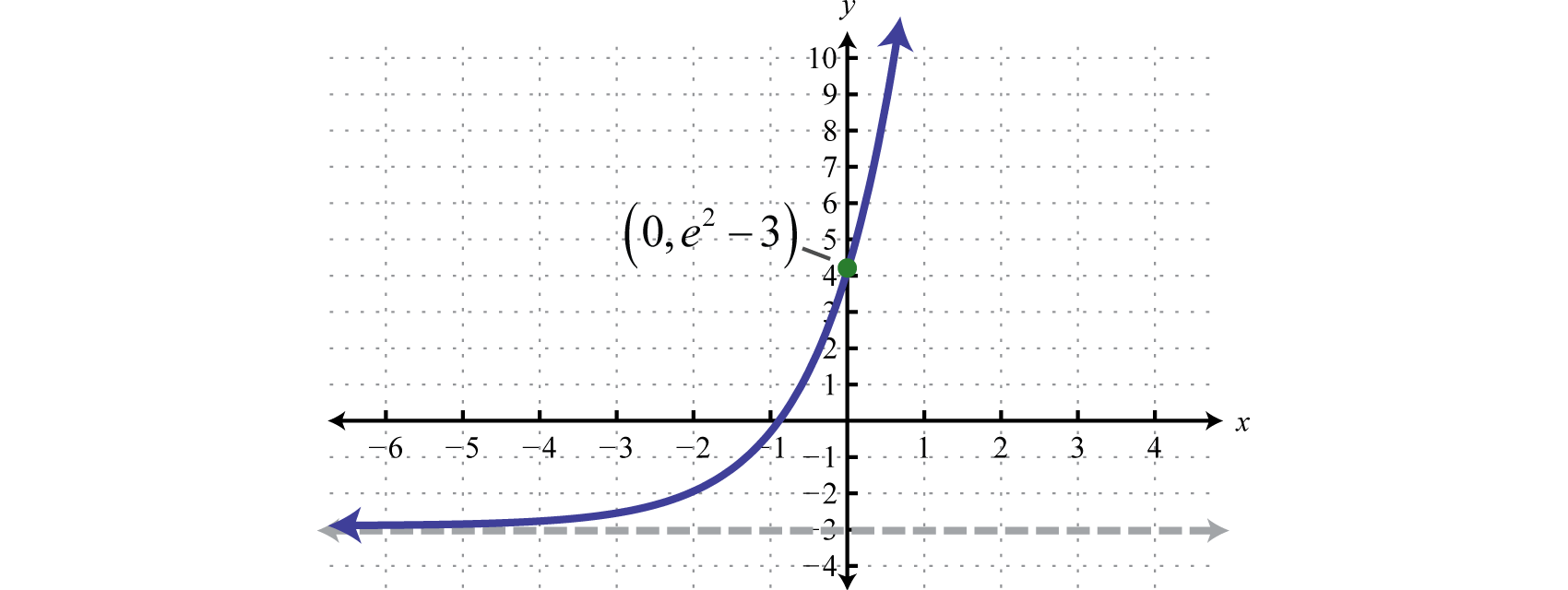
Domain: ; Range:
Try this! Sketch the graph and determine the domain and range:
Answer:
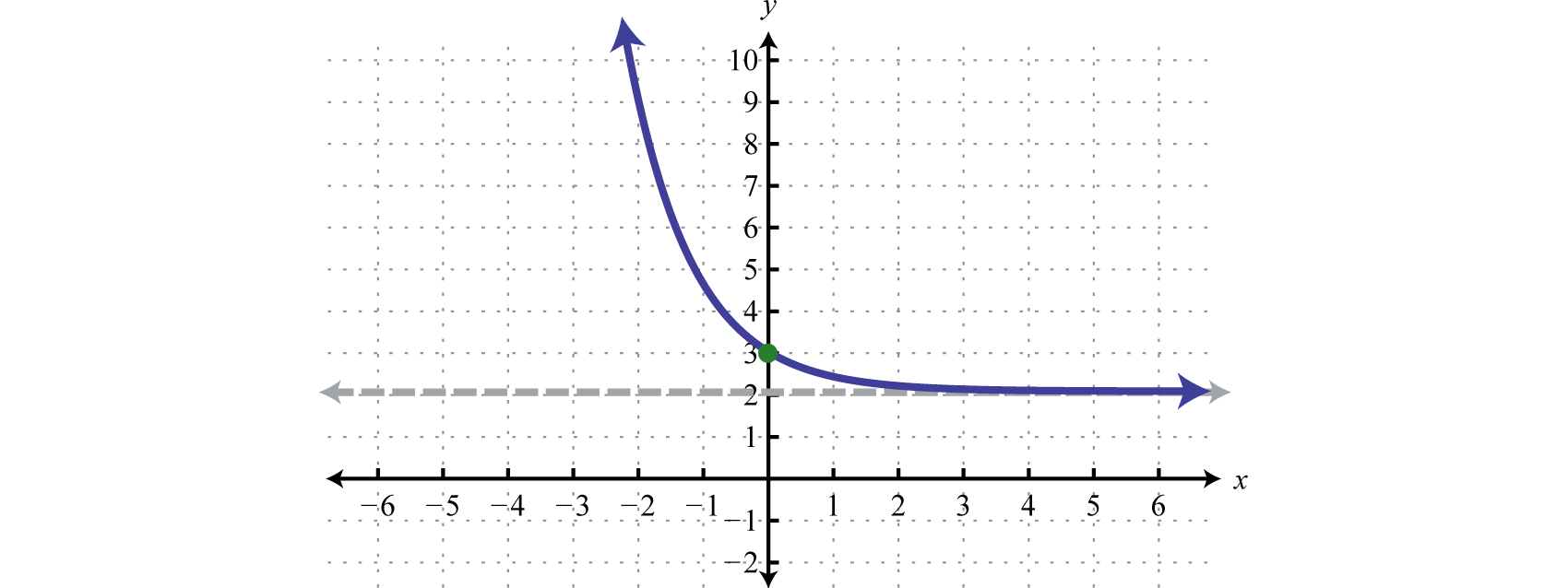
Domain: ; Range:
Exponential functions appear in formulas used to calculate interest earned in most regular savings accounts. Compound interest occurs when interest accumulated for one period is added to the principal investment before calculating interest for the next period. The amount accrued in this manner over time is modeled by the compound interest formulaA formula that gives the amount accumulated by earning interest on principal and interest over time: :
Here the amount A depends on the time t in years the principal P is accumulating compound interest at an annual interest rate r. The value n represents the number of times the interest is compounded in a year.
An investment of $500 is made in a 6-year CD that earns % annual interest that is compounded monthly. How much will the CD be worth at the end of the 6-year term?
Solution:
Here the principal , the interest rate , and because the interest is compounded monthly, The investment is modeled by the following,
To determine the amount in the account after 6 years evaluate and round off to the nearest cent.
Answer: The CD will be worth $654.65 at the end of the 6-year term.
Next we explore the effects of increasing n in the formula. For the sake of clarity we let P and r equal 1 and calculate accordingly.
Annual compounding |
|
|---|---|
Yearly () |
|
Semi-annually () |
|
Quarterly () |
|
Monthly () |
|
Weekly () |
|
Daily () |
|
Hourly () |
Continuing this pattern, as n increases to say compounding every minute or even every second, we can see that the result tends toward the natural base Compounding interest every instant leads to the continuously compounding interest formulaA formula that gives the amount accumulated by earning continuously compounded interest: ,
Here P represents the initial principal amount invested, r represents the annual interest rate, and t represents the time in years the investment is allowed to accrue continuously compounded interest.
An investment of $500 is made in a 6-year CD that earns % annual interest that is compounded continuously. How much will the CD be worth at the end of the 6-year term?
Solution:
Here the principal , and the interest rate Since the interest is compounded continuously we will use the formula The investment is modeled by the following,
To determine the amount in the account after 6 years, evaluate and round off to the nearest cent.
Answer: The CD will be worth $654.98 at the end of the 6-year term.
Compare the previous two examples and note that compounding continuously may not be as beneficial as it sounds. While it is better to compound interest more often, the difference is not that profound. Certainly, the interest rate is a much greater factor in the end result.
Try this! How much will a $1,200 CD, earning 5.2% annual interest compounded continuously, be worth at the end of a 10-year term?
Answer: $2,018.43
Evaluate.
where , , and
where , , and
where , , and
where , , and
where , , and
where , , and
where , , and
where , , and
where , , and
where , , and
Use a calculator to approximate the following to the nearest hundredth.
where
where
where
where
where
where
where
where
where
where
Sketch the function and determine the domain and range. Draw the horizontal asymptote with a dashed line.
Find , , and for the given function. Use a calculator where appropriate to approximate to the nearest hundredth.
Sketch the function and determine the domain and range. Draw the horizontal asymptote with a dashed line.
Jim invested $750 in a 3-year CD that earns 4.2% annual interest that is compounded monthly. How much will the CD be worth at the end of the 3-year term?
Jose invested $2,450 in a 4-year CD that earns 3.6% annual interest that is compounded semi-annually. How much will the CD be worth at the end of the 4-year term?
Jane has her $5,350 savings in an account earning % annual interest that is compounded quarterly. How much will be in the account at the end of 5 years?
Bill has $12,400 in a regular savings account earning % annual interest that is compounded monthly. How much will be in the account at the end of 3 years?
If $85,200 is invested in an account earning 5.8% annual interest compounded quarterly, then how much interest is accrued in the first 3 years?
If $124,000 is invested in an account earning 4.6% annual interest compounded monthly, then how much interest is accrued in the first 2 years?
Bill invested $1,400 in a 3-year CD that earns 4.2% annual interest that is compounded continuously. How much will the CD be worth at the end of the 3-year term?
Brooklyn invested $2,850 in a 5-year CD that earns 5.3% annual interest that is compounded continuously. How much will the CD be worth at the end of the 5-year term?
Omar has his $4,200 savings in an account earning % annual interest that is compounded continuously. How much will be in the account at the end of years?
Nancy has her $8,325 savings in an account earning % annual interest that is compounded continuously. How much will be in the account at the end of years?
If $12,500 is invested in an account earning 3.8% annual interest compounded continuously, then how much interest is accrued in the first 10 years?
If $220,000 is invested in an account earning 4.5% annual interest compounded continuously, then how much interest is accrued in the first 2 years?
The population of a certain small town is growing according to the function where t represents time in years since the last census. Use the function to determine the population on the day of the census (when t = 0) and estimate the population in 6 years from that time.
The population of a certain small town is decreasing according to the function where t represents time in years since the last census. Use the function to determine the population on the day of the census (when t = 0) and estimate the population in 6 years from that time.
The decreasing value, in dollars, of a new car is modeled by the formula where t represents the number of years after the car was purchased. Use the formula to determine the value of the car when it was new (t = 0) and the value after 4 years.
The number of unique visitors to the college website can be approximated by the formula where t represents the number of years after 1997 when the website was created. Approximate the number of unique visitors to the college website in the year 2020.
If left unchecked, a new strain of flu virus can spread from a single person to others very quickly. The number of people affected can be modeled using the formula where t represents the number of days the virus is allowed to spread unchecked. Estimate the number of people infected with the virus after 30 days and after 60 days.
If left unchecked, a population of 24 wild English rabbits can grow according to the formula where the time t is measured in months. How many rabbits would be present years later?
The population of a certain city in 1975 was 65,000 people and was growing exponentially at an annual rate of 1.7%. At the time, the population growth was modeled by the formula where t represented the number of years since 1975. In the year 2000, the census determined that the actual population was 104,250 people. What population did the model predict for the year 2000 and what was the actual error?
Because of radioactive decay, the amount of a 10 milligram sample of Iodine-131 decreases according to the formula where t represents time measured in days. How much of the sample remains after 10 days?
The number of cells in a bacteria sample is approximated by the logistic growth model where t represents time in hours. Determine the initial number of cells and then determine the number of cells 6 hours later.
The market share of a product, as a percentage, is approximated by the formula where t represents the number of months after an aggressive advertising campaign is launched. By how much can we expect the market share to increase after the first three months of advertising?
Why is b = 1 excluded as a base in the definition of exponential functions? Explain.
Explain why an exponential function of the form can never be negative.
Research and discuss the derivation of the compound interest formula.
Research and discuss the logistic growth model. Provide a link to more information on this topic.
Research and discuss the life and contributions of Leonhard Euler.
, ,
, ,
, ,
, ,
, ,
10.66
7.10
1385.46
−1.97
3.99
Domain: ; Range:
Domain: ; Range:
Domain: ; Range:
Domain: ; Range:
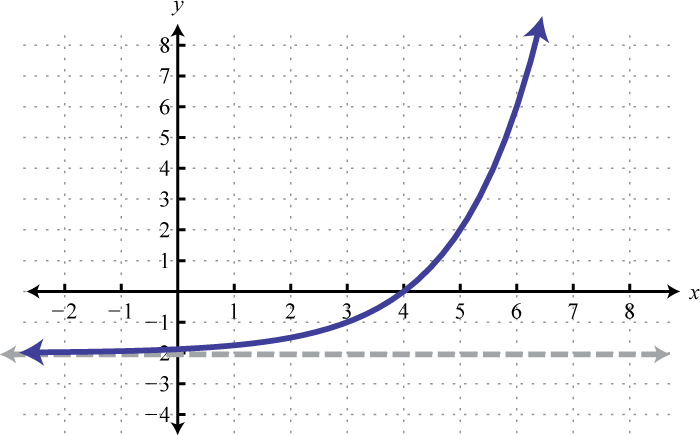
Domain: ; Range:
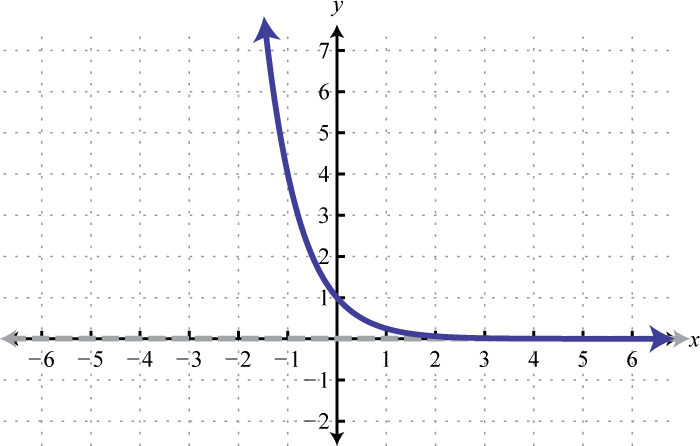
Domain: ; Range:
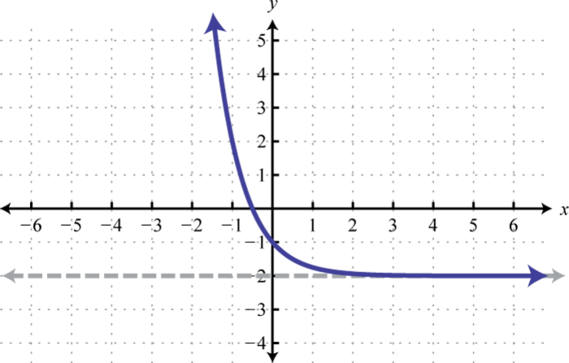
Domain: ; Range:
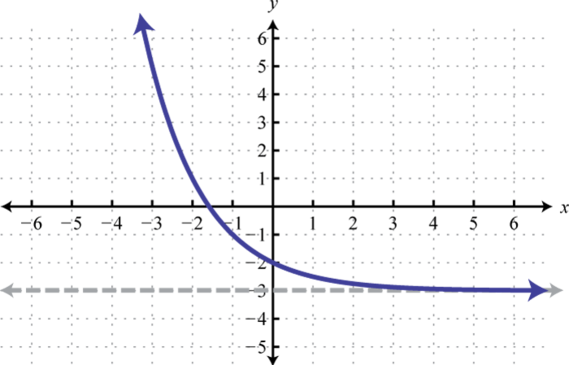
Domain: ; Range:

Domain: ; Range:
Domain: ; Range:
, ,
, ,
, ,
, ,

Domain: ; Range:
Domain: ; Range:
Domain: ; Range:
Domain: ; Range:
Domain: ; Range:
$850.52
$6,407.89
$16,066.13
$1,588.00
$4,685.44
$5,778.56
Initial population: 12,500; Population 6 years later: 14,077
New: $28,000; In 4 years: $13,940.40
After 30 days: 735 people; After 60 days: 540,365 people
Model: 99,423 people; error: 4,827 people
Initially there are 12,000 cells and 6 hours later there are 51,736 cells.
Answer may vary
Answer may vary
Answer may vary
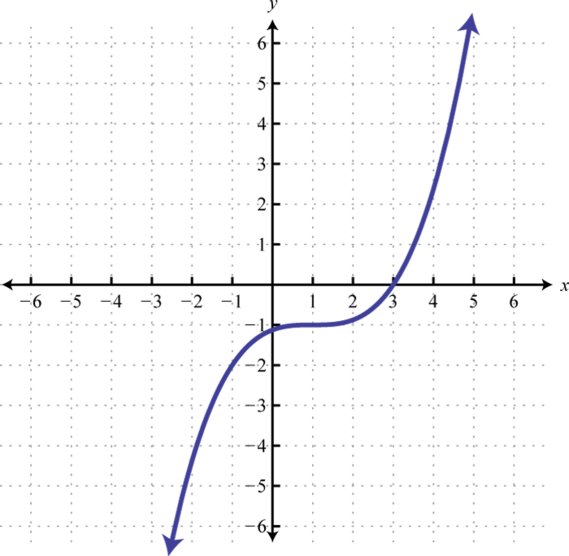
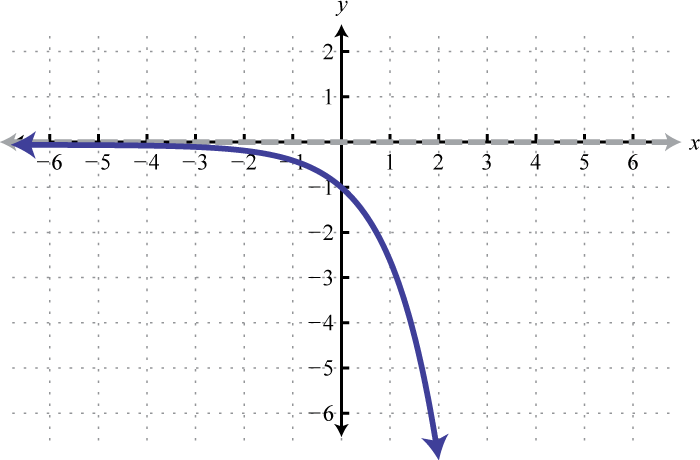
We begin with the exponential function defined by and note that it passes the horizontal line test.
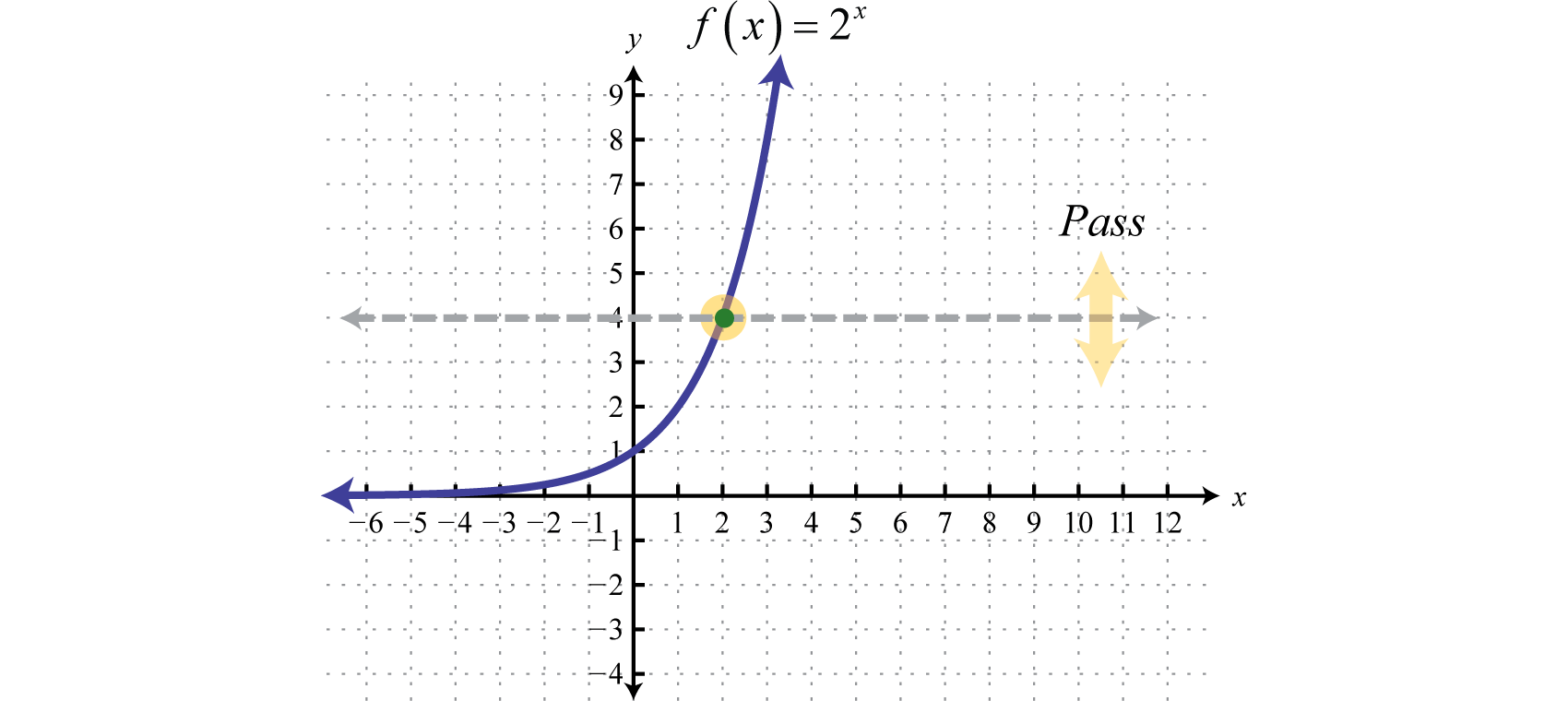
Therefore it is one-to-one and has an inverse. Reflecting about the line we can sketch the graph of its inverse. Recall that if is a point on the graph of a function, then will be a point on the graph of its inverse.
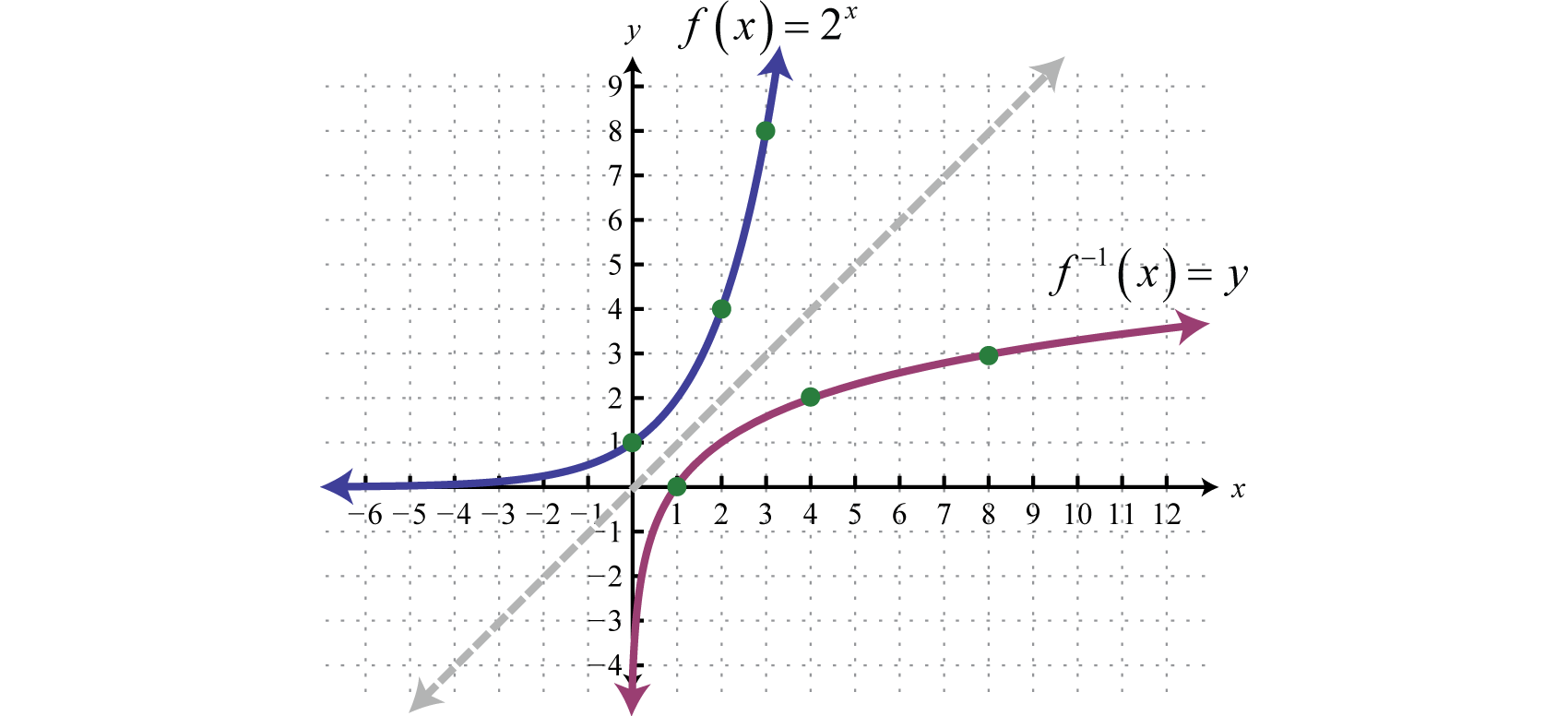
To find the inverse algebraically, begin by interchanging x and y and then try to solve for y.
We quickly realize that there is no method for solving for y. This function seems to “transcend” algebra. Therefore, we define the inverse to be the base-2 logarithm, denoted The following are equivalent:
This gives us another transcendental function defined by , which is the inverse of the exponential function defined by
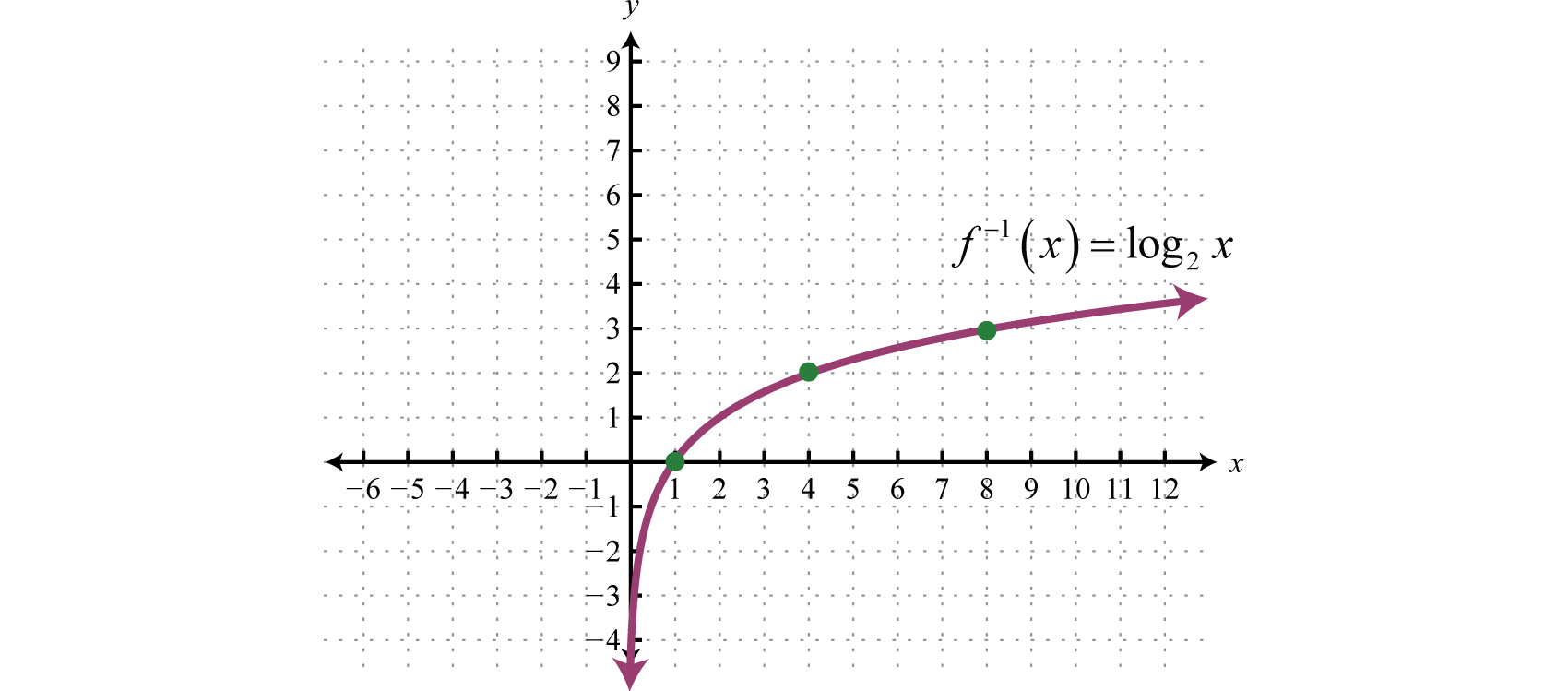
The domain consists of all positive real numbers and the range consists of all real numbers John Napier is widely credited for inventing the term logarithm.
Figure 7.2

John Napier (1550–1617)
In general, given base where , the logarithm base bThe exponent to which the base b is raised in order to obtain a specific value. In other words, is equivalent to is defined as follows:
Use this definition to convert logarithms to exponential form and back.
Logarithmic Form |
Exponential Form |
|---|---|
It is useful to note that the logarithm is actually the exponent y to which the base b is raised to obtain the argument x.
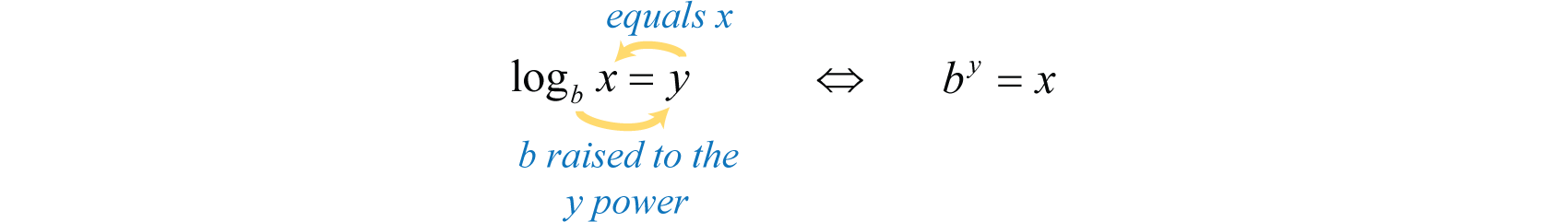
Evaluate:
Solution:
Note that the result of a logarithm can be negative or even zero. However, the argument of a logarithm is not defined for negative numbers or zero:
There is no power of two that results in −4 or 0. Negative numbers and zero are not in the domain of the logarithm. At this point it may be useful to go back and review all of the rules of exponents.
Find x:
Solution:
Convert each to exponential form and then simplify using the rules of exponents.
A logarithm can have any positive real number, other than 1, as its base. If the base is 10, the logarithm is called the common logarithmThe logarithm base 10, denoted .
When a logarithm is written without a base it is assumed to be the common logarithm. (Note: This convention varies with respect to the subject in which it appears. For example, computer scientists often let represent the logarithm base 2.)
Evaluate:
Solution:
The result of a logarithm is not always apparent. For example, consider
We can see that the result of is somewhere between 1 and 2. On most scientific calculators there is a common logarithm button Use it to find the as follows:
Therefore, rounded off to the nearest thousandth, As a check, we can use a calculator to verify that
If the base of a logarithm is , the logarithm is called the natural logarithmThe logarithm base e, denoted .
The natural logarithm is widely used and is often abbreviated
Evaluate:
Solution:
On a calculator you will find a button for the natural logarithm
Therefore, rounded off to the nearest thousandth, As a check, we can use a calculator to verify that
Find x. Round answers to the nearest thousandth.
Solution:
Convert each to exponential form and then use a calculator to approximate the answer.
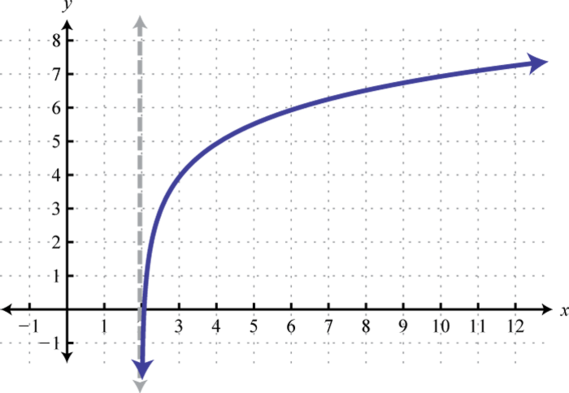
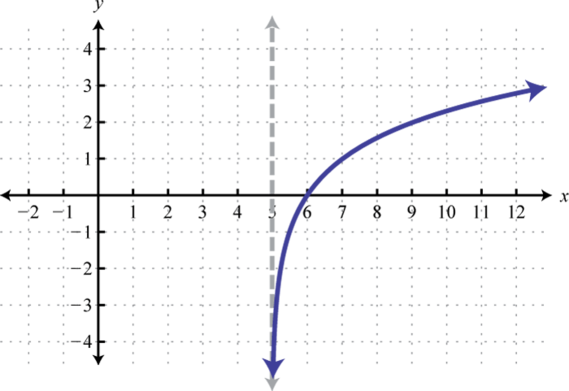
We can use the translations to graph logarithmic functions. When the base , the graph of has the following general shape:
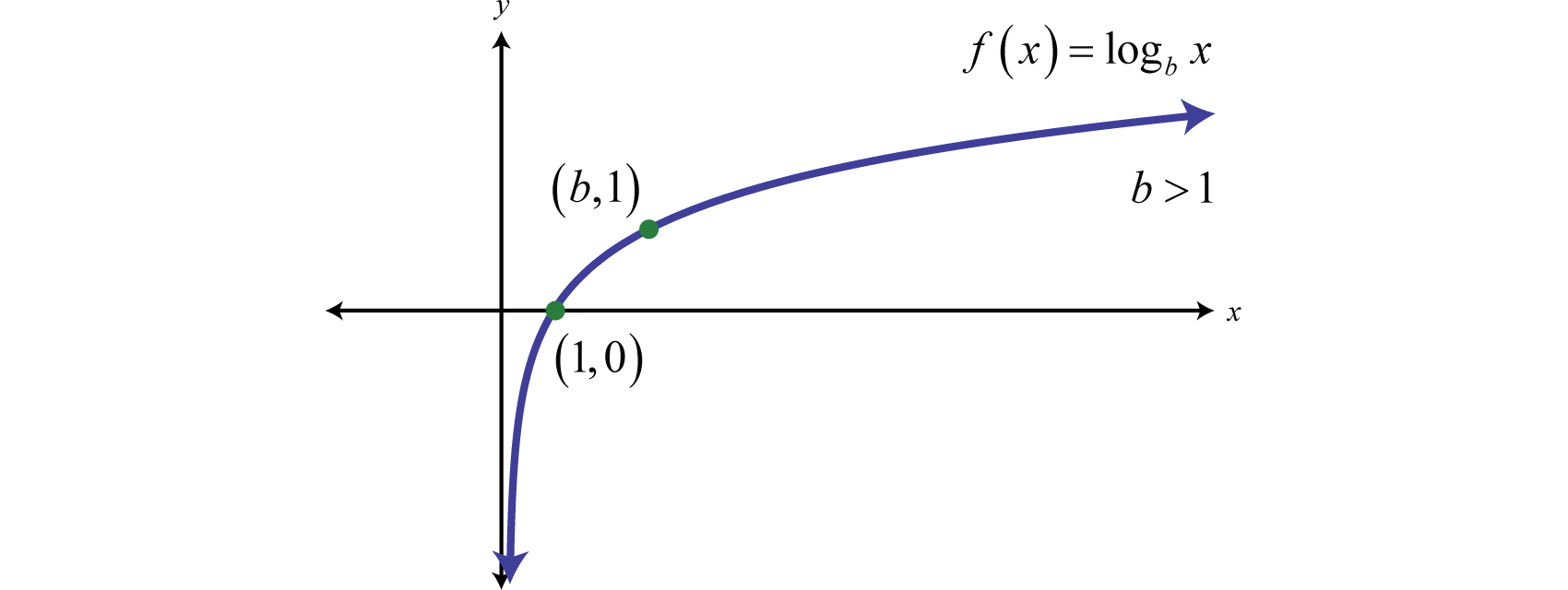
The domain consists of positive real numbers, and the range consists of all real numbers, The y-axis, or , is a vertical asymptote and the x-intercept is In addition, and so is a point on the graph no matter what the base is.
Sketch the graph and determine the domain and range:
Solution:
Begin by identifying the basic graph and the transformations.

Notice that the asymptote was shifted 4 units to the left as well. This defines the lower bound of the domain. The final graph is presented without the intermediate steps.
Answer:
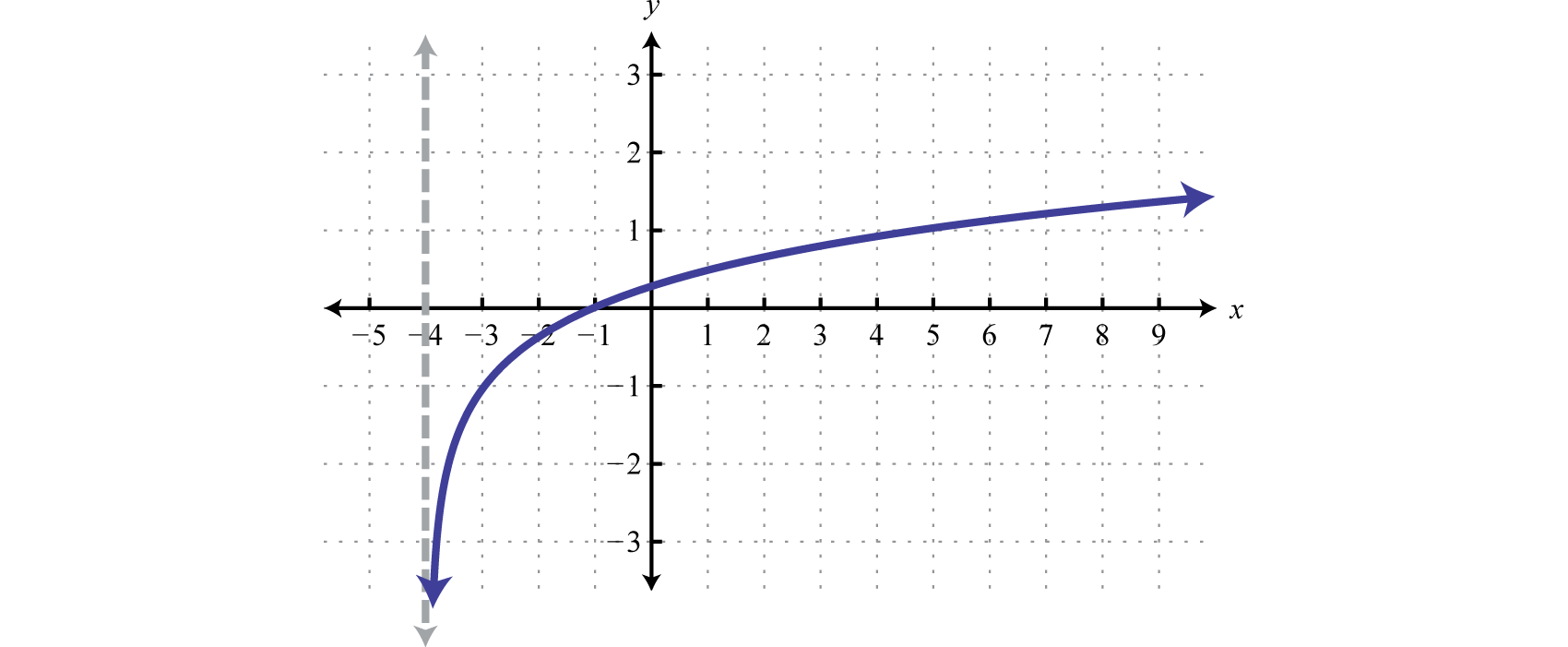
Domain: ; Range:
Note: Finding the intercepts of the graph in the previous example is left for a later section in this chapter. For now, we are more concerned with the general shape of logarithmic functions.
Sketch the graph and determine the domain and range:
Solution:
Begin by identifying the basic graph and the transformations.

Here the vertical asymptote was shifted two units to the right. This defines the lower bound of the domain.
Answer:
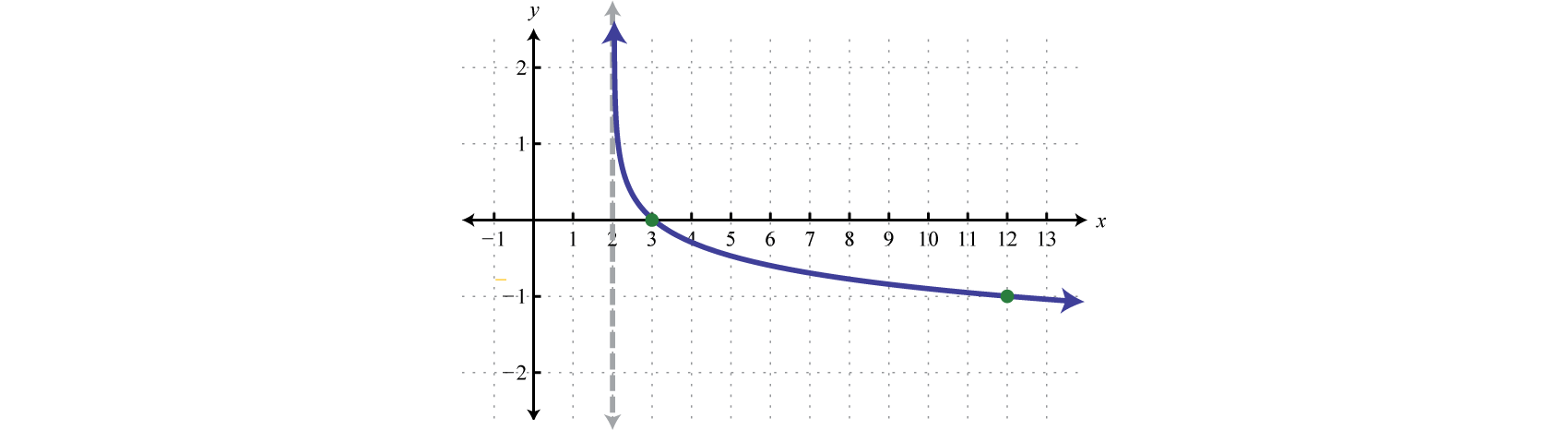
Domain: ; Range:
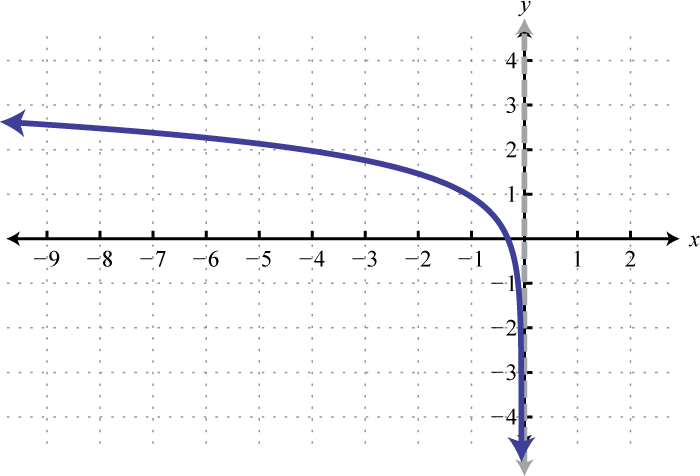
Try this! Sketch the graph and determine the domain and range:
Answer:
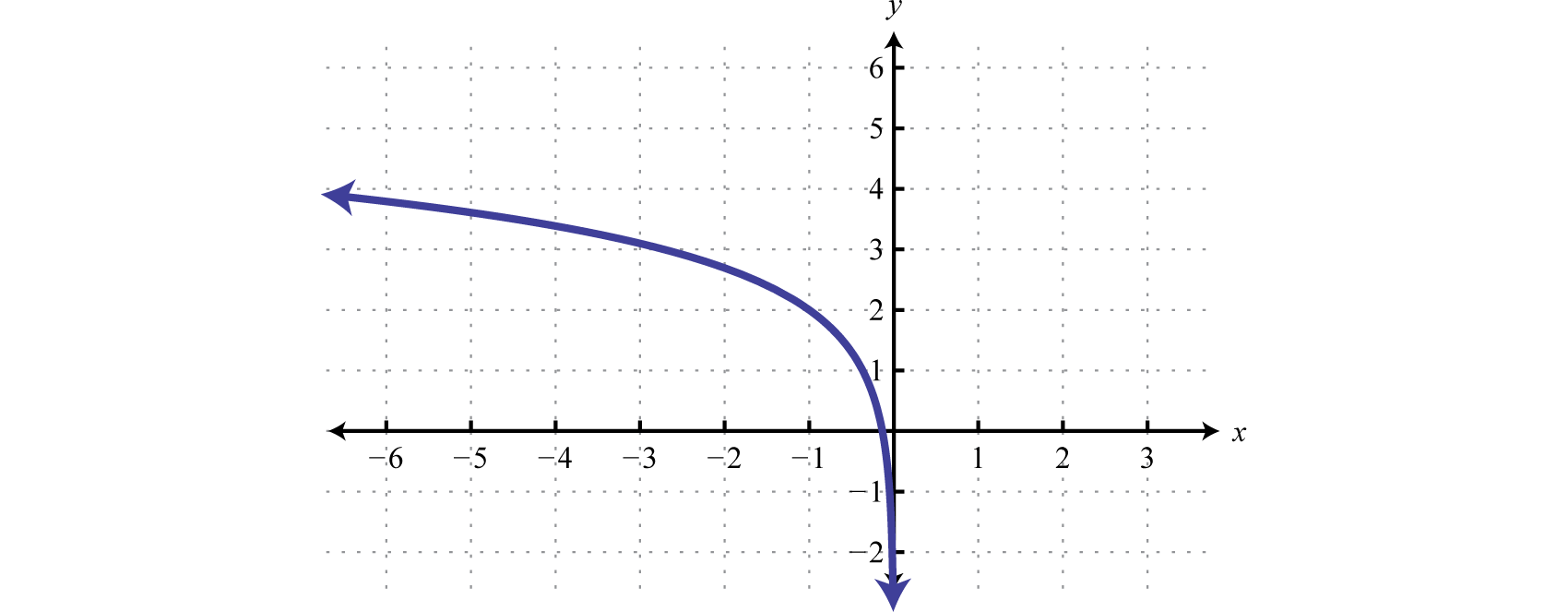
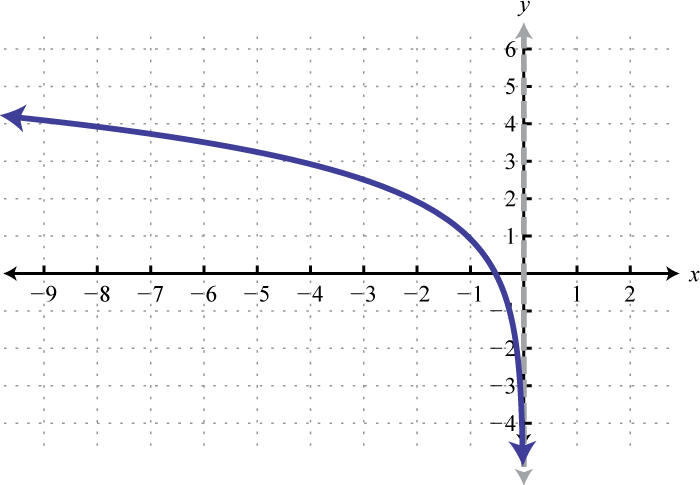
Domain: (−∞, 0); Range: (−∞, ∞)
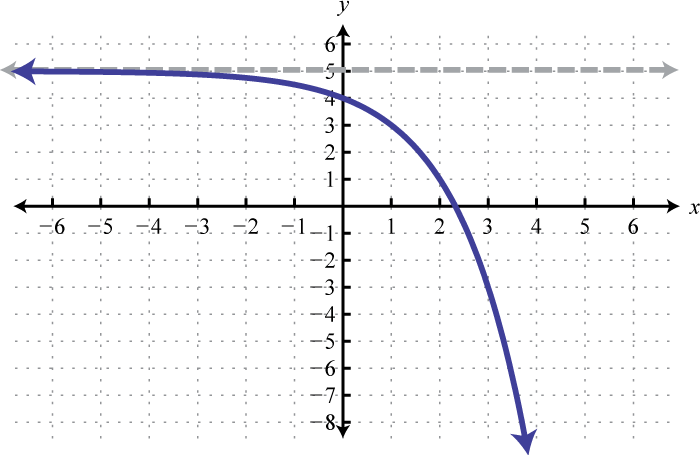
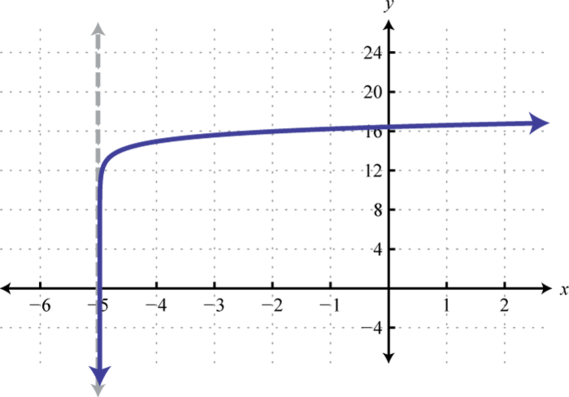
Next, consider exponential functions with fractional bases, such as the function defined by The domain consists of all real numbers. Choose some values for x and then find the corresponding y-values.
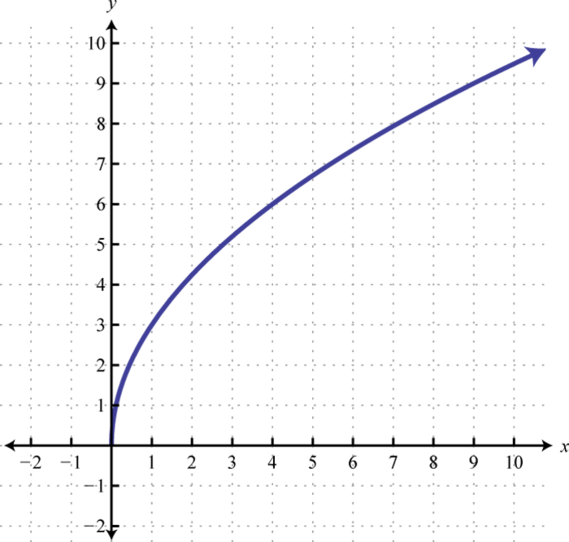
Use these points to sketch the graph and note that it passes the horizontal line test.
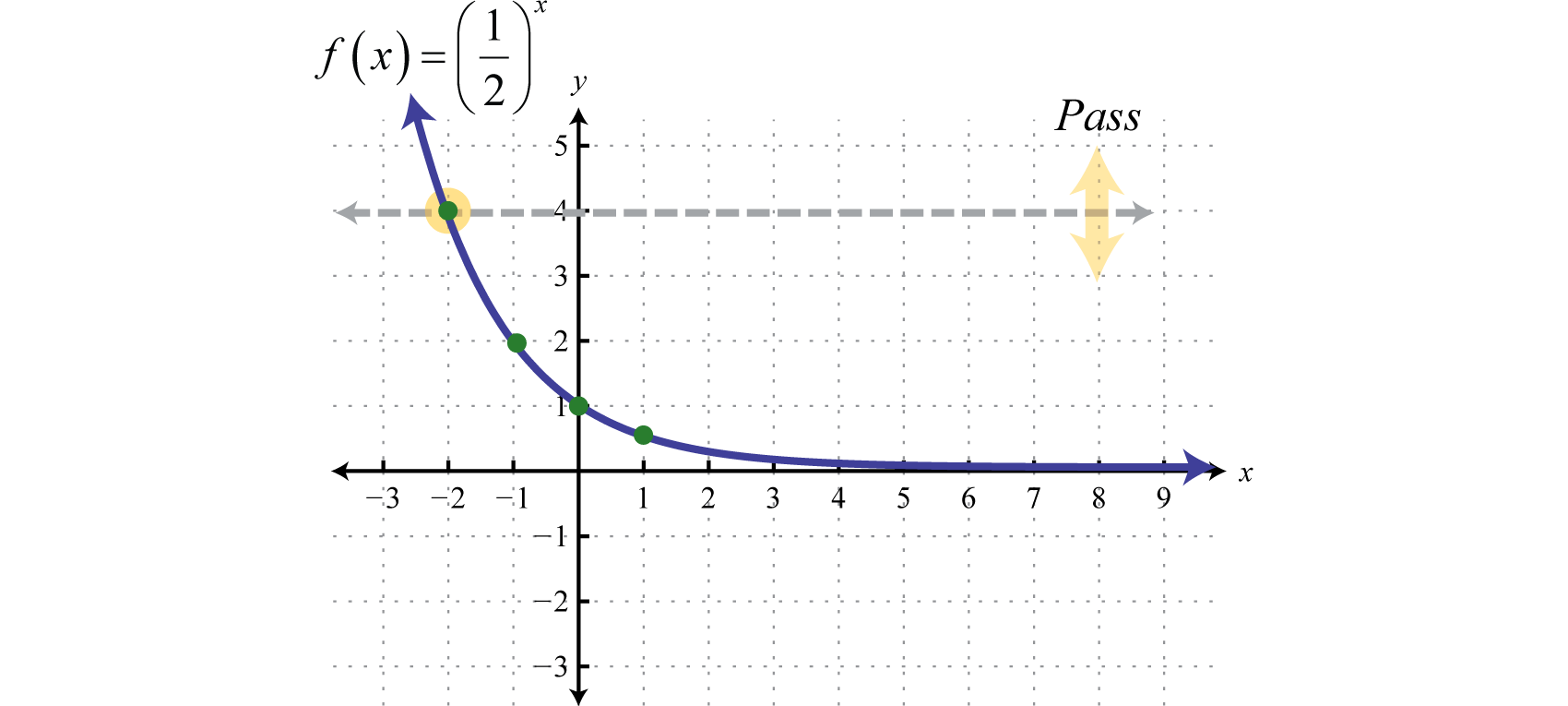
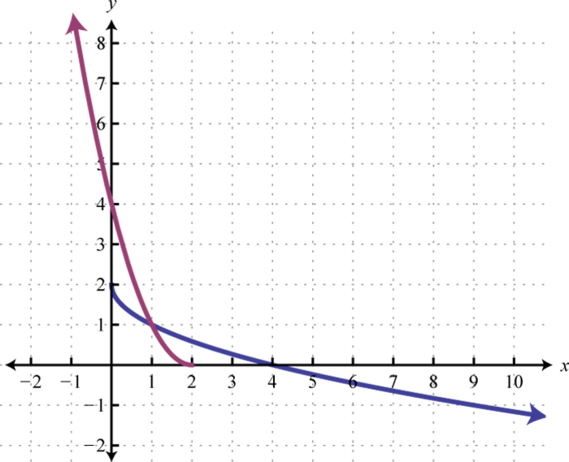
Therefore this function is one-to-one and has an inverse. Reflecting the graph about the line we have:
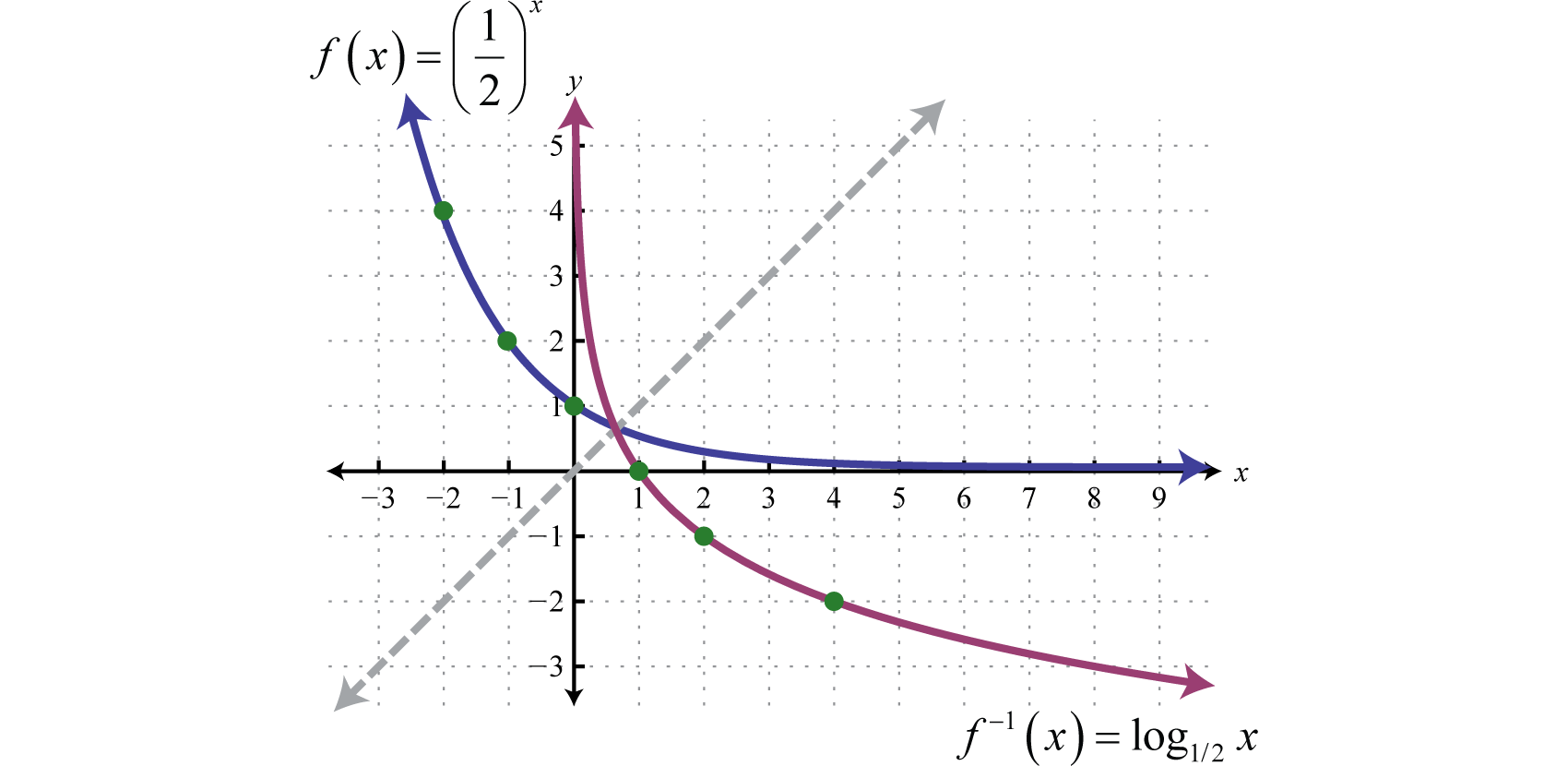
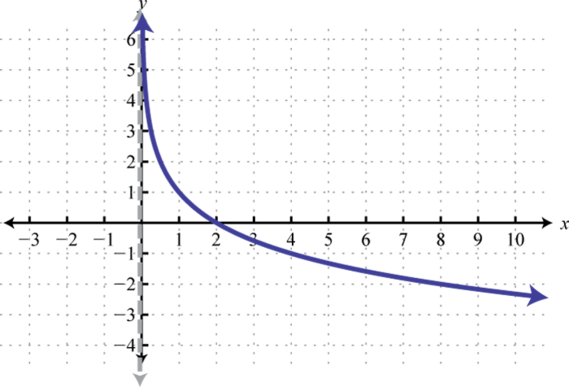
which gives us a picture of the graph of In general, when the base , the graph of the function defined by has the following shape.
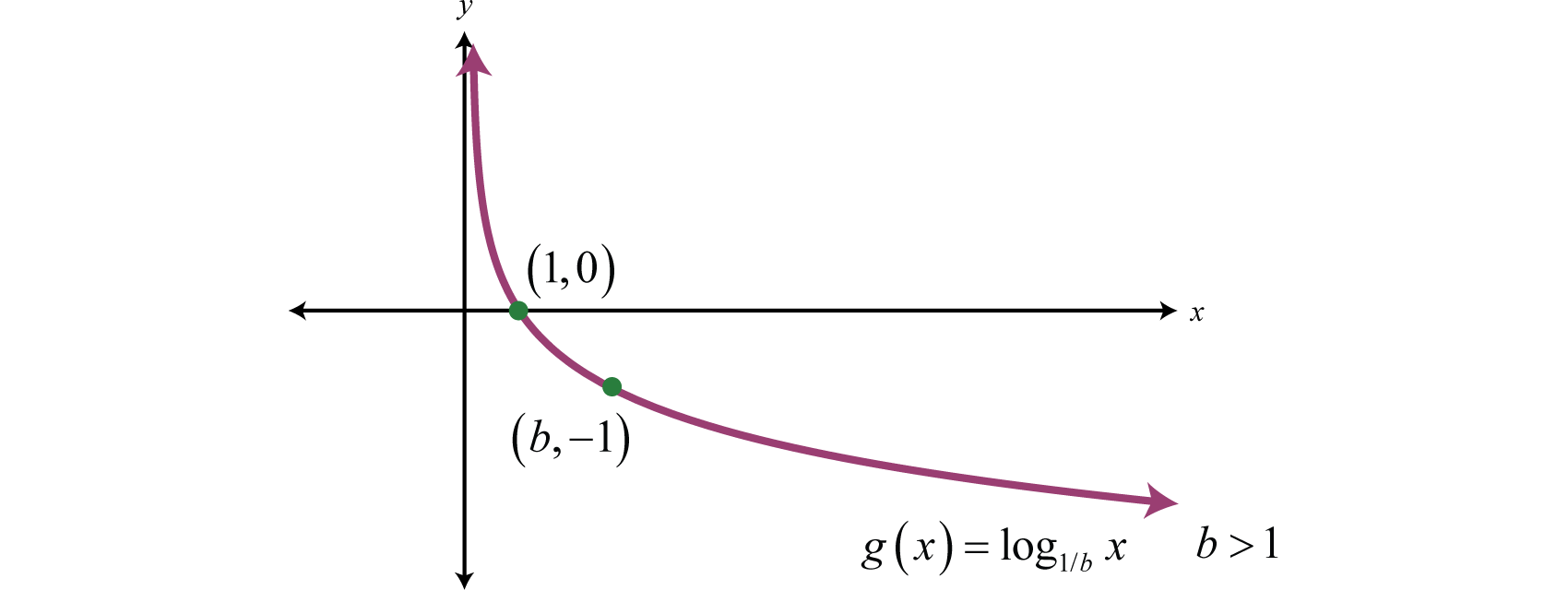
The domain consists of positive real numbers, and the range consists of all real numbers, The y-axis, or , is a vertical asymptote and the x-intercept is In addition, and so is a point on the graph.
Sketch the graph and determine the domain and range:
Solution:
Begin by identifying the basic graph and the transformations.
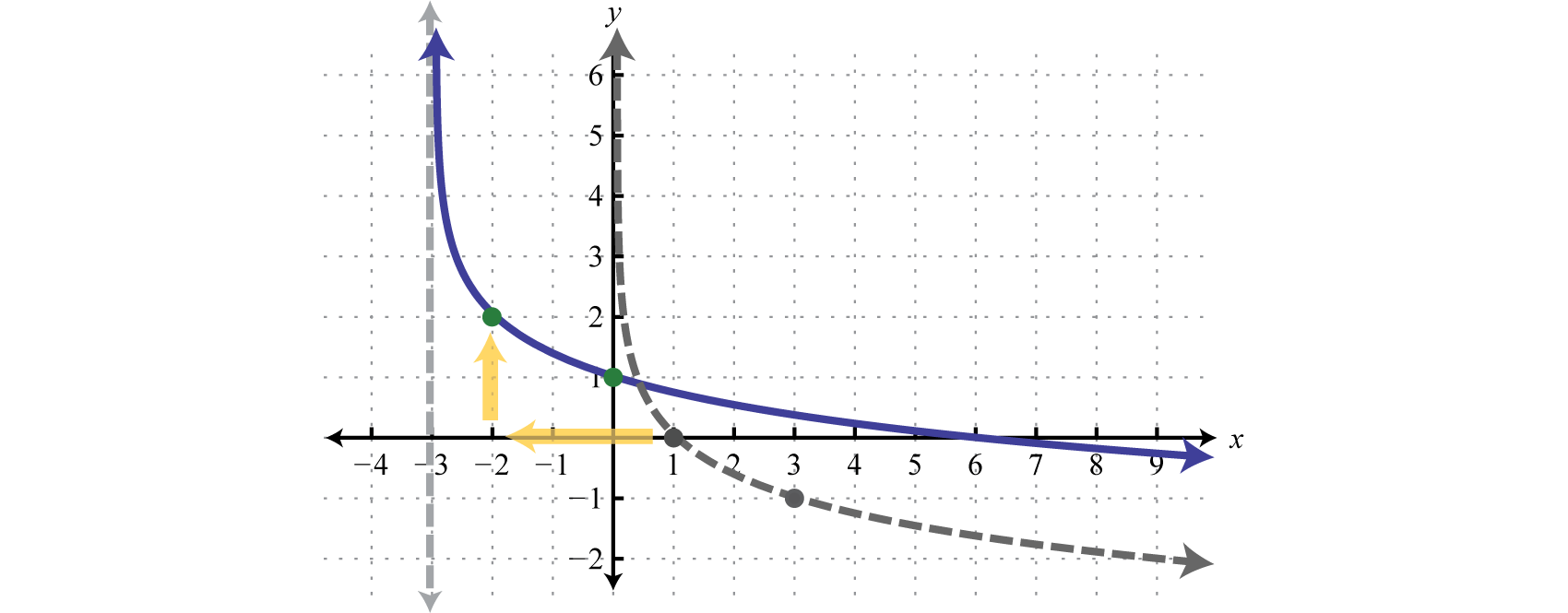
In this case the shift left 3 units moved the vertical asymptote to which defines the lower bound of the domain.
Answer:

Domain: ; Range:
In summary, if
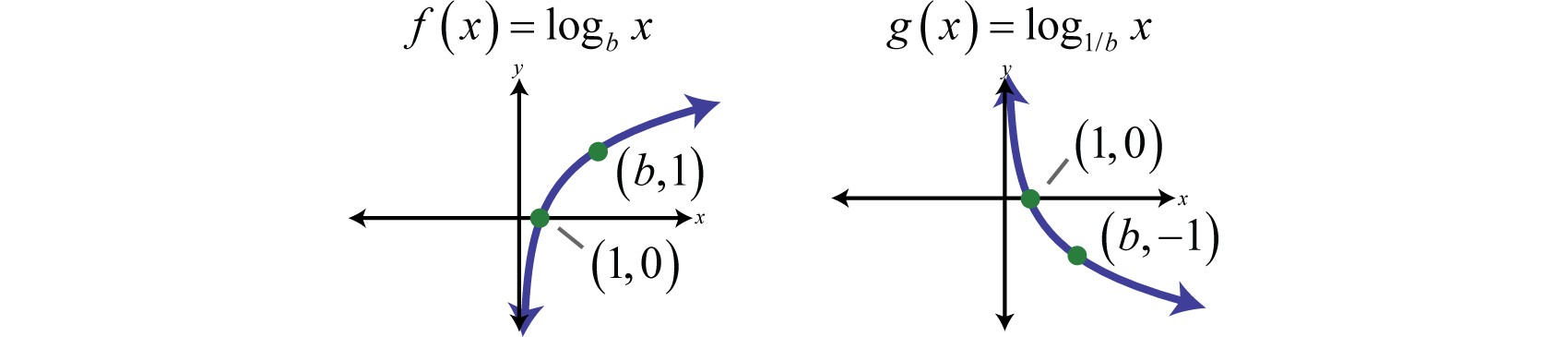
And for both cases,
Evaluate.
Find x.
Evaluate. Round off to the nearest hundredth where appropriate.
Find x. Round off to the nearest hundredth.
Find a without using a calculator.
In 1935 Charles Richter developed a scale used to measure earthquakes on a seismograph. The magnitude M of an earthquake is given by the formula,
Here I represents the intensity of the earthquake as measured on the seismograph 100 km from the epicenter and is the minimum intensity used for comparison. For example, if an earthquake intensity is measured to be 100 times that of the minimum, then and
The earthquake would be said to have a magnitude 2 on the Richter scale. Determine the magnitudes of the following intensities on the Richter scale. Round off to the nearest tenth.
I is 3 million times that of the minimum intensity.
I is 6 million times that of the minimum intensity.
I is the same as the minimum intensity.
I is 30 million times that of the minimum intensity.
In chemistry, pH is a measure of acidity and is given by the formula,
Here represents the hydrogen ion concentration (measured in moles of hydrogen per liter of solution.) Determine the pH given the following hydrogen ion concentrations.
Pure water:
Blueberry:
Lemon Juice:
Battery Acid:
Sketch the function and determine the domain and range. Draw the vertical asymptote with a dashed line.
Research and discuss the origins and history of the logarithm. How did students work with them before the common availability of calculators?
Research and discuss the history and use of the Richter scale. What does each unit on the Richter scale represent?
Research and discuss the life and contributions of John Napier.
2
1
4
−4
−3
10
−2
1
0
81
1
16
3
3
−1
2.21
−1.60
4
−1
3.22
−2.08
316.23
0.06
22.20
0.50
−3
256
12
2
6.5
0
7
2
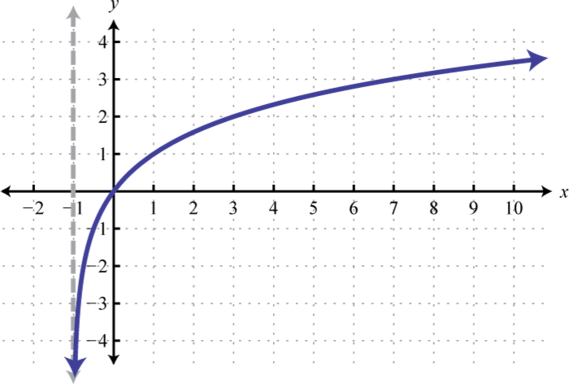
Domain: ; Range:
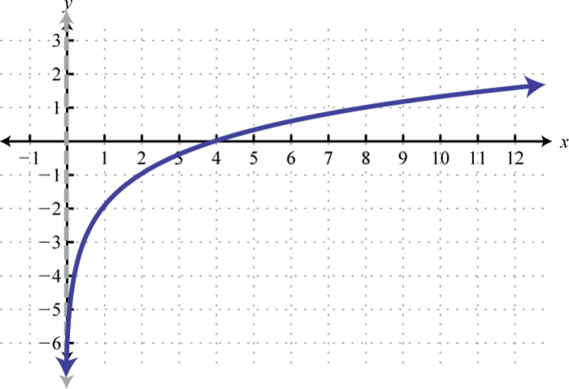
Domain: ; Range:
Domain: ; Range:
Domain: ; Range:
Domain: ; Range:
Domain: ; Range:
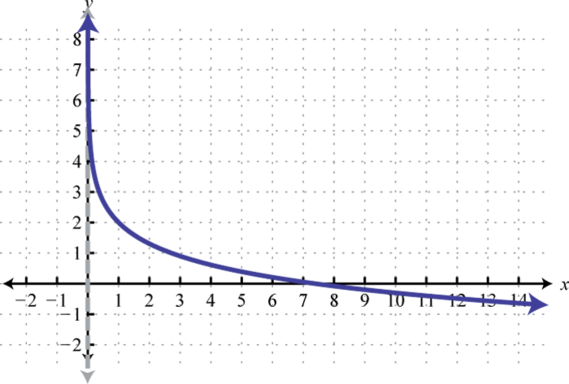
Domain: ; Range:
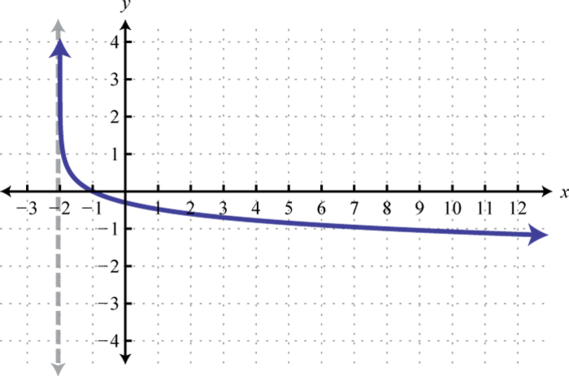
Domain: ; Range:

Domain: ; Range:
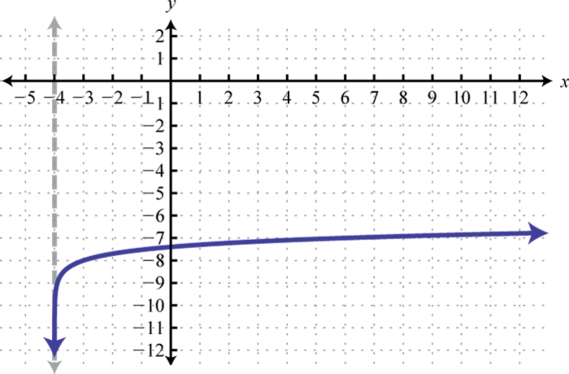
Domain: ; Range:
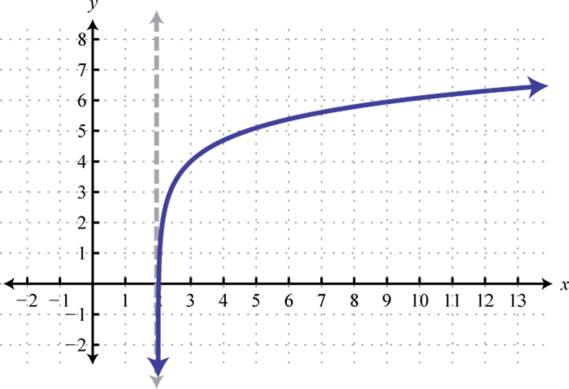
Domain: ; Range:
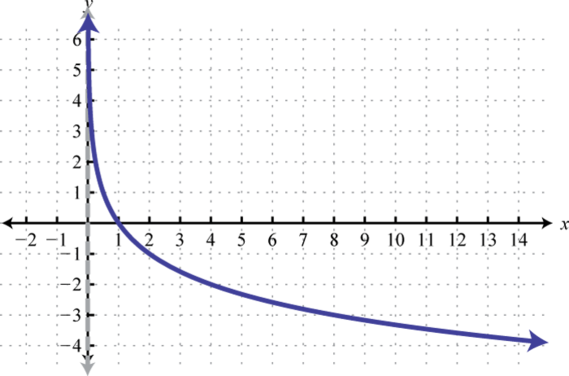
Domain: ; Range:
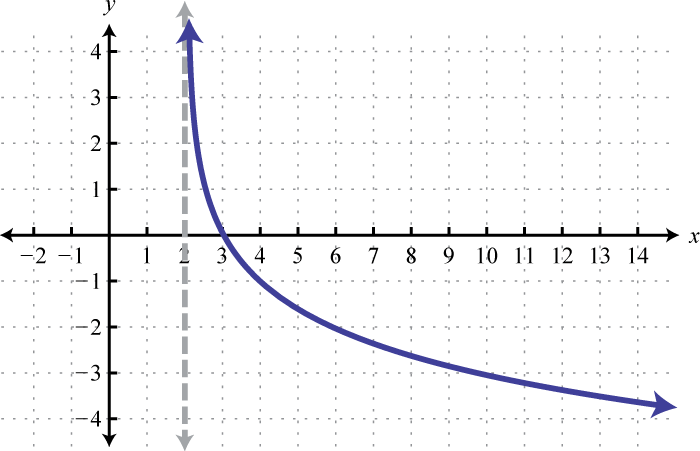
Domain: ; Range:
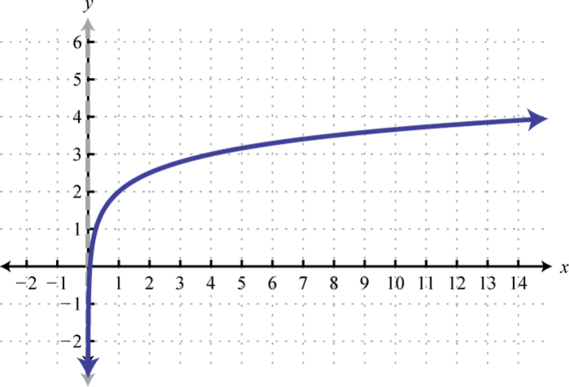
Domain: ; Range:
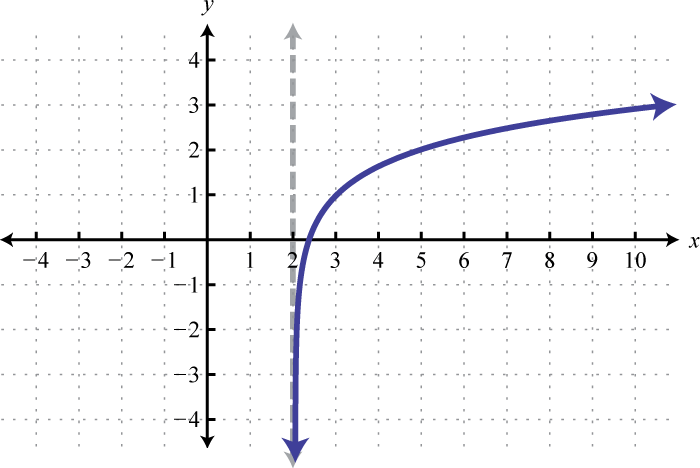
Domain: ; Range:
Answer may vary
Answer may vary
Recall the definition of the base-b logarithm: given where ,
Use this definition to convert logarithms to exponential form. Doing this, we can derive a few properties:
Evaluate:
Solution:
When the base is not written, it is assumed to be 10. This is the common logarithm,
The natural logarithm, by definition, has base e,
Because we have,
Furthermore, consider fractional bases of the form where
Evaluate:
Solution:
Given an exponential function defined by , where and , its inverse is the base-b logarithm, And because and , we have the following inverse properties of the logarithmGiven we have and when :
Since has a domain consisting of positive values , the property is restricted to values where
Evaluate:
Solution:
Apply the inverse properties of the logarithm.
In summary, when and , we have the following properties:
, |
In this section, three very important properties of the logarithm are developed. These properties will allow us to expand our ability to solve many more equations. We begin by assigning u and v to the following logarithms and then write them in exponential form:
Substitute and into the logarithm of a product and the logarithm of a quotient Then simplify using the rules of exponents and the inverse properties of the logarithm.
Logarithm of a Product |
Logarithm of a Quotient |
|---|---|
This gives us two essential properties: the product property of logarithms the logarithm of a product is equal to the sum of the logarithm of the factors.,
and the quotient property of logarithms the logarithm of a quotient is equal to the difference of the logarithm of the numerator and the logarithm of the denominator.,
In words, the logarithm of a product is equal to the sum of the logarithm of the factors. Similarly, the logarithm of a quotient is equal to the difference of the logarithm of the numerator and the logarithm of the denominator.
Write as a sum:
Solution:
Apply the product property of logarithms and then simplify.
Answer:
Write as a difference: .
Solution:
Apply the quotient property of logarithms and then simplify.
Answer:
Next we begin with and rewrite it in exponential form. After raising both sides to the nth power, convert back to logarithmic form, and then back substitute.
This leads us to the power property of logarithms; the logarithm of a quantity raised to a power is equal to that power times the logarithm of the quantity.,
In words, the logarithm of a quantity raised to a power is equal to that power times the logarithm of the quantity.
Write as a product:
Solution:
Apply the power property of logarithms.
Recall that a square root can be expressed using rational exponents, Make this replacement and then apply the power property of logarithms.
In summary,
Product property of logarithms |
|
Quotient property of logarithms |
|
Power property of logarithms |
We can use these properties to expand logarithms involving products, quotients, and powers using sums, differences and coefficients. A logarithmic expression is completely expanded when the properties of the logarithm can no further be applied.
It is important to point out the following:
Expand completely:
Solution:
Recall that the natural logarithm is a logarithm base e, Therefore, all of the properties of the logarithm apply.
Answer:
Expand completely:
Solution:
Begin by rewriting the cube root using the rational exponent and then apply the properties of the logarithm.
Answer:
Expand completely: .
Solution:
When applying the product property to the denominator, take care to distribute the negative obtained from applying the quotient property.
Answer:
Caution: There is no rule that allows us to expand the logarithm of a sum or difference. In other words,
Given that , , and that , write the following in terms of a, b and c:
a.
b.
Solution:
Begin by expanding using sums and coefficients and then replace a and b with the appropriate logarithm.
Expand and then replace a, b, and c where appropriate.
Next we will condense logarithmic expressions. As we will see, it is important to be able to combine an expression involving logarithms into a single logarithm with coefficient 1. This will be one of the first steps when solving logarithmic equations.
Write as a single logarithm with coefficient
Solution:
Begin by rewriting all of the logarithmic terms with coefficient 1. Use the power rule to do this. Then use the product and quotient rules to simplify further.
Answer:
Write as a single logarithm with coefficient
Solution:
Begin by writing the coefficients of the logarithms as powers of their argument, after which we will apply the quotient rule twice working from left to right.
Answer:
Evaluate:
Find a:
Expand completely.
Given , , and , write the following logarithms in terms of a, b, and c.
Given , , and , calculate the following. (Hint: Expand using sums, differences, and quotients of the factors 2, 3, and 7.)
Expand using the properties of the logarithm and then approximate using a calculator to the nearest tenth.
Write as a single logarithm with coefficient 1.
Express as a single logarithm and simplify.
0
14
10
7
1
−1
100
18
4
2.32
0.71
An exponential equationAn equation which includes a variable as an exponent. is an equation that includes a variable as one of its exponents. In this section we describe two methods for solving exponential equations. First, recall that exponential functions defined by where and , are one-to-one; each value in the range corresponds to exactly one element in the domain. Therefore, implies The converse is true because f is a function. This leads to the very important one-to-one property of exponential functionsGiven and we have if and only if :
Use this property to solve special exponential equations where each side can be written in terms of the same base.
Solve:
Solution:
Begin by writing 27 as a power of 3.
Next apply the one-to-one property of exponential functions. In other words, set the exponents equal to each other and then simplify.
Answer: 2
Solve:
Solution:
Begin by writing 16 as a power of 2 and then apply the power rule for exponents.
Now that the bases are the same we can set the exponents equal to each other and simplify.
Answer:
In many cases we will not be able to equate the bases. For this reason we develop a second method for solving exponential equations. Consider the following equations:
We can see that the solution to should be somewhere between 2 and 3. A graphical interpretation follows.
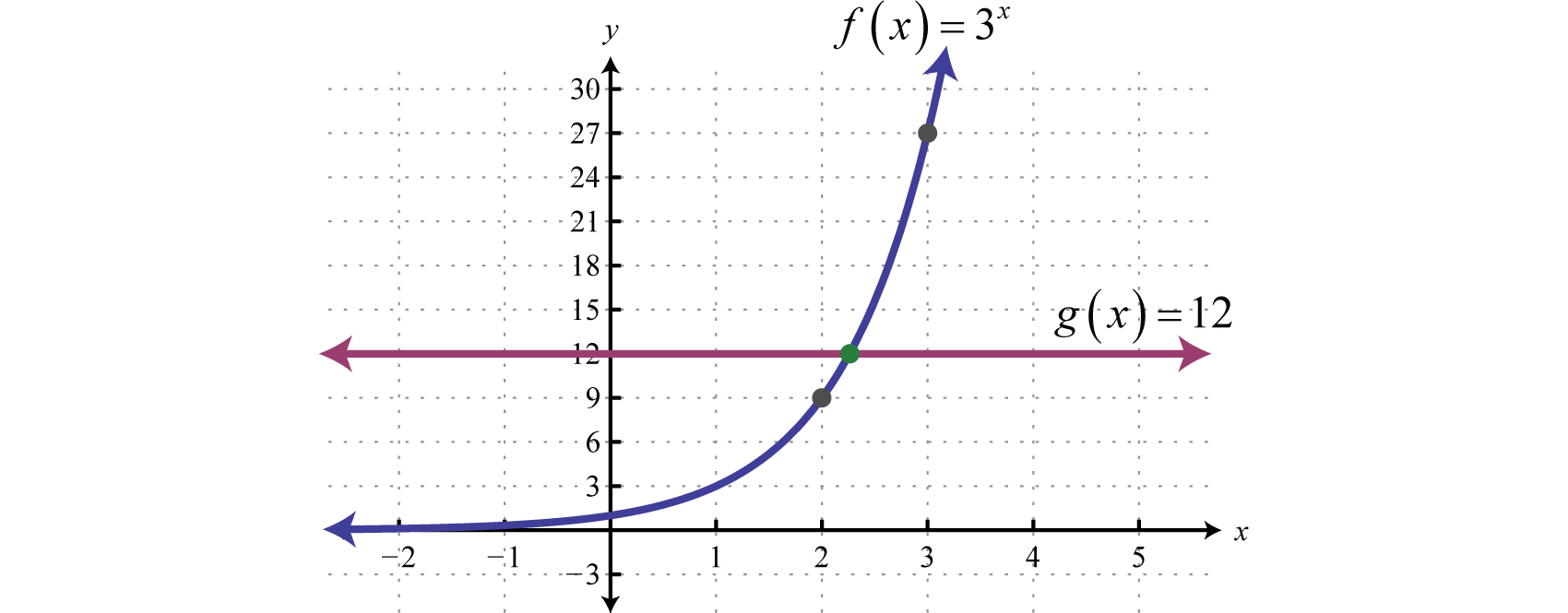
To solve this we make use of fact that logarithms are one-to-one functions. Given the one-to-one property of logarithmsGiven and where we have if and only if follows:
This property, as well as the properties of the logarithm, allows us to solve exponential equations. For example, to solve apply the common logarithm to both sides and then use the properties of the logarithm to isolate the variable.
Approximating to four decimal places on a calculator.
An answer between 2 and 3 is what we expected. Certainly we can check by raising 3 to this power to verify that we obtain a good approximation of 12.
Note that we are not multiplying both sides by “log”; we are applying the one-to-one property of logarithmic functions — which is often expressed as “taking the log of both sides.” The general steps for solving exponential equations are outlined in the following example.
Solve:
Solution:
Step 1: Isolate the exponential expression.
Step 2: Take the logarithm of both sides. In this case, we will take the common logarithm of both sides so that we can approximate our result on a calculator.
Step 3: Apply the power rule for logarithms and then solve.
This is an irrational number which can be approximated using a calculator. Take care to group the numerator and the product in the denominator when entering this into your calculator. To do this, make use of the parenthesis buttons and :
Answer:
Solve:
Solution:
The exponential function is already isolated and the base is e. Therefore, we choose to apply the natural logarithm to both sides.
Apply the power rule for logarithms and then simplify.
Answer:
On most calculators there are only two logarithm buttons, the common logarithm and the natural logarithm If we want to approximate we have to somehow change this base to 10 or e. The idea begins by rewriting the logarithmic function , in exponential form.
Here and so we can apply the one-to-one property of logarithms. Apply the logarithm base b to both sides of the function in exponential form.
And then solve for y.
Replace y into the original function and we have the very important change of base formula; we can write any base-a logarithm in terms of base-b logarithms using this formula.:
We can use this to approximate as follows.
Notice that the result is independent of the choice of base. In words, we can approximate the logarithm of any given base on a calculator by dividing the logarithm of the argument by the logarithm of that given base.
Approximate the nearest hundredth.
Solution:
Apply the change of base formula and use a calculator.
On a calculator,
Answer: 2.46
Try this! Solve: Give the exact and approximate answer rounded to four decimal places.
Answer:
A logarithmic equationAn equation that involves a logarithm with a variable argument. is an equation that involves a logarithm with a variable argument. Some logarithmic equations can be solved using the one-to-one property of logarithms. This is true when a single logarithm with the same base can be obtained on both sides of the equal sign.
Solve:
Solution:
We can obtain two equal logarithms base 2 by adding to both sides of the equation.
Here the bases are the same and so we can apply the one-to-one property and set the arguments equal to each other.
Checking in the original equation:
Answer: 3
When solving logarithmic equations the check is very important because extraneous solutions can be obtained. The properties of the logarithm only apply for values in the domain of the given logarithm. And when working with variable arguments, such as , the value of x is not known until the end of this process. The logarithmic expression is only defined for values
Solve:
Solution:
Apply the one-to-one property of logarithms (set the arguments equal to each other) and then solve for x.
When performing the check we encounter a logarithm of a negative number:
Try this on a calculator, what does it say? Here is not in the domain of Therefore our only possible solution is extraneous and we conclude that there are no solutions to this equation.
Answer: No solution, Ø.
Caution: Solving logarithmic equations sometimes leads to extraneous solutions — we must check our answers.
In many cases we will not be able to obtain two equal logarithms. To solve such equations we make use of the definition of the logarithm. If , where , then implies that Consider the following common logarithmic equations (base 10),
We can see that the solution to will be somewhere between 1 and 10. A graphical interpretation follows.
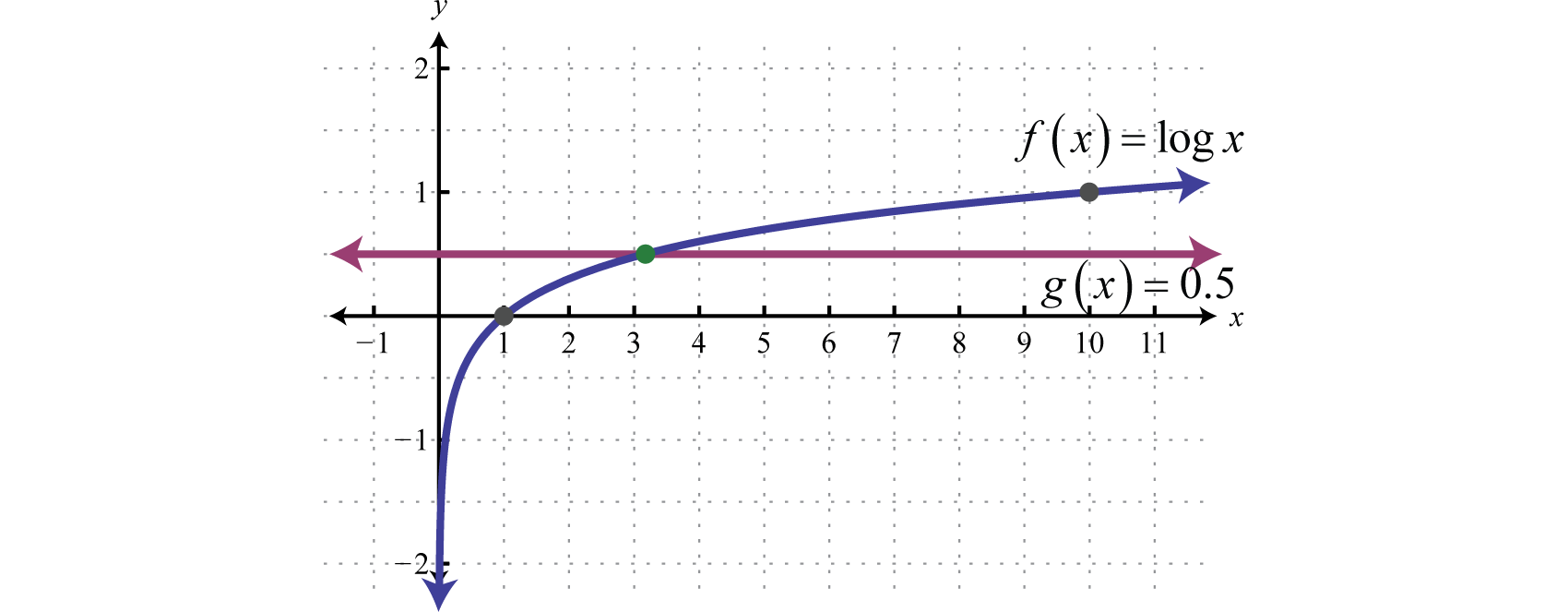
To find x we can apply the definition as follows.
This can be approximated using a calculator,
An answer between 1 and 10 is what we expected. Check this on a calculator.
Solve:
Solution:
Apply the definition of the logarithm.
Solve the resulting equation.
Check.
Answer: 7
In order to apply the definition, we will need to rewrite logarithmic expressions as a single logarithm with coefficient 1.The general steps for solving logarithmic equations are outlined in the following example.
Solve:
Solution:
Step 1: Write all logarithmic expressions as a single logarithm with coefficient 1. In this case, apply the product rule for logarithms.
Step 2: Use the definition and rewrite the logarithm in exponential form.
Step 3: Solve the resulting equation. Here we can solve by factoring.
Step 4: Check. This step is required.
Check |
Check |
|---|---|
In this example, is not in the domain of the given logarithmic expression and is extraneous. The only solution is
Answer: 4
Solve:
Solution:
Begin by writing all logarithmic expressions on one side and constants on the other.
Apply the quotient rule for logarithms as a means to obtain a single logarithm with coefficient 1.
This is a common logarithm; therefore use 10 as the base when applying the definition.
Check.
Answer: −5
Find the inverse:
Solution:
Begin by replacing the function notation with y.
Interchange x and y and then solve for y.
The resulting function is the inverse of f. Present the answer using function notation.
Answer:
Solve using the one-to-one property of exponential functions.
Solve. Give the exact answer and the approximate answer rounded to the nearest thousandth.
Find the x- and y-intercepts of the given function.
Use a u-substitution to solve the following.
(Hint: Let )
Use the change of base formula to approximate the following to the nearest hundredth.
If left unchecked, a new strain of flu virus can spread from a single person to others very quickly. The number of people affected can be modeled using the formula , where t represents the number of days the virus is allowed to spread unchecked. Estimate the number of days it will take 1,000 people to become infected.
The population of a certain small town is growing according to the function , where t represents time in years since the last census. Use the function to determine number of years it will take the population to grow to 25,000 people.
Solve using the one-to-one property of logarithms.
Solve.
Find the x- and y-intercepts of the given function.
Find the inverse of the following functions.
Solve.
In chemistry, pH is a measure of acidity and is given by the formula , where is the hydrogen ion concentration (measured in moles of hydrogen per liter of solution.) Determine the hydrogen ion concentration if the pH of a solution is 4.
The volume of sound, L in decibels (dB), is given by the formula where I represents the intensity of the sound in watts per square meter. Determine the intensity of an alarm that emits 120 dB of sound.
Research and discuss the history and use of the slide rule.
Research and discuss real-world applications involving logarithms.
4
3
−2, 1
, 3
Ø
x-intercept: ; y-intercept:
x-intercept: None; y-intercept:
x-intercept: None; y-intercept:
1
0,
2.32
−0.25
−3.32
1.16
Approximately 31 days
10
−2
, 3
1
13
−5
±3
13
8
2
9
Ø
x-intercept: ; y-intercept:
x-intercept: ; y-intercept: None
x-intercept: ; y-intercept:
55
1
Ø
moles per liter
Answer may vary
Recall that compound interest occurs when interest accumulated for one period is added to the principal investment before calculating interest for the next period. The amount A accrued in this manner over time t is modeled by the compound interest formula:
Here the initial principal P is accumulating compound interest at an annual rate r where the value n represents the number of times the interest is compounded in a year.
Susan invested $500 in an account earning % annual interest that is compounded monthly.
Solution:
In this example, the principal , the interest rate , and because the interest is compounded monthly, The investment can be modeled by the following function:
Use this model to calculate the amount in the account after years.
Rounded off to the nearest cent, after 3 years, the amount accumulated will be $572.12.
To calculate the time it takes to accumulate $750, set and solve for t.
This results in an exponential equation that can be solved by first isolating the exponential expression.
At this point take the common logarithm of both sides, apply the power rule for logarithms, and then solve for t.
Using a calculator we can approximate the time it takes.
Answer:
The period of time it takes a quantity to double is called the doubling timeThe period of time it takes a quantity to double.. We next outline a technique for calculating the time it takes to double an initial investment earning compound interest.
Mario invested $1,000 in an account earning 6.3% annual interest that is compounded semi-annually. How long will it take the investment to double?
Solution:
Here the principal , the interest rate , and because the interest is compounded semi-annually This investment can be modeled as follows:
Since we are looking for the time it takes to double $1,000, substitute $2,000 for the resulting amount and then solve for t.
At this point we take the common logarithm of both sides.
Using a calculator we can approximate the time it takes:
Answer: Approximately 11.17 years to double at 6.3%.
If the investment in the previous example was one million dollars, how long would it take to double? To answer this we would use and :
Dividing both sides by 1,000,000 we obtain the same exponential function as before.
Hence, the result will be the same, about 11.17 years. In fact, doubling time is independent of the initial investment P.
Interest is typically compounded semi-annually (n = 2), quarterly (n = 4), monthly (n = 12), or daily (n = 365). However if interest is compounded every instant we obtain a formula for continuously compounding interest:
Here P represents the initial principal amount invested, r represents the annual interest rate, and t represents the time in years the investment is allowed to accrue continuously compounded interest.
Mary invested $200 in an account earning % annual interest that is compounded continuously. How long will it take the investment to grow to $350?
Solution:
Here the principal and the interest rate Since the interest is compounded continuously, use the formula Hence, the investment can be modeled by the following,
To calculate the time it takes to accumulate to $350, set and solve for t.
Begin by isolating the exponential expression.
Because this exponential has base e, we choose to take the natural logarithm of both sides and then solve for t.
Using a calculator we can approximate the time it takes:
Answer: It will take approximately 9.73 years.
When solving applications involving compound interest, look for the keyword “continuous,” or the keywords that indicate the number of annual compoundings. It is these keywords that determine which formula to choose.
Try this! Mario invested $1,000 in an account earning 6.3% annual interest that is compounded continuously. How long will it take the investment to double?
Answer: Approximately 11 years.
In the sciences, when a quantity is said to grow or decay exponentially, it is specifically meant to be modeled using the exponential growth/decay formulaA formula that models exponential growth or decay: :
Here , read “P naught,” or “P zero,” represents the initial amount, k represents the growth rate, and t represents the time the initial amount grows or decays exponentially. If k is negative, then the function models exponential decay. Notice that the function looks very similar to that of continuously compounding interest formula. We can use this formula to model population growth when conditions are optimal.
It is estimated that the population of a certain small town is 93,000 people with an annual growth rate of 2.6%. If the population continues to increase exponentially at this rate:
Solution:
We begin by constructing a mathematical model based on the given information. Here the initial population people and the growth rate The following model gives population in terms of time measured in years:
Use this function to estimate the population in years.
Use the model to determine the time it takes to reach people.
Take the natural logarithm of both sides and then solve for t.
Using a calculator,
Answer:
Often the growth rate k is not given. In this case, we look for some other information so that we can determine it and then construct a mathematical model. The general steps are outlined in the following example.
Under optimal conditions Escherichia coli (E. coli) bacteria will grow exponentially with a doubling time of 20 minutes. If 1,000 E. coli cells are placed in a Petri dish and maintained under optimal conditions, how many E. coli cells will be present in 2 hours?
Figure 7.3
Escherichia coli (E. coli) (Wikipedia)
Solution:
The goal is to use the given information to construct a mathematical model based on the formula
Step 1: Find the growth rate k. Use the fact that the initial amount, cells, doubles in 20 minutes. That is, cells when minutes.
Solve for the only variable k.
Step 2: Write a mathematical model based on the given information. Here , which is about 3.5% growth rate per minute. However, we will use the exact value for k in our model. This will allow us to avoid round-off error in the final result. Use and :
This equation models the number of E. coli cells in terms of time in minutes.
Step 3: Use the function to answer the questions. In this case, we are asked to find the number of cells present in 2 hours. Because time is measured in minutes, use minutes to calculate the number of E. coli cells.
Answer: In two hours 64,000 cells will be present.
When the growth rate is negative the function models exponential decay. We can describe decreasing quantities using a half-lifeThe period of time it takes a quantity to decay to one-half of the initial amount., or the time it takes to decay to one-half of a given quantity.
Due to radioactive decay, caesium-137 has a half-life of 30 years. How long will it take a 50-milligram sample to decay to 10 milligrams?
Solution:
Use the half-life information to determine the rate of decay k. In years the initial amount milligrams will decay to half milligrams.
Solve for the only variable, k.
Note that is negative. However, we will use the exact value to construct a model that gives the amount of cesium-137 with respect to time in years.
Use this model to find t when milligrams.
Answer: Using a calculator, it will take years to decay to 10 milligrams.
Radiocarbon dating is a method used to estimate the age of artifacts based on the relative amount of carbon-14 present in it. When an organism dies, it stops absorbing this naturally occurring radioactive isotope, and the carbon-14 begins to decay at a known rate. Therefore, the amount of carbon-14 present in an artifact can be used to estimate the age of the artifact.
An ancient bone tool is found to contain 25% of the carbon-14 normally found in bone. Given that carbon-14 has a half-life of 5,730 years, estimate the age of the tool.
Solution:
Begin by using the half-life information to find k. Here the initial amount of carbon-14 is not given, however, we know that in years, this amount decays to half,
Dividing both sides by leaves us with an exponential equation in terms of k. This shows that half-life is independent of the initial amount.
Solve for k.
Therefore we have the model,
Next we wish to the find time it takes the carbon-14 to decay to 25% of the initial amount, or
Divide both sides by and solve for t.
Answer: The tool is approximately 11,460 years old.
Try this! The half-life of strontium-90 is about 28 years. How long will it take a 36 milligram sample of strontium-90 to decay to 30 milligrams?
Answer: 7.4 years
Jill invested $1,450 in an account earning % annual interest that is compounded monthly.
James invested $825 in an account earning % annual interest that is compounded monthly.
Raul invested $8,500 in an online money market fund earning 4.8% annual interest that is compounded continuously.
Ian deposited $500 in an account earning 3.9% annual interest that is compounded continuously.
Bill wants to grow his $75,000 inheritance to $100,000 before spending any of it. How long will this take if the bank is offering 5.2% annual interest compounded quarterly?
Mary needs $25,000 for a down payment on a new home. If she invests her savings of $21,350 in an account earning 4.6% annual interest that is compounded semi-annually, how long will it take to grow to the amount that she needs?
Joe invested his $8,700 savings in an account earning % annual interest that is compounded continuously. How long will it take to earn $300 in interest?
Miriam invested $12,800 in an account earning % annual interest that is compounded monthly. How long will it take to earn $1,200 in interest?
Given that the bank is offering 4.2% annual interest compounded monthly, what principal is needed to earn $25,000 in interest for one year?
Given that the bank is offering 3.5% annual interest compounded continuously, what principal is needed to earn $12,000 in interest for one year?
Jose invested his $3,500 bonus in an account earning % annual interest that is compounded quarterly. How long will it take to double his investment?
Maria invested her $4,200 savings in an account earning % annual interest that is compounded semi-annually. How long will it take to double her savings?
If money is invested in an account earning 3.85% annual interest that is compounded continuously, how long will it take the amount to double?
If money is invested in an account earning 6.82% annual interest that is compounded continuously, how long will it take the amount to double?
Find the annual interest rate at which an account earning continuously compounding interest has a doubling time of 9 years.
Find the annual interest rate at which an account earning interest that is compounded monthly has a doubling time of 10 years.
Alice invested her savings of $7,000 in an account earning 4.5% annual interest that is compounded monthly. How long will it take the account to triple in value?
Mary invested her $42,000 bonus in an account earning 7.2% annual interest that is compounded continuously. How long will it take the account to triple in value?
Calculate the doubling time of an investment made at 7% annual interest that is compounded:
Calculate the doubling time of an investment that is earning continuously compounding interest at an annual interest rate of:
Billy’s grandfather invested in a savings bond that earned 5.5% annual interest that was compounded annually. Currently, 30 years later, the savings bond is valued at $10,000. Determine what the initial investment was.
In 1935 Frank opened an account earning 3.8% annual interest that was compounded quarterly. He rediscovered this account while cleaning out his garage in 2005. If the account is now worth $11,294.30, how much was his initial deposit in 1935?
The population of a small town of 24,000 people is expected grow exponentially at a rate of 1.6% per year. Construct an exponential growth model and use it to:
During the exponential growth phase, certain bacteria can grow at a rate of 4.1% per hour. If 10,000 cells are initially present in a sample, construct an exponential growth model and use it to:
In 2000, the world population was estimated to be 6.115 billion people and in 2010 the estimate was 6.909 billion people. If the world population continues to grow exponentially, estimate the total world population in 2020.
In 2000, the population of the United States was estimated to be 282 million people and in 2010 the estimate was 309 million people. If the population of the United States grows exponentially, estimate the population in 2020.
An automobile was purchased new for $42,500 and 2 years later it was valued at $33,400. Estimate the value of the automobile in 5 years if it continues to decrease exponentially.
A new PC was purchased for $1,200 and in 1.5 years it was worth $520. Assume the value is decreasing exponentially and estimate the value of the PC four years after it is purchased.
The population of the downtown area of a certain city decreased from 12,500 people to 10,200 people in two years. If the population continues to decrease exponentially at this rate, what would we expect the population to be in two more years?
A new MP3 player was purchased for $320 and in 1 year it was selling used online for $210. If the value continues to decrease exponentially at this rate, determine the value of the MP3 player 3 years after it was purchased.
The half-life of radium-226 is about 1,600 years. How long will a 5-milligram sample of radium-226 take to decay to 1 milligram?
The half-life of plutonium-239 is about 24,000 years. How long will a 5-milligram sample of plutonium-239 take to decay to 1 milligram?
The half-life of radioactive iodine-131 is about 8 days. How long will it take a 28-gram initial sample of iodine-131 to decay to 12 grams?
The half-life of caesium-137 is about 30 years. How long will it take a 15-milligram sample of caesium-137 to decay to 5 milligrams?
The Rhind Mathematical Papyrus is considered to be the best example of Egyptian mathematics found to date. This ancient papyrus was found to contain 64% of the carbon-14 normally found in papyrus. Given that carbon-14 has a half-life of 5,730 years, estimate the age of the papyrus.
A wooden bowl artifact carved from oak was found to contain 55% of the carbon-14 normally found in oak. Given that carbon-14 has a half-life of 5,730 years, estimate the age of the bowl.
The half-life of radioactive iodine-131 is about 8 days. How long will it take a sample of iodine-131 to decay to 10% of the original amount?
The half-life of caesium-137 is about 30 years. How long will it take a sample of caesium-137 to decay to 25% of the original amount?
The half-life of caesium-137 is about 30 years. What percent of an initial sample will remain in 100 years?
The half-life of radioactive iodine-131 is about 8 days. What percent of an initial sample will remain in 30 days?
If a bone is 100 years old, what percent of its original amount of carbon-14 do we expect to find in it?
The half-life of plutonium-239 is about 24,000 years. What percent of an initial sample will remain in 1,000 years?
Find the amount of time it will take for 10% of an initial sample of plutonium-239 to decay. (Hint: If 10% decays, then 90% will remain.)
Find the amount of time it will take for 10% of an initial sample of carbon-14 to decay.
Solve for the given variable:
Solve for t:
Solve for t:
Solve for I:
Solve for :
Solve for t:
Solve for I:
The number of cells in a certain bacteria sample is approximated by the logistic growth model , where t represents time in hours. Determine the time it takes the sample to grow to 24,000 cells.
The market share of a product, as a percentage, is approximated by the formula where t represents the number of months after an aggressive advertising campaign is launched.
In chemistry, pH is a measure of acidity and is given by the formula , where is the hydrogen ion concentration (measured in moles of hydrogen per liter of solution.) What is the hydrogen ion concentration of seawater with a pH of 8?
Determine the hydrogen ion concentration of milk with a pH of 6.6.
The volume of sound, L in decibels (dB), is given by the formula where I represents the intensity of the sound in watts per square meter. Determine the sound intensity of a hair dryer that emits 70 dB of sound.
The volume of a chainsaw measures 110 dB. Determine the intensity of this sound.
Which factor affects the doubling time the most, the annual compounding n or the interest rate r? Explain.
Research and discuss radiocarbon dating. Post something interesting you have learned as well as a link to more information.
Is exponential growth sustainable over an indefinite amount of time? Explain.
Research and discuss the half-life of radioactive materials.
5.6 years
year
$583,867
12.7 years
18 years
7.7%
24.5 years
$2,006.44
About 7.806 billion people
About $23,269.27
8,323 people
3,715 years
9.8 days
About 3,689 years old
26.6 days
9.9%
98.8%
3,648 years
Approximately 2.5 hours
moles per liter
watts per square meter
Answer may vary
Answer may vary
Given f and g find and
,
,
,
,
,
,
,
,
Are the given functions one-to-one? Explain.
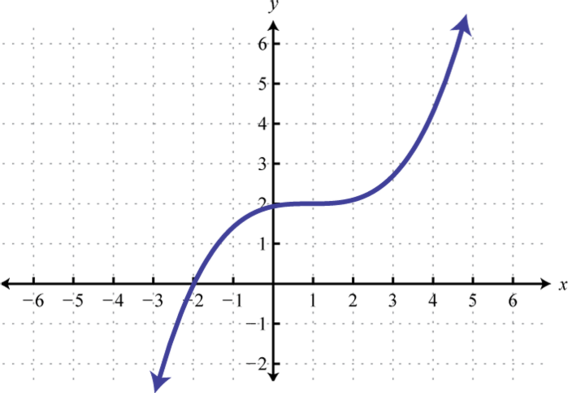
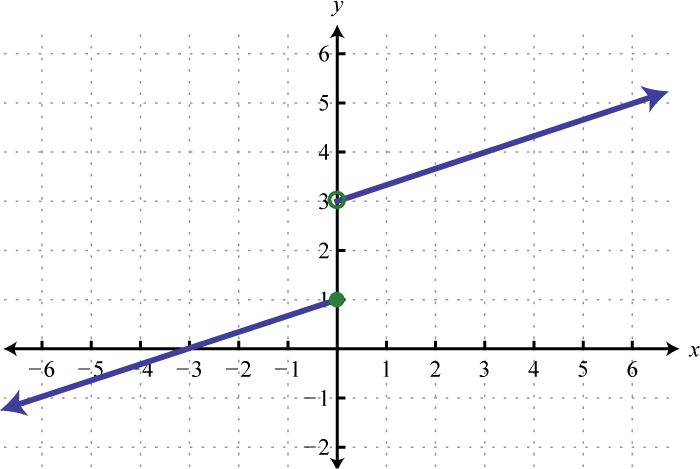
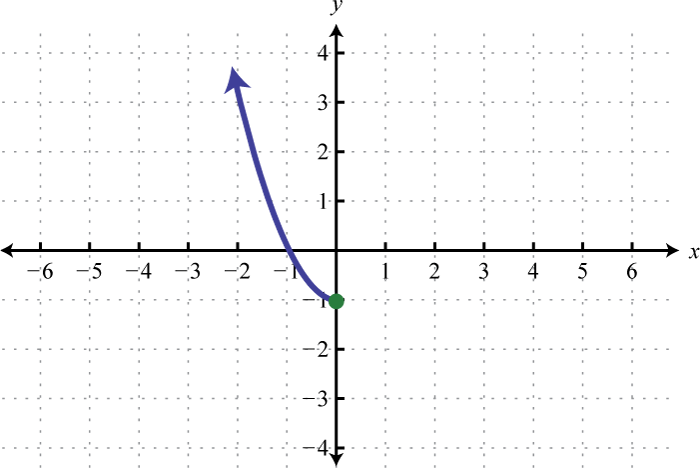
Verify algebraically that the two given functions are inverses. In other words, show that and
,
, ,
,
,
Find the inverses of each function defined as follows:
,
Evaluate.
; find , , and
; find , , and
; find , , and
; find , , and
Sketch the exponential function. Draw the horizontal asymptote with a dashed line.
Use a calculator to evaluate the following. Round off to the nearest hundredth.
; find , , and
; find , , and
; find , , and
; find , , and
Sketch the function. Draw the horizontal asymptote with a dashed line.
Jerry invested $6,250 in an account earning % annual interest that is compounded monthly. How much will be in the account after 4 years?
Jose invested $7,500 in an account earning % annual interest that is compounded continuously. How much will be in the account after years?
A 14-gram sample of radioactive iodine is accidently released into the atmosphere. The amount of the substance in grams is given by the formula , where t represents the time in days after the sample was released. How much radioactive iodine will be present in the atmosphere 30 days after it was released?
The number of cells in a bacteria sample is given by the formula , where t represents the time in hours since the initial placement of 24,000 cells. Use the formula to calculate the number of cells in the sample 20 hours later.
Evaluate.
Find x.
Sketch the graph of the logarithmic function. Draw the vertical asymptote with a dashed line.
The population of a certain small town is growing according to the function , where t represents time in years since the last census. Use the function to estimate the population years after the census was taken.
The volume of sound L in decibels (dB) is given by the formula , where I represents the intensity of the sound in watts per square meter. Determine the volume of a sound with an intensity of 0.5 watts per square meter.
Evaluate without using a calculator.
Expand completely.
Write as a single logarithm with coefficient 1.
Solve. Give the exact answer and the approximate answer rounded to the nearest hundredth where appropriate.
Use the change of base formula to approximate the following to the nearest tenth.
Solve.
Solve.
An amount of $3,250 is invested in an account that earns 4.6% annual interest that is compounded monthly. Estimate the number of years for the amount in the account to reach $4,000.
An amount of $2,500 is invested in an account that earns 5.5% annual interest that is compounded continuously. Estimate the number of years for the amount in the account to reach $3,000.
How long does it take to double an investment made in an account that earns % annual interest that is compounded continuously?
How long does it take to double an investment made in an account that earns % annual interest that is compounded semi-annually?
In the year 2000 a certain small town had a population of 46,000 people. In the year 2010 the population was estimated to have grown to 92,000 people. If the population continues to grow exponentially at this rate, estimate the population in the year 2016.
A fleet van was purchased new for $28,000 and 2 years later it was valued at $20,000. If the value of the van continues to decrease exponentially at this rate, determine its value 7 years after it is purchased new.
A website that has been in decline registered 4,200 unique visitors last month and 3,600 unique visitors this month. If the number of unique visitors continues to decline exponentially, how many unique visitors would you expect next month?
An initial population of 18 rabbits was introduced into a wildlife preserve. The number of rabbits doubled in the first year. If the rabbit population continues to grow exponentially at this rate, how many rabbits will be present 5 years after they were introduced?
The half-life of sodium-24 is about 15 hours. How long will it take a 50-milligram sample to decay to 10 milligrams?
The half-life of radium-226 is about 1,600 years. How long will it take an initial sample to decay to 30% of the original amount?
An archeologist discovered a bone tool artifact. After analysis, the artifact was found to contain 62% of the carbon-14 normally found in bone from the same animal. Given that carbon-14 has a half-life of 5,730 years, estimate the age of the artifact.
The half-life of radioactive iodine-131 is about 8 days. What percentage of an initial sample accidentally released into the atmosphere do we expect to remain after 53 days?
;
No, fails the HLT
Yes, passes the HLT
Proof
Proof
, ,
, ,
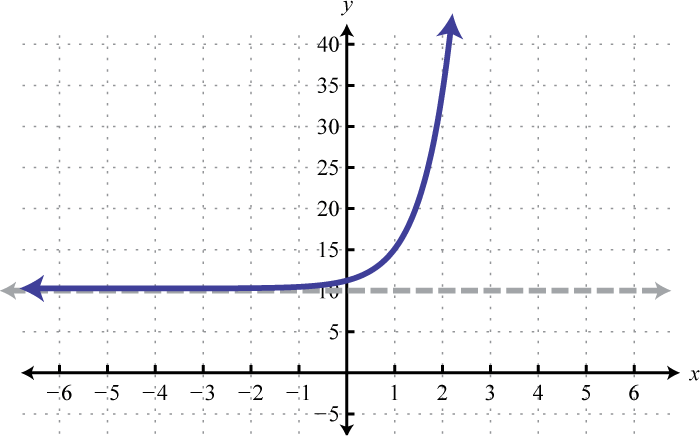
, ,
, ,
$7,223.67
Approximately 1 gram
2
−5
−2
0
Undefined
8
−5
125
0.001
119,229 people
1
−1
17
63
1
5
0
0
1.6
1.2
−2.2
12
2
13
±4
2
0
4.5 years
10.27 years
About 139,446 people
3,086 unique visitors
35 hours
About 3,952 years old
Given and find
Show that and are inverses.
Find the inverse of the following functions:
where
Sketch the graph.
Joe invested $5,200 in an account earning 3.8% annual interest that is compounded monthly. How much will be in the account at the end of 4 years?
Mary has $3,500 in a savings account earning % annual interest that is compounded continuously. How much will be in the account at the end of 3 years?
Evaluate.
Sketch the graph.
Expand: .
Write as a single logarithm with coefficient 1:
Evaluate. Round off to the nearest tenth.
Solve:
Joe invested $5,200 in an account earning 3.8% annual interest that is compounded monthly. How long will it take to accumulate a total of $6,200 in the account?
Mary has $3,500 in a savings account earning % annual interest that is compounded continuously. How long will it take to double the amount in the account?
During the exponential growth phase, certain bacteria can grow at a rate of 5.3% per hour. If 12,000 cells are initially present in a sample, construct an exponential growth model and use it to: a. Estimate the population of bacteria in 3.5 hours. b. Estimate the time it will take the population to double.
The half-life of caesium-137 is about 30 years. Approximate the time it will take a 20-milligram sample of caesium-137 to decay to 8 milligrams.
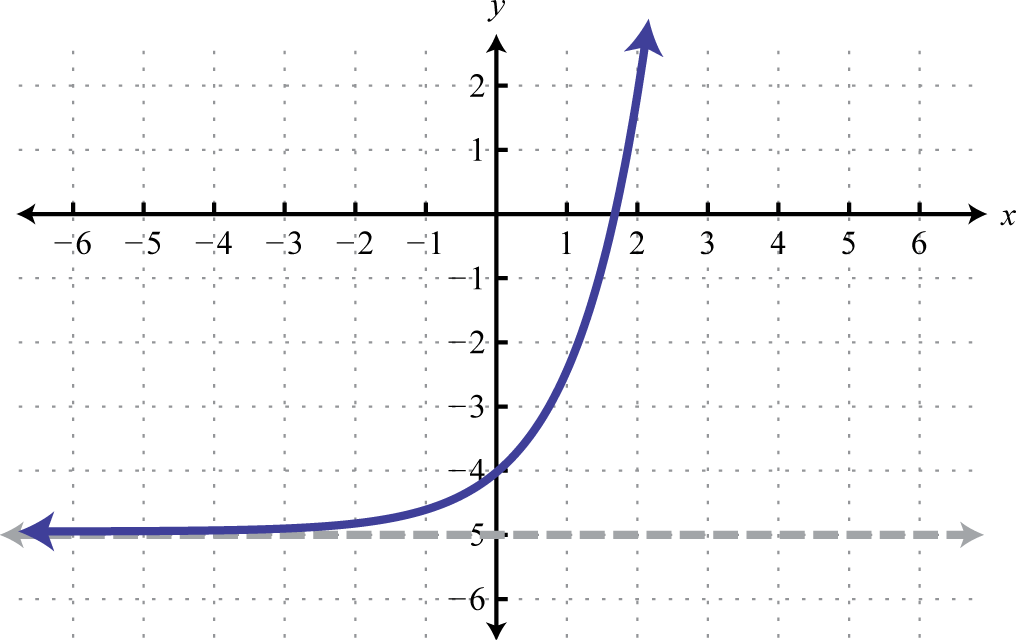
$6,052.18
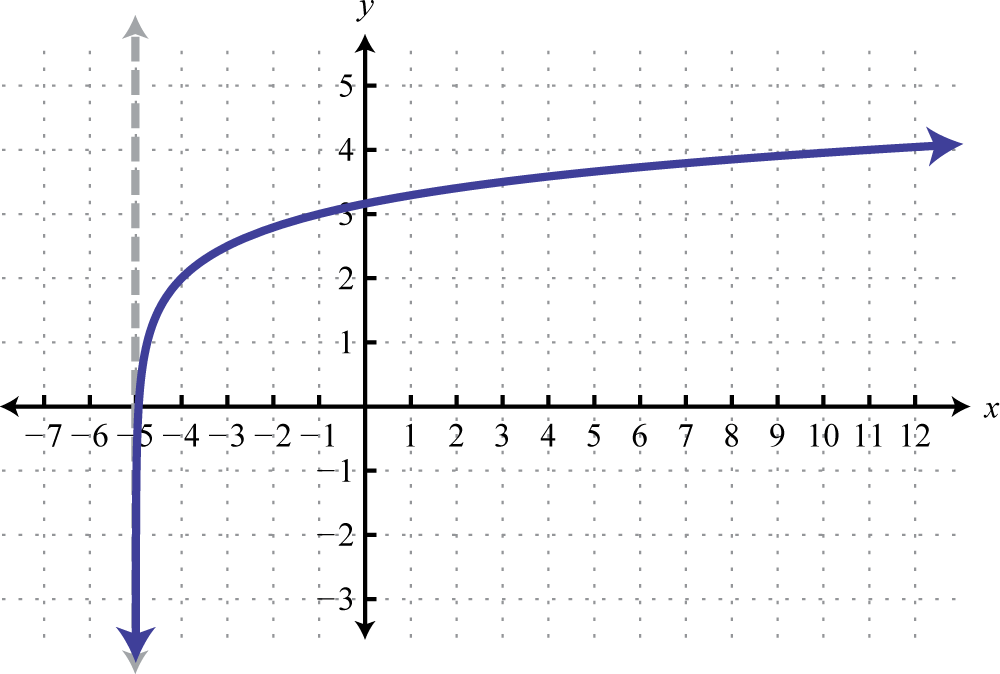
±1
15.4 years
40 years