Значение $1$ соответствует классу клиентов банка, которым выдали кредит и они его успешно вернули.
Значение $-1$ соответствует клиентам, невыполнившим свои кредитные обязанности. \n", "\n", "В банке хотят уметь определять по признакам `a1-a15`, сможет ли новый клиент вернуть кредит или нет? То есть нам надо обучить классификатор! *Обычно, в банках используют скор-карты, но процесс их построения тесно связан с логистической регрессией*" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "Загрузите данные и преобразуйте признаки `a1`, `a9`, `a10` и `a12` из строковых в числовые. В них только 2 возможных значения. Для этого можно использовать функцию DataFrame.replace() в `pandas` или самое обычное присваивание на соответствующих строках." ] }, { "cell_type": "code", "execution_count": null, "metadata": { "collapsed": true }, "outputs": [], "source": [ "# Your code here" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "В признаках `a6`, `a7` присутствуют \"редкие\" значение. Найдите их с помощью фунцкии `.value_counts()` и объедините, присвоив им одно и то же значение, например `'Other'`." ] }, { "cell_type": "code", "execution_count": null, "metadata": { "collapsed": true }, "outputs": [], "source": [ "# Your code here" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "Выделите бинарные признаки `a1`, `a9`, `a10` и `a12` в матрицу `X_binary`\n", "\n", "Преобразуйте категориальные признаки `a5`, `a6`, `a7`, `a13` с помощью `DictVectorizer`. Вы должны получить матрицу `X_cat`.\n", "\n", "Нормализуйте количественные признаки `a2`, `a3`, `a8`, `a11`, `a14` и `a15` с помощью `StandartScaler` или вручную. Вы должны получить матрицу `X_real`.\n", "\n", "Матрица `X_cat` будет sparse-матрицой (разреженной). Преобразуте её в полную матрицу с помощью команд `X_cat = X_cat.toarray()` или `X_cat = X_cat.todence()`\n", "\n", "Используйте функцию np.concatinate(..) или np.c[..] чтобы сцепить матрицы `X_binary`, `X_cat` и `X_real`\n", "\n", "В результате вы должны получить матрицу с преобразованными призанками `X` и вектор ответов `y`" ] }, { "cell_type": "code", "execution_count": null, "metadata": { "collapsed": true }, "outputs": [], "source": [ "# Your code here" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "### Исследование влияния регуляризации\n", "\n", "В случае с логистичесткой регресии, сложность модели выражается в значениях весов $w_j$ при признаках. Больший вес означает большее влияние признака на результат. В таком случае, давайте добавил штрафное слагаемое в функцию оптимизации для логистической регресии. Самый распространенные из них это:\n", "\n", "* Ridge regression\n", "$$L(w) = - \\left(\\sum_i \\log(\\sigma(y^{(i)} \\langle w, x^{(i)} \\rangle)) + \\frac{1}{C}\\sum_j w_j^2\\right) \\rightarrow \\min_w$$\n", "\n", "* Lasso regression\n", "$$L(w) = -\\left(\\sum_i \\log(\\sigma(y^{(i)} \\langle w, x^{(i)} \\rangle) + \\frac{1}{C}\\sum_j |w_j|\\right) \\rightarrow \\min_w$$\n", "\n", "$C$ - называется гиперпараметром регуляризации и он задается вручную. Выбирается он с помощью кросс-валидации. Чем больше $С$ - тем меньше влияние регуляризации.\n", "\n", "\n", "Разделите ваши даннные на обучающую и контрольную выборку в пропорции 70/30 соответственно.\n", "\n" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "Lasso regression называется так, потому что она осуществляет \"отлов\" признаков - т.е. незначимые признаки будут иметь нулевые веса в модели, в то время как в Ridge regression - веса будут постепенно падать у всех признаков.\n", "\n", "
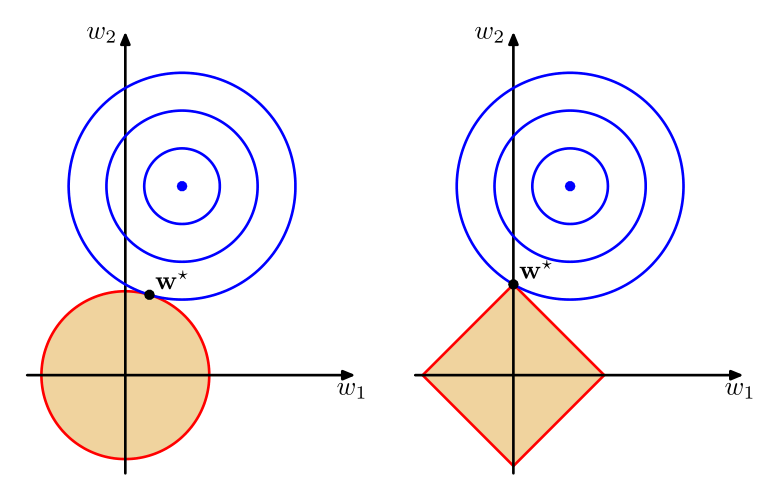 "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Давайте сравним работу регуляризаторов. \n",
"\n",
"1. Разбейте данные на обучающую и валидационную выборки в пропорции 70\\30.\n",
"1. Для $C$ из набора np.logspace(-3, 3, 10) обучите LogisctigRegression c Lasso регуляризацией (`penalty='l1'`). На каждой итерации оцените качество (ROC-AUC) на валидационной выборке и запомните полученные коэффициенты модели\n",
"1. На одном графике выведите значение качества в зависимости от параметра `C` \n",
"1. На другом графике для каждого признака выведите значение коэффициента в модели в зависимости от параметра `C`\n",
"1. Проделайте тоже самое для Ridge регуляризации (`penalty='l2'`)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Your code here"
]
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python [conda root]",
"language": "python",
"name": "conda-root-py"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.12"
},
"nav_menu": {},
"toc": {
"navigate_menu": true,
"number_sections": false,
"sideBar": false,
"threshold": 6,
"toc_cell": false,
"toc_section_display": "block",
"toc_window_display": true
},
"toc_position": {
"height": "44px",
"left": "20px",
"right": "562.667px",
"top": "29px",
"width": "164px"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Давайте сравним работу регуляризаторов. \n",
"\n",
"1. Разбейте данные на обучающую и валидационную выборки в пропорции 70\\30.\n",
"1. Для $C$ из набора np.logspace(-3, 3, 10) обучите LogisctigRegression c Lasso регуляризацией (`penalty='l1'`). На каждой итерации оцените качество (ROC-AUC) на валидационной выборке и запомните полученные коэффициенты модели\n",
"1. На одном графике выведите значение качества в зависимости от параметра `C` \n",
"1. На другом графике для каждого признака выведите значение коэффициента в модели в зависимости от параметра `C`\n",
"1. Проделайте тоже самое для Ridge регуляризации (`penalty='l2'`)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Your code here"
]
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python [conda root]",
"language": "python",
"name": "conda-root-py"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.12"
},
"nav_menu": {},
"toc": {
"navigate_menu": true,
"number_sections": false,
"sideBar": false,
"threshold": 6,
"toc_cell": false,
"toc_section_display": "block",
"toc_window_display": true
},
"toc_position": {
"height": "44px",
"left": "20px",
"right": "562.667px",
"top": "29px",
"width": "164px"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
 "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
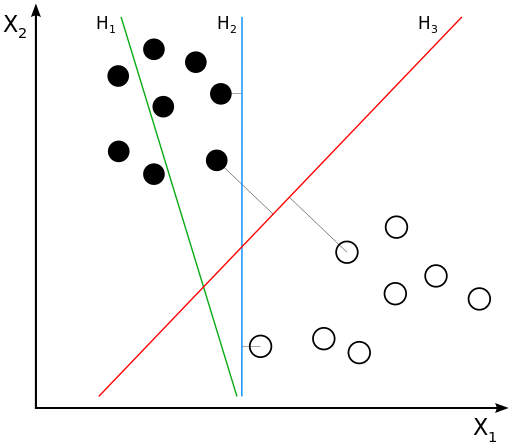
"Нам надо найти уравнение прямой (гиперплоскости), которая бы могла разделить два класса ($H_2$ и $H_3$ подходят). В данном случае, уравнение прямой задаётся как: $$g(x) = w_0 + w_1x_1 + w_2x_2 = \\langle w, x \\rangle = w^\\top x$$\n",
"\n",
"* Если $g(x^*) > 0$, то $y^* = \\text{'черный'}$\n",
"* Если $g(x^*) < 0$, то $y^* = \\text{'белый'}$\n",
"* Если $g(x^*) = 0$, то мы находимся на линии\n",
"* т.е. решающее правило: $y^* = sign(g(x^*))$\n",
"\n",
"Некоторые геометрические особенности\n",
"* $\\frac{w_0}{||w||}$ - расстояние от начала координат то прямой\n",
"* $\\frac{|g(x)|}{||w||}$ - степень \"уверенности\" в классификациий\n",
"* Величину $M = y\\langle w, x \\rangle = y \\cdot g(x)$ называют **отступом**(margin)\n",
"\n",
"Если для какого-то объекта $M \\geq 0$, то его классификация выполнена успешно."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
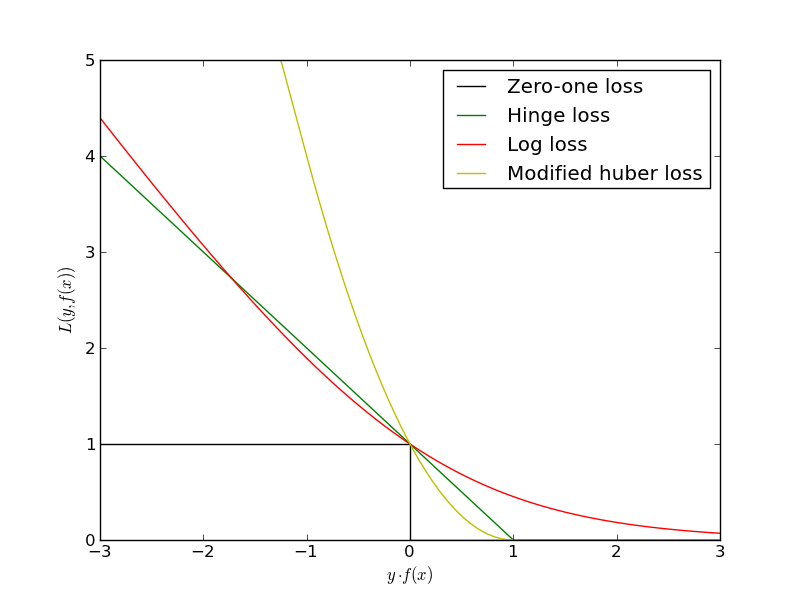
"Отлично! Значит нам надо просто минимизировать ошибки классификации для всех объектов:\n",
"\n",
"$$L(w) = \\sum_i [y^{(i)} \\langle w, x^{(i)} \\rangle < 0] \\rightarrow \\min_w$$\n",
"Проблема в том, что это будет комбинаторная оптимизация. Существуют различные аппроксимации этой функции ошибок:"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"
"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Нам надо найти уравнение прямой (гиперплоскости), которая бы могла разделить два класса ($H_2$ и $H_3$ подходят). В данном случае, уравнение прямой задаётся как: $$g(x) = w_0 + w_1x_1 + w_2x_2 = \\langle w, x \\rangle = w^\\top x$$\n",
"\n",
"* Если $g(x^*) > 0$, то $y^* = \\text{'черный'}$\n",
"* Если $g(x^*) < 0$, то $y^* = \\text{'белый'}$\n",
"* Если $g(x^*) = 0$, то мы находимся на линии\n",
"* т.е. решающее правило: $y^* = sign(g(x^*))$\n",
"\n",
"Некоторые геометрические особенности\n",
"* $\\frac{w_0}{||w||}$ - расстояние от начала координат то прямой\n",
"* $\\frac{|g(x)|}{||w||}$ - степень \"уверенности\" в классификациий\n",
"* Величину $M = y\\langle w, x \\rangle = y \\cdot g(x)$ называют **отступом**(margin)\n",
"\n",
"Если для какого-то объекта $M \\geq 0$, то его классификация выполнена успешно."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Отлично! Значит нам надо просто минимизировать ошибки классификации для всех объектов:\n",
"\n",
"$$L(w) = \\sum_i [y^{(i)} \\langle w, x^{(i)} \\rangle < 0] \\rightarrow \\min_w$$\n",
"Проблема в том, что это будет комбинаторная оптимизация. Существуют различные аппроксимации этой функции ошибок:"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
" "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Знакомьтесь - Логистической регрессия!"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Перед тем как мы начнем, рассмотрим функцию $$\\sigma(z) = \\frac{1}{1 + exp{(-z)}},$$она называется **сигмойда**. Постройте данную фукнцию."
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"[
"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Знакомьтесь - Логистической регрессия!"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Перед тем как мы начнем, рассмотрим функцию $$\\sigma(z) = \\frac{1}{1 + exp{(-z)}},$$она называется **сигмойда**. Постройте данную фукнцию."
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"[