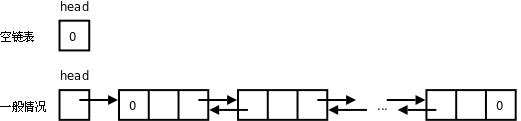
圖 23.6 “鏈表”所示的鏈表即單鏈表(Single Linked List),本節我們學習如何創建和操作這種鏈表。每個鏈表有一個頭指針,通過頭指針可以找到第一個節點,每個節點都可以通過指針域找到它的後繼,最後一個節點的指針域為NULL,表示沒有後繼。數組在內存中是連續存放的,而鏈表在內存中的佈局是不規則的,我們知道訪問某個數組元素b[n]時可以通過基地址+n×每個元素的位元組數得到它地址,或者說數組支持隨機訪問,而鏈表是不支持隨機訪問的,只能通過前一個元素的指針域得知後一個元素的地址,因此只能從頭指針開始順序訪問各節點。以下代碼實現了單鏈表的基本操作。
例 26.1. 單鏈表
/* linkedlist.h */
#ifndef LINKEDLIST_H
#define LINKEDLIST_H
typedef struct node *link;
struct node {
unsigned char item;
link next;
};
link make_node(unsigned char item);
void free_node(link p);
link search(unsigned char key);
void insert(link p);
void delete(link p);
void traverse(void (*visit)(link));
void destroy(void);
void push(link p);
link pop(void);
#endif/* linkedlist.c */
#include <stdlib.h>
#include "linkedlist.h"
static link head = NULL;
link make_node(unsigned char item)
{
link p = malloc(sizeof *p);
p->item = item;
p->next = NULL;
return p;
}
void free_node(link p)
{
free(p);
}
link search(unsigned char key)
{
link p;
for (p = head; p; p = p->next)
if (p->item == key)
return p;
return NULL;
}
void insert(link p)
{
p->next = head;
head = p;
}
void delete(link p)
{
link pre;
if (p == head) {
head = p->next;
return;
}
for (pre = head; pre; pre = pre->next)
if (pre->next == p) {
pre->next = p->next;
return;
}
}
void traverse(void (*visit)(link))
{
link p;
for (p = head; p; p = p->next)
visit(p);
}
void destroy(void)
{
link q, p = head;
head = NULL;
while (p) {
q = p;
p = p->next;
free_node(q);
}
}
void push(link p)
{
insert(p);
}
link pop(void)
{
if (head == NULL)
return NULL;
else {
link p = head;
head = head->next;
return p;
}
}/* main.c */
#include <stdio.h>
#include "linkedlist.h"
void print_item(link p)
{
printf("%d\n", p->item);
}
int main(void)
{
link p = make_node(10);
insert(p);
p = make_node(5);
insert(p);
p = make_node(90);
insert(p);
p = search(5);
delete(p);
free_node(p);
traverse(print_item);
destroy();
p = make_node(100);
push(p);
p = make_node(200);
push(p);
p = make_node(250);
push(p);
while (p = pop()) {
print_item(p);
free_node(p);
}
return 0;
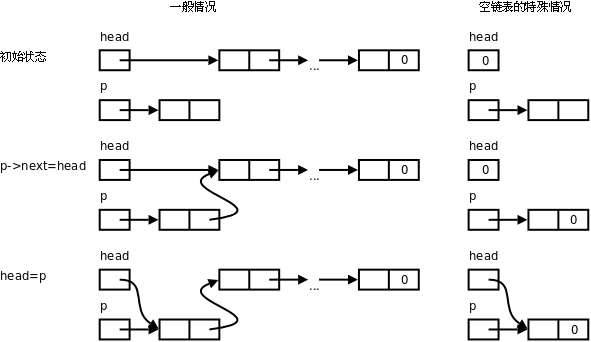
}在初始化時把頭指針head初始化為NULL,表示空鏈表。然後main函數調用make_node創建幾個節點,分別調用insert插入到鏈表中。
void insert(link p)
{
p->next = head;
head = p;
}正如上圖所示,insert函數雖然簡單,其中也隱含了一種特殊情況(Special Case)的處理,當head為NULL時,執行insert操作插入第一個節點之後,head指向第一個節點,而第一個節點的next指針域成為NULL,這很合理,因為它也是最後一個節點。所以空鏈表雖然是一種特殊情況,卻不需要特殊的代碼來處理,和一般情況用同樣的代碼處理即可,這樣寫出來的代碼更簡潔,但是在讀代碼時要想到可能存在的特殊情況。當然,insert函數傳進來的參數p也可能有特殊情況,傳進來的p可能是NULL,甚至是野指針,本章的函數代碼都假定調用者的傳進來的參數是合法的,不對參數做特別檢查。事實上,對指針參數做檢查是不現實的,如果傳進來的是NULL還可以檢查一下,如果傳進來的是野指針,根本無法檢查它指向的內存單元是不是合法的,C標準庫的函數通常也不做這種檢查,例如strcpy(p, NULL)就會引起段錯誤。
接下來main函數調用search在鏈表中查找某個節點,如果找到就返回指向該節點的指針,找不到就返回NULL。
link search(unsigned char key)
{
link p;
for (p = head; p; p = p->next)
if (p->item == key)
return p;
return NULL;
}search函數其實也隱含了對於空鏈表這種特殊情況的處理,如果是空鏈表則循環體一次都不執行,直接返回NULL。
然後main函數調用delete從鏈表中摘除用search找到的節點,最後調用free_node釋放它的存儲空間。
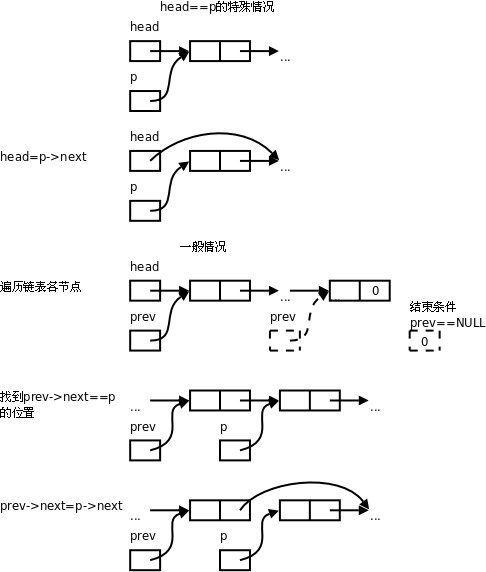
void delete(link p)
{
link pre;
if (p == head) {
head = p->next;
return;
}
for (pre = head; pre; pre = pre->next)
if (pre->next == p) {
pre->next = p->next;
return;
}
}從上圖可以看出,要摘除一個節點需要首先找到它的前趨然後才能做摘除操作,而在單鏈表中通過某個節點只能找到它的後繼而不能找到它的前趨,所以刪除操作要麻煩一些,需要從第一個節點開始依次查找要摘除的節點的前趨。delete操作也要處理一種特殊情況,如果要摘除的節點是鏈表的第一個節點,它是沒有前趨的,這種情況要用特殊的代碼處理,而不能和一般情況用同樣的代碼處理。這樣很不爽,能不能把這種特殊情況轉化為一般情況呢?可以把delete函數改成這樣:
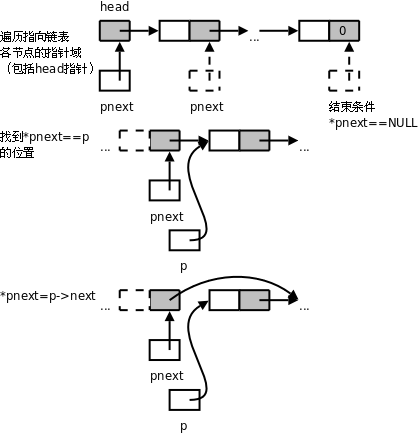
void delete(link p)
{
link *pnext;
for (pnext = &head; *pnext; pnext = &(*pnext)->next)
if (*pnext == p) {
*pnext = p->next;
return;
}
}定義一個指向指針的指針pnext,在for循環中pnext遍歷的是指向鏈表中各節點的指針域,這樣就把head指針和各節點的next指針統一起來了,可以在一個循環中處理。
然後main函數調用traverse函數遍歷整個鏈表,調用destroy函數銷毀整個鏈表。請讀者自己閲讀這兩個函數的代碼。
如果限定每次只在鏈表的頭部插入和刪除元素,就形成一個LIFO的訪問序列,所以在鏈表頭部插入和刪除元素的操作實現了堆棧的push和pop操作,main函數的最後幾步把鏈表當成堆棧來操作,從打印的結果可以看到出棧的順序和入棧是相反的。想一想,用鏈表實現的堆棧和第 2 節 “堆棧”中用數組實現的堆棧相比有什麼優點和缺點?
1、修改insert函數實現插入排序的功能,鏈表中的數據按從小到大排列,每次插入數據都要在鏈表中找到合適的位置再插入。在第 6 節 “折半查找”中我們看到,如果數組中的元素是有序排列的,可以用折半查找算法更快地找到某個元素,想一想如果鏈表中的節點是有序排列的,是否適用折半查找算法?為什麼?
2、基于單鏈表實現隊列的enqueue和dequeue操作。在鏈表的末尾再維護一個指針tail,在tail處enqueue,在head處dequeue。想一想能不能反過來,在head處enqueue而在tail處dequeue?
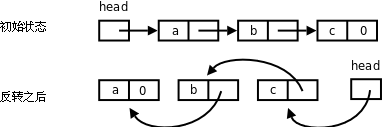
3、實現函數void reverse(void);將單鏈表反轉。如下圖所示。
鏈表的delete操作需要首先找到要摘除的節點的前趨,而在單鏈表中找某個節點的前趨需要從表頭開始依次查找,對於n個節點的鏈表,刪除操作的時間複雜度為O(n)。可以想像得到,如果每個節點再維護一個指向前趨的指針,刪除操作就像插入操作一樣容易了,時間複雜度為O(1),這稱為雙向鏈表(Doubly Linked List)。要實現雙向鏈表只需在上一節代碼的基礎上改動兩個地方。
在linkedlist.h中修改鏈表節點的結構體定義:
struct node {
unsigned char item;
link prev, next;
};在linkedlist.c中修改insert和delete函數:
void insert(link p)
{
p->next = head;
if (head)
head->prev = p;
head = p;
p->prev = NULL;
}
void delete(link p)
{
if (p->prev)
p->prev->next = p->next;
else
head = p->next;
if (p->next)
p->next->prev = p->prev;
}由於引入了prev指針,insert和delete函數中都有一些特殊情況需要用特殊的代碼處理,不能和一般情況用同樣的代碼處理,這非常不爽,如果在表頭和表尾各添加一個Sentinel節點(這兩個節點只用於界定表頭和表尾,不保存數據),就可以把這些特殊情況都轉化為一般情況了。
例 26.2. 帶Sentinel的雙向鏈表
/* doublylinkedlist.h */
#ifndef DOUBLYLINKEDLIST_H
#define DOUBLYLINKEDLIST_H
typedef struct node *link;
struct node {
unsigned char item;
link prev, next;
};
link make_node(unsigned char item);
void free_node(link p);
link search(unsigned char key);
void insert(link p);
void delete(link p);
void traverse(void (*visit)(link));
void destroy(void);
void enqueue(link p);
link dequeue(void);
#endif/* doublylinkedlist.c */
#include <stdlib.h>
#include "doublylinkedlist.h"
struct node tailsentinel;
struct node headsentinel = {0, NULL, &tailsentinel};
struct node tailsentinel = {0, &headsentinel, NULL};
static link head = &headsentinel;
static link tail = &tailsentinel;
link make_node(unsigned char item)
{
link p = malloc(sizeof *p);
p->item = item;
p->prev = p->next = NULL;
return p;
}
void free_node(link p)
{
free(p);
}
link search(unsigned char key)
{
link p;
for (p = head->next; p != tail; p = p->next)
if (p->item == key)
return p;
return NULL;
}
void insert(link p)
{
p->next = head->next;
head->next->prev = p;
head->next = p;
p->prev = head;
}
void delete(link p)
{
p->prev->next = p->next;
p->next->prev = p->prev;
}
void traverse(void (*visit)(link))
{
link p;
for (p = head->next; p != tail; p = p->next)
visit(p);
}
void destroy(void)
{
link q, p = head->next;
head->next = tail;
tail->prev = head;
while (p != tail) {
q = p;
p = p->next;
free_node(q);
}
}
void enqueue(link p)
{
insert(p);
}
link dequeue(void)
{
if (tail->prev == head)
return NULL;
else {
link p = tail->prev;
delete(p);
return p;
}
}/* main.c */
#include <stdio.h>
#include "doublylinkedlist.h"
void print_item(link p)
{
printf("%d\n", p->item);
}
int main(void)
{
link p = make_node(10);
insert(p);
p = make_node(5);
insert(p);
p = make_node(90);
insert(p);
p = search(5);
delete(p);
free_node(p);
traverse(print_item);
destroy();
p = make_node(100);
enqueue(p);
p = make_node(200);
enqueue(p);
p = make_node(250);
enqueue(p);
while (p = dequeue()) {
print_item(p);
free_node(p);
}
return 0;
}這個例子也實現了隊列的enqueue和dequeue操作,現在每個節點有了prev指針,可以反過來在head處enqueue而在tail處dequeue了。
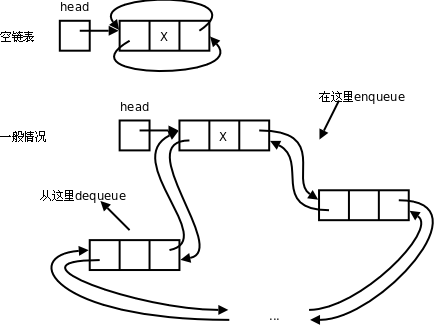
現在結合第 5 節 “環形隊列”想一想,其實用鏈表實現環形隊列是最自然的,以前基于數組實現環形隊列,我們還需要“假想”它是首尾相接的,而如果基于鏈表實現環形隊列,我們本來就可以用指針串成首尾相接的。把上面的程序改成環形鏈表(Circular Linked List)也非常簡單,只需要把doublylinkedlist.c中的
struct node tailsentinel;
struct node headsentinel = {0, NULL, &tailsentinel};
struct node tailsentinel = {0, &headsentinel, NULL};
static link head = &headsentinel;
static link tail = &tailsentinel;改成:
struct node sentinel = {0, &sentinel, &sentinel};
static link head = &sentinel;再把doublylinkedlist.c中所有的tail替換成head即可,相當於把head和tail合二為一了。
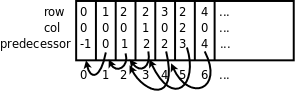
回想一下我們在例 12.4 “用廣度優先搜索解迷宮問題”中使用的資料結構,我把圖重新畫在下面。
這是一個靜態分配的數組,每個數組元素都有row、col和predecessor三個成員,predecessor成員保存一個數組下標,指向數組中的另一個元素,這其實也是鏈表的一種形式,稱為靜態鏈表,例如上圖中的第6、4、2、1、0個元素串成一條鏈表。
1、Josephus是公元1世紀的著名歷史學家,相傳在一次戰役中他和另外幾個人被圍困在山洞裡,他們寧死不屈,決定站成一圈,每次數到三個人就殺一個,直到全部死光為止。Josephus和他的一個朋友不想死,於是串通好了站在適當的位置上,最後只剩下他們倆的時候這個遊戲就停止了。如果一開始的人數為N,每次數到M個人就殺一個,那麼要想不死應該站在什麼位置呢?這個問題比較複雜,[具體數學]的1.3節研究了Josephus問題的解,有興趣的讀者可以參考。現在我們做個比較簡單的練習,用鏈表模擬Josephus他們玩的這個遊戲,N和M作為命令行參數傳入,每個人的編號依次是1~N,打印每次被殺者的編號,打印最後一個倖存者的編號。
2、在第 2.11 節 “本節綜合練習”的習題1中規定了一種日誌檔案的格式,每行是一條記錄,由行號、日期、時間三個欄位組成,由於記錄是按時間先後順序寫入的,可以看作所有記錄是按日期排序的,對於日期相同的記錄再按時間排序。現在要求從這樣的一個日誌檔案中讀出所有記錄組成一個鏈表,在鏈表中首先按時間排序,對於時間相同的記錄再按日期排序,最後寫回檔案中。比如原檔案的內容是:
1 2009-7-30 15:16:42 2 2009-7-30 15:16:43 3 2009-7-31 15:16:41 4 2009-7-31 15:16:42 5 2009-7-31 15:16:43 6 2009-7-31 15:16:44
重新排序輸出的檔案內容是:
1 2009-7-31 15:16:41 2 2009-7-30 15:16:42 3 2009-7-31 15:16:42 4 2009-7-30 15:16:43 5 2009-7-31 15:16:43 6 2009-7-31 15:16:44